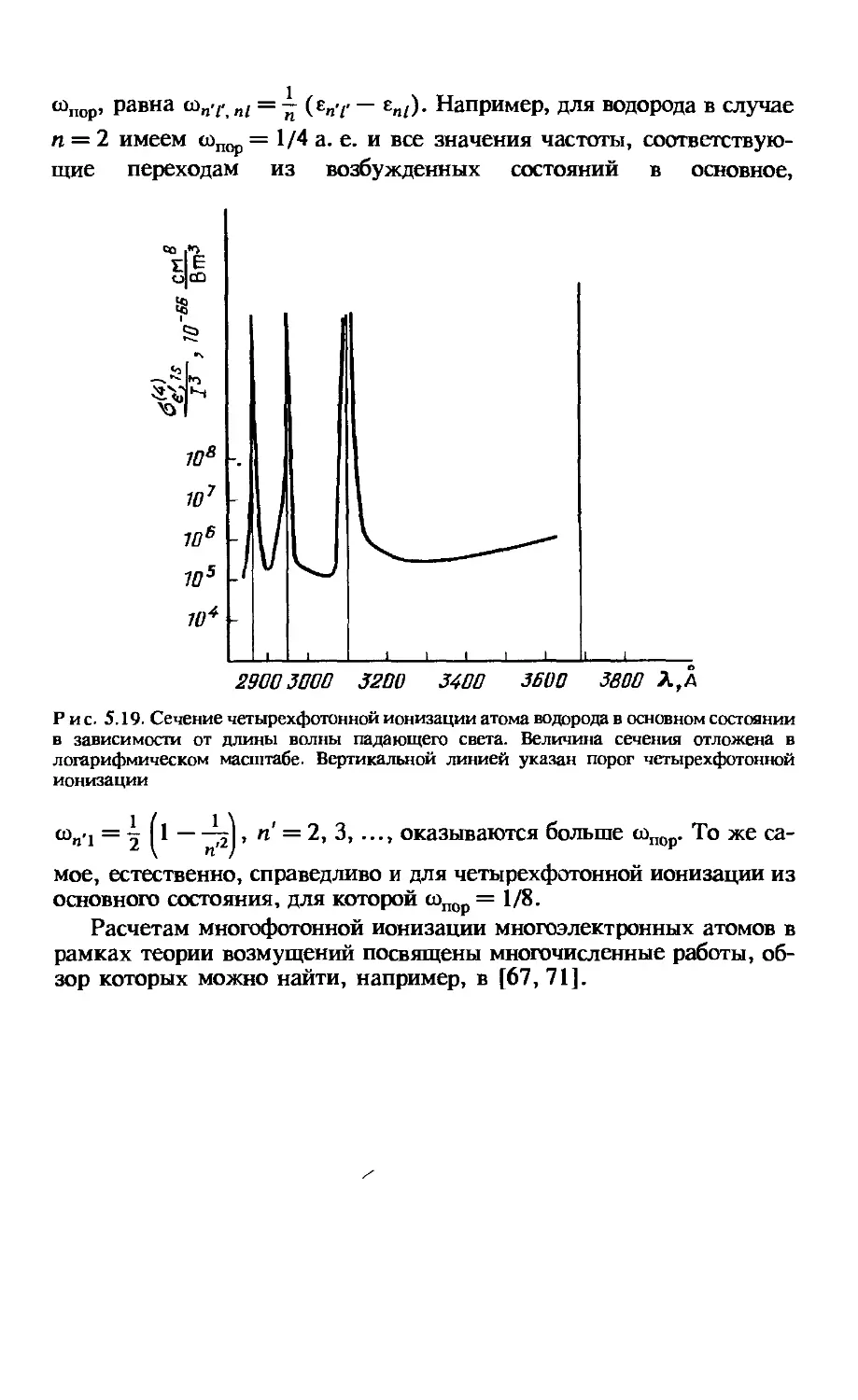
Автор: Лабзовский Л.Н.
Теги: ядерная, атомная и молекулярная физика физико-математические науки физика электродинамика
ISBN: 5-02-015016-9
Год: 1996
Текст
Л.Н.ЛАБ30ВСКИЙ
ТЕОРИЯ АТОМА
Квантовая
электродинамика
электронных оболочек
и процессы излучения
ЛНЛАБЗОВСКИИ
ТЕОРИЯ АТОМА
Квантовая электродинамика
электронных оболочек
и процессы излучения
Рекомендовано Министерством общего и профессионального образования
Российской Федерации для использования в учебном процессе студентами
физических специальностей высших учебных заведений
ш
МОСКВА
НАУКА • ФИЗМАТЛИТ
1996
ББК 22 31 ff Издание осуществлено при поддержке
г. J2 F>cipn Российского фонда фундаментальных
У7ТК ^49 1Я '» исследований по проекту 96-02-30089
а2.4ъ±_
Рецензенты: CD<^
академик АН Украины А И. Ахиезер,
доктор физико-математических наук Н. Ф. Шульга
Лабзовский Л- Н. Теория атома. Квантовая алектродинамика алектронных
оболочек и процессы излзгчения: Учеб. руководство. — М.: Наука. Физматлит,
1996. — 304 с. — ISBN 5-02-015016-9
Представлены как традиционные, так и все значительные новые методы и
результаты теории атома. Подробно рассмотрены релятивистская теория атома водорода, в
том числе релятивистская кулоновская функция Грина. Изложение квантовой
электродинамики атома основано на теории возмущений для S-матрицы в картине Фарри.
Приведена теория радиационных поправок для нерелятивистских и сильно
релятивистских электронов. Рассмотрены процессы мультипольного излучения атомов,
фотоионизация, автоионизация, многофотонные процессы, а также квантовоэлектро-
динамическая теория естественной ширины и формы спектральной линии.
Для научных работников, занимающихся теорией атома, теоретической
спектроскопией, теорией ядра, теорией излучения, а также^дягЯвиирантов и студентов
старших курсов соответствуюц
Табл. 12. Ил. 61. Библи!
Научное издание
ЛАБЗОВСКИЙ Леонтий Нахимович
ТЕОРИЯ АТОМА
Квантовая электродинамика электронных оболочек
и процессы излучения
Редакторы Г. М. Карасева, Л. Л. Русакова, Д. А. Миртова
Оригинал-макет подготовлен в Издательстве МФТИ
Оператор верстки Л. Г. Быканова
Корректоры О. И. Холодкееич, С. А. Холодкееич.
ИБ №41632
ЛР № 020207 от 27.11.91.
Подписано в печать 05.12.96. Формат 60X90/16. Бумага книжно-журнальная.
Печать офсетная. Усл. печ. л. 19. Уч.-изд. л. 20,9.
Тираж 1000 экз. Заказ 859 С-043.
Издательская фирма «Физико-математическая литература» РАН
117071 Москва В-71, Ленинский проспект, 15
Отпечатано в Московской типографии № 2 РАН
121099 Москва Г-99, Шубинский пер., 6
^ 1604090000-043 g^,,^ © Л. Н. ЛабзовСКИЙ, 1996
053(02)-96 ^
ISBN 5-02-015016-9
ОГЛАВЛЕНИЕ
НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ И ЕДИНИЦЫ 5
ПРЕДИСЛОВИЕ 6
ГЛАВА 1
РЕЛЯТИВИСТСКАЯ ТЕОРИЯ АТОМА ВОДОРОДА
§1.1. Уравнение Дирака для электрона во внешнем поле .... 9
§ 1,2. Движение релятивистского электрона в центрально-симметричном поле 15
§ 1,3. Релятивистская задача об электроне в кулоновском поле ядра ... 20
§ 1.4. Релятивистская кулоновская функция Г^ина 27
§1.5. Переход к нерелятивистскому пределу 31
§ 1.6. Преобразование Фолди-Вутха^ена 36
ГЛАВА 2
КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА АТОМА
§2.1. Электромагнитное поле: классическая теория 43
§ 2.2. Разложение потенциалов на плоские волны 51
§ 2.3. Квантование электромагнитного поля 55
§ 2.4. Фотоны с определенным моментом и четностью 59
§ 2.5. Взаимодействие электронов с фотонами 65
§ 2.6. S-матрица в картине Фарри 70
§ 2.7. Электронный и фотонный пропагаюры 78
ГЛАВА 3
РЕЛЯТИВИСТСКАЯ ТЕОРИЯ
ВЗАИМОДЕЙСТВИЯ ЭЛЕКТРОНОВ В АТОМЕ
§ 3.1. Классификация поправок к энергии для связанных электронов в
атомах 82
§ 3.2. Взаимодействие электронов в первом порядке теории возмущений . 85
§ 3.3. Взаимодействие электронов в вьфожденных состояниях 93
§ 3.4. Матричные элементы гамильтониана Брейта 98
§ 3.5. Взаимодействие электронов во втором порядке теории возмущений 104
§3.6. Релятивистский метод Хартри-Фока 109
ГЛАВА 4
РАДИАЦИОННЫЕ ПОПРАВКИ К УРОВНЯМ ЭНЕРГИИ АТОМОВ
§4.1. Квантовая электродинамика свободных электронов 116
§ 4.2. Расходимости в S-матрице 123
§ 4.3. Перенормировка и ре17ляризация 132
§ 4.4. Радиационный сдвиг уровней энергии для нерелятивистских
электронов в атоме 147
§ 4.5. Радиационный сдвиг уровней для релятивистских электронов в атоме 165
ГЛАВА 5
ВЗАИМОДЕЙСТВИЕ АТОМОВ С ИЗЛУЧЕНИЕМ
§5.1. Излучение одного фотона 180
§ 5.2. Спонтанное и вьшужденное излзгчение и поглощение света 189
§5.3. Мультипольное излучение 191
§ 5.4. Вероятности переходов в атоме водорода и одноэлектронных ионах . 202
§ 5.5. Вероятности переходов между уровнями многоэлектронных атомов 212
§ 5.6. Фотоионизация 222
§ 5.7. Автс»10низационные состояния 233
§ 5.8. Излучение атомов в ридберговских состояниях 240
§ 5.9. Рентгеновские спектры атомов и ионов 252
§ 5.10. Многофотонные процессы в атомах 255
ГЛАВА 6
ЕСТЕСТВЕННАЯ ШИРИНА И ФОРМА СПЕКТРАЛЬНОЙ ЛИНИИ
§6.1. Радиационная ширина уровней 268
§ 6.2. Форма спектральной линии: квантовомеханическая теория .... 273
§ 6.3. Форма спектральной линии: квантовоэлектродинамическая теория . 279
ПРИЛОЖЕНИЯ
1. Лэмбовский сдвиг водородоподобных атомов 289
2. Вероятности переходов 290
СПИСОК ЛИТЕРАТУРЫ 299
НЕКОТОРЫЕ ОБОЗНАЧЕНИЯ И ЕДИНИЦЫ
Для обозначения операторов используется буква с крышкой, для
обозначения векторов — полужирный шрифт. Векторное
произведение обозначается ахЬ, коммутатор и антикоммутатор — как
[АВ]:р = АВ + В А. Для обозначения четырехмерных величин
используются греческие индексы [i, v, X, ..., принимающие значения
1, 2, 3, 4, а для обозначения трехмерных величин, — как правило,
латинские. Принята евклидова метрика в четырехмерном
пространстве с мнимой четвертой компонентой 4-векторов: а^^ = (а, Шд)-
Скалярное произведение в 4-пространстве обозначается так:
%К = аЬ + а4*4 = аЬ - а^Ь^.
Наконец, в Jнeкoтopыx случаях используется специальное
обозначение а^7ц = 2 (двойная крышка) для скалярного произведения
произвольного 4-вектора а^^ и матриц Дирака 7^-
В книге используются, в основном, две системы единиц:
релятивистская и атомная. В первой из них h = с = т=\ (h —
постоянная Планка, с — скорость света, m — масса электрона), во второй
Й=е = т=1 (е — заряд электрона). Во многих случаях, однако,
масса электрона m выписывается в формулах явно.
Связь между атомными единицами и единицами в системе СГС
и СИ приведена в первой части книги [I] (см. в предисловии), связь
между атомными и релятивистскими единицами для наиболее
употребительных в теории атома величин дается приводимой таблицей.
Сравнение релятивистской и атомной систем единиц
(а = е /Йс ~ 1/137,036 — постоянная тонкой структуры)
Физическая величина
Заряд
Масса
Момент количества движения
Длина (боровский радиус ао )
Скорость
Импульс
Энергия
Время
Частота
Коэффициент перевода к.
1 а. е. = fc р. е.
V^
1
1
1/а
а
а
а^
1/а^
а
ПРЕДИСЛОВИЕ
В настоящей книге рассматриваются все те задачи, которые требуют
для своего решения применения методов квантовой
электродинамики: это релятивистская теория движения и взаимодействия
электронов в атомах, теория радиационного сдвига уровней и, наконец,
теория излучения и поглощения света атомами. Последняя, как
известно, в нерелятивистском случае может быть изложена на уровне
квантовой механики, как это делается во многих руководствах по
теории атомных спектров. Такое изложение, однако, всегда
является неполным и во многих случаях непригодным (например, для
описания рентгеновских спектров в тяжелых атомах, в которых
внутренние электроны сильно релятивистские). Релятивистская теория
необходима также для описания спектров многозарядных ионов,
изучение которых в последнее время является одной из важнейших
задач атомной физики.
Таким образом, в книге теория излучения атомов излагается с
помощью квантовой электродинамики, а в тех случаях, когда ее
можно не использовать, совершается переход к нерелятивистскому
пределу и применяются методы квантовой механики. Такой подход
позволяет охватить всю совокупность процессов во внешних и
внутренних оболочках атомов и ионов, но требует предварительного
знакомства с методами квантовой электродинамики. Изложение этих
методов в книге наиболее близко к широко известным
руководствам: Ахиезер А. И., Берестецкий В. Б. Квантовая
электродинамика. — М: Наука, 1981 и Берестецкий Б. Б., Лифшиц Е. М., Пита-
евский Л. П. Квантовая электродинамика. — М.: Наука, 1980,
однако не повторяет их. Отличие заключается в том, что изложение
целиком относится к излучению связанных электронов в атомах
(так называемая картина Фарри). Вместе с тем это изложение
последовательно проводится, как и в упомянутых руководствах
начиная с теории невзаимодействующих полей и кончая
перенормировками и регуляризацией 5-матрицы. Это обеспечивает известную
замкнутость содержания книги, хотя, разумеется, большое число
различных конкретных вопросов столь обширной области физики,
как теория взаимодействия атомов с излучением, остается вне
рамок книги. Во всех таких случаях автор старался дать ссылки на
посвященные этим вопросам монографии и обзоры.
В первой главе излагается релятивистская теория атома
водорода, в которой, помимо традиционных вопросов, рассмотрены
импульсное представление для релятивистских водородных волновых
функций, преобразование Фолди—Вутхайзена, а также разработан-
ный относительно недавно атшарат релятивистских кулоновских
функций Грина.
Вторая глава, посвященная общим вопросам квантовой
электродинамики атома, содержит в качестве вступления краткую сводку
результатов классической электродинамики, в частности
классическое описание спина фотона, что приводит непосредственно к
волновой функции фотона, обладающего определенным моментом и
четностью. Последнее особенно важно для описания процессов
излучения в центрально-симметричном поле атома. В этой же главе
содержится формулировка квантовоэлектродинамической теории
возмущений для связанных электронов в атомах (картина Фарри).
Такая теория обладает определенными особенностями по сравнению с
обычной теорией для свободных электронов.
Третья глава посвящена релятивистскому отшсанию
взаимодействия электронов в многоэлектронном атоме. Здесь имеется большое
разнообразие методов и подходов, беглый обзор которых сделан в
предыдущей второй главе. Для конкретных расчетов в книге избран
адиабатический формализм Гелл-Манна и Лоу как один из наиболее
детально разработанных и широко применяемых методов. Глава
содержит как общие формулы для поправок к уровням энергии, так и
результаты конкретных расчетов для простых двухэлектронных
систем, иллюстрирующих относительную важность различных
вкладов в энергию взаимодействия. Завершается глава описанием
релятивистского метода Хартри—Фока, являющегося основой для
современных расчетов тяжелых атомов.
В четвертой главе рассмотрена теория радиационных сдвигов
уровней энергии электронов в атомах. Изложение проводится от
первых принципов электродинамики и позволяет проследить всю
последовательность действий, включая регуляризацию матричных
элементов 5-матрицы, и заканчивается конкретными расчетами
лэмбовского сдвига для различных состояний атомов. Новым
элементом в этой главе является описание расчетов собственной
энергии электрона и поляризации вакуума для релятивистских
электронов в кулоновском поле при произвольных значениях заряда ядра.
Эти расчеты были завершены лишь в самое недавнее время.
Пятая глава книги, наибольшая по объему, содержит описание
процессов взаимодействия атомов со светом на основе квантовой
электродинамики. Здесь наряду с традиционными вопросами,
такими как вероятности переходов и фотоионизация, рассмотрен целый
ряд новых задач, решенных в последние десятилетия. К ним можно
отнести релятивистские расчеты вероятностей переходов для одно-
электронных и двухэлектронных многозарядных ионов с
произвольным зарядом ядра, расчеты фотоионизации многоэлектронных
атомов в приближении случайной фазы, теорию двукратной
фотоионизации, задачу об излучении атомов в ридберговских состояниях,
наконец, теорию многофотонных процессов в атомах.
Последняя, шестая глава книги посвящена проблеме, которая
, обычно не выделяется специально в качестве крупного раздела в
руководствах по теории излучения, — проблеме расчета естествен-
ной ширины и формы спектральных линий. Здесь, однако, эта
проблема рассмотрена более детально. Впервые из квантовой
электродинамики мы получаем замкнутые выражения для радиационной и
автоионизационной ширины, не прибегая к складыванию
вероятностей, а также выводим в общем случае выражение для лоренцевско-
го контура. Результаты этой главы важны для приложения к теории
спектров многозарядных ионов.
Настоящая книга представляет собой вторую часть курса
современной теории атома, первой частью которого является книга:
Веселое М. Г., Лабзовский Л. Н. Теория атома. Строение электронных
оболочек. — М.: Наука, 1986. К сожалению, вторую часть автору
пришлось готовить без непосредственного участия его учителя,
профессора М. Г. Веселова, скончавшегося в 1987 году. Однако автор по
мере возможности старался сохранить стиль изложения первой
части. Этот стиль во многом определялся характером научного
мышления М. Г. Веселова, на первое место ставившего краткость и
четкость формулировок.
Книга рассчитана на студентов физических специальностей
университета, изучающих теоретическую физику. Содержание книги
соответствует курсу лекций по теории излучения, читавшихся
автором на протяжении десятка лет на физическом факультете
Ленинградского университета. Изложение материала в книге построено
таким образом, что для ее чтения необходимо знать лишь основы
квантовой механики (например, в объеме известного курса Л. Д.
Ландау и Е. М. Лифшица «Теоретическая физика»). Необходимые
сведения из квантовой электродинамики содержатся в тексте книги.
Основное внимание при изложении обращается на принципиальную
сторону дела, однако общие вопросы иллюстрируются, как правило,
примерами и вычисления доводятся до окончательных результатов.
Книга может представлять интерес также для физиков-теоретиков,
работающих в области теории атома и в смежных областях, а также
для физиков-экспериментаторов, желающих ознакомиться с
достижениями теории.
Автор предполагает написать также третью, последнюю часть
курса по теории атома, содержащую такие вопросы, как
сверхтонкая структура атомных спектров, описание атомов во внешних
полях, экзотические атомы и некоторые другие вопросы.
Настоящая книга тесным образом связана с первой частью, на
которую в тексте имеются многочисленные ссылки; эти ссылки
начинаются с римской цифры I, за ней следует указание на параграф
или формулу.
Глава 1
РЕЛЯТИВИСТСКАЯ ТЕОРИЯ АТОМА ВОДОРОДА
§ 1.1. Уравнение Дирака для электрона во внешнем поле
Эта глава является продолжением главы 1 части первой [I], в которой
рассматривалась нерелятивистская теория атома водорода. Как и в [I,
гл. 1 ], ядро здесь считается точечной бесконечно тяжелой
бесструктурной частицей (учет поправок на массу и объем ядра, а также
эффекты, связанные с наличием у ядра магнитных и электрических
моментов, см., например, в [1]). Теперь вместо уравнения Шрёдингера
[I, (1.1)] нужно решать уравнение Дирака для электрона в кулонов-
ском поле ядра. В настоящем параграфе мы рассмотрим кратко
некоторые общие свойства уравнения Дирака для произвольного внешнего
поля [2, 3]. Напомним вначале, как выглядит уравнение Дирака для
свободного электрона (в релятивистских единицах):
i^^=h(r^r,t), (1-1)
Л(г) = ар + рт, (1.2)
где а, р — матрицы Дирака
-(°о). f=(i-?)' "•^'
О — матрицы Паули (см. [I, (3.4)]), р = —гУ — оператор
импульса. Волновые функции 4i)(r, t) в теории Дирака являются четырех-
компонентными биспинорами:
-^->=ft£;b
Ф2
Xl
Х2
(1.4)
где спиноры ф, X — так называемые верхняя и нижняя компоненты
биашнора. В уравнении (1.1) функция •ф(г, t) рассматривается как
матрица-столбец.
Матрицы а, {3 обладают следующими свойствами:
[a,ajU = 2b,jI, [а,^и = 0, ^^ = 7 (/=1,2,3), (1.5)
где / — единичная четырехрядная матрица. Все матрицы а, {3
эрмитовы:
at = aj, р+ = р. (1.6)
Часто бывает удобно использовать ковариантную запись
уравнений Дирака. Для этого вводится 4-вектор импульса:
Р = (Р, iPo) = [-'V, - ^j,
а также матрицы
У = (у. Уд' У = Ф«. -¥4 = р. (1 -7)
которые удовлетворяют перестановочным соотношениям
[•Y^'Yv]+=26^v-^ (fi, v=l,2,3,4) (1.8)
и являются эрмитовыми, как и матрицы а, {3.
Умножив обе части уравнения (1.1) на у^, можно переписать его
в виде
(%p^ + '«)^W = o. (l-^)
где X = г, it. Эрмитово-сопряженный биспинор (матрицу-строку)
записываем в виде
Вместо (1.10) удобнее, однако, использовать дираковски
сопряженный биспинор
уравнение для которого принимает вид
'Ф(''уЛ-'«) = 0. (1-12)
причем подразумевается, что в (1.12) оператор р действует справа
налево.
Умножая уравнение (1.9) слева на ijj, а уравнение (1.12) справа
на -ф и вычитая одно из другого, получаем соотношение
'^У^,(Р^-^) + (Р^'^)У^^ = 0, (1.13)
которое можно переписать в виде
э^^^. (1.14)
Вектор
s^(x) = i^x)y^y\>(x) (1.15)
представляет собой плотность тока вероятности и связан с обычным
вектором тока /^^ соотношением
где е — заряд электрона (по абсолютной величине). Компонента
—гуо представляет собой плотность заряда, а компонента — jSq —
плотность вероятности р(х):
-iso(x) = р(х) = я1,+(х)я1,(х). (1.17)
10
Таким образом, (1.14) представляет собой уравнение
неразрывности.
Для стационарных состояний
%(r,t) = y\,^(T)e-'^.', (1-18)
где •ф^(г) — решение стационарного уравнения Дирака
Л(г)я1)Дг) =/?^я1,Дг). (1.19)
Индекс S нумерует различные решения (1.19).
Уравнение Дирака (1.1) имеет решения как с
положительными, так и с отрицательными значениями Е^. В этом проще
всего убедиться, переписав уравнение (1.1) в импульсном
представлении
. д^^ =(ap + ^m)^{p,t) (1.20)
и перейдя от (1.20) к системе уравнений для спиноров (р(р, t) и
Х(р,0 (см. (1.4)):
г|£=(ар)х + АПф, (1.21)
i ^ = (ор)Ч> - тх- (1.22)
В случае стационарных состояний (1.18) эта система уравнений
становится алгебраической:
(£-Ап)ф(р)-(ар)х(р) = 0,
(£ -I- Ап) Х(р) - (ар) Ф(р) = 0.
Из условия разрешимости (1.23) следует:
Е'^-т'^- (ар) (ар) = 0. (1 -24)
Используем известные соотношения для матриц Паули
(оа)о = а -I- г(оха),
(1.25)
о(оа) = а-I-г(а хо),
где а — произвольный вектор. Эти соотношения доказываются с
помощью непосредственно проверяемого равенства
OjO^ = bj^ + if.jki^i (i' k, 1=1,2, 3), (1.26)
где Eji^i — единичный антисимметричный тензор. Из (1.26) следуют
и коммутационные соотношения для матриц с^ как компонент
спинового момента (см. [I, (3.1)])
[Oja^]_ = 2iej^iai (1.27)
и антикоммутационные соотношения
[a.aj, = 26,,. (1.28)
11
Из (1.25) также следует
(оа) (Ob) = (ab) + го(а х b), (1.29)
(oa)(oa) = a^ (1-30)
где а, Ь — произвольные векторы.
С помощью (1.30) из (1.24) получаем
£=±Vp2+An2. (1.31)
Существование решений с отрицательными частотами (энергиями)
приводит к выводу, что в релятивистской квантовой механике
невозможно сохранить обычную интерпретацию собственных
значений оператора Гамильтона как значений энергии частицы. Кроме
того, мы должны придавать различный физический смысл
состояниям с положительными и отрицательными энергиями (см. ниже).
Запишем теперь уравнение Дирака во внешнем
электромагнитном поле, вводя 4-вектор потенциала А (А, IAq), где Aq=V —
скалярный потенциал. Это уравнение получается из (1.9) заменой
{iy^{p^ + eA^) + m)-^ = 0. (1.32)
Сопряженное уравнение принимает вид
Miy^(P^-eAj-m) = 0; (1.33)
потенциал А^, в отличие от р^, является вещественным. В некова-
риантной записи уравнение (1-32) после умножения на {3 принимает
вид (1.1) с гамильтонианом
h(T)=a(p + eA)-eV(T) + ^m. (1.34)
В частности, для электрона, движущегося в кулоновском поле ядра
с зарядом Z,
А = 0, V(r)=f, (1.35)
где г = I г I — расстояние от электрона до ядра. Плотность тока для
электрона во внешнем поле дается теми же формулами (1.15),
(1.16), что и для свободного электрона, в чем легко убедиться,
повторив прежние рассуждения. Прежний вид имеет и уравнение
неразрывности.
Решения стационарного уравнения (1.20) с гамильтонианом
(1.34) могут принадлежать как дискретному, так и непрерывному
спектру. Поскольку собственные значения для свободного электрона
определяются формулой (1.31), областями непрерывного спектра
будут Е> т или Е ^ —т. При —т < Е < т электрон будет
находиться в связанном состоянии и его движение будет финитным.
Таким образом, для электрона во внешнем поле, как и для свободного
электрона, можно говорить о состояниях с положительной и
отрицательной энергией.
12
в качестве условия нормировки для -ф в случае связанных
состояний можно использовать условие
jp(r)dr= (я1,»я1,(г)йг=1. (1.36)
Состояниям с отрицательной энергией в релятивистской теории
придается смысл с помощью преобразования зарядового сопряжения
С, которое заключается, во-первых, в замене А^^ на —А^ и,
во-вторых, в преобразовании биспиноров ij), яр с помощью матрицы
зарядового сопряжения С:
■^^(х) = С^{х); "^^(х) = С-^у\,'(х), (1-.37)
ще символ «т» означает транспонирование.
Матрицу С можно выбрать так, чтобы уравнение Дирака было
инвариантным относительно преобразования зарядового сопряжения
С. Транспонируя уравнение (1.33), умножая его слева на С и меняя
знак у А , получаем
(iCylC-'ip^ + еА^) - лп)я1,с = 0. (1-38)
Чтобы имела место инвариантность, нужно потребовать, чтобы
C/^C-i =-у^. (1.39)
Тогда функция •ф*' после замены А^-^—А^^ удовлетворяет тому же
уравнению (1.32), что и функция -ф. Следовательно, сама по себе
функция -ф*^ удовлетворяет уравнению
(%(Р^ - еА^) + т)^^ = О, (1-40)
т. е. уравнению (1.32) для частиц с другим знаком заряда
(позитронов). Нетрудно убедиться непосредственно, что условию (1.39)
удовлетворяет матрица
C=-Y2'Y4- (1-41)
Можно убедиться также, что эта матрица удовлетворяет условиям
С^С=1, (1-42)
с = -а. (1-43)
Поскольку преобразование зарядового сопряжения (1.37)
содержит комплексное сопряжение, то для стационарных состояний
(1.18) при Е^<0 оно означает переход к состояниям с Е^>0.
Таким образом, можно считать, что функции -ф^, соответствующие
функциям у\>^ с Е^< О, описывают частицы с положительными
энергиями, но с другим знаком заряда — позитроны.
В слабом внешнем поле притяжения для электрона (потенциал
(1.35)) дискретные уровни располагаются вблизи границы
«верхнего» континуума Е = т. В достаточно сильном внешнем поле (впро-
13
чем, недостижимом в реальных атомах) уровни могут перейти
границу Е = 0, т. е. из положительных сделаться отрицательными. В
еще более сильных полях электронные уровни могут погрузиться в
нижний континуум. В этом случае возникает возможность
спонтанного рождения электронно-позитронных пар из вакуума (подробнее
об этом см. в [4]). Следовательно, сама возможность описания
движения электрона в рамках одночастичной задачи (т. е. с помощью
уравнения (1.32)) является ограниченной.
В заключение этого параграфа приведем некоторые
алгебраические соотношения для матриц Дирака. Используя (1.8) и
предполагая, что по одинаковым значкам производится суммирование,
можно получить следующие равенства:
Уу,Уу, = ^у (1-44)
'Ypi'Yv'Ypi =-2'Yv. (1-45)
У^УхУ.Уу^ = ^^х.' (1-46)
'Y^x'Vv'Yp'Y^ = -г-Ур-УЛх- (1 -47)
Введем обозначение а = a^y^^, где а^ — произвольный 4-вектор.
Тогда из (1.8) следует, что
ад + да = 2аХ, (1-48)
SS=a^ (1.49)
а с учетом (1.44)—(1.47) получаем также
'Y^^'Y^ = -2a, (1.50)
"Ypi^ ^"Ypi = 4a^*v' (1-51)
у^адсу^= —2сда. (1.52)
Важное значение имеют формулы для вычисления следов
различных матриц. Рассмотрим тензор
Т,^,,..,„^^Р(У,У,,-У,)- (1-53)
В силу инвариантности следа относительно циклических
перестановок матриц у^ этот тензор инвариантен относительно циклических
перестановок значков и,.. Поскольку матрицы -у,, имеют один и тот
же вид в любой системе отсчета, то и тензор Г„ „ должен иметь
один и тот же вид. Но таким свойством обладает единственный
тензор 6^^, поэтому любой тензор Т^^^^ должен выражаться через
6^^. Из тензора б^^^ можно составить лишь тензоры четного ранга,
поэтому след произведения нечетного числа матриц у всегда равен
нулю. В частности,
T^ = Spy^ = 0, (1.54)
14
что можно увидеть и непосредственно. Далее, используя
циклические перестановки и формулу (1.8), получаем (с учетом Sp 7 = 4):
Г =46 , (1.55)
Spad=abT =ab (1.56)
И т. д.
Помимо матриц у , в релятивистской теории употребляется
также матрица у^:
"Ys ='Yi'Y2'Y3'Y4- (1-57)
Свойства этой матрицы, легко проверяемые непосредственно, таковы:
(•¥5)'= Л (1-58)
[•Y5'yJ+ = 0, (1.59)
а ее явный вид
Из (1.61) следует еще одно свойство:
Sp'Y5 = 0. (1.62)
Наконец, нужно упомянуть еще матрицу
^=(S°). О-бЗ)
которая может быть представлена также в виде
2 = -0^5 (1.64)
(отметим, что матрица у^ коммутирует с матрицами а). С матрицей
S связаны полезные соотношения
[a^aj_=je^^,2:„ (1.66)
которые следуют непосредственно из (1.3), (1.27). Соотношение
(1.66) может быть переписано также в виде
(аха) = г2. (1.67)
§ 1.2. Движение релятивистского электрона
в центрально-симметричном поле
При движении электрона в центрально-симметричном поле
интегралом движения, как 'и в нерелятивистском случае, является полный
момент количества движения электрона
j=T-|-s, (1.68)
15
который складывается из орбитального 1 и спинового s моментов.
Моменты 1 и S в отдельности теперь не являются интегралами
движения. Момент 1 определяется, как и в нерелятивистской механике,
выражением
Т=гхр, (1.69)
а спиновый момент выражается через матрицу 2:
s = i2. (1-70)
Операторы j^, j^ в случае центрально-симметричного поля (1.35)
коммутируют с гамильтонианом (1.34), поэтому они обладают
общей системой собственных функций:
Л^Еум =-Б^Еул/. (1-71)
7г^ЕуМ = Л^^£уМ- (1-73)
Уравнения (1.72), (1.73) могут быть переписаны также в двухком-
понентной форме
0 + Ю'Феум = Я^+1)Феум. (1-''4)
0 + 5)'ХеуМ = Яу+1)Хеум. (1-''5)
0 + Ю.Фяум=^Л/ф^,.^, (1.76)
0+ЮДяум = Л^Х^гум- (1-77)
Построим явно собственные функции операторов (1 -|- s)^,
(T-l-s)^, зная собственные функции операторов!^, 1^, 5^, s^:
\yim = 'nYi„, (1.79)
s^r, =4 Г), (1-80)
V 4 V
Sz%=f*%> (1-81)
где теперь s = ^о, У,^ — сферические функции [I, (1.12)], а т)^ —
двухкомпонентные спиноры (ja = ± 1/2). По формуле [I, (3.29)]
получаем
(\ + §)Ч/л/(п) = /(у + 1)Ц-ш(п), (1-82)
(Т-Ь s),Q^,^(n) = MQji^{n), (1.83)
Ц7м(п) = S C;.t(mfA)y,„(n)r,^, (1-84)
16
m^
где n = r/|r|. Функции (1.84) называются шаровыми спинорами.
Они являются также собственными функциями операторов 1^ и s^ с
собственными значениями
?Q^.,,,(n) = /(/+l)Q.,^(n), (1.85)
и образуют полную систему ортонормированных функций
J Q;,^.(n)Q.,^(n) dQ = bj..\,6^^., (1-87)
вде { dQ означает интегрирование по угловым переменным.
Шаровые спиноры определяют угловую зависимость функций
гEjш = ifEJ,('■Щ-ш(^^) (1-89)
(множитель i поставлен в (1.89) для удобства). Квантовое число /
в нерелятивистской теории определяет значениё^ орбитального
момента электрона и одновременно четность состояния. В
нерелятивистской же теории орбитальный момент не сохраняется, но понятие
четности состояния по-прежнему имеет смысл. _
Рассмотрим операцию пространственной инверсии Р, которая
заключается в замене г—>—г. Уравнение Дирака будет инвариантно
относительно операции Р, если инверсии сопутствует такое
линейное преобразование ^ компонент биспинора
•ф(г, О -* •ф(?г, О = f'4i,(r. О, (1.90)
что
P(iy^(P^ + eA^) + m)^y\, = 0. (1.91)
Если потребовать, чтобы уравнение (1.91) сводилось к (1.32), мы
придем к условиям
у§> = -#>Y, у^§> = §>у^, (1.92)
которым удовлетворяет матрица
^ = rip'Y4- (1-93)
Здесь т)р — числовой множитель, по модулю равный единице. Этот
множитель определяет так назьшаемую внутреннюю четность
частицы. Хотя конкретный выбор т)р может быть различным,
внутренняя четность должна быть противоположной для электрона и
позитрона.
Применим преобразование (1.90) к функции
( 8En(r)Qj,^(n) \ (1.94)
17
Фе/шСО =
1 \ji^a
Тогда
(1.95)
Вспоминая, как преобразуются при инверсии сферические функции
(см. [I, (3.210)]), и используя определение (1.84), получаем
Ч-ш(-п) = (-1)Чш(п)- (^•^^>
Тогда, если потребовать, чтобы функция (1.94) обладала
определенной четностью, из (1.95), (1.96) следует, что число /должно
отличаться от / на единицу. Поскольку, согласно правилам сложения
моментов, / = у ± 1/2, отсюда следует, что
1=2]-I. (1.97)
При этом
^^яушС^»-) = ЛрС-ОЧяушС-)- (1.98)
Как следует из (1.23), спинор Хецм пропорционален (ор)ф£у;м-
Очевидно, то же самое можно сказать и в случае движения во
внешнем поле. Однако при пространственных вращениях величина (ар)
ведет себя так же, как (on). Поэтому угловая часть спинора Xejim
определяется произведением (tm)QjiM. Таким образом, можно
написать
(°п)Чш = «%м^ (1.99)
где а — числовой множитель. Для нахождения а по формуле
« = \ ^Дм(п)(оп)^уш(п) d^ (1100)
нужно записать скалярное произведение (on) в сферических ортах,
учесть выражение [I, (3.83)] для компонент п^ {\i = 0, ±1) через
функции У1ц(п) и воспользоваться формулой [I, (3.44)] для
интеграла от трех сферических функций. Нужно также учесть действие
матриц о на спиноры г]^ (см. в [I] формулы (3.133)—(3.135)) и условие
ортогональности для этих спиноров. Вычисление дает: а = — 1, т. е.
(°п)Ч-ш = -%м- (1101)
Умножая обе части (1.99) еще раз на (on) и используя (1.30),
получаем также
(°п)%м = -^уш- (1-102)
Запишем уравнение (1.32) с потенциалом (1.35) в двухкомпо-
нентной форме аналогично (1.23):
(Е + eV - тЫт) - (ар)х(г) = О, (1.103)
. (E + eV + mЫr)-{ap)^p(г) = 0. (1.104)
18
с помощью (1.101), (1.102) можно написать
(ор)Х = i(ap)f вjl('^Щ^м(.^^) = -i(op)(or) - } /^^ДО^ушСп)-
(1.105)
Используя (1.29), после преобразований получаем
(ор)Х = -г{(Рг) + io(p X г)} i fEji(r)Qji^(n) = Q
= -{div г + (rV) + о(г X p)} i fEj[(r)Qji^(n) =
= -^ + 7/я;Д'-)+7/£уД°0}Цш(п)- (1-106)
При этом мы учли равенства div г = 3, (rV) - = — 7' ^ также (1.69).
Далее, с помощью равенства
а также (1.85), (1.86), переписываем о1 в виде *)
оГ=-(1 + и^.,),
где
'^Л =
I
при j = l — -,
-(/+1) при j = l+j.
Формулу (1.109) можно переписать еще иначе:
«Л =
. , 1 . , 1
у + 2 при у = / - 2,
при i = I + -~.
(1.107)
(1.108)
(1.109)
(1.110)
Наконец, исходя из (1.110) и (1.97), можно написать соотношение
^л = -^п- (1-111)
Тогда вместо (1.106) можно написать
(ар)х = -(^ + Ц^/я;,)£^;ш- (1-112)
Аналогичным путем с помощью (1.111) выводится соотношение
(ар)Ф = /(^ + ^5^,,)о,,м. (1.113)
Подставляя (1.112), (1.113) в (1.103), (1.104), учитывая (1.88),
(1.89) и сокращая в правых и левых частях получившихся уравне-
*) Это равенство справедливо на функциях (1.84).
19
НИИ на шаровые спиноры Qy^^^, ^Дм1 приходим к уравнениям для ^
радиальных функций g^ji, f^ji'. .
^+'-^8Bji-(^- + 'n + eV)f^j, = 0, (1.114)
^ + Ц^ Гвп + (Б-т + eV)g,j, = 0. (1.115) '
®
§ 1.3. Релятивистская задача об электроне
в кулоновском поле ядра
В этом параграфе мы рассмотрим решение уравнений (1.114),
(1.115) с потенциалом (1.35). Выясним вначале вид решения при
г—»0. Пренебрегая членами Е±т в правой части, опуская для
краткости индексы Ejl у функций g, / и у и и вводя новые функции
G=rg, F = rf, получаем
^ + ^G-^F = 0, (1-116)
ar г г
EP + ^F-^G = 0. (1-117)
dr г г
Здесь а = e^/fic — постоянная тонкой структуры. В релятивистских
единицах а = е^.
Будем искать решения уравнений (1.116), (1.117) в виде
G = Ari, F = Br'i. (1.118)
Подстановка в (1.116), (1.117) дает
A{y + -}^)-BZa = 0, (1-119)
AZa + B{y-v.)=0. (1.120)
Величина -у определяется из условия разрешимости уравнений
(1.119), (1.120)
^2 = ^2_(2a)2. (1.121)
В релятивистской теории электрон в кулоновском поле можно
рассматривать только до значения Za< 1, т. е. Z< 137. При Z> 137
энергия основного состояния становится мнимой (см. ниже в этом
параграфе); в этом случае становится обязательным учет конечных
размеров ядра (см. [4]). Поскольку \y.ji\ ^1 при любых значениях
у7, величина -у вещественна при aZ< 1.
Рассмотрим состояния дискретного спектра {Е < т). В этом
случае будем искать решения уравнений (1.114), (1.115) в виде
g = ylm + f?e4ppv-i((2, -I- Q^), (1.122)
/ = -V7;r^rEe-TPpv-i((3j-(22), (1.123)
20
ще p = 2Xr, к = y/rn^ — E^. Такой выбор соответствует асимптотике
решений (1.114), (1.115)
где С — константа. Подстановка (1.122), (1.123) в (1.И4), (1.115)
дает
Р ^ (Qi + Qi) + (•¥ + и)((2, + (Зг) - PQ2 +
+ Za^|^((2,-(2,) = 0, (1.125)
Р ^ (Qi - Qг) + (•¥ - x)(Qi - Qi) + PQ2 -
-Za^f|±f(Qi + Q2)=0. (1-126)
Складывая и вычитая почленно эти уравнения, получаем
pf+(^-¥)a + («-^)a=«. ('•'">
9'-^+[^-^-9)аг+[^ + ^]а^=0. (1.128)
Дифференцируя (1.127) и подставляя производную -^ из (1.128),
а затем действуя в обратном порядке, получаем уравнения для
определения Qj, Qj-
p^ + (2v+l-P)t-(,-¥)Q,=0,®(1.12„
Р-^'
,р. +(27+1-P)^-(7+1-^)Q2 = 0. (1.130)
При этом нужно использовать соотношение
^г_^^'=^г_^^\ (1.131)
которое проверяется непосредственно с помощью (1.121).
Решения уравнений (1.106) (конечные при р-*0) выражаются
через вырожденную гипергеометрическую функцию [I, (П2.1)]:
Q, = AF{y-^,2y+U9Y (1.132)
Q^ = BF[y+\-^,2y+\;p\. (1.133)
Постоянные А к В связаны между собой соотношением
L-^B = -U-^A. (1.134)
21
которое получается из (1.127) или (1.128), если положить там
р = 0. Рассуждая так же, как и при решении нерелятивистского
радиального волнового уравнения (см. [I, § 1.1]), приходим к выводу,
что ряды, с помощью которых определены гипергеометрические
функции (1.132), (1.133), должны обрываться (в противном случае
при р—» 00 эти функции будут возрастать как еР, а функции g, f —
как еР'^).
Условие обрывания рядов можно представить в виде
^_^ = _„^. (1.135)
Если п^= 1, 2, ..., то обе функции (1.132), (1.133) сводятся к
полиномам. Если п^ = О, то обрывается только ряд (1.132). Но при
«г = О из (1.135) имеем y=ZaEIX, а тогда из (1.131) следует
ZamlX= +V.. Если и < О, то, как следует из (1.134), В = 0 и
Q2 = О- В этом случае конечное решение (1.132), (1.133)
существует. Если же и > О, то функция Qj при п^ = О расходится при
р-*оо. Таким образом, радиальное квантовое число п^ в
релятивистской теории может принимать следующие значения:
при и<0, (1.136)
при и > 0.
"^-il.2.3.
Из (1.136) следует выражение для уровней энергии атома водорода
в релятивистской теории (формула Зоммерфельда):
_i
P-n^l = "J
J , (Za)^
{Vx^,-{Za)2+n,)^
(1.137)
Поскольку выражение (1.137) зависит лишь от xji, оно фактически
не зависит от /. Таким образом, уровни энергии с определенными
значениями п^, у двукратно вырождены соответственно двум
возможным значениям / = у± 1/2.
Основному состоянию отвечают значения квантовых чисел
Пг = 0, у = 1/2. При этом возможно лишь одно значение / = О, так
как величина и в этом случае должна быть отрицательной: и = — 1.
Формула (1.137) описывает уровни энергии в водородоподобных
ионах с произвольным зарядом ядра Z< 137 (см. о таких ионах в
§ 5.9). При aZ**; 1 формулу (1.137) можно разложить по степеням
aZ. Ограничиваясь членами порядка (aZ)^, получаем
(i4i Цу
где мы ввели обозначение п = п^ -|- | x.J = п^ + J + 1/2. Можно
убедиться, что таким образом определенное квантовое число п
совпадает с определением главного квантового числа в [I, § 1.1 ]. Тоща,
если рассматривать энергию связи электрона в атоме Е^^ — т, то
22
первый член разложения (1.138) совпадает с формулой Бальмера [I,
(1.22) ], а второй дает поправку на релятивистские эффекты. С
учетом этой поправки энергия электрона начинает зависеть не только
от п, но и от у, т. е. вырождение, имевшее место в нерелятивистском
случае, частично снимается. Как уже говорилось выше, вырождение
по квантовому числу / (т. е. фактически по четности, см. § 1.2)
остается. Это вырождение снимается лишь с учетом радиационных
поправок (лэмбовского сдвига уровней, см. § 4.4). Заметим, что
обозначение энергии тройкой квантовых чисел njl можно использовать
и в общем случае, в формуле (1.137).
Уровни энергии, отличающиеся только квантовыми числами у,
образуют тонкую структуру уровня с определенным значением п.
Тонкая структура обусловлена, как говорилось в [I, §3.12], спин-
орбитальным взаимодействием. Из формулы (1.138) этого
непосредственно не видно, однако становится ясно из полурелятивистского
уравнения Паули (см. § 1.5). Относительный порядок малости
тонкой структуры по отношению к расстоянию между уровнями с
различными значениями п, как следует из (1.138), определяется
параметром (aZ)^, т. е. при Z« 1 составляет 10"^. Для обозначения
состояний в релятивистской теории обычно используется
нерелятивистская символика с дополнительным указанием значения у: (п/)у.
При этом / определяет лишь четность состояния. Тогда
последовательность водородных уровней с учетом тонкой структуры можно
записать так:
Isi, (2si, 2pi), 2pi, Cisi, 3pi), (3/fe, ЗА), ЗЛ, ...
2 22 2 22 22 2
(в скобки взяты уровни, вырожденные по энергии).
Для радиальных функций g, f из условия нормировки (1.36)
следует:
оо
\{^{r)+f\r))r^dr=\. (1.139)
о
Из условия (1.139) определяется нормировочный коэффициент А в
(1.132), коэффициент В связан с А соотношением (1.134).
Вычисление нормировочных интегралов производится, как и в
нерелятивистской теории, с помощью формул интегрирования, приведенных
в [1, (П2.4)]. Приведем окончательные выражения для
нормированных радиальных функций:
g(Ol (2Ц|
/(л) -r(2v+i)
(т±Е)Т(2-1 + п^ + \)
AZam IZam \ .
{2\ry-'^e-^^■ X
xU^- xW(-n^,2-Y + 1; 2Xr) + n^F{\ - n^, 2-у + 1; 2Xr)j,
(1.140)
где верхний и нижний знаки относятся к g{r) и /(л) соответственно.
Приведем отдельно выражения для радиальных функций
состояний с п= 1, 2 [1]:
23
1. Состояние Isi (n= 1, / = 0, /= 1/2):
„ . . (2Zm\ ■'i+i J "i + ^i ^ -1 _Z2
Jm-E.
/iio('-) = -V7J7T£[^i^('')-
2. Состояние 2si (n = 2, / = 0, /= 1/2):
2
. 4_ /2Zm\v.+? J~ (27, + l)(m + £g~
Г 2ZmW2+') ^
.\m-E^ (2y^ + \)lN2 + 2)N2-2lN2 + i)mZr
rVi-'e--^,
TO
(1.142) g(
ГД
(1.143) че
goir.(r). (1.144)
3. Состояние 2pi (n = 2, / = 1, у = 1/2):
2
r Ч = /2Zm\Vi-"?J~(2Yi + l)(m + £^
И
Ф:
/(
л'2-2
2Zm{N^-\)
{27, + 1)Л?2
(27, + 1)Л?|-2{Л?2~ l)"'^''
4. Состояние 2рз (n = 2, / = 1, у = 3/2)
1 Zmr
g^iif)-
(1.145)
rЬ-^e-^r-,
(1.146) m
Л1
• c(3
HI
(1.147)
(1.148)
Здесь использованы следующие обозначения:
7i = V^^^^ToZp", г =1,2
(это согласуется с общим определением (1.121)),
(1.149)
(1.150)
«1
И
ц
а Ef (г= 1, 2, 3) представляют собой энергии состояний, вычисляе- ''
мые по формуле (1.137) (однако обозначаемые тройкой квантовых ^'
чисел njl): g
Е,шЕ,^ = ту/1-(аг)^, (1.151) /
E^^E^^ = E^,=^yfTTTi=^{lTVY^J^^, (1.152) -
E3 = E^^ = m^l-\{aZf. (1.153) '..
24
Перейдем к случаю непрерывного спектра. Из общих формул
(1.132)—(1.134) для функций непрерывного спектра получаются
выражения (отличие от случая дискретного спектра заключается в
том, что мы теперь не требуем обрывания рядов):
^(^Н =^ CiU^*^)^ПЁ±me-^^^'■{2^lr)Цy- ivy^e^^x
X [е'Ч-у + i-v)F{y - iv, 2у + 1; 2щг) ± "
;■ ±t-'\y-i-v)F{y + \-i-v,2y+\;2iv.r)], (1.154)
где С — нормировочная константа. В (1.154) использованы
обозначения
f, = Vf?2_^2 v = :?^, е2'^= ^р^. (1.155)
'^ |х y. + imvlE
Используя соотношение (см. [I, (П2.3)])
\ F{a, Р; х) = е^/'(Р - а, Р; -х), (1.156)
функции (1.154) можно переписать также в виде
^l^jj = ±^ СлГе±Ш{2\>.г)у{у - /v)-i X
(•у + iv)e-^^^'■+^Щy + 1 + /v, 2^ + 1; 2i\ir). (1.157)
^1ш
Нормировочный коэффициент С определяется из сравнения
асимптотического выражения функций (1.154) при г—» » с общей
формулой для нормированной сферической волны. Асимптотическая форма
сферических волн при наличии внешнего поля отличается от
свободных сферических волн лишь дополнительной фазой б^^^^ [2, 3]:
, ^ ;^i 1 . _^"^' I 2 ""П . (1.158)
. ^Епм г ^ ^_VF:r7;^/'Q.,^(n) sin (f.r-f -h б^д)J
При этом функции "^EjiM предполагаются нормированными по
.- «шкале энергий»
Используя асимптотику вырожденной гипергеометрической
функции F{a, ^; х) при X—»<», из сравнения (1.157) и (1.158) при
г-*0 получаем (при этом применяются те же вычислительные
приемы, что ив [I, § 1.1)] или [3]):
;^}=^^j?s^-p[i^-b2.,-b.(i±i)t]x (Ф
I X^(^^f^Uy + iv)e-^^^^^^Щy+l + iv,2y+U2ilJir). (1.160)
В некоторых задачах релятивистской теории атома водорода, как
и в нерелятивистском случае, удобнее использовать волновые функ-
25
ции электрона в импульсном представлении. Уравнение Дирака для (
свободного электрона в импульсном представлении мы уже
использовали в § 1.1. Для электрона во внешнем поле, описываемого
уравнением Дирака, переход к импульсному представлению во всем ана- ' '
логичен соответствующему переходу в нерелятивистском случае
(см. [1,§1.2]).
Уравнение (1.19) с гамильтонианом (1.34) (при А = 0)
аналогично уравнению [I, (1.57)] записывается в виде г
{ap + ^m-E)y^(p)-e^V'(p-p')-^(p')dp' = 0, (1.161)
где •ф(р) — волновая функция электрона в импульсном представле- '
НИИ, представляющая собой четырехкомпонентный спинор. Как и в : i
[I, § 1.2], функция •ф(р) связана с решением 4i)(r) уравнения (1.19)
преобразованием Фурье: |
^W =7rW $ е'Р'я1,(р) dp, (1-162) '
(2л:) ' •' 'i'
^(Р) = -^ \ е-'Р'я1,(г) dr. (1-163) 1
При этом из условия нормировки (1.36) следует: ' |
^я1,+(р)я1,(р)ф=1. ' (1.164) ;'
Переходя к случаю центрального поля, воспользуемся
разложением плоской волны по шаровым спинорам, которое совпадает по • i
виду с [I, (1.43)]^:
е-ф' = 4я2; S S (-0^я(/"-)Пш(^)Ухш(^р)- (1-165).
Х = 0 f=X±i ц X
Формула (1.165) проверяется непосредственно подстановкой яв- ,;
ного выражения для шаровых спиноров (1.84) с учетом
соотношения полноты для спиновых функций
1<%=1 (1.166)'
ц
и соотношения ортогональности [I, (3.32)] для коэффициентов Клеб- .'
ша—Гордана, в результате чего эта формула приводится к [I, (1.43)].
Подставляя в (1.163) функцию •ф(г) в виде (1.94) и используя
(1.165), в результате интегрирования получаем [5]
*.."<р) =(„:;;;,; 4:;^;;]. (...67)
оо
^'EJl(P) = 'Л(-0' J }[{Pr)gEj[(r)r-' dr, (1.168)
о
оо
^яуДР) = #(-0' J Jj{Pr)fEji{r)r-' dr. (1.169)
26
в случае основного состояния Isi вычисление интегралов в
(1.169) дает
Р^
zV
(1.170)
г,2 \
2V,+| I m+Я, Г{7, + 2) Л 13 3
2^+1 J w-^^i r{v, + 3) /l 3 1 5
>(^^ = ^^5;;;^br(2v. + i)-F7ij-/'^[2^i + 2'2^i + 2.2; -i2;;;2j.
(1.171)
где /"(a, p, 7; x) — гипергеометрическая функция.
При aZ«l из (1.170) получается нерелятивистская функция
[I, (1.66)]. Функция (1.171) приобретает малый коэффициент aZ
за счет множителя Vm — Е^. В общем случае переход к
нерелятивистскому пределу в координатном представлении будет
рассмотрен в § 1.5.
§ 1.4. Релятивистская кулоновская функция Грина
В релятивистской теории атома водорода, как и в нерелятивистской
(см. [I, § 1.4]), существует целый ряд задач, которые могут быть
решены с использованием функции Грина уравнения (1.19) —
релятивистской кулоновской функции Грина (РКФГ). Эта функция
Грина определяется уравнением
(h-E)G^{T;T') = b{T-T') (1.172)
и может быть представлена в виде спектрального разложения
ще суммирование производится по полной системе решений
уравнения (1.19). Формулы (1.172), (1.173) по виду аналогичны
соответствующим формулам нерелятивистской теории [I, (1.126)] и [I,
(1.127)]. Однако, как видно из (1.173), РКФГ, в отличие от
нерелятивистской функции Грина, представляет собой мая-рицу 4 X 4 по
спинорным индексам.
Для явного вычисления РКФГ был разработан целый ряд
методов. В частности, построены выражения для РКФГ в виде
разложения по параметру aZ в импульсном [6, 7] и координатном [8]
представлениях. Наиболее удобным для приложений в атомных
расчетах является, однако, парциальное разложение [9, 10],
подобное [I, (1.129)]. В этом случае более удобно использовать вместо
27
функции G^ функцию G^ = G^^, удовлетворяющую вместе зн
(1.172) уравнению са:
Р(Л-/?)С^,(г;г') = 6(г-г'). (1.1741
или, в явном виде, 1 W
jpap-pff? + ^j +лп]с^,(г;г') = 6(г-г'), (1.175) '"''
где а — постоянная тонкой структуры. I Р^
Функцию G£^(r; г') удобно представить в виде I
G^,(r;r') = {-pap + pff? + ^j + лп}ф^,(г; г'), (1.П6ГВ
где функция Ф£(г; г') удовлетворяет «квадрированному» уравне-^ не
нию, получающемуся при подстановке (1.176) в (1.175): | (1
|_Д + ^2 _ ^,2 _ 2£aZ _ (^ _ .^^ ^|ф^(^. ^,^ ^ ^(^ _ ^,^
(1.177L
Ж-
Здесь п = т/г. Разделяя радиальную и угловую части оператора Д;
Лапласа, перепишем (1.177) в виде
Оператор Л^, действующий на угловые переменные, равен
Jv = r2- (aZ)2- iaZan, (1-179;
где 1 — оператор орбитального момента количества движения, опре- ^'
деляемый согласно (1.69). Оператор Л^ можно переписать также
несколько иной форме *) ■
Л^ =
(к^ + к- (aZ)^ -iaZan ^
- iaZan K^ + K-{aZyj
(1.180) ко
-Ю
где А^=-(1+оТ). _ *5
Введение оператора К вызвано тем обстоятельством, что
шаровые спиноры Q^^д^, ^/1м являются его собственными функциями с ■
собственными значениями:
^ и
Щш=-^Лм> (J jgjj но
на
Формулы (1.181) следуют непосредственно из (1.108) с учеток
соотношения (1.111). Теперь можно показать, что собственные
I
*) Выражение (1.180) возникает, если учесть, что согласно (1.29) и перестановоч „
ным соотношениям [I, {1.110)],{аГ){аГ)=Р + 1"а{ГхГ)=Р —(огГ).
28
значения и собственные функции оператора Л^ могут быть
записаны в виде
NP^in; п') = у{у + 1)Р^(п; п'), (1.182)
где величина -у определяется согласно (1.121), а функции Р (п; п')
имеют вид
, Р(п;п')=2
}Ш
^Q,,^(n)Q-^(n') ^Q,,^,(n)Q;j^(n')
iaZ
^%м(п)^;,м(п') ^^м^^Щш^.^^')^
. (1.183)
В уравнении (1.182) в функции Р^(п; п') вектор п является
аргументом, а п' играет роль параметра. Равенство (1.182) проверяется
непосредственно перемножением матриц (1.180) и (1.183) с учетом
(1.181), (1.101), (1.102) и (1.121).
Функции Р^{п; п') обладают следующим свойством:
2/',(n;n') = 6(n-n').
(1.184)
Для доказательства (1.184) заметим, что суммирование по -у
распространяется на два возможных значения, у= ±Vx^— (aZ)^,
отличающихся только знаком. Поэтому
2/',(п;п') = 2
jlM
Цш(п)^;ш(п') о
%м(п)^;Тм(п')^
(1.185)
Используем, далее, условие полноты для шаровых спиноров
' 2 Ч7М(П)^ЛМ(П') = S У/т(п)Уш(п') S %К = *(" - "')'
/W ta ц (1.186)
; которое получается из условия ортогональности преобразования
• Клебша—Гордана [I, (3.32)], условия полноты для сферических
. функций
1Уы(п)^т(п') = 6(п-п') (1.187)
- Im
И правила перемножения матриц: матрица-столбец г]^, будучи ум-
I нежена на матрицу-строку г]^, дает квадратную матрицу. Таким
образом, в правой части (1.184), (1.186) подразумевается
единичная матрица 2x2. Таким же способом получается равенство
2%м(п)£^;7м(п') = 6(п-п'),
JIM
(1.188)
^ и свойство (1.184) тем самым доказано.
29
Пользуясь (1.184), представим трехмерную 6-функцию в виде
6(г - г') = -L 6(г - г') 2 Р,{п; п') (1.189;
гг
у
И разложим Ф£(г; г') также по функциям Р (п; п'):
Ф^(г; г') = -i^ 2 ^vijC'-; '■')P^^^■' «')■ (1-190
Тогда подстановка (1.189), (1.190) в уравнение (1.177) приводит!
следующим уравнениям для радиальных функций:
_4+т2-/?2-^ + ^!^^^1ф.,,(г;г') = 6(г-г'). (1.191
dr"-
+ y(y+llU^(^r;r') = b(r-r'). (1.1
Уравнение (1.191) совпадает с [I, (1.131)], если в последнем еде
лать замену 1—*у, Е—*Е^— т^, Z—*2EaZ (нужно учитывать, чъ
в [I, (1.131)] под Е подразумевалась отрицательная энергия связи
а в (1.191) подразумевается положительная энергия электрона
включающая массу покоя; при этом для связанных состо5ши!
Е< т). Тогда можно воспользоваться результатами из [I, § 1.4] !
написать
л. f . '\ ■^ r-(7 + l-v) ,^ (AEaZ \ „, (^EaZ \
(1.192
где V = -J-—^—5=, а М^^, W^ — функции Уит гекера. Благодар
множителю Г('у+1 —v) выражение (1.192) как функция Е об
ладает полюсами, значения которых совпадают с (1.137). 4to6i
избавиться от аргументов г< можно, как ив [I, § 1.4)], применит
интегральные представления для произведения функций Уиттеке
ра.
Формулы (1.190), (1.192), однако, еще не до конца решают по
ставленную задачу, поскольку необходимо от функции Грин
«квадрированного» уравнения (1.177) перейти к функции Грин
(1.176). Действуя оператором в (1.176) на функцию Ф£(г; г'), по
лучаем
Ge
(«•= «•') = S {'" ^ (~ Ф,^('-г')Р(ап)Р^(п-, n')j -
- ;- %в [Р(«Р) + f^? + ^Ь + ml Р^(п; п')-|. (1.
193
30
Действие операторов an, ар на Р^(п; п') определяется с помощью
формул (1.101), (1.102), (1.106), (1.108):
Р(ап)Р^(п; п') =
' -^^^Jш(^^Щшi^^') -^ ^,-ш(п)^;Тм(п')'
^ Q,7^(n)Q-^(n') ^ Qjj^{n)Q;jUn')^
= 1
jlM
(1.194)
P(ap)P^(n-, n') =
'_ iaZ
If (1 - x)Q.,^(n)Q-^(n') -^(1 - x)Q.,^(n)Q>^(n')
уш[-^(1 + к)%м(п)^;ш(п') -^(1 + «)Цтм(п)^Дм(п')^
(1.195)
Существует целый ряд других эквивалентных (1.193) форм
записи РКФГ (см. по этому поводу [11J). В некоторых задачах нужно
знать редуцированные РКФГ [см. I, § 1.4]. Явные выражения для
таких функций приведены в [11]. Наконец, в релятивистской
теории атома водорода, как и в нерелятивистской, могут быть
построены функции пггурмовского типа [см. I, § 1.5], по которым можно
разложить РКФГ [12-14].
§ 1.5. Переход к нерелятивистскому пределу
Для перехода к нерелятивистскому пределу удобно исходить из
уравнений для двухкомпонентных функций (1.103), (1.104).
Энергию Е для положительно- и отрицательно-энергетических состояний
представим в виде Е^-'* = ±{т + е), где е — энергия связи. В
нерелятивистском случае, как видно из (1.138),
|£| ;=«m(aZ)2<*:m. (1.196)
Для среднего значения V также должно быть справедливо
неравенство V«-m. Тогаа из (1.103), (1.104) следует:
(+);
Ф'
2т ^ '
2т ^ '
(1.197)
(1.198)
Из (1.196) следует оценка для характерного значения импульса
электрона в атоме в нерелятивистском пределе:
'p^maZ. (1.199)
Заметим, что характерное значение скорости атомного электрона
V = р/ш ;=» aZ, и поскольку в используемых нами единицах скорость
света с равна единице, величина aZ представляет собой не что
31
иное, как релятивистский параметр малости vie Из (1.199) получа
ем, что ч^^^« aZip('^\ Ф^~) «s aZx^~\ т. е. что функции ^("^^ ip^")
представляют собой «малые» компоненты дираковских биспиноров
соответственно для положительно- и отрицательно-энергетических
состояний. Подставляя (1.197), (1.198) в (1.103), (1.104) и
используя (1.29), приходим к уравнениям
Таким образом, в нерелятивистском пределе полная система
дираковских биспиноров -ф^ распадается на две полные системы
спиноров, ф^"^) и х1 \ удовлетворяющих уравнениям Шрёдингера
(1.200) или (1.201) и описывающих соответственно электроны или
позитроны. I
Ограничимся в дальнейшем рассмотрением только
электронных состояний и обобщим уравнение (1.200) на случай атома, на-,
ходящегося во внешнем магнитном поле. Согласно (1.34) мы дол-;
жны при этом заменить (1.197) выражением (значки ± теперь
опускаем) 1
^'^i*^(P + ^^)*P- (1.202«
В уравнениях (1.103), (1.104) также нужно произвести замену
р^^р-1- еА.
Для вычисления выражения (о(р-I-еА))^, возникающего при
подстановке (1.202) в (1.103), используем (1.29). Нужно только
учесть, что векторное произведение ((р + еА) X (р-|- еА)) не
обращается в нуль ввиду некоммутативности операторов р и А:
((р -I- еА) X (р -I- еА)) = -/e((V X А) -|- (А X V)) = -ie rot А.
(1.203)
Таким образом, получается уравнение, которое называется
уравнением Паули:
f2^(p-beA)2-eF-b^sd>r-EW = 0. (1-204).
где dS* = rot А — напряженность магнитного поля, s = ^ о — спин
электрона. |
Рассмотрим теперь второе приближение по параметру а^
[2, 3]. Ограничимся при этом случаем, когда внешнее магнитно!
поле отсутствует. С учетом членов следующего порядка малосп
из (1.104) вместо (1.197) получим 1
Х-(1-Ч^)Й>Р- (1-205''
32
Подставляя это выражение в (1.103) и используя (1.30), приходим
к уравнению
Уравнение (1.206) обладает тем недостатком, что оператор в
левой его части (последний член) неэрмитов. Кроме того, функцию ф
теперь нельзя нормировать на единицу, поскольку из (1.36) следует:
\{\^f>{г)\^+Ыт)\^)dг=l. (1.207)
с точностью до членов порядка aZ включительно, т. е. в
нерелятивистском приближении (1.200) или в приближении Паули (1.204)
можно считать, что функция ф нормирована на единицу и условие
(1.207) выполнено, однако учет членов высшего порядка уже не
позволяет этого. Действительно, с точностью до членов, квадратичных
по параметру aZ,
^(1ф(г)|'+к(г)|')ЙГ«$ Лф(г)|2 + _1-|(ар)ф(г)|2| dr.
(1.208)
Преобразуя (1.208) с помощью интегрирования по частям и
используя вновь (1.29), получаем
= \ I Ф| 2 dr -I- -Ц \ ф-рф dr. (1.209)
Из (1.209) следует, что можно ввести функцию, которая будет
нормирована на единицу, с помощью прео!бразования
Ф(г)=[1+£5|ф(г) (1.210)
или
>?('•)= (l-£2) ^РС-)- (1.211)
Получим уравнение для ф(г). Для этого подставим (1.211) в
(1.206) и отбросим члены высших порядков малости по параметру
aZ. При этом возникает уравнение вида
Лф = £ф, (1.212)
где
^=e-^^-£i-ii{(^)^(^)-i(?^+^^)}- (1-213)
Выражение в фигурных скобках преобразуется следующим образом:
(ар) V(ap) = Vp'- i{aVV) (op) = Fp^ -|- /STp - о(5Г х р), (1.214)
pV-Vp^ = -AV + 2iffp, (1.215)
2 л. Н. Лгбзовский ^^
где У = —VV — напряженность электрического поля. Теперь
оператор h принимает вид
h = ^-eV--^ + -^a(Wxp)--^AV. (1.216)
Оператор (1.216) в отличие от оператора в (1.206) является
эрмитовым, в чем легко убедиться непосредственной проверкой.
Используя (1.199), можно проверить также, что три последних члена в
(1.216) являются поправками порядка (aZ)^ по отношению к двум
первым. Действительно, с учетом (1.199) первый член (1.216) имеет
порядок величины m(aZ)^ — это атомная единица энергии. Если в
качестве V взять кулоновский потенциал (1.35) и учесть, что в
релятивистских единицах
^^1^ (1-217)
(это атомная единица длины), а также е^=а, то второй член
(1.216) по порядку величины также равен m(aZ)^. Так и должно
быть, поскольку кинетическая и потенциальная энергии связанного
состояния имеют одинаковый порядок величины в силу теоремы ви-
риала (см. [I, § 4.1]). Наконец, из (1.199) и (1.217) следует теперь,
что три последних члена (1.216) имеют порядок m(aZ)'^.
Первый из поправочных членов представляет собой релятивист-
скую поправку к кинетической энергии электрона (зависимость
массы от скорости). Его происхождение видно из формулы (1.31),
если выражение в правой части этой формулы — энергию
свободного электрона — разложить по степеням pVmh
Первый член в (1.218) дает массу покоя электрона, второй —
обычную кинетическую энергию, третий — рассматриваемую поправку.
Второй из поправочных членов в (1.216}^ представляет собой
оператор спин-орбитального взаимодействия Н^^ (взаимодействия
движущегося магнитного момента с электрическим полем [3]). В
случае центрально-симметричного поля V = V{r)
У= -LEL (1.219)
г dr
и оператор спин-орбитального взаимодействия принимает вид
(см. [I, (3.322)])
^so = ;^^o(rxp)=^^(lS), (1.220)
где 1, S — операторы орбитального и спинового моментов электрона.
В частности, для потенциала (1.35), т. е. в случае атома водорода,
H^=-I^A-([s). (1.221)
34
Наконец, последний из поправочных членов в (1.216) для
потенциала (1.35) принимает вид
Ът"-
2т'-
6(Г).
(1.222)
Поправку к энергии атома водорода, учитывающую
релятивистские поправки aZ«.\, можно получить в первом порядке теории
возмущений, усредняя три последних члена (1.216) с
нерелятивистскими волновыми функциями. Вычисление первой из поправок
производится с помощью соотношения, следующего из уравнения Шрё-
дингера для атома водорода [I, (1.2)]:
(1.223)
p4 = 2mJf?o-|-^Uo,
где -фо и £■() — волновая функция и энергия электрона в
нерелятивистском пределе. Из (1.223) следует:
^^i=-i(p')oo=-ik+
8m
2Za „ ,
— ^0 +
(1.224)
00
где мы использовали принятое в [I] обозначение матричных
элементов. Используя формулы из [I, табл. П2.3] и выражение для
энергии Е^ [I, (1.22)], получаем для поправки (1.224)
выражение [1]
'^'^.= -^(n^-i). с-^")
где п — гл'авное квантовое число, / — орбитальное.
Аналогичное вычисление для второй поправки с учетом
соотношения [I, (3.325)] дает
^E^ = \
о
m(aZ)''
1
2„3 (2/ + 1)(/ + 1)'
m(aZ)'' 1
2п
3 (21+1)1 '
1 = 0,
/ = / - 2.
(1.226)
Наконец, вычисление третьей поправки приводит к формуле
miazy^ (1.227)
АЕ, = -
2п^
Собирая результаты (1.225)—(1.227), убеждаемся, что в сумме
они при любых значениях /, / описываются выражением
I/+ 1/2 4п\- ^ '
АЕ = Af?! -I- АЕ^ + АЕ^ = -
2п^
Как видно, это выражение совпадает с поправочным членом в
(1.138).
35
§ f.6. Преобразование Фолди-Вутхайзена
Недостатком обычной формы записи уравнения Дирака (1.1) или
(1.32), (1.34) является то, что в этой записи невозможно
непосредственно придать физический смысл оператору скорости:
у = ?=г[Лг]_. (1.229)
Действительно, тривиальное вычисление приводит к результату
v = a. (1-230)
Отсюда следует, во-первых, что по модулю скорость электрона
всегда равна скорости света с (напомним, что в используемых единицах
с= 1). Во-вторых, различные компоненты а^ оператора (1.230) не
коммутируют друг с другом, что означает невозможность
одновременного измерения всех компонент скорости. Оба этих вывода
противоречат экспериментальным данным, что наводит на мысль о
возможном существовании другого представления для уравнения
Дирака, в котором эти недостатки отсутствуют.
В том, что такая возможность существует, убеждает также
наличие четырех компонент у дираковского биспинора tj), тогда как для
описания частицы с положительной энергией и двумя возможными
значениями проекции спина достаточно двухкомпонентной
функции. Недостаток оператора (1.230) заключается в том, что он
перемешивает все четыре компоненты биспинора. Необходимо,
следовательно, так переопределить оператор скорости, чтобы он действовал
на двухкомпонентные функции, не перемешивая их друг с другом.
Такое преобразование было найдено Фолди и Вутхайзеном [15].
Заметим, что в нерелятивистском пределе указанное выше
требование выполняется и в обычном представлении, благодаря
(1.197), (1.198):
xjj'^atj) л? ■ф'^о^ + Х^Оф- (1.231)
Для положительно частотных решений, например, отсюда следует,
согласно (1.197), (1.198),
Прежде чем переходить непосредственно к преобразованию
Фолди-Вутхайзена, произведем разбиение различных операторов на
«четно-частотные» и «нечетно-частотные» части [16]. Перейдем к
импульсному представлению и введем знаковый оператор по
определению:
y^gp+Pm (1.233)
где ар -|- {Зш — дираковский гамильтониан (1.2) для свободной
частицы Ер = vpM-m^. Оператор Л, очевидно, коммутирует с
ар -I- {Зш. Кроме того, он эрмитов и унитарен:
Л = Л^ = Л-1. (1.234)
36
Последние свойства легко проверяются непосредственно. Поскольку
Л^ = I, собственные значения Л равны X = ± 1. Различные
значения X соответствуют положительно-частотным (Х=1) и
отрицательно-частотным (Х = —1) решениям уравнения Дирака для
свободного электрона. _
С помощью знакового оператора Л любой оператор, действующий
на волновые функции Дирака, можно разложить на четно-частотную
и нечетно-частотную части. Назовем четно-частотным оператором
такой, который положительно-частотное (отрицательно-частотное)
решение уравнения Дирака переводит вновь в
положительно-частотное (отрицательно-частотное). Напротив, оператор, переводящий
положительно-частотную дираковскую волновую функцию в
отрицательно-частотную и наоборот, назовем нечетно-частотным.
Поскольку все положительно-частотные функции ортогональны
отрицательно-частотным (они принадлежат различным собственным
значениям эрмитового оператора Л), среднее значение любого
нечетно-частотного оператора в состоянии с определенным знаком X равно
нулю. Последовательная одночастичная теория должна содержать
только четно-частотные операторы, поскольку противное означало
бы, например, примесь к электронным состояниям (X = 1) позитрон-
ных состояний, связанных с состояниями Х = —1 (см. § 1.1). Такая
примесь могла бы возникнуть лишь в результате рождения электрон-
но-позитронных пар, т. е. при отказе от одночастичной картины.
Все сказанное до сих пор относилось к свободным электронам, для
которых Одночастичная картина в принципе справедлива. Однако при
взаимодействии электронов с другими частицами, друг с другом или
с внешними полями ситуация меняется. В этом случае эффекты
рождения виртуальных электронно-позитронных пар (радиационные
поправки, см. гл. 4) явно сказываются на движении электронов. В
случае взаимодействия при высоких энергиях (в сильном внешнем поле)
может происходить также рождение реальных
электронно-позитронных пар (см. [2, 3]). В такой ситуации разделение операторов на
четно- и нечетно-частотные части утрачивает смысл. Оно, однако,
полезно в случае слабых внешних полей (при низких энергиях
взаимодействия), пока радиационные поправки остаются малыми и не
происходит рождения пар (см. ниже в этом параграфе).^
Разобьем произвольный одночастичный оператор А на четно-
и нечетно-частотные части:
А = \^^ + А^_у (1.235)
С этой целью рассмотрим следующую серию равенств:
А-^{~) = Л^(-) + А-)^(-)' (^ -^^^^
лЖя1)(+) = ЛЛя1)(^, = ^(+)Я1)(+) - ^-)^(+). (1 -238)
ЛЛЛя1)(_^ = -ЛЛя1)(_) = ^(+)^(-) - \-)\-у (1 -239)
37
где tjj^+j — дираковские волновые функции, отвечающие значениям
X = ± 1. Складывая и вычитая попарно равенства (1.236) и (1.238),
а также (1.237) и (1.239), получаем
Я(^^ = 1(Я±ЛЛЛ). (1.240)
Рассмотрим некоторые примеры. Прежде всего, очевидно,
оператор ар + {Зш является четным, поскольку он коммутирует с Л. То
же самое можно сказать об операторе р. Далее, используя вид
оператора Л (l.i233) и формулу (1.240), можно вычислить
четно-частотные части операторов а, {3. При этом нужно воспользоваться
антикоммутационными соотношениями (1.5):
2(ор + Рт)р; 2рЛ
Аа,А=-а,+ JL_^ =-а.-Ь-^, (1.241)
р
р
В результате в импульсном представлении
а -5^ (1-243)
Р
Р(+) =
!ПА. (1.244)
Е
Р
Таким образом, четно-частотная часть оператора скорости равна
%) = ^- (1-245)
р
Этому выражению, в отличие от (1.230), можно придать
непосредственно физический смысл. Другим способом выражение (1.245)
можно получить, если записать с'помощью (1.240) четно-частотную
часть оператора координаты г в импульсном представлении и затем
воспользоваться уравнением (1.229) [16]. При этом четно-частотная
часть оператора г оказывается равной
р р
где г = V — оператор координаты в импульсном представлении.
По сути дела, переход к четно-частотным частям операторов и,
в частности, формула (1.245) решают поставленную в начале этого
параграфа задачу. Однако при этом мы не получаем в явном виде
представления для дираковской волновой функции в двухкомпонен-
тной форме. Поэтому полезно еще раз рассмотреть ту же самую
проблему теперь уже непосредственно с помощью преобразования
Фолди—Вутхайзена, представляющего собой унитарное
преобразование вида
'^ФВ У/2Е (Е +т) ' ^ '
р Р
38
которому подвергаются волновые функции и операторы в
импульсном представлении. Свойство унитарности
^^в^^ФВ=1 (1.248)
проверяется непосредственно с учетом соотношений
антикоммутации (1.5). Преобразование функций и операторов производится по
формулам
Ч'фв = ^^ФвЧ'. (1-249)
Л1,в = ^^Фв^^^№ (^•25°)
где Ч'фв и Аьв — волновые функции и операторы в представлении
Фолди—Вутхайзена.
Рассмотрим вид различных операторов в ФВ-представлении.
Прежде всего заметим, что оператор импульса р (в импульсном
представлении это оператор умножения) коммутирует с f/фв, поэтому
Рфв = Р- (1-251)
Далее, оператор Гамильтона для свободного движения в
ФВ-представлении принимает совсем простой вид:
Лфв = ^?рР. (1.252)
Пусть -ффв — решение уравнения Дирака в ФВ-представлении:
Лфв^Фв(Р) = 'Б^Фв(Р). (1.253)
'ФфвСр)"!
^Фв(Р) =
^Хфв(Р) j'
(1.254)
где Ффв, Хфв — двухкомпонентные спиноры. Поскольку оператор
■ ^^фв коммутирует с матрицей {3, можно построить двухкомпонент-
: ные функции
', •ФФВ(±) = ^ ^Фв(Р). (^ -255)
■5
; ^ФВ(.) = [^"f^). Ч'ФВ(-) = (^ J(p)). (1-256)
; которые также являются решениями уравнения (1.253). ^
*■ Нетрудно убедиться также, что знаковый оператор Л в ФВ-
f представлении приобретает вид
\ Лфв = Р, (1.257)
откуда следует, что функции ■ффв(±) соответствуют двум возможным
; собственным значениям этого оператора: X = ± 1.
Приведем явный вид еще некоторых операторов в ФВ-представ-
■ лении:
Гфв={/фвГ1/^в = г+'^^Фв(^р1/^в)- (1-258)
39
Подставляя в (1.258) выражение (1.247) и используя определение
(1.240), а также формулы (1.257), (1.248), получаем [16]
«■фв(+) = «■ — 2Е (Е +тУ (^•25^)
р р
?ФВ(-) = 24^(«Р + #Й)- (1.260)
При выводе (1.259) использовано также соотношение (1.66).
Вычисляя четно-частотную часть оператора скорости в ФВ-пред-
ставлении и учитывая (1.252), получаем
^ФВ(+) = '[Лфв. Гфв(+)]- = ^- (1.261)
р
Второй член в (1.259) не дает вклада в (1.261) в силу равенства
нулю коммутатора
[2, Р]_ = 0. (1.262)
Принимая во внимание (1.257), находим, что выражение (1.261)
может быть получено также непосредственно при переходе к ФВ-
представлению в (1.245).
Поскольку, как было продемонстрировано в § 1.5, в
нерелятивистском пределе четырехкомпонентные дираковские спиноры
распадаются на двухкомпонентные, представление ФВ удобно
использовать также при вычислении релятивистских поправок для
электронов во внешнем поле. В этом случае преобразование (1.247) не
сводит дираковские функции в точности к двухкомпонентной
форме, однако отклонения от такой формы оказываются мaJ:ыми
и естественным образом представляют собой релятивистские
поправки.
Продемонстрируем, как с помощью преобразования ФВ получить
релятивистские поправки, приведенные в (1.216). Для этого
перейдем в уравнении Дирака (1.161) к ФВ-представлению; учетом
(1.249), (1.250), (1.252) получаем
(Pf?p - /?)я1)фв(Р) - е j f/(p)F'(P - Р')1/''(Р')^фв(Р') «iP' = 0,
(1.263)
где f/(p) = {/фв(р).
Переходя от функций •ффв(р) к функциям (1.255), получаем
систему уравнений:
фЕ^ - /?)я1)фв(^)(р) - е j (f/(p)f/^(p'))Ml^'(P - Р')^ФВ(+)(Р') Ф'-
-е j ({/(р)1/Чр'))(-)Пр -Р')^ФВ(-)(Р') Ф' = О, (1-264)
(р£р - /?)я1)фв(_)(р) - е j (f/(p)f/^(p'))Ml^'(p - Р')^ФВ(-)(Р') dv'-
- е j (t/(p)f/4p'))(-)l^'(P - р')^Фвм(Р') dv' = 0. (1.265)
40
При этом мы использовали тот факт, что оператор умножения
V'{p — р'), как и любая функция р, р', ввиду (1.251), (1.257)
является четно-частотным.
Из (1.264), (1.265) следует, что теперь уже нельзя написать
независимые уравнения для двухкомпонентных функций ■ффв(±)-
Можно показать, однако (см. ниже), что в низшем порядке по aZ,
соответствующем (1.216), перемешивающие члены (вторая строка в
(1.264) и (1.265)) учитывать не нужно и можно ограничиться
решением двухкомпонентных уравнений. В этом и заключается
преимущество ФВ-представления.
Рассмотрим уравнение (1.264), отбросив перемешивающий член
во второй строке. Проделаем затем следующее преобразование,
учитывая условие унитарности (1.248):
. ^ ,. (Рар + т + Е )(ар'Р + т+Е .)
тиЧр') = 2^Е^ЕХ^тНЕ^,^т/ =
Перейдем, далее, в (1.266) к нерелятивисгскому пределу, оставляя
лишь поправочные члены порядка (aZ)^. При этом используем
разложение для Ер-.
^P = '" + i^ + i5 + -' (^•'^'>
в котором ограничимся лишь первыми двумя членами. Это дает
t/(p)f/+(p') =s 1 -I- (Pap -I- 2m)
g(p'-p)P I P'^-P^
4/71-^
--i^(p'^-p^).
(1.268)
Согласно (1.264) мы должны теперь выделить четно-частотную
часть оператора (1.268). В силу того, что знаковый оператор
совпадает в ФВ-представлении с матрицей {3, при вычислении четно-час-
тогаой части (см. (1.240)) из выражения (1.268) следует исключить
члены, линейные по матрицам а. Тоща мы придем к выражению
(f/(p)f/-(p'))(,,=1+^°р^^°^р;-р» --i^ (р'^- р^). (1.269)
Учитывая (1.65), формулу (1.269) можно преобразовать к виду
(f/(p)f/4p')V)=l-^2:((p'-p)xp)-^^^. (1.270)
Подставим (1.270) в (1.264) и перейдем к координатному
представлению, пользуясь тем обстоятельством, что выражение
(р'~"Р)^^'(р'~ Р) в координатном представлении переходит в
—iVV, а (р' — р)^1^'(р' — р) переходит в —AV (это проверяется
непосредственно дифференцированием фурье-преобразования для по-
41
тснциала). Вместе с тем, импульс р просто заменяется onepaTopoN
импульса р. Тогда, учитывая все три члена разложения (1.267) i
выражая •ффв(+) через двухкомпонентную функцию ффв, мы
получаем для этой функции уравнение, в котором роль гамильтониаш
играет оператор (1.216). Таким образом, мы действительно учли ва
релятивистские поправки порядка (aZ)^ и доказали, что в это*
приближении волновая функция в ФВ-представлении остается двух-
компонентной.
Глава 2
КВАНТОВАЯ ЭЛЕКТРОДИНАМИКА АТОМА
§2.1. Электромагнитное поле: классическая теория
Описывая многоэлектронный атом на языке квантовой
электродинамики, мы рассматриваем его как совокупность электронов,
движущихся во внешнем поле — кулоновском поле ядра. Ядро при этом
считается бесконечно тяжелым, точечным и бесструктурным. В
результате взаимодействия электронов атома с электромагнитным
полем возникает взаимодействие этих электронов друг с другом и
происходят различные атомные процессы — излучение, поглощение
г^ и т. д. Поэтому прежде чем излагать квантовую электродинамику
' атома, мы вначале кратко опишем теорию свободного электромаг-
■ нитного поля, затем перейдем к теории электронно-позитронного
поля и, наконец, к теории взаимодействующих полей [1, 2].
В этом параграфе мы приведем основные результаты классиче-
' ской электродинамики, необходимые в дальнейшем. Уравнения
• Максвел/ia для электромагнитного поля в пустоте имеют вид
rotd*'-f = 4KJ, (2.1)
;: rot5r-h^ = 0, (2.2)
div V = 4згр, (2.3)
divd«'=0, (2.4)
где Sf и dS* — напряженности электрического и магнитного полей,
' р и j — плотности внешних зарядов и токов. При описании взаимо-
' действия атомных электронов с электромагнитным полем эти плот-
I ности создаются атомными электронами. Уравнения Максвелла за-
; писаны здесь в релятивистских единицах. Кроме того, использована
' так называемая гауссова (нерационализованная) система единиц,
г Из уравнений (2.1), (2.3) следует уравнение неразрывности.
Действительно, дифференцируя (2.3) по < и используя тождество
div rot dS* = О, получаем
divj-hf = 0. (2.5)
Электродинамика наиболее удобно формулируется на языке
' потенциалов электромагнитного поля — векторного А и скаляр-
V 43
ного V; эти потенциалы определяются следующими
соотношениями:
^r=rotA. (2.7;
Эти соотношения определяют потенциалы неоднозначно, с
точностью до градиентного (калибровочного) преобразования:
A^A + Vx, (2.8;
v^v-^, (2.9;
где %{т, t) — произвольная функция координат и времени.
Инвариантность выражений для W, dlf относительно калибровочной
преобразования (калибровочная инвариантность) следует из того
что rot Vx = 0.
Неоднозначность в определении потенциалов обычно устраняю'
выбором некоторого дополнительного условия, или калибровки.
Часто употребляется калибровка Лоренца,
divA + ^ = 0, (2.10;
преимуществом которой является ее релятивистская инвариант
ность. Другая часто встречающаяся калибровка — кулоновская,
divA = 0, (2.11;
в которой удобно описывать кулоновское взаимодействие зарядо!
(см. ниже в этом параграфе).
Подставляя выражения (2.6), (2.7) в уравнения Максвелл;
(2.1), (2.3) и используя лоренцеву калибровку, получаем уравне
ния для потенциалов
OA = -43tj, (2.12;
ПУ = -4згр, (2.13;
где П — оператор Даламбера:
П = А--4- (2.14
Уравнения (2.2), (2.4) удовлетворяются при этом тождественно. Ус
ловие Лоренца (2.10) не полностью фиксирует калибровку потенци
алов. Подвергая потенциалы калибровочному преобразованию (2.8)
(2.9) и подставляя в (2.10), находим, что это равенство само инва
риантно относительно калибровочного преобразования с тако!
функцией X. которая удовлетворяет волновому уравнению
□Х = 0. (2.15
Кулоновская калибровка приводит к другим уравнениям для по
тенциалов:
□A-vf = -4KJ, (2.16
ду = -4згр. (2.17
44
1-
' Учитывая явный вид решения уравнения Пуассона (2.17)
nr) = if^, (2.18)
видим, что в кулоновской калибровке скалярный потенциал V
определяет кулоновское взаимодействие. В частности, для точечного
заряда ядра Z с плотностью
р(г) = ге6(г-Го). (2.19)
находящегося в начале координат (Гр = 0), из (2.16) следует (1.35).
Кулоновская калибровка не обладает релятивистской
инвариантностью, однако в атомных задачах это несущественно, поскольку
имеется выделенная система отсчета, связанная с атомом.
Уравнения электродинамики удобно записывать в
четырехмерной ковариантной форме. Потенциалы А, V образуют 4-вектор
(А, iV), который удовлетворяет уравнениям
ПА^ = -4лу^, (2.20)
ще /jj — 4-вектор тока (1.16), р,= 1,2,3, 4. Условие Лоренца-
теперь записывается в виде
П_о (2.21)
дх ~"'
уравнение неразрывности в виде (1.14). Калибровочное
преобразование (2.8), (2.9) принимает вид
А^А +^. (2.22)
^^ ^^ дх^
Вместо векторов напряженностей Sf, dlf в 4-мерной теории
удобно ввести тензор электромагнитного поля
f =^_Hi (2.23)
^^^ дх^ эх/
Видно, что этот тензор по определению антисимметричен,
F^^ = —F^^. Компоненты этого тензора связаны следующими
соотношениями с компонентами векторов W, dlf:
Fjk = bki^i О, k, I =1,2,3),
Уравнения Максвелла (2.1), (2.3) записываются теперь в виде
^-^Hv .„ • (2.24)
тоща как уравнения (2.2), (2.4) по-прежнему удовлетворяются
тождественно.
45
функция Лагранжа *) для свободного электромагнитного поля
(т. е. в отсутствие внешних зарядов и токов) имеет вид
L=^(^-dX^), (2.25)
или, в ковариантной записи,
^= — тг-^ ^ • (2.26)
Эквивалентность выражений (2.26) и (2.25) проверяется
непосредственно подстановкой (2.23). Тот факт, что выражение (2.25)
действительно играет роль функции Лагранжа для электромагнитного
поля, можно установить с помощью прин1щпа наименьшего
действия, построив функционал действия
^=S^(^.'I^)'^'^ (2.27)
и определяя компоненты 4-потенциала из условия экстремума
65 = 0. (2.28)
При этом вариации потенциала на границах четырехмерного объема
интегрирования считаются равными нулю.
Общие уравнения Эйлера—Лагранжа для вариационной задачи
(2.28) имеют вид
J- ( ^^ ^ - i^ = О (2-29) ■
Поскольку, однако, функция Лагранжа (2.26) зависит только от
дА/дх^ и не зависит от А, уравнения (2.29) переходят в
',\d{dAjdx^)j
Непосредственное вычисление с учетом (2.23) дает
d(aAjdxj) = ^^v> (2.31)
откуда следует, что уравнения (2.30) совпадают с уравнениями
Максвелла (2.24) для свободного электромагнитного поля
'^•- 0. (2-32)
— 1^-^ 1=0. (2.30)
эх, Эод/эх,) " ^ ''
fv
эх,
Тем самым доказана справедливость выражений (2.25), (2.26).
Нужно помнить, однако, что к функции Лагранжа (2.25), (2.26)
можно добавлять произвольные члены, имеющие вид 4-мерной
дивергенции. Такие члены исчезают при подстановке в 65 в силу
граничных условий.
Важными характеристиками электромагнитного поля, как и
всякой динамической системы, $шляются сохраняющиеся величины
*) Здесь и повсюду ниже под этим подразумевается плотность лагранжиана.
46
(интегралы движения). Для их определения в самом общем случае
можно использовать теорему Нётер: всякому непрерывному
преобразованию координат, обращающему в нуль вариацию действия
(т. е. преобразованию, относительно которого действие инвариант-
ж)), соответствует некоторая сохраняющаяся величина.
Непрерывные преобразования, о которых идет речь, —
преобразования из собственной группы Лоренца, т. е. трансляции и
повороты в 4-мерйом пространстве, включающем временную координату.
Общий вид этого преобразования (бесконечно малого) таков:
х = X + t + t X , (2.33)
где £^ — бесконечно малая трансляция, е — матрица бесконечно
малого поворота. Из условия ортогональности преобразования
следует: £ = — £vn- При преобразовании координат потенциал А
преобразуется, как всякий 4-вектор:
А' (х') = А(х) + £ А (х). (2.34)
Рассмотрим теперь вариацию действия S, не накладывая на
вариации ЬА^ нулевых граничных условий, т. е. не закрепляя границы
четырехмерного объема интегрирования:
Здесь Q — объем интегрирования в четырехмерном пространстве;
Z — поверхность, окружающая этот объем; dc^ — элемент
поверхности, нормаль к которому совпадает с направлением оси х^. Интех^
рируя по частям в объемном интеграле в (2.35) и рассматривая
вариацию действия для реального движения, т. е. используя
уравнения (2.29), получаем, что объемный интеграл исчезает и вариация
65 сводится к выражению
65 = 1 JZ. 6х, + ^^^ 6aJ^ da, (2.36)
Чтобы вычислить вариацию ЬА, по определению равную
ЬА^ = А'^(х)-А^(х), (2.37)
подставим в формулу (2.34) для А!(х') выражение (2.33) для х'
К^\ + К + V^x) = ^^^v) + V^ (2.38)
и произведем в левой части (2.38) разложение по малым
параметрам. При этом получим
дА дА
бЛДх) = -В, ^ - £,,х, ^ + £^Л- (2.39)
"х
47
Вернемся к теореме Нётер. Из условия исчезновения
вариации 65 получаем
S{^6-v + ^(ra7Hp'^v = o. (2.40)
Рассмотрим вначале преобразование трансляции
4 = V (2.41)
V
Тогда из (2.40) следует:
Е [Т dc =0, (2.43)
X
где
r^v = ^^v - eidAjdxj W- (2.44)
Тензор T^^ называется тензором энергии-импульса
электромагнитного поля.
Поскольку компоненты вектора е произвольны и независимы,
из (2.43) следует:
[Т da =0. (2.45)
X
Пусть теперь Q — объем, не ограниченный в направлении
пространственных координат и ограниченный в направлении
временной координаты двумя пространственными (трехмерными)
плоскостями 2j и ^21 ортогональными оси времени. Такие плоскости
представляют собой пространственные объемы, взятые в различные
моменты времени, т. е. для них da^ = —i dr. Тогда (2.45)
запишется в виде
S Т,^ da^ + S ^.v do^ = -i\ S T^, dT - J T^, drl = 0. (2.
46)
При этом мы предполагаем, что на границах
пространственного объема поле равно нулю; знак минус во втором интеграле
в (2.46) появляется из-за противоположной ориентации
нормалей к плоскостям 5]j и ^2 (об^ эти нормали должны быть
внешними).
Итак, следствием (2.46) является наличие интеграла движения
Р|^ = -i J Г^4 dr = const. (2.47)
Вектор Р называется вектором энергии-импульса
электромагнитного поля.
48
48)
Вычислим теперь тензор Г в явном виде, используя выражение
для лагранжиана (2.26). Непосредственное вычисление дает
— 1 1 1л ^^А
= i { - i ^^яЛк + V^vx + P.X ^}- (2.
В действительности тензор Т^^^ определяется неоднозначно, поэтому
его можно выбрать так, что последний член в (2.48) будет
отсутствовать. На самом деле в выражение для вариации bS входит не сам
тензор Т^^, а интеграл, который с помощью теоремы Гаусса можно
привести к виду
3 i*v V 3 Эх (1*
X п
Поэтому любая добавка Т'^^ к тензору Т^^, удовлетворяющая
условию
~Т' =0, (2.50)
дх (IV "' ^ '
V
не меняет вариации 65 и всегда может быть опущена. Именно
таким свойством обладает последний член в (2.48):
д / дА\ дР, дА д^А ,„ ^,,
-2- /-, —Я = _* _и +/• , ^ = 0. (2.51)
эхД vxaxj эх^ ах, ^'vx эх,эх.
Первый член в (2.51) обращается в нуль в силу уравнений
Максвелла (2.32), а второй — в силу антисимметричности тензора F^j^.
Таким образом, окончательное выражение для тензора
энергии-импульса примем в виде
^.v = 4^{ -i V^x^K + ^x^vx}- (2.52)
Теперь можно вычислить плотности энергии w = —Г44 и
импульса 3ij = —iTj^ (у= 1, 2, 3), которые с учетом (2.24), (2.25)
оказываются равными
w = -^(^ + ^ir^), (2.53)
" = i(^><^- (2-54)
Перейдем теперь к моменту количества движения электромах^
нитного поля. Вновь используем теорему Нётер и рассмотрим теперь
преобразование бесконечно малого поворота. В этом случае вместо
(2.41), (2.42) имеем
*^,х = £^v^v> (2.55)
дА
^\ = -h.\^^ + ^^A- (2-56)
49
Условие исчезновения вариации bS выглядит теперь так:
= -ivH.Xv'i'^v = 0, (2.57)
ще введено обозначение
A^^Xv = -2^'Vx + 2^(g:ya3^^Xa/-2^(aJ7a3^A- (2-58)
Учитывая определение тензора энергии-импульса (2.44), тензор
(2.58) можно преобразовать к виду
Л^.я^ = -2Г,л-2^^^Л,. (2.59)
Поскольку в (2.57) тензор M^^j^^ умножается на антисимметричный
тензор £ ;^, можно переопределить М )^^ следующим образом:
К^. = rxv\ - Т^Л - 2 ^^S^J А- (2.60)
Далее, рассуждая так же, как и при выводе закона сохранения
энергии-импульса, приходим к постоянству интеграла
-'■ S Л^^Я4 dT = М^^ш^ т^^{т) dx = const, (2.61)
ще М )^ — тензор момента количества движения электромагнитного
поля, т )^ — плотность момента количества движения.
Действительно, рассмотрим пространственные компоненты тензора т^ и
ограничимся вначале двумя первыми членами в (2.60). Непосредственные
вычисления для этой части тензора т' ^^ с учетом (2.54) дают:
m'jt = KT^^Xj - Tj^x^) = -(л)Дг)4 + (3t)t(r)^. (2.62)
или, в векторной записи (если ввести вектор т', эквивалентный
антисимметричному тензору второго ранга m'j^):
m' = -(jtxr)=^(rx(Srxd«')). (2.63)
Таким образом, эта часть тензора шц^ отвечает орбитальному
моменту электромагнитного поля.
Оставшаяся часть (2.60) описывает, очевидно, спиновый момент.
Наличие спина у классического электромагнитного поля связано с
его векторным характером, т. е. с существованием внутренних
степеней свободы. Действительно, чтобы задать состояние
электромагнитного поля, недостаточно задать его энергию и импульс —
необходимо еще задать поляризацию. Это и означает наличие
дополнительных степеней свободы. Таким образом, ясно, что поляризаци-
50
онные и спиновые характеристики эластромагнитного поля связаны
друг с другом (см. ниже).
Пространственные компоненты тензора m''j^, соответствующего
последнему члену (2.60), с помощью (2.31) и с учетом
антисимметричности тензора е^^^ можно представить в виде
или, в векторной записи (см. (2.25)):
m" = s = ^(SrxA). (2-65)
§ 2.2. Разложение потенциалов на плоские волны
В отсутствие токов и зарядов мы получаем, согласно (2.20), для
определения потенциалов волновое уравнение
П\ = 0. (2.66)
Общее решение этого уравнения можно представить в виде
суперпозиции плоских волн с произвольными амплитудами:
^Д^) = 1 Ж^^(С,,е^'^'^ + Сие-^*Л). (2.67)
Здесь Л=(к, ico); са=|к| — частота, к — волновой вектор
к = оуу, V — единичный волновой вектор, определяющий
направление распространения фронта волны; е^^^ — 4-вектор поляризации
(X принимает значения 1,2,3,4, причем значения Х=1, 2
соответствуют поперечной поляризации, X = 3 — продольной,
Х=4 — скалярной); V — нормировочный объем; С^^ —
произвольные коэффициенты. При этом к^х^ = —Ш + кг. Выбор
нормировочного множителя (4зг/2Уса)*'^ обосновывается ниже в этом
параграфе.
Электромагнитные волны обладают поперечной поляризацией.
Это значит, что векторы Sf, dS* ортогональны друг другу и вектору
V. Действительно, возьмем монохроматическую плоскую волну
(произвольное решение (2.66)), которую в трехмерных
обозначениях представим в виде
А(г, t) = Аое'С"-"').
Полагая скалярный потенциал F(r) = О и используя уравнения
Максвелла, получаем: Sf = icoA, div Sf = —ca^(vA) = 0, dS* = ica(v X A),
откуда следует:
(vSf) = 0, (2.68)
d«'=(vxSf). , (2.69)
51
Равенства (2.68), (2.69) и доказывают сделанное выше
утверждение.
Таким образом, чтобы задать направление векторов Sf, dS*,
достаточно задать направление одного из них (обычно ST). Это
направление и определяет поляризацию электромагнитной волны. Вектор
поляризации всегда может быть разложен по двум взаимно
перпендикулярным направлениям (осям). Соответствующие орты
обозначим через е^^\ е^^\ Тогда
е = а,е<1> + а^ё^К (2.70)
причем
\а,\^+\а^\^=1. (2.71)
Условие {2.71) можно учесть, переписав (2.70) в виде
е = cos а е^'^ -|- е'Р sin а е^^^ (2.72)
где а, р — вещественные числа. При {3 = 0 получаем, что
проекции вектора Sf на оси е^'\ е^^^ зависят от времени следующим
образом: (Re Sf)j = С cos а sin Ш, (Re Sf)2 = С sin а sin cot. Таким
образом, напряженность поля колеблется вдоль некоторого направления,
одного и того же во все моменты времени. Это случай линейной
поляризации. Если Р = ± 3i/2, а = 3t/4, получаем две круговые
поляризации. Действительно, теперь qj = 1/VJ, а2= ±i/V2, откуда
следует зависимость от времени для компонент вектора Sf:
(Re Sr)i = ;4= sin ш, (Re Sf)2 = ± § cos Ш.
Таким образом, в этом случае вектор W вращается в плоскости,
перпендикулярной направлению распространения волны, оставаясь
неизменным по модулю. В самом общем случае при произвольных
значениях параметров а, {3 имеет место эллиптическая поляризация.
В четырехмерной записи (2.67) не учтено пока условие попереч-
ности, которое должно выражаться в том, что в случае свободного
электромагнитного поля продольная и скалярная *) поляризации не
должны давать вклада ни в какие выражения, имеющие
непосредственный физический смысл. Покажем, что это так и будет, если
потребовать выполнения условия Лоренца (2.21). В применении к
(2.67) это условие дает
дА
л
дх
и
= '■ 1 Ж(С.яе'^Л - С;,е-^М.) = 0. (2.73)
к,Х
Будем считать для простоты, что поляризационные орты совпадают
с ортами координатных осей, т. е.
eW = b,. (2.74)
*) В случае скалярной поляризации вектор поляризации в 4-пространстве
направлен по оси времени.
52
<-ч=
<ч=
<\=
= 0,
:(0,
— СО.
Тогда
(2.75)
(2.76)
(2.77)
Формулы (2.75)—(2.77) получаются непосредственным
вычислением скалярных произведений с учетом равенств
еМл^ = е(^)к-4^)Ло (4^>=i4^)), (2-78)
е(1.2)к = о, (2■7^)
е(%=|к|=а). (2-80)
Тогда из (2.73) следует условие на коэффициенты разложения в
(2.67):
1, ^кг~^ы- (2-81)
' Запишем теперь выражение для тензора электромагнитного поля
[ через плоские волны. Используя (2.23) и подставляя разложение
^ (2.67), получаем
^ ^.v = .'• S ж [^'^\ - <"*v) (Cue^^^^^ - С\^^-''-) ■ (2-82)
к,Х
Вычисляя напряженность электрического поля по формуле (2.25) и
используя (2.81), получаем, что вклады в выражение для Sf от
продольной и скалярной поляризации сокращаются, как это и
ожидалось. Остается (в трехмерных обозначениях)
; Sr = I 2 S ^eW (Ci^^e'C^-"') - С'^е-'У''-"')). (2.83)
>. Точно так же с помощью (2.24) получаем
'■■ <^=i^ 2^(^><eW)(Ckye'^'''""'^-Ck;e-'('''-"0). (2.84)
ky = l,2
\ Вычислим теперь энергию и импульс электромагнитного поля,
заключенного в объеме V. Энергия, согласно (2.53), равна
E = ^\{^ + dX^)dr. (2.85)
V
; При подстановке в (2.85) выражений (2.83), (2.84) существенно, что
интегрирование любого множителя типа е''"' дает нуль при к ч^ 0. Это
просто понять, если взять объем в виде прямоугольного
параллелепипеда со сторонами Lj (у = 1, 2, 3). Тогда компоненты волнового
вектора принимают значения kj = lurijILj, где rij — целые положитель-
53
ные числа. При вычислении возникают интегралы вида
J Г 2лп 1 L.
Sj = ] ехр i -^ X. dxj = г^^ [ехр (2шп^) - 1 ]. (2.86)
о L ' J '
Нетрудно видеть, что при rij =^0 (т. е. к^ 0) Sj = 0. Если же
к = О, то интеграл по объему дает V. Временнйе множители,
содержащиеся в (2.83), (2.84), при этом исчезают, так как равенство
к = О означает также со = 0. Поэтому энергия Е оказывается не
зависящей от времени, как и должно быть.
Учтем, далее, равенства
(еО)еО')) = 6^.^.-,
(V X е(^>) (V X е<^">) = (eW х (v х е^'">) )v =
= (eWeO'))v2- (e(J)v)(eU-)v) = ь..., (2.87)
в последнем из которых использовано условие поперечности.
Тогда, возводя выражения для Sf и dS* в квадрат и интегрируя,
получаем
Ь\^^' = Ъ l^CljC^r (2-88)
V к у = 1,2
^Jd«^dr = 2 So>C*,,C,,, (2.89)
У к у = 1,2
^ = 2 l^^C'ijC^j. (2.90)
к у = 1,2
Аналогично вычисляется импульс (см. (2.54)):
P = J_ j ({rxd»?) dr. (2•^l)
С учетом равенства
е(^> X (V X еО")) = v(ef)ef'>) = v6^.^.. (2-92)
получаем
Р = 2 S»^C*,C,,. (2-93)
к у = 1, 2
Теперь можно сказать, что нормировочный множитель V43t/2Fca в
(2.67) выбирался с целью придать энергии и импульсу
электромагнитного поля вид (2.90), (2.93).
Наконец, для спинового момента электромагнитного поля с
помощью (2.65) тем же способом получаем выражение**)
S = i2 S (е<^>хеО-))(С,,С*,.-С*,,С,,0- (2-^4)
к Л/=1.2
*) При формальной подстановке выражений (2.83), (2.67) в (2.65) один из
значков у, у' в (2.94) будет пробегать значения у - 1, 2, а другой — у - 1, 2, 3, 4. Значения
у - 3, 4 приводят к нефизическим значениям проекции спина (см. следующий
параграф), и их можно заранее опустить. С другой стороны, по формальным соображениям
ниже удобнее считать, что оба значка в (2.94) пробегают значения у - 1, 2, 3.
54
Если поляризационные орты совпадают с координатными, то
векторное произведение в (2.94) можно записать в виде
(е^хе(^')),= Еу^.., (2.95)
где tfjj- — единичный полностью антисимметричный тензор. Тогда
в тензорных трехмерных обозначениях выражение для спина
принимает вид
^i = k^ 1 ^uAc^jClr-c;,jC^r)- (2.96)
к у,/=1,2,3
§ 2.3. Квантование электромагнитного поля
Основное отличие квантовой теории электромагнитного поля от
классической заключается в том, что квантовая теория описывает
процессы рождения и уничтожения квантов электромагнитного
поля — фотонов. При переходе к квантовой теории удобнее всего
использовать разложение потенциалов на плоские волны (2.67). В
квантовой теории величины А^{х) являются операторами. Эти
операторы действуют на вектор состояния электромагнитного поля
IФ), который определяется в пространстве чисел заполнения.
Разложение (2.67) при переходе к квантовой теории заменяется
выражением
^Д^) = 1 Ж<'^ (^и^^*"'^ + Ctx^"^*^'^) ' (2-97)
которое является теперь определением операторов А^^(х) в
гейзенберговском представлении (см. [I, §4.3]). Операторы С^^, С^^^
действуют на вектор состояния и имеют смысл операторов рождения и
уничтожения фотонов. Эти операторы определяются с помощью
перестановочных соотношений
[С^Л'я']- = [СМ'я-]- = О (X, X' = 1, 2, 3, 4), (2.98)
[CuCtrl- = \*'6яя' (^. X' = 1, 2, 3), (2.99)
[С^А%]- = -^ы- (2-100)
Соотношения (2.98) —(2.100) нужно дополнить условием
Си|Фуас> = 0, (2.101)
где I Фуас) — вакуумный вектор состояния электромагнитного поля.
Из перестановочных соотношений следует, что оператор
^*x=Ct,C,, (Х= 1,2,3) (2-102)
55
в качестве собственных значений может иметь любые целые
положительные числа, включая нуль. Это дает возможность
интерпретировать его как оператор числа частиц (фотонов):
Л^*я1^*х> = ^и1^*я>- (2-103)
Здесь Л^^;^ — число фотонов с заданной поляризацией и импульсом,
I ^*л) — соответствующий вектор состояния. В случае X = 4 такая
интерпретация неправомерна из-за" другого знака в правой части
перестановочного соотношения (2.100). Это, однако, не важно, так
как нет нужды говорить о числе скалярных фотонов: при
использовании кулоновской калибровки эти фотоны проявляются только в
виде кулоновского взаимодействия.
Среди матричных элементов операторов С^;^, С^;^ по смыслу
могут быть отличными от нуля только такие: (Л^^х ~ ^ I ^кх I ^ля)'
(Л^^;^ + l\Clj^\Nt^. Тогда из (2.102), (2.103) следует:
^и = <^*я I СГяСи 1^^*я> = <^*я I СГя I ^*я - 1>(Л^и - 11 С, J N,^) =
откуда
<^*х-1|Си1^*я> = '^^' (2-105)
<^и + 11 с;я I ^и> = VA^^T+T- (2.106)
Квантовая теория электромагнитного поля, как и классическая,
является градиентно-инвариантной и требует выбора калибровки
потенциалов. Например, можно попытаться задать калибровку
Лоренца условием, аналогичным (2.81). Однако перестановочные
соотношения (2.98)—(2.100) предполагают, что все операторы С^;^
являются независимыми. Поэтому нельзя наложить дополнительные
условия непосредственно на операторы. В квантовой теории условие
Лоренца накладывается на средние значения операторов:
(Ф|Ги|Ф) = 0. (2.107)
и
При выполнении этого условия продольные и скалярные фотоны, как
и в классической теории, не дают вклада ни в какие физические
величины в случае свободного электромагнитного поля. При наличии
внешних зарядов и при использовании кулоновской калибровки
скалярные фотоны определяют кулоновское взаимодействие (см. § 2.1).
Буквальное повторение выкладок, проделанных для
классического случая, приводит к следующим выражениям для операторов
энергии и импульса электромагнитного поля:
^ = iS<«(C.xCrx + c:xQx). (2-108)
t,x
Р = ^2»^(СиСГя + СГяС*я)- (2.109)
t,x
56
Переходя к средним значениям и используя условие Лоренца
(2.107), получаем (в трехмерных обозначениях)
£ = (Ф|Я|Ф) = 12 1<«(Ф|С,Д, + С-Д,|Ф), (2.110)
к 7 = 1,2
Р = (ф|Р|ф) = 12 ^k{Ф\C^,JCtJ + CtJC^,J\Ф). (2.111)
к У=1, 2
Наконец, используя перестановочные соотношения и формулы
(2.102), (2.103), переписываем выражения для £, Р в виде
^=1 s-k+i). (2.112)
к У=1,2 ^ '
p=s s>^k+i)- (2.113)
к 7 = 1,2 ^ '
Таким образом, энергия и импульс поля совпадают с суммой
энергий и импульсов гармонических осцилляторов со всевозможными
частотами. Поле, следовательно, можно представить как бесконечный
набор осцилляторов. Как видно из (2.112), вакуумное состояние (т. е.
состояние, в котором отсутству1эт фотоны) обладает бесконечной
энергией (суммарный импульс вакуумного состояния, в отличие от
энергии, равен нулю). Если, однако, энергию ачектромагнитного
поля отсчитывать от энергии вакуума, то мы всегда будем иметь дело с
конечными выражениями. Такое изменение начала отсчета энергии
не сказывается, как всегда, ни на каких физических результатах.
Оператор спина электромагнитного поля в квантовой теории
принимает вид (см. (2.96))
^t = il 1 ^tjj<C^Ctj.-CtjC^j.). (2.114)
к у,/" = 1,2,3
С учетом коммутационных соотношений для операторов рождения
и уничтожения, а также свойств антисимметричности тензора £j >,
(2.114) можно переписать в виде
^. = -^1 l^jj^C^- (2.115)
Теперь можно ввести оператор спина для отдельного фотона:
^i = -il^tjj-CtjC^- (2.116)
у,/=1,2,3
Этот оператор записан в представлении вторичного квантования.
Его можно записать в другом представлении, вводя волновые
функции фотона с определенной поляризацией /у. Определим действие
оператора S; на эти функции таким образом:
4j = i4,rfj- (2.117)
57
Тогда матричные элементы этого оператора будут равны
(2.118)
Нетрудно убедиться непосредственным вычислением, что точно
такие же матричные элементы получаются для оператора (2.116), что
и доказывает эквивалентность выражений (2.117), (2.116)._
Построим явные выражения для спиновых операторов Sf и
спиновых функций fj'.
(2.119)
(2.120)
Непосредственным перемножением матриц (2.119) и (2.120)
убеждаемся, что при этом удовлетворяются равенства (2.117). Прямо
проверяются также коммутационные соотношения
[5jS^]_ = i£iytSfc, (2.121)
которые должны выполняться для операторов проекций момента
количества движения (см. [I, § 3.1]).
Далее, таким же перемножением убеждаемся, что
^1 =
го 0 0^
0 0 -I
[о .- oj
, Sj^
л =
rn
0
f 0 f
) I
0 0 0
-i 0 0
. /2=
fo^
1
\
, ^3 ^
>
IQ
-i 0\
i 0 0
1° ooJ
(Q\
. /3 =
0
1
)
s^ = 25? =
1=1
(0 0 0^
0 1 0
(ooij
-1-
(l 0 0^
0 0 0
[ooij
-1-
(l 0 0\
0 1 0
[oooj
= 21, (2.122)
где / — единичная трехрядная матрица. Следовательно, функции
/; являются собственными функциями оператора ?:
sVf = s{s + \)fi = Ifi- (2.123)
Отсюда следует, что спин фотона равен s= 1.
Построим теперь общие собственные функции операторов s^, Sji
Xi= -^(Л + 'Уг). Х-1 = ^(Л-^72), Хо=/з- (2-124)
Вновь проверкой убеждаемся:
b^y. = \^'U (f* = 0' ±1)-
(2.125)
(2.126)
Величина (х имеет смысл проекции спина на некоторое заданное
направление. Трехкомпонентную матрицу-столбец х» можно
рассматривать так же, как трехмерный вектор х„- Нетрудно проверить,
что эти векторы ортонормированы:
\ЛцД»^'/ л^ л^' Jjijji'"
(2.127)
58
Обсудим физический смысл спина фотона. В отличие от спина
электрона, его нельзя толковать как «собственный» момент
количества движения фотона, т. е. как момент фотона в системе покоя,
поскольку такой системы не существует. Поэтому разделение полного
момента количества движения фотона на орбитальный и спиновый,
вообще говоря, лишено смысла. Как мы увидим ниже (см.
следующий параграф), состояния с определенными значениями
орбитального и спинового моментов не удовлетворяют условиям поперечно-
сти; этим условиям удовлетворяют лишь их линейные комбинации.
Существуют, однако, ситуации, когда проекции спина фотона
могут использоваться в качестве квантовых чисел. Рассмотрим
фотон с определенным значением импульса р и направим ось хз вдоль
вектора р. Тоща компонента спина S3 является интегралом
движения, поскольку проекция орбитального момента 1^ равна нулю в
силу тождества р1 = 0 (см. (1.62)). Проекция спина частицы на
направление ее движения называется спиралыюстью. Для фотона
возможны два значения спиральности: \k=+\ (см. (2.126)). Эти
значения спиральности соответствуют двум круговым
поляризациям. Действительно, выпишем явно выражения для векторов ч (в
матричной форме):
^1~ V2
/IN
i
X-i =
J
0^
—i
0
Xo =
0
1
(2.128)
Сравнивая эти векторы с векторами круговой поляризации, также
записанными в виде столбцов (см. § 2.2)
-'' = 72
\ I
—I
О
(2.129)
убеждаемся в справедливости сказанного выше. Из этих же
рассуждений следует, что значение спиральности ja = О для фотона
запрещено условием поперечности: это значение соответствует
продольной поляризации.
§ 2.4. Фотоны с определенным моментом и четностью
В предыдущем параграфе состояния фотона задавались значением
его импульса (энергии) и поляризацией. При этом коэффициент
при операторе С^^^ в (2.97) естественно принять за волновую
функцию фотона в координатном представлении:
(2.130)
4*''H'-'0 = l(^f>e«'cr-coO.
Нужно помнить, однако, что функции (2.130) нельзя придать
обычного для квантовой механики смысла амплитуды вероятности [1].
Это связано с отсутствием системы покоя для фотона и
невозможностью однозначного определения его координаты. Вместе с тем
59
можно говорить о волновой функции фотона в импульсном
представлении, поскольку импульс фотона является вполне
определенной величиной. Волновая функция фотона в импульсном
представлении получается с помощью фурье-преобразования из (2.130).
Функция (2.130) нормирована так, чтобы выражения для энергии и
импульса электромагнитного поля имели вид (2.112), (2.113). В
дальнейшем, при вычислении вероятностей различных процессов с
излучением или поглощением фотонов, можно без ограничения
общности положить V= I.
Для описания состояния фотона можно использовать также
другой набор квантовых чисел, а именно рассматривать состояния
фотона с определенным моментом количества движения и четностью.
Такой набор более удобен при описании поглощения и излучения
фотонов атомами. Полный момент фотона будем обозначать J,
проекцию на некоторое направление — ось z — /3. Обратимся к
импульсному представлению и построим функции этих операторов по
обычной схеме векторного сложения моментов (см. [I, § 3.1]):
Yym(v) = S C;M(mf.)y,„(v)x,, (2-131)
J'Y,,^(v)=/(y + l)Y,,^,(v), (2.132)
^3Y^,m(v)=MY,7m(v)- (2.133)
Функции (2.131) называются векторными сферическими
функциями и образуют, подобно шаровым спинорам (см. § 1.2), полную
систему ортонормированных функций
\ Y),^{v)Yj.,^.{v) rfv = 6.,.6„.6^^.. (2-134)
Каждому значению у ^ О соответствуют три векторные
сферические функции, отличающиеся значениями /: Yyy-Mi Yjj+im> Yjj-\m-
Если у = О, то имеется одна функция Y^jq. Квантовое число /, как
и в случае электронов, определяет четность состояния 9^:
§>Yj,^ = ^Yj,^, (2.135)
где ^ — оператор инверсии. Действие ^ на векторную функцию
определяется следующим образом:
^Y^m(v) =-Y,-,m(-v)- (2.136)
Поэтому, если учесть (2.131) и закон преобразования сферических
функций при инверсии [I, §3.7], четность фотона оказывается
равной
SP = (-1)^+1. (2.137)
Выясним теперь, удовлетворяет ли функция (2.131) условию по-
перечности. Рассмотрим вначале функцию ^jjm и покажем, что она
ортогональна v. Для этого заметим, что векторы % суть сфериче-
60
ские орты (см. [I, § 3.3]). Разложение произвольного вектора А по
таким ортам дает сферические компоненты вектора А:
А=Х(-1)Мд_^. (2-138)
Таким образом, из (2.131) и (2.138) следует:
{-irC%{M-i,, fx)y,^_/v) = (Y.,^)_,, (2-139)
ще {Удм)_^^ — сферическая компонента вектора Yy,^^(v).
Запишем теперь скалярное произведение векторов v и Yjj^ (см.
[1,§3.3]):
^Y,vM = S (-l)4v),(Y,,^)-,, (2-140)
(1
где (v)^ = V43t/3yi^(v). Используя также формулу [I, (3.30)],
можем написать
>'yM-,(v)y,,(v) =
= 1 С%(М- v., f.)(-l)->lP^ [^ ^ ^'j Y,,iv). (2.141)
Тогда
vY,yM(v) = (-1)^-'V27+T 2 C/j^(M- fx, fx) X
X 4'^(M- f., f.) ^^ ^ ^'j y,.^(v). (2.142)
Используя условие ортогональности преобразования Клебша—Гор-
дана [I, (3.31)], которое в данной ситуации дает
2 cii,{M- fx, fx)c;:'^(M- fx, fx) = 6^.^..,
-„„ :;.UM-f.,f.) = 6,,., (2-143)
получаем окончательно
vY,vm(v) = {-ly-'^fWT^ (^ i ^j y,^,(v). (2.144)
Однако (о 0 0 =0 (см. [I, (П4.3)]), поэтому
vY^,^,(v)=0. (2.145)
Итак, функция Yyy^^(v) является поперечной. Принято говорить,
что она описывает фотоны магнитного типа (Му-фотоны); для этой
функции используется также обозначение Yj^J. Название связано с
тем, что излучение таких фотонов определяется магнитным /-поль-
61
ным моментом системы зарядов (см. ниже, §5.3). Четность Mj
фотонов, согласно (2.137), равна
Э^= (-1)7+1. (2.146
Рассмотрим теперь другую поперечную векторную сферическз'в
функцию Y\ J, ортогональную v и функции Y^.^^:
Yf^{v) = HyxY%\v)). (2.147-
Векторное произведение в (2.147) запишем в сферических ортах i
помощью общей формулы [I, (3.112)]. При этом, однако, нужн(
учитывать, что такое определение векторного произведения отлича
ется от обычного множителем —ЬП (это можно установить непос
редственным сравнением). Тогда
iyfj,(y)). = -i^^ 1 C\l{gX)Y,^(v)(Y..^)„ (2.148;
где, согласно (2.139),
(Ууум)я= (-1)'С}]^(Л^+ ^^ -МУум+яМ- (2.149;
Вновь используя (2.141), получаем
(0^))c=(-lV"V2(2/+l)2;[^ I ^') y/..„(v)x
xS (-i)^c{i(9^)qj^(M + X, -х)с;:'^(м+ X, д). (2.150;
qX
Сумма по дк в (2.150) вычисляется с помощью [I, (3.70)]. Этс
дает
(Ос = (-l)^'^°V6(2y + 1)2 VSTTT [> 1 ^'j X
Ь lyj ^"
(M+cr,-a)y..^^„(v). (2.151]
Теперь можно вновь использовать (2.139), что приводит к
выражению
(0„ = V^7nT(-i)^2;V27TT (^ I ^') х|( [ ^}(Y,,.л.)„■
(2.152)
Заметим, что 3/-символ в (2.152) отличен от нуля только при
/ = / ± 1. Следовательно,
y(.^>(v) = a(/)Y..,,^(v) + *(y)Y^^_,^(v). (2.153)
62
Вычисление коэффициентов а, b по формулам, приведенным в [1,
(П4)], дает
.0) = (-,)V6,2;+,)(2y + 3) (U ' J ') {' t' { ;] = -iS^.
(2.154)
bu)=(-i)V6(2,+i)(2/-i) (/; ^- 01) {^- 71 (;.}=-щ.
(2.155)
Фотоны, описываемые функциями (2.145), называются
фотонами электрического типа (£/-фотонами). Излучение таких фотонов
определяется электрическим у'-польным моментом системы (см.
§5.3). Четность электрических £/-фотонов, согласно (2.137), равна
дг> =(_!)/. (2.156)
Таким образом, при одном и том же значении / электрические и
магнитные фотоны различаются четностью. Заметим также, что для
фотонов электрического типа орбитальный момент не имеет
определенного значения.
Рассмотрим, наконец, последний тип векторных сферических
функций — продольные функции YJj(v). Эти функции не
удовлетворяют условию поперечности, однако образуют, совместно с Y^^ и
У)^\ полный набор, по которому можно производить разложение
произвольных функций, функции У^.^, Y^^, Y^ ортонормирсюаны:
5 YW*(v)Yf^)(v) rfv = V6^^.6^., (2.157)
ще значки X, X' соответствуют Е, М, П.
Явное выражение для Yy^ можно построить следующим образом:
Yfл^(v)=vУ,,,(v). (2.158)
В сферических компонентах, с учетом (2.141), получаем
= i-lV-^VU+T ^ (> J j'j 4',,^(М, f.)y.,,,^. (2.159)
Используя свойства симметрии коэффициентов Клебша—Гордана
(3/-символов), приведенные в [I, § 3.2], переписываем (2.159) в виде
(2.160)
63
Теперь, учитывая (2.139), находим
(Yffi). = 1 {-lУ-^V2ГTT [^ J ^'j (Y,,,^(v)),. (2.161)
Отсюда, как и в случае Y^^-функций, следует:
Y,^(v) = a'(/)Y.,,, ^(v) + b'U)Y.._^ ^(v), (2.162)
aV) = (-1)/V27T3 (> I > + Ч = -Щ, (2.163)
*'(/) = (-iyV27+T (^ J '~o']=-{^- (2.164)
Если / = 0, TO no правилу сложения моментов имеется только
одна векторная сферическая функция Yo,o(v). Согласно (2.139) ее
сферические компоненты равны
(Yoio(v)),= (-U'^Ofx, -fx)y,^(v) = -:^ y„(v). (2.165)
Эти компоненты совпадают (с точностью до знака) со сферическими
компонентами вектора vyoo(v), и, таким образом, векторная
функция Yoio(v) 5шляется продольной. Отсюда следует, что не
существует фотонов с моментом, равным нулю.
Таким образом, волновые функции фотона в состоянии с
определенным моментом и четностью в импульсном представлении могут
быть записаны в виде
А^^'лГЧк, О = Сб(а> - |к| )Y(^*^(v)e--', (2-166)
где С — нормировочный множитель *). Переходя в координатное
представление с помощью преобразования Фурье
Ai^-лГЧг, t) = \ e^-^'Al^.--)(к, О dk, (2.167)
используя разложение плоской волны по сферическим гармоникам
е'"'^ = 2 ^%(o''■)УlJ^)KJ^^)' (2-168)
^Дшг) = (2я)1^ /^^.(шг), (2.169)
где п = т/г, Ji^i -^ функция Бесселя, и проводя интегрирование тю
dk= tip- dtii dv в (2.167), получаем волновые функции фотона в ко-
*) Нормировочный множитель С должен быть выбран так, чтобы с учетом
разложения плоской волны по сферическим волнам получалась прежняя нормировка (2.130)
(см. ниже формулу (5.75)).
64
ординатном представлении:
aL^C»-' о = gg/a>r)Y,,^(n)e-^'"' ш ^Ai^CDe"^'"', (2.170)
^^м(г, t) = ^|^g.^,(a>r)Y. .,, ,(n) -
-^^y-i("'-)Yy/-iM(n))e-^'"' = lf^Alf^(r)e-^'"'. (2.171)
При этом мы учли, что нормировочный множитель определяется по-
прежнему формулой (2.130).
§ 2.5. Взаимодействие электронов с фотонами
Уравнение Дирака, по аналогии с уравнениями Максвелла, можно
рассматривать как уравнение для компонент классического
электронно-позитронного поля •ф„(х), ^„(х) (а — спинорный значок)*).
Функцию Лагранжа для электронно-позитронного поля можно
записать в виде
L = ^ i'^y^.P^,-^ - (р^^'Ф)7р1^) - т^-^. (2.172)
Действительно, построив функционал действия
(2.173)
^=$^(^'^'^'§)'^^-
и считая при варьировании функции -ф, -ф независимыми, приходим
к уравнениям Эйлера—Лагранжа.
д ( дь \ dL_f^ (2.174)
__ дь \ _a£^f^ (2.175)
дх^ \Ъ(д^1дх^
Строго говоря, эти уравнения нужно писать для отдельных спинор-
ных компонент -ф^, яр^, однако формальное вычисление
производных в (2.174), (2.175) приводит к правильному результату. А
именно, уравнение (2.174) переходит в (1.9), а (2.175) — в (1.12).
Выражение для тензора энергии-импульса
электронно-позитронного поля получается по аналогии с выражением (2.44) для
электромагнитного поля:
Т =rf\ 31- Эт)) dL Эт)) (2 Пб)
^ (IV -^"^v д(.д-^1дх^) дх^ д^д^flдxJ дх^' ^ ' '
*) «Классическим» это поле является в том смысле, что пока мы не переходим ко
вторичному квантованию и не учитываем тем самым процессов рождения и
уничтожения частиц. В настоящей же классической электродинамике электронно-позитронного
поля вообще нет, а есть лишь заряды и токи.
\ 3 л. Н. Лабзовскии 65
Если считать, что функции -ф, гр в (2.176) являются экстремалями,
т. е. удовлетворяют уравнению Дирака, то L = 0 (это следует
непосредственно из (2.172)). Тогда вычисление производных в (2.176)
приводит к выражению
Т =и^у i2L_iiY J. (2.177)
Отсюда плотность энергии электронно-позитронного поля равна
- = -^..= -{(¥^-^^f) (2-178)
или, с учетом (1.1),
и; = -ф+Ля1,, (2.179)
где оператор h определяется формулой (1.2). Плотность импульса
электронно-позитронного поля получается равной
я = ^(я1)+Уя1)-(Уя1)-")я1)). (2.180)
Если теперь рассматривать взаимодействующие электронно-по-
зитронное и электромагнитное поля как взаимодействующие
классические поля, то полный лагранжиан можно представить в виде
L = L^ + L^ + L,„„ (2.181)
где L — лагранжиан свободного электромагнитного поля (2.26),
Z/g — лагранжиан свободного электронно-позитронного поля
(2.172), а //;„, — лагранжиан взаимодействия. По аналогии с
классической электродинамикой можно положить
^■шг = Цх)А^{х), (2.182)
где/|j(x) — ток, определяемый формулами (1.15), (1.16), А —
потенциал электромагнитного поля.
Теперь нужно варьировать функционал
\ V ц цу
где L определяется выражением (2.181). Подобно тому, как при
варьировании соответствующего действия получались уравнения
(2.32), (1.9), (1.12) для свободных полей, из (2.183) получается
система уравнений:
^ = 4я/^, (2.184)
iiy^.(P^. + eA^) + m)y\> = 0, (2.185)
^У^(р-еА^)-т)=0. (2.186)
Эти уравнения представляют собой уравнения Максвелла в
присутствии зарядов и токов (2.24) и уравнения Дирака во внешнем
электромагнитном поле (1.32) и (1.33).
66
Перейдем теперь ко вторичному квантованию электронно-позит-
ронного поля и рассмотрим для этого разложение произвольного
решения уравнения Дирака ^фСх) по полной системе функций
•ф^(г, t), являющихся решениями уравнения Дирака (1.20).
Разложение представим в виде
^(х) = ^ a^^^ix) + 2 й>Дх), (2.187)
Е >0 Е <0
S S
Щх) = 2 <^Дх) + 2 Ь^%{х). (2.188)
Е >0 Е <0
S S
Вторичное квантование заключается в замене чисел а^, Ь^
операторами уничтожения электронов и позитронов а^, Ь^, а чисел а*, й* —
соответственно операторами рождения 2^, Ь^. Формулы (2.187),
(2.188) заменяются на
Щх) = 2 2,я1)Дх) -I- 2 Ь:%(х), (2.189)
£j > о Ej < О
Г(х) = 2 ^Ш^) +1 *Ж(^)- (2■l^o)
£ >0 £ <0
S S
где ^(х), ^^(х) — операторы электронно-позитронного поля.
Операторы рождения и уничтожения электронов и позитронов
удовлетворяют следующим перестановочным соотношениям:
[a^,aJ^=[a:,a:,U = 0, (2-191)
[Ьь,,и=[Ь:,Ь:,и = 0, (2.192)
[а„а:,и=[Ь^,Ь:,и=Ь^„ (2•1^3)
Я,Ки = [s:,К-и = я, ь:,и= [а^, ь^,и = о. (2■l^4)
Операторы 2^, 2^, й^, Ь^ действуют на вектор состояния
электронно-позитронного поля IФ) , или волновую функцию в пространстве
чисел заполнения (в полной аналогии с ситуацией в случае
электромагнитного поля, см. § 2.3). Запись (2.187), (2.188) соответствует
гейзенберговскому представлению для волновых функций и
операторов: зависимость от времени содержится только в операторах
яр(х), i}j"*'(x), а вектор состояния |Ф) от времени не зависит.
Операторы
«« = 2^2,, (2.195)
nt^ = bth (2■1^6)
67
можно толковать как операторы числа электронов и позитронов
соответственно:
Я(±)|„(±)) = „(±)|„(±)). (2.197)
Здесь I п^~^) — вектор состояния поля с числом электронов
(позитронов) п^-) в состояниях, описываемых волновыми функциями
Из перестановочных соотношений для операторов уничтожения
и рождения следует вьшолнение принципа Паули:
п(-) = 0, 1. (2.198)
Действительно, с помощью (2.193) получаем
(Я(/))2 = а^а^а^а^ = 2^2,(1 - а^а^). (2-199)
Учитывая, что из (2.191) следует 2^ = 0, далее имеем
(Ж/))2 = 2Я = п^''>. (2-200)
откуда и вытекает (2.198). То же самое можно повторить для
оператора Я^").
Перестановочные соотношения (2.191)—(2.194) нужно
дополнить равенством
2J^vac>=*.l^vac> = 0, (2-201)
где I Фуас) — вакуумный вектор состояния электронно-позитронного
поля.
Во вторично квантованной теории все соотношения, приведенные
ранее в этом параграфе и содержащие функции •ф(х), ^(х),
заменяются операторными соотношениями. В частности, из (2.178)
следует выражение для оператора энергии (гамильтониана) свободного
электронно-позитронного поля:
Н^ = J 1})+(х)Л(г)ф(х) dr. (2.202)
Подставляя в (2.202) разложения (2.189), (2.190) и интегрируя,
приходим к следующему результату:
^е = Е ^"^^'s - 1 п<г% + 2 Б,. (2.203)
Е^>0 Е^<0 Е^<0
Последнее слагаемое в правой части (2.203) представляет собой бес- |
конечную энергию вакуума и должно быть отброшено, как и в слу- '
чае электромагнитного поля (см. § 2.3).
С.целью формального устранения таких бесконечностей обычно
вводят так назьшаемое нормальное произведение (Л'-произведенис)
операторов, в котором операторы рождения всегда стоят слева от
операторов уничтожения (см. [I, § 4.4]). Знак нормального
произведения определяется числом перестановок фермионных операторов,
68
которые нужно совершить, чтобы расставить операторы в требуемом
порядке. Если число перестановок фермионных операторов нечетно,
то Л'-произведение приобретает знак минус. Перестановки бозонных
операторов не оказывают влияния на знак. Если использовать Л'^-
произведения операторов, то бесконечная энергия вакуума не
возникает ни для электромагнитного, ни для электронно-позитронного
полей.
Формула (2.203), таким образом, заменяется следующей:
£■ >0 Е <0
S S
Из (2.204) следует очевидное выражение для энергии Е^^^ системы
невзаимодействующих электронов в атоме:
N
f?(0) = (фIя,|Ф) = 2 Е^, (2.205)
где Л'^ — число электронов в атоме.
Оператор плотности тока записывается с помощью Л'^-произведе-
ния операторов так:
7Дх) = -/еЛ^(Г(х)7,Ф(х)). (2-206)
Из (2.206) для оператора заряда
Q=i\7o(x)dT (2.207)
следует выражение, не содержащее бесконечного заряда вакуума:
Q = _е ^ й(+) + е ^ пр. (2.208)
Е >0 Е <0
S S
в случае взаимодействующих полей вторично квантованная
теория приводит вновь к уравнениям (2.184)—(2.186), которые,
теперь, однако, имеют операторный характер. Поэтому единственный
практически осуществимый способ решения всего круга задач кван-
тово-электродинамической теории атома заключается в
использовании теории возмущений по взаимодействию полей. Такую теорию
возмущений удобно развивать в гамильтоновой формулировке, для
чего можно использовать результаты, приведенные в [I, § 4.3]. При
этом полный гамильтониан системы полей представляется в виде
Н=Н^+Н,^„ (2.209)
Н=Н^ + Н^, (2.210)
где Н^ — гамильтониан свободного электромагнитного поля (2.108),
который после перехода к нормальным произведениям приобретает
вид
k,x (2.211)
69
Н^ — гамильтониан свободного электронно-позитронного поля
(2.204), 7/;„, — гамильтониан взаимодействия.
В классической теории функции Лагранжа и Гамильтона для
электромагнитного и электронно-позитронного полей связаны
обычным соотношением:
гг_ г ■ dL SA^ dL Эт)) . dL Эф (-2 212)
^ d(dAjdx^ дх^ "^ ЭОф/Эх ) дх^ "^ ЭОф/Эх^) дх ' ^ ' '
Поскольку, однако, Z^„, не зависит от производных, формула
(2.212) упрощается:
^i„, = -A„.- (2.213)
Сохраняя во вторично квантованной теории выражение (2.182) для
Z/jn,, но заменяя все величины операторами, получаем
К. $7Дх)ЛДх)йг. (2.214)
Таким образом, основой для дальнейших приложений квантовой
электройинамики к теории атома будет разложение оператора
эволюции S{t, to) в ряд инвариантной теории возмущений по
взаимодействию //;„, (см. [I, § 4.3]):
S{t,t^) = l+2S^'Ht,t^), (2.215)
1=1
S^'Ht, to) = ^\ dt, ... \ dt, T{H,,,{t,), ..., Я;„,«,)), (2.216)
0 0
где Г — символ хронологического произведения операторов.
§ 2.6. S-матрица в картине Фарри
Как известно (см. [1, 2]), для квантовой электродинамики
несвязанных электронов характерна такая постановка задачи: любой
процесс рассматривается так, как будто частицы в начальный t = —оо и
в конечный < = 00 моменты времени не взаимодействуют. Тогда,
согласно определению (см. [I, (4.128)]),
|Ф(<»)) = 5(<»,-<»)|Ф(-<»)), (2.217)
где |Ф) — вектор состояния. Оператор 5(оо, —оо) называется 5-мат-
рицей и позволяет по заданному состоянию системы при < = —оо
найти состояние при < = оо. Если взаимодействие отсутствует при
< = ± 00, то функции |Ф(±оо)) соответствуют
невзаимодействующим частицам. Пусть |Ф°) — набор состояний, в которых может
находиться система невзаимодействующих частиц (электронов,
фотонов). Можно считать, что |Ф2) — волновые функции в гейзенбер-
70
говском представлении, совпадающие при отсутствии
взаимодействия с функциями в представлении взаимодействия. В начальный
момент времени система находится в некотором состоянии
|Ф(-~)>= \Ю- Тогда
|Ф(<»)) = 5(<»,-<»)|Ф(-<»)> = 2(Ф0|5|Ф0>|Ф0>. (2.218)
ь
При этом мы произвели разложение |Ф(оо)) по полной системе
функций |Ф^). Матричный элемент 5-матрицы (Фб|5|Ф°)
определяет амплитуду перехода из состояния |Фд) в состояние |Ф^).
Вычисление таких амплитуд и соответствующих вероятностей
различных процессов представляет собой традиционную задачу квантовой
электродинамики. Однако применение этой традиционной схемы к
задаче о связанных состояниях в атоме наталкивается на серьезные
трудности. В частности, трудности связаны с необходимостью
вычислять также сдвиг уровней энергии, как за счет взаимодействия
электронов друг с другом, так и за счет взаимодействия с вакуумом.
Для преодоления этих трудностей использовались различные
методы, так или иначе связанные с теорией возмущений.
Если использовать разложение по параметру малости aZ, то
можно, вообще говоря, распространить полурелятивистский подход,
описанными в § 1.5, на двухэлектронные и многоэлектронные атомы.
Поправки низшего порядка (aZ)^ к межалектронному
взаимодействию приведены в § 3.4. В общем случае многоэлектронного атома
поправки порядка (aZ)^ и (aZ)^ рассмотрены в [3—5]. В таких
теориях упомянутые трудности отсутствуют, поскольку исходным
приближением является обычная квантовая механика, однако
применимость этих теорий ограничена легкими атомами, поскольку в
следующих порядках по aZ возникают сингулярные операторы.
Модификацию полурелятивистского подхода, обходящего эту
трудность, см. в [6].
Другая возможность — использование релятивистского метода
Хартри—Фока, который подробно описан в §3.5 (см. также [7]).
Этот метод является хорошим исходным приближением для
расчетов атомов в рамках квантовой электродинамики, однако он не
представляет собой теорию, в которой последовательно учитываются
все поправки одного порядка по степеням а, без разложения по
степеням aZ. То же самое можно сказать и об усовершенствованиях
такого подхода — релятивистском методе случайной фазы [8] или
релятивистском методе наложения конфигураций [9, 10], дающих,
впрочем, весьма хорошие численные результаты.
Существует также ряд методов, в которых теория строится с
самого начала без разложения по параметру aZ, но с использованием
теории возмущений по а. Это позволяет последовательно учитывать
все поправки по а в каждом порядке; в таком варианте теория
особенно хорошо применима к сильно релятивистским электронам.
71
Один из распространенных методов такого сорта —
адиабатический формализм Гелл-Манна и Лоу [11], изложенный в [I, § 4.3] в
применении к задачам квантовой механики. Применение этого
метода к задачам релятивистской теории атома см. в [12—14]. В
дальнейшем в этой книге мы будем придерживаться именно такого
подхода, поскольку, во-первых, он наиболее близок к традиционному
5-матричному формализму квантовой электродинамики и,
во-вторых, этим методом выполнено значительное число конкретных
вычислений.
Вместе с тем существует целый ряд иных подходов к квантово-
электродинамическому описанию атома, также не использующих
разложения по aZ. Например, другая разновидность 5-матричного
подхода, основанная на другой функции включения
взаимодействия, отличной от функции Гелл-Манна и Лоу, использовалась в [15,
16]. В [17] развивался подход, основанный на методе функций
Грина и квазипотенциальных уравнениях. Модификацию такого
подхода см. также в [18]. В ряде работ предпринимались попытки
построить квантовоэлектродинамическую теорию атома по образцу
нерелятивистской теории атома с эффективными операторами
взаимодействия [19, 20].
Практически во всех используемых методах в качестве исходного
базиса теории возмущений применяются волновые функции
электронов в заданном внешнем поле (например, волновые функции в
кулоновском поле ядра, рассмотренные в гл. 1, или волновые
функции в самосогласованном поле Хартри—Фока, см. ниже). Это
означает, что взаимодействие электронов с полем ядра включено уже в
нулевое приближение. Такая постановка задачи называется
представлением, или картиной, Фарри [21].
Рассмотрим подробнее теорию возмущений и диаграммную
технику в картине Фарри. Как и в квантовой механике (см. [I, § 4.4]),
при подстановке оператора S^^^\ определяемого формулой (2.212), в
амплитуду (Ф^|5|Фд) получаются матричные элементы от так
называемых смешанных произведений операторов, т. е. Г-произведе-
ний от различных //-произведений. При этом выражение для 5-мат-
рицы приобретает вид
5(00, -оо) = 1-|-^5«(оо, -00), (2.219)
1=1
5(')(оо, -оо) =
= Ьр! J d\ ... rf*x, Г(7,,(х,)Л^,(х,), ..., 7^М1)\1Ы)- (2.220)
Переход от смешанных произведений к //-произведениям составляет
содержание теоремы Вика, которая формулируется так же, как в
квантовой механике: смешанные произведения представляются в
виде суммы //-произведений со всевозможными свертками
операторов. Свертка определяется, как и в [I, § 4.4]:
АВ ш Т(АВ) - n(aB) , (2.221)
72
причем сохраняются те же знаковые правила при перестановках
ферми- и бозе-операторов. Из этой суммы, вообще говоря,
необходимо исключить члены со свертками операторов, уже входящих
под знак Л^-произведения в операторе тока в //;„,. Однако в картине
Фарри нельзя на самом деле отбрасывать, как это делается в
квантовой электродинамике без внешнего поля, вакуумное среднее от
оператора тока /ц, поскольку в данном случае оно содержит и ток,
создаваемый в вакууме внешним полем. Поэтому при вычислении
матричных элементов 5-матрицы в картине Фарри символ Л^-произ-
ведения в операторе тока, входящем в //(„„ следует опустить.
Следует также заметить, что операторы рождения и уничтожения
отличных друг от друга частиц не нужно представлять в виде Л^-про-
изведений и, соответственно, не нужно свертывать. В частности, не
нужно свертывать операторы ^{х) и ^{х), так как они содержат
только операторы рождения позитронов и уничтожения электронов;
то же относится и к операторам ф^С^)» ^^{х'), которые содержат
только операторы рождения электронов и уничтожения позитронов.
Свертки операторов уже не являются операторами в
представлении вторичного квантования, а представляют собой с-числа (см.
ниже, а также [I, § 4.4]). Они называются также пропагаторами, т. е.
функциями распространения соответствующих частиц (см. по этому
поводу [I, § 4.4]). Электронный и фотонный пропагаторы
обозначаются следующим образом:
Щх)^'-(х')=8{х,х'), (2.222)
\{x)2^(x')^D^^{x,x'). (2.223)
При этом пропагатор S{x, х') представляет собой матрицу по спи-
норным индексам. Операторы, не участвующие в свертках,
действуют на векторы состояния справа и слева в матричных элементах, в
результате чего появляются волновые функции электронов и
фотонов в начальном и конечном состояниях.
Диаграммная графическая техника, которая используется для
наглядного описания членов ряда теории возмущений для 5-матри-
цы, содержащих различные типы сверток, отличается от той,
которая используется в квантовой механике (см. [I, § 4.5])*).
Сопоставим каждой координате х в (2.220) точку на графике
(вершину), электрону — сплошную линию, соединяющую
вершины, фотону, излучаемому (поглощаемому) электроном в атоме, —
волнистую линию, начинающуюся (оканчивающуюся) в какой-либо
вершине графика (излучение или поглощение будем отмечать
стрелкой). Тогда внешние электронные и фотонные линии
(имеющие свободные концы) будут соответствовать электронам и фотонам
*) Впервые диаграммная техника была использована Фейнманом [22] для
формулировки теории возмущений в квантовой электродинамике, а затем была применена и
в задачах квантовой механики.
73
г j\y\y>^
в начальном и конечном состояниях. Этим линиям сопоставляются
волновые функции электронов и фотонов. Электронные линии на
диаграммах располагаются, вертикально, причем начальному
состоянию атома отвечает низ диаграммы,
конечному — верх. Всего на диаграмме
изображается столько электронных линий, сколько
электронов участвует в рассматриваемом
процессе. Фотонным и электронным пропа-
гаторам сопоставляются фотонные и элект-
'^ ° ронные линии, соединяющие две вершины.
Рис. 2.1. Фейнмановские Т. е. не имеющие свободных концов.
графики в первом порядке д наличии внешнего поля A^4T,t),
теории возмущений в кар- *^ и \ ' /'
тине Фарри действующего на электроны, на графиках
появляются также вершины,
соответствующие взаимодействию с этим полем. Само внешнее поле мы будем
изображать штриховой линией с крестиком на конце. Каждой такой
штриховой линии сопоставляется потенциал A^^{т, t).
Рассмотрим несколько примеров. В первом порядке теории
возмущений возникает смешанное произведение вида
ПЩ^Чх)у^Ч>{х))А^(х)). (2.224)
С учетом сделанных выше замечаний при раскрытии этого
произведения должны появиться следующие члены. Во-первых, член без
всяких сверток, который изображается графиком рис. 2.1а. Этот
график описывает процесс поглощения или излучения фотона электро-
I 1
ном в атоме. Во-вторых, член,, содержащий свертку ^"*'(x)i}J(x).
Этот член по5шляется только в картине Фарри благодаря тому, что
в этой картине мы не учитываем //-произведения в (2.224). Он
изображается графиком рис. 2.16 и описывает взаимодействие
вакуумного тока, возникающего при наличии внешнего поля, с фотоном.
Этот график не описывает никаких процессов в атоме, как и все
графики, не содержащие внешних электронных линий.
Во втором порядке теории возмущений нужно рассмотреть
смешанное произведение
T{N{V{x,)y^^{x,))\{x,)N{^'-{x^)yMx2))Mx2)). (2.225)
Оно, как и (2.224), не 5шляется на самом деле смешанным,
поскольку в картине Фарри знаки //-произведений следует опустить. Тогда
при раскрытии (2.225) по теореме Вика появляются следующие
члены.
Наиболее простым является член (2.225) без сверток.
Соответствующий матричный элемент отличен от нуля только для таких
векторов состояния, в которых имеется не менее двух электронов, так
как иначе один из электронных операторов уничтожения
обязательно действует на вакуум и матричный элемент исчезает согласно
(2.201). Позитронные операторы из (2.187), (2.188) вклада не
дают, поскольку в начальном и конечном состояниях нет позитронов.
74
Таким образом, две вершины xj и х^ могут принадлежать только
двум разным электронным линиям (рис. 2.2а). Поскольку мы
условились изображать электронные линии лишь для электронов,
участвующих в процессе взаимодействия с электромагнитным полем,
рис. 2.2а относится к атомам с числом электронов N^2 и изобра-
'\J-\y^ -Xrs^
ЛУЧ/-
'хух/^ jr\j~w^
■v^^v
Qx^N^
■\yxj^
(~y\y^j^ (~y\y>u^
o^^
QwxO
Рис. 2.2. фейнмановские графики во втором порядке теории возмущений в картине
Фарри
жает либо поглощение двух фотонов атомом, либо излучение двух
фотонов, либо процесс поглощения фотона одним электроном в
атоме и излучения другим (т. е. рассеяние фотона на атоме).
Члену (2.225) со свертками Tp^(xi)ip(x2) или трС^О'Ф^С^г)
соответствует график рис. 2.26. Изображенный процесс есть поглощение
или излучение двух фотонов одним электроном в атоме, либо
рассеяние фотона электроном. Такой процесс может происходить и в
оцноэлектронном атоме.
Если рассматривать следующий член (2.225) со свертками
I ' I I I
\p"*'(xi)ip(x2) И •ф(х1)'Ф"*'(х2) (см. рис. 2.2в), то соответствующий
матричный элемент не содержит электронных операторов и, как
и рис. 2.16, описывает процесс взаимодействия вакуумного тока с
^^Для члена (2.225), содержащего одну свертку A^{xi)A^{x2),
матричный элемент отличен от нуля только в случае атома с числом
электронов N>2. Соответствующая фейнмановская диаграмма
изображена на рис. 2.2г и описывает процесс обмена фотоном между
двумя электронами.
75
Следующий член (2.225) содержит свертки ^(xi)-\\)^{x2) и
JZ Z. • 1 Z Z.
\(xi)AJx2) либо ^^{xi)'^{x2) И \{xi)AJx2). Соответствующая
диаграмма (рис. 2.23) описывает процесс испускания и поглощения
фотона одним электроном. Такие фотоны называются
виртуальными, поскольку в начальном и конечном состояниях фотоны
отсутствуют, а сам процесс представляет собой взаимодействие электрона с
фотонным вакуумом. В картине Фарри, т. е. при наличии внешнего
поля ядра, эта диаграмма приводит к сдвигу уровней электрона в
атоме — лэмбовскому сдвигу (см. гл. 4).
Рассмотрим, наконец, член с тремя свертками Tp^(xi)i}J(x2),
^{xi)^'*'(x2), \(xi)A^(x2). Его матричный элемент не содержит ни
электронных, ни фотонных операторов и изображается так
называемым вакуумным графиком (рис. 2.2е). Можно показать, что при
вычислении вероятностей различных процессов вклад вакуумных
графиков учитывать не нужно. Для этого достаточно заметить, что
пририсовывая к любому графику все вакуумные графики, мы
придем к экспоненте вида [I, (4.265)]. Показатель этой экспоненты
чисто мнимый, что видно, например, из формулы [I, (4.189)]. Таким
образом, учет всех вакуумных графиков эквивалентен умножению
амплитуды вероятности процесса на фазовый множитель, что не
меняет вероятности этого процесса.
Перечислим теперь члены (2.225), возникающие только в карти-
I "■ ■ --■'1 I -■ ■ --■'1
не Фарри. Члену со сверткой Tp^(xi)ip(xi) или ^^{Х2)^{х2)
соответствует диаграмма рис. 2.2ж. Эта диаграмма, как и рис. 2.16,
описывает взаимодействие вакуумного тока с фотоном (и, независимо от
этого, взаимодействие фотона с атомным электроном). Рассуждая
так же, как в случае вакуумных графиков, можно убедиться, что
любые диаграммы, содержащие несвязные (т. е. не связанные
какими-либо линиями с остальной диаграммой) части, не имеющие
внешних электронных линий, не нужно учитывать при расчете
атомных процессов.
Сказанное относится также к члену (2.225), содержащему две
электронные свертки Tp^(xi)ip(xi) и 'Ф^(^2)'Ф(^2)» что соответствует
опять взаимодействию фотонов с вакуумным током (рис. 2.2з).
Рассмотрим теперь член (2.225) с одной электронной и одной фо-
jr -^ Z. :l jr -^
тонной свертками: ■«p"*'(x,)ij)(xi) и A^{xi)A^{x2), либо ■ф"*'(х2)'ф(л:2) и
\(^i)^(^2)- Это единственный член во втором порядке,
возникающий только в картине Фарри и дающий реальный вклад в атомные
процессы. Соответствующая диаграмма изображена на рис. 2.2ы. Ее
отличие от диаграммы рис. 2.2ж заключается в том, что
взаимодействие фотона с вакуумным током передается атомному электрону, т. е.
диаграмма описывает фактически взаимодействие атомного
электрона с вакуумным током — поляризацию вакуума (см. гл. 4).
76
Последний член (2.225), включающий три свертки, •«p"*'(xi)ij)(xi).
гр"*'(х2)'Ф(х2) и A^{xi)A^{x2), соответствует вакуумному графику,
возникающему в картине Фарри (рис. 2.2к). Учитывать этот график,
как и график рис. 2.2е, не нужно.
Расчет любой физической величины с помощью диаграммной
техники разбивается на три этапа: составление графиков Фейнмана,
написание матричных элементов по графикам и, наконец,
вычисление этих матричных элементов. Приведем в окончательном виде
правила сопоставления матричных элементов графикам.
Каждой входящей (снизу) электронной линии на диаграмме
соответствует волновая функция начального состояния электрона
\l)^(x) вида (1.19). Каждой выходящей (сверху) электронной линии
соответствует функция конечного состояния ^^(х). Конкретный вид
функции •ф^(х) связан с выбором Hq. Выбор (2.210) соответствует
исходному приближению невзаимодействующих электронов. В
качестве нулевого можно использовать также любое одноэлектронное
приближение, в частности приближение Хартри—Фока (см. § 3.5).
Перейдем теперь к фотонным линиям. Каждой внешней
входящей фотонной линии (поглощение кванта) соответствует волновая
функция (2.130) (или функции (2.170), (2.171) при другом выборе
квантовых чисел). Каждой внесшей выходящей фотонной линии
(излучение кванта) соответствует комплексносопряженная
волновая функция.
Вершинам диаграммы соответствуют матрицы -уц- Таким
образом, в вершинах, связанных с излучением или поглощением
фотонов, П05ШЛЯЮТСЯ множители "Уцб^^^ = ^•
Внутренним электронным и фотонным линиям сопоставляются
электронные и фотонные пропагаторы. Для внутренних фотонных
линий в теории атома бывает удобно использовать кулоновскую
калибровку и различать кулоновские (т. е. скалярные) и поперечные
фотоны. В таких случаях кулоновские фотоны, в отличие от
поперечных, будем изображать штриховыми линиями, а для поперечных
фотонов сохраним прежнее изображение волнистыми линиями.
Если атом находится в каком-то внешнем поле, то
взаимодействие с этим полем изображается на диаграмме штриховой линией с
крестиком на конце. Каждой такой линии сопоставляется 4-потен-
циал А^^{х).
Нужно также учесть, что всякой диаграмме необходимо
приписывать множитель (—г)"е", где п — порядок диаграммы (число
вершин). Этот множитель возникает при подстановке выражения
для Я(„, в iS^") с учетом (1.15), (1.16), (2.214). При этом
подразумевается, что интегрирование в каждой вершине проводится по
d*x = i dr dt, т. е. после интегрирования появляется еще
множитель (г)". Множитель (п!)~' в S^"^ сокращается с множителем п!,
который возникает при сложении вкладов от эквивалентных
77
вариантов диаграмм, отличающихся лишь расстановкой индексов
Xf в вершинах. Однако каждой диаграмме нужно приписать еще
симметрийный множитель 1/к, учитывающий, сколько раз при
замене индексов в вершинах диаграмма совпадает сама с собой (см.
[1,§4.5]).
Необходимо также учесть все обменные варианты диаграмм,
различающиеся расстановкой индексов электронных состояний вверху
или внизу диаграммы (для определенности будем считать, что
переставляются верхние индексы). Обменным диаграммам
приписываются множители (—l)**-, где 6р — число перестановок пар
индексов. Это правило является следствием антикоммутации фермионных
операторов рождения частиц в различных состояниях (2.191).
Вдоль каждой электронной линии производится суммирование по
биспинорным индексам волновых функций (^^)а, (■ф^)а> матриц
('Уц)ар ^^ электронных пропагаторов (5)„р. На замкнутой
электронной петле последовательность индексов замыкается, т. е. петле
соответствует след произведения расположенных вдоль нее матриц.
Как можно убедиться, этот след всегда появляется со знаком минус.
Действительно, петле с к вершинами отвечает совокупность к
сверток, например такая:
(•ф"^Л-ф)(-ф"^Л-ф) ::: (ij)"^ylij)).
Видно, что полное число перестановок фермионных операторов
здесь нечетно. В простейшей диаграмме с одной сверткой в петле
(см. рис. 2.2ы) знак не определен ввиду неопределенности Г-произ-
ведения при совпадающих временах. Этот знак можно определить,
потребовав, чтобы при разложении по степеням внешнего поля
вклад этой диаграммы давал нужный результат (см. гл. 4).
§ 2.7. Электронный и фотонный пропагаторы
В этом параграфе приведены 5шные выражения для электронного и
фотонного пропагаторов. Электронный пропагатор в картине Фарри
задается выражением, которое получается точно так же, как
выражение [I, (4.228)] для электронного пропагатора в квантовой
механике:
0 s{x,x^) = е(<1 -1^) 2; %{х,)Щх^) - е(<1 -1^) 2; %{х,)Щх^).
в >о Е <о
(2.226)
Здесь •ф^(х) — волновые функции (1.19). Выражение (2.226) можно
переписать в более удобной для вычислений форме [1]:
c^v V Ч - -L f W(o е'^С.-'г) V "^'^'^^'^'^'^'^ (2.227)
78
где суммирование распространяется на положительно- и
отрицательно-частотные состояния.
Действительно, пусть Е^ > 0. Тогда Е^{ 1 — Ю) = Е^ — Ю. Если
<j — <2 > О» то мы интегрируем по верхней полуплоскости, где
ехр [ica(<j — <2)]~*0 при ш—*/oo. При этом вычет в полюсе дает
первую строку формулы (2.226). Если же Е^ < О, t^ — t2>0, то
полюс оказывается в нижней полуплоскости и отрицательно-частотная
часть суммы дает нулевой вклад. Аналогичным образом возникает
вторая строка формулы (2.226).
Действуя так же, как в [I, § 4.4], нетрудно убедиться, что
электронный пропагатор является функцией Грина для уравнения
Дирака (1.32):
[%(Pv + e^(^i)) + '"]^(^i. ^2) = -i6(^i - ^2)- (2-228)
Перейдем к фотонному пропагатору. Используя определение
(2.223), явный вид операторов А^{х) (2.97) и коммутационные
соотношения (2.98), (2.99), получаем
D (х.Х2) = 2я-Це^е'''('.-'г)-'«1'.-'г1, (2.229)
где к = I к I. При этом мы использовали также равенство
S<'>'4" = \v. (2-230)
X
выражающее условие ортогональности и нормировки векторов
поляризации *). Соотношение (2.229) можно переписать также в виде
^,v(^i^2) = —-, S Д,ДЛ)е'^(-.-^. dX (2.231)
где D^^(k) — пропагатор в импульсном представлении
7.^.)=i^, (2-232)
^2 _ |j2 _ (^2^ ^4/^ = i dk doi. Это проверяется непосредственно ин-
тефированием в комплексной плоскости с учетом указанного в
(2.232) правила обхода полюсов:
coj 2 = ± Vk^ - Ю = ± V)?^^ я= ± к + Ю. (2.233)
Наконец, получим еще одно удобное для атомных расчетов
выражение, проинтегрировав в (2.231) по dk. Направив ось z в
*) При переходе к (2.229) произведена также замена
У —Ц t rfk
\ и использована гауссова система апектромагнитньк единиц.
79
к-пространстве по вектору г и вычисляя интеграл по углам,
получаем
(4л:)^6 ^ ^ sin (xT-.-jx rfx ... ., ^ „,,
= -^ [ d(o [ ——Щ еМ«,-«,), (2.234)
"-О0 о
где '■j2= I»*! — fj]. После интегрирования в (2.234) по комплексной
плоскости с учетом полюсов
Kj 2 = ± Vcu^ + Ю « ± to ± гО (2.235)
находим окончательно
6
^^v(^i - ^2) = ъаГ- S e'l^l^^-'^C.-'j) £/(0. (2.236)
—00
В силу калибровочной инвариантности выражение для фотонного
пропагатора определяется неоднозначно. Формулы (2.232), (2.236)
соответствуют так называемой фейнмановской калибровке. Самый
общий вид фотонного пропагатора в импульсном представлении
таков [2]:
^.v(*) = - ^^ + г^{к)к + г^к)К + ^(*')*/v. (2.237)
где Хц(*)> D{k^) — произвольные функции. Действительно, в
выражениях для амплитуды произвольного процесса фотонный пропага-
тор D (к) всегда умножается справа и слева на электронные токи
у , /\„ поскольку выражение D {к) возникает при перестановках
двух фотонных операторов А^, А^, соответствующих двум вершинам
(каждой вершине отвечает свой оператор электронного тока).
Уравнение неразрывности (1.14) в импульсном представлении
принимает вид
Vk = 0- (2.238)
Отсюда становится очевидным, что дополнительные члены в пропа-
гаторе (2.237) не меняют амплитуды.
Обычная для квантовой электродинамики без внешнего поля
фейнмановская калибровка отвечает выбору у^{к) = D{k^) = 0. Ку-
лоновской калибровке соответствует такой выбор:
-^=-^^^ (2.239)
^^ = Р^ ('■=!'2'3), (2.240)
D{k^)=0. (2.241)
80
Подстановка (2.239) в (2.237) дает
^44W=-^, (2.242)
D^.(k)=0 (г =1,2,3), (2.243)
Выражение (2.242) с точностью до числового множителя
представляет собой фурье-образ кулоновского потенциала.
Следовательно, кулоновский пропагатор D^^ можно определить формулой
Далее, поскольку выражение (2.244) удовлетворяет условию попе-
речности в импульсном пространстве
k,D,j{k^) = kp,j{k^)=0, (2.246)
пропагатор поперечных фотонов в кулоновской калибровке можно
записать так:
t
Получим для пропагаторов D^^, Er^^ выражения в координатном
' представлении. Для этого подставим сначала в интеграл (2.231)
'(■ К^{к) в виде (2.245). Проводя вычисления так же, как и в случае
■ ^>ttv(*) (см. (2.234), (2.235)), получаем
^^v(^i - ^2) = - 4 *('i - '2) V6v4- (2.248)
; Для поперечного пропагатора таким же образом получаем
6 "
< ^^v(^i ~^2)=^\гг\ ^^Р [i IWIГJ2 - г(о(<1 - t^) ] do) -
. \
' ' 1 г ехр а\(х>\г„) — I л
•■ -Vi,V,^i S ехр [m{t, - t^)] у^ da>)(l - Ь^,){\ - Ь^,).
(2.249)
^U*)= -^^ P.v--^ (1-V(l-6v4)- (2.247)
Глава 3
РЕЛЯТИВИСТСКАЯ ТЕОРИЯ ВЗАИМОДЕЙСТВИЯ
ЭЛЕКТРОНОВ В АТОМЕ
§ 3.1. Классификация поправок к энергии
для связанных электронов в атомах
В квантовой электродинамике взаимодействие атомных электронсш
друг с другом, как об этом говорилось в предыдущей главе,
описывается с помощью теории возмущений. В квантовой механике такое
взаимодействие в общем случае не считается малым и описывается
оператором взаимодействия в многоэлектронном уравнении Шрё-
дингера. Квантовомеханическое описание справедливо в тех
случаях, когда скорости электронов не слишком велики, т. е. имеет место
нерелятивистская ситуация. Согласно результатам § 1.5 для этого
необходимо, чтобы aZэф<5cl, где г^ф — эффективный заряд ядра
для данного слоя. Таким образом, нерелятивистский подход
непригоден для описания внутренних электронов в тяжелых атомах, а
также для электронов в многозарядных ионах.
В тех случаях когда можно использовать нерелятивистскре
приближение, соответствие между одним и другим способами описания
взаимодействия проще всего установить так. Рассмотрим квантово-
механическую теорию возмущений по взаимодействию между
электронами (см. [I, §4.2]). Каждому порядку такой теории
возмущений в квантовой электродинамике можно сопоставить обмен одним,
двумя, тремя и т. д. кулоновскими фотонами. Следовательно,
соответствующие матричные элементы в нерелятивистском пределе
имеют один и тот же порядок величины по константе
взаимодействия (константе связи) — заряду е. Это обстоятельство
характерно для квантовой электродинамики связанных электронов в
картине Фарри — порядок диаграммы отнюдь не определяется
просто числом ее вершин, как для свободных электронов. Вместе с
тем упомянутые диаграммы с различным числом кулоновских
фотонных линий различаются по степеням параметра 1/Z (если
использовать приближение невзаимодействующих электронов в
качестве нулевого).
Таким образом, решение уравнения Шрёдингера с кулоновским
взаимодействием между электронами эквивалентно суммированию
бесконечной последовательности диаграмм с кулоновскими фотонами
в нерелятивистском пределе. Можно показать, что при этом нужно
учитывать вклад так называемых лестничных диаграмм, на которых
82
кулоновские линии не пересекаются друг с другом. В случае первого
и второго порядков теории возмущений по взаимодействию (во
втором и четвертом порядках по константе связи) это будет
продемонстрировано ниже, в § 3.2 и 3.3.
Итак, в релятивистской теории взаимодействия электронов в
атоме необходимо учитывать влияние двух параметров: а и 1/Z.
Вместо них часто бывает удобнее использовать другую пару: а и
aZ. При этом для многозарядных ионов с небольшим числом
электронов N (//<sc Z) под величиной Z можно понимать
непосредственный заряд ядра, а в остальных случаях — эффективный заряд,
учитывающий экранировку ядра другими электронами.
Для самых легких атомов (водород, гелий) решение
нерелятивистского уравнения Шрёдингера известно (см. [I, § 1.1, 4.1]), а уже
при вычислении релятивистских поправок можно пользоваться
разложением по параметру aZ. В случае водорода такое разложение
было произведено в § 1.5, а в случае гелия будет рассмотрено в
§ 3.4. Для атомов и ионов с числом электронов больше двух и не
слишком большим значением Z главной проблемой является
возможно более точное решение уравнения Шрёдингера, т. е. учет
электронной корреляции (см. [I, гл. 4]). Релятивистские поправки
при этом можно по-прежнему вычислять с помощью разложения по
-6
ЗХда
Рис. 3.1. График сравнительных характеристик различных поправок к энергии
; aZ (см. § 1.5, 3.4). С ростом Z релятивистские эффекты становятся
сравнимыми с корреляционными эффектами и уже не могут рас-
; сматриваться как поправки.
83
в'
в'
Чтобы пояснить, как меняется относительная важность тех ил!
иных поправок к энергии при изменении заряда ядра Z, рассмотри»
основное состояние двухэлектронного иона с произвольным зарядо!
ядра Z. Построим график (рис. 3.1) [1
2], на котором по оси абсцисс отклады
вается заряд Z, а по оси ординат — ве
личина Ig |А£„/А£о|, где А^^ — сум
маркая энергия связи двух невзаимодей
ствующих электронов в атоме, А£„ -
различные поправки к энергии. Согласга
(1.151)
В
в
АЕо = 2т{^/\ -(aZ)2-l). (З.Г
Рис. 3.2. Фейнмановские фа-
фики, изображающие куло-
новское взаимодействие между
электронами в первом порядке
теории возмущений
В'
В'
Кривые Cj и Сг относятся к
поправкам первого и второго порядков по куло
новскому взаимодействию электронов
Эти поправки соответствуют обмену од
ним и двумя кулоновскими фотонам!
и описываются лестничными
диаграммами (рис. 3.2 и 3.5а). Отношения АЕ^/^Е^ (г = 1, 2) при всех зна
чениях Z пропорциональны 1/Z', т. е. имеют порядок единицы npi
Z % 1 и порядок а' при Z »^ 137. Кривая С, построена по формуле
(3.38), а кривая Сг — по формуле
(3.104), приведенным ниже. Кривая £
относится к обмену одним поперечным
фотоном — брейтовскому
взаимодействию (см. [3], а также §3.2 и рис. 3.3),
При малых значениях Z учет брейтов-
ского взаимодействия дает
релятивистскую поправку к энергии порядка
т ■= (aZ)*. Поскольку энергия связи
электрона при малых значениях Z имеет
порядок величины m(aZ)^, получаем
AE^/AEq ^ a^Z. Следовательно, для
Z яг: 1 имеем AE^/AEq »j а^, что и
получается при расчете по формуле (3.40).
При больших значениях Z поправки
В
в
а
Рис. 3.3. Фейнмановские
графики, изображающие брейтов-
ское взаимодействие между
электронами в первом порядке
теории возмущений
AEci и AEg — величины одного порядка. Действительно, если
aZ яг 1, то в теории остается один малый параметр а (или 1/Z), так
что AEb/AEq « AEci/AEq ^ а.
Кривая ВС соответствует обмену одним кулоновским и одним
поперечным фотоном (см. рис. 3.6а—г). При этом АЕд^, можно
рассматривать как кулоновскую поправку к брейтовскому
взаимодействию. Тогда величина АЕ^^^ при всех значениях Z должна быть в
84
Z раз меньше самого брейтовского взаимодействия А£д, что и
отражено на рис. 3.1. Расчет при этом был выполнен по формуле
(3.105). Поскольку приведенные ниже, в § 3.5 формулы (3.104) для
t^E^2 ^ (3.105) для А^вс получены с помощью разложения по
степеням aZ и непригодны при больших значениях Z,
соответствующие кривые ограничены областью Z < 50.
Кривая R на рис. 3.1 соответствует радиационным
поправкам в низшем порядке по константе связи (лэмбовский сдвиг).
Теория таких поправок изложена в гл. 4. При Z ^^ 1 величина
A£'jj»^ma(aZ)*, т. е. AEj^/AEq^^ a{aZ)^. При больших значениях
Z величина AEj^ имеет тот же порядок по константе связи, что и
Д^с!» ^Eg, так как у соответствующих диаграмм (см. в гл. 4 рис. 4.1)
одинаковое число вершин. Таким образом, АЕц ~ та при aZ »j 1.
Кривая А на рис. 3.1 приведена для сравнения и соответствует
одноэлектронным релятивистским поправкам (зависимость массы от
скорости, спин-орбитальное взаимодействие):
А£д = А^о - АЕ^Р = 2т fVl - (aZ)^ - 1 + i (aZ)^^, (3.2)
где А£^Р — нерелятивистская энергия связи.
Из рис. 3.1 видно, какие поправки нужно учитывать в первую
очередь при различных значениях заряда ядра Z. Вклады поправок
АЕс2 и А£д сравниваются уже при Z « 10. Это соответствует
имеющимся представлениям, согласно которым поправки на электронную
корреляцию в атомах становятся сравнимыми с релятивистскими
поправками при Zэф <=» 10. При Z«? 35 поправка А£д превосходит
также AE^i- Релятивистская поправка к взаимодействию электронов
(поправка Брейта) при Z »^ 25 превосходит поправку АЕ^,^! а при
Z«60 сравнима с поправкой A^^i- Радиационные поправки в
низшем порядке при Z »^ 10 уже сравнимы с брейтовскими.
Следовательно, вычисляя поправки к энергии при Z > 10, необходимо
учитывать кулоновское взаимодействие в первом и во втором порядках
теории возмущений, а также брейтовское взаимодействие и лэмбовский
сдвиг. Такой расчет, согласно рис. 3.1, должен давать относительную
погрешность не более а^ ^ 10~*, поскольку при этом учитываются все
кривые на рис. 3.1, лежащие при Z^ 10 выше уровня 2 Ig а.
§ 3.2. Взаимодействие электронов в первом порядке
теории возмущений
Кулоновское взаимодействие электронов в первом порядке теории
возмущений по взаимодействию (во втором порядке по
константе связи) описывается двумя диаграммами, приведенными на
рис. 3.2а, б, из которых вторая диаграмма является обменной; Л, В
относятся к одноэлектронным состояниям в атоме.
85
Для вычисления поправок к энергии в квантовой
электродинамике мы будем применять формализм Гелл-Манна и Лоу (см. [I,
гл. 4]). Основной результат применения этого формализма —
формула для сдвига А£д уровня энергии Е^ через адиабатическую
5„-матрицу:
1 |<Ф°1§„(«'.-«')|Ф°> (3 3)
где оператор эволюции S„(oo, — <») получается из (2.216), если
заменить ^i„t(0 иа «адиабатический» оператор возмущения Гелл-
Манна и Лоу,
Я;„,(<;а) = е-°1'1Я;„,(0, (3-4)
при этом считая а > 0. В таком виде формула (3.3) была впервые
получена в [4]. Производя в (3.3) разложение по степеням е, несколько
первых членов можно записать в виде (см. [5], а также [I, гл. 4])
А£, = lim i ш{(Ф° I S« I Ф1)е + Г2(Ф° | S^^) | Ф°> - (Ф° | SW | ф0)21 ^2 +
+ [3(Ф° IS^) I Ф°> - 3(Ф° 15^2) I Ф°>(Ф° I SO) I Ф0> + (ФОI SO) I Ф0>з] е^ +
+ [ ЧПI ^а > IФ^) - 4(Ф° I SL^> I Ф°>(Ф° 150) I Ф°> +
+ 4(Ф° I Si^) I Ф°>(Ф° I SO) I ФУ - 2(Ф01SO^) IФ^ -
_(ф0|50)|ф0)4]^4+ I (3.5)
Более простой результат можно написать для неприводимых
матричных элементов S-матрицы, т. €. таких, которые не могут
быть приведены к произведению матричных элементов с
обкладками (Фд I и I Ф°). Для диаграмм Фейнмана это означает, что при
сечении диаграммы горизонтальной линией никакое промежуточное
состояние не совпадает с исходным. Например, диаграммы рис. 3.2
и 3.3 (в них вообще нет промежуточных состояний), а также
диаграммы рис. 3.56 и З.бв, г, е — неприводимые, а диаграммы
рис. 3.5а, в и 3.6а, б, д — приводимые.
Для расчета вкладов неприводимых диаграмм можно
использовать более простые формулы (см. [I]):
Д4«) = (Ф°|Р|Ф0>, (3.6)
где матричные элементы оператора эффективной потенциальной
энергии V определяются равенством
(Ф?|5|Ф°>н = -2ш6(£0_£0)^фО|Р|фО)^ (3.7)
а обозначение «н» относится к вкладу неприводимых матричных
элементов.
86
Итак, для вычисления энертетического сдвига в первом порядке по
кулоновскому взаимодействию можно воспользоваться формулами
(3.6), (3.7). Вычислим вначале вклад диаграммы рис. 3.2а согласно
правилам соответствия, перечисленным в § 2.6. Эти правила в случае
применения адиабатических формул (3.3)—(3.5) следует дополнить
еще одним пунктом: каждой вершине дополнительно сопоставляется
адиабатический множитель ехр (—at). В случае применения формул
(3.6), (3.7) в этом, однако, нет необходимости. Получим
(ф0|5(2)|ф0) =
= е^ \ (^AXl)Уt^'^A(Xl))(^AX2)У.'^в(X2)ЩЛXl^2) ^\ ^V (3-8)
Подставляя выражение для кулоновского фотонного пропагатора
(2.248) и производя интегрирование по t^, <2 в (3.8), получаем
<Ф°|5(^)|Ф°> = -2шв^Ш 6(£д.
\Ча-в-ав
+ Ед.-Е^-Е^). (3.9)
При этом мы используем следующие обозначения для матричных
элементов с дираковскими волновыми функциями:
(^)д'д = S ^ж(г)^(г)%(г) dT, (3.10)
(.С)а-в-ав= \ ^\'{^iWB-iJ2)G{r^4)-^AiJi)^Bi4) dT, dr^. (3.11)
Здесь подразумевается, что оператор F представляет собой 4-компо-
нентную матрицу по спинорным индексам, а оператор G — 16-ком-
понентную матрицу. В частном случае в формуле (3.9), когда
G= l/rj2, эта матрица является единичной по спинорным индексам.
Отсюда по формулам (3.6), (3.7) получаем выражение для
оператора эффективной потенциальной энергии
у =^ (3.12)
*= '-12
И для поправки к энергии
АЕ^, = е'Щ . (3-13)
" [Чавав
Заметим, что согласно рассуждениям § 3.1 выражение (3.12) в
рамках нерелятивистской квантовой механики является точным
оператором взаимодействия двух электронов, т. е. в нерелятивистском
пределе все поправки на взаимодействие электронов должны
получаться как итерации потенциала (3.12).
Если в качестве нулевого приближения выбрать приближение
невзаимодействующих электронов, то сдвиг уровня Л^-электронного
атома в первом порядке по кулоновскому взаимодействию с учетом всех
занятых одноэлектронных состояний и обменных диаграмм равен
АЕ^,={е^У. Ш . (3.14)
'}ЛЧав„
АВ
87
При этом мы использовали обозначение для матричных элементов,
аналогичное fl, (2.93) J в нерелятивистской теории
(^)ав; ав = iG)^g^B — (С)дввд. (3.15)
Рассмотрим теперь обмен одним поперечным фотоном
(диаграмма рис. 3.3) и вычислим брейтовскую поправку к энергии А£д.
Поскольку диаграмма рис. 3.3 — приводимая, опять используем
формулы (3.6), (3.7). Согласно правилам соответствия
(ф0|5(2)|ф0) =
= е^ \ (%'(^i)'Yp^%(xi))(^B'(x2)'Yv%(^:2))^J,v(^i^2) dx^ dx^. (3.16)
Подставляя выражение (2.249) для поперечного фотонного пропага-
тора и интегрируя по <j, t^, получаем
J expfi(£:^- — Е^ + w)<j -I- i{Eg. — Eg— со)<Лл, dt^ =
= (2jt)26(co + E^. - Е^)Ь{ш - Eg. + Eg). (3.17)
Теперь интегрирование по со дает (см. [2], а также [3]):
(фо15(2)IфО) = 2шеЧ{Е^ + Eg- Е^-- Eg.) X
е^1^.-^/1-. - (V,a.)(V,a,) /- ^''''"''""^l • (3-18)
Здесь индекс /=1,2 матрицы а^ указывает, что данная матрица
действует на функцию •ф(г^).
Воспользуемся теперь формулами (3.6), (3.7). В прямом
матричном элементе нужно положить А' = А, В' = В и совершить
предельный переход (£д —£д')—»0. После этого зависимость от энергий
£д. Eg внутри обкладок пропадет. В обменном матричном элементе
{А' = В, В' = А) зависимость от £д. Eg в выражении, стоящем
внутри обкладок, остается. Таким образом, уже отсюда видно, что
в общем случае невозможно получить явное выражение для
оператора брейтовского взаимодействия электронов.
При вычислении поправок к энергии необходимо учесть только
действительную часть сдвига АЕд (о роли мнимой части см. § 6.1).
С учетом всех занятых одноэлектронных состояний и обменных
диаграмм окончательно находим
N
АЕд=-1е-
В = 1 l
'12 2
^^(Via,)(V2a2)r,2
АБАБ
, 1 COS (№.-£„)/■„)-!
-COS {{Е^-E,)r^^)-{V,а,)(V^a^)^
АББА!
(3.19)
88
Формула (3.19) допускает упрощение, если воспользоваться
соотношением
((Vla.)(V2a2)/(r,2))д-^,чв=-([Лl[V('-.2)]J-)л'в'дв =
= (£д£в' - Е^Ед - Е^.Е^, + Е^.Ед) {f{r,^) )^.g.^g, (3.20)
ще Л^ — одноэлектронный гамильтониан Дирака (1.34), /(г,2) —
произвольная функция. Из (3.20) следует:
(( V,a,) {^:ft^)f{>'i2))ABAB = 0. (3-21)
((У,а,)(У2а2)/(г,2))дввд = (£д - £в)'(/('■12))дввд- (3-22)
С учетом (3.21), (3.22) преобразуем (3.19) к виду
^Eg =
4^^S
'^ ' '--^ 'а.а,-1 ^ ч . , 1
А,В=\
+ \-^-f—cos{{E^-Eg)r,^) +
ABAS ABBA
(3.23)
Объединяя (3.14) и (3.23), получаем
Д£с1 + А£в =
= 'Л |(^) - f^5^cos((^,-^,).,,)) 1(3.24)
Д,В = 11\ I АВАВ \ I авва)
Наконец, в частном случае эквивалентных электронов, для
которых все £д. Eg одинаковы, формулы (3.23), (3.24) приобретают
Совсем простой вид
A£^=-ie^2 Т? ' (3.25)
'12 ,
А,В = \\ I АВ\АВ
N _
AEc, + AEg = \e^^ [^-~^\ . (3.26)
А, B=l\ ' I АВ\АВ
В нерелятивистском пределе из (3.23) можно получить
известное выражение для операторов взаимодействия Брейта. Для
атомных электронов (£д — Eg) ^ m(aZ)^ (это величина порядка
энергии связи). Далее, характерное значение г,2 в атоме равно
Гц^ a^/Z^i {maZ)~^, ще а^ — боровский радиус. Следовательно,
при aZ«\ показатель экспоненты в (3.18) (эту формулу более
удобно использовать для разложения) мал: {Ej^ — Eg)r^2^^ ctZ> так
что можно разложить экспоненту в ряд:
: f е'1^.-М^. = ^--Н/|£д-£д.|-1(£д-£д.)\,-Ь... (3.27)
89
При вычислении первого слагаемого в матричном элементе (3.18)
можно ограничиться первым членом разложения (3.27), а при
вычислении второго слагаемого в (3.18) необходимо учитывать
третий член разложения (3.27), поскольку первый член (3.27)
исчезает после вычитания единицы в (3.18), а второй не дает
вклада вследствие ортогональности одноэлектронных волновых
функций.
Тогда, используя соотношение
(V,aj (V,a,).,, = - ^ + ^l^I^flli, (3.28)
12 '■j2
формулу (3.18) можно преобразовать к виду
(фо 15(2) I фО) = _2я1(Ф° IV^ I Ф°>6(£° - £°), (3.29)
где Vg — оператор Брейта [3]:
^ в 2
°1°2 (°l'"l2)(°2'"l2)'
(3.30)
Подразумевается, что матричные элементы этого оператора
вычисляются с четырехкомпонентными волновыми функциями.
Для перехода к двухкомпонентной записи нужно прежде всего
представить «малые» компоненты дираковских биспиноров в
матричных элементах в виде (1.202). При этом, поскольку сейчас мы
не рассматриваем атом во внешнем поле, можно гюложить А = 0.
Далее, возникающие при этом произведения о-матриц расписываем
с помощью формул (1.25)—(1.30). Одновременно с преобразованием
матричного элемента оператора (3.30) нужно учитывать также
релятивистские поправки в обкладках матричного элемента оператора
кулоновского взаимодействия (3.12) — они имеют тот же самый
порядок малости. При этом следует учесть преобразование (1.211).
Заметим, что при вычислении матричного элемента (3.30)
учитывать преобразование (1.211) не нужно — это будет превышением
точности.
В процессе описанных выше преобразований при действии
операторов pj = —iVj и Р2= —/Vj на l/rj2 и (arj2)(brj2)/rf2, где а, b —
постоянные векторы, возникают различные сингулярные
выражения. Простейшие из них имеют вид
Р?7- = р1 7- = -(Р1Р2) 7- = -4^6(г,2). (3.31)
Встречается также следующее выражение:
(М)(Р.Ь)^ = :^|аЬ-^^^^|, (3.32)
'"12
которое справедливо, однако, лишь в том случае, когда волновые
функции в обкладках не являются сферически-симметричными. Для
сферически-симметричных функций, как можно убедиться непос-
90
редственно интегрированием по углам, правая часть (3.32)
обращается в нуль. Рассмотрим теперь отдельно сферически-симметричные
волновые функции. В этом случае под знаком интеграла можно
произвести замену
(V,a) (V,b) f = L й, ^ + ah 4 + a A ^1 h (3-33)
'-12 {=' =" dx' У У dy'' ' ' dz") '•,2
Действительно, члены, содержащие перекрестные производные типа
д2
т-д-, исчезают при интегрировании в силу симметрии. Также в силу
сферической симметрии все три члена в правой части (3.33) дают
одинаковый вклад. Поэтому
(V,a)(V,b) ^ = 1 (аЬ)А^= -^ (аЬ)6(г,,). (3.34)
Окончательно, объединяя (3.32) и (3.34), получаем для
произвольного случая:
(р,а) (р,Ь) J- = 4 jab - ^^^^i2Hbr.,)| ^ ^ ^^^^ ^^^^^^ ^^^^^
•2 ''12 [ ''12 J
Собирая все выражения, происходящие как от потенциала
(3.12), так и от потенциала (3.30), получаем в двухкомпонентной
записи следующее выражение для оператора взаимодействия
электронов в атоме [3]:
V=Vc + Vg, (3.36)
^й = m I ~^^^^1г) - ъ-, PiP2 + ;Г 1 +
+ Тг- [-К + 2о2)(Г12 X Pi) -I- (02 -I- 20i)(Г12 XР2)] -I-
+i
''12
(3.37)
' Все члены оператора Брейта представляют собой релятивистские
' шправки порядка {vlc)\ как уже отмечалось в §3.1, их
относительная малость по сравнению с энергией связи равна ^ (aZ)^. Та-
'■ КИМ образом, соответствующие поправки в Z раз меньше, чем реля-
* тивистские поправки в уравнении Дирака (1.216).
Принято говорить, что члены первой строки в (3.37), не
зависящие от спинов, описывают релятивистское взаимодействие
орбита—орбита; члены, второй строки, линейно зависящие от
спинов, — взаимодействие спин—чужая орбита (в отличие от
взаимодействия спина с орбитой для одного электрона (1.221)); наконец,
квадратичная по спинам третья строка описывает спин-спиновое
взаимодействие. ^ ^
Важно отметить, что в отличие от оператора V^ оператор Fg в
виде (3.37) имеет смысл использовать только в первом порядке
\ 91
теории возмущений. То же самое относится и к выражению (3.30).
Причина заключается в том, что при выводе (3.30) и (3.37) мы
существенно использовали, во-первых, разложение (3.27) и,
во-вторых, малость «нижних» компонент дираковских биспиноров. И то и
другое справедливо лишь до тех пор, пока подразумевается, что в
обкладках матричных элементов стоят положительно-частотные од-
ноэлектронные дираковские функции. При переходе уже ко второму
порядку теории возмущений возникает суммирование по полной
системе одноэлектронных состояний, включающей и
отрицательно-частотные состояния.
Приведем некоторые конкретные выражения поправок на
взаимодействие для двухэлектронных атомов и ионов. Для расчета
можно использовать формулы (3.13), (3.23), в которые нужно
подставить конкретные выражения для дираковских волновых
функций (1.88), (1.89), (1.140). Для l/rj2 следует использовать
разложение по сферическим функциям [I, (П1.4)]. После этого
интегрирование по углам производится с помощью формул,
приведенных в [I, § 3.3], а при интегрировании по радиальным
переменным следует воспользоваться формулами, приведенными в [I,
приложение П2.4].
В частности, результат вычисления поправки A^^i Для основной
конфигурации двухэлектронного атома (Isi)^ таков [2] *):
ma2zr(47,-l-l)ffl, 47,-1-1, 27,-1-2; |]
Д£: = 5^ ± (3-38)
" 2'^.-Ч27,-1-1)[Г(27,-1-1)]^
В нерелятивистском пределе (aZ<Kl) выражение (3.38) дает
известный нерелятивистский результат (см. [I, табл. 4.1]):
A£^i = |m(aZ)^ (3-39)
Для той же конфигурации вычисление поправки АЕд дает [2]:
4ma^*Z^Г(4y^ -I- l)f (l, 47, -I-1, 27, + 3; U
АЕ„ = ^- '-. (3.40)
" 2'^.+'3(7,-1-1)[Г(27,-1-1)]^
В нерелятивистском пределе из (3.35) следует:
AE^ = ^ma*Z3. (3-41)
Это совпадает, естественно, с результатом вычислений среднего
значения оператора (3.37) с нерелятивистскими волновыми функция- ]
ми. По формулам (3.38) и (3.40) построены кривые С, и В на
рис. 3.1.
*) Отметим, что вклад обменного графика в этом случае равен нулю.
92 ;
§ 3.3. Взаимодействие электронов
в вырожденных состояниях
Фактически до сих пор все формулы в этом параграфе относились
к невырожденным состояниям. Рассмотрим теперь случай
вырожденных состояний (вновь на примере двухэлектронных систем).
Поскольку решения уравнения Дирака в кулоновском поле описываются
четверкой квантовых чисел njlm (см. гл. 1), в релятивистской теории
естественным образом возникает схема //-связи. При этом
конфигурации задаются набором квантовых чисел («i/i/i)'"', .... (п^/^/^)^.
В случае невырожденных конфигураций функцию |Ф°) можно
представить в виде
где a^ji„ — оператор рождения электрона в состоянии с квантовыми
числами njlm, |Фуас) — вакуумный вектор состояния, N — число
электронов в атоме. В случае вырожденного состояния функция
нулевого приближения (3.42) заменяется на линейную комбинацию
(см. [1,(4.271)])
i^^Smv ij)=lCj^j,c W«i '«N)i^v,/,m w.-^
(3.43)
1де / и M — полный момент и его проекция. Коэффициенты
CjMj I JJ в первом порядке теории возмущений в принципе
должны определяться при диагонализации матрицы энергии. Тем
самым будут определены «правильные» комбинации функций
нулевого приближения, о которых говорилось в [I, § 4.2]. Для определения
«правильных» комбинаций в высших порядках теории возмущений
необходимо диагонализовать секулярный оператор (см. [I, §4.2]).
Построение секулярного оператора в релятивистской теории атома
рассмотрено в [2].
Как и в нерелятивистской теории атома, во многих случаях вид
коэффициентов CjMji JJ может быть установлен из соображений
симметрии, с помощью теории сложения моментов. Формулы (3.42),
(3.43), в которых волновая функция атома записана в представлении
вторичного квантования, соответствуют в координатном
представлении линейной комбинации слэтеровских детерминантов. Определение
коэффициентов в этих комбинациях в случае LS-съязи было
рассмотрено в [I, § 3.10] *). Аналогичный подход возможен и в случае
//-связи (см. [I, § 3.13]). В тех случаях, когда волновая функция полностью
■ *) в [I, § 3.10] использовался, как это обычно делается, метод генеалогических
коэффициентов. Хотя при этом слэтеровские детерминанты непосредственно не
фигурируют в вычислениях, упомянутые коэффициенты векторного сложения получаются
С точностью до нормировки.
93
определяется условиями симметрии, для вычисления энергии можн
пользоваться теми же выражениями, что и в невырожденном случа(
Нужно лишь отметить, что каждому матричному элементу 5-матри
цы, которому в отсутствие вырождения сопоставлялась определенна
диаграмма, теперь сопоставляется совокупность диаграмм, соответст
вующих различным членам линейной комбинации (3.43) и отличаю
щихся проекциями моментов т в наборах квантовых чисел njlm.
Двухэлектронные конфигурации задаются наборами чисе
(пу7, n'j'V). Если исходить из приближения невзаимодействующи
электронов, то необходимо с самого начала учитывать кулоновско
вырождение по числу /, т. е. рассматривать смешанные конфигура
ции, которые могут быть символически записаны в виде
п-1 п'-\
(nj, п'П = 21 (п/^ п'ГП\ j^\.^ j.^,_. (3.44
1=0 /"=0
При учете межэлектронного взаимодействия уу-конфигурации рае
щепляются на уровни (nJ, n'j')j, отличающиеся значениями сум
марного момента / (см. [I, § 3.13]).
Например, при п = п =\ имеется единственная конфигураци
(1^0, 1 ^ 0)о = (Isi, lsi)o. При п = 1, п' = 2 возникают следующн
А • А 2 2
конфигурации:
(li,2i) = (li0,2i0),,o + (li0,2il),,o =
= (i4.24)i,o+(i4'2/'i)i.o. ^^-^^
(1 i, 21) = (1 iО, 211)^, = (l4 , 2р \\,. (3.4«
е
При этом указаны также возможные значения суммарного мс
мента /.
Волновые функции двухэлектронного атома (иона) в случае /j
связи строятся по формуле (здесь мы используем координатнс
представление, см. [I, (3.377)])
= Л^2 С%,(тт'){%;,„(Г,)я1,„..,,,„,(Г2) - %;,„(r2)%vr^'('-l)}. (3-4^
mm
где Л^ — нормировочный множитель. Для эквивалентных электр
нов (п;1 = n'j'V) N= 111. Для неэквивалентных Л^= ЦлП.
Интересно проследить, как постепенно меняются тип связи
расположение уровней при возрастании заряда ядра Z. Для эта
необходимо рассчитать уровни по промежуточной схеме связи, в к(
торой квантовыми числами являются лишь суммарный момент ,
его проекция М и четность. Для нейтральных атомов такой перехс
94
был прослежен на примере конфигурации (пр)^ в [I, § 3.13] путем
параметризации электростатического и спин-орбитального
взаимодействий. Ниже мы продемонстрируем непосредственный
релятивистский расчет для двухэлектронных многозарядных ионов, также
иллюстрирующий этот переход [6, 2].
Вычисляя уровни энергии при произвольных (в том числе
малых) значениях Z, необходимо учитывать, что в пределе LS-съязи
различные волновые функции (3.47) могут перемешиваться.
Поскольку все перемешиваемые уровни в рассматриваемом
приближении имеют различную энергию, это отвечает наложению
конфигураций. Необходимость в таком наложении возникает потому, что
перестает быть справедливой теория возмущений по 1/Z, т. е. по
межэлектронному взаимодействию: матричные элементы
взаимодействия становятся одного порядка с расстоянием между
некоторыми уровнями в схеме //-связи. Например, это относится к уровням
11 13
(1 2 о, 2 ^ l)i и (1- О, 2 ^ l)i. Различие в энергии этих уровней
возникает только в релятивистской теории и обусловлено различием
квантовых чисел / = 1/2 и / = 3/2. Оно велико при больших
значениях Z, а при малых Z имеет порядок m(aZ)^. Следовательно, при
переходе к малым Z, когда межэлектронное взаимодействие
сравнимо с релятивистскими поправками, т. е. ^ = (aZ)^ (см. рис. 3.1),
теория возмущений для указанных уровней становится несправед-
• ливой. Такая ситуация должна иметь место при Z ;=« 30, что под-
' тверждается пересечением кривых С^ и А на рис. 3.1 при Z яг: 35.
Таким образом, в промежуточной схеме связи волновые
функции двухэлектронного иона следует строить в виде
• ^/м(г,Г2) = S S ^JMUnn ^/MjriA^.r^)' (3-4^)
Jj' W
где функции •ф5муу'н' определяются согласно (3.47), а aj^ —
коэффициенты смешивания. В принципе, уровни энергии и
коэффициенты смешивания могут быть найдены и в этом случае диагонали-
зацией матрицы энергии (секулярного оператора), однако такая
диагонализация должна проводиться в рамках адиабатического
формализма до предельного перехода по параметру адиабатического
включения взаимодействия а—*О [2]. Такая процедура является
достаточно сложной, и мы воспользуемся здесь для той же цели более
простым приближенным методом [6].
Вместо точной матрицы энергии мы будем диагонализовать
оператор V=Vc+ Vg, где Vq и Vg определяются формулами (3.12) и
(3.30). Заметим, что для больших значений Z отброшенные в (3.30)
члены имеют тот же порядок малости, что и учтенные. Однако в этом
случае смешивание конфигураций малб: коэффициенты примеси про-
f порциональны 1/Z. При уменьшении Z коэффициенты смешивания
становятся порядка единицы. Как было показано выше, учет
смешивания конфигураций существен при Z :S 30. Однако отбрасываемые в
95
(3.30) слагаемые при малых Z имеют порядок (aZ)^ по отношению к
основному члену Vg. Поскольку само брейтовское взаимодействие
имеет порядок малости (по отношению к энергии связи) ^ (aZ)^, то не
учитываемые в (3.30) члены дают относительную погрешность
2 (aZ)*, что при Z яг: 30 составляет менее 10"*. При этом
диагональные элементы матрицы энергии должны вычисляться без каких бы то
ни было упрощений, через 5-матрицу, по формулам (3.6), (3.7).
Для классификации уровней, полученных в результате диа-
гонализации матрицы энергии, помимо полного момента / следует
в самом общем случае указывать также четность и термы (уровни),
в которые данный уровень переходит в предельных случаях LS- и
уу-связи, т. е. писать Ej+l'^^^^L, jj], где знаки ± указывают
четность. Практически во многих случаях достаточно указать лишь
соответствующий терм в пределе LS-связи, не забывая, однако, что
сами числа L, S теряют смысл при больших значениях Z.
Рассмотрим в качестве примера конфигурацию п = 1, п =2 [2].
В этом случае имеется шесть уровней:
1. £2-М; 2. £о_рР]; 3. E^^'S];
4. E,4'S]; 5. Е,_['Р]; 6. Е.Л'Р].
Первые четыре из них не смешиваются друг с другом, так как они
обладают различными точными квантовыми числами — моментом и
четностью. Энергия этих уровней вычисляется непосредственно по
формулам (3.6), (3.7). Энергии оставшихся двух уровней
определяются как корни секулярного уравнения
£/(lM12,ii01,ii01)-£ £/(lM12,i|01,ii01)
2 2 ' 2 2 ' '"''"''"■• 2 2 ' 2 2
i|01,ii01) £/(lM12,i|01,i|i
= 0,
(3.49)
где
иимпп', ij\l,l\, J2JW2) =11 C^ji}(^i^dCYM<^2^2) X
т.т. т^т^
X '^nj^l^m^.nj\l\m\:nJ^l^m^.n'J'^e^m'^' (3.50)
оператор V=V(,+ Vg задан формулами (3.12), (3.30) и
использовано обозначение (3.15) для матричных элементов двухчастичных
операторов.
Результаты расчетов приведены на рис. 3.4а. По оси абсцисс
отложен заряд ядра Z, по оси ординат — величина E/{ma^Z).
Энергия отсчитана от значения Е^л + E.i, где одноэлектронные энергии
^ 2
Егл_, Ell определены формулой (1.137). Таким образом, расстояние
2 2
ПО вертикали между различными кривыми на рис. 3.4 равно рас-
96
щеплению уровней в атомных единицах, деленному на Z.
Обозначения кривых соответствуют нумерации, приведенной выше. Как
видно из рис. 3.4а, схема LS-связи нарухпается уже вблизи Z л^ 30
(как это и следует из общих соображений). При Z«^50 полностью
f,ae
0.40
азо
D2D
20
40
Рис. 3.4. Зависимость от Z энергии уровней конфигураций пп =12: а — в первом
■ порядке теории возмущений по межэлектронному взаимодействию; б — с учетом
поправки второго порядка по кулоновскому взаимодействию
устанавливается схема у'у'-связи. Отметим, что при малых значениях
' Z точность расчета в первом порядке теории возмущений по меж-
; электронному взаимодействию невелика. В частности, в
нерелятивистском пределе относительное расположение термов ^S и ^Р
оказывается обратным истинному. Причина этого — в пренебрежении
поправками высших порядков по кулоновскому взаимодействию
электронов. На рис. 3.46 приведены уровни конфигурации (1,2) с
■ учетом поправки второго порядка по кулоновскому взаимодействию
А^сг» которая учтена в нерелятивистском приближении *).
Допускаемая при этом относительная погрешность имеет порядок
'., -J (а2^^= а} < 10"* при всех значениях Z.
*) Методы расчета величины А^сг ^ нерелятивистской теории обсуждаются в
[1, § 4.2]. Конкретное значение Д^?с2 Для конфигурации (1, 2) заимствовано из [7].
4 л. Н. Лабзовскии
97
§ 3.4. Матричные элементы гамильтониана Брейта
При вычислении релятивистских поправок к уровням энергии
нейтральных атомов основную роль играет оператор (3.37), который
легко обобщается на случай произвольного многоэлектронного
атома. Этот оператор обычно объединяют с одноэлектронными
операторами (1.216), учитывающими релятивистские поправки, и все
вместе называют гамильтонианом Брейта. Таким образом,
гамильтониан Брейта для произвольного многоэлектронного атома имеет вид
Нв = Но + Н^ + Н2 + Щ + Н^ + Ну (3.51)
Здесь Hq — нерелятивистский оператор Гамильтона [I, (2.3)],
Н,= ЦУр1 (3.52)
J
г = 1
— оператор, учитывающий релятивистский эффект зависимости
массы от скорости,
— оператор взаимодействия орбита—орбита, учитывающий
эффекты запаздывания взаимодействия,
Щ = Щ + Н'' = ^2 6(г.)' - ^ i 6(г,,) (3.54)
1 = 1 i> j
— операторы контактного взаимодействия электрона с ядром (Н'^)
и электронов друг с другом (Н'^), эффективно учитывающие
релятивистские эффекты при взаимодействии,
1 = 1 ' i>i 'i
(3.55)
— операторы взаимодействия спин—орбита (Н'^) и спин—чужая сф-
бита (Я;'),
Щ = Щ + ^^5=-^1 (s.s,)6(r,,) + $i^
i> J i>j'J
s,s.-i^^^
•J
(3.56)
— операторы спин-спинового взаимодействия между электронами.
Гамильтониан Брейта используется для описания релятивистских
эффектов в атомах в тех случаях, когда эти эффекты относительно
невелики и можно ограничиться первым порядком теории возмуще-
98
НИИ по операторам Н- (i = l, ..., 5). В этом случае естественно
использовать схему LS-связи при построении волновых функций.
Вычисление матричных элементов гамильтониана Брейта на волновых
функциях в^схеме LS-связи является нашей дальнейшей задачей. Для
оператора Hq (т. е. для кулоновского взаимодействия F^) и частично
для оператора Н'^ эта задача рассматривалась в [I, § 3.11 и 3.12].
Прежде чем строить выражения для матричных элементов,
необходимо представить все операторы в удобной форме, т. е. выразить
их через неприводимые тензорные операторы [8—12]. Ранее (см. [I,
§3.11]) это было сделано для оператора F^ (оператор
спин-орбитального взаимодействия Н'^ уже приведен фактически к нужному
виду). Аналогично, хотя и несколько более сложно, можно выразить
через неприводимые тензоры и другие операторы. Мы приведем
здесь результаты, пользуясь обозначениями, принятыми в [12].
Выражение для оператора //j через неприводимые тензоры
получается непосредственно с помощью известных соотношений для
оператора Лапласа (см. [I, § 1.1]):
Й= -^ [ЦЩ -Щ = -^ [ЦЩ - ('!-'!)]. (3.57)
ще 1; — оператор орбитального момента.
Выражение для оператора //г является наиболее сложным и
имеет вид
2т'
-^(/c-Dprxc^-f)^^
1 dr. дг
k+l
+ 2г(1 -I- P..) WJTTfTKkTJ) [Cf+1 хЩ x C)+i -
-Л(*^[[сг x7)]'"'xcr]°) ^ (Щ + ^) 5?--
/г k + \ Jt + l-iO
-([[cs"x7)] x[c..,x?J J -
-2[[c;-.x7.]'x[cr-x7;]']°f=iA}, (3,58)
ще неприводимые тензорные операторы Cf определяются согласно
[I, (3.304)], коэффициенты а,^ — согласно [I, (П1.7)], а Pjj представ-
99
ляет собой оператор перестановки индексов i и у. Формула (3.58)
возникает в результате использования разложения [I, (3.303)], а также
известной формулы для градиента (см., например, [10]):
у1 = С'^. + !^^С'хЩ\
Операторы //з и Щ можно представить в виде
ze^ ^ *<'-.)
тт) ^е yrt -^-i'
(3.59)
(3.60)
1=1
— л о
^3 = - ^ S -|5^ S (2Л + 1) [СЧ X С)\ . (3.61)
Формулы (3.60), (3.61) получаются с помощью условия полноты
сферических функций.
Оператор Н'^, как уже говорилось, имеет нужный вид (см. [I,
(3.322)])
(3.62)
I "I • ~11'
Г=Г'
а оператор НЦ преобразуется так:
К = ^1^,[ЪхЩ.
00 са
^"^"^7^ ^ V{2it + i){A:'+it + i) 2 (1 + ^iy) ^
yflm'
k = l К,К' = 1
1>J
0
+ [[ef(i(OxC^] X(?> + 2?;.)] {D,{K)a^)±.^
ef(i(0 = a^^.[cfxcj]''.
, (3.63)
(3.64)
(3.65)
^KK
= i*+i-JfV(2* +l)(K' + k+ l)(lK+ i)(2K' + 1) X
I K\lk 1 k\
0 Ojji /c' Ij'
k + i
0 0
, /i:=*-i,
^/W=^+
--, /i:=*-i-l.
(3.66)
(3.67)
100
Суммирование по К, К' в (3.63) ограничено благодаря свойствам
Зу- и бу-символов в (3.66).
Наконец, выражения для операторов Н'^ и Н"^ таковы:
^i=-|52^[^lx^]°S(2*+l)ptxC^]°. (3.68)
I
&„_£^ 1 Y V V •^к(к + 1)т + 3)(2к-1Т
"s 2^ Z, Z, Z, (2* + l)V(2it + l)
^ ^ „ . .. Х
т
i>j Jt = l А. A' = l
x[[cfxCf]' x[?Jx?;.]'] iD,(K)Dj(K')a,). (3.69)
Рассмотрим теперь матричные элементы операторов Н^
(i= 1, ..., 5) в схеме LS-связи, Из приведенных выше выражений
следует, что операторы //j, Н2, Н'3, Щ, Н'^ являются
скалярными как в спиновом, так и в координатном пространстве. Эти
операторы не дают, таким образом, вклада в расщепление уровней
за счет спин-орбитального взаимодействия и приводят лишь к
сдвигу каждого из термов. Эти сдвиги даются соответствующими
диагональными матричными элементами для каждого из
операторов и представляют собой релятивистские поправки к положению
термов. Расчет таких поправок элементарен в случае одно-
частичных операторов 7/j, //3, а в случае операторов T/j» Щ^ ^
подобен расчету матричных элементов оператора
электростатического взаимодействия (см. [I, §3.11]). Здесь мы приведем
результаты вычислений для конфигурации эквивалентных электронов
(п/)^ [10, 12]:
{l^'yLSl ЩI I'^yLS) = - -^ W{nl) + 21{1 + l)I^\nl) +
-I-1{1 + 1)[/(/ -I- 1) - 6]/f (пО}. (3-70)
о L J
Здесь R^j — радиальная часть одноэлектронной волновой функции
(см. [I, (2.121)], [I, (2.132)]); обозначения для матричных
элементов те же, что и в [I, гл. 3]. Далее,
{l^yLS\H',\l^yLS)=-^N
-'г=0/
(3.72)
101
jk 1 k+ llf
Матричный элемент оператора орбита—орбита, согласно [12],
можно представить в виде
{l^'yLS]%\l'^yLS) = 2 m^{l'^yLS)M^{nl), (3.73)
k = 0
m^il'^yLS) = - ^^^^ + '|^f+ ^^ Щ + l){2l + l)(/||C*||/> X
jil^yLS] [f*+i X f^^Tll^yLS) -^l (3.74)
Л^.(«0 = ^2 i 7^ ^.^C-) 'i'- S r'^R^r') dr'. (3.75)
0 0
Здесь Г* — единичный неприводимый тензор Л-го ранга:
i = \
^ — единичный неприводимый тензор ранга к для одного
электрона; последний определяется равенстве»! *)
mii'^WO = A(lkl')bi^ (k=l,...,2l). (3.76)
Матричный элемент скалярного произведения в (3.74) можно
выразить через генеалогические коэффициенты точно так же, как это
было сделано с аналогичным матричным элементом в [I, § 3.11 ].
Матричные элементы операторов //^', //д различаются лишь
числовым множителем, поскольку сами операторы различаются лишь
благодаря наличию спиновых операторов в (3.68), приведенные
матричные элементы которых, согласно [I, (3.106)], равны:
(s||?4|s) = V3/2. Соответствующие выражения имеют вид
(I'^yLS I Н'з I l^yLS) = - i (l^yLS \ Н'^ \ l^yLS) =
2
^^^^"^^^[S^]'^''''^^'^'^''''^'^
-{21+ \)N
0
V^z.5)-
Q{nl), {Ъ.П)
(3.78)
В отличие от рассмотренных выше операторов, операторы Н\, Н'^,
и Н"^ не являются скалярами отдельно в спиновом и координатном
пространстве. Матричные элементы этих операторов, которые
необходимо вычислять уже с функциями вида [I, (3.326)], оказываются
*) Заметим, что для единичного скаляра t° матричный элемент определяется
иначе (см. [I, (3.109)]).
102
зависящими от значения полного момента электронной оболочки
атома / и, таким образом, определяют тонкую структуру уровней.
Зависимость матричных элементов Т/^» ^'. и ^5 °^ ^ выделяется
в явном виде, если вновь, как ив [I, § 3.12], использовать формулу
[I, (3.120)] для скалярного произведения неприводимых тензоров. В
случае операторов //^, //^' ранг этих тензоров Л = 1 и матричные
элементы имеют вид
(/.5/м|я,|/.5/м) = (-1)^^^^^^ЧЛо(")+Лоо(^'5)){5 f (}'
(3.79)
где константа A^J^LS) связана с константой спин-орбитального
взаимодействия, введенной в [I, § 3.12], соотношением
A{IS) = A^^{LS)\L{L^-\){1.L^-\')S{S+ 1)(25-|- l)]-!'^ (3.8О)
Константа А^ в случае оболочки эквивалентных электронов может
быть представлена в виде
A^J^LS) =VZ(/-|- 1)(2Л- 1)(/л^-у^'5||К"рл^'у^5)5(пО- (3-81)
Здесь F*' — двойной тензорный оператор,
УЧ = УВ?1,, (3-82)
i = \
о
Приведенный матричный элемент тензорного оператора К*' в (3.81)
можно выразить также через генеалогические коэффициенты, как
это было сделано в [I, § 3.12].
Приведем теперь выражения для константы Д.^^ взаимодействия
спин—чужая орбита [10, 12]:
ЛооС^-^) = S 4-i(^'''Yi''S)A^jt-i(nO. (3-84)
m;_,(/^-Yi'5) =
="2^^s-тШ^,шч1)\' ^гSt f W
(Л|?^||/) v'M + l ^\l l L'l
k
X [{l'^yLS\\V'^^\\l'^y'L'S){l'^y'L'S\\fm'^yLS) +
+ 2{l'^yLS\\f'^\\l^y'L'S){l'^y'L'S\\V'^^\\l'^yLS)] -
-3|f f ^Ь^-у^-^ЦК^р^-у/^^)!, (3.85)
'{к + 1)у/Хи+ТТЩ1Г^, K=k + i,
Ы(21 + к+1)(21-к+1), К=к-\.
(3.86)
Интегралы M^^{nl) в (3.84) определяются согласно (3.75)
103
k-l k + l 2 \
L L L'\
В случае оператора Щ ранг образующих его тензорных
операторов (орбитальных и спиновых, см. (3.69)), равен двум и вместо
(3.79) имеет место формула
{LSJM\ir-\LSjM) = {-\)'^^'^^^'A^{LS) + A^,{LS)\^^ I ^|,
(3.87)
где константа спин-спинового взаимодействия А^ определяется
выражением
A^^{LS)^ ml_,{l''yLS)M^_,{nl), (3.88)
к
ml_y{l^yLS) = Ау[5{-\)'^Чк{к + \){2к-\){2к + \){2к + 3) X
^{1\\С'^-Чт\\С'^^'\\1)тЧ1Г'^\\ \ t,
X {l^yLS\\V>'-'^-'^\\l'^y'L'S'){l'^y'L'S'\\V'^*^''^\\l^yLS). (3.89)
Как видно из формулы (3.87), взаимодействие Щ, в отличие от
Щ, приводит к отклонениям от формулы Ланде [I, (3.331)]. Это
отклонение, однако, существенно лишь в случае легких атомов и
невелико для многозарядных ионов. Действительно, как упоминалось
выше,
SO Эф
Таким образом, роль спин-спинового взаимодействия должна быть
наиболее существенной в случае атома гелия.
Рассмотрим низшую триплетную конфигурацию {\s2p)^P,
обладающую тонкой структурой, и вычислим относительную величину
расстояния между отдельными уровнями мультиплета:
Д£,_,-Д£,_,
-1=л4::-ля;::- (з■^l)
Согласно правилу интервалов Ланде [I, (3.336)], должно иметь
место равенство т^^^^р = 2. Экспериментальное значение для
нейтрального атома гелия 11экси(Не) = 0,08 [13].
§ 3.5. Взаимодействие электронов во втором порядке
теории возмущений
Рассмотрим вначале кулонсжское взаимодействие электронов вс
втором порядке теории возмущений по взаимодействию (в
четвертом порядке по константе связи). В общем случае для этого необхо-
104
димо учесть вклады диаграмм рис. 3.5а—г. Все перечисленные
диаграммы, за исключением диаграммы рис. 3.5б, являются
приводимыми и для их вычисления необходимо использовать формулу Гелл-
^ /
\ /
\ /
X
/ ч
/ ч
*
- — ..^ —
а. 5 6 г
Рис. 3.5. Фейнмановские графики, изображающие кулоновское взаимодействие
между электронами во втором порядке теории возмущений
Манна и Лоу (3.3). В случае двухэлектронного атома достаточно
вычислить лишь вклад диаграмм рис. 3.5а, б.
Рассмотрим вначале вклад диаграмм рис. 3.5а. Согласно
правилам соответствия
(фО|5М|фО)= ^4 j ^^^ ^^^^^^ ^^^^^ (Хз)'У^/(ХзХ,)-у^_я1,^(х,) X
хехр [-а(|<,| + \t^\ -h \h\ + \U\)\. (3.92)
Подставляя выражения (2.227) и (2.248) для фотонного и
электронного пропагаторов, получаем
X [f?„_(l - Ю) + a)i]-4^?„^(l - iO) + (oj-i X
X exp \i{Ej^ -I- fJg -I- coj -I- 002)^3] X
xexp[-i(f?^-|-f?g-|-(Oj-|-(02)<i-2a(|<i| -|- \Ц\)\. (3.93)
Вычислим интеграл по <j, входящий в (3.93):
\ ехр [-i(f?^ -I- f?e -I- (01 -I- (ojfj - 2а I <i I ] d<i =
= 4a[(f?^ -I- f?g -I- (Oi -I- Шг)^ + 40^]
21-1
(3.94)
Точно такой же множитель дает интеграл по Ц. Теперь нужно
проинтегрировать по coj, coj, т. е. вычислить интеграл
00 ОО
/= J dcoj J dcoj ME^ -I- fJg -I- coj -I- 002)^ -I- 4a2]-2x
X [f?„ (1 - Ю)-h a)J-H^?„^(l - Ю)-h toj-i. (3.95)
105
Интеграл по coj, входящий в (3.95), вычисляем по теореме о
вычетах:
оо
/j = J dcoi [{Е^ +Ед + (о^ + coj) - 2ш]"^ X
— оо
X [{Е^ + Е^ + (а^ + со^) -I- 2ia]-^[E^ (1 - Ю) -|- coj-i =
- М^ ^^".^^ ~ '^^ ~ '^'* ~ '^в ~ <«2 + 2ш]-21. (3.96)
Верхний (нижний) знаки в (3.96) соответствуют /?„ > О {Е„ <0).
Подставим (3.96) в (3.95) и проинтегрируем по coj. Отметим, что
полюсы выражения (3.96) при Е„ > О находятся в нижней
полуплоскости, а при £■„ < О — в верхней. Поэтому если /?„ > О, а
£■„ < О, то полюс <i>2= —Е„ (1 — Ю) находится в нижней
полуплоскости и интеграл (3.95) равен нулю (поскольку контур
интегрирования можно замкнуть в верхней полуплоскости, где полюсов у
подынтегрального выражения нет). Такой же результат получится,
если £■„ < О, а £■„ > 0. В остальных случаях интеграл отличен от
нуля и равен
I = ^2ni)^U-^^(E„+ Е„^- Е^- E^ + 2ia)-^ +
+ 7^(^„, + ^„,-^л-^« + 2ш)-2|. (3.97)
Верхние знаки в (3.97) соответствуют Е^ > О, /?„ > О, нижние —
отвечают Е„ < О, Е < 0. Подставляя результаты интегрирования в
(3.93), находим
' (E„+E„-E^-E^ + 2ia)-' +
2
^ 77:^2 (^п. + Р-п. -^л-Ев + 2ш)-
(4ia)^ ^ "1
(^)
, (3.98)
где Л(*^ — проекторы на состояния с положительными
(отрицательными) энергиями Е„.
Выделим в матричном элементе (3.98) его неприводимую часть
(см. [I, § 4.3]). Для этого в сумме по «j, «2 выделим члены «j = А,
106
П2 = в и П2 = А, П1 = в. Во всех остальных членах в знаменателях
полагаем а = 0. Тогда
(фо, 5WI фО) = -е* 2 (Лрл(-> - Л(->Л(->)
"."2
(п^п^*АВ)
la''
(^.... ^ Ш
АВАВ
ВААВ
• (3.99)
Запишем теперь поправку к энергии по формуле (3.5) (заметим,
что в нашем случае все матричные элементы нечетного порядка
5^ не дают вклада в Af?):
Af?W = lini| шеП2(Ф°|5^| фО)_(фО 15(f) |фО)2]. (3.100)
Ограничимся далее двухэлектронными атомами и ионами. Тогда
вклад в- матричный элемент (Фа|5(^^|Фа) в (3.100) дают лишь
диаграммы рис. 3.5а, б (с учетом обменных вариантов), а в
матричный элемент (Ф" 15£^^ | Ф") — диаграммы рис. 3.2. Вклад
неприводимой диаграммы рис. 3.56 мы учтем отдельно позднее. При
подстановке (3.99) в (3.100) нужно учесть, что член с квадратичным
знаменателем в (3.99) исчезает в выражении для энергии после
предельного перехода а—»0. Слагаемые в (3.99), содержащие
особенности типа 1/а^, сокращаются с вкладом (Ф" | «S^f^ | Ф"). Кроме
того, под знаком суммы по щ, «2 можно произвести замену (см.
обозначение (3.15)):
\ ' п.пАВ \ ' ВАп п^ \ I пп АВ \ I „ „
.АВ
(3.101)
Таким образом, окончательное выражение для поправки к
энергии А/^сг (вклад диаграммы рис. 3.5а) приобретает вид [5]
лР4"*''-лРл«
. , Е„-Е -Е
А в п п.
■'1"'2
{п^п^*АВ)
(^
"Л
АВ
(3.102)
Вклад неприводимой диаграммы рис. 3.56 можно
вычислить по формуле (3.6). После вычислений, аналогичных про-
107
деланным выше,
получаем [5]:
и выполнения предельного перехода а—» О
й.... й,
А п
-^В-^г.
Е -Е
(3.103)
Суммирование по «j, «2 в (3.102), (3.103) ведется как по
положительно-частотным, так и по отрицательно-частотным состояниям.
В нерелятивистском пределе (aZ*3cl) основной вклад в (3.102)
дает сумма по положительно-частотным состояниям, поскольку для
этих состояний Е^ + Eg — Е„ + £■„ ^^ £х + £в — £„ + £„ , тогда как
для отрицательно-частотных состояний Ey^ + Eg — Е„ — Е„ —*—4т.
"Кроме того, необходимо учесть малость «верхних» компонент
дираковских биспиноров для отрицательно-частотных состояний
"v/xrv"
—
V
г^\
^\i\r\f
V
s"^
а
S
Рис. 3.6. Фейнмановские графики, изображающие обмен одним поперечньпи и одним
кулоновским фотоном (а-г) и обмен двумя поперечными фотонами (д-е)
(см. (1.198)). Положцтельно-частотная часть суммы, как нетрудно
видеть, переходит непосредственно в нерелятивистское выражение
для поправки А^2 (см. [I, § 4.2]). Поправка AfJ^j ^ нерелятивистском
пределе имеет дополнительную малость по параметру aZ по
сравнению с АЕ'(^2у поэтому она не дает заметного вклада при расчетах
кривой Сг на рис. 3.1.
Из наличия проекторов в (3.102) также следует, что обычная
теория возмущений не пригодна для расчета поправок второго
порядка даже по чисто кулоновскому взаимодействию электронов в
релятивистской теории. Тем более это относится к брейтрвскому
взаимодействию. Вычисление смешанных поправок второго порядка АЕд^
по кулоновскому и брейтовскому взаимодействиям (диаграммы
рис. 3.6а—г для двухэлектронных атомов) в обшем производится так
же, как и в случае поправок АЕ(^2> хотя получающиеся выражения
значительно сложнее (см. [14, 15, 2]). Последнее в еще большей
степени относится к поправкам AEg2 второго порядка по
брейтовскому взаимодействию (диаграммы рис. 3.63, е).
108
Расчет поправки Afi'cz Для произвольных значений aZ по
формулам (3.102), (3.103) для основного состояния произведен в [16,
17]. Имеется также результат, полученный с использованием
разложения по степеням aZ [18]. В случае основного состояния двух-
электронного атома этот результат таков:
Af?c2=-'"a^0'15767[H-2,38(aZ)2]. (3.104)
Первый член этого разложения (нерелятивистский предел) мы
приводили ранее, в [I, § 4.2].
Без разложения по степеням aZ найдены также поправки
^Egf, и AEgg для основного состояния двухэлектронного атома [16,
17], Мы вновь приведем результат, полученный с разложением по
aZ [18]:
AEgc = -ma?'{aZf-0,25f>8. (3.105)
Приведенные выше вычисления, как и в первом порядке по
межэлектронному взаимодействию, могут быть обобщены на случай
вырожденных состояний. Если коэффициенты в линейной комбинации
волновых функций (3.43) могут быть определены непосредственно с
помощью сложения моментов, то к вычислению матричных
элементов, рассмотренных в настоящем параграфе, относятся все те слова,
которые были сказаны в § 3.3 по поводу матричных элементов
взаимодействия в первом порядке.
§ 3.6. Релятивистский метод Хартри-Фока
Одним из наиболее распространенных методов учета
релятивистских эффектов в теории многоэлектронных атомов является
релятивистский метод Хартри—Фока (метод
Хартри—Фока—Дирака, ХФД). Преимуществом этого метода является его широкая
область применимости, в частности, он применим в той ситуации,
когда и релятивистские поправки, и взаимодействие электронов между
собой достаточно велики и не могут быть учтены лишь в первом
порядке теории возмущений. Такая ситуация имеет место для
большинства электронов (кроме самых внешних и самых внутренних) в
тяжелых атомах и для многозарядных ионов с достаточно большим
числом электронов.
Впервые релятивистский метод Хартри—Фока сформулировала
Свирлс [19], Впоследствии этот метод развивался многими авторами
(см, обзор современного состояния в [20, 21], а полный
библиографический обзор — в [22]).
Задача о нахождении релятивистских функций Хартри-Фока
может быть поставлена следующим образом. Рассмотрим
приближенный гамильтониан для многоэлектронного атома в виде
N N
г=1 i=i ,09
где Л(г^) — одноэлектронный дираковский гамильтониан (1.34),
V(^ — потенциал кулоновского взаимодействия (3.12). Иногда в это
выражение включают также оператор брейтовского взаимодействия
(3.30), однако более естественно рассматривать брейтовское
взаимодействие, как и все остальные релятивистские поправки, по теории
возмущений, на основе нулевого приближения, определяемого
гамильтонианом (3.106). В гамильтониане (3.106) учитываются
вклады AEJ^, AE^i^ (и частично Afi'cz)» изображенные на рис. 3.1. Таким
образом, как следует из рисунка, этот гамильтониан с точностью до
поправок порядка а (т. е. с погрешностью до 1 %) должен быть
справедлив практически во всем диапазоне значений Z.
Задача свелась к решению приближенного релятивистского
уравнения Шрёдингера
Д^я!) = fJij), (3.107)
для чего можно применить все те же методы, что и в [I, гл. 2], в
частности, аппарат редуцированных матриц плотности. Различие
состоит в том, что теперь одноэлектронная волновая функция
является четырехкомпонентным биспинором, а многоэлектронная
функция для системы из Л^ частиц, в частности детерминант Слэтера,
имеет соответственно 4Л^ компонент. Вводить отдельно спиновую
координату а, как это делалось в [I, гл. 2], теперь нет
необходимости, поэтому одноэлектронные функции •ф^(г) мы будем
рассматривать непосредственно как спинорные функции пространственных
координат.
Соответственно матрицы плотности также являются
многокомпонентными величинами, однако операция Sp теперь включает
суммирование по спинорным значкам. При этом сохраняют силу все
результаты, изложенные в [I, § 2.1 и 2.2]. Мы будем использовать и
вариационный принцип [I, § 2.3], хотя его применение в
релятивистской теории нуждается в дополнительном обосновании (см. ниже
в этом параграфе). Тогда выражение для полной энергии атома в
случае основного невырожденного состояния сохраняет вид [I,
(2.95)], а уравнения для одноэлектронных волновых функций по-
прежнему имеют вид [I, (2.98)]:
N
Л(Гг)я1)„(г) + 2 S Sp «('•')1^с(п-')^„(г')) dr' я1,„(г) -
N
- S $ Sp (^иПУс("-')'^п,(г)Нп(^') dr'= f?„4i,„(r). (3.108)
m = l
Здесь Л (г) — одноэлектронный дираковский гамильтониан (1.34);
•ф„ — одноэлектронные функции Хартри—Фока—Дирака; Е^ —
собственные значения, которые, как и в нерелятивистском случае,
представляют собой одноэлектронные энергии, но включают массу
покоя электрона. В формуле (3.108) символ следа относится уже
только к спинорным значкам.
ПО
Уравнения (3.108) можно записать также в компактной форме,
подобной [I, (2.128)]:
Л^'^(г)^„(г) = ^?„я1,„(г), (3.109)
ЛХФ(г) = Л(г) + ?(г) - к{т), (3.110)
N
/(г)/(г) = S J Sp {Шг')Ус(гт')у\>^т')) dr' f{T), (3.111)
m = l
N
ВД/(г) = S J Sp «(г')Ус(п-')/(г')я1)„(г)) dr'. (3.112)
m = l
Перейдем к отделению угловых переменных в уравнениях
(3,108). Волновые функции представим в виде (1.94):
Действие оператора Л (г) на эти функции определено формулами
(1.106), (1.113). Рассмотрим теперь действие оператора /(г).
Подставляя функции (3.113) в (3.111), в случае заполненных оболочек
находим
Дг)/„(г) = S S $ |^'/''('-')£^Л'м'(^')£^/т-(^') +
nj'f M'=-j'
Для шаровых спиноров Qji^f можно получить аналог теоремы
сложения для сферических функций [I, (П1.3)]. Для этого используем
явный вид шаровых спиноров (1.84):
, м'=-г
= lllC%imV)C%inn.)Y]^.{Q')Y^„(Q)nl,n^. (3.115)
С учетом свойств ортогональности двухкомпонентных спиноров
K'\ = \v (3-116)
из (3.115) получаем
^Q;,^(Q')Q,,^(Q)=2S {c%(mt^)yYU,(^')YiJQ). (3.117)
M-—j М mjji
111
Учитывая свойства симметрии коэффициентов Клебша—Гордана,
следующие из соотношения [I, (3.50)], и свойства симметрии Зу-
символов, используя условие унитарности [I, (3.31)] и формулу [I,
(П1.3)], получаем
2 Щш(^'Щш(^)=11 (qi.(f^))4.(^')>'^(^) =
М m\iL
= 1У:т(^')Уы(^)=^Р,(^У)- (3.118)
М М т\к.
2Л-1
м
Аналогично получается формула
2 Q]j^{Q')Q,j^{Q) =^Pj{cos -у). (3-119)
м
Применяя теорему сложения для шаровых сгшноров к (3.114),
приходим к выражению
n-jV
X
Далее, как и в нерелятивистском случае, используем разложение
кулоновского потенциала в ряд по полиномам Лежандра (формулы
[I, (П1.8)], [I, (П1.5)]). В результате получаем
?(г)я1,„(г) = е^ 2 $ |(2^' + 1)^7г('-') + (2/' + 1)/^,г('-')1 X
где коэффициенты а^{гг') определяются согласно [I, (П1.7)].
Существенно сложнее выглядит в релятивистской теории
определение угловых переменных в обменных членах. Мы рассмотрим
здесь лишь упрощенный вариант учета обмена в уравнениях
Хартри—Фока, предложенный Слэтером [23]. Особенно часто этот
вариант используется в релятивистской теории, где он носит
название метода Хартри—Фока—Дирака—Слэтера. Этот метод
основан на выражении для обменного члена в уравнении [I, (5.173)] в
модели Томаса—Ферми—Дирака. Основываясь на этом выражении,
можно предположить, что на каждый электрон действует
дополнительный локальный потенциал
K{T)=-^a^p\ir), (3.122)
приближенно учитывающий обмен. Для получения р(г) можно
использовать матрицу Фока—Дирака [I, (2.42)].
112
в релятивистской теории в случае заполненных оболочек для
плотности р(г) получим выражение
"" ""="' (3.123)
Вновь используя теорему сложения (3.118), (3.119), получаем
р(г) = 2 {(21 + 1)^;,(г) + (27+ l)flji{r)]. (3.124)
njl
Таким образом,
— 3 "об
2 {(2l'+l)gj^...,(r) + (2?+ 1)/^.,.,(г))]':
п-ГГ
xf«-f'"'r;">]. (3.125)
Собирая результаты (3.121), (3.125) совместное (1.106), (1.113)
и отделяя зависимость от угловых переменных (см. (1.114),
(1.115)), приходим к системе радиальных уравнений Хартри—
Фока—Дирака—Слэтера:
df ir) 1-х, р^7
-t- + —Г- fnj^r) + (f?„,, - m)g„^^{r) + i^ g„ .,(r) -
-e^X \ j(2/'+ U^.^rCO + (2?+ l)/V.,(r'))ao(rr')r'2dr'g„,,(r)+
+ -3-«o6
S {(з/' + и^^гСО + Сг/' + О/^г^ЧО)'
wyi-
(3.126)
''«„,/('■) . 1-х,-
+e^ S \ j(2^' + D^vrC'-') + (2/' + 1)/Ь'('-')Ьо('-'-')'-" 'i'-' /„i^O -
3 "об
2 j(2/' + l)^y,(r) + (2/' + 1)/Sy,(r))
n'yV
/„/,(0=0.
(3.127)
Здесь Xji определяется согласно (1.95), a^ — согласно [I, (5.174)].
В нерелятивистском пределе «малая» компонента /„у,
выражается через «большую» g„^, (см. § 1.5) с помощью соотношения
'njl 2т dr Tmr °njl'
(3.128)
113
в результате этой подстановки уравнение (3.126) переходит в
нерелятивистскую систему уравнений Хартри—Фока [I, (2.140)] за
исключением обменного члена, который в нерелятивистском случае
рассматривался точно. При этом функция g„ji перестает зависеть от
значка у: этот значок в нерелятивистском пределе определяет
тонкую структуру уровней и принимает два значения при заданных п,
к. Таким образом появляется множитель 2 в нерелятивистском
выражении [I, (2.135)] для кулоновского оператора.
При использовании приближенных методов в релятивистской
многоэлектронной задаче, вообще говоря, возникает проблема,
связанная с существованием состояний с отрицательной энергией,
отсутствовавшая в нерелятивистской задаче. Спектр собственных
значений одноэлектронной релятивистской задачи не ограничен снизу,
и вариационный принцип на минимум в релятивистском случае
отсутствует. Хотя формально уравнения Хартри—Фока можно
получить, не прибегая к вариационному началу, например с помощью
уравнений для редуцированных матриц плотности [I, (2.64)], [I,
(5.97)1, при приближенном решении радиальных уравнений эта
проблема дает о себе знать. Приближенные решения в принципе
могут содержать примесь состояний с отрицательной энергией, что
приводило бы к неправильным значениям энергии, лежащим ниже
истинного значения. При численном интегрировании радиальных
уравнений, как правило, трудностей удается избежать, фиксируя,
например, число нулей у радиальной функции, что препятствует
появлению нежелательных добавок. Однако при матричном
решении уравнений устранение таких добавок оказывается более
сложным (см. [24]). *
Как уже упоминалось в § 1.6, приближение Хартри—Фока
можно использовать в качестве нулевого приближения при построении
квантовоэлектродинамической теории возмущений. Рассмотрим,
какие изменения нужно внести при этом в диаграммную технику.
В самом общем случае приближение Хартри—Фока можно ввести,
переопределив операторы Н^ и //;„, (см. § 1.5) следующим образом:
fr^ = ff^ + H', (3.129)
Н'= \ Ч'''(х)^хф(г)Ч)(х) dr. (3.131)
Оператор ^хф('")' согласно (3.99), определяется следующим
образом:
N
Ухф(г)Пт) = 2 $ Sp (■^:,(T')V^(rT').^jT')) dT' f{T) -
^ S $ Sp «(г')К^(гг')я1)„(г'))/(г') dT\
где
m = l
(3.132)
114
где /(г) — произвольный биспинор. Волновые функции •ф„(г)
являются решениями уравнений (3.108), т. е. предполагается, что
процедура самосогласования уже проведена.
Согласно (3.130) (см. также § 2.6) теперь в различных порядках
теории возмущений нужно учитывать, помимо взаимодействия
электронов друг с другом, также взаимодействие с дополнительным
-к
X
-X
—к
—^
X
Рис. 3.7. Графики, описывающие взаимодействие электрона с самосогласованным
полем в первом (а) и во втором (бд) порядках теории возмущений
внешним полем с потенциалом A^^{x) = —1^хф('")^ио- Выясним,
какие диаграммы следует рассматривать при этом в различных
порядках. В первом порядке по константе связи имеется одна диаграмма,
изображенная на рис. 3.7а, во втором порядке — четыре диаграммы
рис. 3.76—3. Однако нужно иметь в виду, что порядок диаграммы,
имеющей 2п вершин и т линий внешнего поля, равен е^""*'^'"
(лишние степени е происходят от выражения (3.132) для Ухф)- Поэтому
диаграмму рис. 3.7а нужно рассматривать совместно с диаграммами
рис. 3.2, а диаграммы рис. 3.76—3 — совместно с диаграммами
рис. 3.5.
Глава 4
РАДИАЦИОННЫЕ ПОПРАВКИ
К УРОВНЯМ ЭНЕРГИИ АТОМОВ
§ 4.1. Квантовая электродинамика свободных электронов
Исследование радиационных сдвигов уровней атомов имеет
принципиальный характер, поскольку именно таким образом впервые была
доказана реальность существования вакуума и подтверждена вся
современная концепция строения материи. Впервые радиационный
сдвиг был измерен в атоме водорода Лэмбом и Резерфордом [1], в
связи с чем он получил название лэмбовского сдвига. Теория
радиационного сдвига впервые была развита Бете [2J. Изложение
современной теории радиационных поправок имеется в большом числе
монографий; наше изложение наиболее близко к [3, 4].
Радиационные поправки к уровням энергии в атомах можно
условно определить как поправки, соответствующие таким графикам
Фейнмана, которые содержат фотонные линии, начинающиеся и
оканчивающиеся на одной и той же электронной линии либо
опирающиеся хотя бы одним концом на замкнутое электронное кольцо. В
низшем порядке по константе связи такими графиками являются
рис. 2.23, и. Как уже говорилось в § 2.6, эти графики описывают
взаимодействие электрона соответственно с фотонным вакуумом и с
вакуумным электронным током. Таким образом, радиационные
поправки учитывают сдвиг атомных уровней в результате
взаимодействия электрона с вакуумом.
Оказывается, однако, что не только энергия вакуума (см.
(2.203)), но и энергия взаимодействия электрона с вакуумом
является бесконечной. Если энергия вакуума может быть попросту
отброшена, поскольку она несущественна при вычислении любых
физических величин, то энергия взаимодействия атомных электронов
с вакуумом, как следует из квантовой электродинамики, должна
быть наблюдаемой величиной. Поэтому для устранения
бесконечностей в радиационных поправках приходится применять сложную
процедуру, получающую оправдание в теории перенормировок. Эта
теория создана в работах Р. Фейнмана, Ю. Швингера, Ф. Дайсона и
С. Томонага (см. [3—6], а также § 4.4).
Формально упомянутые бесконечности возникают как
расходящиеся интегралы при вычислении матричных элементов,
соответствующих диаграммам рис. 2.23, и. Регуляризация этих интегралов '
116
'^^^
Рис. 4.1. Фейнмановские
графики, описывающие
радиационные поправки низшего
порядка для связанных
электронов в атоме
определяется процедурой перенормировок. Последовательная
формулировка процедуры регуляризации обязательно должна быть ко-
вариантной. По этой причине использование картины Фарри для
регуляризации расходящихся графиков неудобно и более
целесообразно использовать картину свободных электронов. В этой главе, чтобы
различать на графиках свободные электроны и электроны во
внешнем поле, последним мы будем
сопоставлять двойные сплошные линии. Тогда
рис. 2.23, и, соответствующие картине
Фарри, должны быть заменены на
рис. 4.1а, б. Таким образом, в качестве
первого подготовительного шага к
вычислению радиационных поправок мы
рассмотрим в этом параграфе
электродинамику свободных электронов. В
принципе, почти все формулы гл. 2 остаются в
силе и в этом частном случае
(отсутствие внешнего поля).
Диаграммная техника для свободных
электронов наиболее удобным образом формулируется в
импульсном представлении [3, 4]. Основные отличия этой диаграммной
техники от сформулированной в § 2.6 диаграммной техники в картине
Фарри заключаются в следующем *).
Во-первых, изменяются одноэлектронные функции,
соответствующие началу и концу (низу и верху) диаграммы. В случае
свободных электронов в качестве таких функций естественно выбрать
плоские волны, т. е. состояния с определенными энергией Е и
импульсом р. Плоские волны имеют вид
4*^W =72ir "(-'') ^*'''"'" = 72ir "(-'') е^'^Р'-'^'^ (4-1)
(см. аналогичное выражение (2.130) для фотонов). Здесь V —
нормировочный объем, и{±р) — постоянные биспиноры, знаки ±
относятся к положительно- и отрицательно-частотным состояниям. Из
уравнения (1.9) следуют уравнения для биспиноров и{±р):
{±i\P^ + m)u{±p)=0. (4.2)
В этой главе, как и в § 1.1, для сокращения записи мы будем
использовать обозначения: -уцР^ = р, причем р^ = iE, Е = Vp^ -|- т^. В
таких обозначениях (4.2) записывается так:
(±ip + m)u{±p) = 0. (4.3)
Уравнение для сопряженного биспинора имеет вид
u{±p){±ip + m) = 0. (4.4)
*) Подчеркнем, что именно диаграммная техника в импулы;ном представлении
для свободных электронов, сформулированная впервые Фейнманом [7], послужила
основой для всех других вариантов диаграммной техники в теории возмущений.
117
в качестве условия нормировки для плоских волн можно
использовать условие (1.36) в объеме V: \
J K*(r,Ol"rfr=l. (4.5)1
V
Из этого условия для биспиноров и{±р) следует:
^и+(±р)и(±р) = 1. (4-6)
Условия нормировки биспиноров и{±р) можно записать и в других,
более удобных формах. Рассмотрим величины и(±р)и{±р),
и{±р)у^и{± р). Первая из них является 4-скаляром, вторая — 4-
вектором. Для свободной частицы существует только один 4-век-
тор — вектор энергии-импульса р. Поэтому
й{±р)у,и(±р) = ар^, (4.7)
где а — некоторая константа. В частности, при v = 4 получаем
u{±p)y^u{±p) = iaE (4.8)
и, сравнивая с (4.6), устанавливаем, что a = 2/i. Теперь, умножив
обе части (4.7) на ip^ и суммируя по v, находим с учетом (1.31)
й( ± р)фи{ ±р) = 2р'^ = 2(Е^ - р2) = -2т\ (4.9)
Отсюда, используя (4.3), получаем •
й{±р)и{±р)= ± 2т. (4.10)
Уравнения (4.2) для каждого из биспиноров и{±р) имеют по
два *) линейно-независимых решения. Эти решения соответствуют
двум различным состояниям поляризации электрона. Состояние
поляризации нерелятивистского электрона можно охарактеризовать,
задав проекцию спина на некоторое произвольное направление. Эта
проекция имеет два возможных значения.
Для релятивистского электрона такой способ задания
поляризации неприменим, так как оператор проекции спина на произвольное
направление не коммутирует в общем случае с гамильтонианом
(1.2). Чтобы описать поляризационные состояния релятивистского
электрона, удобно ввести матрицу iy^v, где v — единичный 4-век-
тор, ортогональный 4-импульсу:
\Р^ = 0, v2=l. (4-11)
Очевидно, в системе покоя электрона (в которой р = 0) этот вектор
можно задать так:
v=(v, 0). (4.12)
*) Число линейно-независимых решений равно числу линейно-независимых
компонент биспинора; последнее равно двум, посколысу нижние компоненты выражаются
через верхние или наоборот.
118
Используя свойства антикоммутации матрицы -уз (1-59) и условие
(4.11), нетрудно проверить, что матрица iy^v коммутирует с р.
Поэтому матрицы р и iy^v имеют общую систему собственных
векторов, причем собственные значения iy^v могут быть равны только
± 1. Действительно, вновь используя свойства антикоммутации у^
получаем
(г^5^)2=1. (4.13)
Следовательно,
1у^Ы^\ ±р) = \лиМ( ± р), (4.14)
причем fA = ± 1 для каждого из двух биспиноров ы{ ± р).
В случае покоящегося электрона "Vs^ ='Ys'Y'v. Р= ■¥4^4 = ~'Y4'"-
Подставляя эти выражения в (4.14), (4.3), комбинируя эти
уравнения и учитывая, что, согласно определению (1.64), S = iy^y^y,
приходим вместо уравнения (4.14) к уравнению
(2v) «(»*)( ±р) = \Jiu(i^\ ± р). (4.15)
Формула (4.15) является еще одним подтверждением того, что
оператор 2 можно считать оператором спина электрона в
релятивистской теории.
В дальнейшем нам понадобится еще формула для суммирования
произведений биспиноров по и{±р) поляризациям:
^ар = S "i'^^C±Р)'^^\±р) = {±т- г^)„р = ±т6„р- i(^)„p.
^ (4.16)
Здесь для ясности указаны спинорные значки а, р. Формулу (4.16)
проще всего доказать так. Найдем вначале след левой части (4.16).
С учетом (4.10) имеем
Sp/'„p=±4m. (4.17)
Далее, согласно (4.3), (4.4)
{±ip+ m)„/'„p = О, /'„р( ± ф + т)„ = 0. (4.18)
С другой стороны, матрица /"„р может быть сконструирована только
из матриц 6„р и (р)„б> а единственная комбинация этих матриц,
удовлетворяющая условиям (4.17), (4.18), как раз и записана в
правой части (4.16).
При подстановке волновых функций (4.1) в матричные
элементы можно без ограничения общности полагать V =\, поскольку
окончательные выражения оказываются конечными. Фактически
это означает, что мы используем нормировку на 6-функцию для
юлновых функций сплошного спектра (см. [I, § 11]). Таким
образом, окончательное выражение для волновых функций, которые
фигурируют в правилах соответствия, таково:
; ^%^{х)=^и<-^\±р)с^^Р^^.. (4-19)
119
Соответственно изменяется также выражение для электронного
пропагатора, который мы будем теперь записывать в виде
S(x) = -^ j S(p)t'P.\ d^p. (4.20)
В силу трансляционной инвариантности электронный пропагатор в
случае свободных электронов зависит только от разностей
координат: ^(xjXj) = 5(xj — Х2). Получим выражение для S(p)
непосредственно из (2.227). Для этого подставим в (2.227) в качестве у\)^
функции
4>fUr)=^u^^\±p)c-'P' (4.21)
((4.21) есть не зависящая от времени часть функции (4.19)).
Суммирование по S в (2.227) заменяется теперь интегрированием по р
и суммированием по двум поляризациям \i. При этом возникает
также коэффициент 1/(2зг)^ (см. аналогичные рассуждения при
выводе формулы (2.229)). Таким образом,
00
S(x)=—Ц { dcoe'"' { dp^. ,\ ■ X
— 00
X j 2: .(^)(p).-(.)(p) еФ' ^^.^,../,_,.o)^, +
+ 2 .(^)(-p).-(^)(-p)e-P' _,^.^,;a-W-fco}- (4-22)
Используя (4.16) и заменяя p на —p при интегрировании второго
члена в фигурных скобках, получаем
S(x) = -L-\d'p e'Pv-v ^ f"^^ , (4.23)
где Pq= (О, d*p= dp dpQ. Сравнивая (4.20) и (4.23), приходим к
выражению
S(p) = i fP-^ . (4.24)
В отличие от электронных, внешние и внутренние фотонные
линии описываются прежними выражениями (2.130), (2.231). То же
самое относится и к вершинам. Переход к импульсному
представлению заключается в том, что мы собираем все экспоненциальные
множители в выражениях для волновых функций и пропагаторов
(2.130), (2.231), (4.19), (4.23) и производим интегрирование по
координатам всех вершин d^x^. При этом возникают множители
(2л;)*6(2р) для каждой вершины, где символ Ир означает сумму
импульсов, подходящих к каждой вершине (с учетом знака). Это
дает возможность приписать каждой фотонной и электронной линии
(как внешней, так и внутренней) определенный импульс.
120
Теперь можно сформулировать в окончательном виде правила
соответствия для диаграммной техники в случае свободных
электронов в импульсном представлении [3]. Каждой внешней входящей
электронной линии соответствует биспинор -т— и^^\±р), каждой
входящей электронной линии — биспинор -^=== ы~(**)(±р). Каждой
внешней фотонной линии (входящей или выходящей) соответствует
матрица 7^==^, где е — 4-вектор поляризации фотона. Каждой
внутренней электронной линии соответствует матрица S(p) (4.24),
каждой внутренней фотонной линии — множитель D^^(k) (2.232).
В электродинамике свободных электронов, как правило,
используется фейнмановская калибровка фотонного пропагатора. Концам
каждой внутренней фотонной линии соответствуют матрицы -уц и
7v- Каждой вершине диаграммы
соответствует 6-функция,
содержащая импульсы всех линий,
сходящихся в этой вершине.
Особая ситуация возникает,
если на диаграмме имеется
замкнутая электронная петля. В
общем случае, как и в картине Фар- а S
^ '' ■' " Рис. 4.2. Фейнмановские графики, ил-
изведения расположенных вдоль люстрирующие доказательство теоремы
нее матриц (см. § 2.6). Однако в Фарри
случае свободных электронов это
выражение обращается в нуль при нечетном числе вершин в
петле (теорема Фарри). Для доказательства теоремы Фарри
рассмотрим замкнутую электронную петлю с произвольным числом
внутренних электронных линий и равным ему числом вершин п (рис. 4.2а).
В петлю могут входить как излучение (поглощение) фотонов, так и
взаимодействие с внешними полями. Одновременно с этой
диаграммой нужно, очевидно, рассматривать и такую же петлю с
обратным направлением обхода, т. е. обратной расстановкой времен
(рис. 4.26).
Диаграммам рис. 4.2а, б соответствуют матричные элементы,
определяемые интегралами вида
^Л=\ '^'^1 - d*x^SvXs{x,-x^)X- Xs{x^-x,), (4.25)
ще Л^ = gj в случае взаимодействия с фотонами и Л^ = F^ в случае
взаимодействия с внешними полями. Под знаком Sp произведем над
всеми матрицами операцию зарядового сопряжения (см. § 1.1):
заменим Af на СА^С'^ и S — на CSC~^. Тогда, согласно определению
матрицы зарядового сопряжения С (см. (1.39)),
121
Пропагатор свободного электрона iS(xi — Xj) удовлетворяет
уравнению (см. (2.228))
(jpi + m)S(xi - Xj) = -/6(xi - Xj). (4.27)
Произведем операцию зарядового сопряжения над обеими частями
равенства (4.27). Это дает
(iCpiC-^ + m)CS(xi - Х2)С-' =
= CS(xi - X2)C-\-ip[ + т) = -j6(xi - xj). (4.28)
В силу того, что свободный электронный пропагатор зависит только
от разности аргументов, (4.28) можно переписать в виде
CS(xi - X2)C-^{i% + т) = -j6(xi - Xj). (4-29)
С другой стороны, транспонируя равенство (4.27)
(iP2 + m)S(x2 — Xj) = -/6(xi - Xj), (4.30)
получаем
S^x^- х,){ф2+ m) = -г6(х, - x^). (4-31)
Из сравнения (4.28) и (4.31) следует:
CS(xi - Х2)С-' = S^(xj - Xj). (4-32)
В целом все выражение для матричного элемента "(4.25) не до;^
жно меняться от операции зарядового сопряжения под знаком Sp,
поскольку под знаком Sp матрицы можно циклически переставить и
использовать условие С~^С= 1. У нас же получается, что все
матрицы становятся транспонированными, сохраняя свой порядок
следования. Однако под знаком Sp для произвольных матриц
Xj, ..., Х^ можно записать равенство
Sp х[,..., к = ^Р К ^ = Sp (Xi :^„)^ = Sp Xi х„.
(4.33)
Кроме того, у всех пропагаторов S(Xj — x^+i) меняются местами
аргументы. Это значит, что мы от петли /j переходим к петле /j или
наоборот. Наконец, все выражение умножается на (—1)", где п —
число вершин в петле ввиду (4.26). Таким образом,
/j = (-l)»/^ (4.34)
и при п нечетном вклады петель рис. 4.2а и б сокращаются.
При п четном петле соответствует след всех расположенных
вдоль нее матриц со знаком минус (см. § 2.6). Таким образом, ококь
чательно числовой множитель при диаграмме в импульсном
представлении в случае свободных электронов таков:
(_l)Jv+z+6 1 (2„)*(л^-), (4.35)
122
те N — число вершин, / — число замкнутых петель, 6 —
четность перестановки индексов в обменных диаграммах, 1/и — сим-
метрийный множитель, s — число внутренних (электронных и
фотонных) линий на диаграмме.
§ 4.2. Расходимости в S-матрице
Выясним теперь, как возникают расходимости при вычислении
матричных элементов S-матрицы. Рассмотрим произвольную
диаграмму, которой соответствует в общем случае многократный интефал
по импульсам внутренних электронных и фотонных линий:
/= \ F{k^ к^) d% ... d%. (4.36)
Здесь F{ki, ..., к^) — некоторая рациональная функция импульсов.
Расходимости в интегралах возникают при больших значениях
импульсов виртуальных частиц (т. е. при больших значениях энергий
или частот), в связи с чем эта проблема в свое время получила
название «ультрафиолетовой катастрофы».
Поскольку расходимости возникают при Л;—*оо, можно
считать, что каждый электронный пропагатор 5(Л^) ведет себя, как
l/ki (см. (4.24)), а каждый фотонный пропагатор ^^v(*i) — как
Р /^+9
р-к
ч/с Лр лул^-^
р р
а Б S г
Рис. 4.3. Типы расходящихся графиков Фейнмана в низшем порвдке
1/Л? (см. (2.232)). В электродинамике имеется всего несколько
типов расходящихся диаграмм. Первый из них — так называемая
диаграмма собственной энергии электрона. Она определяется как
часть произвольной диаграммы, связанная с другими ее частями
только двумя электронными линиями. В низшем (втором) порядке
по константе связи эта диаграмма изображена на рис. 4.3а. Второй
тип расходящихся диаграмм — так называемая вершинная часть,
под которой подразумевается часть произвольной диаграммы,
связанная с другими ее частями одной фотонной и двумя
электронными линиями. В низшем (третьем) порядке она изображена на
рис. 4.36. Часть произвольной диаграммы, связанная с остальной
диаграммой лишь двумя фотонными линиями, называется
фотонной собственно энергетической частью. Эта диаграмма также отно-
123
сится к типу расходящихся и в низшем (втором) порядке
изображена на рис. 4.3в. Наконец, расходящимися, в принципе, являются
также диаграммы типа «рассеяния света на свете». Так условно
называется часть произвольной диаграммы, соединенная с
остальной диаграммой четырьмя фотонными линиями и изображенная в
низшем (четвертом) порядке на рис. 4.3г. Можно убедиться, что
любые расходящиеся сложные диаграммы возникают только при
включении одной из перечисленных выше диаграмм в состав
сложной диаграммы.
Для того чтобы явным образом выделить эти расходимости,
вводится граничный импульс L и интегрирование производится
по некоторой конечной области 4-мерного импульсного
пространства. После регуляризации (см. ниже) выражения, имеющие
физический смысл, становятся не зависящими от Z/ и можно вновь
перейти к интегрированию по всему 4-импульсному
пространству. Рассмотрим в общем случае интегрирование выражений вида
(4.36). В связи со сказанным выше все расходимости фактически
определяются интегралами типа (4.36) с s= 1. Этим случаем
мы и ограничимся в дальнейшем. Функцию F{k) представим в
виде
f(k) = Gm (4.37)
где а|(Л) — полином второй степени по к, G(k) — некоторый
полином. Вычисление интеграла (4.36) удобно проводить методом
параметризации Фейнмана [8]. Для этого нужно воспользоваться
тождеством
1 1 1
' " 0 0 X
X [QjMj ... M„_j + a^Mi ... ы„_2(1 - w„_i) + ... + a„(l - u^)]-"
(4.38
Тождество (4.38) доказывается методом индукции, начиная
п = 2. Это же тождество может быть переписано в другом виде:
1 1 1
^-4-=^ (п - 1)! J dx, \ dx^ ... \ dx„_i X
■ " 0 0 0
X [aix„_, + а2(х„_2- x„_J + ... + а„(1 - х,)]"", (4.39
где
При n = 2 (4.39) имеет вид
^^=\dx[a,x + a^(l-x)]-\ (4.41
124
Рассмотрим вначале вычисление нерасходящихся интегралов.
Подставив (4.49) в (4.37), записываем искомый интеграл в виде
/= (п - 1)! J dx, \ dx^... \ dx„_, /")(х„ ..., х„_,), (4.42)
где
/">(-: -„-:)= $771^^
[(Л-Р)^ + 7]"
(4.43)
а р= P(xi, ..., x„_i), 7= 7(^i> •••> ^n-i)- Под знаком интеграла
сделаем замену переменных к— р—»Л. Тогда мы приходим к интегралу
_ г g(k) d^k
/(")(х., ..., х„ ,) = е1И1^
(4.44)
где е{Щ — полином, с коэффициентами, зависящими от
Xj,..., х„_1. В случае сходящихся интегралов, разумеется, I^J,
kg=-\/k^+m2
кд=\/к^+гп^
Рис. 4.4. Выбор контура в комплексной плоскости ^q при вычислении интегралов в
импульсном пространстве
поскольку интеграл не меняется от замены переменных
интегрирования. Однако для расходящихся интегралов это, вообще говоря,
уже не так (см. ниже). Представим функцию g{k) в виде
g{k) = g^(k^) + g,^(k^)k^ + g2^Sk^)k^K + - (^-^^^
и начнем с интеграла, содержащего функцию goik^).
В этом случае
(4.46)
Интегрирование по к^ в (4.46) производится с учетом правила
обхода полюсов, зафиксированного в формуле (4.23). Это правило
эквивалентно интегрированию по контуру, изображенному на
рис. 4.4а. Но этот контур можно деформировать так, чтобы он про-
125
ходил по мнимой оси, как это изображено на рис. 4.46. Другими
словами, делая замену переменных kQ—*ik'Q, где к'о — вещественная
координата, мы приходим к интегрированию по четырехмерному
импульсному пространству, в котором к'^ = к'^ + к'^. Теперь,
поскольку все Qj в (4.39) представляют собой выражения типа
1/(Л'^ + т^) либо 1/Л'^ можно считать, что -у > О (см. (4.42),
(4.43)) и подынтегральное выражение не содержит особенностей;
Переходя к сферическим координатам в четырехмерном
импульсном пространстве, производим сразу же интегрирование по углам в
(4.46). Это дает (см. [I, § 1.3]) множитель 2п^. Вместо радиальной
координаты в Л-пространстве вводим переменную z= к'^ и
окончательно получаем
/(»)=/JtM/^5^i^. (4.47)
J (z + y)"
Вычисление интегралов с остальными членами разложения
(4.45) сводится к (4.46). Действительно, подставляя в интеграл
giAk^)k^, сразу же из условий симметрии получаем
jW=ih^^^k = 0, (4.48)
а подстановка 82^^к^)к к^ приводит к выражению ,
J (it^-i-v)" ^ **" ^ (к^+чГ
Равенство (4.49) проверяется непосредственно: действительно,
можно положить g2цv(*^) = %Ьу,8г{к^)-> где а^, Ь^ — постоянные
(не зависящие от к) векторы; тогда вместо (4.49) рассмотрим
равенство
Интеграл в левой части (4.50), содержащий функцию g2(k^),
является тензором второго ранга по значкам \л, v, и результат
интегрирования должен выражаться через единственный
имеющийся' в нашем распоряжении тензор 6^^^. Числовой
коэффициент в (4.50) устанавливается сверткой тензоров,в правой и левой
частях.
Приведем теперь результат вычисления сходящихся интегралов
типа (4.46) по формуле (4.47) [4]
г а-к
■f~\n-l){n-2)
(4.51)
126
Соответственно для интегралов типа (4.43) с учетом приведенных
вьппе рассуждений получим
3 {k^ + y-lkg)" {y-gY~4n-l){n-2)
к d4 iK^q
{ ^—
J {k^ + y-
И
2kqr {у-дЪ"~Чп-тп-2)
(«3=3); (4.52)
(n>3); (4.53)
(k^ + y-
k.k.. Л _ '^\'9^
у-2кдГ {у-дЪ"~Нп-1){п-2)
+ , , ""^"^ (n>4). (4.54)
2(7-9 )""^(n-l)(n-2)(n-3)
Перейдем к вычислению расходящихся интегралов. Вначале
рассмотрим логарифмически расходящийся интеграл
Делая замену переменных Л^—»гЛо и вводя граничный импульс в
четырехмерном пространстве, приходим к интегралу
/(2) = i„2 г _±dz =ij,2L^-l], (4.56)
в последнем выражении отброшены члены порядка l/L^, поскольку
они все равно пропадают после регуляризации, в результате
предельного перехода L—*<x>.
Некоторые дополнительные проблемы возникают при
вычислении расходящихся интегралов типа (4.43). В квантовой
электродинамике имеется всего несколько типов расходящихся интегралов,
соответствующих упоминавшимся выше расходящимся
диаграммам. Эти интегралы могут расходиться логарифмически, линейно
или квадратично. Рассмотрим вначале логарифмически
расходящийся интеграл:
d'k_
-2kq)'-
jO-)=t_^l (4.57)
Этот интеграл сводится к (4.55) заменой переменных к — д—* к'.
Однако при такой замене переменных меняется и сама область
интегрирования, т. е. граничный импульс (L—*L'). Учет изменения
граничного импульса может давать дополнительный конечный вклад
в интеграл. Правда, в случае интеграла (4.57) этого не происходит:
если L' отличается от L на конечную величину, то при L-*co
получаем, что 1п L' отличается от 1п L на малую величину порядка
127
L ', и, следовательно, интеграл (4.47) однозначно определяется
выражением
ji^) = m4\n-^-\\. (4.58)
Аналогичные рассуждения могут быть применены и для
вычисления логарифмически расходящегося интеграла:
/3) ^ г Vv'^^ (4.59)
Делая замену переменных к' = к — дк используя (4.48), (4.49),
получаем
'Ji'=¥»..('" ^-|)+¥ 7^- (^-вд
в случае линейно или квадратично расходящихся интегралов
типа (4.43) необходимо уже явно учитывать изменение области
интегрирования при замене переменных. Продемонстрируем это на
линейно расходящемся интеграле:
К2)^г ^'^'^ (4.61)
^ 3 (k^-2gk + y)^
Делая замену переменных к— д= к', получаем
(4.62)
Первый член в (4.62) расходится линейно, однако обращается в
нуль при интегрировании по углам, если не учитывать изменения
области интегрирования. Если такое изменение все же учесть, то от
этого интеграла остается конечный вклад. Продемонстрируем это
непосредственно, вычислив разность [4]
^ 3 (k^-2qk + y9- 3 (^2^^_^2)2
Если не учитывать изменения области интегрирования, то Л^О,
так как оба члена в (4.63) отличаются друг от друга лишь заменой
переменных под интегралом. Очевидно, подынтегральное
выражение в (4.63), записанное в виде разности подынтегральных
выражений двух интегралов, существенно отлично от нуля лишь в области
значений к между L и L'. Отсюда следует, что в (4.63) можно
считать д^'^к . Разложим подынтегральное выражение в (4.63) в ряд
по д и оставим члены первого порядка (члены нулевого порядка по
д взаимно уничтожаются):
г {Щк)к 9 1 .
\=\\ ;" "^ j^^Kd'k. (4.64)
^ 3 |a4v)^ (it^-1-7)^1
128
Далее, используя (4.50) и (4.51), получаем
^ ^ (4.65)
Второй интеграл в (4.62) расходится только логарифмически, и,
используя (4.56), окончательно получаем
•^.'^ = '"Ч (»" :~2-')+^='-Ч (»" ;i^ -1) • (4-66)
Аналогичным путем вычисляется и квадратично расходящийся
интеграл
/2) ^ г Уу'^^ (4.67)
Мы приведем здесь окончательный результат [3]:
С помощью выражений (4.58), (4.60), (4.66), (4.68) могут быть
выделены все основные расходящиеся выражения в S-матрице.
Собственная энергия свободного электрона во втором порядке по
константе связи (диаграмма рис. 4.3а), согласно правилам
соответствия, определяется формулой
2:(^>(Р) = -^ \ \S(p + k)y^D^Jk) c^k, (4.69)
в которой электронный пропагатор определяется выражением (4.24) с
соответствующим правилом обхода полюсов. Фотонный пропагатор,
юобще говоря, определяется согласно (2.232), однако должен быть
модифицирован с учетом так называемой «инфракрасной
катастрофы» в квантовой электродинамике. Эта катастрофа проявляется в
расходимости некоторых матричных элементов S-матрицЫ,
содержащих-интегрирование по импульсам виртуальных частиц, но уже не в
области больших, а в области малых энергий. С самого начала ясно,
что «инфракрасная катастрофа» не может иметь места для связанных
состояний электронов. Действительно, расходимость интегралов при
малых энергиях может возникать только из-за обращения в нуль
знаменателей фотонных и электронных пропагаторов. Фотонные пропа-
гаторы при малых энергиях (Л—»0) всегда дают особенности l/k^,
однако одной этой особенности мало для возникновения расходимостей
при интегрировании. В случае свободных электронов электронные
пропагаторы могут иметь знаменатели типа l/[iCp + Jc) + m], где
р — импульс электрона, к — импульс фотона, поглощенного этим
электроном. Если в обкладках соответствующего матричного
элемента стоят волновые функции свободных электронов •ф^воб» "^^
5 л. II. Лабзовскии
129
(ip + m)-»|)pBo6 = 0 и при к—*О электронный пропагатор также имеет
особенность, которая может уже приводить к расходимости интеграла
по d*k. В случае связанных электронов в обкладках стоят волновые
функции •»|)(,вяз' для которых (гр + т)-»|)рряз ^^ О и дополнительных
особенностей не возникает. Таким образом, инфракрасные особенности,
которые могут появляться на промежуточных этгшах при
вычислениях радиационных поправок для связанных электронов, должны
автоматически исчезать или сокращаться в окончательных выражениях.
Для того чтобы удобнее прослеживать такие сокращения, можно
фотонный пропагатор записать в форме
где Х^ > О, а X имеет смысл «эффективной массы» фотона. Правила
обхода полюсов в (4.70) остаются прежними. В конце вычислений
следует устремить X к нулю.
Подставляя в (4.69) выражения для пропагаторов (4.24) и (4.70)
и используя свойства матриц -у. приведенные в § 1.1 (в частности,
(1.44), (1.50)), получаем
Для вычисления интеграла (4.71) используем формулу (4.41) и
затем формулы (4.58) и (4.66). Это дает [3]:
2 '
о
х1п-5 ~ 5 + (^x-l]p + 2im]. (4.72)
Наличие в выражении (4.72) граничного импульса L указывает
на ультрафиолетовую расходимость собственной энергии
электрона. Формула (4.72) содержит также «массу фотона» X. Правда, в
(4.72) можно положить X = О без ущерба для сходимости всего
выражения, т. е. инфракрасная расходимость здесь отсутствует.
Эта расходимость появляется в выражении для собственной
энергии электрона в результате перенормировки (см. следующий
параграф).
Рассмотрим теперь собственную энергию фотона во втором
порядке (диаграмма рис. 4.3в), которая, согласно правилам
соответствия, определяется формулой
Щт = 7ГЙ Sp J ,^ 4^, у^ fii~A d'p. (4-73)
*^ (2л:)^ •' ^ р^ + т^ (р — к)+т
130
Вычисляя след по формулам (1.55), (1.56), приходим к
выражению
„2 , „2
ще
~,,ч л<>2 г 6 (р +т —pk) — 2p р +(р к +рк ) .
'^^^ ' (2^)" J (p2^.^2)[(p_^)2^^2j
Как будет видно из дальнейшего (см. следующий ггараграф этой
главы), физический смысл имеет лишь поперечная часть фотонной
собственной энергии. Поэтому удобнее вместо (4.74) использовать
другое выражение, удовлетворяющее условию поперечности:
П^1ЧЛ) = (б,. - ^) П(^ЧЛ'). (4.75)
ПР)(Л2) = \ |б,, - ^1 ПР)(Л). (4.76)
Проводя дальнейшие вычисления по методу параметризации
Фейнмана и используя теперь (4.68), после некоторых
преобразований приводим величину П(^)(Л^) к виду [3]
-I- 5 dx [i к^ - nf-- к^х{\ - х)1 In 1 -1--^ х(1 - х) . (4.77)
Перейдем к вершинной функции в третьем порядке по
константе связи (диаграмма рис. 4.36). Согласно правилам соответствия
имеем
^\Pv Р^'>=~;Л ^^^^Р2- *)'Уц5(р, - к) y^JD^»{k) d*k, (4.78)
где фотонный пропагатор определяется формулой (4.70). После
подстановки пропагаторов вершинная часть приводится к виду
Af (Pi. Pi) = —:; I y.U% - ^)\{% - f"h.K -
где
. (4.79)
J (k^-2p^k + p\ + mЪ(k^-2p^k + pl + m^)(k^+xЪ '
_ f *°'^*
°~ ^ ^k^-2p^k + p^ + mЪ^k^-2p2k + pl + mЪ^k^ + >?) '
°^ ~ ^ (k^-2p^k + p\ + тЪ(it^-2pjk + p^ + тЪ(k^ + }?) '
131
Интегралы К, К^, К^^ вычисляются по методу параметризации
Фейнмана. Все выражение (4.79) существенно упрощается, если
считать pj, Р2 импульсами свободных электронов,
удовлетворяющими соотношениям р\ = р'^ = —п9-. Кроме того, в этом случае можно
считать, что при вычислении различных матричных элементов,
куда входит вершинная часть, она всегда умножается слева на Ъ^, а
справа на щ, где и^, щ — постоянные биспиноры, описывающие
электрон в состояниях с импульсами р-^, р^ (см. §4.1). Поэтому
каждую матрицу ipi, стоящую слева, и каждую матрицу ip^,
стоящую справа, можно заменить на —т.
Приведем окончательный результат вычисления вершинной
части A(^)(pi, Р2) (подробности вычислений см. в [3]):
A>.,P.)--^{^(ln?->)-,ilsSUg5<i?-
где
_e,ge-i-iln5[ + 8^(7,?-?7,)^. (4.83)
Я=Рг-Р\' (4.84)
sin^e=-4. ■ ^'-^'^
В порядке комментария к вычислению заметим, что в
ультрафиолетовой области (Л—»оо) расходится только интеграл К^^ в (4.79).
Напротив, в инфракрасной области расходится только интеграл К,
поэтому в интегралах К^, К^^ можно сразу положить X = 0.
Подчеркнем, что в вершинной части инфракрасная расходимость
присутствует с самого начала, т. е. до регуляризации.
Остаются еще расходящиеся диаграммы типа рассеяния света на
свете. Эти диаграммы, однако, не понадобятся нам непосредственно
для вычисления радиационных поправок по константе связи.
Поэтому мы не приводим здесь явных выражений для соответствующих
матричных элементов (эти выражения, в случае необходимости,
можно найти в [3]). Общие принципы устранения расходимостей в
таких диаграммах кратко упоминаются в следующем параграфе
этой главы.
§ 4.3. Перенормировка и регуляризация
Проведение программы перенормировок требует в первую очередь
изучения общей структуры диаграмм матрицы рассеяния, т. е.
выделения основных структурных блоков и принципов
конструирования произвольных диаграмм из этих блоков. Такими блоками яв-
132
ляются определенные в предыдущем параграфе электронная и фо
тонная собственно энергетические части и вершинная часть.
Важную роль играет также выделение компактных (неком
пактных), а также приводимых (неприводимых) собственно энер
гетических и вершинных частей
(диаграмм) *). Компактной электронной
собственно энергетической частью называется
такая диаграмма, которую нельзя разбить
на части, соединенные только одной
электронной линией. Примеры
компактной и некомпактной собственно
энергетических электронных частей в четвертом
порядке по константе связи приведены на
рис. 4.5а, б. Компактной фотонной
собственно энергетической частью называется
такая диаграмма, которую нельзя разбить
на части, соединенные только одной
фотонной линией. Примеры компактной
и некомпактной фотонных собственно
энергетических частей в четвертом
порядке по константе связи приведены на
рис. 4.6а, б. Наконец, компактной
вершинной частью называется такая диаграмма, которую нельзя
разделить на части, связанные между собой только одной элек-
Рис. 4.5. Компактная (о) и
некомпактная (б)
собственно энергетические
электронные части в четвертом
порядке по константе связи
ч/\УЛУ~( С \\/\Г^
Рис. 4.6. Компактная (о) и некомпактная (б) собственно энергетические фотонные
части в четвертом порядке по константе связи
тронной или одной фотонной линией. Пример компактной
вершинной части в третьем порядке представляет собой диаграмма
рис 4.36, примеры некоторых вершинных частей в том же
порядке приведены на рис. 4.7а, б.
Неприводимой диаграммой в квантовой электродинамике
называется такая диаграмма, внутри которой нельзя выделить
собственно энергетические и вершинные части. (При этом в счет не идет
выделение элементарной вершины вида рис. 2.1а.) Существует только
одна неприводимая собственно энергетическая электронная
диаграмма и одна такая же фотонная диаграмма — это диаграммы
низшего порядка рис. 4.3а и рис. 4.3в. Действительно, компактные
*) По установившейся терминологии определение компактной диаграммы в кван-
мой электродинамике соответствует определению неприводимой диаграммы в кван-
шой механике (см. [I, § 4.3, 4.6]), определение же неприводимсй диаграммы вкван-
овой электродинамике имеет совсем иной смьгсл.
133
диаграммы рис. 4.5а и рис. 4.6а являются приводимыми: если их
разрезать так, как указано, каждая из них распадется на две
вершинные части. Так же можно проверить, что и любые другие
собственно энергетические диаграммы являются приводимыми. Однако
ЛУ^ГУ^
ЛУ\У\/^
-•J\J^J^
Рис. 4.7. Некомпактные вершинные
части в третьем порядке по константе связи
Рис. 4.8. Неприводимая (о) и
приводимая (б) вершинные части в пятом
порядке по константе связи
ЧИСЛО неприводимых вершинных диаграмм бесксгнечно. На рис. 4.8а
для примера приведена неприводимая вершинная диаграмма в
пятом порядке по константе связи; на рис. 4.8б для сравнения
приведена приводимая вершинная диаграмма в том же порядке с
указанием разрезов. •
Введем теперь представление о точных пропагаторах (функциях
Грина) для электрона и фотона. Обычный электронный пропагатор
соответствует сплошной внутренней линии на диаграмме. Если в
эту сплошную линию вставить всевозможные собственно
энергетические вставки, то мы получим по определению точный
электронный пропагатор. Такой графической операции соответствует
аналитическое выражение:
G(-)(p) = S{p) + S{p)K^^\p)S{p), (4.86)
где К^^\р) — полная электронная собственно энергетическая часть,
т. е. сумма всех собственно энергетических вставок. В равенстве
(4.86) при этом опущены спинорные значки.
Точно так же можно ввести понятие точного фотонного пропага-
тора:
^ц1ЧЛ) = О^Лк) + D^xWK^Hk)D,^W,
(4.87)
где К^^{к) — полная фотонная собственно энергетическая часть,
т. е. сумма всех собственно энергетических вставок в фотонную
линию.
Наряду со вставками во внутренние линии должны также
рассматриваться и вставки во внешние электронные и фотонные линии;
это приводит к переопределению электронных и фотонных волно-
134
вых функций: вместо исходных функций •»!)(/)) и А (к) мы
приходим к функциям
Щр) = Мр) + S{p)K^'Kp)Mp). (4.88)
а^(к) = А^{к) + л^,(л)4\Чл)Л(*)- (4•^^>
Можно, наконец, ввести полную вершинную часть — сумму всех
компактных вершинных частей T^{piP2k) *). Эта величина зависит
от двух электронных (pj, pj) и одного фотонного (к) импульсов и
является матрицей по спинорным значкам. Величины С^^^{р),
G^^lW^ ^^Чр). ^v4*). ^^{РхРг) представляют собой основные
структурные элементы S-матрицы. Особый интерес представляет
поэтому получение уравнений для этих величин или установление
общих соотношений между ними.
Рассмотрим вначале уравнения для функций С(^\ G^'*). Для этого
. введем понятие массового оператора 2(р), который отвечает сумме
всех компактных собственно энергетических электронных частей. Из
графических соображений можно сразу же установить соотношение
К^-Хр) = Y{p) + Y{p)S{p)Z{p) + Z{p)S{p)Y(p)S{p)np) + ...
(4.90)
Суммируя этот ряд, получаем
K<^^\p) = :Z(p)[l-S{p)T{p)]-\ (4.91)
Подставляя (4.91) в (4.86), получаем
G(-)(p) = S{p) + S{p)Y(p)[l - S{p)E(p)]-'S(p). (4.92)
Преобразуем последнее выражение:
G(-)(p) = {l+ 5{рЩр)[1 - S{p)np)]-'}S{p) =
= [l-S{p):Z(p)]-'S(p). (4.93)
Отсюда
С^Чр) = S{p) + S{p)T{p)G^^\p). (4.94)
Уравнение (4.94) называется уравнением Дайсона для электронного
пропагатора. Из (4.94) также следует:
Т{р). (4.95)
1 1
ФНр) ^(Р)
Такие же соотношения можно получить и для фотонной функ-
; ции Грина G^^{k)y если ввести поляризационный оператор П^^(к).
Этот оператор отвечает сумме всех компактных собственно энерге-
•) в силу сохранения в каждой вершине к — Pi — Р2, поэтому аргумент к в
вершинной функции можно не писать.
135
тических фотонных частей. Уравнение Дайсона для фотонной
функции Грина имеет вид
при этом получается также соотношение, аналогичное (4.95),
[С(^Ч*)]ц' = [D(k)];l - П^ДЛ). (4.97)
Общего соотношения, связывающего вершинную часть Г (pjPj)
с пропагаторами G^^^(p), G^^{k), не существует, однако в частном
случае, при р^ = pj. такое соотношение можно получить. Оно
называется тождеством Уорда и имеет следующий вид [3, 4]:
Г^(р,р)=-^^[С(^Чр)Г'. (4.98)
Помимо вершинной части Г (pjP2) мы будем использовать также
«укороченную» вершинную часть
\(PiP2) = r,(PiP2) - •¥,. (4.99)
С помощью (4.95), учитывая определение (4.24), нетрудно
убедиться, что тождество (4.98) эквивалентно соотношению
ЛДр,р) = ^Др). ^ (4.100)
Чтобы показать, как возникает соотношение (4.100),
продифференцируем тождество
S{p)S-\p) = 1 (4.101)
по
/'ц*-
|l5-i-hS^ = 0, (4.102)
ЭРц 9р^
откуда с учетом (4.24)
Выражение в правой части (4.103), будучи подставлено в 2(р), дает
вершинную часть Л в низшем порядке при к = 0 (т. е.
соответствующую излучению фотона с нулевой частотой). Это можно
увидеть непосредственным сравнением. Таким образом,
дифференцирование электронной линии по р приводит к появлению на этой
электронной линии вершины с нулевым импульсом фотона.
Распространение этого правила на более сложные диаграммы и приводит к
тождеству Уорда (4.100) или (4.98).
Результат всевозможных собственно энергетических вставок к
внешние и внутренние электронные и фотонные линии можнс
описать также иным образом, с помощью перенормировочных
констант. Рассмотрим вначале внешние линии. На самом деле вщ
136
волновых функций свободных электронов и фотонов (плоские
волны) полностью определяется требованиями трансляционной
симметрии и релятивистской инвариантности, поэтому наличие
собственно энергетических вставок может приводить лишь к
возникновению дополнительных множителей, т. е. к изменению нормировки
функций *):
я1,(р) = ZJ'Vp), (4.104)
аДЛ) = Zi/МДЛ). (4.105)
Отметим, что сказанное не относится к тем внешним фотонным
линиям на диаграммах, которые соответствуют взаимодействию с
внешними полями. Действительно, само по себе внешнее поле
считается заданным и не меняется в результате взаимодействия с
вакуумом. Однако за счет взаимодействия с вакуумом возникают
поправки к взаимодействию электрона с внешним полем, которые
необходимо учитывать (см. § 4.4).
Теперь обратимся к пропагаторам. Можно утверждать, что
полюсный характер выражений для пропагаторов свободных
электронов при р^—*пр- и фотонов при к^—*0 не должен меняться при
учете собственно энергетических вставок, поскольку этими
выражениями определяются свойства амплитуд реальных процессов
рассеянря частиц. Например, возможны такие процессы рассеяния,
когда в качестве промежуточных состояний возникают одноэлект-
ронные и однофотонные состояния, которым на диаграммах
соответствуют пропагаторы. Амплитуда процесса в этом случае по
физическим соображениям [4] должна иметь полюс при р^ = пр- или
k^=.Q (р, к — импульсы упомянутого одночастичного состояния).
Этот результат должен сохраниться и при наличии собственно
энергетических вставок в линию промежуточного состояния.
Таким образом, в пропагаторе при включении собственно
энергетических вставок могут произойти следующие изменения: 1)
полюсный член может приобрести дополнительный множитель; 2) могут
добавиться неполюсные члены. При этом, поскольку вычет в
полюсе точного пропагатора представляет собой, как можно ожидать,
произведение точных волновых функций, дополнительный
множитель для электронного пропагатора можно считать равным Zj, а
для фотонного — Zj. Окончательно **)
СЩр) = Z,[S,(p) + g^^Hp)h (4-106)
G(v)(*) = Z,[D^^{k) + g^^(k)], (4.107)
*) Мы используем обозначения для констант перенормировки, принятые,
например, в [5].
*•) Приведенные выше рассуждения являются на самом деле лишь наводящими.
Строгое доказательство равенств (4.106), (4.107), а также (4.104), (4.105) см. в [3-6].
137
где ,^
ip — m,
Sr{p) = i-2 1, (4.108)
g(^)(p), ^^l{k) — неполюсные слагаемые, a смысл обозначения m^
разъясняется ниже.
Переход от пропагаторов S{p) и D (к) к точным функциям
Грина G^^^{p) и С^^1{к) в более общем плане есть переход от теории
невзаимодействующих полей к теории взаимодействующих полей. В
каждом конкретном процессе, помимо непосредственного
взаимодействия реальных электронов и фотонов друг с другом, нужно
учитывать еще и взаимодействие реальных частиц с вакуумом. Оно
присутствует и для каждого отдельного электрона или фотона.
Поскольку это взаимодействие, таким образом, нельзя устранить ни в
каких физических экспериментах, оно и определяет величину
параметров, входящих в уравнения квантовой электродинамики: массу
электрона т и его заряд е. Реальные значения этих параметров
(будем их обозначать в этом параграфе т^ и е^) могут отличаться от
тех «затравочных» значений, которые фигурируют в квантовоэлек-
тродинамической теории возмущений.
Основная идея теории перенормировок [3—6] заключается в том,
что расходимости в квантовой электродинамике рассматриваются
как следствие неправильного выбора исходных параметров гп, е.
Если переформулировать теорию так, чтобы в нее входили лишь
реальные параметры т^, е^, то расходимости исчезнут. Для того чтобы
увидеть, как это получается, установим прежде всего связь между
массами т и т^. Заметим, что, согласно сказанному выше о
полюсах точного пропагатора G^^\p), в формуле (4.106) должна по
смыслу фигурировать масса т^. Тогда в полюсном приближении
(т. е^ опуская неполюсные слагаемые) получаем
-[G(-)(p)]-i«^(?-zmJ. (4.109)
С другой стороны, согласно (^..59),
-[G^^\p)r^ = f-im + I.{p). (4.110)
Здесь, поскольку при выводе (4.95) мы пользовались теорией
возмущений, стоит затравочная масса т.
Массовый оператор 2(р) можно на самом деле рассматривать
как функцию матрицы р: в низшем порядке это видно
непосредственно из выражения (4.72); при этом нужно учесть, что р^ = рр.
Ясно, что такой же характер зависимости сохранится и в высших
порядках. Разложим теперь 1.{р) в ряд Тейлора вблизи р = im^ и
оставим два первых члена разложения:
Z(3) = 5:(rmJ-b(^-rmj[^] +... (4.111)
\ / p=im^
138 '
Подставляя (4.111) в (4.110), получаем
-[GW(p)]-» = {р- im^) + [Z{im^) - im + im^\ +
+ №-'"..)(^).
Теперь из сравнения (4.109) и (4.112) следует:
^i I ар I s .
\ /p=im
m = m + iY.{im).
(4.112)
(4.113)
(4.114)
Разность масс Ь{т) = m^ — m называется электромагнитной массой
электрона, поскольку она обусловлена электромагнитным
взаимодействием.
Переформулируем теперь теорию возмущений так, чтобы в
нулевое приближение входила масса ш^. Полный гамильтониан для
системы взаимодействующих электронно-позитронного и
электромагнитного полей представим в виде (2.209), (2.210):
(4.115)
(4.116)
Н=Щ{т)+Щ,„
Щ{т)=Н^{т)+Н^,
ще явным образом от массы т зависит лишь гамильтониан
свободного электронно-позитронного поля Н^{т), имеющий вид (2.202).
Учитывая эту зависимость, переопределим
гамильтониан свободных полей и гамильтониан
взаимодействия:
"int "ш!
6ш 5 ip-^(x)pip(x) dr. (4.118)
Рис. 4.9.
Графическое
изображение
перенормировки
массы
Таким образом, можно считать, что во всех
формулах, получаемых в рамках теории возмущений, масса
т заменена на ш^, если учитывается дополнительное
взаимодействие в (4.118). Это дополнительное взаи-
мсрействие в графической технике приводит к
вершинам, в которых сходятся лишь две электронные линии. Такие
вершины на графиках отмечаются крестиками (рис. 4.9). По правилам
соответствия этим вершинам отвечает множитель Ьт. Описанная
процедура носит название перенормировки массы электрона.
Вершина с крестиком должна сопутствовать каждому набору
компактных собственно энергетических диаграмм для электрона,
т. е. каждому массовому оператору. Таким образом, можно сказать,
что величина
Y^{p) = Y{p) + ibm (4.119)
139
соответствует перенормированному (по массе) массовому
оператору. Коэффициент i перед Ьт в (4.119) устанавливается
сравнением с (4.112). Используя теперь (4.114), получаем
K(P) = (f-im,)l^]^ +••• (4.120)
Обратимся теперь к перенормировке заряда электрона, т. е. к
установлению соотношения между «затравочным» зарядом е и
реальным зарядом е^. Определением реального заряда электрона может
служить утверждение, что две неподвижные заряженные частицы
на достаточно большом расстоянии друг от друга должны
взаимодействовать по закону Кулона:
V =—. (4.121)
•^ ''и
Если при этом речь идет об электронах, коэффициент при l/r,^
в (4.121) можно определить как квадрат заряда электрона [3]. В
низшем порядке по константе связи потенциал вида (4.121)
возникает из диаграммы рис. 4.10. При этом, в отличие от гл. 3, мы
используем здесь фейнмановскую калибровку для фотонного
пропагатора, что всегда удобнее делать, когда речь идет о
перенормировках. В высших порядках необходимо
учитывать, во-первых, лестничные и
перекрестные диаграммы типа рис. 3.6, во-вторых,
всевозможные собственно энергетические
электронные вставки во внешние линии, а также
всевозможные вершинные части и, в-третьих,
заменить фотонный пропагатор D (к) на диаг-
Рис. 4.10. График, рамме рис. 4.10 точным пропагатором GjjX4^)'
°rr™Se«: Н^РУД™ У-Д^ь, однако, что поправки пер-
ствие электронов в в°го типа при rjj—» °° вклада не дают, посколь-
низшем порядке по ку каждое новое взаимодействие содержит но-
константе связи gj^jg степени 1/г,2. На самом деле, буквально
то же самое получается и для любых графиксш,
содержащих дополнительный фотонный пропагатор. В частном
случае это можно явно увидеть на примере выражения (4.272)
для собственно энергетической электронной части во втором
порядке по константе связи.
Остаются лишь поправки третьего типа, содержащие электрон
ные петли, и построенные на их основе графики. Эти поправки не
дают дополнительной малости, а их учет в полюсном
приближении приводит, согласно (4.107), к умножению потенциала
взаимодействия на Z3. Таким образом,
e^^=Z^e\ (4.12.7)
140
Введем теперь основные регуляризованные структурные функ
ции в квантовой электродинамике. Регуляризованная функция
Грина электрона с учетом (4.106) определяется выражением
g(^) = J-G^^) (4.123)
где G(^) — перенормированная по массе электронная функция
Грина. Последнюю можно определить как решение перенормированного
по массе уравнения Дайсона:
С^е) = s^ + 5^2^ GW. (4.124)
Здесь следует подчеркнуть различие между перенормированными
(по массе) функциями Грина и регуляризованными функциями
Грина. Первые содержат уже зависимость от реальной массы т^, но
могут еще зависеть от затравочного заряда е и поэтому содержат
расходимости. Вторые, как будет показано ниже, зависят уже от
реального заряда е^ и поэтому не содержат расходимостей. Вместе с
тем употребительна и такая терминология: когда говорят просто о
перенормированной величине (без добавления «по массе»), имеют в
виду величину, перенормированную и по массе, и по заряду, т. е.
регуляризованную величину. В случае фотонной функции Грина
расходимости связаны только с затравочным зарядом, поэтому
перенормированная и регуляризованная функции Грина в любом случае
совпадают. Мы будем использовать обозначение (jR^^^ik) и, с учетом
(4.107), запишем
Cf^^ {k) = ^d'\ (4.125)
Регуляризованная вершинная часть Г^ , в согласии с (4.98),
определяется выражением
Г«ц = ^.Г,. (4.126)
Введем также регуляризованную вершинную часть Л (см. (4.99)):
^R^iPxPi) = ^li^iPiPi) - \iimr, 'Ч)). (4.127)
и покажем, что имеет место соотношение
^к^РхРг) = \ + ^rMP2)- (4.128)
Действительно, подставляя (4.127) в (4.128), используя, далее,
тождество Уорда (4.98) и формулу (4.106), а также следующее из
этих соотношений равенство
r^.4,r4)=i-v,. (4-129)
непосредственно приходим от (4.128) к (4.126), что и доказывает
сделанное утверждение.
141
Покажем теперь, что функция G-^' удовлетворяет уравнению
Дайсона вида
c^r\p) = ^Лр) + s^p)^^{p)d^\p), (4-130)
где 2д(р) — регуляризованный массовый оператор:
При этом, как следует из определения (4.120),
i:,(imj = 0. (4.132)
что
Для доказательства (4.130) подставим (4.131) в (4.130) и учтем,
др]^ . \др]~ .
I p = im \ I p = im
После этого, заменяя в правой и левой частях уравнения (4.130)
функцию G^^ на GY', согласно (4.123), получим
i- GW(p) = 5Др) + 5Др)1:Др)СМ(р) - SXp - im^) [f] ^ •
' \ '^ I p=im
(4.133)
Далее, имея в виду, что 5^(р— im^) = 1, а также учитывая ^(4.113),
приводим уравнение (4.133) к виду
^ GW(p) = S, + S^p)Y^G^;){p) + [i; - l) GW(P). (4.134)
из которого сразу же следует (4.124). Это и доказывает уравнение
(4.130).
Проделаем теперь то же самое для фотонной функции Грина
C-^^ik). Запишем уравнение Дайсона (4.96) для поперечной части
функции Грина:
^цХ>(^) = 4v(^) + Чх(^)Пхх(^)^1Ч^). (4-135)
где
D^^Sk) = D{k^)[b,.-^^ (4-136)
D(k^) = j^^ (4.137)
При изучении перенормировок можно ограничиться поперечной
частью функции Грина, поскольку продольная часть не дает на самом
деле вклада во взаимодействие электронов. Действительно,
взаимодействие осуществляется либо путем обмена скалярными фотонами
142
(кулоновское взаимодействие), либо за счет обмена
поперечными фотонами (брейтовское взаимодействие) — см. по этому
поводу гл. 3.
Обратимся теперь к уравнению (4.97). Определим обратные
тензоры равенствами
тк)];1=^П(к-)[ь^^-Щ, (4.139)
[С(^>'(^)]-' = i СЩк^) ib^^ - Щ. (4.140)
Тогда из (4.97) следует:
^,Лк)=Щк')[ь,.-Щ, (4.141)
что и утверждалось в предыдущем параграфе (см. (4.75)). С учетом
(4.139)—(4,141) мы можем опустить в (4.97) и, соответственно, в
(4.96) поперечный множитель и дальнейшие выкладки производить,
оперируя величинами D{k^), С(т)(^^), Щк^).
Покажем теперь, что регуляризованная фотонная функция
Грина С?^\к^), определяемая равенством
С^^^ = С^\к-)[ь^^-Щ, (4.142)
удовлетворяет уравнению
G^^\k^) = D{k^) + D{k^)nj,{k^)d^\k^), (4.143)
ще Пд(^^) — регуляризованный поляризационный оператор:
^R(n = Z,
Щк^)-ЩО)-к^
(4.144)
Для доказательства используем уравнение (4.97), из которого
следует:
[Ф\к'^)\-' = ^ гк^-Щк'^). (4.145)
С другой стороны, при к^—*0 из (4.107) имеем
[Ф\к^)Г'=-^1к\ (4.146)
Разложив П(^^) в ряд при к^—*^0 и сравнивая (4.145) с (4.146),
получаем
П(0) = 0, (4.147)
143
Доказательство (4.143) теперь легко выполняется подстановкой
выражения (4.144) с учетом (4.147), (4.148) и последующим
сведением этого уравнения к (4.135).
Суть теории перенормировок проясняется, когда мы начинаем
вычислять матричные элементы S-матрицы, выражая их через
перенормированные величины. Рассмотрим матричный элемент М^"\
соответствующий некоторой неприводимой диаграмме п-го порядка.
Мы сопоставим всем внутренним электронным и фотонным линиям
на этой диаграмме точные пропагаторы G^'^\ G^^, вершинам —
полные вершинные части Г , а внешним электронным и фотонным
линиям — функции (4.104), (4.105). Обозначим через F^ и F числа
внутренних электронных и фотонных линий, N^ и N — числа
внешних электронных и фотонных линий. Тогда схематически
матричный элемент Л/<") может быть представлен в виде
М<")~е" f (r)"(GW)^.(G(-v))^(W)'v.(a)'v„ (4.149)
где верхние индексы указывают, сколько раз та или иная величина
используется при построении матричного элемента.
Выражение (4.149) записано через неперенормированные
величины. Производим перенормировку, пользуясь формулами (4.104),
(4.105), (4.122), (4.123), (4.125), (4.126). Это приводит к
результату
X f (r)"(GW)^.((4''^)^(4l))'v,(^)'v,. (4.150)
Но для числа электронных линий на любой диаграмме выполняется
соотношение
n = F^+^N^ (4.151)
(это соотношение становится очевидным, если пройти вдоль какой-
либо электронной линии на диаграмме). Имеет место также
очевидное соотношение
n = 2F^ + N^. (4.152)
Тогда
М^")-^ J (Гд)"(c4^^)^'(G^л^)^v(яl,)'v,(yl)^. (4.153)
Формула (4.153) является центральной формулой теории
перенормировок [5]. Она показывает, что матричные элементы 5-матри-
цы, выраженные через перенормированные (регуляризованные)
величины, выглядят точно так же, как и матричные элементы,
выраженные через неперенормированные величины. Следовательно,
проделав в формулах для вершинной части (4.127) и собственно
энергетических частей (4.131) и (4.144) вычитания первых членов и
используя эти формулы в матричных элементах, мы можем заменить
повсюду шна ш^и енае^. Согласно (4.150) вычитательная процедура
144
сводится к мультипликативной — к умножению матричного
элемента на числовой коэффициент. В случае квантовой электродинамики
этот коэффициент оказывается конечным (равным единице), что и
означает перенормируемость квантовой электродинамики.
Вместе с тем эта вычитательная процедура и означает
собственно регуляризацию, поскольку регуляризованные выражения при
подстановке в интегралы уже не дают расходимостей. Поясним это
на конкретных примерах расходящихся выражений, приведенных в
предыдущем параграфе. Отметим, что волновых функций
регуляризация при этом не касается — они остаются теми же, что и в
исходной теории.
Рассмотрим диаграмму собственной энергии электрона во втором
порядке по константе связи*) (выражение (4.72)). Согласно
(4.131) соответствующее регуляризованное выражение имеет вид
Yfip) = i:P)(p) - i:W(rmJ -(3- rmj [^] . (4.154)
Вычисления no формулам (4.72), (4.154) достаточно
прямолинейны, и мы приводим здесь только их результат [3]:
4'^(/') = ё i '^^ {р(1 - ^) - ^''"г]
In
гг?х^ + Х^(1-х)
+
р^х{\-х)+т;х + 1?(\-х)
+ (Р - im')
2т^х{\-х)
m^x^ + xHi-x)
(4.155)
Здесь важно подчеркнуть, что, в отличие от (4.72), выражение
(4.155) расходится логарифмически при X—*0 (это видно из
поведения последнего члена подынтегрального выражения при х—*0).
Таким образом, в результате регуляризации, как уже упоминалось,
в выражении для собственной энергии электрона появляется
инфракрасная расходимость. Эту расходимость удобно выделить в явном
виде, вычисляя (4.155) при Х^О [9, 10],
р^ + гг? р^ + гг?
^— In ^ 1
+ С
г In г—
+
+ 2^('^"'"'"r)ln-^•
(4.156)
Перейдем к собственной энергии фотона во втором порядке.
Регуляризованное выражение для этой величины, согласно (4.144),
имеет вид
(4.157)
n(^^>(;fc2) = n(2)(;fc2) _ п(0) - k-'i-^^
*) в низшем (втором) порядке собственно энергетическая электронная часть
совпадает с массовым оператором, что и отражено в обозначениях. То же самое можно
сказать про фотонную собственно энергетическую часть и поляризационный оператор.
145
Подстановка (4.77) в (4.157) после вычисления интегралов дает [3|:
nf{k^) =
где
— '^^ /с^
(2л)2
sin
1 4m^-2/t^
1 CI fi rtn- ft'* '
g + (i wctgo; ^^2
^e=-A
, (4.158)
(4.159)
4mf
Нам осталось привести выражение для регуляризованной
вершинной части A^\piP2) в низшем (третьем) порядке по константе
связи. Регуляризация в этом случае, согласно (4.127), сводится к
следующему:
Подстановка в (4.160) выражения (4.83) дает [3]:
(4.160)
A>A)=-fv,j(^-l)(ln=^-l)-
S5ig?<(5-|ige)+5!^(v,?-«v,)
tg2e
26
sin 26'
(4.161)
sin2e= --Ц.
4m;
Наконец, необходимо упомянуть о регуляризации приводимых
диаграмм. В принципе нужно доказать, что мультипликативная
теория перенормировок справедлива не только для неприводимого
матричного элемента 5-матрицы (4.149), но и для любого
приводимого матричного элемента. Это достаточно сложное доказательство,
опирающееся в основном на топологические свойства диаграмм
Фейнмана, можно найти, например, в [3—6].
В заключение этого параграфа рассмотрим вкратце, как
производится регуляризация матричного элемента QцvXг(^l^2^з^4)^
соответствующего диаграмме рассеяния света на свете (^^ — импульсы
фотонов). Этот матричный элемент расходится логарифмически,
т. е. содержит члены типа 1п {L?/rrP-), причем расходящимся
является нулевой член разложения по ^iQцvXг(0000) [3]. Однако из
соображений калибровочной инвариантности получаем, что
Действительно, добавление слагаемых типа Xv^a (см- § 2.6) к
каждому из фотонных пропагаторов, присоединяющихся к электронной
петле на рис. 4.3г, не должно менять амплитуду процесса. Отсюда
сразу же следует:
^цvXx(0000)=0• (4.163)
146
Таким образом, благодаря условию калибровочной инвариантности,
расходимости в диаграммах типа рассеяния света на свете
фактически отсутствуют.
§ 4.4 Радиационный сдвиг уровней энергии для
нерелятивистских электронов в атоме
Вычисление радиационных поправок к уровням энергии атомов
производится существенно различными методами в зависимости от
того, являются ли рассматриваемые электроны нерелятивистскими
или, напротив, сильно релятивистскими. Согласно рассуждениям,
приведенным в § 3.1, нерелятивистскими являются электроны, для
которых а2эф«1; для релятивистских электронов aZ^ф » 1.
Причины, по которым расчет поправок для нерелятивистских
электронов обладает особенностями и не может производиться по общей
схеме квантовоэлектродинамической теории возмущений,
обсуждались также в § 3.1. Эти причины сводятся к необходимости
производить расчет поправок к энергии на основе точных шрёдинге-
ровских волновых функций для многоэлектронных атомов. Самый
простой путь в этом случае — построение эффективных
потенциалов типа потенциала Брейта, усреднение которых с точными
шрёдингеровскими функциями дает непосредственно поправки к
энергии. В случае радиационных поправок, однако, как будет
видно ниже, не все выражения удается свести к эффективным
потенциалам.
Высокоэнергетическая часть. Рассмотрим вначале одноэлект-
ронную задачу, т. е. уравнение Дирака для электрона в некотором
Р2
Pi
X
Pi Pi
~vy\.(^—-к
a 5 В
Рис. 4.11. Радиационные поправки к диаграмме взаимодействия с внешним полем
внешнем поле /^^^{^х). Взаимодействие с этим внешним полем
описывается в уравнении Дирака (1.32) выражением
ieU^x) = ie^^Af\x\
(4.164)
которому соответствует диаграмма рис. 4.11а, где величину
et/(x) можно назвать эффективной потенциальной энергией. В
качестве одного из слагаемых eU{x) содержит и действительно
потенциальное взаимодействие с внешним скалярным потенциалом
147
A^^^^{x). Тоща в уравнение (1.19) входит взаимодействие с полем
в виде
ie^U{x) = icPY^4"'^(^)- (4.165)
Попробуем теперь выяснить, какие диаграммы, содержащие
радиационные поправки, будут давать добавки к взаимодействию (4.164).
В предыдущем параграфе подчеркивалось, что волновые функции
начальных и конечных состояний в матричных элементах S-матри-
цы не меняются в результате регуляризации. Это означает, что мы
не должны учитывать собственно энергетических вставок во
внешние электронные линии. Тоща в низшем порядке имеется всего две
возможные диаграммы, приведенные на рис. 4.116, е. При этом
можно сказать, что диаграмма рис. 4.116 учитывает собственную
энергию электрона, а диаграмма рис. 4.11в — поляризацию
вакуума. Действительно, диаграмма рис. 4.116 получается при
разложении диаграммы собственной энергии электрона во внешнем поле
(см. рис. 4.1а) по степеням внешнего поля (см. более подробно в
конце этого параграфа). Диаграмма рис. 4.11в получается в
результате такого же разложения диаграммы рис. 4.16. Последняя же по
смыслу представляет собой поляризацию электронного вакуума
(см. § 1.6).
Введем следующие обозначения для добавки к взаимодействию
(в импульсном представлении):
Ьи{д) = ЫЛ^\д) + Ь[Л^\д), (4-166)
Ьи^'\д) = F^{g)A'^^-*\g), (4.167)
Ьи<-^Кд) = G^{g)A(^-^\g), (4.168)
где 6f/(''^' относятся соответственно к диаграммам рис. 4.116, е;
д= Р2~ Pi- Запишем вначале вклад диаграммы рис. 4.116. Согласно
(4.161), получаем *)
Ьи^(д) = Af^{g)Af'\g), (4.169)
-1^7Ге\^'^^4+ш(Н-\^)Щ- (4.170)
о -• '
Перейдем теперь к вкладу диаграммы рис. 4.11 в:
бг/(2)(^) = Yx^xv(^')n(?(9')4''"^(9). (4.171)
*) в этом параграфе и далее возвращаемся к обозначениям т, е, под которыми
понимаем перенормированные значения массы и заряда электрона.
148
Подставляя выражения (2.232) для Dj^^{g'^) и (4.75), (4.158) для
П(^)(^^), а также имея в виду, что
(4.172)
K\K-'-^]=\-'-f'
получаем
G.(^)=iyxK-'-f
i + (i-ectge)^^
(4.173)
Поскольку величина переданного импульса для
нерелятивистского электрона в атоме мала, д/т» aZ«l (см. (1.199)), разложим
(4.170) и (4.173) в ряд по д, оставляя члены не выше д^ [3]:
''''W=-^{l&('"?-|-^)v--
1 г , i .^
\5т^
Ч + 4 (^\ - V^t)}4"'^(^)- (4-174)
При этом член, содержащий коэффициент —1/5, происходит от
диаграммы поляризации вакуума. Сделав в (4.174) замену ^ —*i-—,
перейдем к координатному представлению:
^^^("^=^ {i (i" f -1 - i) у.^Г'^-) +
+ v.
дх дх
4"'^(^)-8k^HV.^^^"'^(x)
(4.175)
где f^^J"^ — тензор электромагнитного поля, определяемый
формулой (2.23). В трехмерных обозначениях выражение (4.175)
приобретает вид*)
^^^^^^ = 1г {i (^" ^ " t - i) 'Р(°^ - «^А) -
-4(2d*'-iaSr)}, (4.176)
где У, ^f — напряженности электрического и магнитного полей,
V=Ao.
В случае электрона, движущегося в атоме, внешнее магнитное
поле можно считать равным нулю, А = ^f = 0. Далее^ учитывая
Sf(r) = —VF, запишем
еЬи(х) = еЬи{т) =
= ^{i (l"T-|-l)'P^^+4b(«Vn}- (4-177)
*) Предпоследний член в фигурных скобках в (4.175) можно устранить выбором
калибровки (2.21).
149
Чтобы вычислить поправку к энергии уровня, согласно (4.164)
нужно написать
A^; = ie(p6f/)^^, (4.178)
где в обкладках матричного элемента должны стоять дираковские
волновые функции (решения уравнения (1.20) с гамильтонианом
(1.34)). Поскольку в этом параграфе мы рассматриваем
нерелятивистские электроны, в (4.178) необходимо перейти к
нерелятивистскому пределу. В первом члене в фигурных скобках в (4.177) для
этого достаточно просто заменить матрицу {3 единицей и перейти к
шрёдингеровским волновым функциям для атома водорода.
Во втором члене в фигурных скобках в (4.177) перейдем к
нерелятивистскому приближению, используя (1.197). Тогда, по
аналогии с (1.232), имеем
я1)+Р(аVF)^^^^PЧ(oVF)(op) - (op)(oVF))^p. (4.179)
Используя теперь (1.29), получаем
4l)+P(aVF)4l)« -2^ip+(-AF-|-2io(VFxV))ip. (4.180)
В случае сферически-симметричного потенциала
Г^Иг): (4.181)
И, учитывая определение оператора орбитального момента / (см.
(1.69)) выражение (4.180) можно переписать так:
я1,^Р(аУ)Уя1,^ _^^+ду^ + ±^+1^^(оГ)ф. (4.182)
Теперь, собирая все члены и используя (4.178), получим для
поправки к энергии выражение
I АА ■
(4.183)
Низкоэнергетическая часть. Наличие инфракрасной
расходимости в формуле (4.183) говорит о том, что пока не учтен вклад в
радиационный сдвиг от длинноволновых, т. е. низкоэнергетических,
виртуальных фотонов. В случае нерелятивистских электронов этот
вклад может быть получен простым квантовомеханическим
расчетом [2].
В нерелятивистской квантовой механике радиационный сдвиг
уровня А можно определить формулой
|.JWr)A(r).r|^
150
где ]д„ — недиагональный электронный ток:
iAn = ^ (^„Р>л + ^лР^п)^ (4.185)
А — вектор-потенциал электромагнитного поля (2.130) в диполь-
ном приближении (справедливом в случае взаимодействия с
нерелятивистскими электронами — см. по этому поводу §5.1):
Суммирование в (4.184) производится по волновым векторам к и
поляризациям е виртуального фотона и по полной системе
промежуточных состояний для нерелятивистского электрона •фд.
Взаимодействие электрона с фотоном в (4.184) записано согласно (2.214).
Суммирование по состояниям фотона с определенным импульсом
к сводится к интегрированию; при этом подынтегральная функция
должна умножаться на число состояний фотона в интервале значений
импульса от к до к -|- cfk. Это число, очевидно, равно йк/(2л;)^. При
этом, поскольку подынтегральная функция в интеграле по к не
зависит от направления импульса фотона (см. (4.186)), можно сразу
провести интегрирование по углам в к-пространстве. Однако до этого
удобно выполнить еще суммирование по двум направлениям
поляризации е. Такого рода суммирование является операцией, которую
часто приходится выполнять в теории излучения (см., например, § 5.1),
поэтому рассмотрим его подробнее. В общем случае речь идет о
вычислении суммы
Р^^{еа){еЬ), (4.187)
е
которую удобно записать в виде
^-1«ЛЛ.. (4.188)
где
/а = 1(е*)Де),. (4.189)
е
Рассмотрим свойства матрицы /,^^. В силу условия поперечности
(2.75), которое в трехмерных обозначениях имеет вид
(ve) = 0, (4.190)
где V — единичный волновой вектор, должны выполняться
соотношения
SVM = SVi. = 0- (4.191)
k i
Эти соотношения полностью определяют эрмитовскую матрицу /,^^.
Из условия нормировки векторов поляризации также следует:
Sp/i;t = 2. (4.192)
151
Всем требованиям (4.191), (4.192) удовлетворяет матрица вида
fik = ^k-^t^k- (4.193)
Тогда
/■=(ab) = (av)(bv) = (axv)(bxv), (4.194)
и в результате суммирования по поляризациям в (4.184) мы
получаем
2 |е \ j^„(r) rfr|'= |vx J j^„(r) dT\^ = j-^ Ivx (p)^j2. (4.195)
e
Теперь можно вычислить интеграл по углам в к-пространстве,
направив ось ^3 по вектору (р)д„:
J Jv|vx(p)^j2=|(p)^j2-2K5sin3erfe = f |(р)^„|1 (4.196)
о
Собирая все результаты, записываем (4.184) в виде
со 2
д^''= 2 ^ U^ V J®-L. (4.197)
On
Интеграл по частоте со в (4.197) расходится, поэтому
интегрирование ограничено предельным значением со^а^- Формула (4.197) дает,
как уже говорилось, вклад низкоэнергетических фотонов в
радиационный сдвиг, что и оправдывает введение предельной частоты. В
выражении (4.197) нужно произвести перенормировку массы. Для
этого с помощью тождественных преобразований представим (4.197) в
виде
^^::=-lFfiH-
о шах
2 е^ . ^
■ --- со
т
О
1U ^
ш{е^ —е^ + ш)
(4.198)
Напомним рассуждения, связанные с перенормировкой массы,
используя на этот раз квантовомеханическое (а не квантовополевое,
как в § 4.3) описание. Если говорить о свободном электроне, то его
экспериментально наблюдаемая масса т^ состоит из ненаблюдаемой
затравочной массы т и электромагнитной массы 6т, обусловленной
собственной энергией электрона *). При этом мы будем считать, что
Ьт«.т^. (4.199)
Это неравенство не противоречит тому, что в § 4.3 мы считали
величину 6т бесконечно большой (см. (4.114)), поскольку в данном
случае речь идет о низкоэнергетическом вкладе в электромагнитную
*) На протяжении этого абзаца мы вновь используем обозначения т„ т, как в
§ 4.3. Что касается 6т, то теперь так обозначен низкоэнергетический вклад в
электромагнитную массу.
152
массу. В случае нерелятивистского свободного электрона формула
(4.115) приобретает вид
или с учетом (4.199)
ч— Р^ -U ^^^ Р^ -U & -U А> (4.201)
Оператор Я;^, во втором порядке теории возмущений приводит к
изменению энергии свободного электрона, которая дается выражением
(4.198) (записанным с волновыми функциями свободного
электрона). В этом случае, однако, второй член в фигурных скобках
пропадает, поскольку импульс является интегралом движения и
недиагональные матричные элементы оператора р равны нулю. По
определению энергия свободного электрона в состоянии с импульсом р
равна pV2m, т. е. равна математическому ожиданию первого члена
(4.201) с соответствующими волновыми функциями. Таким
образом, мы должны выбрать 6т так, чтобы второй член в (4.201)
уничтожал бы добавку, происходящую от Я;^,. Это дает
(4.202)
о
Эти же рассуждения можно перенести теперь и на связанный
электрон, описываемый гамильтонианом
"e = ^-eV. (4.203)
г
в этом случае, однако, контрчлен с 6т не сокращает полностью
выражение А£'д. Остаток и представляет собой низкоэнергетический
вклад в радиационный сдвиг уровней.
Таким образом, перенормированное выражение для А£'д' имеет
■ вид
со 2
; А^; = f 4 \d<^ Е "^""' Т^^. (4.204)
о п
Будем считать, что частота са^ах достаточна велика, т. е.
<«тах»|£„-£д1- (4.205)
Тогда интегрирование в (4.204) дает
П
■-i4Sl(P)^J^(^«-^Jln^. (4.206)
153
где
j^ -^^л ^п "^"^^ (4.207J
— так называемый логарифм Бете [И]. Ввиду того, что
I £„ — £д| »J m(aZ)^ (см. § 1.5), величина KJm{aZ)'^ не должна
зависеть от Z.
Учитывая явный вид гамильтониана (4.203) и используя простые_
квантовомеханические преобразования, можно написать
S I (Р)д„1'(^„ - Ч) = ([Р^]-. Р)дд = 'e(VF,p)^^ =
П
= e(VF,У)дд =-\ е(АЮдд. (4.208)'
Тогда
Теперь необходимо низкоэнергетическую часть сдвига (4.209)
«сшить» с высокоэнергетической частью (4.183). Для этого
необходимо прежде всего связать эффективную массу фотона К с
минимальной энергией (частотой) фотонов са^;^, которая еще учитывает^-
ся в высокоэнергетической части А£'д. Обычно поступают
следующим образом. Рассматривается процесс излучения фотона
электроном, находящимся в некотором постоянном внешнем поле
(поле ядра). Поскольку речь идет об излучении длинноволновых
фотонов, электрон должен находиться в каком-то состоянии из
сплошного спектра. Тогда внешнее поле достаточно учесть по
теории возмущений, в первом порядке. Фактически при этом мы
приходим к изучению процесса рассеяния электрона на внешнем поле
с испусканием фотона. Начальная энергия £ электрона является
фиксированной, энергия испущенного фотона со считается малой по
сравнению с £, А£<К£ (Де — верхняя граница энергии фотона со).
В отношении нижней границы для величины со можно поступить
двояко *). Можно, во-первых, ограничить возможные значения со
величиной co^in- Во-вторых, можно, не вводя ограничений снизу на
величину со, проводить вычисления с эффективной массой фотона
X. Сравнивая полученные выражения, можно установить искомую
связь между X и со^;^- Приведем здесь результат вычислений [3]:
1п2со„,„ = 1пЛ-ь|. (4.210)
*) Вероятность излучения фотона в области малых энергий обратно пропорциа-
нальна частоте: dW ~ dta/ui; полная же вероятность излучения логарифмически
расходится [3]. Эта расходимость в области малых энергий есть та самая «инфракрасная
катастрофа», о которой говорилось в § 4.3.
154
«Сшивание» формул (4.183) и (4.209) можно осуществить, если
найдется область значений со, в которой удовлетворяются
одновременно условие (4.205) и условие
"min^'"- (4.211)
Последнее возникает в связи с тем, что формула (4.183) получена
при Л—*0. Поскольку единственным энергетическим параметром в
области высоких частот является масса электрона, фактически это
означает Л<*;т, откуда, с учетом (4.210), и следует (4.211). Имея
в виду, что I £„ — £д I <^ та^ при Z л; 1, можно убедиться, что
существует область значений со, в которой одновременно выполняются
условия (4.205) и (4.211):
ma^<3Cca<3Cm. (4.212)
В этой области, т. е. при со f^ та, можно положить са^.^ = са^а^. что
и приводит к «сшиванию» формул (4.183) и (4.209).
В результате «сшивания», с учетом (4.210), получаем выраже-
Д£, = Д£; + Д£;=--^
1^
1^ '^ ' _1_ 5
(АЮдд +
АЛ}
(4.213)
Теперь учтем, что V — кулоновский потенциал ядра, т. е. он имеет
вид (1.35) и удовлетворяет уравнению Пуассона [I, (5.16)]
ду = -4лег6(г). (4.214)
Тогда
^'^. = Sjf('"1?; + 3l)lW0)l^-i(^(oI))J (4.215,
Рассмотрим теперь более конкретно различные состояния
электрона в атоме водорода, расшифровывая символ А = nlj. Возьмем
сначала / = 0. В этом случае последний член в (4.215) обращается
в нуль, а зависимость от / можно не учитывать. Далее, в
релятивистских единицах, согласно [I, (1.26)], имеем
l*.c(0)l^ = i(j;)' = ^(f)', (4.2.6,
где Oq — боровский радиус. Подставляя (4.216) в (4.215), получаем
(в релятивистских единицах)
155
Зяп^ I (aZY m(azr
в случае состояний с 1^0 величину ^д следует переопределить,
поскольку знаменатель в (4.207) обращается в нуль. Удобно
заменить знаменатель в (4.207) другим, соответствующим тому же
значению п, но / = 0. Это значит фактически, что K^i
переопределяется так:
1п
2К^
\%,(0)Г
1п
2К
т(аТр- |1))„о{0)|^ mio2)
2*
(4.218)
Вместе с тем все члены в (4.215), пропорциональные | •фд(О) |^ и не
содержащие 1п К^, в этом случае обращаются в нуль. Вычисляя
второй член в фигурных скобках в (4.215), с учетом результатов [I,
§ 3.12], а также табл. [I, П2.3], получаем
АД
пЦ
4ma^Z''
-in
2^:.
3 у{у + 1)-'(' + 1)-7
16« + 1)U+^U
(4.219)
Формулы (4.217), (4.219) определяют лэмбовский сдвиг для
уровней нерелятивистских электронов в атомах. Этот сдвиг (в
низшем порядке по константе связи) представляет собой поправку
порядка a(aZ)^ к уровням энергии атома. Благодаря различию
поправок при / = 0и/^0и явной зависимости от / в (4.218)
снимается вырождение по четности, о котором говорилось в § 1.1. В
частности, при расчете по формулам (4.217), (4.219) получается
A£'2ji= 1034 МГц, A£'2pi = — 17 МГц. Таким образом, полученное
расщепление составляет 1051 МГц, тогда как экспериментальное
значение приблизительно равно 1058 МГц. Более точное сравнение
с экспериментом с учетом вкладов поправок высших порядков см. в
приложении П4.1.
Значение K^i для некоторых состояний приведены в табл. 4.1
[11]. Как видно, зависимость от п (особенно при 1^0) довольно
слабая.
ш
2К„о
m(aZ)
nl
гк„,
m{aZ)
10
19,77
20
16,64
21
0,97
30
15,93
Т
40
15,64
41
0,96
аб лица4.1
00 0
15,16
Вычисление логарифма Бете. Вычисление логарифма Бете
может быть произведено различными методами, как численными [12],
так и аналитическими [13, 14]. Мы опишем здесь кратко применение
156
г
метода, основанного на кулоновской функции Грина [14]. Для этого
рассмотрим выражение (4.197), в котором выделим сумму по п:
2 ^
^^"^=--kЪ^ ^" "^^('^ ~ ")' (4-220)
т
о
^д(о=1:-^- (4-22»)
п
Для вычисления X^{z) можно использовать нерелятивистскую ку-
лоновскую функцию Грина. С учетом спектрального разложения
[I, (1.127)]
X^(,z) = \ dx dT' я1,:^(г')р'СДг'; г)ря1,^(г), (4.222)
или
X^{t) = \ dT dT' {^■^\{T'))G^{T'', г)(Уя1,^(г)), (4.223)
где ■фд(г) — нерелятивистские волновые функции для электрона в
атоме водорода (см. [I, П2.3]). При этом нужно учитьшать, что в
релятивистских единицах множитель Z в выражениях для волновых
функций в части I повсюду нужно заменить на maZ.
Функцию Грина G^(r'; г) представим в виде разложения по
парциальным волнам [I, (1.129)] и дальнейшие вычисления проделаем
уже непосредственно для состояния А = 1 Sj^j* Тогда после
элементарного интегрирования по углам получаем
оо оо
X^^{z) = 4(maZ)5 j dr J dr' rr' e-'"°2<'^+'^')G^j(r'; r). (4.224)
0 0
В результате подстановки выражения [I, (1.146)] для G^^{r'\ г)
проблема сводится к вычислению интеграла [14]
оо
^ь(0 = ^{maZf \ -^ J|±ij ^ X
оо оо
^\dr\ dr' (гг'У^ g-{mc,z+ty{r+r')/^ (2A;Vrr'(|^-l)) , (4.225)
о о
ще в соответствии с [I, (1.146)] использованы обозначения
V = maZ/k, к = у/—2тг. Интегралы по радиальным переменным
вычисляются разложением функции Бесселя в ряд:
оо оо
/р(а, Y) = J rfr J dr' e-<'-^'">{rr')PIJ2YfrP)
0 0
y^+" тЧр + s + \+ nl2)
s=0
— V V t'tp + s + l+n/.
~ 2j s<(n+S)l д20>+1+1+п/2)
s = 0
VT^lP + l +nl2) I, ( , 1 , n 111" 1 1 V^^ /J ooi:\
- J(,.iUr(„ + i) 2Л[Р+ 1 + 2' P+ ' + 2' "+ '•■^J- (4.226)
157
Полагая n = 3, р= 3/2, что соответствует интегралу в (4.225),
получим
/f (а, V) = ^ Г (4)2 Л и, 4; 4; ^j , (4.227)
а используя формулу для гипергеометрической функции при
совпадающих индексах [15]
^F,{a, Ь; Ь; X) = (1 - ху, (4.228)
приходим к выражению
в результате подстановки (4.229) при а = maZ + ki„ у = ку/^^ — 1
в (4.225) получаем
оо
Х^^{£) = IdimaZ^k^ J rf^ (1 + ^)i+"(^ - 1)'--х
1
X [(maZ)2 + A;2 + 2maZA;^]-'*. (4.230)
Используя далее интегральное представление Эйлера для
гипергеометрической функции
1
^F,{a, b; с; z) = rimhb) S ^""'(l " O^-'^Hl - tzy dt, (4.231)
0
„ ^ s-i
которое подстановкой t = -^^ сводится к виду
2fi(a, b; с; z) =
= "ЙУП,"' j (^- r )>-(»+ ■)-'(l -»|й^)" ds, (4.232)
И сравнивая (4.232) с (4.230), после некоторых преобразований
приходим к выражению
A-j^e) = 128x^(1 + х)-8(2 - хГ\Р^{А, 2 - х; 3 - х; у), (4.233)
где х = maZ/k, >>= (1 — х)^/(1 + х)^. При подстановке Х^^ в
(4.220) нужно положить k = V—2m(£ij — со) = '\/m{a.^Z^ + 2са).
Подстановка (4.233) в (4.220) дает следующее выражение для
сдвига уровня (при этом удобно от интегрирования по со перейти к
интегрированию по х) [14]:
д^„ ^ _ 4т^.9^ г ^^ 1^х__ 2 - х; 3 - х; у).
(4.234)
158
Здесь ^__
m(aZ)^ (4.235)
^0 = /
m(aZ)^ + 2(x>^
Интеграл расходится на нижнем пределе при ы^^^—* оо, т. е. Xq—»0.
Эта расходимость видна из того, что при х—»0 гипергеометрическая
функция в (4.234), с учетом известных соотношений [15]
2^1(0, Ь; с; z) = (1 - zy-^-^Fiic - а, с - Ь; с; z), (4.236)
2^M^b;c;l) = '-S^f§^^, (4.237)
ведет себя следующим образом:
2^ (4, 2 - х; 3 - х; у) ^ ^ х-з. (4.238)
Вычисление менее сингулярных членов требует большей
аккуратности (см. [14]). Поскольку Xq—»-l/to„a^ при tamax~*°°' ^ выражении
для A£'i'j появляются расходящиеся члены, пропорциональные
1/х§~са„ах и 1п Хо~1п со^з^ (члены, расходящиеся как I/xq, не
должны возникать, что следует непосредственно из анализа расходимо-
стей в (4.220)).
Как следует из рассуждений, приведенных выше в настоящем
параграфе, линейно расходящиеся по со^ах члены исчезают в
результате перенормировки массы, а логарифмически расходящиеся
члены — при сшивании АЕ'^ с высокоэнергетической частью сдвига.
В результате выражение для сдвига после некоторых
дополнительных преобразований приобретает вид формулы (4.217) при п= 1, в
которой логарифм Бете равен [14]
,nJ^ = 21n2-h^-
m(aZy f>
1 2
- 16 [ rfx "^^'"^— ./-.(l, 2 - x; 3 - x; y). (4.239)
0
Учет высших поправок. Вскоре после появления
первоначальной работы Бете [2] по теории лэмбовского сдвига в целом ряде
работ [16—19] были получены релятивистские поправки порядка aZ к
формулам радиационного сдвига (4.203), (4.205), т. е. поправки к
энергии уровней порядка ma(aZ)^. Были предприняты попытки
вычисления и поправок более высокого порядка по aZ.
Расчет этих поправок достаточно сложен и основан на разложении
пропагатора для электрона во внешнем поле ядра по степеням
взаимодействия с ядром. В общем случае такое разложение бесполезно,
поскольку ряд не сходится (невозможно получить связанное
состояние электрона и ядра, исходя из приближения невзаимодействующих
частиц), однако для вычисления необходимых поправок достаточно
159
выделить лишь несколько первых членов такого разложения. В
случае диаграммы собственной энергии электрона это разложение
изображено на рис. 4.12. Здесь выделены два первых члена разложения
+ X—-< Ъ +
а S В
Рис. 4.12. Разложение пропагатора для электрона во внешнем поле по степеням
взаимодействия с полем в диаграмме собственной энергии электрона
(диаграммы рис. 4.12а, б); остаток ряда соответствует диаграмме
рис. 4.12в. Расходимости (ультрафиолетовые) имеются лишь в
диаграммах рис. 4.12а, б, остаток ряда свободен от расходимостей.
Трудность при таком подходе доставляет то обстоятельство, что
разложение по степеням потенциала отнюдь не является разложением по
степеням aZ. Более того, отдельные диаграммы рис. 4.12а—в содержат
«ложные» низкие степени aZ, которые сокращаются при сложении
всех вкладов. Далее, сложную проблему составляет выделение и
сокращение инфракрасных расходимостей в разложении рис. 4.12.
Аналогичное разложение по степеням потенциала для
диаграммы поляризации вакуума изображено на рис. 4.13. Первый член
этого разложения дает нулевой вклад по теореме Фарри (см. § 4.1).
Расходящейся является только диаграмма рис. 4.136. При дальней-
'^"^О = '^4D "^ 'W3-^
-I-
¥
I
а
8
I
Рис. 4.13. Разложение пропагатора для электрона во внешнем поле по степеням
взаимодействия с полем в диаграмме поляризации вакуума
шем разложении остатка (диаграмма рис. 4.14), в принципе,
возникает еще диаграмма типа рассеяния света на свете (рис. 4.146).
Однако, как говорилось в конце предыдущего параграфа,
перенормировку этой диаграммы фактически производить не нужно и можно
пользоваться непосредственно разложением рис. 4.13. При этом
нужно лишь позаботиться, чтобы при вычислениях не нарушалась
градиентная инвариантность.
Приведем здесь результат вычислений релятивистских поправок
к лэмбовскому сдвигу, записанный в виде формулы [19]:
'*°'" {[С,, 1п {aZ)-^ + C,^\{aZY + C,{aZY +
А£.,: =
nlj
Ътт'
+ [С,2 In^ (aZ)-2 + С,, In (aZ)-2 + C^oKaZ)^ + ...}. (4.240;
160
в принципе, коэффициенты в (4.240) являются функциями
состояний C^^^ = Cii^{nli), однако для многих из них эта зависимость
сводится лишь к множителю 6^^. Например, С41 = б^^, согласно
к
\-\j\r( j + i\j~\A Vx -ь \\j\r( jj
I
I
X
/5"
Рис. 4.14. Выделение диаграммы типа рассеяния света на свете в диаграмме
поляризации вакуума
(4.217), (4.219). Коэффициент С^^(п1;) определяется также
упомянутыми формулами, а
^5 = 3.[l+3^-iln2-b4]v (^-241)
причем последнее слагаемое в скобках происзОэдит от диаграммы
поляризации вакуума.
Далее,
' c., = 41„2-X+[3(l„f+l+i + ...+i)-gi-^,
Значения Cgj(n/y) для состояний с п= 1, 2 приведены в табл. 4.2.
Коэффициент CgQ в общем виде пока не вычислен.
Таблица4.2
6,п +
-Чо
nlj
2
2si
2
2р1
•^2
Зр|
Сь\
7 In 2-71/80
4 In 2 + 63/40
103/240
29/240
При современной точности эксперимента необходимо также
рассчитывать радиационные поправки четвертого порядка по константе
б л. Н. Лабзовский
161
связи, происходящие от учета двух виртуальных фотонов. Порядок
малости этих поправок к уровням энергии (в низшем по aZ
приближении) ma^(aZ)'*. Поправку четвертого порядка к собственной
энергии связанного электрона во внешнем поле достаточно
вычислять лишь с точностью до первой степени по потенциалу внешнего
поля. Это можно сделать, зная поправки четвертого порядка к
форм-факторам вершины свободного электрона.
Взаимодействие свободного электрона с электромагнитным полем
(т. е. вершинная диаграмма самого общего вида) полностью
описывается выражением
Г^(д) = еи(р + д) [-у.ЛС^") + Ш ^v^v^iC^")] "(Р). ^^'^^^^
где f\(,g^), Рг{Я^) — некоторые функции, называемые
форм-факторами, а матрица с^^ определяется выражением
а =1,(у у -у у ), (4.245)
Это взаимодействие имеет самый общий вид, который
удовлетворяет условиям сохранения тока и четности. Действительно,
выражение (4.244) представляет собой по смыслу электронный ток в
импульсном представлении. Сохранение тока отвечает равенству (см.
(2.238))
^Л(^)=0- (4.246)
Первый и второй члены (4.244) по отдельности удовлетворяют
равенству (4.246), первый — потому, что из уравнения
неразрывности (1.14), записанного в импульсном представлении
(Р,-р;Жр')'У,^(р)=0, (4-247)
с учетом (4.1) следует
"(Р + д)ЫР) = О, (4.248)
а второй — в силу тривиального равенства
^,^.V = 0. (4.249)
Если внешнее поле — электростатическое, то вклад во
взаимодействие дает только форм-фактор F^, который в этом случае
описывает просто взаимодействие электрического заряда с внешним
полем. Этот же форм-фактор описывает взаимодействие дйраковского
электрона, обладающего «нормальным» магнитйым моментом \Iq
(где \jlq — магнетон Бора), с внешним магнитным полем. Однако во
внешнем магнитном поле вклад во взаимодействие дает и форм-
фактор F2, который учитывает так называемый аномальный
магнитный момент электрона, впервые полученный Швингером [20]. В
низшем порядке по константе связи, т. е. с учетом только
диаграммы рис. 4.116, магнитный момент электрона с учетом поправки на
162
аномальный момент равен [20]
f. = f.„(l+^). (4.250)
В низшем порядке по а (во втором порядке по константе связи)
форм-факторы Fi и F2 даются выражением (4.170),
соответствующим диаграмме рис. 4.116. В следующем порядке по а (четвертом
по константе связи) необходимо учесть диаграммы, приведенные на
рис. 4.15. Расчет вкладов этих диаграмм весьма сложен; он прово-
"илух/^
-\j\rCr
■\/vrvo
"Х/Луу/^
•\/\/vr
-xyxrvn
■\/\/\у^
о еж
Рис. 4.15. Радиационные поправки к вершинной части в четвертом порядке по
константе связи
дился различными авторами (см. по этому поводу обзор [21]).
Результаты расчетов даются формулой
А^:.,.- =
nlj
Зл^п^
(aZnCp+Cp)b..,
где
Ср = 1,41, Ср =-0,328.
(4.251)
(4.252)
Помимо поправок к вершинной диаграмме рис. 4.116,
необходимо учесть также поправки к диаграмме поляризации вакуума
(рис. 4.11в), т. е. учесть поляризацию вакуума в четвертом порядке
по константе связи. Для этого нужно вычислить вклад диаграмм
рис. 4.16, что было сделано в [22]. Результат расчета таков:
163
Вклады поправок (4.240), (4.251), (4.253) в величину лэмбовско-
го сдвига A£'(2si) — AE{2pi) приведены в Приложении 1.1. Резуль-
Э 3
\/\/ J^^jT^ "^'М \\у^
\/\/ Vv/vr
■\j\I с V-r
с ■\j^jry\j\.
а 5 в г д
Рис. 4.16. Диаграммы поляризации вакуума в четвертом порядке по константе связи
таты расчетов лэмбовского сдвига для различных состояний атома
водорода и водородоподобных ионов приведены в Приложении 1.2.
В последнее время были вычислены также радиационные
поправки порядка ma^(aZ)^ [23, 24].
В заключение этого параграфа упомянем вкратце о вычислении
радиационных поправок для атомов с несколькими электронами. Как
видно непосредственно из вычислений в настоящем параграфе,
формула (4.215) прямо обобщается на случай Л^-электронного атома. При
этом I •фд(0)|^ нужно заменить на рд(0) — одноэлектронную
плотность на ядре, а о1 заменить на ^ о,-1,-. В определении логарифма Бете
i
In KJ^ (см. (4.207)) также нужно заменить оператор р на ^ р^. Этим,
однако, не исчерпываются поправки порядка тар к уровням энергии.
Как было показано в [25], в гамильтониане Брейта (3.51) следует
заменить собственный магнитный момент электрона на аномальный
момент, что приводит к поправкам того же порядка.
Наконец, тот же порядок имеют вклады, происходящие от двух-
фотонного взаимодействия между электронами. Такое
взаимодействие эффективно сводится к контактному взаимодействию, т. е.
потенциал в координатном представлении пропорционален 6rj2 [25—
27]. Если для волновой функции атома использовать разложение по
1/Z (см. [I, §4.2]), то собственно радиационные поправки имеют
порядок ma(aZ)'*, тогда как двухфотонные поправки, связанные с
дополнительным межэлектронным взаимодействием, имеют порядсж
ma(aZ)'*/Z = ma^Z^. Фактически эти поправки могут быть еще
меньше: среднее значение оператора 6(ri2) для основного состояния
атома Не в 17 раз меньше среднего оператора [6(ri) -|- 6(г2)] [11].
Численные значения логарифма Бете для некоторых состояний
двухэлектронных атомов приводятся в [11]. Вариационные методы
расчета логарифма Бете рассмотрены в [13, 28, 29].
164
§ 4.5. Радиационный сдвиг уровней для релятивистских
электронов в атоме
Для внутренних электронов в тяжелых атомах и многозарядных
ионах методы вычисления радиационных поправок, описанные в
предыдущем параграфе, непригодны, поскольку используется
разложение по параметру aZ. В этом параграфе мы рассмотрим методы
вычисления радиационных поправок для полностью релятивистских
электронов в атоме, считая aZ« 1.
Собственная энергия электрона. Начнем с вычисления
поправки к собственной энергии (см. диаграмму на рис. 4.1а). В принципе
для этого достаточно использовать «разложение», изображенное на
рис. 4.12; трудности, возникающие при этом, уже обсуждались в
предыдущем параграфе. Следует еще добавить, что само
вычисление диаграмм рис. 4.126, в, является очень сложной задачей.
Способ, который впервые позволил обойти эти трудности, был
предложен в [30]. Этим способом в [31, 32] были произведены
расчеты лэмбовского сдвига для внутреннего ls-электрона для ряда
тяжелых атомов. Для вычисления поправки к энергии за счет
диаграммы рис. 4.12 можно использовать формулы (3.6), (3.7). Таким
образом, чтобы получить поправку к энергии, нужно вычислить
матричный элемент
<фО|5Р)|фО) =
= е^ J d% d^x^ ^A'(x2ht^S(x^x^)y^y^{x,)D^^^{XiX^), (4.254)
где пропагаторы определяются согласно формулам (2.226), (2.236).
Аналогичным образом пишутся выражения для каждого из членов
разложения рис. 4.12, при этом появляются свободные электронные
пропагаторы, которые мы будем обозначать здесь через S*'(xiX2), и
вершины, содержащие потенциал V, действующий на электрон в
атоме. Таким образом,
АЕ = АЕ^ + AEf, + АЕ^, (4.255)
где АЕ^, АЕ/^, АЕ^ соответствуют диаграммам рис. 4.12а, б, в.
Рассмотрим вначале диаграмму рис. 4.12а. Вклад этой
диаграммы может быть получен из матричного элемента
<фО|5(2)|фо>^^ = S d\ d% %'(х2)5:(^)(х2Х,)я1,/х,), (4.256)
где 5;^^)(x2Xi) — собственно энергетическая электронная часть для
свободного электрона во втором порядке теории возмущений.
Поскольку величина Ifl^ относится к свободным электронам, она
зависит только от разности Х2 — Xj и в импульсном представлении имеет
вид (4.69). Регуляризация выражения АЕ^, согласно результатам
§ 4.3, должна заключаться в замене величины lP\p) на величину
165
^'яЧр)' определяемую формулой (4.154). Тогда
АЕ, = A£(f) + АЕ,, + АЕ,^, (4.257)
где величины AE,i (i=l,2) соответствуют второму и третьему
членам в правой части формулы (4.154). При этом АЕ,, учитывает
перенормировку массы, а АЕ,2 — перенормировку заряда.
Аналогичным образом, с учетом (4.160), можно написать
АЕ,= АЕ^^^ + АЕ,,, (4.258)
где AEf^i учитывает перенормировку вершинной части. При этом
вклады АЕ^\ А/?^ ' являются конечными.
Далее, в силу тождества Уорда имеет место равенство
АЕ,, = -АЕ,2. (4.259)
Чтобы убедиться в этом, нужно записать в явном виде вклады
АЕ, и AEfj. Подставляя в (4.256) волновые функции в виде (1.18)
и переходя к импульсному представлению, получаем по формулам
(3.6), (3.7):
АЕ, = i \ ^(р)2:Р)(р, f?J ^(Р) dp. (4-260)
Аналогичным путем получается и Af?;,:
АЕ, = \ ^^(p)A,(pf?^; qE^)eV(p - ч)-^Лч) dp dq. (4.261)
Отсюда:
Af?,2 = i(^] ^ $ %(P)(P - i4)%(P) ^P' (4.262)
AE,, = A^(im/, im^) J ^^(p)cF(p - q)y\>^(q) dp dq. (4.263)
Учитывая теперь тождество Уорда (4.100) и тот факт, что функция
Ч'а(р) представляет собой точное решение одноэлектронного
уравнения Дирака в импульсном представлении (1.161), приходим к
равенству (4.259).
Основная идея работы [30] состоит в следующем. Регуляризован-
ное выражение для АЕ, согласно (4.255), (4.257), (4.258), можно
записать так:
АЕ^"^ = АЕ^"^ + A£f) + АЕ^. (4.264)
а О С
с учетом (4.259) формулу (4.264) можно тождественно
преобразовать к виду
Д£(л) =(АЕ- АЕ,) + AESf) + АЕ,^. (4.265)
Преимуществом этого выражения является отсутствие громоздкого
вклада АЕ^. Вместо этого приходится вычислять численно логариф-
166
мически расходящееся выражение АЕ — АЕ^ и возникающую
расходимость сокращать с вкладом АЕ^2- Последний вклад, так же как
и AE^J^^, вычисляется явно без труда.
При таком подходе, однако, возникает дополнительная
трудность. Дело в том, что для выделения расходящегося интеграла в
разности АЕ — АЕ^ удобно использовать так называемую «нековариан-
тную» схему вычислений. Это значит, что элемент объема при
интегрировании в импульсном пространстве удобно представить в виде
d'^k = dQ^^^ d\k\d<i>. (4.266)
Вначале интегрирование производится по углам й,^, связанным с
трехмерным вектором к, и затем по абсолютной величине этого
вектора I к I. Эти интегрирования являются конечными. Расходимости
возникают лишь на последнем этапе при интегрировании по со.
По-иному выглядит последовательность действий при «ковариан-
тном» интегрировании, которое использовалось в § 4.2 для вычисле*
ния АЕ^2 (или, в силу (4.259), AEf^^). В этом случае расходимости
при интегрировании в к-пространстве возникают, когда мы
интегрируем по абсолютной величине 4-вектора к^.
При компенсации расходимостей в (4.265) эти различия
необходимо учесть. Для этого достаточно вычислить тем и другим
способом величину AEfji и учесть разницу в полученных выражениях.
Обращаясь к выражению (4.279) для AjP)(pjP2). в котором
расходимости сконцентрированы в последнем члене, определяемом с
помощью (4.82), полагая р^ = р2= im^ и производя коммутацию
матриц "Yv» видим, что числитель подынтегрального выражения в
расходящемся интеграле может содержать только конструкции типа к^к
или -Yv*^' Вторая из этих конструкций инвариантна относительно
способа интегрирования, «ковариантного» или «нековариантного».
Первая же в результате «ковариантного» интегрирования по углам
4-вектора к сводится ко второй:
Кк^\у.к^- (4.267)
В случае «нековариантного» интегрирования по углам трехмерного
вектора к результат будет другой:
kj^^y^k^ v= 1,2,3, (4.268)
kj^l^kl v = 4. (4.269)
Расходимость при ковариантном и нековариантном
интегрировании будет одна и та же, т. е. компенсация расходимостей в (4.265)
будет иметь место, но результаты вычислений тем и другим
способом будут отличаться на конечную величину. Таким образом, в
правую часть (4.265) нужно ввести поправку АЕ', учитывающую
167
различие между ковариантным и нековариантным вычислениями
AfJjj. Эта поправка получается прямым вычислением интеграла в
(4.82) и последующей подстановкой в (4.263). Результат
вычислений таков [30]:
^E' = -i\aieV),,, (4-270)
где а — постоянная тонкой структуры. Формула (4.265) заменяется
теперь на
^E^R) =(АЕ- AEJ + АЕ<^'> + АЕ^^ + ^^'- (4-271)
Основную трудность при расчетах составляет вычисление разности
АЕ — АЕ^. Это вычисление удобно проводить в координатном
представлении. Подставляя в (4.254) выражения для пропагаторов и
интегрируя по временам и частотам, получаем с помо1цью (3.6), (3.7)
где
2к1
п ^ "^ / АппА
— 00
с учетом определения функции Грина одноэлектронного
уравнения Дирака через спектральное разложение (1.173) выражение
(4.272) можно переписать в виде
X J- ехр {Ы^г^^) я1)д(Г2) dfi dr^. (4.274)
12
Здесь через G'e^'^Si) обозначена функция Грина для уравнения
Дирака. Если использовать уравнение с кулоновским
потенциалом ядра V{r) = Ze/r, то в таком виде выражение (4.274) пригодно
в случае водородоподобных ионов с произвольным зарядом ядра Z.
В принципе здесь можно использовать, как это было сделано в [30],
функцию Грина для уравнения Хартри—Фока—Дирака (3.108).
Вычисление АЕ^ удобно проводить по той же формуле (4.274),
полагая при этом Z = о в выражении для функции Грина.
Функцию Грина Сг^' следует подставить в (4.274) в виде
парциального разложения (1.193), затем выполнить интегрирование по
угловым переменным Qj, Qj и, наконец, по радиальным переменным
rj, г2- После этого остается расходящийся интеграл по со.
Интегрирование в комплексной плоскости нужно производить по контуру,
зафиксированному наличием мнимых добавок в знаменателе в (4.273).
Явное выражение для АЕ^2 (более удобно использовать AEf^i)
получается по формуле (4.263). Выражение АЕ^^ в (4.271) можно
168
получить непосредственно по формуле
д£(л) = i J xi)^(p)2:^,(p, f?J я1,^(р) dp, (4.275)
ще перенормированная собственно энергетическая часть 2^
определяется формулой (4.156). Последний член в (4.156), содержащий
инфракрасную расходимость, согласно тождеству Уорда, сокращается с
аналогичным членом в AfJ^, (входящим в разность Af? — ts.E^). Это
сокращение проверяется так же, как выше проверялось равенство
(4.259). Наконец, последний член в формуле (4.271) (А£")
вычисляется непосредственно по (4.270). Этим завершается, в принципе,
расчет величины лэмбовского сдвига для релятивистского электрона.
Описанный выше способ расчета обладает тем недостатком, что
в различные члены (4.271) при малых значениях aZ входят
«ложные» слагаемые более низкого порядка по aZ, чем это должно
получаться в нерелятивистском пределе. Все эти слагаемые в конце
концов взаимно уничтожаются, однако точность расчетов при этом
понижается настолько, что получить правильный нерелятивистский
предел не представляется возможным.
Этот недостаток устраняется при другом подходе к расчету
лэмбовского сдвига, примененном в [33, 34] специально для кулоновской
задачи при произвольных значениях заряда ядра Z. В этих работах
рассчитывается непосредственно выражение (4.274). При этом
используется другой способ регуляризации [8, 35], когда фотонньш пропагатор
в импульсном пространстве (2.232) заменяется выражением
'\f-
(4.276)
и в конце вычислений берется предел А—* оо. Такой способ позволяет
избежать трудности с «нековариантным» интегрированием. Величина
Л («масса» фотона) связана с электромагнитной массой 6т (см.
(4.114)) соотношением [8]
6т = ^(|1пА^-ь|). (4.277)
Таким образом, перенормированное выражение для сдвига
получается теперь так:
Д£(л) = lim (АДА) -I- ^E^{^.)),
где
Af?„(A) = -6m \ dT я1,^(г)ря1,д(г), (4.278)
а для А£'(А) после подстановки (4.276) в выражение для АЕ имеем
АЕ{А) = ^ J rfr, dr^ dz ^д(г,) [Cf )(г,Г2) - a,Gf )(r,r2)aj X
x_L Ге'Ьг,, _ Qib'r^J ^^^(r^), (4.279)
b=[{E^-z)^-iz]i, b'=[{E^-z)^-A^-it]i. (4.280)
169
При этом мы произвели в (4.274) замену переменной
интегрирования: /^д — со = Z. Картина полюсов и разрезов в комплексной
плоскости Z, соответствующих дискретному и сплошному спектрам
собственных значений Е, приведена на рис. 4.17. На этом рисунке
толстые сплошные линии означают разрезы, точками обозначены
полюсы. Все полюсы лежат между значениями z = OHz = mHa
вещественной оси. Мы будем считать,
что имеем дело с основным
состоянием -фд, соответствующим самому
левому из полюсов. На рис. 4.17
указан также контур
интегрирования С.
Имеются две точки ветвления,
определяемые (4.280), причем
значения корней фиксируются
условием
Re (й) > О, Re (й') > 0. (4.28J)
Точка ветвления b помечена на
рис. 4.17 крестиком, точка
ветвления Ь' при Л —» 00 уходит в левую полуплоскость.
Контур С можно деформировать так, как это изображено на
рис. 4.18, Новый контур делится на две части. Первая часть (Cl) —
Рис. 4.17-Полюсы, разрезы и контур
интегрирования в комплексной
плоскости переменной z—E^ — w при
вычислении интеграла по ш в
формуле для собственной энергии
релятивистского электрона
-R-LD
R+ID
Рис. 4.18- Деформация контура интегрирования в комплексной плоскости z и его
деление на низкоэнергетическую (Сх) и высокоэнергетическую Си части
контур, начинающийся в точке z, на мнимой оси, огибающий точку
ветвления b и оканчивающийся в точке Z2 также на мнимой оси.
Вторая часть (Сд) — интегрирование по дуге большого круга R и
по мнимой оси, за исключением отрезка zj, Z2. Рассмотрим вначале
контур Cl. При е-»0, а также zj, zj—»0 этот контур сводится к изо-
170
[
браженному на рис. 4.19 и состоит из двух частей: Сд и Сд. В силу
условия Re (й) > О знак перед корнем в экспоненте в (4.279) нужно
выбирать следующим образом:
2 + z£U= J~'^^^ ~ ^^' ^ ^ ^«' (4-282)
т-Ь6
-'К^^-^)'+'^1^=1 .•(Z?д-z), .^С
Некоторое неудобство заключается в том, что в пределе е-»О точка
ветвления сливается с полюсом z = Е^^; особенно это неудобно в том
случае, когда Е^ —
возбужденное состояние. Для
преодоления этой трудности можно
сдвинуть все полюсы и разрезы
в нижнюю полуплоскость на ^_,^
величину бив конххе — ^^^
вычислений устремить также -m-iS
6 к нулю [33]. Заметим также,
что часть интеграла (4.279),
содержащая ехр (ii'rj2), дает
нулевой вклад при интег- „ ^,„ гт «
^ . Рис. 4-19-Преобразованный вид низкоэнер-
рировании по Сг, поскольку ^ической ч^ контура Cl
при zj, zj—»0
соответствующее подынтегральное выражение является аналитической функцией
Z внутри контура (нет точки ветвления) и на самом контуре.
В результате вклад от контура Cl в (4.279) не зависит вообще
от Л и записывается в виде
° -«1С(+\б('-1'-2)«2] tJ; sin [(^д - ^)'-12Нд(«-2)- (4-283)
Ввиду того, что интегрирование по z в (4.276) ведется по
ограниченной области значений от О до Е^^, эта часть не содержит расхо-
димостей и определяет вклад области низких энергий в АЕ. В
нерелятивистском пределе выражение АЕ^ содержит «ложные» низкие
(более низкие, чем (aZ)*) степени aZ, которые сокращаются с
аналогичным вкладом из AEyf [33]. В пределе, при е-»0, Zj, zj—»0,
Л—» 00 интегрирование по контуру Cjj сводится просто к
интегрированию вдоль мнимой оси. При этом возникает расходимость,
которая компенсируется расходимостью в АЕ^ [33]. Существенно, что
эту компенсацию можно провести аналитически.
Результаты численного расчета вклада собственной энергии
электрона в энергию уровня для различных водородоподобных
ионов могут быть представлены в виде [34, 36]
AE = ^{aZ)*F{aZ) ^
(4.284)
171
к^ ^ ^ '' „3-
Значения функции FiaZ) для различных значений Z и различных
состояний ионов приведены в табл. 4.3. Как видно из таблицы,
функция F в случае основного состояния монотонно убывает с ростом
Z в интервале от Z= 10 до Z = 90. Возрастание после Z = 90
связано с кулоновской особенностью; для получения правильных
результатов в этой области необходимо учитывать конечные размеры
ядра. В меньшей степени это относится к возбужденным
состоянием, для которых конечный размер ядра становится чувствительным
при больших значениях Z.
Таблица 4.3
Z
10
20
30
40
50
60
70
80
90
100
ПО
Isi
2
4,654
3,246
2,5519
2,1351
1,8644
1.6838
1,5675
1,5032
1,4880
1,5317
1,6614
F{aZ)
2sl
4,893
3,5063
2,8391
2,4550
2,2244
2,0948
2,0435
2,065
2,169
2,387
2,798
2pL
-0,1145
-0,0922
-0,0641
-0,0308
0,0082
0,0549
0,1129
0,1884
0,2934
0,453
0,725
Значения лэмбовского сдвига, полученные по формуле (4.278), в
общем согласуются с результатами расчетов при малых значениях
aZ (формула (4.240) из предыдущего параграфа). По поводу
небольших имеющихся расхождений см., например, [37].
Поляризация вакуума. Помимо собственной энергии
электрона, в первом порядке по константе взаимодействия а нужно
рассчитать еще вклад диаграммы поляризации вакуума (см. рис
4.16). Записывая вклад этой диаграммы, согласно правилам
соответствия (см. § 1.6), получаем для матричного элемента 5-матри-
цы выражение
<ф0|5(2)|ф0> = ^2 J ^^^ й*Х2^д(х,)-у,,^д(Х1) X
X Sp (5(xi, X2)'Y^p£»^_^^(x,X2), (4.285)
172
из которого энергетический сдвиг АЕ получается согласно (3.6),
(3.7). Сам вид этой поправки говорит о том, что ее можно
представить как поправку к взаимодействию (кулоновскому) электрона с
ядром. Действительно, (4.285) можно переписать в виде
где
<ф0|5(2)|ф0) = J d\ ^д(х,)е-уоФ(х,)я1,^(х,), (4.286)
•УоФ(^1) = -е $ «^Ч •Y^.Sp (5(Х2, Х2)-у^^)£>^_^^(х,Х2). (4.287)
Согласно (2.227) выражение 5(х2, Хг) не зависит от fj- Подставляя
в (4.287) фотонный пропагатор в виде (2.236) и интегрируя по <2.
получаем, что функция ip(xi) не зависит от fj и равна
■УоФС»"!) = -ie \ dr^ ^ -у^, Sp
i $ С„(Г2; гг) d(o у^
(4.288)
где G^ — функция Грина для уравнения Дирака (1.173). Формула
(4.288) основана на равенстве
00
•5(^1^2) = 2^ $ е-™('.-'.)-уоС„(г,; г^) do. (4.289)
Далее, вновь вспоминая (2.227), можно заметить, что след в
(4.288) можно записать как след от произведения "Уо^Тц. где
матрица F равна:
(^)ар=«)„(%)р (4•2^o)
(здесь мы явно выписали спинорные значки). Поскольку под знаком
следа матрицы можно коммутировать, то, используя (1.8), сразу
приходим к выводу, что след отличен от нуля только при ja = 0.
Окончательно
/» ^
(4.291)
>P('-i)=-^H'-24Sp
\ С^СГг! «"г) ^(о -уо
Записывая теперь выражение для сдвига энергии с помощью
(3.6), (3.7) в виде
АЕ = ie \ dTy ^д(Г1)-уоФ(«"1)^л(«"1). (4-292)
приходим к выводу, что величина ip(rj) представляет собой
поправку к кулоновскому потенциалу взаимодействия электрона с
ядром — поляризационный потенциал. Можно также считать, что
этот добавочный потенциал возникает в результате появления
поляризационной добавки к электронной плотности
(4.293)
173
Из сравнения (4.293) и (4.291) следует:
Р^''(г2)=-^8р
\ С„(«"2; «"г) doi -уо
(4.294)
Выражение (4.294) (и соответственно (4.292)) расходится. В
координатном представлении эта расходимость связана с
сингулярностью пропагатора 5(ri<; Г2<) при Tj—»Г2 (см. в [38] доказательство
для нерелятивистского случая, которое полностью относится и к
релятивистскому) :
Iim5(r,<;r,0~-T7^. (4•2^5)
Для устранения расходимостей, как и в случае собственной
энергии, можно воспользоваться «разложением», изображенным на
рис. 4.13. Поскольку диаграмма рис. 4.13 а дает нулевой вклад по
теореме Фарри, перейдем сразу к обсуждению вклада диаграммы
рис. 4.136.
Сам вид этой диаграммы говорит о том, что она определяет
поправку к кулоновскому потенциалу взаимодействия электрона с
ядром. Этот поправочный потенциал называется потенциалом
Юлинга [39, 40]. Поправка к энергии за счёт вклада диаграммы
рис. 4.136 получается с помощью формул (3.6), (3.7) из
матричного элемента
<фО|5(3)|фО> = -е2 J d% d^x^ d% (^д(х,)-у^я1,^(х,)) X
xSp (■у,5да(х2Хз)-уя5(°)(ХзХ,))Л^Дх,Х2)Л,(Хз), (4.296)
где А)^{х) = (О, О, О, iVc) — кулоновский потенциал
взаимодействия с ядром. Переходя в импульсное представление, с учетом
определения поляризационного оператора (собственной энергии
фотона) во втором порядке теории возмущений (4.73), после
подстановки выражения для фотонного пропагатора (2.232) и
интегрирования по частям, из (4.296) получаем с помощью
(3.6), (3.7):
А£ = ^ J ^^(p)eFc(k) ^ •у4П^'Чк'. 0)4i,^(q) dp dq, (4.297)
где к = р — q. При этом мы использовали уже регуляризованное
выражение (4.158) для поляризационного оператора. Как уже
говорилось в предыдущем параграфе этой главы, других
расходимостей при вычислении поляризации вакуума не возникает, если все
вычисления проводить градиентно-инвариантным образом.
Из (4.297) следует, что потенциал Юлинга в импульсном
представлении имеет вид
^Pu(Ю = il ^с(к) ~ П(,^)(k^ 0), (4.298)
174
или, после подстановки (4.158),
4>uW =
2{2л)'
Ус(Ю
i+(i-ectge)i^^'^^
]■
(4.299)
где sin^ в = —к^/4т^; V(^(k) — фурье-образ кулоновского
потенциала. Переходя к координатному представлению, из (4.299) с учетом
выражения [I, (1.16)] для Кс(к), можно получить [3]
^Pu(r)=^]c-^"'-[l + ^]
dx.
Асимптотическое поведение этого потенциала таково [3]:
- ^ (I + 2С + 2 In (mr)] , mr«l,
1 „-2mr
mr:«>l,
Ф1/('')
(4.300)
(4.301)
4V^
1тг)г
где С « 0,5772 — постоянная Эйлера.
Формула (4.301) написана в релятивистских единицах, поэтому
на расстояниях порядка воровского радиуса Гд« 1/та функция
^Рц(г) экспоненциально мала: (р(/(г) ~ехр (—2тго)~ехр (—1/а).
Потенциал Юлинга заметно отличен от нуля лишь на малых
расстояниях порядка аг^; на таких расстояниях он дает поправки порядка
aZ к Vf^. При больших значениях Z эти поправки уже не малы.'
Вклад диаграммы рис. 4.13в впервые рассчитывался в работе
[41]. Здесь были, однако, получены лигпь оценки, которые
указывали, что в области значений заряда ядра Z « 70 -г- 90 вклад
диаграммы рис. 4.13в составляет не более 10% вклада диаграммы рис. 4.136.
В [42] была точно рассчитана поправка к поляризационному
потенциалу, определяемому диаграммой рис. 4.13 в, в низшем порядке
при разложении по aZ. Наконец, в [43, 44] вклад диаграммы рис.
4.13в был вычислен точно без разложения по aZ.
Запишем результаты этих вычислений, следуя [44]. Исходной для
расчетов является формула (4.294), в которой удобно развернуть
контур интегрирования в комплексной плоскости вдоль мнимой оси:
P''' = ^$SpG.„(r;r)-Yorfa>.
(4.302)
Для функции Gf^ используем парциальное разложение, котхфое
запишем в виде
Се(г; г') =
ICM в виде
г;г') =
(G^Pj,(r, r)Q,,^(n)Q;,^(n'), iG^^]i{r, r')Q,7^(n)Q;,^(n')
^ [iG%(r, r')Q-j^(n)Q;,^(n'), -G%,(r, r')Qjj^(n)Qjj^(n')
где коэффициенты (^Ejii''' '"') (s=l,2,3,4) определяются
формулами (1.192)—(1.195), и (1.183). После суммирования по М и
вычисления шпура в (4.302) получим
00
9'Чг) = ^кр^{г), k = j + \, (4.304)
*; = !
где
i=j±i -»
Выражение (4.304) является, как и (4.302), расходящимся.
Однако коэффициенты парциального разложения G^Ejii''^ '"') конечны
при г' = г, а расходится сумма по парциальным волнам в (4.304).
Регуляризацию выражения для р^Р удобно проводить, вычитая из
(4.305) линейную по Z часть плотности. При этом из р^^ удаляется
и та часть поляризационной добавки к плотности, которая
соответствует потенциалу Юлинга. Таким образом, перенормированное
выражение для р^ имеет вид
\ / z=o
Приведем окончательные выражения для поправок к энергии,
получающиеся в результате подстановки (4.304), (4.306) в (4.293) и
затем в (4.292) [44]:
AKl = А<, + А£;,,. (4.307)
Здесь A£^ij — вклад, происходящий от потенциала Юлинга (4.300),
ts.E'nij — вклад всей оставшейся части потенциала (4.291) (т. е.
диаграммы рис. 4.13в). Величина AE^ij определяется формулами (4.301),
(4.292), а для AE'^ij в [44] получены следующие выражения:
^^•^Ч = (^ + ТЙЙР) ^;.Д°2) А£;,Даг-0), (4.308)
где A£^;y(aZ—»0) — нерелятивистский предел выражения ts.E'^ij,
F^ij(aZ) — некоторая плавная функция Z. Для АЕ^^ц можно
написать такие формулы:
A£;,.(aZ-0)=i^^*A„-h
+ ^s [225^ l^-ln -?r + C„ - С -h Й4 + 4 *26l,y+lJ
6,,,
A£;,,(aZ-*0) = 128a(aZ)W-3/^-3/-H)(2/-3)! j _ ^ j _ .
(4.309)
176
Здесь С — постоянная Эйлера,
*2 =
1
aiazy
5 r^U'oir) dr = 0,0045105564, (4.310)
*4 =
1
aiaZy
\r'^U^^{r)dr+\ \r'^U^^{r)
2a(aZ)-
225 лг
C„=$(7<|('-)-ie-j
dr =0,004252588,
(4.311)
dr, (4.312)
M — функция Уиттекера (см. [I, § 1.1]), и'о{г) = —е1^1{г),
ур'^{г) — потенциал, получающийся при подстановке (4.304),
(4.306) в (4.293) в нерелятивистском пределе (aZ—»0). В
частности, С2 = 0, Сз = -7/16, С4 =-147/200, €5 =-77/80. Значения
функции F\ij{aZ) приведены в табл. 4.4 для ряда значений Z при
различных nlj. При у = 1/2 выражение A£J,;y имеет особеннссть,
когда Z-» 137; эта особенность выделена явно в (4.308).
nlj
2
2si
2
3.i
4si
2
5si
2
Щ
3pi
4p.
5pl
2p|
3p|
4p|
5p|
10
0,4328
0,4336
0,4335
0,4334
0,4333
0,4825
0,4822
0,4820
0,4819
0,9550
0,9554
0,9555
0,9554
20
0,3896
0,3931
0,3929
0,3925
0,3921
0,4786
0,4779
0,4772
0,4768
0,9166
0,9187
0,9191
0,9191
82
0,3479
0,4315
0,4285
0,4205
0,4139
0,8359
0,8149
0,7936
0,7779
0,9081
0,9574
0,9682
0,9699
100
0,4073
0,5788
0,5709
0,5528
0,5382
1,2782
1,2205
1,1663
1,1279
0,9936
1,0778
1,0966
1,0966
Та
110
0,4749
0,7464
0,7310
0,6997
0,6751
1,7866
1,6745
1,5750
1,5064
1,0708
1,1835
1,2091
1,2133
5лица 4.4
130
0,9135
1,9541
1,8360
1,6737
1,5585
5,9115
5,0967
4,5016
4,1289
1,3589
1,5717
1,6218
1,6302
177
Таблица4.4 (.продолжение)
nlj
3dl
2
4«f3
2
5dl
2
Ml
4dl
2
5dl
2
10
1,0942
1,1052
1,1096
1,0341
1,0385
1,0402
20
1,3001
1,3355
1,3493
1,1020
1,1152
1,1205
Z
82
4,2302
4,6060
4,7415
1,7385
1,8570
1,9037
100
5,9125
6,4957
6,6965
1,9898
2,1622
2,2301
110
7,1949
7,9411
8,1904
2,1592
2,3707
2,4542
130
11,319
12,611
13,014
2,6502
2,9804
3,1119
Приведем также выражение для ^Е^и (aZ—»0) [44]:
A£^,.(aZ^0)=-a(2^)
21+4
(n + l)\wy
8к(21+3) lai + l)!]^(n-Z - 1)!
-2 , ai
[1 + 2 , (2/ + l)(/ + l) 3t 1 ГЛ Qtn^
[27T5+ -^2 \y+ij- (4-313)
Из (4.313), в частности, получается нерелятивистский вклад
поляризации вакуума в лэмбовский сдвиг уровней при / = О,
включенный в (4.217).
Поправки ^Е'^и невелики по сравнению с ts.E^ij, однако они
намного превышают поправки ^Е'^^, пропорциональные а? (см.
(4.251), (4.253)). Так, для 1 Si-состояния при Z= 100 отношение
2
А^:'': А^:"^: А£;^^ равно 400 : 20 : 1. Нужно заметить также, что
при расчете вклада поляризации вакуума в сдвиг уровня энергии
важен учет конечных размеров ядра; это особенно важно в случае
основного состояния, для которого чисто кулоновское выражение
(4.308) расходится при Z—»137. Для сравнения в табл. 4.5
приведены значения поправок А^"^ и аналогичных поправок l^E'',
рассчитанных в [43] с учетом конечных размеров ядра. При этом
сравниваются fT, fr, связанные с А^"^ соотношением
^^r^2iB?^ir.
(4.314)
Приведем еще результаты (табл. 4.6) сравнения значений
поправки на поляризацию вакуума А£ур (с учетом только потенциала
Юлинга) со значениями поправки на собственную энергию
электрона А^^е для основного состояния Isi при некоторых значениях Z
178
[32]. В этой же таблице приведены и суммарные значения лэмбов-
ского сдвига А£ (все величины даны в ридбергах).
Уровень
2
2si
2
2pi
Щ
Hr
Hr
Hr
Hr
Hr
Hr
Hr
Hr
54
0,0059
0,0059
0,0064
0,0064
0,0004
0,0004
0,0001
0,0001
T
z
82
0,0159
0,0150
0,0197
0,0185
0,0036
0,0035
0,0005
0,0005
92
0,0224
0,0207
0,0298
0,0272
0,0072
0,0068
0,0008
0,0007
аблица 4.5
100
0,0303
0.0269
0,0430
0,0377
0,0128
0.0118
0,0010
0,0010
Таблица4.6
z
70
75
80
85
90
Afise
8,95
11,53
14,65
18,47
23,14
Afivp
-1,70
-2,38
-3,29
-4,52
-6,21
^E
7,25
9,15
11,36
13,95
16,93
В заключение этого параграфа укажем, что в самое последнее
время был рассчитан также целый ряд высших радиационных
поправок без разложения по степеням aZ [45—47].
Глава 5
ВЗАИМОДЕЙСТВИЕ АТОМОВ С ИЗЛУЧЕНИЕМ
§ 5.1. Излучение одного фотона
Процесс излучения фотона электроном описывается в низшем
порядке фейнмановской диаграммой рис. 5.1, где индексы А, А'
относятся к начальному и конечному состояниям электрона, а к, е —
волновой вектор и поляризация фотона.
Покажем вначале, что свободный электрон вообще не может
излучать фотоны. Действительно, для свободного электрона
fP- = —m^, где р= (р, Е) (см. (4.9)). Для фотона
А
к^ = О, где к = (к, со) (масса фотона равна
нулю). Пусть pi, р2 — 4-импульсы электрона в
начальном и конечном состояниях. Тогда закон со-
■\улЛ/\^ хранения 4-импульса дает: р^— к = pj- Возводя
' это равенство в квадрат (pj — Ip^k + к^ = р|) и
используя предыдущие соотношения, получаем
Pik = 0. Пусть электрон в избранной нами систе-
Рис 5 1 График ^^ отсчета до излучения покоился, т.е.
Фейнмана, соответ- Pi = (О, ш). Тогда Pik = —mco = О, откуда следу-
ствующий процессу g^, ЧТО СО = 0. То же самое относится и к погло-
излучения кванта щению. Таким образом, излучение (поглощение)
запрещено законами сохранения энергии и
импульса. Поскольку для связанного электрона в атоме справедлив
только закон сохранения энергии, но не импульса, такой электрон
может излучать и поглощать фотоны.
Согласно правилам соответствия (см. § 2.6), матричный элемент
5-матрицы, описывающий излучение фотона (см. также выражение
(2.130)), представляется в виде
<ф0|5^')(к, е)|Ф°> =^ J d^x ^^,(x)?<^)*e-'(''-"0,j,^(x), (5.I)
где е^^^ — 4-вектор поляризации фотона. Интегрируя в (5.1) по
времени
J е'('^/+"-'^^)' dt = 2зг6((о - £д + £д.) (5.2)
180
и учитывая, что с^ ^ = е7 (где е — вектор поляризации), получаем
(см. также (1.1))
<фО|5(»)(к,е)|Ф°>= -^^ ((е-а)е-^''')^,^6(0)-£, + £,.)•
(5.3)
Выясним теперь, как перейти от матричного элемента 5-матри-
цы к вероятности процесса. При этом рассмотрим матричный
элемент общего вида S^j (г — начальное, / — конечное состояния). По
аналогии с только что проведенным вычислением можно понять, что
в общем случае матричный элемент S^j будет пропорционален
?^\^ Efk~^ Eik\< ГД^ ^fk — энергии частиц (электронов, фото-
нов) в конечном состоянии, Ец^ — энергии частиц в начальном
состоянии. Введем амплитуду процесса f/;/ по определению
Sgf = —luiUijb
\
S^/.-S^^
(5.4)
Если теперь считать, что вероятность процесса Wij определяется
величиной I Sif I ^, то эта вероятность оказывается бесконечной.
Чтобы получить результат, имеющий физический смысл, заменим одну
из двух 6-функций, входящих в 15;/1 ^, интегралом
оо
Ь{Е)=^\ё^=Ыи {5.5)
—оо
Далее, в этом интеграле интервал интегрирования по времени будем
считать конечным и равным Г, т. е. произведем замену Ь{Е) на
' г/2
6^(£) = ^ J е''^' dt. (5.6)
-г/2
^ Помня, что выражение bj{E) умножается еще на Ь{Е), заменим
его на
* 6^(0) = Г/2зг. (5.7)
[ Таким образом, вероятность процесса оказывается пропорциональ-
I ной интервалу Г, т. е. времени наблюдения, — поэтому она и
'' сказывается бесконечной при Г—»оо. Физический же смысл
можно придать вероятности, отнесенной к единице времени, т. е.
величине
w,, = \;\S„\^ = 2ii\U„\''.b
S ^/t - S ^ik
(5.8)
Если конечное состояние системы относится к непрерывному
спектру (как в нашем случае), то практический интерес пред-
181
ставляет знание вероятности того, что импульсы частиц в
конечном состоянии находятся в заданных интервалах dp^/^
(индекс к нумерует частицы в конечном состоянии). Такая
вероятность равна
^^^f = ^^fni^s' (5.9)
к
где dpj/{2ji)^ — число состояний частицы в объеме фазового
пространства dpp В нашем случае (один фотон в конечном
состоянии)
Подставляя выражение для амплитуды согласно (5.4), (5.3),
получим
dw^A^, е) = ^ I ((е*а)е-'''') 1 'б(а> -Е^ + Е^.)о, d<x> dv,
' ^'^^ (5.11)
где V = к/со. Интегрирование выражения (5.11) по со дает
вероятность излучения фотона с поляризацией е в заданном направлении
V в единицу времени:
dw^A^, е) = ^ ш^д- I ((е-а)е-'''') 1' dv. (5.12)
I л'А I
Здесь содд' = Е^ — £д' — частота излучения.
Если нас не интересует направление вылета фотона и его
поляризация, то выражение (5.1-2) необходимо проинтегрировать по
углам и просуммировать по поляризациям. Тогда полная вероятность
перехода атома из состояния А в состояние А' с излучением одного
фотона равна
^лл' = i <«дд' S И^ I ((е*«)е-'''Л 1'. (5.13)
е I Л'Л \
Мы не будем теперь в общем случае выполнять суммирование по е
и интегрирование по v в (5.13) — соответствующее выражение
будет получено ниже другим способом (см. § 6.1).
Совершим переход к нерелятивистскому пределу в (5.13).
Рассмотрим вначале одноэлектронный атом. Понимая теперь под
(...)д'д матричный элемент с нерелятивистскими (шрёдингеровски-
ми) волновыми функциями, мы должны считать, что вектор г
имеет характерную для нерелятивистского атома величину
|г| ^si а^= 1/та (в релятивистских единицах). С другой стороны,
|к| =(ofvma^ — частота перехода при излучении также
имеет характерную в нерелятивистском случае величину. Таким
образом, в показателе экспоненты ехр (—гкг) в (5.13) стоит малая
182
величина порядка maxima = а и экспоненту можно заменить
единицей *).
Далее, используя (1.197), в нерелятивистском пределе получаем
^-о^'а = <^'Х^гА + Ха-оФа =i<' {о(ор) + (ор)в}фд, (5.14)
а вспоминая также соотношение (1.25), видим, что в
нерелятивистском пределе
В результате нерелятивистский предел выражения (5.13)
записывается в виде
"'^^'^^'"^^'^ $ dv |(ер)д,д|^ (5.16)
е
Чтобы выполнить здесь суммирование по е, воспользуемся
формулами (4.187)—(4.194) из §4.4. Это дает тот же результат, что и
(4.195):
5:i(eP)A'Al'=l(vxp)A'Al'- (^-1^)
е
Интегрирование по v также выполняется подобно (4.196).
Окончательно имеем 2
"'-' = I^--'I(P)vaI^- (5.18)
Используя известное квантовомеханическое соотношение
^^аА^)а-а = агН]-)А'А = h (Р)а'а' (5.19)
ще Н — одноэлектронный гамильтониан вида [I, (1.1)], и
определение оператора дипольного электрического момента электрона
й = ет, (5.20)
вероятность перехода можно выразить через матричные элементы
оператора d:
"'аа'= 1<'1 (5) a'aI'- (^•^^^
Таким образом, в нерелятивистском пределе излучение атома —
это излучение электрического диполя.
Переход от формулы (5.21) к соответствующему выражению для
многоэлектронного атома заключается в замене одноэлектронного
оператора дипольного электрического момента многоэлектронным:
6 = ^5,. (5.22)
i = l
*) Неравенство | к 11 г | - 2л: а„- / X <к 1 физически соответствует тому, что
длина волны излз^ения X много больше размеров атома а^,.
183
Тогда
• = |<«^'1(б)д'д|', (5.23)
причем в формулу (5.23) нужно подставлять уже многоэлектронные
волновые функции и разности энергий. Выражение (5.23)
представляет собой одну из возможных форм записи вероятности ьУдд' —
форму «длины». Другую форму — так называемую форму
«скорости» — представляет собой выражение (5.18). Эти названия
соответствуют размерности операторов D/e и Vim. В случае
многоэлектронного атома это выражение имеет вид
где
N
P = i:Pi (5.25)
— оператор суммарного импульса электронов в атоме. Формулы
(5.23) и (5.24) переходят друг в друга благодаря существованию
обобщенного на многоэлектронные атомы соотношения (5.19):
<«дд'(К)д'д = ([К^]-)д'д =Ъ (Р)д'д. (5.26)
где
N
а оператор Н теперь представляет собой гамильтониан для
многоэлектронного атома и определяется формулой [I, (2.3)].
Еще одна возможная форма записи выражения для вероятностей
переходов следует из соотношения
' N
<«дд'(Р)д'д = ([Р'^]-)д'д = -г"
(5.27)
дд
где V — потенциальная энергия взаимодействия электронов с ядром
V = ^^. (5.28)
i = l
Формула (5.28) проверяется непосредственно, как и (5.26), с
учетом очевидного соотношения
V,7-=-V,^, (5.29)
ik ik
ИЗ которого следует, что потенциальная энергия взаимодействия
электронов друг с другом не дает вклада в коммутатор (5.27).
184
Помимо вероятностей переходов, в теории излучения атомсв
удобно использовать так называемые силы осцилляторов, которые
определяются так *):
/,,.= -|ma>,,.|(R),.J^ (5.30)
и связаны с вероятностями соотношением
^ЛА'=-^<А'/ЛА- (5.31)
Для сил осцилляторов можно доказать так называемую теорему о
суммах (Томаса—Рейхе—Куна [2]):
1Гал' = ^, (5-32)
А'
где суммирование распространяется на все состояния атома, а Л^ —
число электронов.
Для доказательства используем прежде всего равенство (5.26)
вначале для матричного элемента (К)д'д, а затем для матричного
элемента (И)д'д = (К)дд'. В последнем случае знак в правой части
(5.26) будет противоположный, поскольку сод-д = —<Одд.. Взяв затем
полусумму этих выражений, получим
Е /дд' = - i '■ Е {(Р)д'д(К)дд' - (Р)дд'(К)д'д}- (5.33)
А' А'
Суммируя по полной системе функций А', запишем
2/,,. = i([PR]_),,. (5.34)
А'
Вычисляя, наконец, коммутатор
[PR]_ = -3iN (5.35)
и подставляя его значение в (5.34), приходим к равенству (5.32).
Формулы (5.23), (5.24) и (5.27) эквивалентны друг другу только
при использовании точгалх волновых функций и энергий. При
использовании приближенных функций расхождение между ними
может оказаться значительным. По величине этого расхождения
можно, в принципе, судить о качестве приближения и о его пригодности
для расчетов вероятностей переходов. То же самое можно сказать
относительно теоремы о суммах сил осцилляторов — она также
справедлива лишь для точных функций и может быть использована
в качестве критерия качества приближений.
Рассмотрим теперь подробнее различные формулы для
вероятностей переходов и теорему о суммах в одноэлектронном приближе-
*) Согласно такому определению, сила осциллятора отрицательна для процесса
излучения и положительна для поглощения [1].
185
НИИ, в частности в приближении Хартри—Фока. Вместо (5.26)
теперь можно написать
<«дд'(г)д'д = ([гЛ^'^(г)]_)д.д. (5.36)
При вычислении коммутатора в (5.36) нужно учесть, что
нелокальный обменный оператор [I, (2.104)] не коммутирует с г. В
результате
[гЛХ'^(^)]-/(9) =^р/(9) - \ (г-г')р?(9'; q)v{q'q)f{q') dq'.
(5.37)
Здесь мы использовали запись [I, (2.99)] для обменного оператора и
обозначение q^r, с. Зависимость от спиновой ■ переменной здесь
несущественна, и мы используем переменные q лишь для удобства
сравнения с результатами гл. 2 части I {f{q) — произвольная
функция).
Из (5.37) следует, что из-за нелокальности обменного
оператора эквивалентность различных формул для вероятностей переходсв
нарушается. Поскольку формула (5.26), являющаяся аналогом
(5.37), должна быть использована при доказательстве теоремы о
суммах сил осцилляторов, ясно, что эта теорема в
приближении Хартри—Фока также нарушается. Однако в приближении
Хартри, как и в любом другом приближении с локальным
потенциалом, соотношения между вероятностями выполняются, если
при этом использовать одноэлектронные энергии, являющиеся
точными собственными значениями соответствующих одноэлектрон-
ных уравнений. Для локальных одноэлектронных потенциалов
выполняется также теорема о суммах. В одноэлектронном
приближении она выглядит так:
lfnn'=h (5.38)
п'
причем доказательство полностью аналогично приведенному выше
для точных функций. Суммирование по п' в (5.38)
распространяется на все одноэлектронные состояния, в том числе и на занятые
состояния в многоэлектронном атоме. Таким образом, при
использовании теоремы о суммах, например для валентного электрона,
необходимо учитывать также запрещенные принципом Паули
переходы во все состояния атомного остова.
Покажем теперь, что в приближении случайной фазы
соотношения между вероятностями и теорема о суммах, в отличие от
приближения Хартри—Фока, выполняются строго [3, 4]. Согласно [I,
(4.421)], матричный элемент, соответствующий амплитуде
перехода из состояния А в состояние А' в форме «длины», в приближении
случайной фазы имеет вид
(r)^,^ = Sprpf„^'(^';^). (5.39)
186
Рассмотрим в приближении случайной фазы также матричный
элемент коммутатора [гЛ^'*'(^)]_:
([гЛХ'^(9)]_)д.д = Sp {[Th''*^{g)]-Pt^\g'; д)} =
= Sp {Th'"^{g)p^^\g'; д)} - Sp {h'^'^igypf^-ig'; g)}. (5.40)
Используя эрмитовость оператора h^'^{g) во втором члене в правой
части (5.40), можно заменить под знаком Sp оператор h^'^{g) на
АХФ(9'):
Sp{[Th^'^{g)]_pt^\g';g)} =
= Sp {r(F«'(9) - h'"^{g'))pt^\g'; g)}. (5.41)
В левую часть (5.41) подставим коммутатор (5.37):
Sp {[Th'"^(g)]_pt^\g'; д)} = ^ Sp {ppt^\g'; д)} -
-J (г- r")v(gg")pW' я)9^о\я\ я") dg dg". (5.42)
Для вычисления правой части (5.41) используем уравнение
[I, (4.419)]:
Sp {TiV'^ig) - h''^{g))p't^\g; я)} = Одд.Sp {TpU\g; д)} -
-\ Tv{gg")p^^\g; д")р^,{д"; д) dg dg'' +
+\ Tv{gg")p^^\g"; д)р\{д; д") dgdg". (5.43)
Заметим, что второй член в левой части [I, (4.419)] исчезает при
вычислении Sp и не дает вклада в (5.43). Далее, нетрудно
убедиться, что члены, содержащие интегралы по dg dg" в правых частях
(5.42) и (5.43), одинаковы и взаимно уничтожаются при
подстановке в (5.41). Окончательно имеем
<«лл- Sp {гр^^\я'; д)} = ;^ Sp {Мо(я'; я)), (5.44)
что и представляет собой доказательство справедаивости
соотношения типа (5.26), а следовательно, и эквивалентности формул
«длины» и «скорости» для вероятностей переходов в приближении
случайной фазы. Отсюда же следует и справедаивость теоремы о
суммах сил осцилляторов в виде (5.38).
Нужно, однако, заметить, что во всех этих рассуждениях — как
в приближении Хартри—Фока, так и в приближении случайной
фазы — предполагалось, что исходное и конечное состояния
описываются одним и тем же оператором Хартри—Фока. Само по себе такое
предположение тоже является приближением (см. § 1.2), хотя и
достаточно часто употребляемым.
В заключение этого параграфа приведем оценки порядка
величины для вероятности дипольных переходов. Запишем выражение для
вероятности (5.21) в обычных единицах, т. е. через константы А, с.
187
Для этого нужно, в принципе, сохранить эти константы во всех
выражениях, необходимых для вывода (5.21). Мы не будем этого
делать и приведем сразу ответ:
"'^^-I^^'^Kr)^^!^. (5-45)
Пользуясь таблицей, приведенной в части I, подставим в (5.45)
характерные атомные значения для разностей энергий сод-д *« me'^/tp-
и расстояний г fif а^= h^lme^. При этом оценки будут справедливы
для оптических (валентных) электронов в атомах, для которых
^эф**'!- Тогда
w:
Щ f=л.-'. <^-«'
где <о — атомная единица времени. Подставляя значение t^ из
упомянутой таблицы, получаем
W » 109 (.-1. (5.47)
Величина, обратная вероятности перехода в единицу времени, по
порядку величины определяет, очевидно, «время жизни» атома на
начальном уровне *): t » 10"^ с.
Заметим, что из соотношения Е = Йсо к. ht~^ следует, что и в
атомных, и в релятивистских единицах (при h = l) энергия
измеряется в тех же единицах, что и t~^. В этих же единицах измеряется
W. Отсюда сразу можно увидеть масштаб малости величины w по
сравнению с характерными атомными энергиями EqI в
релятивистских единицах £„ « та^, w «к та^, т. е. w^ а^^о- Значения
вероятностей определяют ширину (т. е. неопределенность в значении
энергии) атомных уровней (см. следующую главу). Полученный
здесь результат w^cEq говорит о том, что уровни энергии в атомах,
как правило, хорошо отделены друг от друга. Это относится и к
компонентам тонкой структуры атома (см. § 1.3) AEf « a^EQ':^w и
даже, в некоторых случаях, к лэмбовским подуровням, для которых
АЕ^ л^ та^ (см. § 4.4), но неравенство АЕ^ > w выполняется
благодаря различию в числовых коэффициентах (как, например, для
подуровней 2Si, 2pi_ — см. § 4.4).
Наконец, введем еще понятие интенсивности излучения /(к, е):
/дд.(к, е) dv= Йсодд, йьУддЧк, е), (5.48)
где dw определяется формулой (5.12), содд. — частота излучения.
Левая часть (5.48) представляет собой энергию, излучаемую в еди-
*) При этом нужно считать, что распад уровня А определяется главньш переходом
А -*А' (подробнее об этом см. в следующей главе).
188
ницу времени в интервал телесного угла dv (имеется в виду энергия
излучения с определенной частотой и поляризацией). Аналогично
определяется полная интенсивность излучения
(проинтегрированная по углам и просуммированная по поляризациям):
^АА' = f^^AA^^^AA^^ (•5-49)
ще ьУдд. определяется формулой (5.13). Все приведенные выше
формулы для вероятностей в нерелятивистском пределе могут быть
использованы также для интенсивностей.
§ 5.2. Спонтанное и вынужденное излучение
и поглощение света
Выше, в § 5.1, рассматривалось так называемое спонтанное
излучение атома. Помимо спонтанного, существует еще вынужденное, или
■индуцированное, излучение. В этом параграфе мы рассмотрим
также индуцированное излучение и установим некоторые общие
соотношения между различными радиационными процессами.
Возьмем состояние электромагнитного поля, в котором имеется
Af„ фотонов данного сорта п (т. е. с определенным импульсом,
поляризацией или моментом и четностью). Тогда матричный элемент
одноквантового перехода, соответствующего излучению фотона,
умножается, согласно формуле (2.106), на VA^„ -|- 1. Вероятность
перехода, таким образом, умножается на Л^„ -|- 1.
До сих пор, производя вычисления матричных элементов с
помощью диаграммной техники, мы не учитывали этого множителя,
т. е. заменяли его единицей. Эта единица в сумме двух членов
N„+ I соответствует спонтанному излучению, а слагаемое N„ —
вынужденному излучению. Вынужденное излучение характерно
тем, что его вероятность растет с ростом Л^„, т. е. наличие фотонов
в исходном состоянии стимулирует (индуцирует) дополнительное
испускание таких же фотонов. Спонтанное излучение, в отличие от
индуцированного, происходит при N„ = 0 в исходном состоянии.
Таким образом, в общем случае ьУ|у~Л^„+1, где w-f —
вероятность перехода с излучением кванта (г, / — начальное и конечное
состояния атома). Матричный элемент обратного перехода f—*i
пропорционален V^, как следует из (2.105). Под обратным
переходом здесь нужно понимать следующее: в системе Stom плюс поле
по-прежнему имеется N„ фотонов, но теперь атом находится в
состоянии /. При этом нас интересует вероятность Wji того, что атом
перейдет в состояние i, поглотив один квант. Из сказанного выше о
зависимости матричных элеменгов от N„ следует соотношение
Эйнштейна:
W., N +1
189
Свяжем теперь число фотонов N„ с интенсивностью падающего
на атом излучения. Энергию излучения, падающего в единицу
времени на единицу площади, запишем как J^^^ dta dv, где Jf^^ —
интенсивность излучения с волновым вектором к и поляризацией е.
Число состояний поля с заданной поляризацией е в интервале к,
к -I- сПс равно (в этом параграфе мы используем обычные единицы)
^^. (5.51)
(2лЙ)
Вспоминая, что са = сЛ, перепишем (5.51) так:
1 ш^ rfto dv
(5.52)
Учитывая также, что £ = Йсо (е — энергия), запишем число
состояний в интервале энергий:
Й^ ш^ rfto dv 1 ш^ rfto dv
ЦтЛ)^ с^ (2л:)^
(5.53)
Энергию излучения, падающего в единицу времени на единицу
площади, получим, умножив (5.53) на энергию кванта Йсо, на
число квантов в данном состоянии поля N^^^, а также на скорость
квантов с. Тогда возникнет равенство
S^i^i^^V . de>rfv, (5.54)
с^ (2л)^ "^^ "^^
откуда
^Ке = -^\е- (5.55)
Рассмотрим следующие вероятности: вероятность спонтанного
излучения фотона (е импульсом к и поляризацией е) с?ьи^9(к, е),
вероятность индуцированного излучения фотона с?ьуЙ^(к, е) и
вероятность поглощения фотона dWfi(Vi, е). Тогда из (5.50) следует:
dwf^{)ii, е) = dWj^{K e) = N^^ dwf/{k, е) =
Если падающее излучение изотропно и неполяризовано (J^^ не
зависит от V, е, т. е. /^^е = .^т)> то интегрирование по v и
суммирование по е в (5.56) дают соотношения между полными
вероятностями радиационных переходов
где
w,j = '^dw,j{k,e). (5.58)
190
Можно ввести также полную спектральную интенсивность
падающего излучения
^. = 1\^-^Ке' (5.59)
е
которая в случае изотропного, неполяризованного излучения равна
7„ = 8л/„. (5.60)
Тогда
(и) л:^ ~ (с) (5.61)
WW = Wf^ г / W./. ^ '
Если состояния атома г и / вырождены, то полная вероятность
излучения или поглощения получается суммированием по всем
вырожденным конечным состояниям и усреднением по всем
вырожденным начальным состояниям. Обозначим соответствующие кратности
вырождения через gj ч gj и рассмотрим для простоты такой случай,
коща переходы одинаково разрешены для всей совокупности
вырожденных состояний. Тогда усреднение ничего не дает, а суммирсва-
ние дает множители g^, gj, и мы получаем
Вместо вероятностей ьу^"\ wy^, Wji иногда употребляют
коэффициенты Эйнштейна
A,j^wfl, B,,^fwf/; B,, = j-wj„ (5.63)
где величина Jjc есть пространственная спектральная плотность
излучения. Записанное через коэффициенты Эйнштейна
соотношение (5.62) выглядит так:
SjBtj = 8^Bj, = gj^,A,. (5.64)
, § 5.3. Мультипольное излучение
В этом параграфе мы рассмотрим вероятности излучения фотонов с
определенными моментами и четностью.
Мультипольное разложение для вероятности. Вероятность
гг)дд'(у7М) излучения фотона с моментом /, его проекцией М и
четностью, определяемой значением /, мы получим непосредственно из
точной формулы (5.13). Для этого используем разложение вектсра
е'ехр (—г'кг) по векторным сферическим функциям (2.131)
e-e-icr = ^ (-04e*Y,,^(v))g^*r)Y;,^(n), (5.65)
jlM
191
к г
где V = ТкГ' " ~ ТгГ' ^'(^''^ ~ 4л/ДЛг), /ДЛг) — сферическая
функция Бесселя (см. (2.169)).
Для доказательства (5.65) используем разложение плоской
волны по сферическим функциям (2.168)
е-^кг = ^ {-i)%{kr)Y^^{v)Y'Jn). (5.66)
Im
Спроецируем обе части равенства (5.65) на тройку базисных
векторов е, V, (е X V). Умножая обе части (5.65) на а (а = е, v, (е х v)),
получаем
(ае*)е-"'' = ^ (-0'(e*Y^,^(v))(aY},^(n))g^*r). (5.67)
jlM
Подставляем выражения для Yj^,^ (2.131):
(ае*)е-"'' = ^ (-0' ^ C%(miK)Y^^{v){e%) х
JIM m\iL
хЕ CiM('«V')yL'(n)(ax;:.)g,(*'-). (5.68)
Используя, далее, условие унитарности [I, (3.32)] для
коэффициентов Клебша—Гордана, преобразуем (5.68) к виду
(ае*)е-"'' = ^ (-0'g,(*'-)y,„(v)y;„(n) ^ {е%){ах;). (5.69)
Поскольку Хц — сферические орты, по которым может быть
разложен любой вектор (см. (2.138)), то
i:(eV(a<) = (e*a). (5.70)
При а = е правая часть (5.70) равна единице, а при а = v, (v х е) она
равна нулю. Таким образом, равенство (5.65) выполняется в
проекциях на все три базисных вектора и его можно считать доказанным.
Подставим теперь разложение (5.65) в формулу (5.13) для
вероятности:
W
АЛ- 2п
jlM j'l'M"
х^ S rfv (e*Y,,^(v))(eY>,^(v)). (5.71)
e
Выполняя в (5.71) суммирование по е, получаем (см. опять (4.195))
2 jrfv(e*Y,,^(v))(eY>,.^(v)) =
= jdv(vxY.,^(v))(vxYJ.,.^^(v)). (5.72)
192
Векторное произведение в (5.72) отлично от нуля, только если
функции Yjii^ образуют линейные комбинации, соответствующие
одной из двух поперечных векторных функций Yy^(v) или
Y^J^(v). В этом случае интеграл (5.72) представляет собой интеграл
ортогональности:
j rfv (VXY%(y)){vX Y^^^(v)) = 6,-.6^^6„, (5.73)
где s, s = E, M. Окончательно выражение (5.71) после подстановки
в него (5.72), (5.73) принимает следующий вид:
"^АА- = ^^АА-^{\ («(«у5; + 1("дд.г)У^^^1д^(п) -
jM
+ l(g;(<«44''-)(«Y^^(n)))^,j2). (5.74)
С учетом определений (2.170), (2.171) формулу (5.74) можно
переписать так:
"'дд' = ^1:||(«А15и'-))д-дР+1(аА1%(г)),.,Р), (5.75)
JM
где А^^-)д^(г), A^lf{r) — волновые функции фотонов. Выражение
(5.73) представляет собой мультипольное разложение для
вероятности однофотонного перехода. Отдельные члены этого разложения
представляют собой вероятности излучения фотона с
определенными моментом и четностью.
Правила отбора при мультипольном излучении возникают
непосредственно при интегрировании по углам и суммировании по
проекциям момента М в (5.75). Эти правила могут быть установлены также из
общих соображений на основе теории углового момента [I, гл. 3].
Пусть /;, М; и Jf, Mf — полный момент и его проекция для
электрона в атоме (фактически пока речь идет об одноэлектронном
атоме) в начальном и конечном состояниях. Тогда из закона
сложения моментов следует
\Ji-J,\^i^Ji + Jf, {5.Щ
М=М. + М^, (5.77)
где /, М — момент фотона и его проекция. Кроме того, существует
правило отбора по четности
Р; = РгРф' (5.78)
где Р; / — четность начального (конечного) состояния электрона в
атоме, Рф — четность фотона. Формулу (5.78) можно переписать,
пользуясь тем, что все четности равны ± 1:
P^ = PiPf (5.79)
7 Л, Н, Лабзовский ' ■'^
Тоща, вспоминая результаты § 2.4, получаем для электрического
мультипольного излучения
P^p. = (-iy, (5.80)
а для магнитного мультипольного излучения
P/P. = (-iy+i. (5.81)
Следующей нашей задачей является поиск вида
мультипольного разложения в нерелятивистском пределе. Эта задача,
однако, проще решается в иной калибровке, нежели та, которая
была использована в § 2.4 для определения волновых функций
фотона. В § 2.4 для калибровки потенциалов электромагнитного
поля мы использовали условие поперечности. В принципе можно
отказаться от этого условия, вводя одновременно продольные и
скалярные фотоны и потребовав кo^iпeнcaции их вкладов
подобно тому, как это делалось в общем случае в § 2.2. Для такой
компенсации достаточно, как мы видели, выполнения условия
Лоренца.
Калибровочное преобразование (2.8), (2.9) в импульсном
представлении принимает вид
A^A + vx(k, О, (5.82)
V^V + xiKt). (5.83)
При этом мы будем требовать, чтобы добавка не меняла квантовых
чисел фотона, т. е. момент, его проекцию и четность. Для фотонов
электрического типа возможен следующий выбор x{ii, t):
Х(к, t) = с6((о - |к| )y.j^(v)e-™'. (5.84)
Тогда, с учетом (2.158), можно написать
^i%(^' О = с6(а> - |к| )(Y(^(v) + CY("^(v))e-™', (5.85)
^соум(»^' О = с6(а> - |к| )CY^.^(v)e-™'. (5.86)
Нетрудно убедиться непосредственно, что условие Лоренца
выполняется для потенциалов (5.85), (5.86).
Поскольку функции Y^^, Y^^,
^S'm' '^^'^ У^^ говорилось в
§ 2.4, образуют полный набор, никакой другой добавки к Y^^
сделать нельзя. По этой же причине к функции Y^^^ добавить вообще
ничего нельзя, так как добавка Y^"^ изменила бы ее четность.
Согласно (2.182), выражение (5.75) теперь нужно заменить
следующим:
W'AA' = e^i: ||(«<м('-) + V^j„(T))^.J^+ |(aA(ff),(r))^.j2J.
JM
(5.87)
194
При переходе к нерелятивистскому пределу удобно использовать
калибровку (5.85), (5.86) и выбрать константу С так:
(5.88)
■=-¥¥■
Если теперь подставить (5.88) в (5.85) и перейти к координатному
представлению для потенциалов А^,^ и V^j,^ так, как это было
сделано в конце § 2.4, то мы получим
<м(г) = {^^Sj.i(kr)Y..,, ^(п), (5.89)
^со/м(г) = 4^^Sj{kr)Y.„(n). (5.90)
При переходе к нерелятивистскому приближению учтем прежде
всего, что кг — малая величина порядка а (см. § 5.1), и разложим
функцию gj{kr) в ряд, ограничиваясь старшими членами.
Используя разложение функций Бесселя (см. (2.169)), получаем
e.(;tr)=^^bM-. (5.91)
Электрические мультиполи. Рассмотрим вначале
электрические мультиполи. Из (5.87), а также из вида потенциалов (5.89),
(5.90) следует, что в нерелятивистском пределе главный вклад дает
член со скалярным потенциалом V^^j^. При этом по-прежнему
скалярные (и продольные) фотоны не дают вклада в выражения для
напряженности поля.
В нерелятивистском пределе часть выражения (5.87),
соответствующая электрическим мультиполям, может быть представлена в виде
^АА- е 2 у[(2/ + 1),.]2 \УЩм)а'а\ ' У^-"^^)
jM
где
^^'^(^•) = lШ^'■^V(") ^^•^'^
— электрические мультипольные моменты атома. При этом
подразумевается, что матричный элемент в (5.92) вычисляется уже с
нерелятивистскими волновыми функциями. Это дает возможность
распространить формулу (5.92) также на случай Л^-электронного атома.
Теперь в качестве функций -фд, -фд. нужно использовать многоэлект^
ровные волновые функции, а оператор (5.93) заменить на
N (5.94)
Q(>„...,r^)=2Q(>,).
Нетрудно убедиться, что при / = 1 формула (5.92) дает результат,
совпадающий с (5.21). Действительно,
^'!^ = h'<A-l\^&A-A\'- (5.95)
3
flf=0. ±1
195
Используя теперь формулы [I, (3.114)], [I, (3.83)], убеждаемся, что
(5.95) содержит скалярное произведение (г)дд-(г)д-д, записанное
через сферические компоненты векторсв, и сводится, таким образом,
к (5.21).
Правила отбора для мультипольного электрического -излучения в
нерелятивистском пределе зависят от схемы связи. В случае LS-свя-
зи эти правила таковы:
\L,-L^\^j^L, + L^, (5.96)
M=M^-Mj^, (5.97)
/
S; - S/ = о, (5.98)
Mg-Mg =0, (5.99)
/
где Li, M^^, Lp M^ — значения суммарного орбитального момента
атома и его проекции в начальном и конечном состояниях, S^, Mg,
Sf, Mg — значения суммарного спинового момента и его проекции.
Правила отбора (5.96), (5.97) являются естественным следствием
(5.76), (5.77), а правила (5.98), (5.99) возникают в силу
независимости операторов перехода (5.94) от спиновых переменных. К этим
правилам нужно добавить также правило отбора по четности (5.80).
Порядок величины вероятностей различных мультипольных
электрических переходов следует непосредственно из (5.91):
(£/)
^=«2^-2. (5.100)
Формула (5.100) относится к переходам, разрешенным правилами
отбора (5.96)—(5.99). В принципе эти правила, в отличие от (5.76),
(5.77), не являются абсолютно строгими и нарушаются при учете
спин-орбитального взаимодействия. Поэтому могут существовать
«запрещенные» мультипольные электрические переходы (например,
при Si^Sf), вероятности которых меньше, чем определяемые
по (5.100).
Магнитные мультиполи. Перейдем к магнитным мультиполям.
В нерелятивистском пределе, пользуясь (5.91), представим
магнитную часть (5.87) в виде
^m = ,2y^J^Ll}}^l^^}^,.^m. .2 (5.101)
/((2у-|-1)!!]^
где величины
^^^(^•) = тЙ^1(^'-^«^^мЧп) (5-^02)
можно назвать магнитными мультипольными моментами атома.
Выражение (5.102) еще не преобразовано, однако, окончательно к
нерелятивистской форме, поскольку в него входят матрицы Дирака и
196
где
матричный элемент в (5.101) пока предполагается с дираковскими
волновыми функ1щями.
Проведем, в связи с этим, дальнейшие преобразования. Прежде
всего, можно написать:
еШ'1^),; = -^^ S ]д-л(г)'-^У^(п) dr, (5.103)
где ]д'д(г) — недиагональный ток (ток перехода) в релятивистской
форме (см. (1.15)). Здесь нам понадобится нерелятивистское
выражение для тока, которое получается из (1.15) предельным
переходом с учетом (1.202), (1.29):
i^"") = ~ 2^ {(ор^)*о^ + я1'*о(аря1))} =
= ш (^*^^ - ^^^*) - 2^ '■0^ Wo^)- (5.104)
Используем теперь иную запись для векторных сферических
функций Y^-^^(v). Для этого вначале покажем, что
Vf)=|k|vf), (5.106)
Vj( ^ — угловая часть оператора градиента Vj^ в импульсном
пространстве. Для доказательства (5.105) нужно взять явное
выражение для вектора V,, который имеет в сферических координатах
всего две составляющие [5]:
у(")= (± -^-^\ (5.107)
* 1эг)' sini) Э<р1'
и подействовать на Yj^, пользуясь правилами дифференцирования
сферических функций. Можно проверить непосредственно, что
получающийся при этом вектор записывается в виде
Vry,M(v) = ЩТТ O-'^T+TY..^, ^(v) + и + 1)V7Y, ._, ^(v)).
(5.108)
Сравнивая (5.108) с (2.153), получаем формулу (5.105).
Векторную сферическую функцию У^'^(У) можно теперь
получить так:
yW(v) = (vxY(^(v)). (5.109)
Очевидно, аналогичное выражение можно записать и в
координатном представлении:
YW(n) = (nxY(^(n)). (5.110)
197
Учитывая (5.105) и переходя в координатное представление, где
V„ = rV, получим
Подставляя теперь (5.111) в (5.103), в результате
интегрирования по частям получаем
e(Q%\-A = jh^T\ (rxj^.,(r))V(r/y,^(n)) dr. (5.112)
Используя выражение для тока (5.104), имеем
<0^>%')а-а = 7ТтШт{ш S ^д-СС-х V)яl^л)V('-^У,м(n)) dr-
-^ S ('•><™^ (^;'0%))V(r^y^fl,(n)) drj. (5.113)
Преобразуем интегралы в (5.113) и введем обозначения
^'^^^л'^^^Д' ^м^-Ш'-'^^м^- (5.114)
Величины С^ представляют собой компоненты неприводимого
тензора ранга у. Тогда, используя формулу
rot Нф = а X Уф -I- 9 rot а, (5.115)
где а, 9 — произвольные вектор и скаляр, запишем второй член
(5.113) в виде
j я1,;^(гX V)41,^.VGW dr = - j у^-^. rot {y\>AT)VG^ dr +
+\ro\Wj,T-^j,)VG^^dT. (5.116)
Поскольку rot r = 0, TO no формуле (5.115) получим
rot(4i,^r) = rxV4i,^. (5.117)
Если учесть также, что div rot а = О для произвольного вектора а,
то последнее слагаемое в (5.116) сводится к поверхностному
интегралу и исчезает. Таким образом, второе слагаемое в (5.113)
равняется первому.
Рассмотрим третий член, подынтегральное выражение в котором
преобразуем с помощью тождества
(ax(bxc))=b(ac)-c(ab), (5.118)
где а, Ь, с — произвольные векторы. Тогда, используя для удобства
тензорные обозначения, запишем
(rx(VxF)), = x,^/',-x,^/',. (5.И9)
198
Подставляем (5.119) в интеграл и применяем интегрирование по
частям, отбрасывая внеинтегральные члены*):
-.0")
= S
эс« д^с]1) э^с^
дх1
dr. (5.120)
Далее используем то обстоятельство, что компоненты тензора (Jj()
представляют собой однородные гармонические полиномы,
являющиеся решениями уравнения Лапласа:
^^Gi4> = Ar^y,.(n) = 0. (^-^21)
дх1
Таким образом, второй член под интегралом в правой части (5.118)
исчезает. Далее, рассмотрим оператор
^rV=r(nV). (5.122)
"'дх.
Градиент в сферических координатах, с учетом выражения (5.107),
может быть записан также в виде [5]:
V = nf-hiv(") = nf-i(nxr), (5.123)
где 1 — орбитальный момент. Отсюда
х.^=г^. (5.124)
' эх,. 9г-
в результате третий член под интегралом в (5.120) приводится к виду
xF l^ = F r-^^ (5.125)
Представляя д/дх,^ с помощью (5.123), находим
Непосредственное вычисление коммутатора в (5.126) дает
([^^.("i-^<nx'))]J^ =
= _(„A_i.,„xD)^=-5|-. <^'27)
*) В этой формуле индексы i, к относятся к декартовым компонентам тензоров,
тогда как индекс М нумерует сферические компоненты.
199
Учитывая также, что из определения О^ следует:
гЬ^^ = 1^г:1^ (5-128)
получаем
&
dS .. ddi]
xF"—^=(i-\)F"—^ (5.129)
i^k
Собирая теперь все члены в (5.120), получим
^(rx(VxF)),-^dr=U + l)\F,-^dT. (5.130)
Теперь, возвращаясь к прежним обозначениям и используя
определение орбитального момента (1.69), выражение (5.113) перепишем
в виде
еШум Va у + 1 V2y + 1 т^
^ S ^Д'(''+^°) ^Д^(г^У.^(п)) dr. (5.131)
При / = 1 величины у/4п/3rY^,^ представляют собой сферические
компоненты радиуса-вектора
Тогда
V(r)fl,= efl„ (5.133)
где е^ — сферические орты (М = 0, ± 1), и выражение (5.131)
содержит сферические компоненты вектора 1 + о. Вводя магнитный
момент электрона по определению
где ? — спиновый момент электрона, ц^ — магнетон Бора, можем
переписать (5.134) так:
К«)л-л = (0^)м)л-л- (5.135)
Подставив (5.135) в выражение для вероятности (см. (5.101)),
»C''^ = K'I:l(«)д'лl^ (5.136)
М=0, il
получаем, переходя от сферических компонент вектора |i к
декартовым:
В «обычных» единицах
<.^' = ф\(i^)л■J'• (5.138)
200
Порядок величины W^^^ легко установить, сравнивая
выражения (5.137) и (5.21) и учитывая, что в релятивистских единицах
d « 1/та, \л « 1/т. Таким образом.
Порядок величины вероятностей различных мультипольных
магнитных переходов, как и в случае электрических переходов, следует из
(5.91):
^^-„2/-2 (5.140)
"^АА
Оценки (5.139), (5.140), как и (5.46), справедливы для
оптических электронов. Как и для электрических переходов,
оценка (5.140) относится к разрешенным магнитным переходам.
Из (5.139) и (5.100) следует, что по порядку величины
W^^^« iV^^^\ если оба перехода разрешены правилами отбора.
Однако фактически Ml-переходы в нерелятивистском
приближении разрешены только между компонентами одного мультиплета
(см. § 5.4, 5.5). В этой ситуации в выражении для W^f^^
возникает дополнительная малость ввиду присутствия частоты
перехода (в данном случае — малой величины) в более высокой
степени. Таким образом, W^-^^wf^'' для переходов внутри
одного мультиплета. Для переходов между различными мульти-
плетами, напротив, W^-^^W^f^^ (так как переход Ml
запрещен).
Правила отбора для мультипольного магнитного излучения в
нерелятивистском пределе в случае LS-связи отличаются от (5.96)—
(5.99) только правилом отбора по четности: вместо (5.80) нужно
теперь использовать (5.81).
Калибровочная инвариантность. В заключение этого
параграфа рассмотрим вопрос о калибровочной инвариантности выражения
(5.87) при использовании приближенных волновых функций [6—
10]. Подставив в (5.87) в качестве А^^ выражение (5.85) в
координатном представлении, запишем добавку к вероятности,
содержащую продольные и скалярные фотоны, в виде
^^AA'=c'^2\Up^A'y^Mr)-i^^.A^^j^(T)}dT\ , (5.141)
jM
а(п) _
где л^!,^ — «продольный» потенциал электромагнитного поля,
Рдд' — недиагональная плотность
Рдд' = е^д'(г)^д(г)- (5-142)
201
JM
Величина А^?д^ определяется формулой (2.158). Переходя к
координатному представлению, можно написать
А^^^мС-) = i ^8j(kr)Yj^{n). (5.143)
Теперь соотношение (5.141) (учитывая также (5.86)) можно
переписать так:
^^ЛЛ- = с ^ S I S {^^AA-pAA-Sj{kr)Yj„{n) -
- WV(g/*Oy,M(n))} dT\\ (5.144)
В случае, если волновые функции в (5.144) являются точными
решениями одноэлектронного уравнения Дирака, добавка (5.144)
обращается в нуль и вероятность, таким образом, не зависит от
выбора калибровочной постоянной С. Чтобы это продемонстрировать,
запишем «недиагональное» уравнение неразрывности (1.14) для
стационарных состояний (1.19):
(^A'-£A)p4A'-divw = 0. (5.145)
Отсюда сразу же получаем, интегрируя по частям в (5.144) и сводя
все выражение к поверхностному интегралу:
6^^,,.= -"^
AA'=Ci^S|Sdi^(W5;(*r)y,^(n))rfr| =0. (5.146)
JM
Калибровочная инвариантность сохраняется и в приближении Хар-
три—Фока—Дирака с локальным обменным потенциалом (3.122).
При этом подразумевается, что начальное и конечное состояния
описываются одним и тем же потенциалом F^*.
§ 5.4. Вероятности переходов в атоме водорода и
одноэлектронных ионах
Вероятности переходов в атоме водорода, пользуясь малостью
релятивистского параметра а = Vfjc^ 1/137, где vq — характерная
скорость электрона (см. § 1.5), можно вычислять в нерелятивистском
приближении. То же можно сказать и об одноэлектронных ионах с
не слишком большим зарядом ядра (aZ*3cl). Начнем поэтому с
электрического мультипольного разложения (5.92), справедливого в
нерелятивистском пределе. Значки А', А теперь расшифруем как
А = nJMj, где п — главное квантовое число; /, Mj — полный
момент электрона и его проекция. Как правило, в атомной физике
измеряется полная вероятность перехода, т. е. вероятность,
просуммированная по значениям проекции момента M'j в конечном состоя-
202
НИИ и усредненная по проекциям момента Mj в начальном
состоянии (см. § 5.2):
^fJK-r = 27ТТ S "'i/M/. П-ГМ-; (5.147)
Здесь величина ьу^5м ; n'j'M" представляет собой соответствующий
член суммы по / в (5.92).
Используем теперь теорему Вигнера—Эккарта [I, (3.100)]:
{QjM)пГМ'/, nJMj ~ ( ^)
f-hf,
'г j /^
Г7- л. л. <п'ГЩ^Чги>. (5.148)
у J J JJ
Подставляя (5.148) в (5.147) и используя для суммирования по
Mj, Mj, M'j [I, (3.31)], получаем
^fJK-r = e^ 2(2y-n)(y + i)co^^„^. ^„,j,||Q(£)||„j^|2. (5.149)
nJ.nJ- (2/+l)((2y + l).4]2 ' "^^ " '
wl
Для вычисления приведенного матричного элемента в (5.149)
нужно учесть, что в нерелятивистском пределе по отдельности
сохраняются орбитальный и спиновый моменты атома L, S (J = L + S,
причем в случае одноэлектронного атома L = 1, S = s, где 1, s — одно-
электронные моменты). При этом оператор перехода в (5.149)
действует только на пространственные переменные. Тогда можно
воспользоваться выражением для приведенного матричного
элемента оператора, действующего на координаты подсистемы [I, (3.121)].
Это дает
/
<n7V/'||Qf >||n/s/> = 6^^.V(2/' + 1)(2/ + 1) X ^
(_1)Г.-.ч/.-Л/^ •^'^4<n7'||Qf)||n/>, (5.150)
причем в нашем случае s= s = 1/2. Подстановка (5.150) в (5.149)
дает
пЛ-.п'П- J[(2j + \)nf
Согласно [I, (3.111)]
<n'l'\\Qf\\nl) = (-l)V(2/' + l)(2/ + l)f^' ^ ОЛЧ),„„ (5.152)
, , . ЛпЧЩ^'ЦШ). (5.151)
где
^\-. т ^ S Rn^r)r'RAr) dr, (5.153)
203
^ ^ni('') — одноэлектронные радиальные волновые функции (см.
[I, (2.132)]). Таким образом, окончательно
fp;. , 2(2/' + l)(2y + l)(y + l)(2Z' + l)(2Z + l)to^i+.l
nJl.nJl Л(2у-1-1)!!]^
'<(oio)T;r,lw,..^.(5..54,
Формула (5.154) определяет вероятность переходов между от^
дельными компонентами тонкой структуры атома, которые
нумеруются квантовыми числами /, /'. При этом в выражении для
частоты са„;; „Y мы пренебрегли тонкой структурой. Этого нельзя
делать, если вычисляются переходы между компонентами тонкой
структуры одного и того же уровня, т. е. при п= п'. В этой
ситуации нужно оставлять зависимость от / в выражении для частоты
^nij; n'l'j' ^^ пользоваться для вычисления разностей энергии
формулой (1.137).
Как правило, однако, в нерелятивистском случае представляет
интерес полная вероятность перехода между двумя уровнями п1,
п'Г. Такая вероятность получается суммированием (5.154) по /' и
усреднением по /. С помощью формулы суммирования [I, (3.60)]
получаем
27Тг2(2/' + 1){^;-;'^/.2}' = ^, (5.155)
откуда следует
" (о о о)'<*'-''• <'•''«
Заметим, что свойства 3/-символа в (5.156) (см. [I, (П4.2)])
полностью определяют сформулированные выше правила отбора для од-
ноэлектронных атомов. Перепишем эту формулу в атомных
единицах, более удобных в нерелятивистской теории (см. таблицу
перехода в начале книги). Формально для перехода нужно сделать
замены е^—»а, со—»та^са, Fy^—*-.—г^ 1с^\ w—»-—т ьу, что приво-
дит к результату
^(.У) г/.1^<^^'>У^'>"^-^'>-^[/' У 1\\^) )2. (5.157)
'^ni.nc у((2; + 1)!!]2 1,0 О oj ^ '^'•'^^'
204
1
Рассмотрим теперь более подробно электрические дипольные
переходы. В этом случае /= 1 и из (5.157) получаем
в формуле (5.158) 3/-символ отличен от нуля при двух значениях
/': Г = 1±1. Вычисляя 3/-символ согласно [I, (П4.2)] и подставляя
в (5.158), получаем
^i^i-i-Z+1 = I а'<;„' 1^1 wr (^Л+i;"')"' (5.159)
4f-i' /-1 = 1 «'<= n /-1 2ГП- ^^^i-v. n/)'- (5.160)
Для матричных элементов, входящих в (5.159), (5.160), имеют
место следующие правила сумм:
1 (J^\.u пд^ = 1 (^Л-п п,)' = <?; ы> (5.161)
причем подразумевается, что в суммирование по п включено и
интегрирование по сплошному спектру. Для доказательства (5.161)
нужно заметить, что радиальные одноэлектронные функции /?„;(г)
удовлетворяют в общем случае уравнениям [I, (2.140)]*). При
фиксированном значении / эти уравнения можно рассматривать как
уравнения на собственные значения для некоторого эрмитового
оператора. Отсюда следует свойство полноты
2Rni('-')Rn;(r) = 6(r'-r), (5.162)
п
а из (5.162) немедленно следует (5.161). В случае чисто кулонов-
ского поля, т. е. атома водорода или одноэлектронных ионов,
равенство (5.161) можно продолжить, используя выражение для I^^lni из
таблицы [I, П2.3]:
^i„/ = ^[5n^+l-3/(/+l)l. ^'-'^'^
Докажем теперь правила сумм для осцилляторов,
соответствующих переходам nl—*n'l + l и п1—*п' I — I. Согласно (5.30),
(5.159), (5.160)
fTn,.i= -f <«„/;„'тЙт(^п'^т=п/)'' (5-164)
fTni-i = -| <"„/=„'/-! 2Гм (^п\-ип,У- (5.165)
*) Таким образом, приводимое доказательство относится не только к одноэлект-
ронным атомам, но и к многоэлектронным атомам в одноэлектронном приближении.
20.'
Рассмотрим сумму
п п'
= 1\ Rn■l^l('■){Щ'-'Чr)r-rЩHr))R^^(r) drx
П
x\Rn-,i-i('-)rR^,{r)dr. (5.166)
Здесь Щ^ — оператор, собственными функциями и собственными
значениями которого являются /?„;(/■) и £„; (см. [I, (2.140)]):
^oV)=-i5-f + ^+n'-). (5.167)
Мы будем считать при этом, что V{r) не зависит от /, что, вообще
говоря, справедливо лишь в отсутствие обменного члена или при его
аппроксимации по Слэтеру (см. § 3.5). В случае чисто кулоновской
задачи V = 0. Учитывая явно различие между Я^'"*"'^ и Н^\ можно
(5.159) переписать в виде
п
х(л„.,^,(г)гЛ„,(г)йг. (5.168)
Используя опять условие полноты (5.162) и условие нормировки
функций /?„;, получаем
S^'r = (г[ЩЧг), г]_)„, „, + / + 1. (5.169)
Вычисляя коммутатор
[Щ\г),г]_=-± (5.170)
и интегрируя по частям, с учетом условия нормировки функций
/г„;(г) находим
(г[Я<')(г),г]_)„,„, = 1 (5.171)
Таким образом,
c{f+i)_2/ + 3 (5.172)
и мы приходим к правилу сумм:
V /^('^i) _» + 1)(2/+3) (5.173)
Z,Jnl\n-l+\ 3(2/ +1) •
п
Аналогичным образом доказывается правило:
V Л^^) — — ^(2/-1)
Z, 1 ni; п-1-\ — з(2/ + 1)- (5.174)
206
Наконец, складывая (5.173) и (5.174), получаем общее правило
(5.32) для //=1:
п
Перейдем к вычислению радиальных интегралов Л^у. ^f.
Радиальные волновые функции в случае кулоновского поля имеют вид [I,
(1.26)] и выражаются через вырожденную гипергеометрическую
функцию. Для определенности рассмотрим интеграл J^nln'i-i- Он
сводится к интегралу
оо
Il^iak; a'k') = j е'^^гУ-'Р^а, у-д; kr)F(a', у-р; k'r) dr, (5.176)
о
где X = - + -; у = 21 + 3; а = -п + 1 + 1; а' = -п' + 1; к = 2Z/n;
к' = iZIn; q= 1; р = 3. Интеграл /^°(аЛ; а к') приведен в формуле
[I, (П2.14)] и выражается через гипергеометрическую функцию*).
Интегралы Ij^(ak; a'k') сводятся к 1^{ак; а'к') с помощью
рекуррентных соотношений для вырожденных гипергеометрических
функций [I, (П2.4)]. Приведем окончательный результат (см. [И],
а также [2]):
d(1) _ (-1)"'"' -Ш+ШКНЕШ (4пп')'+Нп-п')"+"'-^'-^
^п1:пЧ-1 4(2/^1)! 1/(„_/_!)(„-_/), („ + „г+«
xL/'i|-n + /+l,-n' + /;2/; '*""'
(n-n')^j
^^-^] 2^if-n + ^-l.-n' + /;2/; ^^ll- (5.177)
n + n'j I (n — n'r
Поскольку в гипергеометрических функциях 2^i(c'> Р> У' ^) ^
(5.177) параметры а, р отрицательны (или равны нулю), эти
функции сводятся к полиномам (см. [I, (П2.8)]). Это обстоятельство
обеспечивает и само существование интегралов.
Приведем также некоторые квадраты радиальных интегралов для
частных случаев [2]:
ь-";« «.■)'='';:'::,1'Г. <^-'™)
2s-„p: (J^.„.)^=«5^^ttg^ (5.179)
ip-ns-. (да>„„)'='';-^';;;!Г- (5.181)
*) в формуле [I, (П2.14)] имеется опечатка: следует заменить v' на v-
207
При п = п' формула (5.177) непригодна (это видно из того, что
аргументы гипергеометрических функций в (5.177) становятся
бесконечными). В этом случае удобнее производить интегрирование
иным способом, используя запись радиальных функций /?„/(/■) через
обобщенные полиномы Лагерра (см. [I, (П2.0-^12.12)]).
Подставляя в интеграл выражение [I, (П2.11)] для одного из полиномов, а
для второго используя представление [I, (П2.12)], путем повторного
интегрирования по частям можно получить следующее простое
выражение [2]:
/?« =л(1) =^nVn2-/2 (5.182)
Эта формула определяет переходы между компонентами тонкой
структуры уровня.
В приложении П2.1 приведена таблица числовых значений
квадратов радиальных интегралов (5.177) [2] (в атомных единицах).
Далее там же приведена таблица сил осцилляторов (5.164), (5.165)
[2] (приложение П2.2) и таблица вероятностей переходов (5.159),
(5.160) [2] (приложение П2.3). В приложении П2.4 приведена и так
называемая диаграмма Гротриана, дающая наглядное представление
о расположении возбужденных состояний атомов, спектральных
сериях и разрешенных переходах.
Перейдем к магнитному мультипольному излучению. Повторяя
все то, что было сказано в начале этого параграфа об электрическом
мультипольном излучении, можно сразу написать формулу,
аналогичную (5.149):
у(Му)_ _ ^2 2(2у + 1)0- + 1)ш^;^.Г I ^ш,.. „ I 2
пГ.п'Г (2/+l)y[(2y-l-l)!!]^
w):y^.,. = e- -^l<n'/'||Qf>||n/> . (5.183)
Теперь, однако, исходя из вида QJ'**^ (5.131), нельзя утверждать,
что оператор перехода зависит только от координатных или только
от спиновых переменных, и вычисление в общем виде приведенного
матричного элемента Q^*^ становится сложным. Поэтому в
дальнейшем ограничимся вычислением вероятностей дипольных магнитных
переходов. В случае дипольных переходов для одноэлектронного
атома (5.183) принимает вид
"'Sr = I ФгГ I <n'^V/'||f.||-n/./> I', (5.184)
где (,n'l's'J'—\\\Ji\\nlsJ) — приведенный матричный элемент
оператора магнитного дипольного момента (5.134). Для вычисления этого
матричного элемента оператор (5.134) удобнее переписать в виде
|i = -fio(J + S), (5.185)
где J — оператор полного момента атома. Ввиду того, что этот
полный момент является сохраняющейся величиной (он сохраняется до
тех пор, пока мы не учитываем взаимодействие со спином ядра и
208
внешние поля), оператор J вообще не имеет недиагональных по
энергии матричных элементов. Поэтому
{n'l's'J'\\\ji\\nlsJ) = - \iQ(,n'l's'J'\\\ji\\nlsJ).
(5.186)
Теперь можно вновь использовать выражение [I, (3.121)] для при-
; веденного матричного элемента оператора, действующего на коорди-
1 наты подсистемы, на этот раз спиновой (учтем также, что s' = s):
{n'l's'J'MlnlsJ) = -Ho6,^.6„„,V(2/' + 1)(2/+ 1) X
l+s + J) S J' l\
x(-l)'
/ s 1
<s||s||s>. (5.187)
Таким образом, магнитные дипольные переходы возможны лишь без
изменения квантовых чисел п1, т. е. между компонентами тонкой
структуры одного и того же уровня. Подставляя (5.187) в (5.184) и
используя выражение [I, (3.106)] для приведенного матричного
элемента <s||s||s>, получаем (полагая s= 1/2):
i /' /1'
•' 2 '■
(5.188)
Обратимся теперь к расчетам вероятностей переходов в одно-
электронных ионах с произвольным зарядом ядра Z. В этом случае
необходимо сразу воспользоваться релятивистскими формулами.
При этом мы, в отличие от того, что делалось в начале этого
параграфа, будем вычислять непосредственно вероятность излучения фо-
I тона с определенным моментом и четностью. Тогда формулу (5.10)
нужно заменить следующей:
где
dw<-/^.'^\(ojMj) = 2п I l/f^.''\oijMj) I ^6((о -Е^ + Е^.), (5.189)
f//;.-)(a>yM.) = .(7Ai^-->),.„ (5.190)
а выражения для ^^/м^ даются формулами (2.170), (2.171). Вместо
(5.13) теперь имеем
4л'''"Ч/М.) = j rft.i^;.'-)(a>yM.) = 2K^<f^.'->'-P, (5.191)
(Е MjM^^.p(E,M) ч
"АА '^ — \г^Е-Е..)МУАА'-
.(5.192)
Переходя к обозначениям Аш nJlMj, вместо (5.147) теперь
напишем
(£,М) ^ 2па у
пЛ\ nJ'V 2J+\ ^
Ill
(Е, MjM)
(5.193)
209
Для выделения зависимости от проекций моментов и последующего
суммирования по этим проекциям вновь используем теорему Вигне-
ра—Эккарта,
/ / /
M'j Mj Mj
{n'J'l'Wv^^^'^'^WnJl),
(5.194)
и формулу [I, (3.31)]. Общие выражения для редуцированных
матричных элементов в (5.194) достаточно громоздки [12]. Мы приведем
здесь в качестве примера выражения для этих матричных элементов
при переходах с нижних возбужденных уровней пЛ в основное
состояние, т. е. при электрическихдипольных переходах (2-1)—»(1-0),
4 1 11
(2^1)-»(1^0)и магнитном дипольном переходе (2 - 0) -*■ (1 - 0):
оо
<1 i0||^('^')||2i 1> = 2.^ j r^dr rgo(<«'-)Uiio('-)/2io('-) +
о '-
+ J /i ioCO^zio('')) - I 52(<«'')/i ioCO^zi iCOl. (5.195)
<1 iO||^('^')||2| 1> = i±^^]r^dr Шсог)/,.,{г)д,,,(г) +
0 '-
+ i92(<«'-)(/iio('-)g2fo('-)-3gi.o('-)/2fi('-))]. (5.196)
<1 i0||^('^'>||2i 1> = -2i{^ ] r^drg,(o,r)(f,.o{r)g^^o(r) +
Здесь g^ji, f^ji — верхняя и нижняя радиальные компоненты дира-
ковских биспиноров, функции gi^mr) определяются согласно
(2.169), О) — частота соответствующего перехода.
Раскладывая подынтегральные выражения в (5.195)—(5.197) в
ряд по степеням aZ и подставляя результат в (5.193), можно
получить значения вероятностей переходов в нерелятивистском пределе
(в релятивистских единицах):
wm,,., = wm,.,= amiay{^^\ (5.198)
'2"'2" ~2'''2" 13J
"'iTo.iio=9fe°'«(aZ)>o. (5.199)
Результат (5.198) совпадает с получающимся по формуле (5.160)
при п=1, п' = 2, 1=1 в случае подстановки в эту формулу
выражения (5.173) при п = 2.
Выражение (5.199) дает вероятность сильно запрещенного
М1-перехода 2s—Is. Дополнительная (по сравнению с (5.198))
210
буквенная малость в (5.199) обусловлена следующими при-
амплитуде происходит
по сравнению с элек-
10 3D 50 70
чинами. Во-первых, множитель aZ в
от малости магнитного взаимодействия
трическим. В вероятности это дает
(aZ)^. Во-вторых, если не учитывать
релятивистских поправок, матричный
элемент магнитного диполя на
состояниях 2s и Is обращается в нуль
из-за ортогональности
нерелятивистских координатных (радиальных)
волновых функций. Для получения
ненулевого результата нужно учесть
релятивистские поправки к волновым
функциям и к оператору
взаимодействия, т. е. поправки порядка (aZ)^ в
амплитуде или (aZ)* в вероятности [13].
Благодаря дополнительному
множителю (aZ)^, а также малости числового
коэффициента, вероятность однокванто-
вого радиационного перехода 2s—Is при
не слишком больших значениях Z
оказывается очень малой: время жизни
2s-cocтoяния при учете только этого
канала распада составило бы около
двух дней (Z= 1). При малых
значениях Z основным каналом распада
2s-cocтoяния является двухквантовый
переход (см. §5.10). Лишь при Z>40
одноквантовый распад 2s—Is
становится более вероятным, чем двухквантовый,
за счет более резкой зависимости от Z.
Приведем для сведения нерелятивистские пределы для
вероятностей еще двух переходов:
Рис. 5.2. Зависимость от Z
вероятностей переходов
между нижними уровнями одно-
электронного иона:
/-(2^0)-
'(UO)
2-(2^1)-.(1^0)
3-(2|1)-
4-a\l)-
.(1^0)
■(2|0)
5- (2|l)-.(2il).
4f}.2io = «4aZ)io^,
(5.200)
4|\>2., = am(aZ)>^^.
(5.201)
Дополнительная малость в £'1-переходе (5.200) происходит от
малости частоты перехода: разность между подуровнями тонкой
структуры имеет дополнительную малость (aZ)^ по сравнению с атомной
частотой, что в вероятности дает (aZ)^. В М1-переходе (5.201)
добавляется множитель (aZ)^ за счет малости магнитного
взаимодействия.
На рис. 5.2 приведена зависимость от Z вероятностей перехо-
дсв между нижними возбужденными состояниями одно-
211
электронных ионов [12]. По оси ординат отложена величина
т 1
Ig (w/m). Вероятности разрешенных переходов (2^1)—»(1-0) и
(2- 1)—»(1 -0) вычислены в нерелятивистском приближении. Как
видно из рисунка, значения вероятностей разрешенных переходов
4 1 11
(2^1)—»(1-0) и (2-1)—»(1-0), полученные в релятивистсксй
теории, во всей области изменения Z вплоть до Z « 100 практически
совпадают с соответствующими нерелятивистскими значениями
(максимальная погрешность 5%). В то же время для магнитодиполь-
ного запрещенного перехода (2^0)—»(1^0) снятие запретов под
влиянием релятивизма приводит к резкому возрастанию вероятности
с ростом Z.
В приложении 2.5 приведена таблица значений вероятностей
переходов (2i 1)^(1 iO), (2| 1)^(1 io) и (2i0)^(2il) при
различных значениях Z<50 [14].
§ 5.5. Вероятности переходов между уровнями
многоэлектронных атомов
Мы переходим к вычислению вероятностей переходов между
уровнями многоэлектронных атомов и начнем с вычисления
электрических переходов. Прежде всего, формула (5.147) сохраняет свой
смысл для многоэлектронного атома, только теперь нужно считать,
что / и Mj — полный момент всей электронной оболочки атома и
соответствующая проекция. Символ п нужно понимать как набор
всех остальных квантовых чисел, характеризующих электронную
оболочку — фактически в одноэлектронном приближении это
означает задание конфигурации. Точно так же сохраняются в
нерелятивистском приближении формулы (5.148) и (5.149) (см. обсуждение
в § 5.3).
В рамках £5-связи имеет место также формула вида (5.150) для
приведенного матричного элемента:
{n'L'S'J'\\(^^^\\nLSJ) = 65s.V(2/' + l)(2/+l) X
x(-l)^'+s'.-/.-yU' /' ^'|<„r||e('^)||n£>. (5.202)
Подставляя (5.202) в (5.149), получаем
x|<n'r||Q(^||n£>p. (5.203)
^(Bj) , _ _ ^25 2(Z/'+l)(2y + l)0- + l)co^i:^^^y
nJLS: n'J'L'S" SS" y[(2y + l)!!]2
212
Ограничиваясь далее дипольным приближением, заменим (5.203)
выражением (у = 1)
(5.204)
ще D — оператор дипольного электрического момента электронной
оболочки атома.
Приведенный матричный элемент {n'L'\\D\\nL) вцчисляется
просто лишь в случае одного электрона вне заполненных оболочек. В
этом случае квантовые числа LS совпадают с одноэлектронными
квантовыми числами Is для валентного электрона и можно вновь
воспользоваться формулой (5.145), подставляя в радиальные
интегралы волновые функции валентного электрона, например в
приближении Хартри—Фока. В общем же случае необходимо
воспользоваться выражениями для волновых функций, приведенными в [I,
§3.10]. Соответствующие выкладки достаточно громоздки;
результаты можно найти в [1]. Во многих случаях, однако, можно
получить информацию о некоторых особенностях вероятностей
переходов в атомах, не вычисляя явно приведенных матричных элементов.
Прежде всего, с помощью [I, (3.60)] можно написать (см. (5.155))
2Ш11 (2/' + 1)|^' '^ ^} = 27ТТ- (5-205)
Тогда полная вероятность излучения всех линий спектрального
мультиплета при переходе nLS—*n'L'S' равна
41'i;n'L's- = I <Ls;n'L's-^ss' 2Г+Т I <«'^'ll^ll«^> |'■ (5-206)
Относительная вероятность излучения отдельной линии равна
(£1)
Kjls: n-j-L's- = bLs^ss" -jm ' (5.207)
где множитель qji^g определяет вероятность нахождения атома на
уровне с некоторым определенным значением /*). Эта вероятность
равна отношению статистического веса уровня LSJ к полному
статистическому весу терма LS:
Используя (5.208), получаем
KjIs; nVL's- - ^ss 2ST1 \j L 1J ■
*) Мы предполагаем, что все состояния / заселены равновероятно и пренебрегаем
зависимостью частот от /, /', т. е. тонкой структурой уровней.
213
Анализируя формулу (5.209) при различных значениях
моментов, можно установить, что среди компонент мультиплета
наибольшей интенсивностью обладают линии, для которых изменение / и
L при переходе одинаково. Например, если £ = О и соответственно
J= S^ правила отбора дают L' = I, т. е. AL = 1. Тогда, используя
для Зу-символа формулу [I, (3.66)], получаем
^!j'L n'rvs- = 6..' I ^- (5.210)
Наибольшее значение вероятность (5.210) принимает при
J' = J + I, т. е. при А/ = AL = 1. Такие линии называются
главными, остальные — сателлитными.
Суммирование вероятности (5.209) по /' или по / дает (мы
вновь используем [I, (3.60)]):
Y^£i) ,,,, = 2/+J Г521П
Z,""nJLS;n'j'L's' (2L+1)(2S + 1)' i,O.ZllJ
г
V —(Я1) _ 2J'+1
Zj "'nJLs; n'j'L's' ~ (2L +1) (2S +1) ■ (5.212)
J
Таким образом, сумма относительных вероятностей для всех линий
мультиплета, имеющих один и тот же начальный (конечный)
уровень, пропорциональна статистическому весу этого уровня.
Переходим к магнитному излучению, ограничиваясь сразу
магнитными дипольными переходами. Тогда вместо (5.187) можно
записать
{n'L'S'J'WviWnLSJ) = -vi^b^.^bs'sK'n'^{2j' + 1)(2J + I) X
x(-l)i^+s+/+i|^ /' |L5||5||5), (5.213)
где \i — оператор магнитного момента атома, определяемый
согласно (5.185). Используя выражения для приведенного матричного
элемента [I, (3.106)], а также для соответствующего бу-символа
и подставляя все в (5.184), после элементарных преобразований
получаем
3
27+1 ^^nLSJ;nLSJ~l /-riC-L Г_1_1\ч/
^^njLs;nJ-lLS — 2J^"'nj-lLS;nJLS— 3(27+1) У^'^^ -i- J -i- 1)Х
X{L + S-J+l)(J + L-S){J + S-L). (5.214)
Частота перехода c^nLsj;nLsj-i '^Р^ этом определяется формулой [I,
(3.336)]. Таким образом, для вычисления вероятностей магнитных
переходов, разрешенных в нерелятивистском приближении, нужно
знать только частоту.
Для расчета вероятностей электрических переходов
необходимо знать матричные элементы оператора дипольного
электрического момента атома, которые в одноэлектронном приближении в
214
конечном счете сводятся к вычислению радиальных интегралов
типа
Rnr,nl=\'^nr('-)^-^nl('-)dr,
ще iJJn'/'» ■фп/ — радиальные орбитали (например, в приближении
Хартри—Фока). В приближении Хартри—Фока выполнено
большинство современных расчетов вероятностей переходов для атомов [1].
Однако приближение Хартри—Фока не всегда дает хорошие
значения для вероятностей пфеходов, поскольку в этом методе волновые
функции выбираются из условия минимума энергии. Это значит
(см. [I, § 2.3]), что при среднем отклонении волновой функции от
точного решения на величину 6 ошибка в энергии будет порядка
Ь^. Известно, что относительная ошибка при вычислении энергии
уровней в атомах составляет не менее 1 %■ Это значит, что
относительная ошибка для волновой функции и, следовательно, для
матричных элементов различных оператсров может составлять десятки
процентов.
Уточнение расчетов вероятностей переходов достигается либо
применением полуэмпирических методов расчета, либо использова-
Ешем методов, выходящих за рамки приближения Хартри—Фока,
т. е. учитывающих электронную корреляцию. Одним из наиболее
распространенных полуэмпирических методов" является метод
квантового дефекта, впервые примененный для расчета вероятностей
переходов Бейтсом и Дамгаард [15].
Учет электронной корреляции, как правило, приводит к
существенному улучшению согласия расчетов вероятностей переходов (сил
осцилляторов) с экспериментом. Практически все методы учета
электронной корреляции, описанные в § 1.4, были использованы не
только для получения поправок к уровням энергии, но и для
уточнения вероятностей переходов. Мы рассмотрим здесь лишь
результаты применения методов, наиболее приспособленных именно для
расчета поправок к вероятностям переходов. Такими методами
являются, прежде всего, метод случайной фазы [I, §4.12], а также
адиабатический метод [I, § 4.13].
Амплитуда электрического дипольного перехода между
состояниями y\>j( и tjj^ в многоэлектронном атоме, согласно [I, (2.29)],
выражается формулой
A^^ = Spdpf4^';^), (5.215)
1де d — оператор электрического дипольного момента электрона,
pf ^ — матрица перехода. Используя для матрицы перехода
выражение [I, (4.421)], соответствующее приближению случайной фазы,
а также выражение для частоты перехода, полученное при решении
уравнений случайной фазы [I, (4.424)], получаем непосредственно
искомый результат. В таблицах П2.6—Г12.8, заимствованных из [4],
приведены результаты расчетов сил осцилляторов атомов
благородных газов, щелочных и щелочноземельных атомов, вычисленных в
приближении Хартри—Фока в формах «длины» и «скорости» и в
215
приближении случайной фазы с обменом. Там же приведены
известные экспериментальные данные [16]. Сравнивая результаты
расчетов с экспериментом, можно заметить, что в целом метод
случайной фазы дает лучшее согласие с экспериментом, чем метод
Хартри—Фока. Далее, теорема о сумме сил осцилляторов в виде
(5.38) даже приближенно выполняется лишь для щелочных атомов.
В случае щелочноземельных атомов и атомов благородных газов
сумма сил осцилляторов значительно отклоняется от единицы, что
объясняется большей величиной нефизических переходов в занятые
состояния (см. §5.1).
В приближении адиабатического разделения быстрых и
медленных движений в атомах вычисление вероятностей переходов
выглядит следующим образом [17]. Амплитуда перехода из состояния К
в состояние L для атома с одним валентным электроном, согласно
[I, § 4.13], выражается формулой
^KL = S Ф*(9; Q)4>k(Q)^ + ^)Ф{д; Q)^(>t.(Q) dg dQ. (5.216)
Здесь, согласно принятым в [I, §4.13] обозначениям, д —
координаты электронов остова, Q — координаты валентного_электрона.
Поэтому в данной ситуации мы обозначаем через D оператор
дипольного момента внешнего электрона, а через d — оператор
дипольного момента электронов остова (ранее в этой главе
обозначения d и D соответствовали одноэлектронному и
многоэлектронному операторам). В тех же обозначениях (в атомных
единицах)
D = D = R; d = d = 2rp (5-217)
i = l
где R — радиус-вектор валентного электрона, Г; —
радиусы-векторы электронов остова, Л^^ — их число. Заметим, что согласно [I,
(4.478)] волновая функция остова зависит параметрически от
координат внешних электронов, но не зависит от состояний этих
электронов.
В дальнейшем используем теорию возмущений (см. [I, (4.488)])
для волновой функции остова Ф(д; Q). Тогда после усреднения
по спиновым переменным формулу (5.216) можно преобразовать к
виду
^KL = S Фх(К)(К + P(R))*Pi:(R) dR, (5.218)
где
P(R) = 2 Re j 0*(r)dO,(r; R) Зт, (5.219)
Фо(г) — волновая функция невозмущенного остова (нулевое
приближение), Oi(r; R) — поправка первого порядка.
На больших расстояниях от остова, при R^»-a (где а — радиус
остова), пользуясь опять асимптотическим разложением [I, (4.499)]
216
и определением поляризуемости остова а [I, (4.500)], поправку
P(R) сводим к простому выражению
P(R) = aR/l^. (5.220)
Формула (5.220) может быть получена также из простых
классических соображений об остове как об изотропном поляризующемся
шаре (см. [I, §4.13]).
Таблица П2.9 на примере атома лития дает представление об
улучшениях, вносимых в расчеты сил осцилляторов использованием
метода адиабатического разделения в атомах [18]. Из сравнения с
результатами расчетов в приближении случайной фазы (табл. IT2.7) следует,
что метод адиабатического разделения особенно хорошо работает в
случае возбужденных состояний валентного электрона. Это
неудивительно, поскольку для возбужденных состояний наилучшим образом
выполняются критерии применимости метода (см. [I, § 4.13]).
В заключение этого параграфа рассмотрим вычисление
вероятностей переходов в двухэлектронных ионах с произвольным зарядом
ядра Z с помощью квантовой электродинамики [12, 14, 19].
Вероятность одноквантового перехода в этом случае, согласно (5.8),
должна определяться формулами
ш^, = 2пЦФ<',\9\Ф^^\Ч{<о-ЕР^ + Е1)-^^, (5.221)
<ф0|5|ф0> = -2ш<фО| К|фО>6(а)- f?o -I- El). (5.222)
В качестве волновых функций начального и конечного состояний Ь,
а нужно использовать двухэлектронные волновые функции tjjJJ^
(3.46), полученные в схеме промежуточной связи. Мы ограничимся
рассмотрением переходов с изменением только одного из одноэлек-
тронных состояний, входящих в y\)j,^. Вероятность перехода с
излучением одного фотона, просуммированная по проекциям моментов
в конечном состоянии и усредненная по проекциям моментов в
начальном состоянии, равна
= 1JTy1 \<JMj\V<i''^'^\J'M'j)\^io- El + El). (5.223)
Здесь матричный элемент V^^'^ определяется из (5.222).
Вычисление матричного элемента 5-матрицы, соответствующего
графику рис. 5.1, с двухэлектронными волновыми функциями (3.48) дает
<JMj\V<i''^'^^\J'M'j) = 4{-1)^-''-^;
J J J
М. M'j Mj
XS la'j{J,J^l,l^)aj.{J\J'^l[l'^)X
JA^A J'lWz
xN{n,J,n^J^)N{n\J\n'^r^)V^lj'P{J,l^J^l^; /[lU'^l'j). (5.224)
217
Нормировочные множители Л^ определены в § 3.3, там же описанс
вычисление коэффициентов смешивания а. Двухэлектронный
матричный элемент V^^'j^ сводится к одноэлектронному; мы запише№
его сразу через приведенный матричный элемент (5.194):
y^fj-PWx-fili} J'xlWi) = (-1)-'^-'.^-''.[(2/+ 1)(2/' + l)]ix
' j'\J' J
/2 Ji JI
<«;/;/;ll^^'^-''4n,j,h)K.^,.b,.^yb,^^^. (5.225)
По формулам (5.223)—(5.225) можно рассчитать вероятности
различных переходов между уровнями двухэлектронных ионов.
Рассмотрим для примера переходы между уровнями возбужденной
пп'= 1,2 и основной (пп'= 1,1) конфигураций при различны}|
значениях Z [12]. На рис. 5.3 схематически изображены уровни
(п,п'= 1,2)-
г'Р,
Ъ
'Р,
'Л
1 '
1 1
1 1
1 1
1
1 1
1 1
' 1 И
1 1
1 1
1 <
1 V 1
♦ 1
' 1
1 1 1
1 1 1
1 1 1
1 1 *
]1
V
'
1 1 1
1 1 1
1 1 '
1 1
1 1
1 1
1 ^
i
'
1 ^
¥
'
Рис. 5.3. Схематическое изображение переходов между уровнями основной
(и, п'=1, 1) и возбужденной (и, п' = 1, 2) конфигураций двухэлектронных ионов.
Расположение уровней соответствует Z > 30 сотласно рис. 3.46
рассматриваемых конфигураций и указаны возможные переходы.
Сплошной стрелкой показаны электрические дипольные переходы,
разрешенные в нерелятивистском пределе (aZ<cl). Штриховой
стрелкой показаны переходы, запрещенные в нерелятивистскоы
пределе либо по орбитальному моменту и четности (т, е. все, кроме
fJi), либо по спину (интеркомбинационные).
Если обратиться к переходам между возбужденными состояниями,
то оказывается, что в используемом приближении
(невзаимодействующие электроны) вероятности некоторых из них обращаются в нуль
в связи с обращением в нуль частоты перехода ьу^^, в этом приближе-
218
НИИ. Речь идет о переходах с одним и тем же набором
квантовых чисел /,/,/2/2- Например, это относится к переходам
^.-р^. (Щ] ^^..р^. (Н)]=^0-рл (Н)] ^^..р^' [Щ] ^^-
обозначения в § 3.3). В одних случаях указанная трудность
устраняется автоматически при смешивании конфигураций,
описанном в § 3.3. Так, к уровню Ei^rP, (■= ^п оказывается примешанным
уровень Еу
благодаря чему вероятность перехода
E(^Pi) —*E(^Si) оказывается отличной от нуля. В других случаях,
например для перехода f^o-pP, [^^]1 -*£'i+p<S, (^т]]» смешивание
конфигураций отсутствует. При вычислении вероятностей таких
переходов необходимо
переопределить нулевое приближение. В
частности, можно
воспользоваться приближением Хартри—
Фока, в котором снимается вы-
Рис. 5.4. Зависимость от Z
вероятностей переходов между уровнями воз-
буященной (и, и'= 1,2) и основной
(и, и' = 1, 1) конфигураций двухэлект-
ронных ионов. Использованы
сокращенные обозначения уровней согласно
нерелятивистскому пределу; (0)
относится к основной конфигурации:
i-'p,-'sf\
i-V,^'sg";
5 — ^Pj-'^S,;
7 — ■i'l-'^S,;
9 — ^Pi^^Po,
И — ^Pj-'^^o;
13 — V,-.^S,;
IS — V,-»Vo;
2_V,-'sg";
4_^s,-'sg";
6_«P,^«So;
8 — ^P2—^Pi,
10— 'P,-»V,;
/2—¥,-.'So;
14— •/'i-'Vj;
/6-^2-.'So
рождение no / и уровни (2^0) и (2^1) расщепляются, а
следовательно, расщепляются и уровни Eq^I^P, [2^^]] и fi'i+P^, (|^^]1- В
случае многозарядных ионов приближение Хартри—Фока достаточно
использовать лишь при определении частоты перехода, а матричные
элементы перехода можно находить по-прежнему в приближении
невзаимодействующих электронов. Действительно, при достаточно
больших значениях Z поправки, даваемые приближением Хартри—
Фока (поправки на взаимодействие электронов), имеют порядок
219
1/Z. Более того, при вычислении частоты перехода вместо разности
энергий уровней в приближении Хартри—Фока также можно исгюль-
зовать разность поправок первого гюрядка к энергии в теории
возмущений по 1/Z.
Результаты расчета вероятностей всевозможных переходов
между уровнями основной (п, п'= 1, 1) и возбужденной (п, п'= 1, 2)
конфигураций приведены в ло-
Г
-5
-10
20 40 БО 80 100 г
гарифмическом масштабе на
рис. 5.4 [12]. Видно, что гюве-
дение вероятностей с ростом Z
весьма различно для
различных переходов. Так,
вероятность интеркомбинационного
перехода ^Р,—^'S^"^ возрастает
с ростом Z гораздо более
заметно, чем вероятность разре-
шейного перехода Р,
-15
Рис. 5.5. Зависимость от Z ширины
уровней конфигурации и, и'= 1,2 двухэлект-
ронных ионов
Суммируя вероятности
переходов, можно вычислить
радиационные ширины
возбужденных уровней (см. гю этому
поводу §6.1). Эти ширины (в
логарифмическом масштабе)
приведены на рис. 5.5. Как
видно из рисунка, ширины
различных уровней по-разному
ведут себя в зависимости от Z:
при Z«80 ширина Т{^Р^
увеличивается всего в 100 раз
по сравнению с Z = 2, тогда как ширина Т{}Р{) увеличивается в
108 раз, а T{^Si) — в Ю^» раз [12].
Посмотрим теперь, как учесть поправки на взаимодействие
электронов. При больших значениях Z их роль относительно невелика,
но при промежуточных значениях Z может оказаться значительной.
В низшем порядке по межэлектронному взаимодействию для этого
необходимо, в дополнение к диаграмме рис. 5.1, рассчитать также
вклады диаграмм рис. 5.6. Эти диаграммы следует вычислять с
адиабатической 5„-матрицей, поскольку в них возникает
особенность типа 1/а, когда в сумме по промежуточным состояниям
п = Л' {п = А). Эти особенности, однако, уничтожаются при
вычислении вероятности: расходящиеся множители собираются в
экспоненту вида ехр (г/а) [12]. Уничтожение особенностей приводит к
тому, что в сумме по промежуточным состояниям следует опускать
члены п = А' (п = А).
Расчет вкладов диаграмм рис. 5.6а, б может быть выполнен
точно с помощью релятивистской кулоновской функции Грина [14].
220
Другой подход к учету межэлектронного взаимодействия —
использование метода Хартри—Фока—Дирака. Более того,
распространяя формулу (5.215) на релятивистский случай, можно
получить выражение для вероятности перехода в рамках метода реля-
В
В
-\j\/\f\r
■^r\/\r\j^
-\nj-w\r
■'^u\/\r\.
A
л/\ги\у-
P ис. 5.6. Фейнмановские графики, определяющие поправку к вероятности перехода в
первом порядке теории возмзчцений по межэлектронному взаимодействию. Имеются в
виду такие переходы в двухэлектронном атоме, в которых меняется состояние только
Одного электрона
тивистской случайной фазы. Расчеты в приближении
релятивистской случайной фазы можно считать, естественно, наиболее
точными в промежуточной области значений заряда ядра Z.
В таблице П2.10 приведены результаты расчетов различными
методами вероятности магнитодипольного интеркомбинационного
'1 1м . ЖТ1 ric^o^ /1 1\
перехода Е
1+
или, в н^)елятивист-
ских обозначениях, ls2s^5,-»(ls)^'5o [14]. В первом столбце
(wq) приведены результаты расчетов по формуле (5.223) на водо-
родоподобных функциях. Во втором столбце (wi) — результаты с
учетом поправки первого порядка на взаимодействие электронов
[20]. Различие между этими двумя расчетами при малых
значениях Z может быть значительным, однако при больших Z составляет
3—4%. Третий столбец (aJxe) — расчет по методу Хартри—Фока-
Дирака [21], четвертый (м'сф) — по методу релятивистской
случайной фазы [22]. При больших значениях Z различие между
этими двумя методами исчезающе мало, а отличие от ы),
составляет 0,5%.
Наконец в последнем, пятом, столбце приведены для сравнения
значения вероятности по формуле, полученной из (5.223) в не|)еля-
тивистском пределе для рассматриваемого перехода [14]:
<'' = т^°'«(«^)'°-
(5.226)
Оказывается, что различие с Wq составляет 5% при Z«30, около
15% при Z«50 и лишь при Z« 100 превышает 40%.
221
§ 5.6. Фотоионизация
Фотоионизацией называется процесс, при котором в результате
поглощения кванта света атомный электрон переходит из состояния
дискретного спектра в состояние сплошного спектра, т. е. покидает
атом *). Энергия вылетевшего электрона связана с частотой
налетающего кванта соотношением
£ = со - /, (5.227)
где / — потенциал ионизации атома.
При описании фотоионизации, как и любых процессов, в
которых в начальном состоянии присутствуют свободные частицы (в
данном случае — фотон), удобнее вычислять не вероятность, а
сечение. Дело в том, что нормировочный множитель для каждой
свободной частицы в начальном состоянии имеет вид 1/V2FK, где е —
энергия частицы, V — нормировочный объем (см. для фотона
формулу (2.130), для электрона — (4.1)). Для частиц в конечном
состоянии, даже если они являются свободными (подчеркнем, что
выбитый в процессе ионизации электрон, конечно, не является
свободным, но в смысле нормировки не отличается от свободного),
ситуация иная: эти частицы bjoryT быть нормированы, например, на
6-функцию по энергии (см. [I, § 1.1])- Именно поэтому при
вычислении вероятности излучения кванта можно полагать V=l без
ограничения общности. В случае поглощения кванта, в принципе,
этого сделать невозможно, так как нужно задать либо плотность
энергии электромагнитного поля (см. § 2.2), либо плотность потока
квантов, либо какую-то другую физическую характеристику
состояния электромагнитного поля. Переход к сечению подразумеваеп
именно задание плотности потока квантов и позволяет избавить»
от зависимости от объема V.
Сечение процесса da связано с вероятностью dw формулой
da = dw/J, (5.228;
где у — плотность потока частиц, равная
у = v/V (5.229;
(v — скорость частиц). Поскольку выражение для вероятности
фотоионизации при нормировке (2.130) содержит множитель 1/V
сечение (5.228) не зависит от V. В случае фотонов v = с и i
релятивистской системе единиц формулы для dw и для da вообщ(
ничем не отличаются. Учитывая, что вероятность dw имеет размер
ность с~', а поток у — размерность с~'-см~^, видим, что сечени
da имеет размерность плохцади (см^).
*) При поглощении фотона, в принципе, moiyr покинуть атом несколько электро
нов — это «шление назьшается многократной ионизацией и будет рассмотрено в конц
этого параграфа. Возможен и такой процесс, когда электрон покидает атом в результат
поглощения нескольких фотонов — многофотонная ионизация (см. § 5.10).
222
Процессом, обратным фотоионизации, является
фоторекомбинация (захват электрона с испусканием кванта). Сечение этого
процесса а связано однозначно с сечением процесса фотоионизации
o^^ принципом детзльного равновесия [23, 24]:
Ср = 2а„4, (5-230)
Р
где к — импульс испускаемого фотона, р — импульс налетающего
электрона. Подробнее о фоторекомбинации см. в [1, 2].
По аналогии с (5.10) для сечения фотоионизации теперь можно
написать
ЙОдДк, е; р, ^) = 2я| U^J^b(o^-г-I)-^, (5.231)
(2л:)
где к, е — импульс и поляризация начального фотона, р, ^ —
импульс и поляризация (см. § 4.1) конечного электрона, а матричный
элемент амплитуды перехода t/д^ определяется, как и ранее,
формулами (5.3), (5.4). Задание импульса для электрона имеет смысл
асимптотически, на большом удалении от атома, при этом
р^ = £^— т^. Произведя в (5.231) замену
dp = p^ d\p\dv = е\р\ dEdv = eVe^ — т^ dt dv, (5.232)
где v = p/|p|, проинтегрировав по e и используя (2.130), получаем
сечение фотоионизации с вылетом электрона в заданный телесный
угол dv с определенной поляризацией ^:
ЙСдДк, е; V, ^) = ^ iM I ((еа)е-''''),д | ^ rfv. (5.233)
В нерелятивистском пределе (см. § 5.1) формула (5.233)
преобразуется к виду (е « т):
ЙСдДк, е; V, ^) = 2^М I (ep),j2 dv = ^ |р| а>| (ег)^|2 rfv.
(5.234)
Проведем теперь вычисления для водородоподобного атома в
основном состоянии по формуле (5.234), используя форму «скорости» для
матричного элемента. Волновую функцию основного состояния
водородоподобного атома запишем в виде (см. [I, § 1.1]):
где а^ — боровский радиус *). В качестве функции -ф^. следует взять
волновую функцию сплошного спектра, асимптотическая форма
которой содержит плоскую волну ехр (грг) и наряду с ней сфериче-
*) в этом параграфе мы оставляем для наглядности явную зависимость от Од во
всех формулах.
223
скую волну ехр ( ± г | р | r^lr (сходящуюся или расходящуюся — н
данном случае безразлично). Для такой функции, согласно [24J,
можно написать разложение
со
^Р = W 2 ''(2/ + l)e*'^/?,p„(r)P,(v, п), (5.236)
z=o
где /?| |;(г) — радиальные функции сплошного спектра [I, (1.31)],
Pi — полиномы Лежандра, v = p/|p|, п = г/г, а фаза 6;
определяется формулой [I, (1.34)] (вид этой фазы в данном случае
несуществен). В силу правил отбора по / переход из основного состояни*
с / = О возможен лишь в состояние сплошного спектра с / = 1.
Поэтому в (5.236) остается лишь член с /= 1. Опуская
несущественный фазовый множитель и учитывая, что Р\{у, п) = (vn), получаем
Подставляем функции (5.235), (5.237) в матричный элемент:
е(р),д = -ie \ %{r)SI^^{r>, dr. (5-238)
Учитывая, что функция •фд(г) не зависит от углов, можно написат!
(еУ)я1,^(г) = (en) ^ я1,^(г) = -^^{рх)^^{х\ (5.239]
Тогда (вновь опускаем фазовый множитель)
«(Р).л = | Щч^Ы \ ^«">^^"> '^ \ г^^-^^%п(г) dr. (5.240:
Из теоремы сложения для сферических функций [I, (П1.5)] следует:
J (en)(vn)dn = ^(ev), (5-24i:
а радиальная функция Л|р|1, согласно [I, (1.31)], равна *)
^lp|i('-) =
= ^f |PllP^5^'-e-'IP''/'(2 + ix, 4; 2/|p|r), (5.242;
где F — вырожденная гипергеометрическая функция, % = Z/qoIpI-
*) Форл«улы [I, (1.31)] и [I, (1.38)] написаны с ошибкой. Это связано с тем, чт(
в [I, (1.27)] вместо n='-ilk нужно сделать подстановку n~—Zilk Тогда вмест(
[I. (1.31)] получится выражение
Ru(r) =С„ 1^ e-'^'f (f-Ь/ -Ь 1,21 + 2;2.4rJ ,
- выражение
С„ = 2ехр (f)V2SFniP^^=^
а вместо [1, (1.28)] — выражение
В этих формулах Л»« |Р| в обозначениях настоящего параграфа.
224
Интеграл в (5.240) может быть вычислен по формуле [I,
(П2.13)]; в частном случае, соответствующем (5.240), эта формула
сводится к следующей:
со
J e'^''x^-^F(a, у; кх) dx = Т(у)к''-^(к - Л)-°. (5.243)
о
Использование этой формулы с учетом соотношения
rx±iУ'^ = e-2xarc.gx (5.244)
дает
Учитывая выражение для потенциала ионизации / = zy(2alm),
соотношение (5.227) можно переписать в виде
^ = -^ + ^ = -^0 + ^')- (5-246)
Используя (5.246), получаем окончательное выражение для сечения
фотоионизации:
.. = 2W(5)'(i)'^(e.)^<^. (5.247)
Угловое распределение фотоэлектронов определяется
множителем (ev)^. В случае неполяризованных фотонов необходимо
выполнить усреднение по поляризациям е, что, как и в § 5.1, дает
результат
(ё^ = i S (ev)' = i (V X Уф)2, (5.248)
е
где Уф — единичный волновой вектор для падающих фотонов. Для
того же чтобы получить полное сечение фотоионизации, выражение
(5.247) нужно проинтегрировать по углам. Это дает [25]
а = ^г- е
Щ й'е^- <"^')
Видно, что величина с пропорциональна «поперечному сечению»
атома (ao/Z)2.
Вблизи порога ионизации, т. е. при со—»/ (при этом, очевидно,
Х-»оо), из (5.249) получается
(здесь Сд — основание натуральных логарифмов), т. е. сечение
стремится к постоянному пределу. Параметр % можно переписать
225
** л. Н. Лабзовсшш
также в виде х = ^Р(/1РI > ^^ Ро — атомная единица импульса,
или характерный импульс для электрона в атоме водорода (в
основном состоянии). Поэтому значения х<^1 соответствуют быстрым
фотоэлектронам, а значения x^^l — медленным. Поведение
сечения фотоионизации при x^^l описывается формулой (5.250). В
противоположном случае, при х<^1, из (5.249) следует
а=-^еН-!-У\^\\ (5.251)
т-
Таким образом, сечение фотоионизации максимально вблизи порога
и убывает, как са~''^, с ростом частоты налетающего фотона (при
достаточно больших значениях со).
Формула (5.251) соответствует борновскому приближению,
когда вылетающий быстрый электрон можно рассматривать как
свободный и описывать плоской волной. Для кулоновского поля условие
применимости борновского приближения [24] Ze^/hv«l (v —
скорость электрона), что соответствует х**~1-
Аналогичным образом были получены точные формулы для
фотоионизации водородоподобных атомов с уровней п = 2, 3 [2]. Эти
формулы имеют громоздкий вид, однако для приближенных оценок
можно использовать более простые формулы Крамерса, основанные
на квазиклассическом приближении [1]:
Здесь / — по-прежнему потенциал ионизации для основного
состояния атома водорода, а порог фотоионизации определяется условием
<а> 1/п^. Условие квазиклассичности Ze^lhv»\ обратно условию
применимости борновского приближения [24] и соответствует
^>5>1, т. е. области вблизи порога. Действительно, даже при п=\
(известно, что квазиклассическое приближение лучше работает для
высоковозбужденных состояний) отношение приближенного сечения
(5.252) Сприбл к точному (5.250) с^о^н при х**=1 равно
^ = 1^(т)'«Ь25. (5.253)
Формулы для релятивистской фотоионизации, возникающей при
поглощении атомом высокоэнергетических квантов (со»/),
приведены, например, в [23, 2].
Для перехода к изучению фотоионизации многоэлектронных
атомов используем формулу (5.234) в форме «длины». Естественное
обобщение (5.234) дает
226
где D — оператор дипольного электрического момента атома, А по-
прежнему обозначает исходное состояние атома, а А' — состояние
конечного иона. Перейдем в (5.254) к иному описанию вылетевшего
электрона, фиксируя не направление его вылета, а момент и его
проекцию (а также проекцию спина). Для того чтобы понять, как
это сделать, совершим вначале подобный переход в одноэлектрон-
ном атоме, непосредственно в формуле (5.234).
Функцию (5.236), используя теорему сложения для сферических
функций [I, (П1.3)], перепишем в виде
%* = 2T^S/''e*^*''^,p,,y;w(n)y/w(v). (5.255)
I'm
Подставляя ее в (5.234) и интегрируя по v, получаем
Vm
Обобщением (5.256) на случай многоэлектронного атома является,
очевидно, формула
а . =2зг^^У IreDl ., ■, . 1^ (5.257)
Vm
В нерелятивистском пределе, используя схему Z/5-связи, видим,
что значки А, А' соответствуют наборам квантовых чисел:
А = LMi^SMg, А' = L\M'i^ ^[M's • Кроме того, необходимо ввести
полные орбитальный и спиновый моменты системы в конечном
состоянии L' = L[ + I', S' = S[ + s'' и от набора квантовых чисел
Z/'jM^ S'lM'g zl'm'm'^ (сюда мы добавили спиновое квантовое число
для фотоэлектрона m'J перейти к набору L'M'^S'M'gL[S'i\p\l'. Далее
необходимо просуммировать по М^, M'g и усреднить по M^^, М^;
наконец, нужно усреднить по поляризациям и по направлениям
налетающего кванта. Суммирование по поляризациям и интегрирование
по направлениям кванта дает, согласно результатам § 5.1
(усреднение сводится к делению на 8 it) [1] *):
2л тч) 1
^^A,A-t— 3 |р| {2L+1){2S + 1) ^
^11 1\ <LM^SM,IDIL'M'^S'M'^'.S'^\р\П\\ (5.258)
*) Подчеркнем, что мы используем иную, чем в [1], нормировку радиальных
функций СПЛСШ1Н0ГО спектра, чем о&ьясняется различие коэффициенте» в формулах
для сечения.
227
_ Используя формулу [I, (3.103)], а также учитывая, что оператор
D не зависит от спинов, преобразуем (5.258) к виду
2я тсо ^ ^ I f^LS\\D\\L'SL\S\ | р| /'> р. (5.259)
L'
О, ,. =
A'^f- 3 |р| 2L-
Дальнейшие вычисления могут быть проведены для различных
конкретных случаев. Например, в случае одного валентного электрона
в незаполненной оболочке можно использовать генеалогическую
схему: набор квантовых чисел LM^^SMg необходимо дополнить
квантовыми числами Z/jSj, характеризующими терм исходного иона
(остова), и квантовыми числами п1, характеризующими валентный
электрон. Далее, оператор D можно представить в виде
D = Dp + d (5.260)
и считать, что Dq относится к остову, ad — к валентному
электрону. Поскольку при фотоионизации меняются лишь состояния
валентного электрона, оператор Dq не будет давать вклада в матричный
элемент в (5.259) *). Тогда для вычисления матричного элемента с
оператором d можно использовать формулу [I, (3.121)] для
приведенного матричного элемента оператора, действующего на состояние
подсистемы:
{LSLiSinl\\d\\L'SL[Si\p\l'} =
= у/{21+ 1)(2/'-|- 1) (-1)^,+'+^-'+!
Оператор d представим в виде
I LL^
L'I' 1
s.=Wfv
<п/|И|||р|0. (5.261)
(5.262)
тогда, согласно формуле [I, (3.111)],
<п/|И|| I р| О = (-1) V(2/ -I- 1) (21' -I- 1) Г - Чх
/ 1 /'
0 0 0
X J Л„,(г)Л,р,Дг)гЗ ^^ (5.263)
В случае одного электрона вне замкнутых оболочек L^ = О,
L=l, Z/J = О, L'=l\ и, учитывая выражение [1,(3.66)] для Зу-
символа, из (5.259) получаем
^/ 1 /')
Ю О о] „
(5.264)
- 3 |р| 2. У^^ "^ ^)
\ Rnii'')R\M')'''^'
*) Учитывая, что электроны неразличимы, а волновые функции
антисимметричны, можно просто считать, что в матричный элемент (2.259) дает вклад лишь один член
оператора D.
228
в частном случае п, / = 1, О из (5.264) следует выражение (5.249)
для основного состояния атома водорода.
В одноэлектронном приближении общее выражение (5.257)
также упрощается. Особенно простой результат получается в том
случае, когда исходное состояние атома описывается одним слэтеров-
ским детерминантом. В частности, это соответствует случаю, когда
в исходном состоянии все оболочки замкнуты. Тогда конечное
состояние можно рассматривать как однократное возбуждение с
переходом электрона в сплошной спектр. Для вычисления амплитуды
перехода вновь можно воспользоваться формулой (5.215)
^w = Spdpr', (5.265)
где т = nlmitn/, т' = пЧ'т^т'^. Учитывая, что матрица перехода
pf"', согласно [I, (2.65)], имеет вид
РГ' = ^nlm^S^^ ^пГту(9)' (5.266)
приходим вновь к выражению вида (5.256), такому же, как и для
одноэлектронного атома. По значкам /И;, т^ начального состояния
необходимо произвести усреднение.
При использовании одноэлектронного приближения и формулы
(5.263) возникает вопрос, каким образом получать одноэлектрон-
ные функции, описывающие возбужденные состояния (в данном
случае состояния сплошного спектра). Формула (5.263) получена,
вообще говоря, в предположении, что функции -ф^ и -ф^.
принадлежат одному и тому же гамильтониану и, соответственно,
являются ортогональными. Однако (см. обсуждение в [I, §2.4])
функции -ф^. (т' > N) относятся скорее к отрицательному иону и плохо
описывают реальные одноэлектронные возбужденные состояния
(такие функции мы будем обозначать ^Ф^^'^). Более естественным
является использование одноэлектронных функций y'J^-\
получаемых в результате решения уравнений Хартри—Фока
непосредственно для возбужденной конфигурации, т. е. для конфигурации с
дыркой в состоянии т. Такие функции, однако, уже не будут
автоматически ортогональны одноэлектронным функциям основной
конфигурации.
Приведем в качестве примера результаты расчетов сечений
фотоионизации атомов Аг и Хе в приближении Хартри—Фока,
заимствованные из [4]. На рис. 5.7 приведены результаты расчетов как с
функциями ■ф^^ , так и с функциями 'ф'^. Видно, что последние
приводят к лучшему согласию с экспериментом. Однако и те и
другие функции, как и следует ожидать, дают существенно разные
результаты в форме «длины» и «скорости».
Как и в случае вероятностей переходов, результаты расчетов
значительно улучшаются при использовании метода случайной
фазы [4]. При этом вновь используется формула (5.209) и выраже-
229
ние для матрицы перехода [I, (4.421)], соответствующее
приближению случайной фазы. Результаты расчетов для атомов гелия и
аргона [4] приведены на рис. 5.8, Согласие с экспериментом
хореей, MS
б,т
Р и с. 5.7. Сечение фотоионизации Зр подоболочки атома аргона (а) и 3d подоболоч-
ки атома ксенона (б). Штриховая кривая — расчет с функциями т))^^'^ штрихпунк-
тир — с функциями т))^; сплошная кривая — эксперимент. Сечения даны в мегабарах,
связь которых с атомными единицами такова: ао = 27,98 Мб
шее; при этом расчеты в форме «длины» и «скорости» дают
совпадающие результаты (см. §5.1). Подробности расчетов сечений
фотоионизации в приближениях Хартри—Фока и случайной фазы, а
также с учетом различных усовершенствований метода случайной
d,M6
d,Mi5
8
Б
г
о
^^.
. v
1
2,0
^^^^=:,^
1 1 1
г,5 3,0 3,5 a;,Ry
а.
40
3D
го
W
0
3a>,R\^
Рис. 5.8. Сечение фотоионизации атомов гелия (основное состояние) и аргона
(подоболочки Зр*. 3s^). Штриховая кривая — расчет по методу случайной фазы,
сплошная — эксперимент
фазы можно найти в [4]. Там же исследуются и угловые
распределения и поляризация фотоэлектронов (эффекты поляризации
возникают при учете спин-орбитального взаимодействия). Для
расчета фсугоионизации используются также полуэмпирические
методы, являющиеся обобщением метода квантового дефекта на
состояния сплошного спектра [1, 26].
230
Рассмотрим теперь процесс двукратной фотоионизации, т. е.
выбивание двух электронов из атома одним квантом. Такие
процессы (и даже процессы трех- и четырехкратной фотоионизации)
изучались в эксперименте; имеется также целый ряд
теоретических работ по двукратной
фотоионизации (обзор имеющих- и у, v v
ся результатов можно найти в
[27], см. также [4]).
Двукратная фотоионизация с теорети- I 1 fxrk^
ческой точки зрения интересна
тем, что сечение ее равно
нулю в одноэлектронном
приближении, т. е. для расчета этого
сечения с самого начала
необходимо учитывать электронную
корреляцию. Мы опишем здесь
подход, основанный на
приближении теории возмущений [28,
29], поскольку он
естественным образом вытекает из кван-
товоэлектродинамического
описания атома.
В низшем порядке по
межэлектронному взаимодействию
двукратная ионизация описывается фейнмановскими графиками,
приведенными на рис. 5.9. К этим графикам нужно еще
добавить обменные графики, получающиеся заменой значков v,*:sv2.-
Можно сказать, что график рис. 5.9а учитывает корреляцию
электронов в конечном состоянии, а график рис. 5.9б — в
начальном.
Согласно правилам соответствия (см. § 2.6) диаграмме рис. 5.9а
соответствует выражение
S^ = e^[ Л, d% d% (^. (x,)-Y„ Я1) (X,)) X
X (^v,(>^2) V-^C^^i^^s)^^з('^з)^„,(>^з))^,^,(>^1^2)- (5-267)
Подставляя в (5.267) выражения для электронного S(x2X^) и
фотонного (кулоновского) I^f.{xiX2) пропагаторов из §2.6, интегрируя
по временам и по частоте, входящей в выражение для S(x2X^),
получаем
W-
Рис. 5.9. Фейнмановские графики, опи-
сЬшающие двукратную фотоионизацию в
низшем пор51дке теории возмущений по
межалектронному взаимодействию.
Значки «1, «2 соответствуют состояниям
дискретного спектра, значки vj, V2 состояниям
сплошного спектра
'^а = 2я'7к2
(ео е*0„
Е -Е -ш
п п
x6(^v. + ^v,-^„.-^„,-'«)- (5-268)
Аналогичным образом получается вклад диаграммы рис. 5.96.
231
Переход к нерелятивистскому пределу, согласно результатам,
полученным в § 1.5, 5.1, дает (переходим также к атомным единицам)
S„ + S. = 2ш
Чъл
S
+ ; fX
^«-4+'"
X 6(£^_ + £^ - £. - £_ - Ш), (5.269)
где матричные элементы теперь нужно понимать как матричные
элементы операторов со шрёдингеровскими волновыми функциями.
6*40^\z^
16
12
8
4
о
- 1
"6-
1 ./'"■^«.^Ч
7^Г Д
1
^^^"х^
1 1
70
по
150
190 ш.эВ
Рис. 5.10. Результаты расчета а'*"*' для атома гелия в формах «длины» (г) и
«скорости» (V) — сплошные кривые. Результаты экспериментов: треугольники — [30];
кружки — [31]
Используя соотношение (5.19), переписываем (5.269) в таком виде,
где присутствуют матричные элементы оператора перехода в форме
«длины»:
S, + S, = -2nci^|§2
ffr) (->-.. (г) <-)v.
+ . , ..
X
X 6(£^ +£,-£„-£„- ")■ (5.270)
232
Сечение двукратной фотоионизации в общем случае
записывается в виде
6++(к, е; р,^, Р2^2) = 2п\\и\2б(£, + е^ + Г+ - ш) dp, dp^,
(5.271)
где £j, Pj, ^j — энергии, импульсы и поляризации фотоэлектронов,
I'*"*' — потенциал двукратной ионизации атома, а U — матричный
^+*,Мб
Рис. 5.11. Результаты расчета а с для Зр -подобалочки атома аргона в формах
«длины» (г) и «скорости» (V) — сплошные кривые. Результаты экспериментов:
квадратики— [33]; кружки — [31]; треугольники — [34]
элемент амплитуды перехода. При использовании теории
возмущений и определяется соотношением
<v,v2|S|n,n2> = 23t<v,v2|f/|nin2>6(£v +^ -£„ -£„ - ").
(5.272)
где матричный элемент 5-матрицы задается формулой (5.269) или
(5.270). При этом 1^ = -е„_ - £„^.
В заключение приведем результаты расчетов сечений о'*"*'
некоторых атомов, выполненных в рамках теории возмущений. На
рис. 5.10 приведены результаты расчетов а'*"*' для атома гелия [30].
Там же приведены данные экспериментов. На рис. 5.11 — то же для
атома аргона (Зр^-подоболочка) [32].
§ 5.7. Автоионизационные состояния
В этом параграфе речь пойдет об особых возбужденных состояниях
атома, способных распадаться безрадиационным образом, т. е. без
испускания квантов. Такие состояния возникают, во-первых, при
наличии дырок во внутренних оболочках атомов. Эта ситуация
схематически изображена на рис. 5.12. Сплошными горизонтальными
Линиями изображены уровни энергии атома, заполненные в
основной конфигурации. Сплошной кружок означает присутствие элект-
233
рона на уровне, полный кружок — его отсутствие (дырку).
Штриховые горизонтальные линии — дискретные уровни энергии, не
занятые в основном состоянии, жирная сплошная линия — граница
сплошного спектра.
Предположим, что в начальном состоянии имеется дырка во
внутренней оболочке, т. е. мы имеем дело с однократно заряженным
положительным ионом (см. рис.5.12а). Тоща электрон с верхнего
J£-X.
ух^^^//у^^х/х<^ 2222
Рис. 5-12. Схематическое изображение оже-процесса; а — начальное состояние 6 —
конечное. / — потенциал ионизации, Д£ — энергия перехода. Стрелками указаны
переходы электронов
занятого уровня может заполнить эту дырку, т. е. перейти во
внутреннюю оболочку, высвободив при этом энергию АЕ. Эту энергию
он может передать другому внешнему электрону, и если она больше
потенциала ионизации электрона из внешней оболочки /, то другой
электрон окажется в сплошном спектре (см. рис. 5.126). Таким
образом, произойдет безрадиационная ионизация атома (в конечном
состоянии имеется двукратно заряженный ион и несвязанный
электрон). Такой процесс называется эффектом Оже, или
автоионизацией, а соответствующее начальное состояние —
автоионизационным.
В некоторых случаях используют более детальную
классификацию оже-переходов. Собственно оже-переходами при этом
называют такие, когда дырки в начальном и конечном состояниях
находятся в разных оболочках. Если же одна или обе дырки в конечном
состоянии оказываются в той же оболочке (но, естественно, в другой
подоболочке), где была дырка в начальном состоянии, переход
называется переходом Костера—Кронига.
Другой характерный пример автоионизационных состояний -
двукратно возбужденные состояния (рис. 5.13). В этом случае в
начальном состоянии имеется нейтральный атом, в котором оба
внешних электрона возбуждены. Один из них может перейти в основное
состояЕше, высвободив энергию АЕ и передав ее второму
возбужденному электрону. Если (для данного конкретного примера) эта
энергия больше -= I, то второй электрон окажется в сплошном
спектре — произойдет ионизация.
234
Наличие автоионизационных состояний оказывает особо
важное влияние на процесс фотоионизации. Действительно,
рассмотрим однократно заряженный ион, находящийся в основном
состоянии, на который падает квант с энергией ш = АЕ (АЕ —
энергия перехода на рис. 5.12). Если этот квант взаимодействует
с внешним электроном, последний переходит в сплошной спектр
=гЛЕ-1 V'
у/////////////////. у///Щ
J к-
У//////////Л
-о 0-1--
1 }- ZZTI
^ о о ■' о в-^-
Р и с. 5.13. Схематическое изображение процесса автоионизации двукратно
возбужденного состояния атома: а — начальное состояние б — конечное. Обозначения те же,
что и на рис. 5.12
и возникает ситуация, изображенная на рис. 5.126. Это есть
прямой процесс фотоионизации, который был рассмотрен в
предыдущем параграфе. Может, однако, произойти другое: квант может
поглотиться внутренним электроном, поскольку частота ш = АЕ
находится в резонансе с переходом этого электрона во внешнюю
оболочку. Тогда возникает автоионизационное состояние,
изображенное на рис 5.12а, которое уже затем распадается
безрадиационным путем, переходя опять-таки в состояние рис. 5.126. Этот
процесс является резонансным, поскольку, в отличие от прямой
фотоионизации, происходит лишь при определенном значении
частоты. Ясно, что форма зависимости сечения фотоионизации
от частоты с(ш) в области автоионизационных резонансов
заметно искажается.
То же самое относится и к двукратно возбужденным
автоионизационным состояниям. В этом случае резонанс происходит при
поглощении этого кванта электроном внешней оболочки нейтрального
атома, находящегося в основном состоянии. При этом возникает
состояние, изображенное на рис. 5.136. Резонансным процессом в
данном случае является процесс двукратного возбуждения
автоионизационного состояния, изображенного на рис 5.13а *), и
последующего безрадиационного распада этого состояния.
*) Процесс двукратного возбуждения, как и процесс двукратной фотоионизации
(см. § 5.6), не может быть описан в одноэлектронном приближении и в рамках теории
возмз^щений требует учета тех же графиков {§ 5.6).
235
Получим теперь сечение резонансной фотоионизации, следуя
работе Фано [35], в которой впервые была построена
последовательная теория автоионизационных состояний. Говоря (выше в
этом параграфе) о том, что имеются начальные состояния
дискретного спектра (см. рис 5.12а; 5.13а) и конечные состояния
сплошного спектра, мы фактически использовали язык теории
возмущений и нулевое приближение для волновых функций. На самом
деле те и другие состояния смешиваются межэлектронным
взаимодействием, которое в нерелятивистской теории атома не является
малой поправкой и не может, вообще говоря, учитываться по
теории возмущений. Истинная волновая функция
автоионизационного состояния 5шляется суперпозицией «затравочных» состояний
дискретного и сплошного спектра, получаемых в нулевом
приближении, а процесс фотоионизации описывается как переход
из основного состояния атома в «истинное» автоионизационное
состояние.
Гамильтониан атома представим в виде (см. [I, (2.31)])
H = Ho + Hi, (5.273)
где Hq — одноэлектронная часть. Я; представляет собой
возмущение, связанное с межэлектронным взаимодействием. Будем считать,
как и в [35], что гамильтониан Н уже диагонализован на функциях
дискретного спектра, в результате чего получена функция
дискретного спектра «р, для которой *)
<9|Я|9> = /?^. (5.274)
Поскольку функция 9 набирается из функций нулевого
приближения, т. е. из собственных функций оператора Hq, с
коэффициентами, определяемыми путем диагонализации, то фактически диагона-
лизовать нужно лишь оператор //р
Точно так же мы будем считать, что гамильтониан Н
диагонализован на функциях сплошного спектра:
<<Р£»|Я| 9^,) = Е'Ь{Е" - Е'). (5.275)
Функции «рд описывают как вылетевший электрон, так и атомный
остаток, и также 5шляются, в принципе, суперпозициями
собственных функций гамильтониана Hq. Наконец, оставшуюся недиаголи-
зованной субматрицу матрицы оператора Н запишем в виде
<4>E'\ff\4>> = VE'- (5.276)
*) Мы рассмотрим здесь только простейший случай, когда имеется один
дискретный уровень на фоне сплошного спектра. В реальных ситуациях чаще бывает наоборот,
и автоионизационные уровни возникают целыми сериями (см. ридберговские
состояния в § 5.8). Точно так же мы учитываем только один тип сплошного спектра, т. е. один
возможный канал распада автоионизационного состояния.
236
Поскольку функции 9^, «р набираются из различных собственных
функций Hq, то (5.276) можно переписать в виде
<9£,|Я,|9> = У£,. (5.277)
«Истинную» функцию, которая получается в результате полной
диагонализации Н, будем искать в виде
я1)£ = a(f?)9 + j dE' V(^)9£'- (^-^^^^
Коэффициенты a{E) и Ье-{Е) получаются в результате решения
системы уравнений, которая следует из уравнения Шрёдингера для -ф^:
Е^а{Е) + S dE- Уе.Ье-{Е) = Еа{Е), (5.279)
V^.a{E) + ЕЪе,{Е) = ЕЬ^{Е). (5.280)
Формальное решение уравнения (5.280) можно записать в виде
ЬАР.) =
Е-Е'
+ л.г{Е)&(Е - Е')
V^a{E), (5.281)
z(E) = —J'^ _^ . (5.284)
где символ главного значения 9° указывает способ интегрирования
первого слагаемого в (5.281). Второе слагаемое учитывает
сингулярность при Е = Е', а функция z{E) пока остается неопределенной.
Подставляя (5.281) в (5.279) и сокращая на а(Е), получаем
Е^ + F{E) + nz(E) \Ve\'' = E, (5.282)
где
F{E) =^\dE' -^^. (5.283)
J E—E'
Отсюда
E-E -F(E)
f
Коэффициент a(E) определяется из условия нормировки
<^£"1 ^£> = а*{Е")а{Е) + \ dE' Ь*е-{Е")Ье>{Е) = Ь{Е" - Е).
(5.285)
Подставив (5.281) в (5.285), получаем
а*{Е")а{Е)\\ + \ dE' ^^ + ^^^^nz{E) +
^ \ ^ 1Е"-Е')(Е-Е') Е"-Е ^ '
+ l^£i- jtz(f?") -I- I F£|2jtV(f?)6(f?" - f?) 1 = 6(f?" - f?). (5.286)
Второй член в фигурных скобках в (5.286) сингулярен при
Е" = Е. Для выделения этой особенности можно представить
знаменатель в подынтегральном выражении в виде
^ = —^— (— ^—] + f{E', Е", Е)6{Е" - Е),
(Е"-Е')(Е-Е') Е"-Е уЕ-Е' E"-E'j (5 287')
237
a для функции / можно получить выражение [35]:
f{E', Е", Е) = пЧ (е/ - i (Е" + Е)). (5.288)
Далее подставляем (5.287) с учетом (5.288) в (5.286):
\a{E)\^\VE\''^''[l + z\E)]6{E" - Е) +
+a\E")a(E)[l+-^[F{E) - F(E") + nz(E) \V^\^-
- nz{E") I F^,-!^]) = 6(^" - E). (5.289)
Замечая, что выражение в фигурных скобках в (5.289), согласно
определению (5.284), тождественно равно нулю, окончательно
получаем:
1^
\а(Е)\^= _......,!......, = ,. . ll^la..,. ,4- (5.290)
Имея в виду формулу (5.278) для точной волновой функции
автоионизационного состояния, можно сказать, что дискретное
состояние 9 на фоне сплошного спектра «размывается» в результате
взаимодействия с состояниями сплошного спектра и приобретает
ширину. Эта ширина и соответствует безрадиационному распаду
автоионизационных состояний. Ниже, в гл. 6, этот же результат
будет получен и из квантовой электродинамики в рамках теории
возмущений. Сравним (5.290) с обычной формулой Брейта—Вигнера
[24] для распада квазистационарного состояния. При f?»/? —f? ,
т. е. на достаточном удалении от «затравочного» значения энергии
автоионизационного состояния, в выражениях V^, F{E) можно
положить Е = Е^. Тогда (5.290) в точности совпадает с брейт-вигне-
ровской кривой. Величина F{E ) представляет собой сдвиг уровня в
результате взаимодействия со сплошным спектром, а ширина
уровня определяется выражением (см. § 6.4)
r = 2n\V^\\ (5.291)
Получим теперь формулу для сечения процесса резонансной
фотоионизации Ор атома из исходного (основного) состояния -ф^. Это
сечение удобно выразить в виде отношения к сечению прямой
фотоионизации с„, т. е. к переходу непосредственно в состояние
сплошного спектра. Отношение сечений, очевидно,
пропорционально отношению квадратов матричных элементов:
о^_\<^е\ОШ\^ (5.292)
°п l<4>£|t/|li)i>l^'
где и — оператор перехода. В нерелятивистском приближении этот
оператор, вообще говоря, совпадает с оператором электрического
дипольного момента атома f/ = D, однако нужно помнить, что для
238
двукратно возбужденных состояний в нулевом приближении для
функции -фд (т. е. в одноэлектронном приближении без учета
взаимодействия со сплошным спектром) матричный элемент
<-ф£|В|'ф^> равен нулю.
Используя для вычисления матричного элемента в числителе
(5.292) формулы (5.278), (5.281) и (5,.290) и введя обозначение
д(Е) =
(5.293)
отношение сечений (5.292) можно записать в виде (формула Фа-
но [35])
°p_(g(£)+z(£))^ (-5 294)
"п l+zhE)
Числитель этой формулы обращается в нуль при некотором
значении Е = EqI
Для сравнения с экспериментом формулу Фано обычно
параметризуют, полагая д не зависящим от Е (параметр д называется
профильным индексом) и рассматри-
вая зависимость сечения
непосредственно от
«приведенной» энергии Z. Тоща
(5.296)
c„=c.<i±i>^
На рис. 5.14 приведены
значения с^с„ в зависимости
от Z при различных
профильных индексах д.
Заметим, что в формулах (5.292)—
(5.296) нище не
конкретизировался вид оператора U,
поэтому результаты
справедливы, в принципе, и для
других способов возбуждения
автоионизационных состояний.
В частности, формула (5.296)
задает также отношение
сечений резонансного и
нерезонансного процессов
ионизации атома электронами.
При обобщении теории Фано на случай нескольких
автоионизационных состояний, а также нескольких каналов распада оснсвная
проблема заключается в построении волновой функции -ф^ (т. е. в
Рис. 5.14. Зависимость сечения по формуле
Фано от приведенной энергии при различных
профильных индексах
239
обобщении формулы (5.278)). Это традиционная задача теории
рассеяния электронов на атомах, которая решается наиболее строго так
называемым методом сильной связи [36, 37], являющимся
фактически обобщением метода наложения конфигураций (см. [I, § 4.9]) на
состояния сплошного спектра.
Если интересоваться характеристиками автоионизационного
состояния как такового, не вникая в способ его возбуждения, то
важнейшей характеристикой является его ширина, определяемая
формулой (5.297). Можно также сказать, что эта формула определяет
вероятность перехода из начального автоионизационного состояния
в конечное состояние сплошного спектра, хотя нужно помнить, что
возможность такого толкования ограничена применимостью теории
возмущений. Естественно, что при наличии нескольких каналов
распада ширина получается как сумма вероятностей распада по
всем каналам:
r = 2n^\V^^.\\ (5.297)
j
Отметим, что формула (5.297), в отличие от выражения для
вероятностен радиационных переходов, не содержит малых
параметров. Поэтому малость автоионизационной ширины по сравнению
с расстоянием между энергетическими уровнями определяется
только величиной перекрывания функций дискретного и
сплошного спектров в матричном элементе V^ (см. (5.276)).
Например, безрадиационная ширина 252/>-состояния атома гелия равна
Г2,2р = 0,038 эВ [38].
§ 5.8. Излучение атомов в ридберговских состояниях
Ридберговскими состояниями в настоящее время принято называть
высоковозбужденные состояния атомов. Если речь идет об одноэлек-
тронном возбуждении, то возбужденный электрон с хорошей
степенью точности находится в кулоновском поле атомного остатка и
спектр состояний этого электрона является близким к водородному
спектру. Ридберговские атомы обладают весьма характерными
свойствами. Прежде всего, энергия возбужденного электрона, согласно
Бальмеру [I, (1.22)], дается выражением
Е = - -!- е„ (5-298)
где Eq = me^lV- — атомная единица энергии, п — главное кванте- ^
вое число. Энергии таких состояний при больших значениях п
весьма малы, и состояния легко разрушаются, что указывает на
трудность соответствующих экспериментов. Тем не менее, в настоящее
время экспериментально можно наблюдать состояния с n»j 100.
Из (5.298) следует, что размеры ридберговского атома очень
велики: с„ = п^^о, что при п ~ 100 дает а„ л^ 10~* см. Хотя ридбергов-
240
скии атом весьма подвержен внешним воздействиям, его
естественное время жизни достаточно велико. Это можно понять следующим
образом: зависимость "от п вероятностен переходов из возбужденного
состояния с п :«> 1 в нижележащие состояния такова: ьу„ л^ ri~^WQ,
ще Wq — вероятность переходов между нижними уровнями. Эта
зависимость следует, во-первых, непосредственно из точной формулы
(5.177) (на частных примерах (5.178)—(5.181) она видна сразу) и,
во-вторых, из полуклассической теории (см. ниже в этом
параграфе). Хотя время жизни уровня определяется всей совокупностью
возможных переходов, характер зависимости от п и порядок
величины вероятности остаются при их учете прежними. Таким
образом, для времени жизни т„ имеем т„ л^ п^г^, что при tq »j 10~^ с
(см. §5.1) и «яг: 100 дает т^л^ 10~^ с. Разумеется, в лабораторных
условиях время жизни зависит от столкновительного уширения и
других внешних воздействий.
Существенно также то, что естественные ширины в сериях рид-
берговских уровней не перекрываются друг с другом.
Действительно, интервалы между соседними уровнями при п^=^1 убывают,
согласно (5.304),
Af?„ = f?„-f?„,,«^Eo, (5.299)
п
как и ширины Г^. Однако ширина содержит еще малый параметр
а^ (см. (5.46)) и неравенство А£'„5е>Г„ сохраняется при любых
значениях п. Это открывает возможность селективного возбуждения
ридберговских состоянии с помощью узкополосного излучения
лазеров (см. по этому поводу обзор [39]).
Основным теоретическим методом описания ридберговских
состояний является метод квантового дефекта. В рамках этого метода
возбужденный электрон описывается кулоновскими волновыми
функциями с эффективным главным квантовым числом п' и
эффективным зарядом Z* = 1 (см. [I, § 2.5]). При этом п* = п + 6^, ще
6; — добавка, зависящая от орбитального квантового числа и
называемая квантовым дефектом. Уровни энергии в чисто кулоновском
поле описываются формулой Бальмера (5.298). Поправки к
формуле Бальмера можно записать в виде
^E„,= {y\>JV-V^\-^„,), (5.300)
где -фп; — волновая функция возбужденного электрона, а V— V^ —
оператор возмущения, учитывающий отличие потенциала V,
действующего на возбужденный электрон, от кулоновского потенциала
V(,. Благодаря наличию некулоновского потенциала, поправки к
энергии начинают зависеть от квантового числа /.
Обратимся теперь к выражению для радиальной волновой
функции R„i(r) [I, (1.26)] для возбужденного электрона. В области атом-
241
иого остатка, где существенно отлична от нуля разность V — V^,
координата равна г яг: Qq (или, в атомных единицах, г » 1).
Следовательно, в этой области волновую функцию R„i(r) при п»! можно
разложить по степеням г/п. Согласно [I, (1.26)] это дает (при Z= 1)
R_,^J1L,4:,, (5.301)
nl {2Z + 1)! „3/2-
Подставляя (5.301) в (5.300), получаем
6,
д^„/=--
(5.302)
где 6; — некоторая константа [39].
В методе квантового дефекта используется обобщение формулы
Бальмера
^ ^ (5.303)
Р'п1 =
2{п*)2
2{п + 6/
из которого при разложении по Ь[/п следует (5.302). Квантовые
дефекты 6; определяются из сравнения положения серий уровней с
экспериментом. Подробности о методе квантового дефекта, а также
его обобщение на состояния сплошного спектра можно найти в
обзоре [40].
Следует ожидать, что квантовый дефект убывает с ростом
орбитального момента, поскольку при этом убывает вероятность
нахождения возбужденного электрона в области атомного остатка. Для
демонстрации этого факта в табл. 5.1 представлены значения
квантового дефекта для ридберговских серий высоковозбужденных уровней
атома гелия, заимствованные из [41].
Состояние
Квантовый дефект
Isns^S
0,30
Isns^S
0,14
Isnp^P
0,07
Isns^P
0,01
Таблица5.1
Isnd
0,003
\snf
3-10"'*
Особая ситуация возникает для двукратных
высоковозбужденных состояний, которые также могут образовывать ридберговские
серии. Как следует из результатов предыдущего параграфа, такие
состояния являются автоионизационными. При изучении этих
состояний возникает дополнительная трудность, связанная с
невозможностью приписать ридберговской серии уровней определенную
конфигурацию. Так, например, в силу кулоновского вырождения
серии Isnp^P^, 2pns^P9, Ipnd^P^ сходятся к одному и тому же
пределу и в результате сильно взаимодействуют. Поэтому для
классификации таких состояний необходимо использовать специальные
квантовые числа. Одна из классификаций, предложенная Фано [42],
связана с поведением двухэлектронной волновой функции в точке
тройного столкновения и с разложением Фока в окрестности этой
242
точки (см. [I, § 4.1]). Более подробно об этой и других возможных
классификациях двукратных высоковозбужденных состояний можно
прочитать в обзоре [43].
Для вычисления вероятностей переходов между ридберговскими
уровнями, а также для вычисления сечений фотоионизации ридбер-
говских атомов, в принципе, можно воспользоваться точными
формулами, полученными для кулоновского поля (см., например,
выражение (5.177)). Эти точные формулы, однако, слишком громоздки и
представляет интерес получить более простые и наглядные
выражения, пользуясь полуклассическим приближением, которое, как
следует из общих соображений [24], должно быть применимо именно к
состояниям с большими квантовыми числами. Этой задаче было
посвящено большое число работ, в которых использовались различные
методы (см., например, [44—48], а также обзор [39]). Мы изложим
здесь в упрощенном варианте подход, использованный в [45, 46].
Согласно (5.30), сила осциллятора для перехода между
состояниями п1т[ и n'l'm'i водородоподобного атома равна *)
, 2т I , , 12
^п1т^пГт]~ ЗЙ ^n'n\v)n'rm'^nlm\ (5.304)
ИЛИ, после усреднения по т^ и суммирования по mj
■' nl, n'l' 2/ + 1 Zj Zj ^ nlm^ n'l'm'i
V «'''-";• (5.305)
m, m.
Из общей теории квазиклассического приближения в квантовой
механике следует [24], что матричные элементы (f)s,N некоторой
физической величины / при условии на квантовые числа
AN = Ni-N2^Ni, N2, (5.306)
в классическом пределе переходят в компоненты Фурье f^ _^
разложения классической функции f(t) в ряд Фурье.
Рассмотрим связанный электрон в кулоновском поле. В
классической механике траектория его движения представляет собой эллипс,
лежащий в плоскости, перпендикулярной сохраняющемуся вектору
момента количества движения 1. Направим ось z системы отсчета по
вектору 1, тоща движение электрона описывается двумя декартовыми
координатами в плоскости орбиты ху. Параметры орбиты связаны с
сохраняющимися величинами Е, I (энергией и абсолютной
величиной момента импульса) следующими соотношениями (f? < 0):
а=~, (5.307)
1-^'=-^' (5-308)
mZ е*
где а — величина большой полуоси эллипса, е — эксцентриситет.
*) Для наглядности мы не пользуемся здесь атомными единицами и используем
обозначение т, для азимутального квантового числа.
243
Для определения частоты периодического движения необходимо
перейти к переменным действие — угол /|<Р|. Действия
определяются формулами
I, = j^^p,dg, 0=1,...,.), (5.309)
1^£ Pi> 9i — канонически сопряженные переменные: обобщенный
импульс и обобщенная координата; s — число степеней свободы.
Интегрирование в (5.309) ведется по промежутку изменения
(циклу) обобщенной координаты, на котором повторяются значения
обобщенного импульса. Подразумевается, что переменные в задаче
полностью разделяются. Угловые переменные определяются
соотношениями
Ф, = ^Ж, (5-310)
где W — решение уравнения Гамильтона—Якоби. Это уравнение
имеет вид
(5.311)
п( , 9W dW\ „
где Н — функция Гамильтона, W='^ Ж,(^^/1, ..,, IJ.
1=1
В случае кулоновской задачи в полярных координатах г, «р "в
плоскости орбиты вычисление действий приводит к
результату [49]
i^=l> (5.312)
K = -i^ + ^f^- (5.313)
Отсюда
Н=Е= т;. С5 314^
2{/, + у2 10.01Ч;
Частоты периодического движения определяются формулами
a>=6=^ = i^ (5-315)
^i i— dt di:
Из (5,314), (5,315) сразу видно, что движение в кулоновском поле
является вырожденным (две частоты совпадают). Однако
каноническим преобразованием переменных действие — угол всегда можно
добиться такого их выбора, что все ненулевые частоты будут
линейно независимы. Для кулоновской задачи это дает
/ = /+/; /' = /, (5.316)
Н=Е= -^^, (5,317)
244
в результате
= ^Л = Л.{1Ж (5.318)
dl ^7 ^ т '
со— ,, ,
Принцип квантования Бора заключается в квантовании
независимых действий:
1=пК (5.319)
I^=mih, (5.320)
где п — главное квантовое число, т^ — азимутальное квантовое
число, Товда из (5.317) сразу же следует формула Бальмера
(5.298).
После этих предварительных соображений запишем разложение
координат электрона x{t) и y{i) в ряд Фурье:
00
^(0 = S ^. ^"""'' (5.321)
5ЯЯ—оо
OD
yW = S У. е"'^"'. (5-322)
SSX—CO
где частота со определяется формулой (5,318), а значок
суммирования S имеет смысл разности квантовых чисел s = An = п— п' (см.
(5.306)). Зависимость координат х, у от времени удобно
представить в параметрической форме, вводя так называемую
эксцентрическую аномалию и по определению
са< = ы—esinM. (5.323)
При этом предполагается, что в момент t = 0 электрон находится в
перигелии. По смыслу величина at представляет собой угловую
переменную Ф^, канонически сопряженную действию 1^. Выражения
для X, у через аномалию и таковы [50]:
X = a(cos и— г), (5,324)
у = aVl — е^ sin и. (5.325)
Теперь можно определить коэффициенты Фурье х^, у^ в (5.321),
(5.322), вычисляя интегралы
т
x^ = j\ x(t) е""' dt =
о 2я
= ~ \ е"("-'="" ">(cos ы - е) (1 - е cos м) du, (5.326)
о
т
y, = ^\y(t)e'''-'dt =
о ^2л
= ~ VI-е^ J е"("-^"°") sin ы (1 - е cos и) du, (5.327)
245
где Г — период обращения, равный
Т = 2п/(о. (5.328)
Вычисление интегралов (5.326), (5.327) дает [46]
x, = f/;(se), \s\>l, (5.329)
У. = ^^'^^Лsг), 1.1 ^1, (^-330)
Хо=-|ае, (5-331)
>'о = 0. (5.332)
где /^ — функция Бесселя, /^ — производная от нее по аргументу.
Итак, мы приступим теперь к классической аппроксимации
формулы (5.305), считая, что правила отбора для матричных элементов
(r)„7'm'; nim "ам уже известны. Правила эти очевидным образом
следуют из теоремы Эккарта—Вигнера (см, [I, § 3.3]) и для
сферических компонент вектора г имеют вид [2]
(5.333)
(Х -I- iy)n'['m];nlmi~ ^n'n/m,"/,r±l"m,, mj-l'
(Х— i>')„7'm;,n/m, ~ ^п'п/т,"Л/'±1 m,, mj+l' (5.334)
i^fn'l'm',; nlnii ~ ^n' nlm^l, l'±\"m^ m' (5,335)
. Прежде всего заметим, что эти правила отбора могут быть
получены и непосредственно в полуклассическом подходе, для чего
необходимо рассмотреть движение электрона не в полярных, а в
сферических координатах г, -9, ф и, помимо фурье-разложения по
угловой переменной Ф^ = ш, использовать одновременно разложения
по другим угловым переменным, совпадающим с обычными углами
Ф(У = -9, Ф = ф [45]. Для наших целей, однако, проще использовать
известный квантовомеханический результат.
Далее отметим, что при нашем подходе, поскольку отсутствует
движение по оси z, отсутствуют и переходы без изменения
азимутального квантового числа Ат^ = 0. Для наших целей это
несущественно, так как мы претендуем лишь на вычисление выражения
(5,305), просуммированного по всем значениям т^, m'l. На значении
всей суммы не сказывается способ выбора осей системы отсчета в
классической задаче. Однако при желании можно получить и
классический аналог матричных элементов с Ат^ = О, опять-таки
переходя к сферическим координатам и используя принцип
соответствия [45].
Сделаем, наконец, еще одно существенное предположение. В
рамках классической механики естественно считать, что с
увеличением длины вектора момента импульса / (ориентированного по оси
246
z) одновременно увеличивается (а не уменьшается) и его проекция
на ось Z, Иными словами, если А/ > О, то Ат^ > О, и наоборот: при
А/ < О и Anil < О, Из сравнения с (5.333), (5.334) теперь следует,
что переходы с А/ > О описываются матричными элементами
X + iy, а переходы с А/ < О — матричными элементами х — iy.
Основной результат этих рассуждений можно теперь записать в
виде соотношения
■ =_2mcos. .2 (5.336)
где мы использовали также полуклассическое соответствие
са„'„ = (OS [24], s= п — п'. Заметим, что суммирование по
квантовым числам т'[ и усреднение по т^ не приводит ни к каким
дополнительным множителям, поскольку изменение Ат^ фиксировано, а
усреднение в нашем приближении соответствует умножению на
единицу. Подставляем (5.329) и (5.330) в (5.336) и используем для
частоты со еще одно выражение, которое следует из определения
(5.318) и формулы Бальмера (5.298):
_^_mzV (5.337)
Здесь п в принципе не совпадает ни с п, ни с п'. В выборе этого
квантового числа остается произвол, который мы, следуя [46],
устраним так:
п = -^. (5.338)
Та же проблема возникает при определении выражения для
эксцентриситета е в (5,329), (5,330): на самом деле в выражение (5,308)
мы должны подставить некоторое значение /, также не совпадающее
ни с /, ни с /',' Вновь следуя [46], зафиксируем его так:
7=тах (/,/'). (5,339)
При этом с учетом (5,304) эксцентриситет записывается в виде
8^=1-7^Я?. (5.340)
Окончательный результат выглядит следующим образом:
~ Г п 1^ (5.341)
/„Лп7±1=-^Р^е)±у1-1/Д.е)] .
Эта формула, разумеется, значительно проще, чем та, которая
следует из общего выражения (5.177); однако нужно помнить, что она
справедлива лишь для переходов между высоковозбужденными
уровнями.
Для оценки качества приближения приведем сравнение точных
и квазиклассических выражений для ряда переходов [45].
Сравниваются выражения для квадрата дипольного матричного элемента,
247
которые, согласно (5,310), связаны с силой осциллятора
соотношением (см. также (5,313))
Kil; п'1±\ ~ ~ 2mcos ^nl; n'l±\ ~ \^s — ^Уs) ~
= (т) ' [^'Л'') ± l5--^-^.(^^)] '• (5.342)
Результаты сравнения приведены в табл. 5.2 (в атомных единицах).
Видно, что согласие весьма хорошее даже при небольших квантовых
числах. Заметим, кстати, что с учетом (5.298)
где Qq — боровский радиус.
(5,343)
Таблица 5.2
Переход
2s—Зр
4s—5р
6s—7 р
4p-5d
4d-5f
Квантовая
механика
9,393
72,553
274,19
121,86
197,83
Квазиклассика
9,270
73,181
275,25
123,18
200,46
Погрешность, %
3,48
0,86
0,38
1,08
1.33
Используя (5.331), можно получить также выражение для ди-
польного матричного элемента перехода без изменения главного
квантового числа п. В этом случае формально частота перехода cos
равна нулю в классической теории и формулу для силы осциллятора
(5.336) использовать нельзя. Однако непосредственно из (5.331) с
учетом (5.343) следует (в этом случае п = п):
Rlr,nU.. = -l = -An4n--~P), (5-344)
что совпадает с квантовой формулой (5.182),
Существует эмпирическое правило (см. [2]), согласно которому
вероятности переходов, для которых An и А1 имеют одинаковый
знак, больше вероятностей, для которых эти величины
противоположны по знаку. Например, вероятности переходов 2p—*3s и
2p—*3d относятся друг к другу, как 1 : 25. Формула (5.342)
объясняет это правило в случае ридберговских переходов. Действительно,
можно воспользоваться известным свойством нулей функций
Бесселя /^ при v>0 [51]:
v^x; <х, , (5.345)
Iv Iv'
248
где Xj^ — положение первого нуля функции J^, x'l^ — положение
первого нуля функции /^, В формуле (5.342) следует считать е < I
(эллиптическая орбита) и при s>0 (An>0) аргументы функций
/j(se) и J'^(st) соответственно меньше Xj^ и х\^. Поскольку при
х^О (s > 0) /^(х) > О и /^ > О, то в квадратных скобках в (5.342)
оба члена положительны. Следовательно,
^1; п'1+\ > ^1; п7-1> (5.346)
что и требовалось доказать.
Во многих случаях интерес представляет сила осциллятора для
перехода между двумя вырожденными уровнями п и п':
п-\
fnn' — '^Ai (fnl; п7 + 1 + nl: n'l-l)- (5.347)
l = \
Для вычисления /„„< можно воспользоваться приемом,
предложенным в [46]. При этом удобнее не проводить усреднения по т^ при
каждом заданном /, как мы делали выше, но суммировать по ш^ и
затем по / и делить результат на полное число состояний в оболочке
гР: Как показано в [46], результат такого усреднения функции
F(l) можно представить в виде интеграла по е^:
п-1 1
^2('^^+^)^(0^\dt^F(t). (5.348)
/=о о
Чтобы убедиться в справедливости такой замены, достаточно
вычислить сумму при F(l) = 1:
п-1 п 1
^.У{21+\)^\\2Ы1=\ dt\ (5.349)
/=о о о
где мы использовали выражение для эксцентриситета (5.340).
Таким образом,
1
/„„' = \ dt"" (f„i, „'i^,.+ /„,;„.,_i). (5.350)
о
Делая замену переменных y=ts, подставляя (5.341) и вычисляя
интеграл, после ряда преобразований получаем [46]
/««'= -5S 'У^ (^•^.(^)-^;(^)) = -¥^. (5.351)
о
Основная формула для ридберговских переходов (5.342) может
быть получена также другим методом, а именно — непосредствен-
249
ным вычислением радиальных интегралов
•'2
(5.352)
с квазиклассическими волновыми функциями [24]
( < ^
1 г _ , . . .3
Sin
_(vf
^nlif-) - rPXr)
где
Pnlir) =
Id
-T2+f
(5.353)
(5.354)
CO определяется формулой (5.337), a классические точки поворота
r"'2 — условием
pU'-i!2) = o.
(5.355)
Именно таким образом формула (5.342) была впервые получена в
[44] (см. также [52, 53, 48]).
Рассмотрим теперь вопрос о том, какими переходами
определяется время жизни ридберговских атомов. Вероятности переходов,
согласно (5.31), получаются умножением силы осциллятора на
квадрат частоты. Это обстоятельство оказывается решающим и
переходы с наибольшей частотой оказываются наиболее вероятными,
несмотря на то, что сама сила осцилляторов является наибольшей
для переходов с близкими главными квантовыми числами (это
объясняется наилучшим перекрыванием волновых функций), т. е.
когда частота является наименьшей. Например, для переходов с
уровня 4р на Is, 2s, 3s силы осцилляторов относятся друг к
другу как 1 : 3,5: 16, тогда как вероятности переходов относятся
как 23 : 3 : 1. Таким образом, из всех возможных переходов с
излучением из начального состояния п1 наиболее вероятен переход в
состояние с наименьшей энергией, совместимый с правилами отбора.
Таким переходом, очевидно, является переход в состояние п' = I,
Г = I — I (нужно вспомнить, что при заданном I' квантовое число
п' меняется в пределах от /' -|- 1 до <»),
Используя (5.160), (5.177), а также формулу Бальмера для
определения частоты oi^iu-i, запишем точное выражение для
вероятности такого перехода (в атомных единицах):
16 (n + Z + l)! (n-l)^-^(4nl)^
w
nljl-l
= a^
3 (n-l)H2l + iy.
(n-l)^
(5.356)
Эту вероятность удобно сравнивать с вероятностью перехода
2р—» Is в атоме водорода, т. е, с W21 ю = ^с Тогда, используя обыч-
250
ное для ридберговских серий неравенство
1«п,
а также формулу Стирлинга, получаем [39]
3^ е-^'{4/)^' 1
W
ЬУп.
п1,и-1 ^ 121 + 1)1 „3 "'О
(5.357)
(5.358)
Таблица5.3
Орбитальный момент /
3 Ш^,//-!
п
шо
1
6,68
2
1,56
3
0,498
4
0,182
5
0,0723
В табл. 5.3 приведены значения w„[j[-i, вычисленные по формуле
(5,358) для некоторых значений /. Видно, что вероятность резко
убывает с ростом орбитального момента. При п = 2 во втором
столбце табл. 5.3 (/ = 1) стоит 6,68 вместо точного значения 8; различие
объясняется неточным выполнением неравенства (5,357),
использованного при выводе (5.358), для случая /=1, п = 2. Зависимость
^п1,и-\ °^ " согласуется с оценками, использованными в начале
этого параграфа.
Оценим вклад переходов на близлежащие уровни в ширину
ридберговских уровней атомов. Для этого в формуле (5.341) положим
5=1 (п' = п— 1). Будем также считать, что выполняется
неравенство (5.357). Тогда, оставляя в (5.341) лишь главный член, получим
4/;„-U±i=lK(l)]'- (5.359)
Чтобы перейти к вероятности ьу„/;„-1,/±1> умнож'им (5.359) на
—2а^са^ (см, (5.159), (5.160)), где со определяется согласно (5.337).
Результат удобно вновь записать через Wq. Определение числовых
коэффициентов в (5.359) и расчет (5.178) дают возможность записать
результат в виде [39]
^MI,., (5.360)
W.
nl;n-i,l±i
= -^Wr,
Сравнение с (5.358) показывает, что переходы между ридберговски-
ми состояниями вносят малый вклад (~ 1/п^) в полное время жизни
ридберговского атома. Однако такие переходы представляют
практический интерес как возможный способ получения когерентного
длинноволнового излучения (лазера) (см. по этому поводу [39]).
Формулы квазиклассической теории могут быть применены
также для описания переходов с ридберговских уровней в сплошной
спектр, т. е. для описания фотоионизации ридберговских состояний
[44, 48]. При дополнительном условии Ап;«>-1 из этих формул, в
частности, следует формула Крамерса (5.252).
251
§ 5.9. Рентгеновские спектры атомов и ионов
Рентгеновские спектры нейтральных атомов возникают при
наличии вакансий (дырок) во внутренних оболочках. Электроны из
внешних оболочек заполняют эти дырки с испусканием
рентгеновских квантов. Энергия таких переходов имеет порядок величины
Z\q (где Zq — атомная единица эд1ергии), так что при
достаточно больших значениях заряда ядра Z (уже при Z> 10)
излучение будет находиться в области частот, которую принято относить
к рентгеновской. Для классификации рентгеновских спектров
необходимо иметь классификацию состояний атома с
вакансиями во внутренних оболочках — так называемых рентгеновских
термов.
Полный момент заполненной электронной оболочки равен
нулю. При наличии вакансии электронная оболочка приобретает
некоторый момент у, который может принимать те же значения,
что и момент одного электрона: у = 1/2,3/2, ... Можно ввести
также квантовое число l = j±-= (см. §1.2). Таким образом, для
обозначения состояния дырки можно использовать обычные
обозначения одноэлектронных состояний nL: Isi, 2si, 2pi, 2рз и т.д.
■' 2 2 2 2
Для рентгеновских термов приняты, однако, специальные
обозначения:
Isi 2si 2pi 2рз 3si 3pi Зрз. 'idъ 3ds
222222 2 2 2
К L^ Ljj Z^jj Mj Mjj Mjjj Mjy My
Уровни с n = 4, 5, 6 обозначаются аналогичным образом буквами
N, О, Р.
Термы К, L, М всегда достаточно хорошо отделены друг от
друга, поскольку отвечают различным значениям главного квантового
числа п. Группы уровней, соответствующие одинаковым значениям
п, но разным у, образуют так называемые дублеты. Это, например,
Lj, Lji и Ljii или Mj, Мц и Мщ, Mjy и т. д. Релятивистские дублеты
при aZ *« 1 находятся друг от друга на таком же расстоянии, как и
термы, различающиеся главным квантовым числом. При меньших
значениях Z они сближаются и их расщепление определяется
величиной спин-орбитального взаимодействия.
Расщепление же уровней с одинаковыми п, у, но различными
значениями /, связано с отклонением поля, в* котором движутся
электроны, от чисто кулоновского поля ядра, т. е. с учетом
взаимодействия с другими электронами (экранировкой).
Соответствующие группы уровней называют экранировочными дублетами:
например, Lj и Z^, Mj и Мц. Расщепление экранировочных
дублетов уменьшается с ростом Z и составляет величину порядка
1/Z от нормального расстояния между термами К, L, М (см.
§3.1). ■
252
На рис. 5.15 представлена схема наиболее интенсивных
спектральных линий, соответствующих переходам между нижними
уровнями. Наиболее коротковолновой является ^-серия,
возникающая при переходах электронов на ^-терм с более высоких
м^
м.
'ш
Mr
к
1
«1
' 1
•
' '
'
■ \
'
' '
'
(
'
L = серия
^Pi/г
2Рф
^Pi/г
Zs
1/г
К= серая
'•5уг
Р и с. 5.15. Схема рентгеновских переходов между нижними уровнями. На схеме
указаны только наиболее интенсивные £1-переходы
уровней. Эта серия аналогична главной оптической серии
npj^lsi (/=1/2,3/2).
Могут существовать также рентгеновские термы с
несколькими вакансиями в электронных оболочках. Поскольку спин-
орбитальное взаимодействие для электронов внутренних
оболочек превосходит по величине кулоновское взаимодействие
электронов друг с другом, моменты дырок складываются по схеме
уу'-связи.
Ширины рентгеновских термов определяются вероятностями
переходов электронов с более высоких уровней с заполнением
вакансий. Эти вероятности могут быть вычислены по формулам § 5.4
((5.193), (5.194)), а в случае не слишком больших значений Z —
по формулам этого же параграфа с разложением по степеням aZ. В
частности, для электрических дипольных переходов вероятности
пропорциональны a(aZ)'* (см. (5.198)). Это объясняет большую
ширину рентгеновских термов.
В табл. 5.4 приведены значения полных абсолютных и
относительных парциальных вероятностей для ^-серии при различных
значениях Z. Эти величины получены теоретически в приближении
Хартри—Фока—Дирака [54].
253
Таблица5.4
z
Полная
ширина, эВ
20
0,1312
0,1315
0,5061
0,5043
30
0,790
0,1410
0,5142
0,5108
40
2,800
0,1913
0,5225
0,5120
50 .
7.32
0,2230
0.5343
0,5148
60
15.93
0.2504
0,5491
0,5167
70
30,32
0,2634
0,5673
0,5175
80
52.72
0,2788
0,5899
0,5170
90
85,47
0,2952
0.6182
0,5134
В случае меньших значений Z (т, е. для более легких атомов или
более высоких уровней, для которых эффективный заряд ядра
уменьшается благодаря экранированию) более существенную роль
начинают играть оже-процессы (см. § 5.8), Соответствующая
ширина пропорциональна а^ (в релятивистских единицах, см, § 6,4), а
отношение радиационной ширины к автоионизационной оже-шири-
не равно
^^^(aZ^)\ (5.361)
Отсюда следует, что оже-процессы становятся преобладающими при
Z < 10 (при этом нужно помнить, что ширина Гд имеет также
непараметрическую малость, связанную с перекрыванием волновых
функций — см. § 5.8). Так, например, экспериментальное значение
вероятности оже-процесса L^^^—^MM для атома аргона (Z=18)
равно 0,16 эВ (расчет дает 0,19 эВ) [55]. Эта величина сравнима с
радиационными ширинами при тех же значениях (см, табл, 5.4),
В рентгеновской области находятся также спектры
многозарядных ионов, таких, например, как ионы водородоподобного
и гелиеподобного железа Fe XXVI и Fe XXV, наблюдаемые
при солнечных вспышках. Например, резонансная линия Fe XXV
Is^'^Q—Islp'Pj имеет длину волны 0,1851 нм, что отвечает
области мягкого рентгеновского излучения. Наблюдение таких спектров
при солнечных вспышках объясняется высокой температурой
внутренних областей Солнца. Приравнивая потенциал ионизации для
внутренних электронов атома железа к средней энергии частиц в
солнечной плазме кТ, где к — постоянная Больцмана, Г —
абсолютная температура.
Z^ а, е, = кТ,
(5.362)
при Z = 26 получаем оценку Г » 10* К, Эта грубая оценка
указывает, при какой температуре плазмы могут образовываться ионы
водородоподобного железа. На самом деле температура солнечных
недр ближе к Г «» 2* 10' К.
254
Возможность определять температуру плазмы по спектрам
многозарядных ионов обусловливает практическую важность изучения
этих спектров для диагностики плазмы в экспериментальных
термоядерных установках. Более подробно эти вопросы обсуждаются в
обзорах [56—59] и монографиях [6, 60].
Важным лабораторным методом получения высокозарядных
ионов является пропускание пучка ионов через фольгу (beam-foil-
метод) [61], Таким способом оказалось возможным получить ионы
водородоподобного и гелиеподобного урана [62], спектры которых
лежат уже в жесткой рентгеновской области,
В отличие от рентгеновских спектров, нейтральных атомов,
спектры многозарядных ионов по своей структуре больше
напоминают оптические спектры. Действительно, те и другие возникают
при переходах внешних электронов, хотя сами переходы находятся
в разных областях длин волн. Вместе с тем существуют и важные
отличия. Во-первых, наблюдаются значительные отклонения от
схемы LS-связи, а с увеличением Z — приближение к схеме JJ-
связи. Во-вторых, с увеличением Z становятся разрешенными
переходы, запрещенные в оптических спектрах, в частности
интеркомбинационные. Оба эти обстоятельства естественно объясняются
возрастающей ролью релятивизма и отсутствием малости по
параметру aZ (см. § 5.3).
Характерной особенностью спектров многозарядных ионов 5шля-
ется наличие сателлитных линий, возникающих вблизи
резонансных линий данного иона и принадлежащих иону на единицу
меньшей кратности ионизации, у которого возбуждены два электрона.
Такие сателлиты называются диэлектронными. Они связаны с
переходами из автоионизационных состояний и их появление
объясняется ростом вероятности соответствующих радиационных переходов с
ростом Z, в то время как вероятность автоионизации практически
не растет с ростом Z или растет значительно слабее. В качестве
иллюстрации последнего утверждения в приложении 2.11 приведена
таблица автоионизационных ширин двухэлектронных ионов при
различных значениях Z, заимствованная из [60].
Так, например, сателлитами резонансных линий водородоподоб-
ных ионов 2pi_—* Isi, 2рз—* Isi 5ШЛЯЮТСЯ переходы в гелиеподобных
2 2 2 2
ионах типа llnl'LSJ—* IsnV'L'S'J', а сателлитами резонансных
линий гелиеподобных ионов ls2p''^P,—> Is^'Sq являются переходы в
литиеподобных ионах типа ls2lnl'LSJ—*ls^nl"LSJ при всех
возможных значениях индексов /, L, S, J.
§ 5.10. Многофотонные процессы в атомах
В этом, последнем, параграфе главы, посвященной описанию
взаимодействия атомов с излучением, мы рассмотрим процессы с
участием нескольких фотонов. Вообще говоря, это процессы высшего
порядка по электродинамической константе связи а = e^/hc, т. е. их
255
вероятности должны быть малы по сравнению с вероятностями
рассмотренных выше процессов первого порядка. Если, однако, атом
находится в интенсивном внешнем поле, то взаимодействие его с
этим полем уже не является слабым. Фактором усиления здесь
является число квантов поля N, и, поскольку процессы с
несколькими фотонами пропорциональны степеням N (см. ниже), их
вероятности становятся сопоставимыми с вероятностями одноквантовых
процессов.
Такой подход, однако, по-прежнему связан с применением кван-
товоэлектродинамической теории возмущений на состояниях с
определенным числом квантов поля и, безусловно, становится
неприменимым, когда число квантов достаточно большое. Это происходит,
например, в интенсивном электромагнитном поле лазера. Описание
взаимодействия интенсивного электромагнитного поля с атомом
гораздо удобнее проводить с помощью формализма квазиэнергии [63,
64]. В этом формализме электромагнитное поле вводится как
классическое внешнее поле, взаимодействующее с атомом.
Последовательный переход от квантованного электромагнитного поля к
классическому можно совершить, используя так называемые
когерентные состояния (см. по этому поводу [12]). Однако
^/ описание взаимодействия атомов с внешними
полями выходит за рамки этой главы, и мы
рассмотрим здесь только такие процессы с несколькими
фотонами, для которых можно использовать
теорию возмущений, т. е. при не слишком высоких
интенсивностях.
Другая ситуация, когда изучение
многофотонных (в частности двухфотонных) процессов по
теории возмущений является оправданным, —
наличие переходов, запрещенных с испусканием
одного кванта. Примеры таких переходов будут
рассмотрены ниже.
Амплитуда взаимодействия электрона с п
фотонами. Рассмотрим матричный элемент S-
матрицы, описывающий процесс взаимодействия
атомного электрона с п фотонами. Это может
быть поглощение п фотонов, излучение или
рассеяние. Соответствующий график Фейнмана
изображен на рис. 5.16. Согласно правилам
соответствия (см. § 2.6), матричный элемент 5-матрицы
имеет вид (в этом параграфе мы используем сокращенные
обозначения для матричных элементов 5-матрицы)
4"i= (-'^)" \ (%'(^1)ЖХ,)'5(^,^2)Ж^2)-
где Л(х) — оператор излучения. В дальнейшем будем считать, что
атом взаимодействует с полем, в котором имеется N (N^^'it)
одинаковых фотонов. Учитывая вид матричного элемента оператора
х.
а:.
\/\j\r
"X/KTJ-
so.
"WV
Рис. 5.16. График
Фейнмана,
соответствующий
процессу поглощения,
излучения или
рассеяния п квантов
256
рождения фотона (см. § 5.2), видим, что в каждой вершине по5шля-
ется дополнительный множитель y/N+ 1 '«V^ (при N^^n). Тоща
можно использовать следующее выражение для оператора Л(х)
(рассмотрим для определенности случай поглощения):
Л(х) = ■^^fe'C''--'), (5-364)
где V — нормировочный объем *). _
Подставляя в (5.363) выражения для операторов Л(х) в виде
(5.364), а также для пропагаторов (2.227) и интегрируя по
временам и частотам, входящим в выражения для пропагаторов,
получаем
—
^\ --= -2ni(-ier (^)'б(£д + по - Е^.) X
^ 2 (£ -Е.-(п-1)ы]...1е'-Е^-о^Г (^-^^^^
где суммирование по s,, ..., s„_, проводится по всему спектру
уравнения Дирака для атомного электрона. В случае атома водорода это
уравнение (1.1) с гамильтонианом (1.34), (1.35).
Перейдем в (5,365) к нерелятивистскому пределу. Для этого
используем результаты § 1.5, 3.4. Разбирая последовательно
цепочки матричных элементов, с учетом порядка их величины
получаем
<я1,(/)|||я1,(Г)> =-1{<фМ|еа|х1^)> -I- <хГ^|еа|ф(Г)>} =
= - i <фГ^ I (ео) (ор) + (ар)(OS) | ф^Г>> =
= -1<ф(/)|ар|ф(Г)>~0(а) а. е., (5.366)
<4i,(-)|i| 4'Ь = { <хГ| (ap)(os) -I- (os)(ap) | х^Т^ =
= '<хГ^|ор1х^"^>~0(а) а. е., (5.367)
*»-1<хГ^!еа|ф(Г))~0(1) а. е., (5.368)
*t.-i<ip(^)|ea|xir)>~0(l) а. е. (5.369)
Такой анализ приводит к тому, что для п-фотонного процесса в
сумме по Sj, ..., s„_j главный вклад дают члены, в которых либо все
*) в данном случае удобно использовать такую нормировку — см. ниже.
9'/2 л. Н. Лабзовский 257
E^ положительны, либо положительные Е^ чередуются с
отрицательными. Действительно, с учетом порядка величины
энергетических знаменателей, получаем оценки:
(5.370)
(?)^^-^(f)^^~0(l)a.e.,
а
(t)+-(e)-+~0(l)a.e.
(5.371)
Все другие цепочки матричных элементов имеют дополнительную
малость по а.
Выпишем явные выражения для !^?\ и М^Л:
S^^\ = -2nie'
(2kN\ ^,
Ед -I- 2(0 - Ед,) X
X
(ерЬ, (ер) . ,
^,(+)
5<А = -2явЗ (^)^6(Е,-Ь2а. - е,,) X
^1 й;
*,(+)*2(+)
(5.372)
(ер)^,^(ер)у_(ер),_^
— е. —2ш)(е — е. —ш)
*А<*Р^лА
(ер)^г
2 ^ е. —е. —ш 2 ^ е. —е. —2
2ш
^,(+) ■
^,(+) "
(5.373)
При этом мы использовали системы функций ф^ ^ (см. § 1.5) и
соотношение {еа){еа) = 1, которое следует из (1.30). Если также
учесть, что знаменатель в предпоследнем члене в фигурных скобках
в (5.373) с учетом закона сохранения можно преобразовать к виду
Ед. — Ед — (О = —2(0, то два последних члена в фигурных скобках
взаимно уничтожаются. Такая же картина, как можно проверить,
получается при всех значениях п>2: все члены, содержащие
символы Кронекера, т. е. происходящие от суммирований по
отрицательным энергиям, взаимно уничтожаются. При п = 2 такой член
существует лишь для А' = А, т. е. в случае упругого рассеяния
фотона. Итак, в нерелятивистском пределе *)
S^\ = 2Щ-еГ ^Щ'Нг, + пе^ - г,.) X
хУт
..(ер).
(п-1)ш]...(е,-е,-ш]' (5.374)
Для вычислений удобнее перейти от матричных элементов
импульса к матричным элементам координаты, для чего можно
*) в нерелятивистских формулах в дальнейшем значки (+) в суммах по
промежуточным состояниям можно опускать.
258
использовать, во-первых, соотношение (5.19), которое в данном
случае выглядит как
(ер).^.. = '(\-£..)(ег),^... (5.375)
и, во-вторых, соотношение
\.. = 1(\ + \ - 2^.) (ег).^Дег)„_. (5.376)
Последнее соотношение доказывается следующим образом.
Представим правую часть (5.376) в виде
S (\ + \ - 2^.)(е'-).^Дег)„_ = ([[Я, (ег)]_, (ег)]_)^^^_, (5.377)
где Я — одноэлектронный нерелятивистский гамильтониан.
Вычисление коммутаторов в (5.377) дает
([[Я, (ег)]_, (ег)]_),^,_ = -j([(ep), (ег)]-),^,_ = -\,^. (5.378)
Покажем, как проделать переход к матричным элементам
координаты для п = 2. С помощью (5.375), (5.376) представим формулу
(5.372) в виде
^Р^ = -2ш^ (Щ 6(8, + 2^- в,.) X
xS (ег)д-Лег),д ^ _■ ^^ i(s,,-bs,-2s ) . (5.379)
Преобразуем члены в фигурных скобках, используя соотношение
Ед. -I- 2(0:
e_—e .—О)
(s,-ba.-sj U-^—. (5.380)
Таким образом, окончательно
Аналогично в принципе доказывается формула для произвольных
значений п:
^J:\ = 2nii-er [^]'б(Ед + ПС,- Ед,) X
^ ' (ег). (ег) .
X V ^^ '^ (5.382)
1 п-1
Двухквантовый распад. Рассмотрим теперь двухфотонный
процесс распада состояния А с переходом в состояние А' и испусканием
двух квантов с частотами со и со'. Поскольку частоты квантов раз-
259
л/J личны, нельзя сразу воспользоваться формулой (5.387), а нужно
вернуться к началу вычислений, которые, впрочем, проводятся
полностью аналогично. Напомним также, что оператор (5.370)
необходимо заменить комплексно сопряженным в случае испускания и
вместо одной диаграммы рис. 5.16 рассмотреть две (рис. 5.17а, б),
отличающиеся порядком испуска-
л' д' ния квантов. Это дает
S<i^) = —23tic^-23tV(u(u' X
'\J\f\J~'<*-U)'
-\j\j\r^-w
'\r\J>J-'^<0
-\J\J^S\m~W'
xS
X 6(Ед. -I- (o -I- со' — e^) X
(e-r)^,(e'r),^ (e*r)^^(e*'r)^
4-^^+")
A
6
(5.383)
При этом мы полагаем N= I (т. е.
рассматриваем чисто спонтанное
Рис. 5.17. График Фейнмана, описы- излучение) И F= 1 (см. § 2.4).
вающий двухквантовый распад ij
н « Далее переходим к
вычислению вероятности по формулам
(5.4), (5.8), (5.9). В результате применения этих формул получаем
dw2- = 2^1 ^д'^ I '6(ед. -I- со -I- со' - Е.)
(5.384)
где к, к' — волновые векторы испущенных фотонов, а матричный
элемент l/^\ связан с S'^^ соотношением (5.4). Просуммировав
(5.384) по поляризациям фотонов, проинтегрировав по
направлениям их вылета так же, как это делалось в § 5.1 для одного фотона,
и, наконец, проинтегрировав по со', приходим к выражению
ik
где тензор (1//^)д'д определяется так:
iUi,)
ik'A'A
(*P^.(*;
Ц
(5.386)
Полная вероятность двухквантового распада с переходом с
уровня А на уровень А' равна
4i=iM'i'('^)-
(5.387)
Для оценки порядка величины w^^\- учтем, что, согласно (5.385),
(5.387),
4ж««'"д'дй'. (5.388)
260
где а — характерный размер орбиты. По порядку величины в
релятивистских единицах af^ l/(maZ), ьод.д »j m(aZ)^, откуда
и/-^\. »J ma^{aZ)'' p. е. = (aZ)^ a. e. (5.389)
Сравнение с величиной разрешенного одноквантового перехода (см.
(5.198)) дает
w<-^b , (5.390)
а сравнение с величиной запрещенного магнитного перехода (см.
(5.199)) -
Таким образом, при малых значениях Z двухквантовый распад
превалирует над запрещенным магнитным переходом и, в частности,
оказывается главным каналом распада уровня 2s нейтрального
атома водорода (см. ниже).
В случае атома водорода элементы тензора (5.371) могут быть
вычислены точно с помощью кулоновской функции Грина (см. [1, §
1.4]). Для этого в (5.385) запишем скалярные произведения
векторов не в декартовых, а в сферических ортах (см. [I, (3.114)]). Это
дает
ik q'q
ще
С^9',)Д'Д - Z I е^-е^ + ш + е^-е^ + со' j' ^^'^^^^
Вводя функцию Грина одноэлектронного уравнения Шрёдингера [I,
(1.127)], записываем (5.393) в виде
(Ug;)A'A = ('■;. С.,-а>(«-'; «•)'-,)дЧ + ('-;, С,^-а>'(г'; Г)'-,0Д'Д- (5.394)
Для функции Грина используем разложение по парциальным
волнам [I, (1.129)]
СДг'; r)=^,J, G^,(r'; r)y-^Q')y,^Q); (5.395)
векторы г, г' запишем в сферических компонентах [I, (3.83)]
а волновые функции начального А и конечного А' состояний
представим в обычном виде
^A(r)=^R„i{r)Y,JQ). (5.397)
261
Тогда, в результате подстановки (5.395), (5.396) и (5.397) в
(5.394), интегрирование по угловым переменным сводится к
вычислению интегралов от трех сферических функций, для которых
можно воспользоваться формулами [I, (3.110)], [I, (3.111)]. Это дает
п'1'гп\ п1т
[г 1 \\(\ \ t\
0 0 0
/' 1 хИх 1 /
т
(5.398)
= {-\Г'у1{21 + \){21' + \) 2 (2Х -Ы) г J Л |,
где
SW,ni(<^) = \ $ «„r('-')G.„,-<„,x('-'; r)R^i(r)rr' dr dr'. (5.399)
0 0
Далее выражения (5.398), (5.399) следует подставить в (5.392),
(5.385). При этом, однако, нужно еще провести суммирование по
проекциям орбитального момента электрона т' в конечном
состоянии и усреднение по проекциям момента в начальном состоянии т.
Суммирование по т', т, а также по индексам д', д в (5.392) и ja в
(5.398) можно провести в явном виде, пользуясь соотношениями [I,
(3.70)]. В данной ситуации можно, например, вначале провести
суммирование по д', д, \i', \л произведений четырех 3/-символов, в
результате чего зависимость от т', т оказывается сосредоточенной
в произведении двух 3/-символов (формула [I, (3.72)]).
Последующее суммирование по т', т выполняется с помощью [I, (3.31)].
Результатом этих вычислений является следующее выражение
(мы переходим теперь к атомным единицам):
du^% „, = 27ТТ 2,'^-^L-.- „.. = ^ ^42/' -Ы) X
mm
V1 xWx 11\ d' 1 к'] (к' 1 i
Хк'а
x2(2X + l)(2r+l)(2.+ l)^^^^^j^S00Ji000Ji000
|1 1 a
\l' I У
\l I a
\l' I \
+ [^iY;n/('^)^iY;„/("') +
dcu, (5.400)
ще со' = (й„.;'; „; — (О. Формула (5.400) является общей, хотя
радиальные интегралы не могут быть вычислены в общем виде при
произвольных значениях п7', п1.
262
Применим формулу (5.400) для вычисления вероятности двух-
квантового распада атома водорода в состоянии 2s. В этом случае
n'V = 10, п/ = 20 и из (5.400) следует
d^^flio = ^^^'[s\o;2oi^) +S\o;2oi^')\ (5.401)
Займемся вычислением радиальных интегралов [65, 66]. Учитывая,
что радиальные R^i атома водорода имеют вид произведения
полинома на экспоненту, и используя для радиальной части кулоновскои
функции Грина представление [I, (1.144)], [I, (1.145)], можно
заключить, что нам понадобятся интегралы вида
со со со
0 0 0
X ехр j - i [pV + ^r + {r + г') ch x]| X fcth f j '^/2,^, f^ sh Л,
(5.402)
где p = v/n, p' = v/n'. В частности, нужные нам интегралы из
(5.401) могут быть записаны так:
S\,, ^(со) = 2VI [(2»„(v, |; V) - i (2j,(v, |; v)j , (5-403)
V = (-2(Е„, - со)) Ч (5.404)
Аналогично записывается интеграл <S}o. 2о('й')-
Удобно начинать вычисления с интеграла QJ_i ;_i(P', Р; v), а
интегралы при s', s > / — 1 получить затем дифференцированием
по Р', р. Вычисление интеграла QJ_i ;_i(P', Р; v) можно проводить,
например, в следующем порядке: разложить функцию Бесселя в
ряд, после чего интегралы по г, г' берутся элементарно, затем
вычислить интеграл по х и свернуть остающийся ряд к выражению
для гипергеометрической функции. Приведем окончательный
результат [65]:
гЦ /ft' ft. ,л _ 2^'+'(2i+l)!(v)^'+^
x^.
/-, (2/ + 2, л- 1 - v; л- 2 - v; ^P "Ф'-"]. (5.405)
4^ (P + i)(p' + i)j ^ '
Полная вероятность двухквантового распада 2s-aTOMa водорода
равна, согласно (5.387),
•"20,10
<20j'i<20('-)- (5-406)
263
Численный расчет по формулам (5.406), (5.401) дает результат
^?о, 20 = 0,15 с"', тогда как время жизни 25-уровня с учетом только
одноквантового распада составляло бы около двух дней [2].
Многофотонное поглощение и ионизация. Обратимся теперь к
расчетам многофотонного поглощения и многофотонной ионизации.
Используя формулы (5.4), (5.8), (5.9) для перехода от матричных
элементов 5-матрицы (5.382) к вероятности йьид'д и переходя к
сечению процесса с помощью соотнощения
da(^)^ = ^^ (5.407)
где у — плотность потока налетающих квантов, получаем
(*'')л_,' ■■■■ ^^'Ьл
^'А ^ 2 ТГ^ -е^-(п-1)ш) (ё, -Е.-ш)' (5-409)
А
Расшифровывая символы начального состояния как А = п1т, а
конечного как А' = п'Гт', полное сечение п-фотонного поглощения
записываем в виде *)
mm*
В случае п-фотонной ионизации конечное состояние характеризуем
символами ^' = г'Гт' и полное сечение фотоионизации равно
'''^!п1 = 27ТГ S lda<^U nim^ (5.411)
/' mm'
где е' — энергия фотоэлектрона.
Коэффициент в формуле (5.408) удобно записать через
интенсивность падающего излучения. Эта интенсивность, т. е. энергия,
приносимая излучением в единицу времени на единицу
поверхности, равна (в обычных единицах)
I = Nhiuc/V, (5.412)
в наших же единицах (релятивистских)
I = NbilV. (5.413)
Далее, плотность потока квантов в обычных единицах
j = NclV, (5.414)
а в релятивистских
/ = NIV. (5.415)
*) Не путать обозначенные одинаковыми индексами п число квантов и главное
квантовое число для электрона в начальном состоянии.
26
Таким образом,
dcf^ = (2я) V(2Ke2)'>-i/'>-i I /.2\ I ^ (5.416)
Из формулы (5.416) видно, что при достаточно высокой
интенсивности излучения малость взаимодействия е^ в каждом порядке
теории возмущений компенсируется множителем /.
В формуле (5.416) перейдем к обычным единицам, для чего
введем «атомную» единицу интенсивности излучения
/ = 1^=1,4-10»'Вт/см2, (5.417)
где (UQ, Со — атомные единицы частоты и длины, а множитель 1/(2зг)
введен для удобства. Тоща
й = (2.)^(^)
А'А ^.-^-V 1/_| I "АЧ] "С
при этом подразумевается, что величина J^^\ вычисляется в
атомных единицах.
Для численных расчетов сумм У^^ использовались различные
методы |67]. В случае атома водорода эти суммы могут быть вычислены
точно. Используя кулоновскую функцию Грина, по аналогии с
(5.394) можно написать (для удобства направим ось z по вектору е):
Л"а = (^пС(^^+(п-1)а>)(Гп-. «-„-J^n-l. -. ^2С(,^+а,)(Г2; «•i)^i)a'A- (5-419)
Для кулоновской функции Грина можно использовать
представление [I, (1.129)], [I, (1.144)], [I, (1.145)], после чего интегрирование
по угловым переменным в (5.419) может быть произведено в общем
виде, а интегралы по радиальным переменным также факторизуют-
ся и вычисляются с помощью (5.405) [67].
Другой метод заключается в последовательном решении
неоднородных одноэлектронных уравнений вида
(Л —Ej)4i)j = z4i)j. (5.420)
Решение этого уравнения эквивалентно вычислению последнего
интеграла в (5.419)
^T^)=\G^{T^,T,)z,dT„ (5.421)
если положить Ej = Ед -|- со. Точно так же вычисление следующего
(предпоследнего) интеграла в (5.419) эквивалентно решению
неоднородного уравнения _
(к - г^)-^^ = zijjiijjj, (5.422)
при Ег = ^А + 2tu. Таким образом, решая последовательно
неоднородные уравнения, можно получить всю цепочку интегралов в
(5.419). Этот метод применялся для расчетов многофотонных
процессов в работах [68—70].
265
в табл. 5.5 приведены результаты расчетов сечений п-фотонного
поглощения для различных переходов между уровнями атома
водорода, заимствованные из работ [68—70]. Числа приведены для
величины o^^}„i/r~^ (см. (5.410)) в единицах (Bt/cm2)"-i-cm2.
Таблица5.5
Переход
п1
Is
Is
Is
Is
Is
Is
Is
nl
2s
2s
2s
3s
3s
2p
2p
Число фотонов
2
4
6
2
4
3
5
o'l?l„i/l"-\
(Bt/cm^)""' cm^
6,60-10"^*
4,25-10~"
1.14-10~''
5.81-10"^^
2,93-10~"
1,68-lO""**
2.29-10"^
Ha рисунках 5.18, 5.19 приведены заимствованные из тех же работ
результаты расчетов двух- и четырехфотонной ионизации атома во-
•о
S
70*
10^
w
JDOO
12DD HDD 1600 1300 2DDDKA
Рис. 5.18. Сечение двухфотонной ионизации атома водорода в основном состоянии в
зависимости от длины волны падающего света. Величина сечения отложена в
логарифмическом масштабе. Вертикальной линией указан порог двухфотонной ионизации
дорода в основном состоянии в зависимости от длины волны
падающего света. Резонансы в сечении фотоионизации появляются в тех
случаях, когда частота излучения, превышающая пороговое значение
266
(Опор, равна (£>пЧ-,п1 = -ц (^п'г — ^пд- Например, для водорода в случае
п = 2 имеем ол„ар = 1/4 а. е. и все значения частоты,
соответствующие переходам из возбужденных состояний в основное.
со
Z
1
^
«
•ч
h
ID'
29003000 32D0 3400 ЭБОО 3800 A,A
Рис. 5.19. Сечение четырехфотонной ионизации атома водорода в основном состоянии
в зависимости от длины волны падающего света. Величина сечения отложена в
логарифмическом масштабе. Вертикальной линией указан порог четырехфотонной
ионизации
(й„ор. То же са-
(u„'j = ^ 11 jj) > "' = 2, 3, ..., оказываются больше
мое, естественно, справедливо и для четырехфотонной ионизации из
основного состояния, для которой (й„рр = 1/8.
Расчетам многофотонной ионизации многоэлектронных атомов в
рамках теории возмущений посвящены многочисленные работы,
обзор которых можно найти, например, в [67, 71].
Глава 6
ЕСТЕСТВЕННАЯ ШИРИНА
И ФОРМА СПЕКТРАЛЬНОЙ ЛИНИИ
§ 6.1. Радиационная ширина уровней
Ширина уровня по своему физическому смыслу определяется
суммой вероятностей распада этого уровня (в единицу времени) по
всем возможным каналам. Для атомных уровней такими каналами
распада являются радиационные каналы — распад с испусканием
одного или нескольких фотонов — и автоионизационные (с вылетом
одного или нескольких электронов). В этом параграфе мы
рассмотрим радиационные каналы распада, а точнее — одноквантовый
радиационный распад.
Полная радиационная ширина уровня, связанная с таким
распадом, может быть, с одной стороны, получена суммированием
вероятностей, определенных по формулам предыдущей главы. С другой
стороны, эта же ширина может быть получена как мнимая часть
радиационного сдвига уровня энергии. Такой способ вычислений
удобен тем, что он прямо приводит к окончательным выражениям, в
которых просуммированы все возможные вероятности. Этим
способом мы и воспользуемся для вычислений в настоящем параграфе.
Рассмотрим вначале одноэлектронный атом. В низшем порядке
по константе связи мнимые добавки к энергетическому сдвигу
происходят от диаграммы собственной энергии электрона (см.
рис. 4.1а). В общем случае судить о том, какому каналу распада
состояния атома соответствует та или иная диаграмма Фейнмана,
можно, проводя в диаграмме поперечные разрезы между всеми
вершинами. Каждый разрез соответствует определенному каналу
распада. Внутренние линии диаграммы, пересекаемые любым из таких
разрезов, соответствуют частицам, являющимся продуктами
распада в данном канале. При этом нужно считать, что горизонтальные
фотонные линии (т. е. фотонные линии, соединяющие различные
электронные линии), принадлежащие поперечным фотонам, могут
пересекаться разрезами. Действительно, поскольку взаимодействие,
соответствующее обмену поперечными фотонами, не является
мгновенным, вершины, соединяемые поперечными фотонными линиями,
на графиках можно сдвигать относительно друг друга по вертикали.
Этого нельзя делать лишь с вершинами, соединяемыми линиями,
соответствующими мгновенному кулоновскому взаимодействию.
Проводя единственно возможный разрез в диаграмме рис. 4.1а
между двумя ее вершинами, видим, что помимо электрона в поле
268
ядра, который присутствовал и в начальном состоянии, в конечном
состоянии появляется еще фотон. Таким образом, мнимая добавка к
вкладу в энергию от диаграммы рис. 4.1а дает одноквантовую
радиационную ширину, связанную с испусканием одного фотона.
Вещественная часть вклада этой диаграммы дает лэмбовский сдвиг
уровня, описанный в гл. 4.
Исходным для нас при вычислении ширины является выражение
(4.272) для радиационного сдвига, полученное в гл. 4. Мы
обращаемся вновь к вычислению интеграла
I ( \-1 e'l"!''^ rfb) /ж- ,.
—со
Введем обозначение р„д = Е^ — EJ^ и рассмотрим вначале случай
Р„д > 0. Представим /„^ таким образом:
—eo 0
Нетрудно видеть, что первый из интегралов в правой части (6.2)
равен нулю. Действительно, в этом интеграле контур интегрирования
в комплексной плоскости со можно замкнуть в нижней
полуплоскости. При этом интеграл по дуге большого круга исчезает, поскольку
g-i(Rea,-nma,)r,,_^Q „р^ |(^|_»оо^ (6.3)
И весь интеграл оказывается равным нулю, так как полюсы в
нижней полуплоскости отсутствуют при р„д > 0.
Во втором интеграле в правой части (6.2) мнимую добавку
можно положить равной нулю, так как знаменатель нигде в нуль не
обращается. Тогда, используя определения функций интегрального
синуса и косинуса
si(x)=-J^d<, ci(x) = -J^^, (6.4)
X X
получаем
'"г sin ((х —в Jr.,)
Ка = 2i S —^ dx = 2i{ci (P„^r,,) sin (p„^r,,) -
- si (Рпл'-ц) cos (Р„дГ12)}. (6.5)
Если р„д < О, то интеграл /„х можно представить иначе:
г / ^ 1 e-^'urfto fSm(tor,2)rfio
269
где знак минус (плюс) относится к положительно (отрицательно)
энергетическим состояниям*): Е,^^, £'„(-)•
При вычислении первого интеграла в правой части (6.6)
интегрируем по контуру в верхней полуплоскости, так как теперь в этой
полуплоскости исчезает интеграл по дуге большого круга. Есть ли
полюс внутри контура — это зависит от знака Е^ (полюс есть при
£■„ > 0). Во втором интеграле в (6.6) мнимую добавку в
знаменателе можно отбросить, так как знаменатель нигде не обращается в
нуль; удобно также сделать в этом интеграле замену переменных
со—»—со. Тогда, вновь используя (6.4), получаем
^пл(гп) = Я/ |l -I- i^J e-'P-u^2 - 2i{ci (I p„ J r,2) sin (| p„ J r,^) -
-«(iP„Al'-i2)cos(|p„Jr,2)}. (6.7)
Окончательное выражение для /„^ запишем, объединяя (6.5) и
(6.7) [1]:
X {Ci ( I Р„л I r,2) sin ( I P„ J r,2) - si ( I P„ J r,2) COS ( I P„ J r,2)}. (6.8)
Напишем еще разложение 1па(''\2) ^ нерелятивистском пределе,
когда Р„хГ12 *=« aZ<K 1 (при Е^ > 0). Используя известные
разложения для интегрального синуса и косинуса [2]:
si(x)= -f-1-x-l-..., (6.9)
ci(x) = C + lnx-\x'^ + ..., (6-10)
где С = In -у — постоянная Эйлера, получаем
^„a(''i2) = ^i- Щпа'-ц-Н\(^па\- P„a)''i2 +
-Ь2ф„^г,, In (-у I Р„ J г,,) - f (Р„дг,,)^ + i (Р„^г,,)3 +
+ |(1Р„л|-Р„л)Р'„л'-?2-1(Р„л'-12)'1п('У|Р„л1'-12) + - (^-11)
Радиационный сдвиг уровня АЕ получается при подстановке (6.8)
или (6.11) в (4.272). Вещественная часть АЕ при этом расходится.
Эта вещественная часть — лэмбовский сдвиг — рассматривалась
подробно в гл. 4. Здесь мы будем рассматривать только мнимую часть
Im АЕ, которая не расходится и не нуждается в перенормировке.
Мнимая часть АЕ связана с шириной уровня Г соотношением
1тА£: = -Г/2. (6.12)
*) в случае Ь^ > О знак при Я^ определяется однозначно, так как Я^ —
положительно энергетическое состояние.
270
Действительно, рассмотрим волновую функцию квазистационарного
состояния в виде
я1) =-Фо е-'^'^+Д'^)', (6.13)
где добавка АЕ комплексна:
AE = ReAE+iliaAE. (6.14)
Тогда вероятность зависит от времени следующим образом:
UJ= |,J,|2= |^j2e2ImAB, (6.15)
Между тем для распадного состояния должно быть
ьу = ьУое-Г', (6.16)
где Г — полная вероятность распада (ширина уровня). Сравнивая
(6.15) и (6.16), приходим к соотношению (6.12).
Точное выражение для радиационной одноквантовой ширины
получаем, подставив (6.8) в (4.272):
п \ ' \ ' \ ' АппА
(6.17)
Это выражение написано в релятивистских единицах. Заметим, во-
первых, что отрицательно энергетические состояния не дают вклада
в Г^'*^ и, во-вторых, что в сумму по п в (6.17) дают вклад лишь те
положительно частотные состояния, энергии которых меньше, чем
энергия состояния А. Это означает, как и должно быть, что ширина
Г^^ складывается из вероятностей одноквантовых радиационных
переходов во все нижележащие состояния. Ширина основного
состояния равна нулю.
Получим из (6.17) обычное выражение для радиационной
ширины в нерелятивистском пределе. Подставим в (4.272) разложение
(6.11), в котором учтем только реальную часть, что соответствует
мнимой части сдвига АЕ:
Re /„д(г,,) = |l - -f^j sin (I р„ J г,,) =
= -М\^па\ - Р„д)'-12 + 1 (1Р„л1 - Рйд)Йл'12+ •- (^-^^^
Тот член, который не содержит а-матриц в выражении для Г^\
дает нуль при учете только первого члена разложения (6.18) из-за
ортогональности волновых функций. Поэтому здесь необходимо
учитывать следующий член разложения, который дает такой
Г^:
ГГ= -yS (1Р.л1 -Р„л)Йл('-?2)д„„л- (6.19)
"(+)
271
Суммирование теперь распространяется на положительно
энергетические состояния, а в обкладках матричных элементов стоят шрё-
дингеровские волновые функции. Учитывая, что
'■?2 = '-?+'-2-2(г,г,), (6.20)
переписываем (6.19) в виде
ГГ' = Т1 (1Р„л1 -P„л)P^„дl(^•)дJ^ (6-21)
п(+)
а используя соотношение (5.19), получаем вместо (6.21)
гГ=-|1(1Р„л|-Р„л)1(Р)л„1^- (6.22)
п(+)
Теперь рассмотрим член, содержащий а-матрицы в выражении
для Г^'*^ Здесь достаточно учесть только первый член разложения
(6.18), Это дает
ГГ" = е^ S (I Ряд I - Р„л) I («)л„ I ^ (6-23)
"(+)
или, с учетом (5.15),
гГ = е^1(1Р„л1-Р„л)1(Р)л„1'- (6-24)
"(+)
Объединяя (6.22) и (6.24), имеем
r(f) = r(f)' + rr = |e^S(IP„xl-P„x)l(P)x„l^ =
"'"' =|e^S(вд-в„)|(p),„|^ (6.25)
4
3
п<А
где суммирование по п < Л означает £„ < е^. Формула (6.25)
совпадает с суммой вероятностей переходов в нерелятивистском пределе
(см. (5.18)).
В низшем порядке по константе связи, кроме диаграммы
собственной энергии, имеется еще диаграмма поляризации вакуума (см.
рис. 4.16). Однако мнимая часть вклада этой диаграммы в
энергетический сдвиг, как можно убедиться, равна нулю.
Рассмотрим теперь радиационную ширину в двухэлектронных
атомах. В этом случае нужно еще учесть вклады диаграмм рис. 3.3а, б
обмена одним поперечным фотоном (для одноквантовой ширины).
Чтобы получить мнимую часть этих вкладов, достаточно в (3.22)
заменить косинус на синус. При этом видно, что мнимую часть
имеет только обменный матричный элемент. Соответствующая
ширина (будем называть ее брейтовской) Г^^^ равна [1 ]:
Г(«) = 2е-
/l-OjO^
sin (\Е^-Е^\г,^)\ . (6.26)
/ АВВА
272
Видно, что для основного состояния эта ширина равна нулю.
Запишем теперь полную радиационную ширину в двухэлектрон-
ном атоме:
ri^i + r<«i = -2^ 2 [45^ «п (I ^„ - ^л I '-12)] -
п(+) < А \ / АппА
n(+) < В \ / ВппВ
+ 2^2 f-Ц^ sin (I /?д - f?e I '■12)] • (6.27)
Пусть Ej^ < Eg. Тогда (6.27) можно переписать так:
n(+) < А V ' AnnA
-2^S fil^sin(|f?„-f?Jr,2)] • (6.28)
n(+) < в V / BnnB
n*A
Таким образом, учет брейтовской ширины есть не что иное, как
учет принципа Паули: добавление Г^*^ обеспечивает отсутствие
переходов в занятые состояния.
Конкретные расчеты ширины уровней, как правило,
выполняются путем суммирования вероятностей (в большинстве случаев один
какой-либо канал распада является доминирующим). Численные
примеры для одноэлектронных и двухэлектронных, а также
некоторых многоэлектронных атомов были приведены в гл. 5 и
соответствующих приложениях.
§ 6.2. Форма спектральной линии:
квантовомеханическая теория
В предыдущей главе на примере различных процессов шла речь о
вероятностях распадов в единицу времени. Это было связано с тем, что
полная вероятность оказывалась пропорциональной времени
наблюдения. Теперь можно уточнить это утверждение. Это на самом деле
так, если время наблюдения Г много меньше времени жизни уровня
т (Г-зет). В противном случае (Т»х) уровень просто успевает
высветиться полностью за время наблюдения. Например, ситуация
Г:«>т, как правило, реализуется для 2р-уровня атома водорода, где
т »j 10"^ с (см. § 5.1). Ситуация Т«х более реальна для 25-уровня
водорода, где т »^ 7 с (см. § 5.10). В этой главе мы рассмотрим случай
Г is> т и будем интересоваться полными вероятностями.
В принципе, полная вероятность того, что атом из
возбужденного состояния перейдет в основное состояние спустя достаточно
большой промежуток времени, стремится к единице. Однако ввиду ко-
273
Ш л. Н, Лабзовскии
нечности ширины возбужденного уровня испущенный атомом свет
не является строго монохроматическим: частоты будут разбросаны в
интервале Аса « Г. Поэтс»1у можно поставить вопрос о вычислении
полной вероятности как функции частоты са. Обозначим через
dW((o) вероятность излучения кванта с частотой в интервале са,
са + doi и представим эту вероятность в виде
dW{<i>) = /"(са) doi. (6.29)
Функция F(oi) и определяет форму (или контур) спектральной
линии. Очевидно, из условия нормировки вероятности следует
(6.30)
J dW(oi) = 1.
о
В этом параграфе мы рассмотрим квантовомеханическую теорию
контура линии *). Это значит, что мы будем описывать
возбужденное состояние атома волновой функцией вида (6.13)
^а(0 = -Фл e-'(^.-F.)«. (6.31)
Такие состояния в квантовой механике называются
квазистационарными. Ширину уровня Гд мы считаем заданной
феноменологически. Лэмбовский сдвиг Re Af?^ мы в данном случае не учитываем,
поскольку он мало существен в нерелятивистских задачах, а кван-
товомеханическая теория наиболее естественно приложима именно
для таких задач. Конечное состояние атома мы будем считать
основным, т. е. не обладающим шириной:
,j,^,(<) = -ф^, е-^ч'. (6.32)
Далее, введем волновую функцию W^^\t) системы атом -I- поле в
случае, когда эти системы не взаимодействуют. Начальное
состояние этой системы таково, что атом находится в состоянии А, а
кванты поля отсутствуют; это состояние описывается волновой
функцией
Ч'^'2(0=Ч'?о>е-'Мг.)'. (6.33)
Конечное состояние описывается волновой функцией
W(9 (О = W<9 e-'(v+'")'. (6.34)
А coV / А со
Функции W^o, ^Ао^ являются собственными функциями Гамильтона
1Г-^\ описывающего невзаимодействующие электроны и фотоны:
}^{оуц,Ф) ^ ^ ;р(0)^ (6.35)
*) Такая теория была развита Вигнером и Вайскопфом [3], Гайтлером [4] и
другими. Мы здесь следуем изложению [5].
274
ще ^^ — энергия системы атом + поле в отсутствие
взаимодействия. В частности,
^ло=^л-{^Л' ^л'со=^л' + <«- (6-36)
Мы будем искать решение уравнения Шрёдингера
i^=(&^'^ + V)4>, (6.37)
учитывающего взаимодействие V электронов с полем, в виде
разложения по волновым функциям в отсутствие взаимодействия
Щt) = 2 a^(t)4'^^\t) = 2 ajt) e-'V 4^°). (6.38)
V V
При этом V в уравнении (6.37) считается малым возмущением.
Подставляя (6.38) в (6.37), умножая на W^^HO ^ интегрируя,
получаем следующую систему уравнений для коэффициентов a^^^t):
V
в качестве начального условия к этому уравнению потребуем,
чтобы в момент t = 0 система находилась в состоянии v = АО:
а^о=1; а^ = 0 (v^^lO). (6.40)
Найденное с этим начальным условием решение уравнения (6.39)
^А'т(0 определяет вероятность к моменту времени t перехода атома
из состояния А в состояние А' с испусканием кванта в интервале
частот со, со -|- da:
dW(oi,t)=\a^,Jt)\^d(o. (6.41)
Нас будет интересовать полная вероятность, которая получится из
(6.41) при <-»с»:
dW((o) = I ау^(оо) |2 dco. (6.42)
Решая уравнение (6.39) итерациями, в правую часть
подставляем коэффициенты (6.40). Это дает уравнение для определения
^А'т(0- Следующая итерация дает возможность определить
коэффициент адо(0- ^Р^ этом все другие коэффициенты будут оставаться
нулями, поскольку мы считаем отличным от нуля только
матричный элемент <>1'са| F|>10> (только такой переход мы
рассматриваем) . Наконец, еще одна итерация дает уже поправки второго
порядка по F к выражению Од-щ, которые мы считаем малыми. Таким
образом, уравнение для а^.'^ имеет вид
da J , ,•■,
-■ '^^ = <Л'(о| V\AO) ехр{г[(£д- -г^ + (о)+^ Г^]^ (6.43)
dt
275
Интегрируем это уравнение с начальным условием ад'ш(О) = 0.
Получаем
«д'соСО = - <-^'<^И^ИО> ехр{/[(Е^, - Е^ - о) + i г J<]+ const.
Определяем константу из начального условия
1 —exp}i[(e^ —е. —ш)+|-ГЛЙ ., ^^^
«л'.(0 = <АЪ\ V\AO) '^ ^ "^ ,/ ^^ (6-45)
И, согласно (6.42), получаем для вероятности следующее
выражение:
dW((o) = \{A-(o\V\AO)\^ '^"^ , ^. (6.46)
Матричный элемент <>l'ca|F|>lO> в принципе может зависеть от
со. В дальнейшем, однако, мы будем использовать обычное для
теории контура линии (вообще для теории распада) резонансное
приближение, которое сводится в нашем случае к предположению
Гл«£д-£д'- (6.47)
При выполнении неравенства (6.47) знаменатель в (6.46) близок к
резонансу при со = е^ — £д'. Как следует из оценок, приведенных в
§5.1, неравенство (6.47) в случае радиационных переходов в
нейтральных атомах всегда выполняется: даже в случае электрических
дипольных переходов, обладающих наибольшей вероятностью,
возникающая ширина уровней имеет порядок величины Г « а^Ае.
В резонансном приближении в выражении для матричного
элемента V можно положить со = £д — £д' = содд'. Тогда величина
<A'(o\V\AO)\^^^^,= {A'\V\A) (6.48)
определяет обычным образом (см. (5.8)) вероятность перехода в
единицу времени с излучением кванта с частотой со = содд- и с
определенными импульсом, поляризацией и т. д. Зависимость
вероятности от этих характеристик определяется только множителем
I {А' \V\A)\^, т. е. учет распределения фотонов по частоте не меняет
этих характеристик. Поэтому, проводя интегрирование по
направлению вылета фотона и суммирование по поляризациям (см. §5.1),
получаем
dW(<o)=i- ^^""^ ,, (6.49)
где Гдд' — парциальная ширина уровня А, равная вероятности
перехода в единицу времени на уровень А' (формула (5.12), которую
в данном случае нужно записать в нерелятивистском пределе,
поскольку мы пользуемся квантовомеханическим подходом). Распре-
276
деление вероятностей, даваемое формулой (6.49), называется ло-
ренцевским. Следует помнить, что оно справедливо в резонансном
приближении. В общей теории распадных квазистационарных
состояний распределение (6.49) называют также брейт-вигнеровским
(см. § 5.7). В том случае, когда канал распада А—* А' единственный,
Проверим теперь нормировку вероятности. Вычисление
интеграла по со дает при ^а^^^аа'
\ ^VtT^ = T^- (6-50)
Этот результат проще всего получить следующим образом. При
Гд-«;садд' можно считать, что основной вклад в интеграл дает
область значений со вблизи со « содд-. Поэтому интегрирование по со в
(6.50) можно распространить до —<»: от этого результат не
изменится. После этого можно интегрировать по комплексной плоскости со,
замыкая контур интегрирования в верхней или нижней
полуплоскости и вычисляя вычеты в соответствующих полюсах (в каждой
полуплоскости будет по одному полюсу). Используя (6.50), получаем
г
dW{(x>) = ^. (6.51)
о
Величина в правой части (6.51) представляет собой относительную
полную вероятность распада по каналу А^*А'. В том случае, когда
Гдд' = Гд, вероятность, как и должно быть, оказывается
нормированной на единицу:
со
\ dW{oi) = 1. (6.52)
о
Рассмотрим теперь более сложную ситуацию, когда конечное
состояние А' — тоже распадное (возбужденное), обладающее полной
шириной Гд'. Для коэффициента ад'ш(0 мы вместо (6.45) теперь
получим выражение
(^А-^А + '^^+2^А-^А>
Состояние А, обладая конечной шириной, само теперь
высвечивается с испусканием некоторого кванта с частотой со' и переходит в
какое-то третье состояние. Пусть это будет основное состояние А' с
энергией £д". Энергия системы атом -|- поле тогда будет равна
^А"ахо' — ^А" + w + W. Напишем уравнение для коэффициента
277
^A"mm'(0' ^ правую часть общего уравнения (6.39) при этом нужно
подставить
«v(0 = «a'co(0\aV (6.54)
Тоща
^—1Г'= <A"oiOi'\V\A'iii) e'I(v+'"+'"')-('^/+'")+Tr/l'a^,^(i) =
= <Л"саса'| V\Aiii) е''(^'-^+"')+тГу1'а^,^(<). (6.55)
Подставляем в (6.55) выражение (6.53) для aJ^•^{ty, получим
^ '^'^yCшJ ^ {A"w(x>'\V\A'w}{A'(x>\V\AO} ^
X |е''(^'-'^/+"')+тГу]< _ e'Kc/'-c^+co+coO+irj'l. (6.56)
Интегрируя это уравнение с начальным условием ад"^_^'(0) = О,
полагая затем < = 00 и приводя результат к общему знаменателю,
окончательно получаем
/„)= {A"ww'\V\A'w}{A'w\V\AO} (6.57)
[(ш' —ш^^)+|-Г^] [(ш + ш'*-ш^')+J rj
й. л" '(
Полная вероятность процесса, состоящего в переходе с уровня
А на уровень А' и затем на уровень А" с испусканием фотонов со и
со', равна
dW(ci, О)') = I a^'w(~) I^ dci dci' =
А" '\
_J ^A^^.^.f'^"'^"'
(6.58)
1Д^ Гдд', Гд'д" — парциальные ширины. Форму спектральной линии
для перехода А—*А' можно получить из (6.58), проинтегрировав по
со'. В резонансном приближении можно вновь распространить
область интегрирования на всю область значений со' от — оо до оо,
проводить интегрирование в комплексной плоскости и замкнуть контур
интегрирования, например, в верхней полуплоскости.
Подынтегральное выражение имеет в верхней полуплоскости два полюса:
<«(1) = <^А'А" + {^А' <«(2) = ^ЛА" -0^+{^А- (6.59)
Приравнивая интеграл к сумме вычетов, получаем
^aA^AjC f 1
^Ж(а>) = \ dW(<., о') =-^^^1 г ' ,, .,,1 Ч
278
в результате некоторых алгебраических преобразований формула
(б.бО) приводится к следующему окончательному виду:
1 ^А^^л-л" <Га+г^>'^" (б.б1)
^П^)=-2. г. г.
Форма линии для перехода в конечное нестабильное состояние,
как мы видим, отличается от (6.49) лишь тем, что ширина линии
определяется теперь суммой ширин начального и конечного
состояний. От частоты конкретного перехода А'-* А", который мы
использовали в вычислениях, формула (б.б1) не зависит. Нормировочный
интеграл теперь равен
Т. е. равен полной относительной вероятности двойного перехода
Л-*■>!'-*■>!". При Гд = Гдд', Гд' = Гд'д" мы возвращаемся к
нормировочному условию (6.52).
§ 6.3. Форма спектральной линии:
квантовоэлектродинамическая теория
В этом параграфе мы рассмотрим теорию формы спектральных
линий на основе квантовой электродинамики. Это поможет нам
избежать феноменологического введения ширин уровней, как это
делалось в предыдущем параграфе, и сделает теорию способной
описывать такие сугубо релятивистские системы, как многозарядные ионы
(см. § 5.9). Квантовоэлектродинамическая теория естественной
ширины линии для одноэлектронного атома была построена Лоу [6]. В
квантовой электродинамике, однако, в отличие от квантовой
механики, переход от одноэлектронного атома к многоэлектронному не
является тривиальным, как можно было судить по результатам
гл. 3. Одним из методов решения этой проблемы является
применение адиабатического формализма Гелл—Манна и Лоу (см. [1, § 4.3],
а также гл. 3). Этот метод мы используем и здесь для описания
естественной формы спектральных линий в релятивистской теории
атома [7].
Рассмотрим вначале одноэлектронный атом и переход из состоя-
ния А в состояние А с испусканием одного кванта. Амплитуда этого
перехода в низшем порядке по константе связи определяется
диаграммой рис. 5.1. В том случае, когда речь идет о распаде
квазистационарного состояния, естественно использовать адиабатический
оператор эволюции 5„(<», 0), считая, что состояние было
приготовлено в момент < = О и затем распадается. При этом распад не
зависит от способа приготовления. Такая ситуация характерна для
спектроскопии и соответствует постановке задачи в предыдущем
параграфе.
279
Амплитуда перехода вычисляется по правилам соответствия,
изложенным в § 2.6, и равна
<Ф?1^1'^(".0)|Ф°> =
= -ie'{^ Н"" Н' e-°'(^^-(x)c'e-^(V-"»'>4i)^(x)). (6.63)
о
Выполняя интегрирование по t, получаем
А А ф
где
Ф
Здесь мы обозначили через кф, сОф импульс и частоту
испущенного фотона, чтобы не путать их с обозначениями для
переменных интегрирования в выражениях для пропа-
А гаторов.
Рассмотрим теперь диаграмму рис. 6.1 третьего
порядка по константе связи. Эта диаграмма дает
■vy\>'>»- радиационную поправку в низшем порядке к
диаграмме рис. 5.1. Вклад этой диаграммы после
применения правил соответствия можно представить в
виде
Рис. 6.1.Диаг- 0 0 0
рамма, изобра- ^
жающая радиа- X (•фд'(-'^1)^ е"'^"*'!"™*'!^ X
ционный сдвиг
ГяЗприи" Х5(х.х,)7,5(х,хз)7.я»,,(хз))2>,.(х,хз). (6.66)
лучении кванта
Подстановка в (6.66) электронных и фотонных про-
пагаторов приводит к выражению
<фО|5(„з)(со,0)|фо>=-^(Л^Л^ЛзХ
0 0 0
OD OD СО
X t dco С dco, t dm^ exp [j(£'^- + <»>ф -I- со, -|- ia)t^\ x
—CO —CO —CO
Xexp [(coj — CO, — CO -I- ш)<2] exp [—/(tOj + Ej^ + (a— ia)t.^\ X
((F) t^^„f^exp(.|«|r,p]
^-^ X Y — ^"■"'"'^ (6.67)
n.n-.
280
Проведем в (6.67) интегрирование по временам <,, <2> *з> ^ затем
интегрирование в комплексной плоскости со,, coj. Результаты такого
интегрирования выглядят по-разному для положительно и
отрицательно-частотных членов сумм по щ, rij ^ (6.67).
В дальнейшем мы переходим к резонансному
приближению, чему соответствует оставление одного
члена П1 = А в сумме по п, в (6.67). Тогда
„2 ,
А'
'X/vrv*.
<Ф2|5?Ч<».0)|Ф?>„ез =
в'рез
2ra Е^—Е^ — ы.—31а '
Xjdo^
■V " lAnnA
£„ (1—lO)—£^ —Шф —ш —2ia
е(-£ )
+
£ (1-iO)-
-£^-ш-
■la
(6.68)
В формуле (6.68) можно также положить рис. 6.2. Ралиа-
а = О, поскольку, как будет показано ниже, окон- ционные вставки в
чательный ответ является конечным при любом начальное состоя-
значении частоты фотона со^,. Полагая в нерезо- ""^' да^Щ*'^ р^зо-
^ ч) *^ НАнсные вклады
нансных знаменателях в (6.68) Е^- + (аф = Е^ ^\S)
используя формулу (4.272) для радиационного сдвига А£'д,
записываем (6.68) в виде
<ф0|5(„^)(<», 0)|Ф°>р,з= -7^Г-%^^- (6.69)
(£^-£^-Шф)'
Проводя аналогичные вычисления, можно псжазать, что учет
резонансных членов во всех диаграммах типа рис. 6.2 приводит к
следующему выражению для амплитуды перехода:
<Ф0|5^ (со, 0)|ФО„> = -E^E^^ij^E.-Et^^]^- (6.70)
Суммируя возникающую прогрессию, получаем
<Ф?|51'Ч<».0)|Ф°> =
'АА
-Шф + Д£^
(6.71)
Таким образом, выражение (6.71) имеет конечный предел при
а —»О также и в точке резонанса сОф = JE'^ — £^', в которой каждое
из выражений (6.64), (6.69) и т.д. расходится. Формула (6.71)
представляет собой результат аналитического продолжения
разложения (6.70) на всю комплексную плоскость переменной сОф.
281
Учет бесконечной последовательности диаграмм типа рис. 6.2
одновременно уточняет положение резонанса и определяет его
ширину при условии, что у конечного состояния А ширина отсутствует.
Заметим, что формула (6.71) получается непосредственно из (6.64),
если в волновой функции начального состояния заменить £'д на
Е/^ -\- ti.Ej^. Именно так мы и поступали в предыдущем параграфе
при выводе формы линии из квантовомеханических соображений.
Несколько более сложным получается в адиабатической теории
учет радиационного сдвига нижнего уровня. В этом случае
диаграммы, которые нужно суммировать, обладают
особенностями по адиабатическому параметру а. Начнем с
вычисления диаграммы рис. 6.3. Вместо формулы
(6.67) теперь имеем
<00|s(f)(oo, 0)|ФО> =-^ S dt, \ dt^ J dt,x
(2к1У
СО OD
лу\/>».
X J do t doi^ { d<i>2 exp [i(E^. -|- со, -I- со -I- ш)<,] x
— CO —CO
X exp [i((i>2 — <«i — w -I- ш)<2] X
X exp [/(сОф — E^ — ca^'^ io.)h^ X
A
Рис. 6.3. Диаг- I ^°'°' exp (i|ш|TjP| U„.
рамма, изобра- ^ " ' ^"Л'-г if, ^^ч
жающаярадаа- X 2^ ^^ (l-iO) + a),](£ (l-iO)+io,]- УУ>1^)
ционный сдвиг nn ^ ' "2
конечного со- ' ^
стояния при из- Проводя интегрирование по временам и частотам
лучении кванта
coj, coj, оставлял в сумме по п только сингулярный
член п = Л' и полагая при этом в несингулярных и нерезонансных
множителях а = О, получаем
<Ф°|5^(<»,0)|Ф°>,„„="' '
2л:1 Е^—Е^ — <л.—Ъ1о.
^FkrH'"!^
f^expOlioIr,,)] V^^
£ (l-iO)-£v-io •
(6.73)
Используя вновь (4.272), записываем (6.73) в виде
1 v^/^^
<^1\т^'^)\К).«..= -^
£д-£^-Шф-31а'
(6.74)
Аналогичные вычисления в высших порядках теории
возмущений (диаграммы рис, 6.4) с учетом только сингулярных
282
членов дают
п=0 ^ ' *
(6.75)
Полагая в несингулярном множителе в (6.75) а = О, приходим к
выражению
<фО|5„(=о,0)|фо>,_ = -^-з:^^^ехр [-Щ. (6-76)
Однако нужно учесть то обстоятельство, что при разложении
несингулярного множителя в (6.75) по степеням а
возникают члены, не зависящие от а и дающие ,
ненулевой вклад в (6.75). Разложим
несингулярный множитель в ряд:
1
£^-£^-Шф-(2п + 1)1а ~
Е^-Е
I У Г (2« + l)ia -1 * (g 77)
и подставим вначале в (6.75) первый член ряда
(6.77) при Л = 1 (нулевой член при k = 0 дает
(6.76)). Получим
(Е.
(Е.
-i"*)'
х(-^+»)^-р(-т)- (6.78)
Член ряда (6.77) при к = 2 после подстановки в
(6.75) дает
(Е,
^)
4iA£.
+ 1
exp
^)- ('
^/Vrvj»-
Рис. 6.4.
Радиационные вставки
в конечное
состояние,
дающие
сингулярные вклады
79)
Продолжая эти вычисления и собирая члены, отличные от нуля при
а—»О, получаем
<Ф°|5„(оо,0)|Ф°>,„„,=
и
АА
Е.-Е,
ехр
'Ц1
iAE,
Г ^^х 1
^А-^в-'^ф
^ '^^^«Р [ 2а }
^А-^А-^Е^-'^ф
(6.80)
283
Теперь можно учесть одновременно вклад резонансных членов
в диаграммах рис. 6.2 и сингулярных членов в диаграммах
рис. 6.4. Согласно (6.71) для этого достаточно в (6.80) JE'^
заменить на £'д + А£'д, поскольку мы можем считать, что
вычисления в (6.80) с самого начала проводятся с соответствующей
волновой функцией.
Запишем вероятность перехода, определяемую формулой
ЙЖ(кф,е)=ит |<ФО|5„(<»,0)|ФО>|2-^. (6.81)
1-0
(2л)^
Эта формула является аналогом квантовомеханического выражения
(6.42), только здесь явно выписана зависимость вероятности от
направления вылета и поляризации фотона. При подстановке (6.80) в
(6.81) нужно различать два случая. В первом случае Л' — основное
состояние. Тогда Г^- = О, величина АЕ^- вещественна и
lim
а-» о
ехр
{-Щ
г
= 1. (6.82)
Формула (6.81) дает в этом случае после интегрирования по
направлениям вылета фотона и суммирования по по.1яризациям ло-
ренцевский контур (6.49):
(ш^.-Шф) +-Г^
где сбдд' — разность энергий уровней с учетом лэмбовского сдвига
конечного и начального состояний *):
^АА' = -Сд + Re АЕ^ - Е^. - Re АЕ^.. (6.84)
Иной результат получается, если нижнее состояние А' само
обладает шириной. В этой ситуации
lim
а-» о
^^Р [Щ I = «f^ ^^Р ( - Й) = 0. (6-85)
т. е. вклад всех резонансных членов обращается в нуль. Таким
образом, диаграммы рисунков 6.2 и 6.4 не описывают формирования
лоренцевского контура линии при Гд- =^ 0. Такой результат для рас-
падного состояния А' связан с тем, что мы не учитывали явно дина-
*) Можно поставить вопрос о перенормируемости теории, основанной на
использовании «половинной» S-матрицы: в гл. 4, где шла речь о перенормировках,
использовалась только «полная» S-матрица (см. также [8]). Видно, однако, что в резонансном
приближении никаких проблем с перенормировкой не возникает — окончательное
выражение (6.83) содержит лишь матричные элементы оператора собственной энергии
электрона, перенормировка которых описана в гл. 4.
284
мику его распада. На самом деле распад состояний А тл А' нужно
рассматривать одновременно, так как это делалось в предыдущем
параграфе с помощью квантовомеханической теории.
Конкретизируем задачу, считая, как и в § 6.2, что нижнее
состояние А' может, в свою очередь, с помощью одноквантового распада
перейти в основное состояние А". Рассмотрим диаграмму рис. 6.5,
изображающую процесс перехода из состояния А в состояние А' с
испусканием двух квантов. Соответствующая амплитуда равна
1 ^:л V^„U„^
<Ф?|5?Ч<».0)|Ф°> =
Е^-Е^.-ч,,
Ф Ф
Ь^ —Шф—la
(6.86)
В сумме по п в (6.86) нас интересует резонансный член при
п = v4' (как и выше, при вычислении радиационных вставок в
начальное состояние, при этом можно положить а = 0):
<фО|5^>(оо,0)|Ф^>_ =
Va'aVaa
(£,-£^-Шф-шу(£^-£^-ш:,)
-. (6.87)
Учитывая полученные выше результаты, можно сказать, что сум- -^
мирование собственно энергетических вставок с резонансными члена-^w
ми в нижнюю электронную линию на диаграмме рис. 6.5 приведет к
а" а" к
А'
■\r\j-\j~*-W
лук/хг^-о)
"\_Л-Ги-^»<у'
А'
А','
лу\г\г^и>
4
Рис. 6.5. Диаграмма, изображающая переход из состояния А в состояние А!' с
испусканием двух квантов
Рис. 6.6. Диаграмма, изображающая собственно энергетическую вставку во
внутреннюю электронную линию при излучении двух квантов
Рис. 6.7. Диаграмма, изображающая поправку к вероятности перехода на
межэлектронное взаимодействие в начальном состоянии
замене £'д на JE'^ -I- Д£д в (6.87). Суммирование собственно
энергетических вставок в верхнюю электронную линию на диаграмме рис. 6.5
приводит к замене ^д- на £д" -I- ДЕд», причем величина А£д"
вещественна {А" — основное состояние). Таким образом, остается учесть
285
лишь собственно энергетические вставки во внутреннюю электронную
линию диаграммы рис. 6.5, т. е. радиационный сдвиг состояния А.
Рассмотрим с этой целью диаграмму рис. 6.6. Подстановка
выражений для пропагаторов и интегрирование по временам и частотам
приводит после выделения резонансных членов к выражению (мы
вновь полагаем а = 0)
А А ф ф
\ " )АгтА
ИЛИ, с учетом (4.272),
<Ф^|5^(оо,0)|Ф»>р,з=., , ""^^""fff.^^ . 7Гг (6.89)
Суммируя все собственно энергетические вставки во
внутреннюю электронную линию в резонансном приближении, а также
учитывая результаты суммирования таких вставок для внешних
линий, получаем
ху ^^ '-^^^ , (6.88)
<Ф?|5„(<»
со
п=0
.0)|Ф°>рез =
Г ^^А 1
£^, + Д£^,-£^-ш^
(■~<^^-<^'^<^Еа~^а--^^а'~<^'^^
^'A'A^'AA^'^vy-i^r]
{5^„-Шф-ш^-| Г^)(5^^'-ш^-
-{^А^
(6.90)
Переходя от амплитуды к вероятности по формуле
ЙЖ(кф,е;к^,е')=Ит |<фО|5„(со,0)|Ф°>|2-^-^, (6.91)
интегрируя по направлениям вылета фотонов и суммируя по
поляризациям, получим
Эта формула по форме совпадает с (6.58), однако в энергии
переходов включены радиационные поправки. Из (6.92)
интегрированием по со', как и в квантовой механике, получаем (6.61) с заменой
^>^АА' на йдд-.
286
в двухэлектронных атомах, помимо радиахщонных поправок к
диаграмме рис. 5.1, необходимо учитывать еще межэлектронное
взаимодействие. Эта проблема также может быть решена с
применением адиабатического формализма. Для простоты ограничимся такими
состояниями двухэлектронного атома, в которых возбужден лишь
один электрон. Рассмотрим вначале диаграммы типа рис. 6.7,
которые соответствуют переходу из возбужденного состояния >li>li в
основное состояние А!2А\ с учетом кулоновского взаимодействия.
Используя выражение (2.248) для кулоновского пропагатора и проводя
суммирование резонансных вкладов подобно тому, как это было
сделано выше в случае радиахщонных поправок, приходим к
выражению вида
<Ф21^„(°о,0)|Ф°>р,з =
и
м.
(6.93)
Е ^— Ej — ш. — АЯ
=S'
Здесь А£^*^д^ — поправка первого порядка теории возмущений по
межэлектронному взаимодействию (3.14). В эту поправку можно
включить и вклад от обменных диаграмм, которые получаются из
диаграмм рис. 6.7 заменой нижних индексов: Л^«^>1|.
Рассматривая диаграммы рис. 6.8, описывающие кулоновское
взаимодействие электронов в конечном состоянии, и суммируя, как
и в случае радиахщонных вставок,
сингулярные члены, получаем, что выражение (6.93)
нужно заменить на
А',
А',
<Ф°|5„(оо,0)|Ф°>,„„,=
'М
ехр
^-^^-
"Ф
•Д£'
(6.94)
4-
•<
4
■\r\rj^
";
В (6.94) учтены одновременно вклады диаграмм
рис. 6.7 и 6.8. Из результатов вычислений с
собственно энергетическими вставками (см.
выше) ясно, что эти вставки в диаграммы
рисунков 6.7 и 6.8 приводят к появлению
радиационных добавок в знаменателе формулы (6.94).
При этом вещественные части радиационных
сдвигов добавятся к вещественным поправкам
на кулоновское взаимодействие, а мнимая
добавка будет равна ^ Г^ , где Г^ — полная
радиационная ширина одноэлектронного
состояния Ai в приближении невзаимодействующих электронов в атоме.
Остается еще рассмотреть вклады диаграмм типа рис. 6.7 и 6.8,
но с обменом поперечными фотонами. С учетом всех предыдущих
вычислений можно утверждать, что в резонансном приближении это
Р НС. 6.8. Диаграмма,
изображающая
поправку к вероятности
перехода на
межэлектронное взаимодействие в
конечном состоянии
287
приводит к появлению в знаменателе выражения (6.94) брейтовских
поправок t!i.Ef'pA~^^A'\'i определяемых формулой (3.19). Брейтов-
ское взаимодействие помимо этого дает мнимую добавку ^ Г^*^,
определяемую формулой (6.26). Эта добавка происходит от
обменной диаграммы (см. § 6.1) и сокращает тот член в выражении (6.17)
для Гд , который соответствует переходу в состояние ^2 (занятое в
двухэлектронном атоме).
Окончательно для вероятности перехода получаем формулу,
аналогичную (6.83):
где с5д д'. д-д' — энергия перехода с учетом поправок первого
порядка теории возмущений по межэлектронному взаимодействию, а
также лэмбовских сдвигов в начальном и конечном состояниях,
Гд/д'ч = Гд — Г^*^'. Таким же образом, в принципе, в формуле
(6.95) можно учесть и межэлектронное взаимодействие в высших
порядках теории возмущений и другие поправки.
В заключение отметим, что возможны и другие квантовоэлект-
родинамические подходы к описанию формы спектральных линий, в
частности квазипотенциальный подход [8].
ПРИЛОЖЕНИЯ
1. Лэмбовский сдвиг водородоподобных атомов
Таблица П1.1. Вклады различных поправок в величину лэмбовского
сдвига A£(2si.) — АВ(2р!,) в атоме водорода
Поправка
Собственная энергия во втором порядке по
константе связи (формулы (4.217л (4-219))
Поляризация вакуума во втором порядке по
константе связи (формулы (4.217), (4.219))
Формулы (4.240). (4.241)
Формулы (4.240), (4.242). (4.243)
Собственная энергия в четвертом порвдке по
константе связи (формулы (4.251), (4.252))
Поляризация вакуума в четвертом порядке по
константе связи (формулы (4.217), (4.219))
Поправка на отдачу**)
Поправка на конечный размер протона***)
Итого
Порядок
величины*)
ma(aZ)*
ma(aZ)^
ma(aZ)*
ma(aZ)*
ma^(aZ)^
mahaZ)''
Числовое
значение. МГц
1077,640
-27,084
7.140
-0.372
0,342
-0,239
0,359
0.125
1057,911
*) в данном случае следует полагать Z=l.
•*) По поводу поправок на отдачу см. [11,21, 22].
***) По поводу поправок на ксжечный размер протона см. [21, 22].
ТаблицаП1.2. Лэмбовский сдвиг уровней в различных
водородоподобных атомах [22] (в МГц)
Атом
Н (п = 2)
Н (п = 3)
Н (и=4)
D (и = 2)
Не"^ (и = 2)
Не"^ (п = 3)
Не+ (и = 4)
U++ (и = 2)
d+ (и = 2)
Теория
1057,911
344,896
133,084
1059,271
14044,765
4184,42
1769,088
62763,41
783,678-10^
Эксперимент
1057,90 ±0,06
314,810 + 0,052
133,18+0,59
1059,28 + 0,06
14045,4+1,2
4183,17 + 0,54
1769,4+1,2
63031,0+327,0
(744,0+ 7,0) 10^
289
2. Вероятности переходов
Таблица П2.1. Квадраты радиальных интегралов (R^jJ)^
nl
п'Г
п'
1
2
3
4
5
6
7
8
1
п'=9
Дискретный
спектр
Непрерывный спектр
Полная
сумма (5-163)
Is
пр
-
1,666
0,267
0,093
0,044
0,024
0,015
0,010
0,032
2,151
0,849
3,000
2s
п'р
-
27,00
9,18
1,64
0,60
0,29
0,17
0,10
0,31
39,30
2,70
42,00
2р
n's
1,67
27,00
0,88
0,15
0,052
0,025
0,014
0,009
0,025
29.820
0,180
30,00
n'd
-
-
22,52
2,92
0,95
0,41
0,24
0,15
0,42
27.62
2,38
30,00
3s
п'р
-
0,9
162,0
29,9
5,1
1,9
0,9
0,5
1,4
202,56
4.44
267,00
Зр
n's
0,3
9,2
162,0
6,0
0.9
0,33
0.16
0,09
0,22
179,18
0,82
180,00
n'd
-
-
101,2
57,2
8,8
3,0
1,4
0,8
2,0
174,54
5,46
180,00
3d
п'р
-
22,5
101,2
1,7
0,23
0,08
0,03
0,02
0,05
125,88
0,12
126,00
n'f
-
-
-
104,6
11,0
3,2
1,4
0,8
1,8
122,85
3,15
126,00
nl
n'l'
n'
1
2
3
4
5
6
7
8
1
n'=9
Дискретный
спектр
Непрерьшный
спектр
Полная сумма
(5.163)
4s
п'р
-
0,15
6,0
540,0
72,6
11,9
5,7
2,1
4,3
642,7
5,3
648,00
4р
n's
0,09
1,66
29.8
540,0
21,2
2,9
1.4
0,6
1,0
598,7
1,3
600.00
n'd
-
-
1.7
432,0
191.9
19,3
7,7
3,2
5,9
591,7
8,3
600,00
4rf
п'р
-
2,9
57,0
432.0
9.3
1,3
0,5
0,2
0,3
503,50
0,50
504,00
n'f
-
-
-
252,0
197,8
26,9
8,6
3,9
6,9
496.0
8,0
504,00
4/
n'd
-
-
104,7
252,0
2,75
0,32
0,08
0,04
0,07
359,95
0,05
360,00
n'g
-
-
-
-
314.0
27,6
7,3
3,0
4,5
356,4
3,6
360,00
290
Таблица П2.2. Силы осцилляторов для атома водорода
п1
пЧ'
1
п
1
2
3
4
5
6
7
8
п'=9
Дискретный
спектр
Непрерывный спектр
Полная
сумма (5.173),
(5.174)
Is
пр
-
0,4162
0,0791
0,0290
0,0139
0,0078
0,0048
0,0032
0,0109
0,5650
0,4350
1,000
2s
п'р
-
-
0.4349
0,1028
0,0419
0,0216
0,0127
0,0081
0,0268
0,6489
0,3511
1,000
2р
n's
-0,139
-
0,014
0,0031
0,0012
0.0006
0,0003
0,0002
0,0007
-0,119
0,008
-0,111
n'd
-
-
0,696
0,122
0,044
0.022
0.012
0,008
0,023
0,928
0,183
1,111
3s
п'р
-
-0,041
-
0,484
0,121
0,052
0,027
0,016
0,048
0,707
0,293
1,000
Зр
n's
-0,026
-0,145
-
0,032
0,007
0,003
0,002
0,001
0,002
-0,121
0,010
-0,111
n'd
0,619
0,139
0,056
0,028
0,017
0,045
0,904
0,207
1,111
3rf
п'р
-
-0,147
-
0,011
0,0022
0,0009
0,0004
0,0002
0,0007
-0,402
0,002
-0,400
n'f
-
-
-
1,016
0,156
0,053
0,025
0,015
0,037
1,302
0,098
1,400
nl
n'l'
n'
1
2
3
4
5
6
7
8
1
n'=9
Дискретный
спектр
Непрерывный
спектр
Полная сумма
(5.173), (5.174)
4s
п'р
-
-0,009
-0,097
-
0,545
0,138
0,060
0,033
0,082
0,752
0,248
1,000
4р
n's
-0,010
-0,034
-0,161
-
0,053
0,012
0,006
0,003
0,006
-0,126
0,015
-0,111
n'd
-
-
-0,018
-
0,610
0,149
0,063
0,033
0,075
0,912
0,199
1,111
4rf
п'р
-
-0,073
-0,371
-
0,028
0,006
0,002
0,001
0,002
-0,406
0,006
-0,400
n'f
-
-
-
-
0,890
0,187
0,072
0,037
0,081
1,267
0.133
1.400
4/
n'd
-
-
-0,727
-
0,009
0,0016
0,0005
0,0003
0,0006
-0,715
0,001
-0,714
n'g
-
-
-
-
1,345
0,183
0,058
0,027
0,045
1,658
0,056
1,714
291
Таблица
J12.3. Вероятности переходов в атоме водорода (в
Состояние
nl
2s
2р
3s
Зр
3d
4s
4р
4р
4rf
4/
5s
5р
5р
5d
5d
Sf
5g
6s
6p
6p
6d
6d
6/
6/
6«
6Л
пЧ'
п'р
n's
. п'р
n's
п'р
п'р
n's
n'd
п'р
n'd
п'р
n's
n'd
п'р
n'f
n'd
n'f
п'р
n's
n'd
n'p
n'f
n'd
n'g
n'f
n'g
10* c"')
n
1
-
6,25
-
1,64
-
-
0,68
-
-
-
-
0,34
-
-
-
-
-
-
0,195
-
-
-
-
-
-
-
2
-
-
0,063
0,22
0,64
0,025
0,095
-
0,204
-
0,012
0,049
-
0,094
-
-
-
0,007
0,029
-
0,048
-
-
-
-
-
3
-
-
-
-
-
0,018
0,030
0,003
0,070
0,137
0,008
0,016
0,001
0,034
-
0,045
-
0,0051
0,0096
0,0007
0,0187
-
0,0210
-
-
-
4
-
-
-
-
-
-
-
-
-
-
0,006
0,007
0,002
0,014
0,000
0,026
0,042
0,0035
0,0045
0,0009
0,0086
0,0002
0,0129
-
0,0137
-
5
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
0,0017
0,0021
0,0010
0,0040
0,0004
0,0072
0,0001
0,0110
0,0164
292
Таблица П2.4. Диаграмма Гротриана для атома водорода
Горизонтальнью линии на диаграмме указьшают положение уровней энергии,
стрелки — разрешеннью переходы. Цифры рядом со стрелками обозначают длины
волн в ангстремах, цифры у концов стрелок — силы осцилляторов соответствующих
переходов. Изображены три спектральных серии — Лаймана (и' = 1), Бальмера
(и' = 2), Пашена (и' = 3), причем цифры приведены лишь для двух первых.
293
Таблица П2.5. Зависимость вероятностей перехода от Z (в с"')
Z
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
30
35
40
45
50
2iwi|0
6,2650-10*
1,0028-10'"
5,0772- Ю'"
1,6048-10"
3,9181-10"
8,1252-Ю"
1,5054-10'^
2,5684-10'^
4,1146-10'^
6,2721-10'^
9,1842-10'^
1,3009-10'^
1,7922-10'^
2,4110-10'^
3,1778-Ю'^
4,1145-Ю'^
ii2448-10'^
6,5936-10'^
8,1874-Ю'^
1,0054-10'"
1,2224-10'"
1,4728-10'"
1,7600-10'"
2,0872-10'"
2,4582-10'"
5,1061-10'"
9,4729-1 о'"
1,6210-10'*
2,6035- Ю'*
3,9800-10'*
2|1-.1|0
6,2648-10*
1,0027-10'"
5,0764-10'"
1,6043-10"
3,9163-10"
8,1198-10"
1,5041-10'^
2,5654-10'^
4,1084-10'^
6,2604-10'^
9,1636-10'^
1,2975-10'^
1,7865-10'^
2,4022-10'^
3,1645-Ю'З
4,0950-Ю'З
5,2166-Ю'З
6,5539-10'^
8,1324-10'^
9,9797-10'^
1,2124-10'"
1,4596-1 о'"
1,7426-10'"
2,0648-1 о'"
2,42%-1 о'"
5.0206-10'"
9,2627-10'"
1,5725-10'*
2,5048-10'*
3,7935-1 о'*
2|0-»1^
2,4946-10"^
2,5559-10"^
1,4744-10"'
2,6193-10"
2,4406-10'
1,5121-10^
7,0694-10^
2,6895-10^
8,7423-10^
2,5100-10"
6,5181-10"
1,5580-10*
3,4739-10*
7,3003-10*
1,4578-10^
2,7845-10*
5,1153-10*
9,0778-10*
1,5621-10'
2,6149-10'
4,2695-1 о'
6,8155-10'
1,0658-10*
1,6357-10*
2,4673-10*
1,5525-Ю'
7,3939-10*
2,8747-10'"
9,5808-10'"
2,8303-10"
294
Табли ца П2.6. Силы осцилляторов атомоЕ
Переходы
Не
ls-2p
ls-3p
ls-4p
Ne
2p-3s
2p-4s
2p-3d
Ar
3p-4s
3p-Ss
3p-6s
3p-3d
Kr
4p-5s
4p-6s
4p-4d
Xe
5p-6s
Sp-7s
Sp-Ss
5p-Sd
5p-6d
/P
0,260
0,073
0,030
0,156
0,028
0,023
0,296
0,056
0,020
0,162
0,375
0,070
0,267
0,419
0,082
0,031
0,484
0,231
/Г
0,229
0,0642
0,0265
0,144
0,025
0,018
0,266
0,050
0,0183
0,098
0,338
0,063
0,153
0,372
0,072
0,027
0,253
0,11»
t благородных
уСф
0,252
0,070
0,029
0,163
0,028
0,021
0,298
0,031
0,021
0,167
0,353
0,067
0,263
0,403
0,124
0,047
0,385
0,187
газов
Эксперимент
0,276
0,073
0,030
0,174
0,315
0,038
0,199
Таблица П2.7. Силы осцилляторов щелочных атомов
Переходы
Li
2s-2р
2s-3p
2s-4p
ls-2p
ls-3p
Na
3s-3p
3s-4p
3s-5p
К
4s-4p
4s-5p
3p-3d
Cs
5p-5d
уХФ
0,766
0,00339
0,00351
0,344
0,0539
0,988
0,0128
0,00186
1,076
0,0099
0,641
0,222
/Г
0,796
0,00263
0,00304
0,321
0,0498
0,971
0,0120
0,00167
1,024
0,0081
0,363
0,110
усф
0,758
0,00407
0,00387
0,342
0,053
0,968
0,0103
0,00132
1,01
0,0041
0,66
0,25
Эксперимент
0,753
0.00552
0,00480
0,982
0,0142
0,00221
1,02
0,0091
295
Таблица П2.8. Силы осцилляторов щелочно-земельных атомов
Переходы
Be
2s-2р
2s-3p
2s-4p
ls-2p
ls-3p
Mg
3s-3p
3s-4p
3s-5p
Ca
4s-4p
4s-5p
4s-6p
3p-3rf
Ba
6s-6p
6s-7p
6s-8p
Sp-Sd
Sp-bd
Sp-ld
J4
1,90
0,11
0,016
0,37
0,036
2,10
0,31
0,087
2,52
0,35
0,095
2,21
2,91
0,41
0,11
4,11
0,52
0,22
1,01
0,032
0,0023
0,361
0,034
1,16
0,139
0,036
1,23
0,13
0,031
1,21
1,27
0,13
0,030
2,03
0,26
0,11
усф
1,39
0,023
0,0011
0,374
0,035
1,66
0,15
0,035
1,81
0,16
0,035
2,5
2,0
0,10
0,016
3,39
0,29
0,11
Эксперимент
1,36
1,81
0,22
1,75
0,001
0,043
Таблица П2.9. Силы осцилляторов в атоме лития
Переходы
2s-2р
2s-3p
2J-4p
0,766
0,0034
0,0035
уад
0,742
0,0063
0,0050
Эксперимент
0,753
0,0055
0,0048
296
Таблица П2.10. Вероятности перехода ls2s^S
Z
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
30
35
36
40
50
60
70
80
90
100
Wq, с"'
0,1704-2
0,9828-1
0,1746+1
0,1627+2
0,1008+3
0,4713+3
0,1793+4
0,5828+4
0,1673+5
0,4345+5
0,1039+6
0,2316+6
0,4867+6
0,9718+6
0,1856+7
0,3410+7
0,6052+7
0,1041+8
0,1743+8
0,2846+8
0,4543+8
0,7105+8
0,1090+9
0,1645+9
0,2442+9
0,1035+10
0,4929+10
0,6561+10
0,1916+11
0,1887+12
0,1254+13
0,6402+13
0,2716+14
0,1010+15
0,3433+15
LUi, с''
0,179-2
0,360-1
0,4365-1
0,2935+1
0,3190+2
0,1951+3
0,8736+3
0,3172+4
0,9867+4
0,2724+5
0,6838+5
0,1585+6
0,3440+6
0,7059+6
0,1380+7
0,2586+7
0,4672+7
0,8160+7
0,1385+8
0,2289+8
0,3695+8
0,5835+8
0,9033+8
0,1375+9
0,2056+9
0,8928+9
-
-
0,1718+11
0,1730+12
0,1167+13
0,6017+13
0,2572+14
0,9617+14
0,3284+15
ь^ХФ. с"'
0,1253-3
0,2037-1
0,5638+0
0,6731+1
0,4887+2
0,2551+3
0,1052+4
0,3640+4
0,1098+5
0,2966+5
0,7327+5
0,1680+6
0,3614+6
0,7365+6
0,1932+7
0,2672+7
0,4808+7
0,8377+7
0,1418+8
0,2338+8
0,3767+8
0,5939+8
0,9183+8
0,1395+9
0,2084+9
0,9023+9
-
-
0,1729+11
0,1737+12
0,1171+13
0,6032+13
0,2577+14
0,9639+-14
-
,-{\s)-'X
""сф. с"'
0,173-3
0,225-1
0,591+0
0,690+1
0,496+2
0,257+3
0,106+4
. 0,365+4
0,110+5
0,297+5
0,733+5
0,168+6
0,361+6
0,736+6
0,143+7
0,267+7
0,480+7
0,837+7
0,142+8
0,233+8
0,376+8
0,593+8
0,917+8
0,139+9
0,208+9
0,901+9
-
-
0,173+11
0,174+12
0,117+13
0,603+13
0,258+14
0,963+14
0,329+15
и^Р, с-'
0,1703-2
0,9820-1
0,1744+1
0,1624+2
0,1006+3
0,4693+3
0,1786+4
0,5799+4
0,1663+5
0,4313+5
0,1030+6
0,2293+6
0,4810+6
0,9632+6
0,1828+7
0,3353+7
0,5938+7
0,1020+8
0,1703+8
0,2774+8
0,4417+8
0,6889+8
0,1056+9
0,1586+9
0,2348+9
0,9820+9
0,4587+10
0,6080+10
0,1744+11
0,1624+12
0,1006+13
0,4698+13
0,1786+14
0,5799+14
0,1663+14
297
Таблица П2.11. Автоионизационные ширины двухэлектронных ионов
(в электрон-вольтах)
Состояние
Z
10
20
30
40
50
60
70
80
90
100
(2s)^ 'So
0,2357
0,2397
0,2378
0,2517
0,2903
0,3352
0,4267
0,5466
0,7554
1,1033
(2р)^ %
0,01072
0,01553
0,02756
0,03961
0,04769
0,04936
0,04697
0,04250
0,03450
0,02582
(2pf ^Ро
0,000149
0,005451
0,001403
0,002788
0,006809
0,005291
0,011842
0,020253
0,028608
0,052826
apf ^Pi
0,000414
0,028153
0,110744
0,149095
0,155172
0,158546
apf 'г>2
0,2439
0,2084
0,1242
0,0868
0,0376
0,0666
список ЛИТЕРАТУРЫ
1. Веселое М. Г., Лабзовский Л. Н. Теория атома. Строение электронных
оболочек. — М.: Наука, 1986.
К главе 1
1. Бете Г., Солпитер Э. Квантовая механика атомов с одним и двумя
электронами / Пер. с англ. — М.: Физматгиз, 1960.
2. Ахиезер А. И., Берестецкий В. Б. Квантовая электродинамика. — М.: Наука,
1981.
3. Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Квантовая
электродинамика. — М.; Наука, 1980.
4. ЗельдовичЯ. Б., Попов В. С. II Успехи физ. наук. — 1971. — Т. 105. — С. 403.
5. Rubinowicz А. II Phys. Rev. — 1948. — V. 73. — P. 133.
6. Горшков В. Г. II ЖЭТФ. — 1964. — Т. 47. — С. 352.
7. Горшков В. Г. II ЖЭТФ. — 1964. — Т. 47. — С. 1984.
8. Hostler L. II i. Math. Phys. — 1964. — V. 5. — P. 591.
9. Whichmann £.; Kroll N. M. II Phys. Rev. — 1956. — V. 101. — P. 43.
10. Martin P. C, Glauber R J. II Phys. Rev. — 1958. — V. 109. — P. 1307.
11. Запрягаев С. A, Манаков Н. Л., Пальчиков В. Г. Теория многозарядных ионов
с одним и двумя электронами. — М.: Энергоатомиздат, 1985.
12. Шерстюк А. И. II ЖЭТФ. — 1972. — Т. 62. — С. 1238.
13. Христенко С. В. II Теор. и мат. физика. — 1975. — Т. 22. — С. 31.
14. Манаков Н. Л., Мармо С. И., Файнштейн А. Г. II Теор. и мат. физика. —
1984. —Т. 59. —С. 49.
15. Foldy L., Wouthuysen S. II Phys. Rev. — 1950. — V. 78. — P. 29.
16. Давыдов A. C. Квантовая механика. — М.: Физматгиз, 1963.
К главе 2
1. Ахиезер А. И., Берестецкий В. Б. Квантовая электродинамика. — М.: Наука,
1981.
2. Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Квантовая
электродинамика. — М.: Наука, 1980.
3. Araki Н. II Progr. Theor. Phys. — 1957. — V. 17. — P. 619.
4. Sucker J. II Phys. Rev. — 1958. — V. 109. — P. 1010.
5. Браун M. A, Лабзовский Л. H. II ЖЭТФ. — 1967. — Т. 53. — С. 1776.
6. Jankowskl К., Rutkowski A // Phys. Scr. — 1987. — V. 36. — P. 464.
7. Grant I. P. II ku\i. Phys. — 1970. — V. 19. — P. 747.
8. Johnson W. R., Lin С D. II Phys. Rev. — 1976. — V. A14. — P. 565.
9. Desclaux J. P. II Computer Phys. Commun. — 1975. — V. 9. — P. 31.
10. Grant I. P. II Phys. Scr. — 1980. — V. 21. — P. 443.
11. Gell-Mann M., Low F. II Phys. Rev. — 1951. — V. 84. — P. 350.
12. Sucher J. II Phys. Rev. — 1957. — V. 107. — P. 1448.
13. Лабзовский Л. H. II ЖЭТФ. — 1970. — № 59. — С. 168.
14. Дмитриев Ю. Ю., Климчицкая Г. Л., Лабзовский Л. Н. Релятивистские
эффекты в спектрах атомных систем. — М.: Энергоатомиздат, 1984; Labzovsky L.,
299
Klimchitskaya С, Dmitriev Yu. Relativistic effecis in the spectra of atomic systems. —
lOP Publishing, Bristol and Philadelphia, 1993.
15. Васильев A. H., Китанин A Я. II Teop. и мат. физика. — 1975. — Т. 24. —
С. 219.
16. Запрягаев С. А., Манаков Н. Л., ПальчиковВ. Г. Теория многозарвдных ионов
с одним и двумя электронами. — М.; Эиергоатомиздат, 1985.
17. Браун М. А, Гурчумелия А. Д., Сафронова У. И. Релятивистская теория
атома. — М.-. Наука, 1984.
18. Шабаев В. М. //Многочастичные эффекты в атомах. — M.v Наука, 1988. —
С. 65.
19. Sucker J. II Phys. Rev. — 1980. — V. A22. — P. 1167.
20. Mittleman M. H. II Phys. Rev. — 1981. — V. A24. — P. 1167.
21. Furry W. H. II Phys. Rev. — 1951. — V. 81. — P. 15.
22. Feynman R. P. II Phys. Rev. — 1949. — V. 76. — P- 749.
К главе 3
1. Климчицкая Г. Л. ЛабзовскийЛ. И. II ЖЭТФ. — 1971. — Т. 60. — С. 2019.
2. Дмитриев Ю. Ю., Климчицкая Г. Л., Лабзовский Л. Н. Релятивистские
эффекты в спектрах атомных систем. — М.; Эиергоатомиздат, 1984;
Labzowsky L.,Klimchitskaya С, Dmitriev Yu. Relativistic effecis in the spectra of
atomic systems. — lOP Publishing, Bristol and Philadelphia , 1993.
3. Бете Г., Солпитер Э. Квантовая механика атомов с одним и двумя
электронами / Пер. с англ. — М.: Физматгиз, 1960.
4. Sucher J. II Phys. Rev. — 1957. — V. 107. — P. 1448.
5. ЛабзовскийЛ. Н. II ЖЭТФ. —• 1970. — Т. 59. — С. 168.
6. Климчицкая Г. Л., Лабзовский Л. Н. II Опт. и спектр. — 1973. — Т. 34. —
С. 633.
7. Vainstein L. А., Safronova U. I. //At. Data Nuck. Data Tables. — 1978. — V.
21. — P. 49.
8. Marvin H. H. II Phys. Rev. — 1947. — V. 71. — P. 102.
9. Wybourne B. C. II i. Chem. Phys. — 1964. — V- 40. — P. 1457.
10. ЮцисА. П., Савукинас A. Ю. Математические основы теории атома. —
Вильнюс: Минтис, 1973.
11. Сафронова У. И., Лабзовский Л. И. II Вестник ЛГУ. Сер. физ., хим. —
1969. — Вып. 4. — С. 23.
12. Никитин А. А, Рудзикас 3. Б. Основы теории спектров атомов и ионов. —
М.: Наука, 1983.
13. Собельман И. И. Введение в теорию атомных спектров. — М.: Наука, 1977.
14. Тимофеева Т. Е., Лабзовский Л. Н. II Изв. АН СССР. Сер. физ. — 1981. —
Т. 45. — С. 2390.
15. Шабаев В. М. II Многочастичные эффекты в атомах. — М., 1988. — С.65.
16. Blundell S. А, Mohr Р. J., Johnson W. R., Saplrstein J. II Phys. Rev. —
1993. — V. A48. — P. 2615.
17. Lindgren I., Persson H., Salomonson S., Labzovsky L. II Phys. Rev. —
1995. — V. A51. — P. 1167.
18. Запрягаев С. A., Манаков Н. Л., Пальчиков В. Г. Теория многозар11дных
ионов с одним и двумя электронами. — М.: Эиергоатомиздат, 1985.
19. Swirles В. II Ргос. Roy. Soc. — 1936. — V. А157. — P. 680.
20. Grant I. P. II Adv. Phys.1970. — V. 19. — P. 747.
21. Declaux J. P. II Relativistic effects In atoms, molecules and solids / Ed.
G.MaUi. — N. Y.: Plenum Press, 1983. — P. 115.
22. Pyykko P. Relativistic Theory of Atoms and Molecules. — Berlin: Springer-
Verlag, 1986.
23. Slater J. C. Quantum Theory of Atomic Structure. — N. Y.: McGraw-HiU, 1960.
24. Kutzelnigg W. II Int. J. Quant. Chem. — 1984. — V. 25. — P. 107.
300
к главе 4
1. Lamb W. Е.. Retherford R. С II Phys. Rev. — 1947. — V. 72. — P. 241.
2. Bethe H. A. II Phys. Rev. — 1947. — V. 72. — P. 339.
3. Ахиезер A. И., Берестецкий В. Б. Квантовая электродинамика. — М.: Наука,
1981.
4. Берестецкий В. Б., Лифшиц Е. М, Питаевский Л. П. Квантовая
электродинамика. — М.: Наука, 1980.
5. Бьеркен Дж. Д., Дрелл С. Д. Релятивистская квантовая теория / Пер. с англ —
М.: Наука, 1978. Т. 1, 2.
6. Швебер С. Введение в релятивистскую квантовую теорию поля / Пер. с англ —
М.: ИЛ, 1963.
7. Feynman R. Р. II Phys. Rev. — 1949. — V. 76. — P. 749.
8. Feynman R. P. II Phys. Rev. — 1949. — V. 76. — P. 769.
9. Jauch J. M., Rohrlich F. Theory of Photons and Electrons. — Cambridge, Mass.,
1959.
10. Dresden M., Tsu-Teh-Chou II Rev. Mod. Phys. — 1967. — V. 39. — P. 143.
11. Бете Г., Солпитер Э. Квантовая механика атомов с одним и двумя
электронами / Пер. с англ. — М.: Физматгиз, 1960.
12. Harriman J. М. II Phys. Rev. — 1956. — V. 101. — P. 594.
13. Schwartz С, Tiemann J. II Ann. Phys. — 1959. — V. 56. — P. 178.
14. Грановский Я. И. II ЖЭТФ. — 1969. — Т. 56. — С. 605.
15. Справочник по специальным функциям / Ред. М Абрамовиц, И. Стиган; пер.
с англ. — М.: Наука, 1979.
16. Karplus R., Klein А. Schwinger J. // Phys. Rev. — 1952. — V. 86. — P. 288.
17. Baranger M., Bethe H., Feynman R. P. II Phys. Rev. — 1953. — V. 92. — P.
482.
18. Fried H. M.-, Yennie D. R. II Phys. Rev. — 1958. — V. 112. — P. 1391.
19. Erickson G. W., Yennie D. R. II Ann. Phys. — 1965. — V. 35. — P. 271.
20. Schwinger J. II Phys. Rev. — 1949. — V. 75. — P. 1912.
21. Lautrup B. E., Peterman A, de Rafael E. II Phys. Rep. — 1972. — V.
3C. — P. 195.
22. Baranger M., Dyson F. J., Salpeter E. E. II Phys. Rev. — 1952. — V. 88. —
P. 680.
23. Эйдем M. И., Каршенбойм С. Г., Шелюто В. А. II ЯФ. — 1994 — Т. 57 —
С. 1609.
24. Pachucki К., Leibfried D., Weitz М. et al. II i. Phys. — 1996. — V. 29. —
P. 177.
25. Araki H. II Progr. Theor. Phys. — 1957. — V. 17. — P. 619.
26. Sucher J. II Phys. Rev. — 1958. — V. 109. — P. 1010.
27. Браун M. A., ЛабзовскийЛ. И. II ЖЭТФ. — 1967. — Т. 53. — С 1776.
28. Schwartz С. II Phys. Rev. — 1961. — V. 123. — P. 1700.
29. Dmitriev Yu. Yu., Labzowsky L. N. II Phys. Lett. — 1969. — V. 29A. — P. 153.
30. Brown C. E., Langer H. S., Schaejer G. W. II Proc. Roy. Soc. — 1959. —
V.A251. — P. 92.
31. Brown G. E., Mayers D. F. II Proc. Roy. Soc. — 1959. — V.A.251. — P. 105.
32. Desiderio A. M., Johnson W. R. II phys. Rev. — 1971. — V.A3. — P. 1267.
33. Mohr P. J. II Ann. Phys. — 1974. — V. 88. — P. 434.
34. Mohr P. T. II Ann. Phys. — 1974. — V. 88. — P. 52.
35. Pauli W., Villars F. II Rev. Mod. Phys. — 1949. — V. 21 — P. 434.
36. Mohr P. J. II Phys. Rev. Lett. — 1975. — V. 34. — P. 1050.
37. Sapirstein J. II Phys. Rev. Lett. — 198). — V. 47. — P. 1723.
38. Базь A. И., Зельдович Я. Б., Переломов А М. Рассеяние, реакции и распады
в нерелятивистской квантовой механике. — М.: Наука, 1971.
39. Uehling Е. А. II Phys. Rev. — 1935. — V. 48. — P. 55.
40. Schwinger J. II Phys. Rev. — 1949. — V. 75. — P. 651.
41. Whichmann E. H., Kroll N. M. II Phys. Rev. — 1956. — V. 101. — P. 843.
301
42 Blomguist J. II Phys. Rev. — 1935. — V. 48. — P. 55.
43. Spff C, Mohr P. J. II Phys. Rev. — 1988. — V. A38. — P. 5066.
44. Манаков H. Л., Некипелов A. A., Файнштейн A. Г. II ЖЭТФ. — 1989. — T.
95. — С 1167.
45. Scneider S. M., Creiner W.. Soff C. II J. Phys. — 1993. — V. B26. — P. L529.
46. Lindgren I., Persson H., Salomonson S. et al. II J. Phys. — 1993. — V.
B26. — P. L503.
47. Mitrushenkov A., Labzovsky L., Lindgren I. et al. II Phys. Lett. —
1995. — V. A200. — P. 51.
К главе S
1. Собельман И. И. Введение в теорию атомных спектров. — М.: Наука, 1977.
2. Бете Г., Солпитер Э. Квантовая механика атомов с одним и двумя
электронами / Пер. с англ. — М.: Физматгиз, 1960.
3. Thouless D. J. II Nucl. Phys. — 1961. — V. 22. — P. 78.
4. Амусья М. Я. Атомный фотоэффект. — М.: Наука, 1987.
5. Варишлович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория
углового момента. — М.: Наука, 1975.
6. Никитин А. А., РудзикасЗ. Б. Основы теории спектров атомов и ионов. — М.:
Наука, 1983.
7. Веселое М. Г. II Вестник ЛГУ. Сер. физ., хим. — 1953. — № 8. — С. 181.
8. Chen М. Н., Craseman В. II Phys. Rev. — 1984. — V. АЗО. — Р. 170.
9. Scofield J. Н. II Phys. Rev. — 1974. — V. A9. — P. 1041.
10. Листенгартен М. A., Тржасковская М. £., Банд И. М. II Препринт ЛИЯФ
№ 1120. —Л., 1985.
И. Cordon W. II Ann. Physik. — 1929. — Bd. 2. — S. 1031.
12. Дмитриев Ю. Ю., Климчицкая Г. Л., Лабзовский Л. И. Релятивистские
эффекты в спектрах атомных систем. — М.: Энергоатомиздат, 1984; Labzovsky L.,
Klimchitskaya С, Dmitriev Yu. Relativistic effects in the spectra of atomic systems. —
lOP Publishing, Bristol and Philadelphia, 1993.
13. Соколов A. A., Тернов И. М. Релятивистский электрон. М. —; Наука, 1974.
14. Запрягаев С. А., Манаков И. Л., Пальчиков В. Г. Теория многозарядных
ионов с одним и двумя электронами. — М.: Энергоатомиздат, 1985.
15. Bates D. Я, Damgaard А. II Phil. Trans. — 1949. — V. 242. — P. 101.
16. Wiese W. L, Smith M. W., Glennon B. M. Atomic Transition Probabilities. —
NSRDS — NBS 4, 1966, V. I; NSRDS — NBS 22, 1969, V. II.
17. Веселое M. Г., Берсукер И. Б. II Изв. АН СССР. Сер. физ. — 1958. — Т.
22. — С.62.
18. Веселое М. Г., Штофф А В. //Опт. и спектр. — 1969. — Т. 22. — С. 641.
19. Браун М. А., Гурчумелия А. Д., Сафронова У. И. Релятивистская теория
атома. — М.: Наука, 1984.
20. Запрягаев С. А, Манаков И. Л., ПальчиковВ. Г. II Опт. и спектр. — 1979. —
Т. 46. — С. 214.
21. Johnson W. Я. Lin С. D. II Phys. Rev. — 1974. — V. 9А. — P. 1486.
22. Johnson W. Я. Lin С. D. II Phys. Rev. — 1976. — V. 14A. — P. 565.
23. БерестецкийВ. Б., Лифшиц E. М., ПитаевскийЛ. П. Квантовая
электродинамика. — М.: Наука, 1980.
24. Ландау Л. Д., Лифшиц Е. М. Квантовая механика. — М.: Наука, 1974.
25. Stobbe М. II Ann. Physik. — 1930, — Bd. 7. — S. 661.
26. Burgess A., Seaton M. II Rev. Mod. Phys. — 1958. — V. 30. — P. 992.
27. Amusia M. Ya. II Comments At. МЫ. Phys. — 1981. — V. 10 (4). — P. 155.
28. Дмитриев Ю. Ю., Лабзовский Л. И. II Вестник ЛГУ. Сер. физ., хим. —
1971. —№22. — С. 5.
29. Варнавских С- М., ЛабзовскийЛ. Н. II Опт. и спектр. — 1979. — Т. 47. — С.
45.
30. Carter S. L. Kelly Н. Р. II Phys. Rev. — 1981. — V. А24. — P. 170.
302
31. Holland D. M. P., Codling K., West J. B. et al. II J. Phys. — 1979. — V.
В12. — P. 1319.
32. Carter S. L., Kelly H. P. II i. Phys. — 1976. — V. B9. — P. L565.
33. Carlson T. A. II Phys. Rev. — 1967. — V. 156. — P. 142.
34. Samson J. A. R., Haddad G. N. II Phys. Rev. Lett. — 1974. — V. 33. — P. 875.
35. Fano U. II Phys. Rev. — 1961. — V. 124. — P. 1866.
36. Бэрк П., Ситпон М. II Вычислительные методы в физике атомных и
молекулярных столкновений / Ред. Б. Олдер и др.; Пер. с англ. — М.: Мир, 1974. — С. 9.
37. ГайлитисМ. Л. II УФН. — 1975. — Т. 116. — С. 665.
38. Fano и.. Cooper J. W. II Phys. Rev. — 1965. — V. 137A. — P. 1364.
39. Смрнов Б. М. II УФН. — 1980. — Т. 131. — С. 577.
40. Seaton М. 1. II Rep. Progr. Phys. — 1983. — V. 46. — P. 167.
41. Wing W. H.. Lea K. R., Lamb W. E. II Atomic Physics / Ed. S.J.Smith, G. K.
Walters. — N. Y.: Plenum Press, 1973. — V. 3. — P. 119.
42. Fano U. II Rep. Progr. Phys. — 1983. — V. 46. — P. 97.
43. Никитин С. И., Островский В. Н II Физика молекул. — Киев; Наукова
думка, 1980. — Вып. 8. — С. 3.
44. Буреева Л. А. II Астроном, журн. — 1968. — Т. 45. — С. 1215.
45. Naccache Р. F. II J. Phys. — 1972. — V. В5. — Р. 1308.
46. Percival /. С, Richards D. II Adv. in Atgmic and Molec. Phys. / Ed.
D.R.Bates, B.Bederson. — N. Y.: Acad. Press, 1975. — V. 11. — P. 1.
47. Бейгман И. Л., Буреева Л. А. //Изв. АН СССР. Сер. физ. — 1981. — Т.
45. — С. 2277.
48. Гореславский С. П., Делоне И. Б., Крайнов В. П. II ЖЭТФ. — 1982. — Т.
82. — С. 1789.
49. Голдстейн Г. Классическая механика. — М.: Гостехиздат, 1957.
50. Ландау Л. Д., ЛифшицЕ. М. Механика. — М.: Наука, 1973.
51. Справочник по специальным функциям / Ред. М. Абрамовиц, И. Сгиган;
Пер. с англ. — М.: Наука, 1979.
52. Regemorter Н., Hoang Binh Dy., Prud'homme V. II J. Phys. — 1979. — V.
B.12. — P. 1053.
53. Давыдкин В. A, Зон Б. A. II Опт. и спектр. — 1981. — Т. 51. — С. 25.
54. Scofield J. Н. II Atomic Inner Shell Processes / Ed. B.Crasemann. — N. Y.:
Acad. Press, 1975. — V. 1. — P. 265.
55. McGuire E. J. //Atomic Inner Shell Processes / Ed. B. Crasemann. — N. Y.:
Acad. Press, 1975. — V. 1. — P. 293.
56 Пресняков Л. П. II УФН. — 1976. — Т. 119. — С. 49.
57. Виноградов А. В., Скобелев И. Ю., Юков Е. А. II УФН. — 1979. — Т.
129. — С. 177.
58. Житник И. А, Кононов Э. Я., Корпев В. В. и др. II УФН. — 1979. — Т.
129. — С. 722.
59. Jordan С II Progress in Atomic Spectroscopy. — N. Y., 1978. — P. 1453.
60. Аглицкий E. В., Сафронова У. И. Спектроскопия автс»10низационных
состояний атомных систем. — М.: Энергоатомиздат, 1985.
61. Andr'a Н. 1. II Progress in Atomic Spectroscopy. — N. Y., 1978. — P. 829.
62. Munger С Т., Could H II Phys. Rev. Lett. — 1986. — V. 57. — P. 2927.
63. Никишов A. И., Pumyc B. И. II ЖЭТФ. — 1964. — T. 46. — С 776.
64. Зельдович Я. Б. II УФН. — 1973. — Т. 110. — С. 139.
65. Зон Б. А., Манаков Н Л., Рапопорт Л. П. II ЖЭТФ. — 1968. — Т. 55. — С.
924.
66. Грановский Я. И. II ЖЭТФ. — 1969. — Т. 56. — С. 605.
67. Зон Б. А., Манаков Н. Л., Рапопорт Л. П. Теория многофотонных процессов
в атомах. — М.: Атомиздат, 1978,
68. Gontier L, Trahin М. II Phys. Rev. — 1968. — V. 172. — P. 83.
69. Gontier Г, Trahin M. II Phys. Rev. — 1971. — V. A4. — P. 1907.
70. Gontier I., Trahin M. II Phys. Rev. Lett.1971. — V. A36. — P. 463.
71. ДелонеH £., ФедоровМ. В. II УФН. — 1981. — Т. 158. — С. 215.
303
к главе 6
1. Дмитриев Ю. Ю., Климчицкая Г. Л., Лабзовский Л. Н. Релятивистские
эффекты в спектрах атомных систем. — М.: Энергоатомиздат, 1984; Labzovsky L.,
Klimchitskaya С, Dmitriev Yu. Relativistic effects in the spectra of atomic systems. —
TOP PuHishing, Bristol and Philadelphia, 1993.
2. Справочник no специальным функциям / Ред. М. Абрамовиц, И. Стиган; Пер.
С англ. — М.: Наука, 1979.
3. Weisskopf V. F., Wigner Е. Р. II Z. Phys. — 1930. — Bd. 63. — S. 54.
4. Гайтлер В. Квантовая теория излучения. — М.: ИЛ, 1956.
5. Берестецкий В. Б., Лифшиц Е. М., Питаевский Л- П. Квантовая
электродинамика. — М.: Наука, 1980.
6. Low F. Е. II Phys. Rev. — 1952. — V. 88. — P. 53.
7. Лабзовский Л. Н. II ЖЭТФ. — 1983. — Т. 85. — С. 869.
8. Браун М. А. II ЖЭТФ. — 1988. — Т. 94. — С. 145.
9. Лабзовский Л. Н., Рощиненко А В. II Изв. АН СССР. Сер. физ. — 1986. — Т.
50. — С. 1395.
10. Аглицкий Е. В., Сафронова У- И. Спектроскопия автс»10низационных
состояний атомных систем. — М.: Энергоатомиздат, 1985.
"ДОМ КНИГИ"
Ю19ггб"б50098'
20.00
Лабэовс
кий Л.Н
. Теори
я атома
. Кв...