Л. КОЛЛАТЦ, В. КРАБС
ТЕОРИЯ ПРИБЛИЖЕНИЙ
ЧЕБЫШЕВСКИЕ
ПРИБЛИЖЕНИЯ И ИХ ПРИЛОЖЕНИЯ
Перевод с немецкого Б. И. ГОЛУБОВА
Под редакцией С. Б. СТЕЧКИНА
МОСКВА «НАУКА» ГЛАВНАЯ РЕДАКЦИЯ ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ 1978
22.193
К 60
УДК 519.6
APPROXIMATIONSTHEORIE Tschebyscheffsche Approximation mit Anwendungen
Von Dr. phil. Dr. h. c. Dr. E. h. Lothar Collatz o. Professor an der Universitat Hamburg und Dr. rer. nat. Werner Krabs Professor an der Technischen Hochschule Darmstadt
1973
К
20204-173
053 (02)-78
© B. G. Teubner, Stuttgart 1973,
© Перевод на русский язык, Главная редакция ..
физико-математической литературы издательства «Наука», 1978
ОГЛАВЛЕНИЕ
Предисловие ............................................. 7*
I.	Возникновение задач приближения.................... ...	9
1.	Ввод функций в вычислительные устройства.............9
2.	Дискретное приближение и сглаживание.................11
3.	Классификация аппроксимационных задач по применяемым функциональным многообразиям.......................13
4.	Аппроксимационные задачи в дифференциальных уравнениях .................................................13
5.	Одностороннее чебышевское приближение в краевых задачах ................................................20
6.	Комбинированные приближения........................24
А.	Кусочное приближение.............................24
В.	Синхронное приближение . -.......................26
С.	Совместное приближение ..........................26
В. Комбинированное приближение......................27
Е. Условное приближение.............................27
7.	Дальнейшие примеры краевых	задач..................28
А.	Телеграфное уравнение............................28
В.	Другие простые примеры...........................29
С.	Распространение волн в плазме....................33
D.	Совместное приближение...........................33
8.	Другие области анализа.............................34
А.	Интегральное уравнение...........................34
В.	Интегро-дифференциальное уравнение с ядром> зависящим от разности аргументов.......................  .	36
С.	Конформное отображение...........................37
D.	Дифференциально-разностное уравнение.............38
Е.	Численное интегрирование.........................39
9.	Lp-приближение и другие аппроксимационные задачи . . 41
А.	Lp-приближение . . . .^..........................41
В.	Одностороннее М-приближение......................41
С.	Смешанное Li-7-приближение.......................43
D.	Приближение бесконечномерными	подпространствами 43
Е.	Несимметричное Г-приближение.....................44
F.	Приближение с ограничениями на	область ..... 46
G.	Монотонно разложимые операторы...................46
II-	Нелинейное чебышевское приближение. Общая теория ... 49
1.	Постановка задачи..................................49
А.	Общая формулировка задачи........................49
1*
4
Оглавление
В.	Частные случаи......................................50
С.	Постановка задач....................................53
2.	Нижние границы для наилучшего приближения и достаточное условие для элементов наилучшего приближения 54
А.	Общий принцип получения нижних границ...............54
В.	Приложения..........................................58
С.	Достаточное условие для элементов наилучшего приближения ...............................................65
3.	Существование элементов наилучшего приближения	.	.	67
А.	Общие соображения................................67
В.	Примеры..........................................70
4.	Необходимые условия для элементов наилучшего приближения ............................................ 72
А.	Касательный конус в нормированных пространствах	72
В.	Приложение к общей Т-задаче .	 76
С.	Дифференцируемый действительный случай	.	.	.	.78
5.	Характеристика элементов наилучшего приближения	.	.	84
А.	Общее и локальное условие Колмогорова............84
В.	Условие о знаках.................................88
С.	Приложения................................... 91
6.	Единственность......................................93
А.	Достаточное условие единственности ................ 93
В.	Частные случаи...................................99
С.	Необходимое условие единственности..............104
7.	Приближение на действительном отрезке..............109
А. Нижние границы для наилучшего приближения и достаточное условие для элементов наилучшего приближения .............................................ПО
В.	Необходимые условия для элементов наилучшего приближения ...........................................111
С.	Единственность элементов наилучшего приближения 115
8. Непрерывность Т-операторов.........................116
А.	Постановка задачи................................116
В.	Сильная единственность и непрерывность Г-операторов 117
С.	Нормальность и локальная непрерывность Т-оператора 121
D.	Примеры .........................................129
IIГ //-Множества  ........................................131
1.	Я-множества, Ягмножества, Яг-множества.............
2.	Линейное приближение...............................
3.	Примеры Я-множеств.................................
А.	Г-системы.........................................
В.	Линейные функции.................................
С.	Многочлены.........................................
D.	Многочлены двух независимых переменных..........
Е.	Более общие случаи...............................
4.	Тригонометрическое чебышевское приближение в случае двух переменных.......................................
5.	Кусочное приближение многочленами (сплайн-аппроксимация) ...............................................
131
135
137
137
139
140
140
142
142
146
Оглавление
&
6.	Кусочное приближение рациональными функциями . . .148
7.	Яг-множества и монотонность........................150
А.	Принцип монотонности............................150
В.	Трехточечные Яг-множества на прямой.............150
8.	Приложение к дифференциальным уравнениям...........153
А.	Ограниченная область............................153
В.	Неограниченная область..........................155
IV.	Общее рациональное и линейное приближения.............156
1.	Проблема существования при рациональном приближении в действительной области ............................. 156
А.	Общая постановка задачи.......................  156
В.	Обыкновенное рациональное приближение в действительной области......................................159
С.	Рациональное тригонометрическое приближение . . .160
2.	Вычисление наилучшего приближения и характеристика элементов наилучшего приближения.......................163
А.	Теорема двойственности при общей рациональной аппроксимации .........................................164
В.	Характеристика элементов наилучшего приближения 168
С.	Случай линейного приближения.....................170
3.	Дискретное рациональное приближение................172
А.	Двойственность...................................172
В.	Критерий разрешимости 7*-задачи..................173
С.	Случай т = г + s + 2.............................176
D.	Случай линейного приближения.....................180
4.	Метод решения задач дискретной рациональной аппроксимации .................................................182
А.	Теоретические	основы метода......................182
В.	Реализация	метода................................186
5.	Метод решения задачи дискретной линейной аппроксимации ...................................................191
А.	Основы метода....................................192
В.	Теоретическое	описание	метода....................194
С.	Сходимость.......................................196
D.	Практическая	реализация	метода .................198
V.	Нелинейное экспоненциальное приближение.................201
1.	Существование элементов наилучшего приближения . . 201
А.	Постановка задачи . z...........................201
В.	Общая теорема существования.....................202
С.	Приложение к экспоненциальному приближению . . 207
2.	Характеристика и единственность элементов наилучшего приближения...........................................211
А.	Необходимые и достаточные условия для элементов
наилучшего приближения...........................212
В.	Единственность элемента наилучшего приближения . .214
6
Оглавление
VI.	Другие вопросы....................................  216
1.	Теоремы Стоуна и Вейерштрасса.....................216
А.	Постановка задачи..............................216
В.	Теорема Стоуна.................................218
С.	Приложение теоремы Стоуна......................221
2.	Рациональное приближение и задачи на собственные значения ...............................................224
А.	Введение.......................................224
В.	Задачи на собственные значения при общем рациональном приближении.................................224
С.	Обыкновенное рациональное приближение..........230
VII. Приложение..........................................233
1.	Метрические и нормированные пространства..........233
2.	Некоторые свойства выпуклых множеств в векторных пространствах........................................243
3.	Сравнение L2- и Т-приближений.....................247
4.	Дальнейшие примеры	Т-систем......................249
5.	Задачи с решениями................................251
6.	Другие задачи.....................................260
Литература...............................................262
Предметный указатель.....................................270
ПРЕДИСЛОВИЕ
В последнее время появилось так много учебников по теории приближения, что может возникнуть вопрос о правомерности появления еще одной книги. Наша мотивировка исходит из того, что как в журнальной литературе, так и в большинстве учебников по теории приближений сравнительно мало внимания уделяется приложениям. Представляется, что в настоящее время существует известное расхождение между некоторыми областями, достаточно разработанными математиками, и областями, математическое исследование которых с точки зрения приложений было бы чрезвычайно желательным.
Аппроксимационные проблемы, появляющиеся при постановке физических и технических задач, в процессе их развития оказываются весьма многосторонними и часто не похожими на те задачи, которые до сих пор обычно рассматривались в теории. При этом они часто столь интересны и глубоки с точки зрения математики, что появляется исключительно богатое поле деятельности для математического исследования. Очень часто студенты, дипломанты и аспиранты обращались к нам за темами по теории приближения, которые одновременно имели бы практическое значение, а поскольку о таких темах известно сравнительно ма ю, то эта книга является попыткой несколько восполнить пробел между теорией и приложениями. Так как среди приложений различных способов приближения чебышевские приближения по значению, по-видимому, далеко превосходят Другие виды приближения, то эта книга посвящена в основном чебышевским приближениям — как их теории, так и приложениям. Связующим звеном между теорией и приложениями служат также различные задачи и упражнения в конце книги.
8
Предисловие
Первая глава содержит подбор прикладных задач, приводящих к аппроксимационным ‘задачам, в частности, к задачам мало исследовавшихся ранее типов, таких как совместное приближение, одностороннее приближение, комбинированное приближение и др. Затем в главе II излагается общая теория, которая охватывает как линейные, так и нелинейные чебышевские приближения, и в силу этого отличается от многих других изложений. В главе III рассматривается область, близкая к приложениям (а именно, «//-множества»), в то время как главы IV—VI вновь посвящаются теории, но всегда с точки зрения вопросов, важных для приложений. В главе IV даются также некоторые предложения по численному решению задач рационального и линейного приближений. Читателю, интересующемуся больше теорией, предназначены главы II, IV, V, VI, в то время как главы I, III, VII (за исключением первых двух разделов) написаны для читателей, больше интересующихся приложениями.
1973	Л. Коллатц, В. Крабе
I.	ВОЗНИКНОВЕНИЕ ЗАДАЧ ПРИБЛИЖЕНИЯ
Если слово «приближение» понимать достаточно широко, то им может быть охвачена большая часть вычислительной математики. Однако в этой книге слово «приближение» понимается намного уже и охватывает лишь специальный круг задач. В большинства случаев речь будет идти о приближении функций одной или нескольких независимых переменных посредством других функций. Прежде чем эта задача будет уточнена, укажем некоторые важные проблемы численного анализа, которые приводят к аппроксимационным задачам рассматриваемого здесь типа.
1.	Ввод функций в вычислительные устройства
Ввод достаточно точных числовых таблиц в вычислительные машины (вычислительные устройства) потребовал бы слишком- большого объема памяти, поэтому на вычислительных машинах всегда подсчитываются необходимые табличные значения даже простых функций, таких как sin и т. д.
Можно, например, попытаться приблизить функцию
f(x) = e*	(1.1)
на отрезке [0, 1] многочленом
w(x)=^ ajX1	(1.2)
/-о
так, чтобы погрешность
e(x) = w(x)-f(.v)	(1.3)
на рассматриваемом отрезке не превосходила заданной границы, например, >
|8(х)|<1 • 10-8.	(1.4)
10
/. Возникновение задач приближения
Если удастся определить константы а0, ...» вр так, что требование (1.4) будет выполнено, то эти коэффициенты
можно ввести в вычислительную машину и, используя
многочлен (1.2), вычислять значения ех для каждого
Рис. 1.1.1. Приближение функции f (х) многочленом ш (х) (здесь w (х) — многочлен третьей степени).
хе[0,1 ] с точностью до восьмого знака (рис. I. 1.1).
Оказывается, что во многих
случаях, в том числе и в данном, используя вместо многочленов вида (1.2) рациональные функции
.	(1.5)
при том же числе параметров, как правило, можно достичь лучшей точности, т. е. можно понизить максимальное значение ошибки. Поскольку вычислительные машины очень легко могут
подсчитывать также выражения вида (1.5), то в данном случае рациональное приближение имеет преимущество перед приближением много
членами.
Если надо приблизить подобным образом функцию
f(x) = е~х
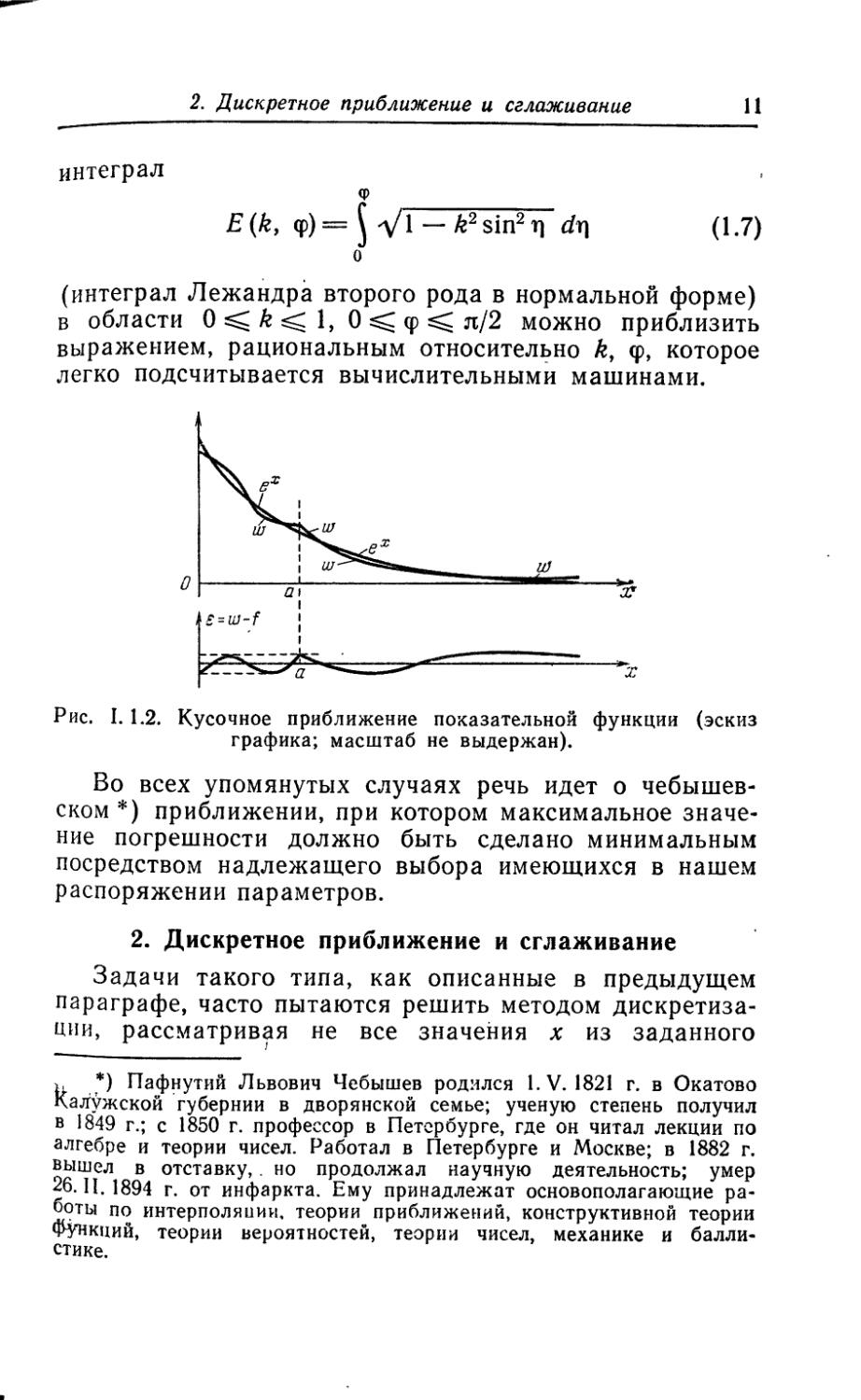
на промежутке / = [0, оо), то представляется естественным на отрезке [0, а] применить приближение многочленом степени р > 0, а на промежутке [а, оо) использовать рациональное приближение (например, рационально^ дробью, обратной по величине некоторому многочлену степени q>0). При этом промежуточное значение а и коэффициенты многочленов надо выбрать подходящим образом (рис. 1.1.2).
Аналогичные задачи возникают и для функций мно^ гих независимых переменных. Например, эллиптический
2. Дискретное приближение и сглаживание
И
интеграл
ф
Е (k, (р) = V1 £2 sin2 Л dr] о
(1.7)
(интеграл Лежандра второго рода в нормальной форме) в области 0 k 1,	л/2 можно приблизить
выражением, рациональным относительно А, ф, которое легко подсчитывается вычислительными машинами.
Рис. I. 1.2. Кусочное приближение показательной функции (эскиз графика; масштаб не выдержан).
Во всех упомянутых случаях речь идет о чебышевском*) приближении, при котором максимальное значение погрешности должно быть сделано минимальным посредством надлежащего выбора имеющихся в нашехм распоряжении параметров.
2.	Дискретное приближение и сглаживание
Задачи такого типа, как описанные в предыдущем параграфе, часто пытаются решить методом дискретизации, рассматривая не все значения х из заданного
*) Пафнутий Львович Чебышев родился 1. V. 1821 г. в Окатово Калужской губернии в дворянской семье; ученую степень получил в 1849 г.; с 1850 г. профессор в Петербурге, где он читал лекции по алгебре и теории чисел. Работал в Петербурге и Москве; в 1882 г. вышел в отставку,. но продолжал научную деятельность; умер 26.11. 1894 г. от инфаркта. Ему принадлежат основополагающие работы по интерполяции, теории приближений, конструктивной теории Функций, теории вероятностей, теории чисел, механике и баллистике.
12
I. Возникновение задач приближения
интервала, а лишь конечное множество х2, - • • > хы значений х. При этом вычисления также проводят лишь с соответствующими значениями функций
=	(2.1)
и погрешностей
ez = wj — fj = w (xj> — f (xf).	(2.2)
Если при этом стремятся сделать величину
|| е || = шах | еу |	(2.3)
как можно меньшей, то приходят к задаче дискретного чебышевского приближения.
Эта задача тесно связана с задачей «сглаживания», когда по заданным точкам измерения (x/.fi) хотят провести гладкую кривую с простым аналитическим выражением а»(х) при наименьшей возможной «общей ошибке». При этом в качестве w(x) выбирают выражение, которое отвечает ожидаемому поведению соответствующего физического процесса, например, многочлен (1.2), рациональную функцию (1.5), при затухающих процессах— экспоненциальное выражение вида
р
w(x)=Lale-bix,	(2.4)
/-1
при периодических процессах — выражение вида
w(x) = ^a/sin0/x —Су)	(2.5)
и т. д. Более сложные задачи возникают при нескольких независимых переменных. В качестве суммарной погрешности (2.3) часто, следуя Гауссу*), берут
*) Карл Фридрих Гаусс, вероятно, самый значительный математик нового времени, «король математиков», родился 30. IV. 1777 г. В 1799 г. дал первое полное доказательство «Основной теоремы алгебры». С 1807 г. стал профессором астрономии в Гёттингене, где протекала его деятельность вплоть до смерти 23. II. 1855 г. С теорией приближений его связывает метод наименьших квадратов.
3. Классификация аппроксимационных задач
13
значение
(2.6)
(метод наименьших квадратов).
3.	Классификация аппроксимационных задач по применяемым функциональным многообразиям
Включим теперь упоминавшиеся до сих пор аппроксимационные задачи в более общие рамки, к которым мы еще вернемся в II. 1. С этой целью сформулируем задачу следующим образом: пусть В — область п-мерного пространства R" векторов х = (хь ..., хп). Пусть, далее, С (В)—пространство непрерывных в В функций g(x), a W — {w (х, а)} — подмножество из С (В), зависящее от некоторого векторного параметра а = (аь ..., aq). Иногда допускается и случай q = оо. Векторный параметр а изменяется в заданной области А ^-мерного векторного пространства R*. Часто А совпадает со всем пространством R<
Пусть для любых двух функций g{x) и h(x) из С (В) определено «расстояние» (метрика) p(g,й), что можно сделать многими способами (см. 1.9 и VII. 1). Например, с помощью положительной непрерывной в В весовой функции р(х) можно ввести норму
I! g У = sup р (х) | g (х) | и расстояние р (g, h) = || g — h ||.
X €= В
т	(3.1)
Часто выбирают р(х)== 1.
Пусть теперь f — фиксированный элемент из С (В), не принадлежащий классу W.
Определение. Число
р0 = inf р (f, w)
w е W
называется расстоянием от f до класса W, а элемент $ такой, что
р(/, й>) = Ро,	(3.2)
называется элементом наилучшего приближения (ближайшим элементом).
14
I. Возникновение задач приближения
Если расстояние определено посредством (3.1), то этим описывается чебышевское приближение.
Аппроксимационные задачи можно классифицировать, исходя прежде всего из того, как класс приближающих функций W(a,x) зависит от параметров ak и как он зависит от переменных х/.
Определение. Аппроксимационная задача называется линейной, если W линейно относительно параметров av (например, является линейным подпространством, натянутым на функции wv(x), v— 1, ..., q), в противном случае задача называется нелинейной.
Как упомянуто выше, возможно также равенство q = оо (например, при приближении гармонической функцией, степенным рядом и т. д.). В линейном случае wv(x) считаются фиксированными функциями из пространства С (В), a W совпадает с множеством
С	Л	1
W = s w (х) = У avwv (х), а е Л	(3.3)
ч	v=i	)
Известны различные частные случаи линейного приближения. Укажем кратко некоторые из них.
Частные случаи. 1а) Полиномиальное приближение многочленами одной или нескольких независимых переменных. При двух независимых переменных х, у класс W может состоять, например, из функций
w = Е	(3.4)
u, v=0
1b) Экспоненциальное	приближение.
В этом случае W состоит из функций
q п
W== s Z	(3.5)
v«l ц—1
где 6^ — фиксированные постоянные; — либо подлежащие определению постоянные, либо подлежащие определению многочлены заданной степени от хь ..., хп: а^у = PpV(xi, ..., хп), причем для степени многочлена Рцу задана фиксированная граница puv* deg Puv Pmv
3. Классификация аппроксимационных задач	£5
1с) Тригонометрическое приближение, В этом случае используются функции
W = Е Е cos &uv (хц — Сцу),	(3.6)
v=l ц = 1
где &ULV и Cgv — постоянные. В простейшем случае полагают
6gv = (v—1)₽и,	v=\,...,q,	|х=1, .... п
при фиксированных 0Ц.
УкажехМ теперь некоторые случаи нелинейного приближения.
2а) Нелинейное рациональное приближение. В этом случае рассматриваются функции
k
У avuv (х)
--------	(3.7)
У, bvvv (х)
V=1
где av, bv — свободные параметры, a uv и vv — фиксированные функции из пространства С (В).
2Ь) Нелинейное экспоненциальное приближение с линейными экспонентами. Применяемые в этом случае функции, как и при линейном экспоненциальном приближении, имеют вид (3.5), однако при этом Ь^у не фиксированы, а являются свободно выбираемыми параметрами. Коэффициенты можно по-прежнему рассматривать как свободные параметры или как многочлены = РЦу(*) с заданной границей Рич для их степеней.
2с) Нелинейное экспоненциальное приближение с квадратическими экспонен-т а м и. В выражении
w	Яцур ехр (ЬцупХрХу СцэХр),	(3.8)
и, v, р
параметры а^ур, b^vp и являются свободными, однако в приложениях часто используются специальные
16
/. Возникновение задач приближения
предположения о зависимостях между или некоторые из них полагаются равными 0.
2d) Нелинейное тригонометрическое приближение. В формуле (3.6) в этом случае все параметры	и cRV являются свободными; очень
важным является содержащийся здесь анализ периодограмм («разыскание скрытых периодов»).
2е) Тригонометрическое экспоненциальное приближение. Полагая в (3.5)
где d^v действительны, отделяя действительную часть получившейся функции и рассматривая все функции в действительной области, приходят к часто встречающемуся в приложениях «смешанному тригонометрическо-экспоненциальному приближению».
Примечание. Встречаются также и другие намного более сложные функциональные классы, которые здесь, естественно, не могут быть перечислены.
4.	Аппроксимационные задачи в дифференциальных уравнениях
Рассмотрим сначала в качестве примера уравнение теплопроводности
^ХХ =='(4.1)
так как уже на нем можно изучить различные типы аппроксимационных задач.
В последующем индексами х, ... обозначаются частные производные, например, ихх = д2и/дх2\ символы Л(х), f(x,y) обозначают заданные (обычно непрерывные) функции, a k — заданную постоянную.
Дифференциальное уравнение (4.1) имеет, в частности, решения
I COS VX I Г V2
< .	> ехр-----г (t — to) ,
tsin vx) L k J
(4.2)
4. Аппроксимации в дифференциальных уравнениях IT
В зависимости от заданных-краевых условий используют те или иные из них.
а)	Пусть заданы следующие краевые и начальные условия:
и (О, /) = и (л, /) = О для i > О, и(х, 0) — h(x) для О^х^л, где /г (0) =/г (л) = О
(рис. 1.4.1,а). Краевым условиям удовлетворяют решения
---/ для v= 1, 2, ...
Таким образом, эти функции следует скомбинировать так, чтобы начальное условие также удовлетворялось как можно лучше.
Принимая
а
w (х)= У, avsin vx & h(x) для О^х^л, (4.4) V» 1
получаем задачу классического линейного тригонометрического приближения. Здесь чебышевское приближение
t
и = h(x)
<*)
Рис. 1.4.1. Краевые задачи для уравнения теплопроводности.
разумно, потому что при нем сразу получается оценка погрешности для приближенного решения
4	2
v (х, /) = av sin (vx) ехр[—у- .
V=l
Именно, для всякого решения и(х, t) уравнения тепло-
проводности (4.1) в каждой области В: ссо < х < он, 0.< t < Т верхняя грань и и верхняя грань |м|
18
/. Возникновение задач приближения
достигаются на границе Г, состоящей из трех отрезков прямых:
/ = О,	0</^Т, х = а0 и х = щ
(так называемый «принцип максимума»).
Если приближение v для и удовлетворяет также однородному уравнению (4.1), то и погрешность (4.1) удовлетворяет уравнению (4.1); если и — решение уравнения (4.1), удовлетворяющее начальным и краевым условиям (4.3), то из неравенства
(4.6)
| v (х, t) — u (х, /) К в	(4.5)
на Г следует также, что (4.5) выполняется и в В (здесь а0 = 0, щ = л).
Ь)	Пусть (см. рис. 1.4.1, Ь)
и (0, /) = 0, и (a, t) == h (/) для t 0
и (х, 0) = h (0) для 0 х а.
Если
а
У av sin Zvx ~ h (0) для 0 x a
V=1
У av sin (Xvn) exp ------ij^h (/) для t :
V = 1
(4.7)
0,
то получаем задачу комбинированного приближения тригонометрическими и экспоненциальными функциями. При заданных Xv приближение линейно, а при переменных нелинейно.
с)	Если значения функции и вдоль всей границы заданы не тождественно нулевыми, то их можно свести к случаям а) и Ь) или же непосредственно применить комбинированное приближение.
d)	Пусть w(0,/) = 0 при /	0, их + уи = 0 при
х = a, t > 0, и(х, 0)=А(х) при О^х^а (см. рис. 1.4.1.с)). При этом пусть у =/= 0 — заданная постоянная. Тогда, если — положительные корни
4. Аппроксимации в дифференциальных уравнениях
19-
уравнения
YtgXva = Xv,	(4.8)
расположенные в порядке возрастания,
v (х, /) = av sin (Xvx) exp^-tj,
V=1
то +	= 0 при x = a.
Считая q w (x) = У av sin (Xvx) « h (x),	(4.9)
v==l
приходим к линейному тригонометрическому приближению с несоизмеримыми частотами Xv.
И здесь, если аппроксимационная задача решена приближенно, можно получить оценку погрешности для искомой функции и(х,/), поскольку справедливы теоремы монотонности (см. Л. Коллатц [1964], стр. 309—311, а также § I. 5 этой книги).
е)	Пусть задана задача Коши с начальными условиями (см. рис. 1.4.Id) u(x, O) = /z(x) для —оо С х < < + оо при lim h (х) = 0. Тогда можно воспользовать-±00
ся формулой
q
V (х, /) = £ av(t + tv)~'h exp ( — J (*) ’» (4-1 °) v=l	V
полагая
A
Z 6vexp(— (x — xv)2) « h (x) для — оо < x < oo, (4.11)
v=i
получаем нелинейную аппроксимационную задачу с квадратичными экспонентами. Если отсюда найти bv, cVf А*, то av, tv определятся равенствами
f) Предположим, что для уравнения теплопроводности
20
I. Возникновение задач приближения
с двумя пространственными координатами для функции и(х, у, t) трех переменных при / = 0 задано начальное условие
и (*, У у 0) — f (*, у) ДЛЯ — оо < х, у < + оо; (4.13) например,
f У) 2 + х2 + у2 + х2у2
Точным решением задачи (4.12), (4.13), которое для каждого t > 0 обращается в нуль на бесконечности (а здесь интересны только такие функции), является функция (для /0 > 0)
V (X, у, /) = (/ + /о)-1 ехр { —	1(Х + х0)2 +
+ (У + i/o)2]}.	(4.14)
Учитывая симметрию (в силу которой хо = уо —0), получаем, что в качестве первого приближения следует аппроксимировать заданные начальные значения f функ* цией
w — ае~ь « f (х, у),
где а и Ь — свободные параметры.
Если выбрать, например, а = 0,46 и b — 0,22, то в начальной плоскости / = 0 будет — f| ^8 = 0,07 и эта же оценка справедлива для соответствующей функции у(х, у, t) из (4.14): |и (х, у, /)— и(х, у, t) | ^0,07 для t > 0.
5. Одностороннее чебышевское приближение в краевых задачах
В 1.4 для оценки погрешности использовался принцип максимума; обсудим теперь принцип монотонности, который обычно ведет к одностороннему чебышевскому приближению и часто дает лучшие границы для погрешности.
Дадим сначала общую формулировку:
Пусть для функции w(x)=u(xi, ..., хп) в области В n-мерного пространства R* с границей Г задано
5. Одностороннее приближение в краевых задачах
21
дифференциальное уравнение Ми = 0 в В
и граничные условия 5и = 0 на Г.
(5.1)
(5.2)
(При этом Su может быть вектором с конечным числом компонент.) Уравнения (5.1) и (5.2) могут быть объединены в одно:
Ти = {Ми, S«} = 0.
Ниже будет предполагаться, что для «функций сравнения» v, v (т. е. для функций, имеющих достаточное количество частных производных) задача обладает свойством монотонности, т. е. является задачей «монотонного типа»:
из Tv^Tv следует	(5.3)
Знак неравенства в (5.3) означает, что оно выполняется поточечно в В, соответственно на Г, при естественном упорядочении действительных чисел. В случае векторов неравенство выполняется для каждой компоненты в отдельности, причем также поточечно.
Этот принцип монотонности справедлив для обширного класса линейных и нелинейных краевых задач для обыкновенных дифференциальных уравнений и для уравнений с частными производными, в частности, эллиптических и параболических (см. Коллатц [1952], [1964], Редхеффер [1962] и др., а также III.8 этой книги).
Если задача (5.1), (5.2) имеет решение и и можно подобрать приближенные решения w, w с неположительным, соответственно неотрицательным «дефектом» (т. е. Tw^O, соответственно Tw^O), то из (5.3) получим оценку погрешности
w w.	(5.4)
Выберем теперь два семейства функций сравнения W — {и (х, at, .... ар)} и W = {w (х, alt ..., ag)}, (5.5) где вектор a = (ait ..., ар) пробегает некоторую область А пространства Rp, а вектор a — (ai......aq) —
область А пространства R7, Для постоянных ац .,,, ар,
22
/. Возникновение задач приближения
aq получаем нелинейную задачу оптимизации | (А)	0 w (х, a) — w (х, а) 6	° |
для хеВ+Г, 6->min	(5.6) |
с бесконечным числом дополнительных условий	|
Tw (х, а) ^0 Tw (х, а) для хеВ + Г. (5.7)
В линейном случае при	\
Ми — Ми — р. (х), Su = Su — а (х),	$
где М, S — линейные операторы ц (х), о (х) — заданные функции и	|
Ти — Ти— r — {Mu — ii, Su — ст), (5.8) J в (5.5) можно использовать линейные выражения: р	ч
w (х) = У, avwv (х), w (х) — У avwv (х).	(5.9) !
У==1	У=1
Тогда получится односторонняя аппроксимационная за- 1 дача с дополнительными условиями, которую можно i записать как линейную задачу оптимизации с контину- f умом дополнительных условий	|
У	Р	|
ОС avwv (х) — S ^vwv	хеВ + Г, 6->min,
V = 1	V=1	|
(AL) У avfwv(x)^r (x) У, avTwv (x)	(5.10) i
v=l	v=l	S
i для всех x e В + Г.	J
Вместо задачи (А) при вычислениях часто исполь- I зуют более простую задачу односторонней аппроксима- | ции с меньшим количеством дополнительных условий:	|
(В)	— Tw (х, а) ^0, 6i-»min (5.11) |
и	е I
0^ Tw (х, а) ^62, d2->min. (5.12) | Обе задачи являются задачами одностороннего чебы- I шевского приближения. В случае (В) имеем следующие ? границы:	в
(х, а) и (х) w (х, а),	(5.13)
5. Одностороннее приближение в краевых задачах
23
которые устанавливаются легче, чем в случае (5.6), соответственно (5.7); однако они, вообще говоря, не столь хороши, как в задаче (А).
Если при этом оператор Г, как в (5.8), линеен, то можно воспользоваться линейными выражениями (5.9), а в случае, если одна из функций Twv и одна из функций Twv постоянны и отличны от нуля, то описанное в задаче (В) одностороннее
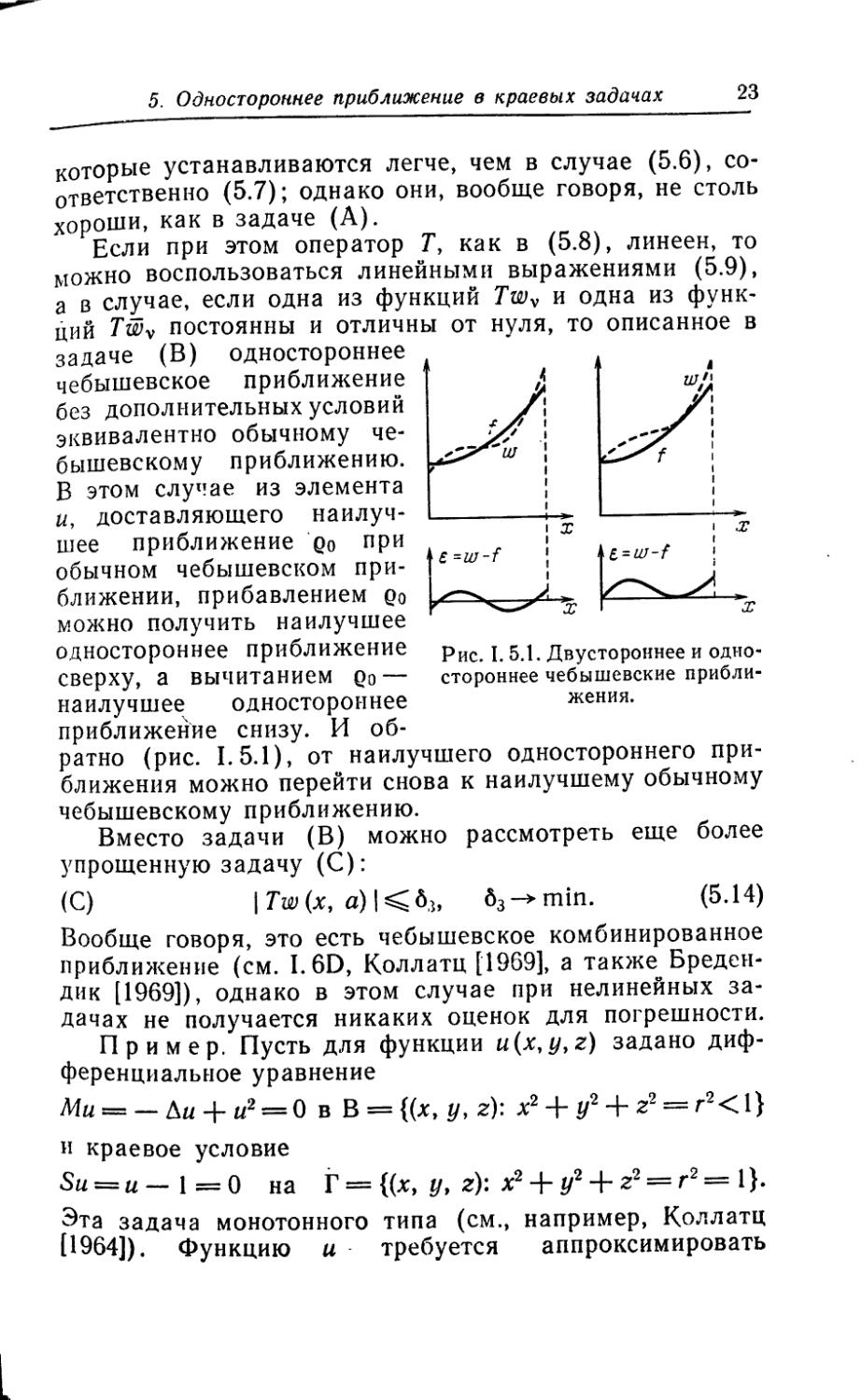
чебышевское приближение без дополнительных условий эквивалентно обычному чебышевскому приближению. В этом случае из элемента и, доставляющего наилучшее приближение р0 при обычном чебышевском приближении, прибавлением Qo можно получить наилучшее одностороннее приближение сверху, а вычитанием Qo —
Рис. I. 5.1. Двустороннее и одностороннее чебышевские прибли-
наилучшее одностороннее	женин.
приближение снизу. И об-
ратно (рис. 1.5.1), от наилучшего одностороннего приближения можно перейти снова к наилучшему обычному чебышевскому приближению.
Вместо задачи (В) можно рассмотреть еще более упрощенную задачу (С):
(С)
\Tw(x, а) |	63 -> min.
(5.14)
Вообще говоря, это есть чебышевское комбинированное приближение (см. I.6D, Коллатц [1969], а также Бреден-дик [1969]), однако в этом случае при нелинейных задачах не получается никаких оценок для погрешности.
Пример. Пусть для функции и(х,у, z) задано дифференциальное уравнение
Ми = — Ди + и2 = 0 в В = {(х, у, z): х2 + у2 + z2 — r2<l}
и краевое условие
Su = u— 1=0 на Г — {(х, у, г): х2 + у2 + г2 = г2 — 1}. Эта задача монотонного типа (см., например, Коллатц [1964]). Функцию и требуется аппроксимировать
24
I. Возникновение задач приближения
функцией w из класса W —	= 1 + (1 —- г2) (ai +'
+ а2г2)}. Для произвольных а2 выполнено краевое условие Sw = 0; функция
Mw — w2 — 6 (я2 — а{) + 20a2r2
на о/резке 0 г 1 должна аппроксимировать функцию, тождественно равную нулю. Вычисления (за провес дение которых мы благодарим Будде и Циммермана) приводят к следующей таблице:
	Обыкновенное Т-приближение ||Ма>Ц-> min (задача (С))	Одностороннее Г-приближение (задача (В))	
		снизу	сверху
		— б < Mw < 0 6 -> min	<б б -» min
«1	—0,13618	-0,13691	-0,13545
а2	—0,01269	—0,01275	-0,01263
• Оценка погрешности	отсутствует	W и	и w
В частности, одностороннее чебышевское приближен ние приводит к следующей двусторонней оценке решения в точке г = 0:
0,86309 и (0, 0,0)	0,86455.
6.	Комбинированные приближения
(Этот термин используется здесь в более общем зна* чении, чем выше, а также в п. I.6.D.)
В приложениях часто встречаются более сложные способы приближения и их комбинации; укажем некоторые из них.
А.	Кусочное приближение (рис. 1.6.1).
Выберем класс К разбиений основной области В на частичные подобласти В0 (о = 1, ..., s), причем число 5 для всех разбиений класса К будем считать фиксированным. Так, например, в случае двух независимых переменных Xi,%2 класс Л можно определить следующимv
6. Комбинированные приближения
£5
образом: покроем область В s прямоугольниками со сторонами, параллельными координатным осям так, чтобы никакие два прямоугольника не имели общих внутренних точек. Каждый прямоугольник должен иметь с областью В общие внутренние точки, однако прямоугольники не обязаны целиком лежать в области В (см. рис. 1.6.1). Пусть, например, задана функция /(х), которую надо приблизить в отдельных областях Ва функцией из класса
Wa = {wa(x, ai(0), apW};	(6.1)
в приложениях часто в качестве w0 берут одни и те же функции. В качестве примера различных функций
приведем уже упомянутую в (1.6) задачу о приближе-
нии функции f(x) = e~x в полуинтервале [0, +°о), а именно — многочленом на отрезке [О, я] и рациональной функцией на полуинтервале [а, + оо).
Пример. Идея кусочного приближения уже давно применяется в теории нелинейных колебаний. Свободные незатухающие колебания системы с
одной степенью свободы (q = Рис. 1.6.1. Кусочное при-—координата, t — вре- ближение на плоскости.
мя) с нелинейной восстанавли-
вающей силой, пропорциональной f(q}> удовлетворяют дифференциальному уравнению

(6.2)
(см. К. Клоттер [1951], стр. 153—162).
Здесь /({/)—заданная функция, которой соответствует при графическом представлении «характеристическая линия». Эта линия кусочно аппроксимируется на конечном {/-отрезке несколькими отрезками прямых (см. рис. 1.6.2). Затем полученное дифференциальное уравнение на каждом из этих {/-отрезков решается в элементарных функциях и полученные решения «склеиваются» друг с другом; если кусочное приближение выбрано
26
/. Возникновение задач приближения
односторонним, то при этом известен знак погрешности приближения для q(t).
Та же самая аппроксимационная задача возникает и при добавлении линейного стабилизирующего члена с постоянным множителем К:
-^+*4г+н<7)=о.	<6-3>
В.	Синхронное приближение. В этом случае требуется приблизить не только функцию f элементом w не-
которого класса W (а, х), но и функцию Tf элементом
Tw. При этом Т — заданный линейный или нелинейный оператор, например, оператор дифференцирования или интегрирования. Конечно, легко привести и нелинейные примеры. В более общем случае могут быть заданы несколько операторов Та (о — = 1, ..., $). Тогда требуется минимизировать расстояние max(p,(7V, T{w), .... ps(Tsf, Tsu))
(6.4)
Рис. 1 6. Характеристи- (при заданных метриках pi, рг, ... ческая линия пружины. ...,ps). См., например, Морсо [1968]).
С.	Совместное приближение. В этом случае требуется приблизить одновременно f и Tf (а возможно и несколько операторов Та) на различных областях BQ (см. Вреден дик [1969]).
Пример. Краевая задача для функции u(xi,x2):
2
Lu=£^(^(Xi’X2)#)=1 В D: х* + х*<1,
в
и —= 0 на Г:	= 1 (v — внутренняя нормаль).
Класс аппроксимирующих функций:
W (х, а) = (w = S a L
6. Комбинированные приближения
27
Здесь р(%1,х2) — заданная функция точки, a q — заранее выбранное натуральное число.
Приближение внутри: В\ = D, T\f = Af, pi = = sup I Lw— 1 |. Приближение на границе:
D
Вг-Г; =	pa = sup|a, — ~
D.	Комбинированное приближение. В этом случае в отдельных областях Ва могут быть заданы различные классы функций Wo.
Три последних типа приближения можно сопоставить с классическим приближением в виде следующей таблицы:
Тип приближения	Оператор	Область	Класс функций
Классическое приближение	Т ] = единичный оператор	В	W
Синхронное приближение	со 1 Л	в	W
Совместное приближение	• II V/	Ва (а=1, .... s) 8>1	W
Комбинированное приближение	й Со	вх (т=1, ..., /)	и С? V 1 Со
Е.	Условное приближение. В этом случае налагаются добавочные ограничения обычно в форме дополнительных условий. Самым известным способом условного приближения, вероятно, является приближение с интерполяцией, при котором значения функции f в определенных точках должны в точности совпадать со значениями приближающей функции:
=	н=1, 2..........s (6.5)
28
/. Возникновение задач приближения
(комбинирование интерполяции и аппроксимации, Тей- ; лор [1969], Шумейкер, Тейлор [1969] и др.).	?
Существуют и другие разнообразные ограничения, например, интегральные условия вида
Ф (х, w (х)) dx = Ф (х, f (*)) dx (6.6) в	в
с заданной функцией Ф.
Наконец, к условному приближению можно отнести также одностороннее чебышевское приближение. Приведем еще несколько примеров для различных, названных здесь способов приближения.
7.	Дальнейшие примеры краевых задач
Рассмотрим еще несколько задач с дифференциалы ными уравнениями.
А. Телеграфное уравнение:
Это уравнение имеет частные решения вида ( COS рх )
e-(VX+uO где ц2 _ v2 _|_ £ J	J. e-ut где р2 ц2_£
’	I, Sin рх)	г i «-
vjJchPQ 2	21 А
е IshpJ’ где P2 = v+*-Пусть, например, и(х, 0) = р(х),
(7.1)
Эи о) = S (х) при х > 0
и и (0, /) = h (/) при i 0, причем lira р (х) = lim s (х) = lim Л (/) = 0 и р (0) = h (0),
Тогда формула
v (х, 0 = X «V exp [— (pvx + Ov0] v-1
7. Дальнейшие примеры краевых задач
29
приводит к комбинированному приближению q	Л
р (х) « £ cive~QvXf s(x) — X ave v=l	v=l
h (/) « У. ау,е~°^,
V=1
где а2 — р2 ПрИ фиксированных pv, Оу получаем линейное, а при переменных pv, ov — нелинейное приближение.
В.	Другие простые примеры. 1. Распределение температуры в поперечном сечении дымовой трубы.
Пусть D—двусвязная область в плоскости (%,у): х2 + у2> 1, |х| <2, |у| <2 (рис. I. 7.1). Пусть и(х, у) в области D удовлетворяет уравнению Лапласа Ди = О, на внутренней границе Г1 пусть и = 1, а на внешней границе Гг пусть и = 0. При z — х + iy, г — |г| и произвольных значениях av функции
w = а01л г + У Uy Re (г2'*)
v=0
удовлетворяют дифференциальному уравнению Ди = 0, и приближение заданных граничных значений и граничными значениями w означает в соответствии с принципом максимума комбинированное приближение (см., например, Коллатц [1964], стр. 305).
2.	Рассматривая ту же задачу и то же выражение для w, что и в примере 1, отбросим ограничение |х| < 2. Тогда получим рисунок 1.7.2, и задачу можно рассматривать как определение потенциала в электростатическом поле плоского конденсатора. Здесь также справедлив принцип максимума, если ограничиться функциями, равными нулю на бесконечности.
3.	При той же самой постановке задачи, что и в примере 2, предположим теперь, что в поле плоского конденсатора находится шар; тогда получаем пространственную задачу (рис. 1.7.3).
Область D теперь задается в системе координат х, z неравенствами х2 + y2-\-z2> 1> \у \ < 2, и снова
30
1. Возникновение задач приближения
Рис. 1.7.1. Распределение температуры в дымовой трубе.
У
Рис. 1.7.2. Электростатическое поле плоского конденсатора.
Я
Рис. 1.7.3. Шар в поле плоского конденсатора.
Рис. 1.7.4. Задача кручения для полукруга.
7. Дальнейшие примеры краевых задач
31
= 0 в D, и — 1 на внутренней и и = О на внешней границе.
4.	Задача кручения полукруга. Пусть D — область х 0, х2 + У2 1 в плоскости (х, у) (рис. 1.7.4); пуСТЬ и = 0 на границе и Au = 1 внутри D. Функцию и можно приблизить, например, многочленом
р
w = у У2 + У, OvWv (х, у), v = l
где wv удовлетворяют уравнению Лапласа (например, wx == 1, W2 = х, w3 = х2 — у2, ...), и задача сводится к приближению граничных значений.
5.	Приближение элементами бесконечномерного подпространства W(x,a). Такая задача возникает в теории линейных однородных дифференциальных уравнений с частными производными Lu = 0, когда функцию f(x) надо приблизить, например, в чебышевском смысле, решениями дифференциального уравнения; эти решения образуют линейное многообразие W бесконечной размерности.
Пример. Пусть в области D (| х |	1, | у |	1) пло-
скости (х, у) требуется приблизить функцию f(x, у) — = х2у2 гармоническими функциями у(Ди = 0). Например, если функцию f приблизить в чебышевском смысле наилучшим образом выражением вида w = С\ + + С2(х4—6х2Г/2 + //4), то для наилучших постоянных получим значения — 0,6 и с2 — —0,2; при этом |/— —	0,6 в D. Если f и v означают распределения тем-
ператур, то спрашивается, насколько распределение f(x,y) уклоняется от стационарного распределения?
6.	Уравнение пластины. Пусть в области D примера 4 (см. рис. 1.7.4) ДДи = 1 (равномерное распределение нагрузки); предположим, что пластина закреплена на границе Г области Z), так что на Г выполняется условие и = ди/ду = 0, где v — направление нормали. Функцию и можно приблизить многочленами
/ уг	i	\
Г. г. .. w(x, t/) = x2l -у- + >, dvFvAx, у) I, '	Ц=1	'
<2
1. Возникновение задач приближения
где многочлены <Рц = х2Р(1 = £	удовлетворяют
однородному дифференциальному уравнению ДД<р = О, например, Рх — \,Р2 = х, ... Тогда
=£(/+*)
i, k
Краевые условия « = -^-=0 на части границы, описываемой уравнением х2 + у2=1, приводят к непосредственно выписываемому комбинированному приближению.
Укажем еще один пример, когда мы не располагаем точными решениями дифференциального уравнения. Пусть и(х, у) — искомый прогиб круглой, закрепленной по краю, неравномерно нагруженной пластины:
ДДм = /(х,	= в В = {(х, у)-. х2 + у2 = г2 < 1},
w = -^- = 0 на Г = {(х, у)-. х2 + у2 = г2 = 1).
Пусть приближенное решение w ищется в виде w = (1 — х2 — у2) [а0 + Я1Х + а2у + а3х2 + а4ху + а5у2].
Если учитывать лишь коэффициенты aQ, ah то
ДДго = 64а0 + 168а! = h.
Итак, заданную функцию f надо приблизить функцией h. Здесь имеет место монотонность: из f h всюду в В следует и w. Таким образом, естественно применить одностороннее приближение. Получаются следующие числовые значения:
	Одностороннее приближение снизу	Одностороннее приближение сверху
	1/144	1/96
	-1/1512	-1/504
7. Дальнейшие примеры краевых задач
83
Итак,
(1 — г2)2 (*144"	1512 ) u (х» у) (! — f2)2 (эв ~ 504") ’
в частности, в центре круга 1/144<ы(0, 0)< 1/96.
При этом выбор наилучших постоянных aQ, at зависит от рассматриваемой точки. Для точки Р(х = 1/2, у = 0) выбор ао= 1/128, Я1 =—1/504 лучше; он дает н( 1/2, 0) 2=г 55/14336 « 0,00382, в то время как данные в таблице значения приводят лишь к оценке и (1/2, 0)	5/1344 а;
0,00372.
С. Распространение волн в плазме. Конечно, и здесь можно указать еще намного более сложные аппроксимационные задачи. В качестве примера приведем уравнение Клейна — Гордона для распространения волн в плазме (например, в куске свинца):
ихх CqU, (7.2)
где са — постоянная, заданная в области Da (о =1,2). При этом Di есть область х < 0, t > 0, а Ог — область х > 0, f>0 (рис. 1.7.5). Далее,пред

х
Рис. 1.7.5. Распространение волн в плазме.
полагаются заданными значе-
ния и(х, 0) и ди(х, O)/dt для —оо < х < оо и требуется непрерывность функцийии ди/дх для х = 0 и всех t 0. Тогда функцию и можно приблизить выражением w вида
w (х, f) = х а‘°' exp (~ b(°}x —	(7.3)
где параметры а^\	подчинены условиям
[ЧаТ = *2[с(а)-]2+ Са> й(1)<0,	&(2)>0> v=l, ...,р.
Функция w удовлетворяет уравнению (7.2) в обеих областях, и на границе областей получаем задачу комбинированного приближения.
D. Совместное приближение. Оно часто возникает тогда, когда не удается задать ни семейство функций,
2 Л. Коллатц, В. Крабе
34	/. Возникновение задач приближения	i

которые в точности удовлетворяли бы дифференциаль-ному уравнению некоторой краевой задачи, ни семейство . функций, в точности удовлетворяющих краевым уело- ; виям. В этом случае требуется приблизить посредством выбранного семейства функций как дифференциальное уравнение
T[U = h(xi,..., хп) в заданной области D. (7.4) так и краевые условия
Таи = ga(xi, .... хп) на границе Г	. |
или на ее частях Га (о = 2, ..., $).	(7.5)
Для нелинейных дифференциальных уравнений возникают и другие, часто необычные, типы аппроксима- : ционных задач, которые до сих пор очень мало исследовались (см. Коллатц [1969]).
Пример. Для нелинейной краевой задачи у"(х) = = 1 + у2, i/(±l) = 0 приближенная формула у~ mw(x)=ai(\—х2) + аг(1—х4) приводит к отличному от обычного полиномиальному приближению
- 1 « 2at + 12а2х2 + [а2 (1 - х2) + а2 (1 - х4)]2.
8. Другие области анализа
Укажем несколько других возможных приложений теории приближений.
А. Интегральное уравнение. Пусть функция y(t) в области В «-мерного пространства точек t = (t\, ..., tn) удовлетворяет линейному интегральному уравнению
y(t) = f(t)+\K(t, s)y(s)ds	(8.1) I
в	?
с заданной функцией f(t) и ядром	>
К (t, s) = К 01tn, st, ..., sn).
Аппроксимируем ядро /( вырожденным ядром К.* вида
/СО. s)=f М>уО)МД (8.2) i
v=l	I
d. Другие области анализа
35
где <pv(0, Фу(О фиксированные функции (например, непрерывные), a &v — подлежащие определению постоянные. Если в уравнении (8.1) заменить ядро К на К*, то решение у* полученного интегрального уравнения при определенных условиях можно представить в конечном виде
а
У (I) = /(/)+ S Cv<Pv(0-	(8.3)
V = 1
При этом если функции q)v выбраны линейно независимыми, то постоянные cv вычисляются из линейной си-
стемы уравнений:
Q
cv === ky Н"	где 4
Ц=1
kv = bv$v (s) f (s) dsf в
av|Ll = ) Мч($)фц ($) ds. в
(8.4)
Снова выясняется, как важно изучать приближение функций нескольких переменных, поскольку в данном случае ключевой задачей является приближение ядра /<(.$,/) ядром №*($,/) (связь с оценкой погрешности см. в I.9.C), и даже если в уравнении (8.1) функция y(t) зависит только от одной переменной /, ядро К зависит от двух переменных s, t.
Численный пример. В уравнении
оо
у (0 = exp (— /2) + exp (— s2 — t2 — s2/2) у (s) ds
— СЮ
заменим ядро Л = ехр[1—(s2 + 1) (Z2+ 1)] на К* — = ехр[—ai — a2(s2 + t2)]- Вычисления, за которые мы вновь благодарим Будде и Циммермана, дают
й| =—0,04866,	а2—1,19127
с погрешностью | е | = | К* — К |	0,04986.
2*
36
1. Возникновение задач приближения
Экстремумы погрешности |е| находятся в точках (рис. 1.8.1):
S	t	8
0	0	+ lle||
0	1,0814	-Hell
0,9178	t = s	+ lle||
t
Соответствующее приближенное решение имеет вид у* (/) = -6,11545е-^2 + е^г.
Численный пример для случая функции двух независимых переменных, и тем самым — приближения ядра, зависящего от четырех действительных переменных, имеется в работе Коллатца [1969а].
В. Интегро-дифференциальное уравнение с ядром, зависящим от разности аргументов.
Пусть функция у(х) удовлет^ воряет уравнению вида
1 у" + у +
о
(8.5) с условиями 1/(0) — z/z (0) = 0.
При этом ядро К зависит лишь от разности х — t, на* пример,
к<*-о=	,о)
Если аппроксимировать ядро экспоненциальной суммой вида
Е cve“v(x-°,	, (8.7)
v»l
Рис. 1,8.1. Экстремальные точки при двумерном нелинейном экспоненциальном приближении.
в. Другие области анализа
37
то уравнение (8.5) перейдет в уравнение
у" + у + Е	(8.8)
V
где	i
Л = J e~a^y(t)dt.	(8.9)
о
Решения уравнения (8.8) можно записать в виде
у (х) = 1 — cosх + -v^v (avsinх+ cosх) —	еа?*,
V	V
(8.10) где для краткости положено
<7v=l+a2v.	(8-11)
а Av вычисляются из линейной системы уравнений. Итак, приходим к нелинейному экспоненциальному приближению
п
в В = [—1, 1].	(8.12)
V«=l
(Этот пример приведен у Коллатца [1969].)
С. Конформное отображение. Пусть в комплексной плоскости задана односвязная область В с границей Г, содержащая внутри себя точку г — 0. Ищется аналитическая функция f(z), нормированная условиями /(0) — 0, Г(0)> 0 и отображающая В внутрь единичного круга.
На границе должно выполняться условие
lf(z)|=l для геГ.	(8.13)
Приближение v для f представим в виде
п
V = Е ^vZV.
V = 1
(8.14)
Тогда на границе круга |о|, а также |о|2 должны наи-
лучшим образом приближать функцию, равную 1. Итак, имеем условие
max геГ
Е av2v
V = 1
min,
(8.15)
38
7 Возникновение задач приближения
где а\ > 0, а в остальном av произвольны. Если границу Г с помощью параметра t представить в виде
z = x + iy = x (t) + iy(t) для 0</<Г,
то получим нелинейную задачу чебышевского прибли-
жения
max
£ av [х (0 + iy (/)]v
V = 1
(8.16)
- 1
—> min.
В частности, если область В симметрична относительно оси х, то av можно считать действительными.
Численный пример. (За проведение счета на вычислительной машине мы благодарим Будде и Циммермана.)	/
Пусть В— квадрат |х|	1, |у|	1.
а) Простейшая формула v — a.\z сразу дает при «! = д/2/3 для погрешности е = |у|2—1 минимальное значение нормы
Ро — max | е | = 1/3 « 0,333. г
Выбор v в двупараметрической форме v — a^z -f-+ ngz5 при a\ = 0,929254, а$ = 0,0588899 дает в десять
раз меньшую норму погрешности ро = max | е |	0,038.
г
Рис. 1.8.2. Счетное множество нулей трансцендентного уравнения.
ЧИСЛО Z == и + iv
О. Дифференциально-разностное уравнение. Пусть функция у (/) в промежутке 1 t < 00 удовлетворяет уравнению
у' (0 + аоУ (/) = а^у (I — 1) (8.17) с действительными постоянными коэффициентами а0, аь Далее, пусть в полуинтервале 0 t < 1 заданы начальные значения у (/): у (/) = = т](/) для 0 t < 1.
Частные решения получаются по формуле у = ezt, где комплексное является корнем трансцендентного
уравнения
z + aQ — а{е-2 = 0.
(8.18)
8. Другие области анализа
39
Это уравнение в общем случае имеет счетное множество корней zr = ur + ivr (с действительными нг, t/r) (рис. 1.8.2). Можно попытаться начальные значения й(/) представить в виде
Л (/) — У. eUrt (сг cos vrt + dr sin vrf). (8.19) r = l
Взяв частичную сумму этого ряда, мы должны будем аппроксимировать h(t) конечной суммой со свободными параметрами cv, dv (v=l, ..., р) (см. В. Келлер [1969]).
Е. Численное интегрирование.
Пример. Пусть требуется найти численными методами интеграл
ь J=	(х) dx,
а
где функции ф(х) и f(x), например, непрерывны; пусть, кроме того, ф(х) дифференцируема.
Один из возможных методов состоит в том, что выбираются дифференцируемые функции vv(x) (v=l, . ..р) и составляются функции wv (х) = — ф' (х) vv (х) + + ^'(х). Тогда интегралы
ь
Jv = J (х) dx а вычисляются точно:
Jv = [e-'p<x>ov(x)]^ поэтому функцию f(x) следует аппроксимировать линейно функциями wv(x). Применяя одностороннее приближение, например,
f(x)- У avwv (х)	0 для а х Ь,
V=1 b
получим НИЖНЮЮ Границу g-Ф W gvwv (х) dx для Л
Л	а	V
Аналогично получается и верхняя граница для /.
40	/. Возникновение задач приближения
Если интервал неограничен с одной или обеих сторон, а <р(х) является многочленом, то в качестве uv(x) целесообразно применять рациональные функции. Тогда ^v(x) также будут рациональными функциями и надо будет осуществить рациональную аппроксимацию. Соответствующим образом можно рассматривать кратные интегралы (например, J e~r2f (х, у) dxdy, где г2 * =
в
= х2 + у2), и прийти к многомерному рациональному приближению. Можно привести и много других примеров и прийти к очень разнообразным аппроксимационным задачам.
Численные примеры:
1.	У = V1 + е~х* dx.
о Так как 00	оо
J е~хг dx = a =	, J (2х2 - 1)е~х’ dx = [-хе~х!]“=О,
О	о
j (Зх2 - 2Х4) е~х2 dx = [^е~хТ = О, О
то функцию f(x) = (1 + x2Y>2 требуется приблизить выражением вида й1 + й!2(2х2+ 1) + «з'(Зх2 — 2х4). Поэтому оценка ‘+4-Т—+	+

сразу приводит к следующим границам для искомого интеграла:
37 г 5	40
32 о	4 а -	32 а.
2. Для преобразования Лапласа
оо
£[/(/)]= $	dt = g(p)
О
9. Lp-приближение и другие аппроксимации
41
известна формула
=	(v = 0, 1,2, ...).
Чтобы найти изображение для функции f (/) = д/1 + /2» можно применить одностороннее приближение функции /(/) многочленами. Тогда из неравенства 0,9 + 0,4/
f(t) гС 1 + /2/2 следует 0,9/р + 0,4/р2 ^g(p)^ \/р 4-+ 1/р3; например, 0,25 g (4)	0,265625.
9.	Lp-приближение и другие аппроксимационные задачи
А.	Lp-приближение. Наряду с описанным в п. 1.3 чебышевским приближением, которому главным образом посвящена эта книга, Lp-приближение является наиболее изученным.
При Lp-приближении в пространстве С(В) непрерывных на В функций g(x) вместо (3.1) вводится норма
llgllp=^?Wlg(-r)lpdxj1/₽» 1<Р<ос,	(9.1)
и расстояние р (g, h) = ||g — h\\p. Вместо непрерывных функций можно рассматривать более общие классы функции, например, классы функций интегрируемых в р-й степени. (См. Люстерник и Соболев [1968], стр. 27.) Функция q(x) фиксированная, положительная и непрерывная на В называется весовой функцией; часто выбирается q(x)=l. При /^-приближении функции f(x) классом функций W (как и в 1.3) ищется минимальное расстояние р0, которое определяется той же самой формулой (3.2), как и при Т-приближении.
Наиболее известным частным случаем является 12-приближение или гауссовское приближение или приближение в смысле среднего квадратического. (Дискретный случай /^-приближения уже встречался в (2.6).) 7-приближение является предельным случаем Лр-приближе-> ния при р->оо. Иногда в приложениях возникает также /^-приближение.
В.	Одностороннее Li-приближение. Пусть J — действительная бесконечная в обе стороны ось х и пусть заданы плотности вероятностей f(x), t^i(x), ..., ^р(х),
(9.2) вида
(9.3)
I
42	7 Возникновение задач приближения	~
определяемые следующими условиями: 00	оо
f (х) dx =	wv (х) dx — 1,
f(x)^>0,	wv(x)^0 в J (v = 1..........p).
Требуется приблизить f(x) функцией
(рис. 1.9.1) р О’ W = Z avffi'v (Д где av > ° (v = 1, ..., р) V=1
так, чтобы в J выполнялось неравенство w(x)^f(x) и чтобы погрешность e = f— w была наименьшей в том смысле, что 00	оо
If — w\dx —	e(x)dx—>min	(9.4)
— оо	—оо
(см. Марсалья [1970]). (Образно выражаясь, требуется
Рис. 1.9.1. Функции распределения.
«исчерпать» наилучшим образом площадь, лежащую между осью х и графиком функции f(x) с помощью распределений вероятностей.) В силу равенства
оо	р
w (х) dx — У av
— оо	V= 1
эта задача эквивалентна
р
У av—>тах,
V=1
av>0,
задаче оптимизации
р
Z avwv (х)< f (х), V-1
V — 1.....р.
(9.5)
9. Lp-приближение и другие аппроксимации
43
Переходя к дискретному случаю, т. е. выбирая конечное число абсцисс xit ..., xs на оси х, получим линейную задачу оптимизации классического типа.
С.	Смешанное £гТ-приближение. Заменив в линейном интегральном уравнении (8.1) ядро К другим ядром К*, а функцию /(/) функцией f*(Z) так, чтобы можно было получить решение y*(t) измененного таким образом уравнения (см. Канторович и Крылов), можно получить оценку погрешности e(t) = y*(t)— y{t). Пусть
s)\ds^d, в	(9.6)
If (OK AT, | f* (/) — f (/) |<т) для всех
Тогда
+	(9.7)
где р зависит от резольвенты интегрального уравнения с ядром К*. Поэтому для достижения требуемой точности стараются приблизить ядро другим ядром /С* так, чтобы величина d в неравенстве (9.6) была возможно меньшей; это приводит к Li-приближению по s и Г-при-ближению по t.
D.	Приближение бесконечномерными подпространствами. Если в предыдущем примере в качестве К* взять вырожденное ядро вида
К* (/, s) = и (t) + v (s),	(9.8)
то полученное уравнение может быть решено в замкнутой форме (см. I.8.A). В связи с этим возникает вопрос, насколько хорошо можно приблизить функцию двух независимых переменных /, s суммой функций вида (9.8), каждая из которых зависит лишь от одной независимой переменной. Этот вопрос исследовался многократно. Однако вопрос о том, насколько хорошо можно аппроксимировать ядро K(tfs) вырожденным ядром вида
Г (6 s) = ах (/) bx (s) + а2 (/) b2 (s)	(9.9)
44
7. Возникновение задач приближения
путем подходящего выбора четырех функций я/, bj или более общим ядром вида (8.2), по-видимому, вряд ли обсуждался.
Е.	Несимметричное Т-приближение. Обычное Т-при-ближение 1.3 и одностороннее 7-приближение 1.5 можно рассматривать как частные случаи несимметричного Т-приближения. Пусть требуется в обозначениях 1.3 приблизить функцию f(x)eC(B) в области В функцией w класса W = {да(х, я)}. Эту задачу можно рассматривать как задачу нелинейной оптимизации с переменными Я1	яр, бь 62 целевой функцией
Q = 6i + 62->min и бесконечным числом ограничений
— 61 < w (х, я) — f (х) < 62
для всех х <= В, di 0, 62 0.
(9.10)
(9.11)
При 61 — 62 имеем обычное Т-приближение, при 61 = = 0 — одностороннее Т-приближение, а при отсутствии ограничений на б» и 62 — общее несимметричное Т-при-
чебышевское приближение.
ближение.
Численный пример. Пусть требуется наилучшим образом приблизить функцию f (х) = х4 на отрезке [0,1] функциями вида w (х, я) = (Я1 + + я2х)2 в смысле (9.10), (9.11). В качестве приближенных оптимальных значений получаем б! « 0,01, 62 = 0,15, 61 + 62 « « 0,16. Функция погрешности 8 = w — f изображена на рис. 1.9.2. Так как 61 =/= 62, то получаем несимметричное Т-приближение.
Обратно, несимметричное Т-приближение можно рассматривать как частный слу-
чай обычного Т-приближения, если для каждого w е W существует хе В, для которого w(x)— f(x) = O. Если
9. Lp-приближение и другие аппроксимации
•45
для всех w е W положить
<р (да) = 62 (w) + 6] (да) =
= max {да (х) — f (х)} + max {/ (х) — да (х)}, х<=В	х<=В
то задача (9.10), (9.11), очевидно, будет равносильна отысканию функции да е W, удовлетворяющей неравен’ ству <р(да) ф(да) для всех да е W.
Пусть теперь W* — множество всех функций вида да + а, где да е W, а а е R. Поскольку ф(да + а) = ф(да) для всех да е W и а е R, то прежде всего inf ф(да)= inf ф(да).
wsW	а>е«7*
Далее из неравенства ф(да)/2	||да— f||, справедливого
для всех да е W*, следует
4- inf ф(да)<р(Д 1Г)< inf ||да-/||. z w e IF*	w e IF*
Утверждение. Справедливо равенство
1 inf <p (да) = p (f, IF).
Доказательство. Предположим, что
4 inf ф(да)<р(Л И-z w<=№*
Тогда найдется функция да е W*, для которой 4<₽(^) < <р(/, IF*). Если положить $*=$ —^S2 (да) — бДй»)], то 62 (да*) = б2 ($) — 2- [б2 ($) _ ($)] = 4 [62 ($) + 61 (да)] > 0 и
6i (®*) = 61 (да) + 4162 (®) — 61 (да)] =
= у [62 (гй) + 61 W] = 62 (t&*), откуда
II да* - /1| = б2 = 4 [62 (^*) + б! (да*)] = 4 Ф (^*),
ЧТО противоречит предположению. □
46
1. Возникновение задач приближения
Для решения несимметричной Г-задачи в классе W можно сначала решить обычную Т-задачу в классе W*. Тогда, если w* = w + d при w е W, а <= R — элемент наилучшего приближения в классе W*, то w — решение несимметрической Т-задачи. Далее, поскольку p(f, 1Г*) р(А Ю, то получаем неравенство
У inf ф(о»)<р(Л W),
которое в общем случае может быть и строгим, как показывает следующий простой пример:
W = {ах | а (= R, х <= [О, 1]},
Г* = {ах + b | a, b е= R, х ее [0, 1]}, f (х) = х2.
С помощью теорем 2.4 и 7.2 главы II можно убедиться, что
p(f, №*) = -£-< р(Л №) = 3-2 д/Г «0,17.
F. Приближение с ограничениями на область. Многие из названных типов аппроксимационных задач могут быть включены в задачу приближения с ограничениями на область, которая формулируется в виде обычной задачи оптимизации: пусть в обозначениях 1.3 В будет заданная область пространства Rn, С (В) — линейное полуупорядоченное пространство непрерывных на В функций g(x), А — заданное подпространство ^-мерного пространства параметров R*, <р(х, а) и G/(x, я) (/= = 1, т)—заданные функции, определенные на В\А; требуется найти векторный параметр а и числа Si, бг, которые минимизируют целевую функцию
Q = б1 + б2 min	(9Л 2)
при ограничениях — 61 <<р(х, а)<б2,
0 < Gj (х, а), / = 1, ..., т
для всех хеВ. (9.13)
Пример задачи приближения с ограничениями на область содержится в следующем пункте.
G. Монотонно разложимые операторы. Пусть R — полуупорядоченное банахово пространство; отношение
9. Lp-приближение и другие аппроксимации
47
порядка будет обозначаться символом < или >; оператор Г, определенный на подмножестве D пространства R и отображающий D в /?, назовем положительным (соответственно— отрицательным)*), если из
v < w следует Tv < Tw
(соответственно Tv > Tw) для всех v, w е D. (9.14)
Оператор Т называется монотонно разложимым опера^ тором, если его можно представить в виде Т —	+ Т2,
где Т\ — положительный, а Т2— отрицательный операторы. Из теории таких операторов мы здесь сформулируем лишь основную теорему (подробное изложение см., например, в книге (Коллатц [1964])):
Теорема (И. Шредер [1956]). Пусть в полуупорядочением банаховом пространстве задано уравнение
и = Ти— Тхи + Т2«,	(9.15
где 7\, Т2 — вполне непрерывные операторы, определенные на выпуклом подмножестве D пространства R; и пусть оператор Т\ — положителен, а Т2 — отрицателен. Кроме того, пусть в итерационных соотношениях
vn+\ = TxVn + T2wn, \
Т IT f « = 0,1,2,...	9.16)
Wn+\ = TxWn+T2Vn, )
начальные элементы v0, D и определенные по ним v{, подчинены условиям
Vq < Vx <w{ < Wq.	(9.17)
Тогда уравнение (9.15) имеет по крайней мере одно решение и такое, что vx < и <. Wx.
Выполняются также соотношения vn < и < wn для каждого п = 0, 1, 2, ... ; для достижения хорошей оценки погрешности следует попытаться сделать разность возможно меньшей; это и есть приближение с ограничениями на область (в применении к действительным функциям обычный символ обозначает поточечное неравенство для всех хеб):
O^^i —Vi^d, d -->min,	(9.18)
*) В оригинале «synton» и «antiton». (Прим, через.)
48
/. Возникновение задач приближения
Пример. В качестве примера приближения с ограничениями на область рассмотрим нелинейное интегральное уравнение типа двойного аргумента
1
£(/)= 1_'_,/(/)г,(s)rfs	(9.19)
О
(Уравнение Чандрасекхара для радиоактивного излучения, см., например, Ортега, Рейнболдт [1970], стр. 18).
К вполне непрерывному оператору
1
Ти (/) = 1 +1 и (I) и (s) ds
* J о 4
и
применима теория монотонно разложимых операторов (здесь Т — положительный оператор, Т = — 1\ для функций н 0 на [0, 1]), и задача заключается в нахождении функций wQ(l), удовлетворяющих условиям
v[==TvQ> w{ = Twq,
Vo (/) < Vi (/) < W1 (0 < w0 (0 (9-20)
Рис. 1.9.3. К решению	гл и
уравнения Чандрасек- Для всех t |у, lj.
хара.	Если выбрать vQ = 0, w0 — 2,
ТО получим — 1, W1 = 1 + + t In (1 + 1//). Условия (9.17) выполнены, и поэтому в полосе О1 (/) h(t) w\(f) расположено по крайней мере одно решение ft(/) уравнения h = Th. Если
мы пожелаем, отправляясь от констант о0 = у, wQ= с, улучшить границы, то (9.20) будет означать приближение с ограничениями на область. Если начинать с констант о0, wQ, то наилучшее из возможных приближений получится при О1 = 1 + (у2/4)/ln(l + 1//), где у==у, с — 2, а у^ 1,28 — решение уравнения
(рис. I. 9.3).
1 + -Гу21п2 = у
II. НЕЛИНЕЙНОЕ ЧЕБЫШЕВСКОЕ ПРИБЛИЖЕНИЕ. ОБЩАЯ ТЕОРИЯ
1. Постановка задачи
А. Общая формулировка задачи. Пусть В — компактное метрическое пространство (см. определение 1.3 главы VII и пояснение после равенств (1.4)), а С (В)—• векторное пространство действительных или комплексных функций, непрерывных на В. Пусть С (В) наделено максимум-нормой
||g|| = max|g(x)|, g^C(B).	(1.1)
х&В
Предположим, что задано непустое подмножество W пространства С (В) и фиксирована функция feC(B). Тогда существует так называемое наилучшее приближение
р(/, F)= inf	(1.2)
we ЦТ
причем
р(Л Ю>0.
Задача чебышевского приближения, кратко Т-задача, состоит в нахождении функции w е W, для которой
110-Л=р(Л W).	(1.3)
Всякая функция е W, удовлетворяющая равенству (1.3), называется элементом наилучшего приближения функции f во множестве W (или ближайшим к f элементом W).
Замечание. Если р<=С(В)— фиксированная действительная положительная на В весовая функция, то можно вместо максимум-нормы (1.1) рассмотреть так называемую максимум-норму с весом вида
||g|| = maxp(x)|g(x)|, g<=C(B).
xt=B
Однако если в этом случае заменить W на pW = == {pw[w е W}, a f на p-f, то получилась бы сформули
50
II. Нелинейное чебышевское, приближение
рованная выше Т-задача. Поэтому мы откажемся от рассмотрения весовой функции, так как при этом получается более экономичная запись и все результаты можно сразу переписать на случай максимум-нормы с весом.
В. Частные случаи. В большом числе приложений W является образом при отображении F: Л->С(В) некоторого множества параметров Л, которое представляет собой непустое подмножество действительного или комплексного n-мерного векторного пространства Rrt или Сл. Отображение F сопоставляет всякому элементу а^А в точности одну функцию	Таким образом,
в этом случае
W = F (Л) = {F (а)\а е= Л).	(1.4)
Компактное метрическое пространство В в большинстве случаев является замкнутым ограниченнььм подмножеством пространства Rs или О, например, замкнутым действительным отрезком [а, 0] (где а<₽), или конечным множеством точек.
Если В — конечное множество, то задачу приближения называют дискретной.
а)	Линейное приближение. В этом случае Л = Rn или Сп. Пусть . ., wn — заданные линейно независимые функции. Тогда W определяется согласно (1.4), причем
п
F (а, х) = У, ая»; (х), х е В.
/=1
Этот случай содержит так называемое полиномиальное приближение, при котором В = [а, ₽] (а < 0), a Wj(x) — — Х]‘-{ (/ = 1, ..., и).
Ь)	Общее рациональное приближение в действительной области. Пусть заданы функции «о, . wT, и0> “•» vs^C(B), где С (В)—пространство непрерывных на В действительных функций. Для а<= Rr+1, соответственно b е Rs+1, положим
г
и(а, х) — ^ашЛх), соответственно v(b, х) — X bkvk (х), /=0	/г=0
хеВ, и предположим, что множество Л={(д, В)е €= Rr+S+2| v(b, х) > 0 для всех хеб} не пусто. Тогда
/. Постановка задачи
51
отображение F: А-*-С (В) задается равенством
F (а, Ь, х) = "	,	(а, Ь) <= А, х<=В.
Как частный случай отсюда получается обычное рациональное приближение в действительной области, если положить
«/(х) = х/ (/ = 0,	vk(x) = xk	(6 — 0, .... s)
иВ = [а, р] (а < р).
В этом случае А является непустым подмножеством пространства Rr+s+2.
с)	Обыкновенное рациональное приближение в комплексной о б л а с т и. В этом случае В является компактным подмножеством пространства С, а С(В)—векторное пространство непрерывных комплексных функций на В,
Множество
А = ( (a, b) <= Cr+1 X Cs+11 и (b, х) = Е bkxk #= О, х е= В }
не пусто. Отображение F: А->С (В) задается равенством
S ajx^
F (a, b, х) = ц.(°’	,	(а,Ь)<=А, х<=В.
У bkXk fe—о
d)	Обыкновенное нелинейное экспоненциальное приближение (см. 1.3). В этом случае В = [а, р] (а < Р)
Л = {(а, ft)eRrXRr|&i<^2< ... <М-
Отображение F: А->С(В) задается равенством
F (а, 6, х) = £ ajebi\ (а, Ь) е Л, х е В. /-1
Если фиксировать bj (/=1, г) и варьировать а} (j — 1, ..., г), то получится задача линейного приближения.	: '
В главах IV и V мы еще остановимся подробно на случаях а) — d). Здесь же для общей картины составим Для них следующую таблицу:
52
П, Нелинейное чебышевское приближение
Способ приближения и вид приближаемой функции f	Приближающие функции F (а, Ь, х), где (а, Ь) «= А, х^В	Л и В
1. Общее рациональное приближение в действительной области (f действительна, непрерывна)	и (а, х) v (Ь, х) ’ где г и (а, х) = У, а .и. (х) /-о S V(J>, х) = У bkvk(x) и., vk действительны, непрерывны	А = {(а, Ь) <= c=Rr+s+2 |v(fc,x)>0 Vx €= В], В — компактное метрическое пространство
2. Обыкновенное рациональное приближение: а)	в действительной области (/ как и в п. 1). Ь)	в комплексной области (/ действительна или ком-плекснозначна, непрерывна)	и (а, х)	. 	77	г как ив п. 1, v (Ь, х) причем «У (х) = х^, / = 0, ..г О* W = хк, k = 0, ...» s	а)	А как и в п. 1 В=[а, ₽] Ь)	А = {(а, Ь) s sCr+s+2|o(6, х)#=0 Ухе В} В — компактное подмножество С
3. Общее линейное приближение в действительной или комплексной области (/ как в п. 2Ь))	и (а, х) как в п. 1 при г == п — 1 ($ = 0, и0(х)=^1) «У — действительны или комплексны, непрерывны	А = R'1 или Сп В как в п. 1
1. Постановка задачи
53
Продолжение
Способ приближения и вид приближаемой функции f	Приближающие функции F (а, Ь, х), где {a, b) g А, х<=В	Ап В
4. Полиномиальное приближение:
а) в действительной области (/ как в п. 1)
Ь) в комплексной области (/ как в
П. 2))
а) А = R", В как в п. 2а.
Ь) А = СЛ, В как в п. 2Ь)
и (а, х), г, s, v0 (х) как в п. 3,
«У как в п. 2
5. Обыкновенное линейное экспоненциальное приближение (f как в п. 1)
btx а.е 1
А = {(a, b) s
<= R2s |&1<&2< ...
... <м.
В = [а, Р1
С. Постановка задач.
1. Существование элементов наилучшего приближения. Вопрос существования элементов наилучшего приближения решается положительно лишь при существенных дополнительных предположениях, о которых речь будет идти в II. 3. В некоторых из названных выше частных случаев к общим утверждениям II. 3 следует сделать специальные добавления.
Вопрос существования элементов наилучшего приближения представляет не только теоретический, но и практический интерес с точки зрения вычислительной практики по следующим причинам:
а) Например, если W задано согласно (1.4), то в случае отсутствия элементов наилучшего приближения параметр а е А часто ведет себя неустойчиво, когда ЦТ7(а) — f|| близко к p(f, W7).
в) Многочисленные способы вычисления элементов наилучшего приближения исходят из необходимых и достаточных признаков для них и в случае несуществования таких элементов вычисления лишаются своего обоснования.
54
//. Нелинейное чебышевское приближение
2.	Единственность элементов наилучшего приближения. Единственность также обеспечивается лишь при существенных предположениях, о которых речь будет идти в II. 6. Она также важна при отыскании элементов наилучшего приближения численными методами.
3.	Характеристика элементов наилучшего приближения. Имеется очень общий восходящий к Колмогорову достаточный признак элемента наилучшего приближения (см. об этом в II.2.C). Наряду с этим известны также весьма общие необходимые признаки элемента наилучшего приближения (см. II. 4). Правда,*как мы увидим в II. 5, требование дать характеристику элементов наилучшего приближения с помощью названных достаточных или необходимых признаков сужает класс допустимых семейств функций W.
4.	Вычисление или оценка наилучшего приближения. При заданных f и W теоретически возможно сколь угодно точно оценить снизу или даже вычислить наилучшее приближение p(f, №). Подходящий для этого принцип будет сформулирован в II. 2. Во многих случаях он допускает также численную реализацию (см. II. 2В, IV. 2 и III. 1). Знание оценки снизу для p(f, W) полезно по следующим двум причинам.
а) Оно позволяет сделать заключение о том, насколько хорошо можно приблизить f функциями класса W по максимум-норме в самом лучшем случае.
в) Оно приводит к двусторонней оценке р(Д IT), так как для каждого w^W величина ||ш—f\\ дает оценку сверху для p(f, W) и позволяет сделать заключение о степени пригодности ||до—f||. На этом мы специально остановимся в главе III.
2. Нижние границы для наилучшего приближения и достаточное условие
для элементов наилучшего приближения
А.	Общий принцип получения нижних границ. Мы рассмотрим сформулированную в II. 1 Г-задачу и оценим снизу р (Л W) — inf || w — f j|.
2 Нижние границы для наилучшего приближения
55
При этом мы применим один геометрический принцип, который сначала поясним «наглядным образом». Для произвольной точки х е В, комплексного числа е(х) с модулем 1 и действительного числа а(х) определим в С (В) множество Н(х) следующим образом:
Н (х) = {h е= С (В) | Re [в (х) h (х)] = а (х)}.
Множество Н(х) является линейным многообразием в С (В), т. е. вместе с двумя функциями h\, /i2^B(x) множеству Н (х) принадлежит и вся прямая, проходящая через Л1 и Л2 и состоящая из всех функций вида AAi 4- (1 — — Х)Л2, X е R. Средствами функционального анализа можно, кроме того, доказать, что Н(х) замкнуто в С (В) (см. определение 1.4 главы VII) и является максимальным действительным линейным подмногообразием С(В), т. е. если Й действительное линейное многообразие в С (В), содержащее Н(х) в качестве подмножества, то Й—С(В) или Й — Н(х). Поэтому мы назовем Н(х) гиперплоскостью в С (В).
Уравнение Re[e(x)ft(x)] ==а(х), определяющее Я(х), является обобщением нормальной формы Гессе гиперплоскости в обычном конечномерном пространстве. А именно, если get(B) — произвольная функция, то наилучшее приближение p(g, Н(х)) или, кратко, — расстояние от g до //(х), задается равенством
Р (g, И (х)) = | Re [е (х) g (х)] — а (х) |.
Доказательство здесь не приводится, так как все эти факты служат лишь для пояснения (см. Дойч и Мазерик [1967]).
Каждая гиперплоскость Н (х) разбивает С (В) на два полупространства, одно из которых задается следующим образом:
Л* (х) = {g е= С (В) | Re [е (х) g (х)] > а (х)}.
Если теперь х пробегает подмножество D из В такое, что объединение всех /?*(х) при x^D содержит
56
IL Нелинейное чебышевское приближение
Рис. II. 2.1. Наглядное пояснение общего принципа.
множество W, но не содержит f (рис. II. 2.1), то «оче-ВИД1Ю», что
inf р(Л Я(х))Ср(А Г).
Это утверждение и составляет содержание теоремы 2.1, которую нам сейчас предстоит доказать. При этом предположение W s (J /?* (х) равносильно допущению (2.1). xc~D
Случай f е U R* (х) также допустим, но при этом xe=D
в силу неравенства т 0 утверждение (2.2) тривиально. Теорема 2.1. Пусть D — непустое подмножество из В такое, что для каждого хе существуют е(х)<= С, |е(х)|=1 и a(x)eR, обладающие следующим свойством: для всякого w W найдется х D, для которого
Re[e(x)w(x)]>a(x). (2.1) Тогда % = inf {а (х) —
-ReJ(x)f(x)]}<p(f,r). (2.2) Доказательство. Предположим, что 0 > p(f, №). Тог
да согласно определению величины p(f, №) найдется w е W, для которого p(f, W) — /|| < т. Но отсюда следует
I w (х) — f (х) | < а (х) — Re [в (х) f (х)]
для всех хе D, а следовательно,
Re {е (х)	(х) — f (х)]} < а (х) — Re [е (х) f (х)],
что влечет
Re [е (х) w (х)] < а (х).
Но это противоречит предположению (2.1). Следовательно, наше предположение ошибочно, и т	р (Д W). □
Замечание. Существенное и, вероятно, вначале не вполне прозрачное предположение (2.1) можно заме-*, нить следующим равносильным предположением;

2. Нижние границы для наилучшего' приближения
57
Не существует функции w е W такой, что
Re [в (х) w (х)] < а (х) для всех xeZ). (2-1*)
Эта формулировка часто легче обозрима, что подтверждает следующий
Пример. Пусть В — действительный отрезок [р0, PiL a W — класс линейных функций вида w = а\ -J- а%х с действительными а\,а^ Множество D состоит из трех произвольных точек Xj^B (/=1, 2, 3), Xi < х2 < х3. Мы должны выбрать значения е/ = е(х;) и а/ = а(х/)
Рис. II. 2.2. Пояснение принципа на линейных функциях.
для / = 1, 2, 3. Пусть, например, ei = 1, е2 = —1, е3 = 1, a ai, —a2, аз — значения произвольной линейной функции Z(x) в точках Xi, х2, х3 (рис. II. 2.2,а)). Тогда не существует w е F, т. е. не существует линейной функции, удовлетворяющей неравенствам
< «Г, — w2 < а2 (или w2 > — «2), ^’з < «з,
где Wj = w(Xj) ддя j = 1, 2, 3.
Действительно, такая функция должна была бы в точках Xi и х3 принимать значения, лежащие ниже графика /(х), а в точке Х2—значение, лежащее выше гра-фика /(х), что невозможно в случае лидайнойфункции (см. рис. II. 2.2, а)). Таким образом, предположение (2.1) выполняется.
Если теперь требуется аппроксимировать произвольную определенную и непрерывную на В функцию f(x) функциями w е Wt то мы можем выбрать произвольные три точки Xi, х2, х3е В и произвольную линейную функцию, принимающую в них значения си, —а2, а3,
58
11. Нелинейное чебышевское приближение
и получить согласно (2.2) оценку снизу для наилучшего приближения:
т = min {<хх — fl, f2 — (— a2), a3 — f3} < p (f, W) = p0.
Для функции f такой, как на рис. II. 2.2, 6) при произвольной линейной функции 1(х) в качестве т получим наименьший из трех отрезков, изображенных на рис. II. 2.2, Ь) жирной линией. Если удастся выбрать функцию /(х) так, что длины этих трех отрезков окажутся одинаковыми (см. рис. II.2.2,г)) и нигде в В отклонение I от f не больше т, т. е. всюду в В \1 — f| т, то 1(х) будет элементом наилучшего приближения. Таким образом, в этом примере теорема 2.1 применима одновременно и как достаточный критерий для элемента наилучшего приближения (об этом см. также теорему 2.4 главы II).
Можно показать, что в случае Q(f, W)> О предположения теоремы 2.1 теоретически допускают оптимальную реализацию, т. е. т = р(Д W) достижимо. Однако применяемая при этом конструкция оптимального множества D непригодна для вычислительных целей и поэтому здесь не приводится (об этом см. Крабе [1969а]).
Вместо этого в IV. 2 мы покажем, что в случае общего рационального приближения в действительной области (а поэтому также и в случае линейного приближения) предположения теоремы 2.1 могут быть оптимально реализованы даже для конечных подмножеств D из В.
В.	Приложения.
а) Общее рациональное приближение в действительной области. Мы рассмотрим за-да^йымД^^формулировке, что и в II. 1 (см. II. 1 ВЬ)). Пусть D — непустое конечное подмножество из В. Так как
w = I Vw" I “(о) = X а1и>' j=o
s
v (*)=У, bkvk k-0
на В
то предположение (2.1) теоремы 2.1 равносильно следующему:
2 Нижние границы для наилучшего приближения
59
не существует вектора (a,6)eRr+1XRH1, удовлетворяющего неравенствам
г	S
— '£1е,(х)и1(х)а1+ 2 a(x)vk(x)bk>0 (2.3) /-0	ь-о
для всех х е D и
S
Е V k (х) ьк > о £=0
(2.4)
для всех хеВ.
Действительно, если бы нашелся вектор (а, Ь)<= е Rr+I X Rs+1. удовлетворяющий неравенству (2.3) для всех хе D и неравенству (2.4) для всех хе В, то было бы w =(ы(а)/о(В))е W, где
Г w(a)= S ^u/f /-о
V (й) = £ bkvk. k~Q
Отсюда следовало бы
— е (х) и (а, х) + а (х) v (b, х) > 0 <=>
<=> Re [е (х) w (х)] — 8 (х) w (х) < а (х)
для всех xeD, т. е. неравенство (2.1) нарушилось бы для w = u(a)!v(b). В противном случае (а, Ь) было бы решением неравенства (2.3) для всех хеО и неравенства (2.4) для всех хек
Пусть, например, D = {хь ..., хт}. Чтобы выполнялось предположение (2.1) теоремы 2.1, надо найти такие действительные числа е(х/) с |e(xz) |= 1 и a(xz) (f = = 1, ..., m), чтобы не существовало вектора (а, 6), удовлетворяющего неравенству (2.3) для всех х = X/ (i = 1, ..., т) и неравенству (2.4) для всех хеВ.
Следующая теорема 2.2 дает достаточные условия для этого. Однако она не очень хорошо приспособлена для вычислительных целей. Поэтому в теореме 2.3 будет показано, как предположения (2.5) теоремы 2.2 могут быть численно реализованы в случае т — г + s + 2 путем решения линейной системы уравнений (см. (2.11)),
60
//. Нелинейное чебышевское приближение '
Теорема 2.2. Пусть (с, р) е Rm X Rm — нетривиальное решение системы
pt^Q, I = 1.......tn,
m
и, (xz) с( = 0, j = 0...г,	(2.5)
i=l m	m
Y.ok(xi)f(Xi)cl='Zlvk(xi)[kt\ci\ + pi], k = Q, s, i-1	i~l
где ...» ^eR -заданные числа. Тогда необходимо с (9/n нулевой вектор пространства Rm). Если положить
( — sign Ci при Ci О,
8fo)=1 «I 1	(2-6)
(, +1 или —1 в противном случае 1 и
a (xz) = Л, + е (Х[) f (xt),	1 = 1,	(2.7)
то система неравенств (2.3) и (2.4) неразрешима и согласно теореме 2.1
tnin Zz^p(f, 17).	(2.8)
/=1, ...» tn
Доказательство. Предположим, что с = Qm. Тогда m
X (х^ Pi = 0, k = 0, ..., s. i—l
Пусть теперь при b е Rs+1
S
v (b, х) = S о* (х) Ьк для всех хе В *=о
(такой вектор b е Rs+1 существует согласно постановке задачи в II. l.Bb)).
Отсюда следует
m
Е V (b, Xi) pi = 0, ( = 1
что влечет р = 0т. Но равенства с = 0m, р — Qm согласно предположению невозможны. Таким образом, С ©т-
2. Нижние границы для наилучшего приближения
6t
Предположим, что система (2.3), (2.4) имеет решение (a, b)^ Rr+1 X Rs+1. Тогда, в частности, было бы
Г	S
— £ е (xf) Uj (xt) а/ + £ a (xz) vk (х{) Ьк > 0,	(2.9)
/=0	fe=0	.	.
s
Е^й(^)&а>0 для Z=1............т. (2.10)
Положим
Г	S
и (а, х) = S cijUj (х) и v (Ь, х) = У bkvk (х).
/=0	k=0
Умножая Ле неравенство (2.9) на |с/|, a Ле неравенство (2.10) на складывая их и суммируя затем по i, получим согласно (2.6) неравенство
т	т
Е Ctu (a, Xi) + £ [a (xz) | ct 1 + р/] v (bt xt) > 0. i=l	i=l
Согласно (2.5) т
У, CiU(a, xz) = 0, » = 1
и, по определению а(х,) и е(х,) (i = 1, .... т), отсюда получим
т	т
— Xv(b, Xi) f (xt) ct + E [A,z |cz 1 + Pi] v (b, Xi) > 0. (=1	i = l
Однако согласно (2.5) вместо этого строгого неравенства должно быть равенство и мы пришли к противоречию.
Тем самым доказано, что система (2.9), (2.10), а тем более и (2.3), (2.4) неразрешима. □
Прямое доказательство импликации (2.5) =>(2.8) имеется у Крабса [1968].
Теперь возникает вопрос о нетривиальной разрешимости системы (2.5). Ответ на него дает
Теорема 2.3. Пусть т = г + s + 2, т. е. пусть D се В состоит из г + s + 2 различных точен Xi е В.
62
II. Нелинейное чебышевское приближение
Далее, пусть матрица
( ul (xi) \
U(W //-0, ..., г, 6-0.........
.... r+s+2
невырожденная. Тогда, если числа Zi^Q, i — 1, ... ..., г + s + 2 не все равны нулю, то система
m
У Uj (xz) Ci = 0, j = О, ..., г,
m " m	(2.Н)
£ Vk (xt) f (xt) ct=yvk (xt) Zt, k = Q, s
t==l	Z = 1
имеет в точности одно нетривиальное решение с = (сх, ...
• • • > Ст).
Если положить
*1 кт при
тах-т^--
с, IM
— *
Ci =И= О,
в противном случае,
и
( О при ct Ф О,
( zt в противном случае,
то (с, р) будет нетривиальным решением системы (2.5), что влечет (согласно теореме 2.2)
min JX-<p(f, ЦТ).	(2.12)
|	| =3*0 |с/|
Доказательство. То, что система (2.11) имеет в точности одно решение, следует из невырожденности ее матрицы. Если бы с — 0« было решением системы (2.11), то мы имели бы
m
Уу(Ь, Xi)Zi = Q для всех &eRs+l, «=1
где v (Ь, х)= У bkVk(x). Выбирая b так, чтобы было 6=0
и (6) > 0, получим z = 0т, что противоречит условию.
2. Нижние границы для наилучшего приближения
63
Из определения X/ и pi непосредственно следует
Zi = ^i\Ci\-Y Pi, i=l, т.
Подставляя z, в (2.11), получим (2.5), что и требовалось показать. □
Теорема 2.3 дает весьма удобный способ получения оценки снизу для p(f, W'). Выбирая при этом г,- > 0, получим согласно (2.12) положительную нижнюю границу для p(f, IT).
Численный пример к теореме 2.3. Пусть
В = {(/ь	f(/b 4) = еЧ г = 0,
s = 1, Ыо (6> Аг)= уо (4. ^2) ~ 1> у1 (Л> Аг)= ^1 4“ Аг-
Тогда множество
А = {(а0, b0, bi) е R31 &о + (^ + 4) > 0 Для (/ь t2) е В) непусто и
ь<*
Пусть D = {(0, 0), (0, 1), (1, 1)} — множество вершин треугольника В. Тогда система (2.11) примет вид
!С1 + Сг + С3 = 0, ci + с2 4- ес3 = zi 4- z2 4- z3, с2 4- 2ес3 = z2 4- 2z3.
Выбирая zi = z2 = z, = 1, получим в качестве решения
с3 = ——г да 1,74593,	с, = 3-----да - 6,49186,
Ci = — с2 — с3ри 4,74593.
Тем самым по теореме 2.3
Z	1
т= min -^-=—-да 0,154039 <р(Д Г).
j I -# J I Cl I I С2 I
В IV. 3 мы снова вернемся к этому примеру и покажем, что
p(f, W) < 0,206284.
64
II. Нелинейное чебышевское приближение
Там мы остановимся также на методе последовательного улучшения Zt с целью увеличения нижних границ т для p(f, W).
В IV. 2 мы увидим, что в принципе согласно теореме 2.2 величину р(/, W) можно оценить снизу как угодно точно или даже вычислить. Правда, вопрос об оптимальном выборе соответствующего множества D еще открыт. В IV. 3 мы еще остановимся на вопросе о наилучшем выборе вектора ге Rm при заданном множестве D, с помощью которого нижняя граница для p(f, W) в (2.12) получается наибольшей.
Вопрос о систематическом улучшении множества D, при котором монотонно возрастали бы оптимальные нижние границы для p(f, W) в (2.12), также еще открыт.
Ь) //-множества. Пусть С (В) — векторное пространство непрерывных действительных функций на В. Согласно Коллатцу [1965] подмножество D множества В называется //-множеством, если D является объединением двух таких непустых множеств Di и D2, что не существует пары функций w, w удовлетворяющих неравенствам
{< 0 для всех х е Db
п
> 0 для всех х е D2.
Если положить
( + 1 для х е Db
8 W — | _ J для х е р2>
и выбрать й» е W, то для каждого w е W найдется х <= D такой, что
е (х) w (х)	в (х) (х),
т. е. для сс(х) = е(х)й»(х), хеО, выполнено предположение (2.1), если D является //-множеством.
Применяя теорему 2.1, получим
inf 8(x)[0(x)-f(x)]<P(A W).	(2.13)
x^D
Чтобы эта оценка не была тривиальной, следует предположить еще, что е(х)[$(%) — f (х)]> 0 для всех x^D. Это приводит к оценке
inf | w(x)-f(x)|<p(f, Г).	(2.14)
хе D
2. Нижние границы для наилучьиего приближения 65
Так как мы еще подробно остановимся на //-множествах в главе III, то здесь мы ограничимся одним простым частным случаем: В — [а, р], где а < р.
Пусть W^C(B) обладает следующим свойством: для всякой пары w, w W разность w — w имеет не более г — 1 нулей либо равна нулю тождественно.
При этом 1—фиксированное натуральное число.
Позднее мы увидим, что это свойство имеет место при полиномиальном приближении, при обыкновенном рациональном приближении и при обыкновенном нелинейном экспоненциальном приближении.
Пусть теперь D = {хь ..., хг+1}, где а X] < < х2 < ... < xr+i Р. Если положить Di = {хь х3, ...} и /)2 = {х2, х4, ...}, то D = Di U /?2 будет //-множеством; действительно, если бы нашлась такая пара w е IF, что
w (xt) — w (xt) < 0 для i = 1, 3, ...,
w (xz) — w (xt) > 0 для / = 2, 4, ...,
то разность v — w имела бы на [а, Р] по крайней мере г нулей, что невозможно, поскольку w — w 0.
С. Достаточное условие для элементов наилучшего приближения. Пусть снова С(В)— пространство непрерывных на В действительных или комплексных функций, a D — непустое замкнутое подмножество В. Тогда D компактно (см. теорему 1.1 главы VII). Пусть w е W такая функция, что
min Re \w (х) — f (х)] [$ (х) — w (х)]	0	(2.15)
xt=D
для всех х е W.
Утверждение. Справедливо неравенство
min | (х) — f (х) К р (f, W). x<=D
(2.16)
Доказательство. Если |w(х) — f(x)| = O для некоторого х е D, то утверждение справедливо.
Поэтому предположим, что
| w (х) — f (х) | > 0  для всех х е D.
3 Л. Коллатц, В. Крабе
66
//. Нелинейное чебышевское приближение
Положим
С/,Л_ |^(x)-f(x)l ’ х^и>
и а (х) = Re [е (х) й> (х)|, хеО. Тогда согласно (2.15) для всякого w е IF найдется такой х е D, что
Re [е (х) w (х)]	а (х).
Но так как
а (х) — Re [а (х) f (x)J = Re {в (х)	(х) — f (х)]} =
= |®(х) —/(х)|, то тем самым оценка (2.16) получается из теоремы 2.1. □
Пусть теперь
Ей, = {хев| |$(х) — /(х)| = ||й — f ||) (2.17) — множество экстремальных точек разности w — /.Тогда Ел, как непрерывный прообраз точки при отображении x->|t&(x)—f(x) | множества В в R замкнуто и поэтому компактно (см. теоремы 1.3 и 1.1 главы VII).
Поэтому из импликации (2.15) =ф(2.16) непосредственно следует
Теорема 2.4. Пусть функция й» е IF такова, что
min Re [w (х) — f (х)] [й» (х) — w (х)] < 0	(2.18)
для всех w е 1F; тогда является элементом наилучшего приближения для f в IF.
Доказательство. Из (2.16) для D = E^> следует
II й> — f || = min | w (х) — f (х) К р (/, 1F) = || — /1|. □ х
Достаточность условия (2.18) для элементов наилучшего приближения впервые была доказана Мейнарду-сом и Шведтом [1964].	. я
Условие (2.18) восходит к Колмогорову [1948], который показал в случае линейной аппроксимации, что (2.18) необходимо и достаточно для элементов наилучшего приближения (см. об этОхМ также теорему 4.4).
3. Существование наилушиего приближения
67
Как показывает следующий контрпример Мейнар-дуса и Шведта [1964], условие (2.18) в общем случае не является необходимым для элементов наилучшего приближения. Пусть В = [—1, 4-1], f = 1,
W = {w(а, х) = а2 4- ах |а е R, хе В}.
Тогда w = w(0, х) является элементом наилучшего приближения для f в W, причем = В. Однако для каждого а е R при | а | > 1 имеем
min [оу (0, х) — f (х)] [w (0, х) — w (а, х)] — min (а2 4- ах) > О, хВ	х^В
т. е. условие (2.18) не выполняется.
3. Существование элементов наилучшего приближения
А. Общие соображения. Рассмотрим сначала, как и в II. 1, общую Т-задачу. Итак, пусть В — компактное метрическое пространство, а С (В) — пространство непрерывных на В действительных или комплексных функций, наделенное максимум-нормой (1.1). Далее, пусть W — непустое подмножество С (В). Для заданной функции feC(B) наилучшее приближение p(f, W) определим согласно (1.2). Поставим вопрос об отыскании элементов наилучшего приближения w е W для f в W, т. е. таких, что
И-Л = р(Л W).	(3.1)
Согласно VII. 1 С (В) является метрическим пространством, если метрику определить равенством p(g, h) = = llg — All, g, h e C(B). Если W — компактное подмножество С (В), то существование элементов наилучшего приближения ®е № вытекает из теоремы 1.8 главы VII. Но эту теорему можно привлекать для доказательства существования элементов наилучшего приближения и тогда, когда W не компактно. А именно, как показывают следующие рассуждения, при отыскании элементов наилучшего приближения можно с самого начала ограничиться определенными подмножествами W. Пусть задан произвольный элемент w* ее W. Тогда, полагая
3*
68
II. Нелинейное чебышевское приближение
будем иметь
Р(/,Ю= inf ш<=Зш»
Но так как || w || —1| f || || w — f ||, то
5да.<=^ = {шё=ИМ<11Л1 + 11^-/11}, откуда следует, что
p(f. W)= inf	(3.2)
W s &w*
Отсюда вытекает
Теорема 3.1. Если для всякого а О множество
Ка(Г) = {ше1Г||М<а}	(3.3)
компактно, то для каждого f^C(B) в W существует элемент наилучшего приближения.
Из необходимого условия существования элемента наилучшего приближения следует
Теорема 3.2. Если для всякой функции f^C(B) во множестве W существует элемент наилучшего при* ближения, то W замкнуто.
Доказательство. Пусть — последовательность из W, причем wn—*g для некоторого g^C(B), т. е. lim || wn — g || — 0. Предположим, что g ф W. Тогда п->оо
найдется такой элемент w е W, для которого
ll^n —gll>p(g, Ю=Н —gll>0
при всех и, что противоречит условию	□
Согласно теореме 1.11 главы VII всякое конечномерное линейное подпространство W пространства С (В) замкнуто. Поэтому справедлива
Теорема 3.3. Если W — конечномерное подпростран-ст во пространства С (В), то для всякого а 0 множество Ka,(W) (см. (3.3)) компактно, так что для каждой функции f^C(B) в W существует элемент наилучшего приближения.
Доказательство непосредственно следует из теоремы 1.10 главы VII и того факта, что Ka(W) ограничено и замкнуто в W. □
Замечание. При доказательстве теоремы 3.3мы пользовались лишь тем, что С (В)—нормиоованное век
3. Существование наилучшего приближения
63
торное пространство. Поэтому утверждение теоремы справедливо также для аппроксимационной задачи в произвольном нормированном пространстве (см. также Ахиезер [1965] и Мейнардус [1964]).
Как показывают уже простые контрпримеры, в нелинейной Г-задаче множество /Ca(IF), вообще говоря, не компактно.
Например, пусть В = [0, 1] и
W — | w (х) =	. I а, й, с е R, b + сх > О
(	7 b + сх I
для всех х<=[0, 1]}. Полагая (х) =	— > n = 1,
2, ... будем иметь wn W и	1 для всех п, т. е.
wn^	Однако последовательность {^} не содер-
жит ни одной подпоследовательности, сходящейся к элементу w е W. Действительно, в качестве предела получилась бы разрывная функция
( 1 при х = 0, g М — | Q При	О
Несмотря на это, мы увидим, что в этом примере для всякой функции	существует элемент наилучшего приближения в W (см. IV. 1).	5
Поэтому простая ссылка на компактность, как в теореме 3.1, для доказательства существования элементов наилучшего приближения в общем случае невозможна.
Рассмотрим теперь частный случай W = F(A)t где А — заданное непустое подмножество R" или С", a F: А-+С(В)—заданное отображение (см. II. 1.В). Мы предполагаем, что R72 или Сп снабжено евклидовой нормой, которую обозначим через || • 11г. По определению 1.6 главы VII отображение F: А-*С(В) непрерывно, если для всякого а^А имеет место импликация:
lim ||	—- а ||2 = 0, ап(=А
П-><х>
при всех n=>lim||F(a„)-F(a)|| = O.
П->оо
На основании теорем 1.4 и 1.9 следующие три условия достаточны для компактности Ka(W) (см. (3.3)), а следовательно, для существования элементов наилучшего приближения:
70
//. Нелинейное чебышевское приближение
1.	А замкнуто.
2.	Отображение F: А-+С(В) непрерывно.
3.	Для всякого а 0 множество Да = {ае Л, \\F(а) ||а} ограничено.
Для доказательства достаточно лишь установить, что при всяком а^О множество Ла замкнуто. Поэтому пусть {tf/J последовательность из Ла и а* —Jim ап. Тогда
М-»оо
и в силу непрерывности отображения а -> ||F (а) || имеем
15m ||F(art)|| = ||F(a*)||<a.
П-»оо
В. Примеры, а) Предположения 1, 2 и 3 выполняются, например, в случае линейного приближения (в этой связи см. доказательство теоремы 1.10 главы VII), когда А — R" или С",
п
F(a)=^afvh	оп^С(В) линейно независимы.
b) Они выполняются также и в случае линейного приближения с линейными дополнительны ми условиями, например, в следующей ситуации.
Пусть отображение F: Rn->C(B) определено, как и выше. Далее, пусть ..., wn, g^C(B) и задано непустое замкнутое подмножество D множества В. Пусть множество А состоит из всех параметров а е R", для ко-
торых
п
Е aj^'i (х) < g (х) /=1
для всех

Предположим, что множество А непусто. Как легко установить, множество А замкнуто, а Аа при всяком а 0 ограничено.
с) При общем рациональном приближении предположение 1 выполняется лишь в частном случае линейного приближения. В этом случае согласно II. l.Bb)
F(a, = где и(а)== Xafu/f и0, «геС(В),
V (b) = s bkvk, vQ, vs<=C (B),
k—\)
3. Существование наилучшего приближения
71
а множество
А = {(a, b) €= Rr+I X Rs+‘ I v (b) > 0 на в}, n = г + s + 2
открыто. Если бы А было одновременно замкнуто и непусто, то это могло бы быть лишь при А = Rn. Поэтому замкнутость А возможна лишь в частном случае линейного приближения. Предположение 2 выполняется, так как согласно И. 4.С отображение F: А->С(В) (при непустом А) удовлетворяет условию дифференцируемости, что по теореме 4.6 влечет дифференцируемость F на А в смысле Фреше, а тем самым и непрерывность (которая непосредственно следует из (4.8)).
Предположение 3 также выполнено, поскольку для доказательства существования элементов наилучшего приближения вместо А достаточно рассматривать множество
Л = {(а, Ь) е Л||| v(&)||= 1}.
Утверждение. Для всякого а множество
Аа = {(а, b) е= А11| F (а, Ь) || < а}
ограничено.
Доказательство. Пусть (а, Ь) е Аа. Тогда \\u(a)\\^[\F(a, b) || • ||t> (6) ||< а,
т. е.
Аа<=Ка = {(а, &)<=Rr+s+2|||w(a)||<a и ||о(&)11<1}.
Но множество Ка ограничено, в чем можно убедиться аналогично доказательству теоремы 1.10 главы VII. Поэтому множество Аа также ограничено. □
Из этих рассуждений следует, что предположения 1, 2 и 3 будут выполнены, если вместо А выбрать множество параметров
{(a, b) €= Rr+s+218 < v (6)< I на В},
где ее (0,1) фиксировано. Для вычислительных целей иногда можно ограничиться достаточно малыми е > 0.
Проблема существования элемента наилучшего приближения при общем рациональном приближении будет еще раз рассмотрена в IV. 1, а при нелинейном экспоненциальном приближении — в V. 1.
72
II. Нелинейное чебышевское приближение
4. Необходимые условия для элементов наилучшего приближения
Сформулированную в II. 1 Лзадачу можно рассматривать так же, как задачу нелинейной оптимизации. А именно, определяя для заданной функции	функционал ф: С(В) ->R равенством
ф(£) = \\g — f IL g^C(B), мы получим Г-задачу, рассматривая задачу нахождения минимума функционала Ф на подмножестве W cz С (В). Тогда всякая точка минимума функционала ф, принадлежащая W, будет элементом наилучшего приближения Т-задачи для f в W и обратно. Ниже мы будем предполагать существование элементов наилучшего приближения и установим для них необходимые условия. Для этой цели мы воспользуемся тем, что с помощью так называемого касательного конуса можно получить весьма общее .необходимое условие для точек минимума функционала ф на W (см. теорему 4.5). Кроме того, мы увидим, что обобщение (2.18) условия Колмогорова, доказанное как достаточное для элементов наилучшего приближения, для выпуклых подмножеств й^сгС(В) также и необходимо (см. теоремы 4.3 и 4.4).
Для этого необходима некоторая подготовка. Сначала рассмотрим
А. Касательный конус в нормированных пространствах. Пусть X — нормированное пространство над полем действительных или комплексных чисел (см. VII. 1). Норму пространства X обозначим через ||-||. Далее, пусть S — непустое подмножество X.
Определение 4.1 (Хестенс [1966]). Элемент X называется касательным вектором к S в точке х St если существует последовательность {%„} элементов xn^S и последовательность действительных положительных чисел Хп, для которых
lim ||xrt —- х || = О	(4.1)
П->оо
и
—*) — И = 0.	(4.2)
П->оо
4. Необходимые условия наилучшего приближения
73
Каждому x^S сопоставим множество Т(х) касательных векторов к S в х. Очевидно Т (х) непусто, так как (0х — нулевой элемент пространства X) принадлежит Т(х).
Кроме того, имеет место импликация
АеГ(х), Лее R, A>0=>UeT(x),
т. е. Т(х)—конус с вершиной
Поэтому мы назовем Т(х) касательным конусом к S в точке х е S.
Пример 1. Если S — непустое открытое подмножество X, то для всякого х е S имеем Т (х) = X. Действительно, пусть задан произвольный элемент хеХ; положим кп = п (п 1) и хп = = X + (1/и) -k.
Тогда xn^S для достаточ о больших и, причем
Игл || хп — х || —1| k || lim — = О
П->оо	П->оо п
И
ИМ*«-*)-*Н=о
для всех п, откуда следует (4.2).
2.	Пусть S — звездное множество относительно хе S, т. е. для вся
кого xeS и Ze [0,1] имеем Хх +(1 — Х)х е S. Тогда Срис. П. 4.1)
S — х = {х — х |х е S) s Т (£). Действительно, если k = х — х при некотором xgS, то положим, как и выше,
Л.„ = п и хп = Л + — • k. tt
Тогда xn^S для всех 1 и (4.1), (4.2} обосновываются аналогичным образом.
Приведем еще несколько вполне конкретных примеров.
3.	Пусть на действительной плоскости X = R2 задана область, имеющая форму линзы, ограниченная, например, двумя дугами окружностей. Пусть dL — ее граница, a L = L + dL. Далее, пусть х и х— две точки
Рис. II. 4.1. Касательный конус звездной области.
74
1L Нелинейное чебышевское приближение
границы dL, одна из которых, х, — угловая точка. На рис. II. 4.2 изображены касательные конусы в точках1^ и х в двух случаях: в одном из них в качестве множества S выбрана граница dL, в другом — в качестве 5 выбрано L.
4.	Пусть
s = if о (х), fl (х)> = {h <= X | fo (х)< h (х) < f, (х)}
— полоса в пространстве X — С[а, 6], где fo, fi — две заданные функции из С[а, Ь], причем f0(x) < fi(x) для
ft] (см. рис. II. 4.2).
Выберем теперь две точки хь х2, а < Xi < Хг < Ь и функцию g(x), график которой касается графика
функции fo в Хг и графика функции fi в Хь Тогда касательный конус T(g) содержится во множестве
{и (х) | и е С [а, 6], ы(Х1)^0, w(x2)^0}.
На рис. II. 4.2 изображен график такой функции и, а волнообразная линия символизирует значения, которые не должна принимать функция и.
Рассмотрим теперь следующую задачу: пусть <р: X -> /? — выпуклый функционал, т. е.
Ф (Лх + (1 — %) t/)< Хф (х) + (1 — X) ф (у)
при всех х, у е X и X е [0,1].
4. Необходимые условия наилучшего приближения
<75.
Кроме того, пусть ф непрерывен на X. Требуется найти минимум функционала ср на непустом подмножестве ScX.
Теорема 4.1. Пусть для некоторого x^S
ф(х)^ф(х) при всех xeS.
Тогда
Ф (х) ф (х + k) для всех k^T (х),
где Т(х) — касательный конус к S в х.
Доказательство. Предположим, что существует элемент Т(х), для которого
ф (х) — ф (х + k) > 6 > 0.
По определению элемента k найдутся последовательность {хп} элементов xn eS и последовательность положительных чисел {Хл}, для которых выполняются условия (4.1) и (4.2). Положим
=== (Хд х).
Тогда из (4.2) и непрерывности ф следует
I Ф (* + kn) — ф (£ + k) | < д
при достаточно больших п. Кроме того,
^пт- = х„ — X, lim|| Аг„ — & II = 0=> lim || kn || = || k ||,
П->ОО
и из (4.1) следует lim -^- = 0, так что для достаточно П-»оо
больших п
Ли = Т_ S [О’ 1] •
Ад
Тем самым для достаточно больших п
Ф (хп) = <р ((1 — л„) % + т)п (X + kn)) <
<(1 — Пп)ф(*) + Ппф(* + У<
<(1 — nnHU)+ пЛф (* + *) +б]<
< (1 — П») Ф (х) + ПлФ (^) = Ф (х),
что противоречит оптимальности х. □
76
IL Нелинейное чебышевское приближение
В. Приложение к общей Т-задаче. Пусть X — С (В) — пространство непрерывных на В действительных или комплексных функций, наделенное максимум-нормой (1.1) (В снова является компактным метрическим пространством). Далее, пусть W по-прежнему непустое подмножество С(В), a f е: С(В) фиксировано.
Функционал
<p(g) = llg-fll, geC(B), как легко проверить, является выпуклым и по теореме 1.5 главы VII непрерывным. Т-задача, как отмечено с самого начала, состоит в нахождении минимума <р на W. Из теоремы 4.1 непосредственно вытекает
Теорема 4.2. Если w — элемент наилучшего приближения для f в, W, то tii> является элементом наи-лучшего приближения для f в
tit> + Т (ш) = {w + k | k e= T ($)},
где T(w) — касательный конус к w в W.
Следующая теорема показывает, что условие (2.18) при некоторых обстоятельствах является также и необходимым для элементов наилучшего приближения. А именно, справедлива
Теорема 4.3. Пусть w е W — элемент наилучшего приближения для f в W и пусть W — звездное множество относительно Из, т. е.
w^W, >.е[0, 1]^-Лда + (1 ~ tyw&.W.
Тогда
min Re (х) — f (х)] [й> (х) — w (х)] 0	(4.3)
х&Еф
при всех w е W, где Е& — множество экстремальных точек разности w— f, заданное формулой (2.17).
Доказательство. Предположим, что для некоторого w е W условие (4.3) не выполнено. Так как Е& компактно, то найдется такое у > О, что
3 (х) = Re (х) — f (х)] [й (х) — f (х)] > у
4. Необходимые условия наилучшего приближения
77
при всех х^Е&. Положим
L'=[.re B\S(x) >-*-}.
Тогда U — открытое подмножество В. Поскольку W звездно относительно w, то
= kw + (1 — X) w = w + X (w — ji>) е W
при всех Хе [0, 1].
Поэтому для каждого х е U имеем
in(*)—f Wl2=
= | w (х) — f (х) I2 + X21 (х) — w (х) |2 — 2XS(х)^ < II & — f II2 — X {у — X || tS — w ||2} < || ji) — f II2,
если ТОЛЬКО 0 < X < X] = V------------tf-.
1 II W — 10 II
Если U = B, то при Хе (О, X), где X = min(Xb 1), имеем
Их — f II < Н — f II,
что противоречит оптимальности
Если же U <= В, но U<£B, то множество В \ U = «= {х е В | х U} компактно и
ц —1| w — f || — max | ji) (x) — f (x) | > 0.
xeB\U
Тогда, если 0 < X < Х2=т—, то для всякого хе В \ U, ’	1 II и> — WII
имеем
|а\(х) — f (х)|<1 й»(х) — f (х)| + |и>к(*) — гН*)1 =
= I w (х) — f (х) | + X | w (х) — Ji) (х) |
<11 — f II— Н + Х|| w — Ji) || < II Ji> — f Ц.
Полагая Х = minfXt, Х2, 1), получим для всех Хе(0,1) Нл-ЛКИ-а
। что противоречит оптимальности и».
Поэтому предположение о том, что (4.3) не имеет места для некоторого jd е W, ошибочно, и теорема до« казана. □
Так как выпуклые множества являются звездными относительно каждой своей точки, то из теорем 4.3 и 2.4
78
II. Нелинейное чебышевское приближение
вытекает следующий критерий элемента наилучшего приближения.	д
Теорема 4.4. Если W выпукло, toweW является элементом наилучшего приближения для f в W тогда и только тогда, когда условие (4.3) выполняется при всех w е W.
Из теорем 4.2 и 4.3 в качестве необходимого условия для элементов на илучшего приближения вытекает
Теорема 4.5. Если w — элемент наилучшего приближения для f, то
min (Х) __ $ (Х)] k (х)<0	(4.4)
при всех T(w), где T(w) —касательный конус к w в W, а Е& — множество экстремальных точек разности w — f, заданное формулой (2.17).
Доказательство. Множество + звездно относительно w, так как если fee T(w) и Хе [0, 1], то
X (w + fe) + (1 ~ X) w — w + Xfe е Ф + Т (ш).
Если w е W — элемент наилучшего приближения для f, то по теореме 4.2 функция w является также элементом наилучшего приближения для f в w + T(w), так что (4.4) сразу следует из теоремы 4.3.
С. Дифференцируемый действительный случай. Как уже упоминалось в II. 1.В, во многих приложениях W является образом множества параметров А при отображении F\ А->С(В). Во многих случаях встречается даже еще более частная ситуация. Пусть С (В)—векторное пространство действительных функций, непрерывных на В. Далее, пусть А — нпустое подмножество действительного n-мерного пространства R" с евклидовой нормой
Огг	X 1/2
£ a -J , ае R".
Пусть До — открытое множество, содержащее А. Наконец, пусть задано отображение F: Д0->С(В) и W = = F(A).
4. Необходимые условия наилучшего приближения
79
Фундаментальное значение имеет следующее условие дифференцируемости отображения F (см. также тео-ррему 4.6).
Определение 4.2. Отображение F удовлетворяет условию дифференцируемости на Ло, если для всякого х е В частные производные
дР , ч , х),
существуют для всех а е Ло и непрерывны в точках (а, х) е Ло X В.
Примеры (см. частные случаи а) —d) в II. 1.В).
1.	Линейное приближение. Л = Ло = R",
F (а, х) = Е Я/&’/ (Д Ш/ С (В),
(a, w) = Wi (х),	/=1, п.
Условие дифференцируемости выполняется.
2.	Общее рациональное приближение. Пусть п = г + s 4- 2. Предположим, что множество
А = Ло= {(a, b) €= Rr+1 X Rs+* I v (b, x) =
— E bkvk (x) > 0 для всех x e В}
/г=0
не пусто. Оно открыто и выпукло. Функции и0, • • • ..., Vs^C(B) фиксированы. Полагая
г
и (а, х) = Е (Д aj R, П/ е С (В)
7=0
(Uj также фиксированы), получим
F (а, Ь, х) = " при (а, Ь) ё= Ло> х е= В
dF .	//у	А	.1 —	Uj(x)	i — n	
daj	— dF	v (b, х) ’ и (а, х) v. (х)	J	v, . . .	(4.5)
	—	и v(btX)2	k — 0, ...	,, s,
и условие дифференцируемости также выполняется.
80
//. Нелинейное чебышевское приближение
3.	Экспоненциальное приближение. В = = [а, Р], а < р. Пусть п = 2г и
A = AQ = {(a, b)^RrXKr\b{<b2< ... <br}. 4 Множество До открыто в R". Отображение F: ДоС (В) определяется равенством
F (а, &, х) — £ а}еь1х, (а, Ь) е До, /=i
и
^-(а. Ь, XI	|
аЛ h ,	j  .............  <46>
(а, b, х) = atxe ' , j
Итак, условие дифференцируемости и в этом случае выполняется.
Теорема 4.6. Пусть F удовлетворяет условию дифференцируемости на До {определение 4.2).
Полагая для каждого h<=Rn и a^AQ
п
Г'а(1г)(х) = ^Ь1-^-(а, х),	(4.7)
м '
получим
\\F{a + h)-F (а) - Fa (Л) || < га (|l h ||2) • || h ||2	(4.8)
для всех Rrt таких, что а + h е До, причем
lim ео(||/г||2) = 0.	(4.9)
Цй||2->0
Кроме того, отображение a->F'a(h) множества До в С (В) непрерывно при каждом фиксированном h, т. е. для всякого а (= До имеем [| F'a (й) — F'b (h) j| е, если Ik — Ь\\2 б(е, а).
Замечание. Условия (4.8), (4.9) на языке функционального анализа означают дифференцируемость отображения F: Aq->C{B) в смысле Фреше.
Справедлива также и обратная теорема: если отображение F; Ао-+С(В) дифференцируемо по Фреше, а отображение a->Ffa \h) непрерывно при каждом фикси
4. Необходимые условия наилучшего приближения
81
рованном /г, то F удовлетворяет условию дифференцируемости на До (по поводу доказательства см. Крабе [1967] или Кудрявцев [1970], т. I, стр. 289).
Доказательство теоремы 4.6. Пусть х е В, деЛ0 и /i^R" выбраны так, что а + Мг е Ао при Ze [0, 1]. Тогда найдется tx [0, 1], для которого
F (а + Л, х) — F (а, х) — (а + СЛ х) —
/~1
п	п
= Zhi^~^a’ х) + £й/(^(а + /Л х)—£-(а, х)). /»| 7 /=! 4 7 7
На основании условия дифференцируемости для всякого фиксированного / и е > 0 найдется такое б = = 6(е, а, х), что
\ dF ,	dF „
Н—(а, х)—т—(&, х)
I да. v ’ 7 да. ' ’ 7
I dF (	dF	{	\	.	I	dF z	ч dF	„	-J
“1— (#,	x) —з—	(я,	x)	+	— (a,	x) —-—	(&,	x)	e
da. '	7 da.	v ’	7	*	da. v ’	7 da^	'
для всех b А при || a — b [|2 б и всех x из некоторой открытой окрестности Vx элемента х. Окрестности Vx образуют открытое покрытие В, когда х пробегает множество В. В силу компактности В по теореме 1.2 главы VII существует конечное число окрестностей Vx. таких, что В= J Vx - Выбирая б(е, а) = min 6(8, а, х), i 1	i
получим
1| < 8 при всех Ь^А0,
если || а — b ||г	6(е, а).
Отсюда вытекает, с одной стороны, непрерывность отображения a—^F'a(h) при любом фиксированном h,
85
II. Нелинейное чебышевское приближение
а с другой стороны,
где
= 8a(||/l2||)||/l||2,
lim еа(||Л||2) = 0. □
II л ||..->0
Пусть теперь задан аеЛ и Т(а)—касательный конус к Л в а. Тогда справедлива
Теорема 4.7. Если отображение F удовлетворяет условию дифференцируемости на Л0(эЛ), то для каждого а^ А и w = F(a) имеем
{F'^h)\he=T(a))<=T(w),
(4.Ю)
где Т(ау) — касательный конус к W — F(A) в w, a F'a (h) определено равенством (4.7).
Доказательство. Пусть задан h^.T(a). Тогда найдутся последовательность {ап} элементов ап е А и последовательность {Хп} положительных чисел, для КО' торых
lim || ап — а ||г = 0 и lim || Л„ (ап — а) — h ||2 — 0.
П->оо	П-»оо
Полагая hn = kn(an~ а), по теореме 4.6 имеем
(*.)!<
oWI*,b (4.Н) причем
lim еа (|| ап — а ||2) = 0.	(4.12)
П->оо
Отсюда в силу
«".КМ-ЗДН
4. Необходимые условия наилучшего приближения
83
следует
П->оо
Наконец, в силу (4.11) и (4.12)
lim || F (а„) — F (а) || = О,
П->оо
откуда следует F'a (Л) е= Т (ш). □
Из теорем 4.5 и 4.7 вытекает следующее необходимое условие для элементов наилучшего приближения:
Теорема 4.8. Пусть F удовлетворяет условию дифференцируемости на До (определение 4.2). Тогда если w — F (а) — элемент наилучшего приближения для f в W = F(A), то
min [/ (х) - (x)J F' (ft) (х) < 0	(4.13)
х Еф
для всех /ге Т(а), где Т(а) — касательный конус к А в а^А, F'a(h)(x) определено равенством (4.7), а Е& — множество экстремальных точек разности w — f, задаваемое формулой (2.17).
Добавления. 1. Если А = Ао, то из предположений теоремы 4.8 следует, что условие (4.13) выполняется для всех h е R”, поскольку, как мы видели в II. 4.А, Т(а) = R" для всех а е А.
2. Если А выпукло, то, как мы видели в II.4.A, А — й^Т(а) для каждого de А, так как А звездно относительно всякого d е А. Поэтому в условиях теоремы 4.8 получаем
min [f (х) — w (х)] F' (а — d) (х)	0 при всех ае А. (4.14)
*
Замечание. Случай А = Ао имеет место при линейном и экспоненциальном приближениях.
При общем рациональном приближении множество А выпукло и А — До, так что условия (4.13) при всех ft е R" и (4.14) при всех аеД оба необходимы для того, чтобы tS> = F(&) был элементом наилучшего приближения для f в W = F(A).
84
11. Нелинейное чебышевское приближение
В заключение сведем полученные результаты в итоговую таблицу:	и
С (В)		Необходимое	Достаточное
		условие для элементов наилучшего приближения	
Векторное• пространство действительных или комплексных функций, непрерывных на В	Произвольное подмножество С (В)	(4.4) для всех k G5 Т (ф)	(4.3) = (2.18) для всех w €= W
	выпуклое подмножество С (В)	(4.3) = (2.18) для всех w е U7	
Векторное пространство действительных функций, непрерывных на В	Г = В(Д), A <= До <= R* До открыто, F удовлетворяет условию дифференцируемости на До (определение 4.2)	(4.13) для всех h е Т (&) — F (&))	
	А = А0	(4.13) для всех Л е	
	А выпукло	(4.14) для всех йеД	
	д = к\ F линейно (=>В (Д) выпукло)	(4.13) = (5.6) для всех (Условие Колмогорова)	
5.	Характеристика элементов наилучшего приближения
А.	Общее и локальное условие Колмогорова. В этом пункте мы ограничимся уже обсуждавшейся в II.4.C частной ситуацией, хотя утверждения частично можно перенести и на случай общей Г-задачи (см. II. 4.1).
Пусть А—непустое подмножество Rrt, а Ло — открытое множество, содержащее А. Кроме того, пусть F:
5. Характеристика элементов
Я5
Aq->C(B) заданное отображение, где С (В)—векторное пространство действительных функций, непрерывных на компактном метрическом пространстве В.
Положим Ц7 = /7(А). Тогда для каждого / еС(В)
р(/, Г)= inf ||F(a)-f||.	(5.1)
a е= А
Всякому а <= А сопоставим (компактное) множество
Ea = {xt=B\F{a, х) — f (x)\ — ^F (а) — f\\}	(5.2)
экстремальных точек разности F(a) —f.
Тогда по теореме 2.4 F(a) (йеА) является элементом наилучшего приближения для f в W, если для всех а е Л имеем
min [F (й, х) - f (х)] [F (й, х) - F (а, х)] < 0.	(5.3)
Условие (5.3) при всех аеЛ будем называть общим условием Колмогорова, поскольку, как уже упоминалось в п. II. 4.С, при линейном приближении оно совпадает с условием Колмогорова, данным в [1948].
Пусть теперь F удовлетворяет условию дифференцируемости на Ао (определение 4.2). Тогда если F(&) (ае А) — элемент наилучшего приближения для f в W, то для всех /г<=Т(а) (Т(й) — касательный конус к А в й, см. II. 4.А) согласно теореме 4.8:
min [f (г) - F (й, х)] F' (А) (х) < 0,	(5.4)
где Еа определено равенством (5.2), а п
х).	(5.5)
/-1 1
Условие (5.4) для всех h е Т(а) будем называть локальным условием Колмогорова. В случае линейного приближения оно также переходит в условие Колмогорова (5.6). Действительно, в этом случае А = Ао = R" п
F (а, х) = £ atWj (х), Wj е С (В),
п
F'a (Л) W = 2 hjWj (x) = F(h, х),
86
//. Нелинейное чебышевское приближение
и так как Т(а)— Rn (см. п. II.4.A), то из (5.4) для всех h е Т (а) следует условие
min [/ (х) — F (а, х)] F (h, х) 0	(5.6)
для всех h е R".
Таким образом, это условие необходимо и достаточно для того, чтобы F(a), а<=А, был элементом наилучшего приближения для f в W. Возникает вопрос, как далеко это утверждение можно обобщить на нелинейные задачи приближения.
Будем исходить из локального условия Колмогорова и исследовать, при каких отображениях F: А->С(В), удовлетворяющих условию дифференцируемости, локальное условие Колмогорова является достаточным для элементов наилучшего приближения. Эти отображения F могут быть охарактеризованы (см. теоремы 5.2 и 5.3).
Аналогичным образом можно поставить вопрос, для каких отображений F: А -+С(В) общее условие Колмогорова является необходимьгм для элементов наилучшего приближения? Это сделал Брозовски в работе [1968а], охарактеризовавший эти отображения. (Он рассмотрел даже случай общего Г-приближения, основываясь на условии (2.18).) Однако мы не будем здесь подробно останавливаться на этом.
Связь между необходимостью общего условия Колмогорова и достаточностью локального условия Колмогорова для элементов наилучшего приближения устанавливается следующей теоремой (см. Брозовски [1968b]).
Теорема 5.1. Если для произвольного f<=C(B) локальное условие Колмогорова (5.4) достаточно для элементов наилучшего приближения в W = F(A), то общее условие Колмогорова (5.3) необходимо.
Доказательство. Пусть f^C(B) и F (а) (аеЛ)—элемент наилучшего приближения для f в W. Для каждого Z > 0 положим
fK = F(a) + ^(f-F (ф).	(5.7)
Утверждение:
IIF — h II == Р (/\> №') для всякого Л > 0.	(5.8)
5. Характеристика элементов
87
Действительно, согласно (5.7) и локальному условию Колмогорова (5.4)
min [7Jx)-F(a, х)]F'(Л) (х)<О
при всех Л^Т’(й), откуда в силу равенства
Еа = {х е В11F (й, х) - fк (х) | = || F (а) - f J|} и предположенной достаточности локального условия Колмогорова следует утверждение (5.8).
Предположим, что
у = min [F (d, х) —• f (х)] [F (я, х) — F (а, х)] > О х е
для некоторого а е А, (5.9) и положим
4)(x) = [F(d, x) — F(a, х)] [F(d, х) — f(x)] для всех хеВ. На Еа имеем
\ty(x)\ = \\F (а)	f\\\F (d, x) — F(a, х)|.
Кроме того, положим
и = | X G= В1ф (х) >	.
Тогда U открыто, содержит Еа, и для всех xg U \F(a, х)-Мх)|2 =
= | F (а, х) - F (й, x)-K(f (х) - F (а, х)) |2 = = I F (й, х) - fK (х) |2 - 2И(х) +1 F (а, х) - F (й, х) |2< < IIF (d) - fк ||2 - Ку +1| F (а) - F (й) ||2 < || F (d) - fr||2, || F(<3)-F(a)||2	,
если выбрать К > 21— — = Лр
Если бы имело место равенство U = В, то это противоречило бы предположению (5.8). Поэтому пусть U s Z3, но U =^=' В. Тогда
и = ||Г(<2)-/||- max | F(&, х) - f (х) |>0, х^в\и
88
11. Нелинейное чебышевское приближение
поскольку Е& s U, и при всех х е В \ U имеем
|F(a, х) — Л,(х)| = | F(d, х) —fK(x) + F(a, х) —F(d, х)]^:’
<Л max \F(d, х) - f (x)\ + \\F (а) - F (а)\\ = xeB\U
= K\\F(d)-f\\- Лр +1| F (а) - F (a) || < || F (d) - ||
если Л> И(й)-Ла) II
vCJln Л ---------------Лп.
И	2
Итак, учитывая все это, получим
И(«) — М<И(<2) — Ml для всех Л > max (Ль Л2),
что противоречит (5.8).
Таким образом, предположение (5.9) ошибочно и теорема доказана. □
В.	Условие о знаках. В этом пункте предполагается, что отображение F удовлетворяет условию дифференцируемости на Ло (см. определение 4.2).
Определение 5.1. Отображение F удовлетворяет условию о знаках на Л, если для всякого непустого замкнутого подмножества. D пространства В и всякой пары (а, 6) еЛ для которой
min| F (а, х) — F (Ь, х) | > О, xgD
(5.10)
существует элемент h^T(a), где Т(а) касательный конус к А в а) такой, что
min [F (й, х) - F (а, х)] F' (й) (х) >0,	(5.11)
xg=D
где F'a (й) (х) определяется равенством (5.5) (см. Крабе [1969b]).
В п. II. 5.С мы покажем, что это условие выполняется при линейном, общем рациональном и экспоненциальном приближениях.
Теорема 5.2. Если F удовлетворяет условию о знаках на Л, то для произвольного	С (В) локальное ус-
ловие Колмогорова (5.4) достаточно, а (согласно теореме 5.1) общее условие Колмогорова (5.3) необходимо для элементов наилучшего приближения.
Доказательство. Пусть для некоторого, С (В) и некоторого а^А условие (5.4) выполняется
5. Характеристика элементов
89
для всех h^T(a). Если мы покажем, что тогда условие (5.3) выполняется для всех аеЛ, то мы докажем оба утверждения теоремы (независимо от теоремы 5.1), Для этого предположим, что условие (5.3) не выполняется, т. е. при некотором b е Л
min[F(d, х) - f (x)][F (d, x)-F(&, x)] > 0. (5.12)
Тогда, в частности, условие (5.10) выполняется при а = а и D = Edi откуда следует существование элемента йе T(d), для которого
min[F(&, x)-F(d, х)] F' (Л) (х) > 0.	(5.13)
Но из (5.12) и (5.13) получаем
min [f (х) - F (d, х)] F' (Л) (х) > 0,
т. е. условие (5.4) не выполняется для элемента Л е Т(а). □
Решающим является то обстоятельство, что теорема 5.2 допускает обращение, так что условие о знаках полностью характеризует отображения F: А-+С(В), для которых локальное условие Колмогорова при произвольном f^C(B) достаточно для элементов наилучшего приближения в W = F(A).
Теорема 5.3. Если при всяком f^C(B) локальное условие Колмогорова достаточно для элементов наилучшего приближения в W = F(A). то отображение F. удовлетворяет условию о знаках на А (определение 5.1).
Доказательство. Пусть D — непустое замкнутое подмножество пространства В, a (a, b) е А X — пара, удовлетворяющая условию (5.10). Предположим, что min [F (b, х) — F (а, х)] F' (Л) (х)	0 для всех h^T (а),
х <= D	а
(5.14) Положим
е(х) = sgn[F(b, х) — F(а, х)], хеО и
ь>+ = {х е£) 1е(х)= 1), D = {хеD |е(х) = — 1),
90
II. Нелинейное чебышевское приближение
где D+ и D~ — два непересекающихся замкнутых подмножества множества D, причем D = D+ U D~.
Если D+ не пусто, то по теореме 1.6 главы VII hW* дется функция g+, непрерывная на В, для которой
( I при х е £)+,
(. 0 при х е D ,
и 0	g+(x) < 1 при всех хей \ D+.
Если D+ пусто, то положим g+ 0. Если D~ — непусто, то аналогичным образом найдется функция для которой
	при х е D~i при х е D+,
и 0	g~(x) <Z 1 при всех х^ В \ D~. Если же D~
пусто, то положим g~ = 0. Тогда g — g+ — g~ есть функция из С (В), для которой
g (х) — е (х) при х е D
И |g(x) | < 1 при всех хе В \ О.
Если положить f = F(a)-{-g, то g = —F(а) + f, F(b, х)— F(a,x) = \F(b, х)— F(a, х) |g(x) при xs Fa = — D, где Ea определено согласно (5.2). Тогда в силу (5.10) и (5.14) имеем
min (х) — F (а, х)] F' (h) (х)	0
для всех йеТ’(а). Таким образом, F(a) является элементом наилучшего приближения для f в W = F(A) и согласно теореме 5.1
min [F (а, х) — f (х)] [F (а, х) — F (с, х)]	0
для всех cs А. Но, с другой стороны, это противоречит условию
min [Е (а, х) — f (х)] [Е (а, х) — F (Ь, х)] =
я= min | F (а, х) — F (Ь, х) | > 0.
5. Характеристика-элементов
91
Поэтому неравенство (5.14) должно нарушаться при некотором йе Т(а), откуда и вытекает условие о зна-□
С.	Приложения. Как и в П.4.В, предположим, что F удовлетворяет условию дифференцируемости на Ао (определение 4.2).
Определение 5.2. Отображение F удовлетворяет на А условию представимости (см. Крабе [1967а]), если для всякой пары (a, b) е А X А существуют положительная непрерывная на В функция <p = q>(a, b, х) и h — h (а, й) е Т(а), для которых
F(b, x) — F(a, х) = <р(а, b, x)F'a(h(a, й))(х), (5.15) где F'a (й) (х) определено формулой (5.5).
Очевидно, что условие представимости достаточно для выполнения условия о знаках.
Частные случаи, а) Линейное приближен и е А = Ао = R",
п
F (а, х) = £ OjWj (х), Wj е С (В).
В этом случае 7'(a) = Rre (см. II. 4.А) и
F (а, х) — F (b, х) = F (а — b, х) = F'a (а — Ь) (х), так что в (5.15) можно выбрать
й (a, b) — b — а и <р (а, 6) s 1.
Ь) Общее рациональное приближение.
В этом случае также Т (а) = R", и из (4.5) имеем
F(&, Ь, x) — F(a, b,
V (о, X) V (Ь, х)
__ у (Ь, х) / и (d, х) _ и (а, х) у (Ь, х) \_
х) \ v (b, х) v(b, х)2	)
' ь- "• *>)-
’ ' *>	д°1	й,	)
92
11. Нелинейное чебышевское приближение
так что в (5.15) можно выбрать
Л((а, Ь), (й,	= Ь) и Ф((а, Ь), (й, Ь), х) = -Ц^.
v (Ь, х)
Так как
Еа^(а' *>*) + £ ь^(а^ Ь, х) =
/=0	1	k=J k
= и (а, х) _ и (а, х) у (&, х) _ ~
= у (Ь, х) у (Ь, х)2
для всех хе В, то в (5.15) можно было бы выбрать
Л ((а, 6), (d, &)) = (d — а, b — 6), a $ ((а, &), (d, b)) взять как и выше.
с) Экспоненциальное приближение. В этом случае условие представимости также выполняется, что мы, однако, не будем доказывать (доказательство см. у Крабса [1967а]). Из теорем 6.7 и 7.5 следует, что F удовлетворяет условию о знаках на А.
Этот раздел мы закончим схемой, которая поясняет логическую связь между различными условиями.
Условие представимости (определение 5.2) . (выполняется, например, при линейном, общем рациональном и обычном нелинейном экспоненциальном приближениях)
Условие о знаках (определение 5.1)
ф (теоремы 5.2 и 5.3)
Локальное условие Колмогорова «(5.4) для всех h^.T (d)» при всяком f cz С (В) достаточно, а тем самым (по теореме 4.8) и необходимо для того, чтобы F(a) был элементом наилучшего приближения для f в W = F (А)
4 (теорема 5.1)
Общее условие Колмогорова «(5.3) для всех аеД» для каждого f е С (В) необходимо, а тем самым согласно теореме 2.4 и достаточно для того, чтобы F(d) был элементом наилучшего приближения для f в W = В (Л).
6.. Единственность
93
6. Единственность
В этом параграфе положена в основу следующая ситуация. Пусть В — компактное метрическое пространство, состоящее по крайней мере из и + 1 точек, а С(В)—пространство непрерывных на В действительных функций. Далее, пусть А — непустое подмножество R", а Ло— открытое множество, содержащее А. Наконец, пусть задано отображение F:	С (В), удовлетво-
ряющее условию дифференцируемости (определение 4.2). Положим W = F(A) и поставим вопрос о нахож-* дении необходимых и достаточных условий для того, чтобы для заданного f^C(B) существовал в точности один элемент наилучшего приближения в W, т. е. лишь один элемент w = F(a) е W, для которого
l!t& —/11 = Р(Л Ю = inf \\F(a) —f И as A
(II • II = максимум-норма (1.1) вС(В)),
А. Достаточное условие единственности. Пусть V — линейное r-мерное подпространство пространства С (В), натянутое на функции гм, ..., vr е С (В).
Следующее определение восходит к Хаару*), который в работе [1918] исследовал вопрос существования и единственности элементов наилучшего приближения при линейной аппроксимации и установил фундаментальную теорему единственности (см. IL6.C).
Определение 6.1. Подпространство V удовлетворяет условию Хаара на В, если всякая не равная тождественно нулю функция v е V имеет на В не более г — 1 нулей.
Лемма 6.1. Подпространство V удовлетворяет условию Хаара тогда и только тогда, когда для всякого
♦) Альфред Хаар, род. 11.10.1885 г. в Будапеште. С 1910 г. при-: ват-доцент в Геттингене, с 1912 г. — профессор в Клуже, затем профессор начертательной геометрии в Сегеде; умер 16.3.1933 г. Ему принадлежат основополагающие работы в теории ортогональных функций, функциональном анализе, теории приближений, теории дифференциальных уравнений, вариационном исчислении, в теории групп.
94
II. Нелинейное чебышевское приближение
набора (xi, ..., хг) различных г точек хь^В матрица
	...» vr(x{)>
< vx (хД vr (хД
неособенная, т. е. ее определитель не равен нулю.
Доказательство. 1. Пусть V удовлетворяет условию Хаара, и пусть (хь ..., хг) — такой набор г различных точек из В, что определитель матрицы (6.1) равен нулю. Тогда найдется ненулевой r-вектор («ь ... ..., аг)т, для которого
/ ид
' vx (хД
т. е. v—^ajVi имеет по крайней мере г нулей, но не является тождественным нулем, что противоречит условию Хаара.
2.	Предположим, что существует с е V, v Ф 0, для которого
fe=l, ..., m, m^r,
г
Тогда, если, например,	то (alt ..., аг) =/=
¥=(0....0)
и поэтому соответствующая матрица особенная, т. е. ее определитель равен нулю. □
Систему (t>i, ..., ог} назовем системой Чебышева*) на В, если натянутое на нее линейное подпространство V пространства С (В) имеет размерность г и удовлетворяет условию Хаара на В.	,
Примеры системЧебышева.
а)	В = [а, р], а < Р, О/(х) = х/-1, /=1,
*) В оригинале система {щ, .,., ог) называется системой Хаара на В. (Прим, перев.)
6. Барственность
95
функции Vj (/=1, ...» г) линейно независимы.
Система {vi, ...» vr} является системой Чебышева на
[a, 0L так как состоит из всех многочленов степени — 1, каждый из которых либо имеет не более г— 1 нулей, либо является тождественным нулем. В этом случае матрица (6.1) является так называемой матрицей Вандермонда, для которой
1,	хь ..х, 1 	.......... = п (*-*/)•
1,	х„ ..., хгг 1
Ь)	В — [0, р], где Р < 2л.
Утверждение. Система {1, cosx, sinx, ...
..., cos rx, sin rx} является системой Чебышева на [0, р].
Доказательство. При f=V —1 имеем
(а/ cos /х + bj sin /х) —
i~o
bi
e~llx) + -~(ellx — e
и правая часть тождественно обращается в нуль лишь в том случае, когда все Cj, т. е. все а/ и bj равны нулю, что влечет линейную независимость системы {1, cos х, sin х, ..., cosrx, sinrx}. Если по крайней мере одно а/ или bj, т. е. по крайней мере одно с/, отлично от нуля, Г	г
ТО X Cje4x, а следовательно, и У (az- cos /х + sin /х) /=о	/=о
имеет не более 2г нулей на [0, р].
С другими примерами мы познакомимся в главе III и в VII. 4.
В случае, когда В является компактным подмножеством обычного конечномерного векторного простран-
96
II. Нелинейное чебышевское приближение
ства, уже Хаар [1918] заметил, что при г 2 г-мерное подпространство пространства С (В) может не удовлетворять условию Хаара, если В содержит по крайней мере двумерный шар. Затем Мерхьюбер [1956] доказал, что если С {В) содержит подпространство размерности г 2, удовлетворяющее условию Хаара, то В необходимо допускает обратимое однозначное и непрерывное (т. е. гомеоморфное) отображение на замкнутое подмножество окружности. Таким образом, условие Хаара реализуется в двух важных для приложения случаях:
1) для действительных отрезков В,
2) для конечных множеств В (дискретная аппроксимация).
Возвратимся теперь к нашей задаче нелинейного приближения и сопоставим всякому параметру а е AQ линейное подпространство V(a) с: С (В), натянутое на
dF z х	dF , v
-7—(а), ..., -5— (а). dcii v 7 дап v 7
Пусть d(a) = dimV(a). Очевидно, что d(a) n. Предположим, что-т—(a), .-%--------(а) линейно незави-
da*i	da^d(a)
симы.
Согласно Мейнардусу [1964] в вопросах единственности основополагающими являются следующие понятия.
Определение 6.2. Отображение F: AQ->C(B) удовлетворяет локальному условию Хаара, если для всякого а^ А система
является системой Чебышева, т. е. если всякая функция из V(а) либо имеет не более d(a) — 1 нулей на В, либо равна нулю тождественно.
Определение 6.3. Отображение F: А0-*С(В) удовлетворяет на А условию о нулях, если для всякого а^А существует такое натуральное число N(a), что всякая разность F(a) — F(b) О, b е А имеет на В не более N(а) — 1 нулей.
6. Единственность
97
Несколько позднее (см. п. II. 6.В, частные случаи) мы остановимся на примерах. Здесь же ограничимся следующей леммой.
Лемма 6.2. Если отображение F: А0->С(В) удовлетворяет на А условию представимости (определение 5.2) и локальному условию Хаара, то F удовлетворяет на А условию о нулях при N(a) = d(a), а^А,
Доказательство. Пусть заданы а, Ь^А. Тогда существуют положительная функция ф(а, b) е С (В) и элемент h = h(a, b) е Т(а), где Т(а)—касательный конус кА в а (см. II.-4.A), для которых
F(6)-F (a) = q)(a, b) F'a(h), причем F'a(h)^V(a) (См. (4.7)) либо имеет не более d(a) — 1 нулей на В, либо равняется нулю тождественно. □
После этой подготовки мы в состоянии сформулировать следующую теорему единственности.
Теорема 6.3. Пусть А = Ао, а отображение F удовлетворяет условию о знаках на А, локальному условию Хаара на А и условию о нулях при N (а) = d(a) -|- 1, «еЛ.
Тогда для всякого	С (В) существует не более од-
ного элемента наилучшего приближения в W = F(A).
Доказательство. Пусть F(a) ф F(b) —два элемента наилучшего приближения для f в W и пусть для определенности d(a) d(b). Тогда
И(а)-Л1 = И(6)-Л1 = Р(А Г)>0.
Для множества экстремальных точек
£a = {xeB||F(a, х) - f (х) | = ||F(а) - f [1}
разности F (a) — f имеем
| F (а, х) - f (х) | > | F (&, х) — f (х) | для всех х е Еа, а так как
F (а) - F (b)== F (а) - f - [F (b) - f], то
[F (а, х) - f (х)] [F (а, х) - F (Ь, х)] > О
для всех х е Еа.
4 Л. Коллатц, В. Крабе
98
II Нелинейное чебышевское приближение
С другой стороны, в силу необходимости условия Колмогорова для элементов наилучшего приближения (теорема 5.2)
min [F (а, х) — f (х)] [F (а, х) — F (Ь, х)]	0.
Поэтому имеется по крайней мере одна точка х е Еа, для которой
F {a, x) — F(b, х) = 0,
и таких точек не более г = d(a), так как иначе F(a) =s ss F(b). Множество всех таких точек х обозначим через {хь .хг} и дополним его в случае необходимости различными точками Хг+1, .... Xd(6) е В. По лемме 6.1 найдется h е R", для которого
п
i-i 1
при &=1, .d(b), причем
п
-[F(a, xk)-f(xk)]Xh/^-(b, xk)>0,	Л=1.г.
/=i	1
Тогда при достаточно малых t b-\~t • Ле А, и
[F (a, xk) - f (х*)] [F (b, Xk)-F(b + t-h, x*)J > 0,
где F(b,xk) = F(a,Xk) для k = 1..............г (теорема 4.6).
Поэтому существует открытое множество U, содер-
жащее {Х1, . . . , Хг), для которого
[F (а, х) - f (х)] [F (а, х) - F (b +1 • Л, х)] > 0 (6.2) для всех х е U.
Если Еа S U, то это противоречит необходимости общего условия Колмогорова для элементов наилучшего приближения.
В противном случае Еа \ U компактно и
[F (а, х) - f (х)1 {F (а, х) - F (Л, х)] > 0	(6.3)
для всех х е Еа \ U.
6. Единственность
99
Согласно теореме 4.6 отображение a—+F(а) дифференцируемо в смысле Фреше на Ао = Л, откуда легко следует, что
|| F (a) — F (с) || е, если || а — с ||2	6 (а, в)
(II-Иг — евклидова норма в R").
Поэтому для достаточно малых t > 0 из (6.3) имеем
[F (а, х) - f (x)][F (а, х) - F (b +t • /г, х)] > О
для всех х е Еа \ U, а согласно (6.2) и для всех х е Еа, что снова противоречит необходимости общего условия Колмогорова для элементов наилучшего приближения. □
Замечание. При доказательстве теоремы 6.3 вместо того, чтобы считать множество А открытым, достаточно сделать более слабое предположение, что для всех а е А и ft е Rn существует tQ > 0, для которого а + t*h^A при всех /е[0,/0]. Это потребуется далее при доказательстве теоремы 6.5. Теорему единственности, подобную теореме 6.3, доказал также Мейнардус [1964] (см. также Мейнардус и Шведт [1964]).
В. Частные случаи, а) Линейное приближение п
А = До = R“, Р (fl) = 2^ ^/;
при этом будем считать, что ..., wn^C(B) линейно независимы.
W = F(A) является n-мерным линейным подпространством С (В). Если {o>i, ..., wn}— система Чебышева на В, то F удовлетворяет локальному условию Хаара (т. е. d(a) = п для всех аеЛ) и условию о нулях при N(a) = п для всех аеЛ. Поскольку F удовлетворяет также условию о знаках на А (согласно П.5.С), то все предположения теоремы 6.3 выполнены, если {шь ..., wn} — система Чебышева.
4*
100
IL Нелинейное чебышевское приближение
Ь) Общее рациональное приближение Я0, • • • , Vq, ..., vs	С (В),
«(«)=£ «/«/. у (Ь) = £ bkvk,
/=0	fc=3
Ао= {(a, b) е= Rr+l X Rs+1 | v (b) > 0 на В},
4>“-НгЬ
для каждого (a, b) е Ао V(a, b) — пространство, натянутое на систему
f up	ur vou (a)	vsu (а) |
I s(J) ’ ” о (b) ’ v (b)2 ’ ' ’ ” у (t>)2 ) ’	' • '
и d (a, b) = dim V(a,b) n = r + s + 2.
Пусть A — произвольное непустое подмножество Ao.
Согласно II. 5.C отображение F удовлетворяет на А условию представимости, а поэтому и условию о знаках. По лемме 6.2 отображение F удовлетворяет на А условию о нулях при А(а, b) = d(a, b), (а, Ь) е А, если F на А удовлетворяет локальному условию Хаара. Это имеет место в важном частном случае обыкновенного рационального приближения. А именно, справедлива следующая лемма (см. Чени [1966]).
Лемма 6.4. Пусть В = [a, Р], a <. р,
«;(х) = х/,	/ = 0, ..., г, vft(x) = x\ k — 0, .... s.
Тогда, если при некотором (й, б)^А многочлены и — = и (&) и v — взаимно просты, то
d(&, 6) = 1 + max {г + deg v (b), s + deg и (d)},
причем при P = 0 следует считать deg P = —оо. Кроме того, всякая функция из V (d, 8) либо имеет не более d(d,6)—1 нулей, либо обращается в нуль тождественно.
Доказательство. Очевидно, достаточно заменить JZ(d, б) линейным подпространством
U + F(d, b)V = {u(a) + F(d, S)v(6)|a«=Rf+l, b e Rs+1} пространства C(B) и для него доказать утверждение леммы. Положим
£ = dim(t/ + F(d, h) V).
6. Единственность
101
Если F(&, ti) = 0, то и (а) = 0 и в силу взаимной простоты и и v, v(6) = 1. Таким образом, k = dimU = r + 1 = I + max {г + deg v (b), s4-deg«(d)}. Пусть F (а, 6) ^0. Тогда
k = dim (U) + dim (F (d, b) V}- dim (t/f| F(&, b)V), причем ’ dim ((/) = r + 1, a dim(F(d, ^)V) = s+l- Кроме того, F (d, b)-v(b)^U тогда и только тогда, когда v(b) = v(b)-Q при degQ — deg и (d).
Так как deg v (b) < s, to deg Q < s — deg v (b). Отсюда следует, что
dim (U П F (d, b) V) = 1 + min {r — deg и (d), s — deg v (o)} и
k = r + s + 1 — min {r — deg и (d), s — deg v (b)} = = 1 4- max {r + deg v (b), s + deg и (d)}.
Предположим теперь, что и (a) + F(d,6)v(b) имеет на [а, р] по крайней мере k нулей; тогда и и(а}о(б) 4-+ u(a)v(b) также имеет по крайней мере k нулей. Однако
deg [и (a) v (Ь) 4- и (d) о (&)} <
< max {г 4- deg v (b), s 4- deg и (d)} = k — 1, а поэтому u(a)v(6) + «(d)u(ft) = 0. □
Предположим, что рассмотренное выше подмножество А множества Ао имеет вид А = {(а, Ь)е Rr+1 X X Rs+11 v (b) > 0 на [а, р]; и (а) и v(b) взаимно просты}.
Тогда справедлива
Т е о р е. м а 6.5. В случае обыкновенного рационального приближения для каждого	и W=F(A)
существует не более одного элемента наилучшего приближения
F (a, b) = (u(a)/v(b)).
Доказательство. Множество А обладает следующим свойством:
(a, b)e=A, (hu ft2)eRr+lXRs+1=Ha + /Ai, H/WeA
102
77. Нелинейное чебышевское приближение
при достаточно малых t > 0, а этого достаточно для доказательства теоремы 6.3 (см. замечание к этой теореме). Из теоремы 6.3 и леммы 6.4 вытекает теорема 6.5. □
с) Обыкновенное нелинейное рациональное приближение
В = [а, р], а < р,
Л = Л0-{(а, 6)^RrXRrl6i<62< ... <М, г
F (а, Ь, х) = У, aiebl*- Обозначим через k(a,b) число отличных от нуля коэффициентов а,. Тогда
{Г	k(a, b)
У, hilebix + У It', а, хе lk* —
j~l 1	k~l ’к 'к
— У (h'j + /г2а;х) ebix | hl, й2 <= Rr j,
где ajk =# 0 для k = 1, ..., k (a, b).
Очевидно,
d(a, b) = dim V(a, b) — r-}-k(a, b).
По поводу следующей леммы см. Полна и Сеге [1956], стр. 60 (а также Мейнардус [1964] и Райс [1962]).
Лемма 6.6. Пусть задана общая экспоненциальная сумма
H(x)=f,Pl(x)ehix, b^R, /=|
my
с различными bi, где Р](х)—У a!kxk,	при
fe=0
s
j = 1, ..., s. Если положить N= У (m/+l), где mj=—l / — 1
при = то H имеет не более N — 1 действительных нулей, если только не все Pj тождественно равны нулю.
Доказательство проведем по индукции. При s = 1 утверждение теоремы справедливо. Поэтому предположим, что s > 1, и пусть утверждение теоремы
6. Единственность
103
верно для случая, когда Н(х) имеет вид
£pt(x)ebix (г=1........s-1).
/=1
Рассмотрим сумму
//(*)= ХрДх) *4 /=1
где без ограничения общности будем считать все Pj Ф 0. Пусть z — число действительных нулей Н. Положим
ж+1
dx s
Если Zi — число нулей Hlt то по теореме Ролля
Zi z — ms — 1.
Поэтому
Ё Qi(x)e^rbs)xt Где degQ^m,, j= 1, ..., s — 1. Согласно индукционному предположению
s—1
Zl<jS(W/+ 1)— 1, т. е.
Z< X (Щ/+ 1)— 1 =#— 1. □ /=1
Теорема 6.7. В случае обыкновенного нелинейного экспоненциального приближения отображение Р: AQ->C(B) удовлетворяет на В локальному условию Хаара и условию о нулях при N(a,b) = d(a,b) для всех (а, Ь) А.
Доказательство. Всякий элемент из V(a,b) имеет вид
Н(х) = g pi (x)ebix, где
( h\: е R	при а, = 0,
Р =<
1	| h\ 4- h2sa .х при а. ф 0.
104
II. Нелинейное чебышевское приближение
По лемме 6.6 либо Н имеет не более
k (a, b) + г — 1 — d (a, b) — 1 нулей, либо оно равно нулю тождественно.
В то же время при каждом (а, Ь) е А разность
F (а, Ь, х) — F (а, Ь, х) — У a;ebix — У dje^'x /=i	/=1
по лемме 6.6 имеет на В не более
k (а, b)-\~ г — \ = d(a, b) — 1 нулей. □
Так как согласно теореме 7.5 отображение F: Ао-> С (В) удовлетворяет на А условию о знаках, то все условия теоремы 6.3 выполнены и имеет место
Теорема 6.8. В случае обыкновенного нелинейного экспоненциального приближения для каждого С (В) в W = F(A) имеется не более одного элемента наилучшего приближения.
С. Необходимое условие единственности. Приведем сначала общее необходимое условие, принадлежащее Брозовскому [1967], в котором на отображение F: А->С(В) не налагается никаких специальных условий.
Теорема 6.9. Если для всякого f^C(B) в W — — F(А) имеется не более одного элемента наилучшего приближения, то выполняется следующее условие-.
пусть D — непустое замкнутое подмножество В, г-. О-Н+1,-1} — непрерывная функция и для некоторого а е Л
min в (х) (F (а, х) — F (6, х)]	0	(6.5)
x^D
для всех b А; тогда имеет место следующая импликация-. из F(a,x) =F(c,x) для всех x^D следует F(a) = ^F(c).
Доказательство. Пусть заданы D, 8 и а^А такие, что (6.5) выполняется для всех b А. Пусть, далее, существует такое сеА, что
F (a, x) = F{c, х) для всех x^D, но F (а) F (с).
6. Единственность
105
Как и при доказательстве теоремы 5.3, можно показать, что существует функция <р е С (В), для которой
<р(х) = е(х) при x&D,
| <р (х) | < 1 при х ф D.
Если положить М (х) — F (а, х) — F (с, х) и g(x) = = ф(х){|| Л1|| — |М (х)|}, то l|gll = l|Af||>0.
Кроме того, полагая f = F (а) — g, получим (см. (5.2))
g=F(a) — f и D = Ea.
Далее согласно (6.5)
min [F (а, х) — f (х)] [F (а, х) — F (&, х)]	0
для всех Ь^А, и по теореме 2.4 F(a) является элементом наилучшего приближения для f в W = F(A). Но в то же время для всех х е В
\F(cy x)-f(x)|<|F(c, x)-F(a, х)| + |В(а, x)-f(x)|<
<|M(x)l + ||Af||-|M(x)| = ||M|| = HI| = ||F(a)-f||t
Таким образом, F(c) также является элементом наилучшего приближения для f в W = F(A), и F(c) ^F(a), что противоречит предположенной единственности элемента наилучшего приближения.
Согласно Крабсу [1970] справедлива
Теорема 6.10. Пусть отображение F: А0-+С(В) удовлетворяет условию о знаках на А (определение 5.1). Тогда, если для всякого f^C(B) имеется не более одного элемента наилучшего приближения в W = F(A), то F удовлетворяет условию о нулях при N (а) — = d(a) 4- 1 для каждого а е А (определение 6.3).
Д оказательство. Пусть задана пара (а, Ь) е е А X Л, для которой
F (я, Xt) — F (b, Xi) = 0 при i = 1, ..., d (а) + 1,
где хь х^(а)+1 — различные точки из В. Предположим, без ограничения общности, что система (dF/dai) (а), .(dF/da^ay) (а) образует базис в V{a).
106
IL Нелинейное чебышевское приближение
Однородная линейная система уравнений
d(a)+ 1
X c^(a’Xi)=0)	•••’d(a)’ (6-6)
i = l	1
имеет нетривиальное решение (сь crf(a)+1). Пусть
D = {Xi | Ci 0}; положим для каждого Xi e D e (xf) = sign ct.
Равенства (6.6) справедливы для всех линейных комбинаций функций
dF , ч	dF . .
да, • • • ’ dad (а)
и поэтому имеют место для всех / = 1, ..., п; умножая /-е уравнение на hj и складывая после этого все уравнения, получим для всех h = (hi, ..., hn) е R":
п
Yj 1С/1е(Х/)£Й/-|г(а> Xi) = 0-
x^D	/=1	7
Отсюда следует
п
min е(хг)У'Л/д— (а, хг)<0
xt^D	j^i /
для всех h= (hi, ..., hn) е Rn. Если бы при некотором с е А было
(6.7)
min — е (х^ [F (a, xt) — F (с, xj] > 0,	(6.8)
xi^D
то в силу условия о знаках нашелся бы элемент h^T(a) (Т(а) —касательный конус к А в а), для которого
п
min [F (с, xi) — F(a, xj] h,-^-(a, xj > 0.
/-1 1
Отсюда и из (6.8) следовало бы	*jr
п
min е (xz) У hj-j- (а, х() > 0,
xi^D fZi 1
что противоречит (6.7).
6 Единственность
107
Таким образом,
min — е (хг) [F (a, xt) — F (с, xz)] 0
при всех с^А, что согласно теореме 6.9 влечет F(a) = F(b). Итак, всякая разность F(a) —F(b) 0 имеет не более d(a) нулей. □
В связи с теоремами 6.3 и 6.10 возникает вопрос, можно ли вывести и локальное условие Хаара из единственности элемента наилучшего приближения для всякого f (когда он существует), если предположить, что отображение удовлетворяет условию о знаках. Этот вопрос еще открыт. Частичным результатом в этом направлении является следующая теорема, в которой условие, что А открыто, заменено несколько более слабым условием, которое в то же время достаточно для доказательства теоремы 6.3 (см. заключительное замечание к теореме 6.3 и доказательство теоремы 6.5). Кроме того, в этой теореме отображение F: А0^С(В) удовлетворяет специальному условию представимости (которое обеспечивает выполнение условия о знаках).
Теорема 6.11. Пусть А обладает свойством:
а^А, h^^n=>aA-th^A
при достаточно малых t =	а отображение
F: А0-+С(В) на А удовлетворяет следующему условию представимости: для любой пары (а,Ь) е Л X Л найдется положительная функция q(a,b) е С (В), для которой
п
F(a)-F (b) = <р (a, b) £ (а, - bt) (а).	(6.9)
/=1 1
Тогда, если для всякого f^C(B) в W = F(A) существует не более одного элемента наилучшего приближения, то F удовлетворяет локальному условию Хаара на А.
Доказательство. Пусть задан а е А. Предположим без ограничения общности, что система
dF . .	dF . ,
dai	dad(a)
108
IL Нелинейное чебышевское приближение
линейно независима. Допустим, что существуют d(a) I различных точек Xi, ..., х^ау е В, для которых матрица |
х<))г’>/=1.....*
— особенная, т. е. ее определитель равен нулю. Тогда найдутся числа Ci, ..., Cd(ay е R, одновременно не рав-ные нулю, для которых
d(a)
x^==Q при
f=l J
и, следовательно, и для / = 1, ..., п.
Положим е(х/) = sign с/, если а =/= 0, и
D = {Xi I С( =0: 0}.
Тогда для всех й е R” имеем
2 । ct । ® (xi) У, h/-^-(a' xi)=°> x^D	/=1	1
а поэтому (см. импликацию (6.6)	(6.7) при доказа-
тельстве теоремы (6.10))
п
min	xz)^0 при всех fteR'1.
xisD	I
Поэтому в силу (6.9)
min е (хг) [F (а, хг) — F (b, хг)] 0 при всех Ь^А.
X^D
Согласно нашему допущению найдется h <= Rd(a) (h ф нулевому вектору), для которого
d(a)
= Z=l, d(a),	(6.10)
/-1 z
причем
d(a)
/=1 z
1
7. Приближение на действительном отрезке
109
Дополним h, если нужно, нулевыми компонентами до вектора h е R". Тогда для достаточно малых t > 0
c = a-\-th^A,
и согласно (6.9)
П
f (а) — F (с) = — /<р (а, с) У fij (а),
/=1 1
что на основании (6.10) влечет
F (a, Xi) — F(c, хг) = 0 для всех xfeD.
Но отсюда согласно теореме 6.9 вытекает, что F(a) —F(c) s= 0. Это противоречит условию
п
Замечание. Теорема 6.11, очевидно, применима к случаю линейного приближения и вместе с теоремой 6.3 приводит к следующей теореме.
Теорема единственности Хаара [1918]. Для всякого f е С (В) элемент наилучшего приближения в W — F(А) является единственным тогда и только тогда, когда W удовлетворяет условию Хаара, т. е. когда каждый элемент w W, w Ф 0, имеет не более (dim W) — 1 нулей на В.
Как уже отмечалось в II. 6.А, по теореме Мерхьюбе-ра [1956] условие Хаара может быть реализовано только на таких множествах В, которые допускают обратимое однозначное и непрерывное отображение на замкнутые подмножества окружности. Отсюда следует, что для функций нескольких переменных теорема единственности Хаара имеет лишь ограниченное значение, например, для функций, заданных на одномерных кусках кривых или на конечных множествах.
7. Приближение на действительном отрезке
В этом разделе рассматривается следующая ситуация. Пусть В= [а, Р], а<Р действительны, а С (В) — пространство непрерывных на В действительных
но
И. Нелинейное чебышевское приближение
функций, наделенное максимум-нормой (1.1). Далее, пусть А непустое подмножество R", a F: А-^С(В) — заданное отображение. В этом случае утверждения, доказанные в разделах 2, 4, 5 и 6 об элементах наилучшего приближения в W = F(A) для f е С(В), могут быть существенно уточнены, что и делается ниже.
А. Нижние границы для наилучшего приближения и достаточное условие для элементов наилучшего приближения.
Теорема 7.1. Пусть отображение F удовлетворяет на А условию о нулях (определение 6.3). Далее, пусть для заданного а^А существуют m = N(d) 4- 1 точек Хь ..., хт е [а, Р], таких, что
а<Х!<х2< ... <хт<р,	(7.1)
min | F(d, Xt) — f (xj | > 0	(7.2)
/«=» 1, ...» m
U
F (й, xt) - f (xt) = e (- 1)' | F (d, xt) - f (xt) I, (7.3)
i=l, m, где e== + l или —1. Тогда
min | F (й, xt)-f (x{) |Cp (f, W) = inf || F (a) - f ||. (7.4) ..., m	ae=A
Доказательство. На основании импликации (2.15)	(2.16) (см. п. II. 2.С) достаточно показать, что
для всякого а е А
т(а)= min [F(d, xt) - f (xt)][F (a, Xi)-F(a, xt)]^0. Z=l, ...» m
Если бы для некоторого Ь^А было т(&)>0, то согласно (7.3) разность F(d) —F(b) по крайней мере в m — = N(&) + 1 различных следующих друг за другом точках принимала бы значения с чередующимися знаками, а следовательно, обращалась бы в нуль в Af(d) различных точках, что противоречило бы условию о нулях.
Теорема 7.1 обобщает соответствующую теорему Валле Пуссена *) [1919] для случая приближения много*'
♦) Шарль Валле Пуссен, род. 14.8.1866 г., учился в Лувене (Бельгия), где стал профессором в 1893 г. Ему принадлежат основополагающие работы в теории рядов Фурье, теории приближений и теории чисел (распределение простых чисел). Умер 2.3.1962 г.
7 П риближение на действительном отрезке
111
членами и теорему Ахиезера [1965] для случая обычного рационального приближения. Она непосредственно приводит к следующему достаточному условию для элементов наи’лучшего приближения.
Теорема 7.2. Пусть отображение F удовлетворяет на А условию о нулях (определение 6.3). Далее, пусть для заданного а^А существуют m = N(a) + 1 точек хь ..., Хщ е [а, р], удовлетворяющих неравенствам (7.1) и
F (d, Xl) - f (х^ = e (- l)z || F (d) - f II, (7.5) i — 1, ..., m, где e = 4-1 или —1. Тогда F(a) является элементом наилучшего приближения для f в W = F(A).
Доказательство. Если || F(d) — f || = 0, то доказывать нечего. Поэтому пусть || F(d) —f || >• 0. Тогда из (7.4) и (7.5) согласно теореме 7.1 следует
l|F(d)-f||<p(A W)^\\F(d)-f\\ = p(f, W). □
В. Необходимые условия для элементов наилучшего приближения. Для дальнейшего нам потребуется одна лемма (см. Чени [1966], стр. 74, 75).
Пусть V — линейное n-мерное подпространство пространства С (В), а {щ, ...,	— базис V (В может
быть произвольным метрическим пространством, состоящим по крайней мере из п + 1 точки).
Лемма 7.3. Пусть V удовлетворяет условию Хаара (определение 6.1). Далее, пусть заданы m п + 1 различных точек Xi, ...,xm^B. Тогда, если существует нетривиальное решение (сь ..., cm) системы
V, (xi) Ci — 0, j = 1, ..., n,	(7.6)
i-1
to m = n-\-\, a Ct^O при всех 1=1.....m.
Если В = [a, p], a < 0 и имеют место неравенства (7.1) Ц Xi < х2 < ... < xm Р, то
sign Ci = е(— 1)‘, i = 1, ..., tn, где е= 4- 1 или — 1.
(7.7)
Доказательство. Если бы было пг <_ п + 1 или Ci = 0 при некотором I, то в случае необходимости мы
112
II. Нелинейное чебышевское приближение
дополнили бы множество {*/: G =И= 0} до п-точечного множества из В. Полагая с/ = 0 для добавленных точек X/, мы получили бы систему (7.6) при т — п с нетривиальным решением (ci, сп), что согласно лемме 6.1 противоречит условию Хаара.
Пусть (7.1) имеет место при т = п + 1. Тогда согласно лемме 6.1 найдется v е V, для которого у(хД = 0 при всех t=/=t0 и i‘o+ 1 (to + 1 m, t0 фиксировано) и =%*о^(х;о+1) =%+i^0- Из (7.6) сле-
дует
0= £ у(х/)с, = с, 4-v,+1с. ...	(7.8)
\ t/ I to to h+1 to +1
Очевидно, v.q и v.q+1 имеют одинаковые знаки, так как иначе v имело бы п различных нулей. Но тогда из (7.8) следует, что с.о и с.о+1 имеют различные знаки. □
Далее будем считать, что F определено на открытом множестве До, содержащем Д, и удовлетворяет условию дифференцируемости (определение 4.2). Кроме того, пусть А обладает следующим свойством:
аеД, h е Rrt=>a + th <= Д, если t — t(h)>Q (7.9)
достаточно мало.
Тогда если задан а е Д, то для касательного конуса Т(а) (см. п. II.4.A) имеем Т(а) = Rn.
Действительно, если задан h е R", то согласно (7.9) найдется последовательность {tk} положительных чисел, для которых
#£ = a Д- tkh £= Д,
lim ||	— а||2 = 0, lim I -т~(^ — а) — /г| =0,
&->оо	й->оо II	Ц2
где II ДЬ обозначает евклидову норму в R". Всякому а е Д сопоставим снова множество
Ea = {x<=B\\F(a, х) - f (х) | = || F (а) - f ||} (7.10) экстремальных точек разности F(a) — f. Тогда справедлива.
Теорема 7.4. Пусть отображение F: Д0->С(В) удовлетворяет на А локальному условию Хаара (определение 6.2). Тогда если F(a), (а^А),— элемент наи*
7. Приближение на -действительном отрезке
ИЗ
лучшего приближения для f С (В) в W = В (А), то существует m = d(a)-f-l различных точек xh ..., xm е Ed, удовлетворяющих условиям (7.1) и (7.5).
Доказательство. Согласно теореме 4.8
min ([F(d, х) — /(*)] У ht-^~ (d, х) 1<0 / /
при всех h^T(d) = Rn (см. выше).
( dF	dF	г
Если —(а),...,	—(а) J — базис пространства
(	п	'I
V(d)^<F'&(h) = '£hl-^-(d)\h^Rn\	(7.11)
<•	/=i	1	'
(т. е. k = d (d) — dim V (d)), то
min f[F (d, x) — f (x)] У hj-^-(d, х)^<0 fz i /
при всех h e R*.
Если || F(a)—f || = 0, то утверждение теоремы тривиально. Поэтому пусть И F(a) —f || > 0. Положим
Kd = {k(x) =
— [F(d, х) — f (x)](-^-(d, х), ..-^-(d, x)|xeEd). x 1	k	)
Тогда Ka — компактное подмножество R*, так как Ed компактное подмножество В, a x-+k(x) непрерывное отображение В в R* (см. теорему 1.4 главы VII). Обозначим через Kd выпуклую оболочку Н (К&).
Тогда согласно теореме 2.2 главы VII 0* е Н (К&), где 0fe — нулевой вектор пространства R*. Поэтому по теореме Каратеодори *) (см. главу VII) существуют
*) Константин Каратеодори, род. 13.9. 1873 г. в Берлине, работал сначала военным инженером; в 1904 г. получил ученую степень? затем его деятельность протекала в Гёттингене, Берлине, Смирне, Афинах и Мюнхене. Ему принадлежат основополагающие работы в вариационном исчислении, дифференциальных уравнениях с частными производными, теории функций действительного и комплексного переменного, механике, геометрической оптике, термодинамике. Умер 2. 2. 1950 г.
114
II. H елинейное чебышевское приближение
т k + 1 различных точек хт^Еа, для которых т
У~дТ. х«)ct ~..............
i-1	1
причем Ci — lF(a, х() — f (х,)] • A.i(	при
т
i= 1, ..., m, а Л/ = 1.
/=|
Отсюда на основании леммы 7.3 следует т =k + 1, а также Ci =И= 0 при i — 1, ..., т. Если расположить точки Xi, ..., е Ей согласно (7.1), то, кроме того, получим
singfz = e(—- 1)\ z = 1, ..т,
где е = +1 или —1. □
Замечание. Теорема 7.4 без утверждения (7.5) для задачи линейного приближения была получена еще Юнгом [1907], а тем самым была доказана достаточность условия Хаара для единственности. В частности, из теоремы 7.4 следует, что при всяком	каж-
дое множество экстремальных точек Еа (см. (7.10)), соответствующее элементу наилучшего приближения F(a) для f в W = F(A), состоит по крайней мере из d(a) 4- 1 точек, если отображение F: Ао-> С (В) удовлетворяет на А локальному условию Хаара.
Если F удовлетворяет на А условию о знаках (определение 5.1), то это утверждение обратимо, что здесь доказываться не будет. По поводу доказательства см. Крабе [1970]. Если утверждение (7.5) назвать альтернантом функции погрешности F(d) —то из теорем 7.2 и 7.4 вытекает
Альтернансный критерий. Пусть отображение F: Aq-^C(B) удовлетворяет на А локальному условию Хаара и условию о нулях при N(a) = d(a) для всех а<=А (определения 6.2 и 6.3).	ТР
Утверждение. Элемент F(a), а е А, является элементом наилучшего приближения для f е С (В) тогда и только тогда, когда существуют m = d(a) + 1 точек xi, хт<=Еа (см. (7.10)), для которых имеет место (7.1) и (7.5).
7. Приближение на действительном отрезке *	115
Согласно II. 6.В альтернансный критерий для элементов наилучшего приближения имеет место, например, в случае -приближения многочленами, обыкновенного рационального приближения и обыкновенного нелинейного экспоненциального приближения.
С. Единственность элементов наилучшего приближения.
Теорема 7.5. Пусть F:A0-*-C(B) удовлетворяет на А локальному условию Хаара и условию о нулях при N(a) = d(a) для всех а^А. Тогда F удовлетворяет условию о знаках на А (определение 5.1).
Доказательство. Пусть D — непустое замкнутее подмножество из В = [а, р], причем для пары (a, b) е А X А справедливо неравенство
min|F(a, x) — F(b, х) | > О, x^D
в то время как
п
min[F(&, x) — F(a, х)] У hj-^-(a, х)<0 x^D	J
при всех h <= Т (а) = R". dF	dF
Если -^-(а), •••>	(а) — базис пространства V (а) (см.
(7.11)), т.е. fe = d(a) = dim V(а)), то
к
min[F(a, х) — F(Ь, х)] У h}(а, х)<0 x<=D	“ °aj
при всех h е Rn. Точно таким же образом, как и при доказательстве теоремы 7.4, отсюда вытекает существование m — k + 1 точек Xi е £>, а С! < х2 < ... < хт
Р, для которых
sing [F (а, xz) — F(b, xz)] = e(—1/,
i = 1, ..., m, где e = +1 или —1. Но отсюда следует, что разность F(a)—F(b) имеет по крайней мере k — ~d(a) нулей на [а, р], что противоречит условию о нулях. □
Из теоремы 6.3 и замечания к ней, а также из теоремы 7.5 вытекает
116
11. Нелинейное чебышевское приближение
Теорема единственности. Пусть отображение F: Л0->С(В) удовлетворяет на А локальному условию Хаара и условию о нулях при N (a) = d(a) для всех а^А. Тогда для всякого С (В) существует не более одного элемента наилучшего приближения в W = F(A).
Заключение. Для случая, когда В — компактный действительный отрезок, а А удовлетворяет условию (7.9), имеют место следующие логические соотношения:
локальное условие Хаара + условие о нулях при N (а) = d (а) для всех а е А
|| [теорема 7.5, 6.3 и
4 альтернансный критерий] единственность + условие о знаках + условие
л	альтернанса (7.5)
[теорема (6.10)] I! '-----------г.------------
условие о нулях	[см. Крабе [1970]]
при N (а) = d (а) + 1 локальное для всех а^А условие Хаара
8.	Непрерывность Т-операторов
А.	Постановка задачи. Как и в ПЛ, начнем с формулировки Т-задачи.
Итак, пусть В — компактное метрическое пространство, а С(В)—пространство непрерывных на В, действительных или комплексных функций, наделенное макси-мум-нормой (1.1). Пусть для заданного непустого множества W пространства С (В) и заданной функции fe еС(В) наилучшее приближение p(f, W) определено формулой (1.2).
Так как С (В) нормированное, а тем самым и метрическое пространство (см. главу VII), то по теореме 1.5 главы VII отображение >р(Д^) пространства С (В) в R непрерывно, т. е. имеет место импликация
Пт (Ил-Л| = °, fn,
=^Птр(/„,	=	W).	t8J)
n>oo
8. Непрерывность Т-операторов
1L7
Теперь предположим, что для всякого /еС(В) существует ровно один элемент наилучшего приближения w е W, для которого
IIw-f|| = р(Л Г).
Тем самым сопоставление f->w = Tf определяет однозначное отображение Т пространства С (В) на W— так называемый оператор Чебышева или, короче, Т-опера-тор *). Как с точки зрения теории, так и с точки зрения вычислительной практики представляет интерес следующий вопрос:
При каких предположениях о W отображение f -+Tf непрерывно, т. е. когда имеет место импликация
Hm ||f„-f|| = O, fn, /ё=С(В)=^ lim||77„-Tf|| = 0?
П->оо	П->оо
(8.2)
В.	Сильная единственность и непрерывность Т-опе-раторов. Положительный ответ на поставленный вопрос можно получить в случае, если Г-оператор обладает так называемым свойством сильной единственности, т. е. если для всякого f^C(B) существуют элемент w е W. и положительное число y = y(f) такие, что
II $ — Л1 + YII $ — II II ю — f II при всех w е W. (8.3)
Так как ||t&—ш||>0 при всех w=/=w, то ||ш—f||< <||о; — f|| при всех w=/=w, т. е. из (8.3) следует, что w — единственный элемент наилучшего приближения для f в W. Тем самым справедлива
Теорема 8.1. (Фройд, см. Чени [1966]). Пусть Т-оператор обладает свойством сильной единственности. Тогда для всякого	существует положительное
число X = X(f) такое, что для любого g С (В)
WTf — Tg\\^K\\f — g\\9	(8.4)
что непосредственно влечет непрерывность оператора 7\
*) Т-оператор называют также метрической проекцией. (Прим, перев.)
118
11. Нелинейное чебышевское приближение
Доказательство. Из (8.3) при w = Tf и w = = Tg следует
y\\Tf — TS\\^\\Tg — f\\ — \\Tf — f\\^
<llf - gll + Hg - g\\ — \\Tf - f||< <llf-gll + ll Tf — g\\ — \\Tf — f\\*^
<11/— gll + llf — gll + ll П — /Ц —1| Tf -f || = 2|| f-g\\.
Тем самым выполняется (8.4) при X = 2/у. □
Теорема 8.2 (см. Ньюман и Шапиро [1963]). Пусть В состоит по крайней мере из п 4- 1 различных точек, а С (В)—пространство непрерывных на В действительных функций. Тогда если W — п-мерное подпространство пространства С (В), удовлетворяющее на В условию Хаара, то Т-оператор обладает свойством сильной единственности (8.3), а поэтому непрерывен.
Доказательство. Пусть задана функция е С(В). Для f W можно выбрать в (8.3) у = 1. Поэтому пусть f ф. W. Тогда по теореме 3.3 в W существует элемент наилучшего приближения w е W для f. Согласно П.5.А элемент w^W характеризуется условием Колмогорова
min [$ (х) — f (х)] w (х) < 0	(8.5)
для всех w^W, где
= U е в 11 W — f (*)I = II ® — HI (> 0)}
(см. (5.6)). Пусть теперь {ze>i, ..., wn} — базис пространства W. Положим
К = {k (х) = [w (х) — f (х)] [о»! (х), .... wn (X)] | X ё= Ew}. Множество Л является компактным подмножеством пространства R", так как компактное подмножество В, а х~>^(х) — непрерывное отображение В в R" (см. теорему 1.4 главы VII). Если выпуклая оболочка множества Jt, то из (8.5) по теореме 2.2 главы VII следует, что 0п^//(Л)(@п—нулевой вектор пространства R'2). Поэтому согласно теореме Каратеодори из VII. 2 найдутся tn (^n+ 1) различных точек xt, xm ее Е&, для которых
Z (xz)Ci = 0, j — 1, ..., п, (8.6) /=i
8. Непрерывность Т-операторов
119
ct = (te> (хг) — f (Xi)) h{, tn
где У, ht =1. Но тогда согласно лемме 7.3 при i=i
/ = 1.....m и m = n-j- 1,
Положим ог, = —signcz, « = 1,	п+1. Тогда
в силу (8.6)
у™ = max otw (xi) > 0 для всех w е W, если w^Q. t-l, ...,n+l
Действительно, сначала из (8.6) имеем
п+1
У w (х() 1 Ci | — 0 для всех w е W, 1 = 1
откуда следует, что yw 0. Однако равенство yw = 0 в силу условия Хаара невозможно, так как из него следовало бы, что w (Xi) — 0 при i = 1, ..., п + 1. Так как отображение w->yw пространства W в R непрерывно (т. е. Wk, w (=W,	— w у 0 => y^^ -> yw^ и так как со-
гласно теореме 1.10 главы VII множество
5 = {дае= W ||| w||=1)
компактно в W, то
у == min у^ > 0.	(8.7)
Пусть теперь задан произвольный элемент w е W. При w = w условие (8.3) имеет место при каждом у > 0. Поэтому пусть а, #= и». Тогда
и существует i е {1, ..., n + 1}, для которого Oiw(xi) у. Отсюда следует
II W — f II > — Oi (w (х{) — f (Xi)) =
= or,- (f (x{) —	(X/)) + Ci (Xj) — w (x,)) >
>11^ — MI + yII^ — t» II-
Если выбрать у согласно (8.7), то будет выполнено
(8.3). □
Сильная единственность Г-оператора при нелинейном приближении, вообще говоря, не имеет места. В случае
120
II. Нелинейное чебышевское приближение
обычного рационального приближения в действительной области, где существование и единственность элементов наилучшего приближения обеспечиваются теоремой 1.2 главы IV и теоремой 6.5 главы II, пример разрывного Т-оператора (а тем самым, не обладающего свойством сильной единственности) построил, например, Чени [1966].
Здесь мы приведем подобный пример. Пусть
W — { w (х) = I Ьъ + Ь\Х > 0 при всех х [0, 1 ]1.
ч	^0 “Г и \Х I	)
Если положить (х) = ~ , х е [0, 1], то wK е W
при всех Л>0 и и\(0)=1.
При X = 0 положим £0о(-к)=—1 для всех хе [0,1].
Рис.II.8.1. Пример разрывного Т-опе-ратора.
Тогда || шх—w0||=2 при всех Z > 0, и при X—>0 wi не сходится равномерно к Wo. Очевидно, при всяком X е [0, 11] существует кусочно-линейная функция fi, для которой разность fi — wK альтернирует в точках х = 0, V2, Уз, 1, т. е. принимает в этих точках максимальные значения с чередующимися знаками (см. рис. II. 8.1, где для некоторого К е [0, 1] график функции wi изображен сплошной линией, а график функции fi — прерывистой). Поэтому согласно альтернансному критерию из П.7.В (достаточно даже теоремы 7.2) и теореме единственности 6.5 wi является элементом наилучшего приближения для fx в W7. Функции fi можно выбрать так, чтобы при Л->0 они сходились равномерно к функции /0 е ^С[0, 1] (на рис. II.8.1 юна изображена тонкой пунктирной линией), для которой элементом наилучшего при-
ближения в W является функция
Wo —1. Таким образом, утверждение о непрерывности (8.2) нарушается.
Приведем следующую теорему, которая обеспечивает
локальную непрерывность, не предполагая существовав
8. Непрерывность Т-операторов
121
ния и единственности элементов наилучшего приближения.
Теорема 8.3. Пусть для заданного f е С (В) существуют у > 0 и w ее W такие, что выполняется неравенство (8.3) при всех w ^W. Кроме того, пусть существует е > 0, для которого множество
V$= {wt=W й||<е}
компактно.
Тогда для каждого С (В) в окрестности uf = {gE c(B)|iig-f IK |eY}
элемента f найдется элемент наилучшего приближения w* s W. для которого
П*-гМ<2у-Ч|£-П	(8.8)
Доказательство. Для каждого §еС(В), очевидно, имеем
(>(.g, inf || да — g||, w^sg
где Sg= {да e IT ||| да — glKIK — g||). Но тогда cor-ласно (8.3) для всякого w e Sg получим
v || W — w IK II w — f II — IK — f IK
< II f — g II + IK — g II — IK — f IK
<llf-gll + IK-gll-IK-/IK
<11/- gll + Ilf - Я11 + II ® -/II -II да -/11 = 211/- g||r откуда ||да —да|К2у~Ч|/ —g||.
Поэтому для всякого g ^Uf отсюда следует s и Sg замкнуто. Таким образом, по теореме 1.1 главы VII Sg компактно, а по теореме 1.8 главы VII найдется w*<=Sg, для которого || да* — gll = Р (g< Ю • Тогда для каждого такого да* имеет место (8.8). □
С. Нормальность и локальная непрерывность Т-оператора. В этом разделе дается достаточное условие, гарантирующее выполнение предположений теоремы 8.3, а тем самым и локальную непрерывность Т-оператора.
122
II. Нелинейное чебышевское приближение
Пусть С (В) — пространство непрерывных на В действительных функций. Далее, пусть U7 = F(A), где А непустое открытое подмножество R", a F: А-> С(В)~ отображение, удовлетворяющее на А условию дифференцируемости (определение 4.2). Тогда по теореме 4.6 F дифференцируемо на А в смысле Фреше, что влечет непрерывность, т. е. из lim Цап — а||2 = 0 (|| • ||2 — евкли-
П->оо
дова норма в R") ап, а е А, следует lim || F (ап) — F (а) ||=
П-»оо = 0.
Кроме того, предположим, что F удовлетворяет на А локальному условию Хаара (определение 6.2) и выполняется условие о нулях при N(a) = d(a), а^А (определение 6.3). При этом для каждого аеЛ: d(a) = = dim У (а), где V(a) — подпространство пространства С (В), натянутое на
Положим
W = maxd(a) «In).	(8.9)
а&А
Лемма 8.4. Пусть задан а*^А u q = d(a*). Далее, пусть Xi, ..., хя^ В — различные точки и
c* = F(a*t xz), /=1, ...» q.
Тогда для всякого достаточно малого е>0 существует б = 6(e) > 0 такое, что уравнения
F(a, Xi) = Ci, /=1, g	(8.10)
при всех Ci, удовлетворяющих условию | — с* | б, i = 1, ..., q, имеют в точности одно решение а = = («i, ..., ап), непрерывно зависящее от ci, причем at = a*, i = q + 1, ..., п
(если предположить без ограничения общности, jito (dF/dai) (а*), ..., (dF/daq) (а*) линейно независимы) и
|| а — а*||2^е, аеА.
Доказательство. Утверждение леммы сразу вытекает из основной теоремы о неявных функциях (см.,
8. Непрерывность Т-оперсторов
123
например, Хестенес [1966], стр. 22, а также Кудрявцев [1970], т. II, стр. 31), примененной к системе уравнений
•••> aq> •••> eq)~
= F(ai....aq, a*+1, .... a*n, x.)-Ci = 0, / = 1, .... q,
так как на основании локального условия Хаара согласно лемме 6.1
х,))(	..^0. □
Лемма 8.5. Если q = d(a*) = N, то для каждого вектора с = (сь ..., сц} найдется не более одной функции F(а)е F(Л), удовлетворяющей равенствам (8.10).
Доказательство. Если (8.10) имеет место для а и а из Л, то разность F(a)—F(a) имеет по крайней мере d(a*) d(a) > d(a)—1 различных нулей и поэтому равна нулю тождественно.
Теорема 8.6. Если при некотором а* е А имеет место равенство d(a*) = N (см. (8.9)), то существует такое 6 > 0, что множество
VF{a*> = {F(a)\a<= А, ||F (а) - F(а*)|| <6} компактно.
Доказательство. Согласно леммам 8.4 и 8.3 существуют е > 0 и б = б(в) такие, что некоторое компактное подмножество множества
{а 11| а - а* || < е} <= А
отображается оператором F на V? (а*). А так как оператор F непрерывен, то согласно теореме 1.4 главы VII множество VF(a*) компактно. □
Определение 8.1. Элемент f^C(B) называется нормальным, ели существует а^А, для которого IIF(а)—f||==p(f, W) и d(a) = N, где N определяется равенством (8.9).
v Цапример, функция feC[0, 1], для которой элементом наилучшего приближения в семействе
^(Л) = {	«ь ьо, и Ьо + Ь1Х>О
ч 4/0 Т и •
при всех х е [0,1]}
124
И. Нелинейное чебышевское приближение
служит некоторая постоянная функция, не является нормальной. Как мы видели выше, в этом случае непрерывность Т-оператора не является обязательной.
В заключение предположим, что В — действительный замкнутый отрезок [а, |3], а < ₽.
Тогда имеет место
Теорема 8.7 (см. Баррар и Лоэв [1970а]). Пусть f^C(B) нормальна. Тогда существуют а<=А и число у > 0 такие, что при всех а^А
IIF (d) - Л1 + YIIР (<*) - F («)11 < IIР (а) - f ||.	(8.3')
Замечание. Из теорем 8.6 и 8.7 вытекает утверждение теоремы 8.3 о локальной непрерывности, если нормальна.
Для доказательства теоремы 8.7 нам потребуется Лемма 8.8. Пусть для f (В)
||F(d)-f|| = p(f, Г)>0 и d(d) = N.
Далее, пусть {ak} — последовательность элементов ak<= А, для которой
lim ||F(a*)-f|| = ||F(d)-f||.	(8.11)
&->оо
Тогда существуют последовательность {dm} элементов dm е А и подпоследовательность последовательности {а*}, для которых
lim || dm — d 112 = 0
и F (aftm) и F (dm) при всех пг, а также d^=-di для г = TV -|- 1, • • •> ti. При этом снова без ограничения общности считается, что система (dF/da^ (d), ..., (dF[daN) (d) линейно независима.
Доказательство. Согласно альтернансному критерию из II. 7.В существуют N + 1 точек Xj е [а, р], для которых
a<Xi<x2< ••• <*у+1<Р	(8112)
и
F(d, Xi)~ f(Xi) = (- l)‘ p||F(d)- f||,
i == 1....M + 1, где p = + 1 или — 1.
8. Непрерывность Т-операторов
125
Из (8.11) следует ограниченность последовательности {|| Л (а*) II}, что влечёт ограниченность всех последовав тельностей
{F(ak, Xj)} при /=1,	#4-1.
Поэтому без ограничения общности можно предположить, что предел
F (х,) = lim F (ak, хг)	(8.13)
fc->oo
существует. Утверждение: справедливо равенство
F(d, Xi) = F(Xi) при z=l, У+1.	(8.14)
Предположим сначала, что (8.14) доказано и зададимся сходящейся к нулю последовательностью {enJ положи-тельных чисел ет. Тогда для достаточно малого е™ со« гласно леммам 8.4 и 8.5 найдется 0, а согласно ра-венствам (8.13) и (8.14) — элемент aktn, для которых
|F(a4 xt)-F(<2, х;)|<бт.
Таким образом, существует в точности одна функция F(am), am^A, для которой
F(am, xt) = F(ak^, хг), i = l, .... #=>
=$• F (d"1) = F (akm) и dT = dh / = #4-1, .... n, причем \\am— й||г^ em. Но это как раз и есть утверждение леммы 8.8. Осталось доказать утверждение (8.14). Прежде всего, при всех i — 1, ..., N + 1 и k имеет место неравенство
||F(a%)-f||>|F(a\
а тем самым на основании (8.11) и (8.13) — неравенство max | F (х{) - f (xz) | < \\F (й) - f ||.	(8.15)
1 < i < /V +1
• Допустим, что для некоторого /ое{1,	N+1}
|F(<I,	(х,.)| = С> 0.	(8.16)
Тогда согласно лемме 8.4 для каждого достаточно малого 8	(0, с/2) существует положительное число
126
II. Нелинейное чебышевское приближение
6 = 6(e) <8 и точно один элемент йЕ/4, для которых F{a, —	%/) + (— 1)7р6 при всех /#=/0	(8.17)
и ||а — й||2	е. Если е достаточно мало, то из непре-.
рывности отображения a-+F(a) следует
||F (a) - F(d)||<c/2.	(8.18)
Кроме того, пусть k выбрано столь большим, что |F(a\x/)-F(x/)|<4(<|), /= 1, .... N+ 1. (8.19)
Из (8.12) и (8.17) следует, что для всех /#= /0 F (a, Xl) - f (xt) = (- 1)' p [|| F (a) - f Щ- 6], откуда с учетом (8.15) и (8.19) имеем I F(a, x/) - f (X1)\>\F(Xj) - f (xj) | + 6 >
>|F(a*, X/)-f(xz)14-6/2. (8.20)
Тем самым F(a, xj) — F(ak, Х/)=И=0 при всех j=£iQ и sign [F (a, Xj) — F (ak, xz)[ =
= sign[F(a, Xj) — f(Xl)] = (— l)'p*). (8.21а)
Рассмотрим следующие случаи. 1. F (d, x/o) — f (x/o)>0.
Тогда из (8.15) и (8.16) следует
и далее из (8.18) и (8.19)
>F^,	- f (я,.) - c/2 = F (x,_) - f (x,_) + c/2 >
>F(a‘.Xl_)-f («,.) - 6/2 + c/2 > F (a', x,t) - f
Тем самым F (a, X/j) — F (a*, Xjjj) > 0.
2. F(&, Xj^ — f (x/o) < 0. Тогда аналогично доказын вается, что
F(«, x,.)-P(a‘, х,_)<0.
*) Для любой пары действительных чисел a, ($ имеет место импликация I a | > | ($ | => sigh a = sign (a — 0).
8. Непрерывность Т-операторов
127
Таким образом, имеем
^ign[F(a, x/o)-F(a\ xj] =
= sign[F(d, */o)~/OJ] = (- l/'p- (8.21b) Но из (8.21a) и (8.21b) следует, что разность F(a)— — F(ak) имеет на [a, p] по крайней мере N различных нулей, что на реновации условия о нулях и максимальности числа N влечет F(a)==F(ak). Это противоречит неравенству (8.20). Таким образом, допущение (8.16) ошибочно и -(8.14) доказано. □
Доказательство теоремы 8.7. Пусть ае А, d(a)=N и Н/Дй) —/||= р(/, №). Если f = F (й), то (8.3) выполняется, например, при у = 1. Поэтому пусть f Ф Ф F (й), т. е. р(/, №)> 0. Положим
1И(а)-л1-ит-л
Y (й>-----\\ F (а) — F (а)	> °)	<8-22>
для каждого аеЛ, для которого F(a)^F(a).
Предположим, что утверждение теоремы ошибочно. Тогда существует последовательность {а*} элементов из А, для которой F(ak)^ F (а) при всех k и
lim у4 = 0, yft = Y(aft)(>0).	(8.23)
k ->оо
Из (8.22) для всех k следует
IIF (ak) - f || = || F (й) - f || + yj| F (ak) - F (Й) ||. (8.24)
Из этого равенства имеем
И(Й) - F(afe)|| — II F(d) - f||<
<И(й) - f 11 + у*И(а*)- /=(<$) ||.
Разделив на || F (й) — F (ак) ||, получим
i < 2||F(d)-f||	.
|| F (&) — F (a*)|| "Г Y*’
Отсюда следует, что последовательность {|| F (а) — ~-F(a*)||} ограничена. Поэтому из (8.23) и (8.24) вытекает
lim ||F(a‘)-fll = ||f(d)-f||.
k~>00
Согласно лемме 8.8 можно, не ограничивая общности,
128
(I. Нелинейное чебышевское приближение
предположить, что a% = di при i = N + 1, п и всех k, и что
lim || ак — <3||2 = 0.
fc->oo
Положим
Е, = {хе[«, ₽]|im x)-f(x)| = ||F(d)-f||}
Н cr (х) = sign (f (х) — F (d, х)) при всех х <= ЕЛ. Тогда из (8.24) для всех k и всех хе£й следует
ук || F (ak) - F (d) || = || F (ак) - f || -1| F (а) - / II >
> о W [f (х) — F (ак, х)] — а (х) [f (х) — F (d, х)] =
— о (х) [F (d, х) — F (ак, х)].	(8.25)
Утверждение. Существует а>0, для которого max cr (х) [F (а, х) — F х)] > а || ak — а ||2	(8.26)
при всех k.
Если бы утверждение (8.26) не имело места, то нашлась бы подпоследовательность последовательности {ak}, которую мы снова обозначим через {а*}, такая, что последовательное™
, ч F(d, х) — F (ak, х)
сходилась бы к пределу ^0.
На основании формулы конечных приращений и, учитывая, что lim || а* — <21|2 = 0, можно предположить, что k ->ОО
при достаточно больших k
max а (х) Гу ~— (ак (х), х)——1 = ak, dai	!!«*- «IhJ
причем ак(х) лежит на отрезке между ак и d. Если по-
ложить с —--------7—, то И с ||2=1 и, не ограничивая
— а*||2
общности, можно считать, что существует с е Ra, для
8. НепрерывностъТ-операторов
129
которого с= lim ck и || с ||2 = 1. Поэтому при &->оо по-k->OQ
лучим
maxaWjc^GJ, х)<0, Z==I i
и, согласно функция
альтернансному критерию (см. II.7.В),
N
1=1	‘
не равная нулю тождественно в силу ||с||2 = 1, имеет по крайней мере W различных нулей, что противоречит локальному условию Хаара.
Таким образом, (8.26) доказано для всех k.
Тем самым, учитывая (8.25), получим
ук || F (ак) - F (а) || > а || ak - d ||2.	(8.27)
Так как ak->a, то на основании формулы конечных приращений для достаточно больших k можно выбрать d >> 0 таким, что
И(а‘) - F(d) ||<d||aft - d||2.
Отсюда и из (8.27) следует
Vfe > - > О
при достаточно больших k, что противоречит (8.23).
D. Примеры, а) Обыкновенное рациональное приближение. В этом случае
F(a, b, х) —
и (а, х) v (Ь, х)
/-о
s	’
У bkxk
k=0
х е [а, р], а < р,
Л = ра, &)eRr+s+2
S	j
У, bkxk > 0 при всех х е [а, р] ?.
к=0	)
5 Л, Коллатц, Б. Крабе
130
//. Нелинейное чебышевское приближение
Согласно II. 4.С и II.6.B все предположения II.8.C выполняются. По лемме 6.4
= 1,
где N определено согласно (8.9), причем d(a,b)=N тогда и только тогда, когда
deg и (а) = г и degv(b) = s.
b) Обыкновенное нелинейное экспоненциальное приближение. В этом случае
F (a, b)= F	6], а < 0,
/=1
Д = {(а, 6)eR2rk <b2< ... <ЬГ}.
Согласно II. 4.С и II.6.B все предположения II.8.C снова выполняются. Кроме того, для N (см. (8.9)) имеем N = = 2г и d(a, b)~N тогда и только тогда, когда й/=/= 0 при / = 1, ..., г.
Замечания. В случае обыкновенного рационального приближения нормальность не только достаточна для локальной непрерывности Г-оператора (как было показано выше), но и необходима. Доказательство этого предложения восходит к работам Мели и Витцгаль [1960], Чени и Лоэб [1964] и X. Вернер [1964] . (см. также [1967]). Распространение этого предложения на случай обобщенного рационального приближения было предпринято в работах: Чени [1965] (см. также [1966]) и Чени и Лоэб [1966].
В случае экспоненциального приближения Шмидт [1968] доказал, что равенство N — 2г не только достаточно, но и необходимо для локальной непрерывности Т-оператора (в смысле теоремы 8.3).
, U - ж
III. H МНОЖЕСТВА
Теоремы альтернанса применимы только к функциям одной независимой переменной. Для функций нескольких независимых переменных вместо множества экстремальных точек возникают Я-множества, соответственно //-множества при одностороннем чебышевском приближении. //-множества часто можно определить также и в нелинейном случае и даже в случаях, когда элемент наилучшего приближения не существует. Они имеют важное значение в практических вычислениях, так как при наличии //-множества удобно применять теорему о двусторонней оценке наилучшего приближения (см. теорему 1.1). Если в этой теореме нижняя и верхняя границы совпадают, то элемент наилучшего приближения найден. Если нижняя и верхняя границы близки друг к Другу, то заключаем, что наилучшее приближение почти достигнуто и что в рассматриваемом функциональном семействе наилучшее приближение не может быть меньше полученной нижней границы. Если эти границы не обеспечивают желаемой точности, то требуется использовать другой (обычно более широкий) класс функций.
1. Я-множества, Ягмножества, Я2-множества
//-множества были введены в II.2.B. Подмножество D (ziB называется Н-множеством для класса приближающих элементов W из С (В), если D является объединением двух непустых множеств D\ и £>2, обладающих свойством: не существует пары w, w е IT, для которой
( >0 при всех x^Dif w (х) — w (х) s л	~
4	( <0 при всех хей2.
(1.1)
5*
132
111. Н-множества
Предполагается, что все встречающиеся в этой главе функции действительны.
Используя //-множества, в II. 2 мы установили оценки (2.13) и (2.14) для наилучших приближений p(f, IF).
Кроме того, из теоремы 2.1 главы II может быть получена следующая удобная в приложениях
Теорема 1.1. Пусть f(x) С(В) и g(x)EW(a,x) — заданные функции. Кроме того, пусть существует множество Н cz В, обладающее следующими свойствами'.
1) погрешность е = g— f отлична от нуля на И;
2) не существует функции ф е W, для которой
e(g —<р)>0 на Н.	(1.2)
Тогда справедлива двусторонняя оценка
inf|8|<p(f, IF)<||8||. н
Доказательство. Если положить
е*(х)=	при любом х<=Н,
И
а (х) = 8* (х) g (х), то согласно предположению для всякой функции ф е W существует точка х для которой
а (х)	8* (х) <р (х),
т. е. выполняется условие (2.1) главы II, если в нем 8* заменить на 8, ф на w и Н на D. Это влечет неравенство (2.2) главы II, а тем самым неравенство
inf | е (х) | = inf {а (х) — е* (х) f (х }< р (f, W). х<=Н	х^Н
Неравенство р(Д lF)^||e|| очевидно. □
Вместо (1.2) можно также потребовать выполнения следующего условия: не существует функции ф е IF, для которой
sign (g — f) = sign (g — <р) на Н. (1.3)
При одностороннем чебышевском приближении функции )(x)eC(fi), например, сверху (для одностороннего чебышевского приближения снизу все последующие рассуждения аналогичны) обозначим через Я? класс «допу-
/. Н-, Hit, Н2тмн&жества
133
стимых функций», т. е. множество функций	для
которых	при всех х^В. Пусть теперь w-^-
допустимая функция; тогда l = w — на В. Далее, пусть Рн (х = 1, k) — точки из В, в которых погрешность равна нулю:
ё (Рх) = О, х = 1, ..., k,
a Qu (р = 1, ...» w)— точки из В, в которых погрешность принимает наибольшее значение:
е (Q ) = max ё (х) = рё, р = 1, ..., т. и х<=В
Теперь можно ввести
Определение. Совокупность точек Рн, Qu образует Н{-множество, если в классе W не существует элемента w, для которого
w (Рх) — w (Рх) > 0,
® (Qg) ~ ® (Qg) < 0.
X = 1, . . . , k, р= 1, ..m.
(1.4)
Справедлива
Теорема 1.2. (Достаточное условие для элементов наилучшего п р и б л и ж е и и я.) Пусть при сделанных предположениях w — допустимая функция для заданной функции f, а точки Рк, образуют Н\-множество. Тогда w — элемент наилучшего одностороннего чебышевского приближения сверху.
Доказательство (от противного). Пусть w не является элементом наилучшего приближения. Тогда существует элемент дающий «лучшее» приближение (существование элементов наилучшего приближения в теореме не предполагается). Соответствующая погрешность 8= w—f неотрицательна на всем В, а верхняя грань ре погрешности ё строго меньше рё; при этом ё*С ^рё < рё на всем В. Тогда для разности
v = е —. § = w (х, av) — w (х, av)	(1.5)
134
111. И-множества
имеем
(х= 1, ..
v(Qg) < 0	(ц= 1, ..т).
(1:6)
Но по определению /Л-множества такой функции v не существует. □
При численной реализации условие (1.3) часто можно заменить несколько более грубыми, но легче проверяемыми условиями.
Определение. Пусть D\ = {Рн} (х=1, ...,£) и D2 — {Qу} (р, = 1, ..., т) — два непустых непересе-кающихся подмножества множества В. Совокупность этих множеств образует Н2-множество для класса приближающих элементов WczC(B), если не существует пары	для которой
{^0 при всех x^D\, < 0 при всех х е О2.
(1.7)
В этом определении аппроксимируемая функция f(x) уже не фигурирует, а всякое //2-множество является одновременно //i-множеством для всякой функции f(x) такой, что найдется функция w е IF, для которой w(x) = = f(x) при всех х Di и w (х) — f (х) = max (w (у) — f (у)) у^В
при всех хеР2. Очевидно, что всякое /72-множество в то же время является //-множеством для того же самого класса приближающих элементов.
Если класс W содержит в качестве параметра аддитивную постоянную «1 и, тем самым, состоит из функций
«» = ai + f(x...... а2, а3.....ар), (1.8)
то задача одностороннего чебышевского приближения эквивалентна обычному чебышевскому приближению. Действительно, если w — решение задачи обычного чебышевского приближения для заданной функции f(x) с наилучшим приближением ро, то w + р0/2 будет решением задачи одностороннего чебышевского приблиШк
2. Линейное приближение
135
ния сверху (и соответственно w — р0/2 будет решением задачи одностороннего чебышевского приближения (Снизу).
2. Линейное приближение
В этом случае для проверки условий (1.1) (соответственно (1.7)) можно использовать алгоритм, подобный методу Гаусса последовательного исключения неизвестных при решении линейных систем уравнений: в линейном случае класс W состоит из линейных комбинаций
р
ш	(*)
V=1
(2.1)
с фиксированными функциями ayv(x)e С (В) и константами av. Всякая разность w — w е IT снова имеет вид (2.1) и требуется проверить, удовлетворяется ли система неравенств
ScOvav^0. v—l,...,k, V=1 р cavav >0,	= £ -(- 1 > • • •» k + т,
V=l
посредством действительных чисел av; при этом полагаем
=®v(P«)	ПРИ <Т=1......k,
Ck+n.v = — wv(Qll) при р = 1,...,т.	' ’
Условия (2.2) можно-привести и к такой форме: требуется выяснить, имеется ли в классе W функция ш, для которой
w(Pa)>0	(o=l,...,k),
MQ^XO (р=1.........т).	1 '
Для проверки условия (1.1) в неравенствах (2.2) (соответственно (2.4)) при о = 1, .... k знак следует заменить на >.
136
III. H-множества
Будем считать, что в (2.2) выписаны только те av, которые действительно появляются, т. е. в каждом столбце матрицы С — (cQV) по крайней мере одно из чисел cov (при фиксированном v) предполагается отличным от нуля. Можно предполагать, что в каждом столбце по крайней мере одно cov > 0, так как в противном случае av можно заменить на —av. Наконец, будем предполагать, что ни в одной строке (т. е. ни при одном о) равенство Cov = 0 не может иметь места при всех о k сразу. Действительно, иначе в случае о k можно опустить соответствующую строку, а в случае о > k неразрешимость системы (2.2) очевидна. Теперь могут встретиться два случая:
Случай 1. В матрице С все элементы cGV 0. Тогда система (2.2) имеет решение av = 1 и точки /\, не образуют ни //-множества, ни /72-множества.
Случай 2. Матрица С имеет отрицательный элемент, например, < 0. Но в первом столбце имеется также положительный элемент, например, cq\ > 0. Тогда неравенства (2.2) можно умножить на положительные числа так, что после сложения коэффициент при «1 будет равен нулю и вместо (2.2) получится новая система неравенств, в которой количество неизвестных и количество неравенств по крайней мере на единицу меньше, чем в системе (2.2). С этой новой системой поступим точно так же, как и с системой (2.2). Продолжая таким образом, уменьшим количество коэффициентов av настолько, насколько это возможно.
Этот процесс оборвется в следующих случаях.
1.	В процессе исключения встретится строка, в которой коэффициенты при всех av равны нулю. Здесь имеются еще две возможности.
а)	Получается противоречие 0 > 0. Тогда точки Рх, образуют //г-множество.
Ь)	Получается неравенство 0^0. Тогда точки Рх, образуют //-множество, так как если в исходных неравенствах всюду знак заменить знаком >, то вместо 0^0 снова получится противоречие 0 > 0.
2.	Получается система неравенств р'
(соответственно >0) сг=1, 2, ..., v=l
3. Примеры' Н-множеств
137
в которых все c'v О и в каждой строке, по крайней мере один элемент c'v > 0; эта система удовлетворяется произвольными положительными числами а'. Но тогда еще нельзя сделать никакого заключения о том, составляют ли заданные точки Н- или //2-множество, а требуется еще проверить, удовлетворяется ли исходная система надлежащими av.
Этот алгоритм не всегда приводит к решению задачи, но все же очень часто подтверждает наличие //-множества или соответственно //2-множества. Подробный пример будет приведен в III. 4.
Часто замечалось, что к отмеченному в случае 2.1 а) противоречию 0 > 0 приходят и тогда, когда в исходных неравенствах (2.2) заменяют знак знаком > и наоборот. Это означает, что если в качестве £>2 взять точки Рк (х = 1, ...,#)> а в качестве Di — точки Qw (ц=1, ..., пг), то также получим //2-множество.
3.	Примеры //-множеств
А. 7-системы. Примеры //-множеств уже даны в П.2.ВЬ): пусть р линейно независимых непрерывных функций кУ](х), ..., wp(x) на отрезке J = [а,Ь} образуют Т-систему, т. е. всякая линейная комбинация w вида (2.1), не равная тождественно нулю, имеет на J не более р— 1 нулей (система Хаара или, согласно П.6.А, однозначно разрешимая система, как в простейшем случае wv(x) = xv~1, v = 1, ..., р); тогда, выбирая в J произвольно р + 1 точек г0 < ?! < ... < zp и объединяя точки ?р с четными р в качестве точек Ра в множество Dit а точки zp с нечетными р в качестве точек Qu в множество D2, мы получим //-множество О = Dili Da-Действительно, функция w, для которой a>(zp)> 0 при нечетных р и ay(zp)<0 при четных р, имеет на / по крайней мере р нулей и поэтому должна тождественно равняться нулю.
Ввиду большого значения Т-систем и их приложений мы сведем в следующую таблицу уже упоминавшиеся и некоторые другие Т-системы (см. П.6.А).
138
///. Н-множества
Некоторые примеры Г-систем &’v(x):
Функции	Замечания	Промежуток
1, X, х2, ..., х^-1	q 1 целое	Произвольный действительный промежуток
/ (х), 1, X, X2, . . ., xq~[	! (,v) <= C« [J], /<<?)+=0 в J	
х^р (х), xvq (х), ц = 1, ...» /; V = 1, . . ., k	Многочлены p (x), q(x) взаимно просты, max [(deg p) — k, (deg q) — j] = 1	
exp (kv х), v = 1, ..., п	kv действительны и попарно различны	
v = 1, ..., п		(0. +00)
1 	г—, v=l, ..., п X ky 1		Произвольный конечный промежуток
cos vx, V = 0, ..., п		[0, л)
cos VX, V = 0, ..., n sin gx, ц — 1, ..., n		[0, 2л)
Система функций {ш¥(х)}, v — 1, 2, 3, ... называется системой Маркова*), если всякий ее «отрезок» {о>ь ..., wm} при любом m образует Т-систему. Из приве* денной выше таблицы сразу получаем примеры систем Маркова, например, wv(x) = xv“1 на всяком действительном промежутке I
*) Андрей Андреевич Марков родился 14.6. 1856 г. Жил и работал в Петербурге, занимался в основном теорией вероятностей. С его именем связаны понятия: цепь Маркова, марковский процесс, распределение Маркова, неравенства Маркова и др. Ему принадлежат также основополагающие работы в области конструктивной теории функций. Умер. 20.7.1922 г.
3. Примеры Н-множеств
139
или
= cos(vx) на промежутке [0, л).
В. Линейные функции. Пусть W— класс аффиннолинейных функций п
W = а0 + 2 avxv.	(3.1)
v=l
Далее, пусть Рь Pk (1 k п)—точки в Rn, а /(+—выпуклая оболочка этих точек. Объединяя точки Ро в множество Db назовем D\ «положительным точечным множеством», поскольку всякая функция w вида (3.1), которая положительна во всех точках Ра, принимает положительные значения на всем К+. Аналогично берется выпуклая оболочка /С_ для точек Qi, ..., Qm Объединим точки в множество D2 и
Рис. III. 3 1 #2-множества для линейных функций на плоскости
Рис HI. 3.2. Яэ-множе-ства для линейных функций в пространстве.
назовем его «отрицательным точечным множеством», поскольку всякая функция w вида (3.1), отрицательная во всех точках отрицательна на К-.
Тогда справедливо следующее утверждение: если выпуклые оболочки /<+ и К- положительного точечного множества (соответственно отрицательного точечного множества) £>2 имеют общую точку Р, то объединение D = D[ U D2 является //-множеством, так как функция w в точке Р не может быть одновременно положительной и отрицательной. Множество D будет даже //2-множеством, так как противоречивы уже неравенства ^(Р)>0 и w(P)<0.
Частные случаи. Плоскость R2, п = 2.\В этом случае /^-множества существуют (см. рис. III. 3.1, где точки Ро обозначены черными кружочками, а точки Qu — светлыми):
140
///. Н-множества
а)	три точки на прямой, из которых две «внешние» точки составляют одно из множеств £>i,£)2, а «внутренняя» точка — другое из этих множеств;
b>	D\ состоит из трех вершин треугольника А, а £)2 — точка внутри А;
с)	пусть V — произвольный выпуклый четырехугольник, Di—пара противолежащих его вершин, а 02 — другая пара вершин.
Пространство R3, п = 3. В этом случае к упомянутым примерам добавляются новые (рис. III. 3.2)
d)	D[ состоит из трех вершин треугольника А, а О2 — из двух точек Qi, Q2, причем соединяющий их отрезок пересекает А.
е)	D{ состоит из четырех вершин тетраэдра, а 02 — из одной внутренней точки Q тетраэдра.
Конфигурации в многомерных пространствах исследованы Тейлором [1972] и Брозовским [1965Ь].
С. Многочлены. Пусть С [/г, л]— класс многочленов п переменных Xi, ..., хп общей степени а W[k/m,n] — класс всех рациональных функций п переменных, у которых числитель принадлежит C[k, и], а знаменатель— С[пг,п], и кроме того, знаменатель положителен во всей рассматриваемой области В. Для проверки условий (1.1) образуем разность двух элементовWj из W [k/m, п\, где Wj = ZjfNj при Z/ <= С [k, л], N}- е С [т, л], на В (/=1,2). Разность — w2 имеет тот же знак, что и многочлен Z\N2— Z2N\, принадлежащий классу C[k + m,n]. Таким образом, решающее значение имеет сумма k-\-m и каждое Н2-множество для класса многочленов С [г, п] является одновременно и Я2-множеством для класса рациональных функций № [k/m, л], если только k + m = г.
D. Многочлены двух независимых переменных. Рассмотрим теперь отдельно случай л = 2 и вместо хЬ) х2 будем писать х, у. Пусть К—связная алгебраическая кривая порядка t= 1 или / = 2 в (х, у)-плоскости. Алгебраическая кривая порядка q либо имеет с К не более tq различных общих точек, либо содержит все точки некоторой ветви К. Теперь на ветви К выберем (tq + 2) точек Pv (v = 1, . ..,/<? +2) и занумеруем их
3. Примеры Н-множеств
141
в том порядке, в котором они располагаются на этой ветви. Пусть Dx состоит из точек Ру с четными v, ай2— из точек Pv с нечетными у. Тогда точки Pv образуют //-множество относительно класса C[q,2]. Действительно, пусть w — многочлен из C[q, 2], причем w > 0 на £>i
Л+ 777=/ к±гп=2
Рис. Ш 3.3. //2-множества при рациональном приближении в случае двух независимых переменных.
и w < 0 на £>2- Тогда в силу непрерывности w на рассматриваемой ветви найдутся по крайней мере tq + 1 точек, в которых w = 0, а следовательно, w должно тождественно равняться нулю на этой ветви. (Если рассматривать и двойные точки, то окажется, что точки Ру образуют даже //2-множество.)
На рис. III. 3.3 представлены различные//-множества Для малых порядков.
142
III. H -множества
Е. Более общие случаи. Принцип, использованный в III. 3.С, часто применяется и в случаях, когда класс W состоит из функций
у
W = Е (Xj,	(3.2)
V=1
где — заданные функции. В разности k
— W2 = Е (*/> 6|iv),	(3*3)
V=1
вообще говоря, можно положить k = 2N и Фдн-v = ФУ при V— 1, ..., N, однако часто можно добиться неравенства k < 2N объединением подходящих членов. Тогда, полагая
ф I	М ПрИ CF=l,...,k,
I — Ov(Qa_A, 6цу) при а = k + 1,.... k + m, мы снова должны проверить, удовлетворяется ли система неравенств
k	s >0, о=1, ..., k,
t > 0, a=k+ I, ...» k + tn
посредством действительных cv, b^y или нет; в последнем случае рассматриваемые точки образуют /^-множество.
Изложенный метод применим и к отношениям выражений вида (3.2) с положительными знаменателями (см., например, (4.3)).
По поводу //-множеств для экспоненциального приближения и рационального экспоненциального приближения см. Коллатц [1965].
4.	Тригонометрическое чебышевское приближение в случае двух переменных
Чебышевское приближение периодических функций одной переменной изучал уже Валле Пуссен [1919]. Этот случай отражен в таблице Т-систем из III. З.А. Здесь мы рассмотрим случай периодических функций f(x,y) двух переменных. Одновременно он будет служить примером применения алгоритма, описанного в III. 2. Пусть В — квадрат 0 jC х 2л, 0 х 2л. Будем рассматри
4. Тригонометрические чебышевские приближения
143
вать либо только функции, значения которых одинаковы в точках, симметричных относительно прямых х — л и у = л, либо только функции, определенные на квадрате О х л, О у л, значения которых продолжаются симметрично относительно прямых х = л, у — л; пусть эти функции требуется приблизить функциями следующего класса W (с параметрами a, bh Cjk)
w = ci + bi cos x + b2 cos у +
+ cos 2x + Ci2 cos x cos у + r22 cos %У-	(4-0
Мы укажем здесь некоторые семейства #2-множеств; для этого выберелМ числа х0, хь х2, #о, У\, Уъ (см. рис. III.3.4,а)), для которых
О < ху < л/2,	/ — 0, 1,2,
о < Уо < (У\ 'и л/2) < у2 < л.
Путем отражения точек (х/, у}) относительно прямой х = л/2 получим шесть точек, три из которых на
Рис. III. 3.4. Н2-множество при тригонометрическом приближении в случае двух независимых переменных.
рис. III. 3.4, а) отмечены светлыми кружочками и составляют множество а остальные три отмечены темными кружочками и составляют множество D2. Разумеется, оси х и у можно поменять местами (см. рис. III.3.4, Ь)). Теперь согласно III. 2 требуется доказать, что ни одна из функций w е W не может быть положительной на 'B'i' и отрицательной на £)2. Алгоритм III. 2 осуществляется с помощью схемы 1.
В строке1 (6) этой схемы единственный отличный от нуля коэффициент cosx0cosz/2 имеет положительный знак, в то время как соответствующий коэффициент в (7), соответственно в (8) (сообразно со знаком cosxj
Схема 1
	Коэффициенты	a	by	b>	Cll	Г.2	^22
№	Операция	1	COS X	cos у	cos 2x	cos xcos у	cos 2y
(1) (2) (3)	Точка х — Xq, у ~ Точка х = л — х0, у — Уъ КО + (2)]	1 —1 0	COS Xq + COS Xq COS Xq	COS yQ — COS yQ 0	cos 2x0 — cos 2x0 0	cos0 x cos yQ + COS X0 cos y0 COS Xq COS yQ	COS 2r/0 — cos 2y0 0
(4)	То же самое для (хь ух)	0	— COS Xi	0	0	— COS X! COS у 1	0
(5)	То же самое для х2, У2	0	COS x2	0	0	COS x2 cos y2	j 0
(6)	(5) cos Xq cos уо — (3) cos х2 cos у 2	0	COS Xq COS X2	0	0	0	0
	COS Уо “ COS у2						
(7)	при cos t/i 0: (3) COS Xi COS у! + (4) COS Xq COS y0 COS #0 —COS#!	0	— COS Xq COS Xi	0	0	0	0
(8)	при cos i/i <0: (4) COS X2 COS у2 + (5) COS Xj COS j/1	0	— COS Xi COS x2	0	0	0	0
	cos у 2 — COS у 1						
III. Н-множества

4. Тригонометрические чебышевские приближения
145
имеет отрицательный знак; неравенства (2.2) приводят к противоречию. Итак, имеет место случай 2.1а) 111.2, поэтому шесть точек образуют //2-множество, а также //-множество.
Исключим пару точек х — х2, у = у2 и х = п — x2t у = у2 и рассмотрим вместо (4.1) класс функций
W = а + cos х + b2 cos у.	(4.2)
Тогда оставшиеся четыре точки (рис. III.3.5,а)) образуют //2-множество для этого класса функций. Это следует из приведенной выше схемы, если рассмотреть лишь
Рис III 3.5. Четырехточечное //2-множество при тригонометрическом приближении.
строки от (1) до (4) и столбцы для 1, cos х, cosy. Действительно, в этом случае коэффициенты при Ь\ в строках (3) и (4) имеют разные знаки, так как cosx0>0, —cos х\ < 0.
Другой пример //-множества образуют четыре точки, расположенные на прямой, параллельной оси х (или оси у);
Di = {(*1, yi), (л — х2, 01)} и D2 = {(%2. 01). (л — Xi, 01)}, где 0 xi < х2 < л/2 (см. рис. III. 3.5b). Действительно, здесь согласно изложенному выше получается схема:
(3) (4)	точка (хь у,), (л —хь yi) точка (х2, yi), (л — х2, ух)	0 0	COS Xi — COS X2	0 0	0 0	COS Xi COS У1 — COS X2 COS у 1	0 0
(5).	(3) cos х2 + (4) cos Xi	0	0	0	0	0	0
145
111, H-множества
Численный пример. Рассмотрим для функции (х, У) = (2 — cos х) 1 — cos у) в классе (4.2) пр^ ближение
w = 2 — cos х — cos у.
Здесь максимальное уклонение достигается в четырех точках (0,0), (0, л), (л, л), (л, 0), причем знаки погрешности e=w—f в этих точках чередуются. Поэтому эти точки можно рассматривать как //-множество, и значит, w является элементом наилучшего приближения.
Схема для класса (4.1) применима и для рационального тригонометрического приближения точно так же как схемы для многочленов в III. З.С приводят к //-множествам и для рациональных функций. Всякое //-множество для класса (4.1), в частности, рассмотренные выше //-множества, являются также //-множествами для класса функций
w — а COS X + cos у	эд
с + d\ cos х + d2 cos у .	' * '
co знаменателями, которые нигде не обращаются в нуль, так как разность W\ —w2 двух таких функций, если не принимать во внимание положительный знаменатель, имеет вид (4.1) (cos2x является линейной комбинацией 1 и cos2x).
5.	Кусочное приближение многочленами (сплайн-аппроксимация)
Рассмотрим сначала простейший случай, когда для функций f(x) одной переменной х на отрезке [а, 6] в качестве класса приближающих элементов (в обозначениях III. З.С) выбирается U?(a, х) = №[/г/0, 1] = C[k, 1], т. ё. функции f(x) приближаются многочленами степени
Если даны два произвольных разбиения Е и 6^ резка [а, 6] на q частичных отрезков точками xv и соответственно х' (v — 0, . .., qY
а = х0 < Xi < х2 <
а = х'
< xq = b, <x'Q — b
.(5.1)
(5<2)
< х,
5. Кусочное приближение многочленами
147
(рис. Ш.*5.1), то в разбиении Е имеется по крайней мере один частичный отрезок Js = [x$-i,x$], который целиком содержится в соответствующем отрезке/'=
/]. В качестве s можно взять наименьшее из чисел г > 0, для которых	Так как х' = х, то такое
г существует.
Пусть теперь Sk,q[af b] (или, короче, S)—класс всех «кусочных многочленов» Р(х), которые характеризуются следующим свойством: для каждого Р(х) существует
такое разбиение (5.1) отрезка [а, &] на q частичных отрезков, что внутри каждого из них Р(х) совпадает с многочленом степени
-----1---1_^-------1---------------£
^2 * * * F* • • •	Хф
-- 1 , 1 ;---------5--------------£
^0 Х1 Х2 ’ ’ ’ Хг * * *
В точке X/ (/ = 1, ..., q — — 1) Р(х) следует опреде-
Рис III. 5.1. Сравнение различных разбиений.
лить как левосторонний ли-
бо правосторонний предел Р(х) в этой точке. Пусть g — фиксированный кусочный многочлен и пусть На (о = 1, ..., q)—некоторое //-множество из отрезка относительно класса С[й; 1]; тогда объединение И всех
//а является //-множеством при кусочном приближении
Рис. III 5.2. Сплайн-аппроксимация (непрерывная ломаная линия).
на отрезке [а, Ь] относительно класса C[k, 1]. Действительно, пусть <р — произвольный кусочный многочлен класса S и пусть Е и Е' — разбиения, отвечающие g и соответственно <р. Согласно
сделанному выше замечанию существует по крайней мере один номер s такой, что для соответствующих отрезков имеет место вложение JS^JS- На Л кусочный
многочлен g — <р имеет по крайней мере k перемен знака и поэтому предположение, что <р является на Js многочленом степени не выше fe, несовместимо с (1.1).
В случае, когда приближаемая функция f(x) на рассматриваемом отрезке [а, Ь\ имеет вторую производную, Сохраняющую знак, в классе С[1, 1] получается непре
148
111. H-множества
рывное кусочное приближение; рис. III. 5.2 иллюстрирует это в случае q = 2. Если в качестве начального значения для Р(х) выбрать f(a)+c, то отправляясь от этой точки, можно построить ломаную, которая попеременно уклоняется от f(x) на экстремальные значения ±с, а абсцисса £ (2<?ч-1)-й экстремальной точки (в предположении, что с > 0) является непрерывной монотонно возрастающей функцией от с, причем limg = 0.
с->0
При этом можно показать, что существует значение с, для которого £(с)=/?; тогда это значение с будет наилучшим приближением при кусочной аппроксимации.
6.	Кусочное приближение рациональными функциями
Рассмотрения III. 5 можно перенести на более общий случай рациональной кусочной аппроксимации. Пусть теперь S — класс функций, определенных на некотором отрезке [а, Ь] и характеризуемых следующим свойством: существует разбиение Е отрезка [п, &] вида (5.1) на q частичных отрезков такое, что внутри каждого из них Q(x) является рациональной функцией класса W[k/m, 1]; непрерывность в конечных точках частичных отрезков не требуется. Пусть теперь g(x)(=S — приближение функции f(x), отвечающее фиксированному разбиению (5.1), и пусть погрешность e=g — f в каждом частичном отрезке Is =	меняет знак в
(k + m + 2) точках xs, г.
sign е (х$, /) = — sign-e (xs, /+1) ¥= 0
s= 1, 2, q, j = 0, 1, ....	+ + (bJ'
Пусть M — множество всех точек xs,/, причем не исключается, ЧТО Xs, о = Xs-1, Xs, k+m+l = Xs.
Утверждение. Справедливы неравенства
min|e(x)|<p(f, S)<||8||.	(6.2)
х^М
(Такая функция g(x) не всегда существует; здесь рассматривается только случай, когда такое приближение имеется.)
6. Кусочное приближение рациональными функциями 149
Доказательство. Условия теоремы 1.1 выполнены (не выполняющееся здесь условие W С (В) в этой "теореме излишне); для того чтобы доказать, что имеет место (1.3), надо установить, что ни при каком w^S равенства
sign(g —^) = sign (g—-f) = sign е на М (6.3)
не выполняются. Докажем это от противного. Предположим, что существует w, для которого выполняется (6.3); элементу w отвечают точки деления х' вида (5.2).
Случай 1. Все точки деления совпадают: xs = xrs при s=l, ..., q. Пусть на Ji — [х0, Xi ] имеем g = u/v, w = й/v, g — w — Z/N, где Z = uv — ilv, N > 0. Степень Z не выше k + m, однако Z должно менять знак на J\ в k + tn + 2 точках; следовательно, (6.3) не выполняется.
Случай 2. Не все точки деления совпадают. Но тогда существует $, для которого Js s и на этом отрезке можно применить те же рассуждения, что и в случае 1. □
Кусочное приближение в случае нескольких независимых переменных. Рассуждения этого и предыдущего пунктов можно обобщить на случай п независимых переменных и класса W[k/m, п]. Пусть заданы натуральные числа 71,72, qn- Рассмотрим разбиение Е следующего вида: координаты Xv0, Xvi, . . . , Xyjq^ (v = l> . . . , ri) ВЫ* браны так, что (ограниченная) область В разбита гиперплоскостями = xVT (v = I, ..., п; т = 0, 1, ...
• • •, qv) на N = qiq2 ... qn частичных областей.
Можно допустить и еще больший произвол в разбиениях; например, при двух независимых переменных х и У можно сначала произвести разбиение области на 72 ’полос, параллельных оси х, а затем каждую полосу разбить на 7! прямоугольников (см. рис. III. 6.1),
Рис. Ш. 6.1.
Сплайн - аппроксимация на плоскости.
150
111. H-множества
7.	Я^-множества и монотонность
Будем вновь придерживаться обозначений III. 1.
А. Принцип монотонности. Пусть V — множество значений w при хеВ, а^А, a ф(г) (действительная) строго монотонная функция аргумента z^V. Тогда при возрастающей функции ср из неравенства
следует ф(и>(Рх))^г cp(ay(QH)), а при убывающей функции ср знак последнего неравенства меняется на противоположный. В итоге введение функции ф не влияет на разрешимость или неразрешимость системы (1.1). Часто в качестве функций ф применяются (в зависимости от интервалов, содержащих V) функции
’ г ’ (г 4- с) ’ * ’ ’ ’ ’
Например, если точки Рх, Qu образуют //-множество для класса функций
w — a, + f (X|, ..., хп, а2, а3, ..., ар), (7.1) то они образуют //-множество и для класса функций
w = ew = d^xpf(xit ..., хп, аъ а3, ...» ар). (7.2)
В.	Трехточечные Я2-множества на прямой. При одномерной чебышевской аппроксимации во многих случаях можно составить простые //2-множества, состоящие из трех точек. А именно, это можно сделать для класса функций, содержащего лишь два параметра (для простоты обозначим их а и Ь):
w = ah(x, b)*,	(7.3)
при этом х может меняться в промежутке /х: х0 <5 х
Х\ (который может быть и неограниченным с одной или с обеих сторон), а b — в промежутке /*: b0 b bi (который также не обязан быть конечным). Пусть а принимает произвольные действительные значения, а /г(х, Ь) положительна и непрерывна при всех рассматриваемых х, Ь. Выберем три точки	*	'
$! < $2 < $3 в 1Х	(7.4)
и введем отношение
Q(x,b,b) = ^±	М
h (х, Ь)
7. Н2-множества и монотонность
151
Теорема. Пусть отношение (7.5) при всех Ь, б е е 1Ь строго монотонно по х; тогда точки sif s2, s3 образуют Н^-множество для класса функций (7.3).
Доказательство. Как и прежде, введем разность
ah (х, Ь) — ah (х, Ь)
и сокращенные обозначения
htb = h{sp his==fl(sp^ Qj = Q(slt b, b).
Исключая из неравенств (1.7)
ah[b — ah^ О, — ah2b + ah2b > 0, ah3b — ah3& 0 параметр а, получим
ЙФ12 > 0, аФ23 > 0,	(7.6)
где
®12 = h2bhlb /Л26» Ф.З = ^2b^b — htffiw
Если мы теперь покажем, что
sign Ф12 = —sign Ф23,	(7.7)
то неравенства (7.6) окажутся несовместными и, следовательно, мы имеем дело с Я2-множеством. Но имеют место равенства
sign Ф12 = sign f 4^- —	== sign (Qt — Q2),
\ "16	"26 J
sign Ф23 = sign (Q3 — Q2).
Далее, в силу предположенной монотонности
Qi < Q2 < Q3, либо Qi > Q2 > Q3,
и в обоих случаях выполняется (7.7). □
На практике свойство монотонности часто устанавливают, доказывая, что производная
q,_ dQ(x,J>, b)	(7.8)
в интервале (хо, Xi) сохраняет знак. Часто это удается сделать, приводя Q' с точностью до положительного множителя к виду <р(Р) — <р(Р) при р = Ьх, Р=5х, где ф(г)—строго монотонная на (Ьх0, Ьх\) функция параметра z. Следующая таблица содержит различные примеры, причем в случаях, когда монотонность непосредственно очевидна, столбцы для Q', <р (г) и т. д. оставлены незаполненными.
Класс W	Q (х, »,5)	Q'	cp(^)	lx,	lb
аеЬх	ехр [(6 — Ь) х]			[Xo> Xj] произволен	[*0. M ' произволен
a cos bx	cos bx cos bx	cosbx r ,2ч , - [ Ф (₽) + Ф (£)] X cos bx при p — bx, p== bx	— ztgz	|0, a] a > 0	(»d9
a sin bx	sin bx sin bx	iin±L{<p(P)-(p(P)] sin bx при ₽ = bx, ^ = bx	•z ctg z	[0, a] a>0	(«£)'
а (х + b)k (k фиксировано)	/x + ft у = /1 b — b\k \x + b) k x + b)			[0, a] a > 0	(0, OO)
152	ill. H-множества
8. Приложение к дифференциальным-уравнениям	153
8.	Приложение к дифференциальным уравнениям
А. Ограниченная область. Пусть функция и(х,у, i), обозначающая температуру, удовлетворяет уравнению теплопроводности
=	=	°<*> у<х> />о <8Л)
с начальным распределением температуры f(x,y) =
= и(х,у, 0) = х(1—х)у(1—у) в области В = = {(х> У) I (0 < х, у <. 1} и граничными значениями и = 0 для (х, у) на границе об- у,.
ласти В при t > 0. Если S„,.„ = sin (тлх) sin (плу), Кп = у (т2 4- П2) Л2, то
= $тп ехр ( hmnt)
является решением дифференциального уравнения (8.1). Аппроксимируя теперь начальные значения f выражением вида
w —	+ п2 (Su + S31), (8.3)
в котором, разумеется, можно добавить еще несколько членов, получаем в случае — f|^6 в В следующую оценку погрешности:
I a1S11e-?l”< + а2 (S13 4- S3,) е~к»< —
— и (х, у, t) | б
при (х, у) е В, / > 0
Рис. III. 8. 1. Приближе-. (СМ., например, Коллатц [1964], ние произведениями сину-стр. 309).	сов.
а)	Если ограничиться одним слагаемым в правой части (8.3), т. е. положить #2 = 0» ТО получим
а = 0,06550 при 6 = 0,00299;
154
HL H-множества
распределение экстремальных точек для этого случая представлено на рис. III.8.1,а).
Ь)	Сохраняя все члены в правой части (8.3), получим (мы благодарим Будде и Циммермана за проведенные вычисления)
= 0,066655, #2 = 0,002458 при 5 = 0,000764;
распределение экстремальных точек в этом случае представлено на рис. 111.8.1,6).
Эти точки образуют //-множество и, таким образом, достигнуто наилучшее приближение в предположении, что w имеет вид (8.3). Проверка признаков //-множеств проводится по следующей схеме, которая вполне аналогична схемам, приведенным в § III. 4 и поэтому не требует дальнейших пояснений. (При этом использована симметрия в расположении точек (см. рис. III.8.1, с); их координаты заданы на схеме; заметим, что на данной схеме t не является временным параметром).
Точка	№	Комбинация из	Множители перед	
X у				Su + -Sai
0,5 0,5 S	S 0,5	t	(V (2) (3)		1 — sin2 (ns) sin (л/)	—2 —2 sin (ns) sin (3ns) sin (3л/) — sin (n/)
	(4)	(1), (2)	0	—2 sin (ns)[sin (ns) 4- 4- sin (3ns)] = = —2 [sin (2ns)]2
	(5)	(2), (3)	0	sin (ns) sin (nt) • Ф
Имеем
Ф = — 2 sin (3ns) + sin (ns) [ Sl” — 11 = I oill	J
= 4 sin (ns) [cos2 nt — 2 cos2 (its)].
При cos (л/) > д/2 cos (ns) имеем Ф > 0, и тогда проверяемое множество является //-множеством. Это условие выполняется при приведенных выше числовых значениях,
8. Приложение к дифференциальным уравнениям 155
с)	Если в правой части (8.3) добавить члены 03S33 Н-+ a4(Si5 + S51), то можно добиться равенства 6 =
0,00030 при 6Z1 — 0,066581, 02 — 0,002503, 03 = = 0,000086, 04 — 0,000559; распределение экстремальных точек для этого случая изображено на рис. III. 8.2.
В. Неограниченная область. Теперь на основе развитой в этой главе теории покажем, что в примере плоского уравнения теплопроводности в (х, у) -плоскости, содержащемся в разделе 1.4 f), полученные в предполо-
Рис. III. 8.2. Экстремальные точки при добавлении новых членов к правой части равенства (8.3)
Рис III.8.3. //-множество при нелинейном экспоненциальном приближении.
женин (4.15) главы I числа дают наилучшее возможное приближённое решение. При х2 = $, у2 = t требуется приблизить функцию f (s, t) = 1/(2 + s + t + st) функцией w(s, t) = 0i exp [—a2(s + /)] в квадранте 0	(s, t) <
< 00. Распределение экстремальных точек показано на рис. III. 8.3. В этом случае имеем четыре экстремальные точки, три из которых являются вершинами треугольника, а четвертая лежит внутри него, как и для линейных функций в разделе III.3.В. В силу монотонности функции. ф(г) = e~z согласно III. 7 эти четыре точки образуют //-множество и для класса функций ехр(— [01 + + «2(5 + /)]).	.
IV. ОБЩЕЕ РАЦИОНАЛЬНОЕ И ЛИНЕЙНОЕ ПРИБЛИЖЕНИЯ
0
1. Проблема существования при рациональном приближении в действительной области
А. Общая постановка задачи. В II. 3 мы рассматривали теоремы существования для общей Т-задачи (см. II. 1) и заметили, что уже в случае обычного рационального приближения доказанная там теорема 3.1 неприменима. Однако в этом случае, как мы увидим, также имеет место теорема существования. Но ее нельзя доказать простой ссылкой на компактность, как при доказательстве теоремы 3.1 главы II.
Будем исходить из следующей аппроксимационной задачи.
Пусть В — компактное метрическое пространство; а С (В)—пространство непрерывных на В действительных функций, наделенное нормой
II g II = max | g (х) |, geC(B).	(1.1)
хе В
Далее, пусть фиксированы функции «о, • • •» ur, Vo, ...
vs<=C(B). Через U (соответственно V) обозначим линейные подпространства пространства С (В), натянутые на «о> • • •. иг (соответственно v0> • • •. ^s) •
Предположим, что множество
V+ — {о е V| v (х) > 0 при всех хе В} непусто, и пусть множество ITsC(B) имеет вид
=	=	ое/+).	(1.2)
Ставится задача: по заданной функции f^C(B) найти функцию w е W, для которой
Н-Л«Р(А W)= inf	(1.3)
we W	4
1, Проблема существования
157
Всякую такую функцию w снова будем называть элементом наилучшего приближения для f в классе W. Существование элементов наилучшего приближения, вообще говоря, не обязательно, как показывает следующий пример:
В = {х|х = 0, 1, 2}, r = 0, s=l,
1/0 = 1, ^0=1» V{(x) = X,
такова, что f(0)=l, f (1) = f (2) = 0. Полагая для е > 0
будем иметь
р(Л 1F) = lim Hu’e — f|| = 0. е->о
Однако не существует функции w = аЦЬх + с), для которой Ьх + с > 0 при х = 0, 1, 2 и || w — f || = 0. Таким образом, задача существования имеет положительное решение лишь при дополнительных предположениях.
Прежде всего ясно, что существует последовательность {wk} = {uk/vk} ик е U, vk V+, для которой
lim || да* — /|| = р(/, W).
Не ограничивая общности, можно считать, что при всех k
II Vй 11=1.
Кроме того, можно предположить, что при всех k выполняется неравенство
ll^ — flKp(A r) + i.
Тогда при всех k имеем
11<М<11^-ЛЖ1Л1<* = р(Л W) + \\H+1, II Uk II <|| да* Illi vk ||<Л.
Согласно теореме 1.10 главы VII множества {« е (7| || и || X} (соответственно {v е V| || v || = 1}) компактны в U (соответственно в V). Поэтому существуют подпоследовательности {uk‘} (соответственно {ой/}) последовательности {ик} (соответственно	для
158
IV. Общее рациональное и линейное приближение
которых lim|| uki — u*|| = 0 (соответственно lim||vki — я*||=^
= 0), где u* е U, [| и* || X, у* V, || и* || = 1, причем ^*(х)	0 при всех хеВ. Однако в общем случае
v* ф. V+.
Если бы имело место включение у* е V4-, то для w* — u*/v*^ W выполнялось бы равенство lim ||wk. — w*| = 0, а так как
IIH-/I-IIW-fill - ®-||, ТО
II®*-f 11 = р(Л ю,
т. е. w* — элемент наилучшего приближения для f в W. Если же с»* ф V+, то для всех хе В, для которых v*(x) > 0,
lim | wk. (х) — w* (х) I — 0, £->оо	'	1
и так как
| I (х) — f (х) | — I w* (х) — f (X) 11 < I Wkl (х) — W* (х) |,
то для этих х справедливо неравенство
ИхН(х)1Ш Г).	(1.4)
Кроме того, так как при всех k имеем || Wk II К то I и* (х) I
при всех хеВ, для которых и*(х) > 0, т. е.
|м*(х) |	A.v*(x) для всех таких х.
Условие (D). Пусть для всякого v^V множество
Рр = {х е В | v (х) =/= 0}
плотно в В, т. е. для всякого хе В существует последовательность {хк} из Pv, для которой Xft->X (см. VII. 1).
Если выполнено (D), то
|и*(х)|Ли*(х) при всех хеВ, (1.5) и тем самым имеет место импликация о‘(х) = 0=>и*(х) = 0.
Возникает вопрос, существуют ли при условии (1.5) элементы й е U и tie V+, для которых
1. Проблема существования
159
пРи всех хеР°*>
4тт== lim при всех х^Рс> (z<=P0*).	(1-7)
Если бы такая пара (й, v) е U X У* существовала, то из (1.4) для w = й/й е W следовало бы
W),
т. е. w был бы элементом наилучшего приближения для f в W. Построение элементов й е U и v е У+, удовлетворяющих условиям (1.6) и (1.7), возможно в двух важных частных случаях.
В. Обыкновенное рациональное приближение в действительной области. В этом случае В = [а, 0] (а < 0) — действительный отрезок, и, (я) = xf, j =0, ..., г, vk (х) — xk, k = 0,	Очевидно, что множество У+
не пусто, а множество Pv плотно в В для всякого v V, т. е. (D) выполняется. В этом случае справедлива
Лемма 1.1. Пусть u*t v* — многочлены степени deg и* г, deg v* s (v*	0) и
I и* (я) | hv* (я) при всех х^В
для некоторого Л > 0. Далее, пусть я0 е В — нуль многочлена и*. Тогда существуют многочлены и и v, для которых deg й < deg н*, deg v <Z deg и*, v (я0) #= 0, йи* = п*й, причем
| й (я) | Лй (я) при всех х е В.
Доказательство. Пусть п — кратность корня я0. Тогда
у* (х) = (я — я0)Л с (я) при всех яе В, причем v (я0) #= 0. Так как v* 0 на В, то !
у* (я) = | я — Яо Г v (я), где с (х) = v (я) sign ((я — я0)п), deg v < deg v*, v (я0) =/= 0 sign0=1 при яое[а, 0) и sign0 = — 1 при Яо = 0. Из (1.5) следует
и (я) = (я — я0)//7 и (я) при m п.
160 IV. Общее рациональное и линейное, приближение
Если положить й (х) = (х — xQ)m п sign ((х — х0)Л) й (х), то deg u < degw*, /w* = w*v, причем выполнено условие (1>5) с заменой (u*, v*) на (й, v). □
Условия (1.6) и (1.7), в частности, выполняются при х = х0. Так как у каждого v е V имеется лишь конечное число нулей, то, применяя лемму, 1.1, получаем следующую теорему.
Теорема 1.2. В случае обыкновенного рационального приближения в действительной области для каждой функции f е С [а, р] в W существует по крайней мере один элемент наилучшего приближения.
Эта теорема впервые доказана Уолшем [35] (см. также Чени [1966] и Вернер [1966]).
С. Рациональное тригонометрическое приближение. В этом случае В — [—л, л]. Множество U состоит из всех тригонометрических полиномов вида
« W = Tm (х) = £ ctj cos (jx) + b, sin (/x)	(1.8)
(r = 2m+ 1), a V — из всех тригонометрических полиномов вида п
v (х) — Тп (х) = У, ck cos kx + dk sin kx (s = 2n + 1).
(1.9)
Очевидно, множество V+ вновь непусто, и при всяком v^V множество Pv = {х е В|у(х) ф 0} плотно в В, так как согласно II. 6.А у всякого г на В имеется лишь конечное число нулей. Решающее значение снова имеет
Лемма 1.3 (см. Чени [1966]). Пусть Тт и Тп— такие тригонометрические полиномы, что Тп 0 и существует X > О, для которого
| Тт (х) | кТп (х) при всех х е R.
Тогда, если хое[—л, л] — нуль полинома Тп, то найдутся тригонометрические полиномы ТЛ и Та, для которых
пг<т, п<п, Тп^О, ТтТЛ = ТЛТп, причем
I Лй(х) |(х) при всех xeR.
1. Проблема существования
161
Доказательство. Сопоставим каждому тригонометрическому полиному Тп алгебраический многочлен следующим образом. Положим
LTn (0 = (1 + fi)n Тп (2 arctg 0,	(1.10)
где х/2 = arctg t. Тогда
it	1 - Р
sinx=T+T2-> cosx==T7p5-.
Как известно,
cos kx = Рк (cos x),
где Pk — многочлен степени k относительно cos x. Дифференцируя это равенство, получим
_! (COS х) = у P'k (cos X).
Отсюда следует
(1 + fir cos kx = (1 + fir Pk ’
(1 + fir sin kx = (1 + fir Qk-x (££) •
Таким образом, LTn(t) является алгебраическим многочленом степени ^2п.
Обратно, если Qzn(t)—алгебраической многочлен степени ^2п, то полагаем при —л < х < л
LQ2nW = (cos|)2'!Q2n(tg|).	(1.Н)
Если Q2n(t) имеет вид
Q2» (0 = Е qktk,
TO
Д?2л(х) = £<?*(sin у) (cos-у)	,	(1.12)
Л=0
и это представление на (—л, л} совпадает с (1.11). Но оно определено однозначно и при х — + л и может быть получено по непрерывности с помощью предельного перехода х —► ±л из (1.11). Кроме того, применяя известные теоремы сложения для синуса и косинуса,. пред-
6 Л. Коллатц, В. Крабе
162
IV. Общее рациональное и линейное приближение
ставление (1.12) для £Q2«(x) можно преобразовать в тригонометрический полином вида (1.9). Ниже мы предполагаем, что LQ2n определено таким образом для всех х е [—л, л] (а следовательно, для всех %gR).
Поэтому из тождества
(1 + /2) cos2 у = 1 при у = arctg t
получаем при всех /е R:
[LLQ2n] (/) = L [(cos |)2" Q2„ (tg 4)] (0 =
= (1 +/2)n [cos (arctg /)2raQ2„(/)] = Q2ra(/).	(1.13)
(Между прочим, имеет место также равенство
[LLTn] (х) = Тп (х) при всех хе R, что, однако, ниже не потребуется.)
Пусть теперь Тт\ Тп — полиномы, заданные условиями леммы. Не ограничивая общности, можно предположить, что Тп (л) =И= 0; в противном случае мы произведем преобразование аргумента вида х->х + а. Итак, пусть хое (—л, л) — нуль полинома Тп. Так как Тп 0, то х0 имеет по крайней мере кратность 2. Поэтому LTn также имеет двукратный корень /0 R, а поскольку
I LTm (/) К Л (1 + t2)m~n LTn (/) при всех t g= R, то LTm имеет тот же корень по крайней мере той же кратности. Итак, LTm и LTn имеют по крайней мере один общий множитель вида (/—/о)2- Полагая
Т* (х) = £[(/- /о)-2 LTm (/)](х),	(1.14а)
Тл (х) = ![(/- /о)’2 LTn (/)] (х),	(1.14Ь)
имеем in < m, it < м, причем Тц Ф 0. Кроме того, не ограничивая общности, можно предположить, что m — m = п — п. Для всех действительных £ не являющихся нулями многочленов LTm и LTn, используя равенства (1.14а и Ь) и (1.13), получим
_(i fY-2_LTnW
LTm(t) V	£?„(/)•
2. Вычисление наилучшего приближения
163
Отсюда, используя определение (1.10) преобразования L и равенство т — in — п — п, будем иметь
ГтМ _ Тт(х)
ЧМ - тп(Х)
для всех хе (—л,л), не являющихся нулями Тт и Тп (тем самым они не являются нулями Tfn и Т „). Но отсюда (в силу непрерывности тригонометрических полиномов) следует, что
Tfn (х) Тп (х)^== Тп (х) Тт (х) и
|Гт(х)|<Л|Тй(х)|
при всех хе[-л, л]. Наконец,
Г«(х)>0 при всех хе[-л, л],
так как L и £ переводят неотрицательные функции в неотрицательные. □
Повторным применением леммы 1.3 (аналогично случаю обыкновенного рационального приближения в теореме 1.2) из общих рассмотрений получаем теорему.
Теорема 1.4. Для всякой действительной функции feC[—л, л] в случае рационального тригонометрического приближения существует по крайней мере один элемент наилучшего приближения в W.
Эта теорема впервые была доказана Чени и Лоэ-вом в [1964] (см. также Чени [1966]).
Замечание. Общие рассмотрения IV. 1.А имеются в работе Ньюмана и Шапиро [1964], где проблема существования обсуждается в несколько более общей форме. Вопросы существования изучали также Боэм [1965] и Голдстейн [1963].
2. Вычисление наилучшего приближения и характеристика элементов наилучшего приближения
Мы придерживаемся той же формулировки Т-зада-чи, что и в IV. 1. В 11,2 (см. теорему 2.2) приведены условия, при которых наилучше^ приближение p(f, W) можно оценить снизу, и показано, что эти условия допускают удобную реализацию (см. теорему 2.3 главы II). В этом параграфе мы покажем, что условия
6*
164
IV. Общее рациональное и линейное приближение
теоремы 2.2 главы II теоретически можно реализовать оптимально.
С этой целью мы с помощью одной теоремы о линейных неравенствах (см. теорему 2.2 главы VII) охарактеризуем наилучшее приближение как максимальное значение в двойственной Т-задаче, дополнительные условия (2.6) которой могут быть получены уточнением предположений (2.5) теоремы 2.2 главы II.
В заключение мы установим связь между решениями Т-задачи (если они существуют) и решениями двойственной задачи (см. теорему 2.4). С помощью теоремы Каратеодори из VII. 2, используя эту взаимосвязь, можно получить характеристику элементов наилучшего приближения (см. теорему 2.5), которая в частном случае линейного приближения содержит известную теорему двойственности.
А. Теорема двойственности при общей рациональной аппроксимации. Пусть л > 0 — заданное действительное число и (u, v) е U X V — заданная пара, т. е.
г
и = X atUi, uQ, ..иг<=С (В), do.....are R,
/-a
v=Yjbkvk, v0......vs^C(B), b0, &ssR.
k-0
Очевидно, выполнение неравенств
o(x)>0,
при всех xsB (2.1)
<Л
равносильно выполнению неравенств
Е «/ (х) а} + (Л — f (х)) vk (х) bk > О,
‘~г	*7	(2-2)
— Ё (х) а, + Ё (А + f (х)) vk(x) bk > О
/=0	й=0
при всех х В. Отсюда непосредственно вытекает

2. Вычисление наилучшего приближения
165
Лемма 2.1. При X > 0 система (2.2) имеет решение (ао, .Qr, bo, ..., bs) тогда и только тогда, когда
W).
Для каждого А>0 определим множество Q^=QJ. U QL где
Q{ = {(“о (*)> • • • > ur W’ Х “ f W) wo W> • • •
• • (h — f (x))vs(x)\x<=B},
QI = {(— «о W.....— ыг (* + f W) °o W> • • •
.... (X + f W) VS (x)) | x e= В].
Тогда Qx—непустое компактное подмножество из Rr+s+2, а система (2.2) не имеет решения тогда и только тогда, когда при всяком у Rr+S+2 справедливо неравенство
min (q, z/)^0, q^Qk
где через (.,.) обозначено скалярное произведение в Rr+s+2. Согласно теореме 2.2 главы VII это утверждение равносильно включению 0пе H(Qi), где &п— нулевой вектор пространства R", п =r + s + 2, a //(Qx) — выпуклая оболочка Qx.
Ниже будем предполагать, что p(f, IF) > 0.
Из проведенных выше рассуждений вытекает
Лемма 2.2. Для всякого % е (0, р (Д IF)) имеем 0„G=tf(QJ.
Теперь предположим, что 0<X^p(f, IF). Тогда из леммы 2.2 и теоремы Каратеодори (см. § VII. 2) следует, что существуют m (^n+l=r + s + 3) различных векторов q\, ..., qn е Qx и чисел М 0, .., . . . , Хл 0, ДЛЯ КОТОРЫХ
тп 1^=1 i = l
И
Гм( = 9«.	(2.3)
1=1
Каждому qt е Qx сопоставим х-еВ с тем, чтобы отнести qt к одному из множеств:	или Q|. Если это
166
IV Общее рациональное и линейное приближение
возможно сделать несколькими способами, то мы зафиксируем один из них. Теперь положим
/2 = {i|^eQ2).
Пересечение П /2 пусто, и (2.3) можно переписать в виде
X (Xi) — Е Xtut (xt) = 0, j = 0, ..., r, l^'	(2 4)
£ А, (A - f (xj) vk (x() + E Kt (К + f (x;)) vk (xz) = 0, e /,	i e h
k = 0, ..., s.
Далее положим
D\ = {x; | i e /J, D2 — {xt | i e /2},
'	А,- при x;eD| \ D2,
— Ki при Xi^D2\D{,
.Kt — Кц при XjSDi, Xi(<^D2 и x/ = x/..
Замечание. Существует лишь один элемент х/., для которого х/(. = х;, так как qt различны и тем самым П /2 ПУСТО.
Положим, кроме того,
D = Di U D2, D* = Dx(\D2, D = D\D*.
Тогда из (2.4) получим
Е С/Иу(Х;) = 0, j — O,...,r, x^D
V fi х i х	(2-5)
Е Cif (х,) vk (xz) =
= Л Е I Ci I Vk (x;) 4- К E + Ay ) Vk (Xi), x^D	risD‘
k — 0, ..., s.
Полагая
( 0	при Xi e D,
Pi t Az -|- Ay(- — | Ci | при Xi €= D*,
i. Вычисление наилучшего приближения
.167
будем иметь р,-^0 при всех х,-е£), а (2.5) примет вид Е CiUj (х,) = О, / = О.................г,
X-<=D
„	~	(2.6)
Е С if (Xi) vk (х,) = X £ (I С/1 + Pi) У* (xt),
Xi €=D	xi^D
k = O, .... s.
При этом D состоит не более чем из г + s + 3 точек. Если Ci — 0 для всех I, то в силу Л > О
Е PiVk (xt) = 0, k = 0, .... s,
и для всякого v е V+
Е Р/и(хг) = 0. xi^D
Отсюда следует, что р, = 0 при всех х,- е D. Но тогда при всех i справедливы равенства X, = 0, что противоре-т
чит условию У, Х/ = 1. Из всех этих рассуждений выте-Х = 1
кает
Теорема 2.3. Пусть p(f,W) >0. Тогда для всякого X, удовлетворяющего неравенствам 0 < X q (f, W), существуют tn (^r + s + З) различных точек Xj, ... . . . , Xm e В и векторы С = (С1, . . . , Ст) #= &т (®т ~~ нулевой вектор), р= (pt, ..., рт), где р,^0 при i= 1, ..., т, для которых справедливы равенства (2.6).
Обратно, если равенства (2.6) выполняются при некотором Хе R для конечного множества D s В и двух векторов с =# 0т и р &т (покомпонентные неравенства), то по теореме 2.2 главы II X p(f, Й7).
Поэтому мы сопоставляем Т-задаче следующую двойственную задачу:
При дополнительных условиях (2.6), где с =/= Qm, Р 0m, найти максимум К. При этом X пробегает все не более чем (г + s + 3)-точечные подмножества множества В.
Итак, из теоремы 2.3 вытекает
' 1€8	/V. Общее рациональное и линейное приближение
Теорема двойственности (см. Крабе [1966а]). Если p(f, W) > 0, то двойственная задача разрешима U Лтах — P(f, И?).
В. Характеристика элементов наилучшего приближения. В этом пункте мы предполагаем, что р(А Ю > 0- Простым следствием теоремы двойственности является
Теорема 2.4. Если Т-задача разрешима, то для всякого решения (c,p,D) двойственной задачи имеем р = где Qm — нулевой вектор.
Если w е W—элемент наилучшего приближения для f в классе W, то при всех Xt е D, для которых Ci =# О, справедливо равенство
f (Xi) — w (Xi) = p (Л F) sign d.	(2.7)
Доказательство. Пусть w = ujv
v e V+) — элемент наилучшего приближения для f в II?, a (c,p,D)—решение двойственной задачи. Тогда из (2.6) имеем
£ с> [( (Xi) — & (Xi)] V (Xi) = x^D
= p(f,W)^(\cl\ + pi)v(x£),	(2.8)
<=D
откуда в силу равенства ||/ —й»|| = р(Л Ю следует, что ' р(Л Ю Z (lGl + pi)v(Xi)<p(/, W) Е \ct\v(Xi).
x^D	xi^D
Это означает, что
S pi^(Xi) = 0, X^D
а поэтому pt — 0 при всех х£ е D.
Тем самым из (2.8) следует, что
Е I с£ | {[/ (xz) — й» (Xi)J sign сг — р (f, W)} v (хг) = 0, c i 0
что возможно лишь в том случае, когда выполняется условие (2.7). □
Теорема 2.4 допускает усиление в том смысле, что D может быть не более чем (г + $ + 2)-точечным подмножеством. Именно, справедлива
2. Вычисление наилучшего приближения
169
Теорема 2.5. Элемент w = u/v (й е U, v е V+) является элементом наилучшего приближения для f в W тогда и только тогда, когда существуют m (^r -Н + 4- 2) точек
Х1, .... xmG=E& = {x<=B\]ti>(x) — f(x)\ = \\tb — fl\} и не равные нулю числа сь ..., cm, для которых
Е CiUj (хг) = 0,	j = 0.....г,	(2.9)
Z = 1
S Cif (*/) vk (Xi) = H — f II S I Ci | Vk (Xi), k = O,...,S, i — 1	i = 1
(2.Ю)
f (Xi) — w (xf) = || $ — f II sign ct. (2.11)
Доказательство. Сначала заметим, что (2.11) следует из (2.9) и (2.10). Тот факт, что условия (2.9) и (2.10) (при Ci =# 0 для всех i) достаточно для того, чтобы w было решением Т-задачи, следует из теоремы 2.2 главы II.
Поэтому остается доказать необходимость.
Согласно теореме 2.4 существуют пг (<г 4- s + 2) точек %1, ..., xm е Е® и отличные от нуля числа С\, ..., ст, для которых выполняются условия (2.9), (2.10) й (2.11). Из (2.10) и (2.11) следует
CiXS) (х;) vk (Xi) = 0, k = 0, ..., s. (2.12) i = l
Полагая
C.
[f(Xi)-w(Xl)]6(Xi) ’	I==I)
в силу (2.11) получим, что X/ > 0 при всех i и условия (2.9), (2.12) переходят в условия
Sxi.[f(Xi)-t&(xi)]^(x/)M/(Xi) = O, / = 0, ...,г, (2.13) 1 = 1
S [/ (Xi) — w (хг)] й (хг) vk (Xi) = 0, k = O.s. (2.14)
i = l
Обратно, для величин X/> 0 из (2.13), (2.14) при
Ci = ^i[f(Xi) — w(x{)]v(Xi), i=l, .... tn (2.15)
170
IV Общее рациональное и линейное приближение
снова получаем равенства (2.9), (2.12) и (2.11), а из них— (2.9) и (2.10). Следовательно, пара систем (2.9), (2.10) эквивалентна паре систем (2.13), (2.14).
Если положить
Q = {[f (Xi) — (хг)] (0 (х,) и0 (xt),	v (х.) иг (хг),
ы (xz) t>o (*Д й(хг) vs(x,))|z = 1, ..., tn}, то равенства (2.13) и (2.14) равносильны утверждению, что
0,+s+2e Н (Q),
где Н (Q) — выпуклая оболочка Q.
Пусть теперь L (Q) — линейное подпространство Rr+s+2, натянутое на Q. Если
« = £ ajUj, й = £ bkvk,
то очевидно, что вектор (яо, .— &о, ...» —bs)^ Ф 0г+$+2 ортогонален L (Q) и поэтому dim L (Q) 2^r + s+ 1- Следовательно, по теореме Каратеодори из VII. 2 0г+$+2 принадлежит выпуклой оболочке не более чем г + s + 2 точек из Q. Это означает, что равенства
(2.13), (2.14), где X/ > 0 при всех I и £ %z = 1, выпол-
i— 1
няются уже при т г + s + 2. Но тогда это верно и для равенств (2.9) и (2.10), если Ct определяются равенствами (2.15).
С. Случай линейного приближения. В этом случае мы можем предполагать, что s = 0 и Уо=1. Разрешимость Г-задачи обеспечивается теоремой 3.3 главы II. Пусть p(f, W) > 0. Теорема 2.5 переходит в следующее
Предложение. Функция u^U является решением Т-задачи для С (В) тогда и только тогда, когда существуют m (^г + 2) точек xb ...,	и числа
Ci, ..., Ст, где Ct =И= 0 при всех i, для которых
£ci«/(x/) = 0,	/ = 0, ...,г,	(2.16)
m '	m
£cJUt)=iifl-fiiSicz|(	(2.17)
f(x{) — ti(Xi) = \\a — f || sign cz, (2.18)
2. Вычисление наилучшего приближения
171
причем условия (2.17), (2.18) эквивалентны (если равенства (2.16) имеют место).
Если имеются /и = г Д-2 различных точек хь ... ..., Хщ В, то система (2.16) имеет нетривиальное решение. Полагая
т
X
т
(2.19)
получим
(2.20)
*<р(Л Г), если задана произвольная функция
Действительно, u&U (= W), то из (2.16) следует
m
Е С if (Xi) = £ с i (и — f (Xi))
т
Sicilia-Л.
т
Так как u^U выбрана произвольно, то сразу приходим к (2.20). Таким образом, имеем удобный способ получения нижних границ для p(f, IT).
Пример. Пусть В — {(х, у) |0 х, у 1}. Далее, пусть f(x, у) — х2-\-у2, Uq(x, у)=\,	и\(х, у) = х и
и2(х, у) — у. Таким образом, г = 2, и мы выбираем четыре точки (0, 0), (1,0), (1, 1), (1/2, 1/2). Тогда система (2.16) принимает вид
с\ + ^2 “1“ С3 4“ £4 = 0,
С2 “Ь С3 = 0,
Сз + 4 С4 = 0, и имеет нетривиальное решение in	1	1
2 ’	^2	^3	2 ’	^4	* •
Из (2.19) получаем X — 1/4, и из (2.20) следует 1/4 <р(А^).
В этом случае можно даже показать, что р(/, W) = = 1/4. Действительно, выбирая
й (х, у) = — y + х + у,
172
IV. Общее рациональное и линейное приближение
получим для всех (х, у) В:
—	у) — f(x, у) =
= -l/4 + x(l-x) + z/(l-i/)<-l/4+l/2 = l/4, т. е. | и — f| = 1/4.
Кроме того, заметим, что (2.18) выполняется для трех точек (0, 0), (1, 1) и (1/2, 1/2). Наконец, имеют место равенства
й(1, 0) —f(1, 0) = й(0, 1) —/(0, 1) = — 1/4.
3. Дискретное рациональное приближение
При численном решении Г-задачи функции, заданные на компактном метрическом пространстве В, часто приходится рассматривать в конечном числе точек из В. Часто приближаемая функция задана лишь своими значениями в конечном числе точек.
Поэтому в этом параграфе Т-задачу, сформулированную в IV. 1, мы рассмотрим для того случая, когда В является конечным подмножеством метрического пространства. Тогда В компактно, а С (В) состоит из всех действительных функций, заданных на В. Обозначим через Xi, ..., Хт точки множества В и предположим, что т г + s + 2.
А. Двойственность. Согласно IV. 2.А имеет смысл сопоставить Т-задаче следующую двойственную задачу:
Найти максимум X при условиях
с = (сь .... cm)=£Qm, p = (Pi, .ptn)>Q,n, (3.1) т
Zciul(xi) = Q, j =	(3.2)
£ Cif (Xi) Vk (Xi) = X £ (I Cd + Pi) Vk (Xi), /=1	i=l
k — 0, ..., s.	(3.3)
Пусть p(f, W) > 0. Тогда из результатов IV. 2.А следует
3. Дискретное рациональное приближение	173
Теорема 3.1. а) Если для тройки (X, с, р) выполнены условия (3.1), (3.2) и (3.3), то k^p(f, W).
b) Для каждого X е (0, р(f, W) ] существуют такие векторы с, р е R"1, что тройка (Л, с, р) удовлетворяет условиям (3.1), (3.2), (3.3), т. е. двойственная задача разрешима и Xmax==p(A F).
с) а) Если Т-задача разрешима, то для каждой тройки (р(Д W), с, р), удовлетворяющей условиям (3.1), (3.2), (3.3) при К — p(f, W), имеем р — @т.
Р) Если w = й/v, (u^U,v е V+)—решение Т-за-дачи, a (q([, W), s, ©т) — решение двойственной задачи, то
f(xi) — w(xi) = p(f,W')signci при Ct 5^0.
Замечание. Утверждение а) можно доказать и непосредственно, без использования теоремы 2.2 главы II следующим образом.
Пусть X > 0 (случай X 0 не требует доказательства). Тогда, если заданы произвольные и е U и v е V+, то из (3.1), (3.2) и (3.3) следует
m
m	m
= л£(|сИ + рг)и(х<)>х£|сг|о(х/) >0, i=l	i=l
откуда m
ZI ci I ° (xi) i-l
Так как и е U и v е V+ произвольны, то сразу получаем *<р(А W).
Утверждение Ь) также может быть очень просто доказано, если воспользоваться теорией линейных нера-> венств (см. Крабе [1967b]).
В. Критерий разрешимости Т-задачи. В этом пункте мы докажем обращение утверждения с) а) теоремы 3.1. С этой целью предположим, что Т-задача не имеет
174
IV. Общее рациональное и линейное приближение
решения, и покажем, что тогда двойственная задача имеет решение (р(Д W), с, р), где р Qm.
Будем исходить из системы линейных неравенств
Г	s
Хи1(х{)а1+ Е(Р(Л W) — f(xi)]vk(xi)bk>0, 7=0	fc=0
г	s
Z-u, (х() а, + Е [р (A w) + f (X/)] Vk (х.) bk > 0,	(3.4)
/=0
s
£ Vk (Xi) bk + Ц > o,
*=o
i = l, ..., tn.
Так как, по предположению, Т-задача не имеет решения, то система (3.4) не имеет решения при ц < 0 Определим 3tn X (г + 5 + 3) -матрицу А:
/ «Дх,)
Л=1 -az(xt)
'AnX(r+l)
[Р((, w)-f(Xi)]vk(X.) em-[Р (А Ю+ /(*<)]	вт
vk(xi)	‘m-
где 0mX(r+i) означает нулевую матрицу размера тХ Х(<+1), 1т = (1, •••, l)eRm, а 0т — нулевой вектор из Rm. Далее положим
где 0r+s+2 — нулевой вектор из Rr+S+2. Тогда согласно
предположению система неравенств
лг>е3т.
dTz<Q
не имеет решения z <= Rs+r+3.
Поэтому согласно лемме Фаркаша (см. Коллатц и Веттерлинг [1971], § 5, теорема 10), найдется У — {У1> У~> у3)^^3"1, для которого
ATy = d,

3. Дискретное рациональное приближение
175
т. е.
z/J > О,	для z =
£ y\uj (х;) - £ у] (xz) = 0, j = 0.г,
i == 1	i = 1
m
Sslfptf, я-ffc)]’.(«.) +
i = l m	m
+ Z »; [p (f.	+ f (x,)] О, (x,) + 2 </’», (A-) = 0,
k = O,...,s.	(3.5)
m
E^=i.
i=l 1
Если положить с. = y\ — z/?,
w?
f'.-sl + s’ + p-ra-N. <3'6»
to (3.5) примет вид
£ci«/(xi) = 0,	/ = 0...r,
£ Cif (x{) vk (Xi) = p (J, W) £ (| ct | + Pi) Vk (Xi),
i = l	/=1
k = 0, ..s, где
E > p(/W) ’ pt^Q’ Z=1..............m’ (3’7)
Равенство c — &m повлекло бы за собой р = Qm, что противоречит (3.7). Тем самым (p(f, 1Г), с, р) есть решение двойственной задачи, причем р#=0т, и мы получаем следующий результат (см. Крабе [19б7Ь]):
Теорема 3.2. Т-задача разрешима тогда и только тогда, когда для всякого решения (p(f, W), с, р) двойственной задачи р = 0«.
176
IV. Общее рациональное и линейное приближение
С. Случай m = г + s + 2. Предположим, что множество В состоит в точности из т = г + $ + 2 точек, а ма-трица
Л= ffx г xJ	(3-8)
\ * \Xi) Vk \Xi) / i—b.Г, k=Q..
t = 1,..., т неособенная (/, k—индексы строк, i — индекс столбца). Кроме того, пусть
— т X /^-матрица, где 0 обозначает нулевую матрицу размера (г + \ )\т.
Если задан вектор z=(zi, ..., Zm)^Qm (покомпонентное неравенство), причем	то согласно тео-
реме 2.3 главы II линейная система уравнений
Ac = Dz	(3.10)
имеет в точности одно нетривиальное решение с = = (сь ст) и
q(z) = min т^тСра, W).	(3.11)
I J=#=0 I ci I
Кроме того, справедлива
Теорема 3.3. Пусть
K={zeR'n|z>6m, г#=0т),	(3.12)
a q(z) определено формулой (3.11). Тогда
p(f, W) = max q(z).	(3.13)
Доказательство. Требуется показать, что существует г е К, для которого
</(*) = Р (Л Ю-	(3.14)
Согласно Ь) теоремы 3.1 существуют векторы с=/=0т и р ©от, для которых
Ac = p(f, W)D(\c\ + p),
W |c| = (|Cl|, ..., \ст |)г.
3. Дискретное рациональное приближение
177
Если положить z = p(f, №) (| с | + р), тозеК и согласно (3.11) q(z)^p(f, IV). С другой стороны, при каждом I, для которого с, =# 0, имеем
ТГТ = Р(Л I-|C I >Р(A
I Li I	I ci I
откуда следует q(z)^p(f, IV), и тем самым (3.14) доказано.
Определим отображение Р: Rm -► R"* равенством P(z) = jAzl, где A=A~1D; А определено согласно (3.8), D — согласно (3.9) и |t/| = (|f/i|, , |f/m|)r. Тогда для q(z), определенного равенством (3.11), имеет место также равенство
<?(?) = min	(3.1 Г)
Ptzy^O r(z)i
Теорема 3.4. Пусть отображение Р монотонно на К и {©«}, Т. е.
©m < Z < У => Р (z) < Р (у).
Тогда для у = Р (z), z^ К имеем
q(z)^q(y).	(3.15)
Доказательство. Согласно (3.11')
©m < q (z) у < Z, поэтому
q (?) р (у) = P(q (z) yXP(z)=у, откуда
?(?)< min ~p7^- = q(y)- □
Таким образом, если Р монотонно на /CU {0m}, то теорема 3.4 дает удобный метод последовательного улучшения нижних границ q(z) для p(f, IF): отправляясь от образуем последовательность {zn} из Kf полагая ^-И = Р(гп),
Тогда для величин
2^
qn+i= min	n = 0, 1, 2,	(3.16)
n+i zi
178
/V. Общее рациональное и линейное приближение
на основании (3.11), (3.1 Г) и теоремы 3.4 имеем
<71<7»<P(A Ю-	(3.17)
Отображение Р будет монотонно на Ли {0™}, если для всех z Л справедливо равенство
I Лг| = | Л ]г,	(3.18)
где |Л| = (|а^|), т. е. если в каждой строке матрицы А отличные от нуля элементы имеют одинаковый знак. Действительно, тогда при Om z у имеем
Р(г) — Р (у) = | Az | — | Ду | = | А |(г — г/)<<Эт.
Но условие (3.18) при всех z^K также и необходимо для того, чтобы Р было монотонно на Ли {0Ш} (по поводу доказательства см. Крабе [1968]).
Численный пример. Поясним полученные результаты еще раз на простом примере, который мы уже обсуждали в II. 2.В:
т = 3, В = {(0, 0), (0, 1), (1, 1)}, r = 0, $=1, ^о(Л, Q 525 L ^о(б> ^2) s 1,	(6» ^) =6 + ^2,
f(/i, 12) = е*'\
В этом случае /111ч	/0	0	0ч
Л = 1 1 1 е I,	0 = 1 1	1	1 )
\ 0 1 2е /	х 0	1	2 /
II
(2е — 1	е	1ч
-2е	- (е+1) -2 1.
1	1	1 /
Очевидно, равенство (3.18) выполняется и поэтому отображение Р(г) = |Лг| монотонно на Л1){®з}. Отправляясь от г° — (1,1, 1)Г, вычислим zn+* = P(zn) и величины <7n+i согласно (3.16). Тогда получим таблицу IV. 1.
Для получения верхней границы для p(f, W) решихМ систему уравнений
h - 1 = -Л,	.	---е = Л
до	до Ч-	до"Ь2д)
(3.19)
3. Дискретное рациональное приближение
179
Таблица IV.1
п		~п + 1 z2	~п + 1 г3	<7п+ 1
0	4,74593	6,49186	1,74593	0,154039
1	23,53993	31,09615	7,55622	0,201612
2	114,3705	150,565	36,19447	0,205822
3	554,5566	729,8072	175,2506	0,206238
относительно неизвестных а0, 6о, b\, X при дополнительных условиях:
6о >0, bQ + b{ > 0, bQ + 2bi > 0.	(3.20)
Если решение найдено, то для /2) =
_________aQ__________
^0 +	(^1 + М
получим
|Л|=11и’-Л1>р(А Ю.
(3.21)
Единственным решением системы (3.19), удовлетворяющим дополнительным условиям (3.20), является
Л = - ^+1 +	-----0,206284,
о	у о	4
а0 = А, 4~ 1 = 0,793716, &0=1, Ь1 = т^у =
= - 0,342016. (3.22)
Таким образом, из (3.17) и (3.21) получается оценка 0,206238 < р (f, W) < 0,206284 = || w - f ||,	(3.23)
где
... и 4 х _	0,793716
® V1, <21 j _ 0,342016 (Л + О) ’
Можно проверить, что
max | w (tu t2) —	| 0,206284,
о<ЛС«»<1
так что оценка (3.23) имеет место также и для «континуальной» 7-задачи при В = {(Л, t2) |0 ti t2 1} вместо В={(0, 0), (0, 1), (1, 1)} (см. также II.2.B).
180
IV. Общее рациональное и линейное приближение
D. Случай линейного приближения. В этом случае s = 0 и у0= 1. Согласно теореме 3.3 главы II Г-задача всегда разрешима, а двойственная задача (со-гласно IV. З.А) формулируется следующим образом:
При дополнительных условиях
с = (сь ...,	(З.Г)
и
2 CiUt (х^ = 0, j = 0, ..., г	(3.2')
найти максимум величины
m
£ (хд
^ = ^ = -4--------•	(3.3')
£ic/i
i=l
Пусть p(f, W) > 0. Из теоремы 3.1 вытекают следующие предложения.
а)	Для всякого решения ceRm системы (З.Г), (3.2') имеем Кс W).
b)	Существует решение с^Кт системы (З.Г), (3.2'), для которого Кс = p(h W).
г
с)	Если с е Rm — такое решение ий — Х — ре-Н
шение Т-задачи, то
f (х^ — й (х^ = р (/, Г) sign при с^в.
На основе этих утверждений Штифель [1959] (см. также [I960]) в предположении, что {и0, ..., иг} — си* стема Чебышева на В (см. II.6.A), разработал так называемый алгоритм обмена, который последовательно увеличивает нижние границы для Кс и после конечного числа шагов приводит к решению Т-задачи (см. об этом также: Коллатц [1964]). Позднее этот алгоритм был распространен Биттнером [1961] и Деклу [1961] на случай, когда {«о, • • •, иг} не обязательно является системой Чебышева на В (см. также Крабе [1963], Голдстейн и Чени [1958].
В IV. 5 мы разработаем один метод на базе критерия Колмогорова (см. II.5.A).
3. Дискретное рациональное приближение
1В1
При этом особую роль играет случай т = г~Н2, который мы рассмотрим в заключение. Предположим, что функции ио, ...» иг линейно независимы на В, т. е. матрица
woUO ... «о(хт)\
(*1) • * * ur (xm)/ (m=r+2)
имеет ранг r+ 1. При этом предположении система однородных линейных уравнений (3.2) с точностью до множителя с модулем 1 имеет ровно одно решение с е R"1, для которого
т
Si ct i=i.	(3.24)
i = l
т
Рассмотрим возможные случаи, a) Zc= £ cj (хг) = 0; f-i
тогда
т. е. p(f, №) = 0.
/-о
т
Ь) Без ограничения общности считаем = £ ctf (xt) > 0.
Тогда на основании проведенных выше рассуждений получим Кс = р (f, W).
Положим
(	1 при с( 0,
sign <?,={	.	. Л
6	‘	— 1 при Ci < 0
и рассмотрим линейную систему уравнений
S Uj(Xi)at — (signc/)T] = f (*<)> i =	(3.25)
/=0
для неизвестных а0, • • •, аг, л*
Соответствующая матрица — неособенная. Действительно, как отмечено выше, с точностью до действительного множителя существует ровно один вектор у — = (f/l, УтУ^=®т> ДЛЯ КОТОРОГО
У Uj (Xi) yt = О при j = 0, ..., г,
182
IV. Общее рациональное и линейное приближение
а именно у = а-с, где cte/?, а^О, но для этого вектора
Е (— sign Ct) yi = — а X I Ci | =/= 0. i — I	i = I
Таким образом, не существует нетривиальной линейной комбинации строк матрицы системы (3.25), равной нулевому вектору из R'71.
Следовательно, система (3.25) имеет в точности одно решение («о, •••, 0г, ц), для которого в силу (3’2') и (3.24) т] = — Кс. Тем самым для
г и = £ afUf J—0
получаем || и — f || = | ц | = р (f, W).
4. Метод решения задач дискретной рациональной аппроксимации
Как и в IV. 3, мы снова берем за основу дискретную задачу, в которой В состоит из tn (^r 4~ s 4~ 2) точек Xi, хт. Для решения задачи мы указываем в этом параграфе итерационный процесс, применение которого приводит к последовательностям нижних и верхних границ для наилучшего приближения, которые сходятся к последнему.
А. Теоретические основы метода (см. Крабе [1966]). Исходной точкой наших рассмотрений является
Задача (Р). Найти минимум ц при условиях
Е«/(х/)й/ + Е (Л — f (х,)) vk (Xi) bk + И > 0, (4.1) /=0	/г=0
г	s
Е — «/ (х,) а, + Е (* + f (х,)) vk (хг) bk + н >0, (4.2) /=о	fe=o
s
E 1>й(х/)^> 1, i = l,	(4.3)
fc=0
Здесь X — фиксированное действительное число, а величины а/, bk, р меняются надлежащим образом.
4. Дискретная рациональная аппроксимация
183
Задача (Р) является задачей линейной оптимизации (см. Коллатц и Веттерлинг [1971]). Двойственной к за* даче (Р) в смысле теории линейной оптимизации является m
Задача (D). Найти максимум S(w)~^ при ус* «=1 ловиях tn	m
'Lui(xl)zi— 'Zul(xi)zi+m = 0, j =	(4.4)
i = 1	i = 1
tn £(Л — vk(Xi)zt + i=l tn	m
+ £	+ f (*/)) Vk (Xi) zi + m+ 2 Vk (Xi) Wi = 0,
1	= 1	1 = 1
fe = 0...s,	(4.5)
tn	tn
2	z< + £ z/+nt= 1,	(4.6)
i=l	1=1
z = (zi, .... z2m)>02m, w = (wt....wm)>em. (4.7)
Теорема 4.1. При любом к, 0 Л р (f, W), задачи (Р) и (D) разрешимы, причем
Hmln == *5щах> т. е. экстремумы совпадают. Кроме того,
Л<р(Д ir)<||f-4||<^+Pn,1n.	(4.8)
где Г	S
й = Х ^jUlt о = 2 hvk /-о	k=o
и (d0) ...,	60> .... bs, pmIn) — решение задачи (P).
r
Доказательство. Если положить и=^а,иг п
S
v = 2 bkVk, то условия (4.1) — (4.3) будут эквивалентны й=0
условиям
|ы(х/) — f (хг) и (xz) к Ло (xf) + [X,	о(х/)>1 (4.9)
при i = 1....tn.
184
IV. Общее рещионалъное и линейное приближение
Тем самым неравенства (4.8) при X > О являются следствием неравенств (4.9), которые выполняются для всякого решения задачи (Р). Так как множество V+ не-пусто, то существует V+, для которого u(xz)Z> 1 при i — 1, ..., т. Если выбрать U произвольно, то условие (4.9), а тем самым и (4.1) — (4.3) будут выполнены при всяком действительном X, если взять р 0 достаточно большим.
На основании Ь) теоремы 3.1 для всякого Хе е(0, р(/, U/)] существуют векторы	и р 0/п,
для которых выполняются условия (3.2) и (3.3). Если положить
1=1 т
где yt = max (0, cf), z/i+m=max (0, — ct) и	I С/1
т .	1=1 .
при /=!,..., т, то для z=(z\, ..., zm) и w — (wb wm) условия (4.4) — (4.7) будут выполнены.
При X = 0 рассмотрим систему
т
22 Uj (Xi) с{ —О, j = 0, ..., г, i = l
т	т
22 f (Xi) Vk (Xt) Ci=^Vk (x,) Wi, k = 0, i = l	i = l
(4.10)
s,
относительно неизвестных Ct и Wi.
Рассмотрим отдельно следующие случаи:
1) m 2> г + s + 2; тогда, полагая wz = 0 для всех /, мы можем найти нетривиальное решение системы (4.10) как системы однородных линейных уравнений с числом неизвестных, большим числа уравнений.
2) т = г + $ + 2; если ранг матрицы левой части системы (4.10) равен г + $ + 2, то выбираем w = = (йч, ..., wm)^0 так чтобы не при всех k — 0t ..., s
т
выполнялись равенства У vk (xj — 0. Это возможно, : = 1
так как для всякого k по крайней мере одно из чисел Vk(Xi) не равно нулю. При таком выборе w система
4. Дискретная рациональная аппроксимация
185
(4.10)	снова будет иметь нетривиальное решение с =
(£h •••, Cm) •
Если же ранг матрицы левой части системы (4.10) меньше г + $ + 2, то, выбирая uJ, = O, можно снова найти нетривиальное решение системы (4.10) относительно Ci.
Итак, система (4.10) всегда имеет решения с — = (й,	^m)¥=0m, W=(Wi, . .., Wm)^®m. ЕСЛИ ПО-
ЛОЖИТЬ
max (ct., 0)	max (—с., 0)
> %i + m	т	’	1 > • • • > ЛЪ
£ I ci I	£ I ci I
i = l	i=l
то условия (4.4) — (4.7) при X = 0 для z е R2m и w е Rw будут выполнены. Поэтому первое утверждение теоремы 4.1 вытекает из известной теоремы существования теории линейной оптимизации (см. Коллатц и Веттерлинг [1971], § 5, теорема 15), которая утверждает, что задачи (Р) и (D) разрешимы и экстремумы совпадают, если выполняются условия (4.1) —(4.3) (соответственно (4.4) — (4.7)), что как раз и было доказано нами выше.
В дополнение к теореме 4.1 справедлива
Теорема 4.2. При X > р (f, W) задача (Р) не имеет решения, так как условия (4.1) — (4.3) при отрицательных ц со сколь угодно большим модулем, выполнимы.
Доказательство. Так как X>p(f, W), то найдутся UG И У Е V+, ДЛЯ КОТОрЫХ
V (Х/)	1
u(xi) v(Ki)
< X при i — 1, ..., m.
И

Полагая
ц = max {| и (xi) — f (xf) v (xz) | — Xv (xz)J, i—1,..., m
будем иметь ц<0и (4.9) выполняется. Таким образом,
186
IV. Общее рациональное и линейное приближение
как мы видели выше, для (а/, bk, р) при Г	S
м = Z «/«/, V = S vkbk /=0	fe=O
условия (4.1) — (4.3) также выполняются. Но это не имеет места для (ап/, abk, ар) при произвольном а 1. □
Для решения задачи (Р) в нашем распоряжении имеется так называемый симплекс-метод (см. Коллатц и Веттерлинг [1971], §§ 3, 4), который в случае 0 X ^p(f, W) дает решение, а в случае X > p(f, W) —конструктивный способ для установления неразрешимости задачи (Р). Он приводит к следующему итерационному процессу.
В. Реализация метода. Сначала положим X = 0 и ц0 = оо. Рассмотрим следующие случаи, которые возможны на n-м шаге (п = 1, 2, 3 ...).
ai) X^p(f, U7), т. е. задача (Р) разрешима. Пусть (u(rt), vw)— решение. Положим ХП = Х. Тогда возможны следующие случаи:
' ~ Цп-1; тогда Иг,=
«(п>
II

тогда Ип = Нп-1-
В обоих случаях положим X = (Xrt + р^) /2.
bi) Х>р(Д U7), т. е. задача (Р) не имеет решения.
Тогда полагаем Хл = Хл_i, рл = X, X = (Хп + Р«) /2.
Согласно этому методу получаем последовательность неравенств
+	••• Р (f»	•••	+	(4.11)
Рассмотрим следующие случаи, аг) После конечного числа шагов получим Х« = рп. Тогда
II II
‘ г>г№ п
т. е. u^/v^ — решение Г-задачи.
4 Дискретная рациональная аппроксимация
187
Ьг) Ki <. Цп при всех п. Тогда для каждого фиксированного п при X = (Х,ч + р«)/2 имеем
А'п+1 = у(Л'п + Ни),	если Л<р(/, №),
^я + 1 ===	Ptz + 1 === ~2	*4“ М-д), если X	р (f, U^).
Отсюда следует
Ртг+1	^п + 1	*2"
и тем самым
lim pn = lim = р (/, W).	(4.12)
п-»сю	гг->оо
Далее возможны следующие случаи.
аг) Существует подпоследовательность {«,}, для ко-„(пг) ||
торой f----т—г-1|	• Тогда из (4.12) следует, что
V' i)	I—1
„(«/) II lim
i->oo	if ||
(4.13)
и можно легко убедиться, что существует подпоследовательность последовательности	сходящаяся к
элементу наилучшего приближения.
р2) При всех n^tiQ имеют место только случаи ai), pi) или bi). Тогда условие (4.12) выполняется, однако ничего нельзя сказать о том, удовлетворяют ли приближенные решения u^/v^ условию (4.13).
Если же при всех п^П\ (^п0) имеют место лишь случаи ai), Pi), то последовательность {рп} при всех п п\ является константой и на основании (4.12) имеем |t„=p(f, U7) при всех n Mi. Исключим этот маловероятный случай и будем считать, что .процесс продолжается до тех пор, пока разность	которая на
каждом шаге уменьшается по крайней мере вдвое, не станет достаточно малой и на последнем шаге реализуется случай bi).
Тогда для известного значения Х>р(Д W) мы решаем следующую задачу.
188
IV. Общее рациональное и линейное приближение
Задача (Р'). Минимизировать величину ц при условиях (4.1), (4.2) и при условии
S
X vk(xt)bk<A, 1=1,	(4.14)
k-о
Это — снова задача линейной оптимизации, которую также можно решать с помощью симплекс-метода. Дей* ствительно, имеет место
Теорема 4.3. Для каждого X > р(Д W) задача (Р') разрешима, причем p,min < 0. Если (djbk, p,min) — ее решение , то, полагая
г
Й = 2 Й/И/, /-0
S
V = Е bkVk,
будем иметь v (х,) > 0 при i = 1, ...» m, а также
|f-||<A + nmIn<X.	(4.15)
Доказательство. Согласно предположению существуют
и* = У, а/u/ <= U, v = У bkvk е V+, /=о	*=о
для которых
и* (х(.) °* К)
<Х при i=l,...,m.

Не ограничивая общности, можно предположить, что »•(«<)	1 при i = 1, ..., m. Полагая
р*= max {| и* (•«/) — f	— Xu*(x»)},
i = l, ..., m
будем иметь ц* < 0 и
lu*(x/)-f(xz) ^(^КЛоЧхО + н*
при i=l, ...,‘аи, что равносильно (4.1), (4.2) для а =а*,	=	Тем самым дополнительные
условия (4.1), (4.2) и (4.14) для ц< 0 выполнимы и поэтому gmin < 0, если задача (Р) разрешима.
Чтобы доказать разрешимость, будем исходить из того факта, что можно ограничиться решениями (а/,
4. Дискретная рациональная аппроксимация
189
pi), для которых р р*. Тогда при
«=Ев/«/> v=Ylbkvk, j-0	k-0
складывая (4.1) и (4.2), получим
О 2 (ц + Av (*/) при 7 = 1, .... tn, что влечет 0 < —ц/А	v(xt). Тем самым задача равно-
сильна задаче нахождения минимума функционала
р = g (и, v) = max {| и (х,) — f (xt) v (хг) | — Av (х,)} i= 1, .... т
при и е U, v е V, 0 v(xi) 1, i = 1, .... т. При этом, как было отмечено выше, можно предполагать, что g(u, v)<p*.
Отсюда следует, что
I и (хг) | — | f (х;) I V (Хг) < I и (xt) — f (Xi) V (Xi) К |A* + A при 7=1, ..., tn, и таким образом, ||Ы||<р* + А + ||Л|.
Поэтому достаточно, найти минимум функционала g(u,v) на компактном множестве
{(«, V) lll«ll<g* + A + Hf||,
0<v(x,-)< 1, i = l, ..., mJ =£/Х V
В силу непрерывности функционала g можно также предположить (см. теорему 1.7 главы VII), что минимум достигается, например, при
г	S
и = й=^ dtujt v = v= У bkvk. i-0	к-0
Тогда (й/, бк, pmIn) будет решением^ задачи (Р') и при этом будет gmin < 0. Если бы было v,(xJ(l) = 0, то согласно (4.1), (4.2) было бы pmin 0. Поэтому
v (х() > 0 при i = 1, ..., т.
190 IV. Общее рациональное и линейное приближение
Наконец,
й(х.)	f(..}
б (*;)	'
+ 777Т Л + Hmln < & v (хи
при всех I. □
Итак, если, как предположено выше, на последнем (для определенности, на n-м) шаге процесса реализуется случай bi), то при известном значении Х(> р(/, W)) мы решаем задачу (Р').
Если (й/, Pmin)—решение, то при
Г	S
Й/ZZ/ и v=£ bkvk
/=0	fe = 0
согласно теореме 4.3 имеем
Л И е й ||	,
Л'п	Рп “Г Pmln ‘С Нм*
Замечания. 1. Теорема 4.3 справедлива и в случае, когда В является компактным метрическим пространством (а не обязательно конечным множеством). Это непосредственно следует из доказательства.
2. На основе задачи (РЛ) можно также разработать итерационный процесс для решения Т-задачи, который дает монотонно убывающую сходящуюся к р(Д W) последовательность верхних границ вместе с соответствующими приближенными решениями. Для получения первой верхней границы можно было бы решить задачу (Р) при X — 0. Дальнейших подробностей мы не приводим, так как этот алгоритм вместе с доказательством сходимости изложен в работе Чени [1966].
Пример. Требуется аппроксимировать бета-функцию Эйлера
а _ Г (s) Г (0 f<s> *> = го + о”
на множестве
В = {(1 + 0, lv, 1 + 0, lo)|0<v 10, v, а — целые}г рациональными-фУйкЦиями вида	' ’ > rf,!
/ Л____ др + at О + 0 + a2St + аз (s2 + t2)
W l) b0 + bt (s + 0 + b2 (s + Z)2
При этом получается таблица IV. 2.
5. Дискретная линейная аппроксимация '
191
Таблица IV. 2
			 п	к	II О(я) II		Ид
0	0					
1	0,0060948	0,0121896	0	0,0121896
2	0,0030474	—	0	0,0060948
3	0,0044807	0,0059140	0,0030474	0,0059140
4	0,0037641	—	0,0030474	0,0044807
5	0,0039610	0,0041579	0,0037641	0,0041579
6	0,0038626	—	0,0037641	0,0039610
7	0,0038998	0,0039370	0,0038626	0,0039370
8	0,0038812	—	0,0038626	0,0038998
9	0,0038859	0,0038906	0,0038812	0,0038906
10	0,0038835	—	0,0038812	0,0038859
11		0,0038858	0,0038835	0,0038859
Таким образом, на 11-м шаге получается оценка
0,003835 <р (Л Г)<0,0038859,
а для коэффициентов и11 и и11 получаем следующие значения: ао — —2,75498, ai = 2,61132, я2 = —1,70414; а3 = = 1,16307, bo = 2,93205, Ьх = —3,96982, Ь2= 1,50190. .
Заключительное замечание. Имеются и другие алгоритмы для решения дискретной задачи рационального приближения, развитые в работах: Чени и Лоэб [1962] (см. также Чени [1966]), Голдстейн [1965] и Лоэб [1960] (см. также Чени и Саутхард [1963]). Однако стандартный метод пока еще не разработан.
5. Метод решения задачи дискретной линейной аппроксимации
Пусть В, как и в IV. 3, — конечное подмножество метрического пространства, состоящее из m различных точек. Далее, пусть С (В) — пространство действительных Функций, заданных на В, наделеннре,<нофмой (1.1). Предположим, что Ui, ..., ип^С(В) линейно независимы на a U есть n-мерное подпространство пространства С(В), натянутое на и,. Наконец, пусть	1. Для
заданного f^C(B) согласно теореме 3.3 главы II
192 IV. Общее рациональное и линейное приближение
найдется й е U, для которого
Пй — f|l = p(f, inf \\u-f\\.
u^U
Каждый такой элемент наилучшего приближения й для f в U характеризуется условием Колмогорова
min [й (х) — f (х)] w(х)< О	/5
при всех u^U (см. II.5.A).
При этом множество Еи для u^U задается соотношением
Е„ = {хе В|| и(х) — f (х) | = ||и — f ||).	(5.2)
А. Основы метода (см. Крабе [1969с]). Если для за-данного u<=U условие (5.1) выполняется не при всех и е U, то й не будет элементом наилучшего приближения для f в U и его можно улучшить. Станем на более общую точку зрения: пусть Е — множество из В, содержащее Ед и пусть существует й е U, для которого
[й (х) — f (х)] й (х) > 0 при всех хе Е. (5.3)
Положим Е — II и — f || и e = min|«(x)|.	(5.4)
хе£
Требуется найти число X > 0, для которого
| й (х) — кй (х) — f (х) К R — Ле,	(5.5)
т. е.
Я, [е — м (х)] < Е — [й (х) — f (х)1,
„	(5.6)
A[e + u(x)]<E-[u(x)-f(x)]
при всех х s В.
Условия (5.6) выполняются при всех хе В тогда и только тогда, когда
Л V = min
niin	~ / v
й (х)>0 е и W
R + [и (х) - f (х)] min -------------г _ 7—г-----
е+й (х)>0 е + И (х) J
(57)
&
5. Дискретная линейная аппроксимация
193
Если й(х) — f(x).;= £ при некотором хеВ, тохе£„ = с Е, и тогда в силу (5.3) и(х) > 0, откуда согласно (5.4) следует, что 8 —й(х)^0. Аналогично доказывается им-плинация
й (*) — f (х) = — R => е + й (х)	0.
Н) отсюда следует, что А* > 0. Поэтому, полагая
и* = й-Кй,	(5.8)
из (5.5) в силу в > 0 получим
И«*-Л1</?-А*е<Я = ||й-/||.	(5.9)
Тем самым мы попутно вновь доказали необходимость условия Колмогорова (5.1).
Таким образом, для заданного ug U, удовлетворяющего условию (5.3), однозначно определены А* равенством (5.7) и и* равенством (5.8), причем выполняется неравенство (5.9).
Для нахождения элемента й е U, удовлетворяющего условию (5.3), рассмотрим следующую задачу: найти максимум числа ц при условиях
У [й (х) — f (х)] Uj (х) Uj — р 0 для всех х s£, (5.10)
|а/|<1,	/=1.....п.	(5.11)
Это задача линейной оптимизации. Очевидно, что при П1 = ... = ап = ц = 0 дополнительные условия (5.10) и (5.11) выполняются. Далее, для всякого (n-f-1)-мерного вектора (а\, ап, ц), удовлетворяющего этим условиям, имеем
Р < R Z II Uj ||.
/-1
Поэтому, как показали Коллатц и Веттерлинг [1971] (§ 5, теорема 16), задача разрешима. Пусть (dj, ...
п
'• • > ап, gmax) —ее решение и й = У, Тогда |imax > i = I
0, причем gmax > 0 тогда и только тогда, когда для й выполняется условие (5.3).	,
Рассмотрим следующие случаи, а) ртах = 0. Тогда не существует элемента й е U, удовлетворяющего условию
7 Л. Коллатц, В. Крабе
1S4 IV. Общее рациональное и линейное приближение
(5.3). В случае Е = Ей согласно условию Колмогорова (5.1) й есть элемент наилучшего приближения для f в [7, Если же Ей является собственным подмножеством £, то ничего определенного сказать нельзя.
Ь) ртах > 0. Тогда условие (5.3) для й выполняется.
Эти рассуждения непосредственно приводят к методу последовательных приближений, который рассматривается в следующем разделе.
В. Теоретическое описание метода. А-й шаг(£=0,1,...) метода проводится следующим образом.
Пусть задано uk е U. Полагаем
Rk = \\uk-f\\.	(5.12)
Если Rk — 0, то || uk — f || = p(f, U) = 0 и процесс обрьь вается.
Если Rk > 0, то выберем б*, удовлетворяющее неравенствам
0<б*<|/?ь	(5.13)
и определим множество
Е (б*) = {х е В | | ик (х) - f (х) | > Rk -	(5.14)
где Rk задается формулой (5.12).
Очевидно, Euk s Е (6J, где Euk определяется соотношением (5.2).
После этого при й = и* и E — E(8k) мы решаем задачу линейной оптимизации (5.10), (5.11). Пусть п
(ак...ак, М*)—ее решение и йк = У, atu.. Тогда
/=1
рл 0.
Рассмотрим следующие случаи.
а) ц* = 0.
а)	Е (6ft) = Euk', тогда для и* выполняется условие Колмогорова (5.1) и ик является элементом наилучшего приближения для f в U.	л-
Р) Euk— собственное подмножество £(бй); тогда полагаем ик+1 — ик и выбираем o*+i из условия 0 < <Jk+i <Z LC о*/2 столь малым, что Euk+i = Е(б* + 1).
Ь)	0 < ц* б*; тогда полагаем б*+1 = <т*/2.
с)	о* < р.*; тогда полагаем бл+i = б*.
5. Дискретная линейная аппроксимация
195
min
ек-йк (х)>0 кк = min 1
I min
I ек+йк (х)>0
Кроме того, в случаях Ь) и с) определяем 8А= min |«fe(x)|,
/?fe-R?(x)-f(x)] ek — йк (x)
Rk + (i? (x) - f (X)] ek + uk (x) Тогда
k> Rk' n
Далее, полагая K= £ ||м/||, получим
8* < II йк || < К при всех К.
(5.15)
(5.16)
(5.17)
(5.18)
Если при некотором хеВ выполняется неравенство uk(x)-f(x)^Rk-t>k,
то согласно (5.13) ик(х) — f(x)> 0, и тем самым i7fe(x)>’
> 0, что на основании (5.15) влечет е* — йЛ(х)^0.
Отсюда следует
{х е В |&к — йк(х) > 0} s {хе В |uk (х) — f(x)<Rk — Sfc).
Аналогично доказывается вложение
{х е= В | ък + йк (х) > 0} S
— {х <= В | — \uk (х) — f (х)] < R* — 6*}.
Принимая во внимание (5.18), из (5.16) получим
Х*>Л>о.	(5.19)
Полагая
ик+1 = ик — Хкйк,	(5.20)
из (5.9) получим
Rk+i = II ик+1 - f || < Rk - Xktk < Rk. (5.21)
Наконец, если Rt+i > 0, то положим
6*+i = min (у Rk+i, 6ft+i),	(5.22)
где 6ft+i определено как в случае Ь) или с).
Таким образом, А-й шаг метода полностью описан.
7*
>196
IV. Общее рациональное < и линейное приближение
С. Сходимость. Отправляясь от и0 € U, будем считать, что реализован метод, описанный в 5.В. Предположим, что процесс не обрывается после конечного числа шагов. Это было бы возможно, если бы для некоторого k при решении задачи линейной оптимизации (5.10), (5.11) при й = ик и £ = £(бй) осуществился бы случай р* = 0 и Е(8к) — Еиъ или было бы ||н* — f || = 0. В обоих случаях ик было бы решением Г-задачи.
Таким образом, если процесс не обрывается, то согласно (5.21) при всех k имеют место неравенства
**>*ft+i>p(A U)-	(5-23)
В частности, /?о = 11ы° — f II > 0, и можно положить, например, бо = £о/2. Кроме того, для последовательности {6ft} по построению
0 < б*+1 ’С -у Rk
(5-24)
(см. также (5.13) и (5.22)).
Из (5.23) следует существование предела
R — lim£ft>p(f, U). /г->оо
(5.25)
В силу {ик} = Uo = {и е £7| || и |] С Ro + II / И } и ком" .пактности множества Uo (см. теорему 1.10 главы VII) существуют сходящаяся подпоследовательность и й е Uо, для которых
lim — й|| = 0, 1->оо
что влечет
Я= lim |rA-H = llfl-fll, (5.26) i-»oo
Утверждение. R — р (f, (7) т. e. й является эле-ментом наилучшего приближения для f в U.
Доказательство. Из (5.24) вытекает существование предела
6 = lim б* ^0.
(5.27)
5. Дискретная линейная аппроксимация
197
Допустим, что б > 0. Тогда при решении задачи линейной оптимизации (5.10), (5.11) для достаточно больших k возможен лишь случай с) (см. В), так как иначе нашлась бы подпоследовательность	для которой
lim б&. = 0, что противоречит неравенству б > 0.
Поэтому из (5.17) для достаточно больших k следует ц, б, б #7 >	°-
Кроме того из (5.19) для достаточно больших k имеем
Итак, б^ > °’
Но это противоречит условию lim Лйе^ = 0, которое вы-fc-»oo
текает из (5.21) и (5.25). Таким образом, допущение б > 0 ошибочно и б = 0.
Далее, предположим, что	U). Так как со-
гласно теореме 3.3 главы II Т-задача разрешима, то существует и* U, для которого || и* — f || = p(f, U).
Пусть теперь {uki} — подпоследовательность из {uk}, для которой выполнено условие (5.26). Так как 6=0, то lim б^. = 0 и для достаточно больших i можно считать, г->оо 1
ЧТО ^<|[Я-р(А С/)1-	(5-28)
Поэтому из (5.28) для всех kt получим
I Uki (х) - и* (х) | > I U i(x) - f (х) I - I U* (x) - f (x) I > >/?ft.-d^-p(f, t/)>
M-p(A С/)_дй >1[^-P(f, [/)] > 0	(5.29)
<• £
Для всех x e E (SjQ, откуда следует, что
min [uk‘ (x) — f (x)] БЛ (x) — u* (x)] > 0. (5.30)
*s£(M
198
IV. Общее рациональное и линейное приближение
Если ПОЛОЖИТЬ
uki =	u* = S
м 1 J	/=1 1 ’
то в силу сходимости последовательности ак* можно предположить, что существует С > 0, для которого
max —	при всех k.
п 1	1
Поэтому из (5.29) и (5.30), а также из определения следует, что
- Ч] [Я-Р (/,{/)].	(5.31)
В силу равенства 6 = 0 из рассмотрения возможных случаев в задаче линейной оптимизации (5.10), (5.11) следует, что существует подпоследовательность {PfcJ последовательности {ца}, Для которой limpfc. = 0. Кроме
Г->оо 1
того, можно предполагать, что эта подпоследовательность удовлетворяет условию (5.31).
Теперь из (5.31), (5.25) и условия lim6*. =0 следует
U)]>o,
что невозможно. Таким образом, предположение R >' > p(f, U) ошибочно, и утверждение доказано. □
Итак, сходимость метода последовательных приближений, описанного в IV. 5В, доказана.
D. Практическая реализация метода. Подходящим начальным шагом для применения метода, описанного в IV. 5.В, служит решение задачи о минимальной квадратической погрешности, т. е. элемент uQ е £7, для которого
Z [U°(x)-f(x)]2< Е [«(x)-f(x)]2 х<е=В	хеВ
при всех u^U. Для нахождения п° можно пользоваться численными методами. Чтобы перейти от uk (= U к uft+l, требуется сделать следующее.
а)	Найти uk е Uy для которого
min [uk (х) — f (х)] йк (х) > 0,	(5.32)
где Е(6*) определено равенством (5.14).
5. Дискретная линейная аппроксимация
199
Ь)	Вычислить Kk согласно (5.16) и положить uk+l — = uk — KkUk.
Для определения uk, удовлетворяющего условию (5.32), рекомендуется, в отличие от теоретического описания, не решать задачу оптимизации (5.10), (5.11) при u = uk и £ = £(6fe), а если возможно, действовать следующим образом.
Если множество Euk — {х е В 11 uk (x)—f (х) |=|| uk—f ||} состоит не более чем из п + 1 точек, то в случае необходимости дополняем Euk до (п 4- 1) -точечного множества из В. Далее, пусть множество Ek выбрано так, что функции ui, ..., ип линейно независимы на Ek. Согласно IV. 3.D это легко сделать, решая Т-задачу на Ek (вместо В). Пусть p*(f, U) — соответствующее наилучшее приближение, a Uk — элемент наилучшего приближения. Очевидно,
р*(Д </)« и)<IIuk-f||.
Рассмотрим следующие случаи. 1. || ик—f ||=р* (Д U). Тогда ик— элемент наилучшего приближения для f в U.
2. || ик — f || > pft (Д U). Тогда при всех х е Euk
ик (х) — йк (х) = [ик (х) — f (х)] — [йк (х) — f (х)] =/= 0 и
sign [ик (х) — йк (х)] = sign [ик (х) — f (х)].
Тем самым при йк = ик — йк имеем
[ик (х) — f (х)] йк (х) > 0 при всех х е Euk.
Тогда, определяя A* = V, согласно (5.7) при й — ик, й = йк, E = Euk и полагая ик+1 ==ик— ^кйк, из (5.9) получим
II «ft+1 - f II < II ик - f || - Kkek <\\uk — f II, где
ek — min | йк (x) |.
Лишь в том случае, если таким способом действовать не представляется возможным (например, если Еик состоит более чем из (n+ 1) точек), следует поступать так, как описано в IV. 5.В.
200
IV. Общее рациональное и линейное приближение
В заключение продемонстрируем этот метод на одном примере: требуется аппроксимировать неполный эллиптический интеграл
Ф , с
j (1 — р2 sin2 %)1/2 о
на множестве
В = {(р, ф)| р = 0,05, 0,10,	0,50;
ф = 0, л/20, ..., л/2)
линейными комбинациями вида и (р, ф) = О1ф + а2 (2ф + sin 2ф) р2 +
+ а3 (12ф + 8 sin 2ф + sin 4ф) р4.
Будем считать, что В занумеровано следующим образом: /=10(5-1) + /,	/ = 1,	10,	5 = 1, И.
Взяв в качестве ц0 решение задачи о минимизации квадратической погрешности, получим следующую таблицу:
Таблица IV. 3
k	f>k tf- U'		i при	€= Euk
0	—	6,0609-10-2	110
1	1,0177- IO-4	4,3826-Ю-2	110, 11
2	8,7311 • IO-3	3,8281 • 10-2	110, 104, 11
3	2.0787-10-2	3,4371 • 10-2	110, 94, 11
4	3,4049-Ю-2	3,4049 • 10-2	110, 105, 94, 11
На 4-м шаге получаем следующие коэффициенты; ai = 1,02187, о2 = 0,0862931, а3 = ~ 0,0180173.
V. НЕЛИНЕЙНОЕ ЭКСПОНЕНЦИАЛЬНОЕ ПРИБЛИЖЕНИЕ
1. Существование элементов наилучшего приближения
А. Постановка задачи. В различных местах главы II уже обсуждалось обыкновенное нелинейное экспоненци-альное приближение. Однако при этом некоторые вопро-сы еще остались открытыми, как например, вопрос о су-ществовании элементов наилучшего приближения. Поэтому в этой главе еще раз систематически изучается экспоненциальное приближение, причем некоторые теоремы даются без доказательства. Начнем с формулировки Т-задачи для обыкновенного экспоненциального приближения.
Пусть В — [а, р], а < ₽, — действительный отрезок, a С (В)— векторное пространство непрерывных на В действительных функций, наделенное максимум-нормой
llgil = max |g(x)|, geC(B). (1.1)
Далее, пусть Wr s С (В) — семейство всех экспонен* циальных сумм
tt> (х) = У. ajebix, хе В,	(1.2)
7=1
где г 1 — фиксированное натуральное число, а а/, Ь, е е R — переменные коэффициенты. Кроме того, не огра-' ничивая общности, предположим, что
bx<b2< ... <br.	(1.3)
Для заданного f<=C(B) требуется найти	для
которого
И-/Н = Р(А^)== inf ||®-f||.	(1.4)
Для произвольного f е С (В) такой элемент	наилучшего
приближения w, вообще говоря, не существует. Для
202
V. Нелинейное экспоненциальное приближение
существования такого элемента согласно теореме 3.2 главы II Wr должно быть замкнутым в С(В), т. е. должна выполняться импликация	j
wk<=Wr, geC(B), lim ||	— g || = 0 => g е= де,..
fe->OO
Но в общем случае она не имеет места, как показывает следующий пример (см. Мейнардус [1964]): г = 2. Пусть
wk (х) — — kex + feexp(l + l/k)x, g(x) = xex.
Тогда
lim Ида* — g|| = 0, wk^W2, но g&W2. fc->oo
Чтобы обеспечить существование элементов наилучшего приближения, рассмотрим подходящее множество, содержащее Wr, а именно семейство W* так называемых общих экспоненциальных сумм вида
w (х) = £ Р. (х) еь1х, ХЕ В.	(1.5)
/-1
Здесь bj действительные коэффициенты, удовлетворяющие неравенствам (1.3) (при s вместо г), а Р}(х) — многочлены степени mj (при этом degP/ = — 1 для Pj = 0) такие, что
S
£(m(+l)<f.
Тогда для всякого f е С (В) существует w s= IF* (теорема 1.5), для которого
и - и=р(г,де;)= mf jiw - f и. (i.6)
O>G= Wr
В. Общая теорема существования. Установим сначала одну теорему существования (теорема 1.2), которая имеет место для произвольного подмножества W из С (В), обладающего определенными свойствами (см. ниже предположения (Л) и (В)), а затем применим ее к экспоненциальному приближению. При этом наибольшую роль играет
/. Существование наилучшего приближения
203
Теорема 1.1 (см. Райс [I960]). Пусть {Ф*}—равномерно ограниченная последовательность функций Ф* е С (В), г. е. существует постоянная М > 0, для которой
ИФлИ^М при всех k.
Кроме того, пусть существует число п, обладающее следующим свойством: если Ф&, то Ф^, — Ф&, имеет на В не более п— 1 нулей. Тогда существует такая подпоследовательность {Ф/^}> что для всякого хе В существует предел
h(x)= lim Фй (х) 1->оо	1
(при этом h не обязательно непрерывна на В).
Доказательство. Не ограничивая общности, будем считать, что в = [0, 1]. Сначала заметим, что теорема справедлива для любого подмножества из В, если она справедлива для В. Кроме того, заметим, что в силу равномерной ограниченности последовательности {Ф*} для каждого хе В из {Ф^(х)} можно выделить сходящуюся монотонно возрастающую или убывающую подпоследовательность. Приведем теперь краткий набросок основных моментов доказательства.
Докажем сначала теорему для п = 1 и п = 2.
Пусть п— 1. Выберем произвольный элемент хе В, а затем такую подпоследовательность {Ф*у}, что {Ф^ (х)} является сходящейся монотонно возрастающей или убывающей последовательностью. Но тогда в силу того, что п—1, последовательность {Ф^(х)} при всех хе В монотонно возрастает или убывает, а поэтому сходится.
Пусть п = 2. Выберем подпоследовательность Fq последовательности F — {Ф*} так, что Во в точках 0 и 1 монотонна и сходится. Если в обеих точках имеет место монотонность одного смысла, т. е. либо возрастание, либо убывание, то в силу того, что п — 2, последовательность Во будет монотонной в том же смысле во всех точках х е В, а поэтому будет сходящейся на В. В противном случае выберем из Во подпоследовательность Bi, которая сходится и монотонна в точке 1/2. Тогда монотонность будет одного смысла либо в точках 1/2 и 0, либо В точках 1/2 и 1. Таким образом, последовательность F\
204
V. Нелинейное экспоненциальное приближение
монотонна во всех точках отрезка длины 1/2. После этого выберем из Fi подпоследовательность F2, которая сходится и монотонна в средней точке оставшегося отрезка. Повторяя проведенное рассуждение, получим, что последовательность F2 сходится на [0, 1] вне некоторого интервала длины 1/4. Итак, подобным способом можно построить последовательность {FJ содержащих друг друга подпоследовательностей последовательности F, причем каждая последовательность Fi сходится поточечно на [0, 1] за исключением, быть может, некоторого интервала длины 1/2*. Тогда соответствующая диагональная последовательность сходится во всех точках, за возможным исключением тех точек, в которые стягиваются те интервалы, на которых не была доказана сходимость последовательностей Fi. Но тогда из диагональной последовательности можно выделить подпоследовательность, которая сходится и в этих точках.
Теперь рассмотрим случай, когда имеются две точки < х2 из В и подпоследовательность Fq последовательности F, которая сходится в этих точках, причем в одной из них она монотонно возрастает, а в другой — монотонно убывает. Будем вести доказательство индукцией по и.
В случае п = 1, как было показано выше, утверждение справедливо и без этого предположения.
Индукционное предположение: пусть теорема верна для всех чисел от 1 до п.
Далее, пусть предположения теоремы выполняются для «+ 1. Так как разность любых двух элементов последовательности Fq имеет на отрезке [хь х2] по крайней мере один нуль, то из индукционного предположения следует, что существует подпоследовательность F\, которая поточечно сходится вне (хь х2). Выберем подпоследовательность Gi последовательности Fb которая сходит-' ся в средней точке отрезка [xb x2J и монотонна. Так как в этой средней точке Gi монотонна в смысле, обратном смыслу монотонности в одной из точек xi или х2, то разность любых двух элементов из Gi имеет на некотором отрезке длины (х2 — Xi)/2 по крайней мере один нуль. Поэтому согласно индукционному предположению существует подпоследовательность F2 последовательности Gb которая поточечно сходится вне некоторого интервала длины (х2 — xi)/2. Подобным образом можно построить
1. Существование наилучшего приближения
205
последовательность FbF2, ... таких подпоследовательностей из F, что Fi поточечно сходится вне некоторого интервала длины (х2— Xj)2z~1. После этого утверждение теоремы получается с помощью диагональной последовательности точно таким же образом, как и в случае п = 2.
Остается еще доказать теорему при следующем предположении: в каждой точке х^В все монотонные подпоследовательности из F монотонны в одном и том же смысле. Очевидно, при доказательстве достаточно считать, что все они не убывающие. Воспользуемся снова индукцией, совершая при этом переход от п к (и 4-2). Случаи п = 1 и п = 2 уже рассмотрены.
Допустим, что теорема уже доказана для п и условия теоремы выполняются для п + 2. Элементы подпоследовательности Fi последовательности F = {Ф*} будем обозначать через Ф*/. Выберем сначала из F подпоследовательность Fo, которая сходится и монотонна (и, значит, не возрастает) в точках х = 0, 1/2, 1. В качестве первого шага покажем, что Fq содержит подпоследовательность, которая поточечно сходится либо на [0, 1/2], либо на [1/2, 1].
Для этого предположим, например, что Fo не содержит ни одной подпоследовательности, сходящейся на [1/2, 1]. Предел подпоследовательности F, из F в точке х ниже будем всегда обозначать через Fz(x) (если этот предел существует). Согласно предположению найдется такой Xi е(1/2, 1), что Fo(xi) не существует. Поэтому из Fo можно выбрать две сходящиеся в точке Xi монотонные подпоследовательности Fi и Gj, для которых F\(xi) < Gi(xi). Таким образом, можно выбрать такой номер k\, что Ф^,1 (xi) < Gi (xi). Отсюда вытекает существование такой подпоследовательности Hi последовательности Gi, что каждый элемент из Hi совпадает с Ф*(1 по крайней мере в одной точке из [1/2, xi) и (xi, 1]. Но по предположению Hi в интервале (1/2, 1) не сходится. Поэтому найдется такой х2, для определенности из (xi, 1), что Я1(х2) не существует. После этого мы можем снова выбрать из Hi две подпоследовательности F2 и G2, сходящиеся и монотонные в точке х2, для которых ^2(х2)< G2(x2). Кроме того, найдется номер fe2, для которого Ф/г,2 (х2) < Gi (х2), a G2 содержит подпоследовательность Н2, каждый элемент которой совпадает с
206
V. Нелинейное экспоненциальное приближение
функцией Ф^2, по крайней мере в одной точке из [хь х2) и (%2, Ц. Так как ^принадлежит F2, а следовательно, и Я1, то разность ФЛ11 — ф£22 имеет на [1/2, 1] по крайней мере два нуля.
Продолжая таким же образом, мы можем построить такую подпоследовательность F* = £ФЛ . 11 = 1, 2, ... ..., Ф^ . е FJ, что разность любых двух элементов из F* имеет на [1/2, 1] по крайней мере два нуля. По индукционному предположению найдется подпоследовательность G* последовательности а следовательно, последовательности Fo, которая поточечно сходится на [0. 1/2].
Таким образом, повторяя эту конструкцию, мы построим такую последовательность {G*} содержащихся друг в друге подпоследовательностей последовательности Fo, что G* сходится поточечно вне некоторого интервала длины 1/2Z+1. Окончательное утверждение получается теперь точно таким же образом, как и в случае п = 2. □
Для установления теорем существования важное значение имеют следующие два предположения.
Условие (Д). Если равномерно ограниченная последовательность {wk} элементов множества W^C(B) сходится поточечно на В к функции Л, то найдется элемент w g=W, который отличен от h лишь на подмножестве из В, имеющем нулевую меру (Лебега).
Условие (В). Для каждой пары w, w^W найдется такое число N — N(w), что N(w) Afmax при всех w е и разность w — w либо имеет на В не более N(w)— 1 нулей, либо обращается в нуль тождественно.
Имеет место следующая (см. Баррар и Лоэб [1970b])
Теорема 1.2. Пусть множество W<=C(B) удовлетворяет условиям (Д) и (В). Тогда для всякого f s С (В) существует элемент наилучшего приближения в W.
Доказательство. По определению наилучшего приближения p(f, IT) найдется последовательность {^} элементов множества W и сходящаяся к нулю последовательность {е*} положительных чисел, для которых
11^ - Л1<р(Л УП + ъ	(1.7)
1. Существование наилучшего приближения
207
при всех k. Не ограничивая общности, будем считать, что Ek ^1. Тогда
II w* II < Р (Л Ю + IIЛ1 + 1 при всех k.
Согласно условию (В) к последовательности {wk} применима теорема 1.1 и поэтому найдется подпоследовательность и функция Л, определенная на В, для которых
lim Wk. (х) — h (х) при всех хе В.
1->оо	1
Отсюда в силу (1.7) получаем
sup | h (х) — f (х) К р (Л №).
Согласно условию (Л) найдется w е IF, для которого w (х) — h (х) для почти всех х е В, т. е.
|w(x) — f (x)|^p(f, W) для почти всех х^В. (1.8)
Если бы нашелся такой х0 е В, что |w(xo)-f(x0)|>p(f, IF), то в силу непрерывности w и f нашлось бы такое е > 0, что было бы справедливо неравенство
I W (х) — f (х) I > р (/, IT) X <= D = [Хо — 8, Хо 4- 8] П В.
Но множество D имеет положительную меру (Лебега), а это противоречит (1.8). Таким образом,
1|ш-Л|<р(Л W),
и поэтому w — элемент наилучшего приближения для f в IF. □
С. Приложение к экспоненциальному приближению. Пусть w е IF* —- общая экспоненциальная сумма вида (1.5). Положим
s
N(w) = £ (т/4- 1).
/=1
Если w W* — произвольный элемент, то из леммы 6.6 главы II следует, что разность w— w либо имеет на
208
V. Нелинейное экспоненциальное приближение
В не более
TV (w) + г — К 2r- 1
нулей, либо обращается в нуль тождественно.
Таким образом, для W = IF* выполняется условие (В). Покажем, что условие (А) также выполняется. Для этого будем исходить из того факта, что каждая функция w е 1F* является решением линейного дифференциального уравнения
<L9>
/-I
если w имеет вид (1.5) *). При этом, не ограничивая общности, будем считать, что все bj различны.
Пусть
L (у) = «о (х) Ум + а\ W У{п~° + • • • + ап W У
— линейный дифференциальный оператор порядка п, в котором
ао (х) #= 0 при всех х е В = [а, р], а
ak^Cn~k(B) при k = 0, п, (1-10)
где С‘(В)— векторное пространство / раз непрерывно дифференцируемых на В действительных функций. Тогда формально сопряженный к L дифференциальный оператор задается равенством
1^) = (-1)"[а0(х) </]<"> +
+ (-1)"'1 [01 (х)//]'"-1’ + ... +ап(х)У-
Пусть теперь С°°(В) — пространство бесконечно дифференцируемых на В действительных функций, а (а, ₽) подпространство всех функций из С°°(В), каждая из которых обращается в нуль вне некоторого компактного подмножества интервала (а, Р). Тогда, если L — линейный дифференциальный оператор порядка п, удовлетворяющий условиям (1.10), a L+ — формально сопряжен
*) По поводу этого и последующих утверждений из теории дифференциальных уравнений см. Коддингтон и Левинсон [1958].
1. Существование наилучшего приближения
209
нЫй к L оператор, то из формулы Грина *) вытекает равенство
3	а
^L(y)®dx = Jz/L+(O)dx	(1.11)
а	а
для всех у ^С°° (В) и всех Ф С™ (а, 0).
Для дальнейшего основной является
Лемма 1.3. Пусть aQi ...» ап С™ (В), а0 =# 0 на В, a L — линейный дифференциальный оператор порядка п с коэффициентами а}-. Тогда, если h = h(x) интегрируе-з
мая по Лебегу на В функция и hL* (Ф) dx = 0 при а
всех Ф <= С~ (а, Р), то существует функция у е С°°(В), отличающаяся от h лишь на множестве меры нуль и удовлетворяющая условию L(y) = 0.
По поводу доказательства см. Данфорд и Шварц [1966], гл. XIII, лемма 2.9.
Лемма 1.4. Семейство W*r общих экспоненциальных сумм (1.5) удовлетворяет сформулированному выше предположению (Л).
Доказательство (см. Баррар и Лоэб [1970]). Пусть {wk} равномерно ограниченная последовательность функций из Wr вида
w. W = S Pkj М ebikx, х(= В, /=1 }
сходящаяся поточечно на В к функции Л = й(х). Не ограничивая общности, можно предполагать, что
— ОО lim b* — &->оо
—ОО
При /	О',
при а < / < т, при т^/‘.
*) Георг Грин, род. 14.7.1793 г. в семье булочника. С 1833 г.— профессор в Кембридже, занимался, теоретической физикой, у мер-31.5.1841 г. в Снейнтоне. Ему принадлежат основополагающие работы в теории дифференциальных уравнений с частными производными, теории упругости, теории колебаний.
210
V. Нелинейное экспоненциальное приближение
При этом следует положить о = 0, соответственно т = $+ 1, если ни одна из последовательностей {б/} не сходится к — оо, соответственно k + оо.
Как отмечено выше, всякая функция Wk удовлетворяет дифференциальному уравнению вида (1.9), которое при не ограничивающем общности предположении, что bkj У= 0 при всех j а и всех / т, можно также запи-
сать в виде

Пусть теперь выбрана произвольная функция ФеС“(а, Р). Тогда из (1.11) следует
&
WkLk (Ф) dx — 0, а
где
/> t
Легко убедиться, что последовательность Lt (Ф) равномерно ограничена и lim Lt (Ф) (х) = L+ (Ф) (х) для всех
х е В, где
-I—г z j	ч т^+1
L+<®)= п (-4-V) ф' о</<т
^)= П
0</<Т
Тогда по теореме Лебега *) о предельном переходе под
*) Анри Лебег, род. 28.6.1875 г. Работал в Париже. Он создал теорию меры и интеграла, носящих ныне его имя; А. Лебег является одним из основателей современного функционального анализа. Его работы тесно связаны с теорией приближения, в частности, с теорией тригонометрических рядов; ему принадлежит особенно простое доказательство теоремы Вейерштрасса о приближении функций многочленами; умер 26.7.1941 г.
2. Характеристика и единственность элементов
211
знаком интеграла получим
3	3
О = lim ( WkLt (Ф) dx = hL+ (Ф) dx. fc-> co J	J
a	a
Так как это соотношение справедливо для всех феС^а, р), то по лемме 1.3 найдется функция е С°°(В), которая отличается на В от h лишь на множестве меры нуль, причем L(w) = 0 на В. Но это и означает, что w е IF*. □
Резюмируя, получаем следующую теорему.
Теорема 1.5. Для всякой функции f^C(B) в семействе Wr всех экспоненциальных сумм (1.5) существует элемент наилучшего приближения.
Эта теорема существования была доказана также Райсом [1962] и Шмидтом [1968]. Приведенное здесь доказательство принадлежит Баррару и Лоэбу [1970b].
2. Характеристика и единственность элементов наилучшего приближения
Ниже Wr снова обозначает семейство обычных экспоненциальных сумм (1.2), а W* — семейство общих экспоненциальных сумм (1.5), заданных на действительном отрезке В = [а, р], а < р.
Если w — общая экспоненциальная сумма вида 1.5, то через
W(w) = У (mf + 1), nij = (fegPj	при Р^О)
(2.1) обозначим степень w, а через
/М = £ 1	(2.2)
mj -1
— длину суммы w, т. е. количество ее слагаемых, отличных от нуля. Если w е Wr, то, очевидно, степень и длина суммы совпадают. В общем случае имеют место нера
венства
0 < I (ш)< N (иуХ г.
(2.3)
212
V. Нелинейное экспоненциальное приближение
Если g^ С (В)—какая-либо функция, то множество точек Х1, ..., хт е В таких, что
а < Х| < х2 < ... < хт С Р g(x;) = (-l)4, |M = |lg!k
назовем альтернансом функции g, а число т — длиной альтернанса.
А. Необходимые и достаточные условия для элементов наилучшего приближения (см. Бресс [1967]). Пусть задана произвольная функция f^C(B). Тогда справедлива
Теорема 2.1. Пусть функция w<^W*r такова, что для разности w — f существует альтернанс длины Л/(ш) + ''+1. Тогда w является элементом наилучшего приближения для f в IFP, т. е, имеет место (1.6).
Доказательство. Как уже отмечалось в начале V. 1.С, согласно лемме 6.6 главы II всякая разность w — w, w е Wr, либо имеет не более N(w) + г — 1 нулей на В, либо равна нулю тождественно. Но тогда доказательство теоремы 2.1 дословно повторяет доказательство теоремы 7.2 главы II.
Следующая теорема дает необходимое условие для элементов наилучшего приближения.
Теорема 2.2. Пусть w ^W*r — элемент наилучшего приближения для f в W* Тогда для разности w — f существует альтернанс длины Z(z&) + r+ 1-
Доказательство. Если w имеет вид
7-1 ^*-0	/	j-N + l
где
t = I (й>), N = N (w),
<2/ = 0 при / = JV + 1.......................г,
< />2 < ... < tf <	< • • • < ^г,
то, очевидно, а> будет также элементом наилучшего приближения для f в семействе всех экспоненциальных
2. Характеристика и единственность элементов
213
сумм вида
I /*/	\	г
F (a, b, х) = £l £ ajkxk]ebix + £ а1еь1х, (2.4) /=1 \fc = J	/	j=N + l
где
а (а10> • • • ’	• • • » а/0» • • • >	aN+V • • • »	’
b = (&P .... bt, bN+l, ...,br)<= br~S+t,	(2.5)
&i < b2 < ... < b[ < bfi+l < ... < br.
Пусть A — множество всех векторов (a, b) R2r~x+i t удовлетворяющих условиям (2.5). Тогда А открыто, a отображение F: A —► С (В), задаваемое равенством (2.4), удовлетворяет на А условию дифференцируемости (определение 4.2 главы II). В частности,
^-(<5, 5, x) = xke^x, k — 0....ttij, j — 1, ..., t,
jk
X) = esix, i=N+l,...,r,
^-(d, b, x) = ( j dlkxk+i)e6ix, j=l,
= j = N + l,...,r.
Линейное подпространство V пространства С(В), натя« нутое на эти частные производные, имеет размерность г Д-t. Каждый элемент из V имеет вид
где а/, ajk eR и по лемме 6.6 главы II имеет не более t
L(m/-|-2)-|-r-JV-l = JV + Z + r-^-l=r4-f-l
нулей на В, если не равняется нулю тождественно. Таким образом, V удовлетворяет условию Хаара. А тогда утверждение теоремы вытекает из теоремы 7А главы IL,
214
V. Нелинейное экспоненциальное приближение
при доказательстве которой использовалось лишь то, что У(й), согласно (7.11), удовлетворяет условию Хаара. □
Из теорем 2.1 и 2.2 получается следующий альтер-нансный критерий, который для случая Wr вместо W* уже был доказан в II. 7.
Теорема 2.3. Функция w е Wr является элементом наилучшего приближения для f е С(В) в классе W*, т. е.
\\w-f\\ = P(h w*r),
тогда и только тогда, когда разность w — f имеет альтернат длины	+1 =A/(w)+ r 4- 1. При этом l(w)
есть количество коэффициентов щ =/= 0, где
W (х) = 2 ще^*.
7=1
Напротив, если l(w)<N(w) (см. (2.1) и (2.2)), то подобный альтернансный критерий не имеет места.
В. Единственность элемента наилучшего приближения. Согласно теореме 6.8 главы II для f е С(В) в классе Wr существует не более одного элмента наилучшего приближения. Следующая теорема (см. Бресс [1967]) показывает, что при приближении общими экспоненциальными суммами единственность не гарантируется.
Теорема 2.4. Пусть г — 2, В = [—1, 1], af е С (В) — положительная четная функция (т. е. /(—x) = f(x), хе е В), которая при х 0 монотонно убывает (например, f.(x) = cosx). Тогда для f существует по крайней мере два элемента наилучшего приближения в W*2*
Доказательство. Предположим, что w^W*z — единственный элемент наилучшего приближения для f в классе Из теоремы 2.2 следует, что w = 0 не может быть элементом наилучшего приближения. Тем самым, l(w)^ 1 (см. 2.2). Тогда согласно теореме 2.2 разность w — f имеет альтернанс длины пг 4. В силу единственности элемента w и четности функции f необходимо будет ш(—х)=й(х) при всех хеВ. Поэтому w имеет вид
й (х) = a ch Лх или ш(х) = а.
Но в общем случае разность w — f имеет не более двух
2. Характеристика и единственность элементов
215
нулей на В и поэтому не может иметь альтернанс длины щ 4. Таким образом, предположение о единственности ошибочно и теорема доказана. □
Однако имеет место
Теорема 2.5. Пусть для w<^Wr и f^C(B) имеем
И-Л1 = р(Л wr).
Тогда w — единственный элемент наилучшего приближения для f в классе W*r.
Доказательство. Так как Wr^W*, то p(f, Wr)^ W*r). В случае p(f, Wr)=O доказывать нечего. Поэтому пусть р (f, Wr) > 0. Согласно теореме 6.7 главы II и теореме 7.4 разность w — f имеет альтернанс
{хь ..., хт}, где tn = l(w) + г + 1 =N(w) + r+ 1.
Пусть теперь для w е W*r выполняется равенство
Н-Л1 = р(Л w*r).
Тогда при всех хг-
1й W -1 (О |=р (/ ч7.) > р (? • »>•:)> | (*,) - f W
и разность w — w имеет на В по крайней мере 2V($) + r нулей, если двойные нули считать дважды. Поэтому согласно лемме 6.6 главы II (которая верна также и с учетом кратности нулей) должно быть w — w = 0, чем и заканчивается доказательство;
Вопрос единственности и существования локальных минимумов тесно связан с распределением знаков коэффициентов а/ в сумме (1.2). Простейшим является случай, когда все aj > 0 (см. Бресс [1967], [1970а, в]).
Вопрос характеристики и единственности элементов наилучшего приближения при общем экспоненциальном приближении исследовал также Райс в работе [1962] (см. также Бресс [1967]).
VI. ДРУГИЕ ВОПРОСЫ
о
1.	Теоремы Стоуна и Вейерштрасса *)
А.	Постановка задачи. Пусть В — компактное метрическое пространство (см. определение 1.3 главы VII), а С(В) — векторное пространство непрерывных на В действительных функций, наделенное максимум-нормой
llg|| = max|g(x) |, geC(B). (1.1)
Если А — какое-либо подмножество пространства С(В), a f е С (В) произвольная функция, то возникает вопрос, при каких предположениях об А функцию f можно сколь угодно точно приблизить элементами h е А в смысле максимум-нормы (1.1), т. е. для любого 8 > 0 найти ЛеЛ, для которого lift —/II <е. Если В = [а, р] (а < Р) — действительный отрезок, а А — множество всех многочленов на В, то на этот вопрос впервые дал положительный ответ Вейерштрасс. Весьма общий положительный ответ дает теорема Стоуна, которая будет доказана в следующем пункте и которая содержит в качестве частного случая обобщение теоремы Вейерштрасса на многочлены и непрерывные функции нескольких переменных.
Для формулировки теоремы Стоуна нам потребуются некоторая подготовка.
*) Карл Вейерштрасс, род. 31.10.1815 г. в Остенфельде, Мюн^ стерланд; сначала изучал юриспруденцию, в 1842—1855 гг. был преподавателем школы в Дойч-Кроне и Браунсберге, Восточная Пруссия. С 1854 г. — почетный доктор в Кёнигсберге, с 1856 г. профессор в Берлине, где он вел очень большую работу до самой смерти 19.2.1897 г. Ему принадлежат основополагающие работы в теории функций, в частности, в теории эллиптических функций, математическом анализе, вариационном исчислении, теории приближений и многих других областях.
I. Теоремы Стоуна и Вейерштрасса
17
Последовательность {£>} функций пространства С (В) называется равномерно сходящейся к g^C(B), если
Игл II gn — g|| = 0.
П~»оо
Последовательность {g,,} из С (В) называется пото чечно сходящейся к g^. С (В), если
lim | gn (х) — g (х) | = О д->оо
для всех х е В. Равномерная сходимость влечет поточечную сходимость. Обратное в общем случае неверно.
Определим в С (В) отношение порядка следую-* щим образом:
/<£<=> f (х) < g (х) при всех х е В,
g > f <=> f < g.
Последовательность {g} из С (В) называется монотонно неубывающей, если gn+i gn при всех и.
Теорема Дини*). Монотонно неубывающая последовательность gn из С (В), сходящаяся поточечно к g^ С (В), сходится также и равномерно к g.
Доказательство. Пусть задано е > 0. Тогда для каждого хе В найдется номер п(х), для которого
g М — gm (х)	е/3 при всех m п (х).
Так как функции g и grt(X) непрерывны, то найдется от-* крытая окрестность V(x) точки х, для которой
для всех х'е V(x). Тем самым имеем g(x') —gn<x)(x')^ е для всех х' е V (х).
Совокупность окрестностей V(x)(xeB) покрывает В. По теореме 1.2 главы VII найдется конечная совокупность окрестностей V(x<) покрывающая В. Пусть п0 = = maxn(xz). Тогда каждая точка хеВ принадлежит
*) Улисс Дини, род. 14.11.1845 г., учился в Париже, ученую степень получил в 1865 г.; с 1867 г. профессор в Пизе. Ему принадлежат важные работы в теории бесконечных рядов, в частности, в теории рядов Фурье, в теории специальных функций, дифференциальной геометрии и геодезии. Умер 28.10.1918 г.
218
VL Другие вопросы
какой-либо окрестности V(x/), и поэтому для всех п п0 g (х) - gn (х) < g (х) - g% (х) < g (х) - gn (Х{} < е,
где п0 зависит лишь от 8. □
Пусть теперь А — какое-либо подмножество пространства С (В). Через А обозначим замыкание множества Д. Множество А состоит из всех таких функций g^C(B)t для каждой из которых в А найдется последовательность {gn}, равномерно сходящаяся к g. Это утверждение равносильно следующему: для каждого е > О найдется йеЛ, для которого || h — g ||	8. Каждая такая функ-
ция g называется предельной точкой множества 4. Итак, поставленный выше вопрос гласит: при каких предположениях о множестве А^С(В) имеет место равенство 4 = С(В)?
Отметим еще без доказательства, что всегда
А = А, т. е.
gn(=A, lim||g„ —g|| = 0,	g<=C(B)^ g ееА.
В.	Теорема Стоуна. Линейное подпространство А пространства С (В) называется алгеброй (в (В)), если
f, gt=A=>f-g^A,
где (f • g) (х)= f (х) • g (х).
Если А — алгебра (в С(В)), то А — также алгебра, так как, если {fn}, соответственно {gn}, равномерно сходится к f, соответственно к g, то {fngn} равномерно сходится к f-g.
Подмножество S пространства С (В) называется разделяющим точки (точечно отделимым), если для всякой пары различных точек х, у^. В найдется функция для которой f(x)=#f(g).
Например, если В компактное подмножество из Rn(n 1), то алгебра S всех многочленов п переменных, заданных на В, является множеством, разделяющим точки (см. теорему 1.8).	. .
Имеет место
1. Теоремы Стоуна и Вейерштрасса
219
Теорема 1.1 (Стоуна). Если А—разделяющая точки алгебра (в С (В)), содержащая постоянные функции, то А = С(В).
Доказательство (по Дьедонне [1974]) распадается на несколько шагов.
Лемма 1.2. Пусть В = [0, 1]. Тогда найдется последовательность многочленов {Рп}, которая монотонно не убывает и равномерно сходится на В к + V t*
Доказательство. Положим Р\ — 0 и пусть
Pn+i(t) = Pn(t) + ±[t-PM (1.2)
при всех п^1. Покажем по индукции, что при . всех п 1
Pn+i(0>P« И P„(/)C + V7 для всех /efi. (1.3)
Очевидно, что при п = 1 (1.3) выполняется. Пусть (1.3) имеет место для всех номеров до п включительно. Тогда V7 - Pn+i (/) = V7 - Р„ (0 - у [(- Рп О)2] -
= [ V7- Рп (/)] [1 -1 (V7 + Рп (0)] •
По предположению, V t~^Pn (О при всех t е В. Отсюда следует, что
уЕV7 + рп (/)]< V7C 1 И V7>Pn+l(0
при всех t<= В. Далее, из (1.2) следует, что Рп+2 Рп+ь Тем самым, (1.3) доказано для всех и 1, откуда вытекает существование предела
v (/) = lim Рп (/) > О
П->оо
при каждом Тогда (1.2) влечет и2(0—/ = 0, а, следовательно, v (/) = + д/ t. Поэтому из теоремы Дини Ьледует, что последовательность {Рп}, определенная рекуррентными равенствами (1.2), равномерно сходится к + V7. □.
Лемма 1.3. Если А —алгебра (в С (В)), содержащая постоянные функции, то имеет место импликация
f €=Л=Н ЛеЛ.
220
VI. Другие вопросы
Доказательство. Пусть {Р„} — последовательность многочленов на [0, 1], удовлетворяющая условиям леммы 1.2. Тогда для всякой функции f е A (f ф 0) имеем
ffn = II f II ’ Л» (ц^г) е X	(1.4)
так как А является алгеброй, содержащей постоянные функции. Из леммы 1.2 следует, что последовательность {gn} (см. (1.4)) равномерно сходится к
HfllVlTF = lf I^X □
Для заданных f, g se С (В) положим
inf (A g)(x) = min(f(x), g(x)), |
sup(f, g) (х) = max (f (х), g(x)), )	'
Тогда
inf (A g) = 4 [f + g — I f — g |],
sup (A g) = 4 + g + If — gIL
и из леммы 1.3 следует
Лемма 1.4. Если А — алгебра (в С (В)), содержащая постоянные функции, то имеет место импликация
A g <= А => inf (A g), sup (f, g) e A, где символы inf и sup определены равенствами (1.5).
Лемма 1.5. Пусть А — алгебра (в С (В)), разделяющая точки и содержащая постоянные функции. Далее, пусть заданы х, у В (х=/= у) м а, ре R. Тогда найдется А, для которой f(x) =а, f (у) = 0.
Доказательство. Так как А разделяет точки, то найдется функция g^A, для которой g(x)^=g(y). Полагая
будем иметь A, f(x) = а и f(y) = 0. □
Лемма 1.6. В предположениях леммы 1.5 для любой функции f е С (В), любой точки хе В и любого е>0 . найдется функция g& А, для которой	,
g(x) = f(x) и g(y)<f(y)-\-e при у <= В. (1.6)
1. Теоремы Стоуна и Вейерштрасса
221
Доказательство. Пусть г^В произвольно. Тогда по лемме 1.5 найдется й2^Д, для которой Л2(х) = = f(x) и hz(z) f (z)+ е/2. Так как f, hz^C(B), то найдется такая открытая окрестность У(г) точки zy что hz(y) /(#) + е для всех y^V(z). Совокупность всех V(z) (zgB) покрывает В. Согласно теореме 1.2 главы VII множество В покрывается конечным числом окрестностей V (zx). Полагая g = inf в силу вложения А^А и леммы 1.4 (по индукции) получим и £ удовлетворяет условию (1.6).
Доказательство теоремы 1.1. Пусть задана произвольная функция f е С (В). Согласно лемме 1.6 для е > 0 и х е В найдется такая функция gx е Д, что
gx (х) = f(x) и gxiyXf (у) + е при всех у^В.
Так как f, gx^ С(В), то найдется окрестность Щх)' такая,что
gx (У) > f (У) — « при всех y<=U(x), причем совокупность всех окрестностей U(x) покры-вает В. Согласно теореме 1.2 главы VII конечное число окрестностей 1/(хг) покрывают В. Положим <p = supgJr. Тогда из леммы 1.4 по индукции следует, что для всякого у^В (который принадлежит некоторой окрестности U(xi)) имеем
f (у) — е < <Р (уХ f (у) + С, что влечет
II f — <Р IK 8.
Таким образом, f является предельной точкой А и принадлежит Д, поскольку А = Д.
С. Приложение теоремы Стоуна. В этом пункте через CR(B) обозначается векторное пространство действительных, а через Сс(В) — векторное пространство комплексных функций, непрерывных на В, наделенное максимум-нормой (1.1).
Разделяющие точки алгебры в Сс(В) определяются точно таким же образом, как и bCr (В) (см. п. VI. 1.В)« Однако теорема Стоуна в Сс(В) в общем случае неверна. Действительно, например, если В —компактное под
222
VI. Другие вопросы.
множество множества С комплексных чисел, а А — алгебра всех многочленов на С с комплексными коэффициентами, то А разделяет точки и содержит постоянные функции. Однако известно, что всякая равномерно сходящаяся на В последовательность многочленов с комплексными коэффициентами сходится к функции, которая является аналитической на некотором открытом множестве, содержащем В. Но эти функции образуют собственное подмножество пространстваСс (В). Несмотря на это, имеет место
Теорема 1.7. Пусть А — разделяющая точки алгебра в Сс (В), причем
f е А А
(z обозначает число, комплексно сопряженное с г). Если_ А содержит постоянные функции, то Д=Сс(В), где А — замыкание множества А.
Доказательство. Пусть Ао — подалгебра действительных функций из А. Тогда Ао непусто, так как при всех feCc(B)
Ref = |[/+f] и = f]
G = V=D.
Вместе с А разделяет точки и До- В До содержатся все действительные постоянные функции. Поэтому _из тео-ремы_Стоуна следует, что Д,> = CR (В). Поэтому А = До+ + /До = Сс(В), так как Д = До + /До и Cc(B) = CR(B) + + iCtt(B). Теорема доказана.
В Cr(B) имеет место общая теорема Вейерштрасса, а именно
Теорема 1.8. Пусть В — компактное подмножество из R". Если А — алгебра всех многочленов п переменных, заданных на В, то
А = С*(В).
Доказательство. Алгебра А содержит постоянные функции и, очевидно, разделяет точки, так как две различные точки х, у е В различаются по крайней мере одной координатой. Требуемое утверждение вытекает и% теоремы Стоуна. □
1. Теоремы Стоуна и Вейерштрасса
2'23
При п = 1 получаем классическую теорему Вейерштрасса. Ниже через Сс обозначается пространство 2л-периодических комплексных, а через С2£—пространство 2л-периодических действительных функций, непрерывных на [0, 2л].
Теорема 1.9. Пусть — пространство всех тригонометрических полиномов
а0 + X ak cos (kt) + bk sin (fe/), n = 0, 1, 2, ... (1.7) k=i
на [0, 2л], где ak)	Тогда А3 = Сц\
Доказательство. Пусть В — граница единичного круга из С, а А — алгебра в Сс(В), порожденная степенями zk, и z&, k = 0,1,2, ... (f снова обозначает число, комплексно сопряженное с z). Тогда А разделяет точки и содержит постоянные функции. Далее, имеем f е А =>
Поэтому из теоремы 1.7 вытекает, что А^Сс(В). Определим отображение ср: Cc(B)->Cq равенством
<Р (/)« = /Л 0</<2л,
и положим Д* = <р(Д). Тогда <р имеет однозначное обратное отображение, определенное на Сс(В) с областью значений CR (В). Кроме того, ср непрерывно (в смысле, определения 1.6 главы VII относительно Сс(В) и Сс\ рассматриваемых как метрические пространства с метрикой, порожденной максимум-нормой). Отсюда следует, что
= ф (Сс (В)) = ф (Л) <= ?(Д) = А* £= С?.
Таким образом,
А* = Cr" + iCr".
Пусть Д*--непустая (см. доказательство теоремы 1.7) подалгебра действительных функций из Д*. Тогда
А = До + iA0 и	До — Cr1 .
Подалгебра До порождается действительными постоянными функциями и произведениями степеней cos / и sin /, а следовательно, совпадает с множеством всех тригонометрических полиномов (1.7).
224
VI. Другие вопросы
2. Рациональное приближение и задачи на собственные значения
А. Введение. Рассмотрим дискретную задачу рационального приближения в формулировке IV. 1 и IV. 3 и предположим, что т — г + s + 2 (см. п. IV. З.С). Как мы видели в II. 2.В, эта задача играет определенную роль при вычислении нижних границ для наилучшего приближения в континуальных задачах. Она возникает также в случае обычной аппроксимации при численном решении континуальных задач с помощью так называемого алгоритма Ремеза (см. об этом Г. Вернер [1962а], [1962b], [1963] и Фразер и Харт [1962], а также Ралстон [1965].
Существует интересная взаимосвязь между названной дискретной задачей приближения и нелинейными, а также общими линейными задачами на собственные значения, которую мы изложим ниже (см. об этом Крабе [1967с] и [1968]).
В. Задачи на собственные значения при общем рациональном приближении. Сохраним обозначения из IV. 2 и IV. 3 и предположим, что p(f, W) > 0. Тогда из теоремы 2.5 главы IV вытекает
Теорема 2.1. Элемент w = u/v (u^U, v е V4-) является элементом наилучшего приближения тогда и только тогда, когда существуют такие числа с\, ...
m
с , . > Ст ЕЕ Rc X | ct | > 0, что i — 1
m
S Uj(xi) с, = 0, j =	(2.1)
E 0* (Xi) f (x{)	(xi) | Cl I, k = 0, ..., s, (2.2)
f = l	i=l
f (x() — Й» (Xi) = К sign Ci при c, =/= 0,	(2.3)
где К = || f — w ||. '
2 Задачи на собственные значения
225
Введя матрицы (uo(xi) ... «f(xiK	/M*i)
•	•	), У = ( •	• I, (2.4)
М*т) • •• MW	'v0(xm) ... Vs{xmY
,f(xd 0 у
F = |	I,
' о ' f(xm)'
запишем равенства (2.1) и (2.2) в виде
Гс=ег+Ь	(2.1*)
У/Гс = ХУ/|с|,	(2.2*)
где 0г+1 — нулевой вектор пространства Rr+1, c = (ci, ... ..., cm), |c| = (|ci|, ..., |cm|)', X', соответственно У\ транспонированная матрица л, соответственно У.
Вводя m X /«-матрицы
Л = (Гт). Mr) М
(см. равенства (3.8) и (3.9) главы IV), где 0 обозначает нулевую матрицу размеров (r-f- 1)Х/«. равенства (2.1) и (2.2) можно записать в виде
Лс = ЛД|с|.	(2.6)
Для дальнейшего мы примем предположение:
матрица А неособенная.	(2.7)
Кроме того, положим A =A~1D. Тогда справедлива
Теорема 2.2. а) Пусть с е R'n нетривиальное решение системы (2.1*), (2.2*) при заданном Х>0. Тогда у = Х|с| является нетривиальным решением уравнения
I Ay | = цу	(2.8)
при ц — 1/Х.
Ь) Пусть у s Rm нетривиальное решение уравнения (2.8) при заданном ц > 0. Тогда с = Ау является нетривиальным решением системы (2.1*), (2.2*) при X = \/р,
8 Л. Коллатц, В. Коабг
226
VI. Другие вопросы
Доказательство, а) Поскольку с =/=©«, то у=.
= Л | с | -Ф @т, а так как с = КА | с |, то
I Ay | = | с | = у = ру.
Ь) Из условия у ф Qm следует Dy 0т. Действительно, в противном случае были бы справедливы равенства
X Vk(хг)Hi = 0 при k = 0, s,
i = l
а тем самым и т У, V (Х{) У[ = 0 при ВСЯКОМ V е V+,
откуда следовало бы y = Qm. Поэтому в силу (2.7) также с = Лу=/=0т, и из (2.8) при Л=1/р. следует
I с 1 = ^ = 4"г/-
Тем самым КА) с } = Ау = с, откуда получаем
Ac = W|c|. □	(2.6)
Уравнение (2.8) является нелинейной задачей на собственные значения для положительного оператора
Р(у) = \Ау\, y<=Rn	(2.9)
(см. п. IV. З.С) и из теоремы 2.1 следует: если Т-зада-ча разрешима, то при K = p(f, №) существует нетривиальное решение cgR™ системы (2.1*), (2.2*), а потому согласно теореме 2.2 существует нетривиальное решение
уравнения (2.8) при р. = - Т)'' Кроме того, имеет место
Теорема 2.3. Существуют такие ц>0 и у=£6т, что равенство (2.8) выполняется, а поэтому (согласно теореме 2.2) найдутся К > 0 и 0m, для которых выполняются равенства (2.1*) и (2.2*).
Доказательство. Пусть К = {у е Rm | у	0m,
Тогда из п. Ь) доказательства теоремы 2.2 для оператора Р, задаваемого равенством (2.9), следует
Р (у) при всех у г К,
2. Задачи на собственные значения
227
Положим
s=Le/<iii//Iii=iS1==4-к	«=1	)
Тогда S — выпуклое компактное подмножество пространства Rm (см. VII. 1 и VII. 2), и непрерывно отображается в себя оператором
?'(«/)= и p[^|h . У^К.
Поэтому по теореме Брауэра*) о неподвижной точке существует y^S, для которого Т ($) = {), т. е. P(y)=z = |Д?7| = цг/, где ц = || PQ/)||i > 0. □
Замечание. Согласно теореме 2.3 главы II для всякого % > 0, для которого существует вектор с =/= Qm, удовлетворяющий системе (2.1*), (2.2*), выполняется неравенство
Л<р(А W),
а поэтому для всякого ц > 0, для которого существует вектор у =/= 0т, удовлетворяющий уравнению (2.8), справедливо неравенство
г*
Предположим теперь, что задана пара X > 0, с =/= 0т, удовлетворяющая условиям (2.1*) и (2.2*). Тогда всякому Ь=(Ь0, ..., bs)', удовлетворяющему неравенству Yb > 0m, т. е. (Уй)( >0 при 1=1, ...,пг, однозначно соответствует диагональная т X т матрица Gb, для которой
c = GbYb.	(2.10)
Для всякой матрицы М = (mik) положим | М | = (| m,k |). Тогда из (2.1) и (2.2) следует
X'GbYb = Qr+b	(2.11)
Y'FGbYb = KY' \Gb\Yb.	(2.12)
*) Л. Е. Д. Брауэр, род. 27.2.1881 г. в Оверши под Роттердамом; широко известен своими топологическими и алгебраическими работами, особенно получившими его имя топологической теоремой о неподвижной точке и брауэровскими алгебрами. Погиб 2.12.1966 г. в автомобильной катастрофе вблизи своего дома в Бларикуме, где он прожил многие годы.	'	’
228
VI. Другие вопросы
Таким образом, Л является собственным числом общей задачи (2.12) на собственные значения. Имеет место
Теорема 2.4. Пусть G — ненулевая диагональная tn\tn матрица. Тогда существует не более одного А,е R, для которого найдется вектор b е 7?s+1, удовлетворяющий условиям
Yb > Qm,	(2ДЗ)
Y'FQYb — kY'\G\Yb.	(2.14)
Доказательство. Предположим, что для <т=1, 2 Yba>&m и Y'FGYba==kaY'\G\Yba,
где Л1 =/= А2. Тогда в силу симметричности матриц Y'FGY и У'| G |У имеем
О = (М - Л2) b'2Y' | G | Ybi = (Xt - Л2) Z IСа | о1 (х,) a2 (хД i-1
где va(xi) = (Yba)i, что влечет равенства Gu = 0 для всех i. Это противоречит предположению. □
Пример. Пусть г = 0, s = 1, так что /п = 3, кроме ТОГО, Х1=(0, 0), Х2=(1, 0), х3 —(1, 1) и «o(t, т]) = = fo 1> vi (В, Л) = t + Л, а также f(|, п) = £2 + Л2-
Тогда для А и D согласно (2.5). получим
(1 1 1\	/о о о\
О 1 2 ) и 0=1 111). 014/	\0 1 2/
Кроме того,
/1 --	-1 -Л
(	2	2 I	12	2 1
0	2 -1 I И Л=Я-1£)=	2	1 О
I О -1	1)	I -1	0 1 I
X 2	2 /	\ 2	2/
Таким образом, нелинейная задача (2.8) на собственные значения при у = (у\,у2,у2)' 0з иц>0в координатной записи примет вид
у г/1+*/2 + -2Уз = 1Ч/1.
2i/i + у2 = 14/2,	(2-8')
yi!/! —^з1
2. Задачи на собственные значения
229
Рассмотрим следующие случаи:
а)	I У\ — Уз I = У\ — Уз.
Тогда единственное положительное собственное число ц, для которого задача (2.8') допускает нетривиальное решение у ©з, задается равенством
|х=и-7з;
и согласно замечанию к теореме 2.3
В качестве решения задачи (2.8'), нормированного условием yi + у2 + Уз = 1, получим
_ Уз	1	1	л/з
У\ 4 ’	2 ’	2	4
В соответстви с п. Ь) теоремы 2.2 для вектора с = Ау, являющегося решением системы (2.1*), (2.2*), получаем следующее распределение знаков:
signci —— 1, signc2 = +l, signc3 = —1.
Поэтому система (2.3) принимает вид
О — -22-=-X, Оо
CLq bo + &1
(2.3')
2
“о _ b0 + 2bt
и единственное положительное X, для которого система (2.3') допускает решение, задается равенством
V3 2	2
Вводя нормировку &о=1, = —1/ (2 + %), что влечет
b0 + bi > 0 и
получим До = X
и bi =»
bo + 2bi>O.
230
V/. Иру гиб вопросы
Отсюда получаем
я = ^--{ = р(А П и
,аа-’|) = —гпг
2 + г) является элементом наилучшего приближения.
b)	If/i — Уз\ = Уз — У\-
В этом случае задача (2.8') имеет два положительных собственных числа, которые, однако, не допускают нетривиальных решений у ©з-
С. Обыкновенное рациональное приближение. Пусть У1(х) = х1, vk(x) = xkt а В — (г + s + 2) — точечное подмножество {х\, ..., хт} (tn = г + s + 2) действительного отрезка [а, Р] (а <Р), причем
а < Xi < х2 < ... < хт < р. Пусть Г	S
й>==-|, й = ^]и/й/)	=
/=0	fe=0
— решение Т-задачи с взаимно простыми многочленами й и v, и
deg 4 = г, degd = s.	(2.15)
Тогда справедлива
Теорема 2.5. В предположении (2.15) существует с точностью до действительного множителя единственная ненулевая диагональная матрица G, удовлетворяющая условиям
X'GYb = @r+i,	(2.16)
Y'FGYb = Mt"\G\Yb,	(2.17)
причем G определяется требованием
X'GY = 0 (0 —нулевая матрица)	(2.18)
Все диагональные элементы матрицы G отличны от нуля, а их знаки чередуются.
2. Задачи На собственные Значения
2.31
Доказательство. Согласно теореме (2.1) существует вектор с Ф Qm, удовлетворяющий равенствам (2.1) — (2.3). Определяя G из равенства
c = GYb ((Г^ = Й(хг)),
на основании (2.1) — (2.3) получим, что условия (2.16), (2.17) выполняются, и
б (х,) И/ (хг) С и — 0,	/ = 0, .... г,
(2.19)
2 й (х/) vk (х{) Git = 0, k = 0, .... s. 4-1
Согласно лемме 6.4 главы II линейное подпространство
L (й, d) = Uv + Уй = {ио + va\и е= U, v €= V) пространства С ([а, р]) имеет размерность r-]-s-|-l. Очевидно, £(й, й) содержится в пространстве Pr+s всех многочленов степени г + $. Поэтому, так как dim Pr+s = г -f- s + 1, то Л(й, v) = Pr+s, и из (2.19) следует
£x'G,,=0,	/ = 0, ..., r + s, (2.20)
1=1
что равносильно (2.18).
Так как Рг+$ удовлетворяет условию Хаара, то матрица системы (2.20) имеет ранг /* + $+ 1, и по известной теореме алгебры Gn определяются однозначно с точностью до действительного множителя. Последнее утверждение теоремы является следствием леммы 7.3 главы II. □
Из доказательства теоремы 2.5 вытекает, кроме того, что для всякого решения w =й/v Т-задачи, для которого выполняется условие (2.15), имеем
Хй — FYb -1 (signG)Yb при	Л = ||0-/||, (2.21)
(signGn	0 v
•	I (G определяется
n ' .im.c 7 условием (2.18)), 0	sign Gmm 7
232
V/. Другие вопросы
и
г	s
Й = X djUj, 6 = £ bkVk.
/“О	fe=O
При этом в является решением системы (2.16), (2.17), а для d из (2.18) и (2.21) получаем
X'\G\Xd = X'\G\FY$>.	(2.22)
Эта система имеет единственное решение d, так как в силу предположения (2.7) ранг системы строк матрицы X равен r + 1 и согласно теореме 2.5 все диагональные элементы матрицы G отличны от нуля.
Поэтому для получения решения Т-задачи можно поступить следующим образом. Сначала определяется отличная от нуля диагональная матрица G, удовлетворяющая условию (2.18). Согласно теореме 2.5 это можно сделать единственным образом с точностью до действительного множителя, разрешая систему (2.20).
После этого определяются R и вектор бе7?s+1, удовлетворяющий условиям (2.16), (2.17) и
5 -
Е&Л(Х()>0 при 7=1, т. ft-0
Если это возможно, то согласно теореме 2.4 X определяется однозначно.
Наконец, вычисляется единственное решение & уравнения (2.22). Если при этом й, б и X удовлетворяют условию (2.21), то для c = GY6 и X выполняются условия (2.1) —(2.3) при
Г	S
“|р т|’ d — й = У ^kvk-/=Э	Л=0
. Таким образом, из теоремы 2.1 следует, что 1 = = p(f, W), а й/6 является элементом наилучшего приближения. Этим путем решение Т-задачи было впервые получено Г. Вернером [1963] (см. также Крабе [1967с] и [1968]).
VII. ПРИЛОЖЕНИЕ
1.	Метрические и нормированные пространства
В главах I—VI многократно рассматривались метрические и нормированные пространства, однако не приводилось определений этих пространств и не исследовались подробно их свойства.
В этой главе частично формулируются, а частично и доказываются результаты, использованные в предыдущих главах.
Определение 1.1. Непустое множество X называется метрическим пространством, если существует отображение р: X X X -> 7?+ (Х+-множество неотрицательных действительных чисел), обладающее следующими свойствами:
а)	р(х, у) = 0 <=> х = у (определенность)
Ъ)	р(х, у) = р(у, х) (симметрия)
с)	р(х, z)^p(x, у) + р(у, г) (неравенство треугольника).
Функцию р называют м етр и ко й пространства, а число р(х, у)—расстоянием между точками х, у^Х.
Свойства а), Ь) и с), очевидно, отражают основные свойства евклидова расстояния в обычном трехмерном пространстве.
Важный частный случай метрического пространства получается с помощью следующего определения:
Определение 1.2. Векторное пространство Е над полем действительных или комплексных чисел называется нормированным векторным пространством, если каждому элементу х<=Е однозначно сопоставлено неотрицательное действительное число || х ||, так называемая норма х, обладающее следующими свойствами:
|| х || == 0	х = 0' (определенность)
(0 — нулевой элемент пространства X),
|| Лх || = | X | • || х ||, X е К, х е Е (однородность)
234
V11. Приложение
(К — поле действительных или комплексных чисел).
II х + УII II х || + IIУII (неравенство треугольника).
Если X — непустое подмножество нормированного векторного пространства Е, то X будет метрическим про-странством, если отображение р: XXX-+R+ задать равенством р (х, у) = || х — у ||.
Примеры нормированных пространств. Е — действительное или комплексное векторное пространство размерности ш, состоящее из всех /n-мерных векторов х == = (xi, хт) с действительными или комплексными компонентами хг.
||х|| = max |xj (максимум-норма),
Z=1..т
Gm	\ 1/р
Е I Xi |₽J , 1 < Р < оо (Lp — норма).
В частности, при т = 1 Е является полем действительных или комплексных чисел и все эти нормы принимают вид || х || = |х|, т. е. превращаются в абсолютную величину числа х. Ниже будем считать, что поле R действительных чисел и поле С комплексных чисел всегда являются нормированными в этом смысле (а следовательно, метрическими пространствами).
Пусть снова X — произвольное метрическое пространство. Далее, пусть задана последовательность{х„}ЛвЬ 2> ( элементов хп е X. Будем говорить:
последовательность {x„}rt==1 2 сходится к хеХ,
и писать
если
lim хп — х или х„->х, /2->оо
lim р (х„, х) = 0.
Я->оо
Элемент х называется пределом (сходящейся) пос ледова* тельности {хп}п=я{ 2	.
Сходящаяся последовательность имеет в точности один предел. Действительно, если
lim хп — х и lim х„ = х,
П-»оо	П~>оо
1. Метрические и нормированные пространства
235
то из неравенства треугольника и симметрии следует р(х, х)<р(хп, х) + Р(хп, х)
при всех п. Это влечет р(х, х) = 0, откуда в силу свойства а) метрики следует х = х. Если последовательность {хл}Д|ж1 2 сходится к х, то всякая подпоследовательность {хп^}йв1 2 также сходится к х.
Определение 1.3. Подмножество К метрического пространства X называется компактным, если для всякой последовательности {хл} из К существует подпоследовательность {xnfe} сходящаяся к некоторому элементу х^К. Если пространство X само компактно, то оно называется компактным метрическим пространством.
Определение 1.4. Подмножество А метрического пространства X называется замкнутым, если имеет место следующая импликация'.
хп^А, хл->х=>хеЯ,
т.	е. если предел сходящейся последовательности из А принадлежит А.
Очевидно, пустое множество и само пространство X замкнуты. Кроме того, конечные объединения и произвольные пересечения замкнутых подмножеств пространства X замкнуты.
Всякое компактное подмножество из X замкнуто.
Обратно, имеет место
Теорема 1.1. Если X — компактное метрическое пространство, а А — замкнутое подмножество X, то А компактно.
Доказательство. Пусть {хл} — последовательность элементов множества А. Тогда найдется подпоследовательность^^} и элемент х^Х такие, что xrtjfe->x. Так как А замкнуто, то хе Л.
Определение 1.5. Подмножество метрического пространства X называется открытым, если оно является дополнением замкнутого подмножества пространства X.
Таким образом, в частности, пустое множество и само пространство X являются открытыми множествами. Кроме того, конечные пересечения и произвольные объединения открытых множеств являются открытыми множествами. Далее, имеет место
236
VII. Приложение
Теорема 1.2*). Если К — компактно? подмножество метрического пространства X, a	— семей-
ство открытых подмножеств пространства X такое, что Ks U и(, то найдется конечное подсемейство {(7J.
(/о — конечно, Iq^I), такое что К U Uit
I /о
Доказательство (см. Чени [1966]) или Рудин [1966], стр. 45). Сначала докажем, что найдется такое е > 0, что всякий шар
К{Х, 8)={0<=Х|р(х, у) < в}, xsK,
лежит в некотором Ui.
Если бы такого е > 0 не существовало, то можно было бы найти последовательность таких шаров К(хп, 1/п), что хп е К при всех п, и ни один из этих шаров не содержится ни в одном Ui. Поскольку К компактно, то найдется подпоследовательность {xnk} последовательности {хп}, для которой Xnk-+x* К, а тем самым U/ при некотором j. Но так как U/ открыто, то существует 6 > О, при котором /С(х*, 6) Если взять k 2/6 столь большим, что р (x„ft, х*) < 6/2, то будут иметь место вложения
К (хп, 1/6) s К (xnk, 6/2) = К (х\ 6) £ U},
и мы приходим к противоречию.
Тем самым доказано существование такого 8 >» 0, что каждый шар К (х, в), х е К, содержится в некотором Uj. Теперь покажем, что К может быть покрыто конечным числом таких шаров К(х, г): Предполагая противное, выберем произвольный Xi <= К, а затем такой х2 е К, что х2 К(х1, е), и такой х3 <= К, что х3 ф К (xi, в) U К (х2, в) и т. д. Тогда последовательность- {хп} не содержит никакой сходящейся подпоследовательности, так как р(х,-, Х/)>:8 при что противоречит компактности множества К.
*) В случае X = R эта теорема принадлежит Борелю. (Прим, пере в.).
1. Метрические и нормированные пространства
237
п
Тем самым К s U K(xt, в) при подходящем выборе точек Xi, ..., хп s Кп, а так как К. (х/, е) s Uje jt е I, то Ks\^Ult. □
Определение 1.6. Пусть X и Y — два метрических пространства. Отображение f: X -> Y назььвается непрерывным в точке х е X, если имеет место следующая импликация:
х„ <= X, хп -* Х=> f (х„) -> f (х).
Отображение f называется непрерывным, если f непрерывно во всех точках х е X.
Теорема 1.3. Пусть f: Х->У— непрерывное отображение. Тогда прообраз замкнутого (открытого) множества есть замкнутое открытое множество.
Доказательство. Пусть ВеУ замкнуто. Если множество
Л = Г1(й) = {хеХ|/(х)еВ}
пусто, то доказывать нечего. Поэтому пусть {хп} — последовательность точек из А, причем хл->х. Так как В замкнуто, то из непрерывности следует /(хл)->/(х)е В. Тем самым хе Л.
Для открытых множеств доказательство получается переходом к дополнениям. □
Замечание. Обратная теорема также справедлива.
Например, если X — метрическое пространство, a f: X->R— непрерывное отображение, то по теореме 1.3 при aeR множества {хеХ|/(х) = а} и {х <= X | f (х) а} замкнуты, а множество {хе X|f(x) > а} открыто.
Теорема 1.4. Пусть отображение f: X-+Y непрерывно, а множество К^Х компактно. Тогда его образ f (К) компактен.
Доказательство. Пусть {уп} — последовательность точек из f(K). Тогда yn — f(xn), хп^К. Так как К компактно, то найдется такая подпоследовательность {x„ft}, что Хп^х^К., откуда следует ynk = f(xnk)->-
/ (К). g	  
238
VII. Приложение
Пусть теперь X — метрическое пространство и А___
произвольное непустое подмножество X. Каждому х е X поставим в соответствие расстояние
р(х, Л)== inf р(х, у) у&А
точки х от Л (р — метрика пространства X).
Замечание. Если А — замкнутое подмножество пространства X, то
р(х, Л) = 0<=>х е Л.
Импликация «ф» очевидна. Обратно, пусть р(х, Л) = 0. Тогда найдется последовательность {хл} из А, для которой
lim р(х, х„) = 0, т. е. хл->х. П->оо
Так как А замкнуто, то х е А.
Теорема 1.5. Отображение х->р(х, Д) пространства X в R непрерывно.
Доказательство. Пусть заданы последовательность {хл} и элемент х из X, причем	Требуется
доказать, что р(х«, Д)->р(х, Д). Из неравенства треугольника и симметричности метрики для любого п и произвольного у е А следует
Р (хп, у) + р (хл, х) > Р (х, у) > р (х, Л).
Поэтому
р (хл, Л) + Р (хп, х) > р (х, Л).
Аналогично,
Р (х, у) + р (х„, х) > р (хл, у) > р (х„, Л).
Поэтому
р (х, Л) + Р (хл, х) > Р (х„, Л).
Следовательно,
| Р (хл, Л) — р (х, Л) К р (хл, х),
откуда и следует утверждение теоремы.
Частные случаи. А — {у}, где уеХ фиксированный элемент. Тогда отображение f(x) = р(х, у), х е X, пространства X в R непрерывно.
1. Метрические и нормированные пространства
239
В частности, функция f(x) = \x\, xeR непрерывна.
Если X, Y и Z—метрические пространства, a f: X-+Y и g- Y^Z — непрерывные отображения, то суперпозиция gof:X^Z отображений f и g также непрерывна, что непосредственно следует из определения.
В частности, если В — метрическое пространство, a f: B->R или f: В—*С — непрерывное отображение, то отображение g(x) = |f(x) | пространства В в R также непрерывно.
Теорема 1.6. Пусть X — метрическое пространство, А — непустое замкнутное, а В — замкнутое подмножество пространства X, не пересекающееся с А. Тогда существует такое непрерывное отображение f: X-*- [О, 1], что f(x) = 0 для всех х е В (если В непусто), f(x) = 1 для всех xeAuj(x)< \ при всех х ф А.
Доказательство. Если В непусто, то положим f (х) =---------------Р_(£1_В)--
1 w р (х, 4) + р (х, В)
Если же В пусто, то положим
f (х, А) +Т-
На основании замечания перед теоремой 1.5 отображение f в обоих случаях обладает всеми требуемыми свойствами (непрерывность следует из теоремы 1.5). □
Теорема 1.7*). Пусть X — метрическое пространство, К — непустое компактное подмножество X, а f: К -► R — непрерывное отображение. Тогда существуют элементы х е К и х* е К, для которых
f (£) = inf f(x) и f (х*) = sup f (x).
x^K	x^K
Доказательство. Пусть m= inf f (x). Согласно x <= К
теореме 1.4 и доказательству теоремы 1.10 tn конечно. Тогда существует последовательность {хл} из К, для которой lim f(xn) = m. Так как К компактно, то найдется П-»оо
такая подпоследовательность и элемент хеХ, что
*) Для X — R эта теорема доказана Вейерштрассом. (Прищ, церев.)
240
VIL Приложение
lim Xnk = x. Непрерывность f влечет f(x) = m. Вторая &->OO
часть утверждения теоремы следует из равенства
sup f (х) = — inf (— f (х)). □ хеК .	х&К
В частности, если В компактное метрическое пространство и f непрерывная действительнозначная или комплекснозначная функция, то функция g (х) = | f (х) |, хеВ, также непрерывна и существует хеВ, для которого
f (х) — max | f (x) |.
xeB
T e o.p e m a 1.8. Пусть X — метрическое пространство, а К— непустое компактное подмножество X. Тогда для всякого х е X существует у е К, для которого
р(х, —	inf р(х, k).
k<=K
Доказательство. Как установлено выше, f(k) = = р(х, k) является непрерывным отображением множества Л в R. Поэтому утверждение теоремы непосредственно вытекает из теоремы 1.7. □
Пусть Е — нормированное векторное пространство над полем R или С.
Определение 1.7. Подмножество В пространства Е называется ограниченным, если существует такое число Р > 0, что ||6|| Р при всех Ь^В,
Теорема 1.9. Пусть пространство Е = R" или Сп наделено максимум-нормой. Тогда всякое замкнутное и ограниченное подмножество Е компактно.
По поводу доказательства отсылаем читателя к работе Чени [1966], стр. 10. (См. также Люстерник и Соболев [1965], стр. 72.)
Теорема 1.10. Пусть Е — п-мерное нормированное векторное пространство над полем R или С, т. е. существует такая система линейно независимых элементов gi, ..., gn^E, так называемый базис пространства Е, что всякий элемент f е Е однозначно представим в виде
п
xtgi, Xi е R или С.
1. Метрические и нормированные пространства
241
Тогда подмножество пространства Е компактно тогда и только тогда, когда оно замкнуто и ограничено.
Доказательство. Пусть В — непустое подмножество Е (для пустого множества доказывать нечего).
а)	Если В компактно, то, как уже отмечалось выше, оно также замкнуто. Предположим, что В не ограничено. Тогда в В найдется последовательность {bk}, для которой lim || bk || = оо. Но эта последовательность не может со-Л->оо
держать никакой сходящейся к элементу из В подпоследовательности, так как для каждой такой подпоследовательности также должно быть lim || bkj || == оо.
/-»ОО
Ь)	Пусть В замкнуто и ограничено. Отображение x = (xi, ..., xn)^f(x) пространства R" (или С), наделенного максимум-нормой, в пространство Е непрерывно, так как
Е у& < Е 1^. — ^||(gJK i=i	t=i || i=i
< ( E II gi II) max | Xt — у1|.
Положим M = {x e R" (или e С) |f(x)e В}. Так как = то в силу теоремы 1.4 достаточно показать, что М компактно, а на основании теоремы 1.9 достаточно показать, что М замкнуто и ограничено. Пусть теперь {х*}—такая последовательность из М, что хь^х (в смысле максимум-нормы). Тогда в силу непрерывности отображения x-*-f(x) и замкнутости множества В имеем
f (xk) -► f (х) <= В, т. е. х s М.
Согласно теореме 1.9 множество S = {х | max | xz | = 1} f=l.........................................n
компактно, а по теореме 1.7 существует xeS, для которого
Ю)|| = а = inf ||f(x)II.
х e=S
Так как {gi, ..., gn}—базис пространства Е, то а > 0. Поэтому для всякого х=/=&п (0« — нуль-вектор R" или
9 Л. Коллатц, В. Крабе
242
VII. Приложение
С") имеем
II / (х) ||=== ||/(17Т)||-||х|| >а||х||)
где ||х|| — максимум-норма элемента х.
Последнее неравенство имеет место также при х=0п<
Так как для всякого f(x)eB выполняется неравенство ||Дх)||^р при некотором р > 0, то для всякого хеА1 имеем || х || p/а, т. е. множество М также ограничено. □
Теорема 1.11. Каждое конечномерное линейное подпространство нормированного векторного пространства замкнуто.
Доказательство. Пусть Е — нормированное векторное пространство, а V — его конечномерное подпространство. Пусть {уЛ}—последовательность элементов из V такая, что vn-^v. Тогда для достаточно больших п справедливо неравенство ||	— vll^l, откуда следует
II vn II II v || + 1. Поэтому для всех достаточно больших п имеем vn е S = {v е V| || v ||	|| v || + 1}- Шар S огра-
ничен и замкнут в пространстве V, а следовательно, согласно теореме 1.10, — компактен. Поэтому найдется подпоследовательность [vn для которой vnk -> v g е S => v е V. □
В заключение займемся еще декартовыми произведениями метрических пространств. Пусть Х\, ...,	—
заданные метрические пространства с метриками pi, ... ..., рг. Если X — так называемое декартово произведение Х\ X Х2х ... хХг, состоящее из всех упорядоченных наборов x = (xi, ..., хг) элементов Xi^Xi, i=l, ..., г, то X превращается в метрическое пространство, если в нем ввести метрику равенством
Р (х, У) = max Pi (x/t/i)	(*)
i-1 г
X = (xb . . ., Xf), у = (У1, .... Уг)-
Теорема 1.12. Пусть, как и выше, Xi, , ХГ — метрические пространства, а ..., Аг — непустые компактные подмножества из Xi, ..., Хг соответственно. Если в X введена метрика (*), а А = Л1Х ... \АГ, то А также компактно в X.
2. Некоторые свойства выпуклых множеств
243
Доказательство. Приведем доказательство лишь для г = 2, так как в общем случае оно проводится совершенно аналогично.
Пусть {х*} —последовательность элементов из А. Тогда всякий элемент xk имеет видх* = (Хр х£), где & е Ль /= 1, 2. Так как компактно, то найдется подпоследовательность {х*/} и элемент хх е А{ такие, что
lim р. (xkJ, х.) = 0.
/-»оо	141	17
Так как Л2 компактно, то в соответствующей подпоследовательности {x*i} снова найдется подпоследовательность {х>} , для которой
lim p2(x2/m> х2) = 0, fn-»oo
где х2еЛ2. Но тогда, конечно, будем иметь также lim р1 (х^м, xt) = 0.
Полагая x = (xb x2) получим хе Л, а из определения метрики р следует
lim р (xfe/m, х) = 0. □ т-»оо
2. Некоторые свойства выпуклых множеств в векторных пространствах
В главах II—IV в различных местах использовались свойства выпуклых множеств. Здесь излагаются и доказываются эти свойства. Изложение тесно примыкает к книге Чени [1966].
Пусть Е — замкнутое пространство над полем действительных чисел.
Определение 2.1. Множество С^Е называется выпуклым, если f, g^ С, O^Z^/=>A/+(1— A,)geC. ' Это означает, что вместе с любыми двумя точками множеству С принадлежит и весь соединяющий их отрезок.
Методом полной индукции доказывается, что множество С <=Е выпукло тогда и только тогда, когда имеет
9*
244
VII. Приложение
место импликация
fi €= С, Л/ 0, i = 1,
г	г
г, 22 — 1	22^ ifi	С.
1=1	х=1
Пусть А — произвольное подмножество Е.
Определение 2.2. Наименьшее выпуклое множество, содержащее А, называется выпуклой оболочкой А и будет обозначаться К(А).
Легко убедиться, что К (А) состоит из всех g^E, которые могут быть представлены в форме
g=ZWo А, ^>0, £х< = 1.	(2.1)
1-1	г-i
Более того, имеет место
Теорема Каратеодори. Пусть Е — векторное пространство размерности п и А — произвольное подмножество пространства Е. Тогда всякий элемент g^K(A)' представим в форме (2.1), где г п + 1.
Доказательство. Требуется доказать лишь следующее: если g<^K(A) — выпуклая комбинация вида (2.1), где г > п + 1, то g представима в виде (2.1), где г заменено на г—1. Тогда после конечного числа шагов этот процесс приводит к представлению g в виде (2.1), где г п + 1. Если в (2.1) X/ = 0, то доказывать нечего. Поэтому пусть все А,/ > 0. Так как Е имеет размерность п, то поскольку г — 1 > п, элементы fi — fr, ...» fr-i — fr линейно зависимы, т. е. найдутся числа ai, .... ar-i, не равные одновременно нулю, для которых
Г-1
У. at — =	(®е—нулевой элемент пространства Е).
Полагая
будем иметь
Г—1 ar= £аг, 1=1 г	г
Еа, = 0 и Z=1	: —1
Определим равенствами
ц/ = Лг — таг при /= 1, г.
2. Некоторые свойства выпуклых множеств
245
и выберем те/? так, чтобы
1	а.	а.
— = maxv- = -7- (так что ak > 0). т	л.
Тогда
Р/^0 при всех z, и = 0.
Кроме того, в силу (2.2) г	г	г
Е = Е = Е — т Е а> = 1
i k	i~l	i = 1	i = 1
И
g = £ Kfi = £ ^ifi + т £ aifi = E ntfi. □
i = l	i=l	i = l	i-l
i = k
Простым следствием теоремы Каратеодори является
Теорема 2.1. Пусть Е — векторное пространство размерности п над полем комплексных чисел, а А — компактное подмножество пространства Е, Тогда выпуклая оболочка К (А) множества А также компактна.
Доказательство. Положим
{п+1
X = (Xi, ..., i) | Л,-	0,	= 1
/=1
Введем в Rrt+1 максимум-норму. Тогда S будет замкнутым и ограниченным множеством в Rrt+1, а следовательно, согласно теореме 1.9 — компактным. Не ограничивая общности, будем считать, что А — непустое компактное множество из Е (в противном случае множество К (Л) было бы пустым и компактным). Тогда по теореме 1.12 декартово произведение S X Лп+1 = S X А X ... XX
(снабженное метрикой (р); см. VII. 1) компактно в R^Xf. Теперь определим отображение <р: R"+1X Еп+{-+ ~+Е равенством
п + 1
ф (Л1, . . ., Л/п+Ь f b • . ., fn+1) — I,
i = 1
).,eR, fi^E, i=l, «4-1. Тогда, очевидно, K(A) согласно теореме Каратеодори совпадает с образом
246
VII Приложение
множества SX^n-bl при отображении ф, и согласно теореме 1.4 компактно, так как ф непрерывно. □
В дальнейшем будем считать, что Е = R", а скалярное произведение в R" обозначим через (.,.).
Теорема 2.2. Пусть Q — компактное подмножество пространства Е. Тогда следующие два утверждения эквивалентны:
а)	@п К (Q), (0П — нулевой элемент пространства £ = R");
b)	для всякого у Е имеем min (у, q) 0.
Замечание. Так как отображение q-+(у, q) множества Q в R (при фиксированном у е Е) непрерывно, a Q компактно, то согласно теореме 1.7 этот минимум достигается.
Доказательство. 1. а) Ь). Пусть 0rte K(Q). Тогда
m	тп
Qi е Q,	22	—	1 >
i = I	i—1
что влечет m о = (у, ©J = X и (у, qi)
при всяком у Е. Но это возможно лишь в случае, если
min {(«/, <?/)}< 0, 1=1, тп
откуда следует Ь).
2.	Ь) => а). Предположим, что K(Q). Так как K(Q) согласно теореме 2.1 компактно, т. е. по теореме 1.8 существует ye K(Q), для которого
0<ИЛ2<ИУ112 при всех yf=K(Q), где	_____
111/112= V(y> У)-
Пусть теперь q е Q. Тогда Х</ + (1 — X) у е К (Q) при всех X е [0, 1]. Поэтому
0 < || Х<? + (1 - X) $ ||2 = 2Х (0, q - 0) + X21|	# II2.
Отсюда при достаточно больших X > 0 следует
(Р. q ~ 0) > 0, т. е. (^, q) > (у, у) > 0.
3. Сравнение L2- и Т-приближений
247
Поэтому (у, q) > 0 при всех q^Q, что на основании сделанного выше замечания влечет
min (у, q) > 0.
я^О. .
Итак, в предположении @n<£K(Q) утверждение Ь) не может иметь места, откуда следует импликация Ь) => а).
3.	Сравнение L2- и Т-приближений
Для заданной функции f(x) и класса приближающих элементов W={w(x, а)} обозначим через wi элемент наилучшего приближения в метрике L2, а через Wt элемент найлучшего чебышевского приближения, если они существуют. Соответствующие функции погрешностей обозначим через
ez = wz — f, et = wt — f.	(3.1)
Будем рассматривать максимум-нормы этих погрешностей. Тогда, очевидно, ||е/||	||е/||. Представляет ин-
терес вопрос, существует ли для заданной области В и заданного класса W постоянная К, так называемая «постоянная переоценки», для которой
ИМ «Не, II,	(3.2)
и как велика должна быть постоянная К, если f пробегает множество всех функций, непрерывных на В, Для случая, когда В является конечным действительным интервалом, a W— классом многочленов степени ш, Пауэлл [1967] доказал, что существуют постоянные К = которые при т—>оо также стремятся к бесконечности, но очень медленно. Например, К\ = 2,4, а 7<ю = 3. Таким образом, это означает следующее: если мы хотим аппроксимировать f(x) в чебышевском смысле многочленами степени не выше 10, то в качестве приближенного решения можно взять элемент наилучшего /^-приближения, полученный путем решения системы ли-н'^йных уравнений, и при этом чебышевская норма погрешности не более чем в три раза может превзойти наилучшее чебышевское приближение, вычислить которое непосредственно несколько труднее.
Покажем теперь, что в случае двух переменных дело обстоит совсем иначе и что в этом случае при L2-annpo-
248
VII. Приложение
ксимации по сравнению с ^-аппроксимацией можно получить в процентном отношении сколь угодно большую погрешность уже в самых
Рис. VII. 3.1. Область (3.3).
простых случаях, а именно даже при приближении многочленами первой степени нельзя задать никакой верхней границы для постоянной переоценки К; в этом смысле
Дг-оператор является не-
Рис. VII. 3.2. Эскиз приближаемой функции.
ограниченным оператором. Пусть а — фиксированное малое число: 0 < а < 1. Далее, пусть В обозначает объ-
единение двух прямоугольников {(*. У) IIX К 1, |1/К1}, {(х, у) || х К а, | у К а~3}
в плоскости (х, у) (рис. VII. 3.1).
Пусть IV — класс функций
W = {ai + а2х + а,у},	(3.4)
и пусть требуется приблизить функцию
при О^х^а,	3,
f (х, у) = •
при а<х<1,
1 — X
1 — а
— f (~“ У) при остальных (х, у)^В функциями класса W (рис. VII. 3.2).
Элемент наилучшего чебышевского приближения получается непосредственно путем использования
4. Дальнейшие примеры Т-систем
249
альтернансного свойства:
wt (х, у) = хх, где х =	.	(3.6)
Элемент наилучшего £2‘приближения ищется в форм wt (х, у) = ох.
При этом постоянная а вычисляется из условия а	1
J = а~3 (а — ~^Ух2^х "Ь J (сх —1 — а У dx^min, (3.7) О	а
ИЛИ
1
+	а^~х) xdx = 0.	(3.8)
о J 1 а
а
Не вычисляя этого интеграла, можно заметить, что при а->0, он стремится к нулю. Поэтому
lim аа = -i-,	(3.9)
а->0	2
и при а—>0 получаем
т —> 1, а->оо, -^-->оо.	(3.10)
Но это означает, что для К нельзя задать фиксированной верхней границы.
4.	Дальнейшие примеры Г-систем (см. главу II)
Теорема. Пусть ki, k2, ..., kn — попарно различные действительные числа и pi, ..., рп — произвольные не* отрицательные целые числа. Тогда функции
{хрем}, р = 0, 1.....pv, v=l,...,n,	(4.1)
а следовательно, и функции
ek'x, xek'x, ..., х₽1е*1Х, ...»	..., xpnek"x,
на всяком сегменте J действительной оси образуют Т-си-стему.
2£0
VII. Приложение
Согласно II. 6 для доказательства наличия свойства Т-системы надо показать, что произвольная линейная комбинация функций (4.1) на действительной оси, которая здесь также обозначается через /, имеет не более N— 1 нулей, если N— число функций (4.1). Это утверждалось в следующей лемме.
Лемма 6.6 из главы II. Пусть Pv(x) — заданные многочлены от х степени pv с действительными коэффициентами, a kv — заданные попарно различные действительные числа. Тогда функция
п
р(х)=Х Pv(x)A‘	(4.2)
V=1
имеет на действительной оси — оо < х < + оо не более N — 1 нулей, где
N = рЛ + п-1. \v= 1	✓
Следствие. Выбирая в качестве kv числа 0, ±qi, (±q2, ..., ±?v из линейных комбинаций показательных функций получим гиперболические функции, откуда вытекает следующая
Теорема. Пусть q\, ..., qn — попарно различные положительные числа, а Pq, ..., рп — произвольные неотрицательные числа. Тогда функции {хр, хр ch (qvx), хр sh(^vX)}, р = 0, 1, ..., pv (v = 1, ..., п) образуют Т-систему на всяком интервале J действительной оси.
Соответствующую теорему для тригонометрических функций таким образом получить нельзя, так как при этом надо было бы использовать линейные комбинации функции elkvx (при действительных &v) с комплексными коэффициентами, что не входит в нашу схему. Вместе с тем, после преобразования ex — s, ek^x = sky}, xQekvx = = skv (log s)p может быть сформулирована
Теорема. При произвольных попарно различных действительных числах kv и неотрицательных целых числах pv (v = 1, ..., п) функции
{xkv (log х)р}, р = 0, 1, ..., pv, v=l, ..., п
образуют Т-систему в открытом интервале (0, оо).
5. Задачи с решениями
251
5.	Задачи с решениями
1.	П р и б л и же н и е многочленами. Найти наи-лучшее Т-приближение для функции f(x) = 1/(1 + х) на отрезке {0, 1]:
а) в классе линейных функций w = a0-j- atx,
b) в классе квадратных трехчленов w = а0 + сцх + + а2х2 (используя результаты а)).
Решение, а) График линейной функции, осуществляющей наилучшее приближение, должен быть паралле-
Рис. VII. 5.1. Приближение многочленами.
лен секущей, проходящей через конечные точки графика данной функции (рис. VII. 5.1а)) и поэтому имеет
Рис. VII. 5.2. Многочлены второй степени.
угловой коэффициент —1/2. Определяем, в какой точке х касательная к гиперболе имеет угловой_ коэффициент, равный —1/2 (это будет в точке х = V2 — 1). Отсюда следует,что w = (1/2) д/2 4- 1/4 — (1/2) х «0,957_— (1/2) х; наилучшее приближение ро — 3/4 — (1/2) д/2 » 0,043; соответствующая функция погрешности ei = w — f изображена на рис. VII. 5.1, Ь).
. . Ь) Теперь попытаемся приблизить наилучшим образом функцию погрешности е(х) многочленом Рг второй степени, график которого на рис. VII. 5.1, Ь) изображен пунктирной линией. В результате получим
йо = 0,9927, й1 = — 0,8283, а2 = 0,3429.
252
VII. Приложение
Наилучшее приближение р0 « 0,0074; норма погрешности достигается в точках Хо = О, Xi « 0,21, х2 ~ 0,71, Хз = 1 с последовательной переменой знака (см. рис. VII.5.1,с)).
2.	Многочлены относительно х2. Для функции f(x) = x на отрезке [0, 1] требуется определить наи-лучшее Т-приближение в классах
a)	w = aQ + aix2,	b) w = а0 + aix2 + a2*4.
Решение.
a)	w = 1/8 4- х2,	р0=1/8, (рис. VII. 5.2, а)
b)	w « 0,0692 + 1,9312х2 - 1,0696х4, р0 « 0,069;
экстремумы функции погрешностей е = w — f находятся в точках х — 0; 0,28; 0,78; 1 (рис. VII. 5.2, Ь)).
3.	Различные примеры. Вычислить наилучшее Т-приближение функции f функциями w класса W в области В и определить наилучшее приближение р0 и эк-стрмальные точки с положительной, соответственно отрицательной погрешностью е = w — f в следующих примерах:
В	f	\		I	W	
V	V/ н	и V/	V/ о	о	X3 хг		ао + а^х + «ах2 аох	1	9 t 3 2 32	16Х + 2 Х 2	.(72" - 1) х
/А * /А СИ	х3 — 6х2 + 6х + 1		аох	« - 0,26х
1<х<2	X		ах + а%х2	17 , 1 2 24 + 3 Х
в	Ро	е>о		е<0
о	о /А	/А *	я А	/А	1 32 с2« 0,17	X = 0, X = у 4 х = a == V2 — 1		11	"S— 1—। И г	'll -Н	я
1 < х < 5	«7,3	«3,4		«5
1<х<2	1 24	х = 1, х = 2		х = 1,5
5. Задачи с решениями
253
4.	Одностороннее чебышевское приближение. Сравнить обыкновенное чебышевское приближение с односторонним чебышевским приближением сверху, соответственно снизу, на примере приближения функции f(x) = 1 на отрезке 1 х 2 функциями класса w = а\х + а2х2.
Решение
	Элемент наилучшего приближения	Погрешность
Обыкновенное Г-приближение Одностороннее Т-приближение сверху Одностороннее Т-приближение снизу	6	8	8 II	II	11 <о| 4» Ьэ| — Ti]00 д.	д	д ОО	СО	СО 1	1	1 X	нН 4Z	z	'	
5. Параболы. Определить наилучшее Т-приближе-
ние снизу функции f(x) = x на отрезке [1, 2] в классе функций ц>(х, а) = 1/2 + а (х2— 1) (параболы, проходя-
щие через точку х= 1; у= 1/2).
Решение. w = x2 наилучшее приближение 0,5, норма соответствующей функции погрешности достигается в точке х = 1.
6. Нелинейное приближение многочленами. Определить наилучшее Г-приближение функции f(x) = x на отрезке [—1, 1] многочленами вида w = (а\ + а2х)3.
Решение, w = ох3, где с ж ж 1,374 — корень уравнения (р— 1) (За) 3/2 = за— 1, экстремальные точки X = ± (Зо)_1/2 И X = = ±1; наилучшее приближение
Рис. VII. 5.3. Нелинейное приближение многочленами.
ро = о — 1 ~ 0,374
(рис. VII. 5.3).
7. Нелинейное приближение многочленами. Определить наилучшее Т-приближение функции f(x) = ex на отрезке [0, 1] в классе w(x, а) = (1 + ах)2.
254
VII. Приложение
Решение. а « 0,62, р0 « 0,09;
8. Линейное приближение в случае двух переменных. Приблизить функцию f(х, у) == = 1/(1 + х + у2) на квадрате 0 х 1, 0 у С 1 в чебышевском смысле в классе w — ai ± а2х ± а3у и
применить теорему о двусторонней оценке наилучшего приближения.
Решение. Уклонение функции до=11/12—(х+у)/3 от функции f в вершинах квадрата поочередно равно е = ±1/2; поскольку четыре вершины квадрата образуют //-множество, то ро 1/12. Норма погрешности е несколько больше. Округляя, получим 1/12 ро 0,1 (1/12 « 0,0833). Оценку можно улучшить, применяя несимметрическую линейную функцию с а2 =/= а3.
9.	Нелинейное приближение в случае двух переменных. Определить наилучшее Г-при-
ближение в классе w = «1+^+ -{-азу+сцху для функции f(x,y) — = еху на квадрате |х| ^1, |#|^1.
Решение. Имеем а2=^з=0; коэффициенты щ, щ являются коэффициентами элемента наилучшего приближения а\ + a±z функции ехр(г) на отрезке —l^z^l. Экстремальные точки указаны на рис. VII. 5.4, а именно погрешность е = w — f принимает зна-
Рис. VII. 5.4. Нелинейное приближение в случае двух переменных.
чения Emax И Emin В Четырех Вер-шинах квадрата и во всех точках ветвей гиперболы, ука-
занных на рисунке.
10.	Рациональная аппроксимация. Приблизить функцию f(x) — ex на отрезке [0, 1] в чебышевском смысле
а)	многочленами второй степени,
Ь)	отношениями двух линейных функций и показать путем сравнения этих двух возможностей с тремя существенными параметрами, что рациональная аппроксимация дает лучшие результаты (см. Мейнардус [1964], стр. 158).
Решение.
а) | ех - (1,008577 + 0,854740х + 0,846029х2) 1 < 0,00878,
м I .	0,995705 + 0,668203* I n ,q9
Iе 1 - 0,388848х	|
5. Задачи с решениями
255
В случае Ь) норма погрешности примерно вдвое меньше, чем в случае а).
11.	Г-систем а. Образуют ли функции я\(х) = = {1, х2, х4, ..., x2s,х25"1} Т-систему на отрезке [—1,1]?
Ответ. Только при s=l. Тот факт, что функции {1, х2, х3} не образуют Т-систему на отрезке [—1, 1], вытекает уже из уравнения 30x3-j- 19х2 — 1 =0, которое
1 1 1
имеет три корня х = ——, “з"’ У ВНУТРИ отрезка [—1, 1]. При s> 1 отрицательный ответ на поставленный вопрос получается путем вычисления соответствующих определителей.
12.	Падё-аппроксимация. Приблизить функцию f(x)=ex при малых х рациональной функцией ш(х), которая является отношением двух многочленов второй степени, так, чтобы тейлоровские разложения функций u’(r) и f(x) имели одинаковые члены до четвертого порядка включительно.
Решение.
13.	Интеграл Гаусса. Приблизить функцию оо
f(x) = J e-s2ds
X
на действительной оси выражениями вида
2
j
W (x) = e-^-V------
fe=0
(Д. К. Хандскомб [1965], стр. 140).
Р е ш е н и е.	-А
f (х) =
_х2 1,69071595 + 1,45117156л + 0,50003230л2 /.	„ _ .„-54
е	1,90764542 + 3,79485940л + 2,90845448л2 + л3 '1 ± 0,0 '1U ''
14.	Задача на собственные значения. К какому типу аппроксимационных задачах приводится
256
VII. Приложение
вычисление наименьшего собственного числа (с собственной функцией не меняющей знака) линейного интегрального уравнения
1 у (х) = К j exiy (/) dt, О
если для этого используется теорема о двусторонней оценке наилучшего приближения с функцией сравнения v (х) = eaiX?
Решение. Отношение
(D (Y\ — р(х) _ еЩХ (Qi + х)
7 1 ~ ^1+^—1
extv (t)
о
должно наименее уклоняться от константы на отрезке /= [О, 1]. Таким образом, надо приблизить функцию f{x)— 1 на отрезке функцией класса
, х	еа'х («1 + х)
w(x, а) = а2 еа,+х_1
Это есть нелинейное приближение, при котором w зависит от параметра ах сложным образом («зацепленное приближение»).
15.	Колебание закрепленной мембраны. Тонкая однородная мембрана, закрепленная по краям, покрывает область В плоскости (х, у). Отклонение и(х, у, t) среднего слоя в момент t удовлетворяет дифференциальному уравнению
ААм = у 4^-, х, у е В, t > О,
краевым условиям н = -|^- = 0 на краю Г области В (п — внутренняя виям
и (х, у, 0) = f (х, у)	и dujdt (х, у, 0) = g (х, у).
Пусть В есть квадрат 0 < х, у < 1, а
f (*, У) = К*~ х2) (у - у2)]2 и g(x,y) = Q.
нормаль) и заданным начальным уело-
5. Задачи с решениями
25Z
Функция f приближается классом функций
W — #1511 + а2 (512 + $21) + ^3^22 + #4 (5i3 + 53i), где
Smn == [1 — cos (2лтх)] [1 — cos (2лш/)].
Тогда функция
v = ciiSii cos (Л-i/) + а2 (512 + 521) cos (Л2/) + • • •, где Л¥ легко подбираются, будет решением указанного
Рис. VII. 5.5. Задача о колебании закрепленной мембраны.
дифференциального уравнения с начальными условиями v = w, dv/dt = 0, требуется вычислить av.
Решение.
Вычисления с коэффициентами	Значения коэффициентов av	II w—f II
ai	ai =0,001029	0,003906
	= 0,0009655; а% = 0,0000690	0,000044
Gl, tZ2> #3> #4	Oj = 0,0009507; а2 = 0,0000623 а3 = 0,0000052; а4 = 0,0000147	0,0000143
На рис. VII. 5.5 показаны соответствующие распределения экстремальных точек. (Мы благодарим Будде и Диммермана за проведенные вычисления.)
f	в	№	Приближение сверху		
			Элемент наилучшего приближения	Ро	8
X2					
X3	-	а\Х	не существует		
1					
X2	1		2х	1	
X3	— 1 < X < 1	а^х + аъх2	X2	2	*
	1<х<3		- Зх + 4х2	«2,1	
1 1		1			
Приближение снизу		
Элемент наилучшего приближения	Ро	8
W = 0	1	
не существует		
W = 0	1	«==-
X	2	
~Х2	2	
—ха2 + 2х2а а = 4 — Уз”	6 (2 - д/З ) «1,6	
VII. Приложение
X2		агх 4- а2у	не существует			г = о	\ 1	п?
х2 4- у2							2	9-^ 6- *-6
х3, ху, ху2	квадрат: |х|<1					не существует		
X3	1у К 1	aix4-a2z/4-«3X2	X2	2	гл	—х2	2	ш
ху		atx + а2у 4-+ а3х2 + aty2	у(Х2+«/2)	2		_^(х2 + у2)	2	
X2						№==0	1	ф
х2 + у2	2РТ:2 х2 + у2	Л1Х 4- а2у	не существует				1	
х3, ху, ху2						не существует		
X2	квадрат 1 х 3		Зх	9/4	л	X	6	□
ху	1 у 1 < 1		4 <*+зу)	3		4 (з^ -	3	14
1		а{х 4- а2у 4-+ а3х2 + а^у2	4 (4х — х2) О	1/3	ш	(4х — х2)	1/4	ш
X2	(х-2)2+у2 < 1	aix + а2у	Зх	9/4	о	X	6	О
5. Задачи с решениями
260
УП. Приложение
16.	Одностороннее чебышевское приближение. Определить для следующих функций f на области В наилучшее одностороннее чебышевское приближение сверху и снизу в классе функций IF. В таблице даны решения вместе со значениями наилучших приближений, а также наброски графиков, причем для погреш-ности & = w— f экстремальные точки, в которых достигается max (в), отмечены темными кружочками, соответственно— линиями, а экстремальные точки, в которых достигается max (в) отмечены пустыми кружочками, соответственно-двойными линиями.
6. Другие задачи
1. Как и в задаче 3 из VII. 5 вычислить наилучшее Т-приближение функции f функциями w класса W в области В (при этом Рп обозначает многочлен степени п).
в	f	W
	X (1 + х«) V1 4- х*	Р2== а0 4-	4- а2х2
-1	|х| VI +|Х|	р<
	|х| (1 + 1 X 1 )2	Яо 4~ cos (а2х)
	(1 4- | х | )к при k = 1 или 2	ехр (а, + а3х2)
0<х<1 0< у < 1	V1 + X + у2	Pt — a0 + atx + а3у Рг (х, у)
	(1 +х + у2)'к	Pi или Р2
— оо < X < оо — оо < у < оо	1 + X2 + у2 1 + X1 + у*	1 Рг (х, у)
6, Другие задачи
261
2. Вычислить наилучшее Т-приближение функции f (х) на [0, оо) сплайнами s(x) с одним свободным узлом при х = а, а именно: пусть s(x) — многочлен Рп(х) на 0
х < а (например, п = 2) и $(х)= [Q^ (х) ] -1 на интервале а < х < оо, где Qn(x)— многочлен степени п (например, п = 2). В качестве f(x) взять одну из функций
>	(1 + x2)e~xt (1—х2)е”х,	д/1+х + х2^-\
3. Вычислить наилучшее приближение сплайнами (как в задаче 2) функции f (х) = (х + х3) е~х* на прямой — оо < х < оо, то же самое для функции f (х) = ех~х* на прямой — ОО < X < °О,
ЛИТЕРАТУРА
Андронов А. А., В и т т А. А., X а й к и н С. Э.
[1959] Теория колебаний. — М.: Физматгиз, 1959.
Ахиезер Н. И.
[1947] Лекции по теории аппроксимации. — М.: Гостехиздат, 1947.
Коддингтон Э. А., Левинсон Н.
[1958] Теория обыкновенных дифференциальных уравнений. — М.: ИЛ, 1958.
Данфорд Н., Шварц Дж. Т.
[1966] Линейные операторы, Т. II. —М.: Мир, 1966.
Дьедонне Ж.
[1964] Основы современного анализа. — М.: Мир, 1964.
Канторович Л. В., Крылов В. И.
[1952] Приближенные методы высшего анализа. М.; — Л.: Гос-техиздат, 1952.
Колмогоров А. Н.
[1948] Замечание по поводу многочленов П. Л. Чебышева, наименее уклоняющихся от заданной функции. — УМН, 1948, т. 3, вып. 1.
Лоран П.-Ж.
[1975] Аппроксимация и оптимизация. — М.: Мир, 1975. Кудрявцев Л. Д.
[1970] Математический анализ. — М.: Высшая школа, 1970. Люстерник Л. А.. Соболев В. И.
[1965] Элементы функционального анализа. — М.: Физматгиз, 1965.
Моисеев Н. Н.
[1969] Асимптотические методы нелинейной механики. — М.: Наука, 1969.
Натансон И. П.
[1963] Конструктивная теория функций. — М.: Гостехиздат, 1949.
Полна Г., Сеге Г.
[1956] Задачи и теоремы из анализа, ч. II. — М.: Гостехиздат, 1960.
Уолш Дж.
[1961] Интерполяция и аппроксимация рациональными функциями в комплексной области. — М.: ИЛ, 1961.
В а г г а г R. В., L о е b Н. L.
[1970а] On the continuity of the non-linear Tschebyscheff Operator.—Pacific J., 1970, v. 32, № 3, p. 587—601.
Литература
263
В а г г а г R. В.. Loeb Н. J.
[1970b] On the convergence in measure of non-linear Tschebyscheff approximations.— Num. Math., 1970, 14, № 3. p. 305— 312.
Bittner L.
[1961] Das Austauschverfahren der linearen Tschebyscheff-Approximation bei nicht erfullter Haarscher Bedingung. Z. Angew. Math. Meeh., 196, v. 41, № 6, p. 238—256.
Boehm B. W.
[1965] Ex’stence of best rational Tschebyscheff approximations.— Pacific J., 1965, v. 15, № 1, p. 19—28.
В r a e s s D.
[1967] Approximation mit Exponentialsummen. — Computing, 1967, № 4, 2, p. 309—321.
В r a e s s D.
[1970a] Uber die Vorzeichenstruktur der Exponeritialsummen, — J. Appr. Theory, 1970, v. 3, № 1, p. 101—113.
В r a e s s D.
[1970b] Die Konstruktion der Tschebyscheff-Approximierenden bei der Anpassung mit Exponentialsummen. — J. Appr. Theory, 1970, v. 3, № 3, p. 261—273.
BredendiekE.
[1969] Simultanapproximation. — Arch. Rat. Meeh. Anal., 1969, 33, № 4, p. 307—330.
BredendiekE.
[1970] Charakterisierung und Eindeutigkeit bei Simultanapproxima-tionen. — Z. Angew. Math. Meeh., 1970, v. 50, № 6—7, p. 403—410.
Brosowski B.
[1965a] Uber die Eindeutigkeit der rationalen Tschebyscheff-Appro-ximationen. — Num. Math., 1965, v. 7, № 2, p. 176—186.
Brosow ski B.
[1965b] Uber Extremalsignaturen linearer Polynome in n Verander-lichen. — Num. Math., 1965, v. 7, № 5, 396—405.
Brosowski B.
[1967] Uber die Eindeutigkeit der asymptotisch konvexen Tschebys-cheff-Approximationen. In: Funktional-analysis, Approxima-tionstheorie, Numerische Mathematik. — Basel, Stuttgart, 1967. — v. 7, p. 9—17.— (Internationale Schriftenreihe zur numerischen Mathematik).
Brosowski B.
[1968a] Nicht-lineare Tschebyscheff-Approximation. — Mannheim: 1968. — B. I.-Hochschulskripten v. 808/808a.
Brosowski B.
[1968b] Einige Bemerkungen zum verallgemeinerten Kolmogoroffs-chen Kriterium. — Schriften des Max-Planck-Instituts fur Physik und Astrophysik Munchen, 1968, v. 7.
Cheney E. W.
[1965] Approximation by generalized Rational functions, r— In: Approximation of functions/H. L. Garabedian, Ed. — Amsterdam; London; New York: 1965, p; 101—110.
264
Литература
С h е п е у Е. W.
[1966] Introduction to Approximation Theory. — New York; St. Louis; San Francisco; Sydney: 1966, p. 259.
Cheney E. W., Loeb H. L.
[1962] On rational Chebyshev approxisation. — Num. Math., 1962, v. 4, № 2, p. 124—127.
C h e n e у E. W., Loeb H. L.
[1964] Generalized rational approximations. — SIAM J. Numer. Anal., 1964, v. 1, № 1, p. 11—25.
Cheney E. W., Loeb H. L.
(1966] On the continuity of rational approximation operators. Arch. Rat. Meeh. Anal., 1966, v. 21, № 5, p. 391—401.
C h e n e у E. W., S о u t h a r d T. H.
[1963] A survey of methods for rational approximation with particular reference to a new method based on a formula of Darboux. — SIAM Review, 1963, v. 5, p. 219—231.
С о d у W. J., M e i n a r d u s G., Varga R. S.
[1969] Chebychev rational approximations to ex in [0, oo) and applications to heat-conduction problems. — J. Appr. Theory, 1969, v. 2, № 1, p. 50—65.
С о 11 a t z L.
[1952] Aufgaben monotoner Art. — Arch. Math., 1952, v. 3, № 5, p. 366—376.
С о 11 a t z L.
[1956] Approximation von Funktionen bei einer und bei mehrer-unabhangigen Veranderlichen. — Z. Angew. Math. Meeh., 1956, 36, № 5—6, 198—211.
С о 11 a t z L.
[1964] Funktionalanalysis und Numerische Mathematik. — Berlin; Gottingen; Heidelberg: 1964, p. 371.
С о 11 a t z L.
[1964a] Einschliefiungssatz fur die Minimalabweichung bei der Segment-approximation. — Proc. Simposio Internazionale sulle applicazioni dell’anaLsi alia fisica matematica 1964, p. 11—21.
С о 11 a t z L.
[1965J Inclusion theorems for the minimal distance in rational Tschebyscheff approximation with several variables. — In: Approximation of Functions/H. L. Garabedian, Ed. — Amsterdam; London; New York: 1965, p. 43—56.
С о 11 a t z L.
[1966] Rationale trigonometrische Tschebyscheff-Approximation in zwei Variablen. — Public. Inst. Math. Beograd, 1966, v. 6, p. 57—63.
С о 11 a t z L.
[1969] Nichtlineare Approximationen bei Randwertaufgaben.— Wiss Z. Hochsch. Architektur u. Bauwesen weimar, V. IKM 1969, p. 169—182.
С о 11 a t z L.
[1969a] Zur Tschebuscheff-Approximation fur Funktionen mehrerer unabhangiger Veranderlichen — Proc. Confer, on constructive theory of functions, Budapest, 1969, p. 89—99.
Литература
265
С о 11 a t z L.
[1971] Some applications of Functional Analysis to Analysis, particularly to Nonlinear Integral equations. — Proc. Symp. Non-lin. Funct. Anal/ed. by Rail, New York; London, 1971, p. 1—43.
С о 11 a t z L.
[1972] Approximationstheorie und Dualitat bei Optimierungsaufga-ben. — Basel; Stuttgart: 1972. — Internationale Schriftenreihe zur numerischen Mathematilk, v. 16, 33—39.
С о 11 a t z L.
[1972a] Anwendungen der Dualitat der Optimierungstheorie auf nichtlineare Approximationsaufgaben. — Basel; Stuttgart: 1972. — Internationale Schriftenre.he zur numerischen Mathe-matik (i. Vorbereitung).
Collatz L., WetterlingW.
[1971] Optimierungsaufgaben. Aufl. 2, Berlin; Heidelberg, New York: 1971, p. 222.
Descloux J.
[1961]	Degenerescence dans les approximations de Tschebyscheff lineaires et discretes. — Num. Math., 1961, 3, № 3, p. 180— 187.
Deutsch F. R., Maserick P H.
[1967] Applications of the Hahn — Banach theorem in approximation theory. — SIAM Review, 1967, 9, № 3, p. 516—530.
Fraser W., H a r t J. F.
[1962]	On the computation of rational approximations to continuous functions. — Comm. Assoc. Comp. Mach., 1962, 5, № 7, p. 401—403.
G о 1 d s t e i n A. A.
[1963]	On the stability of rational approximation. Num. Math., v. 5, № 5, 1963, p. 431—438.
Goldstein A. A.
[1965] Rational approximation on finite point sets/zusammen mit P. Fox und G. Lastman. — In: Approximation of Functions/ H. L. Garabedian, Ed. — Amsterdam; London; New York; 1965. Goldstein A. A., C h e n e у E. W.
[1958] A finite algorithm for the solution of consistent linear equations and inequalities and for the Tschebycheff approximation of inconsistent linear equations. — Pacific J., 1958, v. 8, № 3, p. 415-427.
Haar A.
[1918]	Die Minkowskische Geometrie und die Annaherung an ste-tige Funktionen. — Math. Ann., 1918, v. 78, № 3, p. 415—427. Handscomb D. C.
[1965]	Methods of Numerical Approximation. — Oxford, New York, Toronto, Sydney: 1965, p. 218.
HestenesM. R.
[1966]	Calculus of variations and optimal control theory. New York; London, Sydney: 1966, p. 405.
Keller W.
[1969] Asymptotische Aussagen und Fehlerabschatzungen bei linea-ren Integro — Differenzen-Diffentialgleichungen als Folge von Monotonieeigenschaften. — Dissertation, Hamburg: 1969.
266
Литература
Klotter К.
[1951] Technische Schwingungslehre. V. I. Ayfl. 2. Berlin; Gottingen; Heidelberg: 1951, p. 399.
К r a b s W.
[1963] Einige Methoden zur Losung des diskreten linearen Tsche-byscheff — Problems. — Dissertation. Hamburg, 1963.
К r a b s W.
[1966a] Zur verallgemeinerten reationalen Approximation. — Math. Z., 1966, v. 94, № 2, p. 84—97.
К r a b s W.
[1966b] Ein Verfahren zur Losung der diskreten rationalen Appro-ximationsaufgabe. — Z. Angew. Math. Meeh., 1966, v. 46, Sonderheft, p. 63—68.
К r a b s W.
[1967a] Uber differenzierbare asymptotisch konvexe Funktionenfa-milien bei der nicht-linearen gleichmaBigen Approximation. Arch. Rat. Meeh. Anal., 1967, v. 27, № 4, p. 275—288.
К r a b s W.
[1967b] Dualitat bei diskreter rationaler Approximation. — In: Funk-tionalanalysis, Approximationstheorie, Numerische Mathema-tik. — Basel, Stattgart: 1967. — Internationale Schriftenreihe zur numerischen Mathematik, v. 7, 33—41.
К r a b s W.
[1967c] Eine nichtlineare Eigenwertaufgabe bei rationaler Approximation. — Z. Angew. Math. Meeh., 1967, v. 47, Sonderheft, p. 57—60.
Karbs W.
[1968] Lower bounds for the minimal distance in rational approximation.— J. Appr. Theory, 1968, v. 1, № 2, p. 167—175.
К r a b s W.
[1969a] Duality in nonlinear approximation. — J. Appr. Theory, 1969, v. 2, № 2, p. 136—151.
К r a b s W.
[1969b] Uber die Reichweite des lokalen Kolmogoroff-Kriteriums bei der nicht-linearen gleichmaBigen Approximation. J. Appr. Theory, 1969, v. 2, № 3, p. 258—264.
К r a b s W.
[1969c] Ein Pseudo-Gradientenverfahren zur Losung des diskreten linearen Tschebyscheff — Problems. — Computing, 1969, v. 4, p. 216—224.
Krabs W.
[1970] Charakterisierung der Eindeutigkeit bei der nichtlinearen gleichmaBigen Approximation. — Arch. Rat. Meeh. Anal., 1970, v. 36, № 3, p. 239—244.	Я
L e m p i о F.
Separation und Optimierung in linearen Raumen. — Dissertation, Hamburg, 1971.
L e m p i о F.
[1971a] Lineare Optimierung in unendlich-dimensionalen Vektor-raumen. — Computing, 1971, v. 8, № 3—4, p. 284—290.
Литература	267
L е m р i о F.
[1972] Anwendungen der Lagrangeschen Multiplikatorenregel auf Approximations-, Variations- und Steuerungsprobleme. — Basel, Stuttgart: 1972. — Internationale Schrifttenreihe zur nu-merischen Mathematik (i. Vorbereitung).
Loeb H. L.
[1960] Algorithms for Chebychev approximation using the ratio of linear forms. — SIAM J. 1960, v. 8, № 3, p. 458—465.
Maehly H. J., Witzgall Ch.
Tschebyscheff-Approximationen in kleinen Intervallen.— Num. Math. 1960, v. 2, № 5, p. 293—307.
M a i r h u b e г J. C.
[1956] On Haar’s theorem concerning Chebychev approximation problems having unique solutions. — Proc. Amer. Math. Soc., 1956, v. 7, № 4, p. 609—615.
M a r s a g 1 i a G.
[1970] One-sided approximations by linear combinations of functions.— In: Approx. Theory/edited by A. Talbot. — New York; London: 1970, p. 233—242.
Meinardus G.
[1964] Approximation von Funktionen und ihre numerische Behand-lung. — Berlin, Heidelberg, New York: 1964, p. 180.
Meinardus G., Schwedt D.
[1964] Nicht-lineare Approximationen Arch. Rat. Meeh. Anal., 1964, v. 17, № 4, 297—326.
Meinardus G., Varga R. S.
[1970] Chebuchev rational approximation to certain entire functions in [0, oo)J. Approx. Theory, 1970, v. 3, № 3, p. 300— ' 309.
M о u r s u n d D. G.
[1968] Computational aspects of Chebushew approximation using a generalized weight function. — SIAM J. Numer. Anal., v. 5, № 1, p. 126—137.
Newman D. J., S h a p i г о H. S.
[1963] Some theorems on Cebysev approximation. — Duke Mathem. J., 1963, v. 30, № 4, p. 673—682.
Newman J., Shapiro H. S.
[1964] Approximation by generalized rational functions. — In: On Approximation Theory. — Basel; Stuttgart 1964. — Internationale Schriftenreich zur numerischen Mathematik, v. 5, 245—251.
Ortega J. M., Rheinboldt W. C.
[1970] Iterative solution of nonlinear equations in several variables. — New York, London, 1970, p. 572.
Powel 1 M. I. D.
[1967] On the maximum errors of polynomial approximations defined by interpolation and by least squares criteria. — Computer J, 1967, v. 9, № 4, p. 404—407.
Ralston A.
[1965] Rational Chebyshev-Approximation by Remes-Algorithms. Num. Math., 1965, v. 7, № 4, p. 322—330.
268
Литература
Redheffer R. M.
(1962] An extension of certain maximum principles, Mh. e Math., 1962, 66, № 1, p. 32—42.
Rice J. R.
[1960] The characterization of best nonlinear Tschebyscheff approximation.— Transact. Amer. Math. Soc., 1969, v. 96, № 2, p. 322—340.
R i c e J. R.
[1962] Chebyshev approximation by exponentials. — SIAM J., 1962, 10, № 1, p. 149—161.
R i c e J. R.
The approximation of functions. Reading (Mass); Palo Alto, London, 1964, 1969. —v. I, p. 203, v. II, p. 334.
Schmidt E.
[1968] Normalitat und Stetigkeit bei der Tschebyscheff-Approximation mit Exponentialsummen. — Dissertation, Munster, 1968. Schonhage A.
[1971] Approximationstheorie. — Berlin, New York: 1971, S. 212. Schrouder J.
[1956] Das Iterationsverfahren bei allgemeinerem Abstrandsbeg-riff. — Math. Z. 1956, v. 66, № 1, p. 111—116.
Schumaker L. L., Taylor G. D.
[1969] On approximation by polynomials having restricted ranges.—SIAM J. Numer. Anal., 1969, v. 6, № 1, p. 31—36.
Stiefel E.
[1959] Uber diskrete und lineare Tschebyscheff-Approximationen. Num. Math., 1959, v. 1, № 1, p. 1—28.
S t i e f e 1 E.
[1960] Note on Jordan elimination, linear programming and Tschebyscheff approximation. Num. Math., 1960, v. 2, № 1, p. 1-17.
T a 1 b о t A.
[1970] Approximation Theory. — Proceed. Symp. Lancaster, July 1969, ed. by A. Talbot; New York, London, 1970, p. 353.
T a u I о r G. D.
[1969] Approximation by functions having restricted ranges. — J. Math. Anal. Applic., 1969, v. 27, № 2, p. 241—248.
T а у 1 о r G. D.
[1972] On minimal H-sets. — J. Approx. Theory, 1972, v. 5, № 2, p. 113—117.
T 9 p f e r H. J.
[1971] Einfiihrung in die Approximations theorie (Lineare Tsche-byscheff-Approximation) — Berlin:	Hahn-Meitner-Institut,
1971, p. 157.
de la Vallee Poussin, Ch.
[1919] Le$on sur Tapproximation des fonctions d’une variable reel-le. Collect. Monograph sur la theorie des fonctions. (Nouveau Tirage). — Paris, 1919, p. 150.
Werner H.
[1962a] Tschebyscheff-Approximation im Bereich der rationalen Funktionen bei Vorliegen einer guten Ausgangnaaherung. — Arch. Rat. Meeh. Anal., 1962, v. 10, № 3, p. 205—219.
'Литература
269
Werner В.
[1962b] Die konstruktive Ermittlung der Tschebyscheff-Approximie-rende im Bereich der rationalen Funktionen. — Arch. Rat, Meeh. Anal., 1962, v. 11, № 4, p. 368—384.
Werner H.
[1963] Rationale Tschebyscheff-Approximation, Eigenwerttheorie und Differenzenrechnung.— Arch. Rat. Meeh. Anal., 1963, v. 13, № 5, p. 330—347.
W e r n e r H.
[1964] On the rational Tschebyscheff-operator. Math. Z., 1964, v. 86, № 4, p. 317—326.
W e r n e r H.
[1966] Vorlesung uber Approximationstheorie. — Berlin, Heidelberg, New York: 1966, p. 196, Lecture Notes in Mathematics, v. M. Werner H.
[1967] Die Bedeutung der Normalitat bei rationaler Tschebyscheff-Approximation. Computing, 1967, v. 2, № 1, p. 34—52. Werner H., Schaback R.
[1972] Praktische Mathematik. — Berlin, Heidelberg, New York: 1972, v. 11, p. 355.
Young J. W.
[1907] General theory of approximation by functions-involving a given number of arbitrary parametres. Transact. Amer. Math. Soc., 1907, v. 8, № 3, p. 331—344.
Zuhovickii S. I.
[1951] Ein Algorithmus zur Losung des Tschebyscheffschen Appro-ximationsproblems im Faile eines endlichen uberbestimmten linearen Gleichungssystems. — Dokl. Akadem, Nauk, 1951, v. 79, № 4, p. 561—564.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебра (непрерывных функций) 218
—, разделяющая точки 218
Алгебраическая кривая 140
Алгоритм обмена 180
— определения //-множеств 136
Альтернанс 212
Анализ периодограмм 16
Аппроксимация Паде 255
Базис (конечномерного векторного пространства) 240
Банахово пространство 47
Бета-функция Эйлера 190
Выпуклая оболочка множества 244
Границы для наилучшего приближения 54, ПО
Двойственная задача 172, 180
Двойственность при дискретном приближении 164, 172
Декартово произведение 242
Дифференцируемость отображения
в смысле Фреше 80
Достаточное условие для элементов наилучшего приближения 65, 219 ---единственности элемента наилучшего приближения 93, 97, 99, 100, 101
Единственность элемента наилучшего приближения 54, 115
Задача краевая 17
— кручения полукруга 31
—	монотонного типа 21
—	на собственные значения общая 255
---------при общем рациональном приближении 224
— оптимизации 42
— — линейная 22, 193
--- нелинейная 72
/-задача 49
Интегрирование численное 39
Итерационный процесс 186
Колебание мембраны 256
— нелинейное 25
Компактное метрическое пространство 235
Компактное множество 235
Конус касательный 73-
Критерий альтернансный 114
— разрешимости /-задачи 173
— элемента наилучшего приближения
78
Лемма Фаркаша 174
Максимум-норма 234
— с весом 49
Метод наименьших квадратов 13
— последовательных приближений 194
— решения задач дискретной линейной аппроксимации 191
--------- рациональной аппроксимации 182
Метрическое пространство 233
--- компактное 235
Минимум локальный 215
— от двух независимых переменных 140
Множества Н 64, 131
-	Н1 133
-	Н2 134
Множество выпуклое 243
—	замкнутое 235
-	- звездное 73
—	компактное 235
—	ограниченное 240
—	открытое 235
—	разделяющее точки 218
—	точечное 139
—	экстремальных точек 36
Необходимое условие для существования элемента наилучшего приближения 78, 80
Неравенство треугольника 231
Нижние границы для наилучшего приближения 54
Lp-норма 234
Область неограниченная 155
—	ограниченная 153
Оператор вполне непрерывный 48
—	дифференциальный 208
---сопряженный 208
—	монотонно-разложимый 46
—	отрицательный 47
— положительный 47
— Чебышева 117
/-оператор 116, 117, 121
Оптимизация линейная 42
Предметный указатель
271
Отображение конформное 37
— монотонное 177
— непрерывное 237
Оценка наилучшего приближения 54
Предел (сходящейся последовательности метрического пространства) 234 Приближение бесконечномерным подпространством 43
— дискретное 11, 50
— зацепленное 256
— комбинированное 24, 27
— кусочное 24, 146, 148, 149, 251
— линейное 15, 50, 70, 79, 91. 170, 180, 254
— наилучшее 49
— нелинейное 15, 16, 49, 51, 253, 254
— несимметричное 16, 44, 70, 91, 160
— одностороннее 20
—	полиномиальное 14
—	рациональное 15, 50, 51, 58, 79, 156, 159. 160, 230
—	синхронное 26
—	совместное 33
—	с ограничениями на область 46
—	условное 27
—	экспоненциальное 80
Li-приближение одностороннее 41
Li — Г-приближение смешанное 43
L^-приближение 41
Принцип максимума 18
—	монотонности 150
Разрешимость дискретной рациональной Г-задачи 168
Распределение вероятностей 42
Распространение волн в плазме 33
Симплекс-метод 186
Система Маркова 138
—	Чебышева 94
Т-система 137
Стабилизирующий член 26
Сумма экспоненциальная общая 202
Сходимость (в метрическом пространстве) 234
Теорема Брауэра 227
—	Вейерштрасса 216
—	Дини 217
— единственности Хаара 109
— Каратеодори 244
— Стоуна 216, 218, 219
Уравнение дифференциальное параболическое 21
—	дифференциально-разностное 38
—	интегро-дифференциальное 36
—	Клейна — Гордона 33
—	конденсатора 30
—	Лапласа 29
—	пластины 31
—	телеграфное 28
—	теплопроводности 19, 153
—	трансцендентное 38
— Чандрасекхара 48
Условие дифференцируемости 79
— Колмогорова локальное 66. 85, 86, 88, 89, 72
---общее 86
—	о знаках 88
--- нулях 96
—	представимости 91, 97
—	Хаара 93, 96
Функция аналитическая 37
—	аффинно-линейная 139
—	весовая 13, 41
—	гиперболическая 250
—	- допустимая 132, 133
Характеристика элемента наилучшего приближения 54, 84, 168
Характеристическая линия 26
Элемент наилучшего приближения 14, 49. 157
—	нормальный 123
Ядро (интегрального уравнения) 34, 35
—	вырожденное 43
Лотар Коллатц, Вернер Краба
ТЕОРИЯ ПРИБЛИЖЕНИИ
ЧЕБЫШЕВСКИЕ ПРИБЛИЖЕНИЯ И ИХ ПРИЛОЖЕНИЯ
М., 1978., 272 стр. с илл.
Редакторы А. Л. Гаркави, Г. Я. Пирогова Технический редактор Н. В. Кошелева Корректоры Е, А. Белицкая, Л. С. Сомова
ИБ № 2364
Сдано в набор 26.05.78. Подписано к печати 09.11.78.
Бумага 84Х1081/зг, тип. № 1. Литературная гарнитура. Высокая печать. Условя. печ. л. 14,28. Уч.-изд л. 13,27. Тираж 10 000 экз. Заказ Ns 1126.
Цена книги 1 р. 20 к
Издательство «Наукаэ Главная редакция физико-математической литературы 117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография Ns 2 имени Евгении Соколовой <Союзполиграфпрома» при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли.
198052, Ленинград, Л-52, Измайловский проспект, 29.
. ’ .4

/В'е B-'i