Теория вероятностей и статистика: 7-9 классы - Ященко И.В., Высоцкий И.Р.

Что такое статистика и как она связана с теорией вероятностей

10. Демографическая статистика. Половозрастные пирамиды

Глава III. Описательная статистика. Средние значения и размах

15. Наименьшее и наибольшее значения. Размах

Глава IV*. Описательная статистика. Квартили и частоты

21*. Среднее гармоническое и среднее геометрическое

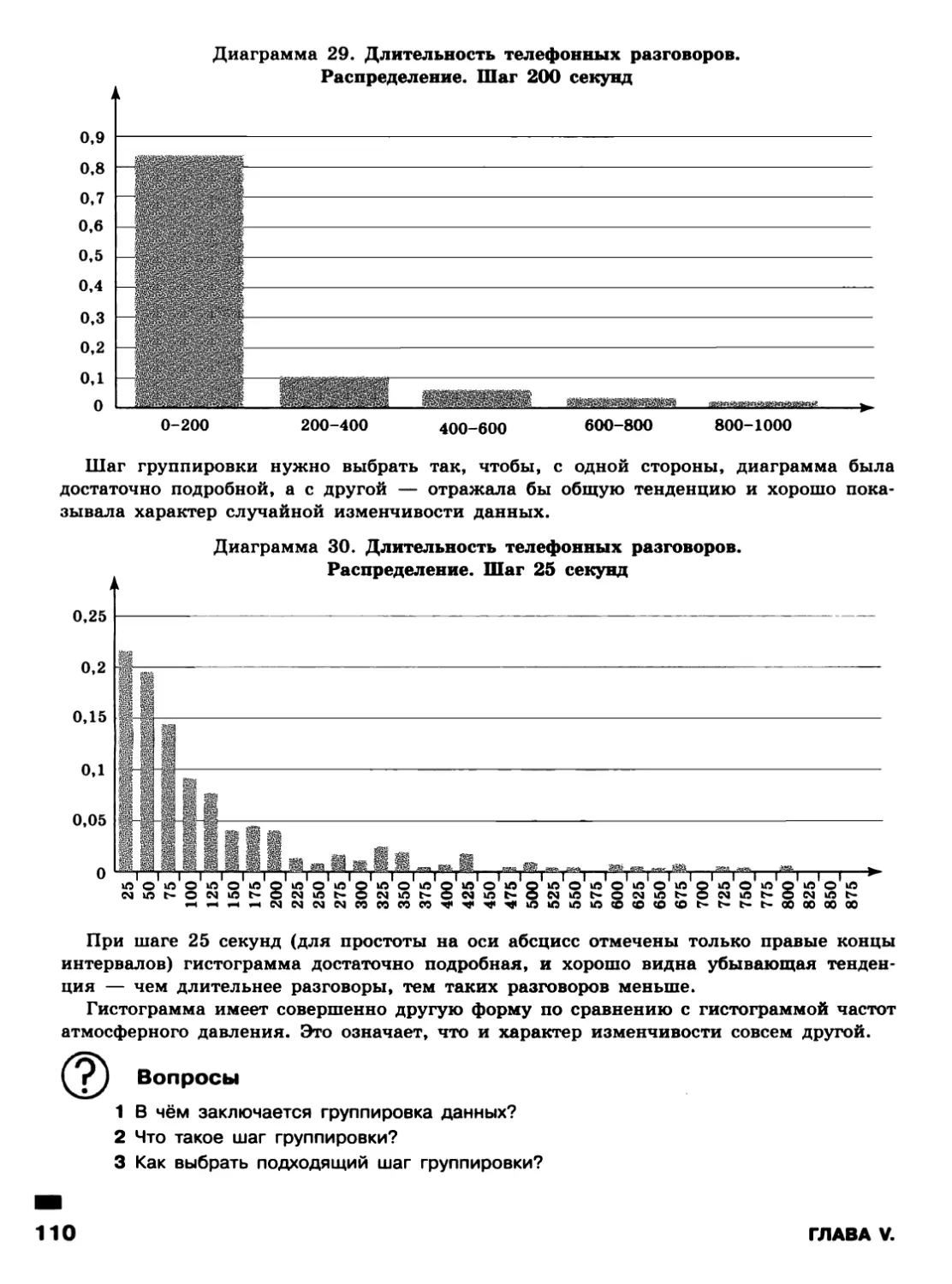
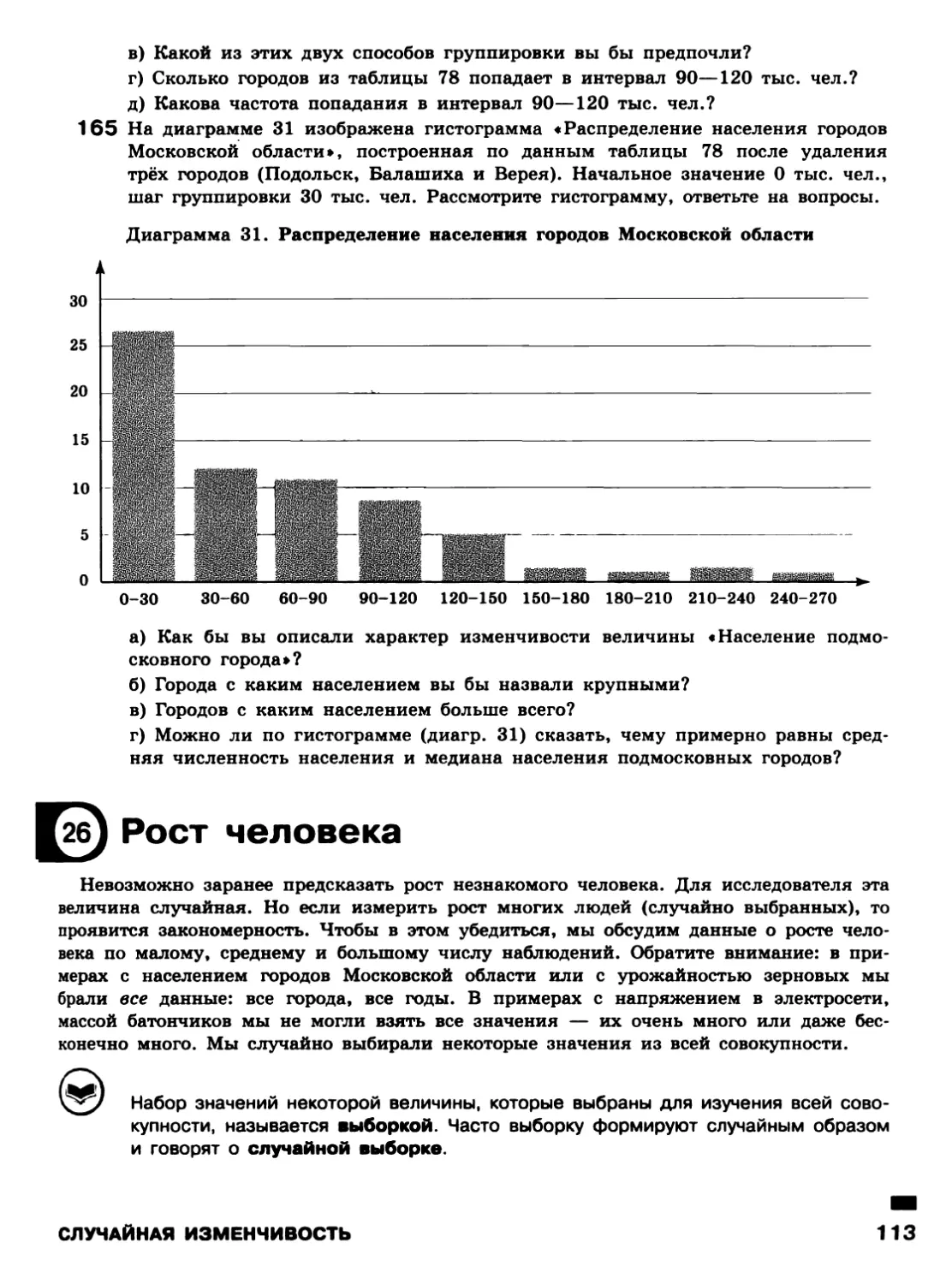
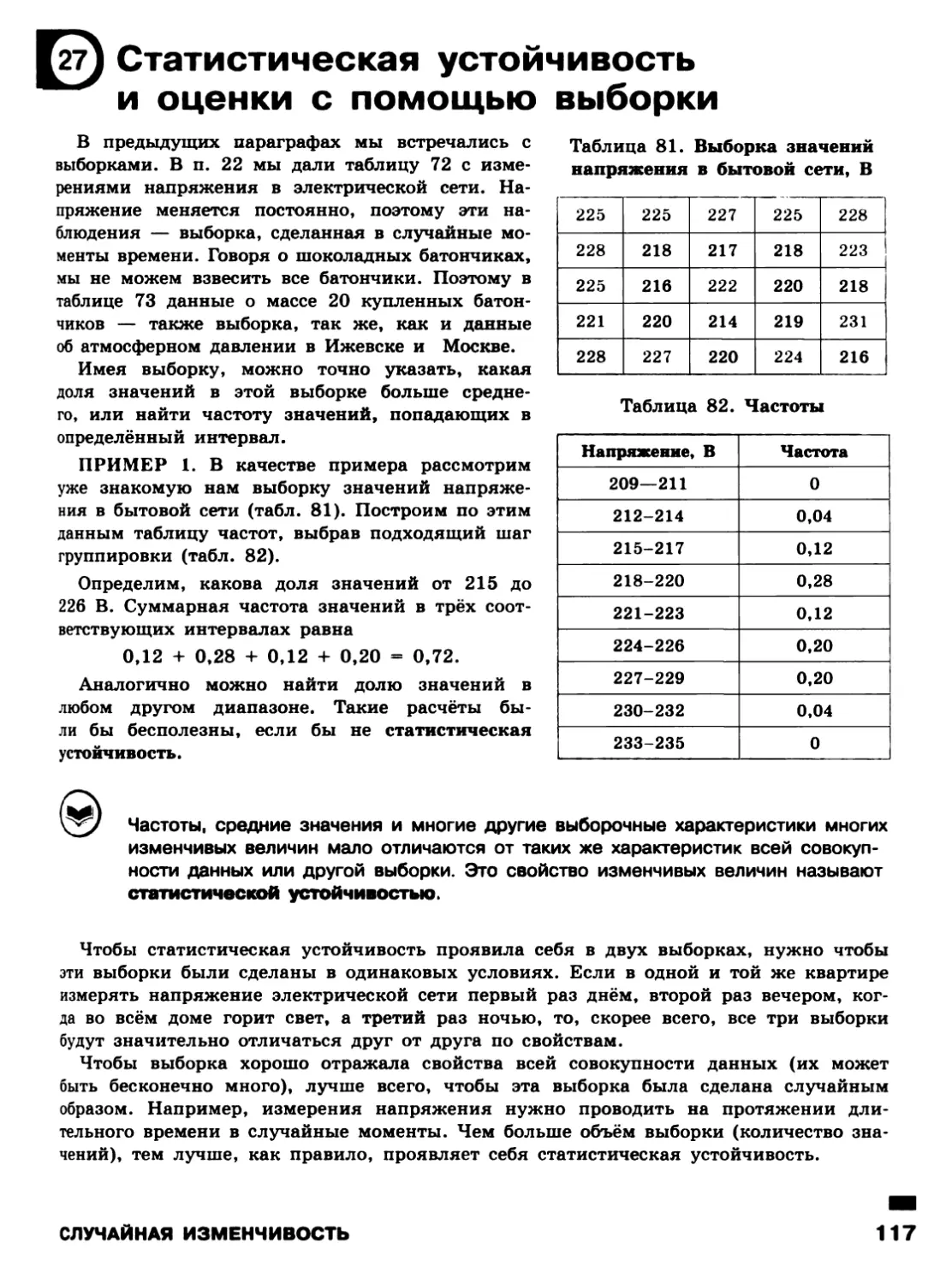
27. Статистическая устойчивость и оценки с помощью выборки

Глава VI. Случайные события и вероятность

30. Монета и игральная кость в теории вероятностей

32. Зачем нужно знать вероятность события

36. Стандартное отклонение числового набора

38*. Свойства дисперсии и стандартного отклонения

39*. Линейная связь на диаграмме рассеивания

Глава VIII. Математическое описание случайных явлений

42. Вероятности элементарных событий. Равновозможные элементарные события

43. Благоприятствующие элементарные события

45. Опыты с равновозможными элементарными событиями

Глава IX. Действия с событиями. Сложение вероятностей

51. Решение задач с помощью координатной прямой

Глава X. Действия с событиями. Умножение вероятностей

55. Об ошибке Эдгара По и о том, как победить стечение обстоятельств

58. Правило умножения и перестановки в задачах на вычисление вероятностей

60. Число сочетаний в задачах на вычисление вероятностей

64. Вероятности событий в испытаниях Бернулли

65*. Случайный выбор из конечной совокупности

67*. Выбор точки из отрезка и дуги окружности

69. Распределение вероятностей случайной величины

70*. Математическое ожидание случайной величины

71*. Закон больших чисел и его применение

Автор: Ященко И.В. Высоцкий И.Р.

Теги: общее школьное образование общеобразовательная школа теория вероятностей и математическая статистика физико-математические науки статистика теория вероятностей комбинаторика

ISBN: 978-5-09-097585-8

Год: 2023

Похожие

Справочник по проектированию электрических сетей.

План электрификации РСФСР

Военная экономика СССР 1941-1945 гг

Органическая химия атмосферы

Текст

И. Р. Высоцкий
И. В. Ященко

И. Р. Высоцкий
И. В. Ященко
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ
И СТАТИСТИКА

УДК 373.167,1:519.2+519.2(075.3)
ББК 22Л72я721
В93
Условные обозначения
Г I J Важно (г у Вопросы I Щ J Справка, комментарий
0 Упражнения ПМ1 Определение Гм) Практическое задание»
^—^ ^**-^ статистическое исследование
I J Начало и окончание материала для углублённого изучения
ИЗ) (или 13*) Пункт, содержание которого не входит в обязательный минимум
содержания ФГОС по математике
120 Задание повышенной сложности
Высоцкий, Иван Ростиславович.
В93 Теория вероятностей и статистика : 7—9-е классы : учебное пособие
И. Р. Высоцкий, И. В, Ященко ; под ред. И. В. Ященко. — 3-е изд., стер. —
Москва : Просвещение, 2023. — 272 с. : ил.
ISBN 978-5-09-097585-8.
Учебное пособие предназначено для знакомства учащихся с формами представления и описания
данных в статистике, случайными событиями, вероятностью и ее свойствами. В пособии в равной
мере уделяется внимание статистике, комбинаторике и теории вероятностей и их роли в изучении
явлений окружающего мира.
УДК 373.167Л;519.2+519.2<075.8)
ББК 22Л72я721
Учебное издание
Высоцкий Иван Ростиславович
Ященко Иван Валериевич
ТЕОРИЯ ВЕРОЯТНОСТЕЙ И СТАТИСТИКА
7—9 классы
Учебное пособие
Центр математики. Ответственный за выпуск Юл:. Голубева. Редакторы Ю. С. Голубева, Л\ В. Кузнецом.
Е.А.Разинко&а* В. Г. Щепеткин, Младший редактор Jb\ А Андреенноеа. Художественный редактор
Т. В. Глушкова. Художники О. В. Попович. Л. В. Масло&а. Компьютерная графика И. В.Губиной. Техниче-
ское редактирование и компьютерная вёрстка О. Л. Карповой. Корректор Д. Д. Нажесткина
Подписано в печать 21.02.2022. Формат 84X108/16- Гарнитура School BookSan Pin. Уч.-изд. л. 16,22.
Усл. печ. л. 28.56. Доп. тираж 8000 экз. Заказ № 70567СМ.
Акционерное общество • Издательство «Просвещение»,
Российская Федерация, 127473, г. Москва, ул. Краснопролетарская, д. 16, стр. 3, этаж 4» помещение L
Адрес электронной почты «Горячей линии» — vopros@prosv.ru.
Отпечатано в филиале «Смоленский полиграфический комбинат» АО «Издательство
«Высшая школа». Российская Федерация, 214020, г. Смоленск, ул. Смольяиинова, 1.
Тел.: +7(4812)31-11-96. Факс? +7(4812)31-31-70. E-mail: spk@smolpk.ru http://www.amolpk.ru
ISBN 978-&~О&Ч)07585-в © АО «Издательство «Просвещение», 2ttZl
© Художественное оформление.
АО «Издательство «Просвещение»»
Все права защищены

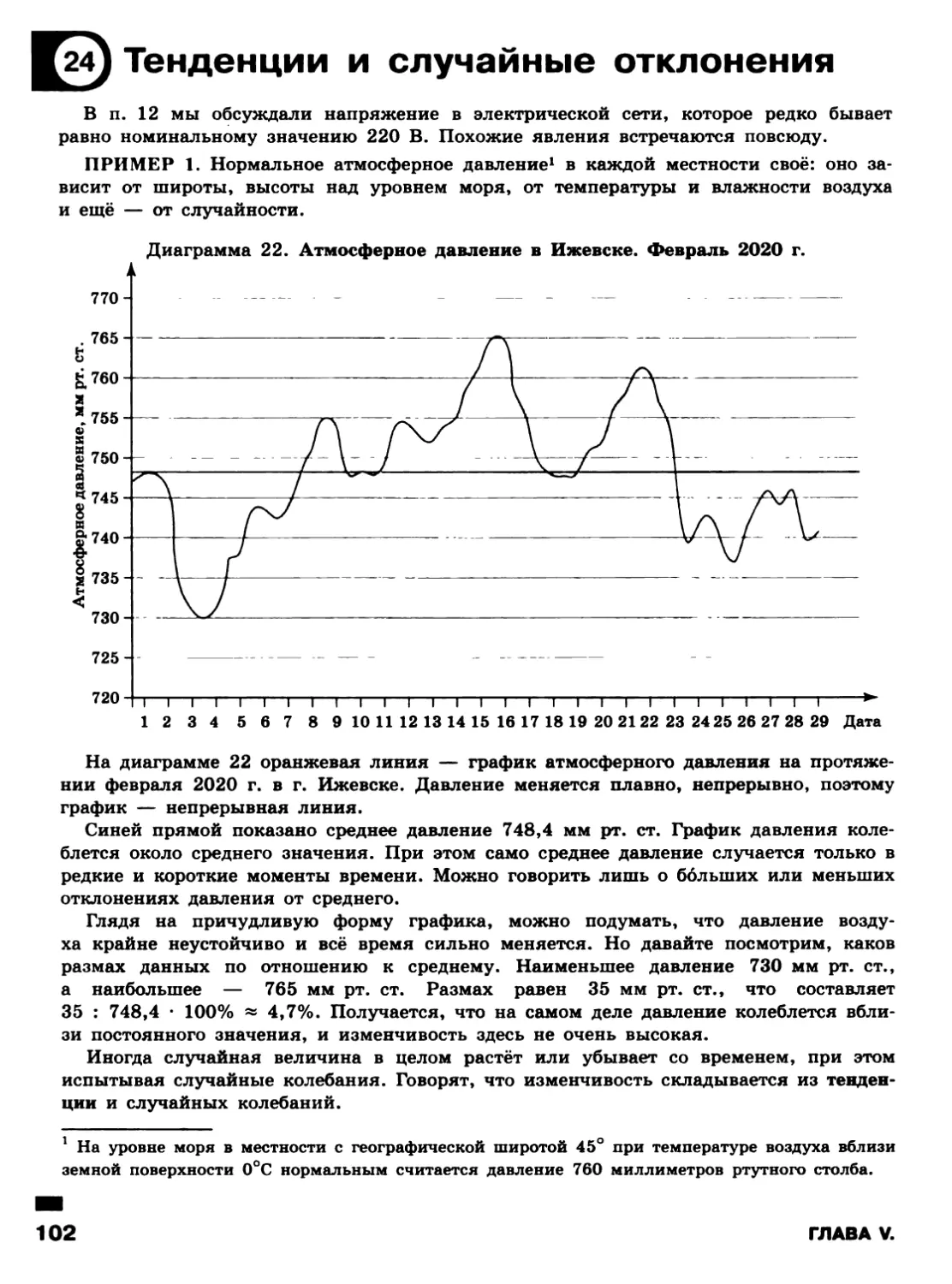
Предисловие
Окружающий мир полон случайностей. Заморозки и оттепели, ураганы, паводки
и засухи, подъёмы и спады экономики, болезни, неожиданные встречи — все эти
события во многом случайны. Однако мысль о том, что в окружающем мире много
случайного, останется бесплодной, если не научиться измерять случайность числом,
вычислять шансы случайных событий, оценивать значения случайных величин.
Теория вероятностей в школе — это общественное признание необходимости фор-
мирования современного мировоззрения, объединяющего представления и о функцио-
нальных зависимостях, и о случайной изменчивости. Без методов теории вероятно-
стей и статистики невозможно эффективное производство, внедрение новых лекарств
и методов лечения, обеспечение страховой защиты граждан от непредвиденных об-
стоятельств, проведение разумной социальной политики.
Особую роль статистика и теория вероятностей играют в современном мире и в со-
временных профессиях. Они важны для развития цифровой экономики. Знание основ
статистики и теории вероятностей позволит школьнику продолжить образование
практически в любой сфере. Особенно эти знания нужны сейчас в инженерном деле,
в сфере управления, в общественных специальностях, в медицине и психологии.
Теория вероятностей начала складываться в XVII в.
Сначала источником вероятностных задач служили игры.
В частности, игра в кости, где главное — подсчёт числа
равновозможных комбинаций. До сих пор во многих на-
чальных курсах теории вероятностей преобладают комбина-
торные задачи, связанные с бросанием монеты или кости,
с выбором случайных комбинаций карточек, шаров и т. п.
Это — анахронизм. Разумеется, такие задачи есть и в этом
учебнике, но они не составляют основу курса и даны для
упражнений и иллюстраций.
Становление теории вероятностей дало толчок бурному
развитию статистики. В XVII в. статистика как наука впер-
вые применяется в демографии и страховании, возникают
идеи о случайных ошибках в измерениях.
Теория вероятностей и статистика долгое время развива-
лись как описательные естественные науки, использующие
математический аппарат. В полноценную математическую
теорию наука о вероятностях превратилась лишь в XX в.
благодаря системе аксиом, созданной академиком Андреем
Николаевичем Колмогоровым.
Не случайно теория вероятностей стала строгой математической наукой так позд-
но: теория вероятностей в некотором смысле сложнее, чем другие школьные матема-
тические дисциплины. Поэтому учебник не претендует на формальное и строгое из-
ложение. В нашем курсе мы не касаемся аксиом Колмогорова, но пользуемся вве-
дёнными им и принятыми во всём мире основными понятиями: случайный опыт,
элементарное событие, вероятностная мера.
Теория вероятностей и статистика в учебнике представлены как естественные нау-
ки, где наибольшую ценность представляет сложившаяся система взглядов, основные
понятия и их связи с реальностью. Математические доказательства отступают на вто-
рой план, а математические методы играют ту же роль, что и в физике или механи-
Андрей Николаевич
Колмогоров
(1903-1987)
ПРЕДИСЛОВИЕ
3

ке. Комбинаторные сведения авторы рассматривают как необходимый, но вспомога-
тельный материал, частично данный в приложении.
Изложение начинается со статистики, поскольку именно статистика, имея дело со
случайными явлениями и величинами, ставит вопросы, решение которых требует ма-
тематической теории. Обсуждается представление данных в виде таблиц и диаграмм.
Изучая совокупности чисел и способы их описания, мы естественным образом прихо-
дим к понятию случайной изменчивости, подготавливая переход к изучению теории
вероятностей.
В качестве учебного материала авторы использовали актуальные сведения о де-
мографии, экономике и сельском хозяйстве России, явлениях повседневной жиз-
ни, окружающих школьника. При этом авторы учитывали возрастные особенности
школьников, которым предназначен учебник.
Весь материал условно можно разбить на три больших раздела:
1. Статистика (представление данных, описательная статистика, понятие о случай-
ной изменчивости).
2. Случайные эксперименты, случайные события и их вероятности.
3. Случайные величины, их характеристики и понятие о законе больших чисел.
Важное место занимает рассказ о последовательностях случайных испытаний,
в том числе о сериях испытаний Бернулли — одной из базовых схем теории вероят-
ностей.
Авторы выражают благодарность Надежде Сошитовой, Александре Кострикиной
и Василисе Шапариной за помощь в подготовке книги.
Авторы будут признательны за отклики, замечания и предложения по совершен-
ствованию учебника. Наш адрес: 119002, Москва, Б. Власьевский пер., 11, МЦНМО,
Теория вероятностей. Email: probinschool@yandex.ru.
4
ПРЕДИСЛОВИЕ

Что такое статистика и как она связана
с теорией вероятностей
Наука, которая занимается способами сбора, обработки и представления больших
массивов данных, называется статистикой. Это название впервые использовал немец-
кий учёный Готфрид Ахенваль. Само слово «статистика» происходит от латинского
слова status — состояние, положение вещей.
Нельзя управлять автомобилем, в котором приборы не работают или работают не-
правильно. Точно так же невозможно управлять государством, городом и даже шко-
лой, если нет достоверной статистической информации.
Статистика нужна не только для управления. Все люди сталкиваются с медицин-
ским обслуживанием, пользуются услугами банков, транспортом, делают покупки в ма-
газинах. В нашем мире, который стремительно становится цифровым, статистическое
мышление даёт человеку преимущество перед тем, у кого статистический кругозор не
развит. Ещё лучше, если статистическое мышление подкреплено знанием математики.
В Российской Федерации сбором и обработкой статистических данных занимается
федеральная служба государственной статистики — Росстат. Росстат собирает и си-
стематизирует сведения о населении, его доходах и расходах, об экономике и транс-
порте, о медицине и образовании, о магазинах и кафе, о том, сколько мы тратим воды
и электроэнергии, бензина и газа, — обо всём, что нужно знать, чтобы планировать
жизнь огромной страны. Очень важно следить, как ведётся строительство жилья —
растёт ли и как быстро количество домов, квартир, какое жильё пользуется наиболь-
шим спросом сейчас и какое будет нужно через несколько лет.
Диаграмма 1. Десять крупнейших метрополитенов мира
Лондон i
Нью-Йорк 1
Токио -\
Москва J
Сеул 1
Шанхай Н
Мадрид J
Париж i
Мехико 1
Пекин J
Гуанчжоу ]
Дели *
Чунцин *
Нанкин 1
!■ Б
1- &:
^'
в .. _.
——< 1-
■
J»
. . м
■В
Q
5i
i .
{ ;_
■ I. , !
1——t »
$
асу;
•И •■'
"Si
Bi; ■ 9>
с\ • tx
£
Sb
' "&
»
и»
... _£
1 1 1 1 t—I 1 1 I
2009 |
Город
Лондон
Нью-Йорк
Токио
Москва
Сеул
Шанхай
Мадрид
Париж
Мехико
Пекин
20
Город
Шанхай
(Пекин
Гуанчжоу
Москва
Сеул
Лондон
Нью-Йорк
[Нанкин
Дели
[ Чунцин
Протяжён
ноешь
линии,км
402 1
370
304
298
287
234
227
220
201
200
>19
Протяжён 1
ноешь
линий,км
676 |
628
476
456
123
402
394
347
343 |
310 "|
50 100 150 200 250 300 350 400 450 500 550 600 650 700
ЧТО ТАКОЕ СТАТИСТИКА И КАК ОНА СВЯЗАНА С ТЕОРИЕЙ ВЕРОЯТНОСТЕЙ 5

Важно не только собрать информацию. Нужно уметь сравнивать её с аналогичны-
ми данными о других странах. Ещё важнее наблюдать, как меняются показатели —
плотность населения, занятость, доходы, как учатся школьники, как развивается
транспорт. Из диаграммы 1 видно, как за 10 лет поменялся состав десяти крупней-
ших метрополитенов мира и как выросла протяжённость линий.
Величины, которые изучает статистика, изменчивы — они подвержены случай-
ным колебаниям. Меняются курсы валют, цены на нефть и газ, температура на ули-
це. Даже в школьной жизни множество изменчивых величин. Например, количество
школьников, присутствующих в классе, меняется день ото дня. Каждый день один
и тот же школьник тратит на дорогу от дома до школы разное время — немного
больше или немного меньше, чем накануне.
Чтобы стать настоящей наукой, чтобы правильно описывать, объяснять и про-
гнозировать изменчивые явления, статистика нуждается в помощи математики. Раз-
дел математики, изучающий случайные явления, называется теорией вероятностей.
Опираясь на математические законы вероятностей, специалисты-статистики могут не
только собирать данные и выдвигать предположения, но и проверять их, а также де-
лать достоверные выводы и полезные прогнозы.
Вы начнёте изучать статистику и теорию вероятностей и увидите, как математика
помогает понять многие сложные и изменчивые явления повседневной жизни. Вам
пригодятся все математические знания: и то, что вы уже знаете, и то, что вам ещё
только предстоит узнать на уроках алгебры и геометрии.
6 ЧТО ТАКОЕ СТАТИСТИКА И КАК ОНА СВЯЗАНА С ТЕОРИЕЙ ВЕРОЯТНОСТЕЙ

Таблицы
Таблицы нужны, чтобы упорядочивать боль-
шие массивы данных. Гораздо легче искать
информацию в таблице, чем в обычном тек-
сте, потому что в таблице каждое значение
находится в своей ячейке, а однородные све-
дения сгруппированы в одной графе. Если
данные подходящим образом помещены в
таблицу, то их удобно сравнивать. Кроме
того, в таблицах удобно проводить неслож-
ные вычисления и подсчёты. А электронные
таблицы позволяют быстро работать даже с
большими массивами данных.
В первой главе мы будем учиться пред-
ставлять статистические данные с помощью
таблиц и извлекать из них информацию.
1 Сбор данных и построение
таблицы
2 Статистические данные
в таблицах
3 Поиск информации
в таблицах
4 Вычисления в таблицах
5 Крупнейшие города России
6 Подсчёты и измерения
в таблицах
7 Упорядочивание данных
в таблицах
8
Таблицы сопряжённости

Таблица — один из самых простых и удобных способов упорядочить данные. С не-
которыми таблицами вы уже знакомы с начальной школы. Это таблицы сложения и
умножения, таблицы спряжения глаголов. Таблицами являются расписание уроков,
страницы школьного дневника, оглавление учебника.
Государственные и коммерческие службы регулярно собирают обширные сведения
об обществе и окружающей среде. Эти данные обычно публикуют в виде таблиц.
Рассмотрим примеры некоторых таблиц и научимся извлекать из них информацию.
MJ Сбор данных и построение таблицы
ПРИМЕР. В образовательном центре был сделан ремонт, и в начале учебного года
руководство центра поручило сотруднице Елене собрать заявки на новую мебель от
всех лабораторий и отделов. Елена принимает заявки по CMC и по электронной поч-
те. В течение двух дней она получила несколько заявок.
I 1 П/1
Лена, здравствуйте. Нам
в библиотеку нужен шкаф для
одежды, 5 столов и 10 стульев.
Ещё мы хотим 2 тумбочки
с ящиками.
Спасибо
<&
Это Алексей. В 201 комнату
нужно: 3 рабочих стола, 3
тумбочки с ящиками, 2
книжных шкафа. А можно еще
шкаф для одежды? Ещё
просят маленький круглый
столик для кофемашины, но
это не обязательно
юбочки вс^°^вмпы настольные
ISSUES^Гэтонужноотдельио
заказывать?
Щ1 Елена
| *"**» Для Олймп^ог^^лУ
няЫЛЧвРа "Р0СИЛИ оранжевый диван
Гриш^воГ НЭМ НУЖвН Зе«
Фиша говорит, что 4 лампы - много
Давайте только 3 лампы купим.
Лена, это снова библиотека.
Извините, нам 10 стульев не
нужно. Нужно только 8. Но
зато мы хотим ещё одну
тумбочку. Тоже с ящиками
Мы хотим маленький
диванчик. Оранжевый. Нам
ещё нужно 2 книжных шкафа,
3 стула и одно кресло.
Ещё 3 рабочих стола.
А правда говорят, что можно
лампы заказать?
Нужно 4
s^** •.$!#*
Как видим, данные поступают в разное время, уточняются, меняются. Всё это
трудно запомнить и неудобно хранить в разных местах. Нужно собрать все сведения
в одну таблицу. Елена использует электронную таблицу. Она уже подсчитала и внес-
ла в таблицу, сколько нужно рабочих столов.
8
ГЛАВА I.

Конечно, часть информации потеряна: мы не видим в таблице, сколько и какой
мебели заказывали разные отделы. Но сейчас это не важно. Главное — собрать об-
щий заказ. Таблицу можно расширить: указать цены и подсчитать общую сумму, ко-
торую придётся затратить на новую мебель. Получится таблица-смета, о которой мы
поговорим позже (см. п. 4).
®
Вопросы
1 Какая информация, нужная для
приобретения и расстановки
мебели, не вошла в электрон-
ную таблицу на рисунке 1?
2 Приведите примеры таблиц, ко-
торые вы видели на улицах, в
торговых центрах, аэропортах,
на вокзалах или автобусных
станциях.
л
1
2
Э
4
5
6
7
8
9
10
11
А
1
2
3
4
5
6
7
8
9
В
Наименование
Стол рабочий
Шкаф для одежды
Стул
Кресло
Тумбочка с ящиками
Книжный шкаф
Настольная лампа
Маленький круглый стол
Зелёный диван
I С I
Количество I
111
0
Упражнения
Рисунок 1. Заказ мебели
Перечертите таблицу из рисунка 1 в свою рабочую тетрадь и заполните её до
конца.
2 Каждый день автобус делает три рейса от железнодорожной станции в посё-
лок: туда и обратно. Первый рейс отправляется от станции утром в 8 часов
32 минуты. На дорогу от станции до посёлка автобус тратит ровно 30 минут.
Такое же время автобус тратит на обратный путь. На конечных остановках
автобус ровно 10 минут ждёт пассажиров и отправляется обратно. Составьте
расписание движения автобуса по образцу (табл. 1).
Таблица 1. Расписание движения автобусов по маршруту
«Ст. Беломошье — пос. Нагорное»
Ежедневно с 25.04.2019
Время отправления от конечного пункта
Ст. Беломошье
8:32
Пос. Нагорное
^2j Статистические данные в таблицах
Население крупнейших городов России
Таблица 2 содержит сведения о числе жителей городов России с населением более
1 млн человек (так называемых городов-миллионеров). Города даны в алфавитном
порядке, а число жителей указано в тысячах человек. Данные приведены за несколь-
ко лет, чтобы можно было судить об изменении численности населения городов.
ТАБЛИЦЫ
9

Таблица 2. Население городов-миллионеров
Город
Волгоград
Воронеж
Екатеринбург
Казань
Красноярск
Москва
Нижний Новгород
Новосибирск
Омск
Пермь
Ростов-на-Дону
Самара
Санкт-Петербург
Уфа
Челябинск
Население, тыс. чел.
1970
926
781
1210
989
795
7854
1342
1309
1016
998
925
1203
4067
977
! 1030
1989
995
882
1363
1085
912
8677
1435
1436
1149
1092
1008
1257
4435
1080
1142
2002
1011
849
1294
1105
909
10126
1311
1426
1134
1002
1068
1158
4661
1042
1077
2006
992
846
1308
1113
921
10 425
1284
1397
1139
993
1055
1143
4581
1030
1093
2010 i
1021
890
1350
1144
974
11504 |
1251
1474
1154
991
1089
1165
4880
1062
ИЗО
2016
1014
1048
1469
1244
1091
12 506
1259
1613
1172
1052
ИЗО
1163
5352
1121
1202
2019
1013
1054
1483
1252
1095
12 616
1254
1618
1165
1054
1133
1157
5384
1124
1201
По этой таблице легко найти ответы на следующие вопросы:
• Сколько было в России городов с населением более миллиона в 2019 г.? Для от-
вета надо пересчитать города в таблице. Их пятнадцать.
• Каково было население Москвы в 2006 г.? Найдём строку, относящуюся к Мо-
скве, и столбец с данными за 2006 г. В Москве в 2006 г. проживало около
10 425 тыс. чел.
• Какой город в России в 2019 г. был третьим по числу жителей? Для ответа на
этот вопрос нужно просмотреть все числа в столбце «2019» и выбрать из них
третье по величине. Это число 1618, Оно находится в строке «Новосибирск».
• На сколько выросло население Москвы за период с 2002 по 2019 г.? Сле-
дует найти разность между числом жителей Москвы в 2019 и 2002 гг.:
12 616 - 10126 s 2490, то есть население Москвы выросло примерно на
2 млн 490 тыс. чел.
10 ГЛАВА I.

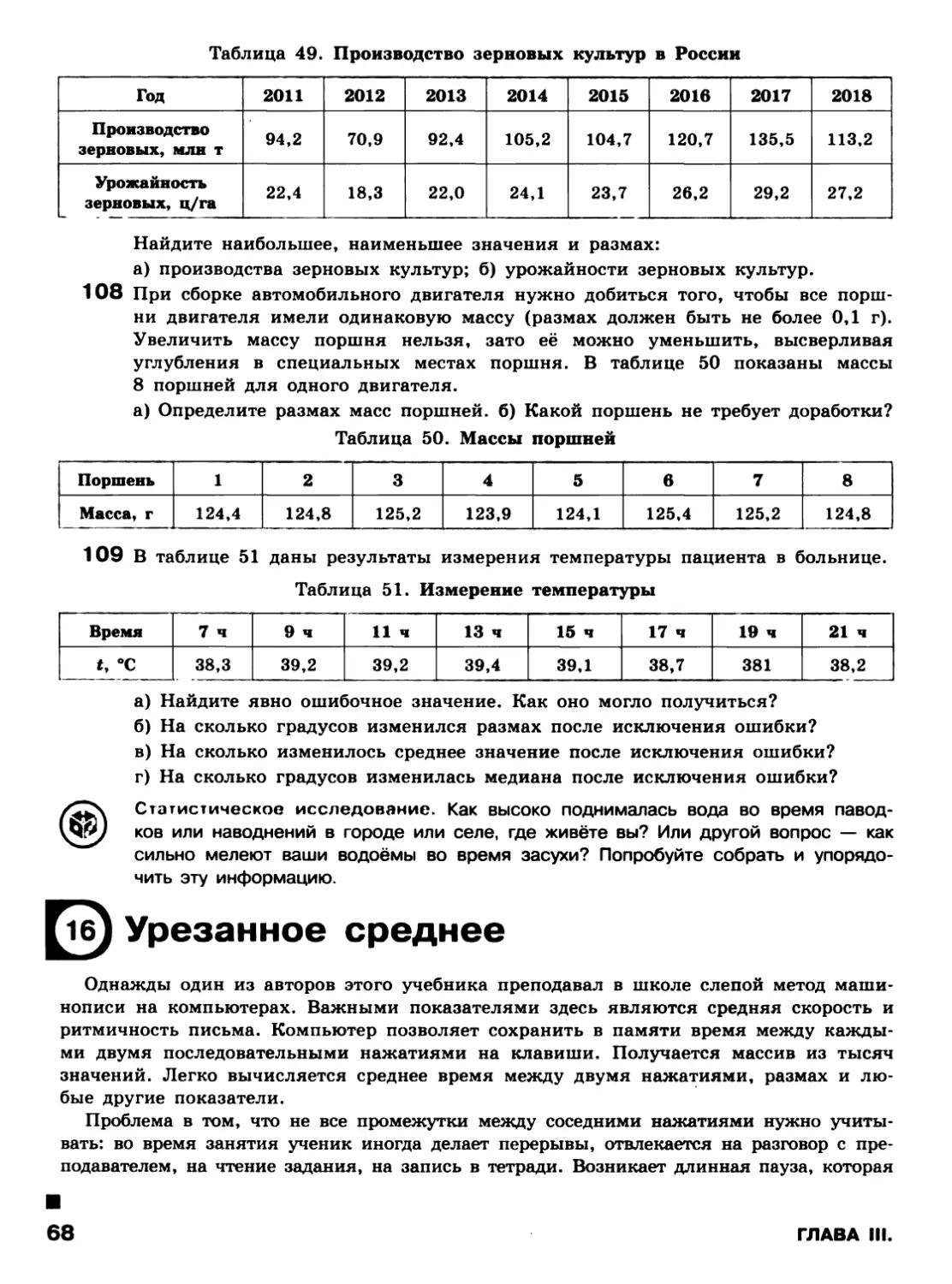
Урожайность зерна
Для России всегда было важно, сколько зерна производит сельское хозяйство. Это
важно сейчас и будет важно в будущем. К зерновым культурам, согласно принятой
классификации, относятся пшеница, ячмень, рожь, гречиха, просо, рис, кукуруза
и некоторые другие культуры (рис. 2). Главной для нас зерновой культурой является
пшеница.
Рисунок 2. Зерновые культуры
Зерно идёт на производство продуктов питания, кормов для скота и на экспорт в
другие страны. По оценкам экспертов, сейчас годовая потребность России в зерне со-
ставляет примерно 105 млн тонн.
Таблица 3 содержит некоторые сведения о зерновом производстве в России с 2011
по 2018 г. Производство зерна и пшеницы дано в миллионах тонн (млн т); урожай-
ность — в центнерах1 с гектара2 (ц/га).
Таблица 3. Производство зерновых культур в России
■ Пад
Промзводство зер-
новых, млн т
Урожайность зерно-
вых, ц/га
Производство пше-
ницы, вин т
Доля пшеницы, %
2011
94,2
22.4
56,3
2012
70,9
18,3
37,8
2013
92,4
22,0
52,1
2014
105,2
24,1
59,7
2015
104,7
23,7
61,8
2016
120,7
26,2
73,3
2017
135,5
29,2
86,0
2018
113.2
27,2
72,1
1 центнер (ц) — 100 кг.
2 1 гектар (га) - 10 000 м2.
ТАБЛИЦЫ

Производство электроэнергии
Важным показателем состояния экономики является объём производства электри-
ческой энергии. Производство электроэнергии практически совпадает с потреблением,
поскольку электрическую энергию очень трудно запасать в большом количестве (бата-
рейки и аккумуляторы не в счёт). Поэтому электричества производят столько, сколь-
ко нужно промышленности, сельскому хозяйству и населению. Годовой прирост про-
изводства электроэнергии даёт представление о росте экономики в стране.
Сейчас появляется всё больше энергосберегающих технологий и в быту, и в произ-
водстве. Поэтому в последнее время рост производства электроэнергии идёт медлен-
нее, чем рост экономики.
В быту количество потреблённой электрической энергии измеряют в киловатт-
часах (кВт * ч); в стране — в миллиардах киловатт-часов. В таблице 4 указано коли-
чество произведённой в России электроэнергии с 2010 по 2019 г.
Таблица 4. Производство электроэнергии в России
Год
Объём произведённой
электроэнергии, млрд кВт * ч
Год
Объём произведённой
электроэнергии, млрд кВт * ч
2010
1038
2015
1050
2011
1055
2016
1072
2012
1069
2017
1074
2013
1045
2018
1091
2014
1047
2019
1096
©
0
Вопросы
Для чего применяются таблицы?
Как вы думаете, почему производство зерновых культур — один из важнейших
экономических показателей?
Почему по количеству произведённой электроэнергии можно судить о росте
экономики в стране?
Почему при обновлении оборудования на фабрике производство может вырасти,
а потребление электроэнергии — снизиться?
Упражнения
С помощью таблиц 2—4 выполните задания и ответьте на вопросы.
3 Найдите численность населения:
а) Новосибирска в 2002 г.; б) Казани в 1979 г.
4 В каком городе население в 1989 г. составляло 1435 тыс. человек?
5 Сколько городов в России имело население более 1 млн человек в 1979 г.;
в 2006 г.?
6 На сколько численность населения Санкт-Петербурга в 2018 г. была больше,
чем в 1989 г.?
7 На сколько численность населения Екатеринбурга в 2018 г. была выше, чем
в 1979 г.?
8 Сколько городов в России в 2002 г. имело население более 1500 тыс. чело-
век?
12
ГЛАВА I.

9 Какой была урожайность зерновых в 2011 г.?
10 В каком-году урожайность зерновых составила 23,7 ц/га?
11 В каком году урожайность была наибольшей?
12 Видно, что в целом год от года урожайность зерновых растёт. Однако в 2012
и 2018 гг. она снижалась по сравнению с предыдущим годом. Какие факто-
ры, по вашему мнению, влияют на урожайность зерновых? Назовите два-три
фактора.
13 Для каждого года в таблице 3 найдите долю пшеницы в урожае зерновых
(в процентах). Заполните нижнюю строку таблицы.
14 В каком году доля пшеницы в урожае зерна была наибольшей?
15 В каком году доля пшеницы в урожае зерна была наименьшей?
16 В какие годы доля пшеницы превышала 60% ?
17 Сколько электроэнергии было произведено в России в 2012 г.?
18 В каком году электроэнергии было произведено больше: в 2012-м или в 2013-м?
19 В каком году в России было произведено больше всего электроэнергии?
20 Назовите один-два фактора, которые влияют на объём годового потребления
электроэнергии в стране.
21 Как вы думаете, чем объясняется спад в производстве электроэнергии
в 2013 г.?
Поиск информации в таблицах
Поговорим подробнее о поиске информации в таблицах на примере расписания
движения поездов Москва—Санкт-Петербург. Фрагмент расписания поездов дан в та-
блице 5.
В расписании много разных сведений о поездах. Для каждого поезда указаны его
номер и название, время отправления из Москвы, дни отправления, время в пути
и время прибытия в Санкт-Петербург.
Для удобства поиска эта информация разбита на столбцы, каждый из которых
имеет свой заголовок. Верхняя строка с заголовками столбцов называется шапкой та-
блицы.
В каждой строке даны сведения только об одном поезде. Порядок столбцов в рас-
писании выбран так, чтобы проще было найти информацию, интересующую пасса-
жира в первую очередь. Звёздочкой отмечено время прибытия, если поезд прибывает
в Санкт-Петербург на следующие сутки.
Для ответа на вопрос о времени отправления конкретного поезда не нужно изу-
чать всё расписание. Достаточно найти в таблице один столбец и одну строку.
Таблицы облегчают поиск необходимых сведений, избавляя от необходимости из-
учать всю имеющуюся информацию. В этом главное преимущество таблицы перед
текстом.
ПРИМЕР. Группа школьников планирует уехать из Москвы в Санкт-Петербург
в пятницу 27 сентября после 19:00, но не позже 22:00. Чтобы выбрать подходя-
щие поезда, не нужно изучать всю таблицу. Достаточно просмотреть колонку «Вре-
мя отправления» и выбрать нужный поезд. Таких поездов всего 2. Это поезда № 778
и 780.
ТАБЛИЦЫ 13

Таблица 5. Расписание движения поездов из Москвы
в Санкт-Петербург (фрагмент)
Номер
и название поезда
20
«Мегаполис*
16
«Арктика»
258
252
242
748
«Невский экспресс»
802
«Ласточка»
778
«Сапсан»
780
«Сапсан»
266
32
«Лев Толстой»
4
«Экспресс»
54
«Гранд экспресс»
2
«Красная стрела»
Время
отправле-
ния
00:20
00:41
12:12
16:20
16:25
16:55
19:45
21:00
22:07
23:10
23:40
23:55
Время
прибы-
тия
08:59
09:14*
20:40
01:24*
01:20*
20:34
00:21*
23:54
00:53*
06:30*
05:49*
08:30*
08:36*
Время
в пути
8 ч 39 мин
8 ч 33 мин
9 ч 04 мин
9 ч 00 мин
4 ч 09 мин
7 ч 26 мин
4 ч 09 мин
3 ч 53 мин
8 ч 23 мин
9 ч 00 мин
8 ч 56 мин
8 ч 00 мин
Дни
отправления
Ежедневно
Ежедневно
с 23 сентября
Ежедневно
4 июля
Ежедневно
с 9 августа
Ежедневно
с 23 сентября
Пн, ср, пт
с 23 сентября
Ежедневно
с 23 сентября
Ежедневно
с 23 сентября
Пн, ср, пт
Ежедневно
Ежедневно
Ежедневно
Ежедневно
Цена, р.
от 2821
от 2228
от 1266
от 1909
от 1909
от 2391
от 1237
от 2064
от 2064
от 1664
от 4067
от 2838
от 2912
от 2838
•J Важно! Таблица не только облегчает поиск информации, но и позволяет лег-
ко сравнивать данные и делать разумный выбор.
Строки и столбцы обычно отделяют друг от друга горизонтальными и вертикаль-
ными линиями. Однако применяются и другие способы зрительного выделения ин-
формации. Часто чередуют цвета строк, отчего таблица становится похожа' на пеше-
ходный переход.
14
ГЛАВА I.

Обязательное страхование гражданской ответственности
Каждый водитель в Российской Федерации должен быть застрахован по програм-
ме обязательного страхования гражданской ответственности (ОСАГО). Срок действия
страхового полиса1, как правило, один год.
Стоимость полиса получается умножением базового тарифа2 на несколько коэффи-
циентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, ре-
гиона, где используется автомобиль, от количества предыдущих страховых выплат и
других факторов. Мы рассмотрим лишь два коэффициента.
Коэффициент «бонус-малус» (КБМ) зависит от класса водителя. Этот коэффициент
понижает или повышает стоимость полиса в зависимости от количества ДТП в пре-
дыдущий год страхования. Сначала водителю присваивается класс 3. Каждый после-
дующий год класс водителя рассчитывается в зависимости от числа страховых вы-
плат в течение истёкшего года, по таблице 6.
Таблица б. Класс водителя и коэффициент «бонус-малус»
Класс
на начало
годового
срока
страхования
М
0
1
2
3
1 4
1 б
в
1 7
1 8
Г в
10
11
12
13
Коэффи-
циент
КБМ
2,45
2,3
1,55
1,4
1
0,95
0,9
0,85
0,8
0,75
0,7
0,65
0,6
0,55
0,5
Класс по окончании годового срока страхования
с учётом наличия страховых случаев
0
страховых
выплат
0
1
2
3
4
5
6
7
8
9
10
11
12
13
13
1
страховая
выплата
М
м
м
1
1
2
3
4
4
5
5
6
6
6
7
2
страховые
выплаты
М
М
М
М
м
1
1
2
2
2
2
3
3
3
3
3
страховые
выплаты
М
м
м
м
м
м
м
м
м
м
4
страховые
выплаты
М
М
м
м
м
м
м
м
м
м
м
м
м
м
м
Страховой полис — документ, удостоверяющий факт страхования. Часто стоимость услуги
страхования называют стоимостью полиса.
2 Наименьшее и наибольшее возможные значения базового тарифа устанавливаются Цен-
тральным банком России. В 2020 году для владельцев легковых машин базовый тариф со-
ставляет от 2746 до 4942 р.
ТАБЛИЦЫ
15

Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость
полиса (табл. 7).
Таблица 7. Коэффициенты возраста и стажа
—-^Стаж, лет
Возраст, лет -^^
| 16-21
| 22-24
25-29
1 30-34
| 35-39
| 40-49
1 50-59
старше 59
0
1,87
1,77
1,77
1,63
1,63
1,63
1,63
1,60
1
1,87
1,77
1,69
1,63
1,63
1,63
1,63
1,60
2
1,87
1,77
1,63
1,63
1,63
1,63
1,63
1.60
3-4
1,66
1,04
1,04
1,04
0,99
0,96
0,96
0,93
б-в
1,66
1,04
1,04
1,04
0,96
0,96
0,96
0,93
7-9
1,04
1,04
1,01
0,96
0,96
0,96
0,93
10-14
1,01
0,96
0,96
0,96
0,96
0,93
более
14
0.96
0,96
0,96
0,96
0,93
Предположим, что в прошлом году некоторый водитель имел класс 5, и у него не
было ни одной аварии, в которой он оказался бы виноват. Поэтому не было страхо-
вых выплат. Следовательно, его класс повысится до б-го, а коэффициент КБМ сни-
зится с 0,9 до 0,85.
Если бы в прошлом году была страховая выплата, то класс понизился бы до 3-го,
а коэффициент вырос бы до 1.
Предположим, что в прошлом году, когда водитель заключал договор со страховой
компанией, ему было 34 года, а за рулём он провёл 3 года. В этом случае его коэффи-
циент КВС в соответствии с таблицей 7 равнялся 1,04. Но в этом году этому водите-
лю уже 35 лет, а стаж составляет 4 года. Коэффициент снизится и станет равен 0,99.
ПРИМЕР. Когда Денис получил водительские права и впервые оформил полис
ОСАГО, ему было 19 лет. Денис страховал свою гражданскую ответственность 3 года.
В течение первого года были сделаны две страховые выплаты, а после этого выплат не
было. В начале третьего года страхования Денис заплатил за полис ОСАГО 25 806 р.
Какой класс будет присвоен Денису на начало четвёртого года страхования и ка-
кие коэффициенты КБМ и КВС будут использованы при заключении договора на
четвёртый год?
Сколько будет стоить полис на четвёртый год, если значения других коэффициен-
тов, кроме КБМ и КВС, не изменятся?
Решим эту задачу, последовательно отвечая на все вопросы. В первый год у Дени-
са был класс 3, но после двух страховых выплат на второй год класс оказался мини-
мальным (М). Так как больше аварий не было, на следующий год класс оказался 0,
а на четвёртый год страхования Денису будет присвоен 1-й класс. Поэтому коэффи-
циент КБМ будет равен 1,55.
На четвёртый год страхования Денису 22 года, и стаж у него 3 года. По табли-
це 7 находим, что КВС на четвёртый год равен 1,04.
В начале третьего года страхования у Дениса был 0-й класс, и КБМ равнялся 2,3,
а КВС равнялся 1,87 (ему был 21 год, а стаж был 2 года). Следовательно, за свой
четвёртый полис Денис заплатит
■
16 ГЛАВА I.

Вопросы
1 Что такое шапка таблицы?
2 В чём преимущество таблицы перед текстом?
3 В расписании поездов указана длительность поездки. Зачем это делают, ведь
длительность поездки можно найти, зная время отправления и прибытия?
4 Как вы думаете, почему в разных регионах России стоимость страхования по
программе ОСАГО различается? С чем это связано?
Упражнения
Пользуясь таблицей 5, выполните задания и ответьте на вопросы.
22 а) В какое время прибывает в Санкт-Петербург поезд № 2?
б) В какое время отправляется из Москвы поезд № 242?
в) Сколько раз в неделю отправляется из Москвы в Санкт-Петербург поезд
№ 266?
г) Сколько времени находится в пути поезд № 258?
23 а) Каждый ли день в сентябре отправляется из Москвы в Санкт-Петербург
поезд № 802?
б) Сколько из данных в таблице поездов отправляется из Москвы в Санкт-
Петербург между 20:00 и 24:00?
в) Перечислите номера поездов, которые в течение всего августа ежедневно
отправляются из Москвы в Санкт-Петербург.
г) Сколько времени находится в пути поезд № 32?
24 Укажите номер поезда, который проводит в пути:
а) наименьшее время;
б) наибольшее время.
25 а) В какое время отправляется из Москвы поезд № 4?
б) Какие поезда не ходят в октябре по воскресеньям?
в) Какие поезда прибывают в Санкт-Петербург между пятью часами вечера
и полуночью?
26 Иван Иванович хочет выехать из Москвы в Санкт-Петербург одним из пере-
численных в таблице поездов и приехать утром не раньше 07:00, чтобы вы-
спаться по дороге, но не позже 08:30, чтобы успеть к началу рабочего дня.
Какие поезда ему подходят? Укажите их номера.
27 Марии Игнатьевне 84 года. Она собирается съездить к внуку в Санкт-
Петербург. Она планирует выехать из Москвы в среду 25 сентября дневным
или вечерним поездом, чтобы приехать в Санкт-Петербург вечером или но-
чью и успеть в метро до закрытия (метро в Санкт-Петербурге закрывает-
ся в 00:30). Из подходящих поездов Мария Игнатьевна хочет выбрать тот,
билеты на который дешевле всего. Какой поезд предложить Марии Игнать-
евне?
28 Школьники решили отправиться из Москвы в Санкт-Петербург поездом,
уходящим из Москвы не позднее 11 часов вечера и приходящим в Санкт-
Петербург не ранее 6 часов на следующее утро. Какие поезда из приведённо-
го расписания им подходят? Укажите их номера.
29 Рассмотрите таблицу 6 с коэффициентами КБМ, которые применяются при
страховании владельцев автомобилей по программе ОСАГО. Предположим,
что владелец автомобиля А имел класс 7, но оказался виновен в ДТП, и его
■
ТАБЛИЦЫ 17

страховая компания сделала одну выплату. Какой будет класс и коэффициент
КБМ в этом году при заключении следующего договора?
30 Рассмотрите таблицу 7 с коэффициентами КВС, которые применяются при
страховании владельцев автомобилей по программе ОСАГО. Предположим,
что владелец автомобиля Б первый договор ОСАГО заключил в 2015 г.,
и тогда ему было 27 полных лет. Каждый договор заключается ровно на
1 год и начинает действовать в день истечения предыдущего. Каков будет
коэффициент КВС для Б при заключении договора в 2020 г.?
Статистическое исследование. Найдите в Интернете расписание движения
электропоездов или междугородных автобусов какого-нибудь направления (на-
пример, того, которым вы пользуетесь сами). Подумайте, почему поезда по од-
ному и тому же маршруту следуют то чаще, то реже. Кто чаще других пользует-
ся этими поездами или автобусами? Как бы вы составили расписание, если бы
вам пришлось это делать? Какая информация потребовалась бы вам для этого?
^4J Вычисления в таблицах
В задачах с расписанием движения поездов мы видели, что иногда значения
в одном из столбцов таблицы вычисляются с помощью значений, стоящих в других
столбцах и строках. С такими таблицами мы часто встречаемся. Вспомните таблицу
умножения или таблицу спортивных состязаний. В этих таблицах одни величины вы-
числяются с помощью других.
Вычислять что-либо в таблицах приходится всем. В любом персональном ком-
пьютере сейчас установлена программа, позволяющая быстро проводить вычисления
с помощью электронных таблиц.
Сметы
Если нужно купить много разных товаров, то удобно составить смету. Смета —
это таблица со списком или планом расходов. В смете указывают нужные товары,
цены и итоговую стоимость.
ПРИМЕР. Спортивный комитет выделил 50 000 р. на закупку спортивного инвента-
ря для летнего лагеря. Было решено купить футбольные, волейбольные и баскетболь-
ные мячи, ракетки, воланы и сетку для бадминтона. Чтобы понять, как распределить
деньги и сколько товаров купить, организаторы составили смету расходов (табл. 8).
Таблица 8. Смета расходов на покупку спортивного инвентаря
п/п
1
2
3
4
5
6
Наименование
Мяч футбольный
Мяч волейбольный
Мяч баскетбольный
Ракетка бадминтонная
Воланы
Сетка для бадминтона
Ед. измерения
шт.
шт.
шт.
шт.
коробка
шт.
Количество
20
20
10
38
15
4
Цена
ед., р.
575,5
500
800
480
750
700
Итого:
Стои-
мость, р.
18
ГЛАВА I.

В столбце «Стоимость» подводятся итоги по строкам: стоимость равна цене, умно-
женной на количество купленных единиц товара. Последняя строка в смете отличает-
ся от предыдущих. В этой строке подводят суммарные итоги в одном или нескольких
столбцах таблицы.
Распределить деньги можно по-разному. Предположим, что спорткомитет решил
купить только футбольные и волейбольные мячи, ракетки для бадминтона и воланы.
Тогда смета может быть такой, как в таблице 9.
Таблица 9. Смета расходов на покупку спортивного инвентаря
№
п/п
1
2
3
4
5
6
Наименование
Мяч футбольный
Мяч волейбольный
Мяч баскетбольный
Ракетка бадминтонная
Воланы
Сетка теннисная
Ед. измере-
ния
шт.
шт.
шт.
шт.
коробка
шт.
Количе-
ство
20
20
0
38
15
0
Цена
ед., р.
575,5
500
690
480
750
700
J Итого:
Стоимость, р.
11510
10 000
0
18 240
11250
0
51000
В последней строке видно, что мы превысили выделенную сумму на 1000 р. При-
дётся менять смету, чтобы уложиться в выделенную сумму. Можно уменьшить коли-
чество волейбольных мячей на два. Тогда как раз получится 50 000 р.
Можно поступить иначе: купить меньше на одну ракетку и на одну коробку вола-
нов. Экономия составит 480 4- 750 = 1230 р., и общая сумма будет равна 49 770 р.
Но в этом случае останется 230 р., на которые уже ничего не купишь.
Доли и проценты в таблицах
Часто приходится вычислять долю одной или нескольких частей в едином целом.
Если исходные данные записаны в таблице, то доли также принято записывать в та-
блицу. Покажем на примере, как это делается.
Наблюдения показывают, что за последние 120 лет структура населения России
сильно изменилась. Россия из сельскохозяйственной страны превратилась в промыш-
ленную. В таблице 10 даны сведения о городском и сельском населении Российской
империи по результатам переписи населения 1897 г. (в границах современной Рос-
сии) и Российской Федерации в 2018 г.
Таблица 10. Население России в 1897 и 2018 гг., млн чел.
Год
1897
2018
Городское население
16,6
109,3
Сельское население
109,1
37,5
Всего
125,7
146,8
Вычислим процентную долю городского и сельского населения в указанные годы.
Доля городского населения в 1897 г. составляла
16,6 : 125,7 • 100 % * 13,2 %,
ТАБЛИЦЫ 19

а доля сельского населения была 86,8 %. Точно так же проводятся вычисления и для
2018 г. Для удобства сопоставления поместим новые сведения в таблицу 11.
Таблица 11. Доля городского и сельского населения России в 1897 и 2018 гг.
Год
1897
2018
Доля городского населения, %
13,2
74,5
Доля сельского населения, %
86,8
25,5
Вопросы
1 Что такое смета?
2 Как вы думаете, зачем нужно знать численность и долю городского и сельского
населения в России?
Упражнения
31 По таблице 8 ответьте на следующие вопросы:
а) Какой из товаров самый дорогой?
б) Какой из товаров самый дешёвый?
в) Какого товара решили купить больше всего? Как вы думаете, почему?
г) Какого инвентаря решили купить меньше всего? Как вы думаете, почему?
32 Начертите таблицу 8 в тетради, найдите стоимость каждого вида товара и за-
полните последний столбец. Ответьте на следующие вопросы:
а) На какой вид инвентаря планируется потратить самую большую сумму?
б) На какой вид инвентаря планируется потратить самую маленькую сумму?
33 Предложите какой-нибудь способ составления сметы по таблице 8 так, чтобы
были куплены волейбольные и футбольные мячи, ракетки, воланы и сетки
и чтобы общая сумма покупки была ровно 50 000 р.
34 Пользуясь данными таблицы 8, составьте собственную смету для покупки
трёх из перечисленных видов спортивного инвентаря на общую сумму от
9900 до 10 000 р.
35 По таблице 11 найдите:
а) какую долю в процентах составляло городское население России в 2018 г.;
б) во сколько раз (примерно) в 2018 г. городское население России превосхо-
дило по численности сельское население.
36 Рассмотрите таблицу 2 «Население городов-миллионеров» (см. с. 9—10).
а) Начертите эту таблицу в тетради, оставив только 1989, 2010 и 2019 гг.
Добавьте справа столбец, в котором укажите, на сколько процентов измени-
лась численность населения каждого города в период с 1989 по 2019 г.
б) В каком городе процентный прирост численности населения наибольший?
в) В каком городе процентный прирост численности населения наименьший?
г) В каких городах произошла депопуляция1 в течение 1990—2019 гг.? Как
вы думаете, с чем может быть связана депопуляция именно в этих городах?
1 Депопуляция — убыль численности населения.
■
20 ГЛАВА I.

д) Найдите в таблице 2 город, где прирост населения за 9 лет с 2010 по
2019 г. превышает 15 %. Как вы думаете, с чем может быть связан такой
резкий рост численности населения в этом городе?
37 Рассмотрите таблицу 4 (см. с. 12). Найдите, как изменялось год от года про-
изводство электрической энергии в России в 2011—2019 гг. в процентах от
показателя предыдущего года. Заполните пустые ячейки в таблице 12.
Таблица 12. Прирост производства электроэнергии в России
Год
Изменение по отно-
шению к предыду-
щему году, %
2011
1,6
2012
2013
2014
0,2
2015
2016
2017
2018
2019
38 Владелец квартиры должен оплатить потребление электроэнергии за сентябрь
2019 г. У него в квартире установлен трёхтарифный счётчик. Один киловатт-
час электроэнергии стоит по-разному в зависимости от времени суток. Владе-
лец квартиры раз в месяц снимает показания со счётчика и заполняет кви-
танцию (табл. 13).
Таблица 13. Заполненная платёжная квитанция
[квитанция
S
j
•
;
:
Получатель плетет» ПАО "Мосэмергосбыг"
Номер лицевого счета
Ф.И.О.
Адрес
Код
плетеше
13
2
15
Тарифная
•ома
Т1
п
ТЗ
Попадания счетчияоа
текущее
10345
9322
1233
предыдущее
10242
9234
•120
Расход
(ивгч)
*Коды платежа:
1 - П (дет) • для одиотарифного и детзстарнфиого учел
13 - Т1 (пин) - для трехтерифного учете
2 - Т2 (мочь) • дум деуятарифиого и трёятарнфиого учета
IS - ТЗ (полупим) • дм трехтарифмого учета
Подпись
Итого
п оплоте:
Период
Тариф
(рувЛвтч)
б£7
2.13
М7
Итого:
1 1
|КодРР |
сем. 19
(меся^год)
Сумма к оплате
<РУв)
РУб. | |коп. ;
Разберитесь в платёжной квитанции, заполните пустые ячейки «Расход»,
♦Сумма к оплате» и «Итого» и ответьте на вопросы:
а) Сколько кВт • ч израсходовано по тарифной зоне Т1 «пик» с момента уста-
новки счётчика к моменту снятия показаний в сентябре?
б) Сколько кВт • ч израсходовано по тарифной зоне Т1 «пик» с момента пре-
дыдущего снятия показаний в августе?
в) Какую сумму владелец квартиры должен заплатить по тарифу Т2 «ночь»?
г) Какую сумму он должен заплатить по квитанции?
Статистическое исследование. Сейчас всё более популярными становятся элек-
тронные платежи. Достаточно передать показания электросчётчика за месяц, и
компания, поставляющая электроэнергию, выставит электронный счёт. Узнайте, как
передают сведения или заполняют квитанции на оплату электроэнергии в вашем
населённом пункте. Если возможно, возьмите на себя эту домашнюю обязанность —
подготовку к ежемесячной оплате электроэнергии.
ТАБЛИЦЫ

Гб) Крупнейшие города России
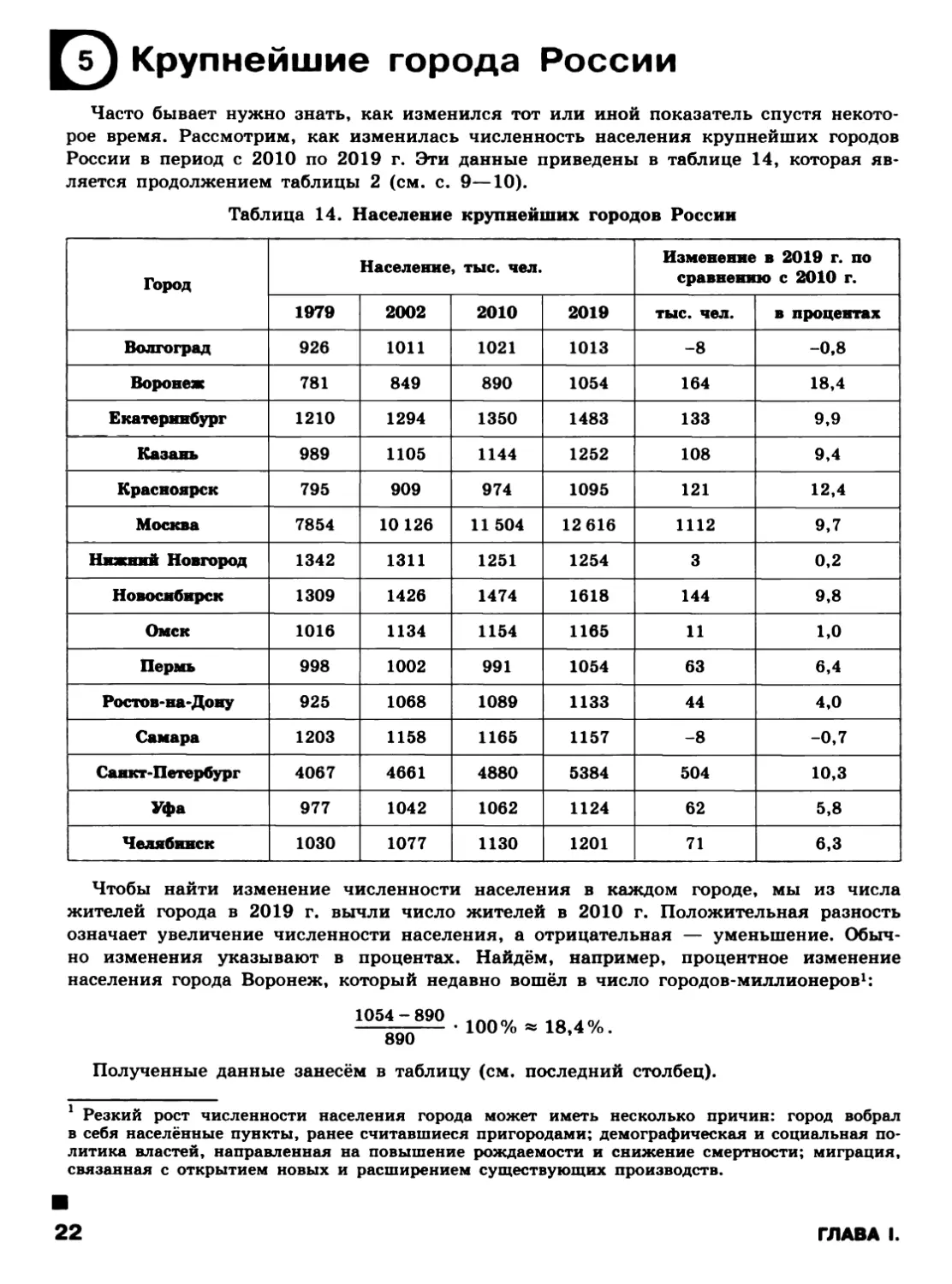
Часто бывает нужно знать, как изменился тот или иной показатель спустя некото-
рое время. Рассмотрим, как изменилась численность населения крупнейших городов
России в период с 2010 по 2019 г. Эти данные приведены в таблице 14, которая яв-
ляется продолжением таблицы 2 (см. с. 9—10).
Таблица 14. Население крупнейших городов России
Город
Волгоград
Воронеж
Екатеринбург
Казань
Красноярск
Москва
Нижний Новгород
Новосибирск
Омск
Пермь
Ростов-на-Дону
Самара
Санкт-Петербург
1 Уфа
Челябинск
Население, тыс. чел.
1979
926
781
1210
989
795
7854
1342
1309
1016
998
925
1203
4067
977
1030
2002
1011
849
1294
1105
909
10 126
1311
1426
1134
1002
1068
1158
4661
1042
1077
2010
1021
890
1350
1144
974
11504
1251
1474
1154
991
1089
1165
4880
1062
ИЗО
2019
1013
1054
1483
1252
1095
12 616
1254
1618
1165
1054
1133
1157
5384
1124
1201
Изменение в 2019 г. по
сравнению с 2010 г.
тыс. чел.
-8
164
133
108
121
1112
3
144
И
63
44
-8
504
62
71
в процентах
-0,8
18,4
9,9
9,4
12,4
9,7
0,2
9,8
1,0
6,4
4,0
-0,7
10,3
5,8
6,3
Чтобы найти изменение численности населения в каждом городе, мы из числа
жителей города в 2019 г. вычли число жителей в 2010 г. Положительная разность
означает увеличение численности населения, а отрицательная — уменьшение. Обыч-
но изменения указывают в процентах. Найдём, например, процентное изменение
населения города Воронеж, который недавно вошёл в число городов-миллионеров1:
1054 - 890
890
100% « 18,4%.
Полученные данные занесём в таблицу (см. последний столбец).
1 Резкий рост численности населения города может иметь несколько причин: город вобрал
в себя населённые пункты, ранее считавшиеся пригородами; демографическая и социальная по-
литика властей, направленная на повышение рождаемости и снижение смертности; миграция,
связанная с открытием новых и расширением существующих производств.
22
ГЛАВА I.

©
Вопросы
1 Чем, по вашему мнению, может объясняться снижение численности населения
в крупном городе (депопуляция)?
2 В чём разница между абсолютным и процентным приростом населения в городе?
3 Как вы думаете, почему компании, поставляющие электричество к нам в дома,
устанавливают разную цену на 1 киловатт-час в разное время суток?
0
Упражнения
39 В каком городе из таблицы 14 абсолютный прирост численности населения
был наибольшим в период с 2010 по 2019 г.?
40 В каких городах произошла убыль численности населения в период с 2010
по 2019 г.?
41 По данным таблицы 14 составьте таблицу изменения численности (абсолют-
ной и относительной в процентах) населения крупнейших городов России
в период с 1979 по 2019 г,
42 В каком из российских городов из таблицы 14 относительный прирост насе-
ления в период с 1979 по 2019 г. был наибольшим? Сколько процентов со-
ставил прирост численности населения в этом городе?
43 Есть ли в таблице 14 два города, в первом из которых абсолютный прирост
населения больше, чем во втором, а в процентном отношении — меньше?
Возможно ли такое?
Статистическое исследование. Составьте таблицу показывающую измене-
ние населения в столицах разных стран за последние 50 лет. Найдите столицы,
в которых абсолютный прирост населения наибольший, а также столицы, в ко-
торых процентный прирост наибольший. Есть ли столицы, где в последние го-
ды наблюдается депопуляция? Для исследования можно взять не все страны,
а 10—20 стран на ваш выбор. Интересно брать для сравнения страны, имею-
щие много общего в географическом положении, в экономике, в культуре и на-
циональных традициях. Отдельно можно сравнить столицы, находящиеся в раз-
ных частях света и имеющие мало общих черт.
им Подсчёты и измерения в таблицах
Подсчёт с помощью таблицы
В классе был проведён опрос о том, какие у кого живут домашние животные. По-
лучился следующий список:
Собака, собака, кошка, никого, кошка, рыбки, кошка, никого, кошка, кошка,
птицы, никого, собака, никого, кошка, птицы, собака, кошка, собака, никого, рыб-
ки, кошка, собака, собака, кошка, никого, черепаха, никого, собака, рыбки, кошка,
собака, кошка.
Список не показывает прямо» сколько каких животных живёт у школьников. Чтобы
ответить на этот вопрос, нужно провести подсчёты. Проще всего это сделать на бумаге
с помощью таблицы, читая список один раз. В первый столбец будем вписывать назва-
ния животных по мере их появления в списке. Во втором столбце будем рисовать
ТАБЛИЦЫ 23

Животное
Собака
Кошка
Никого
Рыбки
Встретилось
в списке
11
Н+4
II
1
Всего
Таблица 16. Подсчёт животных
Таблица 15. Подсчёт животных чёрточки, а последний столбец отведём
для итога. Начало нашей таблицы после
обработки первых десяти ответов выгля-
дит, как показано в таблице 15.
Каждый очередной ответ в списке
будем отмечать вертикальной чёрточ-
кой во втором столбце. Когда число
чёрточек достигнет пяти, пятой го-
ризонтальной чёрточкой перечеркнём
четыре предыдущие, как показано
в строке «Кошка». Запись | | | | озна-
чает пять подсчитанных объектов. Так
делают, чтобы потом проще было под-
считать число чёрточек в каждой стро-
ке. Обработав весь список, получим
таблицу 16.
Теперь легко подсчитать животных
каждого вида. Собак в нашем списке
5 и ещё 4 (НИ ||||), всего 9. Кошек
11. Птиц две, рыбки живут у трёх
школьников, а черепаха только одна.
Составляя таблицу, мы прочитали
список лишь один раз. Если бы мы
считали сначала собак, потом кошек
и т. д., нам бы пришлось просматри-
вать список несколько раз. Чем боль-
ше различных вариантов в списке, тем больше раз его пришлось бы просмотреть.
Такой способ подсчётов часто используют социологи при ручной обработке анкет,
продавцы для учёта проданной продукции.
Разумеется, когда данных очень много, подсчёты можно и нужно проводить с по-
мощью компьютера. Однако подсчёты с помощью карандаша и небольшой таблицы
на бумаге широко применяются и в наше время.
Таблицы с результатами измерений
Таблицы часто используют для записи результатов однотипных измерений. Если
мы хотим сравнить толщину школьных учебников по разным предметам, то можно
составить таблицу числа страниц в учебниках, как это сделано в таблице 17.
Животное
Собака
Кошка
! НИКОГО
Рыбки
Птицы
Черепаха
Встретилось в списке
1 1 1 1 1 1 1 1
1 1 II 1 1 1 1
1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
mi
Всего
9
11
7
3 1
2
1
Точное число страниц указано в описании книги (в выходных данных) на второй
или на последней странице. А вот если мы составим такую таблицу, смотря на по-
следние пронумерованные страницы книг, то можем допустить ошибки, поскольку
одна или несколько последних страниц книги не имеют номеров. Нам придётся са-
мим считать эти страницы, и здесь легко ошибиться.
24
ГЛАВА I.

Таблица 17. Число страниц в учебниках 9 класса
Предмет
Алгебра
Литература
Физика
История
Биология
Химия
Число страниц
384
320
190
424
240
208
Толщина книги, мм
22
20
16
23
16
14
Толщину книги можно измерить линейкой. Результаты измерений занесены в по-
следний столбец таблицы 17. Измерение толщины книги с помощью линейки не очень
точная процедура. Укажем несколько возможных причин погрешностей в измерениях.
Во-первых, между страницами книги есть пустоты; они тем больше, чем более потрё-
пан учебник. Эти пустоты можно уменьшить, сильно сжав книгу. Во-вторых, резуль-
таты измерения зависят от угла, под которым линейка приложена к книге. В-третьих,
если мы видим не целое число миллиметров, то округляем в ту или иную сторону.
Ф
0.
Вопросы
1 Как вы думаете, почему принято считать «пяткйми» — по пять чёрточек?
2 Предложите свой способ подсчёта в таблицах. Может быть, можно использовать
другие фигуры, а не только заборчики из чёрточек?
Какие причины могут приводить к погрешностям при измерениях?
Упражнения
44 Каких животных» согласно таблице 16, чаще всего держат дома?
45 Каких животных из таблицы 16 редко держат в домашних условиях?
46 Возьмите учебники, которые вы принесли с собой в школу.
Определите число страниц в каждом учебнике двумя способами:
а) откройте книгу в конце, найдите последнюю страницу с номером и добавь-
те число ненумерованных страниц;
б) найдите число страниц, которое указано в выходных данных книги. Со-
ставьте таблицу (табл. 18).
Таблица 18. Число страниц в учебниках
Число страниц,
Предмет подсчитанное
самостоятельно
Число страниц
по выходным данным
Число страниц,
измеренное с помощью
линейки
47 Толщина листа офсетной бумаги, на которой печатают современные учебни-
ки, примерно равна 0,86 мм. Измерьте линейкой толщину учебников (без об-
ложки и двух плотных листов в начале и в конце книги). Разделив результат
на 0,86 мм, вы получите приблизительное количество страниц в учебнике.
Заполните в таблице 18 правый столбец. Велики ли с вашей точки зрения
погрешности измерения, полученные при этом способе?
Какой способ самый точный? Самый неточный? Самый быстрый? В каком
случае годится только измерение с помощью линейки?
ТАБЛИЦЫ
25

48 Продавцы небольших книжных киосков часто отмечают число проданных за
день книг в общей ведомости, для того чтобы в конце дня быстро подвести
итоги работы. Часть такой ведомости дана в таблице 19.
Таблица 19. Ведомость продажи книг
п/п
1
2
3
4
б
Название книги
♦Алиса в Стране чудес»
«Властелин колец»
♦Вредные советы»
«Гарри Поттер и Орден Феникса»
«Северное сияние»
Цена,
Р.
590
1100
190
820
460
Продано
м
W4II
III
1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1
1
Всего
Выручка
а) Заполните в таблице 19 столбец
«Всего».
б) Заполните столбец «Выручка».
в) Посчитайте общее число проданных
книг и суммарную выручку и за-
полните соответствующие ячейки.
49 Пользуясь таблицей 19 и результатами
упражнения 48, составьте таблицу долей выручки от продажи каждой книги.
50 В таблице 20 даны четвертные отметки по математике, русскому и иностран-
ному языку всех учащихся класса.
Таблица 20. Отметка за четверть
№ п/п
1
2
3
1 4
1 5
в
1 7
1 8
1 в
Фамилия
Авдеев И.
Андреева 0«
Баранкин С,
1 Бодров О.
Волин С.
Волкова В.
Галкин П.
Данилов М.
Евсеева С.
Математика
4
4
3
5
5
3
3
5
4
Русский
язык
3
4
4
4
5
5
4
3
5
Иностранный
язык
5 1
4 1
3 1
5
5 1
4
3
5
5
26
ГЛАВА I.

Продолжение
№ п/п
10
11
12
13
14
15
16
17
1 18
1 10
1 20
21
1 22
1 23
1 2А
1 25
26
Фамилия
Жуков Д.
Иванова Е.
Караваева А.
Кузнецов И.
Кузовлев П.
Ломов Д.
Макаров А.
Мельникова М,
Надюшнна С.
Норов П.
Оганоа А,
Островая Е.
Петров С.
Петрова И.
Пронина Д.
Шашкнн П.
Яковлева Н.
Математика
5
4
5
3
3
3
4
5
4
4
5
5
4
4
5
4
3
Русский
язык
4
5
4
3
4
3
3
4
5
4
3
4
5
4
5
3
4
Иностранный
язык
4
5
5 1
3 1
3 1
3 1
4 I
3
4
3
4
5
5
5 !
4
4
4
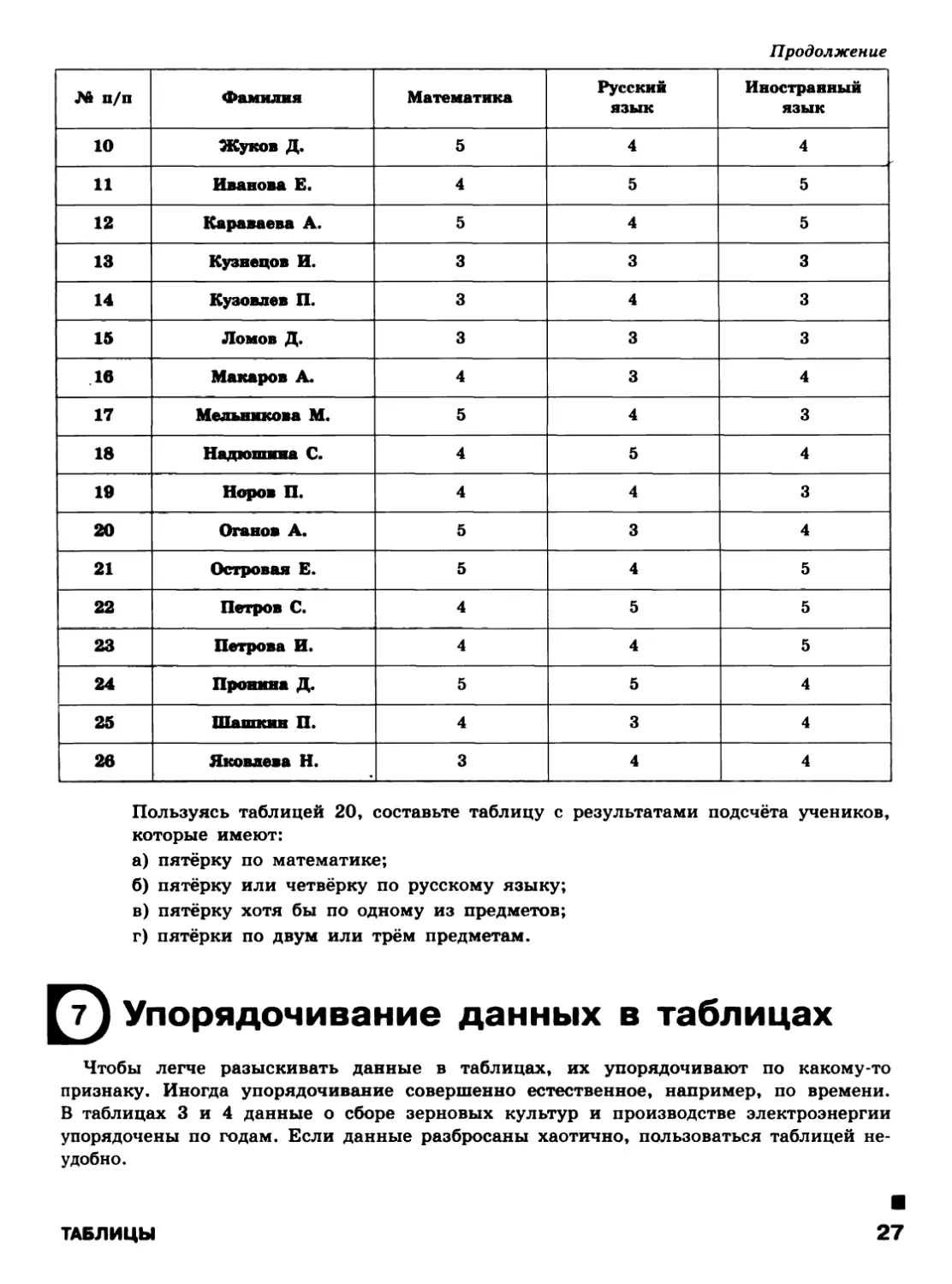
Пользуясь таблицей 20, составьте таблицу с результатами подсчёта учеников,
которые имеют:
а) пятёрку по математике;
б) пятёрку или четвёрку по русскому языку;
в) пятёрку хотя бы по одному из предметов;
г) пятёрки по двум или трём предметам.
Гм Упорядочивание данных в таблицах
Чтобы легче разыскивать данные в таблицах, их упорядочивают по какому-то
признаку. Иногда упорядочивание совершенно естественное, например, по времени.
В таблицах 3 и 4 данные о сборе зерновых культур и производстве электроэнергии
упорядочены по годам. Если данные разбросаны хаотично, пользоваться таблицей не-
удобно.
ТАБЛИЦЫ
27

Таблица 21. Население крупных городов
Щ>
ПРИМЕР 1. В таблице 2, где показано
население городов-миллионеров, можно упо-
рядочить данные по убыванию населения.
Первым городом станет Москва, за ней —
Санкт-Петербург и так далее до Волгограда.
Давайте поступим так (табл. 21) и подума-
ем, чем удобен такой порядок.
По таблице 2 неудобно искать третий
по величине город и города с населением
около 1200 тыс. чел. Зато в таблице 21
это сделать очень просто. Третий по насе-
лению город — третий сверху в таблице.
Правда, теперь мы потеряли другое удоб-
ство — стало трудно найти город по на-
званию. Для этого удобнее таблица 2.
Если нас интересует, в каких городах
самый большой или самый малый при-
рост населения, то нужно взять табли-
цу 14 и упорядочить её по одному из
столбцов «Прирост населения» — по аб-
солютному приросту или по процентному,
в зависимости от того, как нам удобнее.
Очень часто упорядочивание нужно в
таблицах спортивных результатов, эко-
номических достижений и всевозможных
рейтингов1.
Справка. В зависимости от стоящей задачи данные в таблицах упорядочивают
разными способами.
Город
Москва
Санкт-Петербург
Новосибирск
Екатеринбург
Нижний Новгород
Казань
Челябинск
Омск
Самара
Ростов-на-Дону
1 Уфа
Красноярск
Воронеж
Пермь
Волгоград
2019 1
12616
5384 1
1618
1483 1
1254
1252 1
1201 1
1165 1
1157 1
1133 1
1124 1
1095 1
1054
1054
1013 1
ПРИМЕР 2. Рассмотрим таблицу 22 рекордов по прыжкам в длину с места. Упо-
рядочивать данные по имени спортсменов не имеет смысла. Лучше упорядочить дан-
ные по длине прыжка, причём по убыванию. Тогда последние рекорды окажутся на-
верху таблицы. Как вы думаете, что произойдёт, если мы упорядочим рекорды по
времени? Сортировка не изменится, поскольку каждый следующий рекордный пры-
жок выше предыдущего.
Таблица 22. Рекорды по прыжкам в длину с места, см
Имя спортсмена
Пётр
Иван
Алексей
Сергей
Длина прыжка, см
236
241
227
240
1 Рейтинг происходит от английского слова ♦rating» — оценка, определение стоимости, клас-
сификация.
28
ГЛАВА I.

ПРИМЕР 3. В таблице 23 даны результаты спортсменов-мужчин, занимающихся в
спортивном клубе. Для участия в городских соревнованиях по бегу на 100 м тренер
хочет отобрать не более шести лучших бегунов, но только тех, у кого результат не
превосходит 12 с. Как упорядочены данные? Сколько бегунов удовлетворяют этому
условию? Как нужно изменить границу отбора, чтобы отобранных бегунов было ров-
но шесть?
Фамилия
Асташкин
Сычёв
Чернов
Ясенский
Плахотнн
Пережогин
Таблица 23.
Время, с
10,98
11,20
11,23
11,44
11,45
11,47
Результат контрольного забега на 100 м
Фамилия
Карамышев
Ярушевнч
Осадчий
Гостев
Дольнев
Львов
Время, с
11,84
11,86
11,87
12,23
12,30
12,34
Фамилия
Шелепин
Тугарёв
Зверев
Белов
Пилюгин
Богатырёв
Время, с
12,49
12,50
12,65
12,74
13,01
13,12
Очевидно, данные лучше упорядочить по возрастанию времени забега. Время за-
бега у девяти бегунов менее 12 с. Чтобы осталось ровно шесть, тренер может вы-
брать границу 11,5 с. Тогда в число выбранных бегунов войдут спортсмены из перво-
го столбца от Асташкина до Пережогин а.
\jfj Вопросы
1 Зачем упорядочивают данные в таблицах?
0
2 Рассмотрите пример 3. Сколько спортсменов пробежали дистанцию 100 м ме-
нее чем за 12,5 с?
Упражнения
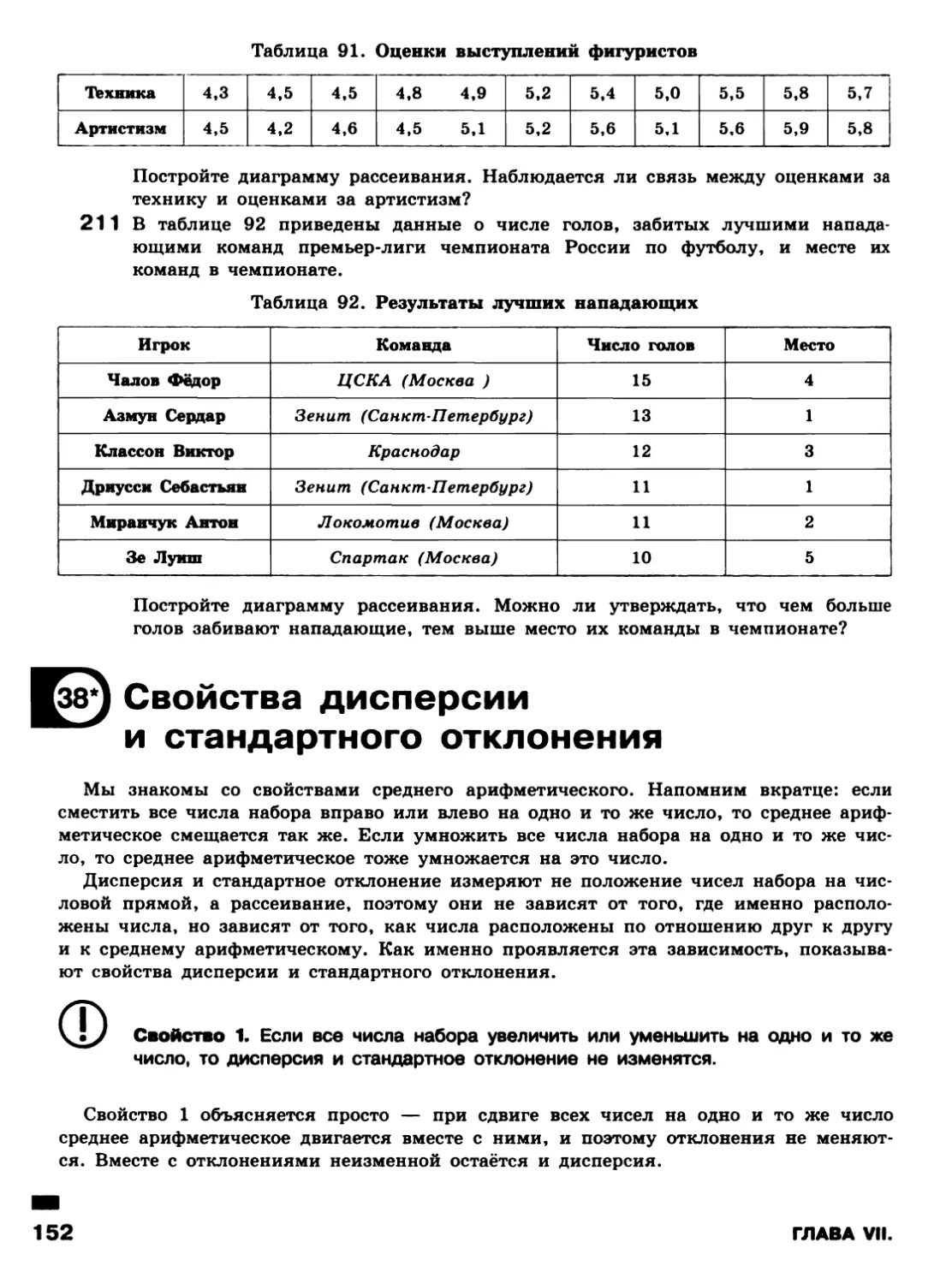
51 В таблице 24 даны нормативы по бегу на 100 м.
Таблица 24. Нормативы по бегу на 100 м, с
Ручной хронометр
Автомат, хронометр
Мастер
спорта
межд.
класса
—
10,28
Мастер
спорта
—
10,64
Кандидат
в мастера
спорта
10,7
10,94
I
разряд
11,2
11,44
II
разряд
11,8
12,04
Ш
разряд
12,7
12,94
Рассмотрите таблицу 23 в примере 3 и ответьте на вопросы.
а) Сколько спортсменов во время контрольного забега выполнило норматив
кандидата в мастера спорта по бегу на 100 м?
б) Сколько спортсменов выполнило норматив I разряда?
в) Сколько спортсменов выполнило норматив II разряда?
ТАБЛИЦЫ
29

52 В математической олимпиаде участвовало 600 учащихся из разных школ го-
рода. Наибольший возможный балл был равен 15. В таблице 25 показано,
как распределились участники по баллам. Найдите:
а) количество участников, набравших не более шести баллов;
б) долю участников (в процентах), которые набрали не менее 11 баллов.
Таблица 25. Распределение баллов
Балл
Кол-во участников
Балл
Кол-во участников
0
3
8
76
1
8
9
54
2
27
10
32
3
44
11
24
4
53
12
20
5
69
13
15
6
88
14
6
7
80
15
1
53 Нужно объявить участникам математической олимпиады (см. предыдущую
задачу) граничный балл, то есть наименьший балл, обладатель которого ста-
новится призёром или победителем олимпиады. Каким должен быть наимень-
ший граничный балл, чтобы общее количество призёров и победителей:
а) не превышало 30 человек;
б) было не более 10% от общего числа участников? Сколько процентов участ-
ников станет победителями и призёрами в этом случае?
Таблицы сопряжённости
Иногда при сборе данных нужно учесть два или даже несколько признаков. При-
знаки могут быть любыми. Если речь о людях, то признаками можно считать воз-
раст, пол, доход, вид деятельности и т. д. Если речь об автомобилях, то можно гово-
рить о типе (легковое авто, грузовик, автобус), о вместимости, цвете и т. п.
ПРИМЕР 1. В небольшом городе интернет-компания проводила исследование ка-
чества домашнего интернета. Была составлена выборка из 1000 случайно выбранных
клиентов, и им был задан вопрос: «Удовлетворены ли вы качеством интернета в ва-
шей квартире?»
Всего в городе два района: Фабричный и Заречный. Чтобы представить данные
была составлена таблица, показывающая, сколько людей из каждого района дали тот
или иной ответ (табл. 26).
Такая таблица называется таблицей сопряжённости двух признаков. В данном слу-
гр - 0£5 п чае признаками являются район прожива-
Таблица 26. Опрос о качестве интернета * л г г
ния респондента1 и качество интернета у
него дома. Даже такое простое представле-
ние данных позволяет сделать довольно
много предположений и выводов. Сначала
перейдём к более полной таблице (табл. 27),
где показаны суммы данных по строкам и
столбцам. В правом нижнем углу общее
число респондентов — 1000.
это тот, кто отвечает на вопросы в социальном исследовании или опросе.
ГЛАВА I.
"^~\Район
Ответ ^ч.
Да
Нет
Фабричный
264
143
Заречный
315
278
Респондент
30

Во-первых, если опрос проводил-
ся качественно, можно предполо-
жить, что в Заречном районе прожи-
вает больше жителей, чем в Фабрич-
ном, поскольку из Заречного района
в выборку попали 593 человека, а
из Фабричного — 407. Можно даже
предположить, что в Заречном райо-
не проживает примерно 59,3% всех
жителей города.
Во-вторых, можно оценить долю
тех, кто доволен и тех, кто недово-
Таблица 27. Опрос о качестве интернета
^\Район
Ответ^\.
Да
Нет
Всего
Фабричный
264
143
407
Заречный
315
278
593
Всего
579
421
1000
579
лен работой домашнего интернета. Доля тех, кто доволен, равна 1QQQ • 100% = 57,9%,
а доля недовольных равна 42,1%.
Мы имеем сведения отдельно по обоим районам, поэтому можем сделать больше.
Попытаемся узнать, в каком из районов интернет работает лучше. В Фабричном рай-
264
оне доля тех, кто доволен, равна -^rz ' 100% « 64,9%.
407
Это значение существенно выше, чем среднее 57,9%. Значит, в Заречном районе
доля довольных должна быть ниже среднего. И действительно, она приблизительно
равна 53,1% (проверьте). Можно подумать, что по какой-то причине качество интер-
нета в Заречном районе заметно ниже, чем в Фабричном. Интернет-компания должна
заинтересоваться этим явлением.
В нашем исследовании оказалось, что качество интернета в квартире каким-то об-
разом зависит от того, в каком районе расположена эта квартира. Если бы доли по
разным районам были близки, можно было бы предположить, что качество интерне-
та и район проживания — независимые признаки.
ПРИМЕР 2. В таблице 20 (см.
с. 26—27) даны четвертные отмет-
ки по математике 26 учащихся не-
которого класса. Выделим признаки
«отметка по математике» и «отмет-
ка по иностранному языку». Будем
считать, что четвёрки и пятёрки —
хорошие отметки, а тройка не явля-
ется хорошей отметкой. Получается
таблица 28.
Доля тех, кто хорошо успевает по
иностранному языку, равна
— • 100% * 69,2%.
А если считать долю тех, кто хорошо учится по иностранному языку, но не среди
всех, а только среди тех, кто хорошо успевает по математике, получается намного
16
19
Таблица 28. Успеваемость по математике
и иностранному языку
-*^^^ Ин. яз.
Математика^—^^
4 или 5
3
Всего
4 или 5
16
2
18
3
3
5
8
Всего
19
7
26
больше:
100% « 84,2%.
Это значит, что нельзя говорить, будто в этом классе результаты по математике и
по иностранному языку независимы. Может быть, тот, кто хорошо понимает матема-
тику, легче осваивает иностранные слова? Или наоборот? Связь может быть довольно
ТАБЛИЦЫ
31

сложной. Нельзя сказать, что одно влияет на другое. Тем не менее, нельзя считать,
что признаки «отметка по математике» и «отметка по иностранному языку» незави-
симы. По крайней мере, в этом классе.
Вопросы
В городе проводился опрос жителей о том, как потратить часть бюджета на
благоустройство — направить деньги на строительство детских площадок или
на озеленение улиц. Какие признаки можно выделить у опрашиваемых респон-
дентов?
Как с помощью таблицы сопряжённости можно сделать предположение о том,
что два признака являются зависимыми или независимыми?
0
Таблица 29. Стиральные машины
^^^^С)ушка
Да
i
Нет
1 Всего
Есть
22
88
Нет
43
1100
Всего
Упражнения
54 Рассмотрите таблицу 20 (см. с. 26—27). Постройте таблицу сопряжённости
признаков:
а) «отметка по математике» и «отметка по русскому языку»;
б) «отметка по математике» и «пол ученика».
Можно ли предположить, что признаки независимы?
55 На сайте интернет-магазина разме-
щена информация об имеющихся в про-
даже стиральных машинах (табл. 29).
Покупатель рассматривает как встраивае-
мые машины, так и не встраиваемые (от-
дельно стоящие). Его также интересует
наличие функции сушки белья. Таблица
сопряжённости показывает результат из-
учения этих признаков у множества мо-
делей,
а) Заполните пустые ячейки таблицы.
б) Найдите долю машин с функцией сушки среди не встраиваемых машин и
среди встраиваемых.
в) Можно ли предположить, что признаки (встраиваемость и наличие сушки)
независимы?
56 Интернет-магазин предлагает сти-
ральные машины различных моделей
(табл. 30). Таблица сопряжённости по-
казывает количество предлагаемых мо-
делей встраиваемых и не встраиваемых
(отдельно стоящих) машин, снабжённых
защитой от протечки воды и без этой за-
щиты.
а) Заполните пустые ячейки.
б) Найдите долю стиральных машин
с функцией защиты от протечки среди встраиваемых и среди не встраивае-
мых машин.
в) Можно ли предположить, что эти признаки (встраиваемость и наличие за-
щиты от протечки) независимы?
Таблица 30. Стиральные машины
^""*"^---^ Защита
Встраив. ^~^-^^
1 Да
Нет
Всего
Есть
54
956
Нет
11
233
Всего
32
ГЛАВА I.

Диаграммы
Диаграммы нужны для графического пред-
ставления данных. В отличие от таблиц, ди-
аграммы не передают информацию совер-
шенно точно, зато они наглядны и позволя-
ют сравнивать величины быстро — на глаз.
Помимо общеизвестных столбиковых и кру-
говых диаграмм существует множество спе-
циальных диаграмм, например демографиче-
ские половозрастные пирамиды, диаграммы
«стебель-листья», лепестковые диаграммы и
множество других.
9 Столбиковые диаграммы
10 Демографическая статистика.
Половозрастные пирамиды
11 Круговые диаграммы
12 Диаграммы «стебель-листья»

Таблицы, как мы видели, удобны для упорядочивания и поиска данных. Однако
они не дают наглядного представления о соотношении величин. Для этого служат
диаграммы: столбиковые1, круговые, картограммы, диаграммы рассеивания, демогра-
фические половозрастные пирамиды и множество других диаграмм.
Ф
Важно! Диаграммы используются для наглядного, запоминающегося изображе-
ния и сопоставления данных.
Диаграммы часто встречаются в Интернете, в газетах, журналах и книгах, они ил-
люстрируют соотношение различных величин.
Гэ) Столбиковые диаграммы
Таблица 31. Продажа шоколада
День неделя
Число
шоколадок
Пн
8
Вт
5
Ср
4
Чт
2
Пт
3
ПРИМЕР 1. В таблице 31 приведены
данные о числе шоколадок, проданных
в школьной столовой в учебные дни
с понедельника по пятницу.
Наглядно эти данные можно изо-
бразить в виде столбиков, каждый из
которых показывает число шоколадок,
проданных за день (диагр. 2).
Диаграмма 2. Количество проданных шоколадок
Понедельник
Вторник
Среда
Четверг
Пятница
Чтобы построить столбиковую диаграмму, мы начертили горизонтальную и вертикаль-
ную прямые линии. На горизонтальной прямой отметили дни недели с понедельника по
пятницу. Над каждой отметкой изобразили стопку проданных шоколадок. На вертикаль-
ную прямую нанесли деления, помогающие понять, сколько шоколадок в каждом столбике.
Диаграмму можно упростить. Вместо шоколадок лучше нарисовать просто стол-
бики разной высоты. Ниже показаны два варианта оформления диаграммы 2
(диагр. 2.1 и 2.2).
1 Столбиковая диаграмма — графическое представление распределения частот для дискретной слу-
чайной величины, образуемое набором столбцов равной ширины, высоты которых пропорциональ-
ны частотам. (ГОСТ Р50779.10-2000: Статистические методы. Вероятность и основы статистики.)
34
ГЛАВА II.

Диаграмма 2.1
Диаграмма 2.2
Ф
Пы
Вт
Ср
Чт
Пт
Важно! При построении столбиковой диаграммы высоты столбиков наглядно от-
ражают соотношение между величинами. Большая точность при этом не нужна.
Важно, чтобы столбики диаграммы были одинаковой ширины. Расстояния между
столбиками тоже должны быть одинаковыми.
Иногда на диаграмме столбики удобно откладывать не от нулевой высоты, а от
другого значения.
ПРИМЕР 2. На рисунке две диаграммы, построенные по данным таблицы 3 «Про-
изводство зерновых культур в России» (см. с. 11). На диаграмме 3.1 столбики от-
кладываются от значения 0 млн тонн, а на диаграмме 3.2 — от значения 60 млн
тонн. На диаграмме 3.1 мельче масштаб: одно деление соответствует 20 млн тонн,
а на диаграмме 3.2 — 10 млн тонн. Поэтому на диаграмме 3.1 различия столбиков
по высоте видны хуже, чем на диаграмме 3.2. В то же время на диаграмме 3.1 мож-
но визуально оценить1, во сколько раз производство выросло по сравнению с преды-
дущим годом, а по диаграмме 3.2 такую оценку сделать трудно. Зато на диаграм-
ме 3.2 лучше видно, на сколько миллионов тонн изменилось производство зерновых.
Выбор начала отсчёта по вертикальной оси и масштаба зависит от природы данных
и от целей, которые стоят перед исследователем.
Диаграмма 3.1 а Диаграмма 3.2
2011 2012 2013 2014 2015 2016 2017
2011 2012 2013 2014 2015 2016 2017
Иногда на одной диаграмме строят сразу несколько рядов данных.
1 Оценить — означает найти приближённое значение.
ДИАГРАММЫ
35

ПРИМЕР 3. Валовой внутренний продукт страны (ВВП) — суммарная сто-
имость всех товаров и услуг, произведённых за год во всех отраслях экономики на
территории государства.
ВВП считают по разным методикам. Можно подсчитывать ВВП просто по стоимо-
сти всех товаров и услуг в долларах США. Другой способ — учитывать при подсчёте
соотношение цен в разных странах. Получается ВВП по паритету покупательной спо-
собности (ВВП по ППС).
Например, в 2004 году весь совокупный продукт России составлял около 600 млрд
долларов США (диагр. 4). Но если пересчитать эту сумму по покупательной способ-
ности рубля в 2004 году, получается уже намного больше — около 2500 млрд долла-
ров.
С помощью ВВП экономисты оценивают состояние экономики, объём финансовой
сферы и производства, направленного на потребление. На диаграмме 4 показан ВВП
по ППС России, Германии, Франции и Италии в период с 1998 по 2018 г.
Диаграмма 4. ВВП (по паритету покупательной способности)
трёх стран, млрд долларов США
■ Германия ■ Россия ■ Франция
^оооо^ечсо^касо^ооФОгнсчео^юсог^ао
0}0>0>QQOQOOOOOQiH^4^Hi-Hi-Hi-Hi-Hi-HfH
0*0*0)0000000000000000000
Линейные диаграммы
Часто данные на диаграммах изображают не столбиками, а точками. Такое изобра-
жение особенно удобно, когда данных много, и столбики «налезали бы друг на дру-
га», мешая воспринимать информацию. Для того чтобы зрительно ряды данных не
смешивались, точки одного ряда соединяют отрезками. Вероятно поэтому такие диа-
граммы иногда называют линейными диаграммами1.
ПРИМЕР 4. Преобразуем столбиковую диаграмму 4 из примера 3 в линейную.
Диаграмма 5 изображает те же данные, но читается легче.
Линейные диаграммы часто называют графиками, но на самом деле это способ изображения
отдельных значений, а промежуточные значения неизвестны. Поэтому такое изображение дан-
ных является всё же диаграммой, а не графиком какого-то процесса или функции.
36
ГЛАВА II.

Диаграмма 5. ВВП (по паритету покупательной способности)
трёх стран, млрд долларов США
t
-•- Германия -•- Россия • Франция
f- 00 0)Oi-<CsJC0^kO?0t^0005Oi-iCsJC0^kO?0t^00
0»0»0»OOOOOOOOOO«H*HfHfHvHf-4*4fHfH
о^о^о^ооооооооооооооооооо
Вопросы
1 Чем диаграмма удобнее таблицы?
2 В каких случаях таблица удобнее диаграммы?
3 Какие требования нужно соблюдать при построении столбиковой диаграммы?
4 Что такое легенда диаграммы?
Упражнения
57 По диаграмме 2 определите:
а) в какой день недели продано больше всего шоколадок;
б) в какой день недели продали меньше всего шоколадок.
58 По диаграмме 2 определите, во сколько раз больше продано шоколадок в по-
недельник по сравнению со средой? с четвергом?
59 Можно ли с помощью диаграммы 2 сделать вывод, что в конце недели про-
даётся меньше шоколадок, чем в начале?
60 За контрольную работу по математике школьники получили 6 отметок
«отлично», 10 отметок «хорошо», 5 отметок «удовлетворительно» и 3 отмет-
ки «неудовлетворительно». Постройте столбиковую диаграмму по этим дан-
ным.
61 В таблице 32 указаны 6 лучших нападающих премьер-лиги чемпионата
России по футболу сезона 2018—2019 гг. и место команды по итогам чемпио-
ната.
ДИАГРАММЫ

Таблица 32. Лучшие нападающие
Игрок
Чалов Фёдор
Азмун Сердар
Классов Виктор
Дрнуссн Себастьян
Миранчук Антон
Зе Луиш
Команда
ЦСКА (Москва)
«Зенит» (Санкт-Петербург)
«Краснодар»
«Зенит» (Санкт-Петербург)
«Локомотив» (Москва)
«Спартак» (Москва)
Число голов
15
13
12
11
11
10
Место
4
1
3
1
2
5
а) Постройте столбиковую диаграмму числа голов, забитых лучшими напада-
ющими.
б) Можно ли сказать, что среди нападающих есть явный лидер?
в) Как вы думаете, есть ли связь между числом голов, забитых нападающи-
ми, и результатами их команд? Иными словами, можно ли утверждать, что
чем больше голов забил игрок, тем выше место его команды в чемпионате?
62 Рассмотрите диаграмму 6, на которой изображён ВВП России, Великобрита-
нии, Индии, Мексики за несколько лет и прочитайте сопровождающий текст.
Диаграмма 6. ВВП России, Индии, Великобритании и Мексики
*•
8
ем
ю
8
СМ
СО
8
ем
t-
8
ем
00
8
см
о>
8
ем
о
1-Н
О
ем
1-Н
1-Н
О
ем
ем
О
ем
со
1Н
О
см
*•
f-H
о
см
ю
1-Н
о
ем
(О
О
ем
t-
О
ем
В конце 2008 г. в мире начался экономический кризис, который проявился
в виде сильного снижения основных экономических показателей в 2009 г.
в большинстве стран с развитой экономикой; некоторые страны оказа-
лись на грани банкротства. Несмотря на это, в некоторых азиатских
странах ВВП имел положительную динамику. Например, в Индии ВВП
в 2010 г. вырос более чем на 30% по сравнению с 2007 г., в то время как,
например, в Великобритании данный показатель за эти 3 года упал более
чем на 20%.
ГЛАВА II.

В России в период 2010—2013 гг. наблюдался стремительный рост эконо-
мической деятельности, поэтому заметно рос ВВП. Но в связи с эконо-
мическими санкциями и падением курса рубля российский ВВП начал сни-
жаться, и в 2014 г. в России зафиксировано падение ВВП по сравнению с
предыдущим годом. В 2015 г. ситуацию усугубило снижение цен на нефть.
Это же обстоятельство негативно отразилось и на ВВП Мексики в 2015 г.,
так как нефтяная промышленность является ведущей отраслью мекси-
канской экономики.
а) На основании прочитанного определите, какой стране какая из линий на
диаграмме соответствует.
б) Как вы думаете, какие причины могли привести к снижению ВВП России
в 2014 г. и двух последующих годах?
в) На сколько миллиардов долларов ВВП России в 2013 г. был выше, чем в
2004 г.? Выразите это увеличение ВВП в процентах.
г) В каком году ВВП Индии и ВВП России сравнялись?
63 Важным экономическим показателем является часть ВВП, которая при-
ходится на одного жителя страны (ВВП на душу населения). Таблица 33 по-
казывает численность населения России, Великобритании, Индии и Мексики
по данным ООН на конец 2017 г. Пользуясь таблицей 33 и диаграммой 6,
оцените ВВП на душу населения в этих четырёх странах в 2017 г. Перечер-
тите таблицу 33 в тетрадь и заполните правый столбец.
Таблица 33. Население и ВВП на душу населения в четырёх странах
Страна
Великобритания
Цм^тр
Мексика
Российская Федерация
Численность населения
на конец 2017 г., млн чел.
67,8
1362,5
133,1
146,8
ВВП на
душу населения
64 В таблице 4 (см. с. 12) приведены данные о выработке электроэнергии в Рос-
сии в период с 2010 по 2019 г. в миллиардах киловатт-часов.
а) Постройте столбиковую диаграмму по данным таблицы 4. Какое значение
удобно взять в качестве начального на вертикальной оси?
б) Можно ли сказать, что выработка электроэнергии сильно меняется год от года?
в) В каком году выработка электроэнергии была самой низкой?
г) В каком году выработка электроэнергии была самой высокой?
д) В каком году прирост выработки электроэнергии был самым низким?
е) Какую тенденцию1 можно заметить в этих данных в период с 2014 по 2018 г.?
65 В таблицах 34 и 35 собраны данные о дальности перелётов некоторых птиц
и других летающих животных. Постройте столбиковые диаграммы по данным
этих таблиц. В каждом случае обращайте внимание на значение, которое
удобно принять за начало отсчёта на вертикальной оси.
1 Тенденция — устойчивое направление развития (рост, снижение, постоянство), наблюдаемое
на протяжении длительного времени.
ДИАГРАММЫ

Таблица 34. Дальность Таблица 35. Дальность
перелётов на зимовку беспосадочного перелёта
Птица
Тонкоклювый буревестник
Европейский белый аист
Сибирская пеночка-весничка
Скандинавская пеночка-таловка
Полярная крачка
Расстояние,
км
9000
10 000 1
11000
13 500
17 000
Животное
Рубнногорлая колибри
Летучая мышь
Перелётная саранча
Бурокрылая ржанка
Расстояние,
км
800
1100
2200
3000
W
Справка. Для сравнения дадим таблицу вместимости и дальности беспосадоч-
ного полёта некоторых пассажирских самолётов (табл. 36).
Таблица 36. Вместимость и максимальная дальность
беспосадочного полёта с пассажирами
Тип самолёта
Аэробус А321
Аэробус
АЗЗО-200
Боинг 737-800
Боинг 747-400
Боинг
777-200LR
Боинг 787-8
Ил-96-400
Число
пассажирских
мест
185—220
253—300
160—189
624
301
242
435
Дальность
полёта*
км
5950
13 400
5400
14 205
17 500
13 600
9000
Тип
1 самолёта
| Ту-154М
1 Ту-204С
1 Сухой SSJ-
100-96LR
Ан-24
Як-42
Ил-114'
МС-21-300*
Число
пассажирских
мест
164—180
210
98
48—52
120
64
163
Дальность |
полёта, км
6600 1
6890 I
4578
1850
2900
6500
6400
Статистическое исследование. В таблице 32 (см. с. 38) даны сведения о фут-
больных игроках, забивших больше всех мячей в ворота противника на чемпио-
нате России по футболу, и о местах, которые заняли их команды. Сделайте по-
хожее исследование: возьмите результаты игроков вашего любимого командно-
го вида спорта (футбол, волейбол и т. п.), соберите результаты лучших игроков
их команд. Составьте таблицу для того, чтобы сопоставить эти данные. Можно
ли высказать какие-то предположения, глядя на полученную таблицу?
Серийный выпуск Ил-114 начинается в подмосковном городе Луховицы в 2020 г.
Серийный выпуск МС-21-300 начинается в Иркутске в 2020 г.
40
ГЛАВА II.

[iq) Демографическая статистика.
Половозрастные пирамиды
В демографии — статистической науке о населении — применяются специальные
диаграммы, которые называются половозрастными пирамидами.
Половозрастная пирамида — это диаграмма, показывающая количество мужчин
и женщин всех возрастов. Половозрастная пирамида состоит из двух столбиковых
диаграмм численности мужского и женского населения в каждой возрастной группе.
Столбики строятся горизонтально по разные стороны от общей оси. На диаграмме 7
изображена половозрастная пирамида России на 1 января 2019 г.
По форме половозрастной пирамиды можно судить о том, какой след оставили вой-
ны и другие социальные потрясения и о том, как реализуется в стране демографиче-
ская политика.
ПРИМЕР 1. На диаграмме 7 изображена половозрастная пирамида России на
1 января 2019 года. Сколько процентов составляет население в возрасте 20—24 лет?
На пирамиде находим соответствующий «слой». Видно, что мужчины в возрасте
20—24 лет составляют 2,4%, а женщины того же возраста — 2,3% всего населения
России.
Зная численность населения России (146,8 млн человек на 1 января 2019 г.),
можно оценить количество россиян в возрасте от 20 до 24 лет:
146,8 • (0,024 + 0,023) * 6,90 млн чел.
ПРИМЕР 2. Чем можно объяснить то, что на момент построения пирамиды граж-
дан России в возрасте 45—54 лет существенно меньше, чем тех, кому 55—59 лет?
Диаграмма 7. Половозрастная пирамида России на 1 января 2019 г.
i
100+-
95—99 -
90—94
85—89
80—84 -
75—79
70—74
65—69 -
60—64
55—59 -
50—54 -
45—49 -
40—44 -
35—39 -
30—34
25—29
20—24
15—19
10—14
5—9
0—4:
Мужчины
0,0% 0,0%
Женщины
0,0% 0,0%
0,1%||0,3%
0,2%|И0,7%
0,7% ■■■1,7%
0,7% 1 И
1.
2,2%
2,9%1
з,з%и
2,7%|
3,2%И
3,5% Щ
4,0% Hi
4,5%И
3,5% |
2,4%|
2,4%|
2,8% |
3,2%Щ
3,2% Щ
*%■■
■
1,6%
| 2,0%
^■3,5%
■1 4,0%
■■4,1%
■ 3,2%
■ 3,4%
■ 3,7%
■ 4,1%
И 4,4%
■ з,з%
| 2,3%
| 2,3%
■ 2,6%
■ зл%
■1 II
1 ►
8% 6% 4% 2% 0% 2% 4% 6% 8%
ДИАГРАММЫ
41

Чтобы ответить на этот вопрос, нужно вспомнить историю нашей страны.
В 1941 г. началась Великая Отечественная война, которая продлилась почти четы-
ре года и стоила нашей стране множества жизней1. На фронтах и в тылу погибло
очень много молодых людей, и у них не родились дети. Кроме того, в годы войны
резко снизилась рождаемость. Очень мало детей родилось в 1942—1946 гг. Поэтому
на пирамиде видно резкое сужение в слоях 70—79 лет. Следующее поколение тоже
оказалось малочисленным: мало родителей — мало детей. Слои 45—54 лет на демо-
графической пирамиде России — это «эхо войны».
Есть и второе эхо войны — внуки военного поколения. Второе эхо нал ожил ось на
период распада СССР и последующие кризисные годы. Рождаемость снова резко сни-
зилась. Поэтому на пирамиде мы видим ещё одно сужение: россиян в возрасте 15—
24 лет намного меньше, чем могло бы быть.
Эхо войн и экономических кризисов сказывается на населении любой страны.
ПРИМЕР 3. Рассмотрим две половозрастные пирамиды Российской Федерации,
построенные по данным на 1 января 2000 г. и на 1 января 2020 г. (диагр. 8.1
и 8.2).
Диаграмма 8.1. Половозрастная
пирамида России в 2000 г.
100+ ]
95—99 \
90—94 \
85—89 \
80—84 \
75—79 \
70—74 \
65—69 j
60—64 1
55—59 \
50—54 \
45—49 \
40—44 \
35—39 \
30—34 \
25—29 \
20—24 \
15—19 \
10—14 1
5—9 J
0—4 И
Мужчины
Женщины
Диаграмма 8.2. Половозрастная
пирамида России в 2020 г.
100+
95—99
90—94
85—89
80—84
75—79 -I
70—74 И
65—69
60—64
55—59 -I
50—54 -I
45—49
40—44
35—39 -I
30—34 \
25—29 -I
20—24
16—19 i
10—14 \
5—9 J
0—4 \
Мужчины
Женщины
4%
2%
0%
2%
4%
Поставим вопрос, как изменилась доля пенсионеров в России. До недавнего вре-
мени возраст выхода на пенсию составлял 55 лет для женщин и 60 лет для муж-
чин2. Соответствующие слои на диаграмме мы ярко окрасили. Видно, что на правой
1 До сих пор не утихают споры, сколько граждан СССР погибло во время войны. В 2015 году
Министерство обороны России опубликовало данные, согласно которым общие потери составили
26,6 млн человек.
2 С 2019 г. в России поэтапно реализуется пенсионная реформа. Пенсионный возраст для муж-
чин и для женщин поднимается на 5 лет: до 65 и 60 лет соответственно.
42
ГЛАВА II.

диаграмме (2020 г.) суммарная площадь «пенсионных» слоев намного больше, чем
на левой. Это значит, что доля пенсионеров в 2020 г. намного выше, чем 20 лет на-
зад — в 2000 г. Это связано не только со снижением рождаемости, но и с ростом
продолжительности жизни в России. Для справки приведём в таблице 37 некоторые
данные о демографии России в 2000 и в 2020 гг.
Таблица 37. Работающее и неработающее население
в 2000 и в 2020 гг.
Год
2000
i
! 2020
i
Численность
населения,
млн чел.1
146,9
146,7
Средняя
продолжительность
жизни, лет
65,3
72,8
Работающее
население,
млн чел.
(%)
72,4 (49,25)
70,7 (48,15)
Дети,
подростки,
студенты,
млн чел. (%)
44,4 (30,25)
37,6 (25,65)
Пенсионеры,
млн чел. (%)
30,1 (20,5)
38,4 (26,2)
ф
Вопросы
1 Как называется специальная демографическая диаграмма, показывающая чис-
ленность мужского и женского населения?
2 За счёт чего может увеличиваться или уменьшаться численность трудоспособно-
го населения в стране помимо войн?
0
Упражнения
66 Рассмотрите половозрастную пирамиду России, составленную на 1 января
2019 г. (диагр. 7). Сделайте прогноз, на сколько процентов и в какую сто-
рону изменится количество взрослых людей в возрасте 30—34 лет к началу
2039 г. по сравнению с началом 2019 г.?
Указание. Нужно сравнить численность тех, кому в 2039 г. будет 30—34 го-
да, с численностью тех, кому 30—34 года было в начале 2019 г.
67 Рассмотрите половозрастные пирамиды Российской Федерации, построен-
ные по данным на 1 января 2000 г. и на 1 января 2020 г. (см. диагр. 8.1
и 8.2).
а) Найдите на пирамиде 2020 г. свою возрастную категорию. Зная общую
численность населения России в 2020 г. (см. табл. 37), оцените количество
ваших сверстников.
б) Как изменилась в России за прошедшие 20 лет потребность в школах —
выросла или снизилась?
в) Как изменилась в России за прошедшие 20 лет потребность в детских
садах?
1 По данным Росстата.
ДИАГРАММЫ
43

68 Выделяют три основных типа воспроизводства и возрастной структуры насе-
ления.
Прогрессивный тип характеризуется высокой долей детей в населении стра-
ны, высокой рождаемостью и низкой средней продолжительностью жизни.
Такой тип характерен для большинства слаборазвитых стран.
Стационарный тип характеризуется почти уравновешенной долей детских и
старших возрастных групп, невысокой стабильной рождаемостью. Такой тип
чаще всего встречается в странах с развивающейся экономикой.
При регрессивном типе доля пожилых людей в составе населения высока, а
детей мало. Наблюдается низкая рождаемость при высокой средней продол-
жительности жизни. Такой тип характерен для современных развитых инду-
стриальных стран.
На диаграмме 9 изображены половозрастные пирамиды трёх стран: Японии,
Афганистана и Исландии. Определите, какая диаграмма какой стране соот-
ветствует.
Диаграмма 9. Половозрастные диаграммы трёх стран
.А. к
100+-
95—99 -
90—94 -
85—89 -
80—84 -
75—79-
70—74-
65—69 -
60—64
55—59
50—54
45—49
40—44 -
35—39
30—34
25—29
20—24
15—19
10—14
5—9
0—4:
^Мужчины Женщины (Б,
1
II
II
II
II
II
■ ■
■ ■
н
ПН
■■■■
■ ■
■ ■■ ■
■ ■■ ■
IB
1 II 1
100+
95—99
90—94
85—89
80—84
75—79
70—74
65—69
60—64
55—59
50—54
45—49
40—44
35—39
30—34
25—29
20—24
15—19
10—14
5—9
L 0—4
Мужчины Женщины
II
Мужчины Женщины
I
I
II
6% 4% 2% 0% 2% 4% 6%
0% 2% 4%
2% 4%
69 По данным Росстата на 1 января 2019 г. население России составляло
146,7 млн человек. Рассмотрите диаграмму 7.
а) Найдите численность детей в возрасте до 4 лет на 1 января 2019 г. в Рос-
сии.
б) На сколько мальчиков в возрасте до 4 лет было больше, чем девочек?
44
ГЛАВА II.

70 На диаграмме 10 изображена половозрастная пирамида населения всей
Земли по данным на конец 2017 г. (общая численность человечества
на этот момент 7,52 млрд чел.). Рассмотрите диаграмму и ответьте на во-
просы.
Диаграмма 10. Половозрастная пирамида
населения Земли (2017 г.)
100+^
95—99 -
90—94 -
85—89 -
80—84 -
75—79
70—74
65—69
60—64
55—59
50—54 -
45—49
40—44 -
35—39
30—34
25—29 -
20—24
15—19
10—14
5—9-
0—4_
Мужчины
Женщины
0,0% 0,0%
0,0% 0,0%
0,1%||0,1%
0,2% || 0,3%
0,4% || 0,6%
0,7% ■■ 0,9%
1,0% ■■1,2%
1,5% | Ц |l,6%
2,0% ■ 12,1%
2,3%
2,8% |
3,1% ■
3,3% ■
3,4%И
3,9% 1
1 4,2% —
4,1%И
4,1% ■
4,2% |
4,5% ■
4,7% Щ
6% 4%
■ ■■ 12,4%
■ ■ ■ 2,8%
■ 3,1%
■ ■ ■ 3,2%
■ ■ ИЗ,4%
■ 3,8%
■4,0%
■ ■ ■ 3,8%
■ ■ ■ 3,8%
■ 4,0%
■ ■■4,2%
щшшщшщшшщ±±±^+
2% 0% 2% 4% 6%
а) Сколько в 2017 г. на планете было детей в возрасте 10—14 лет?
б) Рассмотрим только детей в возрасте до 9 лет. На сколько в 2017 г. в мире
мальчиков было больше, чем девочек?
в) Рассмотрим только людей в возрасте 60 лет и старше.
На сколько мужчин было меньше, чем женщин?
Статистическое исследование. В Интернете есть сайты, содержащие демо-
графические данные обо всех странах мира за последние несколько десятиле-
тий. По данным одного из таких сайтов оцените изменение доли и численности
работоспособного населения России в период с 1980 по 2018 г.
Попробуйте найти данные и провести такое же исследование для региона, в ко-
тором вы живёте. Трудоспособным населением в России в этот период счита-
лись мужчины в возрасте от 16 до 59 лет и женщины в возрасте от 16 лет до
54 лет1.
В разных странах возрастные границы работоспособного населения немного различаются.
ДИАГРАММЫ
45

Jin Круговые диаграммы
Диаграмма 11. Деление
пиццы
И Юрий
Четыре друга в складчину покупают круглую пиццу за
360 р. Иван внёс 50 р., Алексей — 80 р., Юрий — 100 р.
и Пётр — 130 р. Построим круговую диаграмму 8, пока-
зывающую долю каждого (они, конечно, поделят потом
пиццу поровну). Пицца стоит 360 р., поэтому каждому ру-
блю соответствует сектор с углом 1°.
Если бы друзья делили пиццу не поровну, а пропорцио-
нально своим долям в общей сумме денег, то Ивану до-
стался бы сектор пиццы с углом 50°, Юрию — сектор
с углом 80° и т. д.
Деление круга на секторы, пропорциональные частям
целого, настолько наглядно, что его используют в самых
разных случаях. Полученная таким образом схема назы-
вается круговой диаграммой. В английском языке исполь-
зуется слово pie chart (пай чарт), что дословно означает
«схема пирога», или ♦ пи роговая диаграмма».
Определение. Диаграмма, показывающая, как целое делится на части в виде
секторов круга, углы которых пропорциональны долям единого целого, называ-
ется круговой диаграммой.
Чтобы построить круговую диаграмму на бумаге, нужны линейка, циркуль
и транспортир. Чтобы раскрасить секторы, полезно иметь цветные карандаши или
фломастеры. Нет необходимости строить углы очень точно. На рисунке 3 показаны
две круговые диаграммы. На одной из них малый сектор имеет угол ровно 47°, а на
второй угол равен 48°. Попробуйте определить, где какая диаграмма.
Ф
Рисунок 3. Какой угол меньше?
Важно! При построении круговой диаграммы не нужно откладывать углы
с большой точностью. Небольшая погрешность не мешает правильно восприни-
мать диаграмму. Главные достоинства круговой диаграммы — наглядность вос-
приятия и быстрота построения. Для точного представления и анализа данных
диаграммы не годятся, для этого нужны таблицы.
46
ГЛАВА II.

Целое делится на несколько частей, поэтому диаграмма состоит из нескольких секто-
ров. Угол каждого сектора приближённо пропорционален части, которую он показывает.
Иногда лучше обойтись без круговых диаграмм. На рисунке 4, а на диаграмме
«Структура занятости населения города» слишком много секторов. Диаграмма плохо
читается, сравнивать доли неудобно. Лучше объединять близкие отрасли в одну. На-
пример, категории «Торговля» и «Общественное питание» можно объединить.
а) Структура занятости населения города
2,80%
Ц Добыча железной руды
га Обогатительная
^ промышленность
щ Прочие отрасли
^ промышленности
В Здравоохранение
И Культура
0,93%
4,67%
7,48%
12,15%
11,21%
Щ Торговля
ЦЦ Администрация
■ мчс
Щ Транспорт
0 Домохозяйство
| Добыча апатитов
I Слюдяная
I промышленность
!жкх
3 Образование
| Спорт
US Общественное питание
11 МВД
В Финансовый сектор
Щ Связь
Ц Безработные
б) Явка избирателей
в) Продажи разных сортов
газированной воды
не явились
проголосовали
Рисунок 4. Примеры неудачных круговых диаграмм
На рисунке 4, б показано деление целого на две части. Проще сказать: «Примерно
треть избирателей не явилась на участок». На рисунке 4, в диаграмма, где все шесть
долей примерно одинаковы. Лучше было бы написать: «Все шесть сортов газирован-
ной воды пользуются примерно одинаковым спросом».
ДИАГРАММЫ
47

ПРИМЕР 1. В таблице 38 даны сведения о всех океанах Земли.
Таблица 38. Океаны
Океан
Атлантический
Индийский
Северный Ледовитый
Тихий
Южный
Площадь поверхности,
млн км2
91,6
73,6
14,8
169,2
20,3
Объём воды,
млн км3
329,7
292,1
18,1
710,4
72,4
Средняя
глубина, м
3597
3890
1225
4280
3270
Постройте круговую диаграмму, показывающую долю каждого океана в общей
площади поверхности всех океанов Земли.
Решение. Вычислим общую площадь поверхности всех океанов:
91,6 + 73,6 + 14,8 + 169,2 + 20,3 - 369,5 (млн км2).
Найдём долю каждого океана. Доля Атлантического океана равна
91,6 : 369,5 « 0,248,
то есть примерно 24,8 %. Следовательно, сектор, соответствующий Атлантическому
океану, имеет угол 360° • 0,248 =» 89,3°. Аналогично вычислим доли и углы секто-
ров для остальных четырёх океанов. Результаты занесём для удобства в таблицу 39.
Таблица 39. Океаны
Океан
Атлантический
Индийский
Северный Ледовитый
Тихий
Южный
Площадь поверхности,
млн км2
91,6
73,6
14,8
169,2
20,3
Доля в общей
площади
поверхности, %
24,8
19,9
4,0
45,8
5,5
Угол сектора
на диаграмме,
градусы
89,3
71,7
14,4
164,8
19,8
При построении диаграммы округлим углы до целого числа градусов или даже до
углов, кратных 5°. Не забудем раскрасить секторы и добавить легенду, которая упро-
щает чтение и понимание диаграммы.
Видно, что Тихий океан занимает около половины, а Атлантический — примерно
четверть площади всего Мирового океана (диагр. 12).
48
ГЛАВА II.

Диаграмма 12. Площади океанов
^<ШлШ
Ш!Ш1ШВ1йШЩ
'ШУ-Ш?МШ&&;$
^ш^^^я
^Щ1§Я
;„-•,••/;
■-? :у.^М
Атлантический
Индийский
Северный Ледовитый
ШЙ Тихий
0^
Южный
©
Вопросы
1 Почему не требуется строить секторы круговой диаграммы очень точно?
2 В таблице 38 даны средние глубины пяти океанов. Имеет ли смысл использовать
круговую диаграмму для графического изображения этих данных о глубинах?
3 В таблице 38 есть данные об объёме водных запасов в каждом из пяти океа-
нов. Имеет ли смысл использовать круговую диаграмму для графического изо-
бражения этих данных об объёмах воды?
4 Имеет ли смысл использовать круговую диаграмму для изображения долей
мальчиков и девочек в вашем классе?
5 Попробуйте сформулировать общее правило о том, когда лучше строить столби-
ковую диаграмму, а когда — круговую.
0
71
Упражнения
На диаграмме 13 показаны данные о числе учебных и художественных книг
русских и зарубежных авторов в школьной библиотеке. Сколько примерно
учебных книг в библиотеке, если всего в библиотеке 800 книг?
Учебная литература
российских авторов
Диаграмма 13. Школьный библиотечный фонд
Учебная литература зарубежных авторов
Художественная литература
зарубежных авторов
Художественная литература
российских авторов
72 На диаграммах 14.1—14.4 показано содержание питательных веществ в че-
тырёх разных продуктах. Определите по диаграмме, в каком продукте содер-
жание белков превышает 30 %.
ДИАГРАММЫ

Диаграмма 14. Содержание питательных веществ
1) Какао
2) Шоколад
3) Фасоль
4) Грибы
Белки
№'Ы Жиры
шт
Щ Углеводы
щ Прочее*
* К прочему относятся вода, витамины и минеральные вещества.
73 Уральский федеральный округ (УрФО) состоит из шести регионов. На диаграм-
ме 15 представлены сведения о соотношении численности населения в регио-
нах округа по данным на 1 января 2018 г.
а) В каком из регионов УрФО наибольшая численность населения?
б) Найдите примерно долю населения Челябинской области в общей числен-
ности населения УрФО.
Диаграмма 15. Численность населения УрФО
Ямало-Ненецкий АО Курганская
область
Свердловская
область
Ханты-Мансийский АО
74 Пользуясь данными из таблицы 38, постройте круговую диаграмму, показы-
вающую соотношение объёмов воды в пяти океанах Земли.
75 Рассмотрите диаграмму 12. Какие из следующих утверждений верны?
1) Площадь Тихого океана намного превышает площади четырёх остальных
океанов, вместе взятых.
2) Атлантический океан составляет примерно четверть Мирового океана по
площади водной поверхности.
3) Индийский океан превышает Атлантический по площади водной поверхно-
сти.
4) Северный Ледовитый океан — самый маленький океан по площади водной
поверхности.
50
ГЛАВА II.

76 В одной из школ опросили 30 учеников и учителей о домашних животных,
живущих в их семьях (из одной семьи опрашивали только одного человека).
Результаты опроса занесены в таблицу 40.
Таблица 40. Домашние животные
Кошка
18
Собака
10
Птицы
5
Рыбки
2
Другие
7
Нет
6
а) Суммарное число животных больше, чем число опрошенных семей. Чем
это можно объяснить?
б) Предположим, что в каждой семье есть животные не более чем двух ви-
дов. Пользуясь таблицей 40, найдите число семей, где ровно один вид жи-
вотных. Постройте круговую диаграмму, показывающую доли семей: без
домашних животных, с одним видом животных, с двумя видами.
77 В течение четверти Ваня получил следующие отметки: по английскому язы-
ку — 4, 5, 5, 4, 3, 5, 4, 4, 3, 5, 5, 5; по математике — 4, 3, 5, 5, 4, 5, 5, 4.
а) Постройте круговые диаграммы распределения отметок по каждому из
предметов. Сравните диаграммы.
б) Можно ли утверждать, что Ваня примерно одинаково учится по этим пред-
метам?
Статистическое исследование. Соберите данные о числе регионов, площади
и населении своего федерального округа (если вы живёте в УрФО, соберите
данные для Центрального округа). Результаты представьте с помощью таблицы
и круговой диаграммы.
Гт Диаграммы «стебель-листья»
Как мы знаем, диаграммы нужны для быстрого наглядного сравнения данных. Как
правило, диаграммы строят после обработки данных и занесения их в таблицы. Однако
существует способ быстрого построения диаграмм, в чём-то схожий с методом подсчёта
в таблицах (см. п. 6). Помогает привычная десятичная система записи чисел. В готовый
«шаблон» быстро записываются только последние цифры поступающих данных. Особен-
но удобна такая диаграмма, когда данные поступают быстро и не сохраняются.
ПРИМЕР 1. В домашней электрической сети номинальное1 напряжение 220 вольт.
Но часто, особенно в сельской местности, напряжение бывает неустойчивым. Резкие
скачки напряжения опасны для домашней техники. Поэтому Алексей Петрович ре-
шил установить на даче стабилизатор напряжения, но прежде он решил посмотреть,
как меняется напряжение в сети. Он подключил к сети вольтметр2 и в течение дня
время от времени записывал показания. Чтобы сэкономить время и упростить за-
пись, он использовал диаграмму «стебель-листья».
Алексей Петрович заранее заготовил столбец, куда записал десятки вольт от 18 до
26, поскольку он считал, что вряд ли случится меньше 180 или больше 269 вольт.
Справа от столбца десятков он провёл вертикальную черту. Теперь ему оставалось
записывать только последние цифры, которые показывал прибор. Например, если
1 Номинальное значение — правильное, заявленное значение, то, которое должно быть.
2 Вольтметр — прибор, измеряющий напряжение.
ДИАГРАММЫ
51

Алексей Петрович видит на приборе 227 В, то в строчку «22» справа от черты он за-
писывает цифру 7.
Диаграмма 16
18
19
20
21
22
23
24
25
26
27
8
1
4
0
2
3
9
3
1
7
3
1
3
3
7
2
1
1
3
3
4
1
7
2
8 4
9 8
4 2
0 2
4 0
0 4
6
7
1
1
4
0
4
4
3
0
1
3 12 8
4 8
Через некоторое время получилась диаграмма
16. Как видим, пришлось добавить еще строку
«27», поскольку напряжение один раз оказалось
равно 271 В.
Бытовые приборы, как правило, рассчитаны
на напряжение от 180 до 250 В. На даче у Алек-
сея Петровича наибольшее наблюдение показало
271 В, а наименьшее 198 В. Таким образом, стаби-
лизатор Алексею Петровичу действительно нужен.
Кроме наибольшего и наименьшего значения
на построенной диаграмме видно типичные зна-
чения: большинство значений сосредоточено в
строчках «21» — «24».
♦Стеблем» в такой диаграмме называют ле-
вый столбец, а от него вправо растут «листья».
Диаграмма «стебель-листья» является разновид-
ностью столбиковой диаграммы. Значения сгруп-
пированы: все значения внутри одного десятка
(или одного десятичного разряда) попадают в одну
строку. Понятно, что диаграмму «стебель-листья»
можно использовать не для любых данных.
Диаграмму «стебель-листья» иногда можно
встретить на остановках автобусов и электричек.
Чтобы сэкономить место на табличке с расписа-
нием, составители используют тот же принцип.
Часы образуют «стебель», а минуты — «листья»
(рис. 5).
ПРИМЕР 2. На диаграмме 17 показаны среднегодовые температуры в Москве за
100 лет наблюдений с 1918 по 2019 г. В стебле — целые, а листья — десятые доли
градусов Цельсия.
| РАСПИСАНИЕ 1
ДВИЖЕНИЯ МАРШРУТА № 4
61 RMIAI - 11-1 ДАЧ1А1
IT С 1 ДАМП IT 1I-I ДОМ! 1
ЧАС
15
II
■7
■I
■1
11
11
12
13
14
15
11
17
11
11
1 Zl
МИ1УШ
54
27
N,33
11,31
12,45
11,51
24
31
■3.31
11,42
15,41
21,54
27
11.33
11,31
11,41
ЧАС
II
■7
■1
■1
11
11
12
13
14
15
11
17
11
11
21
МИЛЫ II
11,43
11,41
22,55
21
11,34
17,41 |
41 |
11,52
25,51 11
31
И. 37
11,43
11,41
22,55
31,51
Рисунок 5
52
ГЛАВА II.

По диаграмме легко ответить на многие вопросы. В самый холодный год сред-
няя температура составила всего 1,8 °С (это был 1941 г.)- Наибольшая средняя го-
довая температура была 7,8 °С (2010 г,). Самый типичный интервал — от 5,0 °С до
5,9 °С. Обычной можно считать среднегодовую температуру от 3 °С до 7 °С — в со-
ответствующих интервалах расположено подавляющее большинство значений.
1
2
3
4
5
6
7
Диаграмма 17. Среднегодовые температуры в Москве
8
2 7
0012222334558889
000111233444456677788888999
00001111223333444556778888999
02222223345666667779
113 4 8
0
Упражнения
78 Рассмотрите расписание движения автобуса по маршруту №4 (см. рис. 5).
а) Сколько всего раз автобус отправляется от остановки «6-я дачная»?
От остановки «10-я дачная*?
б) Как вы думаете, почему в течение некоторых часовых интервалов авто-
бус отправляется только один раз, а в другие часовые интервалы — по два
раза?
в) Предположим, что на маршруте работает всего один автобус. Когда води-
тель обедает?
г) Если на маршруте работает только один автобус, который ходит
туда-обратно, то сколько примерно времени занимает поездка в одну сторо-
ну? А обратно? Какой из маршрутов занимает больше времени? Как может
случиться, что на путь туда и путь обратно автобус тратит немного разное
время?
79 Алексей Петрович (см. пример 1) сделал 53 наблюдения. Какова доля наблю-
дений, где напряжение было:
а) 220 вольт или больше?
б) больше, чем 250 вольт?
80 Рассмотрите диаграмму 17 из примера 2. В ней 100 наблюдений. Какова до-
ля наблюдений, где температура была:
а) 7 °С или выше;
б) ниже, чем 5 °С;
в) от 4 °С до 5,9 °С?
ДИАГРАММЫ 53

На диаграмме 18 показаны средние температуры августа в Новосибирске
за 50 лет наблюдений с 1970 по 2019 г. В стебле — целые, а в листьях —
десятые доли градусов Цельсия. Рассмотрите диаграмму и ответьте на во-
просы.
а) Какова была самая большая и самая маленькая средняя температура авгу-
ста в Новосибирске за последние 50 лет?
б) Какова доля наблюдений, когда температура превышала 21 °С?
в) Какую среднюю температуру августа в Новосибирске можно считать обыч-
ной?
г) Есть ли в диаграмме две строчки, в которых сосредоточено больше поло-
вины всех значений?
Диаграмма 18. Средние температуры в августе
в Новосибирске (1970—2019 гг.)
15
16
17
18
19
20
21
22
9
99
1466 789
01123355558
03344 5 55669
1111222335778
12 7
25
ГЛАВА II.

Описательная
статистика.
Средние
значения
и размах
В этой главе речь идёт о том, как описать
одним-двумя числами важные свойства
большого массива данных. Отсюда и назва-
ние главы — «Описательная статистика».
Существует множество описательных показа-
телей, по которым можно судить о средних
значениях, рассеивании, асимметричности и
характере изменения статистических данных.
В статистике широко используются среднее
арифметическое и медиана.
Иногда требуются другие средние, напри-
мер, урезанное среднее.
13 Сроднее арифметическое
14 Медиана
15 Наименьшее и наибольшее
значения. Размах
16 Урезанное среднее
17 Как выбрать подходящее
среднее

В этой главе речь пойдёт о наборах чисел и о том, как описать одним-двумя чис-
лами важные свойства набора, в котором много значений. Раздел статистики, изуча-
ющий методы описания данных, называется описательной статистикой.
Чтобы одним числом охарактеризовать весь набор чисел, используют различные
средние, или центральные, меры. Такими центральными мерами являются среднее
арифметическое, медиана. В статистике встречаются и используются и другие сред-
ние, например урезанное среднее.
Ф
Важно! Какое именно среднее лучше выбрать для описания того или иного набора
данных, зависит от природы данных, целей исследования и сложившихся традиций.
Среднее арифметическое
Рассмотрим данные о производстве пшеницы в России в 2011—2018 гг. (в милли-
онах тонн). Они приведены в таблице 41.
Таблица 41. Производство пшеницы в России
Гад
Производство пшеницы,
млн т
2011
56,3
2012
37,8
2013
52,1
2014
59,7
2015
61,8
2016
73,3
2017
86,0
2018 |
72,1
Объём производства пшеницы год от года меняется. Он сильно зависит от погод-
ных условий. По одному году нельзя судить об обычном объёме производства пше-
ницы. Лучше использовать среднее значение за несколько лет. Найдём среднее про-
изводство пшеницы за 8 лет. Для этого нужно сложить годовые сборы и сумму раз-
делить на число слагаемых:
56,3 + 37,8 + 52Д + 59,7 + 61,8 + 73,3 + 86,0 + 72,1 ^0 ол
- = о2,«59.
Найденное значение называется средним арифметическим. Среднее арифметиче-
ское — самая употребительная центральная мера. Поэтому иногда среднее арифмети-
ческое называют просто средним или средним значением.
Определение. Средним арифметическим набора чисел называется число,
равное отношению суммы чисел набора к их количеству.
Чтобы найти среднее арифметическое набора чисел, нужно сумму всех чисел
набора разделить на их количество.
Нанесём данные о производстве пшеницы на числовую ось точками, а среднее зна-
чение укажем стрелкой (рис. 6).
37,8 52,1 56,3 59,7 61,8 73,3 86,0
♦ 1 1 I» » » 1 • I | •—| 1 ♦ ►
к
Рисунок 6. Производство пшеницы в России и среднее значение (млн т)
Четыре значения оказались меньше среднего, а три больше. При этом два числа
59,7 и 61,8 довольно близки к среднему.
■
56 ГЛАВА III.

Среднее арифметическое является в некотором смысле центром рассматриваемого
набора чисел. Поясним, что здесь означает слово «центр». Представим, что числовая
ось является стержнем, на который подвешены одинаковые гири в точках, соответ-
ствующих отмеченным числам (рис. 7).
37,8 52,1 56,3 59,7 61,8 73,3 86,0
Ф I 1 »• Ф • I • I 1 •—I 1 ♦ >
о esqjp оо
Рисунок 7. Среднее арифметическое — точка равновесия
На стержне существует точка равновесия. На эту точку можно «опереть» стержень
с гирями так, что стержень окажется в равновесии. Такой точкой оказывается сред-
нее арифметическое. В физике точку равновесия называют центром масс.
Пример с гирями иллюстрирует главное свойство среднего арифметического: оно оди-
наково зависит от всех чисел набора. И большие, и малые числа входят в среднее ариф-
метическое «с одинаковым весом». В некоторых случаях это достоинство оборачивает-
ся недостатком: если в наборе по ошибке или в силу каких-то особенных причин есть
очень большое или очень малое значение, то оно одно очень сильно влияет на среднее
арифметическое, и тогда среднее не очень корректно описывает весь набор в целом.
Иногда среднее арифметическое используют для описания данных просто в силу
сложившейся традиции. Хороший пример — школьные отметки. Чтобы вывести чет-
вертную отметку, учителя используют среднее арифметическое, хотя отметки не яв-
ляются числами, а поэтому сумма отметок не имеет математического смысла. Ведь
если сложить двойку и тройку, то отметка «пять» не получится. Более того, если
школьник вначале получал двойки, но позже разобрался в материале и стал заслу-
женно получать отличные отметки, среднее арифметическое всё равно будет низким:
средняя отметка не учитывает, какие отметки получены раньше, а какие — позже.
Средняя арифметическая четвертная и годовая отметки — дань традиции.
Вопросы
1 Дайте определение среднего арифметического числового набора.
2 Чему равно среднее арифметическое числового набора, все числа в котором
одинаковы и равны 5, 6?
3 Как можно описать среднее арифметическое с точки зрения физики?
4 Может ли среднее арифметическое числового набора быть больше, чем наи-
большее значение в наборе? Меньше, чем наименьшее?
5 Что произойдёт со средним арифметическим, если все числа набора увеличить на 1 ?
,
В редакторах электронных таблиц на персо-
нальных компьютерах для вычисления среднего
арифметического предусмотрена специальная
функция
СРЗНАЧО
На рисунке показан пример вычисления средне-
го значения массива из четырёх чисел.
Рисунок 8
■
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ 57
I fx | =СРЗНАЧ(С1:С4) ]
С
1
.9
5
I 6
D
Среднее
гг ■
Е
5.25 I

0
Упражнения
82 Найдите среднее арифметическое чисел:
а) 8 и 10; б) 8, 9 и 10.
83 Найдите среднее арифметическое чисел:
а) 3, 9 и 27; б) 6, 10, 16 и 20.
Сколько из данных чисел меньше среднего значения? больше среднего значе-
ния?
84 Придумайте какие-нибудь четыре разных числа, среднее арифметическое ко-
торых равно:
а) второму по величине числу;
б) третьему по величине числу;
в) полусумме второго и третьего по величине из этих чисел.
85 Придумайте какие-нибудь пять разных чисел, у которых среднее значение:
а) больше четырёх чисел, но меньше пятого;
б) больше первого числа, но меньше остальных четырёх.
86 Найдите среднее значение набора чисел, не вычисляя их сумму:
а) 13, 14, 15, 16, 17; г) 20, 25, 30, 35, 40;
б) 16, 17, 18, 19, 20; д) 22, 24, 26, 28, 30;
в) 21, 22, 23, 24, 25; е) 102, 104, 106, 108, 110.
87 Сергею нужно было найти среднее арифметическое всех натуральных чисел
от 1 до 100. Он вычислил его так:
1 + 100
—2—-50,5
а) Верно ли Сергей нашёл среднее арифметическое?
б) Приведите пример другого набора чисел, среднее арифметическое которого
равно полусумме наименьшего и наибольшего чисел.
в) Приведите пример набора, для которого такой способ вычисления среднего
даёт неверный результат.
88 Отметьте числа и их среднее арифметическое на числовой прямой:
а) 1, 2, 3, 4; б) 2, 3, 4, 5; в) 3, 4, 5, 6; г) 10, 11, 12, 13.
89 Вычислите среднее арифметическое числового набора:
а) 2, 4, 7, 8, 9; б) 20, 40, 70, 80, 90; в) 200, 400, 700, 800, 900.
Числовые наборы б) и в) получены из набора чисел а) умножением всех чи-
сел на 10 и на 100. Как средние значения наборов б) и в) можно получить
из среднего значения набора а)?
90 Вычислите среднее арифметическое числового набора:
а) 2, 4, 7, 8, 9; б) 10, 20, 35, 40, 45; в) 50, 100, 175, 200, 225.
Числовые наборы б) и в) получены из набора чисел а) умножением всех чи-
сел на 5 и на 25. Как средние значения наборов б) и в) можно получить из
среднего значения набора а)?
91 Пользуясь данными таблицы 41, ответьте на вопросы:
а) Каков был объём производства пшеницы в 2011 г.? в 2015 г.?
б) Совпадает ли среднее производство пшеницы за эти годы со значением
в каком-нибудь году?
в) В каком году производство пшеницы было ближе всего к среднему показа-
телю?
■
58 ГЛАВА III.

92 В таблице 42 дана урожайность зерновых культур в России за несколько лет.
Таблица 42. Урожайность зерновых культур в России
Гад
ВДюжайность
зерновых, ц/га
2009
22,7
2010
18,3
2011
22,4
2012
18,3
2013
22,0
2014
24,1
2015
23,7
2016
26,2
2017
29,2
2018
27,2
а) Пользуясь таблицей 42, найдите среднюю урожайность зерновых культур
в России за пять лет: с 2009 по 2013 г.
б) Найдите среднюю урожайность зерновых культур в России за пять лет:
с 2014 по 2018 г.
в) Сравните среднюю урожайность за первые пять лет (2009—2013) и за
следующие пять лет (2014—2018). Сильно ли различаются между собой эти
средние значения, с вашей точки зрения?
93 а) Найдите среднюю урожайность зерновых культур в России за весь период
с 2009 по 2018 г. по данным таблицы 42.
б) Назовём год из данного периода (см. табл. 42) годом средней урожайно-
сти, если урожайность зерновых в этот год отличается от средней менее чем
на 5 %. Какие годы были годами средней урожайности?
в) Назовём год из данного периода (см. табл. 42) низкоурожайным, если уро-
жайность зерновых в этот год ниже средней больше чем на 10 %. Какие годы
были низкоурожайными? Каковы, по вашему мнению, причины низкой уро-
жайности в эти годы?
94 В таблице 43 показано число жителей шести крупнейших городов Москов-
ской области (с населением более 200 тыс. чел.) в разные годы. Города пере-
числены в алфавитном порядке.
Таблица 43. Население крупнейших городов Московской области, тыс. чел.
Город
Балашиха
Королев
Люберцы
Мытшци
Подольск
Химки
1969 г.
58,6
41,4
93,3
98,7
129,4
47,8
1970 г.
92.3
105.9
139.4
118,7
168,7
85,0
1979 г.
117,9
133,5
159.6
140,7
201.8
118.0
2002 г.
147,9
142,6
156,7
159,9
181,0
141,0
2010 г.
215,5
183,4
172,6
173,2
188.0
207,4
2019 г.
490,0 |
224,5 |
207,3
222,7
304,2
254.8
Найдите среднее число жителей крупнейших городов Московской области:
а) в 1959 г.; в) в 2010 г.;
б) в 1970 г.; г) в 2019 г.
95 Назовём подмосковный город из таблицы 43 крупным, если численность
населения в нём выше средней численности населения всех шести городов.
Какие подмосковные города были крупными:
а) в 1959 г.; б) в 2019 г.?
Чем, по вашему мнению, можно объяснить изменение списка крупных горо-
дов?
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ 59

Медиана
Не только среднее арифметическое показывает, где на числовой прямой распола-
гаются значения числового набора и где его центр. Другой центральной мерой явля-
ется медиана. Сначала мы на примерах поясним, как найти медиану, а затем дадим
определение.
ПРИМЕР 1. Возьмём какой-нибудь набор различных чисел, например:
1, 4, 7, 9, 11.
Подберём число т так, чтобы в наборе оказалось поровну чисел, которые меньше
числа т и которые больше числа т. В этом наборе числа уже упорядочены по воз-
растанию, поэтому подобрать такое число легко: т — 7. Меньше числа 7 два числа,
больше числа 7 тоже два числа. Следовательно, число 7 делит этот набор на две рав-
ные по численности части. Число 7 — медиана.
В этом примере набор состоял из 5 чисел, записанных в порядке возрастания. Ме-
дианой в этом случае оказывается число, стоящее в точности посередине.
ПРИМЕР 2. Рассмотрим набор 1, 3, 6, 11. Числа тоже записаны по возрастанию,
но их четыре, поэтому среди них нет числа, стоящего точно посередине. Любое чис-
ло из интервала (3, 6) разделяет набор на две равные по численности части. Медиа-
ной этого набора служит любое число, которое находится на отрезке от 3 до 6. Обыч-
но в таких случаях в качестве медианы берут среднее арифметическое двух средин-
ных чисел: * = л к.
2 4'D
Чтобы найти медиану числового набора, его нужно сначала упорядочить: записать
все числа слева направо по возрастанию от наименьшего к наибольшему. Каждое
следующее число не меньше предыдущего. Одинаковые числа окажутся рядом.
Упорядоченный таким образом набор называется вариационным рядом. Разделим
этот вариационный ряд на две части так, чтобы слева и справа от границы деления
чисел оказалось поровну.
Если в наборе нечётное количество чисел, то деление пройдёт в точности по цен-
тральному числу ряда. Это число и будет медианой.
Если в наборе чётное количество чисел, то деление пройдёт между двумя цен-
тральными числами. В качестве медианы можно взять любое из них или любое чис-
ло между ними. Обычно медианой считают среднее арифметическое двух централь-
ных чисел.
ПРИМЕР 3. Найдём медиану набора
12, 2, 11, 3, 7, 10, 3,
в котором семь чисел.
Расположим числа по возрастанию (построим вариационный ряд):
2, 3, 3, 7, 10, 11, 12.
Будем стирать одновременно самое левое и самое правое число до тех пор, пока
не останется одно число, стоящее посередине:
3, Я, 7, Ю, И.
Медиана равна 7.
60 ГЛАВА III.

ПРИМЕР 4. Таким же способом найдём медиану набора
12, 2, 11, 3, 7, 10, 3, 15,
в котором восемь чисел. Упорядочим числа:
2, 3, 3, 7, 10, 11, 12, 15.
Стирая числа по одному слева и справа, в конце концов получим два числа 7
и 10. В качестве медианы можно взять любое из них или любое число между ними.
Как уже говорилось, обычно находят среднее арифметическое двух чисел, стоящих
посередине:
v^"v Определение. Медианой набора чисел называют такое число т, что хотя бы
половина чисел набора не больше числа т и хотя бы половина чисел набора
не меньше числа т.
ПРИМЕР 5. С помощью определения покажем, что число 6 является медианой
числового набора
1, 6, 3, 2, 0, 4, 9, 12, 8, 6.
Всего в наборе 10 чисел, поэтому число 6 будет медианой, если в наборе найдут-
ся 5 (или больше) чисел, которые не больше чем число 6, а также найдутся 5 (или
больше) чисел, которые не меньше чем 6.
Не будем упорядочивать числа, а просто подчеркнём все числа, которые не боль-
ше числа 6, а над всеми числами, которые не меньше чем 6, поставим черту сверху
(надчеркнём их):
1, 6, 3, 2, 0, 4, 9, 12, 8, 6.
Обратите внимание: число 6 входит и в одно, и в другое множество — оно и под-
чёркнуто, и надчёркнуто одновременно.
Всего мы сделали 7 подчёркиваний и 5 надчёркиваний. Значит, в этом наборе
7 чисел, не больших чем 6, и 5 чисел, которые не меньше чем 5. Требование опреде-
ления выполнено, поэтому число 6 является медианой.
Определение позволяет точно сказать, что такое медиана, но использовать его для
поиска медианы неудобно.
Чтобы найти медиану, лучше действовать известным нам способом: упорядочить
числа и найти одно или два числа, стоящие посередине вариационного ряда.
Если всего в ряду п чисел, то медианой будет:
л + 1
— число с порядковым номером при нечетном п;
с*
— любое из чисел с номерами — и — + 1 или любое число между ними (обычно
2 ^
берут среднее арифметическое этих чисел) при чётном п.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ 61

ПРИМЕР 6. Вернёмся к таблице производства пшеницы в России (табл. 44).
Таблица 44. Производство пшеницы в России
ГЬд
Производство
пшеницы, млн т
2011
56,3
2012
37,8
2013
52,1
2014
59,7
2015
61,8
2016
73,3
2017
86,0
2018
72,1
Средний урожай мы уже находили. Он равен 62,39 млн т в год. Вычислим меди-
ану. Упорядочим значения:
37,8; 52,1; 56,3; 59,7; 61,8; 72,1; 73,3; 86,0.
Значений восемь. Медиана — это среднее арифметическое четвёртого и пятого
значений, т. е. 59,7 млн т и 61,8 млн т. Медиана равна 60,75 млн т.
В примере 6 медиана незначительно отличается от среднего арифметического. Так
бывает часто, но не всегда. Если в наборе есть выбросы — резко выделяющиеся зна-
чения, то медиана и среднее арифметическое могут сильно различаться.
ПРИМЕР 7. В России в 2019 г. было 15 городов с числом жителей более 1 млн
человек. Данные о населении этих городов за разные годы приведены в таблице 45.
Таблица 45. Города России с числом жителей более 1 млн человек
Город
Волгоград
Воронеж
Екатеринбург
Казань
Красноярск
Москва
Нижний Новгород
Новосибирск
Омск
Пермь
Ростов-на-Дону
Самара
I Санкт-Петербург
Уфа
Челябинск
Население, тыс. чел. |
2010 г.
1021
890
1350
1144
974
11504
1251
1474
1154
991
1089
1165
4880
1062
ИЗО
2019 г.
1013 |
1054
1483
1252
1095
12 616
1254
1618
1165
1054
1133
1157
5384
1124
1201
Найдём среднее арифметическое численности жителей этих городов по данным пе-
реписи населения 2019 г. Для этого нужно сложить числа соответствующего столб-
ца и сумму разделить на 15. Сумма равна 33 603 тыс. человек (проверьте). Значит,
средняя численность населения города-миллионера в 2019 г. равна
33 603
15
« 2240,2 тыс. чел.
62
ГЛАВА III.

Обратите внимание: в таблице нет города, население которого было бы близко
к получившемуся среднему. В большинстве городов население лишь немного превы-
шает 1 млн человек. Исключение составляют Москва и Санкт-Петербург. Из-за этих
двух городов среднее арифметическое оказалось намного больше, чем население ти-
пичного города. Значит, среднее арифметическое не даёт представления о населении
типичного крупного города России.
Лучше использовать медиану. Упорядочим значения за 2019 г. и найдём медиану:
1013 1054 1054 1095 1124 1133 1157 1165 1201 1252 1254 1483 1618 5384 12 616
Медианой является восьмое по порядку значение (подчёркнуто): 1165 тыс. чело-
век. Это население г. Омска. Можно сказать, что Омск — медианный по численности
город-миллионер в 2019 г., или медианный представитель данного набора.
Мы увидели главное достоинство медианы — устойчивость относительно выбро-
сов, т. е. отдельных сильно выделяющихся значений. Если в наборе есть выбросы,
то среднее арифметическое может не очень хорошо описывать большинство чисел.
Медиана в таких случаях лучше описывает набор, чем среднее арифметическое.
Медиана имеет не только достоинства, но и недостатки. И дело не только в том,
что для поиска медианы приходится упорядочивать набор. Гораздо существеннее, что
приходится отбрасывать все значения, кроме одного-двух. Таким образом, теряется
много полезной информации о массиве данных.
Вопросы
1 В каких случаях среднее арифметическое не очень хорошо описывает большин-
ство значений в числовом наборе? Приведите пример таких данных.
2 Дайте определение медианы числового набора.
3 В упорядоченном по возрастанию числовом наборе 19 чисел. Каким по счёту
числом является медиана в этом наборе?
4 В упорядоченном по возрастанию числовом наборе 24 числа. Между какими
двумя числами (по счёту) заключена медиана этого набора?
5 Что такое выброс?
6 В чём главное достоинство медианы как меры центра?
Г
Чтобы найти медиану массива данных в
электронных таблицах, удобно использовать
функцию
МЕДИАНАО
На рисунке показан пример.
Рисунок 9
Упражнения
96 Вычислите медиану и среднее арифметическое чисел:
а) 1, 3, 5, 7, 9; в) 1э 3, 5, 7, 9, 11;
б) 1, 3, 5, 7, 14; г) 1, 3, 5, 7, 9, 17.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ 63
1 /х | =МЕДИАНА(С1:С5) ]
С
1
9
5
6
3_
D
Медиана
Ё
5\
I ■

97 Пользуясь таблицей 45, укажите:
а) самый большой город России по числу жителей в 2010 г.;
б) второй по численности населения город в России в 2010 г.;
в) третий и четвёртый по числу жителей города в России в 2010 г.
98 Отметьте числа набора и его медиану на числовой прямой:
а) 8, 11, 3; б) 7, 4, 8, 1, 5; в) 10, 3, 9, 8, 4, 5, 7.
99 Отметьте числа набора и его медиану на числовой прямой:
а) 9, 11, 3, 17; б) 7, 4, 8, 1, 5, 6; в) 11, 3, 9, 8, 13, 4, 5, 7.
100 Найдите медиану набора чисел:
а) 11, 3, 21, 4, 17; б) 25, 17, 19, 28, 18; в) 25, 50, 25, 29, 27, 40, 28.
101 Найдите медиану набора чисел:
а) 9, 2, 8, 4; б) 8, 9, 5, 7, 1, 3; в) 12, 11, 18, 10, 22, 17, 11, 14.
102 Пользуясь таблицей 45, ответьте на вопросы.
а) На сколько изменилось среднее число жителей крупнейших городов Рос-
сии к 2019 г. по сравнению с 2010 г.? Можно ли считать, что средняя чис-
ленность населения выросла за эти 9 лет?
б) Найдите медиану числа жителей городов в 2010 г. Сравните её с медиа-
ной, вычисленной для 2019 г. Можно ли считать, что отличие существенное?
103 Рассмотрите данные о числе жителей крупнейших городов России (см. табл. 45),
исключив Москву и Санкт-Петербург.
а) Вычислите среднее значение числа жителей этих городов в 2019 г.
б) Вычислите медиану числа жителей этих городов в 2019 г.
в) Сильно ли, с вашей точки зрения, различаются медиана и среднее значение?
104 В таблице 42 (см. с. 59) приведены сведения об урожайности зерновых куль-
тур в России в 2009—2018 гг. Найдите медиану урожайности и среднюю
урожайность зерновых культур в России за период:
а) 2009—2018 гг.; б) 2009—2013 гг.; в) 2014—2018 гг.
Сравните между собой медиану и среднее за каждый период. Значительно
ли, с вашей точки зрения, они отличаются друг от друга?
105 Средний рост учащихся в классе 165 см. Медиана роста равна 168 см.
а) Обязательно ли не меньше половины учеников выше 165 см?
б) Обязательно ли не меньше половины учеников выше 168 см?
в) Обязательно ли найдётся в этом классе ученик ростом больше 165, но
меньше 168 см?
г) Обязательно ли найдётся в этом классе ученик, рост которого ровно 168 см?
му Наименьшее и наибольшее значения.
Размах
Иногда интересны не только среднее арифметическое или медиана, но и другие
характеристики набора данных, например наибольшее и наименьшее значения.
Если мы хотим узнать, кто победил в прыжках в длину в соревнованиях, то вы-
берем того, кто прыгнул дальше всех, т. е. выберем наибольший результат. Напро-
тив, в соревнованиях по бегу победителем считается тот, кто пробежал быстрее всех,
то есть показал наименьшее время.
■
64 ГЛАВА III.

Нам всегда интересно, какова наименьшая цена на нужный товар. Увидев новый
автомобиль, мы интересуемся, какова его максимальная скорость. Иногда у человека
возникает стремление к рекордам. Существует Книга рекордов Гиннесса, в которой
написано, сколько часов человек простоял на одной ноге, кто выпустил больше всего
мыльных пузырей, у кого самый длинный нос и т. п.
ПРИМЕР 1. Во время подготовки к соревнованиям четыре спортсмена устроили
мини-турнир по прыжкам в длину с места. Каждый из них сделал по пять попыток.
Все результаты занесены в таблицу. Кроме того, в ней указаны средние результаты,
а также наилучший и наихудший прыжок каждого спортсмена.
Таблица 46. Результаты прыжков в длину с места, см
Номер прыжка
1
2
3
4
5
Среднее значение
Наибольшее значение
Наименьшее значение
Пётр
215
228
208
236
205
218,4
236
205
Иван
197
205
212
241
233
217,6
241
197
Алексей
203
212
227
205
215
212,4
227
203
Сергей
208
234
240
212
203
219,4
240
203
Рассмотрите результаты и ответьте на вопросы.
Как вы думаете, почему результаты в разных попытках у ребят различаются?
Какие из перечисленных обстоятельств (факторов) могут влиять на результат: уда-
ча; техника прыжка; рост; вес; тренированность; настроение; плотный обед; уста-
лость; ветер; обувь?
Какие ещё факторы могут повлиять на дальность прыжка? Самое большое среднее
значение прыжка у Сергея. По этому показателю Иван лишь третий. Но рекордсме-
ном всё же стал Иван: в одной из попыток он прыгнул дальше всех.
Во многих спортивных дисциплинах считается, что на отдельный результат влияет
множество различных факторов, особенно если вид спорта связан с риском. В таких
случаях результаты разных попыток нельзя считать равноценными. Кроме того, мо-
гут быть явно неудачные попытки. Поэтому в спорте неразумно использовать сред-
ние показатели для оценки результата; нужно учитывать только лучший.
Тем не менее тренеру есть над чем задуматься: если упорядочить прыгунов по
лучшему прыжку и по среднему значению, то получаются два разных упорядочива-
ния. Сегодня лучшим был Иван, но Сергей уступает лишь немного, а в среднем он
прыгает лучше. Кроме того, худший результат сегодня показал тоже Иван.
Наибольшие и наименьшие значения важны не только в спорте.
ПРИМЕР 2. Каждая судоходная река имеет фарватер (судовой ход) — часть рус-
ла, где возможно движение судов. Течение несёт с собой песок и ил, глубины на
разных участках фарватера меняются, поэтому их приходится промерять несколько
раз в год. В Московском речном бассейне1 фарватеры рек промеряют четыре раза за
1 В Московский речной бассейн входят канал им. Москвы, река Москва, участки рек Оки и Волги.
■
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ 65

период навигации. Каждый раз составляется список глубин, которые наносятся на
карту. Капитану и штурману речного судна важно знать наименьшую глубину, чтобы
понять, может ли судно пройти этот участок реки.
ПРИМЕР 3. В Санкт-Петербурге за всё время наблюдений с 1706 г. случилось бо-
лее 300 наводнений. Самый высокий уровень воды (421 см выше ординара1) зареги-
стрирован 7 ноября 1824 г. Это наводнение описано в поэме А. С. Пушкина «Мед-
ный всадник».
В Санкт-Петербурге наблюдения за уровнем воды в Неве ведутся всё время. Наи-
высший известный уровень воды учитывается при строительстве набережных, дамб,
мостов не только в Санкт-Петербурге, но и в любом другом месте, где существует
опасность наводнения.
Измерение рассеивания. Размах
Часто бывает важно не только знать среднее значение в наборе данных, но и иметь
представление о том, как сильно значения разбросаны, рассеяны на числовой пря-
мой. Самой простой характеристикой, описывающей рассеивание данных, является
размах.
Определение. Размах числового набора — это разность между наибольшим
и наименьшим значениями.
В уже знакомой нам таблице 47 содержатся данные о производстве пшеницы.
Самый большой урожай пшеницы в эти годы был получен в 2017 г. Он составил
86,0 млн т. Самый скромный урожай 37,8 млн т был собран в 2012 г. Размах про-
изводства пшеницы в эти годы составил
86,0 - 37,8 - 48,2 млн т.
Это довольно большая величина по сравнению со средним значением производства
в эти годы — 62,39 млн т.
Таблица 47. Производство пшеницы в России
Год
Производство
пшеницы, млн т
2011
56,3
2012
37,8
2013
52,1
2014
59,7
2015
61,8
2016
73,3
2017
86,0
2018 1
72,1
На производство пшеницы в России сильно влияют погодные условия, и поэтому
разброс этой величины может быть довольно большим.
Во многих случаях наибольшее и наименьшее значения — неудачные характери-
стики. Они часто не являются типичными (вспомните пример с населением городов-
миллионеров, где Москва и Санкт-Петербург сильно выбиваются из общего ряда).
Иногда наибольшее и наименьшее значения оказываются попросту ошибочными.
Ошибка, например, может возникнуть при вводе данных в компьютер.
ПРИМЕР 4. В таблице 48 собраны данные о росте учащихся класса.
Наибольший рост у Евсеевой — 1154 см! Больше чем 11 метров! Ясно, что это из-
мерение — выброс, получившийся по ошибке. Скорее всего, кто-то при вводе данных
в компьютер случайно нажал лишнюю единицу. Лучше не гадать, как получилось
Ординар — средний многолетний уровень воды в водоёме.
■
66 ГЛАВА III.

такое значение, а исключить его
вовсе. Тогда наибольшее значение
167 см. В результате размах со-
кратился с 998 до 11 см.
Посмотрим на медиану. До ис-
ключения ошибочной записи ме-
диана равнялась 160 см, а после
исключения стала равна 159 см
(проверьте).
Этот пример показывает не-
устойчивость наибольшего и наи-
меньшего значений, а также раз-
маха и ещё раз иллюстрирует
устойчивость медианы.
Таблица 48. Рост школьников
Ф
Фамилия
Алексеев
Андреева
Борисов
Вольский
Гетманов
Добромыслов
Рост, см
156
159
162
158
161
156
Фамилия
Евсеева
Железов
Завидов
Коваль
Петровская
Юсуфов
Рост, см
1154
167
163
154
149
165
Важно! Наибольшее и наименьшее значения нередко попадают в набор данных
по ошибке. Начиная работать с данными, полезно обратить внимание на наи-
большее и наименьшее значения — правдоподобны ли они?
©
Вопросы
1 Приведите примеры данных, для описания которых лучше использовать наи-
большее значение, чем среднее или медиану.
2 Приведите примеры данных, для описания которых лучше использовать наи-
меньшее значение, чем среднее или медиану.
3 Что такое размах числового набора?
Для поиска наименьшего и наиболь-
шего значений в электронных табли-
цах есть функции
МИН() и МАКС()
Чтобы найти размах, нужно вычислить
разность:
= МАКС() - МИН()
I fx | =МАКС(С1:С5)-МИН(С1:С5) ]
С D
1
9
5
6
1 з
Наим.
Наиб.
Размах
Е
1
9
8
"
F
0
Рисунок 10
Упражнения
106 Найдите наибольшее и наименьшее значения, размах, среднее значение и ме-
диану набора чисел:
а) 12, 7, 25, 3, 19, 15; б) 17, 19, 5, 41, 47, 13, 19.
107 В таблице 49 приведены данные о производстве зерновых культур в России
в 2011—2018 гг.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ
67

Таблица 49. Производство зерновых культур в России
Год
Производство
зерновых, млн т
Урожайность
зерновых, ц/га
2011
94,2
22,4
2012
70,9
18,3
2013
92,4
22,0
2014
105,2
24,1
2015
104,7
23,7
2016
120,7
26,2
2017
135,5
29,2
2018
113,2
27,2
Найдите наибольшее, наименьшее значения и размах:
а) производства зерновых культур; б) урожайности зерновых культур.
108 При сборке автомобильного двигателя нужно добиться того, чтобы все порш-
ни двигателя имели одинаковую массу (размах должен быть не более 0,1 г).
Увеличить массу поршня нельзя, зато её можно уменьшить, высверливая
углубления в специальных местах поршня. В таблице 50 показаны массы
8 поршней для одного двигателя.
а) Определите размах масс поршней, б) Какой поршень не требует доработки?
Таблица 50. Массы поршней
Поршень
Масса, г
1
124,4
2
124,8
3
125,2
4
123,9
5
124,1
в
125.4
7
125,2
8 _]
124,8
109 В таблице 51 даны результаты измерения температуры пациента в больнице.
Таблица 51. Измерение температуры
Время
t, °С
7 ч
38,3
9 ч
39,2
11 ч
39,2
13 ч
39,4
15 ч
39,1
17 ч
38,7
19 ч
381
21 ч
38,2
а) Найдите явно ошибочное значение. Как оно могло получиться?
б) На сколько градусов изменился размах после исключения ошибки?
в) На сколько изменилось среднее значение после исключения ошибки?
г) На сколько градусов изменилась медиана после исключения ошибки?
Статистическое исследование. Как высоко поднималась вода во время павод-
ков или наводнений в городе или селе, где живёте вы? Или другой вопрос — как
сильно мелеют ваши водоёмы во время засухи? Попробуйте собрать и упорядо-
чить эту информацию.
Пб) Урезанное среднее
Однажды один из авторов этого учебника преподавал в школе слепой метод маши-
нописи на компьютерах. Важными показателями здесь являются средняя скорость и
ритмичность письма. Компьютер позволяет сохранить в памяти время между кажды-
ми двумя последовательными нажатиями на клавиши. Получается массив из тысяч
значений. Легко вычисляется среднее время между двумя нажатиями, размах и лю-
бые другие показатели.
Проблема в том, что не все промежутки между соседними нажатиями нужно учиты-
вать: во время занятия ученик иногда делает перерывы, отвлекается на разговор с пре-
подавателем, на чтение задания, на запись в тетради. Возникает длинная пауза, которая
68
ГЛАВА III.

не связана с умением печатать. Иногда, наоборот, случаются слишком малые проме-
жутки, если палец случайно попадает на две клавиши одновременно. Поэтому слишком
большие и слишком малые промежутки между нажатиями нужно убрать из расчёта.
Так появляется идея отбросить слишком малые и слишком большие значения, а
уже потом вычислить среднее оставшихся значений. Мы не знаем заранее, сколько
значений нужно отбросить. Конечно, можно было бы использовать медиану, но, как
мы знаем, при этом теряется много полезной информации.
С другой стороны, нетипичных значений не может быть очень много. Поэтому
можно отбросить, скажем, 10% самых малых и 10% самых больших значений, оста-
вив 80% значений, которые будут считаться надёжными. Можно принять другое пра-
вило и отбросить снизу и сверху по 5% или по 25% всех значений.
Среднее значение оставшихся данных называется урезанным средним.
Определение. Урезанное среднее массива значений — это среднее ариф-
метическое всех значений, которые остались в массиве после отбрасывания не-
которой доли самых малых и самых больших значений.
Урезанное среднее часто используется» когда в данных могут встретиться ненадёж-
ные слишком большие или слишком малые значения — выбросы. Урезанное среднее
соединяет в себе достоинства среднего арифметического и медианы. Часто урезанное
среднее используется в спорте.
ПРИМЕР 1. Выступления фигуристов оценивают несколько судей. Правила судей-
ства довольно интересные. Каждый элемент (прыжок, вращение и т. д.) имеет базо-
вую стоимость в баллах. Чем труднее элемент, тем выше стоимость. После выступле-
ния фигуриста девять судей ставят оценки за каждый элемент. Оценки ставятся по
11-балльной шкале (от -5 до +5 баллов). Затем применяется специальный алгоритм.
1. За каждый элемент вычисляется урезанное среднее; для этого из девяти оценок
удаляются две — наименьшая и наибольшая.
2. Получившееся урезанное среднее прибавляется к базовой стоимости. Получает-
ся оценка за элемент.
3. Итоговый результат получается суммированием оценок за все отдельные эле-
менты.
На соревнованиях фигурист П. выполнил несколько элементов. В таблице показа-
ны базовые стоимости этих элементов и оценки судей.
Таблица 52. Базовые стоимости элементов и оценки судей
.
Элементы
Тройной садьжов
Каскад прыжков
Четверной тулуп
Двойной аксель
Тройной лутц1
Базовая
стоимость
4,3
6,1
6,7
3,3
5,9
Оценки судей
-1
-2
-2
0
-3
1
-3
-1
1
-1
2
-2
1
2
0
1
-1
0
0
1
1
-2
1
1
0
1
-2
-1
1
1
0
-2
-1
0
0
1
-3
-1
0
0
1
-1
-1
1
0
Сальхов, аксель, тулуп и лутц — виды различных прыжков с вращением в воздухе. Двойной,
тройной и т. п. — указание на количество полных оборотов во время прыжка.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ 69
®

Вычислим, например, оценку за четверной тулуп. Удалим из оценок судей наи-
меньшую оценку -2 и наибольшую оценку 1. Остаётся семь оценок, и урезанное
среднее равно
-1 + 0 + 1-1-1-1-1 4 _„
z - -~ * -0,57.
7 7
Прибавляя это число к базовой стоимости четверного тулупа, получаем:
6,7 - 0,57 - 6,13.
Урезанное среднее в фигурном катании появилось недавно, после одного из скан-
далов, который случился из-за подозрения в предвзятости судейства.
Судьи не могут быть совершенно объективными. Судейство, особенно в творческих
видах спорта и искусстве всегда немного предвзято. Кроме того, если судья поставил
высокую оценку «своим» или «занизил соперникам», то это может спровоцировать
протесты, даже если никакого «подсуживания» на самом деле не было.
Если все судят совершенно честно, то небольшую субъективность можно устранить
с помощью обычного усреднения. Но чтобы избавиться от влияния сознательной
предвзятости в судействе (и обвинений в предвзятом судействе), нужны специальные
средства. Например, урезанная средняя оценка.
ПРИМЕР 2. Обсудим население регионов Российской Федерации. Всего их 85, и
численность населения в них различается (табл. 53).
Таблица 53. Численность населения регионов Российской Федерации
Код
01
04
02
03
05
06
07
08
09
1 10
1 П
1 91
1 12
1 13
Субъект
Российской
Федерации
Республика Адыгея
Республика Алтай
Респ. Башкортостан
Республика Бурятия
Республика Дагестан
Республика Ингушетия
Кабардино-Балкарская
Респ.
Республика Калмыкия
Карачаево-Черкесская
Респ.
Республика Карелия
Республика Коми
Республика Крым
Республика Марий Эл
Республика Мордовия
Население,
млн. чел.
463 453
220 140
4 037 811
986 109
3 111353
506 688
868 174
271 035
465 669
614 628
820 171
1912 025
679 094
790 829
Код
40
42
43
44
45
46
47
48
49
50
51
52
53
54
Субъект
Российской
Федерации
Калужская обл.
Кемеровская обл.
Кировская обл.
Костромская обл.
Курганская обл.
Курская обл.
Ленинградская обл.
Липецкая обл.
Магаданская обл.
Московская обл.
Мурманская обл.
Нижегородская обл.
Новгородская обл.
Новосибирская обл.
Население,
млн. чел.
1 000 070 ]
2 657 758
1 262 549
633 392
826 941 1
1 103 059
1 876 392
1 139 492
140 199
7 687 647
741 511
3 203 818
596 173
2 798 251
По данным Росстата на 1 января 2020 г.
70 ГЛАВА III.

Продолжение
Код
14
15
16
1 17
18
19
20
21
22
75
41
23
24
59
25
1 26
| 27
28
1 29
1 30
1 31
32
33
34
35
36
37
38
1 39
Субъект
Российской
Федерации
Респ. Саха (Якутия)
Респ. Северная Осетия
Республика Татарстан
Республика Тыва
Удмуртская Республика
Республика Хакасия
Чеченская Республика
Чувашская Республика
Алтайский край
Забайкальский край
Камчатский край
Краснодарский край
Красноярский край
Пермский край
Приморский край
Ставропольский край
Хабаровский край
Амурская обл. '
Архангельская обл.
Астраханская обл.
Белгородская обл.
Брянская обл.
Владимирская обл.
Волгоградская обл.
Вологодская обл.
Воронежская обл.
Ивановская обл.
Иркутская обл.
1
Калининградская обл.
Население*
млн. чел.
970 105
697 064
3 902 642
327 388
1 501 005
534 186
1 476 752
1217 820
2 317 052
1 059 657
312 438
5 677 786
2 867 875
2 599 301
1 895 305
2 803 021
1315 310
790 676
1 136 387
1 005 967
1 547 532
1 192 570
1 358 538
2 491 751
1 160 721
2 323 657
997 196
2 390 827
1012 253
Код
55
56
57
58
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
76
77
78
92
79
83
86
87
89
Субъект
Российской
Федерации
Омская обл.
Оренбургская обл.
Орловская обл.
Пензенская обл.
Псковская обл.
Ростовская обл.
Рязанская обл.
Самарская обл.
Саратовская обл.
Сахалинская обл.
Свердловская обл.
Смоленская обл.
Тамбовская обл.
Тверская обл.
Томская обл.
Тульская обл.
Тюменская обл.
Ульяновская обл.
Челябинская обл.
Ярославская обл.
г. Москва
г. Санкт-Петербург
г. Севастополь
Еврейская АО
Ненецкий АО
Ханты-Мансийский
АО-Югра
Чукотский АО
Ямало-Ненецкий АО
Население,
млн. чел.
1 926 562 1
1 956 256 1
733 682 1
1 304 825 1
626 046
4 195 327 1
1 108 924 1
3 179 026
2 421785
488 453
4 310 861 1
934 747 1
1 006 962
1 260 345
1079 051
1 466 025
3 755 778
1 229 687
3 466 960
1 253 189
12 692 466 1
[ 5 392 992
! 448 829
158 381
44 110
1 674 086
50 726
544 008
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ 71

Сначала вычислим среднее арифметическое. Получим (с округлением) 1 млн
753 тыс. чел. Медиана данных равна 1 млн 160,7 тыс. чел. Мы понимаем, отче-
го возникает такая разница: на среднее арифметическое влияют Москва и Санкт-
Петербург, где жителей намного больше, чем в других регионах. Малочисленные ре-
гионы не могут их уравновесить. Можно использовать медиану, как мы уже дела-
ли. Но все же среднее арифметическое тоже подходит, если убрать из расчёта сильно
выделяющиеся большие и малые значения.
Давайте удалим 10% самых малых и 10% самых больших значений, то есть
85 • 0,1 = 8,5 значений с каждой стороны. Восемь с половиной регионов удалить
нельзя, поэтому удалим 8 наиболее населённых и 8 наименее населённых регионов.
Останется 69 регионов, наиболее типичных для России по численности населения.
Урезанное среднее равно 1 млн 443,2 тыс. чел. Эта величина намного ближе к меди-
ане, чем среднее без урезания.
Если удалить не 10%, а 25% значений с каждой стороны, то останется примерно
половина регионов, среднее число жителей в которых равно 1 млн 268,4 тыс. человек.
Ф
Важно! Чем сильнее урезается массив данных с обеих сторон, тем больше ин-
формации теряется.
Какое именно правило следует выбрать при урезании, решает только статистик
в каждом конкретном случае. Ещё раз напомним, что выбор способа описания дан-
ных зависит от природы данных, от целей исследования и от сложившейся тради-
ции. Часто применяется урезание на 25% массива с обеих сторон.
Для урезанного среднего есть специ-
альная функция в редакторах элек-
тронных таблиц
УРЕЗСРЕДНЕЕ()
В примере на рисунке указано, что
нужно обрезать 0,2, то есть 20% всех
значений, то есть по 10% массива с
каждой стороны.
с
1
2
3
4
5
6_
/ж
=УРЕЗСРЕДНЕЕ(С1 :D6;0,2) I
D Ё F
7
8
9
10
11
12_
Урезанное
среднее
о
6,51
Рисунок 11
\jj Вопросы
1 Что такое урезанное среднее? Чем урезанное среднее отличается от среднего
арифметического?
2 В каких случаях применяют урезанное среднее? Почему урезанное среднее часто
используют для усреднения судейских оценок на соревнованиях, конкурсах и т. п.?
0
Упражнения
110 Дан числовой массив: 3, 2, 4, 2, 9, 2, 0, 0, 1, 1, 2, 3, 14, 1.
а) Сколько значений останется в массиве после отбрасывания 10% наимень-
ших и 10% наибольших значений?
72
ГЛАВА III.

б) Найдите урезанное среднее массива при урезании на 10% с обеих сторон.
в) Найдите урезанное среднее массива при урезании на 25% с обеих сторон.
111 В таблице 46 (см. с. 65) даны результаты прыжков в длину. Найдите урезан-
ное среднее результатов при урезании на 20% с обеих сторон:
а) Петра; б) Ивана.
112 В таблице 45 (см. с. 62) дано население 15 городов-миллионеров. Найди-
те урезанное среднее численности населения этих городов при отбрасывании
20% наименьших и 20% наибольших значений с каждой стороны:
а) в 2010 г.; б) в 2019 г.
113 В школе на заключительном туре художественного конкурса три лучших ри-
сунка претендовали на призовые места. Десять судей оценили каждый рису-
нок по шкале от 1 до 10 (табл. 54). Сначала все выставленные оценки просто
усреднили, но один из участников заявил, что в жюри входит мама его со-
перника, поэтому судейство нечестное. Тогда, чтобы исключить возможность
предвзятого судейства, было решено использовать урезанное среднее после
отбрасывания двух самых низких и двух самых высоких оценок.
Таблица 54. Оценивание школьного конкурса
Рисунок
Натюрморт
Портрет учителя
Городской пейзаж
Оценки десяти судей
1
4
4
7
2
5
9
3
3
7
7
6
4
10
5
7
б
7
7
8
в
6
4
6
7
7
10
7
8
4
6
8
9
6
5
3
10
7
7
6
а) Какие оценки получил натюрморт при простом усреднении и при урезан-
ном усреднении?
б) Какой рисунок занял первое место? Какой рисунок занял бы первое место,
если бы методику подсчёта оценок не изменили?
в) Какой рисунок занял третье место? Какой рисунок занял бы третье место,
если бы методику подсчёта оценок не изменили?
Гт Как выбрать подходящее среднее
В предыдущих параграфах мы рассказали о среднем арифметическом, наименьшем
и наибольшем значении, о медиане и об урезанном среднем. Все эти характеристи-
ки по-разному описывают массив данных и используются в разных случаях. Ещё раз
подчеркнём основную мысль.
Ф
Важно! Выбор характеристики массива данных зависит от природы данных, це-
лей исследования и сложившихся традиций.
Чтобы лучше понять, как ведут себя разные характеристики при изменении дан-
ных и как природа данных влияет на выбор подходящего описания, рассмотрим ещё
несколько задач в дополнение к тем, что мы уже решали.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ
73

ПРИМЕР 1. Посмотрим, что произойдёт с разными средними, если каким-либо об-
разом изменить числа в данном наборе. Для иллюстрации лучше выбрать небольшой
набор целых чисел. Возьмём упорядоченный набор из 10 чисел:
0, 1, 1, 3, 5, 5, 6, 7, 12, 128.
Наименьшее значение 0, наибольшее 128. Среднее значение равно 16,8. Медиана
равна 5, а урезанное среднее 4,5 (отбрасываем по 2 числа справа и слева).
Что произойдёт с этими характеристиками, если к каждому числу прибавить одно
и то же число? Например, увеличим все числа на 5. Получится набор:
5, 6, 6, 8, 10, 10, 11, 12, 17, 133.
Ясно, что наименьшее, наибольшее и медиана также увеличились на 5. Они те-
перь равны 5, 133 и 10 соответственно. Интересно, что среднее арифметическое так-
же увеличилось на 5. Чтобы понять, почему так, сложим отдельно числа первого на-
бора и десять добавленных чисел 5.
0 + 1 + 1 + 3 + 5 + 5 + 6 + 7 + 12 + 128 + 10 • 5 - 168 + 50.
Количество чисел в наборе не изменилось. Поэтому, чтобы найти среднее, полу-
ченное выражение нужно разделить на 10:
168 + 50 ,„0 ^
——— - 16,8 + 5.
К старому среднему 16,8 прибавляется число 5.
Легко показать (сделайте это), что урезанное среднее также увеличится на 5.
Что будет, если в наборе поменяются не все числа, а только часть? Проверьте на
этом же примере, что если добавить число 10 к любому одному числу, то:
— среднее арифметическое увеличится на 1;
— медиана может вырасти самое большое на 0,5 и то не всегда.
ПРИМЕР 2. При определении фарватера судоходной реки производится промер
глубин. Затем на основе промеров находят показатель, который называется гаран-
тированная глубина судового хода. Если осадка судна больше, чем гарантированная
глубина, то это судно не может пройти по фарватеру.
Для вычисления гарантированной глубины на участке фарватера к наименьшей
измеренной глубине добавляют минимальный запас воды1 под килем судна. Опреде-
лим гарантированную глубину на участке фарватера реки по данным таблиц 55 и 56.
Таблица 55. Промеры фарватера
Промер
Глубина, м
1
4.2
2
3,8
3
4,5
4
5,3
б
5,8
в
5,1
7
4,8
8
4,3
0 ]
4,1 1
Таблица 56. Минимальный запас воды
Глубина, м
До 1,6
1 1,5—3
1 Более 3
Минимальный запас воды, см
Реки
10
15
20
Каналы |
15
20
30
Минимальное допустимое расстояние от нижней точки корпуса судна до дна.
74 ГЛАВА III.

Наименьшая измеренная глубина в таблице 55 равна 3,8 м. Выбираем из таблицы 56
соответствующее значение минимального запаса воды для рек. Получается, что га-
рантированная глубина равна 3,8 м + 20 см s 4 м.
ПРИМЕР 3. Таблица 57 содержит сведения о площади водной поверхности десяти
крупнейших озёр мира.
Таблица 57. Площади крупнейших озёр
1
2
3
4
5
Озеро
Каспийское море1
Верхнее
Виктория
Гурон
Мичиган
Площадь
376 000
82 100
68 100
60 000
57 800
6
7
8
9
10
Озеро
Аральское море
Танганьика
Байкал
Бол. Медвежье
Ньяса
Площадь
51 100
32 900
31 500
31 326
30 800
Посмотрим на таблицу и без вычислений скажем, что среднее арифметическое
плохо подходит для описания площади типичного крупного озера. Можно использо-
вать медиану или урезанное среднее. Урезанное среднее лучше тем, что оно учитыва-
ет больше данных, чем медиана.
Медиана равна 54 450 км2. Если урезать 10% данных снизу и сверху, то урезан-
ное среднее равно 51 853,25 км2, а если урезать по 20% сверху и снизу, то получает-
ся среднее 50,233 км2.
Какое из этих средних лучше? Отличия небольшие, поэтому можно было бы вы-
брать значение, рассчитанное с наименьшей потерей информации — это урезанное
среднее 51 853,25 км2, полученное урезанием массива на 10% (одно значение) сверху
и снизу.
Упражнения
114 Дан числовой набор. К каждому числу этого набора прибавили число 4.
а) Как изменилось среднее арифметическое этого набора?
б) Как изменилась медиана этого набора?
115 Среднее арифметическое данного набора чисел равно 2,5, а медиана равна 3.
Все числа данного набора умножили на 8. Найдите:
а) среднее арифметическое нового набора;
б) медиану нового набора.
116 Числовой набор состоит из 10 различных чисел. Если наименьшее значение в
этом наборе уменьшить на 8, как изменится:
а) среднее арифметическое;
б) медиана?
1 По классификации водоёмов внутренние моря, такие как Каспийское и Аральское, считаются
бессточными озёрами.
■
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ 75

117 На рисунке схематично показаны четыре числовых набора на координатной
прямой. Охарактеризуйте взаимное расположение среднего арифметического
и медианы: у какого из наборов медиана и среднее приблизительно одинако-
вы, у какого медиана существенно больше, а у какого — меньше, чем сред-
нее арифметическое.
®
©
• — — •
®
®
• —•
•— —
> — — •
Рисунок 12. Четыре числовых набора
118 Таблица 58 содержит сведения о плотности населения стран Южной Европы.
Ознакомьтесь с данными и выберите подходящее среднее для описания этого
массива данных. С помощью калькулятора вычислите это среднее.
Таблица 58. Плотность населения стран Южной Европы
Страна
Черногория
Босния н Герцеговина
Хорватия
Македония
Греция
Испания
Словения
Сербия
Плотность населения,
чел./ км2
46
76
79
83
86
95
98
103
Страна
Албания
Португалия
Андорра
Италия
Сан-Марино
Мальта
Ватикан
Монако
Плотность населения,
чел./ км2
105
117
167
205
350
1315
1818
16500
119В примере 2 описан метод определения гарантированной глубины фарватера.
Пользуясь этим методом, найдите гарантированную глубину участка канала,
если известны результаты промера глубин (табл. 59):
Таблица 59. Промеры глубин фарватера канала
Промер
Глубина, м
1
2,4
2
3,2
3
2,8
4
2,6
5
2,5
в
3,1
7
2,3
76
ГЛАВА III.

120 Таблица 60 содержит данные о контрольном взвешивании партии яиц первой
категории (от 55 до 65 г).
Таблица 60. Контрольное взвешивание
Измерение
Масса яйца, г
1
55,4
2
63,2
3
56,4
4
63,3
5
59,3
6
62,1
7
64,0
8
57,6
9
63,1
10
60,0
Выбрано правило: партия считается неоднородной, если медиана массы от-
личается от среднего арифметического больше, чем на 10% размаха. Можно
ли считать, что в данной партии массы яиц образуют неоднородный массив
данных?
121 Тип климата во многом определяется годовым размахом температуры и её
средним значением. Чем дальше местность от океанов, тем холоднее зима и
жарче лето и тем больше размах температур. Средняя температура связана
с географической широтой местности: чем севернее, тем ниже среднегодовая
температура.
а) На карте (рис. 13) отмечены четыре города: Лиссабон (Португалия), Ашха-
бад (Туркменистан), Берген (Норвегия) и Якутск (Россия).
Рисунок 13
В таблице 61 даны некоторые характеристики температуры в этих четырёх
городах, полученные с помощью многолетних наблюдений. Определите, какой
город какой цифрой обозначен.
Таблица 61. Размах и средняя температура в четырёх городах
Город
1
2
3
4
Минимальная средняя
температура
за январь, °С
1.5
-38,6
3,5
11,9
Максимальная средняя
температура
за июль, °С
14,5
19,5
31,3
24,1
Средняя годовая
температура, °С
7,73
-8,75
17,12
17,66
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. СРЕДНИЕ ЗНАЧЕНИЯ И РАЗМАХ 77

122 Городской муниципалитет принял правило: отопление в домах следует вклю-
чать, если средняя температура в течение трёх предыдущих дней ниже 8 °С.
Всего в городе два района — Прибрежный и Заречный. В Прибрежном рай-
оне правило поняли так: если три дня подряд средняя дневная температура
ниже 8 °С, то на четвёртый день нужно включить отопление. В Заречном рай-
оне правило поняли иначе: если средняя температура за трёхдневный период
ниже 8 °С, то на четвёртый день нужно включить отопление. В таблице 62
показана средняя дневная температура за несколько дней октября. Какого
числа отопление включили в каждом районе?
Таблица 62. Средняя дневная температура в городе
Дата
t, "С
22.10
3
23.10
9
24.10
10
26.10
6
26.10
3
27.10
7
28.10
10
29.10
6
30.10
8
78
ГЛАВА III.

Описательная
статистика.
Квартили
и частоты
В этой главе мы продолжим рассказ об
описательной статистике. Мы познакомим-
ся с квартилями и ещё двумя специальными
средними значениями. Начав использовать
математические обозначения, сумеем прове-
сти математические доказательства некото-
рых фактов.
Чтобы удобнее описывать массивы с повто-
ряющимися значениями, используются час-
тоты отдельных значений. Мы познакомимся
с ними и увидим, как частоты значений мас-
сива связаны со средним арифметическим.
18* Квартили и межквартильный
размах
19* Обозначения в статистике.
Свойства среднего
арифметического
20* Частоты значений
21* Среднее гармоническое
и среднее геометрическое

Квартили и межквартильный размах
В конце параграфа 16 мы сказали, что при урезании числового набора данных ча-
сто отбрасывают по 25% значений с каждой стороны массива. Можно сказать, что
удаляют значения, которые меньше первого квартиля, и те, которые больше третьего
квартиля массива.
Квартили устроены так же, как медиана, только они разбивают массив не попо-
лам, а в отношении 1:3 и 3:1. Определение первого и третьего квартилей массива
можно дать по аналогии с определением медианы.
Определение. Первым квартилем числового набора называется число Кь
если хотя бы 25% значений не больше и хотя бы 75% значений в массиве
не меньше, чем К\.
Третьим квартилем числового набора называется число /С3, если хотя бы 75%
значений не больше и хотя бы 25% значений в массиве не меньше, чем К3.
Термин * второй квартиль» не используется, поскольку второй квартиль — это
просто медиана.
ПРИМЕР 1. Предположим, у нас имеется набор, в котором 17 чисел. Упорядочим
их и получим вариационный ряд, как мы уже не раз делали при поиске медианы.
1122|2]3344457[8]8899
Кг=2 К3=8
Рисунок 14. Первый и третий квартили набора,
в котором 17 чисел
Четверть от числа 17 равна 4,25. Поэтому первый квартиль — это пятое число в
вариационном ряду, то есть число 2. Тогда 5 чисел набора не больше и 12 чисел не
меньше, чем число 2. Третий квартиль — это пятое число с конца, то есть число 8.
Если количество чисел в наборе делится на 4, то нужно поступить так же, как
поступают при поиске медианы — считать, что первый квартиль заключён между со-
ответствующими числами. Например, если в наборе 16 чисел, то первый квартиль
будет между 4-м и 5-м по счёту числами в упорядоченном ряду слева, а третий —
между 4-м и 5-м справа. В примере, который показан на рисунке 16, первый квар-
тиль заключён между числами 3 и 4, а третий — между числами 7 и 8. Например,
можно взять Кх — 3,25 и К3 = 7,75.
1 1 2 з| 4 4 4 5 6 6 6 т| 8 9 10 10
Кх= 3,25 К3= 7,75
Рисунок 15. Первый и третий квартили набора,
в котором 16 чисел
Комментарий. Квартили, так же как медиана, часто определяются неоднознач-
но, но на практике тонкости определения не играют роли. Когда данных много,
результат мало зависит от того, где именно выбирать квартиль — ближе к ле-
вому или к правому значению.
80 ГЛАВА IV*.
щ>

Таблица 63. Данные
для построения диаграммы 19
Существует простой и удобный способ изображе-
ния типичных значений массива с помощью ящич-
ковой диаграммы1. Отдельные значения не изобра-
жают, вместо этого рисуют прямоугольник (ящик)
от первого до третьего квартиля. Таким образом,
длина прямоугольника равна межквартильному
размаху, то есть К3 - Кх.
Медиана изображается перегородкой внутри пря-
моугольника, а среднее арифметическое — точкой.
Для иллюстрации построим ящичковую диа-
грамму по данным о населении регионов России
(табл. 63). Внутрь прямоугольника попадает при-
мерно половина всех значений между первым и третьим квартилями, но это самые
типичные значения. Обратите внимание на большое расстояние между медианой и
средним арифметическим, которое лишний раз говорит о том, что среднее арифме-
тическое не очень хорошо описывает численность населения регионов нашей страны.
Диаграмма 19. Население регионов России
Среднее
Среднее
Первый квартиль
Медиана
Третий квартиль
Межкв. размах
1 753 027
715 373
1 160 721
2 375 242
1 641 869
1
500000
1
1000000
Первый
\
\
\
\
i • 1
1500000 2000000
\ Третий
I
2500
квартиль
Медиана
квартиль
Вопросы
1 Что такое квартиль?
2 Почему не используют название «второй квартиль»?
3 Что такое межквартильный размах?
4 Как вы думаете, почему при построении ящичковой диаграммы на ней не отме-
чают наименьшее и наибольшее значения?
В редакторах электронных таблиц
квартили находят с помощью функции
КВАРТИЛИ)
Последний аргумент в скобках — но-
мер квартиля.
| » /х \ =КВАРТИЛЬ(С1:Е6;3) ]
с
1
2
3
4
5
6
D
7
8
9
10
11
12
Е
F
Первый
квартиль
Третий
квартиль
G
3,75
9,251
—
Рисунок 16
1 Ящичковые диаграммы были предложены в 1970-х г. американским статистиком Джоном Тьюки.
Английское название такой диаграммы box plot. Дословно получается «ящичковая диаграмма».
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. КВАРТИЛИ И ЧАСТОТЫ
81

0
Упражнения
123 Найдите первый и третий квартили числового набора.
а) 0, 4, 3, 2, 4, 5, 3, 2, 1, 0, 12, 4, 6, 4, 1;
б) 4, 3, 2, 1, 2, 0, 4, 2, 7, 8, 9, 2.
124 Первый квартиль числового набора равен 2, а третий квартиль равен 8. При-
ведите пример такого набора, в котором:
а) 9 чисел; б) 12 чисел.
125 Рассмотрите ящичковую диаграмму. Найдите приближённо первый и третий
квартили, медиану, среднее арифметическое и межквартильный размах дан-
ных.
а)
10
Диаграмма 20.
20
30
40
"~1
50
б)
~~Г~
0,2
126 Рассмотрите таблицу 49, содержащую сведения о производстве зерновых
культур в России. Постройте в тетради ящичковую диаграмму для данных:
а) о производстве зерновых культур в России в период с 2011 по 2018 г.
б) об урожайности зерновых культур с гектара в период с 2011 по 2018 г.
При построении диаграммы большая точность не нужна. Больше внимания
обращайте на аккуратность построения, на взаимное расположение отметок
медианы и среднего арифметического.
Кэч Обозначения в статистике.
Свойства среднего арифметического
Обозначения
Наборы данных и отдельные значения в наборах часто приходится обозначать бук-
вами. Использовать отдельно букву для каждого числа невозможно. Поэтому для чи-
сел одного набора используют одну и ту же букву с индексами — номерами. Можно
рассмотреть набор X, в котором пять чисел xl9 jc2, лг3, хА% jc6, или набор У, состоящий
из чисел ух% у2у узз У4> Уы Уь и т« п« Чтобы подчеркнуть, что числа образуют набор,
иногда записывают его значения в фигурных скобках.
ПРИМЕР. Набор чисел 1, 8, 3, 0, -3 можно обозначить X (или любой другой бук-
вой) и записать: X в {1, 8, 3, 0, -3}. В этом наборе хх — 1, х2 = 8 и т. д.
Если чисел в наборе много, то вместо слов ♦и так далее до» используют многото-
чие. Например, набор X, в котором 100 чисел, записывают так:
X в {#1, дг2» *з» •••» *tooi»
82
ГЛАВА IV*.

Среднее арифметическое чисел набора принято обозначать х. Например, среднее
арифметическое набора, в котором пять чисел х1э х2, х3, х4» хы запишется так:
_ Х\ + Х2 + Х3 + Х4 + *5
* б '
а среднее арифметическое набора X, состоящего из п чисел, можно записать, исполь-
зуя многоточие:
_ Хл + Х2 + ••• + *л
х * .
л
Для наименьшего значения набора обычно используется обозначение min, а для
наибольшего — max от латинских слов minimum и maximum. Таким образом, можно
записать:
min {2, 4, 1, 5} * 1, max {2, 4, 1, 5} * 5.
Если набор {2, 4, 1, 5} обозначить буквой X, то можно записать короче:
minX — 1, maxX = 5.
Обозначения не только укорачивают запись, но и делают её ясной, однозначной
и строгой.
Для некоторых описательных характеристик нет общепринятых обозначений. На-
пример, нет общепринятого обозначения для медианы и для квартилей1.
Свойства среднего арифметического
Буквенные обозначения чисел и для среднего арифметического позволяют запи-
сать и доказать свойства среднего арифметического.
\\у Свойство 1. Если каждое число набора увеличить (уменьшить) на одно и то же
число а, то среднее арифметическое набора увеличится (уменьшится) на это
же число а.
Аналогичное свойство верно для умножения.
Ч1У Свойство 2. Если каждое число набора умножить на одно и то же число bt то
среднее арифметическое набора также умножится на число Ь.
Покажем, что эти свойства верны, на примере набора, в котором четыре числа.
Пусть дан числовой набор X = {xlt х2, JC3, xA) и пусть среднее значение равно х.
Прибавим к каждому числу набора число а. Получится набор
{хх + а, х2 -I- а, jc3 + а, х4 + а)-
Нужно показать, что среднее арифметическое нового набора равно х + а. Найдём
среднее арифметическое:
(xi 4- а) + (х2 + а) -I- (х3 + а) + (х4 + а) _ хх 4- х2 + х3 -I- х4 + 4а
4 4 #
„ - .. - хх + х2 + х3 + х4 4а
Разобьем дробь на два слагаемых: -± = н .
4 4
Первое слагаемое равно х — среднему арифметическому первоначального набора X.
Второе слагаемое равно а. Получается, что среднее арифметическое нового набора
равно х + а.
В этой книжке мы обозначаем квартили буквой К, но это не общепринято.
■
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. КВАРТИЛИ И ЧАСТОТЫ 83

Покажем теперь, что верно свойство 2. Умножим каждое число набора X на чис-
ло Ь. Нужно показать, что среднее арифметическое нового набора bxu Ьх2У bx3, ЬхА
равно Ьх.
Вычислим среднее арифметическое нового набора:
Ьхг + ЬХ2 + ЬХ3 + ЬХА Ь(хх + X2 + Х3 + Х4) Jt! +Х2 +ДГз + *4 ._
=■ — О ' : = ОХ.
ф
Вопросы
1 Как называются номера в обозначениях jc5, y2 и т. п.?
2 Как обозначается среднее арифметическое, наименьшее и наибольшее значения?
3 Сформулируйте свойство 1 среднего арифметического.
4 Сформулируйте свойство 2 среднего арифметического.
0
Упражнения
127 Дан числовой набор X, состоящий из чисел 17, 3, 6, 21, 15.
а) Чему равно х2 в этом наборе?
б) Чему равно х5?
128 Среднее арифметическое числового набора X равно 5. Найдите среднее ариф-
метическое числового набора, который получится, если:
а) ко всем числам набора X прибавить число 4;
б) из всех чисел набора X вычесть число 12;
в) ко всем числам набора X прибавить число 8;
г) из всех чисел набора X вычесть число 3.
129 Среднее арифметическое числового набора У равно 8. Найдите среднее ариф-
метическое числового набора, который получится, если все числа набора У:
а) умножить на число 2; в) умножить на -3;
б) разделить на 4; г) разделить на -3.
130 Сначала ко всем числам числового набора X прибавили число 8, а затем все
числа нового набора умножили на 3. Найдите среднее арифметическое полу-
чившегося набора, если среднее арифметическое набора X равно:
а) 2; б) -4; в) 5,2; г) -9,1.
131 Сначала все числа числового набора X умножили на 3, а затем к каждому
числу полученного набора прибавили 8. Найдите среднее арифметическое по-
лучившегося набора, если среднее арифметическое набора X равно:
а) 2; б) -4; в) 5,2; г) -9,1.
132 Средняя цена нефти на протяжении месяца составляла 65 долларов за один
баррель1. Найдите среднюю цену одного литра нефти за этот период, считая,
что в одном барреле 159 л.
133 Средняя зарплата на предприятии составляла 56 000 р. С нового года зарпла-
ту всем сотрудникам проиндексировали (повысили) на 4%. Других изменений
не было. Найдите среднюю зарплату после индексации.
134 В наборе п чисел. На сколько увеличится среднее арифметическое этого на-
бора, если одно число в этом наборе увеличить на 1?
1 Баррель (от англ. Barrel — бочка) — мера объёма, равная 158,9873 л.
■
84 ГЛАВА IV*.

135 В наборе было 100 чисел, а сумма всех чисел равнялась 134. К набору до-
бавили ещё одно число, при этом среднее арифметическое не изменилось. Ка-
кое число добавили?
136 Каждое число набора увеличили на одно и то же число а. Как изменились
наименьшее и наибольшее значения набора?
137 Наименьшее значение набора равно т, наибольшее значение равно М. Каж-
дое число набора умножили на одно и то же число Ь. Найдите наименьшее
и наибольшее значения получившегося набора, если: а) Ь > 0; б) Ь < 0.
138 В наборе было п чисел, их среднее арифметическое равнялось х. К набору
добавили число а. Запишите выражение для среднего арифметического полу-
чившегося набора.
139 Студент в течение семестра выполнил несколько контрольных работ. Когда он
узнал результаты всех работ, кроме последней, он заметил, что если за по-
следнюю контрольную работу он получит 90 баллов, то средний балл за все
работы будет равен 84, а если за последнюю работу он получит 72 балла, то
средний балл за все работы составит 81. Сколько всего контрольных работ
должен выполнить студент?
140 В классе прошёл ежегодный тест по английскому языку. В обеих группах
А и Б средний балл понизился по сравнению с прошлым годом (табл. 64).
Таблица 64. Отметки за тест по английскому языку
Группа Б
1
1 2
3
4
5
6
7
8
9
10
Аверьянов
Воронова
Данилов
Злыднева
Ларионов
Мельникова
Озерова
Рассудова
Уварова
Яхонтов
Средний балл
Средний балл за прошлый год
36
49
31
35
48
32
35
47
35
40
38,8
39,2
Группа А
1
2
3
4
5
6
7
8
9
10
Среда
Среда
Антонов
Белоусова
Григорьев
Дёмин
Исаев
Калинина
Морских
Попов
Сидоров
Филипповская
гай балл
вий балл за прошлый год
31 1
46 1
52 1
51 1
32 1
41 1
59 1
32
44
54
1 44,2
44,4
Учительница хочет, чтобы в обеих группах средний балл оказался выше про-
шлогоднего. Баллы менять нельзя, но можно записать учеников одной груп-
пы в другую. Можно ли таким образом добиться того, что средний балл
в каждой группе окажется выше, чем в прошлом году? Если нет, объясните
почему. Если да, покажите как.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. КВАРТИЛИ И ЧАСТОТЫ 85

20*1 Частоты значений
ПРИМЕР 1. Рассмотрим числовой набор
1, 3, 1, 2, 1, 5, 3, 2, 1, 1.
В этом наборе 10 чисел, но различных чисел только четыре: 1, 2, 3 и 5. Единица
встречается пять раз. Можно сказать, что частота числа 1 в этом наборе равна —,
то есть 0,5. Аналогично частота числа 2 и частота числа 3 равны 0,2, а частота числа
5 равна 0,1. Заметим, что сумма частот равна 1:
0,5 + 0,2 + 0,2 + 0,1 = 1.
Определение. Пусть в наборе всего N значений, и значения, равные а, ветре-
N
чаются Na раз. Частотой значения1 а называется отношение -~.
N
Частоты значений можно подсчитывать не только в числовых наборах, но и там,
где значения не являются числами.
Чтобы в электронной таблице подсчитать, сколь-
ко раз в наборе встречается определённое зна-
чение, используйте функцию
СЧЁТЕСЛИ()
На рисунке подсчитано, что в данном наборе
число 1 встречается 5 раз.
• /х =СЧЕТЕСЛИ(В 1. D5:1)
В
0
1
1
1
2.
С
1
2
2
3
4
D
3
2
1
2
4
Е
5
1
Таблица 65. Частоты значений
Рисунок 17
ПРИМЕР 2. Обратимся к таблице 16 (с. 24)
с результатами подсчёта домашних животных
у школьников одного класса. Различными зна-
чениями в нашем наборе являются виды живот-
ных, а также значение «Никого». Найдём их ча-
стоты. Для этого подсчитаем общее количество
значений:
9+ 11 + 7 + 3 + 2 + 1 = 33.
Значение «Собака» встречается 9 раз. Поэтому
9
частота этого значения равна — « 0,273. В ста-
Зо
тистике принято обыкновенные дроби превращать
в десятичные с округлением при необходимости.
Десятичные дроби удобнее писать в строку, с ни-
ми легче выполнять действия и их легче сравнивать, чем обыкновенные дроби.
Аналогично найдём частоты прочих значений и занесём их в таблицу 65.
Обратите внимание на последнюю строку. Сумма частот снова равна единице.
Животное
Собака
Кошка
Никого
Рыбки
Птицы
Черепаха
Сумма
Всего
9
11
7
3
2
1
33
Частота
0,273
0,333
0,212
0,091
0,061
0,030
1
1 Частота бывает не только у значения в наборе. Позже мы познакомимся с частотой события.
86
ГЛАВА IV*.

ф
Свойство частот. В любом наборе сумма частот значений равна единице.
Докажем это свойство для набора, в котором четыре различных значения а, Ь, с и d,
но каждое может встречаться несколько раз. Предположим, значение а встречается
Na раз, а значения Ь, с и d встречаются Nb, Nc и Nd раз соответственно.
Тогда всего в наборе N = Na + Nb + Nc + Nd значений. Частота значения а рав-
на -rf. Частота значения Ь равна — и т. д. Найдём сумму частот:
N
N N N
N
N
N
N 1'
Аналогичное свойство доказывается для набора, в котором любое количество зна-
чений. Пользуясь тем, что сумма частот всегда равна единице, удобно делать проме-
жуточную проверку в вычислениях.
ПРИМЕР 3. Рассмотрим числовой набор, в котором есть одинаковые значения.
Например, отметки школьника по математике, полученные в течение четверти:
3, 4, 3, 5, 4, 3, 4, 4, 4, 2, 3, 5, 3, 3, 4, 5, 2, 4, 4, 4.
Всего 20 отметок. Чтобы вывести чет- Таблица 66. Частоты отметок
вертную отметку, учитель находит среднее
арифметическое: делит сумму всех 20 чи-
сел на 20. Можно поступить иначе. За-
пишем в таблицу 66 различные значения
и их частоты.
Чтобы убедиться, что мы не ошиблись,
проверим, равна ли сумма найденных частот единице: 0,1 4- 0,3 -I- 0,45 + 0,15 — 1.
Теперь найдём среднее арифметическое: умножим значения на их частоты и сло-
жим произведения:
2 • 0,1 + 3 • 0,3 + 4 • 0,45 + 5 • 0,15 - 0,2 + 0,9 + 1,8 + 0,75 - 3,65.
Проверьте, что обычный способ даёт то же самое значение среднего арифметического.
Значение
Частота
2
0,1
3
0,3
4
0,45
5
0,15
I ТЕОРЕМА. Пусть в наборе N чисел, но среди них только k различных чисел хи
хъ ..., хк. Пусть число хг встречается Nx раз, число х2 встречается N2 раз, и т. д.:
число хк встречается ровно Nk раз. Тогда среднее арифметическое набора равно
+ **• N-
Теорема утверждает, что найти среднее арифметическое можно следующим спосо-
бом: умножить каждое из различных значений на его частоту, а затем полученные
произведения сложить. Для доказательства составим сумму из произведений различ-
ных чисел и их частот:
N± N± N^
Xi • Nx + x2 ; N2 + *з; N3 + ••• + xjk ' Nk _ -
N "*'
Получилось среднее арифметическое. Теорема доказана.
Ф
Вопросы
1 Чему равны частоты значений в наборе, где 10 различных значений, но каждое
встречается ровно один раз?
2 Сформулируйте определение частоты значения.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. КВАРТИЛИ И ЧАСТОТЫ
87

3 Сформулируйте свойство частот.
4 Как найти среднее значение числового набора, зная различные значения и их частоты?
В редакторах электронных таблиц мож-
но быстро вычислить сумму произве-
дений значений и их частот. Для этого
есть функция
СУММПРОИЗВ()
На рисунке показано решение задачи
из примера 5.
Л
т
С
Значение
Частота
Л
[
=CYMMnPOM3B(D2-G2 D3 G3)
Э
2
0.1
Е
3
0.3
F
4
0,45
Среднее
G
5
0.15
З.бб]
■"
J
s00-^ Рисунок 18
\Sj Упражнения
141 Дан числовой набор 5, 4, 8, 1, 1, 3, 4, 5, 8, 1. Найдите частоту:
а) значения 1; б) значения 4.
142 Дана последовательность букв: ФАВЫДОВЛЫДЯЮФЛЧЛИОЫДСОЫЖФ.
Найдите в этой последовательности частоту:
а) буквы Д; б) буквы Ф; в) буквы Ы; г) буквы С.
143 В числовом наборе 5 значений. Частоты четырёх значений известны: 0,35,
0,2, 0,1 и 0,05. Найдите частоту пятого значения.
144 В таблице 20 (с. 26—27) даны четвертные отметки учащихся класса.
а) Найдите частоты различных четвертных отметок по математике. Составьте
таблицу значений и частот.
б) Вычислите среднюю отметку за четверть по математике.
145 Пусть число т является медианой числового набора. Докажите, что:
а) сумма частот всех чисел набора, которые не больше т, не меньше 0,5;
б) сумма частот всех чисел набора, которые не меньше т, не больше 0,5.
146 Частоту букв в русском языке можно приблизительно оценить с помощью худо-
жественных текстов. Прочитайте три отрывка из произведений А.С. Пушкина.
Первый отрывок (*Дубровский*)
По этим приметам немудрено будет вам отыскать Дубровского. Да кто же
не среднего роста, у кого не русые волосы, не прямой нос, да не карие глаза!
Бьюсь об заклад, три часа будешь говорить с самим Дубровским, а не догадаешь-
ся, с кем бог тебя свёл. Нечего сказать, умные головушки приказные!
Второй отрывок (* Выстрел*)
Рассеянные жители столицы не имеют понятия о многих впечатлениях, столь
известных жителям деревень или городков, например об ожидании почтового дня:
во вторник и пятницу полковая наша канцелярия бывала полна офицерами: кто
ждал денег, кто письма, кто газет.
Третий отрывок (* Капитанская дочка*)
Вскоре все заговорили о Пугачёве. Толки были различны. Комендант послал
урядника с поручением разведать хорошенько обо всём по соседним селениям
и крепостям. Урядник возвратился через два дня и объявил, что в степи вёрст
за шестьдесят от крепости видел он множество огней и слышал от башкирцев,
что идёт неведомая сила.
88 ГЛАВА IV*.

а) Посчитайте буквы «а», *о» и «и» в трёх этих отрывках и составьте таблицу частот.
б) Посчитайте буквы *н» и «т» и составьте таблицу частот. Можно ли по полученным
данным судить, какая из букв: «н» или «т» — используется чаще в русском языке?
в) Как вы думаете, почему для оценки частот букв в языке не следует использо-
вать технические или специальные тексты, например учебник по теории вероятно-
стей или инструкцию к телевизору?
D
Историческая справка. На протяжении нескольких веков для печати книг, журна-
лов и газет использовались типографские кассы с набором литер — букв, сделан-
ных из свинца. Наборщик на специальной доске набирал текст каждой отдельной
страницы. Затем набор покрывали типографской краской и делали необходимое ко-
личество оттисков. Поскольку одни буквы встречаются чаще, а другие реже, количе-
ство различных букв в кассе было разным. Таблица частот букв показывает, в каких
пропорциях должны содержаться разные буквы в типографской кассе (табл. 67).
Таблица 67. Частоты букв русского языка
Буква
А
Б
В
Г
д
Е и Ё
Ж
3
и
й
к
Частота
0,075
0,017
0,046
0,016
0,030
0,087
0.009
0,018
0,075
0,012
0,034
Буква
Л
М
н
о
п
р
с
т
У
ф
X
Частота
0,042
0,031
0,065
0,110
0,028
0,048
0,055
0,065
0,025
0,002
0,011
Буква
ц
Ч
Ш
щ
ъ
ы
ь
э
ю
я
Частота
0,005
0,015 1
0,007 1
0,004
0,001 1
0,019
0,016
0,003
0,007
0,022
Не менее важна информация о частотах букв для лингвистов и криптографов1.
Частоты символов лежат в основе некоторых методов расшифровки текстов на
неизвестных языках. Частоты букв, знаков препинания и другие статистические
характеристики текста используют для выяснения авторства, когда точно неиз-
вестно, кто написал произведение.
Статистическое исследование. Пользуясь редактором текстов на компьютере,
можно быстро подсчитать частоту любой буквы, любого сочетания букв и любо-
го слова.
Найдите частоты букв русского алфавита в нескольких больших отрывках (несколько
тысяч слов) ваших любимых художественных произведений. Можно ли считать, что
полученные вами частоты незначительно отличаются от данных таблицы 67?
Подсчитайте частоты слов «что», «где», «откуда», «потому» (нужно количество та-
ких слов разделить на общее количество слов в тексте). Существенно ли отли-
чаются частоты этих слов в произведениях разных авторов?
Криптограф — специалист по шифрованию, расшифровке и защите информации.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. КВАРТИЛИ И ЧАСТОТЫ
89

[2iy Среднее гармоническое
и среднее геометрическое
Среднее гармоническое
Мы говорили, что выбор среднего связан с природой данных. Иногда лучше взять
среднее арифметическое, иногда — медиану. В некоторых случаях важнее знать наи-
большее или наименьшее значение. В статистике встречаются задачи, где требуются
другие показатели. Рассмотрим пример, в котором нужно найти среднюю скорость.
ПРИМЕР 1. Путь разбит на три одинаковых по длине участка. На первом участ-
ке скорость автомобиля составляет 45 км/ч, на втором — 90 км/ч, а на третьем —
60 км/ч. Какова средняя скорость автомобиля на всём пути?
Сначала нужно понять, что такое средняя скорость. Разумно считать, что это та-
кая скорость, двигаясь с которой постоянно, автомобиль пройдёт весь путь за то же
время. Значит, нужно найти время, которое автомобиль был в пути. Но мы не знаем
протяжённость пути. Будем считать, что каждый участок имеет протяжённость 8 км.
о о
Первый участок автомобиль прошёл за — ч, второй участок — за — ч и тре-
45 90
тий — за — ч. На весь путь автомобиль потратил
'" 45*90 + 60 " 445 +90* 6oJ Ч'
Следовательно, средняя скорость автомобиля равна
38 38 3
VCD = — = —; = KM / Ч.
— — — -L + -L + -L
8(45 + 90 + 6о] 45 90 60
уср = 3:—7^7Г- = 3 20 = 60 км/ч.
Вычислим значение этого выражения:
4 + 2 + 3
180
Средняя скорость, которую мы нашли, равна среднему гармоническому данных
скоростей, и она меньше, чем среднее арифметическое, которое в данном случае рав-
45 + 60 + 90 ^с
но = 65 км/ч.
о
Запишем формулу среднего гармонического в общем виде.
Определение. Среднее гармоническое набора положительных чисел
п
Х\% #2i •••• хп равно
J. + JL+...+J,
Х\ %2 Хп
Общепринятого обозначения для среднего гармонического нет. Среднее гармониче-
ское появляется не только как средняя скорость движения на равных участках пути.
Оно возникает в экономических задачах о средних затратах на производство.
ПРИМЕР 2. Предположим, что пять заводов выпускают одинаковые лампочки для
автомобильных фар. В таблице 68 отражены затраты на производство одной единицы
продукции (лампочки) на каждом заводе.
90 ГЛАВА IV*.

Таблица 68. Затраты на единицу продукции
Завод
Затраты на единицу продукции, р.
1
3,5
2
2,8
3
2,9
4
2,3
5
3,4
При одинаковом качестве продукции в условиях конкуренции цена товара во мно-
гом определяется средними затратами на единицу продукции. Что такое средние затра-
ты в данном случае? Предположим, что все пять заводов объединились, каждый вло-
жил в производство Q рублей, и все вместе они изготовили А лампочек, затратив всего
5Q
5Q рублей. Значит, средние затраты на производство одной лампочки равны — рублей.
j\.
Q Q
Первый завод, затратив Q рублей, выпускает — лампочек, второй — — лампо-
чек и т. д. Всего лампочек А штук. Значит, ' '
3,5 2,8 2,9 2,3 3,4
Получается, что средние затраты равны
5Q 5Q
А
Q Q Q Q Q
3,5 2,8 2,9 2,3 3,4
В знаменателе вынесем Q за скобки и сократим дробь на Q
5Q 5
0\— — — — —
^3,5* 2,8* 2,9* 2,3* 3,4
Получилось среднее гармоническое.
11111
3,5 + 2,8 + 2,9 + 2,3 + 3,4
* 2,91 (р.)
Ф
Средняя скорость движения на всём пути равна среднему гармоническому ско-
ростей на каждом из равных по протяжённости участков.
В экономике средние затраты на производство единицы продукции равны сред-
нему гармоническому затрат каждого отдельного производителя.
Среднее геометрическое
Ещё один специальный вид среднего — среднее геометрическое — применяется,
когда нужно усреднить относительное изменение какой-то величины, выраженное
числовым коэффициентом или в процентах.
ПРИМЕР 3. При страховании автомобиля страховая компания вычисляет страхо-
вую стоимость1 автомобиля. Если машина новая, то страховая стоимость совпадает
с ценой машины. Чем старше машина, тем ниже страховая стоимость.
Страховые компании придерживаются разных правил вычисления страховой сто-
имости. Например, правило может быть такое: за первый год эксплуатации маши-
на теряет 15% стоимости, каждый следующий год — ещё 10%, начиная с 6-летнего
возраста машина ежегодно теряет 7,5% стоимости, а автомобили возрастом 10 лет
и старше теряют по 5 % ежегодно (табл. 69). Какова средняя ежегодная потеря стои-
мости в процентах за 10 лет?
1 Стоимость автомобиля, исходя из которой компания рассчитывает страховой взнос и страхо-
вые выплаты в случае ДТП или угона.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. КВАРТИЛИ И ЧАСТОТЫ
91

Таблица 69. Коэффициенты ежегодного снижения страховой стоимости
Возраст автомобиля, лет
Процент уценки
Коэффициент уценки
1
15%
0,85
2—6
10%
0,9
6—9
7,5 %
0,925
10 и старше
5%
0,95
Сначала посмотрим, как меняется стоимость автомобиля. Если новый автомобиль
стоил, скажем, х р., то через год его страховая стоимость стала х • 0,85 р., ещё че-
рез год — х • 0,85 • 0,9 р. и т. д.: каждый год предыдущая цена умножается на со-
ответствующий коэффициент. Через 10 лет автомобиль будет стоить
х • 0,85 • 0,9 • 0,9 • 0,9 • 0,9 • 0,925 • 0,925 • 0,925 • 0,925 • 0,95 * х • 0,39 (р.)
Начальная цена умножена последователь-
но на 10 коэффициентов, и в итоге через
10 лет уценка автомобиля составила при-
мерно 61%. Что же такое средний коэффи-
циент уценки? Это такой неизменный ко-
эффициент fe, что если бы каждый год пре-
дыдущая стоимость умножалась на А, то
результат был бы таким же. Иными слова-
ми, х • к10 - х • 0,39.
Разделим обе части равенства на х и по-
лучим: Л10 - 0,39.
Значит, к — это такое положительное чис-
ло, что его 10-я степень равна 0,39, то есть
произведению 10 данных чисел. Такое чис-
ло называется корнем 10-й степени из чис-
ла 0,39. Подробнее свойства корней будут
изучаться в курсе алгебры. Найти корень
10-й степени можно с помощью калькулято-
1
DEG
МС
X*
у/
t
Я
п!
±
(
0,9101363514
HYP
MA
F-t
М<
О
10»
а
7
4
1
)
М
Sin
k>9
С
8
5
2
0
MS
COS
ЬФ
<я
9
6
3
1
м-
tan
Mod
-r
X
-
+
=
Рисунок 19. Вычисление корня
10-й степени из 0,39
pa. Нужно возвести число 0,39 в степень — (рис. 19).
Получается, что к « 0,910, то есть средняя ежегодная уценка за 10 лет равна при-
мерно 100% - 91% - 9%.
Полученное число к является средним геометрическим данных коэффициентов
уценки. Можно дать общее определение.
Определение. Среднее геометрическое набора положительных чисел хъ х2. ..,
хп равно корню степени п из произведения данных чисел: ^хххгх^»..^хп.
В банковском деле со средним геометрическим приходится иметь дело всякий раз,
когда меняется годовая процентная ставка по вкладу или кредиту.
(г) Вопросы
1 Сформулируйте определение среднего гармонического.
2 Сформулируйте определение среднего геометрического.
3 Приведите пример данных, для усреднения которых применяется среднее гар-
моническое; среднее геометрическое.
92
ГЛАВА IV*.

Если в электронной таблице нужно
вычислить среднее гармоническое или
среднее геометрическое, используйте
функции
СРГАРМ( ) и СРГЕОМ( )
1 • /х | =СРГАРМ(01 D5)
D
2
3
1
5
1 4
*г
F
Среднее гармоническое
2,189781]
G
Среднее геометрическое |
2,605171
0
147
148
149
150
Рисунок 20
Упражнения
Найдите среднее гармоническое четырёх чисел:
а) 1; 2; 4; 6; б) 0,1; 0,25; 0,4; 0,5.
Найдите среднее геометрическое четырёх чисел:
а) 1; 2; 4; 2; б) 3; 9; 1,5; 2.
С помощью калькулятора найдите среднее гармоническое и среднее геометри-
ческое числового набора:
а) 1; 5; 5; 2; 3; 7; 4; 3; б) 3,9; 0,4; 1,2; 3,4; 5,3; 1,6; 4,3.
Даны два различных положительных числа а и Ь. Докажите, что:
а) среднее геометрическое этих чисел больше их среднего гармонического;
б) среднее арифметическое этих чисел больше их среднего геометрического.
Указание. Для решения пункта а) нужно показать, что разность
yfab -
1 1
- + -
а Ь
положительна. Поскольку свойства квадратного корня1 ещё не изучались,
вместо этой разности рассмотрим разность
аЬ-\
1 1
-+ -.
а Ь
Преобразуйте это выражение к виду
ab(a - bf
Поскольку числа а и Ь по ус-
W
(а + Ъ)2
ловию различны, это выражение положительно. Пункт б) решается анало-
гично и даже проще.
Комментарий. Можно показать, что среднее гармоническое меньше среднего
геометрического, а среднее геометрическое меньше среднего арифметического
для любого набора положительных чисел, сколько бы их ни было (если не все
числа в наборе одинаковы). Иногда эти свойства входят в противоречие с инту-
ицией. Рассмотрим две задачи, на которых традиционно «попадаются» не толь-
ко школьники, но и взрослые.
1. Два автомобиля одновременно выехали из города А в город Б. Первый ав-
томобиль весь путь двигался со скоростью 50 км/ч, а второй первую поло-
вину пути ехал со скоростью 40 км/ч. С какой скоростью второй автомобиль
Корень второй степени называют квадратным корнем. В обозначении квадратного корня двойку
не пишут.
ОПИСАТЕЛЬНАЯ СТАТИСТИКА. КВАРТИЛИ И ЧАСТОТЫ
93

должен пройти вторую половину пути, чтобы приехать в город Б одновремен-
но с первым?
Казалось бы, ответ очевиден: полпути второй ехал медленнее первого на
10 км/ч. Значит, вторую половину пути он должен ехать быстрее на 10 км/ч.
Но ведь средняя скорость равна среднему гармоническому скоростей, поэто-
му она меньше чем среднее арифметическое. Ответ 10 км/ч неверный. Обо-
значим х км/ч неизвестную скорость второго автомобиля на второй половине
пути. Нужно решить уравнение
2 2
— г- = 50, откуда х = 66- км/ч.
— + i 3
40 х
Не зря говорится: хуже нет, чем ждать, да догонять.
Похожая ситуация в известной задаче про скидки и наценки.
2. Предположим, владелец магазина решил сделать сезонную скидку на то-
вар на 20%. На сколько процентов затем нужно повысить цену, чтобы она
стала прежней?
Опять хочется сразу сказать, что на 20%. Однако это не так. Ведь среднее
геометрическое меньше, чем среднее арифметическое. Убедитесь, что цену
придётся поднять на 25%.
151 На производство единицы продукции каждый из шести рабочих затрачивает
некоторое время (табл. 70). Найдите среднее время, затраченное на производ-
ство единицы продукции.
Таблица 70. Затраты времени на единицу продукции
Рабочий
Время на единицу продукции, ч
1
2,5
2
3,4
3
2,2
4
3,1
5
3,0
6
2,9
152 В таблице 71 показаны цены на некоторую модель смартфона, менявшиеся
ежемесячно. В июле вышла новая модель смартфона, что вызвало резкое па-
дение цены на предыдущую модель. Найдите средний ежемесячный коэффи-
циент уценки за 11 месяцев года (с февраля по декабрь).
Таблица 71. Цены на смартфон
Месяц
Цена,
тыс. р.
Янв.
9,0
Фев.
9,0
Map.
9,0
Апр.
8,5
Май
8,5
Июнь
8,5
Июль
6,4
Авг.
6,4
Сен.
6,2
Окт.
6,2
Нояб.
6,0
Дек.
6,0
153 Банк предлагает срочный вклад на 5 лет на следующих условиях: если вла-
делец не производит никаких операций (не забирает и не кладёт деньги), то
в конце каждого года сумма вклада увеличивается на некоторое количество
процентов (годовая процентная ставка). После первого года ставка равна
2 %, после второго — 3 %, а после третьего и каждого последующего года —
5 %.
а) Найдите среднюю ставку за 5 лет в процентах (округлите до сотых).
б) Найдите сумму вклада по истечении 5 лет, если сначала владелец поло-
жил на счёт 20 000 р.
94 ГЛАВА IV*.

Случайная
изменчивость
Неизменные величины в жизни встречаются
крайне редко. Даже те величины, которые в
физике называют постоянными обычно под-
вержены изменчивости. Иногда мы можем
указать причины и даже законы изменчиво-
сти. Но помимо закономерной изменчивости
почти всегда присутствует разнонаправлен-
ная случайная изменчивость, причины кото-
рой известны частично, а порой неизвестны
вовсе.
В этой главе мы обсудим несколько важных
примеров изменчивости, которую приходит-
ся учитывать в повседневной жизни. Напри-
мер, мы будем говорить о погрешностях и о
точности измерений.
Кроме того, мы увидим, как разные виды
изменчивости отражаются на диаграммах.
22 Примеры случайной
изменчивости
23 Точность и погрешность
измерений
24 Тенденции и случайные
отклонения
25 Группировка данных
и гистограммы
26 Рост человека
27 Статистическая устойчивость
и оценки с помощью выборки

Очень редко встречаются неизменные величины. Большинство величин, с которы-
ми мы имеем дело в жизни, подвержены случайной изменчивости. Иногда мы мо-
жем указать причины изменений. Иногда причины изменчивости известны частично,
а порой неизвестны вовсе.
Примеры случайной изменчивости
Колебания напряжения в электрической сети
Таблица 72. Измерения В таблице 72 даны результаты 25 измерений
напряжения в бытовой сети напряжения в бытовой электросети. Все измере-
(в вольтах) ния сделаны днём, в случайно выбранные мо-
менты.
В России номинальное1 напряжение в бы-
товых сетях 220 В (вольт). На самом деле на-
пряжение редко равно в точности 220 В. Обыч-
но напряжение несколько выше или ниже этого
значения. Напряжение понижается, если в ва-
шей квартире или у соседей включаются элек-
троприборы. Моменты включения и выключения
электрических приборов случайные и приводят
к случайной изменчивости напряжения. Кроме того, производитель электроэнергии
не может обеспечить напряжение, в точности равное 220 В. Даже если выключить
все электроприборы в городе, напряжение в розетках не будет постоянным.
Электрические приборы в России рассчитаны на колебания напряжения в опреде-
лённых пределах. Если вы посмотрите на заднюю панель микроволновой печи или
холодильника, вы найдёте табличку, где написан интервал рабочего напряжения. На-
пример, от 190 до 250 В. Если напряжение выходит за эти пределы, прибор может
выйти из строя. Поэтому в некоторых случаях люди используют стабилизаторы на-
пряжения, которые уменьшают изменчивость.
Урожайность зерновых культур
Урожайность — очень важный показатель, который отражает эффективность сель-
ского хозяйства. Для формирования экономической и социальной политики государ-
ства, для обеспечения продовольственной безопасности страны необходимо изучать
причины, влияющие на урожайность. Такие исследования ведутся во многих странах
не одно столетие.
Урожайность измеряется в центнерах с гектара. Например, в 2012 г. с одного гек-
тара посевной площади в среднем по России собрано 18,3 ц зерновых культур.
Можно ли найти закономерности в изменчивости урожайности зерновых? Для это-
го следует провести небольшой анализ данных. Построим на диаграмме 21 два ряда
данных: урожайность и средняя урожайность за 5 лет (текущий год и четыре преды-
дущих) по данным с 2000 по 2017 г.
Видно, что урожайность подвержена существенной изменчивости, однако средняя
урожайность за пять последовательных лет колеблется намного слабее. Проявляется
это в том, что ряд средней урожайности «более гладкий». Причина в том, что благо-
приятные и неблагоприятные погодные условия и другие случайные факторы в те-
чение пяти лет уравновешивают друг друга, и их влияние на среднюю урожайность
значительно меньше, чем на урожайность каждого отдельного года.
1 Номинальное значение — объявленное, стандартное значение.
■
96 ГЛАВА V.
225
228
225
221
228
225
218
216
220
227
227
217
222
214
220
225
218
220
219
224
228
223
218
231
216

30
28
26
24
22
20
18
16
14
Диаграмма 21. Урожайность
и средняя урожайность за 5 лет
■♦■ Урожайность, ц/га
-•- Средняя урожайность за 5 лет, ц/га
> \ i i i i i i i i i i i i \ i i i i
2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016 2017
Кроме случайных факторов, в частности погодных условий, урожайность зависит
от усилий людей, качества посевного зерна, удобрений, уборочной техники и мно-
гих других факторов. Усилия людей по повышению урожайности сказываются посте-
пенно. Они влияют на среднюю урожайность не резко, но неуклонно, год за годом.
Поэтому средняя урожайность за несколько лет объективно отражает прогресс в зем-
леделии. За счёт улучшения хозяйствования средняя урожайность к нашему времени
выросла практически в 2 раза по сравнению с серединой 1990-х гг. и в 3 раза по
сравнению с 1950-ми гг.
Массовое производство
На обёртке шоколадного батончика написано, что его масса 50 г. Это номинальная
масса. В таблице 73 даны массы двадцати купленных одинаковых батончиков, полу-
ченные с помощью взвешивания.
Таблица 73. Масса шоколадных батончиков, г
49,1
49,7
50,0
48,8
49,7
51,4
50,5
49,1
48,1
49,6
50,3
50,9
49,7
48,5
51,6
52,0
49,8
50,7
50,1
50,6
Наибольшее значение 52,0 г, а наименьшее 48,1 г. Размах — 3,9 г. И только
один батончик весит в точности 50 г. Но средняя масса всех двадцати батончиков
равна 50,01 г, т. е. практически не отличается от номинальной.
Такая ситуация часто встречается при массовом производстве. Если отклонение
размера, массы мало отличается от заданного стандарта, т. е. находится в пределах
допустимой погрешности, то изделие считается годным. Оно поступает в продажу
или дальнейшее производство. Если отклонение превышает допуск, то изделие счита-
ется бракованным.
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ
97

В случае с шоколадными батончиками невозможно и не нужно контролировать вес
каждого отдельного изделия. Достаточно проверять среднее значение и размах массы
в контрольных партиях.
Большие или систематические отклонения говорят об износе или плохой настрой-
ке оборудования или о низком качестве сырья. В этих случаях приходится останав-
ливать производство, искать и устранять причину.
Для разных изделий допуски разные. Для продуктов питания допуски могут до-
стигать нескольких граммов, для деталей мебели — 1—2 мм, а для точных изделий,
например подшипников, допуски не превышают сотых долей миллиметра.
©
0
Вопросы
1 Приведите примеры изменчивых величин, помимо тех, что описаны в тексте
учебника.
2 Какие факторы влияют на значение напряжения в электросети в случайный мо-
мент времени? Назовите ещё один-два фактора, помимо тех, которые приведе-
ны в тексте учебника.
3 Какие факторы влияют на изменчивость урожайности зерновых культур? Назови-
те ещё один-два фактора, кроме тех, что приведены в тексте учебника.
4 Какие факторы могут влиять на изменчивость массы шоколадного батончика
с арахисом?
5 Что больше подвержено изменчивости — масса каждого отдельного шоколадно-
го батончика или средняя масса в партии батончиков?
Упражнения
154 Рассмотрите таблицу 72. Найдите наибольшее и наименьшее значения напря-
экения*
155 Найдите среднее значение и медиану напряжения по данным таблицы 72.
Сильно ли эти характеристики, по вашему мнению, отличаются от 220 В?
156 Сколько значений из таблицы 72 превышают номинальное и сколько меньше
номинального? Можно ли считать, что шансы событий «напряжение в слу-
чайный момент выше 220 В» и «напряжение в случайный момент ниже
220 В» примерно одинаковы?
157 Рассмотрите таблицу 73. Сколько в купленной партии батончиков массой бо-
лее 50 г? Какую долю и какой процент они составляют?
158 Масса купленного шоколадного батончика может быть больше или меньше
номинальной. Можно ли считать, что шансы этих событий равны, если су-
дить по данным из таблицы 73?
Ггз) Точность и погрешность измерений
Можно точно измерить количество людей в классе или подсчитать деревья в не-
большом сквере. Но чаще всего измерения невозможно выполнить абсолютно точно.
При измерениях возникают неизбежные погрешности, то есть случайные отклонения
от истинного значения. Главный источник погрешности — изменчивость самой изме-
ряемой величины. Кроме того, измерительный инструмент также обладает погрешно-
стью. Обсудим это подробнее.
98 ГЛАВА V.

ПРИМЕР 1. Число жителей города. Численность населения городов измеряется
обычно в тысячах человек (см. табл. 21 на с. 28). Мы понимаем, что число жите-
лей городов дано приближённо, что истинное число жителей, скорее всего, не равно
в точности целому числу тысяч.
Но что такое «истинное число жителей города»? Люди всё время приезжают и уез-
жают, кто-то умирает, кто-то появляется на свет. Поэтому число жителей города посто-
янно меняется. Если подсчитывать людей ежедневно в маленьких городах, то различия
составят десятки человек, в средних городах — сотни. Но число тысяч людей, населя-
ющих город среднего размера, за день, скорее всего, не изменится. Поэтому данные
о населении крупных городов обычно даются в тысячах человек. Более высокая точ-
ность не имеет смысла1.
ПРИМЕР 2. Рост человека. Когда мы говорим о росте человека, мы округляем дан-
ные до сантиметра. Так измеряют рост в России и в континентальной Европе. В США,
Великобритании, Австралии и некоторых других странах рост измеряют в дюймах2.
Рост человека редко равен целому числу сантиметров или дюймов. Казалось бы, мож-
но измерить рост с большой точностью. Но это не нужно: измерение с точностью до сан-
тиметра или дюйма достаточно для практических нужд: пошива одежды, определения
размеров мебели, сидений в автомобилях и т. п.
Кроме того, рост человека не остаётся постоянным в течение суток: утром рост че-
ловека чуть больше, чем вечером. За день под влиянием нагрузки хрящи в суставах
несколько сжимаются, а во время сна вновь расправляются. Поэтому само понятие
«рост человека» не очень точно определено.
ПРИМЕР 3. Расстояние между городами. Расстояние между городами не точ-
но определённая величина. Это расстояние обычно измеряют не по прямой, а вдоль
шоссе или железной дороги, соединяющей города. В России за расстояние между го-
родами принимают расстояние между их центральными почтамтами (главными по-
чтовыми отделениями) вдоль главных дорог. Этот способ определения расстояния по-
явился одновременно с регулярной почтовой службой.
Мы понимаем, как измерить расстояние между двумя точками вдоль некоторой
линии. Но город — это не точка, а обширная территория. К тому же граница города
не всегда отчётлива. Поэтому расстояние между городами точно определить нельзя.
Например, протяжённость автомобильной дороги М10 «Москва — Санкт-Петербург»
равна 697 км. А длина новой автомагистрали МП между этими же городами равна
684 км. Железнодорожники считают, что между Москвой и Санкт-Петербургом 650 км.
Пилоты регулярных рейсов измеряют расстояние от Москвы до Санкт-Петербурга в со-
ответствии со своим полётным планом, который может меняться даже в ходе полёта3.
\2У Важио! Выбирать точность измерения изменчивых величин нужно так. чтобы
погрешность не влияла на последующие выводы.
Слишком высокая точность измерения не нужна, а иногда даже вредна. Излиш-
не точные измерения отнимают время, силы и даже могут порождать ошибки.
В данных Российской службы статистики можно встретить измерения численности населения
городов с точностью до одного человека. Эти данные получены тем или иным методом. Метод
измерения при этом обязательно указывается.
2 Один дюйм (Г) — это примерно 2,54 см.
3 Схема взлёта и захода на посадку зависит от загрузки аэропорта, обстановки в воздухе и на-
правления ветра. Диспетчеры могут сообщить пилоту об изменениях в любой момент.
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ
99

Таблица 74. Допустимая погрешность
весов при эксплуатации
Нагрузка, кг
От 20 до 200
От 200 до 2000
От 2000 до 3000
Допустимая
погрешность, кг
±1
±2
±3
Таблица 75. Допустимые погрешности
автомобильного спидометра
Тем не менее измерительные прибо-
ры должны обеспечивать необходимую
точность. Допустимая погрешность из-
мерительного прибора определяется стан-
дартом.
ПРИМЕР 4. Допустимая погрешность
весов зависит от класса точности весов.
Чем выше класс точности, тем меньше
погрешность и тем дороже весы.
Не очень точные весы (III класс точ-
ности), которые могут взвешивать груз
от 20 до 3000 кг, имеют разные допусти-
мые погрешности при разной нагрузке
(табл. 74).
Знак ± означает, что отклонение воз-
можно в любую сторону — в меньшую
или в большую. Например, если чело-
век весом ровно 65 кг взвешивается на
напольных весах, то они могут пока-
зать от 64 до 66 кг. Наоборот, если на-
польные весы показали, что человек ве-
сит 65 кг, то истинный вес человека т
находится в пределах от 64 до 66 кг.
Это удобно записать двойным неравен-
ством
64 кг ^ т ^ 66 кг.
У лабораторных весов допустимые погрешности намного меньше. Например, точ-
ные лабораторные весы могут иметь допустимую погрешность всего 0,001 г.
ПРИМЕР 5. Согласно государственному стандарту автомобильный спидометр при
температуре окружающего воздуха 20 ± 5 °С не должен иметь погрешности в меньшую
сторону, а допустимые погрешности в большую сторону зависят от скорости и указа-
ны в таблице 75. Обратите внимание: погрешность в большую сторону допускается,
а погрешность в меньшую нет. Это сделано для того, чтобы ошибка спидометра не
приводила к значительному превышению скорости.
До сих пор мы приводили пример абсолютных погрешностей. Иногда погрешности
измеряются в процентах самой величины. Это относительные погрешности. Например,
допустимая погрешность длины верёвки или шнура в мотке
обычно даётся в процентах — это связано со способом изго-
товления мотка.
На рисунке 21 — катушка, на которую намотан шнур.
На ярлыке указана длина шнура: 250 м ± 10 %. Это зна-
чит, что настоящая длина шнура находится в пределах от
250 • 0,9 = 225 (м) до 250 -1,1-275 (м). Это можно выра-
зить двойным неравенством
225 м < / ^ 275 м.
Диапазон
скоростей, км/ч
0—60
| 00—80
80—100
100—120
120—140
Допустимая
погрешность при
Т « 20 ± 5 °С, км/ч
+4
+5
+6
+ 7 !
4-8
Здесь / — истинная длина шнура.
Рисунок 21
100
ГЛАВА V.

Вопросы
1 Численность населения крупной страны обычно измеряется с точностью до ста
тысяч человек. Можно ли совершенно точно определить понятие «численность
населения страны»?
2 Приведите несколько факторов, влияющих на изменчивость числа жителей стра-
ны. Как вы думаете, зачем нужно знать численность населения страны?
3 Почему размеры мебели обычно указывают в миллиметрах, а не в сантиметрах?
4 Приведите примеры измерений длины, когда точность ±1 мм недостаточна.
5 С какой точностью, по-вашему, следует измерять напряжение в бытовой элек-
тросети?
6 Укажите подходящую единицу измерения массы морского судна; железнодорож-
ного вагона; шоколадки; человека.
7 Температуру в России и в большинстве других стран измеряют в градусах Цель-
сия1. Укажите подходящую точность измерения для температуры воздуха в ком-
нате или на улице; тела человека; пламени в газовой плите; температуры на по-
верхности звезды.
Упражнения
159 Рассмотрите таблицу 74. В ней даны допустимые погрешности весов в раз-
ных диапазонах измерения. Предположим, что весы исправны и погрешность
измерения не выходит за пределы допустимой. Запишите с помощью двой-
ного неравенства границы, в которых находится истинное значение массы
т некоторого груза, если при взвешивании этого груза весы показали:
а) 38 кг; б) 129 кг; в) 2956 кг; г) 2543 кг.
160 Рассмотрите таблицу 75. Предположим, что автомобильный спидометр испра-
вен. Укажите с помощью двойного неравенства границы истинной скорости
V автомобиля, если спидометр показывает:
а) 28 км/ч; б) 69 км/ч; в) 96 км/ч; г) 127 км/ч.
161 На мотке верёвки указано, что длина верёвки составляет 30 м ± 5 %. В ка-
ких пределах может быть заключена истинная длина верёвки?
162 При температуре -10 °С дополнительно к допустимой погрешности спидоме-
тра (см. табл. 75) разрешается дополнительная (температурная) погрешность
±6% от верхней границы скорости в измеряемом диапазоне.
Например, если автомобиль движется со скоростью 55 км/ч, то верхняя гра-
ница диапазона скорости равна 60 км/ч. Поэтому дополнительная допусти-
мая погрешность равна ±60 • 0,06 — ±3,6 км/ч. Значит, исправный спи-
дометр при скорости 55 км/ч и уличной температурю -10 °С должен иметь
ошибку в пределах от -3,6 до -1-4 + 3,6 ■» ±7,6 км/ч, т. е. он должен пока-
зывать (после округления) скорость от 52 до 62 км/ч.
Найдите допустимую погрешность и границы показаний исправного спидоме-
тра (округлите до целого), если автомобиль при температуре -10 °С движется
со скоростью:
а) 75 км/ч; б) 96 км/ч; в) 108 км/ч; г) 123 км/ч.
1 В США, Белизе и в нескольких других странах температуру обычно измеряют в градусах
Фаренгейта.
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ 101

^24) Тенденции и случайные отклонения
В п. 12 мы обсуждали напряжение в электрической сети, которое редко бывает
равно номинальному значению 220 В. Похожие явления встречаются повсюду.
ПРИМЕР 1. Нормальное атмосферное давление1 в каждой местности своё: оно за-
висит от широты, высоты над уровнем моря, от температуры и влажности воздуха
и ещё — от случайности.
Диаграмма 22. Атмосферное давление в Ижевске. Февраль 2020 г.
2 3 4
тл—I—I—I—I—I—I—I—I—i—I—I—I—I—I—I—I—I—I—I—I—I—г
5 6 7 8 9 10 1112 13 14 15 16 17 18 19 20 2122 23 24 25 26 27 28 29 Дата
На диаграмме 22 оранжевая линия — график атмосферного давления на протяже-
нии февраля 2020 г. в г. Ижевске. Давление меняется плавно, непрерывно, поэтому
график — непрерывная линия.
Синей прямой показано среднее давление 748,4 мм рт. ст. График давления коле-
блется около среднего значения. При этом само среднее давление случается только в
редкие и короткие моменты времени. Можно говорить лишь о больших или меньших
отклонениях давления от среднего.
Глядя на причудливую форму графика, можно подумать, что давление возду-
ха крайне неустойчиво и всё время сильно меняется. Но давайте посмотрим, каков
размах данных по отношению к среднему. Наименьшее давление 730 мм рт. ст.,
а наибольшее — 765 мм рт. ст. Размах равен 35 мм рт. ст., что составляет
35 : 748,4 • 100% « 4,7%. Получается, что на самом деле давление колеблется вбли-
зи постоянного значения, и изменчивость здесь не очень высокая.
Иногда случайная величина в целом растёт или убывает со временем, при этом
испытывая случайные колебания. Говорят, что изменчивость складывается из тенден-
ции и случайных колебаний.
1 На уровне моря в местности с географической широтой 45° при температуре воздуха вблизи
земной поверхности 0°С нормальным считается давление 760 миллиметров ртутного столба.
102
ГЛАВА V.

В примере с атмосферным давлением можно сказать, что тенденция в феврале от-
сутствовала или была нулевой.
В отличие от тенденции, случайные колебания непредсказуемы, поскольку вызва-
ны кратковременными случайными и разнонаправленными факторами.
\д/ Тенденция (тренд) — характерное, устойчивое изменение во времени. Как пра-
вило, тенденция обусловлена долгосрочными факторами, которые заставляют
величину расти или убывать.
ПРИМЕР 2. На диаграммах 23 и 24 показано, как с возрастом меняется вес дево-
чек и мальчиков1 обычного телосложения. Эти данные медицинской статистики по-
лучены за много лет наблюдений. Средний ожидаемый вес увеличивается плавно —
тенденция показана синей линией.
В случае с весом возрастающая тенденция определена природой — ребёнок ра-
стёт, при этом масса его тела увеличивается. Но каждый конкретный ребёнок может
отставать от тенденции или обгонять её. Эти случайные колебания вызваны индиви-
дуальными особенностями, образом жизни и питания и многими другими фактора-
ми, часть из которых неизвестна.
Диаграмма 23. Вес девочек
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Оранжевой линией на диаграмме 23 показаны результаты взвешивания одной от-
дельной девочки. Видно, что в возрасте 2—3 лет она почти не прибавляла в весе,
1 Данные по центральным регионам России. Разумеется, правильнее было бы говорить о массе
тела, но мы, следуя традиции, пишем слово «вес».
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ
103

зато потом набирала вес очень быстро, компенсируя задержку. К 11 годам вес стал
очень близок к норме, но затем девочка снова оказалась несколько легче ожидаемо-
го. Можно ли сказать, что эта девочка развивалась ненормально? Скорее всего, нет:
отличия от общей тенденции не очень велики и, возможно, вызваны естественной
случайной изменчивостью.
На диаграммах не видны мелкие колебания веса, которые случаются каждый день:
после обеда человек весит на несколько сотен граммов больше, чем утром, а затем
его вес несколько снижается. Если бы можно было взвешивать ребёнка каждый час
и изобразить все измерения на графике, то получилась бы очень сложная линия, по-
хожая на пилу.
Диаграмма 24. Вес мальчиков
60
50
40
30
20
10
0
Ь
5
3,
—
9
V9
4
— Tin
- Ин
12
' 1
эмаль
цивид
14
Ъ
юера
у альн
4=2
^11
\
ЗВИТИ1
>ераз!
19
2^
(итие
23
*,з
25
0,5
28
5,9
31
^2
>,4
31
5.1
35,
U1
39,
44,
ly/
49,
J^
55.
3^
5
61,8
У/*
\
1
—►
1
6
8
9 10 11 12 13 14
15 16
Средний вес в каждом возрасте можно определить, взвешивая и измеряя тысячи
мальчиков и девочек в школах, детских садах и поликлиниках. Поэтому общие тен-
денции в развитии мальчиков и девочек, юношей и девушек известны.
Однако бывает так, что изменчивая величина одна-единственная и не имеет анало-
гов ни в прошлом, ни в настоящем. Таких явлений много в экономике. Если в слу-
чае с весом ребёнка можно опираться на данные тысяч других детей, в случае с по-
годой можно опираться на статистику, полученную за сотни лет, то в экономике это
невозможно: экономическая ситуация в мире уникальна и меняется всё время. На-
стоящее нельзя сравнивать с прошлым, а поэтому прогнозы в экономике делать на-
много труднее, чем предсказывать погоду.
ПРИМЕР 3. Рассмотрим мировые цены на нефть. Мы выбрали два периода —
первое полугодие 2008 г., когда цены на нефть росли, и второе полугодие 2014 г.,
когда они снижались (диагр. 25 и 26).
104
ГЛАВА V.

Диаграмма 25. Цена барреля нефти в первом полугодии 2008 г.
150
оооооооооооооооооооооооророоооооороосророооооооооохооооооооюоооооооооооооо
OOOOppppppOOPPQPQOQQOOpOOOOOOOQpQQPPQO
оооооооооооооооооооооооооооооооооооооо
с*счечечечсчс*с*счечсчсчсчсчсчсчсчсчсчсчсчсчсчсчечм
^ ^ ^ ^ ^ г^ ^н' cvJ cvi eg cvj csj сч nnnnnn^^^^tfioeideioioiodddeed
ooooooooooooooooooooooooooooooooooqoqo
NNNNNeH^d^oiwoo ^oorio6»fiO>eoo6wNNd^©6»fid^o5eobcg
OO*H*Hcgcge0PO*H*Heacgooi-i»Hcgc4OO^*HcgcgoO'H'-'egcgeaoo^^cMCM
Красными пунктирными линиями на обеих диаграммах показаны тенденции. На
диаграмме 25 — по большей части возрастающая тенденция. На диаграмме 26 —
убывающая. Но эти тенденции не были известны заранее, а были определены поз-
же — на основе уже сформировавшихся цен. Мы видим, что в январе — июне
2008 г. цена на нефть в целом росла. Но были дни, когда случались падения: си-
няя линия, показывающая реальные цены, сильно колеблется, прыгает вверх и вниз.
Общее повышение не всегда означает постоянное повышение. Точно так же на диа-
грамме 26 при общем снижении цен часто наблюдаются незначительные, но резкие
краткосрочные повышения.
Какие факторы здесь формируют тенденцию? В начале 2008 г. бурно развивалось
строительство, крупные банки охотно давали кредиты, экономика быстро росла, и ей
требовалось всё больше нефти. Это определило тенденцию: повышение спроса привело
к постоянному росту цен. В 2014 г. сказался экономический кризис: ситуация в миро-
вой экономике ухудшалась, спрос на нефть падал, поэтому она постепенно дешевела.
А какие факторы приводят к кратковременным скачкам цен? Внезапное решение
какой-нибудь крупной компании о покупке нефти или отказ от ожидаемой покупки,
задержка нефтеналивного танкера в океане, заявление влиятельного политика или
экономиста, пожар на морской нефтедобывающей платформе, даже слухи об откры-
тии нового месторождения могут вызвать краткосрочное изменение цены в ту или
иную сторону.
Ф
Важно! Часто изменчивость в природных, экономических и социальных явлени-
ях состоит из двух составляющих. Первая составляющая — тенденция, которая
обусловлена серьёзными и долгосрочными факторами. Вторая составляющая —
случайные отклонения, вызванные разнонаправленными краткосрочными дей-
ствиями, которые зачастую невозможно предвидеть.
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ
105

Диаграмма 26. Цена барреля нефти во втором полугодии 2014 г.
но
100
^* ^Jt ^ ^ ^t ^t ^
ооооооооооооооооооооооооооооооооооооооо
счсчсчсчечечсчсчечсчсчечсчсчсчсчечсчсчсчсчс^
^bhh^h^ooooododoo««aftagioioiddddd6dHHHHHHNcg
OOHHNMNOOHHNNOOOOHHOlMOOHHNMnOHHHNnOOHHNN
Одна из важных задач статистики — научиться выделять тенденции в изменчивых
явлениях и отличать их от незначительных случайных колебаний.
Ф
Вопросы
1 Приведите свой пример величины, имеющей постоянное среднее значение, во-
круг которого наблюдаются случайные колебания.
2 Что такое тенденция?
3 Приведите свой пример величины, имеющей возрастающую тенденцию.
4 Сравните диаграммы 23 и 24. Есть ли участки, где тенденции похожи? Какие
различия в тенденциях вы видите?
5 Какие ещё факторы, помимо перечисленных в тексте, по вашему мнению, могут
влиять на изменчивость веса растущего школьника?
^2б) Группировка данных и гистограммы
Часто наборы данных представляют собой обширные массивы. Среди них встреча-
ются очень близкие друг к другу значения, но полное совпадение встречается крайне
редко, даже если данных очень много. Чтобы понять, насколько плотно распределе-
ны значения на каждом участке числовой прямой, применяют группировку данных.
С группировкой данных мы уже встречались, когда говорили о диаграммах
«стебель-л ист» (см. п. 12). В этих диаграммах значения группируются в один ин-
тервал, если у них совпадают последние десятичные разряды. Например, когда мы
строили диаграмму для наблюдений над напряжением, все значения внутри одного
десятка (от 220 В до 229 В) попадали в один интервал. Длина интервала может быть
не только 10. Она может быть любой. Какой именно интервал группировки лучше,
зависит от конкретной задачи.
106
ГЛАВА V.

Чтобы сгруппировать данные, нужно разбить числовую прямую на одинаковые
промежутки — интервалы группировки. Длина интервала называется шагом группи-
ровки. Затем нужно подсчитать, сколько значений или какая доля значений попа-
ла в каждый интервал, и построить диаграмму. По внешнему виду диаграммы часто
можно увидеть, где именно находится среднее значение, медиана, заметить другие
особенности распределения данных.
ПРИМЕР 1. В таблице 76 приведены результаты ежедневных измерений атмосфер-
ного давления в Москве летом 2019 г.
Таблица 76. Атмосферное давление летом 2019 г. в Москве
749,4
747,3
750,8
755,2
753,7
754,1
754,3
753,8
753,0
752,8
752,3
751,2
755,9
749,4
747,5
748,4
746,1
745,8
748,7
749,6
749,2
749,1
752,4
753,7
756,8
751,7
739,3
730,5
736,8
741,3
738,9
739,8
740,2
743,3
740,8
735,4
738,1
738.4
735,7
735,4
738,2
742,4
743,5
745,6
745,3
743,9
742,6
740,1
740,3
744,6
749,1
748,3
744,7
745,1
748,3
748,9
746,0
741,2
742,2
739,7
736,9
742,9
741,0
738,9
740,3
736,5
740,1
744,2
742,3
735,4
741,8
746,6
750,3
745,8
746,5
746,2
747,1
746,8
743,4
750,1
751,6
754,5
754,3
758,1
753,0
757,0
755,8
751,9
756,7
754,8
752,2
752,1
Всего значений 92, повторяющихся среди них мало. Наименьшее значение 730,5, наи-
большее — 758,1 мм рт. ст. Шаг группировки выберем 4 мм рт. ст., а первый интервал
возьмём 726—730 мм рт. ст. В него не попадает ни одно значение. Последний интервал
тоже сделаем пустым.
Если значение попадает на границу двух интервалов, можно отнести его к любому
из них — это вопрос договорённости. Мы относим граничное значение к левому ин-
тервалу. Например, значение 746,0 мы включили в интервал 742—746. Получается
таблица группировки (табл. 77).
Таблица 77. Группированные данные, шаг 4 мм рт. ст.
п/п
1
2
3
4
5
в
7
8
9
10
Интервал, мм рт. ст.
726—730
730—734
734—738
738—742
742—746
746—750
750—754
754—758
758—762
762—766
Всего
Кол-во попаданий в интервал
0
1
7
18
18
19
17
11
1
0
92
Частота
0
0,011
0,076
0,196
0,196
0,207
0,185
0,120
0,011
0
1,000
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ
107

Чтобы с помощью электронной таблицы
узнать, сколько всего значений в массиве
данных, используйте функцию
СЧЁТ()
1 /х 1 =СЧЁТ(С2:Р7) ]
с
Данные
1.4
1.8
2.3
3,5
2.1
U
D
1.3
2.6
3,1
2,7
1.8
2.6
Е
^
12 1
Рисунок 22
Получилось 10 интервалов. Самые «населённые» — интервалы от четвёртого до седьмого.
Долю значений, попадающих в каждый из интервалов, называют частотой попадания
в интервал, поскольку она показывает, как часто значение попадает в этот интервал.
Частоты находятся в правом столбце таблицы. Частоты выражают в долях единицы1.
Для частот попадания в интервал верно то же свойство, которое мы формулирова-
ли и доказывали для отдельных значений: сумма частот равна единице.
Ф
Важно! Сумма всех частот равна единице.
Чтобы отобразить полученную информацию наглядно, построим гистограмму, то
есть диаграмму частот (диагр. 27).
Диаграмма 27. Давление в Москве летом 2019 г. (гистограмма)
0,250
0,200
0 Л 50
ОД 00
0,050
0,000
I I I I I I П I Г
726-730 730-734 734-738 738-742 742-746 746-750 750-754 754-758 758-762 762-768
На практике частоты часто выражают в процентах. Например, можно сказать, что около 12%
дней летом 2019 г. в Москве было давление от 754 до 758 мм рт. ст.
108
ГЛАВА V.

Гистограммой называется диаграмма частот. Гистограмма позволяет наглядно
представить характер изменчивости данных.
На гистограмме видно, что больше всего дней, когда давление было в пределах
от 738 до 754 мм рт. ст. Дней, когда давление было ниже 738 мм рт. ст. или выше
754 мм рт. ст., было мало — сумма частот соответствующих интервалов невелика.
Данных немного, но видна общая закономерность: очень малые и очень большие зна-
чения редки, в основном значения концентрируются около среднего. От этого гисто-
грамма напоминает горку с двумя склонами.
Далеко не все виды изменчивости характеризуются гистограммами, напоминающи-
ми двускатную горку.
ПРИМЕР 2. Рассмотрим длительность разговоров по мобильному телефону. Мы
собрали данные о длительности всех разговоров одного абонента в течение месяца.
Всего разговоров за месяц было 387. Самый короткий разговор длился всего секунду.
Самый длинный — более 15 минут (924 секунды).
Интересно посмотреть на частоты разговоров разной длительности. Построим
гистограмму по имеющимся данным. Нужно выбрать подходящую группировку.
Если шаг слишком малый, то интервалов очень много, и характер изменчивос-
ти плохо виден из-за «прыгающих» столбиков. Вроде бы информации много,
а общую картину не видно. Мы даже не стали изображать всю получившуюся гисто-
грамму — она слишком длинная. Диаграмма 28 неудачная: слишком мал шаг груп-
пировки.
Диаграмма 28. Длительность телефонных разговоров.
Распределение. Шаг 2 секунды
0,06-
0,05-
0,04
0,03-
0,02-
0,01-
ЕЮ
ш/к
I I I II М I I I I I I I ! I I I I II I И I II И I I I I II I I I I I I I
еаоо^осоеаоо^осречор^оср
«нечеасосо'фдедесосо
м i i i i i i i i i i i i i i i i i i i i i i i i i i г
n оо оо Ф О) о i-ii-ie^eaco^^ioio*©
Если шаг слишком большой, то интервалов мало, и картинка получается очень
грубая — слишком много полезной информации теряется. Диаграмма 29 малоинфор-
мативна из-за слишком большого шага.
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ
109

Диаграмма 29. Длительность телефонных разговоров.
Распределение. Шаг 200 секунд
m^Rwmtwmm
0-200
200-400
400-600
600-800
800-1000
Шаг группировки нужно выбрать так, чтобы, с одной стороны, диаграмма была
достаточно подробной, а с другой — отражала бы общую тенденцию и хорошо пока-
зывала характер случайной изменчивости данных.
Диаграмма 30. Длительность телефонных разговоров.
Распределение. Шаг 25 секунд
хвОьвОьвОЮОЮОЮОЮОЮОКЭОКЭОЮОЮОЮОхвОЮОьвОЮОЮ
NWt-ONkOt-ONke^ON»Ot-OWiflNONiONOCgieb-ONW5b'ONiON
При шаге 25 секунд (для простоты на оси абсцисс отмечены только правые концы
интервалов) гистограмма достаточно подробная, и хорошо видна убывающая тенден-
ция — чем длительнее разговоры, тем таких разговоров меньше.
Гистограмма имеет совершенно другую форму по сравнению с гистограммой частот
атмосферного давления. Это означает, что и характер изменчивости совсем другой.
©
Вопросы
1 В чём заключается группировка данных?
2 Что такое шаг группировки?
3 Как выбрать подходящий шаг группировки?
110
ГЛАВА V.

4 Что такое частота попадания в интервал группировки? Чему равна сумма всех
частот?
5 Что такое гистограмма?
6 Как бы вы объяснили, почему долгих телефонных разговоров меньше, чем ко-
ротких?
Искать количество значений, попавших в
каждый интервал группировки, легко, если
научиться пользоваться функцией
ЧАСТОТА()
На рисунке показан пример: сколько зна-
чений меньше 0, сколько от 0 до 1, от 1
до 2 и т. д.
Внимание! Функция ЧАСТОТА находит не
частоту, а количество значений в интерва-
лах.
I * /х\ =ЧАСТОТА(С2:Р7;Е2:Е7) ~|
С
Данные
I 1>4
1.8
2.3
3.5
2.1
| ^3_
D
1.3
2.6
3.1
2.7
1.8
2.6
Е
Инт-лы
0
1
2
3
4
5_
F
Количество!
ol
о]
5
5I
2
о]
0
163
Рисунок 23
Упражнения
В таблице 78 приведены данные о населении всех городов Московской обла-
сти (данные 2019 г.). Рассмотрите таблицу.
Таблица 78. Население городов Московской области
№
п/п
1
2
3
4
5
6
1 7
8
9
10
11
12
Город
Апрелевка
Балашиха
Бронницы
Верея
Видное
Волоколамск
Воскресенск
Высоковск
Голицы но
Дедовск
Дзержинский
Дмитров
Население,
тыс. чел.
29,1
490,0
22,6
5,0
71,4
19,2
93,2
10,4
17,4
30,1
56,3
68,7
п/п
13
14
15
16
17
18
19
20
21
22
23
24
Город
Долгопрудный
Домодедово
Дрезна
Дубна
Егорьевск
Жуковский
Зарайск
Звенигород
Ивантеевка
Истра
Кашира
Клин
Население,
тыс. чел.
112,0 1
133,5 1
11,3 1
75,0
72,1
107,9
22,9
21,9
79,3
33,5
48,0
79,4
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ
111

Продолжение
№
п/п
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| 44
1 **
| 46
1 47
1 **
1 49
Город
Коломна
Королёв
Котельники
Красноармейск
Красногорск
Краснозаводск
Краснознаменск
Кубинка
Куровское
Ликино-Дулёво
Лобня
Лосино-Петровский
Луховицы
Лыткарино
Люберцы
Можайск
Мытищи
Наро-Фоминск
Ногинск
Одинцово
Озёры
Орехово-Зуево
Павловский Посад
Пересвет
Подольск
Население,
тыс. чел.
141,1
224,5
46,8
26,5
171,8
12,9
42,5
20,1
20,6
29,0
89,3
25,3
30,3
58,6
207,3
30,0
222,7
63,0
102,3
137,5
25,0
118,0
63,9
13,6
304,2
п/п
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
Город
Протвино
Пушкино
Пущино
Раменское
Реутов
Рошаль
Руза
Сергиев Посад
Серпухов
Солнечногорск
Старая Купавна
Ступино
Талдом
Фрязино
Химки
Хотьково
Черноголовка
Чехов
Шатура
Щёлково
Электрогорск
Электросталь
Электроугли
Яхрома
Население, '
тыс. чел.
35,8
106,8 |
20,8 |
119,9 J
107,0 J
20,2 1
13,0 J
102,0 |
124,9 J
51,6 1
22,5 |
66,0 |
12,7 |
60,0
254,7 |
21,2 1
21,1 1
71,9 1
32,4 1
124,8 1
22,8
157,4
20,7 1
14,3
а) Найдите три подмосковных города, где численность населения значительно
отличается от численности населения большинства городов в ту или другую
сторону.
б) Удалите из таблицы три найденных в пункте а) города. Найдите наимень-
шее и наибольшее значения после удаления этих трёх городов.
164 После удаления из таблицы 78 городов Балашихи, Подольска и Вереи нужно
сгруппировать оставшиеся данные.
а) Сколько интервалов группировки получится, если сделать начальное значе-
ние 10 тыс. чел. при шаге группировки 10 тыс. чел.?
б) Сколько интервалов группировки получится, если сделать начальное значе-
ние 0 тыс. чел., а шаг группировки 25 тыс. чел.?
112
ГЛАВА V.

в) Какой из этих двух способов группировки вы бы предпочли?
г) Сколько городов из таблицы 78 попадает в интервал 90—120 тыс. чел.?
д) Какова частота попадания в интервал 90—120 тыс. чел.?
165 На диаграмме 31 изображена гистограмма «Распределение населения городов
Московской области», построенная по данным таблицы 78 после удаления
трёх городов (Подольск, Балашиха и Верея). Начальное значение 0 тыс. чел.,
шаг группировки 30 тыс. чел. Рассмотрите гистограмму, ответьте на вопросы.
Диаграмма 31. Распределение населения городов Московской области
0-30
30-60 60-90 90-120 120-150 150-180 180-210 210-240 240-270
а) Как бы вы описали характер изменчивости величины «Население подмо-
сковного города»?
б) Города с каким населением вы бы назвали крупными?
в) Городов с каким населением больше всего?
г) Можно ли по гистограмме (диагр. 31) сказать, чему примерно равны сред-
няя численность населения и медиана населения подмосковных городов?
Е)
Рост человека
Невозможно заранее предсказать рост незнакомого человека. Для исследователя эта
величина случайная. Но если измерить рост многих людей (случайно выбранных), то
проявится закономерность. Чтобы в этом убедиться, мы обсудим данные о росте чело-
века по малому, среднему и большому числу наблюдений. Обратите внимание: в при-
мерах с населением городов Московской области или с урожайностью зерновых мы
брали все данные: все города, все годы. В примерах с напряжением в электросети,
массой батончиков мы не могли взять все значения — их очень много или даже бес-
конечно много. Мы случайно выбирали некоторые значения из всей совокупности.
W
Набор значений некоторой величины, которые выбраны для изучения всей сово-
купности, называется выборкой. Часто выборку формируют случайным образом
и говорят о случайной выборке.
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ
113

Малая выборка
Таблица 79 содержит данные о росте двадцати случайно выбранных девушек
в возрасте 20—21 года. Наблюдения разбиты на две группы по 10 наблюдений в
каждой.
Таблица 79. Роет 20 случайно выбранных девушек, см (две группы)
Рост девушек, см
Группа 1
Группа 2
164
167
170
164
160
168
163
164
170
167
171
165
166
164
169
158
166
159
165
167
Сред-
нее
166,4
164,3
Меди-
ана
166
164,5
Раз-
мах
11
10
Отдельные значения заметно различаются: размах в первой группе равен 11 см,
во второй — 10 см, а размах значений всех двадцати наблюдений равен 13 см. Од-
нако средние значения и медианы в первой и второй группах различаются значи-
тельно меньше: разность между средними арифметическими всего 2,1 см, разность
между медианами 1,5 см. Причина в том, что среднее арифметическое и медиана
более устойчивы, чем результаты отдельных измерений. Это единственное, что мож-
но заметить, пользуясь небольшим количеством данных.
Средняя выборка
Пополним выборку. К двадцати значениям добавим ещё тридцать новых наблюде-
ний и занесём все пятьдесят в общую таблицу 80.
Таблица 80. Рост 50 случайно выбранных девушек, см
164
167
161
158
163
170
164
169
166
169
160
168
162
168
161
163
164
170
167
162
170
167
168
161
163
171
165
165
167
160
166
164
165
165
166
169
158
166
168
169
166
159
164
165
172
165
167
173
164
160
Среднее значение роста в этой выборке равно 165,3 см, а медиана — 165 см.
Эти значения мало отличаются от тех, что были получены на малой выборке. А вот
размах увеличился до 15 см. Это естественно: чем больше выборка, тем выше шансы,
что в неё попадут очень рослые девушки и девушки малого роста. Размах значений
может увеличиваться, а среднее значение роста остаётся практически неизменным.
Трудно изучать эту таблицу, читая одно число за другим. Построим гисто-
грамму с шагом группировки 2 см (диагр. 32). Начальный интервал пусть будет
155—157 см.
Столбики вблизи среднего значения (165,3 см) высокие, а чем ближе к краям
гистограммы, тем ниже: девушек с ростом гораздо ниже или гораздо выше средне-
го намного меньше, чем девушек, чей рост близок к среднему. Получившаяся гисто-
грамма отдалённо напоминает горку с двумя скатами или колокол.
114
ГЛАВА V.

Диаграмма 32. Распределение роста девушек (объём выборки — 50 наблюдений)
0,25-
0,2-
0,15-
0,1-
0,05-
Ш^Ш:
Жйй
§ЩДЩ|
ИИ'
j.iM..t„.»jijijn;
I I I I I I I 1 Г
155-157 157-159 159-161 161-163 163-165 165-167 167-169 169-171 171-173 173-175
Большая выборка
Добавим к имеющимся 50 наблюдениям ещё 250 новых. Теперь в выборке данные
о росте 300 случайно выбранных девушек. Наименьший рост 151 см, наибольший —
180 см. Построим новую гистограмму (диагр. 33). Внешнее сходство полученной фигу-
ры с колоколом усилилось даже без группировки. На рисунке показана колоколообраз-
ная линия, к которой приближается контур гистограммы с ростом числа наблюдений.
Зная форму этой колоколообразной линии, можно примерно указать долю деву-
шек, рост которых находится в заданных пределах. Например, можно утверждать,
что девушек с ростом от 162 до 170 см примерно 70%, а тех, чей рост превышает
170 см, — около 15%.
Диаграмма 33. Распределение роста девушек (300 наблюдений)
А
0,12-
и N СО
ю ю ю
ТН—1—1—г
(ON000)OHNC0^>fl(0N009>OHC](Q^tA(ON000)O
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ 115

Объяснить, почему получается именно такая форма, можно с помощью мысленно-
го эксперимента. Представим себе, что каждая девушка заняла «своё место» на чис-
ловой прямой (рис. 24). Девушек очень малого роста (например, ниже 155 см) совсем
мало. Точно так же мало очень высоких девушек (скажем, с ростом более 180 см).
Поэтому края получившейся гистограммы низкие. Большинство девушек среднего ро-
ста или около среднего роста, поэтому центральная часть гистограммы высокая.
Опыт показывает, что не только рост людей подчиняется такой закономерности.
Похожий характер имеет изменчивость атмосферного давления (см. диагр. 22), раз-
мера листьев на деревьях, массы шоколадных батончиков и других товаров и мно-
гих других величин. Но не следует думать, что все случайные величины в природе
подчиняются такому или похожему закону. В примере с длительностью телефонных
разговоров мы видели гистограмму другой формы, а значит, другой вид случайной
изменчивости.
Рост 166 см
Рисунок 24. Каждая девушка «встала» на отметку своего роста
D
Важно! Поведение многих изменчивых величин подчиняется некоторым законо-
мерностям, которые проявляются при изучении больших наборов наблюдений.
Разным видами изменчивости соответствуют гистограммы разной формы.
Изучение закономерностей распределения разных случайных величин — одна
из задач математической науки теории вероятностей.
Вопросы
1 Что такое выборка?
2 Как вы думаете, какие факторы влияют на рост человека?
3 Какие факторы могут влиять на длину берёзового листа? На вес домашней кош-
ки? На размер грецкого ореха? На температуру тела человека? На время, кото-
рое находится в пути рейсовый самолёт? На результат измерения высоты по-
толка в квартире?
116
ГЛАВА V.

Статистическая устойчивость
и оценки с помощью выборки
В предыдущих параграфах мы встречались с
выборками. В п. 22 мы дали таблицу 72 с изме-
рениями напряжения в электрической сети. На-
пряжение меняется постоянно, поэтому эти на-
блюдения — выборка, сделанная в случайные мо-
менты времени. Говоря о шоколадных батончиках,
мы не можем взвесить все батончики. Поэтому в
таблице 73 данные о массе 20 купленных батон-
чиков — также выборка, так же, как и данные
об атмосферном давлении в Ижевске и Москве.
Имея выборку, можно точно указать, какая
доля значений в этой выборке больше средне-
го, или найти частоту значений, попадающих в
определённый интервал.
ПРИМЕР 1. В качестве примера рассмотрим
уже знакомую нам выборку значений напряже-
ния в бытовой сети (табл. 81). Построим по этим
данным таблицу частот, выбрав подходящий шаг
группировки (табл. 82).
Определим, какова доля значений от 215 до
226 В. Суммарная частота значений в трёх соот-
ветствующих интервалах равна
0,12 + 0,28 + 0,12 + 0,20 = 0,72.
Аналогично можно найти долю значений в
любом другом диапазоне. Такие расчёты бы-
ли бы бесполезны, если бы не статистическая
устойчивость.
Частоты, средние значения и многие другие выборочные характеристики многих
изменчивых величин мало отличаются от таких же характеристик всей совокуп-
ности данных или другой выборки. Это свойство изменчивых величин называют
статистической устойчивостью.
Чтобы статистическая устойчивость проявила себя в двух выборках, нужно чтобы
эти выборки были сделаны в одинаковых условиях. Если в одной и той же квартире
измерять напряжение электрической сети первый раз днём, второй раз вечером, ког-
да во всём доме горит свет, а третий раз ночью, то, скорее всего, все три выборки
будут значительно отличаться друг от друга по свойствам.
Чтобы выборка хорошо отражала свойства всей совокупности данных (их может
быть бесконечно много), лучше всего, чтобы эта выборка была сделана случайным
образом. Например, измерения напряжения нужно проводить на протяжении дли-
тельного времени в случайные моменты. Чем больше объём выборки (количество зна-
чений), тем лучше, как правило, проявляет себя статистическая устойчивость.
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ 117
Таблица 81. Выборка значений
напряжения в бытовой сети, В
225
228
225
221
228
225
218
216
220
227
227
217
222
214
220
225
218
220
219
224
228
223
218
231
216
Таблица 82. Частоты
Напряжение, В
209—211
212-214
215-217
218-220
221-223
224-226
227-229
230-232
233-235
Частота
0
0,04
0,12
0,28
0,12
0,20
0,20
0,04
0
®

Vi/ Статистическая устойчивость даёт возможность оценивать (приближённо нахо-
дить) частоты и средние значения в недоступных нам массивах данных, пользу-
ясь небольшой известной выборкой.
Важно! При этом нужно помнить, что в силу случайной изменчивости оценки,
сделанные с помощью выборки, приблизительные1.
ПРИМЕР 2. Пользуясь таблицами 81 и 82, найдём примерно, сколько времени на
протяжении суток напряжение в сети превышает 220 В.
Если пользоваться таблицей 81, то нужно подсчитать долю значений, которые
больше, чем 220 В. Этих значений 14 из 25 (выделены красным цветом), то есть до-
ля равна 0,56.
Если пользоваться таблицей 82, то нужно сложить частоты в пяти последних стро-
ках (все интервалы, начиная с интервала 221—223 В):
0,12 4- 0,20 4- 0,20 4- 0,04 = 0,56.
В сутках 24 часа. Общая продолжительность периода, когда напряжение превыша-
ет 220 В, приближённо равна 24 • 0,56 — 13,44 часа, то есть примерно 13 ч 26 ми-
нут.
Ещё раз подчеркнём, что сделанная оценка лишь приблизительно равна истинно-
му значению, да и то если сделанная выборка хорошо отражает колебания напря-
экения.
ПРИМЕР 3. В таблице 73 даны массы 20 купленных шоколадных батончиков. Рас-
смотрим теперь вообще все такие батончики. Сколько процентов из них имеют массу
менее 49 г?
Десятки тысяч этих батончиков сейчас лежат в магазинах, кафе и в самых раз-
ных местах. Миллионы таких батончиков давно уже съедены. А ещё миллионы даже
не выпущены на фабрике. Поэтому взвесить все батончики мы не можем. Но можем
воспользоваться имеющейся выборкой. В этой выборке 3 батончика из 20 легче 49 г.
Следовательно, в силу статистической устойчивости можно предположить, что доля
3
таких «лёгких* батончиков среди всех равна приблизительно ^ = 0,15, то есть 15%.
ПРИМЕР 4. Оценивать доли по выборке можно не только с помощью таблиц, но
и используя гистограммы. На диаграмме 34 гистограмма «Рост девушек», сделанная
по случайной выборке объёмом 300 наблюдений (см. п. 26).
Предположим, что мы хотим заказать футболки с логотипом университета для бу-
дущих первокурсников и первокурсниц. Ограничимся вопросом о женских футболках
для первокурсниц. Известно, что всего их будет 200. Чтобы футболки доставили ра-
дость и никто не был обижен, нужно оценить заранее необходимое число футболок
разных размеров. Определить соответствие между ростом и размером женской фут-
болки можно по таблице 83.
Таблица 83. Соответствие роста и размера женских футболок
Рост, см
Размер
<156
XS
156-162
S
163-168
М
169-174
L
175-180
XL
181-186
2XL
>186 1
3XL
Изучением того, насколько хороши или плохи выборки, занимается теория вероятностей. Она
часто позволяет дать ответ на вопрос, как сильно могут отличаться истинные частоты и средние
от тех частот и средних, которые мы можем найти в сделанной выборке.
118
ГЛАВА V.

Диаграмма 34. Рост девушек
. i
0,12
0,1
0,08
0,06
0,04
0,02
0
{
ш0щШШШШ^ШМ0$
Шя^^^^^^^^^^Ш
шт ив ИЬиИИМЁИИ
^^Щ^^^^^Ш^^^^^ш^^р!^^^
ИЯиШяШНвяя ед »
csj со 3! *° <°
СО СО СО (О (^)
ь-оооонечео^юеьооФо
Определим с помощью диаграммы при-
мерную долю будущих студенток ростом
до 156 см. Разумеется* девушки, чей рост
использован в выборке, и наши буду-
щие студентки — это разные группы. Но
мы будем полагаться на статистическую
устойчивость, то есть считать, что доли
девушек одного роста в этих двух груп-
пах примерно равны. Выделим на диа-
грамме столбики от 151 до 155 см, опре-
делим (приблизительно) их высоты и сло-
жим (рис. 25):
0,003 4- 0,003 + 0,006
0,02
0,006
0,003
0
151 152 153 154 155 156 157
Рисунок 25. Примерное определение
высот столбиков
0,012.
Следовательно, самых маленьких футболок размера XS потребуется примерно
200 • 0,012 - 2,4.
Иными словами, разумно ожидать, что потребуется 2—3 футболки размера XS. Но
это лишь приблизительная оценка. На всякий случай, если есть возможность, следу-
ет купить 3—4 запасных футболки каждого размера.
(2)
Вопросы
1 Что такое статистическая устойчивость?
2 Что значит оценить величину?
3 Почему сделанные с помощью выборки оценки нельзя считать совершенно точ-
ными значениями?
4 Для измерения роста мужчин взяли две выборки. Одну — в Голландии, а дру-
гую — во Вьетнаме. Как вы думаете, можно ли считать, что эти выборки близки
по своим свойствам? Почему?
СЛУЧАЙНАЯ ИЗМЕНЧИВОСТЬ
119

г) Упражнения
166 Пользуясь таблицей 81 или 82, найдите, сколько примерно времени на про-
тяжении суток напряжение в сети:
а) меньше, чем 230 В;
б) отклоняется от 220 В не больше чем на 5 В;
167 В гипермаркет привезли 200 коробок шоколадных батончиков, в точности та-
ких, как мы обсуждали в п. 22. В каждой коробке 24 батончика. Пользуясь
таблицей 73, оцените, сколько примерно в этих коробках батончиков массой
от 49 до 51 г.
168 Можно ли использовать данные таблицы 76 для того, чтобы оценить, сколько
примерно дней летом 2022 г. в Москве атмосферное давление будет меньше
747 мм рт. ст.? Объясните свой ответ.
169 Закончите решение примера 4: определите примерное количество футболок
каждого размера S, M, L, XL, 2XL и 3XL.
170 В университетской баскетбольной секции занимается 100 девушек. Можно ли
оценить, сколько среди них девушек ростом 174—178 см, пользуясь таблицей 83
или диаграммой 34? Объясните свой ответ.
171 Ольге 18 лет, и её рост равен 172 см. Пользуясь диаграммой 34 оцените,
сколько процентов Ольгиных сверстниц:
а) имеют примерно такой же рост;
б) не выше Ольги.
172 В архитектурном институте на специальности «Дизайн» учится в общей
сложности 50 студенток. Сколько примерно среди них девушек ростом
167—168 см? Сделайте оценку, используя данные:
а) таблицы 80;
б) диаграммы 34.
Сравните полученные числа. Можно ли считать их близкими? Какая из двух
сделанных оценок, на ваш взгляд, с большей вероятностью ближе к истинной
доле девушек указанного роста?
120
ГЛАВА V.

Случайные
события
и вероятность
Попытка изучать изменчивость и случай-
ность с помощью математики привела к по-
явлению теории вероятностей. В этой главе
мы познакомимся с основными понятиями
теории вероятностей: случайными опытами
и случайными событиями, которые происхо-
дят в этих опытах.
Вероятность случайного события — это чис-
ловая мера его правдоподобия. Чем боль-
ше шансов на осуществление события, тем
больше его вероятность.
В нашей жизни играют большую роль мало-
вероятные события. Мы расскажем о таких
событиях и о том, как правильно к ним от-
носиться.
28 Случайные события
и случайные эксперименты
29 Вероятности и частоты
событий
30 Монета и игральная кость
в теории вероятностей
31 Как узнать вероятность
события
32 Зачем нужно знать
вероятность события

Случайные события
и случайные эксперименты
О некоторых событиях мы можем твёрдо сказать, что они произойдут. В наступ-
лении других событий мы не уверены. Например, в самый жаркий и солнечный лет-
ний день мы точно знаем, что лето кончится, наступит осень, а затем зима. Но не-
возможно сказать заранее, будет эта зима тёплой или холодной. Мы не можем пред-
видеть, будет ли следующий год влажным или засушливым, урожайным или нет.
В неурожайный год дорожает хлеб, предприятия сельского хозяйства несут убытки,
а некоторые из них могут разориться. Урожайные годы тоже хорошо было бы про-
гнозировать заранее.
Нельзя предвидеть многие события даже недалёкого будущего. Возьмём, напри-
мер, прогноз погоды. В последние годы прогнозы стали намного точнее, чем они бы-
ли 10—15 лет назад. Но всё равно, даже имея грозовой прогноз, нельзя быть уве-
ренным в том, что гроза случится именно в нашем районе в предсказанное время.
Можно лишь говорить о шансах этого события. Поэтому в прогнозах погоды можно
встретить выражения «дождь маловероятен», «вероятность грозы 10 %», «к вечеру
возможно усиление ветра» и т. п.
Для России и других нефтедобывающих стран важны мировые цены на нефть.
Безошибочно прогнозировать эти цены не удаётся, хотя многие стараются это сде-
лать. При составлении бюджета государства на следующий год важно знать, превы-
сит ли средняя цена на нефть некоторый уровень или нет. Если превысит, то в бюд-
жете можно предусмотреть определённые траты, а если нет, то нельзя. Например,
бюджет России на 2020 г. был составлен исходя из предположения, что средняя цена
окажется не меньше 42 долларов за баррель1.
Перед началом футбольного чемпионата мы не можем с полной уверенностью на-
звать ни победителя, ни призёров. Мы можем обсуждать шансы команд, но лишь по
окончании чемпионата станет ясно, кто какое место занял.
Все упомянутые выше события — случайные.
Всякое случайное событие связано с некоторыми условиями. Если мы создаём или
описываем такие условия, мы тем самым производим некоторый случайный экспе-
римент, или случайный опыт. Если случайный эксперимент не описан или описан
плохо, то трудно говорить о вероятностях случайных событий. Например, о шансах
спортивных команд на победу можно говорить, только если эти команды могут встре-
титься и сыграть. О вероятности выпадения какого-нибудь числа очков на игральном
кубике можно говорить, только если кубик бросают.
Случайный эксперимент (случайный опыт) — это условия и обстоятельства,
в которых мы рассматриваем случайные события.
ПРИМЕР 1. Случайный эксперимент — телефонный разговор. Можно говорить
о разных случайных событиях в этом эксперименте. Например, «длительность разго-
вора составит от 5 до 10 минут» или «разговор прервётся из-за плохой связи».
1 Баррель — мера объёма. 1 баррель — 158,9873 л.
122
ГЛАВА VI.

ПРИМЕР 2. Школьник пишет контрольную работу по математике. Это в нашем
понимании случайный эксперимент, и в нём возникают случайные события. Напри-
мер, «школьник сделает не больше трёх ошибок» или «школьник получит отметку
«отлично».
ПРИМЕР 3. Бросание игрального кубика. У игрального кубика (кости) шесть оди-
наковых граней с числами от 1 до 6. Невозможно предсказать, какая грань выпадет.
Выпадение шестёрки — случайное событие. Другое случайное событие — «выпадет
больше двух очков».
ПРИМЕР 4. Подсчёт количества крупных пожаров в определённом городе в буду-
щем году — тоже случайный опыт, поскольку условия определены, а результат не-
известен. Примеры случайных событий: «крупных пожаров не будет» или «крупных
пожаров будет больше шести» и т. п.
ПРИМЕР 5. Денежная лотерея. Случайные события: «выпадение выигрыша на
определённый номер» или «сумма выигрыша на данный билет лотереи превышает
1000 р.».
Примеры случайных экспериментов и связанных с ними случайных событий мож-
но приводить бесконечно.
Если событие не относится к рассматриваемому эксперименту, то оно не является
случайным событием этого эксперимента. Например, в опыте, где школьник пишет
контрольную работу по математике, событие «в этот день отменён урок физкульту-
ры» не является случайным событием.
Другой пример случайного эксперимента — бросание монеты. Мы считаем, что
она может упасть одной из двух сторон (решкой или орлом) кверху. Событие «монета
встала на ребро» или событие «монета закатилась за плинтус» мы в этом опыте не
рассматриваем. Такие события не являются событиями в данном эксперименте.
Поскольку в теории вероятностей речь идёт о случайных событиях в случайных
экспериментах, слово «случайное» мы часто будем опускать.
Вопросы
1 Вообразите, что вы ловите рыбу на озере, где водится только окунь и плотва.
Какие случайные события могут произойти при этом?
2 Случайный эксперимент — определение времени работы некоторого мобильного те-
лефона от батареи. Какие случайные события возможны в этом эксперименте?
3 Игральный кубик бросают один раз. Приведите примеры двух-трёх случайных
событий в этом эксперименте.
4 Автомобиль подъезжает к перекрёстку двух дорог и намерен продолжить движе-
ние. Какие случайные события возможны в этом эксперименте? Приведите не-
сколько примеров.
Вероятности и частоты событий
Часто мы не можем сказать заранее, произойдёт случайное событие в некотором
случайном опыте или нет. Но мы можем говорить о шансах этого события.
Например, обсуждая будущую встречу футбольных команд Л и Б, кто-то мо-
жет сказать, что их шансы на победу относятся как 1 к 3. Всем при этом бу-
дет понятно, что этот человек считает победу команды Б втрое более вероятной,
чем победу команды А. В подтверждение своего мнения он скажет, что команды
А и Б встречались много раз и при этом команда Б побеждала примерно в три
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬ
123

раза чаще, чем команда А. Поэтому он и говорит, что вероятность события * по-
бедит команда А» равна -» или 0,25, а вероятность события «победит команда Б»
3
равна -, или 0,75, опираясь на частоты происходивших событий. В этом примере
4
мы не учитывали матчи, окончившиеся вничью: ничья не входит в условия описан-
ного случайного эксперимента.
Другой пример. При бросании игрального кубика шансы выпадения единицы та-
кие же, как и выпадения двойки. А шансы событий «выпадет шестёрка» и «шестёр-
ка не выпадет» относятся как 1 к 5.
Некоторые случайные события происходят очень редко. Маловероятно, например,
что 31 января следующего года в Екатеринбурге будет гроза или что на конкретный
купленный лотерейный билет выпадет крупный выигрыш.
Другие случайные события происходят очень часто, почти всегда. Таким, напри-
мер, является событие «31 января следующего года в Екатеринбурге грозы не будет».
Шансы случайных событий измеряют числами и называют вероятностями. Со-
бытие, которое никогда не наступает, называют невозможным. Вероятность невоз-
можного события полагают равной 0. Событие, которое наступает в случайном опы-
те всегда, называют достоверным. Его вероятность полагают равной 1. Вероятности
остальных событий — это числа от 0 до 1.
Вероятность случайного события — это числовая мера правдоподобия этого
события.
Невозможное случайное событие — это случайное событие, которое в слу-
чайном эксперименте не наступает, Вероятность невозможного события равна 0.
Достоверное случайное событие — это случайное событие, которое в случайном
эксперименте обязательно наступает. Вероятность достоверного события равна 1.
Иногда вероятности событий можно рассчитать математически, но часто приходит-
ся их оценивать, то есть приближённо находить с помощью частот, повторяя один и
тот же случайный опыт много раз.
Пусть, например, мы провели один и тот же опыт 100 раз, и некоторое событие С
произошло 45 раз. Отношение числа тех опытов, в которых событие С произошло,
45
к общему числу проведённых опытов равно tztz = 0,45.
Число 0,45 в этом случае является частотой случайного события С. Мы уже гово-
рили о частотах значений в числовых наборах, поэтому частота события не является
для нас совсем новым понятием.
Определение. Отношение числа опытов, в которых случайное событие про-
изошло, к общему числу проведённых одинаковых опытов называется частотой
данного случайного события в этой серии опытов.
Если событие не наступило ни разу, то его частота равна 0. Но это не значит, что
оно невозможное. Может быть, в следующей серии таких же опытов это событие всё же
случится. Если событие наступило во всех опытах, то частота этого события равна 1.
Вероятности и частоты связаны. Если опыт повторять достаточно много раз, то
окажется, что частота события близка к его вероятности.
124 ГЛАВА VI.

Близость частот и вероятностей связывает теорию вероятностей с практикой. Мож-
но оценивать вероятности с помощью статистических опытов и прогнозировать ча-
стоты наступления событий, зная их вероятности. Так проявляется статистическая
устойчивость в повторяющихся сериях случайых экспериметнов.
Если вероятность события мала (например, меньше чем 0,001), то такое событие на-
ступает редко. Такие события называют маловероятными. В практических ситуациях,
когда опыт проводят один раз, маловероятные события обычно считают невозможны-
ми. Например, можно выиграть в лотерее большую сумму денег и жить безбедно и не
работая. Но вероятность этого события настолько мала, что разумные люди на это не
рассчитывают.
Тем не менее, пренебрегая маловероятными событиями, надо учитывать возмож-
ные последствия. Вероятность попасть под машину, перебегая через улицу, невысо-
ка, но последствия этого события таковы, что пренебрегать ими нельзя. Поэтому не
нужно перебегать улицу, нарушая правила1.
[YJ Вопросы
1 Что такое частота случайного события? Как частоты и вероятности событий свя-
заны друг с другом?
2 Какие значения может принимать вероятность случайного события?
3 Может ли частота случайного события быть больше единицы?
4 Какие события называют достоверными, а какие — невозможными?
5 Чему равна вероятность достоверного случайного события? невозможного слу-
чайного события?
6 Приведите примеры невозможных и достоверных случайных событий в экспери-
менте, где бросают игральную кость с очками от 1 до 6.
7 Приведите примеры маловероятных событий в эксперименте «прогноз погоды
на завтра».
8 Приведите примеры нежелательных маловероятных событий в жизненных ситуа-
циях. Обсудите с учителем и одноклассниками, какими из них и в каких случаях
можно пренебречь.
0
Упражнения
173 Бросают игральный кубик, на гранях которого числа от 1 до 6. Укажите,
какие из перечисленных событий являются достоверными, а какие — невоз-
можными:
а) выпадет 7 очков;
б) выпадет больше 2, но меньше 5 очков;
в) выпадет от 1 до 6 очков;
г) выпадет больше 3, но меньше 4 очков.
174 Книгу, в которой 256 страниц, открывают на случайно выбранной странице.
Укажите, какие события являются достоверными, а какие — невозможными:
а) номер открытой страницы — дробное число;
б) номер открытой страницы равен 342;
в) номер открытой страницы в книге не меньше 1.
1 Тот, кто бежит, имеет больше шансов споткнуться и упасть. Улицу нужно переходить спокой-
ным шагом, убедившись в безопасности. И водителю проще предсказать действия и движения
спокойно идущего пешехода, чем того, кто внезапно выбегает на проезжую часть.
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬ
125

175 Какова, по вашему мнению, вероятность события:
а) завтра на улице вам встретится живой динозавр;
б) число дней в следующем месяце не превысит 31;
в) на морозе вода в стакане через некоторое время замёрзнет;
г) сборная вашего класса выиграет в футбол у команды «Спартак»?
■зсп Монета и игральная кость
в теории вероятностей
Многие важные и нужные факты первоначально были получены в простых опытах
с обычными монетами и игральными костями-кубиками. Длительное время теория
вероятностей развивалась как исчисление шансов в играх, но давно уже «вышла из
детского возраста». Гораздо важнее и интереснее описывать случайные явления, воз-
никающие в природе, в технике, в общественной жизни, чем вычислять шансы вы-
игрышей или редких игровых комбинаций. Однако монета и игральная кость не уш-
ли из теории вероятностей. Они продолжают играть важную роль, подобно тому как
важную роль играют линейка и циркуль в геометрии.
С помощью монеты, игральных костей и других простых игровых моделей можно
изучать очень сложные и запутанные случайные явления, не поддающиеся анализу
с помощью алгебры.
Математическая монета, используемая в теории вероятностей, лишена многих ка-
честв настоящей монеты. У математической монеты нет цвета, размера, веса и досто-
инства. Она не сделана ни из какого материала и не служит платёжным средством.
Монета с точки зрения теории вероятностей имеет две стороны, одна из которых
называется «орёл», а другая — «решка». Монету бросают, и она падает одной из
сторон вверх. Никакие другие свойства математической монете не присущи.
Название «орёл» для лицевой стороны (аверса) монеты происходит оттого, что на
ней изображён герб Российского государства — двуглавый орёл. Впервые орёл на мо-
нетах появился при великом князе Иване III.
Название «решка» для обратной стороны монеты (реверса) возникло потому, что
в древности монету при чеканке клали на решётчатую наковальню, чтобы она не
скользила при ударе. Решётка отпечатывалась на реверсе монеты. Сейчас на реверсе
чеканят номинал монеты, но название «решка» сохранилось.
Математическая монета считается симметричной. Это означает, что брошенная на
стол монета имеет равные шансы выпасть орлом или решкой. При этом подразуме-
вается, что никакой другой исход
невозможен, — она не может по-
теряться или «встать на ребро».
Настоящая монета не столь иде-
альна, как математическая; она
может быть немного вогнутой, мо-
жет иметь другие дефекты, кото-
рые влияют на результаты броска.
Тем не менее, чтобы проверить на
практике опыты с бросанием ма-
„ ^ ^ ^ тематической монеты, мы бросали
Пробная монета-рубль Аверс монеты образца и будем бросать обычную монету>
126
ГЛАВА VI.

Монета часто помогала и до сих пор помогает людям в сложной ситуации сделать
честный выбор без предпочтений, положившись только на случай. Например, в на-
чале футбольного матча арбитр бросает монету, чтобы решить, какая из команд по-
лучит право начать игру.
Игральный кубик, или игральная кость, также служит пре-
красным средством для получения случайных событий. Игральная
кость имеет удивительную историю. Игры с костями были извест-
ны в глубокой древности в Индии, Китае, Лидии, Египте, Гре-
ции и Риме. Игральные кости в виде кубиков находили в Египте
(XX в. до н. э.) и в Китае (VI в. до н. э.) при раскопках древних
захоронений. Очки на гранях древнеегипетских костей часто изо-
бражались в виде птичьего глаза. Игральная кость
Об играх с костями животных (игры в «лодыжки», «костыги»,
«козули *) в Древней Руси свидетельствуют многочисленные археологические наход-
ки. Отсюда и пошло название игрального кубика — «кость».
Ранние упоминания о костях в древнеиндийской поэзии отражают популярность
игры в кости в Древней Индии. «Гимн игрока» — первый литературный текст, упо-
минающий кости, — изображает их как враждебную человеку магическую стихию:
Ведь кости усеяны колючками и крючками,
Они порабощают, они мучают, испепеляют.
Одаряют, как ребёнок, победителя они вновь лишают победы.
Неудачливый игрок пытается заклясть кости, заключает с ними мир:
Заключите с нами дружбу! Помилуйте нас!
В Древней Греции считалось, что игральные кости придумал мифический герой
Паламед во время Троянской войны. Но по версии философа Геродота, кости изо-
брели лидийцы, населявшие Малую Азию, чтобы отвлечься от голода, болезней или
других напастей.
В Древнем Риме в кости играли все сословия, от рабов до императоров. Импера-
тор Клавдий даже написал книгу об игре в кости. В III в. до н. э. в Риме игра в ко-
сти разрешалась лишь во время ежегодного празднования сатурналий1.
Игру в кости запрещали не только в Древнем Риме. В Древнем Китае за игру
в кости можно было попасть на каторгу.
С появлением христианства кости время от времени запрещались, поскольку, по
мнению духовенства, игра эта была порождением дьявола. В другое время кости бы-
ли разрешены, и игра в них даже поощрялась, при этом каждому сочетанию очков
приписывалось некоторое божественное значение. Очевидно, такие крайности в отно-
шении азартных игр свидетельствуют о том, что изжить их церковь не могла, но пы-
талась использовать страсть к игре.
Во Франции в XIII—XIV вв. многочисленные королевские указы запрещали игру
в кости. Видимо, запреты эти оказались безрезультатными, поскольку королевским
указом от 1396 г. запрещались уже не сами кости, а применение и изготовление
поддельных костей2.
Правильные (симметричные) кости обеспечивают одинаковые шансы выпадения
каждой грани. Для этого все грани должны иметь одинаковую площадь, быть пло-
Праздник в честь бога Сатурна.
2 Поддельная, или шулерская, кость имеет нарушенную разметку, смещённый центр тяжести
или изменённую форму для того, чтобы обеспечить преимущество тому игроку (шулеру), кто
знает об этом. Придумано множество способов сделать симметричные с виду шулерские кости.
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬ
127

скими и одинаково гладкими. Вершины и рёбра кубиков должны иметь правильную
форму. Если вершины скруглены, то все скрутления должны быть одинаковыми.
Сумма очков на противоположных гранях правильной кости равна 7, чтобы затруд-
нить жульничество при игре.
Математическая игральная кость, которая обсуждается и используется в теории
вероятностей, — это математический образ правильной кости. Выпадения всех гра-
ней равновозможны. Подобно математической монете, математическая кость не имеет
цвета, размера, веса и иных материальных качеств.
Как узнать вероятность события
В некоторых случаях вероятность события можно установить, исходя из сим-
метрии в случайном опыте. Например, при бросании симметричной монеты разум-
но считать, что шансы орла и решки одинаковы, и поэтому вероятность выпадения
1
каждой стороны равна -.
с*
То же относится и к правильной игральной кости. Она имеет шесть граней. Кость
симметрична, и поэтому вероятности выпадения всех граней мы полагаем одинако-
1
выми и равными —.
о
Иногда вероятности событий удаётся вычислить, зная вероятности более про-
стых событий. Но даже если вероятность события удалось рассчитать, остаются со-
мнения. Дело в том, что расчёты непременно основаны на каких-либо исходных пред-
положениях. А предположения могут оказаться неточными или даже ошибочными.
Например, мы предполагаем, что монета симметрична. В отношении металлической
монеты это предположение лишь приблизительно верно, так как стороны настоящей
монеты всё же не одинаковы. Для некоторых монет различия могут быть заметными.
Экспериментальный способ определения вероятности основан на наблюдени-
ях. При многократных повторениях опыта частоты случайных событий оказываются
близки к их вероятностям. Поэтому, если опыт можно повторять много раз, то веро-
ятность случайного события можно оценить его частотой.
Рассмотрим связь частот и вероятностей на примере страхования. С 2004 г. в Рос-
сии действует закон об ОСАГО — обязательном страховании автогражданской ответ-
ственности. Владелец автомобиля должен заключить договор со страховой компанией.
По этому договору владелец машины платит компа-
нии определённую сумму (страховой взнос), а ком-
пания взамен обязуется оплатить (до определённого
предела) ущерб, который может быть нанесён этим
автовладельцем другому автовладельцу, городской
собственности или пешеходам в случае ДТП1. Чтобы
определить размер страхового взноса, нужно учесть
две величины:
1) с какой вероятностью автомобиль в течение
срока страхования может попасть в ДТП;
2) какой в среднем ущерб окружающим прино-
сит ДТП.
ДТП — дорожно-транспортное происшествие.
128
ГЛАВА VI.

Зная это, можно вычислить страховые взносы, но подробнее об этом мы расска-
жем позже. Сейчас скажем только, что вероятность случайного события «в течение
года автомобиль попадёт в ДТП» вычисляется по статистическим данным, которыми
располагают страховые компании и Государственная инспекция безопасности дорож-
ного движения. В разных регионах России эта вероятность разная — от 0,04 до 0,1.
Ф
Важно! Вероятности некоторых событий не удаётся ни оценить, ни вычислить,
ни назначить из соображений симметрии. Такими событиями теория вероятно-
стей не занимается.
0
Вопросы
1 Какие три способа определения вероятностей событий вы знаете?
2 На какие предположения мы опираемся, когда говорим, что вероятности выпа-
дения орла и решки при бросании монеты равны 0,5? Верны ли эти предполо-
жения для: а) падающего бутерброда; б) листьев, падающих с дерева?
3 Что нужно сделать для экспериментального определения вероятности случайно-
го события?
4 Как вы думаете, можно ли экспериментально оценить вероятность следующих
событий:
а) вас спросят на уроке;
б) на уроке в классе присутствуют все ученики;
в) вы не сделаете в изложении ни одной ошибки;
г) любимая мамина ваза разобьётся в результате падения на пол?
Упражнения
176 По опыту попробуйте оценить вероятность того, что вас спросят во время
урока.
177 По своим наблюдениям попробуйте определить вероятность того, что на уро-
ке присутствуют все ученики вашего класса.
178 Можно ли оценить вероятность опоздания ученика на урок? Если можно, что
для этого нужно сделать?
■зу Зачем нужно знать вероятность события
Что может дать знание вероятности случайного события? Как эти знания можно
использовать? Частично мы ответили на этот вопрос, рассказывая о страховании ав-
томобиля. Знать вероятность дорожно-транспортного происшествия нужно, чтобы вы-
числить страховой взнос.
Но это не единственная польза, которую может принести знание вероятностей. Ес-
ли мы знаем вероятности каких-либо событий, то часто удаётся найти вероятности
других событий. Это особенно важно при испытании и внедрении лекарств, проекти-
ровании зданий и сооружений, расчёте надёжности систем в автомобилях, самолётах,
судах, на электростанциях и в космических кораблях.
Зная вероятность события, мы можем сказать, насколько часто это событие будет
происходить в жизни. Например, если какое-то событие имеет вероятность 0,99, то
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬ
129

в среднем его следует ожидать в 99 случаях из 100, т. е. почти всякий раз. Напро-
тив, если событие имеет вероятность 0,01, то происходит оно редко, примерно в од-
ном случае из ста.
Предположим, что цри определённых условиях в некоторой местности вероятность
урагана равна 0,25. Это значит, что при многократных повторениях упомянутых ус-
ловий примерно в 25 % случаев случится ураган. Учитывая, что ураган очень опа-
сен, можно считать, что вероятность 0,25 достаточно высока, чтобы объявить штор-
мовое предупреждение. И неважно, что ураган может не случиться. В таком случае
лучше перестраховаться.
Говоря, что событие произойдёт примерно в 25 случаях из 100, мы не утверждаем,
что оно непременно случится ровно 25 раз из 100 возможных. Оно может произой-
ти 22, 23, 24, 25, 26, 27 или 28 раз. Оно даже может произойти всего 18 раз или
32 раза в какой-нибудь серии из 100 опытов. Но такие серии опытов будут встре-
чаться довольно редко.
Если вероятность события равна 0,25, то не следует ожидать его появления, скажем,
1 или 99 раз из 100. Напротив, прогноз «от 22 до 28 раз» можно считать весьма разум-
ным. Как и в каких случаях устанавливаются разумные границы прогноза — сложный
вопрос, ответ на который часто удаётся найти с помощью теории вероятностей.
Роль маловероятных событий в жизни человека
Маловероятные события в повседневной жизни часто считают практически невоз-
можными. Люди следуют правилу: в однократном опыте маловероятное событие не
происходит.
Конечно, в строгом смысле это правило неверно. На него нельзя полагаться, если
от этого зависит чья-то жизнь или здоровье. Нужно помнить, что даже очень мало-
вероятные события иногда случаются. И если такое событие произойдёт — если об-
рушится здание, внезапно выйдут из строя тормоза в автомобиле, — потом будет
поздно вспоминать, как мала была вероятность этого. Поэтому, чтобы предотвратить
несчастье, нужно регулярно проверять тормоза, вовремя ремонтировать или сносить
ветхие здания и принимать другие необходимые меры. Таким образом можно значи-
тельно понизить и без того малую вероятность несчастья.
Есть меткая пословица: «Незаряженное ружьё раз в год стреляет». Это как раз
о маловероятных событиях, которые всё же происходят.
Добиться того, чтобы несчастья и катастрофы не случались совсем, невозможно.
Но можно и нужно делать всё, чтобы вероятности этих событий стали как можно
меньше. К сожалению, часто люди из-за своего легкомыслия недооценивают опас-
ность и ничего не предпринимают.
Например, вероятность столкновения «Титаника» с айсбергом была крайне малой.
Капитан Эдвард Смит мог её ещё уменьшить, снизив скорость судна, но не сделал
этого, считая, что столкновение невозможно. Сотни человек стали жертвами малове-
роятного события в ночь на 15 апреля 1912 г.
Ф
Если же маловероятное событие грозит лишь незначительными потерями или
неприятностями, то люди обычно следуют правилу: «В однократном опыте мало-
вероятное событие не происходит».
И всё же крайне маловероятные события иногда происходят. Как к ним следует
относиться, попробуем объяснить на примере с «упрямой» монетой.
130
ГЛАВА VI.

Вообразим, что ваш приятель у вас на глазах бросает на стол монету 10 раз и все
10 раз выпадает орёл. Это может случиться, хотя это и маловероятно (такое случает-
ся в среднем реже одного раза на 1000 таких опытов). Теперь приятель предлагает
вам угадать, что выпадет при следующем, одиннадцатом броске. Попросите его пока-
зать вам монету и стол поближе.
Предположим, что ваш приятель хитро улыбается и уклоняется под разными пред-
логами. Тогда следует заподозрить, что вам показывают фокус. Например, у монеты
на обеих сторонах орёл. Или в столе скрыто хитрое магнитное устройство, а монета
сильно намагничена.
Другое дело, если приятель соглашается, и вы совершенно ясно видите, что перед
вами обычный стол и обычная круглая монета: на одной стороне орёл, на другой -
решка. В этом случае придётся признать, что вы стали свидетелем редкого, а пото-
му удивительного события: 10 орлов из 10 попыток. Тогда шансы орла и решки при
следующем броске одинаковы. Монете «не надоело» падать орлом вверх — она мо-
жет упасть орлом вверх и в одиннадцатый раз. Монета «не испытывает неприязни к
решке» — она с таким же успехом может выпасть решкой вверх. Это самый трудный
для угадывания случай.
Вероятностная защита от ошибок с помощью двойного ввода
Можно без преувеличения сказать, что мы живём в мире цифр. Цифры сопрово-
ждают нас повсюду и играют важную роль в нашей жизни. У любого человека мно-
жество документов, каждый из которых имеет номер. Почти у каждого взрослого
человека есть банковская карта, а значит, и счёт в банке. Чтобы сделать денежный
перевод, нужно указать номер карты получателя. Нам часто приходится вводить мас-
су данных на разных сайтах. Но человеку свойственно ошибаться. Как избежать слу-
чайных ошибок?
Самый простой способ — двойной ввод. Многие сайты, включая сайты государ-
ственных услуг, запрашивают важную информацию дважды. Например, приходится
два раза вводить новый пароль при создании личного кабинета, два раза подряд вво-
дить адрес электронной почты. Зачем? Для защиты от ошибок.
Если пользователь придумает один пароль, а введёт по ошибке немного другой, то
никто никогда не узнает, какой пароль по ошибке оказался в системе. Пользователь
не сможет войти на сайт, он будет недоумевать и даже может начать возмущаться,
считая, что сайт плохо работает.
Чтобы подтвердить безошибочность ввода, программа регистрации просит ввести
пароль ещё раз: вероятность двух одинаковых ошибок пренебрежимо мала1.
То же и с электронной почтой — если при вводе ошибка, то пользователь не по-
лучит информацию, которую ему добросовестно посылает система. Безошибочность
ввода электронной почты очень важна. Поэтому используется двойной ввод.
Контрольные цифры и суммы
В других случаях применяются иные меры вероятностной защиты. Давным-давно
придумана защита с помощью контрольных цифр. Номер банковской карты не со-
всем случайное число. Кратко расскажем о номерах карт и о том, как теория вероят-
ностей помогает защититься от ошибки при вводе номера.
Некоторых людей такие простые меры защиты раздражают. Они стараются схитрить — ввести
пароль один раз и скопировать его во второе окно. На многих сайтах попытка копирования
паролей блокируется. Но не на всех. Если в первое окно пароль введён с ошибкой, то ошибка
скопируется во второе окно. Человек сам себя накажет.
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬ
131

У большинства платёжных карт номер состоит из 16 цифр. Первая цифра номе-
ра — код платёжной системы. Номер банковской карты «Мир» начинается на циф-
ру 2, у карт JCB первая цифра номера 3, у карт VISA — 4, у MasterCard — 5,
у Maestro — 6. По следующим пяти цифрам можно узнать, какой банк выпустил
карту. Затем идёт девятизначный номер карты. Эти девять цифр можно считать слу-
чайными. И наконец — последняя цифра. Эта цифра контрольная. Чтобы определить
контрольную цифру, применяется специальный алгоритм.
1. Все цифры, стоящие на нечётных местах, умножаются на 2, при этом из дву-
значных произведений вычитается 9.
2. Полученные в результате первого шага цифры и цифры, стоящие на чётных ме-
стах, складываются.
3. Контрольная цифра — это цифра, которой в полученной сумме не хватает до
ближайшего сверху числа, кратного 10.
ПРИМЕР. Предположим, банк выпустил карту, и первые 15 цифр такие:
2200 2476 0343 593_
Нужно определить последнюю контрольную цифру. Умножаем на 2 цифры, стоящие
на нечётных местах, и при необходимости вычитаем 9. Получаются цифры 4, 0, 4, 5,
0, 8, 1, 6. Теперь найдём сумму полученных цифр и цифр, стоящих на чётных местах:
(4 + 0 + 4 + 5 + 0 + 8 + 1 + 6) + (2 + 0 + 4 + 6 + 3 + 3 + 9) = 28 + 27 = 55.
Чтобы получить 60 (ближайшее сверху число, кратное 10), нужно добавить 5. Это
и есть контрольная цифра. Таким образом, карта получает свой номер окончательно
(рис. 26).
Если человек при вводе номера (или сканер при считывании) ошибётся, возникнет
сообщение об ошибке. Можно ли случайно ввести неверный номер с правильной кон-
трольной цифрой? Да, такое возможно, но маловероятно. Защита с помощью одной
контрольной цифры считается достаточной.
Примерно также защищены от ошибки ввода номера банковских счетов, номер на-
логоплательщика, номер пенсионного свидетельства, лицевые счета на квартплату
и многие другие персональные данные.
Похожим образом защищается от ошибок информация при передаче по мобильным
сетям или Интернету. Каждый символ в сообщении кодируется числом, а в конце
группы чисел передаётся их сумма (контрольная
сумма). Если из-за помех информация случай-
ным образом исказилась, то практически навер-
няка контрольная сумма окажется неверной. Ве-
роятность случайного совпадения настолько мала,
что ею можно пренебречь.
Не так важно, что именно использовать для
контроля: одну цифру, сумму, знакочередующую-
ся сумму или другие функции. Важно, что вме-
сте с основной информацией передаётся избыточ-
Рисунок 26. Правильный номер ная информация, позволяющая проверить кор-
карты «Мир» « .
г ректность передачи основной информации.
Вероятностная защита языка с помощью избыточности
Самая известная и всеми нами используемая вероятностная защита информации —
избыточность языка, на котором мы говорим и пишем. Когда мы видим опечатку
в тексте, мы обычно понимаем, что это опечатка, и можем легко догадаться, какое
2200 2476 0343 5935
IVAN IVANOV
МИР
132
ГЛАВА VI.

слово на самом деле должно быть в этом месте. Дело в том, что любой естественный
язык — в частности, русский — избыточный. Если случайно пропала нужная буква,
появилась лишняя или буквы поменялись местами, то на помощь приходят соседние
буквы и слова, иногда даже согласование слов по падежам, родам и числам помогает
нам восстановить смысл написанного. Все языки обладают высокой избыточностью.
Ни у кого не возникнет сомнений в том, что такое «стаитстика», «минная каша»
или «причастный обормот». Смысл пропал, но не совсем. Его можно восстановить.
Чем курьёзнее опечатка, тем легче её исправить. И только в редких случаях избы-
точности языка не хватает, чтобы понять, что имелось в виду. Например, человек
написал, что он «помял машину», а на самом деле он её всего лишь помыл. Смысл
не пропал, он стал другим. Такие незаметные ошибки приводят к недоразумениям,
но они маловероятны, поэтому случаются нечасто.
Избыточность языка позволяет создавать алгоритмы проверки орфографии и ис-
правления опечаток при вводе текста в компьютер или смартфон.
Язык математических символов — это пример языка, где нет избыточности. Поч-
ти любая описка или опечатка в записи числа или в математическом выражении меняет
смысл, и следов не остаётся. Например, хотел школьник написать 72, но почему-то напи-
сал 12 (может быть, в черновике написал семёрку, как единицу, а потом переписал эту
единицу в чистовик). Не очень страшно, если это случилось в домашнем задании. Если же
подобное произойдёт на экзамене, никто потом не сумеет доказать, что имелось в виду не
то, что написано: восстановить задуманное по соседним цифрам или знакам невозможно.
Поэтому математические расчёты и записи, особенно ответы на экзамене, нужно
обязательно проверять два, а то и три раза. Проверка, которую всегда советуют де-
лать учителя математики, — это вероятностная защита от досадных ошибок.
Гу\ Вопросы
1 Падение сосульки с крыши на голову пешехода — событие маловероятное. Что
нужно делать для того, чтобы эту вероятность ещё уменьшить?
2 В каких случаях не следует доверяться правилу: «В однократном опыте малове-
роятное событие не происходит»?
3 Приведите несколько примеров маловероятных событий из жизни.
4 В фантастической повести Аркадия и Бориса Стругацких «Понедельник начина-
ется в субботу» есть эпизод, когда герои сначала находят умершего попугая,
на лапке у которого кольцо с номером 190 573. На следующий день они видят
такого же больного попугая с этим же номером, который умирает на их гла-
зах. Ещё через день к ним в лабораторию влетает весёлый и здоровый попугай
с таким же номером на лапке. Герой повести Александр Привалов рассуждает
следующим образом.
Всё происходящее, рассуждал я, по-настоящему удивительно, только если счи-
тать, что эти три или четыре попугая — один и тот же попугай. Они действи-
тельно так похожи друг на друга, что вначале я был введён в заблуждение. Это
естественно. Я математик, я уважаю числа, и совпадение номеров — в особен-
ности шестизначных — для меня автоматически ассоциируется с совпадением
пронумерованных предметов.
Объясните своими словами, что имеют в виду авторы в последнем предложе-
нии, говоря от имени Привалова о совпадении номеров и предметов.
5 Подумайте, зачем в алгоритме защиты банковской карты умножать цифры на
нечётных местах на 2 перед тем, как складывать цифры. Почему берут остаток
от деления на 9, а не на 10?
СЛУЧАЙНЫЕ СОБЫТИЯ И ВЕРОЯТНОСТЬ
133

rJ Упражнения
179 Обычную симметричную монету, у которой на одной стороне изображён орёл,
а другая сторона — решка, бросили шесть раз. Все шесть раз эта монета вы-
падала орлом. Какое утверждение или какие из утверждений верны?
1. В следующий раз более вероятно, что выпадет орёл, чем решка.
2. В следующий раз более вероятно, что выпадет решка.
3. В следующий раз орёл и решка могут выпасть с равными шансами.
4. Седьмой раз подряд орёл выпасть не может.
5. При седьмом броске тоже выпадет орёл.
180 Для правильной монеты мы полагаем, что вероятность выпадения орла равна
0,5. Разумно ли ожидать, что при 100 бросаниях монеты орёл выпадет:
а) 5 раз; б) 49 раз; в) 90 раз?
181 Подбросьте монету 10 раз. Удалось ли вам с первой попытки выбросить де-
сять орлов? Как вы думаете, можно ли считать такое событие маловероят-
ным?
182 Бросьте игральную кость 6 раз. Выпало ли шесть шестёрок? Можно ли счи-
тать такое событие маловероятным?
183 Вероятность выпадения шестёрки на правильной кости равна -. Сколько раз,
о
по вашему мнению, следует ожидать выпадение шестёрки при 600 бросаниях
кости?
184 Игральную кость бросают 6 раз. Является ли, по вашему мнению, маловеро-
ятным случайное событие:
а) шестёрка не выпадет ни разу;
б) какая-то грань выпала более одного раза?
185 Правильную игральную кость бросили 6 раз. Оказалось, что единица выпала
дважды. Означает ли это, что какое-то число очков не выпало ни разу?
186 В тесте по биологии 16 задач с выбором ответа из четырёх предложенных ва-
риантов. Верный вариант только один. Тройку ставят за 4 правильных отве-
та, четвёрку — за 12, а пятёрку — за 15 правильных ответов. Вася не готов
к тесту и выбирает ответы наудачу. Разумно ли ожидать, что Вася получит:
а) отметку «3»; б) отметку «4»; в) отметку «5»?
134
ГЛАВА VI.

Рассеивание
данных
Занимаясь в главах III и IV описательной
статистикой, мы говорили о центральных
мерах. Но для более полного описания из-
менчивых данных нужно знать не только их
среднее, но и то, как данные рассеяны от-
носительно своего среднего.
Чаще всего для описания и измерения рас-
сеивания числовых данных применяются
дисперсия и стандартное отклонение. Мы
расскажем о них.
Кроме того, в этой главе мы познакомимся
с двумя новыми для нас видами диаграмм.
33 Рассеивание числовых данных
34 Отклонения
35 Дисперсия числового набора
36 Стандартное отклонение
числового набора
37 Диаграммы рассеивания
38* Свойства дисперсии
и стандартного отклонения
39* Линейная связь
на диаграмме рассеивания
40* Диаграмма «ящик с усами»

До сих пор, занимаясь в главе III описательной статистикой, мы говорили в ос-
новном о центральных мерах — среднем арифметическом, медиане, об урезанном
среднем. В отличие от центральных мер меры рассеивания показывают, насколько
далеко значения набора отклоняются от его центра.
Из всех мер рассеивания мы пока обсуждали только размах: разность между наи-
большим и наименьшим значениями. Размах легко найти, но у него есть серьёзный
недостаток: он опирается только на наименьшее и наибольшее значения, которые мо-
гут быть нетипичными или даже ошибочными. Для того чтобы лучше описать рассе-
ивание данных в числовом наборе, обычно используются другие меры — дисперсия
и стандартное отклонение.
Рассеивание числовых данных
На рисунке 27 показаны два числовых набора. У них примерно одинаковое сред-
нее значение. Однако сгруппированы значения совсем по-разному. У первого набора
значения * тяготеют» к краям промежутка. Только две точки находятся где-то посере-
дине.
®
®
Рисунок 27 Два числовых набора на координатной
прямой
Напротив, во втором наборе почти все точки группируются вблизи центральных
значений. Ясно, что это свойство наборов нуждается в каком-нибудь математическом
описании.
Эти два набора отличаются рассеиванием. Если данные сильно рассеяны, то мно-
гие значения сильно отклоняются от некоторого среднего значения и изменчивость
высокая. Напротив, при малом рассеивании большинство значений расположено
близко друг к другу и к среднему. В этом случае изменчивость небольшая.
ПРИМЕР. Сергей и Иван живут в одном доме и учатся в одной школе. Занятия
в школе начинаются в 8:30 утра. Каждое утро Сергей выходит из дома ровно
в 7:55 и идёт в школу пешком. Иван каждое утро выходит ровно в 8:00 и идёт к
остановке автобуса. На автобусе до школы всего одна остановка. В таблице 84 пока-
зано время, когда Иван и Сергей входили в школу. Выборка сделана в разные слу-
чайные дни.
Таблица 84. Время прихода в школу
Сергей
Иван
8:15
8:11
8:14
8:19
8:14
8:27
8:15
8:12
8:16
8:35
8:15
8:17
8:25
8:22
8:15
8:13
8:14
8:18
8:16
8:23
136
ГЛАВА VII.

Сергей тратит на дорогу до школы всегда примерно одно и то же время — око-
ло 20 минут. Если посчитать по имеющимся данным, сколько времени в среднем на
дорогу тратит Иван, то получится около 15 минут. Бывает, что Иван добирается до
школы быстро — его лучшее время 11 минут. Но случается, что он опаздывает или
почти опаздывает на первый урок.
Мы видим без вычислений, что рассеивание данных во втором наборе больше. По-
чему так получается? Время, которое тратит на дорогу Иван, складывается из не-
скольких случайных слагаемых. Среди них есть два очень изменчивых: время ожи-
дания автобуса на остановке и время, которое тратит автобус на то, чтобы проехать
одну остановку. Если автобус почему-то задерживается или стоит в пробке, то Иван
рискует опоздать.
Сергей не пользуется автобусом. Время, которое он тратит на дорогу, зависит
только от скорости ходьбы. Она примерно одинакова во все дни: значительно ниже
только в гололёд. Только один раз Сергей пришёл в школу позже обычного. Может
быть, он встретил по дороге что-то интересное и задержался. Или просто в этот день
он позже вышел из дома.
Для измерения рассеивания, конечно, можно использовать размах. В примере про
время в пути размах данных у Сергея 11 минут, а у Ивана — 24 минуты.
Но размах не самая лучшая мера рассеивания. Посмотрите на два набора на ри-
сунке 27. Мы видим, что у первого набора рассеивание больше, но размах у этих
двух наборов практически одинаковый. Так получается потому, что размах учитыва-
ет лишь два значения — наибольшее и наименьшее, которые, как мы знаем, могут
оказаться нетипичными. Именно это происходит в примере на рисунке 27: у второго
набора наименьшее и наибольшее значения «одиноки». Они далеко отстоят от прочих
чисел, и вычислять рассеивание, опираясь на них, неразумно.
Что делать? Можно урезать набор данных с обеих сторон, а потом найти размах.
Самые нетипичные значения исчезнут. Но урезание не решит главной проблемы. Да-
же после урезания размах учитывает всего лишь два значения.
Нужно поискать другие меры рассеивания, которые учитывают все значения в
данном массиве и поэтому меньше подвержены влиянию отдельных значений, чем
размах. Чтобы найти такие меры, сначала нужно посмотреть, как далеко разные зна-
чения в массиве данных отстоят от среднего. Иными словами, нужно изучить откло-
нения от средних значений.
г^М Вопросы
1 Представьте, что вы живёте в том же доме, где живут Сергей и Иван, и учи-
тесь в той же школе, что и они. Как бы вы добирались до школы — пешком
или на автобусе? Что для вас важнее — никогда не опаздывать или сэкономить
в среднем пять минут на дорогу? Опишите достоинства и недостатки обоих
способов.
2 Почему размах не самый лучший способ описания рассеивания данных?
\fj Упражнения
187 Даны два числовых набора. Нанесите их на числовую прямую или изобрази-
те на диаграмме. Сравните рассеивания этих двух наборов. У какого из них
рассеивание больше?
а) 1, 3, 2, 1, 3, 2, 3 и 4, 4, 5, 5, 6, 6, 6
б) 1, 3, 2, 1, 3, 2, 3 и 2, 4, 5, 5, 6, 6, 8
в) 1, 3, 2, 1, 3, 2, 3 и 7, 7, 7, 8, 8, 9, 9
РАССЕИВАНИЕ ДАННЫХ
137

188 На рисунке 28 изображены два числовых набора на координатной прямой. У
какого из них, на ваш взгляд, рассеивание больше?
(D
• •• • • • • • >
Рисунок 28
189 Рассмотрите таблицу 84 «Время прихода в школу». Чтобы вовремя пригото-
виться к уроку, нужно прийти в школу не позже, чем в 8:20. Какова при-
мерно доля случаев, когда:
а) Сергей вовремя готов к уроку;
б) Иван вовремя готов к уроку.
Е)
Отклонения
Поставим вопрос о том, как числа набора данных расположены по отношению
к своему среднему арифметическому. Зная только размах, мы не можем судить об
этом. Полную информацию даёт набор отклонений.
Определение. В наборе чисел отклонением числа от среднего арифмети-
ческого называется разность между этим числом и средним арифметическим
набора.
ПРИМЕР 1. На рисунке 29 изображён набор чисел: 1; 4; 5; 9; 12. Среднее ариф-
метическое равно 6,2. Отклонение числа 9 от среднего равно 9 - 6,2 = -1-2,8. Знак
«+* можно не писать, но мы написали его, чтобы подчеркнуть, что отклонение по-
ложительно. Число 5 на прямой расположено левее среднего арифметического. Это
значит, что его отклонение отрицательно: 5 - 6,2 — -1,2.
-1,2 +2,8
1 4 б Т 9 12
х* 6,2
Рисунок 29. Отклонения на числовой прямой
ПРИМЕР 2. Отклонения чисел образуют новый числовой набор. Для примера
возьмём набор: 1; 6; 7; 9; 12. Среднее арифметическое этого набора равно 7. Найдём
отклонение каждого числа от среднего:
1 - 7 - -в, 6 - 7 - -1, 7-7 = 0, 9-7 = 2, 12-7-5.
138
ГЛАВА VII.

Если число меньше среднего, то его отклонение отрицательно, если число больше
среднего, то его отклонение положительно. В одном случае — для числа 7, которое
совпало со средним арифметическим, — отклонение равно нулю.
Если не все числа в наборе совпадают друг с другом, то часть отклонений поло-
жительна, а часть — отрицательна. При этом сумма всех отклонений у любого набо-
ра равна 0. Убедимся в этом на нашем примере:
-6-1 + 04-2-1-5*0.
Ф
Основное свойство отклонений. Сумма отклонений от среднего арифметиче-
ского равна нулю. Это свойство удобно использовать для самопроверки при вы-
числении отклонений.
Часто важны не сами отклонения, а их модули, то есть абсолютные значения.
\^/ Модуль отклонения называют абсолютным отклонением.
Абсолютное отклонение показывает, как далеко число отстоит от среднего арифме-
тического, но не показывает, в какую сторону — вправо или влево.
ПРИМЕР 3. Среднее арифметическое числового набора 1; 3; 1; 8; 12 равно 5. Чис-
ло 2 левее числа 5 на 3 единицы, а число 8 правее числа 5 на 3 единицы. Следова-
тельно, абсолютные отклонения у этих чисел одинаковы:
|2 - 5| - 3 и |8 - 5| - 3.
По абсолютным отклонениям можно судить о том, велико ли рассеивание чисел
на числовой прямой. Чем меньше в целом абсолютные отклонения, тем меньше рас-
сеяны значения в наборе. На рисунке 30 изображены два числовых набора. Опреде-
лите, в каком из этих наборов отклонения в среднем больше.
а)
б) • и • •••• | | м • •
0 1
Рисунок 30. Два набора с разным рассеиванием
?) Вопркы
(3
1 Сформулируйте определение отклонения числа в наборе данных от среднего
арифметического.
2 Чему равна сумма всех отклонений чисел набора от их среднего арифметиче-
ского?
3 Чему равно среднее арифметическое всех отклонений от среднего арифметиче-
ского в наборе?
4 Что такое абсолютное отклонение?
Упражнения
190 Найдите отклонения от среднего арифметического чисел набора:
а) 1; -2; 3; 4; 1; 2; б) -2,5; 3,1; 5,3; -1,3; 4,8.
РАССЕИВАНИЕ ДАННЫХ
139

191 Дан некоторый числовой набор. Известно, что сумма отклонений от среднего
всех чисел, кроме последнего, равна:
а) 57; б) -4,37.
Найдите отклонение последнего числа.
192 Могут ли все отклонения некоторого набора от среднего арифметического:
а) быть положительными; б) быть отрицательными; в) равняться нулю?
Если не могут, объясните почему. Если могут, приведите пример.
193 Для числового набора 1; 2; 2; 0; 4; 3 найдите:
а) сумму модулей всех отклонений;
б) сумму квадратов всех отклонений.
194 Для данного числового набора найдите абсолютные отклонения чисел:
а) 1; 5; 3; 5; 2; б) 8,4; 4,5; 6,7; 4,4.
195 Дан числовой набор. Найдите в этом наборе два числа, которые имеют оди-
наковое абсолютное отклонение от среднего арифметического,
а) 3; 6; 4; 1; 8; 2; б) 12; 9; 8; 11; 2; 4; 3.
196 Докажите свойство отклонений от среднего арифметического. Пусть дан на-
бор чисел х19 х29 х3> ..., хп9 и их среднее арифметическое равно х. Покажите,
что сумма всех отклонений равна нулю:
(*! - х) + (х2 - х) + (х3 ~ х) + ... + (хп - х) = 0
Дисперсия числового набора
Наиболее полной характеристикой рассеивания чисел в наборе является набор их
отклонений. Но когда набор велик, рассматривать все отклонения неудобно. Нужно
описать разнообразие чисел в наборе одной характеристикой, одним числом. Нужно
взять какое-то среднее отклонение. Но среднее арифметическое отклонений не годит-
ся, поскольку сумма отклонений всегда равна нулю, а поэтому среднее отклонение
тоже равно нулю.
Чтобы судить о разбросе, принято усреднять квадраты отклонений. Квадраты от-
клонений неотрицательны. Чем больше отклонения по модулю, тем больше будет
средний квадрат отклонений. Эту величину называют дисперсией1.
Определение. Среднее арифметическое квадратов отклонений чисел от их
среднего арифметического называется дисперсией набора чисел.
Обычно говорят короче: дисперсия — это средний квадрат отклонений.
ПРИМЕР 1. Найдём дисперсию числового набора: 4; 3; 0; 5. Поместим числа
в первый столбец таблицы 85. В нижнюю ячейку запишем их среднее арифметиче-
ское.
Во второй столбец запишем отклонения от среднего. Мы проводим вычисления
подробно, хотя, конечно, простые вычисления можно делать в уме, помещая в та-
блицу только результат. Чтобы проверить себя, подсчитаем сумму отклонений. Она
должна равняться нулю. В третий столбец таблицы поместим квадраты отклонений.
В нижней ячейке вычислим дисперсию, усреднив числа третьего столбца.
От латинского слова dispersio — рассеивание, разброс.
140
ГЛАВА VII.

ПРИМЕР 2. Возьмём другой на- Таблица 85. Вычисление дисперсии
бор: 3; 3; 2; 4. Сравним этот набор
с набором из примера 1. Среднее
значение также равно 3. Но диспер-
сия другая — она равна 0,5 (про-
верьте, проделав вычисления так же,
как в примере 1).
Числа во втором наборе распо-
ложены более кучно — ближе друг
к другу и к среднему значению 3,
чем числа в первом наборе. Поэтому
дисперсия второго набора меньше.
ПРИМЕР 3. На рисунке 30 изо-
бражены два числовых набора.
В первом наборе (см. рис. 30, а)
числа расположены более кучно, чем во втором наборе (см. рис. 30, б). Это значит,
что дисперсия первого набора меньше, чем дисперсия второго.
ПРИМЕР 4. Континентальный климат отличается от умеренного более резкими из-
менениями температуры в течение года. В районах с континентальным климатом жар-
кое лето и очень холодная зима. С помощью дисперсии различия между двумя вида-
ми климата можно выразить количественно. Сравним изменение температур в течение
года в Москве и Киеве, где климат умеренный, с изменением температур в Новоси-
бирске и Хабаровске, где климат континентальный. В таблице 86 приведена средняя
месячная температура за 80 лет в Москве, Киеве, Новосибирске и Хабаровске.
Таблица 86. Средняя месячная температура, °С
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Среднее за год, °С
Дисперсия, °С*
Москва
-9,3
-8,6
-3,4
5,1
12,4
16,7
18,4
16,6
10,9
4,4
-2,0
-6,8
4,5
98,9
Киев
-5,9
-5,2
-0,4
7,5
14,7
17,8
19,8
18,7
13,9
7.5
1,2
-3,5
6,0
86,5
Новосибирск
-19,0
-17,2
-10,7
-0,1
10,0
16,3
18,7
16,0
9,9
1,5
-9,7
-16,9
-0,1
185,2
Хабаровск
-22,3
-17,2
-8,5
3,1
11,1
17,4
21,1
20,0
13,9
4,7
-8,1
-18,5
-1,4
228,8
Значение
4
3
0
5
Среднее:
х = 3
Отклонение
4-3-1
3-3-0
0 - 3 - -3
5-3-2
Сумма: 0
Квадрат
отклонения
I2-1
о2 - о
(-3)2 = 9
22 = 4
Дисперсия:
1+0+9+4
4 = 3'5
РАССЕИВАНИЕ ДАННЫХ
141

Средняя температура связана с широтой местности: чем севернее, тем ниже сред-
няя годовая температура. Дисперсии температур различаются очень сильно. Для
Москвы и Киева они составляют 98,9 и 86,5 соответственно, для Новосибирска
и Хабаровска — 185,2 и 228,8 соответственно.
Тип климата определяется на основе разных показателей. Главный показатель —
дисперсия средних месячных температур. Дисперсия температур в приморских мест-
ностях невысокая (морской климат), умеренный климат характеризуется более высо-
кой дисперсией месячных температур, а континентальный климат — очень высокой.
Обозначения и формулы
Дисперсию числового набора X обычно обозначают S2. Символ возведения в ква-
драт подчёркивает, что дисперсия является многочленом второй степени1 с перемен-
ными х1э х2, ..., хп. Если нужно подчеркнуть, что дисперсия относится к набору X,
будем писать S£. Запишем формулу дисперсии:
s2 = (*i - xf + (х2 - xf + (х3 - xf + ... + (хп - xf
п
На первый взгляд может показаться, что дисперсию трудно вычислять. Но, во-
первых, в наше время не приходится находить дисперсию вручную; в калькуляторах
и в электронных таблицах есть специальные функции, которые делают это мгновен-
но. Таким образом, трудоёмкость вычисления не является большим недостатком.
Кроме того, у дисперсии есть свойства, которые позволяют упростить вычисления.
Например, есть более простая формула для дисперсии: S2 = x2-x2.
Чтобы понять эту формулу, вспомним, что с помощью надчёркивания мы обозна-
чаем среднее арифметическое. Символ х2 означает средний квадрат, для вычисления
которого сначала все значения набора нужно возвести в квадрат, а затем найти сред-
нее арифметическое получившихся квадратов. Символ х2 означает квадрат среднего
значения, для вычисления которого сначала нужно найти среднее арифметическое
данных, а потом возвести его в квадрат.
Ф
Формулу S2 = x2-x2 можно прочитать так: «Дисперсия равна среднему квадрату
без квадрата среднего».
Таблица 87. Вычисление дисперсии
Значение
4
3
0
5
Среднее: х = 3
Квадрат значения
16
9
0
25
Среднее: х2 = 12,5
ПРИМЕР 5. Возьмём числа из при-
мера 1 и найдём дисперсию по формуле
S2 = х2 - х2. Таблица становится короче,
а вычислений теперь меньше (табл. 87).
Значит, дисперсия равна
S2 - 12,5 - З2 - 12,5 - 9 = 3,5.
1 Если в формуле для дисперсии заменить среднее арифметическое х выражением —————-,
п
возвести каждую скобку в квадрат, привести все подобные члены, то станет видно, что диспер-
сия является суммой одночленов, каждый из которых имеет степень 2.
142
ГЛАВА VII.

ф
Вопросы
1 Почему размах не всегда является подходя-
щей характеристикой для описания рассеи-
вания значений в наборе данных?
2 Дайте определение дисперсии.
3 Даны два набора: 1; 2; 3 и 2; 4; 6. Без вы-
числений определите, у какого из этих на-
боров дисперсия меньше.
4 Как дисперсия средних месячных темпера-
тур в некоторой местности характеризует
климат этой местности?
5 Может ли дисперсия числового набора быть
отрицательной?
0
Для вычисления дисперсии
числового массива в элек-
тронной таблице используйте
функцию
ДИСПР ()
/х =ДИСПР(С1 С5)
С
3
1
3
7
5
D
4,16
■
Ё
Упражнения
Рисунок 31
197 Для данных числовых наборов вычислите среднее значение. Составьте табли-
цу отклонений от среднего и квадратов отклонений от среднего и найдите
дисперсию:
а) -1; 0; 4; г) 2; 6; 7; 5;
б) 2; 3; 7; д) -2; -1; 1; 2; 5;
в) -3; 1; 2; 4; е) -1; -3; -2; 3; 3.
198 Даны два набора чисел. Отметьте их на числовой прямой. Вычислите диспер-
сию каждого из этих наборов. Дисперсия какого набора больше?
а) 2; 3; 7 и 1; 2; 3;
б) 2; 3; 4; 7 и 1; 5; 6; 8.
199 Даны два набора чисел. Отметьте числа на числовой прямой. Определите на
глаз, у какого из наборов рассеивание значений больше. Проверьте ваш гла-
зомер, вычислив и сравнив дисперсии наборов.
а) 2; 3; 4 и 6; 7; 8;
б) 3; 5; 7; 9 и 12; 14; 16; 18.
[зб) Стандартное отклонение
числового набора
Дисперсия — удобная мера рассеивания. Но всё же у неё есть серьёзный недоста-
ток, который затрудняет её практическое применение. Дело в единицах измерения.
Пусть, например, дан массив расстояний в метрах. Среднее арифметическое, медиана
и другие центральные меры тоже будут измеряться в метрах. А вот дисперсия — мно-
гочлен второй степени. Поэтому дисперсия будет измеряться в квадратных метрах.
В таблице 86 (см. п. 35) мы находили дисперсии средних месячных температур.
Обратите внимание на последнюю строчку таблицы: дисперсия измеряется в квадрат-
ных градусах. Это звучит курьёзно, но так и есть.
Чтобы избавиться от этого недостатка, нужно извлечь из дисперсии квадратный
корень. Получается стандартное отклонение.
РАССЕИВАНИЕ ДАННЫХ
143

Определение. Стандартным отклонением называется квадратный корень из
дисперсии.
Формула стандартного отклонения:
g = /(x1-x)2 + (x2-x)2 + (x3-Jc)2-h... + (xn-Jc)2
п
Стандартное отклонение — некоторое среднее1 отклонение чисел набора. Другая
формула для стандартного отклонения:
S = ylx*-x2.
ПРИМЕР 1. В предыдущем параграфе мы нашли дисперсию числового набора
4; 3; 0; 5. Она равна 3,5. Следовательно, стандартное отклонение этого набора равно
>/3,5 ^ 1,87. Посмотрим, как расположены числа на числовой прямой, и отметим на
этой же прямой их стандартное отклонение.
0 1,13 3 4 4,87 5
• -Ч • • I • »
x-S х x+S
Рисунок 32. Числовой набор, среднее и стандартное отклонение
Точками на рисунке 32 показаны числа набора, синяя линия — отрезок, кото-
рый получается, если от среднего арифметического отступить влево и вправо на
одно стандартное отклонение: [x-S; x + S]. В данном случае получился отрезок
[1,13; 4,87]. Точки 3 и 4 попадают внутрь этого отрезка, точки 0 и 5 — вне отрезка.
ПРИМЕР 2. Рассмотрим данные о населении городов Подмосковья (см. табл. 78
на с. 111—112). Удалим два очень больших и одно очень маленькое значение (насе-
ление городов Балашихи, Подольска и Вереи). Найдём среднее и стандартное откло-
нение после удаления этих трёх городов: х * 67,12 тыс. чел., S = 55,97 тыс. чел.
Если отступить на одно стандартное отклонение от среднего влево и вправо, получит-
ся отрезок от 11,15 до 123,09 тыс. чел.
Если население города попадает в этот отрезок, можно считать такой город типич-
ным по численности населения. Города, население которых меньше чем 11,15 тыс.
жителей, можно считать малыми, а города, где больше 123,09 тыс. жителей, можно
считать крупными городами. Тем самым мы выбрали решающее правило, позволя-
ющее определить, что такое малый и что такое крупный подмосковный город. Это
правило основано на одном стандартном отклонении от среднего значения.
Решающие правила можно выбирать разными способами. Можно опираться не на од-
но, а на полтора, два или три стандартных отклонения. Существуют и другие способы.
Стандартное отклонение играет большую роль в массовом производстве. Значи-
тельный износ оборудования приводит к большому рассеиванию параметров готовой
продукции. Следовательно, измерение рассеивания во время контроля качества про-
дукции позволяет косвенно судить о состоянии оборудования.
1 Это среднее не является средним арифметическим. Квадратный корень из среднего квадрата
называют средним квадратичным. Таким образом, стандартное отклонение — это среднее квад-
ратичное отклонение от среднего арифметического.
144
ГЛАВА VII.

Чтобы найти стандартное отклонение
в электронной таблице, можно из-
влечь корень из дисперсии:
КОРЕНЬ(ДИСПР( ))
Но в современных редакторах есть
специальная функция
СТАНДОТКЛОН.Г ()
Рисунок 33
ПРИМЕР 3. На хлебозаводе производится контрольное взвешивание готовой про-
дукции: булок номинальной массой 200 г. В таблице 88 показаны результаты взве-
шивания двух небольших партий, полученных на двух одинаковых производственных
линиях. В двух правых столбцах указаны среднее арифметическое и стандартное от-
клонение масс по сделанной выборке.
Таблица 88. Контрольное взвешивание двух партий
Номер
пробы
Масса булки, г
Линия 1
Линия 2
1
193
195
2
195
191
3
195
201
4
194
197
5
192
204
в
194
202
7
196
196
8
195
196
9
193
205
10
192
199
Сред-
нее
ариф-
мети-
ческое
193,9
198,6
Стан-
дарт-
ное
откло-
нение
1,30
4,18
Масса готовой булки зависит от количества теста,
которое отмерил дозирующий автомат. В первой пар-
тии среднее отклонение от номинального значения
равно 6,1 г, во второй партии — только 1,4 г. Ка-
залось бы, первая линия работает лучше. Но посмо-
трим на стандартное отклонение: в партии продук-
ции, взятой со второй линии, оно равно 4,18 г, а в
первой партии — только 1,3 г.
Это означает, что вторая линия требует серьёзно-
го ремонта, возможно, замены некоторых деталей.
А первая линия работает нормально и требует всего лишь небольшой регулировки,
чтобы дозатор отмерял примерно на 6—7 г теста больше, чем сейчас.
* fx =СТАНД0ТКЛ0Н.Г(С1:С5)
С
3
1
3
7
<L
D
2,039608
Е
1
F
РАССЕИВАНИЕ ДАННЫХ
145

При производстве массовой продукции высокое рассеивание параметров го-
товой продукции (массы, размеров и т. п.) может говорить о большом износе
оборудования и необходимости ремонта.
Смещение средних значений параметров при низком рассеивании, как правило,
устраняется регулировкой.
Вопросы
1 Что такое стандартное отклонение? Напишите формулу для вычисления стан-
дартного отклонения.
2 Чему равно стандартное отклонение числового набора, если его дисперсия рав-
на 4?
3 Дан массив измерений массы шоколадных плиток в граммах. В каких единицах
измеряется дисперсия? В каких единицах измеряется стандартное отклонение?
4 Может ли стандартное отклонение быть отрицательным?
Упражнения
200 Найдите стандартное отклонение числового набора, если его дисперсия равна:
а) 25; б) 121; в) 3,24; г) 1,69.
201 В числовом наборе 10 чисел, а стандартное отклонение равно 0. Приведите
пример такого набора.
202 Найдите стандартное отклонение набора данных. Результат округлите до сотых.
а) 1; 3; 5; 1; 3;
б) 0,2; 0,4; 1,1; 1,4; 0,7;
в) 234; 432; 521; 211; 424; 233;
г) -0,21; -0,23; -1,34; -0,43; -0,34.
203 Дан набор из десяти чисел: 4; 3; 2; 1; 9; 7; 2; 7; 1; 4.
Найдите среднее и стандартное отклонение (с точностью до сотых).
а) Найдите отрезок, который получается, если отступить от среднего влево
и вправо на одно стандартное отклонение.
б) Какие значения попадают в этот отрезок?
в) Какие значения расположены левее левой границы этого отрезка?
г) Какие значения расположены правее правой границы?
204 Дан набор из десяти чисел: -3; 3; -5; 7; -6; 6; -4; 3; -1; 0.
Найдите среднее и стандартное отклонение (с точностью до сотых).
а) Найдите отрезок, который получается, если отступить от среднего влево
и вправо на одно стандартное отклонение.
б) Какие значения попадают в этот отрезок?
в) Какие значения расположены левее левой границы этого отрезка?
г) Какие значения расположены правее правой границы?
205 Удалите из таблицы 78 города Балашиху, Подольск и Верею. В примере 2
вычислено среднее и стандартное отклонение населения оставшихся городов:'
х = 67,12 тыс. чел., S — 55,97 тыс. чел. Будем считать подмосковный город
малым, если его население меньше чем х - S. Перечислите малые города.
146 ГЛАВА VII.
Ф

206 Удалите из таблицы 78 Балашиху, Подольск и Верею. В примере 2 вы-
числено среднее и стандартное отклонение населения оставшихся городов:
х = 67,12 тыс. чел., S = 55,97 тыс. чел. Будем считать подмосковный город
очень крупным, если его население больше чем х + 2S. Перечислите очень
крупные города. Подумайте, какие общие черты есть у этих городов.
^37) Диаграммы рассеивания
Часто бывает полезно знать, есть ли некоторая связь между изучаемыми величи-
нами и, если есть, то какова она. Разобраться в этом помогает диаграмма рассеива-
ния. Покажем на примере, как её построить.
ПРИМЕР 1. Есть ли связь между ростом и весом человека? Для наглядного ответа
построим диаграмму рассеивания. Данными для этой диаграммы служат пары чисел.
Каждая пара — это рост и вес одного человека. В таблице 89 приведены значения
роста и веса 15 юношей.
Таблица 89. Рост и вес 15 юношей
Рост, см
Вес, кг
Рост, см
Вес, кг
167
62
174
73
169
67
175
66
179
70
180
75
178
72
174
70
177
70
172
67
175
69
178
74
171
63
171
66
181
80
Диаграмма 35. Рост — вес
85
80
70
65
60
1 | | 1 t I i m
I 1111т
II I 1 I т I
Till
1т
—1 t i ? 1**1—
] • I
• T
I | • J I • J I |
• I
Чтобы получить диаграмму рассеива-
ния, нужно в системе координат построить
точки, абсциссы которых — рост, а орди-
наты — соответствующий вес. Получаем
диаграмму 35.
Точки на диаграмме образуют облако
рассеивания, или, более поэтично, созвез-
дие. Видно, что на построенной диаграм-
ме точки группируются вдоль некоторой
наклонной прямой, направленной вправо
и вверх.
Это значит, что между величинами
«рост» и «вес», скорее всего, имеется поло-
жительная связь: в целом чем человек
выше, тем больше он весит. Разумеется,
в каждом конкретном случае это правило может нарушаться. Например, в таблице
есть юноша ростом 179 см и весом 70 кг и юноша ростом 174 см и весом 73 кг. Но
такая ситуация скорее исключение.
Диаграмма рассеивания — способ представления двух совместно наблюдае-
мых величин точками на координатной плоскости. Когда точек много, они обра-
зуют облако рассеивания.
166 168 170 172 174 176 178 180 182
Рост, см
РАССЕИВАНИЕ ДАННЫХ
147

По форме и расположению облака рассеивания можно составить наглядное пред-
ставление об отсутствии связи или наличии связи и её характере. Чтобы лучше
увидеть форму и наклон облака, можно обвести облако фломастером или каранда-
шом.
Диаграмма 36. Длина прыжка —
время забега на 60 м
СО
«
»
О!
S
&
п
121
11,5
11
10,5
10
9,5
9
i
•
< •
х^
\
•
•
•
^v •
\
• \
>
ПРИМЕР 2. На диаграмме 36 наблюдает-
ся вероятная связь между длиной прыжка и
временем забега на 60 м у школьников одной
и той же группы. Видно, что связь отрица-
тельна — чем дальше школьник прыгает, тем
меньше время забега, хотя случается, что тот,
кто далеко прыгает, бегает медленно.
ПРИМЕР 3. Самочувствие человека во мно-
гом определяется температурой тела и арте-
риальным давлением. По данным обследова-
ния нескольких больных построена диаграмма
рассеивания (диагр. 37).
150 170 190 210
Длина прыжка, см
230
Диаграмма 37. Температура тела — артериальное давление
36
36,5
37
37,5 38 38,5
Температура, °С
39
39,5
40
Облако рассеивания овальное, но оно вытянуто вдоль горизонтальной оси и не
имеет наклона. Можно предположить, что связи между давлением и температурой
тела нет: значения одной величины не влияют на значения другой. У человека, за-
болевшего ангиной или гриппом, может быть высокая температура, но артериальное
давление может быть нормальным.
Если облако не имеет явного наклона, то можно предположить, что связь отсут-
ствует.
По форме облака можно не только предположить наличие связи, но и оценить её
силу. Чем уже облако, чем плотнее точки прилегают к некоторой линии, тем сильнее
наблюдаемая связь. На рисунке 34, а—в показаны три случая: сильная связь, слабая
связь и вероятное отсутствие связи.
148
ГЛАВА VII.

а)
У
фф
фф® ф
ффф
фф •
фф •
• ффф
•%• в
фф ф
ф фф
ф
X
Сильная положительная
связь
б)
У
(ft • ®
••• ф
° ° ©
ф • • •
L° • • •
в ф
ф
X
Слабая положительная
связь
в)
0 ф ф © о ®~|
о в ©
° о о о
Q • ° о
°<й °
о
• • ф о •
0 0© |
X
Вероятно, нет связи
Рисунок 34
ПРИМЕР 4. На диаграммах 38 и 39 показано взаимное рассеивание величин «Цена
нефти в долларах США за баррель» и «Стоимость рубля в долларах США». На диаграм-
ме 38 представлены данные за несколько месяцев 2013 г., на диаграмме 39 — данные
Диаграмма 38. Цена нефти — курс рубля, 2013 г.
0,034
Д 0,0335
и
О 0,033
Об
§ 0,0325
Ч 0,032
>>
& 0,0315
й
0,031
"Й8Г*
102,00 104,00 106,00 108,00 110,00 112,00 114,00 116,00 118,00 120,00
Цена нефти, долларов США за баррель
0,0161
4! 0,016
§ 0,0159
О 0,0158
си
об
5 0,0157
О
* 0,0156
«
х§ 0,0155
^ 0,0154
.£ 0,0153
Диаграмма 39. Цена нефти — курс рубля, 2019 г.
0,0152
• ••
г*
• *ч
60,00 62,00 64,00 66.00 68,00 70,00 72,00 74.00 76,00
Цена нефти, долларов США за баррель
РАССЕИВАНИЕ ДАННЫХ
149

за несколько месяцев 2019 г. Если на первой диаграмме хорошо прослеживается по-
ложительная связь, то, судя по второй, можно предположить отсутствие связи или
настолько слабую связь, что визуально её обнаружить невозможно.
Ф
Важно! Диаграмма рассеивания — не доказательство наличия или отсутствия
связи. С помощью диаграммы мы лишь можем предположить, что связь есть или
что её нет. Чем больше наблюдений, тем более обоснованно предположение.
Наличие связи не означает, что одна величина обусловлена другой. Наблюда-
емая связь далеко не всегда причинно-следственная. Механизм связи может
быть сложным. Часто обе величины зависят от какой-нибудь третьей величины,
а не друг от друга.
Например, рассматривая диаграмму 36 «Длина прыжка — время забега на 60 м»,
нельзя сказать, что школьник дальше прыгает потому, что быстрее бегает, или наобо-
рот. Общее физическое развитие, рост, тренированность обусловливают обе величины.
Вопросы
1 Зачем используются диаграммы рассеивания?
2 Как выглядит облако в случае положительной связи? отрицательной связи?
3 Как выглядит облако, показывающее сильную связь между двумя величинами?
4 Что можно предположить, если облако на диаграмме рассеивания вытянуто
вдоль горизонтальной или вертикальной прямой?
0
Упражнения
207 Для следующего набора пар значений постройте диаграмму рассеивания:
а) (1; 2), (2; 2), (3; 2), (3; 4), (4; 5), (5; 6), (4; 3), (4; 4), (в; 6);
б) (1; 2), (2; 3), (3; 3), (3; 4), (3; 2), (4; 3), (4; 4), (5; 2), (6; 3).
Можно ли предположить положительную связь между величинами?
208 В таблице 90 приведены данные о весе и росте 12 девушек.
Таблица 90. Рост и вес 12 девушек
Роет, ем
Вес, кг
165
53
177
67
161
45
162
53
170
60
176
62
177
58
164
60
166
62
161
55
169
55
159
49
Постройте диаграмму рассеивания. Наблюдается ли связь между ростом и ве-
сом девушек?
209 Охарактеризуйте две данные диаграммы рассеивания (диагр. 40—41), ответив
на следующие вопросы:
1) Можно ли предположить наличие связи между двумя величинами?
2) Если связь есть, то положительная она или отрицательная?
3) Если связь есть, то сильная она или слабая, на ваш взгляд?
150
ГЛАВА VII.

Диаграмма 40. Широта местности — среднегодовая температура воздуха
25,0
20,0
15,0
10,0
ее
а
0)
Р 5,0
Я
S
g 0,0
I зо
8
а -5,о
-10,0
-15,0
•
1
•
•
<
•
40
•
•
•
*
•
•
50
•
f
•
•
• 1
•
•
•
•
60
•
• •
•
• 70
•
•
•
-►
Градусы северной широты
Диаграмма 41. Плотность — температура плавления металла
4000
3500
u зооо
о
§ 2500
Я
0)
2 2000
н 1500
1000
500
0
5 Ю 15
Плотность, г/см3
20
25
210 Фигуристы получают две оценки: за технику и за артистизм. В таблице 91
даны оценки одного судьи выступлений различных фигуристов на одном со-
ревновании.
РАССЕИВАНИЕ ДАННЫХ
1

Таблица 91. Оценки выступлений фигуристов
Техника
Артистизм
4,3
4,5
4,5
4,2
4,5
4,6
4,8 4,9
4,5 5,1
5,2
5,2
5,4
5,6
5,0
5,1
5,5
5,6
5,8
5,9
!
5,7 |
5,8
Постройте диаграмму рассеивания. Наблюдается ли связь между оценками за
технику и оценками за артистизм?
211 В таблице 92 приведены данные о числе голов, забитых лучшими напада-
ющими команд премьер-лиги чемпионата России по футболу, и месте их
команд в чемпионате.
Таблица 92. Результаты лучших нападающих
Игрок
Чалов Федор
Азмун Сердар
Классон Виктор
Дриуссн Себастьян
Миранчук Антон
Зе Луиш
Команда
ЦСКА (Москва )
Зенит (Санкт-Петербург)
Краснодар
Зенит (Санкт-Петербург)
Локомотив (Москва)
Спартак (Москва)
Число голов
15
13
12
11
11
10
Место
4
1
3
1
2
5
Постройте диаграмму рассеивания. Можно ли утверждать, что чем больше
голов забивают нападающие, тем выше место их команды в чемпионате?
Свойства дисперсии
и стандартного отклонения
Мы знакомы со свойствами среднего арифметического. Напомним вкратце: если
сместить все числа набора вправо или влево на одно и то же число, то среднее ариф-
метическое смещается так же. Если умножить все числа набора на одно и то же чис-
ло, то среднее арифметическое тоже умножается на это число.
Дисперсия и стандартное отклонение измеряют не положение чисел набора на чис-
ловой прямой, а рассеивание, поэтому они не зависят от того, где именно располо-
жены числа, но зависят от того, как числа расположены по отношению друг к другу
и к среднему арифметическому. Как именно проявляется эта зависимость, показыва-
ют свойства дисперсии и стандартного отклонения.
\^у Свойство 1. Если все числа набора увеличить или уменьшить на одно и то же
число, то дисперсия и стандартное отклонение не изменятся.
Свойство 1 объясняется просто — при сдвиге всех чисел на одно и то же число
среднее арифметическое двигается вместе с ними, и поэтому отклонения не меняют-
ся. Вместе с отклонениями неизменной остаётся и дисперсия.
152
ГЛАВА VII.

\^у Свойство 2, Если все числа набора умножить на одно и то же число к, то дис-
персия умножается на Л2, а стандартное отклонение умножается на | к |.
Например, при умножении всех чисел на 2 дисперсия увеличится в 4 раза, а при
умножении всех чисел на 0,1 дисперсия уменьшится в 100 раз.
Докажем свойства дисперсии на примере небольшого набора, в котором три числа. Ес-
ли чисел в наборе больше, то все рассуждения и преобразования будут точно такими же.
Доказательство свойства 1. Пусть дан набор X = {х1э х2, х3}. Прибавим к каждому
значению некоторое число а. Получим набор чисел:
хх 4- а, х2 + а, х3 + а,
который можно символически обозначить как X + а. Нужно показать, что дисперсия
не изменилась, т. е. S\ + Q * S*.
Среднее арифметическое набора X равно х. Тогда среднее арифметическое набора
X + а равно х + а. Воспользуемся основной формулой дисперсии:
(*х + а - (х + а))2 4 (х2 + а - (х 4 а))2 + (х3 + а - (х + а))2
Sx+u » 3
Раскрывая внутренние скобки и приводя подобные, получаем
С2 _ (*1 Z *)' 1 (*2 Z *)' + (*» " *)' ж С2
0Х+а О £>*•
Дисперсия не изменилась, значит, стандартное отклонение тоже не изменилось.
Доказательство свойства 2. Умножим все числа набора X на произвольное число к.
Получим числовой набор кХ « {кхи кх2, кх3). Среднее арифметическое набора kX
равно кх. Тогда 2 2 _ 2
2 _ (/e*i - кх) 4 (fex2 - foe) 4- (fex3 ~" кх)
ькХ- з
Вынесем множитель к за скобки:
g2 = ^2(*1~*) + (*2~*) + (*8~*) = fe2g2
Чтобы доказать это свойство для стандартного отклонения, извлечём из обеих ча-
стей полученного равенства квадратный корень:
&kx ж yjSkx e yJk2Sx e \k\Sx*
Свойство доказано.
В п. 35 мы указали короткую формулу для дисперсии: S2 = x2-x2. Выведем её.
Для вывода тоже будем использовать набор из трёх чисел. В определении дисперсии
S2 « (*i - *f + (*2 ~ *¥ + (*з ~ xf
возведём каждую скобку в квадрат:
Q2 (xf - 2ххх + х2) 4 (х$ - 2хгх 4 х2) + (xf - 2х& 4 х2)
^ " 3
Теперь перегруппируем слагаемые:
g2 _ xf + xf + xf - 2(xjX 4 X2x -f хэх) 4 3 - x2
РАССЕИВАНИЕ ДАННЫХ
153

Разобьём правую часть на три слагаемых:
е2 х? + *| + *з 2хгх + 2*2* + 2*э* , 3 х2
^ в л ^ ' —л—•
3 3 3
Первое слагаемое равно среднему квадрату значений, т. е. х2. Во втором слагаемом
~ ~ о- 2ххх + 2*2* + 2*а* rt_Xi + х2 + х3 rt_ - 0_9
вынесем за скобки общий множитель 2х: — — — = 2х— = 2х • х = 2х\
3 3
Третье слагаемое равно х2. Получается
S2 - х2 - 2х2 + х2 - х* - х2,
что и требовалось доказать.
©
0
Вопросы
1 Сформулируйте свойства дисперсии и стандартного отклонения.
2 Как изменится дисперсия набора, если все числа уменьшить на 8?
3 Как изменятся дисперсия и стандартное отклонение набора, если все числа ум-
ножить на -3?
Упражнения
212 Дисперсия набора данных равна 4. Все значения в наборе умножили на 3.
Найдите дисперсию получившегося набора.
213 Дисперсия набора равна 4. Все числа набора умножили на 0,5. Найдите дис-
персию получившегося набора.
214 Набор X имеет среднее х = 3 и дисперсию S% = 1,5. Найдите среднее значе-
ние и дисперсию набора:
а) X - 2 (все числа уменьшили на 2); в) X + 0,45;
б) X + 4 (все числа увеличили на 4); г) X - 2,3.
215 Набор X имеет среднее х =-2и дисперсию S* = 1,44. Найдите среднее зна-
чение, дисперсию и стандартное отклонение набора:
а) 2Х (все числа умножили на 2); в) -2,5Х;
б) -ЗХ (все числа умножили на -3); г) 1,5Х.
216 Набор X имеет дисперсию S* e 9. Найдите дисперсию и стандартное откло-
нение набора:
а) 2Х - 1 (все числа умножили на 2, а затем уменьшили на 1);
б) -4(Х + 5) (все числа увеличили на 5, а затем умножили на —4);
в) -1,2Х - 5,4;
г) 2,5(Х - 4,3).
217 Чтобы перевести температуру из градусов Фаренгейта в градусы Цельсия или
обратно, используют формулы
5
tc = -(*F-32) и tF = 1,8*с + 32.
Например, температура замерзания воды равна 0 °С„ Чтобы выразить эту
температуру в градусах Фаренгейта, применим вторую формулу:
tF - 1,8 • 0 + 32 - 32 (°F).
а) Температуру воздуха в помещении измеряли в градусах Фаренгейта каж-
дые 20 минут. Средняя температура равна 86 °F, стандартное отклонение
154
ГЛАВА VII.

равно 1,8 °F. Выразите среднюю температуру и стандартное отклонение
в градусах Цельсия.
б) Температуру тела спортсмена измеряли после каждого упражнения. По-
лучился массив данных со средним 36,8 °С и со стандартным отклонением
0,5 °С. Выразите среднюю температуру и стандартное отклонение в градусах
Фаренгейта. Результаты округлите до десятых.
218 Дан числовой набор X со средним значением 1 и дисперсией 16. Из набора X
X -1
получили набор Z = —-—. Найдите среднее и дисперсию набора Z.
4
219 Дан числовой набор X со средним значением х и стандартным отклонением S.
X — х
Из набора X получили набор Z = —-—. Найдите среднее значение и диспер-
сию набора Z.
Линейная связь
на диаграмме рассеивания
Иногда можно предположить, что между двумя величинами должна быть линей-
ная связь (иногда даже прямая пропорциональность).
ПРИМЕР 1. Количество станций и протяжённость линий метрополитена. Расстоя-
ния между соседними станциями одной линии московского метро различаются, но не
очень сильно. Поэтому можно предположить, что если одна линия метро в два раза
длиннее другой, то и станций на первой линии примерно в два раза больше.
ПРИМЕР 2. Количество жильцов в квартире и расход воды. Если в квартире жи-
вёт семья из трёх человек, то они, вероятно, потребляют в 3 раза больше воды, чем
тот, кто живёт один. В целом это так, но потребление воды зависит от того, сколько
времени люди проводят дома, какие у них привычки, исправна ли сантехника. По-
этому линейная связь есть, но она не жёсткая.
ПРИМЕР 3. Площадь и население города. Можно предположить, что если один город
в пять раз больше другого по площади, то и количество жителей в первом городе при-
мерно в пять раз больше. Сразу скажем, что это предположение неверно. Можете найти
данные в Интернете для двух-трёх десятков городов и построить диаграмму рассеива-
ния. Увидите, что связь между площадью и населением города не прослеживается.
Если есть основания думать, что линейная связь между величинами есть, то с по-
мощью диаграммы рассеивания можно опровергнуть это предположение или, если
связь подтверждается, наглядно оценить её силу. Если же мы не знаем характера
связи, то с помощью диаграммы можно высказать лишь осторожные предположения.
Для проверки нужны более сложные методы.
Из алгебры известно, что линейная зависимость (функция) между двумя перемен-
ными графически описывается наклонной прямой у = kx + Ь. Поэтому можно сфор-
мулировать следующее правило:
Если точки в облаке рассеивания сгруппированы около некоторой наклонной
прямой, то между наблюдаемыми величинами, вероятно, есть линейная связь.
По направлению наклона можно указать характер связи — положительная связь
или отрицательная.
w
РАССЕИВАНИЕ ДАННЫХ
155

ПРИМЕР 4. Рассмотрим диаграмму рассеивания «Длина прыжка — время забега
на 60 м», с которой мы работали в примере 2 на с. 148.
Точки на диаграмме 42 расположены вдоль некоторой прямой. Связь отрицатель-
на, поэтому угловой коэффициент прямой отрицателен, т. е. соответствующая линей-
ная функция убывает.
W
Прямую, около которой группируются точки облака рассеивания, называют осью
диаграммы рассеивания. Если связь положительна, то угловой коэффициент
оси диаграммы также положителен. Если связь отрицательна, то угловой коэф-
фициент отрицателен.
Диаграмма 42. Длина прыжка
время забега на 60 м
v i
N^ 13
12,5
12
11,5
•>
[ забег
>
S
Bpei
*
>
1U
9,5
9
i
v •
•
i >^
•
•
V#
^v <
•
>
•^^
-►
150
170 190
Длина прыжка, см
210
230
Провести ось диаграммы рассеивания можно разными способами1. Мы будем поль-
зоваться простейшим — глазомерным способом, то есть будем на глаз проводить пря-
мую, которая хорошо описывает рассеивание данных. Прямая должна пройти вдоль
облака, «протыкая» его посередине. Чтобы описать линейную связь количественно,
нужно написать уравнение оси.
ПРИМЕР 5. На диаграмме 43 показана связь между протяжённостью линий и ко-
личеством станций на линиях московского метро, включая МЦК2, действующие цен-
тральные диаметры и монорельсовую дорогу. Проведём на глаз ось диаграммы.
1 Чаще всего на практике применяется метод наименьших квадратов. Он состоит в том, что пря-
мую нужно провести так, чтобы дисперсия вертикальных отклонений точек от оси диаграммы
была наименьшей. Отсюда и название метода.
2 МЦК — Московское центральное кольцо — кольцевая железнодорожная пассажирская линия.
156
ГЛАВА VII.

i
OK •
oo"
ОЛ.
oO*
|25-
Количество
D СЛ С
1U"
5"
ь
Диаграмма 43.
' 1 i j
i i i
i
—
—
|
l
t
~r~
1
i
.._.
1
1 1
l>>^
^So: 1,25)
1
^x
•
Протяжённость
1
i
1
i
i
i
i
ii
•
•
• j
•
i i !
1
1 j
1
f
i
\
-H-
•
i
1
—
линий
•—-
i
1
количество <
•
A(36; 20)^,
—
r
i
i !
j
! 1
1 »
»
■'•-
i
,
r
станций
;
1 I
i • !
y-fct + bl^
■L-
K
И^ 1 '
!
1
" "i
. * P4-!
I i
■-ft-
i
—1
1—I
—
—
f 1
'
1
-►
10
20
30
40
50
Протяжённость
линий, км
Чтобы описать предполагаемую связь, нужно составить уравнение проведённой
прямой в виде у -■ kx + b. Масштабы по оси абсцисс и по оси ординат разные, но
это не мешает. Возьмём на прямой две удобные точки.
Первую точку лучше всего взять на пересечении прямой с осью ординат. Это точ-
ка В на рисунке. Её ордината равна примерно 1,25. Значит, Ь = 1,25.
Вторую точку лучше взять подальше от точки В. Есть удобная точка А с ко-
ординатами (36; 20), которые хорошо видны на сетке.
Чтобы найти угловой коэффициент А, подставим координаты точки А и известное
значение Ь в уравнение прямой у = kx + Ь:
20 - к • 36 + 1,25, откуда к « 0,52.
Получаем уравнение оси диаграммы: у = 0,52х + 1,25, где х
линии метро в километрах, а у — количество станций на ней.
протяженность
Ф
Важно! Многие ошибочно считают, что сила связи проявляется в наклоне оси
диаграммы: чем угловой коэффициент больше по модулю, тем связь сильнее.
Это неверно. Угол наклона зависит от соотношения масштабов, выбранных на
координатных осях. Сила связи проявляется в том, насколько плотно облако
рассеивания прилегает к оси диаграммы.
Иногда облако на диаграмме имеет сложную форму. Это означает, что связь между
величинами не является линейной, а имеет более сложный характер. На диаграмме 44
показаны данные о пробеге и цене подержанных автомобилей одной и той же модели.
На горизонтальной оси отмечен пробег (в километрах), на вертикальной — цена
(в рублях).
РАССЕИВАНИЕ ДАННЫХ
157

Диаграмма 44. Пробег — цена подержанного автомобиля
и
i
600 000
550 000 ""
500 000 ~
А **П ППА —
40U UUU
4 ftft ПОП —
Q^OOfin —
оэи иии
Я ПО ООП -
лои иио —
ОЛП ПАП —
&UU UUU
150 000 -
к
•
•
•
•
•
•
•
•
•
•
•
• •
1
•
•
-+
*
•
•
•
• •
• • •
• щ т —
• • • •
•
1 1
•
• •
— •
•
• *
•
•
|
•
•
•
•
-Ч—
•
•
•
•
—н-
•
•
—►
0 20 000 40 000 60 000 80 000 100 000 120 000 140 000
Пробег, км
Облако рассеивания имеет изогнутую форму. Это означает, что связь между про-
бегом и ценой подержанного автомобиля есть, но она нелинейная. Нелинейные связи
изучать сложнее, чем линейные.
• • •
: •
• . .
• • •
• • •:
• •
• • •
Рисунок 35. Примеры нелинейных связей на диаграммах рассеивания
^fj Вопросы
1 Если две случайные величины связаны линейной зависимостью, то как распола-
гаются точки на диаграмме рассеивания этих величин?
2 Как называется прямая, около которой группируются точки на диаграмме рас-
сеивания двух величин, между которыми есть линейная связь?
3 Точки на диаграмме оказались расположены около некоторой прямой. Можно ли
предположить, что между изучаемыми величинами есть линейная связь? Можно
ли это утверждать наверняка?
158
ГЛАВА VII.

4 Между двумя величинами предполагается линейная связь, однако облако рассей-
вания имеет сложную изогнутую форму. Какие выводы можно сделать?
5 Верно ли, что чем больше угол наклона оси облака, тем теснее (сильнее) ли-
нейная связь между двумя изучаемыми величинами?
6 Как проявляется на диаграмме рассеивания сила линейной связи между изучае-
мыми величинами?
Упражнения
220 Рассмотрите диаграммы 40—41 (см. с. 151). Есть ли основания думать, что
наблюдается линейная связь между величинами, представленными:
а) на диаграмме 40; б) на диаграмме 41;
221 На диаграмме рассеивания отражены данные о числе линий и числе станций
в 16 крупнейших метрополитенах мира. Четыре разных человека провели че-
тыре оси на этой диаграмме.
Диаграмма 45. Число линий — число станций крупнейших метро в мире
0
Какая из осей, по вашему мнению, наилучшим образом описывает наблюдае-
мую связь?
РАССЕИВАНИЕ ДАННЫХ
159

222 На диаграммах рассеивания «Дальность прыжка — время забега на 60 м»
(диагр. 46) и «Рост — вес человека» (диагр. 47) глазомерным методом по-
строены оси. Напишите уравнения осей диаграмм (достаточно приблизитель-
но определить коэффициенты).
Диаграмма 46. Дальность прыжка — время забега на 60 м
150 170 190 210
Длина прыжка, см
230
Диаграмма 47. Рост — вес человека
б) 85
165
170
175
Рост, см
180
185
40*1 Диаграмма «ящик с усами»
В п. 18 мы рассказывали о ящичковых диаграммах, с помощью которых числовой
массив изображается прямоугольником (ящиком) на числовой прямой.
Ящичковые диаграммы используются не только для наглядного представления
массива, но и для того, чтобы определить, какие именно значения являются выбро-
сами, то есть слишком далеко отстоят от всех прочих значений. Чтобы определить
выбросы, нужно принять какое-то правило.
160
ГЛАВА VII.

Таблица 93. Площадь лесных
территорий (122 страны), тыс. км2
Первый квартиль
Медиана
Третий квартиль
Среднее арифметическое
Кх - 29,1
82,4
К3 - 193,6
331,1
Во многих приложениях статистики вы-
бросами считают значения, которые оказы-
ваются за пределами интервала длиной че-
тыре межквартильных размаха.
ПРИМЕР. Построим диаграмму по дан-
ным о площади лесных территорий в стра-
нах мира. Будем учитывать только страны,
где есть хотя бы 10 тыс. км2 лесных терри-
торий. Соберём из источников данные и со-
ставим небольшую табличку (табл. 93).
Построим теперь диаграмму. Единичный отрезок — 1 тыс. км2. Тело диаграммы —
сам ящик — заключено между квартилями Кх = 29,1 и К3 = 193,6 и имеет протя-
жённость, равную межквартильному размаху: К3 - Кх = 164,5. Осталось пририсовать
к ящику справа и слева усы длиной по полтора межквартильных размаха, то есть по
1,5(/Сз - Кх) — 246,75. Концы усов удобно отмечать вертикальными засечками.
Сначала левый ус. Чтобы найти его левый конец, от левой границы ящика Кх
отступаем влево полтора межквартильных размаха:
Кх - 1,5(^з - Кх) - 29,1 - 1,5 • 164,5 * -217,7.
Аналогично находим правый конец правого уса:
К3 + 1,5(#з - Кх) * 440,4.
Изобразим все полученные сведения на ящичковой диаграмме.
Диаграмма 48. Площадь лесных территорий (122 страны), тыс. км2
82,4
-217,7
Левый
конец
440,4
— —*-
331.1 I 515,1
Правый
-X-
29,1
193,6
конец
(Бразилия)
809,2
(Россия)
4 межквартильных размаха
Примерно половину значений, а именно — те, которые попали внутрь самого ящи-
ка, можно считать наиболее типичными значениями массива. Те значения, которые не
попали в ящик, но находятся внутри интервала, охваченного усами, можно считать не
очень типичными, но всё же они не очень сильно выбиваются из общей массы.
Те значения, которые находятся за пределами усов — выбросы. В нашем примере
это два значения: тропические леса Бразилии (515,1 тыс. км2) и лесные угодья Рос-
сийской Федерации (809,2 тыс. км2).
Обратите внимание: среднее арифметическое (331,1 тыс. км2) оказалось за преде-
лами ящика, но всё же внутри усов.
Решающее правило определения выбросов, которое мы использовали здесь, очень
распространённое: выбросами считаются значения, не попадающие в интервал дли-
ной четыре межквартильных размаха (по полтора с каждой стороны ящика). Такое
правило не единственное возможное. Можно брать не полтора, а один или два меж-
квартильных размаха с каждой стороны. Иногда длина усов определяется не меж-
квартильным размахом, а связана со стандартным отклонением, и тогда усы откла-
РАССЕИВАНИЕ ДАННЫХ
161

дываются от среднего арифметического. В каждом приложении статистики сформиро-
вались свои правила, зарекомендовавшие себя десятилетиями.
©
0
223
Статистическое исследование. Постройте диаграмму ящик с усами по дан-
ным о численности населения субъектов Российской Федерации. В каких реги-
онах России численность населения можно считать нетипичной? Сделайте такую
же диаграмму для плотности населения регионов.
Вопросы
Что такое межквартильный размах?
Как с помощью диаграммы ящик с усами определить, какие значения в данном
массиве являются выбросами?
Может ли среднее арифметическое не попасть внутрь ящика?
Может ли медиана не попасть внутрь ящика?
Упражнения
Для некоторых данных построен ящик с усами (рис. 36).
Определите примерно квартили, медиану и среднее арифметическое данных.
-8,3
7,7
Рисунок 36
224 Для некоторых данных построен ящик с усами (рис. 37).
а) Определите примерно медиану и среднее арифметическое данных.
б) Является ли выбросом число 12 для этого набора данных?
1.6
5,5
Рисунок 37
225 Дан числовой набор. Постройте для него ящик с усами. Пользуясь правилом
«четыре межквартильных размаха*, найдите выбросы в данном наборе.
а) 1, 0, 3, 1, 2, 2, 1, 5, 2, 3, 2, 1, 12;
б) -8, -4, -4, -3, -5, 4, 0, -1, -2, -2;
в) 741, 743, 741, 742, 745, 760, 767, 751, 743, 743, 743.
226 Для наборов, данных в предыдущей задаче, измените правило: выброса-
ми считайте те значения, которые не попадают в интервал от х - 2S до
х + 2S, где х — среднее арифметическое, a S — стандартное отклонение.
Усы при этом следует откладывать не от краёв ящика, а от среднего арифме-
тического. Сравните результаты, полученные при новом правиле, с результа-
тами задачи 1.
162
ГЛАВА VII.

Математическое
описание
случайных
явлений
В этой главе мы повторим то, что уже знаем о
вероятностях событий, и познакомимся с эле-
ментарными событиями — простейшими собы-
тиями случайного опыта. Все прочие события
состоят из элементарных событий, подобно то-
му как геометрическая фигура состоит из точек.
Интересной разновидностью случайного опыта
служит опыт, в котором все элементарные со-
бытия имеют одинаковые шансы на осущест-
вление: они равновозможны. Чаще всего такие
опыты искусственные; они связаны с играми
или жребиями. Мы научимся вычислять вероят-
ности событий в таких опытах.
41 Случайные опыты
и элементарные события
42 Вероятности элементарных
событий. Равновозможные
элементарные события
43 Благоприятствующие
элементарные события
44 Вероятности событий
45 Опыты с равновозможными
элементарными событиями
46 Случайный выбор

Случайные опыты
и элементарные события
Ещё раз обратим внимание на то, что о случайных событиях можно говорить
только при определённых условиях. Если нет условий, то нет и событий. Например,
случайное событие «выпадение орла» возможно только в опыте с подбрасыванием
монеты. Без этого о выпадении орла нельзя говорить. О случайном событии «элек-
трическая лампочка прослужит более 100 часов» можно говорить, только если имеет-
ся лампочка, которую включают в электрическую сеть.
Условия и действия, при которых может наступить случайное событие, принято
называть случайным опытом или случайным экспериментом.
Точное математическое определение случайного опыта дать можно, но очень непросто.
Для этого требуются абстрактные понятия, которые уведут нас далеко от нашей цели.
Мы не даём определение случайного опыта так же, как учебник геометрии не да-
ёт определение плоскости. Вместо этого мы иллюстрируем понятие случайного опыта
многочисленными примерами.
Иногда случайный опыт — это действительно опыт, вроде бросания игральной ко-
сти или испытания лампочки. А иногда слово «опыт» подходит меньше. Например,
гроза в определённый летний день, без сомнения, случайное событие. Но здесь слу-
чайный опыт проводит не человек, а природа.
Не все случайные события нельзя предсказать. Например, в опыте с электриче-
ской лампочкой можно говорить о событии «лампочка в конце концов перегорит». Мы
твёрдо знаем, что это случится, потому что вечных лампочек не бывает. Это событие
достоверное. Напротив, событие «лампочка никогда не перегорит» — это событие не-
возможное. Невозможное и достоверное события также принято считать случайными.
В случайном опыте могут произойти различные случайные события. Например,
в результате бросания игральной кости можно говорить о событии «выпадет четвёрка»
или о событии «выпадет чётное число очков». Событие «выпадет чётное число очков»
можно разбить на три события: «выпадет два очка», «выпадет четыре очка», «выпадет
шесть очков». А событие «выпадет четвёрка» на более простые события не разделяется.
События случайного опыта, которые нельзя разделить на более простые, назы-
ваются элементарными событиями.
В каждом опыте можно выделить элементарные события, из которых состоят все
остальные события. Здесь снова можно провести аналогию с геометрией. Геометриче-
ские фигуры на плоскости состоят из точек. Точно так же события внутри случайно-
го опыта состоят из элементарных событий.
Ф
Важно! В результате случайного опыта обязательно наступает только одно эле-
ментарное событие.
ПРИМЕР 1. При подбрасывании игральной кости элементарных событий шесть: «вы-
падет одно очко», «выпадет два очка» и т. д., вплоть до события «выпадет шесть очков».
В более сложных опытах элементарных событий больше.
164
ГЛАВА VIII.

ПРИМЕР 2. Рассмотрим, например,
элементарные события в случайном опы-
те, где игральную кость бросают два раза.
В этом опыте 6 • 6 = 36 элементарных
событий, поскольку каждый из шести ре-
зультатов первого броска сочетается с лю-
бым из шести результатов второго. Все
эти 36 элементарных событий удобно
представить в виде таблицы (рис. 38).
В каждой ячейке таблицы пара чисел.
Первое число показывает, сколько очков
выпало при первом броске. Второе число —
число очков, выпавших при втором броске
1; 1
2; 1
3; 1
4; 1
5; 1
6; 1
1; 2
2; 2
3: 2
4; 2
5; 2
6; 2
1;3
2; 3
3; 3
4; 3
6; 3
б; 3
1; 4
2; 4
3; 4
4; 4
5: 4
6; 4
1; 5
2; 5
3; 5
4; 5
5; 5
6; 5
1;6 !
2; 6
3; 6
4; 6
5; 6
6; 6
Рисунок 38. Таблица эксперимента
«двукратное бросание кости»
кости.
щ>
Таким образом, элементарным событием при двух бросаниях игральной кости
является упорядоченная пара чисел.
Что
Гу\ Вопросы
1 Школьник говорит: «Я написал изложение и не сделал ни одной ошибки»,
здесь является случайным опытом, а что — случайным событием?
2 В классе 25 учеников. Учитель во время урока вызывает к доске одного учени-
ка. Сколько различных элементарных событий имеет этот случайный опыт?
3 Могут ли в результате опыта одновременно наступить два различных элементар-
ных события?
4 Перечислите элементарные события опыта, где игральную кость бросают один раз.
5 Назовите элементарные события, которые возникают при бросании математиче-
ской монеты.
6 Что является элементарным событием в опыте, где игральную кость бросают
два раза? Сколько элементарных событий в этом опыте?
7 Почему при двукратном бросании монеты элементарное событие ОР (сначала
выпал орёл, затем — решка) нельзя разделить на два более простых события:
«выпал орёл» и «выпала решка»?
0
Упражнения
227 Игральную кость бросают два раза. Укажите, какие из перечисленных ниже
событий являются невозможными, а какие — достоверными.
а) А «сумма выпавших очков меньше, чем 100»;
б) Б «в сумме выпадет одно очко»;
в) С «в сумме выпадет 13 очков»;
г) D «в сумме выпадет два или больше очков».
228 Из натуральных чисел от 1 до 100 выбирают два различных числа. Какие из
перечисленных ниже событий невозможные, а какие — достоверные?
а) А «одно из чисел больше другого»;
б) В «одно из чисел больше другого на 100»;
в) С «сумма выбранных чисел — положительное число»;
г) D «одно из двух данных чисел меньше половины другого числа».
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ЯВЛЕНИЙ
165

229 Андрей и Борис решили купить мороженое
и встали в очередь перед киоском «Моро-
женое». Сколькими способами они могут
расположиться друг за другом? Выпишите
все эти способы.
230 В киоске продаётся мороженое трёх сор- Рисунок 39
тов: сливочное, шоколадное и клубничное.
Андрей и Борис покупают по одной порции. Выпишите в виде таблицы эле-
ментарные события этого опыта. Сколько всего получилось элементарных
событий? Начало таблицы показано на рисунке 39.
231 Андрей, Борис и Владимир решили купить мороженое и встали в очередь.
Сколькими способами они могут расположиться друг за другом? Выпишите
все эти способы.
232 Игральную кость подбрасывают дважды. Нарисуйте в тетради таблицу эле-
ментарных событий этого эксперимента. Закрасьте в таблице элементарные
события, при которых в сумме выпадет:
а) менее 4 очков; в) ровно 11 очков;
б) ровно 7 очков; г) чётное число очков.
233 При подбрасывании монеты будем обозначать буквой О выпадение орла, бук-
вой Р — выпадение решки. Подбросим монету два раза. Элементарное собы-
тие «выпадет два орла» записывается как ОО. Выпишите все элементарные
события этого опыта. Сколько их?
234 Монету бросают три раза. Выпишите все элементарные события этого опыта,
пользуясь обозначениями О для орла и Р для решки.
235 а) Во сколько раз больше число элементарных событий при трёх бросаниях
монеты, чем при двух бросаниях монеты?
б) Сколько элементарных событий при четырёх бросаниях монеты?
в) Сколько элементарных событий при десяти бросаниях монеты?
236 Монету бросают до тех пор, пока не выпадет орёл. Пользуясь обозначениями
О и Р, запишите несколько элементарных событий этого опыта. Сколько все-
го элементарных событий в этом случайном опыте?
237 Спортивная команда «Математик» проводит встречу из нескольких матчей по
волейболу с командой «Физик». Ничья невозможна. Встреча проводится до
двух побед одной из команд. Победу «Математика» обозначим буквой М, а по-
беду «Физика» — буквой Ф. Одним из элементарных событий является ММ.
а) Запишите все возможные элементарные события.
б) Запишите все элементарные события, при которых встречу выигрывает
команда «Физик».
в) Предположим, что во встрече победила команда «Математик». Какой бук-
вой оканчивается запись соответствующих элементарных событий?
г) Какое наибольшее количество матчей может состояться?
238 В ящике три детали: две исправные детали а и Ь и одна бракованная деталь с.
Из ящика наугад извлекают по одной детали, пока не обнаружат бракован-
ную. Элементарные события этого опыта будем записывать в виде последова-
тельности букв. Например, abc9 ас и т. д.
а) Является ли последовательность cab элементарным событием в этом опыте?
6} Какими буквами может заканчиваться запись элементарного события?
в) Выпишите все элементарные события этого опыта.
Андрей
Сливочное
Борис
Сливочное
166
ГЛАВА VIII.

239 Игральную кость подбрасывают трижды. Сколько элементарных событий
в этом эксперименте?
240 Игральную кость подбрасывают трижды. Найдите количество элементарных
событий, при которых в сумме выпадет: а) 3 очка; б) 4 очка; в) 2 очка.
241 Игральную кость подбрасывают трижды. Найдите количество элементар-
ных событий, при которых в сумме выпадет более: а) 17 очков; б) 16 очков;
в) 15 очков.
^42) Вероятности элементарных событий.
Равновозможные элементарные события
Каждое элементарное событие случайного опыта может осуществиться с некото-
рой вероятностью. У разных элементарных событий эти вероятности могут быть раз-
ными. В некоторых случаях вероятности элементарных событий можно рассчитать.
В других случаях их можно приближённо найти из наблюдений. А в некоторых опы-
тах вероятности элементарных событий остаются неизвестными.
Рассмотрим случайный эксперимент, в котором три элементарных события. Обо-
значим их латинскими буквами а9 Ь9 с. Вероятности этих элементарных событий обо-
значим Р(а), Р(6), Р(с) соответственно. Каждая вероятность — это число от 0 до 1.
В результате эксперимента какое-то одно из элементарных событий обязательно
наступает. Причём только одно, два элементарных события наступить не могут. Из
этого вытекает важное свойство.
В каждом опыте сумма вероятностей всех элементарных событий равна 1. В дан-
ном случае Р(а) 4- Р(Ь) + Р(с) = 1.
Ф
Важно! В любом случайном опыте сумма вероятностей всех элементарных
событий равна 1.
Это свойство вероятностей является отражением такого же свойства частот. Повто-
рим опыт N раз. Пусть элементарное событие а произошло N(a) раз, событие Ь про-
изошло N(b) раз, событие с произошло Щс) раз. Значит, частоты событий a, b и с
равны —, _ и —.
Всего элементарных событий случилось столько, сколько было проведено опы-
тов, — в каждом опыте по одному. Поэтому Ща) + ЩЬ) + Щс) = N.
Значит, сумма частот элементарных событий о, b и с равна 1:
Ща) ЩЬ) Щс) _
N N N
Это свойство частот элементарных событий верно для любого случайного опыта,
который можно повторять много раз.
Интересен случай, когда элементарные события в опыте имеют одинаковые шан-
сы. Например, при одном бросании игральной кости элементарные события — это 1,
2, 3, 4, 5 или 6 очков. Если кость правильная, то шансы этих шести элементарных
событий одинаковы.
\^^У Если в случайном опыте шансы всех элементарных событий одинаковы, то он на-
зывается случайным опытом с равиовоэмоокными элементарными событиями.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ЯВЛЕНИЙ
167

При бросании двух игральных костей элементарных событий 36, и все они равно-
возможны. В дальнейшем мы часто будем рассматривать случайные опыты, в кото-
рых все элементарные события равновозможны. Такие опыты возникают при броса-
нии костей, раздаче игральных карт, в лотереях, жребиях, социологических исследо-
ваниях и других искусственных экспериментах.
Равновозможные события возникают не только в играх или опросах. Есть очень
важная математическая задача — генерация случайных чисел. Мы все пользуемся
мобильными телефонами, а значит — многочисленными алгоритмами шифрования и
защиты данных. Во всех этих алгоритмах используются случайные числа — десятич-
ные дроби, которые с равными шансами выбираются из интервала от 0 до 1. Про-
грамма для создания случайных чисел называется генератором случайных чисел.
В природе опыты с равновозможными элементарными событиями встречаются
очень редко.
Предположим, что в некотором случайном опыте N элементарных событий, и ве-
роятность каждого равна р. Сумма всех вероятностей равна 1: р+р + р + ... + р+р=1.
1 N одинаковых слагаемых
Значит, Np = 1, откуда р — —.
■ В\ Если в случайном опыте ровно N равновозможных элементарных событий, то
^-^ вероятность каждого из них равна —.
N
Хотя в природе опыты с равновозможными элементарными событиями практиче-
ски не встречаются, эти опыты очень важны. Во-первых, с помощью искусственных
опытов с равновозможными событиями часто удаётся находить приближённые реше-
ния сложных и важных задач, причём не только задач по теории вероятностей. Во-
вторых, эксперименты с равновозможными событиями удобны при изучении теории
вероятностей. Традиционно теорию вероятностей начинают изучать именно с таких
опытов. Здесь кроется опасность: из-за * злоупотребления» равновозможными элемен-
тарными событиями при обучении многие люди думают, что во всех опытах события
равновозможны. Вспомним распространённую шутку.
— Какова вероятность встретить на прогулке в центре Москвы живого дино-
завра? — спрашивает преподаватель студента.
— Одна вторая, — отвечает студент.
— Это почему же? — удивляется преподаватель,
— Либо встречу, либо нет.
Это, конечно, шутка. Но, как и во всякой шутке, в ней есть доля правды. Изве-
стен случай, когда подобную ошибку совершил знаменитый учёный Д'Аламбер1, ког-
да писал статью по теории вероятностей для энциклопедии.
Ошибка Д'Аламбера
В опыте, где монету бросают два раза, всего четыре элементарных события: ОО,
ОР, РО и PP. Эти четыре события равновозможны из-за симметричности монет, и ве-
1
роятность каждого из них равна —.
1 Жан Лерон Д'Аламбер — французский учёный, который жил в XVIII в. и занимался матема-
тикой и физикой. В 1764 г. был избран почётным членом Санкт-Петербургской академии наук,
хотя ни разу не был в России.
D
168
ГЛАВА VIII.

Если вместо того чтобы бросать монету два раза, мы одновременно бросим две
одинаковые монеты, то элементарные события ОР и РО покажутся нам одним со-
бытием: ведь монеты одинаковы. Значит, в этом опыте три элементарных события:
«два орла», «две решки» и «орёл и решка». Может возникнуть ошибочное впечатле-
ние, что вероятность каждого из них равна -. Именно так и посчитал Д'Аламбер.
о
На самом деле эти элементарные события не равновозможны: вероятность собы-
тия «два орла» и вероятность события «две решки» равны -, а вероятность события
1 4
«орел и решка» равна —.
(у) Вопросы
1 Какие элементарные события называют равновозможными?
2 Приведите примеры опытов, в которых элементарные события равновозможны.
3 Сформулируйте свойство суммы вероятностей всех элементарных событий слу-
чайного опыта.
4 Могут ли вероятности элементарных событий в случайном опыте быть не равны
друг другу?
5 На какой ответ мог рассчитывать преподаватель из шутки про динозавра?
0
Упражнения
242 Равновозможны ли элементарные события
«выпал орёл» и «выпала решка» при броса-
нии правильной монеты?
243 Автомобиль подъезжает к перекрёстку (рис. 40).
Определим возможные элементарные события:
«автомобиль повернёт направо»,
«автомобиль повернёт налево»,
«автомобиль поедет прямо»,
«автомобиль развернётся и поедет обратно».
Можно ли считать эти элементарные события Рисунок 40
равновозможными? Объясните свой ответ.
Указание. Подумайте, так ли часто автомо-
били разворачиваются и едут в обратном направлении. Какие события будут
случаться чаще, если автомобиль подъезжает к улице с более оживлённым
движением?
244 Команда высшей лиги, встречаясь в матче по футболу с командой первой ли-
ги, может либо победить или проиграть, либо встреча закончится вничью.
Равновозможны ли эти элементарные события? Обоснуйте своё мнение.
245 Случайный опыт может закончиться одним из трёх элементарных событий: а,
Ь или с. Чаму равна вероятность элементарного события с, если:
а) Р(а) = 0,4; Р(6) « 0,2; в) Р(а) - 0,1; Р(6) - 0,01;
б) Р(а) = |;Р(6) = |; г) Р(а)
Какие значения может принимать р?
б) Р(а) = |; Р(6) = |; г) Р(а) = р; Р(6) - 0,8 - р?
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ЯВЛЕНИЙ
169

246 Игральная кость несимметрична. В таблице показаны вероятности выпаде-
ния на этой кости 1, 2, 3, 5 или 6 очков. Найдите вероятность выпадения
4 очков.
Таблица 94. Вероятности выпадения граней
Число очков
Вероятность
1
1
4
2
1
12
3
1
6
4
?
5
1
12
6
1
4
247 В некотором случайном эксперименте все элементарные события равновоз-
можны. Найдите вероятность каждого элементарного события, если всего
в этом эксперименте количество элементарных событий равно:
а) 25; б) 17; в) 100.
248 Все элементарные события случайного опыта равновозможны. Сколько эле-
ментарных событий в этом опыте, если вероятность каждого равна:
а) ^; б) ОД; в) 0Д25; г) ±?
о К
249 В каждом из двух случайных опытов все элементарные события равновозмож-
ны. В каком из этих опытов вероятность элементарного события больше, если:
а) в первом опыте элементарных событий больше, чем во втором;
б) в первом опыте элементарных событий меньше, чем во втором;
в) в этих опытах элементарных событий поровну?
250 При подбрасывании монеты обозначим буквой О выпадение орла и буквой Р
выпадение решки. Подбросим симметричную монету два раза. Равновозмож-
ны ли элементарные события 00, РО, ОР и РР? Найдите их вероятности.
251 Симметричную монету подбрасывают несколько раз. Найдите вероятности
элементарных событий при:
а) 3 бросаниях; б) 4 бросаниях; в) 10 бросаниях*
252 Три богатыря — Илья Муромец, Алёша Попович и Добрыня Никитич — еха-
ли по дороге и увидели развилку, а на ней — придорожный камень с пре-
дупреждением :
Направо поедешь — коня потеряешь,
Налево поедешь — копьё потеряешь,
Прямо поедешь — головы не снесёшь.
Богатыри бросили жребий, разделились, и каждый поехал своей дорогой.
Придумайте систему обозначений для элементарных событий этого опыта, за-
пишите все элементарные события. Считая их равновозможными, найдите ве-
роятность каждого из них.
253 Три первоклассника по очереди выбирают воздушные шарики. Каждый из
них выбирает шарик одного из двух цветов: зелёного (3) или синего (С).
Выпишите элементарные события этого эксперимента. Считая, что все они
равновозможны, найдите вероятность каждого из них.
254 На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 8 с капустой и
3 с вишней. Петя наугад берёт один пирожок. Найдите вероятность того, что
пирожок окажется с вишней.
170
ГЛАВА VIII.

255 В таксомоторной компании в данный момент свободно 25 машин: 3 чёрных,
12 жёлтых и 10 зелёных. По вызову выехала одна из машин, случайно ока-
завшаяся ближе всего к заказчику. Найдите вероятность того, что к нему
приедет зелёное такси.
256 У бабушки десять чашек: шесть с красными цветами, остальные с синими.
Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность
того, что это будет чашка с синими цветами.
257 Оля, Галя, Витя, Артур и Рита бросили жребий — кому начинать игру. Най-
дите вероятность того, что начинать игру должна будет девочка.
258 В девятом классе учатся 11 мальчиков и 9 девочек. По жребию они выбирают
одного дежурного по классу. Какова вероятность того, что это будет мальчик?
259 Три первоклассника по очереди выбирают фломастеры. Каждый из них выби-
рает фломастер одного из трёх цветов: зелёного (3), синего (С) или красного
(К). Сколько у этого опыта элементарных событий? Считая, что все элемен-
тарные события равновозможны, найдите вероятность каждого из них.
260 Игральную кость подбрасывают несколько раз. Равновозможны ли элементар-
ные события такого опыта? Найдите вероятность каждого элементарного со-
бытия при: а) трёх бросаниях; б) четырёх бросаниях.
261 Родительский комитет закупил 25 пазлов для подарков детям на Новый год.
Пазлы с разными рисунками: 12 с автомобилями и 13 с видами городов. По-
дарки распределяются случайным образом между 20 детьми, среди которых
есть Коля. Найдите вероятность того, что Коле достанется пазл с автомобилем.
262 В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Нор-
вегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют,
определяется жребием. Найдцте вероятность того, что первым будет старто-
вать спортсмен из России.
263 В магазине канцтоваров в продаже 100 ручек: 23 красные, 12 зелёных,
17 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность
того, что случайно выбранная в этом магазине ручка будет красной или чёрной.
Благоприятствующие
элементарные события
До сих пор мы обсуждали только элементарные события. Однако в ходе опыта мо-
гут возникать более сложные случайные события. Например, при бросании играль-
ной кости возможно событие «выпадет чётное число очков» или событие «выпадет
более двух очков». Для обозначения случайных событий будем употреблять большие
латинские буквы А, Б, С, D и т. д.
Каждое событие состоит из элементарных событий. Например, событие «выпадет
чётное число очков» при бросании игральной кости состоит из трёх элементарных со-
бытий: «два очка», «четыре очка», «шесть очков». Иными словами, чтобы наступило
событие «выпадет чётное число», должно произойти одно из элементарных событий
«два очка», «четыре очка» или «шесть очков».
Определение. Элементарные события, при которых наступает событие А, назы-
ваются благоприятствующими событию А.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ЯВЛЕНИЙ 171

Мы знаем, что в случайном опыте наступает только одно из элементарных со-
бытий. Но если элементарное событие благоприятствует двум различным событиям
А и В, то события А и В могут произойти одновременно.
ПРИМЕР 1. Андрей, Борис и Владимир (А, Б и В) встают в очередь. Все возмож-
ные события в этом опыте складываются из элементарных событий, которых в дан-
ном случае всего шесть: АБВ, АВБ, БВА, БАВ, ВАБ, ВБА.
Рассмотрим событие «Владимир стоит первым». Оно наступает, если случилось од-
но из двух элементарных событий ВАБ и ВБА (рис. 41). Элементарные события ВАБ
и ВБА благоприятствуют событию * Владимир стоит первым».
Владимир Андрей Борис
Рисунок 41
Владимир Борис Андрей
1; 1
2; 1
3; 1
4; 1
5; 1
6; 1
1; 2
2; 2
3; 2
4; 2
5; 2
6; 2
1; 3
2; 3
3; 3
pi; з
5; 3
6; 3
1; 4
2; 4
3; 4
4; 4
5; 4
6; 4
1; 5
2; 5
3; 5
4; 5
5; 5
1 6; 5
1; 6 1
2; 6 1
3; 6
4; 6
С; 6 |
6; 6
ПРИМЕР 2. В этом же опыте событию * Борис стоит в очереди перед Андреем»
благоприятствуют элементарные события БАВ, БВА и ВБА.
ПРИМЕР 3. Игральную кость бросают
дважды. Таблица элементарных событий
этого опыта нам известна (рис. 42).
Рассмотрим событие А * сумма очков
равна 11». Этому событию благоприят-
ствуют ровно два элементарных события:
(6; 5) и (5; 6). Эти элементарные события
закрашены в таблице оранжевым цветом.
Вместо словесного описания события
можно записать событие А перечислением
благоприятствующих элементарных событий
в фигурных скобках: А = {(6; 5), (5; 6)}.
Событию В «произведение очков при
двух бросках равно 12» благоприятствуют элементарные события (4; 3), (3; 4), (2; 6)
и (6; 2). Они закрашены в таблице голубым цветом. Можно записать: В = {(4; 3),
(3; 4), (2; 6), (6; 2)}.
ПРИМЕР 4. Стрелок в тире стреляет по мишени до тех пор, пока не собьёт её.
Промах обозначим буквой Н (неудача), попадание — буквой У (успех). Элементарные
события в таком опыте имеют вид У, НУ, ННУ и т. д. Последняя буква обязательно У,
поскольку стрельба оканчивается успешным выстрелом. Пользуясь этими обозначе-
ниями, можно записать разные события в этом эксперименте. Например, событию А
♦стрелку потребуется не больше четырёх выстрелов» благоприятствуют элементарные
события: У, НУ, ННУ, НННУ.
Событию В «стрелку потребуется не меньше трёх выстрелов» благоприятствует
бесконечно много элементарных событий: ННУ, НННУ, ННННУ и т. д.
Можно записать: А = {У, НУ, ННУ, НННУ} и В - {ННУ, НННУ, ННННУ, ...}.
Рисунок 42
172
ГЛАВА VIII.

PJ Вопросы
1 Что означает высказывание «элементарное событие благоприятствует событию А»?
Сформулируйте эту мысль иначе.
2 Всякое ли элементарное событие опыта является случайным событием?
3 Верно ли, что случайному событию может благоприятствовать только одно эле-
ментарное событие?
4 Могут ли в опыте два случайных события наступить одновременно?
5 Могут ли в опыте два элементарных события наступить одновременно?
w Упражнения
264 Бросают одну игральную кость. Запишите событие А перечислением элемен-
тарных событий в фигурных скобках, если событие А состоит в том, что:
а) выпадет чётное число очков; в) выпадет больше 2 очков;
б) выпадет меньше 5 очков; г) выпадет от 2 до 5 очков.
265 Монету бросают два раза. Опишите словами следующие события:
а) А = {ОО, ОР}; в) С = {РР, РО, ОР};
б) В = {ОР, РО}; г) D - {ОО, РР}.
266 Шахматисты Андреев и Борисов играют между собой. Игра может окончить-
ся победой одного из них или вничью. Известно, что Андреев не проиграл
Борисову. Какие элементарные события благоприятствуют этому событию?
267 Нарисуйте в тетради таблицу элементарных событий опыта, где игральную
кость бросают дважды. Закрасьте в таблице элементарные события, благопри-
ятствующие событию:
а) «выпадут одинаковые числа»;
б) «при каждом броске выпадет число очков, кратное трём*;
в) «сумма очков при первом и втором бросках равна 5»;
г) «произведение выпавших очков равно 10».
268 Пользуясь таблицей элементарных событий опыта с двумя бросками игральной
кости, укажите элементарные события, которые благоприятствуют событию:
а) «сумма очков равна 7»;
б) «при втором броске выпадет больше очков, чем при первом»;
в) «сумма очков не меньше 6»;
г) «произведение очков равно 12».
269 Биатлонист делает по одному выстрелу в каждую из пяти мишеней. Что яв-
ляется элементарным событием в этом опыте? Сколько элементарных собы-
тий благоприятствует событию:
а) «биатлонист попадёт ровно в четыре мишени»;
б) «биатлонист попадёт ровно в одну мишень»?
270 Симметричную монету бросают дважды. Выпадение орла при каждом броса-
нии обозначим через О, а выпадение решки — через Р. Запишите перечисле-
нием в фигурных скобках событие:
а) «выпадет один орёл и одна решка»; в) «решка выпадет хотя бы один раз»;
б) «во второй раз выпадет решка»; г) «в первый раз выпадет орёл».
271 Симметричную монету бросают три раза. Пользуясь обозначениями О и Р,
выпишите элементарные события, благоприятствующие событию:
а) «выпадет ровно один орёл»; в) «при втором бросании выпадет решка»;
б) «выпадет ровно одна решка»; г) «при третьем бросании выпадет орёл».
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ЯВЛЕНИЙ
173

272 Константин, Леонид и Михаил купили по одной порции мороженого. Всего
было куплено мороженое трёх сортов: абрикосовое, брусничное и вишнёвое.
Введите подходящую систему обозначений для элементарных событий такого
эксперимента: Запишите все элементарные события, благоприятствующие со-
бытию:
а) * Константин купил абрикосовое мороженое»;
б) «Леонид не купил брусничное мороженое»;
в) «Михаил купил либо абрикосовое, либо вишнёвое мороженое»;
г) «У Леонида ни брусничное, ни вишнёвое мороженое».
273 Стрелок в тире стреляет по мишени, пока не собьёт её. Опишите словами
следующие события:
а) А - {НУ, ННУ, НННУ};
б) В = {У, НУ, ННУ, НННУ, ННННУ};
в) С = {ННУ, НННУ, ННННУ, ...} (многоточие означает, что последователь-
ность продолжается до бесконечности);
г) D = {У, ННУ, ННННУ, ННННННУ, ...}.
274 В классе 5 учеников, среди которых учится Петя. Учитель в течение урока
по очереди вызывает к доске двух человек. Сколько элементарных событий
благоприятствует событию «Петю вызовут к доске»?
Щ**) Вероятности событий
Вероятности событий мы будем обозначать буквой Р латинского алфавита по на-
чальной букве латинского слова probabilitae, что означает «вероятность». Например,
вероятность события А обозначим Р(А), вероятность события В — Р(В) и т. п.
Ф
Правило вычисления вероятностей. Вероятность события равна сумме ве-
роятностей элементарных событий, благоприятствующих этому событию.
Запишем это правило формулой. Пусть событию А благоприятствуют элементар-
ные события а, Ь, с, d. Тогда вероятность события А равна сумме вероятностей этих
элементарных событий: Р(А) = Р(а) 4- Р(&) + Р(с) 4- P(d).
Число элементарных событий, благоприятствующих данному событию, и, следова-
тельно, число слагаемых в правой части равенства может быть каким угодно и даже
бесконечным.
Вероятности всех элементарных событий неотрицательны и в сумме равны 1.
Поэтому вероятность события А также неотрицательна и не превосходит 1:
О ^ Р(А) ^ 1.
В частности, вероятность невозможного события равна нулю, а вероятность досто-
верного — единице. Событие, которому благоприятствуют все элементарные события
случайного эксперимента, является достоверным.
ПРИМЕР 1. В шахматной партии, которую Остап Бендер играет с любителем
шахмат из города Васюки, вероятность выигрыша Остапа равна 0,001, вероятность
ничьей равна 0,01. Найдём вероятность события А «Остап не проиграл». Этому со-
бытию благоприятствуют элементарные события «Остап выиграл» и «партия окончи-
лась вничью». Таким образом, Р(А) в 0,001 4 0,01 = 0,011.
174
ГЛАВА VIII.

ПРИМЕР 2. Автомобиль подъезжает к перекрёстку (см. с. 169 рис. 40). Предполо-
жим, что вероятность элементарного события «автомобиль повернёт направо» равна 0,5,
вероятность элементарного события «автомобиль повернёт налево» равна 0,3, вероят-
ность элементарного события «автомобиль поедет прямо» равна 0,18. Найдём вероят-
ность события А «автомобиль не развернётся». Этому событию благоприятствуют три
перечисленных элементарных события. Следовательно, Р(А) — 0,5 + 0,3 + 0,18 = 0,98.
©
0
Вопросы
1 Сформулируйте правило вычисления вероятностей.
2 Бросают одну игральную кость. Событие А заключается в том, что выпадет
целое (не дробное) число очков. Является ли событие А достоверным? Чему
равна вероятность события А?
3 Приведите пример достоверного события в случайном эксперименте с бросани-
ем двух игральных костей.
Упражнения
275 В случайном опыте четыре элементарных события а, Ь, с и d, вероятности
которых соответственно равны 0,1, 0,3, 0,4 и 0,2. Найдите вероятность собы-
тия, которому благоприятствуют элементарные события:
а) а и с; б) а, Ь и d; в) Ь, d и с; г) а и d.
276 В шахматной партии Андрей играет с Борисом. Вероятность выигрыша
Андрея равна 0,3, вероятность ничьей равна 0,2, вероятность того, что пар-
тия не будет закончена, равна 0,1. Найдите вероятность того, что:
а) Андрей не проиграет; б) Борис не проиграет; в) никто не выиграет.
277 Стрелок один раз стреляет в круглую мишень (рис. 43). Вероятности попада-
ния в зоны мишени показаны в таблице 95. Число очков, которое получает
стрелок, равно номеру зоны.
Таблица 95. Вероятности попадания в зоны мишени
Зона
i Вероятность
1
0,001
2
0,002
3
0,004
4
0,006
б
0,021
в
0,065
7
0,138
8
0,243
9
0,334
10
0,186
Найдите вероятность события:
а) «стрелок получит меньше 5 очков»;
б) «стрелок получит больше 7 очков»;
в) «стрелок попадёт в жёлтую зону»;
г) «стрелок не попадёт в голубую зону».
278 Симметричную монету бросают два раза.
Найдите вероятность события:
а) «решка выпадет хотя бы один раз»;
б) «в первый раз выпадет орёл».
279 Игральную кость бросают двазды. С помощью
таблицы этого эксперимента (ей. с. 165 рис. 38)
найдите количество благоприятствующих элемен-
тарных событий и вероятность события:
а) «сумма выпавших очков равна 6»;
Рисунок 43
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ЯВЛЕНИЙ 175

б) «сумма выпавших очков больше чем 5»;
в) «при первом броске выпадет больше очков, чем при втором»;
г) «количество очков, выпавших в первый раз, и количество очков, выпав-
ших во второй раз, различаются на 4».
280 В некотором опыте возможно три элементарных события: а, Ь и с. Вероят-
ность того, что наступит либо событие ft, либо событие с, равна 0,83. Найди-
те вероятность элементарного события а.
281 В некотором опыте возможно три элементарных события: а, Ь и с. Вероят-
ность того, что наступит либо событие а, либо событие ft, равна 0,4; вероят-
ность того, что наступит либо событие а, либо событие с, равна 0,7. Найдите
вероятность каждого из элементарных событий.
t45) Опыты с равновозможными
элементарными событиями
Напомним, что элементарные события называются равновозможными, если все
они имеют одинаковые шансы на осуществление. Значит, эти элементарные события
имеют равные вероятности. Если в случайном опыте N равновозможных элементар-
ных событий, то вероятность каждого из них равна — (см. п. 42).
N
Это обстоятельство позволяет легко находить вероятности всевозможных событий
такого опыта.
ПРИМЕР 1. Игральную кость бросают
два раза. Найдём вероятность события А
♦сумма очков меньше 6». Для этого вос-
пользуемся таблицей элементарных событий
этого эксперимента (рис. 44) и закрасим
в таблице оранжевым цветом элементарные
события, благоприятствующие событию А.
Обозначим через N(A) число элемен-
тарных событий, благоприятствующих со-
бытию А. Таких элементарных событий
десять: N(A) = 10. Общее число элемен-
тарных событий N = 36, а вероятность
1 1
каждого из них равна — = —.
1;
2
3
4
5
6
1
, 1
, 1
, 1
, 1
, 1
1; 2
2; 2
3; 2
4; 2
5; 2
6; 2
1; з
2; 3
3; 3
4; 3
5; 3
6; 3
1; 4
2; 4
3; 4
4; 4
5; 4
6; 4
1; 5
2; 5
3; 5
4; 5
5; 5
6; 5
1; 6 |
2; 6
3; 6
4; 6
5; 6
6; 6
Рисунок 44
Поэтому вероятность события А равна
N(A)
N N
N
N
N
10
36
18'
МЛ) слагаемых
Пользуясь примером 1, мы получили формулу
N{A)
Р(А) =
N
176
ГЛАВА VIII.

Это равенство можно выразить словами:
Щ)
Если в случайном опыте все элементарные события равновозможны, то вероят-
ность произвольного события А в этом опыте равна отношению числа элемен-
тарных событий, благоприятствующих событию А, к общему числу элементарных
событий.
ПРИМЕР 2. Дважды бросают симметричную монету. Найдём вероятность того, что
оба раза выпадет одна и та же сторона.
Выпишем все элементарные события опыта: ОО, ОР, РО и PP.
Всего элементарных событий четыре: N = 4. Так как монета симметричная, эле-
ментарные события равновозможны. Из них ровно два события, ОО и РР, благопри-
ятствуют событию В «оба раза выпадет одна сторона»: ЩВ) — 2. Запишем кратко
решение задачи: N = 4, N(B) = 2, следовательно, Р{В) = = 7 = ^-
ф.
0:
Вопросы
Сформулируйте правило вычисления вероятности случайного события в опыте
с равновозможными элементарными событиями.
Запишите это правило формулой.
Упражнения
282 Бросают одну игральную кость. Найдите вероятность события:
а) «выпадет чётное число очков»;
б) «выпадет число очков, кратное трём»;
в) «выпадет число очков, больше 3»;
г) «выпадет число очков, кратное 7».
283 Бросают одну игральную кость. Вычислите вероятность события:
а) «выпавшее число очков является делителем числа 12»;
б) «выпавшее число очков кратно 5»;
в) «выпадет больше 2 очков»;
г) «выпадет больше 1, но меньше 6 очков».
284 Бросают симметричную монету два раза. Равны ли вероятности событий А
♦два раза выпадет орёл» и В «один раз выпадет орёл, а другой раз — реш-
ка»? Найдите вероятности этих событий.
285 Бросают две игральные кости: жёлтую и зелёную. Вычислите вероятность со-
бытия:
а) «сумма очков на обеих костях равна 7»;
б) «сумма очков на обеих костях равна 11»;
в) «на жёлтой кости выпало больше очков, чем на зелёной»;
г) «числа очков на костях различаются не больше чем на 2».
286 В магазине в коробке 24 одинаковые авторучки. Из них 13 авторучек крас-
ные, 5 — зелёные, остальные — синие. Продавец наудачу достаёт одну авто-
ручку. Найдите вероятность того, что извлечённая ручка:
а) красная;
б) не зелёная;
в) либо синяя, либо зелёная;
г) либо красная, либо синяя.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ЯВЛЕНИЙ
177

287 В ящике 20 синих и 16 красных карандашей. Продавец не глядя вынимает
один карандаш. Найдите вероятность того, что этот карандаш окажется:
а) синим; б) красным.
288 Миша покупает альбом (А), блокнот (Б) и тетрадь (Т). Продавец достаёт эти
товары в произвольном порядке. Найдите вероятность того, что:
а) сначала продавец достанет блокнот;
б) продавец достанет альбом в последнюю очередь;
в) продавец сначала достанет тетрадь, а в последнюю очередь — блокнот;
г) альбом будет извлечён раньше, чем тетрадь.
289 На соревнования приехали гимнастки из трёх стран. Из России 7 гимнасток,
из Германии — 8, из Чехии — 5. Порядок выступлений гимнасток определя-
ется жребием. Найдите вероятность того, что:
а) первой будет выступать гимнастка из России;
б) третьим по счёту будет выступление какой-нибудь гимнастки из Германии;
в) второй по счёту будет выступать гимнастка из России или Чехии;
г) последней будет выступать спортсменка, приехавшая не из Чехии.
290 На день рождения к Паше пришли две Маши и два Саши. Все пятеро рас-
селись за круглым столом. Найдите вероятность того, что Паша сидит между
двумя тёзками.
291 Шахматный слон может за один ход перейти на
любое число полей, двигаясь только по диагона-
ли (рис. 45). Шахматный слон случайным образом
поставлен на доску. Найдите вероятность того, что
он может за один ход перейти на поле:
a) hi; б) а5; в) с4; г) d7; д) d5; e) g3.
292 По правилам игры «Морской бой» на поле 10 х 10
клеток размещаются четыре однопалубных корабля
(по одной клетке), три двухпалубных, два трёхпа-
лубных и один четырёхпалубный (рис. 46). Игрок TT~"r-^^-jr*^^"~f ^T ^
делает первый случайный выстрел. Найдите веро-
ятность того, что он: Рисунок 45
а) попадёт в однопалубный корабль противника;
б) попадёт в трёхпалубный корабль;
в) попадёт в какой-нибудь из кораблей противника;
г) не попадёт ни в какой корабль.
293 При игре в «Морской бой» после первого вашего выстрела противник сооб-
щил, что вы подбили какой-то корабль (но не потопили его). Какова вероят-
ность того, что вы попали: а) в четырёхпалубный корабль; б) в трёхпалубный
корабль; в) в двухпалубный корабль?
294 На рисунке 47 показано положение в игре «Морской бой». Красным цветом по-
казаны потопленные корабли противника. У противника остался только один
двухпалубный корабль, положение которого неизвестно. Клетки, в которых на-
рисованы точки, — это клетки, по которым мы уже стреляли. В них не может
быть корабля. Считая равновозможными любые допустимые положения последне-
го корабля, найдите вероятность того, что мы попадём в него, выстрелив в поле:
а) к4; б) з1; в) к1; г) е7; д) е8.
В какое поле нужно выстрелить, чтобы вероятность подбить последний
корабль была наибольшей?
8 [Т
7|
6 м
5 1
4 Г"
3 II
2 ^
1 I
■
яШр
■
■1
178
ГЛАВА VIII.

абвгдежзик
абвгдежзик
1
2
3
4
5
6
7
8
9
10
р.;;Ц*М="
-. *.. гг —
,•,.:..,-:,;.
\;'Ji'C\y
Щ/ШШ
;,-!">1?7,;;--
• , " 1- '
■'-;'?ЫХ:"'-
ш.
ш
щ
1
2
3
4
5
6
7
8
9
10
11
•
11
•
•
•
•
•
IB
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•■■yjA"
•
•
•
•
•
•
•
I,- /i;':';,':':
•
•
•
Рисунок 46
Рисунок 47
295 Одно время на улицах и вокзалах профессиональные игроки предлагали про-
хожим испытать удачу в простой игре. Зажав в кулаке обычный носовой
платок так» что наружу высовывались только четыре уголка, игрок предлагал
прохожему взять два любых конца и потянуть за них. Если прохожий вы-
таскивал два соседних уголка, то он проигрывал. Если прохожий вытаскивал
два противоположных уголка, то он выигрывал. Найдите вероятность выи-
грыша прохожего.
296 У Андрея в правом кармане брюк шесть монет — две из них по 10 р., а че-
тыре монеты по 2 р. На ощупь монеты неразличимы. Андрей достаёт из пра-
вого кармана три случайно выбранные монеты и перекладывает их в левый
карман. Найдите вероятность того, что обе 10-рублёвые монеты окажутся:
а) в одном кармане; б) в левом кармане.
297 В городе N пять улиц. При атом две из них идут параллельно друг другу
с севера на юг, а остальные проходят параллельно друг другу с запада на
восток. Любые две улицы разных направлений пересекаются. Утром двое
постовых случайным образом встали на два разных перекрёстка. Найдите ве-
роятность того, что они стоят на одной улице.
Кб) Случайный выбор
В задачах предыдущего параграфа мы имели дело с выбором одного случайного
предмета из нескольких. Это выбор наудачу. Выбор наудачу означает выбор бее ка-
ких-либо предпочтений. Выбор наудачу входит как часть во многие игры: наудачу
выбирают номер при игре в лото; наудачу выбирают карты во многих карточных
играх; в лотереях наудачу выбирают номера выигрышных билетов и т. д.
В социологических исследованиях выбор наудачу используется для формирования
группы опрашиваемых людей. При контроле качества продукции также используется
выбор наудачу, чтобы сократить расходы на контроль. Выбор наудачу очень важен
при испытаниях новых лекарств и выяснении, насколько они эффективны и какие
побочные эффекты могут дать.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ЯВЛЕНИЙ
179

Выбор наудачу называют также случайным выбором. Случайный выбор — это
разновидность случайного опыта с равновозможными элементарными событиями.
Элементарным событием в таком опыте является извлечение одного предмета из из-
учаемой группы. Такая изучаемая группа, из которой выбираются предметы, элемен-
ты или люди для опроса или испытаний, называется совокупностью или генераль-
ной совокупностью.
После выбора одного предмета случайный выбор можно продолжить: из всей со-
вокупности или только из оставшихся предметов выбрать ещё один, затем ещё один
и т. д. Собранное таким способом множество называют случайной выборкой из сово-
купности. Численность выборки обычно назначают заранее.
Случайную выборку можно получить иначе: сразу выбрать из общей совокуп-
ности нужное число предметов. Два карандаша из пяти можно выбирать один за
другим, а можно взять два случайных карандаша сразу. Примечательно, что в обо-
их случаях вероятность выбора каких-нибудь двух определённых карандашей одна
и та же.
Организовать по-настоящему случайный выбор непросто. Для этого требуются спе-
циальные методы: нужно бросать жребий, использовать таблицы случайных чисел
и т. д. При разработке шифровальных алгоритмов ещё не так давно использовали
телефонные книги абонентов большого города или страны: последние несколько цифр
в телефонных номерах абонентов, расположенных в алфавитном порядке, можно счи-
тать случайными. В других случаях использовался случайный шум разрядов атмос-
ферного электричества — шум, который мы слышим в радиоприёмнике и называем
помехами. В настоящее время чаще всего для создания случайных последовательно-
стей используются генераторы случайных чисел. Если выбор поручить человеку, то
выбор не окажется случайным. Многочисленные опыты показали, что равномерного
распределения шансов при этом не получается. Например, если учитель пытается по
своему разумению осуществить случайный выбор ученика из списка класса, то чаще
всего шансы учеников, стоящих первыми и последними в этом списке, будут ниже,
чем у тех, чьи фамилии расположены ближе к середине.
с ■ ———— —-^
В электронных таблицах для получения слу-
чайного числа на интервале от 0 до 1 исполь-
зуется функция
СЛЧИС()
Есть другая функция для случайного выбора:
СЛУЧМЕЖДУ()
Эта функция выбирает целое случайное число
на указанном отрезке натурального ряда. На
рисунке показано, как в электронной таблице
| можно имитировать бросание игральной кости.
V J
Рисунок 48
I « Л|=СЛЧИС()
[ с
| 0,616585
D
I
Е
| щ /х I =СЛУЧМЕЖДУ(1.6)|
D
6
Е
F
180
ГЛАВА VIII.

PJ Вопросы
1 Приведите примеры исследований, которые проводят с помощью случайных вы-
борок.
2 Бросают правильную игральную кость. Можно ли считать такой способ случай-
ным выбором одной из её граней?
3 Бросают правильную монету. Можно ли считать такой способ случайным выбо-
ром одной из её сторон?
4 Является ли выбор самого высокого ученика в классе случайным?
5 Зачем для формирования выборки нужны специальные методы?
Щ Практическая работа
Цель исследования. Установить, можно ли «придумать* случайную последователь-
ность из орлов и решек.
Ход работы. Разбейте класс на две команды. В первой команде каждый бросает мо-
нету сто раз и записывает последовательность выпавших орлов и решек.
Во второй команде каждый пытается придумать случайную последовательность ор-
лов и решек, как будто бы он бросает монету. Все листы с записями сдаются учи-
телю. Только учитель знает, где настоящие случайные последовательности орлов
и решек, а где имитация, сделанная кем-то из второй команды.
Учитель по очереди показывает классу последовательности. Задача класса — опре-
делить, настоящая она или придуманная. Удалось ли в большинстве случаев верно
отгадать? После обсуждения ответьте на вопросы, сформулированные ниже.
Обсуждение. Мы провели такой эксперимент. Сначала мы бросили монету 100 раз.
Получилась некоторая последовательность орлов и решек. Во втором эксперименте
мы попросили нашего знакомого придумать последовательность орлов и решек, как
будто бы он бросает монету. Получилась другая последовательность.
Первая последовательность
р
р
О
О
О
р
р
р
р
О
О
о
О
О
О
р
р
р
р
О
р
р
О
О
р
о
р
О
р
О
О
О
р
р
р
р
О
О
р
О
О
О
р
р
О
О
р
О
р
О
О
р
О
р
р
0
0
р
р
о
р
р
р
р
0
0
р
р
0
р
0
0
о
0
р
р
р
0
о
0
0
р
0
0
0
0
о
0
р
р
р
0
о
р
р
р
р
0
р
0
Вторая последовательность
0
о
0
0
0
о
0
р
0
0
0
р
0
р
р
р
р
р
0
р
0
р
р
р
0
р
0
0
р
0
р
0
0
0
0
0
0
0
р
р
р
р
р
р
0
р
р
0
0
р
0
р
0
0
0
р
р
р
0
р
р
р
р
р
р
р
0
р
р
р
0
0
0
р
р
0
0
0
0
0
р
р
р
р
р
р
0
р
0
0
р
р
0
р
0
0
0
р
0
р
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ СЛУЧАЙНЫХ ЯВЛЕНИЙ
181

С первого взгляда почти невозможно понять, где какая последовательность. Но мы
попробуем. Нужно найти характеристику, которая у этих последовательностей сильно
различается. Сначала найдём частоту орлов в каждой последовательности.
В первой последовательности частота орла 0,52 (52 орла из 100 бросков), во вто-
рой — 0,49. Обе частоты довольно близки к 0,5. Частота нам не помогла различить
последовательности.
Подойдём иначе. Стороны монеты могут чередоваться, а может случиться, что од-
на и та же сторона выпадает несколько раз подряд. Получается группа орлов или
группа решек. В первой последовательности сначала две решки, затем орёл, потом
опять две решки и т. д. Подсчитаем в каждой последовательности длины групп и по-
лучим два набора данных (табл. 96 и табл. 97).
Таблица 96. Длины групп, состоящих из орлов или решек, выпавших подряд
Первая последовательность
Вторая последовательность
Длины групп
2, 1, 2, 2, 1, 4, 1, 2, 1, 2, 4, 1, 3, 3, 2, 1, 2, 1, 2, 2, 1, 1,
1, 1, 1, 2, 1, 1, 1, 2, 3, 7, 1, 1, 1, 1, 8, 4, 3, 4, 1, 1, 1, 3,
1, 2, 2, 2, 1
3, 1, 1, 2, 1, 2, 1, 3, 2, 3, 3, 3, 3, 5, 3, 1, 1, 1, 2, 1, 1, 2,
3, 1, 3, 2, 2, 2, 1, 1, 2, 1, 1, 2, 1, 2, 3, 3, 1, 1, 1, 1, 3, 2,
3, 1. 1, 1, 1, 4, 1, 1, 2, 1
Таблица 97. Анализ длин групп
Первая последовательность
Вторая последовательность
Раадичше среднего н дисперсии
Среднее
2
1,85
Небольшое
Дисперсия
2,12
0,94
Большое
Без доказательства скажем, что среднее такого набора данных при случайном броса-
нии монеты должно быть близко к 2 и дисперсия тоже должна быть примерно равна 2.
У первой последовательности средняя длина группы равна 2. Дисперсия равна
2,12. Это не противоречит предположению о случайности первой последовательности.
У второго набора длин среднее значение 1,85, что не очень далеко от числа 2.
А вот дисперсия намного меньше числа 2: она равна 0,94. Возникают сомнения
в том, что эта последовательность действительно случайная.
I Анализ результатов. Если, составляя искусственную последовательность, кто-то су-
I мел хорошо имитировать случайность, то все характеристики придуманной им по-
I следовательности должны быть близки к аналогичным характеристикам настоящих
I случайных последовательностей.
1. Удалось ли хотя бы кому-нибудь придумать последовательность, которую по её
характеристикам трудно отличить от случайной?
I 2. Какая из характеристик (частота орла, средняя длина группы, медиана длин групп,
I дисперсия длин групп, наибольшая длина группы) чаще всего выдавала подделку в
I вашем опыте?
I 3. Можно ли доверить человеку «придумывание» случайной последовательности без ис-
I пользования монет, кубиков или других инструментов, обеспечивающих случайность?
4. За счёт чего дисперсия длин групп в искусственной последовательности может
I оказаться значительно меньше теоретического значения?
182
ГЛАВА VIII.

Действия
с событиями.
Сложение
вероятностей
С событиями, так же как с геометрическими
фигурами или множествами, можно произво-
дить действия. В этой главе рассказывается
о трёх основных действиях с событиями и о
том, как правильно складывать вероятности
двух событий, чтобы найти вероятность их
объединения. Оказывается, способ сложения
вероятностей зависит от того, являются эти
события несовместными или нет.
47 Противоположные события.
Диаграммы Эйлера
48 Объединение событий
49 Пересечение событий
50 Формула сложения
вероятностей
51 Решение задач с помощью
координатной прямой

Мы обсуждаем случайные опыты. Напомним, что случайный опыт оканчивается
каким-либо одним элементарным событием. Какое именно элементарное событие на-
ступит в данном опыте — дело случая. Два разных элементарных события вместе
произойти не могут.
Всякое случайное событие А состоит из элементарных событий. Эти элементарные
события называют благоприятствующими случайному событию А. Если ни одно из
благоприятствующих событию А элементарных событий не произошло, то не произо-
шло и событие А.
Теперь мы дадим определение случайного события, которое не давали прежде.
Определение. Случайное событие — это множество (набор, совокупность)
элементарных событий.
Случайные события можно разными способами сочетать друг с другом. При этом
образуются новые случайные события. Мы обсудим три наиболее часто употребляе-
мых действия с событиями.
Противоположные события.
Диаграммы Эйлера
Рассмотрим какое-либо событие А в некотором случайном опыте. Как и всякому
событию, ему благоприятствуют некоторые элементарные события. Рассмотрим те-
перь все прочие элементарные события этого опыта, то есть те события, которые не
благоприятствуют событию А. Соберём эти элементарные события вместе. Получается
новое событие. Оно состоит из тех элементарных событий, которые не благоприят-
ствуют событию А. Это событие называется событием, противоположным событию А,
Событие, противоположное событию А, обозначают А.
Определение» Событием» противоположным событию А, называют событие Л,
которому благоприятствуют все элементарные события, не благоприятствующие
событию А.
Если событие В противоположно событию А, то есть В = А, то событие А проти-
воположно событию В: А = В. Поэтому события А и А называют взаимно противо-
положными или просто противоположными.
ПРИМЕР 1. Бросают игральную кость. Событию А «выпадет больше четырёх оч-
ков» благоприятствуют элементарные события ♦ пятёрка» и «шестёрка». Не благо-
приятствуют событию А элементарные события «единица», «двойка», «тройка» и
«четвёрка» (рис. 49). Вместе эти элементарные события благоприятствуют событию А
«выпадет четыре очка или меньше».
Событие А •
Событие А
Рисунок 49
184
ГЛАВА IX.

Взаимно противоположные события одновременно произойти не могут, но какое-
либо из них происходит обязательно. Поэтому
Ф
Р(А) + Р(а) = 1.
Сумма вероятностей взаимно противоположных событий равна единице.
Следовательно,
Р(а) = 1 - Р(а) и Р(а) = 1 - Р(а).
Это означает, что для вычисления вероятности одного из взаимно противополож-
ных событий достаточно знать вероятность другого. Это свойство во многих случаях
оказывается полезным.
ПРИМЕР 2. Какова вероятность того, что при двукратном бросании игральной ко-
сти во второй раз выпадет не то же число очков, что в первый?
Решение. Назовём указанное событие А. Ему благоприятствует много элементар-
ных событий. Проще найти вероятность противоположного события А, которое состо-
ит в том, что оба раза выпадет одно и то же число очков. Событию А благоприят-
ствуют шесть равновозможных элементарных событий:
А « {(1; 1), (2; 2), (3; 3), (4; 4), (5; 5), (6; 6)}.
Вероятность каждого из этих элементарных событий равна —. Получаем решение
задачи: _ _ ^щ
N = 36, N{A) = 6, следовательно, Р(а) = —^ = 6— = -.
Тогда
N
Р(А) = 1-Р(а) -1-i-J
36 6
6 6'
Соотношения и связи между событиями удобно
изображать с помощью схематических рисунков —
диаграмм Эйлера1. Весь случайный эксперимент,
т. е. все элементарные события опыта, изобразим
прямоугольником. Событие А изобразим кругом
внутри прямоугольника. Оставшаяся часть прямоу-
гольника изображает противоположное событие А.
На рисунке 50 с помощью диаграмм Эйлера пока-
заны взаимно противоположные события А и А.
Если нужно изобразить несколько событий, то ри-
суют несколько фигур — по одной для каждого
события. Фигуры могут располагаться по-разному,
показывая, как связаны между собой данные события.
Событие А
Леонард Эйлер (1707—1783)
Событие А,
противоположное
событию А
Рисунок 50
1 Леонард Эйлер — великий математик. Эйлер родился в Швейцарии в 1707 г. В 1727 г. Эйлер
приехал в Санкт-Петербург. Вклад Эйлера в мировую математику огромен и неоценим. В России
Эйлер принимал участие в создании университета при Академии, писал учебники. Он возглав-
лял работу по созданию первого географического атласа Российской империи. В интернете вы
найдёте очень много о жизни этого поистине удивительного человека.
ДЕЙСТВИЯ С СОБЫТИЯМИ. СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ 185

/) Вопросы
1 Что такое противоположные события?
2 Обязательно ли события на диаграммах Эйлера изображаются кругами?
3 Сформулируйте словами свойство вероятностей противоположных событий.
^J Упражнения
298 в случайном эксперименте 20 элементарных событий. Событию А благоприят-
ствуют 12 из них. Сколько элементарных событий благоприятствуют событию А?
299 В некотором случайном опыте может произойти событие К. Найдите вероят-
ность события К, если вероятность события К равна:
а) 0,4; б) 0,85; в) 0,13; г) \.
300 Докажите, что события А и Б не могут быть противоположными, если
Р(а) - 0,7, а Р(В) = 0,44.
301 Вероятность события А равна 0,3, а вероятность события В равна 0,7. Обяза-
тельно ли события А и В взаимно противоположны?
302 Предположим, что на некотором производстве из 100 изготовленных сумок
в среднем 3 бракованные (плохой шов, дефект кожи и т. п.). Это означает,
что вероятность события «изготовленная сумка бракованная» равна 0,03.
Найдите вероятность того, что изготовленная сумка качественная.
303 При изготовлении батареек в среднем на 1000 качественных батареек прихо-
дится 4 батарейки с дефектом. Найдите вероятность того,
а) что случайно выбранная батарейка имеет дефект.
б) что случайно выбранная батарейка не имеет дефектов.
304 Вероятность того, что новая шариковая ручка пишет плохо (или не пишет),
равна 0,19. Покупатель в магазине выбирает одну шариковую ручку. Найди-
те вероятность того, что эта ручка пишет хорошо.
305 В каждой четвёртой банке кофе согласно условиям акции есть приз. Призы
распределены по банкам случайно. Аня покупает банку кофе в надежде вы-
играть приз. Найдите вероятность того, что Аня не найдёт приз в своей банке.
306 В среднем из каждых 80 поступивших в продажу аккумуляторов 76 аккуму-
ляторов заряжены. Найдите вероятность того, что выбранный в магазине на-
удачу аккумулятор не заряжен.
307 Могут ли быть противоположными события Си Д если:
а) Р(С) = 0,12; P(D) - 0,78; б) Р(С) - 0,14; Рф) - 0,86.
в) Р(С) = -4т, P(D) = -4т• где а > 0, Ъ > 0;
а + о а + о
г) Р(С) = 0,5 + п; P(D) - 0,5 - п, где -0,5 < п < 0,5?
308 Бросают одну игральную кость. Перечислите элементарные события, благо-
приятствующие событию А, опишите событие А словами и найдите Р(а), ес-
ли событие А состоит в том, что:
а) выпадет шестёрка; в) выпадет число очков, кратное трём;
б) выпадет чётное число очков; г) выпадет от 2 до 5 очков.
309 Игральную кость бросают дважды. Опишите словами событие, противополож-
ное событию А, и найдите его вероятность, если событие А состоит в том,
что в сумме при двух бросках выпадет: а) 2 очка; б) 12 очков; в) менее 4 оч-
ков; г) более 10 очков.
186
ГЛАВА IX.

Таблица 98. Вероятности выпадения
О, 1, 2, 3 и 4 орлов
Число орлов
Вероятность
0
1
16
1
1
4
2
3
8
3
1
4
4
1
16 1
310 В классе 15 мальчиков и 10 девочек. Из класса случайным образом выбира-
ют одного ученика. Событие D — «выбрана девочка».
а) Сколько элементарных событий благоприятствует событию £>?
б) Чему равна вероятность события D?
в) Опишите словами событие D.
г) Чему равна вероятность p(d)?
311 Симметричную монету бросили 4 ра-
за. Орёл при этом может выпасть 1,
2, 3 или 4 раза, а может не выпасть
ни разу. Вероятности этих событий
даны в таблице 98.
Найдите вероятность события, проти-
воположного событию:
а) «орёл не выпадет ни разу»;
б) «орёл выпадет более одного раза»;
в) «решка выпадет менее трёх раз»;
г) «орёл выпадет неизвестно сколько раз, но точно не 2 раза».
312 Из класса выбирают двух учеников. Опишите словами событие Б, если собы-
тие В состоит в том, что:
а) оба выбранных ученика — мальчики;
б) выбраны ученики одного пола.
313 В люстре пять новых лампочек. Опишите словами событие, противоположное
событию:
а) «в течение года перегорит хотя бы одна из лампочек»;
б) «в течение года перегорят ровно две лампочки»;
в) «в течение года перегорит больше трёх лампочек»;
г) «в течение года перегорит меньше четырёх лампочек».
314 На диаграмме Эйлера (рис. 51) изображены события А и В.
Нарисуйте диаграмму в тетради и выделите на ней собы-
тие, которое состоит в том, что:
а) наступило событие А;
б) наступило событие В;
в) событие А наступило, а событие В нет;
г) событие В наступило, а событие А нет.
Рисунок 51
ив) Объединение событий
Пусть А и В — два события, относящиеся к одному случайному опыту. Рассмо-
трим те элементарные события, которые благоприятствуют событию Л, и те элемен-
тарные события, которые благоприятствуют событию В. Все вместе они образуют но-
вое событие. Это новое событие называют объединением событий А и В. Его обозна-
чают лив.
Определение. Объединением двух событий А и В называют событие, которо-
му благоприятствуют все элементарные события, благоприятствующие событию А
или событию в.
ДЕЙСТВИЯ С СОБЫТИЯМИ. СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ 187

Щ)
Объединение A US наступает, если наступает хотя бы одно из событий А и В.
Это означает, что наступает либо А, либо S, либо А и В вместе.
ПРИМЕР 1. Продавец выбирает два костюма, для того чтобы поместить их в витри-
ну магазина. В ассортименте есть чёрные (Ч) и синие (С) костюмы. Элементарные со-
бытия этого случайного опыта представляют собой пары костюмов, которые мы обозна-
чим:
ЧС, ЧЧ, СС и СЧ.
Пусть, например, событие А состоит в том, что первый костюм чёрного цвета.
Этому событию благоприятствуют элементарные события
ЧС и ЧЧ.
Событие В наступает, если второй костюм чёрного цвета; ему благоприятствуют
элементарные события
СЧ и ЧЧ.
Объединению событий AU В в этом случае благоприятствуют элементарные собы-
тия, благоприятствующие хотя бы одному из двух событий А и В, т. е. три элемен-
тарных события: ЧС, ЧЧ и СЧ.
Событие AUB состоит в том, что хотя бы один из костюмов чёрного цвета. Словес-
ная формулировка объединения двух событий часто включает в себя слова «хотя бы*.
ПРИМЕР 2. Игральную кость бросают дваж-
ды. Событие А состоит в том, что в первый
раз выпало больше очков, чем во второй. Собы-
тие В состоит в том, что во второй раз выпало
больше очков, чем в первый.
Тогда событие AUB заключается в том, что
либо в первый раз выпало больше очков, чем
во второй, либо во второй раз больше очков,
чем в первый. Иными словами, событие AUB
можно описать так: «при двух бросаниях кости
выпали два разных числа». В таблице элемен-
тарных событий такого эксперимента событию
AUB благоприятствуют все элементарные собы-
тия, кроме элементарных событий, расположен-
ных на диагонали (рис. 52).
Объединение событий легко изобразить на диаграмме Эйлера
(рис. 53). Левый круг изображает событие А, правый круг — собы-
тие Вj а фигура, состоящая из обоих кругов, — это событие AUB.
Добавив ещё фигуры, можно изобразить объединение трёх, четы-
рёх и более событий.
Рисунок 53
Вопросы
Сформулируйте определение объединения двух событий.
Спортсмен выступает на соревнованиях по прыжкам. Первое событие — «спорт-
смен травмировал левую ногу». Второе событие — «спортсмен травмировал
правую ногу». Опишите словами объединение этих событий.
Событие В является объединением взаимно противоположных событий А и А.
Какова вероятность события S?
[Г;
2;
3
4
|_5,
Гв
1
1
1
, 1
, 1
1
1; 2
| 2; 2 |
3; 2
4; 2
5; 2
6; 2
1; 3 : 1; 4
2; 3 2; 4
3; 3
4; 3
5; 3
в; 3
3; 4
|.4;_4
5; 4
в; 4
1; 5
2; 5
3; 5
[4; 5
1 5; 5
в; 5
1; 6 1
2; в
3; в
4; 6
5; в
6; 6 1
I 2* 1 II Элементарные события, благопри-
*===$ ятствующие событию А
| 3; 5 | Элементарные события, благопри-
ятствующие событию В
Рисунок 52
188
ГЛАВА IX.

Упражнения
315 На диаграмме Эйлера (рис. 54) указано число элемен-
тарных событий, благоприятствующих каждому из
двух событий А и В. Сделайте рисунок в тетради и за-
красьте объединение событий А и В. Сколько элемен-
тарных событий благоприятствует событию AUB?
316 Событию U в ходе некоторого опыта благоприятствуют Рисунок 54
5 элементарных событий. Событию V благоприятствуют
8 элементарных событий, но ни одно из них не благоприятствует событию U.
Сколько элементарных событий благоприятствует событию U U V?
317 Событию А благоприятствуют 6 элементарных событий, а событию В —
8 элементарных событий. Из этих 8 элементарных событий 4 благоприятству-
ют сразу двум событиям. Нарисуйте в тетради соответствующую диаграмму
Эйлера и ответьте на вопросы.
а) Сколько элементарных событий благоприятствует событию А, но не благо-
приятствует событию В?
б) Сколько элементарных событий благоприятствует событию В, но не бла-
гоприятствует событию А?
в) Сколько элементарных событий благоприятствует событию AUB?
318 Монету бросают дважды. Событие А — «первый раз выпадет орёл». Событие
В — «второй раз выпадет орёл». Выпишите элементарные события, благо-
приятствующие каждому из этих событий и событию AUB.
319 Монету бросают дважды. Представьте в виде объединения двух событий событие:
а) «хотя бы один раз выпадет решка»;
б) «оба раза выпадет одна и та же сторона монеты».
320 На диаграмме Эйлера (рис. 55) изображены события А и В.
Нарисуйте диаграмму в тетради и укажите на ней событие С,
которое состоит в том, что:
а) событие А наступило, а событие В нет;
б) событие В наступило, а событие А нет;
в) наступило хотя бы одно из событий А и В; Рисунок 55
г) не наступило ни одно из событий А и В;
д) наступили оба события.
Какое из этих событий является событием AUB? Какое из этих событий яв-
ляется событием A U В?
321 Бросают одну игральную кость. Событие А — «выпадет чётное число очков».
Событие В состоит в том, что:
а) выпадет число очков, кратное 3; в) выпадет число очков, кратное 4;
б) выпадет нечётное число очков; г) выпадет число очков, кратное 5.
Выпишите все элементарные события, благоприятствующие событию AUB.
Найдите P(AUB).
322 На диаграмме Эйлера (рис. 54) указано число элементарных событий, благоприят-
ствующих событиям А и В. Всего в опыте 60 различных элементарных событий.
а) Сколько элементарных событий благоприятствует событию В?
б) Сколько элементарных событий благоприятствует событию А?
в) Сколько элементарных событий благоприятствует событию A U В?
г) Сколько элементарных событий благоприятствует событию AUB?
ДЕЙСТВИЯ С СОБЫТИЯМИ. СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ
ш
189

323 Бросают две игральные кости. Событие А — «на первой кости выпадет еди-
ница*. Событие В — *на второй кости выпадет единица».
а) Выпишите элементарные события, благоприятствующие событию AUB.
б) Есть ли у событий А и Б общие благоприятствующие элементарные собы-
тия? Если да, то сколько их?
в) Опишите словами событие AUB.
г) Найдите вероятность события AUJ3.
324 Бросают две игральные кости. Событие U — «на первой кости выпадет число
очков, кратное 3». Событие V — «на второй кости выпадет число очков,
кратное 3».
а) В таблице элементарных событий этого опыта выделите элементарные со-
бытия, благоприятствующие событиям U и V.
б) Есть ли у событий U и V общие благоприятствующие элементарные собы-
тия? Если да, то сколько их?
в) Опишите словами событие U U V.
г) Найдите вероятность события U U V.
325 Бросают две игральные кости. Событие К — «на первой кости выпадет чёт-
ное число очков». Событие L — «на второй кости выпадет чётное число очков».
а) Выделите в таблице элементарных событий этого опыта элементарные со-
бытия, благоприятствующие событиям К и L.
б) Есть ли у событий К и L общие элементарные события? Если да, то какие
они и сколько их?
в) Опишите словами событие KUL.
г) Найдите вероятность события KUL.
326 Докажите, что для любых событий А и В верны нера-
венства P(AUB) ^ Р(А) и P(AUB) ^ Р(В).
327 На диаграмме Эйлера (рис. 56) показаны события А, В
и С. Нарисуйте диаграммы, изображающие событие:
а) AUB; д) AUBUC;
б) A U С; е) A U BUC; Рисунок 56
в) A U В; ж) AUBUC;
г) AUBUC; з) AUBUC.
^49) Пересечение событий
Предположим, что у событий А и В в некотором случайном опыте есть общие эле-
ментарные события. Эти общие элементарные события образуют новое событие, кото-
рое называют пересечением событий А и В. Его обозначают АПВ. Пересечение со-
бытий А и В наступает, если наступают оба события А и В.
Х^у Определение. Пересечением двух событий А и В называют событие, которо-
му благоприятствуют все элементарные события, благоприятствующие и собы-
тию Л, и событию S.
190
ГЛАВА IX.

ПРИМЕР 1. Вернёмся к продавцу, выбирающему для витрины два костюма из
множества синих и чёрных костюмов. Напомним элементарные события этого опыта:
ЧС, ЧЧ, СС и СЧ.
Пусть событие А, как и прежде, состоит в том, что первый костюм чёрного цвета.
Этому событию благоприятствуют элементарные события
ЧС и ЧЧ.
Событие В «второй костюм чёрного цвета» наступает при элементарных событиях
СЧ и ЧЧ.
Пересечение событий АПВ состоит в том, что оба костюма чёрного цвета. Этому
благоприятствует единственное элементарное событие ЧЧ.
ПРИМЕР 2. Игральную кость бросают дваж-
ды. Пусть событие А — «в первый раз выпало
меньше 3 очков», а событие В — «во второй
раз выпало меньше 3 очков». Тогда событие
АПВ заключается в том, что оба раза выпало
меньше 3 очков (рис. 57).
Событие АПВ можно изобразить на диаграм-
ме Эйлера: нужно выделить общую часть фигур,
изображающих события А и В (рис. 58).
Добавив ещё фигуры, можно закрасить пере-
сечение трёх или нескольких событий.
Если события А и В не имеют общих благо-
приятствующих элементарных событий, то они
не могут наступить одновременно в одном и том
же опыте. Такие события называют несовмест-
ными, а их пересечение — невозможным, или
■щ
■1SIS
рШй
■till
■111
ШШ
щи
ЩИ
ЯП
швш
iWiiftl
1; 3
2; 3
3; 3
4; 3
5; 3
6; 3
1; 4
2; 4
3; 4
4; 4
5; 4
6; 4
1; 5
2; 5
3; 5
4; 5
5; 5
6; 5
1; в I
2; 6
3; 6
4; 6
5; в
в; в J
2; 3
т
щх -^
Элементарные события, благопри-
ятствующие событию А
Элементарные события, благопри-
ятствующие событию В
Элементарные события, благопри-
Ш£*&йМ ятствующие обоим событиям
Рисунок 57
пустым, событием. Оно обозначается символом 0. Можно написать АПВ = 0.
\S^J Определение. События А и В называются несовместными, если их пересече-
ние не содержит элементарных событий.
Вероятность пересечения несовместных событий равна О:
Р(0) =* 0. На диаграмме Эйлера несовместные события изо-
бражаются в виде двух непересекающихся фигур (рис. 59).
ПРИМЕР 3. События «8 марта приходится на пятницу» и
♦8 марта приходится на субботу» являются несовместными
в одном и том же году.
Гу\ Вопросы
1 Сформулируйте определение пересечения двух событий.
2 Сформулируйте определение несовместных событий.
3 Как называется событие, которое не содержит элемен-
тарных исходов?
4 Спортсмен выступает на соревнованиях по прыжкам.
Первое событие — «спортсмен травмировал левую но-
гу». Второе событие — «спортсмен травмировал правую
ногу». Опишите словами пересечение этих событий.
Рисунок 58
Несовместные события
Рисунок 59
ДЕЙСТВИЯ С СОБЫТИЯМИ. СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ 191

(25
328
329
330
331
332
333
Упражнения
Бросают одну игральную кость. Событие А — «выпадет чётное число очков».
Событие В заключается в том, что выпадет число очков:
а) кратное 3; в) большее 4;
б) кратное 4; г) меньшее 3.
Для каждого случая выпишите элементарные события, благоприятствующие
событию АПВ, и найдите вероятность этого события.
Игральную кость бросают дважды. Событие А — «в первый раз выпало мень-
ше 3 очков». Событие В — «во второй раз выпало больше 4 очков».
а) Пользуясь таблицей элементарных событий этого опыта, выделите тремя
разными цветами (или штриховкой) элементарные события, благоприятствую-
щие событиям А, В и АПВ.
б) Опишите словами событие АПВ.
в) Найдите Р(АПВ).
Из класса случайным образом последовательно выбирают двух учеников. Со-
бытие D — «первый выбранный ученик — девочка». Событие С — «второй
выбранный ученик — девочка». Опишите словами события DUC и DO С.
Из класса случайным образом последовательно выбирают двух учеников.
Событие А — «первый выбранный ученик — девочка». Опишите словами
объединение и пересечение событий А и В, если событие В:
а) «среди выбранных учеников есть только одна девочка»;
б) «второй выбранный ученик — мальчик».
В ходе некоторого опыта событию А благоприятствуют 6 элементарных собы-
тий, событию В — 8 элементарных событий. При этом 2 элементарных собы-
тия благоприятствуют событию АПВ. Сколько элементарных событий благо-
приятствует событию:
а) «событие А наступает, а событие В нет»;
б) «событие В наступает, а событие А нет»?
Нарисуйте диаграмму Эйлера, на которой укажите число элементарных собы-
тий, благоприятствующих соответствующим событиям. С помощью сделанно-
го рисунка найдите, сколько элементарных событий благоприятствует собы-
тию A U В.
Запишите формулой событие, изображённое на диаграмме Эйлера (рис. 60,
а, б).
Рисунок 60
334 Изобразите на диаграмме Эйлера событие:
а) АПВ; в) АПВ;
б) АПВ; г) АПВ.
335 Докажите, что Р(АПВ) ^ Р(А) и Р(АПВ) ^ Р(В).
192
ГЛАВА IX.

336 Запишите формулой событие, изображённое на диаграмме Эйлера (рис. 61).
337 Изобразите на диаграмме Эйлера событие:
а)АПВПС; б)ЛПВПС; в)ЛПВПС;
338 Изобразите на диаграмме Эйлера событие:
а) ЛП(ВиС);
г) АПВПО, д) АПВПС.
б) AU(BOC)
в) АП(ВиС)
г) АП(ВиС);
ж) АЦ(ВПС);
з) A U(ВПС).
д) AU(BOC);
е) AU(BnC);
339 С помощью диаграмм Эйлера докажите равенство:
а) АП(ВиС) - (АПВ)ЩАПС); в) АПВ-AUB;
г) A U В'
б) AU(BDC) = (AUB)f)(AUC);
АПВ.
Указание. Для доказательства нужно изобразить оба со-
бытия на диаграмме Эйлера. Если изображения совпада-
ют, то совпадают и события. Рисунок 61
Тып Формула сложения вероятностей
Случай, когда события несовместны
Если события Л и В не имеют общих благоприятствующих элементарных собы-
тий, то они несовместны, их пересечение является невозможным событием. Поэтому
вероятность пересечения несовместных событий равна нулю: Р(Л П В) = 0.
ПРИМЕР 1. Игральную кость бросают дваж-
ды. Рассмотрим событие А «в первый раз вы-
пало больше очков, чем во второй» и событие J5
«в первый раз выпало меньше очков, чем во
второй». Выделим в таблице элементарные со-
бытия, благоприятствующие каждому из этих
событий (рис. 62).
Общих элементарных событий у событий
А и В нет, ведь не может случиться так, что
в первый раз выпало больше и одновременно
меньше очков, чем во второй. События А и В
несовместны.
Поставим вопрос: чему равна вероятность
объединения AUB? Элементарные события рав- гисунок ьг
новозможны. Нужно пересчитать все элементарные события, которые благоприятству-
ют событию А и которые благоприятствуют событию В, сложить полученные числа
и разделить сумму на общее число элементарных событий 36:
15 + 15 _ 5
36 ~~ 6*
Обратите внимание: можно разбить дробь на два слагаемых:
т./ . , . «\ N(A) + N(B) N(A) N(B) , . , .
p(aub) = N - -jjr + ~jr e pU) + p(s)>
т. е. вероятность объединения двух событий оказалась равна сумме вероятностей
этих событий. Это свойство верно для любых двух несовместных событий в любом
случайном опыте.
1 1: 1
2; 1
3; 1
4; 1
5; 1
1 в;1
liLLl
1; 2
2; 2
3; 2
4; 2
5; 2
6; 2
1; 3 1; 4
2; 3 2; 4
| 3; 3
4; 3
5; 3
6; 3
3; 4
4; 4
5; 4
в; 4
1; 5
2; 5
3; 5
4; 5
1; 6 1
2: 6
3; 6
4; 6
| 5; 5 5; в 1
6; 5 | 6; 6 |
Элементарные события, благопри-
ятствующие событию А
3; 5 | Элементарные события, благопри-
ятствующие событию В
r(AUB)-N{A)+NN{B)-
ДЕЙСТВИЯ С СОБЫТИЯМИ. СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ 193

ф
Правило сложения вероятностей несовместных событий. Вероятность объ-
единения несовместных событий равна сумме их вероятностей:
Р(4ив) = Р(4) + Р(в).
Общий случай
Если события Л и Б не являются несовместными, т. е. они совместны и могут
оба наступить в результате одного опыта, то к ним нельзя применить правило для
несовместных событий. Убедимся в этом на примере.
ПРИМЕР 2. Бросают две правильные играль-
ные кости. Событие А — «на первой кости вы-
пало меньше 3 очков». Событие В — «на вто-
рой кости выпало меньше 3 очков».
Событию А благоприятствует 12 элементар-
ных событий. Событию В благоприятствует тоже
12 элементарных событий. Но четыре элемен-
тарных события общие, поскольку события А и
В совместны. Событию AUB благоприятствуют
20 элементарных событий (рис. 63).
Поэтому
шщ
ш:#.
щШ
рнщ-
р>; 1
[»; it*.
щщ
' " *> « *$$. •
:Ьх t
дй§Р
йЩШ?
1; 3
2; 3
3; 3
4; 3
5; 3
6; 3
1; 4
2; 4
3; 4
4; 4
5; 4
6; 4
1; 5
2; 5
3; 5
4; 5
5; 5
6; 5
1; 6 1
2; 6
3; 6
4; 6
5; 6
6; 6 J
2; 3
Элементарные события, благопри-
ятствующие событию А
L %Й„ 1 Элементарные события, благопри-
ятствующие событию В
ШЩШщ Элементарные события, благопри-
ятствующие обоим событиям
Х./.Ч 12 1 , v 12 1
Р<А> = 56 = !• р(в) = 36 - !•
36
6 5
9>9-
5
9*
Рисунок 63 Р(А) + Р(В) - I + I - |f a P(AUB) - §
25 /\/\/\ 112
Очевидно, о ^ о» значит, P(AUB) * Р(А) + Р(В), поскольку - + - = т:
о У о о о
Получается, что формула p(AUB) = Р(а) + Р(в) в этом случае неверна.
Как быть, если события совместны? Изобразим на диаграмме Эйлера события А и Б,
у которых есть общие благоприятствующие элементарные события (рис. 64).
Рассмотрим два события: событие С ♦наступило А, но не на-
ступило В» и событие D ♦наступило Б, но не наступило А». На
диаграмме (см. рис. 64) видно, что события С и АО В несовмест-
ны, поскольку соответствующие фигуры не имеют общих точек.
Вместе эти события образуют событие А. Поэтому по правилу
сложения вероятностей для несовместных событий находим:
Р(А) - Р(С) + Р(АПВ).
Рисунок 64 Точно так же получаем
Р(В) - P(D) + Р(АПВ).
Сложив эти равенства почленно, получим
Р(А) + Р(В) = Р(С) + Р(АПВ) + P(D) + Р(АПВ).
События С, АПВ и D несовместны и вместе образуют событие AUB. Получаем
Р(А) + Р(В) = P(AUB) + Р(АПВ),
откуда
P(AUB) - Р(А) 4- Р(В) - Р(АПВ).
Мы вывели общую формулу, и теперь можно сформулировать правило.
(2D
194
ГЛАВА IX.

\д/ Правило сложения вероятностей. Вероятность объединения двух событий
равна сумме их вероятностей без вероятности их пересечения:
P(AUB) = Р(А) + Р(В) - Р(АГ\В).
Полученная формула справедлива для любых двух событий, в том числе для несо-
вместных, поскольку в случае несовместных событий Р(ЛПВ) — О.
Вопросы
1 Сформулируйте словами правило сложения вероятностей для несовместных со-
бытий. Запишите формулу сложения вероятностей для несовместных событий.
2 Как несовместные события изображаются на диаграммах Эйлера?
3 Запишите формулу сложения вероятностей для двух произвольных событий.
Упражнения
340 Бросают одну игральную кость. Событие А — «выпало чётное число очков».
Событие В — «выпало число очков, кратное пяти».
а) Являются ли события А и В несовместными?
б) Используя правило сложения вероятностей, найдите P(AUB).
341 События U и V несовместны. Найдите вероятность их объединения, если:
а) P(U) = 0,2, P(V) = 0,4; б) Р(С7) * 0,5, P(V) - 0,2.
342 Могут ли события А и В быть несовместными, если:
а) Р(А) = 0,6, Р(В) = 0,5; в) Р(А) « а, Р(В) - 1,2 - а;
б) Р(А) = 0,1, Р(В) - 0,7; г) Р(А) - Р(в) = -^?
343 Вычислите P(AUB), если:
а) Р(А) = 0,8, Р(В) = 0,6, Р(АПВ) = 0,4;
б) Р(А) - 0,5, Р(В) - 0,6, Р(АПВ) - 0,3.
344 Вычислите вероятность пересечения событий А и В, если:
а) Р(А) - 0,8, Р(В) - 0,6, P(AUB) - 0,9;
б) Р(А) - 0,5, Р(В) - 0,6, P(AUB) - 0,8.
345 В торговом центре недалеко друг от друга расположены два автомата, прода-
ющие кофе. Вероятность того, что к вечеру в первом автомате закончится ко-
фе, равна 0,3. Такая же вероятность того, что кофе закончится во втором ав-
томате. Вероятность того, что кофе закончится в двух автоматах, равна 0,12.
Найдите вероятность события:
а) «кофе закончится хотя бы в одном из автоматов»;
б) «кофе закончится в одном из автоматов, а в другом нет».
346 В банке рядом друг с другом стоят два банкомата — старый и новый. Веро-
ятность того, что в течение дня в старом банкомате закончатся денежные ку-
пюры, равна 0,2. Вероятность того, что купюры закончатся в новом банкома-
те, равна 0,1. В двух банкоматах купюры могут закончиться с вероятностью
0,05. Найдите вероятность события:
а) «в течение дня купюры закончатся хотя бы в одном из банкоматов»;
б) «в течение дня купюры не закончатся ни в одном из банкоматов»;
в) «в течение дня купюры закончатся только в старом банкомате»;
г) «к вечеру купюры останутся хотя бы в одном из банкоматов».
ДЕЙСТВИЯ С СОБЫТИЯМИ. СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ
195

347 События С и D имеют вероятности Р(С) — 0,6 и P(D) e 0,7. Какое наимень-
шее значение может иметь вероятность события COD?
348 Пользуясь диаграммой Эйлера, докажите, что несовместны события:
а) А и АПВ; б) АПВ и АПВ.
349 Пользуясь диаграммой Эйлера для событий А, В и С, выведите формулу сло-
жения вероятностей для трёх событий:
Р(Аивис) = Р(А) + Р(В)ч-Р(С)-Р(АПВ)-Р(АПС)-Р(ВПС)ч-Р(АПВПС).
Решение задач с помощью
координатной прямой
Часто на практике случайные эксперименты и события в них связаны с изменчи-
выми или случайными величинами. События состоят в том, что та или иная величи-
на принимает определённое значение или попадает в какой-то промежуток значений.
При этом вся числовая прямая содержит все возможные элементарные события экс-
перимента, поэтому является достоверным событием.
ПРИМЕР 1. Барометр измеряет атмосферное давление Р. Рассмотрим события:
А — {атмосферное давление от 750 до 760 мм рт. ст.},
В = {атмосферное давление больше 740 мм рт. ст.},
С — {атмосферное давление от 755 до 770 мм рт. ст.}.
Изобразим события на числовой прямой промежутками (рис. 65). Это немного по-
хоже на изображение событий на диаграмме Эйлера.
В
. (. rrfVT\IZ~
740 750 755 760 770 Р, мм рт. ст.
Рисунок 65
Данных в условии недостаточно, чтобы найти вероятности этих событий. Но всё
же некоторые выводы можно сделать. Событие А целиком содержится в событии В.
Это означает, что вероятность события А не может быть больше вероятности собы-
тия В. Значит, Р(А) ^ Р(В). В этом опыте можно даже утверждать, что Р(А) < Р(В)
(подумайте, почему). Точно так же Р(С) < Р(В).
Сравнить вероятности событий А и С нельзя, даже несмотря на то, что событие С
изображается более длинным отрезком, чем событие А. Не исключено, что событие А
случается чаще, чем событие С.
ПРИМЕР 2. При продаже автомобильного аккумулятора продавец в присутствии
покупателя измеряет напряжение на клеммах аккумулятора. Замечено, что при про-
верке у 87% новых аккумуляторов напряжение на клеммах больше 11 вольт, а у
95% — не больше 13 вольт. Рассмотрим возможные события в этом эксперименте
и изобразим их на числовой прямой (рис. 66).
11 13 U. вольт
Рисунок 66
196
ГЛАВА IX.

,в
P(F) - 0,13 £ с \ P(G) - 0,05
11 13 С/, вольт
Рисунок 67
Обозначим напряжение U. Событие А «напряжение больше 11 вольт» теперь мож-
но обозначить А = {U > 11 В}. Так же обозначим и другие события: В = {U ^ 13 В},
С - {11 В < U ^ 13 В}, F = {С/ ^ 11 В} и G = {U > 13 В}.
Из условия следует, что Р(А) = 0,87 и Р(В) = 0,95. Найдём вероятности осталь-
ных событий. В этом поможет рисунок. Событие F является противоположным собы-
тию А: лучи, изображающие эти события на рисунке 66, являются продолжениями
друг друга. Значит,
P(F) = P(a) = 1-P(A) = 1-0,87 = 0,13.
Аналогично найдём вероятность события G:
P(G)~P(B) = 1-P(B) = 1-0,95 = 0,05.
Найденные вероятности удобно указывать на числовой прямой (рис. 67).
Теперь вероятность события С легко найти. События F, С и G несовместны, а вме-
сте они занимают всю числовую прямую, т. е. содержат все элементарные события
эксперимента. Поэтому
P(F) 4- Р(С) + P(G) - 1.
Тогда
Р(С) = 1 - P(F) - P(G) = 1 - 0,13 - 0,05 = 0,82.
Вероятность события С можно найти и другим способом. Оно является пересече-
нием событий Л и В. Из формулы сложения вероятностей получаем
P(AUB) = Р(Л) + Р(В) - Р(С).
Объединение AUB — это достоверное событие, занимающее всю числовую пря-
мую, поэтому P(AUB) = 1. Подставим известные значения в формулу:
1 = 0,87 4- 0,95 - Р(С),
откуда
©
0
Р(С) = 0,87 + 0,95 - 1 = 0,82.
Вопросы
1 Чему равна вероятность события, изображение которого на числовой прямой
занимает всю прямую?
2 Как изображаются на координатной прямой взаимно противоположные события?
3 Промежуток, изображающий первое событие, целиком содержится в промежут-
ке, изображающем второе событие. Сравните вероятности этих событий.
Упражнения
350 Аня ждёт автобус на остановке. Изобразите на координатной прямой следую-
щие события:
А = {автобус придёт не меньше чем через минуту},
В = {автобус придёт не меньше чем через 2 минуты},
С = {автобус придёт не меньше чем через 5 минут}.
Расположите события в порядке возрастания их вероятностей.
ДЕЙСТВИЯ С СОБЫТИЯМИ. СЛОЖЕНИЕ ВЕРОЯТНОСТЕЙ 197

351 Мама измеряет температуру воды для купания ребёнка. Изобразите на коор-
динатной прямой следующие события:
А = {температура воды не ниже 35,5 °С},
В — {температура воды не ниже 36,2 °С},
С = {температура воды не ниже 36 °С}.
Расположите эти события в порядке возрастания их вероятностей.
352 На хлебозаводе производится контрольное взвешивание испечённой буханки
хлеба. Изобразите на координатной прямой следующие события:
А = {масса буханки больше 790 г},
В = {масса буханки меньше 810 г},
С = {масса буханки от 792 до 808 г},
D — {масса буханки от 790 до 810 г}.
Укажите событие, которое имеет наименьшую вероятность.
353 Вероятность того, что в случайный момент времени атмосферное давление
в некотором городе не выше 745 мм рт. ст., равна 0,53. Найдите вероятность
того, что в случайный момент давление превышает 745 мм рт. ст. Изобрази-
те соответствующие события на числовой прямой.
354 При изготовлении подшипников диаметром 65 мм вероятность того, что диа-
метр будет отличаться от заданного более чем на 0,01 мм, равна 0,034. Най-
дите вероятность того, что случайный подшипник будет иметь диаметр в пре-
делах от 64,99 до 65,01 мм.
355 При изготовлении шоколадных батончиков номинальной массой 55 г вероят-
ность того, что масса батончика будет в пределах от 54 до 56 г, равна 0,76.
Найдите вероятность того, что масса батончика отличается от номинальной
больше чем на 1 г.
356 Вероятность того, что на тестировании по физике студент П. верно решит не
менее 11 задач, равна 0,61. Вероятность того, что П. верно решит не менее
10 задач, равна 0,69. Найдите вероятность того, что П. верно решит ровно
10 задач.
357 Вероятность того, что новый сканер прослужит больше года, равна 0,96.
Вероятность того, что он прослужит два года или больше, равна 0,87. Найди-
те вероятность того, что сканер прослужит меньше двух лет, но больше года.
358 Термометр измеряет комнатную температуру. Вероятность того, что темпера-
тура окажется не ниже 18 °С, равна 0,78. Вероятность того, что температура
окажется не выше 23 °С, равна 0,63. Найдите вероятность того, что темпера-
тура окажется в пределах от 18 до 23 °С.
359 В роддоме измеряют вес новорождённого. Вероятность того, что вес окажется
не меньше 3 кг, равна 0,87; вероятность того, что вес окажется не больше
3 кг 600 г, равна 0,93. Найдите вероятность того, что вес случайно выбран-
ного новорождённого окажется в пределах от 3 кг до 3 кг 600 г.
360 По данным многолетних наблюдений установлено, что в городе N годовое ко-
личество осадков превысит 2000 мм с вероятностью 0,45, а вероятность того,
что годовое количество осадков окажется меньше 1500 мм, равна 0,24. Най-
дите вероятность того, что количество осадков в городе N в следующем году
окажется в промежутке от 1500 до 2000 мм.
198
ГЛАВА IX.

Действия
с событиями.
Умножение
вероятностей
Когда проводится случайный опыт, наступив-
шие события могут менять вероятности дру-
гих событий. Получаются условные вероят-
ности, т. е. вероятности при определённом
условии. Если же одно событие не влияет
на вероятность другого, то такие события
независимы. Познакомившись с условной
вероятностью и независимыми событиями,
мы узнаем, в каких случаях, почему и как
вероятности событий умножаются.
В этой главе мы обсудим, как можно нахо-
дить вероятности событий с помощью спе-
циальной графической схемы — дерева слу-
чайного эксперимента.
52 Условная вероятность.
Правило умножения
53 Дерево случайного опыта
54 Независимые события
55 Об ошибке Эдгара По и о том,
как победить стечение
обстоятельств

^52) Условная вероятность.
Правило умножения
Часто случайное событие А в случайном опыте приходится рассматривать при ус-
ловии, что произошло некоторое другое событие В. Наступление события В меняет
эксперимент. По сути, при наступлении некоторого события мы получаем новый экс-
перимент, и вероятности других событий при этом могут меняться. Вероятность со-
бытия А при условии события В может вырасти, уменьшиться или остаться прежней.
Определение. Вероятность события А при условии, что событие В произошло,
называется условной вероятностью события А при условии события В. Обо-
значается эта вероятность Р(А\В).
Рассмотрим случайный опыт, вде наступает событие В, а при этом условии наступа-
ет событие А. Изобразим схему этого эксперимента с помощью цепочки1 событий. Собы-
тия будем изображать точками, а переходы от одного события к другому — стрелками.
Начнём опыт с точки S (от англ. start — начало).
Р(В) Р(А|Б) В ходе опыта наступает событие В. Изобразим это со-
s# *з АПв бытие точкой и покажем стрелкой, что из начально-
го состояния S произошёл переход к событию В. Ве-
Рисунок 68 роятность этого события Р(В) укажем около стрелки
(рис. 68).
Мы знаем, что событие В наступило. Предположим, что наступает событие А. Это
значит, что наступают оба события А и В, т. е. наступает событие АПВ. Переход от
события В к событию АПВ также покажем стрелкой и напишем над ней вероятность
Р(А|В) — условную вероятность события А при условии, что событие В уже произо-
шло.
ПРИМЕР 1. Предположим, что в некотором городе 48% населения — мужчины,
а среди мужчин 15 % — пенсионеры. Какова вероятность того, что случайно выбран-
ный житель города окажется мужчиной на пенсии?
Эта вероятность равна доле мужчин-пенсионеров среди всех жителей города. Пусть
событие В «выбранный житель — мужчина». Тогда Р(В) = 0,48, Обозначим А собы-
тие «выбранный житель — пенсионер». Тогда наша задача состоит в вычислении ве-
роятности события АПВ.
Мы не знаем долю пенсионеров в городе, но знаем
0,48 »• °'15 >• Д°лю пенсионеров среди мужчин. Поэтому мы знаем
S В лПв условную вероятность Р(А|В). Она равна 0,15. Цепоч-
Рис ок gg ка событий в этой задаче изображена на рисунке 69.
Найти долю мужчин-пенсионеров несложно. Если чис-
ленность населения обозначить п, то всего мужчин в городе п • 0,48, а мужчин-пен-
сионеров
п • 0,48 • 0,15 = п • 0,072,
т. е. вероятность события АПВ равна 0,072. Эта вероятность получена умножением
Р(В) на Р(А|В). Получилось равенство
Р(АПВ) - Р(В) • Р(А|В).
1 Цепочка или цепь — частный случай графа. В математике графы используются для изобра-
жения различных процессов, событий, объектов и связей между ними. Граф состоит из вершин
(точек) и рёбер — линий, соединяющих некоторые вершины.
200
ГЛАВА X.

Эту формулу мы получили на примере, но она верна для любых случайных собы-
тий в любых случайных опытах.
Ф
Правило умножения вероятностей. Р(АПБ) = Р(в) - Р(А\В).
Очерёдность событий в цепочке может быть другой. Если поменять события места-
ми, получится равенство
Р(А П В) - Р(А) • Р(Б|Д).
Щ>
Правило умножения вероятностей позволяет вычислять вероятности во многих
задачах.
ПРИМЕР 2. В коробке 3 синих и 7 красных карандашей. По очереди извлекают
два карандаша. Найдём вероятность того, что сначала появится красный, а затем —
7
синий карандаш. Вероятность сначала извлечь красный карандаш равна —. После
этого в коробке останется 3 синих и 6 красных карандашей. Значит, вероятность из-
3
влечь теперь синий карандаш равна —. Эта вероятность условная. Для простоты обо-
значим цвета (для нас цвет это событие) буквами if и С и по правилу умножения
получаем
Р(КС) = Р(К) • Р(С]{первый карандаш — красный}).
Подумайте, как найти вероятность последовательности КСК при извлечении трёх
карандашей.
Если вероятность события В больше нуля, то можно выразить Р(Л|Б), разделив
обе части равенства Р(АЛВ) « Р(В) • Р(А\В) на вероятность события В.
Ф
Формула условной вероятности. Если вероятность события В больше нуля, то
ПРИМЕР 3. В торговом центре установлены два автомата, продающие кофе. Вероят-
ность того, что к концу дня кофе закончится в каждом отдельном автомате, равна 0,3.
В обоих автоматах кофе заканчивается к вечеру с вероятностью 0,21. Вечером пришёл
мастер, чтобы обслужить автоматы, и обнаружил, что в первом автомате кофе закончил-
ся. Какова теперь вероятность того, что во втором автомате кофе тоже закончился?
Обозначим события: А «кофе закончился в первом автомате», В «кофе закончился
во втором автомате». По условию Р(А) = 0,3, Р(АПВ) = 0,21. Нужно найти Р(В\А):
Р[В\А) р(А) 0,3 °'7'
(уЛ Вопросы
1 Запишите обозначение для условной вероятности события С при условии события в.
2 Чему равна условная вероятность выпадения двух орлов при двукратном броса-
нии монеты, если в первый раз выпала решка?
ДЕЙСТВИЯ С СОБЫТИЯМИ. УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ 201

3 Чему равна условная вероятность выпадения двух орлов при двукратном броса-
нии монеты, если в первый раз выпал орёл?
4 В некотором опыте произошло событие В. Может ли это увеличить вероятность
другого события? Уменьшить вероятность другого события? Приведите приме-
ры, когда условная вероятность события больше и когда она меньше исходной
-^ вероятности этого события.
\J Упражнения
361 При двукратном бросании монеты в первый раз выпала решка. Найдите ус-
ловную вероятность события:
а) «оба раза выпадет решка»;
б) «выпадет хотя бы один орёл»;
в) «выпадут два орла».
362 При двукратном бросании игральной кости сумма выпавших очков равна 8.
Найдите условную вероятность события:
а) «в первый раз выпадет 3 очка»;
б) «при одном из бросков выпадет 3 очка»;
в) «в первый раз выпадет меньше 5 очков»;
г) «во второй раз выпадет меньше 2 очков».
363 При двукратном бросании игральной кости сумма выпавших очков равна 9.
Найдите условную вероятность события:
а) «в первый раз выпадет 5 очков»;
б) «при одном из бросков выпадет 4 очка»;
в) «в первый раз выпадет меньше очков, чем во второй»;
г) «во второй раз выпадет меньше чем 3 очка».
364 Игральную кость бросают два раза. В первый раз выпало 3 очка. Найдите
вероятность того, что после второго броска сумма очков окажется:
а) равна 9; б) больше чем 7; в) больше чем 10; г) меньше чем 5.
365 В случайном опыте есть события А и В. Найдите вероятность пересечения
событий АПВ, если известно, что:
а) Р(Б) = 0,3 и Р(А\В) = 0,5; в) Р(Б) - 0,72 и Р(А\В) = 0,25;
б) P(£) = J и Р(А|В) = |; г) Р(Б) » 0,34 и Р(А\В) « 0,2.
366 В торговом центре рядом установлены два автомата, продающие кофе. Веро-
ятность того, что к концу дня кофе закончится в первом автомате, равна 0,2.
Если это случилось, то нагрузка на второй автомат растёт, и кофе может за-
кончиться в нём с вероятностью 0,8. Найдите вероятность того, что:
а) к концу дня в обоих автоматах закончится кофе;
б) к концу дня кофе закончится только в первом автомате. (Указание: найдите
сначала условную вероятность того, что кофе во втором автомате не закончится.)
367 В некотором городе 7 % населения — студенты. Из всех студентов 60 % учат-
ся в университете. Найдите вероятность того, что случайно выбранный жи-
тель этого города является студентом университета.
368 В посёлке 40 % взрослого населения занято в сельском хозяйстве, причём
5 % взрослого населения посёлка работают в агропромышленном холдинге
«Нива». Для опроса случайно выбран житель этого посёлка, и оказалось, что
он занят в сельском хозяйстве. При этом условии найдите условную вероят-
ность того, что он работает в холдинге «Нива».
202
ГЛАВА X.

369 В коробке было 2 красных и 3 синих фломастера. Ваня не глядя достал
из коробки 3 фломастера, причём оказалось, что среди них есть и синий,
и красный. Какова вероятность того, что Ваня достал:
а) два синих фломастера и один красный;
б) два красных фломастера и один синий?
370 Игральную кость последовательно бросают до тех пор, пока сумма выпавших очков
не станет 4 или больше. Найдите вероятность того, что будет сделано два броска.
371 На кассе универсама продаются леденцы. В какой-то момент в коробке оста-
лось 10 красных, 9 синих и 6 зелёных леденцов. Таня, Ваня и Маня по оче-
реди покупают по одному леденцу. Кассир не глядя достаёт леденцы из ко-
робки. Найдите вероятность того, что:
а) Таня и Ваня получат зелёные, а Маня — красный леденец;
б) Таня и Маня получат синие леденцы, а Ваня — красный;
в) Таня получит зелёный леденец, Ваня — красный, а Маня — синий;
г) все трое получат красные леденцы.
372 Найдите вероятность получить п разных результатов, бросив игральную кость
п раз, если:
а) п — 3; б) л - 4; в) п = 5; г) п в 6; д) п - 7.
373 В ящике 20 левых и 20 правых перчаток. Сколько нужно достать перчаток,
не глядя в ящик, чтобы среди вынутых перчаток нашлась хотя бы одна ле-
вая и хотя бы одна правая перчатка:
а) наверняка (с вероятностью 1); б) с вероятностью не меньше чем 0,95?
15з) Дерево случайного опыта
Дерево1 случайного опыта, или дерево вероятностей, — удобный инструмент ре-
шения задач. В одних случаях для наглядного представления опыта лучше использо-
вать диаграмму Эйлера или координатную прямую, в других — дерево.
ПРИМЕР 1. Рассмотрим хорошо знакомый нам эксперимент — двукратное броса-
ние монеты. Начальное состояние, когда ни один бросок ещё не сделан, изобразим
точкой S. При первом броске может выпасть орёл либо решка. Изобразим эти два
события точками О и Р и проведём к ним стрелки от точки S вниз влево и вправо
(рис. 70). Стрелки будем называть рёбрами дерева. Начальная точка S, промежуточ-
ные точки и конечные точки называются вершинами дерева.
S S S
2/ \2 2/ \2 2У
а) Первый бросок
б) Выпал орёл при втором
броске
ОО ОР РО РР
в) Законченное дерево
Рисунок 70
Дерево — разновидность графа. Если в графе можно выйти из какой-то вершины и, «пройдя
круг» по рёбрам графа, вернуться в ту же вершину, то говорят, что граф имеет цикл. Дере-
во — это граф без циклов. Все цепи в дереве расходятся, как ветки дерева. Отсюда и название.
ДЕЙСТВИЯ С СОБЫТИЯМИ. УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ 203

Около рёбер напишем вероятности событий: ребро SO имеет вероятность -, и та-
1 г
кую же вероятность - имеет ребро SP.
Ф
' - ._ при кроении «ер** н^но следи.. ЧГОвЫ . ро™й о«о-
ло всех рёбер, выходящих из одной вершины, была равна единице.
Предположим сначала, что при первом броске выпал орёл. При втором броске то-
же может выпасть орёл, и тогда наступит событие «два орла»: ОО. Вероятность вы-
падения двух орлов равна Р(ОО) = —, Но если в первый раз уже выпал орёл, то со-
бытие ОО наступает с вероятностью - — если во второй раз выпадет орёл. То есть
условная вероятность двух орлов при условии, что в первый раз выпал орёл, равна
р(оо|в 1-й раз выпал орёл) = ~. Поэтому, изображая выпадение второго орла в дереве,
около ребра, ведущего из О в ОО, мы напишем условную вероятность - (см. рис. 70, б).
Достроим дерево, проведя ещё три ребра к событиям ОР, РО и РР (см. рис. 70, в).
■ч Элементарные события эксперимента в дереве изображаются конечными вер-
^^Т) шинами дерева. К каждой конечной вершине ведёт единственная цепочка от
точки S. Поэтому можно считать, что элементарные события изображаются не
только конечными вершинами, но и соответствующими цепочками.
Например, элементарное событие ОР на рисунке 70 изображается точкой ОР, к ко-
торой ведёт цепочка S — О — ОР. Она выделена на рисунке красной линией. Вер-
шину ОР и всю цепочку S — О — ОР можно считать изображениями одного и того
же элементарного события «в первый раз выпал орёл, во второй — решка».
■ч Найти вероятность элементарного события можно с помощью правила умноже-
^^Т/ ния вероятностей: нужно найти произведение условных вероятностей вдоль це-
почки, идущей от вершины S к вершине, изображающей нужное элементарное
событие.
Например, чтобы найти вероятность события ОР, нужно умножить вероятности
вдоль цепочки S — О — ОР. Произведение вероятностей вдоль цепочки мы будем
для простоты называть вероятностью этой цепочки:
Р(ОР) = P(S — О — ОР) - P(S — О) • Р(0 — ОР) = \ -\ » \.
Не элементарные, а более сложные события изображаются промежуточными вер-
шинами дерева или какой-нибудь фигурой (например, овалом),
объединяющей благоприятствующие элементарные события.
ПРИМЕР 2. На рисунке 71 изображено дерево некоторого
случайного опыта.
В этом опыте 4 элементарных события: а, Ь, с и d. Направ-
ления рёбер не будем отмечать стрелками, так как ясно, что
цепочки идут от вершины S.
Есть промежуточная вершина, изображающая событие К.
Событие А показано овалом, объединяющим элементарные
события end.
204
ГЛАВА X.

Найдём вероятности событий К и А. Событию К благоприятствуют элементарные
события а, Ь и с. Но нам не нужно искать их вероятности. Сразу видно, что событие К
имеет вероятность
Р(К) « P(S — К) = 0,3.
Осталось найти вероятность события А. Этому событию благоприятствуют элементар-
ные события end. Значит, вероятность события А равна сумме вероятностей цепочек
S — К—с и S — d. Без необходимости в цепочках мы больше не будем писать промежу-
точные буквы и тире. Цепочки S—К—с и S—d кратко можно записать Sc и Sd.
Р(А) - P(Sc) + P(Sd).
Пользуясь правилом умножения вероятностей, получаем
P(Sc) - P(SK) • Р(Кс) - 0,3 • 0,3 - 0,09 и P(Sd) = 0,7.
Следовательно, Р(А) « 0,09 + 0,7 = 0,79.
Можно сформулировать общее правило нахождения вероятностей событий с помо-
щью дерева. Оно получается из правила сложения вероятностей несовместных событий.
Ф
Правило сложения. Чтобы найти вероятность события с помощью дерева, нужно
сложить вероятности всех цепочек, ведущих к этому событию от начальной вершины.
Мл
2/
7
з /
8/
\б
\7
Ч 5
\8
з/
7/
кд
\4
V
Дерево позволяет рассматривать случайный опыт как бы по частям, мысленно рас-
положив случайные события в некотором порядке. Очерёдность эта только мыслен-
ная, и её при желании можно поменять. Деревья очень удобны при решении задач,
связанных со случайным выбором.
ПРИМЕР 3. Решим задачу. В группе 3 мальчика и 5 дево- g
чек. Случайным образом выбирают двух человек. Какова ве-
роятность того, что будут выбраны один мальчик и одна де-
вочка?
Решение. Мысленно разобьём одновременный выбор двоих
на два последовательных выбора и изобразим дерево случайно-
го опыта. Выбор мальчика обозначим буквой М, а девочки — Д.
При первом выборе вероятность выбрать мальчика равна —,
мм^мд Лдм
5
а девочку — -. Укажем эти вероятности около рёбер SM и Рисунок 72
SR (рис. 72).
При втором выборе вероятности выбора мальчика и девочки становятся условны-
ми и зависят от того, кто был выбран в первый раз. Если в первый раз был вы-
бран мальчик, то мальчиков осталось 2 из 7 человек. Поэтому во второй раз мальчик
2
будет выбран (ребро М — ММ) с вероятностью -, а девочка будет выбрана (ребро
5
М — МД) с вероятностью -.
Точно так же, если в первый раз была выбрана девочка, то остаётся 4 девочки и
3 мальчика из 7 оставшихся детей. Вероятности выбора мальчика и девочки теперь
3 4
- и - соответственно.
Событию А «один мальчик и одна девочка» благоприятствуют два элементарных
события, которые изображаются в дереве цепочками S — М — МД и S — Д — ДМ
ДЕЙСТВИЯ С СОБЫТИЯМИ. УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ 205

(выделены на рисунке 72 красным цветом). Пользуясь правилом, найдём вероятности
этих цепочек и сложим результаты:
Р(А) = P(S - М - МД) + P(S - Д - ДМ) = | ■ | + | ■ | = ||.
0
374
375
376
377
378
Вопросы
Как называются точки, изображающие события в дереве?
Как называются линии, изображающие переход от одного события к другому?
Чему равна сумма вероятностей около рёбер, выходящих из одной вершины?
Как изображаются элементарные события в дереве?
Сформулируйте правило вычисления вероятности элементарного события в дереве.
Сформулируйте правило сложения для вычисления вероятностей событий с по-
мощью дерева.
Упражнения
Симметричную монету бросают дважды.
а) Изобразите дерево этого эксперимента, и подпи-
шите около рёбер вероятности соответствующих пе-
реходов.
б) Найдите цепочку, изображающую элементарное
событие РО.
в) Укажите в построенном дереве событие А «в пер-
вый раз выпала решка».
г) Укажите в построенном дереве событие В «орёл
выпал хотя бы один раз».
На рисунке 73 изображено дерево некоторого слу-
чайного эксперимента. Какие ошибки допущены?
На рисунке 74 изображено дерево некоторого слу-
чайного опыта.
а) Перерисуйте дерево в тетрадь и подпишите недо-
стающие вероятности около рёбер.
б) Сколько элементарных событий в этом экспери-
менте?
в) Пользуясь правилом умножения вероятностей,
вычислите вероятности цепочек SAC и SBE.
г) Найдите вероятность события F.
На рисунке 75 изображено дерево некоторого слу-
чайного опыта.
а) Изобразите это дерево в своей тетради и подпи-
шите недостающие вероятности около рёбер.
б) Вычислите вероятности цепочек SAC и SAGF.
На рисунке 76 изображено дерево некоторого слу-
чайного опыта и событие А. Рёбра проведены пунк-
тиром. Известно, что из каждой точки возможные
переходы к следующим событиям равновероятны.
а) Скопируйте рисунок в тетрадь и подпишите око-
ло рёбер соответствующие вероятности.
206
ГЛАВА X.

Клуб
• N
• Ч
У Ч
• ч
• ч
* \ /Т\
' \ / \
' \ t \
/ V—v ! ч
Рисунок 76
Школьный
двор
Рисунок 78
379
380
381
382
383
384
385
б) Обведите сплошной линией цепочки, благоприятствующие событию А.
в) Найдите вероятность события А.
На рисунке 77 изображено дерево некоторого случайного опыта и показаны
события А и В. Рёбра проведены пунктиром. Известно, что рёбра, исходящие
из одной вершины, равновероятны.
а) Скопируйте рисунок в тетрадь. Обведите сплошной линией цепочки, бла-
гоприятствующие событию А. Другим цветом обведите цепочки, благоприят-
ствующие событию Б.
б) Найдите вероятность события А.
в) Найдите вероятность события В.
Сергей Петрович гуляет по своему посёлку. Схема дорожек показана на рисун-
ке 78. Он начинает прогулку в точке S и на каждой развилке с равными шан-
сами выбирает любую из дорожек (но не возвращается).
Найдите вероятность того, что Сергей Петрович в конце концов придёт:
а) на школьный двор; в) на луг;
б) к ферме; г) к ферме или к колодцу.
В группе 18 человек, из них 7 мальчиков, остальные девочки. По сигналу
учителя физкультуры они быстро построились в одну шеренгу в случайном
порядке. Найдите вероятность того, что на концах шеренги окажутся две
девочки или два мальчика.
В классе 30 человек, среди них две подруги — Аня и Катя. Учащихся слу-
чайным образом разбивают на две равные группы. Найдите вероятность того,
что Аня и Катя окажутся в одной и той же группе.
Из ящика, где хранятся 9 жёлтых и 15 зелёных карандашей, продавец не
глядя вынимает один за другим 3 карандаша. Найдите вероятность того, что:
а) два первых карандаша окажутся зелёными;
б) все три карандаша будут жёлтые;
в) цвета будут чередоваться в порядке жёлтый — зелёный — жёлтый.
На фабрике керамической посуды 10 % произведённых тарелок имеют де-
фект. При контроле качества продукции выявляется 80 % дефектных тарелок.
Остальные тарелки поступают в продажу. Найдите вероятность того, что оче-
редная произведённая тарелка попадёт в продажу.
На заводе производят электрические лампочки, причём 5 % всех изготовлен-
ных лампочек неисправны. Система контроля качества выявляет все неис-
ДЕЙСТВИЯ С СОБЫТИЯМИ. УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ 207

правные лампочки, но по ошибке бракует ещё 1 % исправных лампочек. Все
забракованные лампочки поступают в переработку, а остальные — в прода-
жу. Найдите вероятность того, что очередная изготовленная лампочка отпра-
вится в переработку.
386 Автоматическая линия изготавливает батарейки. Вероятность того, что гото-
вая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка
проходит систему контроля. Эта система бракует 99 % неисправных батареек
и по ошибке бракует 3 % исправных батареек. Найдите вероятность того, что
очередная изготовленная батарейка будет забракована системой контроля.
Независимые события
В жизни мы часто встречаемся с ситуациями, когда события каким-то образом
связаны. По наступлению одного события можно судить об изменении вероятности
другого. Например, если на небе тучи, то дождь более вероятен, чем в ясную по-
году.
Если нам сказали, что на игральной кости выпало число, большее 4, то мы
можем ожидать шестёрку (условная вероятность этого 0,5), но не можем ожидать
число 3 (условная вероятность равна нулю).
Бывают события, которые не зависят друг от друга. Например, при бросании двух
костей результат бросания первой кости не влияет на число очков, выпавших на вто-
рой кости. Про такие события говорят, что они независимы.
Разумно считать, что события А и В независимы, если наступление одного из них
не влияет на вероятность другого.
Если вероятности событий А и В больше нуля, то независимость событий А и В
можно выразить равенствами
Р(А\В) = Р(А) и Р(В\А) - Р(В).
Но тогда из известных нам формул
Р(АПВ) = Р(В) • Р(А\В) и Р(АПВ) = Р(А) • Р(В\А)
получается равенство Р(А П В) = Р(А) • Р(В).
Это равенство мы возьмём за определение независимости двух событий1.
Определение. Два события Див называются независимыми, если вероят-
ность их пересечения равна произведению их вероятностей:
Р(АПВ) = Р(А) • Р(В).
Чаще всего о независимости событий судят не по тому, выполняется или нет ра-
венство Р(А П В) — Р(А) • Р(В), а по тому, как устроен случайный опыт, в котором
эти события наступают. Часто независимые события возникают, когда случайный
опыт состоит из нескольких независимых случайных испытаний.
ПРИМЕР 1. Рассмотрим двукратное бросание игральной кости и два события: со-
бытие А «в первый раз выпало более трёх очков» и событие В «во второй раз вы-
1 Аналогично можно говорить о независимости трёх, четырёх и более событий. Если вероят-
ность пересечения любого набора этих событий равна произведению их вероятностей, то собы-
тия называются независимыми.
208
ГЛАВА X.

пало менее трёх очков». Будут ли события А и В независимыми? Элементарные
события, благоприятствующие событиям А, В и АО В, представлены в таблицах
(рис. 79, а—в).
Зная число элементарных событий, благоприятствующих каждому событию, легко
обнаружить, что Р(А) — -, Р(В) ж «, и поэтому Р(А) • Р(В) — ~z. На рисунке 79, в
f% 1
видно, что Р(АЛВ) = — = - Получается, что
Р(АПВ) = Р(А) • Р(В),
и, значит, события А и В независимы.
1
2-
3-
гт
5
Ls,
1
1
1
, 1
, 1
, 1
1; 2
2; 2
3; 2
4; 2
5; 2
6; 2
1; 3
2; 3
3; 3
4; 3
5; 3
6; 3
1; 4
2; 4
3; 4
4; 4
5; 4
6; 4
1; 5
2; 5
3; 5
4; 5
5; 5
6; 5
1; 6
2; 6
3; 6
4; 6
5; 6
6; 6
рЛ~
2; 1
3; 1
4; 1
5; 1
б; 1
"ПТ1
2; 2
3; 2
4; 2
5; 2
6; 2_|
1; 3
2; 3
3; 3
4; 3
5; 3
| 6; 3
1; 4
2; 4
3; 4
4; 4
5; 4
6; 4
1; 5
2; 5
3; 5
4; 5
5; 5
6; 5
1; 6
2; 6
3; 6
4; 6
5; 6
6; 6
18 элементарных событий, благоприят-
ствующих событию А
12 элементарных событий, благоприят-
ствующих событию В
1; 1
2; 1
I 3; 1
14; 1
5> *
[б; j^
1; 2
2; 2
3; 2
4; 2
5; 2
6; 2
1; 3
2; 3
3; 3
4; 3
5; 3
6; 3
1; 4
2; 4
3; 4
4; 4
5; 4
6; 4
1; 5
2; 5
3; 5
4; 5
5; 5
6; 5
1; 6
2; 6
3; 6
4; 6
5; 6
6; 6
6 элементарных событий, благоприятству-
ющих событию АО В
Рисунок 79
Независимые события встречаются не только при независимых испытаниях. Пояс-
ним это на примере.
ПРИМЕР 2. Наудачу выбираем число из ряда 1, 2, 3, 4, ..., 100. Пусть событие А
состоит в том, что это число чётное; событие В — что это число делится на 5. Тогда
событие АГ\В состоит в том, что выбранное число делится и на 2, и на 5. Это зна-
чит, что выбранное число делится на 10.
Покажем, что события А и В независимы. Нужно найти вероятности Р(А), Р(Б),
Р(АПВ) и убедиться в том, что выполняется равенство
Р(АЛВ) = Р(А) • Р(В).
Среди 100 первых натуральных чисел всего 100 : 2 в 50 чётных. Поэтому
Р<А> - ш - °'5-
Среди 100 первых натуральных чисел на 5 делятся числа 5, 10, 15, 20, ..., 95,
100 — всего 100 : 5 = 20 чисел. Поэтому
20
Р(В)
100
= 0,2.
ДЕЙСТВИЯ С СОБЫТИЯМИ. УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ 209

Так же находим, что среди первых 100 натуральных чисел всего 100 : 10 = 10
чисел, кратных 10. Следовательно,
р(АПВ) = ш = 0Д-
Таким образом,
Р(АПВ) = 0,1 и Р(Л) • Р(В) - 0,5 • 0,2 = 0,1.
Получаем, что
Р(АЛВ) - Р(А) • Р(В).
Следовательно, события А и В независимы.
Так получилось потому, что число 100 делится и на 2, и на 5. Если бы мы выби-
рали числа не из 100, а, например, из 99 первых натуральных чисел, то это был бы
другой случайный опыт, и события А и Б не были бы независимыми.
Ф
1 Важно! Не следует путать независимые и несовместные события. Несовмест-
ные события, как правило, зависимы: если произошло одно из них, то мы
заведомо знаем, что не произошло другое.
С г) Вопросы
1 Дайте определение независимых событий.
0
2 События А и А имеют положительные вероятности. Могут ли события А и А
быть независимыми?
3 Являются ли элементарные события в случайном опыте независимыми событи-
ями?
Упражнения
387 События U и V независимы. Найдите вероятность события С/П К, если:
а) P(U) = 0,4, P(V) - 0,6; б) P(U) - 0,1, P(V) = 0,8.
388 События К и L независимы. Найдите вероятность события К, если:
a) P(L) = 0,8, P(KClL) = 0,48; б) P(L) = 0,2, P(KDL) - 0,08.
389 События t/, V и W независимы. Найдите вероятность события UCWDW,
если:
а) P(U) - 0,4, P(V) = 0,6, P(W) - 0,5;
б) Р(Е7) * 0,4, P(V) = 0,3, P(W) - 0,1.
390 События Ку L и М независимы. Найдите вероятность события К, если:
а) P(L) « 0,8, Р(М) = 0,6, Р(КГ)ЬПМ) - 0,096;
б) P(LPIM) - 0,1, Р(КПЬПМ) - 0,06.
391 Монету бросают два раза. Являются ли независимыми события:
а) Л «в первый раз выпадет орёл» и В «во второй раз выпадет решка»;
б) А «при первом броске выпадет орёл» и В «орёл выпадет хотя бы один раз»?
392 Игральную кость бросают дважды. Являются ли независимыми события:
а) А «при первом броске выпадет шестёрка» и В «при втором броске выпадет
меньше трёх очков»;
б) А «при первом броске выпадет больше трёх очков» и В «сумма выпавших
очков меньше девяти»?
210
ГЛАВА X.

393 Случайным образом выбираем натуральное число от 1 до 24. Событие С —
«число чётное». Являются ли события С и D независимыми, если событие D
состоит в том, что:
а) выбранное число делится на 3;
б) выбранное число делится на 5?
394 Бросают одну игральную кость. Событие А — «выпадет чётное число очков».
Являются ли независимыми события Л и Б, если событие В состоит в том, что:
а) выпадет число очков, кратное 3;
б) выпадет число очков, кратное 5?
395 Вероятность того, что лампочка в люстре перегорит в течение года, равна 0,2.
Считая, что лампочки перегорают независимо друг от друга, найдите вероят-
ность того, что в течение года перегорят все лампочки в люстре, если в люс-
тре:
а) 2 лампочки; б) 3 лампочки; в) 5 лампочек.
396 Стрелок в тире стреляет по мишени до тех пор, пока не собьёт её. Рассмотрим
события А «стрелку потребовалось не более трёх выстрелов» и В «стрелку
потребовалось не более пяти выстрелов». Являются ли события А и В неза-
висимыми?
397 В некотором случайном опыте вероятность события А равна 0,4, вероятность
события В равна 0,5. Известно, что события А и В независимы. Найдите ве-
роятность события AUB.
398 События А и В независимы. Докажите, что независимы события А и В.
Об ошибке Эдгара По и о том,
как победить стечение обстоятельств
Знаменитый автор детективов Э. А. По в эпилоге рассказа «Мари Роже» рассуж-
дает о вероятностях, возникающих при бросаниях костей, таким образом: «...обычно-
го читателя почти невозможно убедить, что при игре в кости двукратное вы-
падение шестёрки делает почти невероятным выпадение её в третий раз и да-
ёт все основания поставить против этого любую сумму. Заурядный интеллект
не может этого воспринять, он не может усмотреть, каким образом два броска,
принадлежащие уже прошлому, могут повлиять на бросок, существующий ещё по-
ка только в будущем...»
Разумеется, в ошибку впадает сам Эдгар По. Эта ошибка известна как ошибка
игрока. Действительно, вероятность выпадения трёх шестёрок мала. Она равна
1 1 1 д 1
6 6 6* 216'
Однако если шестёрка уже выпала два раза подряд, то условная вероятность выпа-
1
дения трех шестерок стала равна - — она совпадает с вероятностью выпадения толь-
о
ко одной шестёрки. Когда выпали две первые шестёрки, условия опыта изменились,
и вероятность трёх шестёрок теперь уже не является пренебрежимо малой. Теперь
вовсе нет «оснований поставить против этого любую сумму».
Впасть в ошибку, похожую на ошибку Эдгара По, очень просто. Люди часто не-
дооценивают грозящую опасность и ведут себя легкомысленно, не учитывая, что по
ДЕЙСТВИЯ С СОБЫТИЯМИ. УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ 211

мере наступления различных неблагоприятных событий вероятность опасности может
увеличиваться.
При создании систем безопасности и защиты используются свойства независимых
событий.
Чтобы многократно уменьшить вероятность катастрофы, все жизненно важные си-
стемы автомобилей, судов и самолётов дублируются. При этом каждая такая система
не зависит от работы остальных. Поломки двух независимых систем также являются
независимыми.
Предположим, что в автомобиле две независимые тормозные системы и вероят-
ность отказа одной из них при нажатии на тормоз равна 0,00001. Это большая веро-
ятность. Если бы тормоза в автомобилях отказывали с такой частотой, то в крупных
городах аварии из-за отказа тормозов случались бы много раз в день.
Но вероятность одновременного отказа обеих систем ничтожна. Она равна
0,000012 = = 0,0000000001. Поэтому тормозные системы современных автомобилей
считаются надёжными даже в условиях интенсивного движения в современных мега-
полисах.
В автомобилях два независимых контура системы тормозов. В пассажирских само-
лётах по меньшей мере два двигателя, две системы электроснабжения, две системы
управления, два пилота. И всё равно...
Мы слышим, что автокатастрофа случилась из-за неисправности тормозов. Мы
удивляемся — как же так, ведь тормоза продублированы! А на самом деле один тор-
мозной контур в этом автомобиле не работал уже год, а хозяин всё никак не находил
времени отдать машину в ремонт.
При взлёте разбился самолёт — несчастливое стечение обстоятельств. Плохая пого-
да, обледенел датчик давления на крыле, пилот ошибся в оценке высоты и скорости,
диспетчер не проверил информацию... Каждая из этих неприятностей вполне вероят-
на и сама по себе ещё не смертельна. А вот вероятность совпадения всех независи-
мых обстоятельств событий ничтожна. Но когда случилось одно из них, вероятность
катастрофы многократно возросла. Случилось ещё одно — вероятность несчастья ещё
умножилась, но ни на земле, ни в воздухе этого не знали.
Есть много неприятных обстоятельств, которые никто не может ни предусмотреть,
ни предотвратить. Но есть и такие, про которые говорят — «человеческий фактор».
Обычно это словосочетание звучит по радио и телевидению тогда, когда кто-то пона-
деялся на опыт, надёжность, везение, а надежды не оправдались.
Многие из вас, ребята, скоро сядут за руль автомобиля. Кто-то будет поднимать
в воздух тяжёлые самолёты. Другие поведут железнодорожные составы, морские
и речные суда. Кто-то будет проектировать или строить здания и сооружения, кораб-
ли, самолёты и автомобили. А кто-то будет принимать важные решения.
\^zs Важно! От ошибок не застрахован никто, но уменьшить вероятность беды мож-
но. Для этого не следует оставлять на волю случая то, что должно быть
вовремя предусмотрено и сделано человеком.
С г) Вопросы
1 В чём состоит ошибка Эдгара По?
2 Приведите примеры дублирования важных систем. Зачем это делается?
212
ГЛАВА X.

Элементы
комбинаторики
Часто приходится иметь дело с комбинаци-
ями, составленными из фигур, чисел, собы-
тий или предметов. Предметов может быть
много, но комбинаций из них несравнимо
больше. Их бывает так много, что их невоз-
можно упорядочить или пересчитать непо-
средственно.
В этой главе мы знакомимся с комбинато-
рикой — разделом математики, который за-
нимается перечислением комбинаций раз-
ных объектов.
В теории вероятностей комбинаторика при-
меняется, когда событий в случайном опыте
очень много и их невозможно выписать или
даже просто перечислить без специальных
методов.
56 Комбинаторное правило
умножения
57 Перестановки. Факториал
58 Правило умножения
и перестановки в задачах
на вычисление вероятностей
59 Число сочетаний
60 Число сочетаний в задачах
на вычисление вероятностей

Имея дело с большим количеством чисел, фигур, событий или просто предметов,
часто приходится составлять из них различные комбинации. Эти комбинации труд-
но упорядочивать или пересчитывать непосредственно — их очень много. Нужно на-
учиться устраивать систематический перебор, чтобы не запутаться, не забыть что-то
важное или не посчитать одно и то же дважды.
Методы перечисления и упорядочивания множеств, составленных из чисел, фигур
или предметов, изучаются в специальном разделе математики, который называется
комбинаторика. Типичной задачей комбинаторики является перечисление комбина-
ций, составленных из нескольких предметов.
В теории вероятностей комбинаторика применяется тогда, когда случайный опыт
обширный и количество событий в нём настолько велико, что их невозможно выпи-
сать или даже просто перечислить без применения специальных методов.
Комбинаторное правило умножения
ПРИМЕР 1. Предположим, что имеется белый хлеб, чёрный хлеб, сыр, колбаса
и варенье. Сколько разных бутербродов (хлеб и что-то одно сверху) можно приготовить?
Выпишем сначала бутерброды с белым хлебом. Это бутерброд с сыром (ВС), с кол-
басой (БК) и с вареньем (БВ). Столько же бутербродов можно приготовить и с чёр-
ным хлебом: ЧС, ЧК и ЧВ.
Всего получается 6 разных бутербродов. Это число можно найти с помощью так
называемого комбинаторного правила умножения.
В данном случае у нас два вида хлеба и три вида дополнений к хлебу. Получает-
ся: 2 • 3 - 6.
Ф
Комбинаторное правило умножения. Чтобы найти число пар, составленных из
предметов двух типов, нужно число предметов первого типа умножить на число
предметов второго типа. Если число предметов первого типа равно т, а число
предметов второго типа равно п, то число их комбинаций равно тп.
Такое же правило действует, если имеются предметы трёх или более типов.
Vi/ Комбинаторное правило умножения для нескольких типов предметов. Что-
бы найти число комбинаций из предметов нескольких типов, нужно перемно-
жить количества предметов каждого типа.
Поясним это правило на примере — пересчитаем государственные регистрацион-
ные автомобильные номера в Новосибирской области.
ПРИМЕР 2. Государственные регистрационные автомобильные номера состоят из
буквы, трёх цифр, ещё двух букв и номера региона. Буквы и цифры могут повто-
ряться. Буквы берутся не всякие. Можно использовать только 12 букв: А, В, Е, К,
М, Н, О, Р, С, Т, У, X. (Почему именно эти буквы? Попробуйте догадаться.) Цифры
можно брать любые — от О до 9. Номер региона на автомобильном номере в Ново-
сибирской области может быть 54 или 154.
Сколько всего можно составить регистрационных номеров для автомобилей в Но-
восибирской области?
Будем рассуждать так же, как и в предыдущем примере: первую букву мож-
но взять одну из 12. Первую цифру берём одну из 10, вторую — снова одну из 10
214
ГЛАВА XI.

и третью — снова одну из 10. Затем две буквы подряд. Каждая выбирается из
12 разрешённых букв. И наконец, номер региона. Он может оказаться одним из двух.
12 • 10 • 10 • 10 • 12 • 12 • 2 - 2 • 103 • 123 - 3 456 000.
Номер региона не присваивается произвольно. Сначала всем новосибирским авто-
мобилям присваивали номер 54, поскольку Новосибирская область является 54 субъ-
ектом Российской Федерации. Впоследствии, когда эти номера были исчерпаны, ста-
ли давать номер 154. Возможно, скоро потребуются номера 254 или 754.
Таким образом, в Новосибирской области на данный момент всего может суще-
ствовать почти три с половиной миллиона автомобильных номеров. И это не счи-
тая номеров старого образца, федеральных, дипломатических и номеров автомобилей
спецслужб. Это не значит, что число машин настолько велико. Часть автомобилей
снимается с регистрации, но их номера не присваиваются другим автомобилям во
избежание путаницы.
Гг) Вопросы
1 Сформулируйте комбинаторное правило умножения для подсчёта числа комби-
наций предметов двух типов.
2 Сформулируйте правило умножения для подсчёта числа комбинаций предметов
нескольких типов.
0
Упражнения
399 Сколько можно составить пар, выбирая:
а) первый предмет из 4, а второй из 8 предметов;
б) первый предмет из 6, а второй из 3 предметов;
в) первый предмет из 15, а второй из 12 предметов;
г) первый предмет из 10 предметов, а второй из всех оставшихся после вы-
бора первого предмета?
400 Сколько можно составить троек, выбирая:
а) первый предмет из 4, второй из 8, а третий из 5 предметов;
б) первый предмет из 7, второй из 4, а третий из 9 предметов;
в) первый предмет из 5, второй из 13, а третий из 21 предмета;
г) первый предмет из 8 предметов, второй и третий из оставшихся после вы-
бора предыдущих?
401 В школе есть все классы — с 1 по 11. Каждый из них имеет дополнитель-
ную букву А, Б, В, Г или Д. Например, класс 1А, 7Б и т. д. Сколько всего
классов в этой школе?
402 В автоматических камерах хранения на железнодорожных вокзалах применя-
ется шифр, который состоит из одной буквы и трёх цифр. Буквы берутся от
А до К, исключая буквы Ё и Й, а цифры могут быть любыми — от 0 до 9.
Например, Д195.
Сколько можно составить различных шифров?
403 На каждом барабане игрального автомата изображены символы «вишня*, «ли-
мон» и числа от 1 до 9. Автомат имеет 3 одинаковых барабана, которые вра-
щаются независимо друг от друга. Сколько всего комбинаций может выпасть?
404 Первый класс праздновал Новый год. Каждая девочка подарила каждому
мальчику открытку, а каждый мальчик подарил каждой девочке гвоздику.
Чего было больше — подаренных открыток или подаренных гвоздик?
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
215

405 Составляются различные последовательности из цифр 0 и 1 (двоичные после-
довательности). Сколько существует двоичных последовательностей длины:
а) 1; б) 3; в) 10; г) л?
406 На приёме в посольстве встретились две делегации, в каждой из которых бы-
ло несколько дипломатов (больше одного). Каждый дипломат одной делега-
ции пожал руку каждому дипломату второй делегации. Сколько было членов
в каждой делегации, если всего произошло 143 рукопожатия?
Указание. Если в первой делегации было х дипломатов, а во второй — г/,
то всего рукопожатий было ху. Число 143 можно разложить на натуральные
множители двумя способами: 143 = 1 • 143 и 143 — 11 • 13.
407 Важные данные в компьютере часто защищают паролем. Предположим, что
пароль содержит 8 символов: больших и малых латинских букв, цифр, неко-
торых знаков. Всего разрешённых символов 92. Составьте числовое выраже-
ние для общего числа возможных паролей. Пользуясь калькулятором, вычис-
лите приближённо его значение.
^57) Перестановки. Факториал
Подсчитаем, сколько существует разных способов каждому из троих людей присво-
ить номер от 1 до 3. Тот же самый вопрос можно задать иначе: сколькими способа-
ми можно построить трёх человек в шеренгу?
* ■
lit
Андрей Борис Владимир
f t 1
Андрей Владимир Борис Борис Андрей Владимир Владимир Борис Андрей
Рисунок 80
Воспользуемся комбинаторным правилом умножения. На первое место можно по-
ставить любого из трёх человек. На второе — любого из двух оставшихся. И на по-
следнее место можно поставить только одного оставшегося человека. Первого чело-
века можно выбирать тремя способами, второго — двумя способами, а третьего —
одним-единственным способом.
Таким образом, мы получили 3 • 2 • 1 = 6 способов перестановки трёх человек.
На рисунке 80 показаны все эти способы.
Если людей четверо, то первый номер мы можем присвоить любому из четверых,
а оставшиеся номера распределить 6 способами между тремя оставшимися. Получаем
4 • 6 = 24 способа нумерации. Остаётся напомнить, что 6 мы получали как 3 • 2 • 1.
216
ГЛАВА XI.

Продолжая рассуждения тем же способом, мы обнаружим, что если людей, напри-
мер, семеро, то из них можно составить 7-6-5*4*3-2-1 = 5040 различных
перестановок.
Обобщим полученные результаты. Если есть п предметов, то число способов пере-
нумеровать их равно п • (п - 1) • (п - 2) • ... • 3 • 2 • 1.
Определение. Факториалом натурального числа п называется произведение
всех натуральных чисел от 1 до п. Обозначается факториал п!:
л! = 1 • 2 • 3 • ... - (л - 1) • л.
Для того чтобы в различных формулах не делать исключения для числа 0, при-
нято соглашение 0! = 1.
Подведём итоги. Перестановкой из п предметов называется любой способ нумера-
ции этих предметов (способ их расположения в ряд). Число перестановок п предме-
тов равно л!.
Приведём таблицу факториалов от 0 до 10.
Таблица 99. Факториалы чисел от О до 10
п
п\
0
1
1
1
2
2
3
6
4
24
5
120
6
720
7
5040
8
40 320
9
362 880
10
3 628 800
Факториал п\ быстро растёт с увеличением п.
Поэтому даже для 10 предметов перестано-
вок очень много и выписать все практически
невозможно.
Cf) Вопросы
1 Что такое перестановка?
2 Что такое факториал натурального числа?
3 Чему равно число различных переста-
новок из п предметов?
4 Чему равен факториал нуля?
В электронных таблицах факто-
риалы вычисляются с помощью
функции
ФАКТР()
0
Упражнения
408 Саша, Ваня и Петя получили номера
1, 2 и 3 для участия в соревновани-
ях. Запишите в таблицу все возмож-
ные способы распределения этих но-
меров между участниками.
* /х =ФАКТР(С6)
С
1 Число
11
12
13
I 14
D
Факториал I
39916800
479001600
6227020800
87178291200I
~ |
Рисунок 81
Саша
Ваня
Петя
1-й способ
2-й способ
3-й способ
4-й способ
5-й способ
6-й способ
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
217

409 В автосервис одновременно приехали 3 машины для ремонта. Сколько суще-
ствует способов выстроить их в очередь на обслуживание?
410 Сколько есть способов раздать спортивные номера с 1-й по 5-й пяти хоккеи-
стам?
411 Участники лыжных соревнований стартуют с интервалом в 30 секунд. Чтобы
определить порядок старта, спортсмены тянут жребий, определяющий номер
старта. Сколько существует различных последовательностей выхода лыжников
на старт, если в соревнованиях принимают участие:
а) 6 лыжников; б) 8 лыжников; в) 10 лыжников; г) к лыжников?
412 Сколько различных последовательностей (не обязательно осмысленных) мож-
но составить из букв слова:
а) учебник; б) автор; в) фонарь; г) бабуин?
413 Вычислите значение дроби:
ч 5! ^ч 7! ч 10! ч 100! ч 15! ч 12!
а> ™> б) —; в) —-; г) ——; д) ,ot - е)
2!' ' 5!' ' 8! • ' 99! * "' 13!-2!' ' 3!-9!'
414 Выпишите все натуральные делители числа: а) 4!; б) 5!.
415 Докажите, что если п < т, то т\ делится на п\ без остатка.
Е>
58J Правило умножения и перестановки
в задачах на вычисление вероятностей
Задачи, которые мы будем сейчас решать, отличаются от тех, что мы решали ра-
нее, только числом возможных элементарных событий в опыте.
ПРИМЕР 1. В классе 30 учащихся. Среди них нет двоих одинакового роста. По
команде учителя физкультуры они выстраиваются в одну шеренгу в случайном по-
рядке. Найдём вероятность того, что учащиеся встали по росту.
Решение. Общее число равновозможных событий равно числу перестановок 30 уча-
щихся: N = 30!. Число это настолько велико, что лучше оставить его в таком виде.
Учащиеся по росту могут встать двумя способами: по возрастанию или по убыванию.
Поэтому событию А «встали по росту» благоприятствуют два исхода: N(A) e 2. Тогда
*КА) N 30! *
Это число приблизительно равно 0,000 000 000 000 000 000 000 000 000 000 007 54.
Вот уж действительно маловероятнейшее событие! Рассчитывать на такую случай-
ность не следует.
ПРИМЕР 2. В страховой компании проходит рекламная акция: компьютер слу-
чайным образом выбирает автомобильный номер, и владелец автомобиля с таким но-
мером получает скидку. Найдём вероятность того, что счастливым окажется номер
♦ В 845 МА».
Решение. Как мы знаем, каждая буква в автомобильном номере выбирается из
12, а каждая цифра — из 10 возможных. Поэтому число элементарных событий мож-
но найти по правилу умножения: N - 12 -10 -10 -10' 12 -12 - 103 • 123 - 1 728 000.
Событию А «выбран номер В 845 МА> благоприятствует единственное событие. По-
этому
Р<А> = ITiioOO * 0,0000005787.
218
ГЛАВА XI.

ПРИМЕР 3. Какова вероятность того» что среди последних четырёх цифр в семи-
значном номере телефона есть цифра 8? Мы рассматриваем только последние четыре
цифры, поскольку первые три цифры в телефонном номере не случайны — это мо-
жет быть номер АТС.
Обозначим событие «есть цифра 8» буквой А. Удобнее найти вероятность противо-
положного события А «среди четырёх последних цифр нет цифры 8». Каждую цифру
можно выбрать десятью способами. Общее число комбинаций найдём по правилу ум-
ножения: N - 10 • 10 • 10 • 10 - 10 000.
Это и есть общее число равновозможных элементарных событий опыта.
Теперь нужно найти число элементарных событий, благоприятствующих событию А,
то есть число комбинаций без цифры 8. Каждую цифру можно выбрать одним из де-
вяти способов. Поэтому N(A) = 9 • 9 • 9 • 9 в 6561.
/-ч n(A) 6561
Получаем: Р(А) = —^ = юооо = °'6561в Следовательно, Р(А) = 1 - Р(Л) = 0,3439.
0
Упражнения
416 Найдите вероятность того, что трёхзначный номер случайно проезжающей
мимо машины состоит из цифр 0, 4 и 5, взятых в произвольном порядке.
417 Найдите вероятность того, что среди трёх последних цифр случайного теле-
фонного номера не окажется:
а) цифры 0; б) цифры 2; в) цифр 1 и 6; г) цифр 2, 5 и 7.
418 Какова вероятность того, что среди последних трёх цифр случайного телефон-
ного номера:
а) встретится цифра 7;
б) встретится цифра 2 или цифра 3;
в) встретится хотя бы одна из цифр 4, 0 или 1;
г) будет хотя бы одна из цифр 1, 2, 4 и 9?
419 Десять школьников в случайном порядке заходят на экзамен. Каждый из них
называет фамилию. Председатель экзаменационной комиссии записывает на
листочке фамилии в том порядке, в каком входят школьники. Найдите веро-
ятность того, что фамилии окажутся записаны:
а) в алфавитном порядке; б) в порядке, обратном алфавитному.
420 У вахтёра в комнате доска с крючками. Всего 12 крючков, а на них 12 клю-
чей. Доска упала, и ключи рассыпались. Вахтёр собрал ключи и развесил их
в случайном порядке. Какова вероятность того, что:
а) каждый ключ висит на своём крючке;
б) хотя бы один ключ висит не на своём крючке;
в) два определённых ключа перепутаны местами, а остальные на своих крюч-
ках;
г) ровно один ключ висит не на своём крючке, а остальные — на своих?
421 Слово «АПЕЛЬСИН» написали на полоске картона и разрезали полоску на
буквы. Девочка, играя, выложила их в ряд в случайном порядке. Найдите
вероятность того, что получилось слово «СПАНИЕЛЬ».
422 Найдите вероятность того, что среди последних четырёх цифр случайного семи-
значного телефонного номера есть ровно одна цифра 1 и ровно одна цифра 7.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
219

Число сочетаний
ПРИМЕР 1. Из трёх игроков, заявленных на теннисный матч, надо выбрать двух
для выступления в парном разряде1 (порядок игроков не важен). Сколькими способа-
ми это можно сделать?
Решение. Обозначим игроков различными буквами А, В, С и выпишем все воз-
можные комбинации:
АВ АС ВА ВС СА СВ
Сначала мы брали игрока А и добавляли к нему в пару ещё одного из двух остав-
шихся игроков. Так получились первые две пары АВ и АС в нашем списке. Затем
мы взяли игрока В и к нему добавляли одного из двух оставшихся. Так получились
пары ВА и ВС. Наконец, первым поставили игрока С и добавляли к нему одного из
оставшихся игроков. Получили последние две пары СА и СВ.
Однако среди полученных таким образом комбинаций попадаются перестановки од-
ной и той же пары. Например, АВ и ВА — это одна и та же пара. Совпадают и дру-
гие пары: АС и СА, а также ВС и СВ. Таким образом, всего различных пар три:
АВ АС ВС
Общее число комбинаций букв А, В и С сократилось в 2 раза. Это произошло по-
тому, что из двух разных букв можно составить ровно 2 перестановки.
ПРИМЕР 2. Сколькими способами можно выбрать двух игроков из четырёх заяв-
ленных на матч?
Решение. Обозначим игроков А, В, С и D. Начнём, как и в предыдущем примере,
составлять пары. Первого игрока мы можем выбрать четырьмя способами. Вторым
к нему мы можем взять любого из оставшихся трёх:
АВ AC AD
ВА ВС BD
СА СВ CD
DA DB DC
Получилось 12 комбинаций. При этом, как и в предыдущем примере, каждая па-
ра посчитана дважды. Поэтому различных пар всего 6:
АВ AC AD ВС BD CD
Определение. Число способов, которыми можно выбрать ровно к предметов из
множества, в котором п предметов, называется числом сочетаний из п по к
и обозначается С* (читается «цэ из эн по ка»).
До сих пор мы установили, что с\ = 3 и С\ = 6. Как быть в других случаях?
Если число п небольшое, то число сочетаний Cj можно взять из треугольной
таблицы, которая называется треугольником Паскаля2.
Обычно треугольник Паскаля изображают в виде равнобедренного треугольника,
поэтому столбцы в треугольнике получаются наклонные (рис. 83). Число С* стоит
1 Парный разряд в большом теннисе — это игра «двое на двое»: одна пара игроков играет
против другой пары игроков.
Числовой треугольник, содержащий числа сочетаний, известен по крайней мере с X в. В араб-
ских трудах он появляется не позже XII в. В Иране его называют треугольником Хайама, в
Китае — треугольником Яна Хуэя. Мы называем этот треугольник треугольником Паскаля по
имени французского учёного Блеза Паскаля, который в середине XVTI в. издал «Трактат об
арифметическом треугольнике», где подробно описал его свойства.
220
ГЛАВА XI.

в п-й строке и в А-м столбце. Например, чтобы найти Се, посмотрим, какое число
стоит на пересечении 6-й строки и 4-го столбца. Это число 15. Значит, С% = 15.
Чтобы найти число сочетаний
с помощью электронной таблицы,
удобно использовать функцию
ЧИСЛКОМБ()
| * fx =ЧИСЛКОМБ(ЕЗ.Е2) |
D
К
N
| C(N,K)
Е
4
9
126
F I
■
^/
щ>
Рисунок 82
Столбцы и строки треугольника Паскаля нумеруются начиная с нуля.
п\
Если число п велико, то лучше пользоваться формулой С£ *=
ПРИМЕР 3. Найдём С\.
9!
Решение» Ci —
k\(n-k)\'
9!
9876
41(9-4)! ~ 4!-5! ~ 1-2-3-4
&го же значение можно найти в
треугольнике Паскаля (см. рис. 83)
на пересечении 9-й строки и 4-го
столбца.
Вы, наверное, обратили вни-
мание на то, что каждая строка
треугольника Паскаля начинается
и заканчивается единицей. Это не
случайно: С°п s 1, поскольку вы-
брать О предметов можно един-
ственным способом.
Так же Сп — 1, потому что вы-
брать все п предметов из п имею-
щихся можно тоже только одним
способом.
- 126.
йстолбец
Рисунок 83. Треугольник Паскаля
0
423
424
425
Вопросы
Что такое число сочетаний?
Как обозначить число сочетаний из 6 по 5?
Упражнения
Найдите:
a) Cl; б) С\\ в) Cf; г) С?,; д) С?2; е) С?2.
Сравните числа:
а) С\ и С%\ б) С? и Съг, в) С21 и Cfu г) С\2 и С\2
Найдите значение:
а) С5; б) С%\ в) С°29; г) С?4; д) C°302i e) С\°0\.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
221

426
427
428
429
430
431
432
433
434
435
Сколько существует способов выбрать один объект из совокупности:
а) 50 предметов; б) 67 предметов?
Сколькими способами можно выбрать:
а) 49 предметов из 50 предметов; б) 64 из 65 предметов?
Сколькими способами можно выбрать:
а) 7 предметов из 9; в) 4 предмета из 12;
б) 2 предмета из 6; г) 5 предметов из 13?
Сколькими способами можно отобрать стартовую шестёрку игроков в волей-
больном матче» если всего в команде:
а) 10 игроков; б) 14 игроков?
Предприниматель хочет отправить рекламные объявления в три газеты.
Сколькими способами можно выбрать эти три газеты из:
а) 7 газет; б) 9 газет; в) 15 газет?
Сколько существует способов составить двоичную последовательность из:
а) 5 единиц и 4 нулей; в) 4 единиц и 8 нулей;
б) 3 единиц и 7 нулей; г) 5 единиц и 6 нулей?
Сколько существует последовательностей из шести букв, в которых:
а) три буквы У, остальные буквы Н;
б) пять букв У, остальные буквы Н?
Сколько существует последовательностей, в которых 4 буквы У, а остальные
буквы Н, если всего в последовательностях:
а) 11 букв; б) 12 букв; в) 15 букв; г) 20 букв?
В лотерее разыгрываются несколько выигрышных номеров из общего количе-
ству номеров. Сколько всего существует комбинаций выигрышных номеров,
если разыгрываются:
а) 5 номеров из 36; б) 6 номеров из 49?
Одно время была популярна лотерея * Честная игра*. В билете лотереи име-
ется 20 закрытых букв, ровно 10 из них — буквы слова « АВТОМОБИЛЬ».
Буквы разбросаны случайным образом. По правилам лотереи, если владелец
билета, открыв ровно 10 букв, откроет все буквы слова «АВТОМОБИЛЬ», то
он выигрывает машину.
а) Сколько всего существует способов открыть 10 букв?
б) Сколько существует способов открыть 10 букв так, чтобы выиграть автомо-
биль?
436
Муха ползёт по проволочной решёт-
ке из точки А в точку В (рис. 84),
двигаясь всё время вправо или вниз.
Сколько различных маршрутов может
выбрать муха?
Указание. В случае а), как бы ни
ползла муха, она должна сделать все-
го 6 шагов: три шага вправо (П) и три
шага вниз (Н). Маршрут мухи мож-
но записать в виде последовательно-
сти шести букв. Например, ПНПННП.
а) А
• ill
* * ' 4
б)А
В
Рисунок 84
В
Таким образом, вопрос сводится к тому, сколько существует способов расста-
вить три буквы П в последовательности шести букв.
222
ГЛАВА XI.

Е)
60J Число сочетаний в задачах
на вычисление вероятностей
Умение находить число сочетаний из треугольника Паскаля или по формуле
k _ л!
п ~~ *!(л - k)\
позволяет проще решать многие из уже известных задач. Кроме того, мы теперь на-
учимся решать задачи, к которым раньше было трудно подойти.
ПРИМЕР 1. В группе 5 человек: Ваня, Саша, Маша, Таня и Коля. По жребию
двое из них выбраны дежурными. Найти вероятность того, что это Ваня и Таня.
Решение. Число элементарных событий в этом опыте равно С\, то есть 10. Все
элементарные события равновозможны. Событию А «дежурят Ваня и Таня* благо-
приятствует единственное элементарное событие. Поэтому Р(А) = —g e т^-
ПРИМЕР 2. В ящике 4 красных и 2 жёлтых флажка. Из него наудачу извлекают
3 флажка. Какова вероятность того, что все эти флажки красные?
Решение. Число элементарных событий в этом опыте равно С% = 20. Все они рав-
новозможны. Число благоприятных элементарных событий для события А «вынули три
красных флажка» равно числу способов выбрать 3 красных флажка из 4 красных флаж-
Са 4
ков, имеющихся в ящике. Это число равно С\ — 4. Поэтому Р(Л) — -| = — = 0,2.
I ПРИМЕР 3. Найдём вероятность того, что, извлекая наудачу 5 флажков из ящи-
ка, в котором 8 красных и 7 синих флажков, мы вытащим ровно 3 красных и 2 си-
них флажка.
Решение. Обозначим это событие А. Элементарным событием является комбинация
извлечённых флажков. Всего выбрать 5 флажков из 15 можно N — С\ь способами.
Выбрать 3 красных флажка из 8 можно одним из С% способов. Выбрать 2 синих
флажка из 7 флажков можно С? способами. Пользуясь правилом умножения, нахо-
дим, что всего существует N(a) = С% • С? элементарных событий, благоприятствую-
щих событию А, т. е. способов выбрать комбинацию из 3 красных и 2 синих флаж-
N{A) Cf-C72
ков. Следовательно, Р(А)
" С5,
15
„„ 15! 15 14 13 12 11 олло - м « rt<
Вычислим эту вероятность: Cf5 - gt ... « —ч . Q л е— = 3003, Ci - 56, Ci = 21.
51 ' 101 1 ' £ ' О ' 4 ' О
Значит, Р(А) - -г—- * 0,392. J
3003
0
Упражнения
437 Для участия в телевикторине случайным образом выбирают 3 игроков из
8 претендентов. Какова вероятность того, что будут выбраны 1, 4 и 8-й игроки?
438 В тираже лотереи «Спортлото» разыгрывались 6 случайных номеров из 49.
а) В кинокомедии «Спортлото-82» главный герой зачёркивает номера 1, 2,
3, 4, 5 и 6. Найдите вероятность того, что в тираже выиграют именно эти
шесть номеров.
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
223

б) Какова вероятность того, что в тираже лотереи выиграют номера 4, 28,
17, 8, 12, 32? Отличается ли она от вероятности выигрыша комбинации
1, 2, 3, 4, 5 и 6?
439 На двери установлен кодовый замок с кнопками. На кнопках изображены
цифры от 0 до 9. Чтобы открыть дверь, нужно одновременно нажать три
кнопки неизвестного нам кода. Найдите вероятность открыть дверь с первой
попытки, нажав три кнопки наудачу.
440 В билете лотереи «Честная игра» имеется 20 закрытых букв, ровно 10 из
них — буквы слова «АВТОМОБИЛЬ». Найдите вероятность, открыв случай-
ным образом 10 букв, отгадать все буквы слова «АВТОМОБИЛЬ».
441 На книжной полке 6 романов и 4 повести, расположенные в случайном по-
рядке. С полки сняли 7 первых попавшихся книг. Найдите вероятность того,
что на полке остались:
а) только повести; б) только романы.
Указание. Элементарным событием будем считать комбинацию из трёх
оставшихся на полке книг. Всего таких комбинаций С?0- Событию «остались
только повести» благоприятствуют все комбинации, где все три оставшиеся
книги — повести. Таких комбинаций С*, поскольку повестей всего 4.
442 Известно, что последние четыре цифры в семизначном телефонном номере
некоторого абонента — это 1, 2, 3 и 4. Найдите вероятность того, что номер
оканчивается на 43 или 34.
443 К посольству прибывают три белых и шесть чёрных лимузинов с приглашён-
ными гостями. Машины приезжают в случайном порядке. Найдите вероят-
ность того, что первыми приедут:
а) все белые лимузины; б) все чёрные лимузины.
444 В партии из 15 деталей 3 детали бракованные. Покупатель приобрёл 5 дета-
лей. Найдите вероятность того, что среди них:
а) нет ни одной бракованной детали;
б) есть хотя бы одна бракованная деталь;
в) ровно 2 бракованные детали;
г) ровно 4 бракованные детали.
445 В магазин привезли 10 синих и 10 коричневых костюмов. Продавец случай-
ным образом выбирает 8 из них, чтобы выставить на витрине. Найдите веро-
ятность того, что будет отобрано 3 синих и 5 коричневых костюмов.
446 В билете лотереи * Спортлото 5 из 36» изображены 36 номеров от 1 до 36.
Нужно зачеркнуть ровно 5 из них. При розыгрыше случайным образом вы-
бираются 5 выигрышных номеров. Какова вероятность угадать:
а) ровно 5 выигрышных номеров;
б) ровно 4 выигрышных номера;
в) ровно 3 выигрышных номера;
г) хотя бы один выигрышный номер?
224
ГЛАВА XI.

Испытания
Бернулли
Испытание Бернулли, или просто испытание, —
это простой случайный опыт, в котором
всего два возможных элементарных собы-
тия: успех и неудача. Пример испытания —
бросание монеты. Из таких простых опытов
можно составлять гораздо более сложные.
В этой главе мы рассказываем о важных
случайных опытах:
— испытания до наступления первого успеха;
— серия, состоящая из заранее известного
количества испытаний Бернулли.
Помимо этого, мы займёмся случайным вы-
бором нескольких предметов из множества,
которое состоит из предметов двух или не-
скольких видов.
61 Успех и неудача
Испытания до первого успеха
62 Серия испытаний Бернулли
63 Число успехов в испытаниях
Бернулли
64 Вероятности событий
в испытаниях Бернулли
65* Случайный выбор
из конечной совокупности

Успех и неудача.
Испытания до первого успеха
Успех и неудача
Определение. Испытанием Бернулли' или просто испытанием называют слу-
чайный опыт, который может закончиться одним из двух элементарных событий.
Например, подброшенная монета падает либо орлом, либо решкой вверх. Стрелок
может попасть в мишень, а может промахнуться. Избиратель может проголосовать
или не проголосовать за некоторого кандидата. В жизни мы постоянно встречаемся
с такими опытами.
Одно из двух элементарных событий в таком опыте называют успехом, а дру-
гое — неудачей. Эти названия условны, их можно поменять местами. Например, для
футболиста победа — успех, а для игрока проигравшей команды это же событие —
неудача.
Вероятность того, что испытание Бернулли закончится успехом, обычно обознача-
ют буквой р, а вероятность неудачи — буквой q. Числа р и q в сумме дают единицу,
поэтому q = 1 - р. Чтобы в испытании было действительно два возможных события,
будем считать, что 0<р<1и0<{<1.
Случайные опыты, ^ которых много элементарных событий, часто можно свести
к изучению испытаний Бернулли. Пусть, например, на молочном комбинате в бутыл-
ки наливают по 1 литру молока. Мы знаем, что при массовом производстве возмож-
ны и всегда происходят отклонения в ту или иную сторону от номинальной массы,
размера или объёма. Выберем случайную бутылку для контроля. Будем считать успе-
хом событие «объём молока в бутылке отличается от 1 л не больше чем на 5 мл*.
Противоположное событие можно считать неудачей. Возникает испытание Бернулли.
Испытания до первого успеха
Рассмотрим опыт, в котором одинаковые испытания проводятся до наступления
первого успеха. Как только успех случился, испытания прекращаются.
ПРИМЕР 1. Монету бросают до тех пор, пока не выпадет орёл.
ПРИМЕР 2. Стрелок в тире стреляет по мишени до тех пор, пока не собьёт её.
ПРИМЕР 3. Мобильный телефон в условиях слабой связи пытается отправить
CMC. Если попытка неудачная, телефон предпринимает следующую. Так продолжает-
ся до тех пор, пока очередная попытка не окажется удачной, либо пока не кончится
время, отведённое на попытки.
ПРИМЕР 4. Фрагмент файла загружается из Интернета в компьютер. Загрузка
идёт до тех пор, пока не пройдёт без ошибок.
ПРИМЕР 5. Самолёт осматривают перед каждым рейсом и допускают к полёту,
пока не обнаружено отклонение от нормы в работе жизненно важных систем.
Мы будем предполагать, что в каждом испытании вероятность успеха неизменно
равна р и что все испытания независимы. Исследуем такой случайный опыт.
1 Название дано в честь Якоба Бернулли, который триста лет назад изучал серии испытаний.
Эти простейшие случайные опыты оказались очень важными для науки.
226
ГЛАВА XII.

У У У
Обозначим неудачу буквой Н, а успех —
буквой У. Тогда элементарными событиями
являются последовательности
У, НУ, ННУ, НННУ, ННННУ и т. д.
Будем считать, что попытки могут про-
должаться сколь угодно долго. Значит, тео- Рисунок 85
ретически в этом опыте бесконечно мно-
го элементарных событий. Несложно нарисовать начальный фрагмент дерева такого
опыта (рис. 85).
Элементарные события изображаются цепочками, ведущими из точки S к конеч-
ным вершинам. Например, элементарное событие НННУ (три неудачи и затем успех)
изображается в этом дереве цепочкой SHHHy (выделена красным цветом).
Пользуясь правилом умножения, несложно найти вероятность каждого элементар-
ного события:
Р(У) = р, Р(НУ) = qp, Р(ННУ) = qqp = q2p, Р(НННУ) = q*p
и т. д. Получается общая формула: вероятность элементарного события ННН...НУ,
в котором перед успехом случилось ровно к неудач, равна а неудач
ННН...НУ
к неудач
= qkp.
Разберёмся в интересном вопросе: не может ли случиться так, что успех никогда
не наступит? Сложим вероятности известных нам элементарных событий:
Р + ЯР + Я2Р + Я*Р + — + 9* ~ ХР + -.
Получилась сумма бесконечно убывающей геометрической прогрессии со знамена-
телем q. При этом 0 < q < 1, поэтому сумма существует, и из курса алгебры извест-
но, как её найти:
Р + ЯР + Я2Р + Я*Р + -. + Як ~ 1Р + - - 71- « ^ в *•
1-Я Р
Вероятности элементарных событий, оканчивающихся успехом, в сумме дают еди-
ницу. Следовательно, на долю события «бесконечная цепочка неудач* приходится ве-
роятность 0. Такое событие не произойдёт. Рано или поздно наступит успех, как бы
ни была мала его вероятность р (мы договорились, что р > 0).
ПРИМЕР 6. Стрелок стреляет по мишени до первого попадания. Вероятность по-
падания при каждом отдельном выстреле равна р — 0,2. Какова вероятность того,
что стрелку потребуется:
а) ровно два выстрела; б) не больше пяти выстрелов?
Решение. 1-й способ, а) Вероятность события НУ — сначала промах, а затем по-
падание — равна qp e 0,8 • 0,2 ** 0,16.
б) Событию А «не больше пяти выстрелов» благоприятствуют элементарные собы-
тия У, НУ, ННУ, НННУ и ННННУ. Сложим их вероятности:
Р(А) = р + qp + q2p + q3p + q4p.
По формуле суммы геометрической прогрессии находим:
ИСПЫТАНИЯ БЕРНУЛЛИ
227

2-й способ. Рассмотрим противоположное событие А «потребуется больше пяти вы-
стрелов*. Оно наступает, только если пять первых выстрелов неудачны. Вероятность
этого Р(а) = q5. Следовательно, Р(а) = 1 - Р(а) = 1 - qb.
Подставляя q = 0,8, получаем Р(А) = 1 - 0,85 « 0,672.
С г) Вопросы
1 Что такое испытание Бернулли? Приведите примеры испытаний, помимо тех, что
описаны в примерах.
2 Чему равна сумма вероятностей успеха и неудачи?
3 Сколько элементарных событий в опыте «испытания до первого успеха»?
4 Запишите формулой вероятность события «произошло восемь неудач, а при де-
вятой попытке случился успех».
0 Упраж
447 Обычную симметричную монету бросают до выпадения первого орла. При первых
5 бросках выпала решка. Какое или какие из следующих утверждений верны?
1) Слишком много решек подряд быть не может, поэтому более вероятно, что
в шестой раз выпадет орёл.
2) По какой-то причине в этом опыте решки имеют преимущество перед ор-
лами. Более вероятно, что в следующий раз тоже выпадет решка.
3) При шестом броске орёл и решка имеют равные шансы, так же, как они
имели равные шансы при каждом из предыдущих бросков.
4) Более вероятно, что орёл случится при шестом броске, чем при седьмом.
448 Проведите эксперимент. Возьмите обычную монету и бросайте (лучше трясти
её в пластиковом стаканчике и выбрасывать на ладонь) до тех пор, пока не
выпадет орёл. Сколько бросков для этого потребовалось?
Проведите эксперимент 4—5 раз и запишите, сколько бросков вам пришлось де-
лать каждый раз. Пусть это сделает каждый ученик в вашем классе. Соберите
результаты в таблицу (мы для иллюстрации провели 50 таких экспериментов).
Таблица 100. Бросания монеты до первого орла
Номер броска, при котором
выпал первый орёл
Число экспериментов
1
26
2
14
3
6
4
1
5
2
6
0
7
1
Всего
50
а) Что является элементарным событием в таком эксперименте?
б) Сколько элементарных событий в этом эксперименте?
в) Что происходит чаще — орёл выпадает с первой попытки или со второй?
г) Что происходит чаще — орёл выпадает со второй попытки или с третьей?
449 Монету бросают до тех пор, пока не выпадет орёл. Постройте дерево экспери-
мента. Укажите в дереве событие А и найдите его вероятность, если событие А
состоит в том, что:
а) потребуется ровно два броска;
б) три раза выпадет решка, на четвёртый раз — орёл;
в) потребуется три или четыре броска, чтобы орёл появился в первый раз;
г) первые четыре броска окончатся решкой.
228
ГЛАВА XII.

450 Монету бросают до тех пор, пока не выпадет орёл. Найдите вероятность того,
что к моменту выпадения орла будет сделано:
а) ровно четыре броска; в) больше двух бросков;
б) два или три броска; г) не больше трёх бросков.
451 В испытании Бернулли известна вероятность успеха р. Найдите вероятность
неудачи q, если вероятность успеха р равна:
а) \; б) 0,02; в) |; г) 0,83.
4 7
452 Игральную кость бросают до тех пор, пока не выпадет шестёрка. Найдите ве-
роятность того, что будет сделано:
а) ровно два броска; в) ровно шесть бросков;
б) ровно три броска; г) не более четырёх бросков.
453 Стрелок в тире стреляет по мишени до тех пор, пока не попадёт в неё. Веро-
ятность попадания при каждом отдельном выстреле равна р = 0,6. Найдите
вероятность того, что стрелку потребуется:
а) ровно 5 попыток;
б) от 2 до 4 попыток.
454 Производятся последовательные одинаковые и независимые испытания до тех
пор, пока не наступит успех. В каждом отдельном испытании вероятность
успеха равна р, а вероятность неудачи равна q = 1 - р. Найдите вероятность
события (выразите через р и д), заключающегося в том, что:
а) успех случится при втором испытании;
б) успех случится позже четвёртого испытания;
в) успех случится не позже шестого испытания;
г) для достижения успеха потребуется от трёх до пяти испытаний.
455 Сергей отправляет CMC-сообщение другу. Связь не очень устойчивая, поэтому
каждая попытка отправить CMC имеет вероятность успеха 0,7. На каждую
попытку телефон тратит секунду. Найдите вероятность того, что:
а) CMC будет отправлено со второй попытки;
б) CMC будет отправлено не позже, чем через 6 сфунд.
456 Вероятность того, что новый мобильный телефон выйдет из строя в течение
первого года работы, равна 0,2. Если телефон проработал какое-то время, то
вероятность его поломки в течение следующего года такая же (телефон не со-
держит изнашивающихся деталей, поэтому вероятность его поломки не растёт
со временем). Найдите вероятность того, что новый телефон выйдет из строя:
а) на четвёртый год службы;
б) не позже чем через три года после покупки.
457 Вероятность того, что новый планшет выйдет из строя в течение года после
покупки, равна 0,1. Если планшет проработал несколько лет, то вероятность
его поломки в течение следующего года такая же. Найдите вероятность того,
что новый планшет выйдет из строя:
а) на третий год службы;
б) прослужит больше трёх, но не больше пяти лет.
458 В корабельной артиллерии применяется система управления огнём. Орудие
делает выстрел по цели. Если цель не поражена, делается ещё один выстрел.
Третий выстрел не делается. Предположим, что вероятность поражения цели
каждым отдельным выстрелом равна 0,9. Найдите вероятность того, что:
ИСПЫТАНИЯ БЕРНУЛЛИ
229

а) цель будет поражена только вторым выстрелом;
б) цель вообще не будет поражена.
Как вы думаете, почему систему ограничивают двумя выстрелами?
459 Стрелок в тире стреляет по мишени до тех пор, пока не собьёт её. Вероят-
ность попадания при каждом отдельном выстреле равна р = 0,4. Сколько па-
тронов должен иметь стрелок перед началом стрельбы, чтобы поразить ми-
шень с вероятностью не менее 0,9?
460 Инженеры проектируют систему автоматической передачи информации от ав-
томобиля в кризисный центр в случае аварии. Возможны помехи разного ро-
да, поэтому система должна уметь делать несколько попыток, чтобы достичь
успеха. Число попыток нужно ограничить, чтобы система не зависла. По тех-
ническому заданию вероятность передачи информации должна быть не ниже
0,95, если вероятность успеха в каждой отдельной попытке 0,2. Каким чис-
лом ограничить разрешённое количество попыток?
Серия испытаний Бернулли
В предыдущем параграфе мы рассматривали опыт, в котором испытания проводи-
лись до первого успеха. Рассмотрим другой случайный опыт. Будем проводить испы-
тания несколько раз, независимо от того, успехом или неудачей окончилось предыду-
щее. Важно, чтобы одинаковые испытания можно было проводить много раз и чтобы
они были независимыми — исход каждого не дол-
жен быть связан с предыдущими.
Такую серию испытаний можно устроить далеко
не всегда. Бывают испытания, которые не удаётся
повторить. Вот пример. Новую модель автомобиля
подвергают испытанию на безопасность при стол-
кновении — краш-тест. Если манекен, сидящий
внутри автомобиля, не получил серьёзных повреж-
дений, тест считают успешным.
Однако надёжность выводов при краш-тесте не
очень высокая, поскольку автомобиль разбивается.
Краш-тест автомобиля Повторить испытание много раз невозможно. Мож-
но, конечно, использовать другие такие же автомо-
били, но это слишком дорого — делать множество автомобилей только для того, что-
бы их разбить.
Поэтому для производителей автомобилей, самолётов, железнодорожной техники
очень важно собирать информацию об отказах и авариях, произошедших уже в про-
цессе эксплуатации техники.
Если всё же удаётся провести несколько одинаковых и независимых испытаний
подряд, то говорят, что проведена серия испытаний Бернулли.
Рассмотрим элементарные события в последовательности из трёх испытаний. Каж-
дое испытание оканчивается либо успехом, либо неудачей. Как обычно, в случае
успеха будем писать У, а в случае неудачи — Н. После трёх испытаний мы можем
получить одно из восьми элементарных событий:
УУУ УУН УНУ УНН НУУ ННУ НУН ННН
230
ГЛАВА XII.

Отдельные испытания Бернулли независимы, поэтому вероятность каждого эле-
ментарного события можно найти с помощью правила умножения вероятностей.
Например, элементарное событие УУН имеет вероятность
ppq = p2q.
Занесём результаты вычислений в таблицу 101.
Таблица 101. Элементарные события в серии из трёх испытаний
Элементарное событие
Вероятность
УУУ
р3
УУН
Р2Ч
УНУ
Р2Ч
УНН
рч2
НУУ
Р2Ч
ННУ
рч2
НУН
рч2
ннн
ч3
Таким же способом можно составить таблицу элементарных событий и их вероят-
ностей для серии из четырёх, пяти и более испытаний Бернулли.
Для трёх испытаний мы получили 8 — 23 элементарных событий, для четырёх ис-
пытаний их будет уже 16 — 24, для пяти испытаний их будет 32 = 25 и т. д., для
п испытаний мы получим 2" элементарных событий.
Ф
Важно! Элементарным событием в серии испытаний Бернулли является не от-
дельный успех или неудача, а последовательность успехов и неудач. В серии
из п испытаний Бернулли всего 2" различных элементарных событий.
ПРИМЕР 1. Простейшая серия испытаний Бернулли — бросание симметричной
монеты. В этом опыте вероятности успеха (орла) и неудачи (решки) одинаковы и рав-
ны 0,5. Поэтому вероятности всех элементарных событий одинаковы. Если монету
бросают дважды, то вероятности всех событий ОО, ОР, РО и РР равны 0,25. Если
монету бросают 10 раз, то всего 1024 элементарных события, и вероятность каждого
равНа 1024-
Опыт с многократным бросанием монеты интересен, и мы к нему вернёмся. Но
намного интереснее изучать серии испытаний, где вероятности успеха и неудачи не
одинаковы.
ПРИМЕР 2. Биатлонист делает по очереди 5 вы-
стрелов по пяти мишеням. Известно, что он попадает
в мишень в среднем 8 раз из 10. Какова вероятность
того, что будут поражены первая, третья и четвёртая
мишени, а вторая и пятая нет (рис. 86)?
Такое событие в наших обозначениях имеет вид
УНУУН. И вероятность его равна pqppq = р3?2. Из
условия следует, что р = 0,8, a q = 0,2. Подстав-
ляя эти значения, получаем
0,83 • 0,22 « 0,512 • 0,04
В биатлоне мишени чёрные.
Поражённые мишени
закрываются белыми щитками.
Рисунок 86
pV
0,02048 * 0,02.
Рассуждая таким же образом в общем случае, мы приходим к общему факту.
D
В серии из п испытаний Бернулли вероятность элементарного собы-
тия, в котором произвольным образом чередуются к успехов и п - к неудач,
равна рксГ ~к.
ИСПЫТАНИЯ БЕРНУЛЛИ
231

Вопросы
1 Какими должны быть испытания, чтобы получилась серия испытаний Бернулли?
2 Сколько возможных элементарных событий у одного испытания Бернулли? Как
они называются?
3 Пользуясь обозначениями У и Н, выпишите все элементарные события, которые
могут наступить в серии из двух и из трёх испытаний Бернулли.
4 Каким соотношением связаны вероятности успеха и неудачи?
5 Что является элементарным событием в серии из пяти испытаний Бернулли?
Упражнения
461 Эксперимент состоит из четырёх последовательных испытаний Бернулли.
Пользуясь обозначениями У для успеха и Н для неудачи, выпишите все эле-
ментарные собьгпф, в которых ровно:
а) один успех; б) два успеха; в) три успеха.
462 Пользуясь результатами задачи 461, заполните таблицу 102, в которой указа-
но, сколько может быть элементарных событий без успехов, с одним успехом,
с двумя успехами и т. д. в серии из четырёх испытаний Бернулли.
Таблица 102. Элементарные события в серии из четырёх испытаний
Число успехов
Число благоприятствующих элементарных событий
0
1
2
3
4
463 Эксперимент состоит из пяти последовательных испытаний Бернулли. Поль-
зуясь обозначениями У и Н для успеха и неудачи, выпишите все элементар-
ные события, в которых ровно:
а) 0 успехов; б) 1 успех; в) 3 успеха; г) 4 успеха.
464 Игральную кость бросают четыре раза. Найдите вероятность события, состоя-
щего в том, что шестёрка выпадет:
а) только при первом и третьем бросках;
б) только при втором броске;
в) ровно три раза — при первом, втором и четвёртом бросках.
465 Миша кидает мяч в баскетбольную корзину. Вероятность попадания рав-
на Р ж о- Найдите вероятность того, что, сделав 5 бросков, Миша попадёт
о
в корзину только при втором и четвёртом бросках.
Число успехов в испытаниях Бернулли
В предыдущем параграфе мы описали серии испытаний Бернулли и научились
вычислять вероятности элементарных событий. Поставим другую задачу. Сколько
элементарных событий в серии из п испытаний Бернулли благоприятствует наступле-
нию определённого числа успехов? Например, пусть проводится 5 испытаний. Сколь-
ко элементарных событий этой серии приводит к ровно трём успехам?
Снова применим обозначения У и Н для успеха и неудачи. Элементарные события
серии из 5 испытаний с 3 успехами могут выглядеть следующим образом:
УУУНН УУНУН УУННУ и т. д.
232
ГЛАВА XII.

Таким образом, элементарных событий с 3 успехами в 5 испытаниях ровно столь-
ко, сколько существует способов расставить 3 буквы У в последовательности из
5 букв. Это, как известно, число сочетаний С%.
Обобщим этот результат на произвольное число испытаний п.
Ф
Число элементарных событий, благоприятствующих к успехам в серии из п ис-
пытаний, равно С*.
ПРИМЕР 1. Чтобы быстрее считать мелочь и давать сдачу, кассир в метро зара-
нее складывает монеты столбиками по 10 монет в каждом. При этом кассир кладёт
монеты случайной стороной вверх. Сколько всего есть способов положить 10 монет
в столбик так, чтобы ровно 4 из них лежали орлом вверх?
Решение. Главное — увидеть в задаче знакомый случайный опыт. Положение каж-
дой монеты внутри столбика можно считать испытанием Бернулли с успехом * моне-
та орлом вверх». Выкладывание столбика — серия из п — 10 испытаний. Число тре-
буемых успехов k = 4.
Следовательно, задачу можно переформулировать так: сколько элементарных собы-
тий благоприятствует наступлению 4 успехов в 10 независимых испытаниях Бернул-
ли? Это число равно С\0 = 210 (см. рис. 83 на с. 221).
ПРИМЕР 2* На борту самолёта 100 пассажиров. Им предлагается ужин — кури-
ца с рисом или рыба с картофельным пюре. Каждый пассажир делает свой выбор.
Сколько в этом опыте комбинаций, в которых ровно 67 пассажиров выбирают курицу?
Решение. Задача укладывается в схему испытаний Бернулли. Одно испытание за-
ключается в выборе, который делает очередной пассажир. Успехом назовём выбор ку-
рицы, неудачей — выбор рыбы.
Число испытаний п = 100. Число требуемых успехов k — 67.
Ответ: С^. Число это огромно, но мы всё же запишем его:
С*1о - 294 692 427 022 541 000 000 000 000.
Вопросы
1 Сколько различных элементарных событий благоприятствует 5 успехам в серии
из 7 испытаний Бернулли?
2 Сколько в серии из п испытаний Бернулли элементарных событий, содержащих
ровно к успехов?
Упражнения
466 Выпишите все элементарные события, благоприятствующие:
а) 2 успехам в серии из 4 испытаний Бернулли;
б) 5 успехам в серии из 6 испытаний Бернулли.
467 Сколько элементарных событий в серии из 8 испытаний Бернулли благопри-
ятствует:
а) 2 успехам; б) 6 успехам; в) 5 успехам; г) 3 успехам?
468 Сколько элементарных событий благоприятствует появлению трёх орлов, если
монету бросают:
а) 3 раза; б) 5 раз; в) 7 раз; г) п раз?
ИСПЫТАНИЯ БЕРНУЛЛИ 233

469 Проводится серия из 10 испытаний Бернулли. Каких элементарных событий
больше: тех, в которых 3 успеха, или тех, в которых 7 успехов?
470 Проведена серия из п испытаний Бернулли. Найдите л, если общее число
элементарных событий равно:
а) 16; б) 64; в) 256; г) 2048; д) 2т.
471 Докажите, что в серии из 15 испытаний Бернулли число элементарных со-
бытий, благоприятствующих 6 успехам, равно числу элементарных событий,
благоприятствующих:
а) 9 неудачам; б) 9 успехам; в) 6 неудачам.
472 Проводится серия из п испытаний Бернулли. Выразите формулой число эле-
ментарных событий, которые благоприятствуют появлению:
а) 2 или 3 успехов;
б) не более 5 успехов;
в) ровно 4, 6 или 9 успехов;
г) менее 4 неудач.
473 Найдите число элементарных событий в серии из 134 испытаний Бернулли,
которые благоприятствуют появлению:
а) 133 успехов; б) одного успеха.
Е)
64J Вероятности событий
испытаниях Бернулли
Мы знаем, что при проведении серии из п независимых испытаний Бернулли
каждое конкретное элементарное событие с k успехами и п - k неудачами имеет ве-
роятность pkqn ' к.
Мы также знаем, что число таких элементарных событий с k успехами равно С*.
Следовательно, событие «наступило ровно к успехов» имеет вероятность Cknpkqn ' *.
Эту формулу часто называют формулой Бернулли.
Ф
Формула Бернулли. Пусть проводится серия из п одинаковых и независи-
мых испытаний Бернулли с вероятностью успеха р и вероятностью неудачи
q = 1 - р. Вероятность того, что наступит ровно к успехов, равна
Рассмотрим примеры.
ПРИМЕР 1. Стрелок 7 раз стреляет по мишени с вероятностью попадания - при
3
каждом отдельном выстреле. Какова вероятность события «мишень будет поражена
ровно 3 раза»?
Этот опыт — серия из 7 испытаний Бернулли с вероятностью успеха р = - и ве-
з
2
роятностью неудачи д«1-р = -. Пусть событие А состоит в том, что в этой серии
3
наступило ровно 3 успеха — попадания. По формуле Бернулли получаем
Р(Л) = C?p*q* = 35 • (J) -(I) * 0,256.
234
ГЛАВА XII.

Здесь С? — количество элементарных событий, благоприятствующих событию А,
то есть количество возможных последовательностей из трёх успехов и четырёх не-
удач, a p3q4 — вероятность каждой такой последовательности.
Рассмотрим теперь более сложные события, состоящие в том, что число успехов
заключено в некоторых пределах.
ПРИМЕР 2. Бросаем игральную кость. Успехом будем считать выпадение шестёр-
1 5
ки. Неудачей — выпадение иного числа очков. Таким образом, р = х, 9 = ^. Найдём
о о
вероятность того, что при 8 бросках шестёрка выпадет от 4 до 6 раз.
Чтобы решить эту задачу, нужно отдельно найти вероятности того, что шестёрка
выпала 4, 5 или 6 раз, и их сложить:
QpV-bQW-bClpV-70-Ы4- (|)4+ 56-Ы5. (!]3+28.(£чв
j «0,306.
В некоторых задачах удобно вместо вероятности нужного события сначала найти
вероятность противоположного события.
ПРИМЕР 3. Проводится серия из 6 испытаний Бернулли. Вероятность успеха р
равна 0,3. Найдём вероятность события А, состоящего в том, что в этой серии на-
ступит хотя бы один успех.
Решение. Вместо события А рассмотрим противоположное событие А «наступит
0 успехов». Вероятность этого события найти несложно. Учитывая, что вероятность
неудачи q равна 0,7, получаем: Р(л) - C%p°q6 - 0,76 « 0,118.
Следовательно, Р(л) - 1 - Р(Л) « 0,882.
Чтобы найти вероятность по формуле Бернулли
в электронной таблице, используйте функцию
БИНОМ.РАСП()
На рисунке найдена вероятность того, что
в 10 испытаниях Бернулли с вероятностью успе-
ха р = 0,4, наступит ровно 6 успехов. Обратите
внимание на последний аргумент в скобках. Он
равен 0. Если вместо 0 написать 1, то функция
вычислит вероятность того, что успехов случи-
лось 6 или меньше (от 0 до 6).
/х -БИНОМ.РАСП(Е4,Е2;Е3.0)
D
N
Р
к
Е
10
0,4
6
F
0,1114771
Рисунок 87
ПРИМЕР 4. В 2009 г. в первой части ЕГЭ по математике было 10 заданий с вы-
бором ответа. К каждому заданию предлагалось 4 варианта ответа, но только один
из них был верным. Если участник экзамена выбирал ответы случайным образом, то
для него эти 10 заданий превращались в серию из 10 испытаний Бернулли с вероят-
ностью успеха р в 0,25. Чтобы успешно сдать экзамен, участнику нужно было ука-
зать верные ответы хотя бы к трём заданиям. Какова была вероятность при таких
условиях сдать экзамен, ничего не зная и выбирая ответы наудачу?
ИСПЫТАНИЯ БЕРНУЛЛИ
235

Нужно найти вероятность события А «3 успеха или больше». Найдём вероятность
противоположного события «успехов 0, 1 или 2». По формуле Бернулли получаем:
Р(А) = CUP0?10 + QVg9 + C?op2q* = 0,7510 + 10 • 0,25 • 0,759 + 45 • 0,252 • 0,758 ^ 0,53.
Следовательно, при таких условиях примерно 53% участников, не знавших абсо-
лютно ничего, проваливались, а примерно 47% таких участников успешно сдавали
экзамен. С 2010 г. в ЕГЭ по математике нет задач с выбором ответа.
©
0
Вопросы
1 Запишите формулу вероятности события «наступило 3 успеха в серии из 8 ис-
пытаний Бернулли».
2 Запишите выражение для вероятности события «наступило 2 или 3 успеха в се-
рии из 9 испытаний Бернулли».
3 Как найти вероятность события «хотя бы один успех» в серии испытаний Бер-
нулли?
Упражнения
474 В некотором испытании Бернулли успех наступает с вероятностью р = 0,5.
Найдите вероятность того, что в серии из 4 таких испытаний:
а) наступит ровно два успеха;
б) наступит ровно один успех;
в) наступит ровно три успеха;
г) все испытания окончатся неудачей.
475 Найдите вероятность появления ровно трёх орлов, если монету бросают:
а) 3 раза; б) 7 раз; в) 9 раз; г) п раз.
476 Игральную кость бросают 6 раз. Найдите вероятность того, что шестёрка вы-
падет:
а) 3 раза; г) 6 раз;
б) 5 раз; д) 2 раза;
в) 1 раз; е) ни разу.
477 Перед началом футбольного матча судья бросает монетку, чтобы определить, ка-
кая команда первой будет владеть мячом. Шансы у команд равны. В серии из
пяти матчей между командой «Мотор» и командой «Стартёр» три раза мяч до-
ставался «Мотору». Найдите вероятность того, что в будущем году в такой же
серии матчей повторится то же самое — три раза мяч достанется «Мотору».
478 Случайный эксперимент заключается в пятикратном бросании симметричной
монеты. Найдите вероятность события:
а) «решка выпадет ровно три раза»;
б) «орёл выпадет от двух до четырёх раз»;
в) «решка выпадет либо один раз, либо три раза»;
г) «орёл выпадет нечётное число раз».
479 Система ПВО1 выпускает по летящей цели три ракеты. Вероятность пораже-
ния цели каждой отдельной ракетой равна 0,74. Какова вероятность события:
а) «цель не будет поражена ни одной ракетой»;
б) «все три ракеты попадут в цель»?
1 ПВО — противовоздушная оборона.
236
ГЛАВА XII.

480 В некотором испытании Бернулли неудача наступает с вероятностью ge -.
Найдите вероятность того, что в серии из 5 таких испытаний:
а) наступит ровно два успеха;
б) наступит ровно один успех;
в) наступит более двух успехов;
г) наступит менее четырёх успехов.
481 В некотором испытании Бернулли успех наступает с вероятностью р = 0,4.
Найдите вероятность того, что в серии из 4 таких испытаний:
а) наступит более двух успехов;
б) наступит не более двух неудач;
в) не все испытания окончатся неудачей;
г) наступит менее четырёх успехов.
482 Перед началом шахматной партии с помощью жребия игроки определяют,
кто играет белыми, а кто — чёрными. Остап Бендер проводит сеанс одновре-
менной игры с любителями шахмат города Васюки на 12 досках. Найдите ве-
роятность того, что он будет играть белыми:
а) ровно на трёх досках;
б) ровно на пяти досках;
в) хотя бы на одной доске;
г) по крайней мере на двух досках.
483 Олегу задали 10 одинаковых по трудности задач. Вероятность того, что Олег
решит каждую отдельную задачу, равна 0,75. Найдите вероятность того, что
Олег решит:
а) все задачи; б) не менее 8 задач; в) не менее 6 задач.
(55*} Случайный выбор
из конечной совокупности
Предположим, что в коробке лежат чёрные и синие фломастеры. Если мы выбира-
ем случайным образом один из них, это испытание. Если мы вернём его в коробку
и выберем ещё один случайный фломастер, получится такое же испытание, которое
не зависит от первого. Выбирая и возвращая в коробку фломастеры, мы получаем
серию испытаний Бернулли. Успехом можно считать, например, появление чёрного
фломастера. При этом множество фломастеров в коробке не меняется, ведь мы воз-
вращаем выбранные фломастеры. Поэтому вероятность успеха с каждым разом также
не меняется, а выбор и возвращение можно повторять сколько угодно.
Что произойдёт, если мы не будем возвращать фломастеры в коробку? Тогда каж-
дый раз вероятность успеха меняется: если выбран чёрный фломастер, то вероят-
ность вынуть следующий чёрный фломастер станет меньше. Если выбран синий фло-
мастер, то доля чёрных в коробке увеличилась, вместе с ней увеличилась вероятность
извлечь чёрный фломастер в следующий раз. Значит, при последовательном выборе
из конечной совокупности вероятность успешного или неудачного выбора не остаётся
постоянной. Кроме того, рано или поздно либо синие, либо чёрные фломастеры за-
кончатся.
Как в таком эксперименте найти вероятность того, что случится, скажем, три или
пять или какое-то другое количество успехов? Здесь формула Бернулли не подходит.
ИСПЫТАНИЯ БЕРНУЛЛИ
237

ПРИМЕР 1. Пусть в коробке 4 чёрных и 5 си-
них фломастеров. Из коробки по очереди случай-
ным образом извлекают 6 фломастеров. Найдём
вероятность того, что среди них ровно 2 чёрных.
Решение. Элементарным событием в этом
опыте является комбинация из 6 извлечённых
фломастеров. В силу случайности выбора все
элементарные события равновозможны. Нужно
пересчитать количество элементарных событий,
благоприятствующих событию А «извлечено 2 чёрных и 4 синих фломастера».
Количество способов выбрать 2 чёрных фломастера из 4 равно С\. Количество спо-
собов извлечь 4 из 5 синих фломастеров равно С\. По правилу умножения находим,
что общее число комбинаций, в которых ровно 2 чёрных и 4 синих фломастера, рав-
но N{A) = С\С\.
Всего же способов выбрать 6 фломастеров из 9 штук, лежащих в коробке, равно
N = С69.
Следовательно,
Р(А)
N(A) _ Cl-C$
N (* '
Осталось найти в треугольнике Паскаля (см. рис. 83 на с. 221) нужные числа
и вычислить вероятность. Прежде чем это сделать, обратим внимание на то, как
устроена полученная формула.
Ф
Сумма верхних индексов у чисел С* в числителе равна верхнему индексу
в знаменателе: 2 + 4 = 6. То же с нижними индексами: 4 + 5 = 9.
Это общее правило, которое позволяет проверить, верно ли составлена формула ве-
роятности.
Теперь проведём вычисления:
/ ч 6-5 5
PU) ' "84" - П * °'357'
Последовательный выбор из всей совокупности предметов можно заменить одно-
временным: можно считать, что мы составляем выборку не постепенно, извлекая
предметы один за другим, а сразу. Вероятность собрать ту или иную выборку при
этом не меняется.
Щ)
Не важно, как устроен выбор из конечной совокупности — последовательный он
или одновременный.
Решить задачу, подобную задаче в при-
мере 1, можно в электронных таблицах.
Лучше всего применить функцию
ГИПЕРГЕОМ.РАСПО
Решение примера 1 показано на рисунке.
Последний аргумент равен 0. Если вме-
сто 0 написать 1, то функция вычислит
вероятность того, что выбрано 2 чёрных
фломастера или меньше (от 0 до 2).
I /х =ГИПЕРГЕОМ РАСП(Е4;ЕЗ;Е2;Е1;0) I
С D
Всего фломастеров
Из них чёрных
Выбрано
| Из них чёрных
Е F
9
4
6
2_
G I
0,35714з|
Рисунок 88
238
ГЛАВА XII.

ПРИМЕР 2. В прошлом году в опросе о качестве обедов в школьной столовой уча-
ствовали 10 из 25 учеников класса. В этом году совет школы решил провести такой
же опрос, чтобы сравнить результаты с прошлогодними. Для опроса в этом классе
снова были случайно выбраны 10 человек из тех же 25. Какова вероятность того,
что ровно 4 из них участвовали в прошлогоднем опросе?
Решение. В этой задаче элементарным событием является выборка. Чтобы осуще-
ствилось событие А «ровно 4 участника выборки участвовали в прошлогоднем опро-
се», выборка должна состоять из тех, кто участвовал в прошлогоднем опросе (ровно
4 человека из 10), и тех, кто не участвовал (ровно 6 из 15). Занесём все сведения
в таблицу 103.
Таблица 103. Повторная выборка
Число учащихся
Выбрано в этом году
Всего
Число способов
Участвовавших
в прошлогоднем
опросе
4
10
С?о « 210
Не участвовавших
в прошлогоднем
опросе
10-4-6
25 - 10 - 15
С?5 - 5005
Всего
10
25
С12ь в 3 268 760
Мы расположили графы таблицы так, чтобы из последней строки легко получа-
лась нужная формула. Искомая вероятность равна
PU)
Qo'
425
^15 ^
* 0,322.
Для вычисления приходится использовать калькулятор или компьютер, поскольку
числа, участвующие в выражении, велики.
Можно было бы поставить вопрос иначе. Например, какова вероятность того, что
в выборке оказалось не более четырёх учеников из числа тех, кто участвовал в про-
шлогоднем опросе? Тогда нужно сложить несколько вероятностей: верояЛюсть того,
что их ровно 0, ровно 1, ровно 2, ровно 3 или ровно 4:
^10
Qs + Qo * Qs'
Qo * Cl5 + Qo * Cl6 + Qo ' Q5
^25
« 0,663.
®
Вопросы
1 Что является элементарным событием при выборе нескольких элементов из
имеющейся совокупности?
2 Зависит ли вероятность появления определённой выборки от того, является ли
выбор последовательным или одновременным?
0
Упражнения
484 Из шахматной коробки, где 16 белых и 16 чёрных фигур, вынимают случай-
ным образом одну фигуру. Она оказалась белой. Увеличилась или уменьши-
лась вероятность достать при следующем случайном выборе:
а) белую фигуру; б) чёрную фигуру?
ИСПЫТАНИЯ БЕРНУЛЛИ
239

485 В коробке 9 простых карандашей, из них 4 мягких, остальные твёрдые. Из
коробки не глядя забирают 6 карандашей. Найдите вероятность того, что сре-
ди взятых карандашей окажется:
а) ровно 2 мягких; в) все 4 мягких;
б) ровно 3 мягких; г) более одного мягкого карандаша.
486 Симметричную монету бросили 9 раз. Известно, что орёл выпал 6 раз. Най-
дите вероятность того, что среди первых 5 бросаний выпало ровно:
а) 3 орла; б) 1 орёл; в) 3 решки; г) 1 решка.
487 Игральную кость бросили 8 раз. Известно, что шестёрка выпала трижды.
Найдите вероятность того, что в первых 4 бросаниях:
а) не было ни одной шестёрки; в) выпало две шестёрки;
б) была ровно одна шестёрка; г) шестёрка выпала трижды.
488 В кармане у Сергея 10 монет: 4 двухрублёвые, остальные пятирублёвые.
Сергей на ощупь вынимает из кармана 6 монет. Какова вероятность того, что
среди оставшихся в кармане монет:
а) окажутся ровно 2 двухрублёвые;
б) не окажется ни одной пятирублёвой?
489 В ящике 8 болтов, из них 3 медных, остальные — стальные. Из ящика не
глядя забирают 5 болтов. Найдите вероятность того, что среди выбранных
болтов окажется:
а) менее 2 медных; б) от 2 до 4 стальных.
490 В билете популярной некогда лотереи «5 из 36» всего 36 номеров — от 1
до 36. Участник лотереи выбирает и зачёркивает в билете любые 5 из них —
на свой вкус. Потом проводится тираж лотереи — случайным образом выпа-
дают 5 выигрышных номеров. Если участник угадал хотя бы 3 выигрышных
номера, то он получает денежный выигрыш. Чем больше номеров угадано,
тем выигрыш больше. Найдите вероятность того, что:
а) участник угадает все 5 номеров;
б) участник угадает ровно 4 номера из 5;
в) участник получит какой-нибудь выигрыш.
Составьте выражение для искомой вероятности. Найдите приближённое зна-
чение с помощью компьютера.
491 Группа туристов прилетела в Санкт-Петербург. После приземления тури-
сты ждут 50 своих чемоданов у ленты багажного транспортёра в аэропорту.
Грузчики кладут чемоданы на ленту в случайном порядке, а всего чемоданов
в самолёте было 250. Найдите вероятность того, что все 50 чемоданов этой
группы окажутся среди первых 100 чемоданов, появившихся на ленте.
Составьте выражение для искомой вероятности. Найдите приближённое зна-
чение с помощью компьютера.
492 В коробке 5 красных, 7 синих и 6 белых шаров. Из коробки наудачу выни-
мают 6 шаров. Найдите вероятность того, что среди этих 6 шаров 2 красных,
2 синих и 2 белых.
Указание. В этой задаче выборка состоит из предметов трёх видов. Это не
влияет на способ решения. Нужно отдельно найти число способов выбрать
2 красных шара из 5 имеющихся, 2 синих и 2 белых. Далее следует исполь-
зовать правило умножения для подсчёта общего числа благоприятствующих
комбинаций. В этом выражении будет не два множителя, а три.
240
ГЛАВА XII.

Геометрическая
вероятность
Иногда случайный опыт можно представить
как выбор точки из некоторой фигуры на пло-
скости или из промежутка на прямой. В та-
ком опыте каждое отдельное элементарное
событие имеет нулевую вероятность, поэтому
обычный способ подсчёта вероятностей не
подходит. На помощь приходит геометриче-
ская вероятность.
Интересно, что в геометрических случайных
опытах удобно считать, что событие и фигу-
ра — это одно и то же. Вероятности на
плоскости измеряются отношением площа-
дей фигур, на прямой — отношением длин
промежутков.
66* Выбор точки из фигуры
на плоскости
67* Выбор точки из отрезка
и дуги окружности

Юбч Выбор точки из фигуры на плоскости
Рисунок 89. Неисправный
пиксель на экране
компьютера
Бывает так, что какой-то отдельный пиксель на экране
компьютерного монитора или смартфона перестаёт рабо-
■ I | тать. Тогда на экране появляется чёрная точка (рис. 89).
V_^*W^ I Можно поставить вопрос о вероятности того, что неис-
^^ I правный пиксель попадёт в определённую область экрана.
Пикселей на экране может быть больше миллиона.
Удобно считать, что мы имеем дело с точкой, выбран-
ной случайным образом из прямоугольника.
ПРИМЕР 1. Рассмотрим опыт: из прямоугольника со
сторонами 3 и 4 выбирают случайную точку (рис. 90).
Какова вероятность того, что эта точка попала в левый
нижний квадрат со стороной 1?
В этой задаче речь идёт о так называемой геометри-
ческой вероятности. Элементарными событиями в этом
случайном опыте являются точки прямоугольника. Их
бесконечно много, и вероятность выбрать каждую кон-
кретную точку равна нулю.
Мы столкнулись с опытом, в котором элементар-
ные события имеют нулевые вероятности, но не
являются невозможными.
Определить вероятность событий в этом опыте с по-
мощью суммы вероятностей элементарных событий
нельзя. Нужен другой способ.
Рассмотрим более общий опыт. На плоскости дана
фигура F, которая имеет ненулевую площадь. Из фигу-
ры F выбирают одну случайную точку. Какова вероят-
ность того, что выбранная точка принадлежит фигуре G,
которая содержится в фигуре F (рис. 91)?
Ответ зависит от того, как мы понимаем, что такое
«случайно выбранная точка». Если мы считаем, что все точки должны «иметь рав-
ные шансы», то нужно принять следующее правило:
1* °
1 1
F
Рисунок 90
Щ>
Рисунок 91
Ф
Вероятность события «выбранная точка принадлежит фигуре G» прямо пропорцио-
нальна площади фигуры G и не зависит от расположения и формы фигуры G.
Мы знаем наверняка, что точка выбирается из фигуры F. Поэтому событие ♦точ-
ка принадлежит фигуре F* является достоверным, и его вероятность равна единице:
P(F) - 1.
При таком подходе мы, по сути дела, отождествляем (не различаем) случайные со-
бытия и геометрические фигуры, поэтому событие и соответствующую ему фигуру
мы будем называть одинаково.
Подведём итог.
Ф
Пусть SF и SQ — площади фигур F и G. Вероятность события G «выбранная точ-
ка принадлежит фигуре G, которая содержится в фигуре F» равна P(G) = §г.
242
ГЛАВА XIII.

Площадь фигуры G не больше, чем площадь фигуры F, поэтому P(G) ^ 1.
Вернёмся к нашему примеру. Фигура F — прямоугольник со сторонами 3 и 4 (см.
рис. 90). Следовательно,
SF - 3 • 4 - 12.
Квадрат G, расположенный слева внизу в прямоугольнике F, по условию имеет
длину стороны 1. Поэтому
SG - 1.
Значит, вероятность того, что точка попала в квадрат G, равна
Решая такие задачи, мы предполагаем, что «шансы любой точки» одинаковы.
В большинстве случайных опытов это не так, но при определённых условиях можно
считать, что наше предположение недалеко от истины.
Рассмотрим, например, стрелки, который может попасть в любое место мишени.
Он стреляет не в случайное место, а целится. Значит, вероятность попасть в цен-
тральный круг мишени несколько выше, чем вероятность попасть в такой же круг
где-то с краю.
Но представим себе, что мишень мала, стрелок находится далеко от неё, а слу-
чайное рассеивание пуль во время стрельбы велико (оно вызвано ветром, ошиб-
кой прицеливания, разогревом ружейного ствола и другими факторами). При этих
условиях можно считать, что вероятность попасть в какую-то часть мишени глав-
ным образом зависит только от площади этой части и очень мало — от меткости
стрелка.
ПРИМЕР 2. Стрелок стреляет издалека по круглой
мишени диаметром 5 см. Известно, что стрелок попал
в мишень, которая разбита на три зоны (рис. 92). Ра-
диус центральной круговой зоны равен 1 см, средняя
и внешняя зоны — кольцевые, они имеют одинаковую
ширину 2 см. Найдём вероятность того, что стрелок по-
пал во внешнюю зону мишени.
Решение. Фигурой F в описанном опыте является ми-
шень площадью
SF = 52 • л = 25л см2.
Фигура G — внешняя зона, то есть кольцо, у которого
радиус внешней окружности равен 5 см, а внутренней —
3 см. Площадь зоны равна разности площадей двух кругов:
SG = 25л - 9л = 16л (см2).
Рисунок 92
Следовательно, P(G) e -£- — -гг-
SF 25л
0,64.
Иногда для поиска вероятностей не нужно знать пло-
щади фигур, достаточно уметь находить отношения их
площадей.
ПРИМЕР 3. Из треугольника ABC случайным обра-
зом выбирается точка X. Найдём вероятность того, что
она принадлежит треугольнику, вершинами которого яв-
ляются середины сторон треугольника ABC (рис. 93).
ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ
243

Решение. Средние линии разбивают треугольник ABC на четыре равных малых
треугольника, площадь каждого из которых обозначим Q (см. рис. 93). Значит, пло-
щадь треугольника ABC в 4 раза больше: SABC = 4Q. Интересующее нас событие
состоит в том, что точка X принадлежит малому треугольнику MNK. Вероятность
этого события равна
Smnk Q 1
Р(МА,ЛГ)- S^ 49 4-
О
Вопросы
0
1 Какие события рассматриваются в опыте, состоящем в случайном выборе точки
фигуры на плоскости?
2 Точку выбирают из некоторой данной фигуры. От чего зависит и от чего не за-
висит вероятность попадания выбранной точки в фигуру, содержащуюся внутри
данной фигуры?
3 Напишите формулу для вероятности попадания выбранной точки в фигуру G при
выборе точки из фигуры F, содержащей в себе фигуру G.
4 Точку наудачу выбирают из квадрата ABCD. Какова вероятность того, что вы-
бранная точка принадлежит треугольнику ABC?
Упражнения
493 Внутри треугольника ABC случайным образом выбирается точка. Найди-
те вероятность того, что эта точка попала в треугольник АВМ, где AM —
медиана треугольника ABC.
494 Из прямоугольника случайным образом выбирается точка. Найдите вероят-
ность события:
а) «точка принадлежит ромбу, вершинами которого служат середины сторон
прямоугольника»;
б) «точка принадлежит треугольнику, вершинами которого служат две сосед-
ние вершины прямоугольника и точка пересечения его диагоналей».
495 В квадрате случайным образом выбирается точка. Найдите вероятность того,
что эта точка принадлежит вписанному в этот квадрат кругу.
496 В квадрате ABCD случайным образом выбирается точка X. Найдите ве-
роятность того, что эта точка принадлежит треугольнику ADM, где точ-
ка М:
а) середина стороны CD;
б) делит отрезок CD в отношении 1 : 2, считая от точки С;
в) делит отрезок CD в отношении т : п9 считая от точки С.
497 В квадрате ABCD случайным образом выбирается точка X. Найдите вероят-
ность того, что эта точка принадлежит трапеции AMCD, где точка М:
а) середина стороны ВС;
б) делит отрезок ВС в отношении 1:2, считая от точки С;
в) делит отрезок ВС в отношении т : п, считая от точки В.
498 В круге случайным образом выбирается точка. Найдите вероятность того, что
эта точка принадлежит:
а) вписанному в круг квадрату;
б) вписанному в круг равностороннему треугольнику.
244
ГЛАВА XIII.

499 В прямоугольнике со сторонами 6 см и 20 см нарисованы два непересекаю-
щихся круга диаметром 3 см каждый. Найдите вероятность того, что случай-
но выбранная точка этого прямоугольника:
а) не принадлежит ни одному из этих кругов;
б) не принадлежит хотя бы одному из этих кругов.
500 Буратино посадил в центре прямоугольного листа бумаги размером 20 х 25 см
круглую кляксу радиусом 1 см. Сразу после этого Буратино посадил ещё од-
ну такую же кляксу, которая также целиком оказалась на листе. Найдите ве-
роятность того, что эти две кляксы не соприкасаются.
(S7*) Выбор точки из отрезка
и дуги окружности
Часто случайную точку приходится выбирать не из фигуры на плоскости, а из от-
резка. Важный пример такого эксперимента — срок службы нового прибора (скажем,
мобильного телефона) до первой поломки. Новые телефоны ломаются реже, чем ста-
рые, поэтому поломка в течение первого года службы менее вероятна, чем в течение
второго или третьего. Но если ограничиться небольшим периодом времени, то можно
считать, что телефон может выйти из строя в любой момент этого периода «с равны-
ми шансами».
Рассмотрим опыт, который состоит в случайном выборе одной точки X из некото-
рого отрезка MN. Элементарными событиями служат все точки отрезка.
Пусть отрезок CD содержится в отрезке MN. Нас
интересует событие, состоящее в том, что выбранная • • • • •
точка X принадлежит отрезку CD (рис. 94). Это со-
бытие удобно обозначить так же, как отрезок: собы- Рисунок 94
тие CD.
Применим тот же метод вычисления вероятности *
события CD, какой мы использовали для фигур на плоскости: будем полагать, что
вероятность пропорциональна длине отрезка CD. Тогда вероятность события CD «точ-
ка X принадлежит отрезку CD, содержащемуся в отрезке MN» равна
р<сс> - ш-
Это число неотрицательное и не превосходит 1, как и полагается вероятности слу-
чайного события.
ПРИМЕР 1. Внутри отрезка MN случайным образом выбирается точка X. Найдём
вероятность того, что точка X ближе к N, чем к М.
Решение. Пусть О — середина отрезка MN # 0_^ #
(рис. 95). Указанное событие наступит только тогда, М X N
когда точка X лежит внутри отрезка ON. Тогда его Л
Рисунок 95
вероятность равна 7
р<ОЛГ> = ш = °-5-
Ничего не меняется, если точка X выбирается не из отрезка, а из дуги некото-
рой кривой линии. Например, можно случайным образом выбирать точку на окруж-
ности.
ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ
245

Рисунок 96
ПРИМЕР 2. На окружности даны точки А и В,
причём эти точки не являются диаметрально противо-
положными. На этой же окружности случайным обра-
зом выбирается точка С. Найдём вероятность того, что
отрезок ВС пересекает диаметр окружности, проходя-
щий через точку А.
Решение. Пусть длина окружности равна L. Инте-
ресующее нас событие Е «отрезок ВС пересекает ди-
аметр DA* наступает, только если точка С лежит на
полуокружности DA, не содержащей точку В (рис. 96).
Длина полуокружности равна —. Найдём вероятность
события Е:
X
—•—
т
Ъ п
Рисунок 97
Геометрическую вероятность можно применять
к числовым промежуткам. Предположим, что случай-
ным образом выбирается число х, удовлетворяющее
условию т ^ х ^ л. Этот опыт можно заменить опы-
том, в котором из отрезка [т\ п] на числовой прямой
выбирается точка с координатой х (рис. 97).
Рассмотрим событие, состоящее в том, что точка с координатой х выбрана из от-
резка [а; Ь], содержащегося в отрезке [т; и]. Это событие обозначим а < х ^ Ь. Его
вероятность равна отношению длин отрезков [а; Ь] и [т; п]:
Ь-а
Р(а**х^Ь) = .
п — т
Поясним сказанное на примере.
ПРИМЕР 3. Найдём вероятность того, что точка, случайно выбранная из отрез-
[1 11
ка [0; 1], принадлежит отрезку io» о|
Решение. По формуле геометрической вероятности находим:
1.1
2 3 !
" 6е
«I1 Х
1-0
Ф
0
Вопросы
1 Сколько элементарных событий возникает при выборе случайной точки из фигу-
ры на плоскости или из отрезка?
2 Как найти вероятность события «точка, случайно выбранная из отрезка МЛ/, при-
надлежит отрезку CD, который содержится в отрезке МЛ/»?
Упражнения
501 Отрезок АВ разбит точками Си D на три равные части AC, CD и DB. Из
отрезка АВ выбирают случайную точку X. Найдите вероятность того, что
точка X:
а) принадлежит отрезку CD;
б) не принадлежит отрезку CD.
246
ГЛАВА XIII.

502 Длина отрезка MN равна 3 см. Из этого отрезка наудачу выбирают одну точ-
ку. Найдите вероятность того, что эта точка удалена от точки М:
а) менее чем на 1 см;
б) не более чем на 2 см.
503 Углы АОВ и COD вертикальные. При этом точка С лежит на луче АО и
/LAOB — 60°. Из окружности с центром в точке О случайным образом вы-
бирают точку X. Найдите вероятность того, что точка X лежит:
а) внутри хотя бы одного из углов ВОС или AOD;
б) внутри угла DOC.
504 На окружности с центром О выбрана точка А. Из этой окружности выбирают
случайную точку X. Найдите вероятность того, что угол АОХ:
а) меньше 90°;
б) больше 120°;
в) находится в пределах от 30° до 60°.
505 В окружность вписан равносторонний треугольник ABC. На этой окружности
случайным образом выбирают две точки D и Е. Наймите вероятность того,
что отрезок DE:
а) не пересекает ни одну из сторон треугольника;
б) пересекает ровно две стороны треугольника.
506 Вернувшись из отпуска, Иван Иванович обнаружил, что настенные часы дав-
но остановились. Найдите вероятность того, что время, которое показывают
остановившиеся часы, отличается от действительного времени не больше чем
на 30 минут.
507 Из отрезка [0; 1] случайным образом выбирается число х. Найдите вероят-
ность того, что:
а) х < 0,5; б) х > 0,7; в) х < 0,3; г) х > 0,9.
508 Из отрезка [0; 1] случайным образом выбирается число х. Найдите вероят-
ность того, что:
а) 2х < 0,5; б) 2х - 1 < 0,4; в) 0,4 < 2х ^ 0,6; г) Зл: < 0,3 или Зх ^ 0,9.
509 Иван Иванович обещал позвонить Ивану Никифоровичу между 15:00 и 16:00.
Известно, что Иван Иванович всегда держит своё слово. Иван Никифорович
ждал звонка, но около половины четвёртого отлучился на 10 минут, забыв
взять с собой телефон. Найдите вероятность того, что, когда Иван Иванович
позвонил, Ивана Никифорович был у телефона.
510 Из отрезка [0; 1] случайным образом независимо друг от друга выбираются
два числа хну. Найдите вероятность того, что:
а) *<\> У<\\ в) 0,2 < х < 0,8, 0,3 < у < 0,5;
б) х > 0,7, у < 0,4; г) х < 1, у > 0,4.
511 В самом начале поэмы Н. В. Гоголя «Мёртвые души» два мужика спорят от-
носительно того, как далеко доедет колесо в экипаже Чичикова:
«...Два русских мужика, стоявшие у дверей кабака против гостиницы,
сделали кое-какие замечания, относившиеся впрочем более к экипажу, чем
к сидевшему в нём. «Вишь ты», сказал один другому: «вон какое колесо!
Что ты думаешь, доедет то колесо, если б случилось, в Москву, или не
доедет?» — «Доедет», — отвечал другой. «А в Казань-то, я думаю, не до-
едет?» — «В Казань не доедет», — отвечал другой».
ГЕОМЕТРИЧЕСКАЯ ВЕРОЯТНОСТЬ
247

Предположим, что путь от упомянутой гостиницы в Казань ведёт через
Москву и что до Москвы 140 вёрст, а от Москвы до Казани ещё 760 вёрст.
Будем считать, что колесо обязательно сломается, причём это может случить-
ся в любой момент на пути от гостиницы до Казани. Найдите вероятность
того, что:
а) колесо доедет до Москвы, как и предполагают мужики;
б) колесо не доедет даже до Москвы.
512 Из отрезка [0; 1] случайным образом выбирается число х. Найдите вероят-
ность того, что:
а) х2 < 0,25;
б) х2 ^ 0,09.
513 Из отрезка [2; 5] случайным образом выбирается отрезок [а; Ь] длины 1.
Найдите вероятность события:
а) а < 3;
б) Ь < 4;
в) середина отрезка [а; Ь] заключена между числами 3 и 4;
г) середина отрезка [а; Ь] заключена между числами 2,5 и 4,5.
514 Из отрезка [0; 1] случайным образом независимо друг от друга выбираются
два числа х и у. Найдите вероятность того, что:
а) у > 2х\ б) х < у < Зх; в) - < х < у; г) х + у < -.
515 Хрупкий стержень ломают в двух случайных точках. Какова вероятность то-
го, что из трёх получившихся частей можно сложить треугольник?
248
ГЛАВА XIII.

Случайные
величины
Случайная величина — это величина, значе-
ние которой зависит от элементарного со-
бытия, которым закончился опыт. Чтобы опи-
сать случайную величину, нужно знать все
её возможные значения и их вероятности,
то есть распределение вероятностей случай-
ной величины.
Случайные величины служат для описания
изменчивых величин, которые встречаются в
природе и в повседневной жизни.
68 Примеры случайных величин
69 Распределение вероятностей
случайной величины
70* Математическое ожидание
случайной величины
71* Закон больших чисел
и его применение

Примеры случайных величин
В разных школьных предметах вы изучаете различные величины — длины и рас-
стояния, массу и температуру, скорость и время. В начальной школе обычно рассма-
тривают величины, имеющие постоянные значения. Позже вы познакомились с ве-
личинами, которые зависят друг от друга или меняются со временем. Для описания
таких величин используются функции.
Занимаясь статистикой, мы узнали, что большинство величин в окружающем мире
подвержены случайной изменчивости: на их значения влияет множество известных
или неизвестных случайных факторов. Про некоторые величины мы заранее знаем,
что они случайные. Например, число успехов в серии испытаний Вернулли — за-
ведомо случайная величина. Другие величины принято считать постоянными, но на
самом деле они изменчивы — их значения во многом случайны. Важный пример —
напряжение в электрической сети. В то же время, говоря в главе V о случайной из-
менчивости, мы отмечали, что часто изменчивость подчиняется закономерностям,
проявляющимся при большом числе измерений или наблюдений. Важная задача тео-
рии вероятностей — изучение случайных величин и их числовых характеристик.
Изменчивые величины, возникающие при проведении случайного опыта, мы будем
называть случайными величинами.
Определение. Случайная величина — это величина, значение которой зави-
сит от того, каким элементарным событием закончился случайный опыт.
Чтобы не путать на письме случайные величины и переменные, будем обозна-
чать случайные величины большими латинскими буквами. Приведём несколько при-
меров.
ПРИМЕР 1. Предположим, некто кидает игральную коо^ъ. Случайной величиной X
будем считать число выпавших очков. Поскольку кубик имеет 6 граней и число оч-
ков на каждой грани — целое число от 1 до 6, случайная величина X принимает
значения 1, 2, 3, 4, 5 и 6.
ПРИМЕР 2. Рост наудачу выбранного человека можно рассматривать как случай-
ную величину.
ПРИМЕР 3. Участник лотереи покупает билет. Цена билета фиксирована, но
выигрыш — случайная величина.
ПРИМЕР 4. Время безотказной службы телевизора или стиральной машины —
случайная величина. Свойства этой случайной величины важны, например при уста-
новлении гарантийного срока на новую технику.
ПРИМЕР 5. Число бракованных деталей в контрольной партии — случайная вели-
чина.
ПРИМЕР 6. Напряжение в бытовой электрической сети — случайная величина,
значения которой колеблются около 220 вольт.
ПРИМЕР 7. Масса расфасованных продуктов может несколько отличаться от той,
что указана на упаковке. Пакет крупы номинальной массой 1 кг на самом деле мо-
жет весить несколько больше или меньше. Покупатель такие отличия не замечает.
Зато производителю колебания в весе небезразличны. В случае серьёзного смещения
среднего веса в ту или иную сторону производитель может понести убытки. Можно
250
ГЛАВА XIV.

рассматривать массу расфасованных продуктов как случайную величину, колеблющу-
юся около номинальной массы.
ПРИМЕР 8. Важным примером случайной величины является число успехов в се-
рии испытаний Бернулли. Пусть, например, проводится 10 испытаний Бернулли.
Число успехов в этой серии может принимать любое целое значение от 0 до 10. Чис-
ло неудач также является случайной величиной.
5 3
ПРИМЕР 9. Можно точно вычислить, чему равна сумма чисел - и -. Поэтому
о о
значение этой суммы не является случайной величиной. Однако если дать эту задачу
на контрольной работе в 6 классе, то полученные ответы могут отличаться от верно-
го ответа непредсказуемым образом. Поэтому ответ школьника можно рассматривать
как случайную величину.
ПРИМЕР 10. Монету бросают до первого выпадения орла. Число бросаний — слу-
чайная величина, значением которой может быть любое натуральное число.
Если случайная величина принимает отдельные значения, которые «не сливают-
ся» в интервалы или отрезки, то такую случайную величину называют дискретной.
Например, результат бросания одной игральной кости или сумма выпавших очков
при двух бросках кости — это дискретные величины.
В природе значения многих случайных величин изменяются непрерывно. Напри-
мер, температура воздуха в помещении меняется непрерывно внутри некоторого ин-
тервала. Любое значение из некоторого промежутка может принимать рост случайно
выбранного человека. Такие случайные величины называются непрерывными.
fyj Вопросы
^^ 1 Что такое случайная величина?
2 Приведите два-три примера случайных величин, помимо тех, которые даны
в тексте учебника. Вы можете легко найти примеры, вспомнив игры, в которые
вы играете. Другие примеры можно найти при наблюдениях за погодой.
3 Можно ли рассматривать школьную отметку как случайную величину? Приведите
аргументы за и против.
4 Приведите пример дискретной и пример непрерывной случайной величины по-
мимо тех, что даны в тексте.
\£j Упражнения
516 Рассмотрите примеры 1—8 из текста параграфа. В каких примерах случай-
ные величины дискретные, а в каких — непрерывные?
517 Серия товарищеских матчей проводится до двух побед одной из команд в
трёх матчах. Можно ли считать число матчей случайной величиной? Какие
значения может принимать эта случайная величина?
518 Два шахматиста решили провести дружескую встречу до трёх побед в пяти
партиях. Какие значения может принимать случайная величина ♦ число сы-
гранных партий»?
519 В моментальной лотерее участвуют три типа билетов: без выигрыша (вы-
игрыш 0 рублей), с выигрышем 20 рублей и выигрышем 100 рублей. Можно
ли считать выигрыш играющего случайной величиной? Какие значения мо-
жет принимать эта величина, если играющий покупает:
а) один билет; б) два билета?
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
251

520 В книжке 16 страниц. Вы наугад открываете книжку и смотрите номер стра-
ницы слева. Можно ли считать эту величину случайной? Какие значения она
может принимать?
521 Возьмём произвольное слово русского языка из четырёх букв. Можно ли счи-
тать количество букв «М» в выбранном слове случайной величиной? Какие
значения может принимать эта величина?
522 Какие значения может принимать случайная величина:
а) сумма очков при бросании двух игральных костей;
б) сумма очков при бросании трёх игральных костей;
в) число испытаний в опыте, где испытания проводятся до первого успеха;
г) количество успехов в серии из п испытаний Бернулли?
523 Известно, что в классе 32 ученика. Из них 20 девочек. Какие значения мо-
жет принимать случайная величина:
а) число девочек, присутствующих сегодня в классе;
б) число учеников, отсутствующих сегодня в классе?
Сколько различных значений может принять каждая из этих случайных ве-
личин?
Е)
69) Распределение вероятностей
случайной величины
Случайная величина возникает как результат случайного опыта. Предположим,
что некоторая случайная величина X может принимать несколько значений.
Чтобы описать случайную величину, нужно указать её возможные значения и их
вероятности.
Распределением вероятностей или просто распределением случайной вели-
чины называется закон, который каждому значению случайной величины ставит
в соответствие вероятность того, что величина примет это значение.
Если, например, величина X может принять значение 5, то нужно указать вероят-
ность события «X равно 5». Если величина X может принять значение -4, то нуж-
но указать вероятность события «X равно -4». Такие события принято обозначать
(X - 5), (X = -4) и т. д.
Таблица 104. Число выпавших очков Распределение вероятностей можно
задать таблицей, графиком, диаграммой,
формулами или даже словесным описа-
нием.
ПРИМЕР 1. Случайная величина У
равна числу очков, выпавших при одно-
кратном бросании игрального кубика. Распределение удобно задать таблицей 104.
В этом примере вероятности всех шести значений одинаковые. Вероятность рас-
пределена поровну между шестью возможными значениями.
Найдём, чему равна вероятность события (3 < У ^ 5). Это событие состоит в том,
что при одном броске игральной кости выпало от 3 до 5 очков. Вероятность этого
равна сумме трёх вероятностей:
Р(3<У<5) = - + - + -=2.
Значение
Вероятность
1
1
6
2
1
6
3
1
6
4
1
6
5
1
6
6
1
6
252
ГЛАВА XIV.

ПРИМЕР 2. Рассмотрим случайную величину S — «число выпавших орлов при
пяти бросаниях монеты». Количество выпавших орлов может быть натуральным чис-
лом от О до 5. Вероятность того, что орлов случится ровно А, можно найти по фор-
муле Бернулли: m*me"* г*
p(S_*>.c4|) (|) -|.
Составим таблицу распределения.
Таблица 105. Распределение числа орлов в серии из 5 испытаний
Значения S
Вероятность
0
1
32
1
5
32
2
10
32
3
10
32
4
5
32
5
1
32
Найдём, чему равна вероятность того, что при пяти бросках монеты случится от 2
до 5 орлов. Это событие можно записать (2 < S < 5), и его вероятность равна
п/п лч 10 10 5 1 13
В редакторах электронных таблиц для
вычислений вероятностей по распре-
делениям предусмотрена функция
ВЕРОЯТНОСТИ)
На рисунке показано решение приме-
ра^.
• /х =ВЕРОЯТНОСТЬ(СЗ:С8;РЗ:Р8,2;5)
1 С
|Значения
0
1
2
3
4
| 5_
D
Вероятности
0,03
0.16
0.31
0.31
0,16
0.03
Е
0.8125
F
Рисунок 98
ПРИМЕР 3. Количество попыток в серии испытаний до первого успеха, если веро-
ятность успеха в каждом испытании равна р.
Отличие от двух предыдущих примеров в том, что у случайной величины «число
попыток до достижения первого успеха» (назовём её X) значений бесконечно много —
от 1 до бесконечности. Не будем изображать бесконечную таблицу, а зададим распре-
деление формулой:
Р(Х= к) = pqk\
где q = 1 - р — это вероятность неудачи в каждой отдельно взятой попытке.
ПРИМЕР 4. Иногда распределение вероятностей случайной величины можно изо-
бразить с помощью столбиковой диаграммы. На горизонтальной оси отмечаются зна-
чения, а высоты столбиков равны вероятностям соответствующих значений. Диаграм-
ма 49 построена на основе значений таблицы 105.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
253

ф
Диаграмма 49. Распределение вероятностей случайной величины S
А
Основное свойство распределения. Сумма всех вероятностей в распределе-
нии любой дискретной случайной величины равна 1.
Объясняется это свойство тем, что сумма вероятностей всех значений случайной
величины равна сумме вероятностей всех элементарных событий эксперимента.
Распределение вероятностей значений непрерывных случайных величин обычно
описывают с помощью функций.
Ф
0
Вопросы
Что такое распределение вероятностей случайной величины?
2 Сформулируйте основное свойство распределения случайной величины.
3 Всегда ли различные значения случайной величины имеют равные вероятности?
4 Приведите пример случайной величины, все возможные значения которой име-
ют равные вероятности.
5 Приведите примеры непрерывных случайных величин, помимо тех, которые даны
в тексте параграфа.
Упражнения
524 Задайте с помощью таблицы распределение вероятностей случайной величи-
ны X, равной числу орлов, выпавших при:
а) одном; б) двух; в) трёх бросаниях монеты.
525 Опыт состоит в бросании двух игральных костей. Заполните таблицу распре-
деления вероятностей и постройте соответствующие диаграммы для случай-
ной величины:
а) наибольшее из двух выпавших очков;
б) наименьшее из двух выпавших очков.
Указание. Наибольшее из данных чисел — это число, больше которого нет.
Поэтому, если числа равны, то считается, что каждое из них наибольшее.
254
ГЛАВА XIV.

Например, если оба раза выпало три очка, то считается, что наибольшее вы-
павшее число очков — три. То же самое с наименьшим значением.
526 В таблицах 106 и 107 дано распределение вероятностей некоторой случайной
величины. Одна из вероятностей неизвестна. Найдите её.
Таблица 106
Значение
Вероятность
1
1
9
2
1
3
1 3
I 1
1 в
4
Таблица 107
Значение
Вероятность
-4
0,05
-3
0,1
-2 I
0,15 1
-1
0,18
0
1 1
0,18
5
1 _1
1 4
2
0,15
3
0,1
в
1 1
8
4 1
0,05 1
527 Распределение вероятностей случайной величины X задано таблицей 108.
Таблица 108
Значение X
Вероятность
0
0,1
0,5
0,04
1
0,2
1.5
0,18
2
0,05
2.5
0,15
3
0,11
3,5
0,1
4
0,07 1
Найдите вероятность:
а) Р(1 < X < 2,5);
б) Р(Х - 0,5 или X > 2);
в) Р(Х > 0,4 или X « 2,5);
г) Р(Х — целое число).
70*) Математическое ожидание
случайной величины
Рассмотрим случайную величину X и её Таблица 109
распределение, заданное таблицей.
Если бы у нас был числовой набор
и мы знали бы частоты значений, то мог-
ли бы найти среднее значение как сумму
произведений различных значений и их
частот (см. теорему на с. 87).
В данном случае мы имеем дело не с набором, а со случайной величиной. Вместо
частот нам известны вероятности значений. Если умножить значения случайной ве-
личины на их вероятности и сложить произведения, то получится некоторое среднее
значение случайной величины. Это среднее называют математическим ожиданием.
Математическое ожидание случайной величины X обозначают ЕХ или Е(Х)1. Мы бу-
дем пользоваться скобками только при необходимости.
Значение
Вероятность
*i
р\
*2
Рг
*а
Рз
...
...
*п
р» 1
1 Буква Е — от английского слова expectation — ожидание. Обратите внимание на то, что в
обозначении математического ожидания буква Е пишется прямой, а не наклонной.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
255

Определение. Математическое ожидание случайной величины — это сумма
произведений значений этой величины и их вероятностей:
ЕХ = х1р1 + х2р2 + х3Рз + ... + хпрп.
Математическое ожидание называют также ожидаемым значением или средним
значением случайной величины. Математическое ожидание случайной величины из-
меряется в тех же единицах, что и сама величина (средний рост — в сантиметрах,
средняя температура — в градусах).
ПРИМЕР. Пусть случайная величина X равна числу очков, выпавших на од-
D „ 1
ной игральной кости. Вероятности выпадения каждой грани одинаковы и равны -
(см. табл. 104 на с. 252).
тт «v«l«l«l„l*l,.l 1 + 2 + 3 + 4 + 5 + 6 7 ЛК
Поэтому ЕХ = 1- + 2- + 3- + 4- + 5- + 6- = - - - 3,5.
Наглядный смысл математического ожидания
Смысл математического ожидания можно проиллюстрировать с помощью диаграммы
распределения вероятностей случайной величины. Если представить, что диаграмма
вырезана из листа картона или металла, то математическое ожидание — точка, в ко-
торую проектируется центр масс диаграммы.
На рисунке 99 показано распре-
деление некоторой случайной вели-
чины X. Её математическое ожида-
ние равно 5,09. Если ♦подставить»
под точку с абсциссой 5,09 опо-
ру, то диаграмма будет находиться
в равновесии.
Мы знаем, что таким же свой-
ством обладает среднее арифмети-
ческое, которое служит ♦ центром
масс» числового набора (см. п. 13).
Эта общность свойств среднего зна-
0,3 •
0,25
0,2
0,15
0,1 -Н
0,05 41
0
4 А 6
ЕХ = 5,09
П,1 1,1—!,■—I,»
8 9 10 11
Рисунок 99
чения и математического ожидания ещё раз подчёркивает их общую природу.
Расскажем о двух важных применениях математического ожидания.
Лотерея
С одной стороны, лотерея должна быть привлекательной — должны быть большие
выигрыши, а выигрышных билетов должно быть довольно много.
С другой — лотерея должна приносить доход, то есть суммарный выигрыш должен
быть меньше общей выручки. Добиться этого наверняка невозможно, поскольку неиз-
вестно, сколько билетов будет распродано. Значит, этого нужно добиться с большой ве-
роятностью. Здесь на помощь приходит теория вероятностей. Она помогает установить
цену билета, при которой лотерея практически наверняка принесёт прибыль.
В лотерее должны быть большие выигрыши, поэтому определим, что на 1% би-
летов выпадает выигрыш 2000 р. Выигрышных билетов должно быть немало. Пусть
10% билетов дают выигрыш 200 р.
Участник лотереи случайным образом выбирает один билет. Найдём математиче-
ское ожидание случайной величины X «выигрыш участника». Запишем распределе-
ние в виде таблицы (табл. 110).
256
ГЛАВА XIV.

Таблица 110. Распределение выигрыша
в лотерее
Выигрыш, р.
Вероятность выигрыша
0
0,89
200
0,1
2000
0,01
Математическое ожидание выигрыша
равно
ЕХ = 0 • 0,89 + 200 • 0,1 + 2000 х
х 0,01 = 40 (р.).
Чтобы лотерея приносила доход,
цена билета должна быть больше, чем
средний выигрыш. Если назначить цену билета 50 р., то средний доход от продажи
одного билета будет равен 50 - 40 = 10 р.
Разумеется, может случиться так, что на свой билет участник лотереи получит
большой выигрыш. Но если бы некто решил купить все билеты, то ему достались бы
все выигрыши, но в среднем он достоверно потерял бы по 10 р. на каждый куплен-
ный билет.
Ф
Так устроены все лотереи: математическое ожидание выигрыша на один билет
меньше цены билета. Это условие является непременным, оно обеспечивает
доход организаторам лотереи.
Человек, который решил сыграть в лотерею, должен понимать это. Можно рас-
сматривать лотерею как развлечение, но не как способ получить много денег.
Никакие стратегии, которые якобы позволяют выиграть в лотерею, на самом де-
ле не приносят гарантированный доход — математическое ожидание выигрыша
меньше цены билета.
Чем больше математическое ожидание выигрыша, тем больше билетов требуется,
чтобы устроитель лотереи получил ощутимый доход. Чем меньше математическое
ожидание, тем меньше людей привлекает такая игра. Поэтому организаторы экспе-
риментальным путём определяют наиболее выгодные условия лотереи, придумывают
разнообразную рекламу и часто стараются сделать так, чтобы оценить ожидание вы-
игрыша было невозможно. Это не зна- ^в^___^^_в_^^^и^^и_в-___^_и^^_к
чит, что в лотерею нельзя выиграть.
Иногда люди выигрывают, и даже
крупные суммы, но в конечном итоге
доход всегда имеет организатор лоте-
реи. Когда игроков много, одни вы-
игрывают, другие нет, деньги перерас-
пределяются между ними, и при этом
значительная часть денег достаётся
устроителям лотереи.
Если часть средств, вырученных
от лотереи, идёт на нужды культуры,
спорта, на содержание больниц и дру-
гие благородные цели, то такие лотереи
называются благотворительными. На
любую лотерею и на любой игральный
автомат требуется специальное разре-
шение (лицензия). Если кто-то устра-
ивает игру на деньги или вещи без
лицензии, то это нарушение закона,
а сам хозяин такой лотереи, скорее
всего, мошенник. В такие игры играть
нельзя.
Чтобы найти математическое ожида-
ние в электронной таблице, используйте
функцию
СУММПРОИЗВ()
Решение задачи про лотерею показано
на рисунке.
/х =СУММПРОИЗВ(СЗ:С5;РЗ:Р5)
| " С
Выигрыш
0
200
2000
| Мат.ож
D
Вероятности
0.89
0.1
0.01
I 40
■
Е
i F
Рисунок 100
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
257

Обязательное страхование автомобильной
гражданской ответственности (ОСАГО)
Полис ОСАГО должен иметь каждый владелец автомобиля. Владелец и страхо-
вая компания заключают договор страхования. Продавая автовладельцу полис, стра-
ховая компания берёт на себя обязательство возместить ущерб (в пределах опреде-
лённой суммы), который этот автовладелец нанесёт окружающим в случае дорожно-
транспортного происшествия, случившегося по его вине.
Чтобы определить стоимость полиса, нужно знать две величины: вероятность,
с которой в течение года наступает страховой случай, то есть застрахованный авто-
владелец оказывается виновником ДТП, и среднюю сумму ущерба. Произведение
этих величин даёт математическое ожидание страховой выплаты страховой компании
на один застрахованный автомобиль.
Для каждого отдельного автомобиля эта выплата является случайной величиной.
Разумеется, в стоимость полиса включается доход страховой компании, который идёт
на выплату зарплаты сотрудникам, аренду и содержание офисов, налоги и все теку-
щие расходы.
Поэтому стоимость страхового полиса складывается из дохода страховой компании
и математического ожидания страховой выплаты.
Ф
Вопросы
Что такое математическое ожидание случайной величины?
2 Может ли быть так, что все значения случайной величины положительны, а ма-
тематическое ожидание этой величины отрицательно?
3 Чему равно математическое ожидание числа очков, выпавших при бросании од-
ной игральной кости?
Упражнения
528 В таблице дано распределение вероятностей случайной величины. Найдите
математическое ожидание этой величины.
0
а)
Значение
Вероятность
Значение
Вероятность
1
1
9
2
1
6
3
1
12
-3
0,09
-2
0,12
-1
0,21
0
0,25
4
1
4
5
1
18
6 |
1 1
3
1
0,04
2
0,05
3
0,24
б)
529 Найдите EZ, если случайная величина Z с равными вероятностями принимает:
а) все целые значения от -15 до 15;
б) все чётные целые значения от 2 до 16.
530 На вокзале игрок предлагает прохожим игру. Он зажимает в кулаке носо-
вой платок так, что четыре уголка торчат наружу между пальцами. Прохо-
жий берёт платок за два уголка и вытягивает его. Если прохожий вытяги-
вает платок за соседние уголки, то проигрывает 50 рублей. Если прохожий
вытягивает два противоположных уголка, то выигрывает 50 рублей. Составь-
те распределение и найдите математическое ожидание случайной величины X
«выигрыш прохожего».
258
ГЛАВА XIV.

1
2
3
4
5
в
7
8
9
LO
а
б
ш
•'.': •:.;;":;'::-
в
ШФ.
г
ши
д
ши
е
ШФ.
ж
,'-гА,:.
3
i-:;;;V'.4;
и
Й^=
к
;о-;И
:ЭД
ши
531 По правилам «морского боя» на по-
ле 10 х 10 клеток размещаются четы-
ре однопалубных корабля (по одной
клетке), три двухпалубных, два трёх-
палубных и один четырёхпалубный
(рис. 101). Рассмотрим случайную ве-
личину X «число клеток-палуб в под-
битом корабле противника в резуль-
тате первого выстрела, сделанного на-
удачу». Если первый выстрел мимо,
то X - 0. Найдите EX.
532 Организатор лотереи напечатал всего
10 000 лотерейных билетов. Цена каж-
дого билета 50 р. Известно, что 1000
билетов дают выигрыш 100 р., ещё в
10 билетах — выигрыш 1000 рублей,
а на 1 билет приходится главный вы- Рисунок 101
игрыш 10 000 р. Все прочие билеты без
выигрыша. Найдите математическое ожидание случайной величины «вы-
игрыш на один случайный лотерейный билет». Сравните средний выигрыш с
ценой билета.
Дл^ Закон больших чисел
и его применение
Измерение вероятностей
Когда говорят о бросании симметричной монеты, предполагают, что вероятность
появления орла равна -; говоря о бросании игральной кости, предполагают, что ве-
г 1
роятность выпадения любой из шести граней равна -. В других случаях тоже иногда
делают предположения о вероятностях. Например, считают, что день рождения слу-
чайно выбранного человека с равными шансами может приходиться на любой день
года. Но в большинстве случаев вероятности событий неизвестны.
Владельца магазина интересует вероятность того, что клиент совершит покупку.
Покупателя, приобретающего телевизор или стиральную машину, интересует их на-
дёжность, то есть вероятность того, что купленная вещь прослужит долго. Узнать или
вычислить вероятности в этих случаях мы не можем. Прибора для прямого измерения
вероятностей нет. Но косвенный способ есть. Он основан на законе больших чисел.
Одно из проявлений закона больших чисел состоит в том, что при многократ-
ном повторении одного и того же опыта частоты событий в этом опыте будут
близки к их вероятностям:
Поэтому если число опытов велико, то частоту события можно использовать как
приближённое значение вероятности этого события. Это математическая теоре-
ма, которая обосновывает статистическую устойчивость частот.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
259

ПРИМЕР. Крупная почтовая компания заключила договор с ГГ-компанией
на обслуживание компьютерной системы. Компьютерная система обширная, она
охватывает множество городов, в ней десятки тысяч компьютеров, и нередко случа-
ются сбои или отказы, которые нужно быстро устранить.
Рассмотрим событие А «сбой устранён менее чем за 8 часов». Будем считать это
событие успехом. Оценим неизвестную вероятность р этого события. Каждый отдель-
ный отказ оборудования можно рассматривать как испытание Бернулли. Начнём от-
счёт с какого-то момента.
Известно, что 71,2% отказов из первых 300 были устранены менее чем за 8 часов
после сообщения об отказе. Иными словами, в серии из 300 испытаний событие А
имеет частоту 0,712. Из следующих 300 сбоев только 49 % были устранены менее чем
за 8 часов, т. е. во второй серии из 300 испытаний частота успеха равняется 0,49. Но
если рассмотреть объединённую серию из 600 испытаний, то в этой серии частота успе-
300 0J12 + 300 0,49 л ^ ,
ха равна ^г = 0,601 (мы проводим вычисления с точностью до тысяч-
600
ных). И так далее: каждая следующая серия вносит свой вклад, и частота события А,
которая различна в каждой отдельной серии из 300 испытаний, постепенно стабилизи-
руется в объединённой серии. График этого процесса показан на рисунке (диагр. 50).
Диаграмма 50. Стабилизация частоты события
Чем больше испытаний, тем меньше изменчивость частоты события А. Если ис-
пытаний много, то, скорее всего, частота события А близка к его вероятности (на-
пример, можно считать частоту и вероятность близкими, если различие между ними
менее 0,001). Начиная с какого-то момента эту близость можно считать практически
достоверным событием. Напротив, событие «частота далека от вероятности» малове-
роятно, и его можно не принимать в расчёт.
Точность измерения вероятности
Теория вероятностей не только утверждает, что при большом числе испытаний п
верно приближённое равенство ~
но и позволяет оценить точность этого приближения.
Если мы собираемся использовать частоту события вместо его неизвестной вероят-
ности, мы хотим, чтобы отклонение частоты от вероятности было малым. Предполо-
жим, что нас устроит измерение вероятности р с погрешностью не более 0,05, т. е.
мы хотим, чтобы выполнялось неравенство
S
р - 0,05 < — < р + 0,05.
260
ГЛАВА XIV.

Следовательно, нужно выбрать п так, чтобы вероятность выполнения этого нера-
венства была близка к единице. Зная свойства биномиального распределения, можно
найти, что уже при п в 400 вероятность выполнения этого неравенства больше, чем
0,95. Таким образом, при п =* 400 погрешность измерения с вероятностью 0,95 не
превышает 0,05.
Можно достичь меньшей погрешности и большей достоверности. Например, при
п ^ 1850 погрешность измерения не превышает 0,03 с вероятностью, большей чем 0,99.
При измерении вероятности с помощью частоты следует помнить о двух вели-
чинах: допустимой погрешности измерения и вероятности того, что эта погреш-
ность не будет превышена.
Чем меньше допустимая погрешность и чем выше желаемая вероятность без-
ошибочного измерения, тем больше опытов требуется. На практике это очень важно,
поскольку большое количество опытов требует много времени и средств.
Социологические исследования
При большом числе испытаний Бернулли частота успеха близка к его вероятно-
сти. Этот результат важен для социологических исследований, которые проводятся
с различными целями.
ПРИМЕР 1. Предположим, что нас интересует, какова доля избирателей, готовых
поддержать на выборах кандидата К. С нашей точки зрения, упомянутая доля — это
вероятность р того, что наудачу выбранный избиратель окажется сторонником канди-
дата К. Хорошо бы опросить всех избирателей и узнать, сколько из них поддержи-
вает кандидата К. Но до выборов это невозможно. Кроме того, люди не обязаны от-
вечать на вопросы о своих политических симпатиях. Вместо того чтобы опрашивать
всех, опрашивают небольшую группу избирателей — выборку. Важно, чтобы выбор-
ка правильно представляла всю совокупность избирателей. Оказывается, нет лучшего
способа добиться такого сходства, чем составлять выборку случайно.
Численность выборки обозначим я. Результат опроса каждого человека в выборке
будем считать успехом, если он высказался в пользу кандидата К., а в противном
случае назовём результат неудачей. Неизвестная вероятность успеха равна р, и мож-
но считать, что она остаётся неизменной на протяжении всего опроса.
В отчётах о социологических опросах обычно сообщается не только приближённое
значение р, но также точность приближения и численность выборки. И хотя выборки
бывают разными, обычная их численность — около 2000 человек. Этого объёма вы-
борки достаточно, чтобы обеспечить высокую точность выводов, независимо от того,
как велика изучаемая совокупность.
К сожалению, в отчётах часто не говорят о том, что малая погрешность достигает-
ся не наверняка, а с большой вероятностью.
Ф
Важно! Численность выборки, обеспечивающей нужную точность выводов, не
связана с численностью обследуемой совокупности.
Связь выборочного среднего и математического ожидания
Закон больших чисел позволяет нам с большой точностью вместо неизвестных ве-
роятностей событий использовать их частоты, а вместо математического ожидания —
средние значения, полученные в результате измерений или наблюдений.
т
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
261

Если мы произведём много измерений случайной величины, то получим набор
данных, который является случайной выборкой. Мы найдём среднее арифметическое
этого набора (среднее выборочное), и в силу закона больших чисел это среднее зна-
чение окажется близко к неизвестному математическому ожиданию.
Ф
Важно! Среднее выборочное используется как приближённое значение матема-
тического ожидания.
Таблица 111. Измерение горошин
Диаметр горошины, мм
Частота
5
0,109
в
0,547
7
0,328
8
0,016
ПРИМЕР 2. Мы не зна-
ем точно распределение,
которому подчиняется раз-
мер горошин. Поэтому,
строго говоря, мы не знаем
средний размер гороинф.
Но мы можем произвести много измерений и найти среднее арифметическое. Возь-
мём 1000 горошин определённого сорта, измерим диаметр каждой горошины с окру-
глением до 1 мм и занесём результаты в таблицу 111.
Среднее арифметическое равно
х - 5 • 0,109 + 6 • 0,547 + 7 • 0,328 + 8 • 0,016 - 6,251.
Полученное среднее значение является оценкой математического ожидания слу-
чайной величины «диаметр горошины». Чем больше измерений сделано, тем меньше
дисперсия среднего арифметического, а значит, тем выше точность оценки. Иными
словами, закон больших чисел даёт нам уверенность в том, что диаметр 6,251 мм
очень близок к среднему диаметру всех горошин этого сорта, выращенных в сходных
условиях.
Ф
Важно! Усреднение измерений увеличивает достигаемую точность.
(г) Вопросы
1 Приведите примеры проявления закона больших чисел.
2 Как оценивают математическое ожидание случайной величины?
3 Нужно ли знать общую численность всех жителей России, чтобы с помощью вы-
борочного метода установить, какая доля жителей предпочитает по утрам чай,
а какая — кофе?
4 Как можно увеличить точность не очень точных измерений?
262
ГЛАВА XIV.

Ответы
Глава I
3. а) 1426; б) 989. 4. Нижний Новгород. 5. 8; 11. 6. На 917 тыс. чел.
7. На 259 тыс. чел. 8. 2. 9. 22,4 ц/га. 10. 2015. 11. 2017. 12. Например, погод-
ные условия, качество посевного зерна, качество и количество удобрений, качество
почв, общая культура землепользования. 14. 2018. 15. 2012. 16. 2016, 2017 и 2018.
17. 1069 млрд кВт • ч. 18. В 2012. 19. 2019. 20. Например, погодные условия, пе-
реход на более экономные электроприборы, колебания объёмов производства в про-
мышленности, строительстве и в сельском хозяйстве. 21. Мировой экономический
кризис вызвал снижение производства в России, и промышленность стала потреблять
меньше электроэнергии. 22. а) 7:55; б) 16:20; в) 3; г) 8 ч 28 мин. 23. а) Нет; б) 6;
в) 2, 4, 54, 258, 32 и 20; г) 6 ч 39 мин. 24. а) 780; б) 252. 25. а) 23:30; б) 266,
252, 802; в) 778, 258, 748. 26. 2 и 4. 27. Указание. Подходят поезда № 748 (при-
бытие 20:34, билеты от 2391 р.), № 778 (прибытие 23:54, билеты от 2064 р.), № 258
(прибытие 20:40, билеты от 1266 р.) и формально подходит поезд № 802 (прибытие
0:21, билеты от 1237 р.). Но если говорить о реальной ситуации, а не о формальном
упражнении, то поезд № 802 не следует рассматривать — Мария Игнатьевна может
не успеть добраться от вагона до метро за 9 минут, даже если поезд не опоздает,
даже если она без тяжёлого багажа и хорошо знает дорогу. Поэтому следует рассма-
тривать только поезд 258 с наименьшей ценой билета 1266 р. 28. № 266. 29. 4 и
0,95. 30. 1,04. 31. а) Баскетбольный мяч; б) ракетка. 32. а) На ракетки; б) на сетку.
33. Например
Таблица 9. Смета расходов на покупку спортивного инвентаря
№
1
2
3
4
5
6
Наименование
Мяч футбольный
Мяч волейбольный
Мяч баскетбольный
Ракетки бадминтонные
Воланы
Сетка теннисная
Ед.
измерения
шт.
шт.
шт.
шт.
коробка
шт.
Количество
20
20
0
33
15
2
Цена ед., р.
575,5
500
690
480
750
700
Итого:
Стоимость, р.
11510
10 000
0
15 840
11250
1400
50 000
35. а) 74,5 %; б) примерно в 2,9 раза. 36. г) Нижний Новгород, Пермь и Самара;
д) Воронеж. Возможные причины: демографическая и социальная политика властей
города, появление большого количества рабочих мест. 37. Указание. Производство
электроэнергии в 2011 г. выросло на 17 млрд кВт * ч по сравнению с 2010 г. Изме-
нение составляет 17
100% ^ 1,6%.
1038
Так же вычисляются изменения в другие годы. Если производство электроэнергии в
каком-то году уменьшилось по сравнению с предыдущим годом, следует вписать в та-
блицу отрицательную величину. 38. а) 10 345; б) 103; в) 187 р. 44 к.; г) 1482 р. 26 к.
ОТВЕТЫ
263

39. Москва. 40. Волгоград, Самара. 42. Москва, 60,6 %. 43. Да, возможно. Напри-
мер, Екатеринбург и Новосибирск или Воронеж и Санкт-Петербург. 48. в) 26 книг;
20 570 р. 52. а) 292; б) 11%. 53. а) 13; б) 12; победителей и призёров 7 %.
55. б) ^ 7,4 % и 33,8%. 56. б) * 83,1 % и 80,4 %.
Глава II
57. а) Понедельник; б) четверг. 58. 2; 4. 62. а) 1 — Великобритания, 2 — Индия,
3 — Россия, 4 — Мексика; в) ^ на 1700 млрд; г) « на 280—290 %. 64. в) 2010;
г) 2018; д) 2019. 66. 1 — Афганистан; 2 — Япония; 3 — Исландия. 67. а) « 9 млн
242 тыс.; б) « на 147 тыс. 68. а) « 616,6 млн; б) « на 45,12 млн; в) » на 67,7 млн.
69. Снизится примерно на 39 %. 71. « 400. 72. Грибы. 73. а) Свердловская об-
ласть; б) * 25 %. 75. 2 и 4. 76. б) Без животных — 6; с одним животным — 6;
с двумя — 18. 79. а) * 77,4 %; б) * 22,6 %. 80. а) 5 %; б) 46 %; в) 56 %.
81. а) 22,5 °С и 15,9 °С; б) 10 %; г) нет.
Глава III
82. а) 9; б) 9. 83. а) 13; б) 13. 86. а) 15; б) 18; в) 23; г) 30; д) 26; е) 106.
89. а) 6; б) 60; в) 600; умножением на 10 и на 100 соответственно. 90. а) 6; б) 30; в) 150;
умножением на 5 и на 25 соответственно. 91. а) 56,3 млн т, 61,8 млн т;
в) 2015. 92. а) 20,74 млн т; б) 26,08 млн т. 93. а) 23,41 млн т; б) 2009,
2011, 2014 и 2015; в) 2010 и 2012. 94. а) 78,2 тыс. чел.; б) 118,3 тыс. чел.;
в) 190,0 тыс. чел.; г) 283,9 тыс. чел. 95. а) Люберцы, Мытищи, Подольск;
б) Балашиха, Подольск. Указание. Отвечая на вопрос в), обратите внима-
ние на очень резкий рост населения Балашихи в 2019 г. по сравнению с 2010 г.
Подумайте, чем может быть вызван такой рост населения. 96. а) 5 и 5;
б) 5 и 6; в) 6 и 6; г) 6 и 7. 97. а) Москва; б) Санкт-Петербург; в) Новосибирск и Ека-
теринбург. 100. а) 11; б) 19; в) 28. 101. а) 6; б) 6; в) 14. 102. а) на 168,3 тыс. чел.;
б) 1144 тыс. чел. 103. а) 1200,2 тыс. чел.; б) 1157 тыс. чел. 104. а) 23,2 и 23,41 млн т;
б) 22 и 20,74 млн т; в) 26,2 и 26,08 млн т. 105. а) Нет; б) да; в) нет; г) нет. 106. а) 25;
3; 22; 13,5 и 13,5; б) 47; 5; 42; 23 и 19. 107. а) 135,5; 70,9; 64,6; б) 29,2; 18,3; 10,9.
108. а) 1,5 г; б) 4. 109. а) 381°; б) 341,6°; в) * 42,8°; г) 0,05°. 110. а) 12; б) 2,5;
в) 2. 112. а) 1151,7 тыс. чел.; б) 1207,1 тыс. чел. 113. а) 6,3 и 6,33; б) городской
пейзаж; портрет учителя; в) портрет учителя; городской пейзаж. 114. а) и б) обе ха-
рактеристики увеличились на 4. 115. а) 20; б) 24. 116. а) Уменьшится на 0,8; б) не
изменится. 117. У набора 1 медиана заметно меньше среднего, у наборов 2 и 3 меди-
ана и среднее приблизительно одинаковы, у набора 4 медиана заметно больше, чем
среднее арифметическое. 119. 2,5 м. 120. Нет. 121. 1 — Берген; 2 — Якутск; 3 —
Ашхабад; 4 — Лиссабон. 122. В Прибрежном районе — 28.10, в Заречном — 25.10.
Глава IV
123. а) 1 и 4; б) 2 и, например, 6. 125. а) 15, 47, 35, 25 и 32; б) 0,4, 1,8, 1,1,
1,3 и 1,4. 127. а) 3; б) 15. 128. а) 9; б) -7; в) 13; г) 2. 129. а) 16; б) 2; в) -24;
г) -|. 130. а) 30; б) 12; в) 39,6; г) -3,3. 131. а) 14; б) -4; в) 23,6; г) -19,3.
132. ^ 0,4 доллара. 133. 58 240 р. 134. -. 135. 1,34. 136. Увеличились на а.
п. _
137. а) Ьт и ЬМ соответственно; б) ЬМ и Ьт соответственно. 138. . 139. 6.
л+ 1
140. Да, такое возможно. Указание. Нужно перевести из группы А в группу Б тех
264
ОТВЕТЫ

учеников, у кого балл ниже, чем средний в группе А, но выше, чем средний в группе Б.
141. а) 0,3; б) 0,2. 142. а) 0,12; б) 0,12; в) 0,16; г) 0,04. 143. 0,3. 146. б) «н»:
1) * 0,05; 2) * 0,08; 3) * 0,05; «т»: 1) * 0,05; 2) * 0,07; 3) * 0,05. 147. а) * 2,09;
б) * 0,22. 148. а) 2; б) 3. 149. а) * 2,70 и 3,25; б) * 1,42 и 2,18. 151. * 2,79 ч.
152. * 0,964, т. е. смартфон дешевел в среднем на 3,6 % в месяц. 153. а) * 3,99 %;
б) * 24 324 р. 02 к.
Глава V
154. 231 и 214 В. 155. 222,2 В. 157. 9; ^, т. е. 45 %. 159. а) 37 ^ т < 39;
б) 128 ^ т ^ 130; в) 2953 < т < 2959; г) 2540 ^ т ^ 2546. 160. а) 28 < V < 32;
б) 69 < V ^ 74; в) 96 ^ V < 102; г) 127 ^ V < 135. 162. а) От -4,8 до 9,8 км/ч,
показания от 71 до 86 км/ч; б) от -6 до 12 км/ч, показания от 90 до 108 км/ч;
в) от -7,2 до 14,2 км/ч, показания от 101 до 122 км/ч; г) от -8,4 до 16,4 км/ч,
показания от 115 до 139 км/ч. 163. а) Балашиха, Подольск и Верея; б) 10,4, 254,7.
164. а) 25; б) 11; г) 9; д) * 0,13. 171. а) * 2,4 %; б) * 94,4 %.
Глава VI
173- Невозможное событие в п. а), достоверное в п. в). 174. Невозможное собы-
тие в пп. а) и б), достоверное — в п. в). 185. Да, означает.
Глава VII
187. а) Одинаковые; б) больше у второго; в) одинаковые. 189. а) 0,9; б) 0,6.
190. а) -0,5, -3,5, 1,5, 2,5, -0,5, 0,5; б) -4,38, 1,22, 3,42, -3,18, 2,92.
191. а) -57; б) 4,37. 192. а) Нет, сумма должна быть равна нулю, значит, все откло-
нения не могут быть положительны; б) нет по той же причине; в) да, если все числа
в наборе одинаковы. 193. а) 6; б) 10. 194. а) 2,2, 1,8, 0,2, 1,8, 1,2; б) 2,4, 1,5, 0,7,
1,6. 195. а) 6 и 2; б) 12 и 2 или 11 и 3.
197. а)
Значения
-1
0
4
Среднее: f * 1
Отклонения
-1 - 1 - -2
0 - 1 - -1
4-1-3
Сумма: 0
Квадраты отклонений
4 '
1
9
4 + 1 + 9 14
Дисперсия: 3 e з
198. а) ^ и |; б) 3,5 и 6,5. 200. а) 5; б) 11; в) 1,8; г) 1,3. 202. а) 1,50; б) 0,44;
3 3
в) 120,81; г) 0,42. 203. а) [1,35; 6,65]; б) 2, 3 и 4; в) 1; г) 7 и 9. 204. а) [-4,36; 4,36];
б) -4, -3, -1, 0, 3; в) -6 и -5; г) 6 и 7. 205. Высоковск (не считая Вереи).
206. Люберцы, Мытищи, Химки (не считая Балашихи и Подольска). Общей чертой
можно считать то, что все эти города вплотную примыкают к Москве, являясь частью
Московской агломерации. 209. а) Вероятно, есть отрицательная не очень сильная
связь; б) вероятно, есть положительная слабая связь. 212. 36. 213. 1. 214. а) 1 и
1,5; б) 7 и 1,5; в) 3,45 и 1,5; г) 0,7 и 1,5. 215. а) -4, 5,76 и 2,4; б) 6, 12,96 и 3,6;
в) 5, 9 и 3; в) -3, 3,24 и 1,8. 216. а) 36 и 6; б) 144 и 12; в) 12,96 и 3,6; г) 56,25
и 7,5. 217. а) Средняя температура 30 °С, стандартное отклонение 1 °С; б) средняя
температура 98,24 °F, стандартное отклонение равно 0,9 °F. 218. 0 и 1. 219. 0 и 1.
ОТВЕТЫ
265

220. а) Не исключена линейная связь; б) трудно сказать. 222. а) « у =
= -0,04г + 19,1; б) « у * 1,4дг - 175. 223. Первый квартиль -4,3, третий квар-
тиль 3,3, медиана ~ -2,8, среднее арифметическое - 2,3. 224. а) Медиана - 4,
среднее арифметическое « 3,4; б) является. 225. а) 12 — выброс; б) выбросов нет;
в) значение 767 — выброс. 226. В наборе б) при выбранном правиле значение -8
становится выбросом.
Глава VIII
227. События В и С невозможные, события А и D достоверные. 228. Со-
бытие В невозможное, события А и С достоверные. 229. 2 способа: (Андрей,
Борис) и (Борис, Андрей). 230. 9. 231. 6: АБВ, АВБ, БАВ, БВА, ВАБ и ВБА.
233. 4 элементарных события: ОО, OP, PO, PP. 234. ООО, OOP, ОРО, ОРР,
POO, POP, РРО, РРР. 235. а) в 2 раза; б) 16; в) 1024. 236. Бесконечное чис-
ло элементарных событий: О, РО, РРО и т. д. 237. а) ММ, МФМ, МФФ, ФФ,
ФМФ, ФММ. 238. а) Нет; б) только буквой с; в) с, ас, bcf abc и Ьас. 239. 216.
240. а) 1; б) 3; в) 0. 241. а) 3; б) 6; в) 10. 245. а) 0,4; б) -; в) 0,89; г) 0,2, 0 < р ^ 0,8.
246. £. 247. а) 0,04; б) ^; в) 0,01. 248. а) 3; б) 10; в) 8; г) к. 249. а) Во вто-
ром; б) в первом; в) вероятности равны. 250. Равновозможны; вероятность 0,25.
251. а) |; б) -^; в) т^. 253. 0,125. 254. 0,2. 255. 0,4. 256. 0,4. 257. 0,6.
о 16 1 10Z4
258. 0,55. 259. —. 260. а) —; б) -£-. 261. 0,48. 262. 0,65. 263. 0,47.
сД л1о 1296
264. а) А - {2, 4, 6}; б) А - {1, 2, 3, 4}; в) А - {3, 4, 5, 6}; г) А - {2, 3, 4, 5}.
265. а) Например, «при первом броске выпал орёл»; б) например, «во вто-
рой раз выпала не та сторона, что в первый»; в) например, «решка выпала хотя
бы один раз»; г) например, «оба раза выпала одна и та же сторона». 269. Эле-
ментарным событием является результат всех пяти выстрелов. Например, «по-
пал, промахнулся, попал, попал, попал»; а) 5; б) 5. 270. а) {ОР, РО}; б) {OP, PP};
в) {ОР, РО, РР}; г) {ОР, ОО}. 271. а) {ОРР, POP, РРО}; б) {OOP, ОРО, РОО};
в) {ОРО, ОРР, РРО, РРР}; г) {ООО, ОРО, РОО, РРО}. 273. а) Например, «стрелок
сделает от двух до четырёх выстрелов»; б) например, «потребуется не больше пя-
ти выстрелов»; в) например, «потребуется не меньше трёх выстрелов»; г) например,
«потребуется нечётное количество выстрелов». 274. 8. 275. а) 0,5; б) 0,6; в) 0,9;
г) 0,3. 276. а) 0,6; б) 0,7; в) 0,3. 277. а) 0,013; б) 0,763; в) 0,249; г) 0,644.
278. а) 0,75; б) 0,5. 279. а) ^; б) j|; в) А. г) ±. 280. 0,17. 281. Р(а) = 0,1,
Р(й) = 0,3, Р(с) - 0,6. 282. а) 0,5; б) \% в) 0,5; г) 0. 283. а) |; б) ^; в) |;
О О О «5
2 11
г) -. 284. Нет; в первом случае вероятность 0,25, а во втором — 0,5. 285. а) —; б) —;
3 6 18
в) А. г) ±. 286. а) ±|. б) g. B) U. г) Ц. 287. а) |. б) |. 288. а) |. б) 1.
в) I; г) 0,5. 289. а) £; б) |. в) |. г) ». 290. |. 291. а) |; б) |; в) ±.
г) ^; Д) ^; е) ^. 292. а) 0,04; б) 0,06; в) 0,2; г) 0,8. 293. а) \; б) |; в) |.
294. а) 0; б) \; в) |; г) I; д) J; в поле е8. 295. \. 296. а) 0,4; б) 0,2. 297. 0,6.
7 7 7 7 о
266
ОТВЕТЫ

Глава IX
298. 8. 299. а) 0,6; б) 0,15; в) 0,87; г) -. 301. Не обязательно. 302. 0,97.
303. а) ^т; б) |^. 305. 0,75. 306. 0,05. 307. а) Нет; б) да; в) да; г) да.
308. а) {1, 2, 3, 4, 5}; «выпало меньше шести очков»; Р(Л) = -; б) {1, 3, 5}; «вы-
х 6
пало нечётное число очков»; Р(а) в -; в) {1, 2, 4, 5}; «выпавшее число очков не
п / — \ 1
делится на 3»; р(а) — -; г) {1, 6}; «выпала единица или шестёрка»; Р(Л) = -.
3 35
309. а) «Сумма выпавших очков больше 2»; —; б) «сумма выпавших очков меньше
36
10 35 . . 11 .
12»; —; в) «сумма выпавших очков не меньше, чем 4»; —; г) «в сумме выпало не
11 15
менее 10 очков»; —. 310. а) 10; б) 0,4; в) «выбран мальчик»; г) 0,6. 311. а) —;
" 16
с с О
б) —; в) —; г) —. 312. а) Например, «хотя бы один из выбранных учеников —
девочка»; б) «выбран один мальчик и одна девочка». 313. а) Например, «в тече-
ние года не перегорит ни одна из лампочек»; б) «в течение года перегорит одна,
три, четыре или все пять лампочек»; в) «в течение года перегорят одна, две или
три лампочки»; г) например, «в течение года перегорит четыре или пять лампочек».
315. 49. 316. 13. 317. а) 2; б) 4; в) 10. 318. А - {ОО; ОР}; В - {ОО; РО};
AUB — {ОО; OP; PO}. 319. а) Первый раз выпала решка и второй раз выпала
2
решка; б) оба раза выпал орёл и оба раза выпала решка. 321. а) {2; 3; 4; 6}; -;
б) {1; 2; 3; 4; 5; 6}; 1; в) {2; 4; 6}; |; г) {2; 4; 5; 6}; |. 322. а) 28; б) 43; в) 11;
г) 60. 323. а) {1 — 1; 1 — 2; 1 — 3; 1 — 4; 1 — 5; 1 — в; 2 — 1; 3 — 1; 4 — 1; 5 — 1;
6 — 1}; б) одно: 1 — 1; в) хотя бы на одной кости выпала единица; г) —.
36
324. б) 4 события: 3 — 3; 3 — 6; 6 — 3; 6 — 6; в) хотя бы на одной кости вы-
пало число, кратное трём; г) -. 325. б) 9 событий: 2 — 2; 2 — 4; 2 — 6; 4 —
2; 4 — 4; 4 — 6; 6 — 2; 6 — 4; 6 — 6; в) хотя бы на одной кости выпало чёт-
ное число очков; г) -. 328. а) 6; -; б) 4; -; в) 6; -; г) 2; тт. 329. б) В пер-
4 6 6 6"
вый раз выпало меньше двух, во второй больше четырёх; в) -. 330. DUC:
«хотя бы один из выбранных учеников — девочка»; D П С: «выбраны две де-
вочки». 331. а) Объединение: «хотя бы один из выбранных учеников — девоч-
ка»; пересечение: «сначала была выбрана девочка, затем — мальчик»; б) объ-
единение: «выбраны двое одного пола или сначала выбрана девочка, затем —
мальчик»; пересечение: «сначала была выбрана девочка, затем — мальчик».
333. а) Например, А П В; б) например, АП В. 336. а) Например, (А П В) и (А П В);
- - 2
б) например, (АПВ)и(АПВ), 340. а) Да; б) -. 341. а) 0,6; б) 0,7. 342. а) Нет;
о
б) да; в) нет; г) нет. 343. а) 1; б) 0,8. 344. а) 0,5; б) 0,3. 345. а) 0,48; б) 0,36.
346. а) 0,25; б) 0,75; в) 0,15; г) 0,95. 347. 0,3. 350. СВА. 351. ВСА. 352. Наи-
менее вероятное событие С. 353. 0,47. 354. 0,966. 355. 0,24. 356. 0,08. 357. 0,09.
358. 0,41. 359. 0,8. 360. 0,31.
ОТВЕТЫ
267

Глава X
361. а) 0,5; б) 0,5; в) 0. 362. а) \; б) §; в) |; г) 0. 363. а) \; б) \; в) \;
г) 0. 364. а) |; б) \; в) 0; г) ^. 365. а) 0,15; б) i; в) 0,18; г) 0,068. 366. а) 0,16;
О о О О
б) 0,04. 367. 0,042. 368. |. 369. а) |; б) \. 370. ^|. 371. а) -^; б) —;
о 3 о 41 4о Ц5
в) ^; г) ^. 372. а) |; б) ^; в) ^; г) ^; д) 0. 373. а) 21; б) 5. 376. б) 5;
в) P(SAC) = 0,35, P(SBE) = 0,1. 377. б) P(SAC) = |, P(SAOF) = ^. 378. ||.
379. б) А; в) J. 380. a) i; б) 1; в) ^; г) ^. 381. ^. 383. а) * 0,38;
б) * 0,042; в) « 0,089. 384. 0,92. 385. 0,0595. 386. 0,078. 387. а) 0,24; б) 0,08.
388. а) 0,6; б) 0,4. 389. а) 0,012; б) 0,012. 390. а) 0,2; б) 0,6. 391. а) Да; б) нет.
392. а) Да; б) нет. 393. а) Да; б) да. 394. а) Да; б) нет. 395. а) 0,04; б) 0,008;
в) 0,00032. 396. Нет. 397. 0,7.
Глава XI
399. а) 32; б) 18; в) 180; г) 90. 400. а) 160; б) 252; в) 1365; г) 336. 401. 55.
402. 10 000. 403. 1331. 404. Поровну. 405. а) 2; б) 8; в) 1024; г) 2". 406. 11 и 13.
407. 928 * 5 132 188 731375 620. 409. 6. 410. 120. 411. а) 720; б) 40 320;
в) 3 628 800; г) k\. 412. а) 5040; б) 120; в) 720; г) 360. 413. а) 60; б) 42; в) 90;
г) 100; д) 105; е) 220. 414. а) 1, 2, 3, 4, 6, 8, 12; 24; б) 1, 2, 3, 4, 5, 6, 8, 10, 12,
15, 20, 24, 30, 40, 60, 120. 416. 0,006. 417. а) 0,729; б) 0,729; в) 0,512; г) 0,343.
418. а) 0,271; б) 0,488; в) 0,657; г) 0,784. 419. а) и б) -|- « 2,76 • 10\
420. а) ^ * 2,088 • 10"* б) 1 - ^; в) ^; г) 0. 421. ^ = 2,48 10-5. 422. 0,768.
423. а) 4; б) 10; в) 21; г) 165; д) 924; е) 495. 424. В каждой паре числа равны.
425. Все числа равны 1. 426. а) 50; б) 67. 427. а) 50; б) 65. 428. а) 36; б) 15;
в) 495; г) 1287. 429. а) 210; б) 3003. 430. а) 35; б) 84; в) 455. 431. а) 126;
б) 120; в) 495; г) 462. 432. а) 20; б) 6. 433. а) 330; б) 495; в) 1365; г) 4845.
434. а) 376 992; б) 13 983 816. 435. а) 184 756; б) 1. 436. а) 20; б) 126. 437. ^.
оо
438. а) « 0,715 • 10 8; б) вероятность такая же. 439. « 0,0083. 440. « 5,4 • Ю-6.
441. а) Щ--—; б> \- 442 i 443- а> £!• б> 57- 444' а> 7Т * °'264>
С,3о 30 6 3 84 21 С?5
б) * 0,736; в) ^^ * 0,22; г) * 0,022. 445. '° 8 '° * 0,24. 446. а) * 2,65
10
б) «4,11 • 10 4; в) « 0,0123; г) * 0,549.
Глава XII
447. 3 и 4. 449. а) ±; б) ^; в) ^; г) ^. 450. а) ^; б) |; в) А; г) |.
451. а) ^; б) 0,98; в) |; г) 0,17. 452. а) ^; б) * 0,116; в) * 0,067; г) « 0,518.
4 7 об
268
ОТВЕТЫ

453. а) » 0,015; б) * 0,374. 454. a) qp; б) q*; в) 1 - 9е; г) 92(1 - q3).
455. а) 0,21; б) * 0,9993. 456. а) * 0,102; б) 0,488. 457. а) 0,081;
б) * 0,139. 458. а) 0,09; б) 0,01. 459. 5 патронов (вероятность * 0,922). 460. 14.
461. а) УННН; НУНН; ННУН; НННУ; б) УУНН; НУУН; ННУУ; УНУН; НУНУ;
УННУ; в) НУУУ; УНУУ; УУНУ; УУУН.
462.
Число успехов
Число благоприятствующих
элементарных событий
0
1
1
4
2
6
3
4
4
1
463. а) ННННН; б) УНННН; НУННН; ННУНН; НННУН; ННННУ; в) УУУНН;
УУНУН; УУННУ; УННУУ; УНУНУ; УНУУН; НУНУУ, НУУНУ, НУУУН; ННУУУ;
г) НУУУУ; УНУУУ; УУНУУ; УУУНУ; УУУУН. 464. a) j^g * 0,019; б) * 0,096;
в) * 0,004. 465. -£rz * 0,033. 466. а) УУНН; НУУН; ННУУ; УНУН; НУНУ; УННУ;
б) НУУУУУ; УНУУУУ; УУНУУУ; УУУНУУ; УУУУНУ; УУУУУН. 467. а) 28;
б) 28; в) 56; г) 56. 468. а) 1; б) 10; в) 35; г) Сап. 469. Поровну. 470. а) 4; б) 6;
в) 8; г) 11; д) т. 472. а) С\ + С3„; б) 1 + л + С* + С* + С* + Сьп; в) С\ + С* + С*;
г) 1 + л + Сг„ + С\. 473. а) 134; б) 134. 474. а) |; б) ^; в) ^; г) ^. 475. а) |;
б) -21; в) -|Ь г) §L. 476. а) * 0,054; б) * 0,00064; в) * 0,402; г) * 0,00002;
128 128 2Г
д) * 0,201; е) * 0,335. 477. 0,3125. 478. а) 0,3125; б) « 0,781; в) * 0,469; г) 0,5.
479. а) * 0,016; б) * 0,422. 480. а) * 0,165; б) « 0,123; в) * 0,790; г) * 0,539.
481. а) 0,1792; б) 0,5248; в) 0,8704; г) 0,9744. 482. а) * 0,054; б) * 0,193; в) * 0,9995;
г) * 0,997. 483. а) « 0,056; б) « 0,526; в) 0,922. 484. а) Уменьшилась; б) увели-
чилась. 485. а) * 0,357; б) * 0,476; в) 0,119; г) * 0,952. 486. а) * 0,476; б) 0;
в) * 0,119; г) * 0,357. 487. а) * 0,071; б) * 0,429; в) * 0,429; г) * 0,071.
г5
488. а) * 0,429; б) * 0,005. 489. а) * 0,286; б) 0,982. 490. а) Ь|1 * 0,00000265;
Сзв
б) Щ± s 0>0оо411; в) 10ggl + bfx + С|' * 0,013. 491. ^§ * 7,49 1025.
36 с36 ^250
Глава XIII
493. I. 494. а) |; б) \. 495. J. 496. а) \; б) J; в) ^^_ 497. a) f; б) §;
*> ^tn 498- °> Ь б> '-£.499- *> * ~ & б> *• 50°- * - £•501- а> b б> I•
502. а) |; б) |. 503. а) |; б) g. 504. а) 0,5; б) ^; в) J. 505. а) \; б) |.
506. -^-. 507. а) 0,5; б) 0,3; в) 0,3; г) 0,1. 508. а) 0,25; б) 0,7; в) 0,1; г) 0,8. 509. |.
12 6
ОТВЕТЫ
269

38 7
510. а) 0,25; б) 0,18; в) 0,12; г) 0,6. 511. а) —; б) —. 512. а) 0,5; б) 0,7. 513. а) 0,5;
45 45
б) 0,5; в) 0,5; г) 1. 514. а) 0,25; б) |; в) -; г) —. 515. 0,25.
3 8 18
Глава XIV
516. Дискретные случайные величины в примерах 1, 3, 5, 8. В примерах 2, 4,
6 и 7 — случайные величины непрерывны. 517. Да; возможные значения 2 и 3.
518. 3, 4 и 5. 519. а) 0, 20 и 100; б) 0, 20, 40, 100, 120, 200. 520. Чётные числа
от 2 до 16 (часто несколько первых и последних страниц не нумеруются, но номера у
них все равно есть). 522. а) Натуральные числа от 2 до 12; б) натуральные числа от
3 до 18; в) все натуральные числа от 1 до бесконечности; г) целые числа от 0 до п.
523. а) От 0 до 20 (21 значение); б) от 0 до 32 (33 значения).
524.
а)
Число орлов
Вероятность
0
0,5
1
0,5 |
б)
в)
5
а)
б)
Число орлов
Вероятность
0
0,25
1
0,5
Число орлов
Вероятность
25.
Наибольшее
Вероятность
Наименьшее
Вероятность
0 |
0,125 |
1
0,375
2
0,375
1
1
36
2
3
36
3
5
36
4
7
36
1
11
36
2
9
36
1 3
7
36
4
5
36
2 |
0,25 |
3 |
0,125
5
9
36
6
11
36
5
3
36
6
1
36
526. а) ^-; б) 0,04. 527. а) 0,23; б) 0,48; в) 0,91; г) 0,53. 528. а) ^; б) 0,14.
72 36
50
529. а) 0; б) 9. 530. р., т. е. приблизительно — 16 р. 67 к. 531. 2,5. 532. 12 р.
з
270
ОТВЕТЫ

Оглавление
Предисловие 3
Что такое статистика и как она связана с теорией вероятностей 5
Глава I. Таблицы 7
1. Сбор данных и построение таблицы 8
2. Статистические данные в таблицах 9
3. Поиск информации в таблицах 13
4. Вычисления в таблицах 18
5. Крупнейшие города России 22
6. Подсчёты и измерения в таблицах 23
7. Упорядочивание данных в таблицах 27
8. Таблицы сопряжённости 30
Глава И. Диаграммы 33
9. Столбиковые диаграммы 34
10. Демографическая статистика. Половозрастные пирамиды 41
11. Круговые диаграммы 46
12. Диаграммы «стебель-листья» 51
Глава III. Описательная статистика. Средние значения и размах 55
13. Среднее арифметическое 56
14. Медиана 60
15. Наименьшее и наибольшее значения. Размах 64
16. Урезанное среднее 68
17. Как выбрать подходящее среднее 73
Глава IV*. Описательная статистика. Квартили и частоты 79
18*. Квартили и межквартильный размах 80
19*. Обозначения в статистике 82
20*. Частоты значений 86
21*. Среднее гармоническое и среднее геометрическое 90
Глава V. Случайная изменчивость 95
22. Примеры случайной изменчивости 96
23. Точность и погрешность измерений 98
24^ Тенденции и случайные отклонения 102
25. Группировка данных и гистограммы 106
26. Рост человека 113
27. Статистическая устойчивость и оценки с помощью выборки 117
Глава VI. Случайные события и вероятность 121
28. Случайные события и случайные эксперименты 122
29. Вероятности и частоты событий 123
30. Монета и игральная кость в теории вероятностей 126
31. Как узнать вероятность события 128
32. Зачем нужно знать вероятность события 129
Глава VII. Рассеивание данных 135
33. Рассеивание числовых данных 136
34. Отклонения 138
35. Дисперсия числового набора 140
36. Стандартное отклонение числового набора 143
ОГЛАВЛЕНИЕ 271

37. Диаграммы рассеивания 147
38*. Свойства дисперсии и стандартного отклонения 152
39*. Линейная связь на диаграмме рассеивания 155
40*. Диаграмма «ящик с усами» 160
Глава VIII. Математическое описание случайных явлений 163
41. Случайные опыты и элементарные события 164
42. Вероятности элементарных событий. Равновозможные элементарные события 167
43. Благоприятствующие элементарные события 171
44. Вероятности событий 174
45. Опыты с равновозможными элементарными событиями 176
46. Случайный выбор 179
Глава IX. Действия с событиями. Сложение вероятностей 183
47. Противоположные события. Диаграммы Эйлера 184
48. Объединение событий 187
49. Пересечение событий 190
50. Формула сложения вероятностей 193
51. Решение задач с помощью координатной прямой 196
Глава X. Действия с событиями. Умножение вероятностей 199
52. Условная вероятность. Правило умножения 200
53. Дерево случайного опыта 203
54. Независимые события 208
55. Об ошибке Эдгара По и о том, как победить стечение обстоятельств 211
Глава XI. Элементы комбинаторики 213
56. Комбинаторное правило умножения 214
57. Перестановки. Факториал 216
58. Правило умножения и перестановки в задачах на вычисление вероятностей .. 218
59. Число сочетаний 220
60. Число сочетаний в задачах на вычисление вероятностей 223
Глава XII. Испытания Бернулли 225
61. Успех и неудача. Испытания до первого успеха 226
62. Серия испытаний Бернулли 230
63. Число успехов в испытаниях Бернулли 232
64. Вероятности событий в испытаниях Бернулли 234
65*. Случайный выбор из конечной совокупности 237
Глава XIII*. Геометрическая вероятность 241
66*. Выбор точки из фигуры на плоскости 242
67*. Выбор точки из отрезка и дуги окружности 245
Глава XIV. Случайные величины 249
68. Примеры случайных величин 250
69. Распределение вероятностей случайной величины 252
70*. Математическое ожидание случайной величины 255
71*. Закон больших чисел и его применение 259
Ответы 263