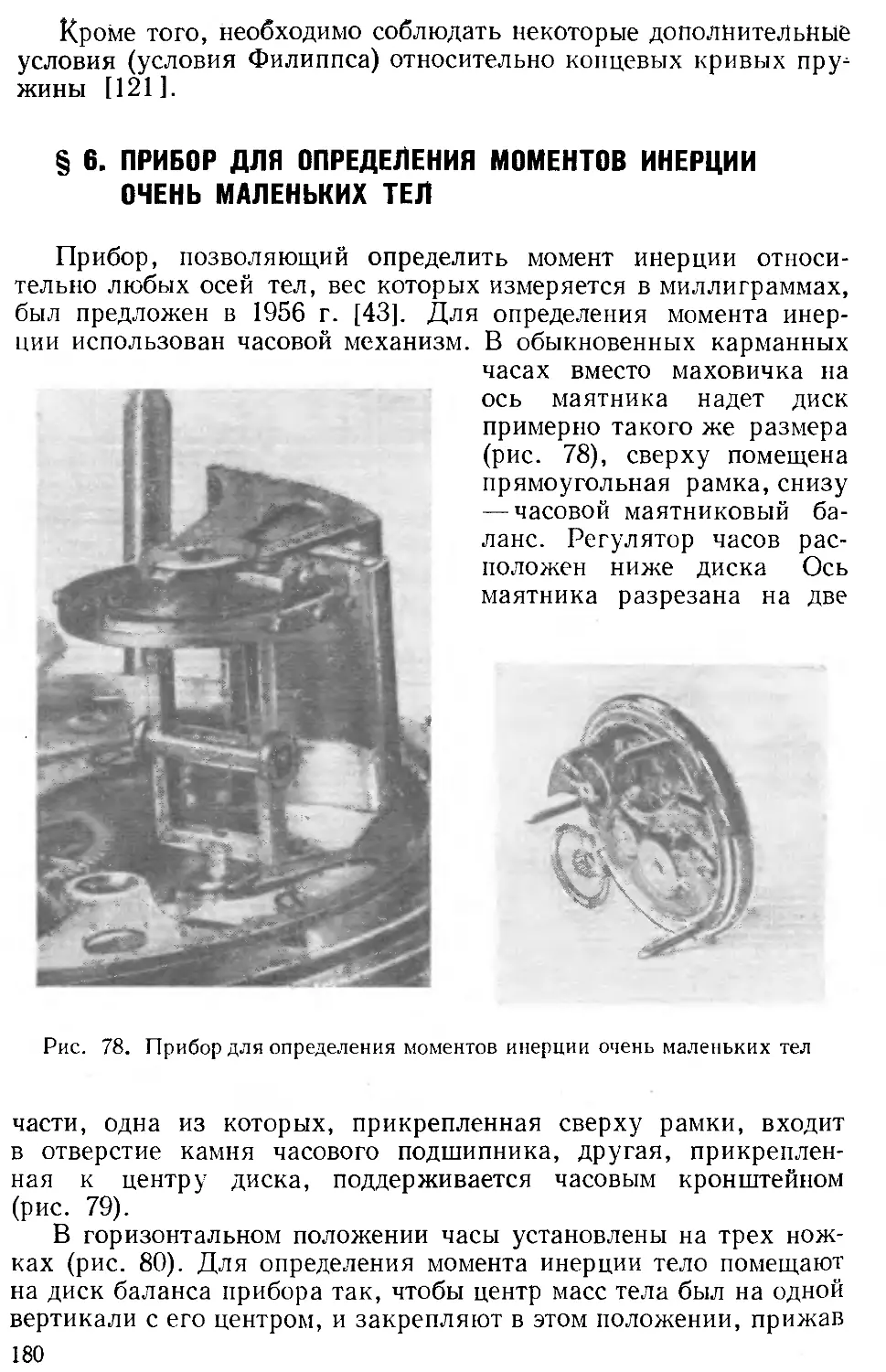
Автор: Гернет М.М. Ратобыльский В.Ф.
Теги: статика силы равновесие притяжение физика механика издательство машиностроение
Год: 1969
Текст
М.М.ГЕРНЕТ
В.Ф.РАТОБЫЛЬСКИИ
Определение
моментов
инерции
М. М. ГЕРНЕТ, В. Ф. РАТОБЫЛЬСКИЙ
ОПРЕДЕЛЕНИЕ
МОМЕНТОВ ИНЕРЦИИ
ИЗДАТЕЛЬСТВО „МАШИНОСТРОЕНИЕ1
Москва 1969
УДК 531.23
Г е р н е т М. М., Р а т о б ы л ь -
с к и й В. Ф. Определение моментов инер-
ции. «Машиностроение», 1969.
В книге изложены различные методы
экспериментального определения момен-
тов инерции, даны их теоретическое обос-
нование, сравнительная оценка (по точ-
ности и сложности эксперимента), а также
практические рекомендации.
Книга предназначена для инженеров-
конструкторов, расчетчиков и научных
работников разных отраслей машинострое-
ния. Она будет полезна преподавателям
и студентам втузов.
Рис. 86, табл. 6, библ. 402 назв.
Рецензент канд. техн. на\к В. В. Юденич
2—4—2
315—69
ВВЕДЕНИЕ
Для определения моментов инерции существуют два прин-
ципиально различных пути — аналитический и эксперименталь-
ный.
Аналитическим путем можно определить моменты инерции
однородных тел правильной геометрической формы. Так как реаль-
ные тела редко имеют простую форму и никогда не бывают одно-
родными, вычислениями не удается точно определить момент
инерции. Поэтому в технике этим способом обычно пользуются
при проектировании отдельных звеньев механизмов и механи-
ческих систем. Однако иногда и при вычислении приходится делать
так много допущений, что конструктор не может удовлетвориться
полученными данными. Тогда изготовляют точную модель проек-
тируемого объекта с подобными размерами, экспериментально
определяют момент инерции и, применяя законы подобия, вычи-
сляют момент инерции проектируемого объекта 1188, 189, 361].
Некоторые экспериментальные методы обладают высокой точ-
ностью (до сотых долей процента), а менее точные привлекают
исследователей простотой эксперимента.
Моменты инерции относительно различных осей тела необхо-
димо знать (с той или иной степенью точности) при решении многих
научных и технических проблем, например, при различных дина-
мических расчетах, исследовании движения испытуемого тела
и его устойчивости, изучении работы машины или показаний
измерительного прибора, определении степени износа механизма,
динамическом уравновешивании испытуемого тела, при контроле
правильности распределения или укладки материальных объектов
и т. д.
Вследствие разнообразия вопросов, при решении которых
необходимо знать момент инерции тела, а также вследствие раз-
нообразия тел и положений их осей задача эксперимента является
чрезвычайно многообразной, обширной и актуальной.
Экспериментальным путем определяют моменты инерции мель-
чайших деталей часовых механизмов и счетных машин [69], ги-
гантских роторов турбин на гидроэлектростанциях, магнитных
стрелок [258, 259, 292-294, 299J, реле, вагонных скатов, зерен
злаков (для проектирования сельскохозяйственных и мельничных
машин) [43, 125], конечностей человеческого тела (для исследова-
ния гимнастических упражнений и определения подготовленности
спортсмена к состязаниям) [45, 56],.автомобилей 147, 48, 178,
308, 328, 399], вагонов [188, 189], подводных лодок, моменты
инерции самолетов [123, 124, 246, 257, 264, 272, 290, 324, 325,
361, 372, 376] и их вращательных производных [130], моменты
инерции гребных винтов [19, 374], церковных колоколов [380],
кристаллов [356], плоских фигур и сечений балок [58, 145, 167,
219] молекул и луны по её орбитальному движению [233|.
Множество несхожих между собой экспериментальных методов
создано на протяжении последних двухсот лет и опубликовано
в многочисленных русских и иностранных журналах, в том числе
и в фундаментальных журналах по экспериментальной физике
или по общему машиностроению, распространенных во всем мире
и известных всем специалистам, и в журналах, выходящих ма-
леньким тиражом и посвященных узким отраслевым вопросам.
Многие работы были опубликованы в различных сборниках трудов,
выпущенных разными институтами.
Весь собранный материал был изучен и систематизирован.
При составлении монографии авторы после тщательного изуче-
ния использовали более четырехсот работ на русском и иностран-
ных языках (латинском, английском, французском, немецком,
итальянском, испанском, польском, венгерском, чешском и др.).
Список использованной литературы дан в конце книги. Авторы
будут признательны читателям, которые укажут работы, не вошед-
шие в этот список. Это в особенности относится к литературе
на некоторых иностранных языках, подбор которой в монографии
носит, к сожалению, почти случайный характер. Если было необ-
ходимо установить первоисточники, то авторы указывали и клас-
сические работы, среди которых сочинения Галилея, Ньютона,
Гюйгенса, Д. Бернулли и др.
В первой главе приведены самые общие сведения по геометрии
масс. Все существующие экспериментальные методы определения
моментов инерции твердых тел рассмотрены в последующих семи
главах. Девятая глава посвящена методу экспериментального
определения эллипсоидов инерции, центробежных моментов, глав-
ных моментов инерции и главных направлений.
При рассмотрении каждого метода авторы старались не только
изложить сущность, но исследовать его историю, определить
сферу применения, точность и вероятные ошибки, дать советы
для применения на практике и найти оптимальные параметры,
при которых эксперимент может быть проведен наиболее точно.
Чтобы не отвлекать внимание читателя длинными или доста-
точно трудными математическими выкладками, авторы отнесли
часть материала в примечания.
♦ ♦♦
Глава I
ОСНОВНЫЕ СВЕДЕНИЯ О ГЕОМЕТРИИ МАСС
§ 1. О ГЕОМЕТРИИ МАСС
Определение центров масс (центров тяжести), моментов инер-
ции тел относительно осей, полюсов и плоскостей, изучение эллип-
соидов инерции, гирационных эллипсоидов, моментов инерции
высших порядков, а также теория потенциала составляют предмет
науки, называемой геометрией масс. Это название предложено
в 1857 г. французским ученым Атоном де ля Гупийером [261],
имеющим крупные работы в этой области.
Задача теоретических и экспериментальных исследований
заключается в изучении распределения масс в пространстве, иссле-
дования сумм вида 2 mkf [хк, ук, zk), распространенных на все
fe=i
принадлежащие данной системе или телу материальные точки.
В частности моменты инерции выражаются суммами, в которых
написанная функция является целой функцией второй степени
относительно координат.
Момент инерции относительно оси
Моментом инерции твердого тела относительно оси назы-
вается мера инерции этого тела при вращательном движении вокруг
данной оси х—х.
В динамике величины, аналогичные моментам инерции тела
относительно оси, впервые появились в 1673 г. в работах Хр. Гюй-
генса [282], однако понятие и термин «момент инерции», а также
основные теоремы были даны Эйлером в 1749 г. [243].
Математически момент инерции тела относительно оси, про-
веденной в теле или вне его, выражается суммой произведений
массы тк каждой материальной частицы на квадрат расстояния г^
ее от данной оси:
J= S m*i- (1)
Точно вычислить момент инерции можно, представив его как
предел суммы бесконечно большого числа произведений бесконечно
5
малых элементов массы dm на квадрат их расстояний от оси
(полюса, плоскости):
J = f г2 dm. (2)
(m)
Следовательно, определение момента инерции тела сводится
к вычислению объемного интеграла.
Если тело отнесено к прямоугольным координатным осям, то,
согласно уравнению (1)
й=1 /e=l *=1
(3)
или
Л- = j (i/2 + г2) dm; Ju = J (г2 + x2) dm; Уг = f (x2 + y2) dm. (4)
§ 2. МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО
ПОЛЮСА И ПЛОСКОСТИ
Наряду с моментом инерции тела относительно оси применяют
понятие момент инерции тела относительно полюса (момент инер-
ции относительно точки, полярный момент инерции) и предложен-
ный в 1813 г. Ж- Бине [196] момент инерции относительно пло-
скости (момент инерции Бине, момент инерции Миндинга). Эти
величины не имеют самостоятельного физического смысла и служат
как вспомогательные для вычисления моментов инерции относи-
тельно оси и для разработки их теории. Математически они выра-
жаются суммой (1), где г — расстояние материальной частицы
от полюса или плоскости.
В прямоугольных координатах момент инерции тела относи-
тельно начала координат и координатных плоскостей выражают
следующими суммами:
J0=kimAxl + yl + ~4) (5)
и
j«*= £mkxi> jzx= §4$ jxy= 244 (6)
*=1 k=\ k=\
Сопоставляя формулы (2), (3), (4), нетрудно увидеть, что момент
инерции тела относительно начала координат равен полусумме его
моментов инерции относительно трех координатных осей или сумме
моментов инерции относительно трех координатных плоскостей.
6
§ 3. ЦЕНТРОБЕЖНЫЙ МОМЕНТ ИНЕРЦИИ
Моменты инерции тела относительно осей, полюсов или пло-
скостей всегда положительны. В отличие от них центробежные
моменты инерции (произведения инерции, моменты девиации) мо-
гут быть положительными, отрицательными или равняться нулю.
Под центробежным моментом инерции тела понимают сумму
произведений массы каждой материальной частицы твердого
тела на две координаты этой частицы в прямоугольной системе
осей:
k—n к=п к-п
Jy.z= H rnkykzk\ J2.x= S mkzkxk\ J,-.,,= £ ткхкук. (7)
k=i ft=i ';=i
Некоторые авторы величину Jx.y называют центробежным
моментом тела относительно осей х, у, другие — центробежным
моментом относительно оси г, второе название представляется
более удачным.
Точку между индексами надо ставить для того, чтобы отличать
обозначения моментов инерции относительно плоскости и произве-
дения инерции. Название «произведение инерции» имеет матема-
тическое объяснение и вызвано тем, что суммы произведений (7)
можно представить как разность моментов инерции тех же точек
относительно равноделящих плоскостей. Название «центробежный
момент инерции» объясняется следующими причинами физического
характера. Как и всякую систему сил, центробежные силы инер-
ции, мысленно приложенные к частицам тела, вращающегося на
неподвижной оси, можно привести к главному вектору, перпенди-
кулярному к оси и к главному моменту центробежных сил, т. е.
к паре сил, лежащих в одной плоскости с осью вращения.
Если центробежный момент инерции тела относительно оси
вращения равен нулю, то и главный момент центробежных сил
инерции равен нулю. Всякую ось, при вращении около которой тела глав-
ный момент центробежных сил инерции равен нулю, называют
главной осью инерции тела. Главные оси инерции были открыты
в 1755 г. Сегнером [3621 и в 1758 г. Эйлером [242]. Через каждую
точку пространства можно провести три главные оси инерции
данного тела. Главные оси взаимно перпендикулярны. В этой си-
стеме осей центробежные моменты инерции тела равны нулю.
Моменты инерции тела относительно главных осей называют
главными.
Всякую ось, проходящую через центр масс, называют цен-
тральной осью тела. При вращении тела вокруг центральной оси
главный вектор центробежных сил равен нулю.
Главные оси, проходящие через центр масс, называют глав-
ными центральными осями инерции тела, а моменты инерции отно-
сительно этих осей — главными центральными моментами инер-
ции тела. Единственное условие, необходимое и достаточное для
7
того, чтобы при вращении твердого тела не было динамических
давлений на ось, заключается в том, чтобы ось вращения была
одной из главных центральных осей инерции тела.
Приведем без доказательств некоторые теоремы геометрии
масс.
§ 4. ТЕОРЕМА О ПАРАЛЛЕЛЬНЫХ ОСЯХ
Теорема позволяет вычислить момент инерции тела относи-
тельно любой оси, если известен момент инерции относительно
оси, проходящей через центр масс тела параллельно данной.
Этой теоремой пользовался Гюйгенс [282] еще в 1673 г., а вполне
общее и строгое доказательство дал Эйлер, опубликовавший его
в 1749 г. в Петербурге [243]. Однако в немецкой и советской-лите-
ратуре теорему несправедливо приписывают Штейнеру, доказав-
шему сто лет спустя [1840 г.] частный случай для системы точек
на плоскости [369]. В формулировке Эйлера теорема читается так:
момент инерции тела относительно какой-либо оси равен моменту
инерции того же тела относительно оси, ей параллельной, но про-
ходящей через центр масс тела, плюс произведение массы тела
на квадрат расстояния между осями:
J = jc-у тс2. (8)
Это позволяет определить момент инерции Jг- относительно
какой-либо оси по известному моменту инерции JZ" относительно
другой оси, параллельной данной даже в том случае, если ни одна
из осей не проходит через центр масс тела, но известны расстояния
сх и с2 от центра масс:
По этой теореме можно показать, что тело обладает наимень-
шим моментом инерции относительно оси, проходящей через центр
масс, а моменты инерции относительно каждой из параллельных
осей, равноудаленных от центра масс, равны между собой.
§ 5. ТЕОРЕМА 0 ПЕРЕСЕКАЮЩИХСЯ ОСЯХ
Теорема позволяет вычислить момент инерции тела относительно
оси, проходящей в заданном направлении через начало прямо-
угольной системы координат, если известны моменты инерции тела
относительно координатных осей (или плоскостей) и центробеж-
ные моменты инерции. Эта задача была поставлена Эйлером
и в 1765 г. решена с помощью так называемых эйлеровых уг-
лов [242]. В 1827 г. Коши дал решение [208], которое можно
вывести и из формулы Эйлера, если функции эйлеровых углов
выразить через направляющие косинусы.
8
Дано тело, прямоугольные координатные оси хОуг и ось, про-
ходящая через начало координат и составляющая с ними углы а, р*
и у. Моменты инерции тела относительно осей координат и центро-
бежные моменты инерции относительно этих осей известны. Тре-
буется определить момент инерции тела относительно этой оси.
По формуле Коши
J = Jx cos2 а Ч- J у cos2 р + J z cos2 у — 2Jy. z cos P cos у —
— 2 Jz_ x cos у cos а — 2JX. y cos^ a cos p. (9)
Если координатные оси являются главными осями инерции
тела, то центробежные моменты инерции относительно главных
осей равны нулю и формула принимает более простой вид
J = Jx cos2 a + J у cos2 P + Jz cos2 у. (9')
По этим формулам можно подсчитать момент инерции тела отно-
сительно любой оси, проходящей через начало координат, если
известны моменты инерции тела относительно главных осей или
моменты инерции и центробежные моменты инерции относительно
любых других координатных осей, пересекающих данную ось под
заданными углами.
§ 6. ЭЛЛИПСОИД ИНЕРЦИИ
Если определить момент инерции тела относительно осей,
проходящих через начало координат (точка О), и на каждой из них
отложить в обе стороны от точки О отрезки ОА ~ ~у=- (J — мо-
мент инерции тела относительно этой оси), то геометрическим
местом концов А отрезков будет эллипсоид с центром в точке О.
Координаты точки А: х = —=■ cos а; и = —=- cos 6; z = —=- cos v-
Определив косинусы и подставив их значения в формулу (9)
или (9'), сократим обе части на / и получим уравнение второго
порядка, связывающее координаты точек А, следовательно,
оно выражает поверхность второго порядка. Эта поверхность
не должна иметь бесконечно удаленные точки, так как J =?= 0.
Следовательно, это эллипсоид, в общем случае трехосный
эллипсоид и главные оси инерции являются его главными осями.
Если два главных момента инерции равны, например, Jx — Jy,
то получим эллипсоид вращения около оси Oz и все перпендику-
лярные к оси диаметры являются главными осями. Если Jx =
= J у = Jz, то эллипсоид инерции — шар, все оси, проходящие
через О, главные, а моменты инерции тела относительно этих
осей равны. Раус такие тела называет одноосными.
Любую точку пространства можем принять за начало коорди-
нат и построить в этой точке эллипсоид инерции данного тела. Но
9
большое практическое значение имеет центральный эллипсоид
инерции. Зная центральный эллипсоид инерции, можно вычис-
лить момент инерции или центробежный момент инерции относи-
тельно любых осей.
Эллипсоид инерции был открыт Коши в 1827 г. [208] и назван
эллипсоидом инерции Коши в отличие от других эллипсоидов,
применяемых в геометрии масс, например, эллипсоида Бине [196],
эллипсоида Мак Куллага [313]. Иногда [180] его называют эллип-
соидом инерции Пуансо. Однако работа, в которой Пуансо дока-
зал (1834 г.), что движение твердого тела с неподвижной точкой
можно представить как катание его эллипсоида инерции по неиз-
менной плоскости, появилась на 7 лет позже работы Коши.
§ 7. РАДИУС ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ
Часто (особенно в английской литературе) наряду с моментом
инерции J тела относительно оси, рассматривают радиус инерции
(плечо инерции, гирационный радиус). Представим момент инер-
ции тела как произведение его массы на квадрат некоторой длины
Га-
J = тг\.
Величину
называют радиусом инерции тела относительно данной оси.
Радиус инерции ги тела можно представить как радиус вообра-
жаемого полого цилиндра, который обладает той же массой,
произвольно распределенной по поверхности, и тем же моментом
инерции относительно оси, что и данное тело. В литературе встре-
чается определение радиуса инерции, как расстояния от оси, на
котором нужно поместить материальную точку массой, равной
массе твердого тела, чтобы получить ту же величину момента
инерции относительно данной оси, как и для тела. Такое опреде-
ление не имеет физического смысла, так как материальная точка
не обладает инерцией во вращении (момент инерции), поскольку
не может совершать вращательного движения; вращение свой-
ственно только телу.
§. 8. МАХОВОЙ МОМЕНТ
Для характеристики распределения масс вращающихся звеньев
машин иногда применяют понятие «маховой момент», понимая
под этим произведение GD'2 веса звена G — mg на квадрат диа-
метра D = 2ги, равного удвоенному радиусу инерции звена отно-
сительно оси вращения [149, 156, 190, 235, 247].
Глава II
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МЕТОДОМ
ФИЗИЧЕСКОГО МАЯТНИКА
§ 1. ИСТОРИЯ МЕТОДА. ТЕОРИЯ МЕТОДА
Физический маятник это тяжелое твердое тело, имеющее воз-
можность свободно вращаться на оси под действием силы тяжести.
Изохронность малых колебаний физического маятника была
открыта Галилеем в 80-х годах XVI века [255, 256]. Первые по-
дробные исследования проведены Христианом Гюйгенсом и опу-
бликованы в 1673 г. [282]. Работа Гюйгенса положила начало
огромному количеству исследований по теории физического маят-
ника в различных случаях его использования.
Со времен Гюйгенса физический маятник является главнейшей
частью маятниковых часов. Точность современных маятниковых
астрономических часов не ниже 0,003 сек в сутки. Маятник
применяют также в ряде других приборов, например, в меха-
нических реле времени, метрономах, сейсмографах, динамомет-
рах и т. д. Физический маятник широко применяют для опре-
деления напряжения поля земного тяготения и фигуры Земли.
Коромысло весов также представляет собой физический маят-
ник, а колебания весоизмерительных приборов имеют большое
значение в современной метрологии.
Физический маятник широко используют для изучения ряда
физических свойств материалов (маятниковые копры для опреде-
ления ударной вязкости материалов, маятниковые склерометры
для определения твердости поверхностей), с помощью маятников
измеряют модуль нормальной упругости материалов, коэффициент
трения, износ материалов и ряд других свойств.
Экспериментальное определение моментов инерции методом
маятниковых колебаний испытуемого тела, по-видимому, впервые
предложено де Прони в 1800 г. [345, 346]. В настоящее время
этот метод наиболее распространен и рекомендован всеми руко-
водствами по теоретической и прикладной механике.
Методика опыта и применяемые для вычисления расчетные
формулы разнообразны.
Однако при всех модификациях момент инерции определяют
по периоду малых колебаний физического маятника или по его
приведенной длине.
11
Первый вариант был известен еще в 1792 г. [345, 346]. Второй
вариант, опубликованный в 1941 г. [35], проще, не требует ника-
кого оборудования, а по точности не уступает предыдущему.
§ 2. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО
МАЯТНИКА ПО ПЕРИОДУ КАЧАНИЙ
Твердое тело (физический маятник) (рис. 1) подвешено на не-
подвижной горизонтальной оси О (ось подвеса), относительно кото-
рой оно может качаться. Трением и сопротивлением воздуха пока
пренебрежем.
Отклоним маятник на некоторый угол ср0 от равновесного
положения и отпустим без начальной скорости.
Дифференциальное уравнение движения маятника составим по
теореме моментов для вращающегося твердого тела
Уф = — mgc sin ф, (11)
J — момент инерции тела отно-
сительно оси вращения;
расстояние оси подвеса от
центра масс;
g — ускорение свободно падаю-
щих тел.
Если угол ф небольшой и можно счи-
тать sin ф = ф, тогда
Уф = — mgcq».
Интегрируя, находим
mgc
где
ОС
[(12)
Рис. 1. Физический маят-
ник
= ф0 Sin
Vf
t.
Следовательно, физический маятник совершает малые коле-
бания, период которых
2я
Г mgc
(13)
Согласно этой формуле период качания не зависит от ампли-
туды. Однако еще в 1671 г. Пикар заметил: «необходимо, чтобы
колебания были малыми; продолжительность их становится не-
одинаковой, если размах превышает некоторую величину» 1339].
Если колебания не малы, то нельзя принимать sin ф — ф. Точное
интегрирование дифференциального уравнения (11) (см. примеча-
ние 1) показывает, что маятник совершает колебания с периодом,
зависящим от угловой амплитуды:
Тф = 4Х ]/
(14)
12
где К — полный эллиптический интеграл первого рода,
к =
\г>
sin2 4г~ sin2 I
(15)
При определении момента инерции значения Тф получают деле-
нием общей продолжительности большого числа колебаний на
их число и, чтобы избежать влия-
ния анизохронности, сообщают
маятнику только малые колебания.
Если положение центра масс
хорошо известно, а вес (mg) изме-
рен на точных весах, то для опре-
деления момента инерции тело
подвешивают на неподвижной го-
ризонтальной оси так, чтобы оно
могло качаться под действием соб-
ственного веса без большого тре-
ния. Повернув тело вокруг оси
подвеса на 5—8°, выведем его из
равновесия и отпустим без началь-
ной скорости. Измерив секундо-
мером (или электросекундомером)
продолжительность 50—100 коле-
баний, вычисляем период одного
полного малого колебания и опре-
деляем момент инерции относитель-
но оси подвеса по формуле
mgc. (16)
J.
4л2
Рис. 2. Определение моментов инер-
ции грузового автомобиля
Результаты определения моментов инерции грузовых авто-
мобилей методом физического маятника приведены Н. Н. Яценко
1178]. Автомобиль со снятыми мостами, колесами и рессорами по-
мещали на платформе (рис. 2), подвешенной к станине с горизон-
тальной осью посредством четырех тяг регулируемой длины.
Благодаря подшипникам качения затухание колебаний оказалось
столь незначительным, что можно было определить время 30—50
колебаний при начальной амплитуде 4—5°. Вычисления проведены
по формуле (16), получены значения моментов инерции автомашин
отечественных марок относительно центральных поперечных осей:
Марка автомобиля
Момент инерции в
кГ-см-сек2 . . .
ГАЗ-63А ЗИЛ-151А МАЗ-502А ЯАЗ-214
46 400 138 400 191800 334 700
13
Формула (16) справедлива лишь для колебаний с очень малыми
амплитудами. Но в действительности эксперимент проводят при
колебаниях с конечными амплитудами, поэтому вычисленное зна-
чение момента инерции не точное (см. примечание 2). Назовем
относительную ошибку, вызванную пренебрежением амплитудой,
относительной ошибкой от анизохронности колебаний, обозначим
бУф и найдем ее величину из сопоставления точного значения
момента инерции, которое определяется формулой
/ — _Л
' точн
и приближенного согласно формуле (16):
н J точн — ^ 1 ^_
•>т',чн ^~
Относительные ошибки для некоторых значений амплитуд коле-
баний приведены в табл. I (см. примечание I).
Частные относительные ошибки вычисления момента инерции
относительно оси подвеса, обусловленные неточностью измерения
периода, массы и расстояния центра тяжести тела от оси подвеса,
следующие:
8JT = 2*Т = 28Т; 67,,, = — = 8т;
8Jr = — = 8с.
с с
Среднеквадратическая ошибка (с учетом ошибки от анизо-
хронности колебаний)
8J = К (в/ф)а + (б/г)2 + (8Jmf + (8JC)\
Следовательно, при неизменных значениях абсолютных ошибок
определения периода AT, массы Am и расстояния от центра тя-
жести до оси подвеса Ас точность определения момента инерции
относительно оси подвеса возрастает с увеличением расстояния с
Часто момент инерции испытуемого тела вычисляют относи-
тельно центральной оси, параллельной оси подвеса. Исследованием
ошибок, получаемых в этом случае, занимался Бауман 1188, 189]
и более обстоятельно Эллет [237].
Момент инерции относительно центральной оси выражается
формулой
Jc — J — mc1 = -л -,- tngc — mc2.
Искомая величина является (особенно при больших значе-
ниях с) разностью близких величин, причем вычитаемое тс1,
ввиду неточности определения с, содержит ошибку.
14
Относительная ошибка от анизохронности колебаний
«с-0-^-)('-Л-
\ НС/
Из формулы следует, что при одинаковых амплитудах колеба-
ний ошибка больше для маятников с с > rUl и меньше, если
£|<V. гДе ^- — центральной радиус инерции.
Рассмотрим относительные ошибки, вызванные неточностью
замера величин, входящих в формулу.
Относительная ошибка, обусловленная неточностью определе-
ния массы подвешенного тела,
Относительная ошибка от неточности замера расстояния оси
центра тяжести С до оси подвеса
,, , J с — tnc1 Ac r,ic ~ с" .
ЫСс = — — = —— Лс.
JC C сгис
Эта ошибка зависит от значения с.
Если с = гис, то 8JCc — 0. При уменьшении с до нуля и неиз-
менной величине абсолютной ошибки (Лс) неограниченно воз-
растает 6/Сс.
Относительная ошибка, возникающая от неточности замера
периода колебаний,
6jc1 = n..Xf^±£LAT.
я г-
ис
Из формулы следует, что с уменьшением с до нуля bJCT неогра-
ниченно убывает.
Суммарная среднеквадратическая ошибка вычисления момента
инерции относительно центральной оси
б/с =- vWJofy + (Мо„у ~г (Мее)2 +тел*:
Относительная ошибка бУСф может быть снижена правильным
выбором амплитуды колебаний, a 8JCm точным взвешиванием
может быть сведена к пренебрежимо малым значениям. Поэтому
общая ошибка вычисления момента инерции почти целиком опре-
деляется значением расстояния с и точностью его определения;
причем не следует принимать очень малые значения, желательно,
чтобы они были одного порядка с гис [65].
15
§ 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО
МАЯТНИКА ПО ПРИВЕДЕННОЙ ДЛИНЕ
С теорией физического маятника тесно связана теория круго-
вого математического маятника, состоящего из одной материаль-
ной точки массой т, совершающей под действием своего веса
плоские колебания около неподвижной точки 0, с которой она
соединена невесомой нерастяжимой гибкой нитью длиной /. Сле-
довательно, если в формулы (13) и (14) подставим вместо момента
инерции J произведение массы т точки на квадрат расстояния /2
ее от оси подвеса и / вместо с, то получим период малых качаний
математического маятника
ТМ=-^У~ (17)
и период качаний конечной амплитуды
TM = 4Ky_Lt (18)
где К выражается формулой (15).
Длина 1пр математического маятника, качающегося синхронно
с физическим маятником, называется приведенной длиной физи-
ческого маятника. Чтобы получить формулу, выражающую приве-
денную длину физического маятника, надо приравнять периоды
качаний физического (13) и математического (17) маятников.
Тогда найдем
Такой же результат получим, приравнивая выражения (18)
и (14) в случае, когда амплитуды качаний обоих маятников не
малы и приблизительно одинаковы. Следовательно, если ампли-
туды качаний обоих маятников одинаковы, приведенная длина
не зависит от амплитуды качания.
Точка 0Ъ отстоящая от оси подвеса за центром масс С физи-
ческого маятника на расстоянии /„ , называется центром качания.
Формула (19) является математическим выражением общего
правила вычисления центра качания, открытого Гюйгенсом.
Задача определения длины математического маятника, изохрон-
ного с данным физическим, была поставлена в 1646 г. Мерсен-
ном [320]. Декарт [227], Роберваль [353], Оноре Фабри, Кавен-
диш, Ричиоли, Пикар [339] дали частные или не вполне точные
решения [232].
По формуле (19) можно вычислить момент инерции, если из-
вестна приведенная длина тела, рассматриваемого как физический
маятник.
16
Для определения приведенной длины проведем следующий
опыт [35].
Подвесим тело на горизонтально расположенную призму.
Привязав к маленькому грузу нитку, перекинем ее через призму,
свободный конец нитки возьмем в руку (рис. 3, а). Подвешенный
таким' образом груз назовем маятником сравнения и примем за
математический маятник. Выведем оба маятника из равновесия и,
изменяя длину маятника сравнения, сравняем периоды качаний.
Даже самое незначительное несовпадение периодов легко обнару-
живается, потому что разность в отклонениях непрерывно ме-
&%
Inp CM
О 50 100
а) Ъ)
Рис. 3. Схема маятника сравнения (а) и относительная
погрешность вычисления (б) момента инерции:
/ — по периоду при ДТ* —0,01 сек; 2 — по приведенной длине
при Llnp = 0,1 см; 3 — то же при Ып„ = 0,5 см
няется, достигая то максимума, то минимума, получается своеоб-
разный нониус.
Метод, основанный на совпадении маятников, применяли в выс-
шей геодезии еще в XVII и XVIII веках. Метод качания маятников,
предложенный Мераном [317] позволил Ж. Кассинии Борда [198]
с высокой точностью определить длину секундного маятника.
Таким образом синхронность маятников можно определить
с точностью, вполне достаточной для данной технической задачи.
Получив из опыта значение приведенной длины физического
маятника, зная массу т и расстояние с центра тяжести от оси под-
веса, определим момент инерции относительно той же оси по фор-
муле
/ = mctnp. (20)
Преимущество этого метода по сравнению с определением мо-
ментов инерции по периоду малых качаний заключается в значи-
тельно большей точности, и, кроме того, колебания не должны
быть так малы, как при измерении периода.
Период качаний обычно измеряют с точностью до 0,01 сек,
а длину маятника сравнения до 0,1 см. На рис. 3, б показано, что
2 М. М. Гернет 2274 17
точность измерения момента инерции по приведенной длине во
много раз превосходит точность измерения по периоду качаний.
И даже если уменьшить точность определения приведенной длины
до 0,5 см, то и тогда для всех тел с 1пр > 25 см (Г> 1 сек), т. е.
для большинства тел методом приведенной длины получают
более точные результаты.
Для того чтобы доказать, что, принимая маятник сравнения
за математический, не вносим большой неточности, необходимо
выяснить:
1) какова погрешность от пренебрежения размером груза;
2) какова погрешность допущения, что нить невесома и не-
растяжима.
Погрешность от пренебрежения размерами груза при достаточно
малых его размерах в этих опытах неощутима. Обозначим момент
инерции груза относительно центральной оси, параллельной к оси
подвеса через Эс. Согласно теореме о параллельных осях момент
инерции груза относительно оси подвеса равен
Э = 9С + ml2,
а период качаний маятника сравнения
^ -2» V4f - * Ут • V^¥ > т«-
Таким образом, 6С несколько увеличивает период качаний
маятника. Но второй член суммы, стоящей под знаком корня,
мал и Тср можно принять равным Тм.
Например, если в качестве груза принять шарик диаметром
15 мм, а длину нити (от точки подвеса до центра шарика) равной
250 мм, то относительная погрешность в определении периода будет
Тм
= 0,00036.
Если приведенная длина равна 100 см, то относительная по-
грешность будет 0,000022, при /„ = 10 см 0,0022, при /„„ =
= 5 см 0,0089.
Погрешность, вызванная тем, что реальная нить принята за
идеальную, тоже незначительна. В опытах удобнее применять
хлопчатобумажную нить, так как при пользовании мягкой и тон-
кой проволокой или отожженной струной труднее изменять длину
маятника сравнения и добиться синхронности маятников.
Рассмотрим влияние веса нити и ее длины.
Период качания маятника сравнения с учетом массы нити
выражается следующей формулой:
f gynl^-^v-l
где ©с — центральный момент инерции груза;
т — его масса;
I и \i — длина и масса нити.
Масса нити мала. Так, масса одного сантиметра балалаечной
струны измеряется миллионными долями Г-сек2!см, масса санти-
метра хлопчатобумажной нити зависит от номера, сорта и пр.,
но согласно ГОСТу выражается в десятимиллионных долях
Г-сек1:см *.
Период качания материальной точки, подвешенной на весомой
нити, должен быть больше, чем математического маятника такой
же длины, потому что вес нити приложен между материальной
точкой и точкой подвеса:
/
3 *
ТСР = 2я |/ ^ = Тм |/ f— < ГЛ
' -Г*
Соответствующим подбором груза и нити можно добиться пол-
ного совпадения периодов качания маятника сравнения и мате-
матического маятника длиной /. Для этого достаточно удовлетво-
рить равенство
6вс = ц/2.
Влияние массы нити проиллюстрируем примером [35]. Вес
стального шарика диаметром 15 мм 13,783 Г. В качестве нити
взята отожженная балалаечная струна, вес 100 см струны ра-
вен 0,595 Г. Если / = 25 см, то Т'ср — Тм, при длине / = 100 см
не получим полного совпадения, но относительная погрешность
тсР ~ тм _ _ 000698i
Тм
т. е. влияние веса нити очень незначительно. При хлопчатобу-
мажной нити погрешность в десятки раз меньше.
Под действием динамической нагрузки (центробежной силы)
даже хлопчатобумажная нить практически не изменяет своей
длины. Натяжение нити меняется в зависимости от угла наклона
маятника в следующих пределах:
Ли in = mg cos ф0; Pmax = mg{\ + фо),
где ф0 — амплитуда качания.
Как видно из табл. 1, при больших амплитудах изменение
натяжения невелико.
При достаточно малом грузе относительное удлинение нити
не влияет на конечные результаты, поэтому нить можно прини-
мать за идеальную, а маятник сравнения за математический.
* лгт^ипп 8015-8025 ,
ОСТ/КНЛП -^т^—^=тг- нитки хлопчатобумажные.
848—858
19
Таблица 1
Амплитуда
Р
г max
5°
1,00 mg
1,00 mg
10°
0,98 mg
1,03 mg
15°
0,97 mg
1,07 mg
20°
0,94 mg
1,12 mg
25°
0,91 mg
1,19 mg
Частные относительные ошибки вычисления момента инерции по
формуле (20) следующие:
6Л
Дт
6т;
б/с =
Ас
= &;
67, - -/- = 6/
Среднеквадратическая ошибка выражается формулой
6/ = 1/(67т)а+ (&/,)*+(6/,)*.
Следовательно, точность возрастает с увеличением расстояния
центра тяжести от оси подвеса.
Пример 1 [39].
Шатун массой 40,00 кг подвешен на горизонтальную призму,
причем расстояние центра тяжести от оси подвеса с = 750,0 мм.
Ввиду больших размеров шатуна применен метод приведенной
длины. Стальной шарик (0 15 мм), просверленный по диаметру,
привязан к одному концу нитки (№ 40), перекинутой через ту же
призму, другой конец ее — в руке экспериментатора.
Отклоненные из равновесного положения шатун и груз сво-
бодно качались в параллельных плоскостях. Изменяя длину нити
между призмой и грузиком, добились совпадения периодов кача-
ния. Длина маятника сравнения (от грани призмы до центра
шарика) равна 1пр = 1079 мм.
Определим сначала по формуле (20) момент инерции шатуна
относительно оси подвеса (в системе СИ)
J = 40,00-0,7500-1,079 = 32,37 кг-м2.
Погрешность от пренебрежения размером груза составляет
2л
т- _ ^-(Увс + тР- УтР)
1 сР —' м _ V g
Тм
v?^'
У0,4- 7,5%г + 1079-ffl — У Ю79Ьп _ 1079,0104 - 1079 Q qqqqj
У\07¥т ~ 1079 ~ •
20
Ошибка от пренебрежения весом нити еще меньше.
Таким образом, результат получен с высокой точностью.
Пример 2.
Определим момент инерции того же шатуна (т — 40,00 кг,
с = 750,0 мм) по периоду качаний. Секундомером измеряем пе-
риод Т = 2,08 сек. Подставим это значение в формулу (16):
У =
I
Л
4л-
mgc
(2,08)»
4(3,14)2
■40-9,81 -0,75 = 32,28 кг-см2.
Если электросекундомером определить период малых колеба-
ний с точностью до тысячной доли секунды (Т = 2,084 сек), то
получим J = 32,41. В формулу (16) входят постоянные величины,
поэтому для получения более надежных результатов их необ-
ходимо определить с точностью до четвертого знака. Примем
4л2 = 39,48; g - 9,808 м/сек2. Тогда
(2.084)2
J ■
39,48
•40-9,808.0,75 = 32,37 кг-м2.
% 4. ОПЫТНОЕ ОПРЕДЕЛЕНИЕ СТАТИЧЕСКОГО МОМЕНТА
ФИЗИЧЕСКОГО МАЯТНИКА
При проведении экспериментов рассмотренными методами необ-
ходимо знать расстояние с. В большинстве случаев положение
центра тяжести можно точно определить экспериментально.
Рассмотрим один из простых
способов. К телу, подвешенному
на острие О призмы, привязывают
нить АВ (рис. 4), конец В которой
присоединяют к динамометру.
Нить оттягивают в сторону, и тело
отклоняется от равновесного по-
ложения на угол а. Если показа-
ние динамометра равно Р, а вес
тела G, то расстояние ОС найдем
из условия равенства моментов
относительно оси подвеса
Ph
с —
где h
G sin a
силы
Рис. 4. Определение центра тяже-
сти с помощью динамометра
натяжения
плечо
нити Р.
В другом случае испытуемое тело устанавливают на острие
призмы так, чтобы оно было уравновешено. Опыт повторяют при
различных положениях тела. Этот способ удобен для определе-
ния центра тяжести тел, имеющих ось симметрии, потому что
можно ограничиться одним опытом, найти центральную плос-
кость, перпендикулярную оси симметрии тела.
21
С. М. Тарг приводит [146] два экспериментальных способа.
Первый состоит в том, что испытуемое тело подвешивают на
нити или тросе. Направление отвеса проходит через центр тяжести
тела. Это направление фиксируют (например, натягивают вдоль
него нить и прикрепляют ее к телу воском), затем опыт повторяют,
подвесив тело за какую-либо другую точку, и опять фиксируют
вертикаль, проходящую через точку подвеса. Точка пересечения
двух направлений определяет центр тяжести тела. Другой способ
показан на следующем примере.
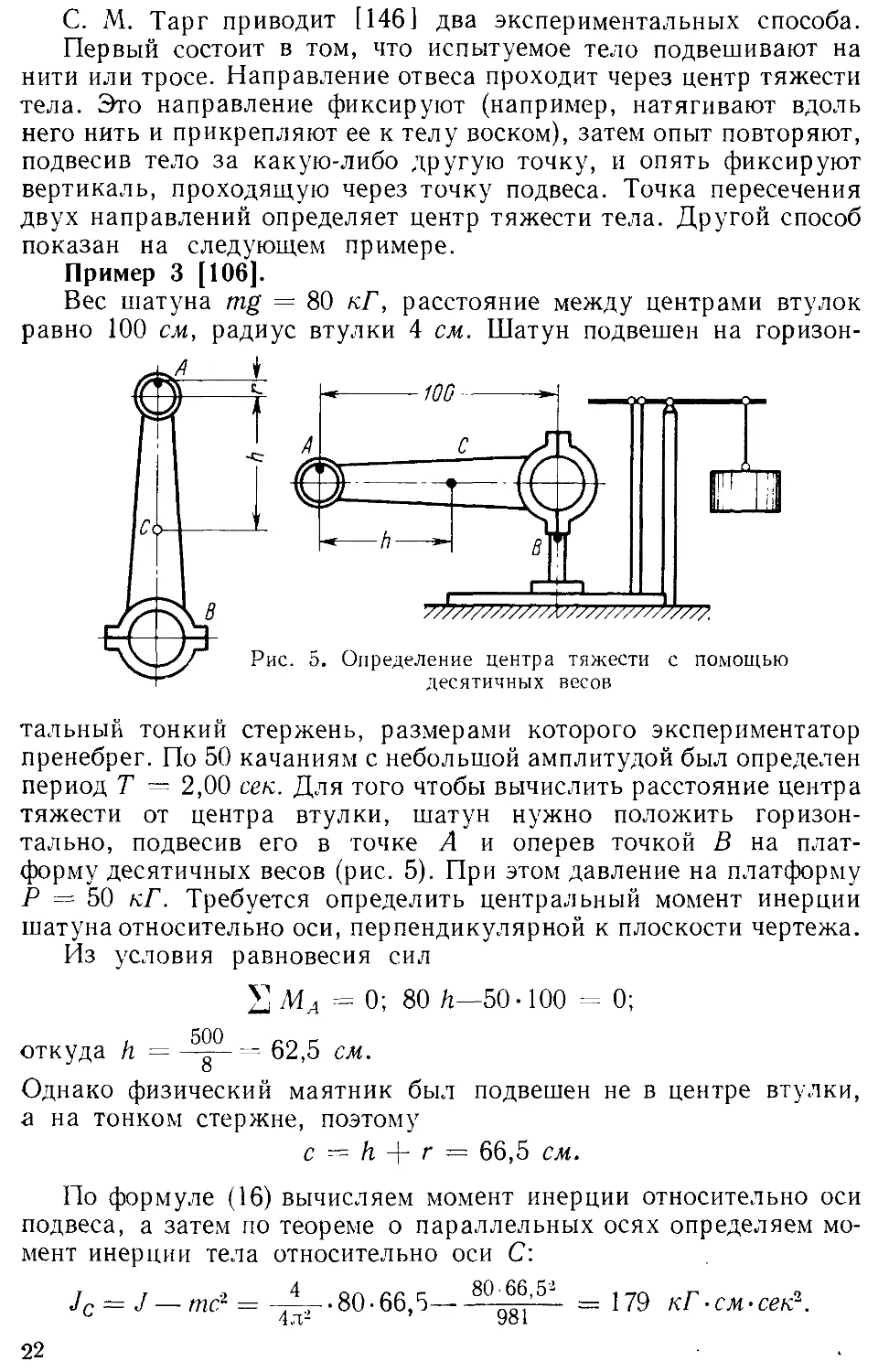
Пример 3 [106].
Вес шатуна mg = 80 кГ, расстояние между центрами втулок
равно 100 см, радиус втулки 4 см. Шатун подвешен на горизон-
тальный тонкий стержень, размерами которого экспериментатор
пренебрег. По 50 качаниям с небольшой амплитудой был определен
период Т = 2,00 сек. Для того чтобы вычислить расстояние центра
тяжести от центра втулки, шатун нужно положить горизон-
тально, подвесив его в точке А и оперев точкой В на плат-
форму десятичных весов (рис. 5). При этом давление на платформу
Р = 50 кГ. Требуется определить центральный момент инерции
шатуна относительно оси, перпендикулярной к плоскости чертежа.
Из условия равновесия сил
YiMA -- 0; 80 ft—50-100 = 0;
I 50° СО С
откуда п = —о— — 62,5 см.
Однако физический маятник был подвешен не в центре втулки,
а на тонком стержне, поэтому
с — h -р г — 66,5 см.
По формуле (16) вычисляем момент инерции относительно оси
подвеса, а затем по теореме о параллельных осях определяем мо-
мент инерции тела относительно оси С:
JC = J — me2 = -i_.80-66,5— -80n^,5a =179 кГ-см-сек\
Ал1 981
22
Результат получен с тремя значащими цифрами, а потому
опыт не требовал особой тщательности и данные, приведенные
автором, по-видимому, несколько округлены. Кроме того, в данном
случае вместо взвешивания на весах следовало повторить опыт
с качанием, изменив ось подвеса маятника на другую, ей парал-
лельную, подвесив шатун второй раз за другую втулку.
§ 5. МЕТОД КАЧАНИЯ НА ПАРАЛЛЕЛЬНЫХ ОСЯХ
Этот метод применяют, если положение центра тяжести не
может быть найдено изложенными способами. Он был предложен
де Прони [345, 346] на заседании Академии наук в Париже
10 марта 1792 г. (см. примечание 3). Прони определял моменты
инерции произвольных тел, центры качания и приведенные длины
по периодам качания тела на двух (или трех) параллельных осях,
лежащих в одной плоскости с центром тяжести.
Пьер Кюри пользовался [1] этим методом для вычисления
моментов инерции коромысел весов.
В СССР метод широко распространен благодаря работам дей-
ствительного члена Академии сельскохозяйственных наук
В. А. Желиговского, успешно применявшего его для определе-
ния моментов инерции деталей сельскохозяйственных машин 157].
Для эксперимента испытуемое тело подвесим на горизонталь-
ной оси А1В1 и, сообщив небольшие колебания, измерим период Т1г
тогда
J с = 4^г т§с — тс2,
где Jc — центральный момент инерции тела относительно оси,
параллельной А^^,
с — расстояние между центром масс С и осью подвеса А1В1.
Для получения второго уравнения тело перевесим на ось АгВг,
проходящую параллельно Л1б] на расстоянии Ь от нее, причем
центр масс С тела должен лежать в плоскости Л1В1Л2В2- Зная
период Г2 малых колебаний тела относительно этой оси, получим
уравнение, не содержащее новых неизвестных,
JcT~ 4:4 mec-2 — mcl,
где с.2 — расстояние между центром масс и осью А.,В2, одно-
значно определяется через с и расстояние Ъ между осями. Гногут
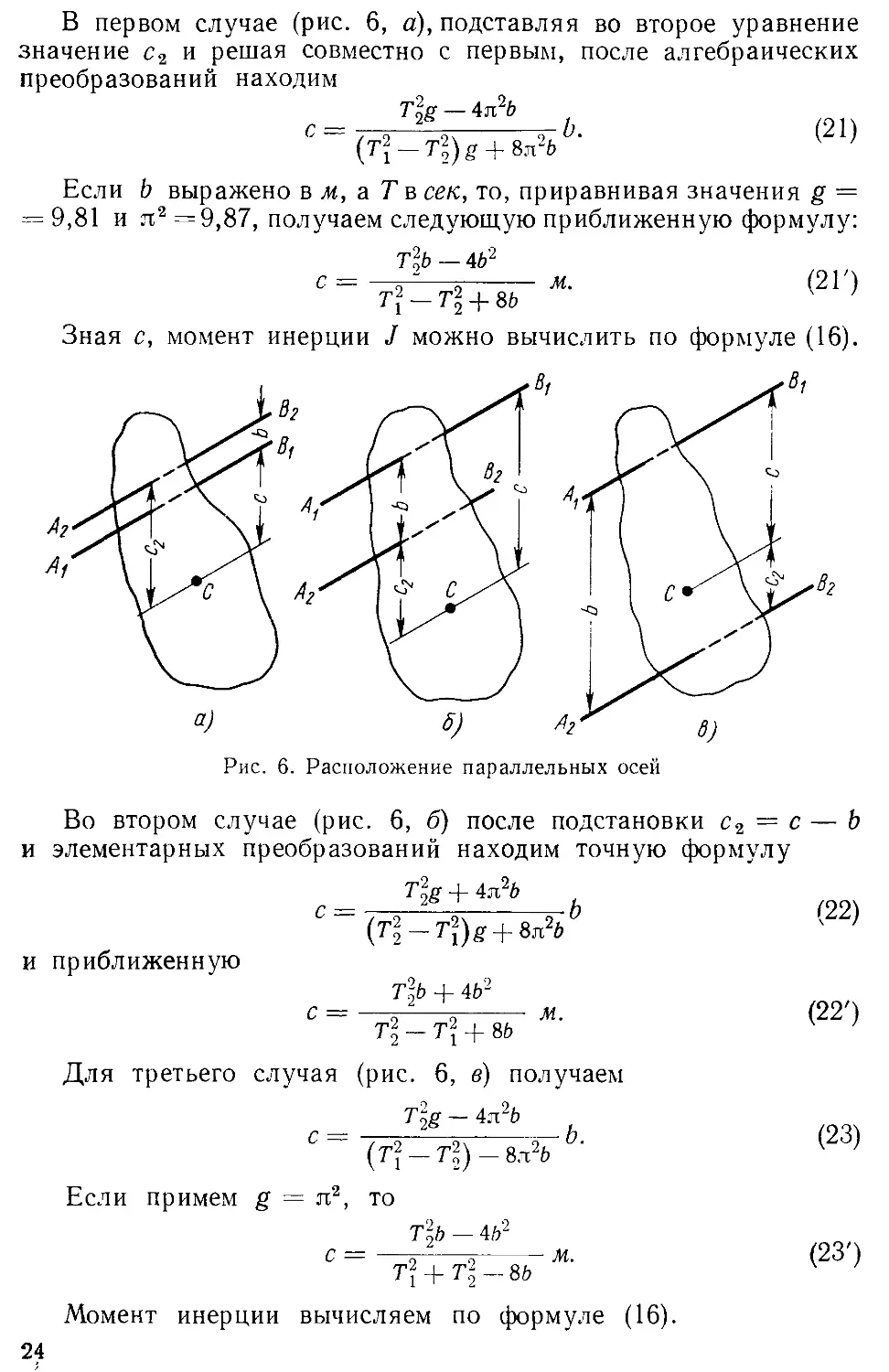
возникнуть три случая, изображенных на рис. 6:
а) ось Л2Й2 и центр масс С расположены по разные стороны
от оси А1В1, тогда с2 =- с + b (рис. 6, а);
б) А2В2 находится между АгВ\ и С; са =■ с — Ь (рис. 6, б);
в) центр масс С лежит между Ах Вг и А2Вг\ с2 -~ Ь —с
(рис. 6, Ь).
23
В первом случае (рис. 6, а), подставляя во второе уравнение
значение с2 и решая совместно с первым, после алгебраических
преобразований находим
с = 7-5 ^ —Ь. (21)
(Tl~Tl)g + Sn2b
Если b выражено в м, а Т в сек., то, приравнивая значения g =
— 9,81 и д2 =9,87, получаем следующую приближенную формулу:
Т\Ь — 4Ь2
с=—^—5 м- (21')
т\ — т\ + &ь '
Зная с, момент инерции J можно вычислить по формуле (16).
Рис. 6. Расположение параллельных осей
Во втором случае (рис. 6, б) после подстановки с2 = с — Ь
и элементарных преобразований находим точную формулу
и приближенную
с =
Tfe + АкЧ
{т\-т\)е + ыЧ
Т\Ь + 4Ь'2
Т\ — Т\ + 86
м.
Для третьего случая (рис. 6, в) получаем
T~2g — 4я2б
{Т\ — Т\) — 8л26
Ъ.
Если примем g = гс2, то
Т\ + Т'\ — 8ft
м.
(22)
(22')
(23)
(23')
Момент инерции вычисляем по формуле (16).
24
Пример 4.
На хлебозаводе № 10 в Москве было проведено динамическое
исследование тестомесильной машины ХТШ выпуска завода
им. В. И. Ленина в Воронеже. Кривошип образован двумя ше-
стернями весом по 121 кГ. На каждой шестерне имеется прилив
в форме сегмента с центральным углом 120', а с диаметрально
противоположной стороны отверстие для пальца кривошипа, на
котором укреплен валик с длинной втулкой; на одном конце
втулки помещен криволинейный месильный рычаг. Момент инер-
ции шестерни был определен методом качания на параллельных
осях с измерением периодов малых качаний, этот метод для ше-
стерен рекомендуют многие авторы, в частности Драгня [231].
Шестерня была подвешена на горизонтальную призму, причем
первый раз призма находилась в отверстии для пальца. По вре-
мени 100 полных колебаний (2 мин 14,7 сек) установлен период
7\ = 1,346 сек, потом было измерено время 103 полных колеба-
ний Т1 = 1,342 сек. Затем было отмечено время некоторого целого
числа колебаний 3 мин 42,0 сек = 222,0 сек, причем число это не
было подсчитано (см. § 17). Разделив это время на полученные
значения периода, находим
-г^-гтг = 164,93 колеб. и т^глг = 165,42 колеб.,
1,34b 1,342 '
заключаем, что полных колебаний было 165 и период
Т1= е = 1,345 сек.
Это значение и было принято для вычислений.
При втором подвешивании призма находилась в центральной
втулке, концентричной с геометрической осью шестерни. Так как
обе оси лежали в плоскости симметрии шестерни и противовеса,
а следовательно, центр масс шестерни находился в плоскости
обеих осей, было выполнено необходимое условие применения
метода. Для проверки выполнения этого условия на шестерне,
находившейся в равновесном положении при первом подвешива-
нии, мелом была проведена вертикальная линия, оказавшаяся
вертикальной и при втором подвешивании.
Расстояние между осями 230 мм. Период малых качаний на
второй оси 72 — 1,555 сек. Вторая ось расположена между пер-
вой осью подвеса и центром масс шестерни, подставляя получен-
ные из опыта данные в формулу (22), находим
с — 312,6 мм.
Тогда момент инерции относительно первой оси
Г2
J\ = -т-- J- mgc = 1733 кГ ■ мм ■ сек2
25
и центральный момент инерции
Jс = Л — тс1 -= 1733—1205 = 528 кГ-мм-сек2.
Расстояние центра масс от второй оси
Ci=c — b= 312,6—230,0 = 82,6 мм.
Диаметр втулки равен 83,0 мм, следовательно, центр масс
шестерни отстоит от оси вращения на расстоянии
82,6 — ^ = 41,1 мм.
Момент инерции шестерни относительно оси вращения находим
по теореме о параллельных осях:
/0 = 528 + -g^-(41,lj2 = 549 кГ-мм-сек2.
Центральный радиус инерции тела
' иС
-1 ,' J с т/528-9810" onfi n
I ИГ = V —121— = 2°6'9 ММ-
Отложив от центра масс С по направлению к оси подвеса отре-
зок СС1 = гис, определим точку Сь при качании на которой маят-
ник имел бы наименьший период. В данном случае точка С\
расположена ближе к первой оси подвеса, этим объясняется тот
факт, что период качания более длинного маятника Т1 оказался
меньше периода качания короткого маятника (коромысла) Т.2.
Момент инерции и положение центра масс удобнее вычислять,
измеряя не период малых качаний, а длину 1пр маятника срав-
нения.
Обозначим длину маятника сравнения при качании тела на
оси AiB1 — /j, а при качании на оси А2В, — /2; расстояние между
осями Ь.
Рассмотрим три возможных случая взаимного расположения
осей подвеса и центра масс тела.
1. с2 — с + Ь; момент инерции тела относительно централь-
ной оси, параллельной оси подвеса,
Jс = J j — те2 — met! — тс2
и
J с = h — mci = т (с + b) 1-, — т (с 4- by.
Из двух уравнений находим
Момент инерции относительно оси А1В1 вычисляют по фор-
муле (20).
26
2. с*
с — b; аналогично случаю 1 находим
k + k
26
(25)
3. с2 = b — с. Центр тяжести лежит между осями подвеса
и расстояние его от оси А1В1 определяется формулой
ti + U
26
(26)
В. А. Желиговским [57] предложен специальный прибор
(рис. 7) для определения моментов инерции этим способом. При-
бор, изготовленный для машиноиспытательной станции сельс-
кохозяйственной академии ^-^
им. Тимирязева, состоит из чы*дт~_^^
двух строго параллельных
и жестко скрепленных между
собой валов. На одном из них
имеется пластина, к которой
винтами прикрепляют испы-
туемое тело. По отвесу прове-
ряют положение центра масс.
Чтобы переменить ось под-
веса, достаточно испытуемое
тело опереть на ножи другим
валом.
Пювре [347] предложил
методом качания на парал-
лельных осях определять мо-
менты инерции автомобилей.
Раму для подвешивания авто-
мобиля сконструировали
Б. Глух, М. Брискин и А. Во-
робьев [48].
На принципе качания ос-
нован прибор проф. Ноак
[332]. Проф. Ф. Виттенбауэр
рекомендует [395] метод качания на трех параллельных осях,
не лежащих в одной плоскости. Об этом же способе писал О. Херр
[280J. Момент инерции тел, которые невозможно последовательно
подвесить на двух осях, расположенных в одной плоскости
с центром масс, можно вычислить после качания на третьей оси,
не лежащей в одной плоскости с первыми двумя. К таким телам
относятся звенья некоторых шарнирных механизмов, имеющие
отверстия для сочленения с соседними звеньями. Подвесив такое
тело в какой-либо точке, проведем вертикальную линию, проходя-
щую через ось подвеса при равновесии. Повторим опыт, подвесив
27
Рис. 7. Прибор В. А. Желиговского
тело в какой-либо другой точке, и на пересечении двух линий
довольно точно определим положение центра масс, а затем по
формуле (16) или (20) вычислим момент инерции тела. Но этим
способом не удается найти центр масс, если, например, тело не
имеет плоской поверхности, на которой можно начертить отвес-
ную линию, или точка пересечения линий находится в полости.
Тогда можно применить метод качания на трех параллельных
осях.
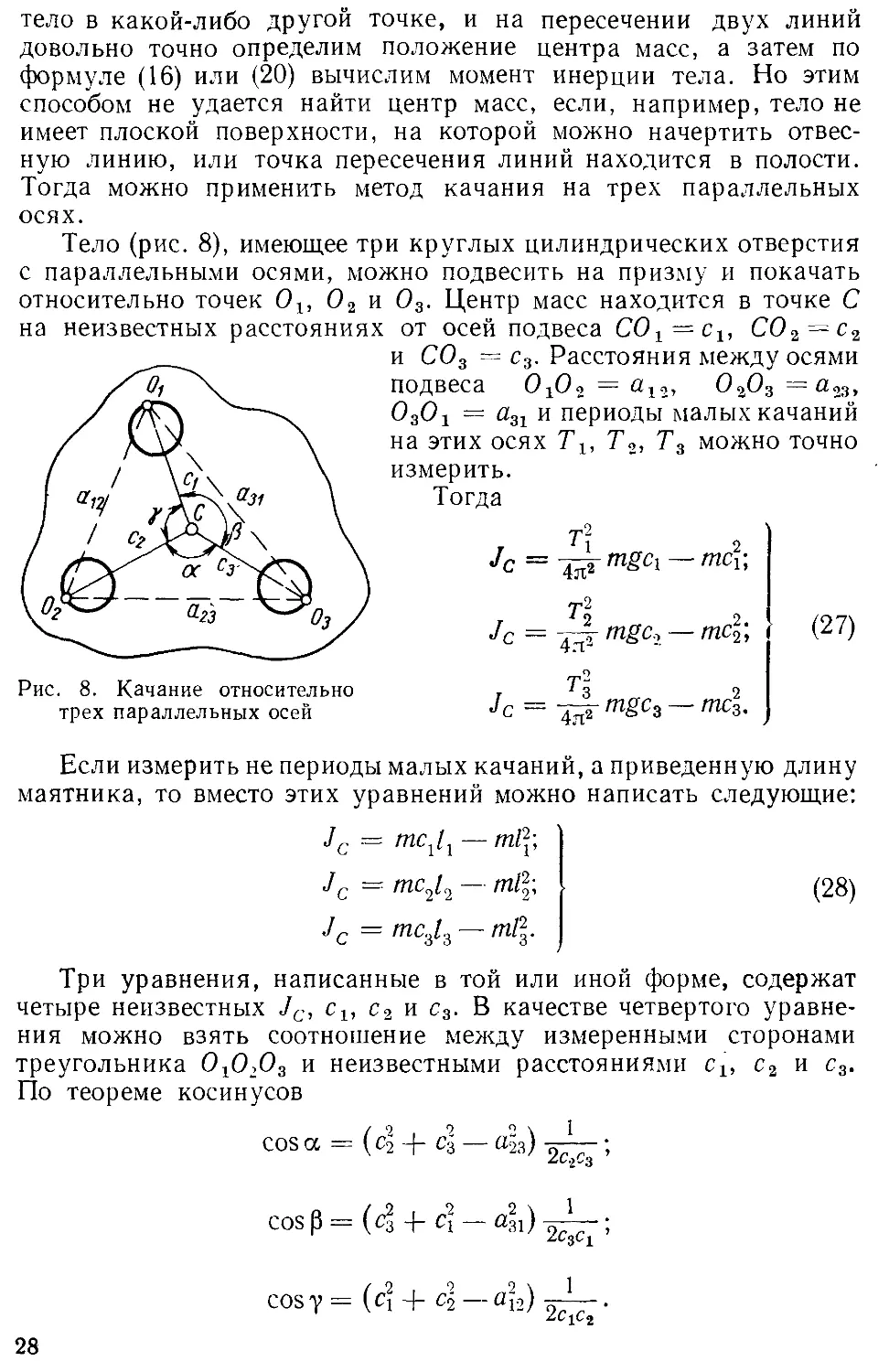
Тело (рис. 8), имеющее три круглых цилиндрических отверстия
с параллельными осями, можно подвесить на призму и покачать
относительно точек 0lt 02 и 03. Центр масс находится в точке С
на неизвестных расстояниях от осей подвеса С01—с1, С02—с2
и С03 = с3. Расстояния между осями
подвеса ОхОг
0*0»
0$! — а31 и периоды малых качаний
на этих осях Т1; Т2, Т3 можно точно
измерить.
Тогда
4я2
mgci
■mc\\
Рис. 8. Качание относительно
трех параллельных осей
Jc
Jc
4я2
п
4rf
% mgc.-, —mc\\ ( (27)
- mgc3 ■
■met
(28)
Если измерить не периоды малых качаний, а приведенную длину
маятника, то вместо этих уравнений можно написать следующие:
J с = mcll1 — ml\\
J c = mc2t2 — mi\,
Jc = тс61г — ml\.
Три уравнения, написанные в той или иной форме, содержат
четыре неизвестных Jc, cu с2 и с3. В качестве четвертого уравне-
ния можно взять соотношение между измеренными сторонами
треугольника 010103 и неизвестными расстояниями cit с2 и с3.
По теореме косинусов
(cl + cl — al3)
cos a
2с,с3
cosp=(c3-f ct — c%i)
\
2csc±
cosy= (c\ + с\ — а\т)
2схсг
28
а + Р + у = 360°, поэтому можно написать соотношение
2 cos a cos P cos у + 1 = cos2 а + cos2 p* + cos2 у.
Подставляя выражения, полученные для косинусов, и умно-
жая на -у21 > получим уравнение, рекомендуемое Виттен-
tCi С-.-)L-*)
бауэром,
(О -) 9 \ / 9 О Q \ / 9 9 9 \ 9 9 9
с; + (5 — аз.,) (сз + с! — flai) (с{ 4- й — ай) + 4c!C2c3 =
= ^(й + с1-ад3)2 + ^(^ + с?~а51)2^^(с^- с^-а?2)2. (29)
Ввиду сложности эксперимента (троекратное перевешивание)
сложности вычислений и в связи с этим невысокой точности, этот
способ следует применять только в тех случаях, когда невоз-
можно использовать более простой и точный метод.
Способом качания на параллельных осях удобно определять
моменты инерции различных прямолинейных звеньев рычажных
механизмов (кривошипов, коромысел, шатунов, кулис), имеющих
по два отверстия, центры которых расположены на одной прямой
с центром масс звена. Этим способом удобно определять моменты
инерции колес и шкивов с противовесами. Положение центра масс
таких звеньев обычно неизвестно, но их можно легко подвесить,
поместив призму один раз во втулке, второй раз оперев на призму
обод так, чтобы новая ось подвеса при равновесии тела находи-
лась в одной вертикальной плоскости с прежней. Главное не-
удобство заключается в том, что необходимо дважды подвешивать
тело, при этом обе оси должны быть строго параллельны между
собой и находиться в одной вертикальной плоскости.
§ 6. МЕТОД КАЧАНИЯ С ЭТАЛОНОМ
Если положение центра масс тела неизвестно, то момент
инерции можно определить методом качания с эталоном [134,
342 и др.]. Использование эталона при наблюдении качаний
физического маятника заимствовано из метода определения мо-
ментов инерции по упругим колебаниям и предложено Гауссом
[258, 259] в 1837 г. Поэтому его часто называют способом Гаусса
[27, 28, 35, 276].
Испытуемое тело подвешивают на горизонтальной оси и ка-
чают как физический маятник. Измеряют приведенную длину
1"Р тс
или период колебаний
Т1 = 2я*\/~—-
t mgc
29
Каждое из этих уравнений содержит два неизвестных: момент
инерции J и расстояние с центра тяжести от оси подвеса.
Для исключения неизвестного с надо отметить (относительно
окружающих предметов) положение равновесия и закрепить эта-
лон, некоторое добавочное тело, положение центра масс и цен-
тральный момент инерции которого известны. Эталон необходимо
присоединить к телу так, чтобы равновесие не нарушилось; только
при этом условии центры тяжести испытуемого тела и эталона
лежат в одной плоскости с острием призмы.
Отклонив тело от равновесного положения, заставляют его
вместе с эталоном качаться подобно физическому маятнику.
Посредством маятника сравнения находят 1.1Пр или секундомером
измеряют период качаний Т.,. Приведенная длина тела с эталоном
lin" ' тс + тэСэ '
где Jэ — центральный момент инерции эталона относительно
оси, параллельной оси подвеса;
т3 — масса эталона;
с3 — расстояние центра масс эталона от оси подвеса.
Определив с из первого опыта через неизвестное пока J:
J
с =
mlnp
и подставив в выражение, полученное для Ln , получим рабочую
формулу
L
J = j— [У, - тс3 (Ln — с3)]. (30)
'2пр hip '
Если обозначить период качания тела Т{, а период качания
тела вместе с эталоном Т2, получим уравнения
Г2 Тт,
J = j^mgc; J =~{mgc+m3gc,)--J, — m3cl,
решение которых приводит к рабочей формуле
J Г?
Г2-Г
(31)
Чтобы выяснить, как влияет расстояние от центра масс эталона
до оси подвеса на параметры маятника, примем эталон за мате-
риальную точку, J3 —■ 0. Тогда из формул (30) и (31) убедимся,
что с присоединением материальной точки к физическому маят-
нику в центре качания (с3 = 1пр = 12пр) приведенная длина маят-
ника и период качания (Г, — Т2) не изменяются (см. Примеча-
ние 4). Поэтому для получения более точных результатов опыта
эталон не следует подвешивать вблизи центра качания. Если
30
эталон подвешен выше центра качания, то 1.2пр <1п„ и Тг <7\.
Если же сэ > 1пр, то и 1.2пр > 1Пр и Га > 7j.
Изменение приведенной длины физического маятника в ре-
зультате присоединения к нему точечной массы тэ на расстоя-
нии с от оси подвеса по направлению к центру масс испытуемого
тела равно
ь-7Пп М1п
/НэСэ (сэ — V)
аир up тс + тзСэ '
Для того чтобы определить значение с,, при котором изменение
приведенной длины маятника достигается посредством груза
наименьшей массы, продифференцируем предыдущее равенство,
считая тэ и сэ переменными и приравняв -т—- нулю:
с = -1-/
Таким образом, эталон следует прикреплять к испытуемому
телу на расстоянии с, от оси подвеса, равном половине значения
приведенной длины физического маятника.
Значение сэ зависит от массы испытуемого тела, его размеров
и формы и эталона.
А. Л. Райх считает [130], что точность можно повысить,
увеличив момент инерции эталона, удовлетворительные резуль-
таты получаются при J3=-^-J.
Интересный вариант метода предложен проф. Крамериусом
в 1892 г. |219], а позже описан Леви-Чивита [309], Линни-
ком |88] и др.
Если подвесить эталон так, чтобы его центр масс лежал на оси
подвеса испытуемого тела, то
тс = (т + тэ) са
и период качания тела с подвешенным эталоном
Т,
J -г J.* Q _. т / J Ч- Jэ
У (т | m3)gc2 f
Тогда
(т | тэ) gc2 У пщс
Т\ J
откуда
т\-т\ - ^'
_ г1
т\ — т\
Если из опыта определяем не периоды, а приведенные длины, то
J + J$ - (m + шэ) c2l,np = md,np
J3 = mc (l,np — lnp).
31
Зная тс, подставим его значение в формулу (20). Тогда
у_ / ^_
•> — J э I _ / -
l-2np hip
Для того чтобы эталон качался синхронно с испытуемым те-
лом, необходимо его жестко соединить с испытуемым телом.
Если испытуемое тело насажено на цилиндрическую ось, качаю-
щуюся в подшипниках, эталон, как предлагает проф. О. Д. Хволь-
сон [161], должен иметь форму кольца, внутренний диаметр
которого равен диаметру вала. Если же испытуемое тело качается
на ребре призмы, то делать такой эталон вряд ли целесообразно.
Для метода Гаусса, как считает проф. Ф. В. Дроздов [55],
момент инерции J3 эталона должен быть «точно высчитан ана-
литически и проверен экспериментально». Поэтому эталонам
обычно придают правильную геометрическую форму (цилиндр,
диск, две пластины). Проф. Е. Гримзель для аналогичного случая
предложил [266] в качестве эталона применять диск с маленьким
концентрическим вырезом, в центре которого находится острие
призмы. По окружности диска расположены небольшие противо-
весы, перемещая которые можно добиться того, чтобы центр тя-
жести диска находился на оси подвеса эталона. Такой диск,
будучи прикреплен к физическому маятнику, совершает посту-
пательное движение и может быть принят за материальную точку.
Изготовив такой эталон из металла, авторы провели специальные
испытания и обнаружили следующий недостаток. Если центр
тяжести диска находится точно на оси подвеса, то при малейшем
сотрясении диск теряет устойчивость. Если с помощью противо-
весов несколько снизить центр тяжести диска, то во время качания
тела эталон приходит в колебательное движение и получается
маятник с двумя степенями свободы.
Поэтому в данном случае диск проф. Гримзеля не следует при-
менять. Эталон надо жестко присоединять к испытуемому телу.
Иногда [106] в качестве эталона используют отдельный физи-
ческий маятник, качающийся на той же оси, что и испытуемое
тело. Для эталонного маятника известны масса тэ, расстояние с,
центра масс от оси подвеса и приведенная длина 13. Сначала
наблюдают качание испытуемого тела, масса которого т; опре-
деляют из опыта его приведенную длину /, расстояние с центра
масс тела от оси подвеса остается неизвестным. Тогда к нему
жестко присоединяют эталонный маятник, подвешенный на той
же оси, и измеряют приведенную длину 1пр маятника, состоя-
щего из испытуемого тела и маятника сравнения:
, mcl -j- тэс31э
пР ~ тс + тэСэ '
откуда
тс (1пр — I) = т,сэ (I, — 1П1)
32
и искомый момент инерции тела выражается уравнением, ана-
логичным формуле (20),
/ = mcl = тэс£ — ~. (32)
Такой эталонный физический маятник должен соответствовать
испытуемому телу. Описание конструкции маятника-эталона при-
водит В. В. Юденич [173]. Для определения моментов инерции
различных тел и даже различных деталей одной машины нужно
иметь ассортимент добавочных тел, для каждого из которых должны
быть известны вес, положение центра тяжести и момент инерции.
Это затрудняет и ограничивает возможность широкого примене-
ния на практике определения моментов инерции методом качания
физического маятника с эталоном.
§ 7. МЕТОД КАЧАНИЯ РОТОРА С ЭТАЛОНОМ
В ПОДШИПНИКАХ РОТОРА
Метод качания маятника с эталоном применяют также в слу-
чае, если испытуемым телом является деталь, вращающаяся во
время работы машины в шариковых подшипниках вокруг непо-
движной центральной оси. К числу таких
деталей принадлежат роторы, маховые ко-
леса, шкивы и пр. Чтобы сообщить телу
маятниковые колебания, надо отсоединить
его от всех соседних звеньев, кроме стани-
ны, и на расстоянии сэ от оси вращения
прикрепить эталон массой тэ (рис. 9).
В качестве эталона обычно применяют
стальную цилиндрическую болванку, мо-
мент инерции J3 которой относительно ее
центральной оси нетрудно вычислить. Роуз
[352] считает, что если сэ приблизительно
равно радиусу г ротора, то вес эталона
должен составлять приблизительно 5%
веса испытуемого тела. При меньшем весе
период качания получается настолько
большим, что наблюдения становятся утомительными и кача-
ния быстро затухают, потому что сильно сказывается влия-
ние трения. При большем весе тело нельзя принимать за мате-
риальную точку и приходится учитывать его момент инерции.
Правильность этого замечания зависит от требуемой точности.
Проф. Грамберг [53] предлагает для уточнения результата
повторить опыт несколько раз с различными эталонами.
При этом способе момент инерции следует определять по пе-
риоду качаний, так как трудно измерить приведенную длину
с использованием маятника сравнения.
3 М. М. Гернет 2274 33
Рис. 9. Качание ротора
с эталоном в подшипни-
ках ротора
Статический момент системы (тело + эталон) относительно
оси вращения в этом опыте равен статическому моменту эталона
тэсэё> и формула для определения момента инерции испытуемого
тела относительно его центральной оси (оси вращения) прини-
мает вид
J = Ш m"c"g — т^ ~~ J$- ^
Если нужно знать приближенное значение момента инерции
испытуемого тела, то моментом инерции эталона можно пре-
небречь и последнее слагаемое в формуле (33) принять равным
нулю.
В эту формулу не входят вес и масса испытуемого тела, следо-
вательно, тело не нужно взвешивать. Это является большим
преимуществом рассматриваемого способа. К числу его недостат-
ков надо отнести трудность точного измерения периода, так как
малые колебания при качании в подшипниках быстро затухают.
Электросекундомером и осциллографом не всегда удается поль-
зоваться, потому что эксперименты обычно производят в завод-
ских условиях.
Большие роторы часто не имеют шариковых подшипников,
поэтому рассмотренный метод невозможно применить там, где
он наиболее удобен, потому что не требует демонтажа машины.
Лучшие результаты можно получить методом атвудовои машины
(см. гл. VI).
§ 8. ВЕСЫ КАЧАНИЯ
Еще один вариант метода качания физического маятника
с эталоном «весы качания» предложил в 1882 г. Е. Брассин [203].
Этот метод отличается от описанного тем, что не эталон, а испы-
туемое тело прикрепляют к физическому маятнику с известным
моментом инерции и качают его вместе с маятником.
Брассин не дает чертежей, но приводит описание весов кача-
ния. Вертикальная трубка пересекает горизонтальную ось под-
веса. Нижняя часть трубки охвачена разградуированным круг-
лым обручем, который можно поворачивать вокруг оси трубки
на любой угол. С обручем жестко соединена вертикальными стой-
ками платформа, на которой можно закрепить испытуемое тело.
Расстояние центра масс системы от оси подвеса можно определить
на тех же весах качания по грузу, прикрепленному к верхней
части трубки, и вызванному им отклонению маятника.
При качании весов вместе с испытуемым телом определяют
момент инерции всей системы относительно оси подвеса и, вычитая
момент инерции весов (постоянная прибора), находят момент инер-
ции тела. Затем переходят к центральной оси инерции испытуе-
34
мого тела, так как расстояние центра масс системы от оси подвеса
и масса испытуемого тела известны.
Повернув платформу вместе с телом вокруг оси трубки на
какой-либо угол, отмеченный по градуированному обручу, можно,
не снимая тела с платформы, определить момент инерции тела
относительно другой оси, лежащей в той же горизонтальной
плоскости. Если же повернуть тело относительно платформы
вокруг какой-либо невертикальной оси, то аналогичными опы-
тами можно получить моменты инерции тела и относительно
других осей (см. гл. IX).
Проф. Крамериус [219] предлагал устанавливать испытуемое
тело на специальном маятнике. На исследованном маятнике,
к которому прикрепляют испытуемое тело, имеется дополнитель-
ный груз. Массу груза и его положение на маятнике можно изме-
нять. Сначала определяют число колебаний в минуту маятника
с испытуемым телом. Затем присоединяют дополнительный груз
и так меняют положение груза или его массу, чтобы число коле-
баний в минуту не изменилось, и на основе полученных данных
находят момент инерции испытуемого тела.
Прибор проф. Крамериуса пригоден для определения моментов
инерции ограниченного числа тел, близких по габаритам и массе,
и имеет учебное, а не практическое значение.
§ 9. МЕТОД КАЧАНИЯ С ПЕРЕМЕЩЕНИЕМ
ДОБАВОЧНОГО ГРУЗА
Основным недостатком всех описанных методов является то,
что необходимо иметь специальные и исследованные эталоны.
Но эксперименты можно проводить и с таким добавочным
телом, момент инерции и положение центра масс которого неиз-
вестны.
В 1934 г. в журнале «Вестник инженеров и техников» была
опубликована статья [33], автор которой предлагал в качестве
эталона использовать любой предмет, например слесарные тиски.
Подвесив испытуемое тело на горизонтальной оси, выводят
его из равновесия и определяют приведенную длину 1Пр или
период Т. Затем прикрепляют к испытуемому телу добавочное
тело, центральный момент инерции J, и положение центра масс
которого могут быть неизвестны; месторасположение его не имеет
принципиального значения, важно только, чтобы равновесие
испытуемого тела не нарушалось от присоединения к нему до-
бавочного. Предположим, что центр масс добавочного тела на-
ходится на расстоянии сэ от оси подвеса испытуемого тела. При-
ведя систему в движение, измеряют приведенную длину физи-
ческого маятника, состоящего из двух тел, или период Т2 его
малых колебаний.
3* 35
При подвешивании к испытуемому телу А добавочного тела В
момент инерции тела А не изменится, а момент инерции всей
системы и ее статический момент относительно оси подвеса станет
равен сумме моментов обоих тел:
или
J + J,
тэс1\
тс + т3с3
Следовательно,
J + J3 + гпэс] = (тс -f тэсэ) /2
(34)
/ + Л -h тэсэ
1^г(™§
тэс&).
(35)
К уравнениям (20) или (16), содержащим два неизвестных
(J и с), присоединим еще одно уравнение (33) или (34), содержа-
щее два неизвестных (J3 и сэ).
Перенесем тело В поступательно на некоторое расстояние Ь по
направлению к оси привеса, не меняя положения испытуемого
тела. В результате перемещения центр масс В будет находиться
на расстоянии с3 — Ь от оси привеса. Найдя из опыта приведенную
длину /3 маятника или период Т3, переместим тело В к оси под-
веса на расстояние d от его начального положения. Тогда расстоя-
ние центра масс тела А от оси подвеса будет сэ—d. Определим
приведенную длину /4 или период Т4 малых колебаний. Это
позволит написать уравнения, не содержащие новых неизвестных.
Таким образом, для метода приведенной длины имеем следую-
щие уравнения с неизвестными /, с, J3 и сэ:
J = mcl;
J = mch -f- ШэСэк — h — гпэСэ;
J = mcls + m, (c3 — b) /3 — J3 — m3 (c3 — b)2; f
J = mclt + шэ (с, — d) lt — J3 — шэ {сэ — d)"1. j
Если замеряем не приведенную длину, а период малых колеба-
ний, то (при тех же неизвестных) получаем следующие уравнения:
(36)
/:
4я2
meg;
4л2
(meg -f- m3c3g) — J3 — тэсэ;
J ^-^[mcg+m3(c3 — b)g]—J3 — m3(c3 — b)1;
J = -^■[mcg + m3{c3 — d)g\—J3 — m3{c3 — df.
(37)
36
Если положение центра масс добавочного тела известно, то
достаточно лишь одного перемещения груза. Заметим, что при
этом способе нет необходимости взвешивать испытуемое тело,
так как величина т может быть исключена из уравнений. Это
является значительным преимуществом метода, так как точное
взвешивание тяжелых тел связано с большими трудностями.
Вносить какие-либо ограничения веса добавочного тела не-
желательно, потому что главное достоинство метода заключается
как раз в отсутствии специальной аппаратуры. Однако слишком
большой вес добавочного тела по сравнению с весом испытуемого
тела уменьшает точность результата. Значения са, b и d зависят
от экспериментатора. В первом положении добавочное тело должно
возможно дальше отстоять от центра качания, потому что, как
было показано при исследовании метода Гаусса, присоединение
добавочной массы в центре качания не сказывается на приведенной
длине и периоде.
Вместе с тем добавочное тело должно возможно дальше от-
стоять от оси привеса. В полученные системы уравнений входит
разность начальной координаты и перемещений тела с3— b и
сэ — d, поэтому относительная ошибка за счет погрешностей
измерения bud будет тем меньше, чем больше значение с,. Сле-
довательно, добавочный груз следует помещать на большом рас-
стоянии сэ и значительно ниже центра качания. Перемещения b
и d должны быть возможно меньшими, но такими, чтобы вызвать
ощутимые изменения в приведенной длине маятника.
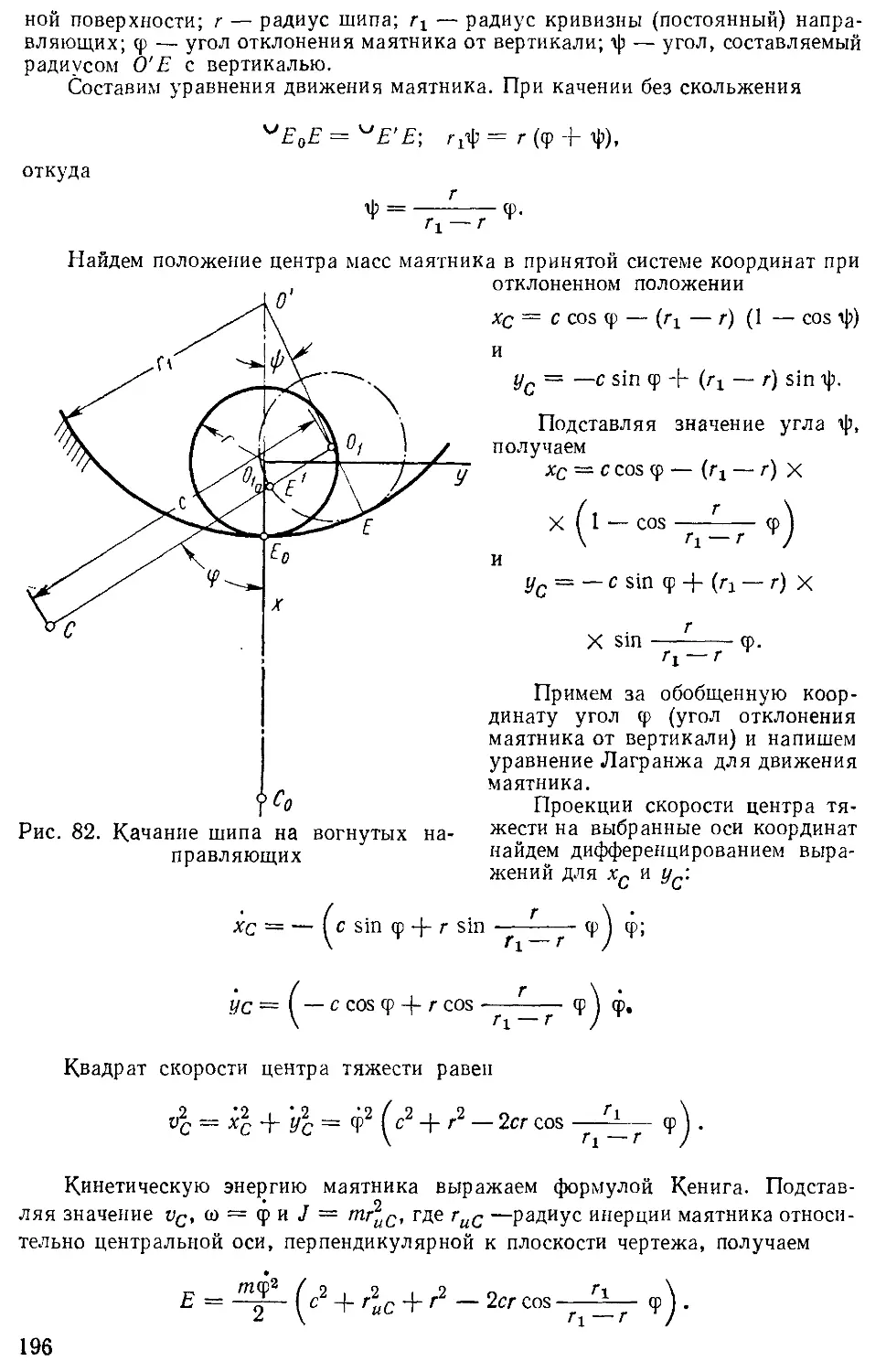
§ 10. МЕТОД КАЧАНИЯ ТЕЛА ПО ВОГНУТЫМ
НАПРАВЛЯЮЩИМ
Если испытуемое тело нельзя подвесить на призму или качать
в собственных подшипниках, то момент инерции можно опреде-
лить следующим методом. Ротор цапфами (шипами) опирают на
две параллельные направляющие (рис. 10) с круглыми углубле-
ниями. Направляющие обычно изготовляют
из тонких стальных полос с выемками, сде-
ланными точно по дуге окружности. Радиус
окружности должен быть подобран так,
чтобы ротор при амплитудах 5—8° качался
без скольжения. При качании маятника на
вогнутых или горизонтальных направляю-
щих скольжение происходит в тех случаях,
когда угол наклона маятника превышает не-
которое предельное значение, называемое
критическим углом отклонения маятника. п 1П _.
Этот вопрос подробно разобран А А Ко- Рис' 10' Качание ро"
робициным [77 781 тара по В0ГНУТЫМ на"
l I i, / о j. . правляющим
37
Период колебаний маятника (см. примечание 5) при качении
без скольжения цапф радиуса г по вогнутым цилиндрическим
направляющим радиуса тх выражается формулой
Т=2л
тп(с — г)'* -f- J с
. meg ( 1 -) j^- J
(38)
где Jc — центральный момент инерции испытуемого тела;
с — расстояние центра масс от оси шипа.
Откуда
^rncg^+^^^-mic-rr (39)
Jc =
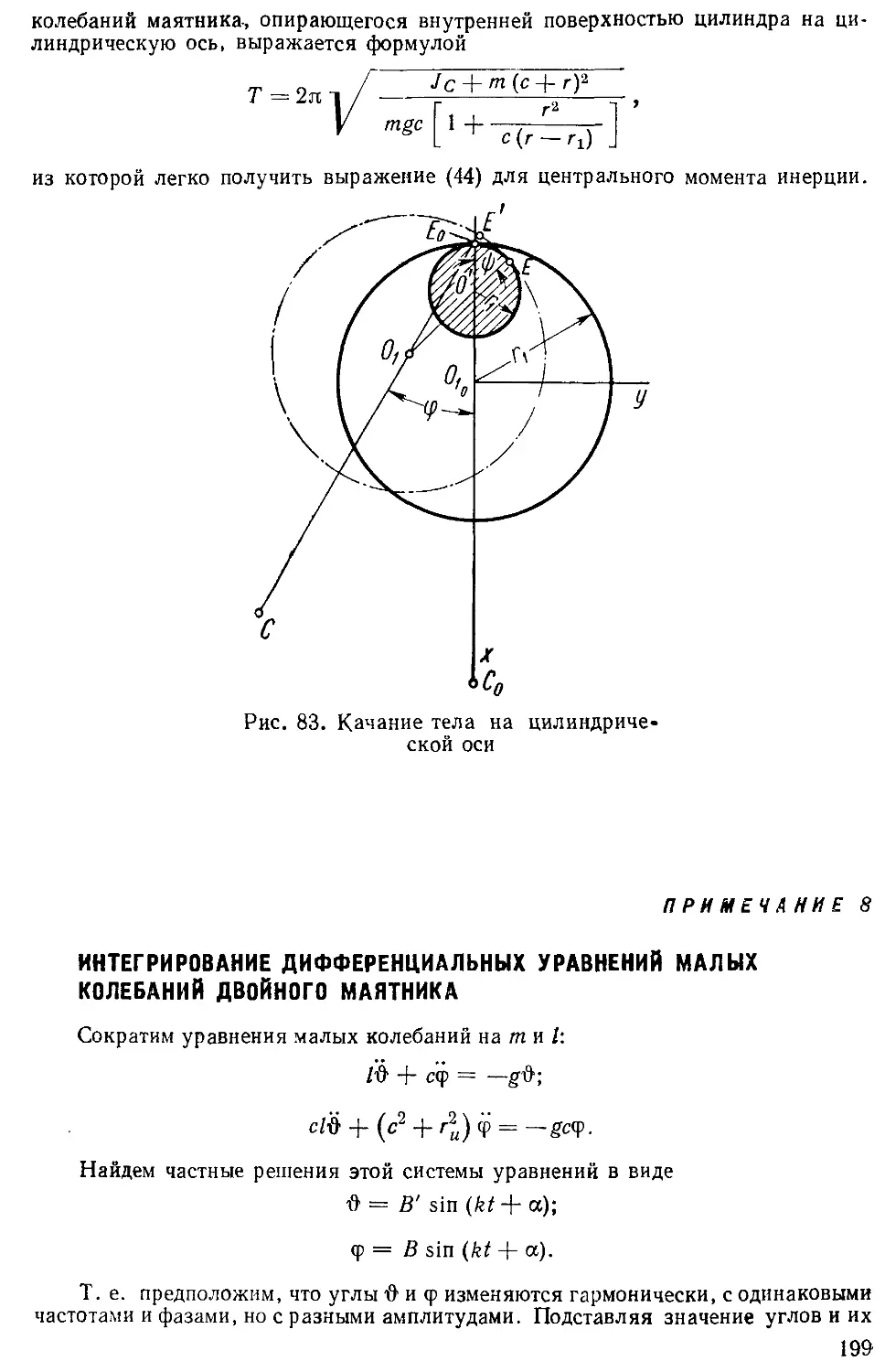
§ 11. МЕТОД КАЧАНИЯ ЭЛЛИПТИЧЕСКОГО МАЯТНИКА
Рассмотрим механическую систему, состоящую из двух точек
(рис. 11, а), соединенных невесомым стержнем ОС, причем дви-
жение точки О ограничено горизонтальной прямой, по кйторой
она может передвигаться без трения, а точка С описывает
эллипс. Такую систему назы-
вают эллиптическим математи-
ческим маятником.
Эллиптический физический
маятник (рис. 11,6) представляет
собой тяжелое тело, положен-
ное круглыми цилиндрическими
шипами на горизонтальные но-
жи. При качании маятника
центр О (ось) шипов совершает
горизонтальные колебания, а
маятник качается относительно
движущейся оси [180, 199, 200,
306, 313].
С помощью такого маятника Дедуи измерил [228] ускорение
поезда с точностью до 0,000lg. Впервые задача о движении эллип-
тического маятника была поставлена и решена Эйлером [244].
Полвека спустя Бессель исследовал [195] движение маят-
ника, опирающегося на подушки из разных материалов (агат,
сталь, латунь). Ребро призмы не может быть абсолютно острым
и ограничено некоторой цилиндрической поверхностью. Поэтому
задачи о качании маятника, опирающегося на плоскость призмой
или цилиндром, по существу идентичны, что значительно повышает
актуальность задачи о качании эллиптического маятника..
Точная, но требующая сложных вычислений формула Дени-
зота [224] для определения четверти периода качания эллипти-
38
Рис. 11. Эллиптический маятник:
а— математический; б — физический
неского маятника, получена из теоремы об изменении кинетиче-
ской энергии. Лаплас [302] и другие авторы применяли здесь
теорему о моментах, считая, что точки, лежащие на оси сопри-
косновения при качении без скольжения, являются неподвиж-
ными. Однако точка соприкосновения (мгновенный центр ско-
ростей) обладает определенным ускорением и ее нельзя считать
неподвижной [74, 75]. Эту ошибку допускают и авторы, предлагаю-
щие применять эллиптический маятник для опытного определения
моментов инерции [27, 68], но здесь эта ошибка имеет несравненно
меньшее значение, чем, например, в гравиметрии, где необходима
высокая точность. Другая ошибка, сделанная некоторыми авто-
рами, заключается в допущении, что центр масс системы (ротор +
+ эталон) находится на оси ротора 168, 383, 384]. Несмотря
на это, полученные ими формулы могут быть приняты как при-
ближенные.
Если в уравнении (39) примем гх = оо, то получим формулу
для определения центрального момента инерции эллиптического
маятника, т. е. тела, качающегося на горизонтальных направ-
ляющих:
Jc = -^mcg — m(c — r)\ (40)
из которой найдем период малых качаний эллиптического маят-
ника [314 и др.]
Т = 2яУ Jc + m{c-r)1.
У meg
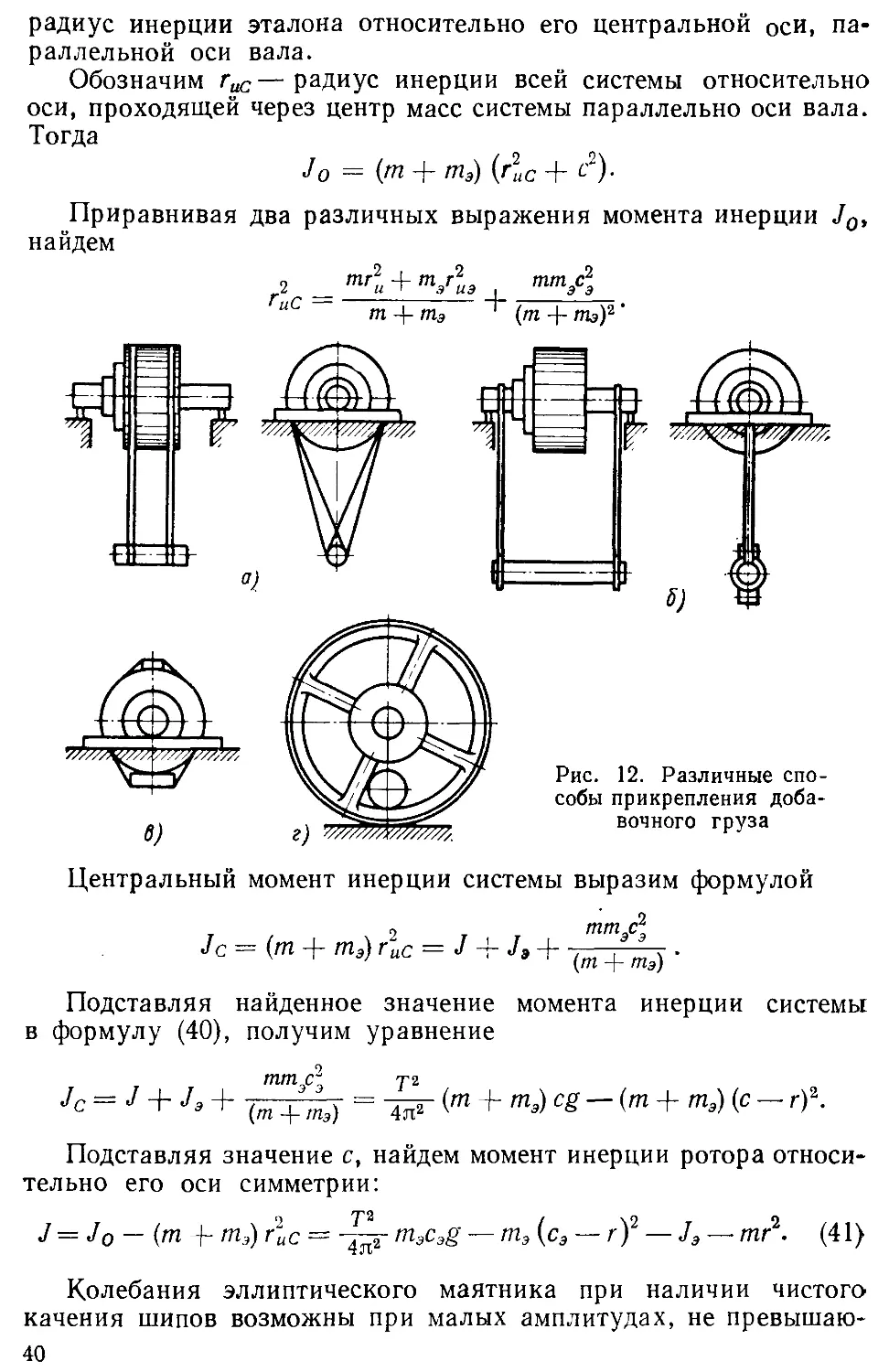
Метод определения моментов инерции качанием эллиптического
маятника часто используют [27, 68, 383, 384 ] для исследования
тел вращения, насаженных на цилиндрический вал и имеющих
центр масс на оси симметрии (роторы электромашин, шкивы,
маховые колеса). Испытуемое тело массы m опирают шипами
(валом) одинакового диаметра на горизонтальные ножи. Чтобы
тело совершало маятниковые колебания, к нему жестко при-
крепляют добавочный груз (эталон) массы пгэ на расстоянии с3
от оси симметрии. Некоторые способы прикрепления изображены
на рис. 12, а—г. Центр масс системы находится от оси симмет-
рии ротора на расстоянии
_ ГПэСэ
m -f- шэ'
Момент инерции J0 относительно оси, проходящей через
центр шипа, равен
J о = J + J, + тэс] = mr\ -f- пгэ {г\э -f- c23),
где J — момент инерции и ги — радиус инерции испытуемого
тела относительно его центральной оси; Jэ — момент и гиэ —
39
радиус инерции эталона относительно его центральной оси, па-
раллельной оси вала.
Обозначим г^—радиус инерции всей системы относительно
оси, проходящей через центр масс системы параллельно оси вала.
Тогда
Jo = (т + тэ) (dc + с2).
Приравнивая два различных выражения момента инерции J0,
найдем
rlc
mrl + m3rla, ттэс1
т-\-тэ
(т + тэ)2 •
v*
т
т.
щж
тЫ
ш%
5)
Рис. 12. Различные спо-
собы прикрепления доба-
с\ i -„„Tj.i.jx,.,, вочного груза
Центральный момент инерции системы выразим формулой
Jc = (m + тэ) rlc = J + J'a +
(т -\- тэ)
Подставляя найденное значение момента инерции системы
в формулу (40), получим уравнение
Jc=J + Ja +
72
(m f тэ) cg — (m + тэ) (с — г)
(т + тэ) 4л2
Подставляя значение с, найдем момент инерции ротора относи-
тельно его оси симметрии:
7*2
J=J0 — {m f тэ) rlc = -j^r m3c3g — тэ (сэ — г) — J3
■mr
(41)
Колебания эллиптического маятника при наличии чистого
качения шипов возможны при малых амплитудах, не превышаю-
40
щих некоторое критическое значение фкр. Проскальзывание в об-
ласти контакта при трении качения изучено А. Ю. Ишлинским
[64]. Скольжение опоры маятника исследовал А. А. Коробицин
[77]. Если амплитуда ф0 превышает критическое значение ц>кв,
то при отклонениях маятника, лежащих между значениями ф0
и ц>кр, шип одновременно катится и скользит, а если ф < фкр,
шип только катится. Следовательно, при ф0 > Ц>кр за одно полное
колебание шип дважды только катится и четырежды катится
с проскальзыванием. В этом случае дифференциальное уравнение
движения и его интеграл значительно усложняются. Поэтому
амплитуды колебаний должны быть меньше критического зна-
чения угла отклонения.
Для качения шипов по плоскости А. А. Коробицин дает при-
ближенную формулу критического угла
*«-/ЬЦ^. (42)
Частные относительные ошибки эксперимента следующие:
&Jm = 6m; 6JC = -^- [~4^г- — 2m(c — r)j Ас;
§у 2т{с-г) bJ Тгш^ьТ.
г Jc Ус2л2
Суммарная среднеквадратическая ошибка вычисления цен-
трального момента инерции по формуле (40)
Нетрудно добиться высокой точности измерения. Массу и
радиус шипа можно точно определить, поэтому основное значе-
ние имеет точность измерения расстояния с и периода Т.
Если центр тяжести симметричного тела лежит на оси ши-
пов, то момент инерции вычисляют по формуле (41). Частные
относительные ошибки
bJm = -£г Am; 6Jms = -±- [ -Qf- c3 — (сэ — г)8] ] Am,;
67'= Ua
Jc
bJr = ~j— [m3 (c3 — r) — mr\ Ar;
41
Суммарная относительная ошибка
Ы0 = Vbfm + Ы1э + bfr + бЛэ + б/' + 5J2r.
Пример 5.
Метод качания по горизонтальной плоскости использован
В. Т. Касьяновым и В. К. Федоровым [68] для эксперименталь-
ного определения момента инерции якоря электромашины.
Дано mg = 2600 кГ; г = 0,099 м\ m3g = 46,7 кГ; сэ = 0,90 м;
Т = 3,97 сек.
Моментом инерции эталона пренебрегли.
Точность замера приведенных величин не указана, однако
судя по их записи, можно предположить, что абсолютные ошибки
не превышали следующих значений:
Amg = 0,5 кГ; Лг = 0,0005 м; Am3g = 0,05 кГ;
Дсэ= 0,005 м; AT = 0,0667 сек.
Подставляя данные эксперимента в формулу (41), найдем
значение момента инерции якоря
J = 11,2 кГ м-сек2.
Суммарная относительная ошибка эксперимента, подсчитан-
ная по данным выше формулам, равна
б/0 = 0,643%.
§ 12. ВЛИЯНИЕ ДИССИПАТИВНЫХ СИЛ НА ПЕРИОД
КОЛЕБАНИЯ МАЯТНИКА
Испытуемое тело при качании претерпевает ряд сопротивлений,
влияющих на период качания. Наиболее значительное влияние
оказывает сопротивление среды и трение в опорах.
Ньютон, наблюдая затухания маятника в воздухе и в воде,
объяснил их различие потерей в весе за счет архимедовой
силы [331].
В 1786 г. Дюбуа [233], а в 1826 г. Бессель [195] указали на
другой важный фактор, влияющий на движение маятника —
присоединенную массу среды, которая увеличивает момент инер-
ции маятника (испытуемого тела) и зависит от его размеров и
формы. По удачному выражению современного английского
исследователя Колин М. Фрей «груз маятника, колеблющийся
в воздушной среде, напоминает веер, который переносит воздух
назад и вперед» [252].
Сопротивление среды зависит от ее плотности, вязкости [139],
температуры, давления, скорости маятника, его размеров и
формы. Во всякое выражение сил сопротивления воздуха входят
42
коэффициенты, значения которых для испытуемых тел неизвестны.
Поэтому в применении к определению моментов инерции методом
качания маятников не имеет большого значения, считать ли со-
противление воздуха зависящим от формы маятника и первой
степени угловой скорости [27, 133, 1401 или же от квадрата ее
[341, 393] или эта зависимость выражается двучленом, содержа-
щим и первую и вторую степень угловой скорости [16], или же
считать момент сопротивления воздуха нелинейной функцией
угловой скорости маятника [71, 79].
Кроме того, если машина, момент инерции детали которой
определяют, предназначена для работы в воздушной среде, то
иногда можно не учитывать поправки на потери вследствие на-
личия воздуха, за исключением случаев, когда требуется большая
точность или испытуемое тело изучено в аэродинамическом отно-
шении (например, самолет).
Влияние трения в опоре маятника впервые было рассмотрено
Л. Эйлером [245]. Этим вопросом занимались Д. И. Менделеев
[100-105], Н. Е. Жуковский [60], Пэнлеве [3361, Буасс [199,
200], Ламб [301], П. М. Агалецкий [4], Б. Л. Очаповский [120]
и др. [10, 225, 370].
Н. Е. Жуковский, интегрируя уравнение движения маятника,
пришел к выводу, что трение в опоре влияет на амплитуду, но не
влияет на изменение периода. Теоретическое и экспериментальное
исследование влияния трения на период по Кулону и по
И. В. Крагельскому проведено А. А. Коробициным [78], пока-
завшим, что на амплитуду маятника при отсутствии скольжения
влияет сопротивление воздуха и незначительно влияют упругие
силы и моменты трения качения. Изменение периода зависит глав-
ным образом от упругости, меньше от амплитуды и незначительно от
сопротивления воздуха, а от моментов трения качения и скольже-
ния не зависит. В случае проскальзывания опор на изменение
амплитуды и периода качаний маятника влияет трение и другие
факторы (см. примечание 6). Если испытуемое тело имеет боль-
шой вес, то его обычно качают не на призме, а на цилиндрическом
шипе и момент инерции определяют без учета момента трения.
Центральный момент инерции тела с учетом трения в шипах
можно вычислить по формуле, предложенной в работе [42]:
где г — число размахов за время /;
Ф0 и ф — начальный и конечный углы поворота.
Для определения момента инерции надо отклонить тело на
начальный угол ср0, отпустить его без начальной скорости, одно-
временно начать счет размахов. В конце опыта остановить секун-
домер и, отметив крайнее положение маятника, измерить конечный
угол отклонения <р.
43
§ 13. ОБЛАСТЬ ПРИМЕНЕНИЯ И РЕКОМЕНДАЦИИ
К ПРОВЕДЕНИЮ ОПЫТА
Метод определения моментов инерции тел по законам качания
физического маятника в том или ином варианте применим к телам
различной формы, размеров и веса.
Некоторые авторы считают, что метод применим только для
определения моментов инерции относительно нецентральных осей,
а относительно центральных его надо вычислять по формуле (8).
Однако качание ротора в собственных подшипниках позволяет
найти момент инерции относительно центральной оси вращения.
Другие авторы [239, 395, 396] рекомендуют его для деталей
«штангообразной формы» или «удлиненной формы». Между тем,
различные варианты метода с успехом применяют к роторам,
шкивам, маховым колесам [53, 319], пластинам [58], автомоби-
лям [47, 48, 178, 347] и другим телам сложной формы [12, 13,
57], хотя для того, чтобы заставить такие тела совершать маят-
никовые колебания, приходится делать специальные подвесы.
Наконец, этим методом возможно определить момент инерции
всякого тела, которое можно закрепить на «весах качания» [203,
219] или укрепить на установке, предложенной Эльжером [236)
и позволяющей найти положение центра тяжести и момент инер-
ции тел весом до нескольких тонн.
Метод неудобен в применении к маленьким легким телам
с небольшим периодом качания [121 ], например к деталям ручных
и карманных часов, так как трудно из опыта определить период
качания маятника меньше 0,5 сек.
Если период качаний превышает 5 сек, то подсчет числа коле-
баний следует производить с применением автоматического счет-
чика. Поэтому его использование целесообразно, если * период
качания тел заключается в пределах от 0,5 до 5,0 сек.
Метод не применим к таким телам, у которых вращающий
момент (момент силы веса) невелик по сравнению с моментом
диссипативных сил, так, например, метод нельзя было бы при-
менить для определения момента инерции дирижабля.
Точность результата зависит от точности производства опыта
и учета различных поправок (конечность амплитуды, трения в оси,
сопротивления среды и пр.). Следовательно, этим методом можно
проводить и ориентировочные и точные измерения моментов
инерции.
И хотя математические вычисления, которые нужно проделать
для получения окончательного результата, несложные, различ-
* Если период мал, то Кольрауш предлагает [292] считать не каждое кача-
ние маятника, а каждое второе или каждое четвертое прохождение, а если
период велик (больше 3 сек), то следует считать не полные колебания, а раз-
махи.
44
ными авторами предложено большое количество разнообразных
номограмм [185, 186, 281, 352], упрощающих эти вычисления.
Большим преимуществом методов, основанных на законе
физического маятника, является то, что при этом не требуется
специальная аппаратура.
§ 14. СПОСОБЫ ПОДВЕШИВАНИЯ
ФИЗИЧЕСКОГО МАЯТНИКА
Способ подвешивания испытуемого тела влияет на точность
эксперимента. Поэтому выбирать его надо осмотрительно и осу-
ществлять тщательно.
Если испытуемое тело имеет круглое
цилиндрическое отверстие (для вала, болта
и т. п.), ось которого параллельна за-
данной оси, то его можно использовать
для подвешивания тела на горизонталь-
ную ось (рис. 13). Если отверстие кони-
ческое, то необходимо вставить в отвер-
стие коническую втулку, имеющую ци-
линдрическое отверстие.
Иногда деталь в месте подвесе необхо-
димо предварительно обработать (напри-
мер, обода маховых колес и шкивов).
Рис. 13. Прибор ТММ-25
(СКБ MB и ССО)
Рис. 14. Приспособление для закрепле-
ния ротора [307]
Если испытуемое тело имеет цилиндрический вал или два
соосных шипа одинакового радиуса, которыми его можно опереть
на горизонтальные ножи или вогнутую поверхность, то момент
инерции можно определить качанием в направляющих. Если
диаметры шипов неодинаковы, то целесообразно сделать специаль-
ные держатели с ножами (рис. 14), как это предлагает Лэр [307],
и установить их на шипы так, чтобы лезвия ножей совпадали
с осью подвеса, параллельной заданной оси.
45
Касьянов и Федоров [68] предлагают на одну из цапф надеть
цилиндрическую втулку. Разница в диаметрах цапф недопустима.
Кроме того, нельзя подкладывать под шкив меньшего радиуса ме-
таллическую полосу, высота которой равна разности радиусов ши-
пов, так как это вызывает скольжение шипов, не предусмотренное
теорией метода, а следовательно, и непригодность выведенных
формул.
Рис. 15. Различные способы подвешивания испытуемого тела
Многие авторы предлагают подвешивать испытуемое тело,
обматывая его проволокой, тесьмой или нитью, в зависимости
от его массивности. Различные способы подвязывания изображены
на рис. 15, а — в [84]. Подвес должен быть коротким [238] и же-
Рис. 16. Установка для качаний автомо- Рис. 17. Неправильный
биля способ подвешивания
тела
Иногда для подвешивания тела сооружают жесткую раму.
Клостерхальфен предложил [2131 конструкцию рамы для качания
закрепленного в ней тела с использованием весов Круппа. На
рис. 16 показана жесткая рама, качающаяся на специальном
штативе, предложенная Б. А. Глух [47].
При конструировании подвесов следует руководствоваться
данными в настоящей главе указаниями об оптимальном периоде
46
качаний одной рамы, рамы с телом, об оптимальном расстоянии
между осями подвеса и качания и др.
Кроме того, необходимо следить, чтобы в подвешенном маят-
нике не возникал опрокидывающий момент относительно гори-
зонтальной оси, перпендикулярной оси подвеса (рис. 17). Под
действием такого момента изменяется плоскость качания маятника
и направление оси подвеса.
§ 15. ОБ УСТРОЙСТВЕ ОСИ ПОДВЕСА
Устройство оси подвеса зависит от веса маятника и требуемой
точности наблюдений. Колебание оси маятника оказывает влияние
на период качаний. Так, при качании штатива с амплитудой
0,04 мк ошибка в полупериоде полусекундного маятника равна
5 • 10"6 сек. Влияние качания штатива интересует не только ме-
хаников, но и физиков, гравиметристов, сейсмо-
логов и др.
Следует отметить исследования в этой области
Н. Е. Жуковского [59], фундаментальные работы
Ю. Д. Буланже [18], П. Л. Капицы [66 и 67]
и другие работы [4, 9, 15, 71, 168, 183, 213, 240,
265, 275, 285, 337].
В зависимости от необходимой точности и веса
тела в качестве оси используют лезвие ножа, спе-
циально изготовленные стальные и агатовые приз-
мы, угловое железо с заостренным ребром, напиль-
ник с ребром, отточенным на наждачном круге, а
также стальные балки различных сечений с зао-
стренным верхним ребром. Сечение призмы обычно
бывает треугольное. Бариффи применяет [185]
призмы с квадратным сечением что увеличивает вдвое жесткость.
Если испытуемое тело подвешено на консольной оси, то конец
консоли закрепляют соответствующими растяжками (рис. 18).
В зависимости от устройства подвеса и его оси следует при-
менять те или иные из полученных формул. Так, если ось подвеса
можно считать неподвижной и ребро призмы абсолютно острым,
то момент инерции тела относительно этой оси следует вычислять
по формулам (16) и (20), если же маятник перекатывается цапфами
по вогнутым поверхностям, то по формуле (39), а если подвешен
в системе «шип—подшипник», то по формуле (43).
В случае, когда маятник, имеющий цилиндрические отверстия
радиуса г1г перекатывается по круглому цилиндрическому прутку
радиуса г, центральный момент инерции маятника следует вы-
числять (см. примечание 7) по формуле
Рис. 18. Кон-
сольная опора
с растяжками
Jr =
4 л2
meg
О-7(^70 )-*(' +'>*■
(44)
47
§ 16. О НАБЛЮДЕНИЯХ С МАЯТНИКОМ СРАВНЕНИЯ
Груз маятника сравнения должен быть небольшим, но таким,
чтобы нитка была натянута и чтобы колебания не затухали.
Привязав к грузу тонкую нитку, не следует тотчас же произ-
водить наблюдения, а нужно на некоторое время подвесить маят-
ник сравнения как отвес, чтобы нитка могла раскрутиться под
тяжестью груза.
Большое несовпадение периодов легко заметить, но если пе-
риоды качаний небольшие и близкие между собой, то бывает
трудно определить, какой маятник качается с большей частотой.
В таком случае рекомендуем сначала следить только за одним
маятником (например, физическим) и вслух считать качания,
затем, продолжая счет по ритму, перейти к другому (маятник
сравнения). Тогда легко установить, обгоняет ли маятник срав-
нения физический или отстает от него. Чтобы обнаружить неболь-
шую разницу в периодах, нужно наблюдать большое число кача-
ний. Анализ показывает, что чувствительность этого метода тем
выше, чем больше амплитуда колебаний маятников. Важно,
чтобы амплитуды обоих маятников были приблизительно одина-
ковы.
Перед маятниками можно поставить узкий высокий экран,
загораживающий маятники при их отвесном положении, и наблю-
дать закрытие качающихся маятников экраном; можно исполь-
зовать широкий экран с вертикальной щелью.
При большой приведенной длине маятника небольшая погреш-
ность в ее измерении не вызывает значительной ошибки. Например,
если 1пр = 100 см, неточность в ее определении даже на санти-
метр не вызывает в результате большей ошибки, чем погрешность
0,01 сек при определении момента инерции по наблюдению периода
малых качаний. Однако асинхронность качаний легче обнаружить
при небольшой приведенной длине.
Оба маятника качаются на параллельных осях: физический —
на верхнем ребре призмы, а маятник сравнения — на боковом её
ребре; длину последнего надо измерять от оси подвеса до центра
тяжести груза.
§ 17. ОБ ИЗМЕРЕНИИ ПЕРИОДА КОЛЕБАНИЙ ФИЗИЧЕСКОГО
МАЯТНИКА И ДРУГИХ МЕХАНИЧЕСКИХ СИСТЕМ
Период качания можно измерить, подсчитав число качаний
за выбранный промежуток времени или определив время по числу
качаний. Первый из указанных способов [292] имел преимущества
в те времена, когда в употреблении не было электросекундоме-
ров и секундомеров. Этот способ иногда применяют и теперь,
так как он позволяет измерить период колебаний с точностью
до 0,1 сек. Энсслин [182, 239] предлагает измерять число z полу-
48
качаний в минуту и определять приведенную длину по формуле
1пр ==—j—. Виттенбауэр [395, 396] рекомендует отсчитывать
число г полуколебаний в минуту и использовать формулу J =
= 365-^р-; Эльзессер [238] предлагает измерить продолжитель-
ность 200 колебаний, затем вычислить число размахов в минуту z
и определить центральный момент инерции по формуле J =
= ~Ш~\—'~- ''Г Аналогичные рекомендации дают дру-
гие авторы ]28]. 'Следует отметить, что пересчет на число полу-
колебаний в минуту только осложняет вычисления и вносит
неточность.
И. И. Артоболевский в одной из своих ранних работ писал:
«Определяя период Т, надо задаваться числом колебаний, время
которых определяется, а нельзя задаваться временем и подсчиты-
вать, какое количество колебаний сделает тело за выбранный
промежуток времени, так как число колебаний может получиться
нецелым, что дает ошибку в опыте» [6]. Поэтому, определив
период качаний, надо измерить промежуток времени, в течение
которого маятник совершает выбранное число колебаний.
Однако возникает вопрос, какое число полных колебаний
нужно выбрать. Некоторые авторы советуют определять время
10 качаний 150, 53], 10—20 качаний [7, 171, 172], другие 25—30
качаний [63], 50 [177, 281] и 200 в зависимости от требуемой
точности. Наблюдатель при пуске секундомера и остановке его
допускает ошибки, причем значение этих ошибок уменьшается
пропорционально увеличению числа качаний. Малые колебания
быстро затухают. Декремент колебаний меньше у тяжелых маят-
ников с большим периодом. Но отсчитывать большое число мед-
ленных колебаний затруднительно, внимание экспериментатора
ослабевает и он иногда сбивается со счета. Поэтому считать коле-
бания надо вслух, и если период большой, то удобнее отсчиты-
вать полупериоды. При пуске секундомера счет надо начинать
со слова «нуль», а не «раз» [7, 171].
Некоторые наблюдатели [145] советуют отсчитывать колеба-
ния от крайнего положения маятника, но большинство [200 и др].
рекомендуют отмечать прохождение маятника через равновесное
положение. Кольрауш пишет: «Время самого поворота неудобно
для непосредственного наблюдения, так как именно в это время
движение тела незаметно. Напротив, вблизи положения равновесия
тело движется с наибольшей скоростью и мгновение прохождения
через это положение можно точно замерить» [292]. Начинать
счет качаний не обязательно при первом прохождении маятника
через равновесие, удобнее это сделать, спустя несколько колебаний.
Гельмгольц [273] сделал следующее предложение: «Нет необ-
ходимости считать качания в течение всего времени; вполне
4 М. М. Гернет 2274
49
возможно отойти после наблюдения в течение небольшого про-
межутка времени и некоторое время спустя повторить наблюде-
ния. Истекшее время должно содержать в себе во всяком случае
целое значение Т, какое? — вытекает без сомнения из первого
приближения для Т, которое можно вывести по немногим кача-
ниям» (см. пример 4). Однако, так как трение влияет не только
на амплитуду, но и на период качания маятников [42], этим спо-
собом подсчета можно пользоваться лишь при полном отсутствии
проскальзывания призмы маятника.
Экспериментатор должен с особой тщательностью измерить
период качаний, поэтому продолжительность заданного числа
качаний надо определить несколько раз и вывести период как
среднее многих наблюдений. Для устранения случайных ошибок
желательно повторять весь эксперимент, начиная с подвешивания
испытуемого тела на ось.
Ввиду того, что погрешность определения периода сказывается
на окончательном результате, наблюдения надо производить
с электросекундомером или, в крайнем случае, с секундомером.
♦ ♦♦
Глава III
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МЕТОДОМ
КАЧАНИЯ ДВОЙНОГО МАЯТНИКА
§ 1. ИСТОРИЯ МЕТОДА. ТЕОРИЯ МЕТОДА
Тяжелая материальная точка А (рис. 19, а) соединена невесо-
мой нерастяжимой нитью I с неподвижной точкой О и нитью с
с тяжелой материальной точкой С. Такая система, будучи выве-
денной из равновесного состоя-
ния, совершает колебания в верти-
кальной плоскости под действием
веса точек и называется двойным
математическим маятником.
Если точку С и нить СА
заменить материальным телом
(рис. 19, б) или если, кроме того,
и точку А с нитью АО заменить
Рис. 19. Двойной маятник (схема)
телом, устроив в точке О неподвижную, а в точке А подвижную
параллельные горизонтальные оси (рис. 19, б), то получится двой-
ной физический вертикальный маятник (рис. 20).
Впервые в литературе двойной маятник описан Клеро [210].
Ряд своих работ, посвященных качанию двойного маятника,
опубликовал в Комментариях Петербургской Академии Наук
Даниил Бернулли. Он же разработал полную теорию качания
двойного маятника [192, 193].
Двойной вертикальный маятник является примером системы
с двумя степенями свободы и описан во многих курсах и статьях
4* 51
Рис. 20 Двойной маятник
[8, 91, 134, 175, 309, 314, 283]. А. И. Лурье приводит [93] урав-
нения движения двойного маятника, учитывая силы веса и со-
противления среды, принятые по квадратичному закону. Много
различных вариантов двойного маятника приводит Буасс [199,
200]. В курсе Кабанна [206] рассмотрен маятник, состоящий
из п точек. Эта задача интересовала и Эйлера [241].
Двойной маятник применяют для различных технических
целей так, например, для маятниковых регуляторов [23]. Поль-
зуясь теорией двойного маятника, пытались найти неподвижную
плоскость на качающемся корабле. Благодаря этой теории удалось
объяснить [380], почему не звонил императорский колокол Кельн-
ского собора. Колокол не может звучать, если в состоянии покоя
центр качания колокола совпадает с центром качания языка.
Приведенная длина колокола Кельнского собора /„ к — 328,2 см,
приведенная длина языка 1пр,я~ 262,9 см, расстояние точки при-
веса языка от точки привеса колокола I = 66,7 см. Таким обра-
зом, центр качания языка отстоял от оси привеса колокола
на расстоянии 262,9 -+- 66,7 = 329,6 см, т. е. почти совпадал
с центром качания колокола. Колокол стал звонить лишь после
того, как была изменена приведенная длина языка.
Для определения моментов инерции двойной маятник впервые
был предложен в 1923 г. В. П. Ветчинкиным и Н. Г. Ченцовым,
ими же была разработана теория метода [25]. С иных позиций
эту теорию подробно рассмотрели Л. Г. Лойцянский и А. И. Лурье
[90].
Метод был принят для определения моментов инерции само-
летов, и в ЦАГИ был сконструирован и построен специальный
подвес ПЭ1, позволяющий качать самолет на бифилярном подвесе
относительно вертикальной оси и как двойной маятник относи-
тельно горизонтальных осей. В подвес были внесены конструктив-
ные улучшения, и новый подвес ПЭ2 вполне отвечал своему
назначению (рис. 21). Оба подвеса и эксперименты подробно
описаны в работах Ю. А. Победоносцева [123, 124]. Для само-
лётов этот метод применяют и за рубежом [262].
Чтобы определить момент инерции относительно главной
центральной оси, тело подвешивают на двух стержнях
АО или на двух тесьмах одинаковой длины, расположен-
ных симметрично относительно центра тяжести, или его пред-
полагаемого местонахождения и так, чтобы при равновесии
системы горизонтальные отрезки АА и 00 были параллельны
заданной оси.
Такая система является маятником с двумя степенями сво-
боды, и испытуемое тело совершает плоское движение в вертикаль-
ной плоскости, перпендикулярной осям. Пересечем тело пло-
скостью, проходящей через его центр масс С, и изучим плоское
движение системы. Масса нитей мала по сравнению с массой
тела и ею можно пренебречь.
52
Рассмотрим малые колебания двойного маятника. Для этого
построим декартовы координаты с началом в точке О, направив
ось Ох вертикально вниз (рис. 22).
Система, выведенная из устойчивого равновесия, совершает
малые колебания. Во всякое мгновение центр тяжести С имеет
координаты
х — I cos ft -1 с cos (f;
у = I sin ft | с sin «p,
где I = АО, с = С A, a ft и cp — углы, составляемые АО и С А
с вертикалью и являющиеся некоторыми функциями времени.
Рис. 21. Подвешивание самолета (подвес ПЭ1 ЦАГИ)
Пренебрегая сопротивлениями, составим уравнения Лагранжа
для находящейся в потенциальном поле механической системы
с двумя степенями свободы. Подсчитаем кинетическую и потен-
циальную энергии.
Кинетическую энергию выразим формулой Кенига
ис , Jc
5 Г
W
Скорость центра масс определим дифференцированием его
координат:
v2c = 'xl +ijc = *V + сУ + 2c/ftcpxos (ф — ft).
Момент инерции тела представим произведением его массы
на квадрат радиуса инерции г„ и получим
[/ft2 + (с2 + г\) ер2 + 2с^''ф cos (ф — ft)].
53
Выражение потенциальной энергии имеет вид
П = mgh + С,
где С — постоянная интеграции, которую можно выбрать про-
извольно, так как важно знать не абсолютную величину потен-
циальной энергии, а ее приращение. За нулевое положение си-
стемы примем положение устойчивого равновесия, тогда
П = trig [I (1 — cos ft) + с 0 — cos ф) ].
При малых колебаниях системы (ft и ф малы) кинетическую
и потенциальную энергии с точностью до малых второго порядка
включительно, можно представить в виде
•2
Е= -.[№ + (С2 + г2и)ф2+2с^ф];
Приняв за обобщенные координаты системы
углы ft и ф, возьмем частные производные по
обобщенным координатам и обобщенным ско-
ростям
m/2ft 4- mc/ф;
дЕ
= 0;
дП
= т.
\<mq
Рис. 22. Колебания
двойного маятника
Подставив эти
дЕ
= 0;
дЕ
aft dft
—'— = т(с2 + г\) ф + tnclb;
дц>
т
в уравнения Лагранжа
дЕ = _д[^
dqi ~ dqt '
уравнения малых колебаний си-
(46)
величины
составим дифференциальные
стемы:
/n/2ft + mclq> = — mgl&;
mcib + m (с2 + r2u) Ф = — mgcq>.
Интегрируя эти уравнения (см. примечание 8), находим сле-
дующее общее решение:
ft = Bjpj sin (kj + «j) + flapg sin (k2t + a2); (47)
Ф = Вг sin (kxt + «i) + B2 sin (k2t + a2),
где Вх и B2, a: и a2 — постоянные интегрирования, определяе-
мые по начальным данным,
54
ki и k2 — частоты главных колебаний, зависящие от параметров
маятника:
7л \с'2 + rl + cl-V {F+rl + clf-Aclri];
^______^ (48>
J_ [с. + г1 + сЦ-У (<* + rl + elf - Aclrl].
k\.
b2 - 8
К2 — -Г-
Из общего решения следует, что изменение каждого из углов,
определяющих положение тела, обусловлено суммой двух главных
колебаний с различными частотами kx и k2. Так как
р\ всегда положительная величина, а р% — отри-
цательная, то, следовательно, первое главное коле-
бание (с низшей частотой) происходит так, что и
нить О А, и прямолинейный отрезок АС в каждое
мгновение бывают отклонены от вертикали по одну
и ту же сторону и проходят через отвесное поло-
жение одновременно, причем отношение углов от-
клонения остается постоянным •&1: <рх = Pi (см.
рис. 22). Во втором главном колебании углы от-
клонения отложены всегда по разные стороны
от вертикали, при неизменном отношении углов
({>2: ф2 - р2) (рис. 23).
Определив из опыта периоды обоих главных
_. I гп 2я ~ 2л \
колебании маятника ( / i = -т—, 12 = ~тг~ )> можно
вычислить момент инерции испытуемого тела. Для
получения рабочей формулы составим сумму и
произведение квадратов частот:
Цтд
Рис. 23. Ко-
лебания
двойного
маятника
J.2
4я"
4л'
l
cl
^1*^2 —
(4я2)2
Т2Т2
'Г2
/z
_с/_
„2
Путем алгебраических преобразований находим уравнение,
определяющее расстояние с до центра масс, и радиус инерции ги:
4лЧ \ / 4л2/
/
\-ыч) (п
71);
/•"« = cl
АпЧ
2 ^т2
J \1 2-
Если расстояние с известно, то, умножая это равенство на т,
находим формулу момента инерции
J=md ШУTlTl (49)
55
Если же это расстояние с достаточной точностью неизвестно,
то, подставляя значение с из предыдущего равенства, получаем
следующую формулу:
'=т12Ш^ЩП-^-)-{^—Т1). (50)
В начале опыта испытуемое тело и подвес отклоняют от верти-
кали на некоторые углы ср0 и Ф0 и отпускают без начальных ско-
ростей (ф0 = 0 и Ь0 = 0). Исследуем колебания тела именно при
этих начальных условиях. Дифференцируя уравнение (47) по
времени и подставляя начальные данные, получим
B^kj cos oci + fi2p2&2 cos a2 = 0;
Bik\ cos ai + 52fe| cos a^ = 0.
Следовательно, начальные фазы обоих колебаний
я
ах =2 a2 = _.
Подставим значения начальных углов и начальных фаз в фор-
мулу (47):
В^ + ВДг -#„;
Откуда
Я1==
В9
Bt + В2 = ф0.
«. + T*(lfe-*1-')
S /г2 т2\
-^ + f.Q-w7l)
Чтобы легче было определить периоды главных колебаний,
выберем такие начальные углы О0 и ф0, при которых одно из двух
главных колебаний системы отсутствует. Так, приравнивая
нулю В 2, находим
<>о = Фо(1 - 4^Г ^)- (51)
Приравнивая нулю Blt будем иметь
*о = -Фо(1§Г7'?-1). (52)
Следовательно, если нить и тело перед началом опыта откло-
нены в одну и ту же сторону, а углы их отклонения от вертикали
56
удовлетворяют условию (51), то механическая система совершает
только низшее главное колебание (см. рис. 22). При таком
движении легко определить период Ту низших колебаний.
Если же в начальное мгновение нить и тело отклонены от
вертикали в разные стороны, причем так, что отношение абсолют-
ных величин углов равняется 1: (-jjrr Т\— l), то система со-
вершает только высшее главное колебание (см. рис. 23). Нить ОА
и прямая АС проходят через отвесное положение в одни и те же
мгновения, но с разных сторон. Период Т2 высших колебаний
также просто измерить.
Однако для облегчения наблюдений периодов главных колеба-
ний нельзя пользоваться формулами (51) и (52), так как они
содержат искомые величины 7\ и Т2. При эксперименте начальные
отклонения находим путем подбора, давая телу и нити раз-
личные начальные углы, добиваемся того, чтобы система совер-
шала только одно из главных колебаний. Измерив период этого
колебания, надо продолжить эксперимент, задавая новые началь-
ные углы, при которых система совершает второе главное коле-
бание [25].
§ 2. ОШИБКИ ОПРЕДЕЛЕНИЯ МОМЕНТА ИНЕРЦИИ
МЕТОДОМ КАЧАНИЯ ДВОЙНОГО МАЯТНИКА
В практике определения моментов инерции методом двойного
маятника могут встретиться два случая. Первый, более общий
случай, заключается в определении момента инерции тела с неиз-
вестным положением центра масс. Второй, частный случай,
возможен при определении момента инерции тела, положение
центра масс которого найдено дополнительным экспериментом,
но тело невозможно подвесить так, чтобы оно качалось как физи-
ческий маятник с одной степенью свободы.
В первом случае рабочей является формула (50); при опыте
надо измерить массу m тела, длину / нити и периоды Т1 и Г2
двух главных колебаний маятника.
Относительная ошибка за счет неточности измерения массы
т т
Относительная ошибка от неточности измерения длины нити
т--2 гр2
57
Относительная ошибка, обусловленная неточностью измере-
ния периода низших колебаний,
2Т
,2 4 л2/
8
«'r, = 2—-T&-67V
4пЧ
Наконец, ошибка измерения периода высших колебаний
4пЧ
g
чт%
6/г, = 2 —р-55 67г.
т' 4 я2/ _2
'м
^ 2
Суммарная среднеквадратическая ошибка определения мо-
мента инерции по формуле (50) равна
Ы = V (&„)* + № + (6А,)2 4- (6/,/-
Как видно из приведенных формул, точность определения мо-
мента инерции зависит не только от точности измерения величин,
но и от значений параметров подвеса, в частности от длины нити /
и расстояния с.
Вычислим относительную ошибку вычисления расстояния
центра масс С тела от точки А привеса
&с = Yibct? 4- (бсг,)« + фсТ1)\
где частные относительные ошибки
г2
бсг =2 . „, 67,;
*yl
Ч = 2-4ЙЧ =78Г«
Для определения момента инерции тела при известном поло-
жении центра масс нужно пользоваться формулой (49). Частные
относительные ошибки вычисления момента инерции по этой
формуле, обусловленные ошибками, допущенными при измерении
массы, длины нити, расстояния с и периодов главных колебаний,
равны
6/„, - 6ш; 6/, = 6/; Ы, = 6c6/Ti -- 267Х; 6/Го = 267,.
58
Тогда общая среднеквадратическая ошибка вычисления мо-
мента инерции определится формулой
б/ = УФ'пУ + (б/)2 + (бс)2 + 4 [(6Г,)2 + (6Т2)2].
§ 3. УСТАНОВЛЕНИЕ ОПТИМАЛЬНЫХ
ПАРАМЕТРОВ МАЯТНИКА
Экспериментатор может по своему усмотрению изменять неко-
торые параметры двойного маятника, например, длину I нити,
а иногда и расстояние с.
А. Н. Волохов[27] пишет: «Если с равно нулю, то ошибка АТг
совсем не скажется на У» и дает следующую рекомендацию: «Итак,
для точности определения момента инерции длина нити подвеса
должна быть возможно больше и точка подвеса должна быть по
возможности ближе к центру тяжести испытуемого тела». Чтобы
убедиться в ошибочности такой рекомендации, достаточно в фор-
мулы (48) подставить с = 0. Тогда получим
*!=0; kt= Y~r-
При условиях, рекомендуемых А. Н. Волоховым, двойной
маятник превращается в математический, испытуемое тело, под-
вешенное в центре тяжести, движется поступательно и, следова-
тельно, момент инерции невозможно определить. Гримзель [2661
предлагал воспроизводить математический маятник, заменив ма-
териальную точку физическим телом, подвешенным в центре тя-
жести, потому что в таком случае твердое тело движется посту-
пательно.
Исследование показывает, что если при постоянных ги к I
увеличивать расстояние с между центром масс и точкой подвеса,
то высшая частота колебания возрастает монотонно, а низшая при
с — -j- (\/12 _|_ 1бг„ I) имеет максимум (см. примечание 9).
Для очень малых и очень больших значений с низшая частота
близка к нулю.
В качестве примера на графике (рис. 24) приведены значения ki
и k\ в зависимости от с при / = г„ = 1.
Для выявления влияния параметров с и I двойного маятника на
точность эксперимента используем равенства, выражающие ошибки
в определении момента инерции от неточности измерений различ-
ных параметров маятника. Учтем, что ошибками измерения массы
тела и длины нити можно пренебречь по сравнению с ошибками
измерения периодов. Абсолютные ошибки измерения периодов
будем считать одинаковыми.
ДГХ = АТ2 = AT.
59
Проведенные исследования (см. примечание 10) показали, что
не существует такой оптимальной длины /, при которой погреш-
ность измерения периода не влияет на момент инерции. Однако
полученные зависимости позволяют сделать некоторые рекомен-
дации. В общем случае, при неизвестном положении центра масс,
но некоторых определенных, хотя и точно неизвестных, значени-
ях с и ги, наименьшая ошибка
получается для
25.6
19,6
9,8С
3,8?
3.72
"у
к. кг
^^-Hl
0.78<t
1
I — 1 / *** ' 2 I Г"
hxcmp —у -ТГ — С- — Ги - \- -^- .
' и
(53)
Если введем параметры q =
= — и и = —, то уравнение (53)
Рис. 24. Зависимость частот колеба-
ний двойного маятника от расстоя-
ния центра масс до точки подвеса
тела к нити
примет вид
1
Яэкстр :
U
Уи*
1.
(53')
Наименьшая ошибка определяется равенством
I
б/п
g (AT)- (и4 + 3« — 2) + 2 У«« — и4 — и2 + 1
л'г и
Ввиду того, что это равенство неудобно для вычислений, со-
ставлена табл. 2. Отношение квадрата минимальной относитель-
Таблица 2
ги
0,1
0,2
0,3
0,4
0,6
0,784
0,8
1,05
1
fэкстр ~ ~У~
9,95
4,90
3,17
2,26
1,25
0,623
0,574
0,104
(«■'mil.)'
е(ьт)'
291
69,8
29,9
16,2
6,25
3,54
3,36
2,09
ги
1,2
1,4
1.6
3
1,8
2,0
5,0
10
100
/
Ькстр = ~
0,578
1,18
1,84
2,31
2,56
3,36
24,5
100
10 000
(^mln)2
2,92
3,41
3,76
3,85
3,96
4,17
6,93
12
102
ной ошибки б/тШ к коэффициенту g
(Д7У
л'ги
характеризует
влияние безразмерных величин и и q или параметров си/ при
радиусе инерции ги, принятом за единицу. Значения и и q надо
выбрать такими, чтобы отношение было небольшим.
60
Приведенные формулы и данные таблицы позволяют заклю-
чить, что параметры двойного маятника влияют на точность опре-
деления момента инерции по формуле (50), т. е. в случае, если
точное положение центра масс испытуемого тела неизвестно.
Относительная ошибка получается минимальной, если вели-
чина q удовлетворяет условию (53'), и может быть подсчитана по
приведенной формуле. Из таблицы видно, что при малых (и <С
-< 0,5) и больших (и >• 10) значениях и ошибка достаточно ве-
лика. Значения и близкие к единице (с близкие к ги) нежела-
тельны, так как длина нити по формуле (53) получается очень
малой.
Для достижения высокой точности и удобства эксперимента
целесообразно выбирать значения и в двух областях: для и <С 1,
т. е. если с < ги, чтобы оно заключалось в пределах 0,5 s=S и ^
^ 0,8, а для и>1 в пределах 1,2 «^ и ==5 10. Значение q3Kcmp
следует определять по формуле (53').
До проведения эксперимента величины ги и с (а следовательно,
и и) точно неизвестны и могут быть оценены ориентировочно.
Поэтому широкие пределы допустимых значений очень удобны.
Приведенные значения параметров двойного маятника являются
только рекомендуемыми, и в зависимости от условий и требуемой
точности опыта экспериментатор может выбирать и другие зна-
чения си I. Однако при этом он должен с большой точностью изме-
рить период главных колебаний, так как ошибка в определении
момента инерции прямо пропорциональна абсолютной ошибке
измерения периода.
Если и выбрана в рекомендуемых пределах и величина q
удовлетворяет условию (53'), т. е. если опыт проводится при
наивыгоднейших условиях, то для грубой количественной оценки
можно принять (см. табл. 2), что
VI A?"
&/;
V ги
Если за единицу длины принять метр, то
б/
Ути
Следовательно, при AT — 0,1 сек относительная ошибка опре-
40
деления момента инерции составит б/ ^= —^=- %, а при AT =
У ги
4
= 0,01 сек и AT = 0,001 сек соответственно 8J = —=■ % и 8J =
Уги
__ 0,4 „,
УУи
Абсолютная ошибка измерения периодов, как правило, не
должна превышать тысячных долей секунды. Такую точность
61
о
о
Я
о
100
о
102
Ш
CD
СМ
О
О
•—'
О
тс
■*
■*
00
—■
о
о
—'
о
О)
ем
<м
г-
ю
о
о
ю
со
■*
~
о
СП
СО
о
о
"
о
_^
~
о
_~
СО
о
о
—
оо
t^
90,
со
LO
СМ
о
t^
Г--
сО
со
77
со
см
СМ
о
со
ю
ю
67,
СО
О
о
—*
ю
ю
60,
о
оо
о
о
-*
**■
50
■w
Ш
о
со
■*
со
СО
43,
1^-
СО
~
о
CD
CN
СМ
35,
ю
_г
о
о
•—1
см
СМ
30,
см
о
о
о
'—1
20,
о
CD
t~~
о
см
о
"
CD
см
ю
о
см"
со
со"
о
CD"
со
со
со
со"
СО
со"
СО
о
о
со"
см
о
■*"
— CD
СМ 00
со" см"
CD.
см"
—. 00
см" —
1Л
о
см
со
см
ОО"
СО
со"
CD
in
о
со"
СП
см
со_
см"
со г-
см" —"
о
СО
г-
со"
со
со"
00
ю
со —
о
со
см — — —
со
1П
см
CD
о"
со,
ю"
■ч-
о
см
о
сп"
о
ш"
со
со"
CD_
см"
о
см"
о
см
в
см
t~-"
§
СП
см"
см"
СП
со
со
CJ>
о"
00
о"
о
со"
<=> с?
СО чр
со —
h- СО
о" о*
см"
о
ю"
о
Г-- 00
О СП
ю
CD
GO
CD О
оо сп
Г-- СО
о" о"
СО — —I
CD 1С ^
о о о"
см ю
СМ ri-
СП со
о" о
I-- см
см г~-
CD 1С
о" о"
с"
СП —
о —
"* СО
о" о
CD
о"
со аз
см ю_
см" —~
СП
00_
о
g g
CD
о"
Г- О
■* со
Ю -Ч"
о" о"
о
со
•* о
о —
со см
о" о"
см
о
см ю
— "Ч-
см" —Г
о
СП
о"
со
m
о
со со
о" о"
m
о"
о — — —
—" см"
in
см"
CD СМ
СО Щ
■* со
Tf"
СО
с"
— о
о —
см —
о" о"
о о
о" о"
— о
нельзя получить обычным секундомером, поэтому необходимо
использовать более современные приборы. Это требование обя-
зательно при малых радиусах инерции испытуемого тела.
Положение центра масс достаточно точно известно. В этом
случае квадрат суммарной ошибки выражается (см. примеча-
ние 10) суммой квадратов двух величин: 1) относительной ошибки
определения расстояния точки прикрепления нити от центра
тяжести и 2) относительной ошибки измерения периодов
<бУ)2 = (бс)2 + -sfc" (A7T-"* + f+1 •
О величине относительной ошибки момента инерции от неточ-
ности измерения периодов колебаний можно судить, пользуясь
табл. 3, в которой приведены значения \~Хт) '
Значения минимальных относительных ошибок в общем случае
несколько больше квадрата относительной ошибки момента инер-
ции от неточности измерения периодов в частном случае. Однако
чтобы судить о точности экспериментального определения момента
инерции, зная положение центра масс, следует учитывать не
только ошибку, обусловленную неточностью измерения периодов,
но и ошибку определения расстояния точки прикрепления нити
от центра масс.
В то же время при сопоставлении ошибок (см. табл. 2 и 3)
можно заключить, что если параметры подвеса выбраны согласно
изложенным рекомендациям, то точность экспериментального
определения моментов инерции тел при неизвестном положении
центра масс получается несколько выше, но ошибки имеют тот же
порядок, что и при известном положении центра тяжести. Разница
в значениях ошибок меньше для 1,2 «^ы s^ 10 и существенна
(на один — два порядка выше) для малых значений и.
Следовательно, предварительное определение положения центра
тяжести каким-либо из других методов желательно для и << 0,5.
При 0,5 «^ и е^ 0,8 и 1,2 sg и «^ 10 оно имеет смысл только
в том случае, если расстояние от точки прикрепления нити до
центра масс было определено с высокой точностью.
Пример 6.
В качестве примера проанализируем данные по определению
момента инерции самолета «15» вокруг его продольной оси, по-
лученные Ю. А. Победоносцевым [124].
Самолет был подвешен на двух тросах равной длины, рас-
положенных в плоскости симметрии самолета. Подбирая началь-
ные отклонения тросов и самолета сначала по одну сторону от
вертикали, добивались, чтобы система совершала первое главное
колебание, и замеряли период 7\. Затем, отклоняя тросы и само-
лет в разные стороны от вертикали, добивались того, чтобы си-
стема совершала второе главное колебание, период которого Т2.
63
Найдено, что 7\ = 4,390 сек, Т2 = 1,766 сек. Среднеквадратические
ошибки измерения периодов Д7\ = 0,001 сек, АТ2 = 0,003 сек.
Длина каждого из тросов / = 3,228 м; масса самолета пг —
= 145 кГсекг1м. Расстояние с от точки прикрепления тросов
к самолету до его центра тяжести было найдено предварительно
(методика определения этого расстояния и точность приводимых
величин не даны) с = 1,145 м.
Так как положение центра тяжести самолета известно, то
момент инерции вычислим по формуле (49):
J = mcl (-jjjsj-V TiT%= 191 кГ-м-сек2.
По приведенным значениям можно предположить, что абсо-
лютные ошибки измерения массы самолета, длины тросов, рас-
стояния до центра тяжести составляли: Am = 0,05 кГсекг/м\
А/ = Ас = 0,0005 м. Тогда частные ошибки вычисления момента
инерции по формулам § 2 равны 8Jm = 0,035%; 8J; = 0,016%;
6/е = 0,044%; 6/Ti = 0,046%; 6JTf = 0,340%.
Общая ошибка
8 J = 0,34%.
Следовательно, / ~ 191 ± 0,6 кГ-м-сек2.
Обработаем приведенные экспериментальные данные в пред-
положении, что расстояние с неизвестно. Вычислим значение с:
«-'(■йг)*-^-^) (^—rf)-i.iw«.
Найдем относительные ошибки вычисления:
6с, = 0,027%; бсТ1 =0,139%; 8сч = 0,108%;
N 6с = 0,195%.
Абсолютная ошибка вычисления с составляет
Ас = ±сбс = ±0,0023 м.
По формуле (50) определим момент инерции
'-^{■ШГУ^ЛЯ-^Г) {~Г~Т1)= 195 кГ.м-сек*.
Относительные ошибки составляют
6/, = 0,0004%; 6/Ti = 0,185%; 6УГ> = 0,23%;
б J = 0,296%.
Следовательно, момент инерции, вычисленный в предположении,
что расстояние с неизвестно, равен
J — 195 ± 0,6 кГ-м-сек.
64
Значения момента инерции оказались разными, так как про*
веденное в |124]с= 1,145 ± 0,0005 м не соответствует с = 1,170 ±
-ь 0,0023 м, найденному методом качания двойного маятника.
Абсолютные ошибки вычисления момента инерции в обоих случаях
получаются одинаковыми и равными 0,6 кГ-м-сек2.
//////,
2Ш22
Рис. 25. Выбор параметров подвеса
§ 4. РЕКОМЕНДАЦИИ ПО ПРИМЕНЕНИЮ МЕТОДА
Метод качания двойного маятника является достаточно точным
и может быть рекомендован особенно в тех случаях, когда иные
методы в силу специфики испытуемого объекта нельзя использо-
вать. Так, при определении момента инерции самолета он должен
находиться в положении, близком к полетному. Применение
методов крутильных колебаний
для определения момента инерции
относительно продольной оси са-
молета нежелательно; но здесь
удобен метод двойного маятника.
Не снимая самолет с подвеса,
можно на тех же нитях методом
бифиляра определить момент инер-
ции самолета относительно верти-
кальной оси.
При этом нет необходимости точ-
но знать положение центра тяжести
испытуемого тела. Однако центр
тяжести должен лежать в вер-
тикальной плоскости, содержащей элементы подвеса (тяги, нити).
Недостатком метода является большой объем эксперимента.
Все полученные в настоящей главе расчетные зависимости
справедливы лишь для малых углов отклонения без учета массы
и деформаций элементов подвеса и трения в местах прикрепления
к штативу и телу. Необходимо, чтобы элементы подвеса были
легкими, а присоединение к штативу и телу шарнирным с возможно
меньшим трением для подвеса на тягах или с исключением изгиба
для подвеса на тросах.
Точность эксперимента зависит от соотношения трех основных
параметров маятника: длины элемента подвеса /; расстояния с
и центрального радиуса инерции ги тела (рис. 25, а, б).
Если нужно получить очень точный результат, то экспе-
римент рекомендуется проводить дважды и в следующем по-
рядке.
1. Подвесив испытуемое тело на двух нитях (тягах), подобрать
начальные углы отклонения, при которых двойной маятник со-
вершает главные колебания, и определить их периоды.
2. По формулам § 1 найти величины си г2.
5 М. М. Гррнет 2274 65
3. Если значение — находится в рекомендуемых пределах,
то по формуле (53) определить длину 1Э нити, при которой ошибка
в измерении периодов меньше влияет на точность опыта. Если же
значение — выходит за указанные пределы, то надо изменить
положение точки А прикрепления нити, приняв рекомендуемое
значение —, а затем вычислить 1Э по формуле (53).
£. 4. Перевесить испытуемое тело на нити (тяги) длиной 1Э.
5. Определить периоды главных колебаний, причем период
колебаний с высшей частотой — из большего числа наблюдений,
чем период колебаний с низшей частотой.
Периоды колебаний после перевешивания тела следует изме-
рять очень точно (электросекундомером).
6. По полученным данным определить момент инерции тела
по формуле (50), а если требуется, то и точное положение
центра тяжести.
♦ ♦♦
Глава IV
♦ ♦♦
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ МЕТОДОМ
КРУТИЛЬНЫХ КОЛЕБАНИИ (УНИФИЛЯР)
§ 1. ИСТОРИЯ МЕТОДА.
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ МЕТОДА
Унифиляр состоит из упругого стержня и укрепленного на
его конце тела, совершающего крутильные колебания вокруг
оси, совпадающей с осью стержня. Унифиляр, как прибор для
научных исследований, был введен в практику эксперимента
Кулоном в 1784 г. [217] и получил широкое распространение.
Он применяется для измерения сил притяжения и отталкивания
между телами: для измерения постоянной всемирного тяготения
[209], измерения магнитного поля Земли [258, 292], для иссле-
дования вязкости жидкости и газов [321], для измерения сил
в потоках малой плотности в экспериментальной аэродинамике;
для изучения механических свойств материалов; в крутильных
весах, с точностью взвешивания до 0,001 мг, и во многих других
экспериментальных исследованиях [120, 129, 184, 205, 214, 218,
223, 335, 401].
В практику экспериментального определения моментов инер-
ции тел унифиляр был введен в начале XIX века Пуассоном
[299] и в настоящее время рекомендуется всеми руководствами
по теоретической и прикладной механике.
Метод крутильных колебаний (унифиляр) является достаточно
точным: искомая величина, при надлежащей тщательности опыта,
определяется с ошибкой в несколько сотых процента. Однако
несмотря на настойчивые усилия ряда исследователей, добиться
более высокой точности не удавалось. Ниже рассмотрены причины
невозможности дальнейшего повышения точности в рамках суще-
ствующей теории метода и предложена уточненная теория и мето-
дика определения моментов инерции с точностью, повышенной
в несколько раз.
Верхний конец упругого стержня (например, проволоки)
жестко закреплен в неподвижном штативе. К нижнему концу
стержня жестко прикреплено зажимное устройство (тиски, патрон
или платформа), на которое помещают испытуемое тело (рис. 26).
По установившейся традиции зажимное устройство будем назы-
вать прибором, а всю систему — унифиляром *. В некоторых
5* 67
случаях испытуемое тело прикрепляют непосредственно к упру-
гому стержню. Для исключения боковых колебаний необходимо,
чтобы ось стержня была главной и центральной осью инерции
всей системы.
Обозначим:
mg — вес испытуемого тела;
m„g — вес прибора;
J — момент инерции испытуемого тела;
Jn — момент инерции прибора.
Повернем прибор вместе с телом вокруг оси стержня на не-
который угол и отпустим его без начальной скорости. Пренебре-
гая ввиду малости сопротивлением воздуха,
дифференциальное уравнение движения мож-
но записать в виде
"///ЛУ//,.
У> + J п. т •> поив) ^2
М = 0,
где
1 'тд
Рис. 26. Унифиляр
М — восстанавливающий момент, обу-
словленный упругостью матери-
ала стержня;
J прив — приведенный момент инерции
подвеса, который учитывает
влияние массы стержня, распре-
деленной по его длине.
Согласно теории колебаний приведенный
момент инерции цилиндрического стержня,
защемленного одним концом и совершающего
крутильные колебания, равен одной трети
его момента инерции относительно оси цилиндра. Так как в ка-
честве подвеса обычно используют длинные проволоки достаточно
малого диаметра, то Jnpue составляет ничтожную часть от момента
инерции и его величиной можно пренебречь, а дифференциальное
уравнение записать в виде
(J + Jn)^ + M = 0.
Если при наибольшем угле закручивания стержня максималь-
ные напряжения сдвига в материале подвеса не превышают пре-
дела пропорциональности, то допустим, что восстанавливающий
момент пропорционален углу закручивания
М = сер.
* Из условий опыта ясно, что тело должно быть подвешено на достаточно
тонком стержне, но не на нити, так как момент кручения тонкой нити равен
нулю. Поэтому нельзя не признать, что общепринятые термины «однонитный
подвес» или «унифиляр» (лат. unus один и лат. filum — нить) неудачны. Тем
более неудачен часто употребляемый термин «монифиляр», так как он образован
из сочетания греческого слова monos — один с латинским filum — нить.
68
Подставляя значение восстанавливающего момента, получим
простейшее дифференциальное уравнение крутильных колебаний*
{J + Jn) ^ + сер = 0. (54)
Проинтегрировав уравнение для случая, когда начальное
отклонение равно ср0, а начальная скорость ср0 равна нулю, по-
лучим
Ф ■= ф0 cos kt.
Частота колебаний
k =
-V:
J + Jn
Период крутильных колебаний
Т = Щ- = 2л ]/ ^±1± . (55)
Отсюда следует, что при сделанных предположениях крутиль-
ные колебания являются незатухающими и изохронными. Первое
заключение противоречит опыту, но затухание колебаний, как
правило, невелико и объясняется влиянием внешней среды (воз-
духа) [216, 251]. Второе заключение большинство исследователей
считает правильным.
Из формулы (55) нетрудно получить выражение момента инер-
ции колеблющейся системы
J + Jn-^TK (56)
Если при эксперименте испытуемое тело закрепляют непосред-
ственно на упругом стержне, то Jn ■= 0. Кроме периода колеба-
ний Т, необходимо знать коэффициент жесткости подвеса с,
обычно называемый в теории унифиляра «направляющей силой».
Некоторые авторы [316] рекомендуют вычислять его по извест-
с j
ной из курса сопротивления материалов формуле с — —р-,
где Jр — -яй полярный момент инерции сечения стержня;
d и / — диаметр и длина стержня; G — модуль сдвига мате-
риала стержня. Но сечение по длине стержня может быть не-
одинаковым, а модуль сдвига определяют с помощью специаль-
ного эксперимента, и он зависит от многих факторов, поэтому
эта рекомендация трудно осуществима [7, 32]. Уолл [384] и не-
которые другие авторы предлагают при каждом эксперименте
коэффициент жесткости измерять динамометрическими устрой-
ствами, для этого нужна хорошо оснащенная лаборатория.
* Это равенство в силу упругого гистерезиса в материале подвеса является
приближенным (см. § 5),
69
У//ЛУ///.
Чтобы избежать необходимости вычисления или опытного
определения коэффициента с, эксперимент проводят так, чтобы
этот коэффициент не входил в окончательную рабочую формулу.
Для этого применяют три способа:
1) измеряют коэффициент с специальным эталоном;
2) наблюдают колебания испытуемого тела и тела с эталоном;
3) наблюдают колебания испытуемого тела на специальной
подставке или в специальном захвате.
1. Применение эталона.
Впервые этот способ был предложен в Англии в прошлом сто-
летии, и многие исследователи 1299] называют его «английским
способом».
Опыт проводят дважды. В первом
опыте к подвесу прикрепляют эталон,
т. е. тело, момент инерции J3 которого
хорошо известен, и измеряют период
крутильных колебаний 7\. Вес эталона
должен быть приблизительно равен весу
испытуемого тела. Для упрощения вы-
числений в качестве эталона обычно
применяют тело цилиндрической формы
[46, 136].
Во втором опыте на том же подвесе
закрепляют испытуемое тело и на-
блюдают период крутильных колебаний
7Y
Рис. 27. Способ Гаусса
Согласно формуле (56) можно написать
Л
° 7? и / = ^- Ц,
4 я2
4я2
откуда
(57)
2. Способ Гаусса.
К. Гаусс в 1837 г. [258] предложил к испытуемому телу
симметрично прикреплять два одинаковых цилиндрических (ра-
диус гэ) груза массой тэ на одинаковых расстояниях а от оси
упругого стержня (рис. 27). В результате присоединения грузов
момент инерции испытуемого тела увеличивается на величину
m,(2a2 + rD=J,.
Эксперимент проводят дважды. Обозначим период колебаний
системы (тело -f грузы) через Т1. Тогда
/+т,(2а» + г2) = ^71
70
Если период колебаний испытуемого тела равен Т2, то
Из этих двух равенств следует, что
J = тэ (2а2 + rl) Т" . (58)
Когда радиус гэ значительно меньше а, величиной г\ можно
пренебречь. Тогда расчетная формула примет вид
J = 2m3a*1^w. (58')
1 1 ~ ' 2
Возможна и иная модификация способа, заключающаяся
в том, что вместо двух грузов к испытуемому телу прикрепляют
одно тело с известным моментом инерции J3, причем таким обра-
зом, чтобы его главная центральная ось инерции совпадала с осью
подвеса. Момент инерции тела определяется так называемой
формулой Кулона [200]
"* = э ~^2 ^2~ ' (^°)
' 1 — 1 2
где Т1 — период крутильных колебаний системы (гело + эталон);
Т2 — период крутильных колебаний тела.
Гаусс подвешивал добавочные грузы на различных расстоя-
ниях а от оси подвеса и находил момент инерции тела как среднее
из вычисленных значений. Этот способ впоследствии использо-
вал X. Бауман как собственный [189].
В первом опыте к испытуемому телу прикрепляют два одина-
ковых груза массой пг'д (момент инерции J'a), таким образом,
чтобы их главные центральные оси совпадали с осью подвеса, и
наблюдают период Т2 крутильных колебаний этой системы.
Во втором опыте наблюдают период 7'2 колебаний тела и грузов,
расположенных на одинаковых расстояниях а от оси подвеса.
В эксперименте, осуществленном по предложению Баумана,
искомый момент инерции определяли формулой
J = 2тэа2 —^—г — 2/э. (60)
т\ -т'2
3. Упругие колебания тела на приборе
Если тело не прикрепляют к упругому стержню, а устанавли-
вают на какой-либо подставке, жестко соединенной со стержнем,
или в зажиме, то эксперимент проводят трижды. Измеряют период
Тх крутильных колебаний прибора, период Тг колебаний прибора
71
с эталоном и период Т3 колебаний прибора с испытуемым телом.
Согласно формуле (56) можно написать уравнения
Jn = !я? Т*' J" + ^ = "1^5" Tv J<* + J ==г "4НГ- Ч-
Из первых двух уравнений находим момент инерции прибора
Jr. = Л
1
г2 г2
2~' 1
Момент инерции испытуемого тела может быть выражен через
момент инерции эталона
Т\-Т\
11 м
или через найденный момент инерции прибора
J = Jn(^r-l)- (6 Г)
Если прибор используют многократно и момент инерции при-
бора хорошо известен, то для определения момента инерции ис-
пытуемого тела достаточно определить период Т3 колебаний
прибора с телом.
§ 2. УТОЧНЕНИЕ ТЕОРИИ.
ВЛИЯНИЕ УДЛИНЕНИЯ НИТИ
Об изменении коэффициента с при нагружении унифиляра.
При подвешивании тел разного веса упругий подвес растя-
гивается пропорционально весу тела, при этом изменяется диа-
метр стержня. Поэтому некоторые авторы, например Лендер [86] и
Волохов [28], справедливо предлагают вводить поправку на из-
менение «направляющей силы».
Если обозначим /0 длину, a d0 диаметр ненагруженного упру-
гого стержня, то коэффициент жесткости ненагруженного подвеса
Ondg
С(|= ТЩГ"
Тело весом mg, прикрепленное к подвесу, вызывает относи-
тельное удлинение -=- стержня, где ст — нормальное напряжение,
равное —jp.
Длина стержня после нагружения равна I = 10 ( 1 -j- -=г
диаметр d --= d0 (\ — И<-7г) » гДе Iх — коэффициент Пуассона (для
стали \i — 0,3).
72
Коэффициент жесткости нагруженного подвеса унифиляра
(.-,■£)'
с = сп
■+т
Так как относительное удлинение значительно меньше еди-
ницы, то можно с достаточной точностью принять
а \4 , . о 1 1 о
+ £
тогда
c^c„(l —4ц-|-) (l —-g-) = c0 [l — |-(1 + ^
Например, для стального подвеса (Е — 2 ■ 10е кГ/смг; \i = 0,3)
при о — 2-Ю3 кГ/см2; -у- -= 10~3; с = 0,9978 с0, т. е. «напра-
вляющая сила» уменьшилась на 0,2%.
Уточним полученные формулы, учитывая возможные измене-
ния коэффициента с.
1. Применение эталона
Если период колебаний эталона равен Гх, то уточненное выра-
жение формулы (56) будет следующим:
■'. = 1^[1--г<1 + 4'*>
Для колебаний испытуемого тела с периодом, равным Т.2,
можно написать аналогичное выражение:
В приведенных формулах -^- а -в относительные удлине-
ния соответственно от веса эталона и испытуемого тела.
Момент инерции испытуемого тела
j = jA*. (62)
' 1
где а — коэффициент, учитывающий изменение крутильной жест-
кости подвеса,
1--)г(1 + 4|х)
а =
1--|-(1 + 4ц)
73
Так как член Щ- (1 + 4ц.) мал, то можно написать приближен-
ное значение
а
1 + -Ч^«т.-а).
Формула (62) аналогична выражению (57), но учитывает изме-
нение крутильной жесткости упругого подвеса.
Относительную ошибку вычисления по формуле (57), т. е. без
учета изменения жесткости подвеса, можно приближенно опре-
делить так:
1+4ц
Ыс-
-(<*» —°).
Из формулы, в частности, следует, что если вес эталона равен
весу тела, то ошибка от пренебрежения изменением крутильной
жесткости подвеса равна нулю, так как относительные удлинения
подвеса от веса эталона и испытуемого тела одинаковы.
2. Способ Гаусса
Если период колебаний испытуемого тела с прикрепленными
цилиндрическими (радиус гэ) грузами массой тэ на расстоянии а
от оси подвеса равен 7\, а период колебаний тела без грузов
равен Т2, то с учетом изменения крутильной жесткости унифиляра
можно написать два равенства:
J+m3(2a + rl)=^Tl
1
0 + 0Э
[1 + 4(1)
^^П[1-^(1 + ^)
Из этих равенств найдем момент инерции испытуемого тела
J = шэ (2а2 + г\)
Т{(\ —а)—Т,
2'
(63)
где
а =
-J- (1 + 4(i)
l_JL(l+4|i)
0э
(1 + 4ц).
Относительная ошибка вычисления момента инерции, которая
будет допущена при использовании формулы (58), определяется
выражением
8JC^ 1 Н , 2 2- а
шэ (2аг + Н,)
74
Если в первом опыте к испытуемому телу прикрепляют не
два груза, а тело с моментом инерции J3, то, заменяя выражение
тэ (2а2 + rj) в формуле (63) на J3, получим
J = J,
Т\(\
■а)-П
(64)
Относительная ошибка без учета растяжения подвеса равна
67^ (!+£)«.
При эксперименте по предложению X. Баумана ввиду того, что
вес колеблющейся системы остается постоянным, крутильная
жесткость не изменяется и момент инерции вычисляют по фор-
муле (60).
Пример 7.
Т. Уолл [384] приводит данные экспериментального опреде-
ления момента инерции чугунной детали весом mg = 15,606 кГ,
подвешенной на стальной проволоке длиной / = 533,4 мм и
диаметром d — 2 мм. Период колебаний детали равен Т2 —
= 4,15 сек. В качестве эталона Уолл использовал стальной стер-
жень весом m3g — 1,871 кГ и длиной L — 0,6096 ж. Следовательно,
момент инерции эталона относительно центральной оси составил
J,
m3L*
' 12
0,00592 кГ-м-сек2.
Период колебаний системы (тело+эталон) равен 7\ =
= 5,20 сек. Момент инерции испытуемого тела по формуле (59)
получается равным J = 0,01035 кГмсек2. Ошибка, вызванная
изменением «направляющей силы» унифиляра, равна 8JC =
= 0,018%, что существенно для точного эксперимента.
3. Упругие колебания тела на приборе
Если Т1 — период колебаний прибора, Т2 — прибора с эта-
лоном, Т3 — прибора с испытуемым телом, то можно написать
следующие выражения:
где ~j}-, ~ и -g -относительные удлинения упругого стер-
жня соответственно под действием веса прибора, эталона и
75
испытуемого тела. Из первых двух уравнений определим момент
инерции прибора
т2
1 1
J „ J g
Т\{\-а,)~Т\
Относительная ошибка вычисления момента инерции прибора
без учета изменения «направляющей силы» унифиляра выражается
формулой
6/„c = (l+-£-)«,.
Момент инерции испытуемого тела найдем из первого и треть-
его уравнений:
-5- (1—«)—1
J = Jn
(65')
где
а
■(1+4ц).
Так как в формуле (65') момент инерции прибора определен
из эксперимента с некоторой ошибкой, то искомый момент инерции
можно выразить и непосредственно через Jэ:
J=J, —Ц- 1 i^ . (65)
!0-О
Относительная ошибка применения формулы (61)
67с = ( 1 + -А- , а,
1 +
JjL
J
а.
Пример 8.
Сотрудник университета в Торонто Джон Сэтерли в 1957 г.
опубликовал 1356] результаты вычислений моментов инерции
различных кристаллов и экспериментальной проверки их на мо-
делях, выполненной методом унифиляра. В качестве подвеса
Сэтерли использовал мельхиоровую проволоку длиной I =
= 315 мм и диаметром d = 0,82 мм. Модели кристаллов он
помещал в специальный прибор. В качестве эталона автор исполь-
зовал стальной шар массой шэ == 439,8 г (момент инерции относи-
тельно центральной оси ]э = 997,9 гсм2). Экспериментально най-
дены период колебаний прибора Тг = 1,502 сек и прибора с эта-
лоном Т2 — 1,708 сек.
Момент инерции прибора, вычисленный без учета изменения
жесткости подвеса, как это сделал Сэтерли, оказался равным
Jn --= 3410 гсм2. Относительная ошибка, обусловленная изме-
нением жесткости подвеса, 6У„ = 0,038%.
76
Зная момент инерции прибора, Сэтерли определял моменты
инерции моделей кристаллов относительно различных централь-
ных осей. Рассмотрим значения, относящиеся к одному из поло-
жений прямоугольного параллелепипеда массой т = 1012 г,
период колебаний на приборе оказался равным Т3 = 2,385 сек.
Момент инерции параллелепипеда автор вычислил по формуле,
тождественной формуле (61), / = 5190 гсм2. Момент инерции,
вычисленный теоретически, равен 5144 гсм2.
Так как автор не учитывал изменения жесткости подвеса, то
подсчитаем относительную ошибку найденного значения момента
инерции. Вычисления показывают, что 8JC — 0,095%.
Из экспериментов Сэтерли (как впрочем и Уолла) следует, что
пренебрежение влиянием изменений жесткости подвеса при-
водит к завышенным значениям момента инерции по сравнению
с действительными. Д. Сэтерли, указывает, что «определен-
ный из опыта момент инерции часто немного больше вычислен-
ного».
Таким образом, изменение растягивающей нагрузки на упру-
гий стержень унифиляра может приводить к ощутимому измене-
нию крутильной жесткости подвеса. Поэтому для точных экспе-
риментов уточненные формулы (62)—(65) предпочтительнее фор-
мул (57)—(61). Приближенные формулы легко получить из уточ-
ненных, если коэффициенты а и аэ принять равными нулю.
§ 3. ОШИБКИ, ДОПУСКАЕМЫЕ
ПРИ ЭКСПЕРИМЕНТЕ
Если момент инерции испытуемого тела определен с приме-
нением эталона по формуле (62), то относительная ошибка, обус-
ловленная неточностью определения момента инерции эталона
eJ3, равна относительной ошибке вычисления момента инерции
эталона 8Э. Аналогично относительная ошибка 8Ja, обуслов-
ленная ошибкой в значении коэффициента а, равна относитель-
ной ошибке ба вычисления этого коэффициента. Относительные
ошибки б/г, и 6Jr2, обусловленные неточностью измерения пе-
риодов 7\ и Т2 колебаний эталона и испытуемого тела, равны
удвоенным относительным ошибкам измерения этих периодов.
Таким образом, среднеквадратическая относительная ошибка
вычисления момента инерции по формуле (62) равна
б/ = Y{b3f + 4 (67\)2 Т~4 (6ТВ)2 +1&05.
Если применен метод Гаусса с двумя дополнительными грузами
и момент инерции тела вычислен с учетом изменения жесткости
упругого стержня по формуле (63), то относительные ошибки,
77
обусловленные неточностью измерения отдельных величин, вхФ
дящих в правую часть формулы, равны
б/тэ = 8тэ;
8Ja = 4тэа
Т\(\-а)-Т\
8а.
Когда а > г3, то
8Ja = 26а; 8Л
«vf
г*(1_а)-г!6Гв;
причем если а ^> гэ, то ошибка 6/, несущественна и ею можно
пренебречь. Следовательно, при использовании способа Гаусса
необходимо точно определить расстояние центров тяжести грузов
от оси подвеса; точность измерения радиусов этих грузов не
столь существенна.
Формулы для определения относительных ошибок момента
инерции от неточности замеров периодов колебаний тождественны
выражениям, полученным для способа эталона:
6Т,
8JTl
8JT,
= 2
= 2
[l +■ J 1
тэ(2с? + г1)
Ги- J ]
6Т2.
Относительная ошибка, вызванная неточностью значения коэф-
фициента обычно бывает мала.
Среднеквадратическая ошибка вычисления момента инерции
по формуле (63) для случая, когда а > гэ, равна
8J
V
(бтэ)2 + 4(ба)2 + 4
1 +
M2fl 2 + г\)
[(67\)2 + (6Т2)]2
Если к испытуемому телу дополнительно прикрепляют тело
с моментом инерции Уэ, то искомый момент инерции надо вычис-
лить по формуле (64). Среднеквадратическая относительная
ошибка определяется формулой
8J = Y{8J3f 4- 4 (1 + -jj)'2 [(6TJ* + (6ВД.
При использовании предложения Баумана момент инерции
78
испытуемого тела можно вычислить по формуле (60). Среднеква-
дратическая ошибка равна
6J =
+ 2^)
(8тэГ + (6а)2 + 41 +
2т'эа2
X
X
(ЬТ'2)2 + (6Т'2)2
+ 4
(б/;)2.
Момент инерции тела по его упругим колебаниям на приборе
можно вычислять по формуле (65').
Относительная ошибка, обусловленная неточностью момента
инерции прибора, равна
6/, = 67„;
8J
г, = 2(1+^-)б7У, б/г, = 2 (1+-^-)бГь
Относительной ошибкой, обусловленной неточностью значе-
ния коэффициента а, можно пренебречь.
Среднеквадратическая ошибка вычисления момента инерции
исследуемого тела выражается формулой
6/ = ]/(б/Л)2 + 4(1+ ^)2 [(67\)8 + фТ3)%
Момент инерции прибора /„ должен быть определен из допол-
нительного эксперимента, ошибка которого
6/„ = У (б/э)3 + 4(l+ -^J [(б^)2 + (6Г2)21,
где б Л
относительная ошибка теоретического вычисления
момента инерции эталона.
Все приведенные в настоящем параграфе формулы, как част-
ных, так и среднеквадратических ошибок, полностью применимы
и для вычисления моментов инерции по приближенным формулам
§ 1, если коэффициенты а и аэ принять равными нулю.
§ 4. 0 ТОЧНОСТИ МЕТОДА
Приведенная теория унифиляра и полученные расчетные фор-
мулы позволяют определить искомую величину с любой точностью.
С. Д. Гидаспов определял моменты инерции коромысла анали-
тических весов [46] методом унифиляра с точностью 0,05%,
а Г. Д. Кокош и Н. А. Смирнова [73] с точностью 0,023%.
Такая точность для неуточненного метода является предельной.
Используя данные, приводимые Д. Крейхгауэром [299], можно
подсчитать, что истинная точность эксперимента этим методом
79
у разных исследователей была следующей: Гаусса — 0,044%;
Вебера — 0,045%; Сарториуса фон Вальтерхаузена—0,297%.
Точность, полученная рядом других исследователей (Ханштейн,
Ламонт, Вильд, Дор и др.), также была недостаточной.
По рекомендации Ф. Кольрауша Д. Крейхгауэр провел боль-
шие теоретические и экспериментальные исследования точности
определения моментов инерции постоянных магнитов методом
унифиляра. Эти определения были необходимы при исследованиях
магнитного поля Земли. Он показал, что система, получающаяся
при подвешивании на нитях или тонких проволочках дополни-
тельных грузов, представляет тройной крутильный маятник;
были получены расчетные зависимости и разработаны рекоменда-
ции, уточняющие методику для случая подвешивания грузов.
Крейхгауэр установил, что на точность метода не оказывают за-
метного влияния такие факторы, как затухание крутильных коле-
баний, присоединенные массы воздуха и др.
На основании уточненной методики Крейхгауэр эксперимен-
тально определил моменты инерции двух различных магнитов,
которые затем вычислил теоретически. Величины, входящие
в расчетные формулы, были замерены с такой точностью, что
ошибка экспериментального определения момента инерции в худ-
шем случае не должна была превышать 0,019%. Однако истинная
точность оказалась равной 0,034% для одного магнита и 0,038%
для другого. Следовательно, истинная точность метода унифиляра
в опытах Крейхгауэра была примерно в 2 раза ниже ожидаемой.
Обстоятельное исследование метода унифиляра было опубли-
ковано Ф. Ф. Лендером в 1911 г. [86]. Он сконструировал
прибор для определения моментов инерции артиллерийских
снарядов.
Ф. Ф. Лендер установил, что период колебания прибора,
определенный по 300 колебаниям, равен 7\ = 8,6720 сек, ошибка
Д7\ = 0,0007 сек. Далее автор наблюдал колебания прибора
с закрепленным в нем цилиндром, причем цилиндр в первой
серии опытов закрепили так, что его геометрическая ось совпадала
с осью упругого подвеса. Период колебаний равен Г2= 10,6847 сек,
ошибка ДГ2 == 0,0007 сек. Во второй серии опытов тот же цилиндр
был закреплен так, что его геометрическая ось была перпенди-
кулярна оси упругого подвеса, и определен момент инерции отно-
сительно центральной оси цилиндра, перпендикулярной его
геометрической оси. В этом случае период колебаний составил
Т3 = 18,1173 сек, ошибка АГ3 = 0,0007 сек.
Момент инерции эталона относительно геометрической оси был
вычислен с высокой степенью точности (б/3 = 0,008%) и ока-
зался равным Уэ == 0,7798 кГсм сек2.
Используя приведенные данные, вычислим по формулам § 2
момент инерции прибора
/„ = 1,5136 кГ-см-сек*.
ад
Затем по формуле (65') подсчитаем момент инерции цилиндра
при его втором положении J = 5,080 кГ-см-сек2.
Относительная ошибка определения момента инерции тела (ци-
линдра при его втором положении) в опытах Лендера равнялась
6V - 0,066%.
В то же время момент инерции испытуемого тела с высокой
степенью точности (отличное качество стали и высокая точность
определения массы и размеров) можно вычислить
Jmeop = 5,0489 кГ-см-сек2,
причем относительная ошибка вычисления dJтеор -- .0,01 %. Зная
теоретическое и экспериментальное значения момента инерции,
можно подсчитать истинную точность метода:
Ыист= J-Jme°P =0,61%.
•I ineop
Сопоставление истинной точности метода унифиляра в опытах
Лендера (0,61%) с предполагаемой (0,066%) показывает, что
в рассматриваемых экспериментах метод унифиляра, в рамках
существующей теории, не показал ожидаемой точности.
Эти несоответствия послужили основанием утверждать (Вильд,
Ханштейн, Крейхгауэр, Лендер), что метод содержит принципиаль-
ные ошибки. Вследствие этого Кольрауш предложил для изучения
земного магнетизма взамен унифиляра использовать бифиляр.
Для объяснения несоответствия между истинной и ожидаемой
точностью Ф. Ф. Лендер высказал предположение, что момент
упругих сил в материале подвеса ввиду влияния зажимов, кото-
рыми упругий стержень прикреплен к прибору и штативу, нели-
нейно зависит от угла закручивания:
М --- сер",
где п — некоторое число, близкое к единице.
Составив дифференциальное уравнение движения унифиляра и
приближенно проинтегрировав его, Ф. Ф. Лендер создал услов-
ную, не имеющую физического обоснования, методику определе-
ния моментов инерции, на основании которой ему удалось повы-
сить точность эксперимента, но все же она осталась недостаточной
(0,36%).
В 1920 г. проф. В. П. Ветчинкин [22], анализируя данные
Лендера, выдвинул предположение, что недостаточная точность
объясняется тем, что прибор Лендера в процессе одного полного
колебания четырежды имел скорость, равную критической. В том
же году Ф. Ф. Лендер [87] доказал, что прибор обладал угловыми
скоростями, значительно меньшими, чем критическая скорость.
Следовательно, предположение В. П. Ветчинкина ошибочно. При-
чины низкой точности метода оставались невыясненными.
(? М. М. Геппет 2274 81
§ 5. АНИЗОХРОННОСТЬ КРУТИЛЬНЫХ КОЛЕБАНИЙ
И УТОЧНЕНИЕ ТЕОРИИ МЕТОДА
Примем, как это установлено рядом исследований, что момент
сопротивления воздуха пропорционален первой степени угловой
скорости, и напишем дифференциальное уравнение
/-HF-r-oW-s- + ccps=0
ИЛИ
rf2cp _u 9„ d<f л- £V - О
где
П-~ 2J~
-V+-
Затухающие колебания характеризуются периодом колебаний
j, _ 2я
и логарифмическим декрементом
Ь - пТ.
Следовательно, затухающие колебания изохронны, т. е. их
период не зависит от амплитуды колебаний, и логарифмический
декремент является постоянной величиной, также не зависящей
от амплитуды.
Однако точные эксперименты показывают, что и период коле-
баний, и логарифмический декремент по мере затухания колебаний
изменяются.
В. Томсон, положивший начало изучению внутреннего трения
и усталости металлов, приводит результаты экспериментов, выпол-
ненных им в 1864—1865 годах, по изучению затуханий крутиль-
ных колебаний проволок. Из этих данных следует, что логарифми-
ческие декременты и периоды колебаний не являются постоян-
ными, причем большие логарифмические декременты соответ-
ствуют большим периодам колебаний, например, значению декре-
мента ■& = 70-Ю"4 соответствует период Т = 4,8 сек, ■& =
= 118-10"* — период Т = 4,9 сёк, v = 156-10~* — период Т =
= 5,0 сек. В работе Ф. Ф. Лендера [86] также отмечена анизо-
хронность крутильных колебаний унифиляра, что и побудило
его создать новую расчетную схему и методику эксперимента.
Так, в одном из опытов с унифиляром Лендером получены следую-
щие значения: за первые 50 колебаний амплитуда изменилась
от 1 до 0,684 рад, а средний период был равен 8,688 сек;
за следующие 50 колебаний амплитуда уменьшилась до
0,476 рад, а средний период 8,680 сек;
82
уменьшилась до
Рис. 28. Петля гистерезиса
За следующие 50 колебаний амплитуда
0,354 рад, а средний период 8,676 сек;
за 50 колебаний амплитуда снизилась до 0,262 рад, а период
8,668 сек;
и, наконец, еще за 50 колебаний амплитуда достигла значе-
ния 0,183 рад, а период снизился до значения 8,664 сек.
Следовательно, опыты Ф. Ф. Лендера говорят о том, что
затухающие колебания унифиляра анизохронны, что период
по мере затухания убывает. Однако объяснений этому явлению
ф. Ф. Лендер не дал.
Физическое объяснение причины ани-
зохронности крутильных колебаний было
дано лишь в 1959 г. [131]. Причина за-
ключается во внутреннем трении в мате-
риале подвеса.
Явлению внутреннего трения, иногда
называемому упругим гистерезисом, по-
священо большое количество исследова-
ний. В работе Я. Г. Пановко[122] изложе-
ны различные гипотезы и математические
описания этого явления, а в библиогра-
фических указателях приведена обширная
литература по этому вопросу.
При периодическом закручивании и раскручивании упругого
стержня касательные напряжения во всех точках его сечения, а
следовательно, и момент упругих сил для стержня в целом не-
сколько отступают от линейной зависимости, вытекающей из
закона Гука. При нагружении момент упругих сил (рис. 28)
изменяется по верхней ветви abc некоторой замкнутой петли, а
при разгружении — по нижней ветви cda (отклонение ветвей петли
от прямой ас, соответствующей закону Гука, мало, поэтому петля
в действительности очень узкая). Площадь, лежащая внутри
петли, пропорциональна энергии, рассеиваемой за одно колебание,
т. е. логарифмическому декременту.
Многими исследованиями установлено, что:
1) рассеиваемая за цикл энергия не зависит от частоты коле-
баний, по крайней мере, в пределах от статических деформаций
до частот в несколько тысяч герц;
2) количество рассеиваемой за цикл энергии зависит от свойств
материала и веса подвешенного тела, с увеличением нормальных
напряжений в подвесе рассеяние энергии несколько уменьшается.
В настоящее время имеется более десяти различных гипотез
упругого гистерезиса, которые можно разделить на две группы.
Первая группа (Фойгт, Шлиппе) проводит аналогию внутреннего
трения с трением жидкостным. Эти гипотезы не соответствуют
экспериментальным данным о независимости рассеяния энергии
от частоты. Вторая группа гипотез основана на опытных данных
6* 83
6 независимости гистерезиса от частоты и зависимости от ампли-
туды.
В свою очередь, гипотезы второй группы можно разбить на
две категории. Первая категория (И. Л. Корчинский, Д. Ю. Панов,
Е. С. Сорокин и др.) приводит к линейным дифференциальным
уравнениям, а следовательно, к изохронности колебаний, что
не может помочь в исследовании анизохронности крутильных ко-
лебаний.
Гипотезы второй категории исходят из нелинейной зависи-
мости напряжения от деформации, которая в общем виде выра-
жается так:
т= G
' * у
У
где v — коэффициент пропорциональности;
— ) — функция, выражающая форму петли гистерезиса;
'Ш
У и Ут — текущее и амплитудное значение относительного сдвига;
я — некоторый показатель, отличный от единицы.
Для функции, выражающей форму петли, предложены две
зависимости.
Первая дана Н. Н. Давиденковым в 1938 г. [54 3:
Вторая предложена Я. Г. Пановко в 1953 г.:
'Ш-^'-Ш'-
Отметим, что форма петли гистерезиса в тех задачах, которые
описаны в литературе, не играет какой-либо роли. Существенно
важно лишь условие, чтобы площадь петли была пропорциональна
энергии, рассеиваемой за один цикл колебания.
Обе указанные нелинейные гипотезы приводят к нелинейным
дифференциальным уравнениям и, следовательно, могут быть
использованы при изучении анизохронности колебаний унифи-
ляра, в частности, в работе [132] была использована гипотеза
Н. Н. Давиденкова. В результате проведенных экспериментов
установлено, что форма петли не полностью совпадает с опытными
данными. Поэтому в основу (см. примечание 11) уточненной теории
унифиляра положена нелинейность между деформацией и напря-
жением, независимо от какой-либо конкретной формы петли.
В примечании 11 получена формула для частоты k анизохрон-
ных крутильных колебаний в зависимости от целого числа г
колебаний унифиляра за время t. Воспользовавшись этой фор-
мулой, можно определить период Т колебания г, происходящего
84
через время I после начала отсчете
z + q In—S-
a
где коэффициент, учитывающий анизохронность колебаний (коэф-
фициент анизохронности),
* = 1Й- <67>
Теперь можно предложить следующую методику эксперимен-
тального определения моментов инерции с учетом внешнего и
внутреннего рассеяния энергии.
В процессе затухающих колебаний унифи"ляра от некоторой
произвольной, но зафиксированной начальной амплитуды а0
надо зарегистрировать времена t1 и tif а также амплитуды а1 и а2
для некоторых чисел колебаний zx и z2. На основании формулы (66)
можно найти значение коэффициента анизохронности
t.ln-^-Mn-^-
(68)
Период незатухающих колебаний подсчитаем по формуле (66):
'Р tj.
U2
Дальнейшее определение момента инерции можно выполнить
по приведенным ранее формулам, в зависимости от способа
исключения «направляющей» силы подвеса (с применением эта-
лона, способом Гаусса или с закреплением тела на приборе).
Пример 9.
Упругий элемент изготовлен из стальной проволоки длиной
10 -- 256 мм и диаметром d0 ~ 1,2 мм. На нижнем конце про-
волоки закреплен цанговый зажим, на который можно наверты-
вать испытуемое тело. Верхний конец проволоки с помощью ана-
логичного зажима прикреплен к штативу Г132 ].
Эксперимент проведен с двумя цилиндрами, один из которых
принят за эталон, а второй — за испытуемое тело. Массы и теоре-
тически вычисленные моменты инерции этих цилиндров были сле-
дующими:
тэ = 1236,2 г, J, = 11101,5 ± 1,3 гсм2;
т = 2849,8 г, J = 58409,5 ± 26,2 гсм2.
Момент инерции цангового зажима равен
Ззаж ~ 23 ± 0,1 гсм2.
85
Эталон, а затем Цилиндр навинчивали на нижний зажим и
наблюдали затухающие колебания каждого из них. В ходе коле-
баний регистрировали амплитуды и время колебаний. Время
регистрировали секундомером с точностью 0,1 сек. Для исключе-
ния случайных ошибок и повышения точности каждый из опытов
повторяли 20 раз.
Данные опытов.
Эталон: а0 = 0,20717 ± 0,00036 рад; ^^ 0,11350 ±
± 0,00029 рад; а2 ~- 0,06140 ± 0,00017 рад; tt = 26,418 ±
± 0,0225 сек; t2 = 92,150 ± 0,0199 сек; гг = 30 колебаний;
г2 = 105 колебаний.
Испытуемое тело: а0 = 0,20872 ± 0,00044 рад; аг = 0,11363-
± 0,00030 рад; а3 - 0,06612 ± 0,00026 рад; t1 -= 50,400 ±
± 0,0195 сек; t2 = 150,810 ± 0,0161 сек; гг -= 25 колебаний;
z2 = 75 колебаний.
Данные эксперимента были обработаны: 1) с учетом удлине-
ния упругого подвеса, но без учета анизохронности, и 2) с учетом
влияния анизохронности колебаний.
1. Периоды изохронных колебаний эталона и испытуемого
тела:
Тэ = 0,8776 ± 0,000189 сек;
Т = 2,0108 ± 0,000215 сек.
Для момента инерции эталона напишем (с учетом растяжения
проволоки)
Js + J,,x = ^Tl[\ -^r(l +Щ],
а для момента инерции испытуемого тела
-?+1заж = 1^Т* [1-"§-(1 +4)1)
откуда момент инерции тела
, _ (Js + J „ж) Т* ' £'('+4^
J —— X * ' /
^^г(1+4ц)
заж-
Относительные удлинения проволоки для эталона и испытуе-
мого тела следующие: ~- — 0,55-10~4 -р- = 1,26-10"4. Под-
ставляя значения величин в формулу момента инерции, найдем
/ = 58370,0 гсм\
Точность искомой величины оценим по формуле
hnf^zL = 0,068 °о.
•> теор
86
2. Применим методику, учитывающую рассеяние энергии.
Коэффициенты неизохронности колебаний эталона и испытуемого
тела, вычисленные по формуле (68), равны q3 = 0,403 ± 0,007;
q = 0,289 ± 0,004. Периоды незатухающих колебаний, вычислен-
ные по фсрмуле (66), учитывающей неизохронность крутильных
колебаний, следующие: Т„ = 0,8735 ± 0,0002 сек; Т = 2,0019 ±
± 0,0003 сек. Момент инерции, вычисленный по той же формуле,
что и в предыдущем случае, оказался равным
J = 58395,3 гсм\
Следовательно, точность в данном примере составляет
Jmeop-J =0)024%.
3 теор
Следовательно, учет рассеяния энергии в материале подвеса
и во внешней среде позволяет существенно повысить точность
определения моментов инерции методом унифиляра.
Относительную ошибку 6/ с учетом рассеяния энергии надо
определять по формулам § 3 в зависимости от способа экспери-
мента. Входящие в эти формулы частные относительные ошибки
измерения периодов колебаний следует вычислять по формулам
87 =
Vw+T^fiw™
+ (ба0)а + (ба2)2 ] ,
где относительная ошибка определения коэффициента анизохрон-
ности
bq = X
аг «1
X
l/Ц [W + W] + {h - hf (бао)2 + t\ {ЬахУ + t\ [batf
6а, 6а1( Ьа2—-относительные ошибки измерения начальной, про-
межуточной и конечной амплитуд;
{^ и б/2 — относительные ошибки измерения времени коле-
баний.
§ 6. ОБЛАСТЬ ПРИМЕНЕНИЯ МЕТОДА
Метод крутильных колебаний получил широкое применение и
занимает первое место по точности среди известных эксперимен-
тальных способов,
?7
т^Н
8 9
.L
5=
ал
Метод широко применяют не только там, где нужна точность
до сотых долей процента, но и при более грубых определениях.
Так в работе [390] методом унифиляра определен момент инер-
ции 56 судовых гребных винтов. Его применяют для определения
моментов инерции артиллерийских снарядов [220], деталей авто-
мобиля [21 ], звеньев мельничных машин [36, 38,40], коромысел
весов [46, 73], в приборостроении [55]
и т. п.
Различные методики и варианты прибо-
ров имеются в трудах многочисленных авто-
ров [107, 136, 167, 173, 177, 226,231,310];
предложены номограммы, облегчающие вы-
числения.
Почти во всех руководствах указано, что
по периоду крутильных колебаний тела, под-
вешенного на упругом стержне, можно опре-
делять моменты инерции только относительно
центральных осей, при этом центр масс тела
должен лежать на оси стержня. Это ограни-
чение является необоснованным, и по кру-
тильным колебаниям непосредственно из
опыта можно определить моменты инерции
тела относительно осей, не проходящих через
центр масс.
На чертеже (рис. 29) показана схема при-
бора для определения моментов инерции
тела относительно нецентральных осей[45].
Стальной стержень 2 цанговыми зажима-
ми / и 3, подобными зажимам в токарном
станке, жестко соединен с неподвижным шта-
тивом 6 и рамой 4, на которой можно закре-
пить испытуемое тело. Под площадкой 5
имеются стержни 7, которые можно повора-
чивать вокруг вертикальной оси, совпадающей с осью упругого
стержня 2. На стержнях 7 имеются подвижные грузы 8, которые
можно закрепить установочными винтами 9 в любом месте и опре-
делить их положение по метрической шкале, нанесенной на стерж-
нях. Для центрирования прибора в центре площадки 5 перпенди-
кулярно к ней расположена стрелка 10. Если центр масс прибора
лежит на оси рамы, то стрела находится на одной вертикали с не-
подвижной стрелкой 11.
Перед опытом прибор центрируем, поворачивая стержни 7,
а'если необходимо, то и перемещая грузы 8, до тех пор, пока
оси стрелок 10 и // не совпадут. Установим испытуемое тело
на площадке 5. Если центр масс лежит на центральной оси при-
бора, то положение стрелки 10 останется неизменным, а если
смещен, то центр масс системы (прибор + тело) не может нахо,-
Рис. 29. Прибор для
определения моментов
инерции тела относи-
тельно нецентральных
осей
диться на оси прибора и стрелка Ю уходит в сторону. Чтобы не
перемещая испытуемое тело на площадке 5, привести центр масс
системы к оси прибора, надо изменить положение центра масс
прибора, поворачивая стержни 7 до совпадения осей стрелок 10.
Момент инерции равен сумме произведений массы каждой частицы
на квадрат ее расстояния от оси, так как при повороте стержня
вокруг оси расстояния частиц от оси не меняются, момент инерции
прибора не меняется при повороте стержней 7 с грузами 8 вокруг
оси прибора.
Вычислив по формуле (56) период крутильных колебаний
системы, определяем момент инерции системы и, вычитая известный
момент инерции прибора (при данных положениях грузов на
стержнях), находим момент инерции тела относительно оси при-
бора, не проходящей через центр масс испытуемого тела.
I Пример 10.
Определение моментов инерции конечностей человеческого
тела. Биомеханические исследования иногда требуют рассмотре-
ния человеческого тела как механической системы, состоящей из
отдельных звеньев, и в первую очередь исследования геометрии
масс этой системы, определения положения центров тяжести и
моментов инерции относительно различных осей всего челове-
ческого тела и отдельных его конечностей [56, 204].
Л. Е. Евгеньева [56] определяла момент инерции отдельных
конечностей на специально сделанной модели. Немецкие ученые
(Брауне и Фишер) экспериментально определяли моменты инерции
ампутированных конечностей [204].
Для определения момента инерции ноги гимнаста относи-
тельно оси, проходящей перпендикулярно к ней через тазобед-
ренный сустав, тело гимнаста было фиксировано на приборе
(см. рис. 29) в положении, указанном на рис. 30, а, причем тазо-
бедренный сустав находился на оси прибора, а правая нога вытя-
нута вдоль оси.Произведя центровку и измерив период колебания,
экспериментаторы предложили гимнасту, не меняя положения рук
и туловища, вытянуть правую ногу вдоль левой. От этого переме-
щения центровка унифиляра нарушилась и была восстановлена
поворотом стержней. Затем был измерен период колебаний уни-
филяра при втором положении гимнаста и вычислены моменты
инерции J'-, и J2 для обоих положений тела. Момент инерции ноги
определен как разность
•'ноги •> 2 •> !•
Таким образом, экспериментаторы пренебрегли моментом инер-
ции ноги относительно оси прибора в первом положении (рис. 30, а)
тела. Ошибка, допущенная при этом, не велика. Для сравнения
укажем, что момент инерции стального прутка массой 9 кг, дли-
ной 1 м и диаметром 4 см относительно оси, перпендикулярной
к нему, в его конце равен 3 /сз-ж2, а относительно его оси равен
89
0,0018 кг-м2, т. е. 0,06% момента относительно перпендикуляр-
ной оси. Можно полагать, что сделанное допущение не повлечет
ошибки большей, чем 1—2%. Аналогично был определен момент
инерции вытянутой руки относительно плечевого сустава.
•Л
Рис. 30. Определение моментов инерции верхних и нижних ко-
нечностей человека
§ 7. РЕКОМЕНДАЦИИ К ПРОВЕДЕНИЮ ОПЫТА
Методом упругих колебаний можно определить моменты инер-
ции самых различных тел и получать результаты с различными
пределами допустимых ошибок. Выбор расчетной формулы и аппа-
ратуры, необходимой для проведения опыта, определяется тре-
буемой точностью.
Наиболее простые и, естественно, менее точные формулы (57),
(58), (59), (61) и (6Г) получены в предположении об изохронно-
сти колебаний и постоянстве коэффициента с унифиляра.
В случае использования этих формул достаточно вычислить
момент инерции эталона (массу грузов и расстояние между ними
для способа Гаусса) и замерить требуемые периоды колебаний.
Для измерения времени колебаний желательно вместо обычно
применяемого секундомера использовать электросекундомер.
Для достижения большей точности эксперимента надо учиты-
вать непостоянство коэффициента с унифиляра, т. е. воспользо-
ваться одной из следующих формул: (62), (63), (64), (65) и (65').
В этом случае, кроме перечисленных величин, необходимо знать
вес эталона (вес дополнительных грузов при способе Гаусса),
а в случае вычисления с измерить также диамегр и длину нена-
90
груженного упругого подвеса, модуль Юнга и коэффициент Пуас-
сона для материала подвеса.
Наконец, наибольшую точность эксперимента можно достичь
при учете анизохронности крутильных колебаний. В этом случае
надо использовать те же расчетные формулы (62), (63), (64),
(65) и (65'), но входящие в них периоды колебаний определить по
формуле (66). При проведении эксперимента необходимо замерить
амплитуды колебаний унифиляра (в начале, в середине опыта,
и в конце опыта). Амплитуды колебаний целесообразно изме-
рять с помощью шкалы, по движению луча света, отраженного
от зеркала, укрепленного на упругом подвесе у нижнего за-
жима.
Независимо от требуемой точности опыты можно проводить
так называемым английским методом, методом Гаусса и с исполь-
зованием прибора. Если имеется прибор, на котором можно за-
крепить испытуемое тело, то, конечно, проще опыт проводить
на приборе. Если прибора нет, то метод Гаусса предпочтительнее
английского, потому что в английском методе на упругом стержне
закрепляют последовательно эталон или испытуемое тело, это
закрепление может быть неодинаковым, а это отражается на точ-
ности результата.
Некоторые исследователи рекомендуют длину и диаметр упру-
гого стержня выбирать такими, чтобы получить период колебаний
более удобный для наблюдений (1 сек < Т < 3 сек).
Диаметр проволоки нужно выбирать таким, чтобы приведен-
ное напряжение па поверхности проволоки, рассчитанное по нор-
мальным напряжениям от веса прикрепленного тела и касательным
напряжениям при амплитудном угле закручивания унифиляра,
не превышало предела пропорциональности для материала под-
веса. Из экспериментальных работ по упругому гистерезису сле-
дует, что с возрастанием веса подвешенного тела рассеяние энер-
гии в материале подвеса несколько снижается. Поэтому большие
значения нормального напряжения вполне допустимы. Однако
приведенное напряжение на поверхности проволоки не должно
превышать предела выносливости материала, так как иначе,
в процессе колебаний, может иметь место нестационарный режим
рассеяния энергии, что приведет к неподдающейся учету анизо-
хронности *.
Выбирая длину упругого стержня, нужно иметь в виду, что
крутильные колебания унифиляра обычно сопровождаются маят-
никовыми колебаниями, мешающими наблюдениям, при большой
Длине устранить их трудно.
* В опытах Ф. Ф. Лендера в подвесе из стальной проволоки нормальные
напряжения от веса прибора и испытуемого тела были равны сгтах = 2500 кГ/см2,
а максимальное напряжение сдвига тшах = 1040 кГ/см2- Следовательно, при-
веденное напряжение в подвесе было слишком велико, порядка 2700 кГ/см2.
91
Поэтому в литературе рекомендуют применять специальные
приспособления, например [3] следующие. По оси прибора снизу
имеется коническое отверстие, а на станине под отверстием распо-
ложен конус, который можно передвигать вверх и вниз. В начале
опыта конус поднимают вверх и вводят в коническое отверстие.
После того как унифиляр сделает несколько колебаний, конус
осторожно опускают вниз и определяют период.
Некоторые авторы предлагают успокаивать маятниковые ко-
лебания ватой. В этом случае удобно по оси прибора установить
две соосные стрелки, одна из которых колеблется вместе с прибо-
ром, а другая неподвижно закреплена на станине, как это сделано
в приборе, описанном в примере 10. Охватив кусочком ваты обе
стрелки, легко устранить маятниковые колебания.
Рис. 31. Цанговый зажим
Иногда рекомендуется [2371 натягивать нить по оси прибора,
но исключить маятниковые колебания можно лишь при условии,
что нить сильно натянута, а это приводит к снижению точности
вследствие изменения коэффициента жесткости унифиляра.
Хотя длина упругого подвеса не входит ни в одну из формул,
необходимо, чтобы концы упругого стержня были жестко соеди-
нены и с телом (или прибором), и со станиной, относительные
смещения недопустимы.
Упругий подвес защемляют верхним концом в зажиме, укреп-
ляемом в неподвижном штативе, а нижний используют для при-
крепления испытуемого тела или прибора. Конструкция должна
быть такой, чтобы, зажимая упругий подвес, он не разрушал формы
и размеров его сечения (рис. 31, 32).
Отметим, что испытуемое тело и эталон не должны иметь каких-
либо перемещений по отношению к прибору, на котором они на-
ходятся. Поэтому прибор должен быть снабжен устройством для
надежного закрепления испытуемого тела и эталона. На рис. 33 и
34 показаны такие устройства в унифилярах Путиловского завода
и СКБ MB и ССО.
Если упругость стержня определяют из опыта или она исклю-
чена из окончательной формулы, то упругий стержень можно при-
паять или приварить к прибору и к станине.
Если при вычислении относительной ошибки определения
момента инерции способом Гаусса пренебречь относительной
92
Ошибкой теоретического вычисления момента инерции эталона,
а в аналогичной формуле для случая прикрепления грузов пре-
небречь ошибками измерения массы грузов и расстояния между
~-Ж
Ш////////////Ш.
Рис. 32. Определение Рис. 33. Прибор Путилов- Рис. 34. Прибор
момента инерции ро- ского завода ТММ-26 (СКВ MB
тора и ССО)
ними, то относительная ошибка эксперимента для обоих вариантов
равна
6/^ 2 (l ■{- ~) ViSTtf + (6T2f.
Введем обозначение 2(1 -Ь ,) — Л, найдем значения коэф-
фициента А в зависимости от отношения:
J :Ja
А
0,1
2,2
0,25
2,5
0,5
3
0,75
3,5
1
4
2,5
7
5
12
7,5
17
10
22
Следовательно, для повышения точности эксперимента надо
выбирать величину /3 по возможности большой. Но увеличение
момента инерции, следовательно, веса подвешиваемых грузов или
эталона приведет к большому изменению крутильной жесткости
Подвеса и изменит характер анизохронности колебаний.
93
В. П. Ветчинкин [22] считает, что моменты инерции эталона и
испытуемого тела должны быть примерно равными. Д. Крейхгауэр
[299] для подвешивания двух грузов рекомендует: «Цилиндры
должны быть настолько тяжелы, чтобы момент инерции увеличи-
вался больше чем вдвое, даже втрое».
Дополнительные грузы к испытуемому телу необходимо при-
креплять так, чтобы центральная ось инерции системы совпадала
с осью подвеса, в противном случае снижается точность экспери-
мента. Эталон должен быть прикреплен к телу жестко. При под-
вешивании эталона на проволоках, нитях и пр. унифиляр превра-
щается в двойной крутильный маятник, что снижает точность.
При экспериментах с постоянными магнитами дополнительные
грузы, по предложению Гаусса, насаживали на острия, укреплен-
ные на магните. Однако измерить расстояния между центрами
тяжести грузов с необходимой точностью не удавалось, поэтому,
по предложению Вебера, их стали подвешивать на тонких шел-
ковых нитях. В этом случае расстояние между центрами тяжести
измеряли компоратором с высокой точностью. Однако, как пока-
зал Крейхгауэр [299], система представляет тройной маятник и
колебания грузов снижают точность эксперимента.
В случае подвешивания тела на приборе для повышения точ-
ности желательно, чтобы момент инерции прибора был несколько
меньше момента инерции эталона и испытуемого тела.
Приведем числовые значения отношений моментов инерции при-
бора и эталона, прибора и испытуемого тела:
Экспериментатор Jп: Jg J : J
Г. Д. Кокош и Н. А. Смирнова 0,29 0,04
Ф. Ф. Лендер 1,94 0,3
В. Н. Тихонов 1,2 0,8—1,4
♦ 44
Глава I/
♦ ♦♦
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
ПО КОЛЕБАНИЯМ НИТЯНЫХ ПОДВЕСОВ
§ 1. ИСТОРИЯ МЕТОДА. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ МЕТОДА
При различных экспериментах в физике и технике применяют
подвешивания на гибких нитях или лентах, верхние концы кото-
рых закреплены неподвижно, а ниж-
ние прикреплены к испытуемому
телу или прибору (рис. 35). Такая -ч^; •
система, выведенная из состояния ^*
равновесия, совершает колебания, *
поэтому нитяные подвесы часто на- 1
зывают нитяными маятниками. j
В зависимости от числа нитей J
нитяные маятники имеют собствен- ;
ные названия. Подвес на двух нитях •
называется бифилярным подвесом, •
или бифиляром (от лат bis — дваж- ■
ды +лат. filum— нить),трехнитяный j
подвес — трифиляром. Трехнитяные, i
четырехнитяные (рис. 36) и подвесы :
на большем числе нитей называют
мультифилярами (от лат. multum —
много + лат. filum — нить) или менее :<- ' '
удачно полифилярами (от греч. poly— ?± ■ -.
много + лат. filum — нить). Щ -') Л$!
Первые научные исследования ко- *^у£•-'-.
лебанийнитяных подвесов проведены ^ ■"'_'•
в Петербурге Д. Бернулли [191]. "* - ;%}^"~^-#>;
Теории нитяных подвесов посвящены -'• :-Т "-с*
работы (1785 г.) Н. Фусса [253, 254], Г* ^
(1815 г.) Боудича [202], (1837 г.) ■ ?
Гаусса [258, 259], (1883) Кольрауша
[293, 294], Люксенберга [312], _ ,, п , тмм „_
/,00! . v геле 1 /innn \ Рис. 35. Прибор ТММ-27
(1884 г.) Хоппа [275], (1909 г.) (СКВ MB и ССО СССР)
Пелльа [338], (1920 г.) Ветчинкина
[22], (1935 г.) Победоносцева [123, 124], (1957 г.) Хигса [278],
(I960 г.) Хаага и Шалеа [269] и др.
95
Для определения моментов инерции вначале был применен
по предложению Гаусса (1837 г.) бифилярный подвес, метод раз-
вит Кольраушем в 1883 г. [293].
Из мультифиляров для определения моментов инерции раньше
других был применен, по-видимому, трифиляр. Опыты проведены
в английской Национальной физической лаборатории для иссле-
дования авиационного мотора «Гном», но работа эта не была опу-
бликована. Проф. В. П. Ветчинкин [22] указывает, что в лабора-
тории Н. Е. Жуковского студент МВТУ Г. Н. Мусинянц в 1915 г.
Рис. 36. Определение момента инерции железнодорожного ва-
гона на четырехнитяном подвесе
применил трифиляр для определения момента инерции артилле-
рийской гранаты. В последующие годы многонитяные подвесы
неоднократно применяли для определения моментов инерции
различных тел.
Теория экспериментального определения моментов инерции
с использованием многонитяного подвеса разработана В. П. Вет-
чинкиным [22] и является развитием теории бифиляра, предло-
женной Ф. Кольраушем [293, 294]. Теория проф. Ф. Коль-
рауша основана лишь на статическом соотношении между весом
подвешенного тела и натяжением нитей. Ту же неточность допу-
скает и теория мультифиляра, приведенная В. П. Ветчинкиным.
В последующем теорию этого метода излагали многие авторы,
среди которых следует отметить Ю. А. Победоносцева [124] и
А. Н. Волохова [27]. Однако все выводы, включая составление
дифференциального уравнения движения испытуемого тела (выра-
96
жение восстанавливающего момента), исходят из условий натяже-
ния нитей, полученных для неподвижного тела, подвешенного
на этих нитях.
В настоящее время автором метода принято считать проф.
В. П. Ветчинкина, впервые (1920 г.) опубликовавшего его в пе-
чати. Но в предисловии к третьей части («Дополнительные статьи»)
курса «Теоретическая механика» проф. Н. Е. Жуковского [25],
изданной в 1925 г. под редакцией В. П. Ветчинкина и Н. Г. Чеп-
цова, сказано, что в основу описания этого способа «была поло-
жена рукопись проф. Н. Е. Жуковского, составленная им в 1915 г.
для аэродинамической лаборатории МВТУ. Этот способ Н. Е. Жу-
ковский излагал на своих лекциях студентам математического
факультета Московского Университета». Таким образом, воз-
можно, что автором метода мультифиляра является проф.
Н. Е. Жуковский. Но этой рукописи Н. Е. Жуковского в его
Музее нет. Не привели к успеху и другие попытки разыскать
рукопись.
Теоретические основы экспериментального определения мо-
ментов инерции на различных нитяных подвесах схожи между
собой. Сначала рассмотрим элементарную теорию бифилярного
подвеса.
Телу, подвешенному на двухнитяном подвесе, можно сообщить
три различных простых движения.
Если тело выведено из равновесия так, что его центр масс пере-
мещается в направлении, перпендикулярном вертикальной пло-
скости, проведенной через равновесное положение нитей, то бифп-
ляр представляет собой двойной маятник (гл. III).
Если центр масс тела получил элементарное перемещение
в плоскости нитей, то тело совершает малые колебания в плоскости
подвеса (§ 8). Если тело подвешено на двух нитях одинаковой
длины и при равновесном положении тела нити параллельны,
следовательно, вертикальны, то тело, выведенное из равновесного
положения так, что центр масс остался в плоскости нитей, совер-
шает поступательное движение и найти его момент инерции невоз-
можно. В 1909 г. Пелльа предложил остроумный метод определе-
ния на таком подвесе ускорения g свободно падающих тел.
Если тело выведено из равновесного положения поворотом
вокруг центральной вертикальной оси, то оно совершает колеба-
ния вокруг этой оси.
В практике экспериментального определения моментов
инерции наибольшее распространение получил третий из этих.
способов, теорию которого можно изложить двумя различными
путями.
Первый путь, предложенный Гауссом в 1837 г. [258], изложен
Кольраушем в 1883 г. [293], а затем и другими исследователями [27,
124], заключается в составлении и интегрировании дифференци-
ального уравнения движения тела под действием восстанавли-
7 М. М. Гернет 2274 97
вающего момента, который определяют как момент статических
реакций нитей
М
А.
Pi
+
sin ф.
где
/j — проекция расстояния между верхними точками
крепления нитей на горизонтальную плоскость;
/2 — то же, для нижних точек закрепления нитей;
за-
Рх и Рг — реакции нитей;
hx и h2 — проекции нитей на вертикальную ось;
Ф — угол поворота тела вокруг вертикальной оси.
Почти все эти величины меняются при движении тела, и интег-
рирование дифференциального уравнения становится невозмож-
Вид С
ным без ряда упрощающих до-
пущений.
Второй путь исследования
колебаний вокруг вертикальной
оси, очевидно, впервые приме-
ненный Улером [378], основан
на теореме об изменении кине-
тической энергии или на урав-
нении Лагранжа в обобщенных
координатах. Не имея решаю-
щих преимуществ, этот способ
позволяет глубже исследовать
зависимость периода колебаний
от основных параметров подвеса
(длины нитей, расстояния между
ними и др.). Поэтому дальней-
шее изложение основано на при-
менении этих уравнений дина-
мики.
Рассмотрим твердое тело,
подвешенное на двух вертикаль-
ных нитях равной длины (рис.
37). Нити будем считать идеаль-
ными, т. е. нерастяжимыми и не обладающими жесткостью. Центр
масс тела находится на оси симметрии подвеса, которую будем назы-
вать осью подвеса. Построим прямоугольнукГсистему координат
xOyzc началом в центре масс при равновесии тела, а ось Oz напра-
вим вертикально вниз. Введем следующие обозначения: / — длина
каждой из нитей; 2а — расстояние между нитями; /ng — вес тела;
/ = тги — момент инерции этого тела относительно оси подвеса.
Примем за обобщенную координату ф — угол поворота бифи-
ляра вокруг оси Oz. Из чертежа видно, что при повороте тела на
угол ф нити отклоняются от вертикального положения на угол г|з.
98
Рис. 37.
Бифиляр с вертикальными
нитями
Связь между углами нетрудно найти из рассмотрения дМЛГО и
дМЛГМ
2аsin— = ^ sin г|з,
откуда
1 л Г
sin ij; = 2 -^г sin -|- и cos г|з = —г- 1/ /2 — 4a2 sin2 ~
Аппликата центра масс тела
zc = — / (1 — cos я|з) = — / + ]/ /2 — 4a
2 sin2 -y-
n • Ф Ф
При малых углах поворота можно принять sin-s- = -к- , тогда
zc = — l + VP — aV .
Скорость центра масс
flZ„ д2ф • а2ф
Обобщенную силу Q найлем из условия
2j dAaKm — Qd<p, т. е. mg dzc = Qa\p или mgzc dt = Qф a7:
mga2 ф
<? =
/
Кинетическую энергию определим по фэрмуле Кенига
mz\ mr\ip m /д4ф2 2\ -2
£ = ~2- + —2— = "Г ("F 4- ги) Ф .
Пренебрегая малыми второго-порядка, получим
9
тг,, ■
£ = ^ф2,
тогда
дЕ ^ дЕ 2 • d д£ 2 ■■
Уравнение Лагранжа принимает вид
2 •• тви'ф*
* Величина с = j называется чувствительностью бифиляра и имеет
размерность, обратную размерности момента силы.
или
Ф + -Чт Ф = О-
Период малых колебаний бифиляра вокруг вертикальной оси
т = 2я-тУт' (69)
откуда
J = ™l = ^T*JL. (70)
Ввиду сделанных допущений полученная формула не учиты-
вает ряда факторов (влияние амплитуды колебаний, перемещение
центра масс, жесткость нитей), поэтому может быть использована
лишь при приближенных вычислениях.
§ 2. ТЕОРИЯ МЕТОДА. ПАРАЛЛЕЛЬНОЕ
РАСПОЛОЖЕНИЕ НИТЕЙ
Точность формулы (70) возрастает с уменьшением амплитуды
колебаний, но амплитуда не может быть очень малой.
Многие исследователи занимались изучением периода крутиль-
ных колебаний бифиляра при больших амплитудах. Полученные
выводы оказались противоречивыми. Курц искал выражение
периода колебаний путем последовательных приближений и при-
шел к выводу, что период колебаний во втором приближении
меньше, чем в первом. Эги выводы по словам Улера «находятся
под большим сомнением», и достоверность их невелика.
Хеун получил выражение периода колебаний в виде гипер-
эллиптического интеграла, на основе которого вывел формулу,
требующую использования таблиц эллиптических интегралов.
Из-за сложности полученной формулы он не смог дать анализа
зависимости периода колебаний бифиляра от его основных пара-
метров.
Улер [378] представил (1923 г.) период колебаний в виде
степенного ряда, исследуя который установил, что период коле-
баний в зависимости от соотношений между параметрами под-
веса (длина нитей, расстояние между ними и радиус инерции
подвешенного тела) может как возрастать, так и убывать с умень-
шением амплитуды. Улер рассматривал сходимость ряда, пред-
ставляющего период колебаний бифиляра, и установил, что при
некоторых значениях амплитуд и параметров подвеса ряд будет
расходящимся. Однако выводы Улера даны в сложной форме и
использование их затруднено.
100
Аналогичное представление периода в виде ряда и исследо-
вание возможностей снижения анизохронности колебаний бифи-
ляра содержится в работе Хаага и Шалеа [269].
Подробное исследование теории бифилярного маятника опуб-
ликовано в работе [44].
Повернем тело (см. рис. 37) вокруг оси Ог на угол cp0. Каждая
из нитей отклонится от вертикали на угол i)50. Если тело затем
отпустить, то оно под действием тяжести и натяжения нитей будет
двигаться, причем центр тяжести С будет перемещаться по оси Ог,
а тело поворачиваться вокруг этой же оси.
Введем следующие обозначения:
Тогда
а , ги
sin ч|з = 2 -г- sin -~- = 2р sin ~y~
1. При a <-g- , т. е. р <-к- или 4р2 < 1, угол г|) растет мед-
леннее, чем возрастает ~- . Когда у- = 90°, то sin i|)max = 2р < 1.
Дальнейшее увеличение ~ приведет к тому, что нити пересе-
кутся и начнут свиваться, угол г|з не изменится. Следовательно,
предельное значение угла ф равно 180°, а угла т|) определяется
выражением
sin ipraax = 2р.
2. При а = -к- , т. е. р = -к- или 4р2 — 1, значению -~ = 90°
соответствует значение г|) = 90°.
3. При а > -„- , т. е. р > -к или 4р2 > 1, угол -ф возрастет
быстрее угла -| . В пределе при лр — 90° sin ф™х- = у- < 1.
Аппликата центра масс подвешенного тела найдена в § 1 : гс =
—■ — /(1—cos г);). Скорость центра масс vc — zc = —/ sin гр -лр.
Напишем следующее соотношение между углами <р и \|з:
Ф = 2arc sin g— sin oj).
Дифференцируя по времени, найдем соотношение между пер-
выми производными
2 cos гЬ ;
Ф = Y=- ф.
l^4p2— sin3 гр
101
Напишем уравнение кинетической энергии бифилярного маят-
ника на участке от начального положения, соответствующего
углу ф0 или ij;0, при котором кинетическая энергия равна нулю,
ло некоторого текущего положения, определяемого углом ф по-
ворота или \\> отклонения нитей:
mv2c tnr\$l
х
mgl (cos \|з — cosij;0)
2 2
Подставим значения tp и %
/ . ., , 4</'-cos2ii- \ ■, 2g , .
откуда
: di|) "|/"2g j/"cos \|з — cos \j^
I /" 4</'2 cos2 \b . . , ,
4p2 — sin3T(:
Разделяя переменные, умножая на 4 и интегрируя, найдем
период колебаний бифилярного маятника:
^0
г 'й | J/ COS lf> — COS tjl0
о'
Подстановкой sin -„- ^ sin -~ sin | --- |/у представим период
колебаний в следующем виде:
л
~2
„ _ . -I/Г] (' УУ*-4 (9'»-р*) Y + 4 (д'*-ръ~- 1) уз + 8у» - 4YJ ~
it
(71')
Интегрируя (см. примечание 12), получаем формулу
102
где bi, b2, b3, ... — некоторые коэффициенты (см. примеча-
ние 12). Эта формула выражает период колебаний бифилярного
маятника в зависимости от угла -фо начального отклонения нитей
от вертикали и справедлива при любом значении этого угла. На
практике вместо этого удобнее пользоваться начальным углом
закручивания ср0 бифиляра вокруг оси Ог. Для этого формулу (72)
представим в виде
T=2n^Y-L[l + -L^sirr^ + -^-(b1 + |б2) />*sln*^ -f-
+ (b1 + ^-b2 + ^rbH)p«sui«^- + -..J. (72')
Использование выражений (72) и (72'), как правило, право-
мерно. Однако исследование сходимости этих рядов (см. приме-
чание 13) показало, что между параметрами бифиляра и ампли-
тудой ф0 существуют такие соотношения, при которых ряд пере-
стает быть сходящимся, а следовательно, использование этих
формул становится невозможным. Если для данного бифиляра
отношение больше некоторого теоретического минимума [44],
определяемого формулой
(4L--&(vtt¥-').
то (72) и (72') применимы при любых амплитудах, а если меньше,
то они применимы лишь для колебаний с амплитудой, не пре-
вышающей некоторого предельного значения ф0, которое может
быть найдено из равенства
<IWa = 2arcsin
Равенство (72') показывает, что период колебаний бифиляр-
ного маятника зависит от амплитуды ф0. При опытном определе-
нии моментов инерции стремятся осуществлять колебания с не-
большими амплитудами, обеспечивающими удобный и надежный
отсчет периода колебаний. Если допустить, что амплитуда коле-
баний ф0 невелика, то множители sin -I2-, входящие в члены
ряда (72), резко убывают при возрастании k, а следовательно,
и значения членов ряда по мере возрастания степени sin -g-
резко убывают. Поэтому для изучения возможности снижения
103
анизохронности колебаний бифиляра рассмотрим наиболее «весо-
мые» члены ряда — второй и третий.
Как показано в работе [44], множитель при sin2-™- в урав-
нении (72') для ги= 1,15а равен 0,25 независимо от отноше-
ния -у. Если ги<С 1,15а, то он возрастает от 0,25 до оо по мере
увеличения -у-.
При гц> 1,15а с возрастанием -у- множитель убывает и обра-
щается в нуль, когда
а Ги
у к-**2
В этом случае период колебаний бифиляра зависит от чет-
вертои и последующих четных степеней sm-^-.
При малых амплитудах членами, содержащими sin4 —, sin6-y-
и т. д. можно пренебречь и выразить период
Еще большее приближение к изохронности можно получить
при — = 1,21 и -у- — 1,93, когда период маятника зависит
только от шестой и более высоких четных степеней синуса. При
небольших амплитудах период качаний такого бифиляра с боль-
шой точностью можно представить^формулой
Т= 1,6л |/^.
Однако снижение анизохронности соответствующим выбором
параметров подвеса можно достичь только путем уменьшения
длины нитей и периода колебаний, что неизбежно приведет
к уменьшению точности измерения периода и поэтому не может
быть рекомендовано в практике экспериментальных определений
моментов инерции.
Бифилярный маятник с найденными параметрами можно реко-
мендовать только для определения моментов инерции тел с боль-
шим радиусом инерции, так как период колебания такого маят-
ника с небольшим моментом инерции невелик и относительная
ошибка вычисления получается большая.
104
§ 3. УСЛОВИЯ РАСПОЛОЖЕНИЯ НИТЕЙ
МНОГОНИТЯНОГО МАЯТНИКА.
ЦИЛИНДРИЧЕСКИЙ МУЛЬТИФИЛЯР
В. П. Ветчинкин считает [22], что нити мультифиляра могут
иметь неодинаковую длину и точки прикрепления их к телу и
штативу могут быть расположены различными способами, того же
мнения придерживается А. Н. Волохов [27]. Это имеет значение
в тех случаях, когда положение точек прикрепления нитей к телу
обусловлено специфической формой тела или когда его нельзя
закрепить в специальной раме. Рас-
смотрим особенно часто встречающие-
ся на практике случаи, когда при
равновесии тела точки М1, М2, ■ ■ ■,
М,г прикрепления нитей к телу лежат
в одной горизонтальной плоскости
М, то же относится и к точкам N v
N2, • •. Nn прикрепления нитей к
штативу (к станине). Плоскость М
неизменно связана с испытуемым
телом. Вторая плоскость (Л/) связана
со штативом и, следовательно, непо-
движна. Нити M1N1, M2N2, . . .,
MnNn считаем идеальными, т. е. не-
растяжимыми, невесомыми и неупру-
гими. Длину и направления нитей
не ограничиваем.
Определим, как должны быть расположены точки Mlt M2, ...
;. . ., Мп на плоскости М и точки Nt, N2, . . ., Nn на плоско-
сти N, чтобы при закручивании мультифиляра на произвольный
угол ф плоскость М оставалась горизонтальной, а все нити на-
тянутыми.
Первое необходимое условие: точки, в которых вертикаль,
проведенная через центр тяжести тела (т. е. линия действия веса),
пересекает плоскости М и N, не должны выходить за пределы
многоугольников М]Л12, . . ., Мп и iVj/Vj, . . ., Nn.
Вывод остальных условий проведем геометрическим путем.
Построим координатные оси (рис. 38) с началом в центре масс
тела при его равновесии, направив ось Oz по вертикали вниз.
Пусть, для определенности, плоскость М при равновесии мульти-
филяра находится над плоскостью хОу на расстоянии h, а пло-
скость N нал плоскостью М на расстоянии I. Рассмотрим нить
MkNk (где k = 1, 2 п) при равновесии мультифиляра.
Рис. 38. Схема мультифиляра
Обозначим х,
к'
Ук
- —h
координаты точки
М
к>
хт< Ут> zNk = —(h + I) — координаты точки Nk; Тк — на-
тяжение нити; cos ak, cos |3ft и cos yk — направляющие косинусы
отрезка прямой, направленной от Мк к Nк.
1Q5
Установим зависимость между координатами точек Mk и Nk,
для чего напишем уравнение прямой, проходящей через Мк в на-
правлении нити:
x — xk _ y — yk _ г — гк
cos аь cos fik cos у*
Координаты точки Nk должны удоглетрорять этому ynaFHe-
нию, и, подставляя вместо текущих координат х, у и z координаты
точки Nk, получим
XNk — Ч yNk — Ук I
cos ak cos pfe cos ук '
является катетом треугольника, гипотенузой которого
cosy*
служит длина sk нити, а так как cosYfe<0. то
I
■ = sh
COSy/j
Из предыдущих уравнений получим следующую зависимость
между координатами точек Mk и Nk:
хмк ~= xk + sk cos ak; yNk -= yk + sk cos pY
Повернем мультифиляр на некоторый угол ф вокруг оси Oz,
Абсцисса и ордината точки Мк получат новые значения:
Чх = xk cos Ф — Ук sin ф; Укг = Ч sin Ф + yk cos ф.
Новое значение аппликаты найдем из условия, что расстояние
между точками прикрепления нити к телу и штативу не изме-
нилось и равно длине нити:
s* = УЫ~\У + 04 -y*iY + (Ч ~\У-
Подставляя значения xk , yk , z^ и s^, получим
* "+(^-/^-^зтф-^со5Ф)2 + (-/г-;-Ч)2.
Из этого равенства путем несложных преобразований опреде-
лим значение аппликаты точки Mk после поворота мультифиляра:
+ /
|/ 1 _ 4 sin -I-
\(4 + у1
-(Л+0 +
xkcosak + ykcos$k\ ф
/ cos уА .' 2
. Уксю a-k—xk cos $k cos _Ф_
/ cos yk 2
106
По условию плоскость М должна оставаться горизонтальной,
следовательно, аппликаты zk точек прикрепления нитей должны
быть одинаковы для всех точек, т. е. не зависеть от значения k.
Как видно из последнего равенства, этому требованию можно
удовлетворить при выполнении двух условий:
2 г 2
xk~r У к xk cos ak + yk cos j5fe
/ cos уk
j/fccos ak — xk cos h _ g
A,
cosy*
где Aug — величины постоянные, не зависящие от k (от номера
нити). Покажем, что 5 = 0. Для этого помножим обе части равен-
ства на вертикальную проекцию натяжения нити:
Tk (yk cos ak — xk cos Pa) ~- BTk cos Vfe-
Составив подобные равенства для всех нитей, просуммируем их:
Yi (yJkcos ak — xkTkcos fy = В £ Tk cos y*.
Левая часть этого равенства выражает сумму моментов отно-
сительно оси Oz всех сил натяжений нити при равновесии мульти-
филяра. На тело, кроме натяжения нитей, действует вес G, на-
правленный по оси Oz. Момент веса относительно оси Oz равен
нулю. Следовательно, левая часть равенства представляет собой
сумму моментов всех сил при равновесии и тоже равна нулю. Сум-
ма, стоящая в правой части, выражает сумму проекций на ту же
ось всех натяжений нитей при равновесии и, следовательно, равна
и противоположна весу тела. Таким образом, предыдущее равен-
ство можно переписать так:
BG = 0.
Вес G не равен нулю, следовательно, В -= 0.
И второе условие принимает вид
yk cos ak ~ xftcosftfe _ q
cos уk
Покажем, что при равновесии мультифиляра каждая его нить
должна лежать в какой-либо вертикальной плоскости, проходя-
щей через ось Oz, т. е. через центр тяжести тела. Проведем пло-
скость через точки Mk, Nk и начало координат. Уравнение пло-
скости имеет вид
х у z
xk У к —h =0
S^li Vb-S?Lht -{h^l)
xk / /у., —
R cos Yft cos \k
107
или
_ (и _)_ h cos Pfe \ t + /x + h cosctfe
\уй г cosy*/' \ fe cos y ft
, j/fe cos a.k — *fe cos ftfe g _ q
cos Yft
Но последний член равен нулю, а потому равенство не содержит
текущей координаты z, т. е. плоскость, проведенная через три
точки, является вертикальной. Это позволяет сформулировать
второе условие расположения нитей. При равновесии мульти-
филяра центр тяжести испытуемого тела должен лежать на линии
пересечения вертикальных
плоскостей, проведенных че-
рез нити; иными словами —
нити мультифиляра должны
быть протянуты так, чтобы
при равновесии тела каждая
нить лежала в какой-либо
вертикальной плоскости, про-
веденной через ось Oz. Эту
ось будем называть осью мул ь-
м« тифиляра. Прямая, на кото-
рой лежит нить, должна пе-
7 ресекать ось или быть ей
параллельной.
На рис. 39 изображено
тело, подвешенное на четырех
нитях. Натяжения этих ни-
тей образуют две взаимно
уравновешенные пары сил,
под действием которых подвешенное тело находится в состоя-
нии устойчивого равновесия. Однако такая система не удовле-
творяет только что выведенному условию, а потому не является
многойитным маятником. Действительно, системе нельзя сооб-
щить поворот вокруг вертикальной оси ни по ходу часовой
стрелки, ни против хода, так как при повороте одна пара нитей
должна удлиниться, а другая укоротиться.
Для выяснения геометрического смысла константы Л при на-
клонном расположении нитей рассмотрим чертеж (рис. 40). Про-
должим нить NkMk до пересечения с осью Oz в какой-то точке Lk,
получим
А + у1 = Л,
где rk = LkMk sin у'к — расстояние точки Mk от оси Oz.
Таким образом, первый член постоянной А равен
4 + у\ 4
Рис.ЗЭ.Четырехнн-
тяной подвес
Рис. 40. Опреде-
ление констан-
ты полифиляра
Из чертежа видно, что
xk = LkMk cos CLk и ijk = LkMk cos $k
108
Умножив первое из этих равенств на cos a'k, а второе на cos $'k
и затем сложив их, найдем
xk cos ak + yk cos $'k = LkMk (cos2 a'k +
+ cos3fQ = L,M,(l-cos2T;)-=
= LkMk sin2 ik - rk sin yk.
Поделим это равенство на cos y'k и учтем, что углы ак и a'k;
f>k и Р*' Yjt и Ya Дополняют друг друга до 180°
xk cos ak -f Уа cos 1
cos уь
rK tg Yfc.
Тогда получим следующее выра-
жение константы А:
Как видно из чертежа, / tg v* ~
=rNk—rk< где r^= V'^+^'k — Рас'
стояние точки 7Vft от оси Ох. Условие
получим в следующем окончательном
виде:
Al -= const.
ritr
v х,
(73)
Рис. 41. Демонеграционный при-
бор, позволяющий различными
способами располагать нити
мультифиляра
Таким образом, произведение
расстояний от оси мультифиляра до
точек прикрепления нити к телу
и штативу должно быть одинаковым
для всех нитей.
На фотографии (рис. 41) изображен прибор, изготовленный
для демонстрации выведенных непременных условий расположе-
ния нитей мультифиляра. Штатив представляет собой неподвиж-
ный горизонтальный диск. Испытуемое тело подвешивают к за-
хвату, такому же диску, подвешенному к первому на нитях. Для
нитей в дисках просверлены отверстия на расстояниях 10, 20, 40,
80 и 160 мм от центра по радиусам через каждые 30°. Если нити
натянуты в плоскостях, в которых при равновесии лежит ось
мультифиляра, и для всех нитей /V/vft 1==" const, то при закручи-
вании мультифиляра на произвольный угол ф вокруг вертикаль-
ной оси все нити остаются натянутыми и нижний диск сохраняет
горизонтальное положение. Если же эти условия не выполнены
полностью, то испытуемое тело не может совершать винтового
колебательного движения, при закручивании тела вокруг оси Oz
109
Натяжение некоторых нитей ослабевает и плоскость М не сохра-
няет горизонтального положения.
Выведенные условия остаются в силе, если точки прикрепле-
ния не лежат в параллельных плоскостях М и N. Важно, чтобы
высота / точки прикрепления нити к штативу над точкой прикреп-
ления ее к телу у всех нитей мультифиляра была одинакова.
Чтобы в этом убедиться, достаточно продифференцировать по
переменному параметру ср выражение, полученное щля zkr
При вертикальном расположении нитей ak --- |3ft = 90°, по-
этому первое условие принимает вид
Х\ + У\ _ .
/ ~Л
или
Следовательно, если тело подвешено на вертикальных нитях,
расстояния всех точек прикрепления от оси мультифиляра должны
быть одинаковыми. Поэтому, вопреки утверждению В. П. Ветчин-
кина, мультифиляр с вертикальными нитями возможен только
в том случае, если нити расположены по образующим круглого
цилиндра.
В случае наклонного расположения нитей экспериментатор
может так расположить нити, чтобы были удовлетворены выведен-
ные в этом параграфе условия и, следовательно, мультифиляр
совершал бы винтовое колебательное движение относительно своей
оси. В частности, нити можно расположить по поверхности круг-
лого конуса с вертикальной осью, но «наклонные конусы», ре-
комендуемые в литературе [22, 27, 61], недопустимы.
Экспериментатор имеет возможность выбрать точки прикреп-
ления нитей. Обычно их располагают на равных расстояниях от
оси мультифиляра и в двух горизонтальных плоскостях. Тогда
гх —- г2= • • • — г„ = 6 в плоскости М и гы = гы — • • • = гмп =
— с в плоскости N. Если Ь = с — а, то имеем цилиндрический
мультифиляр, если b >• с или b <Cc, то конический мультифиляр.
Цилиндрический мультифиляр. При повороте цилиндриче-
ского мультифиляра радиуса а на угол ф аппликата центра масс
определяется равенством
zc = — I + ]//2 - 4а2 sin2-|- = — / (1 — cos т|з),
где гр — угол отклонения нити от вертикали, связанный (см. § 1)
с углом поворота ф соотношением
2а sin-j- = /simp.
ПО
Из двух этих равенств дифференцированием найдем скорость zc
центра масс и угловую скорость ф тела:
, . , • ■ 21 cos гь
гс = — /этгр-ф и Ф = /——^== ^.
У 4о2 —/2 sm2if>
Воспользуемся принятыми обозначениями -j-= р и ~ — q',
выразим кинетическую энергию тела формулой Кенига:
п- w'3 /-2,i 4<7'2cos2tb \ ;2
£=TrH4;_sln;)f.
Сопоставляя выражение кинетической энергии тела, подве-
шенного на многонитяном цилиндрическом подвесе, с выражением
кинетической энергии тела, подвешенного на цилиндрическом би-
филярном подвесе, устанавливаем их полную тождественность.
Это означает, что уравнение малых колебаний тела, подвешенного
на мультифиляре, и его интеграл тождествены уравнению и ин-
тегралу для тела, подвешенного на бифиляре. В частности, период
малых колебаний на мультифиляре выражается формулой, совпа-
дающей с аналогичной формулой бифиляра,
Т = 2п^-У~
Для колебаний с конечными амплитудами применим теорему
об изменении кинетической энергии
4(7' COS2 ф
4^2 _ sin^ + sin У)Ч2 = — (cos г|> - cos ijj0),
полностью совпадающую с записью теоремы об изменении кине-
тической энергии для тела на бифилярном подвесе. Следовательно,
период колебаний тела на мультифиляре при конечных ампли-
тудах может быть представлен бесконечным рядом (72'):
r=2n^]/-^(l+BlSin2^+S2Sin*^4----).
В § 2 подробно разобрана анизохронность крутильных коле-
баний цилиндрического бифиляра, а следовательно, и цилиндри-
ческого мультифиляра.
§ 4. КОНИЧЕСКИЙ НИТЯНЫЙ ПОДВЕС
Рассмотрим сначала двухнитяный подвес с наклонными ни-
тями, расположенными симметрично относительно вертикальной
оси (рис. 42). Такой подвес по аналогии с мультифиляром называют
коническим бифилярным подвесом. Обозначим 2с — расстояние
между верхними точками /V, и N2; 2b — расстояние между точ-
1П
камн Mj и УИ2; длину нитей обозначим через s; расположение
координатных осей сохраним прежнее.
Повернем тело вокруг вертикальной оси Ог на некоторый
угол ф и для повернутого положения тела найдем координаты
точек М1У М2, N± и JV2
М) (b cos ф, —Ь sin ф, — zc); M2 {—b cos ф, b sin ф, —zc);
Nt (с, О, — W — (с — b)2); JV2 (-с, 0, — ]/s2 — (с — b)2);
Расстояние M1N1 = M2N2 равно длине нитей
s = ]/(с — Ъ cos ф)2 + Ьъ sin2 ф + (— Vs2 — (с — b)2' + zcf;
или
Icb (1 — cos ф) — гс (2 l/sa — (с — б)2 — гс). Откуда
Рис. 42. Конический бифиляр Рис. 43. Сравнение конического
бифиляра с бифиляром при вер-
тикальном расположении нитей
Аналогичное равенство можно написать для поворота на бифи-
ляре с вертикальными нитями, выражающее зависимость между ф
и величинами zC) l и а (рис. 43):
cinaJL— ?С (2/ — гс)
ъш 2 ~ №
Из сопоставления обоих равенств следует, что движение би-
филяра с наклонными нитями тождественно движению бифиляра
с вертикальными нитями, если
/ = j/s2 — (р — Ь)\ а = У be. (74)
112
Следовательно, все выводы о периоде и анизохронности ко-
лебаний, полученные в предыдущем параграфе для цилиндри-
ческого бифиляра, могут быть распространены и на конический
бифиляр. Движение конического бифиляра тождественно движе-
нию цилиндрического бифиляра, у которого длина нитей I равна
проекции на вертикальную ось длины нитей s конического би-
филяра, а — среднему геометрическому из половин расстояния с
между верхними точками подвеса и Ь — между нижними точками.
Этот вывод относится ко всем коническим бифилярам, неза-
висимо от того, какая из двух величин с или Ъ больше.
Рассмотрим многонитяный конический подвес. При повороте
такого подвеса на угол ф центр масс подвешенного тела сместится
от начала координат и его аппликата выразится равенством
zc = — / + |//2 — 4bc sin2-J-.
Это равенство тождественно соответствующему равенству для
цилиндрического мультифиляра, если удовлетворяются соотно-
шения (74). Таким образом, все сказанное в этом параграфе от-
носится не только к коническому бифиляру, но и к многонитяным
коническим подвесам, нити которых независимо от их числа рас-
положены по образующим круглого конуса с вертикальной осью.
§ 5. МАЛЫЕ КОЛЕБАНИЯ НИТЯНОГО ПОДВЕСА В СЛУЧАЕ,
КОГДА ПРИ РАВНОВЕСИИ ОСЬ ПОДВЕСА
НЕ ПРОХОДИТ ЧЕРЕЗ ЦЕНТР МАСС
ИСПЫТУЕМОГО ТЕЛА
Пусть испытуемое тело подвешено на цилиндрическом бифи-
лярном подвесе, и в состоянии равновесия центр масс С тела не
лежит на оси бифиляра. Построим неподвижную систему коор-
динат так, чтобы ось Oz была направлена вниз, а две другие
составляли с ней правую систему. При равновесии центр
масс находится в начале координат, а ось нитяного подвеса па-
раллельна Oz и пересекает Ох на расстоянии е от начала коорди-
нат. Подвижная система координат £Сг]£ неизменно связана с ис-
пытуемым телом и в начальное мгновение совпадает с неподвиж-
ной системой. Эти оси не являются главными осями инер-
ции тела.
Положение тела по отношению к неподвижным координатам
хОуг в какое-либо мгновение будем определять тремя коор-
динатами его центра тяжести хс, ус, zc и следующими тремя
углами:
1) поворот вокруг центральной вертикальной оси Cz на
угол ф, который будем называть углом закручивания бифиляра
(рис. 44);
§ М. М. Гернет 2274 113
2) поворот вокруг линии Сг|х на угол й, который назовем углом
прецессии. Очевидно, что угол Ф есть угол наклона прямой Mi ЛТ8
к горизонтальной плоскости;
3) поворот вокруг оси СЕ, на угол ф, который является углом
поворота вокруг оси, параллельной прямой М-^М^, поэтому на-
зовем его углом маятниковых колебаний.
Так как на тело наложены две связи, то из шести координат
независимыми являются только четыре. Примем за обобщенные
координаты тела две координаты центра тяжести хс и ус и два
угла ф и i|).
Методами аналитической геометрии найдем выражения для
двух оставшихся координат (с точностью до малых второго по-
рядка):
ft = «V + yc + h* ф.
гс = — -^ \х2с + у\ + (а2 - е2) Ф2 + h (h + I) г|>2 + 2hyc^\
(где h — расстояние центра масс С от прямой М1Мг),
откуда видно, что угол прецессии Ф и аппликата центра масс гс
являются малыми второго порядка. Малые колебания бифиляра
в рассматриваемом случае описываются дифференциальными урав-
нениями
С
тхс = j- xc\
l
ту с
mg
I
(Ус + fop);
/ЕФ — /^ = — ^f- (a2 — е'2) ф;
Рис. 44. К выводу уравнения j ^ j '„
колебания мультифиляра £* S™
mg
f[h(hj-l)Mp4-hyc].
Проинтегрируем первое уравнение
хс = Л* sin (kxt + рл).
Эго уравнение гармонических колебаний с частотой
*.-V+-
амплитудой Ах и начальной фазой $х, зависящих от начальной
координаты хс0 и проекции начальной скорости центра масс
тела хс0- В частности, при хс„ = хс„ = 0, вне зависимости от
остальных координат, колебания вдоль оси Ох отсутствуют.
114
Для системы трех оставшихся уравнений уравнение частот
имеет вид
т (-г -**){[^' -О —^] [af-ih + d-j^[ -
Общие решения для обобщенных координат ус, ф и ф запишем
в виде
Ус = Л{!) sin {У + pt) + Л|2) sin (k2t f p2) f А[Л) sin (^ + Рз);
Ф = А[Х)№ sin (^ + рО + Л {2,|42) sin (йа* + Ра) +
+ A[3)iii3)sm(ht + Рз);
ф = ЛГ'ui1' sin (М + рО + Л}2)^2' sin (^ + Ра) +
-MiV'sinffcf+Pa).
Постоянные интегрирования — амплитуды А[1), Л{2), Л^3'
и начальные фазы рх, р2, рз — определим по начальным значе-
ниям обобщенных координат и обобщенных скоростей ус0, уса,
фо, фо, хро. фо. а коэффициенты распределения [4 , И-2 . И >
Н-з1', t42>> М'З3* найдем как корни системы двух алгебраических
уравнений
(^-m*»)+|i,^A = 0
и
"^(а2 - е2) - Jtk*] щ + /^Vs = О,
вместо к2 надо последовательно подставлять значения квадратов
частот ku k-2 и fe, вычисленных по уравнениям частот.
Таким образом, если тело подвешено на бифилярном подвесе
и центр масс не совпадает с осью подвеса, а вертикальная ось,
проведенная через центр масс, не является главной осью инер-
ции, то:
1) при движении тела одновременно меняются три обобщен-
ные координаты — ус, ц> и г|з и зависящие от них координаты гс и й;
2) эти движения представляют собой колебания с тремя раз-
Личными частотами, значения которых выражаются корнями
уравнения частот и являются функциями неизвестных осевых
8* 115
моментов </|, У£ и центробежного момента j^. Очевидно, что на-
блюдение и регистрация каждой из частот требуют большого ис-
кусства или сложной аппаратуры. Последовательная подстановка
экспериментально найденных значений kx, k2, k3 в уравнение ча-
стот дает систему трех уравнений с неизвестными J^, J^ и Jg.
Если оси £Ст]£ являются главными, то все центробежные мо-
менты инерции относительно этих осей равны нулю (J^ — 0).
В этом случае дифференциальные уравнения движения тела, как
показано в работе [44], принимают вид
JtV + ^ (а2 — е2) ф = 0;
Так как второе из этих уравнений содержит только угол ф,
который в этом частном случае не входит в два остальных уравне-
ния, то его можно проинтегрировать отдельно:
Ф = Лф sin {kvt + рф),
где частота колебаний
Амплитуда и начальная фаза Лф и рф определяются начальными
данными ф0 и ф0. В практике экспериментального определения
моментов инерции обычно ф0 - 0 и уравнение гармонических ко-
лебаний вокруг вертикальной оси Oz
ф=ф081п(|/ -Т|/ j^ }t).
Два оставшихся дифференциальных уравнения образуют си-
стему
Ус+-^-Ус+1гУ = 0;
Если длина нити / значительно больше вертикального рас-
стояния h центра масс С тела от прямой М1Мг, то можно принять
116
I — h =s I, l + h ^ l. Тогда приближенные значения частот
равны
Общие решения для обобщенных координату и "ф окончательно
можно записать в следующем виде:
j,c=ylS»sm(l/i/-(-p1) + ^!«sm(/xyr^(+fe);
t^'Mv^f'+*)•
Рассмотренный частный случай позволяет сделать вывод о воз-
можности экспериментального определения момента инерции тела
относительно оси С£ путем наблюдения частоты колебаний вокруг
этой оси. Момент инерции тела J^ может быть вычислен на осно-
вании формулы (75). Однако наблюдение периода крутильных
колебаний тела на бифилярном подвесе может быть более слож-
ным, так как они сопровождаются колебаниями по другим обоб-
щенным координатам ус и -ф (и по zc и ■&). Часть этих сопутствую-
щих колебаний можно устранить, приняв ус ~ ус„ = "фо = Фо ~
— 0), другую их часть zc и Ь нельзя устранить.
Необходимые условия, выведенные в § 3, обеспечивают винто-
вое движение многонитяного подвеса. Но могут возникнуть слу-
чаи, что испытуемое тело невозможно подвесить на нитях, распо-
ложенных так, чтобы эти условия были удовлетворены.
Пусть тело подвешено на нитях, которые при равновесии
мультифиляра лежат в вертикальных плоскостях, пересекаю-
щихся на одной прямой (ось мультифиляра). Однако центр масс
испытуемого тела не лежит на этой оси. Проведем две системы
координат с началом в центре масс при ее равновесии: неподвиж-
ную хОуг и подвижную |Crj£, неразрывно связанную с телом.
Повернем тело вокруг оси Ог на малый угол ф так, чтобы абсцисса
хс и ордината ус центра масс оставались равными нулю. Тогда
аппликата гс будет величиной второго порядка малости (см.
примечание 14).
Если тело, подвешенное на мультифиляре, повернуть вокруг
оси Oz на малый угол <р, то его центр тяжести переместится по
117
оси Oz на величину второго порядка малости, определяемую
формулой (см. примечание 14)
z -^D
*с- 2Ти>
где
r\Fl + ^F2 + r\F3
D = ^гк+т^; (76)
г\* г2 и гз — расстояния точек прикрепления трех натянутых
нитей от оси Oz, a Fx, F2, F3 зависят от координат точек прикре-
пления нитей к телу, направляющих косинусов нитей и опре-
деляются формулами, приведенными в примечании 14.
Напишем уравнение малых колебаний мультифиляра в рас-
сматриваемом случае при условии, что тело отпущено без началь-
ной скорости. Кинетическую энергию, с учетом того, что гс, ■&
и ij> — малые второго порядка малости, выразим формулой
Потенциальная энергия определится формулой
тт _ mgip2D
21 "
Уравнение движения тела
^Ф + ^f Ф = 0.
Период малых колебаний
7-2я]/^|/А. (77)
Откуда
Формула справедлива только для малых колебаний, которые
в рассматриваемом случае происходят с одновременным измене-
нием четырех координат, определяющих положение тела. Поэтому
наблюдение периода колебаний связано с некоторыми трудностями.
Множитель D можно вычислить, если известно расположение
нитей и вертикальное расстояние центра масс тела до плоскости
прикрепления нитей к телу. Когда центр масс лежит в плоскости
прикрепления нитей к телу, т. е. когда h — 0, выражения для
Flt F2, F3 значительно упрощаются
Л = х2Уа — У»хя; F2 — у-,х3 — *!//■,; F., ~~- хлУ-г ~ хгУ\-
118
Эти формулы справедливы и для случая вертикального рас-
псложения ни^ей, так как направляющие косинусы нитей с осями
Ох и Оу ггвны нулю cos ak = cos $k = 0.
Если точки прикрепления нитей даны в поляпных координа-
тах, то перио' малых колебаний мультифиляра можно выразить
(см. примечание 15) равенством
T=2nViV~^^)' (77)
где R — радиус окружности, проведенной через точки Mlt M2
и М3 прикрепления нитей, а г — расстояние центра этой окруж-
ности до оси Oz. Тогда
Приводимая теория движения мультифиляра, а следовательно,
и формула (78) справедлива лишь в случае, когда остальные ко-
ординаты тела (аппликата zc, угол прецессии д и угол маятни-
ковых колебаний i|>) есть малые второго порядка, т. е. определи-
тель А (см. примечание 15) не равен нулю.
Если h = 0 или cosak — zosf>k = 0, то можно показать, что
необходимым условием осуществления эксперимента будет:
х2Уз — ЧУ г + ЧУ\ ~ хлуг + ххуг — х2у1 ф 0 (76')
или, переходя к полярным координатам (см. примечание 15),
—гггь sin (02 + 93) + /"i^s sin 93 + гхгг sin 62 =j= 0. (76")
Таким образом, можно сделать следующие выводы:
1. Если точки прикрепления нитей не могут быть расположены
на одинаковых расстояниях от вертикальной линии, проведен-
ной через центр тяжести тела, то число нитей должно быть выбрано
равным трем. Экспериментально момент инерции подвешенного
тела можно определить методом малых колебаний трифиляра.
2. В общем случае период колебаний трифиляра определяется
формулой (77).
3. В частных случаях, когда нити вертикальны или центр
масс лежит в плоскости прикрепления нитей, период колебаний
определяется формулой (77').
4. Малые крутильные колебания тела сопровождаются вра-
щениями вокруг двух других осей. Чтобы эти побочные вращения
были на один порядок меньше крутильных, необходимо выпол-
нить условия (76'), (76") в двух частных случаях.
В. П. Ветчинкин[22] пишет, что специально для проверки
формулы (78) в 1915 г. Г. Н. Мусинянц выполнил эксперименты
U9
»
ft
t
по определению момента инерции цилиндрического эталона. В этих
опытах половина расстояния между нитями а — 10 см, эксцен-
трицитет равен нулю, б и 7 см и найдены значения радиуса инер-
ции ги соотгетстЕенно 23,9; 23,9; 23,86 см, которые близки к
расчетному значению радиуса инерции
г„ = 24,2 см.
Опыты Г. Н. Мусинянца позволили
В. П. Ветчинкину сделать заключение,
что метод бифиляра можно использовать
и для случая, когда центр тяжести не
совпадает с осью подвеса.
Пример 11.
Ротор молотковой дробилки МД-300
представляет собой ряд стальных дисков,
насаженных на один вал. На определенном
расстоянии параллельно оси ротора рас-
положены цилиндрические прутки, на ко-
торые свободно насажены молотки, во
время вращения ротора (п = 3000 об/мин)
под действием центробежной силы прини-
мающие радиальное положение. Требова-
лось определить моменты инерции ротора
при таком их положении. Молотки были
закреплены аркансоном, в состав которого
входят 2/3 канифоли и Vs воска [1]. Для
определения моментов инерции относи-
тельно осей, перпендикулярных к оси вра-
щения, ротор подвесили [38] на четырех
тонких стальных вертикальных проволо-
ках одинаковой длины (рис. 45), защемив
их концы в цангах, ввернутых в отверстия
для болтов подшипников. Верхние концы
проволок были зажаты цангами на крон-
штейнах также в одной горизонтальной
плоскости. Таким образом, все четыре про-
волоки (нити) оказались расположенными
по образующим прямого круглого цилин-
дра радиуса г — 177 мм. Центр масс ро-
тора не лежал на оси этого цилиндра, а
отстоял от нее на расстояние е = 27 мм.
Повернуть ротор вокруг вертикальной
оси, проходящей через центр масс, экспериментатору не удалось,
а потому он был повернут вокруг оси подвеса.
Определив период качаний ротора, по формуле вычислили
момент инерции
т __ T2mg(r*—*2>
}1
^.-
* Ил'
.**•■"". •-
V'
Рнс. 45. Ротор молотко-
вой дробилки на четырех-
нитном гюдвеСе
4л2/
-e-L = 60 850 Г-мм-сек2.
120
Повернув ротор вокруг оси вала на некоторый угол, экспе-
риментатор определил момент инерции ротора относительно дру-
гой оси, также перпендикулярной к оси вращения ротора. Такие
повороты были повторены несколько раз, но это не влияло на
полученную величину момента инерции, следовательно, ротор
был динамически отбалансирован.
§ 6, ВЛИЯНИЕ ЖЕСТКОСТИ НИТЕЙ НА ДВИЖЕНИЕ
НИТЯНОГО ПОДВЕСА
Нити, на которых подвешено тело, не являются идеальными.
'Легкие тела подвешивают на капроновых, хлопчатобумажных,
коконных и кварцевых нитях, тяжелые — на проволоках, ка-
натах, тросах, цепях и стержнях с шарнирами. В точных опытах
необходимо учитывать жесткость нитей.
Влияние упругости подвеса малой жесткости впервые учел
Ф. Кольрауш [293]. В 1951 г. рассмотрел В. К- Нечаев [113]
этот же вопрос несколько иным способом, но в его работе содер-
жатся некоторые неточности. Вопросами жесткости нитей зани-
мались В. В. Туркин [154, 155] и Ю. И. Новиков [118, 119].
Нити подвеса малой жесткости при крутильных колебаниях
претерпевают деформации изгиба и/кручения. В примечании 16
показано, что жесткость нити при изгибе можно учесть, если в фор-
мулы для нитяных подвесов ввести условную длину нитей 1У,
зависящую от усилия V, растягивающего нить, модуля Юнга Е
материала, момента инерции сечения при изгибе, способа прикре-
пления нити к телу и штативу.
Если один конец нити защемлен, а второй прикреплен шар-
нирно, то
/ . / "Л/ EJ изг
ly— L у у •
Практически для экспериментального определения моментов
инерции тел применяют проволоки круглого сечения с моментом
инерции
/ — £^i
где d — диаметр проволоки
Тогда
-\/~EJux _ -\/"Ш1с _ -\f~EV~
У V У W У 4яст2 '
V
Где о = -^р- — напряжение при растяжении нити вертикальной
силой V. Для уменьшения величины поправки на жесткость
121
подвеса следует уменьшать сечение подвеса. Абсолютная вели-
чина поправки на изгиб возрастает с увеличением продольной на-
грузки. Так, для стальной проволоки диаметром 5 мм при на-
грузке 100 кГ поправка / — 1У = 8 см, а при нагрузке 1000 кГ —
25,3 см.
В случае двустороннего защемления поправка на изгибную
жесткость удваивается и условная длина нити выражается форму-
лой
/ / о 1/ " изг
ly — l—6 у у .
Поправку к длине можно рассчитать, подставляя модуль уп-
ругости при растяжении Е, момент инерции сечения при изгибе Ju3e
и принимая продольную силу V, приближенно равной весу под-
вешенного тела mg, деленному на число нитей подвеса.
Величину EJU3a можно, по предложению Ф. Кольрауша,
найти и из опыта. Если короткий отрезок проволоки подвеса за-
щемить, а затем свободный конец нагрузить определенной силой Р,
перпендикулярной к оси проволоки, и измерить прогиб /, то он
определится формулой
Pi3 Pi3
/=Ж7^7' откУда ш«*г = -гГ>
где / — свободная длина испытуемого отрезка проволоки.
Рассмотрим влияние деформации кручения элементов подвеса
(нитей) на движение мультифиляра. Нити присоединены к телу
и штативу. При повороте тела вокруг оси подвеса на некоторый
угол, каждый из элементов подвеса закручивается на тот же
угол.В этом случае на подвешенное тело действует не только вос-
станавливающий момент, обусловленный весом тела, но и моменты
упругих сил в каждом из закрученных элементов подвеса. Сум-
марная величина момента упругих сил равна
G/рФ
М = п
l
где G — модуль упругости при сдвиге; Jp — полярный момент
инерции сечения нити; I — длина нити; ср — угол закручивания
нити (равный углу поворота тела); п — число нитей в подвесе.
Дифференциальное уравнение малых колебаний с учетом упру-
гости нитей принимает вид
2" mga2 GJP
mruw = §— ф — п —f- ф.
Ly I
Изгибная жесткость учитывается введением длины условной
нити 1У, а крутильная жесткость — вторым членом правой части
уравнения.
122
Перепишем это уравнение в следующем виде:
откуда период колебаний
и момент инерции подвешенного тела
'-£(?«, + -!7t)- <8»>
Если вес тела достигает больших значений, то из соображений
прочности элементов подвеса их сечение увеличивают. Так,
Ю. А. Победоносцев [124] при экспериментальном определении
моментов инерции самолетов способом бифиляра применял сталь-
ные тяги диаметром 16 мм. В таком случае крутильная и изгиб-
ная жесткости элементов подЕеса становятся значительными и по-
этому экспериментаторы стремятся так проектировать подвесы,
чтобы исключить деформации. В опытах Ю. А. Победоносцева
были использованы два типа подвесов ПЭ1 и ПЭ2. В первом под-
весе (см. рис. 21) элементы изготовлены из стальных прутков,
а в местах соединения установлены двухрядные шарикоподшип-
ники. Однако в результате испытаний было установлено, что «вы-
ворачивание такого подшипника без вращения вокруг собственной
оси связано со значительными по сравнению с вращением усилиями».
В подвесе ПЭ2 (рис. 46) шарикоподшипники заменены спе-
циальными карданными соединениями, а жесткие тяги — тросом.
В экспериментах по определению моментов инерции валков
мельничных вальцевых станков [41] был применен карданный
подвес (рис. 47), который позволял исключать деформацию из-
гиба. В качестве элементов подвеса был использован трос.
Конструкция подвеса, исключающая изгиб нитей, описана
также в статье Е. С. Веселого [21].
А. Шварц, Б. Малик и И. Фризен [361 ] в 1957 г. опубликовали
результаты экспериментальных исследований точности опреде-
ления моментов инерции на бифилярном подвесе. Первоначально
авторы предполагали, что созданием специальных узлов для при-
соединения элементов подвеса к телу и штативу им удастся исклю-
чить скручивание и изгиб. На рис. 48 и 49 изображены кониче-
ская и двойная ножевая подвески. Однако «обширные исследо-
вания показали, что элементы подвергались крутильным нагруз-
кам, несмотря на все меры, принятые для их устранения».
Шварц, Малик и Фризен провели шесть серий опытов с раз-
личными эталонами и соединительными элементами разной кон-
струкции.
123
Рис. 46. Подвес ПЭ2 ЦАРИ
К
is,-
V —
Рис. 47. Карданный подвес
--1'
Рис. 48. Коническая подвеска
Рис. 49. Двойная ножевая подвеска
На основании полученных
определили моменты инерции
ментов подвеса и сопоставили
\
Рис. 50. Определение момента инер-
ции самолета на бифиляре (США)
статочно точно осуществлен,
ведлива вне зависимости от
экспериментальных данных они
эталонов без учета кручения эле-
их со значениями, вычисленными
теоретическим путем. Оказа-
лось, что относительные ошибки
опытов были равны 4,42; 4,10;
3,90; 4,10; 4,10; 6,55%. Затем
те же данные были обработаны
с учетом скручивания стерж-
ней. В этом случае относи-
тельные ошибки были следую-
щими: 0,55; 0,28; 0.08; 0,28;
0,24; 0,13%.
Следовательно, точность при
учете крутильной жесткости
стержней, возросла почти в 17
раз. На рис. 50 показано уст-
ройство для определений момен-
тов инерции самолета, прове-
денных Шварцем и др.
Опыты Ю. А. Победоносцева,
Шварца, Малика, Фризена и
других позволяют рекомендо-
вать при использовании подве-
сов значительной жесткости
добиваться исключения изгиба
нитей подвеса. Учет же крутиль-
ной жесткости может быть до-
так как формула (79) спра-
величины жесткости.
§. 7. ОШИБКИ ЭКСПЕРИМЕНТАЛЬНОГО ОПРЕДЕЛЕНИЯ
МОМЕНТОВ ИНЕРЦИИ
Ошибки определения момента инерции методами нитяного под-
веса обусловлены факторами, присущими методу, и неточностью
опыта.
К первой категории причин относятся анизохронность
колебаний, и жесткость нитей.
Считая нити идеальными, период колебаний нитяного подвеса
определяют по формуле (72). Если сумму членов ряда, начиная
со второго, обозначить через S:
,2 <Ро
<Ро
S = Вг sin2 -^ + Вг sin* Y- +
126
то момент инерции можно выразить следующей точной фэр-
мулой:
г— Q2"'g т2 1 Г8П
J ~ 4яЧ ' (1+S)» • <01'
Если пренебречь анизохронностью колебаний, приняв 5 = 0,
то получим формулу (70).
Определим ошибку вычисления момента инерции без учета 5
^ф = - j^s ^ ~2S ^ - 2 5isin2 IT •
Эта ошибка может быть значительной.
Пример 12.
В 1937 г. инж. Ю. П. Васильев [19] по заданию судострои-
тельного завода в г. Николаеве экспериментально определил
момент инерции гребного винта танкера. Винт весом 2907 кг
был закреплен в скобах и подвешен на двух параллельных тро-
сах равной длины. На обоих концах тросов были сделаны петли
и крюками присоединены к испытуемому телу и штативу. Чтобы
исключить боковые колебания снизу к винту прикрепляли стер-
жень, помещенный в подпятник.
Опыт повторяли трижды при разных расстояниях 2а между
тросами 84,75; 60,175; 39,95 см (длина тросов / = 402 см).
Средние значения периодов колебаний бифиляра следующие:
7,648; 10,727; 16,154 сек.
Момент инерции автор вычислил без учета анизохронности,
по формуле (70). Для трех значений периодов колебаний моменты
равны 19 858; 19 694; 19 686 кГ■ см -сек2. Окончательное значе-
ние момента инерции автором принято 19 720 кГ-см -сек2.
Ю. П. Васильев указывает, что начальная амплитуда колеба-
ний в его опытах не превышала 5—6°. Если, приняв ср0 = 5°,
подсчитать ошибку анизохронности в наиболее благоприятном
третьем опыте, то окажется, что б/ф = 0,34%.
При конструировании подвеса для точного эксперимента пара-
метры необходимо выбрать так, чтобы была обеспечена максималь-
ная изохронность колебаний или чтобы ошибка не превышала
заданного предельного значения.
Пренебрегая в формуле (72) членами, содержащими синус
в четвертой и более высоких степенях, можем написать
Bl ~ .
2sin2-^-
Как вытекает из примечания 12, величина В1 связана с пара-
метрами нитяного подвеса зависимостью
Вх =
1 4- — I — ~
1 Т /2 о 4
127
При заданной максимальной допустимой погрешности и в за-
висимости от начального угла отклонения гр0 можем вычислить
предельное значение Вл и параметры подвеса. Например, если
ошибка 6/ф не должна превышать 0,02%, то для различных ср„
получим следующие значения Вх:
Фо
в,
12°
0,0091
10°
0,0131
8°
0,0295
6°
0,0365
4°
0,0820
Зная приближенное значение радиуса инерции ги тела и задав-
шись, допустим, величиной а, нетрудно вычислить длину нитей /,
при которой будет выполнено условие б/ф ="=0,02%.
Момент инерции при малых колебаниях мультифиляра с уче-
том изгибной и крутильной жесткостей нитей выражается форму-
лой (80). Условная длина нити подвеса приближенно определяется
формулой
/,
=i-iY-
nEJu
mg
где я — число нитей; / — коэффициент, учитывающий способ при-
крепления нити к телу и штативу (если нить защемлена вверху
и внизу, то / = 2, если защемление одно, то / — 1, при двух
шарнирах / = 0).
Величина, заключенная в скобки в формуле (80), тем меньше,
чем больше модули Е и G, характеризующие упругие свойства
материала подвеса. Обозначим нормальное напряжение в подвесе
mg _ псР 4mg
п ' 4 rmd2
а =
nd4 ltd1
и, учитывая, что для круглого подвеса Jp — -^-, a Ju3e — -щ~,
формулу (80) представим в виде
У =
TWmg
4я?1
G&
jd -l/ Е
41 У а
8а2о
Сравнивая это выражение с формулой (70), легко установить,
что относительная ошибка от пренебрежения жесткостью эле-
ментов подвеса определяется формулой
б/яо =
41 V а
У
41
Е
а
+
G&
8а2а
Ошибка уменьшается с уменьшением й, с увеличением длины /,
расстояния а и нормального напряжения о.
128
Пример 13.
В. Хохман [274] описывает экспериментальное определение
момента инерции коленчатого вала двигателя внутреннего сгора-
ния весом mg = 61 кГ. Подвес состоял из двух стальных про-
волок, защемленных вверху и внизу; а — 14 см, I — 245,25 см.
Если предположить, что о = 500 кГ/см2, то диаметр проволоки
d = 0,3 еж. Тогда, принимая Е -— 2-Ю6 кГ/см2: G = 8 • 10s кГ/см2,
вычислим ошибку, допущенную автором при пренебрежении жест-
костью подвеса,
8JEG = 4,03 + 9,19 = 13,2%.
Эта ошибка складывается из 4% от изгиба элементов подвеса
и 9% от кручения этих элементов.
Вторая категория ошибок связана с неточностью подвешивания
тела и измерения экспериментальных величин.
Если центр тяжести тела сместится на некоторое расстояние е
от оси подвеса, то вычисление момента инерции по формуле (70)
приведет к относительной ошибке
е-
Так как эксцентрицитет е невелик, то можно записать
е2
8Л с^ —S-.
" №■
Ошибки, неизбежные при измерении величин, входящих в фор-
мулу (70), приводят к частным относительным ошибкам.
Ошибка измерения веса
bJms = ^ = bmg.
Ошибка измерения длины нитей
6/, = ~ = Ы.
Ошибка измерения расстояния между нитями
8Ja = 2 — = 28а.
" а
Ошибка измерения периода колебаний
6УГ = 2 ~ = 267\
Среднеквадратическая относительная ошибка определения мо-
мента инерции
Ы = К W + {bJmgf + (bJ,)2 + {Щ2 + (ЫтТ -f (Ыео)*-
9 М. М. Гернет 2274 129
Анализируя формулы ошибок, можно сделать вь!вод, что с уве-
личением / повышается точность определения /.
Пример 14.
Моменты инерции постоянных магнитов методом бифиляра
точно определил Д. Крейхгауэр [299|.
Магнит помещали на приборе, момент инерции которого был
найден из предварительного опыта
JnPu6 = 404 г-см2.
Вес магнита и прибора mg = 279,45 Г, длина нитей|268,872 см;
расстояние между точками прикрепления нитей к телу 2Ь —
= 23,944 см и штативу 2с =-- 24,072 см, период колебаний Т —
— 1,15008 сек. Проволоки подвеса защемлены вверху и внизу,
г = 0,043 см, Е = 434-105 Г/см2; G = 173-105 Г/см2.
При вычислении момента инерции Крейхгауэр учитывал жест-
кость при изгибе и кручении.
Длина условной нити 1У — 267,842 см.
Момент инерции системы по формуле (80) равен
Jcucm ""= 4943,7 г-см2.
Момент инерции магнита
J = 4539,3 г-см2.
Для оценки точности эксперимента вычислим частные относи-
тельные ошибки 8/ф = 0,0016% (принимая ф0 = 2°); bJm —
= 0,0018%; 6У, = 0,0002%; 8Ja = 0,0056%; 8JT = 0,0009%.
Суммарная относительная ошибка определения момента инер-
ции магнита равна
6У = 0,0061%.
§ 8. МЕТОД КАЧАНИЯ В ПЛОСКОСТИ БИФИЛЯРН0Г0 ПОДВЕСА
Телу, подвешенному на двух нитях, можно сообщить колеба-
ния в плоскости бифилярного подвеса.
Положение тела, подвешенного на бифилярном подвесе
(рис. 51), определим точками М1 и М2 прикрепления нитей и
центром масс С. Эти три точки лежат в вертикальной плоскости,
проходящей через точки подвеса нитей Nx и N2. Пусть векторы
скорости точек Мх, М2 и С в начальное мгновение лежат в той же
вертикальной плоскости. Тело будет совершать плоское движение
под действием тяжести и двух связей, наложенных на тело ни-
тями M1N1 и M2N2.
Подвижная система координат |Сг|£ связана с телом так, что
ось С| параллельна отрезку MtM2, ось Ct, перпендикулярна
МХМ2. Ось Сг) перпендикулярна плоскости чертежа и направлена
к нам. Пусть подвижная система в начальное мгновение совпадает
с неподвижной системой отсчета хОуг.
130
Обозначим расстояние между точками подвеса нитей Л^Л/2
через 2с, расстояние между точками прикрепления нитей М1М2
через 26, а расстояние центра тяжести С от отрезка МгМ2
через ft. Пусть центр тяжести лежит посередине между точками
прикрепления нитей Мг и М2. Длину каждой из нитей обозначим
через s *, расстояние по вертикали между верхними и нижними
концами нитей через /.
В примечании 17 составлено дифференциальное уравнение ма-
лых колебаний
| Jn (с — б)2 + m [bl — h(c — b) ]2} х + mgbHx = 0.
Период колебаний
2я у' J^(c-b)* + m\bl-h(c-bW-
г meb^l
mgbH
Откуда момент инерции тела
тЬЧ*
(с - б)2
X
X
\ 4я2* L
h(c-b) H
Ы
(82)
м,
y>/ri
■*
<;
\/_
■2Ь*
I "*"*
м2-у*-
L^Xf%
г Л
Для экспериментального определе-
ния моментов инерции тел методом
качания в плоскости бифилярного под-
веса необходимо, чтобы тело совершало
не поступательное, а плоское движе-
ние, поэтому нити должны быть не-
параллельными между собой.
Исследуем влияние степени непараллельности нитей, которую
будем оценивать коэффициентом
с — Ь
Рис. 51. Качания в плоско-
сти бифилярного подвеса
е =
b ~~ Ь
Преобразуем формулу, приняв Jn
4--1.
тг\:
'-«"/тЛтГ+С
h \2
—г е
* В приводимом ниже выводе нити считаются идеальными, не имеющими
жесткости. В том случае, когда элементы подвеса обладают жесткостью на изгиб,
длину нитей s следует принимать равной
* 5ш?нм ' У
EJ
V
где Е — модуль упругости материала подвеса;
/ — момент инерции сечения нити при изгибе;
V — растягивающая нагрузка, приходящаяся на один элемент (прибли-
m8s\ • п . о
-кг- г, ; = 0; 1; 2 — число защемлении
одной нити.
женно можно принять V '■
9*
131
откуда
[2
4л2/
0-т-)'
Для большей наглядности исключим второстепенный фактор,
смещение центра тяжести тела С с прямой М,уИ2, приняв h
равным нулю. (Отношение —г- обычно не превышает нескольких
десятых долей единицы, а коэффициент е меньше единицы.)
Тогда
J в* \ 4лП 1) •
bJr= „2 2 2 №
Следовательно, коэффициент е должен быть возможно боль-
шим. Но так как анализируемая формула получена для малых
колебаний тела, то чрезмерное увеличение е нежелательно.
Точность вычисления момента инерции J^ по формуле (82)
зависит от точности измерения h, с, b, s, Т. Пользуясь обычными
методами теории ошибок, напишем, что среднеквадратическая от-
носительная ошибка вычисления равна
б/ = V(8JTf + (б/Л)2 {- (Ы,)2 + (б/е)2 + {Ыт)\
где
THg
1г\ъЧ
^Ь£5--'(4-*)]*
8Jm — 8т.
Следовательно, при малых значениях е ошибка эксперимен-
тального определения квадрата радиуса инерции достигает боль-
ших значений.
§ 9. ОБЛАСТЬ ПРИМЕНЕНИЯ МЕТОДА И РЕКОМЕНДАЦИИ
ПО ПРОВЕДЕНИЮ ОПЫТОВ
Метод определения моментов инерции материальных тел по
периоду колебаний нитяных подвесов позволяет вычислить иско-
мую величину с большой точностью.
132
Разнообразие способов подвешивания и расположения нитей
создает благоприятные условия для его использования, поэтому
область применения метода очень обширна. Этим методом опре-
деляют моменты инерции тел весом от нескольких граммов (маг-
нитные стрелки, детали часовых механизмов и т. п.) до десятков
тонн (самолеты, вагоны и пр.). На фотографиях (рис. 52 и 53)
Рис. 52. Определение моментов инерции железнодорожных ваго-
нов относительно вертикальной оси
представлены опыты Баумана [188, 189] по определению момен-
тов инерции железнодорожных вагонов на четырехнитяном под-
весе.
На рис. 54 показано экспериментальное определение момента
инерции самолета на бифиляре проф. Пьетро Теофилато [372],
а на рис. 55 изображен бифиляр конструкции Шварца, Малика
и Фризена [361].
Эти методы пригодны для штангообразных и круглых тел. Как
показано на рис. 56, при определении момента инерции большого
махового колеса без специального прибора, колесо подвешивают
на коническом трифиляре, причем нити закрепляют на испытуемом
теле и на станине (неподвижном диске) посредством цанговых
зажимов.
Этот метод успешно использовали многие исследователи
[70, 82, 83, 85, 94, 186, 221,230,278,279, 280, 350]. Трифи-
ляр и четырехнитяной подвес имеют перед бифиляром то преиму-
щество, что в них центр масс испытуемого тела может находиться
выше плоскости подвеса.
133
Желательно, чтобы длина нитей в 3—5 раз превосходила рас-
стояние между нитями. Такое соотношение имело место почти во
всех известных экспериментах с бифилярными подвесами. Макси-
Рис. 53. Определение моментов инерции тележки ва-
гона относительно горизонтальной продольной оси
мальное соотношение / = 45а было в точных экспериментах Крейх-
граэра при определении момента инерции постоянного магнита,
примененного в экспериментальном измерении магнитного поля
Земли.
С увеличением длины подвесов увеличивается период коле-
баний и тем самым снижается относительная ошибка измерения,
но вместе с тем в них больше сказывается анизохронность и в точ-
ных опытах ее надо учитывать. При длинных подвесах почти не-
избежны маятниковые качания подвеса, которые хотя и не влияют
на период колебаний вокруг вертикальной оси, но мешают наблю-
дениям (см. § 7 гл. IV). При большой длине подвесов меньше ска-
зывается влияние жесткости нити,
134
Для правильного определения длины нитей рекомендуем спе-
циальные (например, цанговые) зажимы. Для исключения изгиба
надо применять специальные узлы (см. рис. 46 — 49), особенно
при испытании тяжелых тел.
В ходе эксперимента необходимо
убедиться, что узлы прикрепления
нитей обеспечивают жесткое сое-
динение[нитей с телом и штативом.
Толщина нитей или сечение
других элементов подвеса должны
быть небольшими, чтобы нормаль-
ное напряжение при статическом
нагружении (от веса тела) было
большим.
Так как анизохронность коле-
баний в основном определяется
членом Вг sin24p, а коэффициент
Вх может быть уменьшен при
—y > -^- , то при любом способе
Рис. 54. Определение моментов
инерции самолета на бифиляре
(Италия)
следует стремиться к снижению
анизохронности, т. е. выбирать
подвес, для которого половина расстояния между нитями а и
радиус инерции удовлетворяют соотношению
а < 0,8ги.
"г-*-*-^""*"'Г.
Nflf
Рис. 55. Схема бифилярного подвеса
самолета
Рис. 56. Определение момента
инерции махового колеса
135
Ориентировочное значение радиуса инерции можно вычислить
теоретически или найти из предварительного (не очень точного)
опыта.
При подвешивании испытуемого тела на любом нитяном под-
Еесе надо стремиться, чтобы его центр масс лежал на оси подвеса.
Если это условие не соблюдено, то появляются дополнительные
колебания. Эти колебания не влияют на период колебаний вокруг
вертикальной оси, но влияют на точность наблюдения, на абсо-
лютную ошибку определения периода. Поэтому, в случае если
центр масс тела не находится на оси подвеса, измерение периода
надо повторить возможно большее число раз.
Угловая амплитуда должна быть наименьшей из достижимых
и, во всяком случае, не более 6°.
Выбор формулы для вычисления момента инерции по получен-
ным периодам зависит от требуемой точности. Формула (70) проста
и удобна, но для точных измерений следует пользоваться фор-
мулой (80), а для еще более точных — формулой (81).
♦ ♦♦
Глава VI
♦ ♦♦
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МЕТОДОМ
АТВУДОВОЙ МАШИНЫ
§ 1. ИСТОРИЯ МЕТОДА. РАЗЛИЧНЫЕ СХЕМЫ ЭКСПЕРИМЕНТА
И ПРИБЛИЖЕННАЯ ТЕОРИЯ МЕТОДА
Дж. Атвуд в 1784 г. [181 ] описал прибор, удобный для демон-
страций при изложении некоторых законов и понятий механики,
и, в частности, для уяснения физической сущности момента инер-
ции вращающегося тела. Твердое тело (рис. 57, 58), закрепляют
на неподвижной оси и при-
водят во вращение посредст-
вом падающего груза, прикре-
пленного к нити, намотанной
на цилиндр, вращающийся
вместе с телом. Эгот прибор
получил название машины
Атвуда.
В 1890 г. чешский профес-
сор М. Кон [295] предложил
использовать машину Атву-
да для экспериментального
определения моментов инер-
ции звеньев механизмов. Он
же предложил и название
«Метод атвудовой машины». Почти одновременно (1888 г.) Обер-
беком [334]", (1892 г.), Хартлем [271] и Мюллером [329, 330]
были предложены демонстрационные и лабораторные приборы,
основанные на том же принципе.
Позже различные ученые, не знавшие работы чешского про-
фессора, неоднократно предлагали аналогичные способы, внося
некоторые видоизменения и усовершенствования этого метода и
его практического применения.
На рис. 59 изображено тело (цилиндр) с моментом инерции J от-
носительно оси вращения. На тело намотана нить с грузом веса Р на
конце, весом нити пренебрегаем. Предположим, что трение в опо-
рах отсутствует и груз Р, опускаясь, поворачивает тело вокруг оси.
137
Рис. 57. Прибор
с горизонтальной
осью
Рис. 58. Прибор
с вертикальной
осью
Напишем следующее уравнение движения (уравнение моментов):
г , Р 2\ da> г.
где со — угловая скорость; г1 — радиус тела
Назовем приведенным весом величину
J
g
Gnp = const.
Тогда
Gnp + P
g
a=P,
где а
Рис. 59. Схема при-
бора для определе-
ния моментов инер-
ции методом опу-
скания груза
г1 —т ускорение груза И.
Начальная скорость груза равна нулю, а
потому время его опускания t и расстояние h
связаны соотношением
Pg Л
Gnp+P ' 2 •
Так как груз движется с постоянным уско-
рением
'пр ~Г "
h =
а —
то из предыдущих уравнений получим рабочую формулу
рг\ , ~™ ч *
J =
8
gt2
2h
О •
(83)
Чтобы определить оптимальные значения параметров Р, h,
rut, проанализируем влияние неточностей, допущенных при их
измерении.
* В практике экспериментального определения моментов инерции, как
правило, наблюдают время t опускания груза без начальной скорости с высоты h.
Это требует тщательного измерения расстояния и времени.
В. В. Юденич [173], описывая методику опытного определения коэффициента
трения скольжения, предлагает начинать замеры времени движения груза не от
начала движения, а лишь после того, как груз приобретет некоторую скорость.
Эту методику можно применять и при определении моментов инерции по времени
опускания груза. Для этого надо включить секундомер не в начале движения
груза, а после того, как груз приобретет заметную на глаз скорость, одновременно
заметив положение груза в это начальное мгновение. Затем надо измерить время t%
опускания на высоту h2, не прерывая эксперимента, замерить время t3 опускания
груза дополнительно на высоту h3.
Если в первой точке скорость равна t»1( то расстояние до второй точки и
скорость в мгновение прохождения этой точки определятся обычными фор-
мулами равноускоренного движения:
at\
К = Мг + -7T'?2V2 = vi + atp
138
Абсолютные ошибки АР, Ah, Art и Д^ вызывают следующие
относительные ошибки определения J:
АР Л/ Л . Рг\ \ ДА
6У,
На рис. 60 представлена зависимость 6/, от отношения —.
Из графика видно, что с возрастанием этого отношения или ускоре-
ния а относительная ошибка 8Jt возра- $j
стает по гиперболическому закону. Сле-
довательно, для ее уменьшения опыт
необходимо проводить с меньшим уско-
рением а, т. е. при достаточно малых
р
значениях Р. Если а = -*—г—sg мало,
то Р <<^ Gnp и приближенно можно при-
нять
а —
Если при проведении эксперимента
выполнено условие а <^. g, то относи-
тельные ошибки J за счет неточностей
замеров h и t можно выразить следующими приближенными
формулами:
Рис. 60. График зависимости
ошибки от ускорения
6Л =
ДА
6J
.-v$
At.
Высота последующего опускания груза выразится аналогично
ati
ati
hs = v2t3 + -~ = v^s + at2t3 -r —~- .
Из выражений для A2 и hs нетрудно найти ускорение груза
п 2(Л8/,-А,<а)
Uh(tt+h)
Составляя и решая уравнение моментов для системы, изображенной на рис. 59,
найдем
Р,1 Г «MjCitW ,1
g L
2(h3t2 — lhts)
139
Среднеквадратическая ошибка определения момента инерции
равна
б./ = VbJ\ + 8J% + 6/2Л +Щ- =-_
Пример 15.
Эдмунде [234] при определении момента инерции ротора элек-
тродвигателя пренебрегал весом нити и трением в опорах, т. е.
провел опыт при допущениях, сделанных в этом параграфе. Дан-
ные эксперимента: Р -= 3,447 кГ; гг— 24,9 мм; h = 3,05 м: t —
= 31,2 сек. На основании формулы (83) J — 3,42 кГ-м-сек2.
Точности измерения экспериментальных величин автор не при-
водит, по они могли быть примерно следующими:
АР - 0,0005 кГ; Аг, - 0,05 мм; ДА - 0,005 м: At = 0,05 сек.
Тогда относительные ошибки вычисления J будут 8Jri — 0,40%;
6JP -- 0,01%; 8Jh - 0,02%: 6/, = 0,32%. 'Среднеквадратиче-
ская ошибка 6У — 0,51%. Из сопоставления значений отдельных
ошибок следует, что в данном эксперименте ошибка в основном
вызвана неточностью измерения радиуса и тем, что радиус г:
очень мал. Ускорение груза а = 0,00626 м/сек2, было выбрано
небольшим, что позволило получить точные результаты. Однако
расчетное значение относительной ошибки является заниженным,
так как зависимости получены без учета трения в опорах.
Пример 16.
Л. Г. Лойцянский и А. И. Лурье [89] приводят следующие дан-
ные опытных определений моментов инерции, проведенных в ка-
бинете механики ЛПИ: t = 4,25 сек при h = 100 см. Вес падаю-
щего груза Р — 0,100 кГ, гг —■■ 2,5 см. J = 0,0558 кГ-см-сек2.
§ 2. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ПО ДВИЖЕНИЮ
СИСТЕМЫ ПОД ДЕЙСТВИЕМ ОДНОГО ГРУЗА
При определении моментов инерции движение системе сооб-
щают, как правило, одним грузом (рис. 61).
Обозначим: J — момент инерции испытуемого тела; J-, — мо-
мент инерции платформы, цилиндра и вала (оси); У2 — момент
инерции вспомогательного блока (постоянные прибора, предпо-
лагающиеся известными): г, и г2 — радиусы цилиндра и блока:
р — вес нити и / — длина нити, включая ту часть, которая на-
мотана на цилиндр: Мт и Мт — моменты сил трения в осях
прибора и блока.
Груз Р выбран так, что он сообщает системе ускоренное дви-
жение. При отсутствии боковых смещений груза система обладает
одной степенью свободы. Примем за обобщенную координату
140
системы положение груза Р на оси Oz, направленной вертикально
вниз, с началом отсчета в точке О касания свисающей части нити
с блоком. В таком случае движение системы может быть описано
следующим уравнением (см. примечание 18):
g
где приведенный вес системы
Unp — У "т~ Jприб) 2~ '
Интегрируя (см. примечание 19), получим
(84)
h
(*«. + ■
I
pg
ЦР+Gnp)
t—\
Отсюда можно было бы определить искомый момент инерции
испытуемого тела, если бы были известны не только приведенный
момент инерции прибора
•>приб — •> i Т J;
2 2
'о
_р_
g
rl
но и приведенная сила трения
чр,
Так как эта сила неизвестна, необходимо
произвести второй эксперимент, который поз-
волил бы ее определить или исключить из урав-
нения. Сначала упростим выражение, полу-
ченное для h.
Обычно при экспериментальном определении
моментов инерции твердых тел этим методом,
вес единицы длины нити-у- составляет малую
часть от суммы веса груза и приведенного веса
системы, время движения груза сравнительно
невелико и поэтому аргумент гиперболического
косинуса значительно меньше единицы. В таком
случае гиперболический косинус с достаточной степенью точности
можно заменить двумя первыми членами разложения в ряд:
Схема си-
стемы с одним гру-
зом:
1 — платформа при-
бора и цилиндр, за-
крепленные на одной
оси; 2 — вспомога-
тельный блок; 3 —
груз: 4— нить; Л —
испытуемое тело
ch
/:
pg
I (P + Gap)
/~1 +
Pg
I (Р + Gnp)
~2~
причем максимальная относительная ошибка такой замены не
превышает
^°5 l-wfo^}
t*.
141
Справедливость приведенных рассуждений можно доказать на
примере 15, используя экспериментальные данные Эдмундса:
-£- = 0,004 кГ/см; Р = 3,447 кГ; Gnp = 54 100 кГ; t = 31,2 сек.
Тогда nnW'r—ч—7-Ю-7, а максимальная относительная ошибка
от замены гиперболического косинуса его разложением в ряд не
превысит пяти сотых от квадрата этой величины, т. е. миллионных
долей процента (2,5-10 ~8).
Используя разложение гиперболического косинуса, можно по-
лучить следующую зависимость между высотой и временем опу-
скания груза:
P-Fmp+^rZ ^
h =
у/ш&/№//Хш;ш
Рис. 62. Устранение влия-
ния веса нити
Р+Опр 2 "
Многие авторы, например проф. Лоран
[303], проф. Николаи [116, 117], выводят
формулы, позволяющие учесть влияние
нити, и рекомендуют пользоваться ими
в тех случаях, когда требуется высокая
точность эксперимента и влиянием веса
свисающей части нити нельзя пренебречь.
Проф. Кон предложил способ, позволяю-
щий устранить влияние свисающей части
нити. Для этого надо так намотать нить
один конец свесился с одной стороны
конец — с другой стороны. Нить должна
на цилиндр, чтобы
цилиндра, а другой
быть настолько длинной, чтобы во время опыта концы ее оста
вались лежать на полу (рис. 62). На нити имеются крючки для
подвешивания грузов. При этом на ось действует только вес
витков, намотанных на цилиндр, и Бес двух кусков длиной от
цилиндра до пола, причем вес нити, действующий на ось, остается
постоянным, а момент относительно оси цилиндра равен нулю.
Такой способ позволяет даже при точных экспериментах не учи-
тывать ускоряющее действие ее свисающей части.
Если вес Р груза больше силы трения Fmp! движение системы
становится равноускоренным и подчиняется закону
I — Fmp gj>_
2 '
h =
P + Gnp
В частном случае, если вес груза равен силе трения, система
находится в состоянии покоя или равномерного движения с той
скоростью, которую ей сообщают. Воспользуемся этим свойством
для следующего способа определения момента инерции испытуе-
мого тела.
1. Равномерное и равноускоренное движения системы. Если
экспериментально установлено, что груз Plt подвешенный к нити,
142
не изменяет начальной скорости, которую сообщили системе, то
действие веса груза, подвешенного на нити, уравновешивается
приведенной силой трения блоков:
Если, остановив систему, снимем груз Я, и вместо него подве-
сим больший груз Р2, то система придет в равноускоренное дви-
жение и груз Я2 за время t опустится на расстояние
Ръ + Gnp' 2 •
Подставив значение Gnp из выражения (84), после алгебраи-
ческих преобразований получим рабочую формулу для определе-
ния момента инерции тела при условии Р± = Fmp:
j=4h ^ - pj -Pjj-- J«»«6- (85)
Определив относительную погрешность, обусловленную ошиб-
кой измерения времени, можно убедиться, что максимальная точ-
ность эксперимента достигается при минимальных ускорениях а
груза Р2. Если ускорение значительно меньше своего предельного
значения 981 см1сек2, то формулы относительных ошибок опреде-
ления момента инерции по формуле (85) можно приближенно пред-
ставить следующими выражениями:
1 fr?
Mr = -т -ir (p* - pJ Ari; ы*** = ^Т^ •
Среднеквадратическая ошибка вычисления момента инерции
для случая малого ускорения а груза Р равна
+ ~(Л/)2 + ( AJ"p"6 V
Изложенный способ рекомендуют некоторые авторы, в част-
ности, проф. Коллиг [296]. Способ обладает существенным не-
достатком, значительно уменьшающим точность определения мо-
мента инерции и не учитываемым выведенными формулами. Этот
недостаток заключается в том, что трудно точно определить груз Ри
уравновешивающий трение.
143
2. Два равноускоренных движения системы. К нити поочередно
подвешивают два груза Р, и Р2, каждый из которых сообщает си-
стеме равноускоренное движение. Если время опускания первого
груза Pi на расстояние h равно tx, а груза Рг — 1г и Р2 > Я,, то
П"'Р1 + 0пр' 2 ' "~P2 + Gnp "2
или
Pi - ^ = Л (Л + Gnp); Р3 - FTP =~(P.2 + Gnp).
Исключая из этих равенств Frp при замене Gnp его значением,
получим следующую рабочую формулу для определения момента
инерции на машине Атвуда по двум равноускоренным движениям
системы:
^ p*(~2T~i[)~Pi(ih~j)
J — ~g" ] J '- Jnpu6- (Щ
Методом, изложенным выше, легко подсчитать относительные
ошибки в определении момента инерции по формуле (86), вызван-
ные неточностями измерения.
Если учесть, что эксперимент следует проводить при неболь-
ших ускорениях грузов, то, полагая, что а, и а2 значительно
меньше g. получим следующие приближенные формулы:
ayPi = (i+-^)T^;
eyPi==(l+i^)_^_;
6Л, = 2 ( 1 +i^)^i-;
s J &J npufj
GJnpu6 ~ j
w
Отсюда следует, что точность определения момента инерции за-
висит не только от отдельно взятых значений ах и а2, но и от их
соотношения. Проанализируем среднеквадратическую ошибку
в предположении, что А^ — At2 — At:
w, =. Уыи 55. - г j/"*+i.^. (i + i~).
Обозначим — через k, тогда формула примет вид
Ы, = аЦ±^, где A=Y^fM.
Определим минимум функции 8Jt — f (k), для чего вычислим
первую производную $Jt no k:
Qfe2 ,
(k-\)— - ]Г\ + fe3
dfe (ft — l)2
Экстремум имеет место при ' — 0, т. е.
(k — 1) 3k2 — 2 (1 + б3) = 0 или б3 — 3k2 — 2 - 0.
Решая полученное кубическое уравнение, получим один ве-
щественный корень, удовлетворяющий этому уравнению:
k- 3,195 ^3,2. (87)
Подставляя значение k в выражение для 8Jt, найдем экстре-
мальное значение среднеквадратической ошибки измерения вре-
мени
8Уга(С„„,= 2,64Л = 3,74]/-5-Д*.
Пример 17.
Проиллюстрируем изложенное результатами исследований ро-
торов электродвигателей врубовых машин, выполненных Я. И. Аль-
шицем, А. Н. Боровицким и др. [5]. Для определения моментов
инерции ротора на валу двигателя устанавливали шкив, на ко-
торый наматывали нить. К концу нити последовательно подве-
шивали грузы различных весов и наблюдали времена опускания
грузов на заданное расстояние. На основании полученных замеров
вычисляли моменты инерции, причем каждое значение момента
определяли по двум различным замерам, среднеарифметическое
значение авторы принимали за окончательное значение момента
инерции ротора.
Приведем некоторые данные эксперимента, их обработку авто-
рами, а также оценим точность вычисления момента инерции на
основании полученных формул.
10 М. М. Гернет 2274 145
Ротор мотора MA 191/11
Радиус цилиндра г± = 40 мм; высота опускания грузов h = 2,26 м.
№ замеров
1
2
3
4
Р в кГ
4,305
6,450
8,615
15,070
t в сек
10,6
8,6
7,2
5,0
а в м/сек2
0,0403
0,0611
0,0887
0,1610
Приведем вычисленные авторами моменты инерции и значения
среднеквадратнческих ошибок, определенных по формулам дан-
ного параграфа.
Сочетание
замеров
1—2
1—3
1—4
J в кГм-секг
0,1626
0,1405
0,1400
6Jti в %
3,54
1,56
0,626
6-/(2 в %
6,81
5,11
5,01
6J, в %
7,63
5,30
5,03
Вычисленные значения получены в предположении, что ошибка
измерения времени А^ —- 0,1 сек. Если принять, что ошибки из-
мерения других величин были АР = 2,5 Г; Ah = 0,5 мм; Агг =
= 0,1 мм, то б/,, - 0,25%; 8Jh = 0,022%; б/Р = 0,12%.
Таким образом, ошибка вычисления момента инерции вызвана
преимущественно ошибкой измерения времени.
Минимальная среднеквадратическая ошибка измерения вре-
мени получается при k = — = 3,195. Поэтому если принять
а1 — 0,0403 м/сек2, то а2 должно быть равно 0,129 м/сек2. При
таком соотношении ах и а2 ошибка должна была бы быть
67, = 3,72 |/^-Д*=4,97%.
Анализ полученных значений показывает, что неправильный
выбор грузов и ускорений привел к ошибке, в 1,5 раза превышаю-
щей значение ошибки при правильном проведении эксперимента.
Ротор мотора 191/35
Методика определения момента инерции ротора была анало-
гичной. Данные эксперимента приведены в таблицах.
Ne замеров
1
2
3
4
P в кГ
4,310
6,450
8,615
10,760
t в сек
10
7,5
6,0
5,3
а в м/сек1
0,0452
0,083
0,125
0,160
Сочетание
замеров
1—2
1—3
1—4
J в кГ-мсек*
0,050
0,480
0,495
W;, в %
2,38
1,13
0,79
6Jh в %
5,93
5,23
5,23
6Jt в %
6,40
5,33
5,30
Из условия k = а2 : ах — 3,195, принимая а — 0,0452 м/сек2,
найдем оптимальное значение а2 = 0,145 м/сек2, при котором
dJ, = 5,27%.
Ротор мотора МА 191/10
Р в кГ
10,76
15,07
t в сек
4,0
3,0
а в м/сек1
0,306
0,544
J в кГмсек2
0,0667
0,0674
6Jti в %
6,41
6./^ в %
15,2
6J; В %
16,5
Оптимальное значение а2 = 0,978 м/сек2, 8Jt = 13,7%.
Сопоставляя минимальные значения а1 для разных роторов
и ошибок 8Jt, убедимся в том, что ускорение груза Р в первом из
экспериментов должно быть небольшим.
При выборе грузов Pt и Р2 необходимо найти такие значения,
чтобы удовлетворить оптимальное соотношение ускорений (87).
Это легко осуществить по следующим этапам:
1. Постепенно увеличивая груз, найти такое его значение Р,
чтобы он приблизительно уравновешивал силы трения в системе.
Такой груз Р не приводит систему в движение, но если ему
сообщить какую-либо скорость, то движется равномерно. Заметим,
что груз может состоять из чашки с разновесками, с сыпучим мате-
риалом или водой.
2. Присоединить к грузу Р небольшой груз qY. Значение qr
зависит от массивности испытуемого тела, но меньший груз
/>! = />+?!
10*
147
должен сообщать системе небольшое ускорение
ai-Gnp + 'p + qig-
3. Присоединить второй дополнительный груз q2, причем боль-
ший груз
Рг = Р + Qi + q*
должен сообщать системе ускорение приблизительно в 3,2 раза
большее, чтобы было справедливо равенство
Решая равенства совместно, определим q.2 в зависимости от qv
Числители в правых частях значительно отличаются друг от друга,
тогда как знаменатели почти одинаковы, а потому, разделив второе
уравнение на первое, с достаточной точностью можем принять
3,2=- Ql + q*
Отсюда находим, что оптимальным значением является q.2 — 2,2ql.
Следовательно,
Pt = P т-3,2^.
3. Применение эталона. В каждую формулу, применяемую для
определения момента инерции тела каким-либо вариантом метода,
в качестве слагаемого входит приведенный момент инерции при-
бора Jnpu6.
Для определения этой величины надо знать моменты инерции
цилиндра и блоков. Эти величины можно определить аналити-
чески или экспериментально.
Jnpu6 определяют на той же установке, для чего вместо
испытуемого тела закрепляют диск, цилиндр или другое тело
с известным моментом инерции J3, наблюдают время t1 и t2 про-
хождения грузами Р1 и Р2 расстояния h и, подставив данные (J3,
tlt t%> Р], Р2) в уравнение, определяют Jnpu6.
И. С. Мясников [112], пользуясь эталоном, определяет не
только приведенный момент инерции, но и приведенную силу тре-
ния установки. В предложенной им методике груз Р остается не-
изменным. Определяют время tt опускания груза на расстояние h
при незагруженном приборе, затем время t2 (прибор с эталоном)
и t (прибор с испытуемым телом), что позволяет написать следую-
щие равенства:
148
/^ -13
Jag
•пр
ч-п
■Р\
F =P — ±L
' rp г Ч
I^—I 1
''прио °э л
Рг\
t\ 8 '
Сопоставление ошибок в определении моментов инерции по
различным формулам показывает, что методы постоянного груза
и эталона приводят к большим ошибкам, чем предыдущий метод.
§ 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ПО ДВИЖЕНИЮ
СИСТЕМЫ ПОД ДЕЙСТВИЕМ ДВУХ ГРУЗОВ
К нити, намотанной на цилиндр прибора, подвешивают одно
временно два груза, стремящихся повернуть цилиндр в противо
положные стороны (рис. 63).
Введем обозначения J — момент
инерции испытуемого тела; J\ — мо-
мент инерции платформы, цилиндра
и вала; У, и J3—моменты инерции
вспомогательных блоков; Рп — вес
правого груза; РЛ — вес левого гру-
за; rlt r2, г3 — радиусы цилиндра
и блоков. Если правый груз опу-
скается с некоторым ускорением,
тогда левый груз должен поднимать-
ся с тем же ускорением, причем,
сумма расстояний правого груза от
правого блока и левого груза от
левого блока всегда постоянна.
Расстояние h (см. примечание20),
проходимое каждым из грузов, и время их движения связаны
соотношением
/j _ ill — P.i — Ftp . _gj^
Ptl -f- P A Grip *
Следовательно, методика такого эксперимента тождественна
методике подвешивания одного груза.
Пусть при первом опыте веса грузов были Р1П и Ри, а время
перемещения грузов на расстояние h равнялось tlt а при втором —
веса Р2П и />,,,, время движения — t2. Тогда из написанных выше
149
Рис. 63. Схема прибора с двумя
грузами
равенств получим следующую точную формулу для определения
момента инерции испытуемого тела:
J =
Роп
(А
2h
-Ргл
g
2h
g
1
1
t2
'2
1 + P" ( 2h + /2
1 " tlpub'
T
h
Если ускорения аг и а.2 значительно меньше ускорения сво-
бодно падающего тела, как это должно быть при правильной
постановке опытов, то величинами -^ — -^- можно пренебречь
и получить приближенную формулу
J = 1(Р,п ~ Р1п) ~ (Ри ~ Ри)] ^~ - JnPu6- (88)
Ошибки вычисления момента инерции по формуле (88) мож-
но выразить формулами
^1„=(1+-%"А)
(Ргп Р\п) \Р%л Ргл) '
«I / 1 _|_ Jnpu6 \ "°
= (\+1^
(Рчп — Р\п) (Ргл Р\л)
si _ I ] | •'приб \ АРгл
Ш Р1Л V Ч- J ) (Ргп - Р1п) - (Ргл - Р1Л)
бУр2л = (1 + -^f6 ^ А/>2л
ДЛ.
прио
(Р2П — P\n) — (**2А — Pia)
Среднеквадрэтическая ошибка, обусловленная неточностью из-
мерения времени,
где k — а2 : ах. Таким образом, все рассуждения о выборе опти-
мальных условий эксперимента, содержащиеся в предыдущем
параграфе, остаются справедливыми.
150
Приближенное значение среднеквадратической ошибки мо-
мента инерции выразится формулой
&/ =
-/*
1 +
' приб
У
(АРщ)» + (ДР2п)2 + (АЯхл)2 + (ДР2Л)2
[(Яг,
Pin) - (Рь
■ Pi,)]2
+
+ (£)*+«(№
(«а
•(АО2
/ AJnpu6 \ ■
Сопоставление основных формул определения моментов инерции
по движению систем под действием одного груза (§ 2) и двух гру-
зов (§ 3) показывает, что метод с двумя грузами в изложенном
виде не имеет преимуществ, а точность его даже несколько ниже.
При выборе основных расчетных формул для всех случаев,
рассмотренных в этой глаЕе, введено допущение, что трение в си-
стеме ярляется постоянным и не зависит от величины подвешивае-
мых грузов, которое, строго говоря, не является обоснованным.
Чтобы сделать это допущение более обоснованным, веса Рп и Рл
следует выбирать так, чтобы в каждом из двух опытов суммарный
вес обоих грузов Рп + Рл не изменялся.
Примем для эксперимента два основных груза Рп и Рл и третий
дополнительный съемный груз q, который можем добавлять или
к правому, или к левому грузу.
Если при первом опыте груз q находится на грузе Ря, тогда
Рщ = Рп, Ри = рл + Ч. причем, Рп > Ря + q. Во втором опыте
съемный груз переложим на груз Р„, тогда
Подставив значения
и точную формулу
*п ~г q, * 2л — * л-
Pin, Р%п> Р\а и Ри, получим простую
2,2
tit
Г2
P — t2
Рп + Рл + Я
8
'Приб-
Пользуясь известными соотношениями равноускоренного дви-
жения, выразим эту формулу в другом виде
а2 — ах
Приближенное значение среднеквадратической ошибки вы-
числения момента инерции по этим формулам следующее:
Ы =
|/ (1 +^)2(^_А)2[(дя„)2 + (дрл)2]+(^)2 +
+ ("У+*№У+¥--4±&гт*+<"'"
h (*,-*!)»
}5{
Пример 18.
М. Кон приводит [295] данные экспериментального определе-
ния момента инерции шкива ременной передачи. Опыт проводили
дважды, причем измеряли перемещения грузов за фиксированный
промежуток времени, равный 2 сек.
Первый опыт: Рп — 0,75 кГ; Рг = 0,50 кГ: q — 0,05 кГ;
Л, -- 0,71 м; ho =-- 1,28 м.
Второй опыт: Рп = 0,85 кГ; Р, --- 0,50 кГ; q — 0,05 кГ;
hx — 1,05 м; h2 — 1,6 м.
Вычислим ускорения грузов:
Первый опыт: а, = 0,355 м/сек2; а., — 0,640 м/сек2.
Второй опыт: а1 = 0,525 м/сек2; а2 ■■= 0,800 м/сек?.
Точность произведенных замеров не указана. Если условно
принять, что At — 0,05 сек, то получим следующие величины сред-
неквадратичных ошибок:
Первый опыт: 8Jtl = 4,6%; 6J,2 - 11,2%; 8Jt - 12%.
Второй опыт: &Jh = 7,8%; 6У,, = 14,6%; б/, - 16,6%.
Низкая точность объясняется тем, что наименьшее из ускоре-
ний было очень велико, а соотношение между ускорениями в каж-
дом из опытов было сравнительно небольшим (а2 '■ ах равнялось
1,48 и 1,25, тогда как оптимально это соотношение должно быть
равно 3,195).
Проф. М. Кон предлагает определять расстояние п, пройденное
телом за заданный промежуток времени t. Такой методики при-
держиваются многие экспериментаторы (например, Хаммерль
[270] и др.). Некоторые авторы предлагают измерять время t,
в течение которого груз опустится с заданной высоты п. Выбор
той или иной методики зависит от наблюдателя. Однако при со-
временных способах измерения времени вторая методика позво-
ляет добиться большей точности.
Выбор грузов, при которых ускорения системы имеют опти-
мальные соотношения (87), рекомендуем проводить по следующим
этапам:
1. Выбрать груз Р, небольшим, но таким, чтобы он натягивал
левую ветвь.
2. Пробными опытами найти груз Рп так, что если подвесить его
к правой ветви, а груз Рл к левой и сообщить Рп скорость, напра-
вленную вниз, то должно сохраниться равномерное движение
системы.
3. Подвесить к грузу Рп небольшой груз q, чтобы система
пришла в движение с небольшим ускорением.
4. Взять два одинаковых груза весом 1,1^ каждый и положить
один из них на груз Рл, а другой на груз Рп. Тогда получим соот-
ношение для первого эксперимента
Ри == P.t+l,\q;
Pln = Pn +2,\q.
152
Для второго опыта груз \,\q переложить на правую ветвь.
Тогда
Р-ы --- Рп + 3,2q.
При первом опыте система получает ускорение
1 Gnp + Р., + Рп + 3,2? *•
а при втором
а* - G„p + Р., + Рп + 3,2? г>
Грузы выбраны так, чтобы отношение ускорений являлось оп-
тимальным и привело к минимальной ошибке эксперимента.
Изложенный опытно-расчетный способ для определения грузов
не является обязательным. Грузы можно выбрать и путем проб,
но для получения наибольшей точности необходимо, чтобы ускоре-
ния в первом и во втором опытах относились друг к другу при-
близительно как 1 : 3,2.
§ 4. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
ПО РАЗГОНУ И ВЫБЕГУ
Влияние трения можно исключить следующим способом. Один
конец нити прикрепить к цилиндру, жестко связанному с плат-
формой прибора, затем несколько раз обернуть ее вокруг цилиндра
и на другом конце закрепить груз. Нить должна быть такой длины,
чтобы при ее полном разматывании подвешенный груз не доставал
до пола. В начале опыта груз должен быть в наивысшем положении;
опускаясь ускоренно, он разгоняет систему, но вследствие ее
инерции не останавливается в низшем положении; нить наматы-
вается на цилиндр, груз поднимается замедленно до тех пор, пока
его скорость не обратится в нуль.
Наблюдая разгон и выбег, можно определить момент инерции
системы. Предложены две модификации этого метода: без отсо-
единения груза и с отсоединением груза в конце участка разгона.
1. Модификация, предложенная 3. А. Хантадзе. 3. А. Хан-
тадзе предложил [159, 160] следующий способ эксперименталь-
ного определения моментов инерции отдельных узлов и деталей
машин. На цилиндр (рис. 64), связанный с испытуемым телом, вра-
щающимся в неподвижных подшипниках, наматывают нить, конец
которой закреплен на цилиндре. К нити подвешен груз Р. Наблю-
дают время t опускания груза с высоты hlt равной длине намотан-
ной на цилиндр нити. Кроме того, наблюдают высоту h.2, на ко-
торую поднимается груз при последующем движении по инерции.
153
Для вывода расчетной формулы целесообразно воспользоваться
теоремой об изменении кинетической энергии системы.
Рассмотрим движение системы под действием веса Р, приведен-
ной силы трения Fmp и веса свисающей части нити, причем длина
всей нити /, а вес р.
Работа этих сил при опускании груза с высоты /гх равна
Ze+A,
A1 = (P-FmD)h1+ j ±-zdz =
При последующем подъеме груза на высоту h2 эти же силы
совершают работу
А,
I
w.
vO-
«Si
а I
,а- -(P + Fmp)h2 +
г0+Л,—h,
" IZ
I
+ J i-zdz
■ (P + Fmp)h2-
pK
21
(гго + 2/i! —Aa).
Обозначая через у максимальную
Рис. 64. схема опыта по скоРость груза при опускании груза,
3. А. Хантадзе получим по теореме об изменении
кинетической энергии
i3^ • 7f = [Р - F'nP + if (2z0 + А,)] К;
а при подъеме
2
J+Jh
= [P + Fmp + -£■ (2z0 + 2h, - Aa)] h,.
Расстояние А груз прошел равноускоренно за время t, поэтому
1h
= —~. Исключив из двух последних уравнений Fmp, получим
рабочую формулу
J
Рг
I r_jVjg_
g L hi (*! + A.)
+
pr\hJ2
+ Ш1(А1 + Аг)(4го + 3^-^-^
(89)
154
Второй член правой части этой формулы учитывает влияние
веса нити. Если при эксперименте не требуется большая точность,
весом нити можно пренебречь и формулу (89) заменить следующей:
J
(89')
Относительные ошибки вычисления
S/P=(l+^)
АР
р
6Л = 1 +
&\=(l +
' пил
jj_ pflhi(IK + К) Л. .
у * аНа1 + а2)2 "
/ (Аг + Й3)2 'а'
s / Д^Чи.1 . с г / 1 г J цил \ г> Art _
6Jt
1 +
2r\Ph2t
Jhx (hx + ft2)
АЛ
Длину /гх можно точно измерить при неподвижном грузе и лю-
бое число раз. Но А2 можно измерить лишь один раз во время од-
ного опыта, при движении машины, а потому абсолютная ошиб-
ка A/i! значительно меньше Ah2-
Эксперимент целесообразно проводить при таком грузе, чтобы
ускорение системы было наименьшим, это позволяет значительно
упростить и формулы ошибок. Среднеквадратическая ошибка вы-
числения момента инерции в таком случае равна
Ы =
-VJ--
AJa
+ (&)'№)' + № + *&)'] + (
Пример 19.
3. А. Хантадзе [160] приводит экспериментальные данные
определения момента инерции молотильного барабана молотилки
МС-1100. При вычислении ошибок принято Ah = 0,005 м; АР =
= 0,005 кГ; At = 0,01 сек.
155
опыта
>,
1
2
3
4
ш
о.
4
5
6
9
=5
^С
1,80
1,80
1,75
1,83
З
■С
1,19
1,24
1,33
1,40
в сек
■"
9,25
8,13
7,10
5,88
^ *
0,832
0,821
0,824
0,816
«■'А,
0,25
0,21
0,21
0,20
«•/л,
0,45
0,44
0,45
0,43
Ыр
%
0,12
0,10
0,08
0,06
6J,
0,22
0,25
0,28
0,34
=■
a а
0,0422
0,0546
0,0696
0,1055
Находим 6Jri = 0,48%, так как г1 — 0,105 м и Arx =^ 0,05 лл.
Наибольшая относительная ошибка была в четвертом опыте
б/ = 0,75%,
что объясняется большим значением ускорения а.
Модификация, предложенная А. Ф. Князевым. Рассмотрим
модификацию метода, описанную А. Ф. Князевым [72]. Систему
из состояния покоя приводит в движение груз Р, подвешенный
на достаточно длинной нити, намотанной на цилиндр, соединенный
с испытуемым телом. В конце разгона груз опускается на пол,
а при последующем выбеге система останавливается за счет сил
сопротивления.
А. Ф. Князев рекомендует измерять не линейные перемещения
груза или точки нити, а пропорциональные им углы поворота вала
испытуемого тела при разгоне и выбеге, а также угловую скорость
в мгновение удара тела о пол. Однако это трудно осуществить
с достаточной точностью, поэтому целесообразно находить обыч-
ные для метода величины: высоту h1 опускания груза при разгоне,
путь выбега h2 и время опускания груза t.
На основании теоремы об изменении кинетической энергии
можно написать для участка разгона груза
J + J4U., i!Lj--£- i!i
2 * ,? *" 8 ' 2
[p-
21
{2z0 + hS\h1
и для участка выбега
J + J
Цил V' Р V~_ _ р .
1 Т „ о — ' трпг-
Решая совместно эти два уравнения и учитывая, что v2 = 4
получим формулу для определения момента инерции
/2
/ =
g (hi + Нг)
V 2АХ Ч^ 4АХ
Prx h2 (2z„ + Ai)
hi + hz
'J цил-
156
Второй член правой части обусловлен весом нити и ввиду его
малости может быть отброшен. Тогда формула приобретает более
простой вид:
Рг\
Относительные ошибки вычисления равны
&/р = ( 1 + ±f-
' цил
АР
р
6Jhl = (l +
А
J 8 (*i + А*)а
g/* (2ftt + Й2)
2h\
— 1
Mi;
8/^(l+^)^
bJt-[\ + }"■') MA*+Ag) •-,
A^i . s г . &J цил
ГГ1 = 2(\+^ш)
6Л = 2 1 + ^ -^ • fi/„„, =
Л( . "" И«л — у
Среднеквадратическая ошибка вычисления момента инерции
выразится формулой
8J=]/ б/2Р + б4х + б42 + 67? + Ы\ + bJ\UJt.
§ 5. ОБЛАСТЬ ПРИМЕНЕНИЯ, ОЦЕНКА МЕТОДА
И РЕКОМЕНДАЦИИ ПО УСТРОЙСТВУ ПРИБОРА
Опытную установку с вертикальной осью применяют для экс-
периментального определения моментов инерции испытуемого тела
как относительно центральных, так и нецентральных осей. Однако
если ось вращения не совпадает с главной центральной осью инер-
ции испытуемого тела, то важно, чтобы ускорение опускающегося
груза было наименьшим, так как в противном случае возникают
значительные динамические давления на подшипники, уменьшаю-
щие точность метода. Если же ось установки горизонтальная и
центр тяжести испытуемого тела не лежит на этой оси, то дифферен-
циальные уравнения движения, положенные в основу вывода ра-
бочих формул, не описывают движение системы. Нарушается ли-
нейность дифференциальных уравнений, что при нецелом числе
оборотов испытуемого тела может существенно повлиять на точ-
ность. Поэтому для определения моментов инерции относительно
нецентральных осей применение машины с горизонтальным рас-
положением оси совершенно недопустимо. Строго говоря, метод
атвудовой машины пригоден для определения моментов инерции
только относительно главных центральных осей инерции.
157
Расчетные формулы выведены в предположении, что сила тре-
ния остается постоянной независимо от скорости. Такое предпо-
ложение не вполне правильно. Поэтому некоторые авторы, на-
пример В. С. Кулебакин [84], А. Н. Волохов [27] и др., рекомен-
дуют применять при опыте лишь опоры качения. В настоящее
время можно рекомендовать подшипники скольжения с фторопла-
стовыми прокладками, коэффициент трения в которых не дости-
гает 0,005.
Для лабораторий и машиноиспытательных станций можно
также рекомендовать антифрикционные механизмы, описанные
в книге В. С. Васильева и П. С. Кут-
ко «Станки и приборы для дина-
мической балансировки». М., Маш-
гиз, 1959.
Б. Е. Горский [52] исследовал
приведенный коэффициент трения
антифрикционного механизма. Он
наблюдал время tt и t2 опускания
грузов Рг = 0,5 кГ и Р2 = 1,0 кГ
с высоты h = 492 мм и, исключив
момент инерции из двух уравнений
движения, определял приведенную
силу трения.
Приведенный коэффициент тре-
ния менялся в пределах от 0,0012
до 0,0035 при изменении расстоя-
Рис. 65. Подвес оси с незначи- ния (Рис- 65) между осями ро-
тельным трением ликов от 200 до 300 мм. Столь
незначительный приведенный ко-
эффициент трения позволяет реко-
мендовать антифрикционный механизм при точных определениях
моментов инерции тел.
Метод достаточно прост в экспериментальном отношении и тре-
бует наличия лишь самой простой аппаратуры (весов, штанген-
циркуля, линейки и секундомера). Но точность результата зависит
от точности измерения времени движения груза (обычно не более
10 сек). Поэтому даже небольшая абсолютная ошибка в измерении
времени сказывается на точности определения момента инерции.
Абсолютная ошибка измерения времени часто бывает значитель-
ной, потому что трудно заметить начало движения системы из
состояния покоя с небольшим ускорением [173].
Точность измерения времени можно увеличить, используя но-
вые методы и приборы экспериментальной физики (см. М. П. Пав-
лов «Техника измерения скоростей и времени», гл. IX. «Приборы
для измерения коротких промежутков времени». М., Машгиз,
1950 г.).
Для пуска и остановки измерителя времени желательно при-
158
менять автоматические устройства, исключающие ошибки экспери-
ментатора. Пуск системы обычно блокируется с включением се-
кундомера, что может быть осуществлено разными путями. Для
метода двух грузов К- П. Яковлев [177] предлагает удерживать
ГРУЗ Рл в верхнем положении магнитным полем соленоида. При
размыкании цепи соленоида (с одновременным включением элек-
тросекундомера той же кнопкой) система начинает движение.
Аналогичный способ удержания груза электромагнитом при спо-
собе одного груза описан Г. Я- Го-
ловниным [50].
В. В. Юденич [173] описывает
прибор ТММ-29, разработанный
СКВ МВО и ССО СССР, в котором
система в исходном положении | С^ 9
удерживается колодочным тормо- •' ' *
зом. Пуск системы осуществляют
замыканием цепи электромагнитов,
которые, преодолевая сопротивле- й
ние прижимных пружин, отводят ,'
тормозные колодки, и система !
приходит в движение. Включение
электросекундомера происходит с
помощью блок-контакта, откиды- чч
ваемого падающим грузом в начале
движения системы.
В ряде приборов груз Р уста-
навливают на специальной пло-
щадке, представляющей собой
рычаг, который удерживается
в горизонтальном положении пру- . ..
жиной, соединенной с якорем -& ' > ^
электромагнита. Пуск системы с
одновременным включением се- Рис. 66. Прибор ТММ-29 СКБ
кундомера осуществляют замыка-
нием цепи электромагнита. Притягиваясь к сердечнику, якорь
освобождает рычаг, который, повернувшись вокруг оси, освобо-
ждает груз Р.
Все эти приборы и приспособления позволяют повысить точ-
ность, но при этом эксперимент усложняется. Поэтому, если тре-
буется определить экспериментально с большой точностью момент
инерции какого-либо тела, нужно применять более точные
методы (унифилярныи и бифилярный подвес или метод
физического маятника). Следует отметить, что этим методом
можно определить момент инерции вращающихся деталей без
разборки машины. Так, например, маховые моменты роторов
электрических машин часто удается определить без демонтажа
машины.
159
§ 6. рекомендации по проведению опыта
Если деталь, момент инерции которой надо определить, напри-
мер маховое колесо, можно отключить от остальных звеньев ма-
шины и вращать в собственных подшипниках, то для проведения
эксперимента проще установить блоки и перекинуть намотанную
на ступицу нить, чем снимать испытуемое звено и устанавливать
на оси прибора.
Предпочтительнее, чтобы ось, относительно которой опреде-
ляют момент инерции, в приборе была расположена вертикально.
При установке ось испытуемого тела должна совпадать с осью
прибора. Испытуемое тело следует закреплять на валу или на
площадке прибора жестко, пробуксовывание недопустимо.
Пробным экспериментом проверить отсутствие перекосов, зае-
даний и прочих помех вращению тела.
В случае горизонтальной оси необходимо проверять статическую
уравновешенность деталей, для чего надо приводить испытуемое
тело во вращение и всякий раз отмечать мелом ту точку, которая
при остановке тела окажется внизу. Если меловые отметки сгруп-
пируются приблизительно в одном месте, это свидетельствует о не-
уравновешенности.
Если испытуемое тело не имеет ступицы или другой цилиндри-
ческой части, то на валу прибора, на котором насажено тело,
строго соосно с валом и жестко закрепляют катушку для наматы-
вания нити. Радиус катушки должен быть таким, чтобы относи-
тельная ошибка его измерения была невелика и составляла не-
большую часть (V4 : V5) общей ошибки, которая допустима при
эксперименте. Относительная ошибка измерения радиуса опре-
деляется формулой
где г1 — сумма радиуса катушки и половины толщины навивае-
мой нити; \г1 — абсолютная ошибка измерения г1.
Задавшись 6УЛ] и зная абсолютную погрешность Arlt определяе-
мую точностью измерительного инструмента (штангенциркуля),
можно найти радиус катушки.
Нить, наматываемая на цилиндр, должна быть достаточно гиб-
кой, чтобы ее жесткость меньше сказывалась при наматывании и
сматывании, не обладать значительным удлинением при подвеши-
вании груза, иметь постоянное сечение, не иметь неровностей,
узлов и пр. Влияние свисающего конца нити на ускорение системы
даже при точных опытах можно не учитывать, но надо нить на
цилиндр намотать так, чтобы оба конца во время опыта лежали
на полу. Нить на цилиндре и свисающая ее часть до груза
должны быть натянуты, иначе груз будет падать некоторое время,
160
не приводя испытуемое тело во вращение. Иногда оказывается
возможным наматывать ее при подвешенных грузах, что обеспе-
чивает нужное натяжение. Нить на цилиндр должна быть намо-
тана в один слой без скольжения, многослойное наматывание при-
водит к изменению расчетного радиуса цилиндра.
В качестве нити на практике применяют тесьму [52], кожаный
шнур [295], цепь [39], тонкую проволоку [159], капроновую
леску и пр. Но тесьму нельзя намотать на цилиндр однослойно
[ПО], кожаный шнур малопригоден для данной цели, потому
что его физические свойства меняются, например, в зависимости
от влажности, цепи применяют для подвешивания только массив-
ных тел.
Высота h, с которой опускается груз, должна быть по возмож-
ности большой, поэтому иногда целесообразно перебрасывать нить
через блоки, прикрепленные к потолку помещения.
Начальное и конечное положения груза необходимо наметить
заранее, выразив расстояние между ними числом, удобным
для подсчетов, так как оно входит в формулы для вычисления
момента инерции. Низшее положение груза при всех вариантах
метода, кроме модификаций, предложенных 3. А. Хантадзе и
А. Ф. Князевым, должно быть заранее отмечено на шкале. При
визуальном наблюдении во избежание параллакса необходимо,
чтобы траектория груза лежала ближе к плоскости шкалы.
Включать и выключать электросекундомер следует электри-
ческим способом посредством контактов, размыкаемых или за-
мыкаемых грузом.
♦ ♦♦
11 М. М. Гернет 2274
Глава VII
♦ ♦♦
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ
МЕТОДОМ КАЧЕНИЯ ТЕЛА ПО ПЛОСКОСТИ
§ 1. ИСТОРИЯ МЕТОДА
Моменты инерции тел, имеющих цилиндрическую форму или
два соосных цилиндрических шипа одинакового диаметра можно
определить методом качения по плоскости. Определив время,
в течение которого тело скатывается по наклонной плоскости, по
соответствующим формулам вычисляют его момент инерции отно-
сительно центральной оси, параллельной мгновенной оси враще-
ния. Плоскость может быть и горизонтальной, но тогда к телу
прикладывают постоянную силу.
Впервые этот метод был изложен в журнале «Physikalische
Zeitschrift» в 1906 г. в статье Луммера и Шефера [311 ]. В том же
журнале появилась статья Ветцмана [382], посвященная анало-
гичному методу. В 1913 г. Лехнер [305] описал прибор для опре-
деления моментов инерции, построенный на том же принципе.
В 1951 г. Ульке [379] предлагал этот метод как новый.
В отечественной литературе этому методу были посвящены
работы проф. Б. И. Турбина, опубликованные в 1939 г. [151],
в 1954 г. [152], в 1957 г. [153], в 1959 г. [150].
§ 2. КАЧЕНИЕ ТЕЛА ПО НАКЛОННОЙ ПЛОСКОСТИ
I Испытуемое тело (рис. 67) скатывается по наклонной плоскости,
опираясь боковой поверхностью или двумя цилиндрическими ши-
пами радиуса г. Движение тела происходит под действием силы
тяжести mg, идеальной реакции R, силы трения скольжения Fmp
и момента М сопротивления качению. Все силы расположены
в одной вертикальной плоскости, начальная скорость равна нулю.
Если ось, проведенная через центр тяжести тела перпендикулярно
к этой плоскости, является главной осью инерции, то тело совер-
шает плоское движение.
Построим координатные оси, направив Ох по наклонной пло-
скости вниз Оу перпендикулярно к ней вверх на центр В шипа
при начальном положении тела. В мгновение t точка В имеет коор-
динаты
х = х (0; у — г.
162
Если центр тяжести тела в начальное мгновение лежал на
оси Оу и координаты его хс = 0, ус = г — е (е — эксцентрици-
тет — расстояние центра тяжести тела от его геометрической оси,
от оси шипов), то в мгновение t координаты центра тяжести и
угол поворота тела будут
xr — x — e sin
Ус
-ecos
Ф =
Взяв первые и вторые производные по времени, получим проек-
ции скорости и ускорения центра тяжести, а также угловую ско-
рость и угловое ускорение тела:
хс = х (l — -^cos -^-);
"хс = х(\ — у cos -j-") + х
цг — х — sin —
зь г г
ус = х--ъ\п-у\ Ф = -^-;
* е . х
X* —5- sin —
X" — COS ; ф = .
Составим дифференциальные уравнения плоского движения
тела
тхс = mg sin a — Fmp
тУс — R — тё cos а'>
;cos
— tfesin —-M,
г
Рис. 67. Качение по наклонной плоскости
где а — угол наклона плоскости; т — масса тела; J = тг2и —
момент инерции относительно центральной оси, перпендикуляр-
ной плоскости хОу.
Определив FmP и R из первых двух уравнений и выражая мо-
мент М произведением идеальной реакции на коэффициент /"
сопротивления качению, подставим полученные выражения
в третье уравнение:
(-.
хс ^ г\ + г2 + е1 — 2re cos — + f"e sin
Л (sin у
= gr | r sin a — /" cos a — e sin (oH )
-cos
t)-
Если центр масс С испытуемого тела лежит на оси шипов,
т. е. совпадает с точкой В, то е = 0 и уравнение принимает вид
х (rl + r2) = £r (r sin a — /"cos a)-
163
Точка В движется прямолинейно. Если эксцентрицитет центра
тяжести не равен нулю, то дифференциальное уравнение дви-
жения является нелинейным, зависимость расстояния, пройден-
ного точкой В, от времени сложная и не может быть использована
для экспериментального определения момента инерции.
Некоторые авторы [151] предлагают в случае, когда центр
тяжести испытуемого тела не лежит на геометрической оси шипов,
измерять время движения точки В на участке, длина которого
кратна длине окружности шипов, полагая, что через каждый
полный оборот тела скорость его центра тяжести возрастает на
одну и ту же величину. Это предположение справедливо лишь
при отсутствии трения качения. Момент трения качения зависит
от давления, следовательно, от ускорения центра тяжести тела,
поэтому приращение скорости за каждый полный оборот не
может быть одинаковым. Но сопротивление качению мало и его
влиянием можно пренебречь.
Принимая /" = 0, получим
х (г2и + г2 + е2 — 2recos— ] + х2еsin — =
= gr Г г sin а — esinfa-t- — j .
Это уравнение также нельзя проинтегрировать в квадратурах.
Для вывода рабочей формулы рассмотрим движение тела при ка-
ком-либо целом числе k оборотов. В таком случае точка В пройдет
за k оборотов путь sk = 2nrk, а ее перемещение равно 2nrk и
направлено параллельно оси Ох, причем k — 1, 2, 3, . . . Такие же
перемещения за k целых оборота тела получат все точки тела и,
в частности, центр тяжести С. Используем теорему об изменении
кинетической энергии тела
mvc mr<pz
—д ( к— — 2nrkmg sin a.
Если обозначим через d расстояние СЕМЦС центра масс тела
от мгновенного центра скоростей в конце рассматриваемого
dx
участка, а vc = — , то из предыдущего уравнения полу-
чаем
Из этого равенства следует, что в конце каждого оборота ско-
рость х оси шипа (точки В) пропорциональна корню квадратному
из числа совершенных оборотов. Поэтому связь между ее пере-
164
мещением, скоростью и временем tk при целых оборотах тела
можно выразить следующим равенством:
sk = 2ял/г = Щ-,
где tk при k = 1, 2, 3, . . . — время, в течение которого катя-
щееся тело делает 1, 2, 3, . . . целых оборота. Тогда
tk у rl + d*
Отсюда определим квадрат центрального радиуса инерции и,
помножив его на массу, получим
, 2 mgr sin a ,2 .2 ,n i \
J = mruZ=-JL——t—md. (91)
Следовательно, для определения момента инерции необходимо
знать d = СЕМЦС при начале движения, эта величина зависит не
только от эксцентрицитета центра масс, но и от того, как тело
установлено на плоскости в начале эксперимента. Однако трудно
установить тело так, чтобы можно было знать с достоверностью
это расстояние. Поэтому в случае, когда центр масс тела не лежит
на геометрической оси шипа, получаются сложные уравнения дви-
жения, не позволяющие получить простые и точные расчетные
формулы. Выбор условий эксперимента (наклон плоскости, пере-
мещение оси шипа) также затруднителен. Не исключено, что в не-
которых случаях движение тела происходит с частичным проскаль-
зыванием, обнаружить которое трудно. Ввиду того, что сила тре-
ния зависит от давления, а следовательно, от сил инерции, условие
качения без скольжения выражается сложным неравенством:
(cos ц>тр j cos [qmp + ~j] ?+
+ -ji sin ( 4>mP + -j-) x2 < g sin (a -- q>mp).
Даже частичное проскальзывание сказывается на точности ре-
шения. Таким образом, если центр тяжести тела не лежит наоси
шипов, этот метод нельзя рекомендовать для точного определения
момента инерции. Однако в некоторых случаях значительно
проще применять этот способ, чем какой-либо другой. Так, на-
пример, момент инерции имеющего протиЁовесы колесного ската
тепловоза можно определить, прокатав скат по наклонному участку
железнодорожного пути,
165
§ 3. ВЫВОД РАБОЧЕЙ ФОРМУЛЫ
С УЧЕТОМ ТРЕНИЯ КАЧЕНИЯ
Если эксцентрицитет центра масс равен нулю или им можно
пренебречь, то, интегрируя дифференциальное уравнение движе-
ния § 1 в предположении, что хс — 0 и хс — О, находим
хс
-о '-о
gt'2 г (г sin а — /"cos а)
-2 7[Т? '
Из этого уравнения определим г2: и, умножив его на массу
тела, получим
j _ mgr (r,in а-Г cos a) fi ^ (92)
-хс
Принимая во внимание дифференциальные уравнения плоского
движения тела, запишем условие качения без скольжения Fmp^.
s=S f'tng cos а в таком виде:
-9mg ,7 (г1 sin a -j- rf" cos a) ^ f'tng cos a.
r; + r v '
Отсюда найдем значение тангенса угла наклона плоскости
tgoKf-^ Г 4"- (93)
Это условие не зависит от ускорений. Если учесть, что трение
скольжения значительно больше сопротивления качению, то усло-
вие (93) можно несколько упростить и написать его в виде, рекомен-
дуемом Л. Г. Лойцянским и А. И. Лурье [89]:
г1 + г2
Если в формуле (92) принять /" —- 0, то получим
г2 <
~2х
г=пщг^_а(,_тг, (92/)
с
Следовательно, пренебрежение трением качения приводит к за-
вышенному значению момента инерции. Чтобы определить допу-
щенную при этом относительную ошибку, нужно разность J' —
— J поделить на J. Для упрощения выкладок поделим разность
на величину /' и, опустив элементарные математические преобра-
зования, напишем следующую приближенную формулу;
e/m,= -L(l+i£)ctga.
166
Из формулы следует, что ошибка от пренебрежения сопротивле-
нием качению возрастает с уменьшением угла наклона и с умень-
шением радиуса шипов. А. Лехнер [305], проверивший влияние
радиуса шипов экспериментально, рекомендует учитывать сопро-
тивление качению при небольшом радиусе шипов.
Чтобы яснее выразить влияние коэффициента трения качения
и радиуса шипов на погрешность, вызванную пренебрежением со-
противлением качению, помножим числитель и знаменатель нера.
венства (93') на т, найдем, что ctg а > -у,—у——г, и подставим
в предыдущее равенство
Например, если шипы и рейки стальные, то /' = 0,2 и /" =
= 0,005 см, bJmp > 0,025—, если же шипы стальные, а рейки
дубовые, то /' = 0,5; /" = 0,35 см и &Jmp = 0,07 --, где г выра-
жено в см. Правые части неравенств равны минимальным значе-
ниям ошибок при максимальных допустимых углах наклона пло-
скости, при меньших углах наклона они значительно превосходят
эти значения.
Не приводя вычислений, напишем окончательные формулы от-
носительных ошибок, причем некоторые из них являются при-
ближенными, так как для упрощения в некоторых случаях при-
нято f" = 0:
SJm = 6m; 8Jr = 2бг; 6Ja = —-;
bJ*c = —7 6*c
Для получения среднеквадратичной ошибки определения мо-
мента инерции методом качения на плоскости надо извлечь квадрат-
ный корень из суммы квадратов этих величин.
Пример 20.
Альфред Лехнер [305] приводит результаты эксперименталь-
ного определения момента инерции модели колесного ската желез-
нодорожного вагона. Масса модели т = 116,6 г, радиус колес
г = 2,87 см. Данные одного из опытов: хс = 37,71 см; а =
= 6° 2' 11". Время определяли секундомером по 10 измерениям
и приняли / = 1,04 сек с среднеквадратической ошибкой At =
= 0,034 сек.
167
Момент инерции модели ската автор вычислил по формуле (92'),
т. е. без учета трения качения. J = 461 гсм3. Определим ошибку
обусловленную пренебрежением трением, принимая/" = 0,005 еж:
dJmp = 5,26%.
Вычислим частные ошибки эксперимента, приняв, как это сле-
дует из данных А. Лехнера, Аг = 0,05 г; Да = 0",05; Ахс =
= 0,005 см; At = 0,034 сек. Тогда bjm = 0,043%; 6/, = 0,35%;
6/а = 0; 6У'х — 0,042%; 8Jt = 20,9%. Суммарная среднеквад-
ратическая ошибка вычисления момента инерции, выраженная
в процентах, равна
6/ = 21,5%.
Как видно из приведенных значений, низкая точность экспери-
мента обусловлена малой точностью измерения времени и прене-
брежением сопротивлением качению.
Пример 21.
Проф. Б. И. Турбин [150] приводит результаты определения
момента инерции шкива методом качения по наклонной плоскости.
Данные эксперимента: г = 0,2 м; tng — 20 кГ; хс = 1,6 м; а —
= 7° 10' (sin а = 0,125); t = 2 сек.
Если шкив и наклонная плоскость изготовлены из стали (/" =
= 5-Ю-3 см), то bJmp = 0,75%.
В этом примере радиус шкива значительно больше, чем в пре-
дыдущем, поэтому ошибка, обусловленная пренебрежением сопро-
тивлением качению, меньше.
Точность измерения времени не указана. Используя другие
работы Б. И. Турбина, где в подобных случаях для измерения
времени применен электросекундомер, можно предположить, что
At = 0,01 сек. Тогда ошибка от неточности измерения времени
6Jt = 3%.
Если t — 2 сек есть среднеарифметическое нескольких замеров,
тогда среднеквадратическая ошибка замера времени меньше
0,01 сек и, следовательно, 8Jt меньше 3%.
§ 4. КАЧЕНИЕ ТЕЛА
ПО ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ
Для определения момента инерции тело иногда катают не по
наклонной плоскости, а по горизонтальной. В таком случае к телу
необходимо приложить движущую силу. В качестве таковой
обычно используют вес р1 груза, привязанного к концу нити,
другой конец которой намотан на испытуемое тело или за-
креплен на его оси (рис. 68). Груз должен быть достаточно боль-
шим, чтобы во время качения тела величина и направление натя-
жения нити не менялись. Измеряют время, в течение которого
168
груз опускается на определенную высоту. Для учета влияния
трения в блоках и прочих диссипативных сил опыт повторяют
при грузе р2. Затем по соответствующим формулам вычисляют мо-
мент инерции испытуемого тела. Такой метод является вариантом
качения по наклонной плоскости или, вернее, комбинацией этого
метода с методом определения момента инерции на машине Атвуда
и не имеет преимуществ перед каждым из них.
Во время качения тела намотанная нить постепенно сматы-
вается с него, поэтому условия опыта меняются. Некоторые авто-
у//аШ>//////////9///ш
Рис. 68. Качение тела по гори-
зонтальной плоскости
й
•<р
Рис. 69. Схема качения тела
по горизонтальной плоскости
ры [153] предлагают один конец нити закрепить на плоскости
между телом и роликом, затем, перекинув нить через тело (или
шипы), другой конец с привязанным к нему грузом перебросить
через блок (рис. 69). Если центр тяжести тела лежит на оси ши-
пов, то скорость его вдвое меньше, чем скорость груза р.
Применив теорему об изменении кинетической энергии системы,
нетрудно вывести формулу для определения момента инерции
_ г2 \2gt\t\ (р, - р2) -Ph{t\-~t\)-~Ah(P,tl~P2t\)\
где р — вес тела.
Условие качения без скольжения в данном случае имеет вид
§ 5. РЕКОМЕНДАЦИИ К ПРОВЕДЕНИЮ ОПЫТА
Метод качения по наклонной плоскости целесообразно при-
менять для определения моментов инерции тел, имеющих цилин-
дрическую форму или цилиндрические соосные шипы одинакового
радиуса. Если радиусы шипов не одинаковы, то метод неприменим
(см. гл. II).
Центр тяжести тела должен находиться на геометрической оси
катящейся цилиндрической поверхности. В случае невыполнения
этого условия можно приближенно определить момент инерции
по наблюдению перемещения оси на расстояние, кратное целому
16?
числу оборотов тела. Ввиду возможности проскальзывания тела
угол наклона плоскости должен быть очень небольшим. Влияние
сопротивления качению в этом случае необходимо учитывать.
Для осуществления плоского движения необходимо, чтобы
центральная ось, перпендикулярная к плоскости движения, была
главной осью инерции тела.
Максимальный угол наклона плоскости для основного случая
(центр тяжести тела лежит на оси цилиндрической поверхности)
определяется формулой (93). Угол наклона следует выбирать не-
большим, но обеспечивающим устойчивое качение тела без замед-
лений и толчков.
Плоскость не должна прогибаться под тяжестью испытуемого
тела. Длина наклонной плоскости должна быть по возможности
большей, что увеличивает время движения, а следовательно, и
точность эксперимента. Однако испытуемое тело не должно раз-
вивать большой скорости.
Основным условием повышения точности эксперимента яв-
ляется многократное и точное измерение времени движения. В ка-
честве прибора для измерения времени обычный секундомер не-
пригоден, необходимы устройства с точностью разового замера
порядка 0,01 сек (например, электросекундомер).
В связи с требованием высокой точности замера времени не-
обходимо исключить субъективные^, ошибки экспериментатора и
предусмотреть специальные устройства для регистрации времени.
В качестве подобных устройств могут быть рекомендованы кон-
такты, устанавливаемые на наклонной плоскости, замыкаемые
катящимся телом.
Этот метод с качением тела по горизонтальной плоскости может
быть рекомендован только в некоторых специфических случаях,
как, например, катание колесного ската по рельсам.
♦ ♦♦
Глава VIII
♦ ♦♦
МЕТОДЫ ОПРЕДЕЛЕНИЯ МОМЕНТОВ ИНЕРЦИИ,
ТРЕБУЮЩИЕ ПРИМЕНЕНИЯ СПЕЦИАЛЬНЫХ
ПРИБОРОВ
§ 1. ПРИБОР Н. Е. ЖУКОВСКОГО С ВИНТОМ И ГАЙКОЙ •
Прибор (рис. 70) основан на так называемом интеграле мо-
ментов, согласно которому сумма моментов количеств движения
точек системы относительно какой-либо оси остается постоянной,
если сумма моментов всех внеш-
них сил системы относительно
этой оси равна нулю. Следует
указать, что описание прибора
впервые опубликовано не в
1891 г. в «Бюллетенях общества
испытателей природы», как ука-
зано в примечании редакции к
Полному собранию сочинений,
а в 1889 г. в малоизвестном
французском журнале «Bulletin
de l'Association francaise pour
l'avancement des Sciences», 1889,
p. 23.
Цилиндр В, на поверхности
которого имеется винтовая резь- Рис 70 Прибор с винтом и га,,кой
ба с большим шагом, может (схема)
вращаться почти без трения во-
круг оси. По резьбе цилиндра может перемещаться массивный диск
А. Испытуемое тело закрепляют на цилиндре, затем поднимают диск
до наибольшей высоты; стрелкой F, неразрывно связанной с ци-
линдром, отмечают начальное положение и отпускают диск без
начальной скорости. Опускаясь, диск поворачивается по ходу
часовой стрелки, при этом испытуемое тело вместе с цилиндром
и стрелкой поворачивается в противоположном направлении. Пред-
положим, что диск повернулся на некоторый угол ср, а цилиндр
с испытуемым телом — на угол q>lt отмеченный стрелкой прибора.
Для вывода рабочей формулы рассмотрим движение системы,
состоящей из диска А, цилиндра со стрелкой F и испытуемого
171
$'-
jr:
Тела D, жестко соединенного с цилиндром. На систему действуют
только вертикальные внешние силы: вес тела и реакция в опоре
С. Внешнее трение отсутствует. Трение между диском и цилинд-
ром является внутренней силой. Моменты внешних сил относи-
тельно вертикальной оси СС равны нулю, поэтому можно написать
fc=i
В начале движения кинети-
ческие моменты всех входящих
в систему тел равны нулю, сле-
довательно, С1 — 0. Кинетиче-
ский момент вращающегося тела
можно выразить через произве-
дение момента инерции на угло-
вую скорость тела. Раскрывая
знак суммы, получим
/coj -\- JBa>i -\- У/й = 0,
где ы1 —■ угловая скорость ци-
линдра и испытуемого
тела;
со — угловая скорость ди-
ска.
Интегрируя это уравнение
и принимая во внимание началь-
ные условия, найдем
(/ f Jв) cpj + JAq> = 0.
Рис. 71. Прибор с винтом и гайкой
Обозначим фх — ф = п (п зависит от геометрических пара-
метров прибора). Исключая из уравнений угол ф, получим ра-
бочую формулу для определения момента инерции испытуемого
тела по углу ф,:
J = JA~
«Pi
«Pi
- — /
в<
(95)
где п, JА и Jв — постоянные прибора. На рис. 71 представлена
фотография одного из таких приборов.
§ 2. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА УДАРОМ
Прибор для определения момента инерции ударом (рис. 72)
был предложен в 1936 г. [34].
Испытуемое тело закрепляем на горизонтальной платформе,
которая может почти без трения поворачиваться вокруг вер-
тикальной оси. На горизонтальной оси закреплен массивный
172
молоток М, который может вращаться почти без трения. В центре
оси закреплен лимб L — неподвижный вертикальный диск с лег-
кой стрелкой F, отмечающей деление, до которого поднялся мо-
лоток. Весь прибор находится на массивной площадке, нивелируе-
мой тремя установочными винтами.
Переведя молоток в наивысшее положение, отпустим его без
начальной скорости. Во время падения молоток увлекает за собой
подвижный индекс. При прохожде-
нии через равновесное положение
молоток ударяет по кулачку К го-
ризонтальной платформы, перпенди-
кулярно радиусу, приводит ее во
вращение и, отдав часть своей ки-
нетической энергии, поднимается до
некоторого положения, отмечаемого
индексом F.
Во время удара на молоток дей-
ствует единственная ударная сила,
реакция кулачка, так как мгновенное
давление на ось устранено соответ-
ствующим подбором длины рукоятки
молотка. Импульс S этой мгновенной
силы определим из уравнения
£ _ Уд (СО! — (02)
где JM — момент инерции молотка;
/ — расстояние от оси вращения до
центра удара; ыг и со2 — угловые
скорости молотка в мгновения, пред-
шествующие и последующие удару, которые можно определить
по начальной h1 и конечной h2 высоте центра масс молотка:
Рис. 72. Прибор для определения
моментов инерции ударом
2mMgh1
Jm
со, =
-V-
2mMgh2
откуда
'-V
Направление импульса горизонтально. Удар приводит во вра-
щение платформу с телом, сообщив им угловую скорость Q.
Если плечо ударного импульса относительно оси платформы обо-
значим г, момент инерции платформы Jn, а испытуемого тела J, то
S = (J + Jn)-?-.
Выражая угловую скорость платформы через со1( со3, а коэф-
фициент восстановления через е, получим новое выражение для
173
мгновенного импульса. Сравнивая два уравнения, после элемен*
тарных преобразований выведем следующую рабочую формулу:
1_]/!Г
J = JM~ L-^-jn. (96)
'+/£
Все величины, входящие в формулу, за исключением h.,,
являются постоянными прибора и заранее известны. Если мо-
лоток отпускать из наивысшего положения, то h2 является функ-
цией только момента инерции испытуемого тела. В приборе, по-
строенном в МТИПП, лимб разградуирован с обеих сторон, при-
чем с одной стороны нанесены значения h2, а с другой — значения
моментов инерции испытуемых тел. Проф. Л. П. Смирнов (МВТУ)
значения моментов инерции, нанесенные на обратную сторону
лимба, определял не по формуле (96), а экспериментально, уста-
навливая на платформе различные тела, моменты инерции которых
известны, и получая соответствующие величины h2, результаты
при этом совпадали. В Томском политехническом институте был
также построен прибор, где испытуемым телом служил цилиндр, ко-
торый можно закреплять в различных положениях. Чтобы на ре-
зультаты не влиял момент мгновенной силы трения, платформа
рассчитана так, чтобы удар происходил не только в центре мо-
лотка, но и вблизи центра удара платформы с испытуемым телом.
Если момент инерции испытуемого тела
гг
то после удара молоток меняет направление вращения и момент
инерции определяется по формуле (96), в знаменателе которой
знак плюс (+) надо заменить знаком минус (—).
Д. М. Беркович [12] исследовал этот метод и установил, что
при соблюдении некоторых условий максимальная ожидаемая
относительная погрешность определения момента инерции состав-
ляет 0,1 %.
% 3. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ НА ВЕСАХ
В 1923 г. проф. Ф. Виттенбауэр [395] предложил определять
момент инерции тела с помощью весов.
Испытуемое тело (рис. 73) в точке А опирают на чувствитель-
ный элемент весового устройства (пружинные весы, пьезодатчик
и пр.), а в точке В прикрепляют к двум нитям, из которых одна
натянута и во время опыта будет пережжена.
Обозначим.те, — вес тела; / — расстояние АВ; Q0 — реакция
в точке А при равновесии тела. Центр масс С тела лежит на пря-
174
мой А В на неизвестном расстоянии а от точки А. Это расстояние
найдем из суммы моментов всех сил относительно точки В:
а =
mg
I.
После пережигания нити тело будет совершать плоское дви-
жение. Для начального момента можно написать следующие урав-
нения движения:
тхс = mg — Q; тус ■■
ускорение тела;
= 0; Jccp = Qa,
Q — динамическая реакция
где ф — угловое
в точке А.
Если элементарное перемещение точки А за бесконечно ма-
лый промежуток времени dt равно нулю (или на один порядок
меньше элементарного перемещения цен- ™^.,
тра масс С тела), то между угловым ^ ^ ^.
ускорением тела и ускорением центра
масс существует соотношение
А)
хс = ера.
Тогда из первого уравнения
тд
Рис. 73. Определение момен-
та инерции на весах
а из третьего уравнения, подставляя значение а, найдем искомый
момент инерции
/ = —g—.^-fa)!/». (97)
mg — Q mg2
Для регистрации динамической реакции Q нужно применять
устройство с возможно малыми перемещениями чувствительного
элемента при изменении нагрузки. С. М. Тарг [146] рекомендует
использовать пьезоэлектрический датчик давления.
Если центр масс тела находится не на прямой, соединяющей
точки опоры А и привеса В, формула (97), как указываете. М. Тарг
[146], справедлива лишь при условии, что трение в точке опоры А
мало.
Если расстояние / между А и В равно приведенной длине
испытуемого тела относительно точки А:
1 = — + а,
та '
то реакция Q равна статической реакции Q0.
Относительная ошибка вычисления момента инерции по фор-
муле (97) равна
8J = у && + ЬА + 6J2Qo + bfQ.
175
Частные относительные ошибки определяются формулами
SJ„
(mg — Q0)(mg — Q)
-6m; 6/, = 26/;
8JC
2Q0
mg — Q,
SQ„; bJr
mg
mg — Q
,6Q,
Л-Л
где 6m, 6/, SQ0, SQ — относительные ошибки определения числен-
ных значений массы длины, статической и динамической реакций.
Проф. В. Касси [207] предложил метод определения моментов
инерции небольших тел с помощью аналитических весов.
Для этого коромысло весов
нужно заменить специальным
устройством корытообразной
формы (рис. 74), имеющим приз-
мы для подвешивания чашек
весов и дополнительного груза.
Центр тяжести системы, состоя-
щей из коромысла и ненагру-
женных чашек, совпадает с осью
опорной призмы. Испытуемое
тело помещают на конусные опо-
ры, сдвигая и раздвигая кото-
рые можно добиться совмещения
центра тяжести тела с осью
коромысла.
К коромыслу подвешивают дополнительный груз и опреде-
ляют период малых колебаний Тг весов.
Положив на чашки весов грузы равного веса Q, измеряют
период колебаний Т».
Затем снимают грузы с чашек и дополнительный груз с ко-
ромысла. Положив на конусные опоры испытуемое тело, переме-
щениями конусных опор добиваются безразличного равновесия
весов. Вновь подвешивают дополнительный груз и находят пе-
риод Т3. Момент инерции вычисляют по формуле
Рис. 74. Определение момента инерции
на коромысле весов
J = 2Qa2
где а — расстояние от опорной призмы до призмы подвешивания
чашки.
Метод Касси не получил применения, так как он требует
сложного прецизионного устройства, размеры которого наклады-
вают ограничения на вес, форму и размеры испытуемого тела.
176
§ 4. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МЕТОДОМ
КОЛЕБАНИЙ ТЕЛА НА КАЧАЮЩЕЙСЯ ПЛАТФОРМЕ
Качающаяся платформа укреплена на валу, помещенном в под-
шипниках качения на неподвижном основании. С одной из па-
раллельных валу сторон устанавливают одну или несколько
пружин. Если на платформу (рис. 75) поместить испытуемое'тело,
а затем вывести платформу из состояния равновесия, то система
совершает колебания. Началь-
ное смещение платформы обычно
мало, и поэтому колебание опи-
сывается следующим дифферен-
циальным уравнением:
(/ + md'1 + /„,) ср + clhp ■= О,
где J — искомый момент инер-
ции; m — масса тела; d — рас-
стояние центра масс тела до оси
платформы; / — расстояние от
оси платформы до оси пружины; ]пл— момент инерции платформы;
Ф—-угол отклонения платформы от ее равновесного положения;
с — суммарная жесткость пружин.
Период малых колебаний системы определится по формуле
7 '
Рис. 75. Определение момента инер-
ции на качающейся платформе
тк
Т
= 2nY~
■ md2 + J пл
~с/2
ШШШШШ
Рис. 76. Определение момента инерции авто-
мобили на качающейся платформе
Отсюда момент инерции
тела относительно цен-
тральной оси, параллель-
ной оси платформы, равен
J = T-^-md*-Jn.v (98)
Момент инерции платформы можно определять, повторив опыт
с ненагруженной платформой. Если период собственных коле-
баний платформы равен Тп„ то
•'пл —
Т2 с/2
4я2
Методика и объем эксперимента, основанного на формуле (98),
могут меняться. Так, жесткость пружин можно найти непосред-
ственными измерениями, либо из дополнительного эксперимента
с телом известного момента инерции. При неизвестном положе-
нии центра масс тела момент инерции можно найти, наблюдая
колебания при двух различных положениях тела на платформе
(гл. II, § 5).
12 М. М. Гернет 2274 \7J
Метод колебаний тела на платформе удобен для тяжелых
объектов (автомобилей, тепловозов, железнодорожных вагонов
и пр.). Е. Лер [308] описал схему (рис. 76) и методику определе-
ния момента инерции автомобиля.
Жесткость пружин желательно подбирать так, чтобы период
колебаний был больше или равен 1 сек.
§ 5. ПРИБОРЫ ДЛЯ ОПРЕДЕЛЕНИЯ МОМЕНТОВ
ИНЕРЦИИ МАЛЕНЬКИХ ТЕЛ
Экспериментальное определение моментов инерции мелких де-
талей различных точных механизмов и приборов весом до 1 Г
представляет собой трудную техническую задачу.
Большинство методов определения моментов инерции основано
на законах свободного колебания тел. Если момент испытуемого
тела мал, то свободные колебания скоро затухают и точно опре-
делить период этих колебаний невозможно.
Для определения момента инерции на машине Атвуда надо
закрепить центральную ось тела. Для применения метода качения
по плоскости надо заставить тело устойчиво катиться по пло-
скости .
Для измерения моментов инерции деталей часовых механизмов
имеется ряд приборов [69, 229]. Например, момент инерции ба-
ланса определяют по периоду колебаний на специальном при-
боре, причем телу сообщают дополнительные вращающие моменты
посредством натяжения нити, намотанной на ось, с привязанным
к ней грузом.
Прибор обладает высокой чувствительностью, но неприго-
ден для измерения моментов инерции иных тел. Другой прибор
НИИчаспрома называется «Прибор для определения моментов
инерции часовых деталей» и по устройству аналогичен прибору
проф. Б. В. Шитикова [55], сконструированному им в годы
войны для определения моментов инерции винтовочных и револь-
верных пуль. Прибор Б. В. Шитикова позволяет определить мо-
менты инерции и других тел весом до 1 Г. Для определения
моментов инерции более легких тел прибор непригоден, так как
колебания его быстро затухают.
Устройство прибора показано на рис. 77. Испытуемое тело
закрепляют зажимными пружинками в специальной рамке, на
которой установлена колодка. Спиральная пружина (волосок)
закреплена одним концом в колодке, а другим в неподвижной
стойке. Отклонив рамку с телом из равновесного положения, на-
блюдают период колебаний системы и определяют момент инер-
ции по формуле (56) гл. IV.
Если бы колебания не были затухающими, то можно было бы
не учитывать массу пружины, так как инерция пружины входит
178
в величину ■/„. Момент упругой силы можно считать пропор-
циональным углу поворота рамы при следующих условиях:
1) концентричном раскручивании пружины баланса, при ко-
тором радиус г деформированной пружины меняется в зависимо-
сти от угла поворота ф по закону, вытекающему из уравнения
1 1 (Г
архимедовой спирали = -*-, где г0 — радиус неза-
крученной пружины и / — ее длина;
2) неизменном совпадении центра масс пружины с осью вра-
щения баланса; в случае несовпадения вес пружины дает доба-
вочный эффект, то увеличивающий, то уменьшающий ее вращаю-
щий момент и возмущающее воздействие силы тяжести на баланс.
12* 179
Кроме того, необходимо соблюдать некоторые дополнительные
условия (условия Филиппса) относительно концевых кривых пру^
жины [121].
§ 6. ПРИБОР ДЛЯ ОПРЕДЕЛЕНИЯ МОМЕНТОВ ИНЕРЦИИ
ОЧЕНЬ МАЛЕНЬКИХ ТЕЛ
Прибор, позволяющий определить момент инерции относи-
тельно любых осей тел, вес которых измеряется в миллиграммах,
был предложен в 1956 г. [43]. Для определения момента инер-
ции использован часовой механизм. В обыкновенных карманных
часах вместо маховичка на
ось маятника надет диск
примерно такого же размера
(рис. 78), сверху помещена
прямоугольная рамка,снизу
— часовой маятниковый ба-
ланс. Регулятор часов рас-
положен ниже диска Ось
маятника разрезана на две
Рис. 78. Прибор для определения моментов инерции очень маленьких тел
части, одна из которых, прикрепленная сверху рамки, входит
в отверстие камня часового подшипника, другая, прикреплен-
ная к центру диска, поддерживается часовым кронштейном
(рис. 79).
В горизонтальном положении часы установлены на трех нож-
ках (рис. 80). Для определения момента инерции тело помещают
на диск баланса прибора так, чтобы центр масс тела был на одной
вертикали с его центром, и закрепляют в этом положении, прижав
180
специальной планкой (см. рис. 78). Планка надета с зажимной
пружинкой на рамку маятника и ее можно перемещать по всей
высоте рамки.
Если прибор при идеально точном ходе имеет период коле-
баний 0,4 сек, то число колебаний баланса за каксй-либо про-
межуток времени в 2,5 раза больше числа секунд, отмеченных
прибором за тот же промежуток
времени.
Б. И. Полозов с высокой точ-
ностью исследовал ход часов в за-
висимости от завода часовой пру-
жины, температуры, положения
планки, закрепляющей на при-
боре исследуемый объект. Соответ-
ствующие поправки были учтены
при особо точных подсчетах момен-
тов инерции.
Рис. 79. Рамка прибора для опре-
деления моментов инерции очень
маленьких тел
К постоянным прибора относятся также момент инерции плат-
формы /„ и жесткость с волоска балансира, для определения кото-
рых пользуются уравнениями
У^\ Tn + AT = 2nY~
где AT — изменение хода часов при увеличении момента инер-
ции платформы после присоединения к ней эталона. В качестве
эталона были взяты шарики шарикоподшипников, моменты инер-
ции J3 которых можно вычислить с любой степенью точности
по весу и диаметру. Оказалось, что момент инерции платформы
и ход часов почти постоянны и не зависят от положения зажимной
планки. Однако значение момента инерции платформы, экспе-
риментально определенное изложенным способом, зависит от
веса шарика. Это объясняется тем, что написанные выше формулы
не учитывают диссипативных сил, а замедление хода прибора
происходит не только вследствие увеличения момента инерции
системы на величину момента инерции положенного на платформу
груза, но и вследствие увеличения сил трения от добавочной
нагрузки на подшипники.
Поэтому, определяя момент инерции J какого-либо тела,
надо брать значение Jn, выведенное из опыта при загрузке
шариком приблизительно такого же веса, что и испытуемое тело.
181
Так, например, при определении момента Инерции пшеничного
зерна весом около 30 мГ момент инерции платформы приняли
равным /„ = 1,34 мГ-мм-сек2, что было получено из опыта при
загрузке платформы шариком диаметром 2,0 мм и весом 32,60 мГ.
1г --
Рис. 80. Прибор для определения моментов инерции очень маленьких тел
Поместив вместо шарика испытуемое тело, можно определить
момент инерции тела относительно его центральной оси, совпа-
дающей с осью платформы, по формуле
J = Jn(^r-l\, (99)
где Jn — момент инерции платформы (постоянная прибора);
Т — период качания платформы с грузом;
Т0 — период качания ненагруженной платформы (постоян-
ная прибора).
Период находят по показаниям часов, устанавливая ход
часов (отставание за 1 ч или за 24 ч) и по соответствующей таб-
лице определяют момент инерции испытуемого тела.
Прибор позволяет определять моменты инерции очень малень-
ких тел относительно различных центральных осей.
Пример 22.
В опытах Б. И. Полозова [125] пшеничное зерно было закреп-
лено планкой на платформе, затем зерно было вынуто, а планка
оставлена на том же месте. По радиосигналам проверен ход ча-
сов и установлено, что в течение 1 ч они отстали на 2,0 сек. После
того как зерно было снова установлено на прежнее место, часы
182
за 3600 сек отстали на 17,5 сек от точного времени. А когда зерно
было опять вынуто, часы с прежним положением планки отстали за
1 ч на 1,0 сек. Приняли, что ход незагруженных часов при таком
положении планки и равен 1,5 сек в час. Момент инерции при-
бора, определенный при загрузке, равной весу зерна, равен
1,3454 мГ • мм • сек2. Тогда по формуле (99) момент инерции зерна
относительно оси балансира равен
= 0,012 мГ-мм-сек2.
J= 1,3454
Г/ 3598,5 \
[Л 3582,5ji
♦ ♦♦
Глава IX
♦ ♦♦
ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ
ЭЛЛИПСОИДОВ ИНЕРЦИИ
§ 1. ИСТОРИЯ ВОПРОСА
И ПОСТАНОВКА ЗАДАЧИ
Требования, предъявляемые к геометрии масс при решении
различных задач динамики механизмов, обычно ограничиваются
точным местоположением центра масс и точным измерением мо-
мента инерции детали относительно оси вращения или параллель-
ной ей центральной оси.
Однако, когда звено машины совершает неплоское движение
или имеет несколько степеней свободы, необхочимо знать момент
инерции относительно различных осей, а иногда и эллипсоид
инерции.
Например, инженеру И. И. Вольф при исследовании сбра-
сывающего аппарата жнеи [29] необходимо было определить
эллипсоид инерции граблей. На приборе В. А. Желиговского были
определены моменты инерции граблей относительно различных
осей (см. стр. 27). Результаты экспериментов и теоретических
расчетов совпали. Была сделана попытка экспериментального
определения и центробежных моментов инерции. Теорию и мето-
дику этих определений автор не привел. Определенные из опыта
центробежные моменты инерции составляли только 77%, 63% и
40% своей величины.
На практике экспериментальные исследования эллипсоидов
инерции часто проводят приближенно. Например, часто ограничи-
ваются определением эллипса, получаемого при пересечении эл-
липсоида инерции самолета плоскостью, принимаемой за пло-
скость симметрии. Но в действительности самолет не имеет пло-
скости симметрии и установить это экспериментальным путем
особенно важно. В 1935 г. Ю. А. Победоносцев, занимавшийся
определением моментов инерции самолетов [124], писал, что этим
способом приходится пользоваться только по необходимости, за
неимением лучшего.
Метод экспериментального определения эллипсоидов инерции
и центробежных моментов инерции предложен в 1950 г. в ра-
боте [37].
184
§ 2. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ ГЛАВНЫХ
МОМЕНТОВ ИНЕРЦИИ, ГЛАВНЫХ НАПРАВЛЕНИЙ
И ЦЕНТРОБЕЖНЫХ МОМЕНТОВ ИНЕРЦИИ
Общее решение задачи определения эллипсоидов инерции [37]
дано в примечании 21. Каким-либо из существующих способов
надо определить моменты инерции тела относительно шести произ-
вольно направленных осей, пересекающихся в одной точке. Пусть
эти оси составляют с осями координат углы ak, §k, yk, где k =
= 1, 2, . . ., 6. Координаты шести точек поверхности эллипсоида
можно вычислить по формулам
1
xk= -^=cosa*
#* = t?==cospY'
V Jk
Zb =
VT,
^cosy^.
Для определения моментов инерции и центробежных моментов
инерции относительно координатных осей нужно вычислить опре-
делитель
D =
А Ж г\
2 2 9
Х2 -У2 22
2у& — 1z\Xx — 2^i J/i
■2y2z2- — 2z2-v~i —2X2I/2
хб Уе z"b — 2(/б2б
■ 2z%x6 — 2хе,У§
и шесть определителей Du Z)2, . . ., De получаемых из D путем
замены в нем элементов к-го столбца единицами. Тогда
D
J* =
•Iу- г —
Pi
D
J,
г D2 .
Jy D •
x D
j D3
J*- D >
' JX.y ~ Q
(100)
В примечании 22 показано, как соответствующим выбором осей
можно упростить решение.
Для этого надо определить три момента инерции Jx, Jy и J2
тела относительно взаимно перпендикулярных осей и три момента
инерции /4, У5 и /6 тела относительно трех биссектрис, составляе-
мых положительными направлениями этих осей. Тогда центро-
бежные моменты инерции выразятся простыми формулами:
J
У- г
_Jy+U
•IX. У —
•>i'< ■'г. х —
J х + J у
Jz + Jx
Л;
(101)
185
Заметим, что оси 4, 5 и 6 можно выбирать в координатных пло-
скостях и не по биссектрисам, но тогда эти формулы несколько
усложняются [14].
Зная моменты инерции и центробежные моменты инерции от-
носительно координатных осей, можно вычислить главные мо-
менты инерции.
Три главных момента инерции /гл1, /гл2 и JeAS получаются
из векового уравнения
•'х "гл "Iх. у •'г. х
•'х.у •> х •'гл Jу. г = U.
•Iг. х ''у- г "г "гл
А для определения главных направлений, т. е. для определения
направляющих косинусов каждой из главных осей эллипсоида
инерции надо решать систему трех уравнений первого порядка
относительно этих косинусов (к = 1, 2, 3):
(/* — J гл. k) C0S агл. k~ h.y COS $гл. k — J г. х COS угЛ, k = 0;
Jx. y cos агл, k + {Jy — JeJl, k) cos р\,л. k~ Jy.z cos yeJ1. k = 0;
J г. x COS агл_ k — Jy.z COS p\,A k + (/2 — Je„, k) COS угд. k = 0.
Пример 23.
Моменты инерции мельничного валка были определены [41]
относительно пяти осей по наблюдениям весьма малых колеба-
ний на бифилярном подвесе с очень большой тщательност ю.
Валик был подвешен на двух вертикальных нитях равной длины
в трех положениях: горизонтальном, вертикальном и наклонном
под углом 45° (рис. 81). При горизонтальном положении валка
проведены две серии опытов. Сначала был измерен период малых
колебаний валка относительно вертикальной оси Ох, перпенди-
кулярной к оси цилиндра. Затем, не вынимая из струбцин валок,
повернули на 90° вокруг его оси, принятой за ось Oz. Тогда ось Ох
приняла горизонтальное положение, осью бифиляра стала ось Оу.
В таком положении была проведена вторая серия опытов и из-
мерен период колебаний относительно оси Оу. Аналогично по-
ступили и при наклонном положении валка.
По этим наблюдениям подсчитаны моменты инерции валка
относительно осей, перпендикулярных оси вращения:
h = К = 90 752 Г-см-сек2;
Jt = Jv = 90 824 Г -см -сек2;
относительно оси вращения валка
J3 — Jz ~ 7766 Г-см-сек2;
186
Рис. 81. Определение эллипсоида инерции валка
относительно наклонных осей (биссектрис)
J4 = 49 524 Г -см -сек2;
Jb = 49 598 Г -см -сек2.
Центробежные моменты, вычисленные по формуле (101), ока-
зались следующими:
^.г = ^±£г —Л-—339 Г-см-сек2;
jtx^Jl±^-J6 = —229 Г-см-сек2.
§ 3. ИЗМЕРЕНИЕ ДИСБАЛАНСА ВРАЩАЮЩЕГОСЯ
ТЕЛА МЕТОДАМИ ОПРЕДЕЛЕНИЯ МОМЕНТОВ ИНЕРЦИИ
В теории уравновешивания показано, что подшипники детали
не претерпевают дополнительных давлений, если ось вращения
является главной центральной осью инерции. В статье [37]
дан метод измерения неуравновешенности вращающегося тела
путем экспериментального определения его моментов инерции,
позволяющий найти величину и положение масс, которые надо
присоединить к вращающемуся телу или отбросить, чтобы
давление, оказываемое вращающимся телом на связи (на под-
шипники), не зависело от скоростей точек тела, иными словами,
чтобы динамически уравновесить вращающееся тело.
Если тело статически уравновешено, то достаточно определить
момент инерции тела относительно пяти осей, а именно, отно-
сительно оси вращения, двух центральных осей, перпендикуляр-
ных между собой и к оси вращения, и двух осей, составляющих
с последними и с осью вращения углы 45°. Д. М. Беркович [12, 13]
развил этот метод для случая, когда уравновешиваемое тело не
отбалансировано статически. В этом случае дисбаланс можно
определить, если известны моменты инерции тела относительно
девяти осей. Для уравновешивания коленчатых валов он скон-
струировал специальные подвесы. При экспериментальной про-
верке Д. М. Беркович, автоматически измеряя время с помощью
электросекундомера, определял периоды колебаний как среднее
12 серий наблюдений с точностью до тысячной доли секунды.
Экспериментальная проверка еще раз подтвердила возможность
точного измерения дисбалансов путем определения моментов
инерции. Он подробно исследовал три экспериментальных метода
определения моментов инерции в отношении их точности и при-
годности к уравновешиванию роторов: метод качения на парал-
лельных осях (гл. II, § 5), метод качания с эталоном (гл. II,
§ 6) и метод удара (гл. VIII, § 2) и пришел к выводу, что
каждый из них точен и пригоден для измерения дисбалансов.
188
Но для определения центробежных моментов инерции нет не-
обходимости в том, чтобы их влияние сказывалось на экспери-
менте, например на периодах колебаний. Центробежные моменты
определяют по формуле (100), в правой части которой имеются
только полученные из опыта моменты инерции относительно
осей. Поэтому принятый для определения центробежных момен-
тов инерции бифиляр [41] в примере 23 можно заменить мульти-
филяром, о котором В. П. Ветчинкин писал [22]: «Весьма важ-
ным является свойство многонитяного подвеса давать весьма малые
погрешности, зависящие от центробежных моментов инерции. Это
свойство позволяет определять моменты инерции одного и того же
тела относительно всевозможных осей, придавая ему последо-
вательно различные наклоны и определяя каждый раз моменты
инерции одинаково непосредственным способом, без всяких раз-
ностей по одному уравнению с одинаковой, весьма большой точ-
ностью».
Динамическая балансировка методом определения моментов
инерции требует точных экспериментов и ее целесообразно при-
менять главным образом для несерийного производства, напри-
мер, для балансировки громадных роторов турбин, где постройка
специальной балансировочной машины нецелесообразна.
♦ ♦♦
ПРИМЕЧАНИЕ 1
КОЛЕБАНИЯ МАЯТНИКА ПРИ КОНЕЧНЫХ АМПЛИТУДАХ
Если амплитуда качания маятника не очень мала, то допущение о равенстве
синуса угла значению этого угла неправомерно. В этом случае необходимо инте-
грировать дифференциальное уравнение (11), которое запишем в виде
d2op mgc .
т — sin ф.
df* J
Умножая обе части равенства на rfcp и интегрируя, получаем
1 / dtp \2 mgc . г
ТЫ) =+-7-coscp + C,
Постоянную интегрирования найдем при t = 0, ср = ср0 и —~ = 0. Тогда
С1== _ cos ср0
и первый интеграл примет вид
2 п mgc , .
2 —f— (cos ф — cos ф0),
т
откуда
dq>
dt =
V-
2mgc j/^cos ф — cos ф0
Период колебаний физического маятника определяется интегралом
Фо
-.у
J
2mgc J j/"cos ф — cos ф0
о
Для вычисления интеграла введем
Ф Фп
sin -£- = sin --~ sin E.
2 2 ъ
При изменении ф от 0 до ф0, новая переменная | изменяется от 0 до -=-.
В результате преобразований получим
я
Т
т = /, I/ - 1 ..___<*!_
.4-1/IZZf
Г mgc \
у 1 — sin2-|^- sin3 |
190
Обозначим
* к.
J УI - sin» -|L sin* 6
0
Тогда период колебаний маятника при конечных амплитудах можно предста-
вить формулой (14):
Т=4К Л[-±— .
V mgc
Величину К называют эллиптическим интегралом первого рода. Численные
значения К. для различных амплитуд ф0 даны в справочных таблицах [97]. Значе-
ния полного эллиптического интеграла первого рода для некоторых амплитуд,
представляющих интерес для практики определения моментов инерции, приве-
дены в табл. I *.
Приближенное значение интеграла можно получить разложением подынтег-
ральной функции в ряд
1 = 1 + -L sin» ^ sin» g +-Ц- sin* -f- sin* I + • • •
V
1 — sin2 -~~ sin2 t
2 й
и почленного интегрирования
К
о
= \ (l + 4 si»2 -у- «п« Б + 4 sin4 -у- sm* l + ■ ■ ■) at =
--г[' + (т)'•"++(-§-)* •"'-¥- + -]■
В таком случае период колебаний физического маятника можно представить
формулой
>■—>^[1+(-1-),"»-++(-1-),'»*-^+-Г
Выражение в квадратных скобках при малых ф0 близко к единице. Так, при
ф0 = 15° оно равно 1,001. Для амплитуд колебаний, меньших 90°, можно прене-
бречь членами с четвертой и более высокой степени sin ^ ;
• Приведение колебании к бесконечно малой амплитуде впервые ввел И. Бернулли
1747 г [194].
** Преобразование формулы к виду Т = 2rt -^ / приводит Пувайн [-ч48].
mgc cos -y-
Фп
/
v0
Относительная ошибка этой формулы при малых ср не превосходит ■
191
фо
Формулу можно упростить, если sin--~^- разложить в ряд по степеням аргу-
Фо
мента —ф-:
ein -VlL __Фо_ L (J^Y j_ JLf <t» \3_
ЬШ 2 ~ 2 6 \ 2 У + 120 V 2 /
Возводя этот ряд в квадрат и удерживая члены только с квадратом аргумента,
получаем
sin'
Тогда
' = 2я у ■
J
mgc
Фо
1 +
Фо
16
Сопоставление этой формулы с точной формулой (14) показывает, что в одной
Т
из них множителем
при у -
mgc
является 4/С, а в другой 2л
1 +
Фо
Для оценки ошибки, допущенной при использовании приближенной формулы,
в табл. I приведены величины 4/С и 2я I I -4-
Фо
16
для различных амплитуд.
Таблица I
Фо
к
4/С
-(■+4)
Фо
/с
4/С
4+4)
*.—^
Фо
/с
4/С
4+4)
".--?
0°
1,5708
6,2832
6,2832
0,00000
10°
1,5738
6,5952
6,5952
0,00377
60°
1,6858
6,7432
6,7110
0,1518
2°
1,5709
6,2836
6,2837
0,00014
20°
1,5828
6,3312
6,3310
0,0154
70°
1,7312
6,9248
6,8694
0,2147
4°
1,5713
6,2852
6,2850
0,00040
30°
1,5981
6,3924
6,3907
0,0351
80°
1,7868
7,472
7,0490
0,2939
6°
1,5719
6,2876
6,2876
0,00140
40°
1,6200
6,4800
6,4749
0,0637
90°
1,8541
7,4164
7,0865
0,3932
8°
1,5727
6,2908
6,2907
0,00244
50°
1,6490
6,5960
6,5823
0,1021
192
В случае малых колебаний значение полного эллиптического интеграла при-
мерно равно -^- и формула (14) обращается в формулу (13). Аналогично, прене-
брегая значением —-^- в последней приближенной формуле, получаем форму-
лу (13) для периода малых колебаний маятника.
ПРИМЕЧАНИЕ 2
ОСНОВНЫЕ СВЕДЕНИЯ О ТЕОРИИ ОШИБОК
Искомая величина F есть функция переменных х, у, г,
рых нужно найти в ходе опыта
F = F (х, у, г О-
t, значения кото-
Теоретическая зависимость носит сложный характер, и ее использование
на практике затруднительно. В то же время пренебрежение некоторыми второсте-
пенными факторами позволяет без существенного снижения точности значительно
упростить точную и рекомендовать приближенную расчетную формулу. Точность
приближенной формулы оценивают относительной ошибкой, определяемой выра-
жением
uF/ipu6A —
Г точн Рприбл
или менее точно
Qr ппиол —
приол ■
РщОЧН FnPu6A
Рцрибл
где Fm04H — значение искомой величины, вычисленное по точной формуле;
Рприбл — значение искомой величины, вычисленное по приближенной формуле,
полученной в результате пренебрежения некоторыми величинами.
Величины х, у, г, . . ., t, входящие в расчетную формулу, определяют экспе-
риментально, поэтому они содержат случайные ошибки. Для повышения точности
каждую величину измеряют несколько раз (8—10 раз). За расчетное значение аргу-
мента, например х, следует принимать среднее арифметическое значение отдель-
ных замеров
- Е**
где Xk — ft-тый замер аргумента; п — количество сделанных замеров.
Точность среднего значения аргумента оценивают средней квадратической
относительной ошибкой
1 -,/Е^-*)2
ЬХ=ТУ п(п-1) ■
Искомую величину F вычисляют по средним значениям ее аргументов
f = F(x,y.z t).
13 М. М. Гернет 2274
193
Значения аргументов определены с некоторыми ошибками бх, by .
этому средняя квадрэтическая относительная ошибка F равна
6F = V(bFx)* -г (bFyf + (6f2)2+ • • • + №)\
где bFx, 8Fy, . . ., bFt — частные средние квадратическме относительные
ошибки искомой величины, обусловленные неточностью измерения аргументов
х, у, . . ., t.
Частная относительная ошибка искомой величины от неточности замера
какого-либо аргумента, например х, выражается формулой
б^ = ( ■ ■ L ) _хЬх,
' х, у, z
дх ,„ „ , t
{ dlnF \ „ „ . ,
где I —ч )_ _— значение частной производной от логарифма функции F
\ 0х / x,~y,~z...t
(такая производная называется логарифмической производной) по аргументу х,
вычисленное для средних значений аргументов х, у, . . ., Т\ Ьх— относитель-
ная ошибка измерения аргумента х.
В дальнейшем будем пользоваться абсолютными средними квадр этическими
ошибками эргументов и искомой величины и называть для краткости средними
квадрэтическими ошибкзми аргументов или искомой величины.
Среднюю квадрэтическую ошибку эргумента, например х, вычисляют по
формуле
-l/JLiffL
-У л (л -
Д* = I/ -, гг—, т. е. Ьх—хох.
". (л —1)
Чэстная средняя квэдрэтическая ошибка искомой величины, обусловленная
неточностью замера аргумента, например х, выражается как
dlnF
дх
ЬРХ = ( ^^- )_ hxF.
.у t
Суммарную среднюю квадрэтическую ошибку искомой величины определяют
по формуле
AF = У№х? + №„)* + (Л/у2 + h (Af()2.
ПРИМЕЧАНИЕ 3
ОБОРОТНЫЙ МАЯТНИК ПРОНИ
Представленный де Прони в Академию Наук мемуар был им расширен и
II Вандемьера IX годэ Республики (4—X—1800 г.) доложен нэ заседании Инсти-
тута. Прони предлэгэл измерять ускорение свободно пздающих тел методом обо-
ротного маятника. Двухметровая модель такого маятника была построена в обсер-
ватории под Парижем, но в 1815 г. была разрушена вместе с обсерваторией
английскими войсками [215].
Позднее аналогичные оборотные маятники были предложены другими иссле-
дователями. Оборотный маятник часто называют маятником Каттера, по имени
энглийского геодезистэ, предложившего его в 1818 г. [288]. Бессель называет
его [195] маятником Бохенбергерэ по имени немецкого ученого, предложившего
его в 1811 г. [197].
194
Для нас важно отметить, что в этой же работе Мари Риш де Прони предло-
жил измерять моменты инерции экспериментальным путем и указал, что пред-
ложенный им метод позволяет определять «вообще положение центра тяжести,
центра качания и момент инерции тел произвольной формы». Более ранние предло-
жения по этому поводу неизвестны.
ПРИМЕЧАНИЕ 4
ИЗМЕНЕНИЕ ПЕРИОДА МАЯТНИКА ОТ ПРИСОЕДИНЕННОЙ МАССЫ
Докажем теорему: от присоединения к физическому маятнику точечной массы
период его качаний уменьшится, если масса присоединена к маятнику между осью
подвеса и центром качания, и увеличится, если масса присоединена к маятнику
ниже центра качания.
Некоторое тело подвешено в точке О и может качаться относительно гори-
зонтальной оси, проходящей через эту точку, с периодом
7\ = 2я]/-^— = 2яТ/ —,
1 V mgc У g '
где т — масса маятника; J = mcl — момент инерции относительно оси подвеса;
/ — приведенная длина.
Присоединим к маятнику, находящемуся в равновесии, в точке М, лежащей
ниже точки О на одной с ней вертикали и на расстоянии ОМ — сэ, некоторую то-
чечную массу тэ. Период малых качаний маятника с присоединенной массой ра-
вен
^/ mcl + ms, -, Г i
/ . , э\ =2яТ/ ±
g (тс + тэсэ) У g
Т2 <С 7\> если второй радикал меньше единицы,
тс -[- тэ —г-
тс -|- тэсэ
тс + тэ — < тс + тэсэ
или
Сэ<1,
в противном случае период качаний увеличится.
ПРИМЕЧАНИЕ 5
КАЧАНИЕ ШИПА НА ВОГНУТЫХ НАПРАВЛЯЮЩИХ
Определим период малых качаний физического маятника, положенного на
направляющие, имеющие круглые углубления (рис. 82). Обозначим 01 — центр
шипа; О' — центр кривизны направляющих; С — центр масс маятника; с =
= OiC — расстояние центра масс от оси шипа; Е — точка касания шипа и опор-
13*
195
ной поверхности; г — радиус шипа; гх — радиус кривизны (постоянный) напра-
вляющих; ф — угол отклонения маятника от вертикали; \|э — угол, составляемый
радиусом О'Е с вертикалью.
Составим уравнения движения маятника. При качении без скольжения
откуда
'Е0Е = ^Е'Е; г$ = г (ф -f- г))),
,|, = .
Найдем положение центра масс маятника в принятой системе координат при
отклоненном положении
XQ = С COS ф — {Гх — г) (1 — COS l|))
и
Ус
-с sin ф + (г\ — г) sin г|>.
Подставляя значение угла i|j,
получаем
хс — с cos ф — (гх ~ г) X
X
О-^тг^г9)
ус = — с sin ф + ('1 — /■) X
X sin
ф.
Рис. 82. Качание шипа на вогнутых на-
правляющих
Примем за обобщенную коор-
динату угол ф (угол отклонения
маятника от вертикали) и напишем
уравнение Лагранжа для движения
маятника.
Проекции скорости центра тя-
жести на выбранные оси координат
найдем дифференцированием выра-
жений для хс и ус:
хс ■
-(
ус=(-
с sin ф -\- г sin
■ с cos ф -)- г cos —
Гл. —г
г
- ф ф
ф ф.
Квадрат скорости центра тяжести равен
v2c = х2с + у% = Ф2 (с2 + г2 -2crcos —^
Кинетическую энергию маятника выражаем формулой Кенига. Подстав-
ляя значение vc, со = ф и J = тт\с, где тиС —радиус инерции маятника относи-
тельно центральной оси, перпендикулярной к плоскости чертежа, получаем
£ =
тф2
(с2 + 4с + Iя ~ 2сгсов-7-^-г ф) ,
196
Найдем члены уравнения (46) Лагранжа
—- = пир (с2 + г\г + г2 — 2crcos —^— Ф ) •
<3ф \ "С '•I—''/'
дф
: гаф I с2 -J- г2 с + г — 2cr cos ■
■%( 2crrl . rt \
дЕ ■ сггх
—— = Шф2 Sin
дф т ^! — г
Обобщенную силу Q определим из условия, что элементарная работа обоб-
щенной силы равна элементарной работе веса маятника. Элементарная работа
силы трения скольжения при качении без скольжения равна нулю:
mg dxc mgxc
dtp
Ф
Q = — mg l с sin ф + r sin —— ф j ,
Подставляя найденные выражения в уравнение Лагранжа, получим неинтег-
рируемое уравнение движения маятника
! + 4c + r2-2crcos „ Г1_г Ф
4- ф2 — sin — ф 4- g I с sin го + г sin Ф ) = О
гг — г гг — г т " \ т тх— г т/
Рассмотрим малые колебания, при которых дифференциальное уравнение
принимает вид
^[(c-rf+rlc] +g(c+ f''_r )ф = 0.
Период малых колебаний маятника при качении без скольжения его шипов
по вогнутой цилиндрической поверхности выражается формулой
Т = 2я
(c-r? + rlc
eg 1 + — '
LL-i
2274
197
ПРИМЕЧАНИЕ 6
ВЛИЯНИЕ ТРЕНИЯ НА ПЕРИОД КАЧАНИЯ МАЯТНИКА
С ПОДШИПНИКОВЫМИ ОПОРАМИ
Для случая колебаний маятника с конечными значениями амплитуд
в работе [42] составлено дифференциальное уравнение движения
Уф = — тдс sin ф — (mg cos rp + nwp'2c) /r sign ф = 0;
множитель sign ф у третьего члена учитывает изменение направления момента сил
трения в зависимости от направления движения маятника: при движении маят-
ника по часовой стрелке ф<0 и sign ф = —1, а при движении против часовой
стрелки ф>0 и sign ф = +1.
Интегрирование этого уравнения показало, что максимальные отклонения
маятника от равновесного положения определяются зависимостью
Ф» = (-1)" Фо-2 £ Aft),
\ 4=1
где Д^ есть сложная функция максимального отклонения (fk-i B предыдущем
полуколебании, коэффициента трения /0 и основных параметров маятника: рас-
стояния с центра тяжести маятника от оси подвеса, радиуса г шипа подшипника,
радиуса инерции гис относительно центральной оси.
Полупериод какого-либо n-го размаха приближенно можно выразить фор-
мулой
+ .(^ «.-)']}•
Из этой формулы следует, что при конечных значениях амплитуды колебаний
маятника полупериод зависит от трения в оси подвеса, амплитуды колебаний
и основных параметров маятника. Выражение в фигурных скобках отличается от
единицы всего на несколько тысячных ее долей, поэтому его нужно учитывать при
особо точных исследованиях.
ПРИМЕЧАНИЕ 7
КАЧАНИЕ НА ЦИЛИНДРИЧЕСКОЙ ОСИ
Часто момент инерции тел, имеющих цилиндрическое отверстие с образую-
щими, параллельными заданной оси, определяют качанием не на ребре, а на ци-
линдрической оси. Однако такая замена оправдана, когда вес тела велик. Под-
робно и с большой точностью эта задача решена А. А. Коробициным [75]. Случай
малых колебаний и качаний без скольжения (рис. 83) аналогичен качанию цилин-
дрического шипа по вогнутым направляющим (см. примечание 5). Период малых
198
колебаний маятника, опирающегося внутренней поверхностью цилиндра на ци-
линдрическую ось, выражается формулой
Т=2я
V:
Jc + т(с-\- г)2
из которой легко получить выражение (44) для центрального момента инерции.
Рис. 83. Качание тела на цилиндриче-
ской оси
ПРИМЕЧАНИЕ 8
ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ МАЛЫХ
КОЛЕБАНИЙ ДВОЙНОГО МАЯТНИКА
Сократим уравнения малых колебаний на т и I:
lb + сф = —gf);
Найдем частные решения этой системы уравнений в виде
т}= В' sm(kt + a)\
ф = В sin (kt + a).
Т. е. предположим, что углы # и ф изменяются гармонически, с одинаковыми
частотами и фазами, но с разными амплитудами. Подставляя значение углов и их
199
вторые производные в дифференциальные уравнения и сокращая на sin (kt + «),
получаем
В' (Ik- — g) + Bck°- = 0;
В'elk2 + в[(с2 + rl) k2 —eg] = 0.
Система двух уравнений, линейных относительно В и В', может иметь реше-
ния, отличные от нуля, если определитель системы равен нулю:
Ik"- — g ck*
elk2 (e2 + rl)k2-cg
= 0
{lk2-g)[{e2 + r2u)k2-cg]-cHk^0.
В теории колебаний это уравнение называют уравнением частот [8], так как
оно позволяет определить частоту колебаний тела.
Для уяснения физического смысла решения и упрощения записей введем обо-
значения
CS _ „2. &
1 —" c2 + rl ^ с2 + г2и
■р
2
п1 — частота качаний математического маятника длиной I (с такой частотой
колебалась бы исследуемая система, если бы вся масса тела была сосредоточена
в точке А); я2 — частота колебаний простого физического маятника (с такой часто-
той колебалось бы испытуемое тело, если бы точка А была неподвижной). Исполь-
зуя обозначения, перепишем уравнение частот:
(к2-п\)(к2-п1)=р2к*
или
(1 - р2) fe4 - {п\ + п\) к2 + п\п\ = 0.
Решим биквадратное уравнение
V-
п2 + п2 j_1/ (n\ + n\f n\n\
4,2 2(1— р2) ~ V 4(1 — р2)2 1—р2
Преобразуем выражение
*1 2(1 -р»)
[л? + 4- V(n2i ~ пЬ + 4рЧ"2 ];
kl= 2(i Lp2) [я? + «1 + 1Лп?-4Y + 4рЧ«2
kx — низшая частота колебаний; /г2 — высшая частота колебаний, причем
низшая частота меньше п^ и п2, а высшая — больше каждой из них (см., например,
в Курсе Л. Г. Лойцянского и А. И. Лурье [89]). Таким обрззом, существует нера-
венство
0 < k1 < (nlt n2) < k2 < oo.
Определитель системы двух линейных однородных уравнений равен нулю,
а потому одно из уравнений должно быть следствием другого и можно найти лишь
отношение амплитуд В' : В = |3, а не их величины.
200
Вычислим отношение амплитуд
В[ ck\ ~Г&1
С ,2
h = ~B7==j^lq= n\-k\ '
Принимая во внимание написанное неравенство, можем заключить, что
Pi>0; pa<0.
Общее решение системы линейных дифференциальных уравнений выражается
суммой частных решений:
О = Bjp! sin (ktt + aj + Вф2 sin (k2t + а2);
Ф = j5x sin (kxt + а,) + B2 sin (k2t + а»).
ПРИМЕЧАНИЕ 9
О ЗАВИСИМОСТИ ГЛАВНЫХ ЧАСТОТ КОЛЕБАНИЙ ДВОЙНОГО
МАЯТНИКА ОТ ЕГО ПАРАМЕТРОВ
Как видно из формулы (48), частоты главных колебаний двойного маятника
зависят от трех величин: /, с и ги. Поэтому для выявления зависимости удобно
воспользоваться следующими безразмерными величинами:
I с
о — —■ и и = — .
ги ги
Тогда квадраты частот колебаний п\ и п| математического и физического
маятников (см. примечание 8) можно выразить равенствами
"l - / - 2ru q '
„2 _ Cg g 2U
Если увеличивать безразмерную величину q,т. е. при данном испытуемом теле
увеличивать длину нити, то п^ будет убывать по гиперболическому закону, стре-
мясь к нулю. С увеличением и величина п| изменяется от нуля при н=0 до своего
2 а
максимального значения я^ = -^— при «=1, а затем будет убывать, стремясь
1Гц
201
к нулю при бесконечном возрастании и Стоке показал («парадокс Стокса»), что ча-
стоты колебаний двойного маятника ни при каких значениях / и с не могут быть
равны между собой.
Используя условия, указанные в примечании 8, выявим изменение квадрата
низшей частоты колебаний двойного маятника в зависимости от параметров. При
очень малых и очень больших расстояниях с квадрат низшей частоты мал. При
значениях с, близких ги, квадрат низшей частоты не превышает значения
/-2-U г2
С0 ь ~Г 'и / О 0\
^-у, если 1< (так как п\ > п^),
s + n,
g
c2 + rl
или значения ■—, если /> — (так как п^угсЛ.
Перепишем в безразмерных величинах выражения (48), полученные для
главных частот:
4 = -£- • ■— [ («2 + яи + 1) + j/(«2 + qu + l)2- 4ди
Полагая а = 0, найдем
(.2 _ л ., Ь2 _ _£ ?. _ „2
2ru q
*f = 0 » fe2 = ^r-lT = "i-
Таким образом, при и = 0 (или с = 0) двойной маятник колеблется как мате-
матический маятник, а испытуемое тело движется поступательно, следовательно,
определить его момент инерции невозможно.
Полагая и= 1, выразим
Ь2 _ g (2 + <?)-У4 + 92 2 _ g (2+9)+lA + ^
И, наконец, полагая и -* оо, получим k\ -* 0 я Щ -*■ оо.
Следовательно, если q (или длина / нити) неизменна, а величину и увеличи-
вать, то высшая частота колебаний двойного маятника будет монотонно возрастать
от п1 до бесконечности.
Для определения максимума fej в зависимости от изменения и при неизмен-
ном q вычислим первую производную
*(*?) g
X
ди 2ruq /(w2 + <?«+ l)2 — Aqu
X [(q + 2и) Vrp~+?« + l)'i-4?« - («2 + qu+l)(q + 2и) + 2?]
Приравняв нулю, получим
2u3 + 9"2 — 2u = 0.
Это уравнение имеет три корня
л. „ _ /?2+16 + ? . /g»+16-
: U, И2 = J > м3 — л
202
Смысл имеет только один корень (и = us), так как и — величина положи-
тельная. Подставляя значение и в выражение k\, найдем максимальное значение
квадрата низшей частоты
1
Klmax 2ru
qyq*-q + 16
У д°- (<?2 + 24) + 128 + 9 (?2 + '6)3/2
4 у'2
ПРИМЕЧАНИЕ 10
ВЛИЯНИЕ ПАРАМЕТРОВ ДВОЙНОГО МАЯТНИКА
НА ТОЧНОСТЬ ИЗМЕРЕНИЯ МОМЕНТА ИНЕРЦИИ
Пренебрегая неточностями измерения / и т, найдем значения I и с, при кото-
рых погрешности в определении главных периодов меньше сказываются на окон-
чательном результате эксперимента.
Сначала рассмотрим общий случай, когда положение центра тяжести не-
известно и момент инерции вычисляют по формуле (50):
б/ = 1^(в/Г1)8 + (°Л2)2-
Для упрощения последующих математических выкладок преобразуем выра-
жения относительных ошибок за счет неточности измерения периода главных коле-
баний
6/г1 =
о 4л2
А?
О 1
" 4я2
4я2/
8
4я2/
/
4аГ1 = 2
1——ki
.Адг,
2я *
и аналогично
в/Г1=2-4
— # —1
2я Л'*-
Предположим, что абсолютные ошибки измерения периодов колебаний оди-
наковы:
АГ,
Тогда квадрат относительной ошибки вычисления момента инерции выразится
формулой
(67)* =
(ЛГ)2
, 2 "г
(--НУ (-Н-)' J'
203
Подставляя значения k1 и k2 и выполняя ряд преобразований, получим сле-
дующее выражение квадрата относительной ошибки через основные параметры
подвеса:
(бУ)^ =
{Д7Т§ с6 + с'1 -с\\ + зЛг2, + cPPri - с\\ - Ыг\ + г6„
пУ\ <*
Для практики эксперимента желательно, чтобы эта ошибка была равна нулю.
Приравняем числитель нулю и решим уравнение относительно /:
'- = ^V[(^-3cVu-^)±c]/"c42,Vu + 9^-84].
Для исследования этого выражения воспользуемся принятым обозначением
с
— = и, тогда
Га
h.2 = -у- 1(2 — Зи3 — и*) ± и Уив + 2и* + 9«2 — 8].
Так как длина нити / — величина вещественная, то необходимо, чтобы вы-
полнялось неравенство
и« + 2м4 + 9и2 — 8 > 0.
Исследуя неравенство, можно установить, что оно выполняется для значений
и 2а 0,86.
В то же время длина нити / должна быть положительная, что возможно при
и < 0,75.
Сопоставляя оба условия для значений и, легко установить их несовмести-
мость. Следовательно, достигнуть абсолютной точности эксперимента невозможно,
так как при любом подборе параметров подвеса / и с относительная ошибка момен-
та инерции 87 не может быть обращена в нуль.
Исследуем экстремумы квадрата относительной ошибки вычисления момента
инерции, определяемой полученной формулой, для чего найдем частные произ-
водные по I и с:
д (Ы>) _ g (АГ)» - с6 + сУи + ^г\ + СЧ - Л
■^Р- = *Щ (2С« + сН - зЛг» + 2А* - *W„ + Mri ~ Ar%).
ас л г'ис I
Необходимым условием экстремума функции двух переменных является ра-
венство нулю каждой из частных производных. Приравнивая нулю, получим си-
стему двух уравнений, а находя I из первого уравнения и подставляя его во второе,
получим уравнение 12-степени относительно с:
cU-7cwr2u + 2бА4„ - 54с6г6„ + 29с4г* + юЛ™ -24^ = 0,
которое подстановкой
г'и
приводится к уравнению шестой степени
г6 — 7г6 + 26г4 — 54г3 + 29г3 + 29г — 24 = 0.
204
Это уравнение имеет четыре вещественных и два комплексных корня и может
быть представлено в следующем виде:
(г- I)2 (г —3) (г+ 0,728) (г2 - 2,73г + 11) = 0.
Так как г — положительная величина, то интерес могут представлять следу-
ющие три корня:
*i, а = 1 и г3 = 3.
—2~. воспользоваться введенным ранее обозначением
Если, помимо г '■
q — , то первое из уравнений можно представить в безразмерных величинах
Ги
г и q:
-г3 + г2 + zq1 + г - 1 = 0,
откуда
гз _ гг _ г _|_ 1
Из трех указанных положительных значений г практически интересно только
= 3, подставляя которое, найдем
16
= 5,33.
(гх, 2 = 1 приводит к и = 0 и поэтому интересовать нас не может).
Итак, проведенный анализ показывает, что соотношения между основным»
параметрами маятника, а именно при
с — ги~у 3 и I = г,
4 УЗ
являются условиями, необходимыми для того, чтобы ошибка в вычислении мо-
мента инерции имела бы экстремальное значение. Но для существования экстре-
мума необходимо, чтобы определитель, составленный пз значений вторых частных
производных,
д2(6Л) д2(6Я)
dp dl дс
<Э2(6/2) &(6J2)
дс dl J дс*
при этих значениях с и / был больше нуля. Если же определитель меньше нуля, та
экстремума в исследуемой точке нет, а имеет место минимакс.
Вычисляя вторые производные, подставляя в них найденные значения и со-
ставляя определитель, убедимся, что он равен
-9,85 g2 (МУ.
Следовательно, относительная ошибка вычисления момента инерции по фор-
муле (50) абсолютного минимума не имеет ни при каких значениях длины нити
и расстояния с.
В практике экспериментального определения моментов инерции методом
двойного маятника расстояние с точки прикрепления нити от центра тяжести
обычно бывает обусловлено формой испытуемого тела и может быть изменено экс-
периментатором лишь в небольших пределах. Длина нити I может быть выбрана
Iбольшом диапазоне значений. Поэтому в дальнейшем будем считать величину с
205
заданной и попытаемся определить оптимальную длину / при различных заданных
значениях с.
Преобразуем формулу, выражающую относительную ошибку вычисления мо-
мента инерции, воспользовавшись величинами q, и и и выведенными формулами:
Ш)2 = 8 (АГ)2 • ("" ~ ц4 ~ ц2 + '} + "2?2 + (ц5 + Зц3 ~2u) q
Если при q ф О положить и -* 0, то (бУ)2 -> со; если и -> со, то (б/)2 -* со.
Следовательно, при очень малых и очень больших значениях расстояния центра
тяжести от точки прикрепления нити относительная ошибка эксперимента резко
возрастает.
Найдем экстремум относительной ошибки при сделанном предположении, что
безразмерное расстояние есть величина постоянная, а безразмерная длина нити
.может изменяться.
Вычислим первую производную от (б/)2 по q
д{{Ы?\ = g(A7T —ие + и* + "2?2 + Я2 — 1
Зд я2/-,, и2?2
Приравнивая производную нулю, находим, что экстремум имеет место при
Vu«— и* — и2+ 1
Яэкстр — .
Это значение qgncmp при всех значениях и^> 0 отлично от куля, за исключе-
нием « = 1, когда q = 0. Следовательно, для всех значений 9 ошибка (бУ)2 имеет
экстремум, кроме случая, когда и= I.
Вычислив вторую производную (б/)2 по q и подставив значение q3itcmp. устано-
вим, что
т. е. имеет место минимум относительной ошибки. Найдем минимальное значение
квадрата относительной ошибки
l0,/'niin „гг.. ' „з
Эта формула показывает, что наименьшее значение
будет при и = 1 и д = 0, вообще говоря, в нереальном случае; при остальных
значениях и ошибка всегда больше этого значения.
В табл. 2 даны значения qSKCmp, соответствующие различным и.
Если положение центра тяжести испытуемого тела заранее известно с достаточ-
ной точностью, величина с = АС измерена непосредственно, а момент инерции
вычислен по формуле (49), то суммарная среднеквадратическая ошибка выра-
жается при малых 6т и 61 следующим равенством:
Если принять ДТ*! = ДТ2 = AT и выразить периоды колебаний через ча-
стоты, то получим
(6jf=(bcf + (*Ly(k\ + kl).
206
Но сумма квадратов частот может быть заменена (см. стр. 55)
(б^ = (а^+(АГ)^.с2 + г" + с/
пЧ
или в безразмерных величинах
(в/)« = (бег- + Щ£*- ■ u* + i» + l
Относительная ошибка 6с определения расстояния точки А прикрепления нити
от центра масс С тела зависит от условий проведения дополнительного экспери-
мента.
Второй член равенства выражает ошибку определения момента инерции за
счет неточностей измерения главных периодов колебаний двойного маятника,
зависит не только от абсолютной ошибки AT измерения периода, но и от пара-
метров с, / и гн и ни при каких значениях этих параметров не может быть обращен
в нуль и не имеет экстремума.
В табл. 3 даны значения 6JT в зависимости от q и и.
ПРИМЕЧАНИЕ 11
КРУТИЛЬНЫЕ КОЛЕБАНИЯ ПРИ НЕЛИНЕЙНОЙ ЗАВИСИМОСТИ МЕЖДУ
ДЕФОРМАЦИЕЙ И НАПРЯЖЕНИЕМ
Примем, что момент сил упругости подвеса определяется выражением
М = сер — г[г (ф),
где f1 (ф) — функция, учитывающая отклонение восстанавливающего момента
от закона Гука;
6 — малый параметр, указывающий на незначительность этого отклоне-
ния.
Момент сил сопротивления среды крутильным колебаниям тела на унифиляре
представим как функцию угловой скорости, причем эта функция может быть не-
линейной:
Мс
*•(-£)■
или, обозначив
Тогда дифференциальное уравнение крутильных колебаний можно записать
в виде
'-$-+«*-['■<*>+'■(-£)]
*-30-м»>+/.(-й-).
-ЙГ + «Р = В/(Ф. -of).
207
Интегрирование полученного уравнения можно выполнить асимптотическим
методом, разработанным Н. М. Крыловым и Н. Н. Боголюбовым [15, 81 ]. Интег-
рал нелинейного дифференциального уравнения в первом приближении можно
выразить равенством
ф = a cos ф,
где амплитуда а и фаза гр определяются линейными дифференциальными уравне-
ниями
dQ . . .
чг = гА1(а);
-^ = ft + eBj (a);
k = \/ —j частота незатухающих колебаний унифиляра.
Функции А1(а) и Bt (а) определяются интегралами вида
Ai(a)—-K—jr f(acosi|j; — a sin i|)) sin if dip;
6
2я
Bl ^ = "2яоГ [ f (a C0S ^' ~a Sin ^ C0S ^ ^
a
/(acos^; —asinif) получается путем подстановки в функцию / ( ф, ——- 1 угла
закручивания ф = a cos ф и его первой производной. Обозначим
2л
/ (a cos я|з; —a sin i|)) cos ij) df
0 afl^a)
**=2lE =^4Г(^Г
/ (a cos ф; —a sin i|)) sin ф d\j)
о
и отметим, что К# учитывает характер рассеяния энергии на трение за один цикл
колебаний. При отсутствии внешнего сопротивления величина Kr определяется
формой петли гистерезиса.
Производная от фазы колебаний по времени есть частота колебаний. Если
колебания изохронны, то частота постоянна, если же колебания анизохронны
то в каждый момент времени значения частоты различны. Обозначим через ft' ча-
стоту, соответствующую какому-либо мгновению или для какого-либо значения
амплитуды
к ~ dt •
Так как фаза колебаний ty и число совершенных колебаний г связаны эле-
ментарным соотношением
Ф = 2лг,
то частота ft' может быть выражена формулой
/ „ dz
к=2*чт-
208
Декремент колебаний есть логарифмическая производная от амплитуды по
времени, взятая с обратным знаком:
а d lna
0 =—ж-
Поэтому можно написать
Тогда
aft = — гАх (а);
к' = k + eB1 (a).
к' = k — К#&.
Таким образом, к' определяется не только количеством энергии, рассеивае-
мой в материале подвеса и окружающей среде за один цикл, но характером этого
рассеяния внутри цикла, учитываемым коэффициентом Kr. В случае пренебрежимо
малого внешнего сопротивления, коэффициент Kr учитывает только форму петли
гистерезиса. Следовательно, это уравнение подтверждает высказанное ранее заме-
чание о влиянии формы петли гистерезиса на анизохронность колебаний унифи-
ляра *.
Чтобы вычислить период колебаний унифиляра, запишем уравнение в виде
0 dz . , „ d In a
Интегрируя это выражение для целого числа колебаний z в предположение,
что время изменяется от нуля до t, а амплитуда — от начального значения а0 до
конечного а, получим
а '
откуда частота колебаний
2я.г + #/?1п-^-
а
ПРИМЕЧАНИЕ 12
ВЫВОД ФОРМУЛЫ ПЕРИОДА КОЛЕБАНИЙ ТЕЛА НА НИТЯНОМ ПОДВЕСЕ
Преобразуем подынтегральное выражение формулы (71'), для чего представим
его многочленом вида с„-гс1у^с2у2 + с3у3 + • • •, коэффициенты с0, сг, сг, с3, с4
которого найдем, приравнивая множители при одинаковых степенях у:
V q'3 — 4(q'2 — р3) y + 4(q'* — р* — l) у2 + 8у3 — 4у4
PV-(p2-r-l)Y + 2Y2-Y3
= с0 -Ь CiY + с2у°- + c3Y3 + c4Y4 +
* Отмеченная нами зависимость анизохронности колебаний от формы петли гисте-
резиса, очевидно, может быть использована для оценки соответствия эксперименту гипо-
тез упругого гистерезиса.
14 М. М. Гернет 2274 209
Возводя обе части равенства в квадрат, группируя в каждой из частей равен-
ства члены с одинаковыми степенями и приравнивая коэффициенты при разных
степенях, получаем
, _ 1' __С!1.
С°~-у- а '
ь = ci _ 4р4~ 5Р2д'г + я'г.
__ _Сг_ = 2>д'1 — ЮрУ' — 8рУ' — 5рУ' + 24ру' — 16р8 _
6з = ~ =-Т~Г7.-164р12 - I44piy! + 92рУ' - 7Ру' +
со 16рУ
+ 48рУ2 — 8рУ * + 7рУ' — 4рУ * — 21рУ' + 5?'')-
Используя найденные коэффициенты, представим подынтегральное выра-
жение формулы (7Г) в виде следующего бесконечного ряда:
У q'' — 4(g'2— p2) y + 4(<7'2—p2 —1)y2 + 8y:)-4y4
J/V — (р2 + 1) у + 2у2 — Y3 ~
= с„(1 +6iY + 62Y2 + b3y3 + ••■)■
Если ряд сходится, то, подставляя его в формулу (7Г), можно получить
выражение периода колебаний в виде бесконечного ряда:
я
о
Заменяя у и с0их значениями и вычисляя интеграл, получаем выражение (72),
ПРИМЕЧАНИЕ 13
ИССЛЕДОВАНИЕ СХОДИМОСТИ РЯДОВ И ОБЛАСТЬ ПРИМЕНЕНИЯ
ПОЛУЧЕННЫХ ФОРМУЛ ПЕРИОДА КОЛЕБАНИЙ
Рассмотрим выражение (71) для периода колебаний бифиляра, которое
можно переписать в иной форме:
■Фо
-I/" / С У4$г — 4ft2 sin2t|: + 4a,2 sin2^— sin4 т|г
Г 2g ,J |/4a2 _ sin 2 ф (/COS 1|) — COS ty0
210
В результате интегрирования этого выражения были получены формулы (72>
и (72')
причем /х и /2 есть бесконечные ряды.
Для установления сходимости рядов (72) и (72') воспользуемся выводам»
теории рядов.
1. Ряд, полученный интегрированием какой-либо подынтегральной функции
сходится, если сходится ряд, в который разложена эта функция; причем радиус
сходимости полученного ряда совпадает с радиусом сходимости исходного-
ряда.
2. Ряд, полученный в результате перемножения рядов сходится, если каждый.
из перемножаемых рядов является сходящимся.
Следовательно, для сходимости рядов (72) или (72') необходимо, чтобы каж-
дый из рядов, полученных при разложении трех корней, стоящих под интегралом
в формуле (71), сходился.
С уЪ//„„//„„„„„„„„, ^
^ШШШ2ЖШ(
077ZV77ZV77777777V777777777T,
О 7W/MW/WWWW/WA.
а)
6)
V
у//л-///////////да/ j
в)
Рис. 84. Область сходимости ряда
Представим корни в виде биноминального ряда
(1 + б)" = i+пб-"("271)б2+-• • + "("-1)-.uj(-^i+ila/+-.
Исследовав их сходимость, можно установить, что ряды, полученные при раз-
ложении выражений
1 1
jAcos \Jj — cos гр0 У 4а2—sin2i|>
сходятся при любых углах отклонения нитей if и любых соотношениях между дли-
ной нитей / и расстоянием 2а.
Сходимость ряда, полученного от разложения выражения
]fW — 4P2 sin2\p + 4a2 sin2i|>— sin4i|) ,
зависит от соотношения трех основных параметров: длины нитей /, расстояния
между ними 2а и радиуса инерции ги подвешенного тела.
Остановлено, что при малых значениях ■— и углах закручивания,
превышающих некоторое предельное значение %пред> РЯД расходится. На
рис. 84 по оси абсцисс отложено отношение и = —^-, а по оси ординат v =
= sin2 -й—• Область сходимости исследуемого ряда ограничена е трех сторон:
14*
211
снизу — осью абсцисс: сверху — прямой АВ, соответствующей предельному
значению угла закручивания бифиляра; слева — кривой OGC (или ее частью).
Заштрихованная область между осью ординат и кривой OGC является областью
расходимости ряда. Рис. 84, а относится к «длинному» подвесу, для которого
1^2а; рис. 84, б — к «короткому» подвесу с 1,15а < I < 2а, а рис. 84, в —
к «очень короткому» подвесу с I <[ 1,15а. Естественно, что такая классификация
•бифилярных подвесов несколько искусственна, но она представляется целесо-
образной.
Верхняя граница области сходимости (прямая АВ) на рис. 84, а отстоит от оси
абсцисс на расстоянии, равном единице; на рис. 84, б — на расстоянии, большем
1/3, а на рис. 84, в — на расстоянии, меньшем 1/3.
Крайняя правая точка области расходимости (G или Н для «очень короткого»
подвеса) имеет координаты
*-£-(у^"-'):
_ 4fl2 — /2
ин - 4^ ;
_ 1г
В табл. II приведены координаты некоторых точек кривой OGC для
«длинного» подвеса с I = 2а (рис. 84, а). Координаты точки G для такого под-
веса оказались равными uq = 0,172; vq = 0,414, что соответствует —— = 0,414
и Чопред --- 80° 00'.
Таблица II
и
0,000
0,025
0,050
0,075
0,100
0,125
0,150
0,172
ги
а
0,000
0,158
0,224
0,274
0,316
0,354
0,388
0,414
VHU0ICH
0,000
0,026
0,056
0,090
0,129
0,180
0,249
0,414
sin Ф°^
0,000
0,161
0,236
0,300
0,360
0,424
0,500
0,645
^опред
00° 00'
18° 32'
27° 20'
35° 00'
42° 00'
51° 10'
60° ОС
80° 00'
vaepx
0,000
0,948
0,894
0,834
0,771
0,694
0,601
0,414
В табл. III [44] приведены координаты точек G к Н для различных подвесов,
а также даны значения отношения—=- и предельных амплитуд ф0лд;д> соответ-
ствующие этим точкам.
212
Если для какого-либо бифилярного подвеса основные параметры и принятая
амплитуда колебаний будут таковы, что ряд станет расходящимся, то на основании
изложенного надлежит сделать вывод о непригодности формулы (72) или (72') и о
необходимости поисков иного математического выражения этой величины. Но, так
как при экспериментальном определении моментов инерции применяют «длинные»
подвесы с I ^> 2а, область расходимости которых мала и предельные амплитуды
колебаний во много раз больше обычно выбираемых значений, то возможность рас-
ходимости ряда (72) или (72') крайне невелика.
Таблица III
а
"Г
0,01
0,1
0,2
0,4
0,5
0,6
0,8
0,865
1,00
1,50
2,0
5,0
VG
0,500
0,495
0,482
0,439
0,414
0,390
0,347
0,333
—
—
—
"G
0,0001
0,01
0,036
0,122
0,172
0,220
0,306
0,333
—
—
.—
^опред
90° 00'
89° 20'
88° 00'
83° 00'
80° 00'
77° 20'
72° 10'
70° 20'
60° 00'
39° 00'
29° 00'
11° 26'
а
0,01
0,1
0,19
0,35
0,414
0,480
0,553
0,578
0,613
0,667
0,696
0,704
"я
—
—
—
—
—
—
0,333
0,250
0,111
0,0625
0,01
"я
—
—
—
—
—
—
0,333
0,375
0,445
0,484
0,495
ПРИМЕЧАНИЕ 14
МАЛОЕ ПЕРЕМЕЩЕНИЕ ЦЕНТРА ТЯЖЕСТИ ТЕЛА ПО ОСИ Ог
ПРИ ПРОИЗВОЛЬНОМ РАСПОЛОЖЕНИИ НИТЕЙ
Положение тела определяем аппликатой гс и тремя углами (<р — углом за-
кручивания мультифиляра, ■& — углом прецессии и \|> — углом маятниковых
колебаний). Так как на тело наложены три связи * и два ограничения на перемеще-
ние его центра тяжести (хс= Ус~ 0), то за обобщенную координату примем
угол ф. Уравнения связей напишем в виде условия, что длина трех нитей неиз-
менна.
Координаты точек прикрепления нитей к телу в системе, связанной с те-
лом, следующие:
I n С
с
м1
м2
м3
0
*1
х2
х3
0
г/i
2/2
Уз
0
—h
—h
-h
* Если нитей в подвесе более трех, то остальные нити являются лишними связями.
213
Направляющие косинусы подвижной системы относительно неподвижной
системы хОуг после малого перемещения тела приближенно будут выражаться
следующим образом:
I Ц I
х cos а2 = 1 cos а2 = г|)Ф — <р cos а3 = ft + фф
у cos Рх = ф cos P2 = 1 cos рз = §ф — \|з
г cos Yt = О cos Y2 = ty cos Y3 = 1
Координаты точки крепления й-той нити к телу найдем по формулам преобра-
зования координат
xk = xc -f- xk cos aj -j- yk cos a2 + zk cos a3;
</*, = Ус + xk cos pj + yk cos P2 + zk cos p3;
г*. = zc + */s cos Yi' + Ук cos Y2 + 4 cos Yr..
Подставляя значение направляющих косинусов, получаем
xkt = xk + Ук № — ф) — л (^ + Ш
Укх = **ч> + % — Л С°ф — W;
z*, = zc - xfl - у$ - h-
Координаты точек Nk прикрепления нитей к штативу получим из условия, что
k-я нить лежит в вертикальной плоскости, проходящей через ось:
cos aft ,
: хь — тггт- I = xk + sk cos aft;
Умк = Ук ■
cosya
cospft
' = У* + sk cos Pa;
HO
поэтому
У
cosy*
(/A cos ak — хЛ cos pA = 0,
Напишем выражение длины &-й нити
Nk xk
Возведя в квадрат, получим
4 = [ук (ч><> — ф) — а (» + ч>ф) — sa cos «*]2 +
+ I ХкЦ> + Ук~ ЦФф — i|0 — ^-(x^ + sftcosa*) ] +
+ (гс - *fttf + УкУ + If-
214
Допустим, что гс, й и ф есть малые второго порядка малости.
В уравнении для sk удержим члены с точностью до малых второго порядка
включительно и после алгебраических преобразований получим следующие
уравнения
2
/.COSC*! \„ / , COS р\ \ г\
6 \ cosYi / \ cos Yt / 21 ^
г„ — Л
cos a,
cos у.2
. cos a3
cosys
х3
и COs Рг \ , 2 „
h — — и~ I Ф = —р ф2;
cos Y2 / 2'
Решая полученную систему относительно г„ найдем, что
= _ф2_ r\Fl + r2f2 + fo 3
гс 2/ ' Ft + F2 + Fs '
где Fj, F8 и fз — миноры определителя системы:
Fx
h™^.-* hSS^h..
cos Ya
cos a3 ,
h - — x3 h
cos Y3
cosy2
cosp3
cos уз
-У2
-Уз
. cos a,
h ~— x,
cos Yi
, cos 6,
h ^~yi
, cos a3 ,
h —-—- — xs h
cos Yi
COSfr)
cos Y3
F* =
cos Y3
cos p\
■Уз
, cos a, ,
h —x, h
cos Yi cos Yi
cos a,
C0SY2
cosp2
COSY2
-Ух
-Уг
Введем обозначение
D =
APi + fa + fa
Fx + F* + Fs »
тогда аппликату центра тяжести тела на мультифиляре запишем в виде
Ф2 ,-.
ПРИМЕЧАНИЕ 15
ПРЕОБРАЗОВАНИЕ ФОРМУЛЫ ПЕРИОДА МАЛЫХ КОЛЕБАНИЙ
МУЛЬТИФИЛЯРА
При эксперименте иногда целесообразнее положение точек прикрепления
нитей к телу определять полярными координатами (рис. 85). Обозначим расстоя-
ния точек прикрепления от вертикали, проходящей через центр тяжести тела, че-
рез гл, гг и г3, а углы между радиусами гх и г2 или тх и г3 соответственно через 92
или 93. Тогда декартовы координаты точек прикрепления нитей к телу можно
записать формулами
хл = ri\ Hi = 0; х-2 ~ Гг cos вг;
у2 — r2 sin 02;
х3 -- r3 cos 9; у3 = — r3 sin Q3.
Используя эти значения, найдем
Fi = -Vs sin (9., + e„);
fa = /V;, sin 93;
f3 = ^i^ sin92.
Рис. 85. Точки прикрепле-
ния нитей в полярных коор-
динатах
D = ггггг3
Подставляя их в равенство, получим
— r1 sin (92 4 9К) + г-2 sin 03 + ^з s'n 82
■ rxr3 sin (G2 + 63) 4- rxr3 sin 93 4- ггг2 sin 02'
Через три точки всегда можно провести окружность. Определим расстояние
от центра этой окружности Ох до линии действия веса (точки О на рис. 85) и угол 0
между гг и г. Обозначая радиус окружности через R и применяя теорему косину-
сов, напишем
R2
г? 4
R*
2 , 2
* = 4 + г1
Решив эту систему, найдем
г — 2rj/-cos 9;
— 2/у cos (02 — 0);
— 2r3/-cos(G3-f-6).
1г.
г* —г2
rx cos 0 — г2 cos (0, — 0)
чН - *г) + г\ (г\ - rjj) cos 92 + л3 (r22 - r\) cos 93
- г2 (г? - 'з) sin 92 + 'з (г2 - r\) sin 0з
1
cos 9 :
Так как R
R2-
■ г' = ггггг3 -
V 1 + tg2 6
— 2/у cos 9, то подставляя 2л и cos 9, найдем, что
—Г] sin (Qs 4- 92) + ra sin 83 + ^8 sin 9г
-/Vs sin (03 4 6г) + 4Г2 sin 9г + м^з sin 03"
216
Сопоставим это выражение со значением D. Для случая, когда нити верти-
кальны, либо наклонны, но центр тяжести тела лежит в плоскости прикрепления
нитей к телу,
D = Р} — г2,
где R — радиус окружности, проходящей через точки приклепления нитей к телу;
г — расстояние центра этой окружности от вертикали, проходящей через
центр масс.
Подставляя значение D в формулу (77), получим известную формулу периода
колебаний тела на мультифиляре.
ПРИМЕЧАНИЕ 16
УЧЕТ ИЗГИБНОЙ ЖЕСТКОСТИ НИТЕЙ ПОДВЕСА
Рассмотрим подвес, обладающий малой жесткостью (например, подвес на
длинных тонких проволоках). При крутильных колебаниях тела на нитяном
подвесе нити претерпевают деформации изгиба и кручения. Упругая линия под-
веса зависит от способа закрепления его концов. Пусть верхний конец защемлен,
а нижний соединен шарнирно и нагружен значительной вертикальной силой V
и некоторой горизонтальной силой Н. Начало коорди-
нат примем в верхней точке подвеса, а оси координат
направим так, как показано на рис.86. Кривизна—;—г
упругой линии и изгибающий момент М (х^ в сечении
х1 связаны зависимостью
1 М (хг)
P(*i) EJu3a '
где Е — модуль упругости; Ju33 — момент инерции
сечения.
В случае больших прогибов, кривизну плоской
кривой определяют по формуле
J.SL
йх\
[' + (£)']"■
Для малых прогибов можно приближенно принять
1 _ <РУ1
Рис. 86. Схема нагру-
жения упругого под-
P(*i)
dx\
При определении моментов инерции на нитяных подвесах угол i]) отклонения
нити от вертикали обычно мал и поэтому для радиуса кривизны упругой липни
может быть использована вторая из приведенных формул.
Изгибающий момент в сечении хх выражается формулой
М (Xj) = Н (I — Xi) — V ({/щах — Ух).
2274
2i:
Дифференциальное уравнение упругой линии запишем в виде
Е/изг -^р- = И {I - *i) - V (ylmax - в1).
Введем обозначения
_К „2. Я ■ «2
. — «j, — Pit
тогда уравнение примет вид
dx\
Интегрируя при граничных условиях
xi == '> </i=i/imax> *i = 0; "j~ = 0>
найдем уравнение упругой линии
п2
Ух — Ух max 9
«1
1 е«1 С— xi) _i_ e—«1 С—*0
J —xx —
a, e«.« + «,-<».'
При дсх = 0 должно быть у1 = 0, поэтому
_ Р1 , 1 *
Лтах-^-U--
Для больших значений аргумента гиперболический тангенс асимптотически
приближается к единице, поэтому для больших aj, т. е. при значительной про-
дольной силе V и большой длине проволоки /, можно приближенно принять
Ух шах '■
или
^"-"гЧ1"^)'
Для идеальной, абсолютно неупругой нити между горизонтальным смещением
нижней точки у1тах, длиной 1и, силами V и Н существовало бы соотношение
_ н i
Ух max — ~у~ '«•
Сопоставление двух последних равенств показывает, что поворот тела вокруг
оси упругого подвеса длиной /, защемленного вверху и шарнирно присоединен-
ного к телу внизу, равнозначно с поворотом тела, подвешенного на идеальных
нитях длиной /ы.
218
ПРИМЕЧАНИЕ /7
ВЫВОД УРАВНЕНИЯ ДВИЖЕНИЯ БИФИЛЯРА
В ПЛОСКОСТИ НИТЕЙ
Движение тела в плоскости подвеса при двух наложенных связях есть дви-
жение с одной степенью свободы. Примем за обобщенную координату абсциссу
центра тяжести х. Две другие координаты тела, аппликата г и угол поворота тела
вокруг оси Ст) — ф могут быть найдены из двух уравнений связей вида
Координаты точек
Nx N3 С Мг ЛГ2
х —с +с х х — Ь cos ф + ft sin ф х + b cos ф + ft sin ф
г — (i-fft) —(/-+- ft) —г — z — b sin ф — ft cos ф —г + 6 sin ф — ft cos ф,
где
/= V&2 — (с — б)2.
Тогда уравнения связей будут следующими:
нить jW4Afa
s2 = (х + 6 cos ф + ft sin ф — с)2 + (—г + Ь sin ф — ft cos ф + / + ft)2;
нить Af1A/1
s2 = (х — b cos ф + ft sin ф + с)2 + (—г — 6 sin ф — ft cos ф + J + ft)2.
Совместное решение этих уравнений позволит найти г и ф в функции обобщен-
ной координаты. Однако эти зависимости достаточно сложны, чтобы их можно
было использовать для написания уравнения движения.
Ограничимся рассмотрением малых колебаний. При малых колебаниях
уравнения наложенных связей, ввиду малости координат, принимают вид
/2 + (с-6)2= [(х+Дф)-(с-&)]2+ [_г+6ф+ Л2;
/2 + (с - б)2 = [(х + top) + (с - б)]2 + [-г - 6ф + I]2.
Решая совместно два уравнения (с точностью до малых второго порядка),
найдем
_ с — Ь
ф_ b(h + t) — hc *'
ЬЧ а
2 2[Ы — к(с — Ь)\* *-
Следовательно, аппликата центра тяжести есть бесконечно малая величина
второго порядка.
Для получения уравнения движения тела воспользуемся теорией малых
колебаний.
Вычислим кинетическую энергию тела
E-JH^ + Jjf.. «,*=,? + *
так как г есть малая величина второго порядка, то
219
Тогда
c — b
М=Ф= bl-h(c-b)
2 "*" 2 [Ы — А (с -б)]2
Потенциальная энергия тела
mgbH
П = — mgz ■■
2[bl — h{c— fe)]2
Вычисляя частные производные от кинетической и потенциальной энергий
и подставляя их в уравнение Лагранжа, получим дифференциальное уравнение
малых колебаний тела в плоскости нитей
{./„ (с — б)2 + т (Ы — h (с — 6) ]2} х + mgbHx = 0.
ПРИМЕЧАНИЕ 18
СОСТАВЛЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
ДВИЖЕНИЯ СИСТЕМЫ
В рассматриваемом случае система имеет одну степень свободы, а потому ее
движение описывается одним уравнением Лагранжа:
dt\dqj dq W-
Если обобщенная координата q есть г, то обобщенной скоростью q является
скорость груза q — г = v. Кинетическая энергия системы выражается формулой
(/ + /,) <*\ Jtf>\ (Р + р) У2
Е = g + —2~+ 2g '
где «>! = — и ш2 = —.
Поэтому
г? ' /| ' «Г | 2
Приведенный момент инерции прибора равен
Обозначим
'1
J Приб = •< 1 4" J 2 2" '
г2
«^ + J приб — J
J' _ Gnp
r\ 8 *
220
где —— приведенная масса системы (без груза). Тогда кинетическая энергия
системы
,, Р + Опр fa
с = ■ —=-.
g 2
Найдем члены левой части уравнения Лагранжа
дЕ . дЕ _ P + Gnp d ( дЕ\_ P + Gnp ■■
dz ' дг S dt \ dz } g
dv
где Z = ^-.
Вычислим обобщенную силу системы. Если сообщить грузу Р перемещение
dz, то элементарная работа обобщенной силы определится так:
0 Мтр Мтр
Qdz = Pdz + -£- zdz ± dz ~ dz,
1 i"\ '%
откуда
о Мтр. Мтр
Q = Р + -f- г - 1 -
I н
Обозначим
Мщр Мтр%
~~- ?тр,
причем Fmp можно назвать приведенной силой трения. Тогда
/
Q = P+-^z-Fmp.
Подставляя значения всех найденных членов уравнения Лагранжа, получим
S ' I
ПРИМЕЧАНИЕ 19
ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ
ДВИЖЕНИЯ СИСТЕМЫ
Проинтегрируем дифференциальное уравнение
P + GnP- р
Z -у Z — Г — tmp.
Обозначим
ЦР + Gnp) ' P + G„p 8'
тогда уравнение примет вид z — 62г == с, или, введя новую переменную и = г +
с ....
+ -Tj- и учтя, что и = z, придем к уравнению
И — ЬЧ - О,
221
Общим интегралом этого уравнения является
поэтому
и = Вхеы + B2e~bt,
г = -~ + В1е»1 + В,е- .
Полагая В1 + Въ = С\ и Вг — 52 — С2> получим
г = — -^- + Сх ch 6* + С2 sh &f.
Для определения постоянных интегрирования найдем г:
г = C-fi sh М + C2b ch 6/.
Используем начальные данные: при t — 0 г = г0, г = 0. Тогда
откуда
Ci = z0 -f- -p"; с2 = о.
Общий интеграл дифференциального уравнения примет вид
-i + (*° + i)^bt-
Если за время t груз Р опустится на расстояние h, то его конечное положение
определится координатой г = га + ft;
откуда
г„ + Л = —£- + («о + -£-) ch 6/,
ПРИМЕЧАНИЕ 20
УРАВНЕНИЕ ДВИЖЕНИЯ ПРИ ОДНОВРЕМЕННОМ
ДЕЙСТВИИ ДВУХ ГРУЗОВ
Примем за обобщенную координату положение груза Рп на оси Ог, направлен-
ной вертикально вниз, с началом отсчета в точке О схода нити с блока. Подсчитаем
кинетическую энергию системы
где f — скорость грузов.
222
Обобщенную силу системы выразим равенством
л_т> о Mmpi Мтр* Mmp3
Г1 '2 '3
Введем обозначения
г2 ?
1 1
Jnpu6 = J\ -Ь J2 ~2~ + ^3 ~2 »
"лр = (^ + Jnpuo) ~2~ •
г\
Назовем приведенной силой трения величину
MmPl Мтр2 МтРз
гтр = — 1 —
г»
Тогда уравнение Лагранжа примет вид
Рц + Рл + Grip "„pip р
— z — fn-\- гл — гтр-
S
Из этого уравнения можно заключить, что система движется равноускоренно
с ускорением
д= Рп-Рл-Fmp
Рп + Рл + Gap ё
и расстояние h, пройденное грузами, связано со временем t соотношением
и Рп-Рл—Fmp gt2
Рп + Рл + Gnp' 2 •
ПРИМЕЧАНИЕ 21
РЕШЕНИЕ ЗАДАЧИ ОБ ЭКСПЕРИМЕНТАЛЬНОМ ОПРЕДЕЛЕНИИ
ЦЕНТРОБЕЖНЫХ МОМЕНТОВ
И ЭЛЛИПСОИДА ИНЕРЦИИ В ОБЩЕМ ВИДЕ
Тензор инерции определяется шестью составляющими, поэтому необходимо
провести шесть опытов.
Построим прямоугольную систему координат хОуг и проведем шесть осей,
проходящих через начало координат и составляющих с координатными осями
углыа1; р\, ylt ol2, p2 Ye. Определив какими-либо из существующих экспе-
риментальных методов моменты инерции испытуемого тела относительно этих
осей, отложим вдоль каждой из них в произвольном масштабе отрезок -у=,
у J
где / — момент инерции тела относительно оси. Координаты концов отрезков
будут иметь следующие выражения:
- cos аъ Ут, = —=- cos р\, гх = — cos Yi
VIZ " " Vb r" l Vh
223
Хп -
VJ,
y^T7Tcosh'
Vh
cos y2
4 ■
- cos ae,
У в
= cos p6,
1
гв = —--_- cos Ye-
Концы этих отрезков расположатся на поверхности, называемой эллипсоидом
инерции и определяемой уравнением
Jxx2 -f Jyy2 + Jzz2 — 2Jy. гуг — 2JZ. xzx — 2JX. yxy = 1,
где x, у и г — текущие координаты;
4- = S m (У2 !- га); Уу = £лг (г2 [- х2); Л = 2 « (*2 + у*) -
моменты инерции тела относительно координатных осей;
Jy-z = 2 тУг> Jz-x — S ™гх и ^*- = 2 ""У —
центробежные моменты инерции относительно тех же осей.
Если вместо текущих координат х, у и г подставим в уравнение эллипсоида
последовательно координаты каждой из шести лежащих на нем точек, то уравне-
ние это удовлетворится и мы получим шесть уравнений:
JA + Jyy\ + JA~2Jy. гУЪ-Ыг. хг1хХ ~ 2Jx. уХ\Ух = 1'
JXX2 + J'у\)ч + Jzz2 ~ 2J у. гУ-2г2 2^г. хг2х2 ~ 2^' х. ух2У2 = *•
Jx4 + ]Л + JA ~2Jy. гУьЧ -Ыг. кЧЧ -2Jx. АУЪ = 1 •
Система шести линейных уравнений с шестью неизвестными \JX, Jy, Jz, Jy z,
Jz.x и Jx.y имеет следующее решение:
D
A.
I — ^1 • i — D*
J - Ds
■^--д-. Jz.x--fi-. Jx.y--fi-.
D — определитель, составленный из коэффициентов при неизвестных:
х\ у\ г\ — 2^ — 2гххх — 2ххух
D-
х2 У2 г2 2^2г2 2г2*2 — 2х2У2
4 у\ 4 - 2у&ч - 2чч - 2х&у&
Dk — детерминант, получаемый при замене элементов k-то столбца определи-
теля D правыми частями уравнений, в данном случае единицами.
Таким образом:
D, =
„2 Л
1 у\ г\ — 2ухгх — 2гЛ — 2ххух
„2 ,2
1 у\ z\ —2y2z2 — 2г2х2 — 2*2г/2
1 у\ 4 ~2Убгб — 2z6x6 —2ЧУб
224
Df =
,2 „2
h У\
-2У\г\
■ 2г^хг 1
Xcf Ijn Z<) JtljnZn ZZftXn \
ХЪ Уй гб 2(/6г6 2г6*6 1
Следовательно, все составляющие тензора инерции (Jx, Jy, Jг, Jy г, Угл:,
•/л:, у) могут быть определены по шести наблюдениям. Зная составляющие
тензора инерции, составим так называемое вековое уравнение
J х J рл Jx. и <lz.x
Jx.
Jz.
•> и •> р
ly.z
iy-г
= 0,
из которого и определим три главных момента инерции'/^ х, }гл 2, ]гл, я. Главные
направления найдем из уравнений
(Jx — J гл. к) cos аел_ к — Jx± у cos %л. к — Jz, х cos угл.к = 0;
— Jx. у cos агл. к + (Jy — JeJt. к) cos %л, к — Jу. г cos угл.к = 0;
— /г. * COS агл. к — Jy.z COS Рг.,. к -I- (Jz — J гл. к) COS ^.л. к = 0.
Подставляя вместо & последовательно 1, 2 и 3, вычислим девять направляю-
щих косинусов cos оселл, ..., cos угл.3, определяющих три главных направления.
ПРИ МЕЧ А НИЕ 22
ВЫВОД РАБОЧИХ ФОРМУЛ ДЛЯ ЭКСПЕРИМЕНТАЛЬНОГО ОПРЕДЕЛЕНИЯ
ЦЕНТРОБЕЖНОГО МОМЕНТА ИНЕРЦИИ
Чтобы упростить методику, изложенную в примечании 21, определим моменты
инерции тела относительно осей, направленных по осям координат и по бис-
сектрисам углов, образованных положительными направлениями осей коорди-
нат; причем координатные оси можно направить произвольно, но так, чтобы
система была прямоугольной [37]. Подсчитаем значения направляющих косину-
сов всех осей и составим таблицу.
Ось коор-
динат
X
У
г
Номер оси, относительно которой измерен момент инерции
1
1
0
0
2
0
1
0
3
0
0
1
4
0
V2
2
V2
2
5
2
0
V2
2
6
1/2
2
1/2
2
0
\5 М. М. Гернет 3274
225
Тогда координаты концов отложенных отрезков равны
Xl = Ti7> л = 0;
*2 =
х3 =
х4 =
*5 =
0;
0;
0;
]
УгГь
\
]/2/в'
Уг-
VT, '
Уз = 0;
У* =
^2/4'
Ув = 0;
if=; у«:
V2J,'
г, = 0;
г2 = 0;
1
i_
1
/27;;
гв = 0.
При выбранном направлении осей /*, J у и /г определяются непосредственно
из наблюдений:
/i = /,t> J%—Jу\ J^ — Jz-
Поэтому вычислим центробежные моменты инерции. Знаменатель D, общий
для всех равенств, после подстановки значений xlt yx г« принимает вид
D =
1
Jl
0
0
0
1
2/5
1
2/„
0
1
J*
0
1
2/4
0
1
2/e
0
0
1
/з
1
2/4
1
2J5
0
0
0
0
1
•/4
0
0
0
0
0
0
1
/5
0
0
0
0
0
0
1
/в
Все элементы, стоящие по одну сторону главной диагонали определителя,
равны нулю, поэтому определитель равен произведению элементов, стоящих на
главной диагонали:
1
D
J \J г' з-м/б/в
Определитель £>5, необходимей для вычисления центробежного моменха
инерции Jz.x, принимает вид
226
£>5 =
1
А
0
0
0
1
27 5
1
2/«
1)
1
0
1
2J4
0
1
2Je
1)
0
1
■А»
1
2^4
1
2Д
0
0
0
0
1
и
0
0
1
1
1
1
1
1
0
0
0
0
0
1
J*
Этот определитель можно привести к определителю третьего порядка. Для
этого разложим его по элементам шестого столбца. Полученный определитель
пятого порядка разложим по элементам чертвертого столбца; детерминант четвер-
того порядка разложим по элементам второго столбца. В результате этих операций
найдем
D,
1
1
J*
1
1
0
2jr "Js
или
J^iJг \ Ji
2Л
hY
2J
Все члены, заключенные в скобки, приводим к общему знаменателю
1 Jl + Ja-2Jb
D.
J Ъ<14J 2 JlJi&Jb
Для определения центробежного момента инерции относительно осей г и
х разделим полученное значение на D.
, J*+Ji 1
••г. х — ■ й Jb>
где индекс 1 соответствует оси Ох, индекс 3 — оси Ог, а индекс 5 —• оси, лежа-
щей в плоскости хОг под углом 45° к осям Ох и Ог.
Аналогично
Jy.z-
Jz + h
-Jt,
где Jj означает момент инерции относительно оси, составляющей 45° с осями Оу
и Oz; J 2 — момент инерции относительно оси Оу.
Для третьего центробежного момента инерции получим
Jx. у
Ji+Jt
-Jo,
15*
227
где Jt — момент инерции относительно оси, составляющей с осями Ох и Оу
углы 45°.
В результате получена теорема: центробежный момент инерции относительно
каких-либо осей равен полусумме моментов инерции относительно этих осей без
момента инерции относительно биссектрисы угла, составленного положительными
направлениями этих осей. Это соотношение можно получить н непосредственно
из известных формул геометрии масс.
Таким образом, для экспериментального определения составляющих тензора
инерции достаточно определить моменты инерции относительно трех координат-
ных осей и трех биссектрис углов между положительными направлениями осей
координат. Составляющие тензора инерции могут быть вычислены по форму-
лам (101). Точность результатов равна точности экспериментальных методов опре-
деления моментов инерции.
♦ ♦♦
♦♦♦
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Абрагам Г. Сборник элементарных опытов по физике. Ч. 1 и 2. Пер.
с фр. Под ред. проф. Вейнберга. Одесса, Изд-во Матезис, 1909—1910 г.
2. А в д е е в Б. А. Техника определения механических свойств материалов.
М., Машгиз, 1958.
3. А в т у х о в М. А. и др. Руководство к лабораторным работам по курсу
теоретической механики. Л., изд-во Высшего военно-морского инженерного
ордена Ленина училища им. Ф. Э. Дзержинского, 1959.
4. А г а л е ц к и й П. М. Способ обнаружения и исключения систематиче-
ских погрешностей маятниковой аппаратуры. Труды ВНИИМ. Вып. II (71),
1950.
5. Ал ьшиц Я. И. Исследование упругих деформаций редукторов привода
режущих цепей с целью возможности их учета при расчете деталей. Ста-
лине, изд. Донецкого индустриального института; 1953.
6. Артоболевский И. И. Определение моментов инерции опытным
путем. М., Изд. МХТИ, 1931.
7. Артоболевский С. И. и др. Лабораторные работы по теории меха-
низмов и машин. М., «Советская наука», 1958.
8. Бабаков И. М. Теория колебаний. М., «Наука», 1965.
9. Бабицкий В. И. Колебание маятника с инерционным подвесом, находя-
щимся в вибрирующей полости. Автореферат диссертации на соискание
ученой степени канд. техн. наук. М., 1964.
10. Б а р б а ш и н Е. А., Табуева В. А. О колебаниях маятника при на-
личии сухого трения. «Известия вузов. Математика», 1959, № 5.
11. Б а у л и н М. И. Определение приведенного момента инерции вращающихся
масс автомобиля и трактора методом затухающего вращения маховика.
Сборник научно-технич. работ. Московский институт механизации и электри-
фикации сельского хозяйства. М., «Советская наука», 1952.
12. Б е р к о в и ч Д. М. Уравновешивание роторов методом опытного определе-
ния их моментов инерции. Сборник докладов. Изд. Львовского политехниче-
ского института, 1957, 2, № 1.
13. Б е р к о в и ч Д. М. Уравновешивание роторов методом опытного определе-
ния моментов инерции. Автореферат диссертации на соискание ученой сте-
пени канд. техн. наук. Львов, 1956.
14. Б е с ш а п о в П. С. О динамической балансировке методом эксперимен-
тального определения центробежных моментов инерции. ВНИИЗ, сообщения
и рефераты. Вып. 4, М., Хлебоиздат, 1956.
15. Блехман И. И. Вращение неуравновешенного ротора, обусловленное
колебаниями его оси. «Известия АН СССР. Отделение технических наук».
1954. № 8.
16. Боголюбов Н. Н. и М и т р о п о л ь с к и й Ю. А. Асимптотические
методы в теории нелинейных колебаний. М., Физматгиз, 1958.
17. Будаев И. С. Теория маятника. Академия наук. Спб. 1853.
18. Б у л а н ж е Ю. Д. О влиянии сокачания при наблюдениях с маятниками.
«Геодезист», 1940, № 12. Труды Сейсмического института. Вып. 107, 1941.
19. Васильев Ю. П. К вопросу определения момента инерции гребного винта
по методу бифилярного подвеса. «Судостроение», 1938, № 3.
20. В е д р о в B.C. Присоединенные массы плоских пластинок. «Техника воз-
душного флота», 1932, № 4.
229
21. Веселый ё. С. Определение моментов инерции и крутильной жесткости
деталей силовой передачи автомобиля. «Известия вузов. Машиностроение»,
1959, № 3.
22. В е т ч и н к и н В. П. Метод экспериментального определения моментов
инерции твердых тел при помощи многонитяного подвеса. «Артиллерийский
журнал», 1920, № 1—2.
23. В е т ч и н к и н В. П. Маятниковые динамометры для измерения средних
величин переменных нагрузок. Труды ЦАГИ. Вып. 74, 1931.
24. Ветчинкин В. П., Поляхов Н. Н. Теория и расчет воздушного
гребного винта. М., Машгиз, 1940.
25. Ветчинкин В. П. иЧенцов Н. Г. Плоский маятник о двух степенях
свободы и определение при помощи его высоты центра тяжести и момента
инерции твердого тела. Труды ЦАГИ. Вып. 3, 1923.
26. В о е в о д и н Ю. М. Определение приведенного момента инерции методом
выбега. «Вестник машиностроения», 1955, № 9.
27. В о л о х о в А. Н. Опытное определение моментов инерции. Труды ЦАГИ.
Вып. 285, 1936.
28. В о л о х о в А. Н. Опытное определение моментов инерции. Труды ЦАГИ.
Вып. 301, 1937.
29. В о л ь ф И. И. Исследование сбрасывающего аппарата жнеи Диринг.
Сб. «Теория, конструкция и производство с.-х. машин», Т. 1. М., Сельхоз-
гиз, 1935.
30. В о р о в и ц к и й А. Н. Об одном способе определения моментов инерции
твердых тел. «Вестник инженеров и техников», 1937, № 11.
31. Г е в о н д я н Т. А., Павлов Е. М. Динамический метод определения
температурного коэффициента модуля упругости тонких материалов. «За-
водская лаборатория», 1956, № 12.
32. ГернетМ. М., Ратобыльский В. Ф. К теории многонитяного
подвеса. Труды МТИПП. Изд. МТИПП. 1969.
33. Г е р н е т М. М. Метод совместного определения моментов инерции и поло-
жения центра тяжести тел. «Вестник инженеров и техников», 1934, № 11.
34. Г е р н е т М. М. Определение моментов инерции твердых тел ударом. Сбор-
ник работ. М., Изд. МТИХП, 1936.
35. Г е р н е т М. М. Метод определения приведенных длин и моментов инерции
физических маятников. «Вестник инженеров и техников», 1941, № 3.
36. Гер нет М. М. Уравновешивание вращающихся масс молотковых мельниц.
Труды ВНИИЗ. Вып. 16. М., Загоиздат, 1949.
37. Г е р н е т М. М. Экспериментальное определение центробежных моментов
инерции и динамическая балансировка без балансировочной машины. Труды
семинара по ТММ АН СССР, т. IX. Вып. 33. М., «Машиностроение»,
1950.
38. Г е р н е т М. М. Геометрия масс рабочих органов машин для измельчения
зерна. Труды МТИПП, т. II. М., Пищепромиздат, 1952.
39. Гер нет М. М. Курс теоретической механики. М., «Высшая школа», 1965.
40. Г е р н е т М. М. Уравновешивание машин пищевых производств. Сб. «Ос-
новы расчета и конструирования машин и аппаратов пищевых производств».
Изд. 2-е М., Машгиз, 1968.
41. Г е р н е т М. М., Ж У P а в л е в В. Ф. Экспериментальное исследование
динамической неуравновешенности валков методом определения моментов
инерции. Сообщения и рефераты ВНИИЗ. Вып. 2, 1951.
42. Г е р н е т М. М., К о р о б и ц и н А. А. Влияние трения на колебание си-
стем с одной степенью свободы. Сб. «Теория механизмов и машин». Изд-во
Харьковского университета. 1969, № 8.
43. Г е р н е т М. М., П о л о з о в Б. И. Экспериментальное изучение некоторых
физических констант злаков, необходимое для конструирования зерноочисти-
тельных и размольных машин. «Пищевое машиностроение», 1956, № 5.
44. Г е р н е т М. М., Ратобыльский В. Ф. К теории бифилярного под-
веса. Труды V конференции по основным проблемам теории машин и меха-
низмов. М., «Наука», 1969.
45. Г е р н е т М. М., Тихонов В. Н. Экспериментальное определение мо-
ментов инерции человеческого тела и его верхних и нижних конечностей.
«Теория и практика физической культуры», 1967, №11.
46. Г и д а с п о в С. Д. Некоторые исследования в области точных весов. Труды
Всесоюзного научно-исследовательского института метрологии им. Д. И. Мен-
делеева. Вып. 19/35/. М.—Л., Изд. ВНИИМ, 1939.
47. Г л у х Б. А. Экспериментальное определение момента инерции и центра
тяжести автомобиля. «Известия НАТИ», 1934, № 2.
48. Г л у х Б. А., В р и с к и н М. И. и В о р о б ь е в А. Экспериментальное
определение момента инерции автомашины. «Вестник металлопромышлен-
ности», 1940, № 1.
49. Г л у ш к о в Г. С. Применение моментов высоких порядков. «Вестник инже-
неров и техников», 1933, № 12.
50. Г о л о в н и н Г. Я. Лабораторные работы по теоретической механике.
М., «Высшая школа», 1967.
51. Гольдберг А. И. Определение моментов инерции тел. Уральский поли-
технический институт, руководство к лабораторным занятиям по физике.
Работа № 9. Свердловск, 1953.
52. Г о р с к и й Б. Е. Регулирование антифрикционного механизма балансиро-
вочного станка. «Известия вузов. Технология легкой промышленности»
1963, № 1 (31).
53. Г р а м б е р г А. Технические измерения при испытании машин и контроле
производственных процессов. М., Макиз, 1927.
54. Д а в и д е н к о в Н. Н. О рассеянии энергии при вибрациях. «Журнал
технической физики». Т. VIII. Вып. 6, 1938.
55. Дроздов Ф. В. Детали приборов. М., Оборонгиз, 1948.
56. Е в г е н ь е в а Л. Я. Исследование изменений движений у гимнастов при
овладении подъемами на брусьях. Автореферат диссертации на соискание
ученой степени канд. техн. наук. М., 1951.
57. Ж е л и г о в с к и й В. А. Прибор для нахождения моментов инерции тел.
«Вестник металлопромышленности», 1924, № 4—6.
58. Ж е л и г о в с к и й А. В. Экспериментальное определение моментов инер-
ции сечений. «Вестник инженеров и техников», 1948, № 6.
59. Ж У к о в с к и й Н. Е. О влиянии колебаний штатива на время качания
маятника. Поли. собр. соч. Т. 1, 1937.
60. Ж У к о в с к и й Н. Е. О движении маятника с трением в точке привеса.
Поли. собр. соч. Т. I, 1937.
61. Жуковский Н. Е. Теоретическая механика. Ч. III. Дополнительные
статьи. Под ред. В. П. Ветчинкина и Н. Г. Ченцова, М., ГТИ, 1925.
62. Жуковский Н. Е. О новом аппарате для определения моментов инерции
тел. Поли, собран, соч. Т. I, 1937.
63. Зельцерман И. М. Описание установок и машин лаборатории приклад-
ной механики. М., Изд. Военной академии механизации и моторизации
РККА, 1933.
64. И ш л и н с к и й А. Ю. О проскальзывании в области контакта при трении
качения. «Известия АН СССР. Отделение технических наук», 1956, № 6.
65. Каневский М. М., Г о п п Ю. А. К вопросу об определении моментов
инерции твердых тел по методу качений. «Вестник инженеров и техников»,
1934, № 2.
66. Капица П. Л. Динамическая устойчивость маятника при колеблющейся
точке подвеса. Журнал экспериментальной и теоретической физики.
Вып. 5, 1951.
67. К а п и ц а П. Л. Маятник с вибрирующим подвесом. «Успехи физических
наук», т. XLIV, вып. I, 1951.
68. Касьянов В. Т., Ф е д о р о в В. К. Определение момента инерции
машин по методу маятника. «Вестник электропромышленности», 1942,
№ 6.
69. Каталог-справочник лабораторных приборов и оборудования. Вып. 20.
Д., «Техучпособие», 1948.
231
70. К и п ш а к б а е в И. К. Исследование влияния приведенного момента инер-
ции машинно-тракторного агрегата и степени нечувствительности регулятора
на показатели работы дизеля Д-35 при неустановившемся характере нагрузки.
Автореферат диссертации на соискание ученой степени канд. техн. наук М.,
1953.
71. К и р н о с Д. П. О некоторых частных случаях вынужденного движения
маятника. Изд. Сейсмического института. Вып. 79/2 1938.
72. К н я з е в А. Ф. Нахождение моментов инерции тел. «Весгник инженеров
и техников», 1937, № 9.
73. К о к о ш Г. Д., Смирнова Н. А. Приложение метода крутильного маят-
ника к исследованию коромысел точных весов. Труды ВНИИМ. Вып. 19(79).
М., Машгиз, 1952.
74. К о р о б и ц и н А. А. Влияние острия призмы на колебания маятника
и коромысла весов. Труды МТИПП. Вып. XVI. М., Пищепромиздат,
1960.
75. К о р о б и ц и н А. А. К вопросу о влиянии закругления призмы на коле-
бания маятника. «Астрономический журнал», т. 38, вып. I, M., 1961.
76. К о р о б и ц и н А. А. Влияние опоры шип-подшипник на колебания физи-
ческого маятника. «Вестник машиностроения», т. 43, 1963, № 12.
77. К о р о б и ц и н А. А. К вопросу о проскальзывании призматических опор
маятников и весов. «Известия вузов. Приборостроение», т. VI, 1963.
№ 6.
78. КоробицинА. А. Исследование колебаний маятника и коромысла весов.
Автореферат диссертации на соискание ученой степени канд. техн. наук,
М., 1965.
79. К о р о б и ц и*н А. А. Определение моментов инерции и физический маят-
ник. Труды МТИПП. Изд. МТ и ПП. 1969.
80. К о р о б о ч к и н И. В. Колебания весоизмерительных приборов. М.,
Машгиз, 1947.
81. Крылов Н. М. и Б о г о л ю б о в Н. Н. Введение в нелинейную меха-
нику. М., изд-во АН УССР, 1937.
82. Кук Г. А. Молочные машины. М.—Л., Машгиз, 1950.
83. К у к Г. А., Селиванов Н. И. К изучению приводного механизма боль-
ших сепараторов. Труды Ленингр. ин-та инженеров молочной пром., т. III,
Л., Ленснабтехиздат, 1934.
84. К у л е б а к и н B.C. Испытания электромашин и трансформаторов.
Изд. 2-е, М.—Л., ОНТИ, 1935.
85. Л а п т е в С. А., К р е с т о в н и к о в Г. А. Определение коэффициента
вращающихся масс автомобиля. «Автомобильная и тракторная промышлен-
ность», 1951, № 7.
86. Л е н д е р Ф. Ф. Прибор для определения моментов инерции. Изд. Пути-
ловского завода, Спб., 1911.
87. Лен дер Ф. Ф. Доклад Главного Конструктора арткомитета Ф. Ф. Лендера
о критических скоростях колебаний прибора для определения моментов инер-
ции снарядов, проектированного им на Путиловском заводе. Пб. Изд. Артко-
митета, 1920.
88. Линии к. Момент. Техническая энциклопедия. Т. XIII, 1941.
89. Л о й ц я н с к и й Л. Г., Лурье А. И. Курс теоретической механики.
Т. II. М., Гостеоретиздат, 1955.
90. Л о й ц я н с к и й Л. Г., Лурье А. И. Теоретическая механика. Т. III.
М.—Л., ОНТИ, 1934.
91. Лоренц Г. Техническая механика. М.—Л., ОНТИ, 1936.
92. Л у к ь я н о в Г. Н. Сопротивление воздуха на шар и на цилиндр. Труды
физического отделения. Общества любителей естествознания, т. XVII. Вып. I.
М., 1905.
93. Л у р ь е А. И. Аналитическая механика. М., Физматгиз, 1961.
94. Малышев А. Бифилярный подвес. Техническая энциклопедия. Изд. 2-е,
т. 2, 1939.
232
95. М а р к е в и ч М. Г. О некоторых вопросах геометрии масс. «Инженерно-
физический журнал», т. 2, 1959, № 8.
96. Мах Э. Механика. Историко-критический очерк ее развития. Спб. «Про-
свещение», 1909.
97. Машиностроение. Энциклопедический справочник. Т. I, кн. I. Инженерные
расчеты в машиностроении. М., Машгиз, 1947.
98. Маятник. Техническая энциклопедия. Спб. «Просвещение», 1910, т. 6.
99. М е л ь н и к о в С. В. К методике экспериментального определения момен-
тов инерции тел на бифилярном подвесе. Записки Ленинградского сельско-
хозяйственного института. Т. 93, Л., 1963.
100. Менделеев Д. И. О логарифмическом декременте качаний. Сочинения.
Т. VII. М., изд-во АН СССР, 1946.
101. Менделеев Д. И. О сопротивлении жидкостей. Сочинения. Т. VII.
М., изд-во АН СССР, 1946.
102. Менделеев Д. И. О колебании весов. Сочинения. Т. VII. М., изд-во
АН СССР, 1946.
103. Менделеев Д. И. Опытное исследование колебания весов и возобновле-
ние прототипа или основной образцовой русской меры массы в 1893—1898 гг.
Сочинения. Т. VII. М., изд-во АН СССР, 1946.
104. Менделеев Д. И. Подготовка к определению абсолютного напряжения
тяжести в Главной палате мер и весов. Т. VIII. М., изд-во АН СССР, 1946.
105. Менделеев Д. И. Возобновление прототипов или основных образцов
русских мер веса и длины в 1893—1989 гг. Т. XXII. М., изд-во АНСССР, 1950.
106. Мещерский И. В. Сборник задач по теоретической механике. Изд. 31.
М., «Наука», 1967.
107. Мещерский И. В. Кабинет теоретической механики Санкт-Петербург-
ского Политехнического института императора Петра Великого. Спб.
тип. «Печатный труд», 1911.
108. М и д г а л А. Б. Сверхтекучесть и моменты инерции ядер. «Журнал экспе-
риментальной и теоретической физики», т. 37. Вып. I (7). М., июль 1959.
109. М и л а е в Ю. А. Упрощенный способ определения моментов инерции.
«Вестник инж. и техников», 1940, № 4.
110. М и н а к о в А. П. Основы теории наматывания и сматывания нити «Тек-
стильная промышл.» 1944, № 10—12.
111. Мунькин В. Б. Исследование и разработка методов и средств автомати-
зации кинопоказа. Автореферат диссертации на соискание ученой степени
канд. тенх. наук. М., 1966.
112. Мясников И. С. Моменты инерции масс. Харьков. «Кубуч», 1939.
113. Н е ч а е в В. К- К вопросу об экспериментальном определении моментов
инерции тел вращения. Известия Томского ордена Трудового Красного
Знамени политехнического института им. Кирова. Т. 68. Вып. I, 1951.
114. Никитин Н. А., Завельский Ф. С. Рационализация метода из-
мерения момента инерции. Труды Всесоюзного заочного политехнического
института. Вып. I, 1952.
115. Н и к и т ю к А. И. К подсчету моментов инерции самолетов. Труды ЦАГИ.
Вып. 94, 1931.
116. Николаи Е. Л. Лекции по теоретической механике. Ч. 3.] Вып. I.
М., ОНТИ, 1926.
117. Николаи Е. Л. Теоретическая механика. Ч. II М., Физматгиз, 1958.
118. Н о в и к о в Ю. И. К расчету упругих элементов подвеса. Сборник мате-
риалов конференции по итогам научно-исследовательских работ за 1962 г.
Вып. III. Красноярск, Изд. Сибирского технологического института, 1963.
119. Н о в и к о в Ю. И. Определение моментов инерции методом полифиляра
при больших амплитудах колебаний его. Сборник материалов конференции
по итогам научно-исслед. работ за 1962 г. Вып. III. Изд. Сибирского техно-
логического института, 1963.
120. О ч а п о в с к и й Б. Л. Гравиметрический маятник малой массы. Ученые
записки Ленинградского университета № 210. Вып. 9. Л., 1956.
121. Павлов М. П. Техника измерения скоростей и времени. М., Машгиз, 1950.
233
122. П а н о в к о Я. Г. Основы прикладной теории упругих колебаний. М., Маш-
гиз, 1957.
123. Победоносцев Ю. А. Экспериментальное определение моментов инер-
ции самолета. Труды Всесоюзной конференции по аэродинамике. Изд. ЦАГИ
1931.
124. Победоносцев Ю. А. Экспериментальное определение моментов
инерции самолета. Труды ЦАГИ Вып. 201, 1935.
125. Полозов Б. И. Определение моментов инерции зерна. М., Изд. МТИПП,
1942.
126. П о п к о Ю. М., Князева Л. А. Руководство к практикуму по физике.
М., Учпедгиз, 1959.
127. Прибор для определения моментов инерции твердых тел. Л., «Техучпо-
собие», 1940.
128. Путилов К- А. Курс физики. Т. I. M., Гостеоретиздат, 1952.
129. П ч е л и н В. А. Новый метод измерения механических свойств тканей и
волокон. «Легкая промышленность», 1952, № 1.
130. Р а й х А. Л. Теория и методика экспериментального определения враща-
тельных производных. Труды ЦАГИ. Вып. 419, М., 1939.
131. Р а т о б ы л ь с к и й В. Ф. Неизохронность крутильных колебаний и экс-
периментальное определение моментов инерции. Автореферат диссертации
на соискание ученой степени канд. техн. наук. М., 1959.
132. Ратобыльский В. Ф. Анизохронность крутильных колебаний и экс-
периментальное определение моментов инерции методом унифиляра. М.,
Изд. ВЗИПП, 1959.
133. Рожанский В. Н. К теории маятникового склерометра. «Журнал
технической физики», т. XIX, вып. 9, 1949.
134. Розе Н. В. Динамика твердого тела. Л., Кубуч, 1932.
135. Сабанеев А. А. О моментах инерции твердого тела. Доклады. XIII на-
учная конференция. Л., Изд. ЛИСИ, 1955.
136. Савелова А. А. Экспериментальное определение моментов инерции
машинных частей при помощи крутильного маятника. Труды Краснозна-
менного Московского механико-машиностроительного института им. Бау-
мана. Вып. 59/3. М., Машгиз, 1940.
137. Савельев В. В. Определение моментов инерции самолета около трех
осей. «Техника воздушного флота», 1939, № 7—8.
138. Савельев В. В. Определение массовых моментов и радиусов инерции
сечений отъемной части крыла и линии центров тяжести отсеков крыла
по размаху. Труды ЦАГИ. Вып. 452, М., 1939.
139. С а в и ч И. И. Об определении сопротивления воздуха движению маятника.
Бюллетень петербургской академии наук, 1866, № 9.
140. Слуцкий А. Я- Влияние сухого трения на колебания в весах и маятни-
ках. Доклады 2-й Всесоюзной конференции по трению. Т. III, 1949.
141. Соколов А. П. Физический практикум. М., Учпедгиз, 1946.
142. Сомов П. Момент инерции. Техническая энциклопедия. Т. 6, Спб., «Про-
свещение», 1910.
143. Сомов П. О. Основания теоретической механики. Спб., «Просвещение»,
1904.
144. Строганов А. Г. Центровка самолета. М., Оборонгиз, 1940.
145. Су р и н Е. И. Определение моментов инерции твердых тел. «Техучпосо-
бие», 1939.
146. Т а р г С. М. Краткий курс теоретической механики. М., «Наука»,
1967.
147. Тимирязев А. К- Кинетическая теория газов. М.( Учпедгиз, 1956.
148. Тимошенко СП. Колебания в инженерном деле. Изд. 3-е. М,, Физ-
матгиз, 1959.
149. Т у л и н С. К- Маховой момент в бурении нефтяных скважин. «Энерге-
тический бюллетень», 1947, № 1
150. Турбин Б. И. Теоретическая механика. М., Сельхозгиз, 1959.
т
151. Ту р бин Б. Й. Определение моментов инерции тел способом качения.
Труды Московского института механизации и электрификации социалисти-
ческого сельского хозяйства. М., 1939.
152. Турбин Б. И. Экспериментальное определение приведенных моментов
инерции сельскохозяйственных машин. Сборник трудов по земледельческой
механике, т. 2. Сельхозгиз, 1954.
153. Турбин Б. И. К определению моментов инерции деталей и узлов сельско-
хозяйственных машин. «Сельхозмашина», 1957, № 6.
154. Т у р к и н В. В. Влияние смещения центра тяжести тела на точность
определения момента инерции методом бифилярного подвеса. «Известия Том-
ского ордена Трудового Красного Знамени политехнического института
им. С. М. Кирова», т. 96, Томск, 1961.
155. Т у р к и н В. В. Влияние деформации нитей на точность метода бифиляр-
ного подвеса. «Известия вузов. Физика», Томск, 1961, № 4.
156. У р н о в К- В. Некоторые вопросы динамики электропривода. «Электри-
чество», 1951, № 10.
157. Физический практикум МВТУ. Часть I. M., Изд. МВТУ, 1929.
158. Фриш С. Э., Т и м о р е в а А. В. Курс общей физики. Т. I. M., Учпед-
гиз, 1956.
159. X а н т а д з е 3. А. Экспериментальное определение момента инерции вра-
щающихся тел и коэффициента трения в подшипниках. Труды Грузинского
сельскохозяйственного института, т. XXXI, 1949.
160. Хантадзе 3. А. Экспериментальное определение момента инерции вра-
щающихся тел и коэффициента трения в подшипниках. «Сельхозмашина»,
1950, № 8.
161. Хвольсон О. Д. Курс физики. В пяти томах. Берлин, Госиздат
РСФСР, 1923.
162. X о х л о в Ю. К- О моменте инерции системы многих частиц. «Журнал
экспериментальной и теоретической физики», т. 36, Вып. I, 1959.
163. Хиус А. А., Грунауэр А. А. Статическая балансировка вращаю-
щихся звеньев машин методом маятниковых колебаний. «Научные доклады
высшей школы. Машиностроение и приборостроение», 1958, № 2.
164. Цирлин Ю. А. и др. Лабораторный практикум по физике, часть I. Ме-
ханика и молекулярная физика. Харьковский ордена Трудового Красного
Знамени сельскохозяйственный институт им. В. В. Докучаева. Харь-
ков, 1959.
165. Чесалов А. В. Испытания опытных самолетов. Труды ЦАГИ. Вып. 358.
М., 1938.
166. Ч и л а е в Ю. А. Упрощенный способ определения моментов инерции.
«Вестник инженеров и техников», 1940, № 4.
167. ЧиликинН. М. Практические занятия по механике. Изд. Комиссаров-
ского технического училища. М., 1912.
168. Чуковский. Влияние колебания штатива на период качания маят-
ника. М., 1883.
169. Шитиков Б. В. Динамическая балансировка роторов турбин при по-
стройке и ремонте. Изд. БТП з-да им. Сталина, Москва, 1948.
170. Шубович С. И. К вопросу об опытном определении моментов инерции
движущихся масс машин. Известия Томского политехнического института
им. Кирова. Т. 68. Вып. I, 1951.
171. Э д е л ь ш т е й н Б. В. Руководство к лабораторным работам по курсу
ТММ. М., Изд. МАИ, 1967.
172. Эдельштейн Б. В., Куровской Ф. М. Руководство к выполне-
нию лабораторной работы: «Определение моментов инерции опытным путем».
Московский ордена Ленина энергетический институт. М., Изд. МЭИ, 1952.
173. Юденич В. В. Лабораторные работы по теории механизмов и машин.
М., «Высшая школа», 1962.
174. Ю д и н В. А. Геометрия масс. М., Изд. Военно-инженерной академии РККА,
1939.
235
175. Яблонский А. А. Курс теоретической механики. Ч. II, М., «Высшая
школа», 1964.
176. Яковлев К- П. Унифилярный подвес. Техническая энциклопедия.
Т. 24. М., Изд-ко «Советская энциклопедия», 1934.
177. Яковлев К- П. Физический практикум. М., ОГИЗ, 1943.
178. Я Ц е н к о Н. Н. Распределение подрессоренных масс грузовых автомоби-
лей. «Автомобильная промышленность», 1959, № 10.
179. Airy G. В. On the vibrations of a free Pendulum in aval differing littl
from a straight line. Phil. Magaz. Vol. 2, 1851.
180. Ap p e 1 1 P. Trate de Mecanique ratiounelle. 3-е edit. Paris, 1911.
181. A t w о о d D. On the rectilinear motion and rotation of bodies. London,
1784.
182. Autenrieth—Ensslin. Technische Mechanik. Berlin. 1922.
183. Baraz. Der Pendelregulator mit beweglichem Drehpunkt. VDI, 1894.
184. В a r b i e r J. С Balance magnetiquc de torsion. Journ. de Physique et de
Radium., v. 15, 1954, N 12.
185. В a r i f f i H. F. Nomogram to determine parallel axis moment of inertia.
Product Eng., 1949, vol. 20, N 7.
186. В a r i f f i H. F. Nomogram for polar moment of inertia by suspension.
Product Eng., 1947, vol. 18, N 7.
187. Bartunek P. F. Some interesting cases of vibrating systems. Amer.
J. Phys. 1956, vol. 24, N 5.
188. Baumann H. Ermittlung der Massentragheitsmomente durch Schwing-
ungsversuch. VDI. Bd. 80. 1936, N 45.
189. Baumann H. Die Ermittelung der Massentragheitsmomente durch
Schwingungsversuche. Organ Fortschritte Eisenbahnwesen. Bd. 73, 1936, N6.
190. Berkley L. H. How to determine WR2 bv running a simple test. Product
Eng. vol. 13, 1942, N 12. Discussion, v. 14," 1943, N 5, 7.
191. В e r n о u 1 1 i D. Theoremata de oscillationibus corporum filo flexili con-
nexorum et catenae verticaliter suspensae. Com. Ac. Sc. Petr. 1738, t. 6.
192. Bernoulli D. Commentatio physico-mechanica specialiter de motibus
reciprocis comppsitis, multifariis nondum exploratis, qui in Pendulis bimem-
bribur facilius observari possunt, in confirmationem principii sui de coexi-
stentia vibrationum simplicium. Novi Comm. Acad. Petrop. t. 19, 1774.
193. Bernoulli D. Vera determinatio centri oscillationis in corporibus
qualibuscunque filo flexili suspensis, ejusque ab regula communi discrepan-
tia. Novi Comm. Acad. Petrop, t. 18, 1773.
194. Bernoulli J. Recherches mecaniques sur la question de la meilleure
maniere de trouver l'heure en mer etc., 1747.
195. В e s s e 1 F. W. Untersuchungen fiber die Lange des emfachen Secunden-
pendels. Abh. der Berl. Ak. 1826.
196. В i net. Memoire sur la theorie des axes conjugues et des moments d'iner-
tie des corps. Journal de l'Ec. polyt. v. IX, 1813.
197. В о h n e n b e r g e r J. Astronomic Tubingen, 1811.
198. Borda, Cassini. Experiences pour connaitre la longueur du pendulc,
qui bat les secondes a Paris. Base du systeme metrique decimal, v. Ill, Paris,
1810.
199. Bouasse H. Cours de Mecanique rationnele et experimental. Paris,
1915.
200. Bouasse H. Pendule, spiral, diapason. Paris LibrairieCh. Delagrave, 1920.
201. Bouton I. Airplane Pitching Moment of Inertia. Journal of Aeronautical
Sciences, v. 18, 1951, N 2.
202. Bowdith N. On the motion of a Pendulum suspended from two points.
Memoirs of the american Academy, v. 3, 1815.
203. Brassine E. Balance d'oscillation employee pour le calcul des moments
d'inertie. Comptes rendus, v. 95, 1882.
204. Braune, Fischer. Leber den Schwerpunkt des menschlichen K.or-
pers. Abhandl d. Konigl. Sachs. Ak. d. Wissensch. (math-physik. Klasse).
Bd. XV, Leipzig, 1889.
236
205. В u r r i i 1 L. and В о g g i s A. Electronics in naval architecture. Ship-
building and Shipping Record, 1951, vol. 78, N 16.
206. Cabannes H. Coitrs de mecanique generale. Paris, 1962.
207. Cassi. e W. R. An Accurate Method of measuring moments of inertia.
Physical Society Proceeding, v. 21, 1909.
208. С a u с h у A. Sur les moments d'inertie. Oeuvres completes, tome VII, 1889.
209. Cavendish. Phil. Trans, vol. 83.
210. С 1 a i r a u t A. Examen des differentes oscillations qu'un corps suspendu
par un fil peut faire iorsqu'on lui donne une impulsion quelconque. Mem.
de l'Acad., 1735.
211. С 1 a i r a u t A. Des centres d'oscillation dans des milieux resistants. Mem.
de l'Acad. 1738.
212. Clausnitzer. Bestimmung des Tragbeitsmoment von Rototionskor-
pern. Elektrotechnische Zeitschrift Bd. 71, 1950.
213. Closterhalfen. Einfache Bestimmung von Tragheitsmomenten. Ma-
schinenbau Gastaltung, Bd. Ill, 1924.
214. С о 1 d i n g E. W. Use of Grassot fluxmeter as a quantity meter; its appli-
cation to the determination of the moment of inertia of a small directcurrent
armature. Journal of the Institution of Electrical Engineers, vol. 76, 1935.
215. Collection de memoires relatifs a la Physique. Publies par la Societe francaise
de physique, tome IV. Memoires sur le Pendule. Paris, 1889.
216. С о r n u, Bailie. Etude de la resistance de l'air dans la balance de tor-
sion. Comptes rendus, v. 86, 1878.
217. Coulomb Ch. A. Recherches theoriques et experimentales sur la Force
de torsion et sur 1'elasticite des fils de metal. Paris, 1784.
218. С г а с е у М. Additional — mass effect of plates as determined by experi-
ments. NACA TN 780, 1940.
219. Cramerius I. Bestimmung des Tragheitsmomentes durch Pendel-
schwingungen. Zeitschr. f. d. phys. und chem. Unterricht., 1892.
220. Cranz С Lehrbuch der Ballistik Bd. 4, Leipzig Teubner, 1912—1918.
221. Crede С. Е. Determining Moment of Inertia. Machine Design., vol. 20,
1948, N 8.
222. Culmann. Qrapischen Statik. Bd. 1, Zurich, 1875.
223. Cyorgyi G. Acta Physica Academial Scientiarum Hungarical, t. 4,
1954.
224. Den i zot A. Ober ein Pendelproblem von Euler. Zeitschrift fur Math,
und Phys. Bd. 46, 1901.
225. D e p r e z M. Sur les lois du frottement. Comptes Rendus, v. 99, 1884.
226. D e г г i m a n W. H. On an Oscillating Table for Determining Moments
of Inertia. The London, Edinburgh and Dublin Philosophical Magazine and
Journal of Science, vol. V, 1903, N 30.
227. Descartes R. Les lettres sur le centre d'oscillation ou d'agitation au
P. Mersenne et a M. Cavendish. Oeuvres de R. Descartes. Ed. Cousin, t. 9.
228. Desdouits. Applications de la methode rationnele aux etudes dynamo-
metriques. Annales des ponts et chaussees, v. II.
229. D о n a t A. Technique Reglage des Appareils horaires systeme balancier
spiral, 1936.
230. D о г n E. Die Reduction der Siemens'schen Eiheit auf absolutes Mass. An.
der Physik und Chemie. Neue Folge, Band XVII, 1882, N 13.
231. Dragnea O. Momente de inertie. Bucuresti, Editura Technica, 1956.
232. D u b а г 1 e D. La theorie du centre d'oscillation et le principe de la con-
servation des forces vives. Revue des questions Scientifiques, v. 16, 1955.
233. Eckert W. I. The moment of inertia of the Moon determined from its
orbital motion. Mantles Earth and Terrests Planets. iLondon—N. Iork—
Sydney. 1967.
234. Edmunds H. Friction Losses in Rotating Parts. Machine design, 1940.
235. Ein elektrisches Verfahren zur Bestimmung des Tragheitsmoments eines Gleich-
stromanker (nach Kapp). Elektrotechnik und Maschinenbau, Bd. 50, 1932, N 17.
237
236. Е 1 ge r G. Pendelschwingmaschine zur Schwerpunkts—und Tragheitsmoment—
Ermittlung. Technics, 1955, N 19, 20.
237. E 1 1 e t t D. How to determine mass moments of inertia for irregular parts.
Product Eng. 1957, v. 28, N 5.
238. E 1 s a s s e r. Ober die Aufnahme von Bremskurven mit dem Oszillografen.
Sicmena—Zeitschrift. 1930, № 3.
239. Ensslin M. Die Traghetskrafte einer Schubstange. Dinglers Polytech-
nisches Journal. Bd. 322, 1907, № 39.
240. E r d с 1 у i. Zeitschrift fur angewandte Math, und Mech. Bd. 14, 1934,
Bd. 16, 1936.
241. Euler L. De oscillationibus fili flexilis quoteunque pondusculis onusti.
Com. Ac. sc. Peter, t. 8, 1741.
242. Euler L. Theoria motus corporum solidorum, 1765.
243. Euler L. Scientia Navalis, 1749.
244. Euler L. De motu oscillatorio penduli circa axem cylindricum piano
horizontali incumbentum. Nova Acta Ac. Petropolitanae, t. VI, 1788.
245. Euler L. De motu Penduli circa axem cylindricum, fulcro datae figurae
incumbentum, mobilis. Remota frictione. Dissertatio prima. Acta Academiae
Scientiarum Petropolitanae, t. IV, 1777.
De motu Penduli circa axem cylindricum fulcro datae figurae incumbentum,
mobilis Habita frictionis rationae. Dissertatio altera, t. IV, 1777.
246. Ferracane V. Studio di un dispositivo per la determiriazione dei momenti
d'inerzia dei vilivoli. Atti di Guidonia, 1940, N 33—34.
247. Fiegehen E. A chart for calculating WR2. Mech. World and Eng. Rec.
vol. 104, 1938, N 2710.
248. Foersterl. Methode de determination experimental d'un moment d'iner-
tie d'une dynamo dans un cas particuler. Revue Cen. de l'Electricite, 1924, N 5
249. Fop pi A. Vorlesungen iiber technische Mechanick. Bd. 1—6, Leipzig,
1921—1925.
250. Fordyce G. Account of a new Pendulum. Phil. Trans., v. 84, 1793.
251. F 6 t t i n g e r H. Ober die Fliissigkeitsreibung umlaufender Scheiben,
Zylinder und Zellenkorper. Zeitschr. fi'jrang. Math, und Mech., t. 17,1937, N 6.
252. Fry e CM. The pendulum. Horolog J. 1956, vol. 98, N 1174, 1175.
253. Fuss N. Determinate motuum Penduli compositi bifili ex primis. Mecha-
nicae principtis petita. Nova Acta Acad. Petrop., 1785, 1, H.
254. Fuss N. Additiones analyticae ad Diss de motu Penduli bifili. Nova Acta
Acad. Petrop. 1 H. 1785.
255. Galilei G. Dialogo intorno ai due massimi sistemi del mondo, Tolemaico
e Copernicano. Ed. 1. Florenzia, 1632.
256. Galilei G. Discorsi e Dimostrazioni matematiche intorno a due nuove
Scienze attenenti alia Meccanica ed ai movimenti locali. Leiden, 1638.
257. Gates S. The determination of the moment of inertia of aeroplanes. Lon-
don. R. and M. 1932, N 1415.
258. Gauss С Ober ein neues Verfahren zur Bestimmung der Horizontalin-
tensitat des Erdmagnetismus. 1837.
259. Gauss С Zur Bestimmung der Konstanten des Bifllarmagnetometers.
Werke V. 1839.
260. Giebel K. Das Pendel. Halle, 1951.
261. Goupilliere H. Memoire sur une theorie nouvelle de la Geometrie
des masses. Journal de l'Ec. polyt. t. XXI, 1858.
262. G г а с е у W. The Experimental Determination of the Moments of Inertia
of Airplanes by a Simplified Compound—Pendulum Method. NAGA, TN
N 1629, 1948.
263. G r a s h о f. Theoretische Maschinenlehre, 1888.
264. Green M. Measurement of the Moments of inertia of Full Scale Airplanes.
NACA, TN N 265.
265. Greenhill. NACA R. and M. N 238, 1915.
266. G r i m s e h 1 E. Ein Tragheitsmomentenapparat und ein Pendel mit direkt
messbarer Pendellange. Zeitschr. f. d. Phys. und Chem. Unterricht. 1905.
238
267. G u t m a n n F. Messung des massentragheitsmomentes von radern und
wellen in getrtiben. VDI. Bd. 83. 1939. N 1235—36.
268. О v D Tali'ku kereszt-^ebzcU-k tohctetlen-egi nvami'tekanak szamitasa.
Ve'ye te f-'J ^ze !e, 1957, t. 7. N 9 -10.
209. i! a a $ J. ft С h a I e a t R Prrblerncs rip the' rie ge'enile des oscillations
i't r'e chron netrie. Paris. 1P60.
270. H я m m e r 1 H. Ein A-parat zit l.ehre von Trrgheitsmoment. Zeitschr.
f. rl. Phys. und chem. Unterricht. 1909.
271. H ;i г t I H. Apparat zur expcrimentellen Behanrilung der Lehre vom
Tr;'gh-'itbmomente. Zeitschr. f. d. phys. und chem. Unterricht. 1891,
1K.2.
272. Hartley S., Sou be A., Mar veil P., Miller. The experi-
mental determination of the moments of inertia of airplanes. NACA T. R.
N 467, 1933.
273. H e 1 m h о I t z. Vorlesungen fiber mathematischen Physik, Leipzig, 1889.
274. Hohmann W. Cber Massentragheitsmomente. Maschinenkonstrukteur.
Bd. 64, 1931. N 12—13.
275. H о р р е R. Oscillationen eines Bifilarpendels. Arch, de Grunert, 70, 1884.
276. H о г t H. Auswuchtfragen. Maschinenbau Gastalting, 1923.
277. H о г t W. Technische Schwingungslehre. Berlin, 1922.
278. H у g h e s G. The trifilar pendulum and its application to the experimental
determination of moments of inertia. Paper Amer. Soc. Mech. Eng. 1957,
N SA—51.
279. Hunt I. T. Determing radius of gyration. Machin. Design, vol. 22, 1950,
N 8.
280. Herre O. Beobachten und Messen. VDI, 1917.
281. Hirsch P. Zeits. fur ang. Math, und Mech. Bd. 10, 1930.
282. H u у g e n s. Horologium oscillatorium sive de motu pendulorumad horlogia
aptato. Paris, 1673.
283. I а с к w i t z. Die unendlich kleinen Schwingungen eines aus zwei Massen-
punkten bestehenden Pendels (im Raume). Progr. des Posener Gymnasiums.
1882.
284. I a n к u V. Elementarni odvozeni momentu setrvacnosti nekterych teles
pravidelnych. Gasopis pro pestovany math, a fysiki, Praga, 1900—1901.
285. I s e 1 у М. Influence du ressort de suspension sur la duree des oscillations
du pendule. Bull, de Neuchatel, v. 5, 1859—1861.
286. Ivory J. On rolling Pendulum. Phil. Magaz. v. 58, 1821.
287. К а р р G. Journal of the Institution of Electrical. Engineers, 1909.
288. К a t e r H. An account of experiments for determining the length of the
Pendulum vibrating seconds in the latitude of London. Phil. Trans., vol. 108,
1818.
289. Ker Wilson W. Practical solution of torsional vibration problems.
London, vol. 1, 1940, vol. II, 1941.
290. К i r s с h b a u m H. W. Estimation of moments of inertia of airplanes
from design data NACA, N 575, 1936.
291. К п a u e r F. und Schulze E. Neue Methoden zur Bestimmung des
Tragheitsmoments elektrischen Maschinen. Electrotechnik und Maschinenbau,
1923, Electrotechnische Zeitschrift, 1922.
292. Kohlrausch F. Lehrbuch der praktischen Physik, Drezden, 1896.
293. Kohlrausch F. Ueber den Polabstand den Inductions- und Temperatur-
Coefficient emes Magnetes und flber die Bestimmung von Tragheitsmoment
durch Bifilarsuspension. Gottingere Nachrichten, 1883, N 13.
294. Kohlrausch F. Absolute Messungen mittels bifilarer Aufhangung
insbesondere zwei Methoden zur Bestimmung der erdmagnetischen Horison-
talintensitat ohne Zeitmessung. An. der Physik und Chemie. Band XVII,
1882, N 13.
295. К о h n M. Experimented Bestimmung des Tragheitsmomentes rotirender
Afaschinentheile. jjer Civilingenieur, Leipzig, 1890.
239
296. К о 1 1 i g E. Apparat zur Bestimmung der Tragheitsmomente von beliebig
geformten Massen in bessug auf verschiedene Drehungsahsen. Zeitachr. f. d.
phys. und chem. Unterricht, 1912.
297. К о p p e M. Das Tragheitsmoment. Zeitschr. f. d. phys. und chem. Untericht,
1891, 1892.
298. Kramerius I. Ueber H. Hartl's Apparat zur Bestimmung von Trag-
heitsmomenten. Zeitschr. f. d. phys. und chem. Unterricht, 1892.
299. Kreichgauer D. Zur Bestimmung von Tragheitsmomenten durch
Schwingungsversuche. Ann. den Physik und Chemie. Neue Folge. Bd. XXV,
1885.
300. К r i s h n a i у a r N. С Experimental determination of the inertia of
a sphere vjbrating in a liquid. Phil. Magaz. vol. 46, 1923.
301. Lamb H. Dynamics. Cambrige, 1927.
302. La Place. Sur la langueur du pendule a seconde. Conaissence des temps
pour 1820. Paris, 1818.
303. Laurent H. Traite de Mecanique Rationnelle Paris, 1870.
304. Lazarescu A. Consideratiuni cu privire la determinarea experimentala
a momentelor de inertie mecanice si, i geometrice (polare). Metalurgia si Con-
structia de Masini, 1955, N 10.
305. Lechner A. Experimentelle Bestimmung der Tragheitsmomente von
Laufradern. Dinglers Polytechnisches Journal, 1913.
306. Lecornu L. Cours de mecanique, t. II. Paris, 1915.
307. L e h r E. Schwingungstechnik. Berlin, 1930.
308. L e h r E. Die Sehwingungstechnischen Eigenschaften der Kraftwagens und
ihre messtechnische Ermittlung. VDI, Bd 78, 1934, N 10.
309. Levi Civita a Amaldi. Lezioni di meccanica razionale,
vol. II, parte II. Bologna, 1927.
310. L u k e n s A. F. How to determine WR2? Power Plant Eng. v. 4, 1942, N 8.
311. Lummer und Schafer M. Physikalische Zeitschrift. 1906, S. 269.
312. Luxenberg M. Ueber das Zweigliedrige Pendel. Z. fur Math, und Phys.
Bd. 28, 1883.
313. M а с - С u 1 1 a g h. On the rotation of a solid body round a fixed point.
The collected works. 1880.
314. M а с m i 1 1 a n W. Dynamics of rigid bodies. New Iork and London 1936.
315. Maggi G. Sulla teoria del pendolo. Giornale di Mathem., Napolit. 38,
1900—1901.
316. Maine A. Moment of inertia torsional oscillation. Electronic Engineering,
v. 25, 1953, N 302.
317. M a i r a n J. J. d'Ortous de: Recherches sur la pesanteur des corps et de
l'acceleration. Paris, 1747.
318. Martin O. Bestimmung des Tragheitsmoments von Ringkorpern Bauzei-
tung, 1954, Bd. 72, N 23.
319. M a t z W. Bestimmung der Schwungmomente von Schwungradern. Maschi-
nenbau Gestaltung. Bd. 2, N 14, 1923.
320. Mersenne P. Propose aux savants le probleme du centre d'agitation ou
de balancement du penbule. 1646. Cogitata physico-mathematica. Parisiis, 1644.
321. Meyer O. Ueber den Einfluss der Luft auf Pendelschwingungen. Poggen-
dorff's Ann., t. 125, 1865.
322. Meyer O. Pendelbeobachtungen. Poggendorff's Ann., t. 142, 1871.
323. Milikan, Roller and Watson. Mechanics. Molecular Physics,
Heat and Sound. Ginn & Company, 1937.
324. Miller M. P. An accurate method of measuring the moments of inertia
of airplanes NACA, N 351, 1930.
325. Miller M., Soule H. Moments of inertia of several airplanes. NACA.
T. N. N 375, 1931.
326. Mischpeter E. Die Behandlung des Tragheitsmomente in der Schule.
Zeitschr. f. d. phvs. und chem. Unterricht, 1897.
327. Moll ier R. "Der Beschleunigungsdruck der Schubstange. VDI, 1903,
S. 1638—1640.
328. Mr к va F., Ratinger H. Metody mefeni momentu setrvacnosti
soucasti vozidel. «Automobil» (GSR), 1957, N 10.
329. M ii 1 1 e r F. Cber einen neuen Tragheitsmomenten Apparat. Zeitschr. f. d.
phys. und chera. Unterricht, 1905, S. 194—198.
330. Miiller F. Zeitschr. f. d. phys. und chem. Unterricht, 1887—1888.
331. Newton. Philosophica Naturalis Plincipia Mathematica, London, 1687.
332. N о а с к К- Apparat fur Einfiihrung in die Lehre vom Tragheitsmoment.
Zeitschr. f. d. phys. und chem. Unterricht, 1892.
333. N u 1 t у Е. Solution of a general case of the simple Pendulum. Trans, of
Amer. Phil. Soc. v. 2, 1825.
334. Oberbeck. Zeitschr. f. d. phys. und chem. Unterricht, 1887—1888.
335. P a g n i n i. Journal de Physique, v. 6, 1907.
336. P a i n 1 e v ё P. Lecons sur ie frottement. Paris, 1895.
337. P a r о d i M. Petites oscillations d'un pendule dont le point de fixation est
anime d'un mouvement periodique verticale. Comptes Rendus., v. 212,
1943, N 2.
338. P e 1 1 a t M. H. Sur le pendule bifilaire. Comptes rendus, t. 149, 1909.
339. P i с а г d I. La mesure de la Terre. Memoires de l'Ac. des sciences de
Paris, t. 7, 1671.
340. P о i n s о t. Theorie nouvelie de ia rotation des corps., 1834.
341. P о i s so n. Traite de mecanique. 2 ed. t. 2. Paris, 1833.
342. P б s с h 1 T. Lehrbuch der technischen Mechanik. Berlin, 1930.
343. Preobrajensky B. Demonstration de la formule du pendule. Journ.
de la Soc. phys.-chem. russe a l'Universite de S. Peterb. 1883, p. 65.
344. Prescott J. Electrical method for determining the moment of inertia
of a directcurent armature. Journal of the Institution of Electrical Engineers,
v. 69, 1931.
345. P г о n у G. Methode pour determiner la longueur du pendule simple qui
bat les secondes et pour trouver, en general, les positions des centres de gravite
et d'oscillation et le moment d'inertie d'un corps de forme quelconque. Me-
moire presente a la premiere Classe de l'lnstitut dans la seance du II vende-
miaire an IX (4/X 1800) .
346. P г о n у G. Recherches sur les moyens de determiner ia longeur de Pendule.
(Memoire presente a l'Acad. des Sc. 1. 10 mars 1792). Rapport a l'Academie
sur ce memoire le 28/IV—1792 par le Roi, Laplace, Legendre et Delambre.
347. P u v r e z P. Contribution a l'etude de la suspension et de la tenue de route
des vehicuies, Paris, 1933.
348. Puwein M. G. Die mutverte Pendellange. Osterreichisches Ingenieur-
Archiv, Bd. 8, H. 1, 1954.
349. Rice P. Moment of inertia experiments. Amer. J. Phys., vol. 9, 1941.
350. Ritchie H. Measuring moment of inertia of heavy rotors. Engineering,
v. CXXV, N 3253, 1928.
351. Rogers J. Greanwoodl. Electronic Instruments. Massachusettes
Institute of Technology, vol. 21, 1948.
352. Rose G. Determination of flywheel effect WRa. Machine Design, v. 13,
N 11, 1941.
353. Roberval G. Observation sur le sujet de la presante lettre de M. Des-
cartes a M. Cavendish, ofl il marque ses fautes. Oeuvres d. R. Descartes. Ed.
Cousin, t. 9, 1824.
354. R о u t h. Advanced part of a Treatise on the Dynamics of a system of Rigid
Bodies. 1884.
355. R u b i о S. Elementos de la teoria de momentos de inercia у calculo de los
mismos. 2 ed., Barcelona, 1955.
356. SatterlyJ. Moments of inertia of solid rectangular parallelepipeds, cubes,
and twin cubes, and two other regular polychedra. Amer. J. Phys., vol. 25,
1957, N 2.
357. Schneider K- Die geschichtliche Entwicklung der experimentellen
Ermittelung von Tragheitsmomenten nach der schwingungsmethode. Nature,
Bd. 12, 1921, N 21, N 22.
16 М. М. Гернет 2274 241
358. Schneider К- Experimented Ermittlung von molekularen tragheis-
momenten insbesondere die des Wassermolekules auf Grund der Bjerrumsche
Theorie und Rotationsspektrum der Gase. Natur, Bd. 13, 1922.
359. Schneider K. Experimentelle Bestimmung des Haupttraghetsmomentes
der Erde. Natur, Bd. 14, 1923.
360. Sang E. Notice of an expeditions method for computing the time of descent
in a circular arc. Proc. Edinb. Roy. Soc. 1859—1860.
361. Schwartz A., Ma lick S., Friesen J. Measurement of the
moment of inertia of missiletype bodies. Aircraft Engineering, vol. 29, 1957,
N 332.
362. Segner I. A. Specimen Theorie. Turbinum, 1755.
363. Shortt W. Herolog. J., vol. 93, 1951, N 1108.
364. Simpson T. Essays on several curious and useful subjects in speculative
and mixt Mathematics. London, 1740.
365. Spaeth W. Geraet zum Bestimmen von Traegheitsmomenten. VDI, v. 76,
1932, N 13.
366. Szebehely V., Niederer O. Unsteady and amplitude effects on
the moment derivatives of a prolate spheroid. David W. Taylor Mod. Basin
Rept., 1953, N 828.
367. S p e e r B. Orgon Fortschritte. Eisenbannwesen, Bd. 88, 1933.
368. Spies P. Ein Apparat fur das Tragheitsmoment. Zeitschr. f. d. phys. und
chem. Unterricht, 1907, S. 136.
369. S t e i n e r I. Vom Puncte der mittleren Entfernung Gesammelte Werke,
Bd. 2, Berlin, 1882.
370. Stokes G. On the Effect of the Internal Friction of the Motion of Pendu-
lum, Trans, of the Phil. Soc. Cambridge, vol. IX, 1856. Phil. Magaz — v. 1,
1851, Biblioth. de Geneve t. 21, 1852.
371. Sutton R. Demonstration experiments in Physics. New-York and Lon-
don, 1938.
372. T e о f i 1 a t о P. Sulla determinazione sperimenale die moment d'inerzia.
Atti di Guidonia, 1940, N 36.
373. Tessarotto. Ingegneria mecc. 1953, N 1.
374. The moment of inertia of propellers. Shipbuilder and marine Engine — Builder,
vol. 55, 1948, N 476.
375. T о m i t a. Trans. Assoc. Mach. Tech., vol. 8, 1958, N 4.
376. Turner, Howard L. Measurement of the Moments of Inertia of an
Airplane by a Simplified Method. NACA, T. N.. N 2201, 1950.
377. T u 11 1 e L. and S a t t e г 1 у J. The Theory of Measurements. Long-
mans., 1925.
378. U h 1 e г Н. Period of the bifilar pendulum for large amplitudes. Journal
of the Optical Soc. of America and Review of Sc. Instr., vol. 7, 1923, N 3.
379. U Ike R. Bestimmung des schwungmomentes von maschinen. Werkstatt
und Betrieb, 1951, N 10.
380. V e 1 t m a n n. Ueber die Bewegung einer Glocke. Dinglers Pilytechnisches
Journal, Bd. 220, 1876.
381. Volkmann P. Theoretische Physik, Leipzig, 1900.
382. Waetzmann. Einfache Methode zur annaherden Bestimmung von Trag-
heitsmomenten. Phys. Zeitschr. 1907, N 15.
383. Wall T. The separation of the iron losses in asynchronous machines. Elec-
trician, vol. LIX, 1907, N 1518.
384. Wall T. Determination of the moment of inertia of an electrical rotor.
Engineering, vol. CXXV, 1928, N 3241.
385. Walker E. On Pendulums. Phil. Magaz., vol. 36, 1810.
386. Watss W. Observations on the resistance of fluids. Edinburgh Phil.
Journal, v. 4, 1821.
387. Weinhol d A. Physikalische Demonstrationen Anleitung zum experi-
mentiren in Unterricht an Gymnasien, Realgymnasien, Re. lschulen und
Gewerbschulen. Leipzig, 1889.
242
389. Weishampel J., Wochling J. Physical method for obtaining
properties of a section. Ingineering and Contracting, vol. 71, 1932.
390. W h i t а к е г I. Notes of the moment of inertia of small marine propellers.
Shipbuilder and marine Engine—Builder, vol. 56, 1949, N 483.
391. Whitehurst J. An attempt toward obtaining invariable measures of
length, capacity and weight from the mensuration of time, independent of the
mechanical operations requisite to ascertain the centre of oscillation, or the
true length of Pendulums. London, 1787.
392. Wild. Wied. Ann. Bd. 10. 1880. Bull, de l'Acad. de st. Petersb., v. 8, 1898.
393. W i 1 1 e r s F. Pendelschwingungen bei einer dem Quadrat der Geschwindig-
keit proportionalen Damfung. Zeitschr. f. Instrumentenkunde, 1933, N 53.
394. Willis. System of Apparatus for the Use of Lecturers and Experimenters
in Mechanical Philosophy, London, 1898.
395. Wittenbayer F. Graphische Dynamik. Berlin, 1923.
396. Wittenbayer F. Aufgaben aus der technischen Mechanik, II Bd.
Berlin, 1927.
397. W о 1 к о f f W. Demonstration elementaric de la formule du Pendule. Jour-
nal de la Societe physico-chimique russe a l'Universite de Saint-Petersbourg,
v. 15, 1883, p. 16.
398. Wolkowitsch D. Sur les applications de la notion de moment d'inertie
en geometrie. Mem. des Sc. mathematiques., 1952, N 121.
399. W r i g 1 e у Н. В. Determining center of gravity and moment of inertia.
Automobile, 1916, N 35.
400. Young T. A course of Lectures on natural Philosophy and the mechanical
Arts. London, 1807.
401. Yu Yee-Tak. Virtual masses and moments of inertia of disks and cylin-
ders in various liquids. Journ. of applied physics, vol. 13, 1942, N 1.
402. Zawadzki I. Moment derwlandnosci ciaglichcecha podstawowa przy
okreslaniu zastepezych mas dynamicznich i zredukowanych. Przegl. mech.
1955, N 9,
♦ *♦
♦ #♦
ОГЛАВЛЕНИЕ
Введение 3
Глава I. Основные сведения о геометрии масс 5
§1.0 геометрии масс 5
§ 2. Моменты инерции относительно полюса и плоскости 6
§ 3. Центробежный момент инерции 7
§ 4. Теорема о параллельных осях 8
§ 5. Теорема о пересекающихся осях 8
§ 6. Эллипсоид инерции 9
§ 7. Радиус инерции тела относительно оси 10
§ 8. Маховой момент 10
Глава II. Определение момента инерции методом физического маят-
ника 11
§ 1. История метода. Теория метода 11
§ 2. Определение момента инерции физического маятника
по периоду качаний 12
§ 3. Определение момента инерции физического маятника
по приведенной длине 16
§ 4. Опытное определение статического момента физиче-
ского маятника 21
§ 5. Метод качания на параллельных осях 23
§ 6. Метод качания с эталоном 29
§ 7. Метод качания ротора с эталоном в подшипниках ротора 33
§ 8. Весы качания 34
§ 9. Метод качания с перемещением добавочного груза 35
§ 10. Метод качания тела по вогнутым направляющим . . 37
§ 11. Метод качания эллиптического маятника 38
§ 12. Влияние диссипативных сил на период колебания маят-
ника 42
§ 13. Область применения и рекомендации к проведению
опыта 44
§ 14. Способы подвешивания физического маятника ... 45
§ 15. Об устройстве оси подвеса 47
§ 16. О наблюдениях с маятником сравнения 48
§ 17. Об измерении периода колебаний физического маят-
ника и других механических систем 48
Глава III. Определение момента инерции методом качания двойного
маятника 51
§ 1. История метода. Теория метода 51
§ 2. Ошибки определения момента инерции методом качания
двойного маятника 57
§ 3. Установление оптимальных параметров маятника • • 59
§ 4. Рекомендации по применению метода 65
244
Глава IV. Определение моментов инерции методом крутильных колебаний
(унифиляр) 67
§ 1. История метода. Элементарная теория метода .... 67
§ 2. Уточнение теории. Влияние удлинения нити .... 72
§ 3. Ошибки, допускаемые при эксперименте 77
§ 4. О точности метода 79
§ 5. Анизохронность крутильных колебаний и уточнение тео-
рии метода 82
§ 6. Область применения метода 87
§ 7. Рекомендации к проведению опыта 90
Глава V. Определение моментов инерции по колебаниям нитяных
подвесов 95
§ 1. История метода. Элементарная теория метода .... 95
§ 2. Теория метода. Параллельное расположение нитей . • 100
§ 3. Условия расположения нитей многонитяного маятника.
Цилиндрический мультифиляр 105
§ 4. Конический нитяной подвес 111
§ 5. Малые колебания нитяного подвеса в случае, когда при
равновесии ось подвеса не проходит через центр масс
испытуемого тела 113
§ 6. Влияние жесткости нитей на движение нитяного под-
веса 121
§ 7. Ошибки экспериментального определения моментов
инерции • ... 126
§ 8. Метод качания в плоскости бифилярного подвеса . . 130
§ 9. Область применения метода и рекомендации по прове-
дению опытов 132
Глава VI. Определение моментов инерции методом атвудовой ма-
шины 137
§ 1. История метода. Различные схемы эксперимента и при-
ближенная теория метода 137
§ 2. Определение момента инерции по движению системы
под действием одного груза 140
§ 3. Определение момента инерции по движению системы
под действием двух грузов 149
§ 4. Определение момента инерции по разгону системы гру-
зом и выбегу 153
§ 5. Область применения, оценка метода и рекомендации по
устройству прибора 157
§ 6. Рекомендации по проведению опыта 160
Глава VII. Определение момента инерции методом качания тела по пло-
скости 162
§ 1. История метода 162
§ 2. Качение тела по наклонной плоскости 162
§ 3. Вывод рабочей формулы с учетом трения качения . . 166
§ 4. Качение тела по горизонтальной плоскости 168
§ 5. Рекомендация к проведению опыта 169
Глава VIII. Методы определения моментов инерции, требующие приме-
нения специальных приборов 171
§ 1. Прибор Н. Е. Жуковского с винтом и гайкой ... 171
§ 2. Определение момента инерции тела ударом 172
§ 3. Определение момента инерции на весах 174
245
§ 4. Определение момента инерции методом колебаний тела
на качающейся платформе 177
§ 5. Приборы для определения моментов инерции маленьких
тел 178
§ 6. Прибор для определения моментов инерции очень ма-
леньких тел 180
Глава IX. Экспериментальное определение эллипсоидов инерции .... 184
§ 1. История вопроса и постановка задачи 184
§ 2. Экспериментальное определение главных моментов инер-
ции, главных направлений и центробежных моментов
инерции 185
§ 3. Измерение дисбаланса вращающегося тела методами
определения моментов инерции 188
Примечание 1. Колебания маятника при конечных амплитудах ... 190
Примечание 2. Основные сведения о теории ошибок 193
Примечание 3. Оборотный маятник Прони 194
Примечание 4. Изменение периода маятника от присоединенной массы 195
Примечание 5. Качание шипа на вогнутых направляющих 195
Примечание 6. Влияние трения на период качания маятника с подшип-
никовыми опорами 198
Примечание 7. Качание на цилиндрической оси 198
Примечание 8. Интегрирование дифференциальных уравнений малых ко-
лебаний двойного маятника 199
Примечание 9. О зависимости главных частот колебаний двойного маят-
ника от его параметров 201
Примечание 10. Влияние параметров двойного маятника на точность из-
мерения момента инерции 203
Примечание 11. Крутильные колебания при нелинейной зависимости
между деформацией и напряжением 207
Примечание 12. Вывод формулы периода колебаний тела на нитяном под-
весе 209
Примечание 13. Исследование сходимости рядов и область применения
полученных формул периода колебаний 210
Примечание 14. Малое перемещение центра тяжести тела по оси Ог при
произвольном расположении нитей 213
Примечание 15. Преобразование формулы периода малых колебаний
мультифиляра 216
Примечание 16. Учет изгибной жесткости нитей подвеса 217
Примечание 17. Вывод уравнения движения бифиляра в плоскости нитей 219
Примечание 18. Составление дифференциального уравнения движения
системы 220
246
Примечание 19. Интегрирование дифференциального уравнения движе-
ния системы 221
Примечание 20. Уравнение движения при одновременном действии двух
грузов 222
Примечание 21. Решение задачи об экспериментальном определении
центробежных моментов и эллипсоида инерции в общем
виде 223
Примечание 22. Вывод рабочих формул для экспериментального опре-
деления центробежного момента инерции 225
Использованная литература 229
Михаил Михайлович ГЕРНёТ,
Всеволод Фёдорович РАТОБЫЛЬСНИЙ
ОПРЕДЕЛЕНИЕ МОМЕНТОВ
ИНЕРЦИИ
Редактор издательства 3. 3. Анчурина
Технический редактор Н. В. Тимофеева
Корректор Г. И. Сурова
Переплет художника А. Я. Михайлова
Сдано в производство 20/IX 1968 г.
Подписано к печати 14/IV 1969 г.
Т-05917. Тираж 7000 экз. Печ. л. 15,5
Бум. л. 7,75 Уч.-изд. л. 14,75
Формат бумаги 60Х90У1в
Цена 1 р. 01 к. Зак. № 2274
Издательство «МАШИНОСТРОЕНИЕ»,
Москва, Б-66, 1-й Басманный пер., 3
Ленинградская типография № 6
Главполиграфпрома
Комитета по печати
при Совете Министров СССР
Ленинград, ул. Моисеенко, 10