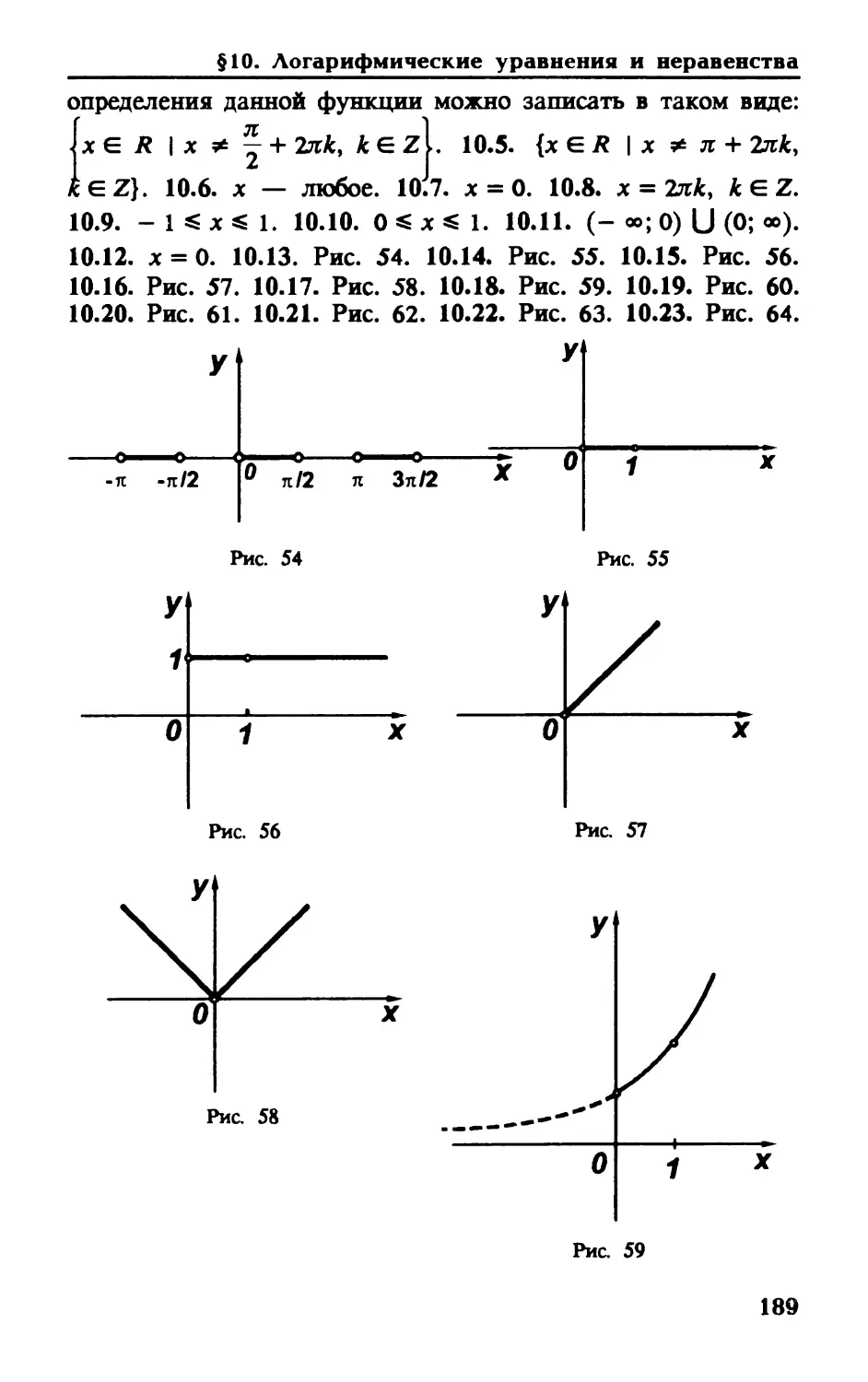
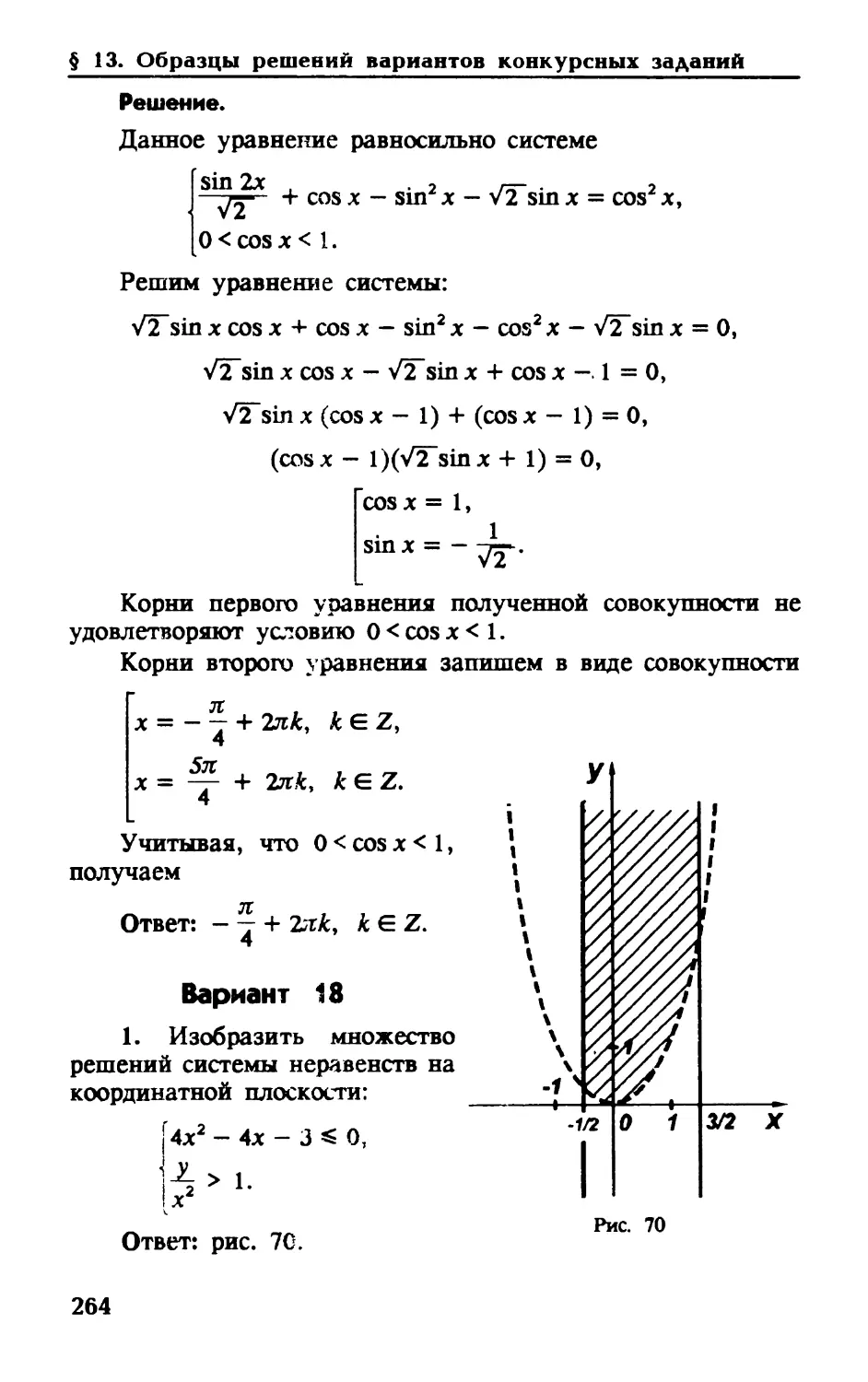
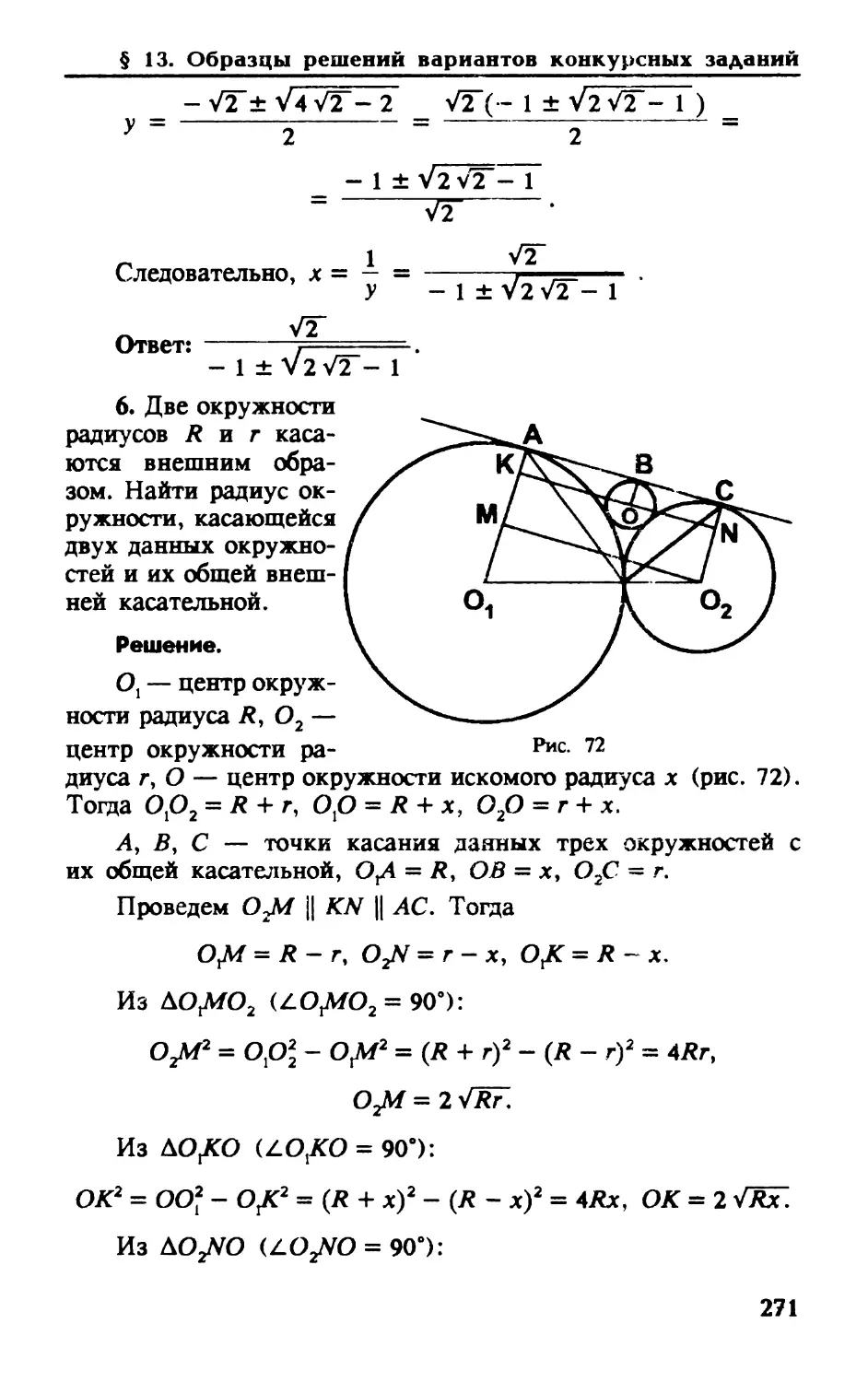
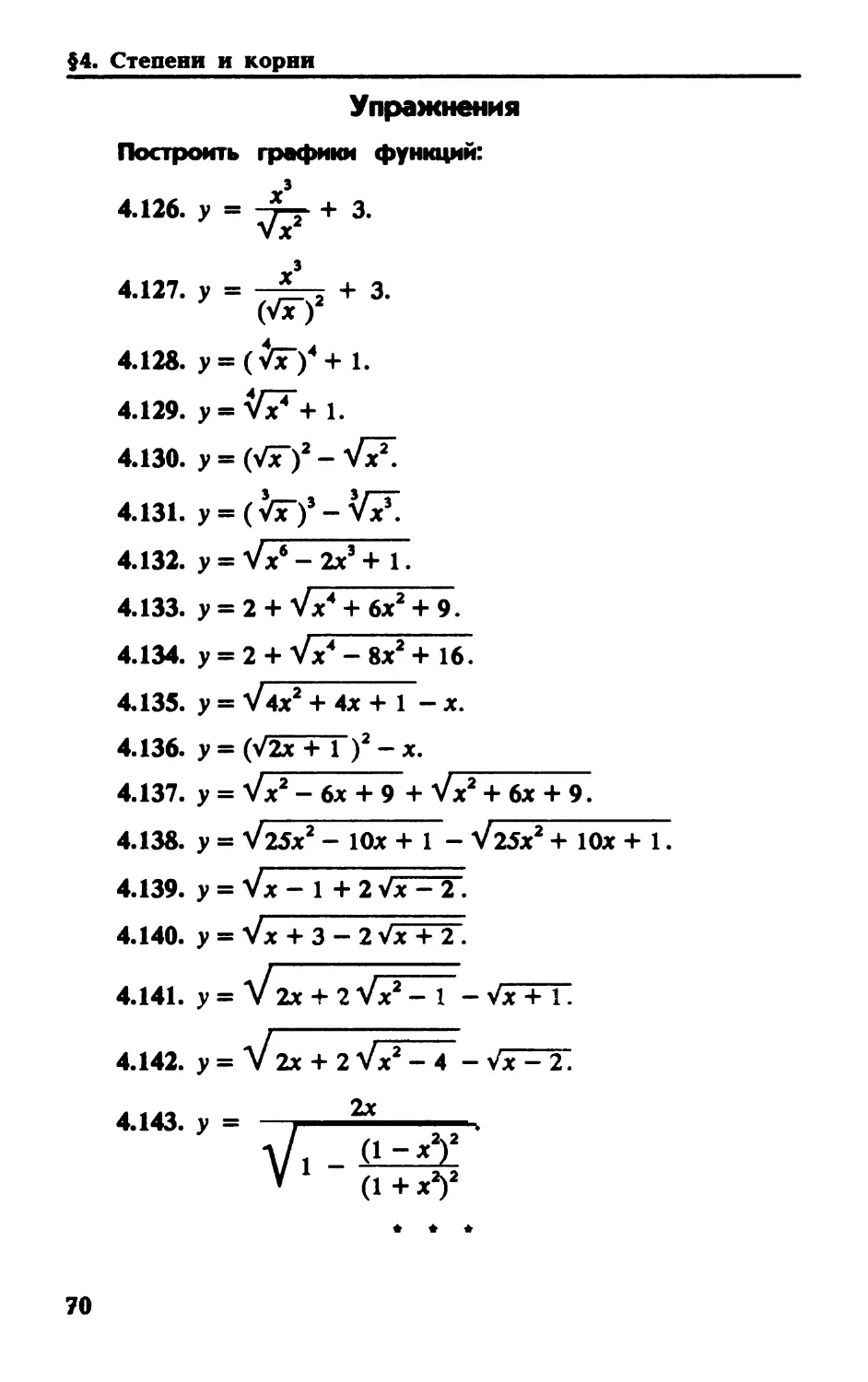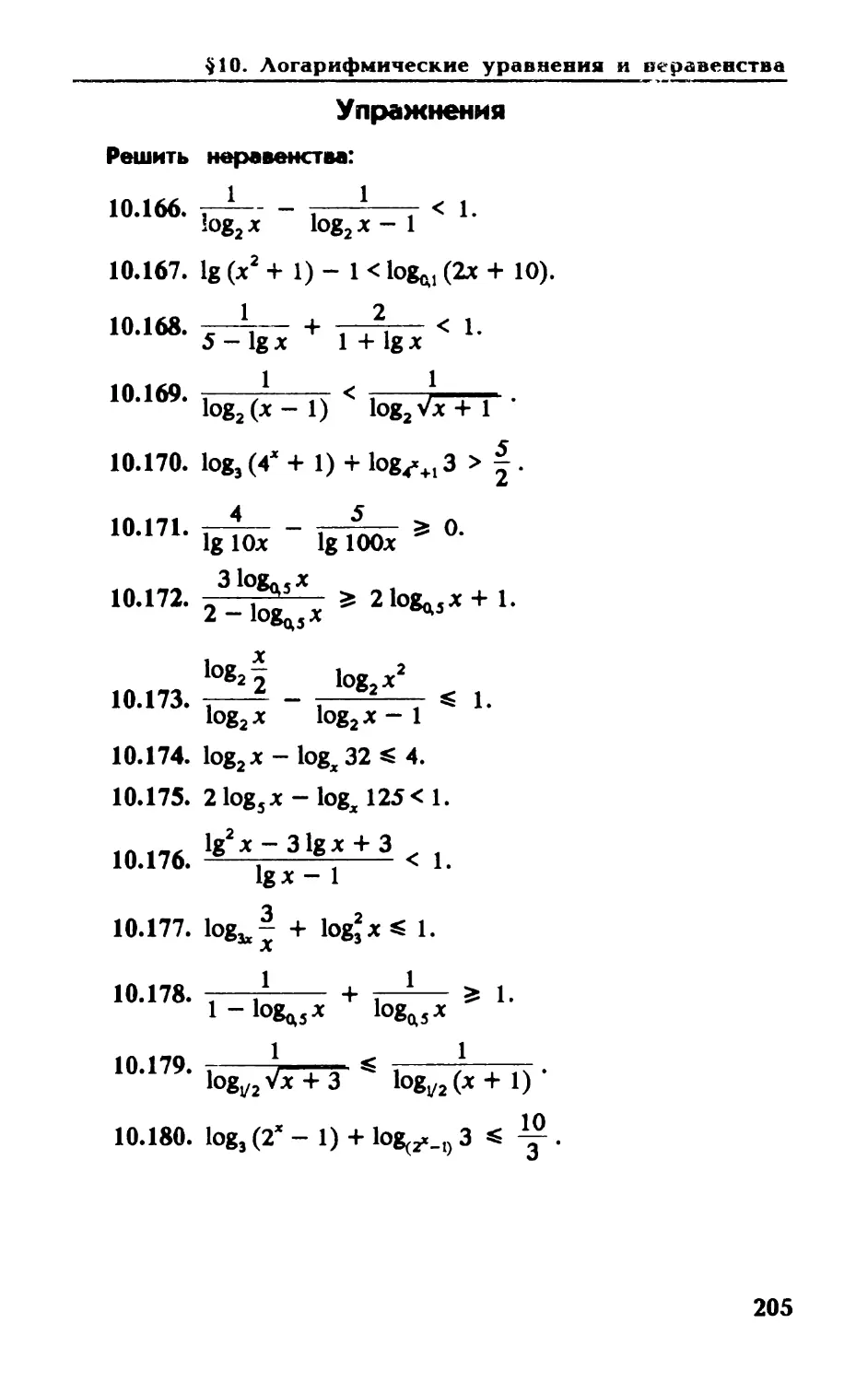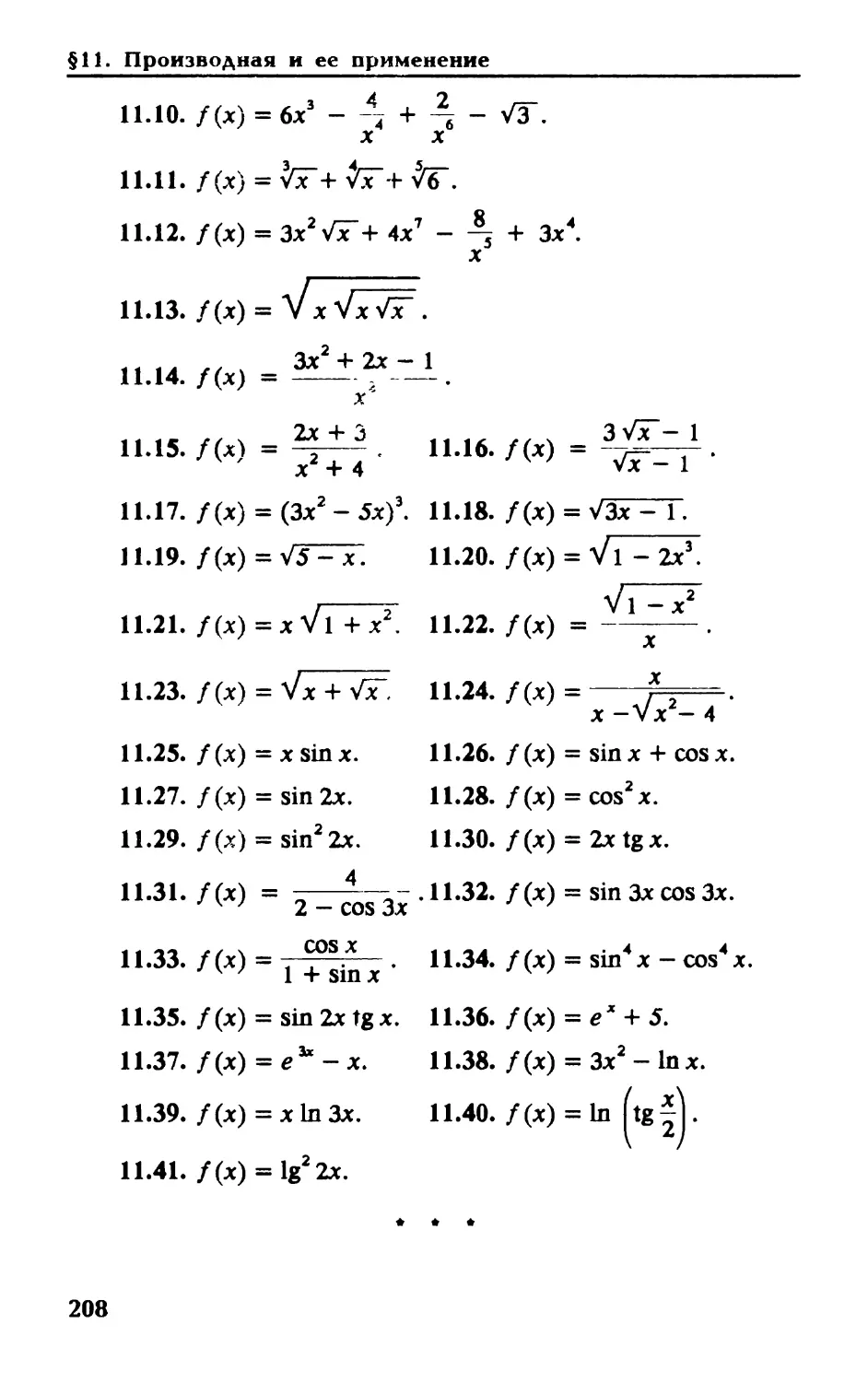Автор: Мерзляк А.Г. Полонский В.Б. Якир М.С.
Теги: алгебра математика
ISBN: 978-5-89237-022-6
Год: 2007
Текст
9С/1адовая ш/(олъной juamejitamuiQi
ШИК, ШИНОЙ, Ш»
А.Г. Мерзляк,
В.Б. Полонский,
М.С. Якир
Алгебраический
тренажер
Пособие для школьников и абитуриентов
«ИЛЕКСА»
Москва
2007
5БК 22.14
М52
А. Г. Мерзляк, В. Б. Полонский, М. С. Якир
М52 Алгебраический тренажер: Пособие для школьников
и абитуриентов / Под ред. Мерзляк А.Г., Полон-
ский В.Б., Якир М.С.— М.: Илекса, 2007,— 320 с.
ISBN 978-5-89237-022-6
В настоящем пособии представлены основные разделы курса
школьной алгебры и начал анализа. Книга построена по схеме «клю-
чевая задача + упражнения». Ее можно рассматривать как обучаю-
щий сборник задач с широким диапазоном применения: от справоч-
ника по методам решений до дидактического материала. В конце
пособия дополнительно приведены образцы вариантов вступитель-
ных экзаменов в вузы с экономическим профилем.
Для учащихся 7-11 классов, учителей математики, абитуриентов
ББК 22.14
ISBN 978-5-89237-022-6
© Мерзляк А.Г.,
Полонский В.Б.,
Якир М.С., 1998
© ООО «Илекса», 1998
От авторов
Даже самый превосходный торт вряд ли до-
ставит вам удовольствие, если кто-то его предва-
рительно пожует. Так же и самую хорошую задачу
можно испортить, преждевременно показав ее ре-
шение. Правда, и в том, что «видит око, да зуб
неймет», мало радости: от задачи, решение которой
вы никогда не узнаете, немного проку.
«Голые» решебники, с одной стороны, и «чи-
стые» сборники задач, с другой, — две крайности
учебной литературы. Первые совсем не оставляют
места для творчества. Работа со вторыми, как пра-
вило, возможна лишь под руководством опытного
наставника. Желательно иметь нечто среднее, ска-
жем, обучающий сборник задач. разъяснения.
В каждой теме есть базисные (опорные) задачи,
идея решения которых группирует вокруг них це-
лый класс аналогичных задач. Таким образом, на-
учившись решать ключевую задачу, мы открываем
путь к решению «задач-родственников». На наш
взгляд, решение именно базисных задач следует
демонстрировать в сборнике, а аналогичные рас-
сматривать как упражнения.
з
Мы надеемся, что настоящее пособие как раз
и является сборником задач подобного рода. В нем
представлены основные разделы курса школьной
алгебры и начал анализа. Книга построена по схеме
«ключевая задача + упражнения». Её можно рас-
сматривать как сборник задач с широким диапазо-
ном применения: от справочника по методам ре-
шений до дидактического материала. В конце по-
собия дополнительно приведены образцы вариантов
вступительных экзаменов в вузы с экономическим
профилем.
Авторы выражают искреннюю благодарность
Ю.Б.Боженко, М.Е.Рабиновичу, Е.М.Рабиновичу и
А.О.Романенко, чья дружеская помощь и ценные
советы в процессе работы над книгой во многом
способствовали ее улучшению. Также авторы бла-
годарны всем своим ученикам, участвовавшим в
апробации рукописи этой книги.
4
§ 1. Абсолютная величина числа (модуль)
Немного теории
Определение.
Абсолютной величиной числа а (обозначается \а\) на-
зывается расстояние от точки, изображающей данное чис-
ло а на координатной прямой, до начала отсчета.
Из определения следует, что
|а| =
а, если а О,
- а, если а =£ О.
(*)
Отметим, что здесь значок { не обозначает логическую
операцию. Он использован лишь для придания записи ком-
пактной формы.
Основные свойства модуля
1) |а| £0;
3) |а| 2 а;
я |1|=
7) |а + 6| = |а| + |6|
2) |а| = |-в|;
4) |а6| = |а| |6|;
6) 1а + 6| |а| + |6|;
тогда и только тогда, когда
8) |а| + |6| = а + 6 тогда и только тогда, когда а & О и
6^0;
9) 1а — 6| = |а| + |6| тогда и только тогда, когда
ab =5 О;
10) |а| - |6| &0 тогда и только тогда, когда
а2 - б2 О.
Полезные упражнения
Раскрыть модуль:
1.1. а) |л-3|;
в) IVT+VTI;
д) |х2|;
© ll-VTl;
г) IVT-2I;
е) lx4+ 11;
5
} 1. Абсолютная величина числа (модуль)
ж)
и)
з) |х2 + 2х + 21;
к) |-х2 + Зх-4|.
Решить уравнения:
1.2. \х2- 4х + 3| = -2.
1.4. |х| = -х2- 1.
1.6. |х| =- |х + 1|.
1.8. |х| =- 4-
X
1.10. - = - X2.
X
1.12. 2х -х2 - 1 = |х|.
1.14. |х| -х = 1 - VT.
1.16. |х| = -х2.
1.18. |х —31 = 6х — х2 —
1.19. lx + 31 +(х + 3)2 =
1.20. |х + 2| = — |х2 —4
1.3. |х2-6х-7| =vT-2.
1.5. |х| = — (х — 2)2.
1.7. х2 + 4 |х| + 1 =0.
1.9. х |х| = -
х
1.11. х2 + х+ 1 = - |х|.
1.13. |х| - х = - 1.
1.15. х- Ixl = |х + 1|.
1.17. |х — 2| = -(2-х)2.
9.
О.
1.21. х-|х| =х2. 1.22. |х|=х.
1.23. |2х - 31 = 2х - 3. 1.24. |х2 - 11 = 1 - х2.
1.25. 1.26. — = 1.
X - 1 1-х X
1.27. *-3’ =1. 1.28. |х-2| = 12-х|.
J X
Решить неравенства:
1.30. |х| > - 1. 1.31. |х2 - Зх - 21 < - 1.
1.32.
1 1
х + 3 2х-5
> — 2.
б
} I. Абсолютная величина числа (модуль)
1 1 1 ^4 1 vl SA
1«ОО« X2- 1 * 2- 1.0**. 1X 1 V.
1.35. х| >0. 1.36. |х| <0.
1.37. х2- 4| 0. 1.38. |х| -х2.
1.39. х| >- х2. 1.40. |х| >- |х-4|.
1.41. х| > - IX (х — 1)1.
1.42. х| >- |х(х- 1)1.
1.43. X (х - 1)1 >- 1х|.
1.44. X (х - 1)1 1x1.
1.45. 1 >- X 1x1. 1.46. |х| >х.
1.47. х| > х. 1.48. |х| - х.
1.49. Х| >- X. 1.50. |х| <х.
1.51. х| 3 х. 1.52. |х| <-х.
1.53. х| 3 - X. 1.54. - > - . X X
1.55. >1. 1.56. —- > 1.
X X
1.57. |х| 1. 1.58. —- < 1.
X ** X
1.59. |х| +х - х2. 1.60. jxi + х> -- х2.
1.61. |х| + х 3 - х2. 1.62. |х| +х< -х2.
1.63. х- |х| < А- 1.64. | х 1 - х - X
X X
1.65. х |х- 1| >0. 1.66. х |х- 1| <0.
1.67. х |х + 11 > 0. 1.68. х |х + 1| <0.
1.69. х|х + 1| 3 0. 1.70. ,/1( >0.
1.71. X |Х- 11 > 0. 1.72. Ix:lt<o.
1.73. X lx + 11 3 0.
7
$ 1. Абсолютная величина числа (модуль)
Решить уравнения:
1.74. |х| = а.
1.76. |х| = -а2.
Решить неравенства:
1.78. а |х| >0.
1.80. а 1x1 <0.
1.75. |х| = -а.
1.77. |х| + |а| =0.
1.79. а |х| £0.
1.81. а |х| « 0.
Комментарии, указания, ответы
При решении упражнения 1.1 следует воспользоваться
одним важным правилом, которое непосредственно следует
из соотношения (*): чтобы раскрыть модуль, надо знать знак
выражения, стоящего под модулем.
1.1. а) л-3; ® VT-1; в) VT4-V5"; г) VT-2; д) х2;
е) х4 + 1; ж) х2 - х + -у. Указание, х2 - х + -у = |х - ^| Э 0;
4 4 121
з) х2 4- 2х + 2. Указание, х2 + 2х 4- 2 = (х 4- I)2 4- 1 > 0;
х2
и) — — х 4- 1; к) х2 — Зх 4- 4. Указание. Воспользуйтесь свой-
4
ством квадратного трехчлена с отрицательным дискрими-
нантом.
Заметим, что в упражнениях 1.2-1.73 нет необходимости
раскрывать модуль. Достаточно лишь воспользоваться свой-
ствами 1)-3) и соотношением (*).
1.2-1.15. Нет решений. 1.5. Указание. Левая часть урав-
нения неотрицательна, правая — неположительна. Однако
левая и правая части обращаются в нуль при различных
значениях х. 1.9. Указание. Правая и левая части уравнения
имеют разные знаки. 1.13-1.15. Указание. Воспользуйтесь
свойством 3). 1.16. 0. 1.17. 2. 1.18. 3. 1.19. -3. 1.20. -2. 1.21.
0. Указание, х - |х| 0 в то время, как х2 0. 1.22. х 0.
1.23. х^|. 1.24. -1<х<1. 1.25. х<1. 1.26. х>0. 1.27.
х < 3. 1.28. х — любое. 1.29. х < 3 или х > 3. 1.30. х — любое.
1.31. Нет решений. 1.32. х < — 3 или х > — 3 и х # Указание.
Решением данного неравенства является область его опреде-
ления. 1.33. х < — 1 или - 1 < х < 1, или х > 1. 1.34. х < 0 или
х>0. 1.35. х — любое. 1.36. Нет решений. 1.37. х = 2 или
8
$ 1. Абсолютная величина числа (модуль)
х = —2. 1.38. х — любое. 1.39. х < О или х > О. Указание.
Обратите внимание на то, что данное неравенство строгое.
1.40. х — любое. Указание. Заметим, что при х = О правая
часть неравенства отрицательна. 1.41. х — любое. 1.42.
х<0 или х>0. 1.43. х<0 или х>0. 1.44. х — любое. 1.45.
х < О или х > О. 1.46. х — любое. 1.47. х < О. 1.48. х — любое.
1.49. х > О. 1.50. Нет решений. 1.51. х J О. 1.52. Нет решений.
1.53. х < 0.1.54. х < О или х > 0.1.55. х > О. 1.56. Нет решений.
1.57. х < О или х > О. 1.58. х < О. 1.59. х — любое. Указание.
При любом х |х| + х^О. 1.60. х<0 или х>0. 1.61. х = О.
1.62. Нет решений. 1.63. х < О или х > О. 1.64. Нет решений.
1.65. х>0 и х # 1. 1.66. х < О или х = 1. 1.67. х = — 1 или
х £0. 1.68. х < О и х# — 1. 1.69. х « О. 1.70. х > О и х * 1.
1.71. х^О и х # 1. 1.72. х<0 и х # - 1. 1.73. х<0 и
хх-1. 1.74. Если а<0, то нет решений; если а = О, то
х = О; если а > О, то х = — а или х = а. 1.75. Если а > О, то
нет решений; если а = О, то х = О; если а < О, то х = - а или
х = а. 1.76. Если а # О, то нет решений; если а = О, то
х = О. 1.77. Если а # О, то нет решений; если а = О, то
х = О. 1.78. Если а О, то нет решений; если а > О, то х —
любое, кроме нуля. 1.79. Если а < 0, то х = О; если а & О, то
х — любое. 1.80. Если а О, то нет решений ; если а<О, то
х — любое, кроме нуля. 1.81. Если а О, то х — любое;
если а > О, то х = О.
Основные типы задач
1.82. Построить график функции у = 12х ~ 3 L
Решение.
Поскольку мы не знаем, каков знак выражения, стоящего
под модулем, то рассмотрим две возможности. Если
3
2х - 3 < О, т.е. х < -, то у = 3 - 2х; если 2х - 3 О, т.е.
£
х , то у = 2х — 3. Полученный результат удобно записать
в таком виде:
3
3 - 2х, если х < •
у= 3
2х — 3, если х .
9
} 1. Абсолютная величина числа (модуль)
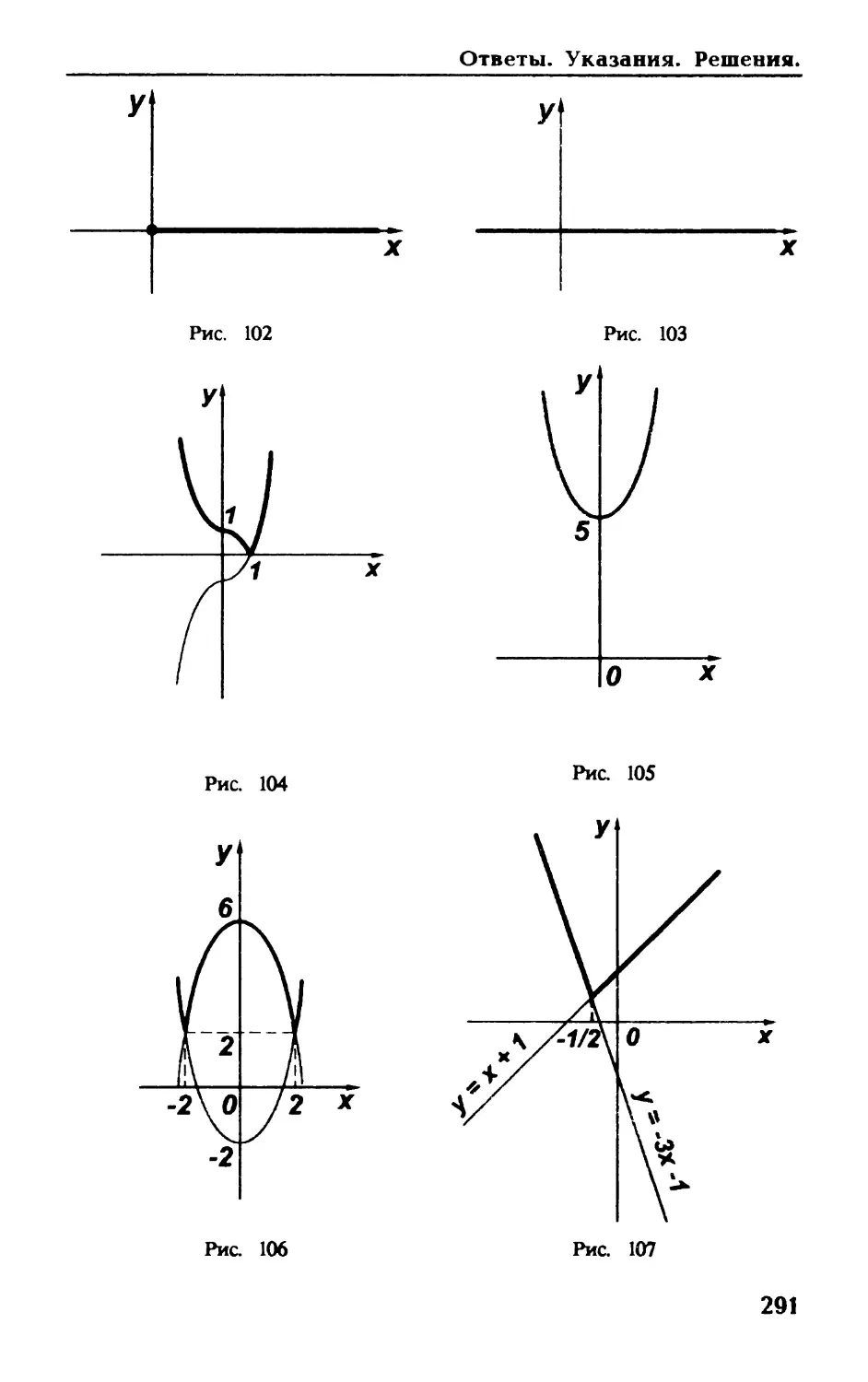
График данной функции изображен на рис. 1.
1.83. Построить график функции у = -ру (х2 — 4х + 3).
Решение.
Очевидно, что следует рас-
сматривать два случая: х > О и
х<0. Имеем:
График данной функции
состоит из двух соответствую-
щих парабол (рис. 2).
10
} 1. Абсолютная величина числа (модуль)
Упражнения
Построить графики функций (1.84-1.100):
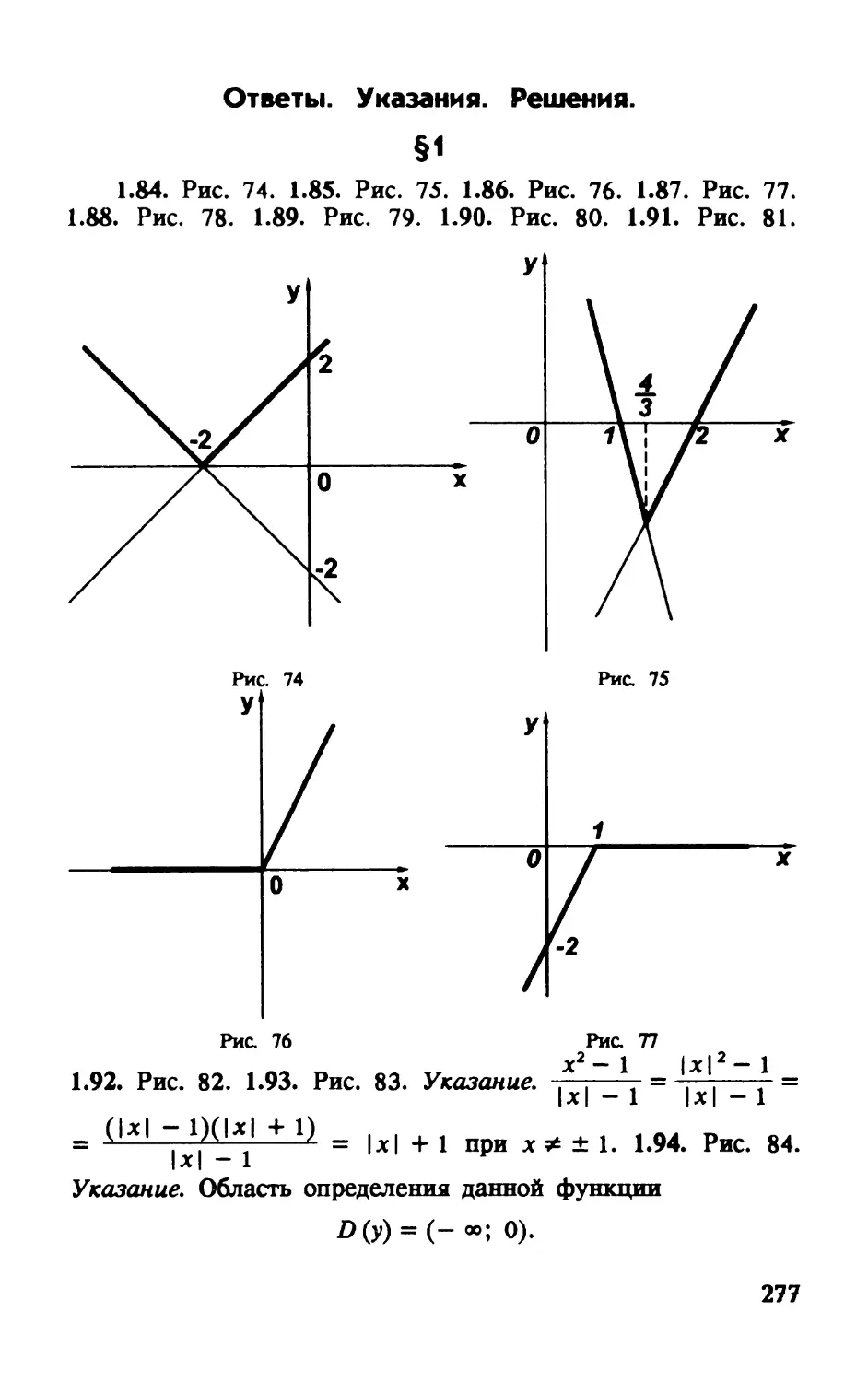
1.84. у = |х + 2|. 1.85. у = |Зх-4| - х.
1.86. у = |х| + х. 1.87. у = х - 1 - |х — 11.
1.88. у = |х| (х - 2). 1.89. у = |х + 41 х.
1.90. у = -ру. 1-91. у = .
z |х| х+1
х2 — 1 х2 - 1
1.92. у = , , * . 1.93. у = , , \ .
7 |х| +1 7 |х| - 1
1.94. у = —. 1.95. у = , * .
7 |х| -х 7 |х| +х
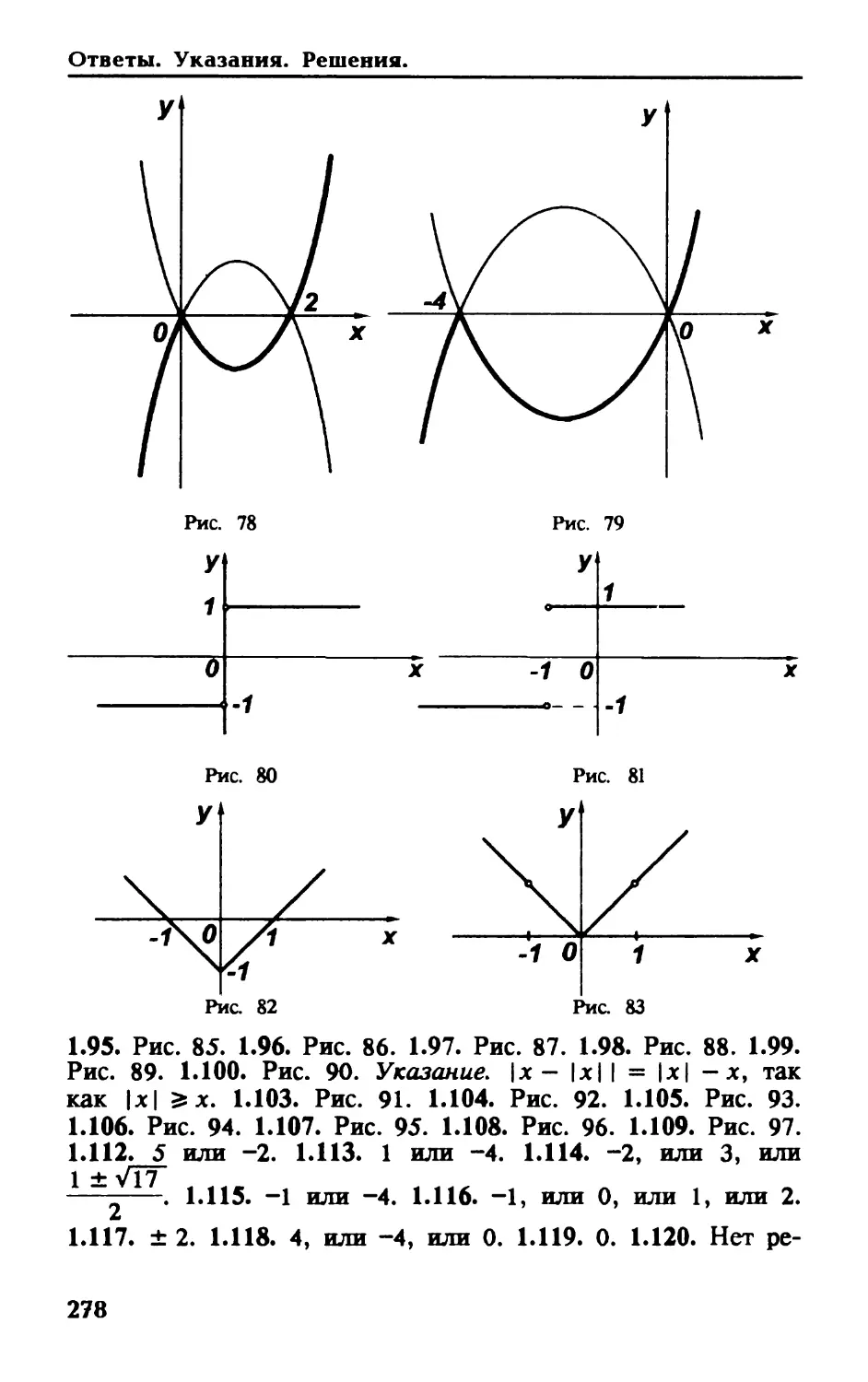
1.96. у = -рт(х2- 1). 1.97. у = |х4ч' (*2 + 4х + 3).
7 |х| v 7 7 х + 2 v 7
, х2 - х - 2 . „ х2 - 5х - 6
••“•’’-йзгг- 1W),= ix + ii
1.100. у = 1,11 .
7 X
1.101. Построить график функции
у = |х + 21 + 2 |х - 1| -х.
Решение.
Выражения, стоящие под модулем, принимают нуле-
вые значения в точках х = — 2 их = 1, разбивающих число-
вую прямую на три промежутка: (- - 2), [-2; 1 ],
(1; оо). Рассмотрим данную функцию на каждом из этих
промежутков.
Если х < — 2, тох + 2<0их — 1<0. Значит,
у = - х — 2 - 2х + 2 - х, у = - 4х.
Если - 2 х =5 1, то х + 2 г О и х - 1 $ О. Поэтому
у = х + 2 — 2х + 2 — х, у = — 2х + 4.
11
§ 1. Абсолютная величина числа (модуль)
Если х>1, то х + 2>0 и
х — 1 > О. Следовательно,
у = х + 2 + 2х-2-х, у = 2х.
1.102. Построить график,
функции
у = х(|х + 2| + |х —21).
Решение.
Если х< - 2, то
у = х (- х - 2 - х + 2),
Рис. з
у = - 2х2.
Если - 2 =5 х 2, то
у = х (х + 2 - х + 2),
у = 4х.
Если х >2, то
у = х (х + 2 + х - 2),
у = 2х2.
Итак,
У =
- 2х2, если х < - 2,
4х, если — 2 х =5 2,
2х2, если х > 2.
График изображен на
рис. 4.
Рис. 4
12
§ I. Абсолютная величина числа (модуль)
Упражнения
Построить графики функций:
1.103. у= |х- 1| + |х + 1|.
1.104. у= |х-2| - |х + 2|.
1.105. у = |х-3| + |2х — 1|.
1.106. у= |х + 31 + |2х + 1| -х.
1.107. у = х(|х-2| + 1x4-11).
LIU.,.
1.110. Решить уравнение |5х + 4| = 3.
Решение.
Ясно, что здесь есть две возможности: 5х + 4 = 3 или
5х + 4 = - 3. Откуда несложно получить
1 7
Ответ: х = - — или х = - —.
О о
Отметим, что при решении уравнений вида |/(х)| = а
(а Э О) наиболее рациональный путь — переход к сово-
купности
7(х) = а,
/(*) = - а.
1.111. Решить уравнение |х2 — 2х — 7| =4.
Решение.
Здесь указанный выше прием освобождает нас от необ-
ходимости находить интервалы знакопостоянства квадратного
трехчлена с «неприятвдми» корнями.
Имеем:
х2 - 2х - 7 = 4,
х2 - 2х - 7 = - 4;
13
§ 1, Абсолютная величина числа (модуль)_
х2-2х- 11 =0,
х2 - 2х - 3 = 0.
Ответ: х = - 1 или х = 3, или х = 1 ± 2 VT
Упражнения
Решить уравнения:
1.112. |2х-3| =7. 1.113. |2х + 31 = 5.
1.114. |х2-х-5| = 1. 1.115. |х2 + 5х + 61 = 2.
1.116. |х2 —х — 1| = 1. 1.117. х2 — |х| -2 = 0.
1.118. I |х| -21 =2. 1.119. 11x1 +21 =2.
1.120. I |х| +2| = 1. 1.121. |х2- 4х| =4.
1.122. 2 (х — I)2 + |х — 11 — 1 = 1.123. (х + 2)2 = 2 |х + 2| + 3. 0.
1.124. Решить уравнение
|2х+1|х — Зх — 4 = 0.
Решение.
Данное уравнение равносильно совокупности двух систем
Первая из полученных систем решений не имеет, а второй
удовлетворяет лишь х = 2.
Ответ: х = 2.
14
$ 1. Абсолютная величина числа (модуль)
Упражнения
Решить уравнения:
1.125. х |х| + 8х - 7 = О.
1.126. |х - 2| х - 6х + 8 = О.
1.127. х2 - 5х ——- 14 = О.
х - 2
1.128. х2 + 2х + 3 ——г- = О.
х - 1
1.129. |Х ~Х~21 = 3.
х + 1
1.130. х2 - х - 7
4
= 0.
1.131. |х2-3 |х| + 1| = 1.
1.132. х2 —2 |х - 1| =2.
1.133. Х + 5Х ~ 6 = 2.
|х - 2|
1.134. Решить уравнение |х2 — х — 81 = — х.
Решение.
При решении уравнений вида |/(х)| = g(x) распростра-
ненной ошибкой является переход к совокупности
’f(x) = g(x),
f(x) = -g(x),
что, скорее всего, связано с неверным обобщением метода,
приведенного в 1.110. Однако отсутствие требования
g (х) 0 может привести к появлению посторонних решений.
Таким образом, равносильным является переход к системе
Г/(*) = «(х),
. [/(x) = -g(x),
g(x) ^0.
Получаем
15
§ 1. Абсолютная величина числа (модуль)
х2 - х - 8 = - х,
х2 — х — 8 = х,
- х > О.
Ответ: х = — 2 или х = — 2 V2".
1.135. Решить уравнение | Зх - 41 = 4х2 + Зх - 2.
Решение.
Это уравнение принципиально не отличается от предыду-
щего. Однако здесь более комфортным представляется путь,
связанный с раскрытием модуля. Имеем:
Зх - 4 = 4х2 + Зх - 2,
Зх - 4 •» О,
Подчеркнем, что выбор того или иного из двух предло-
женных путей решения уравнений вида |/(х) I = g (х) связан
лишь с вопросом, какие из неравенств g(x) О (см. 1.134)
или /(х) 0 (см. 1.135) решить легче.
Упражнения
Решить уравнения:
1.136. 1x4-21 =2 (3-х).
1.137. |3х-1|-^.
1.138. 1x4-31 = х2 + х-6.
1.139. х2 - 4 |х + 11 + 5х + 4 = О.
1.140. |х2 + х —31 =х.
1.141. |х2 + х- 1| =2х- 1.
1.142. |5х + 2| = 3 — Зх.
16
§ 1. Абсолютная величина числа (модуль)
1.143. |х2- 2х| = 3 - 2х.
1.144. |3х2-х| = 8 + х.
1.145. |х*-х| = х + 4.
1.146. |х - 31 = - х2 + 4х - 3.
1.147. х2 + 4 |х - 31 - 7х + И = О.
1.148. lx lx - 1| -2х| = х2 — 2.
1.149. |х- |х- lx-ЦП = |.
лл
♦ ♦ ♦
1.150. Решить уравнение | х | - 2 | х 4- 11 =5.
Решение.
Данное уравнение равносильно совокупности трех систем:
1) ?<-1’ 2) {-*«*«>•
м |-х + 2х + 2 = 5; |-х-2х-2 = 5;
{х О.
х - 2х - 2 = 5.
Ответ: нет решений.
1.151. Решить уравнение
|х2 —4x4-31 4- |х2 - 4х - 5| =8.
Решение.
Находя интервалы знакопостоянства трехчленов
х2 - 4х + 3 и х2 - 4х - 5 (рис. 5), приходим к необходимости
решения пяти систем:
17
$ 1. Абсолютная величина числа (модуль)
2) - 1 х< 1, х2 - 4х 4- 3 - х2 4- 4х 4- 5 = 8;
3) 1 « х<3, - X2 4- 4х - 3 - X2 4- 4х 4- 5 = 8
4) • 3 х < 5, х2 - 4х 4- 3 - X2 4- 4х 4- 5 = 8;
5) < х 5, х2 - 4х 4- 3 4- X2 - 4х - 5 = 8.
Объединяя полученные результаты, имеем
Ответ: - 1 < х < 1 или 3 х £ 5.
Упражнения
Решить уравнения:
1.152. |х-2| + |х — 4| =3.
1.153. |х| + |х-6| =6.
1.154. |х + 2| - |х —31 = 5.
1.155. |х — 2| — 3 |3 — х| 4-х = О.
1.156. |х2- 91 + |х —3| =6.
1.157. |х2 - 5х + 4| + |х2 - 5х + 61 = 2.
1.158. |х| - 2 |х + 11 + 3 |х + 2| = О.
1.159. |х4- 1| 4- |х-5| =20.
1.160. |х4-5| + |х —81 = 13.
1.161. |х| - |х —21 = 2.
1.162. |7х — 12| - |7х — 111 = 1.
1.163. |х| 4- |х - 2| 4- 2 |х - 5| = 6.
1.164. |х| + |Зх + 2| + |2х — 1| =5.
1.165. |2х 4-2| 4- |х — 5| 4- 1 = 0.
1.166. |4 — х| 4- |2х — 2| = 5 — 2х.
1.167. |х 4- 31 - 15 - 2x1 = 2 - Зх.
1.168. |х-31 4-2 1x4- 1| =4.
1.169. |х - 11 4- |х - 2| = |х - 31 4- 4.
1.170. |х2 - 4х 4- 31 4- |х2 - 5х 4- 61 = 1.
1.171. |х2 —9| 4- |х —2| =5.
18
§ 1. Абсолютная величина числа (модуль)
1.172. |х2- 4| - |х2- 9| =5.
1.173. х |х| +2 |х — 2| =3.
1.174. |х2- Зх + 2| + |х2-5х + 6| =2.
1.175. ||х+ 1| - lx-ЗЦ = |х|.
1.176. ||х+ 2| - |х — 611 = |х|.
1.178. Решить неравенство |2х - 31 <5.
Решение.
Разумеется, это неравенство можно решить, раскрыв мо-
дуль. Однако в подобных примерах удобно пользоваться сле-
дующей теоремой.
Теорема.
Неравенство вида l/(x) I <g(x) равносильно системе
/(x)<f(x),
/(*)>-<(«)•
В частности, неравенство вида |/(х)| <а (а>0) равно-
сильно системе
f(x)<a,
f(x)>-a.
Итак, система
2х - 3 < 5,
2х — 3 > — 5
равносильна исходному неравенству. Отсюда
Ответ: - 1 < х < 4.
1.179. Решить неравенство х2 + 6 I Зх + 2| - 7х.
Решение.
И здесь, раскрывая модуль, можно добиться результата.
Но если записать исходное неравенство в таком виде:
19
§ 1. Абсолютная величина числа (модуль)
|Зх + 2| «х2 + 7х + 6,
то переход к равносильной системе
Зх + 2 х2 + 7х + 6,
Зх + 2^-х2-7х-6
несколько облегчит работу. Имеем:
(х + 2)2 О,
(х + 5 + ЛТ) (х + 5 - V17") 0.
Ответ: х — 5 — VTT или х > — 5 + VTT
1.180. Решить неравенство |х2 — 4| + 2х+1>0.
Решение.
Перепишем данное неравенство в таком виде:
|х2 —4| > — 2х — 1.
Воспользуемся следующей теоремой.
Теорема.
Неравенство вида l/(x) I > f (х) равносильно совокупности
В частности,
совокупности
7(х)>а,
[/(х)<- а.
Имеем:
7(Х)>< (X),
/(*)<-*(*)•
неравенство вида |/(х)| >а равносильно
-3 1-{б 1 1+/б х
Рис. 6
х2 - 4 > - 2х - 1,
х2- 4<2х + 1;
’(х- 1)(х + 3)>0,
(х - 1 + VD(x - 1 - V6“) < О.
С помощью рис. 6 получаем
Ответ: х < — 3 или х > 1 —
20
$ 1. Абсолютная величина числа (модуль)
Упражнения
Решить неравенства:
1.181. |4х + 5| <3. 1.182. |х2 — х - -31 <9.
1.183. |х — 1| <1. 1.184. |2х - 1| <3.
1.185. |2х-5| ^х. 1.186. |3х + 1|
1.187. |х2 + 5х| <6. 1.188. 3 |х — 1| х + 3.
1.189. 1.191. 1.193. 1.194. 1.195. 1.196. 1.197. 1.198. 1.199. 1.200. 1.201. 1.202. 1.203. 1.204. 1.205. 1.206. |х2- 4| <3х. 14х2 - 11 < х + 2. х2 - Зх + 2 к х х2 + Зх + 2 х2- 5х + 9> |х - 61. |х2 —6х + 8| <5х —х2. |2х2 — 9х+ 15| £20. 2 |х + 1| £х — 1. |2х + 1| £ 1. |х2 —2х| £ 1. 2х - 3 £1. х —5 2х — 1 £ 3. х2 —3 Зх —2| >2х + 1. |Зх-5| >9х+ 1. |х| >х + 2. х2 —х —2< I5X-3I. 1.190. 1.192. |х2 + Зх х + 1 2х - 1 I < х + 4. < 1.
1.207. |х2 + Зх| £ 2 — х2.
1.208. |х2 —Зх| £х + 5.
1.209. |хэ— 1| £ 1 -х.
21
} 1. Абсолютная величина числа (модуль)_________________
1.210. Решить неравенство |2х - 11 > |х + 2|.
Решение.
Здесь целесообразно применить следующую теорему.
Теорема.
Неравенство вида I/ (х) I > I у (х) I равносильно неравен-
ству f2(x)>y*(x).
Имеем (2х - I)2 > (х + 2)2, т.е. Зх2 - 8х - 3 > О.
Ответ: х < — ^ или х > 3.
Упражнения
Решить неравенства:
1.211. |Зх-2| > |2х+ 1|.
1.212. |х2 + х — 2| > |х + 2|.
1.213. |х + 4 — х2| « |х2-5х + 4|.
1.214. |х + 2| < |х-2|.
1.215. |3 + х| |х|.
1.216. |2х - 1| < |Зх + 1|.
1.217. |4х— II 3= |2х + 31.
1.218. |2х2 + х- II > |х+ 1|.
1.219. 124х2 - 39х - 81 118х2 - 25х + 321.
ее*
В следующем цикле задач довольно трудно избежать
операции раскрытия модуля.
1.220. Решить неравенство х |2х - 31 < 2.
Решение.
Данное неравенство равносильно совокупности двух си-
стем:
22
§ 1. Абсолютная величина числа (модуль)
[2х —3<0,
х (3 - 2х) < 2;
2х - 3 5: О,
[х (2х - 3) < 2.
Отсюда
[Ь < 1.
12х2 - Зх + 2 > О; Г < 3
2 ’
[х > | < х < 2.
X Л»
[х + |)(х-2) <0;
\ ** /
Ответ: х<2.
1.221. Решить неравенство |х — 11 + |х — 21 >х + 3.
Решение.
Это неравенство равносильно совокупности трех систем:
1) х< 1, 1-х-х + 2>х + 3; i<i: ’<о;
2) < Г1 «х^2, lx-1-х + 2>х + 3; 1 ^х^ 2, нет решений; х< —2,
х>2, х>2,
3) х>6.
х-1+х-2>х + 3; х>6,
Ответ: х<0 или х>6.
Упражнения
Решить неравенства:
1.222. |3х —2|х<1.
1.223. |х-4| (x + 2)=s4x.
1.224. |х- 1| —2 1x4-31 >х + 7.
23
§ 1. Абсолютная величина числа (модуль)
1.225. 2 |х — 31 4- 1x4- 1| 3x4- 1.
1.226. |х| —2 |х —2| 4-3 1x4-51 £ 2х.
1.227. 2 1x4- 1| - |х — 1| >3.
1.228. 1x4- 1| 4- |х- 1| < 2.
1.229. |х| -2 1x4- 11 4-3 1x4-21 54.
1.230. |х| —2 1x4- 1| 4-3 |х 4- 2| >4.
1.231. 1x4- 1| - |х — 1| >1.
1.232. х2 — 4 |х| < 12.
1.233. х2 4- 3 |х| > 10.
1.234. х2+ |5х-4| - 1 « |Зх-2|.
1.235. х2 4- 2 |х - 1| 4- 7 « 4 |х - 2|.
1.236. |4-х| -X lx-61-2
1.237. 12 — х| -х < |х - 31 - 1
1.238. 1x1 ~ 12 2. х - 3
1.239. х2 + 5х + 6
1.240. з 1x4-31-1 * |х + 2|‘
♦ ♦ ♦
Задачи для самостоятельного решения
С-1
1. Построить график функции у — |2х - 11 — Зх.
2. Решить уравнение:
а) |Зх + 5| =6;
б) 1x4- 1| =3(2-х);
в) 12x4- 1| 4- |х4-3| =4.
3. Решить неравенства:
а) |1 -2x1 <3;
24
} 1. Абсолютная величина числа (модуль)
б) |х2- 2х| >х;
в) |х- II < |х|.
С-2
1x1 2
1. Построить график функции у = (х — 4)..
2. Решить уравнения:
а) I х | = - х - 2;
б) х2 + |х| -2 = 0;
в) |х2- 41 + |х —2| =2.
3. Решить неравенства:
а) |х2- 2х - 31 <4;
б) х |3х - 1| <3;
в) |х+ 1| -3 |х-21 >х + 4.
С-3
1. Построить график функции у — |х — 21 + 12х — 11.
2. Решить уравнения:
б) 1x4-31 -2 |1 -Зх| + 5х = 0;
3. Решить неравенства:
а) (2х - 1) |х + 31 Зх;
б) 3 |х — 31 - 14 + 3x1 <х + 3;
в) |х| —2 |х — 1| +4 |х —31 <5х.
25
§2. Рациональные уравнения
Немного теории
Определение.
Областью определения уравнения f(x) = g (х) называ-
ется множество D(f) П D (g), где D(f) и D(g) — области
определения функций fug.
Определение.
Число а называется корнем уравнения f(x) = g(x), если
при подстановке его вместо х в уравнение получается верное
числовое равенство f(a) = g(a).
Определение.
Функция вида
Р(х) = аох" + а, Xя-1 + а2х""2 + ... + а„.,х + аЛ>
где п — натуральное, a*, ах,...,ап — некоторые действи-
тельные числа, называется целой рациональной функцией.
Определение.
Уравнение вида Р (х) = О, где Р (х) — целая рациональная
функция, называется целым рациональным уравнением.
Определение.
Уравнение вида
Л(х) . ЛОО + . ЛОО =п
Q,00 Q,(x) Q.00 *
где Pt(x), Р2(х), ... ,Ри(х). Q.(x), Q2(x),..., - це-
лые рациональные функции, называется рациональным
уравнением.
Полезные упражнения
Решить уравнения:
2.1. = О. 2.2. Х-= 1.
х - 1 х - 1
26
§2. Рациональные уравнения
2.9. (а2 - 4)х = 2. 2.10. (а2 - 4) х = а + 2.
л /% «/% Л (Х " 1) Л
2.11. - = О. 2.12. —----------------= О.
х х - 1
2.15. -—J = О. 2.16. —а^Х = О.
х - 1 х - 2
Комментарии, указания, ответы
2.1. Нет решений. 2.2. х<1 или х>1. 2.3. -5. 2.4. Нет
решений. 2.5. х < - 3 или х > — 3. 2.6. х < 3 или х > 3. 2.7.
Если а = О, то нет решений; если а # О, то х = . 2.8. Ес-
ли а - О, то х — любое; если а # О, то х = О. 2.9. Если
2
а = ± 2, то нет решений; если а # ± 2, то х = . 2.10.
а — 4
Если а = 2, то нет решений; если а = — 2, то х — любое;
если а # ± 2, то х = д 1 2- 2.11. Если а # О, то нет решений;
если а = 0, то х < О или х > О. 2.12. Если а # 0, то нет решений;
если а = 0, то х < 1 или х > 1. 2.13. Если а = 1, то нет решений;
если а # 1, то х = 1. 2.14. Если а # 1, то нет решений; если
а = 1, то х < 1 или х > 1. 2.15. Если а = 1, то нет решений;
если а # 1, то х = а. 2.16. Если а = 2, то х - 1; если а = 1,
то х = 1; если а # 2 и а # 1, то х = а или х = 1. 2.17. Если
а = 1, то х = 4; если а = 4, то х = 1; если а#4иа#1, то
х = 1 или х = 4. 2.18. Если а = 4 или а = 1, то нет решений;
если в#4 и а# 1, то х = а.
27
$2. Рациональные уравнения
Основные типы задач
х 1 2
2.19. Решить уравнение ——;-------;-----г--- = О.
х+1 х- 1 х - 1
Решение.
Сложив дроби, стоящие в левой части, получим уравнение
х2 — 2х — 3 л ~__
—^2—J— = °’ равносильное исходному. Это же уравнение,
в свою очередь, равносильно системе
х2 - 2х - 3 = О,
х2# 1.
Квадратное уравнение имеет корни х = 3, х = - 1. Оче-
видно, что последний корень — посторонний.
Ответ: х = 3.
Упражнения
Решить уравнения:
2.25. ——--------------- = -------
хэ-1 4х2 + 4х + 4 2(1-X)’
2.26. 1 + ---------5-Ц.
2х2 + 8х 2х2 + 7х - 4 2х - 1
28
§2. Рациональные уравнения
2.27. + -----г-Ц*------------О.
2х + 12х + 10 4х2+16х—20 х3+ 5х- х - 5
2х — 7 1 1
2.28. — ------------=—-------- = —Ц-.
х - 9х + 14 х - Зх + 2 * “ 1
2.29. Решить уравнение
(х2 + Зх + 1)(х2 + Зх + 3) + 1 = О.
Решение.
Пусть х2 + Зх + 1 = t. Тоща х2 + Зх + 3 = Г + 2, и данное
уравнение становится таким:
t(t + 2) + 1= 0.
Отсюда (t + I)2 = О, t = — 1. Следовательно, исходное урав-
нение равносильно такому: х2 + Зх + 1 = — 1. Имеем:
х2 + Зх + 2 = О, ^ = - 2.’
Ответ: х = — 1 или х = - 2.
2.30. Решить уравнение
Решение.
Пусть х +х—- = t. Тогда 2 Отсюда
х х + х - 5 t
t + | + 4 = 0, t2 + 4t + 3 = 0, (= - 3 или (= - 1.
Следовательно, исходное уравнение равносильно совокуп-
ности
2 + х - 5
х2 + 4х - 5 = О,
х2 + 2х - 5 = 0.
X
х2 + х - 5 _ _ р
X — ’
Ответ: х = 1 или х = — 5,
или х = —1+ V6".
или х = — 1 — V6",
29
§2. Рациональные уравнения
Упражнения
Решить уравнения:
2.31. 2х4 + х2 - 1 = 0.
2.32. (х + З)4 - 3 (х + З)2 + 2 = 0.
2.33. -г—— х2 + 4х = 6. х - 4х + 10
2.34. х- 1 _ Зх = _5 х 2х - 2 2 '
2.35. ^-+ ! =0 (2х + З)2 2х + 3
2.36. х2 - Зх - 6 8х - , = - 2. х х2 - Зх - 6
2.37. 1 + 2 = 6 х2 - 2х + 2 х2 - 2х + 3 х2 - 2х + 4 2 2 . л
2.38. х - х _ х - х + 2 _ 1 х2 - х + 1 х2 — х — 2
2.39. 24 15 = 2 х2 + 2х — 8 х2 + 2х — 3
2.40. х2 + 2х + 1 х2 + 2х + 2 _ 7 х2 + 2х + 2 х2 + 2х + 3 ” 6 '
2.41. х2 + 2х + 7 2 х2 + 2х + 3
2.42. (х2 + х + 1)(х2 + х + 2) = 12.
2.43. - 2 = 3 - х - х2. 1 + X + х2
2.44. Зх2 —9х 12 2 х2-3х
2.45. х2 + х - 3 3 _ J 2 2х2 + 2х-6 ~
30
______________________________§2. Рациональные уравнения
2.46. Решить уравнение (х2 - 6х)2 - 2 (х - З)2 = 81.
Решение.
Имеем: (х2 - 6х)2 - 2 (х2 - 6х + 9) = 81.
Пусть х2 — 6х = t. Тогда данное уравнение становится
таким: t2 - 2 (t + 9) = 81. Отсюда /2 - 2t - 99 = О, Z = - 9 или
t = 11. Далее,
х2 - 6х = - 9,
х2- 6х = 11.
Ответ: х = 3 или х = 3 — V20, или х = 3 + V20.
2.47. Решить уравнение
(2х2 + Зх — I)2 - 10х2 — 15х + 9 = О.
Решение.
Данное уравнение выгодно переписать так:
(2х2 + Зх — I)2 - 10х2 - 15х + 5 + 4 = О,
(2х2 + Зх - I)2 - 5 (2х2 + Зх - 1) + 4 = 0.
Пусть 2х2 + Зх - 1 = t. Получаем:
t2 - St + 4 = О, t = 1 или t = 4.
Итак,
’2х2 + Зх - 1 = 1,
2х2 + Зх — 1 = 4.
Ответ: х = - 2 или х = или х = - ^, или х = 1.
л» л»
Упражнения
Решить уравнения:
2.48. (8х2 - Зх + I)2 = 32х2 - 12х + 1.
2.49. (х2 + х + I)2 - Зх2 - Зх - 1 = О.
Х'Эи-х(х + 2) (х + 1)» 12*
31
$2. Рациональные уравнения_________________________________
2.51. (х2 + 2х)2 - (х + I)2 = 55.
•> о ______6_____ j. _______?_______ — 1
(х + 1)(х + 2) (х - 1)(х + 4)
2.53. (х2 - 5х + 7)(х - 2)(х - 3) = 2.
2.54. (х2 - 5х)(х + 3)(х - 8) + 108 = 0.
2.55. (х + 4)2(х + 10)(х - 2) + 243 = 0.
2« 16_______________20 _
(х + 6)(х - 1) (х + 2)(х + 3) " *•
♦ ♦ ♦
2.57. Решить уравнение (х - 1) х (х 4- 1)(х + 2) = 24.
Решение.
При решении уравнений подобного вида не следует спе-
шить раскрывать скобки. Надо найти выгодный способ груп-
пировки множителей. В данном примере он будет таким:
((х - 1)(х + 2)) (х (х + 1)) = 24.
Имеем: (х2 + х — 2)(х2 + х) = 24. Замена х2 + х = I. Тогда
t(t - 2) = 24, t2 - 2t - 24 = О, t = - 4 или t = 6.
Получаем:
х2 + х = — 4,
х2 + х = 6.
Ответ: х = — 3 или х = 2.
Упражнения
Решить уравнения:
2.58. (х - 4)(х - 5)(х - 6)(х - 7) = 1680.
2.59. х (х + 3)(х + 5)(х + 8) = 100.
2.60. (х - 4)(х + 2)(х + 8)(х + 14) = 1204.
2.61. (х + 3)(х + 1)(х + 5)(х + 7) = - 16.
2.62. (х - 1)(х - 7)(х - 4)(х + 2) = 40.
2.63. х (X + 1)(х + 5)(х + 6) + 96 = О.
32
____________________________$2. Рациональные уравнения
2.64. (12х - 1)(6х - 1)(4х - 1)(3х - 1) = 5.
2.65. (2х - 3)(2х - 1)(х + 1)(х + 2) = 36.
2.66. Решить уравнение
(2х2 - Зх + 1)(2х2 + 5х + 1) = 9х2.
Решение.
Непосредственной проверкой устанавливаем, что х = О
не является корнем данного уравнения. Тогда, вынеся из
каждой скобки х, перейдем к равносильному уравнению
Опять-таки с учетом того, что х # О, запишем равносильное
уравнение
2х + - - 31 12х + - + 5| =9.
X II X )
Замена 2х + - 3 = t. Отсюда
Г (Г+ 8) = 9, t = 1 или t = -9.
Далее,
1
х
1
X
2х2 - 4х + 1 = О,
Ответ: х = —-— или х = —-—, или
х =
2
Упражнения
Решить уравнения:
2.67. (х + 2)(х + 3)(х + 8)(х + 12) = 4х2.
2.68. 4 (х + 5)(х + 6)(х + 10)(х + 12) - Зх2 = О.
2 Алгебраический тренажер
33
$2. Рациональные уравнения
2.69. (х + 6)(х + 3)(х - 1)(х - 2) - 12х2 = О.
2.70. (х - 3)(х + 4)(х + 6)(х - 2) = 10х2.
2.71. (2х - 1)(х - 2)(2х2 + 7х + 2) = - 20х2.
2.72. (х - 4)(х + 5)(х + 10)(х - 2) = 18х2.
2.73. Решить уравнение х4 — Зхэ — 8х2 + 12х + 16 = О.
Решение.
Очевидно, что х = О не является корнем данного урав-
нения. Тогда, разделив обе части уравнения на х2, получим
уравнение, равносильное исходному. Имеем:
х2-Зх-8 + — + ^| = О,
х х
х2 + ^4 - 3 (х - -1 - 8 = О.
х2 х)
Пусть х - — = t, тогда х2 + ^4 = t2 + 8. Отсюда
х х2
t2 + 8 — 3/ — 8 = 0, t(/-3) = 0,
t = О или t = 3.
Далее,
х ~ х ~ °’ х2 — 4 = О,
х - - = 3, х2-Зх-4 = О.
X
Ответ: х = - 2 или х = 2, или х = - 1, или х = 4.
х2 48 (
2.74. Решить уравнение — + —= 10 Н
3 х
Решение.
Данное уравнение выгодно записать так:
34
§2. Рациональные уравнения
rr * 4 . х2 . 16 .2,8
Пусть - - - = t, тогда — + = t2 +
исходное уравнение в таком виде:
3 ft2 + = 10t.
Отсюда 3t2 + 8 = 10t, t = 2 или t = Имеем:
О
Запишем
X _ 4 _
3 х ~ 2’ х2 - 6х - 12 = О,
х _ 4 _ 4 . х2 - 4х - 12 = О.
3 х 3’ L
Ответ: х = 3 + V2T или
х = 3 - V2T,
или х = 6, или х = — 2.
Упражнения
Решить уравнения:
2.75. х2 + х + - + Л=4.
х X
2.76. 7 |х + -1 - 2 (х2 + -У = 9.
\ Х/ \ х)
2.77. 4х2 + 12х + — + 4 = <7.
х х2
2.78. 6х“ - 35хэ + 62х2 — 35х + 6 = О.
2.79.
х (х - I)2 _ 2
(х2 - х + I)2 9 '
2.80.
(х2 + I)2 = 625
х(х+1)2 П2’
2.81.
2.82.
2.83.
Л2_х\ _ 2. xi 4
Д* 3j “ х2 18 3 '
2 36 112 /х 3\
Х х2 5 ^2 х) *
2 1 ( 1 \
12х + -Ч + 10 2х + + 11 =0.
Зх I 3х/
35
$2. Рациональные уравнения
2.85. (хэ + + (*2 + А') + (х + -) = 6.
\ х7 \ х) \ *'
2.86. х4 - 2х3 - 18х2 — 6х + 9 = О.
2.87. 4х4 - 8хэ + Зх2 - 8х + 4 = О.
2.88. Зх2 + 5х + - + А = 16.
х х
2.89. х4 - 2хэ - 13х2 - 2х + 1 = О.
2.90. Решить уравнение
(х2 - 2х + 2)2 + Зх (х2 - 2х + 2) = 10х2.
Решение.
Поскольку х = О не является корнем данного уравнения,
(х2-2х + 2)2 , 3(х2-2х + 2)
то уравнение ----р-----+ —*-------------- 10 = О рав-
_ х2 - 2х + 2
посильно исходному. Пусть-----------= t. Тогда
t2 + 3t - 10 = О, t-2 или t = - 5.
Имеем:
х2 - 2х + 2 _ л
х ~ 2» х2 - 4х + 2 = О,
х2 - 2х + 2 _ х2 + Зх + 2 = О.
— О. L
X
Ответ: х = 2 + V2” или х = 2 — V2”, или
х = — 1, или х = — 2.
2.91. Решить уравнение (х2 + х + I)2 = х2 (Зх2 + х + 1).
Решение.
Преобразуем исходное уравнение:
(х2 + х + I)2 = х2 (2х2 + х2 + х + 1),
36
§2. Рациональные уравнения
(х2 + х + I)2 = 2х4 + х2 (х2 + х + 1).
Очевидно х = О не является корнем уравнения. Тогда
перейдем к равносильному уравнению
(х2 + х + I)2 Л , х2 + х + 1
----------2-------- = 2 + 2-•
X----------------------------X2
+ X + 1
Пусть----------- = t. Отсюда t2 — t — 2 = 0, / = — 1 или
t = 2. Имеем:
х2 + х + 1 _
х2 “ *» |2х2 + х + 1=0,
х2 + х + 1 _ х2 - х - 1 = 0.
2 ~ L
X
_ 1 + V3- 1 - VS"
Ответ: х = —-— или х = —z—.
Упражнения
Решить уравнения:
2.92. 2 (х2 + х + I)2 - 7 (х - I)2 = 13 (хэ - 1).
2.93. х4 + 5х2 (х + 1) = 6 (х + I)2
. _ . /х — 2\2 „ (х + 2\2 , ЛГ1 х2 — 4
2.94. 20 —гт ~5 ------------г +48 -ч-------- = О.
I* + 1J (х - 1J X2 - 1
2.95. (х2 - х + I)4 - 6х2 (х2 - х + I)2 + 5х4 = О.
2.96. (х2 - Зх + I)2 + 3 (х - 1)(х2 - Зх + 1) = 4 (х - I)2.
2.97. (2х - I)2 + (2х - 1)(х + 2) - 2 (х + 2)2 = О.
2.98. (х2 - х)4 - 5 (х2 - х)2 х2 + 6х4 = О.
2.99. (Зх2 + 7х - 2)2 + 5х2 (Зх2 + 7х - 2) - 24х4 = О.
2.100. Решить уравнение
2х + Зх _ _5
х2 - 4х + 2 х2 + х + 2 4 *
37
$2. Рациональные уравнения
Решение.
Поскольку х = О не является корнем данного уравнения,
то, разделив числитель и знаменатель каждой дроби, стоящей
в левой части, на х, получим уравнение, равносильное ис-
ходному:
2 3 = _ 5
„ 2 2 4 *
х-4 + - х + 1 + —
X X
О 2 15
Замена х 4- - = t. Тогда -—- 4- . . 4- - = О,
X I — 4 Г т 1 4
t2 + t-12 R = - 4,
4(1 —4)(1+1) "°’ t = 3.
Имеем
х + х ~ ~ 4’ х2 + 4х + 2 = О,
х + 2 _ з; х2 - Зх + 2 = 0.
Ответ: х = - 2 - VT или х = - 2 + V2~,
или х = 1, или х = 2.
Упражнения
Решить уравнения:
2.101. - —------- + 2 ----- = 1.
4х2 - 8х + 7 4х2 — 10х + 7
2.102. —------------------- = |.
х2 + 1 - 4х х2 + 1 + х 3
х2 - 10х + 15 _ 4х
X.lUOa 9 9
х - 6х 4- 15 х - 12х 4- 5
BillTti 9 9 ---- 1.
Зх - х + 2 Зх + 5х + 2
2.105. J.
х2 - 2х + 5 х2 + 2х + 5 8
2.106.--------------------2— ---------------j— - = ±.
X2 + Зх + 2 х2 + 5х + 2 24
38
}2. Рациональные уравнения
9 1Л7 х2 - Зх + 1 2х _ 7
4.1 и /•
X х2 - 2х + 1 2 ’
хг + 5х +4 х2 - х + 4 13
2.108. 2 “ = 0.
х - 7х + 4 х2 4- X + 4 3
х2 — 6х — 9 _ х2 - 4х - 9
2.109.
X х2 - 6х - 9 ’
2х2 + х + 2 _ 2х2 - Зх + 2
2.110.
Зх - х + 3 X - X -4 1
2.111. Решить уравнение (х + I)'1 + <х + 5)4 = 32.
Решение.
Пусть х = t — , т.е. х = t - 3. Тогда х + 1 = t - 2,
х + 5 = t + 2, и исходное уравнение станет таким:
(t - 2)4 + (t + 2)4 = 32.
После возведения в степень и приведения подобных сла-
гаемых получим уравнение t4 + 24Z2 = 0. Отсюда t = О, а
х = - 3.
Ответ: х = - 3.
Упражнения
Решить уравнения:
2.112. (х + З)4 + (х + I)4 = 20.
2.113. (х - 2)4 + (х - З)4 = 1.
2.114. (х + 5)4 + (х + З)4 = 2.
2.115. (х - 6)4 + (х - 4)4 = 82.
2.116. (х - З)4 + (х + I)4 = 256.
2.117. (х - 2)4 + (х + I)4 = 17.
2.118. х4 + (х - I)4 = 97.
39
§2. Рациональные уравнения
2.119. Xs + (6 - х)5 = 1056.
2.120. (х - 2)* + (х - 4)6 = 64.
2.121. (х - I)5 + (х + З)1 = 242 (х + 1).
2.122. (х - З)4 + (х - 2)4 - (2х - 5)4 = 0.
81х2
2.123. Решить уравнение х2 + ; = 40.
(х + 9)2
Решение.
Выделим квадрат разности в левой части уравнения:
2 _ 18х2 , 81х2 18х2 _
Х х + 9 (X + 9)2 Л + 9
Пусть g = t Тогда t2 + 18Г — 40 = 0, t = — 20 или
t = 2. Отсюда
7+"9 = ~ 20, Г*2 + 20х + 180 = 0,
х2 _ х2 - 2х - 18 = О.
х + 9
Ответ: х = 1 — V19”или х = 1 + V19.
Упражнения
Решить уравнения:
2.124. х2+ М-й =8.
I х - 11
/ \2
2.125. х2 + I—4тI =3.
х + 1
40
§2. Рациональные уравнения
2.126.
2.127.
2.128.
2.129.
2.130. х2 +
2.131. х2 + = 7.
(х + 3)2
2.132. Решить уравнение
х - 3 х + 4
х + 3 х - 4
Решение.
Имеем:
5х — 8____________5х + 12
(х - 1)(х - 4) (х + 2)(х + 3)
5х2 + 5х - 16
(х - 1)(х - 4)(х + 2)(х + 3)
Ответ: х =
-5-У345~
10
ИЛИ X
-5 +У345~
10
41
$2. Рациональные уравнения
Упражнения
Решить уравнения:
2х - 1 Зх - 1 х - 7 , .
х + 1 х + 2 х - 1
х + 4 х - 4 _ х + 8 х - 8 _ 8
х-1х4-1“х-2х4-2 3'
X2 * + 4х + 4 _ 2х 4- 6 = х2 4- х + 1 _ 2х 4-9
X 4-4 х 4-2 х 4- 1 х 4-3 '
х - 1 х - 2 _ х - 4 х - 5
х + 2 х + 3 ~ х + 5 х 4-6 ’
х - 1 х - 2 _ х - 3 х — 4
X 4- 1 ” х 4- 2 “ X 4- 3 х 4-4 '
2 X2 4- 8х 4- 20 _ X2 4- 4х 4- 6 X2 4- 6х 4- 12
+ х 4-4 “ х 4-2 + X 4-3
2.133.
2.134.
2.135.
2.136.
2.137.
2.138.
2.139.
/24 —5х , 5—6х
31 ---TV + —
1x4-1 X 4- 4
2.140.
4- 370 = 29
/17 —7х 8х 4-55\
X 4-2 X 4-3 J
112 4-19
/8 - Зх
х 4-3
3 — 2х\
X 4- 7 J
/15-х 314-2х\
“ 17 | ~ ’ । , I •
1x4-4 х 4- 6 I
Задачи для самостоятельного решения
Решить уравнения:
1. 4- = 2,9.
х х2 4-1
2. (х - 2)(х 4- 1)(х 4- 4)(х 4- 7) = 19.
3. (Зх2 + 7х - 2)2 -г 5.с2 (Зх2 4- 7х - 2) - 24х4 = 0.
42
§2. Рациональные уравнения
4. (х + 4) 4 + (х + 10)4 = 462.
$ 2х 7х
’ Зх2 - х + 2 Зх2 + 5х + 2 ~
С-2
Решить уравнения:
i х + 2 х + 6 х+10
1. —;—г • —;—z’ » ----;—~ — о.
х + 1 х + 3 х + 5
2. (2х2 - х + 5)2 + 3 (2х2 - х - 1) - 10 = 0.
3. 2 (х - I)2 - 5 (х - 1)(х - а) + 2 (х - а)2 =
4. 6х4 + 7хэ - 36х2 - 7х + 6 = О.
О.
С-3
Решить уравнения:
1 -aL- + x + 1 = —I____________1-
X2 _ 4 2 (х - 2) 2-х х + 2*
2. (х - I)4 + (х + 7)4 = 100.
3. х4 + 1 = 2 (х + I)4.
4 + Sx = -
’ х2 + х — 2 х2 + 2х - 2 3‘
5. (х - 1)(х - 8)(х + 2)(х + 4) + 36х2 = О.
43
§3. Рациональные неравенства
Немного теории
Определение.
Р.(х) Р2(х) Р(х) .
Неравенство вида „ , ч ч + ... + ( £ О, где
QiW Q2W QmW
Л (*)> Л (*)’•••> Лн (*)» С1 (*)> Q1 (*)» — . От (*) - целые ра-
циональные функции, называется рациональным неравен-
ством.
Определение.
Квадратным трехчленом называется выражение вида
ах2 + bx + cf где а, Ь, с — некоторые действительные числа
(параметры), причем а* О.
Теорема.
Если х{ и х2 — корни квадратного трехчлена ах2 +
4- Ьх + с, то ах2 + Ъх + с = а(х- х^(х - xj.
Теорема.
Если дискриминант квадратного трехчлена отрицатель-
ный, то его знак зависит от знака старшего коэффициен-
та: если а > 0, то ах2 + Лх + с > 0 при всех х; если а < 0, то
ах2 + Лх + с < 0 при всех х.
Определение.
Функция вида
у = ах2 + Ьх + с,
где ах2 4- Ьх 4- с —
квадратный трех-
член, называется
квадратичной.
Фактически все
основные свойства
квадратичной фун-
кции определяются
таблицей — рис. 7.
Рис. 7
44
§3. Рациональные неравенства
Решение неравенств вида
' W (* " «««Х* " «м+г) - aj С °*
Изобразим числа ар а2,..., ап на координатной прямой.
Эти числа, расположенные в порядке возрастания, разобьют
координатную прямую на п + 1 промежутков знакопостоян-
ства функции /(х), т.е., если а{ и ак — соседние точки, то
для любого х е (at; а*) функция /(х) сохраняет знак. Таким
образом, определив знак функции / в любой (удобной для
вычислений) выбранной точке каждого из п + 1 промежутков,
мы установим знак / на каждом промежутке. Такой прием
решения неравенств называется методом интервалов.
Полезные упражнения
Решить неравенства:
3.1. х2>0. 3.2. х2 0.
3.3. Л + 1 > 0. X 3.4. х(х2+ 1)>0.
„ _ х2 + 1 „ , х4 + 1
3.5. < 0. 3.6. х— > 0.
X х2
- - х — 1 Л Л х — 1
3.7. -—> 0. 3.8. 0.
х - 1 х - 1
3.9. 3.10. =£ 1.
х - 1 2 X - 1
/ 2
(х — 2\ _ _ (х — 2\
3.11. -—£ > 0. 3.12. -—= > 0.
\х “ 3/ V “ 3/
3.13. X + - > - - 1. 3.14. ~ > 0.
X X х - 4
3.15. (х- 1)(х —2)2>0. 3.16. (х - 1)(х + 2)2 0.
3.17. (х + 2)(х + З)2 < 0. 3.18. (х + 2)(х - З)2 « 0.
3.19. х2<а. 3.20. х2 Э а.
3.21. х2 - а2. 3.22. х2> - а2.
45
§3» Рациональные неравенства
3.23. ах > О. 3.24. ах < 1.
3.25. ах а. 3.26. а х 0.
3.27. (х - 2)(х - а) < 0. 3.28. (х - 3)(х - а)2 > 0.
3.29. (х - 3)(х - а)2 > О. 3.30. (х - а)(х + 2)2 < 0.
3.31. (х - а)(х + 2)2 О. 3.32. О.
3.33. (х-5)(х-а) $
х — а
Решить систему:
3.34.
3.36.
х< 1,
х> а.
х2 - 1 £ О,
х<а.
х2 - 4 < О,
Комментарии, указания, ответы
Заметим, что в этих упражнениях нет необходимости
применять метод интервалов.
3.1. х<0 или х>0. 3.2. 0. 3.3. х<0 или х>0. 3.4. х>0.
3.5. х<0. 3.6. х<0 или х>0. 3.7. х<1 или х>1. 3.8. х<1
или х>1. 3.9. х<1 или х>1. 3.10. х<1 или х>1. 3.11.
х<3 или х>3. 3.12. х<2, или 2<х<3, или х>3. 3.13.
-1<х<0 или х>0. 3.14. 1<х<4 или х>4. 3.15. 1<х<2
или х>2. 3.16. х=—2 или х 1. 3.17. —3<х<— 2 или
х < - 3. 3.18. х = 3 или х =5 - 2. 3.19. Если а О, то нет
решений; если а>0, то -Та"<х<Та! Указание. При а>0
данное неравенство равносильно неравенству |х| <Va. 3.20.
Если а О, то х — любое; если а > О, то х S - Та" или
х Та! 3.21. Если а # 0, то нет решений; если а = О, то
х = О. 3.22. Если а = 0, то х < О или х > О; если а # О, то х —
любое. 3.23. Если а = 0, то нет решений; если а < 0, то
х < О; если а > О, то х > О. 3.24. Если а = О, то х — любое;
если а < О, то х > —; если а > 0, то х < —. 3.25. Если а = О,
а а
то х — любое; если а > О, то х г 1; если а < 0, то х < 1.
46
$3. Рациональные неравенства
3.26. Если а = О, то х — любое; если а # О, то х О. 3.27.
Если а = 2, то нет решений; если а < 2, то а < х < 2; если
а > 2, то 2 < х < а. 3.28. Если а 3, то х > 3; если а>3, то
3 < х < а или х > а. 3.29. Если а = 3, то х & 3; если а < 3, то
х = а или х 3; если а > 3, то х 3. 3.30. Если а = — 2, то
х< - 2; если а> — 2, то — 2<х<а или х< — 2; если а< — 2,
то х < а. 3.31. Если а = — 2, то х =£ - 2; если а > - 2, то
х а; если а<-2, то х « а или х = - 2. 3.32. Если а = 5,
то х>5; если а<5, то а х < 5 или х>5; если а>5, то
х & а. 3.33. Если а = 5, то х < 5; если а<5, то а<х<5 или
х < а; если а > 5, то х < а. 3.34. Если а 1, то решений нет;
если а<1, тоа<х<1. 3.35. Если а « - 2, то-2<х<2; если
-2<а<2, то х< 2; если а > 2, то решений нет. 3.36.
Если а^-1, то х<а; если то х^-1; если
а> 1, то 1 х<а или х — 1.
Основные типы задач
3.37. Решить неравенство
(х + 1)(3 — х)(х — 2)2<0.
Решение.
Согласно описанному выше методу интервалов изобразим
числа -1, 2, 3 на координатной прямой. Получим че-
тыре промежутка, на каждом из которых функция
/(х) = (х + 1)(3 - х)(х - 2)2 ----
сохраняет знак. «Мето- _____________________________У
дом пробной точки» не- 2
следуем знак / на по-
лученных промежут-
ках (рис. 8.) Теперь 8
можно записать
Ответ: х < - 1 или х > 3.
„ „о г, (х - 1)3(х + 2)4(х - 5) л
3.38. Решить неравенство д--------------е-л—=—4 < О.
(2х + 1)(х - 4)2
Рис. 9
47
§3. Рациональные неравенства
Решение.
Изобразим числа -2, - —, 1, 4, 5 на координатной прямой.
С помощью рис. 9. получим следующий
Ответ: (- оо; - 2) и 2; - U (1; 4) U (4; 5).
1 лл I
Упражнения
Решить неравенства:
3.39. (х - 2)(х + 4)(х - 7) О.
3.40. (х - 4)(х + 7)(2х - 5)(х + 2) « О.
3.41. (2х + 3)(х - 5)(х + 4)2 > О.
3.42. (х - 3)2(х - 1)(х + 8)(х - 6) Ъ О.
3.43. (х + 6)(х + 1)(х - 2)2(х - 3) « О.
(х + 3)(4 — х)(2х + 5)
(Зх - 1)(х + 4)
3.46. —* (х~ 0 (х + 5)— < о.
(1 - 4х)(х + 3) (х - 8)
(х - 5)(2 - х)2 (х - 6)4 (х + 9)
х2(1-5х)’(х-7)
3.48.
(х + 1)(4х + 7)(х - 10)2
(х + 4)(3х - 6)
> О.
349 (Зх + 1)(5х — 6)(х — 11)2 $ 0
(х — 4)(1 — 7х)2(х —3)
3.50. Решить неравенство
(х - 4)(х - 3)(3х -7-х2) > 0
х2 + х — 2
48
§3. Рациональные неравенства
Решение.
Поскольку дискриминант квадратного трехчлена
Зх - 7 - х2 отрицательный, то Зх - 7 - х2 < О при всех х. Сле-
довательно, данное неравенство равносильно такому:
W - 3) < 0.
х2 + х - 2
Для удобства квадратный трехчлен, стоящий в знаменателе,
разложим на множители. Имеем:
(X - 4)(х - 3)
(х + 2)(х — 1) <0-
Рис. 10
Теперь легко исследовать знак выражения, стоящего в
левой части последнего неравенства — рис. 10.
Ответ: (- 2; 1) U (3; 4).
Упражнения
Решить неравенства:
3.51. (х2 - 4)(х + 1)(х2 + х + 1) > 0.
3 52 ~ 2)(х2 — 1)(4х — 5 — Зх2) <
х + 7
3.53. (*2-2х + 8)(х2-8) + 2х(2х-х2-8) < Q
49
$3. Рациональные неравенства
3.57.
- 2х + Зх + 2
3.58.
3.59.
3.60.
3.61.
3.62.
(х2 - 9)(х2 - 7х + 10)(х2 - 7х + 13) > 0
(2х2 + 7)(3 - 2х)
(х4 - 5х2 + 4)(х4 + 7х2 - 18) >
(х — 4)2 (Зх - 5)
____(х3-8)(*2~6х-7)________ 0
(Зх - 2х2 - 4)(3х2 - 10х + 3)
(х4 - Зх2)(х4 + х3 - 8х - 8)
(х — 1)(2 + х)
х* + Зх4 - х2 - 3 л
-----з----------< О.
х - 64х
3.63. + - 27^ > о.
2х2 - 5х + 2
3.64. Решить неравенство (х2 - 4)(х2 + х — 2) 0.
Решение.
Имеем: (х + 2)2 (х - 1)(х - 2) 0. На рис. 11а показан
знак выраже-
ния, стоящего в
левой части не-
равенства. Важ-
но не упустить,
что х = — 2 вхо-
Рис. 11а
ДИТ в
Ответ: [1; 2] U {- 2}.
Упражнения
Решить неравенства:
3.65. (х - 5)(х + 4)(х2 + 6х + 9) £ О.
з.бб. -~3х + 2 О.
6-х
50
$3. Рациональные неравенства
3.67. (х2 + 2х - 15)(х2 - 4х + 3)(х - 1) « О.
3.68. (х2 - 9)2 (х + 1)(х2 - 2х - 3)(х - 1) « О.
3.69. (х3 - 4х)(х2 + 2х - 8)(х2 + 7х + 10) О.
3.70. (х3 - 27)(х3 + 1)(2х + 3 - х2) » О.
3.72. (х2 - 4)(х2 - 4х + 4)(х2 - 6х + 8)(х2 + 4х + 4) » О.
3.73. (2х2 - х - 5)(х2 - 9)(х2 - Зх) О.
3,74. (*2-;°* + 21Х*г-^-7) s 0
(х + 5х + 6)(х - 4)
3.75. Решить неравенство 2 1 х 4- < 1.
Решение.
Преобразуем данное неравенство к виду
g(x)
< О. Имеем:
2 + х + 10 — 5х — 4 + х2 х2 — 4х + 8
(2 - х)(2 + х) °’ (2 - х)(2 + х) °'
Поскольку х2 — 4х + 8 > О при всех х, то данное неравен-
ство равносильно такому: (2 — х)(2 + х) < О.
Ответ: (— <»; — 2) U (2; «).
3.76. Решить неравенство (х2 + Зх + 1)(х2 + Зх — 3) 5.
Решение.
Пусть х2 + Зх + 1 = t. Тогда t (t — 4) 5. Отсюда
t2 - 41 - 5 » О, (t - 5)(Г + 1) О,
t - 1 или t 5 5.
Итак, исходное неравенство равносильно совокупности
х2 + Зх + 1^-1, Гх2 + Зх + 2«0,
х2 + Зх + 1 £ 5; х2 + Зх - 4 О;
51
}3. Рациональные неравенства
(х + 1)(х + 2) О,
(х + 4)(х - 1) £ О;
Ответ: (— ®; - 4 ] U [— 2; - 1 ] U [1; °0).
Упражнения
Решить неравенства:
3.77. - < 1. X 3.78. < 4-х 2.
3.79. -*-= > |. 3.80. < 3
_ л.
х - 5 2 х + 2 х - 3
а Я1 2х~5 < 1 1 Я“> J.
< 1
х - 6х - 7 * - 3 Э.Оа. | т 1 -х
3.83. —- - < 2. 3.84. 2 ~ —-—
х х - 1 х (х - 6) х - 1 ’
„ 2x4-3 „ 1 „ х + 7 . Зх + 1
3.85. -Z i. 3.86. т + —~0.
х + х - 12 2 х - 5 2
3.87. ~. 3.88. —Ц +
х2 - 9 * + 2 х - 2 х - 1 X
3.89. 7 гг + о —+ 1 < 0.
(х - 2)(х - 3) х - 3
3.90. (х2 - х - 1)(х2 - х - 7) < - 5.
3.91. (х2 + Зх)(2х + 3) - 16 • * О-
3.92. х2- 6х + 11 |.
3.93. (х2 + 2х + 1)(х2 + 2х - 3) 5.
3.95. 2х2 + 2х + 1--------------< 0.
х2 + х + 1
52
$3. Рациональные неравенства
|х — 3|
3.96. Решить неравенство —$--------- 2.
х2 - 5х + 6
Решение.
Данное неравенство равносильно совокупности двух си-
стем (а и ®.
х^ 3,
,3~* г 2.
х2 - 5х + 6
Преобразовав второе неравенство системы, получим
а)
х^ 3,
2х2 — 9х + 9 к
х2 - 5х + 6 ’
х 3,
(х-3)[х - I'
(х - 2)(х - ЗУ
Схема реше-
ния полученной
системы изобра-
жена на рис. 116.
Итак, имеем:
3
2 х < 2. Рис. U6
« О.
Поскольку 2х2 - 9х + 15 > О при всех х, то последняя
система равносильна такой:
х>3,
(х - 2)(х - 3) < О.
Понятно, что эта система решений не имеет.
Ответ: 2 ].
3.97. Решить неравенство
х2 - 5х + 4 <
х2 - 4 "
53
$3. Рациональные неравенства
Решение.
В данном неравенстве в отличие от предыдущего нет
необходимости раскрывать модуль. Достаточно, воспользовав-
шись соответствующей теоремой, перейти к системе, равно-
сильной исходному неравенству. Имеем:
х2-5х + 4
х2 — 4 "
х2 - 5х + 4
х2- 4
Рис. 12
Решение неравенств системы показано на рис. 12 а, б
соответственно. Найдя пересечение полученных множеств,
запишем следующий
Ответ:
Упражнения
Решить неравенства:
3.98.
|х| -3 < 2 •
3.99. |Х --—- < 2.
X
3.100. 12L+2L+* > L
х + 2
злм.
х - 3
2х.
54
§3. Рациональные неравенства
3.102. 2х- 1 х - 1 £ 2.
3.103. Зх 2 1.
х - 4
3.104. (|х| — 3)(|х| + 7)<0.
3.105. (|х| - 5)(|х| -7)^0.
3.106. (|х| — 17)(|х| + 6) =5 О.
3.107. х2 - 8х - , 3 + 18 « О.
|х - 4|
3.108. х2 + 10х - f - + 1 >0.
IX т 31
3.109. х + 4 х + 2 1.
3.110. со «о 1 1 X X 1.
3.111. - |2х - с2 + х - 11 - 2 3.
3.112. - |х- 11 ~ О s 1
х + 2 X J i * х + 2
3.113. 2 . < - 1. х |х - 1|
3.114. х2- 7 |х| + 1 х2 - 6х + 9 — < 0.
3.115. х2 - Зх + 2 < 1.
х2 + Зх + 2
Задачи для самостоятельного решения
С-1
Решить неравенства:
1. (х + 4)(5 — х)(3 — х)2 < О.
2 (х-1)2(х + 7)(х + 3)э * о
х2 + 6х + 9
55
§3. Рациональные неравенства
3 - —
л х х - 4
4. (х2 -6х + 1)(х2 - 6х + 3) « 80.
х2 — 9х + 8
х2 - 9
С-2
Решить неравенства:
1. (х - 6)(х - 4)(х + I)2 « 0.
3. ~2-----£----------2---------- < Т •
х2 + 2х + 2 х2 + 2х + 3 6
5. х2(х2 —7 |х| — 8)>0.
Решить неравенства:
3 ---------------- + ---------------<
Х (х - 1)(х - 4) + (х - 6)(х + 1)
5
з •
< 3.
5. -V---------- 2.
х2 - 5х + 6
56
§4. Степени и корни
Немного теории
Определение 1.
Степенью числа а с натуральным показателем п > 1
называется произведение п множителей, каждый из которых
равен а.
Определение 2.
а1 = а.
Определение 3.
а~я = Дг, где nGN и а* О.
<Г
Определение 4.
а0 = 1, где а # О.
Определение 5.
ви/я = уП", где mGZ, nGN, п > 1, а > О.
Определение 6.
О’"'" - 0, где т G N и п G N.
Свойства степени с рациональным показателем
Если а > 0, Ъ > 0, р G Q, q G Q, то справедливы следующие
теоремы:
Теорема 1. of • o’ = а'’*’.
Теорема 2. а*: а* = а*’-*.
Теорема 3. (ab)p -tf • V.
(а\р
Теорема 4. М = —.
Теорема 5. (tf)" - <F.
Замечание 1. Если pGZ и qGZ, то ограничение а>0
и Ь>0 можно ослабить до а # 0 и b # 0. Если pGN и
q е N, то ограничение а х О и М О остается лишь для теорем
2 и 4 соответственно.
57
§4, Степени и корни
Определение 7.
Корнем п-ой степени (nEN} г>1) из числа а назы-
вается такое число Ь, п-ая степень которого равна о, т.е.
У = а.
Замечание 2. Если п — нечетное, то корень n-ой степени
яз числа а обозначается Если п — четное, то корень
1-ой степени из числа а обозначения не имеет.
Определение 8.
Арифметическим корнем п-ой степени (nEN, п > 1)
из числа а называется неотрицательное число Ь9 п-ая сте-
пень которого равна а
Замечание 3. Арифметический корень n-ой степени из
числа а не зависимо от четности п обозначается
Свойства корней
Теорема 6. у а = I al.
Теорема 7. (>Га)п — а, причем если п — четное, то
а 0, если л — нечетное, то а — любое.
Если а О, b^O, пе N, п> 1,то справедливы следующие
теоремы:
Теорема 8. yfaS~ = 'Га- уЛГ.
Теорема 9. 4*0.
Теорема 10.
V Те” ="7а’, hi G N, т > 1.
Теорема 11. (v'a’)'" = '/сГУ meN.
Теорема 12. VoF = v'a", m е N.
Замечание 4. Если пит — нечетные, то ограничения
а >0 и Ь^О можно снять.
Замечание 5. Если n = 2k, kGNviab^O, то справедливы
следующие теоремы:
58
§4. Степени и корни
Теорема 13.
Теорема 14.
, если а & О, Ь > 0;
если а < 0, Ь < 0.
Полезные упражнения
4.1. Вынести множитель из-под корня:
а) 'J-a-, б) -а9;
в) Vx4y5; г) У/аЬт-,
д) у/9с?Ь, где а<0; е) Ч25а2Ь\ где а>0;
ж) 4cib\ где а<0, Ь<0\
з) ^а‘х‘; и) Ча2Ь2с\
K)lV-x’.
X
4.2. Внести множитель под корень: а) аТз”; б) аV— а; в) ат/а-З; г) (а + 2) V . ' 7 т а + 2
д> ж) aVF; з) хУз", где х<0;
и) л) avT; к) bcVc~; *2 у| ; м) 2аьу[^., IX 1
59
$4. Степени и корни
н) — ab V — + 4 > где а > О, Ь < О.
» а о
4.3. При каких а верно равенство:
а) ((а - 1Н* = а - 1;
б) V(a-2)2 = Va —2;
в) V?r= 4;
г) аТз’=7заГ;
д) а$Т= - Убе?-,
е) V(a- I)4 = VI - а;
ж) Va - 2 • Va + 1 = V(a - 2)(а + 1);
4-------
а + 4 _ V— а — 4
а-2 ~ ^2"—"а" ’
4.4. Известно, что выражение у/с?Ь определено. Что мож-
но утверждать о знаке числа Ъ1
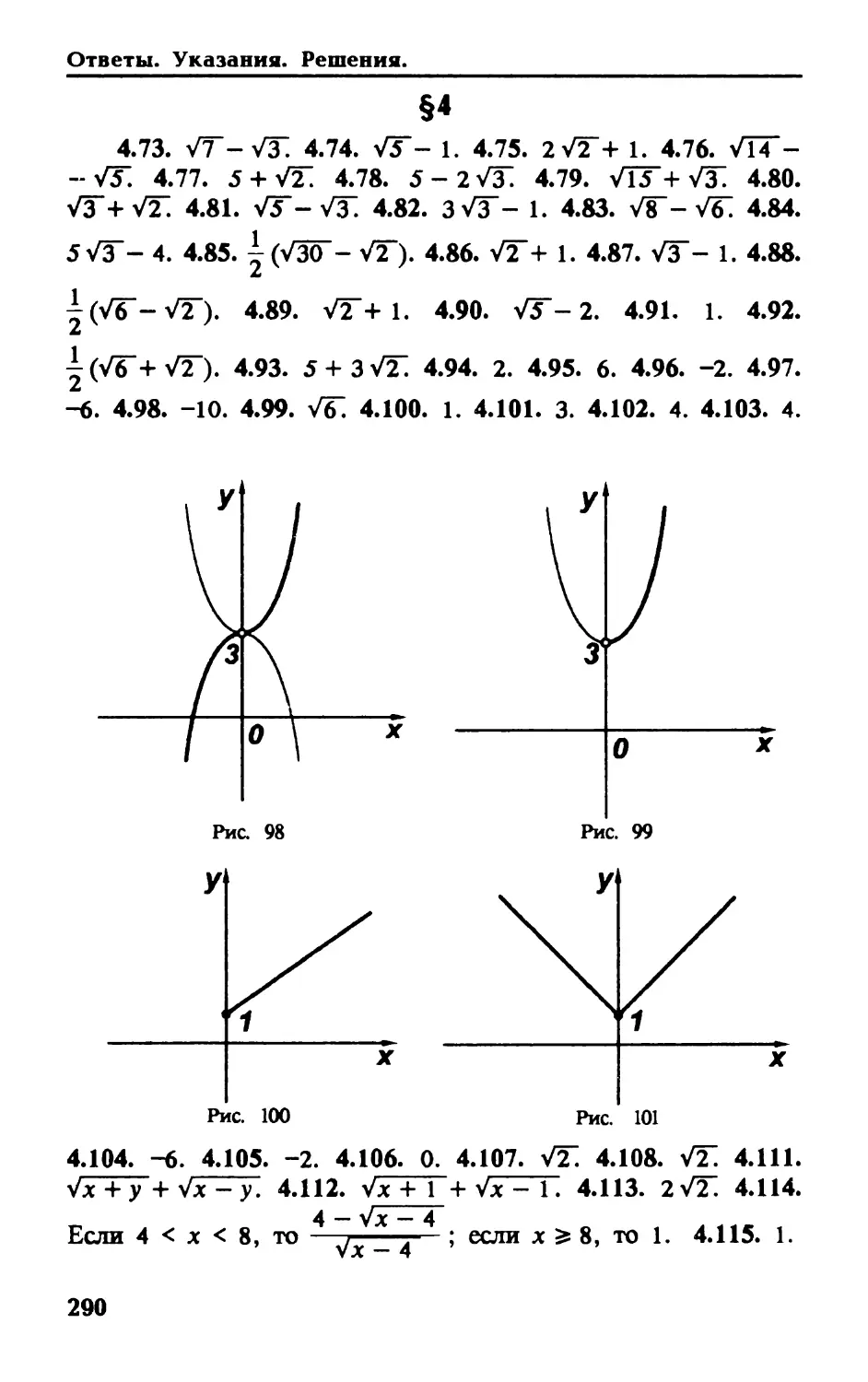
Построить графики функций:
4.5. у = V-x2.
.Ч Л/221
4.7. у= у-х-х -9.
4.9. у = Vx - 3 + V3 - х.
4.11. у = VF"ix.
4.13. у = (vGF)’.
4.15. у = (х-,/э)_э.
Решить уравнения:
4.16. Vx = - х2.
4.18. = - х2.
4.20. Vx- =х - |х|.
4.6. у = V— Vx”.
4.8. у = V- |х-2|.
4.10. у = Vx — |х|.
4.12. у = (Vx-)4.
4.14. у = (xVi)3.
4.17. VF= - |х|.
4.19. хиз = - 2.
4.21. VF= - (х + I)2.
60
§4. Степени и корни
4.22. х Vx”= - х.
4.23. Vx- 1 + |х - 11 = О.
4.24. Vx - 2 + V4 — х2 = О.
4.25. VP”= х2‘.
4.26. Vx2’= х.
4.27. Vxr= - x.
4.28. Vx - 2 Vx - 3 = 0.
4.29. Vx (x + 1) = Vx”Vx + 1.
4.30. V(x - l)(x - 2) = VI - x V2 - x.
4.31. x Vx - 2 = 0.
4.32. (x2 - 4) Vx”= 0.
4.33. Vx - 3 + V2 - x = 1.
4.34. Vx” = a.
4.35. a Vx — 1 = 0.
4.36. (x — 1) Vx — a = 0.
4.37. (x - a) Vx - 2 = 0.
Решить неравенства:
4.38. Vx”< - 1. 4.39. V5x + 2 < 3- VTo.
4.40. Vx - 2 > - 3. 4.41. V | x | > — 5.
4.42. VTxT>0. 4.43. V—jm V x + 3 JO.
4.44. Vx~0. 4.46. Vx”- Vxl 4.45. Vx”< 1. 4.47. Vx”> - Vjg
4.48. Vx”> x - |x|. 4.49. Vx”> x - | x|.
4.50. Vx”x — | x 1. 4.51. Vx”< x - | x|.
4.52. Vx2^ x. 4.54. x Vx + 3 >0. 4.53. VxF>x. 4.55. (x + 2) Vx
4.56. (x + 2) VF« 0. 4.57. |x+ 21 Vx>0.
4.58. |V2x + 3 -21 >- 1. 4.59. £--2 > — 3.
61
$4. Степени и корни
4.60. Ух~> а.
4.62. а уГх О.
4.64. (х — а) /х S О.
4.66. х Vx — а > О.
4.68. |х - а\ Ух”О.
4.61. Ух"а.
4.63. a ViT< О.
4.65. х Vx — а < О.
4.67. (x-a)VT<0.
4.69. |х - 1| Vx + а >0.
Комментарии, указания, ответы
4.1. а) — аЧ— а. Указание. Область определения данного
выражения а £ О; 6) а2^— а; в) x2y2Vy; г) absVa’, если
А О; — аЬ*>1а\ если 6<0; 0) — 3aVF; е) 5ab'JT>\ ж)
ab'TaF; з) ах2 Уд", если в О; — ах2 V— а, если а< О; и)
ab Ус", если а О, 6^0 или а О, 6<0; — ab Ус", если
а>0, 6<О или а<0, А>0; к) - х. 4.2. а) УЗд2, если
а О; - У Зв2, если a<О; б> — V— в2; в) Уд2 (в — 3); г)
Ув + 2; 3) - V2 - в; ё) у а- ; ж) ''J а*Ь, если a S О;
— у/с^Ь, если, в < О; з) - У5х2; a) V^Zo3; к) у/th?, если 5^0;
— УЛ?, если 5<О; л) у/1?', м) у/2с?Ь; н) у/al? + c?b. 4.3. в)
аЯ. Указание. См. определение 5; 6) а 2; в) aEN и
а # 1; г) а О; д) а О; в) а 1; ж) а 2; з) а — 4. 4.4.
Если а # О, то b О; если а = О, то Ь — любое. Особенностью
функций, рассматриваемых в задачах 4.S-4.9, является то,
что областью их определения служит всего лишь одна точка.
4.S-4.6. Искомый график — точка (О; О). 4.7. График —
точка Н; 0|. 4.8. График — точка (2; О). 4.9. График —
1 J /
62
}4. Степени и корни
точка (3; О). 4.10. Рис. 13. Ука-
зание. Область определения дан-
ной функции — все неотрица-
тельные числа. 4.11. Рис. 14.
4.12. Рис. 15. 4.13. Рис. 16. 4.14.
Рис. 14. Указание. См. опреде-
ление 5. 4.15. Рис. 17. Указание.
См. определение 6. 4.16. О. 4.17.
О. 4.18. Нет решений. 4.19. Нет
решений. 4.20. О. 4.21. Нет ре-
шений. 4.22. О. 4.23. 1. 4.24. 2.
4.25. х — любое. 4.26. х > О.
4.27. х 0. 4.28. 3. Указание. Область определения данного
уравнения х > 3. 4.29. х JO. См. теорему 13. 4.30. х < 1.
4.31. 2. 4.32. х = О или х = 2. 4.33. Нет решений. 4.34. Если
а < О, то нет решений; если а О, то х = а2. 4.35. Если
а#0, то х = 1; если а = 0, то хЯ. 4.36. Если а<1, тэ
х = а или х = 1; если а 1, то х = а. 4.37. Если а 2, то
х = 2; если а > 2, то х = а или х = 2. 4.38. Нет решений. 4.39.
Нет решений. 4.40. х > 2. 4.41. х — любое. 4.42. х < О или
х > О. 4.43. х > - 3. 4.44. О. 4.45. О х < 1. 4.46. х 5 О. 4.47.
х > О. 4.48. х > О. 4.49. х > О. 4.50. О. 4.51. Нет решений. 4.52.
х — любое. 4.53. х < О или х > О. 4.54. х = — 3 или х £ О.
4.55. Нет решений. 4.56. О. 4.57. х О. 4.58. х > -4.59.
х>0. 4.60. Если а<0, то х » О; если а&О, то х>а2. 4.61.
Если а < О, то нет решений; если а»О, тоО^х^а2. 4.62.
Если а < О, то х = О; если а 3= О, то х г О. 4.63. Если а > О,
63
§4. Степени и корни____________________________
то нет решений; если а < О, то х > О. 4.64. Если а О, то
х & О; если а > О, то х а или х = О. 4.65. Если а £ О, то
а < х < О; если а > О, то х = а. 4.66. Если а & О, то х > а; если
а<О, то х >О. 4.67. Если а > О, то О < х < а; если а О, то
решений нет. 4.68. х г О. 4.69. Если а — 1, то х > — а; если
а> - 1, тох>-аих*1.
Основные типы задач
4.70. Упростить выражение V? — 2
Решение.
Обычно, упрощая выражения вида Va + b'fc, есть смысл
попытаться представить а + b >Гс в виде квадрата двучлена.
Имеем: V7 - 2 V12 = V7 - 4 73~ =
= V4 - 4<Г+ 3 = V(2 - /З")2 = |2 - V3"| = 2 - VT
4.71. Упростить выражение V2 + V3”.
Решение.
г*- -\/4 + 2V3’ 1/1 +2V3"+3
V2 + V3-=V —J— = V---------2----- =
V(Vr +1)2 VT+ 1
2 “ VT ’
4.72. Упростить выражение V5V2~+ 7 — V5V2”— 7.
Решение.
Пусть
V5VT+ 7 - V5VT-7 = х. (*)
Тогда ( ^5V2~+7 - V5vT-7 )3 = х3,
5V2_+7-5V2-+7-3Vf5V2_+7 • V5<2”- 7 X
X ( V5VT4-7 - V5VT-7 ) = х3.
С учетом (*) имеем х3 + Зх — 14 = О. Отсюда
64
___________________________________§4. Степени и корни
х3 - 2х2 + 2х2 - 4х + 7х - 14 = О,
х2 (х - 2) + 2х (х - 2) + 7 (х - 2) = О,
(х - 2)(х2 + 2х + 7) = 0, х = 2.
Ответ: 2.
Упражнения
Упростить выражения:
4.73. У10 - 2 <21”. 4.74. Уб - 2<5.
4.75. У9 + <32*. 4.76. У19 - 2 <70”.
4.77. У27 + 2 V5Q. 4.78. Уз7 —5<48”.
4.79. У18 + 2<45". 4.80. Уз + <24~.
4.81. Ув -<бб”. 4.82. У 28 - <108”.
4.83. У14 - 8 <3”. 4.84. У91 - 40 <3”.
4.85. Ув-<1Т. 4.86. У17 + 12 <2”.
4.87. У28 - 16 <3”. 4.88. N97 - 56 <3".
4.89. А/б — У17 — 12 <2” ж
4.90. V 17 - 4 У9 + 4 <5”.
4.93. у 13 + 30 V 2 + У9 + 4<2”.
4.94. Уз + <8” - Уз-<8”.
4.95. Vll + 2<ТГ + У|2<18”- 1ТГ
4.96. Ув - <28” - Ув + <28”.
3 Алгебраический тренажер
05
}4. Степени и корни
4.97. V|12VT- 291 - V12VT+29.
4.98. V|2OVT-531 - +53.
4.99. V4 + V15" - V4-VT3-.
4.100. V2 + VT + ^2-VT.
4.101. ^9 +V86" + ^9-VSiT
4.102. ^20+ 14 VF + ^20- 14 VT.
4.103. ^26+ 15 vT + V26- 15 VT.
4.104. a/29vT-45 - V29VT+45.
4.105. (V5+2VF + Vvy+ vT) • Vvr-vr.
4.106. 1-------- L_-----.
V7-V2T+1 V7 + V2T-1
. ... 2 + VT 2-vT
4.107. f=== + ~zz—i _k
VT+V2 + VT vT-V2-VT
4.108.
4% - VvT+ 1
4.109. Упростить выражение
A = Vx + 2 Vx — 1 + Vx — 2 Vx — 1
при l<x<2.
Решение.
A « Vx - 1 + 2 Vx - Г+ 1 + Vx - 1 -2Vx- Г+ 1 »
= V(Vx — 1+ l)a + V(Vx — 1— I)2 =
= I Vx^T+ 11 + I VF=T- 11 =
= Vx- 1 + 1 + |Vx - 1 - II.
66
§4. Степени и корни
Поскольку по условию 1 £ х < 2, то х - 1 1. Следова-
тельно, А = Vx - 1 + 1 - Vx - 1 +1=2.
Ответ: 2.
4.110. Упростить выражение А =
V25 + 2 V? - 4
V52-4 + b + 2
Решение.
Из условия следует, что Vd2 - 4 - Ь. Отсюда нетрудно
показать, что Ь^2. Тогда
V52- 4 = V5- 2 • V5 + 2, b - 2 = V(5- 2)2,
5 + 2 = V(5 + 2)2.
V5-2 + 2V52- 4+ 5 + 2
Имеем. A - + + + ~
_ 'J(V5 - 2 + V5 + 2 )2 _ 1
“ V5 + 2(V5-2 +V5 + 2) “ VS + 2 ‘
Ответ: VFFT-
Упражнения
Упростить выражения:
4.111. V2x + 2Vx2-y2 при x y>0.
4.112. V 2x + 2 Vx2 - 1 при x £ 1.
4.113. Vx + 2 V2x - 4 - Vx - 2 V2x - 4 при x 4.
Vx - 4 Vx - 4 + 2
4.114. 1 -- .
Vx + 4 Vx-4 - 2
67
§4. Степени и корни
V 2а + 2 Va2 - 4b2 -Ча-2b
4.117. V 10х + 2 V25x2 - у2 - V 10х - 2 V25x2 - у2.
4.118. Vx2 +2 + 2>/х2+1 - Vx2 + 2-2>/x2+1 .
4.119. V 2а + 3 - 2 Va2 + За + 2 + Va+ 1.
4.120. V 2 — V4 — а2 при О < а < 2.
4.121. V д-2>/а*-а2.
4.122. V а2 + 2 Via2 - 4 + V а2 - 2 Тга2 - 4.
V2а + 2Va2 — b2’ — Ча — b
4.123. । -------, где b>Q.
V2а — 14 а2 - Ь2 + 'Га^Т
4.124. Построить график функции
у = V 2х — 2 Vx2 — 1 + Vx — 1.
rwmvmve
Имеем:
у = Vx - 1 - 2 Vx2 -1+x+l + Vx - 1.
Отсюда у = | Vx - 1 - Vx + 1 I + Vx - 1.
Поскольку Vx + 1 > Vx - 1, to
у = Vx + 1 — Vx — 1 + Vx - 1, у = Vx + 1.
При построении графика функции важно помнить, что
область определения исходной функции D(y) = [1; 00), тогда
как преобразования привели к функции у = Vx + 1, область
определения которой D(y) = [- 1; 00). Искомый график изо-
бражен на рис. 18.
68
$4. Степени и корни
Рис. 18
4.125. Построить график функции
/х Vx*
х + 1 |х-1| •
~7Г +
х + 1 + х - 1
Если 0<х < 1, то у = = х;
х + 1 _ х - 1
Vx* Vx*
х + 1 _ х - 1
если х > 1, то у = = —.
’ X + 1 X - 1 X
Vx* 4х
Искомый график изображен на рис. 19.
69
§4. Степени и корни
Упражнения
Построить графики функций:
4.126. у = -т-Г + 3.
NX
4127,у = ё/гу + 3*
4.128. y = (VT)4+ 1.
4.129. у = \/хГ+ 1.
4.130. у = (Vx)2 - Vx\
4.131. у = (Vx")’ - Vx\
4.132. у = Vx‘-2x’+ 1.
4.133. у = 2 + Vx4 + 6x2 + 9.
4.134. у - 2 + Vx4 - 8х2 + 16.
4.135. у = V4x2 + 4х + 1 - х.
4.136. у - (V2x + 1 )2 - х.
4.137. у = Vx2 - 6х + 9 + Vx2 + 6x + 9.
4.138. у = V25x2- 10х + 1 - V25x2 + 10х + 1.
4.139. у = Vx - 1 + 2Vx-2.
4.140. у - Vx + 3-2Vx + 2.
4.141. у = V2x + 2Vx2- 1 - Vx + 1.
4.142. у = V2x + 2Vx2-4 - Vx - 2.
70
§4- Степени и корни
Задачи для самостоятельного решения
С-1
1. Упростить выражения:
a) V4-2V3*; б) V6-V8”;
в) Vlx + 1 - 2 V2x".
2. Построить графики функций:
а) у = б) у = Vx2 - 4х + 4 + 2х.
С-2
1. Упростить выражения:
a) V6-2VS- + V6 + 2V8";
б) V2-VT;
в) V2 + 2VT- х2.
2. Построить графики функций:
б) у = V2X + 2 Vx2- 9 - Vx + 3.
С-3
1. Упростить выражения:
б) V8 + 2V1O + 2V5* + A/в — 2 V10 + 2 V3” .
2. Построить графики функций:
а) у = Vx2 + 2x + 1 - Vx2 - 2х + 1 ;
б) у = Vx + 2 Vx - 1 + Vx - 2 Vx - 1 .
71
§5. Иррациональные уравнения
Немного теории
Определение.
Два уравнения (х) = g1 (х) и f2 (х) = g2 (х) называются
равносильными (эквивалентными), если множество всех
корней первого уравнения совпадает с множеством всех
корней второго уравнения.
Определение.
Два уравнения (х) = (х) и f2 (х) = g2 (х) называются
равносильными на множестве М, если совпадают множе-
ства всех их корней, принадлежащих множеству М.
Определение.
Если множество корней уравнения f2 (х) = g2 (х) со-
держит множество корней уравнения (х) = gx (х), то
уравнение f2 (х) = g2 (х) называется следствием уравнения
ft 00 = ft 00-
Теорема.
Уравнение (/ (х))2" = (ft (х))**, nGN, является следстви-
ем уравнения / (х) = g (х).
Теорема.
Пусть для любого х G М / (х) 2= 0 и g (х) г 0. Тогда
уравнения / (х) = ft (х) и (f (х))“ = (ft (х))“, п G N, равносиль-
ны на множестве М.
Полезные упражнения
5.1. Какие из пар уравнений являются равносильными?
Какое из уравнений в парах является следствием другого?
а) х2 = 1 и |хI = 1;
6) х2 = х3 и х = 1;
в) х3 = 1 и | х I = 1;
г) х”4 =1 и х2 = 1;
д) х + 1 = 0 и (х + 1)(х2 + 1) = 0;
72
______________________ $5. Иррациональные уравнения
е) х2 + 2х+1=0их + 1=0;
ж) |х + 31 = 12 - х| и (х + З)2 = (2 - х)2;
з) — = 1 и х = х;
х
х) *—ц—= О и х2 - 1 = О;
х2 - 1
Л) Y+T
л<>^| = О.х!-1=О;
и) 2х - 3 = 3 - 2х и ——
х - 1 х - 1
о) Vx” =1 и х2 = 1;
п) Vx2” =1 и х2 = 1;
р) = 1 и Vx = 1;
с) Vx” = - 2 и = О;
m) VF+ 3 = О и х”91 + х”*4 + ... + х2 + х + 1 = О;
у) Vx + 1 = х — 1 и х + 1 = (х — I)2;
ф) V(x + 1)(х - 1) = О и (х + 1)(х - 1) = О;
х) Vx + 1 Vx — 1 = О и V(x + 1)(х — 1) = О;
ц) (х - 1) Vx + 1 = О и (х + 1)(х - 1) = 0;
ч) (х + 1) Vx - 1 = О и (х + 1)(х - 1) = О;
ш) х — 1 = О и (х + 1) Vx — 1 = 0;
щ) 2х + 3 = х - 1 и (2х + 3) Vx” = (х - 1)Vx”;
э) 2х + 3 = х - 1 и (2х + 3) Vx + 6 = (х - 1) Vx + 6;
ю) х2 + Vx”= Vx" + 1 и х2 = 1.
73
§5. Иррациональные уравнения
5.2. При каких значениях параметра а уравнения рав-
носильны?
а) х - 1 = 0 и (х - а)(х - 1) = 0;
б)х + 1= 0и(х + 1)(х2 + а) ж О;
в) Vx” = а и х = а2;
. X2 — 1 2 _
г)------- = О и х - 1 0;
х - а
_ х2 — 1 „ .
3)------« О и х - 1 = О;
х-в
х2- 1
е)------» 0 и х + 1 = 0;
X л
ж) |х| = а и х2 = а;
з) ах = 1 и х2 + х + 2 « О;
u) Vx” = а н ах » 1;
к) = а и ах = 1;
л) Vx” + а ж О н (а — 1) Vx” ж 1;
ж) х2 — а = О и | х | = а + 1;
н) a Vx”« 0 и х2 - а = 1;
о) eVx — 1 = О и х - а2 » О;
п) вVx” = 0 и |х| = ах2;
р) в2х » а и ах « 0;
с) — » 1 - а и — = 0;
х х
m) V(x — а)(х + 1) ж О и (х - a) Vx + 1 = 0;
у) V(x - а)(х + 1) » 0 и (х + 1) Vx - а = 0;
ф) х2 + Vx"ж Vx" + а и х2 = а;
х) 2х + 3“х + аи2х + 3 + Vx"«х + а + Vx”;
74
§5. Иррациональные уравнения
Комментарии, указания, ответы
5.1. а) (1) * (2); б) (2) * (1); в) (1) * (2); г) (1) * (2); 3)
(1) * (2); е) (1) ♦ (2); ж) (1) «► (2); з) (1) * (2); и) никакое
из данных уравнений не может являться следствием другого;
к) (1)*(2); л) (1)*(2); м) (1)*(2); н) (1)*(2); о)
(1) * (2); n) (1) ♦ (2); р) (1) * (2); с) (1) «► (2). Указание.
Данные уравнения не имеют решений, а следовательно, рав-
носильны; т) (1) ♦ (2). Указание. Первое уравнение решений
не имеет, Значит, любое уравнение (с одной переменной)
может являться его следствием. Кстати, второе уравнение
имеет по крайней мере один действительный корень, напри-
мер, х = -1; у) (1) => (2); ф) (1) *• (2); х) (1) * (2); ц)
(1)*(2); ч) (1)*(2); ш) (1)«*(2); щ) никакое из данных
уравнений не может являться следствием другого; э)
(1) * (2); Ю) (1)*(2).
5.2. а) а = 1; ® а>0; в) а О; г) а * ± 1; д) а = - 1;
ё) а=1; ж) а^О или а=1. Указание. При а<0 данные
уравнения решений не имеют, а следовательно, равносильны;
з) а = О. Указание. Второе уравнение корней не имеет, тогда
равносильность уравнений может обеспечить требование от-
сутствия корней у первого уравнения; и) а = 1; к) а = О или
а = 1. Указание. При а = О уравнения корней не имеют. Вто-
рые значения параметра находим, решив уравнение = —
<г а
л) 0<а^1. Указание. Равносильность данных уравнений
обеспечивается лишь требованием отсутствия корней у по-
следних, так как уравнение — а = д । решений не имеет;
м) а< - 1; н) а = - 1. Указание. Если а = О, то уравнения
не являются равносильными. Если а * 0, то достаточно по-
требовать, чтобы а = - 1; о) а= ± 1; п) a<Q. Указание. Если
а = О, то первое уравнение имеет бесконечно много корней,
а второе — один. Если а # О, то первое уравнение имеет
единственный корень х = 0, следовательно, второе уравнение
будет иметь своим корнем лишь х = О при условии а < О;
р) а = 0; с) а = 0. Указание. Если а # 0, то второе уравнение
корней не имеет; т) а^-1. Указание. Если а<—1, то
х = а не является корнем второго уравнения; у) а — 1;
ф) а 0; х) а 3. Указание. Данные уравнения равносильны,
75
§5. Иррациональные уравнения
если первое уравнение имеет неотрицательный корень; ц)
а< — 2 или а > - 2. Указание, Надо потребовать, чтобы первое
уравнение имело корень, отличный от 1.
Основные типы задач
5.3. Решить уравнение Vx2 + х - 3 = VI - 2х.
Решение.
Возведя обе части уравнения в квадрат, переходим к
уравнению-следствию: х2 + х — 3 = 1— 2х,
Гх = 1,
х = - 4.
Понятно, что найденные значения переменной должны
быть подвергнуты проверке. Она покажет следующий
Ответ: х = - 4.
Данное уравнение можно решать и методом равносильных
переходов. Для этого достаточно исходное уравнение заменить
равносильной системой
1 - 2х £0,
х2 + х — 3=1— 2х.
В этом случае проверку делать не надо.
Упражнашя
Решить уравнения:
5.4. Vx + 2 = V2x - 5.
5.5. V7x + 1 = 2Vx + 4.
5.6. Vx2 - 5x + 1 = Vx - 4.
5.7. Vx2 —8 «
5.8. V5x - 1 - V3x + 19 = 0.
5.9. V2x - 9 = V6 — x.
5.10. Vx2 - 36 = V2x- 1.
5.11. V8-5x « Vx2 - 16.
70
§5- Иррациональны^ уравнения
5.12. Vx2- 4х + 5 = Vx^T.
5.13. V6x2 + 2х - 10 = Vx2 — х — 2.
5.14. V&x2 + 2х - 14 = Vx2 — х — 6.
5.15. Vx + 7 • V3x — 2 = 3 Vx - 1 • Vx + 2.
♦ ♦ ♦
5.16. Решить уравнение Vx - 1 Vx + 4 = V6".
Решение.
Перейдем к системе, равносильной данному уравнению:
(х - 1)(х + 4) = 6,
х 1;
х = -5,
х = 2,
х > 1.
Ответ: х = 2.
Упражнения
Решить уравнения:
5.17. Vx - 1 V2x + 6 = х + 3.
5.18. Vx - 2 Vx + 5 =x.
5.19. V3-x V2-x = <2.
5.20. Vx + 1 Vx + 2 « 4.
5.21. Vx - 1 Vx + 1 = VjL
5.22. VI - x v7= x.
5.23. Vx + 2 V5 — x = 2.
ее*
5.24. Решить уравнение V1 + 4x - x2 = x — 1.
Решение.
Запишем систему, равносильную исходному уравнению:
1 + 4х - х2 = (х - I)2,
77
§5. Иррациональные уравнения
х = О,
х = 3,
х Я.
Ответ: х = 3.
Упражнения
Решить уравнения:
5.25. V4 + 2X-X2 = х - 2.
5.26. 7б - 4х - х2 = х + 4.
5.27. Vx2 + 8 = 2х + 1.
5.28. Vlx2 - 7х + 5 = 1 - х.
5.29. 1 + V1 + х Vx2"- 34 = х.
5.30. V12-X = х.
5.31. V7 -х = х - 1.
5.32. V5x + 1 = х - 1.
5.33. 2 Vx + 5 = х + 2.
5.34. V5x + 1 = 1 - x.
5.35. Vx2 —4x + 13 = |x + 2.
5.36. Vx + 7 - x + 3 = 0.
5.37. V2x2 + 8x + 7 - 2 = x.
5.38. x + V2x2 - 14x + 13 = 5.
5.39. 3x - V18x + 1 +1=0.
5.40. V3x2 —3x + 21 = x - 5.
5.41. V3 + Vj-x" = Vxl
78
§5. Иррациональные уравнения
5.42. V 1 + х Vx2 + 42 = х + 1.
5.43. ^5-Vx+l + V2x2 + x + 3 = 1.
5.44. 9 - V81 - 7хэ = у .
* * *
5.45. Решить уравнение (х - 3) Vx2 - 5х + 4 = 2х - 6.
Решение.
Перепишем данное уравнение в таком виде:
(х - 3) (Ух2 - 5х + 4 - 2) = О.
Казалось бы, х = 3 — корень данного уравнения. Однако
число 3 не входит в его область определения. Чтобы избежать
подобных неприятностей, решение проведем по такой схеме.
Данное уравнение равносильно системе
х2 - 5х + 4 » О,
. Гх — 3 = О,
Ух2 - 5х + 4 = 2.
Теперь понятно, что исходное уравнение равносильно
такому: Ух2 - 5х + 4 =2, х2 - 5х = О.
Ответ: х = О или х = 5.
Упражнения
Решить уравнения:
5.46. (х + 1) Vx2 + x - 2 = 2х + 2.
5.47. (х + 2) V16x + 33 = (х + 2)(8х - 15).
5.48. (х - 1) Vx2 - х - 6 = 6х - 6.
5.49. (х + 1) V16x + 17 = (х + 1)(8х - 23).
79
§5. Иррациональные уравнения
5.50. 3 (4х + 3) V16x + 17 = (4х + 3)(8х + 5).
5.51. (х + 2) Vx2-x - 20 = 6х + 12.
5.52. (х + 1) Vx2-6x + 17 = Зх + 3.
5.53. (х 4- 4) V2x - 4 = (х + 4)(х - 1).
5.54. Решить уравнение V2x - 3 + V4x + 1 = 4.
Решение.
На области определения уравнения (7 =
части принимают неотрицательные значения
3 \
—; оо обе его
X J
г Тогда данное
уравнение равносильно системе
2х — 3 + 2 V(2x - 3)(4х + 1) + 4х + 1 = 16,
Отсюда
V8x2 - 10х - 3 = 9 - Зх,
8х2 - 10х - 3 = 81 - 54х + 9х2,
' 2 ’
9 - Зх Ъ О;
х2 - 44х + 84 = О,
2 ’
х £ 3;
х = 42,
х = 2,
I < X « Э;
х = 2.
Ответ: х = 2.
80
$5. Иррациональные уравнения
5.55. Решить уравнение V3x + 1 — Vx + 4 = 1.
Решение.
Имеем: V3x + 1 = Vx + 4 + 1. Обе части этого уравнения
на его области определения принимают неотрицательные зна-
чения. Возведя их в квадрат, получим уравнение, равносиль-
ное исходному: Зх + 1 = (Vx + 4 + I)2. Тогда
Зх + 1= х + 4 + 2 Vx + 4 + 1,
2 Vx + 4 = 2х — 4, Vx + 4 = х — 2,
х + 4 = (х - 2)2, х2 - 5х = О,
х - 2 » О, х £ 2,
х (х - 5) = О,
х 2,
Ответ: х = 5.
Упражнения
Решить уравнения:
5.56. V2x + 6 - Vx + 1 = 2.
5.57. Vx + 5 - Vx"= 1.
5.58. V2x-4 - Vx + 5 = 1.
5.59. V2x + 5 = 8 - Vx - 1.
5.60. Vx + 3 + V3x —2 = 7.
5.61. Vllx-2 + 3 VF= 6.
5.62. Vx + 5 + V5-x = 4.
5.63. 2 V3x + 2 - V6x" = 2.
5.64. V3x + 1 + V16 - 3x = 5.
5.65. 3 Vx + 3 - Vx - 2 = 7.
81
$5. Иррациональные уравнения
5.66. Vx - 13 = Vx + 8 - 3.
5.67. Vx - 3 + V6 - x = V3~.
5.68. V3x-2 + V2x + 5 = 5.
5.69. V3x-5 = 3 - Vx-2.
5.70. Vx + 2 + V3-x = 3.
5.71. V4x + 8 - V3x — 2 = 2.
5.72. Vx + 4 + V2x + 6 = 7.
5.73. V3x — 7 - Vx + 1 = 2.
5.74. 2 Vx - 1 + Vx + 3 = 2.
5.75. Vx + Vx + 1~ + Vx - Vx + 1~ = 4.
5.76. Решить уравнение V2x — 5 + Vx + 2 = V2x + 1.
Решение.
На области определения данного уравнения G =
обе его части принимают неотрицательные значения. П
данное уравнение равносильно системе
Зх - 3 + 2 V2x-5 Vx + 2 = 2х + 1,
xU.
' 2
Отсюда
2 V2x - 5 Vx + 2 = 4 - х,
х - 2.
Обе части уравнения системы принимают неотрицатель-
ные значения на множестве Н = —; 4 С G. Следовательно,
исходное уравнение равносильно системе
82
___________§5. Иррациональные уравнения
8х2 - 4х - 40 = х2 - 8х + 16,
-2-6VTT
Х 7
-2 + 6VTF
* 7
| £ х £ 4.
Лл
- 5 x $ 4:
[2 *
7x2 + 4x - 56 = 0,
5 x * 4;
_ -2 + 6VTT
Ответ: x = ----------.
Заметим, что это уравнение, впрочем, как и все, приве-
денные выше, можно решать методом перехода к уравнени-
ям-следствиям. Однако это целесообразно делать тогда, когда
«подозреваемые» корни удобны для проверки, чего нельзя
сказать о последнем примере.
Упражнения
Решить уравнения:
5.77. V3x + 4 + Vx - 4 = 2 VT
5.78. Vx + 1 - V9 -х = V2x - 12.
5.79. 2 Vx - 1 - Vx + 2 - V5x - 10 = 0.
5.80. V8x + 1 + V3x — 5 = V7x + 4 + V2x-2.
5.81. Vx + 3 - V2x - 1 - V3x — 2 = 0.
5.82. Vx + 1 - V2x — 5 - Vx - 2 = 0.
5.83. V5x + 1 - V6x - 2 - Vx + 6 + V2x + 3 = 0.
5.84. V2x + 1 + Vx-3 = 2 VT
5.85. Vx + 2 - V2x — 3 = V4x-7.
5.86. Vx - 2 + V4 - x = V6 - x.
5.87. Vx" + Vx-3 - V3(x - 1).
5.88. Vx + 1 + Vx - 1 = V3x - 1.
5.89. V8 -x - V9 + 5X - V4 - 5x + V5 + x = 0.
83
$5. Иррациональные уравнения ___________________
5.90. V2x + 3 + V3x + 2 = V2x + 5 + ТЭГ.
5.91. Vllx + 3 - >12-x = V9x + 7 - Vx - 2.
♦ ♦ ♦
5.92. Решить уравнение
V4xi + 9x + 5 - V2x2 + x - 1 = Vx2 - 1.
Решение.
Выгодно разложить квадратные трехчлены, стоящие под
радикалами, на множители:
V(x + 1)(4х + 5) - V(x + 1)(2х — 1) = V(x - 1)(х + 1).
Теперь важно не совершить распространенную ошибку,
а именно: применить теорему о корне из произведения в
таком виде: На самом деле записанная формула
справедлива лишь при а > О и 5^0, а если а 0 и 5 < О,
то Va5~= V- а >/- Ь.
Поскольку областью определения данного уравнения есть
множество (—«>’, -4 U [1; °0) U {- 1}, то последнее урав-
I 4
некие равносильно совокупности двух систем и одного урав-
нения:
х Ъ 1
Vx + 1 V4x + 5 - Vx + 1V2x — 1 = Vx - 1 Vx + 1 ;
ХЭ 1,
V4x + 5 - V2x - 1 = Vx - 1;
x > 1,
2 V4x + 5 V2x - 1 = 5x + 5;
x > 1,
4 (4x + 5) (2x - 1) = 25x2 + 50x + 25;
x & 1,
x = 5,
9
7
x = 5.
84
§5. Иррациональные уравнения
б)
V-x — 1 V-4x — 5 — V-x - 1V—2х + 1 = V—х + 1V—х - 1 ;
V— 4х — 5 — V- 2х + 1 = V— х + 1 ;
V— 4х — 5 = V—2х + 1 + V—х + 1
2 V(2x - 1)(х - 1) = - х - 7;
х - 7,
7х2 - 26х - 45 = О;
Понятно, что эта система решений не имеет.
в) х + 1 = 0, х = - 1.
Ответ: х = - 1 или х = 5.
Заметим, что данное уравнение можно решать методом
следствий. Наметим схему решения.
Уравнение
V|x + 11 V|4x + 5| - V|x + 1| V|2x — 1| = V|x - 11V|x + 11
является следствием исходного. Последнее в свою очередь
равносильно совокупности
х = - 1,
VI4X + 5I -V|2x- 1| = V|x- 1|.
Заметим, что техническую работу по раскрытию модулей
можно значительно сократить, обратившись к области опре-
деления исходного уравнения.
85
$5. Иррациональные уравнения
Упражнения
Решить уравнения:
5.93. Vx24-x —2 + Vx2-4x4-3 = Vx2 - 1.
5.94. Vx2 - 4x 4- 3 - Vx2 —Зх 4-2 = Vx2-x.
5.95. Vx2 - 4 + Vx24-2x —8 = Vx2-6x4-8.
5.96. Vx2 —3x4-2 + Vx2 —6x + 8 = Vx2- llx+ 18.
5.97. V2x2 + 5x + 2 - Vx2 + x-2 = V3x4-6.
5.98. Vlx2 - 5x + 2 - Vx2 —x —2 = Vx2-3x4-2.
5.99. 2Vx2 - 2x - 8 - Vx2 - 16 = V3x2- 13x4-4.
5.100. Vx2 —3x- 10 4- Vx2 4- 3x 4- 2 = Vx24- 8x 4- 12.
5.101. Решить уравнение
(VI 4-х 4- 1)(V1 4- x 4- 2x - 5) = X.
Решение.
Умножим обе части уравнения на выражение V1 4- х -1.
Получим уравнение-следствие
X (VI 4- х 4- 2х - 5) = х (Vx 4- 1 - 1).
Это уравнение равносильно совокупности
х = О,
VI 4-х 4- 2х - 5 = Vx 4- 1 - 1.
Решим второе уравнение совокупности. Его следствием
будет 2х — 5 = - 1. Отсюда х = 2.
Осталось произвести проверку. Ей подвергнем значения
х = 2, х = О. Легко убедиться, что первый корень подходит,
а второй — нет.
Ответ: х = 2.
Прежде чем приступить к раэбору следующего примера,
отметим, что выражение VI 4- х - 1 обращается в нуль при
х = О. Именно это значение и оказалось посторонним корнем.
86
$5. Иррациональные уравнения
5.102. Решить уравнение
V21 + х + V21 — х
V21 + х - V21 - х
21
х
Решение.
Умножим числитель и знаменатель дроби, стоящей в
левой части уравнения, на V21 + х + V21 — х.
Эта операция приведет к следующему уравнению, рав-
21 + V21 - х V21 +х 21
носильному исходному:-------------------- = —.
Это уравнение, в свою очередь, равносильно совокупности
1*21 — х = О,
21 + х = 0.
Ответ: х = 21 или х = - 21.
Упражнения
Решить уравнения:
5.103. Vlx2 + Зх + 5 + V2xI-3x + 5 = Зх.
5.104. (Vx + 1 + l)(Vx + 10 - 4) = х.
5.105. (Vx + 1 + 1)(V1 + x + xa + x - 7) = x.
c t(wt Vx + 6 — V6-x _ X
5.106.
5.107. Vxa-5x + 2 - Vxa + x + 1 = 1 - 6x.
5.108. V5x + 7 - Vx + 4 = 4x + 3.
5.109. V2xa + 8x + 6 + Vxa- 1 = 2x + 2.
5.110. V17 + x + V17 -x = 4 •
4
5.111. V20 + x + V20 - x =
S.112. V20*' + V-— = VT
V X v X
V2O + x д/20-х
------ ~ V--------- =6.
x V x
87
$5. Иррациональные уравнения
5.114. Решить уравнение
х2 + Зх - 18 + 4 Vx2 + Зх - 6 = О.
Решение.
Пусть Vx2+ Зх - 6 = Г, t О. Тогда х2+ Зх - 18 = t2- 12,
и исходное уравнение становится таким:
Г2 - 12 + 4t = О.
Тогда
t = - 6,
t = 2.
Понятно, что подходит липп» t = 2. Итак, исходное урав-
нение равносильно такому:
Vx2 + Зх - 6 = 2, х2 + Зх - 6 = 4.
Ответ: х = — 5 или х = 2.
Упражнения
Решить уравнения:
5.115. vGF +г7Р"= з.
5.116. = 2.
VT+2 5
5.117. xVT- УхГ= 2.
5.118. xVT + 2 УхГ= 3.
5.119. х2** + х*42 = 12х’Л
о
ЛоЬг-'/го^г-2'
5.120.
5.121.
5.122.
з._ 1Г~з
х'Гх - 1 Vx - 1
Vx2 - 1 vT + 1 ”
88
$5. Иррациональные уравнения
5.123. х >Гх — 4 Vx2" +4 = 0.
5.124.
X '/х = 56.
5.125. х2 + 11 + Vx2 + 11 = 42.
5.126. х2 - 2 Vx2 - 24 = 39.
5.127. х2 + 2 V41 - х2 = 26.
5.128. Vx~- 3 + 6 = 5Vx-3.
5.129. Vx2 + 32 - 2 Vx2 + 32 = 3.
5.135. -*
5.136. x Vx2 + 15 - Vx" • Vx2 + 15 = 2.
5.137. 2x2 + 3x - 5 V2x2 + 3x + 9 +3 = 0.
5.138. x2 + Vx2 + 2x + 8 = 12 - 2x.
5.139. 2x2 + V2x2- 4x + 12 = 4x + 8.
5.140. x2 - 4x + 6 = V2x2- 8x + 12.
5.141. 3x2 + 15x + 2 Vx2 + 5x + 1 = 2.
5.142. Vx2 - 3x + 7 = Зх + (x - 3)2 - 22.
89
$5. Иррациональные уравнения
5.143. (Vx + 1 + Vx-)’ + (Vx + 1 + Vx-)2 = 2.
5.144. Vx2 + x + Vx2 + x + 5 = Vzx2 + 2x + 17.
5.145. Vx2 + x + 4 + Vx2 + x + 1 = V2x2 + 2x + 9.
♦ ♦ ♦
5.146. Решить уравнение
Vx + 4 + Vx - 4 , ,/-5—— .
---------------- = x + Vx - 16 - 6.
Решение.
Пусть Vx + 4 + Vx - 4 = t,t^O. Тогда, возведя в квадрат
обе части последнего равенства, получим
2х + 2 Vx2 — 16 =t2.
t t2
Теперь данное уравнение становится таким: 2 = 2~ ~
Отсюда t = 4 или t = - 3. Следовательно, исходное уравнение
равносильно такому: Vx + 4 + Vx — 4 = 4. Далее,
х ^4, (х 4,
2х + 2 Vx2 - 16 = 16; Vx2 - 16 = 8 - х;
4 £ х 8,
х2 - 16 = 64 - 16х + х2.
Ответ: х = 5.
5.147. Решить уравнение
х2 + х Vx + 1 - 2 (х + 1) = О.
Решение.
Поскольку х = О не является корнем данного уравнения,
, Vx+T 2(х + 1) Л
го уравнение 1 + — -----------—4 = О равносильно ис-
^одному. Пусть —-— = t, тогда 2t2 — t - 1 = О. Отсюда
t = 1 или t = - . Имеем:
90
§5. Иррациональные уравнения
Ответ: х = —— илл х = 2 — 2 >/2.
5.148. Решить уравнение +
1 = 5
V 13-х2 6 ’
Решение.
Возведя обе части данного уравнения в квадрат, перейдем
к уравнению-следствию. Имеем:
1 1 2 = 25
х2 13 - х2 х V13 - х2 36 '
„ 13 2 25 _ л
ЮДах2(13-х2) х V13 - х2 36
Теперь замена * 2 = t стала очевидной.
25
Находя корни уравнения 13?2 + 2t - -тг =0, переходим
□О
к совокупности
1 = j_
х <13 — х2 6 ’
1 = _ 25
х V13 - х2 78 ’
□с ~ ~ V48T±13
решениями которой являются числа 2, 3 и--------—----.
„ V48T- 13
Проверка показывает, что х =---------не удовлетворяет
исходному уравнению.
_ V48T+13
Ответ: х = 2 или х = 3, или х =--77.---.
91
$5. Иррациональные уравнения
Упражнения
Решить уравнения:
5.149. Vx - 1 + Vx + 3 + 2 V(x - 1)(х + 3) = 4 - 2х.
5.150. V2x + 3 + Vx + 1 = Зх + 2 V2x2 + 5x + 3 - 16.
х2 ,______
5Л51-72?+5 +<2ГТУ=2Х-
5.152. (х + 4)(х + 1) - 3 Vx2 + Зх + 2 = 6.
5.153. 4Х2 + 12х VI +х = 27 (1 + х).
5.154. х + V(x + 6)(х — 2) = 2 + Vx + 6 + Vx — 2.
5.155. (34-х)^х+Т-(х + 1)^4^Т =
V34 — х — Vx + 1
5.156. 6 + &Г=~2 = 5 V(x - 3)(х - 2).
5.157. 5 Vx + 1Vx + 3 = 2 V2"(x2 + 4x).
5.159. Решить уравнение
у/(2 - х)1 + ^(7 + х)2 - % (7 + х)(2 - х) = 3.
Решение.
Пусть у/2-х = а, у/7 + х = Ь. Тогда
а2 + б2 - ab = 3,
а* + 6*« 9;
(а + Ь)г — ЗаЬ = 3,
а + Ь « 3;
а2 + б2 - ab = 3,
(а + д)(а2 + *2-а6)®9;
’|а= 1,
ab = 2, р * 2;
а + 4»3; (а «2,
16= 1.
92
$5. Иррациональные уравнения
Теперь можно записать
>12-х — 1,
|^Г+Т= 2; гх e j
▼ А — л — щ
$7+Т=1;
Ответ: х = 1 или х = — 6.
Упражнения
Решить уравнения:
5.160. ^9-Vx + Г + V7+VxTT = 4.
5.161. Vx+T-v*3x + 2 = 0.
5.162. yfx + 7 - Vx + 3 « 0.
5.163. Vx + 8 -v'x-fc =2.
5.164. ^18 + 5x + v*64-5x = 4.
5.165. ^12 -x + V14 + x » 2.
5.166. ^13 -x + V22 + x « 5.
5.167. Vx - 2 + Vx - 1 « 5.
5.168. vT=x"= 1 - Vx^E
5.169. ^14+ x + V12-X = 6.
5.170. v^43 + x - ^x - 16 = 1.
5.171. ^54 + VT + >/54-Vx =
5.172. v5T=T + vT+T= 2.
5.173. yfx - 16 » ^x + 3 - 1.
5.174. V*2 + llx + ^2- llx = 4.
93
$5. Иррациональные уравнения
5.175. V80 + х + V2 — х = 4.
5.176. V97 — х + йс"= 5.
5.177. Vx — 4 = 1 - Vx+ 1.
5.178. V(x + З)2 + а/(6 —х)2 - V(x + 3)(6 - х) = 3.
5.179. У/(х + 4)2 + А/(х - 5)2 + V(x + 4)(х - 5) = 3.
5.180. V(8-х)2 + Л/(27 + х)2 = V(8 - х)(27 + х) + 7.
♦ ♦ ♦
5.181. Решить уравнение
Vx + 3 - 4 Vx - 1 + Vx + 8 —6Vx — 1 = 1.
Решение.
Имеем:
Vx - 1 - 4 Vx - Г+ 4 + Vx - 1 - 6 Vx - Г+ 9 = 1,
V(Vx - Г- 2)2 + V(Vx - 1 - 3)2 = 1,
IVx- 1 -2| + |Vx- 1 -31 = 1.
Это уравнение равносильно совокупности трех систем.
Vx - 1< 2, [Vx — 1< 2,
-Vx-1 4-2-Vx-l + 3 = 1; I Vx - 1 = 2.
Эта система решений не имеет.
2 Vx-1 =£ 3,
б) ,_____ ._________
Чх - 1 - 2 - Vx - 1 +3 = 1;
4 £ х - 1 9,
1 = 1;
5 sS х 10.
94
}5. Иррациональные уравнения
Vx — 1> 3, Vx - 1> 3,
в) ______ __________ • ______________
Vx - 1 - 2 + Vx — 1 — 3 = 1; [Vx — 1 « 3.
Эта система решений не имеет.
Ответ: 5 < х < 10.
Упражнения
Решить уравнении:
5.182. Vx + 6 + 2Vx + 5 + Vx + 6 —2Vx + 5 «6.
5.183. Vx —4 + 4Vx —8 - Vx-4-4Vx-8 «2.
5.184. Vx + 2Vx - 1 - Vx - 2Vx - 1 « 3.
5.185. Vx-2 + V2x-5 + Vx + 2 + 3V2x-5 = 742.
5.186. Vx2 + 2VF=T- Vx-2Vx-1"« 2.
5.187. Vx2 + 5 —4Vx + 1 + Vx + 2 —2Vx+ 1 » 1.
5.188. Vx + 2 + 2a/x + 1 + Vx + 2 —2Vx + l « 2.
Задачи для самостоятельного решения
С-1
Решить уравнения:
1. V4x- 1 - х = 1.
2. Vx2 - 32 » <^4jg
V3x2 + x _ yl х2-1 3
x2 - 1 ’ Зх2 + x " 2’
4. Vx - 10 + yfx - 17 « 3.
5. 4х-5 + 24х~=Т + Vx-2 + 2VTzT » 8.
95
§5. Иррациональные уравнения
С-2
Решить уравнения:
1. Vx - 2 Vx - 3 = 4.
2. V2x - 7 + Vx - 3 = 2.
3. Vx2- Зх + 11 - 4x2 + 12x = 11.
4. У/5Х + 2 - y/5x-2 = 2.
5. 10x2 - 2x - 1 - 3x V2x + 1 = 0.
C-3
Решить уравнения:
1. (x + 5) Vx2 - 6x + 5 = 2x + 10.
2. Vx"+ Vx - 5 = V10 - x.
3. V?6 + Vx" + V?6-Vx" = 8.
5. Vzx2 + x- 1 + Vx2 —x —2 = Vx2 - 3x - 4.
96
§6. Иррациональные неравенства
Немного теории
Определение.
Два неравенства f (х) > g, (х) и f2 (х) > g2 (х) называются
равносильными (эквивалентными), если множество решений
первого неравенства совпадает с множеством решений вто-
рого неравенства.
Определение.
Два неравенства (х) > g, (х) и f2 (х) > g2 (х) называются
равносильными на множестве М, если совпадают множе-
ства их решений, принадлежащие множеству М.
Определение.
Если множество решений неравенства f2 (х) > g2 (х) со-
держит множество решений неравенства f (х) > gt (х), то
неравенство f2 (х) > g2 (х) называется следствием неравен-
ства Ъ (ж) > g, (х).
Теорема.
Пусть для любого х G М f (х) э 0 и g (х) 0. Тогда
неравенства/(х)>g(х) и (f (х))">(g(ж))", neN равносиль-
ны на множестве М.
Теорема.
Неравенство V/ (ж) > Vg (ж), п е N, равносильно системе
/(x)>g(x),
g(x)=?0.
Теорема.
Неравенство V/(x) > g (х), п е N, равносильно совокуп-
ности двух систем:
’Jg(x)<0,
|/(х)^0,
|/(х) >(«(«))*•
4 Алгебраический тренажер
97
$6. Иррациональные неравенства
Теорема.
Неравенство *7(х)< g (х), п G N, равносилию системе
I (*) >0.
/(x)<(g(x))*,
/(*) £0.
Полезные упражнения
6.1. Какие из пар неравенств являются равносильными?
Какое из неравенств в парах является следствием другого?
а) х > 1 и х > 2;
® х2>1 и |х| >1;
е> х’> 1 и |х| > 1;
е) х4>1 и х2> 1;
® х + 1 >0 и (х + 1)(х2 + 1)>0;
е) х2 + 2х + 1 >0 и х + 1 >0;
ж) |х + 3|>|2 —х| и (х + З)2> (2 - х)2;
з) (х - 1)(х — 2) > О и х - 2 > 0;
и) -—< 0 и х - 1 > О;
X в л»
к) ——Ц < 0 и х - 1 < 0;
(х - 2)2
л) —Ц > О и х - 1 >0;
(х - 2)2
ж) (х — 1)2(х — 2) J0 и х - 2^0;
н) (х - 1)(х - 2)2 0 и х - 1 О;
о) - > 0 и х > О;
х
п) — > 1 и х < 1;
х
х + 1
с) 1 и х> 1;
98
$6. Иррациональные неравенства
т) Vx~<1 и х< 1;
и х2> 1;
ф) -/х > - 2 и х > 4;
х) Vx”< - 2 и х < 4;
ц) V(x + 1)(х - 1) > О и (х + 1)(х - 1) > О;
ч) Vx + 1 Vx — 1 > О и V(x + 1)(х — 1) > О;
ш) (х - 1) Vx + 1 < О и х < 1;
щ) (х + 1) Vx — 1 > О и х > — 1.
6.2. При каких значениях параметра а неравенства рав-
носильны?
а) х - 1 >0 и (х - а)(х - 1) > О;
® х — 1 >0 и (х — а)2(х - 1) >0;
в) х — а > О и (х — 1)2(х — а) > О;
г) Vx”> а и х > а2;
д) Vx~> а и —-—5 > О;
(х + I)2
е) Vx~<а и х<а2;
ж) Vx”< а и 0 х < а2;
з) Vx”< а и х2 + 1 0;
и) Vx”> - 1 и х>а;
к) Vx”> - 1 и х а;
л) Vx”< - 1 х — а Л и . . < 0;
м) V(x - а)(х - 1) > О и (х - а)(х - 1) > О;
м) Vx — а Vx — 1 >0 и V(x — а)(х - 1) >0;
о) (х - 1) Vx - а > О и х > 1;
я) (х - а) Vx - 1 >0 и х> а;
р) х + Vx”> Vx” + а и х > а.
99
$6. Иррациональные неравенства
Комментарии, указания, ответы
6.1. а) (2) *> (1); ® (1)0(2); в) (1) * (2); г) (1)*(2); 3)
(1)о(2); е) (2)*(1); ж) (1)о(2); з) (2) о (1); и) (1) о (2);
к) (1)о (2); л) (1)о(2); м) (2)-> (1); н) (1)о(2); о)
(1)о(2); п) (1)о(2); р) (2) о (1); с) (1)о(2); m) (1) о (2);
у) (1)о(2); ф) (2)о(1); х) (1)о(2); ц) (1)о(2); ч)
(1) о (2); ш) (1) о (2); щ) (1) о (2).
6.2. а) нет таких значений параметра а; б) а<1;
в) а 1; г) а О; 3) а = О; е) нет таких значений параметра
а; ж) а > О; з) а О. Указание. Поскольку второе неравенство
решений не имеет, то и решением первого неравенства должно
быть пустое множество; и) нет таких значений параметра
а. Указание. Решением первого неравенства является проме-
жуток [О; о), однако второе неравенство является строгим,
поэтому число 0 не может являться его решением; к) а = 0;
л) а = - 1. Указание. Первое неравенство решений не имеет,
второе неравенство не имеет решений только при а = — 1;
м) а — любое; и) нет таких значений параметра а;
о) а 1; п) а > 1; р) а & 0.
Основные типы задач
6.3. Решить неравенство
Vx2 - Зх + 1 > V3x - 4.
Решение.
Данное неравенство равносильно системе
х2 - Зх + 1 Зх - 4,
Зх - 4 » О;
1.
(х - 5)(х - 1) £ О,
х =U;
Л " 3’
Ответ: х 5.
100
§6. Иррациональные неравенства
Упражнения
Решить неравенства:
6.4. Vx + 2>Ve—х2.
6.5. Vx + 1 > Vx - 1.
6.6. Vx2 + 5x < Vl -x2 + 4x.
6.7. V2x2 + 5x-6 > V-x - 3.
6.8. V2x2 + 6x + 3 Э V-x2-4x.
6.9. Vx2 - 7x + 5 V3x —4.
6.10. V4x2 —4x + 2 =5 Vl + x-2x2.
6.11. Vlx2 —x —6 =s Vx2-4.
6.12. VT^x"Ъ
6.13.
x - 2
x + 2
2x - 3
4x- 1
6.16. Решить неравенство Vlx2 — Зх —5 < x — 1.
Решение.
Данное неравенство равносильно системе
х- 1>0,
2х2-Зх - 5<(х - I)3,
2х3 - Зх - 5 0;
х>1,
(х — 3)(х + 2) < О,
(х + 1) [х ~ ^0;
101
$6. Иррациональные неравенства
X - 1
Х>А.
2
Ответ: < х < 3.
Упражнения
Решить неравенства:
6.17. Vx + 7< х.
6.18. Vx2-3x — 10 <8 - х.
6.19. Vx2 + 3х + 3< 2х + 1.
6.20. х + 4>2V4-x2.
6.21. V4x - х2 < 4-х.
6.22. V(x - 6)(х - 12) <х - 1.
6.23. V(x - 3)(2 - х) < 3 + 2х.
6.24. Vx2 - Зх - 18 < 4-х.
6.25. Vx2 — Зх<5 —х.
6.26. V5- |х + 1| 2 + х.
6.27. <4^.
6.28. V4 -VI -х~ - V2 -х >0.
6.29. Решить неравенство Vx2 + 7х + 12 > 6 - х.
Решение.
Данное неравенство равносильно совокупности двух си-
стем.
а)
6 —х<0,
X2 + 7х + 12 £ 0;
х>6,
х - 4, х > 6.
х Ъ -3;
102
96. Иррациональные неравенства
6 - х £ О,
х2 + 1х + 12 > (6 - х)2;
24
Ответ: х > —.
24 „ .
19 < Х * 6
Упражнения
Решить неравенства:
6.30. V2x + 4>x + 3.
6.31. Vx2 —2х > 4 - х.
6.32. V — х2 + 6х — 5 > 8 - 2х.
6.33. Vx + 4 > V2 - V3 + х.
6.34. Vx2-5x-24>x + 2.
6.36. V2x2 + 5x-6>2-х.
6.37. V(x + 4)(х + 3) > 6 - х.
6.38. V-x2-8x- 12>х + 4.
6.39. Vx2 —4х>х - 3.
6.40.
хэ+ 27
х
> х - 3.
6.41. Решить неравенство (х - 3) Vx2 + 4 х2 - 9.
Решение.
Перепишем исходное неравенство в таком виде:
(х - 3) (Vx2 + 4 - х - 3) « 0.
Это неравенство равносильно совокупности двух систем.
а)
х - 3 £ О,
Vx2 + 4 « х + 3;
х Э 3,
х2 + 4 х2 + 6х + 9;
103
$6. Иррациональные неравенства
хЭЗ,
X - 3 О,
Ух2+ 4 Ъ х + 3;
х « 3,
О' |о»
Ответ!
и [3; оо).
Упражнения
Решить неравенства:
6.42. (х + 1) Ух2 + 1 >х2 - 1.
1 - У1 — 4х
Ув — 2х — х2 Ув-2х-х2
х + 10 2х + 9
У12 — х — х2 V12 -х -х2
2х - 7--------х - 5
Уб + х — х2 Уб + х-х2
2х + 5 х + 4 •
Уз - 2х - х2 Уз - 2х - х2
х + 8 2х + 1
У15 + 2х - х2 У15 + 2х -J
Зх + 9 4х + 5
У2-Х-Х2 Уг-х-х2
х-4 2х + 11 ’
104
§6. Иррациональные неравенства
6.52. Решить неравенство (х - 1) Vx2 - х - 2 0.
Решение.
Вероятно, наиболее рациональный путь решения нера-
венств подобного вида — это переход к следующей совокуп-
ности:
(х - 1) Vx2 - х - 2 = 0,
(х - 1) Vx2 - х - 2 > 0.
Решим уравнение совокупности. Оно равносильно системе
х2 - х - 2 0,
2 Л Л Г* = 2,
Гх — 1 = 0, х Х 2 - °’ |х = - 1.
х2 - х - 2 = 0;
Неравенство совокупности равносильно системе
х - 1 >0,
х>2.
х2 - х - 2 > О;
Ответ: х = — 1 или х г 2.
Упражнения
Решить неравенства:
6.53. (х+ 10) Vx - 4 « 0.
6.54. (х + 2) V(4 - х)(5 - х) Э 0.
6.55. (х - 12) Vx-З « 0.
6.56. (х + 1) Vx + 4 Vx + 7 « О.
6.57. (х + 2)2 (х - l)2Vx=T2 0.
6.58. (х - 3) Vx2 + x —2 Ъ 0.
6.59. (х - 1) Vx2-x —2 ЭО.
6.60. (х - 2) 716-х2 « О.
105
§6. Иррациональные неравенства
6.62. (7х + 2) V9 -х2 £ О.
6.63. (х + 8) Vx2 —5х + 4 0.
6.64. (2х + 3) V9x2- 10х + 1 3= 0.
6.65. (х2 - 1) Vx2 - 4 О.
6.66. (х2 - 9) V16 - х2 Э 0.
6.67. (х2 + Зх - 10) Vlx2 + 5х + 2 3= 0.
♦ ♦ ♦
6.68. Решить неравенство Vx - 2 + Vx — 5 * Vx - 3.
Решение.
Данное неравенство равносильно системе
х 3> 5,
х — 2 + 2 V(x — 2)(х — 5) + х- 54х-3;
х 3: 5,
2 V(x - 2)(х - 5) < 4 - х,
Понятно, что эта система решений не имеет.
Ответ: решений нет.
Упражнения
Решить неравенства:
6.69. 3 Vx"- Vx + 3 > 1.
6.70. V1 - х2 + V4-x2< 2.
6.71. Vx^T- VxVlO < 1.
106
______________________§6. Иррациональные неравенства
6.72. Vx + 3 — Vx — 1 > V2x - 1.
6.73. Vx + 3 < Vx - 1 + Vx —2.
6.74. Vl -3x - V5 + x> 1.
6.75. Vx — 2 + V2x + 5 > 3.
6.76. V2x- 1 + Vx + 15 « 5.
6.77. 3 Vx + 3 - Vx — 2 £ 7.
6.78. Vx~ + Vx - 5 V10 - x.
6.79. 2 Vx" + V5 - x > Vx + 21.
6.80. А/х + Л+ Д/х-Л >-•
V x2 V x2 x
* * *
6.81. Решить неравенство
V3x2 + 5x + 7 - V3x2 + 5x + 2 > 1.
Решение.
Пусть Зх2 + 5x + 2 = t, t&O. Тогда
VF+T-VF>1, VFF5’>VF+1.
Это неравенство равносильно системе
гэо, ft&o,
t + 5>t+2VF+l; VF<2.
Отсюда OS t<4. Теперь
достаточно решить систему
Зх2 + 5х + 2 О,
Зх2 + 5х + 2 < 4.
(х + 1)^х + 3s О,
(x + 2)fx " I) < 0;
107
§6. Иррациональные неравенства________
Г рх а£ - 1,
2
• [* " 3’
- 2 < х <
л 2 1
Ответ: - 2 < х =S - 1 или - -z х < -г.
•J «j
Упражнения
Решить неравенства:
6.82. V4x2 + х + 9 + V4x2 + x >3.
6.83. Vx2-х + 2 + Vx2-x + 14 >6.
6.84. Vx2-5x + 4 + Vx2 - 5x + 20 Э 4.
6.85. Vx2-2x-2 + Vx2-2x + 6 < 4.
108
§7. Системы алгебраических уравнении
Немного теории
Теорема.
Система уравнений
F (х; у) = Ф (х; у),
У = /(«)
равносильна системе
У = /(*)•
Теореме.
Система уравнений
Л(х; у) = Ф1(х; у),
у) = ф2(»; у)
равносильна каждой из следующих систем:
Z (х; У) + Р2 (х; у) = Ф, (х; у) + Ф2 (а; у),
>,(х; у) = Ф,(х; у);
Р, (х; у) + J2 (х; у) = Ф, (х; у) + Ф2 (х; у),
Л(х? У) = Ф2(х; у);
Л (х; У) - Р2 (х\ У) = Ф( (х; у) - Ф2 (х; у),
>,(х; у) = Ф,(х; у);
[#, (х; у) - Р2 (х; у) = Ф1 (х; у) - Ф2 (х: у),
[Л(*5 У) = Ф2(х; у);
(х; у) + Р2 (х; у) = Ф, (ж; у) + Ф2 (х; у).
' (х; у) - F2 (х; у) = Ф, (х; у) - Ф2 (х; у).
109
§7. Системы алгебраических уравнений
Теорема.
Система
Л (* у) • Л (*; у) = ф, (»; у) • ф2 (*; у).
Л (*; у) = ф> (*; у)
является следствием системы (*).
Теорема.
Если в множество решений уравнения
F2(x; у) = Ф2(х; у)
не входят такие пары (х; у), при которых обе части этого
уравнения обращаются в нуль, то каждая из следующих
систем
Л (* у) • Л (»; у) = ф1 (*; у) • ф2 О; у).
F, (х; у) = Ф, (х; у);
Zfo у) = ф1 (у. у)
Л (* у) фз (»; у)’
F,(x; у)-Ф1(х; у)
равносильна системе (♦).
Определение.
Однородным многочленом от двух переменных х и у
называется многочлен вида
+ а/’-’у + + ... + ап_^Г' +
где at (i = 0, 1,..., п) — некоторые действительные числа.
Определение.
Симметричным многочленом от двух переменных х, у
называется многочлен, который не изменяется при замене
х на у и у на х.
110
§7. Системы алгебраических уравнений
Основные типы задач
7.1. Решить систему
1________1 = 1
, у - 1 у + 1 X ’
у2 - х - 5 = О.
Решение.
Имеем:
Подставив в первое уравнение вместо у2 двучлен х + 5,
получим систему, равносильную исходной:
2 _ 1
х + 4 х ’
у2 = х + 5;
х « 4,
у2 = 9;
Ответ: (4; 3), (4; -3).
Упражнения
Решить системы уравнений:
7.2.
х2 + у2 + 6х + 2у - О,
х + у + 8 = О.
х2 + Зху - у2 = 92,
х + Зу = 18.
7.4.
Зх + у
х - 1
х - у = 4.
х-У
2у
= 2,
Зх + 2у = 7,
2х2 + у2 = 6.
111
$7. Системы алгебраических уравнений
7.8.
7.10.
7.14.
7.16.
ху _ 9
х - 3 2 ’
х + у = 12.
2х + у2 = 3,
Зх + / = 4.
у4 + ху2 - 2х2 = О,
X + у = 6.
х - 1 у + 1
4 = 2
х + 5 у '
2х2 + у — z = - 1,
Z + у - 2х = 1,
х4 + zy - у = 1.
7.9.
7.11.
7.13.
У-2
х - 1
= 2,
у - 2х = х2 - 1.
х3 + у = 1,
у3 — 4у2 + 4у + х6 = 1.
х3 + у = 35,
х2 - ху + у2 = 7.
7.15.
Зх = 2у = z,
х2 + у2 + z2 = 196.
7.17. Решить систему
х2 + у2 - х = 2,
(х - 1)(у + 3) = 2х2 - х - 1.
Решение.
Второе уравнение системы преобразуем следующим об-
разом:
(х - 1)(у + 3) = (2х + 1)(х - 1), (х - 1)(у - 2х + 2) = 0.
Тогда исходная система равносильна совокупности двух
систем.
а)
х2 + у2 - х = 2,
х = 1;
х = 1,
у = ТУ,
х = 1,
у = — VT.
б)
х2 + у2 - х = 2,
у = 2х - 2;
х2 + (2х - 2)2 - х = 2,
у = 2х - 2;
112
§7. Системы алгебраических уравнений
9 + V4T
Г 9 + V4T Х ~ 10 9 - V4T ” 10 Х ~ 10 - 1 + VTT = 5 9 - V4T
у = 2х - 2; Х 10 - 1 - VTT Г = 5
Ответ: (1; Т2~), (1; - V2~),
'9 + V4T - 1 + V4T \ /9 - V4T - 1 - V4T
10 ’ 5 ’ 10 ’ 5
Упражнения
Решить системы уравнений:
7.18.
4х2 + у2 - 2ху = 7,
(2х - у) у = у.
7.19.
(х - 2)(у + 2) = О,
х2 + 2у2 - Зх = 5.
7.20.
2х2 - Зху + 5у = 5,
(х - 2)(у - 1) = 0.
7.21.
(х + 4)(у - 1) = х2 + 5х + 4,
х2 - у2 - Зх + 8 = 0.
7.22.
х2 - 5у2 - Зх - у + 22 = 0,
(х - 3)(у - 2) = у2 - Зу + 2.
7.23.
2х2 - ху - Зу = 7,
2х2 + х - 3 = (х - 1)(у + 5).
ИЗ
$7. Системы алгебраических уравнений
7.24. х2 + у2 + 2х + 2у = 23, х2 + у2 + 2ху = 9.
7.25. Зх - 5ху +1=0, (У - 4х)2 = 4.
7.26. х2 - 2ху + у2 = 9, 4х2 + ху + 4у2 = 18.
7.27. х2 + у2 = 25 - 2ху, х - у = 5.
7.28. • х2 + у2 = 2 (ху + 2), х + у = 6.
7.29. х’ - у’ = 19 (х - у), х’ + у’ = 7 (х + у).
7.30. Решить систему
х2 + у2 - 2х = О,
х2 - 2ху +1=0.
Решение.
Сложим уравнения системы. Получим
х2 - 2ху + у2 + х2-2х + 1=0,
(х - у)2 + (х - I)2 = О.
Данная система равносильна такой:
(х - у)2 + (х - I)2 = 0,
х2 + у2 - 2х = О.
Первое уравнение полученной системы, в свою очередь,
равносильно системе
114
$7. Системы алгебраических уравнений
X = 1,
решение которой — пара (1; 1). Непосредственной подста-
новкой пары (1; 1) во второе уравнение системы (*) получа-
ем решение исходной системы:
х = 1,
\у= Ь
Ответ: (1; 1).
Упражнения
Решить системы уравнений:
7.31. х2 + у2 = 20, ху = 8.
7.32. х2 + у2 = 13, ху = 6.
7.33. х2 + ху = 15, у2 + ху = 10.
7.34. • х2 - ху = 6, у2 - ху = 3.
7.35. ху — х 4- у = 7, ху + х - у = 13.
7.36. х2 + Зху = 18, ху + 4/ = 7.
7.37. • х2 + у2 + х + у = 2, 2х2 - у2 + 2х - у = 4.
115
$7. Системы алгебраических уравнений
7.38.
7.39.
7.40.
7.41.
7.42.
7.43.
7.44.
7.45.
7.46.
7.47.
7.48.
Зх2 + ху-2х + у-5- О,
2х2 -ху-Зх-у-5 = 0.
х3 - х + 1 = у,
у3 - у + 1 = X.
х4 + хУ = 20,
у4 + х2у2 = 5.
2х2 - Зху + Зх - 2у = 2,
5ху - 2х2 + 7х - 8у = - 22.
Зх2 + Зу2 — 11х — 7у + 10 = О,
х2 + у2 - 4х - Зу + 5 « 0.
х2 + у2 + 2х = 23 - 2у,
2х2 + 2/ + 5у = 27 + Зх.
5х2 - Зу2 + 10х - 12у = 17,
2х2 + у2 + 4х + 4у = - 2.
х3 + 2х2у + ху2 - х - у = 2,
у3 + 2ху2 + х2у + х + у = 6.
х + у = 3,
у + z = 7,
z + х = 2.
у + z - х = 2,
z + x-y = 8,
х + у - z = 12.
х3 + у3 = 7,
ху (х + у) = - 2.
116
________________}7. Системы алгебраических уравнений
7.49. Решить систему
х* + у* = 7,
ху (х + у) = — 2.
Решение.
Покажем еще один способ решения этой системы, отлич-
ный от метода сложения. Разделим первое уравнение системы
на второе. Имеем:
(х + у)(х2- ху + у2) _ _7
ху (х + у) ~ 2 ’
х2 - ху + у2 _ _ 7 х + 2 _ i _ _ 7
ху 2 ’ у х 2 ’
Пусть у = Тогда
t = - . Следовательно,
t + 7 = - 7. Отсюда t = - 2 или
€ X
исходная система равносильна сово-
Ответ: (2; -1), (-1; 2).
Упражнения
Решить системы уравнений:
7.50. х2 - у2 = 16, х + у = 18. 7.51. х + у = 3, хэ + х2у = 12.
7.52. • х2 + у2 = 5, у6 + у*х2 = 80. 7.53. • хуэ + х3у = - 10, х У + х4у2 = 20.
7.54. • х*у‘ = 64, х‘у* = 256. 7.55. • (х - у)(9 - х) = 10, (х - у)(12 - у) = 20.
117
§7. Системы алгебраических уравнений
7.56. 2ху + 6х - у2 — Зу = 14, 7.57. • 2х2 + 4х - ху - 2у = 35. х2 - у2 = 3, х2 - ху = 2.
7.58. х’ - у’ = 26, 4 4 7.59. ' х — у = 20 (х + у). х2 + ху = 15, у2 + ху = 10.
7.60. (х - у)(х2 - у2) = 24, 7 б1 X + у = 6. (X + у)’(х - у)2 = 27, (х - у)*(х + у)2 = 9.
7.62. ху = 1, yz = 2, 7.63. zx = 8. ху + yz = 3, yz + zx = 10, zx + ху = 9.
7.64. (х + у)(у + z) = 1, (y + z)(z + x) = 1, 7.65. < (z + х)(х + у) = 4. II II II О>|Ы Ь>|О> O'
♦ * ♦
7.66. Решить систему
(х + у)(х2 - у2) = 9,
(х - у)(х2 + у2) = 5.
Решение.
Пусть у = xt, где t е R, 1*0. Тогда
(х + xt)(x2 - x2t2) = 9,
(х - xt)(x2 + х21 ’J = 5.
Отсюда
(i + 0(i-Q = 9
(1-0(1 +12) 5'
Г = 2.
Исходная система равносильна совокупности двух систем.
118
§7. Системы алгебраических уравнений
у = 2х,
х’= -1;
X = - 1,
У = -2.
Ответ. (2; 1), (-1; -2).
Заметим, что левые части уравнений системы — одно-
родные многочлены. Именно для таких систем целесообразен
вышеописанный метод решения.
Упражнения
Решить системы уравнений:
7.67. х2 - ху + у2 = 21, у2 - 2ху + 15 = 0. 7.68. х2- 5ху + 6у2= 0, Зх2+ 2ху - у2= 15.
7.69. х2 - ху + 2у2 = 0, 2х2 + Зху - 5у2 = 0. 7.70. 2х2- ху + у2= 28, х2+ Зху - Зу2= 28.
7.71. х2 — Зу2 = 1, 2х + у2 = - 3. 7.72. • 2х2— Зху + 2у2= 14, х2 + ху - у2 » 5.
7.73. х2 - 2ху - 5у2 — - 2, Зх2 + 2ху + у2 - 2. 7.74. х2у3 + х3у2 = 12, х2у3 - х3у2 = 4.
7.75. • х2 - у2 = 3, х3 - у3 = 7 (х - у). 7.76. х2 - 5/ = - 1, Зху + 7у2 « 1.
7.77. • х3 у3 = 19, ху(х-у) = 6. 7.78. х2 + у2 = 10, у2 - ху = 6.
7.79. • 2х2— Зху + Зу2= 80, х2+ ху - 2у2= - 56. 7.80. х2 - 2ху - у2 = 2, ху + у2 = 4.
119
§7. Системы алгебраических уравнений
7.81. 5х2 - бху + 5у2 = 29, 1х2 - Зху + 7у2 = 43. 7.82. < Зх2- х2 - - 4ху + 2у2= 17, у2 = - 16.
х2 + у2 = 5 х3 - у’= 7,
7.83. ху 2 ' 7.84. 2
7.85. х2 - у2 = 3. 2х2 + Зху + у2 = 3, Зх2 - ху + 2у2 = 16. X у - 1- ху2 = 6.
7.86. Решить систему
х2 + у2 + х + у = 8,
х3 + у3 + х^ + /х = 15.
Решение.
Обратим внимание на то, что данная система является
симметричной, т.е. не изменяется при замене х на у и у на
х. Для таких систем удобно использовать замену х + у = и,
ху = V.
Подготовим данную систему к замене. Имеем:
(х + у)2 - 2ху + х + у = 8,
(х + у)((х + у)2 - Зху) + ху (х + у) = 15.
Отсюда
и2 - 2v + и = 8, - 2v = 8 - и2 - и,
и (и2 — Зи) + uv = 15; и (и2 — 2v) = 15.
Тогда и (и2 + 8 - и2 - и) = 15, и2 - 8и 4- 15 = О,
и = 5,
и = 3.
Имеем:
и = 5,
и = 11;
u = 3,
v = 2.
120
§7. Системы алгебраических уравнений
Исходная система равносильна совокупности двух систем.
а)
х + у = 5,
ху = 11.
Эта система решений не имеет.
б)
х + у = 3,
ху = 2,
х = 1,
У = 2,
Ответ: (1; 2),
]х = 2,
|у= 1.
(2; 1).
7.87. Решить систему
X + у + 2 = 1,
ху + yz + zx = — 4,
X3 + / + 23 = 1.
Решение.
Эта система, как и предыдущая, является симметричной.
Для нее целесообразна замена
X + у + z = и, ху + yz + zx = о, xyz = W.
Легко показать, что х3 + у3 + z3 = и3 — Зии + 3w. Отсюда
и = 1,
v= - 4,
и3 - 3uv+ 3w = 1,
и = 1,
о = - 4,
w = — 4.
Имеем
X + у + Z = 1,
ху + yz + zx = — 4,
xyz = - 4.
Здесь выгодно воспользоваться теоремой Виета. Действи-
тельно, х, у, z — корни уравнения t3 — t2 — 4t + 4 = О,
t2(t- 1) - 4 (t — 1) =0,
0-l)02-4) = 0,
121
§7. Системы алгебраических уравнений__
‘t~ 1,
Г= -2,
1 = 2.
Ответ: (1; -2; 2), (1; 2; -2), (2; -2; 1),
(2; 1; -2), (-2; 2; 1), (-2; 1; 2).
Упражнения
Решить системы уравнений:
7.88. х + у + ху = 5, х2 + у2 + ху = 7.
7.89. х + 2ху + у = 10, х - 2ху + у = - 2.
7.90. х + у + х2 + у2 = 42, ху = 15.
7.91. . х2 + у2 - х - у = 18, х2 + у2 - ху = 13.
7.92. ху + 2х + 2у = 5, х2 + у2 + Зх + Зу = 8.
7.93. х2 + у2 = 17, х + ху + у = 9.
7.94. (х-1)(у-1) = 1, х2у + ху2 = 16.
7.95. ху(х- 1)(у- 1) = 72, (х + 1)(у + 1) = 20.
7.96. (х + 1)(у + 1) = 10, (х + у)(ху + 1) = 25.
7.97. х2у + у2х = 20, 1 + 1 * х у 4
122
§7. Системы алгебраических уравнений
7.98. Г .( х2 + 1)(у2 + 1) = 10. х + У)(ху - 1) = 3.
7.99. Д д с3 + х’у3 + у3 = 12, t + ху + у = 0.
7.100. х2 + у2 + 2 (х + у) = 23, х2 + у2 + ху = 19. [х2 у2 — + г = 12,
7.101. — | со II + к
7.102. х4 - х2 + у4 - у2 = 612, х2 + ху + у2 = 39.
7.103. • х4 + у4 - х2 - у2 = 12, 2х2 — ху + 2у2 = 8.
7.104. 5 (х4 + у4) = 41 (х2 + у2), х2 + у2 + ху = 13.
7.105. (х + у)(ху + 1) = 18ху, (х2 + у2)(х2у2 + 1) = 208х2у2. х + у + z = 0,
7.106. x2 + y2 + z2 = x3 + y3 + z3, xyz = 2. X + у + z = 1,
7.107. x2 + y2 + z2= 1, х’ + у3 + z’= 1. , . 7 x + y + z = -,
7.108. г^|сч II + + 11 т SL
123
§7. Системы алгебраических уравнений
7.109. Решить систему
i(x2-2y2) = 4,
£ (х2 + 2/) = 3.
Решение.
х
Путь — = t. Тогда данная система становится такой:
Г(у2Г2-2у2) = 4,
|(у2Г2 + 2у2) = 3.
Отсюда = 4 , 3/4 - ЮГ2 - 8 = О,
t2 + 2 3
Исходная система равносильна совокупности двух систем.
а)
х = 2у,
^(х2-2у2) = 4;
х - 2у,
у2=1;
х = 2,
у= 1;
х = - 2,
у = - 1.
б)
х = - 2у,
|(х2-2у2) = 4.
Эта система решений не имеет.
Ответ: (2; 1), (-2; -1).
7.110. Решить систему
х (X + 1)(3х + 5у) = 144,
х2 + 4х + 5у = 24.
Решение.
Перепишем данную систему в таком виде:
124
________________§7. Системы алгебраических уравнений
(х2 + х)(3х + 5у) - 144,
х2 + х + Зх + 5у = 24.
Пусть х2 + х = и, Зх + 5у = и Тогда
ии= 144,
и + v = 24.
Отсюда
и = 12,
v = 12.
Далее,
х2 + х = 12,
Зх + 5у = 12;
х = 3,
х = - 4,
Зх + 5у = 12.
Ответ: (з; [- 4; у
Упражнения
Решить системы уравнений:
*о| II 1 Х|
7.111. 1 II О» Ох
7.112. 3|« • - 2 si° 11 II + + + Х| iX^X ,и
7.113. < х _ X _ 35 ух 6 [_!_ + 1 = 1.
7.114. ^1’4- со II -IV 1 Oi Z—S X о
125
§7. Системы алгебраических уравнений
7.115. 7.116. 7.117. • 7.118. 7.119. 7.120. 7.121. 7.122. 7.123. 7.124. 2х + у + Х 3’ [2^= -4- 1 1 _ 1 х у 36 ’ ху2 - х2у = 324. х2у + ху2 = 30, i + 1 = t X у 6 х + у + х-у _ 5 х — у х + у 2 ’ х2 + у2 = 20. х3 + у3 = 7, х3у3= -8. V _ Z _ 2 у х 2 ’ 1 2_1 у х 2' 2 2 х у - ху =6, ху + х - у = — 5. (х + у)4 + 4 (х + у)2= 117, х - у = 25. (х + у + I)2 + (х + у)2 = 25, х2 - у2 = 3. *У + х + Зу = 2 х + Зу ху ’ ху + Х-у _ 5 х — у ху 2 *
126
§7. Системы алгебраических уравнений
ху 4- 1 4- - 4- = 13.
7.125. ху У X
ху - 1 _ X 4- = 12.
ху У X
7.126. (х24-у2)х = 6у, (х2 - у2) у = X.
7.127. X (х 4- 1)(3х2 4- 5у) = 144, 4х2 4- х 4- 5у = 24.
7.128. х2 4- у2 - х - 2у - 5 = 0, 2х2 4- Зу2 - 2х - бу - 13 = 0.
7.129. х4 4- у4 = 17, ху = 2.
7.130. Решить систему
fyx + 2у 4- ^х - у + 2 = 3,
2х + у = 7.
Решение.
Запишем
^х + 2у + у/х-у + 2 = 3,
х4-2у4-х-у4-2 = 9.
Очевидна замена Vx + 2у = и, Vx - у + 2 = и Имеем:
[и = 1,
и + о=3, и2 - uv 4- х? = 3, |»=2;
и* 4-t? = 9; u + o=3; [и = 2,
]о= 1.
Исходная система равносильна совокупности двух систем.
127
13
х ~ 3 ’
5
у = -3-
§7. Системы алгебраических уравнений
Vx + 2у = 1, fx + 2у = 1,
а)
Vx - у + 2 = 2; Ь-У + 2-8
Vx + 2у = 2, [х + 2у = 8, [х = 2,
б) •
v^x-y + 2 = 1; [^-у + 2-1; [у-3.
/1 з
Ответ: —; -- , (2; 3).
1 J О /
Упражнения
Решить системы уравнений:
7.131.
V2x + у + 1 - Vx + у = 1,
Зх + 2у = 4.
7.132
-5=5,
х2 + у2 = 13.
7.133.
3
4
х + у = 20.
3,____ 3,
7.134.
ху = 8.
7.135.
3__ 3___
Vx - Vy = 2,
ху = 27.
7.136.
Vx + у 1 / 5х _ 34
5х V х + у ~ 15 ’
х + у= 12.
128
$7. Системы алгебраических уравнений
7.137.
7.138.
7.139.
7.140.
7.141.
7.142.
7.143.
7.144.
7.145.
7.146.
V у V Зу - 2х
3 (х2 + 1) = (у + 1)(у - х + 1).
VI + 5х + 45 —у = 3,
5х - у = 11.
2 / 2
х + х Уху = 80,
2 »/ 2
у + ууух = 5.
9х2 + V9x2 + 2у + 1 = 1 - 2у,
6х + у = 2.
V4 — х + у + V9 — 2х + у = 7,
2у - Зх = 12.
Vx + у + V2x + у + 3 = 7,
Зх + 2у = 22.
х2 + 7зх2- 2у + 3 = |у + 5,
Зу - 2х = 5.
х2 + 4х + у2 - Зу = О.
з_____ ___
7 vxy - 3 4ху = 4,
х + у = 20.
х + Vx2 - у2 х - Vx2 - у2 _ 17
х - Vx2 — у2 х + Vx2 — у2 *
х (х + у) + Vx2 + ху + 4 = 52.
5 А;п ебраическии тренажер
129
§7. Системы алгебраических уравнений
7.147.
Vx - у 20
..............,
X + у X + у
х2 + у2 = 34.
7.148.
7.149.
4_____ 4_______
Vx + у + Vx — у = 4,
Vx + у - Vx - у = 8.
7.150.
(х2 + 1) у + (у2 + 1) X = 4ху.
Задачи для самостоятельного решения
С-1
Решить системы уравнений:
ху + 4 = 0,
х + у = 3.
х2 - ху + у2 = 7,
х - у = 1.
х3 + у3 = 35,
ху (х + у) = 30.
х2 + у2 + х + у = 8,
х3 + у3 + х2у + у2х = 15.
130
§7. Системы алгебраических уравнений
С-2
Решить системы уравнений:
х2 + у2 = 2 (ху + 2),
X + у = 6.
|х2 + у2 + 5х + у = О,
’ |х + у + 11 =0
+ < - 3.
о X 3
£ . 3 = 3
2 у 2 *
х + у 4- z = 12,
ху + XZ = 11,
х2 + у2 + Z2 = 66.
С-3
Решить системы уравнений:
(х - у)(х2 - у2) = 16,
(х + у)(х2 + у2) = 40.
2.
X + у + Z = 6,
ху + xz - yz = 7,
х2 + у2 + z2 = 14.
Vx + у + 4 + Vy + 7 = 4,
х + 2у = 5.
131
§8. Тригонометрические уравнения и
неравенства
Немного теории
Свойства функции у = sin х.
1) Область определения D (у) = R.
2) Область значений Е(у) = [- 1; 1 ].
3) Функция периодическая, основной период Т = 2л.
4) Функция нечетная.
5) Нули функции х = лк, Ле Z.
6) Функция принимает положительные значения на каж-
дом из промежутков (2лЛ; л + 2лЛ), к е Z; отрицательные —
на каждом из промежутков (- л + 2лЛ; 2лЛ), к е Z.
7) Функция дифференцируема на R.
8) Функция возрастает на каждом из промежутков
- + 2лЛ, + 2лк , kEZ, функция убывает на каждом
Гл Зл "1
из промежутков — + 2лк, — + 2лА , к € Z.
Зл ____ J
2 ' Л » ~ —
л
9) Точки максимума х = — + 2лЛ, к е Z. Точки миниму-
ма х = — — + 2лЛ, к 6 Z.
10) График функции изображен на рис. 20.
Свойства функции у = cos х.
1) Область определения D(y) = R.
2) Область значений Е(у) = [- 1; 1].
3) Функция периодическая, основной период Т = 2л.
132
§8. Тригонометрические уравнения и неравенства
4) Функция четная.
я
5) Нули функции х = — 4- лк, кЕ Z.
6) Функция принимает положительные значения на каждом
из промежутков + 2яЛ; -I- 2я^ Д GZ; отрицательные
(я Зя \
— + 2я&; — + 2я& , к G Z.
7) Функция дифференцируема на R.
8) Функция возрастает на каждом из промежутков
[—л 4-2я£, 2я£], к G Z; функция убывает на каждом из
промежутков [2лк; я 4- 2я£], к G Z.
9) Точки максимума х = 2яЛ, к G Z. Точки минимума
х = я 4- 2яЛ, к G Z.
10) График функции изображен на рис. 21.
Свойства функции у = tg х.
1) Область определения
2)
3)
4)
5)
D (у) = х G Я | * у 4- лк, к G ZI.
X I
Область значений Е (у) = R.
Функция периодическая, основной период Т = я.
функция нечетная.
Нули функции х = яЛ, к €= Z.
6) Функция принимает положительные значения на каж-
(f1 я _ \ _
ях; — 4- лк , к €= Z; отрицательные —
я \
- — 4- лк\ лк , к Е. Z.
X у
133
§8. Тригонометрические уравнения и неравенства
7) Функция дифференцируема на D(y), т.е. на объеди-
(л Л \
— — + л к; — + л к , к G Z.
8) Функция возрастает на каждом из промежутков
(Л « « __
- — + лк\ — + лЛ , к G Z.
9) Экстремумов нет.
Свойства функции у = ctg х.
1) Область определения D (у) = {х G R | х # лк, kEZ}.
2) Область значений Е (у) = R.
3) Функция периодическая, основной период Т = л.
4) Функция нечетная.
л
5) Нули функции х = — 4- лк, кЕ Z.
6) Функция принимает положительные значения на каж-
(л \
лк; — 4- лк , к G Z; отрицательные —
(л \
на каждом из промежутков - — 4- лк; лк , к G Z.
134
__________Тригонометрические уравнения и неравенства
7) функция дифференцируема на D (у), т.е. на объеди-
нении промежутков (лк; л + лк), к GZ.
8) Функция убывает на каждом из промежутков
(лк; л + лк), kGZ.
9) Экстремумов нет.
10) График функции изображен на рис. 23.
л л_
2’ 2
Свойства функции у — arcsin х.
1) Область определения D(y) - [- 1; 1].
2) Область значений Е (у) =
3) функция нечетная.
4) Нуль функции х — О.
5) функция принимает положительные значения на
(О; 1], отрицательные — на [-1; О).
б) функция дифференцируема на D(y).
7) Функция возрастает на D(y).
8) Экстремумов нет.
9) График функции изображен на рис. 24.
135
§8. Тригонометрические уравнения и неравенства
Свойства функции у = arccos х.
1) Область определения D(y) = [- 1; 1].
2) Область значений Е (у) = [0; л ].
3) Функция ни четная, ни нечетная.
4) Нуль функции х = 1.
5) Функция принимает положительные значения на
[- 1; 1).
6) Функция дифференцируема на D(y).
7) Функция убывает на D (у).
8) Экстремумов нет.
9) График функции изображен на рис. 25.
Свойства функции у = arctg х.
1) Область определения D (у) = R.
2) Область значений Е(у) =
3) Функция нечетная.
4) Нуль функции х = 0.
5) Функция принимает положительные значения на
(0; оо), отрицательные — на (- оо; 0).
6) Функция дифференцируема на D(y).
7) Функция возрастает на D (у).
8) Экстремумов нет.
9) График функции изображен на рис. 26.
136
§8. Тригонометрические уравнения и неравенства
Свойства функции у = arcctg х.
1) Область определения D(y) = R.
2) Область значений Е(у) = (О; л).
3) Функция ни четная, ни нечетная.
4) Нулей нет.
5) Функция принимает положительные значения на R.
6) Функция дифференцируема на R.
7) Функция убывает на R.
8) Экстремумов нет.
9) График функции изображен на рис. 27.
137
§8. Тригонометрические уравнения и неравенства_______
Общий метод решения неравенств
Теорема.
Если функция /определена и непрерывна на промежутке
(а; Ь) и не имеет корней на этом промежутке, то для любого
хе (а Ь) функция / сохраняет знак (рис. 28).
Рис 28
Пусть / — непрерывная функция. Найдем ее корни и
область определения. Корни делят область определения функ-
ции / на промежутки постоянного знака. Тогда «методом
пробной точки» можно определить знак / на каждом из по-
лучившихся промежутков. Те промежутки, на которых / при-
нимает положительные (отрицательные) значения, составля-
ют решение неравенства /(х) >0 </(х) <О).
Полезные упражнения
Построить графики функций:
о в sinx > - Них- 8.2. зшх у = . smx
8.3., = z 8ШХ 8.4. у = tg X COS X.
8.5. y = ctgxsinx. 8.6. у = tgxctgx.
138
§8. Тригонометрические уравнения и неравенства
8.7. у
8.8. у
8.9. у
8.10.
8.11.
8.12. ;
8.13.
8.14. ;
8.15. ;
8.16. ;
8.17. ;
8.18. ;
8.19. ;
8.20. ;
8.21. ;
8.22. ;
8.23. ;
8.24. ;
8.25.
= tg2x-------
COS X
= Ctg2X------7^—.
Sin X
_ sin x - sin 3x
- 2 cos 2x
f = sin2 tg x + cos2 tg x.
= sin2 Vl - x2 + cos2 Vl - x2
2
1 +tg2X
22i
_ tg 2x - tg x
“ 1 + tg 2x tg x ’
1 - —1“
sin X
= V2"*x - 2.
sin х - 2 sin х + 1.
= sin (arcsin x).
= arctg x + arcctg x.
= arcsin x + arccos x.
= Varccos x - л.
. 2 Я2
arcsin x------
4
139
§8. Тригонометрические уравнения и неравенства
8.26. Применить теорему корень из произведения к вы-
ражениям:
a) V(sm х - 3)(sin х - 2);
б) /(tg х — l)(sin х - 2).
8.27. Найти наибольшее и наименьшее значения функции:
. COS X (1 4- cos 2х)
а) у =----------------
cosx
б) у = sin х ctg х + 1.
8.28. Какие из пар уравнений являются равносильными?
Какое из уравнений в парах является следствием другого?
ч sin2x Л Л
а) —;---- = 0 и sin 2х = 0;
sinx
в) cos х tg х = 0 и sin х = 0;
г) sin х ctg х = 0 и cos х = 0;
д) sin х tg х = 0 и sin х = 0;
е) cos х ctg х = О и cos х = 0;
ж) sin х = 3 и tg2 х = - 1;
ч х ~ cos х
з) cos х tg х = 2 и —— = 2;
ctgx
и) v sin2 х cos х = 0 и I sin х I Vcosx = 0.
Решить уравнения:
8.29. л cos х = — . 8.30. Л smx =
8.31. tgx = —— . ® cosx 8.32. (1 + tg2x)ctg2x = 1.
8.33. tg 2х - tg х _ 1 + tg х tg 2х 8.34. sin x + sin | x I =0.
8.35. sin x + | sin x | =0. 8.36. cosx = cos |xI.
8.37. cos x = | cos x |. 8.38. sinx = x2 + 1.
140
§8. Тригонометрические уравнения и seравенства
8.39. 2 cos лх = Xх — 4х + 6.
8.40. tg2 х + 1 - sin 4х = 0.
8.41. sin х + sin у = 2.
8.42. cosx - arccosх = 1.
8.43. arccos x + Vl - x2 = 0.
Решить неравенства:
8.44. sinx > 1. 8.45. sinx > - 1.
8.46. sinx> - 1. 8.47. cosx< 1.
8.48. cosx « 1. 8.49. cosx =5 — 1.
8.50. sin 2x < 2. 8.51. sin 2x > - 2.
8.52. arccos x ? n. 8.53. arccos x > 0.
Л JT
8.54. arcsin x =£ - — . 8.55. arcsin x > — .
8.56. arctg x =£ - у . 8.57. arctg x < - —
8.58. arcctg x > 0. 8.59. arcctg x г 0.
8.60. При каких значениях параметра а уравнения рав-
носильны?
a) sin х = а и sin х = а2 — 2;
б) cos х = а и Vcosx = а;
в) Vsinx = а и sin х = а2;
г) I cos х | = а и cos2 х = а2;
d) | cos х | = а и cos х = а;
2 2 1
е) 1 + tg х = а и cos х = -;
а
ж) arccos х = а и arcsin х = — - а.
8.61. Вычислить:
а) arcsin (sin 6); б) arccos (cos 16);
в) arctg (tg (- 8)).
141
§8. Тригонометрические уравнения и неравенства
Комментарии, указания, ответы
8.1. Рис. 29. 8.2. Рис. 30. 8.3. Рис. 31. 8.4. Рис. 32. 8.5.
Рис. 33. 8.6. Рис. 34. 8.7. Рис. 35. 8.8. Рис. 36. 8.9. Рис. 37.
Рис. 31
142
§8. Тригонометрические уравнения и неравенства
Рис 34
-ЗЙ2
О я/2 Зя/2 х
8.10. Рис. 38. 8.11. Рис. 39. 8.12. Рис. 40. 8.13. Рис. 41.
8.14. Рис. 42. 8.15. Рис. 43. 8.16. Рис. 44. 8.17. Рис. 45.
143
§8. Тригонометрические уравнения и неравенства
8.18. Рис. 46. 8.19. Рис. 43. 8.20. Рис. 47. 8.21. Рис. 48. 8.22.
Рис. 49. 8.23. Рис. 50. 8.24. Рис. 51. 8.25. Рис. 52. 8.26.
a) V3 - sinx • V2 - sin х; б) Vl - tgx • V2 - sinx. 8.27. a)
max у = 2, наименьшего значения не существует; б) наиболь-
144
§8, Тригонометрические уравнения и неравенства
145
§8. Тригонометрические уравнения и неравенства
У
-Зя/2 -л/2 • п!2 Зя/2 5л/2 *
Рис. 48
146
§8. Тригонометрические уравнения и неравенства
л/2
О
Рис. 49
Рис. 51
Рис. 52
8.28. а)
(1)о(2);
шего и наименьшего значений не существует.
(1)=>(2); б) (1)о(2); в) (1)о(2); г) (1)о(2); д)
е) (1) о (2); ж) (1) о (2); з) (1) о (2); и) (2) о (1). Указание.
В первом уравнении если sin х = 0, то косинус может при-
нимать отрицательные значения. 8.29. Нет решений. 8.30.
Нет решений. 8.31. Нет решений. 8.32. Нет решений. 8.33.
Нет решений. Указание. Переход к уравнению tg х = 1 рас-
ширяет область определения исходного уравнения ровно
л лк
на множество — + —, к 6 Z. 8.34. х 0 или х = лк, к& N.
8.35. л + 2лЛ х 2л + 2лЛ, к 6 Z. 8.36. х — любое. 8.37.
- ^ + 2лк < х у + 2лк, kEZ. 8.38. х = О. Указание.
sinx 1, вместе с тем, как х2 + 1 > 1. 8.39. х = 2. Указание.
х2 - 4х + 6 = (х - 2)2 + 2 =s 2. 8.40. Нет решений. Указание.
Данное уравнение равносильно системе sin х = 0 и
sin 4х = 1. 8.41. х = ~ + 2лЛ и у = + 2л т, кит — целые.
Указание. Данное уравнение равносильно системе sin х = 1 и
sin у = 1. 8.42. Нет решений. 8.43. х = 1. 8.44. Нет решений.
8.45. х — любое. 8.4о. х — любое, кроме х = - ^ + 2лк,
k&Z. 8.47. х — любое, кроме х = 2лк, k&Z. 8.48. х —
147
§8. Тригонометрические уравнения и неравенства
любое. 8.49. х = л 4- 2л&, к G Z. 8.50. х — любое. 8.51. х —
лкАоъ. 8.52. х = -1. 8.53. -1 х < 1. 8.54. х = -1. 8.55. Нет
решений. 8.56. Нет решений. 8.57. Нет решений. 8.58. х —
любое. 8.59. х — любое. 8.60. а) а< — VT, или а = - 1, или
а > уГз. Указание. Достаточно решить уравнение а2 — 2 — а и
систему
|а| >1,
а2 — 2> 1.
б) а < — 1, или а = О, или а 1; в) а 0 или а < — 1; г)
а 0 или а < - 1; д) а < - 1, или а = О, или а > 1; е) а О
или а 1; ж) а — любое. Указание. Воспользуйтесь тож-
л
деством arcsin х + arccos х = —. 8.61. а) 6 - 2л. Указание.
sin 6 = sin (6 - 2л); б) 6л - 16; в) Зл - 8.
Основные типы задач
2 •
8.62. Решить уравнение cos
Решение.
тг Л
Имеем: 2х + — = ± arccos
о
GZ,
Л , И ) Л . I
6 Т + Х = ± 8 " 12
/ч Зл л , , „
Ответ: х = ± —------— + лЛ, k G Z.
о 1Z
Упражнения
Решить уравнения:
8.63.
8.65.
8.67.
8ш(х+з) =2-
( л\
tg * + 7 = 1.
V2~
sin (2х - 3) = •
8.64. COS |х - vl = - 1-
I 4 1
8.66. tg (Зх - 1) = 2.
8.68. ctg
148
§8. Тригонометрические уравнения и неравенства
8.69. tg (х - 1) = 7. 8.70. sin (я sin х) = - 1.
8.71. cos лх = - i 8.72. cos— = .
2 х 2
8.73. Решить уравнение 3 cos х + 5 sin х = 4.
Решение.
В левой части уравнения вынесем за скобки число, равное
V32 + 52, т.е. Т34~. Имеем:
+ V5Tsinx) =4-
( з \2 ( 5 \2
Поскольку I ^д + ^/зд = 1, то можем положить
3 5 _ L я\
sin а = ^зд> cos а = где a G 10; — , т.е. можем счи-
3 '
тать, что, например, а = arcsin^—. Далее,
<34~(sin a cos х + cos a sin х) = 4,
4
sin (х + а) = ,
4
х = (- 1)" arcsin а + лп, пЕ Z.
Ответ: х = (- 1)" arcsin — arcsin + лп, nEZ.
Заметим, что при решении данного уравнения мы ис-
пользовали метод преобразования двучлена a sin х + b cos х в
произведение.
Упражнения
Решить уравнения:
8.74. V3~cos Zx - sin 2х = 1.
vT
8.75. cos 4х + sin 4х = —.
149
§8. Тригонометрические уравнения и неравенства
8.76. 3 sin х + 4 cos х = 5.
8.77. 2 cos х + 2 sin x = V6~.
8.78. cos 3л - sin x = V3~(cos x - sin 3x).
v 3 1
8.79. sin 3x + — sin 5x + — cos 5x = 0.
8.80. sin 8x — cos 6x = V3~(sin 6x + cos 8x).
8.81. sin 1 lx + -^-sin7x + ^cos7x = 0.
2 2
8.82.
4 cos2 x = 2 + cos 2x I——- + . \ j.
2 I cos 2x sin 2x I
8.83. sin 2x + cos 2x = V2~sin 3x.
8.84. Решить уравнение sin 2х — sin Зх + sin 8х = sin 7х.
Решение.
sin 2х - sin Зх + sin 8х - sin 7х = 0,
„ . х 5х . _ . х 15х
- 2 sin - cos — + 2 sm - cos -т- = 0,
2 2 2 2’
2 sin [cos - cos =0, sin sin 5х sin = °-
2 I 2 2 2 2
Sx
Поскольку корни уравнения sin — = 0 содержатся среди
корней уравнения sin 5х = 0, то последнее уравнение равно-
х
сильно такому: sin — sm 5х = 0,
sin | = 0,
sin 5х = 0,
х = 2яЛ, к G Z,
ял „
х = — , п G Z.
О
Заметим, что при n =
лп
Юк получаем х = -=- = 2лк. Сле-
О
довательно, все корни первого уравнения совокупности со-
держатся среди корней второго уравнения.
гч ЯП ~
Ответ: х = , п G Z.
О
150
§8. Тригонометрические уравнения и неравенства
Упражнения
Решить уравнения:
8.85. 2 cos х cos Зх = Уэ~cos Зх.
8.86. cos Зх + sin 2х - sin 4х = 0.
8.87. VTcosx + cos2x + cos4x = 0.
8.88. cos 9х - cos 7х + cos Зх - cos х = 0.
8.89. sin х + sin 7х - cos 5х + cos Зх = 0.
8.90. cos 5x + cos 7x + cos 6x = 0.
8.91. sin x + sin 2x + sin 3x = cos x + cos 2x + cos 3x.
8.92. sin x + 2 sin 2x + sin 3x = 0.
8.93. sin x + sin 2x + sin 3x = 1 + cos x + cos 2x.
( 2л\ ( Jt\
X - -r — sin x + — = COS X + T .
6J 3 j \ 4/
8.95. sinx + sin 5x = 0.
8.96. sin (15* + x) + cos (45* + x) +1 = 0.
* ♦ ♦
8.97. Решить уравнение
sin Зх + sin 5x = 2 (cos2 2x - sin2 3x).
Решение.
В правой части уравнения применим формулу понижения
. „ . . , /1 + cos 4х 1 - COS 6х\
степени: sin Зх + sin 5х = 2 -------------2----1 >
sin Зх + sin 5х = cos 6х + cos 4х,
2 sin 4х cos х = 2 cos 5х cos х,
cos х (sin 4х - cos 5х) = 0,
(. (я \ \
sin 4х - sin рг - 5х|| =0,
(9х л\ (х л\
COSXSinly - -Icosl---I =°,
151
§8. Тригонометрические уравнения и неравенства
х = — + лк,
9х
2
л
— = ЯП>
4
X
2
л л
- = лт + -,
к, п, т — целые,
х
х
х
л
= у + л£,
_ л 2л п
~ 18 + 9
Зл , „
= — + 2лт,
к, п, т — целые.
Ответ: х = — + 2лт или х = — 4- —— ,
где п и к — целые.
Упражнения
Решить уравнения:
8.98. sin2|x = |.
J 4
8.99. cos2~~ = |.
Z 4
8.100. sin2 2z + sin2 3z + sin2 4z + sin2 5z = 2.
8.101. 0,5 (cos 5x + cos lx) - cos2 2x + sin2 3x = 0.
8.102. cos2 3x + cos2 4x + cos2 5x = .
8.103. cos 2x + cos 6x + 2 sin2x = 1.
8.104. sin2 3x + sin2 4x = sin25x + sin2 6x.
о i Л i о ( Л i
8.105. sin2 x + — - cos x - — = 0,5.
\ I \ 1
О.ЛГ 2X , z2x 23x
8.106. cos - + cos — = cos -z- .
0
8.107. sin2x + sin25x = 1.
152
§8. Тригонометрические уравнения и неравенства
8.108. 2 cos2 2х + cos 10х — 1 = 0.
8.109. sin2x + sin2 2х = cos2 Зх + cos2 4х.
8.110. Решить уравнение 1 4- cos t + cos 2t + cos 3t = 0.
Решение.
1 4- cos 2t 4- cos t 4- COS 3t = 0,
2 cos21 4- 2 cos t cos 2t = 0,
cos t (cos t 4- cos 2t) = 0,
cos t cos - cos — = 0.
3t t t
Поскольку cos — = 4 cos2 — - 3 cos — , то среди корней урав-
3t t
нения cos — = 0 содержатся все корни уравнения cos — = 0.
X X
Следовательно, исходное уравнение равносильно такому:
3t „
cos t cos — = 0,
cos t = 0,
cos у = 0;
Ответ: t = — 4- лк или
t = 4- лк, k^Z>
л 2л n ~
t = — 4- —— , nEZ.
л 2лп .
t=- + -у—, где пик — целые.
Упражнения
Решить уравнения:
8.111. (1 + cos 4х) sin 2х = cos2 2х.
8.112. 1 - cos (л + х) - sin * = 0.
8.113. (cos 6х - 1) ctg Зх = sin Зх.
8.114. V2"(l +cosx) = ctg^.
153
§8. Тригонометрические уравнения и неравенства
8.115. 2 (1 - cos 2х) = VTtgx.
8.116. 1 + cosx + cos 2х = 0.
8.117. sin х + cos 2х = 1.
8.118. cos2x + 3 sinx = 2.
8.119. (l+cosx)tg^ =0.
8.120. 1 - cos x = 2 sin .
8.121
Решить уравнение tg x + tg 2x - tg Зх = 0.
Имеем:
Решение.
sinx sin2x
COSX COS2X
sin3x _
cos3x '
sin3x
cosx cos 2x
Sin3x _
cos3x
. „ cos Зх - cos x cos 2x „
sin 3x------------r-----z— = 0,
cos x cos 2x cos 3x
cos3x -
sin3x
1 1
уCOSX - ~COS3x
—-------------- = 0.
COS X cos 2x cos 3x
. cos 3x - cos x sin x sin 2x sin Зх л
Sin 3x -----------r-----z— = 0, ----------z-----— - 0,
cos x cos 2x cos 3x cos x cos 2x cos 3x
sin x sin 2x sin 3x = 0,
cosx * 0,
cos 2x # 0,
cos3x * 0.
Поскольку
sin Зх = 3 sin x - 4 sin3 x и sin2xB=2sinxcosx,
го уравнение системы равносильно такому: sin Эх cos х = 0.
Теперь становится понятным, что достаточно решить систему
sin Зх = 0,
cosx # 0,
cos 2х х 0,
cos3x # 0,
154
§8. Тригонометрические уравнения и неравенства
которая, в свою очередь, равносильна уравнению sin Зх = О.
Ответ: х — , к 6 Z.
Упражнения
Решить уравнения:
8.122. cos 2х ctg Зх — sin 2л — V2"cos 5х = О.
8.123. tg 2х cos Зх + sin Зх + V2~sin 5х = 0.
8.124. tg Зх + tg х = — 2 sin 4х.
8.125. ctg х - tg х - 2 tg 2x - 4 tg 4x + 8 = 0.
8.126. tg 5x - tg 3x - 2 tg 2x = 0.
8.127. tgx + tg 2x - 2 tg 3x » 0.
8.128. tg 6x cos 2x - sin 2x - 2 sin 4x = 0.
8.129. 6 tg x + 5 ctg 3x = tg 2x.
8.130. tg x ctg 3x = 4.
8.131. tg2x + cos 4x = 0.
wee
8.132. Решить уравнение
cos 2x = 72”(cos x - sin x).
Решение.
Имеем: cos2 x - sin2 x = V2~(cos x - sin x),
(cos x - sin x)(cos x 4- sin x) = 7T(cos x - sin x),
(cos x - sin x)(cos x •+• sin x - 72”) = 0,
cos x - sin x = 0,
cos x + sin x = 72”;
COS I x 4- — I =0,
\ * }
( л\
cos x - — = 1;
I 4 I
155
§8. Тригонометрические уравнения и неравенства
Л л
х + — = — + лп,
4 2
х - v = 2лк, п, к — целые.
4
Объединим полученные корни в
Л л ~
Ответ: х = — 4- лп, пЕ Z.
4
Упражнения
Решить уравнения:
8.133. sin 2л = cos4 - sin4 .
2 2
8.134. 4 sin 2л sin 5л sin 7л - sin 4л = О.
8.135. 4 sin 5л cos 5л (cos4 л - sin4 л) = sin 4л.
8.136. 2 ^tg ~ — = cos л.
1 + V3~
8.137. cos 2л = —-— (cos л + sin л).
8.138. ctg л - tg л = sin л + cos л.
8.139. 1 + sin л + cos л + sin 2л + cos 2л = О.
8.140. Решить уравнение
cos31 cos 3t + sin31 sin 3t = — .
4
Решение.
Воспользовавшись формулами тройного угла для синуса
и косинуса, запишем
(cos 3t + 3 cos t) cos 3t + (3 sin t - sin 3t) sin 3t = V2~,
cos2 3t — sin2 3t + 3 (cos t cos 3t - sin t sin 3t) = V2”,
cos 6t + 3 cos 2t = V2~,
4 cos’ 2t - 3 cos 2t + 3 cos 2t = VT,
156
§8. Тригонометрические уравнения и неравенства
V2
cos 2t = — .
Ответ: х = ± — + тгЛ, к G Z.
о
Упражнения
Решить уравнения:
8.141. sin’ х sin Зх + cos’ х cos Зх = cos’ 4х.
8.142. 4 sin’ х cos Зх + 4 cos’ х sin Зх = 3 sin 2х.
8.143. sin’x cos Зх + cos’x sinЗх + ^ = 0.
О
* * ♦
8.144. Решить уравнение sin 6х + sin 2х = tg 2х.
Решение.
Имеем: 3 sin 2х - 4 sin’ 2х + sin 2х = tg 2х,
X
4sin2x 1-Sin22x - 8^4 =0,
sin2x Icos22x —
sin 2x = 0,
з 1
cos 2x = -,
8 cos 2x I ’
sin 2x = 0,
„ 1
COS2x = — .
+ лп, к и n — целые.
Упражнения
Решить уравнения:
8.145. sin 9х = 2 sin Зх.
8.146. cos 6х = 2 sin I — + 2x1.
157
§8. Тригонометрические уравнения и неравенства
8.147. sin Зх + sinx = 4sin’x.
8.148. sin 6х + 2 = 2 cos 4х.
, з 7з~
8.149. sin 3x4-sin х = —-— sin2x.
4
а 3
8.150. cos Зх - cos х 4- - sin 2x = 0.
4
8.151. Решить уравнение
(я \ . (л
— 4- 2x1 sin — - Зх
4 I 14
Решение.
Имеем: sin Зх - sin х + 4 cos 5х + cos Зх =
2 2 2 2
1 r 1 /л \
= -cos5x - -cos l^-xI,
(Jt\
Зх + -? I = О,
4 J
Л
Зх 4- — = лп, nEZ.
4
л л лп
Ответ: х = - — + —, п е Z.
12 3
Упражнения
Решить уравнения:
х Зх
8.152. cos - cos .-sin х sin Зх - sin 2х sin Зх = 0.
8.153. cos x cos Зх - cos 4x cos 8x = 0.
8.154. sin I-- + 5x| cos|v + 2x| = sinl^ + x| sinl^ - 6x
14 I 14 I 14 J 14
8.155. sin -y cos + sin cos + sin 2x cos 7x = 0.
8.156. cos 3x cos 2x - sin x sin 6x = cos 7x.
158
§8. Тригонометрические уравнения и неравенства
8.157. sin 5х - sin х cos 4х = О.
8.158. 2 sin 5х cos 6х + sin х = sin 7х cos 4х.
8.159. Решить уравнение sin4 2х + cos4 2х = sin 2х cos 2х.
Решение.
Выделим в левой части уравнения квадрат суммы. Имеем:
(sin2 2х + cos2 2х)2 - 2 sin2 2х cos2 2х = sin 2х cos 2х.
Пусть sin 2х cos 2х = t. Понятно, что I /| < у. Получаем
X
т.е.
__ л лк t
Ответ: х = - + —, к G Z.
о X
Упражнения
Решить уравнения:
8.160. 3sin22x + 7cos2x-3 = 0.
8.161. 2cosax + 2 VTsinx - 3 = 0.
8.162. cos 2x — 5 sin x — 3 = 0.
8.163. cos 2x + 3 sin x = 2.
8.164. 5sin£ - cos£ + 3 = 0.
o 3
8.165. tgax - 2tgx — 3 = 0.
8.166. 8 sin2 2x - 2 cos 2x = 5.
8.167. 7 + 4cosxsinx + 1,5(tgx + ctgx) = 0.
8.168. sin4x + cos4x = sin 2x - 0,5.
159
§8. Тригонометрические уравнения и неравенства
/ 271 \
8.169. cos 2х + — + 4 sin
1 J I
8Л70. sinx + 2cos2x = 1.
8.171. sin Зх - 3 cos 6x = 2.
8.172. cos2x + sin4x = 1.
8.173. 2cos2x + 2 V2"sinx - 3 = 0.
o r» ___ ctg 2л . ctgx , _
8.174. Решить уравнение -7— 4- * % 4-2 = 0.
ctgx ctg2x
Решение.
Пусть
J ctgx
Имеем: =
ctgx
= t. Тогда t
- 1,
cos 2х
sin 2х
+• у = - 2. Отсюда I = - 1.
= О,
smx
sin 3x
. „ . = О,
sin 2х sin х
x
Понятно, что
лк
У’
лп
Т’
лт, к,п,т — целые.
лк . ~
из множества —, к G Z, следует исключить
О
множество чисел вида л /, t е Z. Получим
Ответ: х = ± - + лк, Ле Z.
Упражнения
Решить уравнения:
8.175. 2 tg х - 2 ctg х = 3.
8.176. | = 0.
tg 2х tg 4х 2
160
§8. Тригонометрические уравнения и неравенства
8.177. ctg’x + -----3ctgx — 4 = 0.
sin х
8.178. 2tg2x + 3 = —— .
cosx
8.179. tgx + —V- = 3.
COS X
8.180. —------2 VTctgx -6 = 0.
sin x
8.181. tg4x + tg2x + ctg4x - ctg2x = .
8.182. tg4x + ctg4x + tg2x + ctg2x = 4.
8.183. tgx + ctgx + tg2x + ctg2x + tg’x + ctg’x = 6.
8.184. —= ctgx + 3.
sin x
1 2
8.185. -----------~2---12 tgx - 16 = 0.
cos x cos x
8.186. tg2 x + tg x - 3 ctg2 x - 3 ctg x - 2 = 0.
* * *
8.187. Решить уравнение
2 sin2 x + cos2 x 4- 3 sin x cos x = 3.
Решение.
Преобразуем это уравнение к однородному уравнению
второй степени относительно синуса и косинуса. Имеем:
2 sin2 х + cos2 х 4- 3 sin х cos х = 3 sin2 x 4- 3 cos2 x,
sin2 x - 3 sin x cos x 4- 2 cos2 x = 0.
Покажем, что множество чисел вида — 4- лЛ, к G Z, не
являются корнями данного уравнения. Действительно, если
cos х = 0, то из данного уравнения следует, что sin х = О,
однако cos2 х 4- sin2 х = 1, следовательно, cos х # 0. Разделим
обе части последнего уравнения на cos2x. Учитывая выше-
сказанное, получим уравнение, равносильное исходному:
6 А.Л1 ебриическии >ренажер
161
§8. Тригонометрические уравнения и неравенства________
tg2x-3tgx + 2 = O,
"tgx = 1,
tgx = 2.
Ответ: x = — + лк или х = arctg 2 + лп, пик — целые.
4
Упражнения
Решить уравнения:
8.188. sin2x - 2sinxcosx = 3cos2x.
8.189. 6sin2x + sin xcosx - cos2x = 2.
8.190. 2 sin’x + 2 sin2x cos x — sin x cos2x — cos’x = 0.
8.191. 2 sinx cos2 |x - x| + 3cos2|x + x| cosx -
|2 j \2 /
- 5cos2x sin |зг + х| =0.
I Z I
8.192. 3sin2xcos (^г + xl + 3sin2xcosx~
2 (2 2^ 2 2
- sinxcos2x = sin2 (x + o') cosx
22 12 21 2
8.193. 5 sin4 2x - 4 sin2 2x cos2 2x - cos4 2x + 4 cos 4x - 0.
8.194. sin2x - cos 2x = 2 - 2 sin 2x.
8.195. sinx + cosx = —-—.
cosx
* e *
8.196. Решить уравнение
5 (1 - sin 2x) — 16 (sin x — cos x) + 3 = 0.
Решение.
Пусть sinx - cosx = t. (Заметим, что lit V2). Тотда
sin2 x - 2 sin x cos x + cos2x = t2,
1 - sin 2x = t2.
162
§8. Тригонометрические уравнения и неравенства
Получаем 5t2 - 16t + 3 = О,
'z = 3,
'Ч-
Т, 1
Теперь достаточно решить уравнение sinx — cosx = —.
Имеем: v2 sin л - -- = sin х - — = 'ух- .
I 41 5 I 41 5v2
л 1
Ответ: x = — + (- 1) arcsin + лл, n G Z.
Упражнения
Решить уравнения:
8.197. 1 + sin 2x = cos x + sin x.
8.198. sin 2x + 5 (sin x + cos x) + 1 = 0.
8.199. 1 — sin 2x = cos x — sin x.
8.200. 4-4 (cos x - sin x) - sin 2x = 0.
8.201. 5 sin 2x — 11 (sin x + cos x) + 7 = 0.
8.202. Решить уравнение (tg2 x + ctg2 x) = 2 + ctg 2x.
Решение.
Имеем: (tg x - ctg x)2 + 1 = 2 + ctg 2x,
(cos2 x - sin2 x)2
2 sin2 x cos2 x
+ 1 = 2 + ctg 2x,
2 ctg2 2x - ctg 2x - 1 = 0,
ctg 2x = 1,
ctg2x =
- Л . 71П 1 . ( t Лк
Ответ: x = - + —илих = - arcctg - - + — ,
о Z Z I Z / z
где n и k — целые.
163
§8. Тригонометрические уравнения и неравенства
8.203. Решить уравнение
tg2 х + ctg2 x + 3tgx + 3ctgx + 4 = O.
Решение.
Пусть tg х + ctg х = t. Тогда
tg2x + ctg2x + 2 tgx ctgx = t2,
tg2x + ctg2x = t2 - 2.
Отсюда t2-2 + 3t + 4 = 0,
‘t = - 2,
t = - 1.
Имеем:
'tgx + ctgx = - 2,
tgx + ctgx = - 1.
Второе уравнение совокупности корней не имеет. Из
первого получаем tgx = - 1.
л
Ответ: х = - — + лп, nEZ.
4
Упражнений
Решить уравнения:
_ l+sin2x Л 1+tgx
8.204. ----г-- + 2 • ------------3 = 0.
1 - sin 2х 1 - tg х
8.205. 7 + 4 sin х cos х + (tg х + ctg х) = О.
8.206. tg2 J + ctg2 - 2 = 4 tg x.
8.207. tg4 x + tg2 x + ctg4 x - ctg2 x. = .
8.208. 2 sin2 x + sin x + -4— + —= 6.
smx sin2x
, I 1 \ 2
8.209. 18 cos x + 5 3cosx + ----- + —+ 5 = 0.
I COS X I cos2 x
164
§8. Тригонометрические уравнения и неравенства
8.210. -Ц- + |ctg2x + 10 (2tgx + = 1.
COS X 3 \ 3 у
1 2
8.211. —--------------12 tgx - 16 = 0.
cos x cos x
8.212. Решить уравнение
. 5x
cos Зх + cos — = 2.
Решение.
Поскольку I cos 3x I 1 и
5х
cos т
$ 1, то данное урав-
некие равносильно системе
cos Зх = 1, х = ,
cos~~ = 1; Алк
2
Ответ: х = 4лт, т G Z.
8.213. Решить уравнение
15 + . \ | (2 - sin6x) = 7 + cos 2у.
sin2 х)
Решение.
Заметим, что 5 + ---- £ 8, а 2- sin6x 1. Тогда
sin2x
|5 + -rV|(2 - sin’x) > 8.
I surxj
Вместе с тем 7 + cos 2у 8. Следовательно, исходное
уравнение равносильно системе
jsin2x = 1,
jcos 2у = 1.
л ,
Ответ: х = — + лкиу = лп, где п и к •— целые.
165
§8. Тригонометрические уравнения и неравенства
Упражнения
Решить уравнения:
8.214. cos 2л + cos —— 2 = 0.
4
8.215. cos2 ^2х + + cos2 - xj =0.
8.216. | cos2x + —“ | (1 + tg2 2y)(3 + sin 3z) = 4.
cos x I
8.217. 12 + —4~l(4-2cos*x) = 1 + 5sin3y.
cos x)
8.218. cos 6x + sin = 2.
8.219. (tgx - tg2 x)2 - cos (x + 4 tgx) = - 1.
13
8.220. (4 - cos 2x)(2 + 3 siny) = 12 + 2 .
cos 3z
8.221. sin5x + cos5x = 2 - sin4x.
8.222. Решить неравенство 2 cos2 x + 5 cos x + 2 0.
Решение.
Пусть cosx = t, Id 1. Тог-
да запишем 2t2 + 5t + 2 Э 0. От-
сюда t - 2 или t . Сле-
довательно, данное неравенство
равносильно совокупности
cos х - 2,
1
cos х .
Теперь достаточно решить
неравенство cos х Схема решения показана на рис. 53.
-2k/3
Рис. 53
27Г 27t
Ответ: —— + 2лк x £ — + 2лЛ, k 6 Z.
3 3
166
§8. Тригонометрические уравнения и неравенства
Упражнения
Решить неравенства:
8.223. tg2x - tgx - 2>0.
8.224. 2cos2x - sinx> 1.
8.225. ТУ sin2 х + cosx < 0.
8.226. ctg2 x + ctg x > 0.
8.227. 2sin2^ + cos2x<l.
8.228. sin4x + cos4x < .
8.229. sin* x + cos4 x > sin 2x.
8.230. 8 sin4x - 8 sin2x + sinx - 1 < 0.
8.231. 2 + tg2x + ctg2x<0.
8.232. 2 cos x (cos x - V8~tg x) < 5.
8.233. 2sin2x - 7sinx + 3>0.
8.234. tgx + ctgx < - 2.
8.235. sin x + cos 2x > 1.
8.236. sin2x - 3sinxcosx + 2cos2x<0.
8.237. 3sin2x - 4 sinxcosx + 5cos2x >0.
♦ ♦ •
8.238. Решить неравенство sin x + sin 2x + sin 3x > 0.
Решение.
Для решения данного неравенства удобно воспользоваться
общим методом. Рассмотрим функцию
/(х) — sin х + sin 2х + sin Зх.
Эта функция периодическая с периодам Т = 1л. Поэтому
достаточно определить знак функции / на промежутке
[0; 2л). Найдем корни уравнения /(х) = 0 на промежутке
[О; 2л). Имеем:
167
$8. Тригонометрические уравнения и неравенства
sin х 4- sin 2х 4- sin Зх = О,
2 sin 2х cos х 4- sin 2х = О,
sin 2х = О,
cos х = - ~ ,
ли _ ~
х ~ ~2 ’ neZ>
2л
х = ± — + 2лк, kGZ.
принадлежат такие корни:
на R,
2; Т ’
Промежутку [0; 2л)
2л 4л Зл _ .
—, л, —, —. Поскольку функция / непрерывна
& Ал
г L
то на каждом из промежутков = 0; — ,
_ /2л \ _ / 4л \ _ /4л Зл\
73 = —; л I, I4 = I л; — , 15= —; — она сохраняет по-
1 / I J X /
стоянный знак.
Методом пробной точки несложно установить знак функ-
ции f на каждом из промежутков. Имеем:
л;
• если х G (, то /(х) >О;
• если х 612, то /(х) < 0;
• если хе/,, то f (х) > 0;
• если х 6/4, то /(х)<0;
• если х G /5, то /(х) > О.
Итак, на [0; 2л) У(х)>0 при хб/, или х6/э, или
х е/,.
л 2л
Ответ: 2лк < х < ^ + 2лк, + 2лк < х < л + 2лк,
4л Зл
— 4- 2лк < х < — 4- 2лЛ, к G Z.
Упражнения
Решить неравенства:
8.239. sin х 4- sin 2х > 0.
8.240. sin2 х cos х 4- cos2 х sin х < 0.
168
§8. Тригонометрические уравнения и неравенства
8.241. cosx - VTsin^ > 1.
8.242. cos х - sin 2х - cos Зх < 0.
8.243. 5 sin2 x + sin2 2x > 4 cos 2x.
8.244. sin 2x + tg x 3= 2.
8.245. sin 3x > 4 sin x cos 2x.
8.246. (sin x + cos x)(V3”sin x - cos x) > 0.
8.247. cos2 x + cos2 2x + cos2 3x + cos2 4x < 2.
8.248. ctgx>ctg3x.
8.249. cos x - cos 2x > sin 3x.
8.250. sin2 x + sin2 2x - sin2 3x > 0.
8.251. cos x cos 3x < cos 5x cos 7x.
8.252. sin 5x cos 3x > sin 7x cos x.
8.253. cos2xtgx>0.
Задачи для самостоятельного решения
С-1
Решить уравнения:
1. tg(3x + 2) = — 1.
2. 5 cos 2х = sin2 х.
3. tg(2x — l)tg(3x + 1) = 1.
4. 3 cos2 x + 4 sin x cos x + 5 sin2 x = 2.
5. 1 + sin x cos x - sin x - cos x = 0.
C-2
Решить уравнения:
1. sin2 x - cos2 x - cos 3x = 0.
2. sin 3x + cos 3x - '/2~.
169
$8. Тригонометрические уравнения и неравенства
3. 6 sin х — 4 cos х — --3—.
smx
4. cos Юх - cos 8x - cos 6a + 1 = 0.
S. Решить неравенство sin 5x sin 3x > sin 7x cos x.
C-3
Решить уравнения:
1. cos 4x = cos 2x - sin 2x.
2. Sln£ + Sini - sta-UJ.
XX X
3. 2 cos 2x + 2 cos 4x + 3 sin2 2x = 1.
. 1 + tgx . . (n . t'n \
4. -—t5----2sm — + x sin — - x =0.
1 - tgx 14 j i4 j
5. Решить неравенство sin4x + cos4x > .
О
§9. Показательные уравнения и неравенства
Немного теории
Определение.
Функция, заданная формулой у = а*, где а> 0 и а # 1,
называется показательной функцией с основанием а.
Свойства показательной функции
1) £>(у) = Я.
2) Е(у) = (О; оо).
3) Если а>1, то функция возрастает на R; если
О < а < 1, то функция убывает на R.
Теорема.
Уравнение af{x} = а*(х} при а>0 и а#1 равносильно
уравнению f (х) = <р (х).
Теорема.
Неравенство а/(х) >а^(х) равносильно совокупности двух
систем:
\а> 1,
1/(*)>?(*);
[О < а < 1,
1/(«Не-
полезные упражнения
Решить неравенства:
9.1. 2Х> — 1. 9.2. 21/х>- 1.
9.3. 2^> - 1. 9.4. 2,,х>0.
9.5. 2*™"х > - у. 4 9.6. 2^ х > - |.
9.7. 2х>sinx - 1. 9.8. 2й* х>cosx - 1.
„ „ , . л 9.9. 2 > arcsin х - р 9.10. 2“'““ х> arccos х - л.
171
$9. Показательные уравнения и неравенства
9.11. 2vV > — . 9.12. 2х2 Ъ sinx.
X
9.13. 2х2 > cos х. 9.14. 2"х2 Э х2 + 1.
9.15. 2~х* =s |sinx| + 1. 9.16. 2W Э 1 - х2.
Решить уравнения:
9.17. 2“* х = х2 + 2. 9.18. 2*'““ х = 1 - х2.
9.19. | = х2+1. 9.20. 2м = cos х.
Комментарии, указания, ответы
9.1. х — любое. 9.2. (- »; 0) U (О; »). 9.3. х 0. 9.4.
х — любое, кроме х = у + лк, к& Z. 9.5. — 1 х 1. 9.6.
х — любое. 9.7. х — любое. 9.8. х — любое, кроме х = лк,
kGZ. 9.9. - 1 < х < 1. 9.10. — 1 « х « 1. 9.11. х >0. 9.12.
х — любое. 9.13. (— оо; о) U (0; °0). 9.14. х = 0. 9.15. х = 0.
9.16. х = 0. 9.17. х = 0. Указание. 2“" х 2, вместе с тем
х2 + 2 £ 2. 9.18. х = 0. 9.19. х = 0. 9.20. х = 0.
Основные типы задач
9.21. Решить уравнение 2х ” 3 • 5х “ 3 = 0,01 • (10х-1)3.
Решение.
(2 • 3 = 10-2 • Ю*1-3,
10х2" ’ = Ю*-5, х2 - 3 = Зх - 5.
Ответ: х = 1 или х = 2.
Упражнения
Решить уравнения:
9.22. = 128. 9.23. (5 х +х-2)3'х = 1.
172
§9. Показательные уравнения и неравенства
9.24. 0,5 х2-вх+17’5 = . 9.25. • V'93х-1 = IT3'3.
9.26. (0,5/ • 2^= ^.9.27. 2 = у-1^.
9.28. 16 V 8 х2-ь"3 = 128.
9.30. 2х • 5х = 0,1 • (10х-1)3.
9.32. 7 1-W = 49.
х+5 х+17
9.35. 32 х-7 = 0,25 • 128 х-э.
9.36. 52 • 5* • 5* • ... • 5* = 0,04-2*.
9.37. 4х • 5х-1 = 0,2 • 20’“&.
9.38. Зх+1 • 4х = 0,25 • 12to_‘.
9.39. 16 У/ (0,25) ” * = 2
9.40. 5&г-х = 6 ъ?~х.
9.41. 8 • 7 x2-s,+T -7-8 x2_s,+7 = о.
9.42. Решить уравнение
21Ь-1
- 44х“1 + e41-1 - 161х"1 = 1280.
Решение.
2^-1
212х-2 + 212х-3
- г1*-4 = 1280,
173
§9. Показательные уравнения и неравенства
212x-4 (23 - 22 + 2 - 1) = 1280,
212х-4 _ 256, 21*-4 _ 2»
Ответ: х = 1.
9.43. Решить уравнение 2 • 3х”1 — 3х-2 = 5х-2 + 4 • 5х-3.
Решение.
3х-2(2 • 3 - 1) = 5х-3 (5 + 4),
5 • 3х-2 = 5х-3 • З2, 3х-4 = 5х"4,
3х-4 , /з\х’4 f3\°
F24 ’ [J) = И •
Ответ: х = 4.
Упражнения
Решить уравнения:
9.44. Зх+2 - 3х = 72.
9.45. 2х - 2х-4 = 15.
9.46. 2х2+х-‘ - 2хЧх~9 = 56.
9.47. 3х-1 + 3х-2 + 3х-3 = 3159.
9.48. Зх’+1 + 3х2-1 = 270.
9.49. 2 • Зх+3 - 5 • 3х-2 = 1443
9.50. 10х - 5х"1 • 2х’2 = 950.
9.51. 2 • 16х - 241 - 42х“2 = 15.
9.52. 2** + 3 • 2Э'Т“‘ = 20.
9.53. 'ТзГ* - 7 V3x-“ = 162.
9.54. З12”1 - 96х~1 - г?*1-1 + в!3**1 = 2192.
9.55. 2Л+2 - 2vV+1 = 12 + 2Л“’.
9.56. 9х - 2 * 2 = 2 + 2 - З2*-1.
9.57. 6х + 6х+1 = 2х + 2х+1 + 2х+2.
174
§9. Показательные уравнения и неравенства
9.58. 52'-1 + 4х = S2* - 4х41.
9.59. 5х"3 - 5х"4 - 16 • 5х"5 = 2х”3.
9.60. 4х - 3х’*5 = Зх+0>3 - 2*~1.
9.61. 2х’'1 - 3х* = 3х2"1 - 2х*42.
9.62. 5*-Т-35 • 5* + 35 • 7х = 0.
9.63. х • 3х-1 + 3 • 3^ - 3х + х • 3^.
9.64. х2 • 4Л=Г + 424х = 16 • г27^ + х2 • 2*.
9.65. Решить уравнение 8х - 4х40’5 — 2х + 2 = 0.
Решение.
2Ь - г2*4' - 2х + 2 • 0, 2Ь — 2 • 2Ь — 2х + 2 = О.
Пусть 2х = /, ! >0. Тогда
/ 3 — 2/2 — / + 2 = О, r2(f-2)-(r-2) = 0,
(/— 2)(/— l)(t + 1) = О,
t-2,
1=1,
t = - 1.
Исходное уравнение равносильно совокупности двух урав-
нений:
2х = 2,
2*= 1.
Ответ: х = 1 или х = 0.
Упражнения
Решить уравнения:
9.66. 4* - 5 • 4Л + 4 = 0.
9.67. 4х - 10 • 2х-1 = 24.
9.68. J2*-1 + 5х41 = 250.
175
§9. Показательные уравнения и неравенства
9.69. 9х’-1 - 36 • Зх2-Э + 3 = 0.
9.70. 641/х + 22+з/х _ 12 = о.
9.71. 27^ = 4 - 3^ - 3.
9.72. 4 x-Vx2-5 -12-2 + 8 = о.
9.73. 3 • Л2""1 - 2 • 5х-1 = 0,2.
9.74. 9х-1 - 36 • 3х"3 + 3 = 0.
9.75. 8х+1 - в*-1 = 30.
9.76. 27х + Зх+4 = 702.
9.77. 4 2x41 + 2 2х+* = 4 • 8Х+1.
9.78. 2 - 2 Л - 8 = 0.
9.79. 3 • 2^"' - 8 2 -4 = 0.
9.80. «О |м 1 ГО II сч 1 к со +
9.81. - -1 = 2. 2х + 2 2х - 3
9.82. 4х2-х - 17 • 2х2-х+2 + 256 = 0.
9.83. 4x+Vx2-2 _ 5.2x+Vx2-2 - 1 _
9.84. * 1 и» р fe’loo 1 X СО + II К)
9.85. 2С“ 21 = 3 2С“2 х - 4. 1 2
9.86. 4‘* х + 8 = 3 • 2 с“ х.
9.87. Решить уравнение 51+*2 - 51 х2 = 24.
Решение.
Имеем: 5 • 5х2--— = 24. Пусть 5х2 = L Тогда
176
§9. Показательные уравнения и неравенства
St - у = 24.
Отсюда 5t2 - 24/ - 5 = 0, t = 5 или t = - . Следователь-
О
но, исходное уравнение равносильно такому: 5х = 5.
Ответ: х = 1 или х = — 1.
Упражнения
Решить уравнения:
9.88. 5* - 24 = — . 9.89. 22+х - 22~х = 15.
5х
9.90. 101+х2 - 10’-*2 = 99. 9.91. 2х + 8 • 2~х = 16,5.
9.92. 9 - 2х = 23-х. 9.93. 31+х - 2 • 3,-х = 7.
9.94. 5х-1+ 5 • 0,2х-2= 26. 9.95. 9 • 5*"* + 4 • З*-2* = 325.
9.96. 2х - 2 (0,5)* - (0,5)х -1=0.
9.97. 2’1"2 х + 2“*2 х = 3.
* * *
9.98. Решить уравнение 27х + 12х = 2 • 8х.
Решение.
Имеем: Зь 4- 3х • 2^ = 2 • 23*. Разделим обе части полу-
, (2\ (2\
ценного уравнения на 3. 1 + — = 2 • —
I J / I I
= t. Тогда 2t3 - t2 - 1 = 0,
2t3 - 2t2 + t2 - 1 = 0, 2t2 (t - 1) + (t - 1)(/ + 1) = 0,
(/ - 1)(2/2 + t + 1) = 0, t = 1.
Отсюда - =1.
Ответ: х = 0.
177
§9. Показательные уравнения и неравенства
Упражнения
Решить уравнения:
9.99. 64 • 9х — 84 • 12х + 27 • 16* = О.
9.100. 4 • 2* - 6х = 18 • З2*.
9.101. 3 • 4х + 2 • 9х « 5 • 6х.
9.102. 2 • 81х = 36х + 3 • 16х.
9.103. 3 • 16х + 37 • 36х = 26 • 81х.
9.104. 2-7*-3-2* = б| • 14**
9.105. 4-1/х + 6~Vx = 2 •
9.106. 6 • 25* - 5 • 10х - 4х = 0.
9.107. 4 • 3х - 9 • 2х = 5 ♦ бЛ
9.108. 6VT +6VT- 13vT=0.
9.109. 8х + 18х = 2 • 27х.
9.110. 4х+и + 9х = 6х+‘.
9.111. 5 • З2* + 15 • 52*-1 = 8 • 15*.
9.112. Решить уравнение 2х + 5х = 7х.
Решение.
Легко заметить, что х = 1 — корень данного уравнения.
Покажем, что других корней нет. Имеем:
1.
Понятно, что функция f(x) = убывающая. Тогда
горизонтальная прямая (в частности, у = 1) может пересечь
график функции / не более, чем в одной точке. Следовательно,
исходное уравнение имеет не более одного корня.
Ответ: х = 1.
178
§9. Показательные уравнения и неравенства
Упражнения
Решить уравнения:
9.113. 2х = 3-х.
9.114. 3х + 4х = 5х.
9.115. 7б-х = х + 2.
9.116. (V2 + vT)x + (V2 - V3")x = 2х.
9.117. 3х-1 + 5х-1 = 34.
9.118. 4х-2 + 6х-3 = 100.
9.119. 3х’2 =
X
9.120. 4Ux - 1 = г*-1.
9.121. 5х = V26 —х.
9.122. Решить уравнение (х — 3)х +х = (х — З)7х-3.
Решение.
Прежде всего заметим, что функция у — не явля-
ется показательной. Существуют две точки зрения, оценива-
ющие область определения данной функции. Первая исходит
из требования /(х)>0, вторая позволяет f(x) принимать от-
рицательные значения при условии, что g (х) принимает целые
значения, или /(х) = 0 при условии g(x) >0.
Решим данное уравнение, придерживаясь второй точки
зрения. Вначале проверим, какие из решений совокупности
х-3 = - 1,
х - 3 = 0,
х - 3 = 1
являются корнями данного уравнения. Проверка покажет,
ЧТО ПОДХОДЯТ ТОЛЬКО X = 3 или X = 4.
Теперь установим, какие из корней уравнения х2+ х =
= 7х — 5 удовлетворяют исходному уравнению. Имеем:
х = 1 или х = 5.
179
$9. Показательные уравнения и неравенства
Легко убедиться, что найденные значения подходят.
Ответ: х = 1 или х = 3, или х = 4, или х = 5.
Замечание. Если придерживаться первой точки зрения
на область определения функции y=f(x)*x\ то корни
х = 1 и х = 3 из ответа следует исключить.
Упражнения
Решить уравнения:
9.123. х* = 1.
9.124. (х2 — х - 1)х2“’= 1.
9.125. (х - 3)х’“х = (х - З)2.
9.126. (х - I)**1 = (х - I)2**4.
9.127. (х + 2/ = (х + г)*-2.
9.128. xx’_Sx+6= 1.
9.129. |х|х2-х’2=1.
9.130. (х + 1)х2*ь = (х + I)10*’12.
9.131. (х + 5)х2-х-1 = х + 5.
9.132. (х + 4)x2+,x+s = 1.
9.133. (1 - х2)(2+х>2 = (1 - х2)(8х"2)(х+2).
9.134. х^ = Xх’3.
, . Vx+X , . Vx2+3x+4
9.135. Решить неравенство I — I > I —I
I j I \ I
Решение.
Данное неравенство равносильно такому:
Vx + 4 < Vx2 + Зх + 4.
180
§9. Показательные уравнения и неравенства
Отсюда
х + 4 < х2 + Зх + 4,
х + 4 Э: 0 ;
'х < - 2,
х>0,
х Э - 4.
Ответ: [- 4; - 2) U (0; °0).
Упражнения
Решить неравенства:
х+1
9.136. 2 х’2» 4.
9.138. (0,3) х~2 < (0,3)х-1.
9.137. 16х >0,125.
ж+5
9.139. б”’>1.
9.141. 8 • 2х2-3х < (0,5)-1.
9.142. 36аь,2_1 2 ||
9.143. (0,36)ftix2_J
9.144. (0,25)э_аь2 « 8.
9.145. 125
9.146. 25 • 0,042х > 0,2^’-х).
9.147. 4 • О.Л4"*3’ < 0,2^.
9.148.
9.150.
9.152.
9.153.
9.149. 2х2+1х - 8 • 2х >0.
9.151.
9.154. 4'Л+1 < 64 • 2^.
9.155. - 4 =£ Зх2-2х_| - 5 «S 4.
181
§9. Показательные уравнения и неравенства______________
9.156. Решить неравенство 4х — 22'х-1) + 82Гх-2)/э > 52.
Решение.
Имеем: 2* - 2&“2 + 2&-4 > 52,
2ь-< (2* - 22 + 1)> 52, г2"-4 > 22,
2х - 4 > 2, х > 3.
Ответ: (3; »).
Упражнения
Решить неравенства:
9.157. 2х+2 - 2х+1 + 2х-1 - 2х-2 « 9.
9.158. 2х-2х-4 >15.
1 1
О 1 * х “ 2
9.159. 2 +8 - 4 <10.
9.160. З2*"1 + Э*"2 - З*-4 « 315.
/iV Z1V"2
9.161. | | >5.
9.162. «= 26.
I О I I О I
9.163. 5 • 2^ - 3 • 2Л“‘ 2 56.
9.164. 2х+2 - 2х+э - 2х+4 > 5х*1 - 5х*2.
9.165. 7х - 2х+2 < 5 • 7х-1 - 2х-1.
9.166. 3х - 2х+4 > Зх“* - 55 • 2х-2.
9.167. Зх+2 + 7х < 4 • 7х"1 + 34 • 3х-1.
9.168. г2”1 + 2&“3 - г2*'1 > 27-х + 2i-x - 2Э-Х.
9.169. Решить неравенство
4 * * 2 — 7 • 2-х — 4 < О.
182
$9. Показательные уравнение и неравенства
Решение.
Имеем: 2 • 4“* - 7 ♦ 2"х - 4 < 0. Пусть 2“х = t. Тогда
2t2 — It — 4<0, |Г + ||(Г-4)<0,
\ 1
- | < t < 4.
Поскольку t>Q, то исходное неравенство равносильно
такому: 2~* <4, 2~х < 22, - х < 2, х > - 2.
Ответ: (- 2; »).
Упражнения
Решить неравенства:
9.170. 25*<6 • 5х-5.
9.171. 5**‘>Г + 4.
9.172. 25"х + 5-х+19= 50.
9.173. Зь+1 + 3*+2 + 6 > 0.
9.174. — 21-х —8<0.
14 I
9.175. 9х*1 — 2 • 3х <7.
9.176. 4х + 2х+э>20.
9.177. 2* + 2 > 3 • 2х.
9.178. 2*** - 21 • + 2 =е 0.
9.179. 2х + 2“х*‘ - 3 < 0.
9.180. (т) « 2,-х - 16.
9.181. (0, if - 6 • (0,2)х + 5 « 0.
9.182. 5 • (0,04)х - 126 • (0,2)х + 25 < 0.
9.183. 2^ - 2'~^ 1.
9.184. 3 • (vT)x - 7 • 2х74 - 20 0.
183
§9. Показательные уравнения и неравенства
9.185. Решить неравенство 4х — 2 - Л2* + 10х >0.
Решение.
Имеем: I2* — 2 • S2* 4- (2 • 5)х > 0. Разделим обе части не-
/2\(2\х
равенства на 52х>0. Получим: —I 4- — -2>0.
1 0 I I 0 I
= t Тогда t2 4-1 - 2 > 0. Отсюда с учетом того,
/2'
что />0, получаем />1, т.е. —
1
Ответ: (- оо; о).
Упражнения
Решить неравенства:
9.186. 3 • 4х + 2 • 9х - 5 • 6х < 0.
9.187. 22х-1 + Зх+‘ • 2х-1 - 2 • 3* < 0.
9.188. 5 • 4х + 2 • 25х « 7 • 10х.
9.189. 9 • 4-,/х + 5 • 6-17х < 4 • 9-1/х.
9.190. 5 • 25Vx + 3 • Ю17' 2 • 41/х.
9.191. 2 • 7х - 3 • 2х > • 14х72.
9.192. 3 • 16х + 2 • 81х - 5 • 36х < 0.
9.193. 22**1 - 5 • 6х + 3&+1 « 0.
9.194. 10** + 251/х Ъ 4,25 • 5^х.
9.195. 4 • 3х - 9 • 2х - 5 • 6х72 <0.
184
§9. Показательные уравнения и неравенства
Задачи для самостоятельного решения
С-1
1. Решить уравнения:
2. 2 • 9х — Зх+1 -9 = 0;
3. З**5 - 2*+7 + 3*+4 - 2*+4 =
4. 5 • 3* + 2 • 15х - 3 • 5* = 0.
2. Решить неравенства:
2. 2х+э + 10 • 1Г+2< 11х+э + 2х+2;
3. + 4.
С-2
1. Решить уравнения:
1. 5х+1 — 5х-2 = 620;
2. 4х+1 + 19 • 2х - 5 = 0;
3. 7^' + 4 • 21х — З**1 = 0;
4. |x-4|V-x2-Sx = |х-4|2.
2. Решить неравенства:
2. 2* - 3 • 2х + 2 « 0;
3. 2V™ -КЗ- 22"^.
185
§9. Показательные уравнения и неравенства
с-з
1. Решить уравнения:
1. 3 • 9х*2 - 26 • 3х*' - 1 = 0;
2.
0;
3. 9 ♦ 16х - 7 • 12х - 16 • 9х = 0;
4. 12 - хI^х’-х-2 = |х-2|2
2. Решить неравенства:
2. З2**2 — 3х*4 < 3х — 9;
3. 2 • З7* — 5 > 31-1/х.
?86
§10. Логарифмические уравнения. и неравенства
Немного теории
Определение.
Логарифмом положительного числа N по основанию
а (а>0 и а^ 1) называется такое число а, что = N.
Основные свойства логарифмов
1) Если .У>0, то a'°t“N = N.
2) Если М>0 и N>0, то loge(MN) = logeМ + logeN и
10g“^ = lo&aN-
3) Если N > О, to loge N" = p loga N, где p G R.
log. W
4) Если N>0, b>0, ft # 1, to log,N = .
logta
Основные свойства логарифмической функции
У = loga*, a>0 и a # 1.
1) Z>(y) = (O; оо).
2) Е (у) = R.
3) Если a>l, то функция возрастает на (0; оо); если
0 < а < 1, то функция убывает на (0; оо).
4) Если х = 1, то у = 0; если х > 1 и a > 1, тоу>0; если
х > 1 и 0 < а< 1, тоу<0; если 0 < х < 1 и а > I, тоу<0; если
0 < х < 1 и 0 < а < 1, то у > 0.
Теорема.
Уравнение log,/(х) = log,<р (х), где а> 0 и a * 1, равно-
сильно каждой из следующих систем:
(/ (*) = Р (*)’ и,и (X) = У (X).
|/(х)>0 или ^(х)>0.
Теорема.
Неравенство loga/(x) >ioga^> (х) равносильно совокуп-
ности двух систем:
187
$10. Логарифмические уравнения и неравенства
а> 1,
/(»)>?(*).
р(*)>0;
0<в< 1,
/(*)<?(*).
/(*)>о.
Полезные упражнения
Найти область определения функции:
10.1. У = lg (- X). 10.2. у = Igx2.
10.3. - 1 10.4. у = lg(1 - sinx).
У lg(*2+l)‘
10.5. у = 1g (1 4- cosx). У = Vlog^l + х2) 10.6. y = Vlg(l+x2).
10.7. . 10.8. у = Vlg cos x.
10.9. у = 1g (arccos х). 10.10. у = 1g (arcsin х).
10.11. y = lg(|x| -х). 10.12. у = lglog,,2W.
Построить график функции:
10.13. у = lg tg х + lg ctg x. 10.14. У = log* 1.
10.15. y = logxx. 10.16. y = 2,o,<
10.17. y = 22 . 10.18. log 2 y = Xх .
10.19. у = 10 10. 10.20. у = Vlg sin x.
10.21. y = V2C“X- 2.
10.22. У = log2 (x2 - 1) - log2 (x - 1).
10.23. = lg(x2+l) lg(*2+l)‘
Комментарии, указания, ответы
10.1. (- оо; 0). 10.2. (- «•; 0) U (О; -»). Ю.З. (-<»; 0) U
U (0; «•). 10.4. х — любое, кроме х = + 2лк, kEZ. Область
188
§10. Логарифмические уравнения и неравенства
определения данной функции можно записать в таком виде:
Я I х # + 2яЛ, к G zl. 10.5. {хЕЯ | х # л + 2лк,
xGZ}. 10.6. х — любое. 10.7. х = О. 10.8. х = 2лк, kGZ.
10.9. - 1. 10.10. О « х « 1. 10.11. (- »; 0) U (0; ®).
10.12. х = О. 10.13. Рис. 54. 10.14. Рис. 55. 10.15. Рис. 56.
10.16. Рис. 57. 10.17. Рис. 58. 10.18. Рис. 59. 10.19. Рис. 60.
10.20. Рис. 61. 10.21. Рис. 62. 10.22. Рис. 63. 10.23. Рис. 64.
189
§10. Логарифмические уравнения и неравенства
190
§10. Логарифмические уравнения и неравенства
Основные типы задач
10.24. Решить уравнение 1g (х + 1,5) = - 1g х.
Решение.
Имеем: 1g (х + 1,5) + 1g х = 0. Заметим, что переход к
уравнению 1g х (х + 1,5) = 0 расширяет область определения
исходного уравнения. Поэтому возникает угроза приобретения
посторонних корней. Однако система
|х>0,
[1g х (х + 1,5) = 0
равносильна данному уравнению. Далее,
х>0,
х>0, Гх = - 2,
ха+1,5х = 1; ' 1
2*
Ответ: х =
log2(9 —2я)
10.25. Решить уравнение —-------- = 1.
Решение.
Данное уравнение равносильно системе
х #3, (х # 3,
log2 (9 — 2я) = 3 - х; [9 — 2* = г*-*;
х # 3,
2я + - 9 = 0 ;
2я
х # 3,
х = 0,
х = 3.
Ответ: х = 0.
Упражнения
Решить уравнения:
10.26. logj (х - 2) + log^y (х3 - 2) + log^ (х - 2) = 4.
10.27. log, (Зх - 11) + log, (х - 27) = 3 + log, 8.
191
§10. Логарифмические уравнения и неравенства
10.28. log, (х - 2) - log, (х + 2) = 1 - log, (2х - 7).
10.29. log, (х + 1) - log, (1 -х) = log, (2х + 3).
10.30. log4 (х + 3) - log4 (х - 1) = 2 - log4 8.
10.31. 1g (х - 1) + 1g (х + 1) = 31g 2 + 1g (х - 2).
10.32. 1g (5 - х) - 11g (35 - x3) = 0.
10.33. log2^ + log2(x2 - 25) = 0.
10.34. log^ (4х - 6) - log^y (2х - 2) = 2.
10.35. log2 (4 • 3* — 6) — log2 (9х - 6) = 1.
10.36. 2 log3 (x - 2) + log3 (x - 4)2 = 0.
10.37. 2 1g x - 1g 4 = - 1g (5 - x2).
10.38. Igx (x + 9) + lg^^ = 0.
10.40. logj (9х + 9) = x + log, (28 - 2 • 3х).
10.41. x + 1g (1 + 2х) = x 1g 5 + 1g 6.
10.42. A8-*" = 1.
1g (6x - 5)
10.43. log,., 3 - log,., 2 - | = 0.
10.44. 4 210*«(2x-2) • 0,25 lo*« (k_5) = yfW.
10.45. log2(9 - 2х) = 10 “ (3-x>.
10.46. Решить уравнение log^34x + log2-^- =8.
Решение.
2
i log Ax \
Имеем: ,—+ log,x2 - log, 8 = 8,
Uog20,5) 2 2
192
§10. Логарифмические уравнения и неравенства
(log24 + log2x)2 + 21og21 л I -11=0.
Поскольку x > 0, то последнее уравнение можно перепи-
сать так: 4 + 4 log2 х + log2 х + 2 log2 х - 11 = 0.
Пусть log2x = t, тогда t2 + 6t - 7 = О,
't = - 7,
t = 1.
Отсюда
log2x = - 7,
log2x = 1.
Ответ: x = 2-7 или x = 2.
10.47. Решить уравнение
log, x - 1 _ , ,
---------+ 2 log, vGF + log, x = 3.
loM
Решение,
log, x - 1 t , ,
+ bg,x + lo8,«-3.
«Исчезновение» первого слагаемого в левой части данного
уравнения расширит область определения уравнения. Поэтому
исходное уравнение равносильно системе
х # 3,
log*х + log3x -2 = 0;
х # 3,
log3x = - 2,
log,x = 1;
x # 3,
1
X~9
x = 3.
_ 1
Ответ: x =
Упражнения
Решить уравнения:
10.48. Vlog, x* - 4 log, V3x~ = 1.
10.49. 9')
О
3
lg(x - 9)34 *
7 Ain ебраическии гренажу
193
§10. Логарифмические уравнения и неравенства
10.50. 31g2 (х - 1) - 101g (х - 1) + 3 = 0.
10.51. —~— = 1.
5 - 1gх 1 + Igx
10.52. 1g2 (100х) + 1g2 (Юх) = 14 + lg|.
10.53. V2 log8 (- x) - log, VZ = 0.
10.54. 2 Igx2 - (1g (- x))2 = 4.
10.55. 31gx2- log2(-x) = 9.
10.56. log2 (x - I)2 - log^ (x - 1) = 5.
10.57. lg2x-lgx2 = lg23- 1.
10.58. logL 4x + log2 — = 8.
О
10.59. log2xs- 51og2x’ = 10.
10.60. 1g (Юх) • 1g (0,lx) = Igx’ - 3.
in ai 2 + 9 = 13
‘ 7 - Igx 11 + Igx 12 '
10.63. logj^F + ^log2 x = j .
10.64. log2(2x) = log2x4.
10.65. log, (3х - 1) log, (3x+’ - 3) = 6.
10.66. Решить уравнение
loga5x x2 - 141 loglbt x3 + 40 log^ VF= 0.
Решение.
Безопасный путь решения этого примера — переход к
основанию 2. Переход к основанию х сужает область опре-
деления исходного уравнения ровно на один элемент х = 1,
который как раз и является корнем данного уравнения (в этом
194
§10. Логарифмические уравнения и неравенства
легко убедиться). Поэтому, выбирая переход к основанию х,
следует записать, что данное уравнение равносильно сово-
купности:
X = 1,
log, х2 14 log, хэ 40 log, Vx”
------±----- _----------f--------------±---- — 0
logx 0,5 + log, X logx 16 + logx x logx 4 + logx x
Решим второе уравнение совокупности. Имеем:
____?__________42___ + _J0_______ =
1 - logx 2 4 logx 2+1 2 logx 2+1
Пусть logx 2 = t, тогда получим
_J-------21 + 10 =
1-1 41+1 21+1
После необходимых преобразований запишем:
212+ 31- 2_______________________
(1-1)(41+1)(21+1) " •
Отсюда 1 = или 1 = - 2. Имеем:
Ответ: х = 1, или х = —, или х = 4.
Упражнения
Решить уравнения:
10.67. logx 9х2 log, х = 4.
10.68. 2 logx 27 - log^x = 1.
10.69. log5x + logx 25 = 3.
10.70. logx 9 + logx2 729 = 10.
10.71. V log2 x + log2 5 + 2 = 2,5.
195
§10. Логарифмические уравнения и неравенства
7
10.72. logx2-log4x + 6 = 0.
10.73. logx 125xlog23x = 1.
10.74. 5 log^jX + logVx x3 + 8 logfc2 x2 = 2.
10.75. logx+1 (x - 0,5) = logx_a5(x + 1).
10.76. logx* 16 + log^ 64 = 3.
10.77. 310gx 4 + 2 log^ 4 + 310g16x 4 = 0.
10.78. logx+1 (x3 - 9x + 8) logx_| (x + 1) = 3.
imo 2~41°8i22 _ bg6(8-x)
log12(x + 2) log6(x + 2)’
* * *
U X 4- 5
10.80. Решить уравнение x 3 =105+lg x.
Решение.
Поскольку на области определения обе части уравнения
положительны, то можем записать уравнение, равносильное
данному:
Igx 3 = 1g 105+1‘х, 18* + 5 • Igx = 5 + Igx.
Пусть lg х = t. Тогда t2 + 2t - 15 = 0. Отсюда t = - 5 или
1 = 3.
lg x = - 5,
lg x = 3.
Ответ: x = 10-5 или x = 103.
10.81. Решить уравнение 51*x = 50 - x'*s.
Решение.
Пусть x1*5 = t, t> 0. Тогда lg x'g 3 = lg t,
lg51gx = lg t, IgJ* * = lg t, отсюда t = 5 й x.
Запишем t = 50 — t, t = 25. Имеем:
196
§10. Логарифмические уравнения и неравенства
х“ 5 =25, х = l-S10»’10, х = (5,ot110)2, х = 100.
Ответ: х = 100.
Упражнения
Решить уравнения:
10.82. я1»’* - 51»х = 0,0001.
10.83. х1*х = 10000х2.
10.84. х 2-^х~'*х2 = 1.
X
10.85. х 2 '*’* = 10х3.
10.86. хlgx’2 = 1000.
10.87. (х + 7)'‘(,+Т) = Ю.
10.88. (х- 18)“
10.89. 9х“ х + 91Х-1** = 60.
10.90. 7“* = 98 - х Ч
10.91. хк>,гЖ+2 = 256.
10.92. х 3+1*И = 8000.
10.93. х10*5*-^
10.94. х = 2 3<к’!‘х+3).
10.95. VxlgVr = 10.
10.96. 61О*‘Х + х |<*'х = 12.
10.97. х'” + 3 = 54.
10.98. Решить уравнение
(х + 1) log*х + 4х log3x - 16 = 0.
197
§10. Логарифмические уравнения и неравенства
Решение.
Рассмотрим данное уравнение как квадратное относи-
тельно log3x. Тогда получим:
log,x=—4, Гх = 3"4,
1ое>* = 1оь* = ГГг
Очевидно, что х = 3 — корень второго уравнения сово-
4
купности. Поскольку функции у = log, х и у = х + t имеют
разный характер монотонности, то рассматриваемое уравне-
ние больше корней не имеет.
Ответ: х = З-4 или х = 3.
Упражнения
Решить уравнения:
10.99. log7 (х + 8) = - х.
10.100. logV3 (х - 5) = х - 9.
10.101. 3х = 10 —log2x.
10.102. log2x + (х - 1) log2x = 6 - 2х.
10.103. Зх2 - 2х’ = log2 (х2 + 1) - log2x.
10.104. Решить систему уравнений
'4х/у + у/х _ 32
logj (X - у) = I - log, (х + у).
Решение.
Имеем:
22х/у + 2у/х _ 25
log, (х - у) + log, (х + у) = 1.
Из первого уравнения системы следует, что — +
2 = 5
х 2 ‘
198
§10. Логарифмические уравнения и неравенства
Отсюда у = 2 или ~ = Следовательно, исходная си-
стема равносильна совокупности двух систем.
х = 2у,
а)
log, (х - у) + log3 (х + у) = I.
Имеем: log3 у + log3 Зу = 1, log3y + I + log3y = 1, у=1.
Тогда х = 2.
у = 2х,
б)
log3 (х - у) + logj (х + у) = 1.
Имеем: log3(—х) + log33x = 1. Понятно, что это уравне-
ние, а следовательно, и система, решений не имеет.
Ответ: (2; 1).
Упражнения
Решить системы уравнений:
10.105. lg V5 - х + 1g 2 = 1g (х + 3), х2 + 7х - 8 = 0. 2х-у „ f2\ „ /2\ 2 , „
10.106. • 3 +7Н -6 = 0, 1 J 1 1 л I ,1g (Зх - у) + 1g (х + у) - 41g 2 = 0.
10.107. 51og2x = log2y3 - 1о^2, log2y = 8 - log^x.
10.108. < OQ 0Q 1 41 О 1 0Q _ * М QQ 1 » * ч II II й (Л г X +
10.109. log2 (х + у) + log2 (х2 - ху 4- у2) = 1.
10.110. . logx (Зх + 2у) = 2, log,, (2х + Зу) = 2.
199
§10. Логарифмические уравнения и неравенства
10.111. х1*’’ = 2, ху = 20. 1 _ 1 _
10.112. х у 15 ’ log3x + log, у = 1 + log, 5.
10.113. logyx 4- logxy = 2, x2 + у = 12. log3 (x + 2y) + log^3 (x - 2y) = 1,
10.114. x2 + y2 = 4 + |y.
10.115. fi . i 5 logj,x + logxy = 2 , xy = 27.
10.116. < x ,ow’ + у'°*** = 4, log4x - log4y = 1.
10.117. < 2 (log№ 2-2 logxj y) + 15 = 0, xy2 = 32.
10.118. (x + y)3’-' = ^, 310g5 (X + y) = x - y.
10.119. Решить неравенство
logV2 (Зх - 4) < log^j (х - 2).
Решение.
Данное неравенство равносильно системе
j Зл - 4 >х - 2, fx > 1,
р - 2>0; ]х>2.
Ответ: х > 2.
200
§10. Логарифмические уравнения и неравенства
Упражнения
Решить неравенства:
10.120. log5(3x - 1)< 1.
10.121. log(X2(4 - 2х)> - 1.
10.122. loga4 (2х - 5) > loga4 (х + 1).
10.123. log4 (Зх — 1) < log4 (2х + 3),
10.124. logj/2 (х2 - 5х + 6) > - 1.
2 — Зх
10.125. log, ^ =s - 1.
10.126. logl/4 Ss - |.
10.127. log, (х2 - 4х + 3) « 1.
10.128. log, |3 - 4x1 >2.
10.129. logy3 (х + 4) > logV3 (х2 + 2х - 2).
10.130. 1 + log2 (х - 2) > log2 (х2 - Зх + 2).
10.131. log^ (х + 1) > log, (2 - х).
10.132. ioga,log6 < 0.
10.133. logajlog8 С °-
10.134. loga7log2 > О.
10.135. 1g (х - 2) + 1g (27 - х) < 2.
10.136. log2 (2 - х) + logy2 (х - 1) > logyj 3.
10.137. log, (x + 2)(x + 4) + logy, (x + 2) < | 10^7.
10.138. Решить неравенство logx —j--- > 0.
201
§10. Логарифмические уравнения и неравенства
Решение.
Перепишем данное неравенство так: log, —-----> log, 1.
х + 1
Это неравенство равносильно совокупности двух систем.
а)
0<х< 1,
Зх - 1
2 , , <
1,
0;
“ < х < 1,
х2 - Зх + 2 > 0;
| < х < 1,
О
(х - 1)(х - 2) > 0;
Зх “ 1
2 _1_1
б) * 3% 1
1
3
х > 2,
х < 1,
1.
1
3
.2
1;
х2-Зх + 2<0; \(х - 1)(х - 2)<0;
Ответ:
11 U (1; 2).
О /
Упражнения
Решить неравенства:
10.139. log,_,| > |.
10.140. logt/j log2 log,_. 9 > 0.
10.141. log, log, (3х - 9) < 1.
10.142. log, log, (9х - 6) Ъ 1.
10.143. log* (x2 - 5x + 6) < 1.
10.144. log,2 (3 - 2x) > I.
10.145. log, (x2 + 3x - 3) > 1.
10.146. log,2 -^4 « |.
10.147. log,_4 (2x2 - 9x + 4) > 1.
202
§10. Логарифмические уравнения и неравенства
10.148. log^ (6 + 2х - х2) « |.
10.149. logx_3 (х2 - 4х)2 « 4.
10.150. logx2+Jx (х + 3) < 1.
10.151. logx (х2 - х) > 1.
10.152. log(x_3) (2 (х2 - Юх + 24)) =s log(X_3) (х2 - 9).
10.153. Решить неравенство
log2 (х - I)2 - log^ (х - 1) > 5.
Решение.
_ log2(x-l)
Имеем: (2 log2 I х - 11 )2-------—- > 5.
Поскольку х > 1, то можем записать
4 log2 (х - 1) + log2 (х - 1) - 5 > 0.
Пусть log2 (х - 1) = t. Тогда 4i2 + t - 5 > О,
|Г + 4|0- 0>0, К -4 или Г>1.
I 4 J 4
Получаем совокупность
log2 (х - 1) < -
log2(x- 1) > 1;
1 <х< 1
х>3.
0<х - 1 <2-*4,
х - 1 > 2;
+ тк-
V32
Ответ:
Упражнения
Решить неравенства:
10.154. log*2(x- 1) > 4.
203
§10. Логарифмические уравнения и неравенства
10.155. log^2 (л - 3) > 1.
10.156. ig2x + 6<51gx.
10.157. lg2x + lgx>2.
10.158. lg2(-x) + lgx2<3.
10.159. log2+2 (x - 1) - 3 log,+2 (x - 1) + 2 < 0.
10.160. log2 (2x + 1) - logx (2x + 1) — 2 > 0.
10.161. 51ogft3x 6 + log^jX.
10.162. log2 (6 - x) + 2 logm (6 - x) + log, 27 =s 0.
10.163. log2 (x - x2 + 2) + 3 logj/2 (x - x2 + 2) « - 2.
/ э\2
10.164. (log2x)4- Hog^yj + 9 log2 < 4 (log^ x)2.
♦ ♦ *
10.165. Решить неравенство log^, x < logx 3 - y.
Решение.
Пусть log,x = t. Тогда t + у - у > 0. Отсюда
° < t <
t>2.
Далее,
log,x >2,
0<log,x <
x>9,
1 <x<vT
Ответ: (1; V3~) U (9; <»).
204
§10. Логарифмические уравнения и неравенства
Упражнения
Решить неравенства:
10.166. ---------,----------г
log2 X log2 X - 1
1.
10.167. lg (х2 + 1) - 1 < log^ (2х + 10).
10Л68- 5 —Igx + rfe < L
10.169. iOg^x _ i) < ]og2Vx + 1 '
10.170. log, (4х + 1) + log/+13 > |.
10.171. 5—^-----1 5» 0.
lg 10х 1g 100х
10.172. :> Zlog^x + 1.
2 - log^ х
10.173.
log2 2 _ log2x2
log2x log2x-l
1.
10.174. log2 x - logx 32 « 4.
10.175. 2 logjX - logx 125 < 1.
10.176. ^х-З^х + .З < j
Igx - 1
10.177. log^ j + logjX « 1.
10.178. -г----- + j—-— 1.
i-tog^x logft3x
У log^7x + 3 log^/x+l)
10.180. logj (2х - 1) + log^ 3 « у.
205
§11. Производная и ее применение
Немного теории
Правила дифференцирования
Если функции и и v дифференцированы в точке
ху то и их сумма, произведение, частное (при
условии v (Xq) * 0) дифференцируемы в этой же
точке, причем
(и 4- и)' = и' + v,
(ии)' = и’ v + d и,
Если функция f дифференцируема в точке ху а
функция g дифференцируема в точке f(x^, то
функция h(x) = g(f(x)) также дифференцируема
в точке Xq, причем
Л'(*о) =«'</(*<>)) ’/'(Jo)-
Геометрический смысл производной
Угловой коэффициент касательной, проведенной к гра-
фику функции f в точке (x0,/(Xq)), равен /' (jQ. Уравнение
этой касательной имеет вид у = /' (х0)(х - xj 4-/(х0).
Достаточное условие возрастания (убывания) функции
Если функция f имеет положительную (отрицательную)
производную в каждой точке промежутка (а; Ь), то f возра-
стает (убывает) на этом промежутке.
Достаточное условие существования экстремума в точке
Если функция f непрерывна в точке х0, a f' (х) > 0 на
интервале (a; xj и /'(х)<0 на интервале (х0; Ь), то х0 —
точка максимума функции /.
Если функция f непрерывна в точке х0, a f' (х) < 0 на
интервале (a; xj и /'(х)>0 на интервале (х0; Ь), то х0 —
точка минимума функции /.
206
§11. Производная и ее применение
Основные типы задач
11.1. Найти производную функции f(x) = V2 - Зх3 .
Решение.
г м _ <гЗ*’)' _ -К2
1 1 ' 2 V2 - Эх’ 2 V2 - Эх’ ‘
11.2. Найти производную функции f(x) = xlg2x.
Решение.
/' (^) = (х)’ 1g 2х + х (1g 2х)' = 1g 2х + =
= lg 2х + = 1g 2л + 1g е = 1g 2ех.
. 2
11.3. Найти производную функции f(x) = * COs 2х
Решение.
и zz \ Sin2X 1 . 2
Имеем: /(х) - |8 х.
Упражнения
Найти производные функций:
11.4. /(х) = х3 - Зх2 + VF+ 5.
11.5. /(x) = x3Vx~- |.
11.6. /(х) = VxVF.
1L7- = ГТзГ
11.8. /(х) = 5х4 - 7х3 - 2 Vx"+ .
V 1 Я
11.9. f(x) = xVx 4- ----j.
X X
207
§11. Производная и ее применение
11.10. /(х) = 6х3 - 4 + 4 - 'Гз-
X X
11.11. /(х) = у/х~ + Vx" + ^6~.
11.12. /(х) = 3x2Vx~ + 4х7 —+ Зх4.
X
11.13. /(х) = V х Vx
11.14. f(x) = X' 1 1 1 C f \ 11 .15. j(x\ = , x2 + 4 11. 17. f (x) = (3x2 - 5x)3. 11 .19. /(x) = V5-x. 1 ,z . 3Vx"- 1 11.16./(«) = vj--! • 11.18. /(x) = V3x- 1. 11.20. /(x) = Vl - 2x3.
11.21. /(x) = xVl +x2. Vl - x2 11.22. /(x) = x
11.23. /(x) = Vx + Vx-. П.24. /(x) _ JL_^. x -Vx - 4
11.25. /(x) = x sinx. 11.27. /(x) = sin2x. 11.29. /(x) = sin22x. 11.26. f (x) = sinx + cosx. 11.28. /(x) = cos2x. 11.30. /(x) = 2xtgx.
11.31. /(х) = -------1- ,11.32. /(х) = sin Зх cos Зх.
v 7 2 - cos Зх ' '
11.33. / (х) = , gV- . 11.34. / (х) = sin4 х - cos4 х.
1 v 7 1 + sin X v 7
11.35. /(x) = sin 2x tgx. 11.36. /(x) = e* + 5.
11.37. /(x) = e* - x. 11.38. /(x) = 3x2 - Inx.
11.39. /(x) = x In 3x. 11.40. /(x) = In (tg .
11.41. /(x) = lg22x.
208
§11. Производная и ее применение
11.42, Написать уравнение касательной к кривой
/ (х) = V2 - 5х в точке пересечения этой кривой с осью ор-
динат.
Решение.
Очевидно, что абсцисса точки касания х0 = О. Тогда
/ Оо) = V2. Имеем: /' (х) = —, /' (Хо) = - —
X ▼ At Ол At V At
Подставляем полученные числовые значения в общее
уравнение касательной. Получаем у — — “ 0) + т-е-
Упражнения
Составить уравнение касательной к графику функции:
11.43. у = х3 в точке х = - 1.
11.44. у = sinx в точке х = 0.
2
11.45. у =---в точке х = 1.
х
11.46. у = Vx" в точке х = 4.
11.47. у = х3 - Зх в точке х = 2.
11.48. у = 3 - 2х2 в точке х = - 2.
3
11.49. у = —у в точке х = 1.
х
11.50. У = tg |х - I в точке х = .
I 4 j х
11.51. у = (е^2 + е -х/2) в точке х = 2 In 2.
Л
11.52. у = sin 2х в точке х = — .
1X
11.53. у = V2x - 1 в точке х = 5.
11.54. у = (Зх - 7)3 в точке х = 3.
209
§11. Производная и ее применение
,. __ X2 — 1
11.55. у =------в точке х = - 2.
х
11.56. у = sin2 Зх в точке х = .
1X
11.57. у = х2 е ~х в точке х = 1.
11.58. у = х Vx-1 в точке х = 2.
11.59. у = А—— в точке пересечения с осью абсцисс,
х + 1
11.60. у = х2 — 4 в точке пересечения с осью ординат.
11.61. у = 2х2 — 4х в точках пересечения с осью абсцисс.
♦ * *
11.62. На кривой /(х) = х2 - х 4- 1 найти точку, в которой
касательная параллельна прямой у = Зх - 1.
Решение.
Поскольку касательная параллельна прямой у = Зх — 1,
то угловой коэффициент касательной равен 3. Следовательно,
если х0 — абсцисса точки касания, то /' (х0) = 3. Имеем:
2х0 ~ 1 = 3, х0 = 2.
Ответ: (2; 3) — точка касания.
Упражнения
11.63. Существует ли на кривой у = Vx2 4- 1 точка, в
которой касательная параллельна прямой у = х?
11.64. Существуют ли на графике функции у = 2х34-
4- х2 4- 5х 4- 3 точки, в которых касательная параллельна оси
абсцисс?
11.65. Написать уравнение касательной к кривой
у = х2 - 7х 4- 3, которая параллельна прямой 5х 4- у - 3 = 0.
11.66. На графике функции у = х (х — 4)3 найти точки,
в которых касательная параллельна оси абсцисс.
11.67. При каких значениях а и b прямая у = 7х — 2
касается графика функции у — ах2 4- Ьх 4- 1 в точке А (1; 5)?
210
§11. Производная и ее применение
11.68. На параболе у = х2 взяты две точки с абсциссами
х = 1 и х = 3. Через эти точки проведена секущая. В какой
точке параболы касательная к ней будет параллельна секу-
щей? Записать уравнение этой касательной.
11.69. При каком значении х касательная к линии
у = х2 - 2х + 5 параллельна прямой у = 2х?
11.70. Найти касательные к графику функции
у = 2х2 4- 2, проходящие через точку (0; 1).
11.71. Записать уравнения всех касательных к кривой
у = х3 - Зх 4- 1, которые параллельны прямой 9х - у = 5.
11.72. Найти угол между касательными к графику функ-
ции у = х3 - х в точках с абсциссами Xj = — 1 и х2 = 1.
11.73. Определить, под какими углами парабола
у = х24- 2х - 8 пересекает ось абсцисс.
11.74. Написать уравнение касательной к кривой
у = V2x - 1, образующей с осью абсцисс угол 45°.
11.75. В какой точке нужно провести касательную к
х + 5
х 4- 3’
графику функции у =
чтобы она прошла через начало
координат?
11.76. Найти координаты точки, в которой касательная
к кривой у = 5 — х2 образует с осью абсцисс угол 75°.
11.77. На кривой у = х2 - х 4- 5 найти точку, касательная
в которой образует угол 45° с осью абсцисс.
11.78. В каких точках касательная к графику функции
х 4" 2
у = х образует с осью абсцисс угол в 135°?
11.79. Найти промежутки возрастания и убывания, а
также точки максимума и минимума функции
/ (х) = х4 - 4х3 - 8х2 4- 3.
Решение.
Данная функция определена и дифференцируема на
D(f) = Я. Имеем: /' (х) = 4х3 - 12х2 - 16х
= 4х (х2 - Зх - 4) = 4х (х - 4)(х 4- 1).
211
§11. Производная и ее применение
Исследуем знак
производной методом
интервалов — рис. 65. __ _________________
Теперь можно сделать—_Г---------------------------_
вывод, что функция f ~~ 4 Х
возрастает на каждом из РпС 55
промежутков [-1; 0] и
[4; оо), а убывает на (-<»;- 1 ] и [0; 4]. Учитывая характер
смены знака производной, получаем, что х = — 1 и х = 4 —
точки минимума, а х = 0 — точка максимума.
Упражнения
Доказать, что функция является монотонной на всей
числовой прямой:
11.80. у = |х3-|х2 + х-5.
О X
11.81. у = 6 - 6х-2х3 + Зх2.
11.82. у = х + —
1 + х
11.83. у = 2х 4- sinx.
Найти промежутки возрастания и убывания функции,
а также точки максимума и минимума:
11.84. у — 2х3 + Зх2 - 2.
11.85. у= х3 + х2 - 6х.
3 2
* * ох х3 3 2 _ , 25
11.86. У = -р + -7Х - 5х + — .
О 4 1Z
11.87. у = Зх2 — х3.
11.88. у = - |х4 + 4х3 - 6х2 + 5.
11.89. у = х4- 2х3.
11.90. у = х5- х3- 2х.
11.91. у = |х4 -|х2 + 5.
11.92. у = — х (х - 2)2.
11.93. у = - х4 + 4х3 + 8х2 - 3.
212
§11. Производная и ее применение
11.94. ) 11.96. ) 3 X П 95 у = х * *6
х2 + 3 ‘ +". 4 х 1 у 2 X 2
и.»’. , - ?1.
11.98. у 11.100. 11.102. х’ + 4 ' = —2 ~ X х + 3 11.99. у = (J1 ~ . х+1 11101 v — * +
у ~ х1 - 4 ’ х2 + 1 11.1U1. у — х - 1 111 л» —
У — 2 1 • х - 1 11.1 иэ. у — э х2+ 1
11.104. - Зиг у = х • е 11.105. у = х — In х.
11.106. у = х - е~х . 11.107. у = х + 1п(1-2х).
11.108. у = х2-1п(1 -2х). 11.109. у = х2е
11.110. у = х3 е ~х. 11.111. у = —- . X
11.112. е У ~ X 11.113. у = х21пх.
11.114. _ х2 у ~ 1пх ’ 11.115. у = х2ех\
11.116. 11.118. 2 X У = - 2 • ех у = In sin х. 11.117. y = x-6sin^ .
11Л19. Найти наибольшее и наименьшее значения функ-
х 3
ции /(х) = - + - на отрезке [1; 4].
«5 х
Решение.
1 3
Имеем: /'(х) = ------Найдем критические точки функ-
3 х
тт 1 3
ции. Для этого достаточно решить уравнение —----------2 = О-
J X
213
§11. Производная и ее применение
Получим х = 3 или х = — 3. Из двух найденных критических
точек рассматриваемому промежутку принадлежит лишь
х = 3. Теперь осталось найти значение функции на концах
промежутка [1; 4], а также в точке х = 3 и сравнить по-
лученные результаты. Имеем:
/(1) = з|,/(4) = Ц,/(3)-2.
Следовательно, max /(х) = 3 , min /(х) = 2.
ft О 3 ft 0
Упражнения
Найти наибольшее и наименьшее значения функции на
заданном отрезке:
11.120. /(х) = |х4-6х + 3, [-1; 2].
11.121. /(х) = |х3 - |х2 + 2, [-2; 2].
О X
11.122. /(х) = х3 — 4х2 + 4х + 3, [1; 3].
11.123. /(х) = 2sinx + cos2х, [О; л].
11.124. / (х) = 12х — х3, [-1; 3].
11.125. /(х) = х4 - | + 1, [-1; 1].
11.126. /(х) = х5- 5х4 + 5х3 + 2, [-1; 2].
11.127. /(х) = х V3--cos 2х,
11.128. /(х) =x2V3^x", [1; 3].
11.129. /(х) = 7 + ^. [1; 5].
11.130. /(х) = 1-2; 2].
х2 + 1
11.131. / (х) = V2x -х2 , 2 .
11.132. /(х) = sin22x, - 7 •
214
§11. Производная и ее применение
Л
°' 2 '
11.133. /(х) = х + cos2x,
11.134. f(x) = х2еь. [-2-/1].
11.135. f(x) = cos2x + sinx,
11.136. f(x) = 2x2 —Inx, [1; e].
Задачи для самостоятельного решения
С-1
1. Найти производную функции:
ч .. . Vx- + 1
а) = VF ;
б) /(х) = 2xctgx;
в) /(х) = 5* - 251п5х.
2. Найти уравнение касательной к графику функции
х- Л
f (х) = sin 2х в точке с абсциссой х0 = — .
3. Найти промежутки монотонности и экстремумы функ-
ции f(x) = х4 - 2х2.
С-2
1. Найти производную функции:
a) f(x) = V3 - 4х ;
б) /(х) = tg23x;
в) /(х) = In ^sin^.
2. На графике функции /(х)=|х3-|х2 найти точки,
в которых касательная параллельна прямой у = 2х + 5.
3. Найти промежутки монотонности и экстремумы функ-
ции f(x) = xlnx.
215
§ 12. Знакомство с параметром
Эта небольшая по объему глава адресована в
первую очередь читателям, имеющим минималь-
ное представление о задачах с параметрами.
Известно, что в программах по математике для неспе-
циализированных школ этим задачам отводится незначитель-
ное место. Поэтому, в первую очередь, укажем разделы об-
щеобразовательной математики, в которых вообще присутст-
вует сама идея параметра.
Так, с параметрами учащиеся встречаются при введении
некоторых понятий. Не приводя подробных определений, рас-
смотрим в качестве примеров следующие объекты:
• функция прямая пропорциональность: у = кх (х и у —
переменные; к — параметр, к # 0);
• линейная функция: у = кх+b (х и у — переменные; к и
Ь — параметры);
• линейное уравнение: ах 4- Ъ = 0 (х — переменная; а и Ъ
— параметры);
• уравнение первой степени: ах 4- Ь = 0 (х — переменная;
а и Ь — параметры, а # 0);
• квадратное уравнение: ах2 4- Ьх 4- с = 0 (х — переменная;
а, Ь ис — параметры, а # 0).
К задачам с параметрами, рассматриваемым в школьном
курсе, можно отнести, например, поиск решений линейных
и квадратных уравнений в общем виде, исследование коли-
чества их корней в зависимости от значений параметров.
Естественно, такой небольшой класс задач многим не
позволяет усвоить главное: параметр, будучи фиксированным,
но неизвестным числом, имеет как бы двойственную природу.
Во-первых, предполагаемая известность позволяет «общаться»
с параметром как с числом, а во-вторых, — степень свободы
общения ограничивается его неизвестностью. Так, деление
на выражение, содержащее параметр, извлечение корня чет-
ной степени из подобных выражений требуют предваритель-
ных исследований. Как правило, результаты этих исследова-
ний влияют и на решение, и на ответ.
216
§ 12. Знакомство с параметром
Основное, что нужно усвоить при первом знакомстве с
параметром, — это необходимость осторожного, даже, если
хотите, деликатного обращения с фиксированным, но неиз-
вестным числом. Этому, по нашему мнению, во многом будут
способствовать примеры настоящей главы.
Необходимость аккуратного обращения с параметром хо-
рошо видна на тех примерах, где замена параметра числом
делает задачу банальной. К таким задачам, например, отно-
сятся: сравнить два числа, решить линейное или квадратное
уравнение, неравенство и т.д.
Рассмотрим ряд примеров.
12.1. Сравнить: - а и За.
Решение.
Естественно рассмотреть три случая:
если а < 0, то -а > За;
если а - 0, то -а = За;
если а > 0, то -а < За.
12.2. Решить уравнение ах = 1.
Решение.
На первый взгляд представляется возможным сразу дать
ответ: х = Однако при а = 0 данное уравнение решений
не имеет, и верный ответ выглядит так:
Ответ: Если а = 0, то нет решений;
если а # О, то х = - .
а
12.3. Решить уравнение (а2-1)х = а+1.
Решение.
Нетрудно сообразить, что при решении этого уравнения
достаточно рассмотреть такие случаи:
1) а = 1; тогда уравнение принимает вид Ох = 2 и не
имеет решений;
2) а = — 1; получаем Ох = О, и очевидно х — любое.
3) а # ± 1; имеем х = — Ц-.
а— I
Сделаем одно замечание. Существенным этапом решения
задач с параметрами является запись ответа. Особенно это
217
§ 12. Знакомство с параметром
относится к тем примерам, где решение как бы «ветвится»
в зависимости от значений параметра. В подобных случаях
составление ответа — это сбор ранее полученных результатов.
И здесь очень важно не забыть отразить в ответе все этапы
решения.
В только что разобранном примере запись ответа прак-
тически повторяет решение. Тем не менее мы считаем це-
лесообразным привести
Ответ: Если а = -1, то х — любое; если а = 1,
то нет решений; если а # ± 1 , то х = .
12.4. Решить неравенство ах < 1.
Решение.
Как и ранее, анализ трех возможностей а > 0, а = О,
а < О позволяет получить следующий
Ответ: Если а < 0, то х > - ; если а = О,
а
то х — любое; если а > 0, то х < -.
а
В плане рассматриваемых вопросов полезно разобрать
следующие два примера.
12.5. Решить неравенство |х+3 I > - а.
Решение.
Ясно, что при а # 0 правая часть неравенства отрица-
ельна, и тогда при любом х левая часть больше правой. В
лучае, коща а = 0, важно помнить, что исходному нера-
венству удовлетворяют все действительные числа, кроме
: = -3.
Ответ: Если а # 0, то х — любое;
если а = О, то х < — 3 или х > — 3.
12.6. Решить уравнение |х2—1 |+ |а(х-1) 1=0.
Решение.
Это уравнение равносильно системе
|х2-1|= 0,
|а(х—1) 1 = 0.
218
§ 12. Знакомство с параметром
Имеем:
х2-1 = О,
и а(х—1) = 0.
При а # 0 второе уравнение системы, а значит, и сама
система, имеет единственное решение х = 1. Если же а = 0,
то из второго уравнения получаем х — любое. Следовательно,
в этом случае система имеет два решения: х = 1 или
х = -1.
Ответ: Если а * 0, то х = 1; если а = 0, то х = ±1.
Обратим внимание, что во всех решенных примерах об-
ластью допустимых значений как для переменной, так и для
параметра являлось все множество действительных чисел.
Разумеется, следует познакомиться с задачами иного рода.
12.7. Решить уравнение у/х~ = а173.
Решение.
Легко увидеть, что х = а — единственный корень данного
уравнения. Однако, этот результат — еще не ответ. Специ-
фика задач с параметрами предполагает даже в таком три-
виальном уравнении, как х—а = 0, отмечать, что х = а —
корень при любом а.
Ответ: Если а О, то х = а\
если а < О, то нет решений.
~ х—а
12.8. Решить уравнение = О.
Решение.
Как и в предыдущем примере, х = а — единственный
корень. Понятно, что условие х # 1 влечет за собой требование
а # 1.
Ответ: Если а # 1, то х = я;
если а = 1, то нет решений.
12.9. Решить неравенство (a— l)Vx"О.
Решение.
Понятно, что ответ зависит от знака двучлена а — 1. При
а 1 очевидно данному неравенству удовлетворяет любое
значение х из области определения, т.е. х 0. При а > 1
219
§ 12. Знакомство с параметром
левая часть неравенства неотрицательна, поэтому в рассмат-
риваемом случае х = О — единственное решение.
Ответ: Если а 1, то х 0; если а > 1, то х = 0.
12.10. Решить уравнение (x-l)Vx-a = О.
Решение.
Данное уравнение равносильно системе
х а,
• х = 1,
х = а.
Отсюда х = а — корень исходного уравнения при любом а,
а х = 1 — корень лишь при а 1.
Ответ: Если а < 1, то х = а или х = 1;
если а = 1, то х = 1; если а > 1, то х = а.
Выскажем два соображения по поводу роли параметра в
приведенных примерах 12.1 — 12.10. Во-первых, искомые
значения х выступали в роли зависимой переменной, а па-
раметр — независимой. Отсюда и возникло «расслоение» ре-
шения с учетом определенных значений параметра. Во-вто-
рых, условие задач отводило параметру скромное место, —
не ясно было, повлияет ли его присутствие на ход решения.
Дальнейшее знакомство с параметром поведем в несколь-
ко ином направлении.
Выделим класс задач, где за счет параметра на переменную
накладываются какие-либо искусственные ограничения. Для та-
ких задач характерны следующие формулировки: при каком
значении параметра уравнение (неравенство, система) име-
ет одно решение, два, бесконечно много, ни одного; реше-
нием уравнения (неравенства, системы) является какое-то
подмножество множества действительных чисел и др.
Обратимся к конкретным примерам.
12.11. При каких а неравенство (х-а)(х-2) 0 имеет
единственное решение?
Решение.
Легко догадаться, что а = 2 удовлетворяет требованию
задачи. Действительно, при а = 2 получаем неравенство
220
§ 12. Знакомство с параметром
(х-2)2 0, имеющее единственное решение. Для случая, ког-
да а # 2, решением неравенства очевидно будет отрезок.
Ответ: а = 2.
12.12. При каких а решением неравенства
(х—а)2(х—2)(х+3) О
будет отрезок?
Решение.
Так как (х-а)2 О, то данное неравенство равносильно
совокупности
(х—2)(х+3) О,
х = а.
Решением неравенства совокупности будет отрезок
[-3; 2]. Следовательно, при a G [-3; 2] решением совокуп-
ности также будет отрезок.
Ответ: -3 а 2.
12.13. При каких а уравнение ах2-х+3 = О имеет един-
ственное решение?
Решение.
Прежде всего обратим внимание на распространенную
ошибку: считать исходное уравнение квадратным. На самом
деле это уравнение степени не выше второй. Пользуясь этим
соображением, естественно начать решение, рассмотрев слу-
чай, когда а = 0. Итак, если а = 0, то очевидно данное урав-
нение имеет единственное решение. Если ж,е а # 0, то имеем
дело с квадратным уравнением. Его дискриминант 1 —12а
1
принимает значение, равное нулю, при а = —.
Ответ: а = 0 или а =
12.14. При каких а уравнение (а-2)х2 +(4—2а)х +3 = 0
имеет единственное решение?
Решение.
Понятно, что надо начинать со случая а = 2. Но при
а = 2 исходное уравнение вообще не имеет решений. Если
а # 2, то данное уравнение — квадратное, и, казалось бы,
искомые значения параметра — это корни дискриминанта.
221
§ 12. Знакомство с параметром
Однако дискриминант обращается в нуль при а = 2 или
а = 5. Поскольку мы установили, что а = 2 не подходит, то
Ответ: а = 5.
Вероятно, в двух последних примерах ничего сложного
нет (тем более, если они уже решены). Однако, на наш
взгляд, параметр в этих задачах проявляет свое «коварство»,
особенно для начинающих. Поэтому полезно рассмотреть еще
несколько примеров, где параметр «расставляет ловушки».
12.15. При каких а уравнение ах2— 4х4-а4-3 = 0 имеет
более одного корня?
Решение.
При а = 0 уравнение имеет единственный корень, что не
удовлетворяет условию. При а # О исходное уравнение, бу-
дучи квадратным, имеет два корня, если его дискриминант
16-4а2-12а — положительный. Отсюда получаем-4<а<1.
Однако в полученный промежуток (— 4; 1) входит число О,
которое, как мы уже проверили, неприемлемо.
Ответ: -4<а<0 или 0<а<1.
12.16. При каких а уравнение
а(а4-3)х24-(2а4-6)х—За—9 = О
имеет более одного корня?
Решение.
Стандартный шаг — начать со случаев а = 0 и а = -3.
При а = О уравнение имеет единственное решение. Любопыт-
но, что при а = — 3 решением уравнения служит любое дей-
ствительное число. При а # -3 и а# 0, разделив обе части
данного уравнения на а 4- 3, получим квадратное уравнение
ах2 4- 2х — 3 = О, дискриминант которого 4(1 4- За) положите-
лен при а > — . Опыт предыдущих примеров подсказывает,
О
/ 1 \
что из промежутка I - —; » надо исключить точку а = О,
\ J I
а в ответ не забыть включить а =—3.
Ответ: а =-3 или - < а < 0, или а > 0.
О
222
__________________________§ 12. Знакомство с параметром
12.17. При каких а уравнение (уГх — 1)(х - а) = 0 имеет
единственное решение?
Решение.
При любом а х = 1 — корень данного уравнения, и
требование единственности решения сводит задачу к поиску
условий, при которых уравнению «запрещено» иметь корни,
отличные от единицы. В то же время множитель х — а как
бы предлагает еще один корень х = а, и, на первый взгляд,
значение а = 1 представляется достаточным для ответа. Но
более внимательный анализ позволяет «отмести» х = а за
счет области определения уравнения: при а < О х = а не
является корнем.
Ответ: а = 1 или а < О.
Заметим, что если начать решение с записи равносильной
уравнению системы, а именно
х £ О,
- х = а,
х = 1,
то, возможно, мы уменьшим вероятность того, что в ответ
не войдет промежуток (- »,0).
Завершим рассматриваемый цикл задач еще одним по-
учительным примером.
„ х2—ах-Ы Л ___
12.18. При каких а уравнение —— = 0 имеет един-
ственное решение?
Решение.
Данное уравнение равносильно системе
х2-ах4-1 = О,
х * —3.
Наличие квадратного уравнения и условие единственно-
сти решения, естественно, приведут к поиску корней диск-
риминанта. Вместе с тем условие х # -3 должно привлечь
внимание. И «тонкий момент» заключается в том, что квад-
ратное уравнение системы может иметь два корня! Но обя-
зательно только один из них должен равняться —3. Имеем
223
§ 12. Знакомство с параметром
D = а2—4 , отсюда D = 0, если а = ±2; х = - 3 — корень
уравнения х2—ах4-1 = О при а = “Др причем при таком зна-
чении а второй корень квадратного уравнения отличен от — 3.
~ 10
Ответ: а = ±2 или а = —— .
&
Как мы отмечали, в примерах 12.11 — 12.18, благодаря
параметру регулировались свойства решений уравнений (не-
равенств). Продолжая эту тему, покажем, как параметр вли-
яет на условия равносильности уравнений и неравенств.
12.19. При каких а уравнения х2—а = 0 и а = О
равносильны?
Решение.
Очевидно, что при а > 0 первое уравнение имеет два
различных корня, а второе — только один, и в этом случае
о равносильности речь идти не может. Так же ясно, что при
а = 0 решения уравнений совпадают. При а < О ни первое,
ни второе уравнения решений не имеют. Однако, как известно,
такие уравнения считаются равносильными.
Ответ: а О.
12.20. При каких а уравнение ах = а2 равносильно не-
равенству |х—3 | а 2
Решение.
При а # О уравнение имеет единственное решение, а
неравенство - бесконечно много. Если а = 0, то решением
как уравнения, так и неравенства является все множество
действительных чисел. Следовательно, требованию задачи
удовлетворяет только а = 0.
Ответ: а = 0.
12.21. При каких а неравенство 2х4-а > 0 является след-
ствием неравенства х4-1-За > 0 ?
Решение.
Перепишем данные неравенства в виде х > — — и
х > За-1. Учитывая условие, отметим, что множество реше-
224
§ 12. Знакомство с параметром
ний неравенства х > —— должно содержать множество реше-
ний неравенства х > Зд-1. Это требование выполняется, если
- За-1, т.е. а у .
Ответ: а -.
12.22. При каких а неравенство х > а является следствием
неравенства | х | < а?
Решение.
Нетрудно догадаться, что а > 0 не подходит. Действи-
тельно, при а > О рассматриваемые неравенства не имеют ни
одного общего решения. При а 0 неравенство I х I < а не
имеет решений. А это нас устраивает, так как неравенство
х > а, играющее роль неравенства-следствия, имеет решения.
Ответ: а 0.
Надеемся, что самостоятельное решение упражнений со-
здаст неплохой задел для дальнейшей работы.
Упражнения
Решить уравнения: 12.23. (а2 - 4)х = а + 2. 12.24. (а2 - 6й + 5)х = а - 1
12.25. ах = Ь. . _ _, х - 2 12.26. ;— = 0. х + а
12.27. ^4 = 0- х + 3 12.28. Л - = 0. а - 2
х - 7 12.29. -2—Ц = 0. х - а х + 2а 12.30. —-— = 0. х + а
12.31. —2 = 0. х - 4х + 3 12.32. ^~4лс--^ = о. х - а
12.33. а^Х ~ = 0. х — а 12.34. “iiZjQ = 0. х - 2
12.35. Vx - 3 = а. 12.36. VF= - а.
12.37. аГх = 0. 12.38. (х - a) Vx - 1 =0.
8 Алгебраический 1ренажер
225
§12. Знакомство с параметром
12.39. —«0. УХ - 1 12.40. (x - 1) Vx + a = 0.
х — 1 12.41. 1 = 0. Vx + а 12.43. (х — а) у/х +а = 0. 12.42. Vx~Vx - a = 0. 12.44. (x + dyJx - a = 0.
12.45. (х - a)Vx2 -1=0. 12.46. (x2 - l)Vx - a = 0.
12.47. VF+ Vx + a = 0. 12.48. Vx - 1 + a2Vx~ = 0.
12.49. a2Vx - 1 + Vx"= 0. 12.50. |x| = a.
12.51. |x - 31 + a2|x| = 0. 12.52. Vx - 3 + a2|x| = 0.
12.53. а\х - 3 + |х|=0.
Решить неравенства:
12.54. x(x - a) < 0. 12.55. (x —a)(x - 2a) < 0.
12.56. (x — a)2(x — 2a) < 0. 12.57. (x - a)2(x - 2a) « 0.
12.58. Vx"+ a2 S 0. 12.59. aVx">0.
12.60. a Vx"0. 12.61. Vx"> a.
12.62. Vx" a. 12.63. Vx" + Vx - a > 0.
12.64. (x - a)Vx" 5= 0. 12.65. x Vx - a 0.
12.66. |x — l|Vx + a>0. y/x - a 12.67. —- 3= 0. lx - 21
12.68. lx - 21 < a. 12.69. |x2 + a| «0.
12.70. |x|(x + a) «= 0. 12.71. |x|(x-a)>0.
12.72. (x - 1)lx - al >0. 12.74. a2x «£ a2. 12.76. x2 - 2x + 2й > 0. 12.73. (x - 2)|x + a| <0. 12.75. a22x>a.
226
§ 12. Знакомство с параметром
12.77. При каких а система
х>3,
х а
не имеет решений?
12.78. При каких а система
х £5,
х 3 - а
имеет единственное решение?
12.79. При каких а существует ровно три целых числа,
являющихся решением системы неравенств
|х 2,
[х < а!
12.80. При каких а решением системы
1х > 3,
|х а
является промежуток а) (3; °°); 6) [5; <»)?
12.81. При каких а уравнение (а + 4)х2 + 6х - 1 = 0 имеет
единственное решение?
12.82. При каких а уравнение
(2а 4- 8)х2 - (а + 4)х + 3 = О
имеет единственное решение?
12.83. При каких а уравнение
а) (а 4- 6)х2 - 8х 4- а = 0;
б) а(2а 4- 4)х2 - (а 4- 2)х - 5а - 10 = 0
имеет более одного решения?
12.84. Найти все значения параметра а, при которых
графики функций у = (а 4- 5)х2 - 7 и у = (За 4- 15)х - 4 не
имеют общих точек?
12.85. При каких а неравенство (х - a)Vx 4- 3 О имеет
единственное решение?
227
§ 12. Знакомство с параметром
12.86. Найти все значения а, при которых уравнение
имеет единственное решение?
а) (х - a)(VJT- 9) = О,
б) (х - a) logjX = О,
в) (х - 3) log2a = О,
г) (х — a) arccos(x + 3) = О,
д) (х - 1) arccosa = 0.
12.87. При каких а решением неравенства
(х - а)2(х + 4) 0
является луч?
12.88. При каких а неравенство 2х — а > 0 является след-
ствием неравенства х + 2а — 3 > 0?
12.89. При каких а из неравенства 0<х< 1 следует не-
равенство х2 — а2 О?
12.90. Найти все значения а, при которых уравнение
(Vx~ - 1) log3(l - а) = О равносильно неравенству аЛГ О.
12.91. Найти все значения а, при которых уравнения
sin х = а - 3 и Vx + 3 = 2а + 1 равносильна.
12.92. При каких а большее из двух чисел 5а - 1 и
12а | равно квадрату меньшего?
228
§ 13. Образцы решений вариантов
конкурсных заданий
Киевский государственный экономический
университет
Вариант 1
1. Решить уравнение sin3x 4- cos’x = 1 4- sin 2х.
Решение.
(sin х 4- cos x)(sin2 x - sin x cos x 4- cos2 x) = (sin x + cos x)2.
Следовательно, данное уравнение равносильно совокупности
sin х 4- cos х = 0,
1 - sin х cos х = sin х 4- cos х.
Из первого уравнения совокупности получаем:
tg х = - 1, х = - — + лк, kGZ.
4
Преобразуем второе уравнение:
2 - 2 sin х cos х = 2 (sin х + cos х),
2 - ((sin х + cos х)2 - 1) = 2 (sin x + cos x),
3 - (sin x + cos x)2 = 2 (sin x + cos x).
Замена sin x + cos x = t, I 11 VT. Тогда
t = - 3,
t = 1.
Учитывая, что I t I V2~, получаем:
, 1.^1 1
sin X + COS X = 1, sin X + cos X = ,
t2 + 2t — 3 = 0,
sin x 4- —
I 4
л JI _ ~
x 4- — = - 4- 2л n, n e Z,
4 4
л 3л ~
x 4- - = 4- 2лт, m E Z,
4 4
229
§13. Образцы решений вариантов конкурсных заданий
х = 2лп, n G Z,
я
х = — 4- 2лт, те Z.
Ответ: х = - -- 4- ля, или х = 2яп, или
4
х = — 4- 2ят, где Л, и, т — целые.
2. Одновременно начали гонки с одного места два мото-
циклиста: один со скоростью 80 км/ч, второй — 60 км/ч.
Через полчаса с того же старта и в том же направлении
отправился третий гонщик. Найти скорость третьего гонщика,
если известно, что он догнал первого гонщика на 1 ч 15 мин
позже, чем второго.
Решение.
Пусть скорость третьего гонщика была х км/ч, и он
догнал первого гонщика через t ч после своего старта. Тогда
место встречи первого и третьего гонщиков на расстоянии
60 11 4- — км или xt км от старта. Следовательно,
\ X I
60
= xt.
км,
К моменту встречи второго и третьего гонщиков второй был
117
в пути t + — 4-1— = t + — часов и проехал 80
2 4 4
а третий — 114- 41 часов и проехал х 11 4- 41 км* Следова-
I 41 I 41
/ 7\ 7 / 5\ Х 7
тельно, 80 и 4- — I = х р4-— . Получим систему уравнений:
I 41 I 4)
60t + 30 = xt,
80t + 14O = xt + 4
4
Вычитая из второго уравнения первое, имеем:
2ОГ+11О = 4*. t =
4 1о 2
Тогда 60 (утх - + 30 = х - -у-),
110 Z I I 1О Z I
230
§ 13. Образцы решений вариантов конкурсных заданий
х2 - 148х 4- 4800 = 0, х = 100 юш х = 48.
Корень х = 48 не удовлетворяет условию задачи, так как
при скорости 48 км/ч третий гонщик не мог бы догнать
первых двух.
Ответ: 100 км/ч.
о 6х 11х
3. Решить уравнение -3--------+ 5------------ = 2.
х2 + 2х + 3 х2 + 1х + 3
Решение.
Так как значение х = 0 не является корнем данного
уравнения, то, разделив на х числитель и знаменатель каждой
дроби в левой части уравнения, получим уравнение, равно-
6,11
сильное данному: --------- 4---------- — 2.
х 4- 2 4-— + U
X X
3
Выполнив замену х 4- — = /, получим уравнение
+ _п__ = 2.
i 4- 2 t 4- 7
Тогда = °, z = 4 или f - - |. Следователь-
но, исходное уравнение равносильно совокупности
Тогда
х2 - 4х 4- 3 = 0,
2х2 4- 9х 4- 6 = 0;
х = 3,
х = 1,
— 9 ± V33"
Х ~ 4
о * -9±<33
Ответ: 3; 1:-------.
4
4. Решить неравенство
з^ + х^б.
231
§13. Образцы решений вариантов конкурсных заданий
Решение.
Перепишем данное неравенство в виде
(3,о«,у^ + х'°4/ < 6
Тогда х‘°‘зх + х1с«>* < 6, 2х'°1зж < 6, х1о‘зж < 3,
log3xl’*’JI<log33, log3x<l, - l<log3x<l, ^<х<3.
О
„ fl \ в с
Ответ: 3J. д-------------~71
5. В параллелограмме ABCD / \ /
АА = 60% В£ = ~ , СЕ = ^, / \/ /
где Е — середина стороны AD. А Е D
Найти стороны параллело- Рис. 66
грамма.
Решение.
Пусть АЕ = ED = х, АВ = у (рис. 66). Из ЛАВЕ:
BE2 = АВ2 4- АЕ2 - 2АВ • AEcos ZA,
| = х2 4- у2 - 2ху cos 60°,
х2 4- у2 - ху = 7 . (1)
4
Из \CDE-. СЕ2 = ED2 + CD2 - 2ED CD cos Z.D,
= х2 + у2 — 2xycos 120°,
ч
х2 4- у2 4- ху = -у . (2)
4
Складывая и вычитая уравнения (1) и (2), переходим к
системе уравнений
[2.x2 + 2/ = у ,
W=1-
Тогда
232
§13. Образцы решений вариантов конкурсных заданий
х2 + у2 = , (х + у)2 - 2ху = ,
2ху = 1; 2ху = 1;
/ _1_ \2 , $ (х + У)2 = т»
(х + yf - 1 = -, v " 4 ’
2ху= 1; ху = |.
Учитывая, что по условию задачи х > 0 и у > 0, получаем
Следовательно, стороны параллелограмма 2 и — или 1 и 1.
Ответ: 2 и | или 1 и 1.
6. Решить уравнение
log3(VF + |VF- 1|) = log^VF- 3 + 4 |VF- 11).
Решение.
Замена Vx” = t, t&O. Тогда уравнение примет вид
log3(t + \ t- 11) = 1о^(4Г - 3 + 4 |t - 1|). (1)
При t 1 имеем:
log3(Z + r- 1) = log3(4/ — 3 4- 4Z — 4),
2 log3 (2t — 1) = log3 (8t — 7),
f(2t — l)2=8t-7, t2 —3t + 2 = 0,
|2/-l>0; t>|;
“t=l, lx=l,
t = 2; x = 4.
L L
При 0 t < 1 имеем:
log, (t - t + 1) = log, (4t — 3 — 4/ + 4), log, 1 = log, 1.
233
§13. Образцы решений вариантов конкурсных заданий
Следовательно, в этом случае решением уравнения (1)
являются все значения t из промежутка [0; 1) и 0 s х< 1.
Ответ: [0; 1) U {4}.
7. Решить систему уравнений
х + у = 3,
х4 + у4 = 17.
Решение.
х = 3 - у, (х = 3 - у,
' ((3 - у)2)2 + У4 = 17; 1 (9 - бу + у2)2 + у4 = 17;
(х = 3 - у,
[81 + у4 + Зб/ + 18/ - 108у - 12у’ + у4 = 17;
х = 3 - у,
у4 - б/ + 27/ - 54у + 32 = 0;
(х = 3 - у,
|у4 - У3 - 5/ + 5/ + 22/ - 22у - 32у + 32 = 0;
х = 3 - у,
/(у - 1) - 5/(у - 1) + 22у (у - 1) - 32 (у - 1) = 0;
х = 3 - у,
• Гу» Ъ
/ - 5/+ 22у - 32 = 0;
х = 3 - у,
Гу» 1,
/ - 2/ - 3/ + бу + 16у - 32 = 0;
х — 3 - у,
Гу -1.
[/(у-2)-Зу(у-2) + 16 (у - 2) = О;
х ~ 3 - у,
Гу» I,
У» 2,
/ - Зу + 16 = 0;
234
§ 13. Образцы решений вариантов конкурсных заданий
X = 2,
У = 1
Ответ: (2; 1) и (1; 2).
х = 1,
У = 2.
Вариант 2
1. Два пешехода вышли одновременно навстречу друг
другу из пунктов А и В. При встрече оказалось, что первый
прошел на 2 км больше, чем второй. После того, как они
продолжили после встречи свой путь с теми же скоростями,
то первый прибыл в В через 40 мин после встречи, а второй
в А через 1 ч 30 мин после встречи. Определить расстояние
между Л и В.
Ответ: 10 км.
4
2. Решить уравнение I tg х 4- ctg х | = .
л л ли _ _
Ответ: х = ± — + — , и G Z.
о Z
3. Решить неравенство 3**+2< + З1*"*^ 28.
Ответ: (— °°; — 2] U [1; + »).
4. Решить систему уравнений
у^'4=1,
log2x = У-
Ответ: (4; 2), (2; 1).
5. Решить уравнение 6 — —=——----= 4х - х2.
х2 — 4х + 10
Ответ: 1; 3.
6. Решить уравнение
V1 + logx/27 • log3x + 1=0.
Ответ: .
7. Найти площадь прямоугольного треугольника, гипоте-
нуза которого делится точкой касания вписанной окружности
на отрезки а и Ь.
Ответ: ab.
235
§13. Образцы решений вариантов конкурсных заданий
Вариант 3
1. Решить неравенство — >1.
„ ( 3V5" \ | , / 3V5”\
Ответ: ---—; - 1 U 1; ~т— •
О / \ ^ /
2. Решить систему уравнений:
(х2 + ху + у*) Чх2 4- у2 = 185,
(х2 - ху + у*) >/х2 4- у2 = 65>
Ответ: (4; 3), (3; 4), (-4; -3), (-3; -4).
3. Из города А в город В отправился почтовый грузовик.
Через 30 мин вслед за грузовиком отправился мотоциклист
со скоростью 50 км/ч; догнав грузовик, передал ему допол-
нительную почту и в тот же час вернулся обратно, прибыв
в А одновременно с прибытием грузовика в В. Определить
скорость грузовика, если расстояние между А и В равно
180 км.
Ответ: 40 км/ч.
4. Решить уравнение х 4- 1g (1 4- 2х) = х 1g 5 4- 1g 6.
Ответ: 1.
5. Решить уравнение
(х2 - х 4- I)4 - 6х2 (х2 - х 4- I)2 4- 5х4 = 0.
V5" + 1 ± V2 + 2 V5"
Ответ: 1; -------------------.
2 2 2 3
6. Решить уравнение sin х 4- sin 2х 4- sin Зх = - .
_ л ли л
Ответ: х = — 4- — или х = ± — 4- лк,
о 4 3
п и к — целые.
7. В прямоугольной трапеции отношение длин ее осно-
ваний равнс 4, а отношение длин диагоналей равно 2. Найти
величину острого угла.
~ 2
Ответ: arctg - .
О
236
§ 13. Образцы решений вариантов конкурсных заданий
Вариант 4
1. Две окружности радиусов R и г касаются внешним
образом. Найти расстояние от точки касания до общей каса-
тельной, проведенной к этим окружностям.
- _ ZRr
Ответ: —.
R + г
2. Решить уравнение sin4 х + cos4 х = sin 2х - .
Л л
Ответ: — + лп, п G Z.
4
log (—| • log Зх . 2. ,
3. Решить неравенство (0,4) > (6,25) *’
Ответ: (о; U (243; + »).
4. Решить уравнение
Vx + 3 - 4 Vx - 1 + Vx + 8 - 6 Vx - 1 = 1.
Ответ: [5; 10].
5. Решить уравнение (3 х -7,2х+Л’ - 9 VT) 1g (7 - х) = 0.
Ответ: 6; -L
О
6. Решить систему уравнений
Vx" + vy= ю,
4- yfy = 4.
Ответ: (81; 1), (1; 81).
7. Две точки движутся по окружности в одном направ-
лении. Первая точка проходит окружность на 2 с быстрее
второй и догоняет ее через каждые 12 с. За какое время
каждая точка проходит окружность?
Ответ: 4 с; 6 с.
Вариант 5
1. Решить уравнение
logx+, (** - 9х + 8) log,.! (х + 1) = 3
23"
§ 13. Образцы решений вариантов конкурсных заданий
Решение.
Данное уравнение перепишем в таком виде:
log*+i (х* ~ 9х + 8)
l°8x+i (х - О
Уравнение (1) равносильно системе
log,., (х3 - 9х + 8) = 3,
х + 1 >0,
х + 1 # 1.
Тогда
х3 - 9х + 8 = (х - I)3,
х - 1 >0,
х - 1 # 1,
Х> - 1,
х # 0;
х3 - 1 - 9х + 9 = (х - I)3,
х> 1,
х # 2;
(х — 1)(х2 + х + 1) - 9 (х - 1) = (х - I)3,
х> 1,
х # 2;
(х - 1)(х2 + х - 8) = (х - I)3,
х> 1,
х # 2;
х2 + х - 8 = х2 - 2х + 1,
х>1, х = 3.
х # 2;
Ответ: 3.
2. Решить систему уравнений
1х4 + у4 = 17 (х + у)2,
1ху = 2 (х + у).
Решение.
Очевидно, что пара (0; 0) является решением этой сис-
темы. Прих#0иу*0 данная система равносильна системе
238
§13. Образцы решений вариантов конкурсных заданий
х* + у4 = 17 (х + у)2,
х2 у2 = 4 (х + у)2,
ху (х + у) > 0.
(1)
Разделив первое уравнение системы (1) на второе, по-
лучаем:
х4 + у4 = 17 х2 у2 = 17
х2^ 4 у2 х2 4
Обозначим —г = t, ОО. Тогда
Г
1 + 4 = ^, 412- 171 + 4 = 0,
t 4
1 = 4 или 1 = 4-
4
Следовательно, система (1) равносильна совокупности
двух систем:
ху = 2 (х + у),
ху (х + у) > 0
или
ху = 2 (х + у),
х2 _ 1
у2 “ 4’
ху (х + у) > 0,
которая в свою очередь равносильна совокупности четырех
систем:
ху = 2 (х 4- у),
У = 2х;
или
ху = 2(х + у),
у = - 2х.
Тогда
х = 2у, х = - 2у,
„ 2 , или Л 2
2/ = бу - 2/ = - 2у;
[у = 2х, [у = - 2х,
12х = 6х , | - 2х = - 2х.
Учитывая, что х # 0 и у # 0, получаем решения системы (1):
(6; 3), (-2; 1), (3; 6), (1; -2).
Ответ: (0; 0), (6; 3), (-2; 1), (3; 6), (1; -2).
239
§ 13. Образцы решений вариантов конкурсных заданий
3. Решить уравнение tg х 4- tg 2х 4- tg Зх 4- tg 4х = О.
Решение.
Перепишем данное уравнение в виде
sin5x + sin 5х _
cos х cos 4х cos 2х cos Зх ~
Тогда
sin 5х (cos 2х cos Зх 4- cos х cos 4х)
cos х cos 2х cos Зх cos 4х
= О,
sin 5х = О,
cos 2х cos Зх 4- cos 4х cos х = О,
cos х * О,
cos 2х * О,
cos Зх * О,
cos 4х # 0.
Первое уравнение совокупности имеет корни х = -z- ,
О
к G Z, удовлетворяющие требованиям системы.
Так как cos Зх = cos Зх + cos х - cos х =
= 2 cos 2х cos х - cos х = cos х (2 cos lx - 1),
перепишем второе уравнение совокупности так:
cos 2л cos х (2 cos 2х - 1) + cos х (2 cos2 2х - 1) = 0,
cos х (2 cos2 2x - cos 2x + 2 cos2 2x - 1) = 0,
cos x (4 cos2 lx - cos lx - 1) = 0.
Учитывая, что cos x # 0, и рассматривая уравнение
4 cos2 lx — cos lx — 1 = 0 как квадратное относительно cos lx,
1 ± 717"
8
получаем: cos 2x =
----- 4- лп, п G Z.
о
x = ± arccos
_ Л* 1 1 ± 7ГГ ,
Ответ: —; ± — arccos----=-- + nn, пик — целые.
0 Z о
4. В классе писали контрольную работу. Среди выстав-
ленных за нее оценок были: «2», «3», «4», «5». Оценки «2»,
240
§ 13. Образцы решений вариантов конкурсных заданий
«3», «5» получило одинаковое число учеников, а оценок «4»
было поставлено больше, чем всех остальных оценок вместе
взятых. Оценку выше «3» получило менее 10 учеников. Сколь-
ко троек и сколько четверок было поставлено, если конт-
рольную писало не менее 12 учеников?
Решение.
Пусть оценки *2», *3», «5» получило по х учеников, а
оценку «4» — у учеников. Так как четверку получило больше
учеников, чем всех остальных оценок вместе взятых, то
у > Зх. Так как оценку выше «3» получило менее 10 учеников,
то х 4- у < 10. Так как контрольную писало не менее 12 уче-
ников, то Зх 4- у 12. Получили систему неравенств:
у>3х,
х + у<10, <1>
Зх + у =s 12.
Тогда х 4- у > х 4- Зх = 4х, 4х < 10, х < 2,5.
Так как х — целое неотрицательное число, то из нера-
венства х < 2,5 следует, что х = 0, или х = 1, или х = 2.
При х = 0 два последних неравенства системы (1) обра-
зуют систему
у< 10,
У > 12,
не имеющую решений.
При х = 1
решений.
При х = 2
[у <9,
получаем систему К, > 9
имеем:
также не имеющую
у<8,
у =s 6, откуда у = 7-
Следовательно, оценку «3» получили 2 ученика, оценку
«4» — 7 учеников.
Ответ: 2 ученика, 7 учеников.
2
5. Решить неравенство 5 1°'3 х + х10131 < 10.
Решение.
Перепишем данное неравенство в виде
(5,о«зх)1о*зх + х,о<зХ<10.
Тогда х 1о»зХ + х< 10, х 1о»зХ < 5, log3x < log3 5,
241
§ 13. Образцы решений вариантов конкурсных заданий
log,х< 1, - 1 <log,х<1,4<х<5.
О
Ответ: j; 5
6. Решить уравнение
Vx-3 - 2Vx - 4 + Vx - 4 Vx -T = 1.
Решение.
Перепишем данное уравнение в таком виде:
Vx-4-2Vx-4'+l + Vx - 4 - 4 Vx - 4' + 4 = 1.
Следовательно, V(Vx - 4 - I)2 4- V(Vx -4- 2)2 = 1,
|Vx - 4 - 1| + |Vx - 4 - 21 = 1.
Замена Vx - 4 = t, t&O. Тогда 11 - 11 + 11 - 21 =1.
Рассмотрим случай t > 2. Имеем: t - 1 + t - 2 = 1, f = 2,
что не удовлетворяет условию t>2>
При 1 Г 2:
t- 1 - t + 2 = 1, 0 • t = 0.
Следовательно, в этом случае t — любое число из про-
межутка [1; 2].
При 0 К 1: 1 - t - t + 2 = 1, t = 1 — не удовлетворяет
условию t< 1. Следовательно, 1 Vx - 4 2,
1 х - 4 4, 5 х 8.
Ответ: [5; 8].
7. Две окружности ради-
усов R и г касаются внешним
образом в точке С. К этим
окружностям проведена об-
щая касательная АВ, где А
и В — точки касания. Найти
длины сторон ЛАВС.
Решение.
О1 — центр окружности
радиуса R, О2 — центр ок-
ружности радиуса г, R > г Рис 67
242
§13. Образцы решений вариантов конкурсных заданий
(рис. 67). Тогда О]О2 = Л + г, 0/1 = Л, OJi = r. Проведем
OJrf ± 0/1. Тогда OjAf = R — г.
Из ЛО,Л/О2:
ОМ R-г
cos LAO.С = sin LCOyM = _ _ = ;
1 r 0,0^ R + r
O^f2 = OXO2 - OJtf2 = (R + r)2 - (R - r)2 = 4Rr.
AB = O?M = 2 VRr. Из AAOjC:
AC2 = AO2 + O,C2 - 20/1 • OXC cos LAOXC =
= 2^-2^ "/ = 2«/'l -
лс=2я
4R2r .
R + r'
Из ДВО2С:
BC2 = O2C2 + O^2 - 2O2C • cos LCOzB =
= 2r 2 - 2r 2 cos (90° + LCO^f) = 2r 2 + 2r 2 sin LCOJA =
= 2r 2 + 2r 2
= 2,2^ + л-r) = ^R.
R + r Я + rJ R + r'
VD
Ответ: 2/ffr-; 2R
; 2r
Вариант 6
1. Около дома посажены липы и березы, причем общее
их число не меньше 14. Если увеличить вдвое количество
лип, а количество берез увеличить на 18, то берез станет
больше, чем лип. Если же увеличить вдвое количество берез,
не изменяя количество лип, то лип все равно будет больше
берез. Сколько лип и сколько берез было посажено?
Ответ: 10 лип и 4 березы или
11 лип и 5 берез.
243
§ 13. Образцы решений вариантов конкурсных заданий
2. Решить неравенство (3 х+2 4- 3 "x)*e х ~ 1в (2х +Зх) < 1.
Ответ: (0; 3).
1 D 4 ЙГ+ 3 „
3. Решить уравнение---- 4- —-—г = 2.
йГ+2 5
Ответ: 8; 27.
4. Решить уравнение 15|о,зЭ • х|о’3*,+| = 1.
„ 1 1
Ответ: .
О х 0
5. Решить уравнение sin х sin Зх 4- sin 4х sin 8х = 0.
лп лк ,
Ответ: —; —, п и к — целые.
/ 0
6. Решить систему уравнений
Vx 4- у 4- V2x 4- у 4- 2 = 7,
Зх 4- 2у = 23.
Ответ: (5; 4), (-9; 25).
7. В круге с диаметром d проведены две взаимно пер-
пендикулярные хорды АВ и CD. Чему равно AD? 4- СВ2?
Ответ: d2.
Вариант 7
1. Определить острый угол ромба, если известны его
площадь 5 и площадь вписанного в него круга Q.
4Q
Ответ: arcsin .
2. Два автохозяйства отправили несколько машин для
перевозки грузов. Число машин, отправленных из второго
автохозяйства, меньше удвоенного числа машин, отправлен-
ных из первого. Если бы первое автохозяйство послало на
две машины больше, а второе — на две меньше, то машин
из второго автохозяйства было бы больше, чем машин из
первого. Сколько машин отправлено из каждого автохозяй-
ства, если всего было отправлено не менее 18 автомашин?
Ответ: 6 машин и 11 машин.
244
§ 13. Образцы решений вариантов конкурсных заданий
3. Решить неравенство (0,5) 1 1/3 < 1.
Ответ: -1;-----у- U ~у—; 1 .
4. Решить систему уравнений
х + у + z = 11,
• ху + yz + ZX = 36,
xyz = 36.
Ответ: (2; 3; 6), (2; 6; 3), (3; 2; 6),
(3; 6; 2), (6; 2; 3), (6; 3; 2).
5. Решить уравнение
V12 + х , V12 + х 64 г—
+ -12- ” 3 ”'
Ответ: 7=1-7=-
127 129
6. Решить уравнение
2 sin Зх sin х + (3 VT- 1) cos 2х = 3.
Л
Ответ: ± — + лк, kSZ.
О
7. Решить уравнение
bg,+1 (X - 0,5) = logx_a5 (х + 1).
Ответ: 1.
Вариант 8
1. Сумма квадратов цифр некоторого положительного
трехзначного числа равна 74. В этом числе цифра сотен равна
удвоенной сумме цифр десятков и единиц. Найти это число,
если известно, что разность между этим числом и числом,
записанным теми же цифрами, но в обратном порядке, рав-
на 495.
Ответ: 813.
2. Решить неравенство log2_x (х + 2) • logx+3 (3 - х) 0.
Ответ: (-2; - 1 ] U (1; 2).
245
§ 13. Образцы решений вариантов конкурсных заданий
3. Решить уравнение
2 + х 2-х -.эуру
72 + Vx + х V2~- V2 + х
Ответ: - 2; 1 + V5~.
4. Решить систему уравнений
х + у + z = 3,
' х2 + у2 + z2 = 3.
Ответ: (1; 1; 1).
5. Решить уравнение
sin х - cos х - 1 _ 4 (sin х - cos х)
sin х — cos х - 2 — 9 + 3 sin 2x
Ответ: (- 1/ arcsin + у + лк, kSZ.
3 4
6. Решить уравнение
27^-7 • 9^-21 • 3^ + 27 = 0.
Ответ: 1; 100.
7. В прямоугольном треугольнике АВС биссектриса AD
острого угла А делится центром О вписанной окружности в
АО VT+ 1
отношении QD - .
Найти величину острых углов
треугольника.
Ответ: 30е; 60е.
Вариант 9
1. Решить уравнение
^(13 + х)2 + 4 \<(13 -х)2 = 5 ^169-х2.
Решение.
Учитывая, что х = 13 не является корнем данного урав-
нения, разделим обе его части на 7(13 - х)2:
у/ /13 + х\~
V (13 -xj
V13 +х
13-х
+ 4 = 5
246
§ 13. Образцы решений вариантов конкурсных заданий
Замена
V 13 -Ьх
13-х
= t Тогда
t2 - 5t + 4 = 0, t = 1 или t = 4,
13 + х
13-х
13 + х
13 — х
х = 0 или х = 12,6.
Ответ: 0; 12,6.
2. В треугольнике ABC LC = 120°, —- . Найти
ДО 2
угол В.
Решение.
Пусть LB = х. Тогда LA = 60° - х. По теореме синусов
sin LA _ ВС _ У3~ - 1
sin LB ~ АС ~ 2
_ sm (60 — х) УТ- 1
Тогда-----—L = —-—
sin х 2
sin 60° cos х - cos 60° sin x _ УЗ - 1
sinx ~ 2
УТ t i Уз i 4
— ctgx - 2 = -2- - 2’ ct*x = 1
Учитывая, что LB — острый, имеем x = 45е.
Ответ: 45е.
3. Решить систему уравнений
х2 - бху 4- ву2 = 0,
х2 + Зу2 - ху = 45.
Решение.
Очевидно, что пара чисел вида (х; О) не является реше-
нием данной системы. Разделив обе части первого уравнения
на у2, имеем:
247
§13. Образцы решений вариантов конкурсных заданий
X2 + 3/ - ху = 45.
Положив ~ = имеем t2 - Ы 4- 8 = 0, откуда t = 4 или
t = 2. Следовательно, исходная система равносильна совокуп-
ности двух систем:
{х = 4у, (х = 2у,
х2 4- Зу2 - ху = 45 и7™ |х2 4- Зу2 - ху = 45.
Тоща
{х = 4у, (х = 2у,
16/+ Зу2- 4/ = 45 ]4/ + 3/ - 2/ = 45,
х = 4у, (х = 2у,
/ = 3 н™ |/ = 9.
Отсюда получаем
Ответ: (4<3~; V3~); (-4V3"; -V3~);
(6; 3); (-6; -3).
4. Из бочки, в которую налит спирт, отлили часть и
долили водой. Потом из этой бочки отлили столько же смеси
и после этого осталась смесь, содержащая 49 л спирта. Сколько
литров спирта было отлито из бочки в первый и второй раз,
если ее емкость равна 64 л?
Решение.
Пусть в первый раз из бочки отлили х л спирта. Тогда
64 — х
в ней осталось (64 — х) л спирта, что составляло —“—
п X * 64-х
части смеси. Во второй раз из бочки отлили ——— • х л
64
спирта. Следовательно, в бочке осталось после /х отливаний
(64 —х \ 4 — х
64-х-------- - • х л спирта. Тогда 64 - х - —• х = 49,
64 1 64
(64 - х) j = 49, (64 - х)2 = 64 • 49,
64 - х = 8 • 7, х = 8.
248
§13. Образцы решений вариантов конкурсных заданий
Следовательно, в первый раз из бочки отлили 8 л спирта,
А 64 — 8 „
а во второй раз —~— • 8 - 7 л.
64
Ответ: 8 л; 7 л.
5. Решить уравнение
sin (2х2 4- х) • cos х2 — sin (х2 + х) • cos 2х2 = 0.
Решение.
Разложим произведения тригонометрических функций,
стоящих в правой части уравнения, в сумму:
(sin (2х2 4- х 4- х2) + sin (2х2 4- х - х2)) -
- (sin (х2 4- х 4- 2Х2) 4- sin (х2 4- х — 2л2)) = 0.
Тогда
sin (Зх2 4- х) 4- sin (х2 4- х) - sin (Зх2 4- х) - sin (х - х2) = 0,
sin (х2 4- х) 4- sin (х2 - х) = 0,
sin х2 cos х = 0,
х2 = лк, к = 0; 1; 2;...,
JT г,
х = — 4- лп, n&Z.
4- лп, Л = 0;1;2;...; п G Z.
sin х2 = 0,
cos х = 0;
6. Решить неравенство logi n < (х2 - Зх 4- 2) 2.
Решение.
*°8v3/2 (х* ~ Зх + 2) =5 2.
Данное неравенство равносильно системе
х2 - Зх + 2 « |,
х2 - Зх + 2 > 0.
Тогда
249
'> 13. Образцы решений вариантов конкурсных заданий
4х2 — 12х + 5 «£ О, [0,5« х« 2,5,
Гх< 1, < Гх< 1,
х>2; [ х>2;
[0,5 « х< 1,
2 < х « 2,5.
Ответ: [0,5; 1) U (2; 2,5].
7. Решить уравнение 10 ' + х vTo‘110 = 200.
Решение.
Обозначим Vlgx = Г, t>0. Тогда Igx = t\ х = 10* .
Данное уравнение равносильно уравнению
10* + (10'2)1/г= 200.
Имеем 10 * + 10 * = 200, 10 * - 100, t = 2.
Следовательно, х = 104.
Ответ: 104.
Вариант 10
1. В треугольнике АВС высота, опущенная из вершины
А, равна половине биссектрисы внешнего угла при той же
вершине. Найти АВ — LC.
Ответ: 60°.
2. Решить уравнение х + lg (1 + 2х) = х 1g 5 + 1g 6.
Ответ: 1.
3. Решить систему уравнений
х3 - у3 = 19 (х - у),
х3 + у3 = 17 (х + у).
Ответ: (0; 0), (<17; vTT), (-<17"; - <17"),
(<19"; - <19”), (- <191 <ПГ), (2 + <5"; - 2 + <5"),
(2 — <5”; — 2 — <5"), (- 2 + <51 2 + <5”),
(- 2 - <5"; 2 - <5”).
4. Решить неравенство 2 log2 (х - 1) - log2 (2х - 4) > 1.
Ответ: (2; 3) U (3; + <»).
250
§ 13. Образцы решений вариантов конкурсных заданий
5. Решить уравнение cos2 Зх - tg2 Зх - sin2 Зх + 1 = 0.
л л , лп „
Ответ: — + —, п G Z.
12 о
6. Из двух однородных кусков сплава с разным процен-
тным содержанием меди с массами соответственно тип,
отрезали по куску с равными массами. Каждый отрезанный
кусок сплавили с оставшимися частями другого куска, после
этого процентное содержание меди в полученных сплавах
оказалось одинаковое. Какая масса каждого из отрезанных
кусков?
7. Решить уравнение
Vx2 + 2>/x2 — 1 - Vx2 - 2 Vx2 - 1 = 1.
Ответ:
Вариант 11
1. Решить систему уравнений
log»х • log2(y+ О2 = з •
Ответ: (2; 3), (VT; 15).
2. Решить уравнение
2 sin2 х + 2 tg2 х - 4 tg х - 2 V2~sin x + 3 = 0.
Ответ: — + 2лк, kGZ.
4
3. В равнобедренном треугольнике АВС, где АВ = ВС,
высота BD делится точкой М так, что ВМ: MD = т:п. В
каком отношении сторона ВС делится прямой, которая про-
ходит через точки А и Af?
Ответ: .
2п
251
$13. Образцы решений вариантов конкурсных заданий
4. Решить неравенство
log3 (4х+ 1)4-10^^ 3^2,5.
Ответ: (- оо; log4(V3~- 1)] U [1,5; + °0)-
5. В каких пределах изменяется скорость точки, движу-
щейся равномерно по прямой, если известно, что при уве-
личении скорости на 3 м/с промежуток времени, в течение
которого эта точка проходит расстояние 630 м, сокращается
не менее чем на 1 с и не более чем на 280 с?
Ответ: 1,5 м/с 42 м/с.
6. Решить уравнение 2Ь------ 6 |2Х------У = 1.
2 2 J
Ответ: 1.
7. Решить уравнение
1 2 = 6
х2 - 2х 4- 2 х2 - 2х 4- 3 х2 - 2х 4- 4 ’
Ответ: 1.
Вариант 12
1. Решить систему уравнений
V2x 4- у 4- 1 - Vx 4- у = 1,
’ Зх 4- 2у = 4.
Ответ: (2; -1).
2. Решить неравенство
(ТУ + 2)1’1=s (ТУ - 2)***.
Ответ: [- 2; - 1) U [1; + °0)-
3. Пассажир, едущий из города А в город В, половину
пути ехал автобусом, а другую половину — автомобилем.
Если бы весь путь он ехал автобусом, тс для этого он потратил
бы в 1,5 раза больше времени. Считая, что скорость автобуса
и автомобиля постоянные, определить, во сколько раз скорость
автомобиля больше скорости автобуса.
Ответ: в 3 раза.
252
§ 13. Образцы решений вариантов конкурсных заданий
4. Решить уравнение log2 (4* + 4) = х + log2 (2x+1 - 3).
Ответ: 2.
5. Конус, образующая которого наклонена к плоскости
основания под углом а, вписан в шар. Объем конуса равен
У. Найти объем шара.
~ У
Ответ: -----*----.
2 sin a cos а
6. Решить уравнение 1 — sin4 х — cos4 х = 0.
Ответ: ~ 4- лЛ; ± ~ + лп, кип — целые.
2 о
7. Найти действительные корни уравнения
(х — 2,5)4 + (х — 1,5)4 = 1.
Ответ: 1,5; 2,5.
Вариант 13
1. Решить систему уравнений
х+ у + Vx + у = 20,
х2 + у2 = 136.
Решение.
Обозначим Vx + у = t, t > 0. Тогда первое уравнение си-
стемы принимает вид t2 + t — 20 = 0 и 1 = 4.
Следовательно, данная система равносильна системе
Vx + у = 4,
' х2 + у2 = 136.
Тогда
х + у = 16,
(х + у)2 - 2ху = 136;
[х = 10,
J , или
|у = 6
Ответ; (10; 6), (6; 10).
х + у = 16,
ху = 60;
х = 6,
у = 10.
253
§ 13. Образцы решений вариантов конкурсных заданий
2. Решить неравенство 4- * > 1.
Решение.
Обозначим 1gх = t. Тогда у - - 1 > О,
t2- t 4- 1
Г(Г-1)
< О,
Q<t< 1, 0<lgx< 1,
1 <x< 10.
Ответ: (1; 10).
3. В течение года завод дважды увеличивал выпуск про-
дукции на одно и то же число процентов. Найти это число,
если известно, что в начале года завод выпускал 600 изделий,
а в конце года стал выпускать ежемесячно 726 изделий.
Решение.
Применим формулу «сложных процентов»
АП = Ло + 755j ПРИ ло = 600, п = 2, Ап = 726.
(V 2
1 + Тпл I =
Ivv I
/ п \2 121
Тогда 1 4- т5л| = и, учитывая, что р>0, имеем
I lUv / lUv
. , р 11 _Е___________L _ ,п
1 + 100 10 ’ 100 10 ’ р 10,
Ответ: 10%.
л ™ sin х
4. Решить уравнение ctg х 4- । + = 2-
Решение.
Имеем
cosx
sinx
sinx
1 4- cosx
cos х 4- cos2 x 4- sin2 x Л 1 4- cos x
------------------ = 2 --------------- = 2
sinx (1 + cosx) ’ sinx(l+cosx) ’
254
$13. Образцы решений вариантов конкурсных заданий
-А- = 2, 1
• sin X sin X = - ,
cos х # - 1;
х = (- 1)" • + лп, п G Z.
о
Ответ: (- 1)" • ^ + лп, nEZ.
О
5. Решить уравнение
|х - 21 + |х —31 + |2х —8| - 9 = 0.
Решение.
Применяя метод интервалов, раскрываем знаки модуля.
1) х 4. Уравнение принимает вид
х — 2 + х — 3 + 2х — 8 — 9 = 0.
Тоща х = 5,5.
2) 3 х < 4. Тогда
х—2 + х—3 - 2х + 8 - 9 = 0, Ох = 6.
Уравнение не имеет корней на интервале [3; 4).
3) 2 х < 3. Имеем х-2-х + 3- 2х + 8- 9 = 0, х = 0.
Найденное значение х не удовлетворяет условию х G [2; 3).
4) х < 2. Тогда — х + 2 — х + 3 — 2х + 8 — 9 = 0, х = 1.
Ответ: 5,5; 1.
6. Вычислить
у log23 + log2|| - log2 3J • logy, 2.
Решение.
V log2 3 + log2- log2 з] • logy, 2 =
= (Vlog2 3 + log216 - log2 81 - log2 3) • logy, 2 =
= (Vlog2 3 — 4 log2 3 + 4 - log2 3) logy, 2 =
= (V(log23 - 2)2 - log2 3) • logy, 2 =
255
§13. Образцы решений вариантов конкурсных заданий
2 - log2 3 - log2 3 2-2 log2 3
= 1-юг;з
О
Ответ: 2.
7. Параллелограмм, периметр которого 44 см, разделен
диагоналями на четыре треугольника. Разность между пери-
метрами двух смежных треугольников равна 6 см. Найти
стороны параллелограмма.
Решение.
В данном параллелограмме
ABCD (рис. 68)
AD 4- АВ = 22 см.
PKAOD - РКАОВ = АИ-АВ = Ьы. Рис. 68
AACZD ЛАС/л
Решая систему уравнений
AD 4- АВ = 22,
AD - АВ = 6,
получаем AD =14 см, АВ = 8 см.
Ответ: 14 см, 8 см.
Вариант 14
1. Решить уравнение sin6x 4- cos6x = у .
4
Ответ: , к G Z.
2. В параллелограмме ABCD величина угла BAD равна
Л
—, АВ = 3 см. Биссектриса угла А пересекает сторону ВС в
точке Е. Найти площадь треугольника АВЕ,
~ 9VT
Ответ: ——-.
. 4
3. Решить уравнение
Ix + ll - |х| + 3|х-1| - 2 |х - 21 = |х + 2|.
Ответ: (- »; - 2] U [2; + °0)-
256
§ 13. Образцы решений вариантов конкурсных заданий
. ~ о • 1 iro 1 х-о Sin 60°
4. Вычислить 2 sin 15 cos 15 + —.--------------;--
sin4 15° - cos4 15'
„ 1
Ответ: - - .
5. Решить систему уравнений
= Vx + у + Vx - у,
= ^х +У - ^-У-
Ответ: (5; 4).
6. Решить уравнение
2l I J Л I 21 /Л | \ 2 . i I ' А1Л т QI
* Og2 ГкГ “ Х 1o8i/2^2+3x) = х ~ 4 + 2,08^ I------П)------1 ’
Ответ: 2; 1.
7. В начале года в сберегательную кассу на книжку было
внесено 1640 руб., а в конце года взято с книжки 882 руб.
Еще через год на книжке снова оказалось 882 руб. Сколько
процентов начисляют в сберегательной кассе в год?
Ответ: 5%.
Вариант 15
1. По окружности радиуса R равномерно движутся в
одном направлении две точки. Одна из них делает полный
оборот на t с быстрее второй и время между последователь-
ными встречами равно Т. Определить скорости этих точек.
Ответ:
/ (Vf2 + 477 + t)
2Tt
I pit2 + 4Tt - t)
zft
2. Решить уравнение
log2 x • log2 (x - 3) 4- 1 = iog2 (x2 - 3x).
Ответ: 5.
, 8-12x
3. Решить неравенство 5 > 25.
Ответ: 11 (J (2; 6).
I О I
9 Алгебраический гренажер
257
§13. Образцы решений вариантов конкурсных заданий
4. Решить уравнение cos Зх 4- sin х • sin 2х = 0.
л л л лк
Ответ: — 4- лп\ -- 4- —, п и к — целые.
Z 4 2
5. Решить систему уравнений
Гх 4- у = 3,
|х4 + у4= 17.
Ответ: (2; 1), (1; 2).
6. Решить уравнение
(5 - х) (х - 3) Ух - 3
V5-x -h Vx-3 2
Ответ: 3; 5.
7. Площадь прямоугольного треугольника равна 5, один
из острых углов равен а. Найти периметр треугольника.
Ответ:
V2S”(cos а 4- sin а 4- 1)
Vsin a cos а
Вариант 16
1. Дан параллелограмм, в котором величина острого угла
равна 60е. Найти отношение длин сторон параллелограмма,
если отношение квадратов длин диагоналей равно ~ .
Ответ: 1:1.
2. Решить систему уравнений
|x3 + / = 35,
|ху (х 4- у) = 30.
Ответ: (2; 3), (3; 2).
3. Решить неравенство log2 (х 4- 1) > 1ogx+116.
Ответ:
4. Решить уравнение
|х - 2| - 3I2X-1I +5|Зх-2| =4.
1 9
Ответ: - ; — .
2 8
258
§ 13. Образцы решений вариантов конкурсных заданий
5. Решить уравнение sin7 х cos3 х — cos7x sin3 л = cos 2х.
я лп ~ „
Ответ: — 4- — , п G Z.
6. По двум окружностям равных диаметров равномерно
вращаются две точки. Одна из них совершает полный оборот
на 5 с быстрее, чем другая, и поэтому успевает сделать в
1 мин на два оборота больше. Сколько оборотов в минуту
совершает каждая точка?
Ответ: 6 об/м, 4 об/м.
(5.___ 4
( v27 )
Ответ: 10.
= у?.
Вариант 17
1. Найти все значения параметра а, при которых функция
/(х) = 1 хэ + (а- 1) х2 + 2х + 5 возрастает на R.
О
Решение.
Функция у = /(х) возрастает на R, если для всех дейст-
вительных значений х /' (х) 0.
/' (х) = (а2 - 1) х2 + 2 (а - 1) х + 2.
При а = 1 f (х) = 2 > 0. Следовательно, значение а = 1
принадлежит искомому множеству.
При а = - 1 /' (х) = - 4х 4- 2, следовательно, а = - 1 не
принадлежит искомому множеству.
При а # ± 1 /' (х) — квадратичная функция. Она при-
нимает неотрицательные значения при всех х, если D < 0 и
а2 - 1 > 0.
V = (а - I)2 - 2 (а2 - 1) = - а2 - 2а + 3.
4
Имеем:
-а2 -2а + 3^0,
а2 — 1 >0;
|а2 + 2а - 3 =s 0,
[а2 — 1 > 0;
259
§13. Образцы решений вариантов конкурсных заданий
-3,
а 1;
а> 1,
а< - 1;
- 3,
а> 1.
Объединив найденные значения для а, получим
Ответ: а - 3 или а 1.
2. Числа х, у, z (в указанном порядке) образуют геомет-
рическую прогрессию, а числа х4-у, y4-z, x4-z — арифме-
тическую. Найти знаменатель геометрической прогрессии.
Решение.
Пусть q — искомый знаменатель геометрической про-
грессии. Тогда у = xq, z = х^2, х # 0.
Так как х 4- у, у 4- z, х 4- z — последовательные члены
, V . (* + у) + (х 4- z)
арифметической прогрессии, то у 4- z = ---f L .
Тогда 2х = у + z, 2x = xq + xq1, 2 = q + q2,
q2 + q - 2 = 0, q = \ или q = — 2.
Ответ: q = 1 или q = — 2.
_ . 3te2-lta+3
3. Решить уравнение I x - 31 = 1.
Решение.
Данное уравнение равносильно совокупности
х - 3 = 1,
х - 3 = - 1,
Зх2 - 10х + 3 = 0,
х — 3 * 0.
Тогда
х = 4,
х = 2,
х = 3,
х = 4,
х # 3;
1
3 ‘
Ответ: 4; 2; .
О
260
§ 13. Образцы решений вариантов конкурсных заданий
. п 6 cos3 2л + 2 sin3 2л
4. Решить уравнение —---------х— = cos 4л.
3 cos 2л-sin 2л
Решение.
Данное уравнение равносильно системе
[6 cos3 2л + 2 sin3 2л = cos 4л (3 cos 2л - sin 2л),
|tg 2л * 3.
Решим уравнение системы:
6 cos3 2л + 2 sin3 2л = (cos2 2л - sin2 2л)(3 cos 2л - sin 2л),
sin3 2л + 3 sin2 2л cos 2л + sin 2л cos2 2л + 3 cos3 2л = О,
sin 2л (sin2 2л + cos2 2л) + 3 cos 2л (sin2 2л + cos2 2л) = О,
sin 2л + 3 cos 2л = 0, tg 2л — — 3.
1 Jtk
Следовательно, л = — . arctg 3 + у, к G Z.
X X
Ответ: - arctg 3 + ~, к G Z.
X X
5. Решить систему уравнений
х3 4- хУ 4- у3 = 17,
ху 4- х 4- у = 5.
Решение.
Обозначим х 4- у = а, ху = Ь.
х34- у3=(х4-у)(х24- у2- ху) = (х 4- у)((х 4- у)2- Зху) = аСа2- ЗЬ).
Тогда данная система принимает вид
а (a2 - 3ft) 4- ft3 = 17,
а 4- b = 5.
Имеем:
а3 4- ft3 - ЗаЬ = 17, ((а 4- Ща2 - ab 4- ft2) - ЗаЬ = 17,
а 4- ft = 5; 4- ft = 5;
5 (а2 - ab 4- ft2) - ЗаЬ = 17,
а 4- ft = 5;
261
§13. Образцы решений вариантов конкурсных заданий
5 ((а + 5)2 - Заб) - ЗаЬ = 17,
а 4- b = 5;
125- 15ab- ЗаЬ= 17,
а 4- b = 5;
ab- 6,
а 4- b = 5;
а = 3,
5 = 2
или
а = 2,
5 = 3.
Следовательно, исходная система равносильна совокуп-
ности
х 4- у = 3,
ху = 2
или
х 4- у = 2,
ху = 3.
Первая из полученных систем имеет два решения: (2; 1)
и (1; 2), вторая система решений не имеет.
Ответ: (2; 1), (1; 2).
6. В конус с радиусом основания R и углом а между
образующей конуса и его высотой вписан цилиндр так, что
его боковая поверхность относится к боковой поверхности
конуса, как т: и. Найти объем цилиндра.
Решение.
ЛАВС — осевое сечение данного
конуса, прямоугольник MNKE — осе-
вое сечение вписанного в него цилин-
дра (рис. 69).
ВО — высота конуса, ОА — ра-
диус его основания. По условию
LABO = а, ОА = R.
Тогда образующая конуса
I = АВ = — , Н = ВО = Л ctg а,
sin а
Рис. 69
боковая поверхность конуса 5, = лЛ/.
Пусть радиус основания цилиндра FN = г, высота цилин-
дра FO - Л. Тогда боковая поверхность цилиндра S2 = 2nrh.
S2 2rtrh 2rh m -
По условию j- = тогда
262
§ 13. Образцы решений вариантов конкурсных заданий
mR2
, mRl mR2 , mR2
rh = —--- = ----;--- , n = -----;-- .
2n 2n sin a 2rn sin a
Из &BFN: BF=rctga. Тогда
h = H - r ctg a = R ctg a - r ctg a.
Следовательно, 2r^jna = ^ctga ~ rctga,
mR2 = 2rRn cos a — 2r 2n cos a,
2r 2 n cos a — 2rRn cos a + mR2 = 0,
2r 2-2rR + mRi = 0.
ncosa
(1)
Найдем корни полученного квадратного уравнения (1):
Объем цилиндра V = лг 2h = л • г • rh =
mR2
2nsina
Ответ:
7. Решить уравнение
х I + 008 х ~ s*®2 х ~ v<2"sin х I =2.
263
§13. Образцы решений вариантов конкурсных заданий
Решение.
Данное уравнение равносильно системе
Sill 2Х 2 /75“ • 2
4- cos х - sin х - v 2 sin х = cos x,
О < cos x < 1.
Решим уравнение системы:
V2~sin х cos x + cos x - sin2 x - cos2 x - VYsin x = 0,
VT"sin x cos x - 7Уsin x 4- cos x -1 = 0,
V2Tsinx (cosx - 1) + (cosx - 1) = 0,
(cosx - l)(V2Tsinx 4- 1) = 0,
cos x = 1,
sinx = _vT-
Корни первого уравнения полученной совокупности не
удовлетворяют условию 0 < cos х < 1.
Корни второго уравнения запишем в виде совокупности
х = - у 4- 2лк, kEZ,
4
5л
х = — 4- 2л4, к G Z.
4
Учитывая, что 0 < cos х < 1,
получаем
Ответ: + 2лк, iGZ.
4
Вариант 18
1. Изобразить множество
решений системы неравенств на
координатной плоскости:
Ответ: рис. 70.
Рис. 70
264
§ 13. Образцы решений вариантов конкурсных заданий
2. Найти площадь треугольника АВС. если LACB = 30е,
АС = ВС и периметр треугольника равен 5.
~ 25
Ответ: ----------—- .
4(2 +V2-VT)
3. Решить уравнение (х + 1) log,x + 4х log,x — 16 = 0.
Ответ: 3; -у .
О I
4. Решить уравнение sin (л tg х) 4- cos (л tg х) = 1.
Ответ: arctg 2k + лп; arctg ^2/ 4- + лт,
k. п. I. т — целые.
5. При каких значениях параметра а график функции
ах - х3 л
у = —-— пересекает ось абсцисс под углом а = — хотя бы
4 4
в одной точке?
Ответ: а = 4.
6. Решить уравнение 2(2V7+3)27x - V 16 = 0.
Ответ: 9.
7. Среди 11 членов арифметической прогрессии первый,
пятый и одиннадцатый являются последовательными членами
геометрической прогрессии. Найти эту прогрессию, если ее
первый член равен 24.
Ответ: - 24; d = 3
или ах = 24; d = 0.
Вариант 19
1. На координатной пло-
скости изобразить множество
решений системы неравенств
уС -|л + 3.
Ответ: рис. 71.
Рис. 71
265
§13. Образцы решений вариантов конкурсных заданий
2. Числа ху, Xх, у являются последовательными чле-
нами геометрической прогрессии, а числа log*(y + 1), — ,
log* (2 - у) — последовательные члены арифметической про-
грессии. Найти х, у.
Ответ: х = , у = 1.
х2-2х
3. Решить уравнение |х| =1.
Ответ: - 1; 1; 2.
4. Решить уравнение
sin 2х = sin4 х + cos4 х.
Ответ: -—Ц- • arcsin (<3~ - 1) + ^ , п G Z.
5. При каких значениях а и b прямая у = 7х - 2 касается
графика функции у = ах2 + bx + 1 в точке А (1; 5)?
Ответ: а = 3, b = 1.
6. В конус, образующая которого наклонена к плоскости
основания под углом а, вписан шар. Найти отношение объемов
шара и конуса.
~ , 3 <2
Ответ: 4tg — ctg а.
7. Решить уравнение log^ (125х) • log^x = 1.
О™"* 625*
Вариант 20
1. Решит систему уравнений
5хг - бху + 5/ = 29,
' 7х2 - 8ху + 7/ = 43.
Ответ: (3; 2), (-3; -2), (2; 3), (-2; -3).
2. Решить уравнение 25 '* * = 5 + 4х '*3.
Ответ: 10.
266
§ 13. Образцы решений вариантов конкурсных заданий
3. Число членов геометрической прогрессии четное. Сум-
ма всех ее членов в три раза больше суммы ее членов,
имеющих нечетные номера. Найти знаменатель прогрессии.
Ответ: 2.
4. Решить уравнение Vlog* V5x~ = - log* 5.
/ч 1
Ответ: — .
5. Решить уравнение sin х sin 2х sin Зх = 4 sin 4х.
4
_ лк л лп
Ответ: — ; - + — , к, п — целые.
L о 4
Й'х-П t (*"2)
6. Решить неравенство 4—2 7 + 8 >52.
Ответ: (3; 4- °°).
7. В шар радиуса R вписана пирамида, основанием ко-
торой является прямоугольник с острым углом а между его
диагоналями. Боковое ребро пирамиды образует с плоскостью
основания угол <р. Найти объем пирамиды.
Ответ: R3 sin3 Ър tg <р sin а.
Вариант 21
1. При каких значениях параметра а уравнение
25х - (а - 4) 5х - 1с? + 10а - 12 = 0
не имеет действительных корней?
Решение.
Произведем замену 5х = у, у > 0. Тогда получаем квад-
ратное уравнение
у2 - (а - 4) у - 2а2 + 10а -12 = 0.
Отсутствие корней у исходного уравнения обеспечивают
следующие случаи:
1) квадратное уравнение не имеет корней;
2) оба корня yt и у2 отрицательны;
3) оба корня равны нулю;
267
§ 13. Образцы решений вариантов конкурсных заданий
4) один корень равен нулю, другой — отрицательный.
Для случая 1) имеем
D = (а - 4)2 - 4 (- 2а2 4- 10а - 12) < 0,
9а2 - 48а 4- 64 < 0, (За - 8)2 < 0.
Следовательно, этот случай не выполняется ни при каких
значениях а.
Случай 2) имеет место, если выполняется система нера-
венств
D £ 0,
У! + у2<0,
Для данного уравнения D 0 при всех значениях а. По
теореме Виета 4- у2 = а - 4, уу2 = - 2а2 4- 10а - 12. Тоща
44 — *t V, а
-2а2+ 10а- 12>0; 12<а<3;
Случай 3) имеет место, если
а — 4 = 0,
- 2а2 + 10а - 12 = 0,
что не выполняется ни при каких а.
Случай 4) имеет место, если
а — 4 < 0,
-2а2 4- 10а- 12 = 0,
что выполняется при а = 2 или а = 3.
Соберем полученные результаты в
Ответ: 2 а 3.
2. Решить неравенство log^ log2 log^ 9 > 0.
Решение.
Имеем: 0 < log2 log^ 9 < 1,
1 < log,.! 9 < 2, logx_! x - 1 < logx—19 < logx_t (x - I)2.
Последнее неравенство равносильно совокупности двух
систем:
268
§ 13. Образцы решений вариантов конкурсных заданий
X - 1 > 1,
X - 1 <9,
(х - 1)2>9
0<х - 1 < л,
х - 1 >9,
(л - 1)2<9,
х > 2,
х< 10,
х - 1 > 3,
х - 1 < - 3
ИЛИ
0<х<2,
х> 10,
(х - 1)2<9.
(1)
Первая система совокупности (1) имеет место при
4<х< 10, вторая система решений не имеет.
Ответ: (4; 10).
3. Решить уравнение sin = х2 — 2 /3~х 4- 4.
Решение.
Перепишем данное уравнение в таком виде:
sin = (х - VT)2 + 1. (1)
Очевидно, при всех значениях х
sin (утг) 1( (я-^)2* 1 ь
Следовательно, равенство (1) имеет место при
’ . ( ЛХ \
.sm (гтт) = *’
(х - vT/ + 1 = 1.
Второе уравнение полученной системы имеет единствен-
ный корень х = 7з~, являющийся также корнем первого урав-
нения.
Ответ:
4. Решить систему уравнений
х + у + z = 9,
- + - + - = 1,
xyz
ху + yz + zx = 27.
269
§ 13. Образцы решений вариантов конкурсных заданий
Решение.
Перепишем данную систему уравнений в таком виде:
Гх + у 4- z = 9,
j yz 4- xz 4- ху _ j
| xyz ’
[ху 4- yz 4- zx = 27.
Следовательно, данная система равносильна системе
х 4- у 4- z = 9,
< ху 4- yz 4- zx = 27,
xyz = 27.
Тогда х, у, z — корни кубического уравнения
t3 - 9t2 4- lit - 27 = 0 или (t - 3)э = 0.
Следовательно, х = у = z = 3.
Ответ: (3; 3; 3).
5. Решить уравнение х4 - 4х3 — 1=0.
Решение.
Очевидно, что х = 0 не является корнем данного урав-
нения. Тогда, разделив обе части его на х4, получим уравнение
1 4 1
1 - - - ^ = О, равносильное данному.
Произведем замену = у. Имеем:
у4 4- 4у — 1 = О, у4 4- 2/ 4- 1 - 2/ 4- 4у - 2 = О,
(/ + I)2 — 2 (у — 1)2 = 0,
(у2+1-V2 (у- 1))(/ + 1 + V2~(y - 1)) = О,
'у2-у'/Г+1+\Т=0,
y2 + yVT+ 1 -VF=O.
Дискриминант первого уравнения полученной совокуп-
ности Dj = 2 - 4(1 4- vT) = -4<2’-2<0.
Дискриминант второго уравнения
В2 = 2 - 4(1 - V2) = 4<2~-2>0и
270
§ 13. Образцы решений вариантов конкурсных заданий
- V2± V4VT- 2 V2"(- 1 ± V2vT- 1 )
у ~ 2 ~ 2
- 1 ± V2 vT- 1
- 1/2
г, 1 VT
Следовательно, х = — = ---1—.
У - 1 ± V2VT- 1
6. Две окружности
радиусов Янг каса-
ются внешним обра-
зом. Найти радиус ок-
ружности, касающейся
двух данных окружно-
стей и их обшей внеш-
ней касательной.
Решение.
Ot — центр окруж-
ности радиуса R, О2 —
центр окружности ра- Рис- 72
диуса г, О — центр окружности искомого радиуса х (рис. 72).
Тогда О{О2 = R + г, О{О = R 4- х, О2О = г 4- х.
А, В, С — точки касания данных трех окружностей с
их общей касательной, О^А = Л, ОВ = х, О2С - г.
Проведем || KN || АС. Тогда
= Я - г, О// = г - х, OJC = R - х.
Из UOtAfO2 = 90°):
OJA2 = Ор22 - OJA2 = (Я 4- г)2 - (R - г)2 = 4Rr,
OJA = 2 jRr.
Из ДО^О (LOJCO = 90е):
OK2 = ОО2 - OJC2 = (R 4- x)2 - (R - x)2 = 4Rx, OK =2 VRx.
Из &OJW (LOJW = 90е):
271
§ 13. Образцы решений вариантов конкурсных заданий
ON2 = OO22 - О^2 = (г + х)2 - (г - х)2 = 4rx, ON = 2 Vrx.
Тогда КО 4- ON = KN = МО2,
2 'JRx + 24rx = 2 '/Rr, Vx~+ Vr ) = VrF,
Rr
(V/?~+ Vr )2 ’
Ответ:
Rr
(fR + '/r)2 ‘
7. Пункт А находится в поле на расстоянии 8 км от
прямолинейного шоссе. На шоссе расположен пункт В. Из
А в В выезжает автомобиль, который может выбрать маршрут
движения или только по полю, или частично по полю, а
частично по шоссе. Известно, что скорость автомобиля по
шоссе в 2 раза больше, чем по полю,
и что даже при самом удачном выборе
маршрута, проходящего по полю и
по шоссе, на это уйдет не меньше
времени, чем потребуется, если ехать
напрямик по полю. Найти, какое
максимальное расстояние может
проехать автомобиль, если его мар-
шрут будет проходить по полю и по
шоссе.
Рис. 73
Решение.
Пусть расстояние от л до В равно s (рис. 73). Расстояние
AD от пункта А до дороги по условию равно 8 км, $ 8.
С — точка, в которой автомобиль выезжает с поля на шоссе.
Рассмотрим только случай, когда участок дороги АС по полю
прямолинейный, так как любой криволинейный путь от Л до
С длиннее отрезка АС и требует большего времени движения.
Очевидно, точка С лежит между точками В и D.
Пусть v — скорость движения автомобиля по полю. Тогда
s АС . СВ 1
по условию - -- + -г—, s АС + — СВ.
J v v 2v 2
Пусть СВ = х. Тогда BD = Vs - 64, DC = Vs2 - 64 - х,
AC = у/AD2 + DC2 = Уб4 + (УР-64 -x)2.
272
§ 13. Образцы решений вариантов конкурсных заданий
Неравенство s АС 4- СВ примет вид
s « V 64 + (VP - 64 - х)2 +
Тогда s - $ V64 + (Vs 2 - 64 - х)2.
(V 2
s - ~ | 64 + (Vs 2 - 64 - х)2,
X I
х2 _______
s2 - sx + -J- 64 + s 2 — 64 — 2х Vs 2 - 64 + х2,
4
ог2 _______
— + х (s - 2 Vs2 - 64 ) г о,
х \х - ± (2 Vs 2 - 64 - s)| 5 О.
I J /
Полученное неравенство должно выполняться при всех
значениях величины х, определяющей положение точки С,
в которой автомобиль выезжает с поля на шоссе.
Для того, чтобы это неравенство выполнялось при всех
х 0, необходимо и достаточно, чтобы выполнялось условие
(2 Vs 2 - 64 - s) «= 0.
J
Тогда s 2 Vs 2 - 64, s 2 4 (s 2 - 64) и, учитывая, что
s 8, получаем 8 s Следовательно, максимальное
расстояние, которое может проехать автомобиль, равно
16
VT км
Ответ: км.
Вариант 22
1. Решить неравенство (х - 4) > 0.
Ответ: (4; 3 4- V2~) U (5; 4- оо).
273
§ 13. Образцы решений вариантов конкурсных заданий
2. При каких значениях параметра а уравнение
36х + (а - 1) 6х + а - 2а2 = О
имеет два действительных различных корня?
Ответ: 2<а<5.
3. Решить уравнение sin10 х + cos10 х = ?? cos4 2х.
1о
Ответ: ± , kGZ.
о 2
4. Решить уравнение
4х- 3х 2 = 3 х 2 - 2
Ответ: 1,5.
5. В треугольнике ABC LB = 60е, AD и СЕ — биссек-
трисы углов А и С треугольника. Найти сумму
LCEB 4- LADB.
Ответ: 180е.
6. Решить систему уравнений
Ух 4- у 4- УЗу 4- z = 4,
• УЗу + z 4- Уг - х = 5,
Уг - х 4- Ух 4- у == 3.
Ответ: (-1; 2; 3).
7. Два поезда выехали одновременно в одном направлении
из городов А и В, расположенных на расстоянии 60 км друг
от друга, и одновременно прибыли на станцию С. Если бы
один из них увеличил скорость на 25 км/ч, а другой на
20 км/ч, то они также прибыли бы на станцию С одновре-
менно, но на 2 часа раньше. Найти скорости поездов.
Ответ: 50 км/ч, 40 км/ч.
Вариант 23
1. Решить уравнение sin (л sin х) 4- cos (л sin х) = 1.
Ответ: лп, (-1/^4-лЛ,
п и к — целые.
274
§ 13. Образцы решений вариантов конкурсных заданий
2. В квадрате ABCD точка М является серединой стороны
ВС, О — точка пересечения DM и АС. Найти угол МОС.
Ответ: arccos^rj^.
3. Решить систему уравнений
[х (у + Z) - 20,
5У(г + х) = 18,
[z(x + у) = 14.
Ответ: (4; 3; 2), (-4; -3; -2).
4. Решить неравенство
logx (10х + 3) • log1Qx (Зх + 10) Ъ 0.
Ответ: (0; 0,1) U (1; + °0)*
5. При каких значениях параметра а уравнение
(а - 1) • 9х - (2а - 1) • 3х - 1 = 0
имеет два различных действительных корня?
V3"
Ответ: а < —— .
6. Решить уравнение (х — 2)х ~х = (х - 2)12.
Ответ: -3; 1; 2; 3; 4.
7. Два экскаватора роют траншею навстречу друг другу
и заканчивают работу за 60 дней. Если бы первый экскаватор
проработал 18 дней, а другой 16 дней, то вместе они прошли
2
бы 60 м траншеи. Если бы первый экскаватор выполнил —
&
всей работы второго экскаватора, а второй 0,3 всей работы
первого, то первому понадобилось бы на эту работу на 6
дней больше, чем второму. Сколько метров в день проходит
каждый экскаватор?
Ответ: 2 м/день; 1,5 м/день.
Вариант 24
1. Два круга одного и того же радиуса R расположены
так, что центр каждого из них лежит на окружности другого.
275
§13. Образцы решений вариантов конкурсных заданий
Найти радиус круга, вписанного в общую часть этих кругов
и касающегося их линии центров.
~ 3R
Ответ: — .
о
2. При каких значениях параметра а уравнение
sin6 х + cos6 х = а
имеет решение?
Ответ: 4 а 1-
3. Решить уравнение loglul ж 2 • log,ul^ 3 = 1.
Ответ: (-1)" arcsin 2 + an, n&Z.
4. Решить уравнение (х - 3)х -1х = (х — З)7 8*-30.
Ответ: 2; 4; 5; 6.
5. Решить неравенство log2 (2 - х) - 8.1oga23 (2 - х) а 5.
Ответ: (- «о; О] U 1 4^; 2|.
6. Решить систему уравнений
х4 + у4 = X,
X* + у3 = 1.
Ответ: (1; 0),
>11'
7. От пристани А к пристани В, находящихся на рассто-
янии 12 км, вниз по течению реки отходит моторная лодка,
скорость которой в стоячей воде ц = 6 км/ч. Одновременно
с ней из В в А выходит катер, скорость которого в стоячей
воде v2 = 10 км/ч. После их встречи они мгновенно разво-
рачиваются и возвращаются к своим пристаням. Определить
все возможные значения скорости течения реки и, при ко-
торых лодка приходит в Л не раньше, чем через час после
возвращения катера в В.
Ответ: 2 и < 6.
276
Ответы. Указания. Решения.
§1
1.84. Рис. 74. 1.85. Рис. 75. 1.86. Рис. 76. 1.87, Рис. 77.
1.88. Рис. 78. 1.89. Рис. 79. 1.90. Рис. 80. 1.91. Рис. 81.
= (1£L_JX12LLL11 _ |х|+1 при х # ± 1. 1.94. Рис. 84.
Указание. Область определения данной функции
D(y) = (-«; 0).
277
1.95. Рис. 85. 1.96. Рис. 86. 1.97. Рис. 87. 1.98. Рис. 88. 1.99.
Рис. 89. 1.100. Рис. 90. Указание. |х - |х| I = |х| - х, так
как |х| 5= х. 1.103. Рис. 91. 1.104. Рис. 92. 1.105. Рис. 93.
1.106. Рис. 94. 1.107. Рис. 95. 1.108. Рис. 96. 1.109. Рис. 97.
1.112. 5 или -2. 1.113. 1 или -4. 1.114. -2, или 3, или
1 ± V17"
--------. 1.115. -1 или -4. 1.116. -1, или 0, или 1, или 2.
1.117. ± 2. 1.118. 4, или -4, или 0. 1.119. 0. 1.120. Нет ре-
278
Ответы. Указания. Решения.
279
Ответы. Указания. Решения.
шений. 1.121. 2 или 2 ± V8~. 1.122. или 1.123. 1 или -5.
1.125. - 4 4- V23^ 1.126. - 2±273"или4 + 2/Г 1.127. ± 7.
У
или ±2, или ±3. 1.132. или 2. 1.133. ---------.
1.136. 4- 1-137. -рг. 1.138. ±3. 1.139. -8 или -1, или 0. 1.140.
о IX ___
— 3 + V17 1 5
73~ или 1. 1.141. ---z---- или 1. 1.142. - или -1.143.
Z о L
1 или - -/3. 1.144. 2 или - 1.145. 2 или - 1.146. 2
О
280
Ответы. Указания. Решения.
11 — л/29~ 3 + VI3 1
или 3. 1.147. —— или — . 1.148. ± 2. 1.149. | или
2 2 о
13 3 9
— , или 1.152. — или — . 1.153. О х 6. 1.154. х 3.
2 2 2 2
11 — 1 + V73”
1.155. у или 7. 1.156. 2 или -3, или ----------. 1.157.
1 х 2 или 3 х 4. 1.158. - 2. 1.159. - 8 или 12. 1.160.
—5 х 8. 1.161. х 2. 1.162. х -у- . 1.163. Нет решений.
2 2
1.164. -1 или 1.165. Нет решений. 1.166. 1. 1.167.
*5 О
5 9 + V17
1.168. -1. 1.169. ± 4. 1.170. 2 или или 1.171. -3
или 2, или —1 . 1.172. х < — 3 или х 3. 1.173.
- 1 - V2” или 1. 1.174. 1 или 3. 1.175. -4
2
или —, или 2, или
О
281
Ответы. Указания. Решения.
Рис. 94
4 2 1
. 1.176. -8, или —, или 4, или 8. 1.177. - —, или —, или 2.
«j X
1.181. - 2 < х < - |. 1.182. - 3 < х < 4. 1.183. О < х < 2. 1.184.
X
< 2 2
— 1<х<2. 1.185. ^0 4 5. 1.186. -=;<х<--. 1.187.
3 7 3
-6<х<-3 или -2<х<1. 1.188. О =£ х £ 3. 1.189.
<х< 4. 1.190. —1 — V5~<x < - 2 или -2<х<-1 + V5~.
.191. -?<х<1. 1.192. х<0 или х>2. 1.193. х 3= 0. 1.194.
4 __ _____________
. . 11-V3T 11+V57" . ,Л, „ 1
< 1 или х>3. 1.195. ------- <х<--------. 1.196. х — -z
4 4 Z
282
Ответы. Указания. Решения.
или х 5. 1.197. х — любое. 1.198. х - 1 или х 0. 1.199.
3
х 1 - V2~ или х = 1, или х 1 4- /2~. 1.200. 0 < х < — или
283
Ответы. Указания. Решения.
3
^<х<6. 1.201. х^-3 или 1^х<5, или х>5. 1.202.
1+V3T . Л5- 4 -1+V3T
---------- х < - v3 или -v3 < х < - - , или------------
«J «J
х < 73~, или VT< х 2. 1.203. х < или х > 3. 1.204. х < -L
О о
9
1.205. х<-1. 1.206. - 5<х<3 + 2>/Т. 1.207. х « - | или
х . 1.208. х - 1 или х 5. 1.209. х - 1 или х 0.
1.211. х<7 или х>3. 1.212. х<-2, или -2<х<0, или
з
х > 2. 1.213. х « О или 2 «£ х « 3. 1.214. х < 0. 1.215. х 2 .
1.216. х< — 2 или х>0. 1.217. или х 2. 1.218.
О
5 2
х<-1 или -1<х<0, или х>1. 1.219. - — х — или
| « х « 4. 1.222. х < 1. 1.223. - 4 « х « 2 или х 5s 3 + 7ГГ
1.224. Нет решений. 1.225. х . 1.226. х — любое. 1.227.
о
х<-6 или х>± 1.228. - 1 « х « 1. 1.229. х«-4 или
О
284
Ответы. Указания. Решения.
х^- 1. 1.230. х< — 4 или х>0. 1.231. х>у. 1-232.
- 6<х < 6. 1.233. х< — 2 или х>2. 1.234. 4 - ЛГ0 4 1.
1.235. - 1. 1.236. 4<х<6 или 6<х<8. 1.237. х<2, или
з + Тзз-
х = 3, или х > 4. 1.238. - 2 « х < 3 или х 5 ----------z----. 1.239.
□
- 2<х< - . 1.240. - 5 « х< - 4 или - 2<х« - 2 + vT
х = -3. 2.24.
2.27. х = у.
х = - 4, или
2.20. х = 3. 2.21. х = - J . 2.22. х = - |. 2.23. х = 3 или
о X
7 1
х = 9. 2.25. х = — 1 или х = —— . 2.26. х = — —.
X о
V2” у/2
2.28. х = 0. 2.31. х = или х = - ~ 2.32.
X X
х = - 2, или х = - 3 — ТУ, или х = - 3 4- ТУ
2.33. х = 1 или х = 3. 2.34. х = -у или х = 2. 2.35. х = - 1
4
или х = 3. 2.36. х = - 3 или х = - 1, или х = 2, или х = 6.
2.37. х = 1. 2.38. х = 0 или х = 1. 2.39. х = 0 или х = — 2,
-2+Тбб" -2-/66" „
или х =-----------. 2.40. х = 0 или х = —2.
X
2 или х = 1. 2.43. х = - 2 или
= 1. 2.44. х = - 1 или х = 1, или
2, или х = 1,
3 — Т73~
16
или х =-------
2.41. х = - 1. 2.42. х = -
х = - 1, ИЛИ X = О, ИЛИ X
х = 2, или х = 4. 2.45. х = - 3 или х =
3
или х = 2. 2.48. х = 0 или х = — , или х
о
ИЛИ
3 + V73"
16
. 2.49. х = — 1 или х = О, или х =
или
—-----. 2.50. х = - 3 или х = 1. 2.51
или
х = 2. 2.52. х =
- 3 или х = 0. 2.53. х = —-—
5-<УГ
х = - 1 ИЛИ X = 6, или X =----
или
или
х = - 7, или х = - 1, или х = - 4 - 3 /3~,
2
х = - 4
5 + VT ...
х = —2-54*
5+V9T э__
х =-----. 2.55<
или х = - 4 + 3 ТУ 2.56. х = 2 или х = - 7. 2.58. х = - 1
285
Ответы. Указания. Решения.
или х = 12. 2.59. х = - 4 - V2T” или х = - 4 4- V2R 2.60.
х = - 5 - V95" или х = - 5 4- V95\ 2.61. х = - 4 - V3” или
5 _ V89
х = - 4 4- а/5~. 2.62. х = 2 или х = 3, или х =---, или
5 + <89“ „ . .. 1 1
х =------. 2.63. Нет решений. 2.64. х = — или х = - —.
XIX
2.65. х = ” 2 ИЛИ * = 2- 2.67. х = - 6 или х = -- 4, или
- 15 - <129" - 15 4- 7129" _о
х =----------, или х =--------. 2.68. х = - 8, или
15 -35-Т265- — 35 4-V265”
х = - —, или х =------------, или х = ------------. 2.69.
XX X
„ „ — 7 —/73~ — 7 +/73“
х = — 2, или х = 3, или х =---, или х =-------------.
2.70. х = -3, или х = 4, или х = -3-V21, или х = -34-V2F
2.71. х = - 2 или х = - ^. 2.72. х = - 4 или х = 5, или
X
х = — 5 - 3 V5", или х = - 5 4- 3 /5". 2.75. х = 1 или
-3-/5“ -3 + /5“ 1 о
х =------, или х =----------. 2.76. х = — или х = 2. 2.77.
2 2 __ 2
1 „ -11-/105“ -11+/105“
X = —, ИЛИ X = 2, ИЛИ X = ----, ИЛИ X =-------------.
2.78. х = или х = 2, или х = или х = 3. 2.79. х = 2, или
X О
х = или х = 2-<3", или х = 2 + /Г 2.80. х = 7 или х = у.
2.81. х = - 3 - /15“ или х = - 3 + /15". 2.82. х = 5 - /ГТ
3 + <159“ л „
или х = ——z-----. 2.83.
О
или х = 5 + V31, или х =
3-/159
5
х = - 1 или х = - у. 2.84. х = + 1 или х = - <2“- 1, или
О
х = 41 — 1, или х = 1 — >/2. 2.85. х = 1. 2.86. х = — 1 или
х = - 3, или х = 3 - /б", или х = 3 + 2.87. * = 1 или
X
ол 5 — V2T
2.89. х =------т---- или х =
X
5 + V2T -3-/5“
------, ИЛИ X =-------, или
о’ о ’
х = —. 2.92. х = 2 или х = 4, или х = - 1, или
286
Ответы. Указания. Решения.
1 ___ ____________________
х = - - 2.93. х = - 3 - /3 или х = - 3 4- /3, или
X
х = -—, или х = 1 • 2.94. х = 3 или х = . 2.95.
Ал Ал J
1- V5+V2-2V5" 1 - VT- V2-2V5-
X = 1 или X = -----------------, ИЛИ X = ------------------- ,
2 2
/Г + 1 - V2 + 2VT V5~ + 1 + V2 + 2V5”
ИЛИ X =---------------------, ИЛИ X = -----------Z----------.
2 ’ 2
— 1 — /13”
2.96. х = 2 - /2~ или х = 2 4- ТУ, или х =-----------, или
-14- /ТУ я
х =---------. 2.97. х = 3 или х = - 2.98. х = О или
Z 4
х = ТУ 4- 1, или х = - /У 4- 1, или х = /У 4- 1, или х =
э _ 7 _ д/1 Я 7
= - ТУ 4- 1. 2.99. х = — или х = ----------—-------, или
- 7 4-/137” . 1Л1 1 7 5-/21”
х =------—-----. 2.101. х = - или х = 2.102. х =---------
22 2 2 2
5 4- ТТГ ____
или х =--------. 2.103. х = 3 или х = 5, или х = 9 — /66,
Л1 — 11—/97” -114-/97”
или х = 9 4- /66. 2.104. х =-------------- или х =------------
о 6
2.105. х = 1 или х = 5. 2.106. х = 1
-11-/ТГУ -11 4-/ПУ
X =----------, или X =-----------.
или х = 2,
2.107. х = ~
X
х = 2, или х = 3 - 2 4Т, или х = 3 + 2 ТУ. 2.108. х = 1
х = 4. 2.109. х = — 1 или х = 9, или х = -—,
х = 2.110. х = 1. 2.112. х = Тз ТУ- 3 - 2
ИЛИ
или
или
или
или
х = - 7з Т2 - 3 - 2. 2.113. х = 2 или х = 3. 2.114. х = - 4.
2.115. х = 3 или х = 7. 2.116. х=-1 или х = 3. 2.117.
х = 0 или х = 1. 2.118. х = - 2 или х = 3. 2.119. х = 2 или
х = 4. 2.120. х = 2 или х = 4. 2.121. х = - 2 или х = - 1, или
х=0. 2.122. х = 2 или х = 3. 2.124. х =? 2 или х = -1-
- Тз~, или х = -1 4- Тз~. 2.125. х = -—или х = * ^2^ •
1 -1-V3" -14-/3" -
2.126. х=1, или х =--------——, или х =--------------. 2.127.
/Г -ТЗ" 3/ТГ 3/ГГ
х = — или х = —-— , или х = --—.— , или х =------------—— .
X X 11 11
287
Ответы. Указания. Решения.
„ 11—V55* ll+VST
2.128. х =----—----или х =--------—----, или х=-1, или
х = 3. 2.129. х = 1 или х = - у. 2.130. х = - 1 или х = 2.
1-/13" 14-/13"
2.131. х =--------- или х =------------. 2.133. х = 5 или
Ал L
х — - 7 . 2.134. х = 4 или х = - 4, или х = х, или х = - х-
4 2 2
. ... Л -5 + VT -5-VT „
2.135. х = 0 или х = ----------, или х =------------. 2.136.
2 2
х = —— или х = - 4. 2.137. х = - или х = 0. 2.138.
X X
х = — 77 или х = 0. 2.139. х = — . 2.140. х = — 5.
2 2
§3
3.39. [-4; 2] U П; оо). 3.40. [-7; -2]U [2,5; 4]. 3.41.
(-оо; - 4) и (- 4; - 1,5) и (5; оо). 3.42. [-8; 1 ] U [6; oo)[J
U {3}. 3.43. (-оо; -6] и [- 1;3]. 3.44. (- f; 2 . 3.45.
(- оо; - 4) и (- 3; - 2,5) и 4^. 3.46. (- оо; - 5) U
I о I
и fo; и (8; оо). 3.47. (- оо; - 9] U 5 U (7; оо) (J
I ’ J I
и {6}. 3.48. (- оо; - 4) и - lj U (2; 10) и (10; оо).
I U (3; 4) и {11}. 3.51. (-2; -1) U
- оо; - 7) и (- 1; 1) U (2; оо). 3.53.
- 2) U
г). 3.58. (-оо; -3] U
[-2; -VTiUl-i; HU
- I; и [2; 3) и
- 2) и [- VT; - 1 ] и (I; vT] и
>; — 8) и (— I; о) и (1; 8).
оо; —4] U [5; оо) U {-3}.
3.49. -
U (2; «).
(- •; - 3) и (- 2; 4). 3.54. (- 8; 1 ]. 3.55. (-
U [1; °0). 3.56. (- 1; 5). 3.57.
U (1,5; 2] U [3; 5]. 3.59.
U vT; и [2; 4) и (4; «).
и 17; «).'
и [2; оо) и {0}. 3.62. (- о
3.63. 2] и (3; оо). 3.65. (-
3.61.
7’ 5
3.60.
288
Ответы. Указания. Решения.
3.72.
3.66. (- оо; - 2] и (6; оо) U {1}. 3.67. (-оо; - 5] U {1; 3}.
3.68. [1; 3]U{-3;-l}. 3.69. (-oo;-5]U [- 4; 0] U {2}.
3.70. {- 1; 3}. 3.71. (- оо; - 4) U (3; •) U {|}.
„ 1 - V4
3; 4
U {3}. 3.74. (-3; - 2) U (- 2; - 1 ] U
U
«>; - 5) U (5; оо). 3.80. (- 4,5; - 2) [J
°°; -1) U (1; °°).
- оо; о) U (1; 6).
- оо; - 4) и ['- 3; 3) и [6; оо). 3.86. [1; 3] [J (5; оо).
(-оо; - 3) и (-2; 3). 3.88. [-VT; 0) U (1; VT] U
(- -2] U [4; оо) [J {2}. 3.73.
। . Гл 1 + V4T'
U О; ----------
U (2; 3] U {7}. 3.77. (- оо; О) U (1; •). 3.78. (- оо; о) U
и (4; оо). 3.79. (-
U (3; оо). 3.81. (- оо; -1) [J (3; 7). 3.82. (-
3.83.
3.85.
3.87.
U (2; оо). 3.89. (- 5; 1) U (2; 3). 3.90. (- 2; - 1) U (2; 3).
3.91. [-4; - 3) U - о) и [1; *). 3.92. (0; 1 ] и [2;3].
3.93. [-1 - vT; -1 + V5~]. 3.94. (- оо; — 5] (J (- 3; U
и [- 2; - 1). 3.95. (- 2; 1). 3.98. (- оо
U (5; оо). 3.99. (- оо; о) U (1; •).
U(-1; •)• З.Ю1. (-оо; з). З.Ю2. J 11 U(1; <»). з.юз.
-5)U(- з; 3)U
3.100. (- 5; - 2) U
3. | , ,л,
4’ J '*
(-оо;-4] и [-1; 1] U [4; оо). 3.104. (-3; 3). 3.105.
[-7;-5] U [5; 7]. 3.106. (-<»;-17] U [17; <»). 3.107.
[3; 4) U (4; 5]. 3.108. (-°°; - 10) U (0; «>). 3.109. (-оо; -3].
3.110. [4; 5) U (5; «). 3.111.
1 3.112. (-2; 1 - VT) U (2 V2; оо). 3.113.
6---;’2
и 6
[- 1; 0). 3.114. (- 5; - 2) U (2; 3) U (3; 5). 3.115. (0; оо).
10 Ат ебраический |ренажер
289
Ответы. Указания. Решения.
£ £
§4
4.73. /Г-/3*. 4.74. /5*- 1. 4.75. 2/2*+ 1. 4.76. /14*-
- vT 4.77. 5 + /Г 4.78. 5 - 2 /Т 4.79. /15* + /X 4.80.
/3*+ /Г 4.81. /5*- /X 4.82. 3 /3*- 1. 4.83. /8"- VF. 4.
5 /3*— 4. 4.85. | (730*- /Г). 4.86. /Т+ 1. 4.87. /3*- 1. 4.
|(/6*-/T). 4.89. /2*+l. 4.90. /5*-2. 4.91. 1. 4.92.
| (/6* + /2"). 4.93. 5 + 3/2; 4.94. 2. 4.95. 6. 4.96. -2. 4.97.
-6. 4.98. -10. 4.99. /67 4.100. 1. 4.101. 3. 4.102. 4. 4.103. 4.
4.104. -6. 4.105. -2. 4.106. 0. 4.107. /Г 4.108. /Г 4.111.
Vx 4- у 4- Vx - y. 4.112. Vx 4- 1 4- Vx - 1. 4.113. 2V2”. 4.114.
4 — Vx — 4
Если 4 < x < 8, то —77TT4— » 607111 * 8, то 1. 4.115. 1.
290
Ответы. Указания. Решения.
Рис. 104
Рис. 106
Рис. 105
291
Ответы. Указания. Решения.
4.116. 1. 4.117. Если у<0, то 2 + у"; если у О, то
2/5х=у. 4.118. 2. 4.119. Va+2. 4.120. +| - ^1 .
4.121. Если Ь 2а, то ЧЪ — а - Va”; если а Ь^2а, то
Va”- V6 - а. 4.122. Если a< - 2 или a> 2, то 2 Va2 - 2; если
- 2 « а « - '/2 или V2”C а « 2, то 2 VT. 4.123. 1. 4.126.
Рис. 98. 4.127. Рис. 99. 4.128. Рис. 100. 4.129. Рис. 101. 4.130.
Рис. 102. 4.131. Рис. 103. 4.132. Рис. 104. 4.133. Рис. 105.
4.134. Рис. 106. 4.135. Рис. 107. 4.136. Рис. 108. 4.137. Рис.
109. 4.138. Рис. ПО. 4.139. Рис. 111. 4.140. Рис. 112. Указание.
292
Ответы. Указания. Решения.
X = 5. 5.18.
10
Х ~ 3 ’
Преобразовав правую часть
Vx + 3- 2Vx + 2 = |Vx + 2 -II,
запишите данную функцию в виде
1 - Vx + 2, при -2Sx< —1,
Vx + 2 - 1, при х > - 1.
4.141. Рис. 113. 4.142. Рис. 114.
4.143. Рис. 115.
У =
§5
5.4. х = 7. 5.5. х = 5. 5.6. х = 5. 5.7.
х = - 4. 5.8. х = 10. 5.9. х = 5. 5.10.
х = 7. 5.11. х = - 8. 5.12. х = 2 или
5.14. Нет корней. 5.15. х = 2. 5.17.
Уб5~ - 3
2
5.19. х = 1. 5.20. х
293
Ответы. Указания. Решения.
1 з — Тзз”
5.21. х = 2. 5.22. х = 0 или х = — . 5.23. х =------------- или
х = -° у -° . 5.25. х = 3. 5.26. х=-1. 5.27. х = 1. 5.28.
19
х = 1. 5.29. х = у . 5.30. х = 3. 5.31. х = 3. 5.32. х = 7. 5.33.
7- Тдр
х = 4. 5.34. х = 0. 5.35. х = 2 или х = 6. 5.36. х =-----------
5.37. х =-1. 5.38. х = - 2. 5.39. х = 0 или х = ± . 5.40. Нет
корней. 5.41. х = 4. 5.42. х = 9,5 или х = 0. 5.43. х = - 37
или х = 6. 5.44. х = О или х = 2. 5.46. х = - 3 или х = 2.
5.47. х = - 2 или х = 3. 5.48. х = - 6 или х = 7. 5.49.
3
х = - 1 или х = 4. 5.50. х = - — или х = 2. 5.51. х = - 7 или
4
х = 8. 5.52. х = - 1 или х = 2, или х = 4. 5.53. Нет корней.
5.56. х=-1 или х = 15. 5.57. х = 4. 5.58. х = 20. 5.59.
х = 10. 5.60. х = 6. 5.61. х = 1. 5.62. х = 4 или х = - 4. 5.63.
э
х = - . 5.64. х = 0 или х = 5. 5.65. х = 6. 5.66. х = 17. 5.67.
х = 3 или х = 6. 5.68. х = 2. 5.69. х = 3. 5.70. х = - 1 или
х = 2. 5.71. х = 2 или х = 34. 5.72. х = 5. 5.73. х = 8 + 4 7Г
5.74. х = 1. 5.75. х = 5. 5.77. х = 4. 5.78. х = 8. 5.79. х = 2.
5.80. х = 3. 5.81. х = 1. 5.82. х = 3. 5.83. х = 4 или х = 3.
4
12
5.84. х = 4. 5.85. х = 2. 5.86. х = или х = 4. 5.87. х = 4.
О
5.88. х=1. 5.89. л = -| или х=-1. 5.90. х = 3. 5.91.
6
х = 2. Указание. Область определения данного уравнения
5—2 V7"
G={2}. 5.93. х = 1. 5.94. х = 1 или х =------------|. 5.95.
—2 — 4 VT3~
х = 2 или х =--------------. 5.96. х = 0 или х = 2. 5.97. х = 1,
«э
или х = -2, или х = 13. 5.98. х = 2 или х = —— . 5.99.
—2 + 2 VoT
х = 4. 5.100. х = — 2 или х =-------------. 5.103. х = 4. 5.104.
х = - 1. 5.105. х = 2. 5.106. х = 6 или х = - 6. 5.107. х = .
о
294
Ответы. Указания. Решения.
3
5.108. х = - — . 5.109. х = 1 или х = - 1. 5.110. Нет корней.
5.111. х = 16. 5.112. х = 12. 5.113. Нет корней. 5.115.
27
х = - — или х = 1. 5.116. х = 8 или х - 27. 5.117. х = - 1
о
или х = 2\'Т. 5.118. х=1. 5.119._36/5 5.120. х = 3. 5.121.
х = 9. 5.122. х = 8. 5.123. х = 2 V2 или х = - 2 VT. 5.124.
х - 1024. 5.125. х = - 5 или х = 5 5.126. х = - 7 или х = 7.
5.127. х = — 4 или х = 4. 5.128. х -- <9 или х = 84. 5.129.
х = 7 или х = — 7. 5.130. х = ^. 5.131. х = £ 5.132. х = - 2.
о X
5.133. х = 5. 5.134. х = |. 5.135. х = - - 5.136. х = 1. 5.137.
о
х=~- или х = 3. 5.138. х = - 4 или х = 2. 5.139.
х = 1 - VT или х = 1 + V3^ 5.140. х = 2 5.141. х = - 5 или
х = 0. 5.142. х = 6 или х = - 3. 5.143. х = 0. 5.144.
-1-VTT -1+VTT
х =---------или х —------2----• 5.145. х = 0 или х = — 1.
5.149. х = 1. Указание. Произвести замену
Vx - 1 + Vx + 3 = у.
Тогда /= 2х+2+2 V(x - 1)(х + 3). 5.150. х = 3. 5.151. х = 5.
Указание. Разделив обе части уравнения на х (х # 0), пе-
х V2x + 15 _
рейти к уравнению ^jx + 15 + ---------х--- = 5.152.
„ ~ е 81 - 9 V97~ „ е
х = - 7 или х = 2. 5.153. х =---------или х = 3. 5.154.
о
х = 3. Указание. Умножив обе части уравнения на 2, получаем
2х + 2 V(x + 6)(х - 2) =4 + 2 (Vx+ 6 + Vx - 2 ).
Теперь, произведя замену Vx + 6 + Vx-- 2 = у, следует за-
метить, что 2х + 2 V(x + 6)(х - 2) — у2 — 4. 5.155. х = 7 или
г .« 190 2185 _ _ ,_о
х = 26. 5.156. х = — ~ или х = _-о . 5.157. х=1. 5.158.
03/Хо
7 11/1 ___
х = ^ или х= у j(49 + 5V7T) 5.160. х = 0. 5.161.
х = 2. 5.162. х = 1. 5.163. х = 8. 5.164. х = - или х =
О о
295
Ответы. Указания. Решения.
5.165. х = - 15 или х = 13. 5.166. х = - 14 или х = 5. 5.167.
х = 10. 5.168. х = 1 или х = 2, или х = 10. 5.169. х = - 24,
или х = - 88, или л - 3. 5.170. х = 80 или х = - 109. 5.171.
х = 4416. 5.172. х = 7. 5.173. х = - 11 или х = 24. 5.174. Нет
корней. 5.175. х = - 79 или х = 1. 5.176. х = 16 или х = 81.
5.177. х = 3. 5.178. : - - 2 или х = 5. 5.179. х = - 3 или
х - 4. 5.180. х = -19 или х = 0. 5.182. х = 4. 5.183. Нет
корней. 5.184. Нет корней. 5.185. х = 15. Указание. Умно-
жить обе части данного уравнения на VT. 5.186. х 2. 5.187.
0 х 3. 5.188. - 1 х 0.
§6
6.4. 2 < х < 2VT 6.5. О 1. 6.6. 0 « х < |. 6.7.
х < ——. 6.8. - 4 < х — 3 или — х € 0. 6.9. х > 9.
X о
6.10. “ 2 х з 117111 2 х 1- 6.11. х -2 или х £ 2. 6.12.
х 2"^"* 6’13- 2 х 4. 6.14. Решений нет. 6.15.
1 4- Т29
- 1 <х - 2 + ТУ или х >0. 6.17. х >------------. 6.18. х -2
или 5 х < . 6.19. х > . 6.20. —2 х < — — или 0 < х 2.
1 о о о
6.21. О « х < 2. 6.22. 7~ < х « 6 или х =s 12. 6.23. 2 $ х $ 3.
16
4ТЗ~
6.24. х - 3. 6.25. х 0. 6.26. 0 х 4. 6.27. 1 < х — .
VTV— 5 R
6.28. --------<х^ 1. 6.30. Решений нет. 6.31. х>—. 6.32.
- з - V3"
3<х 5. 6.33. — 2---------<х 1. 6.34. х - 3. 635. х - 2
24
или х>0. 6.36. х<-10 или х>1. 6.37. х > —. 638.
___ о
- 6 х < - 4 + ТУ 639. х 0 или х > - . 6.40. х - 3 или
х > 0. 6.42. х > - 1. 6.43. х < 2 или х > 5. 6.44.
-20 х < 0 или х > 5. 6.45. - ~ х и х # 0. 6.46. х = 2
X X
296
Ответы. Указания. Решения.
или - 4 х 1. 6.47. х = — 4 или 2 х 3. 6.48. х = 3 или
- 2 х -1. 6.49. х = - 3, или - | < х 1, или 4 х 5.
6.50. “ 3 < х < - ^ или х 4. 6.51. х = -2 или х = 1. 6.53.
х = 4. 6.54. - 2 х 4 или х 5. 6.55. 3 х 12. 6.56.
-4^х^--1. 6.57. х 7. 6.58. х = - 2, или х = 1, или
х 3. 6.59. х = - 1 или х 2. 6.60. - 4 х 2 или х = 4.
17 2
6.61. х —— или 1 х < 10. 6.62. х = - 3 или - - х 3.
3 1
6.63. х — 8. или х = 4, или х = 1. 6.64. - — х — или
х 1. 6.65. х = 2 или х = - 2. 6.66. - 4 х - 3 или
3 х 4. 6.67. х - 5, или х 2, или х - - 2, или
х = - р 6.69. х > 1. 6.70. х 1 или - 1 х < - —РГ
L 4 4
6.71. х Z 6. 6.72.
7 - vT
4
6.73. х > 2 VT 6.74.
—6.75. х>2. 6.76. 1. 6.77.
о Z
6.78. х = 5. 6.79. 4 < х <
. 6.82. х < -
X 6.
1
— или
х > 0. 6.83. х < -1 или х > 2. 6.84. х 1 или х 4. 6.85.
1 + vT^ х < 3.
§7
7.2 (-6; -2); 6-4; -4). 7.3. (6; 4); (192; -58). 7.4. (5; 1).
7.5. <1;
(1; -1).
/ 3
7.8. (9; 3),
(1; 1); ]. 7.7. (1; 1);
125 25 Г ’
27\ ' '
у . 7.9. (-1; -2). 7.10. (1; 1);
1 « х<
— . 7.6.
L; г :
7.12. (4; 2); (9; -3
; - — . 7.11. (1; 0); (0; 1); (-1; 2).
13. (2; 3); (3; 2). 7.14. (-15; -5); (3; 4).
7.15. (4; 6; 12); (-4; -6; -12). 7.16. (1; 0; 3); (-1; -2; 1). 7.18.
Ко]; (-1; -3); (|;2). 7.19.
(2; у j. 7.20. (2; 3>: (0; 1); (1,5, 1). 7.21. (-4; 6); (-4; -6);
297
Ответы. Указания. Решения.
7.22. (О; 2); (3; 2); (2 + 75; 75); (2 - 75; - 75).
7.23. ^1; - ; (-1; ” f) ‘ 7,24‘ (-1; 4): (4: -1); (-5: 2); (2; -5)-
(—7 — 7129" 13 - 7129") (—7 + 7129’ 13 + 7129")
7-25- I—«Г" ; - То }' ( 40—;~To~г
(13 + 7249" - 7 + Т24*Г\ . (13 - 7249", - 7 - 7249")
( 40 10 р ( 40 ; 10 /’ 7’26’
(2; -1); (-1; 2); (-2; 1); (1; -2). 7.27. (5; 0): (0; -5). 7.28.
(2; 4); (4; 2). 7.29. (0; 0); (7Т ТТ); (- 7Т; - 77);
(719; - 719"); (- 719"; ТЙГ); (2; 3); (-2: -3); (3; 2); (-3; -2).
7.31. (4; 2): (-4; -2); (-2; -4); (2; 4). Указание. Умножить
обе части второго уравнения системы на 2, затем сложить и
вычесть уравнения системы. 7.32. (3; 2); (2; 3); (-3; -2);
(-2; -3). 7.33. (3; 2); (-3; -2). 7.34. (2; -1); <—2; 1). 7.35.
/ 7\ ( 7\
(5; 2); (-2; -5). 7.36. (3; 1); (-3; -1); !12;-^ ; - 12;^1.
\ 2/ \ 2/
7.37. (-2; 0); (-2; -1); (1; О); (1; -1). 7.38. (2; -1); (-!;(),
где t — любое число. 7.39. (1; 1). Указание. Сложить
уравнения системы. 7.40. (2; 1); (-2; -1); (-2; 1); (2; -1).
7.41. (-1; 1); (-2; О). 7.42. (3; 1); (1; 2). Указание. Умножить
обе части второго уравнения системы на 3 и вычесть из первого.
7.43. (2; -5); (3; 2). 7.44. (-1 +72;-2); (-1-7Г;-2).
7.45. (1; 1). Указание. Сложить уравнения системы и получить
(х + у)3 = 8. 7.46. (-1; 4; 3). Указание. Каждые два уравне-
ния сложить и вычесть третье. 7.47. (10; 7; 5). 7.48 (2; -1);
(-1; 2). 7.50. (5; 3). 7.51. (2; 1); (-2, 5Ч 7.52. (-1; 2); (1; 2);
(-1; -2); (1; -2). 7.53. (2; -1); (-2; 1); (1: -2); (-1; 2). 7.54.
(1; 2); (-1; -2); (1; -2); (-1; 2). 7.55. (4: 2); (11; 16). 7.56.
/ з з\
(3; -1); |-6—;-4-т . Указание. Разложить левые части
\ о 4/
каждого из уравнений на множители. 7.57» (2; 1); (-2; -1).
7.58. (З'Тз’; - vHT); (-1; -3); (3; 1). 7.59. (3; 2):
(-3; -2). 7.60. (4; 2); (2: 4). 7.61. (2; 1). 7.62. |2; |; 41;
I X 1
2; - - 4]. Указание. Каждые два уравнения умножить
и результат разделить на третье. Получить систему-следст-
вне. 7.63. (г; 4); (-2: - - 4). 7.64. ft ft
\ 2 / \ 2 / \ 4 4 4/
298
Ответы. Указания. Решения.
7.65. (1: 2; 3); (-1; 2; 3); <-1; 2; -3):
(1; -2; -3). 7.67. (4; 5); (-4; -5); (- ЗУз~; - Уз~); <3<3":/3,.
7.68. (2; 1); (-2;-1); (-3^ ;
\ ’ JZ ’ О£ / \ V JZ Т о£ /
7.69. (0; 0). 7.70. (4; 2); (-4; -2). 7.71. (-2; -1); (-2; 1):
(- 4; V5-); (- 4; - vT). 7.72. L ;
' ' ' /VT VTa
(3; 4); (-3; -4). 7.73. (1; -1); (-1; 1); :
t О J i
( VT ТзЛ
7-74- 2>- 7-75- <2; i>; <-2; -d:
I A); (4s •7-76- (i; -1): ( г I!; <2; -n:
(-2; 1). 7.77. (3; 2); <—2; -3). '7.78. (-2VT; vT);
(2vT;-V2); (1; 3); (-1; -3). 7.79. (2; 6); (-2; -6);
(V^8VM (-VrT-8VM im- <з; i,:
(-3; -1); (~V2]2VT); (vT; - 2V2j. 7.81. (2; 3); (-2; -3);
(3; 2); (-3; -2). 7.82. (3; 5); (-3; -5); 11 j; 4|j:
(_1з:-41/ 7’83’ (2; 1); (“2; -1)- 7,84‘ (2: lb 7,85‘
(2; -1); (-2; 1); 7.88. (1;
2); (2; 1). 7.89. (3; 1); (1; 3). 7.90. (3; 5); (5; 3);
/-9 + V2T -9-V2T\ f-9 - V2T - 9 + V2T\ qj
\ 2 ’ 2 j’ 2 ’ 2 } ’ 7‘9 *
(3; 4); (4; 3); (-2 - VT; - 2 + vT); (-2 + vT; - 2 - vT).
7.92. (1; 1). 7.93. (4; 1); (1; 4). 7.94. (2; 2); (-2-2VT;
-2 + 2V2”); (-2 + 2VT; — 2 — 2V2~). Указание. Раскрыть
скобки в первом уравнении системы. 7.95. (3; 4); (4; 3);
(11 + 2V3T; 11 - 2V3T); (11 - 2 V3T; 11 + 2 V3T). 7.96.
(4; 1); (1; 4). 7.97. (4; 1); (1; 4); 5 ;
(~5 2^’ ~5 2^^)' 7’98’ (2; 1); <1; 2>; (”2; 1)1 (1; “2>;
(О; -3); (-3; 0). 7.99. (1 + VT; 1 - 7з~); (1 - V3"; 1 + VT).
299
Ответы. Указания. Решения.
7.100. (2; 3); (3; 2); (-5; 2); (2; -5). 7.101. (6; 6);
(3(УТ- 1). _ 3(УУ+ 1)\. (_ 3(УТ+ 1). 3(УТ- 1)\
\2’ 2/’!, 2 ’ 2 ) '*1UZ*
(5; 2); (2; 5); (-5; -2); (-2; -5). 7.103. (2; 1); (1; 2);
(-2; -1); (-1; -2); (0; 2); (2; 0); (0; -2); (-2; О). 7.104.
(1; 3); (3; 1); (-1; -3); (-3; -1). 7.105. (7 + 4VT; 2 + VT);
(2 + VT; 7 + 4 VT); (7 - 4 VT; 2 + VT); (2 + VT; 7 - 4 VT);
(7 + 4 VT; 2 - VT); (2 - VT; 7 + 4 VT); (7 - 4 VT; 2 - VT);
(2 - VT; 7-4VT); (0; 0). 7.106. (2; -1;.-1); (-1; -1; 2);
(-1; 2; -1). 7.107. (0; 0; 1); (0;l; 0); (1; 0; 0). 7.108.
(l;|;z); (2;1); (|;i;z); 2; 1).
7.111. (3; 2); (-3; -2). 7.112. (2; 3); (3; 2); (-2; -3); (-3; -2).
7111 (9-3Ы 21-631 7114 (П. 241 7114 ( ,.9V
7.H3. 40’2бГ 7Л14‘ 1ДЗ’"ТГ 7Л15‘ \ l,4/’
(4; -9). 7.116. (9; 12); (-12; -9). 7.117. (3; 2); (2; 3); (-6; 1);
(1; -6). 7.118. (-3VT;-VT); (-3VT;VT); (3VT; - VT);
(3VT.VT). 7.119. (-1; 2); (2; -1). 7.120. (-1; -2); (2; 1).
Указание. Замена x — y — u, xy = v. 7.121. (-1; 2); (-2; 1).
7.122. (14; -11); (11; -14). 7.123. (--£ -^1; (2; 1).
,l о о I
7.124. (в; f); (-4; 7-125. 51; (2; 5); [ - - 5l;
(-2; -5). 7.126. (fovT); (-- fc); (^77);
(^27 £зЛ
I; (0; 0). Указание. Очевидно, что (0; 0) —
решение. Далее, рассмотрев случай, когда у # 0, воспользо-
ваться заменой — = t. 7.127. (3; -3); (-4; -7,2). Указание.
У
Замена Зл24-5у = и, х (х 4- 1) = и. 7.128. (-1; -1); (-1; 3);
(2; -1); (2; 3). Указание. Замена х2 - х = и, y2 — 2y = v.
7.129. (2; 1); (1; 2); (-2; -1); (-1; -2). 7.131. (2; -1).
Указание. Преобразовать второе уравнение системы к виду
2х 4- у + 1 -t- х 4- у = 5, затем сделать замену VZv 4- у + 1 = и,
/.132. (2; 3); (-2; -3); (-2; 3), <2; -3). 7ЛЗЗ.
(4; 16); (16, 4). 7.134. (8; 1); (1; 8). 7.135. (27; 1); (-1; -27).
7-136- (4 4); ОН111£)-7Л37-<1; 2,: <2; 4>-7л38-
(3; 4); (0; -11). 7.139. (8; 1); (8; -1); (-8; 1); (-8; -1).
300
Ответы. Указания. Решения.
(2 1
—; -21. 7.141. (-2; 3);
(12; 24). 7.142. (-10; 26); (4; 5). 7.143. (2; 3); уу].
\ у ^1
7.144. (-4; 0); . 7.145. (10 + З/ТГ; 10 - 37ТГ);
(10-3/ТГ; 10 + зТТГ); (16; 4); (4; 16). 7.146. (5; 4);
(-5; -4); (15; -12); (-15; 12). 7.147. (5; 3); (5; -3);
(-V¥VT); (~V¥ - VT)-7л4в- <*•4>-7-14’-
(41; 40). 7.150. (1; 1). Указание. Разделить обе части второго
уравнения системы на ху.
§8
8.63. х = 77 + 2лк или х = - + 2лк. 8.64. х = — + 2лк.
2 6 4
8.65. х = лк. 8.66. х = | + |arctg2 + . 8.67. х = (-1)*х
jt 3 лк _ л _ _ _
х — + ^ + —. 8.68. х = - — 4- 2лЛ. 8.69. х = arctg 7 + 1 + лк.
о 2 2 4
8.70. x = (-l)i+1- ? + 2лЛ. 8.71. х = ± | + 2к. 8.72.
О о
х = • 8.74. х = у + 2л к или х = - ~ + 2лк. 8.75.
12к zt 1 о 2
7л лк л лк _ _. 3 ~
х = ~~ + -- или х = - . 8.76. х = arctg- + 2лЛ. 8.77.
4о 2 4о 2 4
л 5л л
х = — + 2лк или х = — 4- 2лЛ. 8.78. х = ~- 4- лк или
л лк л лк 5л > « лл
х = - -h -у . 8.79. х = - — + y или х = - 2 лк. 8.80.
л лк л , „ о < л лк
х = — 4- — или х = — 4- лк. 8.81. х = - Л х -
12 / 4 Юо 9
7л лк л лк л
= - + 8.82. х = - + -г- или х = - i лк, или
24 2 4 2 12
5л яЛ л Зл 2лк
х = . 8.83. х = - + 2лЛ или х = — * . 8.85.
Зо 3 2 ЮЗ
л лк л лк _ л 2лЛ
х = —+ — -. 8.86. х = т+_. 8.87. х = ±-+—z~ или
О 3 О 3 4 3
««« лк л лк „ „„ лк
х = — + лк. 8.88. х = — или х = — 8.89. х = — иля
2 5 О 3 4
301
Ответы. Указания. Решения.
Зл лк _ лл л лк 1л , л
х = — 4- —- . 8.90. х = — 4- — или х = ± — 4- 2лк. 8.91.
о х 1x0 3
л . лк 2л , лк о
х = — + -- или х = ± — + Злк. 8.92. х = — . 8.93.
ОХ 3 X
х = (-1)‘ у + лк или х = + лк, или х = ± ~ + Злк. 8.94.
Ох 3
л , Л лк л лк п
х = -- 4- лк. 8.95. х - -— или х = - 4- — . 8.96. х = ± 120 +
4 3 4 х
л Злк 1л 1лк
+ 15° + 360%. 8.98. х = ± - + . 8.99. х = ± ~ .
XX У о
_ ЛЛ л лк л лк _ л
8.100. х - ту + — или х = — 4- — 8.101. х = 7 4- лк или
14 / 4 х х
2лА Л л лк л , Л
х = —- . 8.102. х = — 4- — или х = ± _ + лк. 8.103. х =
11 16 8 3
л лк л лк лк лк
= ± — + — или х = — + — . 8.104. X = — или х = - .
8.105. х = ± - 4 arccos + лк. 8.106. х = ±
12 х 6 I 4 х
. 5 ' 1 - vTF л лк
или х = ± — arccos---+ 5лк. 8.107. х = т: + — или
х 4 1х О
л лк „ <Л„ л лк л лк .
х = тг + ~г . 8.108. х = -7 + — или х = . 8.109.
о 4 и 3 14 /
л лк л , лк о ,,, . ,.. л , лк
х = 7 + тилих = — + — . 8.111. х = (-1)* • — + 7 или
х = ~: + -^-. 8.112. х = ± + Алк или х=л + 3лк. 8.113.
4 2 3
2л 2лк . л
х — ± — Ч—— . 8.114. х = (— 1)* • — + лк или х = л + 2лк.
8.115. х = (-1)* • или х = лк. 8.116. х = ^ + лк или
х = ± ~3* + 2лк. 8.117. х = лк или х = (- 1/ • + лк. 8.118.
х = + 1лк или х = (— 1)* • 77 + лк. 8.119. х = Тлк. 8.120.
X 6
Л
х = Злк или х = л + Алк. 8.122. х = — + лк или
х = (-1/ • -7 + -Т-. 8.123. х = или х = ± + лк. 8.124.
1х 3 □ о
л лк „ л лк „ лк
х = ± - + лк или х = 8.125. х =- — + —. 8.126. х = —
3 4 Зх о х
302
Ответы. Указания. Решения.
л лЛ лЛ лк
или х = — 4- — . 8.127. х = — . 8.128. х = — или
16 о 3 2
л лк Л 1 1 1
х = ± — 4- — . 8.129. х = ± — arccos — 4- лк или х = ± —х
1 о 3 2 3 2
х arccos | - -у) + лк. 8.130. х = ± х arccos | - т I + лк. 8.131.
\ 4/ 2 I 6)
л лк 1 V3" - 1 7 , „ ,
х = + -z- или х = ± - arccos-------------~— т лк. 8.133.
4 2 2 2
z v t л _ л г _ . —. л лк
х = (-1)* • V + лк или х = — + лк. 8.134. х = — + — или
О X Х^т 1X
лк о л лк лк о л ~ ,
х = — . 8.135. х = — 4- — или х = — . 8.136. х = — 4- 2лк.
2 12 О 4 2
8.137. х = - 4- лк или х = - 4- 2лк, или х = - +
4 3 6
2 - VT .
+ 2лк. 8.138. х = - — + лк или х = — — ± arccos —z— +
4 4 2
4-2лЛ. 8.139. х = - ^ + лк или х = ± 4- 2лк. 8.141.
х = • 8-142. х = лк или х = 4- . 8.143. х = (~1)л+1 х
О о о
л лп „ . лк л лк _ . .. л
х — + —. 8.145. х = — или х = ± -z- + —. 8.146. х = — +
24 4 3 1о 3 4
яЛ л лк „ . ... , л лк „ .
+ — или х = ± — + — . 8.147. х = лк или х = — + —. 8.148.
2 6 2 4 2
. < лк лк о . л . _________
х = (- 1) • — + — или х = — . 8.149. х = ± — + 2лк или
' 7 12 2 2 6
лк п л лк . в .1 л . _ .л
х = -г-. 8.150. х = — или х = (-1)* • — + лк. 8.152. х — — +
XX О 7
л о лк лк о
4—т— или х = л 4- 2лт. 8.153. л= — или х = — . 8.154.
7 О ’ /
х = . 8.155. х = 8.156. X = ? + лк. 8.157. х = 8.158.
4 о 2 4
л лк лк л ^к
х = — + -z- или х = — . 8.160. х = — + -z- . 8.161. х =
14 / 4 4 2
= (-1)* • J + лк. 8.162. х = (-l)t+1 • + лк. 8.163. х = j +
+ 2лк или х = (— 1)* • + лк. 8.164. х = (-1)**1 • л + Ьлк.
О
л л
8.165. х = arctg 3 + лк или х = — — + лк. 8.166. х = ± -г +
303
Ответы. Указания. Решения.
4- лк или л = ± ~ arccos + лЛ. 8.167. х = (-1/+1х
<л лк Л Л » а л л _
х — 4- — . 8.168. х = — 4- лк. 8.169. л = (-1)* • — - — 4- лк.
12 2 4 6 3
8.170. х = + 2лк или х = (-l)k+i +лк. 2 6 8.171.
л 2лк 1 ( . .5 .\ а --а _ лк
х = - — 4- —— или х = — 1 (-1) arcsin — +лк 1. 8.172. х "Т*
8.173. х = (-1)* • 4- лк. 8.175. л = arctg 2 4-л£ или
х = - arctg 4- лк. 8.176. х = ± arctg V2~ 4- или
г - Jtk Л Л — Л - Л .
х = ± arctg v5 4- — . 8.177. х = - — 4- лк или х = ± — 4- лк.
2 4 6
8.178. х = 2л к. 8.179. х = — + лк или х = - arctg 2 4- лк.
4
8.180. х = 4- лк или х = - 4- лк. 8.181. х = ± 4- лк или
6 3 3
X = ± arctg V 11 + лк. 8.182. х = у+ . 8.183.
V 6 4 2
х = v 4- лк. 8.184. х = arctg 4- лк или х = - 4- лк. 8.185.
4 __________ 2 4
1 ± Уб УГ-Т , „ л , о .„<»
х = arctg---------------- + лк. 8.186. х = ± — + лк. 8.188.
х = - ^ + лк или х = arctg 3 + лк. 8.189. х = - v + лк или
4 4
3 л V2~
х = arctg . + лк. 8.190. х = — — + лк или х = ± arctg — +
4 4 2
4- лк. 8.191. х = v + 8.192. х = - 4- лк или х = ± 4-
4 4 6
_ _ . _ — <л л л л лк о Л * <л _
4- лк. 8.193. х = — 4- — или х = ± — 4- —. 8.194. х = — 4-лЛ
о 4 6 2 2
3 Л
или х = arctg — 4- лк. 8.195. х = лк или х = — 4- лк. 8.197.
4 4
х = - у 4- лк, или х = 4- 2лк, или х = 2лк. 8.198.
4 2
х = —^ + лк. 8.199. х = ^4-лЛ или х = - 4- 2лЛ, или
4 4 2
х = 2лк. 8.200. х = 2лк или х = — 4- 2лк. 8.201. х = ±
2 4
304
Ответы. Указания. Решения.
± arccos + 2л к. 8.204. х = лк или х = arctg 2 + лк. Указа-
„ 1 + sin 2л (1 +tgx\2 „ . ..1..
ние. Доказать --.—_ = -—-— . 8.205. х = (-!)* х
1 - sin 2х 11 - tgx I v ’
х ~ 8.206. х = у + лк. Указание, tg2 + ctg2 - 2 =
12 2 4 2 2
(\ 2
ctg* - tg^l = 4ctg2x. 8.207. х = ± + лк нлн х =
х X J О
= ± arccos - *—- + лЛ. 8.208. х = у + 2лЛ или
х = (-l)t+1 7 + лк. 8.209. х = ± + 2лк или х =
О J
(2\
— — + 2тгЛ. Указание, При замене 3cos* +
Ч----— = t имеем 18 cos2* + —= 2 (t2 - 6).
cos х cos х
8.210. х = - v + или х = - arctg ~ + лк. 8.211.
4 и
1 ± VevT- 1
X = arctg----------+ лк.
Указание. Применяя формулу ^2* = 1 tg2jc, несложно
получить tg4* — 12tg* — 17 = 0. Отсюда
tg4 * + 2 tg2 * + 1 - 2 (tg * + З)2 = О или
(tg2* + I)2 - (V2"tg* + 3 7Г)2 = 0.
8.214. * = Ълк. 8.215. * = — + лк. 8.216. * = лк. у = — ,
Л . X, Г) 2 . 1 Ъ
z = - — + -Z-. Указание. Заметим, что cos * + —х—2,
6 3 cos2*
1 + tg2 2у 1, 3 + sin 3z 2. Тогда
(cos2* + —| (1 + tg2 2y) (3 + sin 3z) 4.
I cos^*y \ /
8.217. х=лк, y = ~ + ^. 8.218. х=л + 4лк. 8.219. x =
6 3
= 2лк. 8.220. * = + лк. у = + 2лп. • 8.221. * =
л
2
2лк. Указание. Складывая почленно неравенства
305
Ответы. Указания. Решения.
sin3x sin2x и cos5x cos2x,
получаем sin3x + cos3x 1. Теперь ясно, что исходное урав-
нение равносильно системе
sin3* + cos3x = 1,
2 - sin4x = 1.
8.223. - — + лк<х< — -? + лк или arctg2 + лк<х< — + лк.
2 4 2
JT л 5л Зл
8.224. - — 4- 2лк <х< — + 2л к или — 4- 2л к <х< — + 2лк.
2 6 О 2
8.225. + 2лк <х< + 2лк. 8.226. лк<х <+ лк или
4 4 2
— + лк < х < лк. 8.227. — + 2лк < х < 2лк или 1лк < х <
л 1 . 2 . лп л 1 . 2 лп
< — + 2лк. 8.228. -т arcsin — + — < х < - тг arcsin — + — .
2 232 2232
8.229. - у - z- arcsin + лк < х < ± arcsin + лк. 8.230.
л _ , „ л лк Зл лк
х * — + 2лк. 8.231. — + — < х < — + — или
2 4 2 8 2
+ -£-<х<^ + 8.232. — у + 2лк < х < + 2лк или
8 2 2 2 4 2
л 5л 1л л
- + 2лк < х < — + 2лк. 8.233. - — + 2лк < х < - + 2лк.
2 4 6 6
8.234. +лк <х<^- + 2лк или + 2л к <х<л + 2лк.
2 4 4
8.235. 2л к < х < ~ + 2л к или + 2лк < х < л + 2лк. 8.236.
6 6
4- лк < х < arctg 2 4- лк. 8.237. х — любое.
4
2л 2л
8.239. - л + 2лк < х < —— + 2лк или 2лк < х < — + 2лк.
и и
8.240. — л 4- 2лк < х < — у 4- 2лк или — 4- 2лк < х < 2лк,
л Зл л
или — 4- 2лк<х<— 4- 2лк. 8.241. - — 4- Алк < х < Алк или
2 4 2
5л Л
2л + 4лк < х < — + Алк. 8.242. - л + 2лЛ < х < - — + 2лЛ или
2л£ < х < + 2лк, или + 2лк < х < + 2лЛ.
6 2 6
306
Ответы. Указания. Решения.
J¥. JJl
8.243. - + лк < х < — + лк. 8.244. - + лк < х < - + лк.
6 6 4 2
5л л
8.245. — л + 2л к < х < —— 4- 2лЛ или — — + 2лЛ < х < 2лЛ,
6 6
или + 2лк < х < + 2л£. 8.246. + лк < х <^~ + лк. 8.247.
оо 6 4
л f тс t Зл f л _
— + лк < х < — + лк или — + лк < х < — + лк, или
10 4 10 2
л 7л Зл 9л
— + лк < х < — 4- лк, или —г + лк<х<— 4- лк.
2 10 4 10
8.248. лк < х < — 4- лк или — + лк<х< — 4- лк.
и L J
л 2л 5л 4л
8.249. — 4- 2лк < х < — 4- 2лк или 4- 2л к < х < — 4- 2л к,
4 3 4 3
или “ 4- 2лк < х < 2л 4- 2л к. 8.250. v 4- лк< х < 4- лк или
2 6 2
л , 5л , л л лк л лк
~ 4- лк < х < — 4- лк. 8.251. — 4-—-<*<—4- — или
2 6 8 2 4 2
л лк Зл лк л , л
-г + -^г<*<-7г~ + — . 8.252. лк < х < 4- лк, или
4 2 о 2 о
Зл ~ л t 5л _ 7л w _
— + лк < х < — + лк, или — + лк < х < — 4- лк. 8.253.
о 2 о о
- 4- лк < х < лк или + лк <х<^г + лк.
4 4 2
л 1л
8.254. - — 4- 2лк < х < 2лк или л 4- 2л к < х < — 4- 2л£, или
6 6
1 л
arcsin — 4- 2лЛ < х < — 4- 2лк, или
о 6
4- 2лк <х<л - arcsin4- 2лк.
6 о
7
9.22. — . 9.23. х = - 2 или х = 1, или х = 3. 9.24. х = 4
или х = 5. 9.25. 1. 9.26. х = 4 или х = - 2. 9.27. х = 1 или
7
х = 5. 9.28. х = 5 или х = - 2. 9.29. х = - — или х = 2. 9.30.
|. 9.31. л = - | или л = 3. 9.32. Нет решений. 9.33. 3. 9.34. -1.
307
Ответы. Указания. Решения.
9.35. 10. 9.36. 7. 9.37. 1. 9.38. 1. 9.39. 24. 9.40. х = 0 или
х = 9.41. х = 2 или х = 3. 9.44. 2. 9.45. 4. 9.46. х = — 4
или х = 3. 9.47. 8. 9.48. х = - 2 или х = 2. 9.49. 3. 9.50. 3.
9.51. 1. 9.52. 1. 9.53. 66. 9.54. 4- 9-55. 9. 9.56. |. 9.57. 0.
4 2
9.58. 1. 9.59. 5. 9.60. |. 9.61. х = VT или х = - VX 9.62. О.
9.63. х = 2 или х = 3. 9.64. х = - 4 или х = 4, или х = 2. 9.66.
1. 9.67. 3. 9.68. 2. 9.69. х = ± 1 или х = ± VT 9.70. 3. 9.71.
1 О
х = ± или х = 0. 9.72. х = — или х = 3. 9.73. О. 9.74. х =2
2
или х = 1. 9.75. х = или х = log ,60. 9.76. х = log ,6. 9.77.
2. 9.78. 9. 9.79. 9. 9.80. х = 1 или х = log, 1,25. 9.81. х = 1
или х = — 1. 9.82. х = — 2 или х = 3, или х = 2, или
х = -1. 9.83. |. 9.84. 1. 9.85. х = лп, п е Z. 9.86.
х = ± + лп, nEZ или х = arctgVT + лк, k&Z. 9.88. 2.
9.89. 2. 9.90. х = ± 1. 9.91. х = — 1 или х = 4. 9.92. х = 3 или
х = 0. 9.93. 1. 9.94. х = 1 или х = 3. 9.95. х = 3 или
х = log 5 у + 2. 9.96. 1. 9.97. х = у , iez. 9.99. х = 1 или
х = 2. 9.100. -2. 9.101. х = О или х = 1. 9.102. 0,5. 9.103. |.
9.104. 2. 9.105. Нет решений. 9.106. О. 9.107. 4. 9.108. Нет
решений. Указание. Область определения данного уравнения
х>1 и xEN. 9.109. 0 9.110. x = logV22 или x = 21ogV22.
9.111. х = 0 или х = 1. 9.113. 1. 9.114. 2. 9.115. 5. 9.116. 2.
Указание. Разделить обе части уравнения на 2х. 9.117. 2.
9.118. 5. 9.119. 3. 9.120. 1. 9.121. 1. 9.123. х = 1 или
х = - 1. 9.124. х = 1 или х = - 1, или х = 2. 9.125. х = 2
или х = 3, или х = 4, или х = - 1. 9.126. х = 1 или х = 2,
или х = 3. 9.127. х = - 3 или л = -1, или х=1, или
х = 2. 9.128. х = 1 или х = 2, или х = 3, или х = - 1. 9.129.
х = 1 или х = — 1, или х = 2. 9.130. х = — 2 или х = 0, или
х = 3, или х = 4. 9.131. х = - 4 или х = - 6, или х = - 5,
или х = 2, или х = - 1. 9.132. х = - 3 или х = - 5, или
х = - 8, или х = - 1. 9.133. х = 0 или х = 1, или х = - 2,
308
Ответы. Указания. Решения.
или х = у. 9.134. х = 1 или х = 5. 9.136. (2; 5]. 9.137.
х>-^. 9.138. (-оо; 1) и (2; 3) U (4; «). 9.139. (-5; -3) U
4
и (3; со). 9.140. (-1; 3) и (6; оо). 9.141. (1; 2). 9.142.
(-oo;-2]U[2; оо). 9.143. [-3; 3]. 9.144. [-3; 3]. 9.145.
(-oo;-3]U •). 9.146. (-2; 1). 9.147. (-оо;-i) U
и (2; оо). 9.148. (-2; - U (- 1; оо). 9.149. (-оо; -3) U
I О I
и (1; »)• 9.150. (-7; -3) и (-3; 9.151. (2; оо).
9.152. (f; 2j. 9.153. (-оо; о). 9.154. [-1; 35]. 9.155.
[-1; 1 - V2 ] U [1 + vT; 3]. 9.157. (- оо; 2]. 9.158. (4; оо).
9.159. (—оо; 5). 9.160. (-оо; 3]. 9.161. (-оо; О). 9.162.
[-1; оо). 9.163. [16; оо). 9.164. (0; оо). 9.165. (- оо; 2). 9.166.
(2 \
2 оо . 9.170. (0; 1). 9.171.
(О; оо). 9.172. (- оо; -1 j. 9.17J. х — любое. Указание. Левая
часть неравенства положительна при любых х. 9.174.
(-2; оо). 9.175. (- оо; О). 9.176. (1; оо). 9.177. (- оо; 0) U
U (1; »)• 9.178. |(log2|-lj; *)• 9Л79* <°: °-
х = — 2. 9.181. [-1; О]. 9.182. [-2; 1]. 9.183. [О; 1 ].
[8; оо). 9.186. (0; 1). 9.187. (0; оо). 9.188. [О; 1 ].
(-1; о). 9.190. [-1; 0) U (О; оо). 9.191. (2; оо).
[о; I). 9.193. [-1; 0]. 9.194. -1; 0J U [О; | .
9.180.
9.184.
9.189.
9.192.
9.195.
(- 4).
§ю
VT- 1
10.26. х = 3. 10.27. х = 37. 10.28. х = 9. 10.29. х =—.
10.30. х = 5. 10.31. х = 3 или х = 5. 10.32. х = 2 или х = 3.
10.33. х = 6. 10.34. х = 2. 10.35. х = 1. 10.36. х = 3 или
х = 3 + vT 10.37. х = 1 или х = 2. 10.38. х = - 10. 10.39.
х = 29. 10.40. х = 2 или х = - 1. 10.41. х = 1. 10.42. х = 5.
309
Ответы. Указания. Решения.
10.43. х = - 7 . 10.44. х = 2. 10.45. х = О. 10.48. х = 3 или
4
х = 81. 10.49. X = 1009 или х = 9,001. 10.50. х = 1001 или
х = ^10'+1. 10.51. х = 100 или х = 1000. 10.52. х = 10-*2
или х = 10. 10.53. х = - 64 или х = - 1. 10.54. х = - 100.
10.55. х = - 1000.
10.56. х = 3
или х = 1 + —1— . 10.57.
2V2"
х = — или х = 30.
или х = 2. 10.60.
10.58. х = или х
12о
х = 10 или х = 100.
= 2. 10.59. х = г'2'5
10.61. х = 10 или
х = 10**и. 10.62. х = 0,1 или х = ’^ТсГ 10.63. х = 2. 10.64..
х = 2. 10.65. х = log или х = log 310. 10.67. х = — или
х = 3. 10.68. х = или х = 27. 10.69. х = 25 или х = 5.
10.70. x = vT
х = 25. 10.72. х = ~~ или х = 8.
V4"
10.73. х = или х = 5.
10.74. x = vT или х = 3. 10.75. х = 1. 10.76. x = 0,5vT
или х = 4. 10.77. х = или х = . 10.78. х = 3. 10.79.
х = 7. 10.82. х = 100, или х = 0,01, или х = 10, или
х = 0,1. 10.83. х = 0,1 или х = 1000. 10.84. х = 0,001 или
х = 1, или х = 10. 10.85. х = или х = 10 2 . 10.86. х = 0,1
или х = 1000. 10.87. х = 3 или х = — 6,9. 10.88. х = 1 или
х = 27. 10.89. х = 10* 11 (1Э/3) или х = 10* U (7/Э). 10.90. х = 100.
10.91. х = или х = 4. 10.92. х = 20 или х = 0,001. 10.93.
64
х = 3 или х = 27. 10.94. х = или х = 64. 10.95. х = 0,01 или
о
х = 100. 10.96. х = I или X = 6. 10.97. х = 1000. 10.99.
6
х — -1. 10.100. х = 8. 10.101. х = 2. 10.102. х = или х = 2.
10.103. х=1. 10.105. х = 1. 10.106. (2; 2). 10.107. (4; 16).
10.108. (-10; 20); ^|. 10.109. (1; 1);
I о о / у J J ]
310
Ответы. Указания. Решения.
10.115. (3; 9); (9; 3). 10.116. (8; 2);
(2; 4); (4 VT; 2 $2). 10.118. (4: 1).
10.110. (5; 5). 10.111. (2; 10) (10; 2). 10.112. (3; 5). 10.113.
(3; 3). 10.114. (;
10.117.
k2 8J
10.120. 2|. 10.121. (-0,5; 2). 10.122. (2,5; 6). 10.123.
Н; 4i. 10.124. (1; 2) U (3; 4). 10.125. (О; 0,6]. 10.126.
[-7; - V35") U [5; V35"). 10.127. [-1; 1) U (3; 5]. 10.128.
(-4; -3) и (8; «). 10.133. (3; 4] и [6; о»), 10.134. (-оо; -2).
10.135. (2; 7)U (22; 27). 10.136. ^1; . 10.137. (-2; 3).
10.139. 2^. 10.140. (4; 10). 10.141. (log, 10; оо). 10.142.
(log, 7; 1)U(1; *). 10.143. (0; 0,5) U (1; 2) U (3:6). 10.144.
(-3; -1). 10.145. (^~ 3-; 1) U(l;oo). 10.146. (-оо; - 1)U
(J [5; оо). 10.147. (5; оо). 10.148. (<>; U [2; 1 + vT) U
U (-1; о) U (1 - VT; - 1 ]. 10.149. (з; U (4; | .
10.150. ^0; (J (1; «о). 10.151. (О; 1) U (2; «о).
10.152. (10 - V43; 4) U (Ю + V43; оо). 10.154. (1; 1,04) U
и (26; оо). 10.155. (3; 3,5] U [6; оо). 10.156. (100; 1000).
10.157. (О; 0,01) U (Ю; оо). 10.158. (-10;-0,001). 10.159. Нет
решений. 10’60. (О; 0,5) U (1 + VT; оо). 10.161. [О; | U
. 10.162. (-оо; - П9] U [1; 6). 10.163. [О; 1].
10Л64.
/ -5-V21
I 51 2
I. 10.166. (О; 1) U (2; оо). 10.167.
5; о). 10.168. (О; 0,1) U
X /
311
Ответы. Указания. Решения.
и (Ю; 1000) и (100 000; <»). 10.169. (3; «) U (1; 2). 10.170.
(-®;log4(VT-l))U(l,5; •). 10.171. (о; -jU U feiooo).
\ 1VU / \ 1V j
|; || и [2; оо). 10.173. (о; | U (i; vT ] U
(о; | и (1; 32]. 10.175. (о; U
Г1 i\ . .
10.172. Р; J
\4 L
и (2; «). 10.174.
и (1; 5VT). 10.176. (0; 10). 10.177. U (1; 3]. 10.178.
(0,5; 1). Ю.179. (- 1; 0) U [1; »). 10.180.
9’ 3
§11
11.4. Зх2 - 6х + Д—. 11.5. Jx2Vx“ + \ . 11.6. -Я- . 11.7.
2VF 2 х2
----Д=. 11.8. 20х3 - 21х2 - -т 4- lL9- 4 +
2x2V3F vx хг 3 х3
+ Х. 11.10. 18х2 + 1* - 1J. 11.11. —1== + —|-т. 1Ы2.
х х х 3vx 4Vx
7,5xVx~+28x6 + 12x3. 11.13.-2-. 11.14. 2—11.15.
* 8vx **
- 2x - 6x + 8 ,, ,, 1
(x2 + 4)2 L16, /F(VF-17’ 11,1 ( }
x(3,= -5»=. 11.18. JTsk- ll'1’- -2-vT^T-
— 11 21 л- _ 11.22 — —-j-------
Vl — 2л3 ‘ * Vl + x2 * * x2 Vl - x2
11.23,
+ 1 n24 4
4 Vx2 4- x Vx~ * (x - Vx2 - 4 )2 • Vx2 - 4
11.25. sinx +
+ xcosx. 11.26. cosx-sinx.
11.27. 2cos2x. 11.28. - sin 2x.
11.29. 2sin4x. 11.30. 2tgx + -^-. 11.3.. -
cos2 x (2 - cos 3x)
11.32. 3cos6x. 11.33. - ——• И.34. 2sin2x. 11.35. 2sin2x.
1+sinx
11.36. e\ 11.37. Зе3*-!. 11.38. 6x -11.39. In3x + 1.
x
312
Ответы. Указания. Решения.
—— . 11.41. И 43. у =3x4-2. 11.44. у = х.
sinx л in 10 ' 7
11.45. у = 2х - 4. 11.46. у = |х 4- 1. 11.47. у = 9х - 16. 11.48.
у = 8х 4- 11. 11.49. у = - 6х 4- 9. 11.50. у = 2х 4- 1 - л. 11.51.
3 3. , 5 м л^З
у = -Х--\п2 + -.
у = зх + з-
У = Зх4-|-
7 2 2
Не существует. 11.64. Не существует. 11.65. у = — 5х 4- 2.
11.66. х = 4 или х = 1. 11.67. а = 3, 6=1. 11.68. (2; 4);
У = 4х - 4. 11.69. х = 2. 11.70. у = 2VTx+ 1, у = -2VTx + 1.
11.71. у = 9х - 15, у = 9*+17. 11.72. 0°. 11.73. arctg (-6)
(___________________________________ 5 + /пг \
и arctg 6. 11.74. у = х. 1L75. (/ПГ-5; ------- 1;
\ 5 3 J* 11,76, х 2(1 - vT) * 1L77’ Х L
11.78. х - 0 или х = 4. 11.84 Возрастает на (-<»;- 1 ] и
[0; °°); убывает на [-1; 0]; х = -1 — точка максимума,
х = 0 — точка минимума. 11.85. Возрастает на (- <»; — 3] и
[2; »); убывает на [-3; 2]; х = - 3 — точка максимума,
х = 2 — точка минимума. 11.86. Возрастает на (-«>;- 5] и
[2; »); убывает на [-5; 2]; х = - 5 — точка максимума,
х = 2 — точка минимума. 11.87. Возрастает на [0; 2];
убывает на (- »; 0] и [2; оо); х = 2 — точка максимума,
х = 0 — точка минимума. 11.88. Возрастает на (- »; 0];
убывает на [0; »); х = 0 — точка максимума. 11.89. Возра-
стает на [1,5; ®); убывает на (- »; 1,5];х = 1,5 — точка
минимума. 11.90. Возрастает на (— °°; — 1] и [1; <®
вает на [-1; 1 ]; х = - 1 — точка максимума, х = 1 — точка
минимума. 11.91. Возрастает на [-1; 0] и [1; оо); убывает
на (- оо; - 1 ] и [0; 1 ]; х = 0 — точка максимума, х = — 1 и
Н
11.40.
11.52. у = хУТ-
11.54. у = 36х - 100 11.55.
Я Я Г 1
-. 11.57. у=-х.
11.60. у = - 4. 11.61. у = - 4х, у = 4х - 8. 11.63.
11.58.
1
2 •
12
у = |х 4- 1.
4
у = 2х - 2.
11.53.
11.56.
11.59.
11.75.
. 11.76. ?
); убы-
х = 1 — точки минимума. 11.92. Возрастает на
убывает на
2
3
и [2; ®); х = 2 — точка максимума,
313
Ответы. Указания. Решения.
= — — точка минимума. 11.93. Возрастает на (-<»;- 1 ] и
[0; 4]; убывает на )~1; 0] и [4; оо); х = — 1 и х = 4 — точки
максимума, х = 0 — точка минимума. 11.94. Возрастает на
ьсей числовой прямой. 11.95. Возрастает на (0; 3,2]; убывает
а (- оо; 0) и [3,2; оо); х = 3,2 — точка максимума. 11.96.
Возрастает на (—°°;-4] и [4; оо); убывает на [-4; 0) и
0; 4]; х = — 4 — точка максимума, х = 4 — точка миниму-
3____________________________ з________________________
ма. 11.97. Возрастает на [- V2, 0]; убывает на (-оо; - V2 ],
[0; 1) и (1; оо); х = 0 — точка максимума, х = - ^2~ —
точка минимума. 11.98. Возрастает на (- оо; о) и [2; оо);
убывает на (0; 2]; х = 2 — точка минимума. 11.99. Возра-
стает на (- оо; - 4] и [2; оо)* убывает на [-4; -1) и (-1; 2];
х = — 4 — точка максимума, х = 2 — точка минимума.
И.100. Возрастает на [-3-^5; - 2) и (- 2; - 3 + V5*];
убывает на - 3 - V3”], [- 3 + Vs”; 2) и (2; оо);
л = - 3 + V3” — точка максимума, х = - 3 - /У — точ-
ка минимума. 11.101. Возрастает на (-<»; 1 -/З”] и
[l+VT;oo); убывает на [1 - V3~; 1) и (1; 1 + 73”];
х = 1 - /3~ — точка максимума, х = 1 4- Уз” — точка мини-
мума. 11.102. Возрастает на (- оо; — 1) и (- 1; 0]; убывает
на [0; 1) и (1; оо); х = 0 — точка максимума. 11.103.
Возрастает на [-1; 1]; убывает на (- оо; - 1 ] и [1; оо);
х = 1
точка максимума, х=-1 — точка минимума,
убывает на
1. оо’-
—: оо ।:
[з’ /’
4.104. Возрастает на
Л = 3 — точка максимума. 11.105. Возрастает на [1: »);
убывает на (0; 1]; х = 1 — точка минимума. 11.106. Возра-
Г г--- ! *1 / -- П
стает на
V2
— оо;------
’ 2
. -
2 » 001J х = ”2----точка максимума, х = —-----------точка
; убывает на
—; — ; убывает на
и
2
минимума. 11.107. Возрастает на «
“4; ^1; х = _ 4 — точка максимума. 11.108. Возрастает
XX/ X
1
2
на
оо:
1
— — точка
X
314
Ответы. Указания. Решения.
минимума. 11.109. Возрастает на [0; 2]; убывает на
(- 00; 0] и [2; оо); х = 2 — точка максимума, х = 0 — точка
минимума. 11.110. Возрастает на (- оо; з]; убывает на
[3; оо); х = 3 — точка максимума. 11.111. Возрастает на
(0; е]; убывает на [е; оо); х = е — точка максимума. 11.112.
Возрастает на [1; оо); убывает на (- оо; о) и (0; 1 ]; х = 1 —
точка минимума. 11.113. Возрастает на
L 1
; убывает на
х = — точка минимума. 11.114. Возрастает на
[VF; оо); убывает на (0; 1) и (1; vF ]; х = VF — точка
минимума. 11.115. Возрастает на [0; оо); убывает на
(- оо; о]; х = 0 — точка минимума. 11.116. Возрастает на
(- оо; - 1] и [0; 1]; убывает на [-1; 0] и [1; оо); х=-1и
х — 1 — точки максимума, х = 0 — точка минимума. 11.117.
Возрастает на каждом из промежутков вида [я + 6тгЛ;
5л 4- бяк], kEZ; убывает на каждом из промежутков вида
[- я 4- 6лЛ; я 4- бяк ], кЕ Z; х = - я 4- 6лЛ, кЕ Z, — точки
максимума, х = я 4- бяк, кЕ Z, — точки минимума.
11.118. Возрастает на каждом из промежутков вида
х = я 4- бяк,
Возрастает на
^2лЛ; — 4- 2лЛ ; убывает на каждом из промежутков вида
4- 2лЛ; я 4- 2як |, к Е Z; х = 4- 2лЛ, к Е Z, — точки мак-
2 р ’ 2
симума. 11.120. max f(x) = 15,
[-и а
4
max/(х) = 2; min/(x) = -
[-2; ZJ [-2; ZJ J
min/(x) =
t-t а
11.122.
11.121.
max /(х) = 6,
tt 3)
min/(x) = 3. 11.123. max/(x) = —; min f(x) = 1. 11.124.
[ft 5 (0 я] 2 (<X я]
max f(x) = 16; min f(x) = - 11. 11.125. max/(x) =
[-t 5 [-t 5 I-t 1] 2
min/(x) = 11.126. max f(x) = 3; min f(x) = - 9. 11.127.
[ —t 1] 16 [-1; jg [-1; Я
max f(x) = 1 + min /(x) = 1 - 11.128.
[-H 2 [-H
max /(x) = V I ; ““ A*) = °- 1L129’ max/(x) = з|;
tt 31 20 “ ° tt 3 tt 4 J
315
Ответы. Указания. Решения.
min/(x) = 2. 11.130. max/(x) = min/(л) = - . 11.131.
[» 4 [-4 Я * (-4 29 2
max /(х) = 1; min /(х) = О. 11.132. max /(х) = 77;
[1: 2] [1= 2] [_й: в]
min /(*) = °- 11133. max /(х) = min /(х) = 1. 11.134.
-и н 2 и
max /(х) - е 2; min f(x) = 0. 11.135. max f(x) =
[o^] 4
min f(x) = 1. 11.136. max f(x) = 2e2 - 1; min f(x) = 2.
§12
12.23. Если a = -2, то x — любое; если a = 2, то решений
нет; если a # ± 2, то х = —Цг. 12.24. Если а = 1, то х —
а - 2
любое; если а = 5, то решений нет; если a # 1 и а* 5, то
х = ——12.25. Если а = ОиА = О, тох- любое; если
а - 5
а = 0, а 6*0, то решений нет; если a # О, то х = ^. 12.26.
Если а = —2, то решений нет; если a # - 2, то х = 2. 12.27.
Если а = -3, то решений нет; если a # - 3, то х = a. 12.28.
Если a # 2, то х = а. 12.29. Если а = -7 или а = 7, то
решений нет; если a # ± 7, то х = 7. 12.30. Если a = 0, то
решений нет; если a # О, то х = - 2a. 12.31. Если a = 1 или
a = 3, то решений нет; если a # 1 и a # 3, то х = а. 12.32.
Если а=1, то х = 3; если а = 3, то х = 1; если а#1 и
а # 3, то х = 1 или х = 3. 12.33. Если а = 0, то х < 0 или
х > О; если а = 2, то решений нет; если а # 0 и а * 2, то
х = а. 12.34. Если а = 0, то х < 2 или х > 2; если а = 2, то
решений нет; если а * О и а * 2, то х = а. 12.35. Если
а< 0, то решений нет; если а 0, то х = а2 + 3. 12.36. Если
а>0, то решений нет; если а 0, то х = а2. 12.37. Если
а = 0, то х £0; если а 0, то х = 0. 12.38. Если а 1, то
х = 1; если а > 1, то х = 1 или х = а. 12.39. Если а 1, то
решений нет; если а>1, то х = а. 12.40. Если а -1, то
х = —а; если а>-1, то х = 1 или х = —а. 12.41. Если
316
Ответы. Указания. Решения.
а^ -1, то решений нет; если а>-1, то л= 1. 12.42. Если
а 0, то х = О; если а>0, то х = а. 12.43. Если а 0, то
х = -а; если а > 0, то х = а или х = -а. 12.44. Если а <0,
то х = а или х = -а; если а 0, то х = а. 12.45. Если
I а | > 1, то х = а, или х = — 1, или х = 1; если |а| 1, то
х = 1 или х = -1. 12.46. Если а<-1, то х = а, или
х = -1, или х = 1; если -1 а < 1, то х = а или х = 1; если
а 1, то х = а. 12.47. Если а = 0, то х = 0; если а # 0, то
нет решений. 12.48. Если а = 0, то х = 1; если а # 0, то нет
решений. 12.49. Нет решений. 12.50. Если а 0, то
х = ± а; если а<0, то нет решений. 12.51. Если а = 0, то
х = 3; если а # 0, то нет решений. 12.52. Если а = 0, то
х = 3; если а * О, то нет решений. 12.53. Нет решений.
12.54. Если а < О, то а < х < 0; если а = 0, то нет решений;
если а > О, то 0<х< а. 12.55. Если а<0, то 2а < х < а; если
а = 0, то нет решений; если а>0, то а<х<2а. 12.56. Если
а < 0, то х < 2а; если а = 0, то х < 0; если а > О, то х < а или
а < х < 2а. 12.57. Если а < 0, то х = а или х 2а; если а = О,
то х 0; если а>0, то х 2а. 12.58. Если а = 0, то х = 0;
если а * 0, то нет решений. 12.59. Если а>0, то х>0; если
а 0, то нет решений. 12.60. Если а 0, то х 0; если
а>0, то х = 0. 12.61. Если а <0, то х 0; если а 0, то
х > а2. 12.62. Если а О, то 0 х а2; если а < 0, то нет
решений. 12.63. Если а<0, то х 0; если а = 0, то х>0;
если а > 0, то х а. 12.64. Если а 0, то х 0; если а > О,
то х а. 12.65. Если а 0, то а^х^О; если а>0, то
х = а. 12.66. Если а^-1, то х> -а; если а>-1, то
-а<х< 1 или х> 1. 12.67. Если а <2, то х<2 или х>2;
если а = 2, то х > 2; если а > 2, то х а. 12.68. Если а > О,
то 2 — а<х^ а + 2; если а 0, то нет решений. 12.69. Если
а 0, то х = ± V-а; если а > 0, то нет решений. 12.70. Если
а > 0, то х = 0 или х -а; если а 0, то х - а. 12.71.
Если а<0, то а<х<0 или х>0; если а 0, то х>а. 12.72.
Если а< 1, то х = а или х 1; если а 1, то х 1. 12.73.
Если а > -2, то -а < х < 2 или х < —а; если а —2, то х < 2.
12.74. Если а О, то х — любое; если а>0, то х < log^.
12.75. Если а< 0, то х — любое; если а = 0, то решений нет;
если а>0, то x>-log2a. 12.76. Если а Ф 0, то х — любое;
если а = 0, то х<1 или х>1. 12.77. а 3. 12.78. а- -2.
317
Ответы. Указания. Решения.
12.79. 4<а^5. 12.80. а) а 3; б) а 5. 12.81. а = -4 или
а =-13. 12.82. а = 20. 12.83. а) -8<а<-6 или -6<а<2;
1 19
б) а = — 2 или - — < а < 0, или а > 0. 12.84. —— < а -5.
12.85. а^-3. 12.86. а) а = 81 или а<0; б) а=1 или
а 0; в) 0<а<1 или а>1; г) а<-4 или а -2;
д) -1 « а< 1. 12.87. а 3= -4. 12.88. а « |. 12.89. а « -1 или
а 1. 12.90. а = 0. 12.91. а< — . Указание. Первое уравне-
ние или имеет бесконечно много корней, или вообще их не
имеет. Второе уравнение имеет один корень или ни одного.
Следовательно, о равносильности может идти речь только
тогда, когда данные уравнения корней не имеют. 12.92.
. 6 - vTT
а = 1 или а = ——— .
318
СОДЕРЖАНИЕ
От авторов........................................ 3
§ 1. Абсолютная величина числа (модуль) 5
§ 2. Рациональные уравнения...................... 26
§ 3. Рациональные неравенства.................... 44
§ 4. Степени и корни............................. 57
§ 5. Иррациональные уравнения 72
§ 6. Иррациональные неравенства.................. 97
§ 7. Системы алгебраических уравнений 109
§ 8. Тригонометрические уравнения и неравенства 132
§ 9. Показательные уравнения и неравенства 171
§10. Логарифмические уравнения и неравенства 187
§11. Производная и ее применение 206
§12. Знакомство с параметром................... 216
§13. Образцы решений вариантов конкурсных заданий 229
Ответы. Указания. Решения........................277
Мерзляк Аркадий Григорьевич,
Полонский Виталий Борисович,
Якир Михаил Семенович
АЛГЕБРАИЧЕСКИЙ ТРЕНАЖЕР
Пособие для школьников и абитуриентов
Под редакцией авторов
Художник Курдюмов МЛ
Печать офсетная Формат 84x108/32
Тираж 10 000 зкз Заказ Ne 3422
ООО «Илекса», 105187, г. Москва, Измайловское шоссе, 48а,
тел. (495) 365-30-55
О1печа1ано в О/\О ордена Трудового Красною Знамени
«Чеховский поли! рафичсский комбинат»
142300. г Чехов Московской облает.
1ел /факс (501) 443-92-17, (272) 6-25-36
Г-mail market ingC^chpk ru