A. в. МАНЖИРОВ, А. Д. ПОЛЯНИН
МЕТОДЫ РЕШЕНИЯ
ИНТЕГРАЛЬНЫХ
УРАВНЕНИЙ
СПРАВОЧНИК
МОСКВА
«ФАКТОРИАЛ»
1999

ББК 517.2
М-23
УДК 517.9
М-23 Манжиров А. В., Полянин А. Д. Методы решения
интегральных уравнений: Справочник. — М.: «Факториал», 1999.—272 с. — ISBN
5-88688-043-7.
В книге излагаются точные, приближенные аналитические и численные
методы решения линейных и нелинейных интегральных уравнений. Помимо
классических методов описаны также некоторые новые методы. Для лучшего понимания
рассмотренных методов во всех разделах книги даны примеры решения
конкретных уравнений. Приведены некоторые точные и асимптотические решения
интегральных уравнений, встречающихся в приложениях (в механике и физике).
Справочник предназначен для широкого круга научных работников,
преподавателей вузов, аспирантов и студентов, специализирующихся в различных
областях прикладной математики, механики, физики, теории управления и инженерных
наук.
Библиогр. 108 назв.
Справочное издание
МАНЖИРОВ Александр Владимирович
ПОЛЯНИН Андрей Дмитриевич
МЕТОДЫ РЕШЕНИЯ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
СПРАВОЧНИК
Компьютерная верстка А. И. Журов
Формат 60 X 90/16. Усл. печ. л. 17. Бумага офсетная № 1. Гарнитура литературная.
Подписано к печати 05.05.1999. Тираж 600 экз. Заказ № 829 .
Издательство «Факториал», 117449, Москва, а/я 331; ЛР № 063537 от 22.07.1994.
Отпечатано с готовых диапозитивов
в ППП «Тип. «Наука» 121099, Москва, Шубинский пер., 6.
© А. В. Манжиров, А. Д. Полянин, 1999
ISBN 5-88688-043-7 © «Факториал», оформление, 1999

Оглавление
Предисловие 9
1. Основные определения и формулы. Интегральные преобразования 10
1.1. Предварительные замечания 10
1.1-1. Некоторые определения 10
1.1-2. Структура решений линейных интегральных уравнений 11
1.1-3. Интегральные преобразования 12
1.1-4. Вычеты. Формулы для вычислений 12
1.1-5. Лемма Жордана 13
1.2. Преобразование Лапласа 14
1.2-1. Определение. Формула обращения 14
1.2-2. Обращение рациональных функций 15
1.2-3. Теорема о свертке для преобразования Лапласа 15
1.2-4. Предельные теоремы 15
1.2-5. Основные свойства преобразования Лапласа 16
1.2-6. Формула Поста-Уиддера 16
1.3. Преобразование Меллина 17
1.3-1. Определение. Формула обращения 17
1.3-2. Основные свойства преобразования Меллина 17
1.3-3. Связь преобразований Меллина, Лапласа и Фурье 18
1.4. Преобразование Фурье 18
1.4-1. Определение. Формула обращения 18
1.4-2. Несимметричная форма преобразования 19
1.4-3. Альтернативное преобразование Фурье 19
1.4-4. Теорема о свертке для преобразования Фурье 20
1.5. Синус- и косинус-преобразования Фурье 20
1.5-1. Косинус-преобразование Фурье 20
1.5-2. Синус-преобразование Фурье 21
1.6. Другие интегральные преобразования 21
1.6-1. Преобразование Ханкеля 21
1.6-2. Преобразование Мейера 22
1.6-3. Преобразование Конторовича-Лебедева 22
1.6-4. У-преобразование и другие преобразования 22
2. Методы решения линейных уравнений вида J^ K(x,t)y(t) dt ^ f(x) ... 25
2.1. Уравнения Вольтерра первого рода 25
2.1-1. Структура уравнений. Классы функций и ядер 25
2.1-2. Существование и единственность рещения 26
2.2. Уравнения с вырожденным ядром: К(х, t) = g-^(x)h-^(t) + • • • + g^(x)h^(t) . 26
2.2-1. Уравнения с ядром K(x,t) = g-^(x)h-^(t) +5'2(^)^2(^) ^^
2.2-2. Уравнения с вырожденным ядром общего вида 27
2.3. Сведение уравнений Вольтерра первого рода к уравнениям Вольтерра второго
рода 28
2.3-1. Первый способ 28
2.3-2. Второй способ 28
2.4. Уравнения с разностным ядром: К(х, t) = К(х — t) 29
2.4-1. Метод рещения, основанный на преобразовании Лапласа 29
2.4-2. Случай рационального образа рещения 30
2.4-3. Представление рещения в виде композиции 30
2.4-4. Использование вспомогательного уравнения 31
2.4-5. Сведение к обыкновенным дифференциальным уравнениям 32
2.4-6. Связь уравнений Вольтерра и Винера-Хопфа 33
Страница 3

Оглавление
2.5. Метод дробного дифференцирования 33
2.5-1. Определение дробных интегралов 33
2.5-2. Определение дробных производных 34
2.5-3. Основные свойства 35
2.5-4. Решение обобшенного уравнения Абеля 35
2.6. Уравнения с ядрами, имеюшими слабую особенность 36
2.6-1. Метод преобразования ядра 36
2.6-2. Ядро с логарифмической особенностью 37
2.7. Метод квадратур 38
2.7-1. Квадратурные формулы 38
2.7-2. Обшая схема метода 39
2.7-3. Алгоритм на основе формулы трапеций 40
2.7-4. Алгоритм для уравнения с вырожденным ядром 40
2.8. Уравнения с бесконечным пределом интегрирования 41
2.8-1. Уравнение с переменным нижним пределом интегрирования 41
2.8-2. Приведение к уравнению Винера-Хопфа первого рода 42
3. Методы решения линейных уравнений вида у(х) — J^ К(х, t)y(t) dt= f (х) 43
3.1. Интегральные уравнения Вольтерра второго рода 43
3.1-1. Предварительные замечания. Уравнения для резольвенты 43
3.1-2. Связь между решениями интегральных уравнений 44
3.2. Уравнения с вырожденным ядром: К(х, t) = g-^(x)h-^(t) + • • • + g^(x)h^(t) . 44
3.2-1. Уравнения с ядром К(х, t) = ^(х) -\- ^(x)(x — t) 44
3.2-2. Уравнения с ядром К(х, t) = ip{t) -\- ф{1){1 — х) 45
3.2-3. Уравнения с ядром K{x,t) = J2m=i ^mi^)i^ ~ t)'^~^ 46
3.2-4. Уравнения с ядром К{х, t) = Em=i ^тШ^ - ж)"^"^ 46
3.2-5. Уравнения с вырожденным ядром обшего вида 47
3.3. Уравнения с разностным ядром: К(х, t) = К(х — t) 48
3.3-1. Метод решения, основанный на преобразовании Лапласа 48
3.3-2. Метод, основанный на решении вспомогательного уравнения 50
3.3-3. Сведение к обыкновенным дифференциальным уравнениям 50
3.3-4. Приведение к уравнению Винера-Хопфа второго рода 51
3.3-5. Метод дробного интегрирования для уравнения Абеля 51
3.3-6. Системы интегральных уравнений Вольтерра 53
3.4. Операторные методы решения линейных интегральных уравнений 53
3.4-1. Использование решения «укороченного» уравнения 53
3.4-2. Использование вспомогательного уравнения второго рода 54
3.4-3. Метод решения «квадратных» операторных уравнений 56
3.4-4. Решение операторных уравнений полиномиального вида 57
3.4-5. Некоторые обобшения 58
3.5. Построение решений уравнений со специальной правой частью 58
3.5-1. Обшая схема 58
3.5-2. Порождаюшая функция экспоненциального вида 59
3.5-3. Порождаюшая функция степенного вида 61
3.5-4. Порождаюшая функция, содержашая синусы или косинусы 62
3.6. Метод модельных решений 63
3.6-1. Предварительные замечания 63
3.6-2. Описание метода 64
3.6-3. Модельное решение для экспоненциальной правой части 64
3.6-4. Модельное решение для степенной правой части 66
3.6-5. Модельное решение для синусоидальной правой части 67
3.6-6. Модельное решение для косинусоидальной правой части 67
3.6-7. Некоторые обобшения 67
3.7. Метод дифференцирования интегральных уравнений 68
3.7-1. Ядро содержит сумму экспонент 68
3.7-2. Ядро содержит сумму гиперболических функций 69
3.7-3. Ядро содержит сумму тригонометрических функций 70
3.7-4. Ядро содержит комбинации различных функций 71
Страница 4

Оглавление
3.8. Сведение уравнений Вольтерра второго рода к уравнениям Вольтерра первого
рода 71
3.8-1. Первый способ 72
3.8-2. Второй способ 72
3.9. Метод последовательных приближений 72
3.9-1. Общая схема 72
3.9-2. Формула для резольвенты 73
3.10. Метод квадратур 74
3.10-1. Общая схема метода 74
3.10-2. Применение формулы трапеций 75
3.10-3. Случай вырожденного ядра 75
3.11. Уравнения с бесконечным пределом интегрирования 75
3.11-1. Случай переменного нижнего предела интегрирования 76
3.11-2. Приведение к уравнению Винера-Хопфа второго рода 77
4. Методы решения линейных уравнений вида J K(x,t)y(t) dt ^ f(x) ... 78
4.1. Предварительные замечания 78
4.1-1. Интегральные уравнения Фредгольма первого рода 78
4.1-2. Интегральные уравнения первого рода со слабой особенностью 78
4.1-3. Интегральные уравнения типа свертки 79
4.1-4. Парные интегральные уравнения первого рода 80
4.2. Метод Крейна 80
4.2-1. Основное и вспомогательное уравнения 80
4.2-2. Рещение основного уравнения 81
4.3. Метод интегральных преобразований 82
4.3-1. Уравнение с разностным ядром на всей оси 82
4.3-2. Уравнения с ядром K(x,t) = K(x/t) на полуоси 82
4.3-3. Уравнение с ядром K(x,t) = K(xt) и его обобщения 82
4.4. Задача Римана для действительной оси 83
4.4-1. Связь интеграла Фурье с интегралом типа Кощи 84
4.4-2. Односторонние интегралы Фурье 85
4.4-3. Теорема об аналитическом продолжении и теорема Лиувилля 86
4.4-4. Краевая задача Римана 87
4.4-5. Задача Римана с рациональными коэффициентами 93
4.4-6. Исключительные случаи. Однородная задача 94
4.4-7. Исключительные случаи. Неоднородная задача 96
4.5. Метод Карлемана для уравнений типа свертки первого рода 99
4.5-1. Уравнение Винера-Хопфа первого рода 99
4.5-2. Интегральные уравнения с двумя ядрами первого рода 99
4.6. Парные интегральные уравнения первого рода 102
4.6-1. Метод Карлемана для уравнения с разностными ядрами 102
4.6-2. Точные рещения некоторых парных уравнений первого рода 104
4.6-3. Приведение парных уравнений к уравнению Фредгольма 105
4.7. Асимптотические методы рещения уравнений с логарифмической особенностью 109
4.7-1. Предварительные замечания 109
4.7-2. Рещение при больщих значениях характерного параметра 109
4.7-3. Рещение при малых значениях характерного параметра ПО
4.7-4. Интегральные уравнения теории упругости 112
4.8. Методы регуляризации 112
4.8-1. Метод регуляризации Лаврентьева 112
4.8-2. Метод регуляризации Тихонова 113
5. Методы решения линейных уравнений вида у(х) —/^ К(х, t)y(t) dt= f(x) 114
5.1. Предварительные замечания 114
5.1-1. Уравнения Фредгольма и уравнения со слабой особенностью 114
5.1-2. Структура рещений 115
5.1-3. Интегральные уравнения типа свертки второго рода 115
5.1-4. Парные интегральные уравнения второго рода 115
Страница 5

Оглавление
5.2. Уравнения Фредгольма второго рода с вырожденным ядром 116
5.2-1. Простейшее вырожденное ядро 116
5.2-2. Вырожденное ядро в обшем случае 117
5.3. Решение в виде ряда по степеням параметра. Метод последовательных
приближений 120
5.3-1. Итерированные ядра 120
5.3-2. Метод последовательных приближений 120
5.3-3. Построение резольвенты 121
5.3-4. Ортогональные ядра 122
5.4. Метод определителей Фредгольма 123
5.4-1. Формула для резольвенты 123
5.4-2. Рекуррентные соотношения 124
5.5. Теоремы и альтернатива Фредгольма 125
5.5-1. Теоремы Фредгольма 125
5.5-2. Альтернатива Фредгольма 125
5.6. Интегральные уравнения Фредгольма второго рода с симметричными ядрами . 125
5.6-1. Характеристические числа и собственные функции 125
5.6-2. Билинейный ряд 127
5.6-3. Теорема Гильберта-Шмидта 128
5.6-4. Билинейные ряды итерированных ядер 128
5.6-5. Решение неоднородного уравнения 129
5.6-6. Альтернатива Фредгольма для симметричных уравнений 130
5.6-7. Резольвента симметричного ядра 130
5.6-8. Экстремальные свойства характеристических чисел 131
5.6-9. Интегральные уравнения, приводимые к симметричным 131
5.6-10. Кососимметричное интегральное уравнение 132
5.7. Операторный метод решения интегральных уравнений второго рода 132
5.7-1. Простейшая схема 132
5.7-2. Решение уравнений второго рода на полуоси 132
5.8. Метод интегральных преобразований и метод модельных решений 133
5.8-1. Уравнение с разностным ядром на всей оси 133
5.8-2. Уравнение с ядром K(x,t) = t~^Q(x/t) на полуоси 135
5.8-3. Уравнение с ядром K{x,t) = t^Q{xt) на полуоси 136
5.8-4. Метод модельных решений для уравнений на всей оси 137
5.9. Метод Карлемана для интегральных уравнений типа свертки второго рода ... 137
5.9-1. Уравнение Винера-Хопфа второго рода 137
5.9-2. Интегральное уравнение второго рода с двумя ядрами 141
5.9-3. Уравнения типа свертки с переменным пределом интегрирования 146
5.9-4. Парное уравнение типа свертки второго рода 148
5.10. Метод Винера-Хопфа 149
5.10-1. Некоторые замечания 149
5.10-2. Однородное уравнение Винера-Хопфа второго рода 151
5.10-3. Обшая схема метода. Проблема факторизации 154
5.10-4. Неоднородное уравнение Винера-Хопфа второго рода 156
5.10-5. Исключительный случай уравнения Винера-Хопфа второго рода 157
5.11. Метод Крейна для уравнения Винера-Хопфа 158
5.11-1. Некоторые замечания. Проблема факторизации 158
5.11-2. Решение уравнения Винера-Хопфа второго рода 159
5.11-3. Формула Хопфа-Фока 161
5.12. Методы решения уравнений с разностным ядром на конечном отрезке 162
5.12-1. Метод Крейна 162
5.12-2. Ядра с рациональными преобразованиями Фурье 163
5.12-3. Сведение к обыкновенным дифференциальным уравнениям 164
5.13. Метод замены ядра вырожденным 166
5.13-1. Аппроксимация ядра 166
5.13-2. Приближенное решение 167
Страница 6

Оглавление
5.14. Метод Бейтмена 168
5.14-1. Общая схема метода 168
5.14-2. Некоторые частные случаи 169
5.15. Метод коллокации 171
5.15-1. Общие замечания 171
5.15-2. Приближенное рещение 172
5.15-3. Собственные функции уравнения 173
5.16. Метод наименьщих квадратов 174
5.16-1. Описание метода 174
5.16-2. Построение собственных функций 175
5.17. Метод Бубнова-Галеркина 176
5.17-1. Описание метода 176
5.17-2. Характеристические числа уравнения 176
5.18. Метод квадратур 178
5.18-1. Общая схема для уравнений Фредгольма второго рода 178
5.18-2. Построение собственных функций 179
5.18-3. Особенности применения квадратурных формул 179
5.19. Системы интегральных уравнений Фредгольма второго рода 180
5.19-1. Некоторые замечания 180
5.19-2. Метод преобразования системы уравнений в одно уравнение 181
5.20. Метод регуляризации для некоторых уравнений второго рода 181
5.20-1. Основное уравнение и теоремы Петера 181
5.20-2. Регуляризующие операторы 182
5.20-3. Метод регуляризации 183
6. Методы решения сингулярных интегральных уравнений первого рода .... 185
6.1. Предварительные замечания 185
6.1-1. Интегральные уравнения первого рода с ядром Кощи 185
6.1-2. Интегральные уравнения первого рода с ядром Гильберта 185
6.2. Интеграл типа Кощи 186
6.2-1. Определение интеграла типа Кощи 186
6.2-2. Условие Гёльдера 187
6.2-3. Главное значение сингулярного интеграла 187
6.2-4. Многозначные функции 189
6.2-5. Главное значение сингулярного криволинейного интеграла 190
6.2-6. Формула перестановки Пуанкаре-Бертрана 192
6.3. Краевая задача Римана 192
6.3-1. Теорема об аналитическом продолжении и теорема Лиувилля 192
6.3-2. Интерполяционный полином Эрмита 194
6.3-3. Понятие индекса 194
6.3-4. Постановка задачи Римана 196
6.3-5. Рещение однородной задачи 198
6.3-6. Рещение неоднородной задачи 199
6.3-7. Задача Римана с рациональными коэффициентами 201
6.3-8. Задача Римана для действительной оси 204
6.3-9. Исключительные случаи задачи Римана 206
6.3-10. Задача Римана для многосвязной области 210
6.3-11. Случаи разрывных коэффициентов и разомкнутых контуров 213
6.3-12. Краевая задача Гильберта 213
6.4. Сингулярные интегральные уравнения первого рода 214
6.4-1. Простейщее уравнение с ядром Кощи 214
6.4-2. Уравнение с ядром Кощи на действительной оси 214
6.4-3. Уравнение первого рода на конечном отрезке 215
6.4-4. Общее уравнение первого рода с ядром Кощи 216
6.4-5. Уравнения первого рода с ядром Гильберта 217
6.5. Метод Мультоппа-Каландия 218
6.5-1. Рещение, не ограниченное на концах отрезка 218
6.5-2. Рещение, ограниченное на одном конце отрезка 220
6.5-3. Рещение, ограниченное на обоих концах отрезка 221
Страница 7

7. Методы решения полных сингулярных интегральных уравнений 222
7.1. Некоторые замечания 222
7.1-1. Интегральные уравнения с ядром Коши 222
7.1-2. Интегральные уравнения с ядром Гильберта 223
7.1-3. Об уравнениях Фредгольма второго рода на контуре 224
7.2. Метод Карлемана для характеристических уравнений 226
7.2-1. Характеристическое уравнение с ядром Коши 226
7.2-2. Уравнение, союзное с характеристическим 229
7.2-3. Характеристическое уравнение на действительной оси 230
7.2-4. Исключительный случай характеристического уравнения 232
7.2-5. Характеристическое уравнение с ядром Гильберта 234
7.2-6. Уравнение Трикоми 234
7.3. Полные сингулярные интегральные уравнения, разрешаемые в замкнутой форме 235
7.3-1. Замкнутое решение при постоянных коэффициентах 235
7.3-2. Замкнутое решение в обшем случае 236
7.4. Метод регуляризации для полных сингулярных интегральных уравнений .... 238
7.4-1. Некоторые свойства сингулярных операторов 238
7.4-2. Регуляризуюший оператор 240
7.4-3. Способы регуляризации слева и справа 241
7.4-4. Проблема равносильной регуляризации 242
7.4-5. Теоремы Нётера 243
7.4-6. Способ регуляризации Карлемана-Векуа 244
7.4-7. Регуляризация в исключительных случаях 246
7.4-8. Полное уравнение с ядром Гильберта 246
8. Методы решения нелинейных интегральных уравнений 250
8.1. Некоторые определения и замечания 250
8.1-1. Нелинейные интегральные уравнения Вольтерра 250
8.1-2. Нелинейные уравнения с постоянными пределами интегрирования .... 251
8.2. Нелинейные интегральные уравнения Вольтерра 252
8.2-1. Метод интегральных преобразований 252
8.2-2. Метод дифференцирования интегральных уравнений 253
8.2-3. Метод последовательных приближений 254
8.2-4. Метод Ньютона-Канторовича 256
8.2-5. Метод коллокации 258
8.2-6. Метод квадратур 258
8.3. Уравнения с постоянными пределами интегрирования 260
8.3-1. Нелинейные уравнения с вырожденными ядрами 260
8.3-2. Метод интегральных преобразований 262
8.3-3. Метод дифференцирования интегральных уравнений 263
8.3-4. Метод последовательных приближений 264
8.3-5. Метод Ньютона-Канторовича 264
8.3-6. Метод квадратур 267
8.3-7. Метод регуляризации Тихонова 267
Список литературы 269
Страница 8

Предисловие
ПРЕДИСЛОВИЕ
Интегральные уравнения встречаются в различных областях науки и
многочисленных приложениях (в теории упругости, теории пластичности,
гидродинамике, теории массо- и теплопереноса, теории управления, химической технологии,
биомеханике, теории массового обслуживания, экономике, медицине и др.).
В книге излагаются точные, приближенные аналитические и численные
методы решения линейных и нелинейных интегральных уравнений. Помимо
классических методов описаны также некоторые новые методы. При отборе материала
авторы отдавали безусловное предпочтение практической стороне вопроса
(конструктивным методам, позволяющим эффективно «строить» решения). Для
лучшего понимания рассмотренных методов во всех разделах книги даны примеры
решения конкретных уравнений.
Приведены некоторые точные и асимптотические решения интегральных
уравнений, встречающихся в приложениях (в механике и физике).
Для удобства широкого круга потенциальных читателей с разной
математической подготовкой авторы по возможности старались избегать использования
специальной терминологии. Поэтому некоторые методы излагаются схематически и
упрощенно (с необходимыми ссылками на книги, в которых эти методы
рассмотрены более детально).
Расположение уравнений внутри всех разделов отвечает принципу «от
простого к сложному». Это существенным образом облегчает работу с материалом.
Многие разделы книги могут читаться независимо друг от друга, что позволяет
быстро вникать в суть вопроса. Достаточно подробное оглавление поможет
читателю находить искомую информацию.
Отдельные разделы книги могут быть использованы в качестве основы для
специальных курсов по иптегральным уравнениям и уравнениям математической
физики для студентов и аспирантов университетов и технических вузов.
Авторы надеются, что справочник окажется полезным для широкого круга
научных работников, преподавателей вузов, инженеров и студентов,
специализирующихся в различных областях прикладной математики, механики, физики, теории
управления и экономике.
А. В. Мансисиров
А. Д. Полянин
Страница 9

1. Основные определения и формулы.
Интегральные преобразования
1.1. Некоторые определения, замечания и формулы
1.1-1. Некоторые определения
Функция f(x) называется квадратично интегрируемой (квадратично
суммируемой, интегрируемой с квадратом) на отрезке [а, 6], если f^(x) интегрируема
на [а, 6]. Совокупность всех квадратично интегрируемых на [а, Ь] функций
обозначают L2(a, b) или коротко L2*. Совокупность всех интегрируемых на [а, Ь]
функций обычно обозначают Li(a,b) или коротко Li.
Основные свойства функций из L2:
1°. Сумма двух квадратично интегрируемых функций есть квадратично
интегрируемая функция.
2°. Произведение квадратично интегрируемой функции па константу есть
квадратично интегрируемая функпия.
3°. Произведение двух квадратично интегрируемых функпий есть интегрируемая
функция.
4°. Если f(x) G iv2 и д(х) G iv2, то имеет место неравенство Буняковского —
Шварца:
if,9f ^ WffWgf, if,9) = j f(x)g(x)dx, ll/f = (/,/) = f f{x)dx.
Число (f,g) называется скалярным произведением функпий f(x) и д(х), а. число
11/11 —нормой функпий f(x) в L2.
5°. Для f(x) G iv2 и д(х) G L2 имеет место неравенство треугольника:
II/+5IK 11/11+ II5II-
6°. Пусть функции /(ж) и /i(x), /2(ж),..., /гг(ж),... квадратичпо интегрируемы
на отрезке [а, 6]. Если
рЬ
^(x)-f(x)?dx = 0,
lim / [М
п—>оо /
J а
ТО говорят, ЧТО последовательность функций /i(x), /2(ж), ... сходится в среднем
квадратичном к функпий f(x).
Если последовательность функций {fn(x)} из L2 сходится равномерно к /(ж),
то f(x) G iv2 и {fn(x)} сходится к f(x) в среднем.
Аналогичным образом вводится понятие интегрируемой (суммируемой)
функции нескольких переменных. Например, функция f(x,t) называется квадратично
интегрируемой в области S = {a^x^b, a^t^b}, если f(x,t) измерима и
\\ff= [ [ f(x,t)dxdt<+^.
Здесь, как и ранее ||/|| обозначает норму функпий f(x,t).
* В общем случае рассматриваются измеримые функции и интеграл Лебега. Как обычно,
эквивалентные функции (т. е. равные почти всюду или отличающиеся на множестве меры
нуль) считаются одним и тем же элементом L2.
Страница 10

1.1. Некоторые определения, замечания и формулы 11
1.1-2. Структура решений линейных интегральных уравнений
Линейное интегральное уравнение с переменным пределом интегрирования
имеет вид
13у{х)+ / K{x,t)y{t)dt^f{x), A)
J а
где у{х) — неизвестная функция.
Линейное интегральное уравнение с постоянными пределами интегрирования
имеет вид
ру{х)+ I K(x,t)y(t)dt = f(x). B)
При /3 = 0, уравнения A) и B) называются линейными интегральными
уравнениями первого рода, а при Р фО —линейными интегральными уравнениями
второго рода.
Уравнения вида A) и B) при специальпых условиях, накладываемых на
их ядра и правые части, образуют различные классы интегральных уравнений
(уравнения Вольтерра, уравнения Фредгольма, уравнения типа свертки и др.),
которые подробно рассмотрены в главах 2-7.
В ряде случаев, для краткости, будем использовать операторную форму записи
линейных интегральных уравнений A) и B):
L[y] = f{x). C)
Линейный оператор L обладает следующими свойствами:
L[yi -\-у2] = L[yi] +Ь[у2],
L [ау] = aJj [у], а = const.
При f(x) = О линейные уравнения называются однородными , а при
f(x) ^ О — неоднородными.
Любое линейное однородное интегральное уравнение имеет тривиальное
решение у = 0.
Если yi = yi(х) иу2 = У2(х) —частные решения линейного однородного
интегрального уравнения, то их линейная комбинация Ciyi +С2У2 с произвольпыми
постоянными Ci, С2 также будет решением данного уравнения (в физических
задачах это свойство называют принципом липейной суперпозиции).
Общее решение линейного неоднородного интегрального уравнения C) равно
сумме общего решения Y = Y(x) соответствующего однородного уравнения
L [Y] = О и любого частного решения у = у(х) данного неоднородного уравнения
L[y] = /(x):
y = Y^y. D)
Если однородное интегральное уравнение имеет только тривиальное решение
У = О, то решение соответствующего неоднородного уравнения будет
единственным (если оно существует).
Пусть yi иу2 — решения линейных неоднородных интегральных уравнений с
одинаковыми левыми и разными правыми частями: L [yi] = /i (ж) и L [у2] = /2(ж).
Тогда функция у = yi -\- у2 является решением уравнения L [у] = fi(x) Ч- /2(ж).
Преобразование
x = g(z), t = g(r), у(х) = (р(г)и)(г)-\-ф(г), E)
где g(z), ^(z), ф(г) — произвольные непрерывные функции (g'z ф 0), приводит
Страница 11

12 Основные определения и формулы. Интегральные преобразования
уравнения A) и B) к линейным уравнениям того же вида относительно
неизвестной функции w = w(z). Такие преобразования часто используются для построения
точных решений линейных интегральных уравнений.
1.1-3. Интегральные нреобразовання
Интегральные преобразования имеют вид
гЬ
J а
Функция f(x) называется оригиналом, /(Л) —изобрасисением (или образом)
функции /(ж), а (/?(ж, Л) —ядром интегрального преобразования. Пределы
интегрирования а и b — действительные (как правило а = О, 6 = оо или а = —оо, 6 = оо).
В разд. 1.2-1.6 описаны наиболее распространенные интегральные
преобразования (Лапласа, Меллина, Фурье и др.), которые встречаются в этой книге при
решении конкретных интегральных уравнений. В этих же разделах даны
соответствующие формулы для обратных преобразований, которые имеют вид
f{x) = j i,{x,\)J{\)d\
и позволяют по заданному изображению /(Л) восстановить оригинал f{x). Контур
интегрирования С при этом может проходить как по действительной оси, так и по
комплексной плоскости.
Интегральные преобразования используются для решения различных
дифференциальных и интегральных уравнений. На рис. 1 приведена принципиальная
схема решения интегральных уравнений при помощи интегральных
преобразований (в случае, приведенном на схеме, использование подходящего интегрального
преобразования позволяет получить линейное алгебраическое уравнение первого
порядка относительно изображения /(A)).
Во многих случаях для вычисления определенных интегралов, в том числе для
определения обратных преобразований Лапласа, Меллина и Фурье, используют
методы теории функций комплексного переменного, включая теорему о вычетах
и лемму Жордана, которые излагаются ниже в пп. 1.1-4 и 1.1-5.
1.1-4. Вычеты. Формулы для вычнсленнй
Вычетом функции f{z) в изолированной особой точке z = а комплексной
плоскости Z называется число
res fiz) = —^ / f(z) dz, i^ = -1,
3s/(^) = —- / f(z)dz, г
где Се — окружность достаточно малого радиуса г, которая описывается
уравнением \z — а\ = е.
Если точка z = а есть полюс гг-го порядка* функции /(^), то
res fiz) = lim \(z - a)"/(^)l.
Для простого полюса, что соответствует гг = 1, отсюда имеем
res f(z) = lim Uz - a)f(z)].
В окрестности этой точки f{z)^ const (z — a) ^.
Страница 12

1.1. Некоторые определения, замечания и формулы 13
Рис. 1. Принципиальная схема решения интегральных уравнений при
помоши интегральных преобразований
Если f(z) = —^^, причем (р(а) т^ О, а ф(z) имеет в точке z = а нуль первого
ф(г)
порядка, т. е. ф(а) = О, а V^i(a) ^ О, то
res f(z) =
Шо)
1.1-5. Лемма Жордана
Если функция f{z) непрерывна в области \z\ ^ Ro,lmz ^ а (а —
фиксированное действительное число) и lim /(^) = О, то для любого Л > О выполняется
Z—>00
предельное равенство
lim / е* ^ f(z) dz = О,
lim
R
Страница 13

14 Основные определения и формулы. Интегральные преобразования
где Cr — дуга окружности \z\ = R, лежащая в рассматриваемой области.
(•) Литература: М. Л. Краснов, А. И. Киселев, Г. И. Макаренко A968), А. Г. Свешников,
А. Н. Тихонов A970).
1.2. Преобразование Лапласа
1.2-1. Определение. Формула обращения
Преобразование Лапласа для произвольной (комплекснозначной) функции
f(x) действительного переменного х (х ^ 0) определяется следующим образом:
Яр) = Г
■Jo
'f{x)dx, A)
где р = S -\-ia — комплексная переменная.
Функция f(x) называется оригиналом, а f(p) — изобрасисением {образом)
функции f{x).
Преобразование Лапласа существует для непрерывных и
кусочно-непрерывных функций, удовлетворяющих условию |/(ж)| < Ме'^о^, где М>Оисго^О —
некоторые числа. Далее считаем, что в указанной оценке взято наименьшее из
возможных чисел сто, которое называется показателем роста функции /(ж).
Для всякого оригинала f{x) функция f{p) определена в полуплоскости
Rep > сто и является в этой плоскости аналитической функцией.
Формулу A) кратко будем записывать так:
}{p)^S.{f{x)] или }{p)^Z{f{x\p}.
По известному изображению f{p) оригинал находится с помощью обратного
преобразования Лапласа
-, rc-\-ioo
f(x) = ^ f(p)e^''dp, г^ = -1, B)
где путь интегрирования расположен параллельно мнимой оси комплексной
плоскости справа от всех особых точек функции /(р), что соответствует с > ctq.
Интеграл в B) понимается в смысле главного значения:
/»с+гоо nc-\-iuj
/ f(p)e^''dp= lim / f(p)e^''dp.
J с — гоо J c — xuj
В области ж < О формула B) дает /(ж) = 0.
Формула B) справедлива для непрерывных функций. Если в точке ж = жо
ж = жо > О, функция /(ж) имеет конечный разрыв первого рода, то правая часть
формулы B) в этой точке дает значение у[/(жо — 0) + /(жо + 0)] (при жо = О
первый член в квадратных скобках должен быть опущен).
Формулу обращения преобразования Лапласа B) кратко будем записывать так:
/(х) = £-1{/(р)} или /(х) = £-Ч/(р), ж}.
1.2-2. Обращение раниональных функций
Рассмотрим важный случай, когда изображение является рациопальной
функцией вида
Страница 14

1.2. Преобразование Лапласа
15
где Q{p) и R{p) — многочлены переменной р, причем степень многочлена Q{p)
больше степени многочлена R{p).
Пусть все нули знаменателя простые, т. е. справедливо равенство
Q{p) = const (р - Xi){p - А2)... (р - Хп).
Тогда оригинал можно определить по формуле
RD)
к=1 ^ '^^k)
где штрихом обозначены производные.
Пусть многочлен Q{p) имеет кратные корни, т. е.
Q{p) = const (р - Al)'l (р - А2)'2 . . . (р - \mf
в этом случае оригинал вьгаисляется по формуле
т^Т.
1
к=1
(s^ - 1)! P^Sfe dp'^k
lim ^-^[(p-Afcf'/We^l.
D)
1.2-3. Теорема о свертке для преобразования Лапласа
Сверткой (по Лапласу) двух функций f{x) я д(х) называется выражение
f(x)^g(x)= Г f(t)g(x-t)dt
Jo
Справедлива теорема о свертке:
2.{f{x)*g(x)}=2.{f{x)}2.{g{x)},
которая часто используется при решении уравнений Вольтерра с разностным
ядром.
1.2-4. Предельные теоремы
Пусть 0^x<ooH/(p) = ii{/(x)} —преобразование Лапласа функции f{x).
Если существует предел f{x) при ж ^ О, то
lim /(ж) = lim [pj{p)\.
X—>{j р—>00
Если существует предел f(x) при ж ^ ос, то
lim f{x) = \im [pf{p)].
X—>00 p—>(j
1.2-5. Основные свойства преобразования Лапласа
Ниже в таблице приведены основные формулы соответствия оригиналов и
изображений нреобразования Лапласа.
Страница 15

16
Основные определения и формулы. Интегральные преобразования
ТАБЛИЦА 1
Основные свойства преобразования Лапласа
Ъй
1
2
3
4
5
6
7
8
9
10
11
12
Оригинал
аД(ж) +6/2 (ж)
f{x/a), а > 0
/(ж - а),
/@ = 0 при С < 0
ж^/(ж); гг= 1,2,...
7/(-)
е--/(ж)
/i(^)
/i"^(^)
ж^4^^(ж), т>гг
к^/(жI, т>гг
Г f{t)dt
Jo
Г h{t)f^{x-t)dt
Jo
Изображение
afM^bf^iP)
af{ap)
e--Pf{p)
{-^Tli^\p)
/"OO
/ l(q) dq
Jp
f{p - a)
p1(v) - /(+0)
fc=l
(-i'fv-m
d^ ~
/1(P)/2(P)
Операция
Линейность
Изменение маспттаба
Сдвиг аргумента
Дифференцирование
изображ:ения
Интегрирование
изображ:ения
Смегцение в
комплексной плоскости
Дифференцирование
Дифференцирование
Дифференцирование
Дифференцирование
Интегрирование
Свертка
Существуют таблицы прямых и обратных преобразований Лапласа (см.
литературу в конце раздела), в которых сведены вместе конкретные функции и их
изображения. Эти таблицы удобно использовать при решении линейных интегральных
и дифференциальных уравнений.
1.2-6. Формула Поста-Уиддера
Для нриложений имеется возможность определять значения оригинала /(ж),
если известны значения изображения f{t) на действительной полуоси при t=р ^ 0.
Для этого можно использовать формулу Поста-Уиддера:
а^)
lim
п—>оо
(-1)^ ( П \^-
(г) /;"'G)
E)
Для получения приближенной формулы обращения можно в E) вместо предела
взять конкретное (достаточно большое) целое значение п.
(•) Литература'. И. И. Хиршман, Д. В. Уиддер A958), Г. Бейтмен, А. Эрдейи A969),
Г. Дёч A971), J. W. Miles A971), В. А. Диткин, А. П. Прудников A974), В. Davis A978),
Yu. А. Brychkov, А. Р. Pmdnikov A989), W. П. Beyer A991), А. D. Polyanin, А. V. Manzhirov
A998).
Страница 16

1.3. преобразование Меллина 17
1.3. Преобразование Меллина
1.3-1. Определение. Формула обращения
Пусть функция f{x) определена при положительных х и удовлетворяет
условию
г»!
/
/О
И условию
[
|/(ж)|ж~^^ж<оо
\f{x)\x'"'~^dx<oo
ч
при подходящем выборе чисел cri и сг2 (cri < сг2).
Преобразование Меллина функции f{x) вводится следующим образом:
/»оо
Jo
dx, A)
где s = сг Ч- гт — комплексная переменная (cri < а < сг2).
Функция f{x) называется оригиналом, а f{s) —изобрасисением f(x).
Формулу A) кратко будем записывать так:
/(s) = m{f{x)},
или в ряде случаев в форме
J{s) = m{f{x),s}.
По известному изображению f(s) оригинал находится с помощью обратного
преобразования Меллина:
-. rcr-\-ioo
/(^) = 7Г- / J(s)x~' ds, 0-1 < о- < 0-2, B)
где путь интегрирования расположен параллельно мнимой оси комплексной
плоскости S, а интеграл понимается в смысле главного значения.
Формула B) справедлива для непрерывных функций. Если в точке х = хо
ж = жо > О, функция f(x) имеет конечный разрыв первого рода, то правая часть
формулы B) в этой точке дает значение у[/(жо — 0) + f{xo + 0)] (при жо = О
первый член в квадратных скобках должен быть опущен).
Кратко формулу B) будем записывать так:
f{x)^m-'Cfis)} или fix)^m-'{J{s),x}.
1.3-2. Основные свойства преобразования Меллина
Ниже в таблице приведены основные формулы соответствия оригиналов и
изображений нреобразования Меллипа.
2 А. В. Манж:иров, А. Д. Полянин
Страница 17

18
Основные определения и формулы. Интегральные преобразования
ТАБЛИЦА 2
Основные свойства преобразования Меллина
Ъй
1
2
3
4
5
6
7
8
9
10
11
12
Оригинал
аД(ж) +6/2 (ж)
f(ax), а > 0
x-fix)
П^')
fi^^)
x^f{axl='), a>0,f3^0
Г.И
^fU^)
&Н^)
(^i)"^(^^
/•оо
х'- t^f,{xt)f^{t)dt
Jo
x"l^°°t^f,{j)f^{t)dt
Изображение
a/i(s) + 6/2(s)
a-7(s)
/(s + a)
i/(is)
/(-s)
1 ^+^ - / С ^ Л \
/5 -^ V /5 У
-(s-l)/(s-l)
-s/(s)
(-^^^T(^^(^-^^
i-lTs-Jis)
Ji{s^a)%{l-s-a^C)
/i(s + c.)/2(s + a+/5 + l)
Операция
Линейность
Изменение маспттаба
Сдвиг аргумента
у изображения
Квадратичный аргумент
Изменение знака у
аргумента изображения
Преобразование оригинала,
содержагцее степени
Дифференцирование
Дифференцирование
Многократное
дифференцирование
Многократное
дифференцирование
Слож:ное интегрирование
Сложное интегрирование
1.3-3. Связь преобразований Меллина, Лапласа и Фурье
Существуют таблицы прямых и обратных преобразований Меллина (см.
литературу в конце раздела), которые удобно использовать при решении конкретных
интегральных и дифференциальных уравнений. Преобразование Меллина связано
с преобразованиями Лапласа и Фурье следующими формулами:
m{f{x),s} = £{/(е^),-5} + £{/(е-^),8} = dlfie'^lis},
что позволяет использовать также более распространенные таблицы прямых и
обратных преобразований Лапласа и Фурье.
(•) Литература: Г. Бейтмен, А. Эрдейи A969), Г. Дёч A971), В. А. Диткин, А. П.
Прудников A974), Yu. А. Brychkov, А. Р. Prudnikov A989), А. D. Polyanin, А. V. Manzhirov A998).
1.4. Преобразование Фурье
1.4-1. Определение. Формула обращения
Преобразование Фурье вводится следующим образом:
1 [°^
Л/27Г J_^
Формулу A) кратко будем записывать так:
Ли) = d{f(x)} или Пи) = d{f(x), и}.
A)
Страница 18

1.4. Преобразование Фурье 19
По известному изображению f{u) оригинал f{x) находится с помощью
обратного преобразования Фурье:
f(x)^-^j f{u)e''^^du. B)
Формула B) справедлива для непрерывных функций. Если в точке ж = жо
ж = жо > О, функция f{x) имеет конечный разрыв первого рода, то правая часть
формулы B) в этой точке дает значение \[f{xo — 0) + f{xo -\- 0)].
Кратко будем записывать B) так:
fix) = 5"Ч/(«)} или fix) = d-'Cfiy-), х}.
1.4-2. Несимметричная форма преобразования
В ряде случаев бывает удобно пользоваться преобразованием Фурье в форме
/оо
/(x)e-^''^dx, C)
-ОО
где C) запишем следующим образом: f(u) = J'{f(x)} или f(u) = J'{f(x),u}.
В этом случае по известному изображению f(u) оригинал f(x) находится с
помощью формулы обратного преобразования Фурье в виде
1 Г°° .
(ж) = — / f{u)e'''' du
/(^) = 7^/ f{u)e''''du, D)
причем для D) вводится символическая запись f{x) = J^ {/(^)}
fix)^J^\fiu\x}.
1.4-3. Альтернативное преобразование Фурье
Иногда, например в теории краевых задач, используют альтернативное
преобразование Фурье (его называют просто преобразованием Фурье) в форме
^(")-^/_>(^^^
E)
Формулу E) кратко будем записывать следующим образом:
Tiu) = F{fix)} или :Fiu) = F{fix),u}.
По известному изображению J-"(и) оригинал f(x) находится с помощью
обратного преобразования:
f{x)^-^j Tiu)e-^-^du. F)
Формулу F) кратко будем записывать так:
/(х) = F-^^^)} или /(х) = F-^^^), х}.
Функция Т{и) называется также интегралом Фурье от функции /(ж).
Аналогично тому, как было проделано для преобразования Фурье, можно
ввести несимметричную форму и для альтернативного преобразования Фурье:
^{^) = / /(ж)е'''^ dx, f(x) = -— / J^(u)e '""^ du, G)
при этом прямое и обратное преобразования G) обозначают f'(u) = F{/(x)} и
/(х) = ¥~^{Т(и)} илиТ(и) = ¥{/(х), и} и/(х) = ¥~^{Т(и)х}
соответственно.
2*
Страница 19

20 Основные определения и формулы. Интегральные преобразования
1.4-4. Теорема о свертке для преобразования Фурье
Сверткой (но Фурье) двух функций f{x) и р(ж) называется выражение
f{x) * д{х) =^ Г fix - t)g(t) dt.
Путем замены неременных х — t = и легко установить, что свертка симметрична
относительно свертываемых функций: f(x)^g(x) = д(х) ^ f(x).
Теорема. Преобразование Фурье свертки равно произведению
интегралов Фурье свертываемых функций:
d{f(x)^g(x)}^d{f{x)}d{9{x)}. (8)
Для альтернативного преобразования Фурье теорема о свертке выражается
соотношением
F{f(x)*g(x)}^F{f{x)}F{g{x)}. (9)
Формулы (8) и (9) будут использованы в главах 4 и 5 для решения линейных
интегральных уравнений с разностными ядрами.
(•) Литература: Г. Бейтмен, А. Эрдейи A969), J. W. Miles A971), В. А. Диткин, А. П.
Прудников A974), В. Davis A978), Yu. А. Brychkov, А. Р. Prudnikov A989), W. И. Beyer A991),
А. D. Polyanin, А. V. Manzhirov A998).
1.5. Синус- и косинус-преобразования Фурье
1.5-1. Косинус-преобразование Фурье
Пусть функция f(x) интегрируема на полуоси О ^ ж < оо. Косинус-
преобразование Фурье вводится следующим образом:
(и) = \ —
у ^ Jo
(и) = \ — / f (х) cos(xu) dx, О < и < оо. A)
По известному изображению fc(u) оригинал f(x) находится с помощью
обратного косинус-преобразования Фурье:
^ Jo
f(x) = \ — / fc(u) cos(xu) du, 0 < ж < oo. B)
Косинус-преобразование Фурье A) обозначают fc(u) = ^^{Кх)}- Пз
формулы B) следует, что косинус-преобразование Фурье обладает свойством ^^ = 1.
Существуют таблицы косинус-преобразования Фурье (см. литературу в конце
раздела), которыми удобно пользоваться при решении конкретных интегральных
уравнений.
Иногда пользуются несимметричной формой косинус-преобразования Фурье,
задаваемой парой формул
fc(u) = / f (х) COS(xu)dx, f(x) = — / fc(u) cos(xu) du. C)
Jo ^ Jo
прямое и обратное косинус-преобразования Фурье C) обычно обозначают
%{и) = J^c{f{x)} И f{x) = J^^{fc{u)} соответственно.
Страница 20

1.6. другие интегральные преобразования 21
1.5-2. Синус-преобразование Фурье
Пусть функция f{x) интегрируема на полуоси О ^ ж < ос. Синус-
преобразование Фурье вводится следующим образом:
-/
(и) = \ — / f(x) sm(xu) dx, О < и < оо. D)
По известному изображению fs(u) оригинал f(x) находится с помощью
обратного синус-преобразования Фурье:
^ Jo
f(x) = \ — / fs(u)sm(xu)du, О < ж < оо. E)
Синус-преобразование Фурье D) кратко обозначают %(и) = S^s{/(^)}- Из
формулы E) следует, что синус-преобразование Фурье обладает свойством ^^ = 1.
Существуют таблицы синус-преобразования Фурье (см. литературу в конце
раздела), которыми удобно пользоваться при решении конкретных интегральных
уравнений.
В ряде случаев бывает удобнее использовать несимметричную форму синус-
преобразования Фурье, задаваемую следующей парой формул:
fs(u)= / f(x)sm(xu)dx, f(x) = — / %(и)зт(хи) du. F)
Jo ^ Jo
Прямое и обратное синус-преобразования Фурье F) часто обозначают
соответственно %(и) = J^s{f(x)} И/(ж) = J^^{%(u)}.
(•) Литература: И. Снеддон A955), И. И. Хиршман, Д. В. Уиддер A958), Г. Бейтмен,
А. Эрдейи A969), В. А. Диткин, А. П. Прудников A974), А. D. Polyanin, А. V. Manzhirov
A998).
1.6. Другие интегральные преобразования
1.6-1. преобразование Ханкеля
Преобразование Ханкеля вводится следующим образом:
/»оо
%(и) = / xJu{ux)f{x)dx, о < и < оо, A)
-'о
где zy > — ^, а 7гу(ж) — функция Бесселя первого рода порядка и.
По известному изображению fu(u) оригинал f(x) находится с помощью
обратного преобразования Ханкеля:
{х)= [
Jo
f(x)= / uJu(ux)fu(u)du, О < ж < оо. B)
Отметим, что если функция f(x) такая, что f(x) = 0(х^) при ж ^ О,
а -\- и -\-2 > О и f(x) = 0(х^) при ж ^ оо, /3 + -|- < О, то интеграл A) сходится.
Формула обращения B) справедлива для непрерывных функций. Если f(x) в
некоторых точках имеет конечный разрыв первого рода, то левую часть
формулы B) следует заменить на 4" [/(^ ~ 0) + /(^ + 0)] •
Преобразование Ханкеля A) кратко обозначают %(и) = S^jy{f(x)}, Пз
формулы B) следует, что преобразование Ханкеля обладает свойством S^^^ = 1.
Страница 21

22 Основные определения и формулы. Интегральные преобразования
1.6-2. Преобразование Мейера
Преобразование Мейера вводится следующим образом:
fi^{s) = \— / ^/sxK^{sx)f{x)dx, О < s < ОС, C)
V 7г Jo
где Ki^(x) —модифицированная функция Бесселя второго рода (функция Макдо-
нальда) порядка /х.
По известному изображению fi^(s) оригинал f(x) находится с помощью
обратного преобразования Мейера:
-1 rc-\-ioo
f(x) = — / VsxIi^(sx)Ji^(s) ds, О < ж < ОС, D)
гл/27г Jc-ioo
где /^ (х) —модифицированная функция Бесселя первого рода порядка /х. Для
преобразования Мейера определена свертка и построено операциопное исчисление.
1.6-3. Преобразование Конторовича-Лебедева
Преобразование Конторовича-Лебедева вводится следующим образом:
/»оо
F(r) = / Kir(x)f(x) dx, О < т < ОС, E)
-'О
где Ki^(x) —модифицировапная функция Бесселя второго рода (функция Макдо-
нальда) порядка /х, а г — мнимая единица.
По известному изображению F(r) оригинал f(x) находится с помощью
обратного преобразования Конторовича-Лебедева:
2 /"°°
(х) = -^— / Ts}i{iiT)Kir{x)F{T)dT, О < ж < ОС
1.6-4. У-преобразование и другие преобразования
Интегральное У-преобразование вводится соотношением
/»оо
Fi^(u) = / y^iixYu(ux)f(x)dx, G)
-'О
где Yiy(x) — функция Бесселя второго рода порядка и.
По известному изображению Рг^{и) оригинал f{x) находится с помощью
обратного У-преобразования:
/»оо
f(x)= / y^ux'iiu(ux)Fiy(u)du, (8)
где Нгу(ж) — функция Струве, определяемая формулой
(-1У(ж/2)^+2^'+1
Н.(х)= Е
^r(i+f)r(^ + i + f) •
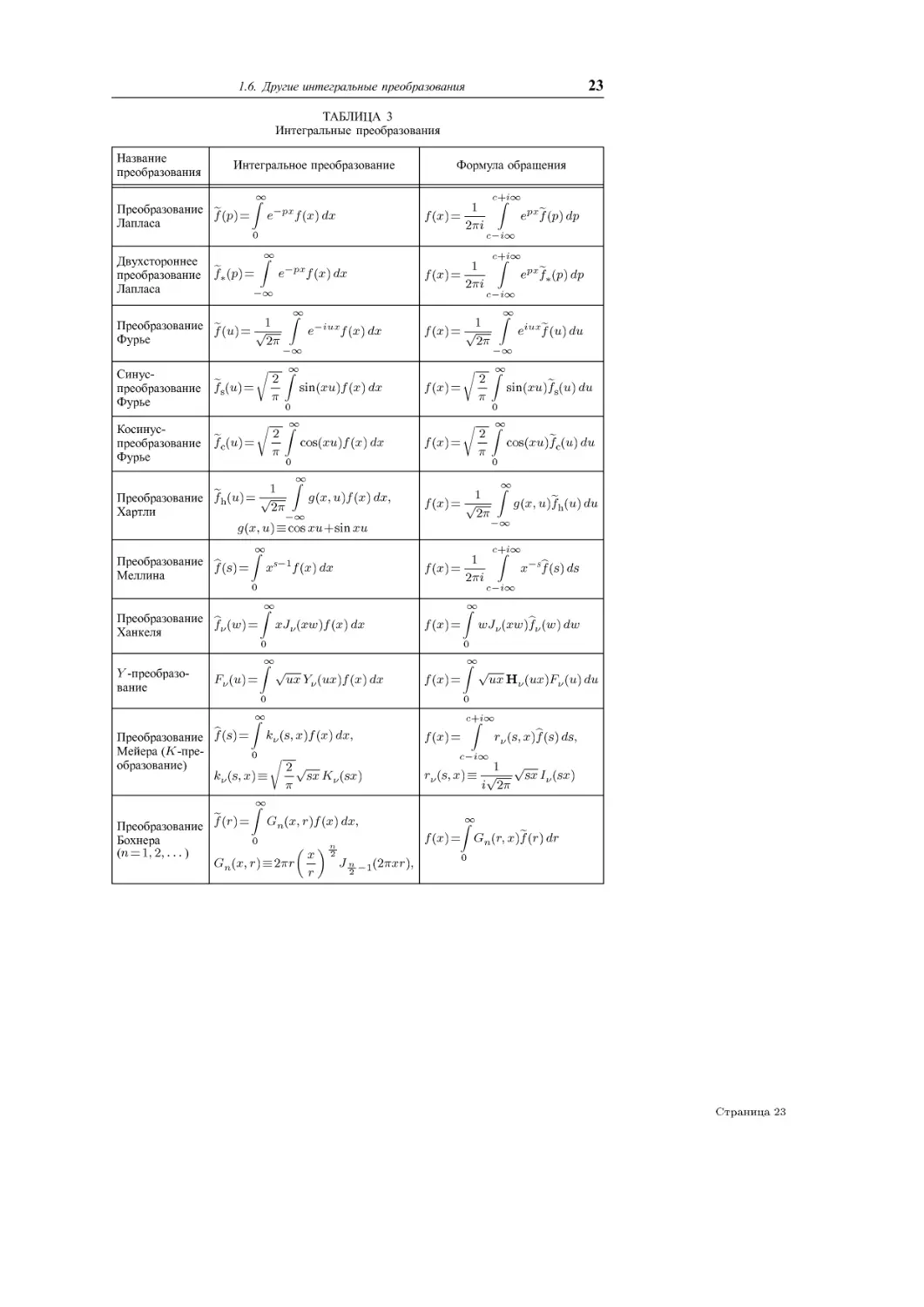
Существуют и другие интегральные преобразования, основные из которых,
наряду с указанными выше преобразованиями, приведены в табл. 3 (об
ограничениях, накладываемых на функции и параметры преобразований, см. в литературе,
приведепной в конце раздела).
Страница 22

1.6. другие интегральные преобразования
23
ТАБЛИЦА 3
Интегральные преобразования
Название
преобразования
Преобразование
Лапласа
Двухстороннее
преобразование
Лапласа
Преобразование
Фурье
Синус-
преобразование
Фурье
Косинус-
преобразование
Фурье
Преобразование
Хартли
Преобразование
Меллина
Преобразование
Ханкеля

У-преобразование
Преобразование
Мейера
(X-преобразование)
Преобразование
Бохнера
(гг = 1,2,...)
Интегральное преобразование
оо
J(p) = J e-P-f(x)dx
0
оо
УЛр)= J е P''f{x)dx
— ОО
оо
— ОО
/s(^) = Y — / sin(xw)/(x) йж
0
/с(^)-у - / cos{xu)f{x)dx
0
оо
— оо
д{х^ и) = cos xu-\-sm хи
оо
J(s) = J x'-^f(x)dx
0
оо
?Л^)= / xJ^(xw)f(x)dx
0
оо
Fj^(u)= / y/uxY^(ux)f{x)dx
0
оо
7(s)= / k^{s,x)f{x)dx,
0
оо
J(r) = jG^(x,r)f(x)dx,
0
С^(ж,г) = 27гг{ -J JrL_iB7rxr),
Формула обращения
с+гоо
с —гоо
с+гоо
С —гоо
оо
— ОО
/— °°
f{x) = J — / sin(xwOg(w) dw
0
/(^) = Y — / cos(xu)J^{u) du
0
оо
— oo
с+гоо
c —гоо
oo
f(x)= / wJ^(xw)%(w)dw
0
oo
0
с+гоо
с —гоо
r^(s, x) = —^^y/~sxl^{sx)
гл/2тт
oo
f{x)=lG„{r,x)J{r)dr
0
Страница 23

24
Основные определения и формулы. Интегральные преобразования
Преобразование
Вебера
оо
F^(u)= / Wj^(xu,au)xf(x) dx,
W,i/3,ti) = J,il3)Y,iti)-
-J,(M)y,(/?)
f{x)= / Wj^(xu,au)F^(u)du,
0
^ W^{xu, au)u
J^(au)^Y^(au)
Преобразование
Конторовича-
Лебедева
оо
F(t) = J K,^(x)f(x)dx
f(x)= f D(x,T)F(T)dT,
D(x,t)= -^r-T shGVT)K^^(x)
Преобразование
Мелера-Фока
F(r):
ОО
^{x)f{x) dx
f{x) = J L{x,r)F{T)dr,
Ь(х,т)%тЩ7гт)Р_^^,^(х)
Преобразование
Гильберта*
7Г J X — S
fix
TV J S — X
ds
Обозначения: г = л/^, J^(x) и Y^(x) — функции Бесселя первого и второго рода,
/^(ж) и К^(х) —модифицированные функции Бесселя первого и второго рода, Р^{х) —
сферическая функция Лежандра второго рода.
* Примечание. В прямом и обратном преобразованиях Гильберта интегралы
понимаются в смысле главного значения.
(•) Литература: Г. Бейтмен, А. Эрдейи A969), J. W. Miles A971), В. А. Диткин, А. П.
Прудников A974), В. Davis A978), D. Zwillinger A989), Yu. А. Brychkov, А. P. Pmdnikov A989),
W. H. Beyer A991).
Страница 24

2. Методы решения линейных уравнений
вида £ К(х, t)y(t) dt = f(x)
2.1. Уравнения Вольтерра первого рода
2.1-1. Структура уравнений. Классы функций и ядер
В главе 2 излагаются методы решения линейных интегральных уравнений
Вольтерра первого рода, которые имеют вид:
J а
K(x,t)y(t)dt = f(x), A)
где у(х) — неизвестная функция (а ^ х ^ 6), K(x,t) —ядро интегрального
уравнения, f(x) — некоторая известная функция, которая называется свободным
членом или правой частью уравнения A).
Функции у(х) и f(x) обычно считают ненрерывными, либо квадратично
интегрируемыми на [а, 6]. Ядро интегрального уравнения K(x,t) полагают
непрерывным в квадрате S = {a^x^b, a^t^b}, либо удовлетворяющим условию
/ / К^(x,t) dx dt = В^ <оо,
J а J а
B)
где В — постоянная, т. е. квадратично интегрируемым в этом квадрате. В
формуле B) полагается, что К(х, t) = О при t > х.
Ядро интегрального уравнения K(x,t) называется выроэюденным, если оно
представимо в виде K(x,t) = gi(x)hi(t) Ч- • • • -\- gn(x)hn(t).
Ядро интегрального уравнения K(x,t) называется разностным, если оно
зависит от разности аргументов: К(х,t) = К(х — t).
Рассматривают также полярные ядра
K(x,t)= ,^^ \^^ ^M(x,t), 0</3<1, C)
L{x,t)
(х - ty
и логарифмические ядра (ядра, имеющие логарифмическую особенность)
K{x,t) = L(x,t)\n(x - t) -\- M(x,t), D)
где L(x,t) (L(x,x) ф 0) и М(ж, t) — непрерывны в S.
Полярные и логарифмические ядра составляют класс ядер со слабой
особенностью. Уравнения, содержащие такие ядра, называются уравнениями со слабой
особенностью.
Частным случаем уравнения A) с ядром C) является обобщенное уравнение
Абеля:
рх
J а
.dt = f(x), 0</3<1.
(х - ty
Для непрерывных K(x,t) и f(x) правая часть уравнения A) должна
удовлетворять следующим условиям:
1°. Если К (а, а) ф О, то должно выполняться условие /(а) = 0.
Страница 25

26 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
2°. Если К{а,а) = К'^{а,а) = - - - = K^J'-^Xa.a) = {), 0< \K^J'\a,a)\ < оо, то
правая часть уравнения должна удовлетворять условиям
/(«) = /i(a) = --- = /i"'(«) = 0.
3°. Если /Г(а,а) = /Г^(а,а) = • • • = /Г^^~"^''(а,а) = 0, i^^^ (о^? о^) = сю, то правая
часть уравнения должна удовлетворять условиям
/(а) =/^а) = • • • =/i"-'4«) = 0.
Для полярных ядер вида D) и непрерывных f{x) на правую часть
интегрального уравнения дополнительные условия не накладываются.
Замечание 1. Случай, когда а = — ос, вообще говоря, не исключается.
2.1-2. Существование и единственность решения
Если в уравнении A) функции f{x) и K(x,t) —непрерывны и ограничены
вместе со своими первыми производными на [а, 6] и в 5* соответственно, причем
К(х,х) ф О (х е [а,Ь]) и /(а) = О, то существует единственное непрерывное
решение у(х) уравнения A).
Замечание 2. Вопрос о существовании и единственности решения уравнения
Вольтерра первого рода тесно связан с условиями, при которых оно приводится к
уравнениям Вольтерра второго рода (см. разд. 2.3).
Замечание 3. Уравнение Вольтерра первого рода можно трактовать как
уравнение Фредгольма первого рода, ядро которого K(x,t) обращается в нуль при t>x
(см. главу 4).
(•) Литература: Э. Гурса A934), Г. М. Мюнтц A934), С. Г. Михлин A959), Ф. Трикоми
A960), П. П. Забрейко, А. И. Кошелев и др. A968), М. Л. Краснов, А. И. Киселев,
Г. И. Макаренко A968), Л. Я. Цлаф A970), J. А. Cochran A972), С. Corduneanu A973),
В. И. Смирнов A974), В. Вольтерра A982), А. J. Jerry A985), А. Ф. Верлань, В. С. Сизиков
A986), А. D. Polyanin, А. V. Manzhirov A998, 1999).
2.2. Уравнения с вырожденным ядром:
K(x,t) = gi(x)hi(t) Н \-9n(x)hn(t)
2.2-1. Уравнения с ядром K(x,t) = g:i(x)hi(t) -\- g2{x)h2{t)
Рассматриваемое уравнение можно записать так:
ГХ fX
9i(x) hi{t)y(t)dt + g2(x) h2{t)y(t)dt^f(x). A)
J a J a
Считается, что выполнены условия: gi{x) ф const д2(х), hi(t) ф const h2(t),
0<Р?(а)+р|(а)<оо,/(a) = 0.
Замена
u(x)= I hi(t)y(t)dt B)
J a
И последующее интегрирование по частям второго интеграла в A) с учетом
равенства и(а) = О дает уравнение Вольтерра второго рода
[g4x)hi(x)+g2(x)h2{x)]u(x)-g2(x)hi(x)r[^]'u{t)dt^hi(x)f{x). C)
Страница 26

2.2. Уравнения с выроэюденным ядром: К(х, t) = g-^(x)h-^(t) + • • • + g^(x)h^(t) 27
Подстановка
w(x
J a
h^(t)
h,{t)
u{t) dt
D)
Приводит C) к линейному обыкновенному дифференциальному уравнению
первого порядка
[gi(x)hi(x)-\-g2(x)h2(x)]w'^-g2(x)hi(x)
h^ix)
h-^(x)
w = f(x)hi(x)
h^ix)
h^{x)
E)
1°. При gi(x)hi(x) + g2(x)h2(x) ф 0, решение уравнения E), удовлетворяющее
условию w{ci) — О (которое является следствием замены D)), имеет вид
W{X) = Ф(Х) г I ^2^^^
J а
Ф(ж) = ехр-^ /
f(t)h^(i)dt
/ii@Jt*(<)bi@/»i(<) + 92@/»2@]
h^(t)
h,{t)
g^{t)h^{t)dt
t 9i{t)K(t) + g^i^h^it)
F)
(V)
продифференцируем обе части D) и подставим в полученное выражение
зависимость F). После интегрирования по частям с учетом равенств /(а) = О,
w{a) = О, при / ф const р2 получим
и(х)
д2(х)Н-^(х)Ф(х)
g^{x)h^{x) -^g2{x)h2{x)
Г
J а
т
dt
При помощи формулы B) находим решение исходного уравнения в виде
У{х)
92_
h-^(x) dx \ g^{x)h
^) J а
fit)
dt
92@Jt*(<) J'
(8)
где функция Ф(х) дается выражением G).
Если f(x) = const р2(ж), то решение дается формулами (8) и G), в которых
индекс 1 должен быть заменен на 2 и наоборот.
2°. При gi(x)hi(x) Ч- g2(x)h2(x) = О решение имеет вид
У(х)
1 d
h^ dx
{fl92)'.
{9\l92)'x
1 d
h^ dx
{f/92)'.
{h^/K)'..
2.2-2. Уравнения с вырожденным ядром общего вида
Уравнение Вольтерра первого рода с вырожденным ядром общего вида можно
записать так:
^ дт{х) /
т=1 -^(^
hm(t)y(t)dt = f(x).
J а
Используя обозначения
Wm{x)= I hm(t)y(t)dt, ш = 1,2,... ,n,
J а
запишем уравнение (9) следующим образом:
п
^ дт{х)гюш(х) - /(ж).
(9)
A0)
A1)
Страница 27

28 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
Дифференцируя формулы A0) и исключая из полученных выражений у (ж),
приходим к линейным дифференпиальным уравнениям для функций Wm = Wm(x):
hi {x)w'm = hm {x)w[, Ш = 2, 3,..., п, A2)
(штрих соответствует производной по ж) с начальными условиями
Wm(ci) = 0, ттг = 1, 2,..., гг.
Если найдено решение системы уравнений A1), A2), то решение исходного
интегрального уравнения (9) определяется с помощью любого из выражений
У(^)=^Ц4' гп = 1,2,...,п,
которые получены путем дифференпирования формулы A0).
Систему A1), A2) (путем неоднократного дифференпирования уравнения A1)
с учетом A2)) можно свести к линейному дифференпиальному уравнению
(п — 1)-го порядка для любой функции Wm(x) (т = 1,2,... ,п).
(•) Литература: Э. Гурса A934), А. Ф. Верлань, В. С. Сизиков A986).
2.3. Сведение уравнений Вольтерра первого рода к
уравнениям Вольтерра второго рода
2.3-1. Первый способ
Пусть ядро и правая часть уравнения
K(x,t)y(t)dt = f(x), A)
/■
J а
имеют непрерывные производные по ж и выполняется условие К(х,х) ^0. Тогда
после дифференпирования A) с последующим делением обеих частей полученного
выражения яа К(х,х), приходим к уравнению Вольтерра второго рода:
К(х,х)
Уравнения этого типа рассматриваются в главе 3. Если К(х,х) = 0,то дифферен-
пируя дважды уравнение A) по ж при К'^(x,t)\t=x^O имеем уравнение Вольтерра
второго рода
Если же К'х{х,х) = О, то вновь можно применить дифференпирование и т. д. В
случае, когда первые ттг — 2 частные производные ядра по х тождественно равны
нулю, а (ш — 1)-я производная не равна нулю, то ш-кратное дифференпирование
исходного уравнения дает следующее уравнение Вольтерра второго рода:
Ki'-"(^.t)l,„ Kl"-'>(a-,t)|,.
2.3-2. Второй способ
Введем новую переменную
У(х)= Г y(t)dt,
J а
Страница 28

2.4. Уравнения с разностным ядром: K(x,t) = К(х — t) 29
а затем проинтегрируем по частям правую часть уравнения A) с учетом равенства
/(а) = 0. В результате после деления обеих частей полученного выражения
яа К(х,х), приходим к уравнению Вольтерра второго рода:
ДЛЯ которого должно выполняться условие К(х,х) ф 0.
(•) Литература'. Э. Гурса A934), В. Вольтерра A982).
2.4. Уравнения с разностным ядром: К{х^ t) = К(х — i)
2.4-1. Метод решения, основанный на нреобразованнн Лапласа
Уравнения Вольтерра первого рода с ядром, зависящим от разности
аргументов, имеют вид
-'О
K{x-t)y{t)dt = f{x). A)
/о
Для решения этих уравнений используют преобразование Лапласа (см.
разд. 1.2). Для дальнейшего понадобятся образы ядра и правой части
интегрального уравнения, которые вычисляются по формулам
/»оо /»оо
к{р)^ K{x)e-^^dx, ]{р)^ f{x)e-^^dx. B)
Применяя преобразование Лапласа ii к уравнению A) и учитывая, что
интеграл с ядром, зависящим от разности аргументов, преобразуется в произведение
по правилу (см. п. 1.2-3):
£ II" К{х - t)y{t) dt\ = К{р)у{р),
Приходим к уравнению для образа искомой величины у(р):
к(рШр) = f(p)- C)
Решение уравнения C) определяется формулой
т = #^. D)
К{р)
Применяя к D) обратное преобразование Лапласа (если оно существует), получим
решение уравнения A) в виде
2^^ Jc-ioo К(р)
при использовании указанного аналитического метода решения могут
возникнуть следующие технические трудности:
~ /"ОО
1°. Получение изображения К(р) = / К(х)е~^^ dx для данного ядра К(х).
Jo
2°. Получение оригинала D), задаваемого формулой E).
Для вычисления соответствующих интегралов применяют таблицы прямых
и обратных преобразований Лапласа, причем во многих случаях для обратного
преобразования используют методы теории функций комплексного переменного,
включая теорему о вычетах (см. п. 1.1-4).
Замечание. Если нижний предел в интеграле уравнения Вольтерра с ядром,
зависящим от разности аргументов, равен а, то его можно свести к уравнению A)
с помощью замены х = х — a,t = t — а.
Страница 29

30 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
2.4-2. Случай рационального образа решения
Рассмотрим важный частный случай, когда образ решения D) является
рациональной функцией вида
К(р) Qip) '
где Q(p) и R(p) — многочлены переменной р, причем степень многочлена Q(p)
больше степени многочлена R(p).
Если все нули знаменателя Q(p) простые, т. е. справедливо равенство
Q(p) = const (р - Xi){p - А2)... (р - Хп)
и Лг 7^ Xj При г 7^ j, ТО решение интегрального уравнения имеет вид
^(^) = J2 п/^м ^ exp(Afcx),
к=1 ^ ^"^^^
где штрихом обозначены производные.
Пример 1. Рассмотрим интегральное уравнение Вольтерра первого рода
["^ e-^^^-^^y(t) dt = Ash(bx).
Jo
Применяя к нему преобразование Лапласа, получим
-у{р)
р -\- а р'^ — Ь'^
Отсюда находим, что
АЬ(р-\-а) _ АЬ(р-\-а)
у{р) ^
р2_52 (р_5)(р + 6)'
Имеем Q(p) = (р — Ь)(р -\- 6), Я(р) = АЬ(р -\- а) и Х-^ = Ь, Х2 = —Ъ. Поэтому решение
интегрального уравнения может быть записано в виде
у{х) = ^А{Ь + а)е^^ + ^А{Ь - а)е-^^ = АазЦЬх) + АЬсЦЬх).
2.4-3. Представление решения в виде комнозинии
При решении интегральных уравнений Вольтерра первого рода с разностным
ядром К(х — t) с помощью преобразования Лапласа иногда полезно использовать
следующий прием.
Представим образ решения D) в следующем виде:
у(р) = N(p)M(p)f(pl N(p) ^ ^ . F)
К{р)М{р)
Если удается подобрать такую функцию М(р), что существуют
£-1{М(р)} = М{х), S^-'{N(p)} = N(x), G)
ТО решение интегрального уравнения можно записать в виде композиции:
у(х)= I N(x-t)F(t)dt, F(t)= I M(t-s)f(s)ds. (8)
Пример 2. Рассмотрим уравнение
/ sm{kV^^^^)y(t)dt = f(x), /@)=0. (9)
^0
Страница 30

2.4. Уравнения с разностным ядром: K(x,t) = К(х — t)
31
Используя преобразование Лапласа, получим изображение решения в виде
у(р) ■
/ттк
p^^'^eM^/pffipl а=^к''
Перепишем правую часть A0) в эквивалентном виде
2
у(р) ■
л/тг/с
р2[р-1/2ехр(а/р)]/(р), а=^к\
A0)
A1)
Здесь в квадратных скобках выделен сомножитель, соответствуюший М(р) в формуле F),
N(p) = const р^.
Применяя обратное преобразование Лапласа по указанной схеме к формуле A1) с
учетом равенства
dx^
находим решение интегрального уравнения
2 d^ /-^ сЦку^¥^^)
У{Х) :
7тк dx^ Jo \/х — t
fit) dt.
2.4-4. Использование вспомогательного уравнения
Рассмотрим уравнение
J а
K(x-t)y(t)dt = f(x),
A2)
где ядро К(х) имеет интегрируемую особенность при х = 0.
Пусть W = w(x) —решение вспомогательного более простого уравнения при
fix) = ha = 0:
f
Jo
Kix-t)wit)dt = 1.
A3)
Тогда решение исходного уравнения с произвольной правой частью A2)
выражается через решение вспомогательного уравнения A3) с помощью формулы
у{
х) = — / wix-t)fit)dt = fia)wix-a)-\- wix - t)fiit)dt. A4)
dx J a J a
Пример 3. Рассмотрим обобшенное уравнение Абеля
Г- yit)dt
^ /(^),
1а ix - t)
Решение соответствуюшего вспомогательного уравнения
wit) dt
О < /i < 1.
Г
Jo
/о ix - t)^
ишем методом неопределенных коэффициентов в виде
wix) = Ах^.
О < /i < 1,
A5)
A6)
A7)
Подставим A7) в A5), а затем сделаем в интеграле сделаем замену переменной t = х^.
Учитывая связь
Г(р)Г(д)
B{p,q)-
Jo
(i-O'-^dC
Г(р + q)
Страница 31

32
Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
между бета- и гамма-функциями, имеем
А
Г(/? + 1)ГA-м)^^^,_, ^ ^
rB + /5-/i)
Из этого равенства находим коэффициенты Аи C:
/5 = /i-l, А:
sinGr/i)
Г(/х)ГA - /i)
A8)
Формулы A7), A8) определяют рещение вспомогательного уравнения A6) и позволяют с
помощью формулы A4) получить рещение обобщенного уравнения Абеля A5) в следующем
виде:
У{Х) :
sinGr/i) d
L
f{t) dt _ sinGr/i)
7Г dx J a (X — ty~^
/(«)
fl{t)dt
(s-a)l-f Ja (x-ty-t^
A9)
2.4-5. Сведение к обыкновенным днфференннальным уравнениям
Рассмотрим специальный случай, когда образ ядра интегрального
уравнения A) можно представить в виде
К{р)
М{р)
N{p)
B0)
где М(р) и N(p) некоторые многочлены степеней тип соответственно:
m п
M{p) = Y,Akp\ N{p) = Y,Bkp\ B1)
fc=0
fc=0
в этом случае решение интегрального уравнения A) (если оно сугцествует)
удовлетворяет линейному неоднородному обыкновенному дифференциальному
уравнению ш-го порядка с постоянными коэффициептами:
к=0 к=0
Уравпение B2) можно кратко записать в операторном виде
d
dx
B2)
M(D)y(x) = N(D)f(x), D
Начальные условия для дифференциальпого уравнения B2), а также условия,
которые необходимо наложить на правую часть интегрального уравнения A),
получаются из равенства
m fc —1
п к—1
y: а, ^/-i-'2/W(o) - y: в,^р'-'-^л^\о)=о
B3)
fc=0 s=0
к=0 s=0
путем выделения членов при одинаковых степенях параметра р.
Доказательство этого утверждения проводится с помощью применения
преобразования Лапласа к дифференциальному уравнению B2) и последующим
сравнением полученного выражения с уравнением C) с учетом равенства B0).
Страница 32

2.5. Метод дробного дифференцирования 33
2.4-6. Связь уравнений Вольтерра н Вннера-Хонфа
Уравнение Вольтерра первого рода с разностным ядром вида
К(х - t)y(t) dt = f(x), О < ж < ОС, B4)
/
/о
можно привести к уравнению Винера-Хопфа первого рода в форме
/■
К^(х - t)y{t) dt = f(x), О < ж < ОС, B5)
/о
где ядро К-^(х — t) дается соотношением
/^ /.^_ i K{s) при s>0,
^ + ^^^~\0 при s<0.
Методы решения уравнения B5) приведены в главе 4.
(•) Литература: П. П. Забрейко, А. И. Кошелев и др. A968), М. Л. Краснов, А. И. Киселев,
Г. И. Макаренко A968), Г. Дёч A971), В. А. Диткин, А. П. Прудников A974), В. И. Смирнов
A974), Ф. Д. Гахов, Ю. И. Черский A978).
2.5. Метод дробного дифференцирования
2.5-1. Определение дробных интегралов
Функция f(x) называется абсолютно непрерывной на отрезке [а, 6], если для
любого £ > О можно найти такое ^ > О, что для любой конечной системы
попарно непересекающихся отрезков [а^^Ьк] С [а,6], к = 1,2,... ,гг, такой, что
п п
Y^ (bk — ак) < 8, справедливо неравенство J^ |/(^fc) — 1{ак)\ < s. Класс всех
к=1 к=1
таких функций обозначается АС.
Через АС^, где п = 1,2,..., обозначим класс функций /(ж), непрерывно
дифференцируемых на [а, Ь] до порядка гг — 1, причем f'^^~'^\x) G АС.
Пусть (р(х) G Li(a,b). Интегралы
с) = -—— / ^ ^\; dt, х> а
г{р) Л (x-ty-f^
Г^^ф) ^ -f- / ^ ^ _^^ dt, х>а, A)
'^-^^'''шl^^^-^
1>^_ф)^-±- —Щ_^М, х<Ь, B)
где /х > О, называются интегралами дробного порядка fi. Первый из них
называют иногда левосторонним, а второй — правосторонним. Операторы Ij^^, 1{^_
называют операторами дробного интегрирования.
Интегралы A), B) принято называть также дробными интегралами Римана-
Лиувилля.
Справедлива формула
/ 'Р{хЖ+Ф{х)^х= I ^{x)l^_ip{x)dx, C)
называемая иногда формулой дробного интегрирования по частям.
Дробное интегрирование обладает свойством
Г,ХМ^)='^аХ^Ф)^ 1ЧЯ-Ф)=Ч^^^{^), М>0, /?>0. D)
Свойство D) называется полугрупповым свойством дробного интегрирования.
3 А. В. Манж:иров, А. Д. Полянин
Страница 33

34
Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
2.5-2. Определение дробных производных
Дробное дифференцирование естественно ввести как операцию, обратную
дробному иптегрировапию. Для функции /(ж), заданной на отрезке [а, 6],
выражения
1 d Г f(t)
d::+/(x) =
ГA - IJ,) dx
1 d
J а
Г
J X
{х - ty
fit)
-dt,
-dt
E)
F)
ГA - fi) dx J^ {t - ж)/^
называются соответственно левосторонней и правосторонней дробными
производными порядка /х. В этих формулах считается, что О < /х < 1.
Дробные производные E), F) называют обычно производными Римана-
Лиувилля.
Заметим, что дробные интегралы определены для любого порядка /х > О, а
дробные производные — пока только для порядка О < /х < 1.
Если f{x) G АС, то функция f{x) имеет почти всюду производные D^^/(x)
и В^_/(ж), О < /X < 1, причем В;^+/(ж),В^_/(ж) G Lr(a,b), 1 ^ г < 1//х, и их
можно представить также в виде
d::+/(x)
1
ГA-/х)
1
(х - ау Л (^ - ^)^
т _ [' _jm
ху J^ (t-x
G)
(8)
ГA -/х) [ F-ж)/^ J^ (t-ж)/^
Перейдем, наконец, к дробным производным порядков /х ^ 1. Будем
пользоваться обозначениями: [/х] — целая часть числа /х, {/х} — дробная часть числа /х,
О ^ {м} < 1^ так что
М = М + {М}- (9)
Если /X — целое число, то под дробной производной порядка /х будем понимать
обычное дифференцировапие:
D*:
dx
М = 1,2,.
Если же /X — не целое, то D^_|_/(a;), 1)^_/{х) вводятся по формулам
D|:+/(x)
Таким образом.
dx
Ы]
^'Л'П-)=[^)
dx
il-J'^m,
dx
I^l'Jfix) =
dx
fix)
A0)
A1)
A2)
- fj.) \dx J J^
m
(x-t)
/X —n + l
dt,
M + 1, A3)
D^ fix) = -^
fit)
■dt, n=[fi]-\-l. A4)
Достаточное условие существования производных A3), A4) состоит в том.
чтобы
J а
fit) dt
АС^^\
la ix-t)M
Для выполнения этого условия достаточно, чтобы fix)e АС^^\
Страница 34

2.5. Метод дробного дифференцирования
35
Замечание. Определения дробных интегралов и дробных производных
можно обобщить на случай комплексных /а (см., например, С. Г. Самко, А. А. Килбас,
О. И. Маричев A987)).
2.5-3. Основные свойства
Через I^^(Li), /х > О, обозначим класс функций /(ж), представимых
левосторонним дробным интегралом порядка /а от интегрируемой функции:
f(x) = 1^^(/?(ж), ip(x) е Li(a, 6), 1 ^ _р < ОС.
Для того чтобы f(x) G I^^(Li), /х > О, необходимо и достаточно, чтобы
и.^{х) = К+'^Дх) G АС", A5)
где гг = [/х] Ч-1, и чтобы*
/f-V(«) = 0' fc = 0,l,...,n-l. A6)
Пусть /X > 0. Будем говорить, что функция f(x) G Li имеет интегрируемую
дробную производную D^^/(x), если 1^^^/(ж) е АС^, п = [/а] -\-1.
Другими словами, этим определением введено понятие, использующее только
первое из двух условий A5), A6), описывающих класс I^^(Li).
Пусть /X > 0. Тогда равенство
выполняется для любой интегрируемой функции (р(х), а равенство
Га+'0^а + /{х) = fix)
выполняется для функции
fix) е l^+(Li).
Если вместо A9) предположить, что функция f(x) G Li(a,b) имеет суммируемую
производную D^^/(x), то A8), вообще говоря, неверно и заменяется формулой
п-1
A7)
A8)
A9)
r,+-D':+fix) = fix) - Y,
(х - a)t^-
/•(n—k — l)
k=0
Г(М - к)
fr.'ia),
где n = [fj] -\-l и fn-i^(x) = 12_^^ f(x). В частности, при О < /x < 1 имеем
Z+Ti^a+fix) = fix) ■
/i-m(«)
Г(М)
(z — a)
M-l
B0)
B1)
2.5-4. Решение обобщенного уравнения Абеля
Рассмотрим интегральное уравнение Абеля в форме
yit)
f
J а
■ dt = f(x)
B2)
где О < /X < 1. Будем считать, что х G [а, 6], f(x) G АС, y(t) G Li, и применим
технику дробного дифференцировапия. Разделив обе части уравпения B2) на
ГA — /х), на основании A) запишем это уравнение в виде
у(х) =
_ /М_
Т{1-р)
X > а.
B3)
* Здесь и далее в разд. 2.5 запись f^^\x) обозначает гг-ю производные
функции f{x) по ее аргументу, а f^^\a) = f^^\x)\ _ .
3*
Страница 35

36
Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
Подействуем на обе части равенства B3) оператором дробного
дифференцирования D^^^. Тогда на основании свойств операторов дробного интегрирования и
дифференцирования получим
ууи.
' ГA-м) '
или в развернутой записи
( \ ^
^^""^ V{p)V{l-p)
.(x-a)i-M Л
Теперь с учетом соотношения
1 sinGr/i)
im
(x-t)
Т{р)Т{1 -р) 7Г
придем к решению обобщенного уравнения Абеля в форме
1-/Х
-dt
B4)
B5)
у{х)
sinGr/i)
/(а)
(ж-а)!-*'
B6)
которая совпадает с полученной ранее в п. 2.4-4.
(•) Литература: К. В. Oldham, J. Spanier A974), Ю. И. Бабенко A986), С. Г. Самко,
А. А. Килбас, О. И. Маричев A987).
2.6. Уравнения с ядрами, имеющими слабую
особенность
2.6-1. Метод преобразования ядра
Рассмотрим интегральное уравнение Вольтерра первого рода с полярным
ядром
L{x,t)
K(x,t)
О < а < 1.
(x-t)"^
Тогда исследуемое интегральное уравнение можно записать в форме
L(x, t)
f
Jo
-y(t)dt = f(x),
A)
B)
/о (^-*)°
причем предполагается, что функции L(x, t) и дЬ{х, t)/dx являются
непрерывными и ограниченными. Для решения уравнения B) умножим обе его части на
dx/{^ — xY~°' и проинтетрируем от О до S,. Тогда
ULiB^M^^-L
Полагая
Jo
f{x) dx
L(x, t) dx
(С-жI-°^(ж-^)°^ '
f{x) dx
V^(O) = 0,
{i-xY-^
будем иметь другое интегральное уравнение первого рода с неизвестной
функцией y(t):
Jo
K*{^,t)y{t)dt = ip{0,
C)
В котором ядро К*(^, t) не имеет особенностей.
Страница 36

2.6. Уравнения с ядрами, имеющими слабую особенность
37
Можно показать, что любое решение уравнения C) является также решением
уравнения B). Таким образом, после преобразования уравнения B) к виду C), к
последнему применимы методы, пригодные для непрерывных ядер.
2.6-2. Ядро с логарифмической особеииостью
Рассмотрим уравнение
/ \n{x-t)y{t)dt = f{x), /@) = 0.
-'О
Для его решения применим преобразование Лапласа. Заметим, что
ii {хП = Г е-^^х^ dx = ^^^+/\ 1У > -1.
.и+1
продифференцируем соотношение E) по и. Тогда
1^ J р^ + 1
При I/ = О в силу F) имеем
г> +1)^1,1
Т{и + 1)
D)
E)
F)
гA) - ^'
где С = 0.5772. .. —постоянная Эйлера. С учетом последнего равенства
формула F) принимает вид
£{Ых} =
1пр + С
Р
G)
Применяя к уравнению D) преобразование Лапласа, с учетом G) получим
у{р) = f{p),
откуда
Запишем теперь у(р) в виде
у{р)
Pfjp)
Inp + C
Я@)
^^"^^ рAпр + С) рAпр + С)
Так как /@) = О, то
s.{fU^)}=p''~f{p)-fUo)-
Перепишем формулу E) следующим образом:
1
Г(^ + 1)
Р'
,^+1 '
(8)
(9)
A0)
(И)
И проинтегрируем обе части A1) по z^ в пределах от О до ос. Тогда
du 1
^\Уо Г(^ + 1)'^''/ Уо
Воспользовавшись формулой для преобразования Лапласа при изменении
масштаба переменной (см. табл. 1 из п. 1.2-5), будем иметь
[Jo Г(г. + 1) J Уо Р"+^ Pln^P р{1пр-
+ 1па)
Страница 37

38
Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
Если положить а = е , то
Л r(i. + 1
■ du
1
1) J p(lnp + C)
Обратимся к равенству (9). В силу соотношения A2)
/i@)
S.lf:
poo jy .
■ dzy
A2)
A3)
p(inp + c) Г^""'Л r(i. + i)
Учитывая A0) и A2), первое слагаемое в правой части (9) можно рассматривать
как произведение изображений. Для отыскания этого слагаемого воспользуемся
теоремой о свертке:
Р^/(р)-/^@)
рAпр + С)
= £
ПХ ПС
/ fuit) /
(x-t)^e-^^
dp dt
A4)
На основании соотношений (9), A3) и A4) получим решение интегрального
уравнения D) в виде
у(х) = - f,[{t) ^ /^ \ dudt-fUO) / Л^ -^z^
Л Л r(i. + l) '"^ Vo r(i. + l)
A5)
(•) Литература: М. Л. Краснов, А. И. Киселев, Г. И. Макаренко A968), В. Вольтерра
A982).
2.7. Метод квадратур
2.7-1. Квадратурные формулы
Методом квадратур называется метод построения приближенного решения
интегрального уравнения, основанный на замене интегралов конечными суммами
по некоторой формуле. Такие формулы называются квадратурными и в общем
случае имеют вид
/ ф(х) dx = ^ Aiф(xi) + еп[ф],
-'а ■_-,
A)
где Xi (г = 1, 2,..., гг) — абсциссы точек разбиения промежутка интегрирования
[а, Ь] или узлы квадратуры (или интерполирования), Ai —числовые
коэффициенты не зависящие от выбора функции ф(х), еп[ф] —остаточный член (ошибка)
п
формулы A). Как правило Ai ^ О и ^ Ai = b — а.
i=l
Существует довольно много квадратурных формул вида A). Наиболее
простыми и часто применяемыми на практике являются следующие (h — постоянный шаг
интегрирования):
Формула прямоугольников:
А,
h =
--А2 =
b — а
п-1
: Ап-1 =h, Ап= о,
= a-\-h(i-l) (i = l,
Формула трапеций:
А1=Агг = \Н, А2= А2, = --= Агг-1 = Н,
b — а
h =
Xi = а -\- h(i — 1) (г = 1,
.,п)
B)
C)
Страница 38

2.7. Метод квадратур
39
Формула Симпсона {парабол):
Ai = А2т-\-1 = -jh, А2 = • • • = А^т = y/i, As = • • • = A^m-l = y/i;
h:
b — a
■ a Ч- h(i — 1) (n = 2m + 1, г = 1,..., n),
D)
n-1 '
где vfi — натуральное число.
Широкого применяются также квадратурные формулы Чебышева и Гаусса с
разным количеством узлов интерполирования. Проиллюстрируем эти формулы на
примере.
Пример. На отрезке [—1,1], параметры формулы A) принимают следующие значения:
Формула Чебышева (п = 6):
Аг
2 _ 1
гг ~ 3 '
^2 = -^5 = -0.4225186538,
Формула Гаусса (п = 7):
А, = Av = 0.1294849662,
3818300505,
-0.9491079123,
-0.4058451514,
= -Xq = -0.8662468181,
: -Ж4 = -0.2666354015.
= Aq = 0.2797053915,
= 0.4179591837,
= -Xq = -0.7415311856,
= 0.
E)
F)
Заметим, что квадратурным формулам посвящена обширная литература,
которую заинтересованный читатель сможет найти, например, в книгах Н. С.
Бахвалов A973), С. М. Никольский A979), Г. Корн, Т. Корн A984).
2.7-2. Общая схема метода
Рассмотрим линейное интегральное уравнение Вольтерра первого рода
K{x,t)y{t)dt = f{x), /(а) = 0, G)
J а
И Применим для его решения на отрезке а ^ х ^ b метод квадратур. Процедура
построения решения состоит из двух этапов:
1°. Во-первых, определим начальное значение у (а). Для этого
продифференцируем уравнение G) по х. Тогда
К(х,х)у(х)+ / KUx,t)y{t)dt = fUx).
J а
Полагая х = а, найдем
yi = у{а) = ';^ \ = '^j^.
К(а,а) К-^-^
2°. Возьмем постоянный шаг интегрирования h и рассмотрим дискретное
множество точек Xi = а -\- h(i — 1), г = 1, 2,..., гг. При х = Xi уравнение G) примет
вид
' K{xi,t)y{t) dt = f{xi), г = 2, 3,..., гг. (8)
Г
J а
Заменяя интеграл в (8) квадратурной формулой A) и выбирая Xj (j = 1, 2,..., г)
узлами квадратуры (по переменной t), получим следующую систему уравнений:
^AijK(xi,Xj)y(xj) = f(xi) -\-€i[y], г = 2,3,.
(9)
Страница 39

40 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
где Aij —коэффициенты квадратурной формулы на отрезке [а, Жг], Si[y\ — ошибка
аппроксимации. Полагая Si[y\ малыми и отбрасывая их, получим систему липей-
пых алгебраических уравпений в форме
г
J2AijKijyj=fi, г = 2,...,гг, A0)
j=i
где Kij = K(xi,Xj) (j = 1,...,г), fi = f(xi), yj —нриближенные значения
искомой функции у (ж) в узлах Xi.
Теперь система уравнений A0) позволяет последовательно определить при
AiKii фО (i = 1,2,... ,п) искомые приближенные значения посредством формул
п-1
г/ / \ г л т^ ^"^ ^ ^nj-'^njyj
У1 = -^, У2= . г. ^ •••' Угг =
^11 ^22^22 ^пп^п
конкретный вид которых зависит от выбора квадратурной формулы.
2.7-3. Алгоритм на основе формулы траненнй
В соответствии с формулой трапеций C), имеем
Ац = Ац = ^h, Ai2 = ■ ■ ■ = Ai^i-i = h, i = 2,... ,n.
Примепение этой формулы в общей схеме приводит к следующему пошаговому
алгоритму:
2h
Y^PiKayA, Pj = \l
^ii\h ~[ J U при J > 1,
где обозначения совпадают с введенными в п. 2.7-2. Формула трапеций достаточно
проста, эффективна и часто используется на практике для решения интегральных
уравнений с переменным пределом интегрирования.
На основании 2.7-1 и 2.7-2 можно выписать аналогичные выражения с
использованием других квадратурных формул. Однако существуют особенности в
их применении. Например, применение формулы Симпсона должно чередоваться
для нечетных узлов с каким-либо другим правилом, скажем, с формулой
прямоугольников или формулой трапеций. Для уравнений с переменным пределом
интегрирования возникают сложности и в применении формул Чебышева и Гаусса.
2.7-4. Алгоритм для уравнения с вырожденным ядром
Общее свойство алгоритмов метода квадратур при решении уравнений Воль-
терра первого рода с произвольным ядром состоит в пропорциопальной
зависимости количества вычислений на шаге от номера шага: все операции предыдущего
шага повторяются с новыми дапными на следующем шаге и добавляется еще один
член суммы.
Если же ядро в уравпений G) вырожденное, т. е.
т
K(x,t) = Y,Pk{x)qk(t), A1)
Страница 40

2.8. Уравнения с бесконечным пределом интегрирования 41
или возможна приближенная замена произвольного ядра вырожденным, то можно
построить алгоритм, для которого количество операций пе зависит от номера узла
дискретизации. С учетом A1) уравпение G) нринимает вид
к=1 "^«^
qk{t)y{t)dt = f{x). A2)
Применяя к A2) формулу трапеций, получаем рекуррентные выражения для
решения уравнения (см. формулы п. 2.7-3):
т г—1
У(^)= т "^ : yi = —
к=1 к=1
/,
^ -^Pki^PjflkjVj
к=1 3=1
где yi —приближенные значения неизвестной функции у (ж) в узлах Xi, fi= f(xi),
Pki = Pk(xi), qki = qk(xi).
(•) Литература: H. C. Бахвалов A973), В. И. Крылов, В. В. Бобков, П. И. Монастыр-
ный A984), А. Ф. Верлань, В. С. Сизиков A986).
2.8. Уравнения с бесконечным пределом
интегрирования
представляют интерес интегральные уравнения первого рода с одним
переменным, а другим бесконечным пределами, содержащие разностное ядро. Часто
ядра и функции таких уравпений не принадлежат описанным в начале главы
классам. Исследование этих уравнений проводится методом модельных решений (см.
разд. 3.6) или методом сведения к уравнениям типа свертки. Рассмотрим
отмеченные методы на примере уравнения первого рода с переменным нижним пределом.
2.8-1. Уравнение с неременным нижним пределом интегрирования
Рассмотрим уравнение первого рода с разностным ядром:
Kix-t)y{t)dt = f{x). A)
[
J X
Уравнение A) нельзя решить путем непосредственного применения
преобразования Лапласа, так как здесь теорема о свертке не применима. В соответствии с
методом модельных решений, подробное изложение которого приведено в разд. 3.6,
рассмотрим вспомогательное уравнение с экспоненциальпой правой частью
f
K(x-t)y(t)dt = e''\ B)
Решение B) имеет вид
Y{x,p) = ^-^e''^ к{-р) = Г K{-z)e^' dz. C)
K(-V) Jo
Тогда на основании этих формул и формулы A1) из разд. 3.6 получим решение
уравнения A) для произвольной правой части /(ж) в форме
^^^^ "''"dp, D)
^("^ = il
К(-р)
где f(p) — изображепие функции /(ж), нолученное с помощью преобразования
Лапласа.
Страница 41

42 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
Пример. Рассмотрим интегральное уравнение первого рода с переменным нижним
пределом интегрирования
J X
е
<''-^^y{t) dt = Asm{bx), а > 0. E)
F)
В соответствии с формулами C) и D) получим выражения для /(р) и К(—р):
Ah Г°° 1
р^ -\-Ь^ Jo а-р
а также решение уравнения E) в форме
1 /■'=+^°° АЬ{а - р) р.
Теперь, воспользовавшись таблицами обратного преобразования Лапласа, получим точное
решение
у(х) = Aasm(bx) — Abcos(bx), а > О, (8)
которое можно легко проверить подстановкой (8) в уравнение E) с использованием таблиц
интегралов.
2.8-2. Приведение к уравнению Винера-Хонфа первого рода
Уравнение A) может быть приведено к одностороннему уравнению первого
рода
/»оо
/ K-(x-t)y(t)dt = -f(x), 0<ж<оо, (9)
-'О
где ядро К- (х — t) имеет следующий вид:
т^ / ч _ Г О при S > О,
^-(^)- \-K(s) при s<0.
Методы исследования уравнения (9) описаны в главе 4.
(•) Литература: Ф. Д. Гахов, Ю. И. Черский A978), А. Д. Полянин, А. В. Манжиров
A997).
Страница 42

3. Методы решения линейных уравнений
вида у{х) - £ К{х, t)y{t) dt = f{x)
3.1. Интегральные уравнения Вольтерра второго рода
3.1-1. предварительные замечания. Уравнения для резольвенты
В главе 3 излагаются методы решения интегральных уравнений Вольтерра
второго рода, которые имеют вид:
у(х)- / K(x,t)y(t)dt = f(x), A)
J а
где у(х) — неизвестная функция (а ^ х ^ 6), K(x,t) —ядро интегрального
уравнения, f(x) — свободный член или правая часть интегрального уравнения.
Классы функций, которым могут принадлежать у (ж), f{x) и K(x,t), определены
в п. 2.1-1. В этих классах функций решение интегрального уравнения Вольтерра
второго рода существует и единственно.
При f(x) = О уравнение A) называют однородным , а при f(x) ф О —
неоднородным.
Ядро интегрального уравнения K(x,t) называется выроэюденным, если оно
представимо в виде K(x,t) = gi(x)hi(t) + • • • -\- gn(x)hn(t).
Ядро интегрального уравнения K(x,t) называется разностным, если оно
зависит от разности аргументов: K(x,t) = К(х — t).
Замечание 1. Однородное интегральное уравнение Вольтерра второго рода
имеет только тривиальное решение.
Замечание 2. Вывод о существовании и единственности решения
интегрального уравнения Вольтерра второго рода справедлив и для гораздо более широкого
класса ядер и функций.
Замечание 3. Уравнение Вольтерра второго рода можно трактовать как
уравнение Фредгольма второго рода, ядро которого K(x,t) обращается в нуль при t>x
(см. главу 4).
Замечание 4. Случай, когда а = —оо и/или b = оо, вообще говоря, не
исключается, но при этом следует внимательно проверять выполнение условия
квадратичной интегрируемости ядра K(x,t) в квадрате S = {а^х ^Ь, a^t ^Ь}.
Решение уравнения A) можно представить в виде
y{x) = f{x)+ г R(x,t)f(t)dt,
J а
B)
тдс резольвента R(x,t) не зависит от свободного члена f(x) и нижнего предела
интегрирования а, а определяется только ядром интегрального уравнения.
Резольвента уравнения Вольтерра A) удовлетворяет двум интегральным
уравнениям
R(x,t) = K(x,t)-\- K(x,s)R(s,t)ds, C)
R(x,t) = K(x,t)-\- I K(s,t)R(x,s)ds, D)
в которых интегрирование ведется по различным парам переменных ядра и
резольвенты.
Страница 43

44 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f(x)
3.1-2. Связь между решениями интегральных уравнений
Приведем две полезные формулы, выражающие решение одного
интегрального уравнение через решения других интегральных уравнений.
1°. Пусть решению уравнения Вольтерра второго рода с ядром K(x,t) отвечает
резольвента R(x,t). Тогда решению уравнения Вольтерра второго рода с ядром
K''(x,t) = —K(t,x) отвечает резольвента W{x^t) = —R(t,x).
2°. Пусть имеются два уравнения Вольтерра второго рода с ядрами Ki(x,t)
и K2(x,t), которым соответствуют резольвенты Ri(x,t) и R2(x,t). Тогда
уравнение Вольтерра с ядром
Ki(x,s)K2(s,t)ds E)
имеет резольвенту
R{x,t) = Ri{x,t) -\- R2{x,t) -^ / Ri{s,t)R:
2{x,s)ds. F)
Отметим, что в формулах E) и F) интегрирование ведется но различным нарам
неременных.
® Литература: Э. Гурса A934), Г. М. Мюнтц A934), С. Г. Михлин A959), Ф. Трикоми
A960), П. П. Забрейко, А. И. Кошелев и др. A968), М. Л. Краснов, А. И. Киселев,
Г. И. Макаренко A968), Л. Я. Цлаф A970), J. А. Cochran A972), С. Corduneanu A973),
В. И. Смирнов A974), В. Вольтерра A982), А. J. Jerry A985), А. Ф. Верлань, В. С. Сизиков
A986), А. D. Polyanin, А. V. Manzhirov A998, 1999).
3.2. Уравнения с вырожденным ядром:
K(x,t) = gi(x)hi(t) Н \-9n(x)hn(t)
3.2-1. Уравнения с ядром K(x,t) = (р(х) -\- ф(х)(х — t)
Решение уравнений Вольтерра с таким ядром можно представить в виде
формулы
y = w'^x, A)
где W = w(x) —решение линейного неоднородного обыкновенного
дифференциального уравнения второго порядка
^хх - ^(x)w'^ - ф(x)w = f(x), B)
удовлетворяющее начальным условиям
w(a) = Wx(a) = 0. C)
Пусть wi=wi (х) —нетривиальное частное решение соответствующего линейного
однородного дифференциального уравнения B) при f(x) = 0. Пусть wi(a) ф 0.
Тогда другое нетривиальное частное решение указанного линейного однородного
дифференциального уравнения W2 = W2(x) можно записать в виде
W2{x) = wi{x) -—yr^dt, Ф(ж) = ехр[/ cp{s)ds\.
Решение неоднородного уравнения B), удовлетворяющее начальным условиям C),
дается формулой
w{x) = W2(x
fi|/«)*-».(.)/'^/«)... <4)
Страница 44

3.2. Уравнения с выроэюденным ядром: К(х, t) = g-^(x)h-^(t) + • • • + g^(x)h^(t) 45
Подставляя выражение D) в формулу A), получим решение исходного
интегрального уравнения
yix) = f(x)+ г R(x,t)f(t)dt,
J а
где
R(x,t) = [W2(x)wi(t) - Wi(x)w2(t)]-—— =
Здесь Ф(х) = ехр / (p(s)dsL штрихами обозначены производные по
переменной X.
Для вырожденного ядра рассматриваемого вида резольвенту можно
определить по формуле
ri[X^ t) ^ Uxx •)
где вспомогательная функция и является решением линейного однородного
обыкновенного дифференциального уравнения второго порядка
и'^^ - (^{х)и^ - ф(х)и = о, E)
удовлетворяющим следующим начальным условиям при х = t:
и\ ^ = О, u'l ^ = 1. F)
\x=t ' ^\x=t ^ ^
Параметр t входит лишь в начальные условия F), при этом само уравнение E) не
зависит от t.
Замечание 1. Ядро рассматриваемого уравнения можно записать в виде
K(x,t) = Gi(x) + tG2(x), где Gi(x) = ^(х) + хф(х), G2(x) = —(р(х).
3.2-2. Уравнения с ядром K(x,t) = (p(t) -\- ip(t)(t — х)
Для вырожденного ядра рассматриваемого вида резольвента определяется
выражением
R(x,t) = -v'tt, G)
где вспомогательная функция v является решением линейного однородного
обыкновенного дифференциального уравнения второго порядка
у[[^ср(г)у[^Ф(г)у = о, (8)
удовлетворяющим следующим начальным условиям при t = х:
И,_=0, ^:L_ = 1. (9)
Величина х входит в начальные условия (9) лишь параметрически, при этом само
уравнение (8) не зависит от х.
Пусть VI = VI (t) —нетривиальное частное решение уравнения (8). Тогда общее
решение этого дифференциального уравнения дается формулой
vit) = СгУгЦ) + C,v,(t) £ -Щ^^^^ т = ехр[£ ф) ds].
Удовлетворяя начальным условиям (9), находим зависимость постоянных
интегрирования Ci и С2 от параметра х. В результате получим решение задачи (8), (9):
Страница 45

46 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
Подставляя выражение A0) в формулу G) и исключая вторую производную с
помощью уравнения (8), найдем резольвенту
Замечание 2. Ядро рассматриваемого интегрального уравнения можно
записать в виде i^ (ж, t) = Gi{t) + xG2{t),TjxQ Gi{t) = ip{t)+til){t),G2{t) = -^{t).
3.2-3. Уравнения с ядром K{x^t) = YlZi=i ^^ (x)(x — ty
Для определения резольвенты R(x,t) введем вспомогательную функцию
которая при x = t обращается в нуль вместе со своими п—2 первыми производными
по ж, а производная порядка п — 1 при х = t равна единице. Кроме того,
D/ +^ (^)/ +^ (^) d'^u{x,t)
R{x,t)=u), \x,t), и], ^ = —^^^ . A1)
Подставляя A1) в уравнение для резольвенты C) из п. 3.1-1, будем иметь
u^^\x,t) = K{x,t)+ I K{x,s)u^r\s,t)ds. A2)
Применяя к интегралу в правой части A2) формулу интегрирования по частям,
получим
u^:^\x,t)=K{x,t)+^(-i)'"i^i'"Hx,sL"-'"-'4s,i)i:::- A3)
m=0
Подставляя теперь в A3) выражения для K(x,t) и u(x,t), придем к линейному
однородному обыкновенному дифференциальному уравнению гг-го порядка
относительно функции u(x,t).
Таким образом, резольвенту R(x,t) интегрального уравнения Вольтерра с
вырожденным ядром указанного вида можно получить при помощи A1), где u(x,t)
удовлетворяет следующему дифференциальному уравнению и начальным
условиям:
ui""^ - (pi(x)ui''~^^ - (p2(x)ui''~^^ - 2ip2,{x)u^^~^^ (n - 1)! ipn{x)u = 0,
\x=t •^\x=t -^ \x=t ' -^ \x=t
Величина t входит в начальные условия лишь параметрически, при этом само
уравнение не зависит от t.
Замечание 3. К ядру рассматриваемого вида элементарными преобразовани-
п
ЯМИ приводится ядро K(x,t) = Y1 фт(хI^~'^.
3.2-4. Уравнения с ядром К(х, t) = YlZi=i ^^ (^)(^ ~ ^У
Представим резольвенту заданного вырожденного ядра в виде
ЩхЛ) = —V2 (хЛ), V2 ' = ^ -,
Страница 46

3.2. Уравнения с выроэюденным ядром: К(х, t) = g-^(x)h-^(t) + • • • + g^(x)h^(t) 47
причем вспомогательная функция v(x,t) при t = х обращается в нуль вместе с
п — 2 производными по t, а гг — 1-я производная по t при t = х равна единице.
Подставляя выражение для резольвенты в уравнение C) из н. 3.1-1, получим
vi''\x,t)= I K(s,t)v^''\x,s)ds-K(x,t).
Применим к интегралу в правой части формулу интегрирования по частям. Тогда,
учитывая свойства вспомогательной функции v(x,t), придем к следующей задаче
Коши для обыкновенного дифференциального уравнения гг-го порядка:
г;^"^ + МЫ""''^ + МЫ''~''^ + 2(^3(t)i;^"'^ + • • • + (гг - 1)! Mt)v = О,
I П (^-2I п (^-1I 1
\t=x ''\t=x "^ \t=x ' "^ \t=x
Величина x входит в начальные условия лишь параметрически, при этом само
уравнение не зависит от х.
Замечание 4. К ядру рассматриваемого вида элементарными преобразовани-
п
ЯМИ приводится ядро K(x,t) = Y1 фт{1)х^~^,
3.2-5. Уравнения с вырожденным ядром общего вида
В данном случае уравнение Вольтерра второго рода можно представить в виде
"^ пх
У{Х) - Y, 9т{х) / hm{t)y{t)dt = fix). A4)
m=l "'"
Используя обозначения
Wj{x)= [ hj{t)y{t)dt, j = l,2,...,n, A5)
J a
запишем уравнение A4) следующим образом:
п
У(^) = X! 9m(x)Wm(x) + f(x). A6)
Дифференцируя выражения A5) с учетом формулы A6), приходим к системе
линейных дифференциальных уравнений для определения функций Wj = Wj(x):
п
Uj = hj(x) ^ gm(x)wm + f (х)
i = i,2,.
с пачальными условиями
Wj(a) = 0, j = l,2,...,n.
Если найдено решение этой системы, то решение исходного интегрального
уравнения A4) определяется по формуле A6) или с помощью любого из выражений
У{х)
Wj (х)
hj(x)
1,2,...,гг,
которые получены путем дифференцировапия формулы A5).
® Литература: Э. Гурса A934), Г. М. Мюнтц A934), А. Ф. Верлань, В. С. Сизиков A986),
А. D. Polyanin, А. V. Manzhirov A998).
Страница 47

48 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
3.3. Уравнения с разностным ядром: К{х^ i) = К(х — i)
3.3-1. Метод решения, основанный на нреобразованнн Лапласа
Уравнения Вольтерра второго рода с ядром, зависящим от разности
аргументов, имеют вид
у(х)- г K{x-t)y(t)dt = f(x).
JO
A)
применяя преобразование Лапласа ii к уравнению A) и учитывая, что
интеграл с ядром, зависящим от разности аргументов, по теореме о свертке (см. п. 1.2-3)
преобразуется в произведение К(р)у(р), приходим к уравнению для образа
искомой величины
у{р) - к{р)у(р) = }(р). B)
Решение уравнения B) определяется формулой
1 - К(р)
которую можно записать в эквивалентном виде
у{р) = ?{Р) + R{p)f(p), R(p) = т^%7Т- D)
1 - к{р)
Применяя к D) обратное преобразование Лапласа, получим решение уравнения A)
в виде
у(х) = /(х)+ г R{x-t)f{t)dt,
При использовании формулы E) могут возникнуть технические трудности:
_ /"ОО
1°. при получении изображения К(р) = / К{х)е~^^ dx для конкретного
ядра К{х).
2°. При нахождении оригинала резольвенты E), изображение которого R{p)
находится по формуле D).
Для вычисления соответствующих интегралов применяют таблицы прямых
и обратных преобразований Лапласа, причем во многих случаях для обратного
преобразования используют методы теории функций комплексного переменного,
включая теорему о вычетах (см. п. 1.1-4).
Замечание. Если нижний предел в интеграле уравнения Вольтерра с ядром,
зависящим от разности аргументов, равен а, то его можно свести к уравнению A)
с помощью замены х = х — a^t = ~t — а.
На рис. 2 приведена принципиальпая схема решения интегральных уравнений
Вольтерра второго рода с разностным ядром с помощью интегрального
преобразования Лапласа.
Пример 1. Рассмотрим уравнение
у{х) + А / sin [\{х - t)] y{t) dt = fix), F)
Jo
которое является частным случаем уравнения A) при К(х) = —Asm(Xx).
Страница 48

3.3. уравнения с разностным ядром: K(x,t) = К(х — t) 49
Рис. 2. Схема решения интегральных уравнений Вольтерра второго рода
с разностным ядром с помошью интегрального преобразования Лапласа.
к{р)
R(x) —оригинал функции R{p) ■
К(р)
Сначала, используя таблицы преобразований Лапласа [Г. Бейтмен, А. Эрдейи A969,
стр. 138)], получим образ ядра интегрального уравнения в виде
к{р). ^^
р2 + Л2 '
Затем по формуле D) найдем образ резольвенты:
АЛ
R{p):
р2 + Л(А + Л)
Используя далее таблицы обратных преобразований Лапласа [Г. Бейтмен, А. Эрдейи
A969, стр. 207)], получим оригинал резольвенты:
1АЛ
sm{kx) при Л(А + Л) > О,
^\ где /с = |Л(А + Л)|1/2.
s\v{kx) при Л(А + Л) < О,
к
Заметим, что в частном случае при Л = — А получаем R{x) = А^ж. Подставляя эти
выражения в формулу E), находим решение интегрального уравнения F). В частности, при
4 А. В. Манж:иров, А. Д. Полянин
Страница 49

50 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f(x)
Л(А + Л) > О это решение имеет вид:
y(x) = f(x)-^- J sm[k(x-t)]f(t)dt, /с = УЛ(А + Л). G)
3.3-2. Метод, основанный на решении вспомогательного уравнения
Рассмотрим интегральное уравнение
Ау{х) + В Г К(х - t)y{t) dt = fix). (8)
J а
Пусть w = w(x) — решение вспомогательного более простого уравнения при
fix) = 1,а = 0:
Aw(x) -\-В К(х - t)w{t) dt = 1. (9)
Тогда решение исходного уравнения с произвольной правой частью (8) выражается
через решение вспомогательного уравнения (9) с помощью формулы
у{
х) = — / w(x-t)f(t)dt = f(a)w(x-a)-\- w(x - t)fi(t)dt. A0)
dx J a J a
Докажем это утверждение. Перепишем выражение A0) (в котором предварительно
сделано переобозначение параметра интегрирования t на s) в виде
у{х) = -^1(х), 1{х) = г w{x - s)f(s) ds, A1)
dx Ja
и подставим его в левую часть уравнения (8). В результате некоторых преобразований и
изменения порядка интегрирования в двойном интеграле с учетом (9) получим
— А/(ж) + б/ K{x-t)—I{t)dt=—AI{x)^—Bf K{x-t)I{t)dt =
dx Ja dt dx dx Ja
dx
d
dx
d
dx
dx
что и требовалось доказать.
[рх р X pt
А w(x-s)f(s)ds^B / K(x-t)w(t-s)f(s)dsdt
J а J а J а
I / f{s) \Aw{x -s)^B I K{x - t)w{t - s) dt] ds\ =
fis) \Awix -s) + B Kix -s- Л)гу(Л) d\\ ds\
^jy(s)ds = fix),
3.3-3. Сведение к обыкновенным дифференниальным уравнениям
Рассмотрим специальный случай, когда образ ядра интегрального
уравнения A) можно представить в виде
l-i^(p) = ||, A2)
где Q(p) и R(p) некоторые многочлены степени п:
п п
Qip) = Y,Akp\ Rip) = Y,Bkp\ A3)
Страница 50

3.3. уравнения с разностным ядром: K(x,t) = К(х — t)
51
В этом случае решение интегрального уравнения A) удовлетворяет линейному
неоднородному обыкновенному дифференциальному уравнению гг-го порядка с
постоянными коэффициентами:
к=0 к=0
Уравнение A4) кратко можно записать в операторном виде
dx
Начальные условия для уравнения A4) получаются из равенства
J2 Аи X:/-^-'2/i'^@) - J2 в. E/-^-7i^'@) = о
A4)
Q{D)y{x) = R{D)f{x),
A5)
fc=0
fc=0
путем выделения членов при одинаковых степенях параметра р.
Доказательство этого утверждения проводится с помощью применения
преобразования Лапласа к дифференциальному уравнению A4) и последующим
сравнением полученного выражения с уравнением B) с учетом равенства A2).
Другой метод сведения интегрального уравнения к обыкновенным дифферен-
циальным уравнениям описан в разд. 3.7.
3.3-4. Приведение к уравнению Винера-Хонфа второго рода
A6)
A7)
Уравнение Вольтерра второго рода с разностным ядром вида
у{х) + / К{х - t)y{t) dt = f{x), О < ж < ОС,
можно привести к уравнению Винера-Хопфа в форме
/»оо
у(х) + / К^(х - t)y{t) dt = f(x), О < ж < ОС,
-'О
где ядро К-^(х — t) дается соотношением
/^ /.^_ i K(s) при s>0,
^ + ^^^~\0 при s<0.
Методы исследования уравнения A7) описаны в главе 5, где приведен и
пример построения решения уравнения Вольтерра второго рода с разностным
ядром посредством решения соответствующего уравнения Винера-Хопфа второго
рода (см. п. 5.9-3).
3.3-5. Метод дробного интегрирования для уравнения Абеля
Рассмотрим обобщенное уравнение Абеля второго рода в форме
у(х) - л
J а
y{t)
(х - ty
dt = fix),
X > а,
A8)
где О < /х < 1. Будем считать, что х G [а, 6], f(x) G АС, y(t) G Li, и применим
технику дробного интегрирования (см. разд. 2.5). Положив
■/?,
0</?<1,
Л:
Г(/3)
A9)
4*
Страница 51

52 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
на основании B.5.1) запишем уравнение A8) в виде
{l-u\l+)y(x) = f{x), х>а. B0)
Теперь решение обобщенного уравнения Абеля второго рода можно символически
представить следующим образом:
y{x)={l-uli^)-'f{x), х>а. B1)
Разлагая операторное выражение в скобках в ряд по степеням оператора при
помощи формулы для геометрической прогрессии, получим
У{Х) :
1 + ЕК+)"
f{^\
X > а.
B2)
В развернутой записи с учетом равенства A^+)^ = 1а+ формула B2) принимает
вид
у(х) = f(x) +
ti Г(/Зп) л
{x-tf"-'f{t)dt,
X > а.
B3)
Поменяем в выражении B3) порядок суммирования и интегрирования, и заметим,
что
Е
г^^(ж-^)^^-1
Г(/5гг)
d
dx
Е
i^^(x-t)^^
ГA+/5гг)
гг=1 ^ ^ гг=1
Тогда с учетом замены A9) решение обобщенного уравнения Абеля второго рода
примет вид
X > а,
y{x) = f(x)+ г R{x-t)f(t),
J а
где резольвента R(x — t) определяется формулой
[XT{l-/i){x-t)(^-^^]''
R(x - t)
dx
E
Г[1 + A - 1л)п]
B4)
B5)
Ряд в представлении резольвенты B5) удается в некоторых случаях
просуммировать и получить для нее явное выражение.
Пример 2. Рассмотрим уравнение Абеля второго рода (в уравнении A8) полагаем
s/(t)
■ dt = /(ж), X > а.
В силу формулы B5) резольвента для уравнения B6) задается выражением
Известно, что
Е
R{x - t)
d ^ [Лд/7г(ж — t)]^
п=1
dx ^, ГA+ ^п
^ erf л/ж, erix= ——■ / е ^ dt,
л/тг Jo
B6)
B7)
B8)
^1^A+1гг)
где erf X — интеграл вероятностей. Тогда на основании B7) и B8) выражение для
резольвенты можно записать в форме
R(x-t)= -^{exp[A27r(x-t)]erf[Ay7r(x-t)]}. B9)
Воспользовавшись соотношениями B4) и B7), получим решение интегрального уравнения
Абеля второго рода, которое имеет вид
у{х) = f{x) + / 1ехр[Х^7т{х - t)] eYi[X^7T{x-t)] \f{t) dt, x > a. C0)
dx J a
Заметим, что в рассмотренном случае решение построено в замкнутом виде.
Страница 52

3.4. Операторные методы решения линейных интегральных уравнений 53
3.3-6. Системы интегральных уравнений Вольтерра
Преобразование Лапласа можно применить для решения систем интегральных
уравнений Вольтерра вида
Ут(х)-2_^ Ктк(х -t)yk(t)dt = fm(x), Ш = 1, 2, . . . , П. C1)
Подействуем на систему C1) преобразованием Лапласа. Тогда будем иметь
п
Ут(р) - ^ктк(р)Ук(р) = fm(p), Ш = 1, 2, . . . , П. C2)
к = 1
Решая эту систему линейных алгебраических уравнений, определим Ут{р), и
решение рассматриваемой системы уравнений примет вид
-, pc-\-ioo
Ут(х) = -— / ут(р)е^'' dp. C3)
преобразование Лапласа можно применить для построения решения систем
уравнений Вольтерра первого рода и интегродифференциальных уравнений.
(•) Литература: В. А. Диткин, А. П. Прудников A965), П. П. Забрейко, А. И. Кошелев
и др. A968), М. Л. Краснов, А. И. Киселев, Г. И. Макаренко A968), В. И. Смирнов A974),
К. В. Oldham, J. Spanier A974), Ф. Д. Гахов, Ю. И. Черский A978), Ю. И. Бабенко A986),
С. Г. Самко, А. А. Килбас, О. И. Маричев A987), R. Gorenflo, S. Vessella A991).
3.4. Операторные методы решения линейных
интегральных уравнений
3.4-1. Использование решения «укороченного» уравнения
Рассмотрим линейное уравнение второго рода
yix)+L[y] = f{x), A)
где L — некоторый линейный (интегральный) оператор.
Пусть решение вспомогательного «укороченного» уравнения первого рода
L[u]=gix), B)
может быть представлено в виде
и(х) = М[Цд]], C)
где М — некоторый известный линейный оператор. Формула C) означает, что
L~^ =ML.
Подействуем оператором L~^ на обе части уравнения A). В результате
получим
М[Цу]]+у{х) = М[Ц/]]. D)
Исключая у(х) из A) и D), приходим к следующему уравнению:
M[w] -w(x) = F(x), E)
где использованы обозначения
w = L[y], F{x) = M[L[f]]-f{x).
Страница 53

54 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
В ряде случаев уравнение E) оказывается проще, чем исходное уравнение A).
Это бывает, например, когда оператор М является константой (см. п. 5.7-2) или
дифференциальным оператором:
M = a^D"+a^-iD"
7^ Т^ d
ах
В последнем случае уравнение E) представляет собой обыкновенное линейное
дифференциальное уравнение относительно функции w.
Если решение w = w{x) уравнения E) получено, то решение уравнения A)
дается формулой у{х) = М [L[il']] .
Пример 1. Рассмотрим уравнение Абеля второго рода
y{t) dt
у(х) + л
л/ж - t
: fix).
F)
Для его решения будем использовать небольшую модификацию схемы, описанной выше,
которая соответствует случаю М = const .
dx
Перепишем уравнение F) следуюшим образом:
J а
y(t)dt _ f(x)-y(x)
\fx
■t
л
G)
Считая правую часть известной, будем рассматривать G) как уравнение Абеля первого рода.
Его решение можно записать в виде (см. пример из п. 2.4-4)
]__d_ Г fit) - y(t)
7Г dx J а Лл/Ж — t
ИЛИ
у{х)
-dt
у{х) +
1
y{t) dt
dt:
1 d
7гЛ dx
" f{t)dt
(8)
7ГЛ dx J a \/x — t 7ГЛ dx Ja \/X — t
продифференцируем обе части уравнения F) по ж, затем умножим обе части (8) на
—7гЛ^ и сложим почленно полученные выражения. В результате придем к линейному
обыкновенному дифференциальному уравнению первого порядка для функции у = у (ж):
■■K\^y = F',{x),
где
F{x) = fix) - А
J а
f(t) dt
л/ж — t
уравнение (9) следует дополнить «начальным» условием
у(а) = f(a),
которое является следствием F).
Решение задачи (9)-A1) имеет вид
у(х) = F{x) + 7гЛ^ / ехр[7гЛ^(ж - t)]F{t)
J а
И определяет решение уравнения Абеля второго рода F).
dt
(9)
A0)
A1)
A2)
3.4-2. Использование вспомогательного уравнения второго рода
Решение уравнения Абеля второго рода F) можно было получить также
другим методом, который излагается ниже.
Рассмотрим линейное уравнение
2/(ж) - L [у] =/(ж), A3)
Страница 54

3.4. Операторные методы решения линейных интегральных уравнений 55
где L — линейный оператор. Пусть решение вспомогательного уравнения
w{x) - L"H = Ф(ж), L"H = L [L"-'H], A4)
содержащего гг-ю степень оператора L, известно и определяется формулой
11;(ж) = М[Ф(ж)]. A5)
Тогда решение исходного уравнения A3) имеет вид
у{х) = ШЩхI Ф(ж) = Ь'^-1[/]+Ь'^-2[/] + ...+Ь[/]+/(ж). A6)
Это утверждение доказывается применением оператора L^~^4-L^~^4----4-L4-l
к обеим частям уравнения A3) с учетом операторного равенства
A - L) (L"-' + L"-^ + ... + L + 1) = 1 - L"
и формулы A6) для Ф(ж). в уравнении A4) вместо w{x) можно писать у{х).
Пример 2. Используем теперь операторный метод (при гг = 2) для решения
обобщенного уравнения Абеля с показателем 3/4:
Рассмотрим сначала интегральный оператор с разностным ядром
Ъ[у{х)]= г K{x-t)y{t)dt.
Jo
Посмотрим как действует L^:
L2[y]=L[L[y]] = Г I K(x-t)K(t-s)y(s)dsdt
Jo Jo
= f y{s)ds f K{x-t)K{t-s)dt= f K^{x-s)y{s)ds, A8)
^0 Js Jo
Щ{г)= Г K{i)K{z-i)di.
Jo
При выводе этой формулы менялся порядок интегрирования и делалась замена ^ = t — s.
Для ядра степенного вида
к{^) = ье
имеем
K^(Z) = 62-L_Vi:L^^l+2M. A9)
6=
|Г2A + м)^
ГB + 2ц)
-а' а
1+2/х_
Для уравнения A7) имеем
3
Поэтому вспомогательное уравнение A4), соответствующее значению гг = 2, имеет вид
у(х)-а[''У^=Ф{х), B0)
Jo VX - t
Ф{х) = /{х)^Ь
Г
Jo
fit) dt
(Х - tK/4
уравнение B0) с точностью до переобозначений А ^ — Л, Ф ^ / совпадает с уравнением F),
его решение может быть получено по формуле A2).
Замечание. Из формулы A9) следует, что решение обобщенного уравнения
Абеля с показателем Р
yjt) dt
(х - ty
сводится к решению уравнения аналогичного вида с другим показателем степени
'^^^^'[f^ = f^^^
Pi = 2/3 — 1. В частности, уравнение Абеля F), соответствующее значению /3 = ^,
сводится к решению уравнения с вырожденным ядром при /3i = 0.
Страница 55

56 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
3.4-3. Метод решения «квадратных» операторных уравнений
Пусть известно решение линейного (интегрального, дифференциального и др.)
уравнения
у{х) - XL [у] = fix) B1)
ДЛЯ произвольной правой части f(x) и любого Л из интервала (Aminj ^maxj'
Обозначим это решение так:
y = Y(f,X). B2)
Построим решение более сложного уравнения вида
у(х) - аЪ [у] - Ы? [у] = fix), B3)
где а и b — некоторые числа, f{x) —произвольная функция. Для этого представим
левую часть уравнения B3) в виде произведения операторов:
A - aL - Ь1?)[у] = {1- AiL)(l - A2L)[y], B4)
где Ai и А2 — корни квадратного уравнения
А^ - аА - 6 = 0. B5)
Пусть Amin < Ai, А2 < Amax.
Решим вспомогательное уравнение
уо{х)-\2Ъ[уо] = !{х), B6)
которое является частным случаем уравнения B1) при А = А2. Его решение дается
формулой
w{x) = Y{f,\2). B7)
Уравнение B3) с учетом B4) и B6) можно записать в виде
A - AiL) A - A2L) [у] = {1- A2L) Н
или, с учетом тождества A — AiL)(l — A2L) = A — A2L)A — AiL), в виде
(l-A2L){(l-AiL)[y]-^(x)}=0.
Это равенство будет выполняться, если искомая функция у{х) будет удовлетворять
уравпению
yix)-ML[y] = wix). B8)
Решение уравнения B8) дается формулой
yix) = Yiw,\i), где w = Yif,\2). B9)
Если однородное уравнение у{х) — A2L[y] = О имеет только тривиальное*
решение у = О, то формула B9) определяет единственное решение исходного
уравнения B3).
Пример 3. Рассмотрим интегральное уравнение
^ь/Лт^--)
у{х)- , ^^B)y{t)dt = f{x).
Из результатов примера 2 (см. п. 3.4-2) следует, что его можно записать в виде
уравнения B3):
Vix) - AL [у] - ^BL2 [у] = fix), L [у] = Z'' ^^.
Jo у^Х - t
* Если однородное уравнение у{х) — X2'Li[y] = О имеет нетривиальные решения, то в
правой части уравнения B8) вместо w{x) должна стоять функция w{x) -\- Уо{х), где уд —
общее решение указанного однородного уравнения.
Страница 56

3.4. Операторные методы решения линейных интегральных уравнений 51
Поэтому решение интегрального уравнения (в квадратурах) дается формулами
y{x)=Y{w,X^), w = Y(f,\^),
У(/,Л) = ^(ж)+7гЛ2 / e:^p\TT\^(x-t)\F(t)dt, F(x) = f(x)^X -^} ^ ,
Jo Jo Vx-t
где Л]^ и Лз —корни квадратного уравнения Л^ —АЛ —В = 0.
Этот метод применим также для решения (в квадратурах) более обших уравнений вида
где /5 — рациональное число, удовлетворяюшее условию О < /5 < 1 (см. пример 2 из п. 3.4-2).
3.4-4. Решение операторных уравнений нолиномиального вида
Метод, описанный в п. 3.4-3, допускает обобщение на случай операторных
уравнений полиномиального вида. Будем считать, что решение линейного
неоднородного уравнения B1) дается формулой B2), а соответствующее однородное
уравнение имеет только тривиальное решение.
Построим решение более сложного уравнения с полиномиальной левой частью
относительно оператора L:
п
2/(x)-^^fcL'=b] = /(x), L'==L(l'=-1), C0)
fc = l
где Ак —некоторые числа, f(x) —произвольная функция.
Обозначим Ai, Л2,..., А п корни характеристического уравнения
п
A'-^AfcA""'' =0. C1)
fc=i
Левую часть уравнения C0) можно представить в виде произведения операторов:
п п
y{x)-J2AkL''[y] = l[{l-XkL)[y]. C2)
fc = l fc = l
Решение вспомогательного уравнения B6), в котором переобозначены w -^ Уп-i,
А2 ^ An, дается формулой yn-i{x) = Y(f,Xn). Рассуждая аналогично тому, как
это делалось в п. 3.4-3, получим, что решение уравнения C0) сводится к решению
более простого уравнения
п-1
l[{l-Xk-L)[y]=yn-i(^), C3)
fc = l
которое имеет меньшую степень (на единицу) относительно оператора L, чем
исходное уравнение. Аналогичным образом можно показать, что уравнение C3)
сводится к решению более простого уравнения вида
п-2
]^A - AfcL)[y] =угг-2(х), Уп-2(х) = Y (уп-1 , Xn-l) •
к = 1
Продолжая последовательно процесс попижепия порядка уравнения, придем в
итоге к уравнению B8), в правой части которого стоит функция yi (х) = У (у2, А2).
Решение этого уравнения дается формулой у(х) = Y(yi, Ai).
Решение исходного уравнения C0) определяется рекуррентно с помощью
формул
yk-i(x) = У(ук,Хк); к = п,...,2,1, где уп(х) = /(х), уо(х) = у(х).
Отметим, что здесь используется убывающая последовательность к = п,... ,2,1.
Страница 57

58 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
3.4-5. Некоторые обобщения
Пусть левая часть липейного (интегрального) уравнения
у{х) - Q [у] = fix) C4)
может быть представлена в виде произведения
п
у{х)-€1[у] = \{{1-Ъф1 C5)
fc=i
где Lfc — линейные операторы. Будем считать, что решения вспомогательных
уравнений
y{x)--Lk[y] = f{x), к = \,2,...,п, C6)
известны и даются формулами
y{x) = Yk[f{x)\, к = 1,2,...,п. C7)
Решение вспомогательного уравнения C6) при к = п,в котором
переобозначено у ^ Уп-1, дается формулой yn-i(x) = Yn [f(x)]. Рассуждая аналогично тому,
как это делалось в п. 3.4-3, получим, что решение уравнения C4) сводится к
решению более простого уравнения
п-1
ll{l--Lk)[y]=yn-i{x).
к = 1
Продолжая последовательно процесс «попижепия порядка» уравнения, придем
в итоге к уравнению C6) при к = 1, в правой части которого стоит функция
yi(x) = Y2 [у2 (ж)]. Решение этого уравнения дается формулой у(х) = Yi[yi(x)].
Решение исходного уравнения C5) определяется рекуррентно с помощью
формул
yk-i(x) = Yk[yk(x)]; к = п,...,2,1, где уп(х) = /(х), уо(х) = у(х).
Отметим, что здесь используется убывающая последовательность к = п,... ,2,1.
(•) Литература: А. D. Polyanin, А. V. Manzhirov A998).
3.5. Построение решений уравнений со специальной
правой частью
в этом разделе описаны способы построения решений интегральных
уравнений со специальпой правой частью. Эти способы основаны на использовании
вспомогательных решений, зависящих от свободного параметра.
3.5-1. Общая схема
Рассмотрим линейное уравнение, которое для краткости будем записывать в
виде
L[j/] = /g(a;,A), A)
где L — некоторый линейный (интегральный, дифференциальный и др.) оператор,
который действует по переменной ж и не зависит от параметра Л; fg(x,X) —
конкретная функция, которая зависит от переменной х и параметра Л.
Будем считать, что решение уравнения A) известно:
у = у(х,Х). B)
Страница 58

3.5. Построение решений уравнений со специальной правой частью
59
Пусть М — некоторый линейный (интегральный, дифференциальный и др.)
оператор, который действует по параметру Л и не зависит от неременной х. Будем
считать, что операторы L и М коммутативны. Подействуем оператором М на обе
части уравнения A). В результате получим, что уравнение
L \w] = !м{х), /м(х) = М [fg(x, Л)], C)
имеет решение
w = M[y(x,X)]. D)
Выбирая различным образом оператор М можно получить решения для
других правых частей уравнения A). Исходную функцию /g(x, Л) будем называть
пороэюдающей функцией для оператора L.
3.5-2. Порождающая функция экспоненциального вида
Рассмотрим линейное уравнение с экспоненциальной правой частью
LM = e^^ E)
Будем считать, что его решение известно и дается формулой B). В таблице 4
приведены решения уравнения L [у] = f{x) с различной правой частью, которые
выражаются через решение уравнения E).
Замечание 1. При использовании указанных в таблице формул не надо знать
левую часть линейного уравнения E) (уравнение может быть интегральным,
дифференциальным и др.), если известно его частное решение для экспоненциальной
правой части. При этом важна лишь самая общая информация о том, что левая
часть уравнения пе зависит от параметра Л.
Замечание 2. При использовании указанных в таблице формул необходимо
проверять сходимость интегралов, входящих в полученное решение.
Пример 1. Решение уравнения с экспоненциальной правой частью
/.
у{х) + К(х- t)y(t) dt
F)
ищем в виде у{х, Л) = ке^
у(х,Х) =
' методом неопределенных коэффициентов. В результате получим
——e^^ В(Х) = 1 + / K(-z)e^^ dz. G)
J^W Jo
Из п. 3 таблицы 4 следует, что решение уравнения
/"ОО
у(х) + / К(х- t)y(t) dt
J X
: Ах
(8)
имеет вид
1^ = 1 +
f
Jo
у(х)
э
К{-
D
z) dz,
AC
С:
zK{—z) dz.
Для того чтобы такое решение сушествовало, должны сушествовать несобственные
интегралы от функций K{—z),zK{—z). Поэтому функция K{—z) должна убывать быстрее,
чем z~'^ при Z ^ оо.Ъ противном случае решения не сушествует. Интересно отметить, что
для растуших по степенному закону функций K{—z) при z ^ оо ъ случае Л < О решение
уравнения F) сушествует и дается формулой G), а решения уравнения (8) не сушествует.
Поэтому следует быть осторожным при использовании формул из таблицы 4 и проверять
сходимость интегралов, входяших в решение.
Страница 59

60
Методы решения линейных уравнений
ВИДА у(ж)
-j^K{x,t)y{t)dt = f{x)
ТАБЛИЦА 4
Решения уравнения L [у] = f{x) с порождаюшей функцией экспоненциального вида
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Правая часть f(x)
gAx
A^e^i^^ hA^e^^^
Аж + Б
гг = 0, 1, 2, •••
А
X -\- а
0
Аж^е^^,
гг = 0, 1, 2, •••
а^
АсЬ(Лж)
Ash(Ax)
Аж^ сЬ(Лж)
m = 1,3,5,.
Аж^ сЬ(Лж)
m = 2,4,6,.
Аж^ 8Ь(Лж)
m = 1,3,5,.
Аж^ 8Ь(Лж)
m = 2,4,6,.
Асо8(/5ж)
А81п(/5ж)
Аж'^со8(/5ж),
гг = 1,2,3,...
Аж'^8т(/5ж),
гг = 1,2,3,...
Ае^^ со8(/5ж)
Ае^^ 81п(/5ж)
Аж^е^^со8(/5ж),
гг = 1,2,3,...
Аж^е^^8т(/5ж),
гг= 1, 2, 3, ...
Решение у
у(ж,Л)
А1у(ж,Л1)+---+А^у(ж,Л^)
у(ж,Л)
1 дХ^
_ +Бу(ж,0)
у(ж,Л)
J л=о
/•оо
А/ е-^^у(ж,-Л)ЙЛ
А
у(ж,Л)
у(х, In а)
^-л[г/(гк, л) + г/(гк,-А)]
iA[?/(x, Л) - г/(х, -А)]
Qm
\A^^[v(xA)+v(x,-\)\
Qm
Qm
\А^^[у{хА)-у{х,-Щ
АКе[у(ж, 1E)]
А1т[у(ж, г/5)]
^4i&H^'^)]},=,,
А1ш\^^\у(х,Х)\\
АКе[у(ж, )U + i/5)]
А1т[у(ж, )U + i/5)]
^^HI^H-^)]},^,,,
^-{^Н-^)]Ц,,
Как получено
Исходное уравнение
Следствие линейности
Следствие линейности
И результатов п. 4
Следствие результатов
п. 6 при Л = 0
Интегрирование
по параметру Л
Дифференцирование
по параметру Л
Следствие п. 1
Линейность И связь
с экспопептой
Линейность И связь
с экспопептой
Дифференцирование по Л,
И связь с экспопептой
Дифференцирование по Л,
И связь с экспопептой
Дифференцирование по Л,
И связь с экспопептой
Дифференцирование по Л,
И связь с экспопептой
Выделение действительной
части при Л = г/5
Выделение мнимой
части при Л = г/5
Дифференцирование поЛ,
выделение действительной
части при Л = г/5
Дифференцирование по Л,
выделение мнимой
части при Л = г/5
Выделение действительной
части при Л = /i + г/5
Выделение мнимой
части при Л = /i + г/5
Дифференцирование по Л,
выделение действительной
части при Л = /i + г/5
Дифференцирование по Л,
выделение мнимой
части при Л = /i + г/5
Страница 60

3.5. Построение решений уравнений со специальной правой частью
1 +
K{—z)cos{Xz)dz, В,
[В^ sin(Ax) — Бд cos(Ax)],
K{—z)sm{Xz) dz.
61
Из п. 15 таблицы 4 следует, что решение уравнения
/•оо
у{х)-\- К{х-t)y{t)dt = А sm{Xx)
J X
дается формулой
у{х)
(9)
3.5-3. Порождающая функция степенного вида
Рассмотрим линейное уравнение со степенной правой частью
L[2/]=x\ A0)
Будем считать, что его решение известно и дается формулой B). В таблице 5
приведены решения уравнения L [у] = f{x) с различной правой частью, которые
выражаются через решение уравнения A0).
ТАБЛИЦА 5
Решения уравнения L [у] = /(ж) с порождающей функцией степенного вида
УФ.
1
2
3
4
5
6
7
8
9
Правая часть /(ж)
х^
п
к=0
Alnx^B
А1п^ж,
гг = 0,1,2,...
гг = 0, 1, 2, ...
Acos{C\nx)
Asm{f3lnx)
Ах^ cos{Clnx)
Ах^ sm(Clnx)
Решение у
у(х,Х)
п
к=0
''Jr[»<''*']«..+'"'"'»>
■'Ш"'-'']}.^
d^ г 1
АКе[у(ж, 1E)]
А1ш[у{х, 1E)]
АКе[у(ж, р^гE)]
А1ш[у{х, р + гE)]
Как получено
Исходное уравнение
Следствие линейности
Следствие линейности
и результатов п. 4
Следствие результатов
п. 5 при Л = 0
Дифференцирование
по параметру Л
Выделение действительной
части при X = iE
Выделение мнимой
части при X = iE
Выделение действительной
части при X = р -\- iE
Выделение мнимой
части при X = р -\- iE
Пример 2. Решение уравнения со степенной правой частью
у(х)^ г -K(-)y{t)dt = x^
Jo X V ж /
Страница 61

62 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
ищем в виде у(ж, Л) = кх^ методом неопределенных коэффициентов. В результате получим
1 .л „,.^_ /-^/.^.л
у{х,\) =
В(Х) = [ K(t)t^
Jo
dt.
1 + В(Л) '
Из п. 3 таблицы 5 следует, что рещение уравнения с логарифмической правой частью
У{'
ж)+ / —K( — )y(t)dt = Aln^.
Jo X \ X J
имеет вид
у{х)
А А1^
■ In ж -
1 + ^0 A + ^о)^'
/q = / K{t)dt, /i = / K{t)lntdt.
Jo Jo
3.5-4. Порождающая функция, содержащая синусы или косинусы
Рассмотрим линейное уравнение с синусоидальной правой частью
L [у] = sin(Ax).
A1)
Будем считать, что его решение известно и дается формулой B). В таблице 6
приведены решения уравпения L [у] = f(x) с различной правой частью, которые
выражаются через решение уравнения A1).
ТАБЛИЦА 6
Рещения уравнения L [у] = f{x) с синусоидальной порождающей функцией
№
1
2
3
4
5
6
7
Правая часть f{x)
sin(Ax)
п
^ AfcSin(Afcx)
к=1
т = 1, 3, 5, ...
Ax^sin(Ax),
m = 2, 4, 6, ...
Ах"^ cos(Xx),
m = 1, 3, 5, ...
sh{Cx)
m = 2, 4, 6, ...
Решение у
y(x,X)
n
k=i
m—l
A(-l)^
Г d^ 1
I dA^ ^ ^J
л=о
m (j^
A(-l)~ y(x, A)
m-1 (]yi
A(-l) 2 y(x, X)
-iy(x,if3)
m+2 г fj-m П
i(-l)^^ y{x, A)
Как получено
Исходное уравнение
Следствие линейности
Следствие результатов
п. 5 при А = 0
Дифференцирование
по параметру А
Дифференцирование
по параметру А
Связь с гиперболическим
синусом, А = г/3
Дифференцирование по А,
связь с гиперболическим
синусом, А = г/5
Рассмотрим липейное уравнение с косинусоидальной правой частью
L[y] = cos(Ax). A2)
Будем считать, что его решение известно и дается формулой B). В таблице 7
приведены решения уравпения L [у] = f(x) с различной правой частью, которые
выражаются через решение уравнения A2).
Страница 62

3.6. Метод модельных решений
63
ТАБЛИЦА 7
Решения уравнения L [у] = f(x) с косинусоидальной порождающей функцией
Ъй
1
2
3
4
5
6
7
Правая часть /(ж)
С08(Лж)
п
к=1
т = 0, 2, 4, ...
Аж'^со8(Лж),
т = 2, 4, 6, ...
Ax^sin(Ax),
?тг = 1, 3, 5, . ..
сЬ(/5ж)
ж^сЬ(/5ж),
т = 2, 4, 6, ...
Решение у
у(х,Х)
п
к=1
т
А{-1)-
Г d^ 1
[ ^дт yV ^J
л=о
га rjm
m+1 rjm
A(-l)^~ y{x, A)
y{x,iE)
m г //'"T' -1
(-1)— y(x, A)
Как получено
Исходное уравнение
Следствие линейности
Следствие результатов
п. 4 при А = 0
Дифференцирование
по параметру А
Дифференцирование
по параметру А
Связь с гиперболическим
косинусом, А = г/3
Дифференцирование по А,
связь с гиперболическим
косинусом, А = г/5
3.6. Метод модельных решений
3.6-1. предварительные замечания*
Рассмотрим линейное уравнение, которое для краткости будем записывать в
A)
- неизвестная функ-
виде
l^[y{x)] = f{x),
где L — некоторый линейный (интегральный) оператор, у{х)-
ция, f{x) — известная функция.
Зададим пока произвольно некоторое пробное решение
Уо=Уо{х,\), B)
зависящее от вспомогательного параметра А (считается, что оператор L не зависит
от А и уо ^ const). Из уравнения A) определим правую часть, которая будет
соответствовать пробному решению B):
/о(ж,А) = Ь[уо(ж,А)].
Умножим обе части уравнения A) при у = уои f = /ояа. некоторую функцию v^(A),
а затем проинтегрируем полученное равенство по А на отрезке [а, 6]. В результате
получим
'^[у^(х)] = U{x), C)
где
Уср(х)
-I
J а
yo(x,X)(p(X)dX,
,(х)
J а
(x,X)(p(X)dX.
D)
Из формул C), D) следует, что для правой части / = fcp(x), решением
исходного уравнения A) будет у = уср(х). За. счет произвола в выборе функции ^(Х) (и
отрезка интегрирования) функцию f^{x) в припципе можно сделать любой.
Основная проблема здесь состоит в том, как подобрать функцию v^(A), чтобы
получить заданную функцию fcp(x). Эту проблему можно решить, если удается найти
До чтения этого раздела полезно просмотреть разд. 3.5.
Страница 63

64 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
такое пробное решение, для которого правая часть уравнения A) будет ядром
известного обратного интегрального преобразования (такое пробное решение будем
обозначать У (ж, Л) и называть модельным решением).
3.6-2. Описание метода
Действительно, пусть ^ — некоторое обратимое интегральное
преобразование, которое любой функции-оригиналу f{x) ставит в соответствии
изображение F{X) по правилу
F{X) = Щ/{х)}. E)
Считаем, что обратное интегральное преобразование ^~ имеет ядро ф(х,Х) и
действует следующим образом:
^-'{F{X)} = f{x), ^-4f(A)}= Г^(АЖх,Л)ЙЛ. F)
J а
Пределы аиЬи путь интегрирования в F) могут лежать в комплексной плоскости.
Пусть удалось найти модельное решение Y(x,X) вспомогательной задачи для
уравнения A), в правой части которого стоит ядро обратного преобразования ^~ :
Ь[¥(х,Х)] = Ф{х,Х)- G)
Умножим обе части G) на F(Л), а затем проинтегрируем по Л в тех же пределах,
которые стоят в обратном преобразовании F). Учитывая, что оператор L не
зависит от Л и используя равенство ^~ {F(X)} = /(ж), получим
Ь[У Y(x,X)F{\)dx\ =/(х).
Отсюда следует, что решение уравнения A) при произвольной функции f(x)
выражается через решение более простого вспомогательного уравнения G) по
формуле
у(х)= [ Y(x,X)F(X)dX,
J а
(8)
где F(X) — изображение функции /(ж), полученное с помощью
преобразования E).
В качестве правой части вспомогательного уравнения G) можно, например,
взять экспоненциальпую, степенную и тригонометрические функции, которые
соответственно являются ядрами обратных преобразований Лапласа, Меллина, синус
и косинус преобразований Фурье (с точность до постоянного множителя). В
ряде случаев методом неопределенных коэффициентов удается сравнительно просто
найти модельное решение (задав его структуру). После этого для построения
решения уравнения с произвольной правой частью можно использовать формулы,
выписанные далее в пп. 3.6-3-3.6-6.
3.6-3. Модельное решение для экспоненниальной правой части
Пусть удалось подобрать модельное решение Y = У (ж, Л), соответствующее
экспоненциальной правой части:
L[У(x,A)] = e^^ (9)
Рассмотрим два случая.
Страница 64

3.6. Метод модельных решений 65
1°. Уравнение на полуоси, О ^ ж < ос. Обозначим f(p) изображение функции /(ж),
полученное с помощью преобразования Лапласа:
/»оо
f{p) = Q{f{x)}, Q{f{x)}= f{x)e-^^dx. A0)
Решение уравнения A) при произвольной правой части f{x) выражается через
решение более простого вспомогательного уравнения с экспоненциальпой правой
частью (9) при \= рпо формуле
-, pc-\-ioo
у{х) = —- / Y(x,p)f(p)dp. A1)
2°. Уравнение на всей оси, — ос < ж < ос. Обозначим f{u) изображение
функции /(ж), нолученное с помощью преобразования Фурье:
1{и) = Ъ{1{х)}. Ъ{!{х)}^^ f^
/(ж)е-^""^ж. A2)
Решение уравнения A) при произвольной правой части f{x) выражается через
решение более простого вспомогательного уравнения с экспоненциальпой правой
частью (9) при Л = г г^ по формуле
у{х) = ^= / Y{x,iu)f{u)du. A3)
Для вычисления интегралов в правых частях формул A1) и A3) используют
методы теории функций комплексного переменного, включая лемму Жордана и
теорему о вычетах (см. пп. 1.1-4 и 1.1-5).
Замечание 1. Модельное решение У (ж, Л) может иметь структуру, отличную
от ядра обратного преобразования Лапласа или Фурье.
Замечание 2. При использовании указанного метода не обязательно знать
левую часть уравнения A) (уравнение может быть интегральным,
дифференциальным, функциональным и др.), если известно его частное решение для эксно-
ненциальной правой части. При этом важна лишь самая общая информация, что
уравпение линейно и его левая часть пе зависит от параметра Л.
Замечание 3. Указанный метод может использоваться также при
решении линейных интегральных (дифференциальных, интегро-дифференциальных и
функциональных) уравнений со сложным аргументом у искомой функции.
Пример 1. Рассмотрим уравнение Вольтерра второго рода с разностным ядром
/•оо
у{х) + / К{х- t)y{t) dt = f{x). A4)
Это уравнение нельзя решить путем непосредственного применения преобразования
Лапласа, так как здесь теорема о свертке не применима.
В соответствии с методом модельных решений рассмотрим вспомогательное уравнение
с экспоненциальной правой частью
/"ОО
у(х)^ K{x-t)y{t)dt = e^\ A5)
J X
Его решение имеет вид (см. пример 1 из п. 3.5-2)
Y{x,p) = i-—e^^ к(-р) = Г K(-z)eP^ dz. A6)
1 + К{-р) Jo
5 А. В. Манж:иров, А. Д. Полянин
Страница 65

66 Методы решения линейных уравнений вида у(х) — J^ К(х, t)y(t) dt = f{x)
Отсюда с помошью формулы A1) получим решение уравнения A2) для произвольной правой
части
1 /-с+гоо ^/ ч
У{^) = 1Г- / ,J^^ в^- ф, A7)
2Ш Jc-ioo 1 + К(-р)
где f(p) —изображение функции /(ж), полученное с помошью преобразования Лапласа A0)
(см. также разд. 3.11).
Отметим, что более сложным путем решение уравнения A2) было получено в книге
М. Л. Краснова, А. И. Киселева, Г. И. Макаренко A968, стр. 42, 43).
3.6-4. Модельное решение для степенной правой части
Пусть удалось подобрать модельное решение Y = Y(x,s), соответствующее
степенной правой части уравнения
L[Y(x,s)]=x-', X = -s. A8)
Обозначим f(s) изображение функции /(ж), полученное с помощью
преобразования Меллина
/»оо
J{s) = m{f{x)}, m{f{x)}= / f{x)x'-Ux. A9)
-'о
Решение уравнения A) при произвольной правой части f(x) выражается через
решение более простого вспомогательного уравнения со степенной правой
частью A8) по формуле
-1 pc-\-ioo
y(^)^^-J Y(x,s)Jis)ds. B0)
/ с — гоо
Для вычисления соответствующих интегралов в правой части формулы B0)
используют методы теории функций комплексного переменного, включая лемму
Жордана и теорему о вычетах (см. пп. 1.1-4 и 1.1-5).
Пример 2. Рассмотрим уравнение
у{х)^ г ^K(-)y{t)dt = f{x). B1)
Jo X V ж /
в соответствии с методом модельных решений рассмотрим вспомогательное уравнение со
степенной правой частью
у{х)+ г ^K(-)y{t)dt = x-\ B2)
Jo X \ X у
Его решение имеет вид (см. пример 2 из п. 3.5-3 при Л = —s)
1
1 +~B(s)
Y(x,s)= ^ /^^ ^ х-'\ B(s)= [ K(t)t-'dt. B3)
Отсюда на основании формулы B0) получим решение уравнения B1) для произвольной
правой части
у(х) = -^ / ''^ \ ^ x-'ds, B4)
^^ ^ 27гг Jc-ioo 1 + B{s) ^ ^
где f(s) —изображение функции /(ж), полученное с помошью преобразования
Меллина A9).
Страница(

3.6. Метод модельных решений 61
3.6-5. Модельное решение для сннусондальной правой части
Пусть удалось подобрать модельное решение Y = Y(x,u), соответствующее
синусу в правой части:
L [У(ж,г^)] = sm{ux), X = и. B5)
Обозначим fs(u) изображение функции /(ж), полученное с помощью
несимметричной формы синус-преобразования Фурье:
Jo
f(x) sm(ux) dx. B6)
Решение уравнения A) при произвольной правой части f(x) выражается через
решение более простого вспомогательного уравнения с синусоидальной правой
частью B5) по формуле
2 f°°
(х)= — / Y(x,u)fs(u)du
^ Jo
у(х) = - / Y(x,u)fs(u)du. B7)
3.6-6. Модельное решение для косинусоидальной правой части
Пусть удалось подобрать модельное решение Y = Y(x,u), соответствующее
косинусу в правой части:
L [У(ж,г^)] = cos(ux), X = и. B8)
Обозначим fc(u) изображение функции /(ж), полученное с помощью
несимметричной формы косинус-преобразования Фурье:
/»оо
fc(u)= J^c{f(x)}, J^c{f(x)}= / f(x)cos(ux)dx.
Jo
B9)
Решение уравнения A) при произвольной правой части f(x) выражается через
решение более простого вспомогательного уравнения с косинусом в правой
части B8) по формуле
у(х) = - / Y(x,u)fc(u)du. C0)
^ Jo
3.6-7. Некоторые обобщения
Как и ранее, будем считать, что ^ — обратимое преобразование, которое
любой функции-оригипалу f(x) ставит в соответствие изображепие F(X) по
правилу E). Обратное преобразование определяется формулой F).
Пусть удалось найти модельное решение Y(x,X) следующей вспомогательной
задачи для уравнения A):
Ь,[У(ж,Л)] = Нл[^^(ж,Л)]. C1)
В правой части уравнения C1) стоит некоторый обратимый линейный
(интегральный, дифференциальный или функциональный) оператор, который не
зависит от неременной х и действует но параметру Л на ядро обратного
преобразования ф(х,Х), см. формулу F). Для паглядности оператор в левой части
уравнения C1) помечен индексом х (он действует по переменной ж и не зависит от Л).
Подействуем на обе части C1) обратным оператором Н^^. В результате в
правой части получим ядро ф(х,Х), а в левой части переставим операторы по
правилу H^^Lx = LxH^^ (это как правило можно сделать, так как операторы
Страница 67

68 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
действуют по различным переменным). Умножим далее обе части полученного
равенства на изображение F{X), а затем проинтегрируем по Л в тех же пределах,
которые стоят в обратном преобразовании F). В результате с учетом равенства
^~^ {FW} = fix) получим
L. [J Г(Х)Щ'[У(х,Х)]с1х\ = fix). C2)
Отсюда следует, что решение уравнения A) при произвольной функции f(x)
в правой части выражается через решение более простого вспомогательного
уравнения C1) по формуле
у(х)= f Р(Х)Щ'[¥{х,Х)]с1Х, C3)
J а
где F(X) — изображение функции /(ж), полученное с помощью
преобразования ^ по формуле E).
Такой подход за счет произвола в выборе оператора Нл расширяет
возможности метода модельных решений.
(•) Литература: А. D. Polyanin, А. V. Manzhirov A997, 1998).
3.7. Метод дифференцирования интегральных
уравнений
в ряде случаев дифференцировапие (однократное, двукратное и т. д.) ипте-
гральных уравнений с последующим исключением интегральных членов с
помощью исходного уравнения позволяет свести их к обыкновенным
дифференциальным уравнениям. Иногда с помощью дифференцировапия удается свести
рассматриваемое уравпение к более простому интегральному уравнению, решение
которого известно. Ниже перечислены некоторые классы интегральных уравнений,
которые сводятся к обыкновенным дифференциальным уравнениям с постоянными
коэффициентами.
3.7-1. Ядро содержит сумму экспонент
Рассмотрим уравнение
у(х)-\-
/ж г ■"-
^^gA,(x-t)
y(t)dt = f(x). A)
Это уравнение в общем случае можно свести к линейному неоднородному
обыкновенному дифференциальному уравнению гг-го порядка с постоянными
коэффициентами.
В широком дианазоне измепения параметров Ак, Хк решение можно
представить в виде:
y(x)^f{x)+ r^Bfc
f{t)dt,
-к = 1
где параметры решения Вк, 1Лк связаны алгебраическими соотношениями с
параметрами уравнения Ак, Хк.
Пример 1. Рассмотрим уравнение
у{х
) + /" [A^e^i^^-^) + ^26^2^^-^)] y{t) dt = fix).
J a
Страница(

3.7. Метод дифференцирования интегральных уравнений
69
1°. Введем обозначения
J а
.Ai(x-t)
y{t) dt,
rx
J a
^X^ix-t)
y(t) dt.
Продифференцируем дважды интегральное уравнение. В результате имеем (первым
записано исходное уравнение)
y^A^I^+A^I^ = f, f = f(x), B)
у', + {А, + А2)у + А,Х,1, + AjAj/j = /;, C)
V'L + (^1 + Л^)У'. + (^lAi + A2X2)V + ^iA?/i + AjAi/j = fj,. D)
Исключая отсюда величины /^ и /3, приходим к линейному обыкновенному
дифференциальному уравнению второго порядка с постоянными коэффициентами
. + (^l+^2-^l-^2)?/i + (^1^2-
-^2^l)y = fxx-i^l^^2)fx^^l^2f- E)
Подставляя значение х = а в равенства B) и C), получим начальные условия
у(а) = f{a), у',(а) = f,(a) - (А^ + A^)f(a). F)
Решение дифференциального уравнения E) с условиями F) позволяет найти решение
интегрального уравнения.
2°. Рассмотрим характеристическое уравнение
/i^ + (Ai + Аз - Ai - \^)р + Л^Лз - А^Лз - А^\ = О, G)
которое соответствует однородному дифференциальному уравнению E) при f(x) = 0.
Структура решения интегрального уравнения зависит от знака дискриминанта квадратного
уравнения G):
D = (Ai - Аз - Ai + X^f + 4AiАз-
В случае D > О квадратное уравнение G) имеет действительные (и различные) корни
^1 ^^2-
f^i
i-(Ai+A2-Ai-A2) + ^v^,
^2
^(Ai+A2-Ai-A2)-
При этом решение исходного интегрального уравнения имеет вид
iv^-
y(x) = f(x)^ / [B,e^i(--'^ ^B^e^^(--'^]f(t)dt,
где
f^i
■+A.
f^i -^1
f^2
+ A.
f^2
f^2 - /^1 /^2 - /^1 /^1 - /^2 /^1 - /^2
В случае D < О квадратное уравнение G) имеет комплексно сопряженные корни
р-^ = а -\- if3, Р2
-if3,
a=i-(Ai+A2
■Л,1 /5=^л
При этом решение исходного интегрального уравнения имеет вид
у(х) = f(x) + /""{Б^е-^"-^) cos[f3(x - t)] + В^е'^^''-'^ sm[f3(x - t)]}f(t) dt,
J a
где
В,
Во
j[A^^2-
■a)+A2(Ai -a)
3.7-2. Ядро содержит сумму гиперболических функций
Уравнения с разностным ядром вида
гх
у(х)+ / K(x-t)y(t)dt^f(x),
J а
т. S
К(х) = ^ Afc ch(Afcx) -\-^Вк sh(/ifc^),
(8)
с помощью формул ch/3 = ^(е^ + ^~^) и sh/3 = ^(е^ — е~^) могут быть
представлены в виде уравнения A) при п = 2т + 2s. Поэтому они сводятся
к линейным неоднородным обыкновенным дифференциальным уравнениям с
постоянными коэффициентами.
Страница(

70 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
3.7-3. Ядро содержит сумму тригонометрических функций
Уравнения с разностным ядром вида
у{х) + / К{х- t)y(t) dt = f(x), К(х) = J2^^ cosiXk^^
•^«^ k=i
px ^
y(x) + / K(x- t)y(t) dt = f(x), K(x) = J2^^ sin(Afca
(9)
A0)
также можно свести к линейным неоднородным обыкновенным
дифференциальным уравнениям 2гг-го порядка с постоянными коэффициентами.
Пример 2. Рассмотрим подробнее уравнение A0).
1°. Обозначим
1^{х)= f\m[X^{x-t)]y{t)dt. A1)
J а
Продифференцируем A1) дважды по ж. В результате имеем (штрихи обозначают
производные по ж)
II = Afc Г cos[Afc(x - t)]yit) dt, I'^ = XkVix) - Xl Г sm[\k(x - t)]v(t) dt. A2)
J a J a
Из сопоставления формул A1)иA2) получим связь между 1'^ и 1^\
1к=Чу(^)-Фк,
■■1кИ-
Интегральное уравнение с помощью A1) можно записать в виде
п
у{х) + Y, A^h = f(^)-
A3)
A4)
Дифференцируя A4) дважды по ж, с учетом равенств A3) имеем
п п
Ухх(х) + (^пУ(х) - Y1 ^кФк = fxx(x)^ ^n = Y. ^кЧ- A5)
к=1 к=1
Исключая интеграл /^ из A4) и A5), получим
п-1
Дифференцируя равенство A6) дважды по ж и исключая интеграл I^-i ^^ полученного
выражения с помощью A6), придем к аналогичному равенству, в левой части которого будет
стоять линейный дифференциальный оператор четвертого порядка с постоянными коэффи-
п-2
циентами (действующий на у) и сумма вида Y1 ^к^к- Продолжая далее с помощью дву-
к=1
кратного дифференцирования и соотнощения A3) последовательно исключать слагаемые
/гг-2' ^п-З' • • •' придем в итогс к линейному неоднородному обыкновенному
дифференциальному уравнению с постоянными коэффициентами порядка 2гг.
Начальные условия для функции у(х) находятся в результате подстановки значения
ж = а в интегральное уравнение и все его следствия, полученные с помощью
дифференцирования.
2°. Найдем корни Zj^ алгебраического уравнения
V А^^ + 1 = 0,
A7)
Страница 70

3.8. Сведение уравнений Волътерра 2-го рода к уравнениям Волътерра 1-го рода 71
которое после приведения к общему знаменателю сводится к задаче об определении корней
характеристического многочлена гг-й степени.
Пусть все корни z^ уравнения A7) действительны, различны и не равны нулю. Все
корни в зависимости от их знака разобьем на две группы:
z^> ()^ 2;2>0, ..., Zg> () (положительные корни);
^s+i < О' ^s+2 < О' • • •' ^п < О (отрицательные корни).
Рещение интегрального уравнения можно представить в виде
y{x) = f{x
A8)
k=s+l
Коэффициенты В^ и С^ находятся из системы линейных алгебраических уравнений
^k^^k , Y^ ^k^^k
Е
'о ^™ + П
k=s+l
XI
о,
-f^k
f^k
^Ы.
m = 1,2,
A9)
Случай с нулевым корнем 2;^ = О рассматривается с помощью введения новой
постоянной D = BgPg и предельного перехода /i^ ^ 0. В результате в рещении A8) вместо члена
В^ sh [/^^(ж — t)\ возникает слагаемое D(x — t), а в системе A9) появляются
соответствующие слагаемые DX^.
Уравнение с разностным ядром, содержащим сумму косинусов и синусов,
также сводится к линейному неоднородному обыкновенному дифференциальному
уравнению с постоянными коэффициентами.
3.7-4. Ядро содержит комбинации различных функций
Любое уравнение с разностным ядром, содержащим линейную комбинацию
слагаемых вида
(x-t)"^ (ш = 0, 1, 2,
ехр[а(ж — t)],
ch.[P(x — t)], sh[7(^ —t)], cos[X(x — t)], sin[/i(x — t)],
B0)
также с помощью дифференцировапия может быть сведено к линейному
неоднородному обыкновенному дифференциальному уравнению с постоянными
коэффициентами. Экспоненциальпая, гиперболические и тригопометрические функции
могут быть умножены также на (ж — t)^ (гг = 1, 2,...).
Замечание. Метод дифференцировапия с успехом может использоваться
также для решения более сложных уравнений с неразностным ядром, к которым
неприменимо преобразование Лапласа.
3.8. Сведение уравнений Вольтерра второго рода
к уравнениям Вольтерра первого рода
уравнение Вольтерра второго рода
у(х)- [ K(x,t)y(t)dt = f(x)
J а
МОЖНО свести к уравнению Вольтерра первого рода двумя способами.
A)
Страница 71

72 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
3.8-1. Первый способ
Проинтегрируем обе части уравнения A) по ж от а до ж, а затем изменим
порядок интегрирования в двойном интеграле. В результате приходим к уравнению
Вольтерра первого рода
J а
M(x,t)y(t)dt = F(x), B)
в котором использованы следующие обозначения:
/X ПХ
K(s,t)ds, F(x)= f(t)dt. C)
3.8-2. Второй способ
Пусть выполнено условие /(а) = 0. Тогда уравнение A) приводится к
уравнению Вольтерра первого рода для производной искомой функции
J а
N{x,t)y't{t)dt = f{x), j/(a) = 0, D)
J а
где
N{x,t) = 1- / K(x,s)ds. E)
Действительно, интегрируя по частям правую часть D) с учетом формулы E),
приходим к уравнению A).
Замечание. При f(a) ^^ о из уравнения A) следует, что у(а) = f(a). В этом
случае замена z(x) = у(х) — f(a) приводит к уравнению Вольтерра второго рода
t)dt,
z(x)- Г K{x,t)z{t)dt = ^{x), Ф(х) = /(х)-/(а)^/(а) Г К{х,
J а J а
ДЛЯ правой части которого выполняется условие Ф@) = О и которое уже может
быть сведено вторым способом к уравнению Вольтерра первого рода.
(•) Литература: В. Вольтерра A982), А. Ф. Верлань, В. С. Сизиков A986).
3.9. Метод последовательных приближений
3.9-1. Общая схема
A)
1°. Рассмотрим интегральное уравнение Вольтерра второго рода
пх
у(х)- / K{x,t)y{t)dt = f{x).
J а
Будем считать, что f(x) непрерывна на отрезке [а, 6], а ядро K(x,t) непрерывно
при а^х^Ь, a^t^x.
Будем искать решение методом последовательных приближений. Для этого
положим
оо
у{х) = f{x) + Y^ ^п{х), B)
Страница 72

3.9. Метод последовательных приблиэюений 73
где (^п{х) определяются по формулам
<pi{x)= / K{x,t)f{t)dt,
J а
Мх)= [ K(x,t)ipi(t)dt= I K2(x,t)f(t)dt,
Mx)= I K(x,t)ip2(t)dt= I Ks(x,t)f(t)dt, ...
J a J a
Здесь
PX
Kn{x,t)= K{x,z)Kn-i{z,t)dz, C)
J a
где n = 2,3,..., причем Ki(x,t) = K(x,t), Kn(x,t) = 0 при t > x.
Функции Kn(x, t), даваемые формулами C), называются итерированными ядрами. Для
них справедливо соотношение
Кп(х, t)= Кт(х, s)Kn-m(s, t) ds, D)
J а
где т — любое натуральное число, меньшее п.
2°. Последовательные приближения можно построить и по другой, более общей
схеме:
Уп(х) = /(х)^ [ K(x,t)yn-i(t)dt, гг = 1,2,..., E)
J а
где уо(х) —какая-либо непрерывная на [а, Ь] функция. Получаемые таким образом
функции yi(x),y2(x), ... также непрерывны на отрезке [а, 6].
При сделанных выше предположениях относительно /(х)иК(х,1)
последовательность {уп(х)} СХОДИТСЯ при гг ^ ОС к непрерывному решению у(х)
интегрального уравнения. Удачный выбор «нулевого» приближения уо(х) может
привести к быстрой сходимости процесса.
Следует отметить, что в частном случае уо(х) = f(x) данный метод переходит
в метод, изложенный в 1°.
Замечание 1. Если ядро K(x,t) квадратично интегрируемо в квадрате
S = {а ^ X ^ Ь, а ^ t ^ Ь} и f(x) G L2(a,6), то последовательные
приближения сходятся в среднем к решению у(х) G L2(a,b) уравнения A) при любом
выборе начального приближения уо(х) G L2(a,b).
3.9-2. Формула для резольвенты
Резольвента интегрального уравнения A) определяется через итерированные
ядра формулой
оо
R{x,t) = Y,Kn{x,t), F)
п=1
где сходящийся ряд, стоящий в правой части, называется рядом Неймана
ядра K(x,t). Решение уравнения Вольтерра второго рода A) может теперь быть
записано в традиционной форме
/
2/(х) = /(х)+ / R{x,t)fit)dt. G)
Страница 73

74 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
Замечание 2. В случае ядра со слабой особенностью решение уравнения A)
может быть получено рассмотренным выше методом последовательных
приближений. При этом ядра Кп(х, t), начиная с некоторого значения гг, непрерывны.
При а < Y непрерывным будет уже ядро К2(х, t).
(•) Литература: У. В. Ловитт A957), С. Г. Михлин A959), М. Л. Краснов, А. И. Киселев,
Г. И. Макаренко A968), В. И. Смирнов A974), В. Вольтерра A982).
3.10. Метод квадратур
3.10-1. Общая схема метода
Рассмотрим линейное интегральное уравнение Вольтерра второго рода
у(х)- [ K(x,t)y(t)dt = f(x) A)
J а
на отрезке а ^ ж ^ 6, и применим для его решения метод квадратур. Будем считать
ядро и правую часть уравнения непрерывными функциями.
На основании уравнения A) найдем, что у (а) = f(a). Возьмем постоянный шаг
интегрирования h и рассмотрим дискретное множество точек Xi = а -\- h(i — 1),
г = 1, 2,..., гг. При х = Xi уравнение A) примет вид
y(xi)- K(xi,t)y(t)dt = f(xi), г = 1,...,гг. B)
J а
Заменяя интеграл в B) квадратурной формулой (см. п. 2.7-1) и выбирая Xj
(j = 1,2,...,г) узлами квадратуры (по переменной t), получим следующую
систему уравнений:
i
y(xi) -^^ijK(xi,Xj)y(xj) = f(xi) -\-€i[y], г = 2,...,n, C)
где Aij —коэффициенты квадратурной формулы на отрезке [а, Жг], ei[y] — ошибка
аппроксимации. Полагая €i[y] малыми и отбрасывая их, получим систему липей-
пых алгебраических уравпений в форме
i
У1 = /ь Vi-Yl "^^з^^зУз = fi^ г = 2,..., п, D)
j=i
где Kij = K(xi,Xj) (j = 1,...,г), fi = f(xi), yj —нриближенные значения
искомой функции у(х) в узлах Xi.
На основании D) получим следующую рекуррентную формулу:
yi=fi, yi = /~\ ^ , г = 2,...,гг, E)
справедливую при условии
1 - АиКи ф О, F)
чего всегда можно добиться за счет выбора узлов и обеспечения достаточной
малости коэффициентов Ац.
Страница 74

3.11. уравнения с бесконечным пределом интегрирования IS
3.10-2. Применение формулы транений
В соответствии с формулой трапеций (см. п. 2.7-1), имеем
Ац = Аи = ^/г, Аг2 = • • • = Ai^i-i = h, г = 2,3,..., гг.
Использование формулы трапеций в общей схеме метода квадратур для решения
интегрального уравнения Вольтерра второго рода приводит к следующему
пошаговому алгоритму:
Л + ^Е CjK,jyj
х.=а + (г-1)/г, n = А^ + 1, /3, = ( ^ ^^^{ = \^
h -^ i 1 при J > 1,
где обозначения совпадают с введенным в п. 3.10-1. Формула трапеций
достаточно проста, эффективна и часто используется на практике. Некоторые особенности
применения метода квадратур для решения интегральных уравнений с
переменным пределом интегрирования отмечены в п. 2.7-3.
3.10-3. Случай вырожденного ядра
В случае решения интегрального уравнения Вольтерра второго рода с
произвольным ядром по мере увеличения номера шага нарастает и объем вычислений.
Если же ядро оказывается вырожденным, то возможно построение алгоритмов с
неизменным объемом вычислений на шаге. Действительно, для вырожденного яд-
т
ра K(x,t) = Е Pk(x)qk(t) уравнение A) можно записать в виде
к=1
У(^) = ^Рк(х) / qk(t)y(t)dt-\- f(x).
k=i -^^
Применение формулы трапеций позволяет получить следующее рекуррентное
выражение (см. п. 3.10-2):
m г—1
fi + hY. PkiT. f^jQkjVj
f, k = \ j = l
yi=/l, Уг =
1 - T^ E PkiQki
k=i
где yi —приближенные значения искомой функции у(х) в узлах Xi, fi = f(xi),
Pki = Pk(xi), Qki = qk(xi), из которого видно, что количество вычислений на
каждом шаге остается неизменным.
(•) Литература: В. И. Крылов, В. В. Бобков, П. И. Монастырный A984), А. Ф. Верлань,
В. С. Сизиков A986).
3.11. Уравнения с бесконечным пределом
интегрирования
представляют также интерес интегральные уравнения второго рода с одним
переменным, а другим бесконечным пределами, содержащие разностное ядро.
Ядра и функции таких уравнений могут не принадлежать описанным в начале
главы классам. В этом случае их исследование проводится методом модельных
решений (см. разд. 3.6) или методом сведения к уравнениям типа свертки. Для
определенности рассмотрим далее уравнения второго рода с переменным нижним
пределом интегрирования.
Страница 75

76 Методы решения линейных уравнений вида у{х) — J^ К(х, t)y(t) dt = f{x)
3.11-1. Случай переменного нижнего предела ннтегрнровання
Интегральное уравнение второго рода с неременным нижним пределом в
случае разностного ядра имеет вид
/»оо
у(х)+ K(x-t)y(t)dt^f{x),
J X
О < Ж < ОС.
A)
Оно принципиальным образом отличается от уравнений Вольтерра второго рода,
рассмотренных выше, для которых решение существует и единственно. Решение
соответствующего однородного уравнения
/»оо
у{х)+ / K(x-t)y(t)dt = 0
J X
B)
может быть и нетривиальным.
Собственные функции иптегрального уравнения B) определяются корнями
следующего трансцендентного (или алгебраического) уравнения относительно
параметра Л:
/■
к(-
' dz ■■
-1.
C)
Левая часть этого уравнения есть изображение функции K(—z), полученное с
помощью преобразования Лапласа с параметром Л.
Например, простому действительному корню Л^ уравнения C) соответствует
собственная функция ук(х) = ехр(—Afcx). Общее решение однородного
уравнения представляет собой линейную комбинацию (с произвольпыми постоянными)
собственных функций уравпения B).
Ниже в примере 1 даны общие решения конкретного уравнения типа B) для
случаев кратных и комплексных корней C).
Общее решение интегрального уравнения A) представляет из себя сумму
общего решения однородного уравнения B) и частного решения неоднородного
уравнения A).
Пример 1. Рассмотрим однородное интегральное уравнение Пикара-Гурса
'L
у(х) -\-А (t- x)'^y(t) dt = О,
0,1,2,
D)
E)
которое является частным случаем уравнения A) при K(z) = A(—z)^.
Общее решение однородного уравнения имеет вид
m
У(^) = Y1 <^fcexp(-Afcx),
к=1
где Cj^ —произвольные постоянные, Л^. —корни алгебраического уравнения
Л^+1 + Ап\ = О, F)
удовлетворяющие условию Re Л^. > О (т — число корней уравнения F), для
которых это условие выполняется). Уравнение F) есть частный случай уравнения C) при
K(z) = A(—z)^. Корни уравнения F), для которых ReA^. ^0 должны быть отброшены,
поскольку интеграл в C) для них расходится.
Уравнение F) имеет комплексные корни. Рассмотрим два случая, которые
соответствуют разным знакам величины А.
1°. Пусть А < 0. Решение уравнения D) имеет вид
у{х) = Се-^^, Л = {-Ап\) гг+1 ,
где С — произвольная постоянная. Это решение единственно при гг = 0,1, 2, 3.
G)
Страница 76

3.11. уравнения с бесконечным пределом интегрирования 11
При п^А, выделяя в E) действительную и мнимую части, придем к общему решению
однородного уравнения Пикара-Гурса в форме
[гг/4]
у{х) = Се-^- + Y. ехр(-а,а^) [С^^^ cos(/5,a^) + cf ^ sin(/5,a^)], (8)
k=i
где С^ \ C^fc — произвольные постоянные, [а] — целая часть числа а, Л определено в G),
а коэффициенты а^ ia E^ даются выражениями
а^ = \Ап]\ п+1 cos(^--^j, /5fc = |Агг!| -+i sml^—^y
Заметим, что решение (8) содержит нечетное число слагаемых.
2°. Пусть А > 0. Выделяя в E) действительную и мнимую части, получим обшее решение
однородного уравнения Пикара-Гурса в форме
[^]
у(х)= Y1 exp(-afcx)[c(i)cos(/3fcx) + cf sin(/3fcx)], (9)
fc=0
где Cl \ Cj^ ^ —произвольные постоянные, а коэффициенты а^ и f3^ даются формулами
Заметим, что решение (9) содержит четное число слагаемых. В частных случаях при п = О
и гг = 1, выражение (9) приводит к тривиальному решению у{х) = 0.
Пример 2. Рассмотрим неоднородное интегральное уравнение Пикара-Гурса
/•оо
у{х)^А {t-x)''y{t)dt = Be-^"", гг = 0,1,2,..., A0)
J X
которое является частным случаем уравнения A) при K(z) = A(—z)^ и/(ж) = Ве~^^.
Будем считать, что р > 0. Рассмотрим два случая.
1°. Пусть /2^+-*^ + Ап\ ф 0. Частное решение неоднородного уравнения имеет вид
5(.) = De--, !>= Д;";^,. A1)
при А < о, обшее решение неоднородного уравнения Пикара-Гурса является суммой
решений (8) и A1). При А > О, обшее решение уравнения A0) есть сумма решений (9) и A1).
2°. Пусть р^^^ + Ап\ — 0. Поскольку р положительно, то А должно быть отрицательным.
Частное решение неоднородного уравнения имеет вид
D гг+2
-y(x)=Exe-^^\ Е=—^—-. A2)
А\п + 1)!
Обшее решение неоднородного уравнения Пикара-Гурса есть сумма решений (8) и A2).
3.11-2. Приведение к уравнению Винера-Хонфа второго рода
Уравнение A) может быть приведено к одностороннему уравнению второго
рода типа
/»оо
у(х)- K-(x-t)y(t)dt = f(x), О < ж < оо, A3)
где ядро К- (s) = О при s > О и К- (s) = —K(s) при s < 0.
Методы исследования уравнения A3) описаны в главе 5, где рассматриваются
уравнения второго рода с постоянными пределами. Там же в п. 5.9-3 изучено
уравнение второго рода с разностным ядром и переменным нижним пределом
интегрирования посредством приведения его к уравнению Винера-Хопфа второго
рода.
(•) Литература: Ф. Д. Гахов, Ю. И. Черский A978).
Страница 77

4. Методы решения линейных уравнений
вида J^ К(х, t)y(t) dt = f(x)
4.1. Предварительные замечания
4.1-1. Интегральные уравнения Фредгольма первого рода
Линейные интегральные уравнения первого рода с постоянными пределами
интегрирования имеют форму
K(x,t)y(t)dt^f(x), A)
/
где у(х) —неизвестная функция (а^х^ 6), К(х, t) —ядро интегрального
уравнения, f(x) —некоторая известная функция, которая называется свободным членом
или правой частью уравнения A). Функции у{х) и f{x) обычно считают
непрерывными, либо квадратично интегрируемыми на [а, 6]. Если ядро интегрального
уравнения A) непрерывно в квадрате 5' = {а^ж^6, a^t^6}, либо квадратично
интегрируемо в этом квадрате, т. е.
/7'
K^(x,t)dxdt = В^ < ОС, B)
где В — постоянная, то его называют фредголъмовым ядром. Уравнения с
постоянными пределами интегрирования вида A), имеющие фредгольмово ядро, называют
уравнениями Фредгольма первого рода.
Ядро интегрального уравнения K(x,t) называется выроэюденным, если оно
представимо в виде K(x,t) = gi(x)hi(t) Ч- • • • -\- gn(x)hn(t).
Ядро интегрального уравнения K(x,t) называется разностным, если оно
зависит от разности аргументов: K(x,t) = К(х — t).
Ядро интегрального уравнения K(x,t) называется симметричным, если оно
удовлетворяет условию K(x,t) = K(t,x).
Интегральное уравнение, полученное из A) заменой ядра K(x,t) на K(t,x),
называется союзным с A) или транспонированным к нему.
Замечание 1. В общем случае переменные t и х в уравнении A) могут
изменяться в различных пределах (например, a^t^bnc^x^d).
4.1-2. Интегральные уравнения первого рода со слабой особенностью
Если ядро интегрального уравнения A) является полярным:
^(^' *) = ^3^ + ^(^' *)' о < а < 1, C)
либо логарифмическим:
K(x,t) = L(x,t)\n\x-t\ -\-M(x,t), D)
где L(x,t), M(x,t) непрерывны в S и L(x,x) ^ О, то оно называется ядром со
слабой особенностью, а само уравнение —уравнением со слабой особенность.
Страница 78

4.1. Предварительные замечания 79
Замечание 2. Ядра с логарифмической особенностью и полярные ядра при
О < а < ^ являются фредгольмовыми.
Замечание 3. Случай, когда пределы интегрирования а и/или b могут быть
бесконечными, вообще говоря, не исключается, но при этом следует внимательно
проверять выполнение условия B).
4.1-3. Интегральные уравнения тнна свертки
Интегральное уравнение первого рода с разностным ядром на всей оси (его
называют иногда уравнением типа свертки первого рода с одним ядром) имеет
вид
f
J —с
К(х -t)y(t)dt = f(x), -ОС < ж < ОС, E)
где у(х) — искомая функция, К(х) —ядро интегрального уравнения, f(x)
—правая часть интегрального уравнения (введенные обозначения будем использовать и
далее).
Интегральное уравнение первого рода с разностным ядром на полуоси имеет
вид
/»оо
/ K{x-t)y{t)dt = f{x), 0<ж<оо. F)
-'О
уравнение F) называется также односторонним уравнением первого рода или
интегральным уравнением Винера-Хопфа первого рода.
Пятспргтьяое уравнение типа свертки с двумя ядрами первого рода имеет вид
/»оо гО
/ Ki{x-t)y{t)dt+ /
Jo J -с
Ki{x-t)y{t)dt-\- K2{x-t)y{t)dt = f{x), -оо<ж<оо, G)
«V —oo
где Ki(x) и K2(x) —ядра интегрального уравнения G).
Функция д(х) удовлетворяет на действительной оси условию Гёльдера, если
для любых действительных xi и Ж2 выполняется неравенство
\д{х2) - 9{xi)\ ^ А\х2 -xi\^, О < Л ^ 1,
и для любых достаточно больших по модулю Ж1 и Ж2 справедливо
\д(х2) - g(xi)\ ^А
0< Л^ 1,
где АиХ — положительные числа (последнее условие является условием Гёльдера
в окрестности бесконечно удаленной точки).
Предположим, что функции у(х), f(x) и ядра К(х), Ki(x), К2(х) таковы,
что их изображения, полученные с помощью преобразования Фурье,
принадлежат L2(—ОС, оо) и, кроме того, удовлетворяют условию Гёльдера.
Для того чтобы некоторая функция у(х) принадлежала введенному классу
функций, достаточно, чтобы функция у(х) принадлежала L2(—оо,оо), а ху(х)
была абсолютно интегрируема на (—оо, оо).
Замечание 4. Иногда класс функций и ядер для уравпений тина свертки (в
частности, для уравнения Випера-Хопфа) отличается от введенного в п. 4.1-3. Это
обстоятельство будет оговариваться в каждом отдельном случае.
Страница 79

80 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x
4.1-4. Парные интегральные уравнения первого рода
Парное интегральное уравнение первого рода с разностными ядрами {типа
свертки) имеет вид
/оо
Ki(x-t)y(t)dt = /(ж), О < ж < оо,
.Г (8)
/ К2(х -t)y(t)dt = f(x), -оо < ж < О,
J —оо
где обозначения, класс функций и ядер совпадают с введенными ранее для
уравнений тина свертки.
Парное интегральное уравнение первого рода в достаточно общем случае
имеет вид
/»оо
/ Ki(x,t)y(t)dt = fi(x), a<x<b,
J а
/»oo
/ K2(x,t)y(t)dt = f2(x), b<x<oo,
J a
где /i(x), /2(ж) и Ki(x,t), K2(x,t) —известные правые части и ядра
уравнения (9), а у (ж) — функция, подлежащая определению. Его различные формы будут
рассмотрены в пп. 4.6-2 и 4.6-3.
Интегральные уравнения, полученные из E)-(8) заменой ядра К(х — t) на
K(t — х), называются союзными с ними или транспонированными к ним.
Замечание 5. К уравнениям E)-(8) приводятся некоторые уравнения, ядра
которых содержат произведение или отношение переменных ж и t.
Замечание 6. Уравнения типа свертки E)-(8) иногда записывают в форме,
где перед интегралами ставят множитель I/V^tt.
® Литература: И. Снеддон A955), С. Г. Михлин A959), Б. Нобл A962), И. Ц. Гохберг,
М. Г. Крейн A967), П. П. Забрейко, А. И. Кошелев и др. A968), М. Л. Краснов, А. И. Киселев,
Г. И. Макаренко A968), Л. Я. Цлаф A970), Я. С. Уфлянд A977), Ф. Д. Гахов, Ю. И. Черский
A978), А. J. Jerry A985), А. Ф. Верлань, В. С. Сизиков A986), L. А. Sakhnovich A996),
А. D. Polyanin, А. V. Manzhirov A998, 1999).
4.2. Метод Крейна
4.2-1. Основное н вспомогательное уравнения
Опишем здесь метод построения точных аналитических решений линейных
интегральных уравнений первого рода со слабой особенностью и произвольной
правой частью. Метод основан на построении вспомогательного решения более
простого уравнения с правой частью равной единице. Вспомогательное решение
используется для построения решения исходного уравнения при произвольной
правой части.
Рассмотрим уравнение
f
J —с
K(x-t)y(t)dt = f(x), -а^х^а. A)
Считаем, что ядро интегрального уравнения A) является полярным или
логарифмическим, а К(х) —четная положительно определенная функция, пред ставимая
Страница 80

4.2. Метод Крейна 81
в виде
К{х) = C\х\-^ + М(х), О < м < 1,
К(х) = р\п-^^М(х),
\х\
где Р > О, —2а ^ X ^ 2а, М(х) — достаточно гладкая функция.
Одновременно с A) будем рассматривать вспомогательное уравнение,
зависящее от параметра ^ (О ^ (J ^ а):
K(x-t)w(t,^)dt = l, -^^х^С B)
-С
/:
4.2-2. Решение основного уравнения
Для любой непрерывной функции f(x) решение исходного уравнения A)
может быть выражено через решение вспомогательного уравнения B) по формуле
у(х) = — / w(t,a)f(t)dt\w(x,a)
^^ ^ 2М'{а) Ida J_^ У ^ JJ У J J У ^ J
-- [ w(x,n—\^--— [ w(t,nf(t)dt\dC C)
где M(^) = w(x,^) dx, штрих обозначает производную, a последний внутрен-
ПИЙ интеграл берется по Стилтьесу
Формула C) позволяет получить некоторые точные решения интегральных
уравнений вида A) с произвольной правой частью.
Пример 1. Решение интегрального уравнения
которое встречается в теории упругости, дается формулой C), где функции М(^) и w(t, ^)
определяются выражениями
2Ал-1 / ^ч _ ^@
M(^)={ln—) , ^(t,0
Пример 2. Рассмотрим интегральное уравнение
j:m-'">' «<-'■
\x-t\^
которое встречается в теории ползучести. Его решение дается формулой C), где
функции М(^) Hw(t,^) определяются выражениями
(•) Литература: Н. X. Арутюнян A959), И. Ц. Гохберг, М. Г. Крейн A967).
6 А. В. Манж:иров, А. Д. Полянин
Страница 81

82 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
4.3. Метод интегральных преобразований
Метод интегральных преобразований позволяет привести некоторые
интегральные уравнения на всей оси и на полуоси к алгебраическим уравнениям для
изображений. Последние элементарно разрешаются относительно изображения
искомой функции. Решение исходного интегрального уравнения получается в
результате применения обратного интегрального преобразования.
4.3-1. Уравнение с разностным ядром на всей оси
Рассмотрим интегральное уравнение
К(х -t)y(t)dt = f(x), -ОС < ж < ОС, A)
Г
J —с
где /(ж), у(х) G L2(—ОС, оо) и К(х) G Li(—оо, оо).
Применим к уравнению A) преобразование Фурье. Тогда с учетом теоремы о
свертке (см. п. 1.4-4) получим
V2^K(u)y(u) = ]{и). B)
Таким образом, с помощью преобразования Фурье нам удалось свести
решение исходного интегрального уравнения A) к решению алгебраического
уравнения B) для изображения искомого решения. Решение последнего уравнения имеет
форму
л/27г К{и)
причем функция f(u)/K(u) должна принадлежать L2(—оо, оо).
Тем самым изображение решения исходного интегрального уравнения
оказалось выраженным через изображения заданных функций — ядра и правой части
уравнения. Само решение может быть выражено через его изображение с
помощью формулы обратного преобразования:
г/(х) = —^=- / у(и)е^^^ du = — / ~ е'^^ du. D)
4.3-2. Уравнения с ядром К(х, t) = K(x/t) на полуоси
f
Jo
Интегральное уравнение первого рода
K(x/t)y(t) dt = f(x), О ^ ж < оо, E)
/о
заменой переменных х = е^, t = е^, w(r) = ty(t) приводится к виду A). Его
решение может быть также получено путем непосредственного применения
преобразования Меллина, что будет в аналогичной ситуации проделано в следующем
разделе.
4.3-3. Уравнение с ядром K(x,t) = K(xt) н его обобщения
1°. Рассмотрим сначала следующее уравнение:
K(xt)y(t) dt = f(x), О ^ ж < оо. F)
/■
Страница 82

4.4. Задача Римана для действительной оси 83
Его заменой переменных х = е^, t = е~^ можно привести к виду A), но
здесь удобнее использовать преобразование Меллина (см. разд. 1.3). Умножая обе
части F) на ж^~^ и интегрируя по х от нуля до бесконечности, получим
/»оо /»оо /»оо
/ y(t) dt / K(xt)x'-^ dx= f(x)x'-^ dx.
Jo Jo Jo
Bo внутреннем интеграле двойного интеграла сделаем замену z = xt.B результате
получим
/»оо
K(s) / y(t)t-'dt = J(s). G)
-'о
Учитывая равенство
/»ос
y{t)t-'dt = y{l-s),
f
Jo
/о
перепишем уравнение G) в следующем виде:
K(s)y(l - s) = /(s). (8)
Заменяя в (8) 1 — s на s и разрешая полученное выражение относительно y(s),
находим изображение искомого решения
y(s) = р-'\ (9)
^^ ^ K{l-s) ^^
По формуле обращения Меллина получим решение интегрального
уравнения F) в виде
^^"^ = i/
•' ^ ' X ds.
K(l-s)
2°. Рассмотрим теперь более сложное уравнение
^0
K{ф)ф{t))g{t)y(t)dt = f{x). A0)
/О
Считаем, что выполнены условия (р@) = О, v^(oo) = оо, ср^ > О, '0@) = О,
ф(оо) = оо,фх > 0.
преобразование
z = ^), г = ф(г), y{t) = ^w{T)
приводит A0) к уравнению вида F)
K(zr)w(r)dr = F(z),
f
Jo
Jo
где функция F{z) задается параметрически: F = f {х), z = Lp{x) .Во многих
случаях, исключая из этих равенств ж, удается получить явную зависимость F = F(z).
(•) Литература: В. А. Диткин, А. П. Прудников A965), М. Л. Краснов, А. И. Киселев,
Г. И. Макаренко A968).
4.4. Задача Римана для действительной оси
краевая задача Римана служит одним из основных инструментов построения
решений интегральных уравнений, к которым могут быть применены различные
интегральные преобразования, и при этом возможно использование теорем типа
свертки. Ее исследование проводится на примере интегрального преобразования
Фурье.
Страница 83

84 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x
4.4-1. Связь интеграла Фурье с интегралом типа Коши
Пусть У{т) — функция, интегрируемая на замкнутом или разомкнутом
контуре L, расположенном в комплексной плоскости z = и -\- iv {т — комплексная
координата точек контура). Рассмотрим интеграл типа Коши (см. разд. 6.2):
27гг Jj^ г- Z
Он определяет функцию, аналитическую в комплексной плоскости с разрезом по
контуру L. Если L — замкнутая кривая, то интеграл будет функцией,
аналитической в каждой связной части плоскости, ограничиваемой L. Пусть контур L есть
вещественная ось, тогда
^г y(-Ldr={y;(i "р«^^>0' A)
27гг J_^ T-Z \3^ (^) при Im^ < 0. ^ ^
Кроме того, существуют предельные значения функций 3^ (^) па
действительной оси и они будут связаны с плотностью 3^ интеграла следующими формулами
Сохоцкого-Племеля:
°° B)
У-{и) = -Ыи) + ^ ^^dr
2 27гг ,/_^ т-и
У+{и)-у-{и)=У{и), у+{и) + у-{и) = — Г ^^dT.
тгг J_^ т-и
C)
Интеграл в последних формулах понимается в смысле главного значения по Коши.
В интеграл Фурье*
^") = ^/_
З^(г^) = / у(х)е^^^ dx
действительный параметр и входит посредством аналитической функции, поэтому
в нем можно и заменить на комплексное z. Функция комплексного
переменного З^(^), определяемая интегралом
1 f°^
= -у^ / y(x)e'^''dx
Л/27Г J_^
y{z) = ^ y{x)e^'^dx, D)
будет аналитической в той области комплексной плоскости z = и -\- iv, где
интеграл D) абсолютно сходится. Если такая область не сводится к одной
действительной оси, то интеграл D) даст аналитическое продолжение интеграла Фурье в
комплексную плоскость z = u-\-iv. Интеграл D) будем также называть интегралом
Фурье.
Установим связь между этим интегралом и интегралом типа Коши с
плотностью З^(г^), взятыми по оси. Будем иметь
— / —^—^dr = ^— / у(х)е dx, Im^ > О,
тгг J_^ T-z л/27г Jo
— Г ^^ dr = - -^ / у(ж)е'"" dx, Im ^ < 0.
E)
F)
В разд. 6.4-6.6 используется альтернативное преобразование Фурье (см. п. 1.4-3).
Страница 84

4.4. Задача Римана для действительной оси 85
4.4-2. Односторонние интегралы Фурье
Если З^(^) = З^^(^) ^сть аналитическая в верхней полуплоскости
функция, имеющая своим предельным значением на действительной оси функцию
У [и) = З^^(г^) G L2(—оо,оо), то функцию З^^(^) можно представить
интегралом Коши. Отсюда в на основании E) будем иметь
1 f°°
^ dx,
причем в силу непрерывности интеграла предельные значения на оси можно
получить простой заменой в последнем равенстве ^ на г^ :
1 f°^
" dx,
где у(х) есть, согласно E), оригинал для З^(г^). Правую часть можно рассматривать
как интеграл Фурье от функции, равной тождественно нулю для отрицательных х.
Отсюда в силу единственности нредставления функции 3^^ (г^) интегралом Фурье
следует, что у(х) = О яа отрицательной полуоси.
Наоборот, если у(х) = О для ж < О, то ее интеграл Фурье принимает вид
^"^ = ^/о
З^(г^) = / у(х)е^^^ dx.
От замены параметра и на число z, лежащее в верхней полуплоскости, сходимость
интеграла только улучшается. Отсюда следует аналитичность функции
V2¥ Jo
y{z) = ^ y{x)e"^dx
В верхней полуплоскости.
Случай нижней полуплоскости рассматривается аналогично.
Интегралы
y^{z) = -^ Г у(х)е'^''dx, y-(z) = -^ Г y(x)e'^-dx G)
называются односторонними интегралами Фурье, правым и левым
соответственно. Значки ± над символами функций, как и в формуле A), будут означать
аналитичность этих функций соответственно в верхней или нижней полуплоскостях.
Введем функции
,. /^^ _ / У{х) при ж > О, . /^ч _ Г О при ж > О,
^+^^^ - \ О при ж < О, ^-^^^ ~ \ -у{х) при ж < 0. ^^^
Будем называть их правой и левой односторонними функциями для у{х)
соответственно, а иногда просто правой и левой функциями. Очевидно, будет справедливо
равенство
у{х) = у+{х)-у-{х). (9)
Используя известную функцию sign ж:
Г 1 при ж > О, .^^.
sign ж = i -, ^ Pi A0)
^ 1—1 при ж < О, ^ ^
можно у±{х) выразить через у{х) в следующем виде:
У±{х) = ^(±1+signx)y(x). A1)
У односторонних функций значки ± будем всегда писать внизу.
Страница 85

86
Методы решения линейных уравнений вида /^ K(x,t)y(t) dt = f(x)
Интегралы Фурье правой и левой односторонних функций есть краевые
значения функций, аналитических соответственно в верхней и нижней полуплоскостях.
Приведем аналоги формул Сохоцкого-Племеля C) в интегралах Фурье:
У {и) = —7^ \ у{х)е'''' dx = —= / у(х)е''''' dx-\-
+ ^/' y(x)e'''''dx = y^(u)-y-(u),
тгг J_^ г-и
1 f°° . iux
= / y(x)signx е'^^ dx.
л/27г J_^
Таким образом, первая из формул Сохоцкого-Племеля (представление
произвольной функции в виде разности краевых значений аналитических функций) здесь
является тривиальным следствием разбиения интеграла Фурье на правый и левый.
Вторую из формул можно записать еще в следующей форме:
A2)
" dx ■■
-J /»оо л;/ \
F{y(x)signx} = — / —^^ dr.
A3)
4.4-3. Теорема об аналитическом продолжении и теорема Лиувилля
Ниже приведены теорема об аналитическом продолжении и обобщенная
теорема Лиувилля в форме единого утверждения, которое будет использовано далее
в главах 4 и 5.
Пусть функции 3^1 (^) и3^2(^) апалитичпы соответственно в верхней и нижней
полуплоскостях за исключением может быть точки z^ ф оо, где они могут иметь
полюс. Если 3^1 (^) и 3^2 (^) ограничены на бесконечности, причем главные части
их разложений в окрестности точки z^ имеют вид
^1 _| £2 |_ _| ^т — ^m-l(^J
z-z^ {z-z^Y {z-z^)^ ~ (z-z^)^'
a сами функции совпадают на действительной оси, то они представляют единую
во всей плоскости рациопальную функцию
У(^)
■ со-\-
(z-z^)"^
где Со —постоянная, Vm-i —полином степени т — 1. Полюс z^ может лежать
как в полуплоскостях, так и на действительной оси.
Ниже приведена более общая объединенная формулировка теорем.
Если функции y-^(z)Hy2(z) аналитичны соответственно в верхней и нижней
полуплоскостях за исключением может быть конечного числа точек Zq = со, z^ (/с = 1, 2,..., гг), где
они могут иметь полюсы, причем главные части разложений этих функций в окрестности
полюсов имеют вид
_0 ^ГПп
C^Z + C^Z^ + •
+ ••• +
---^m,{^)
В точке z.
-i(^)
(^ - Ч?
0'
В точках Zu
(Z-Z„)"^k (Z-Z„)"^k
Страница <

4.4. Задача Римана для действительной оси 87
а сами функции совпадают на действительной оси, то они представляют единую во всей
плоскости рациональную функцию
y(z) = C + V^^{z) + Y^
fi (^-
где С — постоянная. Полюсы z^ могут лежать как в полуплоскостях, так и на
действительной оси.
4.4-4. Краевая задача Римана
Решение задачи Римана в этом разделе будет отличаться от традициопного тем,
что оно будет выражаться не в интегралах тина Коши (см. н. 6.3-7), а в интегралах
Фурье. Для решения рассматриваемых уравпений тина свертки последний аппарат
является более удобным.
Индексом непрерывной не обращающейся в нуль комплексной функции М (и)
(М(и) = Mi(u) + гМ2(и), —ос < и < оо, М(—оо) = Л^(оо)) называется
изменение ее аргумента на действительной оси, выраженное в полных оборотах:
IndMiu) = -L[argA4(„)]^^ = _1_[1пЛ4(и)]Г^ = iy dlnMiu).
Если М (и) не дифференцируема, но имеет ограниченную вариацию, то интеграл
нужно понимать в смысле Стилтьеса. Из правил действий над аргументом
вытекают следующие свойства индекса:
lnd[Mi(u)M2(u)] = lndMi(u) + lndM2(u),
Ind J^^^liM = IndMUu) - lndM2(u), IndWiu) = nlndM(u).
M2(U)
Если функция Л4 (и) является краевым зпачением аналитической, за исключением
может быть конечного числа полюсов в верхней или нижней полуплоскости
функции, то
lndM(u) = ±(N-P),
где знак плюс берется для верхней, а минус — для нижней полуплоскости, Л^ —
число нулей, а Р — число полюсов в соответствующей полуплоскости, причем
нули и полюсы считаются с учетом их кратности.
Если в окрестности некоторой точки zq аналитическая функция З^(^) имеет
представление
У{г) = {Z - zorViiz),
где 3^1 (^) аналитична и yi(zo) ф О, то целое число ш (положительное,
отрицательное или нуль) называется порядком функции З^(^) в точке ^о- Если ттг > О, то
порядок функции есть порядок ее нуля, если ш < О, то порядок ее есть порядок
полюса с противоположным знаком. Если порядок функции в ^о есть пуль, то в
такой точке функция нринимает конечное, отличное от нуля, значение. При
рассмотрении бесконечно удаленной точки разность z — zq^ следует заменить на 1/^.
Сформулируем задачу Римана. Пусть на действительной оси заданы две
функции: Т>(и) — коэффициент задачи и 1-L(u) — свободный член, причем
выполнено условие нормальности Т){и) ф 0. Функции l-i{u) i^T){u) — \ принадлежат
L2(—ОС, оо) и при этом удовлетворяют условию Гёльдера (см. н. 4.1-3). Требуется
найти две функции 3^^ (^) — аналитические соответственно в верхней и нижней
Страница 87

88 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x
ряют краевому условию
у+{и) = V(u)y- (и) + Щи). A4)
Из представления V(u) вытекает, что Р(оо) = 1. Последнее условие не
ограничивает общности дальнейших рассуждений, поскольку, разделив краевое условие A4)
на Р(оо), всегда можно получить необходимую форму задачи.**
Если Т>(и) = 1, то задача Римана называется задачей о скачке. Если ?{(и) = О,
то задача Римана называется однородной. Индекс и коэффициента краевой задачи
V(u) называется индексом задачи Римана.
Рассмотрим задачу о скачке, т. е. определим 3^^ (z) по краевому условию
У^(и)-у-(и) = П(и). A5)
Решение этой задачи дает первая формула A2):
y^{z) = ^= Г H{x)e''''dx, y-{z) = ^ / Я(ж)е'""^ж, A6)
где
Н(х) = —^ П 'ЯAг)е-'"" du. A7)
Построим необходимое для дальнейших исследований частное решение А'(^)
однородной задачи Римана A4):
Х^{и) = V{u)X~ {и), Р(оо) = 1, A8)
не обращающееся на действительной оси в нуль с дополнительным условием
А'^(оо) = 1. Обозначим через Л^+ и Л^- числа нулей функций X^{z) и Х~ {z)
соответственно в верхней и нижней полуплоскостях. Вычисляя индекс обеих
частей краевого условия A8), на основании свойств индекса получим
N+ + N-= lndV{u) = и. A9)
Пусть сначала ly = О.В этом случае \iiT>(u) будет однозначной функцией. Из
соотпошения A9) следует, что Л^+ = Л^- = О, т. е. решение не имеет нулей во
всей плоскости. Поэтому функции InA'^(^) и 1пА'~(^) будут аналитическими в
своих полуплоскостях и, следовательно однозначными вместе со своими краевыми
значениями In Х~^(и) и In А'" (г^). Логарифмируя краевое условие A8) будем иметь
\пХ^{и)-\пХ~{и) = \nV{u). B0)
Выбирая для \iiT>(u) такую ветвь, чтобы InP(oo) = О (можно показать, что
окончательный результат не зависит от выбора ветви), придем к задаче о скачке.
Тогда на основании A5)-A7) и B0) решение задачи A8) можно представить в
форме
^'^^^^^^/Ш 9{x)e^''dx, g~(z) = --^ g(x)e'''dx, ^^1)
1 /"°° -iux
g(x) = / \nV(u)e ^^^ du.
л/27г J_^
* Пару функций y^(z) можно трактовать как одну кусочно аналитическую во всей
комплексной плоскости функцию y{z). В ряде случаев мы будем использовать последнее
обозначение.
** Поскольку основным аналитическим выражением задачи Римана является ее краевое
условие, то при ссылках на соответствующую задачу будем часто указывать только ее
краевое условие и писать, например, задача Римана A4).
Страница <

4.4. Задача Римана для действительной оси
89
Соотношения B1) позволяют сделать важный вывод о том, что не
обращающуюся в нуль на действительной оси функцию нулевого индекса V{u), такую что
Р(оо) = 1, можно представить в виде отношения функций, являющихся краевыми
зпачениями функций, аналитических и не обращающихся в нуль соответственно в
верхней и нижней полуплоскостях.
Перейдем к случаю произвольного индекса однородной задачи Римана A8).
Канонической функцией (однородной задачи Римана) ?^{z) называют функцию,
удовлетворяющую краевому условию A8), условию А'^(оо) = 1 и имеющую
пулевой порядок всюду, за исключением может быть точки —г, где ее порядок
равен индексу задачи Римана v. Ее можно построить, приведя однородную задачу
Римана к рассмотренному случаю нулевого индекса. Действительно, запишем
краевое условие однородной задачи Римана A8) в форме
Х+{и) =
и -\- г
V{u)
и -\-г
Х-[и]
B2)
Тогда стоящая в первых квадратных скобках функция имеет нулевой индекс и
может быть представлена в виде отношения краевых значений аналитических в
верхней и нижней полуплоскостях функций. Отсюда и из краевого условия B2)
получим выражение для канонической функции
X+{z) = е^+(^'
6^{z)
f
Jo
9{х)
X-{z) =
д{х)е^'' dx, G~ (z) = -
1
1°
J —ОС
f
J —с
In
и -
V{u)
.^"(^)
g(x)e^^^ dx, B3)
du,
и -\- i ^
i пуль порядка z^, a в случае и < 0-
где Х~ (z) в случае и > О имеет в точке
нолюс порядка \iy\.
Коэффициент краевой задачи Римана V(u) может быть представлен в виде
отношения краевых значений канонической функции (см. B2) и B3)):
^ ' Х-(и)
B4)
Такое представление Т>(и) в виде отношения краевых зпачений канонической
функции часто называют факторизацией.
Рассмотрим теперь однородную задачу Римана с краевым условием
у^(и) = V(u)y- (и), Р(оо) = 1. B5)
Подставляя в B5) выражение для V(u) в форме B4), приведем краевое условие к
виду
Х+{и) Х-(и) ' ^ ^
Согласно формулам B3) для X(z)b левой и правой частях равенства B6) стоят
краевые значения функций аналитических соответственно в верхней и нижней
полуплоскостях, за исключением может быть точки —г, где порядок равен и. Для
выбранного класса функций их зпачение на бесконечности есть нуль. Тогда по
теореме об аналитическом нродолжении и обобщенной теореме Лиувилля (см.
н. 4.4-3) при jy > О будем иметь
y+{z) _ y-{z)
i(^)
X^(z) X-(z) {z^iy
B7)
Страница <

90
Методы решения линейных уравнений вида /^ K(x,t)y(t) dt = f(x)
где Vv-i{z) — произвольный многочлен степени р — 1 (степень числителя ниже
степени знаменателя в силу З^(оо) = 0). Отсюда
y{z) = X(z)-
i(^)
(z + iy
При I/ ^ О в силу У{оо) = О по обобщеииой теореме Лиувилля y{z)
B8)
0.
Итак, однородная краевая задача Римана при zy > О имеет точно v линейно
независимых решений вида
^ = 1,2,..
, ^,
{z + iY
при zy ^ о нетривиальных решений нет.
Правая часть равенства B8) имеет во всей плоскости ровно v нулей, включая и
нуль на бесконечности. Эти нули могут быть расположены в любых точках верхней
и нижней полуплоскостей или действительной оси. Если обозначить число нулей
на действительной оси через Л/'о, то формула A9) в общем случае (без условия об
отсутствии нулей на действительной оси) заменяется следующей:
N+ + N-+Nq= lndV{u) = и. B9)
Перейдем к решению неоднородной задачи Римана с краевым условием A4).
Воспользуемся соотношением B4) и приведем краевое условие к виду
У^(и) _ у-(и)
Щи)
+ "^^'^ . C0)
л:+(и) л:-(и) л:+(и) ^ ^
представим последнее слагаемое как разность краевых значений аналитических в
верхней и нижней полуплоскостях функций (см. задачу о скачке), т. е.
Щи)
W^{u)-W~{u).
A'+(w)
где
W
VZTT Jq V2-!T J_^
, , 1 p Щи)
w(x)e^^^ dx,
л:+(и)
du.
Подставляя C1) в C0), получим
3^+(w)
W^{u)
у-{и)
yV~{u),
C1)
C2)
C3)
X+{u) ' ' ' ' X-{u)
По теореме об аналитическом продолжении и обобщенной теореме Лиувилля при
v > О будем иметь
X+(z)
Откуда при zy > О получим
W^{z)
X-{z)
■yV~{z)
{z^iy
y{z) = X{z)
yV{z) +
i(^)
C4)
{z^i)-
В правой части формулы C4) присутствует в качестве слагаемого общее
решение B8) однородной задачи. Таким образом, получено общее решение
неоднородной задачи.
Страница 90

4.4. Задача Римана для действительной оси
91
При zy ^ О следует положить Vv-i{z) = О, и искомое решение запишется в
виде
y{z) = X{z)y\;{z). C5)
Однако только при v = 0 формула C5) дает решение удовлетворяющее всем
условиям. Если zy < О, то функция А'(^) будет иметь в точке —г полюс порядка |z^|. В
этом случае для существования решения в выбранном классе функций
необходимо, чтобы второй множитель имел в точке —г нуль соответствующего порядка. На
основании соотношений F) и C2) представим функцию W~ {z) в форме
W~{z)
1 Г°° Щт) dr
2ш ]_^ Х+{т) T-Z
Разлагая последний интеграл в ряд по степеням ^ + г и приравнивая нулю
коэффициенты при {z -\- г) ~^ (/с = 1, 2,..., |zy|), получим условия разрешимости
задачи в виде
f
J —с
Щи)
du
= 0, A; = l,2,...,|zy|.
C6)
Х+{и) (u^i)^
Для наглядности на рис. 3 приведена принципиальпая схема метода решения
задачи Римана на действительной оси.
Сформулируем окончательные результаты, касающиеся решения задачи
Римана. Если индекс задачи и > О, то однородная и неоднородная задачи Римана
безусловно разрешимы и их решения
y^{z) = X^iz)-
i(^)
y^(z) = X^{z)
(z + гУ
(однородная задача), C7)
. (неоднородная задача) C8)
зависят от V произвольных комплексных постоянных, где Vv-\{z) — полином
степени zy — 1. Если zy ^ О, то однородная задача имеет лишь тривиальное нулевое
решение, а неоднородная задача имеет единственное решение
y^{z) = X^{z)y^^{z) C9)
при соблюдении |zy| условий C6). При этом
In
и + \
1 /"°°
X+(z) = e^^^'\ X-(z) =
V{u)
du,
1 Г
g{x)e^''dx, Q (z) = -—^ g{x)e^
Щи)
' dx,
-ъих 1
-e du,
D0)
D1)
D2)
D3)
w{x) = —^=- /
W+(^) = ^= г w{x)e''''dx, W~{z) = ^ / w(x)e''''dx. D4)
Последовательность действий для получения решения можно представить
следующим образом:
1°. По формуле D0) отыскивается д(х), а по ней с помощью D1) —
функция 0^(^).
Страница 91

92 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x
Рис. 3. Схема решения краевой задачи Римана для функций y~^(z)
и y~{z), аналитичных соответственно в верхней и нижней
полуплоскостях комплексной плоскости z = и -\- iv. Считается, что Т>(и) т^ О и
V^_i{z) = Оприг^ ^0.
Страница 92

4.4. Задача Римана для действительной оси 93
2°. По формулам D2) находится каноническая функция X {z).
3°. По формуле D3) определяется w{x)^ а затем с помощью D4) —
функция W^(^).
После этого по формулам C7)-C9) и D2) находится решение однородной и
неоднородной задач. В случае z^ < О необходимо еще проверить выполнимость
условий разрешимости C6).
4.4-5. Задача Римана с рациональными коэффициентами
Полученное решение задачи Римана требует вычисления ряда интегралов
Фурье. Легко можно было бы выразить решение также через интегралы типа Коши.
Как правило, интегралы не берутся в конечном виде, а вычисляются различными
приближенными методами. Это трудоемкий процесс, поэтому представляет
интерес выделить те случаи, когда решение можно получить по краевому условию
методом аналитического продолжения, минуя квадратуры.
Пусть в краевом условии A4)
Viu) = Щ^
П_{и)
Q+{u) Q_{u)
Здесь lZ^{u)^ Q^{u) и 7l-(u), Q-(u) —многочлены, нули которых лежат
соответственно в верхней и в нижней полуплоскостях (не следует смешивать их с
введенными ранее, имеющими аналогичные обозначения, односторонними
функциями). Обозначим степени многочленов 7^+, 7^_, Q+, Q- соответственно ш+,
т-, гг+, п-. Так как по условию задачи Т>(оо) не может обращаться ни в нуль, ни
в бесконечность, будет выполняться соотношение ш+ + ш_ = гг+ + гг_. Индекс
задачи выразится равенством
jy = liidT>(u) = 771+ — гг+ = —(т- — гг_).
Умножив краевое условие на Q-{u)/lZ-{u), будем иметь
7^_(w) Q+W 7^_(w)
Если свободный член 1-L{u) также есть рациопальная функция, то легко решается
задача о скачке
W+ {и) - W- {и) = ^^Щи). D5)
iZ_{u)
Для этого достаточно правую часть разложить на сумму простых дробей. Тогда
W^{u) и W~ {и) будут соответственно суммами дробей с полюсами в нижней и
в верхней полуплоскостях. К полученному равенству
-У^{и) - У\^^{и) = + ,У~(и) - yV~(u)
П_{и) Qj^{u)
можно непосредственно применить теорему об аналитическом продолжении и
обобщенную теорему Лиувилля. Единственной исключительной точкой, где
единая во всей комплексной плоскости аналитическая функция может иметь
ненулевой порядок, будет бесконечно удаленная, где порядок функции будет равен
I/ — \ = ш+ — гг+ — 1 = гг_ — тп- — 1.
При zy > О решение запишется в виде
У^{^) = ^^[^^^(z)^v.-,(z)], y-(z) = |±^[w-(^) + ^.-i(^)].
Q_(z) /^+(^J
Страница 93

94 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f(x)
При zy ^ О нужно положить Vv-1 = о и при zy < о выписать еще условия
разрешимости, получаемые приравниванием нулю \ь'\ начальных членов разложения
рациональной функции W(^) в ряд в окрестности бесконечно удаленной точки (по
степеням 1/ z).
Решение задачи о скачке D5) можно получить или используя метод
неопределенных коэффициентов, как это делается при интегрировании рациопальных
функций, или же используя теорию вычетов аналитических функций. Пусть Zk есть
полюс кратности т функции \Q-[z)/lZ- {z)\l-L{z). Тогда коэффициенты главной
части ее разложения в окрестности точки Zk
4 _^ ... _^ ^'^
могут быть получены по формуле
к 1 d^-
Сп
(j-l)\ dzJ-
n_(z)
n(z)
Рассмотренный случай нередко встречается на практике. Он важен также и как
один из возможных путей решения задачи при общих предположениях.
Аппроксимация произвольных коэффициентов рассматриваемого класса рациопальными
функциями является одним из распространенных способов приближенного
решения краевой задачи Римана.
4.4-6. Исключительные случаи. Одиородиая задача
Пусть в краевой задаче Римана коэффициент Т>(и) имеет нули соответственно
порядков ai, ..., «г в точках ai,..., аг и полюсы* порядков /3i, ..., Д в точках
6i, ..., 6s (ai, ..., «г, /?1, ..., Ps — целые положительные числа). Таким образом,
коэффициент представляется в виде
г
V(u) = ^^ Vi(u), Vi(u)j^O, —оо<и<оо, \^а^=ш, У^ Cj = п.
1 i=l
D6)
Функцию Vi (и) в свою очередь представим (см. п. 4.4-5) в виде
i>i(»)=^;"g-;>2w, D7)
где 71-\-(и), Q-^(u) и 71-(и), Q-(u), так же как и выше — многочлены степеней
соответственно ш+, гг+ и ш_, гг_, имеющие нули в верхней и нижней
полуплоскостях. Функция Т>2 (и) удовлетворяет условию Гёльдера, имеет нулевой индекс и
нигде на действительной оси не обращается в нуль. Кроме того, на нее могут быть
наложены некоторые условия дифференцируемости в окрестности точек а^, bj и,
может быть, в окрестности бесконечно удаленной точки.
* В случае, когда функция Т>(и) не аналитическая, термином «полюс» будет обозначаться
точка, где функция обращается в бесконечность целого порядка.
Страница 94

4.4. Задача Римана для действительной оси 95
Краевое условие однородной задачи Римапа запишется в виде
г
\{{и-а,Г^П^{и)П_{и)
У^{и) = ^ V2(u)y-(u). D8)
Решение будем искать в классе функций, ограпичепных на вещественной оси и
обращающихся в нуль на бесконечности:
З^(оо) = 0. D9)
Коэффициент Т>(и) на бесконечности имеет порядок
rj = п -\- п-^ -\- п- — т — т^ — тп-. E0)
Число
ь/ = т^ — гг+ E1)
назовем индексом задачи. Введем обозначение
h = п- — гп-. E2)
Тогда порядок на бесконечности выразится формулой
rf = h — р -\- п — т. E3)
Приступим теперь к решению задачи D8). Применяя общие приемы, положим
Q^{z) = —7^ \ д(х)е'^'' dx, G~ {z) = --7^ / д(х)е'^''dx
и запишем краевое условие в виде
Д (w - а^Г^П_ (w)e^^^"^ П (^ - ^•)^' Q+{u)e^~ ^"^
Применяя, аналогично тому, как это сделано ранее, аналитическое
продолжение и обобщенную теорему Лиувилля, получим в качестве единственной
возможной особенности полюс на бесконечности.
Возможны два случая:
1°. Пусть порядок коэффициента краевой задачи на бесконечности ?7 > О, т. е.
Т>(и) имеет на бесконечности нуль порядка г]. Пз E3) следует n — iy^m — h.
Приравнивая левую и правую части равенства E5) многочлену Vu-n-i(z), получим
решение краевой задачи в следующем виде:
;+(.) = fliz - а.Г Ы^е^^<^^Т..^.,{г),
y-{z) = fliz-b,f^^e^-<^^V..^.,{z).
У'
E6)
n.{z)
3=1
Задача имеет v — n линейно независимых решений при i/ — п > О и имеет лишь
тривиальное нулевое решение при г^ — п < 0.
Страница 95

96
Методы решения линейных уравнений вида /^ K(x,t)y(t) dt = f(x)
2°. Пусть ?7 < О, т. е. Т>{и) имеет на бесконечности полюс порядка —ту. В
этом случае т — h>n — и^и общее решение получим из E6), если в нем
заменим Vu-n-i(z) naVh-m-iiz). В этом случае задача имеет h — т решений
при /г — ш > О и лишь тривиальное нулевое при h — т ^ 0.
Согласно E3) имеем
h — т = 1У — п-\-г]. E7)
Таким образом, в обоих рассмотренных случаях число линейно независимых
решений равно индексу минус суммарное число полюсов (включая и полюс на
бесконечности) коэффициента V(u). Следовательно, число линейно независимых
решений однородной задачи Римана не изменяется от наличия нулей
коэффициента и уменьшается на суммарный порядок его полюсов.
4.4-7. Исключительные случаи. Неодиородиая задача
Предположим, что свободный член имеет те же полюсы, что и коэффициент.
Краевое условие можно представить в виде
У+{и) = i=i V2{u)y-(u) + , ^1^"^
3 = 1 J = l
E8)
где Т>2(и), 1-Li{u) удовлетворяют условию Гёльдера и, кроме того, некоторым
условиям дифференцируемости в окрестности точек аг, hj, ос.
1°. Пусть порядок коэффициента краевой задачи на бесконечности ту ^ 0. В силу
того, что первые два члена равенства E8) на бесконечности обращаются в нуль,
минимально возможный порядок Tii (и) на бесконечности равен 1—гг. Заменяя, как
и в однородной задаче, Т>2(и) отношением двух функций E4), запишем краевое
условие в виде (под фигурными скобками выписаны порядки соответствующих
функций на бесконечности)
S г
11(и- b^fo Q_{u)y+{u) Д (n - а,Г^П^{и)у-{и)
П_{и)е^^(^)
Q^{u)e^ (^)
-h
n_{u)e^^(^)
l — n — h l — m — v 1 — n — h
Допустим, что многочлен S(u) степени n-\-h — l представляет главную часть
разложения последнего члена в окрестности бесконечно удаленной точки (в случае,
если гг + /г — 1 > 0)
n_iu)e^4u^ -S{u) + W{u)^ moo) = 0.
Заменив W{u) разностью краевых значений аналитических функций
W{u) = W"'{и) -W~{и),
где
w(x) = , / yV(u)e *^^ du,
Л/27Г J_oo
E9)
F0)
dx,
Страница{

4.4. Задача Римана для действительной оси
97
приведем краевое условие к виду
ll{u-bjfjQ_{u)y+{u)
j=i
П_{и)е^^(^)
-S(u)-W^(u)--
11{и-а,Г^П^{и)у-{и)
i=l
-W~(u).
Применяя теорему об аналитическом продолжении и обобщенную
теорему Лиувилля и учитывая, что единственной особой точкой рассматриваемой
функции может быть лишь бесконечно удаленная точка, а также тот факт, что
—п — h ^ —т — 1У (г] ^ 0), получим
y+(z)
7г_B)е5'^(^)
3=1
-[W+(z)+Siz)+r,+^-i(z)],
y-(z) = , ^+^'^''^ ^^^ [W-iz)+V.+^-iiz)].
F1)
Последние формулы определяют решение, имеющее в точках аг, bj полярные
особенности. Чтобы получить ограниченное решение, воспользуемся
канонической функцией неоднородной задачи.
Канонической функцией V(z) неоднородной задачи Римана в исключительном
случае называется кусочно аналитическая функция, удовлетворяющая краевому
условию E8), имеющая во всей конечной части плоскости, включая точки ai
и bj, нулевой порядок и обладающая на бесконечности наинизшим возможным
порядком.
Пусть Ыр(г) —интерполяционный многочлен Эрмита с узлами
интерполяции порядков ai, Pj соответственно в точках а^, bj. Такой многочлен степени
р = т-\-п — 1 существует и определяется единственным образом (см. п. 6.3-1). На
заданные функции T>i (и), TCi (и) нужно наложить дополнительное условие, чтобы
в окрестности точек а^, bj они имели производные порядков ш, f3j соответственно,
удовлетворяющие условию Гёльдера. Тогда каноническая функция неоднородной
задачи запишется в виде
+ ('у\ —
V^{z)
U(^-bjf^Q_{z)
-[W^(z)^S(z)-Up(z)],
V-{z)^^r^+^ [W-{z)-U,{z)].
\{(z - air^n+(z)
F2)
Складывая V(^) с полученным ранее общим решением однородной задачи,
получим общее решение рассматриваемой неоднородной задачи:
y+{z) = V+(.) + fliz - а,Г' |^e«+(^V.-„-i(.),
:y-(.) = V-(.) + П(. - 6,y^ |±Le^-Wp._„_i(.).
F3)
7 A. B. Манж:иров, A. Д. Полянин
Страница 97

98
Методы решения линейных уравнений вида /^ K(x,t)y(t) dt = f{x)
При zy — гг > О задача имеет р — п линейно независимых решений. В случае zy — гг ^ О
нужно положить Vu-n-i(z) = 0. При 1У — п<0 каноническая функпия V(^) имеет
на бесконечности порядок zy — гг < О и, следовательно, перестает быть решением
неоднородной задачи. Однако, подчиняя свободный член п — и условиям, можно
добиться повышения порядка на бесконечности функции V(u) на гг — zy единиц и
тем самым вновь сделать каноническую функцию V(^) решением неоднородной
задачи.
Чтобы обеспечить выполнимость указанных операций, достаточно
потребовать, чтобы функции и 7{i(u) и Т>2{и) имели на бесконечности производные
порядков до гг — zy, удовлетворяющие условию Гель дера.
2°. Пусть ?7 < 0. Наинизший возможный порядок 7{i(u) на
бесконечности h — и — т -\- 1. Тогда в условии E8) функция [Hi(u)Q-(u)]/[JZ-(u)e^ ^^'']
будет иметь па бесконечности порядок, равный 1 — т — и. В этом случае после
выделения главной части разложения [Hi(u)Q-(u)]/[JZ-{u)e ^'^^] в
окрестности бесконечно удаленной точки при т -\- и — 1 > О краевое условие запишем в
виде
Yl{u-bjf^Q_{u)y^{u)
j=i
7г_(«)е^+(^)
-W^(u) = -
11{и-а,Г^П^{и)у-{и)
-W~(u)^S(u).
Каноническая функция пеоднородной задачи выражается через иптерполяциопный
многочлен следующим образом:
V+(^)
-[W+(z)-Up(z)],
■bAibQ_{z)
vriz) =
Q+(z}
=ff-(^)
F4)
Y[{z - aX'T^^iz)
i = l
Общее решение задачи E8) примет вид
y+iz) = V+{z) + f[{z-air
i = l
s
-[W-(z)-S(z)-UAz)l
n_{z)_ c+
(^)
Vh-
n^(z)
F5)
y-(z) = V^(z)^l[(z-
j=i
При h — m > 0 задача имеет h — m линейно независимых решений. В случае
h—m^O многочлен Vh-m-i(z) нужно положить тождественно равным нулю, а от
свободного члена в случае /г—ш < О потребовать выполнения ш—/г условий такого
же вида, как и в предыдущем случае. При выполнении этих условий неоднородная
задача E8) будет иметь единственное решение.
Замечание. В разд. 4.5 будут рассмотрены уравнения, которые приводятся
к задаче Римана посредством применения теоремы о свертке для преобразования
Фурье. Аналогично можно исследовать уравнения, к которым применимы теоремы
о свертке для других интегральных преобразований, например для преобразования
Меллина.
(•) Литература: Н. И. Мусхелишвили A968), Ф. Д. Гахов, Ю. И. Черский A978),
S. G. Mikhlin, S. Prossdorf A986).
Страница!

4.5. Метод Карлемана для уравнений типа свертки первого рода 99
4.5. Метод Карлемана для уравнений типа свертки
первого рода
Методом Карлемана назовем метод приведения интегрального уравнения к
краевой задаче теории аналитических функций, в частности, к задаче Римана. Для
уравнений типа свертки такое приведение осуществляется с помощью
интегральных преобразований. После решения краевой задачи искомая функция может быть
получена посредством обратного интегрального преобразования.
4.5-1. Уравнение Вннера-Хонфа первого рода
Рассмотрим уравнение Винера-Хопфа первого рода
K(x-t)y(t)dt = f(x), 0<ж<оо, A)
— Г
л/2^ Jo
которое часто встречается в приложениях. Доопределим его на отрицательной
полуоси путем введения односторонних функций
у^(^)={f^ Z X; S: /-(-)={1^'^ Z X; S: ^-(-)=о при. > 0.
Используя односторонние функции, запишем уравпение A) в виде
К(х — t)y^{t) dt = f-\-(x) Ч- У- (ж), —ОС < X < ОС. B)
— Г
n/2^ У-с
Всномогательная функция у-(х) введена для того, чтобы доопределить левую
часть уравнения B) при х < 0. Заметим, что у-(х) в области х < О неизвестна и
находится в процессе решения задачи.
Применяя теперь к уравнению B) преобразование Фурье, получим
следующую краевую задачу:
/С{и) /С{и)
Если а — порядок JC(u) на бесконечности, то порядок коэффициента краевой
задачи на бесконечности г] = —а<0. Общее решение задачи C) можно получить на
основании соотношений F5) из п. 4.4-7, заменив в них Vh-m-i(z) на Vu-n-\-r]-i(z).
Решение исходного уравнения A) получим из решения задачи C) по формуле
обращения
у(х) = у+{х) = -^ / З^+Не-^^^ du, х>0. D)
Л/27Г J_oo
Отметим, что в формуле D) явно присутствует только функция З^^(г^), которая
связана с У~ (и) соотношением C).
4.5-2. Интегральные уравнения с двумя ядрами первого рода
Рассмотрим интегральное уравнение первого рода
^= / Ki{x-t)y{t)dt-\-^^ / K2{x-t)y{t)dt = f{x), -оо<ж<оо.
E)
Преобразование Фурье уравнения E) приводит к решению следующей краевой
задачи:
у+(и)^^^у-(и) + р^, -оо<и<оо. F)
7*
Страница{

100
Методы решения линейных уравнений вида /^ K(x,t)y(t) dt = f{x)
Ее коэффициент представляет собой отношение функций, обращающихся в пуль
на бесконечности, и, следовательно, в отличие от предыдущего случая, может
иметь в бесконечно удаленной точке нуль или полюс некоторого порядка.
Пусть ]Ci{u) = Ti(u)/u^, а JC2(u) = Т2(и)/и^, где функции Ti(u) и Т2(и)
имеют на бесконечности нулевой порядок. В зависимости от того, будет ли
разность Г] = /а — X отрицательна или положительна, могут представиться два
случая. Для общности будем считать, что имеются также исключительные точки
на конечном расстоянии. Пусть функции JCi(u) и 1С2{и) имеют представления
S Р
JCi(u) = ll(u-bjf^ll(u-Cky^JCii(u),
j=i
k=i
р
i=l к=1
кроме общих нулей в точках Ск кратности 7fc, функции JCi(u) и }С2(и) имеют
па бесконечности общий нуль порядка min(A,/i).
Коэффициент задачи Римана можно представить в виде
г
V{u) = ^ V2{u).
3 = 1
Пз F) следует, что эта задача и интегральное уравнение E) будут разрешимы, если
J^(u) в точках Cfc, являющихся общими нулями функций /Ci (г^), }С2(и), имеет нуль
порядка 7fc, т. е. Т(и) имеет вид
р
:F{u) = l[{u-cky'':Fi{u).
Для этого необходимо выполнение 7i + ''' + 7р = ^ условий
И''''(«)]„=с, =0- ifc=0,l,...,7fc-l,
или, ЧТО все равно, условий
/»оо
f(x)x^^e^^^^ dx = 0.
f
J —с
(V)
(8)
К этим условиям в рассматриваемом случае уравнения первого рода добавятся еще
d = min(A,/i)+ 1 (9)
условий, накладываемых на поведение Т(и) на бесконечности, так как функции
JCi(u), }С2(и) имеют на бесконечности общий нуль порядка min(A,/i).
Следовательно, Т(и) должна удовлетворять условиям (8) и иметь на бесконечности
порядок не ниже d.
Если эти условия выполнены, то краевая задача F) принимает вид
11{и-а,Г^П^{и)П_{и)
У^(и) = ^
-V2(u)y-(u)^
Щ{и)
3 = 1
3 = 1
Страница 100

4.5. Метод Карлемана для уравнений типа свертки первого рода
101
Ее решение приведено ранее в п. 4.4-7. В случае г] ^ О (/j. ^ X) оно записывается
в виде
.•-1 ^-V^J
y-(z) = V-(z)^l[(z-bj
j=i
n^{z)^ /.-n+l(^J.
A0)
в случае г] < О (fi < X) оно дается в виде
y+{z) = Vtiz) + f[iz - а^Г^^^е^^^^^Тн-ш-ф),
.•—1 ^-V^J
y-(z)^V^{z) + ll{z-
3 = 1
TZj^iz)
A1)
Решение исходного интегрального уравнения в обоих случаях может быть
получено путем подстановки выражений A0), A1) в формулу
y(x) = ^J ^ [У+ (и) - у- («)]е-™- du.
Пример. Рассмотрим уравнение первого рода
—= / К^{х - t)y{t) dt + —= / К^{х - t)y{t) dt = fix),
A2)
^iW = {
при ж > 0, т^ / \
'27г(еЗ^-e^^) при ж < О, ^2(^J ^ | q
27Г ie ^^ при ж > О,
при ж < О,
J.. ч _ Г О при ж > О,
^^^^ ~ \ л/2^(е^^ - е^^) при ж < 0.
A3)
Применяя преобразование Фурье к функциям из A3), получим
/Ci(w)
1
(и - 2i){u - 3i)
Краевая задача F) здесь имеет вид
, JC^iu)
1
u-\-2i
, :f(u)
(и - 2i){u - 3i)
и -\-2г
Коэффициент Т>(и) имеет в бесконечно удаленной точке полюс первого порядка
(i^ = —1). Тогда
т_^ = 2, п_^ = 0, г^ = т_^ — п_^ = 2, min(A, р) = 1, d = 2.
Функция Т(и) имеет на бесконечности нуль второго порядка, следовательно, необходимое
условие разрещимости уравнения выполнено.
Однородная задача
и -\-2г
в классе функций, обращающихся в нуль на бесконечности, имеет следующее рещение:
y+(z)
С
z-\-2i
где С — произвольная постоянная.
у-(^)
с
(z-2i)(z -Зг) '
Страница 101

102
Методы решения линейных уравнений вида /^ K(x,t)y(t) dt = f{x)
у{х) :
Число линейно независимых решений задачи A3) меньше индекса на единицу, так как
Т>(и) имеет полюс первого порядка на бесконечности.
Решение неоднородной задачи в классе функций, обрашаюшихся в нуль на
бесконечности, имеет вид
-л/27ггСе-2^ при ж > О,
/2^С(е2^ - е^^) - 4гл/2^е2^ + 5гл/2^е^^ при х < 0.
При выбранной выше правой части уравнение оказывается разрешимым. Возьмем
теперь, например,
О при ж > О,
л/27ггEе^^ - 46^^) при х < 0.
Тогда J-"(и) = (и -\- 2i)/[{u — 2i){u — Si)]. Соответствуюшая краевая задача Римана имеет
вид
(и — 2i)(u — Si)
fi^)
A4)
У^{и) :
-У~{и) +п + 2г.
п + 2г
Ее решение в классе функций, ограниченных на бесконечности, можно представить в форме
C-Z . C-Z- (^ + 2гJ
y+{z) :
у-(^)-
A5)
^ + 2г' " '"' {z-2i){z-Si)
Ни при каком подборе постоянной С решение не обрашается в нуль на бесконечности,
следовательно, уравнение с правой частью, заданной выражением A4), не имеет решений,
интегрируемых на вешественной оси.
(•) Литература: Н. И. Мусхелишвили A968), Ф. Д. Гахов, Ю. И. Черский A978),
S. G. Mikhlin, S. Prossdorf A986).
4.6. Парные интегральные уравнения первого рода
4.6-1. Метод Карлемана для уравнения с разностными ядрами
Рассмотрим парное интегральное уравнение тина свертки
^= / Ki(x-t)y(t)dt = f(x), 0<ж<оо,
л/27г J_^
1 f°^
—^= \ К2(х- t)y(t) dt = /(ж), -ОС < ж < о,
A)
где функция у(х) подлежит определению.
С целью дальнейшего использования интегрального преобразования Фурье
(см. ПН. 1.4-3, 4.4-1, 4.4-2) доопределим соотношения A) на всю действительную
ось. Для этого добавим в правые части обоих соотношений новые неизвестные
функции. Эти функции должны быть выбраны так, чтобы заданные на полуосях
уравнения оставались справедливыми. Таким образом, к правой части первого
уравнения A) следует прибавить функцию, исчезающую на положительпой
полуоси, а к правой части второго уравнения A) — функцию, исчезающую на
отрицательной полуоси. В итоге парное интегральное уравнение принимает вид
-^ Г K,(x-t)y(t)dt = f(x)^^-(x),
-^ Г К2(х - t)y(t) dt = fix) + U(x),
где ^±(x) — неизвестные правая и левая односторонние функции
ос < ж < ос,
Страница 102

t.6. Парные интегральные уравнения первого рода
103
применяя интегральное преобразование Фурье, получим
K:i{u)y{u) = Т{и) + ^~{и), }С2(и)У(и) = Т{и) + Н+Н.
B)
Соотношения B) содержат три неизвестные функции З^(г^), Н^(г^), и Н (
Исключая У {и) из соотношений B), придем к краевой задаче Римана в форме
ос < 1/ < ос.
-+(.;
_ М^Е-^и) + Щ;:^Ы±:г^и\
/Ci(w) ' ' /Ci(w)
В данном случае коэффициент краевого условия представляет собой
отношение функций, обращающихся в пуль на бесконечности, и, следовательно, может
иметь в бесконечно удаленной точке нуль или полюс некоторого порядка.
Решение краевой задачи Римана может быть построено на основании пп. 4.4-6 и 4.4-7,
а решение интегрального уравнения A) определится по формуле
У{х)
V2^ J-,
-{u) + J=-{u)
du
■E-{u)+J'(u)
IC,{u)
du.
C)
Пример. Рещим парное уравнение первого рода A), где
К,{Х):
27Г (е^
■ е^^) при ж < О,
при ж > О,
К^{х)
27vie
при ж < О,
при ж > О,
Найдем интегралы Фурье
1
27ге^
27ге-
при ж < о,
при ж > 0.
)С,(и):
(и - 2i){u - 3i)
JC^(u) :
-2г
Т(и).
w^+4
Соответствующая этому уравнению краевая задача B) запищется в виде
Е+{и)
(и — 2i)(u — Зг) „_
W +
-Зг
D)
п + 2г '"' ' (п + 2гJ w^ + 4 "
Коэффициент Т>(и) имеет на бесконечности полюс первого порядка (индекс г^ = — 1),
Функции JCi{u) и /C2(w) имеют в бесконечно удаленной точке общий нуль первого порядка.
Тогда
т_^ = 2, п_^ = 0, г^ = ?тг^ — п_^ = 2.
Представляя краевое условие в форме
и — 3i 1
(и + 2i)S+(«) —- = (и- 2i)(u - 3i)E-(и) —
и -\-2г и — 2г
и используя аналитическое продолжение и обобщенную теорему Лиувилля, получим, что
общее рещение задачи D) в классе функций, обращающихся в нуль на бесконечности, дается
выражением
^+
(^)-
-2г
Зг
+ С , Z-{Z):
1
-2г
+ С
^ + 2г ' J' ''' (z-2i)(z-3i)
где С — произвольная постоянная.
Рещение рассматриваемого интегрального уравнения находится по формуле
E+{u)^J=-{u) ■
E)
У(Х) :
— Г
\/2^ J-
JC^iu)
^ du.
Так как функция /Сз (w) имеет на бесконечности нуль первого порядка, то S+ (w) + JF(w)
должна иметь в бесконечно удаленной точке нуль, по крайней мере второго порядка. Из
этого условия находим С = — 1.
Страница 103

104 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f{x)
При С = — 1 решение E) принимает вид
Ы , , 1 + 2г -
-(^)
-, Z-{Z):
7ТГ. У{х) '■
{;
27ге^
при ж < о,
(^ + 2гJ' " ^^ {z-2iY{z-Zi)' "^' [5л/27ге-^^ при ж > 0.
Таким образом, условию разрешимости, вытекаюшему из наличия обшего нуля
функций fC^ {и) и fC^iu), удалось удовлетворить путем подбора входяшей в обшее решение
произвольной постоянной, и интегральное уравнение оказалось однозначно разрешимым.
4.6-2. Точные решения некоторых парных уравнений первого рода
В приложениях (например, в теории упругости, теплопроводности,
электростатике) встречаются парные интегральные уравнения, которые имеют вид
/■
Ki(x,t)y(t)dt = fi(x) при О < ж < а,
F)
K2(x,t)y(t)dt = f2(x)
При а < X < ОС,
где Ki(x,t), K2(x,t), /i(x), /2(ж)—известные функции, у(х) — функция,
подлежащая определению.
Методы решения различных типов таких уравнений описаны, например, в
приведенной в конце раздела литературе. Ниже приведены решения некоторых
классов парных интегральных уравнений, которые наиболее часто встречаются в
приложениях.
1°. Рассмотрим парное интегральное уравнение в форме
/»оо
/ Jo(xt)y(t)dt = f(x)
Jo
/»оо
/ tJo(xt)y(t)dt = 0
Jo
при о < ж < а,
при а < X < ОС,
G)
где Jo (ж) — функция Бесселя пулевого порядка. Решение уравпений G) можно
получить, используя преобразование Хапкеля. Оно определяется формулой
-Г
dt Jo
sf{s) ds
vw
dt.
2 f" I
y{x) = — / cos{xt)
^ Jo I
2°. Точное решение парного интегрального уравнения
tJo(xt)y(t)dt = f(x) при О < ж < а,
/
-'о
/■
-'о
(8)
(9)
Jo(xt)y(t)dt = 0
при а < X < ОС,
где Jo (ж) — функция Бесселя пулевого порядка, построенное при помощи
преобразования Хапкеля, дается формулой
у(х) ■■
— / sm{xt) —- I
7г Jo idt Jo
sf(s) ds
dt.
Vt'^ - s'^
3°. Точное решение парного интегрального уравнения
tJi^(xt)y(t)dt = f(x) при О < ж < а,
/■
Jo
f
Jo
A0)
A1)
J^(xt)y(t)dt = 0
при a < X < 00,
Страница 104

4.6. Парные интегральные уравнения первого рода
105
где Ji^(x) — функция Бесселя порядка /х, определяется следующим выражением
(здесь также применяется преобразование Ханкеля):
У(х)
2х_ f
V 7Г Уо
t^/V,
/х+^
(Xt)
/
Jo
г/2
sin^^'Оf{t sin 0)dO
dt.
4°. Рассмотрим парное интегральное уравнение в форме
/•
t'^Mxt)y(t)dt = f(x)
J^{xt)y{t)dt = 0
при о < ж < 1,
при 1 < ж < ОС,
A2)
A3)
где Ji^(x) — функция Бесселя порядка /х.
Решение уравнения A3) можно получить, используя преобразование Меллина.
При Р > О это решение определяется формулами
BжI-/5
у{х) =
у(х) ■■
Г(/5)
B0^)-
Jo
e+>'j^+0(xt)F(t)dt,
F{t)= Г f{toc+4i-cy-'dc.
Jo
при P > —1 решение парного уравнения A3) имеет вид
1+/3 J / ч / ,/x+l/-, ,2ч/3 ,
ГA + /5)
^^+/з(ж) /
t^^\l-tyf(t)dt^
Ф(х
Jo
■/'
Jo
+ / e^'il-ty^{x,t)dt
2^/з,l
A4)
A5)
ixo'+^j^+0+i(xOfmdc
Формула A5) справедлива при /3 > — 1 и —/х —^<2/3</х+-|-. Можно показать,
что при Р > О решение A5) можно привести к виду A4).
5°. Точное решение парного интегрального уравнения
/■
/■
tp
,(chx)y(t)dt = f(x)
при о < ж < а,
A6)
th.Gvt)P_j^_^^^(ch.x)y(t)dt = О при а < х < оо,
где Pi^(x) — сферическая функция Лежапдра первого рода, а г — мнимая единица,
может быть построено при помощи интегрального преобразования Мелера-Фока
(см. разд. 1.6) и дается формулой
/(s)shs
у(х]
Заметим, что
P-^+it{chx)
= / sin(xt) /
^ ^0 Uo
л/ch t — chs
- ds
dt.
A7)
cos(ts)
■ ds.
x> 0,
л/ch ж — ch ^
где интеграл в правой части равенства называется интегралом Мелера.
4.6-3. Приведение парных уравнений к уравнению Фредгольма
Одним из эффективных методов приближенного решение парных
интегральных уравнений первого рода является метод их сведения к интегральным
уравнениям Фредгольма второго рода (см. главу 5). Ниже приведем некоторые парные
уравнения, которые встречаются в задачах механики и физики, и связанные с ними
уравнения Фредгольма второго рода.
Страница 105

106 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f{x)
1°. Решение парного интегрального уравнения первого рода
g(t)Jo(xt)y(t)dt = f(x) при О < ж < а,
tJo(xt)y(t)dt = О при а < ж < ос,
I
I
где д(х) — известная функция, а Jo(x) — функция Бесселя нулевого порядка,
имеет вид
у(х) = / ip(t)cos(xt)dt. A9)
-'О
функция (р(х) в равенстве A9) определяется из решения уравнения Фредгольма
второго рода следующего вида:
(р(х)-— K{x,t)Lp{t)dt = ilj{x), О < ж < а, B0)
^ Jo
симметричное ядро K(x,t) и правая часть ф(х) которого даются соотношениями
K(x,t) = 2 [ [l-g(s)]cos(xs)cos(ts)ds, ф(х) = —— [ -^Щ== dt, B1)
Jo ^ ^^ Jo V ^ - ^
Методы исследования таких уравнений изложены в главе 5.
2°. Решение парного интегрального уравнения первого рода
tg(t)Jo(xt)y(t)dt = f(x) при О < ж < а,
Jo(xt)y(t) dt = О при а < ж < ос,
/о
где д(х) — известная функция, а Jo(x) — функция Бесселя нулевого порядка,
имеет вид
уС
х)= ip(t)sm(xt)dt, B3)
Jo
Функция (р(х) в равенстве B3) определяется из решения уравнения Фредгольма
второго рода B0), где
K(x,t) = 2 / [1 — p(s)]sin(xs) sin(ts) ds, ф(х) = — /
Jo ^ Jo
*^W at.
Vx'^ - t'^
Заметим, что ядро K(x,t) — симметричное.
3°. Решение парного интегрального уравнения первого рода
/»оо
/ g{t)Ji^{xt)y{t)dt = f{x) при О < ж < а,
^'оо B4)
/ tJi^(xt)y(t)dt = О при а < ж < ос,
Jo
где д(х) — известная функция, а J^(x) — функция Бесселя порядка /х, имеет вид
dt. B5)
У(^) = \1^ Г VtJ,^{xt)^{t)
V ^ Jo
Страница 106

4.6. Парные интегральные уравнения первого рода 107
Функция Lp{x) в равенстве B5) определяется из решения уравнения Фредгольма
второго рода B0), в котором
/»оо
К{х, t) = TvVxi / [1 — g(s)]s J^_ j_ (xs)J^_ j_ (ts) ds,
Jo 2 2
ф(х) = AJ/(o)+ / [фтО)^-^ fixsinO) ^ x(smOY f (xsinO)] с
где f' (x sin 0) = —^-^ , причем ядро К(х, t) — симметричное.
d^ I ^=x sin в
4°. Решение парного интегрального уравнения первого рода
tg(t)Ji^(xt)y(t)dt = f(x) при О < ж < а,
B6)
Ji^(xt)y(t) dt = о при а < ж < ос,
f
Jo
f
Jo
где g(x) — известная функция, а Ji^(x) — функция Бесселя порядка /х, имеет вид
. . I 7VX
J VtJ^^^{xt)ip{t)dt. B7)
Функция (^{х) в равенстве B7) определяется из решения уравнения Фредгольма
второго рода B0), в котором
. (ts) ds,
K(x,t) = 7TV^ / [l-g(s)]sJ^^i(xs)J^
Jo ^
ф(х) = — / /(xsin6>)(sin6>)^+' dO,
^ Jo
причем ядро K(x,t) — симметричное.
5°. Решение парного интегрального уравнения первого рода
/»оо
/ g(t)Ji^(xt)y(t)dt = f(x) при О < ж < а,
-'О
/»оо
/ Jij,(xt)y(t)dt = о при а < ж < ОС,
где д(х) — известная функция, а Ji^(x) — функция Бесселя порядка /х, имеет вид
y{x)^xJ^ rVij^_i(xtMt)dt. B9)
\ ^ Jo
функция (р(х) в равенстве B9) определяется из решения уравнения Фредгольма
второго рода B0), в котором
B8)
га 1 — 11 /«оо
K{x,t) = x^V2^t f / [l-g{s)]s'^'j,
Jx VP -^ Jo
(ps)J i(ts)dsdp,
^ Jx V P^ ■
■ dp.
д/р2 — Ж^
6°. Решение парного интегрального уравнения первого рода
t^^g{t)J^{xt)y{t)dt = f(x) при О < ж < а,
f
Jo
/»оо
/ J,
Jo
C0)
(xt)y(t) dt = о при a < X < ОС,
Страница 107

108 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f{x)
где О < /3 < 1, д{х) — известная функция, а J^(x) — функция Бесселя порядка /х,
имеет вид
у{х) = х1^х^~^ [ Vij^^f3(xt)ip(t)dt. C1)
V ^ Jo
Функция (р(х) в равенстве C1) определяется из решения уравнения Фредгольма
второго рода B0), в котором
K{x,t) = 7TVxi / [1-p(s)]s J^+/3(xs)J^+/3(ts)ds,
-'О
ф(х)= ^^X —x^ /^ f(xsme)(sme)^^\cosef^-Ue,
Г(/5) V 7Г Jo
причем ядро K(x,t) — симметричное.
7°. Решение парного интегрального уравнения первого рода
/»оо
/ g{t)P_j^_^^^{ch.x)y{t)dt = f{x) при О < ж < а,
/»оо
/ tth.GTt)P_X-^it(^^x)y(t)dt = О при а < ж < ос,
-'о ^
C2)
где Pfi(x) — сферическая функция Лежандра первого рода, i — мнимая единица,
а д(х) — известная функция дается формулой
у{х) = / cos{xt)cp{t)dt. C3)
-'О
Функция (р(х) в равенстве C3) определяется из решения уравнения Фредгольма
второго рода B0), в котором
/»оо
К(х, t) = [1 - g(s)]{cos[(x + t)s] + cos[(x - t)s]} ds,
7Г dx Jq vchX — chs
причем ядро K(x,t) — симметричное.
8°. Решение парного интегрального уравнения первого рода
/»оо
/ tg(t)P_j^_^^^(ch.x)y(t)dt = f(x) при О < ж < а,
-'О ^
/»оо
/ th.GTt)P_j^_^^^(ch.x)y(t)dt = О при а < ж < ос,
-'О ^
C4)
где Pi^(x) — сферическая функция Лежандра первого рода, г — мнимая единица,
а д(х) — известная функция, дается формулой
га
у(х) = / sm(xt)(p(t)dt.
Jo
C5)
Функция (р(х) в равенстве C5) определяется из решения уравнения Фредгольма
второго рода B0), в котором
K(x,t)= [7l-g(s)]{cos[(x-t)s]-cos[(x^t)s]}ds, ф(х) = — [^—Ш^^ ds,
Jo 7т Jo vchx-chs
причем ядро K(x,t) — симметричное.
® Литература: Е. Титчмарш A948), И. Снеддон A955), Я. С. Уфлянд A977), Ф. Д. Гахов,
Ю. И. Черский A978).
Страница 108

4.7. Асимптотические методы решения уравнений 109
4.7. Асимптотические методы решения уравнений с
логарифмической особенностью
4.7-1. Предварительные замечания
Рассмотрим интегральное уравнение Фредгольма первого рода
/
K{^]y(t)dt^f(x), -is;xs;i, A)
С характерным параметром Л, где О < Л < оо.
Будем считать, что ядро К = К(х) является четной непрерывной (при х j^ 0)
функций, которая имеет логарифмическую особенность при ж ^ О и экспоненци-
альным образом убывает при ж ^ оо. Уравпения с таким ядром возникают при
решении различных задач механики сплошной среды со смешанными граничными
условиями.
Пусть f(x) нринадлежит пространству функций, первые производные которых
удовлетворяют условию Гёльдера с показателем а > ^ на отрезке [—1,1]. В этом
случае решение интегрального уравнения A) в классе функций, удовлетворяющих
условию Гёльдера, существует и едипственно при любом Л G (О, оо), причем оно
имеет следующую структуру:
/ \ и;(х)
V1 — х^
где о;(ж) — непрерывная функция, которая пе обращается в нуль на концах отрезка
при X = ±1.*
Из формулы B) следует, что решение уравнения A) неограничено при ж ^ ±1.
Это важное обстоятельство будет учтено в п. 4.7-3 при построении
асимптотического решения в случае Л ^ 0.
Заметим, что более общие уравнения с разностным ядром и произвольными
конечными пределами интегрирования всегда можно заменой переменных
привести к A). Здесь форма A) взята для удобства дальнейшего изложения.
4.7-2. Решение при больших значениях характерного параметра
Пусть для ядра интегрального уравнения A) справедливо следующее
представление при X ^ 0:
оо оо
K{x) = \n\x\Y,ar.\xr + Y,br,\x\", C)
п=0 п=0
где ао ф 0.
Из выражения C) видно, что в уравнение A) при Л ^ оо входят два разно
масштабных больших параметра Л и In Л. Второй «квазипостоянный параметр»
растет существенно медленнее, чем первый (например, при Л = 100 и Л = 1000
имеем соответственно In Л ~ 4, б и In Л ~ б, 9).
Отбросим в уравнении A) все слагаемые, затухающие при Л ^ оо. С учетом
C), для главного (нулевого) приближения получим
г»!
(aoln|x-t| -aolnA + 6o)yo(t)(it = /(x), -1 ^ ж ^ 1. D)
/:
* Равенства С(;(±1) = О могут выполнятся лишь в исключительных случаях при особых
значениях параметра Л.
Страница 109

110
Методы решения линейных уравнений вида /^ K(x,t)y(t) dt = f{x)
Следует отметить, что в подынтегральном выражении нельзя было сохранить
только одно слагаемое, пропорциональное In Л (так как соответствующее «укороченно-
е» уравнение было бы неразрешимым). Константа bo также должна быть включена
в D), чтобы уравнение для главного приближения было инвариантным
относительно перенормировки параметра Л в уравнении A).
Для построения асимптотического решения уравнения A) при Л ^ ос удобно
поступить следующим образом. Рассмотрим сначала вспомогательное
интегральное уравнение с двумя параметрами Л и /3:
г1
/С(ж - t, /3, \)y{t) dt = f(x), -1 ^ ж ^ 1,
-1
oo oo E)
n=0 n=0
Его решение ищем в виде регулярного асимптотического разложения по обратным
степеням Л (при фиксированном /3). В итоге для первых Л^ членов получим:
£
у{х,р,Х) = ^Х "уп{х,р)+о{Х
F)
Подставляя F) в E), для последовательного определения функций уп(х,Р)
получим рекуррентную цепочку интегральных уравнений вида D):
г»!
(aoln|x-t| - аор -\- bo)yn(t, C) dt = дп(х, C), -1 ^ ж ^ 1, G)
/:
правые части которых дп(х,Р) зависят только от предыдущих членов разложения
Учтем, что вспомогательное уравнение E) при /3 = In Л совпадает с
уравнением A), в которое подставлено разложение C). Поэтому асимптотическое решение
уравнения A) получается с помощью выражений F) и G) при /3 = In Л.
Контактные задачи теории упругости часто приводятся к уравнению A),
в котором ядро может быть представлено в виде C) при а^ = О для всех
гг > О и b2m-\-i = О при т = 0,1,2,... В этом случае в решении F) следует
положить уп(х,Р) = О при гг = 1,3, 5,... Для практических целей обычно можно
ограничиться удержанием членов порядка до Л~^.
4.7-3. Решение при малых зиачеииях характерного параметра
При анализе предельного случая Л ^ О учтем особенности решения на концах
отрезка — 1 ^ ж ^ 1 (см. формулу B)). Для этого рассмотрим вспомогательную
систему двух интегральных уравнений
t
/ос
-1
/'
J —о
к
к
л
yi(t)dt = h(x)^ / к
п
J —oo
л
2/2(t)di = /2(a;) +
i:
к
л
y2(t)dt,
yi(t)dt,
-1 ^ X < oo.
(8)
-oo < X ^ 1.
Первое уравнение способствует выделению особенности решения при х
второе — выделению особенности решения при ж = +1,
Функции fi(x) и /2 (ж) таковы, что
/1(X) + /2(X) = /(X), -l^X^l,
/i(x) = 0(e-"i") при ж^оо,
/2(ж) = 0(е"^^) при X -^ —оо.
-1, а
(9)
Страница 110

4.7. Асимптотические методы решения уравнений 111
где а\ > О, «2 > 0.
При выполнении первого условия (9) решение интегрального уравнения A)
отыскивается как сумма решений интегральных уравнений (8), т. е.
у{х) = yi(x) + у2(х), -1 ^ Ж ^ 1. A0)
Отметим, что в силу двух последних условий (9) справедливы соотношения
yi{x) = 0{e~'^^'') при ж ^ ОС,
У2(х) = 0(е^2^) при X -^ —ос,
где р1 >0,р2> 0.
Напомним, что ядро К(х) является четной функцией. Поэтому если
функция f(x) в интегральном уравнении A) четная или нечетная, то в системе (8)
следует положить*
/i(x) = ±/2(-x), уг(х)^±у2(-х). A2)
В обоих этих случаях система уравнений (8) путем перехода к новым
переменным сводится к одному интегральному уравнению
/»оо /»оо
/ K(z-r)w(r)dr = F(z)± KB/X-z-r)w(r)dr, О ^ ^ < оо, A3)
Jo J2/X
в котором использованы следующие обозначения:
z=^, г=^, wiT) = y{t), Fiz)=^Mx). A4)
С учетом свойств ядра К(х) (см. п. 4.7-1) и первого соотношения A1) можно
получить равномерную по т асимптотическую оценку
/»оо
= / К{2/Х - Z - r)w{r)dr = 0{е-
J2/\
2/3i/AN
I{w)= / K{2/\-z-T)w{T)dT = 0[e-'^^'^), A5)
/2/л
Согласно A5), иптегральное уравнение A3) при малых Л можно решать
методом последовательных приближений по схеме
/»оо
/ K{z-T)wn{T)dT = F{z)±l{wn-i), гг = 1, 2, ..., A6)
-'О
отбрасывая в главном приближении интеграл I{wq) в правой части. Полученные
интегральные уравнения Винера-Хопфа первого рода A6) решаются в замкнутом
виде (см. п. 4.5-1).
Пз формул A0), A2) и A4) следует, что главный член асимптотического
разложения решения интегрального уравнения A) при Л ^ О имеет вид
y{x) = w^[^^±w,(^^y A7)
где wi = wi(r) —решение уравнения A6) при гг = 1 и it;o = 0.
Для практических целей обычно бывает достаточно использовать форму-
лу A7).
* В формулах A2), A3), A6) и A7) знак плюс берется для четной функции /(ж), минус -
для нечетной функции f(x).
Страница 111

112 Методы решения линейных уравнений вида /^ К(х, t)y(t) dt = f{x
4.7-4. Интегральные уравнения теории упругости
В контактных задачах теории упругости часто встречается интегральное
уравнение A), в котором ядро задается с помощью косинус-преобразования Фурье
Х(х)= [ I^cos(ux)du, A8)
Jo ^
Здесь функция L(u) непрерывна и положительна при и G (О, оо), причем для нее
справедливы асимптотические равенства
L(u) = Аи-\-0(и^) при и ^ о,
При и -^ оо,
п=0
где А > О, Бо > 0.
Из формулы A8) следует, что ядро является четной функцией: К(х) = К(—х).
Обычно считается, что L(u)u~^ и u[L(u)]~^ как функции комплексного
переменного w = и -\- iv соответственно регулярны в полосе \v\ ^71 ив полосе
1^1 ^ 72- Отсюда, в частности, следует, что ядро К(х) убывает на бесконечности
не слабее, чем ехр(—7i|t|).
Из формул A8) и A9) следует, что ядро интегрального уравнения К(х)
имеет логарифмическую особенность при х = 0. Ири этом справедливо
представление C), где an =0 при гг = 1, 3, 5,...
Таким образом ядро, заданное с помощью формулы A8), имеет те же самые
характерные особенности, которые предполагались выполненными для ядра
интегрального уравнения A). Поэтому для асимптотического анализа уравнения A) с
ядром A8) при Л ^ оо и Л ^ О можно использовать результаты пп. 4.7-2 и 4.7-3.
(•) Литература: И. И. Ворович, В. М. Александров, В. А. Бабешко A974), В. М.
Александров, Е. В. Коваленко A986), В. М. Александров A993).
4.8. Методы регуляризации
4.8-1. Метод регуляризации Лаврентьева
Рассмотрим интегральное уравнение Фредгольма первого рода (см. также
замечание 3 из п. 5.6-5)
гЬ
K(x,t)y(t)dt = f(x), a^x^b, A)
/
J а
где f(x) G L2(a,b), y(x) G L2(a,b), ядро K(x,t)—квадратично суммируемое,
симметричное и положительно определенное (см. п. 5.6-2).
В выбранных классах функций и ядер задача отыскания решения уравнения A)
является некорректно поставленной, т. е. неустойчивой по отношению к малым
изменениям правой части интегрального уравнения.
Согласно методу регуляризации Лаврентьева наряду с уравнением A)
рассмотрим также регуляризованное уравнение
еуе(х) + / K(x,t)ye(t)dt = f(x), a^x^b, B)
J а
где е > О — параметр регуляризации, которое является уравпением Фредгольма
второго рода и может быть решено методами, изложенными в главе 5, причем его
решение существует и единственно.
Страница 112

4.8. Методы регуляризации 113
Задавая в уравнении B) параметр е достаточно малым, найдем решение
уравнения уе{х) и подставим это решение в уравнение A). В результате получим
K(x,t)ye(t)dt = fe(x), a^x^b. C)
/
J а
Если полученная таким образом функция fe(x) мало отличается от /(ж), т. е.
\\f{x)-Mx)\\^S, D)
где 6—некоторое заранее известное малое положительное число, то решение fe (х)
считается достаточно хорошим приближенным решением уравнения A).
Обычно параметр 6 определяет погрешность исходных данных, когда правая
часть уравнения A) задается или определяется в эксперименте с некоторой
точностью.
В случае, когда при заданном е условие D) не выполняется, выбирается новое
значение параметра регуляризации, и повторяется описанная процедура.
В следующем пункте описан метод регуляризации, пригодный для уравнений
первого рода с произвольными квадратично интегрируемыми ядрами.
4.8-2. Метод регуляризации Тихонова
Рассмотрим интегральное уравнение Фредгольма первого рода
гЬ
K(x,t)y(t)dt = f(x), c^x^d. E)
/
J a
Будем полагать, что K(x,t) есть любая квадратично суммируемая в области
{а ^ t ^ Ь, с ^ X ^ d} функция, f(x) G L2(c,d) и у(х) G L2(a,b). Задача
отыскания решения уравнения E) также является некорректно поставленной в
указанном выше смысле.
Согласно методу регуляризации Тихонова (нулевого порядка), наряду с
уравнением E) рассмотрим интегральное уравнение Фредгольма второго рода
(см. главу 5)
€уе(х)-\- K*(x,t)ys(t)dt = f*(x), а^х^Ь, F)
J а
где
/а па
K{s,x)K{s,t)ds, Г{х)= K{s,x)f{s)ds,
G)
а число е>0 — параметр регуляризации. Уравпение F) называется регуляризован-
ным интегральным уравнением, причем его решение существует и единственно.
Задавая в уравнении F) параметр е достаточно малым, найдем решение
уравнения уе(х) и подставим это решение в уравнение E). Тогда
гЬ
K(x,t)ye(t)dt = fe(x), C^X^d. (8)
/
J а
Сравнивая найденную правую часть уравнения fs(x) с заданной f(x) по
формуле D) в соответствии с описанным выше простейшим алгоритмом, либо сочтем
полученное приближенное решение Уе(х) удовлетворительным, либо продолжим
поиск при новом значении параметра регуляризации.
Выше изложены простейшие принципы выбора приближенного решения
уравнения Фредгольма первого рода. Более совершенные и сложные алгоритмы можно
найти в цитируемой ниже литературе.
(•) Литература: А. Н. Тихонов, В. Я. Арсенин A979), М. М. Лаврентьев, В. Г. Романов,
С. П. Шишатский A980), А. Ф. Верлань, В. С. Сизиков A986).
8 А. В. Манж:иров, А. Д. Полянин
Страница 113

5. Методы решения линейных уравнений
вида у{х) - £ К{х, t)y{t) dt = f{x)
5.1. Предварительные замечания
5.1-1. Уравнения Фредгольма н уравнения со слабой особенностью
Линейные интегральные уравнения второго рода с постоянными пределами
интегрирования имеют форму
у{х)-Х / K{x,t)y{t)dt = f{x), A)
J а
где у{х) —неизвестная функция (а ^ ж ^ 6), К{х^ t) —ядро интегрального
уравнения, f{x) —некоторая известная функция, которая называется свободным членом
или правой частью уравнения A). Для удобства анализа в интегральном
уравнении A) по традиции принято выделять числовой параметр Л, который называют
параметром интегрального уравнения. Классы рассматриваемых функций и ядер
были определены ранее в пп. 4.1-1 и 4.1-2. Отметим, что уравнения с постоянными
пределами интегрирования вида A), имеющие фредгольмовы ядра или ядра со
слабой особенностью, называются соответственно уравнениями Фредгольма второго
рода или уравнениями со слабой особенностью второго рода.
Число Л называется характеристическим числом или характеристическим
значением интегрального уравнения A), если существует нетривиальное решение
соответствующего однородного уравнения (/(ж) = 0). Само же это
нетривиальное решение называется собственной функцией интегрального уравнения,
соответствующей характеристическому числу Л. Если Л является характеристическим
числом, то величина 1/Л называется собственным числом интегрального
уравнения A). Правильным или регулярным значением параметра Л называется такое
его значение, при котором упомянутое однородное уравнение имеет только
тривиальное решение. Иногда характеристические числа и собственные функции
интегрального уравнения Фредгольма называют характеристическими числами и
собственными функциями ядра K(x,t).
Ядро K(x,t) интегрального уравнения A) называется выроэюденным, если оно
имеетвид i^(x,t) =gi(x)hi(t)-\ h5'n(ж)/in(t), разностным, если оно зависит от
разности аргументов: K(x,t) = К(х — t), симметричным, если оно удовлетворяет
условию K(x,t) = K(t,x).
Интегральное уравнение, полученное из A) заменой ядра K(x,t) на K(t,x),
называется союзным с A) или транспонированным к A).
Замечание 1. Иеременные t и х могут изменяться в различных интервалах
(например, a^t^bnc^x^d). Для определенности далее будем считать, что
с = а и d = b (этого всегда можно добиться линейной подстановкой х = ах -\- Р с
помощью надлежащего выбора постоянных а и Р).
Замечание 2. Случай, когда пределы интегрирования а и/или Ь могут быть
бесконечными, вообще говоря, не исключается, но при этом следует внимательно
проверять выполнение условия квадратичной интегрируемости ядра K(x,t) в
квадрате S = {a^x^b, a^t^b}.
Страница 114

5.1. Предварительные замечания 115
5.1-2. Структура решений
Решение уравнения A) может быть представлено в форме
гЪ
y(x) = f(x)^X f R(x,t;X)f(t)i
J a
где резольвента R(x,t;X) не зависит от свободного члена f(x) и определяется
только ядром интегрального уравнения.
Резольвента уравнения Фредгольма A) удовлетворяет двум интегральным
уравнениям
R(x,t;X) = K(x,t)-\- I K(x,s)R(s,t;X)
J а
ds,
(X,t)+ /
J a
R(x,t;X) = K(x,t)-^ / K(s,t)R(x,s;X)ds,
в которых интегрирование ведется по различным парам переменных ядра и
резольвенты.
5.1-3. Интегральные уравнения типа свертки второго рода
Интегральными уравнениями типа свертки (см. также п. 4.1-3) называются
уравнения, которые при применении к ним некоторого интегрального
преобразования и теоремы о свертке для этого преобразования приводятся к алгебраическим
уравнениям для изображений или к краевым задачам теории аналитических
функций. Рассмотрим уравнения типа свертки второго рода, связанные с
преобразованием Фурье.
Интегральное уравнение второго рода с разностным ядром на всей оси (его
называют иногда уравнением типа свертки второго рода с одним ядром) имеет
вид
/»оо
у(х)-\- К(х-t)y(t)dt = f(x), -ОС < ж < ОС, B)
где f(x) и К(х) — известные правая часть и ядро интегрального уравнения, а
у(х)—искомая функция.
Интегральное уравнение второго рода с разностным ядром на полуоси имеет
вид
/»оо
у(х) + / К(х - t)y{t) dt = f(x), О < ж < ОС. C)
Уравнение C) называется также односторонним уравнением второго рода или
интегральным уравнением Винера-Хопфа второго рода
Интегральное уравнение типа свертки с двумя ядрами второго рода имеет
вид
/»оо пО
- / Ki(x-t)y(t)dt^ /
Jo J -с
у{х)+ Ki{x-t)y{t)dt^ K2{x-t)y{t)dt = f{x), -оо<ж<оо, D)
-'О -'-оо
где Ki(x) и К2(х) —ядра интегрального уравнения D). Класс функций и ядер
для уравнений типа свертки введен ранее в п. 4.1-3.
5.1-4. Парные интегральные уравнения второго рода
Парное интегральное уравнение второго рода с разностными ядрами (типа
свертки) имеет вид
Страница 115

116 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
/оо
Ki(x-t)y(t)dt = f(x), О < ж < оо,
/оо \*^/
К2(х - t)y(t) dt = f(x), -оо < ж < о,
-оо
где обозначения, класс функций и ядер совпадают с введенными для уравнений
типа свертки в п. 4.1-3.
Парное интегральное уравнение второго рода в достаточно общем случае
имеет вид
/оо
Ki(x,t)y(t)dt = fi(x), а < X <b,
/^оо F)
у(х)-\- K2(x,t)y(t)dt = f2(x), b < X < оо,
J а
где /i(x), /2(ж) и Ki(x,t), K2(x,t) —известные правые части и ядра
уравнения F), а у(х) — функция, подлежащая определению. Такие уравнения можно
исследовать методами различных интегральных преобразований с приведением
к краевым задачам теории аналитических функций, а также другими методами
развитыми для парных интегральных уравнений первого рода (см., например,
И. Снеддон A955), Я. С. Уфлянд A977)).
Интегральные уравнения, полученные из B)-E) заменой ядра К(х — t) на
K(t — х), называются союзными с ними или транспонированными к ним.
Если правые части уравнений A)-F) тождественно равны нулю, то их
называют однородными. Если же правые части не обращаются в нуль всюду в области
их определения, то уравнения A)-F) называют неоднородными.
Замечание 3. К уравнениям B)-E) приводятся некоторые уравнения, ядра
которых содержат произведение или отношение переменных ж и t.
Замечание 4. Уравнения типа свертки B)-E) иногда записывают в форме,
где перед интегралами ставят множитель 1/\/27т.
Замечание 5. Если класс функций и ядер для уравпений тина свертки (в
частности, для уравнения Випера-Хопфа) отличается от введенного в п. 4.1-3, то
это будет особо оговариваться в каждом случае (см. разд. 5.10 и 5.11).
® Литература: Г. Виарда A933), Э. Гурса A934), Г. М. Мюнтц A934), И. И.
Привалов A935), И. Г. Петровский A951), М. Г. Крейн A958), С. Г. Михлин A959), Ф. Три-
коми A960), Б. Побл A962), П. П. Забрейко, А. И. Кошелев и др. A968), М. А.
Красносельский, Г. М. Вайникко, П. П. Забрейко и др. A969), М. Л. Краснов, А. И. Киселев,
Г. И. Макаренко A968), Л. Я. Цлаф A970), J. А. Cochran A972), В. И. Смирнов A974),
А. П. Колмогоров, С. В. Фомин A976), Л. В. Канторович, Г. П. Акилов A977), Ф. Д. Га-
хов, Ю. И. Черский A978), Ф. Рисе, Б. Сёкефальви-Падь A979), А. Г. Бутковский A979),
L. М. Delves, J. L. Mohamed A985), A. J. Jerry A985), A. Ф. Верлань, В. С. Сизиков A986),
А. Golberg A990), D. Porter, D. S. G. Stirling A990), C. Corduneanu A991), J. Kondo A991),
S. Prossdorf, B. Silbermann A991), W. Hackbusch A995), R. P. Kanwal A996), K. E. Atkinson
A997), A. Д. Полянин, A. B. Манжиров A998), A. B. Манжиров, A. Д. Полянин A998),
A. D. Polyanin, A. V. Manzhirov A998, 1999).
5.2. Уравнения Фредгольма второго рода с
вырожденным ядром
5.2-1. Простейшее вырожденное ядро
Рассмотрим интегральное уравнения Фредгольма второго рода с простейшим
Страница 116

5.2. Уравнения Фредгольма второго рода с выроэюденным ядром
117
вырожденным ядром
у(х) - л / д(х
J а
)h{t)y{i)dt = f{x), ai^xi^b.
A)
Решение уравнения A) ищем в виде
у(х) = fix) + \Ад{х). B)
Подставляя выражения B) в уравнение A), после простых преобразований будем
иметь
/ h{t)g{t)di\ = [
J а А J а
f{t)h{t)dt.
C)
Считается, что оба интеграла, входящие в C), существуют. На основании A)-C), с
учетом того, что единственное характеристическое число Ai уравнения A) дается
выражением
Ai =
/
h{t)g{t)dt
D)
получим следующие результаты.
1°. Если А ф Ai, то при произвольной правой части существует единственное
решение уравнения A), которое можно записать в виде
у(х) = fix) + -^Щд(х),
-Г
f(t)h(t)dt.
E)
Ai -А
2°. Если А = Ai и /i = О, то решение уравнения A) можно представить в форме
У = f(x)-\-Cyi(x), yi(x)=g(x), F)
где С — произвольная постоянная, yi(x) — собственная функция,
соответствующая характеристическому числу Ai.
3°. Если A = Aih/i7^0 решения не существует.
5.2-2. Вырожденное ядро в общем случае
Интегральное уравнение Фредгольма второго рода с вырожденным ядром в
общем случае имеет вид
у{х) - А /
J а
^ gk(x)hk(t)
y(t)dt = f(x)
Перепишем уравнение G) в форме
п „ь
y(x) = f(x)^Xj29k(x) hk(t)y(t)
k=i -^"^
dt,
п = 2,3,
п = 2,3,.
Предполагая, что уравнение (8) имеет решение, с учетом обозначения
Ак= [ hk(t)y(t)dt
J а
будем иметь
У(х) = f(x) + ^'^ AkQkix),
G)
(8)
(9)
A0)
Страница 117

118 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
из которого видно, что решение интегрального уравнения с вырожденным ядром
сводится к определению постоянных А^.
Умножим обе части равенства A0) на hm (ж) и проинтегрируем по ж в пределах
от а до Ъ. Тогда получим систему линейных алгебраических уравнений, которой
удовлетворяют коэффициенты А]^:
п
Am- \^^SmkAk = fm, Ш = 1, 2, . . . , П, A1)
fc = l
где
гк = hm(x)gk(x)dx, fm= f(x)hm(x)
J a J a
dx, 771, /c = 1, 2,... ,n. A2)
при вычисления коэффициентов Smk ^ fm для конкретных вырожденных ядер
можно воспользоваться таблицами интегралов из справочников И. С. Градштейна,
И. М. Рыжика A975), А. П. Прудникова, Ю. А. Брычкова, О. П. Маричева A981,
1983, 1986).
Если построено решение системы уравнений A1), то построено и решение
интегрального уравнения с вырожденным ядром G). Значения параметра Л, при
которых определитель системы A1) обращается в нуль, являются
характеристическими числами интегрального уравнения G), причем их ровно п штук с учетом
кратности.
Теперь можно сформулировать основные результаты о решении уравнения G).
1°. Если Л — правильное, то при произвольной правой части f{x) существует
единственное решение интегрального уравнения Фредгольма с вырожденным
ядром, которое можно представить в форме A0), где коэффициенты Ак являются
решением системы линейных алгебраических уравнений A1). Постоянные Ак
можно определить, например, по формулам Крамера.
2°. Если Л — характеристическое и f{x) = О, то решение однородного уравнения
с вырожденным ядром имеет вид
р
y{x) = Y,Ciyi{x), A3)
г=1
где d —произвольные постоянные, а уг(ж) —линейно независимые собственные
функции ядра, соответствующие характеристическому числу Лг:
п
yi(x) = Y1 Ak(i)gk{x). A4)
fc=i
Здесь постоянные Ak(i) составляют р (р ^ п) линейно независимых решений
следующей однородной системы алгебраических уравнений:
п
Am(i) - X^SmkAk(i)=0; т = 1,...,п, i = l,...,p. A5)
fc=i
3°. Если Л — характеристическое и f(x) ф О, то для разрешимости
неоднородного интегрального уравнения G) необходимо и достаточно, чтобы правая часть
уравнения f(x) удовлетворяла р условиям
п
^Bk(i)fk =0, г = 1,...,р, р^п. A6)
Страница 118

5.2. Уравнения Фредгольма второго рода с выроэюденным ядром
119
Здесь постоянные В/с(г) составляют р линейно независимых решений однородной
системы алгебраических уравнений, транспонированной к системе A5). В этом
случае решение уравнения G) имеет вид
У(х) = Уо(х) + Y^ Ciyi(x),
A7)
где уо(х) —частное решение неоднородного уравнения G), а сумма представляет
собой общее решение соответствующего однородного уравнения (см. 2°).
В частности, если f(x) ф О, но все Д равны нулю, то
V
2/(ж) = /(ж) + ^а№(ж). A8)
г=1
Пример. Решим интегральное уравнение
у{х) — X (х cost-{-t'^ sin X-\-cos xsmt)y{t) dt = X, —тт^х^тт. A9)
J —7Г
Введем обозначения
y(t)costdt, А2 = / t^y(t)dt, A3 = / y(t)smtdt, B0)
-ТГ ^ —7Г ^ —7Г
где А^, ^2, Аз —неизвестные постоянные. Тогда уравнение A9) примет вид
у{х) = А-^Хх -\- A2Asinx + АзЛсо8ж + х. B1)
Подставляя выражение B1) в равенства B0), получим
А^ = {A-^Xt-\-A2Xsmt-\-A^Xcost-\-t)costdt,
J — 7Г
^2 = / {A-^Xt-\-A2Xsmt-\-A^Xcost-\-t)t^dt,
J — ТГ
Аз = / (A-^Xt-\-A2Xsm t-\-A^Xcost-\-t) sin tdt.
J — IT
Вычисляя входящие в эти уравнения интегралы, получим систему алгебраических
уравнений для нахождения неизвестных А^, А2, A3:
А^ - ЛтгАз = О,
А2 + 4Л7гАз = О, B2)
-2Х7тА-^ - ХттА^ + Аз = 27Г.
Определитель этой системы отличен от нуля:
I 1 О -Лтг!
А(Л) = О 1 4Х7т\=1^2Х^7т^фО.
I -2Л7Г -Лтг 1 I
Таким образом, система B2) имеет единственное решение
^~ 1 + 2Л27Г2' 2~ + 2Л27г2' ^ ~ ТТ2Л^^'
Подставляя найденные значения А^, А2, A3 в B1), получим решение данного интегрального
уравнения в виде
(Лтгж — 4Л7Г sin X -\- cos х) -\- х.
(•) Литература: С. Г. Михлин A959), М. Л. Краснов, А. И. Киселев, Г. И. Макаренко
A968), И. С. Градштейн, И. М. Рыжик A975), А. J. Jerry A985), А. П. Прудников,
Ю. А. Брычков, О. И. Маричев A981, 1983, 1986).
Страница 119

120 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
5.3. Решение в виде ряда по степеням параметра. Метод
последовательных приближений
5.3-1. Итерированные ядра
Пусть имеем интегральное уравнение Фредгольма второго рода
у{х) -X [ К(х, t)y(t) dt = f(x), a^x^b. A)
J a
Будем искать его решение в виде ряда по степеням параметра Л:
оо
2/(а;) = /(а;) + ^А>„(а;). B)
п=1
Подставим ряд B) в уравнение A). Приравнивая коэффициенты при
одинаковых степенях Л, получим рекуррентную систему соотношений для определения
функций фп(х):
фг(х)= [ K(x,t)f(t)dt,
J а
rb rb
Ф2(Х)= K{x,t)^lji{t)dt= K2(x,t)f(t)dt,
J a J a
rb rb
)dt,
ф^(х)= f K{x,t)ilj2{t)dt= [ Ks(x,t)f(t)i
J a J a
Здесь
Kn(x,t)= I K(x,z)Kn-i(z,t)dz, C)
J a
где n = 2,3,..., причем Ki(x,t) = K(x,t). Функции Kn(x,t), определяемые
HO формулам C), называются итерированными ядрами. Для них справедливо
соотношение
Kn(x,t)= / Km(x,s)Kn-m(s,t)ds,
J а
D)
где т — любое натуральное число, меньшее п.
Птерированные ядра Кп(х, t) можно непосредственно выразить через данное
ядро K(x,t) по формуле
Kn(x,t)= / " K(x,si)K(si,S2).. .K(sn-i,t)dsids2 ... dSn-1.
Ja J a Ja
n-l
Bee итерированные ядра Kn(x,t), начиная с K2(x,t), будут непрерывными
функциями в квадрате S = {a^x^b, a^t^b}, если начальное ядро K(x,t)
квадратично интегрируемо в этом квадрате.
Если данное ядро K(x,t) симметрично, то все итерированные ядра Кп(х, t)
тоже симметричны.
5.3-2. Метод последовательных нрнблнженнй
Результаты п. 5.3-1 могут быть также получены с помощью метода
последовательных приближений. Для этого следует использовать рекуррентное соотношение
Уп(х) = f(x) + А / K(x,t)yn-i(t)dt, п = 1,2,...,
J а
В котором нулевое приближение уо(х) = f(x).
Страница 120

5.3. Решение в виде ряда. Метод последовательных приблиэюений 121
5.3-3. Построение резольвенты
Резольвента интегрального уравнения A) определяется через итерированные
ядра формулой
оо
i?(x,t;A) = ^A"-'i^^(x,t), E)
где ряд, стоящий в правой части, называется рядом Неймана ядра K(x,t). Он
сходится в среднем к единственному квадратично интегрируемому решению
уравнения A), если
Если, кроме того.
|Л| < ^, ^=\ [ [ K^(x,t)dxdt. F)
/ K^(x,t)dt^ А, а^х^>
J а
где А — некоторая постоянная, то ряд Неймана сходится на [а, Ь] абсолютно и
равномерно.
Решение уравнения Фредгольма второго рода A) выражается формулой
у(х) = f(x)-\-X R(x,t;X)f(t)dt, а ^ х ^ b. G)
J а
Неравенство F) является существенным для сходимости ряда E). Однако
решение уравнения A) может существовать и для значений |Л| > 1/В.
Замечание 1. Решение уравнения второго рода со слабой особенностью
у(х)-Х K(x,t)y(t)dt = f(x), a^x^b,
J а
где ядро К(х, t) имеет вид
K{x,t)= ,^^^^^^ , 0<а<1,
а функция L(x,t) —непрерывна в квадрате S = {a^x^b, a^t^b}, можно
построить методом последовательных приближений при условии
|Л| < ^—-^^ , Б* =sup\L(x,t)\.
Само же уравнение со слабой особенностью можно привести к уравнению
Фредгольма вида
у{х)-Х' I Kn(x,t)y(t)dt = F(x), a^x^b,
J а
F{x) = fix) + Y.^4 Kp(^,t)f{t)dt,
где Kp(x,t) (p = l,2,...,n)—p-oe итерированное ядро, причем Kn(x,t) —
фредгольмово при гг>^A — а)~^и ограниченное при гг > A — а)~^.
Страница 121

122 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Пример 1. Решим интегральное уравнение
у{х)-Х xty{t)dt = f{x), 0^ж^1,
методом последовательных приближений. Здесь K(x,t)=xt,a = 0,b=l. Последовательно
найдем
/■1 xt
K-^(x,t) = xt, K2(x,t) = / (xz)(zt) dz
Jo
3
1 / xt xt
Согласно формуле E) для резольвенты
R{x,t]X) = Y^ y-^K^{x,t) =xtY^
Л\"-^ 3xt
14"/ 3-Л'
72 = 1 72 = 1 ^ ^
Причем |Л| < 3, и в силу формулы G) решение данного интегрального уравнения запишется
в форме
/-1 Q^f
y{x) = f{x)^X -f{t)dt, O^o^^l, Л 7^3.
Jo о — л
В частности, при f{x) = х получим
Зх
у(х) = , 0^ж^1, Л 7^3.
5.3-4. Ортогональные ядра
Для некоторых уравнений Фредгольма ряд Неймана E) для резольвенты
сходится при любых значениях Л. Покажем это.
Пусть имеем два ядра: K(x,t) и L(x,t). Будем называть эти ядра
ортогональными, если выполняются два условия:
/ K(x,z)L(z,t)dz = 0, / L(x,z)K(z,t)dz = 0, (8)
J а J а
При любых допустимых значениях ж и t.
Существуют ядра, ортогональные самим себе. Для таких ядер K2(x,t) = О,
где K2(x,t) —второе итерированное ядро. В этом случае, все последующие
итерированные ядра также равны нулю и резольвента совпадает с ядром K(x,t).
Пример 2. Найдем резольвенту ядра К(х, t) = sin(x — 2t), О ^ ж ^ 27г, О ^ t ^ 27г.
Имеем
/•27Г /-277
/ sin(x — 2z) sm{z — 2t)dz=^ / [cos(x -\-2t — 3z) — cos(x — 2t — z)] dz =
Jo Jo
= T [~ T ^i^(^ -^2t- 3z) + sin(x - 2t - z)] ^Z^J = 0.
Таким образом, в этом случае резольвента ядра равна самому ядру:
R{x,t]X) = sin(x -2t),
так что ряд Неймана E) состоит из одного члена и, очевидно, сходится при любом Л.
Замечание 2. Если ядра M^^^(x,t), M^^^(x,t), ..., М^''^(ж, t) попарно
ортогональны, то резольвента, соответствующая их сумме
п
7тг=1
равна сумме резольвент, соответствующих каждому из слагаемых.
(•) Литература: С. Г. Михлин A959), М. Л. Краснов, А. И. Киселев, Г. И. Макаренко
A968), J. А. Cochran A972), В. И. Смирнов A974), А. J. Jerry A985).
Страница 122

5.4. Метод определителей Фредголъма
123
5.4. Метод определителей Фредгольма
5.4-1. Формула для резольвенты
Решение уравнения Фредгольма второго рода
у(х)-Х [ K(x,t)y(t)dt = f(x),
J а
дается формулой
y{x) = f{x) + \ j R(x,t;X)f(t)dt,
J а
где резольвента R(x,t; Л) определяется равенством
D(x,t]X)
а ^ X ^ b,
а ^ X ^
R(x,t;X) =
D(X) ф 0.
D(A) '
Здесь D(x^ t; Л) и D(X) —степенные ряды по Л:
D(x,t;X) = V ^^A.(x,t)A", D(X) = V ^^Б.Л",
A)
B)
C)
D)
коэффициенты которых определяются формулами
Ao(x,t) = K(x,t),
K(x,t) K(x,ti)
pb pb
in(x,t)= / ••• /
J a J a
K{tn,t) K{tn,tl)
K(x,tn)
K(tn,tn)
dti...dtn, E)
Bo
rb rb
J a J a
K(t2,ti) K{t2M)
K(t2,tn)
dt\... dtn-
F)
; \K(tn,ti) K(tn,t2) ••• K(tn,tn
Функция D(x,t;X) называется минором Фредгольма, a D(X) —
определителем Фредголъма. Ряды D) сходятся для всех значений Л и, значит, являются
целыми аналитическими функциями от Л. Резольвента R(x,t;X) есть аналитическая
функция от Л, кроме тех значений Л, которые являются корнями D(X).
Последние совпадают с характеристическими числами уравнения и являются полюсами
резольвенты R(x,t; Л).
Пример 1. Рассмотрим интегральное уравнение
Имеем
у{х)-Х [ xe'y{t)dt = f{x),
Jo
AQ(x,t) =хе^, A-^(x,t)= /
A^{x,t)= f f
Jo Jo
0 ^ж ^1, Хф1.
xe'^ же''!
dt-^ = 0,
xe же 1 же 2
^2е^ ^2е^1 ^2е^2
dt-^ dt^ = 0,
Страница 123

124 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
так как определители под знаком интеграла равны нулю. Очевидно, что и все последующие
А^(х, t)=0. Находим коэффициенты В^:
г1 г1
В-^= K{t-^, t-^)dt-^ = / t^e^i dt-^ =1, В^= I /
Jo Jo Jo Jo
Очевидно, что и все последующие В^ = 0.
Согласно формулам D) имеем
D(x,t;X) = K(x,t) =хе^; D(X) = 1 - Л.
Таким образом,
D(x,t;X) хе^
R(x,t]X) = ^ ] \ ^ = ,
^ ' ' ^ D{X) 1 - Л '
и рещение уравнения можно записать в форме
/■1 хе^
y(x) = f(x)^X -f(t)dt, O^o^^l, Л 7^1.
Jo i — А
В частности, для f(x) = е~^ получаем
у(ж) = е~^ + X, 0^ж^1, Л 7^1.
1 — Л
dt^ dt^ = 0.
5.4-2. Рекуррентные соотношения
Вычисление но формулам E) и F) коэффициентов Ап(х, t) и Вп рядов D)
практически возможно лишь в очень редких случаях, но из этих формул
получаются следующие рекуррентные соотношения:
An(x,t) = BnK(x,t)-n I K(x,s)An-i(s,t)ds, G)
J а
Вп= An-i(s,s)ds. (8)
J а
Пример. Пользуясь формулами G) и (8), найдем резольвенту ядра K(x,t) = х — 2t,
где О ^ ж ^ 1, О ^ t ^ 1.
Действительно, Bq = 1, Aq(x, t) = х — 2t. По формуле (8), найдем
В^= {-s)ds
Jo
X — 2t f^
A^{x,t) = / (x - 2s){s - 2t) ^
2 Jo
2 •
^ и
По формуле G) получим
-X -t-\-2xt-\- ^.
Далее будем иметь
: [ (-2s + 2s2 + i:)ds= ^,
A^{x,t) = ^-^-2 f {x-2s){
^ Jo
3 / '^'^
0, Аз(ж, t) = A^(x, t) = ••• = 0.
Следовательно,
D(A)
Резольвента данного ядра будет иметь вид
D{X) = 1+ |-Л+ -|-Л^; D{x,t]X) = х - 2t ^ Х{х ^ t - 2xt - |-).
R{x,t]X) :
ж - 2t + Х{х + t-2xt- \
(•) Литература: С. Г. Михлин A959), М. Л. Краснов, А. И. Киселев, Г. И. Макаренко
A968), В. И. Смирнов A974).
Страница 124

Интегральные уравнения Фредголъма 2-го рода с симметричными ядрами 125
5.5. Теоремы и альтернатива Фредгольма
5.5-1. Теоремы Фредгольма
Теорема 1. Уравнение Фредгольма имеет не более счетного множ:ества
характеристических чисел, которые могут сгугцаться только на
бесконечности.
Теорема 2. Если значение Л правильное, то как данное интегральное
уравнение, так и союзное с ним уравнение, разрешимо при любом свободном
члене и решение каукдого из этих уравнений единственно. Соответствуюгцие
однородные уравнения имеют только тривиальные решения.
Теорема 3. Если значение Л характеристическое, то однородное
интегральное уравнение, так ж:е как и союзное с ним однородное уравнение,
имеет нетривиальные решения. Число линейно независимых решений
однородного интегрального уравнения конечно и равно числу линейно
независимых решений однородного союзного уравнения.
Теорема 4. Для того чтобы неоднородное интегральное уравнение было
разрешимо, необходимо и достаточно, чтобы его свободный член f(x)
удовлетворял условиям
гЬ
/(х)фк(х)Aх = 0, А; = 1,...,гг,
/
J а
где фк (х) — совокупность всех линейно независимых решений соответству-
югцего союзного однородного уравнения.
5.5-2. Альтернатива Фредгольма
Из теорем Фредгольма вытекает так называемая альтернатива Фредгольма ,
которой чаще всего пользуются при исследовании интегральных уравнений.
Альтернатива Фредгольма. Либо неоднородное уравнение разрешимо,
какова бы ни была его правая часть, либо соответствуюгцее однородное
уравнение имеет нетривиальные решения.
Первая часть альтернативы имеет место, если данное значение параметра
правильное, вторая — если оно характеристическое.
Замечание. Теория Фредгольма справедлива и для интегральных уравнений
второго рода со слабой особенностью.
(•) Литература: С. Т. Михлин A959), М. Л. Краснов, А. И. Киселев, Г. И. Макаренко
A968), J. А. Cochran A972), В. И. Смирнов A974) А. J. Jerry A985), D. Porter, D. S. G. Stirling
A990), C. Corduneanu A991), J. Kondo A991), W. Hackbusch A995), R. P. Kanwal A996).
5.6. Интегральные уравнения Фредгольма второго рода
с симметричными ядрами
5.6-1. Характеристические числа и собственные функнии
Симметричными интегральными уравнениями называются уравнения, ядра
которых симметричны, т. е. K(x,t) = K(t,x).
Каждое симметричное ядро, не равное тождественно нулю, имеет по крайней
мере одно характеристическое число.
Страница 125

126 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Совокупность характеристических чисел гг-го итерированного ядра при
любом п совпадает с совокупностью гг-ых степеней характеристических чисел
первого ядра.
Собственные функции симметричного ядра, соответствующие различным
характеристическим числам, ортогональны, т. е. если
пЪ пЪ
(pi(x) = Xi K(x,t)(pi(t)dt, (р2(х) = Х2 K(x,t)(p2(t)dt, Ai7^A2,
J а J a
TO
rb
((pi,(P2) = o, ((р,ф)= ^р{х)ф{х)ах
I
J a
Характеристические числа симметричного ядра действительны.
Собственные функции можно сделать нормированными: достаточно каждую
из них разделить на ее норму. Если некоторому характеристическому числу
соответствуют несколько линейно независимых собственных функций, например,
(/?i(x), ^2(х), ..., ^п(х), то каждая их линейная комбинация также является
собственной функцией и эти линейные комбинации могут быть выбраны так, что
полученные при этом собственные функции будут ортопормировапы.
Действительно, функция
llv^ill
имеет норму, равную единице: ||V^i|| = 1. Образуем комбинацию афг + (/?2 и
выберем а так, что
(аф1 -\-(р2, ф1) = О,
т. е. возьмем
Функция
(^1,^1)
-(^2,ф1
Ф2{Х) = 11 / , "^^11
\\аф^ +(/9211
Ортогональна к ф1(х) и имеет норму, равную единице. Далее выбирается
комбинация афг Ч- Рф2 Ч- v^3 и постоянные а и Р находятся из условий ортогональности
(аф1 + C(р2 + ^3, ф1) = О, (аф1 + (Зф2 + (рз, Ф2) = 0.
С найденными таким образом коэффициептами а и Р функция
^ аф1 + /?У^2 + ^2
\\аф^ ^E^2 +^^з11
ортогональна к V^i, V^2 и имеет норму, равную единице, и т. д.
Собственные функции, соответствующие разным характеристическим числам,
как было отмечено ранее, ортогональны. Отсюда вытекает, что последовательность
собственных функций симметричного ядра можно сделать ортонормированной.
В дальнейшем будем считать, что последовательность собственных функций
симметричного ядра ортонормирована.
Условимся также нумеровать характеристические числа в порядке возрастания
их абсолютных величин. Таким образом, если
Ai, А2, ..., An, ... A)
есть последовательность характеристических чисел некоторого симметричного
ядра, и ей соответствует последовательность собственных функций
(/?1, (/?2, ..., ^гг, ... B)
Страница 126

Интегральные уравнения Фредгольма 2-го рода с симметричными ядрами
111
так что
ipn{x)-\n / K(x,t)(pn(t)
J а
dt = О,
/'
J а
(pi(x)(pj(x)dx = l^
. О при г ф j,
C)
D)
|Ai|^ |Л2|^---^ |А.|^--- E)
Если характеристических чисел бесконечно много, то по теореме 1
Фредгольма они сгущаются только на бесконечности и потому Лп ^ ОС при 77/ > ОС.
Совокупность всех характеристических чисел и соответствующих им ортонор-
мированных собственных функций симметричного ядра называются системой
характеристических чисел и собственных функций данного ядра. Система
собственных функций называется неполной, если существует отличная от нуля квадратично
интегрируемая функция, ортогональная ко всем функциям системы. В противном
случае система собственных функций называется полной.
5.6-2. Билинейный ряд
Пусть ядро K(x,t) допускает разложение в равномерно сходящийся ряд по
ортонормированной системе своих собственных функций
K(x,t) = y^^ak(x)(pk(t)
F)
для каждого фиксированного значения х в случае непрерывного ядра или почти
всех X в случае квадратично интегрируемого ядра.
Тогда будем иметь
аф)= [ K{x,t)Mt)dt=^^,
Ja ^к
И, следовательно,
^к(ФМ
А,
Обратно, если ряд
сходится равномерно, то
Kix,t) = J2
к=1
K{x,t) = Y,
G)
(8)
(9)
Имеет место следующее утверждение: билинейный ряд (9) сходится в среднем
кядру i^(x,t).
Если симметричное ядро K(x,t) имеет лишь конечное число
характеристических чисел, то оно вырожденное, так как в этом случае
K{x,t) = Y^
к=1
^ki^)^kii)
Ль
A0)
Страница 127

128 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Ядро K(x,t) называется полосисителъно определенным, если для всех
функций (/?(ж), отличных от тождественного нуля,
по по
/ / К{х, t)(p(x)(p(t) dx dt > О,
J а J а
И ЛИШЬ для (р(х) = о указанный выше квадратический функционал равен нулю.
Такое ядро имеет только положительные характеристические числа. Аналогично
определяется отрицательно определенное ядро.
Всякое симметричное непрерывное положительно определенное (или
отрицательно определенное) ядро разлагается по собственным функциям в билипейный
ряд, абсолютно и равномерно сходящийся относительно переменных ж, t.
Утверждение остается верным, если допустить, что ядро имеет конечное число
отрицательных (соответственно положительных) характеристических чисел.
Если ядро интегрального уравнения K(x,t) симметрично, непрерывно в
квадрате S = {a^x^b, а^1^Ь}и имеет в последнем равномерно ограниченные
частные производные, то оно разлагается по собственным функциям в равномерно
сходящийся билинейный ряд.
5.6-3. Теорема Гильберта-Шмидта
Если функцию f(x) можно представить в виде
f{x)= [ K{x,t)g{t)
J а
dt.
(И)
где K(x,t) —квадратично интегрируемое ядро, g(t) — некоторая квадратично
интегрируемая функция, то f(x) может быть представлена своим рядом Фурье
относительно ортонормировапной системы собственных функций ядра K(x,t):
где
ак
Если, кроме того.
к = 1
= / f(x)(pk(x)dx
J а
f
J а
A2)
к = 1,2,.
K^{x,t)dt < А < оо,
A3)
ТО ряд A2) сходится абсолютно и равномерно для каждой функции f{x) вида A1).
Замечание 1. В теореме Гильберта-Шмидта полнота системы собственных
функций не предполагается.
5.6-4. Билинейные ряды итерированных ядер
По определению итерированных ядер
Km(x,t)
-
J а
К(х, z)Km-i(z,t) dz,
ттг = 2,3,...
A4)
Коэффициенты Фурье ak(t) ядра Km(x,t), рассматриваемого как функция ж,
отпосительпо ортонормированной системы собственных функций ядра K(x,t)
равны
ak(t)
= [ Km{x,t)M^)dx=^^
Ja ^к
A5)
Страница 128

Интегральные уравнения Фредголъма 2-го рода с симметричными ядрами 129
Применение теоремы Гильберта-Шмидта к A4) дает
i^^(.,t)=f:^^M^, ж=2,3,... A6)
в формуле A6) сумма ряда понимается как предел в среднем. Если же
дополнительно выполняется неравенство A3), то в формуле A6) ряд сходится равномерно.
5.6-5. Решение неоднородного уравнения
Представим интегральное уравнение
у(х)-Х K(x,t)y(t)dt = f(x), a^x^b, A7)
J а
где значение Л правильное, в виде
у(х) - fix) = Х f K{x,t)y{t)dt A8)
J а
И Применим теорему Гильберта-Шмидта к функции у(х) — f(x):
оо
у(х) - f(x) = Y^ Ак(рк(х),
к=1
^к= [у(х)-f(x)](pk(x)dx= / y(x)(pk(x)dx- / f(x)(pk(x)dx = yk-fk-
Ja J a Ja
сепия (8) будем иметь
nb оо
л / K{x,t)y{t)dt = \Y
•^«^ к=1
Тогда с учетом разложения (8) будем иметь
сЪ
^'^-(/^fc(x)
и, таким образом.
^к к — к —
Следовательно,
оо
у{х) = fix) + Л^ -IJ^^,(x). B0)
к=1 к
Если же значение Л характеристическое, т. е.
Х = Хр = Лр+1 = • • • = Ад, B1)
то при кфр^р-\-1^... ^q члены B0) сохраняют свой вид. При /с = р, р Ч-1, • • •, ^ из
формулы A9) следует Д = Ак{\ - Хк)/Х и в силу B1) fp = /p+i = ••• = fq =0.
Последнее означает, что
гЬ
f(x)(pk(x) dx = о
I
J а
При к = р, р+1,..., д^, т. е. свободный член уравнения должен быть ортогональным
к собственным функциям, соответствующим характеристическому числу Л.
Решения уравнения A7) в этом случае имеют вид
оо q
у(х) = f(x) + л ^ ^]^^,(х) + J2 СкМ^): B2)
к=1 ^к~^ к=р
где в первой из сумм B2) должны быть опущены члены при к=р,р-\-1,... ,q, для
которых одновременно обращаются в нуль fk и Л — Afc. Коэффициенты во второй
сумме Ск — произвольные постоянные.
9 А. В. Манж:иров, А. Д. Полянин
Страница 129

130 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Замечание 2. Аналогично проделанному выше можно на основании
билинейного разложения (8) и теоремы Гильберта-Шмидта построить решение
симметричного интегрального уравнения Фредгольма первого рода
сЪ
К(х, t)y(t) dt = f(x), а^х ^b,
I
J a
В следующей форме:
oo
k=l
Причем необходимыми и достаточными условиями существования и
единственности такого решения из L2(a,b) являются полнота системы собственных функ-
оо
ций (рк(х) ядра K(x,t) и сходимость ряда J^ /^А|, где Хк —соответствующие
характеристические числа.
Следует отметить, что проверка последнего условия для конкретных
уравнений затруднительна. Обычно при решении уравнений Фредгольма первого рода
пользуются методами, изложенными в главе 4.
5.6-6. Альтернатива Фредгольма для симметричных уравнений
Полученные результаты можно объединить в следующей альтернативной
форме.
Симметричное интегральное уравнение
у(х) -X [ К(х, t)y(t) dt = f(x), a^x^b, B3)
J a
При заданном Л либо имеет для всякой произвольной функции f(x) G L^(a, b) одно
и только одно квадратично интегрируемое решение, (в частности, у = 0 для / = 0),
либо соответствующее однородное уравнение имеет конечное число г линейно
независимых решений Yi(x), 1^2(ж), ..., Yr(x), г > 0.
Во втором случае неоднородное уравнение имеет решение тогда и
только тогда, когда заданная функция f(x) ортогональна всем функциям Yi(x),
Y2(x), ..., Yr(x) па отрезке [а, 6]. При этом решение определяется с точностью
до аддитивной линейной комбинации AiYi(x) + A2Y2(x) + • • • + ArYr(x), где
Ai (i = 1,2,..., г) — произвольные постоянные.
5.6-7. Резольвента симметричного ядра
Решение уравнения Фредгольма второго рода B3) можно записать в виде
у(х) = fix) + л / R{x,t; A)/(i) dt, B4)
J а
где резольвента R(x,t; Л) имеет вид
fl(x,i;A) = V^^^(^l^^^. B5)
^—^^ Хи — л
к=1 '^
Здесь совокупности ^к(х) и Хк составляют системы собственных функций и
характеристических чисел уравпения B3). Пз формулы B5) вытекает, что
резольвента симметричного ядра имеет только простые полюсы.
Страница 130

Интегральные уравнения Фредголъма 2-го рода с симметричными ядрами 131
5.6-8. Экстремальные свойства характеристических чисел
Введем обозначения
{u^w) = \ u(x)w(x)dx, \\и\\ = (и,и),
J а
{К
рЬ рЬ
и,и) = / K(x,t)u(x)u(t)dx dt,
J а J а
где (u,w) —скалярное произведение функций и{х) и w{x), \\и\\ —норма
функции и{х), а {Ки^ и) —квадратичная форма норожденная ядром К{х^ t).
Пусть Ai — наименьшее по абсолютной величине характеристическое число
симметричного ядра K(x,t) и пусть yi(x) — соответствующая этому числу
собственная функция. Тогда
-—— = max —-——— B6)
|Ail у^о \\уР
в частности, максимум достигается иу = yi является точкой максимума.
Пусть Ai, А2, ..., An —первые п характеристических чисел
симметричного ядра K(x,t) (в порядке возрастания их абсолютных величин), а yi(x),
У2(х), ..., уп(х) —соответствующие им ортонормированные собственные
функции. Тогда для характеристического числа A^+i, следующего за An, справедлива
формула
^^=^^Щу1, B7)
\K+i\
причем максимум берется на множестве функций у, отличных от тождественного
нуля и ортогональных к собственным функциям yi, у2, • • •, У^:
{y,yj) = 0, j = l,...,n; B8)
В частности, максимум в B7) достигается и у = уп+i является точкой
максимума, где Уп+1 —собственная функция, соответствующая характеристическому
числу Агг+1 и ортогональная ку1,у2, ..., Уп.
Замечание 3. Для положительно определенного ядра K(x,t) знак модуля в
соотношениях B6) и B7) может быть опущен.
5.6-9. Интегральные уравнения, приводимые к симметричным
Уравнение вида
у(х) - л / K(x,t)p(t)y(t)dt = fix), B9)
J а
где К(х, t) — симметричное ядро и непрерывная функция p(t) > О па [а, 6], можно
привести к симметричному Действительно, умножая обе части B9) на \Jр{х)
и вводя новую искомую функцию z{x) = лУр(х)у(х), придем к иптегральному
уравнению
fb ^ ^
z(x)-X L(x,t)z(t)dt = f(x)y^p(x), L(x,t) = K(x,t)y^p(x)p(t), C0)
J a
где L(x,t) —симметричное ядро.
9*
Страница 131

132 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
5.6-10. Кососимметричное интегральное уравнение
Кососимметричным интегральным уравнением называется уравнение, ядро
которого кососимметрично, т. е. в уравнении
у{х) - л / K{x,t)y{t)dt = fix) C1)
J а
ядро K(x,t) обладает следующим свойством:
K{t,x) = -K{x,t). C2)
Уравнение C1) с кососимметричным ядром C2) имеет но крайней мере одно
характеристическое число и все его характеристические числа — чисто мнимые.
(•) Литература: Э. Гурса A934), Р. Курант, Д. Гильберт A951), С. Г. Михлин A959),
Ф. Трикоми A960), М. Л. Краснов, А. И. Киселев, Г. И. Макаренко A968), J. А. Cochran
A972), В. И. Смирнов A974), А. J. Jerry A985), D. Porter, D. S. G. Stirling A990),
C. Corduneanu A991), J. Kondo A991), W. Hackbusch A995), R. P. Kanwal A996).
5.7. Операторный метод решения интегральных
уравнений второго рода
5.7-1. Простейшая схема
Рассмотрим линейное уравнение второго рода специального вида
yix)-\L[y] = fix), A)
где L — некоторый линейный (интегральный) оператор, удовлетворяющий
условию Jj^ = к, к = const.
Подействуем оператором L на обе части уравнения A). В результате получим
Ъ[у]-кХу(х) = Ъ[/(х)]. B)
Исключая из A) и B) слагаемое L [у], находим решение:
Замечание. В разд. 3.4 описаны различные обобщения указанного метода.
5.7-2. Решение уравнений второго рода на полуоси
1°. Рассмотрим уравнение
/»оо
у(х) - Л / cos(xt)y(t) dt = f(x). D)
-'О
Оператор L в данном случае с точностью до постоянного сомножителя
совпадает с косинус-преобразованием Фурье:
/»оо /
L [у] = / cos(xt)y(t) dt = J^dM E)
Jo V ^
и действует по правилу L^ = /с, где к = ^ (см. п. 1.5-1).
Решение получим по формуле C) с учетом равенства E):
2
у{х) =
2-7ГЛ2
f(x) + л / cos(xt)f(t) dtV \ф ±J
Хф±\1-- F)
Страница 132

5.8. Метод интегральных преобразований и метод модельных решений 133
2°. Рассмотрим уравнение
/»оо
у{х) - Л / tMxt)y(t) dt = /(ж), G)
-'О
где Ju{x) — функция Бесселя, Леи > — ^.
Оператор L здесь с точностью до постоянного сомножителя совпадает с
преобразованием Ханкеля:
/»оо
/ tJ^{xt)y{t)dt (8)
и действует по правилу L^ = 1 (см. п. 1.6-1).
Решение получим по формуле C) при к = 1 с учетом равенства (8):
1
У{х)
/»оо
/ tJ.{xt)f{t)i
Jo
/(ж) + Л / tJ4xt)f(t)dt
1-Л2
(•) Литература: А. D. Polyanin, А. V. Manzhirov A998, 1999).
5.8. Метод интегральных преобразований
и метод модельных решений
л 7^ ±1. (9)
5.8-1. Уравнение с разностным ядром на всей оси
Рассмотрим интегральное уравнение типа свертки второго рода с одним ядром
у(х) + —= / К(х - t)y(t) dt = f(x), -ОС < ж < ОС, A)
Л/27Г J_^
где f(x) и К(х) — известные правая часть и ядро интегрального уравнения, а
у(х) — искомая функция. Применим к уравнению A) альтернативное
преобразование Фурье. Тогда с учетом теоремы о свертке (см. п. 1.4-4)
y(u)[l^JC(u)]=J^(u). B)
Таким образом, с помощью преобразования Фурье решение исходного
интегрального уравнения A) приводится к решению алгебраического уравнения B) для
изображения искомого решения. Решение уравнения B) имеет вид
У(и) = ^^. C)
1 + /C(w)
Формула C) выражает изображение решения исходного интегрального уравнения
через изображения заданных функций — ядра и правой части уравнения. Само
решение может быть получено при помощи обратного преобразования Фурье:
Формула D) фактически решает задачу, однако она не всегда удобна для
использования, так как требует вычисления изображения J^(u) для каждой правой
части /(ж). Во многих случаях более удобным оказывается представление решения
неоднородного интегрального уравнения через резольвенту исходного уравнения.
Чтобы получить требуемое представление, заметим, что формула C) может быть
преобразована к виду
у (и) = [1 - Щи)]:Г(и), Щи) = ^^;j . E)
1 + /V-(WJ
Страница 133

134 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
На основании E) при помощи обратного преобразования Фурье и теоремы о
свертке (для изображений) получим
у{х) = /(х) - -1= У" Д(х - t)f{t) dt,
F)
R{x) = ^ Г ^^^е—^ du. G)
V27r J_^ H-/C(f'
где резольвента Д(ж — t) интегрального уравнения A) задается соотношением
-)С{и)
Таким образом, для определения решения исходного интегрального уравнения A)
достаточно найти функцию R(x) по формуле G).
Функция R(x) представляет собой решение уравнения A) при специаль-
ном виде функции f(x). Действительно, из формул C) и E) следует, что при
У (и) = lZ{u) функция Т{и) равна }С(и). Это означает, что решением уравнения A)
при f(x) = К(х) является функция у(х) = R(x),t. е. резольвента уравнения A)
удовлетворяет интегральному уравнению
1 f°^
R{x) + -^= / К{х - t)R{t) dt = К{х), -ОС < ж < ОС.
л/27г J_^
(8)
Отметим, что для вычисления прямых и обратных преобразований Фурье
существуют соответствующие таблицы в книгах Г. Бейтмена, А. Эрдейи A969),
В. А. Диткина, А. П. Прудникова A965, 1974).
Пример. Решим интегральное уравнение
/оо
е:><:р[а\х — t\)y(t) dt = f(x), —оо < ж < оо, (9)
-оо
которое вытекает из уравнения A) при конкретном ядре К(х — t), задаваемом выражением
Х(ж) = -л/2^Ле-^1, а>0. A0)
Найдем функцию R{x), для чего вычислим
/оо 9г>Л
д^-«|х|^гих ^^ ^ ^щ
-оо w^+a^
Тогда по формуле E)
^, . fCiu) 2а\ .._.
1 + /C(w) w^ + а^ — 2а\
7Ш Л ^(")^""^ ^" = V V /I IJ^T^r^^— '- ^13)
откуда
R(x)
Положим, что л < ^а. Тогда интеграл A3) имеет смысл и может быть вычислен с помощью
теории вычетов путем применения леммы Жордана (см. пп. 1.1-4 и 1.1-5). После некоторых
выкладок найдем
R(x) = -у/^ __^ рур(-|^|л^/гу2 - 9гуЛ ) A4)
и, окончательно, в соответствии с F) получим
у(ж) = /(ж)+ ^ =^ / ехр(-|ж-^|Уа2 -2aX)f{t)dt, -оо<ж<оо. A5)
л/о;2 — 2аХ J-00
Страница 134

5.8. Метод интегральных преобразований и метод модельных решений 135
5.8-2. Уравнение с ядром K(x,t) = t Q(x/t) на нолуосн
Рассмотрим здесь уравнение на полуоси
у{х) - |°° }q (j) y{t) dt = fix). A6)
Для решения будем использовать преобразование Меллина, которое определяется
следующим образом (см. также разд. 1.3):
/»оо
J{s)=m{f{x),s}= f{x)x'-Ux,
Jo
A7)
где s = а -\- ir — комплексная переменная (ai < а < сг2), f(s) — изображение
функции f(x). Далее для краткости преобразование Меллина будем обозначать
m{f{x)} = m{fix),s}.
По известному изображению f(s) оригинал находится с помощью обратного
преобразования Меллина
fix) = m-'{f(s)} ^ -^ / J(s)x-4s, ai < с < а2, A8)
где путь интегрирования расположен параллельно мнимой оси комплексной
плоскости S, а интеграл понимается в смысле главного значения.
Применяя преобразование Меллина к уравнению A6) и учитывая, что интеграл
с таким ядром преобразуется в произведение про правилу (см. п. 1.3-2)
Шу^ jQ[j)y{t)dtj =Q{s)y{s),
Приходим к уравнению для изображения искомой величины y(s):
y(s) - QisMs) = f(s).
Решение этого уравнения определяется формулой
Vis) = -^^f ^ . A9)
l-Q(s)
Применяя к A9) обратное преобразование Меллина A8), получим решение
исходного интегрального уравнения
у(х) = J- /"'"^'°° ^^!^ X-'ds.
2жг J,_i^ l-O(s)
B0)
Это решение можно записать также с помощью резольвенты в виде
y(x) = f{x) + j°°jN[j)mdt, B1)
где приняты обозначения
Щх) = m-'{N(s)}, N(s) = -^^f-. B2)
1 - Q{s)
При использовании указанного аналитического метода решения могут
возникнуть технические трудности: 1) при получении изображения для заданного
ядра К(х) и 2) при нахождении оригинала решения по его изображению y(s). Для
вычисления соответствующих интегралов применяют таблицы прямых и обратных
преобразований Меллина. Во многих случаях сначала используют связь между
преобразованием Меллина и преобразованиями Фурье и Лапласа:
m{f{x),s} = S{f{e%is} = £{f{e^),-s}+Q{f{e-^),s}, B3)
а затем применяют таблицы прямых и обратных преобразований Фурье и Лапласа.
Страница 135

136 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f(x)
Замечание 1. Уравнение
y(x)-J H[j)x''t-"-'y{t)dt = f{x)
МОЖНО записать в форме A6), если обозначить K(z) = z^H(z).
B4)
5.8-3. Уравнение с ядром K(x,t) = t^Q(xt) на нолуосн
Рассмотрим уравнение на полуоси
/»оо
у{х)- / t^Qixt)y{t)dt = f{x).
Jo
B5)
Для решения будем использовать преобразование Меллина. Умножая обе
части B5) на х^~-^ и интегрируя по х от нуля до бесконечности, получим
/»оо /»оо /»оо /»оо
/ y(x)x'~^dx- y(t)t^dt Q(xt)x'~^dx= f(x)x'~^dx. B6)
-'О -'О -'О -'О
Сделаем замену z = xt.B результате получим
/»оо
y(s)-Q(s) y{t)t^-^t = J{s).
Jo
B7)
Учитывая равенство
y(ty-'dt = y(l^p-s),
перепишем уравнение B7) в следующем виде:
y(s)-Q(s)y(l+/3-s) = /(s).
Заменяя s в соотношении B8) на 1 Ч- /3 — s, имеем
уA +/3 - S) - Q(l +/3 - s)^(s) =/A +/3 - S).
B8)
B9)
Исключая из равенств величину уA -\- Р — s) и разрешая полученное уравнение
относительно y(s), находим изображение искомого решения
y(s)
f{s)^Q{s)f A^C-8)
l-Q(s)Q(l^C-s)
C0)
По формуле обращения Меллина получим решение интегрального
уравнения B5) в виде
Замечание 2. Уравнение
f{s)^Q{s)f{l^f3-s)
l-Q{s)Q{l^f3-s)
X ' ds.
C1)
/»оо
у(х)- / H(xt)x4''y(t)dt = f(x)
Jo
можно записать в форме B5), если обозначить Q(z) = z^H(z), Р = q — р.
Страница 136

5.9. Метод Карлемана для интегральных уравнений типа свертки второго рода 137
5.8-4. Метод модельных решений для уравнений на всей оси
Проиллюстрируем возможности обобщенной модификации метода модельных
решений (см. разд. 3.6) на примере уравнения
Ау{
/оо
Q{x + t)e'^'y{t)dt = f{x), C2)
-ОО
где Q = Q(z), f(x) —произвольные функции, А, C — произвольные постоянные,
удовлетворяющие некоторым ограничениям.
Для наглядности вместо исходного уравнения C2) будем писать
Ь[у{х)] = fix). C3)
В качестве пробного решения возьмем экспоненту
Уо = е^"". C4)
Подставляя C4) в левую часть уравнения C3), после некоторых преобразований
получим
/оо
д{г)е^^+^'^Ыг. C5)
-ОО
правую часть C5) можно рассматривать как функциональное уравнение
относительно ядра обратного преобразования Лапласа е^^. Для его решения заменим р
в C5) на —р — /3. В результате получим
L [е-^^+^^"] = Ае-^^+^^" + q{-p - f3)e''\ C6)
Умножим обе части равенства C5) на А, а обе части равенства C6) на —q(p) и
сложим почленно полученные выражения. В результате имеем
L Ие"^ - <z(p)e-(^+'''l = [А^ - q{p)q{-p - /3)]e''^ C7)
Поделив обе части C7) на постоянную А^ — q{p)q{—p — /3), получим исходное
модельное решение
^ = ^;r~fw'"^'^r^ L [Y(x,p)] = е^\ C8)
А2 - q(p)q(-p - C)
Здесь — оо < ж < оо, поэтому следует положить р = iu и воспользоваться
формулами из п. 3.6-3. Тогда решение уравнения C2) для произвольной функции f(x)
можно записать в виде
-. /»оо /»оо
у(х) = ^ Y(x,iu)~f{u)du, ~f(u)= f(x)e-'"^dx. C9)
V27T J_oo J_oo
(•) Литература: П. П. Забрейко, А. И. Кошелев и др. A968), М. Л. Краснов, А. И. Киселев,
Г. И. Макаренко A968), В. И. Смирнов A974), Ф. Д. Гахов, Ю. И. Черский A978),
А. Д. Полянин, А. В. Манжиров A997), А. D. Polyanin, А. V. Manzhirov A998).
5.9. Метод Карлемана для интегральных уравнений
типа свертки второго рода
5.9-1. Уравнение Вннера-Хонфа второго рода
В приложениях часто встречаются уравнения типа свертки второго рода вида*
у(х) + -^ [ К(х - t)y(t) dt = /(ж), О < ж < оо, A)
Перед чтением этого раздела рекомендуется ознакомится с разд. 4.4 и 4.5.
Страница 137

138 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
где ядро К{х) определено на всей действительной оси.
Доопределим A) на отрицательной полуоси путем введения односторонних
функций
Тогда получим уравнение
fix) прих>0, ^_(^) = Оприх>0.
О при ж < О, ^ ^ ^
у+{х) +
n/2^ У-с
К{х - t)y+{t) dt = у-(х) + U(x)
-ос < ж < ОС, B)
которое совпадает с A) при х > 0.
Вспомогательная функция у- (х) введена для того, чтобы доопределить левую
часть уравнения B) при х < 0. Заметим, что у-(х) в области х < О неизвестна и
находится в процессе решения задачи.
Переходя в равенстве B) к интегралам Фурье (см. пп. 1.4-3, 4.4-1, 4.4-2),
получим задачу Римана в форме
+
-ОС < и < ОО.
1 + /C(w) 1 + /C(w) '
1°. Предположим, что выполнено условие нормальности, т. е.
и запишем задачу Римана в ее обычной форме
У^{и) = V{u)y~(и) + Щи), -ОС <и<оо,
где
Т{и)
V(u) =
Щи) =
C)
D)
E)
1 + /C(w) ' ' ' 1 + /C(w)
Задача Римана D) равносильна уравнению A): они одновременно разрешимы
или неразрешимы, имеют в общих решениях одинаковое число произвольных
постоянных. Если индекс задачи Римана
F)
и = Ind ■
1 + /C(w
который иногда называют индексом уравнения Винера-Хопфа второго рода
положителен, то однородное уравнение A) (/(ж) = 0) имеет ровно v линейно
независимых решений, а неоднородное уравнение безусловно разрешимо, и его решение
зависит от v произвольных комплексных постоянных.
В случае z^ ^ О однородное уравнение не имеет отличных от нуля решений.
Неоднородное уравнение при v = О безусловно разрешимо, причем решение
единственно. Когда индекс р отрицателен, условия
Т{и) du
f
J —с
О,
1,2,.
G)
Х+{и)[1^1С{и)]{и^г)^
необходимы и достаточны для разрешимости неоднородного уравнения (см.
п. 4.4-4).
Во всех случаях, когда решение уравнения A) существует, его можно найти
по формуле
У{
1 Г
х) = у+{х) = —= /
Л/27Г J _^
У^{и)е ^^^ du,
ж > О,
(8)
где З^^(г^) — построенное по схеме из п. 4.4-4 (см. рис. 3) решение задачи
Римана D) и E).
Отметим, что в формуле (8) явно присутствует только функция З^^(г^), которая
связана с У~ (и) соотношением D).
Страница 138

5.9. Метод Карлемана для интегральных уравнений типа свертки второго рода 139
2°. Исследуем теперь исключительный случай интегрального уравнения A), когда
нарушается условие нормальности для задачи Римана C) (см. пп. 4.4-6 и 4.4-7).
В этом случае отсутствуют нули коэффициента D(u) = [1 + ]С{и)\~^ и порядок
его на бесконечности т] = 0. Общее решение краевой задачи C) можно получить
по формулам F3) из п. 4.4-7 при а^ = 0. Решение исходного интегрального
уравнения A) определится из решения краевой задачи по формуле (8).
На рис. 4 изображена схема решения интегральных уравнений Винера-Хопфа
(см. также п. 4.5-1).
Пример. Рассмотрим уравнение
/•оо
у{х) + / {а^Ь\х- t|)e-l"-^ly(t) dt = f{x), х >(), (9)
где постоянные а и 6 вещественны и 6 т^ 0. Ядро К{х—1)ъ уравнении A) дается выражением
К{х) = л/2^(а + 6|ж|)е-1^1.
Найдем изображение ядра:
и^ (а - Ь) -\-а-\-b
JC(u) :
/оо
(а + 6|ж|)б
-оо
-Ы+гих ^^ ._
(и^ + 1J
Отсюда
1+/C(W) :
Р{и)
P(Z):
- 2(а - 6 + l)z^ + 2а + 26 + 1.
(w2 + 1J
Исходя из условия нормальности, предполагаем, что постоянные а и 6 таковы, что
многочлен P{z) не имеет вещественных корней. Пусть а -\- гE — корень биквадратного уравнения
P{z) = О, причем а > О, /5 > 0. Тогда, в силу вещественности коэффициентов уравнения,
величины (а — г/5), {—а -\- ijS) и {—а — ijS) будут тремя остальными корнями. Также в силу
вещественности функция 1 + 1С{и) имеет нулевой индекс, так что рещение уравнения (9)
существует и единственно.
Разлагая на множители, находим 1 + 1С{и) = Х~ (и)/Х^(и), где
(w + iJ
Х+{и) :
Х-{и):
(и-
■if3)(u-
-iC)
(и-\-а-\-if3){u — а-\-if3) ^ ^ ^ (и — i)^
Используя этот результат, представим краевое условие D), E) в виде
У+(и) (u-i)^T+(u) _ у-(и)
л:-(и)'
оо < w < оо.
A0)
Л:+{и) (и-а- if3){u + а - г/5)
Применяя теорему об аналитическом продолжении и обобщенную теорему Лиувилля (см.
п. 4.4-3), получаем возможность приравнять обе части равенства величине
и — а — ijS и-\- а — ijS^
где постоянные С^ и С^ подлежат определению. Отсюда
{u-ifT+{u) , Ci
У^{и) = A'+(w)
+ ■
С,
(и — а — iC)(u-\-а — iC) ' и — а — iC ' и-\-а — iC
Для устранения полюсов (а + г/5) и (—а + г/5) необходимо и достаточно положить
(a^iC-i)^J='+(a^iC) _ (-а ^ iC - i)^J='+(-a ^ iC)
С,
2а
Со
-2а
A1)
A2)
Ввиду громоздкости переход от изображения A1) к оригиналу осуществим в два этапа.
Сначала найдем оригинал слагаемого
у,{и) = л:+{и)
(w-iJ^+(w)
(и — а — iC)(u -\- а — гE)
-JC(u)
■Т^{и) = Т^{и) + Щи)Т+{и).
Страница 139

140 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f(x)
Рис. 4. Схема решения интегральных уравнений Винера-Хопфа. При
/5 = 0 имеем уравнение первого рода, при /5 = 1 — уравнение второго
рода.
Здесь
Щи) ■
2и'^ (а - Ь)-\-2а-\-2Ь _ /^ Д
-(а + г/5J][«2-(а-г/5J] ~ и^ - (а ^ iC)^ ^ и^ - (а - iC)^
Страница 140

5.9. Метод Карлемана для интегральных уравнений типа свертки второго рода 141
р = г-
Найдем оригинал первой дроби:
р
(а + г/5J(а- 6) + а + 6
2сф '
У w^ — [а
: + г/5J
оригинал второй дроби запишем в виде
Д
F-1
и^ -{а- iEY J \ 2 (З^га
1_ Д ^-{15-гсА\х\
2 /5 - га
^ Д .g-(/3+ic.)|x|_
Таким образом,
A3)
R{x) = J — р[е^^+^'^\^\ + Q-ie-ic^\x\^^^-C\x\ ^ у^ре-(^\^\ 008F» + а\х\)
y^{x) = f{x)^p / e-^l^-^lcosF' + a|x-t|)/(t)dt, ж > О, ре''
Jo
C — га
A4)
Заметим, что одновременно мы нашли резольвенту R{x — t) интегрального уравнения на
всей оси
/оо
{a^b\x-t\)e-\^SQ{t)dt = fQ{x),
-оо
Теперь рассмотрим оставшуюся часть изображения A1):
-оо < ж < оо.
У^(и)=Х+{и)(-
Ci
С,
Вычислив интегралы
F-H3^2W}
с,
а — гC и-\- а — гC
(и -\- if3 — а){и -\- if3 -\- а){и — а — гE)
+ ■
Со
(w + iJe-^^^dw
5 {и -\- гC — а){и -\- гC -\- а){и -\- а — г/5)
с помошью теории вычетов (см. пп. 1.1-4 и 1.1-5) и подставив вместо постоянных С^ и С^
их значения A2), получим при ж > О
У2{^) ■
4а2/5
/•оо
/ е-^^^+^^ со8[а(ж - t)]/(t) dt+
^ i:^ Г ^"'^"' ^^^f'^ ^ "(^ ^ *^]^(*^ ''^ '*'"=Ш^
A5)
Так как У~^{и) = 3^^^ (и) +3^2 ('^)' '^^ искомое решение будет суммой функций A4) и A5).
5.9-2. Интегральное уравнение второго рода с двумя ядрами
Рассмотрим интегральное уравнение тина свертки второго рода с двумя
ядрами в форме (—оо < X < оо)
у(х)-\-
— Г
V^ Jo
Ki(x-t)y(t)dt^
\/2^ J-OC
K2{x-t)y{t)dt = f{x). A6)
Заметим, что каждое из ядер Ki(x) и К2(х) задано на всей вещественной оси.
Представляя искомую функцию в виде разности односторонних:
у(х) = у^(х)-у-(х), A7)
Страница 141

142 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
запишем уравнение в виде
у+(х) + -= / K^{x-t)y+{t)dt-y-{x) ^= / K2{x-t)y-{t)dt = f{x).
л/2ТТ J_oo л/ZTT J-00
A8)
Переходя от оригиналов к изображениям при помощи интегрального
преобразования Фурье (см. п. 1.4-3), получим
[1 + JCi(u)]y^(u) - [1 + }С2(и)]у-(и) = J^(u). A9)
Откуда будем иметь
у^(и) = 1±!^у-(и) + -^Р-. B0)
1 + /Ci(w) 1 + /Ci(w)
Здесь JCi(u), }С2(и) и J^(u) —интегралы Фурье известных функций.
Неизвестные изображения З^^(г^) и У~ (и) являются краевыми значениями функций,
аналитических соответственно в верхней и нижней полуплоскостях. Таким образом,
получена краевая задача Римана.
1°. Предположим, что выполнены условия нормальности, т. е.
и запишем задачу Римана в ее обычной форме (см. п. 4.4-4):
y^(u)=V(u)y-(u)^n(u), -оо<и<оо, B1)
где
Viu) = l±b(^, Щи) = ^Р^. B2)
1 + /Ci(w) 1 + /Ci(w)
Задача Римана B1), B2) равносильна уравнению A6): они одновременно
разрешимы или неразрешимы и имеют в общих решениях одинаковое число
произвольных постоянных.
Если индекс
т J 1 +''^2(^) /лоч
1 -\-JC-^{u)
положителен, то однородное уравнение A6) (f(x) = 0) имеет ровно ly линейно
независимых решений, а неоднородное уравнение безусловно разрешимо, и его
решение зависит от 1у произвольных комплексных постоянных.
В случае и ^ О однородное уравнение не имеет отличных от нуля решений.
Неоднородное уравнение при i/ = О безусловно разрешимо, причем решение
единственно. Когда индекс и отрицателен, условия
-^(")'^" -о, к = 1,2,...,-и, B4)
f
J —с
л:+{и)[1^}с^{и)]{и^1)к
необходимы и достаточны для разрешимости неоднородного уравнения.
Во всех случаях, когда решение уравнения A6) существует, его можно найти
по формуле
1 f°^
у(х) = / [З^^(^) — У~ (г^)]е~*'^^ du, —ос < ж < ос,
л/27г J_^
B5)
где З^^(г^), 3^ (г^) —построенное по схеме из п. 4.4-4 (см. рис. 3) решение задачи
Римана B1), B2).
Птак, решение уравнения A6) равносильно решению краевой задачи Римана
и сводится к вычислению некоторого числа интегралов Фурье.
Страница 142

5.9. Метод Карлемана для интегральных уравнений типа свертки второго рода 143
2°. Исследуем теперь исключительный случай интегрального уравнения A6).
Допустим, что функции 1 -\- ]Ci{u), 1 -\- ]С2{и) могут иметь нули, причем эти
нули могут быть как в различных, так и в совпадающих точках контура. Напишем
разложение этих функций, выделив совпадающие нули:
1+/Ci(^) = П(^ - ^^^^' П (^ - ^о^'^пЫ,
3 = 1 к = 1
г р
fc=i
р
fc=l
B6)
Здесь ai ф bj, но возможно, что отдельные точки dk (к = 1,... ,р) могут совпадать
либо с ai, либо с bj. Это будет соответствовать тому случаю, когда функции
1 Ч- }Ci(u) и 1 Ч- JC2(u) имеют общий нуль разной кратности. Мы не выделяем
такие точки особо, потому что их наличие не оказывает влияния на условия
разрешимости и число решений задачи.
Из равенства A9) и условия конечности на контуре решения вытекает, что
для разрешимости задачи, а следовательно, и уравнения A6), необходимо, чтобы
Т(и) во всех точках dk обращалась в нуль порядка 7fc, т. е. Т(и) должна иметь
вид
р
T(u) = l[(u-dky'^Ti(u).
к=1
Для этого необходимо выполнение 7i + 72 + • • • + 7р = ^ условий
:f(j^)(dk) = o, jfc = o,i,...,7fc-i,
или, что все равно, условий
/»оо
I
J —с
B7)
B8)
Так как функции JCi(u) и }С2(и) обращаются в нуль на бесконечности, то
бесконечно удаленная точка является обыкновенной точкой V(u).
Допустим, что условия B8) выполнены. Тогда краевую задачу Римана B0)
можно записать в виде (см. пп. 4.4-6 и 4.4-7)
У^(и) = ^ V2(u)y-(u) +
Щ{и)
B9)
Найдя в этом исключительном случае ее общее решение, получим общее
решение исходного уравнения по формуле B5).
Сформулируем выводы об условиях разрешимости и числе решений
уравнения A6). Для разрешимости уравнения A6) необходимо, чтобы преобразование
Фурье свободного члена уравнения удовлетворяло / условиям B7). Если эти
условия выполнены, то при 1у — п> О задача B0) и интегральное уравнение A6) имеют
ровно 1У — п линейно независимых решений. Ири 1у — п ^0 многочлен Pj^-n-i (^)
следует положить тождественно равным нулю, причем от свободного члена в
случае 1У — п < О необходимо потребовать выполнения еще п — р условий. Ири
выполнении последних интегральное уравнение будет иметь единственное решение.
Страница 143

144 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Пример. Рассмотрим уравнение A6), для которого
где а и /5 — вещественные постоянные. Тогда К^ (ж — t) = О для ж < t и ^2 (ж — t) = О для
X < t. Следовательно, заданное уравнение имеет форму
у{х) - A + а) /" e-^^'-'^vit) dt-{l + C) f e-^"-'^y(t) dt = О, ж > О,
у(ж) - A + /5) I e-^^-^^y(t) dt = -л/2^е^, ж < 0.
^ — оо
Вычислим интегралы Фурье
Jo "■ ' "
и -\- г и -\-1
и — ijS
Т(и)= г, ^W
краевое условие запищем в виде
у^^и) = ^^^^у-(и) + -Щ±11—. C0)
и — га (и — г)(и — га)
Рещение задачи Римана будет различным в зависимости от знаков а и /5.
1°. Пусть а>0иC>0. В этом случае i^ = lndV{u) = 0. В левой и правой
частях краевого условия стоят функции, аналитически продолжимые соответственно в
верхнюю и нижнюю полуплоскости. Применяя непосредственно теорему об аналитическом
продолжении и обобщенную теорему Лиувилля (см. п. 4.4-3), будем иметь
у+(,) = о, ±^у-(.) + ^(£±1Ц = о.
Z — га [z — г){г — га)
Отсюда
у+{х) = о, у{х) = -у_ {х)=-^ г %+'^ е-'- du.
^ л/27г J_oo {и-г){и-гE)
Вычисляя последний интеграл в предположении C ф 1, по теореме о вычетах (см. пп. 1.1-4
и 1.1-5) получим
О при ж > О,
у(х) = { _^ j2e- - A + /3N"-] при X < 0.
В случае /5=1 имеем
{'
. . _ I О при ж > О,
УК^) - 1 -л/2^е^A + 2ж) при ж < 0.
2°. Пусть а < О и /5 < 0. Здесь по-прежнему г^ = О, Л'+B;) = B; — iE){z — га)~^,
Х~ {z) = 1. Группируя члены, содержащие краевые значения аналитических в каждой
из полуплоскостей функций и применяя затем теорему об аналитическом продолжении и
обобщенную теорему Лиувилля (см. п. 4.4-3), найдем
y+{z) , /5 + 1 1 _ y-{z)
X+{z) i{C -1) z-iC X- {z) i(/5 - 1) z-i
:0.
Страница 144

5.9. Метод Карлемана для интегральных уравнений типа свертки второго рода 145
Отсюда
y+{z) :
/5 + 1
C — 1 Z — га
у-(^)
у{'
1 Г°°
X) = -^j^Jy+(u)-y-(u)] е—
2г 1
/5-1 z-i'
du --
/5-1
2л/2^
/5-1
при ж > О,
при ж < 0.
3°. Пусть а < О и /5 > О, тогда г^ = 1. В этом случае, краевое условие C0) запишем в виде
У+{и) +
гA + а)
и — ijS
1 — а и — га и — га
у-{и)-
2г
1 — а и — г
Применяя теорему об аналитическом продолжении и обобшенную теорему Лиувилля (см.
п. 4.4-3) получим, что
y+{z) +
Поэтому
y+{z)=(c-
гA + а)
z-iE
1 — а Z — га z — га
у-{^)-
2г
С
1 — а Z — г Z — га
1 + а
1 — а J Z — га
у-(^)-
с
2г
Z — ijS 1 — а (z — i)(z — ijS)
где С — произвольная постоянная. Теперь при помоши обратного преобразования Фурье,
получим обшее решение интегрального уравнения в форме
у{х) = {
27Г гС +
гС +
1 + а '
1-а ,
2(а-/5)
2л/27г
1-/5
при ж > О,
е^ при ж < 0.
A-а)A-/3).
4°. Пусть а > О и /5 < О, тогда г^ = — 1. По теореме Лиувилля (см. п. 4.4-3)
i{z -\-i)
y^{z) = ^^y-{z)^
y+{z)=0, y-{z):
(z — i)(z — ia)
i{z -\-i)
0,
{z-i){z-iC)
Из выражения для y~{z) видно, что особенность функции У~ (z) в точке г/5 исчезнет, если
положить /5 = — 1. Последнее равенство и будет условием разрешимости задачи Римана. В
этом случае имеем единственное решение
Г О при ж > О,
\ —л/27ге^ при ж < 0.
У(Х) :
— Г
' du --
Замечание 1. К рассмотренным в н. 5.9-2 уравнениям приводятся некоторые
уравнения, в ядра которых входят не разности, а другие их комбинации:
произведения или, чаще, отношения. Так, например, уравнение
C1)
становится обычным уравнением с двумя ядрами, если сделать следующие замены
функций и их аргументов: ^ = е^, т = е^, A^i(C) = Ki(x), Л^2@ = К2(х),
9@ = fi^l Y@ = У(х).
10 А. В. Манж:иров, А. Д. Полянин
Страница 145

146 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
5.9-3. Уравнения тнна свертки с неременным пределом интегрирования
1°. Рассмотрим интегральное уравнение Вольтерра второго рода
у{х) + -^ / К{х - t)y{t) dt = f(x), О ^ X < Т,
C2)
где промежуток [О, Т) может быть как конечным, так и бесконечным. В отличие от
уравнения A), где ядро задается на всей оси, здесь ядро задается на положительной
полуоси.
Уравнение C2) можно рассматривать как частный случай одностороннего
уравнения A) из п. 5.9-1. Для этого достаточно записать его в виде
у{х)-\-
1 /"°°
^ / К^{х - t)y{t) dt = f{x), О < ж < ОС,
27Г Jo
ЮЩС!
Приводящемся к следующей краевой задаче:
у-(и)
Т+(ь
l + /C+(w) l + /C+(w)
Здесь коэффициент [1 + JC~^(u)]~'^ задачи есть функция, аналитически продолжи-
мая в верхнюю полуплоскость, за исключением конечного числа возможных
полюсов, являющихся нулями функции 1 -\- JC~^(z) (считаем, что на действительной
оси 1 Ч- АС^(^) ф 0). Поэтому индекс и задачи всегда неположителен, и ^0.
Переписав задачу в виде [1 + 1С~^ (и)]У~^ (и) = У~ (и) + Т~^(и), видим, что У~ (и) = О,
так что
_ ^+(^)
l + /C+(w) '
Рассмотрим следующие случаи.
1.1. Функция l-\-JC~^(z)ue имеет нулей в верхней полуплоскости (это означает,
что jy = 0). Следовательно, уравнение C2) при любой правой части f(x) имеет
единственное решение, которое можно выразить через резольвенту:
У^(и) =
C3)
где
у(х) = f(x) +
R(x) =
1 Г
V2^ У-оо 1
R(x-t)f(t)dt, ж > О,
C4)
/C+(w)
du.
. + /C+(w)
1.2. Функция 1 + АС^(^) имеет нули в точках z = ai,a2,...,am верхней
полуплоскости (тогда z^ < О, причем 1у равно взятому со знаком минус суммарному
порядку нулей). Могут представиться две возможности:
(а) Функция J-'~^(z) в точках ai, а2,..., am обращается в пуль, причем
порядки этих нулей не ниже порядков нулей функции 1 + /С^(^). В этом случае функция
JF+(^)[1 Н- /С^(^)]~^ опять не будет иметь полюсов, так что по-прежнему
уравнение имеет единственное решение C4).
Предложение d^T^{aj)/dz^ = О об обращении J^^{z) в нуль равносильно
условиям
f
J —с
f{t)e-'''^4^dt = ^,
k = 0,...,r]j -1, j = 1,
,ш,
C5)
где rjj —кратность нуля функции 1 -\- JC~^(z) в точке aj. Условия C5)
накладываются уже непосредственно на правую часть уравнения.
Страница 146

5.9. Метод Карлемана для интегральных уравнений типа свертки второго рода 147
(Ь) Функция ^^(^) не обращается в нуль в точках ai,a2,...,am (или,
если обращается, то с кратностями, меньшими, чем 1 + /С^(^)). Тогда функция
JF+(^)[1 -\- /С^(^)]~^ имеет полюсы, и поэтому функция C3) не принадлежит
условленному классу. Уравнение C2) не имеет решений в выбранном классе
функций. В рассматриваемом случае условия C5) не выполняются.
Последний результат не противоречит известному факту, что уравнение Воль-
терра всегда имеет единственное решение. Уравнение C2) принадлежит классу
уравнений типа Вольтерра и поэтому в случае (Ь) будет также разрешимо, но в
более широком пространстве функций с показательным ростом.
2°. Другим простым частным случаем уравнения A) из п. 5.9-1 будет уравнение
с переменным нижним пределом:
у{х) + —= / К{х - t)y(t) dt = /(ж), О < ж < ОС. C6)
Л/27Г J^
Это соответствует случаю, когда в уравнении A) функция К(х) будет левой
одпосторонней: К(х) = К- (х). Задача Римапа при условии 1 + /С~ (г^) ф О примет
вид
yUu)=-^^ + -^^. C7)
1 -\- /С [и) 1 -\- /С [и)
2.1. Функция 1+/С~ (^) не имеет нулей в нижней полуплоскости. Это означает,
что оригиналом функции 3^~(г^)[1 Ч- /С~(г^)]~^ служит левая односторонняя, а
последняя не окажет влияния при ж > О на соотношение между оригиналами
равенства C7). Итак, введя для удобства функцию
П-(и)= ^"("^
l + /C-(w)
применяя к обеим частям равенства C7) обратное преобразование Фурье и полагая
ж > О, получим единственное решение уравнения C6)
у(х) = f(x) + ^= / R-(x- t)f(t) dt, х>0.
Л/27Г J^
2.2. В нижней полуплоскости у функции 1 + /С~ (z) есть нули. Так как эта
функция на всей вещественной оси, в том числе и на бесконечности, отлична от
нуля, то число ее нулей конечно. Задача Римапа C7) имеет положительный индекс,
как раз равный числу нулей функции в нижней полуплоскости (нули считаются
столько раз, какова их кратность):
1У = Ind = - Ind[l + /С~ (и)] =Г]1-\-"'-\-Г]п>0.
1 + /V- [и)
Здесь rik —кратности нулей Zk функции 1 -\- JC~ (z), к = 1,2,...,гг.
Пусть
^1к I ^2к I - - - I "^f"^
есть главная часть разложения функции 3^~(^)[1 Ч- 1С~{z)]~^ в ряд Лорапа по
степеням {z — Zk),k = 1,2,... ,п. Тогда равенство C7) можно представить в виде
^+W ,v^^ с,^
^ ^ > 1+/С-Н ^tih ^'-'^^'
C8)
10*
Страница 147

148 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
где многоточие означает функцию, оригинал которой равен нулю при ж > 0.
Переходя в равенстве C8) к оригиналам, при ж > О получим
2/(ж) =/(ж) +-^ / R-{x-t)f{t)dt^y^Pk{x)e-''>'\ х>0. C9)
Здесь Рк(х) — многочлены степеней rik — 1. Можно проверить, что C9) будет
решением уравнения C6) при произвольных коэффициентах многочленов. Так как
число линейно независимых решений однородного уравнения C6) равно индексу,
то найденное решение C9) будет общим решением неоднородного уравнения.
5.9-4. Парное уравнение тнна свертки второго рода
Рассмотрим парное интегральное уравнение второго рода
1 /"°°
у{х) + —^1 Ki(x-t)y(t)dt = f(x), О < ж < ОС,
л/27г J_^
1 f°^
у{х) + —= / К2{х - t)y{t) dt = f{x), -ОС < ж < о,
Л/27Г J_^
D0)
где функция у(х) является искомой.
Для примепения нреобразования Фурье (см. пп. 1.4-3, 4.4-1, 4.4-2)
доопределим оба условия в уравпении D0), формально записав их для всех действительных
значений х. Этого можно достигнуть путем введения в правые части новых
неизвестных функций. Последние должны быть выбраны так, чтобы они не нарушали
заданных на полуосях условий. Следовательно, верхнее условие D0) должно быть
дополнено слагаемым, которое обращается в нуль на положительной полуоси, а
нижнее — слагаемым, равным нулю на отрицательной. Таким образом, парное
уравнение может быть записано в форме
1 /"°°
у(х)^-= / K,(x-t)y(t)dt = f(x)^^-(x),
у(х)^^ [ K2{x-t)y{t)dt = f{x)+U{x).
ОС < ж < ОС, D1)
где ^±{х) — пока неизвестные правая и левая односторонние функции.
Воспользовавшись иптегральным преобразованием Фурье, получим
[1 + Ыи)]У{и) = Ни) + ^~(и), [1 + JC2(u)]y(u) = Т{и) + Е-^{и).
Здесь неизвестными являются три функции З^(г^), Н^(г^) и Н~(г^).
Теперь можно на основании D2) найти
^(w)+S+(w)
У{и)
^(ц) + ^-(ц)
1 + /Ci(w)
1+/С2(«)
D2)
D3)
и, исключая при помощи равенства D3) функцию У {и) из соотношений D2),
получить краевую задачу Римана в виде
Н+(^) :
1 + /C2(w)_^_ ^ JC^ju) - JC^ju)
1 + /Ci(w) ^ ' 1 + /Ci(w)
1°. Предположим, что выполнены условия нормальности, т. е.
-ОС < и < ОС.
D4)
Страница 148

5.10. Метод Винера-Хопфа 149
и запишем теперь задачу Римана D4) в ее обычной форме (см. п. 4.4-4)
E'^{u)=V{u)E~{u)+rL{u), -оо<и<оо, D5)
где
Задача Римана D5), D6) равносильна уравнению D0): они одновременно
разрешимы или неразрешимы, имеют в общих решениях одинаковое число
произвольных постоянных.
Если индекс
1У = Ind ^) D7)
положителен, то однородное уравнение D0) (f(x) = 0) имеет ровно и линейно
независимых решений, а неоднородное уравнение безусловно разрешимо, и его
решение зависит от и произвольных комплексных постоянных.
В случае ly ^ О однородное уравнение не имеет отличных от нуля решений.
Неоднородное уравнение при и = О безусловно разрешимо, причем решение
единственно. Когда индекс ly отрицателен, условия
/С,(п)-/С,(п) dn ^ j^^^^ D8)
A'+(«)[1+/Ci(«)] ^ \u^i)f^ ^ ^
необходимы и достаточны для разрешимости неоднородного уравнения.
Во всех случаях, когда решение уравнения D0) существует, его можно найти
по формуле
J —с
D9)
где E~^(u), E (u) —построенное no схеме из п. 4.4-4 (см. рис. 3) решение задачи
Римана D5), D6).
2°. Исследуем теперь исключительный случай интегрального уравнения D0).
Допустим, что функции 1 Ч- }Ci(u), 1 Ч- JC2(u) могут иметь нули, причем эти
нули могут быть как в различных, так и в совпадающих точках контура. Возьмем
разложение этих функций, выделив совпадающие нули в форме B6), и далее
повторим все рассуждения, проведенные для уравнения типа свертки второго
рода с двумя ядрами. Найдя в этом исключительном случае общее решение
краевой задачи Римана D4) (см. п. 4.4-7), получим общее решение исходного
уравнения D0) по формуле D9).
Выводы об условиях разрешимости и числе решений уравнения D0)
аналогичны сделанным для уравнения с двумя ядрами в п. 5.9-2.
Замечание 2. Рассмотренные в разд. 5.9 уравнения иногда называют
характеристическими уравнениями типа свертки.
(•) Литература: Ф. Д. Гахов, Ю. И. Черский A978).
5.10. Метод Винера-Хопфа
5.10-1. Некоторые замечания
Пусть существует преобразование Фурье функции у(х) (см. п. 1.4-3):
y{z) = ^ Г y{x)e*'''dx. A)
Л/27Г J_oo
Страница 149

150 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Будем считать, что параметр ^, входящий в преобразование A), может принимать
и комплексные значения. Исследуем свойства функции З^(^), рассматриваемой как
функция комплексной переменной z. Для этого представим функцию у{х) в виде*
у{х) = у^{х)+у~{х), B)
где функции у^{х) иу~ (х) соответственно равны
,.+ /^^ _ Г У(х) при ж > О, - . . _ Г О при ж > О,
^ ^^^ ~ \ О при ж < О, ^ ^^^ ~ \ у(ж) при х<0. ^^^
Изображение З^(^) функции у(х) при этом, очевидно, равно сумме изображений
У-^(г), З^-(^) функций у~^(х) и у~(х). Выясним аналитические свойства
функции З^(^), установив аналитические свойства функций 3^+(^) и У- (z). Рассмотрим
функцию у~^(х), задаваемую соотношениями C). Ее изображением является
y^(z) = ^ y+{x)e'^-dx. D)
Можно показать, что если функция у^{х) удовлетворяет условию
|у (ж)| < Ме"~^ при X -^ ОС, E)
где М — некоторая постоянная, то функция 3^+(^), определенная формулой D),
является аналитической функцией комплексной переменной z = и -\- iv в области
lmz> V-, причем в этой области 3^+(^) -^ О при \z\ ^ ос. Можно также показать,
что функции у~^(х) и y-\-(z) связаны следующим соотношением:
-. poo-\-iv
у+(х) = ^ y+{z)e-'^''dz, F)
V^TT J-oo-\-iv
где интегрирование производится по любой прямой Imz = v > v-, параллельной
действительной оси на комплексной плоскости z.
Ири г;- < О (т. е. для убывающих на бесконечности функций у(х)) область
аналитичности функции y-\-(z) содержит действительную ось и в формуле F) можно
проводить интегрирование вдоль действительной оси. Если г;- > О (т. е.
функция у~^(х) растет на бесконечности, но не быстрее, чем экспонента с линейным
показателем), то область аналитичности функции 3^+(^) лежит над
действительной осью комплексной плоскости z (при этом на действительной оси интеграл D)
может расходиться). Аналогично, если функция у~ (х) из соотношений C),
удовлетворяет условию
\у~(х)\ < Ме^+^ при X -^ —ос, G)
то ее изображение, функция
\/2^ J-C
y_{z) = -^j y-{x)e'^''dx, (8)
является аналитической функцией комплексной переменной ^ и в области
Im Z <v^. Функция у~ (х) выражается через функцию 3^- (z) с помощью
соотношения
-1 /»оо+гг;
у~(х) = / y-(z)e~^^^ dz, Imz = V < v-\-. (9)
V ^7Т J—oc,-\-iv
-oo-\-iv
* Введенные в этом разделе функции у (х) и У±{х) не следует путать с функциями
у±(х) и У^(х), введенными в п. 4.4-2 и использовавшимися при решении краевой задачи
Римана на действительной оси.
Страница 150

5.10. Метод Винера-Хопфа
151
Если v^ > О, то область аналитичности функции У- (z) содержит
действительную ось.
Очевидно, при v- < v-\- функция З^(^), определенная по формуле A), является
аналитической функцией комплексной переменной z в полосе v- < Im^ < г;+.
При этом функции у(х) и З^(^) связаны обратным преобразованием Фурье:
у{х)=-^ y(z)e-''^dz, A0)
где иптегрировапие производится по любой прямой, параллельной действительной
оси комплексной плоскости z, лежащей в полосе v- < Im^ < г;+. В частности,
при V- <0 иу-\- > О функция З^(^) является аналитической в полосе, содержащей
действительную ось комплексной плоскости z.
Пример 1. Функция К(х) = е""'^' при а > О обладает изображением
}C{Z):
У27Г а^ -\- z^ '
являющимся аналитической функцией комплексной переменной z в полосе —а< Im z < а,
содержащей действительную ось.
5.10-2. Однородное уравнение Вннера-Хонфа второго рода
Рассмотрим однородное интегральное уравнение Винера-Хопфа второго рода
в форме
У(Х) :
/»оо
/ К{.
Jo
X — t)y{t) dt,
(И)
где функция К(х) задана на всей действительной оси. Решение этого уравнения,
очевидно, находится с точностью до произвольного множителя. Он может быть
найден из дополнительных условий задачи, например условий нормировки.
Будем считать, что уравнение A1) определяет функцию у(х) для всех значений
переменной ж, как положительных, так и отрицательных. Введем функции у~(х)
иу~^(х) но формулам C). Очевидно, у(х) = у~^(х)-\-у~(х), и уравнение A1) можно
переписать в виде
/»оо
у^(х)= / K(x-t)y^(t)dt,
Jo
/»оо
у-(х)= / K(x-t)y+(t)dt,
Jo
х>0
X <0.
A2)
A3)
То есть функция у~^(х) определяется из решения интегрального уравнения A2),
а функция у~(х) выражается через функции у~^(х) и К(х) с помощью
формулы A3). При этом имеет место соотпошение
/оо
K{x-t)y+{t)dt,
-ОО
эквивалентное исходному уравнению A1).
Пусть функция К(х) удовлетворяет условиям
\К{х)\ < Ме^-"^ при X-
\К{х)\ < Ме"+'' при X-
где V- < 0,1;+ > 0. Тогда функция
оо,
—оо,
/С(г
л/2^ У-<
К{х)е^^^ dx,
A4)
A5)
A6)
Страница 151

152 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
является аналитической в полосе v- < 1т z < v-\-.
Будем искать решение уравнения A1), удовлетворяющее условию
\у^(х)\ < Mie^"" при ж ^ ОС, A7)
где 11 < v^ (такое решение существует). При этом интегралы в правых частях
соотношений A2) и A3), как можно проверить, являются сходящимися, причем
для функции у~ (х) имеет место оценка
\у~(х)\< М2е''+'' при ж ^-ОС. A8)
Из условий A7) и A8) следует, что изображения 3^+(^) и З^-(^) функций
у~^(х) и у~ (х) являются аналитическими функциями комплексной переменной z
при Im Z > /1 и Im z < v-\- соответственно.
Перейдем к решению интегрального уравнения A1) или эквивалентного ему
уравнения A4), для чего воспользуемся преобразованием Фурье. С помощью
теоремы о свертке (см. п. 1.4-4) на основании A4) получим
y^)^y-{z) = V27T}C{z)y+{z),
или
W{z)y+{z)^y-{z) = 0, A9)
где
W(z) = 1 - V2^JC(z) ф 0. B0)
Птак, с помощью преобразования Фурье удалось перейти от исходного
интегрального уравнения к алгебраическому уравнению для изображений. Однако
теперь в уравнение A9) входят уже две неизвестные функции. Вообще говоря, из
одного алгебраического уравнения нельзя однозначно определить две неизвестные
функции. Метод Випера-Хопфа позволяет решить эту задачу для определенного
класса функций. Оп в первую очередь связан с изучепием областей апалитичпости
входящих в уравпение функций и специальным представлением этого уравнения.
Основная идея метода Випера-Хопфа заключается в следующем.
Пусть уравнение A9) пред ставимо в виде
y^^{z)y^) = -y^-{z)y-{z\ B1)
где левая часть является аналитической в верхней полуплоскости Im^ > /х, а
правая — аналитической в нижней полуплоскости Im^ < г;+, причем /х < г;+,
так что существует общая полоса аналитичности этих функций \i < 1т z < v-\-.
Тогда в силу едипственности аналитического продолжения можно утверждать, что
существует единственная целая функция комплексной переменной, совпадающая
с левой частью B1) в верхней и правой частью B1) в нижней полуплоскости
соответственно. Если при этом известно, что функции, входящие в B1), растут па
бесконечности не быстрее, чем конечная степень ^, то в силу обобщенной теоремы
Лиувилля (см. п. 4.4-3) данная целая функция есть полином. В частности, в случае
ограниченной на бесконечности функции получим
W+(z)y+(z) = -W-(z)y-(z) = const. B2)
Отсюда функции 3^+(^) и У- (z) определяются однозначно.
Птак, применим данную схему к решению уравнения A9). Пз проведенных
выше рассмотрений следует, что области аналитичности функций 3^+(^), 3^- (^) и
W(^) = 1 —л/27г/С(^) соответственно представляют собой верхнюю полуплоскость
lm.z> /а, нижнюю полуплоскость Im ^ < г;+ и полосу v- < Im ^ < г;+. Тем самым
Страница 152

5.10. Метод Винера-Хопфа 153
это уравнение справедливо в полосе* /х < Im z <v^^ являющейся общей областью
аналитичности всех входящих в это уравнение функций. Для нреобразования урав-
нения A9) к виду B1) предположим, что возможно разложение функции W(^):
Щ,) = Щ).^ B3)
где функции yV-\-(z) и W- (z) являются аналитическими при 1т z > /а и1т z < v-^
соответственно. Кроме того, предположим, что в областях своей аналитичности
эти функции на бесконечности растут не быстрее, чем z^, где п — некоторое
положительное целое число. Представление B3) аналитической функции 'W(z)
часто называют ее факторизацией.
Итак, в результате факторизации исходное уравнение приведено к виду B1).
Из предыдущих рассмотрений следует, что оно определяет некоторую целую
функцию комплексной переменной z.
Так как y±(z) -^ О при \z\ -^ оо, а 'W±(z) растут на бесконечности, как z^,
то данная целая функция может быть лишь нолиномом Vn-i(z) степени не
выше п — 1.
Если функции yV±(z) растут на бесконечности, лишь как первая степень
переменной z, то из соотношений B2) в силу теоремы Лиувилля следует, что
соответствующая целая функция есть постоянная С. Тогда для неизвестных 3^+(^)
и У- (z) получим выражения
определяющие изображения искомого решения с точностью до постоянного
множителя, который может быть найден хотя бы из условий нормировки. В общем
случае выражения
определяют изображения искомого решения интегрального уравнения A1) с
точностью до неопределенных постоянных, которые можно найти из дополнительных
условий задачи. Само решение определяется с помощью обратного
преобразования Фурье F), (9) и A0).
Пример 2. Рассмотрим уравнение
/"ОО
у(х) = Л / e-l^-^ly(t) dt, О < Л < оо, B6)
ядро которого имеет вид К(х) = Ле~1^1.
Найдем изображение функции К(х):
JC(z) = -= / К(х)е'^^ dx=J ^--. B7)
Л/27Г J_oo V 7Г Z^ -\-1
Функция JC(z) является аналитической функцией комплексной переменной z в полосе
— 1 < Im^; < 1. Представим выражение
2;2 _ о \ _|_ 1
W(z) = 1 - V2^K{z) = ^-^ B8)
Z"^ -\- 1
* Для определенности положим р > v_. В противном случае общей областью
аналитичности будет полоса v_ < 1т z < v_^.
Страница 153

154 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
в виде B3), где
W+(^)= ^, W_{z)=z-i. B9)
Функция yV^B;) в B9) является аналитической и отличной от нуля функцией z в области
Im Z > Im л/2Л — 1. При О < Л < ^ эта область определяется условием Im z > л/1 — 2Л,
причем л/1 — 2Л ^ /i < 1. При А > ^ функция УУ^B;) является аналитической и отличной
от нуля в области Im^; > 0. Функция W_{z), очевидно, представляет собой отличную от
нуля аналитическую функцию в области Im^; < 1. Поэтому при О < Л < ^ обе функции
удовлетворяют требуемым условиям в полосе /2 < 1т z < 1.
При А > ^ общей областью аналитичности функций 'W_^(z) и УУ_ (z) является полоса
О < Im^; < 1. Таким образом, необходимая факторизация функции B8) произведена.
Рассмотрим выражения y_^{z)'W^{z). Так как y±{z) -^ О при \z\ ^ оо, а 'W^{z),
согласно B9), растут на бесконечности, как первая степень z, то целая функция V^_i{z),
совпадающая с У_^(г)УУ_^(г) при Im^; > /i и с У_(г)УУ_(г) при Im^; < 1, может быть
лищь полиномом нулевой степени. Поэтому
y+{z)W+{z) = C. C0)
Отсюда
и, согласно F),
У+(Ж) :
^+(^^ = ^7^^^ГТТ ^''^
с /'°°+^^ z^i
, ^ e-'^'^dz, C2)
/27Г
где /i < г; < 1.
Замкнув контур интегрирования при х > О дугой полуокружности в нижней
полуплоскости и оценив интеграл по этой дуге с помощью леммы Жордана (см. пп. 1.1-4 и 1.1-5),
после ряда вычислений получим
у^{х) = с
со8(л/2Л- 1х) +
8т(л/2Л -1х)
C3)
л/2Л- 1
где С — постоянная. При О < Л < ^ это рещение экспоненциально возрастает с ростом ж,
при -^ < Л < оо — ограничено на бесконечности.
5.10-3. Общая схема метода. Проблема факторизации
В общем случае задача, решаемая методом Випера-Хопфа, сводится к
следующей. Требуется определить фупкпии 3^+(^) и З^-(^) комплексной перемеппой z,
аналитические соответственно в полуплоскостях Im z> v- и Im z <v-\- (v- < v-\-),
стремящиеся к нулю при \z\ ^ ос в своих областях аналитичности и
удовлетворяющие в полосе (v- < Im z < v-\-) функциональному уравнению
A(z)y+(z) + B(z)y-(z) + C(z) = 0. C4)
Здесь A(z), B{z), C{z) —заданные функции комплексной переменной z,
аналитические в полосе V- < 1т. Z < v-\-, причем A(z) и B(z), отличны от нуля в этой
полосе.
Основная идея решения этой задачи основана на возможности факторизации
выражения A(z)/B(z),t. е. возможности представления его в виде
A{z) _ W^(z)
B(z) W_(z)
C5)
где функции W+(^) и 'W-(z) являются аналитическими и отличными от нуля
соответственно в полуплоскостях Im^ > v'_ и Im^ < v'_^, причем полосы
Страница 154

5.10. Метод Винера-Хопфа 155
V- < Im z < v-\- и vL < Im z < v'_^ имеют общую часть. Тогда с помощью C5)
уравнение C4) можно переписать в виде
W+(z)y+(z) + W- (z)y- (z) + W- (z) ^ = 0. C6)
B(z)
Если последнее слагаемое в C6) можно представить в виде
B(z)
где функции V-^(z) и V-(z) являются аналитическими в полуплоскостях
Im^ > v'l и 1т Z < v'\. соответственно, и все три полосы v- < 1т z < v-\-,
v'_ < Im z < v'_^ Hv'l < Im z < v'^ имеют общую часть — полосу v^ < Im z < v^,
TO в этой полосе имеет место функциональное уравнение
W+(z)y+(z)^V+(z) = -W-(z)y-(z) - V-{z). C8)
Левая часть C8) представляет собой функцию, аналитическую в полуплоскости
v^ < 1т. Z, правая — функцию, аналитическую в области Im^ < г;^-. Из равенства
этих функций в полосе v^ < 1т z < v^ следует, что существует единственная
целая функция, совпадающая соответственно с левой и правой частями C8) в
областях их аналитичности. Если все функции, входящие в правые части C5)
и C7), растут па бесконечности в своих областях аналитичности не быстрее,
чем z^, то из условия y±(z) -^ О при |^| ^ оо следует, что эта целая функция
является полиномом Vn-i(z) степени не выше п — 1. Тем самым равенства
^^ ^ W^{z) ^ ^ \ ) W_{z) ^ ^
определяют искомые функции с точностью до постоянных. Иоследние могут быть
найдены из дополнительных условий задачи.
Ирименение метода Винера-Хопфа основано на представлениях C5) и C7).
Если функция G{z) является аналитической в полосе v- < Im^ < г;+, причем в
этой полосе G{z) равномерно стремится к нулю при |^| ^ оо, то в данной полосе
возможно представление
g{z) = g+{z) + g-{z),
где функция G-\-(z) — аналитическая в полуплоскости
ция Q- (z) — в полуплоскости Im ^ < г;+, причем
y+{z) = / —^—^dr, V- < v_
Im^
< Im
>
z <
V-,
^+,
a
D0)
функ-
D1)
oo-\-iv_
poo-\-iv'.
g_{z) = - / ^^^^dr, V- <lmz<vL<v+. D2)
27Гг 7_оо+г^^ r-Z
Интегралы D1) и D2), как интегралы, зависящие от параметра, определяют
аналитические функции комплексной переменной z при условии, что точка z не
лежит на контуре интегрирования.
В частности, G+{z) является аналитической функцией в полуплоскости
Im^ > vL, а Q-(z) —в нолуплоскости Im^ > v'_^.
Кроме того, если функция H(z) является аналитической и отличной от нуля
в полосе V- < 1т Z < ^7+, причем 7Y(^) равномерно в этой полосе стремится к
единице при \z\ -^ ос, то в данной полосе имеет место представление
n{z)=n+{z)n-{z), D3)
Страница 155

156 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
H-\-(z) = exp
H- (z) = exp
27гг ./_^_^iyf^
2ш ]_
2ш J_
oo-\-iv 1 o// \
- InHjr) ^^
roo+iv^ ln?i(T) ^
—^ dr
2ш
V- <v'_ < Im^ < г;+, D4)
V- < Im^ < г;^ < г^+, D5)
где функции 71+{z) и 7{-(z) являются аналитическими и отличными от нуля
соответственно в полуплоскостях Im^ > г;- и Im^ < v-\-. Представление D3)
называется факторизацией функции 7{(z).
5.10-4. Неоднородное уравнение Вннера-Хонфа второго рода
Рассмотрим уравнение Випера-Хопфа второго рода
/»оо
у{х) - К{х- t)y{t) dt = fix). D6)
-'О
Будем предполагать, что ядро уравнения К(х) и его правая часть f(x)
удовлетворяют условиям A5), и будем искать решение у~^(х) уравнения D6), для которого
выполняется условие A7).
Тогда, проводя рассуждения, аналогичные рассуждениям при выводе
функционального уравнения A9) для однородного иптегрального уравнения, получаем,
что в случае уравнения D6) в полосе /а < Imz < v-^ должно удовлетворяться
функциональное уравнение
y+(z) + У-(г) = V27T )C(z)y+{z) + :F+{z) + Г-iz) D7)
или
W{z)y+{z) + У- {z) - T(z) = О, D8)
где W(^), как и в случае однородного уравнения подчинена условию B0).
Заметим теперь, что уравнение D8) является частным случаем уравнения C4).
Функция W{z) в полосе v- < 1т z < v-\- является аналитической и равномерно
стремится к единице при \z\ ^ ос, так как |/С(^) | ^0 при \z\ ^ ос. Тогда ее можно
представить в виде (см. D3)-D5))
где W+(^) является аналитической функцией в верхней полуплоскости Im^ > v-,
а yV-(z) — в нижней полуплоскости Im^ < г;+, причем функции yV±(z) растут
па бесконечности не быстрее, чем z^.
На основании представления D9) уравнение D8) принимает вид
yV^(z)y^(z) + yV-(z)y-(z) - yV-(z)T-(z) - yV-(z)T^(z) = 0. E0)
Для приведения уравнения E0) к виду C8) достаточно разложить последнее
слагаемое:
:F+{z)W-iz) = V+{z)+V.{z), E1)
на сумму функций V^{z) и V- (^), являющихся аналитическими в полуплоскостях
Im ^ > /х и Im Z < v^ соответственно.
Для обоснования возможности представления E1) заметим, что J^+{z)
является аналитической функцией в верхней полуплоскости Im ^ > г;- и равномерно
стремится к нулю при \z\ ^ ос. Функция W- {z) является аналитической в нижней
полуплоскости Im^ < ^7+, и по способу ее построения можно так провести
факторизацию D9), чтобы W- {z) оставалась ограниченной в полосе v- < Im ^ < г;+
Страница 156

5.11. Метод Крейна для уравнения Винера-Хопфа
157
при 1^1 -^ ОС. Отсюда следует (см. D0)-D2)), что для функции T^{z)W-{z) в
полосе V- < Im^ < г;+ выполнены все условия, достаточные для обоснования
представления E1).
Проведенные рассуждения позволяют с учетом того, что функции W±{z)
растут па бесконечности не быстрее, чем z^, представить изображения решения
неоднородного интегрального уравнения D6) в виде
y-{z) =
-T„_,(z) + W_{z)r_(z) + V_{z)
YV.(z)
E2)
Само решение может быть получено из E2) с помощью формул обратного
преобразования Фурье F), (9) и A0).
5.10-5. Исключительный случай уравнения Винера-Хонфа второго рода
Рассмотрим исключительный случай уравнения Винера-Хопфа второго рода,
когда функция W(^) = 1 — л/^тг /С(^) имеет конечное число нулей Л^ (с учетом их
кратности) в полосе v- < Im^ < г;+. Возможность факторизации сохраняется и в
этом случае. Для этого достаточно ввести вспомогательную функцию
Wi(^) = ln
{z' + b')''/'W{z)\{{z-z.)-
E3)
где ai —кратность нулей Zi, а постоянная Ь> {\v-\, \v^\} выбирается из условия,
чтобы функция, стоящая под знаком логарифма, не имела донолнительпых нулей
в полосе V- < Im^ < г;+.
Однако в исключительном случае метод Винера-Хопфа приводит к
результату только тогда, когда число нулей функции W{z) четно. Это связано с тем, что
только в случае четного числа нулей можно добиться необходимого для
применения метода Винера-Хопфа поведения функции {z^' -\- 6^)^/^ па бесконечности
(см. Ф. Д. Гахов, Ю. И. Черский A978), стр. 144-146). Последнее обстоятельство не
мешает широкому использованию метода Винера-Хопфа для решения прикладных
задач, где обычно ядро интегрального уравнения К{х) является четной функцией,
и поэтому все проводимые рассуждения безупречны.
Замечание 1. Уравнение Винера-Хопфа второго рода для функций,
убывающих па бесконечности, приводится к краевой задаче Римана на действительной
оси (см. п. 5.9-1). Тогда предположения о четности числа нулей функции W{z)
или четности ядра интегрального уравнения К{х)ъ исключительном случае
несущественны.
Замечание 2. Полное решение уравнения Винера-Хопфа второго рода для
функций растущих па бесконечности приведено в упомянутой книге Ф. Д. Гахова,
Ю. П. Черского A978).
Замечание 3. Метод Винера-Хопфа можно использовать и для решения
интегральных уравнений Винера-Хопфа первого рода при условии четности ядер
этих уравнений.
(•) Литература: Б. Нобл A962), А. Г. Свешников, А. Н. Тихонов A970), В. И. Смирнов
A974), Ф. Д. Гахов A977), Ф. Д. Гахов, Ю. И. Черский A978).
Страница 157

158 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
5.11. Метод Крейна для уравнения Винера-Хопфа
5.11-1. Некоторые замечания. Проблема факторизации
Рассмотрим уравнение Винера-Хопфа второго рода
/»оо
у{х) - / К{х - t)y{t) dt = f(x), О ^ ж < ОС,
-'о
A)
где /(ж), у(х) G Li@, оо) и К(х) G Li(—оо, оо). Будем использовать классы
функций, представимых как изображения преобразования Фурье (альтернативного
преобразования Фурье в несимметричной форме, см. п. 1.4-3) функций h3Li(—оо,оо),
Li@,oo) hLi(—00,0). Для краткости вместо этих символов будем просто писать
L, L+ и L-. Пусть функции /г(ж), hi(x), и h2(x) принадлежат соответственно L,
L+ и L_, тогда их изображения можно представить в форме
щ
и)= г
J — с
h(x)e^^^ dx, l-ii{u)
/»оо
= / hi{x)
Jo
dx, i-i2(u)
-f
J —ОС
h2(x)e^^^ dx.
Через Q, C+ и Q- обозначим классы функций, представимых соответственно в
виде
vv(^) = 1 + п(и), т(и) = 1 + ni(u), т(и) = i + П2(и), B)
где функции из C+ или Q-, рассматриваемые как функции комплексной
переменной Z = и -\- iv, аналитичны при Im ^ > О или Im ^ < О и непрерывны вплоть до
вещественной оси.
Пусть Т(х) принадлежит L, а Т(и) —ее изображение, причем
l-t{u)j^O, Ind[l-t(«)] = ^|arg[l-t(M)]r =0,
ZTT L J — оо
тогда существует такое q(x) G L, что
/оо
q(x)e'
-ОО
" dx.
-оо <и<оо, C)
D)
Пз этой формулы непосредственно следует, что 1п[1 — Т(и)] -^ О при г^ ^ ±оо.
В дальнейшем будем использовать факторизацию непрерывных на
промежутке —оо ^ г^ ^ оо функций М(и) класса Q. Под этим будем понимать нредставление
функции ЛЛ(и) в виде произведения
М{и) = М+{и)
и -
и -\- i
М-(и),
E)
где J\4-(z) и J\4-\-(z) — аналитические функции в соответствующих
полуплоскостях Im ^ > О и Im Z < О, непрерывные вплоть до вещественной оси. Кроме того,
M^(z)^0 при Imz^O и M-(z)^0 при Im^ ^ 0. F)
Пз E) можно заключить, что
k = lndM{u).
Факторизация E) называется канонической, если к = 0.
В дальнейшем будем рассматривать лишь функции вида
М(и) = 1-Т(и), G)
такие что М.(±оо) = 1. Можно также считать, что
Л1+(±оо) = М- (±оо) = 1. (8)
Страница 158

5.11. Метод Крейна для уравнения Винера-Хопфа
159
Сформулируем основные результаты, касающиеся проблемы факторизации.
Для того чтобы функция G) допускала каноническую факторизацию,
необходимо и достаточно наличия двух условий:
М{и)фО, lndM{u) = 0. (9)
При этом каноническая факторизация единственна. Кроме того, при выполнении
условий (9) существует функция М(ж) из L такая, что
ЛЛ{и) = ехр
М_^(и) = ехр
Г
Jo
f
•J —с
М(ж)е^"" dx
М(ж)е^"" dx
, М-{и) = ехр
/"
V —с
М(ж)е'''^ dx
A0)
A1)
Отсюда следует, что М(и) G Q и J\4±(u) G Q±. Множители в канонической
факторизации определяются также следующими формулами:
\М(г)
27гг J_^ T-z
2ш J_^ T-z
A2)
A3)
В общем случае факторизации имеет место следующее предложение. Для того
чтобы функция G) допускала факторизацию E), необходимо и достаточно, чтобы
выполнялось условие
М{и) ф О, —ос <и < оо.
В этом случае равенство E) можно переписать в виде
w + г
М{и) = М-{и)М^{и),
-ос < 1/ < ОС.
Последнее означает каноническую факторизацию для функции
Mi{u)
и — г
и -\- i
М(и).
Следовательно, для множителей J\A±(u) справедливы формулы A0)-A3), если в
них заменить М(и) на Mi (и).
Вернемся теперь к уравнению A), для которого
/оо
К(х)
-оо
' dx.
A4)
5.11-2. Решение уравнения Винера-Хонфа второго рода
Теорема 1. Для того чтобы уравнение A) при любом f(x) из L+ имело
одно и только одно решение из L-^, необходимы и достаточны следующие
условия:
1 - JC{u) ф О, -оо <и<оо, A5)
zy = - Ind[l -/C(i/)] = 0. A6)
Теорема 2. Если выполнено условие A5), то неравенство z^ > О является
необходимым и достаточным условием того, чтобы однородное уравнение
У{х)
Г
Jo
K(x-t)y(t)dt = 0
A7)
Страница 159

160 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
имело в L^ отличные от нуля решения. Множ:ество этих решений имеет
базис, СОСТОЯ1ЦИЙ из v функций (рк{х) (к = 1,2,... ^и), стремятцихся к нулю
при X ^ оо и связанных меж:ду собою следуютцими соотношениями:
^к(
х)= I Lpk+i{t)dt, к = 1,2,...,1У-1, (рг.(х)= I ф{1)(И + С, A8)
Jo Jo
где С —некоторая отличная от нуля постоянная, а функции (pk(t) п фA)
принадлеукат L+.
Теорема 3. Если выполнено условие A5) пиУО, то при любом f(x) G Ь+
уравнение A) имеет бесчисленное множ:ество решений из L^.
Если же z^ < О, то при данном f{x) G Ь+ уравнение A) либо вовсе не имеет
решений из L+, либо имеет единственное решение. Для того чтобы имел место
последний случай, необходимо и достаточно выполнение следующих условий:
f
Jo
/{х)фф)с1х = 0, к = 1,2,...,\и\, A9)
/о
где фк(х) — какой-либо базис множества всех решений транспонированного
однородного уравнения
/»оо
Ф(х)- / к(г-х)ф(г)(И = о. B0)
-'О
1°. Если выполнены условия A5), A6), то имеется единственная факторизация:
[1 - 1С(и)]-^ = М^(и)М-(и), B1)
причем
/»оо /»оо
М^(и) = 1-\- / i?+(t)e^"' dt, М-(и) = 1-\- / R-(t)e~^"' dt. B2)
Резольвента определяется формулой
/»оо
R(x,t) = R^(x-t)-\-R-(t-x)-\- / R^(x-s)R-(t-s)ds
Jo
B3)
где О ^ X < ОС, О ^ t < ОС, i?+(x) = О и R- (х) = О при ж < О, так что при f(x)
из L+ решение уравнения определяется выражением
/»оо
y(x) = f(x)^ / R(x,t)f(t)dt. B4)
-'О
Формулу B3) можно записать в следующем виде:
/»оо
R(x, t) = R(x - t, 0) + R@, t-x)-\- R(x-s, 0)R@, t - s) ds. B5)
Если K(x — t) = K(t — ж), TO формула B5) имеет вид
R(x,t) = R(\x-t\,0)-\- / R(x-s,0)R(t-s,0)ds. B6)
Отметим, что R-\-(x) = R(x,0) и R-(x) = R@,x) — единственные в классе L+
решения уравнений следующего вида (О ^ ж < ос):
/»оо
R^(x) + / К(х - t)R^(t) dt = К(х),
Jo
/»оо
R-(x)-\- / K(t - x)R-(t) dt = К(-х).
Jo
B7)
Страница 160

5.11. Метод Крейна для уравнения Винера-Хопфа 161
2°. Положим, что выполнено условие A5), но
гу = - Ind[l - t{u)] > 0.
В этом случае функция [1 — }С{и)]~^ допускает следующую факторизацию:
[i-jc(u)]-^ = д-(и)(:!^\ д^(и), -оо<и<оо. B8)
Для функций М-(и) и М.-\-(и), онределенных равенствами
М-(и) = д-(и) и МАи)=(^) §+Ы, B9)
\и-\-г J
имеет место представление B2) и формула B3) для резольвенты.
Кроме того, для к = 1,2,... ,1у имеют место нредставления
-.—^т^ = / 9к(х)е dx, C0)
{и-гГ Jo
причем дк(х) —решения однородного уравнения A7). Через них можно,
естественно, выразить и решения (рк(х), упомянутые в теореме 2.
3°. Если и = — Ind[l — К.(и)] < О, то у транспонированного уравнения
у{х
/»оо
)- / K(t-x)y(t)dt = f(x) C1)
-'О
индекс —1У>0. Если формула B8) определяет факторизацию для уравпения A),
то для транспонированного уравнения имеем факторизацию
[1 - 1С(и)]-^ = М-(-и)М^(-и),
причем М.-(—и) играет роль М.-^(и) и J\4-\-(—u) —роль Л4-(и).
5.11-3. Формула Хопфа-Фока
Приведем здесь полезную формулу, позволяющую выразить решение
уравнения A) для произвольной правой части f(x) через решение более простого
вспомогательного интегрального уравнения с правой частью экспоненциальпого вида.
Пусть в уравпении A)
f{x) = e*^\ ImC>0, у{х) = ус{х) C2)
И, кроме того, выполнены условия A5), A6). Тогда
/»оо
у^(х) = е'^" + / R(x, t)e'^' dt, C3)
где R(x,t) имеет вид B5). После некоторых преобразований можно получить, что
у^х) = М-{-0
I
1+ / R{t,0)e-'^'dt
е'^\ C4)
Полагая ж = О в C4), будем иметь
2/с@) = А1-(-С), C5)
Причем при четной функции К{х), описывающей ядро интегрального уравнения
2/с@) = M+iC). C6)
11 А. В. Манж:иров, А. Д. Полянин
Страница 161

162 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Располагая формулой C4), можно получить решение уравнения A) и в общем
случае f{x) (см. также разд. 3.6):
-j /»00 /»00
У(^)=^1 ^+(-CJ/c(a;)dC, К{и) = j /(x)e^"^dx. C7)
Замечание 1. Все полученные в разд. 5.11 результаты, касающиеся
уравнения Винера-Хопфа второго рода справедливы также для непрерывных,
квадратично суммируемых и ряда других классов функций, которые подробно обсуждаются
в работе М. Г. Крейна A958) и книге С. Corduneanu A973).
Замечание 2. Решение уравнения Винера-Хопфа в других классах функций
может быть построено и в исключительном случае, когда 1 — ]С{и) = О (см. пп. 5.9-1
и 5.10-5).
(•) Литература: В. А. Фок A942), М. Г. Крейн A958), П. П. Забрейко, А. И. Кошелев и др.
A968), С. Corduneanu A973), В. И. Смирнов A974).
5.12. Методы решения уравнений с разностным ядром
на конечном отрезке
5.12-1. Метод Крейна
Рассмотрим метод ностроения точных аналитических решений линейных
интегральных уравнений с произвольной правой частью. Метод основан на
построении двух вспомогательных решений более простых уравнений с правой частью
равной единице. Вспомогательные решения используются для построения
решения исходного уравнения при произвольной правой части.
1°. Пусть дано уравнение
у(х)- [ K(x,t)y(t)dt = f(x), a^x^b, A)
J а
Одновременно с A) будем рассматривать два вспомогательных уравнения,
зависящих от параметра ^ (а ^ ^ ^ Ь):
w(x,^)- K(x,t)w(t,^)dt = l,
"^^ ^ B)
W
\х,0>- [ K{t,x)w\t,^)dt = l,
J а
где а ^ ж ^ (J. Пусть для любого ^ вспомогательные уравнения B) имеют
единственные непрерывные решения w{x^^) и il'*(x,(J), удовлетворяющие условию
^(С?0^*(С?0 Ф ^ (а ^ ^ ^ Ь). Тогда для любой непрерывной функции f(x)
единственное непрерывное решение уравнения A) может быть получено по
формуле
y{x) = F{b)wix,b)- [ wix,OFUOd^, ^@=-^^ I w'{t,i)f{t)dt,
C)
где
Формула C) позволяет строить решение уравнения A) с произвольной правой
частью f(x) с помощью решений двух более простых вспомогательных
уравнений B) (зависящих от параметра ^) с постоянной правой частью равной единице.
Страница 162

Методы для уравнений с разностным ядром на конечном отрезке
163
2°. Рассмотрим теперь уравнение с ядром, зависящим от разности аргументов:
у{х) + / К{х- t)y(t) dt = f(x), a^x^b.
J a
D)
Считается, что К(х) —четная функция, интегрируемая на отрезке [а — b,b — а].
Одновременно с D) будем рассматривать вспомогательное уравнение, зависящее
от параметра ^ (а ^ ^ ^ Ь):
w(x,^)-\- K(x-t)w(t,^)dt = l, а^х^С E)
J а
Пусть для любого ^ вспомогательное уравнение E) имеет единственное
непрерывное решение w(x,^). Тогда для любой непрерывной функции f(x)
решение уравнения D) может быть получено по формуле C), если в ней
положить W* (x,t) = w(x,t).
Укажем здесь еще одну полезную формулу для уравнения с ядром, зависящим
от разности аргументов:
J —а
у{х) + / К{х - t)y{t) dt = f(x), -а^х^а.
F)
Считается, что К(х) — четная функция, интегрируемая на отрезке [—2а, 2а].
Одновременно с F) будем рассматривать вспомогательное уравнение, зависящее
от параметра ^ (О < ^ ^ а):
w(x, О + / ^(х - t)w(t, ^)dt = l, -С ^ ж ^ <J. G)
Пусть для любого ^ вспомогательное уравнение G) имеет единственное
непрерывное решение w(x,^). Тогда для любой непрерывной функции f(x)
решение уравнения F) может быть получено по формуле
у(х) =
2М(а)
Г w(t,a)f(t)
J —а
dt
w{x,a)
- Гw(x,o—\—^— ( w(t,of{t)dt\di
2 dx 4| M@ [J_^ V'^^ M J
(8)
где M(^) = ^^(C?0' ^ последний внутренний интеграл берется по Стилтьесу
5.12-2. Ядра с рациональными нреобразованиями Фурье
Рассмотрим уравнение вида
у{
х)- Г К{.
Jo
x-t)y{i)dt = f{x),
(9)
где О ^ ж ^ Т < ос. Если ядро К{х) интегрируемо в промежутке [—Т, Т], то к
этому уравнению применима теория Фредгольма.
Поскольку в уравнение входят значения ядра К{х) лишь для [—Т, Т], то
можно продолжить ядро любым образом вне этого отрезка. Пусть ядро продолжено на
всю ось с сохранением интегрируемости. Тогда в пространстве L2@,T)
уравнение (9) в общем случае сводится к краевой задаче теории аналитических функций
(задаче Римана) для двух пар неизвестных функций.
11*
Страница 163

164 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Если преобразование Фурье ядра
/оо
К{х)е'^^ dx
-оо
рационально, то уравнение (9) решается в замкнутом виде. Пусть 1 — ]С{и) ф О
(—оо < и < оо). Тогда изображение решения интегрального уравнения (9) дается
формулой
^'С") = 1 I, , [Ни) - >V+(«) - e-^^^VV- (и)], A0)
1 — K.(u) ^ ^
в которой
где 6J и 6^ —полюсы функции 1 — JC(u), лежащие соответственно в верхней
и нижней полуплоскости, р^ — их кратности. Постоянные M^j^ могут быть
определены из условий
^ [VV+(«) + e-'^"W-{u) - Я«)]„^„+ =0, S = 0,1,..., g+ - 1,
^[VV+H+e-^''-^(«)]__=0, s = 0,l,...,q--l,
где а J и а~ —нули функции 1 — JC(u), лежащие соответственно в верхней и
нижней полуплоскости, Qn —ИХ кратности. Постоянные M^j^ можно определять также
с помощью подстановки решения в исходное уравнение. Решение интегрального
уравнения (9) получается обращением формулы A0).
5.12-3. Сведение к обыкновенным днфференннальным уравнениям
1°. Рассмотрим специальный случай, когда образ ядра интегрального уравнения
(9), полученный с помощью преобразования Фурье, можно представить в виде
Ци) = §^, A1)
N{u)
где М (и) и Я/(и) некоторые многочлены степеней тип соответственно:
m п
M{u) = Y,Aku\ U{u) = Y,Bku\ A2)
fc=0 fc=0
в этом случае решение интегрального уравнения (9) (если оно существует)
удовлетворяет линейному неоднородному обыкновенному дифференциальному
уравнению ттг-го порядка с постоянными коэффициентами
M{il)yi.)=M{il)fi.), 0<х<Т. A3)
Решение уравнения A3) содержит т произвольных постоянных, которые
определяются подстановкой решения в исходное уравнение (9). При этом для
определения постоянных получается система линейных алгебраических уравнений.
2°. Рассмотрим уравнение Фредгольма второго рода с разностным ядром,
содержащим сумму экспонент:
У(^)+ t(yAue^''^''-'\\y{t)dt = f{x). A4)
/»6 / '^
Страница 164

Методы для уравнений с разностным ядром на конечном отрезке 165
Это уравнение в общем случае можно свести к линейному неоднородному
обыкновенному дифференциальному уравнению 2гг-го порядка с постоянными
коэффициентами.
Пример. Рассмотрим уравнение
у{х) + I e^\--'\g{t)y{t) dt = fix), a^x^b,
J a
которое при g{t) = const будет частным случаем уравнения A4).
1°. Раскроем модуль в подынтегральном выражении. В результате получим
у{х) + г еМ—')9(t)j/(t) dt+ I еМ*—K(t)j/(t) dt = f{x). A5)
Дифференцируя A5) дважды по ж, имеем
y'Ux)+2\g{x)y(x)+\' f\^(--''>g(t)y(t)dt + \^ f e^(*-)g(«)?/(«) dt =/^,(x).
J a J X
A6)
Исключая из A5) и A6) интегральные члены, приходим к следующему обыкновенному
дифференциальному уравнению второго порядка для функции у = у{х)\
y'i, + 2\д(х)у - А\ = Г^^(х) - ХУ{х). A7)
2°. Выведем граничные условия для уравнения A7). Будем считать, что пределы
интегрирования удовлетворяют условиям —оо<а<6<оо. Полагая вA5)ж = аиж = 6, имеем
два следствия:
у(а)+е-^^ / e'''g(t)y(t)dt = f(a),
"^" A8)
УF)+е^^ / e-'''g{t)y{t)dt = f{b).
Выразим из уравнения A7) произведение д{х)у через у'^^ и f'J^ и подставим в A8). После
интегрирования по частям получим
e^VUfe) - e^VL(a) = Ae^V(a) + Ae^VW, ^ _
e-^VLF)-e-^V;(a) = Ae-^Xa)+Ae-^V(b),
Отсюда после некоторых преобразований найдем граничные условия для функции у(х):
VU») + Х<р{а) = о, <p'Jb)-\<p{b) = 0; <р{х) = у{х) - f{x). A9)
Уравнение A7) вместе с граничными условиями A9) описывает рещение исходного
интегрального уравнения. При g(t) = const соответствующее рещение приведено в книге
А. Д. Полянина, А. В. Манжирова A998, стр. 261).
3°. Уравнения с разностным ядром, содержащим сумму гиперболических
функций:
/Ь п
К(х - t)y(t) dt = f(x), К(х) = J2Ak sh{Xk\x\) B0)
k=i
также с помощью дифференцирования сводятся к линейным неоднородным
обыкновенным дифференциальным уравнениям 2гг-го порядка с постоянными
коэффициентами.
4°. Уравнения с разностным ядром, содержащим сумму тригонометрических
функций:
К(х - t)y(t) dt = f(x), К(х) = J2Ak sin(Afc\x\) B1)
k=i
Страница 165

166 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
также можно свести к линейным неоднородным обыкновенным
дифференциальным уравнениям 2гг-го порядка с постоянными коэффициептами.
® Литература: W. В. Davenport, W. L. Root A958), И. Ц. Гохберг, М. Г. Крейн A967),
П. П. Забрейко, А. И. Кошелев и др. A968), А. Д. Полянин, А. В. Манжиров {\9Щ,
А. D. Polyanin, А. V. Manzhirov A998).
5.13. Метод замены ядра вырожденным
5.13-1. Аппроксимация ядра
Для приближепного решения иптегрального уравнения Фредгольма второго
рода
у(х)- K(x,t)y(t)dt = f(x), а^х
J а
^b,
A)
где функции f(x) и K(x,t) для простоты будем считать пепрерывными,
ядро i^ (ж, t) заменяют близким к нему вырожденным ядром
к=0
B)
Укажем несколько способов такой замены. Если ядро K(x,t) достаточное
число раз дифференцируемо по х на отрезке [а, 6], то в качестве вырожденного
ядра i^(n) (ж, t) можно взять конечный отрезок ряда Тейлора:
K(n)(x,t)=J2 ^^^^Ki'^4xo,t),
C)
где хо — некоторая точка отрезка [а, 6]. Аналогичный прием можно применить
также, если K(x,t) достаточное число раз дифференцируема по t на отрезке [а,Ь].
Для построения вырожденного ядра можно также использовать конечный
отрезок двойного ряда Тейлора:
^(n)(^,t) = ^^apqix-xoYit-toY
р=0 q=0
D)
где
1 ^Р+'З
ana = К(хЛ)
^^ p\q\ dxPdt^ ^ ' ^
а ^ Хо ^ Ь, а ^ to ^ Ь.
Непрерывное ядро K(x,t) допускает также аппроксимацию
тригонометрическим полиномом периода 2/, где I = b — а.
Например, можно положить
п
K^ri){x,t) = —ao(t) + y^afc(t)cos
k=i
кттх
где ak(t) (/с = 0,1, 2,...) — коэффициенты ряда Фурье:
К(х, t) cos dx.
E)
F)
Страница 166

5.13. Метод замены ядра еыроэюденным
167
Аналогичное разложение получается, если поменять ролями переменные х
и t. Можно также использовать конечный отрезок двойного ряда Фурье, полагая,
например.
ак{
11
^ и
ИЗ формул E)-G) имеем
п
К^гг) (x,t) = —аоо + — ^ ttfco COS
к=1
п п
rmrt
кттх
/с = 0,1,.
G)
п
IE
акт COS
кттх
rmrt
rriTvt .
aom COS I —;— I +
где
dkr
= _i f' f'KC;^t)cos(^) cosi ^ ] dxdt. (8)
Существуют и другие приемы аппроксимации ядра K(x,t).
5.13-2. Приближенное решение
Если K(^n)(x,t) есть вырожденное ядро, аппроксимирующее ядро K(x,t), и
функция fn(x) близка к /(ж), то решение Уп(х) интегрального уравнения
Уп (х) - / K^rb){x,t)yn
J а
(t)dt = fn(x)
МОЖНО рассматривать как приближение решения у(х) уравнения A).
Пусть справедлива следующая оценка погрешности:
/'
J а
\K(x,t) - K(n)(x,t)\ dt ^ е, \f(x) - U(x)\ ^ 6,
И резольвента Rn(x,t) для уравнения (9) такова, что
J а
\Rn(x,t)\dt^ Мгг
При а ^ X ^ Ь, причем выполнено неравенство
q = s(l^Mn) < 1.
Тогда уравнение A) имеет единственное решение у(х) и
\у{х) - у^(х)\ ^ е^A + ^»)' +S, N= те^ \f{x)
Пример. Найдем приближенное решение уравнения
/-1/2 2,2
У(х)- / е— ' y(t)dt=l.
Jo
Пользуясь разложением в двойной ряд Тейлора, ядро
заменяем приближенным вырожденным ядром
(9)
A0)
A1)
Страница 167

168 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Отсюда вместо уравнения A1) получаем
/•1/2
у^{х) = 1 + / A - x'^t^ + ^xH'^)y^{t) dt.
Jo
Следовательно,
где
1/2
У2{х) = 1 -\- А-^ -\- А^х'^ + -4зЖ^,
A2)
A3)
/•1/2 -|^ /•l/^
y2(x)dx, А2 = — x^y2(x)dx, ^s — — / x^y2(x)dx. A4)
Ha основании формул A3) и A4) получим систему трех уравнений с тремя
неизвестными, решив которую, с точностью до четырех значаших цифр будем иметь
Ai =0,9930, А2 = -0,0833, A3 = О, 0007.
Следовательно,
у{х) ^У2{х) = 1,9930-0,0833^2 +О, 0007ж^
Оценку погрешности приближенного решения A5) можно произвести по формуле A0).
О^х^^. A5)
(•) Литература: С. Г. Михлин A959), Л. В. Канторович, В. И. Крылов A962), Б. П. Деми-
дович, И. А. Марон, Е. 3. Шувалова A963), М. Л. Краснов, А. И. Киселев, Г. И. Макаренко
A968).
5.14. Метод Бейтмена
5.14-1. Общая схема метода
Может оказаться полезной часто не только замена данного ядра вырожденным,
но и приближенное его представление в виде суммы ядра, для которого
резольвента известна, и вырожденного ядра. Для ядер последнего вида резольвента может
быть дана в конечном виде.
Рассмотрим интегральное уравнение Фредгольма второго рода
у(х)-Х [ k(x,t)y(t)dt = f(x) A)
J а
С ядром k(x,t), резольвента которого r(x,t;X) известна, т. е. решение A) может
быть представлено в форме
гЬ
)dt.
y(x) = f(x)^X f r(x,t;X)f(t)i
J a
Тогда для интегрального уравнения с ядром
K(x,t)-.
1
k(x,t) gi(x)
hi(t) an
9n(x)
din
A(a,,0
hn{t) ttni
где gi{x), hi{t) и aij (i,j = 1,2
числа соответственно, резольвента дается в виде
\r(x,t;X) ^i(x)
1
A{aij)-
ац ai2 • • • ain
tt21 tt22 • • • Ci2n
dnl Cin2
B)
C)
R(x,t;X)
A(a^. + Xb^,
n) — произвольные функции и произвольные
;ается в виде
c,t;A) ^i{x) '" ^п{х)
фг (t) an + Л611 • • • ain -\- Xbin
^n{t) ani-\-Xbni "' ann-\-Xbnn
D)
Страница 168

5.14. Метод Бейтмена
169
где
рЪ рЬ
(рк(х) = дк(х)-\-X r(x,t;X)gk(t)dt, фк(х) = hk(x)-\-X r(x,t;X)hk(t)dt,
J а J а
-
J а
gj(x)hi(x)dx, /с, г, j = 1,... ,гг.
5.14-2. Некоторые частные случаи
Предположим, что
K(x,t) = k(x,t) - y^^gk(x)hk(t),
E)
F)
т. е. в формуле C) aij = О при i^ j иац = 1. Резольвента для этого случая примет
вид
G)
x,t;X) = ^
А* =
r(x,t;X)
Фп{1)
1 + Xbii
Л621
Xbni
ipi(x) "
1 + Л611 ••
Xbni
Xbi2
1 + Л622 • •
Xbn2
(Pn(x)
Xbin
• 1 + Xbnn
Xbin
Xb2n
1 + Xbnn
Пусть, кроме того, k(x, t) = 0, т. е. ядро К(х, t) —вырожденное:
п
K(x,t) = -^gk(x)hk(t).
k=i
В данном случае, очевидно, что г(ж, t; Л) = О, и ввиду G)
(рк(х) = дк(х), фк(х) = hk(x), bij = / gj(x)hi(x)dx.
J а
(8)
Поэтому резольвента принимает вид
О
I h
R(x,t;X) = —
9i(x)
hi(t) 1 + Л611
9n(x)
Xbin
(9)
\hn(t) Xbni ••• l-\-Xbnn
Рассмотрим интегральное уравнение с некоторым ядром Q(x,t). Выберем
произвольно в промежутке (а, Ь) точки xi, Ж2, ..., ж^ и ti, t2, ..., tn, и положим
в равенстве C)
k(x,t) = О, дк(х) = Q(x,tk), hk(t) = -Q(xk,t), aij = Q(xi,tj).
Тогда, очевидно, r(x,t; Л) = О и ядро К(х, t) принимает вид
О Q(x,ti) ••• Q(x,tn)
Q(xi,t) Q(xi,ti) ••• Q(xi,tn)
K(x,t):
D
Q(Xn, t) Q(Xn, tl) • • • Q(Xn, tn)
D-.
Q(xi,ti) • •• Q(xi,tn)
^{Xn^tlj ' ' ' y^yXn^tn)
Страница 169

170 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Выражение для ядра удобно записать в виде
K{x,t) = Q(x,t) ■
D
Q(x,t) Q(x,ti)
Q(xi,t) Q(xi,ti)
Q(xn,t) Q(xn,ti
Q{x,tn)
Q{xi,tn)
^{Xfi: tn)
A0)
Это ядро вырожденное и обладает тем свойством, что совпадает с Q(x,t) на
прямых X = Xi, t = tj (i,j = 1, 2,..., n). Действительно, если положить х = Xi
или t = tj, то определитель, стоящий в числителе второго члена, будет иметь две
одинаковых строки или столбца и, следовательно, обратится в нуль, а поэтому
K(xi,t) = Q{xi,t), K(x,tj) = Q(x,tj).
Такое совпадение на 2п прямых позволяет рассчитывать на то, что K(x,t) близко
к Q(x,t), а решение уравнения с ядром K(x,t) —к решению уравнения с
ядром Q(x,t). Следует заметить, что если Q(x,t) вырожденное, т. е. имеет вид
Q(x,t) = y^^gk(x)hk(t),
A1)
то определитель в числителе тождественно равен нулю, а потому в этом случае
K(x,t) = Q(x,t). A2)
Для ядра K(x,t) резольвента может быть составлена на основании следующих
равенств:
r(x,t;A) = 0, (pi(x) =gi(x) = Q(x,ti), ^j{t) = hj(t) = -Q(xj,t),
Л A3)
bij = - Q(x,tj)Q(xi,x)dx = -Q2(xi,tj), ij = 1,... ,n,
J a
где Q2(x, t) —второе итерированное ядро для Q(x,t):
h(x,y)= / Q(x,s)Q(s,t)ds,
J a
И, следовательно.
R(x,t;X)
D.
0 Q(x,ti) ••• Q(x,tn)
Q{xi,t) Q{xi,ti) - XQ2{xi,ti) • • • Q{xi,tn) - XQ2{xi,tn)
Q(Xn,t) Q(Xn, ti) - XQ2(Xn,ti) • • • Q(Xn, tn) - XQ2(Xn,tn)
A4)
где
Dx=D- XD2
D2
?2(xi,ti)
Q2{Xn,ti)
h(xi,tn)
h{xn,tn)
С помощью резольвенты R(x,t;X) можно получить приближенное решение
уравнения с ядром Q(x,t).B частности, приближенные значения для собственных
значений Л этого ядра найдем, приравнивая нулю определитель Da, стоящий в
знаменателе A4).
Страница 170

5.15. Метод коллокации \1\
Пример. Рассмотрим уравнение
у{х)-Х Q{x,t)y{t)dt = 0, 0^ж^1, A5)
^0
Q{x,t) :
x(t — 1) при X ^t,
t(x — 1) при X ^ t.
Найдем его характеристические числа. Для этого воспользуемся формулой A4), где для
второго итерированного ядра будем иметь
2(x,t) = 1 Q(x,s)Q(s,t)
Jo
J ^х{1 - t){2t - ж2 - t^) при X ^t,
■^t(l - x)Bx -x^ - t^) при X ^t.
Выберем равноотстоящие точки x^ ntj и возьмем гг = 5, тогда
Xi = t-^ = -g-, X2 =t2 = -g-, ^3=^3 = -g-, X^ =t^ = -g-, X^ =t^ = -g-.
Приравняем нулю определитель, стоящий в знаменателе A4). Тогда после некоторых
преобразований придем к уравнению
130/i^ - 441/i^ + 488/i^ - 206/i^ + 30/i - 1 = О (Л = 216/i),
которое можно записать в форме
{/1 - l)B/i - l)E/i - l)A3/i2 - 22/i + 1) = 0. A6)
После рещения A6) найдем
Ai = 10,02, Л2=43,2, Лз = 108, Л4 = 216, Л5 = 355, 2.
Точные величины характеристических значений рассматриваемого уравнения известны:
Л^ = 7г2 = 9, 869 ..., Лз = B7гJ = 39, 478 ..., Л3 = (Зтг)^ = 88, 826 ...,
следовательно, ощибка при определении первого собственного значения 2%, второго — 9%,
третьего — 20%.
Результат можно улучщить выбором другой совокупности точек ж^ и у^ (г = 1, 2,..., 5).
Однако при таком числе ординат очень высокая точность не может быть достигнута, так как
само ядро Q{x,t) имеет особенность: производная его разрывна при х = t вследствие чего
невозможна хорощая аппроксимация его такими ядрами.
(•) Литература: Н. Bateman A922), Э. Гурса A934), Л. В. Канторович, В. И. Крылов A962).
5.15. Метод коллокации
5.15-1. Общие замечания
Запишем интегральное уравнение Фредгольма второго рода в форме
е[у(х)] = у(х) -X f K{x,t)y{t) dt - fix) = 0. A)
J a
Будем искать приближенное решение уравнения A) в виде функции вида
Уп(х) = Ф(х,А1,А2,...,Ап) B)
со свободными параметрами Ai, А2, ..., An. Подставляя выражение B) в
уравнение A), получим невязку
s[Yn(x)] = Yn(x)-X [ K(x,t)Yn(t)dt-f(x). C)
J а
Страница 171

172 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Если у{х) является точным решением, то невязка £ [у (ж)] равна нулю. Поэтому
стараются подобрать параметры Ai, А2, ..., An так, чтобы невязка £[у(ж)] была бы
в определенном смысле возможно малой. Минимизировать невязку £[у(ж)] можно
различными способами. Обычно для простоты выкладок берут функцию Yn(x),
линейно зависящую от параметров Ai, А2, ..., An. Найдя параметры Ai,
А2, ..., An, получают приближенное решение B). Если
D)
An, найти
lim Yn(x) = у(х),
то можно, взяв достаточно большое число параметров Ai, А2,
решение у(х) с любой наперед заданной степенью точности.
Перейдем теперь к изложению одного из конкретных методов построения
приближенного решения Yn(x).
5.15-2. Приближенное решение
Положим
Yn{x)
: ^0
{x)-\-^Aicpi{x),
E)
где ^о(х), ^i(x), ..., ^п(х) —известные координатные функции и Ai, А2, ...,
An — неопределенные коэффициенты, причем функции (pi(x) (i = 1,2,... ,гг)
линейно независимы. Заметим, что в частности, можно положить ^о(х) = f(x)
или (ро(х) = 0. Подставляя выражение E) в левую часть уравнения A), получим
невязку
п /»Ь Г ■"- ■
e[Yn(x)] = ipo(x) + Yl ^^М^) - /(^) -^ K(x,t) ipo(t) + Yl ^^V^^W
или
n
e\Yn{x)] = фо(х, A) + ^ Aiфi(x, A),
где
фо(х,Х) = (po(x) - f(x) - A / K(x,t)(po(t)dt,
J a
rb
фъ{х^Х) = Lpi{x) — \ I K(x,t)(pi(t) dt, i =
J a
dt,
F)
G)
1,... ,n.
Согласно методу коллокации потребуем, чтобы невязка £[Угг(ж)] обращалась
в нуль в заданной системе точек коллокации Ж1,Ж2, ...,ЖггИЗ отрезка [а, 6], т. е.
полагаем, что
£[Yn(xj)] = 0, j = 1,...,п,
где
а ^ XI < Х2 < • • • < Хп-1 < Хп ^ Ь.
Обычно полагают xi = а и Хп = Ь.
Отсюда, на основании формулы F) для определения коэффициентов Ai,
А2, ..., An получим систему линейных алгебраических уравнений
^ AiV^i(xj,A) = -фo(xj,X), j = 1,2,..
(8)
Страница 172

5.15. Метод коллокации
173
Если определитель системы (8):
det[ilji(xj,X)] =
Ф2{Х1,Х) Ф2{Х2,Х)
ф1(Хп,Х)
ф2(Хп,Х)
7^0,
\фп(х1,Х) фп(х2,Х) ••• фп(Хп,Х)\
ТО из системы (8) можно однозначно определить Ai, ^2,..., An и, следовательно,
найти приближенное решение Yn(x) по формуле E).
5.15-3. Собственные функннн уравнения
Приравнивая нулю определитель системы (8), получим уравнение
de^i(xj,X)] = 0,
которое, вообще говоря, позволяет найти приближенные значения
характеристических чисел Л/с (А; = 1, 2,..., гг) ядра К(х, t).
Если положить
f(x) = 0, ipo(x) = 0, Х = Хк,
то вместо системы (8) будем иметь однородную систему
^lfVife,AO = 0, i = l,2,
. ,n.
(9)
Определив ненулевые решения А\ -" (г = 1, 2,..., гг) системы (9), получим для
ядра K(x,t) приближенные собственные функции
i=l
отвечающие его характеристическому числу Л^ ~ А^.
Пример. Методом коллокации решить уравнение
^(^) ~ / о , ^о dt = x arctg —,
Jo х^ -\-t^ X
Положим
Y^{x) = A^^A^x.
Подставляя это выражение в уравнение A0), получим невязку
A0)
e[Y^(x)] :
-А-^х arctg \- А2
1 ж^ , Л 1
— + ^-1п 1+^
2 2 V ж2
■ X arctg ■
Выбирая точки коллокации х-^ = О, Х2 = 1 ii учитывая, что
lira X arctg — =0, lira ж^ In I 1 -\ —
x—^O X x—^0 \ x^
для определения коэффициентов A^ и A2 будем иметь систему:
= 0,
О X Ai - i-A2
О,
Отсюда получаем А 2
2 ^^2
: О и А;!^ = —1. Таким образом,
Y^(x) = -1.
(И)
Найденное решение A1), как легко проверить является точным.
(•) Литература: Л. Коллатц A958), Б. П. Демидович, И. А. Марон, Е. 3. Шувалова A963),
А. Ф. Верлань, В. С. Сизиков A986).
Страница 173

174 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f(x)
5.16. Метод наименьших квадратов
5.16-1. Описание метода
Для уравнения
г[у(х)] = у(х) -X [ К(х, t)y(t) dt - f(x) = О,
J а
аналогично методу коллокации, полагаем
п
Yn{x) = lfo(x) + ^ Ацрг{х),
A)
B)
где ^о(х), ^i(x), ..., ^п(х) — известные функции и Ai, А2, ..., An —
неопределенные коэффициенты, причем ^i(x) (i = 1, 2,..., n) линейно независимы.
Подставляя B) в левую часть уравнения A), получим невязку
R[Yn(x)] = фо(х, А) + ^ Aiilji(x, Л),
C)
где фо(х,Х) ифi(x,X) {г = 1, 2,..., гг) определяются формулами G) из п. 5.15-2.
Согласно методу наименьших квадратов, коэффициенты Ai (i = 1,...,гг)
отыскиваются из условия минимума интеграла
1= [ {е[Уп(х)]У dx = [ Uo(x,A) + ^A,V^i(x,A)
Ja Ja L г^1
Это требование приводит к системе алгебраических уравнений
^^ о, j = l,2,...,n,
dx.
дА^
D)
E)
откуда на основании D), дифференцируя по параметрам Ai, ..., An под знаком
интеграла, будем иметь
1 dl
~2 дА,
/»Ь г ^
J а L л 1
dx = 0, j = l,2,...,n. F)
С помощью обозначений типа
j{X)= / фi{x,X)фj{x,X)dx
J а
систему F) можно записать в виде
cii(A)Ai + ci2(A)A2 + • • • + cin{X)An = -cio(A),
C2l(X)Ai + C22(X)A2 + • • • + C2n(X)An = -C2o(X),
Cnl{X)Ai + Cn2{X)A2 H h Cnn{X)An = -Cno(A).
G)
(8)
Заметим, что если (po(x) = О, то фо(х) = —f(x). Кроме того, так как dj (А) = Cji(A),
то матрица системы (8) симметричная.
Страница 174

5.16. Метод наименьших квадратов
175
5.16-2. Построение собственных функций
Метод наименьших квадратов применяется и для определения
характеристических чисел и собственных функций ядра K(x,t). Действительно, полагая
f(x) = О и (ро(х) = О, откуда фо(х) = О, определим приближенные значения
характеристических чисел из алгебраического уравнения
det[ci,(A)] = 0. (9)
После этого приближенные собственные функции находятся из однородной
системы (8), где вместо Л подставлено соответствующее приближенное значение.
Пример. Методом наименьших квадратов найти приближенное решение уравнения
у{х) = ж^ +
.L''^
X + t)y{t) dt
A0)
Для приближенного решения полагаем 1^2(^) — ^^ -\- А2Х -\- А-^. Отсюда
Учитывая, что
1 /•! /•!
sh(x-\-1) dt = а sh X, / t sh(x-\-1) dt = bshx, / t^ sh(x-\-1) dt = с sh x,
-1 J-1 J-I
a = 2shl = 2,3504,
:2e-
: 0, 7358,
:6shl-4chl = 0,8788,
на основании формул G) из п. 5.15-2 имеем
ф^ =1 — ashx^ Ф2 = X — bchx, ф^-
-cshx.
Далее находим (с точностью до четырех значаших цифр после запятой)
c-L^ =2 + a2(^sh2-l) =6,4935, С22 = |- + ^^(^ sh2 + l)
С12 = -4(ае-^ + 6sh 1) = -86"^ sh 1 = -3, 4586,
c-^Q = ac(^ sh2- 1) = 1,6800, c^q = -2ce~^ = -0,6466,
и получаем систему для определения коэффициентов А^ и А2
6,4935Ai -3,4586^2 = -1,6800,
-3,4586Ai + 2,1896^2 = О, 6466.
Отсюда имеем А-^ = —О, 5423, А2 = —О, 5613. Таким образом,
Y2{x) = ж^ - о, 5613ж - О, 5423.
Так как в уравнении A0) ядро
К(х, t) = sh(x -\-t) = sh ж ch t + ch ж sh t
вырожденное, то можно получить точное решение:
у(х) = х^ -\- ashx -\- f3chx,
: 2,1896,
A1)
A2)
а= ^^bl-4chl ^ /5 = a(ish2-l)
2-(ish2)^ ' ' ^ ^2 )
-0,5548.
Из сравнения формул A1) и A2) заключаем, что приближенное решение ^2(^) близко к
точному у(х), если |ж| —малая величина. На концах ж = ±1 расхождение \у(х) — 1^2(^I
довольно значительно.
(•) Литература: Л. В. Канторович, В. И. Крылов A962), Б. П. Демидович, И. А. Марон,
Е. 3. Шувалова A963), М. Л. Краснов, А. И. Киселев, Г. И. Макаренко A968).
Страница 175

176 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
5.17. Метод Бубнова-Галеркина
5.17-1. Описание метода
Пусть
е[у{х)] = у{х) -X [ К(х, t)y(t) dt - f(x) = 0. A)
J а
Аналогично предыдущему, будем искать приближенное решение уравнения A) в
виде конечной суммы
п
Уп(х) = f(x) + Y^ Aiipi(x), г = 1, 2,..., n, B)
i=l
где (pi(x) (i = 1,2,..., n) — некоторые известные линейно независимые функции
(координатные функции) и Ai, А2, ..., An—пеопределенные коэффициепты.
Подставляя выражение B) в левую часть уравнения A), получим невязку
s[Yn(x)] = J2^jWj(x)-^ K(x,t)ipj(t)dt\-X K(x,t)f(t)dt. C)
j — l I J a ] Ja
Согласно методу Бубнова-Галеркина, искомые коэффициепты Ai
определяются из условия ортогональности певязки ко всем координатным функциям ^i(x),
(р2(х), ..., (рп(х). Это дает систему уравнений
гь
s[Yn(x)](pi(x)dx = О, г = 1,...,гг,
/
J а
ИЛИ В силу C)
п
J2(^ij - ^Pij)^J = ^Ъ, i = l,2,...,n, D)
где
rb rb fb
OLij = / (pi(x)(pj(x)dx, Pij = / / K(x,t)(pi(x)(pj(t)dtdx,
Ja Ja Ja
ъ
pb pb
= K(x,t)ipi(x)f(t)dtdx.
J a J a
Если определитель системы D)
D(X) = det[aij - Xpij]
отличен от нуля, то из этой системы можно однозначно определить коэффициепты
Ai, А2, ..., An. Тогда формула B) дает приближенное решение интегрального
уравнения A).
5.17-2. Характеристические числа уравнения
Пз уравнения D(X) = О находятся приближенные характеристические числа
Ai, Л2, ..., An уравнения. Найдя ненулевые решения однородной линейной
системы
п
Страница 176

5.17. Метод Бубнова-Галеркина 111
можно построить приближенные собственные функции Yn (ж), соответствующие
характеристическим числам Л^:
i=l
Можно показать, что метод Бубнова-Галеркина равносилен замене
исходного ядра K(x,t) некоторым вырожденным ядром i^(^)(x,t). Поэтому для
приближенного решения Yn(x) имеется оценка погрешности, аналогичная приведенной
в п. 5.13-2.
Пример. Найдем первые два характеристических числа интегрального уравнения
s[y(x)] = у(х) -X [ К(х, t)y(t) dt = О,
где
K(x,t) = \' при t^o.,
^ ' ^ IX при t > X. ^ ^
На основании E) имеем
е[у{х)] = у{х) - хИ ty{t)dt^J xy{t)dt\.
Положим 1^2(^) = ^1^ -\- А^х'^. Тогда
е^^(х)\ = А,х + А^х^ -Х[^А,х^ + ^А^х"" +х{^А, + ^А^) - {^А,х^ + 1^2^')]
Ортогонализуя невязку £[У2(з?)]5 будем иметь систему
/.
1
£[Y2(x)]xdx = о,
о
1
2.
/ s[Y2(x)]x'^dx = 0,
Jo
или однородную систему двух алгебраических уравнений с двумя неизвестными:
AiA20 - 48Л) + ^2(90 - 35Л) = О
AiF30 - 245Л) + ^2E04 - 180Л) =0. ^ ^
Приравнивая нулю определитель системы F), получим уравнение для определения
характеристических чисел:
I 120-48Л 90-35Л 1
630 - 245Л 504 - 180Л
D{X).
Откуда
:0.
Л^ - 26, ОЗЛ + 58,15 = 0. G)
Из уравнения G) будем иметь
Ai =2,462... и Л2 =23,568...
Для сравнения укажем точные характеристические числа
Л^ = ^тг^ =2,467... и Л2 = |-7г2 =22,206...,
полученные из решения краевой задачи, эквивалентной исходному уравнению:
y'^Jx) + Xy{x) = 0; у{0) = 0, у'М) = 0.
Таким образом, погрешность Л^^ равна примерно 0,2%,аЛ2 —6%.
(•) Литература: Л. В. Канторович, В. И. Крылов A962), Б. П. Демидович, И. А. Марон,
Е. 3. Шувалова A963), А. Ф. Верлань, В. С. Сизиков A986).
12 А. В. Манж:иров, А. Д. Полянин
Страница 177

178 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
5.18. Метод квадратур
5.18-1. Общая схема для уравнений Фредгольма второго рода
Сведение задачи решения интегральных уравнений к решению систем
алгебраических уравнений, получаемых заменой интегралов конечными суммами,
является одним из самых эффективных методов. Метод квадратур относится к ап-
проксимационным методам. Он широко распространен в практике, поскольку
достаточно универсален в отношении принципа построения алгоритмов решения как
линейных, так и нелинейных уравнений.
Так же как это было в случае уравнений Вольтерра, в основе метода лежит
некоторая квадратурная формула (см. п. 2.7-1):
сЪ ^
Lp{x) dx = Y^ Ajcp{xj) + Sn[^l A)
j=l
где Xj — узлы квадратурной формулы, Aj — известные коэффициенты, не
зависящие от функции ^(х), еп[^] —ошибка замены интеграла суммой (остаточный
член квадратурной формулы).
Если в линейном неоднородном интегральном уравнении Фредгольма второго
рода
у(х) -X [ К(х, t)y(t) dt = f(x), a^x^b, B)
J a
Принять X = Xi (i = l,2,...,n), TO получим исходное для данного метода
соотношение
J а
y(xi) - А / K(xi,
J а
t)y{t)dt = f{xi), г = 1,2,...,п, C)
ИЗ которого после замены интеграла конечной суммой получается система
уравнений:
п
y(xi) -X'^AjK(xi,Xj)y(xj) = f(xi)-\-Xen[y]. D)
j=i
После отбрасывания в ней малой величины A£n[y] для отыскания приближенных
значений yi решения у(х) в узлах xi, Х2, ..., Хп получается система линейных
алгебраических уравнений
п
yi-X^AjKijVj = fi, г = l,2,...,n, E)
где Kij = K(xi,Xj), fi = f(xi).
Решение системы E) дает значения yi, у2, • • •, Уп, но которым путем
интерполяции находится приближенное решение интегрального уравнения B) на всем
отрезке [а,Ь]. При этом в качестве приближенного решения можно принять
функцию, полученную линейной интерполяцией, т. е. совпадающую с yi в точках Xi и
липейную в каждом из промежутков [xi, Жг+i]. Кроме того, в качестве
аналитического выражения приближенного решения уравнения принимается функция
п
у(х) = f(x) + Л^ ^^^(ж,ж,)у,', F)
также имеющая в узлах xi, Ж2, ..., Хп значения yi, у2, • • •, Уп.
Страница 178

5.18. Метод квадратур 179
5.18-2. Построение собственных функций
Метод квадратур применяется также для решения однородных уравнений
Фредгольма второго рода. В этом случае система E) становится однородной
{fi = 0) и имеет нетривиальное решение лишь в том случае, когда ее определитель
D{X) равен нулю. Алгебраическое уравнение D{X) = {) степени п относительно Л
позволяет найти корни Ai, Л2, ..., А^, представляющие собой приближенные
значения п характеристических чисел уравнения. Подстановка любого из значений А^
(/с = 1, 2,..., гг) в E) при fi = 0 приводит к системе уравнений
У,
^^^ -XkJ2 ^J^ijvT^ =0' г = 1, 2,..., n,
ненулевые решения которой у\ ^ позволяют получить приближенные выражения
для собственных функций интегрального уравнения:
п
Если А не равно ни одному из корней А^, то неоднородная система линейных
алгебраических уравнений E) имеет единственное решение. Однородная система
уравнений E) в этом же случае имеет только тривиальное решение.
5.18-3. Особенности применения квадратурных формул
Точность получаемых решений существенно зависит от гладкости ядра и
свободного члена. При выборе квадратурной формулы необходимо учитывать, что
чем более точную формулу предполагается применить, тем большие требования
должны быть предъявлены к гладкости ядра, решения и правой части.
Если правая часть или ядро имеют особенности, то целесообразно
предварительно преобразовать исходное уравнение с целью получения более точного
приближенного решения. При этом применяются следующие приемы.
Если особенности имеет правая часть /(ж), а ядро гладкое, то можно
вместо у(х) ввести неизвестную функцию z(x) = у(х) — f (х), использование которой
в исходном уравнении позволяет получить уравнение
z(x)-X K(x,t)z(t)dt = X K(x,t)f(t)dt,
J а J a
В котором правая часть сглажена, а следовательно, и решение z(x) будет более
гладким. По найденной функции z(x) легко пайти искомое решение у(х).
В тех случаях, когда ядро K(x,t) или его производные по t имеют разрывы
на диагонали х = t, решаемое уравнение целесообразно записать в эквивалентном
виде:
У{х)
1
X K(x,t)dt\-X K(x,t)[y(t)-y(x)]dt = f(a
J а J J a
где нодынтегральная функция во втором интеграле не имеет особенностей,
поскольку на диагонали х = t разность y{t) — у(х) обращается в нуль, а вычисление
интеграла / K(x,t)dt выполняется без искомых функций и часто возможно в
явном виде.
12*
Страница 179

180 Методы решения линейных уравнений вида у{х) — /^ Х(ж, t)y(t) dt = f{x)
Пример. Рассмотрим уравнение
у{х) -
\ [ xty(t)
Jo
Выберем узлы х-^ = О, Х2 =
f(x) = -|-ж и ядра К(х^ t) = xt\
dt = ^х.
1 И вычислим в них значения правой части
/@)=0, f{\)--
Х@,0)=0, Х@, |-)=0, Х@,1):
5
12 •
/A) =
Ч\Л)
KA,0) = 0, K(l, ^
^0, К[\,\
КA,1) = 1-
Используя квадратурную формулу Симпсона (см. п. 2.7-1)
L
О
ДЛЯ определения приближенных значений у^ (г = 1, 2, 3) решения у{х)ъ узлах ж^, получим
систему
У1 =0,
12 У2 24 УЗ — 12 '
12 У2 + 12 УЗ - 6 '
решением которой являются у-^=0^у2 = ^, Уз = 1- Приближенное решение в соответствии
с выражением F) можно представить в виде
у(х)= fx-
1
i(o + 4
X
X
■^х -\-1 X 1 X х) = X.
Легко видеть, что оно совпадает с точным решением.
(•) Литература: Н. С. Бахвалов A973), В. И. Крылов, В. В. Бобков, П. И. Монастыр-
ный A984), А. Ф. Верлань, В. С. Сизиков A986).
5.19. Системы интегральных уравнений Фредгольма
второго рода
5.19-1. Некоторые замечания
Система интегральных уравнений Фредгольма второго рода имеет вид
yi{x)-\\^l Kij(x,t)yj(t)dt = fi(x), a^x^b, i = l,...,n. A)
j=l ^^
предположим, что ядра Kij(x,t) непрерывны или квадратично интегрируемы в
квадрате S = {а ^ х ^ Ь, a^t^6},a свободные члены fi(x) непрерывны или
квадратично интегрируемы на [а,Ь]. От искомых функций yi(x) также потребуем,
чтобы они были на [а, Ь] непрерывны либо квадратично интегрируемы. На такие
системы полностью распространяется теория, развитая для уравнений Фредгольма
второго рода. Так, можно показать, что для системы уравнений A)
последовательные приближения сходятся в среднем к решению этой системы, если Л
удовлетворяет неравенству
|А| < ^, B)
где
В^
\Kij{x^t)\ dxdt = В^ < ОС.
C)
Страница 180

5.20. Метод регуляризации для некоторых уравнений второго рода 181
Если ядра Kij(x,t) удовлетворяют еще и условию
гЬ
I
J а
Kfj (х, t) dt^ Aij, а^х ^ b, D)
где Aij — некоторые постоянные, то последовательные приближения сходятся
абсолютно и равномерно.
Если все ядра Kij(x,t) вырожденные, то система A) сводится к линейной
алгебраической системе. Можно установить, что для системы интегральных
уравнений Фредгольма справедливы все теоремы Фредгольма.
5.19-2. Метод преобразования системы уравнений в одно уравнение
Систему уравнений A) можно преобразовать в одно интегральное уравнение
Фредгольма второго рода. Действительно, определим функции Y(x) и F(x)
на [а, пЬ — (п — 1)а], положив
Y{x) = yi{x-{i- 1){Ь - а)), F{x) = fi{x-{i- 1){Ь - а))
при
(г - 1N - (i - 2)а ^ X ^ ib - (i - 1)а.
Ядро интегрального уравнения K(x,t) зададим в квадрате
Sn = {а ^ X ^ пЬ — (п — 1)а, а ^ t ^ пЬ — (п — 1)а},
положив
K{x,t) = Kij{x - (г - 1){Ь -a),t- (j - 1){Ь - а))
при
(г - 1N - (i-2)a^x ^ib- (i- 1)а, (j - 1N - (j - 2)a ^ t ^ jb - (j - l)a.
Теперь система A) записывается в виде одного уравнения Фредгольма
гпЬ— (п—1)а
У(х) - Л / К(х, t)Y(t) dt = F(x), а^х ^nb- (п- 1)а.
J а
Если ядра Kij(x,t) квадратично интегрируемы в квадрате S = {а ^ х ^ Ь,
а ^ t ^ 6}, а свободные члены fi(x) — на [а, 6], то ядро К(х, t) квадратично
интегрируемо в новом квадрате Оп, а свободный член F(x) квадратично интегрируем
на [а, пЬ — (п — 1)а].
Если выполнено условие D), то ядро K(x,t) удовлетворяет следующему
неравенству:
I
J а
K^(x,t)dt ^ А^, а < X < пЬ — (п — 1)а,
где А* — некоторая постоянная.
(•) Литература: С. Г. Михлин A959).
5.20. Метод регуляризации для некоторых уравнений
второго рода
5.20-1. Основное уравнение и теоремы Нетера
Рассмотрим интегральное уравнение второго рода в форме
у{х)-\-
I foo 1 Г°
^ Ki(x-t)y(t)dt^^= K2(x-t)y(t)dt^
27Г Jo v27r J_^
/oo
M(x,t)y(t)dt = f(x), -oo < ж < oo. A)
-oo
Страница 181

182 Методы решения линейных уравнений вида у{х) — /^ К(х^ ^)у{^) ^^ — /(^)
Будем считать, что функции у (ж), f{x) и ядра i^i(x), К2(х), M(x,t) таковы, что
их изображения, полученные при помощи интегрального преобразования Фурье,
принадлежат L2(—оо,оо) и удовлетворяют условию Гель дера, причем для ядра
М(х, t) — по каждой переменной. Кроме того,
/оо /»оо
/ \M{x,t)\^dxdt< оо.
-оо «V — оо
Можно заметить, что уравнение A) при M(x,t) = О переходит в изученное ранее
в п. 5.9-2 интегральное уравнение типа свертки с двумя ядрами.
Союзное с A) однородное уравнение имеет вид
/.оо 1 Г°
ip(x)^^= / Ki(t-x)ip(t)dt^^= / K2(t-x)ip(t)dt^
л/27г Jo v27r J_^
/оо
M{t,x)y{t)dt = 0, -оо < ж < оо. B)
-оо
Будем считать, что выполнены условия нормальности (см. п.5.9-2), т. е.
l-\-JCi(u)^0, l-\-JC2(u)^0, -оо<и<оо. C)
Теорема 1. Числа линейно независимых решений однородного
уравнения A) (f{x) = 0) и союзного с ним однородного уравнения B) конечны.
Теорема 2. Для разрешимости неоднородного уравнения A)
необходимы и достаточны условия
Г
J —с
f(t)ipk(t)dt = 0, k = l,...,N, D)
где (рк(х) —конечное число всех линейно независимых решений союзного
однородного уравнения B).
Теорема 3. Разность числа линейно независимых решений однородного
уравнения A) и числа линейно независимых решений однородного союзного
уравнения B) равна индексу
1+/С2(«)
1 + /Ci(w) 27Г
arg
1 + /Ci(w)
E)
5.20-2. Регуляризующие операторы
Одним из методов как теоретического исследования, так и практического
решения рассматриваемых уравнений является их регуляризация, т. е. приведение
к уравнению Фредгольма второго рода.
Обозначим через К оператор, определенный левой частью уравнения A):
К[у{х)] = у(х) + ^1°° Кг (х - t)y{t) dt+
-н гО гоо
+ ^=/ K2(x-t)f(t)dt^ M(x,t)y(t)dt, F)
И введем еще один аналогичный оператор
1 /"°°
L[u;(x)]=u;(x)-\-^^ / Li(x - t)u;(t)dt-\-
-| rO /«оо
+ ^=/ L2(x-t)u;(t)dt-\- Q(x,t)u;(t)dt. G)
л/27Г J_oo J-oo
Страница 182

5.20. Метод регуляризации для некоторых уравнений второго рода 183
Найдем оператор L такой, чтобы произведение LK определялось левой
частью уравнения Фредгольма второго рода с ядром K(x,t):
/оо /»оо /»оо
K(x,t)y(t)dt, / / \K(x,t)\^dxdt<oo. (8)
-оо J — оо J — с
-оо ^/ — оо
Оператор L называется регуляризующим слева или левым регуляризатором.
Для того чтобы оператор К интегрального уравнения A) имел регуляризу-
ющий слева оператор L вида G), необходимо и достаточно, чтобы выполнялись
условия нормальности C).
Если условия C) выполнены, то регуляризующий слева оператор L имеет вид
1 /"°°
Ъ[ио{х)] = ио{х)- —=^ / Ri{x-t)uj{t)dt-
л/27г Jo
-= I R2(x-t)u;(t)dt-\- Q(x,t)u;(t)dt, (9)
V-^Т* J—оо J — оо
где резольвенты Ri(x — t) и R2(x — t) ядер Ki(x — t) и К2(х — t) задаются
выражениями (см. п. 5.8-1)
R (х) = ^ Г ^'^''] e-'^'^du, }Cj{u) = ^ Г Kj{x)e'''^dx, A0)
где j = 1,2, а функция Q(x,t) может быть любой, удовлетворяющей условию
оо оо
/ / \Q(x,t)fdxdt< оо.
— оо —оо
при условии C) оператор L, определенный формулой (9), для оператора К
является одновременно и регуляризующим справа:
/оо /»оо /»оо
K^{x,t)y{t)dt, / / \K^{x,t)\^ dxdt<oo. {П)
-оо J —оо J —оо
5.20-3. Метод регуляризации
Пусть дано уравнение в виде
Щу{х)] = f(x), -оо < ж < оо, A2)
где оператор К определен выражением F).
Существует несколько способов его регуляризации, т. е. приведения к
уравнению Фредгольма. Во-первых, можно привести это уравнение к уравнению с ядром
Коши. Регуляризовав последнее одним из способов, изложенных в разд. 7.4, можно
считать цель достигнутой. Этот путь приемлем, если удается найти по заданным
функциям Ki(x), К2(х), M(x,t) и f(x) простые выражения для их интегралов
Фурье. В противпом случае естественно проводить регуляризацию уравпения A2)
непосредственно, без перехода к изображениям.
Регуляризация слева уравнения A2) заключается в применении к обеим его
частям построенного в предыдущем пункте регуляризующего оператора L:
1Ж.[у{х)] = Uf{x)]. A3)
В силу (8) уравнение A3) есть уравнение Фредгольма
/оо
K{x,t)y{t)dt = -L[f{x)]. A4)
-ОО
Страница 183

184 Методы решения линейных уравнений вида у{х) — /^ К(х^ ^)у{^) ^^ — /(^)
Итак, уравнение A2) регуляризацией слева преобразуется в уравнение Фред-
гольма с той же неизвестной функцией у (ж) и известной правой частью L[/(x)].
Известно, что регуляризация слева пе приводит к потере решений: среди решений
регуляризованного уравнения содержатся все решения исходного уравнения A2).
Однако в общем случае не всякое решение регуляризованного уравнения будет
решением исходного.
Регуляризация справа заключается в подстановке в уравнение A2) вместо
искомой функции выражения
y{x) = Uuj{x)l A5)
где и{х) — новая неизвестная функция. В результате приходим к иптегральному
уравнению, которое в силу A0) также является фредгольмовым:
/оо
K,{x,t)u{t)dt = f{x),
-оо
-оо < Ж < ОО. A6)
Таким образом, от уравнения A2) отпосительпо неизвестной функции у{х)
удалось перейти к иптегральному уравнению Фредгольма относительно новой
неизвестной функции ио{х). Решив уравпение Фредгольма A6), но формуле A5)
найдем решение исходного уравнения A2). Регуляризация справа не может
привести к посторонним решениям, но известно, что она может привести к потере
решений.
Представляет значительный теоретический и практический интерес решение
вопроса о равносильной регуляризации, когда не происходит ни потери решений,
ни появления посторонних «решений».
Для того чтобы уравнение A2) допускало равносильную регуляризацию слева
при любой правой части /(ж), необходимо и достаточно, чтобы индекс v,
определенный формулой E), был неотрицательным числом. В качестве равносильно
регуляризующего оператора можно взять оператор L°, определенный выражением
J^[uj{x)] = uj{x) -=^ I Ri{x-t)uj{t)dt -=^ I R2{x-t)uj{t)dt.
л/27г Jo v2^ ^-оо
Итак, уравнение Фредгольма L°K[y(x)] = Ь°[/(ж)],в случае z^ > О имеет те
и только те решения, какие имеет уравнение A2). В случае, когда индекс р число
неположительное, оператор L° осуществляет равносильную регуляризацию справа
уравнения A2) при любой правой части /(ж). Действительно, при zy ^ О, найдя
решение уравнения Фредгольма KL°[a;(x)] = /(ж),по формуле у{х) = Jf[u;(x)]
можно получить все решения исходного уравнения A2).
Известен еще один способ регуляризации Карлемапа-Векуа, основывающийся
на решении соответствующего характеристического уравпения. Уравнение A2)
формально записывается в виде уравнения с двумя ядрами
У(х)
+ ^ / Ki(x-t)y(t)dt^^ [ K2(x-t)y(t)dt = fi(x),
л/27г Jo v2^ ^-оо
/оо
Mix,t)y{t)dt.
-оо
A7)
Затем, функция fi(x) временно считается известной, и решается уравнение A7)
(см. п. 5.9-2). Анализ формулы, нолученной в результате для функции у(х),
показывает, что эта формула при 1у = 0 является интегральным уравнением Фредгольма
с неизвестной у(х).В случае и > О полученное уравнение будет содержать и
произвольных постоянных. Ири отрицательном индексе ly к уравнению добавляются
условия разрешимости.
(•) Литература: Ф. Д. Гахов, Ю. И. Черский A978).
Страница 184

6. Методы решения сингулярных
интегральных уравнений
первого рода
6.1. Предварительные замечания
6.1-1. Интегральные уравнения первого рода с ядром Кошн
Сингулярное интегральное уравнение первого рода с ядром Коши имеет вид
±f^dr = m, г' = -1, A)
где L — гладкий замкнутый или разомкнутый контур в комплексной плоскости
Z = х-\-гу, t и т — комплексные координаты его точек, Lp{t) —неизвестная функция,
ядро Коши, f(t) —некоторая функция, которая называется свободным
т — t
членом или правой частью уравнения A). Интеграл в левой части существует
только в смысле главного значения по Коши (см. п. 6.2-5).
Частными случаями уравнения A) являются простейшее сингулярное
интегральное уравнение, когда L — гладкий замкнутый контур, уравнение на
действительной оси
-Г
t — X
а также уравнение с ядром Коши на конечном отрезке
dt = f(x), —ОС < X < ОС, B)
а
^f!^dt = f{x), a^x^b. C)
Общее сингулярное интегральное уравнение первого рода с ядром Коши имеет
вид
^f^^^ir)dr = m, D)
где M(t, т) —известная функция. Его также записывают и в другой эквивалентной
форме, которая приведена в п. 6.4-4.
Будем считать, что все функции в уравнениях A)-D) удовлетворяют условию
Гёльдера (см. п. 6.2-2), причем функция M(t, т) — по обеим переменным.
6.1-2. Интегральные уравнения первого рода с ядром Гильберта
Простейшее сингулярное интегральное уравнение первого рода с ядром
Гильберта имеет вид
j-j\tg(^i^^^{Od^ = f{x), E)
где ^(х) —неизвестная функция (О ^ ж ^ 27г), ctg [^(^ — х)] —ядро Гильберта,
f(x) —заданная правая часть уравнения.
Общее сингулярное интегральное уравнение первого рода с ядром Гильберта
имеет вид
N{x,Octg(^)^iOd^ = fi^), F)
2^ Л
Страница 185

186 Методы решения сингулярных интегральных уравнений первого рода
где N(x,^) —известная функция. Уравнение F) часто записывают в
эквивалентной форме, которая приведена в п. 6.4-5.
Будем считать, что все функции в уравнениях E) и F) также удовлетворяют
условию Гёльдера (см. п. 6.2-2), причем функция N(x, ^) —по обеим переменным.
Если правые части уравнений A)-F) тождественно равны нулю, то уравнения
называются однородными, в противном случае — неоднородными.
(•) Литература: Н. И. Мусхелищвили A968), Ф. Д. Гахов A977), А. И. Гусейнов,
X. Ш. Мухтаров A980), S. G. Mikhlin, S. Prossdorf A986), S. Prossdorf, В. Silbermann A991),
A. Dzhuraev A992), И. K. Лифанов A995).
6.2. Интеграл типа Коши
6.2-1. Определение интеграла тина Коши
Пусть L — некоторый гладкий замкнутый контур* на плоскости комплексного
переменного z = х -\- iy. Область, лежащую внутри контура L, будем называть
внутренней и обозначать П^, а дополнительную к П^ U L область, содержащую
бесконечно удаленную точку, будем называть внешней и обозначать П~.
Если f{z) — функция, аналитическая в П^ и непрерывная в П^ U L, то
согласно известной из теории функций комплексного переменного формуле Коши
^ [ li^dT=[f^'^ при^еП+, ^.
2ш Jj^ т - Z \ О при Z еО. .
Если же /(^) аналитична в области П~ и непрерывна в П~ U L, то
2ш Jl т- z \ -f{z) + /(оо) при ^ G П . ^ ^
За положительное направление обхода контура L, как обычно, будем принимать
то, при котором область Q~^ остается слева.
Формула Коши дает возможность вычислить значения функции в любой точке
области, если известны ее значения на границе области, т. е. формула Коши решает
краевую задачу для аналитических функций. Интеграл, стоящий в левой части
формул A) и B), называется интегралом Коши.
Пусть теперь L — гладкий замкнутый или незамкнутый контур, целиком
расположенный в конечной части плоскости, т — комплексная координата его
точек и (р(г) — непрерывная функция точек контура. Тогда интеграл
^^^г, C)
Ф(^) = — [
fL ' - ^
построенный так же, как и интеграл Коши, называется интегралом типа Коши.
Функция (/?(т) называется его плотностью, а 1/(т — z) —ядром.
Для интеграла типа Коши с непрерывной плотностью ^{т) единственными
точками, где подынтегральная функция перестает быть аналитической
относительно Z, являются точки линии интегрирования L. Последняя является особой линией
для функции Ф(^).
Если L — незамкнутый контур, то Ф(^) будет функцией, аналитической во
всей плоскости с линией особенностей L. Пусть теперь L — замкнутый контур.
* Под гладким контуром будем понимать простую (без точек самопересечения)
замкнутую или незамкнутую линию с непрерывно меняющейся касательной и не имеющую точек
возврата (заострения).
Страница 186

6.2. Интеграл типа Коши 187
Тогда Ф(^) распадается на две самостоятельные функции: Ф^(^), определенную
в области П^, и Ф~(^), определенную для точек в области П~. Функции эти,
вообще говоря, не являются аналитическим продолжением друг друга.
Аналитическую функцию Ф(^), определяемую в двух дополняющих друг
друга до полной плоскости областях П+, П~ двумя самостоятельными выражениями
Ф+(^), Ф~(^), будем называть кусочно аналитической функцией.
Отметим одно важное свойство интеграла типа Коши. Функция Ф(^),
представленная интегралом типа Коши C), в бесконечно удаленной точке обращается
в нуль, т. е. Ф~ (ос) = 0. Это условие является также и достаточным для
представимости кусочно аналитической функции интегралом типа Коши.
6.2-2. Условие Гёльдера
Пусть L — гладкая кривая на плоскости комплексного переменного z = х-\-гу
и Lp{t) — функция точек этой кривой. Говорят, что функция Lp{t) удовлетворяет на
кривой условию Гёльдера, если для любых двух точек этой кривой
|(/^(t2)-(/^(tl)|^A|t2-ti|\ D)
где А и Л — положительные числа. Число А называется постоянной Гёльдера, а
Л — показателем Гёльдера. Если бы Л было бы больше единицы, то из условия D)
вытекало бы, что производная ^' {t) всюду равна нулю и функция Lp{t) была бы
тождественно равна постоянной. Поэтому мы будем считать, что О < Л ^ 1. Если
Л = 1, то условие Гёльдера часто называют условием Липшица. Иногда условие
Гёльдера называют условием Липшица порядка Л.
Если ti, t2 достаточно близки друг к другу и условие Гёльдера выполняется
для некоторого показателя Ai, то оно будет, очевидно, выполняться и для
всякого показателя Л < Ai. Обратное, вообще говоря, несправедливо. Таким образом,
меньшему Л соответствует более широкий класс функций. Наиболее узким
классом будет класс функций, удовлетворяющих условию Липшица.
На основании последнего свойства легко установить, что если функции
V^i@, 4^2{t) удовлетворяют условию Гёльдера соответственно с показателями
Ai, А2, то их сумма, произведение, а также частное при условии, что
знаменатель не обращается в нуль, удовлетворяют условию Гёльдера с показателем
А = min(Ai, А2).
Если Lp{t) дифференцируема и имеет конечную производную, то она
удовлетворяет условию Липшица. Обратное, вообще говоря, неверно.
6.2-3. Главное значение сингулярного интеграла
Рассмотрим интеграл
dx
I
J а
а < С <
X — с
Вычисляя его как несобственный, получим
f'^^= Иш (- П" ^^+ /' J^\ =\п А^+ lim In ^. E)
Предел последнего выражения зависит, очевидно, от способа стремления £i и £2
к нулю. Следовательно, интеграл, понимаемый как несобственный, не существует.
Его называют сингулярным интегралом. Можно, однако, ему придать смысл, если
Страница 187

188 Методы решения сингулярных интегральных уравнений первого рода
установить некоторую зависимость между ei и €2- Полагая, что вырезаемый
интервал расположен симметрично относительно точки с, т. е.
£1 = £2 = £, F)
мы приходим к понятию главного значения сингулярного интеграла по Коши.
Главным значением по Коши сингулярного интеграла
гЪ
I
J а
dx ,
, а < с < о,
называется
dx
lim { Г~' ^^ /
Учитывая формулу E) и условие F), будем иметь
:1П^^. G)
/
dx . b -
- с
Рассмотрим теперь более общий интеграл
/
J а
' ^^dx, (8)
где (р(х) — некоторая функция, удовлетворяющая условию Гёльдера. Этот
интеграл аналогично рассмотренному выше будем понимать в смысле главного
значения, которое определим следующим образом:
^(^^ dx
dx
Записывая тождество
f ^P^dx= f'^^M^^^dx^^ic) f
Ja X-C J a X-C J^
замечаем, что первый интеграл в правой части сходится как несобственный,
поскольку в силу условия Гёльдера
ip{x) - ip{c)
а второй интеграл совпадает с G).
Таким образом, получаем, что сингулярный интеграл (8), где ^(х)
удовлетворяет условию Гёльдера, существует в смысле главного значения по Коши, причем
Ja ^-С J a X-C
c)\n^
Для обозначения сингулярного интеграла, некоторые авторы употребляют
специальные символы, например v.p. / (valeur principale). Однако в этом нет особой
необходимости, потому что, с одной стороны, если интеграл (8) существует как
обыкновенный или как несобственный, то он существует и в смысле главного
значения, причем их значения совпадают, с другой же стороны, сингулярный интеграл
всегда будем понимать в смысле главного значения. Поэтому сингулярный
интеграл будем обозначать обычным знаком интеграла.
Страница 188

6.2. Интеграл типа Коши 189
6.2-4. Многозначные функннн
В задании комплексного числа z = ре* модуль р определяется однозначно,
аргумент же ^ с точностью до слагаемого, кратного 27г. Последнее обстоятельство
не приводит к многозначности представления числа в силу того, что аргумент
входит в это представление через посредство функции е*^, имеющей период 27г.
Но если аналитическая функция такова, что в ее выражение аргумент входит
посредством функции не периодической, то она окажется многозначной. Среди
элементарных функций к таким принадлежат логарифм:
1п(^ — ^о) = In 1^ — ^о| + i8iXg(z — zo) = Inp + гв, (9)
и степенная функция с нецелым показателем:
{z-zoy=p^e'^^=p''[cos{p\np)^ism{p\np)y^'e'^''''\ -f = a^ip. A0)
Во всех рассуждениях иод логарифмом модуля комплексного числа всегда
понимается его действительное значение согласно обычному определению. Общее
представление аргумента в имеет вид S = О -\-27тк, где к может нринимать
любые целые значения (к = 0,±1,±2,...), ав качестве О можно взять наименьшее
по абсолютной величине значение аргумента.
Каждому выбранному значению к будет соответствовать определенная ветвь
многозначной функции. У логарифмической функции число ветвей бесконечно. У
степенной при иррациопальном или комплексном показателе также бесконечно.
Если же показатель рациопальный, 7 = р/я, где p/q — несократимая дробь, то
степенная функция имеет q ветвей. Ветви логарифма отличаются друг от друга па
слагаемое вида г27гш, а ветви степенной функции па множитель е*^^^^ (т —
целое число). Для задания многозначной функции, очевидно, необходимо указать
выбранную ветвь. Однако, в отличие от функций действительного переменного, этого
еще недостаточно для полного определения многозначной функции
комплексного переменного. Для последних существуют на плоскости точки, обладающие тем
свойством, что, когда переменное, изменяясь по замкнутому контуру,
окружающему эту точку, возвращается к начальному значению, выбранная ветвь функции пе
остается неизменной, а переходит в некоторую другую ветвь. Такие точки
называются точками ветвления многозначной функции.
Для рассматриваемых функций (9) и A0) точками ветвления будут zq и
бесконечно удаленная. Если переменное описывает контур, окружающий точку zq в
положительном или отрицательном направлении, то аргумент в изменяется на 27г
или на — 27Г. При этом логарифм получает слагаемое г27г или — г27г, а степенная
функция множитель е*^^^ или е~*^^^. Следовательно, ветвь, соответствующая
выбранному значению к = п, переходит в соседнюю ветвь, соответствующую
значению к = п -\- 1 или к = п — 1. Псследование в бесконечно удаленной точке
производится, как обычно, путем подстановки z = 1/(^ и исследования в точке
С = о.
Сохранить выбранную ветвь функции удастся лишь в том случае, если
сделать невозможным обходы вокруг точек ветвления. Последнее достигается
проведением в плоскости разрезов, соединяющих точки ветвления. В
рассматриваемых случаях логарифмической и степенной функций нужно провести разрез вдоль
некоторой линии, исходящей из точки zq и удаляющейся в бесконечность.
Границы измепения аргумента в определяются положением разреза. Если,
например, разрез проведен по лучу, образующему с осью абсцисс угол во, то для
главной ветви (к = 0) во ^ S ^ во -\- 27v. В частности, для разреза, направленного
по положительной полуоси абсцисс, О ^ в ^ 27г, по отрицательной полуоси.
Страница 189

190 Методы решения сингулярных интегральных уравнений первого рода
—7г ^ в ^ 7г. Если разрез криволинейный, то границы изменения аргумента будут
функциями точки. Начальное значение аргумента соответствует левому (если
смотреть от точки zq) берегу разреза, конечное — правому. Обозначим значение
аргумента на левом и правом берегах разреза соответственно в^ и в~. Тогда
в~ — в^ = 27Г. Разрез для выбранной ветви будет линией разрыва. На берегах
разреза выполняются соотношения
1п(^~ — ^о) = 1п(^ — ^о) Н- ^27г, (z~ — гоУ = е ^^{z — ^о)^-
Свойство разрывности ветвей многозначных функций на берегах разреза
широко используется при решении краевых задач с разрывными граничными
условиями. Логарифм используется в том случае, когда разрывная функция входит
в краевое условие в качестве слагаемого, стененная функция, — если множителем.
6.2-5. Главное значение сингулярного криволинейного интеграла
Пусть L — гладкий контур, г и t — комплексные координаты его точек.
Рассмотрим криволинейный сингулярный интеграл
^^^dr. A1)
/.
/ L
Проведем из точки t контура, как из центра, окружность радиуса р, и пусть
ti, t2 —точки пересечения этой окружности с кривой. Радиус будем считать
настолько малым, чтобы окружность не имела с кривой L других точек нересечения,
кроме ti и t2. Обозначим часть контура L, вырезаемую окружностью, через / и
возьмем интеграл
/ ^dr. A2)
Jl-1 ^-t
предел интеграла A2) при р ^ О называется главным значением сингулярного
интеграла A1). Представляя его в виде
Ш-=/.-^^^--<')/^
dr
fL ' - '^ JL ' - '^ JL ' - '^
И рассуждая так же, как и ранее, получим, что сингулярный интеграл A1) для
функции v^(t), удовлетворяющей условию Гёльдера, существует в смысле
главного значения но Коши.
Во всех точках гладкости его можно представить в двух видах:
где а иЬ — концевые точки контура L.
В частности, для замкнутого контура, полагая а = Ь, получим
Пусть L — гладкий контур (замкнутый или незамкнутый) и (р(г) — функция
точек контура, удовлетворяющая условию Гёльдера. Тогда интеграл тина Коши
Страница 190

6.2. Интеграл типа Коши 191
имеет предельные значения Ф^(t), Ф~(^) во всех точках контура L, не
совпадающих с его концами, при приближении к контуру слева или справа по любому
пути, и эти предельные значения выражаются через плотность интеграла (/?(t) и
сингулярный интеграл A3) по формулам Сохоцкого-Племеля:
Вычитая и складывая формулы A4), получим пару равносильных им формул
Ф+(t)-ф-(t) = v^(t), A5)
Ф+(t)+ф-(t) = — / ^dr, A6)
которыми часто пользуются вместо A4).
Формулы Сохоцкого-Племеля для действительной оси имеют вид
^ ' 2^^ ' 2пг J_^ т-х ^ ' 2^^ ' 2ш J _^ т - х
A7)
Причем
ф+(оо) = ^(р(оо), Ф~(оо) = -^(р(оо).
Отсюда и из A7) имеем
Ф+(оо) + Ф~(оо) = 0, A8)
lim / ^ilL(ir = 0. A9)
функция, представимая интегралом типа Коши на действительной оси,
необходимо удовлетворяет условию A8). Это условие является также и достаточным
для представления кусочно аналитической в верхней и нижней полуплоскостях
функции интегралом по действительной оси.
Рассмотрим интеграл типа Коши по действительной оси, считая z не лежащим
на ней:
4z) = ^ Г ^^dx, B0)
27гг J_^ X-Z
где (р(х) —комплексная функция действительного переменного ж,
удовлетворяющая на действительной оси условию Гёльдера (см. п. 4.1-3).
Если аналитическая в верхней полуплоскости функция (p(z) непрерывна в
замкнутой полуплоскости и на действительной оси удовлетворяет условию Гёльдера,
то
ip(x) 7 _ Г ^(^) - Т^^(^) при Im^ > О,
27гг J_^ X — Z \—^(/?(оо) при Im^ < 0.
-Г
27гг J_,
Также справедлива формула
-Г
ip{x)-ip{oo) ^^ ^ г tV^(^) при Im^ > О,
X — Z \ —(/?(^) Ч-^V^(oo) при Im^ < О,
если аналитическая в нижней полуплоскости функция (p(z) непрерывна в
замкнутой полуплоскости и удовлетворяет на действительной оси условию Гёльдера.
Страница 191

192 Методы решения сингулярных интегральных уравнений первого рода
6.2-6. Формула перестановки Пуанкаре-Бертрана
Рассмотрим пару следующих повторных сингулярных интегралов:
Nit) = ^ [ J^± [ ^("'"i) dri, B3)
где L — гладкий контур, a функция К (г, ri) удовлетворяет условию Гёльдера по
обеим переменным.
Оба интеграла имеют смысл, и хотя N и М отличаются лишь порядком
интегрирования, они не равны, что показывает следующая формула перестановки
Пуанкаре-Бертрана:
^(^'-^^ -dr,
1 f dr If К(т,т,) , r^,, г, 1 f , 1 f
— 7—/ ^ ' " dTi=K{t,t)+— dri —
B5)
которую можно записать еще и в следующем виде:
Jl ^-^ Jl ^1-^ Jl Jl (^-Щ^1-^)
Пример. Вычислим интеграл типа Коши, взятый по единичной окружности |2;| = 1, с
плотностью v^(t) = 2/[т(т — 2)], т. е.
Ф(.) = ^/^ ^_^/1^?^.
27гг J L т — 2 т — Z 2ш J l т т — z
Функция 1/B; — 2) аналитична в П+, а 1/^; аналитична в П~ и обращается на бесконечности
в нуль. Первый интеграл по формуле A) равен 1/B; —2) для 2; G П+ и равен нулю для z^Vl~.
Второй интеграл по формуле B) для z ^Vl~ равен — 1/^;, а для 2; G П+ равен нулю. Отсюда
ф+(^) = -^. ф-(^) = |-
Z — 1 Z
(•) Литература'. Н. И. Мусхелишвили A968), Ф. Д. Гахов A977), S. G. Mikhlin, S. Prossdorf
A986).
6.3. Краевая задача Римана
6.3-1. Теорема об аналитическом продолжении и теорема Лнувилля
Теорема об аналитическом продолжении (принцип непрерывности).
Пусть две области Qi и Q2 граничат вдоль некоторой гладкой кривой L.
В областях ^1 и ^2 заданы аналитические функции fi{z) и f2{z). Пред-
нолож:им, что при стремлении точки z к кривой L обе функции стремятся
к предельным значениям, непрерывным на кривой L, причем эти
предельные значения равны меж:ду собой. При этих условиях функции fi(z) и f2(z)
будут аналитическим иродолукением друг друга.
Пусть в области П, ограниченной контуром L, функция f(z) аналитична, за
исключением конечного числа точек, где она может иметь полюсы. Выпишем
разложение в ряд в окрестности некоторой точки zq:
f(z) = Cn(z - zo)"" -\- Cn+i(z - zo)""^^ -\ = (z-zo)''fi(z), fi(zo) = On 7^0.
Страница 192

6.3. краевая задача Римана 193
Число п называется порядком функции в точке zq. Если п > О, то порядок
функции есть порядок ее нуля, если гг < О, то порядок ее есть порядок полюса с
противоположным знаком. Если порядок функции в zq есть нуль, то в такой точке
функция принимает конечное, отличное от нуля, значение. При рассмотрении
бесконечно удаленной точки разность z — zq нужно заменить на 1/^. Если точка zq
лежит на контуре L, то порядком функции будем считать число ^гг.
Пусть Nq, Pq и Nl, Pl соответственно числа нулей и полюсов в области
и на контуре, причем каждый из них берется столько раз, какова его кратность.
Символом [5]ь обозначим приращение величины 5 при обходе контура в
положительном направлении. Положительным обходом, как всегда, считается тот, при
котором рассматриваемая область остается слева.
Принцип аргумента. Пусть f(z) есть функция, аналитическая и
однозначная в многосвязной области Q, ограниченной гладким контуром
L = Lq -\- Li -\- • • • -\- Lm, за исключением конечного числа точек, где она
мож:ет иметь полюсы, непрерывная в замкнутой области Q -\- L и имеет на
контуре не более чем конечное число нулей целого порядка. Тогда
справедлива формула
Nu-Pu+ Unl - Pl) = ^[arg/@)]i.
Z ZTT
Обобщенная теорема Лиувилля. Пусть функция f(z) аналитична во
всей плоскости комплексного переменного, за исключением точек а о = сю, ак
(к = 1,2,... ,п), где она имеет полюсы, причем главные частиразлоэюений
функции f(z) в окрестности полюсов имеют вид
/^ / \ о I о 2 I 1 О тпп
Qo(z) = CiZ-\-C2Z -\-• • •-\-c^qZ ^ в точке ао,
L \ Ci Со т 7
Z ± \ ± h • • • Н в точках ак.
Ч/ ^-^к i^-cik)^ i^-cik)'^^
Тогда функция f(z) есть рациональная функция и мосисет быть представлена
формулой
п. /
1
/(г) = С + до(г) + ^
где С — постоянная. В частности, если единственная особенность функции f(z)
есть полюс порядка т в бесконечно удаленной точке, то f(z) есть многочлен
степени т:
f{z) = Co-\-CiZ-\ h CmZ"^.
Обычно используют следующие обозначения:
a) f(z) — функция, сопряженная с данной функцией f(z);
b) f(z) — функция, получаемая из f(z) путем замены в ней ^ на ^, т. е. у на —у
в/(г); _
c) f(z) — функция, определяемая условием f(z) = f(z).
Если Z = X -\- iy и f(z) = и(х, у) Ч- iv(x, у), то
f(z)=u(x,y)-iv(x, у), f(z)=u(x, -y)-\-iv(x, -у), f(z)=u(x, -y)-iv(x, -у).
п
В частности, если f(z) задана рядом f(z) = Y1 CkZ^, то
f(^) = J2^^^^^ f(^) = J2^^^^^ /(^) = Х1
- к
CkZ .
13 А. В. Манж:иров, А. Д. Полянин
Страница 193

194 Методы решения сингулярных интегральных уравнений первого рода
Для функции, представленной интегралом типа Коши
будем иметь
^ ^ 2ш Jl f-z ' ' ^ ^ 2ш Jl T-Z ' '^ ^ 2ш Jl т- Z
Заметим, что если функция удовлетворяет условию /(^) = /(^), то для
вещественных значений z она припимает чисто действительные значения. Справедливо
также и обратное предложение.
6.3-2. Интерполяционный нолнном Эрмнта
Интерполяциопный полипом Эрмнта используется для построения
канонической функции неоднородной задачи Римана в пп. 4.4-7 и 6.3-9.
Пусть заданы различные точки ^^ (А: = 1, 2, ..., ттг) и пусть каждой точке Zk
сопоставлены числа А^'^'' (j = 0,1,..., п/с — 1), где Пк —заданные натуральные
числа. Требуется построить полином Up{z) наинизшей степени, удовлетворяющий
условиям
U^J\zk) = ^^i\ ^ = 1,2,...,ш, j = 0,l,...,nfc-l,
где Up (zk) —значения производных j-ro порядка полинома в точках Zk. Числа Zk
называются узлами интерполирования, an к — кратностями интерполирования в
узлах Zk.
Такой полином существует и имеет следующий вид (см. В. И. Смирнов,
Н. А. Лебедев A964)):
С(^) \
Up{z) = J2
^k,r\Z Zk
j\{r-j)\
у, Р = ^Пк-1
к=1
_ dz'^-^ C,{z)
,=1 (---fc)"' f^,
m r
C{z) = \{{z-Zkr\ Ak,r = Y.-
k=l 3=0
k = l,2,...,m, r = 0,1,...,Пк -1,
причем он определяется единственным образом.
Интерполяционный полином Up(z), построенный для функции f(z), в
точках Zk должен удовлетворять условиям
U^'\zk) = А['^ = f^'\zk), к = 1,2,...,т, j = 0,l,...,nk-l,
где f^^\zk) —значения производных j-ro порядка этой функции в точках Zk.
6.3-3. Понятие индекса
Пусть L — гладкий замкнутый контур и D{t) —заданная на нем непрерывная
функция, не обращающаяся в нуль.
Индексом V функции D(t) по контуру L называется разделенное на 27г
приращение ее аргумента при обходе кривой L в положительном направлении:
i/ = IndD(i)=^[argD(i)]L. A)
Страница 194

6.3. краевая задача Римана 195
Так как InD(t) = ln|D(t)| + zargD(t) и после обхода контура L
функция \D{t)\ возвращается к начальному значению, то [lnD(t)]b = z[argD(t)]b и
следовательно,
V = Л_[\пОЦ)]ь. B)
Индекс можно представить в виде интеграла
р = lndD(t) = — [ d\nD(t) = — [ dargD(t). C)
27гг Jl 27Г Jl
При этом, если D(t) не дифференцируема, но имеет ограниченную вариацию, то
интеграл понимается в смысле Стилтьеса. В силу непрерывности D(t) образ Г
замкнутого контура L будет также замкнутым контуром и приращение
аргумента D(t) при обходе контура L будет кратным 27г. Следовательно, справедливы
следующие утверждения.
1°. Индекс функции, непрерывной на замкнутом контуре и нигде не
обращающейся в нуль, есть целое число (возможно, нуль).
2°. Индекс произведения функций равен сумме индексов сомножителей. Индекс
частного равен разности индексов делимого и делителя.
Пусть теперь D(t) дифференцируема и представляет собой краевое значение
аналитической внутри или вне контура L функции. Тогда
1У= — [ d\nD(t) = — [ ^^ dt D)
2ш Jl ^ ^ 2ш Jl D(t)
оказывается равным логарифмическому вычету функции Z)(t). Из принципа
аргумента (см. п. 6.3-1) вытекают следующие свойства индекса:
3°. Если D(t) есть краевое значение функции, аналитической внутри или вне
контура, то индекс ее равен числу нулей внутри контура или соответственно числу
нулей вне контура, взятому со знаком минус.
4°. Если функция D(z) аналитична внутри контура, за исключением конечного
числа точек, где она может иметь полюсы, то индекс ее равен разности числа
нулей и числа полюсов внутри контура.
Нули и полюсы считаются при этом столько раз, какова их кратность. Заметим
еще, что индексы комплексно сопряженных функций обратны по знаку.
Пусть контур L описывается уравнением
t = ti(s) -\-it2(s), О ^ s ^ /.
Подставляя выражение комплексной координаты t в функцию D(t), получим
D(t) = D{ti(s) + it2(s)) = <e(s) + гф). E)
Будем рассматривать ^ и ?7 как декартовы координаты. Тогда
C = C(s), V = v(s)
представляет собой параметрическое уравнение некоторой кривой Г. В силу
непрерывности функции D(t) и замкнутости контура L кривая Г будет замкнутой.
Число витков кривой Г вокруг начала координат, т. е. число полных оборотов
радиуса-вектора, когда переменная s изменяется от О до /, и будет, очевидно,
индексом функции D(t). Число это иногда называют порядком кривой Г относительно
начала координат.
Если кривую Г удается построить, то число витков усматривается
непосредственно. Можно привести много примеров, когда индекс может быть определен по
13*
Страница 195

196 Методы решения сингулярных интегральных уравнений первого рода
виду кривой г. Например, если D(t) —действительная или чисто мнимая функция,
не обращающаяся в нуль, то Г есть отрезок прямой (проходимый четное число раз)
и индекс D(t) равен нулю. Если действительная часть ^(s) или мнимая часть ri(s)
не меняет знака, то индекс, очевидно, также равен нулю и т. п. Если функцию D(t)
можно представить в виде произведения или частного функций, являющихся
предельными значениями аналитических внутри или вне контура функций, то индекс
вычисляется на основании свойств 2°, 3° и 4°.
В общем случае вычисление индекса может быть произведено по формуле C).
Полагая в ней на основании формулы E)
dargD(t) = darctg^
и Предполагая ^ и г/ дифференцируемыми, получим
2^7г ^2 + ^2 2^ Л ^4s)^v4s) ' ^^
Пример. Вычислить индекс D(t) = f^ по любому контуру L, окружающему начало
координат.
1-й способ. Функция f^ есть краевое значение функции z^, имеющей один нуль
порядка п внутри контура. Следовательно,
iy = lndr =п.
2-й способ. Если аргумент t есть (/?, то аргумент t^ равен п^. Когда точка t, обойдя
контур L, возвращается к начальному значению, ^р получает приращение 27г. Следовательно,
Indt^ =п.
Индекс может быть определен и при помощи численных методов. В силу
целочисленности значений индекса приближенное его значение, найденное с
погрешностью, меньшей ^, и округленное до ближайшего целого числа, даст
точное значение.
6.3-4. Постановка задачи Римана
Даны простой гладкий замкнутый контур L, делящий плоскость
комплексного переменного на внутреннюю область П^ и внешнюю П~, и две функции
точек контура D(t) и H(t), удовлетворяющие условию Гёльдера (см. п. 6.2-2),
причем D(t) не обращается в нуль.
Задача Римана. Найти две функции (мож:но говорить об одной кусочно
аналитической функции): Ф^(^) — аналитическую в области Q~^, и Ф~ (z) —
аналитическую в области Q~, включая z = оо, удовлетворяющие на
контуре L линейному соотношению
Ф+(t) = D(t)Ф~(t) (однородная задача) G)
ф+(t) = 0(г)Ф (t) + H(t) (неоднородная задача). (8)
Функцию D(t) будем называть коэффициентом задачи Римана, а
функцию H(t) — ее свободным членом.
Рассмотрим предварительно задачу Римана частного вида, которую называют
задачей о скачке. Пусть на замкнутом контуре L дана функция (p(t),
удовлетворяющая условию Гёльдера. Требуется найти кусочно аналитическую функцию Ф(^)
Страница 196

6.3. краевая задача Римана 197
(Ф(^) = ф+(^) при Z е П+, Ф(^) = Ф~(^) при Z ^ Q ), исчезающую на
бесконечности и испытывающую при переходе через контур L скачок (/?(t), т. е.
удовлетворяющую условию
Функция
Ф(^) = -^ / ^^^ dr + const. (9)
на основании формул Сохоцкого-Племеля (см. п. 6.2-5) дает единственное
решение этой задачи.
Таким образом, заданную на замкнутом контуре произвольную функцию v^(t),
удовлетворяющую условию Гёльдера, можно единственным образом представить
в виде разности функций Ф^(^) и Ф~(^), являющихся краевыми значениями
аналитических функций Ф^(^)иФ~(^), при дополнительном условии Ф~ (оо) = 0.
Если отбросить дополнительное условие Ф~ (ос) = О, то решение задачи будет
даваться формулой
_ 1 ( ^(г)
"^TTi Jl r-z
Будем искать частное решение однородной задачи G) в классе функций, не
обращающихся на контуре в нуль. Пусть Л^+, Л^_ —число нулей искомых функций
соответственно в областях П^, П~. Взяв индекс обеих частей равенства G), на
основании его свойств 2° и 3° получим
N++N-= IndD(t) = zy. A0)
Индекс и коэффициента D{t) будем называть индексом задачи Римана.
Пусть v = 0. При этом условии \n.D{t) будет однозначной функцией. Пз A0)
следует Л^+ = Л^_ = О, т. е. решение не имеет нулей во всей плоскости. Функции
1пФ (^) будут поэтому аналитическими в своих областях и, следовательно,
однозначными вместе со своими краевыми значениями In Ф (t).
Логарифмируя краевое условие G), получим
lnФ+(t)-lnФ~(t) = \nD{t). A1)
Для \n.D{t) можно выбрать любую ветвь, поскольку окончательный результат не
зависит от ее выбора. Таким образом, необходимо найти кусочно аналитическую
функцию 1пФ(^) по заданному на L скачку. Решение этой задачи при
дополнительном условии 1пФ~(оо) = О дается формулой
1пФ(г) = ^ /i^i^llldr. A2)
Обозначим для краткости
Решениями краевой задачи G), удовлетворяющими условию Ф~(оо) = 1,
будут, как это непосредственно вытекает из формул Сохоцкого-Племеля, функции
ф+(^) = е^^^"^ и ф-(^) = е^"^"\ A4)
Если отбросить дополнительное условие Ф~ (ос) = 1, то в формуле A2) нужно
добавить произвольное постоянное слагаемое и решение задачи будет иметь вид
Ф+(^) = Се^^^"\ ф-(^) = Се^"^"\ A5)
Страница 197

198 Методы решения сингулярных интегральных уравнений первого рода
где С — произвольная постоянная. Так как С~(оо) = 0, тоС представляет собой
значение Ф~(^) на бесконечности.
Таким образом, в случае zy = О и при произвольном Ф~(оо) ф О решение
содержит одну произвольную постоянную, следовательно, имеется одно линейно
независимое решение. Если Ф~(оо) = О, то С = О и задача имеет только
тривиальное решение — тождественный нуль, что естественно в силу Л^- = 0.
Отсюда можно получить важное следствие. Заданную на контуре L
произвольную функцию D{t) фО, удовлетворяющую условию Гёльдера и имеющую индекс
нуль, можно представить в виде отношения функций Ф^(^) и Ф~(t), являющихся
краевыми значениями функций, аналитических в областях П^, П~ и не имеющих
в этих областях нулей. Функции эти определяются с точностью до произвольного
постоянного множителя и даются формулами A5).
Переходя теперь к общему случаю, будем искать кусочно аналитическую
функцию, удовлетворяющую однородному краевому условию G) и имеющую
нулевой порядок во всей плоскости, кроме одной бесконечно удаленной точки,
где ее порядок равен индексу задачи.
Канонической функцией (однородной задачи Римана) X{z) назовем функцию,
удовлетворяющую краевому условию G) и кусочно аналитическую всюду в
плоскости, за исключением бесконечно удаленной точки, где порядок ее равен индексу
задачи.
Эту функцию можно построить приведением к случаю нулевого индекса.
Действительно, запишем краевое условие G) в виде
Ф+(t) = t-"D(t)t"ф-(t).
Представляя имеющую нулевой индекс функцию t~^D(t) как отпошение краевых
значений аналитических функций
получим выражение для канонической функции:
X^(z) = е^^^'\ X-(z) = z-''e^~^'\ A7)
Пз X~^(t) = D(t)X~ (t) следует, что коэффициент задачи Римана может быть
представлен в виде отношения канонических функций:
Dit) = 1^. A8)
Представление A8) часто называют факторизацией.
При zy > О каноническая функция, имея па бесконечности нуль порядка и,
является одним из частных решений краевой задачи G). При 1у < О каноническая
функция имеет на бесконечности полюс порядка |zy| и уже не является решением,
но она и в этом случае используется в качестве вспомогательной функции при
решении неоднородной задачи.
6.3-5. Решение однородной задачи
Пусть 1У = Ind D(t) есть любое целое число. Представляя D(t) по формуле A8),
приведем краевое условие G) к виду
Ф+(^) _ ф-(^)
X+(t) X-(t)
Страница 198

6.3. краевая задача Римана 199
В левой части последнего равенства стоит краевое значение функции,
аналитической в П^, а в правой — краевое значение функции, имеющей па бесконечности
порядок не ниже —ly. По принципу непрерывности (см. п. 6.3-1), функции в
левой и правой частях являются аналитическим нродолжением друг друга па всю
плоскость, за исключением разве что бесконечно удаленной точки, где в случае
и > О возможен полюс порядка не выше и. Отсюда, при zy > О по обобщенной
теореме Лиувилля (см. п. 6.3-1) эта единая аналитическая функция является
многочленом степени и с произвольными коэффициептами. Если и < О, то вновь по
обобщенной теореме Лиувилля (п. 6.3-1), функция есть постоянная. Но так как на
бесконечности она должна обратиться в нуль, то отсюда следует, что она есть
тождественный нуль. Следовательно, получаем, что при zy < О однородная задача имеет
только тривиальное решение — тождественный нуль. Будем называть
неразрешимыми задачи, не имеющие других решений, кроме тривиального. Таким образом,
однородная задача G) при отрицательном индексе неразрешима.
При zy > О, обозначая многочлен степени р с произвольными коэффициептами
через Pv{z), получим решение в виде
^{z) = P,{z)X{z),
ИЛИ
ф+(^) = Р,(^)е^^^"\ ф-(^) = ^-"Р.(^)е^"^"\ A9)
где G{z) определяется формулой A6).
Птак, если индекс р краевой задачи Римана неотрицателен, то однородная
задача G) имеет v -\-1 линейно независимых решений
Ф+(г) = ^^«^W^ Ф^-(г) = /-'е°"М (fc = 0,l,...,^). B0)
Общее решение содержит zy +1 произвольных постоянных и определяется
формулой A9). При отрицательном индексе задача G) неразрешима.
Многочлен Pv{z) имеет в комплексной плоскости точно v нулей. Пз
формул A9) следует, что число всех пулей решения однородной краевой задачи Римапа
точно равно индексу v. В зависимости от подбора коэффициептов многочлена эти
нули могут попасть в любую из областей П , а также и на контур. Обозначая, как
и ранее, N± число нулей решения в областях П^, а Л^о число нулей на
контуре L, получим, что в общем случае (без ограничения отсутствия нулей на контуре)
формула A0) примет вид
ЛГ+ + ЛГ_ + ЛГо = и. B1)
6.3-6. Решение неоднородной задачи
Заменяя коэффициепт D{t) краевого условия (8) отпошением краевых
значений канонической функции по формуле A8), приведем (8) к виду
X+{t) X-(t) X^(t) ' ^ ^
функция H{t)/X^{t) удовлетворяет условию Гёльдера. Заменим ее разностью
краевых значений аналитических функций (см. задачу о скачке из п. 6.3-4):
где
^^^^ 2^гУ^ Х+(г) r-z- ^^^>
Страница 199

200 Методы решения сингулярных интегральных уравнений первого рода
Тогда краевое условие B2) можно будет записать в виде
X+{t) ^ ' X-(t)
Заметим, что при zy ^ О функция Ф~ (z)/X~ (z) будет иметь на бесконечности
полюс, а при и < О — нуль порядка \iy\.
Рассуждая совершенно так же, как это делалось при решении однородной
задачи, получим следующие результаты.
Пусть г^ > О, тогда
X+it) ' ' Х-(€)
Отсюда имеем решение
Ф(^) = X{z)\^{z) + P.{z)\ B4)
причем X{z^ и Ф(^) выражаются формулами A7) и B3), а Pv{z) —многочлен
степени v с произвольными коэффициентами.
Легко видеть, что формула B4) дает общее решение неоднородной задачи,
так как оно содержит в качестве слагаемого общее решение однородной задачи
X{z)Pr,{z).
Пусть zy < 0. В этом случае Ф {z)lX {z) равно нулю на бесконечности и
X+(t) ^^ X-(t) ^^ ^'
откуда
^{z) = X{z)^{z). B5)
В выражении функции Ф~(^) первый множитель на основании формулы A7)
имеет на бесконечности полюс порядка — z^, а второй, как интеграл типа Коши B3),
имеет на бесконечности в общем случае нуль первого порядка. Следовательно,
Ф~(^) имеет на бесконечности полюс порядка не выше чем —v — \. Таким
образом, если z^ < — 1, неоднородная задача, вообще говоря, неразрешима. Она
будет разрешима лишь тогда, когда свободный член удовлетворяет некоторым
дополнительным условиям. Для получения их разложим в ряд интеграл типа
Коши B3) в окрестности бесконечно удаленной точки:
Ф (z) = ^c,z , где cfc = -—у ^^^^г dr.
Для аналитичности Ф~(^) в бесконечно удаленной точке нужно, чтобы
первые —1У — 1 коэффициентов разложения Ф~(^) обратились в нуль. Отсюда
получаем, что для разрешимости неоднородной задачи в случае отрицательного
индекса (jy < —1) необходимо и достаточно, чтобы удовлетворялись следующие
—и — 1 условий:
-^^т^-' dT = 0, к = 1,2,...,-и-1. B6)
Птак, в случае z^ > О неоднородная задача Римана разрешима при любом
свободном члене и ее общее решение дается формулой
/.
Страница 200

6.3. краевая задача Римана 201
где каноническая функция X{z) определяется из A7), а Pv{z) —полином
степени zy с произвольными комплексными коэффициептами. Если zy = — 1, то пеодно-
родная задача также разрешима и имеет единственное решение.
В случае zy < — 1 пеоднородная задача, вообще говоря, неразрешима. Для того
чтобы она была разрешима, необходимо и достаточно, чтобы свободный член
задачи удовлетворял — zy — 1 условиям B6). При выполнении последних едипственное
решение задачи дается формулой B7), где нужно положить Pv{z) = 0.
Важные примепения имеет решение с донолнительпым требованием, чтобы
оно обращалось в нуль в бесконечно удаленной точке. В этом случае вместо
многочлена степени р нужно взять многочлен степени zy — 1. Для разрешимости
задачи в случае отрицательного индекса придется потребовать обращения в нуль
также и коэффициепта с_гу.
Следовательно, при условии Ф~ (оо) = О решение будет задаваться при zy ^ О
формулой
Ф(г)=Х(г)[Ф(г) + Р._1(г)], B8)
где при zy = О нужно положить Pjy-i(^) = 0.
Если zy < О, то решение по-прежнему будет выражаться формулой B8), где
P^_i[z) = О, при соблюдении —р условий разрешимости:
^^^^ T^-^dT = 0, к = 1,2,...,-и. B9)
В этом случае утверждение о разрешимости неоднородной задачи принимает
более симметричный вид. При zy > О общее решение неоднородной задачи
линейно зависит от р произвольных постоянных. При zy < О число условий
разрешимости равно —р. Заметим, что здесь при zy = О неоднородная задача
безусловно разрешима и притом единственным образом.
На основании изложенного решение краевой задачи Римана сводится в
основном к двум следующим операциям:
1°. Представление произвольной функции, заданной на контуре, в виде разности
краевых значений функций, аналитических в областях П^ и П~ (задача о скачке).
2°. Представление неисчезающей функции в виде отпошения краевых значений
аналитических функций (факторизация).
При этом вторая операция может быть сведена к первой путем
логарифмирования. Некоторые осложнения при ненулевом индексе вносит только
неоднозначность логарифма. Первая операция для произвольной функции равпосильпа
вычислению интеграла типа Коши. В связи с этим решение задачи по формулам
A7), B3)-B5) выражается явно (в замкнутой форме) через интегралы типа Коши.
/.
6.3-7. Задача Римана с рациональными коэффициентами
Рассмотрим краевую задачу Римана с контуром, состоящим из конечного
числа простых кривых, коэффициент D{t) которой есть рациопальная функция, не
имеющая нулей и полюсов на контуре. Заметим, что произвольная непрерывная
(а тем более удовлетворяющая условию Гёльдера) функция может быть с любой
точностью приближена рациопальными и решение задачи с рациопальными
коэффициентами может стать основой ее приближепного решения в общем случае.
Предположим, что задача Римапа имеет вид
^+{t) = ^^-{t) + H{t), C0)
Страница 201

202 Методы решения сингулярных интегральных уравнений первого рода
где многочлены p(z) и q(z) можно разложить в произведение
P{z) =p+{z)p-{z), q{z) = q^{z)q-{z), C1)
причемP-\-(z), q-\-(z) —многочлены, корни которых лежат в П+, ар- (z), q- (z) —
многочлены с корнями в П~. Из свойства 4° индекса (п. 6.3-3) легко получить, что
и = т^ — гг+, где ш+ и гг+ —числа нулей многочленов p+{z) и q+{z).
Ввиду того, что коэффициент задачи есть функция, аналитически продолжи-
мая в области П^, здесь целесообразно не пользоваться общими формулами
решения, а получить последнее непосредственно, пользуясь аналитическим
продолжением, причем роль стандартной функции типа t^, используемой для сведения
индекса к нулевому, способно играть произведепие Y\ (t~CLj)^ где ai, а2 ,..., «г^ —
любые точки области П^. Представляя краевое условие в виде
p-(t) q+(t) p-{t)
где каноническая функция определяется выражениями
ХЧ^) = Щ, Х-{г) = Щ, C2)
па основании тех же соображений, что и в п. 6.3-6, получим решение в форме
где
т/ ч 1 / ^-М H{T)dT ^-, , ^
^ ^ 27гг Jl Р_ т r-z ' ^ ^
L
Если индекс отрицательный, то нужно положить Pjy-i(^) = О и добавить
условия разрешимости
^:z!^H(T)T^-^dT = {), A; = l,2,...,-zy, C4)
L P-i^)
которые согласуются с общей формулой B9) с учетом того, что каноническая
функция имеет вид C2).
Заметим, что и в общем случае при практическом решении задачи Римана
бывает удобно коэффициент представлять в виде
где Di (t) — функция с пулевым индексом, а многочлены р± (t) и q± (t)
подбираются, исходя из вида коэффициента. При удачном подборе таких многочленов
решение может быть получено наиболее простым путем.
Пример. Рассмотрим задачу Римана
при условии, что Ф~ (оо) = о и L — произвольный гладкий замкнутый контур следующего
вида:
1°. Контур L содержит внутри себя точку z-^ = О и не содержит точек Z2 = 1, z^ = —1;
2°. Контур L содержит внутри себя точки z-^ = О, Z2 = 1 яяс содержит точки z^ = —1;
Страница 202

6.3. краевая задача Римана 203
3°. Контур L содержит внутри себя точки z^ = (), z^ = 1, z^, = —1',
4°. Контур L содержит внутри себя точки 2:2 = 1, 2:3 = —1 и не содержит точки z^ =().
Рассмотрим случаи 1°-4° по порядку. Для рещения используем метод из п. 6.3-7.
1°. В этом случае будем иметь
P+(t)=t, p_(t) = l, m+ = l,
q^{t) = 1, q_ (t) = t^ — 1, гг^ = 0, и = m_^ — n_^ = 1.
Запищем краевое условие в виде
(t^ -1)Ф+(^) -^ф-(^) = —{t^ -t2 + l)(t + l).
Отсюда
Ф(^) = / ^—^Н(т) = / dr + / — dr,
2ттг Jl Р-{ч t — z 2ш Jl t — z 2ттг Jl т — z
и, значит, в силу формул для интеграла Кощи (см. п. 6.2-1) имеем
ф+(^) = z^ -z^l, Ф~(^) = .
Z
Общее рещение задачи содержит одно произвольную постоянную. По формуле C3) находим
Z \ Z ) Z^ Z
где С — произвольная постоянная. Заменяя С на С — 1, можно рещению придать еще и
такую форму:
Ф+(.) = г + ^^, ф-(.) = -14^ + ^.
z^ — \ z^ Z
2°. Имеем
p^(t)=t, p_(t) = l, q^(t)=t-l, q_(t)=t^l, т^=гг^ = 1, и = О,
t-1 '' 4t-i)
2ш Jl T-Z 2ш Jl t-z I . _ ^.
Задача имеет единственное рещение:
Z ^CL~
Ф+(.) = ^Ф+(.) = ^(.^+ .) = ..
^ ^ P+{z) ^ ^ Z [ z{z-l)
z^\
3°. Имеем
p^(t)=t, p_(t) = l, g^(t)=t2-l, g_(t) = l, m^ = 1, n^=2, гу = -1,
^{z) = / dr + / -^^-^ — dr = {
2ш JL T — z 2ш Jl t — z
z{z - 1)
z G n~.
Страница 203

204 Методы решения сингулярных интегральных уравнений первого рода
Решение задачи сушествует лишь при выполнении условий разрешимости C4) или, в данном
случае, одного условия:
.(
Il Р-(г)
Вычисляя этот интеграл, находим
dr f dr
г - 1 Jl т
■ dr = I rdr ^ I '—r - I — = 0 + 27гг - 27гг = 0.
Условие разрешимости, таким образом, выполняется, и единственным решением задачи
будет
z^
4°. в этом случае имеем
p^(t) = 1, p_(t)=t, q^(t)=t^-l, q_(t) = l, 1^ = m^-n^ = -2<0.
Для разрешимости задачи необходимо выполнение двух условий:
/.
^-^^^ Н{т)т^-^ dT = 0, /с = 1,2.
Il Р-{г)
Вычисляя последний интеграл при /с = 1, находим
/- тЗ-т2 + 1 , /Л 1 1 1 \ , ^ . . .
Jl г(т^-т) Jl\ г т^ r-lj
Таким образом, условие разрешимости не выполнено, и поэтому задача не имеет решения.
Заметим, что если формально вычислить функцию ^{z), то она будет иметь полюс в
бесконечно удаленной точке и, следовательно, не может являться решением задачи.
6.3-8. Задача Римана для действительной оси
Пусть контур L есть действительная ось. Как и ранее, задача Римана
заключается в том, чтобы найти две ограниченные аналитические соответственно в
верхней и нижней полуплоскостях функции Ф^(^), Ф~(^) (кусочно аналитическую
функцию Ф(^)), предельные значения которых на контуре удовлетворяют
краевому условию
Ф^(х) = 0(х)Ф~(х)-\-Н(х), -ОС < ж < ОС. C5)
Заданные функции D(x) и Н(х) удовлетворяют условию Гёльдера как в
конечных точках, так и в окрестности бесконечно удаленной точки контура.
Считаем также, что D(x) ф 0.
Главное отличие от рассмотренного ранее случая конечной кривой состоит
в том, что здесь бесконечно удаленная точка и начало координат лежат на самом
контуре и потому не могут быть приняты в качестве исключительной точки, где для
канонической функции допустим ненулевой порядок. Вместо употреблявшейся в
предыдущем вспомогательной функции t, имеющей по L индекс, равный единице,
здесь будет введена обладающая тем же свойством на действительной оси дробно-
линейная функция
Аргумент этой функции
х-% {x-%f . ..
arg —— = arg . = 2 arg(x - г)
ж + г ж^ + г
Страница 204

6.3. краевая задача Римана
205
изменяется на 27г, когда х пробегает действительную ось в положительном
направлении. Таким образом.
Ind^^ = l.
X -\- 1
Если IndD(x) = zy, то функция
X -\- i
D{x)
имеет индекс, равный нулю. Ее логарифм будет на действительной оси функцией
однозначной.
Построим каноническую функцию, для которой исключительной точкой будет
точка —г:
X+{z) = e''^^'\ X-{z) =
z -\-г
где
G{z)
2vri J_^
т -\- i
D{r)
„G-(z)
dT
C6)
Пользуясь предельными значениями этой функции, преобразуем краевое
условие C5) к виду
Ф+(ж) _ ф-(ж)
+
Н{х)
Х+{х) Х-{х) Х+{х)
Далее, вводя аналитическую функцию
{{г) dr
ф(^)
Х+(г)
C7)
представим краевое условие в форме
—-^^-Ф+(ж)= \-L-y^ (х).
Х+{х) ^ ^ Х-{х) ^ ^
Заметим, что, в отличие от случая конечного контура, здесь, вообще говоря,
Ф~ (ос) ф 0. Применяя теорему об аналитическом продолжении и учитывая, что
единственной особенностью рассматриваемой функции может быть лишь полюс
в точке z = —г порядка не выше v (при v > 0), на основании обобщенной теоремы
Лиувилля (см. п. 6.3-1) будем иметь
-, ^>о,
X+{z) ' ' X-{z) ' ' {z + iY
где Pv{z) —многочлен степени не выше р с произвольными коэффициептами.
Отсюда получаем общее решение задачи
Ф(^) = X(z)
Ф(^) +
РЛ^)
при г^ > О,
C8)
C9)
(z^i)-
Ф(z)=X(z)[^(z)^C] при 1У<0,
где С — произвольная постоянная. При и < О функция X(z) имеет в точке
Z = —i полюс порядка — z^, поэтому для разрешимости задачи нужно положить
С = — Ф~(—г). При zy < — 1, кроме того, должны выполняться еще следующие
условия:
Н(х) dx
f
J —(
Х+(ж) (x^if
= 0, /с = 2,3,
D0)
Страница 205

206 Методы решения сингулярных интегральных уравнений первого рода
Таким образом, получены результаты, аналогичные тем, которые имели место в
случае конечного контура.
Действительно, при zy > О однородная и неоднородная краевые задачи Ри-
мана для полуплоскости безусловно разрешимы и решение их зависит линейно
от zy + 1 произвольных постоянных. При и < О однородная задача неразрешима.
Неоднородная задача при 1у < О разрешима однозначно, причем в случае i/ = —1
безусловно, а при и < —1 лишь при выполнении —и — 1 условий D0).
Остановимся на случае исчезающих на бесконечности решений (см. также
п. 4.3-4). Подставляя Ф^(оо) = Ф~ (оо) = О в краевое условие, получим Н(оо) = 0.
Следовательно, чтобы задача Римана имела решение, исчезающее на
бесконечности, свободный член краевого условия должен на бесконечности обращаться в
нуль. Будем считать это условие выполненным. Для получения решения в
рассматриваемом случае следует в C8) вместо Р^ (z) взять Pu-i(z), а в C9) постоянную С
приравнять нулю. Таким образом.
Ф(^) =X(z
Ф(^)+ ^^-'^'^
{z + iy
D1)
При zy ^ О в этой формуле нужно положить Pjy-i(^) = O.K условиям
разрешимости D0) добавится еще одно: Ф(—г) = О, и в результате они примут вид
«w '"-=0. t = i.2....,-.. т
f
J —(
Х+{х) {x^if
Теперь при zy > О будем иметь решение, зависящее от v произвольных
постоянных, при zy ^ О решение единственно, причем при zy < О для его
существования необходимо и достаточно выполнения —v условий.
6.3-9. Исключительные случаи задачи Римаиа
В постановке краевой задачи Римана требовалось, чтобы коэффициент D{t)
удовлетворял условию Гёльдера (что исключало возможность обращения его в
бесконечность) и нигде не обращался в нуль. Ограничения эти, как было видно
из хода решения (использование InD(t)), существенны. Пусть теперь D{t) в
отдельных точках контура обращается в нуль или бесконечность целых порядков.
Будем считать, что контур L состоит из одной замкнутой кривой.
Рассмотрим однородную задачу. Запишем краевое условие однородной задачи
Римана в виде
Ф+(*) = п'=^^ГУГД1(^)Ф"^)- D3)
Здесь а/с {к = 1, 2,..., /х) и /3j (j = 1, 2,..., х) — некоторые точки контура, гпк
и pj — целые положительные числа, Di(t) — функция, удовлетворяющая условию
Гёльдера и пе обращающаяся в нуль. Точки а к будут нулями функции D(t).
Точки Pj будем называть ее полюсами. Так как функция D(t) пеаналитическая, то
нрименение термина «полюс» не вполне законно. Будем употреблять этот термин
для краткости, понимая под этим точку, где функция (неаналитическая) обращается
в бесконечность целого порядка. Обозначим
lndDi(t) = 1У, ^pj=p^ У^тк=т.
j=i к=1
Решение будем искать в классе функций, ограпичепных на контуре.
Страница 206

6.3. краевая задача Римана 207
Пусть X{z) есть каноническая функция задачи Римана с
коэффициентом Di(t). Подставим Di(t) = X~^(t)/X~(t) в D3) и запишем краевое условие в
виде
применим к последнему равенству теорему об аналитическом продолжении и
обобщенную теорему Лиувилля (см. п. 6.3-1). Точки а^, Pj не могут быть
особыми точками единой аналитической функции, так как это противоречило бы
предположению об ограниченности Ф^(^) или Ф~(t). Следовательно, единственной
возможной особенностью является бесконечно удаленная точка. Порядок на бес-
конечности Х~{z^ есть zy, а порядок П (^ ~ 0зУ^ равен —р. Отсюда порядок на
бесконечности функции Ф~ (^)/ \Х~ (^) П (^ ~ ft Y^ ] ^^ть — zy + р. При zy — р > О,
согласно обобщенной теореме Лиувилля, имеем
Ф+(^) _ ф-(^)
:Р.-р(^).
Поэтому
fc=l i=l
D5)
Если zy — р < О, то нужно положить Pu-p(z) = о и, следовательно, задача не
имеет решений.
Назовем краевую задачу с коэффициептами Di (t) приведенной задачей. Пп-
декс приведенной задачи 1у назовем вместе с тем и индексом исходной задачи.
Формулы D5) показывают, что степень присутствующего в них многочлена на р
единиц меньше индекса задачи 1у.
Отсюда следует, что число решений задачи D3) в классе функций,
ограниченных на контуре, не изменяется от наличия нулей у коэффициента задачи и
уменьшается на суммарный порядок всех полюсов. В частности, если индекс
оказывается меньше суммарного порядка полюсов, то задача неразрешима. Если
задача разрешима, то ее решение дается формулами D5), в которых каноническая
функция приведенной задачи X(z) находится по формулам A6) и A7), причем
в них D(t) нужно заменить на Di(t). Если наложено дополнительное условие
Ф~(оо) = 0, то число решений уменьшается на единицу и многочлен в D5) нужно
взять степени и — р — 1.
Расширим теперь класс решений, допуская, что одна из искомых функций
Ф^(^) или Ф~(^) может обращаться па контуре в некоторых точках в
бесконечность целого порядка, в то время как другая в этих точках остается ограниченной.
Легко усмотреть, что такое допущение пе повлечет никаких измепений в
неисключительных точках. Здесь ограничепность одной из функций автоматически влечет
за собой ограниченность другой. Иначе обстоит дело в исключительных точках.
Запишем краевое условие D3) в виде
X^(t) X-(t) ' ^ ^
Рассуждая аналогично предыдущему и учитывая, что правая часть имеет на
Страница 207

208 Методы решения сингулярных интегральных уравнений первого рода
бесконечности полюс порядка ly -\- т, получим общее решение в виде
^+(z) = X+(z)l[{z-ak)-"'''P,+m(z), ф-{z)=X-(z)l[{z-pj)-''^P,+^(z).
к=1 j=i
D7)
Формулы D7) показывают, что в классе решений с допустимой полярной
особенностью у одной из функций число решений по сравнению с классом ограниченных
на контуре функций увеличивается (при zy > 0) на суммарный порядок всех нулей
и полюсов коэффициента.
Рассмотрим теперь неоднородную задачу. Запишем краевое условие в форме
ф+(*) = ^'С1^^-У)Гд1^)ф"(^) + H(t)-
D8)
Легко видеть, что краевое условие не может быть удовлетворено конечными Ф^(^)
и Ф~(^), если допустить, что H(t) имеет полюсы в точках, отличных от Pj, или
если в последних точках порядки полюсов H(t) превышают pj. Исходя из этого,
примем как условие, что H(t) может иметь полюсы только в точках Pj и порядки
их не превышают pj. Для проведения дальнейших рассуждений необходимо также
потребовать, чтобы функции Di(t) и П (t — PjY^ H(t) в исключительных точках
были дифференцируемы достаточное число раз.
Заменим, как и в однородной задаче, Di (t) отношением канонических
функций X~^(t)/X~ (t) и запишем краевое условие D8) в виде
j=i ^ ^ к=1 ^ ^ j=i ^ ^
Заменив функцию, представленную вторым слагаемым в правой части D9),
разностью краевых значений аналитических функций
H{t)
П(* -/?i)'':|т^ = *^w - *"(*)'
где
2ш Jj^ ^J^ Х+{т) т- Z
приведем краевое условие к виду
применяя теорему об аналитическом продолжении и обобщенную теорему Ли-
увилля, получим
Последние формулы дают решения, которые, вообще говоря, обращаются в
бесконечность в точках а/с, Рк- Для того чтобы решение было ограниченным,
необходимо, чтобы функция Ф^(^) + Piy-^rn(z) имела нули порядков pj в точках Pj, а
Страница 208

6.3. краевая задача Римана 209
функция ^~{z) -\- Pi^^rniz) — нули порядков TTifc в точках а/с. Эти требования
накладывают т-\-р условий на коэффициенты многочлена Pv+m {z). Если
коэффициенты многочлена Pv+m {z) подобрать в соответствии с наложенными условиями,
то формулы E1) дадут решение неоднородной задачи D8) в классе ограниченных
функций.
Рассмотрим другой, более удобный способ решения, основанный на
построении специального частного решения.
Канонической функцией неоднородной задачи Y{z) называется кусочно
аналитическая функция, удовлетворяющая краевому условию D8), имеющая всюду в
конечной части плоскости (включая и точки а^, Pj) нулевой порядок и
обладающая на бесконечности наинизшим возможным порядком.
При построении канонической функции будем исходить из решения, даваемого
формулами E1). Построим многочлен Un(z) так, чтобы он удовлетворял
следующим условиям:
uL'\pj) = ^^^'\pj), г = 0,1,... ,р,- - 1, j = 1, 2,..., X,
и^\ак) = ^~^^\ак), 1 = 0,1,...,тк-1, /с = 1, 2,... ,/х,
где '^~^^'^\Pj), Ф~*^ (o^fc) —значения производных г-го и /-го порядков в
соответствующих точках. Таким образом, Un{z) есть интерполяциопный многочлен
Эрмита для функции
y^(z) = [ ^Ч^) в точках f3j,
^ ^ \^ {z) в точках ак
с узлами иптерполяции f3j и ак кратпостей соответственно pj и тпк (см. п. 6.3-2).
Такой многочлен определяется единственным образом и его степень п не выше
т-\-р — 1.
Каноническая функция пеоднородной задачи выражается через иптерполяци-
оппый многочлен следующим образом:
Для ностроения общего решения неоднородной задачи D8) воспользуемся тем,
что это общее решение складывается из некоторого частного решения
неоднородной задачи и общего решения однородной. Используя формулы D7) и E2),
получим
ф+(^) = Y^{z) + X^{z) \{{z- akr'P.-p(z),
':' E3)
ф-{z) = Y-{z)^X-{z)l[{z-PJrP.-,{z).
В случае, если ly — р <0, нужно положить Pu-p(z) = 0. Пользуясь формулой E2),
нетрудно подсчитать, что порядок У~ (z) на бесконечности равен и — р-\-1. Если
1У < р — 1, то Y~ (z) имеет в бесконечно удаленной точке полюс и каноническая
функция перестает быть решением неоднородной задачи.
Однако, подчиняя свободный член H{t) р — р — 1 условиям, можно добиться
повышения порядка на бесконечности функции Y{z) ndi р — v — 1 единиц и
тем самым вновь сделать каноническую функцию Y{z) решением неоднородной
задачи. Для этого, очевидно, необходимо и достаточно, чтобы в разложении
функции ^{z)—lAn{z)B окрестности бесконечно удаленной точки первыер — z^ — 1
коэффициентов обращались в нуль. Это и даст р — v — 1 условий разрешимости
14 А. В. Манж:иров, А. Д. Полянин
Страница 209

210 Методы решения сингулярных интегральных уравнений первого рода
задачи в этом случае. Выясним характер этих условий. Разложение Ф(^) — Un(z)
можно представить в виде
'^(z)-Vln(z) = -anz'^-an-iz'^~ ao-\-a-iz~ -\-a-2z~ -\ \-a-kZ~ Н ,
где ао, «1, ..., an —коэффициенты многочлена Un{z), а а-к —коэффициенты
разложения функции Ф(^), вычисляемые по формуле
Условия разрешимости будут иметь вид
dn = CLn-l = • • • = an-p+v+2 = 0.
Если на решение наложено дополнительное условие Ф~(оо) = О, то при
jy — р > О в формулах E3) нужно взять многочлен Pjy-p-i(^), а при 1у — р < О
понадобится удовлетворить р — и условиям.
6.3-10. Задача Римана для многосвязной области
Пусть L = Lo-\-Li-\ hLm — совокупность ш +1 непересекающихся
контуров, причем контур Lq содержит внутри себя все остальные. Пусть Q~^ — (ттг Ч-1)-
связная область, лежащая внутри контура Lq и вне контуров Li, L2,..., Lm, а П~
дополнение Q^ -\-L до полной плоскости. Для определенности будем считать
начало координат расположенным в области П^. Положительным обходом контура L
считается тот, который оставляет область Q~^ слева, т. е. контур Lq нужно обходить
против часовой стрелки, а контуры Li, L2, ..., Lm — по часовой.
Прежде всего укажем, что задача о скачке
Ф+(t)-Ф~(t) = H{t)
решается при помощи той же формулы
27Ti Jl T-Z '
что и в случае односвязной области. Это вытекает из формул Сохоцкого-Племеля,
которые имеют для мпогосвязной области тот же вид, что и для односвязной.
Задача Римапа (однородная и неоднородная) формулируется совершенно так
же, как для односвязной области.
Обозначим Uk = ^[argZ)(t)]b/, (все контуры обходятся в положительном
направлении). Индексом задачи назовем величину
т
y = Y,i^k. E4)
fc=0
Если Рк (/с = 1, 2,..., ттг) для внутренних контуров равны нулю, то решение задачи
имеет совершенно тот же вид, что и для односвязной области.
Для приведения общего случая к простейшему вводим функцию
т
к=1
где Zk —точки, лежащие внутри контуров Lk (к = 1, 2,... ,т). Учитывая, что
[arg(t - Zk)]L. = О, если к ф j.n [arg(t - zj)]l. = -27г, получим
1
^Ylit-^kY
— [^vg(t-ZjY^]^^ =-iyj, J = 1,2,
Страница 210

6.3. краевая задача Римана
211
Откуда
^xg(D(t)l[(t-Zkr
:0, j = 1,2,...,т.
Вычислим изменение аргумента функции D(t) Yl (t — ZkY'^ но контуру Lq:
k=i
1
~2^
^xglD{t)l[{t-Zkr
^ k=i
k=l k=l
Так как начало координат лежит в области П^, то
[argt]L;, =0, /с = 1,2,...,ш, [argt]Lo = 27г.
Поэтому
^rg[t-''l[(t-Zkr'D(t)
= 0.
1°. Однородная задача. Запишем краевое условие
Ф+(t) = D(t)Ф~(t)
в виде
Ф+it) =
nT=iit-^kr
г'''[[{г-гкУ''0{г))ф-{г)
E5)
E6)
E7)
функцию t~^ Yl (t — Zky^D{t), имеющую па каждом из контуров Lk
к=1
(к = 1,2,... ,т) индекс нуль, можно представить в виде отношения
t~''l[(t-^kr'D(t) =
aG-(t) '
где
Каноническая функция задачи дается формулами
E8)
E9)
-.gG+M^ Х-(г) = г-^е«"(^\
F0)
X+iz) = '[[iz-z,)
к = 1
Теперь краевое условие E7) может быть записано в форме
Ф+(^) _ ф-(^)
X+{t) ~ X-{t)'
Применяя теорему об аналитическом продолжении и обобщенную теорему
Лиувилля (п. 6.3-1), получим
к=1
'^e^^^'^Pr^iz), ф-(^) = ^-"е^ ^"^P.{z). F1)
14*
Страница 211

212
Методы решения сингулярных интегральных уравнений первого рода
Решение, как видим, отличается от полученного ранее решения задачи для од-
носвязной области лишь наличием у функции Ф^(^) множителя YI (^
Zk)
при дополнительном условии Ф~(оо) = О в формулах F1) следует брать
многочлен Pu-l(z).
Воспользовавшись формулами Сохоцкого-Племеля, будем иметь
G^(t) = ±^\n[t-''U(t)D(t)]^G(t),
где G(t) есть главное значение интеграла E9) и
m
Il{t)=l[{t-Zkr.
к=1
Переходя теперь в формулах F0) к пределу при z ^ t, получим
1
X^(t)
Dji) Git)
X-{t):
G{t)
F2)
t^n(t) ' ' ^t^U(t)D(t)
Знак корня определяется выбором ветви функции \n[t~^Il(t)D(t)], которая может
быть взята произвольно.
2°. Неоднородная задача. Рассуждая совершенно аналогично тому, как это
делалось ранее, представим краевое условие
Ф+(t) = D(t)ф-(t)+Я(t)
в виде
F3)
Ф+(«)
Ф+(*) =
Ф-(«)
X+{t) ^ ' X-(i)
где ^{z) определяется следующей формулой:
Ф(,) = J- f -ElL _
^ ' 2ш J^ Х+{т) т
*-(i),
dT
Отсюда получаем общее решение
Ф(г)=Х(г)[Ф(г) + Р4г)]
F4)
F5)
Ф(г)=Х(г)[Ф(г) + Р._1(г)],
если на решение наложено условие Ф~ (ос) = 0.
При zy < О неоднородная задача разрешима тогда и только тогда, когда
выполнены условия
: о, {66)
L
"^t'-ut
где к принимает значения от 1 до —z^ — 1, если ищутся решения, ограниченные на
бесконечности, и от 1 до —z^, если считать, что Ф~(оо) = 0.
При выполнении условий F6) решение можно получить из формул F4)
или F5), полагая в них Pu(z) = О или Piy-i(z) = 0.
Если отсутствует внешний контур Lq и область Q~^ представляет собой
плоскость с дырами, то главное отличие от предыдущего случая состоит в том,
что теперь нулевой индекс относительно всех контуров Lk (к = 1,2,...,?7г)
т
имеет функция YI (t — Zk)^'^D(t), в которую не входит множитель t~^. Поэтому
fc=i
для получения решения задачи достаточно повторить все прежние рассуждения,
опустив этот множитель.
Страница 212

6.3. краевая задача Римана 213
6.3-11. Случаи разрывных коэффициентов и разомкнутых контуров
Пусть функции D{t), H(t) в краевом условии задачи Римана F3) всюду на L
удовлетворяют условию Гёльдера, за исключением точек ti, t2, ..., tm, где они
имеют разрывы 1-го рода, причем L — замкнутая кривая. Никакое из предельных
значений не обращается в нуль и краевое условие выполняется всюду, кроме точек
разрыва, где оно теряет смысл.
Решение задачи разыскивается в классе функций, интегрируемых на контуре.
Отсюда вытекает, что решение непрерывно в смысле Гёльдера всюду, кроме разве
что точек tfc. В этих точках имеются разные возможности.
1°. Можно требовать ограниченности во всех точках разрыва, отыскивая решение
всюду ограниченное.
2°. Можно требовать, чтобы решение было ограниченным в некоторых точках
разрыва, допуская интегрируемую бесконечность в остальных точках разрыва.
3°. Можно допустить обращение решения в бесконечность интегрируемого
порядка во всех точках, где это допускается условиями задачи.
Первый класс решений является наиболее узким, второй класс является более
широким, и самым широким является последний класс. Число решений зависит от
того класса, в каком оно отыскивается, и может оказаться, что задача, разрешимая
в более широком классе, будет неразрешимой в более узком.
Несколько слов о задаче Римана для разомкнутых контуров. Пусть контур L
состоит из совокупности т простых гладких непересекающихся кривых Li,
L2 ..., Lm, концы которых ttfc И 6fc (положительный обход производится от а к
к 6fc), и пусть D(t), H(t) —заданные на L функции, удовлетворяющие условию
Гёльдера, причем всюду D(t) ф 0.
Требуется определить функцию Ф(^), аналитическую на всей плоскости, кроме
точек контура L, граничные значения Ф^(t), Ф~(^) которой при приближении
к L слева и справа суть интегрируемые функции, удовлетворяющие краевому
условию F3).
Задача Римана для разомкнутого контура, как видно из постановки, принци-
пиально отличается от задачи для замкнутого контура тем, что вся плоскость с
разрезом по кривой L составляет одну область и приходится отыскивать пе две
самостоятельные аналитические функции Ф^(^) и Ф~(^), а одну аналитическую
функцию Ф(^), для которой контур L является линией скачков.
Сформулированную задачу можно свести к задаче для замкнутого контура с разрывными
коэффициентами.
Более подробно о краевой задаче Римана с разрывными коэффициептами
и разомкнутыми контурами можно прочитать в цитируемой в конце раздела
литературе.
6.3-12. Краевая задача Гильберта
Пусть дан простой гладкий замкнутый контур L и действительные функции
дуги S контура a(s), 6(s), c(s), удовлетворяющие условию Гёльдера.
Краевой задачей Гильберта будем называть следующую задачу. Найти
аналитическую в области П^ и непрерывную на контуре функцию
f{z) =и(х,у) -\-iv(x,y),
предельные значения действительной и мнимой частей которой удовлетворяют на
контуре линейному соотношению
a(s)u(s) + b(s)v(s) = c(s). F7)
Страница 213

214 Методы решения сингулярных интегральных уравнений первого рода
При c(s) = 0 будем иметь однородную задачу, а при c(s), отличной от нуля, —
неоднородную. Краевая задача Гильберта может быть сведена к краевой задаче
Римана. Способы такого сведения можно найти в цитируемой ниже литературе.
(•) Литература: Н. И. Мусхелишвили A968), Ф. Д. Гахов A977).
6.4. Сингулярные интегральные уравнения первого рода
6.4-1. Простейшее уравнение с ядром Кошн
Пусть дано сингулярное интегральное уравнение первого рода
±[Щаг = т, A)
где L — замкнутый контур. Построим его решение. Заменим в обеих частях
1 dr^
переменную t на ri, умножим на ^, проинтегрируем по контуру L и
7гг т-^ — t
переставим по формуле Пуанкаре-Бертрана (см. п. 6.2-6) порядок интегрирования.
Тогда
B)
Вычислим второй интеграл в правой части B):
Таким образом,
^(t) = — I ^dr. C)
ш Jl T-t
Последняя формула дает решение сингулярного интегрального уравнения первого
рода A) для замкнутого контура L.
Сингулярное интегральное уравнение A) для произвольного контура L
является частным случаем характеристического интегрального уравнения с ядром
Кошн (см. ПН. 7.1-1 и 7.2-1).
6.4-2. Уравнение с ядром Кошн на действительной оси
Рассмотрим сингулярное интегральное уравнение первого рода на
действительной оси
— / ^f^dt = f{x), -оо<ж<оо. D)
^^ J-00 ^-^
уравнение D) является частным случаем характеристического интегрального
уравнения на действительной оси (см. п. 7.2-4) и в классе исчезающих на бесконечности
функций имеет решение
1 f°° fit)
(^(х) = — / ''^ ' dt, -ОС < ж < ОС. E)
^^ J-00 ^-Х
Обозначая f{x) = F(x)i~^ запишем соотношения D) и E) в форме
^ ^ dt, -ОС < ж < ОС. F)
7Г J_^ t-X 7Т J_^
t — X
Пару формул F) называют преобразованием Гильберта (см. п. 1.6-4).
Страница 214

6.4. Сингулярные интегральные уравнения первого рода 215
6.4-3. Уравнение первого рода на конечном отрезке
Рассмотрим сингулярное интегральное уравнение первого рода на конечном
отрезке
^ Ja i-^
^ Ъ- G)
Его решения можно построить, опираясь на теорию краевой задачи Римана
для разомкнутого контура (см. п. 6.3-11). Приведем окончательные результаты.
1°. Решение, не ограниченное на обоих концах:
где С — произвольная постоянная, причем
/ cp{t)dt = C. (9)
J а
2°. Решение, ограниченное на конце а и не ограниченное на конце Ь:
Ф) = -1ЯЕ1ГД^Ж,г. A0)
тгу b — X J^ V i — ci t — X
3°. Решение, ограниченное на обоих концах:
^ J а ^{t-0){b-t) t-X
При условии
f{t)dt
A1)
/
J а
, = 0. A2)
la ^(t-a){b-t)
Можно построить и решения, имеющие точку сингулярности s внутри
отрезка [а, 6]. Они имеют следующий вид.
4°. Сингулярное решение, не ограниченное на обоих концах:
,,(х) = -1^=4==(Г v^l^HMEII/(,)di + G, + ^, A3)
7г л^{х-а){Ъ-х) \Ja t-X x-sj
где Ci и С2 —произвольные постоянные.
5°. Сингулярное решение, ограниченное на одном конце:
гЬ
ф) = -1^(х-а)(Ь-х)( f\l^^dt^
^ \Ja V t-d t-X
С
X — s
где С — произвольная постоянная.
6°. Сингулярное решение, ограниченное на обоих концах:
^(х) = --^(х-а){Ь-х){ Г—=Щ==^+ ^
A4)
0 = --ч/(ж-а)F-ж)(/ -=М
^ /•! f(t) dt
У_1 V(t-a)F-t)
)(b-t) t-X
f(t) dt
A5)
Страница 215

216
Методы решения сингулярных интегральных уравнений первого рода
6.4-4. Общее уравнение первого рода с ядром Кошн
Рассмотрим общее уравнения первого рода с ядром Коши
A6)
где интеграл, понимаемый в смысле главного значения, берется по замкнутому
или разомкнутому контуру L. Заданные на L функции f{t) и M(t,r) считаются,
как обычно, удовлетворяющими условию Гёльдера, причем последняя по обеим
переменным.
Проведя преобразование
M{t,T)
M(t,r) - M(t,t) M(t,t)
и обозначив
M{t,t) = b{t),
запишем уравнение A6) в виде
b(t) f ф)
1 M{t,T)- M{t,t)
Tvi т — t
K{t,r)
A7)
1 f ^dr+ f K(t,rMr)dr = f(t).
г Jl ^-i Jl
A8)
Из формул A7) следует, что функция b(t) удовлетворяет условию Гёльдера па всем
контуре L, а K(t, т) всюду, кроме точек г = t, где для нее справедлива оценка
\K(t,r)\ ^ , ^ ,, , А = const < ОС, 0^Л<1.
Общее сингулярное иптегральное уравнение первого рода с ядром Коши часто
записывают в форме A8).
Общее сингулярное интегральное уравнение первого рода является частным
случаем полного сингулярного интегрального уравнения, теория которого
рассматривается в главе 7. Обычно оно не решается в замкнутой форме. Однако имеется
ряд случаев, когда такое решение возможно.
Пусть функция M(t, т) в уравнении A6), удовлетворяющая условию Гёльдера
по обеим переменным на гладком замкнутом контуре L, аналитически продолжима
в область Q~^ по каждой переменной. Если M(t, t) = 1, то решение уравнения A6)
можно получить при помощи формулы Пуанкаре-Бертрана (см. п. 6.2-6). Оно
дается формулой
M{t,T)
^(t)
^г Jl
-fir) dr.
A9)
Уравнение A6) можно решить и не ограничивая функцию M(t,r) условием
M(t,t) = 1. Действительно, пусть функция M(t,r) аналитически продолжима
в П+ по каждой переменной, и пусть M(z,z) ф О для z G П+. Тогда решение
уравнения A6) имеет вид
1 1 i M(t,r) f(r)
Ф)
(t.t) II
■dr.
B0)
Ш M{t,t) Jj^ M{t,t) T-t
В разд. 6.5 дан также численный метод решения одного вида общего уравнения
первого рода, представляющий самостоятельный интерес с точки зрения его
использования для решения прикладных задач.
Замечание 1. Построенные в п. 6.4-4 решения полных сингулярных
интегральных уравнений применимы в случае, когда контур L представляет из себя
совокупность конечного числа гладких замкнутых контуров без общих точек.
Страница 216

6.4. Сингулярные интегральные уравнения первого рода 217
6.4-5. Уравнения первого рода с ядром Гильберта
1°. Рассмотрим простейшее сингулярное интегральное уравнение первого рода с
ядром Гильберта
^ ^ \tg{^^^ ^(^)d^ = f(x), О ^ X ^ 2^ B1)
27Г Jq ^\ 2
при дополнительном условии
Г27г
(р(х) dx = 0. B2)
/о
Уравнение B1) может иметь решение только при соблюдении условия
разрешимости, которое получается интегрированием обеих частей B1) по ж от нуля до 27г
и, с учетом
f
Jo
I
'\tg(^]dx = 0,
имеет вид
Л27Г
/
f(x) dx = 0. B3)
/о
Для построения решения уравнения B1) воспользуемся решением
простейшего сингулярного интегрального уравнения первого рода с ядром Коши, считая
контур L окружностью единичного радиуса с центром в начале координат (см.
п. 6.4-1). Запишем уравнение с ядром Коши и его решение в форме
^ dT = h(t), B4)
^ Jl ^-t
Mt) = -- f ^dr, B5)
которая получается подстановкой в соотношения из п. 6.4-1 функции (pi(t) вместо
(p(t) и функции fi{t)i~^ вместо /(t).
Полагая t = е*^ и г = е^^ найдем соотношение между ядрами Коши и
Гильберта:
dr 1 , / £ — ж \ ,, i 1^ ^^^ч
-TTCtg^^— Ue+-6^e B6)
r-t 2 ^\ 2 J 2
Подставляя теперь соотношение B6) в уравнение B4) и его решение B5), с учетом
замены переменных (р(х) = (pi(t) и f(x) = fi(t) получим
^ £' ctg(^i^) ^@ d^+^ fj V@ d^ = fi^), B7)
Ф) = -^/^"ctg(l^) fiOd^-^l'^fiOd^. B8)
Уравнение B1) при дополнительном условии B2) совпадает с уравнением B7),
а значит его решение дается выражением B8). Учитывая условие
разрешимости B3), на основании B8) запишем решение уравнения B1) в виде
Формулы B1) и B9) вместе с условиями B2) и B3) называются формулами
обращения Гильберта.
Страница 217

218 Методы решения сингулярных интегральных уравнений первого рода
Замечание 2. Уравнение B1) является частным случаем
характеристического сингулярного интегрального уравнения с ядром Гильберта (см. ни. 7.1-2
и 7.2-5).
2°. Рассмотрим общее сингулярное интегральное уравнение первого рода с ядром
Гильберта
-Г
З'г Jo
N(x,0ctg(^^^^@d^ = f(^)- C0)
Представим его ядро в форме
iV(x,Octg ^^ = [N(x,0 - N(x,x)] ctg ^^ + iV(x,x)ctg ^^.
Вводя обозначения
N(x,x) = -b(x), j-[N(x,0-N{x,x)]ctg^^ = K{x,0, C1)
запишем уравнение C0) в следующем виде:
Г»27Г / ^ \ /»27Г
2тт
1 ^ ^^&{^^)viOdi + jj K{x,0v@di = f{x), C1)
Из формул C1) следует, что функция Ь(х) удовлетворяет условию Гёльдера, а
ядро К(х,^) удовлетворяет условию Гёльдера, всюду, кроме, может быть, точек
X = ^, где для него справедлива оценка
1^(^:01 ^ 1 пг: ^ = const < (X), о ^ л < 1.
Общее сингулярное интегральное уравнение первого рода с ядром Гильберта часто
записывают в форме C2). Оно является частным случаем полного сингулярного
интегрального уравнения с ядром Гильберта, которое рассматривается в пп. 7.1-2
и 7.4-8.
(•) Литература: Н. И. Мусхелишвили A968), Ф. Д. Гахов A977), Ф. Д. Гахов и Ю. И.
Черский A978), S. G. Mikhlin, S. Prossdorf A986), И. К. Лифанов A995).
6.5. Метод Мультоппа-Каландия
Рассмотрим общее сингулярное интегральное уравнение первого рода с ядром
Коши на конечном отрезке [—1,1] вида
^ Г ^ + ^ Г Kix,tMt)dt = f(x).
Т J_i t-X 7Г J_i
A)
Это уравнение часто встречается в приложениях, особенно к аэродинамике и
плоской теории упругости.
Приведем способ приближенного решения уравнения A) в предположении,
что оно допускает решение в указанных ниже классах.
6.5-1. Решение, не ограниченное на концах отрезка
Такое решение согласно общей теории сингулярных интегральных уравнений
(см., например, Н. И. Мусхелишвили A968)) может быть представлено в виде
ф)=4^, B)
Страница 218

6.5. Метод Мультоппа-Каландия
219
где ф{х) — ограниченная функпия на [—1,1]. Подставим выражение B) в
уравнение A) и введем новые переменные в ia т равенствами х = cos О, t = cost,
0^^^7г,0^т^7г. Тогда уравнение A) примет вид
— / —5^ \ / i^(cos ^, cos t)V^(cosт) с/т =/(cos ж). C)
7V Jq cos Т — COS 9 TV Jq
Построим интерполяционный полином Лагрансиса для искомой функции ф{х)
по чебышееским узлам
2т-1
Хт =COSUm, Ощ = " 7Г, Ш = 1, 2, . . . , П.
2п
Известно, что такой полином имеет вид
п
Ь„{ф;С08в) = 1 V(-1)'+V(COS0O^
п f—^ cost;
cos пв sin в^
cos и — cos 6
D)
Заметим, что дробь в правой части формулы D) представляет собой при
любом / четный тригонометрический полином степени ^ п — 1. Определив
коэффициенты этого полинома с помощью известных равенств
О ^ ^ ^ 7г, п = 0,1,2,..., E)
1 f^ cos?
7Г Jq cost -
- COS и sm 6
запишем формулу D) в виде
п п—1 п
Ьп(ф; COS0) = — ^ ф(cosOl) ^ cosmOi cosтО ^ ф(cosOl). F)
1 = 1 т=0 1 = 1
На основании двух предыдущих равенств выпишем квадратурную формулу
для сингулярного интеграла:
-Г
^ J-1
ip(t) dt
t — X
■^V^(cos^;) ^ COS mOI sin mO.
G)
1 = 1 m=l
Эта формула точна всегда, когда ф(t) — полином от t порядка ^ п — 1.
Ко второму интегралу в левой части уравнения A) применим следующую
формулу:
1Г I^ = l±Picose,), (8)
TV J_i VI -Ж2 ^ ^
справедливую всегда, когда Р(х) — полином степени ^ 2гг — 1. Тогда в силу (8)
будем иметь
— / K(x,t)ip(t)dt= —У^ K(cose, cosвl)ф(cosвi
(9)
Подставляя соотношения G) и (9) в уравнение A), получим
п п—1 п
^V^(cosOi)^2 COSmOi sinm^H ^i^(cos 0, cosOl)ф(cos Oi) = /(cos0).
nsmu ^—^ ^—^ n
1 = 1 m=l 1 = 1
Полагая 0 = Ok (k = 1,2,... ,n), с учетом формулы
у ^ COS mOi sm тОк = — ctg —^ ,
A0)
A1)
Страница 219

220
Методы решения сингулярных интегральных уравнений первого рода
где знак плюс берется, когда число |А; — /| четное, а минус, когда оно нечетное,
получим систему линейных алгебраических уравнений для нахождения
приближенных значений ф1 искомой функции ф(х) в узловых точках в форме
п
^ак1ф1 = fk, fk = f(cosOk), /с = 1,2,... ,n,
1=1
dki -
■ CtQ
,±<
^-\-К (cos Ok, cos Oi)
A2)
После решения системы A2) приближенное решение уравнения A) находится
по формулам B) и D).
6.5-2. Решение, ограниченное на одном койне отрезка
В этом случае полагаем
(р(х) =
1-х
1-\-х
ф),
A3)
где С(х) —ограниченная на отрезке [0,1] функция.
Оставив узлы интерполяции такими же, как и в п. 6.5-1, заменим С(х)
многочленом
п
п. ■^——'^
COS п9 sin (:
COS и — COS е
A4)
и подставим результат в сингулярный интеграл, входящий в выражение A). Тогда,
аналогично предыдущему, получим квадратурную формулу
/I . . п п—1 п
^й^ = 21^^2ii у C(cos ^0 У cos тв, sin тв - ^У C(cos в,
и-
A5)
Эта формула точна, если C,{t) —многочлен степени ^ гг — 1.
Формула (9) для второго слагаемого в левой части уравнения имеет вид
— / K(x,t)if(t)dt=—У"A-COSвЛК(cosв, COSOACicosел. A6)
"'-I 1 = 1
Она будет точной, если подынтегральное выражение есть полином от t степени
^ 2гг - 2.
Подставляя соотношения A5) и A6) в уравнение A) и полагая в = вк
(к = 1, 2,... ,гг), с учетом формулы A1) получим систему линейных
алгебраических уравнений для приближенных значений ("г искомой функции С (О в узлах в
форме
^bkiCi = fk, fk = f(cosOk), /с = 1,2,... ,n.
^2 2
l + 2sin^-^i^(cos6>fc, cos6>0
A7)
После решения системы уравнений A7) приближенное решение уравнения A)
определяется по формулам A3)иA4).
Страница 220

6.5. Метод Мультоппа-Каландия
111
6.5-3. Решение, ограниченное на обоих концах отрезка
Ограниченное на отрезке решение A) обращается в нуль на концах отрезка:
^A) = ^(-1) = 0. A8)
Будем приближать функцию ^{х) четным тригонометрическим полиномом от в,
построенным по узлам интерполяции, являющимися корнями полинома Чебышева
второго рода:
Xk=cosOk, Ok = -, к = 1,2,...,п.
гг + 1
Полином этот будет иметь вид
2
Мп((р;cos0) = y^V^(c^^^O 2^ smmOismmO.
^ 1 = 1 m=l
Тогда получим следующую квадратурную формулу:
A9)
B0)
1 [' ^
^ J-1 t-
гг +
— 2_. ^(cosOi) 2_. sinm^; cosтО. B1)
1 = 1 m=l
Она точна всегда, когда ^(х) — нечетный тригонометрический полином
степени ^ п.
К регулярному интегралу в уравнении A) применим формулу
/1 ^
Vl-x2P(x) dx = —!^- у sin^ Oi Р(cos Oi), B2)
 1=1
имеющую ту же точность, что и формула (8). На основании B2) будем иметь
— / K(x,t)ip(t)dt= y"smOiK(cosO,cosOi)ip(cosOi). B3)
Подставляя соотношения B1) и B3) в уравнение A) и полагая О = Ок
(к = 1, 2,..., гг), аналогично предыдущему получим систему линейных
алгебраических уравнений в форме
2jcfcZ(/?Z = fk,
/с = 1,... ,гг,
Ckl = -
'2sj^
--\-K(cosek, cosOi)
, Skl =
B4)
0 при четных I /с — /1,
cos и I — cos Uj^ ^ ' j ll при нечетных | /с — /1,
где fk = f (cos Ok), a ^pi —приближенные значения функции (p(t) в узлах.
После решения системы B4) нриближенное решение интегрального уравнения
определяется по формуле B0).
При решении сингулярного уравнения методом Мультоппа-Каландия
существенно, чтобы искомые решения представлялись в виде
ф) = A-хГA^х^х(х), B5)
где а = ±^,/3 = ±^,а х(х) — ограниченная функция на отрезке, припимающая
определенные значения на концах. При наличии нредставления B5) метод при-
мепим к полному сингулярному иптегральному уравнению, которое изучается в
главе 7.
Другие методы численного решения сингулярных иптегральных уравнений
можно найти в цитируемой ниже литературе.
(•) Литература: Н. И. Мусхелишвили A968), А. И. Каландия A973), С. М. Белоцерков-
ский, И. К. Лифанов A985), И. К. Лифанов A995).
Страница 221

7. Методы решения полных сингулярных
интегральных уравнений
7.1. Некоторые замечания
7.1-1. Интегральные уравнения с ядром Кошн
D)
Полное сингулярное интегральное уравнение с ядром Коши имеет вид
a(t)^(t) + ^ / ^^^^(т) dr = fit), е = -1, A)
где интеграл, понимаемый в смысле главного значения, берется но замкнутому
или разомкнутому контуру L, а t и т — комплексные координаты точек контура.
Заданные на L функции a(t), f (t), М(t, г) и искомая (p(t) удовлетворяют условию
Гёльдера (см. н. 6.2-2), причем M(t, г) — по обеим переменным.
Интегральное уравнение A) можно также записать в часто используемой
эквивалентной форме. Для этого рассмотрим преобразование ядра
M{t,T) _ M{t,T)-M{t,t) M{t,t)
J. J. "•" J. ' ^^
T — t T — t T — t
где обозначим
Mit,t) = bit), 1-ММ1^Ш^=КЦ,г). C)
7гг т — t
Тогда уравнение A) с учетом B) и C) примет вид
a(t)^(t) + ^ / ^ dr + / K{t, т)ф) dr = fit),
ш Jl T-t Jl
Из формул C) следует, что функция b{t) удовлетворяет условию Гёльдера на всем
контуре L, а K{t, т) всюду, кроме точек г = t, где для нее справедлива оценка
\K(t,r)\^- —, А = const < ОС, о ^ л < 1.
\т — Ц
Естественно, что уравнение D) также называют полным сингулярным
интегральным уравнением с ядром Коши. Функции a{t) и b{t) называются коэффициентами
уравнения D), ядром Коши, а известная функция fit) —правой частью
т — t
или свободным членом уравнения. Первое и второе слагаемые в левой части
уравнения D) составляют характеристическую часть или характеристику полного
сингулярного уравнения, а третье — его регулярную часть, причем функция K(t,r)
называется ядром регулярной части. В силу полученной для ядра регулярной
части оценки K(t,r) является ядром со слабой особенностью либо фредгольмовым
ядром.
Для уравнений A) и D) будем использовать и операторную форму записи,
которая имеет вид
K[^it)] = f(t), E)
где оператор К называется сингулярным оператором.
Уравнение
fit) F)
Страница 222

7.1. Некоторые замечания 11Ъ
называется характеристическим уравнением^ соответствующим полному
уравнению D), а оператор К° —характеристическим оператором.
Вводя для регулярной части уравнения обозначение
K,Hi)] = |7f(t,TMr)fl!T,
где оператор Кг называется регулярным {фредголъмоеым) оператором, запишем
полное сингулярное уравнение еще в одной операторной форме:
K.[p{t)] = K°[^(i)] + Kr[^(i)] = fit), G)
которая будет использоваться в дальнейшем.
Уравнение
K*[^(i)] = a(i)^(i)-— / ^(lMldr+ f К{т,1)ф{т)ат = д{1), (8)
получаемое из уравнения D) перестановкой переменных в ядре, называется
союзным с D) или транспонированным к нему Оператор К* называется союзным с
оператором К или транспонированным к нему
В частности, уравнение
K°*[V^(t)] ^ а{1Ж1) -^ [ M^^{r)dT = g(t) (9)
ш Jj^ r-t
будет уравнением, союзным с характеристическим уравнением F). Следует
отметить, что оператор К°*, союзный с характеристическим оператором К°, не
совпадает с оператором К*°, характеристическим для союзного уравнения (8).
Последний определяется формулой
K*°[V^(t)] ^ am(t) -^ [ ^dr. A0)
7^* Jl ^-^
Всюду в дальнейшем будем считать, что контур L состоит в общем случае из
ш + 1 замкнутых гладких кривых: L = Lq -\- Li -\- • • • -\- Ьщ. Об уравнениях для
разомкнутых контуров можно прочитать, например, в книгах Н. И. Мусхелишвили
A968), Ф. Д. Гахова A977).
Замечание 1. Установленная связь между уравнениями A) и D),
включающая свойства этих уравнений, нарушается, если предположить, что в уравнении A)
функция M(t,T) удовлетворяет условию Гёльдера всюду на контуре за
исключением конечного числа точек, где они имеют разрывы первого рода. В этом
случае полное сингулярное интегральное уравнение следует каким-либо отличным от
преобразования B) и C) способом представить в форме D) с выделенными
характеристической и регулярной частями, поскольку упомянутое преобразование
уравнения A) к такому выделению не приводит. Об уравнениях с разрывными
коэффициентами можно прочитать в упомянутых выше книгах.
7.1-2. Интегральные уравнения с ядром Гильберта
Полное сингулярное интегральное уравнение с ядром Гильберта имеет вид
а{х)ф) + j- J ' N{x,0ctg^v{0d^ = f(^)' A1)
где действительные функции а (ж), /(ж), N(x,^) и искомая (р(х) удовлетворяют
условию Гёльдера (см. и. 6.2-2), причем N(x,^) по обеим переменным.
Страница 223

224 Методы решения полных сингулярных интегральных уравнений
Интегральное уравнение A1) можно также записать в часто используемой
эквивалентной форме. Для этого преобразуем его ядро следующим образом:
N(x,Octg^^ = [N(x,0-N(x,x)]ctg^^ +N(x,x)ctg^^, A2)
где обозначим
N(x,x) = -b(x), -l.[N(x,0-N(x,x)]ctg^^ =К(х,0- A3)
Тогда уравнение A1) с учетом A2)иA3) примет вид
а(хЫх) - ^ р ctg ^ viO di + р K{x,OviO di = fi^)- A4)
Из формул A3) следует, что функция Ь(х) удовлетворяет условию Гёльдера, а
ядро К(х,^) удовлетворяет условию Гёльдера, всюду, кроме, может быть точек
X = ^, где для него справедлива оценка
А
Уравнение в форме A4) также называют полным сингулярным интегральным
уравнением с ядром Гильберта. Функции а(х) и Ь(х) называются
коэффициентами уравнения A4), ctg [^(^ —ж)] —ядром Гильберта, а известная функция f(x) —
правой частью или свободным членом уравнения. Первое и второе слагаемые в
левой части уравнения A4) составляют характеристическую часть или
характеристику полного сингулярного уравнения, а третье — ото регулярную часть, причем
функция К(х,^) называется ядром регулярной части.
Уравнение
а(хМх) - -^ р ctg ^ ^(i) di = fix), A5)
называется характеристическим уравнением, соответствующим полному
уравнению A4).
Все рассмотренные и последующие уравнения, правые части которых равны
нулю всюду в области их определения, будем, как обычно, называть однородными,
в противном случае — неоднородными.
\^(^^0\^——ПХ' ^ = const < ОС, 0^Л<1.
7.1-3. Об уравнениях Фредгольма второго рода на контуре
Теория Фредгольма и методы решения интегральных уравнений Фредгольма
второго рода, представленные в главе 5, остаются справедливыми, если все
функции и параметры в уравнениях считать комплексными, а отрезок действительной
оси заменить некоторым контуром L. Здесь приведем только некоторые сведения
и запишем интегральное уравнение Фредгольма второго рода в форме, удобной
для использования в этой главе.
Рассмотрим интегральное уравнение Фредгольма в форме
^(t) + \j K{t, тЫт) dr = f(t), A6)
где L — некоторый гладкий контур, t и г — комплексные координаты его точек,
(p(t) — искомая функция, f(t) — свободный член или правая часть уравнения,
K(t,r) — его ядро.
Если при некотором значении параметра Л однородное уравнение
Фредгольма имеет нетривиальное решение (или нетривиальные решения), то Л называется
Страница 224

7.1. Некоторые замечания 225
характеристическим числом (характеристическим значением)^ а сами
нетривиальные решения — собственными функциями ядра K(t,r) или уравнения A6).
Уравнение A6) имеет не более счетного множества характеристических чисел.
Если это множество бесконечно, то его предельной точкой является бесконечно
удаленная точка. Каждому характеристическому числу соответствует конечное
число собственных функций. Множество характеристических чисел интегрального
уравнения называется его спектром. Спектр интегрального уравнения Фредгольма
есть множество дискретное.
Если значение параметра Л не совпадает ни с одним характеристическим
числом (в этом случае его называют правильным или регулярным), т. е. однородное
уравнение имеет только тривиальное решение, то неоднородное уравнение A6)
разрешимо при любой правой части f(t).
Общее решение дается формулой
'fiit) = f(t)- j Rit,T;X)f(T)dT, A7)
где функция R(t,r;X) называется резольвентой уравнения или резольвентой ядра
K(t,r) и выражается через последнее.
Если значение параметра Л характеристическое для уравнения A6), то
однородное интегральное уравнение
ip(t) + Л / K(t, r)ip(r) dr = О, A8)
также как и союзное с ним однородное уравнение
Ф(г)^х1 к(т,гЫт)
dr = О, A9)
имеют нетривиальные решения, причем число линейно независимых решений
уравнения A8) конечно и равно числу линейно независимых решений
уравнения A9).
Общее решение однородного уравнения может быть представлено в виде
п
^{t) = Y,CkMt). B0)
к=1
где Lpi (t), Lpi{t),... ,Lpn (t) —конечное число всех линейно независимых
собственных функций, соответствующих характеристическому числу Л, а Cfc
—произвольные постоянные.
Если однородное уравнение A8) разрешимо, то неоднородное уравнение A6),
вообще говоря, неразрешимо. Оно будет разрешимо тогда и только тогда, когда
выполнены условия
/.
f{t)^k{t)dt = 0, B1)
/L
где фk(t) (к = 1, 2,..., гг) есть конечный набор всех линейно независимых
собственных функций союзного уравнения, соответствующих характеристическому
числу Л.
Если условия B1) выполнены, то общее решение неоднородного
уравнения A6) дается формулой (см., например, п. 5.6-5)
V(t) = fit)- / Rg(t,T; X)f(T)dT + J2CkMt),
B2)
15 A. B. Манж:иров, A. Д. Полянин
Страница 225

226 Методы решения полных сингулярных интегральных уравнений
где Rg(t,r;X) называют обобщенной резольвентой^ а сумма в правой части B2)
есть общее решение соответствующего однородного уравнения.
Рассмотрим теперь уравнение второго рода со слабой особенностью на
контуре
V^@ + /^ УЗ^^(^) ^^ = ^(^)' (^^^
где M(t, т) —непрерывная функция и О < а < 1. Такое уравнение при помощи
итерации можно привести к интегральному уравнению Фредгольма второго рода (см.
замечание 1 из разд. 5.3). Оно обладает всеми свойствами уравнения Фредгольма
(см. замечание из разд. 5.5).
В теории сингулярных интегральных уравнений в силу сказанного обычно
не делают различий между уравнениями Фредгольма и уравнениями со слабой
особенностью и используют общую для них форму записи
'/.
M{t,T)
Lp{t) + Л / K{t, t)lp{t) dr = 0, K(t, r) = , ^ Y , 0 ^ a < 1, B4)
причем интегральное уравнение B4) так же, как и его ядро, называют просто
фредголъмовыми.
Если в уравнении B4) известные функции удовлетворяют условию Гёльдера,
причем M(t,r) —по обеим переменным, то любое ограниченное интегрируемое
решение уравнения B4) также удовлетворяет условию Гёльдера.
Замечание 2. Ядра регулярных частей рассмотренных выше сингулярных
интегральных уравнений в силу приведенных для них оценок являются фредголь-
мовыми.
Замечание 3. Полные и характеристические сингулярные иптегральные
уравнения называют иногда сингулярными иптегральными уравнениями второго рода.
(•) Литература: С. Г. Михлин A959), Ф. Трикоми A960), Н. И. Мусхелишвили A968),
Ф. Д. Гахов A977), А. И. Гусейнов, X. Ш. Мухтаров A980), S. G. Mikhlin, S. Prossdorf
A986), S. Prossdorf, В. Silbermann A991), A. Dzhuraev A992), И. K. Лифанов A995).
7.2. Метод Карлемана для характеристических
уравнений
7.2-1. Характеристическое уравнение с ядром Коши
Рассмотрим характеристическое уравнение с ядром Коши
K^Mt)] ^ a(tMt) ^^ [ ^dr = fit), A)
ш Jl r-t
где контур L состоит из ттг Ч-1 замкнутых гладких кривых: L = Lo-\-Li-\-- • •-{- Lm •
Решение уравнения A) можно свести к решению краевой задачи Римана
(см. н. 6.3-10) и дать решение уравнения в замкнутой форме.
Введем кусочно аналитическую функцию, заданную интегралом Коши,
плотностью которого служит искомое решение характеристического уравнения
Согласно формулам Сохоцкого-Племеля (см. н. 6.2-5)
^(*) = Ф+(*)-Ф-(*),
± [ ^(^dr = Ф+{t)+ф-(t). ^^^
Страница 226

7.2. Метод Карлемана для характеристических уравнений
227
Подставляя C) в уравнение A) и решая его относительно Ф^(t), получим, что
кусочно аналитическая функция Ф(^) должна являться решением краевой задачи
Римана
$+(t) = 0(t)$-(t) + H(i), D)
где
D{t) = ^^
-b(t)
H(t) = ^(^)
^ ^ a{t) + b{t)
E)
a(t) + b(t)
В силу того, что искомая функция Ф(^) представлена интегралом типа Коши, она
должна удовлетворять дополнительному условию
ф-(оо) = 0. F)
Индекс и коэффициента D(t) задачи Римана D) будем называть индексом
интегрального уравнения A). Решив краевую задачу D), по первой формуле C)
найдем решение уравнения A).
Таким образом, интегральное уравнение A) свелось к краевой задаче
Римана D). Чтобы установить равносильность уравнения и краевой задачи, отметим,
что, и обратно, v^(t), найденная указанным образом из решения краевой задачи,
удовлетворяет уравнению A).
Рассмотрим сначала нормальный (не исключительный) случай, когда
коэффициент D{t) задачи Римана D) не обращается в нуль или бесконечность, что
соответствует для уравнения A) условию
a{t) ± h{t) ф 0. G)
Для упрощения дальнейших формул будем считать, что коэффициенты
уравнения A) удовлетворяют условию
a^{t)-b^{t) = 1. (8)
К такому случаю всегда можно привести исследуемое уравнение делением обеих
его частей на у a2(t) — ^^(t).
Выпишем решение краевой задачи Римана D), считая zy ^ О, и вычислим по
формулам Сохоцкого-Племеля предельные значения соответствующих функций
(см. ни. 6.2-5, 6.3-6 и 6.3-10)
где
Ф+(t) = X+(t)
2 X+(t)
1 Hit)
2 X+(t)
27гг Л ^+'
+ ^(t)-
+ ^(t)-
iW
iW
dr
(r)
(9)
A0)
Произвольный многочлен взят в форме
обозначений.
Отсюда по формуле C)
x-{t)'
~Pj^_i(t) ДЛЯ удобства дальнейших
vit) =
1
1 +
X+(t)
H(t) + X+(t)
x-(t)
X+(t)
*(i)-^p._l(i)
представляя коэффициент задачи Римана в виде D{t) = X~^(t)/X (t), и заменяя
функцию ^(t) ее выражением по формуле A0), будем иметь
^it)=^
1+
D(t)i
H{t)+X+it)
D(t)
— [-
2ni Jl X^
(r) dT
X+(t)
-jP'^-lit)
15*
Страница 227

228 Методы решения полных сингулярных интегральных уравнений
Подставляя, наконец, вместо X~^(t) ее выражение, задаваемое формулой F2)
из п. 6.3-10, и значения D(t) и H(t) из E), получим
^(t) = a{t)f(t) - -^^^H!I / ^JL^ + b{t)Z(t)P..^{t), A1)
где
Z{t) = [a{t) + b{t)]X+{t) = [a{t) - b{t)]X-{t) = -^^щ,
Git) = J- f ы\г-^Щг)^^^)-^]^, uit) = ±it-z,r,
27гг Jl I а(т) + Ь(т) j т-t ^
причем коэффициенты a(t) и b(t) удовлетворяют условию G). Здесь n(t) = 1
в случае, когда L — простой контур, охватывающий односвязную область. Так
как функции a(t), 6(t), f(t) удовлетворяют условию Гёльдера, то па основании
свойств предельных значений интеграла типа Коши функция (p(t) также будет
удовлетворять условию Гёльдера.
Последний член формулы A1) представляет собой общее решение
однородного уравнения (f(t) = 0), а первые два члена — некоторое частное решение
неоднородного уравнения.
Частное решение уравнения A) можно записать как R[/(t)], где R—оператор,
определяемый равенством
Тогда общее решение уравнения A) примет вид
V
(^(t) = R[/(t)] + ^Cfc(^fc(t), A3)
к=\
где (/?fc(t) = b(t)Z(t)t ~^ (к = 1,2,..., ь>) — собственные функции
характеристического уравпения.
Если р < О, то задача Римана D), вообще говоря, неразрешима. Условия ее
разрешимости
^M-r^^-^dr^O, к = 1,2,...,-1У, A4)
/.
Х+(г)
будут вместе с тем и условиями разрешимости уравпения A).
Заменяя Н(г) и Х~^ (г) их выражениями из E) и A2), можно записать условия
разрешимости в виде
^^^Уг^-^с1г = 0, к = 1,2,...,-и. A5)
/
Если условия разрешимости соблюдены, то решение неоднородного
уравнения D) дается формулой A1) при Pjy-i(t) = 0.
1°. Если z^ > О, то однородное уравнение K°[(/?(t)] = О имеет 1у линейно
независимых решений
ipk(t) = b(t)Z(t)t''-\ к = 1,2,...,и.
2°. Если z^ ^ О, то однородное уравнение неразрешимо (имеет только тривиальное
решение).
Страница 228

7.2. Метод Карлемана для характеристических уравнений 229
3°. Если zy ^ О, то неоднородное уравнение разрешимо при любой правой
части f{t) и его общее решение линейно зависит от v произвольных постоянных.
4°. Если zy < О, то неоднородное уравнение разрешимо тогда и только тогда, когда
его правая часть / удовлетворяет —v условиям:
j Mt)f{t)dt = О, Mt) = ^- A6)
сравнивая перечисленные свойства характеристического сингулярного
интегрального уравнения со свойствами интегрального уравнения Фредгольма (см.
п. 7.1-3), можно усмотреть между ними существенные различия. Для уравнения
Фредгольма в случае разрешимости однородного уравнения неоднородное,
вообще говоря, неразрешимо и, наоборот, в случае неразрешимости первого второе
безусловно разрешимо. Для сингулярного же уравнения при разрешимости
однородного безусловно разрешимо и неоднородное, при неразрешимости же первого,
вообще говоря, неразрешимо и второе.
Введем аналогично уравнению Фредгольма в ядро характеристического
уравнения параметр Л и рассмотрим уравнение
ш Jl r-t
,dr = 0.
' L
Как было показано, последнее уравнение разрешимо, если
^ , a(t) - Xb(t)
V = Ind -Н ГГ7Т- > О-
a{t) + Xb{t)
Индекс непрерывной функции изменяется скачкообразно, причем только для
таких значений Л, для которых a(t) ^ Xb(t) = 0. Если в комплексной плоскости
Л = Ai -\-iX2 провести кривые Л = ±a(t)/6(t), то они разделят плоскость на области,
в каждой из которых индекс будет постоянным. Таким образом, собственные
значения характеристического интегрального уравнения заполняют целые области,
следовательно, спектр его, в отличие от спектра уравнения Фредгольма, является
не дискретным, а сплошным.
7.2-2. Уравнение, союзное с характернстнческнм
Уравнение
K°*[V^(t)] ^ а(г)ф(г) -^ I ^AЖ1 dr = g(t), A7)
союзное с характеристическим уравнением K°[(/?(t)] = f(t), само не является
характеристическим. Однако путем подстановки
Ь{1)ф{1) = ио{1) A8)
оно превращается в характеристическое уравнение относительно функции uj{t):
a{t)oj{t) -^ f Щ dr = b(t)g(t).
A9)
Определив из последнего уравнения u;(t) но формуле получающейся
сложением равенств A7) и A8), найдем искомую функцию фA):
Ф{1) =
a{i)+b(t) [
1 f ^(r)
T^i Jl '^-^
w(t) + — / ^^dT + g{t)
Страница 229

230 Методы решения полных сингулярных интегральных уравнений
Вводя кусочно аналитическую функцию
придем к краевой задаче Римана
+ ait)+b{t) b{t)g(i)
* ^> a{t) - b(t) * ^> + a(t) - b(t) ■ ^ '
Коэффициент краевой задачи B1) есть величина, обратная коэффициенту задачи
Римана D), соответствующей уравнению K°[(/^(i)] = f(t). Следовательно,
.* = Ind Щ±Щ = - Ind 44^ = — B2)
a{t) - b{t) a{t) + b{t) ^ ^
Заметим, что в силу формул A7) из п. 6.3-4 канонические функции X* (z) для
уравпения B1) и Х(^) для D) будут обратим по величине:
Аналогично проделанному в п. 7.2-1 получим решение сингулярного
интегрального уравнения A7) при и* = —и '^ О в виде
где Z(t) задается формулой A2), а Qu*-i(t) — многочлен степени zy* — 1 с
произвольными коэффициептами. Если z^* = О, то следует положить QT^*-i(t) = 0.
Если jy* = —jy < О, то для разрешимости уравпения A7) необходимо и
достаточно выполнение условий
/ b{t)Z{t)g{t)t^~^dt = 0, к = 1,2,...,-и% B4)
при соблюдении которых решение дается формулой B3), где нужно положить
O,*_i(t) = o.
Результаты одновременного исследования характеристического и союзного с
ним уравнений показывают существенное отличие их свойств от свойств
уравнений Фредгольма (см. п. 7.1-3). Характеристическое и союзное с ним однородные
уравнения никогда не бывают одновременно разрешимы. Они или оба
неразрешимы при и = О, или, при ненулевом индексе, разрешимо то из них, которое имеет
положительный индекс.
Отметим, что разность чисел решений характеристического и союзного с ним
однородных уравнений равна индексу и.
Утверждения 1°, 2° и 3°, 4°, сформулированные в п. 7-2.1, называются первой
и второй теоремами Нётера для характеристического уравнения, а отмеченная
здесь связь индекса уравнения с количеством решений однородных уравнений
K°[(/?(t)] = О и K°*[V^(t)] = о — третьей теоремой Нётера.
7.2-3. Характеристическое уравнение на действительной оси
Теория интеграла типа Коши показывает (см. разд. 6.2), что если плотность
интеграла типа Коши, взятого по бесконечной кривой, равна нулю на
бесконечности, то свойства интеграла в случаях конечного и бесконечного контуров во всем
существенном совпадают. Поэтому теория сингулярного интегрального уравнения
Страница 230

7.2. Метод Карлемана для характеристических ураенений 231
на бесконечном контуре в классе исчезающих на бесконечности решений
совпадает с теорией уравнения на конечном контуре.
Так же, как в случае конечного контура, характеристическое интегральное
уравнение
а{х)^{х) + -^ Г ^^ dr = fix) B5)
ш J_^ т-х
с помощью интеграла типа Коши
27гг J_^ T-Z
B6)
И формул Сохопкого-Племеля (см. п. 6.2-5) приводится к краевой задаче Римана
для действительной оси (см. п. 6.3-8)
^А_. . ШХ) — OlX) ^_. . fix) ,^„^
* 0^ = -Н гН* 0^ + ,,;,,, -ОС < ж < ОС. B7)
^ ^ а(ж) + 6(ж) ^ ^ а(ж)+6(ж)
а^(ж)-6^(ж) = 1, B8)
а{х)-Ь{х) ^-^^^ , fix)
aix]
Будем считать, что
поскольку уравнение B5) всегда можно привести к случаю B8) делением обеих
его частей на y^a'^it) — b'^it) с последующими переобозначениями, и заметим, что
индекс v интегрального уравнения B5) дается формулой
aix) - bix)
'^ = ^"^а(.)+6(.)- ^^'^
Тогда при г^ > О получим
■ X ' ^ ^ ^ ^ (ж + г)^
,.(х) = а(х)/(х)-^М^(^ Г f(j) ^- ^bix)Zix)^J^^^, C0)
тгг J_^ Zir) т- -
где
Z(x) = [а(ж) + bix)]X^ix) = [aix) - 6(ж)]Х-(ж) = (^^)
С(ж) = ^— In
^ ^ 2vri J_^
air) - bir)
г -\-i J air) -\- bir)
В случае ly ^0 следует положить Pj^-i (ж) = О и потребовать при zy < О выполнения
условий разрешимости
fix) dx
f
J —с
z(.)(. + .)^-0' ^ = М,...,- C1)
о решении уравнения B5) в классе ограниченных на бесконечности функпий
можно прочитать в книге Ф. Д. Гахова A977).
На действительной оси аналогом характеристического уравнения является
уравнение вида
а(ж)(/?(ж)
+ ^^ Г ^^^ ^^dr = fix), C2)
тгг J_^ г-Zq r-x
где Zq — точка, не лежащая на контуре. Для него справедливы все качественные
результаты и формулы, полученные для характеристического уравнения на
замкнутом конечном контуре. В частности, оказываются справедливыми формулы
обращения интеграла типа Коши
V;(x) =^ Г ^^^ ^(IL dr, ф) =^ Г ^^^ ^^^ dr. C3)
тгг J_^ г-Zq r-x тгг J_^ г - Zq r-x
Страница 231

232
Методы решения полных сингулярных интегральных уравнений
7.2-4. Исключительный случай характеристического уравиеиия
При исследовании характеристического уравнения в н. 7-2.1 исключался
случай, когда функции a(t) ± 6(t) обращались на контуре L в нуль. Это было вызвано
тем, что коэффициент D{t) задачи Римана, к которой приводится
характеристическое уравнение, имеет в этих случаях на контуре нули и полюсы, и, следовательно,
такая задача не подчиняется общей теории. Рассмотрим указанный
исключительный случай.
Будем предполагать, что коэффициенты исследуемых сингулярных уравнений
таковы, что обеспечивается выполнение дополнительного требования дифферен-
цируемости функций, которое вводилось при рассмотрении исключительных
случаев задачи Римана (см. 6.3-9).
Рассмотрим характеристическое уравнение с ядром Коши A) в
предположении, что функции a{t) — b(t) и a(t) -\- b(t) имеют на контуре нули соответственно
в точках ai, «2, ..., о^/х и /3i, /^2, ..., P-q целых порядков и, следовательно, пред-
ставимы в виде
a(t) - b(t) = П (t - a^r^rit), a(t) + b(t) = f[(t - pjY^sit),
k=i j=i
где r(t) и s(t) нигде не обращаются в нуль. Все ак и Pj предполагаются
различными.
Будем считать, что коэффициенты уравнения A) удовлетворяют соотношению
к=1 3 = 1
C4)
К такому случаю исследуемое уравнение всегда можно привести делением обеих
его частей на у s(t)r(t) с последующими очевидными переобозначениями.
Уравнение A) в исключительном случае, аналогично проделанному в п. 7.2-1,
приводится к задаче Римана
П(*-"^Г'=
+ т - _!s=i
$+(t) =
j=i
-L>i(t)$-(i) +
m
C5)
П («-/?,■ )^-'s(«)
3=1
где Di(t) = r(t)/s{t). Решение этой задачи в классе фзшкций, удовлетворяющих
условию Ф(оо) = О, определяется формулами
Ф+(г) =
г, ^^^'^ [4!+{z)-U,{z)+A,{z)P..,.,{z)l
X-{z)
^(^-<^кГ
-[ф-(г)-МЛг) + Ло(г)Р.-р-1(г)],
C6)
где
^ > 2ш J^ 8(т)Х+{т) т - Z
C7)
Страница 232

7.2. Метод Карлемана для характеристических уравнений
233
а lAp{z) —интерполяциопный полипом Эрмита (см. п. 6.3-2) для функции ^{z)
степени р = т -\- р — 1 с узлами в точках ак и Pj соответственно кратностей
гпк и pj, тдс т = J2 '^к, Si р = J2 Pj'
Условимся многочлен Vlp(z) рассматривать как оператор, ставящий в
соответствие свободному члену f(t) уравнения A) полином, интерполирующий
указанным образом интеграл типа Коши C7). Обозначим этот оператор
^T[f{t)]=U,iz).
C8)
Коэффициент Y здесь взят для удобства дальнейших преобразований.
Далее, аналогично тому, как это было сделано в нормальном случае, из C6)
найдем
Ф+(*)
X+{t)
1
fit)
[ 2 s{t)X+{t)
2-Ki J^ s{i
fir)
dr
)X+(r)
ф-(*)
x-(t)
i\it-ock)
fit)
2 s{t)X+{t)
- JT[/(i)]-l^o(i)P.-p-i(i)
_,J_f f(r) dr
27гг Л s{t)X+{t) T-t
rT[/(t)]
-Ao{t)P^-p-i{t)
Коэффициент — i в последних слагаемых этих формул взят для удобства
дальнейших преобразований в силу произвольности коэффициентов многочлена
Pt,_p_i(i). Следовательно,
.(.) = Ф-(.)-ф-(.) = ^^+
+ A2(i)
где
L / f±.
тг J^ s{t)X+{
Al(t) =
)dT
T){T-t)
X+(t)
+
'^tlit-Pj)"^ 2П(«-а,
3=1 k=l
X+(t) X-{t)
T[/(i)]-^o(i)P.-p-i(i)
x-(t)
, C9)
A,{t) =
2Ylit-Pj)^^ 2П(<-а^Г'
j=i fc=i
Воспользовавшись обозначением
Z(t) = s(i)X+(i) = r(t)X~(t),
a также соотношением C4), представим формулу C9) в виде
D0)
Vit) =
Mt)
a{t)f{t)
b(t)Z(t)
L
fir) dr
IL Z(t) T-t
+ b{t)Z{t)T[f{t)]
+
+ b{t)Z{t)P^-p-i{t).
Страница 233

234 Методы решения полных сингулярных интегральных уравнений
Вводя оператор Ri[/(t)] формулой
Ri[/(i)] = -±^ \a(t)fit) - М|(^ j^m.j^+b{t)zm[f{i)]
D1)
Л@
окончательно получим
^{t) = Ri[/(t)] + 6(t)Z(t)P._p_i(t). D2)
Формула D2) дает решение уравнения A) в исключительном случае при
р — р > О, которое линейно зависит от 1у — р произвольных постоянных. Если
и — р < О, то решение существует лишь при выполнении р — и специальных
условий разрешимости, налагаемых на свободный член f(t) и вытекающих из
условий разрешимости соответствующей этому случаю задачи Римана C5).
7.2-5. Характеристическое уравнение с ядром Гильберта
Рассмотрим характеристическое уравнение с ядром Гильберта
а(хЫх) - ^ р ctg ^ ^{0 di = fix). D3)
Как характеристическое интегральное уравнение с ядром Коши связано с краевой
задачей Римана, так и характеристическое уравнение D3) с ядром Гильберта
аналитически непосредственно приводится к задаче Гильберта. Задача Гильберта в
свою очередь может быть сведена к задаче Римана (см. п. 6.3-12), а значит можно
построить аналитическое решение уравнения D3).
При и > О однородное уравнение D3) (f(x) = 0) имеет 2iy линейно
независимых решений, а неоднородное безусловно разрешимо и зависит линейно от
2iy действительных постоянных.
При и < О однородное уравнение неразрешимо, а неоднородное разрешимо
лишь при выполнении —2iy действительных условий разрешимости.
Учитывая, что комплексный параметр содержит два действительных, а
комплексное условие разрешимости равносильно двум действительным, заключаем,
что при zy 7^ О качественные результаты исследования характеристического
уравнения с ядром Гильберта полностью совпадают с соответствующими результатами
для характеристического уравнения с ядром Коши.
7.2-6. Уравнение Трикоми
Сингулярное интегральное уравнение Трикоми имеет вид
V^W-A^ (Т^~ - ' ^^ o^.V@^e-/W, O^x^l. D4)
-С-2^С
Ядро этого уравнения состоит из двух слагаемых. Первое слагаемое
представляет собой ядро Коши. Второе слагаемое непрерывно, если хотя бы одна из
переменных X и ^ меняется строго внутри отрезка [0,1], но если х = ^ = О или
X = ^ = 1, то это слагаемое становится бесконечным и неинтегрируемым в
квадрате {О ^ ж ^ 1, О ^ С ^ 1}.
При помощи кусочно-аналитической в верхней и нижней полуплоскостях
функции
z^^-2z^
Страница 234

Полные сингулярные уравнения, разрешаемые в замкнутой форме 235
уравнение D4) можно привести к задаче Римана с краевым условием на
действительной оси. Решение уравнения Трикоми имеет вид
Lp{x)
1 + Л27г2
/(^) +
/Лт^
^ / Jo V 1 - с
^C{l-xf
-2xi )" ^"^-""J ■ ж1+/3
OL= — arctg(A7r) (-1 < a < 1), tg — = Лтг (-2 < /3 < 0),
7Г 2
где С — произвольная постоянная.
(•) Литература'. Ф. Трикоми A960), Н. И. Мусхелишвили A968), П. П. Забрейко, А. И. Ко-
шелев и др. A968), Ф. Д. Гахов A977).
7.3. Полные сингулярные интегральные уравнения,
разрешаемые в замкнутой форме
Полные сингулярные интегральные уравнения, в отличие от
характеристических и союзных с ними, не решаются в общем случае в замкнутой форме. Однако
имеется ряд случаев, когда и полные уравнения могут быть решены в замкнутой
форме.
7.3-1. Замкнутое решение нрн постоянных коэффнннентах
Рассмотрим полное сингулярное интегральное уравнение с ядром Коши в
форме (см. п. 7.1-1)
a(t)^(t) + ^^ / ^ dr + / K{i, тЫт) dr = fit), A)
ш Jl T-t Jl
где L — произвольный замкнутый контур. Покажем, что уравнение A) решается в
замкнутой форме, если a{t) = aiAb{t) = b постоянны, а i^(t, т) —любая функция,
аналитически продолжимая в область П^ по каждой переменной.
Уравнение A) при указанных предположениях имеет вид
J_ f M{t,T
T^i Jl ^-t
a^(t) + ^ / ^^^A^v^(r) dr = fit), B)
где M(t,r) = b -\- 7vi(t - r)K(t,r), так что M(t,t) = b = const. Пусть b j^ 0.
Обозначим
ФИ) = Л_[т11^^г)аг. C)
бтгг J j^ I — L
Согласно п. 6.4-4 функция (p(t) выражается через ф(t) точно так же, как ф(t)
через (p(t). Тогда уравнение B) запишем в виде
a^(t) + Ьф{1) = fit). D)
Применяя к обеим частям операцию C), получим
aV^(t) + 6(/?(t) =w{t), E)
где
w{t)
= ^fM(hllf^r)dr.
Ъш Jl r-t "^ ^ ^
Страница 235

236 Методы решения полных сингулярных интегральных уравнений
Решая систему уравнений D) и E), найдем (p(t):
1
^{t) =
а^ -b^
т^г Ji^ T-t
F)
При условии, что а ф ^b.
Таким образом, при а т^ ±6 и аналитически продолжимом ядре K(t,r)
уравнение A) или B) разрешимо и имеет единственное решение, даваемое формулой F).
Уравнение A) рассматривалось при b ф 0. Это предположение естественно
ввиду того, что при b = О уравнение A) перестает быть сингулярным. Однако,
получаемое при b = О фредгольмово уравнение
a(p(t) + / K(t, r)(p(r) dr = f(t), a = const G)
разрешимо в замкнутой форме при аналитически продолжимом ядре K(t,r).
Пусть функция K(t,r) аналитически продолжима в область П^ по каждой
переменной и непрерывна при t, т G L. Тогда
1°. Функция
ф+(t)= / K(t,r)ip(r)dr
аналитически продолжима в область Q~^ для любой функции (p(t),
удовлетворяющей условию Гёльдера.
2°. Если функция (p~^(t), удовлетворяющая условию Гёльдера, аналитически
продолжима в область П^, то
/ K(t,r)ip^(r)dr = 0. (8)
Отсюда следует, что
/ K(t, т) / К(г, ri)ip(ri) dri dr = 0 (9)
J L J L
ДЛЯ любой (удовлетворяющей условию Гёльдера) функции ^(t). Поэтому из G)
находим
а [ КЦ,ф{т)с1т = [ K{t,T)f{T)dT,
J L J L
A0)
И тогда
f(i)- j K{t,T)f{T)dT\.
Следовательно, если ядро K(t,r) аналитично в области П^ по каждой
переменной и непрерывно при t, т G L, то уравнение G) разрешимо при любой правой
части и его решение дается формулой A0).
7.3-2. Замкнутое решение в общем случае
Перейдем к общему случаю разрешимости уравнения A) в замкнутой форме
при условии, что функция K(t,r)[a(t) -\- b(t)]~^ апалитичпа по т и мероморфна
по t в области П^.
Обозначим для краткости
Kr[ip(t)]= [ K(t,r)ip(r)dr
Страница 236

Полные сингулярные уравнения, разрешаемые в замкнутой форме
237
и заметим, что
K,[^+(t)] = 0 A1)
для ВСЯКОЙ функции v^^(t), аналитически продолжимой в область П+. Полагая
Lp{t) = (p~^(t) — (р~ (t). Приводим уравнение A) с учетом A1) к соотношению типа
задачи Римана
V^^W - и^\и^^Л^~(^)] = D(t)^-(t) + Я(t), A2)
где
D(t)
a{t) + b{t)
a{t) - b{t)
a{t) + b{t)
По предположению имеем
H(t)
fit)
a(t) + b{t)
K{t,T)
a(t) + b(t)
A+(t,T)
n+(t)
Tl+{t)=\{{t-zuT
A3)
fc=i
где Zk £ fi"'', гпк —целые положительные числа, а функция Л"'"(^, т) аналитична
по i и по т в
Соотношение A2) принимает вид
n+(i)vp+(t) + A+[vp-(t)] = n+(t)p(t)^-(t) + H{t)], A4)
где A^ — интегральный оператор с ядром A^(t,T). Так как функция A^(/?~(t)
аналитична в П^, то последнее соотношение представляет собой обычную задачу
Римана, из которой определяются функции n^(t)(/?^(t) Ч- A^[(/?~(t)l и (р~ (t), а
следовательно, и v^(t). В самом деле, записывая D(t) в виде D(t) = X^(t)/X~ (t),
где X (z) —каноническая функция задачи Римапа, и приводя соотпошение A4)
к виду, допускающему применение обобщенной теоремы Лиувилля (см. п. 6.3-1),
п
Придем к многочлену степени zy — 1 Ч- Х^ гпк с произвольными коэффициептами
к=1
п
(в случае ^ + Х^ гпк > 0). Однако наличие множителя n^(t) перед v^^(t),
к=1
п
обращающегося в нуль в П^ с суммарным порядком нулей ^ гпк, уменьшит
к=1
число произвольных постоянных в общем решении.
Замечание 1. Аналогично проделанному в п. 7.3-2 может быть рассмотрен
случай, когда ядро K(t,r) мероморфно и по т. Тогда уравнение A) можно свести
к задаче Римана типа A2) и некоторой линейной алгебраической системе.
Замечание 2. Построенные в разд. 7.3 решения полных сингулярных
интегральных уравнений применимы в случае когда контур L представляет из себя
совокупность конечного числа гладких замкнутых контуров без общих точек.
Пример 1. Рассмотрим уравнение
1 f cos(t — t)
7vi Jl
X^{t) +
-t
-^{T)dT = f{t),
A5)
где L — произвольный замкнутый контур.
Заметим, что функция МA,т) = cos(t — t) обладает свойством M(t,t) :
воспользоваться формулой F), так что для уравнения A5) имеем
■ 1. Остается
VP(«):
1
А2
А/(«)
7тг Jl
cos(t — t)
f{r)dT
X^±l.
Страница 237

238
Методы решения полных сингулярных интегральных уравнений
Пример 2. Рассмотрим уравнение
Хф) +
1 Г sin(
тгг Jl (г
sin(T — t)
V(T)dT = f(i),
тгг Jr. [T-ty
A6)
где L — произвольный замкнутый контур.
Функция M(t, т) = [sin(T — 1)]/[т — t] обладает свойством M(t, t) = 1.
Воспользовавшись формулой F), для уравнения A6) получим
Ф):
1
Л2-1
(•) Литература: Ф. Д. Гахов A977).
тгг Jl {г - ty
\ф±1.
7.4. Метод регуляризации для полных сингулярных
интегральных уравнений
7.4-1. Некоторые свойства сингулярных операторов
Пусть Ki, К2 —сингулярные операторы:
Ki[v.(t)] ^ а,{1Ы1) + ^ / М1^ф)
dr.
K2[a;(t)] = a2(t)a;(t) + — /
7^^ Jl
T-t
u;(r)dr.
A)
B)
Оператор К = K2K1, определяемый формулой K[(/?(t)] = К2 [Ki[(/?(t)]], будем
называть композицией или произведением операторов Ki и К2.
Составим выражение для оператора К:
K[(^(t)] = K2Ki[(^(t)] = a2(t)
± f Щ
ai(t)v?(t) +
{t.r)
ai(r)(p(r) +
1 f Mi(t,T
TTi Jl r-t
J_ f M,(r,r,
^^ Jl ^1-^
(p(r) dr
(p(ri)dri
dr, C)
и выделим его характеристическую часть. Для этого проделаем следующие
преобразования:
Jl ^-i Jl ^-i Jl ^-^
I ^li^}M2(hll^(r)dr = a,(t)M,(t,t) I ^^dr^
Jl ^-t Jl ^-t
{t,t)
(p(r) dr,
+
f a^{T)M^{t,T)-a^
Jl r-t
(t)M^(t,t)
(p(r)dr,
1- I ^h(hAdrl- I Mi^iiiA^,)dr, = M,{t,t)M,{t,t)^{t)-
7П Jl r-t 7тг Jl r-^ - r
+
т^г Jl '^^ Jl ("^i
(t,r)Mi(r,ri)
r)(r - t)
dr.
D)
Здесь использована формула перестановки порядка интегрирования Пуанкаре-
Бертрана (см. п. 6.2-6). Легко видеть, что все ядра интегралов в последних
слагаемых правых частей формул D) являются фредгольмовыми.
Страница 238

7.4. Метод регуляризации для полных сингулярных интегральных уравнений 239
Обозначая
Mi(t,t) = 61 (t), M2(t,t) = 62 (t), E)
получим, что характеристический оператор К° композиции (произведения) К
двух сингулярных операторов Ki и К2 выражается формулой
K°b(t)] = (K2Ki)°[vp(t)] =
= [a,{t)a,{t) + b,(t)b,{t)Mt) + -2it)bAt) + b,(t)a,(t) f <^(r^ ^^ ^^^
Ш Jl T-t
Запишем операторы Ki, К2 в форме C) с явно выделенной
характеристической частью:
G)
KiHt)] = ai(t)(^(t) + MI / ^dT+ [ K,(t,rMr)dr,
ш Jl T-t Jl
K2[c^(t)] = a2(t)c^(t) + MI / i^^dT+ [ K2(t,r)u(r)dr. (8)
T^f' Jl ^-t Jl
Таким образом, коэффициенты a(t) и b(t) характеристической части
произведения операторов К1К2 выражаются формулами
a(t) = a2(t)ai(t) + b2(t)bi(t), b(t) = a2(t)bi(t) + b2(t)ai(t). (9)
Эти формулы не содержат регулярных ядер Ki, К2 и они симметричны
относительно индексов 1 и 2. Отсюда заключаем, что характеристическая часть
произведения сингулярных операторов не зависит от их регулярной части и не зависит от
порядка следования этих операторов в произведении.
Таким образом, изменение порядка операторов, а также изменение их
регулярной части оказывает влияние только на регулярную часть произведения
операторов, не затрагивая ее характеристической части.
Вычислим коэффициент задачи Римана, соответствующей
характеристическому оператору (K2Ki)°:
^' a{t)+b(t) [«2D) + 62D)] K(t) + 6i(t)] ^^' '^'' ^ ^
где через
обозначены коэффициенты задач Римана, соответствующих операторам К?, К2.
Отсюда вытекает, что коэффициент задачи Римана оператора (K2Ki)° равен
произведению коэффициентов задач Римана операторов К" и К2, и, следовательно,
индекс произведения сингулярных операторов равен сумме индексов
перемножаемых операторов:
1У = 1У1 -\-1У2. A2)
Полный вид оператора К2К1 будет определяться выражением
K2Ki[(^(t)] = a(t)(^(t) + ^ / ^^dT+ f K(t,rMr)dr,
ш Jl T-t Jl
где a{t) и b{t) определяются формулами (9), a на основании формул D) можно
выписать явное выражение для регулярного ядра K(t,r).
Для сингулярного оператора К и союзного с ним К* (см. п. 7.1-1) справедливы
соотношения:
/ Ф(г)К[ср(г)] dt= [ срК*[ф(г)] dt
Jl J l
для любых функций (p{t) иф{1), удовлетворяющих условию Гёльдера, и
(K2Ki)* = KtK;.
Страница 239

240 Методы решения полных сингулярных интегральных уравнений
7.4-2. Регуляризующий оператор
Метод регуляризации состоит в приведении сингулярного интегрального
уравнения к фредгольмову. Сам процесс такого приведения называется регуляризацией.
Если сингулярный оператор К2 таков, что оператор К2К1 является
регулярным (фредгольмовым), т. е. в нем отсутствует сингулярный интеграл {b{t) = 0),
то К2 называется регуляризующим оператором по отношению к сингулярному
оператору Ki или, коротко, его регуляризатором. Заметим, что если К2 является
регуляризатором, то регулярным будет и оператор К1К2.
Найдем общий вид регуляризующего оператора. По определению, должно
выполняться равенство
b{t) = a2(t)bi(t) + b2(t)ai(t) = О, A3)
из которого следует, что
a2{t) = 9{t)ai{t), b2{t) = -9{t)bi{t), A4)
где g(t) — произвольная не обращающаяся в нуль функция, удовлетворяющая
условию Гёльдера.
Следовательно, если К — сингулярный оператор:
KMt)] ^ a(tMt) + ^ / ^ dr + / K(t, тЫт) dr, A5)
ш Jl T-t Jl
то его регуляризатор К можно в общем случае представить в форме
K[a;(t)l = g{t)a{t)uj{t) - ЯШ^ [ i^^ dr + / K(t, r)u;(r) dr, A6)
7^^ Jl ^-t Jl
где K(t, r) — произвольное фредгольмово ядро, a g(t) — произвольная функция,
удовлетворяющая условию Гёльдера.
Так как индекс регулярного оператора (b(t) = 0), очевидно, равен нулю, то из
свойства произведения операторов вытекает, что индекс регуляризующего
оператора равен по абсолютной величине и обратен по знаку индексу регуляризуемого
оператора. Это же заключение можно сделать непосредственно по виду
регуляризующего оператора A6), исходя из того, что
£)(^)_ т-т _ a{t)^b{t) _ 1
a{t) + b{t) a{t) - b{t) D{t)
Таким образом, для любого сингулярного оператора с ядром Коши A5)
нормального типа (a(t) ± b(t) ф 0) существует бесчисленное множество регуляризу-
ющих операторов A6) с характеристической частью, зависящей от произвольной
функции p(t), и содержащих произвольное регулярное ядро K(t,r).
Произвольными элементами g(t), K(t,r) можно, при случае, распорядиться
так, чтобы регуляризующий оператор удовлетворял некоторым дополнительным
условиям. Можно, например, добиться в регуляризованном уравнении
нормирования коэффициента при v^(t), сделав его равным единице. Для этого нужно
положить g(t) = [a^{t) — b^(t)]~^. Если никаких условий не налагается, то естественно
воспользоваться простейшими регуляризаторами. Пх можно получить, если в
формуле A6) положить g(t) = 1, K(t,r) = О, после чего регуляризатор будет иметь
вид
K[a;(t)] = K*°[a;(t)] = a(t)u;(t) - ^ [ i^^ dr, A7)
^'^ Jl ^-^
Страница 240

7.4. Метод регуляризации для полных сингулярных интегральных уравнений 241
или же положить g{t) = 1, А (t, т) = — —^ —^, тогда
7гг т — t
K[a;(t)l = K°*[a;(t)l = a{t)uj{t) - — / .К^М^! ^^_ ^^g^
Простейшие операторы К*° и К°* употребляются в качестве регуляризаторов
наиболее часто.
Так как перемножение операторов не переместительно, то следует различать
два вида регуляризации: регуляризацию слева, когда в результате получается
оператор КК, и регуляризацию справа, когда она приводит к оператору КК. На
основании сделанного выше замечания регуляризатор справа является одновременно
и регуляризатором слева, и наоборот. Таким образом, операция регуляризации пе-
реместительпа.
Если оператор К является регуляризующим для оператора К, то и обратно,
оператор К является регуляризатором для оператора К. Операторы КК и КК
могут отличаться друг от друга лишь регулярной частью.
7.4-3. Способы регуляризации слева и справа
Пусть дано полное сингулярное интегральное уравнение
Щ^{1)] ^ a(tMt) + ^ / ^ dr + / K(t, тЫт) dr = fit). A9)
Используются три способа его регуляризации. Первые два основаны на
композиции данного сингулярного оператора и его регуляризатора (регуляризация слева
и справа). Третий способ существенно отличается от первых двух, в нем
устранение сингулярного интеграла производится путем решения соответствующего
характеристического уравнения.
1°. Регуляризация слева. Возьмем регуляризующий оператор A6)
K[a;(t)] = g{t)a{t)uj{t) - ЯШ^ [ i^^ dr ^ [ k(t, r)u;(r) dr. B0)
^'^ Jl ^-^ Jl
Подставляя в K[a;(t)] вместо функции a;(t) выражение K[(/?(t) — /(t)], придем
к интегральному уравнению
KKb(t)] = K[/(i)]. B1)
По определению оператор КК фредгольмов, так как К — регуляризатор.
Следовательно, уравнение B1) есть уравнение Фредгольма. Таким образом, мы
преобразовали сингулярное интегральное уравнение A9) в интегральное уравнение
Фредгольма B1) относительно той же неизвестной функции (p(t).
В этом состоит первый способ регуляризации, который называется
регуляризацией слева.
2°. Регуляризация справа. Подставив в уравнение A9) вместо искомой функции
выражение B0):
^{t) = Що{1I A1)
где и{1) —некоторая новая неизвестная функция, придем к иптегральному
уравнению
KK[c..(i)] = /(i), B3)
которое также является фредгольмовым. Таким образом, от сингулярного ипте-
грального уравнения A9) относительно неизвестной функции Lp{t) мы перешли
16 А. В. Манж:иров, А. Д. Полянин
Страница 241

242 Методы решения полных сингулярных интегральных уравнений
к интегральному уравнению Фредгольма относительно новой неизвестной
функции u;(t).
Решив уравнение Фредгольма B3), но формуле B2) найдем решение
исходного уравнения A9). Применение формулы B2) требует только вычисления
квадратур (один интеграл обыкновенный и один сингулярный).
В этом состоит второй способ регуляризации, который называется
регуляризацией справа.
7.4-4. Проблема равносильной регуляризации
В процессе приведения сингулярного иптегрального уравнения к
регулярному над уравнением производится некоторое функциональное преобразование. Это
преобразование может, вообще говоря, или внести посторонние решения, не
удовлетворяющие исходному уравнению, или вызвать потерю некоторых из них.
Поэтому получаемое уравнение, вообще говоря, не равносильно исходному.
Рассмотрим связи между решениями этих уравнений и выясним когда уравнения
равносильны.
1°. Регуляризация слева. Пусть дано сингулярное уравнение
Kb(t)] = f{t) B4)
И соответствующее ему регулярное
KKb(t)] = K[/(i)]. B5)
Запишем B5) в форме
K[KHt)]-/(i)]=0. B6)
Так как оператор К однородный, то всякое решение исходного уравнения B4)
(функция, обращающая выражение K[(/?(t)] — f{t) в нуль) удовлетворяет также
уравнению B6). Следовательно, регуляризация слева пе приводит к потере
решений. Но не всякое решение регуляризованного уравнения является решением
исходного.
Рассмотрим сингулярное интегральное уравнение, соответствующее регуляри-
зующему оператору
K[a;(t)] = 0. B7)
Пусть a;i(t), uo2{t), • • •, ojp{t) — его полная система решений, т. е. совокупность
всех линейно независимых собственных функций регуляризующего оператора К.
Рассматривая уравпение B6) как сингулярное уравнение вида B7) с искомой
функцией uj{t) = K[(/?(t)] — /(t), будем иметь
р
KMt)]-f(t) = J2^J^j(t), B8)
j=i
где aj — некоторые постоянные.
Таким образом, регуляризованное уравнение равносильно не исходному
уравнению B4), а уравнению B8).
Птак, уравнение B5) равносильно уравнению B8), в котором aj —
произвольные или определенные постоянные. Может оказаться, что уравнение B8)
разрешимо только при условии, что все aj = 0. В этом случае уравнение B5) будет
равносильно исходному уравнению B4), и регуляризатор будет равносильным. В
частности, если регуляризатор не имеет собственных функций, то правая часть
Страница 242

7.4. Метод регуляризации для полных сингулярных интегральных уравнений 243
уравнения B8) тождественно равна нулю, и он обязательно является
равносильным. Такой оператор заведомо существует при zy > 0. Например, им может быть
регуляризатор К*°, не имеющий в этом случае собственных функций, так как
индекс регуляризатора К*° равен — zy ^ 0.
2°. Регуляризация справа. Пусть имеем уравнение B4) и регуляризованное
уравнение
KK[w(i)] = /(i), B9)
полученное подстановкой
K[c^(i)] = ф). C0)
Если Uj (t) есть какое-нибудь решение уравнения B9), то из формулы C0)
получаем соответствующее ему решение исходного уравнения
^pj(t)=K[LOj(t)].
Следовательно, регуляризация справа не может привести к посторонним
решениям.
Пусть, наоборот, ^k(t) есть некоторое решение исходного уравнения. Тогда
решение регуляризованного уравнения B9) может быть получено как решение
неоднородного сингулярного уравнения
K[u;{t)] = ipk{t),
которое, однако, может оказаться неразрешимым. Таким образом, регуляризация
справа может привести к потере решений. Такой потери не произойдет, когда
уравнение C0) разрешимо при любой правой части. В этом случае оператор К
будет равносильным регуляризатором справа.
3°. Равносильная регуляризация. Оператор К = К*° является при любом индексе
равносильным регуляризатором, причем при zy > О следует применять
регуляризацию слева, а при и ^0 — регуляризацию справа.
В последнем случае получается уравнение относительно новой функции <x;(t),
но если она найдена, то можно построить все решения исходного уравнения
в квадратурах, причем по свойству регуляризации справа не может возникнуть
посторонних решений.
О других способах равносильной регуляризации можно прочитать в
цитируемой в конце раздела литературе.
7.4-5. Теоремы Нётера
Пусть дано полное сингулярное интегральное уравнение
Kb(t)] = f{t). C1)
Теорема 1. Число решений сингулярного интегрального уравнения C1)
конечно.
Теорема 2. Необходимым и достаточным условием разрешимости
сингулярного уравнения C1) является выполнение равенств
J f{t)ijj{t)dt = 0, j = l,2,...,m, C2)
где фl(t), ф2(t), ..., фm(t) —максимальный линейно независимый набор
решений союзного однородного уравнения K*[V^(t)] = 0.
16*
Страница 243

244 Методы решения полных сингулярных интегральных уравнений
Теорема 3. Разность числа п линейно независимых решений
сингулярного уравнения K[(/?(t)] = О и числа т линейно независимых решений
союзного уравнения K*[V^(t)] = О зависит лишь от характеристической части
оператора К и равна его индексу, т. е.
п — т = 1У. C3)
Следствие. Из всех сингулярных уравнений, имеющих данный индекс z^,
наименьшее число решений имеют характеристические.
7.4-6. Способ регуляризации Карлемаиа-Векуа
Перенесем регулярный член сингулярного уравнения в правую часть и
запишем его в следующем виде:
a(tMt) + ^ / ^ dr = fit) - I K(t, тЫт) dr C4)
или, в операторной форме,
K°[^{t)] = fit)-KrMt)]. C5)
Решим последнее уравнение как характеристическое, рассматривая временно
правую часть как известную функцию. Тогда (см. п. 7.2-1)
^рA) =
а(ь)т-Щ^ I ;у; - ^ +bit)z{t)p.-,it)
f fir) dr
Jl Z{t) T-t
Jl t» Jl Z{t-^){t-^ -t) Jl
, C6)
где при zy ^ О следует положить Pj^-i (t) = 0. Меняя в двойном интеграле порядок
интегрирования, запишем выражение в последних круглых скобках следующим
образом:
JlV ^^ Jl Z{r^){r^ -t)
(p(r) dr.
i
Так как функция Z(t) удовлетворяет условию Гёльдера (следовательно,
ограничена) и не обращается в нуль, а K(ri,r) вблизи п = г имеет оценку
\K(ri,r)\ ^ А\г1 — т|~^ (О ^ Л < 1), то и весь интеграл
IL Z{T,){r,-t)
имеет ту же оценку, что и /Г(т1, т). Следовательно, ядро
Щг,г) = атЦ,г) - mm I /G>-) dr. C7)
7^^ Jl Z{r^){r^ -t)
является фредгольмовым. Перенося все члены, содержащие v^(t), в левую часть,
получим
^{t) + j N(t,rMr)dr = /i(t), C8)
где N(t, т) — фредгольмово ядро, определяемое формулой C7), а /i(t) —
свободный член, имеющий вид
hit) = a{t)f(i) - т^^^ [ iP-J^+b{t)Z(i)P.-,{t). C9)
Страница 244

7.4. Метод регуляризации для полных сингулярных интегральных уравнений 245
Если индекс уравнения C4) zy < О, то наряду с уравнением Фредгольма C8)
функция должна удовлетворять соотношениям
JlUl Z(t) J^^ ^ Л Z(t)
D0)
Итак, если и > О, то решение полного сингулярного интегрального
уравнения C4) приводится к решению интегрального уравнения Фредгольма C8).
Если zy < О, то уравнение C4) приводится к уравнению C8) (где нужно положить
P^_i{t) = 0) совместно с условиями D0), которые можно записать в форме
/.
Рк{т)(р{т)Aт = fk, к = 1,2,...,-и,
. , /■ K{t,T).k-i,. f f fit) ,k-i.. ^ '
где рк{т) — известные функции и fk —известные числа.
Равенства D1) есть условия разрешимости регуляризованного уравнения C8).
Однако не все они являются условиями разрешимости исходного сингулярного
интегрального уравнения C4). Часть их может оказаться условиями равносильности
этих двух уравнений. Выделим условия указанных двух типов.
Пусть среди функций рк (t) имеется h линейно независимых. Можем выбрать
нумерацию так, чтобы это были pi(t), p2(t), ..., ph(t). Тогда будем иметь
[ Pk(t)ip(t)dt = fk, /с = 1,2,...,/г. D2)
Кроме того, будут выполняться г] = \iy\ — h независимых линейных соотношений
o^jiPi{t) + \-aj\^\p\^\{t) = 0, j = l,2,...,r/.
Умножим равенства D0) последовательно на aji, aj2, ..., Q^jii^i и сложим.
Учитывая последние равенства, будем иметь
1 '"'
/(t)V^,(t)dt = 0, ф^(г)= J2^^^t'~'^ j = l,2,...,r/. D3)
'^ ^ ^ к=1
Эти равенства, не содержащие искомой функции ^(t), будут условиями
разрешимости, которым необходимо должен удовлетворять свободный член f(t) для
того, чтобы исходное сингулярное уравнение и его регуляризованное были
разрешимы. Равенства D2) будут условиями равносильности уравнений исходного
сингулярного и регуляризованного. Из решений фредгольмова уравнения C8) данному
сингулярному уравнению C4) будут удовлетворять лишь те, которые
удовлетворяют условиям D2).
Таким образом, при zy ^ О регуляризованное уравнение C8) равносильно
исходному сингулярному. Ири zy < О исходное уравнение будет равносильно
регуляризованному (вместе с общими для них условиями разрешимости D3)) и
условиям D2).
Замечание 1. Если ядро регулярной части полного сингулярного
интегрального уравнения с ядром Коши вырожденное, то способом регуляризации
Карлемана-Векуа это уравнение можно привести к исследованию системы
линейных алгебраических уравнений (см., например, С. Г. Михлин, X. Л. Смолицкий
A965)).
Замечание 2. Способ регуляризации Карлемана-Векуа иногда называют р^-
гуляризацией решением характеристического уравнения.
L
Страница 245

246 Методы решения полных сингулярных интегральных уравнений
7.4-7. Регуляризация в исключительных случаях
Рассмотрим полное сингулярное уравнение с ядром Коши
KMt)] ^ a(tMt) + ^ / ^ dr + / K(t, тЫт) dr = fit) D4)
ш Jl T-t Jl
при тех же предположениях относительно функций a{t) ± 6(t), что и в п. 7.2-4.
Представив его в виде
К°И*)] =/(i) - У" i^(i,rMr)dr,
I L
Применим метод регуляризации Карлемана-Векуа. Тогда по формуле D2) из
п. 7.2-4 получим уравнение
^{t) + Ri
/ K(t,r)(p(r)dr
:Ri[/(t)]+6(t)Z(t)P._p_i(t), D5)
где оператор Ri определяется формулой D1) из п. 7.2-4.
В выражении для второго слагаемого в левой части D5) операция Ri по
переменной t и онерация иптегрировапия по т перестановочны. Тогда уравнение D5)
можно записать в форме
^(t) + / К\ [K(t,r)]^(r) dr = Ri[/(t)] + b(t)Z(t)Pr.-p-i(t), D6)
где индекс t у символа оператора Ri указывает, что операция производится по
переменной t.
Так как оператор Ri ограниченный, то полученное интегральное
уравнение D6) является фредгольмовым и, следовательно, задача регуляризации
сингулярного уравнения D4) решена.
Из общей теории регуляризации следует, что при ly — р ^ О уравпение D4)
равносильно уравнению D6), а при и — р < О — уравнению D6) и системе
некоторых функциональных уравнений.
В заключение заметим, что для рассмотренных случаев сингулярных
интегральных уравнений теоремы Нётера оказываются, вообще говоря,
несправедливыми.
Замечание. Исключительные случаи сингулярных интегральных уравнений
с ядром Коши можно привести к уравнениям нормального типа.
7.4-8. Полное уравнение с ядром Гильберта
Рассмотрим полное сингулярное интегральное уравнением с ядром Гильберта
(см. п. 7.1-2)
а(х)ф) - ^ j'j ctg {^^) ^@ dC + £^ К(х, 0^@ dC = /(^)- D7)
Покажем, что уравнение D7) можно привести к полному сингулярному
интегральному уравнению с ядром Коши, в связи с чем вся теория последнего может
быть непосредственно перенесена на уравнение D7). Так как регулярные части
у обоих типов уравнений имеют одинаковый характер, то достаточно
воспользоваться соотношением между ядром Гильберта и ядром Коши (см. п. 6.4-5)
= -ctg ^-^]d^^-dC D8)
t 2 ^\ 2 J 2
Страница 246

7.4. Метод регуляризации для полных сингулярных интегральных уравнений
247
Откуда
-ctg
- X
d^:
dr
1 dr
~2^'
D9)
2 "\ 2 J T-t
где t = e^^ иг = е^^ — комплексные координаты точек контура L, представляющего
из себя окружность единичного радиуса.
Заменяя в уравнении D7) ядро Гильберта выражением D9) и подставляя
х = —i\iit,^ = —i\iir,d^ = —idr/r, после очевидных переобозначений приведем
уравнение D7) к полному сингулярному интегральному уравнению с ядром Коши
в форме
ai(t)ipi(t) ■
ib^(t)
f ^l(ll^r+ [ KAt,T)dT:
Jl ^-t Jl
hit)-
E0)
E1)
/L ' - ^^ JL
Коэффициент задачи Римана, соответствующий уравнению E0), имеет вид
jj(^\ ^ ai(t) +i6i(t) ^ а(ж)+г6(ж)
^ ^ a-^(t) -ib-^(t) а(х) - ib(x) '
а индекс выражается формулой
IndD(t) = 21nd[a(x)-\-ib(x)]. E2)
Пример. Произведем различными способами регуляризацию следующего
сингулярного интегрального уравнения:
K[^{t)] = {t^t-^Mt)^ ^~\ [ ^illdr--i^ [ {t^t-^){T^T-^MT)dT = 2t^
ттг Jl ^ -t 2ш Jl
E3)
где L — единичная окружность.
Регулярная часть ядра является вырожденной, поэтому тем же способом, который
применяется при решении уравнений Фредгольма с вырожденным ядром (см. разд. 5.2),
уравнение может быть сведено к исследованию характеристического уравнения и линейного
алгебраического уравнения и, следовательно, решено в замкнутой форме. Таким образом,
здесь нет необходимости в регуляризации. Однако рассматриваемое уравнение удобно для
иллюстрации на нем обших методов, поскольку окончательный результат можно получить
в замкнутом виде.
Для удобства дальнейших рассуждений предварительно решим данное уравнение.
Обозначая
E4)
— / (т + т~^)(/9(т)йт = А,
ттг Jl
E5)
2ш Jl
запишем его в форме характеристического:
(t + t-^Mt) + ^~^~' / ^^ dr = 21" + A{t + t-i).
Ш J L г — t
Для соответствуюшей краевой задачи Римана
Ф+(^) = t-Ч- (t) + t + ^АA + t-2)
индекс h' = —2 и условия разрешимости (см. п. 7.2-1) будут выполняться только при А = 0.
При этом Ф~^{г) = Z и Ф~{г) = 0. Отсюда получим решение уравнения E3) в форме
(^(t) = Ф+(^) — Ф~ (t) = t. Подставляя последнее выражение в равенство E4), убедимся
в том, что оно удовлетворяется при А = 0. Следовательно, данное уравнение разрешимо и
имеет единственное решение
ip{t) = t.
1°. Регуляризация слева. Так как индекс уравнения г^ = — 2 < О, то любой его регуляризу-
юший оператор будет иметь собственные функции (не менее двух), поэтому регуляризация
слева приводит, вообше говоря, к уравнению, не равносильному исходному.
Страница 247

248 Методы решения полных сингулярных интегральных уравнений
Рассмотрим сначала регуляризацию слева при помоши простейшего регуляризато-
ра К*°. Найдем собственные функции уравнения
K*°[io{t)] = {t^ t-^)uj{t) - ^—^ / ^^^ dr = 0.
ттг Jl т -t
Соответствуюшая краевая задача Римана
Ф+(^) =Ь^ф-{1)
имеет теперь индекс г^ = 2. Находя по формулам из п. 7.2-1 собственные функции
оператора К*°, получим
Регулярное уравнение K*°K[(/9(t)] = K*°[/(t)] на основании обшей теории (см.
п. 7.4-4) будет равносильно следуюшему сингулярному уравнению:
K[^{t)] = fit) + a^uj^it) + a^uj^it), E6)
где a-^, a2 —некоторые постоянные, которые могут оказаться или произвольными или
определенными. Учитывая E4), запишем уравнение E6) в форме характеристического:
(t^t-^)^{t)^^^^ / ^ilIdr = 2t2+A(t + t-i)+ai(l-t-2)+a2(^-^~^)-
7гг Jl т — t
Соответствуюшая ему краевая задача Римана имеет вид
Ф+(^) = t-Ч-(t) + t + ^АA + t-2) + ia^(t-^ + t-^) + ^a^il - t-2).
Ее решение представляется в форме
Ф+(^) = ^ + |-А + 1-^2, Ф"(^) = |-^^[ai^-^ + (^2 - A)z-'^ - a^z-^].
Условия разрешимости дают а^^ = О и 0=2 = ^- Тогда решение уравнения E6) определяется
формулой
^(t) = Ф+A) - ф-(^) = t + А.
Подставляя найденное значение ^(t) в равенство E4), получим тождество А — А.
Следовательно, постоянная а^ — А остается произвольной, и регуляризованное уравнение
равносильно не исходному уравнению, а уравнению
K[(^(t)] = /(t)+a2^2W,
имеюшему решение ^р{€) — t ^ А, где А — произвольная постоянная. Последнее решение
удовлетворяет исходному уравнению только при А = 0.
2°. Регуляризация справа. В качестве регуляризатора справа возьмем простейший
оператор К*°. Полагая
V9(t)=K*°[a;(t)] = (t + t-i)a;(t)- ^^^^ / ^^^dr, E7)
тгг Jl ^ -t
получим уравнение Фредгольма относительно функции u;(t):
KK*°[a;(t)] = u;{t) --^ [ [t{T^ - 1 + r'^) + 2т-^ + t'^r^ + 3 + т'^)-
47гг Jl
-2T-^T-^]u;{T)dT= \t^. E8)
Решая последнее уравнение как вырожденное, будем иметь
uo{t) = \t^ + a{t - t-^) + /5A - t-2),
где a, C — произвольные постоянные.
Таким образом, регуляризованное уравнение имеет относительно ио{1) два линейно
независимых решения, тогда как исходное уравнение E3) решалось однозначно. Подставляя
найденное значение uo{t) в формулу E7), получим
i^{t) = К*° [^^2 + a{t - t-i) + /5A - t-2)] = t,
где (p{t) — решение исходного сингулярного уравнения. Результат согласуется с обшей
теорией, так как при отрицательном индексе регуляризация справа оператором К*° является
равносильной.
Страница 248

7.4. Метод регуляризации для полных сингулярных интегральных уравнений 249
3°. Регуляризация Карлемана-Векуа. Этот способ регуляризации проводится по формулам
C6)-C9). Однако нужно помнить, что эти формулы применимы к уравнению, для которого
выполняется условие a^{t) — b'^(t) = 1. Поэтому предварительно нужно разделить
уравнение E3) на 2. Тогда будем иметь
a=i-(t + t-i), b=^{t-t-^), f{t)=t', X(t,T) = -^(t + t-i)(T + T-i),
-iw2 {t-t-^)t f t2 dr
X+(.) = l, Z(t) = (a+6)X+=t, f^(t)=^(t^t-')t'-^' '~ ^' f ^^=t,
^ 27гг Jb T T — t
(t-t-l)t(T + T-l) /• rj>rf^^(Tj_^ L(^ + ^-l).
2 47гг
+ -
27гг • 47гг
Регуляризованное уравнение имеет вид
^{t) -J-f(r^ r-'Ыг) dr = t. E9)
27гг Jl
К нему нужно добавить еше условия D1) при /с = 1, 2. Решая его как вырожденное, найдем
обшее решение ^(t) = t-\-A, где А — произвольная постоянная. Выпишем условия D2), D3).
Здесь
Pl(r) = 0, p2(r) = -i(r + r-l), f^ = j^M-t^-Ut = j^t^dt, /i=/2 = 0.
Функции p^ (t), P2@ линейно зависимы. Зависимость a^^p^ (О +''' + ^jVI /^bl @ ~ ^
(cm. П. 7.4-6) имеет вид
^iPiW+0-p2W = 0-
Отсюда условие разрешимости D3) выполняется тождественно. Условие
равносильности D2)
j Р2{т)^{т) dT = -\ j {т + т-^){т + А) dr = о
удовлетворяется лишь при А = 0. Следовательно, из множества решений регуляризованного
уравнения (^{t) = t -\- А исходному сингулярному удовлетворяет лишь функция (^{t) = t.
(•) Литература: Н. И. Мусхелишвили A968), Ф. Д. Гахов A977), S. G. Mikhlin, S. Prossdorf
A986).
Страница 249

8. Методы решения нелинейных
интегральных уравнений
8.1. Некоторые определения и замечания
8.1-1. Нелинейные интегральные уравнения Волътерра
Нелинейные интегральные уравнения Вольтерра могут быть нредставлены в
следующем виде:
K{x,t,y{t))dt = F{x,y(x)), A)
Г
J а
где К(^х, t, y(t)) —ядро нелинейного интегрального уравнения, у(х) —
неизвестная функция (а ^ X ^ Ь). Все функции в A) обычно считают ненрерывными.
Вид A) не охватывает все возможные формы нелинейных интегральных
уравнений Вольтерра, однако включает часто встречающиеся и более всего
изученные. Нелинейное интегральное уравнение A) называется интегральным
уравнением Вольтерра в форме Урысона.
В ряде случаев уравнение A) удается записать в виде
J а
K{x,t,y(t))dt = f(x). B)
Уравнение B) называют уравнением Вольтерра первого рода в форме Урысона.
Аналогично уравнение
Г K{x,t,y{t))dt = f{x
J а
у{х)- / K{x,t,y{t))dt = f{x) C)
называют уравнением Волътерра второго рода в форме Урысона.
Уравнение C) заменой и{х) = у(х) — f(x) можно привести к канонической
форме
гх
D)
и(х) = / }C(^x,t,u(t)^ dt,
J а
где /C(x,t,i^(t)) —ядро* канонического интегрального уравнения.
Ядро K[x^t^y{t)) называется выросисденным, если
п
K{x,t,y(t)) =Y,9k(x)hk{t,y(t)).
k=i
Если в уравнении A) ядро K(^x,t,y(t)) = (Э(ж,t)Ф(t,y(t)), причем Q(x,t) и
Ф(t,y) —известные функции, то получаем интегралъное уравнение Волътерра в
форме Гаммерштейна:
пх
/ Q(z,i)Ф(i,2/(i))di = F(z,2/(z)),
J а
E)
где функции у(х), Г(х,у),ФA,у) и ядро интегрального уравнения Q(x,t) обычно
считают непрерывными.
* Существуют и другие способы приведения уравнения C) к форме D), при этом вид
функции /С изменится.
Страница 250

8.1. Некоторые определения и замечания
251
В ряде случаев уравнение E) удается записать в виде
Q{x,t)^{t,y{t))dt = f{x).
рх
J а
F)
Уравнение F) называют уравнением Волътерра первого рода в форме Гаммер-
штейна. Аналогично уравнение
У{х)
Г
Q{x,t)^{t,y{t))dt = f{x)
называют уравнением Волътерра второго рода в форме Гаммерштейна.
Уравнение G) можно привести к канонической форме
и{
х)= / Q{x,t)^.{t,u{t))dt,
J а
G)
(8)
тд^и{х) = у{х) - f{x).
Замечание 1. Поскольку уравнения Вольтерра в форме Гаммерштейна
являются частным случаем уравнений Вольтерра в форме Урысона, то все
рассмотренные ниже методы для последних безусловно применимы и к первым.
8.1-2. Нелинейные уравнения с ностоянными пределами интегрирования
Нелинейные интегральные уравнения с постоянными пределами
интегрирования могут быть представлены в виде
гЬ
K{x,t,y(t)) dt = F(x,y(x)), а^х ^ р, (9)
/
J а
где К(^х, t, y(t)) —ядро нелинейного интегрального уравнения, у(х) —
неизвестная функция. Обычно все функции в (9) считают непрерывными и рассматривают
случай а = а и Р = Ь.
Вид (9) не охватывает все возможные формы нелинейных интегральных
уравнений с постоянными пределами интегрирования, однако, аналогично форме A)
для уравнений Вольтерра, включает часто встречающиеся и более всего
изученные. Нелинейное интегральное уравнение с постоянными пределами
интегрирования (9) будем называть интегральным уравнением типа Урысона.
Если уравнение (9) удается записать в виде
гъ
K{x,t,y(t))dt = f(x), A0)
/
J а
ТО A0) называют уравнением Урысона первого рода. Аналогично уравнение
у(х
)- / K{x,t,y(t))dt = f(x)
J а
(И)
называют уравнением Урысона второго рода.
Уравнение Урысона второго рода можно записать в канонической форме
гЬ
I dt. A2)
и(х) = / JC[x,t,u(t)) (
J а
Замечание 2. Условия существования и единственности решения уравнения
Урысона обсуждаются ниже в пп. 8.3-4 и 8.3-5.
Страница 251

252 Методы решения нелинейных интегральных уравнений
Если в уравнении (9) ядро K[x^t^y{t)) = Q{x^t)^{t^y{t))^ причем Q(x,t) и
Ф(t, у) —известные функции, то получаем интегральное уравнение типа
Гаммерштейна:
гЬ
0(x,t)Ф(t,y(t)) dt = F{x,y(x)), A3)
/
J а
где все функции уравнения, обычно, считаются непрерывными.
Если уравнение A3) удается записать в виде
гЬ
Q{x,t)^{t,y{t))dt = f{x), A4)
/
J а
ТО A4) пдзываУдт уравнением Гаммерштейна первого рода. Аналогично уравнение
у{х)- 1 Q(x,^{t,y(t))dt = f(x) A5)
J а
называют уравнением Гаммерштейна второго рода.
Уравнение Гаммерштейна второго рода можно записать в канонической
форме
и(х)= Q{x,t)^^{t,u{t))dt. A6)
J а
Существование канонических форм D), (8), A2) и A6) свидетельствует о том,
что различие между неоднородными и однородными нелинейными
интегральными уравнениями носит не принципиальпый характер и составляет отличительную
особенность по отношению к линейным уравнениям. Еще одной отличительной
особенностью нелинейных уравнений по отношению к линейным является
наличие, как правило, нескольких решений.
Замечание 3. Поскольку уравнения Гаммерштейна являются частным
случаем уравнений Урысона, то все рассмотренные ниже методы для последних
безусловно применимы и к первым.
(•) Литература'. Н. С. Смирнов A951), М. А. Красносельский A956), Ф. Трикоми A960),
П. П. Забрейко, А. И. Кошелев и др. A968), М. Л. Краснов, А. И. Киселев, Г. И. Макаренко
A968), М. А. Красносельский, Г. М. Вайникко и др. A969), А. Ф. Верлань, В. С. Сизиков
A986).
8.2. Нелинейные интегральные уравнения Вольтерра
8.2-1. Метод интегральных нреобразованнй
Рассмотрим интегральное уравнение Вольтерра с квадратичной
нелинейностью
^у{х) -X [ у(х- t)y(t) dt = f(x). A)
Для его решения используют преобразование Лапласа, которое с учетом теоремы
о свертке (см. разд. 1.2) приводит к квадратному уравнению относительно
изображения у(р) = £^{у(х)}:
fiy{p) - Ху^{р) = f{p).
Отсюда имеем
p±^p^-4Xf{p) ^.,
У(Р) = -^^ • B)
Страница 252

8.2. Нелинейные интегральные уравнения Вольтерра
253
Оригинал у(х) = ^~ {у(р)} (если он существует), полученный с помощью
обратного преобразования, будет решением уравнения A). Отметим, что разным знакам
в формуле для изображений B) отвечают два решения исходного уравнения.
Пример 1. Рассмотрим интегральное уравнение
у(х - t)y(t) dt = Ах"^, т > -1.
Применяя к обеим частям рассматриваемого уравнения преобразование Лапласа, с учетом
равенства /С{ж^} = Г(?тг + 1)р~^~^ имеем
у2(р) = АГ(т + 1)р-^-\
где Г(?тг) —гамма-функция. Извлекая из обеих частей квадратный корень, получим
изображения
m + l
у{р) = ±^АТ{т^1)р 2 .
Используя обратное преобразование Лапласа, находим два решения исходного
интегрального уравнения
уЛ^) ^
^АГ(т + 1)
^/ m + l л
X 2
_ уАГ(т + 1) 211^
У2{^)- /ш + 1л ^
8.2-2. Метод дифференцирования интегральных уравнений
В ряде случаев дифференцирование (однократное, двукратное и т. д.)
нелинейных интегральных уравнений с последующим исключением интегральных членов
с помощью исходного уравнения позволяет свести их к нелинейным
обыкновенным дифференциальным уравнениям. Ниже кратко перечислены некоторые
уравнения такого типа.
1°. Уравнение вида
у(х)+ / f{t,y(t))dt = g(x)
J а
C)
с ПОМОЩЬЮ дифференцировапия приводится к пелипейному уравнению первого
порядка:
Ух -\- f(x,y) - д'х{х) = О
с начальным условием у(а) = д(а).
2°. Уравнение вида
у(х)+ / (x-t)f{t,y(t))dt = g(x).
J а
D)
С помощью двукратного дифференцировапия (с последующим исключепием ип-
тегрального члена с помощью исходпого уравнения) приводится к нелинейному
уравнению второго порядка
УXX + f{x,y) - дхх{х) = 0.
Начальные условия для функции у = у(х) имеют вид
у(а) =д(а), у^(а) = gU^)-
3°. Уравпение вида
2/(х)+ re^<^-*V(i,2/(i))rfi = ff(x)
J а
E)
F)
(V)
Страница 253

254
Методы решения нелинейных интегральных уравнений
С помощью дифференцирования (с последующим исключением интегрального
члена с помощью исходного уравнения) приводится к нелинейному уравнению
первого порядка
Ух -\- f(x,y) - Ху-\-Хд(х) -gUx) = 0. (8)
Искомая функция у = у(х) должна удовлетворять начальному условию у {а) =д(а).
4°. Уравнения вида
у(х)^ [ ch[X(x - t)]f{t,y(t)) dt = д(х),
J а
у{х)+ [ sh[\{x-t)]f{t,y{t))dt = g{x),
J а
y{x)+ f cos[X(x-t)]f{t,y(t))dt = g{x),
y{x)+ f sm[\(x-t)]f{t,y(t))dt = g{x)
J a
(9)
A0)
A1)
A2)
также приводятся к обыкновенным дифференциальным уравнениям второго
порядка с помощью двукратного дифференцировапия.
Пример 2. Остановимся подробнее на уравнении A2). Дифференцируя его два раза по
ж, получим
v',(x) + \ coslX{x-t)]f(t,y{t))dt=g'Ax), A3)
J а
y'i,{x) + \f(x,y(x)) - A2 /" sin[A(rK - t)]f(t,y{t)) dt = g'^,{x). A4)
Исключая из равенства A4) интегральное слагаемое с помощью исходного уравнения,
приходим к нелинейному обыкновенному дифференциальному уравнению второго порядка
г/^', + Xf{x,y) + Х^у - Х^д(х) - g'^Jx) = 0. A5)
Полагая х = ав исходном уравнении и равенстве A3), имеем следующие начальные условия
для функции у = у{х):
у(а)=д{а), у',{а) = д',(а). A6)
Уравнение A5) с условиями A6) определяет рещение исходного интегрального
уравнения. Точные рещения нелинейных обыкновенных дифференциальных уравнений второго
порядка A5) для различных функций f{x,y) и д{х) можно найти в книгах В. Ф. Зайцева,
А. Д. Полянина A995, 1997).
8.2-3. Метод последовательных приближений
1°. Метод последовательных приближепий во многих случаях может быть
успешно применен к решению различных видов интегральных уравнений. Принцип
построения итерациопного процесса остается таким же, как и в случае липейных
уравнений. Для уравнения Вольтерра второго рода в форме Урысопа
гх
у(х) - / К{х, t, y(t)) dt = f(x), a^x ^b,
J a
соответствующее рекуррентное выражение имеет вид
гх
yk+i{x) = f{x)+ K{x,t,ykit))dt, к = 0,1,2,...
J а
В качестве начального приближения уо(х) обычно выбирается уо(х) = О или
Уо(х) = f(x).
A7)
A8)
Страница 254

8.2. Нелинейные интегральные уравнения Волътерра 255
В отличие от случая линейных уравнений метод последовательных
приближений имеет более ограниченную область сходимости. Приведем условия
сходимости итерационного процесса A8), одновременно представляющие и условия
существования решения уравнения A7). Пусть для определенности уо(х) = f(x).
Если для любой пары величин zi,Z2 имеет место соотношение
\K(x,t,Zi) - K(x,t,Z2)\ ^ (p(x,t)\zi - Z2\
и, кроме того.
причем
Г K{x,t,f{t))dt
J а
^ Ф(х),
пх пЪ пх
/ 2lj^(t)dt^N^, / / ip^(x,t)dtdx^M^,
J а J а J а
где N и М — постоянные, то последовательные приближения сходятся к
единственному решению уравнения A7) почти всюду абсолютно и равномерно.
Пример 3. Используем метод последовательных приближений для решения уравнения
"^ ' Jo 1 + *2
Если Уо(^) = О' то
dt
■- arctgx,
-t2
.2,
„3.
уЛх) = / —
Jo 1 -
, , f" 1 + arctg^t , -, о
У2(х) = / —-^ dt = arctgx + f arctg''
p 1 + arctg t + 4- arctg^ t
y^(-^ = J, TTi^ "'* =
= arctg X -\- ^ arctg^ x -\- -^ arctg^ x -\- y^- arctg^ x.
Продолжая этот процесс, можно заметить, что У]^{х) -^ tg(arctgx) = х при /с ^ оо,
т. е. у{х) = X. Подстановка этого результата в исходное уравнение подтверждает его
правильность.
Пример 4. Для нелинейного уравнения
у{х)= [\ty\t)-l]dt
Jo
необходимо получить три первых приближения. Если принять Уо(^) — ^^ '^^
гх
уЛ^) = / {-l)dt= -ж,
У2(х)= [ (tз-l)dt = -ж+^ж^
Уг(^) = Г [t{^t' - ¥' + *') -l]dt=-x+ \х^ - ^х^ + ^^10.
2°. Метод последовательных приближений применим к решению и других видов
нелинейных уравнений, например, уравнений вида
y{x) = F(x,j К{х,
t)y{t)dt],
объединяемых тем, что они разрешимы относительно у{х), а интеграл имеет х в
качестве верхнего предела. Это позволяет при численной реализации получить
решение путем движения малыми шагами по ж и линеаризации на каждом шаге, что
также обычно обеспечивает единственность результата итераций при
произвольном начальном приближении.
Страница 255

256
Методы решения нелинейных интегральных уравнений
3°. Начальное приближение существенно влияет на количество итераций для
получения результата с необходимой точностью, поэтому при его выборе обычно
пользуются некоторыми донолнительпыми соображепиями. Так для уравнения
Ау(х)
f
Jo
Q(x-t)^{y(t))dt = f(x)
где А — некоторая постоянная, хорошее начальное приближение уо{х) иногда
может быть найдено из решения следующего, в общем случае трансцендентного,
уравнения относительно уо(р):
Ауо(р) - Ш-^Ыр)) = ?(Р),
где уо(р), Q(p) и f(p) —изображения соответствующих функций, полученные
при помощи преобразования Лапласа. Если уо(р) определено, то начальное
приближение можно найти, воспользовавшись обратным преобразованием Лапласа:
уо{х) = И~^{уо{р)}.
8.2-4. Метод Ньютона-Канторовича
Достоинством итерациопных методов примепительпо к липейным
уравнениям Вольтерра второго рода является их неизбежная сходимость при слабых
ограничениях на ядро и правую часть. При решении нелинейных уравнений область
сходимости метода простых итераций сужается, а если процесс и сходится, то
во многих случаях скорость сходимости может оказаться очень низкой. Одним
из эффективных методов, позволяющих преодолеть указанные трудности,
является метод Ньютона-Канторовича. Основным назначением данного метода является
решение нелинейных интегральных уравнений второго рода с постоянными
пределами интегрирования. Тем не менее он оказывается полезным и при решении
многих задач для уравнений Вольтерра, позволяя значительно ускорить сходимость по
сравнению с методом последовательных приближений.
Применим метод Ньютона-Канторовича к решению уравнения Вольтерра
второго рода в форме Урысона
y(x) = f(x)^ [ K{x,t,y(t))dt.
J а
Тогда получим следующий итерациопный процесс:
^к
Ук(х):
г(х):
-■ Ук
■■ £к-
-i(x) -\-(pk-i(x)
.i(x)+ Г К'у
J а
x,t,yk-i(t))(pk-
i{t)dt,
I
Sk-i(x) = f{x) + / K{x,t,yk-i{t))dt-yk-i(x).
A9)
B0)
B1)
B2)
В основе алгоритма лежит решение линейного иптегрального уравнения B1)
относительно поправки ipk-i(x) с изменяющимися от шага к шагу ядром и правой
частью. Такой процесс обладает быстрой сходимостью, однако достаточно сложен
из-за необходимости решения нового уравнения на каждом итерациопном шаге.
Упрощение может быть достигнуто путем использования вместо B1) уравнения
или уравнения
(pk-i(x) = €k-i(x)-\- / Ky(x,t,yo(t))(pk-i(t)dt
J а
fX
ipk-i{x) = ek-i{x) + I Ky[x,t,ym(t))(pk-i(t)dt,
J a
B3)
B4)
Страница 256

8.2. Нелинейные интегральные уравнения Волътерра 257
ядра которых неизменны. В уравнении B4) т фиксированно и удовлетворяет
условию т < к — 1.
Уравнение B3) целесообразно использовать при удачно выбранном начальном
приближении. В противном случае можно остановиться на некотором ш-м
приближении и, начиная с него, использовать упрощенное уравнение B4).
Получающийся в результате итерациопный процесс представляет собой модифицированный
метод Ньютона-Канторовича. В припципе он сходится медленнее, чем исходный
процесс B0)-B2), однако менее сложен при вычислениях.
Пример 5. Применим метод Пьютона-Канторовича к решению уравнения
Г[Ьу\1)-1]с
■Jo
у{х)= / [ty''{t)-l]dt
производная подынтегрального выражения по у имеет вид
K;^{t,yit))=2tyit).
Принимая в качестве нулевого приближения Уо(^) = ^^ получим согласно B0) и B1), что
(Pq{x) = —X и yi{x) = —X. Далее, У2{х) = yi{x) -\- ^i{x). Согласно B2) имеем
е-^{х)= [t{-tf-l]dt^x= ^х"^
Jo
4
Уравнение относительно поправки имеет вид
ip^(x) = -2 / t'^^iit) dt + —ж^
Jo 4
и может быть решено любым из методов решения линейных уравнений Вольтерра второго
рода. В данном случае воспользуемся методом последовательных приближений, который
приводит к следуюшим результатам (номер шага указывается верхним индексом):
@) 1 4
1 — 4 ^ I 4 — 4 ^ 14 "^
^0
Ограничившись здесь вторым приближением, получим
и перейдем к третьему итерационному шагу метода Ньютона-Канторовича:
Р (^^ - ^_^10 ^^13 ^^16 I 1 ^19 , 1 ^22
^2\^^) — 160 "^ 1820 "^ 7840 "^ ^ 9340 "^ ^ 107800 "^ '
-2\^^) — 160 1820 7840 ^ 9340 '
^^{х) = e^ix) + 2 /" t{-t + ^t^ - -^t" + ^ti0)(^2 W dt.
Jo
Ограничившись нулевым приближением при решении последнего уравнения, получим
УЗ^-^у» — -^ ^ 4 "^ 14 "^ ^ 112 "^ 1820 7840 ^ 9340 ^ 107800 *
Применение метода последовательных приближений к исходному уравнению приводит к
такому же результату на четвертом шаге.
При численном решении интеграл, как обычно, заменяется квадратурной
формулой. Основная трудность реализации метода в этом случае может заключаться
в определении производной от ядра. Задача упрощается, если ядро задано в виде
аналитического выражения, допускающего дифференцирование в аналитическом
виде. Если же ядро задано таблицей, то дифференцировапие должно выполняться
численно.
17 А. В. Манж:иров, А. Д. Полянин
Страница 257

258 Методы решения нелинейных интегральных уравнений
8.2-5. Метод коллокации
Применительно к решению уравнений Вольтерра первого рода в форме Уры-
сона
/■
J а
K{x,t,y{t))dt = f{x), a^x^b, B5)
метод коллокации состоит в следующем. Промежуток [а, Ь] разбивается на
Л^ участков, на каждом из которых искомое решение представляется в виде
функции определенного вида
у(х) = Ф(х, Ai,A2,..., Am), B6)
зависящей от свободных параметров Ai (i = 1,2,..., т).
Решаемое уравнение записывается на каждом (/с Ч- 1)-м участке Хк ^ х ^Xk-\-i
(k = 0,l,...,N - 1) в виде
Г K{x,t,y(t)) dt = f(x) - ^fc(x), B7)
где интеграл
y^k(x)= [ ' K{x,t,y(t))dt B8)
J a
всегда может быть вычислен по известному на промежутке а^х^Хк
приближенному решению у(х), полученному предварительно для к — 1 участков. Начальное
значение у (а) искомого решения находится каким-либо вспомогательным
способом или считается заданным.
Для решения уравнения B7) используется представление B6), а свободные
параметры Ai (i = 1,2,..., т) определяются из условия обращения в нуль невязок
6\Ai, Xk,j)
I "^^^ K{xk,j,t,^{t,Ai,... ,Ат)) dt - f{xk,j) -^k{xk,j), B9)
где Xk,j {j = 1,2,..., m) — узлы, соответствующие разбиению отрезка [xk,Xk+i\
на т частей (подотрезков). Выражение B9) представляет собой систему т
уравнений относительно Ai, А2, ..., Ащ.
Для удобства вычислений искомое решение на участке целесообразно
представлять в виде какого-либо полипома
т
y(x) = Y,AiVi(x), C0)
i=l
где ^i(x)—липейно независимые координатные функции. В качестве ^i(x)
часто выбираются степенные и тригонометрические полиномы, в том числе,
(pi(x) = ж""-^.
в приложениях конкретный вид функций ^i(x) в формуле C0), а также вид
функции Ф в B6), иногда задается из физических соображений или определяется
структурой решения более простого модельного уравнения.
8.2-6. Метод квадратур
К решению нелинейного уравнения Вольтерра можно применить метод,
основанный на использовании квадратурных формул. Методика составления
аппроксимирующей системы уравнений остается такой же, как и в линейном случае (см.
п. 3.10-1).
Страница 258

8.2. Нелинейные интегральные уравнения Вольтерра 259
1°. Рассмотрим нелинейное уравнение Вольтерра второго рода в форме Урысона
у{х)- Г K{x,t,y{t))dt = f{x) C1)
J а
на отрезке а ^ х ^ Ь. Будем считать, что K(^x,t,y(t)) и f(x) —непрерывные
функции.
На основании уравнения C1) найдем у (а) = f(a). Возьмем постоянный шаг
интегрирования h и рассмотрим дискретное множество точек Xi = а -\- h(i — 1),
где г = 1,2,...,гг. В точках х = Xi уравнение C1) принимает вид
у{
Xi) - I ' K{xi, t, y{t)) dt = f{xi). C2)
J a
Выбирая Xi в качестве узлов квадратурной формулы (см. п. 2.7-1), для которой
ошибкой аппроксимации будем пренебрегать, и заменяя ею интеграл в
выражении C2), получим следующую систему нелинейных алгебраических (или
трансцендентных) уравнений:
i
yi=fi, yi-^AijKij{yj) = fi, г = 2,3, ...,n, C3)
j=i
где Aij —коэффициенты квадратурной формулы на отрезке [а,Жг], yi
—приближенные значения решения у(х) в узлах Xi, fi = f(xi) и Kij(yj) = K(xi,tj,yj).
Соотношения C3) можно записать в виде последовательности рекуррентных
нелинейных уравнений
г-1
У1= fi, Vi- AiiKii(yi) = fi-\-Y^ AijKij(yj), г = 2,3,... ,n, C4)
для определения приближенного значения искомого решения в узловых точках.
2°. Применительно к уравнению Вольтерра второго рода в форме Гаммерштейна
у{х)- г Q{x,t)^{t,y{t))dt = f{x) C5)
J а
основные соотношения метода квадратур имеют вид {xi = а)
г
yi=fi, yi-^AijQij^j(yj) = fi, г = 2,...,гг, C6)
j=i
где Qij = Q(xi,tj) и ^j(yj) = Ф(tj,yj). Они приводят к последовательности
нелинейных рекуррентных уравнений
г-1
У1= fi, yi- AiiQiiФi{yi) = fi-\-Y^ AijQijФj{yj), г = 2,... ,n, C7)
решения которых дают приближенные значения искомой функции.
Пример 6. При решении уравнения
У(х)- Г e-^^-'^y\t)dt-.
Jo
О ^ж ^0,1,
где Q(x,t) = е *^^ ^\ Ф{1,уA)) = y^(t) и f(x) = е ^, аппроксимируемое выражение
имеет вид
у{х,)- r\-^-^-'^y\t)dt = e--^.
Jo
17*
Страница 259

260
Методы решения нелинейных интегральных уравнений
Используя для замены интеграла формулу трапеций (шаг /г = О, 02) и отыскивая решение
в узлах х^ = О, 0,02, 0,04, 0,06, 0,08, 0,1, получаем согласно C3) следуюшую систему
расчетных соотношений:
г-1
2,3, ...,6.
,6.
j=i
Таким образом, для нахождения приближенного решения необходимо решить квадратное
уравнение для каждого значения у^, что позволяет записать
г ^-1 П 1/2
У, = 50 ± 50 1 - О, 04(Д + 5] О, 02 Q.^yf^
(•) Литература: П. П. Забрейко, А. И. Кошелев и др. A968), М. Л. Краснов, А. И. Киселев,
Г. И. Макаренко A968), А. Ф. Верлань, В. С. Сизиков A986).
8.3. Уравнения с постоянными пределами
интегрирования
8.3-1. Нелинейные уравнения с вырожденными ядрами
1°. Рассмотрим уравнение Гаммерштейна второго рода в канонической форме
у(х)= [ 0(x,t)Ф(t,y(t))
J а
dt.
где Q(x,t), Ф(t, у) —заданные функции, у(х) — искомая функция.
Пусть Q(x, t) —вырожденное ядро, т. е.
т
Q(x,t) = y^^gk(x)hk(t).
k=i
В этом случае уравнение A) нринимает вид
У{х)
= Y.9k(x) / hk(m{t,y(t))dt.
k=i ^"^
Положим
Ak= hk{t)^{t,y{t))dt, к = 1,2,...,т,
J а
где Ak — пока неизвестные постоянные. Тогда в силу C) будем иметь
т
A)
B)
C)
D)
E)
Подставляя в равенства D) выражение E) для у(х), получим в общем случае
т трансцендентных уравнений вида
Ак = ^fc(Ai,A2,...,Am), А; = 1,2,...,ш, F)
содержащих т неизвестных величин Ai, ^2, ..., Am-
В случае, когда ^(t,y) —многочлен относительно у, т. е.
Ф(t,y) = po(t) +pi{t)y + • • • +Pn(%", G)
гдеро(t),pi(t),... ,рп(t) есть, например, непрерывные функции t на отрезке [а, 6],
система F) превращается в систему нелинейных алгебраических уравнений
относительно Ai, ^2, ..., Am.
Число решений интегрального уравнения C) равно числу решений
системы F). Каждое решение системы F) порождает решение E) интегрального
уравнения.
Страница 260

pb ^
+ / fm(t,h(t)^Y,Xkgk(t))dt = 0, ш = 1,2,...,гг. A0)
8.3. уравнения с постоянными пределами интегрирования 261
2°. Рассмотрим уравнение Урысопа второго рода с упрощенным вырожденным
ядром следующего вида:
Его решение имеет вид
п
у(х) = h(x) + ^ Хк9к(х), (9)
fc=i
где постоянные Хк определяются путем решения алгебраической
(трансцендентной) системы уравнений
рЬ
к=1
Различным корням этой системы отвечают различные решения нелинейного
интегрального уравнения. Возможны ситуации, когда (действительные) решения
отсутствуют.
Решение уравнения Урысопа второго рода с вырожденным ядром в общей
форме
/(х,у(х))+^ H29k{x,y(x))hk{t,y(t))\dt = () A1)
можно записать в неявном виде
п
f{x, у{х)) + ^ Хкдк (ж, у{х)) = О, A2)
к=1
где параметры Хк определяются путем решения системы алгебраических
(трансцендентных) уравнений
Хк-Нк(Х) = 0, к = 1,2,...,п,
Нк(Х)= hk{t,y{t))dt, Л = {Л1,Л2,...,Л.}.
J а
в систему A3) следует подставить функцию у{х) = у(х,Х), которая получается
путем разрешения A2).
Число решений интегрального уравнения определяется числом решений,
полученных из A2) и A3). Возможны ситуации, когда решения отсутствуют.
Пример 1. Решим интегральное уравнение
у(х) = Л / xty^{t)dt
Jo
A4)
с параметром Л. Положим
А= [ ty^{t)dt. A5)
Тогда из A4) будем иметь
у(х) = ХАх. A6)
Подставляя у(х) в форме A6) в соотношение A5), получим
А= [ tX^A^t^dt.
Jo
Страница 261

262 Методы решения нелинейных интегральных уравнений
Откуда
5
При Л > О уравнение A7) имеет три решения:
А=\\^А^. A7)
О, А^
5 л _ / ^
л^' ^^- V л^'
Следовательно, интегральное уравнение A4) также имеет три решения при любом Л > 0:
при л ^ о уравнение A7) имеет только одно тривиальное решение у{х) = 0.
у^(х) = 0, У2(х) = \/^^х, у^(х) = -^ —X.
8.3-2. Метод интегральных нреобразованнй
1°. Рассмотрим нелинейное интегральное уравнение с квадратичной
нелинейностью на полуоси
fiy{x)-xj°° jy[j)y(t)dt = f(x). A8)
Для его решения используют преобразование Меллина, которое с учетом теоремы
о свертке (см. разд. 7.3) приводит к квадратному уравнению относительно
изображения y(s) = ^Ш{у(х)}:
fiy{s)-Xy'{s) = J{s)
Отсюда имеем
y(s) = '-^^ • A9)
Оригинал у(х) = ШТ~ {y(s)} (если он существует), полученный с помощью
обратного преобразования, будет решением уравнения A8). Разным знакам в
формуле для изображений A9) отвечают два решения исходного уравнения.
2°. С помощью преобразования Меллина можно решать также нелинейные
интегральные уравнения вида
/»оо
(х)-Х t^y{xt)y(t)dt = f{x).
Jo
у{х) - А / fy{xt)y{t) dt = f(x). B0)
Преобразование Меллина (см. табл. 2 из разд. 1.3) приводит B0) к
функциональному уравнению для изображения y(s) = Ш1{у(ж)}:
vis) - Ху(8)уA - S + /3) = /(s). B1)
Заменяя в B1) s на 1 — s Ч- /?, имеем следствие
y{l-s + p)- \y{s)y{l -s + p) = J{l-s + p). B2)
Исключая из B1) и B2) квадратичный член, получим связь
yis) - J{s) = y{l-s + p)-Jil-s + р). B3)
Выражая отсюда у{1 — s -\- C) ia подставляя в B1), приходим к квадратному
уравнению относительно изображения
\y\s) - [1 + lis) - 7A - s + P)\y{s) + /(s) = 0. B4)
Разрешив B4) относительно y{s) с помощью обратного преобразования Меллина
можно найти решение исходного интегрального уравнения B0).
Страница 262

8.3. Уравнения с постоянными пределами интегрирования 263
8.3-3. Метод дифференцирования интегральных уравнений
B5)
B6)
B7)
1°. Рассмотрим уравнение
у{х)+ f \x-t\f{t,y(t))dt = g{x).
J а
Раскроем модуль в подынтегральном выражении. В результате получим
у{х)+ [ {x-t)f{t,y{t))dt+ [ {t-x)f{t,y{t))dt = g{x).
J а J X
Дифференцируя B6) по ж, имеем
рх рЪ
У'х{х)+ f{t,y{t))dt- f{t,yit))dt = gUx).
J а J X
Дифференцируя B7), приходим к следующему обыкновенному
дифференциальному уравнению второго порядка для функции у = у(х):
Ухх + ^f(x,y) = g'L{x). B8)
Выведем теперь граничные условия для уравнения B8). Считаем, что
—оо<а<6<оо. Полагая в B6) ж = а и ж = 6, имеем два следствия:
у{а)+ ( (t-a)f{t,y{t))dt = g(a),
ь B9)
2/F)+ / {b-t)f{t,y{t))dt = g{b).
J а
Выразим из уравнения B8) функцию f(x,y) и подставим в B9). После иптегри-
ровапия по частям получим искомые граничные условия для функции у(х):
у (а) + у(Ь) + F - а) [gUb) - yUb)] = 9(a) + 9(b), ^^^^
у(а) + у(Ь) -\-(а-Ь) [gU^) - Ух(а)] = 9(a) + 9(b)-
Отметим полезное следствие этих равенств:
Ух (а) + Ух (Ь) = 9х (а) + 9х (Ь),
которое можно использовать вместо одного из условий C0).
Уравнение B8) вместе с граничными условиями C0) описывает решение
исходного интегрального уравнения (отметим, что решений может быть несколько).
2°. Уравнение вида
у(х) + [ e^l^-*l/(i,2/(i)) dt = д(х) C1)
J а
С ПОМОЩЬЮ двукратного дифференцировапия (с последующим исключепием ипте-
грального члена с иснользованием исходного уравнения) приводится к
нелинейному уравнению второго порядка
у^^ + 2Xf(x,y) - Х^у = g'L(x) - \^д(х). C2)
О граничных условиях для этого уравнения см. в книге А. Д. Полянина, А. В.
Манжирова A998, стр. 392).
3°. К обыкновенным дифференциальным уравнениям второго порядка с помощью
дифференцирования приводятся также уравпения вида
у(х)+ [ sh{X\x - t\)f{t,y(t)) dt = д(х), C3)
J а
у{х)+ [ sm{X\x-t\)f{t,y{t))dt = g{x). C4)
J а
Об этих уравнениях см. в книге А. Д. Полянина, А. В. Манжирова A998, стр. 393).
Страница 263

264 Методы решения нелинейных интегральных уравнений
8.3-4. Метод последовательных приближений
Рассмотрим нелинейное интегральное уравнение Урысона в канонической
форме
у(х) = / JC{x,t,y(t))dt, а
J а
^х^Ь. C5)
Итерационный процесс для этого уравнения строится по формуле
yk(x)= [ K:{x,t,yk-i(t))dt, к = 1,2,... C6)
J а
Если функция JC(x,t,y) непрерывна вместе с производной JCy(x,t,y) по
совокупности переменных а ^ х ^ Ь, а ^ t ^ Ь, \у\ ^ р и
пЪ пЪ
I sup|/C(x,t,y)|dt ^ р, / sup|/C^(x,t,y)|dt ^/3 < 1, C7)
Jay Jay
ТО при любой непрерывной функции начального приближения уо{х) из области
{\у\ ^ р.а^х ^Ь} последовательные приближения C6) сходятся к непрерывному
решению у*(ж), которое расположено в той же области и единственно в ней.
Скорость сходимости определяется неравенством
* C^
\У (ж) - ук(х)\ ^ sup \yi(x) - уо(х)\, a^x^b, C8)
J- Р ж
которое дает априорную оценку погрешности /с-го приближения. Апостериорная
и, вообще говоря, более точная оценка имеет вид
|у*(ж) -ук{х)\ ^ sup|yfc(x) -yk-i{x)\, а^х ^b. C9)
J- Р ж
Решение уравнения вида C5) с дополнительным слагаемым f(x) в правой
части может быть построено аналогичным образом.
Пример 2. Применим метод последовательных приближений для решения уравнения
У(х)= xty^(t)dt- ^х^1.
Jo
Соответствующая рекуррентная формула имеет вид
Ук{х)= [ xtyl_^{t) dt - ^х ^ 1, к = 1,2,...
Jo
В качестве начального приближения возьмем Уо(^) — ^- Вычисления показывают, что
у^(ж) = 1+ 0,083ж, у2{х) = 1^0,Ых, у^{х) = 1^0,lSx,
Уз(ж) = 1 + 0,27ж, уд{х) = 1^0,26х, ^^(ж) = 1 + О, 29ж,
y^Q{x) = 1 + 0, 318 ж, У1г{х) = 1 + 0, 321 ж, yigix) = 1 + 0, 323 ж, ...
Таким образом, приближения сходятся к точному решению у(ж) = 1 + -^ж. Видно, что
скорость сходимости очень мала.
В п. 8.3-5 это уравнение будет решено более эффективным методом.
8.3-5. Метод Ньютона-Канторовича
Решение нелинейных интегральных уравнений является сложной задачей
вычислительной математики, что обусловлено трудностями как принципиальпого,
Страница 264

8.3. Уравнения с постоянными пределами интегрирования 265
так и вычислительного характера. В связи с этим разрабатываются методы,
специально предназначенные для решения нелинейных уравнений. К таким методам
относится метод Ньютона-Канторовича, который во многих случаях позволяет
решать вопросы обеспечения и ускорения сходимости итерациопных процессов.
Рассмотрим данный метод примепительпо к уравнению Урысона в
канонической форме C5). Птерационный процесс строится следующим образом:
Ук{х) = yk-i(x) -\-ipk-i(x), к = 1,2,..., D0)
(pk-i(x) = €k-i(x)-\- / JCy{x,t,yk-i(t))(pk-i(t)dt, D1)
J а
Sk-i(x) = / JC{x,t,yk-i(t)) dt-yk-i(x). D2)
J a
Ha каждом шаге алгоритма решается линейное иптегральное уравнение
относительно поправки ipk-i(x). Процесс D0) при онределенных условиях обладает
быстрой сходимостью, однако достаточно сложен, поскольку на каждой итерации
необходимо получать новое ядро JCy(^x,t,yk-i(t)) для уравнения D1).
Упрощение алгоритма достигается путем использования уравнения
(pk-i(x) = Sk-i(x)-\- / JCy{x,t,yo(t))(pk-i(t)dt D3)
J а
вместо D1). При удачном выборе начального приближения интегральные
операторы в D1) и D3) отличаются мало. При этом ядро в D3) в процессе решения
остается неизменным.
Метод приближенного решения, состоящий в нрименении формул D0), D2)
и D3), называется модифицированным методом Ньютона-Канторовича. В
принципе он сходится медленнее, чем исходный (немодифицировапный) метод, однако
менее сложен при вычислениях и потому часто оказывается предпочтительным.
Пусть функция JC(x,t,y) непрерывна вместе с производными JCy(x,t,y) и
JCyy(x,t,y) по совокупности переменных а^х^Ь, a^t^bn выполнены
следующие условия:
1°. При начальном приближении уо(х) ядро JCy[x,t,yo(t)) имеет резольвенту
lZ{x,t) такую, что
гъ
\n(x,t)\dt ^ А< оо, а^х ^Ь.
I
J а
2°. Невязка €о(х) уравнения D2) для приближения уо(х) удовлетворяет
неравенству
\£о(х)\
^ В < оо.
/ JC{x,t,yo(t)) dt - уо(х)\
I «^а I
3°. в области \у(х) — уо(х)\ ^ 2A Ч- А)В имеет место соотношение
/ sup\JCyy(x,t,y)\ dt ^ D < оо.
J а у
4°. Постоянные А, В и D подчинены условию
Н= {l-\-AfBD^ ^.
Тогда при выполнении условий 1°^° процесс D0) сходится к решению у*(х)
уравнения C5), расположенному в области
\у(х) - уо(х)\ ^ A - VT^^2H)H-\l - А)В, а^х^Ь,
Страница 265

266 Методы решения нелинейных интегральных уравнений
и единственному в области
\у(х) - уо(х)\ ^ 2A + А)В, а^х^Ь.
Скорость сходимости определяется оценкой
\у*{х) - yk{x)\ ==: 2'-\2Hf-\l - А)В, a^x^b.
Таким образом, приведенные условия устанавливают сходимость алгоритма,
существование, область расположения и область единственности решения нелинейного
уравнения C5). Они также предъявляют определенные требования к начальному
приближению уо(х), выбор которого является важной самостоятельной задачей,
не имеюгцей единого подхода. Обычно начальное приближение определяется либо
более детальным априорным анализом решаемого уравнения, либо физическими
соображениями, вытекающими из существа задачи, описываемой этим
уравнением. При удачном выборе начального приближения метод Ньютона-Канторовича
обеспечивает высокую скорость сходимости итерационного процесса для
получения приближепного решения с заданной точностью.
Замечание. Пусть правая часть уравнения C5) содержит донолнительпое
слагаемое f(x). Тогда такое уравнение может быть представлено в виде C5) с
подынтегральным выражением K(^x,t,y(t)) -\- (b — a)~^f(x).
Пример 3. Применим метод Ньютона-Канторовича для решения уравнения
у(х) = / xty^(t) dt - -^х + 1. D4)
В качестве начального приближения возьмем Уо(^) — 1- Определим согласно D2) невязку:
^о(^) = / ^^У%{^) ^^ - -Т2^ + 1 - Уо(^) = X tdt- -j^x + 1 - 1 = -^х.
Jo Jo
Необходимая в расчетах производная от ядра /С(ж, t, у) = xty^(t) имеет вид JCy(x, t, у) =
= 2xty(t). В соответствии с D1) составим относительно ^q{x) уравнение
V^o(^) = -W^ + 2а? / tyQ(t)^Q(t) dt,
Jo
в котором ядро оказывается вырожденным, что позволяет получить ^q(x) = -^х. Теперь
определим первое приближение искомой функции: yi{x) = Уо(^) +V^o(^) — ^ + т^*
Продолжая итерационный процесс, получим
е^{х) = [ xt{l + ^t) dt + A - -^х) - A + ^х) = -^х.
Jo
уравнение относительно ^i{x) имеет вид
V^iW= Ж^ + 2^ / t{^ ^ it) dt ^ {1 - ^х) - {1 ^ ^х),
Jo
и его решение ^i(x) = -^х. Отсюда У2(х) = 1 + -^х -\- -^х = 1 + 0, 325ж. Максимальное
отличие точного решения у(х) = 1 -\- ^-х от приближенного решения У2{х) наблюдается
при ж = 1 и составляет менее 0,5%.
Данное решение не единственное. Второе решение также может быть получено, если
в качестве начального приближения выбрать функцию Уо(^) — ^ + О, 8ж. В этом случае
повторение приведенной выше последовательности приближений приводит к следуюшим
результатам:
у^(ж) = 1+ 0,82ж, У2{х) = 1^1,13х, y^{x) = 1^0,9Sx, ...,
Страница 266

8.3. Уравнения с постоянными пределами интегрирования
267
и последующие приближения стремятся к точному решению у{х) = 1 -\- х.
Мы видим, что скорость сходимости итерационного процесса связанного с методом
Ньютона-Канторовича существенно выше, чем для случая метода последовательных
приближений (см. пример 2 из п. 8.4-4).
Сравним также скорости сходимости итерационных процессов метода Ньютона-
Канторовича и модифицированного метода. Применение модифицированного метода дает
/Cq
0
К
0,25
^2
0,69
/Сз
0,60
/с^
0,51
Ч
0,44
/Cg
0,38
/С7
0,36
/Cg
0,345
у^{х) = 1 + /с^ж;
Итерационный процесс модифицированного метода также сходится к точному
решению у(х) = 1 + -|-ж.
Видно, что модифицированный метод Ньютона-Канторовича менее эффективен, чем
метод Ньютона-Канторовича, но более эффективен, чем метод последовательных
приближений (см. пример 2 из п. 8.4-4).
8.3-6. Метод квадратур
К решению любого нелинейного уравнения можно применить метод,
основанный на использовании квадратурных формул. Методика составления
аппроксимирующей системы уравнений остается такой же, как и в линейном случае (см.
п. 5.18-1). Рассмотрим ее на примере уравнения Урысона второго рода
У
Положим X
(х)- [ K{x,t,y(t))dt = f(x)
J а
, гг), тогда
= Xi (i = 1,2,.
y(xi)- / K{xi,t,y(t))dt = f(xi)
J a
a ^ X ^
г = 1,2,..
D5)
D6)
Воспользовавшись квадратурной формулой из п. 5.18-1 и пренебрегая ошибкой
аппроксимации, преобразуем соотношения D6) в систему нелинейных уравнений
. ,n,
D7)
относительно приближенных значений yi решения у{х)ъ узлах Ж1,Ж2, ...,Xn, где
fi = f(xi), Kij(yj) = K(xi,tj,yj), a Aj —коэффициенты квадратурной формулы.
Решение нелинейной системы D7) дает значения yi, у2, •••, Уп, по
которым путем интерполяции находится приближенное решение интегрального
уравнения D5) на всем отрезке [а,Ь]. В качестве аналитического выражения
приближенного решения уравнения может быть взята функция
у{х) = f{x) -\-^AjK{x,Xj,yj).
D8)
8.3-7. Метод регуляризации Тихонова
Применительно к нелинейному интегральному уравнению Урысона первого
рода
J а
K{x,t,y{t))dt = f{x),
с ^ ж ^
D9)
Страница 267

268 Методы решения нелинейных интегральных уравнений
где f(x) G L2(c,d) и y(t) G L2(a,b), метод регуляризации Тихонова приводит к
регуляризованному нелинейному интегральному уравнению в форме
ауо,(х)-\- / M{t,x,yo,(t),yo,(x))dt = F{x,yo,(x)), а ^ х ^ Ь, E0)
J а
I'd
M{t,x,y(t),y(x))= I K{s,t,y{t))K'y{s,x,y{x))ds, E1)
,y{x))= / K'y{t,x,y{x))f(t)dt
J С
F{x,y{x))= I Ky{t,x,y{x))f{t)dt, E2)
где a — параметр регуляризации.
Метод квадратур с использованием формулы транеций, например, приводит
уравнение E0) к системе нелинейных алгебраических уравнений. Приближенное
решение D9) строится по принципу, описанному для линейных уравнений (см.
разд. 4.8).
(•) Литература: Н. С. Смирнов A951), Ф. Трикоми A960), П. П. Забрейко, А. И. Кошелев
и др. A968), А. Ф. Верлань, В. С. Сизиков A986).
Страница 268

Список литературы
Абрамовщ М, Стиган И. Справочник по специальным функциям.—М.: Наука,
1979.
Александров В. М. Асимптотические методы механики сплошной среды: задачи со
смешанными граничными условиями // ПММ. Т. 57. Вып. 2. 1993.
Александров В. М., Коваленко Е. В. Задачи механики сплошных сред со
смешанными граничными условиями. —М.: Наука, 1986.
Арутюнян Н. X. Некоторые вопросы теории ползучести. — М.-Л.: Гостехиздат,
1952.
Арутюнян Н. X. Плоская контактная задача теории ползучести // ПММ. Т. 23.
Вып. 5. 1959.
Бабенко Ю. И. Тепломассообмен: Метод расчета тепловых и диффузионных
потоков. — М.: Химия, 1986.
Бахвалов Н. С. Численные методы.—М.: Наука, 1973.
Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Том 1. — М.: Наука,
1973.
Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Том 2. — М.: Наука,
1974.
Бейтмен Г., Эрдейи А. Таблицы иптегральных преобразований. Том 1. — М.:
Наука, 1969.
Беллман Р., Кук К Дифференциальпо-разностные уравнения.—М.: Мир, 1967.
Белоцерковский С. М, Лифанов И. К Численные методы в сингулярных
интегральных уравнениях. —М.: Наука, 1985.
Бутковский А. Г. Характеристики систем с распределенными параметрами. —
М.: Наука, 1979.
Верланъ А. Ф., Сизиков В. С. Методы решения интегральных уравнений с
программами для ЭВМ. — Киев: Наукова Думка, 1986.
Виарда Г. Интегральные уравнения.—М.-Л.: ОНТП, 1933.
Волътерра В. Теория функционалов, интегральных и интегро-дифференциальных
уравнений.—М.: Наука, 1982.
Вороеич И. И., Александров В. М, Бабешко В. А. Неклассические смешанные
задачи теории упругости. — М.: Наука, 1974.
Гахов Ф. Д. Краевые задачи. — М.: Наука, 1977.
Гахов Ф. Д., Черский Ю. И. Уравнения типа свертки. — М.: Наука, 1978.
Гохберг И. Ц., Крейн М. Г. Теория вольтерровых операторов в гильбертовом
пространстве и ее приложения. —М.: Наука, 1967.
Градштейн И. С, Рыэюик И. М. Таблицы интегралов, сумм, рядов и
произведений.— М.: Наука, 1975.
Гурса Э. Курс математического анализа, т. 3, часть П. Интегральные уравнения.
Вариационное исчисление.—Л.: Гостехиздат, 1934.
Гусейнов А. И., Мухтаров X. Ш. Введение в теорию нелинейных сингулярных
уравнений.—М.: Наука, 1980.
Демидович Б. П., Марон И. А., Шувалова Э. 3. Численные методы анализа. — М.:
Физматгиз, 1963.
Дёч Г. Руководство к практическому применению преобразования Лапласа и
Z-преобразования. — М.: Наука, 1971.
Страница 269

270 Список ЛИТЕРАТУРЫ
Диткин В. А., Прудников А. П. Справочник по операциопному исчислению. —М.:
Наука, 1965.
Диткин В. А., Прудников А. П. Интегральные преобразования и операционное
исчисление. — М.: Наука, 1974.
Забрейко П. П., Кошелев А. П., Красносельский М. А. и др. Интегральные
уравнения.— М.: Наука, 1968.
Зайцев В. Ф., Полянин А. Д. Справочник по линейным обыкновенным дифферен-
циальным уравнениям. —М.: Факториал, 1997.
Зайцев В. Ф., Полянин А. Д. Справочник по нелинейным обыкновенным
дифференциальным уравнениям.— М.: Факториал, 1997.
Зайцев В. Ф., Полянин А. Д. Справочник по обыкновенным дифференциальным
уравнениям: Точные решения.—М.: Наука, 1995.
Каландия А. И. Математические методы двумерной упругости. — М.: Наука, 1973.
Камке Э. Справочник по обыкновенным дифференциальным уравнениям. —М.:
Наука, 1976.
Канторович Л. В., Крылов В. И. Ириближенные методы высшего анализа. — М.-Л.:
Физматлит, 1962.
Канторович Л. В., Акилов Г. П. Функциональный анализ. — М.: Наука, 1977.
Коллатц Л. Числепные методы решения дифференциальных уравнений. — М.:
Иностранная литература, 1958.
Колмогоров А. П., Фомин С. В. Элементы теории функций и функционального
анализа. — М.: Наука, 1976.
Корн Г., Корн Т. Справочник но математике. —М.: Наука, 1984.
Краснов М. Л., Киселев А. К, Макаренко Г. И. Интегральные уравнения. —М.:
Наука, 1968.
Красносельский М. А. Топологические методы в неории нелинейных интегральных
уравнений. — М.: Гостехиздат, 1956.
Красносельский М. А., Вайникко Г. М., Забрейко П. П. и др. Ириближенное решение
операторных уравнений. — М.: Наука, 1969.
Крейн М. Г. Интегральные уравнения на полупрямой с ядром, зависящим от
разности аргументов // Успехи математических наук. Т. 13. Вып. 5 (83). 1958.
Крылов, В. П., Бобков, В. В., Монастырный, П. И. Начала теории вычислительных
методов. Интегральные уравнения, некорректные задачи и улучшение
сходимости.— Минск: Наука и техника, 1984.
Курант Р., Гильберт Д. Методы математической физики. Том 1. — М.-Л.: Физмат-
гиз, 1951.
Лаврентьев М. М., Романов В. Г., Шишатский С. П. Некорректные задачи
математической физики и анализа. — М.: Наука, 1980.
Лифанов И. К. Метод сингулярных интегральных уравнений и численный
эксперимент.—М.: ТОО "Янус", 1995.
Ловитт У. В. Линейные интегральные уравнения. —М.: Гостехиздат, 1957.
Манлсиров А. В., Полянин А. Д. Интегральные уравнения. —М.: МГАИИ, 1998.
Математическая энциклопедия, т. 2. —М.: Советская энциклопедия, 1979.
Математическая энциклопедия, т. 5. —М.: Советская энциклопедия, 1985.
Михайлов Л. Г. Интегральные уравнения с ядром, однородным степени —1. —
Душанбе: Дониш, 1966.
Михлин С. Г. Интегральные уравнения и их приложения. — М.-Л.: Гостехиздат,
1949.
Михлин С. Г. Лекции по липейным интегральным уравнениям. —М.: Физматгиз,
1959.
Страница 270

Список литературы 271
Михлин С. Г., СмолщкийХ. Л. Ириближенные методы решения дифференциальпых
и иптегральных уравнений. —М.: Наука, 1965.
Мусхелишеили Н. И. Сингулярные иптегральные уравнения.—М.: Наука, 1968.
Мюнтц Г. М. Интегральные уравнения.—Л.: Гостехиздат, 1934.
Никольский С. М. Квадратурные формулы.—М.: Наука, 1979.
Нобл Б. Ирименение метода Винера-Хопфа для решения дифференциальпых
уравнений в частных производных. — М.: Изд-во иностранной литературы,
1962.
Петровский И. Г. Лекции но теории интегральных уравнений. —М.: Гостехиздат,
1951.
Полянин А. Д., Манлсирое А. В. Метод модельных решений в теории линейных
интегральных уравнений // Докл. АН. Т. 354. № 1. 1997.
Полянин А. Д., Манэюирое А. В. Справочник но интегральным уравнениям: Точные
решения. — М.: ^'Факториал", 1998.
Привалов И. И. Интегральные уравнения.—М.-Л.: ОНТИ, 1935.
Прудников А. П., Брычкое Ю. А., Маричее О. И. Интегралы и ряды. Элементарные
функции.—М.: Наука, 1981.
Прудников А. П., Брычкое Ю. А., Маричее О. И. Интегралы и ряды. Снециальные
функции.—М.: Наука, 1983.
Прудникое А. П., Брычкое Ю. А., Маричее О. И. Интегралы и ряды. Донолнитель-
ные главы. — М.: Наука, 1986.
Рисе Ф., Сёкефалъеи-Падъ Б. Лекции но функциональному анализу. — М.: Наука,
1979.
Самко С. Г., Килбас А. А., Маричее О. И. Интегралы и производные дробного
порядка и некоторые их приложения. —Минск: Наука и техника, 1987.
Свешников А. Г., Тихонов А. П. Теория функций комплексного переменного. — М.:
Наука, 1970.
Смирное В. К, Лебедев П. А. Конструктивная теория функций комплексного
переменного.—М.-Л.: Наука, 1964.
Смирнов В. И. Курс высшей математики. Том 4, часть 1. — М.: Наука, 1974.
Смирное П. С. Введение в теорию нелинейных интегральных уравнений. —М.:
Гостехиздат, 1951.
Снеддон И. Иреобразования Фурье.—М.: Иностранная литература, 1955.
Титчмарш Е. Введение в теорию интегралов Фурье. — М.-Л.: Гостехиздат, 1948.
Тихонов А. П., Арсенин В. Я. Методы решени некорректных задач. — М.: Наука,
1979.
Трикоми Ф. Интегральные уравнения. —М.: Иностранная литература, 1960.
Уиттекер Э. Т., Ватсон Дэю. П. Курс современного анализа. Часть 1. — М.:
Физматлит, 1963.
Фок В. А. О некоторых интегральных уравнениях математической физики. Докл.
АН СССР, 1942, т. 26, Ш 4^5, с. 147-151.
Хиршман И. П., Уиддер Д. В. Иреобразования типа свертки. — М.: Иностранная
литература, 1958.
Цлаф Л. Я. Вариациопное исчисление и интегральные уравнения. —М.: Наука,
1970.
Atkinson К. Е. The Numerical Solution of Integral Equations of the Second Kind. —
Cambridge: Cambridge Univ. Press, 1997.
Bateman П. On the numerical solution of linear integral equations // Proc. Roy. Soc. (A).
Vol. 100. No. 705, 1922.
Beyer W. П. CRC Standard Mathematical Tables and Formulae. — Boca Raton: CRC
Press, 1991.
Страница 271

272 Список ЛИТЕРАТУРЫ
Brakhage К, Nickel К., Rieder P. Auflosung der Abelschen Integralgleichung 2. Art. —
ZAMP, 1965, Vol. 16, Fasc. 2, S. 295-298.
Brychkov Yu. A., Prudnikov A. P. Integral Transforms of Generalized Functions. —New
York: Gordon & Breach Sci. Publ., 1989.
Cochran J. A. The Analysis of Linear Integral Equations. —New York: McGraw-Hill
Book Co., 1972.
Corduneanu С Integral Equations and Stability of Feedback Systems. — New York:
Academic Press, 1973.
Corduneanu С Integral Equations and Applications. — Cambridge-New York:
Cambridge Univ. Press, 1991.
Davenport W. В., Root W. L. An Introduction to the Theory of Random Signals and
Noise. —New York: McGraw-Hill Book Co., 1958.
Davis B. Integral Transforms and Their Applications. — New York: Springer-Verlag,
1978.
Delves L. M., Mohamed J. L. Computational Methods for Integral Equations. —
Cambridge-New York: Cambridge Univ. Press, 1985.
Dzhuraev A. Methods of Singular Integral Equations. —New York: J. Wiley, 1992.
Golberg A., Ed. Numerical Solution of Integral Equations. —New York: Plenum Press,
1990.
Gorenflo R., Vessella S. Abel Integral Equations: Analysis and Applications. —Berlin-
New York: Springer-Verlag, 1991.
Gripenberg G, Londen S.-O., Staffans O. Volterra Integral and Functional Equations. —
Cambridge-New York: Cambridge Univ. Press, 1990.
Hackbusch W. Integral Equations: Theory and Numerical Treatment. — Boston:
Birkhauser Verlag, 1995.
Jerry A. J. Introduction to Integral Equations with Applications. —New York-Basel:
Marcel Dekker, 1985.
Kanwal R. P. Linear Integral Equations. — Boston: Birkhauser, 1996.
Kondo J. Integral Equations. — Oxford: Clarendon Press, 1991.
Mikhlin S. G, Prossdorf S. Singular Integral Operators.—Berlin-New York: Springer-
Verlag, 1986.
Miles J. W. Integral Transforms in Applied Mathematics. — Cambridge: Cambridge
Univ. Press, 1971.
Oldham, K. B. and Spanier, J., The Fractional Calculus. — London: Academic Press,
1974.
Polyanin A. D., Manzhirov A. V. Handbook of Integral Equations. — Boca Raton-New
York: CRC Press, 1998.
Polyanin A. D., Manzhirov A. V. Handbuch der Integralgleichungen. — Heidelberg:
Spectrum Akad. Verlag, 1999.
Polyanin A. D., Zaitsev V. F. Handbook of Exact Solutions for Ordinary Differential
Equations. — Boca Raton-New York: CRC Press, 1995.
Porter D., Stirling D. S. G Integral Equations: A Practical Treatment, from Spectral
Theory to Applications. — Cambridge-New York: Cambridge Univ. Press, 1990.
Prossdorf S., Silbermann B. Numerical Analysis for Integral and Related Operator
Equations — Basel-Boston: Birkhauser Verlag, 1991.
Sakhnovich L. A. Integral Equations with Difference Kernels on Finite Intervals. —
Basel-Boston: Birkhauser Verlag, 1996.
Zwillinger D. Handbook of Differential Equations. — San Diego: Academic Press, 1989.
Страница 272