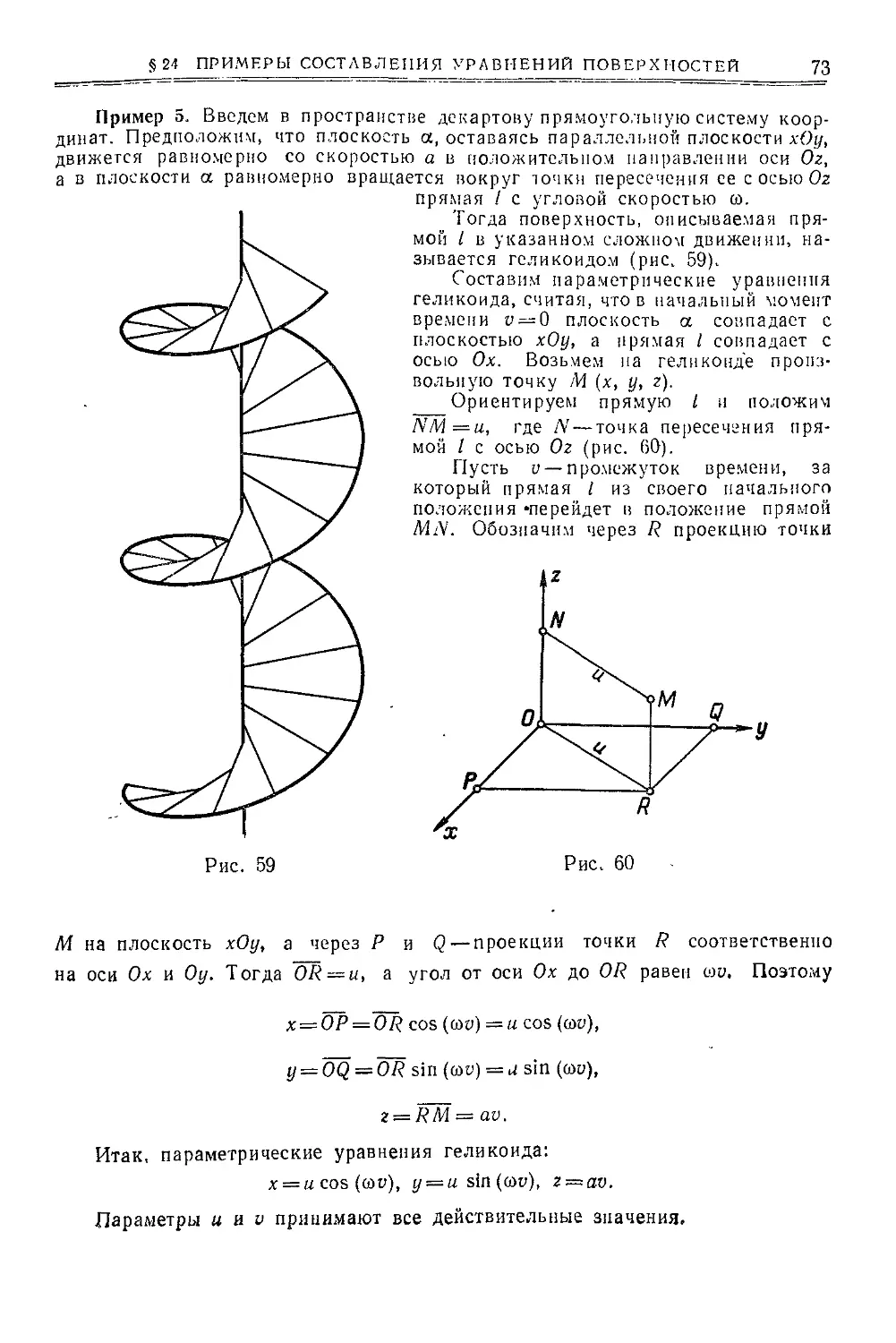
Текст
УДК 516
Настоящая книга предназначена в качестве
учебника по аналитической геометрии для студентов меха-
нпко-матечатичесьих, физических и физико-матег.гати-
ческих факультетов университетов и педагогических
институтов. Наличие в книге задач с решениями и
задач для самостоятельного решения (с ответами)
позволяет использовать заочниками эту часть книги
как материал семинарских занятий. Помимо
традиционного материала по аналитической геометрии is книге
дано понятие о линейном пространстве и линейном
многообразии. Линейное отображение определяется как
коллинеания. при которой сохраняется простое
отношение Изложено понятие собственных векторов Дана
метрическая теория инвариантов в аффинной системе.
Рассмотрены произвольные плоские сечения
поверхности второго порядка Проективные координаты и
теоремы Дезарга, Паскаля и Бриаишона даны в до-
потнешш в основном тексте — только однородные
координаты
Печатается по постановлению
Редакиионно-изда1ельского совета
Московского университета
2-2-3
ПРЕДИСЛОВИЕ
В главе I вводится понятие направленного отрезка, а затем
известное соотношение между тремя точками, лежащими на
прямой (теорема Шаля). Обобщением понятия направленного отрезка
(упорядоченная пара точек) является понятие ориентированного
треугольника (упорядоченная тройка точек) и ориентированного
тетраэдра (упорядоченная четверка точек). Имеют место
соотношения, аналогичные теореме Шаля. Включение этого материала в
книгу позволяет дать общие выводы формул, относящихся к
простейшим задачам по аналитической геометрии (расстояние между
двумя точками, деление отрезка в данном отношении, площадь
треугольника, объем тетраэдра), а также получить необходимое
и достаточное условие принадлежности трех точек одной прямой
и принадлежности четырех точек одной плоскости. Простейшие
вопросы по аналитической геометрии изложены последовательно
на прямой, на плоскости и в пространстве. Это обстоятельство,
а также введение понятия ориентированной плоскости л
ориентированного пространства позволяет с самого начала изучения курса
значительно расширить тематику задач на практических занятиях
(главы I — II). Глава III посвящена понятию уравнений линии и
поверхности (задачи 23—25, 29, 30 на сгр. 87—88 лучше решать
после прочтения глав IV — VI). В главе IV изложена векторная
алгебра.
Линейные образы на плоскости и в пространстве изложены в
главе V (прямая линия на плоскости) и в главе VI (плоскость
и прямая линия в пространстве).
В главе VII содержится материал, относящийся к
преобразованию декартовой системы координат (сюда включены углы Эйлера).
В главе VIII дан традиционный материал но каноническим
уравнениям линий второго порядка, а в главе IX изложены
канонические уравнения поверхностей второго порядка. В главе X
даны сведения о комплексной плоскости и комплексном
пространстве. В главе XI изложена общая теория линий второго порядка,
а в главе XII—общая теория поверхностей второго порядка.
В главу XIII выделены понятия отображения, преобразования
и группы преобразований.
ПРЕДИСТОВHE
Линейное отображение (и преобразование) определяется как
отображение, при котором сохраняется принадлежность трех точек
одной прямой и сохраняется простое отношение Aлава XIV); этим
удается охватить вырожденные линейные преобразования. Аффинное
преобразование определяется как линейное взаимно однозначное.
В той же главе XIV даны сведения о собственных векторах
линейного преобразования и доказана основная теорема о
представлении аффинного преобразования в виде произведения
ортогонального на самосопряженное. Все изложение ведется одновременно
для плоскости и пространства.
В главе XV изложены элементы проективной геометрии.
В книгу включены четыре дополнения.
В дополнении I вводится понятие ориентации плоскости и
пространства рассмотрением цепей из ориентированных треугольников
и тетраэдров; все относящиеся сюда определения используют
лишь аксиомы соединения и порядка (и потшу, например, могут
быть без всяких изменений отнесены к плоскости и пространству
Лобачевского).
В дополнении II излагается метрическая теория инвариантов
многочлена второй степени от двух и трех переменных по
отношению к преобразованию одной общей декартовой системы координат
в другую. Даются понятия ковариантных и контравариантных
координат вектора и точки; излагается понятие метрического тензора.
В III дополненич исследуются типы и расположение в
пространстве произвольных плоских сечений поверхности второго порядка,
заданной общим уравнением, в частности круговые сечения и
омбилические точки.
В дополнении IV излагается понятие проективных координат
на проективной плоскости и в проективном пространстве и
приводятся доказательства теорем Дезарга, Паскаля и Брианшона. В
основном тексте я ограничился рассмотрением однородных координат.
Выражаю глубокую благодарность академику П. С.
Александрову за просмотр рукописи, обсуждение ее на кафедре высшей
геометрии и топологии, за ссе сделанные замечания и советы. Много
ценных замечаний я получил от 1фофессора Ю. М. Смирнова.
Особую признательность и благодарность я приношу доценту
кафедры высшей геометрии и топологии МГУ А. С. Пархоменко,
который провел очень большую работу над рукописью при ее
редактировании и дал мною ценных советов.
Г Л А В А I
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПРЯМОЙ
§ 1. Направленные отрезки
Направленным отрезком АВ называется упорядоченная пара
точек А и В. Первая точка А называется началом направленного
отрезка АВ, а вторая точка В — его концом
(рис. 1).
В обозначении направленного отрезка АВ
порядок точек определяется порядком их записи;
Л —первая точка, В — вторая. Если точки А и рис j
В различны, то направленный отрезок АВ
называется ненулевым (или невырожденным), а если точки А я В
совпадают, то направленный отрезок АВ называется нулевым (или
вырожденным).
§ 2. Ось. Координата направленного отрезка
Осью называется прямая, на которой фиксировано
положительное направление и выбран масштабный отрезок*.
Координатой ненулевого направленного отрезка А В, лежащего на
оси I, называется число АВ, модуль которого равен длине АВ на-
правленного отрезка АВ, измеренной масштабным отрезком оси I;
оно положительно, если направленный отрезок АВ и ось I имеют
одинаковое направление, и отрицательно в противном случае.
Координата пулевого направленного отрезка по определению равна
нулю.
* Часто осью начинаю! прямую, на которо,"; фиксировано положительно;
направление. В аналитической геометрии понятие ос-и употребляется чаще
всего в том смысле, как только что указано в основном тексте.
Гла-.а I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПРЯМОЙ
§ 3. Ось координат. Координата точки
Осью координат называется ось, на которой фиксирована точка
О, называемая началом координат.
Координатой х точки М, лежащей на оси координат,
называется координата направленного отрезка ОМ:
Точку М, имеющую координату х, обозначают так: М(х).
Точка £A) называется единичной точкой. Отрезок, концами
которого являются начало координат и
0 £• единичная точка, равен масштабному
о— о *~дг отрезку (рис. 2).
Ось координат можно задать, фикси-
PlIC- 2 руя на прямой две различные точки О и
Е (начало координат и единичную точку),
так как при этом на прямой устанавливается положительное
направление (от О к £), фиксируется масштабный отрезок ОЕ и
начало координат О.
Направленный отрезок ОЕ, началом которого является
начало координат, а концом — единичная точка Е оси координат,
называется масштабным (или единичным) и обозначается буквой е:
Координата масштабного направленного отрезка ОЕ равна 1.
Направление масштабного отрезка ОЕ совпадает с положительным
направлением оси координат.
При помощи системы координат на прямой осуществляется
взаимно однозначное соответствие между множеством всех точек
прямой и множеством всех действительных чисел, т. е.
1) каждой точке оси координат ставится в соответствие одно
и только одно действительное число х (координата этой
точки) и
2) каждое действительное число х является координатой одной
и только одной точки этой прямой.
Для построения этой точки в случае хфО надо отложить от
начала координат отрезок ОМ, длина которого равна \х\; при
этом отрезок ОМ откладывается в положительном направлении
оси, если х>0, и в отрицательном, если х < 0. Конец М
отложенного отрезка и будет точкой, координата которой равна х.
ТЕОРЕМА ШЛЛЯ
§ 4. Теорема Шаля. Координата направленного отрезка,
заданного двумя точками декартовой оси координат. Расстояние
между двумя точками, лежащими на оси координат
Теорема 1 (Шаля). Вели А, В, С —три -гюбые точки оси, то
А5 + ЙС = ~АС.
Доказательство. Предположим, что точки Л, В, С
попарно различны. Если точка В лежит между точками А и С, то
длина отрезка АС равна сумме длин отрезков ЛВ и ВС:
\~АВ\ + \ВС\=>\~АС\\
но так как в рассматриваемом случае направленные отрезки АВ, ВС
и АС имеют одинаковое направление, то числа АВ, ВС и АС
имеют один и тот же знак, а потому
Л~В г ВС = АС.
Если точка С лежит между Л и В, то
СВ=-В~С, ~АВ+Ж=~АС.
Если точка Л лежит между точками В и С, то В А + АС = ВС,
Ш+~вс^Тс, b~a = -Jb, 7[в + в~с = лс~.
Если точки А и В совпадают, то АВ + ВС = ВС— АС.
Если точки В и С совпадают, то АВ + ВС= АВ = АС.
Наконец, если точки А и С совпадают, то
ДВ -\-~BC = АВ +~ВЛ = 0 = Ж.
Теорема 2. Координата АВ направленного отрезка АВ,
заданного двумя точками А (хг) и В (хг) оси координат,
вычисляется по формуле
АВ = x2—xv
Доказательство. На основании теоремы Шаля ОА-\-
-\-А~В-=ОВ, откуда
Теорема 3. Расстояние d между точками A(Xj) и В(х2) оси
координат вычисляется по формуле
Эта теорема является следствием предыдущей.
Глава I AT'\ 1ИТИЧПСКЛЯ 1П0МЕТР11Я НЛ ПРЯМОЙ
§ 5. Деление направленного отрелка в данном отношении
Пусть на одной и той же прямой лежшь два направленных
отрезки АВ и CD, причем CD невырожденный направленный
гг -, ~АВ
отре-юк. Тогда отношением — в случае, если направленный
CD
отрезок А В также невырожденный, называется число К, абсолют-
АВ
пая величина которого равна отношению -^ и которое
положительно, если АВ и CD имеют одинаковое направление, и
отрицательно в противном случае. Если отрезок АВ вырожденный, а
—h дв
отрезок CD невырожденный, то будем считать, что =^ = 0. Если
CD
7^. .. ~АВ
отрезок CD вырожденный, то отношение ■=^ не определяется.
CD
Если отношение АВ к CD равно К, то пишут
АВ,
"■"ццу — Л.
CD
Пусть на некоторой прямой задан невырожденный
направленный отрезок АВ и пусть С—какая-нибудь точка этой прямой,
отличная от точки В.
Отношением, в котором точка С делит невырожденный
направленный отрезок АВ, называется число X, определяемое соотношением*
АС
л = z=p .
СИ
Из этого определения следует, что X > 0, если точка С лежит
между точками А и В, и X < 0 в противном случае. При этом
|л|<1, если точка А лежит между точками В и С, и |Х|> 1,
если точка В лежит между точками А и С. Заметим, что
отношение, в котором точка С делит невырожденный направленный от-
,резок АВ, никогда не равно — 1.
Теорема 1. Если на оси координат заданы две различные точки
А (Ху) и В (х2) и ест точка С (х) делит направленный отрезок АВ
* Опюшепке ^^ называют также простым отношением точек А, В, С и
СВ
обозначают (ABG).
<> -, ДЕЛЕНИЕ НАПРАВЛЕННОГО OTPF.3K.A В ДЛН'.ЮМ ОТНОШЕНИИ 9
в отношении Я, то
. Х — Хх X-t — Ujj
Л. = И X — -;—г-; ,
х.2 — х 1 -р X
Доказательство. Из данного определения отношения Я,,
в котором точка С делит направленный отрезок АВ, а также из
определения координаты направленного отрезка, лежащего на оси,
следует
ев с~в'
значит, на основании теоремы 2, § 4
Х.г — X
откуда
Следствие. Координата середины отрезка равна полусумме
координат его концов:
В самом деле, для середины отрезка Я = 1.
Теорема 2. Каково бы ни было число Хф-—1, существует и
притом только одна точка С, которая делит невырожденный
направленный отрезок АВ в отношении К.
Доказательство. Введем на прямой АВ систему координат.
Предполагая, что некоторая точка С (х) делит направленный
отрезок АВ в отношении К, на основании предыдущей теоремы найдем
где a'i и х2 —координаты точек А и В. Этим доказана
единственность точки С, делящей направленный отрезок АВ в данном
отношении X, т. е. доказано, что если такая точка существует, то
только одна.
Далее, точка С с координатой
делит направленный отрезок АВ в отношении X, так как из
написанного соотношения следует
X) = .Vj + U2, .¥—.<! - Л (,г2 — л), Л С =
|0 Р,а@ I. АНАЛИТИЧЕСКАЯ rFOMETPHfl НА ПРЯМОЙ
Точки С и В различны, так как разность их координат не
ра^на нулю; в самом деле,
Поэтому СВфО и из последнего равенства следует, что
Ш СВ
§ 6. Преобразование системы координат на прямой
Пусть на прямой введены две системы координат с одним и
тем же положительным направлением оси и одним и тем же
масштабным OTpejKOM. Пусть О —начало координат в одной из этих
систем (эту систему координат будем называть старой), а О' —
начало координат в другой (эту систему координат будем называть
новой). Пусть М — произвольная точка оси, х—координата
точки Ж в старой системе (эту координату будем называть старой),
х' — координата точки М в новой системе (эту координату будем
называть новой); наконец, пусть а — координата нового начала О'
в старой системе. Тогда имеет место формула
х = х -\-а,
т. е. старая координата точш, лежащей на оси координат, равна
новой координате этой точки, сложенной с координатой нового
начала в старой системе.
Доказательство. На основании теоремы Шаля (§ 4,
теорема 1)
ом==дб~'+(Ш,
т. е.
Рассмотренное в этом параграфе преобразование системы
координат называется переносом системы координат. При переносе
системы координат координата направленного отрезка не меняется.
Это сразу следует из теоремы 2 § 4.
§ 7. Векторы
В настоящем параграфе дается определение вектора в
трехмерном евклидовом пространстве (понятия Бектора на плоскости и
вектора па прямой являются частными случаями этого
определения]. Предварительно введем ряд дополнительных определений.
§7. ВЕКТОРЫ
Два невырожденных направленных отрезка А В и CD называются
коллинеарнымиу если прямые А В и CD или параллельны, или
совпадают.. Вырожденный направленный отрезок считается коллине-
арным любому направленному отрезку.
Будем говорить, что два невырожденных направленных отрезка
АВ a CD, лежащих на параллельных прямых, имеют
одинаковое направление, если точки В и D лежат по одну сторону
от прямой АС. Если же точки В и D лежат по разные
стороны от прямой АС, то направленные отрезки АВ и CD имеют
противоположное направление (рис. 3). В
случае, если невырожденные направленные
отрезки АВ и CD лежат на одной прямой а, они ^-^у--— п
имеют одинаковое направление, если на любой
прямой Ь, параллельной а, найдется
невырожденный направленный отрезок PQ, имеющий
одинаковое направление с каждым из
направленных отрезков АВ и CD. Если же любой
невырожденный отрезок PQ (лежащий на
прямой Ь, параллельной прямой а) имеет одинако- рнс о
вое направление с одним из отрезков АВ или
CD и противоположное с другим, то направленные отрезки АВ
и CD имеют противоположное направление. Наконец, условимся
считать, что вырожденный направленный отрезок имеет одинаковое
направление с любым направленным отрезком.
Если направленные отрезки АВ и CD коллинеарны, то будем
писать AB\\CD; если при этом они имеют одинаковое направление,
то АВЦСЕ), а если противоположное, то AB[\CD.
Два направленных отрезка АВ и CD называются равными
АВ --CD, если выполнены следующие условия:
1) равны длины отрезков АВ и CD;
2) направленные отрезки АВ и CD коллинеарны;
3) направленные отрезки АВ и CD имеют одинаковое направление.
Свободным вектором а называется класс всех равных между
собой направленных отрезков. Нулевым вектором называется класс
всех вырожденных направленных отрезков.
Свободный вектор а часто обозначают и изображают любым
из направленных отрезков АВ того класса направленных отрезков,
которым является вектор а.
12 Глава I. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ EIA ПРЯМОЙ
Отложить свободный вектор а от точки Л —значит построить
направленный отрезок АВ входящий в класс направленных
отрезков, образующих, вектор а.
В дальнейшем под словом «вектор» мы будем понимать
«свободный вектор».
Рассмотрим два произвольных вектора а и Ъ. Пусть АВ —
направленный отрезок из класса направленных отрезков,
образующих вектор a, a CD— направленный отрезок из класса
направленных отрезков, образующих вектор Ь.
Векторы а и Ь называются коллинеарными, если коллинеарны
направленные отрезки АВ и CD. Если при этом направленные
отрезки АВ и CD имеют одинаковое направление, то векторы а
и Ь имеют одинаковое направление, а если направленные отрезки
АВ и CD имеют противоположное направление, то векторы а и Ь
имеют противоположное направление. Если векторы а и Ь
коллипеарны, то будем писать а\\Ь; если при этом они имеют
одинаковое направление, то будем писать аЦЬ, а если
противоположное, то а\\Ь. Если направленные отрезки АВ и CD равны,
то будем говорить, что векторы а и Ь равны, и писать а = Ь.
Длиной или модулем вектора а называется длина* отрезка АВ.
Длина вектора обозначается так: \АВ\, АВ, \а\, а.
Если определения, относящиеся к свободным векторам,
формулируются при помощи направленных отрезков, то надо каждый-
раз устанавливать независимость формулировок от выбора
направленных отрезков из тех классов, которыми являются
рассматриваемые векторы. Эта независимость ясна для только что
рассмотренных простейших случаев: определение длины вектора,
коллинеарности и равенства двух векторов. В более сложных
случаях (см. ниже определение координат вектора, определение
суммы векторов и др.) полезно применять следующую теорему.
Теорема. Необходимым и достаточным условием равенства
направленных отрезков АВ и CD является совпадение середины,
отрезка** AD с серединой отрезка ВС.
Доказательство необходимости. Дано AB = CD.
Требуется доказать, что середина отрезка AD совпадает с
серединой отрезка ВС.
Пусть О—середина отрезка AD. Рассмотрим преобразование S
симметрии относительно точки О. При этом преобразовании каждой
* Длину вырожденного отрезка считаем равной нулю.
** Если отрезок вырожденный, то серединой будем считать точку, с кото-
рои совпадают его концы.
$7 ВЕКТОРЫ
13
точке /VI ставится в соответствие точка М', симметричная точке М
относительно точки О, т. е. такая, что точка О является
серединой отрезка ММ'.
Каждый направленный отрезок PQ при преобразовании 5
переходит в направленный отрезок P'Q', такой, что P'Q' = QP (рис. 4).
Пусть В'—точка, в которую при преобразовании S перейдет
точка В. Так как точка А переходит в точку D, то направленный
отрезок АВ перейдет в направленный отрезок
и, значит, точки В' и С совпадают, т. е. точка О является также
и серединой отрезка ВС.
Доказательство достаточности. Предположим, что
середина отрезка AD совпадает
с серединой отрезка ВС и дока- /?И ^??' R'
жем, что
Пусть О—середина отрезка
AD; по условию точка О является
и серединой отрезка ВС. Значит,
при преобразовании S симметрии
относительно точки О точка А
перейдет в D (рис. 5), а точка В в точку С, поэтому AB — CD.
Следствие. Если AB — CD, то АС = Вй.
Понятие вектора и векторное исчисление возникло в связи
с рассмотрением в физике и механике таких понятий, как
скорость, ускорение и пр. К понятию свободного
вектора мы пришли из определения равенства
направленных отрезков.
Существуют и иные определения равенства
двух направленных отрезков: будем говорить,
что направленные отрезки АВ и CD равны,
если выполнены следующие условия:
1) длины отрезков АВ и CD равны;
2) отрезки АВ и CD принадлежат одной
прямой;
3) направленные отрезки АВ и CD имеют одинаковое
направление.
Тогда класс всех равных между собой направленных отрезков
называют скользящим вектором.
Рис. 5
Главе I АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ HA ПРЯМОЙ
Понятие скользяще о сектора и векторное исчисление
скользящих векторов возникло в механике (статике) при изучении
взаимодействия сит, приложенных к твердому телу; (силу «нельзя»
переносить параллельно самой себе, но «можно» переносить вдоль
линии ее действия).
ГЛАВА II
ПРОСТЕЙШИЕ «ОПРОСЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
I. КООРДИНАТЫ ТОЧКИ Я ВЕКТОРА НА ПЛОСКОСТИ
И 15 ПРОСТРАНСТВЕ
I
§ 8. Параллельное проектирование
В геометрии рассматриваются следующие три вида
параллельного проектирования.
1. Проекция точки М на прямую / параллельно
прямой т. Пусть на плоскости заданы две пересекающиеся
в точке О прямые / и т.
Если точка М не лежит
на прямой т, то проекцией
точки /VI на прямую /
параллельно прямой т
называется точка М' пересечения
прямой / с прямой,
проходящей через точку М
параллельно прямой т. Если же Рис. 6 Рис. 7
точка М лежит на прямой т,
то ее проекцией на прямую / параллельно прямой т называют
точку О (рис. 6).
Если прямые/ и «взаимно перпендикулярны, то рассмотренный
вид проектирования оказывается ортогональным проектированием
на прямую /.
Ортогональной проекцией М' точки М плоскости на прямую I,
лежащую в этой плоскости, называется точка пересечения прямой /
с прямой, проходящей через точку М перпендикулярно прямой /
(рис. 7).
2. Проекция точки М на плоскость л
параллельно прямой /. Пусть в пространстве задана плоскость л
и пересекающая ее в точке О прямая /.
16
Глава П. ПРОСТГЯШИЕ ВОПРОСЫ
Если точка М не лежит на прямой /, то проекцией Л! ее на
плоскость л параллельно прямой / называется точка пересечения
плоскости л с прямой, проходящей через точку М параллельно
прямой I. Если же точка М лежит на прямой /, то ее проекцией
на плоскость я
параллельно прямой /
называют точку О
(рис. 8).
Если фямая /
перпенди к у ля рна
плоскости я,
то'рассматриваемый вид
проектирования
оказывается
ортогональным.
Ортогональной
проекцией М' точки
М на плоскость л
называется точка
пересечения плоскости
л с прямой,
проходящей через точку М
пер печдн куля рно
плоскости л(рис. 9).
3. Проекция
точки /И на
прямую / пара л-
прострачетве задана плос-
М
о
W7
Рис. 10
Рис 11
лельно плоскости л. Пусть в
кость л и пересекающая ее в точке О прямая /.
Если точка М не лежит на плоскости к, то ее проекцией на
прямую / параллельно плоскости л называется точка М'
пересечения прямой/ с плоскостью, проходящей через точку М параллельно
плоскости л. Если же точка М лежит на плоскости л, то ее
проекцией на прямую / параллельно плоскости л называют точку О
(рис. 10).
Если прямая / перпендикулярна плоскости л, то
рассматриваемый вид проектирования оказывается ортогональным.
Ортогональной проекцией точки М на прямую / называется
точка М' пересечения грямой / с плоскостью, проходящей через
точку М перпендикулярно прямой / (рис. 11).
Ортогональное проектирование точки М на прямую в
пространстве можно определить и так:
ортогональной проекцией точки М на прямую / называется
точка М' пересечения прямой / с прямой, проходящей через точку М
и пересекающую прямую / иод прямым углом (рис. 11).
i9. ДЕКАРТОВА СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
§ 9. Общая декартова и декартова прямоугольная системы
координат на плоскости
Общей декартовой (или аффинной) системой координат на
плоскости называется упорядоченная совокупность двух
пересекающихся осей координат с общим началом координат О на каждой
из них (рис. 12).
Масштабные отрезки этих осей могут быть различны. Первая
ось называется осью Ох, или осью абсцисс, вторая — осью Оу, или
осью ординат.
Пусть /VI—произвольная точка плоскости. Пусть Р — проекция
точки М на ось Ох параллельно оси Оу, а к — координата точки Р
на оси Ox; Q —проекция точки М на ось Оу параллельно о^п Ох,
а у — координата точки Q на оси Оу.
Числа х, у называются общими
декартовыми (или аффинными) коорди-
патами точки М. Первая координата
х называется абсциссой точки /И,
вторая координата у называется
ординатой точки М. Точка М с
координатами х, г/обозначается М(х, у).
Абсцисса точки М равна нулю
тогда и только тогда, когда точка
М лежит на оси Оу; ордината у
точки М равна нулю тогда и толь- Рис. 12
ко тогда, когда точка М лежит на
оси Ох. Для начала координат О (и только для этой точки) обе
координаты хну равны нулю. Точки Е1A, 0) и /:2@, 1)
называются единичными точками осей координат; точка ЕA, 1)
называется единичной точкой системы координат, параллел)грамм
ОЕгЕЕг— масштабным параллелограммом.
Отрезки OEt и ОЕг являются масштабными отрезками
соответственно осей Ох и Оу. Векторы
называются масштабными векторами соответственно осей Ох и Оу.
Общую декартову систему координат на плоскости можно задать
упорядоченной парой пересекающихся прямых и единичной точкой Е,
не лежащей ни на одной из них.
В самом деле, пусть О — точка, в которой пересекаются эти
прямые, Ех — проекция точки Е на первую из данных, прямых
параллельно второй, а Е% — проекция точки Е на вторую прямую
параллельно первой. Тогда положительные направления прямых
определяются направлениями векторов ОЕХ и ОЕ,2, отрезки ОЕХ
18
Глава I) ПРОСТЕЙШИЕ ВОПРОСЫ
и 0Е„—масштабные отрезки соответственно для перво;": и второй
осей координат.
При помощи общей декартовой системы координат на плоскости
устанавливается взаимно однозначное соответствие между
множеством всех точек плоскости и множеством всех упорядоченных пар
действительных чисел, так как:
1) каждой точке М плоскости соответствует одна определенная
упорядоченная пара действительных чисел х, у — координат этой
точки;
2) каждая упорядоченная пара х, у действительных чисел
ставится в соответствие одной и только одной точке /VI, для которой
первое число х — абсцисса, а второе число у— ордината.
Для построения этой точки /И . ел\чае хФО, у^=0 надо
построить на оси Ох точку Р с координатой х, а на оси Оу—точку
Q с координатой у. Точка М является точкой пересечения прямых,
проходящих через точки Р и Q,
параллельных соответственно осям Оу и Ох.
Если ц = О или х = 0, то дело сводится
к построению точки на оси Ох или на оси
Оу.
Декартовой прямоугольной системой
координат на плоскости называется
упорядоченная совокупность двух взаимно перпен-
дикулярных осей координат с равными масш-
0j i £^ ^~~*-Х табными отрезками ОЕ 1 = О£2 и с общим
началом координат О на каждой оси (рис.
13).
Определение декартовых прямоугольных
координат точки формулируется аналогично соответствующему
определению общих декартовых координат точки: пусть Р и
Q—ортогональные проекции точки М соответственно на оси Ох и Оу,
х—координата точки Р на оси Ох, а у — координата точки Q на
оси Оу. Числа х, у называются декартовыми прямоугольными
координатами точки М.
Отметим, что часто масштабные векторы осей Ох и Оу в
декартовой прямоугольной системе координат обозначают так:
О£1 = /, О£2=/.
ч
j
Рис. 13
§ 10. Общая декартова и декартова прямоугольная системы
координат в пространстве
Общей декартовой, или аффинной, системой координат в
пространстве называется упорядоченная совокупность трех осей
координат, не лежащих в одной плоскости и проходящих через одну
§10. ДЕКАРТОВА СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ
19
точку О, являющуюся началом координат на каждой оси.
Масштабные отрезки осей координат, вообще говоря, различны (рис. 14).
Точка О называется началом координат Первая ось называется
осью Ох, или осью абсцисс, вторая—осью Оу, или осью ординат,
третья — осью Oz, или осью аппликат. Плоскость, проходящая через
Рис. 14
Рис. 15
две оси из трех Ох, Оу, Oz, называется координатной плоскостью;
координатных плоскостей три; они обозначаются так:
yOz, zOx и хОу.
Пусть М — произвольная точка пространства. Обозначим через
Р проекцию точки М на ось Ох параллельно плоскости yOz, a
через х — координату точки Р на оси Ох. Через Q обозначим
проекцию точки М на ось Оу параллельно плоскости гОх, а через
у — координату точки Q на оси О у. Через R обозначим проекцию
точки М на ось Oz параллельно плоскости хОу, а через г —
координату точки R на оси Ог (рис. 15). Три числа х, у, г, взятые
в этом порядке, называются общими декартовыми (или аффинными)
координатами точки М. Первая координата х называется абсциссой
точки М, вторая г/—ординатой точки М, третья г — аппликатой
точки М. Точка М с координатами х, у, г обозначается М (х, у, г).
Абсцисса точкч М равна нулю тогда и только тогда, когда
точка М лежит на координатной плоскости yOz. Ордината точки М
равна нулю тогда и только тогда, когда точка /И лежи г на
координатной плоскости гОх, Аппликата точки М равна нулю тогда и
только тогда, когда точка М лежит на координатной плоскости хОу.
Отсюда следует, что точка М (х, у, г) лежит на оси Ох тогда
и только тогда, когда у = 2 = 0; на оси Оу тогда и только тогда,
когда z — x — 0 и на оси Ог тогда и только тогда, когда v = y — O.
Для начала координат (и только для этой точки) все три
координаты равны нулю.
20 Гю-<а 1! ПРОСТЕЙШИЕ ВОПРОСЫ
Точки 1^A, 0 0), £2 @, 1, 0), Е3 @, 0, 1) называются
единичными точками осей координат. Точка ЕA, 1, 1) называется
единичной точкой системы координат. Параллелепипед с вершиной
в начале координат О и с ребрами OEV ОЕ2, OES называется
масштабным параллелепипедом. Отрезки ОЕ1г ОЕг, ОЕ3 являются
масштабными отрезками соответственно осей Ox, Oy, Oz. Векторы
называются масштабными векторами соответственно осей Ox, Oy, Oz.
Общая декартова система координат в пространстве может быть
задана упорядоченной тройкой прямых, не лежащих в одной
плоскости, и проходящих через одну точку, и единичной точкой Е (не
лежащей в одной плоскости ни с какой парой из заданных прямых).
В самом деле, проектируя единичную точку Е па каждую из
заданных прямых параллельно плоскости, содержащей две другие
прямые, мы построим единичные точки Ev E2, Е3; этим самым
будут определены и масштабные отрезки, и положительные
направления на данных прямых.
При помощи общей декартовой системы координат
устанавливается взаимно однозначное соответствие между множеством всех
точек пространства и множеством всех упорядоченных троек
действительных чисел. Здесь для построения точки М, имеющей
координатами заданные числа х, у, z, поступают так: если х=^=0, у ^0.
z-/=0, то строят на осях Ox, Oy, Oz точки Р, Q, R, имеющие на
этих осях координаты, соответственно равные х, у, z, и проводят
через точки Р, Q, R плоскости, соответственно параллельные
координатным плоскостям yOz, zOx, хОу; точка М есть точка
пересечения этих плоскостей. Если одна из координат х, у, z равна
нулю, например 2 = 0, то точка М лежит в координатной плоскости
хОу и имеет в этой плоскости
относительно общей декартовой системы координат,
заданной осями Ох и Оу, координаты хну;
построение точки М для этого случая ука-
' зано в § 9. Аналогично строится точка
М, если у = 0 (в этом случае она лежит в
4-—9гг—*^У плоскости zOx) и если х — 0 (в этом случае
z точка М лежит на плоскости yOz).
Декартовой прямоугольной системой
координат в пространстве называется упоря-
Рис 16 доченная тройка попарно перпендикулярных
осей координат с общим началом координат
О на каждой из них и с одним и тем же масштабным отрезком для
каждой оси (рис. 16).
Определение декартовых прямоугольных координат точки
формулируется аналогично соответствующему определению общих декар-
КООРДИНАТЫ ВИКТОРА
21
товых координат точки, а именно: пусть Р, Q, R — ортогональные
проекции точки М на оси Ох, Оу, Ог (рис. 17); х— координата
точки Р на оси Ох, у—координата
точки Q па оси Оу, а г— координата
точки R на оси Ог. Три числа х,
у, г называются декартовыми
прямоугольными координатами
точки М.
Отметим, что часто масштабные
векторы осел Ох, Оу, Ог в
декартовой прямоугольной системе
координат обозначаются
ucx = i, uc,=j, ис3 = к. Рис 17
§ 11, Координаты вектора на плоскости и в пространстве
Проекцией* вектора АВ называется вектор А'В', где А' и В' —
проекции точек А и В.
Это определение обосновывается следующей теоремой.
Теорема 1. Проекции равных направленных отрезков равны.
Доказательство. Пусть АВ ~CD. Обозначим проекцию
направленного отрезка АВ через А'В', а проекцию направленного
отрезка CD через CD'. Так как АВ — CD, то середина отрезка AD
совпадает с серединой отрезка ВС (теорема § 7, условие
необходимости), а так как при параллельном проектировании середина
отрезка проектируется в середину его проекции, то середина отрезка
A'U совпадает с серединой отрезка
J/ В'С, значит (теорема §7, условие до-
f^r— . пВ статочности),
18
Впедем па плоскости общую
декартову систему координат. Пусть
АВ — произвольный вектор,
лежащий в этой плоскости, а А'В' и А"В"—
его проекции на оси Ох и Оу параллельно осям Оу и Ох (рис. 18).
Координатами вектора АВ в общей декартовой системе
координат называются числа х, у, где х— координата вектора А'В' на оси
Ох, а у — координата вектора А "В" на оси Оу.
* Имеется в виду любой из трех видов параллельного проектирования (§8).
22
Глава И ПРОСТЕЙШИЕ ВОПРОСЫ
Аналогично определяются координаты вектора АВ в общей
декартовой системе координат в пространстве: это упорядоченная тройка
чисел х, у, г, где х — координата на оси Ох проекции Л'И ректора
АВ на ось Ох параллельно плоскости yOz и т. д. (рис. 19).
X
Рис 19
Если вектор а имеет координаты х и у (на плоскости) или
х, u, z (в пространстве), то будем обозначать его {х, у} (на
плоскости) и {х, у, г] (в пространстве) и писать а = {х, у} и
соответственно а-- {х, у, г).
Из теоремы 1 и определения координат точки следует, что
координаты вектора а являются координатами его конца Р, если
вектор а отложен от начала координат:
ОР = а.
Итак, вводя на плоскости общую декартову систему координат,
можно каждому вектору а этой плоскости поставить в соответствие
упорядоченную пару чисел х, у — координат этого вектора в
выбранной системе координат Обратно, каждая упорядоченная пара чисел
х, у является координатами некоторого вектора а. Для построения
этого вектора достаточно построить точку Р (х, у) в выбранной
системе координат. Класс всех направленных отрезков, равных
направленному отрезку ОР, и является вектором а с
координатами х, у.
Аналогичное положение имеет место и в пространстве
Это соответствие между Гекторами плоскости ч упорядоченными
парами чисел (и соответствие между векторами пространства и
«Ml КООРДИНАТЫ ВЕКТОРА 23
упорядоченными тройками чисел) взаимно однозначно, так как два
вектора а и Ь равны тогда и только тогда, когда равны их
соответствующие координаты.
В самом деле, отложим векторы а и Ь от начала координат:
Соотношение а = Ь имеет место тогда и только тогда, когда
точки Р и Q совпадают, г е. тогда и только тогда, когда равны
их соответствующие координаты.
Теорема 2. Если чектор АВ задан своим началом А(х1, /д) и
концом В (х.2> уг) относительно общей декартовой системы
координат, то его координаты х и у вычисляются по формулам
х = ха xi> У — У% Ух-
Доказательство. Пусть A'(xlt 0) и В'(х.,, 0)— проекции
точек Л и В на ось Ох параллельно оси Оу. Тогда вектор А'В
является проекцией вектора АВ на ось Ох параллельно оси Оу;
теперь на основании определения координаты вектора и теоремы 2
§ 4 имеем
JQ —L- ^*-J £5 2tl!— Лп ' ' ' ' All
Аналогично выводится формула у = у2—У\-
Теорема 3. Если вектор АВ задан своим началом Л(хг, уг, гх)
и концом В{х2, у2, г2) относительно общей декартовой системы
координат в пространстве, то его координаты х, у, z вычисляются
по формулам
Х = Хо ACj! У ~ У% Уц 2 = 22 Z].
Доказательство аналогично доказательству предыдущей
теоремы (только проектирование параллельно координатным осям
заменяется проектированием параллельно координатным плоскостям).
Теорема 4. Координата ортогональной проекции вектора А В
на ось I равна длине А В этого вектора, умноженной на косинус
угла ф между вектором АВ и осью I:
коорд. пр.г АВ = АВ cos ср.
Доказательство. Так как проекции равных направленных
отрезков равны между собой, то можно считать, что вектор АВ
отложен от произвольной точки А оси /. Обозначим тогда через
С проекцию точки В на ось /. Если вектор АВ ненулевой и угол
между вектором А В и осью / острый (рис. 20), то
коорд. пр., АВ =- Ж; --= АС = АВ cos q>.
24 Глава И ПРОСТПЙШИЕ ВОПРОСЫ
Если вектор АВ ненулевой и угол меж чу вектором Л В и осью /
тупой (рис. 21), то
коорд. np.f Хв -= АС — — АС = -~ AB'cos -ф = Л В cos ф.
Случаи ф = 0, ф = 90°, ф=180°, а также случай, когда вектор
АВ пулевой (в этом случае ф—любое число) предоставляется
рассмотреть читателю.
Рис 21
Теорема 5. Пусть I и т—две оси, образующие между собой
угол ф. Пусть АВ —вектор, коллинсарный оси т, а АВ — его
координата на этой оси. Тогда координата ортогональной проекции
вектора АВ на ось I равна координате А В этого вектора на оси т,
умноженной на косинус угла ц> между осями I и т:
коорд. пр.г АВ = АВ cos:p.
Доказательство. Если направление вектора АВ совпадает
с направлением оси т, то АВ—АВ, а, кроме того, угол ф между
осями / и т равен углу между вектором АВ и осью /. Поэтому
на основании предыдущей теоремы
коорд. пр.г АВ = АВ cos ср=* АВ cos ф.
Если же направление вектора АВ противоположно направлению
оси т, то АВ — —АВ, а, кроме того, угол между вектором A3 я
осью / равен я — ф. Поэтому на основании предыдущей теоремы
коорд. пр.г АВ^АВ cos (л — ф) = — АВ созф== АВ cos ф.
Определение. Назовем ломаной А±АгАл.. ■ Ап упорядоченную
совокупность п точек пространства (порядок точек определяется
порядком их записи). Направленные отрезки 41/42, A2AS, ... ,
Ап_хАп будем называть звеньями ломаной, a ALAn—замыкающей
ломаной А1А2...Ап
«12 РАССТОЯНИЕ МЕЖДУ ДВУМЯ ЮЧКЛ.«!1 25
Теорема 6. Координата проекции замыкающей ломаной на ось
равн-х сумме координат проекции ее звеньев на ту же ось.
Доказательство. Пусть Аи А\ ..., Л',—соответственно
проекцпч точек Av ,1,, ..., Ап на ось /. Тогда ча основании
теорем ! Шаля и:;еем
коорд. пр., /4,/42Н- коорд. пр., Л,Л,+ ...-'г
+ коорд. пр., Дп_1.4„= АгА«-г A.2AS+ ...
'^ . пр., АхАп.
ii. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ. ДЕЛЕНИЕ НАПРАВЛЕННОГО
ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ. ПЛОЩАДЬ ТРЕУГОЛЬНИКА.
ОВЬЕМ ТЕТРАЭДРА
§ !2. Расстояние между двумя точками на плоскости и в
пространстве
Теорема I. Расстояние d между двумя точками М1(х1, у{) и
M2(Xt, у2), заданными относительно прямоугольной системы
координат на плоскости, равно корню квадратному из суммы
квадратов разностей соответствующих координат этих точек, т. е
-У1)Г. A)
Доказательство. Предположим сначала, что ххфхг и
Ц\Ф Уг- Рассмотрим точку М (х2, у-,). Пусть М1 (xv 0) и М' (xz, 0)
— проекции точек М1(х1, ух) и М (х2, у{) на ось Ох, а М2 @, у.,)
и М" @, уг) — проекции точек M2(xit yz) и М (х2, у,) на ось Оу.
На основан,in теоремы 3 § 4 длины отрезков М1М'и М'2М"
равны
М, М' =; х, - хх |, М', М" = | у, - у, |.
Так как точки /И, (д;^ yt) ц M{xi,yl) имеют одинаковые
ординаты, то отрезок МХМ лежит на прямой, параллельной оси Ох,
или па самой оси Ох. Поэтому мина отрезка МгМ' равна длине
отрезка М,М:
М1М = \хг—х1\.
Аналогично доказывается, что
Далее, Д М>ММг — прямоугольный (^/ MtA^M, = 90°), так как
отрезок MLM лежит па прямой, параллельной "оси Ох, или на
26 Глава И ПРОСТЕЙШИЕ ВОПРОСЫ
самой оси Ох, а отре.юк ММ, лежит на прямой, параллельной
оси Оу, или на самой оси Оу. Значит,
Д^М!? = Л^М2 -'- ММ\ = |хй — х1 Г2-Ь\уг-уг |2,
или, обозначая MtM2 через d и замечая, что квадрат модуля
числа равен квадрату самого этого числа, получим
f/2 = (x2— xvJ + (yt — yj\
откуда следует формула A).
Если iJi=y2, то отрезок МгМ2 лежит на прямой,
параллельной оси Ох, или на самой оси Ох. В этом случае длина отрезка
равна длине его проекции на ось Ох, т. е. \х2—х1\. Но при
У1—У2 т0 же самое получится и из формулы A):
й = V\x2—Xlf-T-(y2—yJi = V(X2 — Xj1 == I Xo —X! ].
Аналогично доказывается правильность формулы (J) в случае
1 ==~ *^2
Теперь предположим, что направленный отрезок М.^Ж2~
ненулевой. Из предыдущих рассуждений ясно, что координаты
проекций этого направленного отрезка MLM2 па оси Ох и Оу
соответственно равны хг — х1 и у2 — у1 (теорема 2, § 11). С другой
стороны, обозначая через а и JS углы направленного отрезка
МгМ2 с осями Ол; и Оу, на основании теоремы 4 § 11 заключаем,
что координаты проекций отрезка М1М2 на оси Ох и Оу равны
dcosa и dcosjS, где d—длина отрезка М1М2.
Итак,
откуда
COSa = ^p, cosp = ^=^. B)
Углы аир, которые образует направленный отрезок М1М, с
осями Ох и Оу, называются его направляющими косинусами. Из
формул A) и B) следует, что
cos2 a + cos2 Р = 1,
т. е. сумма квадратов направляющих косинусов равна единице.
Из формул A) и B) как следствие находим расстояние г от точки
М (х, у) до начала координат (в декартовой прямоугольной системе
координат) и направляющие косинусы направленного отрезка ОМ:
cosa-i,
Теорема 2. Расстояние d между двумя точками М1(х1, ух, zx)
и Мг(х2, у2, z2), заданными относительно декартовой прямоуголь-
§ 12. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ 27
ной системы координат в пространстве, равно квадратному корню
из суммы квадратов разностей соответствующих координат этих
точек, т. е.
d = V{x2 -xxf + (у2 -ytf + (z2 -z,J. C)
Доказательство. Предположим сначала, что х1 Фх2,
У\ ФУ^ Ч Ф г2- Рассмотрим точку М (х2, у2, гх). Пусть М, (хг, yv 0)
и М'(х2, у2, 0) —проекции точек M1(xv yv zt) и М (х2, у2, гг)
на плоскость хОу, а М'2{0, 0, г2) и М"@, 0, г^ —проекции точек
М2(х2, уг, г2) и М (х2, у2, гА) на ось Oz. На основании теоремы 1
этого параграфа и теоремы 3 § 4 имеем
М\М' = K(x2-x^ + (y2-yiJ, М';М" = |2a-Zl|. (А)
Так как точки Мх и М имеют одинаковую аппликату, то отрезок
Л^М леж.\п в плоскости, параллельной плоскости хбу, или в
самой этой плоскости, а значит М1М' = М1М. Далее, так как
точки М и М2 имеют соответственно одинаковые абсциссы и
ординаты, то отрезок ММ2 лежит или на прямой, параллельной оси
Oz, или па самой оси Oz; следовательно, ММ2 = М"М2. Из
предыдущих рассуждений следует также, что Д МгММ2 прямоугольный
(J/MMM = 90°), поэтому
Отсюда и из формул (А) следует, что
= (х2 - хгJ + Q/2 - r/iJ +! г2 -гх \\
М! Ml = (х2 - хг) + Q/2 - r/i) +! г2 -гх \
или
где d—длина отрезка М^а. Из последней формулы следует
формула C).
Пусть теперь равны две какие-нибудь соответствующие
координаты точек М1(х1, у,, Zj) и М2 (х2, у2, z2), например хг = х2.
Тогда отрезок М1М2 лежит в плоскости, параллельной плоскости
уОг, или в самой этой плоскости, и его длина равна расстоянию
между проекциями Р^О, yv zx) и Р2 @, г/2, г2) этих точек
Mi(*i, f/i, zj и М2 (х2, у2, г2) на плоскость yOz. Но
расстояние между точкам!! Р, и Р2 по теореме 1 равно
и это число равно длине отрезка Л^Мг. С другой стороны, при
хх = х2 правая часть формулы C) обращается в тот же радикал:
\ (yz-yif + iZt-W'
28 Глава II ПРОСТЕЙШИЕ ВОПРОСЫ
Аналогично доказывается правильность формулы C) в случае
У1~Уъ и в случае zL — z2. Итак, формула C) доказана полностью.
Рассуждениями, аналогичными тем, которые мы проводили для
плоскости, получим формулы
D)
где а, р\ у —углы ненулевого направленного отрезка М1М2
соответственно с осями Ох, Оу, От, d — его длина; xlt uly zx —
координаты начала М{, x%, уг, га —координаты конца Мг. Из формул D)
и C) находим
cos2 а + cos2 Э + cos2 у — 1,
т. е. сумма квадратов направляющих косинусов направленного
ненулевого отрезка равна единице. В частном случае из формул
C) и D) находим расстояние г от точки М(х, у, г) до начала
координат и направляющие косинусы направленного отрезка ОМ (в
предположении, что он ненулевой)
cos ос = — , cos В = — , cos v = — .
§ 13. Деление направлгниого отрезка в данном отношении
Теорема I. Если относительно общей декартовой системы
координат на плоскости заданы две различные точки А (хх, ух) и В(х.1гуг)
и точка С(х,у) делит направленный отрезок АВ в
отношении К, то К равно тому из соотношений
х—х, у—у,
-1 или -—— ,-
#2 * У 2 У
в котором знаменатель не равен нулю, и любому из них
х, A)
если оба знаменателя хг—х и у2—у не равны нулю. Координаты
х, у точки С выражаются через координаты точек А и В
соотношениями
' J
Доказательство. Спроектируем точки А, В. и С на ось
Ох параллельно оси Оу; проекциями будут соответственно точки
А'(хх,0), В'(хг,0), С'(х,О).
«13. ДЕЛЕНИЕ НАПРАВЛЕННОГО ОТРЕЗКА В ДМ1П0М ОТНОШЕНИИ 29
Предположим, что точки А' и В' различны, т. е. кхфх2. Так
как при параллельном проектировании сохраняется порядок
точек, лежащих на прямой, и отношение отрезков, лежащих на
одной прямой, то точка С делит направленный отрезок А' В' в том
же отношении К и, значит (§ 5, теорема 1):
X— X] |
л X— X]
/V — , л, —
2—X 1 -J-/,
Если точки А' и В' совпадают, то с ними совпадает и точка С",
т. е. х1 = х2 = х. Формула
у, — х~х^
л. —
х2—х
в этом случае не имеет места. Однако формула
верна, так как при х1 — х2 правая часть обращается в хх.
Аналогично доказывается остальная часть теоремы.
Следствие. Координаты середины отрезка равны
полусуммам координат его концов:
g > У— 2 " *■ '
Теорема 2. £сл« относительно общей декартовой системы
координат в пространстве заданы две различные точки A (xv y1} zt) и
В (х2, у2, z2) и точка C(x,y,z) делит направленный отрезок АВ
в отношении X, то X равно тому из отношений
— Ui z—
в котором знаменатель не равен нулю, и любому из них:
если все знаменатели не равны нулю. Координаты точки С через
координаты точек А и В выражаются соотношениями
Xi 4~ }>Х2 {/l 4" \У2 г1 4~ ^г2
14-А. ' У~~ 14-А." ' 2~ м-А, •
Доказательство этой теоремы аналогично доказательству
предыдущей теоремы. Надо только проектирование параллельно
координатным осям заменить проектированием на оси координат
параллельно координатным плоскостям.
Следствие. Координаты середины отрезка равны
полусуммам координат его концов:
х = - —, у = Т , z -— „ .
30 Глава И ПРОСТЕЙШИЕ ВОПРОСЫ
§ 14. Ориентированный треугольник. Ориентированная плоскость.
Площадь треугольника
Треугольником будем называть тройку точек. Если эти точки
не принадлежат одной прямой, то треугольник будем называть
невырожденным, а если они принадлежат одной прямой, то —
вырожденным. Площадь вырожденного треугольника будем считать
равной нулю.
Ориентированным треугольником ABC называется
упорядоченная тройка точек А, В, С. В обозначении ABC ориентированного
треугольника порядок точек определяется порядком их записи:
Л —первая точка, В—вторая, С — третья.
Если точки Л, В, С не принадлежат одной" прямой, то
ориентированный треугольник ABC называется невырожденным, а если
точки Л, В, С принадлежат одной прямой, то —вырожденным.
Плоскость, на которой фиксирован невырожденный
ориентированный треугольник Е LE2O, называется ориентированной.
Рассмотрим произвольный невырожденный ориентированный
треугольник ЛВС, лежащий на плоскости, ориентированной
треугольником £\£20.
Будем говорить, что треугольник ABC имеет положительную
ориентацию, если треугольники ABC и Е^^О имеют одинаковую
ориентацию; если же треугольники ABC и Ь\£20 имеют
противоположную ориентацию, то треугольник ABC имеет
отрицательную ориентацию.
Определение одинаковой и противоположной ориентации двух
невырожденных ориентированных треугольников, лежащих в одной
плоскости, дано в дополнении I в конце книги. Можно
пользоваться и следующим наглядным определением, если обходы
контуров треугольников ABC и ELE2O в направлении от первых
вершин ко вторым и третьим совершаются в одном направлении (оба
против часовой стрелки или оба по часовой стрелке), то
треугольники ABC и ЕкЕ.гО имеют одинаковую ориентацию (рис. 22), а
если указанные обходы совершаются в противоположных
направлениях (один против часовой стрелки, а другой по часовой
стрелке), то треугольники ABC и ЕхЕ%0 имеют противоположную
ориентацию (рис. 23).
Вырожденному ориентированному треугольнику ABC не
приписывается никакой определенной ориентации (ни положительной,
ни отрицательной). Введем на плоскости декартову прямоугольную
систему координат; ориентируем ее треугольником ЕгЕЛО, где О —
13 ДЕЛЕНИЕ НАПРАВЛЕННОГО ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ 31
начало координат, а £, и ^--соответственно единичные точки
осей Ох и Оу.
/,'лощадь'о ABC невырожденного ориентированного
треугольника ABC, лежащего в плоскости, ориентированной треугольником,
ЕгЕ^О, называется число, абсолютная неличина которого равна
площади треугольника ABC, измеренной масштабным квадратом (т. е.
квадратом со стороной ОЕг = ОЕ2), и которое положительно,
если треугольник ABC имеет положительную ориентацию, и
отрицательно в противном случае.
Итак,
ABC | = пл. Д ABC,
причем ABC > 0, если треугольник ABC имеет положительную
ориентацию, и ABC < 0 в противном случае.
Если ABC — вырожденный треугольник, то будем считать, что
его площадь ABC равна нулю: АВС = 0.
При перестановке двух вершим невырожденного треугольника
ориентация его меняется на противоположную, поэтому при
круговой перестановке вершин треугольника ABC ориентация не
меняется, а при нарушении кругового порядка вершин ориентация
меняется на противоположную. Отсюда следует, что
ABC = ВС А = CAB = — ВАС = — АСВ =
-СВА.
Эти соотношения верны, конечно, и для вырожденного
ориентированного треугольника.
Теорема 1 (теорема Шаля для площадей). Пусть А, В, С, D —
четыре произвольные точки, лежащие на плоскости п. Введем на
этой плоскости декартову прямоугольную систему координат хОу.
Пусть 0—начало координат, а 0Ех и ОЕ2—масштабные точки
соответственно осей Ох и Оу(ОЕ1 — ОЕ2). Ориентируем плоскость
32
Глава 11 ПР0СТЕПП1ИЕ ВОПРОСЫ
л. ориентированным треугольником ЕХЕ2О. Тогда*
Доказательство Предположим сначала, что треугольник
ABC не вырождается.
1 П\сть точка D лежит внутри треугольника ABC (рис 24);
тогда * "
пл Д BCD -|- пл. Д CAD + пл Д ABD = пл. Д ЛВС,
или
~ " B)
BCD
+ ABD\= ABC\ .
В рассматриваемом сл>чае все треугольники BCD, CAD, ABD
и ABC имеют одинаковую ориентацию, поэтому все числа,
стоящие иод знаком модуля в соотношении B), имеют один и тот же
знак Если все они
положительны, то знак модуля (по определе- С
нию модуля или абсолютной
величины числа) можно снять. Если
В
Рис. 24
Рис. 25
все они отрицательны, то при снятии знака модуля перед каждым
выражением и слева, и справа надо поставить знак минус и после
перемены знака опять получим равенство A).
2 Предположим, что точка D лежит в области, ограниченной
отрезком АВ и лучами, полученными продолжениями отрезков
* Формулу A) можно переписать в виде АВС +BAD-\-CBD-{-ACD =0.
Запомнить се можно так- треугольник ABC ориентируется любым из двух
возможных способов, например ABC, каждый из остальных трех
треугольников ориентируется так, что общие сторочы двух любых треугольников
оказались бы ориентированными в протипопотожных направлениях (например,
в треуготьчике ЛВС первой является вершина А, второй — вершина В,
значит, при ориентации треугольника с вершинами А, В, D надо взять первой
вершим\ В, второй А, а третьей D)
** Площадь измеряем масштабным квадраюм.
§14 ОРИЕНТИРОВАННЫЙ ТРЕУГОЛЬНИК
СА и СВ за точки Лий (рис. 25). Тогда
пл. Д BCD i- пл. Д CAD — ал. Д Л££> = пл. Д ABC,
или
\cId\—\~abd\ = \abc\.
BCD
C)
В рассматриваемом случае треугольники BCD, CAD и ABC
имеют одинаковую ориентацию, а треугольник ABD имеет
ориентацию, им противоположную. Значит, BCD, CAD, ABC—числа
одного знака, а число ABD имеет знак, им противоположный.
Если, например,
BCDyO, CAD>0, ABC>0, ABD < О,
то из равенства C) сразу следует равенство A), а если
BCD<0, CAD<0, ABC<0, ABD>0,
то после перемены знаков в левой и правой частях равенства C)
снова приходим к равенству A).
Аналогично доказывается правильность формулы A) для
случая, когда точка D лежит в области, ограниченной отрезком ВС
и лучами, полученными продолжением отрезков
А В а АС за точки В и С, и для случая, когда
точка D лежит в области, ограниченной
отрезком СА и продолжениями отрезков ВС и ВА
за точки С и Л.
3. Предположим, что точка D лежит внутри
угла, вертикального с внутренним углом А
треугольника ABC (рис. 26). Тогда
пл. /\BCD~пл. ДС/Ш-пл.
= пл. Д ABC,
или
\BCD\-\CAD\—\ABD\=\ABC\. D)
Теперь числа BCD и ЛВС имеют одинако-
им
Рис. 26
вые знаки, а числа CAD и ABD — знаки,
противоположные, поэтому из равенства D) опять следует
равенство A).
Аналогично доказывается правильность формулы A) для
случая, когда точка D лежит внутри угла, вертикального с
внутренним углом В или с внутренним углом С треугольника ABC.
4. Предположим, что точка D лежит на прямой ВС между
точками В и С (рис. 27).
2 П. С. Моденов
Ггава П ПРОСТЕЙШИЕ ВОПРОСЫ
В этом случае
пл. Д CAD + пл. Д ABD = пл. Д АВС,
или
E)
В рассматриваемом случае треугольники CAD, ABD и ABC
имеют одинаковую ориентацию, поэтому числа CAD, ABD и ABC
Рис. 28
одного знака, и из равенства E) следует равенство A) (так как
в рассматриваемом случае BCD = 0).
Аналогично доказывается правильность формулы A) в случае,
если точка D лежит на стороне СА между точками С и А или
на стороне АВ между точками А и В.
5. Предположим, что точка D лежит на продолжении отрезка
ВС за точку В. Тогда (рис. 28)
пл. ДСЛО—пл. /\ ABD = пл. А АВС,
или
\CAD\-
ABD\ = \ABC . F)
В рассматриваемом случае треугольники CAD и АВС имеют
одинаковую ориентацию, а треугольник ABD имеет ориентацию,
им противоположную, поэтому числа CAD и АВС одного знака,
знак, противоположный им. Если, например,
a ABD имеет
CAD > 0, АВС > 0, А~Ш < 0, то из равенства F) сразу следует
равенство A) (надо еще учесть, что BCD = 0), если
CAD < 0, 1ВС < 0, ABD > О,
то, поменяв в обеих частях равенства F) знаки, опять придем
к равенству A).
§ 14 ОРИЕНТИРОВАННЫЙ ТРЕУГОЛЬНИК
Аналогично доказывается правильность формулы A) Для
случая, когда точка D лежит на продолжении отрезка ВС за точку С,
а также когда она лежит на прямой С А (на продолжении
отрезка СА за точку А или за точку С) или на прямой АВ (на
продолжении А В за точку А или за точку В).
Наконец, читатель без труда проверит, что формула A) верна
и в том случае, когда точка D совпадает с одной из точек
А, В или С.
Остается рассмотреть случай, когда точки А, В, С
принадлежат одной прямой. Если при этом и точка D принадлежит той
же прямой, то соотношение A), очевидно, верно (оно обращается
в равенство 0 = 0). Предположим поэтому, что среди точек А, В,
С, D есть три точки, не принадлежащие одной прямой. Пусть,
например, точки В, С, D не принадлежат одной прямой. Тогда
по доказанному имеем
BCA+CDA+DBA = BCD,
BCD —CD A—DBA = ВС А,
или
или
Теорема 2. Если относительно общей декартовой системы
координат хОу на плоскости заданы точки A(xv уг), В(х2, у2),
С (xs> Уз) и выбран масштабный отрезок т для измерения длин и
площадей (за единицу измерения площадей выбирается квадрат со
стороной т), то площадь ABC ориентированного треугольника
ABC вычисляется по формуле
АВС =
2
ч
х2
хз
У1
Уг
Уз
1
1
1
или
G)
(8)
где So — площадь масштабного параллелограмма, т. е.
параллелограмма, двумя сторонами которого являются масштабные отрезки
О£х и ОЕ2 соответственно осей Ох и Оу.
Доказательство. Сначала предположим, что точка А лежит
на осн Ох и не совпадает с началом координат (х1^=0, (/1 = 0),
точка В лежит на оси Оу и не совпадает с началом координат
(*2 = 0, УъФО), а точка С совпадает с началом координат
( О)
36 Глава 11. ПРОСТЕЙШИЕ ВОПРОСЫ
Тогда
I ЛВС I пл.ДЛВС 1 пл.ДЛВО 1 О А ОВ
So So 2 пл. Д EiE3O 2 О£х О£3
' I v 1 I II I v II I /Q\
— ~2 I xi 11 У а —~% I i1 " v '
Далее, если л;^ > 0 (т. е. точки Л и В лежат на
положительных полуосях Ох и Оу или на их продолжениях), то треугольники
АВО и ЕХЕ2О имеют одинаковую ориентацию, т. е. АВО > 0.
Если же хху2 < 0, то треугольники АВО и ЕгЕ%0 имеют
противоположную ориентацию, т. е. ЛВО<0. Таким образом, xty2 и
АВО—числа одного знака, а потому из соотношения (9) следует, что
ЛВО = уХ1уа. A0)
Последнее соотношение верно, конечно, и тогда, когда одна
из точек Л или В (или обе) совпадает с началом координат.
Пусть теперь точки Л и В занимают на плоскости какое угодно
положение, а точка С совпадает с началом координат. Обозначим
через Лх и Вг параллельные проекции точек Л и В на ось Ох
параллельно оси Оу. Применяя теорему 1 Шаля для точек Л, В,
О, Av будем иметь
С другой стороны, ориентация и площадь треугольника не
меняются, если одну из его вершин переместить по прямой,
параллельной стороне, противолежащей этой вершине,
следовательно,
и предыдущее соотношение примет вид
Применяя теорему 1 для точек Л, Bv О, Av получим
— Л R П ()9\
и так как В1ОЛ1 = 0, то из соотношений A1) и A2) следует, что
где Ла и В2 — параллельные проекции точек А и В на ось Оу
параллельно оси бх.
14 ОРИЕНТИРОВАННЫЙ ТРЕУГОЛЬНИК
37
Применял формулу A0), будем иметь
Пусть, наконец, точки А, В и С занимают на плоскости какое
угодно положение. Тогда
АВС =
■АВ0 =
Ч У г
Ч Уз
Ч Уз
Ч J/i
Ч
Ух
Ч Уг
So
—
Ч Ух 1
Ч Уг 1
Ч Уз [
Отнимая из элементов первой и второй строк соответствующие
элементы третьей строки и разлагая полученный определитель по
элементам последнего столбца, получим
х
хх хз Ух Уз
Х2 ХЪ Уч. Уз
Следствие 1. Площадь S треугольника ABC, заданного
своими вершинами A(xv yx), В{х2, у2), С (х8, у3) относительно
общей декартовой системы координат, вычисляется по формуле
s=
So
2
mod
Ч
ч
ч
Ух
Уг
Уз
1
1
1
= 4?-mod
Ч—Ч Ух-Уз
Х2 Х3 У2 Уз
A3)
(mod — знак модуля или абсолютной величины).
Следствие 2. Для того чтобы три точки
А(Ч>
B{xz, yt), C(x3, y8),
заданные относительно общей декартовой системы координат на
плоскости, принадлежали одной прямой, необходимо и достаточно,
чтобы выполнялось равенство
= 0,
ч
х,
ч
Ух
Уг
Уз
1
1
1
или
хх хз Ух Уз
хч хз Уч. Уз
-0.
Следствие 3. Пусть А(хи ух) и В(х2, у2)— две различные
точки, заданные относительно общей декартовой системы
координат. Тогда, если точки С(х, у) и С'(х', у') лежат по одну сторону
38
Глава II ПРОСТЕЙШИГ. ВОПРОСЫ
от прямой АВ, то определители
Д =
X
Ч
Ц
У
Ух
Уг
1
1
1
и Д' =
х'
хх
х2
У'
Ух
1
1
1
имеют один и тот же знак. Если же точки С(х, у) и Сг(х', у')
лежат по разные стороны от прямой АВ, то эти определители
имеют различные знаки.
В самом деле, если точки С н С" лежат по одну сторону от
прямой АВ, то треугольники CAB и С АВ имеют одинаковую
ориентацию, а если точки С и С" лежат по разные стороны от
прямой АВ, то треугольники CAB и С АВ имеют
противоположную ориентацию.
Замечание. Площадь So масштабного паргаллелограмма
записывают в виде
где g = gng22— g*2> причем glt = ОЕ\, g22 = OEl, g12=OE1-OE2 cos со
(со —угол меж а у осями Ох и Оу). ■
Таким образом, формулы G) и (8) можно записать в виде
АВС =
-VJL
хх Ух
хз Уз
-Уз
хз У 2 —Уз
Х1 Х3
соответственно изменятся формулы A3).
§ 15. Ориентированный тетраэдр. Ориентированное пространство.
Объем тетраэдра
В этом параграфе сформулируем определения и основные результаты для
тетраэдров, аналогичные результатам предыдущего параграфа для
треугольников. Доказательства этих положений могут быть даны аналогично тому,
как это было сделано в § 14 для треугольников. Однако проще всего эти
результаты получаются нз § 41 и 42 (смешанное произведение трех векторов).
Тетраэдром будем называть четыре произвольные точки А, В, С, D
пространства. Если эти точки А, В, С, D не принадлежат одной плоскости, то
тетраэдр будем называть невырожденным, а если они принадлежат одной
плоскости, то вырожденным, Объем вырожденного тетраэдра условимся считать
равным нулю.
Ориентированным тетраэдром A BCD называется упорядоченная четверка
точек А, В, С, D, В обозначении ABCD ориентированного тетраэдра порядок
15. ОРИЕНТИРОВАННЫЙ ТЕТРАЭДР
39
точек определяется порядком их записи: А —первая точка, В —вторая, С —
третья, D—четвертая. Если точки А, В, С, D не принадлежат одной
плоскости, то ориентированный тетраэдр ABCD называется невырожденным, а
если точки А, В, С, D принадлежат одной плоскости, то ориентированный
тетраэдр ABCD называется вырожденным.
Пространство, в котором задан невырожденный ориентированный тетраэдр
ElE2EsO, называется ориентированным* Если в пространстве введена общая
декартова система координат, то ориентируем пространство тетраэдром
Е^^ЕзО, где О —начало координат, а Еъ Е2, £3 —соответственно единичные
точки осей Ох, Оу, Ог.
Рис. 29
Будем говорить, что невырожденный ориентированный тетраэдр ABCD
пространства, ориентированного тетраэдром Е1Е2Е3О, имеет положительную
>■ ►
ориентацию, если тетраэдры ABCD и Е1Е2Е3О имеют одинаковую ориентацию.
Если же тетраэдры ABCD и Е^^Е^О имеют противоположную ориентацию,
то тетраэдр ABCD имеет отрицательную ориентацию.
Определение одинаковой и противоположной ориентации двух
ориентированных тетраэдров дано в дополнении I в конце книги.
Можно пользоваться и следующим наглядным определением:
ориентированные тетраэдры ABCD и Е-^Е^Е^О имеют одинаковую ориентацию, когда
обход контура треугольника EiE2Es, если смотреть на плоскость ЕХЕ2Е3
с той стороны от плоскости £1£2£13, где расположена точка О, кажется
происходящим в том же направлении, в каком обходится контур треугольника
ABC, если смотреть на плоскость этого треугольника с той стороны от
плоскости ABC, где расположена точка D (рис. 29). Если же указанные обходы
40
Глава II. ПРОСТЕЙШИЕ ВОПРОСЫ
производятся в противоположных направлениях (один — по часовой стрелке,
другой—против часовой стрелки), то будем говорить, что тетраэдры ABCD
и ЕхЕ^ЕзР имеют противоположную ориентацию (рис. 30).
Вместо вершин D и О можно взять две другие с одинаковым номером,
например С и £j, и сравнивать направления обходов треугольников BAD и
ЕгЕхО, рассматривая их соответственно из точек С и £5. Если направления
этих обходов одинаковые, то тетраэдры ABCD и ExEtE3O имеют одинаковую
ориентацию, а если противоположные, то тетраэдры ABCD и ЕхЕ2Е3О имеют
протииоположную ориентацию Читателю предлагается убедиться геометри-
Рис 30
чески в том, что данное определение одинаковой и противоположной
ориентации двух тетраэдров не зависит от выбора вершин (D и О, или С и Е3,
или В и £2, или А и £j3.
Вырожденным ориентированным тетраэдрам никакой определенной
ориентации из приписывается (ни положительной, ни отрицательной).
Пусть пространство ориентировано тетраэдром £1£2£3О; параллелепипед
с ребрами 0Ец ОЕ2, OES назовем масштабным. Выберем масштабный отрезок
т и за единицу измерения объемов примем куб, ребро которого равно
масштабному отрезку (единичный куб)
Объемом ABCD невырожденного ориентированного тетраэдра ABCD,
находящегося в пространстве, ориентированном тетраэдром £1£2£3О,
называется число, абсолютная величина которого равна объему V тетраэдра ABCD
и которое поло*игелыю, если тетраэдр ABCD имеет положительную
ориентацию и отрицательно в противном случае.
Итак,
\IMd\=v,
причем ABCL)> 0, если тетраэдр ABCD имеет положительную ориентацию и
ABCD < 0, если тетраэдр ABCD имеет отрицательную ориентацию
§ 15. ОРИЕНТИРОВАННЫЙ ТЕ I РЛЭДР
41
Если тетраэдр ABCD— вырожденный, то его объем считаем равным нулю:
При перестановке двух вершин ориентированного тетраэдра его
ориентация меняется на противоположную, поэтому ABCD = — BACD = BADC =
=— DABC и т. д.
Теорема 1 (теорема Шаля для объемов). Для пяти произвольных точек
А, В, С, D, Е ориентированного пространства имеет место соотношение*:
АВСЕ4- BADE-\-CBDE + ACDE = ABCD. (I)
Теорема 2. Ест относительно общей декартовой системы координат заданы
вершины тетраэдра A (xlt ух, ?{), В {х2, у2, г2), С (х6, у3, гЛ) и D {xit yit гй),
то
х2 щ
или
ABCD =
у2—у4
Уз —У*
B)
C)
где Vo — объем масштабного параллелепипеда, т. е. параллелепипеда, ребрами
которого служат масштабные отрезки OElt OE2, OES осей координат, Эют
объем Vo может быть вычислен по формуле
D)
* Условимся считать поверхность тетраэдра ABCD ориентированной, если
ориентированы все его грани, притом так, что ориентации двух любых граней
порождают на ребре, принадлежащем им обоим, противоположные
ориентации. Для того чтобы ориентировать поверхность тетраэдра ABCD, достаточно
ориентировать лишь одну его грань, так как ориентация одной грани
порождает в соответствии с принятым соглашением ориентации всех остальных.
Таким образом, поверхность всякого тетраэдра ABCD можно ориентировать
только двумя способами:
BAD, CBD, ACD и ВАС, АвЪ, ВСЪ, CAD.
Порядок первых трех точек каждого слагаемого левой части равенства A)
выбран так, что соответствующие этому порядку ориентации граней тетраэдра
ABCD образуют ориентацию его поверхности (в правой части вместо ABCD
можно записать BADC или CBDA, или ACDB).
Отметим, что теорема Шаля для площадей (§ 14, теор ма 1) может быть
записана так:
ABC + BAD+CBD+ ACD = Q.
Ориентированные грани ABC, BAD, CBD, ACD образуют ориентацию
поверхности вырожденного тетраэдра ABCD. Теоремы Шаля для площадей и объемов
относятся к элементарной геометрии (см., например, Ж. А дам а р.
Элементарная геометрия, ч. II, стереометрия. М., Учпедгиз, 1938, прибавление G —
о понятии объема, стр. 498—501, где изложено элементарное доказательство
теоремы Шаля для объемов).
42
Глава /Л ПРОСТЕЙШИЕ ВОПРОСЫ
где
?п Su
E)
§31 8з2 ЙЗЗ
а числа gik определяются соотношениями
2 = OEi-OE2 COSCO3, £2з = (
0Ег-ОЕ] cosco2
F)
(со3—угол между осями Ол; и Оу, coj — угол между осями Ог/ и Ог, соа —угол
между осями Ог и Ох)
Из теоремы 2 вытекают следующие следствия.
. Следствие 1. Пели в пространстве введена общая декартова система
координат и выбран масштабный отрезок т для измерения длин, причем куб,
ребро которого равно масштабному отрезку т, служит для измерения объемов,
то объем тетраэдра ABCD с вершинами
А (хъ i/i, z{), В i
вычисляется по формуле
2, г2), С (х3, уа, г3) и D
4, г4)
V =
А", Г/1 Zt
Ч Уз Ч
^з 1)л Ч
Ч 1
G) или У =
(8)
где g—квадрат объема масштабного параллелепипеда — вычисляется по
формуле E), причем gtk вычисляются по формулам F),
Следствие 2, Для того чтобы четыре точки
i/i.
2. г2), С (*3. Уз. гз). D (xit yit z4),
заданные относи 1елыю общей декартовой системы координат, принадлежали
одной плоскости, необходимо и достаточно, чтобы выполнялось равенство
= 0, т е.
Ч J/i Ч
х2 у2 ?а
*.- Уз гз
= 0,
или
1 —** ^1— £/4 *! — г4
2 — -«4 У2—У4 г2 —г4
3 ^4 Уз Hi гЗ г4
= 0.
Следствие 3 Пусть относительно общей декартовой системы координат
заданы три точки
A (*i, УХ, гО, S (х2, 1/г, г2), и С (х3, у3, г3),
не принадлежащие одной прямой. Тогда, если точки D (х, у, г) и D'(x',y',z')
лежат по одну сторону от плоскости ABC, то определители
Д =
х у г
Ч У\ 2)
х2 у2 г2
Ч Уз г3
х — *Л У —Уз г —г3
«1—*з г/i — Уз ч—ч
Ч — Xi г/г—г/з г2—г3
v'
x2
у' г'
Vi ?i
y2 22
§ 15.
1
I
УГЛЫ
x x3
Xi — Xq
x2 — x3
у —
«i —
У2 —
Уз
Уз
Уз
г' — г.л
*1 — 23
г2~ Z3
43
имеют один и тот же знак, а если точки D (х, у, г) и D' (х', у', г') лежат по
разные стороны от плоскости ABC, то определители Д и Д' имеют
противоположные знаки.
§ 16. Углы
1. Определение угла
Углом, называется совокупность двух лучей р и q, выходящих из
одной точки О. Точка О называется вершиной угла, а лучи р к q —
его сторонами. Если лучи р и q совпадают, то угол называется
нулевым, а если один из них является продолжением другого, то
развернутым.
Углы обычно измеряют в радианах или градусах. Если угол
измеряется в радианах, то его величина ф принимает значения
от 0 до л (величину 0 имеет нулевой угол, а величину it —
развернутый). Если угол измеряют в градусах, то его величина
принимает значения от 0 до 180° (величину 0° имеет нулевой угол,
величину 180° — развернутый угол).
2. Ориентированный угол. Его величина. Равенство,
сумма и разность величин ориентированных углов
Ориентированным углом pq называется упорядоченная пара лучей
р и q, выходящих из одной точки О. В обозначении pq
ориентированного угла порядок его сторон определяется порядком их
записи! р — первая сторона, <? —вторая.
Пусть на плоскости, ориентированной треугольником ЕгЕгО,
лежит ориентированный угол pq с вершиной в точке О, отличный
от нулевого и развернутого. Возьмем на лучах р и q соответственно
точки А и. В, отличные от вершины О угла pq. Будем говорить,
что ориентированный угол pq имеет положительную ориентацию,
если положительную ориентацию имеет треугольник А ВО (т. е. если
треугольники АВО и ЕХЕ2О имеют одинаковую ориентацию). Если
же треугольник АВО имеет отрицательную ориентацию, то будем
говорить, что угол имеет отрицательную ориентацию. Это
определение не зависит от выбора точек А и В на лучах р и q, так
как если А и А'—две точки, отличные от точки О и лежащие
на луче р, а В и В'—две точки, также отличные от точки О а
44 * Глава 11 ПРОСТЕЙШИЕ ВОПРОСЫ
лежащие на л\че q, то треугольники АВО и А'В'О имеют
одинаковую ориентацию.
Нулевому и развернутому углу не приписывается определенной
ориентации (ни положительной, ни отрицательной).
Отсюда, между прочим, следует, что плоскость можно
ориентировать, задав на ней ориентированный угол pq (ненулевой и
неразвернутый). В таком случае плоскость считается
ориентированной треугольником АВО, где А я В — любые точки, отличные от
вершины угла pq и лежащие соответственно на его сторонах р и q.
Величине (р, q) ориентированного угла pq, лежащего на
ориентированной плоскости, приписывается бесконечное множество
значений:
{р,Я) = а + 2кя A)
(k принимает все целые значения), где |а| = ср; а ф — величина угла
со сторонами р и q\ при этом а > 0, если угол pq имеет
положительную ориентацию, а < 0, если угол pq имеет отрицательную
ориентацию, а = 0, если pq — нулевой угол, и а = я, если pq-—
развернутый угол.
Заметим, что а в формуле A), называемое главным значением
ориентированного угла pq, можно заменить любым другим значением
величины ориентированного угла pq. Так, например, если а = -~ , то
каждое из выражений
+ 2kn
+ 2kn, + 2kn, ^+2кл и т. д.,
где k принимает все целые значения, определяет одно и то же
множество чисел.
Главное значение а величины ориентированного угла pq
заключено в полуинтервале (—it, я], т. е. —я<а^я.
Заметим, что два любых значения (р, q) величины
ориентированного угла обладают тем свойством, что их разность кратна 2л
(т. е. отношение этой разности к числу 2л есть число целое). В связи
с этим обстоятельством формулу A) часто записывают в виде
(р, q)~a(mod2n) B)
(читается так: «(р, q) сравнимо с а по модулю 2л»). В последней
формуле B) число а можно считать любым значением величины
ориентированного угла {pq).
Будем считать величины {р, q) и {р', q') двух ориентированных
углов pq и p'q', лежащих на ориентированной плоскости, равными,
если множество всех значений величины одного из них совпадает
с множеством всех значений другого.
. 16. углы 45
Величины (р, q) и (р', q') ориентированных углов pq и p'q',
лежащих на ориентированной плоскости, равны тогда и только
тогда, когда разность любых двух значений величин этих углов
кратна 2я (т. е. отношение этой разности к числу 2л есть число
целое). Это обстоятельство записывают так:
(р, q)=z(pr, q') (mod 2л). C)
Таким образом, в формуле C) можно считать, что (р, q) — любое
из значений величины угла pq, a (p', q') — любое из значений
величины угла p'q'.
Суммой (р, q) ~- (p1, q') величины (р, q) ориентированного угла pq с
величиной (р\ q'), ориентированного угла p'q', лежащих па
ориентированной плоскости, называется бесконечное множество чисел,
которое получится, если каждое из значений величины угла pq
сложить с каждым из значений величины угла p'q'.
Сумма (p,q) + (p',q') величин ориентированных углов pq и p'q'
равна сумме двух любых значений (р, q) и (р', q') величин этих
углов, сложенной с 2/гл, где k принимает все целые значения.
Например,
(р, q)+(q, p)~0 (mod 2л), D)
так как среди всех значений (р, q) и (q, p) ориентированных
углов pq и qp найдутся два таких, сумма которых равна нулю.
Разность (р, q) — (p', q') величин ориентированных углов pq и p'q',
лежащих на ориентированной плоскости, определяется аналогично
тому, как была определена сумма этих величин. При вычислении
разности (р, q) — (p', <?')> и здесь можно вычесть любое из
значений (р', q') из любого значения (р, q) и добавить 2/гл, считая,
что k принимает все целые значения. При этом удобно пользоваться
формой записи, аналогичной соотношению A). Например,
(р, q) — iP, <7)ssO (mod 2л). E)
3. Угол между двумя осями. Угол от одной оси до
другой и его величина
Пусть / и т—две оси, имеющие общую точку О; тогда углом
между осями / и т называется угол с вершиной О, сторонами
р \\ q которого являются лучи, лежащие на осях / и т,
выходящие из точки О и идущие в положительных направлениях этих
осей; ориентированный угол pq называется углом от оси / до оси т.
Если оси / и т имеют общую точку О и _лежат на
ориентированной плоскости, то величине (/, т) угла Ст. от оси / до оси т
4G Глава И ПРОСТЕЙШИЕ ВОПРОСЫ
приписывается бесконечное множество значений:
(/, m) = a + 2kn, F)
где а — любое из значений угла от оси I до оси т, a k принимает
все целые значения. Формулу F) можно записать так:
(I, m) = a(mod2ji). G)
Если лучи / и т параллельны и направлены в одну сторону,
то говорят, что они образуют пулевой угол и приписывают
величине угла от оси / до оси т бесконечное множество значений 2/гл,
где k принимает все целые значения:
(/, m) = 0 (mod 2л). (8)
Если лучи / и т параллельны и направлены в разные стороны,
то говорят, что они образуют развернутый угол и приписывают
величине угла от оси I до оси т бесконечное множество значений
Bk-\-l)n, где k принимает все целые значения:
(/, m) = n (mod 2л). (9)
Равенство, сумма и разность величин (I, т) и (/', т') углов
1т и I'm' от оси / до оси т и от оси /' до оси т' определяются
соответственно как равенство, сумма и разность величин
ориентированных углов, являющихся углами от оси / до оси т и от оси
/' до оси т'.
В записях равенств этих углов, значений их суммы или
разности естественно пользоваться той же формой записи,
заимствованной из теории сравнения, которая была указана в п. 2 настоящего
параграфа.
4. Углы между двумя прямыми. Угол от одной
прямой до другой и его величина
Две прямые а и Ь, имеющие общую точку О, образуют четыре
угла; любой из этих углов называется углом между прямыми а и Ь.
Любой из углов между двумя прямыми а и Ь, стороны которого
упорядочены, притом так, что первой стороной угла является та,
которая лежит на прямой а, а второй —та, которая лежит на
прямой Ь, называется углом от прямой а до прямой Ь и
обозначается ab.
Если прямые а и b лежат на ориентированной плоскости и
имеют общую точку О, то величине (a, b) угла ab от прямой a
до прямой Ь приписывается бесконечное множество значений: это
множество всех значений только что указанных четырех
ориентированных углов. Если a—одно из значений (а, Ь) ориентированного
угла ab от прямой а до прямой Ь, то все значения (a, b) заклю-
16. УГЛЫ 47
чаются в формуле
(а, Ь) = а + йп, A0)
где k принимает все целые значения. Формулу A0) можно
записать и так:
(а, 6) = а (mod n). A1)
Если прямые а и Ъ параллельны, то говорят, что они образуют
нулевой угол и считают
(a, b)==Q (mod я). A2)
Главным значением а угла ab от прямой а до прямой Ь,
лежащими на ориентирова шой плоскости, называется то из
значений этого угла, которое заключено в полуинтервале [0, я), т, е.
0<а<п.
Величины (а, Ь) и (а', Ь') двух углов ab и а'Ь' от прямой а
до прямой Ь и от прямой а! до прямой Ь' считаются равными, если
множество всех значений (а, Ь) угла ab совпадает с множеством
всех значений (а', Ь') угла а'Ь', иначе гопоря, разность двух
любых значений (а, Ь) и (а', Ь') углов ab и а%' кратна л:
(а, Ь)э=(а', Ь') (mod я). A3)
Сумма и разность величин (а, Ь) и (а', Ь') углов ab и а'Ь'
определяются так же, как сумма и разность величин ориентированных
углов. Однако во всех соотношениях между величинами (а, Ь), (а', Ь"),
(а", Ь") и т. д. углов аЪ, а'Ь', а"Ь" сравнение следует брать по
модулю п. Например, если прямые а и b взаимно перпендикулярны, то
(а, Ь) = ^ (mod я).
Для двух любых прямых а я b имеют место соотношения!
(a, b) + (b, а)==0 (mod л),
(а, b) — (a, b)~0 (mod л).
Замечание. В-дальнейшем слово „угол" употребляется и в
других ситуациях, например: угол между двумя направленными
отрезками О А и ОБ — это угол с вершиной О, на сторонах р и q
которого лежат соответственно точки А и В; при этом углом от
направленного отрезка О А до направленного отрезка ОВ считается
ориентированный угол pq.
Далее, угол между двумя векторами а и Ь — это угол, вершина
которого берется в любой точке О пространства, а стороны р и q
идут соответственно в направлении векторов а и Ь (заметим, что
здесь угол определяется неоднозначно, однако все полученные таким
48 Глава П ПРОСТЕЙШИЕ ВОПРОСЫ
образом углы равны, иначе конгруэнтны). Или еще: угол, который
вектор а образует с осью / — это угол, вершиной которого
является произвольная точка О оси /, а сторонами р и q — соответственно
луч р, выходящий из О и идущий в положительном направлении
оси /, и луч q, выходящий из О и идущий в направлении вектора а.
При этом ориентированный угол pq называется углом от оси / до
вектора а. И здесь определение угла между вектором и осью
неоднозначно, по все получаемые в соответствии с этим
определением углы будут равны между собой (конгруэнтны).
§ 17, Теорема Шаля для ориентированных углов
Пусть р, q, г — три луча, выходящие из точки О, лежащие на
ориентированной плоскости. Тогда
(р, q)-\-(q, л) = (р, r) (mod 2л). A)
Доказательство. Предположим сначала, что лучи р, q, r
попарно различны и ни один из них не является продолжением
,р другого. Обозначим через аи a2, а3
соответственно главные значения углоз pq, qr и рг.
Случай 1. Луч q проходит внутри угла
рг (рис. 31). Тогда сумма величины угла,
образованного лучами р и q, и величины
угла, образованного лучами q и г, равна
величине угла, образованного лучами р и г,
т. е.
Рис. 31 |а \-\-\a i = ! а I.
Но так как углы pq, qr, pr имеют одинаковую ориентацию, то
ai> а2> аз—числа одного знака, а потому из последнего равенства
следует, что
Ctj ~j- C&2 := 0-з
и, значит,
(р, q)-\-(q, r) = (p, r) (mod 2л).
Случай 2. Луч г проходит внутри угла pq (рис.32). Тогда,
на основании уже доказанного
(Р, r)-\-(r, q)=(p, q) (mod 2л),
или
(р, q) — {r, q) S2 (р, г) (mod 2л),
или
(р, q) + (q, r)=(p, r) (mod 2л).
17. ТЕОРЕМА ШЛЛЯ ДЛЯ ОРИЕНТИРОВАННЫХ УГЛОВ
49
Случай 3. Луч р проходит внутри угла qr (рис. 33). Тогда
(<7. Р) + (Р, '•) = (<?. г) (mod 2л),
-(<?, p) + (q, /•)==(/>, г) (тос12я),
(Р, 9) +(9. r)=s(p, r) (mod 2л).
Случай 4. Лучи р, q, r попарно различны, ни один из них
не проходит внутри угла, образованного двумя другими и ни один
из них не является продолжением другого. В этом случае
причем числа ах и а2 одного знака, а а3 —число знака, им противо-
■Р >*
0^— г
Рис. 32
Рис. 33
положного (для случая, изображенного на рис. 34, ах > 0, а2 > О,
а3 < 0, а для случая, изображенного на рис. 35, аг < 0, а2 < О,
а3 > 0). Таким образом, имеет место одно из двух равенств:
или
ах -j- а2 = а3 ± 2л.
Отсюда (р, q) + (q, r)==(p, r) (mod 2я).
Рис. 35
Случай 5. Среди лучей р, Ц, г есть совпадающие. Пусть,
например, совпадают лучи р и q. Тогда аг = 0, а2 = а3и, значит,
= а3,
50
Г i a s a 11 ПРОСТЕПШИГ ВОПРОСЫ
т. е.
(р, q)\-(q, r) = (p. r) (mod 2л).
Аналогично доказывается это равенство в случае, если
совпадают лучи q и г. Если совпадают лучи р и г, то а1 = — а2, а3 = 0
и, значит, опять а1-[-а2 = а3.
Случай 6. Один из лучей р, q, r является продолжением
другого. Пусть, например, луч р — продолжение луча г. Тогда
либо а14-аа = л;> «я = л (рис. 36), либо
а1 + «2=—л,а3 = л (рис. 37), значит, либо
a1-i-a2 = a3, либо a1 + a2 = a3—2л.
Из обоих равенств следует, что
(р, q) + (q, r) = (p, r) (mod 2л).
Следствие. Пусть I, m, n — три луча,
имеющие общую точку О и лежащие на
ориентированной плоскости. Тогда
(/,
(т, п)==A, п) (mod 2л).
B)
Теорема 2 (теорема Шаля для прямых).
Пусть а, Ь, с — три прямые, лежащие на
ориентированной плоскости и имеющие общую
точку О; тогда
(а, Ь) f ф, с) = (а, с) (mod л). C)
Доказательство. Пусть р, q, /- — соответственно лучи,
лежащие на прямых а, Ь, с и выходящие из точки О. На основании
теоремы Шаля для углов
(р, q) + (q, r)=(p, r) (mod 2л),
следовательно,
(р, q) + (q, 0 = (Р. г) (той к).
Но так как какое-нибудь значение (р, q) есть одно из
значений угла ab, одно из значений (q, r) есть одно из значений угла
be, а одно из значений (р, г) есть одно из значений угла ас, то
из последнего соотношения следует, что
(a, b) + (b, c) = (a, с) (mod л).
III. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
§ 18. Полярная система координат на плоскости
Говорят, что на плоскости введена полярная система
координат, если эта плоскость ориентирована, на ней выбраны точка О —
полюс, луч Ох, выходящий из точки О—-полярная ось и
масштабный отрезок.
§18 ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ НЛ ПЛОСКОСТИ
51
Рис 38
Пусть М — произвольная точка плоскости, не совпадающая с
полюсом (рис. 38).
Первой полярной координатой точки М, или полярным
радиусом, называется расстояние г от точки М до полюса О. Второй
полярной координатой точки М, или
амплитудой, называется угол ср от полярной оси
(от луча Ох) до луча ОМ.
Для полюса О считают /- = 0, ср — любое
число.
В некоторых вопросах (например, при
задании линии полярным уравнением)
удобно полярному радиусу г приписывать знак;
именно считают г < 0, если амплитуду ср измеряют от полярной
оси до луча, который получается продолжением луча ОМ за
точку О.
Полярные координаты г, ср в случае, если для первой
координаты г допускаются и отрицательные значения, называются
обобщенными полярными координатами.
Пусть на плоскости введена полярная система координат.
Введем декартову прямоугольную систему координат, принимая
полюс О за начало координат, и за положительную полуось Ох—
полярную ось. За ось Оу примем
ось, которая получается поворотом
оси Ох вокруг точки О на угол +90°,
т. е. положительное направление на
оси Оу выбирается таким, чтобы угол
от оси Ох до оси Оу был равен
-(-90°. Масштабный отрезок
полярной системы координат примем и за
масштабный отрезок декартовой
системы (рис. 39). Пусть г и гр —
полярные координаты произвольной
точки М плоскости, не совпадающей с полюсом, ахи у—ее
декартовы прямоугольные координаты в указанной выше системе.
По определению тригонометрических функций имеем
Рис. 39
откуда
Так как
то
cos ср = у , sin ср = у
р( г/ = г sin ф.
A)
B)
C)
52
Глава II ПРОСТЕЙШИЕ ВОПРОСЫ
Формулы A) позволяют вычислить декартовы прямоугольные
координаты хну точки М по ее полярным координатам г и ф.
Формулы B) и C) позволяют вычислить полярные координаты г
и ф точки М по ее декартовым координатам х и у.
Отметим, что формулы A) верны и для обобщенных полярных
координат (т. е. для радикала Ух2 + у2 во всех формулах B)
и C) можно брать и отрицательное значение).
Рис 40
§ 19. Полярная система координат в пространстве. Полярные и
сферические координаты
Рассмотрим в пространстве ориентированную плоскость П.
Пусть Oz — ось, перпендикулярная плоскости П и пересекающая
ее в точке О, а Ох — луч, лежащий в
плоскости П и выходящий из точки О.
Выберем масштабный отрезок.
Ориентированная плоскость II
называется экваториальной, ось Oz
—зенитной, луч Ох—полярной осью, а точка
О —полюсом.
Совокупность этих элементов
называется полярной системой координат в
пространстве (рис. 40).
Цилиндрическими координатами точки /И, не лежащей на
зенитной оси, называется упорядоченная тройка чисел р, ср, z, где
р и ф —полярные координаты ортогональной проекции Р точки М
на экваториальную плоскость (в полярной системе
экваториальной плоскости с полюсом О, полярной осью Ох и выбранной
единицей масштаба), a
z—координата на зенитной оси Oz проекции Q
точки М на зенитную ось (рис.
41). Для точек зенитной оси
считают р = 0, ф—любое число, а
z определяется так, как указано
выше.
Заметим, что при помощи
цилиндрических координат не
устанавливается взаимно однозначного
соответствия между множеством
всех точек пространства и
множеством упорядоченных троек
действительных чисел.
Сферическими координатами точки М, не лежащей на
зенитной оси, называется упорядоченная тройка чисел г, ф, 0, где/- —
длина отрезка ОМ, ср —угол от полярной оси Ох до луча ОР
Рис. 41
§19. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ
53
(Р—проекция М на экваториальную плоскость), а0— угол между
лучами ОР и ОМ, который принимает значения в интервале
(—£- , ~), причем считается, что 0 = 0, если точка М лежит в
экваториальной плоскости, 0 > 0, если луч ОМ образует острый
угол с зенитной осью, и 0 < 0, если луч ОМ образует с зенитной
осью тупой угол (рис. 42).
Если точка М лежит на зенитной оси и не совпадает с
полюсом О, то считают, что ср — любое число, а Q—-\--~
или
0 = —^- в зависимости от того, совпадает ли направление луча
ОМ с направлением зенитной оси или противоположно ему. Для
полюса считают г = 0, ср и 0 — любые числа. При помощи
сферических координат не устанавливается взаимно однозначного
соответствия между множеством всех точек пространства и
множеством упорядоченных троек действительных чисел.
Пусть в пространстве введена полярная система координат.
Введем еще декартову прямоугольную систему координат,
принимая за положительную полуось Ох полярную ось, за ось Оу —
ось, полученную из оси Ох поворотом ее вокруг полюса в эква-
П
Рис. 42
Рис.43
ториальной плоскости на угол +90° и зенитную ось за ось Oz
(рис. 43). Пусть Р — проекция точки М на экваториальную
плоскость. Обозначая через р длину отрезка ОР, находим
x = pcoscp, £/ = р sin ф.
С другой стороны, p = rcos0, значит,
Кроме того, ясно, что
: = rcos0 cos cp,
/ = rcos0 sin cp.
A)
54 Глава II ПРОСТЕЙШИЕ ВОПРОСЫ
Формулы A) верны и для того случая, когда точка М лежит
на зенитной оси и когда она совпадает с полюсом (при
дополнительных соглашениях о величинах ц> и 0 в этом случае).
По формулам A) вычисляются декартовы прямоугольные
координаты точки М в случае, если известны ее сферические
координаты.
Из формул A) следует, что
х2 |-£/3 = р2 = г2 cos2 G,
откуда
г cos 6 = ]/х2 -f У2,
значит,
COS ф = ,
■ л/ .л \
sincP^^7=f=
sin 0 ~
B)
По этим формулам вычисляются сферические координаты г, ф,
8 точки М, не лежащей на зенитной оси по ее декартовым
прямоугольным координатам х, у, z (при указанном взаимном
расположении этих двух систем координат).
Замечание. Вторую сферическую координату ф часто
называют долготой, третью G — широтой. Иногда вместо широты 0
рассматривают угол я|з между положительным направлением
зенитной оси и лучом ОМ, идущем из полюса О в данную точку М;
величина я|з изменяется в пределах от 0 до л. Величина i|)
называется зенитным расстоянием.
Так как 9 —-^- — г|>, то в формулах A) и B) (в случае, если за
третью сферическую координату принимается зенитное
расстояние) cos0 и sin 0 следует заменить соответственно на sin г|) и cos i|).
§ 20. Задачи к главе II
1. Задачи с решениями
Пример 1. Точка С делит невырожденный направленный отрезок АВ
в отношении к (Ф ± 1) Точка D делит тот же отрезок в отношении —X. В
каком отношении делит отрезок А В середина М отрезка CD.
Решение. Введем на прямой АВ систему координат, принимая точку Л
за начало координат, а ючку В за единичную точку. Тогда коор инаты х'
и х" точек С и D будут
X „ —X
i 20. ЗАДАЧИ К ГЛАВЕ II 55
Х =7-П-> X =■:
X • л ~ 1 _ X '
а координата л середины М отрезка CD
__*' + **. X2
Х~ 2 ~ 1->,2'
Отсюда находим
^ _
AM Ш ^_ 1~Л2 _
Отсюда, между прочим, следует, что точка М лежит вне отрезка АВ.
Пример 2. В точках A (xt) и В (х2) сосредоточены массы т-^ и т2. Найти
координату центра тяжести этой систеуы материальных точек.
Решение. Центр тяжести С лежит между точками Л и В и дели:
отрезок АВ в отношении тг:т\. Поэтому координата х центра тяжести
определяется по формуле
Замечание. Методом полной индукции доказывается, что координата л:
центра тяжести системы из п точек:
М1(х1), М2(х2) Мп(кп),
в которых помещены массы, соответственно равные mlt /n2, ..., тп,
определяется по формуле
=
т1-\-т2+...-\-т„
Пример 3. Найти координаты центра М (х, у) и радиус окружности,
описанной вокруг треугольника ABC с вершинами
ЛA, 2), В(-1, 0), СC, -1).
Решение. Имеем МА — МВ = МС, МА2 = МВ^ = МС2, или (х— ]J4.
2J (lJb2 CJ+(+lJ
Решая эту систему уравнений, получим * = ttj> У~~7п1 Центр
.. /11 1 \
м ilo- —ToJ; радиус
r = AM=V [1-Го) +B+Го] =
Пример 4. Найти центр М {х, у) » радиус г окружности, вписанной в
треугольник ABC с вершинами:
А (9, 2), В@, 20), С (-15, -10).
56
Глава //.ПРОСТЕЙШИЕ ВОПРОСЫ
Решение. Пусть D(x', у') —точка пересечения биссектрисы
внутреннего угла А треугольника ABC со стороной ВС (рис. 44) Тогда точка D
делит направленный отрезок ВС в отношении
ВР_АВ_ У(9 — 0)Ч-B— 20J .. . 3
DC ~ АС ~ /"(9+15J+B+10)г~ 4
fAC,2) Поэтому координаты точки D будут
т • С-15>
в(о,го)
х := -
У ==-
Далее, так как
:=У (— 15 — 0J+(— 10 — 20J=15
7
Т'
BD_3 BD + DC_7 ВС _ 7
4 gO
потому DC=y • 15 J/5=—;
DC
■. Далее,
С 12 J/T.7 7
CD 60
а потому координаты точки М будут
=—5 \ 7^=о, £/=—Ц.2-=5.
45
" 7 •
f .(-10)
_50
Центр вписанной окружности М @, 5). Радиус МК вписанной окружности
можно найти из соотношения
4-8С-/И/С = пл. ДВСМ,
или
15
МК = j mod
0 20 1
— 15 —10 1
0
5 1
МК-
152
" ""ч — 2 '
Пример 5. На ориентированной плоскости задан невырожденный
ориентированный треугольник ABG. Пусть М — произвольная точка плоскости.
Числа
САМ 1Ш
ВСМ
ABC'
ABC
ABQ
§20. ЗАДАЧИ К ГЛАВЕ II
57
называются барицентрическими координатами точки М относительно
ориентированного треугольника ABC
ABC, то все треугольники
Если точка М лежит внутри треугольника
ВСМ, САМ, ABM, ABC
имеют одинаковую ориентацию и, значит, все числа ВСМ, САМ, АВМ и
ABC имеют один и тог же знак; поэтому для любой точки М, лежащей внутри
треугольника ABC, имеем а > 0, р > 0, у > 0. Если точка М переходит через
какую-нибудь одну из сторон треуготьника ABC, то соответствующая
барицентрическая координата меняет знак; например, для всех точек области,
ограниченной отрезком ВС и продолжениями отрезков AS и АС за точки В
и С, имеем а < 0, р > 0, у > 0. Наконец, если точка М лежит иа одной из
прямых ВС, СА или АВ, то соответствующая барицентрическая координата
равна нулю.
На рисунке 45 показано распределение знаков барицентрических
координат точки М в зависимости от ее положения относительно прямых ВС,
Рис 45
СА и АВ (стороны изображены в виде полос). Если вершины невырожденного
ориентированного треугольника заданы относительно общей декартовой
системы координат A (xlt у{), В (х2, у2), С (х3, у3), а точка !Л имеет координаты
х и у, то
х2
Ч
X
Ч
ч
ч
г/г
Уз
г/
г/i
£/2
Уз
1
1
1
1
1
1
х3
Ч
к
Xl
хг
Хз
Уз 1
г/i i
г/ 1
1Л 1
г/г 1
Уз 1
ч
ч
X
Ч
ч
ч
г/i
г/2
г/
г/i
г/г
Уз
1
1
1
1
1
1
58
Глава 11. ПРОСТЕЙШИЕ ВОПРОСЫ
и, вычисляя а, р, у, можно по их знакам (без чертежа) определить
расположение точки М относительно треугольника ABC.
Пример 6. Относительно общей декартовой системы координат заданы
четыре точки А (хи у{), В (х2, у2), С (х3, ys) и D (х4, </„). При каком
необходимом и достаточном условии эти четыре точки могут служить вершинами
выпуклого четырехугольника?
Решение. Это будет тогда и только тогда, когда треугольник ABC
невырожденный, а точка D находится с одной из трех областей, каждая из
которых ограничена стороной треугольника ABC и продолжениями двух других
за граничные точки этой стороны Пусть а, Р, у — барицентрические
координаты точки D относительно треугольника ABC. Только одно лз чисел а, р, у
должно быть отрицательно, а два других — положительны. Значит, искомое
необходимое и достаточное условие ару < 0, или
х2
х3
X,
г/2
Уз
г/4
1
1
1
X-i
Х1
Xi
г/з
г/i
г/4
1
1
1
xi
х2
X,
г/г
£/4
1
1
1
Х1
х2
х3
Hi
г/г
г/з
1
1
1
2. Задачи для самостоятельного решения
1. Доказать, что если А, В, С, D — четыре произвольные точки, лежащие
на оси, то
~АВ .CD+1C- Ш+ТЬ- SC = 0.
2. Точки Р и Q делят невырожденный направленный отрезок АВ в
отношениях, соответственно равных А, и ц (X Ф ц, ц Ф 0). В каком отношении
точки А и В делят отрезок PQ?
3. Точки Р, Q и /? делят невырожденный отрезок АВ в отношениях,
соответственно равных К, [д, и v. В каком отношении точка R делит отрезок
PQ (v ф ц)?
4. Точки Р и Q делят невырожденный направленный отрезок ЛВ в
отношениях, соответственно равных К и ц,. Пусть i? — середина отрезка PQ. В
каком отношении точка R делит отрезок ЛВ (X+|iy=— 2)?
5. В точках с координатами 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 помещены массы,
соответственно равные 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Найти координату центра
тяжести системы.
Отв 7.
6. На оси Оу найти точку, равноудаленную от точки ( — 8, —4) и от
начала координат.
Отв @, —10).
7. Найти точку М (х, у), симметричную точке А B, —3) относительно
прямой, проходящей через точки В (Ь 3) и С (—6, *-4).
Отв. (—5, 4).
§20. ЗАДАЧИ К ГЛАВЕ II 59
8. Найти точки пересечения с осями координат прямой, проходящей через
точки ЛC, 4) и В B,-1).
Отв. (У-, о), @, -И).
V о 1
9. Найти координаты х и г/ центра тяжести треугольника /?i5C с вершинами
A (xv r/i.), В (*2, у2) и С (,г3, j/3).
10. Даны две смежные вершины Л ( — 4, — 7) и В B, 6) параллелограмма
и точка М C, 1) пересечения его диагоналей. Найти две другие вершины.
Отв. A0,9) и D, —4).
11. На прямой, проходящей через точки D,2) и @,-1), найти точки,
отстоящие от точки (— 4, —4) на расстоянии 5.
Отв. (-8, -7) и @, -1).
12. Найти расстояние от точки B, 0) до прямой, проходящей через точки
A,1) и F,4).
Отв. 1.
13. Две вершины треугольника находятся в точках E, I) и ( — 2, 2); третья
вершина лежит на оси Ох. Найти координаты третьей вершины, зная, что
площадь треугольника равна 10.
Отв. C2,0) и ( — 8,0).
14. Относительно общей декартовой системы координат даны вершины
A (Xi, iji), В(х2,Уг), С(х3, у3) невырожденного треугольника ABC. Пусть а, р\
■у—барицентрические координаты точки М относительно треугольника ABC.
Доказать, что декартовы координаты точки М выражаются следующими
формулами:
+ Pf + P + A)
Обратно, если a+P + Y=l> то точка М, декартовы координаты которой
выражаются формулами A), имеет барицентрические координаты а, {5, у.
15. В вершинах невырожденного ориентированного треугольника ABC
помещены массы тъ т2, тъ. Найти барицентрические координаты центра
тяжести этой системы материальных точек относительно треугольника.
_ т, о т2 т3
Отв. а = ;——. , В = :—— , v= :—*-; , Отсюда
16. Относительно невырожденного ориентированного треугольника ABC
заданы две различные точки Р (аъ fS1( Yi) и Q (a2> Рг> Y2) своими
барицентрическими координатами. Точка М делит направленный отрезок PQ в
отношении X. Найти барицентрические координаты точки М.
<"■'■ «"^ ^ № _^
17. Относительно невырожденного ориентированного треугольника ABC,
лежащего на ориентированной плоскости, заданы три точки Р (alt p1( yi).
60
rtaea II ПРОСТЕЙШИЕ ВОПРОСЫ
Q (а2> $2, Y2). Я (аз> Рз> Уз) своими барицентрическими координатами. Найти
~PQR
ABC
в частности, найти необходимое и достаточное условие принадлежности трех
точек Р, Q, R одной прямой.
Отв.
PQR
Твс
«1
«3
b
Pa
Yi
Y2
Ys
I
a3 В
l Vi
2 Y2
3 Ys
= 0.
18. Найти в плоскости Oxz точку, равноудаленную от трех точек! А A, 1, 1),
(—1. 1,0) и СC, 1, —1).
19. Определить внутренние углы треугольника с вершинами А A,2, —4),
В D, 0, —10), С (-2, 6,8).
/1 / 89\ D 23
Ome ^=arccos — ^r , o = arccos
7/И
= arccos я=-
13]All
ГЛАВА III
ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
I. ЛИНИЯ И ЕЕ УРАВНЕНИЯ
§ 21. О понятии линии и ее уравнениях
Понятие линии является одним из самых трудных понятий
математики. Общее определение линии дается в специальной
математической дисциплине — топологии. Оно было получено лишь в 20-х
годах текущего столетия советским математиком П. С. Урысоном.
Не останавливаясь на определении линий*, мы дадим лишь
определение того, что называется уравнением линии.
Определение I. Уравнением линии в декартовой системе
координат называется уравнение
F(x, j/) = 0, A)
которому удовлетворяют координаты х, у всех точек этой линии
и только координаты таких точек.
В частности, уравнение линии может иметь вид
U = f(x). B)
Уравнением линии в полярной системе координат называется
уравнение
Ф(/-,Ф) = 0, C)
которому удовлетворяют полярные координаты г и ср всех точек
этой линии и только координаты таких точек.
В частности, уравнение линии в полярных координатах может
иметь вид
г = г(ц). ■ D)
* См., например, А. С. Пархоменко. Что такое линия. М., Гостехиз-
дат. 1954, или П. С. Урысон. Труды по топологии и другим областям
математики, т. II, о канторовых многообразиях, ч. II, канторовы кривые.
62
Глава III ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
Определение II. Параметрическими уравнениями линии в
декартовой системе координат называются уравнения вида
x = x(t), y = y(t),
где функции x(t) и у (t) имеют одну и ту же область определения,
каждому значению t из этой области соответствует точка
M(x(t), у(t)) рассматриваемой линии и каждая точка М этой
линии соответствует некоторому значению t из области
определения функций x(t) и u(t), т. е. для любой точки М линии
найдется такое значение t, что x{t) и y(t) будут координатами точки М.
Аналогично определяются параметрические уравнения линии в
полярных координатах.
§ 22. Примеры составления уравнений линии
Пример 1. Рассмотрим окружность S радиуса г с центром в точке С(а,Ь)
заданной относительно декартовой прямоугольной системы координат (рис. 46)
Пусть М (х, у) — произвольная точка плоскости. Точка М лежит на окружно
М(х,у)
о
Рис. 46
Рис. 47
сти S тогда и только тогда, когда расстояние между точками М а С равно
радиусу г окружности S.
Расстояние между точками М и С равно
поэтому уравнение окружности S имеет вид
ИЛИ
или
(х—а
(х—а
—&J — г2 = 0.
0)
A')
В частности, уравнение окружности радиуса г с центром в начале
координат имеет вид (рис. 47)
х2-(-уг = Л B)
или
х* + У°- — '2 = 0- B')
§22. ПРИМЕРЫ СОСТАВЛЕНИЯ УРАВНЕНИЙ ЛИНИЙ 63
Уравнение (Г) (и B')) называется нормальным уравнением окружности.
Замечание. Пусть М(х, у) — произвольная точка плоскости, а А я В —
точки пересечения с окружностью S прямой, проходящей через центр С
окружности A') и точку М. Тогда, выбирая на этой прямой положительное
направление, имеем
{х—аJ + (у — bf — г2=МС2 — г2 =
==/ИС2 —"Ж
: + СА){МС—СА) =
= (МС-г~СА) (МС-\-~C~B) = М~А-МВ.
Произведениео = MA-MB равно произведению MP-MQ, где Р и Q—точки
пересечения с окружностью S любой секущей (на которой произвольным
образом выбрано положенное направление), проходящей через точку М; оно
называется степенью точки М относительно окружности S.
Таким образом, левая часть (х — аJ + ((/—бJ—/-2 нормального уравнения
окружности S, где х и у — координаты любой точки М плоскости есть степень
точки М относительно окружности S:
o^(x-af+(y-bf-r\
Если точка М лежит вне окружности S, то координаты МР и MQ иа-
правленных ненулевых отрезков МР и MQ имеют одинаковые знаки, значит
a > 0, а если точка М лежит внутри окружности S, то а < 0; впрочем, это
ясно и из того, что 0=Л1С2 — г2; отсюда также следует, что если точка М
лежит вне окружности S, то ее степень относительно этой окружности равна
квадрату длины отрезка МТ, где Г—точка прикосновения к окружности S,
касательной к ней, проведенной из точки М.
Если точка М лежит на окружности S, то по крайней мере один из
направленных отрезков МР или MQ— нулевой и, значит, а = 0—степень точки М,
лежащей на окружности относительно этой окружности, равна нулю.
Пример 2. Составить уравнение линии, отношение расстояний каждой
точки которой до двух данных различных точек А и В равно числу m—одному
и тому же для всех точек линии.
Решение. Введем на плоскости декартову прямоугольную систему
координат, принимая за начало координат середину О отрезка АВ, а точку А —
за единичную точку оси Ох; тогда координаты точки А будут 1, 0, а
координаты точки В будут—1,0.
Пусть М (х, у) — произвольная точка плоскости. Она будет лежать на дан-
нон линии тогда и только тогда, когда
МА
-гт-g =/Л, ИЛИ
или
или, считая m ф\ после ряда тождественных преобразований, получим
2_ 4т2
Vv ~(l-nflf "
Это уравнение является уравнением окружности * с центром в точке
_ ,'Н-т2 Л 2т
С г-з. О и радиусом г = . ..
* Эта задача была рассмотрена Лпполоинем в работе о конических
сечениях. Поэтому окружность, определяемую свойством, указанным в условии
задачи, называют иногда окружностью Апполоння.
64 Глава 111. ЛИНИИ. ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
Пример 3. Найти геометрическое место точек, для каждой из которых
сумма квадратов расстояний до трех данных точек А, В, С равна данному
числу т.
Решение. Введем на плоскости декартову прямоугольную систему
координат, Пусть хъ уу\ х2, у2; хл, у.— координаты точек А, В и С. Точка
М (х, у) принадлежит данному геометрическому месту тогда и только тогда,
когда
(х-Х1)Ч-(У-<лГ--{ (х-х^-[-(у-у2У-\-(х-х.
или
или
I 3 / V 3——j ^"з"^*2— 3> +Wj-Уз) -r
или окончательно
(x-x
где
0
a a, b, с — длины отрезков ВС, СА u AB.
Таким образом, если
т<
то данное геометрическое место пустое Если
то данное геометрическое место точек содержит только одну точку Мо (хп, и„).
а2 + Ь2 + с2
Если т. > ——^—■— , то данное геометрическое место точек является окруж-
о
ностью с центром в точке Мо (xQ, yQ) и радиусом г = -^- |/"Зш —(о2 + 62-}-с2).
Заметим, что если точки А, В, С неколлинеарны, то Мо — точка
пересечения медиан треугольника ABC, а а, Ь, с — длины его сторон.
Замечание. На основании предыдущего
а2 -4- Ь2 4- г2
Значит, сумма квадратов расстояний от точки Л1 до точек А, В, С имеет
наименьшее значение, если точка М совпадает с точкой /Ио (иначе с центром
тяжести системы равных масс, помещенных в точках А, В, С).
Имеет место (и аналогично доказывается) следующее положение! сумма
/Их/И2 + М2М2 + ... + М„Л12
имеет минимальное значение, если точка М совпадает с центром тяжести
системы п равных масс, помещенных в точках Mlt /И2, .., Мп (точки /Ид,
М2, ..,, М„ могут и не лежать в одной плоскости).
§22. ПРИМЕРЫ СОСТАВЛЕНИЯ УРАВНКНИЙ ЛИНИИ
65
Пример 4. Составить уравнение линии, произведение расстояний любой
точки которой до двух данных точек Fi и F2 равно данному числу &2.
Решение. Пусть расстояние между точками Ft и F2 равно 2а. За
начало О декартовой прямоугольной системы координат на плоскости примем
середину отрезка F^i, а прямую FiF2 с положительным направлением от О kF3
примем за ось Ох. Точка F1 в выбранной системе координат имеет
координаты—а, 0, а точка F2—а, 0.
Согласно условию задачи
или
MF\-MF\—b*.
Применяя формулу расстояния между двумя точками, находим
и соотношение MF^-zMf2 =64 принимает вид
(х* -Ь У2J + 2о2 (у2 — х2) = б4 — а4.
Линии, определяемые этим уравнением, называются овалами * Кассини.
Изображения их (для случаев а > Ь, а — b, а < &) даны на рис. 48. Если а = &,
Рис. 48
т. е. если произведение расстояний от точки М до точек Я^и/^ равно квадрату
половины расстояния между точками Fx и Fit то опал Кассини называется
лемнискатой Бернулли (рис. 49). Уравнение лемнискаты имеет вид
(х2-Ь(/2J = 2а2(*2 — у2).
Составим уравнение лемнискаты еще в полярной системе координат,
принимая точку О за полюс, а положительную полуось Ох за полярную ось.
* Овалы Кассини не всегда являются овалами в собственном смысле
этого термина (выпуклая замкнутая линия).
3 II. С. Моденов
66
Рлавй 111 ЛИНИИ ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
Заменяя и уравнении лемнискаты х и у их выражениями через полярные
координаты
i
получим
или
r4=2aV2(cos2q>—sin2q>),
r = o |/~2cos2q>
При изменении ср от —- до 0 функция а
возрастает от 0 до
a У~2, а ПРИ изменении ф от 0 до -\--т- эта функция убывает от а У~2 до 0,
получается петля, расположенная в первой и четвертой четвертях, при измене-
Зл 5я
нии ф от — до —т- получается другая петля, расположенная во второй н
третьей четвертях, симметричная
первой относительно полюса.
Значениям ф, для которых
со$2ф<0 соответствуют мнимые значения
функции У 2tos 2ф, следовательно, этим
значениям ф не соответствуют никакие
точки лемнискаты.
Что касается построения овалов
Кассипи, то точки этих линий удобнее
всего строить, исходя из геометриче
ского определения линии
Уравнения линий иногда удобло
составлять в полярной системе координат.
Рассмотрим следующий пример.
Пример 5. Дана окружность С диаметра О А—а и на ней точка О. Вокруг
точки О вращается луч ОТ Пусть прямая, на которой лежит этот луч,
пересекает окружность в точче Р Па этой прямом от точки Р в направлении
рис 49
Рис 50
Рис 5!
луча откладываем отрезок РМ=Ъ Составить уравнение линии, описываемой
точкой М (рис 50)
* Сокращая на г\ мы не теряем полюса, принадлежащего лемнискате, так
как приф = -2~ из уравнения г = а V 2 cos 2 ф находим /-=0,
$22 ПРИМРРЫ СОСТ ЧВЛЕНИЯ Ур\ППЕНИЯ '1Н11ИИ
E7
Решение Примем точку О за полюс, а луч ОА — за полярную ось Ох.
Пусть г и ф—обобщенные полярные координаты точки М, а ги ф—обобщенные
полярные координаты точки Р. Тогда
г = Г1 + Ь
Но
Гх — а cos ф,
где ф—угол от оси Ох до вращающегося луча *.
Поэтому полярное уравнение данной линии будет
г = b -f- a cos ф
Эта линия называется улиткой Паскаля. Строить ее проще всего исходя
из геометрического определения (рис. 51).
Рис 52
Пример 6. Рассмотрим окружность радиуса а с центром в начале О
декартовой прямоугольной системы координат.
Введем полярную систему координат, принимая начало координат за полюс,
а за полярную ось —положительную полуось Ох (ориентация плоскости
определяется выбранной декартовой системой координат, а масштабный отрезок
декартовой системы координат берем в качестве масштабного и в полярной
системе).
Пусть х и (/—декартовы координаты произвольной точки М окружности,
а а и t — полярные координаты топ же точки. Тогда
, с Зя Згг \f2
* Если, например ф=—, то cos—= ^—
и гх =
a V2
это значит
(в соответствии с определением обобщенных координат), что при ф = -^- отре-
а Y2
зок —-г— надо откладывать на продолжении луча ОТ за точку О. Так именно
и строится точка Р линии, соответствующая положению луча ОТ в сдул ie,
когда угол от полярной оси до луча ОТ лежит, например, в интервале f-у, л \ .
3*
68
Глава 111 ЛИНИИ ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
где параметр I принимает все значения от 0 до 2зх Эти уравнения являются
параметрическими уравнениями окружности.
Пример 7. Рассмотрим на плоскости снова две системы координат: яекар-
тову прямоугольную и полярную, находящиеся в том же отношении друг к
другу, что и в предыдущем примере
Спиралью Архимеда называется линия, уравнение которой в обобщенных
полярных координатах илеет вид
где а—фиксированное число, отличное от нуля, а г и t — полярные координаты
точки (г — полярный радиус, t — амплитуда), параметр / принимает все дейст-
рительные значения (рис 52). Параметрические уравнения спирали Архимеда
в указанной выше декартовой прямоугольной системе координат имеют вид
x = alcost, y-*=at sin t.
Строить спираль Архимеда проще всего исходя из ее полярного уравнения.
Замечание. Составим параметрические уравнения траектории,
описываемой точкой М в следующем сложном движении: точка М движется
равномерно со скоростью v по прямой, проходящей через полюс О, а прямая
равномерно вращается в плоскости вокруг
точки О с угловой скоростью ш
Примем за начало отсчета времени
тот момент, когда точка М была в точке
О и предположим, что в этот момент
вращающаяся прямая совпадала с осью
Ох. За время t точка М вращающейся
прямой пройдет путь, равный r~vt, a
прямая повернется на угол <p = (ot.
Таким образом, полярные координаты
х'
точки М:
Отсюда
где а =
= vt, m =
т. е. точка движется по
спирали Архимеда.
Уравнения r = ut, cp = ro< являются параметрически ли уравнениями спирали
Архимеда в полярных координатах (считаем, что в этих уравнениях параметр t
принимает все действительные значения)
Пример 8. По прямой / катится без скольжения окружность радиуса а.
Составить параметрические уравнения линии, которую описывает произвольная
точка катящейся окружности (циклоида)
Решение. Пусть Со — начальное положение катящейся окружности, Л'о—
ее центр, а О —точка, в которой эта окружность касается прямой / (рис. 53).
Примем точку О за начало декартовой прямоугольной системы координат, а
прямую /, ориентированную в сторону движения, за ось Ох. Произвольное
положение катящейся о'кружности обозначим через С, ее центр — через N,
точку, в которую перейдет точка О окружности Со, когда эта окружность Сд
займет положение С, обозначим через М и наконец точку касания окружности С
с осью Ох обозначим через S.
Пусть Р и Q —проекции точки М соответственно на оси Ох и Оу.
Проведем через точку N оси Л'дг' и Ny' соответственно параллельные и одинаково
направленные с осями Ох и Оу Обозначив через / — (Л'УИ, NS) значение
ориентированного угла от направленного отрезка NM до направленного отрезка
§23. ПОВЕРХНОСТЬ И ЕЕ УРАВНЕНИЕ
69
NS, имеем:
Так как
(NM,
£-,
(NM,
~
то координаты SP и N0Q проекций направленного отрезка NM на оси Ох и
Оу (соответственно параллельные осям * Nx' и Ny') будут
SP = a cos ( t + -o- ) = — a sin <,
iV0Q = a cos (/-f-n) = —a cos t
и потому координаты x n у точки /И:
x — OP = OS-\-SP = a{— a sin t — a (t—sin t),
Уравнения
x = a(t — sin t), y = a(\—cost),
где параметр t принимает все действительные значения, и являются
параметрическими уравнениями циклоиды (рис. 54).
Рис 54
Наглядное представление о циклоиде мы получаем, наблюдая за движением
какой-либо точки колеса, катящегося по прямой.
II . ПОВЕРХНОСТИ И ЛИНПИ В ПРОСТРАНСТВЕ
§ 23. Поверхность и ее уравнение
Определение понятия поверхности еще труднее, чем понятие
линии, и останавливаться на нем мы не будем.
Уравнением поверхности в общей декартовой или в
прямоугольной системе координат называется уравнение
F(x,y,z) = 0,
* Так как оси Ох и Nx' параллельны и направлены в одну сторону, то
угол от оси Ох до направленного отрезка NМ равен углу от оси Nx' до того
же направленного отрезка. Аналогичное заключение имеет место и по
отношению к осям Оу и Ny'.
70 Глава III ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
которое удовлетворяется координатами любой точки, лежащей на
этой поверхности и не удовлетворяется координатами точек, не
лежащих на поверхности.
Аналогично определяется уравнение поверхности в сферических
координатах
и в цилиндрических координатах
F(p, ф,г) = 0.
В частности, уравнение поверхности в декартовой системе
координат может быть задано в виде, разрешенном относительно
одной из координат, например в виде
2 = /(х, у).
Наконец, поверхность может быть задана параметрическими
уравнениями.
Параметрическими уравнениями поверхности П в декартовой
системе координат называются уравнения вида
x = x(u,v), y = y(u,v), z = z{u,v),
где функции х(и, v), у (и, v) и z(u, v) имеют одну и ту же область
определения D (которая представляет собой множество
упорядоченных пар чисел и, v); каждой паре чисел и, v из этой области D
соответствует точка M(x(u,v), y(u,v), z(u,v)) поверхности II, и
для любой точки М поверхности П найдется пара чисел и, v из
области D, такая, что х(и, v), у (и, v), z(u, v) будут координатами
точки М. Числа и и v называются криволинейными (или
внутренними) координатами точки М. Аналогично определяются
параметрические уравнения линии в цилиндрических и сферических
координатах.
§ 24. Примеры составления уравнений поверхностей
Пример 1. Введем в пространстве декартову прямоугольную систему
координат. Рассмотрим сферу S радиуса а с центром в точке С (х0, у0, г0). Точка
М (х, у, г) лежит на сфере S тогда и только тогда, когда длина отрезка СМ
равна а (рис 55) или тогда и только тогда, когда СМ2 = аг или (см. § 12)
В частности, уравнение сферы радиуса а с центром в начале координат имеет
вид
Пример 2. Введем в пространстве декартову прямоугольную систему
координат Охуг, а кроме того, — полярную, принимая положительную полуось Ох
§24 ПРИМЕРЫ СОСТАВЛЕНИЯ УРАВНЕНИЙ ПОВЕРХНОСТЕЙ
71
за полярную ось, за экваториальную плоскость —плоскость хОу, причем
ориентируем ее треугольником £1£20 (£i и £2—масштабные точки осей Ох и Оу),
а за зенитную ось — ось Ог. Рассмотрим сферу S радиуса а с центром в начале
координат. Возьмем на этой сфере произвольную точку М (х, у, г), обозначим
Рис. 55
Рис. 56
ее долготу и широту соответственно через и и v (рис. 56). Тогда (см § 19,
формулы A))
х=а cos v cos и, y = acosvsin и, г = a sin с;
таковы параметрические уравнения рассматриваемой сферы S.-Криволинейные
координаты точки М — это ее долгота и и широта а. Область D изменения
параметров и, v такова:
Заметим, что сферу S в сферических
координатах можно записать
уравнением г = а.
Пример 3. Составим уравнение
прямой круговой конической
поверхности д\ вершина которой находится
в начале декартовой прямоугольной
системы координат, а острый угол
между образующими поверхности и
осью Ог (положительное направление
на оси Ог не учитывается) равен а.
Пусть М (х, у, г) —произвольная
точка поверхности д; тогда
расстояние MQ от этой точки М до оси
Ог равно расстоянию М'О от
проекции М' (х, у, 0) точки М (х, у, г) в
плоскость хОу до начала координат
(рис. 57), т. е.
MQ=M'0= j/>-j-y2.
С другой стороны,
MQ = OQ\ga,
Рис 57
а так как OQ = |z|, то из последних соотношений находим
откуда
72
Глава III. ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
Обратно, если координаты некоторой точки М (х, у, г) удовлетворяют
последнему уравнению, то
х* + if* = гг \g* а,
откуда
V"xT+J2 = \z\ tga или ,MQ=OQtga,
а значит, точка М лежит на прямой, проходящей через начало координат и
наклоненной к оси Ог под углом а, т. е. точка М лежит на поверхности К-
Наряду с декартовой прямоугольной системой координат введем
полярную, как это сделано в § 19 (и в предыдущем примере). Обозначим через и
расстояние от точки /И до начала координат, а через v—долготу точки М.
Т огда
х = и cos i> sin a, y = u sin v sin a, 2 = ucosa
Однако этими параметрическими уравнениями не задается вся поверхность К
(так как г = «со5аэ0). Для задания параметрическими уравнениями всей
поверхности К следует считать, что и принимает все действительные значения.
Таким образом, область D изменения параметров и и v такова:
О < и < 2л, — оо < и < — оо.
(D)
При таком выборе области D изменения параметров и и v предыдущие
урапнсния являются параметрическими уравнениями поверхности К.
Заметим, что часть поверхности К, соотве1С1вующая неотрицательным
значениям и (т. е. одна полость конической поверхности К), в сферических
координатах может быть записана ура-
2 " внецием вида
0 = 7;—а,
а обе полости, т. е. вся поверхность
К, — двумя уравнениями:
П
.-*(!-.)
(знак + соответствует „верхней" части
поверхности К, знак — „нижней").
Пример 4. Докажем, что уравнение
x2-f y2 = a2, где а > О,
58
в декартовой прямоугольной системе
координат является уравнением прямой
круговой цилиндрической поверхности П
с образующими, параллельными оси Ог,
причем плоскость хОу пересекает
ЭТу поверхность по окружности С
радиуса а с центром в начале координат.
В самом деле, координаты точки М (х, у, z) удовлетворяют уравнению
х2+</2==°2 тогда и только тогда, когда координаты М'(х, у, 0) проекции
точки М на плоскость хОу удовлетворяют этому уравнению, а это значит, что
точка М лежит на поверхности, заданной уравнением x2 + i/2 = a2 тогда и
только тогда, когда ее проекция М' на плоскость хОу лежиг на окружности
С (угх2-\-у2 = 0М1). Значит, х2-{-у2 — а2 есть уравнение цилиндрической
поверхности II, описанной выше (рис. 58).
§24 ПРИМЕРЫ СОСТАВЛЕНИЯ УРАВНЕНИЙ ПОВЕРХНОСТЕЙ
73
Пример 5. Введем в пространстве декартову прямоугольную систему
координат. Предположим, что плоскость а, оставаясь параллельной плоскости хОу,
движется равномерно со скоростью а в положительном направлении оси Ог,
а в плоскости а равномерно вращается вокруг точки пересечения се с осью Ог
прямая / с угловой скоростью w.
Тогда поверхность, описываемая
прямой / в указанном сложном движении,
называется геликоидом (рис. 59).
Составим параметрические уравнения
геликоида, считая, что в начальный момент
времени v — 0 плоскость а совпадает с
плоскостью хОу, а прямая I совпадает с
осью Ох. Возьмем на геликоиде
произвольную точку М (х, у, г).
Ориентируем прямую / и положим
NM=u, где Л' — точка пересечения
прямой / с осью Ог (рис. 60).
Пусть у —промежуток времени, за
который прямая I из своего начального
положения 'перейдет is положение прямой
ММ. Обозначим через R проекцию точки
Рис. 59
Рис. 60
М на плоскость хОу, а через Р и Q —проекции точки /? соответственно
на оси Ох и Оу. Тогда Wt — u, а угол от оси Ох до OR равен ыи. Поэтому
х = О~Р = O~R cos (сои) = и cos (tot)),
у = O~Q =OR sin (во) = и sin (too),
z = RM = av.
Итак, параметрические уравнения геликоида:
х = « cos (tot»), у —и sin (wu), z = av.
Параметры и и v принимают все действительные значения.
74
Г лава ИГ ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
§ 25. Цилиндрические и конические поверхности
1. Цилиндрические поверхности
Цилиндрической поверхностно называется поверхность,
образованная параллельными между собой прямыми К, называемыми ее
образующими.
Если какая-нибудь плоскость, пересекающая все образующие
цилиндрические поверхности, пересекает ее по линии С, то эта
линия называется направляющей этой цилиндрической
поверхности.
Теорема 1. Если в пространстве введена общая декартова
система координат, и уравнение
F(x, y) = 0
в плоскости хОу является уравнением некоторой линии С, то это
уравнение в пространстве есть уравнение цилиндрической поверх-
Рис 61
нести П с направляющей линией С, а образующие параллельны
оси Oz (рис. 61).
Доказательство. Точка М(х, у, г) лежит на
цилиндрической поверхности II тогда и только тогда, когда проекция
М'(х, у, 0) точки М на плоскость хОу параллельно оси Oz лежит
на линии С, т. с. тогда и только тогда, когда выполняется
уравнение F (х, у) = 0.
Теорема 2 (обратная). Если П — цилиндрическая поверхность,
направляющей которой является плоская линия С, а образующие
поверхности П параллельны некоторой прямой I, не лежащей в
плоскости линии С, то существует система координат, в которой
уравнение поверхности П имеет вид
F(x, y) = 0.
Доказательство. Введем общую декартову систему
координат Охуг, совмещая плоскость хОу с плоскостью, в которой
25. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ 75
расположена линия С, и принимая за ось Ог—ось, параллельную
прямой /. Пусть
F(x, у) = 0
уравнение линии С в плоскости хОу. На основании предыдущей
теоремы это уравнение в пространстве во введенной системе
координат является цилиндрической поверхностью И.
Замечание 1. Аналогичные заключения имеют место для
уравнений вида F(y, z) = 0 и F(z, х) = 0 (рис. 62 и 63).
Замечание 2. Если линия С на плоскости хОу задана
параметрическими уравнениями х — х(и), у = у(и), то
параметрические уравнения поверхности П с направляющей С, образующие
которой параллельны оси Ог, можно записать в виде
х = х(и), у = у{и), г = у.
Пример 1. Уравнение
в декартовой прямоугольной системе хОу на плоскости является уравнением
окружности С с центром в точке (х0, у0) и радиусом а. Если ввести ось Ог,
не лежащую в плоскости хОу, то в полученной общей декартовой системе
координат Охуг это же уравнение в пространстве является уравнением
наклонного цилиндра, образующие которого параллельны оси Ог, а
направляющая— окружность С. Сечения этой цилиндрической поверхности плоскостями,
параллельными плоскости хОу,—окружности, полученные переносом
окружности С вдоль оси Ог,
Пример 2. Уравнение
у = ах*-\-Ьх-\-с, где афО,
в декартовой прямоугольной системе координат хОу на плоскости является
уравнением параболы С. Присоединяя ось Ог, не лежащую в плоскости хОу,
получим пространственную систему координат Охуг, относительно которой
уравнение у = ах2-\-Ьх-\-с является уравнением цилиндра, направляющая
которого—парабола С, а образующие параллельны оси Ог (параболический
цилиндр).
2. Конические поверхности
Определение 1. Конической поверхностью называется
поверхность, образованная множеством прямых К, проходящих через
одну точку S, называемую вершиной этой поверхности. Прямые К
называются образующими конической поверхности.
Если какая-нибудь плоскость, не проходящая через вершину
конической поверхности и пересекающая все ее образующие,
пересекает коническую поверхность по линии С, то эта линия
называется направляющей конической поверхности.
Определение 2. Функция F (х, у, г) называется однородной, ест
она обладает следующими свойствами:
76 Глава lU ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
1) если точка (х, у, z) входит в область определения функции
F (х, у, г), то точка (kx, ky, kz), где k—любое число, также
входит в область определения этой функции;
2) существует такое число п, что для любой точки (х, у, г)
из области определения функции F (х, у, z) и для любого числа k
выполняется соотношение
F(kx, ky, kz) = k"F(x, у, z).
Число п называется показателем однородности.
Теорема. Если уравнение
F (х, у, z) = О,
где F (х, у, г) — однородная функция, в декартовой системе
координат является уравнением поверхности К, то эта поверхность
коническая, причем вершина конуса лежит в начале координат.
Доказательство. Если точка М (х, у, г) (отличная от начала
координат) лежит на поверхности, заданной уравнением
F(x, у, г) = 0, то на той же поверхности лежит точка (kx, ky, kz),
где k—любое число. В самом деле,
F (kx, ky, kz) — kn F (x, у, г) = 0. A)
Если k принимает все действительные значения, то точка
(kx, ky, kz) описывает всю прямую, проходящую через точку М
и начало координат О, так как точка (kx, ky, kz) в случае ':фО
делит направленный отрезок МО в отношении -^— .
Действительно, вычисляя координаты делящей точки по формулам § 13,
получим
, 1-/г . , \—k „ , \-k .
: -г- — kx, : т- = k\j, j г- = kZ.
1 _i_ '~д I i ' Z 1 4- ' ~~k
k k k
Начало координат (в случае п > 0) также принадлежит
поверхности, заданной уравнением F (х, у, г) = 0, так как, полагая в
соотношении A) k — О, получим
F@, 0, 0) = 0.
Таким образом, если на поверхности К лежит какая-нибудь
точка, не совпадающая с началом координат, то на ней лежит вся
прямая, проходящая через эту точку и начало координат. Итак,
поверхность образована прямыми, проходящими через начало
координат, т, е. является конической поверхностью с вершиной в
начале координат.
Замечание. Обратная теорема интереса не представляет, так
как для любой конической поверхности К с вершиной в начале
координат функцию F (х, у, г) можно определить так: она равна
<i 26 ПОВЕРХНОСТИ ВРАЩЕНИЯ 77
пулю во всех точках этой поверхности и не определена ни в одной
другой точке пространства. Такая функция F (х, у, г) однородна
и уравнение F (х, у, г) —0 является уравнением поверхности К.
§ 26. Поверхности вращения
Поверхностью вращения называется поверхность, обладающая
следующим свойством: любое ее сечение плоскостью, проходящей
через точку поверхности, перпендикулярной к некоторой прямой I
(ось вращения), содержит окружность (параллзль), центр которой
лежит на прямой I и которая проходит через взятую точку.
Меридианом поверхности вращения называют ее сечение
плоскостью, проходящей через ось вращения. Иногда меридианом
называют сечение поверхности вращения полуплоскостью,
ограниченной осью вращения.
Говорят, что поверхность
вращения получается вращением ее
меридиана (любого) вокруг оси I
(рис. 64).
Теорема. Пусть относительно
декартовой прямоугольной
системы координат хОу на плоскости,
задан меридиан * С поверхности Рис. 64
вращения уравнением
F(x, y) = 0. A)
Тогда уравнение поверхности П, образованной вращением линии
С вокруг оси Ох в декартовой прямоугольной системе координат
Oxyz (рис. 65), будет иметь вид
F(x, |//+Т2) = 0. B)
Доказательство. Расстояние от произвольной точки
М (х, у, z) пространства до оси Ох равно YxfA^-z1. Поэтому
точка М (х, у, г) пространства лежит на поверхности П тогда и
только тогда, когда точка Р плоскости хОу с абсциссой х и
ординатой Vll2---z2 лежит на данном ее меридиане, т. е. тогда и только
тогда, когда выполнено соотношение B).
Замечание. Если уравнением F (х, у) — Озадано сечение
поверхности II положительной полуплоскостью хОу (т. е. полуплоскостью,
для всех точек которой </>0), то уравнение поверхности П имеет вид
F(x, Vy^+7') = 0 C)
(см. ниже пример 3 и пример 4, случай b>a>0), a если
уравнением F(х, у)~0 задано сечение поверхности П отрицательной
* Здесь под меридианом мы понимаем сечение поверхности вращения
плоскостью хОу.
Рлава 111. ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
полуплоскостью хОу (т. е. полуплоскостью, для всех точек которой
г/<0), то уравнение поверхности П имеет вид
F(x, -
D)
(см. ниже пример 4, случай —)
Если, наконец, уравнение F (х, у) —0 определяет на различных
интервалах изменения х сечение поверхности II, то положительной,
то отрицательной полуплоскостью хОу,
то перед радикалом надо брать знак-}-
(уравнение C)) или знак —(уравнение
D)) соответственно интервалу
изменения х (см. пример 5).
Пример 1. Рассмотрим уравнение
окружности радиуса а с центром в начале декартовой
прямоугольной системы координат хОу. При
вращении этой окружности вокруг оси Ох
получим сферу радиуса а с центром в начале
координат. Уравнение этой сферы на
основании предыдущей теоремы имеет вид
Рис. 65
i-22J = a2, или
Пример 2. Рассмотрим прямую, заданную уравнением y = kx относительно
декартовой прямоугольной системы координат.
Уравнение поверхности вращения, полученной при вращении этой прямой
вокруг оси Ох, т. е. уравнение прямого кругового конуса с вершиной в
начале координат, имеющего своей осью Ох, имеет вид
± Vy'l-r^ = kx
(знак-f берется для тех значений х, для которых kx > 0, а знак —для тех
значений х, для которых kx < 0), или
Тангенс угла а между осью Ох и образующей этого конуса равен
tga=ft.
Пример 3. Рассмотрим прямую, параллельную оси Ох, заданную
уравнением !/ = &(& >0) относительно декартовой прямоугольной системы координат.
Уравнение поверхности, полученной при вращении этой прямой вокруг оси Ох,
т. е. уравнение прямого круглого цилиндра радиуса Ь, ось которого
совпадает с осью Ох, имеет вид
Vy* + I2 = b, или i/2+22 = 62.
Пример 4. Рассмотрим окружность радиуса а с центром в точке @, 6),
лежащем на оси Оу, заданную уравнением
х2+(у— ЬJ = а2
относительно декартовой прямоугольной системы координат.
Поверхность, полученная вращением этой окружности вокруг оси Ох,
имеет уравнение
У¥Тг
«26 ПОВЕРХНОСТИ ВРАЩЕНИЯ
79
причем, если 6 > а > 0, то перед радикалом надо взять только знак +, если
— 6>а>0, то только знак — . Если \Ь\<а, то ±. Упрощая последнее
уравнение, получим
x2-;-y2+z2-ffe2-a2=±2fe ^7?
Рис. 66
которое эквивалентно уравнению
(х2 + у2 + г2 -j- б2 — а2J = 462 (г/2 + г2).
B)
Если 6 > а > 0, то эта поверхность называется тором (рис. 66). Получим
параметрические уравнения этого тора. Пусть С —центр окружности произ»
Рис. 67
вольного сечення тора полуплоскостью, проходящей через ось Ох; М (х, у, г)—'
произвольная точка, лежащая на окружности (С); R — проекция точки М на
плоскость гОу, а Р и Q —проекции точки R на оси Ог и Оу (рис. 67).
Обозначим через и угол от оси Оу до оси ОС в плоскости цОг, а через v — угол о»
луча ОС до луча СМ в плоскости СОх (которая ориентирована ориентирован-1
—> —*
ным углом ОС, Ох, см. § 16, п. 2).
80 Глава 111. ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
Тогда
х—~RM = С Msmv = a s\n v, y = O~Q — OR cos и = (ОС + CR~)cos и =(b +a cos v)cos и,
z = OP~OR cos I и у-] —OR sin u = (b-]-acosv) sin u.
Итак, параметрические уравнения тора:
x = asinv, у — (b-{-a cos v) cos и, z — (b-\-a cos v) sin a. C)
Область D изменения параметров и и v такова:
0<ц<2д, 0<и<2я (П)
Параметр и называется долготой точки М тора, а параметр v — широтой.
Исключим из уравнений C) параметры и и v Имеем
Х2_|_у-г_[,г2 = a2 bin2 и + (fe + a cos иJ = аг + b* + 2aS los и,.
откуда
2Ч2 + &2 2
Далее,
у2 -j- г2 = (b -j- a cos иJ,
значит,
(*2 + S/2 + г2 -f &2 — а2J = 462 (^ -|- г2)
то же уравнение, что и полученное выше.
Замечание. Можно (а если не опираться на первый способ решения,
то и нужно) доказать, что если координаты х, у, г точки М удовлетворяют
последнему уравнению, то найдутся такие числа и и у из полуинтервала [0,2л),
что х, у, г будут выражаться формулами C).
Пример 5. Поверхность, полученная при вращении вокруг оси Ох
синусоиды, заданной уравнением i/ = sinx относительно декартовой прямоугольной
системы координат, выражается уравнением
± J^{/2+z2 = sin х, или i/3 + 2a = sin2 х,
а поверхность, полученная вращением той же синусоиды вокруг Оу,
выражается уравнением
y = sin (± Ух2 + г2), или (/2 = sin Y~x2+z*.
§ 27. Линия в пространстве и ее уравнения
Линия в пространстве может быть задана двумя уравнениями
F(x,y,z) = 0, Ф(х,у,г) = 0 (I)
поверхностей, пересекающихся по этой линии. Линию в
пространстве иногда задают параметрически:
х = *@, y = y(t), z = z{t), B)
причем параметрические уравнения линии в пространстве
определяются так же, как и параметрические уравнения линии на
плоскости.
Если поверхность S задана параметрически:
x--=x(u,v), y = y(u,v), z = z{u,v), C)
то линию С, лежащую на этой поверхности, часто определяют
одним уравнением f(u,v) = 0 (в частности u = u{v) или v = v(u))
между криволинейными координатами и и v. Уравнение
/(ы, v) = 0 D)
§28. ПРИМЕРЫ УРАВНЕНИЙ ЛИНИЙ В ПРОСТРАНСТВЕ 81
называется уравнением линии С, если любая пара значений и, v,
удовлетворяющая уравнению D), не выходит из общей области
определения D функций х(и, v), у (и, v) и г {и, v), а точка М с
координатами х(и, v), у (и, v), z(u, v) лежит на линии С. Обратно, для
любой точки М линии С найдется пара чисел и, v, входящая
в область D и такая, что f (и, v) = 0, а х(и, и), у (и, v), z(u, v)—■
координаты точки М.
В частности, линии, выражаемые уравнениями u = C1, v — C2,
где Сх и С3 — постоянные, называются координатными линиями
поверхности S, заданной параметрическими уравнениями C). Вместо
одного уравнения D) линию С на поверхности S задают и
параметрически (в криволинейных координатах и, v):
u = u(t), v = v(t). E)
Эти два уравнения называются внутренними уравнениями линии,
лежащей на поверхности S, заданной уравнениями C), если
функции u(t) и v (t) имеют общую область определения Dx; любому
числу t из области Dx соответствует пара чисел u(t), v(t), не
выходящих из области D и таких, что точка M[x(u(t), v(t)),
y(u(t), v (t)), z(u(t), v(t))] лежит на линии С. Обратно, для
любой точки /Иллинии С существует число t, обладающее укаэгаа^
ным свойством'. * "'
§ 28. Примеры уравнений линий в пространстве
Пример 1. Уравнения
х2 + Уа = а2. z = 0
относительно декартовой прямоугольной системы координат выражают
окружность С радиуса а с центром в начале координат, лежащую в плоскости хОу,
так как первое уравнение, т. е. \2-\-у2 = аг есть уравнение круглого цилиндра
радиуса а, ось-ю которого является Oz, a 2 = 0 есть уравнение плоскости хОу.
Эти две поверхности пересекаются по окружности С
Пример 2. Пусть точка М движется равномерно по окружности радиуса а
так, что радиус ОМ этой окружности вращается с постоянной угловой
скоростью со, а плоскость окружности движется равномерно и поступательно
в пространстве так, что ее центр перемещается по прямой, перпендикулярной
плоскости окружности, с постоянной скоростью v. Тогда точка М описывает
линию, называемую обыкновенной винтовой линией
Примем центр окружности в начальном ее положении за начало
координат, плоскость, в которой она расположена,— за плоскость хОу, а прямую,
проходящую через центр окружности перпендикулярно ее плоскости,— за
ось Oz (рис. 68) (оси Ох и Оу взаимно перпендикулярны)
Пусть Мо (а, 0, 0) — начальное положение движущейся точки За время t
точка Мо пройдет по окружности дугу, равную со£, а в направлении оси Ог
пройдет путь vt
Следовательно, ее координаты в момент / будут:
x = acosco£, i/ = asinco?, z = vt.
Произведем замену параметра, полагая
(ot — u, vt = — u = ku, где k — — ;
О) £))
82
Глава III ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
A)
получим
x = acos«, г/= a sin u, z = ku.
Эти уравнения и являются параметрическими уравнениями винтовой линии
Они выражают закон движения точки по этой винтовой линии. Параметр
и принимает все действительные значения Если заменить на
противоположное направление вращения радиуса (или перемещение плоскости
окружности), то получим винтовую линию
противоположной нарезки.
Различают прапую и левую винтовые
линии (рис. 69).
Математически имеет смысл говорить
лишь о винтовых линиях противоположных
или одинаковых ориентации; понятие о
правой и левом винтовых линиях имеет лишь
физический смысл.
Пример 3. Рассмотрим параметрические
уравнения сферы с центром в начале
координат и радиусом а (система координат
декартова прямоугольная):
х = a cos v cos и,
у = а cosy sin и,
г = a sin и
я
т
и < 2я,
д
Рис 68
- (см пример 2, § 24).
У Координатными линиями и = С, где С —
число из полуинтервала [0,2л;), являются
сечения этой сферы полуплоскостями,
проходящими через ось Ог; это — полумеридианы сферы I если за полюсы принять точ-
О, 0, ± -^-) ) . Координатными линиями £> = С, где С—число из интервала
, являются сечения сферы плоскостями, перпендикулярными оси
я_ п_
~Т'
г; это—параллели Уравнения и
л
я
о= -^- выполняются
соответстя
венно только для полюсов/ 0, 0, —-^-
и (о, 0, ■"-
Пример 4. Рассмотрим прямой
круговой цилиндр радиуса а, ось которого
совпадает с осью Oz. Уравнение этого
цилиндра можно записать в виде
х"-\-и =с
но можно записать
ской форме;
в параметриче-
х = а cos и,
у —a sin и,
f-V,
Рис. 69
2л,
— оо < v < -f- оо,
§29. ЗЛДАЧИ К ГЛАВЕ Ш 83
где и —угол от оси Ох до луча ОМ', а М'— проекция произвольной точки
М (х, у, г), лежащей на поверхности цилиндра, в плоскость хОу. Линейное
однородное уравнение
v ■= ки, где к Ф О,
есть внутреннее уравнение винтовом липни, лежащей на рассматриваемом
цилиндре. Параметрические уравнения этой винтовой линии:
x = acos и, y = asinu, z = ku
(см. уравнения A) примера 2 этого параграфа).
В заключение отметим координатные линии цилиндра, заданного
параметрическими уравнениями A). Линии и=С—это прямолинейные образующие
цилиндра, так как если и имеет постоянное значение из полуинтервала
[0,2д), то точка М (х, у, г) поверхности цилиндра проектируется в
фиксированную точку М' (a cos С, а sin С, 0), и при изменении и от —оо до -f- oo
точка Л) (a cos С, а sin С, v) описывает прямолинейную образующую,
проходящую через точку М'. Линии с = С (где С — любое число) являются
окружностями, по которым плоскость, перпендикулярная к оси цилиндра, пересекает
этот цилиндр
§ 29. Задачи к главе III для самостоятельного решения
1. На плоскости фиксированы две различные точки А и В; фиксировано
положительное число к. Найти геометрическое место точек М, для каждой из
которых
АВг
Отв. Пустое множество, если к < —к~\ середина отрезка АВ, если
k=—y-; окружность с центром в середине отрезка АВ, если к > —^- .
2. На плоскости фиксированы две различные точки А и В; фиксировано
число к. Найти геометрическое место точек М, для каждой из которых
MA2 —
Отв. Прямая, перпендикулярная АВ.
3. Дана точка О и прямая /, не проходящая через О. Пусть Р
—переменная точка прямой I. На луче ОР берется точка М, такая, что OP-OM = k,
где к — дачное положительное число. Найти геометрическое место точек М
Отв. Окружность
4. Написать в полярных координатах уравнение прямой,
перпендикулярной полярной оси и отсекающей на ней отрезок ОА = а.
Отв. г —
COS ф
5. Написать уравнение окружности радиуса а в полярных координатах,
принимая за полюс точку О на окружности, а за полярную ось проходящий
через нее диаметр ОА.
Отв. r = 2a cos tp.
6. Прямоугольник, две стороны которого совпадают с осями координат,
изменяется так, что его диагональ сохраняет постоянную величину а. Линия,
описываемая основанием перпендикуляра, опущенного из вершины
прямоугольника, противоположной началу координат, на его диагональ, называется
Глава III. ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
астроидой. Найти ее уравнение, принимая за осп координат неподвижные
стороны прямоугольника (рис, 70).
_2_ 2 _2_
Отв. х3 +У3 =а3 .
7. Даны точка О и прямая, находящаяся от точки О на расстоянии ОА=а.
Вокруг точки О вращается луч, пересекающий данную прямую в переменной
точке В. На этом луче по обе
стоВ откладываются
i = b. Написать и
точки
роны от
отрезки B
полярных координатах уравнение
линии (конхоида Никомеда),
описываемой точками Мх и уИ2 при
вращении луча, принимая за полюс
точку О, а за полярную ось
—перпендикуляр ОА, опущенный из точки
О на данную прямую; перейти затем
к декартовым координатам,
принимая за начало системы точку О, а
за ось абсцисс прямую ОА (рис. 71),
Отв. /■ = -
cos tp
(х—
± 6, или
J — 6
Рис.
8. Даны точка О и прямая,
находящаяся от точки О на
расстоянии О А = а. Вокруг точки О
вращается луч, пересекающий прямую в
переменной точке В. На этом луче по обе стороны от точки В откладываются
равные отрезки ВМ1 = ВМ2 — АВ. Составить уравнение линии (строфоида),
описываемой точками Mt и М2 при вращении луча, в полярных координатах,
Рис. 71
Рис. 72
Рис.
принимая за полюс точку О и за полярную ось перпендикуляр ОА, опущенный
из О на данную прямую. Перейти затем к декартовым координатам, принимая
за начало коорднна т точку О и за ось абсцисс прямую ОА (рис. 72).
«29. ЗЛДЛЧИ К ГЛАВЕ III
Отв. г-
£0S ф
± a tg ср, или (х2 ~t- у2) (л: — оJ—а2</ =
9. На окружности радиуса а изята точка О и через точку К, диаметрально
противоположную точке С, к окружности проведена касательная. Вокруг
точки О вращается луч, пересекающий
окружность и касательную соответственно в точках
Л и В. На этом луче от точки О откладываем
отрезок ОМ, равный отрезку АВ луча,
заключенному между окружностью и касательной.
Линия, описываемая точкой М при
вращении луча, называется циссоидой Диоклеса.
Написать ее уравнение в полярных
координатах, принимая за полюс точку О и за
полярную ось диаметр ОК< Перейти затем к
декартовым координатам (рис. 73).
la sin2 ф
Отв. г— ! , или
cos ф
la — x
Рис. 74
10. На окружности радиуса а взята точка О и через нее проведен
диаметр ОА. Вокруг точки О вращается луч, пересекающий окружность в
переменной точке В. На этом луче по обе стороны от точки В откладываются
отрезки В{Лх=.ВМг — АВ. Написать уравнения линий, описываемых точками
Мх и Ai2 при вращении луча. »
Отв. Две окружности ' ,1
(х— аJ + ((/-аJ = 2а2, (x-aJ + (t/-faJ = 2a2.
11. Отрезок постоянной длины 2а скользит своими концами по сторонам
прямого угла. Найти линию, описываемую при этом движении отрезка
основанием перпендикуляра, опущенного из вершины прямого угла на отрезок
(в полярных и декартовых координатах) (рис. 74).
Отв. r=--asm1(f, (х2-|-у2K^ Аагхгу2.
12. На окружности радиуса а взята точка О Через точку К, диаметрально
противоположную О, к окружности проведена касательная. Вокруг точки О
вращается прямая, пересекающая окружность и касательную соответственно
в точках А к В. Из точки А проводится прямая, параллельная касательной, а
из точки В — прямая, параллельная диаметру ОК.. Найти геометрическое место
точек пересечения этих прямых (верзьера Марии Аньези), принимая за начало
прямоугольной системы координат точку О, а за ось абсцисс диаметр ОК
(рис. 75).
Отв. % =
; х= 2 2
13. Круг радиуса г катится по кругу радиуса R, оставаясь вне его.
Найти параметрические уравнения линии, описываемой точкой катящегося
круга (эпициклоида), принимая за начало координат центр неподвижного
круга, а за параметр — угол ( между положительным направлением оси
абсцисс и радиусом неподвижного круга, идущим в точку касания подвижного
круга с неподвижным. В начальном положении подвижная окружность
касалась неподвижной в точке пересечения последней с осью абсцисс (рис. 76).
П I р
Отв. x = (RJr r) cost —r cos ——■ t.
= (R-\-r)sm t —
86
Глава III. ЛИНИИ. ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
14. Круг радиуса г катится по кругу радиуса R, оставаясь внутри пего
Написать параметрические уравнения линии, описываемой точкой катящегося
круга (гипоциклоида). Выбор системы координат и обозначений такой же,
как и в предыдущей задаче (рис. 77)
Отв. x—(R — г) cos t -\- r cos t,
R — r
(/ = (/? —г) sir] t —г sin t.
f
15. Показать, что ври R = 4r
гипоциклоида обращается в астроиду
М(ъу)
Рис 75
16. Показать, что при
движного круга.
Рис. 76
гипоциклоида обращается в диаметр непо-
Рис. 77
Рис. 78
17. Отрезок постоянной длины движется так, что один его конец
скользит по окружности х2-}-у2 = г2, а другой — по оси Ох (шатунно-кривошипный
механизм). Составить уравнение кривой, которую описывает точка отрезка,
разделяющая его на части а и Ь.
§29. ЗАДАЧИ К ГЛАВЕ ПГ
Отв. 4aVll-fc) = (r*-a2~x*-^y>
18. По окружности %2 + (/2 = г2 катится прямая, начальное положение о-
Topoii х=г. Определить траектори.о точки катящейся прямой, принимая за
начальное ее положение точку (г, 0) (эвольвента окружности) (рис 78).
Отв. x = r (cos t-\-1 sin t), y = r (sin t — / cos t).
19. Уравнением какой поверхности является уравнение
х = у
в декартовой прямоугольной системе координат?
Отв. Плоскость, делящая пополам вертикальные двугранные углы,
образованные координатными плоскостями хОг и yOz.
20. Какие поверхности выражаются уравнениями
х = а (а ф 0), у — Ь (ЬфО), г = с {сфЩ
в общей декартовой системе координат?
Отв. Плоскости, параллельные координатным.
21. Какие поверхности выражаются уравнениями
* = 0, y = 0, г = 0
в общей декартовой системе координат?
Отв. Координатные плоскости.
22. Какую поверхность определяет уравнение
в декартовой прямоугольной системе координат?
Отв. Две биссекторнальпые плоскости между координатными плоскостями
yOz и zOx.
23. Составить уравнение цилиндрической поверхности, направляющей
которой является окружность г = 0, x2-\-y% = 2Ry (R>0), а образующие
параллельны вектору {а, Ь, 1}.
Отв. (x-az
24. Составить уравнение цилиндра, описанного около сферы х2 + уг-\-г2 —
образующие которого параллельны вектору {/, т, л}.
Отв. (x2-ft/4-z2)(
25. Состащпь уравнение конической поверхности с вершиной в точке
@, 0, с), направляющей которой является лемниската Бернулли (х2+(/2J =
= 2а2(х2—у2).
26. Составить уравнение поверхности вращения, полученной вращением
параболы у2 = 2рх вокруг оси Оу.
Отв. у* = 4р2(х2-{-г2).
27. Составить уравнения поверхностен вращен'ия, полученных вращением
лемнискаты Бернулли (х2+ t/2J = 2a2 (х2—у2) вокруг осей Ох и Оу.
Отв. Вокруг оси Ох: (х2+ у2-\- г2J = 2а2 (х2—у2 — г2).
Вокруг оси Оу: (x2 + y2 + z2J = 2a2 (х2—у2 + г2).
Глава 111 ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
28. Плоскость вращается вокруг одной из своих прямых с постоянной
угловой скоростью. Прямая, лежащая в этой плоскости, вращается вокруг
одной из своих точек с угловой скоростью, пдвсе меньшей угловой скорости
вращения плоскости. Составить
параметрические уравнения
поверхности, образованной движением этой
прямой
Указание. Направим ось Ог
по оси вращения, а ось Ох
расположим в начальном положении
вращающейся плоскости
перпендикулярно оси Ог (рис. 79). Допустим,
кроме того, что прямая,
вращающаяся вокруг точки' Л?, в начальном
своем положении была параллельна
оси Ог и точка N отстоит от оси
вращения на расстоянии, равном а
(так, что эта точка описывает
окружность радиуса а с центром О,
расположенную в плоскости хОу).
Обозначая угол от оси Ох до луча
Рис- ^Э ON через 1и и полагая NM =v,
получим
х=(а — v sin и) cos2м,
у = (а—t)sin и) sin 2м,
z = y cos «.
Исключая и и v, получим уравнение поверхности в
декартовых'координатах:
Чтобы представить себе вид этой поверхности, достаточно взять не
бесконечную прямую MN, а конечный отрезок, длина которого меньше а; тогда
полученная поверхность будет так
называемым листом Мебиуса (рис. 80).
29. Составить уравнение поверхности,
образующие которой параллельны плоскости
хОу, пересекают ось Ог и линию, заданную
уравнениями хуг — а3, x2-}-y2 = b2.
Отв. Ь2хуг = а3(х2 + у2). Рис. 80
30. Две равные параболы имеют общую вершину в начале координат;
главные оси лежат на оси Ох, но противоположны по направлению; одна
парабола лежит в плоскости хОу, другая — в плоскости хОг. Составить
уравнение поверхности, образованной прямыми, параллельными плоскости у — г=0
и пересекающими данные параболы.
Отв. уг—г2=2рх.
31. Вокруг оси Ог вращается линия x = f(z), y = g(z). Составить
уравнение поверхности вращения.
Отв. x2+(/2 = f2(z) + g2(z).
32. Вокруг оси Ог вращается прямая, по которой пересекаются плоскости
а-г а и у —кг. Составить уравнение поверхности вращения.
Отв. х2-^у2 = аг+к2г\
ЗАДАЧИ К ГЛАВЕ IIT
89
33. Со ставить параметрические уравнения линии Вивиани, по которой
сфера Ar2-f-y2 + z2 = a2 пересекается с цилиндром х2-{-у2 — в(/==0.
Отв. x=asin tcost, y = asin2t, z—acost.
Рис. 81
34. Плоскость, первоначально совпадающая с плоскостью xOz и
содержащая прямую, выходящую из начала координат под углом а к оси Oz,
вращается вокруг оси Oz с постоянной угловой скоростью <в Одновременно
точка, выходящая из начала координат, движется по указанной прямой с
постоянной скоростью V. Составить уравнения траектории движущейся точки
(коническая спираль) (рис. 81).
Отв. x = vt sin acosco?, y=vt sin asm at, z = vt cosa.
ГЛАВА IV
ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
В § 7 гл. II дано определение вектора (класс всех равных
между собой направленных отрезков), а в § 11 гл.
II—определение координат вектора. В дополнение к сказанному в § 7 и
11 введем следующее определение: если вектор а есть класс всех
направленных отрезков, равных направленному отрезку АВ, то
класс направленных отрезков, равных направленному отрезку ВА,
называется вектором,' симметричным вектору а, и обозначается — а.
В этой главе излагаются основы векторной алгебры, причем
для координат вектора будет дано еще одно определение (по
существу эквивалентное тому, которое дано в § 11). Векторная
алгебра позволяет решать с полной общностью и проще многие
задачи, решение которых в координатах достаточно трудно
(например, расстояние между двумя точками в общей декартовой
системе координат, объем ориентированного тетраэдра в общей
декартовой системе координат и т. д.). Кроме того, векторная
алгебра служит удобным средством для изложения теории прямой
линии на плоскости, теории плоскости и прямой в пространстве,
в вопросах,-связанных с линейными преобразованиями, а также
с линиями и поверхностями второго порядка.
§ 30. Сумма векторов
Суммой а + Ь векторов а и Ь называется вектор, начало
которого находится в произвольной точке А пространства, а конец
строится следующим образом: отложим от точки А вектор АВ,
30. СУММА ВЕКТОРОВ
равный вектору а, а от точки В вектор ВС, равный вектору Ъ;
тогда точка С и будет гонцом вектора а-\-Ь (рис. 82.).
Если произвести указанное построение, взяв вместо А любую
другую точку Р, то получим направленный отрезок PR, равный
направленному отрезку АС.
В самом деле, пусть Р—
произвольная точка пространства,
a Q и R — такие точки, что PQ =
= а и QR — b. Из равенства
= CR, а потому (снова
] = PQ следует AP = BQ (см.
теорему § 7), а из равенства
~BC=~QR следует BQ = CR, значит
применяем теорему § 7) АС = PR.
Сумму двух неколлииеарных векторов а и b можно построить
и так: откладываем от произвольной точки О векторы а и b
и строим параллелограмм ОАСВ со сторонами ОА и ОВ. Тогда
а
а
Рис. 83
(рис. 83).
Р Сумма двух векторов обладает
следующими свойствами:
а + Ф + с) = (а -+■ Ь) + с
(ассоциативность), A)
B)
C)
(коммутатив ность).
D)
Доказательство ассоциативности суммы.
Рассмотрим три произвольных вектора а, Ь, с.
Пусть А — произвольная точка, а В, С и D—такие точки, что
Тогда
Свойства B) и C) очевидны.
Доказательство коммутативности суммы.
Рассмотрим два вектора а и Ь. Отложим вектор а от произвольной
92 Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
точки А
а от точки В отложим вектор Ь:
Жс = ь.
Тогда
а + Ь=Ае.
Отложим теперь сначала от точки А вектор Ь:
Тогда в силу равенства AD = ВС имеем DC— АВ = а, т. е. DC
есть вектор а, отложенный от точки D. Таким образом, 6 +
= AC и потому
§ 31. Разность векторов
Разностью а—Ь векторов а и b называется такой вектор х,
что х-\-Ь — а.
Разность а — Ь двух векторов всегда существует и единственна.
В самом деле, докажем сначала существование разности, т. е.
докажем, что каковы бы ни были векторы а и Ь, всегда существует
такой вектор х, что х-\-Ь = а.
Отложим векторы а и Ъ от одной и той же точки О:
ОА=а, ОВ = Ь.
Тогда на основании определения суммы двух векторов
т. е.
—*■
полагая ВА — Х, будем иметь (рис.
84)
Рис 84 Докажем, что существует только
один вектор х, удовлетворяющий
последнему равенству. Предположим, что существует еще вектор
Xi, такой, что Ь-\-хх~а. Тогда
§32. ПРОИЗВЕДЕНИЕ ЧИСЛА НА ВЕКТОР 93
откуда
Отметим еще равенство
a-b = a + (-b).
В самом деле,
§ 32. Произведение числа на вектор
Произведением Ха числа X на вектор а в случае аФО, X
называется вектор, коллинеарный вектору а, модуль которого
равен | X11 а | и который направлен в ту же сторону, что и вектор
а, если X > 0, и в противоположную, если X < 0. Если Х = 0 или
а = 0, то по определению Ха = 0.
Произведение числа X на вектор а обладает следующими
свойствами:
\-а = а, A)
B)
a, C)
b. D)
Свойство A) сразу следует из данного определения произведения
числа на вектор.
Для доказательства свойства B) заметим, что в случае Х^О,
[х^=0, афО) оба вектора Я(|ла) и (Х\х) а имеют одну и ту же длину,
равную | X11 |л 11 а |, и одно и то же направление (такое же, как а,
если X и |л—числа одного знака, и противоположное с а, если
X и [х — числа разных знаков).
Соотношение B), очевидно, также верно, если Я = 0, или,и = 0,
или а = 0.
Докажем свойство D). Предположим, что векторы а и 6 не-
коллинеарны, а Я=£0. Отложим вектор а от точки Л
~АВ = а.
а вектор 6 от точки В
ВС = Ь.
Тогда
Построим векторы АВ' = Ха и АС = Х(а-\-Ь) (рис. 85). Из
подобия треугольников ABC и АВ'С следует (как в случае Я > О,
94
Глава IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
так и в случае X < 0), что В'С' = ХЬ. Но А В' + В'С = АС,
следовательно,
Случай коллинеарности векторов а и Ъ предоставляется
рассмотреть читателю (вопрос в этом случае сводится к свойствам
C) и B)). Доказательство
свойства C) предоставляется
читателю (надо доказать, что
векторы (X 4- ц) а и Ха + \ia имеют
одинаковые модули и
направление).
Замечание 1. Вектор
—а, противоположный
вектору а, равен — 1 -а.
Замечание 2. Частное
-f , где ХфО, определяется
Рис. 85 Л
как произведение j-a.
Замечание 3. Если а^=0, то вектор
есть единичный вектор, имеющий то же направление, что и вектор а.
Отсюда
а = \а\а°.
Замечание 4. Если векторы а и Ь коллинеарны и а=£=0,
то отношением — называется число X, такое, что Ха = Ь.
Если екторы а и Ь коллинеарны и направлены в одну
сторону, то
Ь _ \Ь\
а \а\'
а если — в разные стороны, то
\а\ •
Если 6 =
Отношение пеколлинеарных векторов не определяется.
Замечание 5. Из замечания 4 и определения координаты
точки, лежащей на оси координат (§ 2), следует, что координату
точки М на оси координат с началом О и единичной точкой Е
33 ТЕОРЕМЫ О ПРОЕКЦИЯХ ВЕКТОРОВ
можно определить так:
ОМ ОМ.
* = —, или * = — ,
ОЕ е
т. е. координата точки М, лежащей на декартовой оси координат»
равна отношению вектора ОМ к масштабному вектору.
Из последнего соотношения следует, что
ОМ = хе.
§ 33. Теоремы о проекциях векторов
Теорема 1. Проекция суммы двух векторов (имеется в виду
любой из трех видов параллельного проектирования) равна сумме их
проекции'
пр. (а + Ь) = пр. а-\- пр Ь.
Доказательство. Отложим вектор а от произвольной
точки А:
а от точки 6 отложим вектор Ь:
Тогда
Пусть А', В', С —проекции точек Л, В и С. Тогда по определению
проекции вектора
пр. а =/!'#', пр. Ь = В'С', пр. (а-\-Ь) — А'С
и так как
lVB' + ВХ' = WC',
то
пр. (я + Ь) = пр. а + пр. 6.
Теорема 2. Проекция произведения числа X на вектор а равна
произведению числа К на проекцию вектора а, т. е.
пр. {Ха) = X пр. а.
Доказательство Отложим векторы а и Ха от
произвольной точки А: г
АВ = а, АС = Ха =
gg Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
отсюда
АВ
Пусть А', В' и С — проекции точек А, В и С. Так как при
параллельном проектировании сохраняется порядок точек на
прямой и отношение отрезков, лежащих на одной прямой, то,
предполагая, что точки А' и В' различны (в этом случае различны
и точки А и В), имеем
АВ А7/?
lVC' = хЖв', или пр.
Если точки А' и В' совпадают, но точки А и В различны, то
точка С совпадает с точками А' и В' и соотношение
пр. (Яа) = Япр.а
верно и в этом случае. Оно, очевидно, верно и в том случае, если
совпадают точки А и В(а — 0).
§ 34. Теоремы о координатах векторов
Теорема 1. Если векторы а и Ь лежат на оси, то координата
их суммы равна сумме координат слагаемых, т. е. коорд. (а-{-Ь) =
= коорд. а-[-коорд. Ь.
Доказательство. Отложим вектор а от любой точки А
оси координат, на которой лежит этот вектор:
а от точки В отложим вектор Ь:
ВС = Ь.
Тогда
АС = а-\-Ь.
Далее,
коорд. а = AS, коорд. Ь = ВС, коорд. {а + Ь) = АС
и на основании теоремы Шаля:
коорд. (а+ 6) = коорд. а. + коорд. Ь.
Теорема 2. Если вектор а лежит на оси, то координата произ'
ведения числа К на вектор а равна произведению числа К на коор*
§35 СУММА, РАЗНОСТЬ И ПРОИЗВЕДЕНИЕ ЧИСЛА НА ВЕКТОР 97
динату вектора а:
коорд. (ка) = % коорд. а.
Доказательство. Предположим, что ХфО и афО.
Отложим векторы а и ка от произвольной точки А оси:
~АВ = а, АС = Ы.
Тогда коорд. а = АВ, коорд. (ка) = АС и требуется доказать, что
Имеем
|ЛС| = АС = \ка\ = \1\\а\ = \к\ АВ = |Х|| АВ\ = \1А~В\.
Если X, > 0, то векторы АВ и АС имеют одинаковое
направление, значит, АВ и АС — числа одного знака и АС — 'кАВ. Если же
Я < О, то векторы АВ и АС имеют противоположное направление,
значит, АВ и АС—числа разных знаков, а АВ и ХАС — числа
одного знака, следовательно, ЛС = ^Лб.
Равенство коорд. (ка) = X коорд. а верно также в случае ^ = 0
и в случае а = 0.
§ 35. Сумма, разность и произведение числа на вектор
в координатах
Теорема 1. Координаты суммы двух векторов равны суммам
соответствующих координат слагаемых, т. е. если относительно
общей декартовой системы координат на плоскости заданы векторы
a = {xv У1} и b = {x2, y2},
то
Если относительно общей декартовой системы координат в
пространстве заданы векторы
a={xv yv гх} и 6 = {х2) уг, гг],
то
2,
Доказательство. Пусть в общей декартовой системе
координат па плоскости а — {х1У ух), Ь = {х2, у2]. Спроектируем векторы
a, b и а-\-Ь на ось Ох параллельно оси Оу. Пусть пр. а, пр. &
и пр. (а+ 6) —эти проекции. На основании теоремы 1 § 33 и
теоремы 1 § 34 имеем
коорд. пр. (а + 6) = коорд. (пр. а-}-пр. &) = коорд. пр.а + коорд.
пр. Ь. Но по определению координат вектора
4 П. С. Моденов
98 I' л а ] a IV ОСНОВЫ ВГ.КТОРНОЙ АЛГЕБРЫ
коорд. i p a-xlt косрд пр. Ь — хъ, а коорд. пр. (а-\-Ь) есть
первая координата вектора а-\-Ь.
Таким образом, первая координата вектора а-\-Ь равна х1 + х2.
Аналогично доказывается, что вторая координата вектора а4-Ь
равна t/i + y2-
В случае пространства надо проектировать данные векторы на
оси параллельно координатным плоскостям.
Следствие. Координаты разности а—Ь двух векторов равны
разностям соответствующих координат а и Ъ, т. е. если
относительно общей декартовой системы координат на плоскости даны
векторы
a = {xv Ух) !i b = {x2, у2},
то
Если относительно общей декартовой системы координат в
пространстве даны векторы
«Н*1. Уи zi) и Ь = {х2, у2, гг),
то
Для доказательства достаточно заметить, что
а—Ь=*а + (— Ь)
Теорема 2. Координаты произведения числа на вектор равны
произведениям этого числа на соотве/пствующие координаты вектора,
т е. если относительно общгй декартовой системы координат
задан вектор а = {х, у} (на плоскости) или а = {х, у, z} (в
пространстве), то
%а = {'кх, Ку} (на плоскости),
Ха = {Хх, Ку, Кг] (в пространстве).
Доказательство Проведем доказательство для плоскости
(доказательство для пространства аналогично). Пусть пр. а
—проекция вектора а на ось Ох параллельно оси Оу, В силу теоремы 2
§ 33 и теоремы 2 ^ 34 имеем
коорд. пр. (Ка) = коорд (К пр а) = А (коорд. пр. а) = Хх.
Аналогично доказывается, что вторая координата сектора %а
равна %у.
36 ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВИКТОРОВ 99
§ 36
§ 36. Линейная зависимость векторов. Линейная комбинация
векторов. Коллинеарность векторов.
Компланарность векторов
Определение. Векторы alt аг, ... , ak называются линейно
зависимыми, если существуют числа ^1, %2, ,.. , Kk, среди которых
есть по крайней мере одно, не равное нулю, такие, что
Сумма произведений чисел %.х, А2, ... ,%k на векторы av аг
ak, т. е. вектор
называется линейной комбинацией * векторов а1г а2, ... , ak.
Если вектор р представлен в виде линейной комбинации
векторов alt a2, ... , ak, то говорят также, что вектор р разложен по
векторам ах, а2, ... , ak.
Данное выше определение линейной зависимости векторов
alt a2, ... , ak, очевидно, эквивалентно такому: векторы аи а2,... ,ak
линейно зависимы, если один из них можно представить в виде
линейной комбинации остальных (или разложен по остальным).
Теорема 1. Для того чтобы два вектора аг и а2 были линейно
зависимы, необходимо и достаточно, чтобы они были коллинеарны.
Доказательство необходимости. Дано: векторы ах
и а2 линейно зависимы. Требуется доказать, что они коллииеар-
ны. Так как векторы ах и а2 линейно зависимы, то существуют
числа Хг и Я2, не равные нулю одновременно, и такие, что
Пусть, например, Х1Ф^; тогда
отсюда следует, что векторы аг и а2 коллинеарны.
Доказательство достаточности. Дано: векторы ах и
а2 коллинеарны. Требуется доказать, что они линейно зависимы.
Если а1 = 0, то имеет место равенство 1 •a1-f0-a2 = 0, а это
означает, что векторы а1 и а2 линейно зависимы (Х1 = \ф0).
Если же агф0, то, полагая — = Я, находим а2 = Яа1,или \-а2 —
— Я-а1 = 0, значит векторы ах и a2 линейно зависимы.
Определение. Три вектора называются компланарными, если,
будучи отложенными от одной точки, оказываются лежащими в
одной плоскости.
* В этом определении не исключается случай \l = %2= ...=%k = 0. Тогда
линейная комбинация векторов аь а2, ■.., ай дает нулевой вектор.
100 Глава IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Теорема 2. Для того чтобы три вектора ах, а2, az были
линейно зависимы, необходимо и достаточно, чтобы они были
компланарны.
Доказательство необходимости. Дано: векторы ах,
а2, а3 линейно зависимы. Требуется доказать, что они компланарны.
Так как векторы ах, а2, а3 линейно зависимы, то существуют
числа Х1( Я2, Х3, среди которых есть хотя бы одно, не равное
нулю, такие, что
Ка1 + ^2^
Пусть, например, Я3^0". тогда
Векторы —j~ai и —rfl2 коллинеариы соответственно
векторам ах и а2; очевидно, сумма таких векторов, т. е. вектор а3
будет компланарен с векторами аг и а2.
Доказательство достаточности. Дано: векторы alt
аг, as компланарны. Требуется доказать, что эти векторы
линейно зависимы.
Если векторы ах и а2 коллинеарны, то они линейно зависимы
(теорема 1 настоящего параграфа), т. е. найдутся числа кх и Я2,
из которых по крайней мере одно не равно пулю и такие, что
Я1а1 + Я2а2 = 0, по тогда и Я1а1 + Я2а2 + 0-а3 = 0, т. е. векторы
alt а2, а3 линейно зависимы. Пусть векторы ах и а2 неколли-
неарны. Отложим векторы а1У а2 и а3 от одной и той же точки О:
Так как векторы ах, а2, а3 компланарны, то точки О, Ах, А2,
А3 лежат в одной [[лоскосги. Спроектируем точку А3 на прямую
ОАг параллельно прямой ОА2; пусть Р — эта проекция. Тогда
ЪА3=оР-\-Р~А3 и так как
ОР\\ах и ахФ0, РЛ3||а2 и а2ф0,
то, полагая
ОР. РА3 .
находим
так что
Я2а2,
т. е. векторы alt а2 и а3 — линейно зависимы.
Теорема 3. Всякие четыре вектора ах, а2, а3, а4 в
пространстве линейно зависимы.
§36. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ Ю1
Доказательство. Предположим, что векторы аъ а2, а3
некомпланарны. Отложим все векторы alt а2, а3, а4 от одной и
той же точки О:
Пусть Р — проекция точки А4 на плоскость ОА1А2 параллельно
прямой 0А3, a Q — проекция точки Р на прямую 0А1
параллельно прямой ОА2. Тогда
Векторы OQ, QP, PAi соответственно коллинеарны векторам
аи а2 и аг. Полагая
OQ . QP . РЛ4 .
получим
и, следовательно,
а4 = Я^! + Я2а3 -f X3a3,
т. е. векторы alt a2, а3, а4 линейно зависимы.
Теорема 4. Для того чтобы два ненулевых вектора ах и а2 были
коллинеарны, необходимо и достаточно, чтобы их координаты
были пропорциональны*.
Докажем теорему для случая, когда векторы заданы своими
координатами относительно общей декартовой системы координат
в пространстве.
Доказательство необходимости. Дано: векторы аг=*
= {х1>у1, Zy] и а2 = {х2, у2, z2] коллинеарны; требуется доказать,
что их координаты пропорциональны.
Так как «х^О, то, полагая ^==Я, получим аа = Яа1) т. е.
{*2> Уг> 22} = ^{x1, yv гг},
или
х2 = Kxlt у2 = %ylt г% = Хгг.
* Упорядоченная совокупность чисел называется ненулевой, если среди чисел
этой совокупности есть по крайней мере одно, не равное нулю. Будем
говорить, что упорядоченные ненулевые пары чисел хь у1 и х2, ц2
пропорциональны, если существует такое число ^ 5й 0, что x2~Xxv у2 = ^У1- Аналогично
определяется пропорциональность двух ненулевых упорядоченных троек чисел.
Пропорциональность двух упорядоченных пар чисел кх, ух и х2, у2 мы будем
писать и в форме—= — , причем условимся, что если какой-либо знамена-
х2 у2
тель в этой пропорции равен нулю, то это означает, что равен нулю
соответствующий числитель. Аналогично будем понимать пропорцию — = — = — .
х2 у., 23
При указанном соглашении относительно пропорции это определение
пропорциональности совпадает с тем, которое дано в начале сноски.
102
Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Доказательство достаточности. Даноз координаты
векторов
<*i = {*i. 01. «i> и а2 = {х2) у2, г2}
пропорциональны. Требуется доказать, что эти векторы колли-
неарны.
Пусть
х2 = %xv у2 — Цх, г2 = Xzt\
тогда аг = 'ка1 и, значит, векторы ах и а2 коллинеарны.
Теорема 5. Для того чтобы два вектора ахи а2, заданные
своими координатами относительно общей декартовой системы
координат на плоскости
или относительно общей декартовой системы координат в про-
странстве
al = {xv ylt гх}, a2 = {*2> Уг» гг}»
были коллинеарны, необходимо и достаточно, чтобы
= 0 (в случае плоскости),
A)
У 1
ЧУх
= 0 (в случае пространства). B)
Докажем теорему для случая, когда векторы ах и а2 заданы
своими координатами относительно общей декартовой системы
координат в пространстве.
Доказательство необходимости. Дано: векторы ах~
~{xi> lJi> zi\ и «2 = {X2' Ун гг} коллинеарны. Требуется доказать,
что выполнены соотношения B). Если векторы ах и а2 ненулевые
и коллинеарпы, то их координаты пропорциональны, а потому
равенства B) выполнены (определитель, в котором две строки
пропорциональны, равен нулю). Если ах = 0 или а2 = 0(или ах =
= а2 = 0), то равенства B), очевидно, также выполнены.
Доказательство достаточности. Дано, что
соотношения B) выполнены. Требуется доказать, что векторы ах и а2
коллинеарны.
Если xx = yx = zx = 0 (т. е. ах—0), то векторы ах и а2
коллинеарны. Пусть хотя бы одно из чисел хх, ух, гх не равно нулю,
например ххФ0. Положим — = Х,. Тогда х2 = 'кх1, и из соотноше-
ния
= 0,
или
§36. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ REKTOPOB
103
находим
и так как х1Ф0, то уг — Ъу1 = О, т. e. у2 —^yx.
Аналогично из соотношения
1 1
= 0, или гххг—г2хг — 0,
находим
и так как
г1кх1—х1г2 = 0, x1(kz1 — 22) = 0,
, то Kzl — z2 = 0, т. е. г2 = Х.2г. Итак,
= Xzt илл a2 =
т. е. векторы ах и а2 коллинеарны.
Теорема 6. Необходимым и достаточным условием
компланарности трех векторов
«i = {*i. Уи Zj], a2 = {x2, у2, г2}, as = {xs, ys, zs\,
заданных своими координатами относительно общей декартовой
системы координат, является равенство
х1у1г1
Уз
-0.
Доказательство. На основании предыдущей теоремы
векторы av a2, a3 будут компланарны тогда и только тогда, когда
найдутся три числа Xlt %2, л.3, не равные нулю одновременно,
такие, что
или
или
Ух,
У2,
Уз,
Эта система соотношений относительно Х1( %it k3 линейная и
однородная. Но для того чтобы линейная однородная система п
уравнений с п неизвестными имела ненулевое решение (т. е.
решение, в котором хотя бы одно из неизвестных не равно нулю),
необходимо и достаточно, чтобы определитель этой системы был
равен нулю.
Из доказанных теорем вытекают такие следствия.
Три попарно различные точки Ml(xvyl), M2(x2,y2), М3(х3,у8),
заданные своими координатами относительно общей декартовой
104
Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
системы координат на плоскости, лежат на одной прямой тогда
и только тогда, когда векторы М3М1 и М3М2 коллинеарны, т. е.
тогда и только тогда, когда координаты их пропорциональны:
ИЛИ
з У\ Уз
Х3 У 2 Уз
= 0*
Три попарно различные точки Mi(xv yv z±), М2(х2, y2, z2),
М3(я3, Уз> гз). заданные своими координатами относительно общей
декартовой системы координат в пространстве, принадлежат одной
прямой тогда и только тогда, когда векторы M3MX и MSM2
коллинеарны, т. е. тогда и только тогда, когда выполнены
соотношения
(см. сноску на стр. 101),
или
У\ Уз zi сз _q
'3 Л1"
= 0,
-Уз
-Уз
= 0.
У2— Уз Ч-
Точки
1\A I v it 7 \ Лд (v 11 у \ АА t v it у \ Лд (v it "у \
/V11\A1* У\, с\I ^У12\Л2» £/2> ^2/' /К13\Л3» УЗ» ^3h 1'1&\Л1* У&, ^4/»
заданные своими координатами относительно общей декартовой
системы координат в пространстве, принадлежат одной плоскости
тогда и только тогда, когда векторы М^МЬ М^М2, М4М3
компланарны, т. е. тогда и только тогда, когда
xi xi У\ — У\ г1 Z
Х2 Х4 У 2 У 4 ?2 2
гЗ
= 0.
§ 37. Базис и координаты вектора
Базисом на плоскости называется упорядоченная пара неколли-
неарных векторов ег и е2, лежащих в этой плоскости.
Базисом в пространстве называется упорядоченная тройка
некомпланарных векторов ev e2, е3.
* Эта форма записи необходимого и достаточного условия
принадлежности точек Мь М2, М3 одной прямой не требует оговорки, сделанной в
начале формулировки следствия; иначе говоря, среди точек Mi, Mit M3 могут
быть совпадающие (и даже все три точки Ми М8, Мв могут сливаться в одну). *
§37. БАЗИС И КООРДИНАТЫ ВЕКТОРА !05
Теорема 1. Всякий вектор а, компланарный с двумя неколлине-
арными векторами ех и е2, может быть и притом единственным
образом разложен * по этим векторам.
Доказательство существования разложения.
Обложим все векторы ev е2 и а от одной и той же точки О:
Тогда в силу компланарности векторов ev е2, а точки О,
Е2, А лежат в одной плоскости.
Пусть Р — проекция точки А на прямую 0£х параллельно
мой 0Е% (рис. 86). Тогда
а так как векторы ОР и РА соответственно коллинеарны
ненулевым векторам eL и е2, то, полагая
ОР _ РА _
будем иметь
OP = xelt РА = уе2,
так что Рис. 8б
Доказательство единственности разложения.
Пусть существует еще другое разложение
2
Тогда
хе1 + уе2 = x'el + y'eit
или
Если хотя бы одна из разностей х—х' и у—у' была не равна
нулю, то последнее соотношение означало бы, что векторы ех и е3
линейно зависимы, а потому коллинеарны (§ 36, теорема 1), значит,
х—х' = 0, у—у' = О, т. е. х~х', у = у'.
Теорема 2. Всякий вектор а пространства может быть и
притом единственным образом разложен по трем некомпланарным
векторам еи е2, е3.
* См. начало § 36, где дано определение понятия разложения любого
вектора по нескольким векторам.
106
Глаза IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Доказательство существования разложения.
Отложим все векторы еи ег, es, а от одной и той же точки О:
Пусть Q — проекция точ.ш А па плоскость Е1ОЕ2 параллельно
прямой ОЕ3, а Р — проекция точки Q на прямую ОЕг параллельно
прямой ОЕ2 (рис. 87).
Так как
и векторы OP, PQ и QA соответственно коллинеарны векторам
в\> е,г, е3, то, полагая
будем иметь
значит,
ех
xev PQ = ye2,
a = xe1 + ye2 -f
Доказательство единственности разложения.
Предположим, что
существует еще разложение
Тогда
z'es,
или
Если хотя бы одна из
Рис 87 разностей к—х', у—у',
„—г'была отлична от нуля,
то последнее соотношение означало бы, что векторы elt e2, е3
линейно зависимы, а потому компланарны (§ 36, теорема 2),
значит,
х—х' = 0, у—у' = 0, г — г' = 0,
т. е.
Теорема 3. Коэффициенты в разложении вектора а, лежащего
в некоторой плоскости, по масштабным векторам е1 и е2 общей
декартовой системы координат на этой плоскости являются
координатами вектора а.
5 38. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ Ю?
Доказательство. Пусть вектор а лежит на плоскости,
в которой введена общая декартова система координат хОу с
масштабными векторами ОЕ1 = е1 и ОЕ2 = е.1.
Отложим вектор а от начала координат ОА = а и разложим
его по векторам е1 и е2:
а = xev -\-уе2.
Выберем на осях Ох и Оу точки Р и Q, такие, что
ОР = хеи OQ = ye.z. A)
Тогда
и, значит, ОР — проекция вектора О А на ось Ох параллельно оси
Оу, a 0Q — проекция вектора О А на ось Оу параллельно оси Ох.
Далее, из соотношений A) следует, что
Х-°Е и-9Я
л о » У — о '
т. е. х и у—координаты вектора а (см. § 11, гл. II, а также
замечание 5 к § 32).
Теорема 4. Коэффициенты в разложении вектора а по
масштабным векторам ev e2, еъ общей декартовой системы координат
в пространстве являются координатами вектора а.
Доказательство аналогично доказательству предыдущей теоремы.
Замечание 1. Назовем радиусом-векторо]\1 произвольной
точки М плоскости или пространства вектор ОМ, где
О—фиксированная точка плоскости (или пространства). Из доказанных
теорем 3 и 4 этого параграфа следует, что общие декартовы
координаты точки М равны координатам ее радиуса-вектора ОМ, где
О—начало координат.
Замечание 2. Теоремы 3 и 4 являются уточнениями теорем
1 и 2 в части, касающейся существования разложения любого
вектора по двум неколлинеарным векторам на плоскости и по трем
некомпланарным векторам в пространстве.
Замечание 3. Утверждение теорем 3 и 4 может быть
принято и за определение координат вектора.
§ 38. Скалярное произведение двух векторов
Скалярным произведением аЬ двух векторов а и Ь в случае, если
эти векторы ненулевые, называется произведение их модулей на
косинус угла между ними
аЬ — | а | \ Ь | cos ф.
108 Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Если ненулевые векторы а и b коллинеарпы и направлены в
одну сторону, то угол между ними считается равным нулю, а если
ненулевые векторы а и Ь коллинеарны, но имеют
противоположное направление, то угол между ними считается равным я.
Наконец, если а = 0 или й = 0 (или а = й = 0), то скалярное
произведение ab по определению считается равным пулю.
Если считать величину угла нулевого вектора с любым
вектором равной любому числу, то скалярное произведение двух
векторов мож'но определить для любых двух векторов как произведение
их модулей на косинус угла между ними (считая этот угол любым
числом, если один или оба вектора равны нулю).
Из этого определения следует, что скалярный квадрат а2
вектора а, т. е. скалярное произведение аа равно квадрату модуля
вектора а.
В самом деле,
а2 = аа = | а [ [ а | cos 0 = [ а [а.
Отсюда
т. е. модуль вектора равен квадратному корню из его скалярного
квадрата.
Скалярное произведение двух векторов обладает следующими
свойствами:
ab = ba (коммутативность), A)
а (%Ь) — к (ab) (ассоциативность умножения на число), B)
а {Ь-\-с) = ab-\-ас (дистрибутивность). C)
Свойство A) сразу следует из определения скалярного
произведения.
Для доказательства свойств B) и C) заметим, что в силу
теоремы 4 § 11 имеем
ab = \a ||&|cos(p = |«| коорд. пр. аЬ.
Доказательство свойства B):
а (Щ = | а | коорд. пр. а (Щ = | а \ коорд. (к пр. а Ь) =
= | а | к коорд. пр. а Ь = К (ab).
Доказательство свойства C):
а (Ь + с) = | а | коорд. пр. а (Ь + с) —
= | а|(коорд. пр. аЬ + коорд. пр.„с) =
— \а\ коорд. пр.аЬ-f |а | коорд. пр. ас = ab + ас.
§39 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТАХ 109
§ 39. Выражение скалярного произведения в координатах
Ортоноржированным базисом называется упорядоченная тройка
i, j, k единичных и попарно ортогональных векторов.
Пусть относительно ортонормированного базиса заданы два
вектора своими координатами *:
a={xlt yu Zj], й = {х2, у2, г2},
т. е.
На основании свойств A) — C) скалярного произведения (§ 38)
находим
ab={x1i + yj+ zYk) (x2i + yj+z2k) =x1x2i2 + ytyj2 + 2хг2кг +
+ (хм +Х2У1) U+ (yi*2 + \1гг\)№ + (ztx2 + z2Xj) M.
Но так как /, j, k — единичные и попарно ортогональные
векторы, то
/»=/! = Л* = 1, ij=jk = ki = Q,
значит,
A)
т. е. скалярное произведение двух векторов, заданных своими
координатами в ортонормированном базисе, [равно сумме произведений
их соответствующих координат.
В частности, *
а2 = | а21 = Ух2 + у2 + z2, B)
где
а = {х, у, г},
т. е. модуль вектора равен корню квадратному из суммы квадратов
его координат, взятых относительно ортонормированного базиса.
Теперь из формулы
ab
находим косинус угла <р между двумя ненулевыми векторами,
заданными своими координатами
a = {xv У1, <?i}, b = {x2, y2, z2}
относительно ортопормировашюго базиса; именно
cos ф == г = > =-. C)
У х\ + У\+г1 У х\+у\+г\
* В дальнейшем можно считать, что /, j, k—единичные векторы осей Ох,
Оу, Ог декартовой прямоугольной системы координат. Однако фиксирование
начала координат в пространстве не обязательно при определении координат
вектора, '<ак коэффициентов разложения его по векторам базиса.
110 Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Из формулы C) находим следующее необходимое и достаточное
условие перпендикулярности двух ненулевых векторов:
*1*2+1/11/2+^2= 0, D)
т. е. необходимым и достаточным условием ортогональности двух
ненулевых векторов является равенство нулю суммы произведений
соответствующих координат, взятых относительно ортонормиро-
ванного базиса.
Теорема. Координаты х, у, z вектора а относительно орто-
нормированного базиса равны скалярным произведениям этого
вектора на единичные векторы базиса.
Доказательство. На основании теоремы 4 § 37 имеем
а = xi -f- yj+ zk.
Умножая скалярно обе части этого равенства поочередно на
/, J, к в силу свойств скалярного произведения и соотношений
получим
x — ai, y — aj, z — ak. E)
В частности, если вектор а единичный, то
х = at — cos а, у = aj— cos р, г — ак — cosy,
где а, р, у — углы между вектором а и векторами I, j, к.
Так как вектор а единичный, то
а2= |а|2=1,
а в силу формулы B)
| а I2 = cos2 а -f- cos2,8 + cos2 у.
Таким образом,
cos2 a + cos2 £ + cos2 у = 1. F)
Косинусы углов вектора а с векторами /, /, к ортонормировап-
ного базиса называются направляющими косинусами вектора а или
направляющими косинусами оси, имеющей направление вектора а.
Мы видим, что сумма квадратов направляющих косинусов
оси равна 1.
Если вектор а не единичный, то из соотношений E) находим
x=\a\cosa, y = \a\cos$, z = | а | cos у
и так как |а| = Vx2 + y2 + z2, то
i P y тяу = -—г G)
§39. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТАХ Ц1
Пусть М (х, у, г) — произвольная точка, заданная своими
координатами относительно декартовой прямоугольной системы
координат, а г —ОМ- ее радиус-вектор. Как было доказано,
где /, j, к—единичные векторы соответственно осей Ох, Оу
и 02.
Умножая скалярно обе части этого равенства поочередно на
/, j, к, получим
x = ri, y — rj, z = rk, - (8)
т. е. декартовы прямоугольные координаты точки М равны
скалярным произведениям радиуса-вектора этой точки на единичные
векторы осей координат.
На плоскости формулы A) —(8) примут вид:
скалярное произведение
а& = х1х2 + у1г/2, (Г)
модуль вектора
|а| = К*Чг/2, B')
угол между ненулевыми векторами
гпяф^-—-£*»+у« C')
у *1+у\у *:+»!
необходимое и достаточное условие перпендикулярности векторов
координаты вектора относительно ортонормировашюго базиса
x=ai, y = aj, E')
соотношение между направляющими косинусами оси
cos2 a + cos2 P = 1, F')
выражения для направляющих косинусов оси, заданной
ненулевым вектором
декартовы прямоугольные координаты точки (или координаты
ее радиуса-вектора г)
x^ri, y = rj. (%')
Базис /, j предполагается ортоиормированным, а координаты
всех векторов в формулах (Г) — (S') предполагаются заданными
относительно этого ортонормированного базиса.
112 Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
§ 40. Угол от одного вектора до другого на ориентированной
плоскости
Теорема 1. Введем на плоскости ортонормированный базис i, j
(этим самым плоскость ориентирована). Пусть a = {xlt ух} и
Ь = {х2, у2} — ненулевые векторы, координаты которых даны
относительно базиса i, j. Обозначим через (а, Ь) любое из значений
ориентированного угла ab. Тогда имеют место формулы:
cos (а, Ь)= г ***'+у.' A)
У *\+у\У *\+у\
sin {a, b) = ^ryi^=, B)
у х\+у
tg(a, ь) = чу*~Х2Ух , C)
&К ' ЧХ2 + У1Ч2 K '
причем последняя формула имеет место тогда и только тогда,
когда векторы а и b не взаимно перпендикулярны.
Доказательство. На основании
теоремы Шаля имеем
а (I, a) + (a, b) = (t, b) (mod 2л), D)
или
{а, &) = (/, &) — (/, a) (mod 2л). E)
ОТ i' зв"г Введем декартову прямоугольную систему
рис 88 координат, выбирая произвольно начало
координат О; направим ось Ох по вектору
/, ось Оу по вектору j и примем эти векторы / и j за
масштабные соответственно для осей Ох и Оу (рис. 88).
На основании определения тригонометрических функций имеем
cos(/, a)= ^_fl=, sin (/, a)=—~L=; F)
f 1 1 F 1 1
cos (i, b) = r *2 ■-, sin (/, b) = ■ r У2 . G)
У 4+'Л У *1+у1
Отсюда и из соотношения E) находим
cos (a, b) = cos (/, a) cos (/, b) + sin (/, a) sin (/, b) =
V х\ + У
sin (a, ft) = sin(/, b)cos(i, a) — sm(i, a)cos(i, b) =
*1+у1
§40 УГОЛ ОТ ОДНОГО ВЕКТОРА ДО ДРУГОГО ЦЗ
Из полученных выражений для cos (a, Ь) и sin (a, Ь) в
случае {а, Ь)ф-у- (modя) получаем формулу C).
Замечание. Если на плоскость введен ортонормироваиный
базис, то координаты единичного вектора а (а:!=1) равны
соответственно cos а и sin а, где а — угол от вектора i до вектора а,
т. е. а = (/, а). Это следует из формул F) (х\-\-у\ — \).
Теорема 2. Если на плоскости введен ортонормированный
базис i, J (этим плоскость ориентирована) и относительно этого
базиса задан ненулевой вектор
а = {х, у},
а вектор b получен из вектора а поворотом на угол а*, то
b = {xcosoc — у sin a, x sin а -f и cos а}. (8)
Доказательство. Из соотношения D) находим
cos (/, b) = cos (/, a) cos (a, b) — sin (/, a) sin (a, b), > „
sin (j, 6) = cos(j, a) sin (a, 6) + sin(/, a) cos (a, b). ]
По определению тригонометрических функций
cos(/, а) = щ, sin (I, а) = |-^Г|,
cos(/, Ь) = щ, sin(/, *)=j^|T,
где х', у' — координаты вектора b.
Из этих формул и соотношений (9) следует,
A;' = A;cosa—у sin а, у' = x sin a -f г/ cos a.
Следствие. Будем обозначать через [a]
вектор, полученный из ненулевого вектора а,
лежащего в ориентированной плоскости,
поворотом на угол + -к-. Тогда если в ортонормированием базисе
а = {х,у},
то
В самом деле, это сразу следует из формул A0), если положить
в них а==~ (рис. 89).
* То есть (a, &)=a(mod2jt) и |а| = 1&|.
114
Глава IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
§ 41. Объем ориентированного параллелепипеда
Назовем параллелограммом ABDC совокупность граничных
точек А, В, С, D двух равных между собой направленных
отрезков AB = CD. Точки А, В, С, D назовем вершинами
параллелограмма ABDC; отрезки АВ, CD, AC, BD назовем сторонами
параллелограмма, а отрезки AD и ВС — его диагоналями. Если
j, вершины А, В, С, D
параллелограмма принадлежат одной прямой, то
такой параллелограмм будем называть
вырожденным.
Совокупность вершин двух
параллелограммов ABDC и A'B'D'C,
симметричных друг другу относительно
некоторой точки О, назовем
параллелепипедом (точки А, В, С, D
симметричны соответственно точкам А', В',
С, D' относительно точки О). Назовем
вершинами параллелепипеда вершины
этих параллелограммов; отрезки АА',
ВВ', СС, DD' — диагоналями парал-
,4 лелепипеда; стороны
параллелограммов ABDC, A'B'C'D', а также отрезки
AD', DA', ВС, В'С — ребрами
параллелепипеда. Гранями параллелепипеда
назовем параллелограммы ABDC,
A'B'D'C, ABC'D', A'B'CD, ACB'D',
A'C'BD (рис. 90).
Если вершины параллелепипеда принадлежат одной плоскости,
то он называется вырожденным.
Параллелепипед однозначно определяется заданием трех его
направленных ребер, выходящих из одной вершины, например
DA', DB, DC.
Ориентированным параллелепипедом называется параллелепипед,
у которого упорядочены три ребра, выходящие из одной вершины.
Ориентированный параллелепипед будем обозначать так] (DA',DB,
DC), где DA', DB, DC — три его направленные ребра, выходящие
из одной вершины и упорядоченные записью DA' — первое ребро,
DB — второе, DC — третье.
Замечание. Каждому ориентированному параллелепипеду
(DA1, DB, DC) можно поставить в соответствие ориентирован-
§41. ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА Ц5
ный тетраэдр A'BCD (§ 18) и, обратно, всякий
ориентированный тетраэдр A'BCD ставится в соответствие и притом только
одному ориентированному параллелепипеду (DA', DB, DC). Так
как всякий невырожденный тетраэдр можно ориентировать только
двумя различными противоположными способами (см. § 15), то
и всякий невырожденный параллелепипед можно также
ориентировать только двумя противоположными способами.
Пространство, в котором введен невырожденный
ориентированный параллелепипед @Elt 0Е2, 0Е3) (базисный
параллелепипед), называется ориентированным.
Будем говорить, что невырожденный ориентированный
параллелепипед ПфЛ', DB, DC) имеет положительную ориентацию,
если он одинаково ориентирован с базисным параллелепипедом;
если же эти параллелепипеды имеют противоположные
ориентации, то параллелепипед П имеет отрицательную ориентацию.
Произведем кратчайший поворот от направленного отрезка DA' к
направленному отрезку DB в плоскости DA'B и будем
наблюдать его с той стороны от этой плоскости, где расположена
точка С. Произведём кратчайший поворот от направленного
отрезка ОЕХ к направленному отрезку 0Ег в плоскости ОЕгЕ2 и
будем наблюдать его с той стороны от этой плоскости, где
расположена точка Е3. Если эти повороты совершаются в одном
направлении, то упорядоченные тройки DA', DB, DC и OEV 0E2,
0Е3 имеют одинаковую ориентацию (см. § 15, а также
дополнение I), а параллелепипед П и базисный параллелепипед имеют
одинаковую ориентацию. В противном случае —противоположную.
Каждому ориентированному параллелепипеду (DA', DB, DC)
можно поставить в соответствие упорядоченную тройку свободных
векторов а, Ь, с, определяемых соотношениями
a = DA', b = DB, c = DC.
Если же задана упорядоченная тройка а, Ь, с векторов, то
имеется бесконечное множество ориентированных
параллелепипедов, каждому из которых ставится в соответствие эта
упорядоченная тройка векторов: точка D выбирается произвольно, а
затем от точки D откладываются векторы а, Ь, с:
DA'^a, DB^b, DC = c.
Все такие параллелепипеды получаются всеми переносами
любого из них. Понятие ориентации (положительной и отрица-
116
Глава IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
тельной) упорядоченных точек направленных отрезков DA', DB,
DC (не лежащих в одной плоскости) переносится и на
упорядоченные тройки а, Ь, с пекомпланарных векторов, а именно,
говорят, что упорядоченная тройка некомпланарпых векторов
ориентированного пространства имеет положительную ориентацию,
если положительную ориентацию имеет упорядоченная тройка
направленных отрезков DA', DB, DC, которые мы получим, от-
Рис. 91
Рис. 92
кладывая векторы а, Ь, с от произвольной точки D. Если же
упорядоченная тройка DA', DB, DC имеет отрицательную
ориентацию, то и упорядоченная тройка векторов а, Ь, с имеет
отрицательную ориентацию. Это определение не зависит от выбора
точки D.
Замечание. Иногда вводят понятия правой и левой
упорядоченных троек пекомпланарных векторов; именно,
упорядоченная тройка а, Ь, с пекомпланарных векторов называется правой,
если по векторам а, Ь, с можно направить соответственно
большой, указательный и средний пальцы правой руки (рис. 91) или
если кратчайший поворот от вектора а = ОА к вектору Ь — ОВъ
плоскости ОАВ кажется происходящим против часовой стрелки,
если смотреть на плоскость ОАВ со стороны конца С вектора ОС —с
(рис. 92).
Аналогично определяется левая упорядоченная тройка
пекомпланарных векторов (рис. 93 и 94). Однако эти понятия имеют
лишь физический смысл. В математике имеет смысл говорить
лишь об одинаковой или противоположной ориентации двух
упорядоченных некомпланарных троек векторов; этим самым
множество всех таких троек делится на два класса: две
упорядоченные некомпланарные тройки векторов принадлежат одному
§41. ОБЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА
11?
классу, если они одинаково ориентированы, и к разным, если они
ориентированы противоположно. Какой из классов упорядоченных
некомпланарных векторов назвать «правым», а какой «левым» —
безразлично.
Определение. Объемом невырожденного ориентированного
параллелепипеда (DA1, DB, DC), находящегося в ориентированном
пространстве, называется число, равное по абсолютной величине
объему параллелепипеда с ребрами DA', DB, DC, положительное,
Рис. 93
если упорядоченная тройка направленных ребер DA', DB, DC
имеет положительную ориентацию, и отрицательное, если
упорядоченная тройка DA', DB, DC имеет отрицательную
ориентацию.
Объем вырожденного ориентированного параллелепипеда
условимся считать равным нулю.
Поставим в соответствие упорядоченной тройке направленных
отрезков DA', DB, DC упорядоченную тройку а, Ь, с векторов:
a = Dk', b = DB, c = DC.
Имеется бесконечное множество ориентированных
параллелепипедов, каждому из которых ставится в соответствие та же
упорядоченная тройка а, Ь, с векторов. Эти ориентированные
параллелепипеды получаются всеми переносами любого из них и имеют
поэтому один и тот же объем; этот объем мы будем обозначать
abc и говорить, что это объем ориентированного параллелепипеда,
построенного на векторах а, Ь, с (взятых в этом порядке).
Объем abc ориентированного параллелепипеда, построенного
на векторах а, Ь, с, обладает следующими свойствами:
abc = Ьса = cab = — bac = — acb = — cba A)
118 Глава IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
(т. е. от круговой перестановки множителей он не меняется, а при
нарушении кругового порядка множителей меняет знак, сохраняя
абсолютную величину),
ab (с + d) = abc + abd (дистрибутивность), B)
ab (kc) = Я (abc) (ассоциативность по отношению к числу). C)
Доказательство. Для доказательства свойства A)
достаточно только заметить, что упорядоченная тройка а, Ь, с
некомпланарных векторов не меняет ориентации при круговой
перестановке этих векторов и меняет ориентацию при нарушении
кругового порядка.
Для доказательства свойств B) и C) докажем предварительно
следующую лемму.
Лемма. Объем abc ориентированного параллелепипеда,
построенного на векторах а, Ь, с, равен площади S параллелограмма,
построенного на векторах а и Ь, умнооюенной на координату
ортогональной проекции вектора с на ось I, единичный вектор е
которой перпендикулярен к векторам а и b и в случае, если
векторы а и b неколлинеарны, направлен так, что тройка
векторов а, Ь, е имеет положительную ориентацию:
abc = S коорд. пр.е с. D)
Доказательство. Предположим, что векторы а, Ъ, с
некомпланарны. Отложим векторы а, Ь, с, е от одной и той же
ТОЧКИ!
Тогда абсолютная величина координаты проекции вектора с
на вектор е будет высотой параллелепипеда с ребрами О А, О В
и ОС, а значит,
| abc \ = S\ коорд. пр.е с |,
так как и abc и 5[коорд. и.е с\ равны объему параллелепипеда
с ребрами О А, ОВ, ОС.
Далее, если тройка а, Ь, с имеет положительную ориентацию,
то точки С и Е лежат по одну сторону от плоскости ОАВ и,
значит, коорд. пр.ес>0, а если тройка а, Ь, с имеет
отрицательную ориентацию, то точки С и Е лежат по разные стороны
от плоскости ОАВ я, значит, коорд. пр.,, с < 0.
В первом случае а6с>0, во втором abc < 0, значит, числа
abc и коорд. пр.е с одного знака,
В случае, если векторы а, Ь, с компланарны, соотношение D),
очевидно, также выполняется @ = 0).
Теперь свойства B) и C) доказываются так!
5коорд. пр.е (c+d) = S (коорд. пр.е c-f-коорд.пр.* й) =
= S коорд. пр.е с 4-5 коорд. пр.е d — abc + abd.
§ 42. ОГ.ЪЕМ ОРИЕНТИРОВАННОГО ПАРАЛЛЕЛЕПИПЕДА В КООРДИНАТАХ Ц9
Доказанное свойство дистрибутивности объема
ориентированного параллелепипеда относительно сложения верно по отношению
к любому множителю.
В самом деле, имеем, например:
a(b + c)d = — (ad(b + c)) = — (adb + adc) =
= — adb — adc — abd -f acd-
Доказательство свойства (З):
ab (Xc) = S коорд. iip.e (Xc) = S коорд. (к пр.е с) ==
= XS коорд. пр., с; = X (abc).
§ 42. Объем ориентированного параллелепипеда в координатах.
Объем тетраэдра
Ориентируем пространство ортоиормироваппым базисом I, ], /г.
Пусть относительно этого базиса заданы три вектора своими
координатами:
Тогда
abc = (xj -f yj -!- zxk) (xj -|- yj + z2fe) (x3t + Уз/ + z3ft).
В силу того, что объем ориентированного параллелепипеда,
построенного на векторах а, Ь, с, обладает свойствами
дистрибутивности и ассоциативности по отношению к умножению любого
множителя на число (свойства B) и C) § 41), правая часть
последнего равенства может быть представлена в виде суммы
двадцати семи слагаемых Cx3x3=^27):
(xj) (xj) (x.J) + (xj) (x2i) (yj) + ...
В этой сумме смешанных произведений обратятся в пуль все
те, которые образованы тремя компланарными векторами.
Останется
abc = (xj) (yj) (zsk) +■ (x,/) (z2fe) (ya/) -f- (yj) (x2t) (zsk) +
+ (yj) (z2fe) (*8') + (zik) (x-2l) (yJ) -1- (z,fe) {yd) (xsi) =--
ly23j
+ x3yxzjki
и так как
ijk =jki = kij = 1, ikj=jik = kji = -1,
то
abc = x^jzZg —XjZ2ij3—x2ytzs + x3ytz2
или
xx
x9
x~3
Ui
У 2
Уз
Ч
Ч
г3
abc = x., i/a г2 . A)
120
Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Замечание 1. Если пространство ориентировано
произвольным базисом е1( е2, е3, то вместо формулы A) получим
abc =
Ч У\ z\
Ч У% Ч
3
Уз Ч
B)
Замечание 2. Предположим, что известны длины базисных
векторов ех, е2, е3 и углы между ними. Это равносильно тому,
что известны скалярные произведения efik (i, k=\, 2, 3).
Обозначим эти скалярные произведения так:
Введем в пространстве ортонормированный базис /, J, к и
пусть векторы elt е2, е3 в этом базисе имеют координаты
ei = K> blt cj, e2 = {a2, b2, cs}, e3 = {a3, b3, c3};
тогда па основании доказанного выше
а1 Ьг
а2 Ь2
C)
и, значит (используем формулу для умножения двух
определителей, выполняя умножение «строк на строки»),
а2 Ь2
а3 Ь3
Яза1 + Ь3Ьг
2
1
+ <
+ <
'2С1
'8^1
el
е^г
е3ех
аха2-\
а
а3а2Н
ехеъ
е\
е3е2
-ЬгЬг-
Сг
l+b'l+c\
h &3^2 + С3С1
ехеа
еге3
el
=
in
£-21
а2с
in
£22
§32
Ц +
al-i
§13
§23
§33
ЬгЬз + СгСз
it О 1 £ Q
Обозначая последний определитель буквой g, получим
abc=Vg
xl
x2
xs
Уг
y2
Уз
zi
4
C')
Если в пространстве относительно декартовой прямоугольной
системы координат заданы четыре точки:
Мх(хх, yv zx), М2{х2, уг, z2), M3(xs, y3, z8), М4(л4, yv г4),
§ 43 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
121
то объем V ориентированного параллелепипеда с ребрами MtMlf
M
2, MtM3 вычисляется по формуле
V =
X2 Xi У 2 У* Z% Zi
XS Xi Ув У$ Z3 Zi
D)
Доказательство следует из формулы A) этого параграфа и того
обстоятельства, что
= {х2 — xit y2 —
z1 — г4},
z2 — zt},
Следствие. Объем ориентированного тетраэдра
(см. § 15) вычисляется по формуле
Zl Z4
x3 x4 Уз yi z3 — zu
E)
Замечание. В случае общей декартовой системы координат
перед определителями в формулах D) и E) следует поставить
множитель Vg (см. формулу C')). Если надо вычислить йбъем
параллелепипеда или тетраэдра (неориентированных),
определители в формулах D) и E) надо взять по модулю.
§ 43. Векторное произведение
Определение. Если векторы а и Ь, лежащие в ориентированном
пространстве, неколлинеарны, то векторным произведением [ab]
вектора а на вектор b называется вектор, определяемый
следующими тремя условиями.
1. Модуль векторного произведения [ab] равен произведению
модулей перемножаемых векторов на синус угла между ними:
2. Векторное произведение [ab] перпендикулярно и вектору а и
вектору Ь:
[ab] I a, [ab] 16.
3. Упорядоченная тройка векторов
a, bj [ab]
имеет положительную ориентацию.
122
Глава IV ОСНОВЫ BFKTOPHOfl АЛГЕБРЫ
Если векторы а и b коллинеарны, то их векторное
произведение равно нулю по определению, если а \\ Ь, то [ай] = 0.
Замечание Вели ориентировать пространство правой
тройкой, то направление векторного произведения [ab] (в случае, если
Рис 95
Рис 96
векторы а и Ь неколлинеарпы) определяется по следующему
правилу
если большой палец правой руки направить по вектору а,
указательный —по вектору Ь, а средний расположить
перпендикулярно большому и указательному, то
средний палец укажет на направление
вектора [ab] (рис. 95).
Или если смотреть на плоскость
векторов а н Ь, отложенных от одной точки
со стороны стрелки векторного
произведения [aft], отложенного от той же точки,
то кратчайший поворот от вектора а к
вектору Ь кажется происходящим
против часовой стрелки (рис. 96).
Если пространство ориентировать
левой тройкой, то направление векторного
произведения определяется
аналогично по правилу трех пальцев левой руки (рис. 97).
Лусть векторы а и Ь неколлинеарны. Отложим их от одной
и гой же точки О:
Рис. 97
На основании данного определения векторного произведения
модуль векторного произведения равен площади параллелограмма
со сторонами ОА и ОВ; иногда говорят так: модуль векторного
произведения двух неколлииеарных векторов равен площади
параллелограмма, построенного па этих векторах, отложенных от одной
точки.
5 44. СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ТРЕХ ВЕКТОРОВ ]23
Если рассматривать и вырожденные параллелограммы, причем
считать, что площадь вырожденного параллелограмма равна нулю,
то модуль векторного произведения [ab] равен площади
параллелограмма, построенного на векторах а и Ъ во всех случаях.
§ 44. Смешанное произведение трех векторов
Определение. Смешанным произведением трех векторов а, Ь, с,
лежащих в ориентированном пространстве, называется скалярное
произведение вектора [ab] на вектор с, т. е. [ab] с.
Теорема. Смешанное произведение [ab] с равно объему
ориентированного параллелепипеда, построенного на векторах а, Ъ, с.
Доказательство. В § 38 для скалярного произведения
двух векторов была доказана формула
pq = \p\ коорд. пр.р<7.
Пусть векторы а, Ь, с иекомпланариы. Тогда на основании
леммы § 41 имеем
[а&]с = |[а&]| коорд. np.c = S коорд. np.c = abc,
причем проектирование ведется на ось, имеющую направление
вектора [ab].
В случае, если векторы а, Ь, с компланарны, равенство
[ab] с = abc,
очевидно @ = 0).
Следствие.
[ab]c = a[bc].
Доказательство.
[ab] с = abc = bca = [be] a-=a [be].
§ 45. Координаты векторного произведения
Пусть i, ], k — ортонормированный базис. Пусть в этом базисе
a = {xv yv zj, b = {x2, уг, г2}.
Координаты вектора в ортонормированном базисе можно
рассматривать как скалярные произведения этого вектора на векторы
базиса. Пользуясь формулой A) § 42 для объема ориентированного
параллелепипеда в координатах и замечая, что
/ = {1, 0, 0}, /={0, 1, 0}, fc = {0, 0, 1},
124
Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
находим координаты векторного произведения:
[ab] i = abl =
[ab]j=abj =
% Уг
1 О О
Хх Ух ?i
Х-2 У* 22
О 1 О
х2
0
Уг
Уч
0
ч
1
=
Уг
Z,
_ Хх У!
Итак, если в ортонормированием базисе
то
Уч
2, г,},
У\
Уг
§ 46. Свойства векторного произведения
Векторное произведение двух векторов обладает следующими
свойствами:
B)
. C)
Они вытекают из выражений для векторного произведения
в координатах. Докажем, например, последнее свойство. Пусть
в ортонормированном базисе
{х у±
Тогда
и, следовательно,
Уг+Уз
Ух г,
= {х3, у3, z3}.
Ух
Уз
»
22
Ух Ч
Уг 22
УгЧ
Уз
гз
Ч
+ 2
ч
ч
3 X
хг
х2
Ч
Ч
г3
ХХ
1 1 Хз
х2
Х1
х3
Ч
Ч
•
*
X-2 У2
хз Уз
Ч Уз
§ 47. ДВОЙНОЕ ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
125
§ 47. Двойное векторное произведение
Вектор [a [be]] называется двойным векторным произведением. Векторы
Ь, с и [a [be]] компланарны; в самом деле это так, если векторы b и с кол-
липеарны. Если же векторы b и с неколлинеарны, то вектор [be] им
перпендикулярен, а вектор [а[йс]], перпендикулярный вектору [be], будет
компланарен с векторами b и с. Отсюда следует, что вектор fa [be]] можно
разложить по векторам & и с.
Приводимая ниже формула и дает разложение этого вектора по векторам
& и с:
[a[bc]] = b(ac)-c(ab).
Для доказательства этой формулы введем ортоиормировапный базис, взяв
первый единичный вектор i базиса коллинеарным вектору а и расположив
второй единичный вектор j этого базиса перпендикулярно i и так, чтобы
векторы a, b, j были компланарны/
Тогда
а = {хъ 0, 0}, & = {х2, уг, 0), с = {х3, f/3, z3},
значит,
= {угг3, — хгг3, x2ys—x3y2},
, 0}—
ас = х1х3, ab = x1xz,
) — с(аЬ}=хгх3{х2, уг, Q}—x1xl{xi, ys, z3} =
~{XiX2X3, XiX22/3. X1X2Z3}={0,
= {0, — хх(х2уа—xsy2), —
Отметим еще формулу
[[ab]c] = b(ac)~ a(bc).
Доказательство:
[[ab] c]= — [с [ab]] = -(a (cb) — b (ac)) = & (ac)-a (cb).
§ 48. Площадь параллелограмма и треугольника в пространстве
Площадь параллелограмма, построенного на двух неколлинеарных
векторах а={хь ylt Zx} и &={х2, г/г, ^г}» отложенных от одной точки и
заданных своими координатами относительно ортонормированпого базиса, равна
| [ab] I и, следовательно, вычисляется по формуле
У I г/г г2
Уг
Пусть относительно прямоугольной системы координат в пространстве
заданы три вершины параллелограмма:
А (хх, Ух, гг), В (х2, г/г, г2), С (х3, г/з. г3).
Тогда его площадь вычисляется по формуле
2—г/з z2—
хз "
12S
Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
В самом деле, площадь параллелограмма с тремя данными вершинами
А, В, С равна S = \[CACB]\. Остается заметить, что
/"• А == I У , V II . It у _ у \
/~> а j v у it it „ ~ \
O£) — ^Л2 Лз, У2~~ УЗ» *2 "~" гЗ[*
'й™"™ '3 SS^~ 3 2 " 3 У 2 "~ S/3 \}
и что модуль вектора равен корню квадратному из суммы квадратов его
координат.
Замечание. Площадь S треугольника ABC с вершинами
A (*i, 2/1, Zi), В (х2, #2) z2), С (х3, #3. г3),
заданными относительно декартовой прямоугольной системы координат,
вычисляется по формуле
Ух ~~* Уз **i. ~™ ^з
2/2 — 2/3 z2 — г3
а — гз -'■г—
i — ^з 2/1 — 2/3
— Ха г/а — Уз
§ 49. Примеры и задачи к главе IV
1. Задачи с решениями
Пример 1. Рассмотрим произвольный треугольник ABC (рис. 98). Пусть
АВ = С, АС = Ь, ВС = а. Тогда а = Ь—с. Возводя обе части этого равенства
а+Ь
Рис. 98
Рис 99
скалярно в квадрат, получим а2 — Ьг-\-сг — 1Ъс. Но а2 = а2, &2 = 62, с2 = с2,
be = bccos Л, поэтому аг = Ьг + с2 — 26сcos Л—теорема косинусов. Заметим,
что эта формула верпа и для вырожденного треугольника.
Пример 2. Рассмотрим ромб (рис. 99). Составим скалярное произведение
вектора а-\-Ь на вектор а—Ь:
(а — &) = а2— &2 = а2—62 = 0.
Но если скалярное произведение двух ненулевых векторов а-\-Ь и а — Ь равно
нулю, то эти векторы взаимно перпендикулярны. Таким образом, доказана
теорема! диагонали ромба взаимно перпендикулярны.
§ 49. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ IV 127
Пример 3. Пусть AD — биссектриса внутреннего угла Л треугольника ABC.
Выразим длину х биссектрисы AD через длины с и 6 сторон АВ и АС и
угол А между ними. Полагая AD=x, имеем (рис. 100)
с _ВР_~ВР_ х—с
Отсюда
_bc-\-cb
значит,
26с cos тг
F +сJ
Пример 4. Найти проекцию вектора а на ненулевой вектор Ь.
Рассмотреть числовой пример: а = {1, 4, 8}, & = {1, 2, —2}.
Решение. Отложим векторы а и & от одной точки О: О А—а, ОВ = Ь.
Пусть С —проекция точки А на прямую ОВ. Искомая проекция ОС. Очевидно,
ОС = ХЬ, остается определить X. Так как АС_\_ОВ и АС — ОС — ОА^'кЬ—а,
то (Х& — а)& = 0, откуда Х=-р-. Итак, пр.{,а=т^ Ь. В случае а= {1, 4, 8},
& = {1, 2, —2} имеем
Пример 5. В вершине куба приложены три силы, разные по величине
1, 2, 3 и направленные по диагоналям граней куба. Определить величину
равнодействующей.
Р е ш е п и е. Примем данную вершину за начало координат, а исходящие
из нее ребра—за оси координат. Пусть, например, сила Flt величина
которой равна 1, лежит в плоскости хОу; тогда ее координаты
o
Пусть сила F2, величина которой равна 2, лежит в плоскости уОг; тогда
ее координаты
Пусть сила Fs, величина которой равна 3, лежит в плоскости гОх; тогда
ее координаты
Равнодействующая этих трех сил
следовательно, ее величина
25
128
Глава IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Пример 6. Одна из вершин параллелепипеда находится в точке М A, 2, 3),
а концы ребер, выходящих из этой вершины, — н точках А (9, 6, 4), В C, 0, 4)
и С E, 2, 6). Найти косинус угла между диагональю MD этого
параллелепипеда, выходящей из точки М, и его ребром МЛ Система координат
прямоугольная.
Решение
MD = МА + MB + МС,
откуда
= {8, 4, 1}, лГй = {2,-2, 1}, МС = {4, 0, 3},
= {14, 2, 5},
MA ML
Л,
\
Ъ\ У
\с
У
Рис
8-14+4-
«.-1-4.-!-, V
зЛ
X
101
2+ 1-5
И2 + 22 + 5
25
,2 27
Пример 7. Вычислить длину d диагонали OD параллелепипеда, зная длины
ОА=а, ОВ = Ь, ОС = с трех его ребер, выходящих из вершины О, и углы
между ними. Вычислить также углы фь ф2, ср3 между OD и ребрами О А, ОВ, ОС.
Решение. Имеем (рис. 101)
d=a+ftfс
Отсюда
Далее,
= lAa2 + &3 + с2 -|- 2bc cos a -f 2ca cos p + 2a6 cos у
_ ad _ a (a -f Ь + с) _ а2 + ab cos y + ас cos P _
~~ ad~ ad ad ~
cos Y
у a24 &2-f c2-j-2&ccosa + 2cacos p + 2ab cosy
Аналогично найдем
a cos у + b + с cos а
cos фа =
cos ф8 =
у аг + b2 -г с2 -f- 2ic cos я -j- 2ca cos p + 2a6 cos у
a cos \i-\-b cosa +c
§49- ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ IV
129
Пример 8. Доказать тождество
[аЬ] \ху\ = (ах) (Ьу)-(ау) (Ьх).
Доказательство.
[аЬ] [ху] = а [Ь [ху] ] = а (х фу) - у (Ьх)) = (ах) (by) - (ay) (bx).
Пример 9. Вычислить внутренние двугранные углы трехгранного угла,
плос не углы которого а, Ь, с.
Предвари тельное замечание. Для вычисления двугранных углов
методом векторной алгебры можно поступать так: найти вектор х,
перпендикулярный грани р двугранного угла н направленный внутрь * этого угла.
Найти вектор у, перпендикулярный
грани q угла и направленный во
внешнюю сторону двугранного угла.
Тогда угол между векторами хну
будет равен линейному углу
рассматриваемого двугранного угла
(рис. 102). Для нахождения вектора
х, перпендикулярного грани р,
можно найти пару неколлннеарных
векторов, лежащих в этой грани, и
взять их векторное произведение.
Аналогично находится н вектор у.
Решение. Рассмотрим
единичные векторы р, д, r, идущие по
ребрам данного трехгранного угла
(рис. 103). Найдем косинус
линейного угла для двугранного угла, по
ребру которого направлен вектор р.
Вектор \рд\ перпендикулярен гра-
Рис.
103.
ни ОАВ и направлен во внешнюю
сторону двугранного угла В (АО) С.
Вектор [рг] перпендикулярен грани ОАС
же угла. Обозначая внутренние двугранные
угла буквами А, В, С, имеем:
[рд] [рг] __ рг (gr)-(pr) (qp) _ cos a —cos Ь cose
sin & sin с ~ sin & sin с
и направлен
углы данного
внутрь того
трехгранного
cos A =
Аналогично находим
cos Ь — cos a cos с
smasmc
— , cosC =
cos c — cos a cos b
sinasinu
Замечание. Построим сферу радиуса 1, центром которой является
вершина данного трехгранного угла. Грани трехгранного угла высекут из сферы
сферический треугольник ABC (ограниченный дугами ВС, СА и АВ больших
кругов построенной сферы). Так как радиус сферы равен 1, то длины сторон
* Отложим вектор х, перпендикулярный грани р, от любой точки этой
грани; если его конец н точки другой грани q лежат по одну сторону от
плоскости, в которой расположена грань р, то будем говорить, что вектор
х направлен внутрь двугранного угла pq. Если же конец вектора х,
отложенного от любой точки грани р, и точки грани q лежат по разные стороны от
плоскости, в которой расположена грань р, то будем говорить, что вектор х
направлен во внешнюю сторону угла pq.
5 п, С. Моденов
130
Глава IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
ВС, СА и АВ сферического треугольника ABC соответственно равны а, Ъ, с
Углом А сферического треугольника ABC при вершине А назовем угол,
стороны которого касаются дут АВ и АС в точке А, причем эти стороны идут
в направлении от А к В и от Л к С (рис. 104). Аналогично определяются
углы В и С сферическою треугольника ABC. Ясно, что угол А сферического
треугольника ABC является линейным углом внутреннего двугранного угла
В (АО) С Таким образом, полученные выше формулы дают решение следующей
задачи сферической тригонометрии: пай
ти углы А, В, С сферического треуголь
ника ABC, если даны его стороны
ВС = а, СА = Ь, ДВ=е
Пример 10. Л BCD —произвольный тет
раэдр (невырожденный). Возьмем на какой-
нибудь его грани, например на грани
ABC, произвольную точку S и отложим
от этой точки вектор SS'*=d, модуль ко
торого равен площади грани ABC,
перпендикулярный грани ABC и направленный
так, что точки S' и D лежат по разные
стороны от плоскости грани ЛВС. Анало
г и чпо построим вектор РР'=а для грани
BCD, вектор QQ' =Ь для грани ACD и
вектор RR' —с для грани ABD (рис 105)
Доказать, что
Рис. 104
Доказательство Положим DA—x, DB=y, DC = z Тогда СА =
х — Z, СВ=у— г. Ориентируем пространство тетраэдром A BCD. Тогда
будем иметь
a
= —\xz\, с = у [jut],
-j[{x-z) (у-г)]
Отсюда
Пример П. Доказать тождество:
ах ау аг
(аЬс) (хуг) =
bx by Ьг
сх су cz
Рис. 105
Доказательство Пользуясь формулой для двойного векторного
произведения, имеем
ЦаЬ][рс]]=р(аЬс) — с\
«40 ПРИМЕРЫ И ЗЛДЛЧИ К Г/ПВЕ IV
131
Положим в этом тождестве р = [ху\, получим
\ху\ (abc)-c(ab [ху])-\-Ь([ху] са) — а({ху] cb) =
= c({ab\ [xy\)-\-b ([xy] [ca]) — a([xy] [cb]) —
= с ((ах) (by)- (ay) (bx)) + b ((xc) (уa) -(xa) (yc))~a((xc)(yb)~(xb) (yc)).
Умножая обе части этого равенства скалярно на г, найдем
(abc) (хуг) = (сг) {(ах)фу)~(ау) фх))-{-фг) ((хс) (уа)-(ха) (ус)) —
ах ау аг
— (аг) ((хс) (yb) — (xb) (ус)) =
bx by Ьг
сх су сг
Замечание. Доказанное соотношение выражает собой формулу для
умножения доух определителей третьего порядка;
Рис. 106.
(cti, а2, а3 — координаты вектора а в ортонормированием базисе i,J, k; 61, Ьг, 6Я —
координаты вектора Ъ в том же базисе и т. д.)
Пример 12. Вычислить объем V параллелепипеда, зная длины его ребер
ОА — х, ОВ = у, ОС = г, выходящих из одной вершины О, и плоские углы
между ними (рис 106):
Решение (см. предыдущий пример)
= хуг~у
1 cos с cos 6
cos с \ cos a
cos 6 cos a 1
-\-2 cos a cos Ъ cos с —cos2a — cos26—cos2c.
132
Глава IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Пример 13. В треугольной пирамиде О ABC даны длины ребер О А—а,
ОВ = Ь, ОС —с и плоские утлы при вершине О; ЙО?Г=а, бЬ~А—?>, *АОВ =у
Вычислить кратчайшее расстояние между прямыми ОА и ВС и найти положение
точек Р я- Q соответственно на прямых О А и ВС, для которых отрезок PQ
перпендикулярен прямым ОА и ВС (рис 107)
Решение. Сначала выведем общую формулу для кратчайшего расстояния
между двумя скрещивающимися (или пересекающимися) прямыми (рис. 108).
Назовем направляющим вектором прямой всякий ненулевой вектор, коллине-
Рис 107
Рис 108
арный этой прямой. Пусть а и Ь—направляющие векторы двух
скрещивающихся (или пересекающихся) прямых р и q. Вектор [ab\ имеет направление
общего перпендикуляра к прямым р и q. Пусть дан еще вектор МхМ2, концы
которого лежат соответственно на прямых р и q. Тогда кратчайшее расстояние
б равно длине проекции вектора М1М2 на общий перпендикуляр к двум прямым
р и q или (что то же самое) — длине проекции вектора MiM2 на вектор [ab\:
Но
следовательно,
| \аЬ]
= | [аи] 11 пр |eftJAf jyw, | = 8 | [аи] |,
M1Mtab\
|[а»1| " \[ab]\
Введем теперь векторы
ОА — а, Ъв = Ь, ОС = с.
§ 49 ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ IV
138
Тогда СВ = Ь—с—направляющий вектор прямой ВС. В качестве вектора
можно взять, например, вектор ОВ = Ь и, значит,
б =
\Ьа(Ь — с)\
\аЬс\
\аЬс\
[a(b — c)\\ | [aft]-[ас] | "" |/([aft] -[ a]J
laftcl
2 — 2 [аи] \ас]
abcl
У aWs\n2y-\-aWsin*fi — 2 (a2 (be) — (ас) (abj)
\abc\
У a2bis'm2yJra2c'"s\n2li — 1dlbc (cosa—cos p cosy)
_abc УI + 2 cos a cos P cos y — cos2 a—cos2 (J — cos2 у _
a Y№ч\п-y-\-cl s\n-\\--'2bc (cosa — cos [] cos v)"
be У 1 -|-2cosacos p cos Y — ccs2a — cos'2 p — t с s2 у
У u2sin2Y — c2sin2 f— Ibc (cosa—cosp cos"v)
Для определения положения точек Р и Q на прямых ОА и ВС заметим,
что ОР = Ха, CQ = yi(b—с), и вопрос сводится к нахождению чисел л и и,
(если 0 < X < 1, то точка Р лежит между точками О и Л и ОР—-Х | a ] и т. д.).
Имеем:
и так как P~Q _[_a и PQ _]_& — с, то а Р<2=0, (й-с) PQ=0, т. е.
ac-ffia (ft — с) — Xa2 = 0,
с(й —с)-Ь[х(& —сJ —?.a(& —c)=0.
Мы получили линейную систему двух уравнений относительно X и (.г.
Ха2 — \ia (b — с) = ас.
Решая эту систему, получим
ас —а(Ь — с)
c(b — c) —(ft—сJ
(aft — ac)(cb — с2)—
2 — 2Ьс)
— а2 (о2 -- с2 — 2&с) + (aft — асJ
a2 —a (ft —с)
а(Ь — с) —(Ь — сJ
(ab cosy —ас cos р) (с& cosa— с2) — ас iosP (&2 + c2 — 2&c cosa)
— а2 (Ь2-гс2 — 2&с cosa)-|- (a&tcsy — ас cos (iJ
_ с [(bcosу — cccsp) (b cosa —с) — cos f5 (&2-| c2 — 2te cosa)j
— a [b2-|-c2—26c cosa-t- (b Ccsy^c tcs fiJ1
ac
a(b—c) с (ft —с)
a2 (eft—c2) — ac (ab — ac)
:—a'2(ft—cJ-!-(a0—acJ ~~ — a2(ft — cJ-j- (a& — acJ
с [b cosa—с — cos p (b cos у — с cos P)]
"" —b2 — i.'2 -j- 2bc cos a -, (b cos у — с cos Р)я *
134
Глава IV. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Пример 14. ABCD — прямоугольник (рис. 109). Отрезок EF параллелен
плоскости этого прямоугольника и проектируется на эту плоскость в отрезок
GH\\AD\\BC, причем точки G и Н находятся на равных расстояниях от АВ и
CD, а отрезок GH — на равных расстояниях от AD и ВС. Дано:
АВ = а,
1) Найти косинус двугранного угла
С (FD) А. 2) Найти кратчайшее
расстояние между прямыми BE н АС
(многогранник EFABCD называется клином).
Решение. 1) Принимая точку В
за начало координат, В А — за ось Ох,
ВС— за ось Оу и располагая ось Ог
перпендикулярно плоскости ABCD,
будем иметь
В@, 0, 0), А (а, 0, 0), D(a, Ъ, 0),
С @, Ь, 0),
b+c
F(a
М 2 ' 2
Отсюда находим
D
-с, 0|,
Рис. 109
[FEFD] =
Далее,
-с О
Ь — с
— h
0
— ft
0
а
»
0
а
~2
— с
Ь — с
2
, о, «}=/,,
[FC FD] =
— ft
— ft
-
а
а
~h т
)
а й — с
Т ~2~
а Ь—с
~2~
= io, -aft, -a
Таким образом,
0, -2ft, -(b-c)}=q.
-аф-с)
cos ф = cos С (FD) А=?—=
РЯ
Отметим, что если с<Ь (как на рис. 109), то созф<0, угол ф тупой;
если с >b, tocos9/>0, угол ф острый; если с = 6, то созф = 0, ф = —; в этом
§49 ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ IV 135
случае клин превращается в прямую призму,
2) АС = {-а, Ь, 0}=х, S£ = j-J, b-=± , ft} || {a, b-c, 2h}=y,
[ху] = {Ш, 2ah, а{с-Щ); Те=\-~, ^.
Кратчайшее расстояние б между АС и BE равно.
mod
a
')
— a
a
b — c
2
b
b — c
h
0
2h
AE [xy]\ a b — c 2h 2abh
(c — 2u)a /~4ft2 (a2 + b2) + aa (с— ?й)а
Пример 15. Найти векторы jc и _}*, если известны их сумма a ^ 0, скалярное
произведение р и векторное произведение Ь Ф 0. Дано, что векторы а и &
ортогональны (если векторы а \\ b не ортогональны, то задача не имеет решений).
Решение Имеем систему
х-\-у = а, ху — р, [ху]=Ь, причем а& = 0
Из первого уравнения находим у.
у = а — х.
Подставляя это значение у во второе и третье уравнения, получим
х(а — х) = р, [ха]=Ь.
Из соотношения [ха] = Ь следует, что вектор х ортогонален вектору &,
а так как векторы а и & ортогональные и ненулевые, то вектор х
компланарен векторам а и [ab]; эти векторы ненулевые и ортогональные, значит,
по ним можно разложить вектор х:
[ab].
Подставляя это значение х в уравнение [ха]—Ь, получим
[(Ха + ц[а&])а]=&,
(х[[а&]а]=&, &-а2ц = &,
значит,
1 , . [ab]
Теперь соотношение х{а — х)=р, или ах—хг=р, примет виз
откуда
Л-
Если а* < 4 F2 + ра2), то задача не имеет решений. Если a* = 4F2-j-Pa2)>
ю Я = -ц- и задача имеет одно решение:
a [a&l a [ab]
136 Г лае, а IV ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
Накокец, если а4 > 4 (Ь2 -\- ра-), то задача имеет два решения:
Г а*) „ , [aft]
2а2
или
__a2 — t/a1 — 4(fc2 + pa2) \db\
Х~
[а]
а Ф
2. Задачи для самостоятельного решения
1. Даны радиусы-векторы rlt r2, rd трех последовательных вершин А, В, С
параллелограмма. Найти радиус-вектор четвертой вершины D.
Отв. ri + Гз—ff
2. Доказать, что для четырех любых точек А, В, С, D пространства
выполняется соотношение
ВС +
3. Доказать, что
4. Даны три некомпланарных вектора а, Ь, с и скалярные
произведения а, р\ у неизвестного вектора х на эти векторы: ах = а, &jc = p, cx = y.
Найти вектор х.
Отв х^
abc
5. Даны три вектора ОА=а, ОВ = Ь, ОС —с. Векторы а и & неколли-
неарны. Пусть /У —проекция точки С на плоскость ОАВ. Найти вектор СН.
Отв. Ctf—
6. Даны два пеколлинеариых вектора ОА=а и ОВ = Ь. Окружность
с центром S касается прямых ОВ и ОА в точке А. Найти вектор OS.
Отв -Bs^
7. Даны три компланарных вектора х, а, Ь, причем а и & неколлинеарны.
Выразить коэффициенты разложения вектора х по векторам а и & через эти
векторы
(xb[ab])a + (x[ab]a)b
Отв. х- ^р .
8. Даны три компланарных вектора ОА = а, ОВ = Ь, ОС = с, причем
векторы а и & неколлинеарны, Пусть М<—точка пересечения прямых АВ и ОС.
Найти вектор ОМ=х.
[aft]2
?49. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ IV 137
9. Даны три некомплапарп-ых вектора ОЛ=а, ОВ = Ь, ОС = с. Пусть S —
центр сферы, проходящей через точки О, А, В, С. Найти вечтор OS.
Ome. 5s = gii^l + &:lca]+c2[a^-.
laoc
10. Даны векторы ОА=а, 08 = 0, 0С~с. Векторы Ь и с неколлиш'арны.
Пусть Я —проекция точки А на плоскость ОВС. Найти вектор ОН.
Отв. 0Н = а — ^~, \Ьс].
II. Даны четыре вектора ОА -— а, ОВ = Ь, ОС = с и OU = d. Векторы а, Ь, с
некомпланарны. Пусть М — точка пересечения прямой OD с плоскостью ABC.
Найти вектор ОМ.
Ото ОЛ1 = ., , а.&С --,— d.
ГЛАВА V
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
§ 50. Уравнение прямой, проходящей через данную точку в данном
направлении
Направляющим вектором прямой называется любой ненулевой
вектор, коллинеарный этой прямой.
Теорема 1. В общей декартовой системе координат уравнение
прямой р, проходящей через точку Мо (х0, у0) с направляющим
вектором а = {/, т}, имеет вид
—хо У-Уо
I m
= 0,
A)
или
I ~ m '
Доказательство. Рассмотрим произвольную точку М (х, у)
плоскости. Точка М (х, у) лежит на прямой р тогда и только тогда,
когда векторы М~^М — {х — х0, у — у0} и {I, т] коллинеарны.
Условием коллинеарности этих векторов является равенство (§ 36,
теорема 5):
X
У—У о
т
= 0,.
ИЛИ'
х—Хр __ У ffo
/ т
Уравнение (I) или (Г) называется каноническим уравнением
прямой.
* Если один из знаменателей / или т. равен нулю, то уравнение (!')
означает, что равен нулю соответствующий числитель.
§51. ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ 239
§ 51. Общее уравнение прямой
Теорема I. В общей декартовой системе координат прямая
выражается уравнением первой степени:
Ах + Ву + С = 0. A)
Доказательство. Перепишем каноническое уравнение
прямой (§ 50) в виде
тх — 1у-\-1у0— тх0 = 0.
Полагая т = А, —1 — В, 1уо—тхо = С, приведем eFo к виду
Это уравнение первой степени, так как вектор а — {1, т)
ненулевой, а потому А и В одновременно в нуль ае обращаются (А = т,
В = -1).
Теорема 2 (обратная). Всякое уравнение первой степени
Ах + Ву + С = 0 B)
в общей декартовой системе координат является уравнением прямой.
Доказательство. Пусть х0, у0 — какое-нибудь решение
уравнения
0, т. e. Axo + ByQ + C = Q. C)
Данное уравнение будет эквивалентно уравнению, которое мы
получим, отняв почленно из уравнения B) равенство CI
или
х—х0 у-~у0
В А
_
По доказанному в предыдущей теореме это "уравнение, а
следовательно и уравнение B), является уравнением прямой,
направляющим вектором которой является вектор а = { — В, А} и которая
проходит через точку (х0, у0).
Уравнение Ах-{-Ву-{-С = 0 называется общим уравнением
прямой.
§ 52. Направляющий вектор прямой
Из предыдущего параграфа следует, что если прямая задана
общим уравнением
относительно общей декартовой системы координат, то вектор
{— В, А} и всякий ненулевой вектор, с ним коллинеарный, является
направляющим вектором этой прямой.
140 Гласа V ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Теорема. Необходимым и достаточным условием того, что
вектор а—{1,т} коллинеарен прямой, заданной относительно общей
декартовой системы координат уравнением
является цсловие
А1 + Вт = 0. A)
Доказательство. Отложим вектор а = {1,т) от любой
точки М0(х0,у0) данной прямой. Конец Р отложенного вектора
будет иметь координаты хо + 1, у^+т. Вектор а = {1,т} колли-
неарен данной прямой тогда и только тогда, когда точка Р лежит
на данной прямой, т. е. тогда и только тогда, когда выполнено
равенство
или
(Ах0 + Вуп + С = 0, так как точка Мо лежит на данной прямой).
Если прямая задана общим уравнением
относительно декартовой прямоугольной системы координат, то
вектор
перпендикулярен этой прямой.
В самом деле,
ап = — В-Л-М-В = 0,
значит, вектор п перпендикулярен направляющему вектору {—В, А)
данной прямой, а потому вектор п перпендикулярен и самой
прямой.
Для общей декартовой системы координат это положение, вообще
говоря, не имеет места. Вектор п=-{А,В], координаты которого
служат коэффициентами в общем уравнении Ах + By + С — 0
прямой относительно общей декартовой системы координат, будем
называть главным вектором этой прямой.
Главный вектор п={Л,£>} прямой, заданной уравнением
Ах + Ву + С — 0 относительно общей декартовой системы
координат, неколлинеарен этой прямой. В самом деле A = А, т — Б),
АА+ВВ А* + Вгф<д
§53. ЧАСТНЫЕ СЛУЧАИ РАСПОЛОЖЕНИЯ ПРЯМОЙ J41
§ 53. Частные случаи расположения прямой относительно
системы координат
Прямая Ах + В у -f С = 0 коллинеарна оси Ох тогда и только
тогда, когда Л = 0, так как направляющий вектор {— В, А} прямой
Ах-\-Ву-\-С = 0 коллинеарен оси Ох тогда и только тогда, когда
вторая координата этого вектора равна пулю.
Уравнение прямой Ах -f By -j-С — 0 в случае, если эта прямая
коллинеарна оси Ох, имеет, таким образом, вид By -\-C = 0, или
у-=Ь (где b = — -J-).
Аналогично доказывается, что прямая Ах + Ву + С = 0
коллинеарна оси Оу тогда и только тогда, когда В = 0, т. е. тогда и
только тогда, когда общее уравнение Ах-{-Ву + С = 0 прямой имеет
вид Ах + С = 0, или х = а(а — г
Необходимым и достаточным условием того, что прямая
Ах-г By-{-С — 0 проходит через начало координат, является
равенство С = 0, так как в случае С = 0 и только в этом случае
уравнение Ах-\-Ву-\-С = 0 удовлетворяется координатами начала
координат.
Таким образом, общее уравнение прямой, проходящей через
начало координат, имеет вид Ах + Ву = 0, и обратно (т. е. любое
однородное уравнение Ах + Ву — 0 первой степени определяет
прямую, проходящую через начало координат).
§ 54. Параметрические уравнения прямой
Параметрические уравнения прямой, проходящей через точку
Мо (х0, у0) и имеющей направляющий вектор а = {I, т}, в общей
декартовой системе координат имеют вид
Доказательство. Пусть М{х, у) — произвольная точка
плоскости. Точка М(х, у) будет лежать на данной прямой тогда и
только тогда, когда векторы М0М = {х — х0, у — у0} и а = {1,т}
коллипеарны, т. е. тогда и только тогда, когда они отличаются
числовым множителем
M?M = ta, A)
или в координатах
х — xo = lt, y — yo = mt,
откуда
x — xo-\-lt, y = yo + mt.
142
Глава V ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Если t принимает все действительные значения, то точка М
с этими координатами описывает всю данную прямую.
Замечание 1. Из соотношения A) находим
,.. дуй
т. е. t есть координата точки М на данной прямой в следующей
системе координат: Мо — начало координат, а —масштабный вектор.
Замечание 2. Вводя радиусы-векторы ОМ0 = г0 и ОМ = г
точек Мо и М, можно соотношение A) переписать так;
r—ro = ta,
откуда
Это уравнение называется параметрическим уравнением прямой
в векторной форме, проходящей через точку М0(г0) и имеющей
направляющий вектор а.
§ 55. Уравнение прямой, проходящей через две точки
Теорема. Уравнение прямой, проходящей через две точки
Ml(xv ух) и М2(х2, у2), заданные относительно общей декартовой
системы координат, можно записать в одном из следующих видов:
или
или
X — X]
Х2-Х
Х—Хх
X
х\
b
У
Уг
У—Ух
У г —Ух
У-Ух
1
1
_(
= 0,
^
B)
C)
(в этих уравнениях / есть координата точки М на прямой МгМ2
в следующей системе координат: Мх — начало координат, М2 —
единичная точка).
Доказательство. За направляющий вектор прямой можно
взять вектор
или в параметрической форме
далее остается применить результаты § 50 и 54.
§ 56 УРАВНЕНИЕ ПРЯМОЙ В ОТРЕЗКАХ 143
§ 56. Уравнение прямой в отрезках
Пусть прямая р не проходит через начало общей декартовой
системы координат и пересекает обе оси координат: ось Ох
в точке (а, 0), а ось Оу в точке @, Ь).
Абсцисса а и ордината Ь точек пересечения прямой с осями
Ох и Оу часто называются отрезками, отсекаемыми прямой на осях
координат.
Уравнение прямой р будет иметь вид
х у 1
а 0 1
= 0, или 4-
У
а
0 Ь 1
Это уравнение называется уравнением прямой в отрезках.
§ 57. Угловой коэффициент прямой
Определение. Угловым коэффициентом k прямой р, заданной
относительно общей декартовой системы координат, называется
отношение второй координаты направляющего вектора а = {/, т}
этой прямой к его первой координате:
/г- —
к— г .
Прямые, параллельные оси Оу, и сама ось Оу не имеют
углового коэффициента, так как первая координата любого направляю
щего вектора всех таких прямых равна нулю.
Для каждой прямой, пересекающей ось Оу, угловой коэффициент
имеет вполне определенное значение, не зависящее от выбора
направляющего вектора
В самом деле, если {/, т\ и {/ , т'\ — два направляющих вектора
одной и той же прямой, пересекающей ось Оу, то 1ф0, V =£0 и,
следовательно (§ 36, теорема 4),
. __ т т'
Т ~Т '
В декартовой прямоугольной системе координат угловой
коэффициент k прямой, пересекающей ось Оу, равен тангенсу угла а
от оси Ох до направляющего вектора этой прямой:
k = tg a.
В самом деле, если угол от оси Ох до вектора а равен а, то на
основании теоремы 4 § 11 координата / ортогональной проекции
вектора а на ось Ох равна
I = I a i cos a.
144 Глава V ПРЯМАЯ ЛИНИЯ НЛ ПЛОСКОСТИ
Угол от оси О у до вектора а равен а—у, а потом} на
основании той же теоремы
т = | а | cos (а — -|-) = [ а | sin a.
Из этих соотношений и следует, что
&=T = tga.
§ 58. Уравнение прямой с угловым коэффициентом
Уравнение прямой, проходящей через точку М0(х0, у0) и
имеющей угловой коэффициент k, в общей декартовой системе
координат имеет вид
хо). A)
Уравнение A) следует из канонического уравнения прямой (§ 50).
Уравнение прямой р, имеющей угловой коэффициент k и
пересекающей ось Оу в точке @, Ь), в общей декартовой системе
координат имеет вид
y=*kx + b. B)
Доказательство. Уравнение B) следует из уравнения A),
если в нем положить у0 = Ь, х0 =- 0.
Число b называют иногда «начальной ординатой» прямой р,
а уравнение B)—уравнением прямой с данной начальной
ординатой и данным угловым коэффициентом.
§ 59. Взаимное расположение двух прямых
Теорема. Пусть относительно общей декартовой системы
координат даны уравнения двух прямых
А.х + В.у + С^О, А,х + Вгу + С2^0. A)
Тогда необходимое и достаточное условие того, что эти прямые
пересекаются, имеет вид
Необходимое и достаточное условие того, что эти прямые
параллельны, имеет вид
«59 ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ
145
Необходимое и достаточное условие того, что эти прямые
совпадают, имеет вид
^I — Ej. —£l (A)
Лг £>2 ^2
Необходимое и достаточное условие совпадения двух прямых,
заданных общими уравнениями
относительно общей декартовой системы координат, можно
сформулировать и так: существует такое число ^=^0, что
или так: существует такое число Ъ=/=0, что имеет место тождество
относительно х и у
Агх -f- B1yJrCx^'k (AoX-\- Вгу-\-С„).
Эта теорема следует из того, что условия B) — D) являются
необходимыми п достаточными признаками того, что система A)
имеет соответственно только одно решение, не имеет решений или
является неопределенной (т. е. имеет бесконечное множество
решений).
о \г А, , ВЛ
«замечание. Условие -^ф-^- можно записать в виде
А 2 О2
А, Вх
А В А В
а условие -~ — -~ в виде .1Й1 =0.
Условие
—- = —^- И Ч И
В*
А1В1
А2Вй
-0,
есть необходимое и достаточное условие того, что две прямые,
заданные относительно общей декартовой системы координат
уравнениями
Ахх -|- Bty -f Cx = 0, /l2x + В2// + С3 --= 0,
или параллельны, или совпадают (иначе, что эти прямые колли-
неарны).
146
Глава V. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
§ 60. Пучок прямых
Собственным пучком прямых называется множество всех прямых,
проходящих через одну точку (центр пучка) и лежащих в одной
плоскости.
Несобственным пучком прямых называется множество всех
параллельных между собой прямых, лежащих в одной плоскости.
Теорема 1. Для того чтобы три прямые, заданные общими
уравнениями
4 0
A)
относительно общей декартовой системы координат, принадлежали
одному пучку (собственному или несобственному) необходимо и
достаточно, чтобы выполнялось условие
1 Вх С,
А =
/1 о О О v> о
= 0.
Доказательство необходимости. Дано: три прямыеA)
принадлежат одному пучку. Требуется доказать, что А — 0.
Пусть три прямые, заданные уравнениями A), принадлежат
одному собственному пучку. Это означает, что существует точка
(х0, у0), принадлежащая всем этим прямым. Координаты этой
точки удовлетворяют всем трем уравнениям A):
Таким образом, столбцы определителя Д линейно зависимы,
значит, он равен пулю.
Если прямые, заданные уравнениями A), принадлежат одному
несобственному пучку, то первые два столбца определителя Д
пропорциональны, и, значит, он также равен нулю.
Доказательство достаточности. Дано А = 0.
Требуется доказать, что прямые, определяемые уравнениями A),
принадлежат одному пучку.
Предположим, что прямые не принадлежат одному пучку;
тогда среди них есть пересекающиеся. Пусть, например,
пересекаются первая и вторая прямые. Подстактяя координаты
Л,г\ —
С, В,
С R
лГд,
Ац Вг
Л, С,
А, С*
By
Вг
§60 ПУЧОК ПРЯМЫХ
точки пересечения первой и второй прямых в левую часть
уравнения третьей прямой, получим
-в,
*1 Су
Ay By
А2 S2
So Co
-B-,
Ay C,
Л, C2
+c3
Лх Sx
Л, So
Л!
л2
Ay By
Л2 B2
= 0,
значит, точка (л:0) y0) пересечения первых двух прямых лежит на
третьей прямой, а это значит, что три данные прямые
принадлежат одному пучку вопреки предположению.
Теорема 2. Пусть в общей декартовой системе координат
заданы две различные прямые V и I" общими уравнениями
Для того чтобы третья прямая I, заданная также общим
уравнением
относительно той же системы координат, принадлежала пучку,
определяемому двумя первыми прямыми, необходимо и достаточно,
чтобы левая часть уравнения прямой I была линейной комбинацией
левых частей уравнений прямых V и Г.
Доказательство необходимости. Дано: прямая
/принадлежит пучку прямых, определяемых прямыми [' и I". Требуется
доказать, что найдутся два таких числа 1 и ц, что будет
выполнено тождество, справедливое при всех значениях х и у;
В самом деле, если прямые /', /", / принадлежат одному пучку,
то А = 0 (теорема 1); по первые две строки определителя Д
линейно независимы (так как прямые /' и I" различны), значит
(в силу условия А —0), третья строка есть линейная комбинация
двух первых, т. е. существуют такие числа % и ц, что
Умножая обе части первого равенства на произвольное число
х, обе части второго равенства на произвольное число у, обе части
третьего на 1 и складывая, получим
Доказательство достаточности. Дано:
148 Глача V ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
(тождество, справедливое при всех значениях х и у). Требуется
доказать, что А = 0.
В самом деле, из данного тождества следует
С3
а значит, Д = О, так как третья строка определителя А есть ли-
/Й|#ная комбинация двух первых.
Уравнение
C2) = 0, B)
где X и ц не равны нулю одновременно, называют уравнением
пучка прямых, определяемых двумя различными прямыми /' и /",
общие уравнения которых в общей декартовой системе имеют вид
2 = 0. C)
Как было доказано, уравнение всякой прямой пучка,
определяемого двумя различными прямыми C), может быть записано в
виде B).
Обратно, если уравнение B) (при X и ц, не равных нулю
одновременно)— уравнение первой степени (т. е. коэффициенты при
хну одновременно в нуль не обращаются), то оно является
уравнением прямой, принадлежащей пучку прямых, определяемому
прямыми C), так как для трех уравнений C) и B) условие Д = 0
выполнено.
Если прямые /' и Г пересекаются, то при любых % и ц, не
равных нулю одновременно, уравнение B) будет уравнением
первой степени, так как если бы коэффициенты при х и у в этом
уравнении оба были равны нулю:
то прямые /' и/"были бы коллинеарны, что противоречит
предположению.
Но если прямые V и /" параллельны, то коэффициенты при х
и у в уравнениях C) пропорциональны, а значит, найдутся числа
X и \i, не равные пулю одновременно, при которых уравнение B)
не будет уравнением первой степени (например, или при Х = В2,
)i = —Въ или при Х~—Л2, [г —Лх).
Это следует учитывать, если пользоваться уравнением B) пучка
прямых, определяемо! о двумя параллельными прямыми.
§в! ВЗАИМНО!; РАСПОЛОЖЕНИЕ ТРЕХ ПРЯМЫХ
149
§ 61. Взаимное расположение трех прямых
Пусть относительно общей декартовой системы координат
заданы общие уравнения трех прямых:
Введем следующие обозначения:
А, В, С,
А2 В2
А3 5,
А3 В, С8
А, В,
На основании предыдущего получаем следующие необходимые
и достаточные признаки взаимного расположения трех данных
прямых.
1. Если Д=^0, &1ф0, 62^0, 83=^0, то три данные прямые
попарно пересекаются и не принадлежат одному пучку, т. е.
ою
Рис. ПО
точки пересечения попарно различны и не принадлежат одной
прямой (рис. ПО,а).
2. Если А =^0, но только один из трех определителей 8lf б2,
б3 равен нулю, то три данные прямые не принадлежат одному
пучку (Д^О); две прямые параллельны, а третья их пересекает
(рис. 110,6).
3. Если Д = 0, ЬуфО, 62=£0, б3=т^0, то три данные прямые
попарно различны и проходят через одну точку (рис. 110,s).
4. Если Д = 0, но только один из определителей б1( б2, б3
равен нулю, то две прямые совпадают, а третья их пересекает
(рис. 110,г).
5. Если б1 = б2 = б3 = 0 (в этом случае и Д = 0), но
коэффициенты ни одной пары уравнений не пропорциональны, то три
данные прямые попарно параллельны (рис. 110,3).
150 Глава V. ПРЯМЛЯ ЛИНИЯ НА ПЛОСКОСТИ
6. Если бх = б2 = б3 = 0 и коэффициенты только одной пары
уравнений пропорциональны, то две прямые совпадают, а третья
им параллельна (рис. 110, е).
7. Если соответствующие коэффициенты всех уравнений
пропорциональны, то уравнения определяют совпадающие прямые
(рис. 110, ж).
§ 62. Геометрический смысл неравенства первой степени
с двумя неизвестными
Теорега 1. Пусть относительно общей декартовой системы
координат прямая линия задана общим уравнением
Тогда для координат х, у всех точек М (х, у), лежащих по одну
сторону от этой прямой, выполняется неравенство
Ах + Ву + С>0,
а для координат х, у всех точек М (х, у), лежащих по другую
сторону от этой прямой,—неравенство (рис. 111)
Ах + Ву + С <0.
Доказательство. Пусть Ml (xv yj и М2 (х2, у2)—две
произвольные точки, лежащие по разные стороны от прямой /,
заданной уравнением
Ах + By -[- С = 0.
+ Ах+Ву+С>0
+ + + + 4
+ + •+ + +
+ + + + + +
Ах+Ву+С<0
Рис. 111 Рис. 112
Это значит, что существует внутренняя точка М (х, у) отрезка
М,, М2, лежащая на прямой /. Пусть X — отношение, в котором
точка М делит направленный отрезок МгМ.у Тогда координаты
$62 ГЕОМЕТРИЧЕСКИЙ СМЫСЛ НЕРАВЕНСТВА ПЕРВОЙ СТЕПЕНИ M1
точки М через координаты точек Мх и Мг выражаются
соотношениями
Так как точка М лежит па прямой I, то координаты точки М
удовлетворяют уравнению прямой /:
откуда
А =="
Точка М — внутренняя точка отрезка MtM2, поэтому к > 0, значит,
числа Ахх + Ву1 + С и Лха -f By2 -f-С — разных знаков. Если теперь
считать точку М, фиксированной, а точку М2 переменной (по
лежащей все время по разные стороны с точкой Ми относительно
прямой /), то становится ясно, что Ах.г + Вуг + С имеет один и тот
же знак (противоположный знаку Ах1-{-Ву1+С) Для переменной
точки Мг. Фиксируя точку М2, и считая, что Мг — переменная
точка (лежащая с точкой М2 по разные стороны от прямой /),
Ах+Ву+С>0
+ н- +
\ М0(хд,у0)
Ах+Ву+С<0
Рис. 113
Рис. 114
докажем, что Ах1-\-Ву1-{-С имеет один и тот же знак,
противоположный знаку Ахг -f By2 + С. Полуплоскость, для координат
всех точек которой Ах-±-Ву-\-С> 0, будем называть положительной,
а полуплоскость, для координат всех точек которой Ах -f- By -f С < О,
будем называть отрицательной.
Теорема 2. Пусть относительно общей декартовой системы
координат прямая линия задана общим уравнением Ах-гВу-\-С ==0.
Тогда, если отложить главный вектор п = {А, В} этой прямой от
любой точки М0(х0, у0) этой прямой М0Р = п, то конец Р
отложенного вектора будет находиться в положительной полуплоскости
от данной прямой (рис. 112).
152 Глава V ПРЯМАЯ ЛИНИЯ ПА ПЛОСКОСТИ
Доказательство. Точка Р имеет координаты хй~-А,
уо-'гВ. Подставляя их соответственно вместо а: и у в левую часть
уравнения Ах -j- By -{- С ~ О, получим А (х0 -|- А) + В (у0 -f В) -)- С =
= Ах0 + Ву0 -|- С +' А2 + В2 = Аг + В2 > 0.
Если система координат декартова прямоугольная, то (см. § 52)
главный вектор «—{Л, В} при этом еще ортогонален прямой
Ax+Bj + C = 0 (рис. 113).
Рассмотрим ненулевой вектор а = {1, /я}, заданный
относительно общей декартовой системы координат, и прямую X,
заданную общим уравнением Ах-\- By -}-С = 0 относительно той же
системы координат.
Возьмем на прямой К произвольную точку Мо (х0, у0) и
отложим от нее вектор а: М0Р = а. Тогда точка Р будет иметь
координаты Jco-f/, t/0-J-m. Подставим эти координаты в левую часть
Ах-\-Ву-\-С данного уравнения. Получим А (х0 + /) -\-В (уо-\- т) +
+ С = Ахо-'г Вуо-'ГС -г А1 + Вт. Так как топка М0(х0, у0) лежит
на данной прямой, то число Л v0+ £(/„ +С равно нулю, значит,
результат подстановки координат точки Р в левую часть Ах+Ву + С
уравнения данной прямой будет равен Л1-\-Вт. Отсюда следует,
что если А1-\- Вт> 0, то коней Р вектора а, отложенного от
любой точки прямой К, лежит в положительной полуплоскости от
прямой, заданной уравнением Ах^-Бг/ + С = О. Будем говорить,
что в этом случае вектор а направлен в положительную
полуплоскость от прямой, заданной уравнением Ах-}-Ву-\-С = 0. Если же
А1 + Вт<0,
то конец Р вектора а~{1, т}, отложенного от любой точки Мо
прямой Ах I By-{-C—-Q, лежит в отрицательной полуплоскости от
этой прямой В этом случае будем говорить, что вектор а—[1, т]
направлен в отрицательную полуплоскость от прямой ЛлН-5</4-С = 0.
Эти соображения используются в общей теории линий второго
порядка при исследовании направления вектора, коллпнеарпого
оси параболы, заданной общим уравнением (причем систему
координат можно считать общей декартовой).
§ 63. Расстояние от точки до прямой
Теорема. Расстояние d от точки Мо (х0, у0) до прямой,
заданной общим уравнением
относительно декартовой прямоугольной системы координат,
вычисляется по формуле
\Ах + Ву + С\
У А*
НОРМАЛЬПОП УРАВНЕНИЕ ПРЯМОЙ 153
Доказательство. Пусть М1(х1, уг) — произвольная точка
данной прямой. Так как вектор п = {А, В} является нормальным
к данной прямой (система координат декартова прямоугольная),
то (рис. 114)
o-f C\
так как A1x1Jr Ву1-{-С = 0 и значит,— Лхх — Вух = С.
§ 64. Нормальное уравнение прямой
Уравнение
Лх-f By-f-C = O
прямой, заданной относительно декартовой прямоугольной системе
координат, называется нормальным, если нормальный вектор
п = {А, В}
к этой прямой является единичным, т. е. если Аг-{-В2=1.
Для приведения к нормальному виду общего уравнения
прямой Ах -{- By -г С = 0, заданной относительно декартовой
прямоугольной системы координат, следует умножить левую часть
данного уравнения на число М
и выбрать М так, чтобы вектор {AM, BM) был единичным;
(АМJ + (ВМJ= 1;
отсюда
1
Таким образом, для каждой прямой всегда получим два
нормальных уравнения
Это ясно и из того, что существуют два различных единичных
вектора, перпендикулярных к данной прямой.
Множители ± , ■ -, при умножении на любой из которых
у Л2-г в2
левой части общего уравнения
154 Глача V ПРЯМАЯ ЛИНИЯ НЛ ПЛОСКОСТИ
прямой, заданной относительно декартовой прямоугольной системы
координат, уравнение переходит в нормальное, называются
нормирующими множителями. Радикал }/"Л2 + В2 есть модуль
нормального вектора п — {А, В} к данной прямой, так что М~±г—\ .
Коэффициенты нормального уравнения прямой, заданной
уравнением
Ах + Ву + С = 0 (Л24-Я2=1)
относительно декартовой прямоугольной системы координат, имеют
простой геометрический смысл:
/! = «/ = cos a, 8 = «/ = cosp, \C\=p,
где а и £—соответственно углы между масштабными векторами
/ и / осей координат Ох, Оу и главным вектором п = {А, В}
прямой Ах -j- By -р С = 0, а р — расстояние от
начала координат до этой прямой (положить
хо = Уо — О В формуле A) § 63 и учесть,
что Л2Ч-82= 1)-'
Если относительно декартовой
прямоугольной системы координат прямая задана
С 0
_ нормальным уравнением Ах-\-у +
~ т. е. Л2+S2=l, причем С < 0, то А и В
рис Ц5 являются косинусом и синусом угла а от
положительного направления оси Ох до
вектора ОР, гдеР — основание перпендикуляра, опущенного из начала
координат на данную прямую, а \С\ = р — длина этого
перпендикуляра (рис. 115).
В самом деле, если С < 0, то начало координат лежит в
отрицательной полуплоскости от прямой Ах-\-Ву-\-С = 0 (см. §62),
значит, векторы ОР и {А, В} не только коллинеарны (оба они
перпендикулярны данной прямой), но и направлены в одну
сторону. Поэтому угол а от оси Ох до вектора ОР равен углу а от
вектора / = {1, 0} до главного вектора {А, В} данной прямой и,
значит (см. § 40, формула (8))
п — 1* = {cos a, sin а}.
То обстоятельство, что \С\ = р, где р — расстояние от начала
координат до данной прямой, следует из формулы A) § 63, в которой
надо положить хо = уо — О, Л2 + Б2=1. Таким образом, нормальное
уравнение прямой, не проходящей через начало координат, можно
записать (а часто так и пишут) в виде
х cos а -[- у sin а—р = 0, A)
где а и р имеют значения, указанные выше.
E 65. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ J55
Для приведения общего уравнения прямой Ах + Ву + С = 0
к нормальному виду A) следует воспользоваться теоремой § 59,
в силу которой существует множитель (нормирующий множитель),
такой, что соответствующие коэффициенты уравнений
АМх + ВМу-\-СМ = 0, xcosa + y sin a—p = 0
соответственно равны
AM — cos а, ВМ = sin а, СМ = — р.
Отсюда
1
причем из условия СМ —— р<0 следует, что знак М
противоположен знаку С.
Если прямая задана нормальным уравнением относительно
декартовой прямоугольной системы координат, то расстояние d
от точки М0(х0, у0) до этой прямой равно абсолютной величине
результата подстановки координат точки Мо в левую часть
нормального уравнения (см. § 63):
или
d — | х0 cos а + у0 sin а — р\
(см. уравнение A)).
Замечание. Иногда расстояншо от точки до прямой
приписывают знак, называют такое расстояние отклонением и
полагают
б = х0 cos a -f- y0 sin а—р.
Если прямая xcosa-\-y sin a—р = 0 не проходит через начало
координат, то начало координат лежит в отрицательной
полуплоскости от прямой xcosa-j-r/ sin a — р — 0. Поэтому 6<0 для
полуплоскости, содержащей начало координат, а для полуплоскости,
не содержащей начало координат, б > 0.
§ 65. Угол между двумя прямыми; условие перпендикулярности
двух прямых
Пусть две прямые заданы относительно декартовой
прямоугольной системы координат общими уравнениями
Л^-Ь В ,(/ + (?! = 0, Агх + Вгу + С2 = 0. A)
Тогда угол между векторами
156 Глава V ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
равен одному из углов, образованных этими прямыми, а значит,
косинусы этих углов будут вычисляться но формуле
cos Фь2 = ± _ML^l£l= . B)
Отсюда находим необходимое и достаточное условие
перпендикулярности двух прямых
А1А2 + В1В2 = 0.
Заметим, что если данные прямые параллельны, то векторы пг
и п2 коллинеарны, и мы получим coscpli2 = ±l (в этом случае
считаем ср^О, щ — л).
Замечание. Так как главный вектор п={А, В} прямой,
заданной общим уравнением Ах -\- By-f С = 0 относительно
декартовой прямоугольной системы координат, перпендикулярен этой
прямой и направлен в положительную
полуплоскость от данной прямой (рис. 116),
то по формуле
гпяф^—jjHi-t-BiB» . C)
V A\ + B\VА\^В\
(где для радикалов берутся положительные
значения) вычисляется косинус того угла
между двумя прямыми
Рис- И6 А^ + Вд + С^О, Аях + Вгу + Съ = 0
(заданными относительно декартовой прямоугольной системы
координат), внутри которого лежат точки, принадлежащие
разноименным полуплоскостям от данных прямых (положительной
полуплоскости для одной прямой и отрицательной для другой). Конечно,
это обстоятельство зависит от уравнений, которыми заданы
прямые; например, при перемене знаков в левой части одного из
уравнений (I) по формуле C) будет вычислен косинус угла,
смежного с ф (так как при перемене знаков в левой части уравнения
прямой положительные и отрицательные полуплоскости меняются
местами).
§ 66. Угол от одной прямой до другой в ориентированной
плоскости
При вычислении угла от прямой /' до прямой Г
^0 A)
(система координат декартова прямоугольная) заметим, что угол ф
от вектора nl={Al, Вг) до вектора nz — {A2, Вг} равен одному
66 УГОЛ ОТ ОД ПОП ПРЯМОЙ ДО ДРУГОЙ 157
из значений угла от прямой /' до прямой /". Поэтому, вычислив
этот угол ф по формулам A) и B) § 40
B)
sin Ф - J^1TA^= , C)
VA\ + B*V A\ + B\
следует в качестве всех его значений взять ф-ffai, где k
принимает все целые значения.
Если данные прямые не взаимно перпендикулярны, то
tg(D= AiB*~A4EL D)
Обозначая через фх угол от оси Ох до первой прямой /' через
ф2, угол от оси Ох до второй прямой Г через ф2, угол от первой
прямой /' до второй /" через Я (рис. 117) у
на основании теоремы Шаля для прямых,
будем иметь
(Ох, /') + (/', 1")~в@х, I") (mod я),
или
ф1 + Ф=:ф2 (mod я),
ИЛИ "I
Ф==Ф2 — фх (mod л). E)
Если прямые /' и /" не перпендику- Рис. 117
лярны и ни одна из них не коллине^рна
оси Оу, то, обозначая через kx и k2 их угловые
коэффициенты, из соотношения E) находим
1+tg фх-tg ф2 '
или окончательно
Формулу можно получить и из формулы D), если последнюю
переписать так:
и заметить, что так как направляющие векторы данных прямых
таковы {—-Bv Ax} и { — В2, А2}, то их угловые коэффициенты
К\— ft" И Й2 R--
153 Г iaaa V. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Нсли две прямые (I) не параллельны и не совпадают с осью Оу, то неоэ
ходнмое и достаточное условие их перпендикулярности Л1Л2 + В1Ва, которое
следует из форм7Лы B), можно переписать так:
ИЛИ
^2+1=0,
или
?де /ех и k2 — угловые коэффициенты этих прямых.
§ 67. Примеры и задачи к главе V
1. Задачи с решениями
Пример 1. Составить уравнение прямой, проходящей через точку A,3)
параллельно прямой Зх + 5(/+1=0. Система координат общая декартова.
Решение. 1-й способ. Разрешая данное уравнение относительно у
находим угловой коэффициент данной прямой: k±=:—- . Угловой коэффици-
о
ент k2 искомой прямой равен kxi k2 = —"?. Искомое уравнение (§ 58)
о
у — 3=-J-(x— 1), или Зх + 5у—18 = 0.
2-й способ. Искомое уравнение можно взять в виде
Так как эта прямая должна проходить через точку A, 3), то
3+15+С = 0, С=-18,
и искомое уравнение
3-й способ. Уравнение прямой, проходящей через данную точку (х0, уй),
коллинеарную прямой Ax-\-By-\-C = Q, имеет вид
А(х-хй)-\-В(у-уй)=0.
Поэтому искомое уравнение
3(х—1L-5 (у — 3) = 0, или Ъх + Ьу—18 = 0.
Пример 2. Составить уравнение прямой, проходящей через точку A, 3)
перпендикулярно прямой 2>х-\-Ъу-\-1 =0. Система координат прямоугольная.
Решение. 1-й способ. Разрешая данное уравнение относительно у
3 1
§67. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ V
159
находим угловой коэффициент данной прямой: kL= — •=-. Угловой
коэффициент искомой прямой &2=-— Искомое уравнение
о
5
у—3 = -^-(х—1), или Ъх — 3i/-j-4 = 0
2-й способ. Искомое уравнение можно взять в виде
Ъх — 3(/ + С = 0.
Так как эта прямая должна проходить через точку A, 3), то
5-1— 3-3-|-С = 0, откуда С = 4,
и искомое уравнение
Ъх — 2>у + 4 = 0.
3-й способ. Уравнение прямой, проходящей через точку (х0, у0)
перпендикулярно прямой Ах-\-Ву-]-С = 0, имеет вид
В(х-хо)-А(у-уо)=О
Поэтому искомое уравнение
Ъ(х— 1) — 3((/ —3) = 0, или Ъх — 3(/ + 4 = 0.
4-й способ. Вектор {3, 5} перпендикулярен данной нрямон, поэтому он
является направляющим вектором искомой прямой Искомое уравнение (§ 50)
х-\ у-Ъ
= 0, или Ъх —
Пример 3. Составить уравнение прямой, проходящей через точку М A, 3)
и образующей с прямой /, заданной уравнением 3.*-j-оу-\- 1 = 0, острый угол ф,
4
такой, что tg ф = —. Система координат (rfv i /i-t?
прямоугольная
Решение. 1-й способ. Искомых
прямых две (рис. 118). Угол от одной из
искомых прямых до данной равен ф, а от
другой из искомых до данной равен —ср.
Угловой коэффициент данной прямой равен
kx = —i- Пусть k2 — угловой коэффициент
искомой прямой Для одной из искомых
з L
прямых будем иметь
tgcp = -
для другой
tg(-cp)=-
или
4 _
У~ —
160
Г.iaa a V ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Раиая эти уравнения получим
41 » 1
k2—~2i' k2 — ~Jj-
Искомые уравнения
_. О . 31 ( у 1 \ ,1 ^ г^ — —1, (у 1 )
23 ' 47
или
4U-J-23!/— 110 = 0, х + 47у —142 = 0.
4
2-й способ. Так как 1§ф = ^ и ср —острый угол, то
sin ф = -^^,
cos
/65
Понорачкзая вектор п = {3,5}, нормальный к данной прямой, на углы <р и —<р,
получил векторы, нормальные к искомым прямым (рис 119).
/\
М
Рис 119
Рис. 120
Пусть я^,—вектор, попученный из вектора а = {х, у) поворотом на угол <р;
тогда a. = {xcos ф — i/sm ф, xsin ф + i/cos ф} (§ 40, формула (8)).
Таким образом,
/65 /65' ' /65 ' /65
{1,47},
я-.= 13 ■
7 l-5-i- -'
^ + 5-4=
/65 /65' /65 ]/65
Искомые уравнения:
х— 1 -г-47 (у— 3) = 0, 41 (х— 1) + 23 (// — 3) = 0,
или
• х + 47у—142 = 0, 41х-!-23(/—110 = 0
Пример 4. Основанием равнобедренного треугольника служит прямая
х-\-2у~Л), а одной из боковых сторон —прямая х~у-\-Ъ — 0. Составить
уравнение другой боковой стороны, зная, что она проходит через точку М D,2).
Решение Угловой коэффициент стороны основания k, = — ■=-.
Угловой коэффициент данной боковой стороны ft2=l.
Тангенс }гла от основания до данной боковой стороны
:<х=
- = 3.
х ~~-"
§ 67. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ V
161
Тангенс угла 8 от основания до искомой боковой стороны равен тангенсу угла
от основания до данной боковой стороны, но имеет противоположный знак
(рис. 120). Следовательно, tg{5 = —3; с другой стороны,
k.—kt
где k3 — угловой коэффициент другой боковой стороны. Так как
1
tg|3 = ~3, ftx=—=•, то -3 =
отсюда &3 = 7.
Уравнение искомой боковой стороны
у —2 = 7 {х —4), или
7л: —(/ — 26 = 0.
2-й способ. Так как тангенс угла а от основания до данной боковой
3 1
стороны равен 3, то (а—острый угол) sinsc=; _^, cosoc = ——., значит,
sin 6= т=, cos 8 = —^= C = —ос—угол от основания до искомой боковой
/10 У10
стороны). Направляющий вектор основания а={ — 2,1}. Направляющий вектор
искомой стороны
~2.-JL + l~
Искомое уравнение
х-4 у-2
= 0, или 7л:—(/—26 = 0.
Схема
Пример 5. Составить уравнение прямой, отстоящей от точки М0(х0, у0) на
расстоянии d и образующей с прямой Ах-\- Ву-{-С — 0 острый угол а.
Решение. Искомых прямых
четыре (рис. 121). Поворачивая
вектор я = {Л, В}, нормальный к
данной прямой, на углы ф и —ср,
получим векторы
Яо={Л соэф — В sin ф,
A sin ф-j-B cos ф},
Я_«. = {;4 СОЭф + ВвШ ф,
— A sin ф + В cos ф},
нормальные к искомым прямым.
Возьмем искомые уравнения в виде у X А=-ф1Ч*\
(А созф^ Bs\ncp)(x—xo)-i- ' П-<Р " П(Р
(±Л sin ф + S cosф) (у — (/„) -f- С — 0.
Так как расстояние от точки
(хо> Уа) До искомой прямой должно
быть равно d, то, нормируя последнее уравнение и полагая затем х=х0,
У = Ий> получим
\С\
6 II. С. Моденов
162
Главы I-' ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
отсюда
Итак, искомые уравнения:
(A cos ф — В sin ф) (х —хо) + (Л БШф -f В cos ср) (у —
(А совф —Ssin ф) (х—хо)+ (A sin ф-J-В cos <p)fe> — #0) —
{A cosq~\-Bs\n <р)(х — л-0) + ( — A sin ф
(A cos ф + В sin ф) {х — хо)-\-( — A sin ф-ЬВсозф)A/ —у0) —
Пример 6. Определить положение точки <W A,5) относительно
треугольника ABC с вершинами
А B, -1), ВC, 1), С D, 0).
Решение 1-й способ Составляем уравнения прямых АВ, ВС, АС:
2х — у—5 = 0, (АВ)
х + у-А=0, (ВС)
x-2y — A-=Q (CA).
Подставляя координаты точек С, А, В соответственно в уравнения
противоположных сторон АВ, ВС и СА, получим
2-4 — 0— 5 = 3>0, 2— 1— 4 = — 3 < 0, 3 — 2 — 4 = — 3 < 0.
Подставляя координаты точки М в уравнения тех же сторон АВ, ВС и
СА, имеем
2.1—5—5 = —8 < 0, 1+5 — 4 = 2 > 0, 1 — 10—4 =—13 < 0.
3)' чит, точка М лежит по разные стороны с точкой С относительно АВ,
по разчые стороны с точкой А относительно ВС и по одну сторону с точкой В
относительно АС (сделать точный чертеж).
2-й с и о с о б. Вычислим барицентрические координаты точки М
относительно треугольника ABC:
3 1 1
4 0 1
1 5 1
САМ
4 0 1
2 —1 1
1 5 1
всм
Твс
2 —1 1
3 1 1
4 0 1
V ~^2 -
АВМ
2 -1 1
3 1 1
1 5 1
— 3
= -1Г<0
ЛВС -3
Выводы re же.
Пример 7. Составить уравнения биссектрис углов между прямыми
Ъх—4у + 7 = 0, Ъх-\-\2у —1=0.
Решение. Точка М (х, у) лежит на одной из биссектрис углов,
образованных данными прямыми тогда и только тогда, когда расстояния dj и d2 от
9той точки М до данных прямых равны между собой: dj = d2) т. е
\Ъх~Ау-\-7\
5
- = 0.
§67. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ V
163
Для всех точек М (х, у) одной яз биссектрис функции Зх — 4у-\-7 и
5x4- 12г/— 1 имеют одинаковые знаки (и обращаются в нуль в точке
пересечения прямых); для всех точек М (х, у) другой биссектрисы эти функции разных
знаков (рис. 122).
Значит, уравнение одной из биссектрис имеет вид
а уравнение другой
5 ~ 13 '
Зх-~4у-\-7 5х+12у — 1
5 ~ 13
или
7х — 5
32* + Ау + 43 = 0.
Пример 8. Составить уравнение биссектрисы того угла между двумя
прямыми х + г/ + 2 = 0, х + 7г/ + 3 = 0, в которо.м лежит точка А B, —1)
Решение. Подставляя
координаты точки А в левые части
уравнений данных прямых, получим
2—1+2 = 3 > 0, 2 —7+3 = —2<0.
Значит, точка А лежит в тех
полуплоскостях от данных прямых, для
координат точек которых х + г/ +
+2>0, х + 7у-\-3 <0. Искомая
биссектриса проходит, следова гельно,
в тех областях (на которые
плоскости делятся данными прямыми), для
координат точек которых функции
х + г/ + 2 н х + 7г/ + 3 имеют разные
знаки. Значит, уравнение искомой
биссектрисы:
х + У + 2
Схема
Рис. 122
или
6л--|-
Пример 9. Составить уравнение биссектрисы внутреннего угла треугольника,
стороны которого ВС, С А и А В заданы соответственно уравнениями
х—у =
Решение,
гольника
х + 2у+1=0.
Решая данные уравнения попарно, находим
(СА)
{АВ)
вершины треу-
А A,-1), й(-1, -4), С
@, 0).
Подставляя координаты точки С в уравнение АВ, получим
0+2-0+1 = 1 >0.
Подставляя координаты точки В в уравнение прямой АС, получим
1
"Г
•!<»■
Значит, для координат всех точек, лежащих внутри внутреннего угла А
треугольника ABC, имеем х-\-2у-\-1 > 0, х-\-у<0, а потому искомая
биссектриса проходит в тех областях, на которые плоскость делится прямыми АВ
и АС, для координат точек которых функции х+2(/+1 и х + г/ имеют разные
164 Глаза V ПРЯМАЯ ЛИНИЯ НЛ ПЛОСКОСТИ
знаки. Поэтому искомое уравнение имеет вид
У2~ У 5 '
ИЛИ
(V2+ К)х+(К + 2 у2)у+ j/~2=0.
Пример 10. Найти косинус внутреннего угла Л треугольника, уравнения
сторон которого:
х-у = 0, {ВС) x + y = 0, (СА) х + 2у+1=0. (АВ)
Решение. 1-й способ. Решая данные уравнения попарно, найдем вершины
треугольника
А{\, -1), в(-1, -IV С@, 0).
3 '
Теперь находим векторы
Jg = i_i_l, -j.
вместо вектора АВ можно взять вектор { — 2,1}, который коллипеарен
вектору АВ и направлен в ту же сторону. Внутренний угол А треугольника
есть угол между векторами {—2,1} и {—1,1}, значит,
л (— 2)( — 1) -1~ 1 • 1 3
COS Л — ' ■■■= = .
Y( — 2J+12 У ( — 1 J —J— 12 у 10
2-й способ. Подставляя координаты точки С в левую часть уравнения
АВ, получим 1 > 0, а подставляя координаты точки В в левую часть уравне-
112
ния АС, получим — -g-—- =—- <0. Значит, из уравнений
угол А определяется по формуле C) § 65:
L1 + 1-2
cos А =
Пример 11. Определить тангенсы внутренних углов треугольника, стороны
которого заданы уравнениями
2* + 3y — 6 = 0, 2х—у — 5 = 0, х—Зу—4 = 0.
Решение. Обозначш: стороны треугольника цифрами 1, 2, 3 в том
порядке, как они заданы, и пусть их угловые коэффициенты соответственно
равны ki, k2, k3:
2 _ __ 1
Тогда тангенсы углов ф12, ф23 и ф81 от первой стороны до второй, от
второй до третьей и от третьей до первой будут:
§67. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ V
165
Но три угла от первой стороны до второй, от второй до третьей и
от третьей до первой являются либо все внутренними углами треугольника,
либо все внешними. Так как в данном случае все три тангенса — числа
отрицательные, то углы ф12, ф23 и ф31—внешние. Внутренние углы треугольника
дополняют их до 180°, поэтому тангенсы внутренних углов треугольника бу-
9
дут 8, 1 и y ■
Пример 12. Относительно декартовой прямоугольной системы координат
даны две пересекающиеся и невзаимно перпендикулярные прямые:
Дана точка М0(х0, у0). При каком необходимом и достаточном условии
точка Мо лежит в остром угле, образованном данными прямыми?
- М0(х0,у0)
Рис. 123
Рис. 124
Р е ш е н и е. Предположим сначала, что угол между векторами «i = { Alt St }
и И2 = { А2, В2 } острый (рис. 123). Тогда их скалярное произведение я1иг =
= А1Лг+В1й2 положительно: AlA2-!rB1Bi> 0. Если точка М0(х0, у0) лежит
в остром угле, образованном данными прямыми, то числа ^ + S + C
и /42хо-т-52г/о-г С2 разных знаков. Таким образом,
(А2х0
A)
Если же угол между векторами щ и щ тупой (рис. 124), то АхА2-\-Вф?, < 0,
и если точка УИ0 лежит внутри острого угла, образованного данными
прямыми, то числа ЛjXo-j-В^о-f Сг и А2ха-\-В2у0-\-С2 одного знака, значит,
соотношение A) снова выполняется. Таким образом, соотношение A) является
необходимым условием того, что точка Мо (х0, уд) лежит внутри острого угла,
образованного данными прямыми. Повторяя аналогичные рассуждения,
докажем, что необходимое условие того, что точка М0(х0, у0) лежит внутри
тупого угла, образованного данными прямыми, имеет вид
■ 0. B)
Отсюда следует, что соотношение A) является и достаточным условием
того, что точка М0(х0, у0) лежит внутри острого угла, образованного
прямыми Л1х-гВ1г/-|-С1 = 0 и А2х-{~В2у-\-С2 = 0.
Пример 13. Составить уравнение биссектрисы острого угла между двумя
прямыми
х + у + 1 = 0, х—Ту — 3 = 0.
Решение. Так как для координат х, у всех точек, лежащих внутри
острого угла, образованного данными прямыми, выполняется неравенство
166
Глава V ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
то функции х-\-у-\-\ и х — 1у — 3 для координат всех внутренних точек острых
углов имеют одинаковые знаки. Значит, уравнение искомой биссектрисы
( 1 у 7*i Q
_= = ^= , ИЛИ
У 2 |^50
Пример 14. Вычислить площадь ABC ориентированного треугольника ABC,
стороны которого относительно декартовой прямоугольной системы координат
заданы уравнениями
A1x-\-B-ly-\-C1=0, (ВС)
А2х+В2у + С2=0, (С А)
(АВ)
Обозначим через
A)
матрицу, присоединенную к матрице
*i fli Ca
А2 В2 С2 ; B)
3 Сд/
элементы матрицы A) являются алгебраическими дополнениями
соответствующих элементов матрицы B), например,
= ВгС3 — В3С2 и т. д.
Тогда вершины А, В, С треугольника ABC будут иметь координаты
В
с2
и, следовательно,
i- 1
1
— 1
2
*- 1
2 C
as
Но
а2
А2
Л,
С2
д
0
0
0
д
0
0
0
д
= Д% где Д =
Ах Вх d
Аг В2 С2
Аг В9 С8
i 67. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ V
167
Следовательно,
и окончательно
0-2 Oey C%
G3 0g Cg
1
2
At B,
A3 B;
A
A
A
Аг fli
A2 B2
A3 B3
1 Bt С
a B2 С
з Bs С
A3 fl»
Аг Вг
С
С
С
1
3
'2
•>
2
Пример 15. Найти косинус внутреннего угла А треугольника ABC,
стороны которого заданы уравнениями
Рис 125
Рис.126
Решение (см. предыдущий пример) Подставляя координаты вершины
— , —— j в левую часть уравнения стороны С А, получим
^+В^ + С^; где Д =
Л2 В2 С2
А3 В3 С3
А3 В3
„ / ач Ь., \
Подставляя координаты вершины С ( —— , —=-) в левую часть уравнения
\ Ч сз /
стороны АВ, получим
Таки\ образо'м, если числа
ь3 = —> гДе с*~
А3 В
о о
Л2 В
Аг Вг
разных знаков, то коси»
нус угла между векторами п2 = { А2, В2\ и яа = { Л3> В3} равен косинусу
внутреннего угла А треугольника ABC (рис. 125):
А2АЯ+В2В3
Если же числа
cos Л
ASBS
Аг
имеют один и тот же знак, то косинуо
\ г 2 г!
угла между векторами яа = { Аг, В2} и п3 = \Аг, Bz\ от косинуса виутрешшгэ
угла А треугольника ABC отличается знаком, т. е. (рис. 126)
A2AS±B2BS
COS /1 -— ■—■ *
168
Глава V ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Пример 16. Найти барицентрические координаты а, C, у точки М (х, у)
относительно треугольника ABC, стороны которого заданы уравнениями
= 0, (ВС)
= 0, (С А)
А3х+В3у+С3 = 0 (АВ)
Решение (см пример 14).
мвс
X
аг
с2
_Оз_
У
С%
Ьз_
1
1
'ABC
Далее находим
х у 1
В3 Со
схс2со
х у I
£?2 £?2 ^2
аг bjCs
О
О
и окончательно
Д
О
о
д
Аналогично находим $ и у. Итак,
Аг В2
Аг В3 „
Л,
лй в3 с3
ЛJ Bt Сх
Лг Вг С2
А3 В6 С3
Y =
Л
л
лг
1
2
в
в
в
В\
в2
1 С1
г ^2
з С
3
2. Задачи для самостоятельного решения
!. Составить уравнение прямой, проводящей через точку B,5) и
равноудаленной от точек (— 1,2) и E,4)
Отв. х—2 = 0, х—Зу+13 — 0.
2. Найти проекцию точки ( — 5,6) на прямую 7л:— 13у—105 = 0
Отв B, —7)
3. Найти точку, симметричную точке (—2,J) относительно прямой 2х—3у +
•J- 18 = 0
Отв B,3).
§67. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ V 169
4. Даны две вершины (—6,2) и B, —2) треугольника и точка A, 2)
пересечения его высот. Найти третью вершину.
Отв. B,4).
5. Составить уравнения сторон треугольника, зная одну из его вершин
C, —4) и уравнения двух высот 7х — 2у— 1=0, 2х —7у—6 = 0.
Отв. 2х + 7г/ + 22 = 0, 7л: -)- 2х/—13 = 0, х—у + 2 — 0.
6. Найти косинус угла между прямыми 2х—7у-{-3 = 0, х + 5г/ = 0, в
котором лежит точка C, 1).
33
Отв. arccos , ■
• /26
7. Составить уравнения прямых, перпендикулярных к прямой 2х-\-6у—3 = 0
!• отстоящих от точки E,4) на расстоянии |/"l0.
Отв. Зх — у — 21=0, Зх — у—1 =0.
8. Составить уравнение прямой, отстоящей от точки A,1) на расстоянии 2,
а от точки B,3) на расстоянии 4.
Отв. 4х ЬЗу + 3 = 0, [/4-1=0.
9. Даны уравнения боковых сторон равнобедренного треугольника 7х —
— г/-J— 4 = 0, x-j-i/— 2 = 0 и точка C,5) на его основании. Составить уравнение
основания.
Отв. Зх + у — 14 = 0.
10. Даны уравнения 4x-fy—6 = 0, 2х-\-у—2 = 0, я — 2 = 0 медиан
треугольника и его площадь 5 = 3. Найти вершины треугольника.
Отв. B, -4), A,2), C, —4), или B, 0), C, -6), A, 0).
11. Составить уравнения сторон треугольника, зная одну из его вершин
B, —4) и уравнения биссектрис двух углов х + у—2 = 0, л:—Зг/ — 6 = 0.
Отв. х + 7у — 6 = 0, к—у—6-=0, 7*-fу— 10 = 0.
12. Лапы уравнения х>]-4 = 0, 4х-т-?г/-|-5 = 0 биссектрис двух внутренних
углов треугольника и уравнение 3x-\-4y — Q стороны, соединяющей вершины, из
которых выходят данные биссектрисы Составить уравнения двух других сторон.
Отв. Зх~4i/-i-24 = 0, 5,v+ 12r/ f 16 = 0.
13. Даны уравнения 3.v + y —3 = 0, .Ъс+4{/ = 0 двух сторон треугольника
и уравнение х — «/-j-5 = 0 биссектрисы одного из его внутренних углов.
Составить уравнение третьей стороны
Отв. х + Зу—13 = 0.
14. Даны три прямые А^х-\- 3ftt/ = 0, й = 1, 2, 3. При каком необходимом
и достаточном условии третья прямая проходит в остром угле, образованном
двумя первыми?
Отв.
ГЛАВ А Т1
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
§ 68. Уравнение плоскости, проходящей через данную точку
компланарно двум неколлинеарным векторам
Теорема. В общей декартовой системе координат уравнение
плоскости л, проходящей через точку Мо (х0, у0, z0),
компланарной двум неколлинеарным векторам
a — {lvmv л1}и& = {/2, тг,пг], имеет вид
х—х0 у—у0 z—z0
ly tU1 t
L
/п,
= 0.
Рис 127
Доказательство. ПустьЛ1(л',г/,г) —
произвольная точка пространства. Точка
М(х, у, z) лежит на плоскости л тогда и только тогда, когда век-
горы М0М = {х—х0, у—yQ, z—z0}, а и Ь компланарны (рис. 127).
Необходимое и достаточное условие компланарности этих
векторов имеет вид (§ 36, теорема 6)
х—х0 у—у0 z—z0
т1
§ 69. Общее уравнение плоскости
Теорема 1. В общей декартовой системе координат плоскость
выражается уравнением первой степени
/Доказательство. Фиксируем на плоскости я произвольную
точку Мо (х0, у0, z0) и возьмем два неколлинеарных вектора
a — {lvmvn1} и Ь = {1г, т2, п%}, каждый из которых компланарен
i 69. ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
171
плоскости л. Тогда на основании предыдущего параграфа
уравнение плоскости я можно записать в виде
х—х0 у-~у0 z—z0
т.
= 0,
или
т1 п1
т2 п2
(X Xq) ,
«1 h
п2 12
т1
U
(г-го) = 0.
A)
Так как векторы а и Ь неколлинеарны, то по крайней мере один
из определителей
m2
«i
n2
у
B =
«2
h
h
c=
h
h
mx
m2
не равен нулю (§ 36, теорема 5), следовательно, уравнение A) первой
степени относительно х, у, г. Если еще положить
—хп
Щ n2
— Уо
n1 /j
n2 /2
— 20
lt mx
=D,
то уравнение A) примет вид
Уравнение Ах-\-By + Cz+D = 0 называется общим уравнением
плоскости.
Теорема 2 (обратная). Всякое уравнение первой степени
0 B)
в общей декартовой системе координат является уравнением
плоскости.
Доказательство. Пусть х0, у0, г0 —какое-нибудь решение
данного уравнения> т. е.
Axo+Byo + Czo + D = 0. C)
Данное уравнение будет эквивалентно уравнению, которое мы
получим, отняв почленно из уравнения B) равенство C):
-zo) = O. D)
(б)
Одно из чисел А, В, С не равно 0; пусть, например,
тог/щ уравнение D) эквивалентно уравнению
х—х0 у—у0 z — z0
-В А
-C 0
о
А
--=0.
172
Глава VI ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
Л
0
0
Л
= А2,
0
А
— В
— С
= АВ,
— В
Q
А
0
В самом деле, последнее уравнение после раскрытия
определителя примет вид
А2 (х-х0) + АВ (у-уо)+АС (г — г0) - О,
или (так как А Ф 0)
Л (л-- х0)-Ь £ (у - уо) +С (г - г0) = 0.
Далее, векторы
г = { — £, А, 0} и д={ — С, 0, Л}
неколлинеарны, поскольку один из определителей
= АС
не равен нулю (в силу условия А Ф 0 не равен нулю первый
определитель). Поэтому уравнение E), а значит и данное уравнение A),
определяет (на основании предыдущей теоремы) плоскость,
проходящую через точку (хй, yo,zo) компланарно двум неколлинеарным
векторам (в случае АфО):
г = {-В,А, 0} и д = {-С, 0, А}.
Аналогично доказывается, что данная плоскость (в случаеВфО)
компланарна векторам р={0,—С, В} и г = {-— В, Л, 0}, между
собой неколлинеарным, а в случае С=^0—векторам
р={0, -С, В} и д = { — С,0, А},
которые также неколлинеарны. В декартовой прямоугольной системе
координат вектор п = {А, В, С} перпендикулярен плоскости,
заданной уравнением Ax + By + Cz+D = 0. В самом деле, возьмем на
плоскости, заданной общим уравнением Ах + By + Cz-\-D = 0
относительно декартовой прямоугольной системы координат, две
произвольные различные точки М1{х1, ух, гг) и М2(х2, у2, z2). Тогда
Ахх + Вуг
= 0, Ах2
уг -f Cz2+D = 0,
Л (х2—хх) + В (у^—уг) -г С {z2 — z1) = 0,
откуда
или
Значит, вектор п перпендикулярен любой прямой МгМ2,
лежащей на данной плоскости, значит, перпендикулярен самой плоскости.
В общей декартовой системе координат вектор п={А,В,С}
может и не быть перпендикулярным плоскости, заданной
уравнением Ax-\-By + Cz + D = 0; этот вектор п={А, В, С} будем
называть главным вектором плоскости, заданной уравнением AxJrBy-\~
-\rCz-\-D = 0 относительно общей декартовой системы координат.
$71. ЧАСТНЫЕ СЛУЧАЛ РАСПОЛОЖЕНИЯ ПЛОСКОСТИ [73
§ 70. Условие компланарности вектэра и плоскости
Теорема. Пусть относительно общей декартовой системы
координат в пространстве заданы вектор а = {1,т,п} и плоскость
своим общим уравнением
Тогда необходимое и достаточное условие компланарности
вектора а и данной плоскости имеет вид
Доказательство этой теоремы такое же, как и доказательство
теоремы § 52.
Из доказанной теоремы следует, что главный вектор п= {А, В, С}
плоскости, заданной общим уравнением Ах-\- By + Cz + D — O
относительно общей декартовой системы координат, некомпланарен
этой плоскости. В самом деле,
§ 71. Частные случаи расположения плоскости относительно
системы координат
Из предыдущего параграфа следует, что плоскость, заданная
общим уравнением
относительно общей декартовой системы координат, будет или
параллельна, или проходить через ось Ох тогда и только тогда,
когда А = 0, так как в качестве направляющего вектора оси Ох
можно взять вектор {1,0, 0}.
Аналогично условия В —0 и С = 0 являются необходимыми
и достаточными условиями того, что плоскость соответственно
параллельна или проходит через ось Оу, параллельна или
проходит через ось Oz.
Отсюда следует, что плоскость параллельна или совпадает о
одной из координатных плоскостей тогда и только тогда, когда
в оба(ем ее уравнении Ax + By + Cz-\-D = 0 два из коэффициентов
А. В, С обращаются в нуль.
Таким образом, уравнения Ax-\-D = §, By-\-D~Q, Cz-\-D = Q,
или
х = а, y = b, z — c
и только уравнения первой степени такого вида в случае ф,
Ь0 е=й=О являются уравнениями плоскостей, параллельных
174 Глава VI ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ ^
координатным. В частности, уравнения координатных плоскостей
имеют вид
х=0 (плоскость yOz)
t/ = 0 (плоскость zOx)
2 = 0 (плоскость хОу).
Отметим, наконец, что необходимым и достаточным условием
того, что плоскость, заданная общим уравнением A), проходит
через начало координат, является равенство
§ 72, Параметрические уравнения плоскости
Параметрические уравнения плоскости, проходящей через точку
Mti(xo> Уо' 2о) компланарно двум неколлинеарным между собой
векторам:
a = {lv mv nj, Ь = {1г, тг,пг),
в общей декартовой системе координат имеют вид
z = zo + un1 + vn.z. A)
Доказательство. Произвольная точка М (х, у, z)
пространства лежит на дайной плоскости тогда и только тогда, когда векторы
М0М = {х—х0, у—у0, z—z0}, а и b компланарны, иначе, когда
они линейно зависимы. Но так как век-
торы а и b неколлинеарны, то вектор
М0М является линейной комбинацией
векторов а и Ь:
liCM = ua + vb. B)
Переходя к координатам, получим
х—xQ = u
Рис. 128
откуда и следуют соотношения A).
Замечание 1. Параметры и и v имеют следующее
геометрическое значение: это общие декартовы координаты точки М данной
плоскости в системе координат; Мо—начало координат, а и b —
масштабные векторы соответственно первой и второй осей координат
(рис. 128).
Замечание 2. Если г0 = ОМ0, г = ОМ — радиусы-векторы
точек Мо и М. то соотношение B) можно переписать так:
r—ru = ua-\-vb, или г = r0-J-иа-J-vb.
§73. УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ТОЧКИ 175
Это уравнение называется векторным параметрическим
уравнением плоскости, проходящей через точку М0(г0) компланарно двум
неколлииеарным между собой векторам а и Ь.
§ 73. Уравнение плоскости, проходящей через две точки
компланарно данному вектору
На основании § 68 уравнение плоскости, проходящей через две
различные точки M1{xl, ylt zx) и М2 (х2, уг, z.2) компланарно
вектору а= {/, tn, n), который неколлинеарен вектору
в общей декартовой системе координат имеет вид
1—4 Уг — Ух
I m
= 0.
§ 74. Уравнение плоскости, проходящей через три точки,
не принадлежащие одной прямой
На основании § 68 уравнение плоскости, проходящей через три
точки
Л Л i y II У \ 1\А (Y 11 У \ l\A IY II У \
I V 2 1 \ «^ 1ч hi * tvi !■ i г X л 1 дл * wo* ^О/ч «гаО1 «^ Оч иО 1 ^о/а
заданные относительно общей декартовой системы координат и не
принадлежащие одной прямой, как плоскости, проходящей через
точку Ms (x3, y3, z3) компл'анарно двум неколлинеарным векторам
j/i3ivi1 — \ax л3, ух ys> ^i ^31 и '"з'"г — \Х2 хз> Уг—Уз> *2 — •'зЬ
имеет вид
х х3 у у3 z zs
■"-2 XS У2 Уз %Ъ
-о,
или
X
Xi
хь
У
Уг
Уъ
z
zi
Z3
1
j
1
= 0.
Параметрические уравнения этой плоскости я можно записать
так;
X = Xs + U (Хх — Xs) + V {Х% ~Х3),
y = ys + u(y1 — y!i) + v(yi~y3),
г = г8 + и (zx ~ z3) + v {z2 — z9).
[76 Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
Параметры и и v имеют следующее геометрическое значение:
это общие декартовы координаты точки7 плоскости л в общей
декартовой системе координат, в которо1Уза начало координат берется
точка М3, а за единичные точки осгй М3и и Msv соответственно
точки М1 и /И3.
§ 75. Уравнение плоскости в отрезках
Если плоскость не проходит через начало координат и
пересекает все оси общей декартовой системы координат соответственно
в точках (а, 0, 0), @, Ь, 0) и @, 0, с), то ее уравнение на
основании предыдущего параграфа можно записать в виде
х — а у z I
а 0 —с =0,
или
х 1 У i г _ j
a b с
Это уравнение называется уравнением плоскости в отрезках.
§ 76. Взаимное расположение двух плоскостей
Пусть относительно общей декартовой системы координат две
плоскости заданы своими общими уравнениями
= 0, A)
= 0. B)
Тогда имеют место следующие утверждения.
1. Для того чтобы плоскости, заданные уравнениями A) и B)
в общей декартовой системе координат, пересекались, необходимо
и достаточно, чтобы соответствующие коэффициенты при х, у, г
в уравнениях A) и B) не были пропорциональны.
2. Для того чтобы плоскости, заданные уравнениями A) и B)
в общей декартовой системе координат, были параллельны,
необходимо и достаточно, чтобы соответствующие коэффициенты при
х у, г в уравнениях A) и B) были пропорциональны, но чтобы
свободные члены не были им пропорциональны, т. е. чтобы
существовало такое число X Ф0 что
или
Ахх + В1У + C1z+D1 = X (Л2х + Вгу -f C2z + D2). C)
3. Для того чтобы плоскости, заданные уравнениями A) и B)
в общей декартовой системе координат, совпадали, необходимо и
достаточно, чтобы коэффициенты уравнений A) и B) были пропор-
§ 76. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ177
циональны, т. е. существовало такое число Х=^0, что
Докажем сначала достаточность признаков.
1. Если тройки Ац Blt Сг и А2, В2, С2 непропорциональны, то
найдутся пары соответствующих чисел из этих троек, например
А1У В1 и Л2, В2, которые также непропорциональны.
Полагая в данных уравнениях A) и B) 2 = 0, получим
уравнения
определяющие в плоскости хОу уравнения прямых, по которым
плоскости A) и B) пересекают плоскость хОу (следы плоскостей
A) и B) на координатной плоскости хОу). В силу того, что пары
Av BL и А2, В2 непропорциональны, эти следы пересекаются,
следовательно, пересекаются и данные плоскости.
2. Уравнение B) эквивалентно следующему;
bA1x-{-%B1y-'rbC1z-\-Di = 0, или Л^ + ^И-^Н-у ==0. B')
Свободные члены Dx и -у уравнений A) и B') в силу условия
П2ФЮ1 различные, значит, любое решение уравнения A) не
является решением уравнения B'); это значит, что ни одна из точек,
лежащих на плоскости, заданной уравнением А1х-}~В1у-{-
-i-Clz-\-D1 = 0, не лежит на плоскости, заданной уравнением
А.2х + В2у -j- C2z+D2 = 0, следовательно, эти плоскости параллельны.
^ 3. Если А2 = ХА1, B2 = KBlt C2 = KClt Di^W1 (кфО), то
левые части данных уравнений A) и B) отличаются числовым
множителем, не равным нулю, а значит, эквивалентны.
Необходимость всех признаков доказывается сразу методом от
противного.
Замечание. Для того чтобы плоскости, заданные общими
уравнениями
относительно общей декартовой системы координат, пересекались,
необходимо и достаточно, чтобы выполнялось любое из следующих
условий.
1. Хотя бы один из определителей
в
2
с,
в,
в»
был отличен от нуля.
178
Г лав а VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
2. Главные векторы щ — {А1, Вг, СХ\А\ п2 = {А2, В2, С.2\
данных плоскостей были бы неколлинеарн^.
3.
Необходимое и достаточное условие параллельности двух
плоскостей заключается в выполнении одного из условий.
1.
В, С, |СХ А,
В» Со
л, в,
Аг В2
__ Q
но хотя бы один из определителей
Аг D1
Л2 D2
>
В2 D2
Л* Г)
не равен нулю.
2. Главные векторы л1 = {Л1, S^ С^, п2 = {А2, В2, С3} данных
плоскостей коллинеарны, по
3. Rg
!!
^ 2 2
2 2 2
Необходимое и достаточное условие совпадения двух
плоскостей заключается в выполнении одного из условий.
1.
в,
в,
л,
А2
Сг
с2
д2
с2
в,
Во
Аг\
D1
D2
Аг
А,,
Сг
с2
в,
Вг
1)г
D2
= 0.
2. Главные векторы п1 — {Л1, В1У CJ и я2 = {Л2, Б2) С3}
данных плоскостей коллинеарны и
3.
Л, Б, d D
2 в2 с2
Все это лишь Другие формулировки уже доказанной теоремы.
§77 УР4ВНЕППЯ ПРЯМОМ 179
§ 77. Уравнения прямой, проходящей через данную точку в данном
направлении. Параметрические уравнения прямой
В общей декартовой системе координат уравнения прямой,
проходящей через точку Мо (х0, у0, г0) и имеющей направляющий
вектор а = {1, т, п), будут
x—xo_y—yo_z—zo ,..
Т т ~ A>
(эти уравнения называются каноническими уравнениями прямой),
или в параметрической форме
x = xo-\-lt, y = yo + mt, z = zo + nt, B)
или в векторно-параметрической форме
г = г0 -I- ta.
Действительно, пусть М(х, у, г) — произвольная точка; она
лежит на прямой, проходящей через точку М0(х0, у0, z0), колли-
неарной вектору а = {1, т, п] тогда и только тогда, когда
векторы М0М — {х~х0, у~—у0, г — г0} и а — {1, т, п\ коллинеариы,
т. е. тогда и только тогда, когда координаты этих векторов
пропорциональны:
х—х0 _ у— г/0 __г—г9
I m n '
Так как афО, то необходимое и достаточное условие
коллинеарности векторов М0М и а- можно записать еще и так:
М0М = ta,
или
{х — х0, у—у0 z — zo} = t{l, m, п},
откуда сразу получаются уравнения B).
Соотношение
7AJA = ta
эквивалентно такому:
r—ro = ta,
где г0 — радиус-вектор точки Мо, г —радиус-вектор точки М. Из
последнего уравнения находим
Параметр t есть координата точки М данной прямой в
следующей системе координат па этой прямой: Мо—начало координат,
а —масштабный вектор.
180
Глава VI, ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
§ 78. Уравнения прямой, проходящей через две точки
Уравнения прямой, проходящей через две различные точки
ML(x, ylt г^) и Мг(х2, уг, z2), заданные относительно общей
декартовой системы координат, можно записать в виде
или в параметрической форме
Доказательство. За направляющий вектор прямой можно
взять вектор M1M2 = {xi~x1, у2 — yv z2 — Zj), после чего остается
применить результаты предыдущего параграфа.
§ 79. Взаимное расположение двух прямых
Следующие утверждения выражают необходимые и достаточные
признаки взаимного расположения двух прямых в пространстве,
заданных каноническими уравнениями
Т
m1
/„
n2
относительно общей декартовой системы координат.
Прямые скрещиваются, т. е. не
лежат на одной плоскости
Прямые пересекаются
Прямые параллельны
Прял'ые совпадают
Д =
Хъ — Ху Уз—lJi Zl — Zl
1й m2 n2
Д = 0, но векторы a = \lv my, п^ и
& = {/2>т2, п2} неколлинеариы (иначе
их координаты непропорциональны)
векторы а = \1ц mlt n^ и&={/2, «2, п2}
коллинеарпы, но вектор A/f1/M2 =
= {xt—x1, Уч — yv г% — гх\ им ие кол-
линеареп
Все три вектора: а = {/ь
Ь = {1.2, пг2, п2\, /И1М2 =
Уя—Уи г2—Zl\ — коллинеарнь
тъ пу),
\xz-Xl,
Доказательство. Докажем достаточность указанных
признаков.
§ 80. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
181
1. Рассмотрим вектор
M1Mi=-{x2—x1, y2 — ylt
и направляющие векторы данных прямых
{1 mlt nx} и Ь=={12,
Если
А =
lt
Х2 Х1
/2
2 Ul Z2 ■"
т.! пх
ГЛ.*, По
то эти векторы некомпланарны, следовательно, данные прямые не
лежат на одной плоскости.
2. Если Д = 0, то векторы а, Ь, МгМ2 компланарны,
следовательно, данные прямые лежат в одной плоскости, а так как в
случае 2 направляющие векторы а и & этих прямых предполагаются
неколлинеарными, то прямые пересекаются.
3. Если направляющие векторы а и & данных прямых колли-
неарны, то прямые или параллельны, или совпадают. В случае 3
прямые параллельны, так как по условию вектор МхМг, начало
которого находится в точке Мг первой прямой, а конец — в точке
М2 второй прямой, не коллинеарен этим векторам а и Ъ.
4. Если все векторы а, Ь и МХМ2 коллинеарпы, то, очевидно,
прямые созпадают.
Необходимость признаков доказывается методом от противного.
§ 80. Взаимное расположение прямой и плоскости
Следующие утверждения дают необходимые и достаточные приз-
паки взаимного расположения прямой, заданной каноническими
уравнениями
х—х0 __ у— г/о _ г — г0
I m n ' A)
и плоскости, заданной общим уравнением
Ax + By + Cz+D = 0 B)
относительно общей декартовой системы координат.
Плоскость и прямая пересекаются: А1~-Вт-\-СпфО.
Плоскость и прямая параллельны: Al -f Вт -f Cn = О,
Axo + By C
Прямая лежит на плоскости: А1-\-Вт-{-Сп
A B C
182 Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВ!-:
Докажем сначала достаточность указанных признаков.
Запишем уравнения данной прямой в параметрическом виде:
x = xo-\-lt, y = yo + mt, г = го + п/. C)
Подставляя в уравнение B) координаты произвольной точки
данной прямой, взятые из формул C), будем иметь
или
(Л/ + Вт + Cn)t + Ах0 + Ву0 + Cz0 +D = 0. D)
1. Если А1-\- Вт-\-СпфО, то уравнение D) имеет относительно
t единственное решение:
, _
Al + Bm + Cn
а, значит, данная прямая и данная плоскость имеют только
одну общую точку, т. е. пересекаются.
2. Если
то уравнение D) не удовлетворяется ни при каком значении t,
т. е. на данной прямой нет ни одной точки, лежащей на данной
плоскости, следовательно, данные прямая и плоскость параллельны.
3. Если
Al + Bm + Cn==0, Axo + Byo-\-Czo+D = Q,
то уравнение D) удовлетворяется при любом значении t, т. е.
все точки данной прямой лежат на данной плоскости, значит,
данная прямая лежит на данной плоскости.
Выведенные нами достаточные условия взаимного расположения
прямой и плоскости являются и необходимыми и доказываются
сразу методом от противного.
Из доказанного следует необходимое и достаточное условие
А1-\-Вт-т-Сп = 0 того, что вектор а = {/, т, п} компланарен
плоскости, заданной общим уравнением Ах-\- By-\-Cz-\-D = 0
относительно общей декартовой системы координат.
§ 81. Прямая как линия пересечения двух плоскостей
В общем случае прямую р в общей декартовой системе
координат можно задать уравнениями двух плоскостей:
= 0, A)
пересекающихся по этой прямой.
Для приведения прямой, заданной двумя пересекающимися
плоскостями A), к каноническому виду надо найти какое-нибудь
решение х0, у0, z0 системы A). Точка М0(х0, у0, z0) лежит на пря-
§82. ПУЧОК ПЛОСКОСТЕЙ
183
мой, по которой пересекаются плоскости A). Далее, вектор а
с координатами
с,
111 =
[Сг At
С2 Л.2
п-
Л, В,
Л, В,
является направляющим вектором данной прямой, так как он
ненулевой и компланарен каждой из данных плоскостей. В самом
деле, применяя необходимое и достаточное условие компланарности
вектора и плоскости, получим
2 ^2
Л Si Сх
"« Оа Со
с\ лх
= 0
Л, В,
и аналогично
так что вектор а — {1, т, п) коллинеарен прямой, по которой
пересекаются плоскости A).
Канонические уравнения прямой A) можно записать в виде
X — Хо
Вх Сг
В, С9
У~Уо
С Л
с л
§ 82. Пучок плоскостей
Собственным пучком плоскостей называется множество всех
плоскостей, проходящих через одну прямую.
Несобственным пучком плоскостей называется множество всех
параллельных между собой плоскостей.
Теорема 1. Для того чтобы три плоскости, заданные общими
уравнениями
A
относительно общей декартовой системы координат, принадлежат
одному пучку, собственному или несобственному, необходимо и
достаточно, чтобы ранг матрицы
!АХ В, С,
В2 С2 D2
был равен или двум, или единице.
184 Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
Доказательство необходимости. Пусть три
плоскости A) принадлежат одному пучку. Требуется доказать, что
RgM<2.
Предположим сначала, что три данные плоскости принадлежат
собственному пучку. Тогда система A) имеет бесконечное множество
решений; это будет тогда и только тогда, когда Rg/W<[2, так
как если Rg/W = 3, то система A) или имеет единственное
решение, или несовместна, смотря по тому, будет ли определитель,
составленный из коэффициентов при неизвестных, отличен от
нуля или равен нулю.
Если три данные плоскости принадлежат несобственному пучку,
то ранг матрицы
/А, Вх
2 В2
3 "8
равен 1, а значит, ранг матрицы М равен или двум, или единице.
Доказательство достаточности. Дано: Rg/W<[2.
Требуется доказать, что три данные плоскости принадлежат одному
пучку.
Если Rg/W<2, то и Rgm<2. Пусть Rg/W = Rgm = 2. Тогда
система A) совместна, имеет бесконечное множество решений, а
среди данных плоскостей есть пересекающиеся, т. е. три данные
плоскости принадлежат одному собственному пучку.
Если Rg/n=l, RgM = 2, то все плоскости коллинеарны (две
из них непременно параллельны, а третья может и совпадать
с одной из параллельных плоскостей).
Если Rg/W = l, то и Rgm=l, и все плоскости совпадают.
Теорема 2. Пусть в общей декартовой системе координат заданы
две различные плоскости л1 и л2 общими уравнениями:
Для того чтобы третья плоскость я, заданная также общим
уравнением
A
относительно той же системы координат, принадлежала пучку,
определяемому плоскостями п1 и л2, необходимо и достаточно, чтобы
левая часть уравнения плоскости л была линейной комбинацией
левых частей уравнений плоскостей п1 и л2.
Доказательство необходимости. Дано: плоскость л
принадлежит пучку плоскостей, определяемому плоскостями л1 и
л2. Требуется доказать, что существуют числа Аир,, такие, что
будет выполнено тождество, справедливое при всех значениях
х, у, г\
A
§82. ПУЧОК ПЛОСКОСТЕЙ 185
В самом деле, если три плоскости л, лх и л2 принадлежат
одному пучку, то RgM<[2, где
/А, В, С, ОЛ
М = [ Аг В2 С2 Da .
\А.г В3 С3 Dj
Первые две строки этой матрицы линейно независимы (поскольку
плоскости л1 и л2 различны), а так как RgM<2, то третья
строка есть линейная комбинация двух первых, т. е. существуют
числа Я и (X, такие, что
Умножая обе части первого равенства на х, обе части второго
па у, обе части третьего на г и складывая почленно полученные
равенства и равенство D3 = KD1-lrixDi, получим доказываемое
тождество.
Доказательство достаточности. Пусть тождество
справедливо при всех значениях х, у и г. Требуется доказать,
что плоскость я принадлежит пучку, определяемому
плоскостями л1 и л2.
Из данного тождества следуют соотношения
так что третья строка матрицы М есть линейная комбинация двух
первых, а потому RgM^2.
Уравнение
= 0, A)
где Я и |л не равны нулю одновременно, называются уравнением
пучка плоскостей, определяемого двумя различными плоскостями
л1 и л2, уравнения которых в общей декартовой системе
координат таковы:
A^ + B^ + C^ + D^O, A2x + B2y + C2z+D, = 0. B)
Как было доказано, уравнение всякой плоскости пучка,
определяемого различными плоскостями B), может быть записано
в виде A).
Обратно, если уравнение A), в котором хотя бы одно из чисел
Я и ц не равно нулю, есть уравнение первой степени, то оно
186 Глава VI ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
является уравнением плоскости, принадлежащей пучку,
определяемому плоскостями B). В самом деле, третья строка матрицы М,
составленной из коэффициентов уравнений B) и A), имеет вид
XAj. + vlA,, Я^ + цВ,, ЯС^ + цС,, KDx-\-\xD2,
т. е. является линейной комбинацией двух других, поэтому
Rg/W<2.
Если плоскости ях и л2 пересекаются, а Я и р. не равны нулю
одновременно, то все коэффициенты при х, у, г в уравнении A)
ие могут быть равны нулю, так как если бы имели место
соотношения
то плоскости nt и л2 были бы коллинеарны вопреки предположению.
Но если плоскости я, и я2 параллельны, то существуют такие
числа к и (X, среди которых хотя бы одно ие равно нулю, и такие,
что в уравнении A) все коэффициенты при х, у и z равны нулю.
§ 83. Взаимное расположение грех плоскостей
Пусть относительно общей декартовой системы координат
заданы три плоскости общими уравнениями:
= (),
0, A)
Введем следующие обозначения;
Л1В1 С
6 =
2 2 ^ 2
А.д Bs C3
и обозначим главные векторы данных плоскостей так:
ft^Mi. fli. cib «2 = {^3- fla, Q}. th = {A3, 8„ Са}.
На основании предыдущего получаем следующие необходимые
и достаточные признаки взаимного расположения трех плоскостей.
1. Если 6=5^=0, то три данные плоскости имеют и притом
только одну общую точку, так как в случае 6=^=0 система A)
имеет п притом только одно решение: это решение, т. е.
координаты единственной общей точки, принадлежащей трем данным
плоскостям, мы получим, решив систему A) (например, по
формулам Крамера) (рис. 129, а).
2 Если Rgm = 2, Rg M = 3 и среди главных векторов пъ п2, nt
нет коллинеарных, то система несовместна (Rg М > Rg m); нло-
j 84. СВЯЗКА ПЛОСКОСТЕЙ
187
скости попарно пересекаются, прячем прямые пересечения попарно
различны (рис. 129,6).
3. Если Rgm — 2, RgA4 = 3, но среди главных векторов
пх, пг, п3 есть два коллипеарных (они не могут быть все три
коллинеариы, так как Rgm = 2), то система несовместна; причем
две плоскости параллельны, а третья их пересекает (рис. 129, б).
4. Если Rgm-— 2, RgM = 2 и среди главных векторов nlt n2, п3
нет коллипсарпых, то плоскости попарно различны и проходят
через одну прямую (рис. 129, г).
Рис. 129
5. Если Rgm —2, RgM = 2 и среди главных векторов nlt n2,
п3 есть два коллипеарных, то две плоскости совпадают, а третья
их пересекает (рис. 129, 3).
6. Если Rgm=l, но коэффициенты любой пары из уравнений
A) непропорциональны, то "плоскости попарно параллельны (рис.
129, е).
7. Если Rgm=l, но среди уравнений A) есть только два,
коэффициенты которых пропорциональны, то две плоскости
совпадают, а третья им параллельна (рис. 129, ж).
8. Если RgM—l, то все плоскости совпадают (рис. 129, з).
§ 84. Связка плоскостей
Собственной связкой плоскостей называется множество всех
плоскостей, проходящих через одну точку (центр связки).
Несобственной связкой плоскостей называется множество всех
плоскостей, компланарных одной прямой.
Теорема 1. Для того чтобы четыре плоскости, заданные
относительно общей декартовой системы координат уравнениями
1 = О,
9 = 0, A)
188
Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
принадлежали одной связке (собственной или несобственной),
необходимо и достаточно, чтобы
AlBlClD1
А =
A3B3CSD3
= 0.
Доказательство необходимости. Дано: четыре
плоскости A) принадлежат одной связке. Требуется доказать, что
А-0.
Если четыре данные плоскости принадлежат одной собственной
связке, то, обозначая через (x0, y0, z0) центр этой связки, будем
иметь
Таким образом, столбцы определителя Д линейно зависимы,
значит, он равен нулю.
Если четыре данные плоскости, заданные уравнениями A),
принадлежат одной несобственной связке, то существует ненулевой
вектор {/, т, п), компланарный всем этим плоскостям, и, значит,
п = 0,
А31 -Ь Bsm-f Csn --- 0, AJ. +
так что первые три столбца определителя Д линейно зависимы,
а значит Л—-О.
Доказательство достаточности. Дано: Д = 0.
Требуется доказать, что четыре плоскости A) принадлежат одной связке.
Если ранг матрицы / AlBlCl
А2В2С2
равен трем, то среди четырех данных плоскостей есть три такие,
которые имеют единственную общую точку Мо (х0, у0, z0).
Пусть, например,
A.Bfi,
А3ВЯСЪ
¥=0,
тогда это будут три первые плоскости.
Первые три строки матрицы
A1BlC1D1
§84. СВЯЗКА ПЛОСКОСТЕЙ
189
линейно независимы, а так как Д = 0, то последняя строка есть
линейная комбинация первых трех:
Л4 = IЛх + \х Л2 + vЛ8, В4 -= КВ1 -j- цВ, -h vB3.
С4 = КС1 + рСг -f vC3, D4 = XDX -(- \iD2 + vD3;
отсюда следует тождество, справедливое при всех х, у, г:
Из этого тождества следует, что точка М0(х0, у0, г0),
являющаяся пересечением первых трех плоскостей, лежит и на
четвертой плоскости, т. е. четыре данные плоскости принадлежат одной
собственной связке.
Если RgM <3 (отсюда уже следует, что Д = 0), то среди
главных векторов пг, пг, я3, я4 данных плоскостей есть не более двух
линейно независимых.
Пусть пх и пг линейно независимы, следовательно неколли-
неарны, а векторы га3 и я4 —их линейные комбинации:
Лз == Л7*1 ~г |Л/*д, Д4 = Л rli I F " V*/
Система уравнений
имеет ненулевое решение
например, / =
В силу соотношений B) будем также иметь
т —
;2л2
п =
АгВг
)•
т. е. четыре данные плоскости принадлежат одной несобственной
связке, так как ненулевой вектор {/, пг, и} всем им компланарен.
Если наконец, Rgm=l, то четыре данные плоскости колли-
пеарны, а значит также принадлежат одной связке.
Теорема 2. Пусть
^Q C)
три плоскости, не принадлежащие одному пучку. Для того чтобы
плоскость
A^x + B^ + C^ + D^O D)
принадлежала связке, определяемой плоскостями C), необходимо и
достаточно, чтобы левая часть уравнения D) была линейной
190
Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
комбинацией левых частей уравнений C):
Atx + Bty-|-Схг +- D4 = A.(AlX
+ ix (A.zx + B.2y + C2z + D,) -f v (A3x
+ Csz + D,)
E)
(тождество при всех значениях х, у, г).
Доказательство необходимости. Дано: плоскость D)
входит в связку, определяемую плоскостями C). Требуется
доказать, что существуют такие числа К, \i и v, при которых
соотношение E) является тождеством.
Так как плоскости C) не входят в один пучок, то ранг
матрицы
равен 3, а так как плоскость D) входит в связку, определяемую
плоскостями C), то
д =
A2B.2C2D2
= 0.
F)
Отсюда следует, что четвертая строка этого определителя есть
линейная комбинация первых трех:
G)
Поэтому соотношение E) есть тождество относительно х,
У, г.
Доказательство достаточности. Предположим, что
существуют такие X, \i и v, при которых соотношение E) есть
тождество относительно х, у, г. Требуется доказать, что плоскость
D) входит в связку, определяемую плоскостями C).
Если соотношение E) есть тождество относительно х, у, г, то
из него следуют равенства G), а следовательно Д = 0, так как
четвертая строка определителя Л есть линейная комбинация трех
первых. Но если Д = 0, то четыре плоскости, заданные
уравнениями C) и D), принадлежат одной связке.
$>cl СВЯЗКА ПЛОСКОСТЕЙ
191
Уравнение
X(A1x-\-B1y-\-C1z]-D1)-\-
(8)
в котором хотя бы одно из чисел X, \х, v не равно нулю, а
(9)
общие уравнения трех плоскостей, заданных относительно общей
декартозой системы координат и не принадлежащих едиому пучку,
называется уравнением связки плоскостей, определяемой тремя
даниь/мя плоскостями.
Как было доказано, в таком виде может быть записано
уравнение всякой плоскости, входящей в связку плоскостей,
определяемую тремя данными плоскостями.
Обратно, если X, \х, v выбраны произвольно, но так, что
уравнение (8) есть уравнение первой степени относительно х, у, г, то
оно ость уравнение плоскости, входящей в связку, определяемую
тремя плоскостями (не входящими в один пучок), уравнения
которых в общей декартовой системе координат таковы:
A1x-\-B1y-\-C1z~-D1 = 0,
Если плоскости (9) имеют только одну общую точку, а среди
чисел X. (X, v хотя бы одно не равно нулю, то в уравнении (8)
коэффициенты при х, у, z одновременно в нуль не обращаются,
так как если X, \i, v не равны пулю одновременно и
:+vA8 = 0,
-j-vfl8 = 0,
A0)
то
Ail
A2l
Ad
= 0,
и три данные плоскости или не имеют ни одной общей точки,
или имеют бесконечное множество общих точек.
192 Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
Если же три данные плоскости попарно пересекаются по трем
различным прямым (рис. 129, б) или две из них траллельны и
третья их пересекает (рис. 129, в), то существует непулевой
вектор {%, (х, v}, компланарный каждой из плоскостей (9), т. е. будут
выполнены соотношения A0), а в таком случае уравнение (8) не
будет уравнением первой степени (коэффициенты при х, у, z
равны нулю).
§ 85. Геометрический смысл неравенства первой степени с
тремя неизвестными
Теорема!. Пусть относительно общей декартовой системы
координат задана плоскость л общим уравнением
Ax + By-\-Cz+D = Q. A)
Тогда для координат х, у, z всех точек М (х, у, z), лежащих по
одну сторону от плоскости я, выполняется неравенство
Ах + By -\- Cz -j- D > 0,
п-Ы ВС} а ^ЛЯ к0°рдинат х, у, z всех точек
рГ "' М (х, у, г), лежащих по другую сто-
\ з рону от плоскости к,— неравенство
\
Плоскость л делит пространство
на два полупространства. То
полупространство, для координат всех
точек которого
/bt-f By + Cz+D>0,
Рис. 130.
будем называть положительным, а
другое, для координат всех точек которого
Ax + By + Cz+D <0,
— отрицательным.
Теорема 2. Пусть относительно общей декартовой системы
координат плоскость я задана общим уравнением
Тогда, если отложить главный вектор п={А, В, С} этой
плоскости от любой точки Мо этой плоскости М0Р = п, то конец
Р отложенного вектора будет находиться в положительном
полупространстве от данной плоскости л (рис. 130).
Теоремы 1 и 2 доказываются аналогично тому, как были
доказаны теоремы 1 и 2 в § 62.
§87 НОРМАЛЬНОЕ УРАВНЕНИЕ ПЛОСКОСТИ 193
Если система координат—декартова прямоугольная, то
главный вектор п — {А, В, С} перпендикулярен к данной плоскости.
Рассуждениями, вполне аналогичными тем, которые были
проведены на стр. 152, доказывается, что условие
является необходимым и достаточным условием того, что вектор
а = {1,т,п\, заданный относительно общей декартовой системы
координат, направлен в положительное полупространство от
плоскости, заданной уравнением
Ах -f By + Cz + D = О
относительно той же системы координат.
Это соображение может быть использовано при определении
направления вектора, коллинеарного особому направлению
эллиптического параболоида, заданного общим уравнением
относительно общей декартовой системы координат (§ 166), а также при
определении направления вектора, имеющего особое направление
относительно параболического цилиндра (§ 166), заданного общим
уравнением относительно общей декартовой системы координат.
§ 86. Расстояние от точки до плоскости
Теорема. Расстояние d от точки М0{х0, у0, z0) до плоскости,
заданной относительно декартовой прямоугольной системы
координат общим уравнением
Ax-\-By-\-Cz+D = Q>,
вычисляется по формуле A)
\A + BCD\
d
Va2-'B*± С2
Доказательство теоремы ничем не отличается от доказательства
теоремы § 63.
§ 87. Нормальное уравнение плоскости
Уравнение
D = Q A)
плоскости, заданной относительно декартовой прямоугольной
системы координат, называется нормальным, если главный
вектор и — {А, В, С}, перпендикулярный к этой плоскости,
единичный, т. е. если
Л2-г Я2-г С2 =1. B)
7 П. С. Моденов
194 Глаза VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
Для приведения к нормальному виду общего уравнения
плоскости, заданной относительно декартовой прямоугольной системы
координат, надо умножить левую часть данного уравнения на
такое число /И (нормирующий множитель), чтобы в уравнении
МАх + МВу + MCz + MD = О
вектор {AM, BM, СМ} стал единичным, т. е. чтобы
М2Аг+М2В2 + МгСг = \,
откуда
х C)
±Y лч-ч'Ч- с2
Таким образом, для каждой плоскости всегда получим два
нормальных уравнения
Ах + Ву\С?+П
" [
И это естественно: для любой плоскости существуют два и
только два различных единичных вектора, перпендикулярных
к ней. Множители
М = + ~7= ' E)
называются нормирующими множителями уравнения Ах-\-Вц-\-
+ Cz + D = 0. f
Радикал \ А1-\-Вг ■{■ Сг есть модуль главного вектора п —
— {А, В, С}, который в случае декартовой прямоугольной системы
координат является нормальным к плоскости
Q, \n\ = V A2 + fi2 + C2. F)
Таким образом,
M = ±TiT. G)
Коэффициенты нормального уравнения плоскости, заданной
уравнением
относительно декартовой прямоугольной системы координат, равны
косинусам углов а, р, у, которые нормальный вектор п = {А, В, С}
к плоскости, заданной уравнением Ах + Ву + Сг-\-О = 0,
образует с осями координат. В самом деле,
Л = {Л, В, С}{1, 0, 0} = «/ = cosa,
В = {А, В, С} {0, 1, 0} = ц/= cos (J, (8)
С={А, В, С] {О, 0, 1} = п/г
§87. НОРМАЛЬНОЕ УРАВНЕНИЕ ПЛОСКОСТИ 195
Наконец, \D\ = p, где р — расстояние от начала координат
доданной плоскости (для доказательства в формуле A) § 86 следует
положить xo = yo = zo = O и заметить, что Л2 + В2 + С2 = 1).
Если относительно декартовой прямоугольной системы
координат плоскость задана нормальным уравнением
т. е. А2 + В2 + С2 — 1, причем D < О, то Л, В, С являются
направляющими косинусами cos a, cos p, cosy луча /, выходящего из
начала координат и пересекающего данную плоскость, причем
\D\ = p, где р — расстояние от начала координат до
рассматриваемой плоскости. Действительно, если D < О, то начало
координат лежит в отрицательном полупространстве плоскости,
заданной уравнением
Ах + By -f Cz + D = О
и, значит, луч I, выходящий из начала координат и
пересекающий данную плоскость, одинаково направлен с нормальным
(главным) вектором п = {А, В, С} плоскости Ах -f- By -j- Cz -f- D = 0. Fo
так как |D| = p, где p— расстояние от начала координат до
плоскости, заданной нормальным уравнением, то нормальное
уравнение Ax-\-By-\-Cz + D = 0 плоскости в случае D<0 имеет вид
t/cos р + гсоэ у — Р = 0, (9)
где cos a, cos p, cosy — направляющие косинусы луча,
выходящего из начала координат и пересекающего плоскость, а р —
расстояние от начала координат до этой плоскости.
Для приведения к нормальному виду (9) общего уравнения
плоскости, заданной относительно декартовой прямоугольной
системы координат в случае, если эта плоскость не проходит через
начало координат, воспользуемся результатами § 76 (см. § 76,
соотношение C)), согласно которому существует такое число МО
что имеет место тождество (относительно х, у, z)
МАх + МВу + MCz + MD = х cos a + у cos (J + z cos у—р,
или
/ИЛ = cos a, /WB = cosp, МС — cos у, MD=—
Так как направляющие косинусы любого луча в декартовой пря
моугольной системе координат связаны соотношением cos2a + cos2 C
+cos2y=1, то (МЛJ + (МВJ + (/ИСJ=1, откуда
196 Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
причем в силу того, что
MD = - р < О,
знак /И следует выбрать противоположным знаку р.
Если плоскость задана нормальным уравнением
относительно декартовой прямоугольной системы координат, то
расстояние d от точки Мо (ха, у0, г0) до этой плоскости
вычисляется по формуле
d A B
т. е. расстояние от точки до плоскости, заданной нормальным
уравнением относительно декартовой прямоугольной системы
координат, равно абсолютной пеличине результата подстановки
координат данной точки в левую часть уравнения плоскости (см. §86).
Если плоскость не проходит через начало координат и задана
относительно декартовой прямоугольной системы координат
уравнением
х cos a -f у cos $ -\-z cos у — р = О,
гдесоэа, cos p\ cosy — направляющие косинусы луча,
выходящего из начала координат и пересекающего эту плоскость, а р—
расстояние от начала координат до рассматриваемой плоскости,
то расстояние d от произвольной точки Мо (х0, у0, г0) до этой
плоскости вычисляется но формуле
d — | х0 cos а + у оcos Р + гоcos Y ~ Р !•
§ 88. Угол между двумя плоскостями. Условие
перпендикулярности двух плоскостей
Косинусы углов между двумя плоскостями, заданными
уравнениями
A1x + B1y + C1z + D1 = 0, A)
А2х-тВ2у — C22 + D2 = 0 B)
относительно декартовой прямоугольной системы координат,
выражаются формулой
соэф1,2 = ± - I—* 2Т-Л-1==== . C)
V A\-]-B\ + C\V Л\ + В\ + С1
Угол между векторами П1 = {А1, Вг, Сг} и п2~{Аг, В2, С2},
нормальными соответственно к данным плоскостям, равен одному
из углов, образованных этими плоскостями, именно тому из углов,
образованных плоскостями A) и B), внутренние точки которого
находятся в положительном полупространстве от одной плоскости и
УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
197
в отрицательном полупространстве от другой плоскости (рис. 131).
Поэтому, обозначая через срх один из углов, образованных
данными плоскостями, а через ср2 — угол, смежный с углом срх, и
, ab
применяя формулу cosa = , & | для
косинуса угла а между непулевыми
векторами а и Ь, мы и получим
формулу C).
Следствие. Необходимым и
достаточным условием
перпендикулярности двух плоскостей, заданных
общими уравнениями
Рис. 131
относительно декартовой прямоугольной системы координат,
является равенство
§ 89. Угол между двумя прямыми. Условие перпендикулярности
двух прямых
Углом между двумя прямыми в пространстве называется любой
из углов между двумя параллельными им прямыми, проходящими
через произвольную точку пространства. Таким образом, две
прямые в пространстве (если они неперпендикулярны) образуют
между собой два различных угла: один острый, другой тупой.
Сумма этих углов равна л.
Пусть a = {llt tnv nx} и b — {l2, m2, n2) — направляющие
векторы данных прямых, заданных относительно декартовой
прямоугольной системы координат. Угол между этими векторами равен
одному из углов, образованных данными прямыми. Следовательно,
косинусы углов между двумя данными прямыми выражаются
формулой
cos ф, , = ± ' 2 ' ' -
Отсюда получаем необходимое и достаточное условие
перпендикулярности двух прямых:
/j/, -\-mlm2 + п{п2 = 0;
для того чтобы две прямые были взаимно перпендикулярны,
необходимо и достаточно, чтобы сумма произведений
соответствующих координат направляющих векторов этих прямых была равна
нулю.
198
Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
§ f,0. Угол между прямой и плоскостью. Условие
перпендикулярности прямой и плоскости
Углом между прямой и плоскостью (если они неперпендикулярны)
называется меньший из двух углов между этой прямой и ее
ортогональной проекцией на эту плоскость. Если же прямая и
плоскость перпендикулярны, то угол между ними считается
равным у. Пусть относительно декартовой прямоугольной системы
координат задана плоскость П общим
У** уравнением
7 Ах-
/ и прямая р—каноническими уравие-
7 нпями
х—хо_у—у(, __г — г„
I m n
Косинус угла гр между вектором
п={А, В,С}, перпендикулярным
данной плоскости, и направляющим
вектором а — {1, т, п) данной прямой по
абсолютной величине равен синусу угла гр
между данной прямой и данной плоскостью (рис 132). Но
косинус угла ф между векторами и и а равен
А1-\- Вт~Сп
cos гь = ,,
Рис
л
132
следовательно, синус угла <р межд^ данной прямой и данной
плоскостью определится по формуле
„;„„_ \А1 + Вт + Сп\
Если прямая,
перпендикулярна
г УА'<
заданная
х—х0
i
плоскости
Ах +
ЧйЧС2
у /2+
уравнениями
У—Уо
т
Ву + Сг-
г —г0
п
f D =
>
о,
то направляющий вектор а = {1, т, п} прямой коллинеареи
вектору п — {А, В, С}, перпендикулярному данной плоскости. Поэтому
координаты этих векторов пропорциональны, т. е. существует такое
отличное от нуля число К, что
или
т
§92. ОБЩИЙ ПЕРПЕНДИКУЛЯР К ДВУМ ПРЯМЫМ 199
Обратно, если выполнены эти соотношения, то векторы
а = {/, т, п) и я = {Л, В, С} коллинеарны, т. е. направляющий
вектор данной прямой коллинеарен вектору п = {А, В, С},
перпендикулярному данной плоскости, следовательно, данная прямая
и плоскость взаимно перпендикулярны.
Итак, для того чтобы прямая и плоскость, заданная
относительно декартовой прямоугольной системы координат, были
перпендикулярны, необходимо и достаточно, чтобы координаты
направляющего вектора прямой были пропорциональны
коэффициентам при х, у, z в уравнении плоскости.
§ 91. Уравнения перпендикуляра, опущенного из данной точки
на данную прямую
Уравнения перпендикуляра, опущенного из точки
Mi(*i> Уъ zi)
па прямую, заданную каноническими уравнениями
х — Хр _У — Уо __2—г0
I m n
относительно декартовой прямоугольной системы координат, можно
записать в виде
•*• хо У У о г z0
Л1 ЛО »1 УО с\ СО
I m n
= 0,
так как первое из этих уравнений выражает плоскость,
проходящую через точку М1(х1, ylt zt) перпендикулярно данной прямой,
а второе — плоскость, проходящую через данную точку и данную
прямую. Эти две плоскости пересекаются по прямой, проходящей
через точку Мх и пересекающей данную прямую, под углом 90°
(рис. 133).
§ 92. Уравнения общего перпендикуляра к двум
неколлинеарным прямым
Пусть две прямые р и ^ заданы своими каноническими
уравнениями
х—*i _ у—yt==z—?!
U mi ni ' \
X — Х2 У — У2 г — г2
относительно декартовой прямоугольной системы координат.
Предположим, что направляющие векторы этих прямых
a={llt тг, пх\ и Ь = {1г, т2, пг)
200
Р лава VI ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
неколлинеарны, т. е. что данные прямые или скрещиваются, или
пересекаются. Пусть / — прямая, которая пересекает обе прямые
под углом 90°.
Тогда за направляющий вектор прямой / можно взять
векторное произведение [ab] направляющих векторов данных прямых:
/п,
пг
По
По
к
к
к
к
т1
Общий перпендикуляр / к двум данным прямым можно
определить как прямую, по которой пересекается плоскость л;1(
проходящая через прямую р компланарно вектору [ab], с плоскостью л2>
проходящей через прямую q компланарно [ab] (рис. 134).
а={1„т,,п(}
Рис 133
Рис. 134
Уравнение плоскости лг имеет вид
х—хх
у—
1г т
Ш2 По
«2
Уг
г-
1 '
к
к
1
к
~*1 '
т1!
Шо\
= 0,
A)
так как эта плоскость проходит через точку М1(х1, уг, гг)
прямой р и компланарна векторам а н [ab] Аналогично составляем
уравнение плоскости л2:
= 0.
X— Хг
У — У2
z-z2
к тг пг
/п, п2
Пг к
п-2, к
Общий перпендикуляр I к данным прямым выражается
уравнениями A) и B).
94. КРАТЧАЙШЕЕ РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ
201
§ 93. Расстояние от точки до прямой з пространстве
Пусть в пространстве заданы точка Ml(x1, ylt гг) и прямая/
каноническими уравнениями
х — х0 у—у» г—?0
п
относительно декартово»"; прямоугольной системы координат.
Расстояние d от точки /VI х до прямой / можно определить как
вы-оту параллелограмма, сторонами которого служит вектор
М, МОМХ и направляющий вектор а
прямой /, отложенный от точки Мо
этой прямой. Поэтому для
определения расстояния d рассмотрим
модуль векторного произведения:
но
sincp = d, следовательно (рис. 135),
1 а | sin
откуда
Так как
\а\
1 = {х1—х0, y
а = {1, т, п},
то
поэтому
/ т
'•]}.
т п
i — Уо
m
— /—; •
. У № + т ~\~ni
§ 94. Кратчайшее расстояние между двумя прямыми
Если две прямые скрещиваются, т. е. не лежат в одной
плоскости, то кратчайшее расстояние между ними (как доказывается
е элементарной геометрии) есть длина отрезка общего
перпендикуляра к этим двум прямым, концы которого лежат на этих
прямых. Отсюда следует, что кратчайшее расстояние между двумя
202
Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В 'ПРОСТРАНСТВЕ
скрещивающимися прямыми равно величине ортогональной
проекции любого отрезка МХМ2, концы которого лежат на этих
прямых (рис. 136), на любую прямую, перпендикулярную к данным;
это очевидно при проектировании точек Мх и М2 на общий
перпендикуляр к данным прямым; величина проекции не изменится,
если спроектировать
отрезок МХМ2 па любую
прямую, параллельную этому
перпендикуляру. Пусть две
скрещивающиеся прямые
заданы каноническими
уравнениями
nL
i2 т2 п2
относительно декартовой
Рис. 136
прямоугольной системы
координат. Кратчайшее расстояние между ними равно абсолютной
в'еличине проекции вектора
= {х2 —x
lt
начало М1(х1, ух, zx) и конец М2(х2, у2, z2) которого лежат
соответственно на первой и второй прямых, на прямую,
параллельную вектору
перпендикулярному направляющим векторам
}■
= {/1; m
lt
= {l2, т2, п2}
данных прямых.
Так как
| [аЬ] МХМ21 = | [аЬ] \ |пР[я6] лТД | -1 [ад] | d,
то кратчайшее расстояние d между данными скрещивающимися
прямыми вычисляется по формуле
или в координатах
d =
т/ \
Г \
I [ab\ |
/я i.
т2 п2| "|п.2
п2
($95. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ VI 203
Отметим, что эта формула верна и для двух пересекающихся
прямых: числитель обратится в нуль, знаменатель отличен от нуля,
и мы получим d = Q в соответствии с определением кратчайшего
расстояния между двумя пересекающимися прямыми.
Если две прямые параллельны, то кратчайшее расстояние
между ними равно расстоянию от любой точки первой прямой до
любой точки второй прямой.
§ 95. Примеры и задачи к главе VI
1. Задачи с решениями
Пример 1. Составить уравнения перпендикуляра, опущенного из точки
B, 3, 1) на плоскость
г — 11=0.
Решение. В прямоугольной системе координат вектор ^3, 1, 2|
перпендикулярен данной плоскости, поэтому для искомой прямой известна точка
B, 3, 1) и направляющий вектор \3, lt 2}.
Ее уравнения:
х — 2__ у— 3_2 — 1
3 1 2 "
Пример 2. Составить уравнение плоскости, проходящей через точку
A, 2, —1) компланарно векторам {1, 7, 0} и {4, 3, 2}.
Решение.
х— 1 у—2 г+1
1 7 0 =0,
4 3 2
Ых- Чу — 25г — 35 = 0.
Пример 3. Составить уравнение плоскости, проходящей через точку C, 2, 1)
и прямую
х—2_у+3_г—1
4 ~"Т~~ 2 "
Решение. Искомая плоскость проходит через точки /М1C, 2, 1) и
/И2 B, —3, 1) и параллельна вектору а = {4, 1, 2), следовательно, она
параллельна вектору
М^Мг = \ — 1, —5, 0^
и, значит, ее уравнение
х — 3 у —2 г—1
4 1 2 =0,
— 1 —5 0
или
Юх— 2(/— 19г — 7 = 0.
Пример 4. Составить уравнение плоскости, проходящей через три точки
Мх{2, 5, 1), М2F, 3, 2), /И3A, 1, 1).
Решение. Искомая плоскость параллельна векторам
/И7/Й2 = {4, -2, 1} и aT^Mj. = {1, 4, 0},
204
Глава VI ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
поэтому ее уравнение
или
х—1 у—1 г—1
4 — 2 1
1 4 0
= 0,
4х — у— 18г+15 = 0.
Пример б. Составить уравнение плоскости, проходящей через начало
координат и перпендикулярной прямой
х-2_ у+7_г+3
3 ~ 4 ~ I '
Решение. Направляющий вектор {3, 4, 1} данной прямой служит
нормальным вектором плоскости, поэтому уравнение плоскости будет
Пример 6. Составить уравнение плоскости, проходящей через точку C, 1, 1)
И перпендикулярной плоскостям
Зх— у + 2г + 4 = 0, х-\-2у — г + 5 = 0
Решение Так как векторы
{3, —1, 2} и {1, 2, -1}
Перпендикулярны соответственно первой и второй из данных плоскостей, а
искомая плоскость должна быть перпендикулярна данным плоскостям, то
искомая плоскость будет параллельна этим векторам, а поскольку она к тому
же проходит через точку C, 1, 1), то ее уравнение будет
= 0,
х-3
3
1
— 1
2
г—
2
— 1
1
или
Зх — Ъу—7г + 3 = 0.
Пример 7. Найти проекцию точки A, 2, 5) на плоскость
— z = 0.
Решение. Уравнения прямой, проходящей через данную точку
перпендикулярно данной плоскости, будут
х—1_у—2_z—5
~~2Г~ 1 ~~^Т'
или в параметрической форме:
х=1+2*, y = 2 + t, г = 5 — t.
Подставляя это в уравнение данной плоскости, получим
отсюда
Координаты проекции:
29
§95 ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ VT 205
Проекция
М 13 29 \
\' 6' Т)'
Пример 8. Найти проекцию точки <3, 2, 1) на прямую
х — 2 (/ + 3 г ,.
~Т~ = ~Т~" = 1Г' (
Решение. Составим уравнение плоскости, проходящей через данную
точку C, 2, 1) перпендикулярно данной прямой:
х — 3+у—2+2B—1) = 0, или х + у-\-2г — 7 = 0. B)
Решаем систему A), B):
г _И,
~ 3 '
х-2+—=— =-3+—=-— -А
3 3' 3 3 3
Замечание. При составлении уравнений прямой не следует всегда
стремиться получить уравнения прямой в виде
— C)
т
Часто удобнее найти уравнения двух различных плоскостей проходящих
через прямую:
эти два уравнения и будут уравнениями прямой, и их вовсе не обязательно
приводить к виду C). Рассмотрим ряд примеров.
Пример 9. Найти проекцию прямой
х — 2 __«/+2 _г — 1
_________
на плоскость
Решение Так как проекция лежит в дайной плоскости, то
—О
есть одно из уравнений проекции
Второе уравнение будет уравнением проектирующей плоскости.
Проектирующая плоскость проходит через данную прямую, следовательно, она
проходит через точку B, —2,1) и компланарна вектору {3, 4, \\. Так как
проектирующая плоскость перпендикулярна плоскости
t —0,
то она компланарна вектору {1, 2, 3j, перпендикулярному этой алоскоепи
Итак, уравнение проектирующей плоскости
х—2у+2г—1
3 4 1
1 2 3
= 0,
206 Глава VI ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
ИЛИ
Ъх — 4у + г —19 = 0.
Искомые уравнения проекции:
x + 2</+3z+4 = 0, Блг — 4г/+2— 19 = 0.
Пример 10. Составить уравнения перпендикуляра, опущенного из точки
3, 2, 1) на прямую
х_ у_г + 3
~2~~1 Г~
Решение. Рассмотрим плоскость ль проходящую через данную точку
C, 2, 1) и перпендикулярную к данной прямой, т. е к вектору {2, 4, 1}
Уравнение этой плоскости
(!/ — 2) + г—1=0,
или
2х-\-4у + г — 15 = 0
Рассмотрим плоскость т2, проходящую через данную точку и данную
прямую
Эта плоскость проходит через ючки '!iC, 2, 1) и Л12@, I), —3) и
параллельна направляющему вектору данной прямой {2, 4, \\. Имеем
М,Мг = {3,/, 4}.
Следовательно, уравнение плоскости- я2
х У г + 3
3 2 4 =0,
2 4 1
или
14л: — 5(/ — 8г— 24 = 0
Плоскости jtj и Иг пересекаются по прямой /, которая проходит через
данную точку и перпендикулярна данной прямой, поэтому" уравнения
2х + 4у+г— 15 = 0, 1 4аг — 5у — 8г—24 = 0
и будут уравнениями прямой I.
Пример 11. Дана прямая
х—1_у_г
2 ~~ 3 ~ 4
и плоскость
х-\-2у—г = 0.
Через точку, в которой эта прямая пересекает данную плоскость,
проведена прямая, перпендикулярная к данной прямой и лежащая в данной
плоскости. Составить уравнения этой прямой.
Решение. Одно из уравнений прямой есть уравнение данной плоскости
* х + 2у — г = 0
Составим уравнение плоскости я, проходящей через исковую прямую
и данную, эта плоскость проходит через точку A, 0, 0) и параллельна вектору
О = {2, 3, 4} Далее, вектор Ь — {\, 2, —1} перпендикулярен данной плоскости,
поэтому вектор [а&] = { —11, 6, 1} будет направляющим вектором искомой
прямой и, значит, параллелен плоскости я Таким образом, уравнение
плоскости и
х — 1 у г
2 3 4
— 11 6 1
= 0,
§ 95. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ VI
207
или
21х + 46(/ — 45г — 21 =0.
Итак, искомая прямая определяется уравнениями
х-т-2у — г = 0, 21* + 46j/ —45г —21=0.
Пример 12. Составить уравнения прямой, проходящей через точку B, 1, 0)
и пересекающей две прямые: ^
х-\-\__у— 1 _ г л: — 2 у_+2 ^_
~~2~~~"П~3~ " ~3~~~ 4 ~Т'
Решение. Искомую прямую можно рассматривать как прямую, по
которой пересекаются две плоскости, проходящие через данную точку и одну
из данных прямых.
Уравнения этих плоскостей (см. пример 3)
= 0,
4-
2
1
1
У-1
1
0
г
3
0
= 0,
х — 2
3
0
у + 2
4
1
или
3(/—г—3 = 0, х — Зг—2 = 0
— искомые уравнения прямой.
Пример 13. Составить уравнения общего перпендикуляра к двум прямым:
х— 1 _у—2_г—3 х __ у __ г
8 ~~4~~~Т~ И Т~—2~ 1 '
Решение. Направляющими векторами данных прямых являются
соответственно векторы а = {8, 4, 1} и & = {2, —2, 1}. Вектор с = [а&],
являющийся векторным произведением вектора а на вектор Ь, перпендикулярен
векторам а н Ь. Вектор
с = {6, -6, -24} || {1, -1, -4}.
Искомый общий перпендикуляр к двум данным прямым можно
рассматривать как линию пересечения двух плоскостей: одна плоскость проходит
через первую из данных прямых компланарно вектору с, другая — через вторую
данную прямую компланарно вектору с. Уравнения этих плоскостей:
х — 1 у — 2 z —3
= 0,
1
4
— 1
1
х у г
2 -2 1
1 —1—4
= 0,
или
5х—ll(/-f-4z-j-5 = 0, х-\-у = 0.
Пример 14. Составить векторно-параметрическое уравнение прямой /,
проходящей через точку Мо, определяемую радиусом-вектором ОМ0 = г0, и
пересекающей под острым углом а прямую пг, которая проходит через точку Мг,
определяемую радиусом-вектором ОуИ1=г1, и коллинеарна единичному вектору а.
Точка Мо не лежит на прямой т.
Решение. Вектор [[(г0 — /ч) а] а] лежит в плоскости и, проходящей
через точку Мо н прямую т, и перпендикулярен вектору а. Вектор
b==[[(£v^£il£LE]
I Кгй—fi)a] I
будет единичным вектором, лежащим в плоскости я и перпендикулярным
вектору а (рис. 137). Векторы
/? = acosa-j-&sin a и q = — acosa+ftsina
208
Г лава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
будут единичными направляющими векторами искомых прямых (их будет две).
Уравнения этих прямых:
'-"+' (-
Пример 15. Прямая р с направляющим вектором а проходит через точку Ми
определяемую радиусом-вектором О/И1 = г1; прямая q с направляющим
вектором ft проходит через точку /И2, определяемую радиусом-вектором 0М.х = г2.
Прямые р и q неколлинеарны. Найти радиусы-векторы ОР н OQ концов Р и Q
Рис. 137
Рис. !38
наименьшего отрезка PQ, концы которого лежат соответственно на данных
Прямых р и q.
Решение. Очевидно, OP = rl-\-'ka, OQ=r2-{-\ib (рис. 138). Отсюда
Так как PQ _[_а и PQ _L&, то PQ а = 0, PQb = 0, или подробнее!
— ц&2 = Ь (r2—^J,
или
(г2 —
Яа2 — цай = а(г2—rx). J
Разрешая эту систему относительно I и |i, получим
ЬA
и аналогично
rz—ri) —
ab —ft2
а2 —аЬ
аЬ
*(a(r1-r1))-<a»)F(r,-r1))
a2*2—(aftJ
[aft]2 [аи]2
[ab]*
§95. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ VI 209
Итак,
Пример 16. Составить уравнение прямой /, проходящей через начало
координат, образующей угол ас прямой т, не проходящей через начало
координат и заданной уравнением r = ra-\-ta (а — единичный вектор), при условии,
что кратчайшее расстояние между прямыми / и т равно б.
Решение. Вопрос сводится к определению направляющего вектора Ь
искомой прямой; будем считать этот искомый вектор Ь единичным. По условию
4 \Ьага\ \Ь[агй]\ и иг 1
о = 1ГГ,—^4-=-!—1—'Ш-, ab = cosa, Ь2=1.
|[Ьа\ | sm а
Разложим вектор Ь по векторам а, \агй] и [[аг0] а)'.
Ь = Ха-\-ц lar^ — v \[ar0] а].
Умножая обе части этого равенства скалярно один раз на а, другой раз
на [аг0], получим
ba = l,
или
Но |&aro| = 6sin a, значит, baro= ± 6 sin a.
Итак,
, б sin a
Таким образом,
, б sin a , , , . , ,
b = acosa± [ar0\+v[\ar0]a].
Так как Ь2= 1, то
, , . б2 sin8 a , »r ,,
1 = cos2 a+ -f—p- + v2 [«'"ol8.
v- ±
Если [ar0]2 < б2, то задача не имеет решения. Если [аго]8"»^2' то v=0
и задача имеет два решения:
б sin a. А .
-p- [arg]j t,
б sin
Если [ar0]2 > б2, то задача имеет четыре решения:
/ , б sin a , . sin a ./■■ ^—^rrr , ,\
г = (a cosa + j^-p-[ar0] + ^rp V[ar0]2-б2 [[ar0] a] J<,
/ б sin a , . , sin a ./--. r=—rrrr , \ .
r = ( acosa-j—rj-farol + T—y2 V [aro]2-62 [[aro\ a\ }t,
\ lM'0J it*» 0}
210 Глава VI, ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
2. Задачи для самостоятельного решения
1. При каком необходимом и достаточном условии точка (х0, уй, г0) лежит
между двумя параллельными плоскостями:
Лх + б(/ + Сг+О = 0, Ах+Ву-\-Сг+Е = 0 (D ф £)?
Отв. (Аха + Ву0+Сг0+ D) (Лхо+ Вуо+Сг0+ Е) < 0.
2. Через начало координат провести плоскость, перпендикулярную
плоскости 5х — 2у-\-ог—10 = 0 и образующую с плоскостью х — \у—8г+12 = О
угол 45°.
Отв л: + 20(/+7г = 0 и х — г = 0.
3. Найти угол между двумя плоскостями Ъх-\-у — 2г + 4 = 0, х—
в котором лежит точка A, 1, 1).
Отв. arccos ( ■?=.
V 3/2
4. При каком необходимом и достаточном условии точка (х0, у0, г0) лежит
в остром угле, образованном двул!я пересекающимися и не взаимно
перпендикулярными плоскостями
Отв.
(АХА2+ BiBt + CiC2) {А^о+ВгУо + Cl2o + Ог) (А2х0 + В2уй + С2г0 + D2) < 0.
5. Доказать, что плоскости 11х+10(/ + 2г = 0, Зх + 4(/ = 0, л: — у + г —1=0
образуют призму и вычислить ее внутренний двугранный угол, образованный
первыми двумя плоскостями.
73
Отв. arccos=^.
/о
6. Составить уравнение биссекторной плоскости угла между двумя
плоскостями 2>х-\-Ьу — 4г+1 =0, х —г—5 = 0, в котором лежит начало координат.
Отв. 8х + 5у—9г— 24 = 0.
7. Составить уравнение биссекторной плоскости острого угла между
плоскостями Зх —4|/ + 6г—2 = 0 и yOz.
Отв. C+ У"&\)х — 4(/+6г—2 = 0.
8. Через прямую 2х=г/ = 2г провести плоскость р так, чтобы данная
прямая была биссектрисой угла, образуемого линиями пересечения плоскости р
с плоскостями (/ = 0 и х-|-У = 0.
Отв г/—2г = 0.
9. Найти точку, симметричную точке B, 7, 1) относительно плоскости
х — 4г/ + г + 7 = 0.
Отв. D, —1, 3).
10. Найти точку, симметричную точке D, 3, 10) относительно прямой
х— 1_у—2_г—:3
2 ~ 4 ~~ 5 '
Отв. B, 9, 6).
11. Даны две вершины треугольника А (— 4, —1,2) и S C, 5, —16). Найти
третью вершину С, зная, что середина стороны АС лежит на оси Оу, а
середина стороны ВС— на плоскости хОг.
Отв. С D, —5, —2).
IS. ПРИ.ЧЕРЬГ И ЗАДАЧИ К ГЛАВЕ VI
211
12. Вычислить объем ABCD ориентированного тетраэдра ABCD, грани
которого заданы уравнениями
= 0 (CBD),
= 0 (ACD),
+ Д) = 0 (BAD),
= 0 (ABC).
Отв.
Л4 В4 C4 D4
А2 В2 С2
As В, С3
A-2 02
A, fl, C
4 S» С4
13. Даны четыре точки А (хъ уи 2Х), В (х2, уг, г2), С (.r3, i/3, г3) и
^(-^4. Уь г4,), не принадлежащие одной плоскости. Как определить положение
точки М (х, у, г) относительно тетраэдра ABCD?
Решение. Пусть в ориентированном пространстве задан
ориентированный невырожденный тетраэдр ABCD. Пусть М —произвольная точка
пространства. Числа
CBDM ACDM
ABCD ' ^ IBCD
BADM
ABCD
АВСМ
ABCD
называются барицентрическими координатами точки М относительно
тетраэдра ABCD. Если точка М лежит внутри тетраэдра ABCD, то все тетраэдры
CBDM, АСОМ, ВАША, АВСМ и ABCD
имеют одинаковую ориентацию и, значит, все числа
CBDM, ACDM, BADM, АВСМ, ABCD
одного знака, следовательно, а > 0, р1 > 0, у > О, S > 0. При переходе точки
М через одну из плоскостей граней тетраэдра ABCD соответствующая
барицентрическая координата меняет знак. Если точка М находится в плоскости
одной из граней тетраэдра ABCD, то соответствующая барицентрическая '.оор-
дината равна нулю. Если точки А, В, С, D, М заданы своими координатами
4 (*i> Уи гх), В(х2, (/2. 2г). С (х3, у3, г3), D (х4, уА, г4), М (х, у, г) относительно
аффинной системы координат в пространстве, то
*i Ух Ч 1
Н Уз г3 1
Xi ijt г4 1
х у г 1
ч
х2
х»
X
Ч
х2
х3
х4
Уз
У2
^4
У
У1
Уг
Уз
'Ji
г3
Ч
г4
г
Ч
22
ч
24
1
1
1
1
1
1
1
1
Ч У\ Ч 1
Xi у2 Ч 1
х3 Уз Ч 1
Xi У* 24 1
212
Глава VI. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
xi УхЧ
х2 г/2 г2 1
*з Уз гг 1
х у г 1
Xj Ул 2i
*з Уз ^з
x4 //4 z4
Зная знаки a, P, y> ^> можно определить положение точки М (х, у, г)
относительно тетраэдра ABCD. Пусть, например, a > О, р > О, Y < °> б < 0.
Тогда точка М лежит в области, ограниченной продолжениями граней CAB
и DAB за ребро АБ и продолжениями граней DCA и ВВС за вершины А и В.
Если, например, a < 0, р = 0, у > 0, б < 0, то точка М лежит в плоскости
ACD внутри угла, вертикального углу ACD
Точка М может занимать 65 различных положений относительно
плоскостей, в которых расположены грани тетраэдра ABCD, и прямых, по которым
пересекаются эти плоскости Каждому такому положению точки /И будет
соответствовать своя комбинация знаков для a, f5, у, 8.
14. Относительно общей декартовой системы координат даны вершины
А (хъ уъ гг), В (х2, у2, г2), С (х3, у3, г3) и D (х4, г/4, г4) невырожденного
тетраэдра ABCD. Пусть a, f5, y. б — барицентрические координаты точки М
относительно тетраэдра ABCD. Доказать, что декартовы координаты точки М
выражаются формулами:
0)
Обратно, если a-f-p + Y + ^==^. т0 точка М, декартовы координаты
которой выражаются формулами A), имеет барицентрические координаты а, \°>, у, б.
15. В вершинах А, В, С, D невырожденного тетраэдра помещены массы,
соответственно равные mj, m2, m3, mx. Найти барицентрические координаты
центра тяжести этой системы материальных точек относительно тетраэдра
"авсо.
у=ау1 + р#2
Отсюда
a: E: у: б = mx: m2: m3: m4.
16.„Относительно невырожденного ориентированного тетраэдра ABCD,
лежащего s ориентированном пространстве, даны четыре точки Р (ait pi( ylt 6t),
Q (a2. P2. Y2. S2), ^ (a3, p3, уз. б3) и S (a4, p4, y*> б4) своими барицентрическими
координатами. Найти
PQRS
Jbcd
Найти, в частности, необходимое и достаточное условие принадлежности
четырех точек Р, Q, R, S одной плоскости.
§95. ПРИМЕРЫ И ЗАДАЧИ К ГЛЛВЕ VI
213
Отв.
PQRS
~ШсЪ
Pi Yi
$2 у2
Рз Ys
Pi Yi
a2
Р Ys
a4 Pi Y4 64
17. Относительно общей декартовой системы координат даны три точки
А(хъ Уъ ?i), В (х2, уг, г2), С(х3, г/3. гз)> «е лежащие в одной плоскости с
началом координат. Дана еще точка М (х, у, г), не совпадающая с началом
координат. При каком необходимом и достаточном условии прямая ОМ
пересекает плоскость треугольника ABC в его внутренней точке?
Отв. Числа
X
Ч
х3
У
Уг
Уз
г
гг
г3
X
*з
*i
Уз
Ух
г
?з
zx
X Г/
xi У1
•^г Уг
г
г2
одного знака.
18. Вычислить барицентрические координаты а, Р, y> S точки /И (*, у,
относительно тетраэдра ABCD, грани которого заданы уравнениями
■£>!=(), {BCD),
-£>2 = 0, {ACD),
= 0, (ЛВО),
= 0. (ABC).
Отв.
где
л4
Y = -~ (А Зх + Въу + С3
Д =
А% в% С2 L/g
Л3 Я3 С3 Ds
At B4 C4 D4
А. В,
в4 с4
х В,
ГЛАВА VII
ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ
НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
§ 96. Перенос декартовой системы координат
Рассмотрим на плоскости две общие декартовы системы
координат хОу и х'О'у', имеющие соответственно одинаковые масштабные
векторы (рис. 139). В таком случае говорят, что одна из этих
систем получена переносом другой.
Систему хОу будем называть старой,
а систему х'О'у' — новой.
Обозначим через хй, yQ
координаты нового начала О' в старой
системе.
Рассмотрим проекцию О* точки
О на ось Ох параллельно оси Оу и
введем промежуточную систему
координат x*O*if, полученную
переносом системы хОу, при котором точ-
ка О переходит в точку О*. Точка О*
в системе хОу имеет координаты х0,
О, а точка 0' в системе х*О*у* имеет
координаты 0, у0.
Пусть М — произвольная точка плоскости; х, у — координаты
точки М в системе хОу; х*, г/* —координаты точки М в системе
х*О*г/*; х', у' — координаты точки М в системе х'Оу'.
На основании § 6 имеем
х'
х = х + х0, у у
и аналогично, рассматривая переход от системы x*Q*y* к системе
х'О'у', будем иметь
* ' * '
A)
Таким образом, окончательно
х = х'+х0, у = у'-гуо,
§96. ПЕРЕНОС ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ 215-
т. е. старые координаты х, у точки М соответственно равны
суммам новых координат х', у' этой точки М с соответствующими
координатами х0, у0 нового начала координат в старой системе.
Для двух общих декартовых систем координат Oxyz и О'х'у'г',
полученных одна из другой переносом, т. е. имеющих
соответственно одинаковые масштабные векторы е1( е2, е3 (рис. 140), имеют
место формулы
B)
где х, у, z — координаты любой точки М в системе Oxyz; x',y',z' —
координаты точки М в системе O'x'y'z'; х0, у0, z0 — координаты
точки О' в системе Oxyz.
Рис.
В самом деле, пусть О*(хй, у0, 0) —проекция точки О'на
плоскость хОу параллельно оси Oz. Рассмотрим систему координат
O*x*y*z*, полученную переносом системы Oxyz. Тогда
В системе О*х*у*г* точка О' имеет координаты 0, 0, г0.
Следовательно, х* = х', у*^=у', z*=z' + z0. Отсюда и из предыдущих
соотношений получаем формулы B). Формулы A) и B) называют
формулами переноса системы координат.
Так как координаты вектора АВ, заданного двумя точками
А (*i> Ух, zx) и В(хг, уг, z2), равны хг—xlt уг — у1г гг — гг, то из
формул A) и B) следует, что при переносе общей декартовой
системы координат, координаты вектора не меняются.
216 Глава VII. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОП СИСТЕМЫ КООРДИНАТ
§ 97. Преобразование общей декартовой системы координат
на плоскости
Рассмотрим на плоскости две общие декартовы системы
координат хОу и х'Оу', имеющие общее начало координат О. Пусть
ч системе хОи масштабные векторы осей Ох и Оу будут соответст-
венно ег и е2, а в системе х'Оу'
масштабные векторы осей Ох' н Оу'
будут е1 и е2 (рис. 141).
Рассмотрим произвольную точку М
плоскости; пусть х и у —ее координаты
в системе хОу, ах' и у'— в системе
х'Оу'. Обозначим, наконец, через г
радиус-вектор точки М, т. е. положим
Разлагая радиус-вектор г точки
М по векторам е1 и ег, а также по
векторам ех и е2> будем иметь
Разложим векторы ех и е2 по векторам ех и
е, =
A)
B)
2 2"
Подставляя в соотношение A) вместо ех и е2 их выражения
из формул B), получим
г = x'ei -f y'e2 = дс' (fli^! + о21е2) + у' (a12ex + a22e3) =
= (altxr + a12y') ex -f (a21Jc' -f ai2y') e2. '
С другой стороны,
г = хег-\-уе2.
Отсюда и из предыдущего разложения г по векторам ех и еа
в силу единственности разложения вектора по базису находим
C)
Матрица
Л __
12
a31 a22
называется матрицей перехода от системы хОу к системе х'Оу'.
Числа, расположенные в ее первом столбце, являются
координатами вектора ех оси Ох' в системе хОу (или в базисе ev e2), а чис-
? 97. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ
217
ла, расположенные во втором столбце, — координатами вектора еа
в системе хОу (или в базисе е,, е2).
Так как векторы et и е2 иеколлинеарны, то
D)
т. е. матрица А —невырожденная.
Обратно, если D) —любая невырожденная матрица и на
плоскости введена общая декартова система координат хОу, то,
рассматривая векторы е, и е2, определяемые формулами B), можно
утверждать, что эти векторы
неколлинеарпы, и
интерпретировать соотношения C) как
формулы, связывающие
координаты х, у произвольной точки М
плоскости в системе хОу с
координатами х', у' той же точки
М в системе х'Оу' с тем же
началом координат и
масштабными векторами е, и е2 осей
Ох' и Оу'.
Рассмотрим теперь на плоскости две общие декартовы системы
координат хОу и х'О'у' (рис. 142); обозначим масштабные векторы
осей Ох и Оу в системе хОу соответственно через е1 и е2, а в
системе х'О'г/' масштабные векторы осей OV и О'г/ обозначим
соответственно через е, и е2. Введем промежуточную систему
координат х"О'у" с началом координат в точке 0', полученную
переносом системы хОу. Обозначим координаты произвольной точки
М плоскости в системах хОу, х"О'у" и х'О'у' соответственно через
Тогда
х, у; х", у"; х', у',
х" = апх' + а12у', у" = ай1х' + а22у',
E)
в базисе e
lt
a a
12
где аг1 и о21 — координаты вектора
а22 —координаты вектора ег в базисе ev ea.
Далее, на основании § 96
х = х" + аи У = у"+аг, F)
где а1 и о2 — координаты начала координат О' системы х'О'у'
относительно системы хОу. Из формул E) и F) находим
х = апх' +а12у' + av у=аг1х' + a2iy' + a2. G)
Так как координаты вектора равны разностям соответствующих
координат его конца и начала, то старые координаты х, у вектора
218 ГлаваУП ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ
через его новые координаты х', у' при общем преобразовании
общей декартовой системы координат имеют вид
l2y', y = a21x' i-a22y'. (8)
§ 98. Преобразование общей декартовой системы координат
в пространстве
Аналогично доказывается, что если в пространстве введены
две общие декартовы системы координат Oxyz и O'x'y'z' с общим
началом 0 и если масштабные векторы осей Ox, Oy, Oz
соответственно ev е2, е3, а масштабные векторы осей Ox', Oy', Oz'
соответственно еи е2, е3, то, обозначая через х, у, z координаты
произвольной точки М пространства в системе Oxyz, а через
х'
■3 2
Рис. 143
Рис. 144
х, у, z, а через х', у', z' — координаты той же точки М в системе
O'x'y'z'', будем иметь (рис. 143)
х^аих' + a{iy'-t- auz',
y^=anx'-i-ai2y' + a2Sz', A)
причем
B)
(координаты векторов ех, е2, е3 даны в базисе е17 е2, ег) и, далее,
матрица перехода
Л = ( а21 а22 а23
C)
iS9 ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ 219
невырожденная, т. е.
о,, а
11 "-12 3
¥=0.
Обратно, если Л— любая невырожденная матрица ив
пространстве введена общая декартова система координат, то соотношения A)
связывают координаты х, у, г и х', у', z' одной и той же
точки М пространства в системе Охуг и в системе Ох'у'г' с началом
координат в точке О и масштабными векторами осей Ох', Оу', Oz',
заданными равенствами B) относительно системы Охуг.
Нсли в пространстве введены две общие декартовы системы
координат Охуг и О'х'у'г' (рис. 144), то координаты х, у, г любой
точки М пространства в системе Охуг через координаты х', у', г'
той же точки М в системе G'x'y'z' выражаются соотношениями
х = «пх'-fo12(/'-j-a13?'■
г/ = о21х'+а2,у' + а23г' + а2, D)
г = а31х' + а32г/' + aSsz' -f а8>
где а/й имеют прежний геометрический смысл, а ах, д2, я3—
координаты начала координат О' системы О'х'у'г' в системе Охуг.
При этом общем преобразовании общей декартовой системы
координат старые координаты х, у, г вектора а через его новые
координаты х', у', z' выражаются соотношениями
х = аих' + апу' + alsz',
У = а.21х' + аг2у' + a23z',
z = о<цХ т ^згУ ~т~ Озз^ •
§ 99. Преобразование декартовой прямоугольной системы
координат на плоскости
1. Переход от одной декартовой прямоугольной
системы координат на плоскости к другой
декартовой прямоугольной системе с той же
ориентацией и с тем же началом координат
Предположим, что на плоскости введены две декартовы
прямоугольные системы координат хОу и х'Оу' с общим началом
координат О, имеющие одинаковую ориентацию (рис. 145).
Обозначим единичные векторы осей Ох и Оу соответственно через i и /,
а единичные векторы осей Ох' и Оу' чере: V и /'. Наконец, пусть
а—угол от оси Ох до оси Ох'. Пусть х и у—координаты
произвольной точки М в системе хОу, а х и у' — координаты той же
точки М в системе х'Оу'.
220 ГлаваУП. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАГ
Так как угол от оси Ох до вектора / равен а, то координаты
вектора I'
cos a, sin а.
Угол от оси Ох до вектора /" равен a -f -2-; поэтому координаты
вектора /":
cos|a + -2-J = —sin a, sin
Формулы C) § 97 принимают вид
-я- = cos a.
A)
x = x cos a — y sin a,
у = x' sin a -f- (/' cos a.
Матрица перехода от одной декартовой прямоугольной системы
координат хОу к другой прямоугольной системе х'Оу' с той же
ориентацией имеет вид
Wcosa-sin«\
\sin a cos a/
Матрица
'?' Г1) C)
«21 2 /
называется ортогональной, если сумма
квадратов элементов, расположенных в каждом
столбце, равна 1, а сумма произведений соответствующих
элементов разных столбцов равна нулю, т. е. если
-а» = 1. D)
Таким образом, матрица B) перехода от одной прямоугольной
системы координат к другой прямоугольной системе с той же
ориентацией ортогональная. Отметим еще, что определитель этой
матрицы равен -f-1:
cos a—sin a I ,
I — 1- E)
sin a cos a
Обратно, если задана ортогональная матрица C) с
определителем, равным +1, и па плоскости введена декартова прямоугольная
система координат хОу, то в силу соотношений D) векторы /'=
= {an, a21} и/ = {а12, а22} единичные и взаимно перпендикулярные,
следовательно, координаты вектора /" в системе хОу равны cos a
и sin a, где а —угол от вектора / до вектора/', а так как вектор
§ S9. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ 221
/ единичный и получен нз вектора /' поворотом на -j-y', то
либо/=={— sina, cosa}, либо /' = {sina, —cosa}.
Вторая возможность исключается, так как если бы мы имели
/" = {sina, cosa}, то Det A = —1, а нам дано, что Det A — I.
Значит, #12=—sina, a22 = cosa и матрица А имеет вид
^s a —sin aN
sina cosa
т. е. является матрицей перехода от одной прямоугольной системы
координат хОу к другой прямоугольной системе х'Оу', имеющей
ту же ориентацию, причем (Ох, Ох') = а.
2. Переход от одной декартовой прямоугольной
системы координат на плоскости к другой
прямоугольной системе с противоположной ориентацией
и с тем же началом коордилат
Пусть на плоскости введены две декартовы прямоугольные
системы координат хОу и х'Оу' с общим началом координат О, но
имеющие противоположную ориентацию. Обозначим угол от оси
Ох до оси Ох' через а (ориентацию
плоскости зададим системой хОу).
Так как угол от оси Ох до
вектора /' равен а, то координаты вектора I'
cosa, sina.
Теперь угол от вектора V до
вектора У равен —y (рис. 146),
поэтому угол от оси Ох до вектора j" равен
(по теореме Шаля для углов) a-f-f—y)=a— й потому
координаты вектора /'
cos (a—-^-) = sina, sin (а—-5-) = —cosa.
Формулы C) § 97 принимают вид
x = x' cosa-f-у' sina, у = x' sina — у cosa. F)
Матрица перехода
, /cos a sin a\
A -
4sin a —cosa/
ортогональная, но ее определитель равен — h
Det A = - 1. G)
222 Глава VII ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ
Обратно, любая ортогональная матрица с определителем,
равным— 1, задает преобразование одной прямоугольной системы
координат на плоскости в другую прямоугольную с тем же началом,
но противоположной ориентации. Итак, если две декартовы
прямоугольные системы координат хОу и х'Оу' имеют общее
начало, то
х = Сцх' +с12у', у = с21х' + с2гу\
где х, (/ — координаты любой точки в системе хОу; х и у' —
координаты той же точки в системе х'Оу', а
•-21
ортогональная матрица.
Обратно, если
^С21 С22/
произвольная ортогональная матрица, то соотношениями
выражается преобразование декартовой прямоугольной системы
координат ь декартову прямоугольную систему с тем же началом
■координат; си, с21— координаты в системе хОу единичного
вектора /', дающего положительное направление оси Ox'; cVi, с22 —
координаты в системе хОу единичного вектора f, дающего
положительное направление оси Оу'.
В случае
С21
= 1
системы координат хОу и х'Оу' имеют одинаковую ориентацию,
а в случае Д =—1—противоположную.
3. Общее преобразование одной декартовой
прямоугольной системы координат на плоскости в
другую прямоугольную систему
На основании пунктов 1 и 2 этого параграфа, а также на
основании § 96 заключаем, что если па плоскости введены
прямоугольные системы координат хОу и х'О'у'', то координаты х и у
произвольной точки М плоскости в системе хОу с координатами
х' и у' той же точки М в системе х'О'у' связаны соотношениями
x = A:'cosa—у' sin a, + х0, y = x's\na-\-y'cosa + y0, (8)
если системы хОу и х'О'у' имеют одинаковую ориентацию, и
соотношениями
х = х'cosa + y' s\na-\-x0, y = x' sin a — y'cosa + j/0, (9)
если системы хОу и х'О'у' имеют противоположную ориентацию.
§ 100. ПРЕОБРАЗОВАНИЕ ПРЯМОУГОЛЬНОЙ СИСТЕМЫ 223
В формулах (8) и (9) х0 и у0 — координаты точки О' в системе
хОу, а а = @х, О'х'), причем ориентация плоскости определяется
системой хОу.
Общее преобразование декартовой прямоугольной системы
координат в декартову прямоугольную можно записать и в виде
где
Ли с12\
\С21 С22/
ортогональная матрица, а си с2 — координаты начала О' системы
координат х'О'у' в системе хОу.
Заметим, что старые и новые координаты х, у и х', у' вектора
при общем преобразовании декартовой прямоугольной системы
координат связаны соотношениями
je = A''cosa—у' sin a, у = х' sin a -4- у' cos a
в случае, если системы хОу и х'О'у' имеют одинаковую
ориентацию, и соотношениями
х = х' cos a-f-у' sin a, y = x' sin a—y' cosa
в случае, если эти системы имеют противоположную ориентацию,
или же с виде
* = cux' + c12y', у = сг1х' + сг2у', A1)
где
\С21 С22/
ортогональная матрица. Преобразование A0) и A1) будем называть
ортогональным.
§ 100. Переход от одной декартовой прямоугольной системы
координат к другой прямоугольной системе в пространстве
Введем в пространстве две прямоугольные системы координат
Оху~ и Ox'y'z' с общим началом координат. Обозначим через i,
j, k единичные векторы осей Ox, Oy, Oz, а через i', f, k' —
единичные векторы осей Ох', Oy', Oz' (рис. 147).
Координаты единичного "вектора в ортонормированном базисе
h j> k, т. е. в базисе, векторы которого единичные и попарно
ортогональные, являются косинусами углов между этим
единичным вектором и векторами i, j, k. Обозначая углы между
вектором /' и векторами /, j, k через alf px, Yi, углы между вектором
224 Глава VII ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ
A)
j' и векторами i, j, k через a2, p2, Y2 и углы между вектором k'
и векторами i, j, k через a8, P3, ys, будем иметь (§ 98)
л: = х' cos ax -f- у' cos a2 -j- z' cos a3,
у = л:' cos px + y' cos p2 -\- z' cos p3,
z = л;' cos Yi -f- y' cos y2 + z' cos Ys>
где x, у, г —координаты произвольной точки /И в системе
а х', у', г' — координаты той же точки М в системе Ox'y'z'.
Матрица перехода имеет вид
/ cos ax cos a0 cos a3N
A = cos px cos p2 cos I
\cosyi cos y2 cosy3/
Она ортогональная, т. е. сумма квадратов элементов,
расположенных в каждом столбце, равна 1, так как векторы /', /, k'
единичные, а сумма произведений
соответствующих элементов двух
любых различных столбцов равна нулю
(так как векторы /', /, k' попарно
ортогональные).
Так как определитель Det А
равен
cos аг cos a2 cos a3
P cos p2 cos P3
cos |
COS"
cos
cos
= /'/*'.
Рис. 14.
а векторы V, j, ft'—единичные и
попарно ортогональные, то этот
определитель равен ±1; он равен +1,
если упорядоченная тройка векто-
ро.. i/, f, k' имеет ту же ориентацию, что и упорядоченная
тройка I, j, ft, и —1, если эти упорядоченные тройки векторов
имеют противоположную ориентацию.
Можно сказать и так: детерминант матрицы А равен ±1 в
зависимости от того, имеют ли системы Oxyz и Ox'y'z' одинаковую
или противоположную ориентацию.
Отметим частный случай преобразования декартовой
прямоугольной системы координат в декартову прямоугольную той же
ориентации при условии, что оси Oz и Oz' совпадают. В этом
случае формулы A) принимают вид
p — у' sin ф, у — х' sin cp + y' coscp, z = z',
B)
где ф — угол от осп Ох до оси Ох' в плоскости хОу, причем
ориентацию этой плоскости задаем системой координат хОу. В этом
§ 100 ПРЕОБРАЗОВАНИЕ ПРЯМОУГОЛЬНОЙ СИСТЕМЫ
225
частном случае будем говорить, что система Ox'y'z' получается из
системы Oxyz поворотом вокруг оси Oz на угол ср.
Обратно, пусть задана ортогональная матрица третьего порядка:
А= а
flu a
11 2
а,, а.
'21 2
'81
т. е.
C)
D)
а12ап
Введем в пространстве прямоугольную систему координат
Oxyz. Векторы
l' = {an, C21, C31}, /={Ol2, ^22. Д32}. ^' = {а13. Д23> йЗз) E)
в силу соотношений D) единичные и попарно ортогональные.
Рассмотрим систему Ox'y'z' с
единичными векторами V, J, к'.
Тогда формулы
х = anxf -f- a12y' -f alsz',
y = a21x' + ai2y' + a23z',
z = aslx' + aS2y' + a3Sz'
F)
связывают координаты х, у, г и х , у , г
одной и той же точки М в системах Oxyz
и Ox'y'z'.
Если в пространстве введены две
декартовы прямоугольные системы
координат Oxyz и O'x'y'z', то координаты х, у, Рис. 148
z любой точки М пространства в
системе Oxyz через координаты х', у', г' той же точки в системе
O'x'y'z' выражаются соотношениями (рис. 148):
х = х' cos аг -(- у' cos а2 4- г' cos a3 -f x0,
у = х' cos р\ + у' cos р2 + z' cos p3 + г/о.
г = л:' cos Yi + {/' cos y2 + z' cos y8 + г0,
8 П, G. Моденов
226 Глава VII. ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ
где а1г Pj, Yi, «2. Ра. Уг> аз> Рз> Уз~углы между осями Ох, Оу,
Oz, О'х', 0'y't O'z'i
О'х'
о'у
O'z'
Ох
а2
а3
Оу
Pi
Р2
Ра
Oz
Yi
Ya
Y3
а х0, у0, г0—координаты точки О' в системе Oxyz.
Старые и новые координаты х, у, г и х', у', z' вектора а при
общем преобразовании декартовой прямоугольной системы
координат в декартову прямоугольную имеют вид
Ar = Af'cosa1 -j-г/'cos a2-f г' cosa3.
у = х' cos px-f y' cos p2-f z'cosP3,
z — x' cos уг + у' cos y2 + z' cos y8.
Матрицей А', транспонированной к матрице А, называется
матрица, полученная из матрицы А заменой строк матрицы А
столбцами.
Нетрудно видеть, что матрица А будет ортогональной тогда и
только тогда, когда
АА' = Е,
где
/1 0 On
£=0 1 0
\0 0 X/
единичная матрица.
Так как определитель произведения матриц равен
произведению определителей' сомножителей, то
Det (AA') = Dei A • Det A' = (Det Af = Det E = 1
и, следовательно,
Det A =
т. е. ортогональная матрица Л —невырожденная и ее детерминант
равен или -fl. или —1.
Из соотношения АА' = Е следует, что А'= А'1 (и обратно),
т. е. ортогональная матрица может быть определена как такая,
для которой сопряженная равна обратной.
Так как определитель ортогональной матрицы А равен ±1,
то для ортогональной матрицы алгебраическое дополнение каж-
101. УГЛЫ ЭЙЛЕРА 227
дого ее элемента или равно элементу, расположенному
симметрично рассматриваемому относительно главной диагонали (в
случае Det Л = 1), или отличается от него знаком (в случае Det А——1).
Например, если матрица
А = (а21 а22 а,
fl31 °32 Й33
ортогональная и Det^ = l, то алгебраическое дополнение
элемента с21 будет
Алгебраическое дополнение элемента а31:
а22 а
Это свойство ортогональной матрицы третьего порядка можно
установить, введя в пространстве две декартовы прямоугольные
системы координат: одну Oxyz с единичными векторами /, ], к,
другую Ox'y'z' с единичными векторами
i' = {an, a21, asl}, }' = {a12, a22, as2}, k' = {a13, a2s, a3S}.
Рассмотрим векторные произведения [j"k']t [k'i') и [i'f]. Они
соответственно равны /', j', к', если базисы i, j, k и I', j', к'
имеют одинаковую ориентацию, и — V, —)', —к', если
противоположную.
§ 101. Углы Эйлера
Преобразование декартовой прямоугольной системы координат
Oxyz в декартову прямоугольную систему координат Ox'y'z'
с тем же началом О определяется формулами A) предыдущего
параграфа. Между девятью коэффициентами (cos a{, cos p,-, cos yt,
t = l, 2, 3) имеется шесть соотношений, а именно:
»! ?|
Значит, преобразование одной прямоугольной системы
координат в другую прямоугольную с тем же началом зависит от трех
параметров.
Эйлер показал, что если Oxyz и Ox'y'z'—две прямоугольные
системы координат, имеющие одинаковую ориентацию, то
преобразование одной системы координат в другую можно заменить
тремя преобразованиями, каждое из которых является поворотом
вокруг осей координат одной из данных систем и
вспомогательных прямоугольных систем координат.
228 Глава \'П ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ
Так как плоскости хОу и х'Оу' имеют общую точку, то они
имеют и общую прямую. Ориентируем эту прямую, получим ось
01 (рис. 149).
Рассмотрим еще ось Оц, перпендикулярную осям Oz и Ос, и
направленную так, что системы Oxyz и Oc,r\z имеют одинаковую
»/
ориентацию; эти системы
имеют общую ось Oz,
поэтому вторая система
получается из первой поворотом
вокруг оси Oz на некоторый
угол ф, значит (§ 100,
формулы B))
JC = g COS cp — Т] Sin ф, /,ч
y = g sinq>-f-'»icosq>. * '
Перейдем теперь от
системы О^цг к
прямоугольной системе О1ц'г' (ось Oz'
перпендикулярна оси 0%,
так как ось Ос, лежит в
плоскости х'Оу'; ось Оц' перпендикулярна осям 0%, и Oz' и
направлена так, чтобы обе системы 0%цг и О\ц'г' имели
одинаковую ориентацию).
Система О\ц'г' из системы О&цг получается поворотом вокруг
оси 01 на некоторый угол 6; значит,
ц = ц' cos 6—г' sin 9, ,„.
z = r)'sin 9 +г'cos 9. K)
Система О\ц'г' имеет ту же ориентацию, что и система Oxyz,
а значит ту же ориентацию, что и система Ox'y'z', Поэтому
система Ox'y'z' получается из системы О\ц'г' поворотом вокруг
оси Oz' на некоторый угол -ф, следовательно,
Рис. 149
ц'—х' sin^-L-t/'cos^. ^'
В формулах A) — C) х, у, z—координаты произвольной точки М
пространства в системе Oxyz; g, ц, z— координаты той же точки
в системе 0\цг, \, ц', z' — координаты той же точки в системе
О\ц'г' и х', у', г' — координаты той же точки в системе Ox'y'z'.
Исключая из написанных соотношений g, tj, г|', получим
х=л;'(соз ф cos г|>—sin ф sin г|> cos 9)—у' (cos ф sin ф+вШф cos ty cos 9)-f-
+ z'sin фз}п9,
y = x' (sin фсоэ tp -|- cos ф sin i[)cos9) — у' (эф
—cos ф cos iC cos 9)—z' cos ф sin 9,
z = x' sin я|) sin 0 (-f/'cos\j) sin 9-f-z'cos 0.
sin ty —
§ 101. У! ЛЫ ЭЙЛЕРА 229
Углы ф, ty, 9 называются углами Эйлера. Матрица этого
преобразования ортогональная, так как она является матрицей
перехода от одной декартовой прямоугольной системы координат к
другой прямоугольной системе (той же ориентации); это следует и
из того, что она является произведением матриц
/cos ф—sin ф 0\ /1 0 0 \ /cos гр — sin -ф 0\
(sincp coscpO), I 0 cos0 — sin9 ), (sinip cos\jH],
V 0 0 1/ V0 sin 9 cos 9/ \ 0 0 1/
каждая из которых—ортогональная.
Если какая-нибудь из осей Ox, Oy, Oz совпадает с
соответствующей осью Ox', Oy', Oz', то формулы упрощаются (одну систему
координат можно перевести в другую одним поворотом).
Замечание. Углы ф, 9 и ij; могут принимать значения от
0 до 2л (как углы от одного луча до другого на соответствующей
координатной плоскости). Однако если положительное
направление оси Ос, выбрать так, чтобы тройка лучей Oz, Oz', 01 имела
такую же ориентацию, как и тройка Ox, Oy, Oz, то угол 9 будет
принимать значения от 0 до я.
ГЛАВА Vffl
ЛИНИИ ВТОРОГО ПОРЯДКА, ЗАДАННЫЕ КАНОНИЧЕСКИМИ
УРАВНЕНИЯМИ
М(х.Ч)
§ 102. Эллипс и его каноническое уравнение
Определение. Эллипсом называется геометрическое место точек,
для каждой из которых сумма расстояний до двух фиксированных
точек плоскости, называемых фокусами, есть данное число 2а,
большее, чем расстояние 2с между фокусами.
Пусть М — произвольная точка эллипса, a Fx и F2~evo
фокусы. Отрезки MFX и MF2 так же, как и длины этих
отрезков, называются фокальными
радиусами точки М эллипса. В силу
данного определения эллипса (рис. 150)
MFX + MF2 = 2а. A)
Из определения эллипса вытекает
следующий способ его
вычерчивания. Воткнем в чертежную доску
две булавки и накинем на них
замкнутую нить, длина которой равна
2а-'г2с. Натянем нить карандашом
(рис. 151) и будем передвигать его,
держа нить все время натянутой. Карандаш опишет эллипс, так как
сумма MFx-\- MF^ расстояний от острия М карандаша до точекFx
и F2, в которые воткнуты булавки, во время движения острия
карандаша по бумаге не будет изменяться, оставаясь равной 2а.
Введем на плоскости прямоугольную систему координат,
принимая середину отрезка F^ за начало координат, а за ось Ох—
прямую FXF%, ориентированную от точки Fx к точке F2. В
выбранной системе координат фокус Fx будет иметь координаты —с,
0, а фокус /^ — координаты с, 0. Обозначая координаты точки М
эллипса через х и у, будем иметь
/И/г1= У\х -j-'c)i+~yi
/j(c,o)
Рис. 150
102 ЭЛЛИПС И ЕГО КАНОНИЧЕСКОЕ УРАВНЕНИЕ
231
н соотношение A) принимает вид
V (x + cy + i/ + ^(
у* = 2а,
или
B)
Возводя обе части уравнения B) в квадрат, получим
х2 + 2сх + с* + у2 = 4а2 + х2 — 2сх + с2 + у2 — 4aV(x —c)*
или
а У х2 —
или
Рис. 151
Возводя обе части этого уравнения в квадрат, получим
• а2х2 — 2а2сх + а2с2+с2у2 = а* — 2а2сх + с2х2,
(а2 — с2) х2 + а У = а2 {а2 — с2).
Так как по условию а>с, то а2—с2 > 0. Обозначая а2 —са
через б2
получим
или
с2—с2 =
— + — =1
о2 ^ б2
C)
D)
Мы доказали, что координаты любой точки М(х, у) эллипса
удовлетворяют уравнению D). Однако уравнение D) еще нельзя
назвать уравнением эллипса, так как не доказано обратное
предложение, а именно: если числа х и у удовлетворяют уравнению D),
232
Глава VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
то точка М с координатами х и у удовлетворяет соотношению
MFj. + MF2 = 2а,
т. е. лежит на эллипсе.
Докажем это. Пусть координаты точки М (х, у) удовлетворяют
уравнению D). Тогда
MF, =
/с2л:2
сх
-
и аналогично
Так как
MFt =
СХ
то ]д;|^а, а так как 0<с<а, то а + — >0 и а— — > 0, сле-
довательно,
E)
откуда
X -f MF2 = 2a.
Таким образом, D) есть уравнение эллипса, так как доказано,
что координаты любой точки М эллипса, т. е. любой точки, для
которой
удовлетворяют уравнению D), и, обратно, если два числа х и у
удовлетворяют уравнению D), то точка М с этими координатами
х я у удовлетворяет соотношению
т. е. лежит на эллипсе.
Уравнение
называется каноническим уравнением эллипса.
103. ИССЛЕДОВАНИЕ ФОРМЫ ЭЛЛИПСА
233
§ 103. Исследование формы эллипса
Так как в каноническое уравнение эллипса координаты х и у
входят в четной степени (именно во второй), то если на эллипсе
лежит точка М(х, у), т. е. координаты этой точки удовлетворяют
уравнению A), то на том же эллипсе лежат точки М'(х, —у) и
М" {—х, у), симметричные с
точкой М относительно осей Ох и Оу,
и точка ЛГ"( — х, —у),
симметричная с точкой М относительно
начала координат (рис. 152).
Поэтому оси координат Ох и Оу для
эллипса, заданного каноническим
уравнением
х=-а
1
Рис. 152
являются осями симметрии, а
начало координат — центром
симметрии. Ниже мы покажем, что всякий эллипс имеет
единственный центр симметрии, а если он не является окружностью, то —
только две оси симметрии.
Из уравнения эллипса
следует, что для координат любой его точки имеют место
соотношения
Геометрически это значит, что эллипс расположен внутри
прямоугольника, сторонами которого являются прямые
Точки пересечения эллипса с его осями симметрии называются
вершинами эллипса. Таким образом, эллипс
имеет четыре вершины:
А^-а, 0), А, (а, 0), B^O.-fr), £2@, Ь).
Полуосью эллипса называется отрезок (а также длина этого
отрезка), одним концом которого является центр симметрии эллипса,
а другим — одна из его вершин; а называется большей полуосью
эллипса, a b — меньшей полуосью,
234 Глава VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
Отрезок AlAi, граничными точками которого являются
вершины At и Д2 эллипса, расположенные на оси симметрии,
содержащей фокусы (а также длина 2а этого отрезка), называется
большей осью эллипса, а отрезок ВхВг и его длина 2Ь — меньшей осью
эллипса.
Разрешая уравнение эллипса относительно ординаты у, беря
для у лишь неотрицательное значение
и считая, что О^х^а, получим точки эллипса A), лежащие
в первой четверти. Из уравнения B) следует, что функция у на
сегменте 0^х^а— убывающая
функция, причем х — О при у — b ил: = апри
у = 0 (рис. 153).
График эллипса в целом мы
получим, добавив к дуге, заданной
уравнением B), дуги, ей симметричные от-
—■"х носительно осей координат и начала
координат. В результате получим
замкнутую линию (см. рис. 152).
Рис. 153 Замкнутая линия является
выпуклой, если любая прямая
пересекает ее не более чем в двух точках. Эллипс есть выпуклая
замкнутая линия, так как решая уравнение A) эллипса совместно
с уравнением прямой y — kx-~tn или х — р, получим уравнение
второй степени относительно х или у, значит, любая прямая
пересекает эллипс не более чем в двух точках.
Итак, эллипс —замкнутая выпуклая линия, имеющая центр
симметрии и две (взаимно перпендикулярные) оси симметрии.
Условимся уравнение
называть каноническим уравнением эллипса и в том случае,
когда а = Ь и когда а < Ь.
В случае а = Ь уравнение принимает вид
т. е. является уравнением окружности радиуса а с центром
в начале координат. Таким образом, мы рассматриваем
окружность как частный случай эллипса. Этот частный случай
соответствует совпадению фокусов Fx и F2 с центром окружности. В
случае а < b большей полуосью будет Ь, меньшей а, фокусы
расположены на оси Оу на расстоянии Vb — а2 от центра эллипса.
В дальнейшем, если не будет специальной оговорки, мы будем
предполагать, что в каноническом уравнении A) эллипса а>&.
§ 104 ДИРЕКТРИСЫ ЭЛЛИПСА 235
Отношение половины расстояния между фокусами эллипса
(фокальное расстояние) к большей полуоси эллипса называется
эксцентриситетом эллипса и обозначается буквой е:
Так как О^с<а, то 0^е<1, т. е. эксцентриситет эллипса
есть неотрицательное число, меньшее 1.
Отметим, что
Следовательно, эксцентриситет определяется отношением
полуосей эллипса, и, обратно, отношение полуосей эллипса
определяет его эксцентриситет. Если эксцентриситет равен нулю е = 0,
то а = Ь и эллипс является окружностью. Чем ближе
эксцентриситет е к 1, тем меньше ]/l— e2 и, значит, тем меньше
отношение меньшей полуоси к большей. Таким образом, эксцентриситет
характеризует степень «вытянутости» эллипса.
Формулы E) § 102 теперь можно записать:
г1 = а-\-ех, г2 = а—ех, C)
где
§ 104. Директрисы эллипса
Две прямые, перпендикулярные оси эллипса, на которой
расположены его фокусы, и отстоящие от центра эллипса на
расстоянии — , где а—большая полуось эллипса, а е — его
эксцентриситет, называются директрисами эллипса.
Окружность (для которой е = 0) не имеет директрис; таким
образом, понятие директрис дается собственно для эллипса, т. е.
для эллипса с неравными полуосями. Если эллипс задан
каноническим уравнением
„2 ,,2
ZУ 1
Ь2 ~ '
а2
причем а > b (фокусы расположены на оси Ох), то уравнения
директрис имеют вид
а а
х-— И Х=
е е
Так как собственно для эллипса 0<е<1, то— > а и, зпа-
чит, директрисы эллипса отстоят от его центра дальше, чем
вершины (рис. 154). Фокус и директриса эллипса, расположенные по
236
Глава V111 КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
одну сторону от меньшей оси эллипса, называются
соответствующими друг другу.
Таким образом, фокусу Fx{— с, 0) соответствует директриса
х — —— , а фокусу F2(c, 0)—директриса х = ~ .
Теорема. Для того чтобы точка лежала на эллипсе, необходимо
и достаточно, чтобы отношение расстояния от этой точки до
фокуса эллипса к расстоянию от
той же точки до директрисы,
соответствующей
рассматриваемому фокусу, было равно
эксцентриситету эллипса.
Доказательство
необходимости. Рассмотрим,
например, фокус F% (с, 0) и
соответствующую ему директрису х =— .
Ряс. 154 е
Расстояние г2 от точки М (х, у)
эллипса до фокуса F2 (с, 0) вычисляется по формуле г2 = а—ех
(§ 103, формулы C)).
Расстояние d2 от той же точки М (х, у) эллипса до прямой
вычисляется по формуле
а
X
е
(что следует из рис. 154, но может быть получено и по формуле
расстояния от точки до прямой; см. § 63, уравнение х ——=0
■— нормальное).
Итак,
а
е
ех—а
е
ех—а
а—ех
Отсюда
Аналогично доказывается, что
■ = е,
где гх есть расстояние от точки М эллипса до его фокуса Flt a
d1 — расстояние от той же точки до директрисы х~——>
соответствующей фокусу Fx.
§101. ДИРЕКТРИСЫ ЭЛЛИПСА 23/
Доказательство достаточности. Возьмем каноничес-'
кое уравнение эллипса
2 2
где а>Ь. Рассмотрим, например, фокус F2(c, 0) этого эллипса и
соответствующую ему директрису х = — •
Пусть М (х, у)—такая точка, что
где r2 — расстояние от точки М до фокуса F2, a d2—расстояние
от точки М до директрисы х = — .
Докажем, что точка М(х, у) лежит на эллипсе
В самом деле, так как
~=е , или г\ —егй\,
то из соотношения
находим
Упрощая это уравнение, получим
— 4-— = 1
аа i- ba — J.
а это и означает, что точка М (х, у) лежит на эллипсе.
Расстояние т от фокуса эллипса до его директрисы равно
а эксцентриситет определяется формулой
£_
Из этих соотношений находим
те е2т
Отсюда следует, что если на плоскости задана произвольно
точка F, прямая, не проходящая через эту точку F (отстоящая
238 Глава VIII КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
от точки F па расстоянии т.) и задано произвольное
положительное число е, меньшее 1, то существует эллипс, для которого
точка F — фокус, заданная прямая —директриса, а е —
эксцентриситет. Центр этого эллипса находится на расстоянии
"-1-е»
от точки F (по одну сторону с точкой F от данной прямой), а
большая полуось
те
О =
Отсюда и из только что доказанной теоремы следует, что
эллипс можно определить как геометрическое место точек, для
каждой из которых отношение расстояния от данной точки F к
расстоянию до данной прямой d, не проходящей через точку F,
равно данному положительному числу, меньшему 1.
Исключение составляет окружность, которая указанным
свойством не обладает.
§ 105. Эллипс как образ окружности при равномерном сжатии
к ее диаметру
Фиксируем на плоскости прямую /, а также число 1гФ§
(положительное или отрицательное).
Пусть М — произвольная точка плоскости. Проведем через
точку М прямую т, перпендикулярную прямой /; обозначим через
Р точку пересечения прямых / и т. Поста-
"' вим в соответствие точке М точку М', такую,
что
(такая точка М' существует и притом толь-
—I ко одна). Заметим, что если k>0, то точки
М и М' лежат по одну сторону от прямой /,
/л а если k < 0, то —по разные.
Рассмотрим преобразование точек плос-
Рис. 155 кости, при котором точке М ставится в
соответствие точка М' (рис. 155). Это
преобразование называется равномерным сжатием плоскости к прямой
/, число k — коэффициентом сжатия. Точка М' называется образом
точки М, а точка М —прообразом точки М' при рассматриваемом
преобразовании.
Если прямую / ориентировать и принять ее за ось Ох
декартовой прямоугольной системы координат, то координаты обра-
; 105. ЭЛЛИПС КАК ОБРАЗ ОКРУЖНОСТИ
239
за М'(х', у') через координаты прообраза М{х, у) будут
выражаться соотношениями (рис. 156)
у'= ky, х' — х (на рис. 156 k выбрано равным-!^
ч 3 /
A)
Заметим, что если |&|> 1, то фактически происходит
растяжение плоскости от прямой /; однако и в случае | k | > 1 это
преобразование будем называть сжатием (с коэффициентом сжатия,
таким, что \k{> 1).
При сжатии плоскости к прямой / каждая точка М прямой /
совпадает с ее образом М'. То же обстоятельство, но уже для
всех точек плоскости имеет место, если k=l. Если k — — 1, то
имеем симметрию
относительно прямой /. Подробно
о преобразованиях
плоскости и пространства см.
гл XIII и XIV.
*М(х,у)
р
Рис. 156
-Я
Рис. 157
Теорема. При равномерном сжатии плоскости к диаметру
окружности образом окружности является эллипс.
Обратно, каждый эллипс может быть получен как образ
окружности при равномерном сжатии плоскости к диаметру этой
окружности.
Доказательство. Рассмотрим окружность
X2 + Y2 = а2
B)
радиуса а с центром в начале координат.
Произведем равномерное сжатие плоскости к оси Ох с
коэффициентом сжатия 0< k <. 1.
Пусть при этом сжатии образом точки @, а) будет точка (О, Ь)
(рис. 157); тогда b — ka и коэффициент k сжатия выразится в виде
ь
k==J> C)
240 Глава VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ _^^
Таким образом, формулы A) принимают вид
х = Х, У = ~¥, D)
откуда
Х — х Y=r —
и, значит, координаты любой точки (х, у), являющейся образом
точки окружности
удовлетворяют уравнению
или
Обратно, если координаты х и у удовлетворяют уравнению
вида E), то координаты
удовлетворяют уравнению B), т. е. произвольный эллипс E)
является образом окружности при равномерном сжатии плоскости
к диаметру окружности.
§ 106. Параметрические уравнения эллипса
Пусть дан эллипс каноническим уравнением
53 + 5* = 1- 0)
Рассмотрим окружность
Х2 + К2 = й2, B)
которая переходит в данный эллипс в результате сжатия
х = Х, y=^Y. C)
Пусть М (х, у) — произвольная точка данного эллипса, Р (X, Y)—
ее прообраз на окружности B). Обозначим через ф угол от
положительного направления оси Ох до луча ОР.
Тогда
X = acoscp, K = asincp
и, следовательно,
p, у — — Y — — a sin cp = 6 sin <p.
§ 107. ПОСТРОЕНИЕ ЭЛЛИПСА ПО ТОЧКАМ
241
Уравнения
= acoscp, у = fr sin
и являются параметрическими уравнениями эллипса.
Параметр ср называется эксцентрическим углом точки
эллипса. Если задана точка М эллипса, то для нахождения ср надо
построить окружность на
большей оси эллипса как па диаме- У
тре и через точку М провести
прямую, параллельную малой
оси эллипса. Точка Р (X,Y)
пересечения этой прямой с
окружностью, лежащая по ту
же сторону от большей оси
эллипса, что и точка М, является
прообразом точки М(х, у) при
равномерном сжатии C); угол
от оси Ох до луча ОР и
является эксцентрическим углом ср,
соответствующим взятой точке
М на эллипсе (рис. 158):
= {Ох, ОР).
Рис. 158
§ 107. Построение эллипса по точкам
Построим две окружности с центром в начале координат,
радиусы которых а и Ь равны соответственно большой и малой
полуосям эллипса. Проведем из начала координат произвольный луч,
пересекающий эти окружности соответственно в точках А и В.
Проведем через точку А прямую, перпендикулярную оси Ох, а
через точку В —прямую, перпендикулярную оси Оу. Пусть М —
точка пересечения этих прямых. Тогда точка М лежит на эллипсе
с полуосями а и Ь, для которого оси координат являются осями
симметрии. В самом деле, координаты точки А
а координаты точки В
acoscp, asmcp,
frcoscp, 6 sin ср.
Так как точка М лежит на прямой, проходящей через точку А
перпендикулярно оси Ох, то точки А и М имеют одинаковые
абсциссы, а так как точка М лежит на прямой, проходящей
через точку В перпендикулярно оси Оу, то точки М и В имеют
одинаковые ординаты, поэтому абсцисса точки М равна л: = acoscp,
242
Глава VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИИ
а ордината y=:bs'm((i. Следовательно, точка М лежит на эллипсе
v2 <<2
Проводя через точку О различные лучи, мы указанным путем
построим сколько угодно точек эллипса (рис. 159).
*-х
Рис 159
Рис. 160
§ 108. Вычерчивание эллипса непрерывным движением
Пусть отрезок АВ постоянной длины скользит своими концами
Л и В по двум взаимно перпендикулярным прямым. Примем эти
прямые за оси декартовой прямоугольной системы координат
(рис. 160). Фиксируем на движущейся прямой АВ произвольную
точку М(х, у), отличную от точек А и В. Докажем, что точка М
при указанном скольжении отрезка АВ опишет эллипс
где
а=:АМ, Ь = ВМ.
В самом деле,
х = коорд. пр. ox AM, у = коорд. ар.оуВМ.
Если векторы AM и ВМ имеют одинаковое направление, то,
полагая {Ox, AM) — ф, будем иметь (теорема 4§ 11) x — i
109 ЭЛЛИПС КАК ПРОЕКЦИЯ ОКРУЖНОСТИ
243
Если же векторы AM и ВМ имеют противоположное
направление, то, полагая
(AM, Ох) = ф,
будем иметь
(Ох,А~М) = ~(AM, Ох) = — ц>,
(Оу, В~М) = (Оу, Ох)-\-(Ох, А~М) + (А~М,
= g ф + Я = -^ ф
и, значит, по-прежнему
х = асозф, w = ocos -s—ю =osinro.
В обоих случаях ф изменяется от 0 до 2л, значит, точка
М(асозф, Ь sin ф) описывает эллипс
у2 „2
целиком.
На указанном принципе основан
прибор, называемый эллиптическим
циркулем. В металлической доске
сделаны два прореза под прямым
углом. В этих прорезах ходят
ползуны, к которым прикреплена
шарнирами А и В линейка АВ. На
линейке в любом ее месте при помощи
муфты М может быть закреплен
карандаш. Из предыдущих
рассуждений следует, что при непрерывном движении линейки острие
карандаша опишет эллипс (рис. 161).
§ 109. Эллипс как ортогональная проекция окружности
Пусть в плоскости а дан эллипс с полуосями а и Ъ\ его можно
рассматривать как образ окружности С при равномерном сжатии
плоскости а к ее диаметру с коэффициентом сжатия k = —.
ПроМ
Рис. 161
ведем через большую ось эллипса плоскость
к плоскости а под углом со, таким, что
наклоненную
COSO)=— ,
а '
и построим в плоскости § на большей оси эллипса как на
диаметре окружность С* (рис. 162). Тогда данный эллипс является
244
Глава VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
Я
ортогональной проекцией построенной окружности С* на
плоскость а.
В самом деле, пусть R— произвольная точка окружности С*,
а М— ее ортогойальная проекция на плоскость а. Докажем, что
точка М лежит на данном
эллипсе. Опустим из точки R
перпендикуляр RQ набольшую
ось эллипса и соединим точку
Q с точкой М. Прямая QM
также будет перпендикулярна
АВ (на основании теоремы о
трех перпендикулярах). Таким
образом, угол MQR является
линеййым углом двугранного
угла между плоскостями а и
§, а потому
QM = QR cos со = RQ - ,
Рис. 162
откуда
QM_ Ь
QR~ a '
Продолжим луч QM за точку М до встречи с окружностью С
в точке Р. Так как QR = QP и направленные отрезки QM и QP
направлены в одну сторону, то
QM
QP
и, следовательно, точка М лежит на эллипсе. Обратно, пусть
точка М лежит на рассматриваемом эллипсе, т. е.
QM
Обозначим через R точку плоскости §, проекцией которой
является точка М. Тогда QR±AB, а потому
Итак,
откуда
MQ_MQ
QR PQ '
и, значит, точка R лежит на окружности С*.
110 КАСАТЕЛЬНАЯ К ЭЛЛИПСУ
245
Аналогичными рассуждениями можно до-казать, что всякий
эллипс можно спроектировать ортогонально в окружность; для этого
надо в качестве плоскости проекции взять плоскость, проходящую
через малую ось эллипса и наклоненную к плоскости, в которой
лежит эллине, под углом со, таким,
что (рис. 163)
cos со = — .
а
Обратно, если некоторая плоская
линия проектируется в окружность,
то эта линия является эллипсом.
Отсюда следует, что плоскость,
пересекающая все образующие
какого-нибудь прямого круглого
цилиндра, рассекает его по эллипсу, так
как если это сечение
спроектировать в плоскость, пересекающую все
образующие цилиндра под прямым углом, то в проекции получится
окружность.
§110. Касательная к эллипсу
Уравнение касательной в пеособой точке (х0, у0) к линии,
заданной неявным уравнением*
Рис. 163
= 0,
пишется в виде
F'x(x0,
A)
где Fx(x0, Уо) и Fy(x0, Уо) — значения частных производных от
функции F(x, у) в точке (х0, у0).
Для эллипса, заданного каноническим уравнением
Х2 „2
уравнение касательной в точке (х0, у0), лежащей на этом эллипсе,
имеет вид
/ х2 у2 \
(так как -^ + -р-= I)
УоУ _
исчисления
См. Г. М. Фихтенгольц. Курс дифференциального и интегрального
тения, т, I. M., Физматгиз, 1958» гл. VII, § 2, стр. 530.
246 Глава VI// КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИИ
. ■ , ' '. ■■■■ - ■ - ,_ , ■■-;.■ ■■ _;
§ 111. Оптическое свойство эллипса
Теорема. Касательная к эллипсу в произвольной его точке Мй
является биссектрисой внешнего угла Мо треугольника F1F2M0,
имеющего своими вершинами фокусы Ft и F2 эллипса и данную
точку Мо.
Доказательство. Рассмотрим уравнение касательной к
эллипсу
а2 + Ь* -1
в данной на нем точке MQ (xQ, у0):
хох I УаУ 1 __ л
а2 + Ь2 —I-"-
Отношение расстояний пг и h2 от фокусов F1 (—с, 0) и F2 (с, 0)
эллипса до касательной в точке М0(х0, у0) равно отношению
модулей результатов подстановки координат фокусов F1 и Fa в
левую часть уравнения касательной:
:
сх0 ,
а2
а
а
Отметим, что результаты подстановок Ц- — 1 и Щ- — 1
координат фокусов Fx(—с, 0) и F2{c, 0) в левую часть уравнения
касательной —числа одного знака:
поэтому оба фокуса Fj и F2 расположены по одну сторону от
касательной к эллипсу в произвольной его точке.
Обозначим через Рх и Р2 основания перпендикуляров,
опущенных из фокусов эллипса на касательную к нему, проведенную
в точке Мо (рис. 164). Тогда Д /11Р1М0~Д F2P2M0, так как оба
они прямоугольные, и по доказанному
поэтому
/.F.M.P^^F.M.P,,
следовательно, угол РХМОРХ равен углу РХМ^, где точка Q
лежит на продолжении отрезка F2M0 за точку Мо.
Из этой теоремы непосредственно вытекает способ построения
касательной к эллипсу в произвольной его точке.
§112 ГИПЕРБОЛА И ЕЕ КАНОНИЧЕСКОЕ УРАВНЕНИЕ
247
Доказанной геореме можно дать следующую физическую
интерпретацию: если поместить в один из фокусов эллипса источник
света, то лучи после отражения от эллипса соберутся в другом
Рис. 164
Рис 165
фокусе, так как световой луч отражается от эллипса, как от
касательной, проведенной к эллипсу, в точке падения луча (рис. 165).
Слово «фокус» по латыни означает «очаг».
§ 112. Гипербола и ее каноническое уравнение
Определение. Гиперболой называется геометрическое место точек,
для каждой из которых абсолютная величина разности расстояний
до двух фиксированных точек плоскости, называемых фокусами, есть
—..и
Рис. 166
данное положительное число 2а, меньшее, чем расстояние 2с между
фокусами.
Пусть М —произвольная точка гиперболы, a Fx и F2—ее
фокусы. Отрезки FXM. и F%M так же, как и их длины, называются
248 Глава VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
фокальными радиусами гиперболы. Поэтому
Из определения гиперболы вытекает следующий способ ее
вычерчивания (рис. 166). Берем линейку, длина которой больше 2а,
и к одному ее концу прикрепляем нить такой длины, чтобы
разность между длиной линейки и длиной нити была равна 2а.
Второй конец линейки закрепляем в одном фокусе так, чтобы
линейка могла свободно вращаться вокруг него, а второй конец
нити закрепляем в другом фокусе. Если удерживать острием
карандаша нить в натянутом вдоль линейки положении, как
указано на рис. 166, то при вращении линейки карандаш
перемещается и его острие описывает ветвь гиперболы, внутри которой
лежит-тот фокус, в котором закреплена нить.
Введем на плоскости прямоугольную систему координат,
принимая середину отрезка FXF2 за начало координат, а за ось Ох —
прямую /г1/?г, ориентированную от точки Fx к точке F%. В
выбранной системе координат фокус Fx имеет координаты —с, 0, а
фокус F2 — координаты с, 0. Обозначая координаты точки М гиперболы
через хну, будем иметь
MF, = V(x + c)* + y\ MF2 = У(х-
и соотношение A) принимает вид
1 = 2а.
Преобразуя это уравнение так же, как и для эллипса (§ 102)
2a,
и т. д.,
получим уравнение
(а2 — с2) х2 + а2у2 = а2 (а2 — с2).
Однако теперь а<.с. Обозначая разность а2 —с2 через —б2:
а2-с2 = —б2,
или
с2 = а2 + 62, B)
имеем
или
о2 b2 ( '
Итак, координаты любой точки гиперболы удовлетворяют
уравнению C). Докажем обратное: если координаты некоторой
§112. ГИПЕРБОЛА И ЕЕ КАНОНИЧЕСКОЕ УРАВНЕНИЕ 249
точки М(х, у) удовлетворяют уравнению C), то
\MF1-MFt\ = 2a.
Для этого найдем расстояния r1 — MFl и rz = MF% от этой
точки до точек Ft и F2'
r^MF^Vix-
— |/ x* 4- lex -\ c2-
и аналогично
Из равенства
, i2.v2
y2
5з"
= T/
P2 =
i/2
7(
ex
a
(* +
a2 +
o2
— a
1
сJ + Ь2(~—Л =
b2 x2 + 2cx -f с2 Ь2
л; \а_
ca:
-
•
следует, что \х\^а.
Если х^а, то в силу соотношения с>а>0 будем иметь
а потому
ex
2
= a
a
если xssa. D)
Если же л; ^ — а, то
а потому
) ( } если ^<-а. (б)
Таким образом, если х^а, то гг — г2 = 2а, а если х^ — а, то
гх — гг = —2а; в обоих случаях
Итак, мы доказали, tito координаты любой точки гиперболы
удовлетворяют уравнению
* э
а2 б2
250 Глава VIII КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
и обратно: если координаты точки удовлетворяют этому уравнению,
то эта точка лежит на рассматриваемой гиперболе.
Следовательно, уравнение
a2 i2 1
является уравнением гиперболы; оно называется каноническим
уравнением гиперболы.
§ 113. Исследование формы гиперболы
Так как в каноническое уравнение гиперболы координаты х и у
входят во второй степени, то оси Ох и Оу являются осями
симметрии гиперболы, заданной уравнением
а начало координат — центром симметрии. Ниже мы покажем, что
каждая гипербола имеет единственный центр симметрии и только
две (взаимно перпендикулярные) оси симметрии.
Из уравнения A) следует, что
т. е. или х^а, или #^—а. Геометрически это означает, что
между прямыми х — а и х = — а нет ни одной точки гиперболы A).
Ось симметрии Оу не пересекает гиперболу, заданную
уравнением A), и называется мнимой осью; ось Ох пересекает гиперболу
A) в двух точках:
Аг(— а, 0) и А% (а, 0).
Эта ось называется действительной осью гиперболы. Точки, в
которых действительная ось пересекает гиперболу, называются
вершинами гиперболы.
Числа а и Ъ в каноническом уравнении A) гиперболы
называются соответственно действительной и мнимой полуосями
гиперболы.
Решая уравнение A) относительно у, беря для у лишь
положительное значение:
и считая х^а, мы получим точки гиперболы A), лежащие в первой
четверти. Из уравнения B) следует, что у в полуинтервале
^ оо есть возрастающая функция; при этом
Ит у— -\- оо.
Х-* +(Я
§113 ИССЛЕДОВАНИЕ ФОРМЫ ГИПЕРБОЛЫ
251
Всякая прямая пересекает гиперболу не более чем в двух
точках, так как прямая определяется уравнением первой степени, а
гипербола — второй.
Рассмотрим уравнение прямой
»-!*■ C)
Найдем расстояние d от точки М (х, у), лежащей на дуге
гиперболы, определяемой уравнением B), до прямой C); переписывая
уравнение C) в виде Ьх—ау~0, находим
йа2
Отсюда следует, что на полуинтервале [а, +°°) расстояние d
от точки М (х, у) рассматриваемой части гиперболы до прямой C)
есть убывающая функция от х и lim d = 0 (рис. 167). Прямая,
X -++00
определяемая уравнением
называется асимптотой гиперболы
В силу того что гипербола,
заданная каноническим уравнением, сим- Рис. 167
метрична относительно начала
координат, расстояние от точки М (х, у), лежащей на дуге гиперболы,
заданной уравнением у= ——Ух2 —а2, до прямой у = — х
стремится к нулю при х"-^-—оо. Так как гипербола, заданная
каноническим уравнением, симметрична и относительно оси Оу, то
она имеет вторую асимптоту
которая обладает свойством, аналогичным свойству первой
асимптоты по отношению к дугам гиперболы, расположенным во
второй и четвертой четвертях.
Асимптоты гиперболы являются диагоналями *
прямоугольника с вершинами Р(а, b), Q(a, —b), R{ — a, b), S( — a, —b).
* Здесь под диагональю прямоугольника мы понимаем всю прямую,
соединяющую противоположные вершины прямоугольника.
252
Глава VIII КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
При одной и той же абсциссе х ординаты точки ветви
гиперболы, лежащей в первой четверти, с ординатой точки асимптоты
у——х связаны неравенством
Отсюда и из того, что гипербола симметрична относительно
осей координат, следует, что она имеет две ветви, заключенные в
Рис. 168
двух областях: одна из них ограничена отрезком PQ и
продолжениями отрезков ОР и 0Q за точки Р и Q, другая
симметрична этой области относительно мнимой оси гиперболы (рис. 168).'
Гипербола, у которой полуоси равны, называется
равносторонней. Каноническое уравнение равносторонней гиперболы имеет вид
Уравнения асимптот равносторонней гиперболы таковы:
это биссектрисы углов между ее осями симметрии. Асимптоты
равносторонней гиперболы взаимно перпендикулярны.
Обратно, если асимптоты гиперболы взаимно
перпендикулярны, то ее полуоси равны между собой и, значит, гипербола
равносторонняя.
254
Глава Vin, КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
Теорема. Для того чтобы точка лежала на гиперболе,
необходимо и достаточно, чтобы отношение расстояния от этой точки
до фокуса гиперболы к расстоянию от той же точки до директрисы,
соответствующей рассматриваемому фокусу, было равно
эксцентриситету гиперболы.
Рис 169
Доказательство необходимости. Рассмотрим,
например, фокус F2(c, 0) и соответствующую ему директрису
Расстояние г2 от точки М (х, у) гиперболы
а2 б*'
до фокуса F2(c, 0) равно
гг = \ех—а\,
а расстояние от той же точки М (х, у) до директрисы лг = —
равно
Отсюда
\ех—а\ _г2
Аналогично доказывается, что
где rt есть расстояние от точки М(х, у) гиперболы до ее фокуса
F{{—c, 0), a rf, —расстояние от той же точки М до директрисы
х = , соответствующей фокусу £\.
114. ЭКСЦЕНТРИСИТЕТ И ДИРЕКТРИСЫ ГИПЕРБОЛЫ
255
Доказательство достаточности такое же, как и в теореме § 104.
Расстояние от фокуса F2 до директрисы х — — гиперболы равно
а эксцентриситет
отсюда
те
с —•
те ■
Если задана произвольная точка F, прямая d, не проходящая
через точку F, и число е> 1, то существует, и притом только
одна, гипербола, эксцентриситет которой равен е, F — фокус, а
d—соответствующая директриса.
Центр О этой гиперболы отстоит от точки F на расстоянии
те1-
причем точки О и F расположены по разные стороны от прямой
d (рис. 170), а большая полуось этой гиперболы равна
а =
те
Рис. 170
Доказанная теорема и последнее утверждение позволяют дать
гиперболе другое определение, эквивалентное принятому выше:
гипербола есть геометрическое место точек, для каждой из которых
отношение расстояния от данной точки F к расстоянию до
данной прямой d, не проходящей через точку F, равно данному
числу е > 1.
256 Глава VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
§ 115. Параметрические уравнения гиперболы
Перепишем уравнение гиперболы
в виде
\а b )\а • bj l-
Отсюда видно, что
a b ~^ ' (х ' b
Положим
тогда t ^0 я
У II 1
следовательно,
Мы доказали, что координаты любой точки гиперболы могут
быть представлены в виде A), где ^=0. Обратно, при любом t~£0
точка с координатами A) лежит на гиперболе
в чем можно убедиться, подставляя в уравнение
вместо х и (/ их выражения из формул A). Следовательно,
уравнения A) являются параметрическими уравнениями гиперболы
£!_£!_ 1
а2 б2"'
Если точка М (х, у) лежит на той ветви гиперболы, для точек
которой х^га, то
следовательно, ^ > 0. Обратно, если t > 0, то х^а, т.е. точка
М (д:, (/) лежит на указанной ветви гиперболы. При изменении t
в полуинтервале @, 1] значение х убывает от -j-oo до а, а
значение у возрастает от —оо до 0; при изменении t в полуинтервале
[1, -j-oo) значение х возрастает от а до -(-оо, а значение у воз-
S116. СОПРЯЖЕННЫЕ ГИПЕРБОЛЫ
257
растает от 0 до-f °° (рис. 171). При t = l получаем правую
вершину (а, 0) гиперболы. При отрицательных значениях t получаем
левую ветвь. При этом если / изменяется в полуинтервале (—оо, —1],
то значение х возрастает от —оо до —а, а значение у возраста-
+00
+0
Рис 171
ет от —оо до 0, а если t изменяется в полуинтервале [ — 1, 0), то
значение х убывает от —а до — оо, а значение у возрастает от
О до + оо.
§ 116. Сопряженные гиперболы
Две гиперболы, заданные уравнениями
а2 Ьг аг б2"
в одной и той же декартовой прямоугольной системе координат
с одними и теми же значениями полуосей а и Ъ, называются
сопряженными (рис. 172).
Выше доказано, что всякая гипербола
* У 1
а2 б2
может быть выражена параметрическими уравнениями
параметрические уравнения гиперболы, сопряженной с данной, будут
9 П. G. Моденов
258
Глава \'1П. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
§ 117. Уравнение гиперболы, отнесенной к асимптотам
Перепишем уравнения асимптот гиперболы в виде
Введем новую систему координат, принимая за начало
координат по-прежнему центр О гиперболы, а за масштабные векторы
осей Ох' и Оу'— единичные направляющие векторы асимптот*
i~\T >~Tf' е*~\Т •Т/*
Рис. 172
Тогда формулы преобразования координат будут иметь вид
следовательно,
ix'y'
4.x 'у'
-7Г-.
и, значит, уравнение гиперболы, отнесенной к асимптотам, имеет вид
Обратно, при любом С^О уравнение х'у' = С определяет
гиперболу; осями координат служат ее асимптоты и если ввести но-
* Из этих выражений находта кееинус того угла ф между асимптотами
гиперболы, в котором лежит сама гипербола:
' ' а2—йг 2-е2
cos Ф =» «1 в2 = —J5- = -^- .
«118. КАСАТЕЛЬНАЯ К ГИПЕРБОЛЕ
25Э
в у ю декартову прямоугольную систему координат, принимай за
новые оси ориентированные прямые, являющиеся биссектрисами
углов между асимптотами Ох' и Оу', то получим каноническое
-/равнение гиперболы.
Сопряженные гиперболы определяются уравнениями
х'у' = С и х'у'=—С (СфО>).
§ 118. Касательная к гиперболе
Уравнение касательной к гиперболе, заданной каноническим
уравнением
£!
в точке М0(х0, у0), лежащей на этой гиперболе, можно записать в
виде (см. § 110)
2х0, _ ,2
а2 (Х Х°> М
-yo) = O, или
§ 119. Оптическое свойство гиперболы
Теорема. Касательная к гиперболе в произвольной ее точке
является биссектрисой внутреннего угла Мо треугольника F1M0Fa,
имеющего своими вершинами фокусы гиперболы и данную точку Мо.
Рис. 173
Доказательство. Опустим из фокусов Рг ч F2
перпендикуляры FvPl и F^P2 на касательную. Так же как для эллипса
(§ 111) доказывается, что (рис. 173)
9*
260
Г л а в а VIII КАНОНИЧЕСКИЙ УРАВНЕНИЯ ЛИНИЙ
i, и, следовательно,
поэтому
Результаты подстановок координат фокусов Fx{—с,0) и F2(c,0)
в выражение *Щ — Щ — 1 —числа разных знаков, откуда следует,
что фокусы гиперболы лежат по разные стороны от любой
касательной к ней.
Рис. 174
Указанное геометрическое свойство позволяет построить
касательную к гиперболе в произвольной точке Мо: точку Мо
соединяем с фокусами Fx и F2 гиперболы и угол /'1М0/;'2 делим
пополам; биссектриса этого угла и является касательной к гиперболе
в точке Мо.
Доказанной теореме можно дать оптическое истолкование,
аналогичное тому, какое было дано для эллипса (рис. 174).
§ 120 ПАРАБОЛА И ЕЕ КАНОНИЧЕСКОЕ УРАВНЕНИЕ
261
§ 120. Парабола и ее каноническое уравнение
Параболой называется геометрическое место точек, для каждой из
которых расстояние до некоторой фиксированной точки плоскости,
называемой фокусом, равно расстоянию до некоторой фиксированной
прямой, не проходящей через фокус, и называемой директрисой.
Рис. 175
Расстояние от фокуса параболы до ее директрисы называется
параметром параболы.
Эксцентриситет параболы принимается равным единице. Из
определения параболы вытекает способ ее построения. Закрепим
вдоль директрисы линейку. К линейке
приставим меньшим катетом угольник, и
к вершине противолежащего острого
угла прикрепим нить, равную по длине
другому катету. Второй конец нити
закрепим в фокусе. Если перемещать
угольник вдоль линейки, удерживая нить
натянутой карандашом, как указано на рис.
175, то карандаш опишет параболу.
Опустим из фокуса F перпендикуляр
на директрису d и точку пересечения
этого перпендикуляра с директрисой
параболы обозначим буквой D. Введем на
плоскости декартову прямоугольную
систему координат, поместив начало
координат О в середине отрезка FD, принимая за ось Ох прямую D/\ о
положительным направлением от О к F (рис. 176).
Расстояние FD от фокуса F до директрисы d обозначим бук-
ьой р (параметр параболы). В выбранной системе координат фо-
Рис. 176
262
Глава V1U. КАНОНИЧЕСКИЕ СРАВНЕНИЯ ЛИНИЯ
кус F имеет координаты
уравнение директрисы
f о,
»--•!
Пусть М {х, у)— произвольная точка плоскости. Обозначим
через г расстояние MF отточки М до фокуса параболы, а через d —
расстояние МР от точки М до директрисы этой параболы.
Точка М (х, у) лежит на дайной параболе тогда и только
тогда, когда
Так как
то уравнение параболы имеет вид
Г
а й-.
X "Т о
УЧ*-*)'+и-
B)
го уравнение эквивалентно следующему;
или
уг==2рх. C)
Уравнение C) называется каноническим уравнением параболы.
£ 121. Исследование формы параболы
Так как ордината у в каноническое уравнение параболы
входит во второй степени, то ось Ох является осью симметрии
параболы:
A)
Ниже мы докажем, что это единственная ось симметрии
параболы (и что парабола не имеет центра симметрии).
Точка пересечения параболы с ее осью симметрии называется
вершиной параболы. Парабола A) имеет только одну вершину @, 0).
Из уравнения A) следует, что х^О (так как р>0, a *=f-)-
Разрешая уравнение у2 = 2рх относительно у и беря для у лишь
неотрицательное значение
5 121. ИССЛЕДОВАНИЕ ФОРМЫ ПАРАБОЛЫ
263
видим, что в полуинтервале [0, + °°) # —возрастающая
функция х, причем
limy — -)-оо.
X -*■ +00
у2~~ 2рх
р>0
О
Рис. 177
Рис. 178
У
Всякая прямая пересекает параболу не более чем в двух
точках (так как прямая определяется уравнением первой степени, а
парабола —уравнением второй
степени). Проведенное исследование даег
представление о форме параболы (рис.
177).
О
Рис. 180
Замечание. Уравнение
ф = — 2рх, B)
где р > О, сводится к уравнению у2 = 2рх заменой х на —х, т.е.
путем преобразования системы координат, которое соответствует
изменению положительного направления оси Ох на противополож-
264
Г л а. а VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
ное. Отсюда следует, что парабола у2=—2рх симметрична с па-
раРолой у2 — 2рх относительно сси Оу (рис. 178). Аналогичными
рассуждениями устанавливаем, что каждое из уравнений
= 2ру,
C)
D)
где р > 0, определяет параболу с вершиной в начале координат
и осью симметрии Оу (рис. 179, 180).
Уравнение C) и D) пишут часто в виде, разрешенном
относительно ординаты у:
= ах2,
где а ф 0
а =,
§ 122. Построение параболы по точкам
Пусть М0(х0, у0) — какая-нибудь фиксированная точка
параболы у2=2рх, а М (х, у) — произвольная точка той же параболы.
Обозначим через Р (х1, у0) точку
пересечения прямой ОМ с прямой
M0D, проходящей через точку Мо
параллельно оси параболы. Пусть S
и Т — проекции точек М и Р на ось
параболы, а К — проекция точки М
на прямую, проходящую через
вершину параболы перпендикулярно
ее оси (рис. 181). Докажем, что
DP OK
Рис. 181
Далее,
значит,
откуда
В самом деле, из подобия
треугольников OMS и ОРТ имеем
X
7
Уа'
fiV-1.
\Уо/ хо
DP KM DP
- таг0=ор > или ш^:
OS'
123 КЛСАГЕЛЫ1ЛЯ К ПЛРЛБОЛЕ
2бЭ
Отсюда вытекает следующий
способ построения параболы по
точкам, если заданы ось
симметрии параболы,ее вершина и какая-
нибудь точка Мо, лежащая на
этой параболе: пусть О — вершина,
Ох — ось, направленная в сторону
вогнутости параболы, и Мо —
какая-нибудь точка параболы.
Опустим из точки Мо
перпендикуляр M0D па ось Оу,
перпендикулярную к оси Ох; разделим
отрезок 0D па п равных между
собой частей и отрезок DM0 — па
такое же число п равных между
собой частей. Перенумеруем точки
деления так, как указано на
рис. 182. Точка пересечения пря- Рис 182
мой Oi с прямой, параллельной
оси Ох и проходящей через точку того же номера i оси Оу, лежит
на параболе.
Аналогично строятся точки параболы, лежащие в четвертой
четверти.
§ 123. Касательная к параболе
В курсах математического анализа доказывается*, что если
функция y = f(x) в точке х = х0 имеет производную, то уравнение
касательной к линии, выражаемой уравнением y = f(x) в точке
(хо,уо), где yo = f(xo), имеет ВИД
Если парабола задана уравнением
y—Q^ Q-^0, A)
то уравнение касательной к ней в точке (х0, у0) имеет вид
У У0 == 6U-Xq (X %о)г
ИЛИ
у 4-1/0 = 2ахох, B)
так как
* См. В. А. Ильин, Э. Г. Поз н як. Основы математического анализа
М„ „Наука", 1965, гл. I, § 2.
266
Глава VIII КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
Ьсли парабола задана уравнением
C)
то уравнение касательной к ней в точке (х0, у0) имеет вид
уоу = р (х + х0)
Полагая в уравнении B) х = 0, находим точку 5@,— у0),
пересечения касательной к параболе C) с ее осью симметрии.
Отсюда вытекает следующий способ построения касательной
к параболе в данной на ней точке Мо. Опускаем из точки Мо
перпендикуляр М0Р на ось симметрии параболы и откладываем
на оси симметрии параболы отрезок ОВ = ОР (рис, 183).
Прямая М,>В —касательная к параболе в точке Мо.
§ 124. Оптическое свойство параболы
Теорема. Касательная к параболе является биссектрисой угла FMD
между фокальным радиусом MF точки касания и
перпендикуляром MD, опущенным из нее на директрису.
Доказательство. Имеем (рис. 184)
Но
следовательно,
= ОВ, QD*=OF,
ц 125. полярной уравнение
267
Поэтому треугольник BFAI равнобедренный и, значит,
= Z.FBM;
но /_FBM=-/_BMD, следовательно, £ £
Эта теорема имеет следующее оптическое истолкование! если
в фокусе F параболического зеркала поместить источник света, то
лучи, отразившись от зеркала, образуют пучок параллельных лучей.
Указанное свойство параболического зеркала применяется при
устройстве зеркальных прожекторов (рис. 185).
§ 125. Полярное уравнение эллипса, гиперболы и параболы
Пусть L—какая-нибудь из изученных нами линий второго
порядка! эллипс, гипербола или парабола (в случае, если
L—гипербола, мы имеем в виду лишь одну ее ветвь).
== В
Рис 185
Рис. 186
Будем называть фокальной осью линии L ту из ее осей еим»
метрии, которая проходит через фокус линии L.
Введем полярную систему координат, совмещая полюс с фоку-
сом F линии L (в случае гиперболы мы берем фокус, ближайший
к вершине рассматриваемой ветви); пусть D—основание
перпендикуляра, опущенного из фокуса F на директрису, соответствующую
этому фокусу (в случае параболы— просто на директрису) (рис. 186).
Полярную ось расположим на прямой DF, причем ее
положительное направление примем от D к F. Обозначая через г расстояние
от произвольной точки М линии L до фокуса F, а через
d—расстояние от той же точки М до директрисы, соответствующей атому
268 Глава Mill КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
фокусу, будем иметь
где е—эксцентриситет линии L.
Находим
d= QM = DF + FN =DF + r ens ф.
Проведем через фокус F перпендикуля, кфокальной оси линии L,
и пусть Р — одна из точек пересечения этого перпендикуляра с
линией L. Так как соотношение A) верно для всех точек линии L,
в частности и для точки Р, то
FS-e
SP~ '
откуда
sp-Ц-.
Половина длины фокальной хорды (т. е. хорды, проходящей
через фокус перпендикулярно к фокальной оси) называется
фокальным параметром*.
Таким образом,
и, следовательно,
Отсюда и из равенства A) находим полярное уравнение линии
в виде
1 — е cos ф * '
Уравнение B) используется в механике и астрономии.
§ 126. Эллипс, гипербола и парабола как конические сечения
Рассмотрим поверхность прямого кругового конуса,
неограниченно простирающуюся по обе стороны от его вершины.
Плоскость, проходящая через вершину конуса, может занимать
относительно этого конуса следующие три положения:
1) иметь с конусом только одну общую точку (вершину конуса,
рис 187);
* В том случае, когда линия L — парабола, FP = PS, следовательно,
фокальный параметр p=DF, т е. параметр параболы равен расстоянию от фокуса
этой параболы до ее директрисы. В этом случае величина р совпадает с
параметром параболы, с которым мы встречались ранее, обозначая его той же
буквой.
§ 126 КОНИЧЕСКИЕ СЕЧЕПИЯ
269
2) касаться конуса вдоль его образующей (рис. 188);
3) пересекать конус по двум различным его образующим
189).
Рис. 187
Рис. 188
Рис. 189
Поэтому плоскость, не проходящая через вершину конуса,
может занимать относительно конуса следующие три возможных
положения:
1) пересекать все образующие конуса;
2) быть параллельной только одной образующей конуса;
3) быть параллельной двум различием образующим конуса.
Теорема. Плоскость, не проходящая через вершину прямого
кругового конуса, пересекает его по эллипсу, если она пересекает все
Рис. 190
Рис 191
Рис 192
образующее конуса (рис. 190^ по параболе, если она параллельна
только одной образующей конуса (рис. 191), и по гиперболе, если
она параллельна двум образующим конуса (рис. 192).
Доказательство. Пусть плоскость я, не проходящая через
вершину прямого кругового конуса (и не перпендикулярная ее оси),
пересекает поверхность конуса по линии С (рис 193). Впишем
в этот конус сферу, касающуюся плоскости п. Обозначим через F
точку прикосновения сферы с плоскостью п, через S — окружность,
по которой сфера касается конической поверхности, а через я'—
плоскость, в которой лежит окружность S. Возьмем на линии G
270
Глава VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
произвольную точку М и проведем через нее образующую конуса,
точку пересечения этой образующей с плоскостью п' обозначим
через А. Пусть Р — ортогональная проекция точки М на плос-
Рис ШЗ
кость п', а В —ортогональная проекция точки Р на прямую б,
по которой пересекаются плоскости я и я' (тогда MB J_ б).
Имеем MF=MA (как отрезки касательных, проведенных из
точки М к одной и той же сфере) и далее:
= MA sina«=MFsina, МР = MB sin $,
где а—угол образующих конической поверхности с плоскостью я',
а р —острый угол между плоскостями л и я'*
Из последних соотношений находим
MF_ sin p
MS ~ sin a '
т. е. все точки линии С принадлежат либо эллипсу Г, либо
гиперболе Г, либо параболе Г; F—фокус, б — соответствующая этому
фокусу директриса, а %~~== в—эксцентриситет.
$120 КОНИЧЕСКИЕ СЕЧЕНИЯ
271
Если плоскость п пересекает L'ce образующие конической
поверхности (рис. 194), то а> р. Значит, sin a > sin р,
эксцентриситет е<1; если гл—$, т. с. плоскость л параллельна только
одной образующей, то эксцентриситет е—1, если, наконец, а<{5,
то плоскость л параллельна двум образующим и эксцентриситет
е> 1.
Докажем, что и обратно: любая точка линии Г принадлежит
линии С; тогда можно утверждать, что линия С совпадает с
линией Г, т. е. что сечение С прямого
кругового конуса плоскостью, не
проходящего через ее вершину, есть или
эллипс, или гипербола, или парабола.
В самом деле, предположим, что
па линии Г есть точка М, не лежа
щая на линии С. Проведем через точку
М прямую, лежащую в плоскости л и
пересекающую коническую поверхность
в двух различных точках Р и Q; точки
Р и Q лежат очевидно на линии С, а по
доказанному, следовательно, и на
Рис. 194
Рис. 195
линии Г. Мы пришли к противоречию, заключающемуся в том, что
прямая линия MPQ пересекает линию Г (эллипс, гиперболу или
параболу) в трех различных точках М, Р и Q.
Замечание. Второй фокус F' эллипса или гиперболы
является точкой прикосновения к плоскости я второй сферы,
вписанной в коническую поверхность и касающейся плоскости я.
При этом для любой точки линии С, плоскость которой
пересекает есе образующие (рис. 195), имеем MF = MA, Ml\ = MB
272 Глава VIII КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
и MFx-\- MF= AB = const, а для любой точки линии С, плоскость
которой параллельна двум образующим конической поверхности,
MF = MA, MFX=MB и MF1 — MF = AB = const (рис. 196).
Рис. 196
Сферы, касающиеся конической поверхности и секущей
плоскости, называются шарами Данделена.
§ 127. Примеры и задачи к главе VIII
1. Задачи с решениями
Пример 1. Составить уравнения касательных к эллипсу
32 + 18 = 1>
проведенных из точки А A2, —3).
Решение. Уравнение касательной к эллипсу
X | У |
имеет вид
где (х0, у0)—точка касания. Уравнение касательной к данному эллипсу будет
иметь вид
хох . УоУ _ .
2"+ 18
§ 127 ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ VIII 273
Так как касательная проходит через точку А A2, —3), то координаты
точки А должны удовлетворять этому уравнению; подставляя в последнее
/равнение вместо х и у координаты точки А, получим
—5-^ = 1, или 9*0-4y0 = 24. A)
Но точка прикосновения (х0, у0) лежит на данном эллипсе, поэтому
х2 и2
Решая систему уравнений A) и B), находим два решения
*о=4> г/'о=3- *о=у y'o = --g--
Искомых касательных две, их уравнения получим, подставляя в уравнение
Мл-М —I
32 т 18
4 21
вместо х0 и у0 один раз 4 и 3, другой раз -=- и —=-j
о о
1 21
Зг"^" ' 32 18 '
или
Зх + 4у —24 = 0, Зг — 28у—120 = 0.
Пример 2. Составить уравнение гиперболы, асимптотами которой являются
прямые
У=±2х
и которая проходит через точку А A, 3).
Решение. Биссектрисы угла между асимптотами гиперболы являются
осями гиперболы. Но биссектрисами углов между данными прямыми служат
оси координат. Значит, осями гиперболы служат оси координат и потому ее
уравнение можно записать в виде
если действительная ось совпадает с осью Ох, и в виде
если действительная ось совпадает с осью Оу. Так как мы не зиаем, какой
из этих случаев имеет место в данной задаче, то необходимо исследовать обе
возможности. Предположим сначала, что уравнение гиперболы имеет вид A),
тогда из условия прохождения гиперболы A) через данную точку A, 3) имеем
Так как угловой коэффициент одной из асимптот гиперболы A) равен — ,
то в нашем случае
|-=2, или ^ = 4. D)
274 Глава VIII, КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИГ)
Решая совместно систему уравнений C) и D) относительно а2 и й2,
находим
а2= — -т-< °> 62= —5 < О,
что невозможно. Таким оСразом, не существует гиперболы, действительной
осью которой является ось Ох \\ которая удовлетворяет условиям задачи.
Возьмем теперь искомое уравнение в виде B). Подставляя в это
уравнение вместо хну координаты точки А, получим
и, кроме того, по-нрсжиему
' Ь п б2 „
■— = 2, или -5 = 4.
а а*
Решая теперь эту систему, находим
и искомое уравнение
х2 у2
^___ = _1.
4
Пример 3. Через точку А B, 1) провести такую хорду параболы у* = 4х,
которая делилась бы в данной точке пополам.
Решение. Пусть у — кх-\- Ь— уравнение искомой хорды. Ординаты уг и у2
точки пересечения этой прямой с данной параболой определяются из уравнения
Откуда следует, что
4
k
Но - 1Х —ордината середины хорды, и эта ордината должна быть равна
2
ординате данной точки. Таким образом, -r- = l> откуда й = 2 и искомое
уравнение
у—1=2 (х — 2), или 2х — у—3==0.
Пример 4. Доказать, что произведение расстояний от фокусов эллипса до
любой касательной к нему равно квадрату малой полуоси.
Доказательство. Пусть
уравнение эллипса. Возьмем уравнение касательной к нему в произвольной
точке (х0, у0):
•^Г+ £2 *=1-
Находим расстояния от фокусов F1(—c, 0) и F2(c, 0) до этой касательной
CXq
, о2 ■
<*»=■-— "г--
„9 *
1^
§127 ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ VIII
275
Отсюда
-—1
J
(а*-Ь*)х*
а4
^—1
&4
*о , "в
1 „2 + „4
2
v,2
il
ii
б4
Пример 5. Фокус линии второго порядка находится в точке F C, 0),
директрисой, соответствующей этому фокусу, является прямая лг == 12. Определить
вид линии и составить ее уравнение, зная, что она проходит через точку А G, 3).
Решение. Расстояние от точки А до точки F равно
AF = |/"G-3)Ч-C-0J = 5.
Расстояние от точки А G, 3) до директрисы равно
do = |7— 12| = 5.
Так как AF = d0, то эксцентриситет линии равен 1 и, значит, искомая линия—»
парабола
Пусть М (х, у) — произвольная точка этой параболы. Тогда
а расстояние от точки М до директрисы х—12=>0 равно
Отсюда
или
]8дг— 135 = 0.
Пример 6. Найти фокусы и директрисы равносторонней гиперболы xi/ = 8.
Решение. Действительной осью данной гиперболы является биссектриса
первого и третьего координатных углов.
Решая ее уравнение у = х совместно с уравнением гиперболы ху>=>8, найдем
вершины гиперболы
Ai[V~l, V"S), A2{-f% -V~8).
Длину действительной полуоси гиперболы найдем как расстояние от центра
гиперболы до ее вершины: а = 4. Так как эксцентриситет равносторонней
гиперболы
iV то с =
Так как фокусы лежат иа действительной оси гиперболы, совпадающей с
биссектрисой первого и третьего Координатных углов, и отстоят от центра гиперболы
на расстоянии е = 4 ]/2, те координаты фокусов Ft D, 4), F2( — 4, —4).
Расстояние от центра до директрисы
276 Глава VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
поэтому координаты точки пересечения директрисы с действительном осью
0^2, 2) и D2( — 2, —2).
Так как директрисы перпендикулярны действительной оси гиперболы, а
угловой коэффициент последней равен 1, то угловой коэффициент директрисы
равен —1, поэтому уравнения директрис будут:
у—2 = —(х—2), или х-\-у — 4=0,
или
Пример 7. Найти точки эллипса
х2 и2
^ + £-1. «>*.
в которых нормаль к эллипсу наиболее удалена от его центра. Найти это
наибольшее расстояние.
Решение. Пусть (х0, у0) — искомая точка. Уравнение нормали к данному
эллипсу в этой точке имеет вид
—(**) + -@И) = О
или
или
б2
Расстояние d от центра данного эллипса до этой нормали равно
с2
ТШл I хоУо \
Подставим сюда выражения для х0 и у0 через эксцентрический угол ср точки
(*о. Уо) данного эллипса:
х0 = о cos ф, {/о = ^
получим
sin2m cos2 ф У а2 siS2 ф + б2 cos2 q>
В силу того что эллипс симметричен относительно своих осей, можно
oi раничиться рассмотрением значений ф из интервала ( 0, -^ \ . В таком
§ 127 ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ VIII 277
случае
с2 sin ф ros ф
}/"a2sin2(p-f Ь2соз2ф У а''
У а2( 1 + tg2cp) + б2A + ctg2?) ]/а2 + б2 + о2 tg2 Ф + б2 ctg2 ф
У + + + (atg ф — b ctg фJ
Отсюда следует, что d будет наибольшим, если a tg ф — 6 ctg ф = 0, и это
наибольшее значение d равно
a + b
Решая уравнение
a tg ф —
находим
следовательно,
in ф = -
' Уа+Ь'
Искомая точка ( для 0 < ф < — имеет координаты
\ ^ 1
а У~а Ъ У~Ь
Всего искол!ых точек четыре:
, аУ~а Ь У~Ь
4- — ■■'- 4- *'Ц'—;
Уа~+Ь Уа+t
2. Задачи для самостоятельного решения
1. Составить уравнение семейства всех эллипсов, имеющих одни и те же
фокусы F1( — c, 0) и F2(c, 0)
2. Составить уравнения касательных к эллипсу
25+16~Ь
проходящих через точку A0,4).
Оте у = 4, \6х— 15у—100 = 0
3. При каком необходимом и достаточном условии прямая
1) касается эллипса
х2 у2
278 Рлаза VIII. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
2) пересекает эллипс,
3) не пересекает его?
Отв 1) 42аЧ-Я2Ь2 — С2 = 0; 2) Л2а2+Й262—С2 > 0; 3) Л2а2+ /№-- С2 < 0
4. Доказать, что касательные к эллипсу отсекают на двух касательных
к нему, проведенных в копнах большей оси, отрезки, произведение которых
равно квадрату малой полуоси эллипса.
5. Доказать, что отрезок любой касательной к эллипсу, заключенный
между каса1ельными, проведенными в копнах большем оси, виден из любого
фокуса пол прямым углом.
6. Найти геометрическое \.есто точек, из которых эллипс
виден под прямым углом
Отв Окружность *2+ i/2 =
7. Эллипс при движении по плоскости касается двух взаимно
перпендикулярных прямых. Какую линию описывает его центр?
Отв. Окружность.
8. Составить уравнение эллипса, фокусы которого (— 3, 0) и C, 0) и
который касается прямой х-\-у — 5 = 0.
Отв. £ + !=,.
9. Найти геометрическое место проекций какого-нибудь фокуса эллипса
на касательные к нему.
Отв. Окружность.
10. Найти геометрическое место точек, симметричных с каким-либо фокусом
эллипса относительно касательных к нему.
Отв Окружность.
11. Найти произведение расстояний от любого фокуса эллипса до
параллельных, касательных к нему.
Отв. Квадрат меньшей полуоси.
12. При каком условии из точки (x0, </0) можно провести касательные к
эллипсу
X2 I/2
а2 + б2 Ь
Составить уравнение линии, распадающейся на касательные, проведенные
к данному эллипсу из этой точки.
Л2
13. Найти углы между касательными, проведенными из точки (х0, у0) к
эллипсу
х* ■ JL 1
а2 Т l>» ""*
§127 ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ V11I 279
Отв.
Ы~
14. Доказать, что сумма квадратов обратных величин длим двух взаимно
;ерпсндикулярных радиусов эллипса есть величина постоянная.
J5. Доказать, что сумма обратных величии отрезков, па которые фокус
эллипса делит проходящую через него хорду, есть величина постоянная.
Доказать, что и отношение произведения этих отрезков к длине хорды также
постоянно.
16. Найти длину отрезков (считая от центра гиперболы), отсекаемых
директрисами гиперболы
х2 £_
W ь2
иа ее асимптотах.
Отв. а.
17. Доказать, что директриса гиперболы проходит через проекцию
соответствующего ей фокуса на любую из асимптот. Найти также расстояние от
любого фокуса гиперболы до любой из асимптот.
Отв. Длина мнимой полуоси
18. Доказать, чтс произведение расстояний от любой точки гиперболы до
ее асимптот есть величина постоянная.
19. Составить уравнения касательных к гиперболе
,2-11 = 1
проходящих через точку М A, 4).
Отв. х=1, 5.x —2j/ + 3 = 0.
20. При каком необходимом и достаточном условии прямая Ах-\-Ву-\-
+С = 0 1) касается гиперболы:
*2 У2 ,
2) пересекает гиперболу; 3) не пересекает ее?
Отв. 1) aM2-&2fi2-C2 = 0; аМ2-Ь2В2 ф 0; 2) аМ2-62В2-С2 < 0
(исключая асимптоты); 3) а2Л2 — 62В2— С2 > 0.
21. Определить произведение расстояний от любого фокуса гиперболы
а2 б2
до любой касательной к пей.
Oms. fe2.
22. Определить геометрическое место вершин прямых углов, стороны
которых касаются гиперболы
Отв. Пустое множество, если а2 < Ь2; окружность х8 + у2 = а2—б2, еслио>6.
23. Доказать, что расстояние от любой точки М гиперболы до ее фокуса F
равно отрезку прямой, проходящей через эту точку параллельно асимптоте,
заключенному между точкой М и директрисой, соответствующей фокусу f.
280 Глава VIH. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ЛИНИЙ
24. Составить уравнение гиперболы, зная уравнения ее асимптот !/=±-„-х
и уравнение 5х — 6у — 8 = 0 одной из касательных в ней.
Отв. — i/2= 1
25. Найти геометрическое место проекций какого-либо фокуса гиперболы
на касательные к пей.
Отв Окружиесть.
26. Найти геометрическое место точек, симметричных с каким-нибудь
фокусом гиперболы относительно касательных к ней*
Отв. Окружность.
27. 1) При каком условии из точки (х0, у0) можно провести к гиперболе
две различные касательные? Составить уравнение пары этих касательных.
U) При каком условии из точки (х0, у0) к данной гиперболе можно провести
только одну касательную? Составить ее уравнение.
а3 б2 7 V аг~ ~W /~['a*'~~W~
г2 у2
2) При условии —° аГ — ^1' причем х0 и у0 не равны нулю одиовре-
менно, или при условии, что —| аГ ■ Если —j-—p- =1, то уравнение
х2 у2
касательной имеет вид ^г—^¥ = 1> а если -|— dr = 0' но го и у0 не равны
нулю одновременно, т.. е. точка (х0, у0) лежит на асимптоте гиперболы, но не
сбвйадает с ее центром, то уравнение касательной имеет вид
(S \ / 2 \
г/ —+U г/ "f ^ =
Н—г/ —+U г/ "f ^ = о(если точка (дс0, (/о) лежит на асимптоте
Ь
« = — к
а
28. Найти углы между касательными к гиперболе
проведенными из точки (х0, Уо).
Отв.
I/ _il+iL
6 К аг б2
29. Доказать, что произведение отрезков, отсекаемых касательной к
гиперболе на ее асимптотах (считая от центра), равно квадрату расстояния от
центра до фокуса.
30. Вычислить площадь треугольника, образованного асимптотами
гиперболы
а2 Ь*
и произвольной касательной к ней.
Отв. ab.
? 127. ПРИМПРЫ И ЗАДАЧИ К ГЛАВЕ VIII 281
3!. Доказать, что отрезок касательной к гиперболе л точке Мо, заключен-
ньп" между ее асимптотами, точкой Мо делится нополам.
32. Вычислить площадь параллелограмма, одна из вершин которого есть
точка гиперболы
а две стороны параллелограмма лежат на асимптотах.
Отв. -у ab
33. При каком необходимом и достаточном условии касательные,
проведенные из точки (дс0, (/о) к гиперболе
*2 У2 _,
W
касаются различных ее ветвей?
34. При каком необходимом и достаточном условии точка (дг0. J/о) лежите
области, ограниченной одной из ветвей гиперболы
и двумя соответствующими лучами, выходящими из центра гиперболы и
идущими по ее асимптотам?
Отв. 0<^— ^-<1.
35. Доказать, что софокусные эллипс и гипербола (т. е. эллипс и
гипербола, имеющие общие фокусы) пересекаются ортогонально.
36. Доказать, что отрезок произвольной касательной к гиперболе,
заключенный между двумя данными касательными к этой гиперболе, виден из
любого фокуса под прямым углом.
37. Доказать, что точки пересечения касательной к гиперболе с ее
асимптотами лежат на одной окружности с фокусами.
38. Доказать, что прямые, соединяющие какие-либо две фиксированные
точки гиперболы с произвольной переменной точкой той же гиперболы,
отсекают на любой ее асимптоте отрезок постоянной длины.
39. Доказать, что две равносторонние гиперболы, асимптоты одной из
которых являются осями симметрии другой, ортогональны.
40. Доказать, что сумма обратных величин отрезков, на которые фокус
гиперболы делит проходящую через него хорду, постоянна. Доказать, что
отношение произведения этих отрезков к длине хорды также постоянно.
4!. При каком необходимом и достаточном условии прямая Ax~\-B\jJrC = Q
1) касается параболы уг = 2рх; 2) пересекает параболу у2=2рх; 3) не
пересекает параболу.
Отв. 1) В2р—2ЛС = 0; 2) В2р— 2АС > 0, 3) В2р — 2АС < 0.
42. Найти геометрическое место проекций фокуса параболы на
касательные к ней.
Отв. Касательная к параболе в ее вершине.
282 Глава VIII. КАНОИИЧЕСКИГ УРАВНЕНИЯ ЛИНИЙ
48. НаЙ1и геометрическое место точек, симметричных фокусу параболы
относительно касательных к ней
Отв, Директриса.
44. Найти геометрическое место точек, для каждой из которых касатель
ные, проведенные к параболе, взаимно перпендикулярны,
Отв Директриса
45. Доказать, чго фокус параболы и точки прикосновения двух
касательных к параболе, проведенных из любой точки директрисы, принадлежат одной
прямой,
46. Доказать, что отрезок произвольной касательной к параболе,
заключенный между двумя фиксированными касательными к ней, проектируется на
директрису в отрезок постоянной длины
47. Доказать, что если точка перемещается по одной из касательных к
параболе, то угол между прямой, соединяющей эту точку с фокусом, и
второй касательной к параболе, проходящей через ту же точку, сохраняет
постоянную величину,
48. Пусть М — точка пересечения касательных к параболе в точках Mj и
М2, a F—фокус параболы. Доказать, что
49. Доказать, что пря\;ые, соединяющие основания перпендикуляров,
опущенных из каждой точки одной стороны треугольника на две другие его стороны,
касаются одной и той же параболы. Фокусом этой параболы служит
основание соответствующей высоты треугольника. Директрисой является прямая,
соединяющая основания двух других высот,
50. Доказать, что сумма обратных величин отрезков, на которые фокус
параболы делит проходящую через него хорду, постоянна. Доказать, что
отношение произведения длин этил отрезков к длине хорды также постоянно.
51. Фок.>с эллипса проектируется в переменную точку М на переменную
плоскость, проходящую через касательную к эллипсу и образующую с
плоскостью эллипса постоянный угол. Доказать, что OM = const (О —центр эллипса).
52. Рассмотрим семейство Сх линий второго порядка:
Исследовать линию при условии, что к принимает все действительные
значения Вычислить ее полуоси и эксцентриситет
Отв. Со —парабола; Сх при к > 0— эллипс (Cj —окружность), С\ при X < 0
и К ф — 1 —гипербола; С_х—две пересекающиеся прямые. Если к ф 0, то
координаты центра "К, -у-
Если %. Ф 0, то уравнение преобразуется к виду
Центр / f X, -«-)• производя параллельный перенос осей
с — л, х —у— ,
получим
12? ПРИМЕРЫ И ЗАДАЧИ К ГЛЛВП VIII 283
Если 0 < X < 1, то фокальной осью является ось / Y, полуоси
а_ |/ -."Г" < у —jj—^sb, эксцентриситет е= УГ^Х. В случае \ > 1
фокальной осью является ось IX. Полуоси а«= 1/ —г—> |/ ~р—— ^
эксцентриситет е= 1/ 1 — у. В случае — 1<Х,<0 фокальная ось гиперболы
Ск — ось /У, полуоси! действительная 6= |/ —Х—, мнимая а= I/ J— ,
эксцентриситет е= ]/"! — X. В случае ?v < — 1 цокальиая ось —ось /А, полуоси
в=_ |/ .— i— , Ь- у ~- , эксцентрисите!• е —
ГЛАВА IX
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА, ЗАДАННЫЕ
КАНОНИЧЕСКИМИ УРАВНЕНИЯМИ
§ 128. Эллипсоид
Эллипсоидом называется поверхность, уравнение которой в
некоторой специально выбранной прямоугольной системе координат,
имеет вид
Будем считать, что а^Ь^с. Если на эллипсоиде A) лежит
точка (х, у, г), то на нем лежат и точки (±х, ±у, ± г) (с
любым набором знаков плюс и минус). Отсюда следует, что для
Рис !97
эллипсоида A) начало координат О является еге центром
симметрии и называется центром эллипсоида; оси координат являются
осями симметрии и называются главными осями; плоскости
координат являются плоскостями симметрии и называются
главными плоскостями.
128. ЭЛЛИПСОИД
285
Если а>Ь>с, то эллипсоид A) называется трехосным
Если а>Ь = с, то эллипсоид A) называется вытянутым
эллипсоидом вращения; он получается вращением эллипса
X2 II1
а2 + &2 - '
вокруг его большой оси (рис. 197).
Если а — Ь^>с, то эллипсоид A) называется сжатым
эллипсоидом вращения; он получается вращением эллипса
вокруг его малой оси (рис. 198).
1'ис 198
Если а—Ь = с, то эллипсоид A) является сферой рллиуса а с
центром в начале координат.
Вершинами трехосного эллипсоида называются точки
пересечения эллипсоида с его главными осями. Трехосный эллипсоид имеет
шесть вершин (±а, 0, 0), @, + 6, 0), @. 0, ±с).
Из уравнения A) следует, что
Это означает, что эллипсоид A) лежит внутри прямоугольного
параллелепипеда с вершинами (+а, ±Ь, ±-_с). Каждая грань
этого параллелепипеда имеет с эллипсоидом A) только одну
общую точку — его вершину.
286 Глава IX КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
Плоскость хОу пересекает эллипсоид A) но линии,
выраженной уравнениями
v2 ,,2 ?J
£. ' i-4- —=1 2 — 0
или эквивалентной системой
— 4- —— 1 2 — 0 B)
Аналогично плоскость уОг пересекает эллипсоид A) по линии,
уравнения которой
£ + $=1, * = 0, C)
а плоскость гОх по линии
5 + -3-1. *»0. D)
Линии B), C), D) суть эллипсы. Эти эллипсы, т. е. сечения
эллипсоида A) его главным;' плоскостями, называются главными
сечениями.
Рассмотрим сечения эллипсоида A) плоскостями,
параллельными какой-нибудь координатной плоскости, например плоскостями,
параллельными плоскости хОу, т. е. плоскостями, выражаемыми
уравнением
2 = h,
где h—произвольное действительное число.
Уравнения линии сечения имеют вид
3S + F + C* ' '
или
или
v-2 ,i2 /,2
* |_г_—1 „ 2 = ft. E)
Если |А|>с, то первому уравнению этой системы не
удовлетворяет ни одна пара действительных чисел х, у, т. е. система E)
не имеет действительных решений х, у, z. Это означает, что
плоскость z — h при |/?|>с не пересекает эллипсоид A).
При h=±c первое уравнение системы E) имеет вид
$ 128. ЭЛЛИПСОИД
287
откуда х = у — 0. 1аким образом, плоскости г = ±.с встречают
эллипсоид A) в его вершинах @, 0, ±с). Наконец, если |/г|<с,
то систему уравнений, выражающих линию сечения, можно пере-
писагь так:
У"
ill
f.i
или
Эти уравнения являются уравнениями эллипса, лежащего в
плоскости сечения z = h\ центр этого эллипса — точка @, 0, /г), оси
симметрии параллельны осям Ох и Оу, а полуоси равны
х
Рис 199
Рассмотренные сечения дают представление о форме
эллипсоида (рис, 199). Отметим, что эллипсоид A) может быть получен
из сферы A + F2 + Z2= 1, если произвести три равномерных
сжатия :
= аХ, tj — bY,
288
Глава IX. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
к трем попарно перпендикулярным плоскостям yOz, zOx и хОу,
проходящим через центр этой сферы *.
§ S29. Однополостный гиперболоид
Однополостным гиперболоидом называется поверхность,
уравнение которой в некоторой специально выбранной прямоугольной
системе координат имеет вид
Будем считать, что а^Ь. Так же как в предыдущем пара-
Графе доказывается, что для однополостного гиперболоида A) на-,
чало координат является
центром симметрии (центр), оси
координат—осями симметрии
(главные оси), а
координатные плоскости —
плоскостями симметрии (главные
плоскости).
Если в уравнении A) а = Ь,
то однополостный гиперболоид
A) называется однополостным
гиперболоидом вращения, так
как может быть получен
вращением гиперболы
вокруг ее мнимой оси (рис.
200).
Вершинами однополостного
гиперболоида называются тонки
пересечения гиперболоида с его
главными осями. Гиперболоид
A) в случае а=/= Ь имеет четыре
вершины (± а, 0, 0), @, ± Ь, 0).
Плоскость хОу пересекает однополостный гиперболоид A) по
эллипсу, выражаемому уравнениями
Рис. 200.
* Равномерное сжатие пространства к плоскости определяется аналогично
тому, как было определено в § 105 равномерное сжатие плоскости к прямой:
фиксируем в пространстве плоскость П и фиксируем число k ф 0. Пусть М —
произвольная точка пространства, а Р — ее ортогональная проекция ив
плоскость П. Поставим в соответствие точке М точку /И', такую, что РМ' = k PM-
Это соответствие и называется равномерным сжатием пространства к
плоскости П с коэффициентом сжатия, равным к.
ч 129 ОДНОПОЛОСТНЫЙ ГИППРБОЛОИД 289
называемому горловым эллипсом однополостпого
гиперболоида A). Плоскость уОг пересекает однополостный гиперболоид A)
по гиперболе, выражаемой уравнениями
У ? 1 v — O
Ь2 С2 — . * — U.
а плоскость xOz — по гиперболе, выражаемой уравнениями
v2 ,2
1 Г\
аг С2 • J — •
Рассмотрим сечения однополостного гиперболоида A)
плоскостями, параллельными координатной плоскости хОу, т. е. плоско-
С1ями г = /г.
Уравнения линии сечения будут
эта система уравнений эквивалентна следующей:
х2 у2 /г2 , ,
се2 Ъ^ с^ ' *
или
Этими уравнениями выражается эллипс с полуосями
с центром на оси Ог и точке @, 0, /г) и осями, параллельными
соответственно осям Ох и Оу. Из выражений B) следует, что
а' > а, &' > &,
т. е. горловой эллипс является наименьшим из всех эллипсов, по
которым однополостный гиперболоид A) рассекается плоскостями,
параллельными плоскости хОу.
Плоскость A' = ft, параллельная плоскости уОг, пересекает одно-
иолостный I иперболоил (I) по ;нш :и, выражаемой уравнениями
или
&2 С2 — ! а2 ! Л—ft.
11. С, Моденов
2S0 Глава IX КЛНОПИЧ1ХКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
Если |/г|<й, то этими уравнениями определяется гипербола С
с центром в точке (/г, 0, 0), лежащая в плоскости x = h,
действительная ось которой параллельна оси Оу, а мнимая —оси Ог.
Полуоси этой гиперболы:
Ъ у \ — — (действительная полуось),
с у 1 2 (мнимая полуось).
Если \h\-a, то уравнения линии сечения имеют вид
Уравнения
У2 г2 а
~W—? —и> х = а
являются уравнениями двух пересекающихся прямых р и q:
-Г- + —= 0, х=а — прямая р;
О С
-т- — — = 0, х=а — прямая q.
О С
Аналогично уравнения
1 L — П Y — П
являются уравнениями двух прямых:
JL.L 1 А у — пи У г О •/ п
Если |Л|>а, то в сечении получается гипербола, уравнения
которой
У2l L
У2
С I/ —s—I
Действительная ось этой гиперболы параллельна оси Oz,
мнимая — оси Оу; центр лежит в точке (h, 0, 0).
Асимптоты всех гипербол, получающихся при пересечении одно-
полостного гиперболоида A) плоскостями х—к(кф±_а),
параллельны прямым, получающимся при пересечении гиперболоида
плоскостями х=±а.
Сечения плоскостями y = h, параллельными плоскости хОг,
аналогичны рассмотренным.
<s 130 лвупо.гасшын гиперболоид
291
Все эти сечения дают представление о форме поверхности
однополостного гиперболоида (рис. 201).
Всякий однополостный гиперболоид
^г + -р 7* = ^
можно получить из однополостного гиперболоида вращения
производя равномерное сжатие
к плоскости
Однополостный гиперболоид A)
можно получить из
равностороннего однополостного гиперболоида
вращения X2 + Y2—Z2=l,
производя равномерные сжатия х — аХ,
y — bY, z — cZ соответственно к
плоскостям уОг, гОх и хОу с
коэффициентами сжатия, равными а,
Ь, с.
§ 130. Двуполостный гиперболоид
Двуполостным гиперболоидом
называется поверхность, уравнение ко- Рис 2oi
торой в некоторой специально
выбранной прямоугольной системе координат имеет вид
~a?Jr~b2 c2"= 1-
A)
Начало координат является центром симметрии (центр)
двуполостного гиперболоида, оси координат —осями симметрии
(глав иые оси), координатные плоскости — плоскостями
симметрии (главные плоскости).
Если в уравнении A) а — b, то двуполостный гиперболоид A)
называется двуполостным гиперболоидом вращения, так как может
быть получен вращением гиперболы
вокруг ее действительной оси Ог (рис. 202).
Ю*
292
Гласа IX КАНОНИЧЕСКИЙ СРАВНЕНИЯ ПОВЕРХНОСТЕЙ
Вершинами двуполостного гиперболоида называются точки его
пересечения с главной осью Oz. Двуполостный гиперболоид A) имеет
две вершины @, 0, ±с).
Плоскости \Oz и yOz пересекают двуполостный гиперболоид
А
==о и
1, х=-0
Рис 202
по гиперболам
ь2 с2
Сечение двуполостного i ипербо-
лоида плоскостью z = h выражается
■. равнениями
Если j h | < с, то первое
уравнение не имеет действительных
решений—плоскость z = h не
пересекает поверхности.
Если /г = + с, то
откуда
плоскости г = ±с встречают поверхность двуполостного
гиперболоида в его вершинах @, 0, ± с). Если |ft|>c, то уравнения ли-
ьии сечения можно переписать в виде
у1
1 /й* 1
-,= 1, 2 = А.
Этими уравнениями выражается эллипс с полуосями
с центром в точке (О, О, И) и осями, соответственно параллельными
осям Олг и Оу.
Плоскость x — h пересекает поверхность двуполостного
гиперболоида по линии, выражаемой уравнениями
Ь2 *i2 ?2
Л_ i У _ — 1 v — h
U С/ С
§ 131. КОНУС ВТОРОГО ПОРЯДКА
293
или
= h,
г. е. по гиперболе с центром в точке (Л, 0, 0), лежащей в
плоскости x = h. Действительная ось этой гиперболы параллельна оси Oz,
мнимая — оси Оу.
Аналогично исследуются сечения
поверхности плоскостями y = h (рис. 203).
Двуполостный гиперболоид
можно получить аффинным сжатием
X — —
а '
= y, Z =
к плоскости yOz двуполостного
гиперболоида вращения
1,
с2
или из равностороннего двуполостного
гиперболоида вращения
тремя сжатиями
§ 131. Конус второго порядка
Конусом второго порядка называется поверхность, уравнение
которой в некоторой специально выбранной прямоугольной системе
координат имеет вид
■Л 1,2 ,2
а* ■ Ъ* с% ~и (I)
(считаем, что в этом уравнении а^Ь). Начало координат, оси
координат и координатные плоскости являются соответственно
центром симметрии, осями симметрии и плоскостями симметрии и
называются вершиной, главными осями и главными плоскостями.
Осью конуса A) обычно называют ось Oz.
Основное свойство конуса: если на конусе A) лежит точка
Мо(*о> Уо> zo) (не совпадающая с вершиной), то на нем лежат все
294
Глава IX. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
точки прямой ОМ0, проходящей через вершину 0 и эту точку Мо.
В самом деле, если М (х, у, г)—произвольная точка, лежащая на
прямой ОМ0, то
и потому
%1 yi 22 / X' у' „ ,
Таким образом, поверхность A) образована прямыми,
проходящими через начало координат. Поэтому для представления вида
этой поверхности достаточно рас-
hz смотреть ее сечение какой-нибудь
плоскостью z = h, параллельной
плоскости хОу. В сечении
получится эллипс, уравнения которого
= 1, z — h.
Центр этого эллипса С лежит
на оси Ог в точке @, 0, К), а
значит, поверхность A) образована
прямыми, соединяющими начало
координат со всеми точками
эллипса С (рис. 204).
Конус A) может быть получен
в результате равномерного сжатия
Рис. 204
к плоскости yOz конуса вращения
полученного вращением вокруг оси Ог прямой
или в результате сжатий к плоскостям yOz, zOx, хОу: х — аХ,
y = bY, z — cZ из равностороннего конуса вращения X2 -\- Y2 —-Z2 = 0.
§ 132. Асимптотический конус гиперболоидов
Два гиперболоида (один однополостиый, другой двуполостмый)
Х^ U" 2*^
W + W~~ Ж = ^ * (!)
называются сопряженными.
132. АСИМПТОТИЧЕСКИЙ КОНУС ГИПЕРБОЛОИДОВ
295
Конус второго порядка, выражаемый уравнением
B)
называется асимптотическим конусом для обоих
гиперболоидов.
Докажем, что любая плоскость, проходящая через ос^ Oz,
пересекает поверхность A) по сопряженным гиперболам, а
асимптотический конус B)—по двум прямым, которые для этих
сопряженных гипербол являются
асимптотами. В самом деле,
повернем оси координат
вокруг оси Oz па угол а.
Уравнения A) и B) в повой
системе координат Ox'y'z'
будут иметь вид
Рис 205
Рис. 206
(х' cos а — у' sin аJ (*' sin а + у' cos аJ г2 _
2 I 2 72" —
(х' cos а — у' sin аJ . (х' sir а-\-у' cos аJ г2
Ji I ь2 7J
( ' )
B')
Сечения этих поверхностей плоскостью x'Oz выражаются
уравнениями
sin2a\ _i2_ = + j у, = 0. A„,
-7F = °. У' = °- B")
Из уравнений видно, что сечениями являются две сопряженные
гиперболы A") с полуосями а' — —т=—- ., Ь' = с, а пря-
J /fc2cos2a + a2srn2a i
мые B") —асимптотами этих гипербол (рис. 205).
29G Глава IX. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ.
Заметим, что все гиперболоиды семейства
*-л.Л1. *2 -г
а2 + ь* ~"?~°
имеют общий асимптотический конус
§ 133. Эллиптический параболоид
Эллиптическим параболоидом называется поверхность, уравнение
которой в некоторой специально выбранной прямоугольной системе
координат имеет вид
Т=2г- где
Будем считать, что p^q. Если p — q, то эллиптический
параболоид A) - это параболоид вращения, так как получается
вращением параболы
вокруг оси Ог, являющейся осью параболы.
Ось Ог является осью симметрии эллиптического параболоида (I)
(она называется осью параболоида), а плоскости хОг и
yOz~плоскостями симметрии (главные плоскости) Начало координат для
эллиптического параболоида A) является точкой пересечения этой
поверхности с ее осью и называется вершиной.
Плоскость z = h пересекает эллиптический параболоид A) по
линии
** 4- У* — 9 — h х* У2 О
р q ' ' р ' ~q~ ' ^ П. B,)
Если h < О, то первое уравнение не имеет действительных
решений, так как р > 0, q > 0; это означает, что плоскость z = /z
при h < 0 не пересекает эллиптический параболоид A). Если г = 0,
то л- = г/ = О, т. е плоскость хОу имеет с эллиптическим
параболоидом только одну общую точку - вершину @, 0, 0). Если h > 0,
то переписав уравнения B) в виде
..9 2
-I 2 = 1 у—U
видим, что сечением_является эллипс с центром в точке @, 0, h)
и полуосями a = Viph и b = ]/2qh.
Плоскость хОг пересекает эллиптический параболоид A) по
параболе
133 ЭЛЛИП1ИЧ НСКИП ПАРАБОЛОИД
297
а плоскость yOz — no параболе
f = 2qz, x = 0.
Таким образом, числа р и q •- параметры парабол, получающихся
в сечении параболоида его плоскостями симметрии (рис. 207)
Рассмотрим сечения эллиптического параболоида плоскостями,
параллельными плоскости xOz, т. е. плоскостями, выражаемыми
уравнением
Уравнения линии сечения:
,,2
■£-= 2г, y =
q y
Рис 207 Рис 2U8
ИЛИ
ИЛИ
Эти уравнения выражают параболу вершиной
298 Глава IX КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
ось которой выражается уравнениями
х = 0, y = t
и одинаково направлена с ссью Ог. Параметр параболы
равен р, т. е. параметру главного сечения эллиптического пара-
Солоида плоскостью хОг.
Аналогичная картина получается и для сечений эллиптического
параболоида A) плоскостями, параллельными плоскости yOz.
Таким образом, эллиптический параболоид может быть
образован параллельным переносом параболы С1г при котором вершина
параболы С1 перемещается по параболе С2; плоскость параболы С2
перпендикулярна плоскости параболы С\, а оси этих парабол
параллельны и одинаково направлены (рис. 208).
Эллиптический параболоид A) является образом параболоида
вращения X'1-\-Y'i — 2qZ при равномерном сжатии пространства
к плоскости yOz (коэффициент сжатия 1/ — ].
§ 134. Гиперболический параболоид
Гиперболическим параболоидом называется поверхность,
уравнение которой в некоторой специально выбранной прямоугольной
системе координат имеет вид
j—^ = 2z, где р>0 и q>0. A)
Для гиперболического параболоида
* У_ — 2г
р я
плоскости хОг и yOz являются плоскостями симметрии, а ось
Ог — осью симметрии.
Ось симметрии гиперболического параболоида называется просто
его осью. Точка, в которой ось гиперболического параболоида
пересекает эту поверхность, называется вершиной.
Гиперболический параболоид A) имеет вершину в начале координат.
Плоскости хОг и yOz, являющиеся для гиперболического
параболоида A) плоскостями симметрии, называются главными
плоскостями гиперболического параболоида.
Гиперболический параболоид
§ 134 ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД 299
в случае рфц имеет только одну ось симметрии (ось Oz), если же
p — q, то параболоид имеет еще две оси симметрии:
у = х, 2 = 0 и у= —х, г = 0.
В самом деле, если координаты точки М(х, у, г)
удовлетворяют уравнению
то этому же уравнению удовлетворяют координаты точки
М'(у,х,—г), симметричной с точкой M{x,y,z) относительно
прямой у = х, z = 0. Так же доказывается, что прямая у=—х,
2 = 0 является осью симметрии.
Плоскость хОу пересекает гиперболический параболоид
по двум прямым:
- ^- = 0, z = 0, или ~^=-\—т= = 0, 2 = 0,
р Я Уруя
--^ = 0,2 = 0.
Vp Vq
Плоскость 2 =/г, параллельная плоскости хОу, пересекает
гиперболический параболоид по гиперболе Сх:
£ У_ — о/» у — и
Р Я
Еели h > 0, то эти уравнения можно переписать в виде
это гипербола, расположенная в плоскости 2 = h с центром в точке
@, 0, /г), действительная ось которой параллельна оси Ох, а
мнимая— параллельна оси Оу.
Если ft<0, то уравнения линии сечения можно представить
в виде
= 1, z = h,
(У'-2ркУ
это гипербола С2, расположенная в плоскости z = h с центром
в точке @, 0, /г), действительная ось которой параллельна оси Оу,
а мнимая — оси Ох. Асимптоты всех гипербол, получающихся при
пересечении гиперболического параболоида A) плоскостями z = h,
300
Глава IX. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
/2=^=0, параллельны прямым, по которым этот параболоид
пересекается с плоскостью' 2 = 0.
Плоскость хОг пересекает гиперболический параболоид A) по
параболе С3:
х* = 2рг, у = 0,
а плоскость уОг—по параболе С4:
Мы видим, что числа р и q являются параметрами парабол,
получающихся в сечении гиперболического параболоида A) его
главными плоскостями.
Рассмотрим сечения
гиперболического параболоида A)
плоскостями, параллельными
плоскости хОг, т. е.
плоскостями, выражаемыми
уравнением
Рис 2С9
Уравнения линии сечения
имеют вид
X2 IIе
— = 2z, y = t,
р q y
или
Эти уравнения выражают
параболу Съ с нсршиной в точке
Рис 210
ось которой выражается
уравнениями
а направление оси совпадает с положительным направлением оси Ог.
Параметр параболы
равен р, т. е. параметру главного сечения гиперболического
параболоида плоскостью хОг.
Аналогичная картина получается и для сечений
гиперболического параболоида плоскостями, параллельными плоскости иОг
(рис. 209).
135 ЦИЛИНДРЫ ISJOPO1O ПОРЯДКА
301
Таким образом, гиперболический параболоид может быть
образован параллельным переносом параболы С4, при котором вершина
параболы С4 перемещается по парасоле С3; плоскость параболы Ся ■
перпендикулярна плоскости параболы С4, а оси этих парабол
параллельны и противоположно направлены (рис. 210).
§ 135. Цилиндры второго порядка
Существует тгп типа цилиндров второго порядка:
эллиптический (рис. 211)
а2 "г №
гиперболический (рис. 212)
A)
B)
Рис. 211
Рис. 213
Рис. 212
параболический (рис. 213)
У2 = 2рх. C)
Эллиптический, гиперболический и
параболический цилиндры суть
поверхности, образованные прямыми линиями,
проходящими через точки эллипса,
гиперболы и параболы перпендикулярно
плоскости каждой из этих линий. Эти
линии — эллипс, гипербола, парабола —
называются направляющими, а прямые,
лежащие на поверхности цилиндра,—его
образующими. Для цилиндров, заданных
уравнениями A),- B) и C),
направляющими лилиями являются соответственно
эллипс
~Ж + "ьГ = 1 > 2 = 0,
302 Глава 1Х{ КАНОНИЧЕСКИЕ УРЛВШЧ1ИЯ ПОВЕРХНОСТЕЙ
гипербола
л-2 и2
± °_ — 1 7 — 0
а2 Ь2 ""' *' Z"~U>
парабола
у2 = 2рх, z = 0,
а образующие параллельны оси Oz.
§ 136. Прямолинейные образующие однополостного гиперболоида
и гиперболического параболоида
1, Прямолинейные образующие однополостного
гиперболоида
Определение. Прямая, все точки которой лежат на поверхности
второго порядка, называется прямолинейной образующей этой
поверхности.
Мы знаем, что конические и цилиндрические поверхности вю-
рого порядка имеют прямолинейные образующие, причем каждая
из этих поверхностей может быть образована движением прямой
в пространстве.
Оказывается, что среди всех поверхностей второго порядка,
кроме цилиндра, конуса и пар плоскостей, прямолинейными
образующими обладают еще одпополостный гиперболоид и
гиперболический параболоид, причем, так же как в случае цилиндра и
конуса, обе эти поверхности могут быть образованы движением
прямой в пространстве.
В этом пункте мы рассмотрим прямолинейные образующие
одиополостного гиперболоида.
Теорема 1. Через каждую точку однополостного гиперболоида
проходят две и только две его прямолинейные образующие.
Доказательство. Пусть (х0, у0, г0) — произвольная точка
однополостного гиперболоида
,2 ,,2 ,2
±LJt1 /11
x = xo + lt, y = yc-i-mt, z=--zQ-{-nt B)
параметрические уравнения проходящей через нее прямой.
Чтобы найти точки, общие поверхности A) и прямой B),
подставим в уравнение A) вместо х, у, г их выражения из формул B).
Ш-11Г , (Уо-rmty (zo + ntf .
а2 ' Ь2 с2 '
ИЛИ
_Р_. т2 п2 \ ,2 , 0Aх0 ту0 nzo\ , Х1 у1 г1 .
«2 + й2 ~"W) 1 ~1 [7?"*~Т2 "с2 )l r!?^~W~~~&-1'
4- 136. ПРЯМОЛИНЕЙНЫЕ ОБРАЗУЮЩИЙ
Так как точка (х0, yQ, г0) лежит на поверхности A), то
■А ,,2 7г
-14--^- —il-1 И")
о2 ^ й2 с2 ~~ l> V '
и последнее уравнение принимает вид
-0 C)
Для того чтобы прямая B) целиком лежала на поверхности A;,
необходимо и достаточно, чтобы все ее точки лежали на этой
поверхности, т. е. чтобы уравнение C) удовлетворялось при всех
значениях /, а это возможно тогда и только тогда, когда оба
коэффициента при t2 и t равны нулю:
£+£-?-«■ A>
хо1 . уот гоп _ п ,г
Мы получили два уравнения относительно координат /, m, a
направляющего вектора прямой B). Из уравнения D) следует,
что пфО, так как в противном случае (п = 0) мы имели бы
Так как для определения направления прямой B) играют роль
лишь отношения 1:т:п и по доказанному пфО, то можно
положить п — с. Тогда система уравнений D) и E) примет вид
- + ^ = 1 ' D')
. а2 Т- Ь2 — 1. 14- J
а2 "■" б2 с ' *■ '
Эта система имеет два действительных и различных решения.
В самом деле, присоединяя к системе D'), E') тождество*
в силу уравнений D'), E') и (Г) находим
^-^ = 1, или ^_
об ab ab
* Тождество (a\-{-al) ( b\-\-b\)— (axb1-i-aibiJ==(a1b2—albxf называется
тождеством Лаграижа и проверяется раскрытием скобок в левой части.
Тождество F) получается из тождества Лагранжа, если положить
а [ п - т h х° h Уй v
304 Inn /A. KAHOHHHttKllt УРАВНЕНИЯ ПОВЕРХ I-. ОСТ ЕЙ
Итак, для определения координат / и т направляющего вектора
{I, т, с] прямолинейных образующих однополостного
гиперболоида A), проходящих через точку (х0, у0, г0), мы имеем систему
аг "г Ь2 — с . (Ч
эквивалентную системе D'), E'). Серя в правой части уравнения
(8)+ 1, получим
ас b be а .
кЬ(9)
Если же в правой части уравнения (8)'взять —1, то получим
ас Ь , be a .
го 2 2 > "*2 2 9 > 2 I 2/
а2 + й3 "о2""^"^
Таким образом, найдены направляющие векторы {^, тх, пх}
и {/8, т2, п2} прямолинейных образующих однополостиого
гиперболоида A), проходящие через его точку (хA, у0) г0). Теорема
доказана.
Каждая из образующих пересекает плоскость хОу в точке,
лежащей на горловом эллипсе
Поэтому за точку (х0, у0, z0) образующей всегда можно взять
точку (*0, у0, 0). Для такой точки
х2 у2
и формулы (9j) и (92) принимают вид
■ • *=х m=- ^=c; (lo)
Разобьем множество образующих на два семейства1 к первому
семейству отнесем образующие
jg.--.jcp д—Уо __ z /Ь
13b ПРЯМОЛИНЕЙНЫЕ ОБРАЗУЮЩИЕ
'Ю5
ко второму
х — хо_у —
Ьхп
(II)
где х0, у0, 0—координаты точки горлового эллипса.
Теорема 2. Две прямолинейные образующие однополостного ги~
перболоида, принадлежащие к разным семействам, всегда лежат
в одной плоскости и параллельны в том и только в том случае,
когда они проходят через диаметрально противоположные точки
горлового эллипса.
Доказательство. Пусть (хи ylf 0) и (х2, у2, 0) —
произвольные точки горлового эллипса, а
x—xl_y~y1 _ г
ayl bxx с '
~Ь~ а"
t — x2_y — y.
проходящие через них образующие разных семейств.
Применяя необходимое и достаточное условие компланарности
двух прямых, будем иметь
хг — ху у2—ух 0
__Ьхх
Т о"
i с
= с
а
Ьх9
= abc A —l) = 0
Образующие параллельны в том и только в том случае, если
откуда
Георема 3. Две прямолинейные образующие однополостного
гиперболоида, принадлежащие одному семейству, скрещиваются.
Глава IX КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
Доказательство. Пусть
bxl
х—х2 _ у — у2 _ г_
ау2 Ьх% с
Ь а
Ь а
две различные образующие одного семейства. Имеем
x2~xi У2—У1 О
Точно так же убедимся в том, что скрещиваются две любые
образующие другого семейства.
Из теорем 1 и 3 следует, что через каждую точку однополост-
ного гиперболоида проходят две образующие, принадлежащие
разным семействам.
Рис. 214
Отсюда следует, что однополостный гиперболоид есть
геометрическое место точек, принадлежащих всем прямолинейным
образующим одного семейства (рис. 214).
Однополостный гиперболоид вращения можно получить
вращением одной нз его прямолинейных образующих вокруг оси
вращения.
Теорема 4. Никакие три прямолинейные образующие однопо-
лостного гиперболоида, принадлежащие одному семейству, не
параллельны одной плоскости.
j> 130 ПРЯЛЮЛПНПППЫЕ ОБРАЗУЮЩИЕ
307
Доказательство. Рассмотрим направляющие векторы
___ i_ p
jay2 __&£з Д
\ Ь ' а ' С ( '
3 bxs \
трех образующих одного семейства.
Имеем
ay i
~b~
~F
ays
b
bXl
a
a
a
С
С
С
= С
Ч
х3
\)\
Уг
Уз
1
1
1
так как точки (xlt уг, 0), (х.2, у2, 0), (х3, у3> 0) как точки
горлового эллипса не лежат на одной прямой. Таким образом,
направляющие векторы рассматриваемых образующих некомпланарны.
Для отыскания двух семейств прямолинейных образующих од-
нополостного гиперболоида практически можно поступать так:
перепишем каноническое уравнение
однополостного гиперболоида в виде
а с) V1 ' b А1 ь
и рассмотрим два семейства прямых, одно, заданное уравнениями
— -г — =^ и
\-4-
х г 1 I. у
— — I 1 i—т~
а с и \ b
дополненное двумя прямымих
(I')
* Первая из этих двух прямых соответствует значению и = 0, второе
значению « = оо. Доказательство то; о, что плоскости, заданные уравнениями
(!'), пересекаются, предоставляется читателю
308
Г.чае а IX КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВП'ХПОСТЕП
и другое, заданное уравнениями
а
а с
дополненное двумя прямыми
а
У
Т> >
-т=о
Из уравнений (Г) и (II') следует, что
Xs U2 ?2
__!_ £ — 1
_.<Э 1 »_О _•) ^ 1
(II')
т. е. все эти прямые лежат на поверхности заданного однопо-
лостного гиперболоида.
Для нахождения уравнений образующих, проходящих через
данную точку (х0, у0, г0), следует в уравнения (Г) и AГ)
подставить х0, у0, z0 вместо х, у и г. Тогда будут найдены и и v.
Таким образом могут быть получены, например, уравнения
1 УО \ / Л I ^
1 г — + —
X Z
а с
— х° М
~ а Г
(I")
1
т+т =т 0+1 ■
(П")
образующих, проходящих через любую точку (х0, у0, 0)
горлового эллипса
х2 и2
— + — = I z = 0
однополостного гиперболоида
Из уравнений (I") и (II") находим направляющие гекторы
соответственно прямых (I") и (II"):
, ,1 О(/п б*п 1
§ 136. ПРЯМ0ЛШ1ГГШЫЕ ОБРАЗУЮЩИЕ
Таким образом, семейстсо прямолинейных образующих (Г)
совпадает с тем семейством, которое выше было названо
семейством (I), а семейство образующих (II') совпадает с семейством (II).
2. Прямолинейные образующие гиперболического
параболоида
Теорема 1. Через каждую точку гиперболического параболоида
~-у = 2г, где р>0 и <7>0, A)
проходят две и только две его прямолинейные образующие.
Доказательство. Пусть (х0, у0, z0)—произвольная точка
гиперболического параболоида A), а
у-Уо + mt, z = z^-\-nt B)
параметрические уравнения прямой, проходящей через эту точку.
Для того чтобы прямая B) целиком лежала на поверхности
A), необходимо и достаточно, чтобы уравнение
или
\Т> я~
или
выполнялось при всех значениях /, а это возможно тогда и
только тогда, когда
^. — ^. = 0 х°1- УйП » = 0
Р q ' Р я
Из первого уравнения находим
р
Решая это уравнение совместно с уравнением
Р Я
находим
310 Глава IX КАНОНИЧЕСКИЕ УРАВНЕНИЯ IIOBFPX ПОСТЕЙ
Теорема доказана. Мы видим, что прямолинейные образующие,
параллельные вектору {llt mx> п^, параллельны плоскости
а прямолинейные образующие, параллельные вектору {/2, /па> пг}>
параллельны плоскости
Разобьем множество всех прямолинейных образующих
гиперболического параболоида на два семейства, относя к первому
семейству все образующие, параллельные плоскости
Vp П~0'
а ко второму семейству — образующие, параллельные плоскости
п
p V я
Как мы видели в § 134, плоскость хОу пересекает
гиперболический параболоид
V2 „2
Р ч
по паре прямых
Т-7Т = 0 z=° W
УТ+
Прямая % принадлежит первому семейству, а прямая ц. —
второму. Выше было доказано, что через каждую точку
гиперболического параболоида проходит по одной образующей из каждого
семейства. Следовательно, через каждую точку прямой %
проходит еще по одной образующей второго семейства. Прямая fj.
принадлежит второму семейству и, следовательно, через каждую ее
точку проходит еще по одной образующей из первого семейства.
Образующими, пересекающими прямые К или \а, исчерпываются
все прямолинейные образующие гиперболического параболоида A).
В самом деле, прямые % и \л пересекают друг друга; всякая
же другая прямолинейная образующая, гиперболического
параболоида A) пересекает плоскость хОу, а значит, и одну из прямых
л- или \i, ибо плоскости, параллельные плоскости хОу, пересекают
гиперболический параболоид A) по гиперболам и, значит, не
содержат его прямолинейных образующих.
136. ПРЯМОЛИНЕЙНЫ!; ОБРАЗУЮЩИЕ
311
Таким образом, первое семейство прямолинейных образующих
гиперболического параболоида A) является множеством всех
прямолинейных образующих, пересекающих прямую ц:
а второе семейство есть множество всех прямолинейных
образующих гиперболического параболоида A), пересекающих прямую К:
■77= — J^^O, г = 0.
VР Уя
Гиперболический параболоид есть геометрическое место точек,
принадлежащих всем прямолинейным образующим одного семейства
(рис. 215).
Рис. 215
' Теорема 2. Две прямолинейные образующие гиперболического
параболоида из разных семейств пересекаются.
Доказательство. Возьмем две прямолинейные образующие
разных семейств:
Y"p
Vp
x—x2 _ y~-tj2
Y"p
V7+
V7
проходящие через точки (xlt ylt гг) и (х2, у2, z2)
гиперболического параболоида. Эти прямые непараллельны (их направляющие
312
Глава IX КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
векторы неколлнгеарны) и лежат в одной плоскости, так как
хъ — хх уг — у
Vp Vq
Vp ~Vq
—г,
Jh
Vp V q
Vp
= V pq
u\-y\
Поэтому прямые пересекаются.
Теорема 3. Две прямолинейные образующие гиперболического
параболоида, принадлежащие разным семействам, скрещиваются.
Доказательство. Возьмем две разные образующие,
принадлежащие, например, первому семейству. Они проходят через
две разные точки прямой ц:
V
p
и параллельны плоскости
Vp Vq
пересекающей прямую \i. Таким образом, эти образующие лежат
в параллельных плоскостях и потому не пересекаются. Но они не
могут быть и параллельны, так как в противном случае все
образующие второго семейства, пересекая эти две образующие в силу
теоремы 2, лежали бы в плоскости, проходящей через эти две
параллельные образующие. Это противоречиво, так как параболоид
есть геометрическое место точек, принадлежащих всем образующим
одного семейства.
Замечание Уравнения двух семейств прямолинейных
образующих гиперболического параболоида
137. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ IX
313
можно взять в виде: одна серия
_х__ , _JL _ 2м — ^-_i_
У"р Уя ' У р \fq~~~u"
дополненная еще одной прямой
C)
и другая серия
дополненная прямой
JL.~1. Л L._9y
-£= ^= = 0, г=0.
Ур Vq
D)
Нетрудно видеть, что уравнениями C) задается та серия
прямолинейных образующих, которая выше была названа «второй»,
а уравнениями D) —серия, которая выше была названа «первой».
§ 137. Примеры и задачи к главе IX
1. Задачи с решениями
Пример 1. Определить вид и расположение поверхности
Решение.
-fl) — 2—3(/2 — 3(г2 — 2г + 1)-}-3—5 = 0,
2(*+1J — Згу2 — 3B— 1J = 4,
f у* (г-1)"_1
4 4'
Положим
х+
тогда уравнение примет вид
1 JL
4_ •
3
', z-l = Z,
£1 = — 1
4
A)
Это уравнение определяет двуполостный гиперболоид вращения (вокруг
оси О'Х).
Формулы A) можно переписать и виде
314 Глава IX КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
Отсюда видно, что уравнение приводится к каноническому виду
параллельным переносом осей координат Начало новой системы O'XYZ находится
в точке ^— 1, 0, 1) эта точка является центром гиперботоида Ось вращения/
совпадает с новой осью О'Х, т е прямой, проходящей через точку (— 1, 0, 1)
параллельно оси Ох Полуоси гиперболоида
Уз
Этот гиперболоид можно получить вращением вокруг действительной оси
гиперботьь
Y2 X2
з
уравнения которой даны относительно повой системы координат.
Пример 2. Определить вид и расположение поверхности
Зх2 + 4(/2 — 12* -i- 8(/ + 17г = О
Решение
3(х2— 4х-г4)-12 + 4(г/2+2у~М) — 4+172 = 0,
30с — 2J-Н (у+ 1J-1-17г—16 = 0,
ТГ +17
6 8
Положим
ж-2-Х, (/+
или
16
Последнее уравнение примет вид
X2 К2
_ 4-1— о/
17 +17 ~ ZZl
6 8
Оно определяет эллиптический параболоид, для которого
17 17
Ось параболоида имеет отрицательное направление оси O'Z, вершина
находится в точке [2,-1, -р=
Пример 3. Определить вид и расположение поверхности
г2 = 3*-Иг/+ 15
Решение Повернем оси координат вокруг оси Ог на угол,
определяемый соотношениями
4 3
-=-, smcp = —=-,
<! 137 ПР1.МКРЫ И ЗАДАЧИ К 1ЛЛЫ-. IX
формулы преобразования будут иметь вид
5
Отсюда
3x-f4y=5y* A)
и уравнение
" " ' '/-1-15
принимает вид
г*2 =5«/*-|-15, ил» г*2=5((/* + 3).
Положим
я* = Х, i/*-f3==y, г*=2, B)
тогда получим
Z2 = 5y,
т. е. уравнение параболического цилиндра. Из формул A) и B) находим
Направляющей этого цилиндра служит парабола с параметром р — —,
лежащая в плоскости Х=0, т. е. в плоскости
4л—3|/=0.
Плоскость симметрии цилиндра, перпендикулярная к плоскости напрлч-
ляюшей, есть плоскость Z = 0, или г = 0, т. е. плоскость хО(/.
П юскость, касательная к цилиндру, лерпеидикулярная к указанной
плоскости симметрии, будет 7 = 0, т. е.
Для всех точек цилиндра Y > 0, т. е. цилиндр лежит в том
полупространстве от плоскости Зл + 4(/+ 16 = 0, для всех точек которого
3*-М«/-;-15 >0.
Пример 4. Определить вид и расположение поверхности
z2 = 2;cy.
Решение. Проиаводя поворот осей вокруг оси Oz на угол а, будем иметь
х = х' cos а— у' sin а, j/==*'sina+«/' cos a, z = z'
и уравнение !1римет вид
г'2 =2 [х'2 cosasin <x-\-x'y' (cos2a—sin2a) — у'2 sin acosa].
Подберем угол а так, чтобы в этом уравнении обратился в нуль
коэффициент при x'y'i
cos2a—sin2a = 0.
Отсюда можно пзять cosa = sina, следовательно, a = 45°. Так как при этом
1 V
cosa = sm a =—yr=., то попедпое уравнение примет вид
это конус вращения с вершиной в начале координат.
316 Глава 1К КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
^ гол иегьду осью вращения и образующими рапен 45°. Осью конуса
является новая ось Ох', т. е. биссектриса угла хОу.
Пример 5. Подобным образом приводится к каноническому виду уравнение
z = xy.
После поворота осей вокруг оси Ох на угол 45" получим
х'2-{/'2 =2г',
это гиперболический параболоид.
2. Задачи для самостоятельного решения
1. Дан однополостный гиперболоид
9 + 4 1
и плоскость а'= 5. Найти вид и полуоси линии пересечения данной
поверхности и данной плоскости.
4
Отв Гипербола, действительная полуось равна —, мнимая полуось
о
g
равна -=-, центр E, 0, 0); действительная ось параллельна оси Ог, мнимая
о
ось параллельна оси Оу.
1. Составить уравнения прямолинейных образующих однополостного
гиперболоида
16+ 9 4 '
проходящих через его точку D, 3, 2)
<»-■*+*-'+!■ f-*->-*■
Т-7-» '-!-•
3 Определить вид и расположение поверхности
Зг> + 4(/2— 12х + 2 = 0
Отв Эллиптический параболоид, вершина B, 0, 12); ось параболоида
имеет отрицательное направление оси Ог; каноническое уравнение
Y2 V2
T+T=2Z
6 8
4. Составить уравнение эллипсоида, оси которого совпадают с осями
координат, если известно, что он проходит через окружность лга+ t/2-j-za = 9,
z — x, и через точку C,1,1).
л2 , уг , г2
Отв __r_.T_ = i.
5. Доказать, что сумма чисел, обратных квадратам длин трех любых
попарно перпендикулярных радиусов эллипсоида, постоянна.
6. Доказать, что плоскости, проходящие через концы трех попарно
перпендикулярных радиусов эллипсоида, касаются шара, вписанного в куб,
который (куб) вписан в эллипсоид.
137 ПРИМЕРЫ Ii ЗАДАЧИ К ГЛАВЕ IX 317
7. Определить угол между прямолинейными образующими однополостно:о
гиперболоида хг-\-у2 — 22 = 1, проходящими через произвольную его точку.
Отв. Если х — г--=и A— у), и (х + г) = 1 + </ и х — z = v (I -\-y), v(x + z) =
•_ 1__^_две образующие, то
(UV— IJ
8. Доказать, что проекции прямолинейных образующих поверхности
. ~~j = 2z (р>0, <?>0)
на плоскость xOz касаются параболы >2 = 2рг, # = 0.
9. На гиперболическом параболоиде хг— y2 = 2z найти геометричеспоа
место точек пересечения двух взаимно перпендикулярных образующих.
Отв. Две прямые (образующие): 1) х — у = 0, 2 = 0
и 2) x-j-t/ = O, 2 = 0.
10. Доказать, что проекции на плоскость горлового эллипса линий, по
которым поверхность однополостного гиперболоида рассекается касательными
плоскостями к его асимптотическому конусу, касаются этого эллипса.
11. Доказать, что-проекция прямолинейной образующей однополостного
гиперболоида на плоскость горлового эллипса касается последнего.
12. Пусть С — сечение параболоида вращения некоторой плоскостью.
Доказать, что проекция С па плоскость, перпендикулярную оси параболоида,
есть окружность.
13. Доказать, что если р' и q'— параметры парабол, получаемых в
сечении эллиптического пара!олоида
j+~ = 2z (p>0, ?>0)
двумя его взаимно перпендикулярными плоскостями, проходящими через
ось Ог, то
1+11+1
14. Найти геометрическое место точек, равноудаленных от двух данных
скрещивающихся прямых в пространстве.
Отв Гиперболический параболоид.
15. Доказать, что любая плоскость, проходящая через прямолинейною
образующую одной из серии однополостного гиперболоида, проходит через
прямолинейную образующую другой серии.
16. Доказать, что любая плоскость, проходящая через прямолинейную
образующую гиперболического параболоида в случае, если она не параллельна
оси этой поверхности, проходит еще через одну прямолинейную образующую
этого гиперболического параболоида другой серии.
17. Прямая
вращается вокруг оси Ог. Составить уравнение поверхности вращения.
Отв. A'2~f у2— 13г2— 142-f 10 — одиополостный гиперболоид.
18. Найти геометрическое место центров сфер, касающихся плоскости
хОу и сферы A-2-f-i/2 + z2=^a2.
Отв. х2~\- у2 = а2 ± 2az—два параболоида вращения.
318 Глава IX. КАНОНИЧГ-СКИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
19. Найти поверм.ость, образованную прямой, которая пересекает па
ра1олы
у2 = 2х, 2 = 0 и 22= — 2х, у = 0,
оставаясь параллельной плоскости у— 2 = 0.
Отв. у2 — г2 = 2х — гиперболический параболоид.
20. Составить уравнение геометрического места прямых, касающихся
С(|.еры х2+(/2+22=1 и пересекающих две прямые
х = 1, «/ = 0 и х= — 1, г = 0
Отв. х2 i 2yz — 1 —однополостные гиперболоиды.
21. Найти прямолинейные образующие однополостного гиперболоида
x2-:-(/2 = 2(Z2-f 1),
проходящие через точку A, 1, 0).
Отв.
х—\ у—\_г л: — 1 у — 1 г
1 =ТГГ~Т' ~Т~ ~ ~^Т ~~ ~ "
22. Определить угол прямолинейной образующей однополостного
гиперболоида х2-\-у2—22=1 с касательной к окружности горлового сечения в той
точке, в которой эта окружность пересекается с рассматриваемой образующей.
Отв. 45°.
23. Найти проекции прямолинейных образующих гиперболического
параболоида
хг и2
— -^- = 22 (р>0, <?>0)
в плоскость хОу.
Отв. Два семейства параллельных прямых
77+77=с- г=° и с °
где Ci и С2 принимают все действительные значения.
24. При каком необходимом и достаточном условии точка (х0, у0, г0)
лежит внутри эллипсоида
v2 /i2 ?2
Отв.
25. Найти геометрическое место точек, для каждой из которых отношение
расстояний до двух скрещивающихся прямых пространства равно данному
числу k.
Отв. Однополое!ный гиперболоид, если k Ф 1; гиперболический
параболоид, если k = 1.
S 137. ПРИМЕРЫ II ЗАДАЧИ К ГЛАВЕ IX 319
26. Составить параметрические уравнения
1° эллипсоида,
2° одпополостного гиперболоида,
3° двуполостного гиперболоида,
4° гиперболического параболоида.
Отв 1° х = a cos и cos v, у = й cos и sin v, z = csinu.
„. uv+\ ,v — u uv—\
2 x=a—:—, ij — b—■—, z = c—;—
u-f-v u-\-v u-\-v
(координатные линии —прямолинейные образующие).
Q
3" A- = acos и tg v, y = bsmu\gv, z=
4° a-= Vp (u + u), y=Vi(u — v), z = 2uv
(координатные линии —прямолинейные образующие).
27. Доказать, что проекции прямолинейны^ образующих однополостного
гиперболоида
на плоскость хОг касаются гиперболы
*2 ——1 — О
являющейся сечением данного одпополостпого гиперболоида плоскостью хОг.
ГЛАВАХ
КОМПЛЕКСНАЯ ПЛОСКОСТЬ
И КОМПЛЕКСНОЕ ПРОСТРАНСТВО.
АЛГЕБРАИЧЕСКИЕ ЛИНИИ
И АЛГЕБРАИЧЕСКИЕ ПОВЕРХНОСТИ
§ 138. Комплексная плоскость и комплексное пространство
1. Комплексная плоскость
Комплексной плоскостью назовем множество всех
упорядоченных пар комплексных чисел, а каждую такую упорядоченную
пару комплексных чисел—точкой комплексной плоскости.
Направленным отрезком комплексной плоскости назовем
упорядоченную пару точек этой плоскости.
Если на комплексной плоскости заданы четыре точки:
A{xv уг), В(х2, </2), С(х3, уз), D(x4, y4)
(х,, у{ — комплексные числа), то два направленных отрезка АВ
и CD условимся считать равными тогда и только тогда, когда
выполнены равенства
x2—x1 = x4—xs и у2 — у1 = у4 — у!1.
Совокупность всех равных между собой направленных отрезков
назовем вектором комплексной плоскости.
если направленный отрезок АВ задам своим началом А (х1, уг)
и концом В(х2, У2)> то числа хг — х1 и уъ — уг будем называть
координатами вектора а, являющегося классом всех
направленных отрезков, равных направленному отрезку АВ. При этом
будем писать
* ISS КОМППГКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО 321
Суммой а + Ь вектороь а и b и произведением ha числа К на
вектор а, где а={х1. ух), b={xit у2}, будем называть векторы;
\a = {\xlt \yt). B)
Вектор а = {0, 0} будем называть нулевым или
нуль-вектором. Если а — нулевой вектор, то будем писать а = 0.
Векторы а — {х, у} и Ь={ — х, —у} будем называть
противоположными друг другу и писать Ь =— а или а—— Ь.
Сумма векторов и произведение числа на вектор обладают
следующими свойствами:
Iе а + (& +с) = (а + *) + с,
2е а + 0 = а,
Зь a-f(-a) = 0,
4е a + b = b + а, C)
5е 1. а = а,
6° А (ца) = (Х|х) а,
7° (Х + ,и)а = ^а-Ь!ла,
8° ? (а + 6) = Ъа -f- Я6.
Замечание. При изучении операций сложения, вычитания
векторов и умножения вектора на число в главе IV мы по
существу пользовались только этими свойствами векторов.
Пусть в произвольном множестве М определены две операции над
его элементами: 1) операция сложения, т. е. двум любым элементам
а и Ь, входящим в множество М, ставится в соответствие элемент
того же множества М, называемый их суммой: с = а-\-Ь,
2) любому комплексному числу X и любому элементу а из
множества М ставится в соответствие элемент b из множества М,
называемый произведением числа А па этот элемент: Ь = ка
Если при этом выполнены все свойства C), то множество М
называется линейным пространством, а его элементы — векторами
(свойство 2° при этом формулируется так: в множестве М
существует элемент 0, такой, что для любого элемента а из
множества М выполняется равенство а-]-0 = а; свойство 3°—так: для
любого элемента а из множества М найдется элемент b из
множества М, такой, что а + 6 = 0; этот элемент b обозначается —а).
Теория линейных пространств изучается в курсах линейной
алгебры *.
Определение линейной зависимости векторов комплексной
плоскости такое же, как и в § 36. Два линейно зависимых
вектора называются также коллинеарными. Векторы а и b кол-
линеарпы тогда и только тогда, когда или 6 = Яа, или a— Kb.
* Свойство 4е может быть доказано из остальных (даже без использования
свойства 6°).
11
П. С. Моденов
32? ГяаваХ КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
Необходимым и достаточным условием коллинеарности
векторов а = {х1, ух} и b = { x2 уг} является равенство
=0.
На комплексной плоскости существуют два линейно
независимых вектора (например, {1, 0} и {0, 1}), но всякие три
вектора линейно зависимы.
Базисом на комплексной плоскости называется упорядоченная
пара неколлинеарных векторов е1 и е2.
Всякий вектор а можно и притом единственным способом
разложить по базчсу е1, е2, т. е. существует и притом только
одна пара чисел х и у, таких, что
а — хе1 + уе<ь-
Числа хну называются координатами вектора а в базисе
t',, е.2 (то, что выше названо координатами вектора, это его
координаты в базисе ^ = {1, 0} еа = {0, 1}).
Декартовой системой координат на комплексной плоскости
называется совокупность точки О (начало координат) и базиса ег, е.2.
Направленный отрезок ОМ, где М —любая точка
комплексной плоскости, а О—фиксированная точка (в частности, начало
координат), называется радиусом-вектором точки М. Координаты
хну радиуса-вектора ОМ точки М в декартовой системе
координат (О, ev ёг)
называются координатами точки М в этой системе (то, что
г.азаано координатами точки,— это ее координаты, если за начало
координат принята точка 0@, 0), а за базис — векторы ех —
= |1,0}, *2 = {0,1}).
Если на комплексной плоскости введены две системы
координат @, еи е2) и @', еи е2), то координаты хну точки М
is системе (О, elf e2) через координаты х' и у' той же точки
и системе @', elt e2) выражаются соотношениями х = апх' +
+ в121/'-7**0> 9 — *цХ'-\-а22у'-)-у0, где хй, у0 —координаты топки О'
г. системе @, е17 ё%), а (аи, а21} и {а12, а22} — координаты
векторов е,, е2 в базисе elt ег.
В самом деле, разложим векторы е\ и е2 по векторам ех и ег\
e1 = aue1 + a21e2, e2 = alze1 + e2iei. D)
Тогда
= хйег + уйе2 + x'e[ + у'е, =
хое1 -f г/0в2 + д:' (оцв! + «2,6^ + г/' (а12ех + аггеъ)
' f-^o) ех + {а21х'
5 П8 КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО 323
С другой стороны,
ОМ — х
Значит, в силу единственности разложения вектора по базису
имеем
x = a11x' + aliy' + x0, у = а21х' + аг2у' + у0. E)
Введем на комплексной плоскости систему координат (О, еъ е2).
Пусть а—{1, т} — какой-нибудь ненулевой вектор; фиксируем
еще точку М0(х0, у0). Пусть ОМ0 = г0 — ее радиус-вектор.
Множество концов М радиусов-векторов ОМ = г, определяемых
соотношением
r = r^-\-ta, F)
где t принимает все комплексные значения, называется прямой,
лежащей на комплексной плоскости. Вектор а называется
направляющим вектором прямой F). Координаты хну точки М прямой
F) через координаты /, т направляющего вектора а и через
координаты х0, уй точки Мо выражаются соотношениями
x=*xo-\-lt, y = yo + mt, G)
'это параметрические уравнения прямой.
Уравнение прямой, проходящей через две различные точки
A(xi> Уг) и В (х2, у2), можно записать в виде
г^Г1 — 1{Гъ-гх), (8)
где г1 — ОА, гг = ОВ, а г —радиус-вектор ОМ произвольной точки
прямой АВ. В параметрической форме
x=zx1-\-t(xi~ хг), y = yi + /(y2—Уг). (9)
Из уравнений G) следует, что уравнение прямой, лежащей на
комплексной плоскости, можно записать в виде!
= 0, A0)
—х0 у—у0
I m
или
тх—1у-\- 1у0—тх0 = 0,
или
Ах + Ву + С = 0, A1)
т. е. уравнение любой прямой, лежащей на комплексной
плоскости в любой системе координат (9, elt e3),— уравнение
первой степени
Обратно, пусть на комплексной плоскости введена система
координат @, е1г е%) и задано уравнение первой степени
О. A2)
11*
324 Глава X КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
Пусть х0, у0 — какое-нибудь решение этого уравнения, i. e.
имеет место следующее числовое равенство;
Уравнение A2) эквивалентно уравнению
или
= 0. A3)
с~хо У — Уо
— В А
Уравнение A3), следовчтельно и эквивалентное ему
уравнение A2), является уравнением прямой линии, проходящей через
точку (х0, у0), направляющий вектор которой а = {—В, А}.
Теорема. Для того чтобы точки А, В и С комплекс ой
плоскости лежали на одной прямой, необходимо и достаточно, чтобы
векторы АС и СВ были коллинеарны.
Доказательство необходимости. Пусть точки А,
В, С лежат на прямой
Обозначая через гх, г2 и г3 их радиусы-векторы, будем иметь
r1 = r0-\-t1a, г2 = г0 + /2з, r3 = r0 + tsa.
Отсюда
значит, векторы АС и СВ коллинеарны.
Доказательство достаточности. Пусть векторы АС
и СВ коллинеарны. Если точки В и С совпадают, то существует,
очевидно, прямая, на которой лежат точки А, В и С. Если
точки В и С различны (но векторы АС и СВ коллинеарны), то
существует такое число t, что
или
Г3 Гг = I (Г2 Гд),
или
Г1 = Гл + 1(Г9 — Гг),
т. е. точка А лежит на прямой
r = rs + t(r3—г,),
проходящей через точки В и С
§ 138. КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО 325
Если точки А, В, С принадлежат одной прямо,i, а точки В
и С различны, то как указывалось выше, существует такое
число К, что
АС^ХВС.
Это число \ называется отношением направленного отрезка
~АС к направленному отрезку ВО
. _ лс
ВС
Если точки A(xv yt) и В (х2, у2) различны, а точка С(х, у)
лежит на прямой АВ, не совпадает с точкой В и если
— — Я
ев
то говорят, что точка С делит направленный отрезок АВ в
отношении Я. Координаты точки С через координаты точек А и В
выражаются соотношениями
Обратно, каково бы ни было комплексное число Хф—1,
формулами A4) определяются координаты точки, делящей
невырожденный направленный отрезок АВ в отношении I. В частности,
* = £!+£*, у-Ь+Ь A5)
координаты середины отрезка с концами А (хг, уг) и В (х2, у2).
2. Комплексное пространство
Комплексным пространством будем называть множество всех
упорядоченных троек (х, у, z) комплексных чисел, а любую такую
тройку чисел (х, у, г)—точкой комплексного пространства.
Числа х, у, z будем называть координатами этой точки.
Определение направленного отрезка, вектора, его координат,
определение суммы векторов и произведения числа на вектор
даются аналогично соответствующим определениям этих понятий
для комплексной плоскости. При этом имеют место все
соотношения C), т. е. множество всех векторов комплексного
пространства является линейным пространством.
Определение линейной зависимости векторов комплексного
пространства такое же, как и для комплексной плоскости (см.
также § 36). Два линейно зависимых вектора называются колли-
326 Глава X КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
неарными. Три линейно зависимых вектора комплексного
пространства называются компланарными.
В комплексном пространстве имеются три линейно независимых
вектора, например {1, 0, 0}, {0, 1, 0}, {0, 0, 1}, но всякие
четыре вектора линейно зависимы.
Базисом комплексного пространства называется упорядоченная
тройка ех, е2, е3 некомпланарных координат.
Всякий вектор а может быть и притом единственным образом
разложен по базису ех, е2, е3:
a = xex + ye2 + ze3. A6)
Числа х, у, г называются координатами вектора а в базисе
#1, #2> бз- Вместо соотношения A6) мы часто будем писать
а = {х, у, г}.
Векторы
а = {хх, У\, «lb b = {x2, у2, г2},
заданные относительно базиса ех, e2, е3, линейно зависимы тогда
и только тогда, когда ранг матрицы
i Ух гЛ
2 Уч Ч)
меньше 2.
Три вектора
«={*i. Ул., г1], b = {x2, y2, z2), с = {х3, уз, z3)
компланарны тогда и только тогда, когда
= 0. A7)
Ч Уг
хз Уг гз
Декартовой системой координат в комплексном пространстве
называется совокупность точки О и базиса е1) е2, е3.
Направленный отрезок ОМ называется радиусом-вектором
точки М комплексного пространства. Координаты ОМ, т. е. числа
х, у, z такие, что
называются координатами точки М в системе (О, е1г е2, е3)
(таким образом, то, что мы называли координатами точки М
в начале этого пункта,— это координаты точки М в системе
О @, 0, 0), {1, 0, 0}, {0, 1, 0}, {0, 0, 1}).
Если в комплексном пространстве введены две системы
координат (О, ех, е2, е3) и (О', ех, е2, е3), то координаты х, у, г
точки М в системе (О, ех, е%, es) через координаты х', у', z
^ 138 КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО 32?
той же точки М в системе (О', е\, е\, es) выражаются
соотношениями
х-аих' + alsy' + а1вг' +ха,
у~ал1х +аы!,' + а2Яг'+у0, A8)
г = а31х -\-ай2у' -Ь а33г' -f-z0,
где х0, г/о. г0 —координаты точки О' в системе (О, elt е2, е3), a
коэффициенты aik имеют следующий смысл!
е\ = {ап, а21, а31},
е2 = {а12, а22, а82}, A9)
е, = {а18, «аз. азз}
(координаты векторов е',, е'2> е'^ даны в системе О, ег е2, е3).
Доказательство такое же, как в случае комплексной плоскости.
Прямой комплексного пространства, проходящей через точку
Л'о^о. !/о> го) коллипеарно вектору а = {/, т, п}=^0, называется
множество концов всех ради усов-векторов ОМ, определяемых
соотношением
r=ro + ta, B0)
где t принимг-.ei все комплексные значения. В параметрической
форме уравнения прямой имеют иид
x=*xo + U, y = yu + mt, z = za + nt. B1)
Уравнение прямой, проходящей через две различные точки А
и В, определяемые радиусами-векторами ОА = гх и ОВ = г2, имеет
вид
r^r^ + tir.-rj, B2)
или в параметрической форме
У = У1 + 'Л1Л-У1), ' B3)
z = z1 + t(z2 — zl).
Теорема п. 1 этого параграфа имеет место и для комплексного
пространства и доказывается так же.
Так же, как и на комплексной плоскости, определяется поня-
тие отношения, в котором точка С делит направленный отрезок АВ;
имеют место формулы, аналогичные формулам A4) и A5)
(добавляется еще по одному соотношению).
Пусть а = {/1, тх, nt} и & = {/2, т2) п2}—два неколлинеарных
вектора, М0(х0, у0, г0) —произвольная точка комплексного
пространства, а ОМ0 = г0 ее радиус-вектор. Плоскостью П, проходя-
328 ГлавоХ КОМПЛРКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
щей через точку Мо компланарно векторам а и Ь, называется
множество концов ОМ всех радиусов-векторов ОМ = г,
определяемых соотношением
B4)
где параметры и и и принимают все комплексные значения. Числа
и и у —это координаты вектора М0М, где М — любая точка
плоскости П в базисе а, Ь.
В параметрической форме плоскость 11 определяется
уравнениями
y = yo-\-m1u-\-miv, B5)
z — zo-\- nxu-\-n$.
Отсюда следует, что координаты х, у, г всех точек
комплексной плоскости П удовлетворяют уравнению
х хо У У о
11 т1
= 0 B6)
и обратно: если координаты некоторой точки (х, у, z)
удовлетворяют этому уравнению, то в силу линейной независимости
второй и третьей строк определителя А первая его строка
является линейной комбинацией второй и третьей:
х—хо = ы/1 + у/2, y — yo = um1 + vm2, z — zo = «n
откуда следуют отношения B5), т. е. точка (х, у, z) принадлежит
плоскости П.
Из уравнения B6) сразу следует, что любая плоскость
выражается уравнением первой степени:
Ах + Ву + Сг + D = 0. B7)
Обратно, уравнение B7) первой степени всегда можно
записать в виде B6) (см. §69); поэтому всякое уравнение первой
степени является уравнением плоскости.
Отложим вектор я = {/, т, п) от любой точки плоскости. Если
его конец при этом также будет лежать на этой плоскости, то
будем говорить, что вектор а компланарен плоскости.
Необходимым и достаточным условием компланарности вектора
а — {1, т,п} и плоскости, заданной общим уравнением B7),
является равенство
(доказательство такое же, как и в § 70).
« 139 ГМОСКНЕ MfFRP.ViMECKHE ЛИНИИ
329
Отметим, что в комплексном пространстве главный вектор
{Л, В, С} плоскости, заданной уравнением B7), может быть ей
компланарен. Пример:
Имеем
{А, В, С} = {3, 4, 5i}
и далее
Наконец, прямую в комплексном пространстве можно задать
парой различных плоскостей
+ Dx = 0, B8)
■ + D, = 0, B9)
имеющих общую точку.
В самом деле, если множество всех решений уравнения B8)
не совпадает с множеством всех решений уравнения B9) (плоскости
различны!), но имеется точка (х0, уа, га), лежащая как на
плоскости B8), так и на плоскости B9), то множество всех решений
системы B8), B9) имеет вид
х —
C0)
а эти уравнения являются уравнениями прямой, проходящей
через точку (х0, у0, г0) с направляющим вектором
в2
с,
с2
А,
А2
Сг
С2
Аг
Аг
Вг
В-г
В1 С1
в2 с2
С, At
С 2 A.z
>
Al В,
Аг В2
}■
§ 139. Плоские алгебраические линии
1. О п р е д е л е н ие плоской алгебраической линии
и ее порядка
Целой рациональной функцией над полем комплексных чисел
называется функция, которая получается, если над аргументами
и комплексными числами производятся только операции сложения,
вычитания и умножения*.
Например,
« = C-1-40 xi/~~-\-2 + i
* Деление на комплексное число, не равное нулю, рассматривается кап
умножение на число, обратное этому числу.
330 Глава X, КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
целая рациональная функция от грех аргументов. Аналогично
формулируется определение целой рациональной функции над
полем действительных чисел.
Степенью целой рациональной функции и называется максималь
ное значение суммы р + q + /"+... показателей аргументов в выра
жении вида
Ах" у9 г1...,
суммой которых является функция и.
В приведенном выше примере функция и третьей степени.
Алгебраическим уравнением называется уравнение, которое мы
получим, приравняв нулю целую рациональную функцию.
Степенью алгебраического уравнения
/■■(*, у, ?. ...)== о
называется степень целой рациональной функции F. Множество
всех точек М(х, у) комплексной плоскости, координаты которых
удовлетворяют алгебраическому уравнению
F(x, y) = 0,
называется плоской алгебраической линией. Порядком
алгебраической линии, заданной уравнением
F(x, у) = 0,
называется степень этого уравнения, иначе степень целой
рациональной функции F (х, у).
Пусть
F(x, y) = 0 A)
уравнение алгебраической линии п-ro порядка в системе
координат (О, elt e2). Перейдем к другой системе (О', elt e2).
Тогда (см. п. 1 предыдущего параграфа)
х = аих' + а12у' + х0, у = а21х' + а22у' + у0
и уравнение F (х, у) = 0 в новой системе координат примет вид
' ' + уо) = О, B)
т. е. снова является алгебраическим.
Так как х и у через х' и у' выражаются линейными
соотношениями, то степень последнего уравнения не выше степени
уравнения F(х, у) = 0. Но степень последнего уравнения B) не может
быть и ниже степени уравнения F(x, у) —0, так как х' и у'
через х и у также выражаются линейно, а потому, если бы степень
уравнения B) была ниже степени F (х, у) = 0, то при замене х' и
у их выражениями через х и у в уравнении B) получили бы
уравнение F (х, у) = 0 степени более низкой, чем п.
139. ПЛОСКИЕ АЛГЕБРАИЧЕСКИЕ ЛИНИИ 331
Таким образом, во всех декартовых системах координат
алгебраическая линия определяется алгебраическим уравнением и имеет
одни и тот же порядок. Говорят, что алгебраический характер
уравнения алгебраической линии и ее порядок инвариантны (т. е
неизменны) по отношению к преобразованию декартовой системы
координат.
В аналитической геометрии на плоскости изучаются главным
образом алгебраические линии первого и второго порядка, т. е,
линии, заданные относительно общей декартовой системы
координат уравнениями
Ах + By + С = 0, Ах2 + Вху + Су2 + Dx
2. Пересечение алгебраических линий. Пересечение
алгебраической линии с прямой
Пусть заданы уравнения двух алгебраических линий:
F(x, у) = 0, Ф{х,у) = 0 C)
(F и Ф —целые рациональные функции от х и у). Для
нахождения координат точек пересечения линий, заданных уравнениями
C), надо решить эту систему C), так как координаты каждой
точки, лежащей на обеих линиях, должны удовлетворять обоим
уравнениям этих линий.
Докажем, в частности, следующую теорему.
Теорема 1. Прямая линия или совсем не имеет общих точек с
алгебраической линией, или целиком входит в ее состав, или
пересекает ее в конечном числг точек, причем это число не превосходит
порядок линии.
Доказательство. Пусть
F(x, y) = 0 D)
уравнение алгебраической линии n-го порядка (т. е. F — целая
рациональная функция от х и у степени п).
Рассмотрим произвольную прямую, заданную параметрическими
уравнениями
х = хй-\-Н, у = уо + т(. E)
Для определения координат точек, принадлежащих одновременно
алгебраической поверхности D) и прямой E), надо исследовать
следующее уравнение относительно t:
t, y0 +mt) = 0. F)
Это уравнение относительно t имеет степень не выше п. Может
представиться три случая.
1. Уравнение F) не имеет корней. Это значит, что прямая
(.5) и поверхность D) не имеют ни одной общей точки.
332 Г л а ю X КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
2. Соотношение F) является тождеством относительно t. Это
значит, что все точки прямой E) лежат на линии D), иначе
прямая E) входит в состав линии D)
3. Соотношение F) является уравнением относительно t степени
k, большей или равной 1 (но меньшей или равной п, как укачано
выше). В таком случае прямая E) пересекает поверхность D) в k
точках Если среди k корней есть кратные, например, число
t — ll является s-кратпым корнем уравнения F), то будем говорить,
что точка (*0-j-//i, Уо+tnty) является s-кратной точкой
пересечения прямой с линией
Примеры 1 Прямая
x = t, y = t
не имеет ни одной обшей точки с линией
так каь соотношение F) здесь принимает вид —1=0.
2. Прямая
x = t, y = t
входит в состав линии
х2—1/2=0,
так как соотношение F) обращается в тождество 0=0.
3. Прямая
х=и y
пересекает пинию второго порядка
в одной точке В самом деле, уравнение F) принимает вид
/2— t2—2(— 1—1=0,
откуда t — — 1 и, значит, единственная точка пересечения имеет координаты
х=—1, у=0.
4. Прямая
x=t, у = 0
пересекает линию второго порядка
в двух точках A, 0) и ( — 1, 0).
5. Прямая х=1, y = t пересекает линию
в двух совпадающих точках A,0), так как уравнение F) здесь принимает вид
*2=0
и имеет двойной корень {=0.
134 ПЛОСКПР А1ГЕБРЛИЧЕСКHP ПИНИИ
3. Распадение алгебраических линий
Если левая часть уравнения алгебраической линии разлагается
в произведение двух целых рациональных функций, степень
каждой из которых больше или равна 1, т. е.
F(x, i^sbF^x, у) -Fz(x, у),
где Fх{х, у) и F2(x, у) — целые рациональные функции от х и у,
степень каждой из которых больше или равна 1, то говорят, что
данная алгебраическая линия распадается на алгебраические
линии, определяемые уравнениями
Fl(x, t/) = 0 и F2(x, у) = 0.
Например, линия
х2 — if = 0
распадается на две:
к + у = 0, х — у = 0;
каждое из этих уравнений является уравнением прямой,
проходящей через начало координат.
Линия
х2 + у2 = О
также распадается на две!
= 0, y—ix = O;
имеется только одна точка @, 0) с действительными координатами,
лежащая на этой линии.
Докажем теперь следующую теорему.
Теорема 2. Если в состав алгебраической линии
F(x,y) = Q G)
порядка п > 1 входит прямая
Ах + Ву + С = 0, (8)
т. е. координаты всех точек прямой Ах -\- В у -\- С = 0 удовлетворяют
и уравнению F (х, у) = 0, то левая часть F (х, у) уравнения G) может
быть представлена в виде
F(x,y) = (Ax + By + C)F1(x,y),
где Ft(x, у) —целая рациональная функция от х и у, степень
которой на единицу меньше степени F(x, у).
Доказательство. Целую рациональную функцию F(х, у)
степени п от двух аргументов х и у можно представить в виде
F{x,y) = айх" + al(y)xn-> + ..,+ а„ (у), (9)
334 Г леи а X КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛРКСНОР ПРОСТРАНСТВО
где а0 — число, а а1(у), ...,ап(у) — целые рациональные функции
от у, степеней, соответственно не больших 1,2, .,., п. Предположим,
что /4=^=0, тогда уравнение (8) можно разрешить относительно х\
По условию
поэтому на основании теоремы Безу функция (9) делится на
Частное
Ф (к, у) = aax"-i + [ах (у) - (А у + ^-) а0] л;"" + ...
является целой рациональной функцией ф (х, у), степень которой
на 1 меньше степени F(x,y). Итак,
F(x, y) = ^x + Ty + -£J(p(x, у),
или «
где
§ 140. Алгебраические поверхности
1. Определение алгебраической поверхности
Алгебраической поверхностью называется множество всех точек
М (х, у, г) комплексного пространства, координаты которых
удовлетворяют алгебраическому уравнению
F(x,y>z) = 0. A)
Порядком алгебраической поверхности называется степень целой
рациональной функции F(x,y,z). Так же, как п. 1. § 139,
доказывается, что алгебраический характер уравнения A) и порядок
алгебраической поверхности инвариантны по отношению к
преобразованию декартовой системы координат.
В аналитической геометрии в пространстве изучаются главным
образом поверхности первого и второго порядка, т. е. поверхности,
140 Л ЧГЕВР \ИЧНСКПК ПОВЕРХНОСТИ 33"*
заданные относительно декартовой системы координат уравнениями
Ax + By + Cz + D = 0,
Ах2 + By2 + Сг2 + Dyz -\- Егх + Fxy -f Gx -f Hy+Kz+L = 0.
2. Пересечение алгебраической поверхности
с прямой и плоскостью
Теорема 1. Прямая линия или совсем не имеет с алгебраической
поверхностью общих точек, или целиком принадлежит этой
поверхности, или пересекает ее в конечном числе точек; в последнем
случае число точек пересечения не более порядка алгебраической
поверхности.
Доказательство этой теоремы вполне аналогично доказательству
теоремы 1 § 139; пусть
F(x,y,4 = Q A)
уравнение алгебраической поверхности, а
лг = хо + //, y = yo-rmt, г = го-\-п( B)
параметрические уравнения произвольной прямой. Для нахождения
координат точек, принадлежащих одновременно заданной
поверхности A) и прямой B), надо исследовать уравнение относительно t:
zo + n() = O. C)
Степень этого уравнения не выше п. Если оно не имеет корней,
то прямая B) и поверхность A) не имеют ни одной общей точки.
Если соотношение C) выполняется при всех значениях * /, то все
точки прямой B) лежат на поверхности A),. иначе прямая B)
целиком лежит на поверхности A). Если, наконец, уравнение C)
относительно / имеет степень k, такую, что 1^/г^п, то прямая B)
пересекает поверхность A) в k точках (среди которых могут быть
и совпадающие).
Примеры. 1. Прямая
не имеет ни одной общей точки с поверхностью второго порядка
х2 — у2 — 2z = 0.
2. Прямая
x = t, y = t, г = 0
целиком лежит на поверхности
* Для этого достаточно, чтобы равенство C) выполнялось при я + 1
различных значениях t.
336/" л ава X КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
3. Прямая
х=0, t/ = 0, г = /
и поверхность второго порядка
х2—уг—2г = 0
имеют только одну общую точку @, 0, 0).
4. Прямая
x = t, y = 0, г=1
пересекает поверхность второго порядка
в двух точках
(^2, 0, 1) и (-\Г2, 0, 1).
5. Прямая
x—t, у = 0, г = 0
пересекает поверхность
х2—у- — 2г = 0
в одной двойной точке: @, 0, 0) (сравнить с примером 3).
Теорема 2. Плоскость или совсем не имеет с алгебраической
поверхностью общих точек, или целиком входит в ее состав, или
пересекает ее по плоской алгебраической линии, порядок которой
не больше порядка данной поверхности
Доказательство. Пусть
F(x, у, г) = 0 D)
уравнение алгебраической поверхности п-ro порядка (F— целая
рациональная функция от х, у, z степени п).
Рассмотрим произвольную плоскость П, проходящую через
точку М0(х0, у0, г0) компланарно двум иеколлинеарным векторам
a={llt /Пц п\ и b = {L, ;n2, nt\.
Параметрические уравнения этой плоскости
x = xo-Jrl1u + liV, y=-yo-\-mlu--'r'n2v, г = го + п1« + «2у, E)
где и и v—координаты точки М этой плоскости в системе
координат с началом в точке Мо и базисными векторами а и Ь.
Уравнение, связывающее координаты и, v точки М плоскости П, которая
(точка М) лежит и на поверхности D), имеет вид
F (xo + ^u + l^v, уо + т^ + тл, zo + nlu+n1v) = Q. F)
Если это уравнение относительно и и v ue имеет ни одного
решения, то поверхность D) и плоскость E) не имеют ни одной
общей точки.
Если соотношение F) является тождеством относительно и и v,
то все точки плоскости E) лежат на поверхности D), иначе
плоскость П входит в состав данной алгебраической поверхности.
§ 140 АЛГЕБРАИЧЕСКИЕ ПОВЕРХНОСТИ 337
Если, наконец, соотношение F) является уравнением
относительно и и v степени 1 s^&sSCn, то оно является в указанной выше
системе координат (Мо, а, Ь) уравнением алгебраической линии
порядка k.
Примеры. 1. Плоскость
х = и, у = и, z = y
не имеет с поверхностью (также плоскость!):
х—у-\-\=0
ни одной общей точки.
2. Плоскость
х = и, у = и, г —и
входит в состав поверхности
х* — у*^0.
3. Плоскость
X=U, у -U, Z=iO
пересекает поверхность второго порядка
х2 —t/z —2г = 0
по прямой
V----0
(т е. по линии первого порядка).
4. Плоскость
х — и, y = v, г —0
пересекает поверхность второго порядка
*2 + #2 + г2 = 1
по линии второго порядка
3. Распадение алгебраических поверхностей
Если левая часть уравнения
F(x, у, г) = 0
алгебраической поверхности разлагается в произведение двух целых
рациональных функций, степень каждой из которых больше или
равна 1
F (х, у,г) = ц> (х, у, г) ■ \|з (х, у, г),
то говорят, что данная алгебраическая поверхность распадается
на алгебраические поверхности, определяемые уравнениями
(f(x,y,z) = Q и ty(x,y,z) = 0.
Например, поверхность второго порядка, заданная уравнением
338 Глава X, КОМПЛFКСНАЯ П НОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО
ИЛИ
или
(х + у + г)(х + у — г) = 0
распадается на две поверхности первого порядка (плоскости),
уравнения которых
Х + У + 2 = 0, A'-f у — 2 = 0.
Теорема 3. Если в состав алгебраической поверхности
F(x,y,z) = 0 G)
порядка п > 1 входит плоскость
Ах + By -|- Сг -Ь D = 0, (8)
то целая рациональная функция F (х, у, г) может быть
представлена в виде
F {х, у, г) = {Ах + Ву+Сг+ D) Fx (x, у, г),
где Ру(х, у, г) —целая рациональная функция от х, у, г, степень
которой на единицу меньше степени F(x, у, г).
Эта теорема доказывается так же, как и теорема 2 § 139, только
здесь коэффициенты av a2, ...,ап в выражении
F(x,y, z) = a0x2 + a1x"-t+ ■■■+an
являются целыми рациональными функциями от у и г степеней
соответственно не больше 1, 2, ...,п (о0 — число).
ГЛАВА XI
ЛИНИИ ВТОРОГО ПОРЯДКА, ЗАДАННЫЕ ОБЩИМ
УРАВНЕНИЕМ
§ 141. Теорема о том, что всякое уравнение второй степени
с двумя неизвестными определяет эллипс, гиперболу, параболу или
две прямые
Общее уравнение линии второго порядка будем писать в виде
апх2 + 2а12ху + а22у2 + 2ахх + 2а2у + а = 0.
Все коэффициенты обозначены одной буквой а с индексами,
указывающими, какая координата и в какой степени умножается
на этот коэффициент (аи — коэффициент при х2 — х-х и т. д.).
Через й12, а, и а2 обозначены соответственно половины
коэффициентов при ху, хну для симметрии последующих формул.
Все эти коэффициенты можно предполагать и комплексными,
так же как и значения хну. Однако мы ограничимся
рассмотрением того случая, когда ои, а12, о22, о1, о2, а— действительные
числа. Комплексные прямые и комплексные точки будем вводить
лишь в связи с рассмотрением точек пересечения линии второго
порядка с прямой и в связи с распадением линии второго порядка
на две прямые. Систему координат можно предполагать общей
декартовой, однако в § 141 —143 предполагаем, что система
координат прямоугольная.
Теорема I. Общее уравнение
anxZ+2altxy + a2iif + 2axx + 2a2y + a = 0 A)
линии второго порядка, заданной относительно прямоугольной
системы координат, при помощи поворота и переноса осей коорди-
340 Слава XI ЛИНИИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
наш можно привести к одному из следующих видов*\
'X' YDO V О 'О
где Vu =£ О,
где
li где
Эти уравнения будем называть простейшими уравнениями линии
второго порядка.
Доказательство. Докажем сначала, что можно повернуть
оси хОу на такой угол се, что в преобразованном уравнении
коэффициент при произведении х'у' новых координат обратится в нуль **.
Итак, предполагая, что о12 ф О, повернем оси хОу пока на
произвольный угол се. Тогда координаты х и у точки М в системе хОу
через координаты х' и у' той же точки М в системе х'Оу' будут
выражаться соотношениями
х = х' cos се — у' sin се, у = х sin се -f- у' cos а,
а уравнение A) примет вид
ап (х' cos се — у' sin аJ + 2а12 {х cos а —у' sin а) (а;' sin а + у' cos а) +
+ о22 (х' sin а +1/' cos аJ + 2ах (х cos а—у' sin а) +
+ 2а2 (х' sin а + у cos а) -j- а — О,
или
где
а\ 1 = ап cos2 а + 2^12 cos а sin а + а22 sin2 а, B)
a'i2 =a12 (cos2a— sin2a) + (a22 — eu) sin acosa, C)
аг2 ==an sin2 a—2a12cosasina-f a22cos2a, D)
d^ = al cos a -f-a2 sin a, E)
a^ = — flj sin a + a2cosa. F)
Условие
* Здесь по существу речь идет о том, и это будет доказано, что при
помощи ортогонального преобразования целую рациональную функцию (а не
уравнение!)
апх2 + 2а12ху + а2г«/2 + 2«ix+2a2i/ + a
можно преобразовать к одному из следующих простейших видов:
OnX= + a22K2+O, a'11X* + 2a'aY, a'^X'+D, где а'п ф 0, ах2ф0, а\ф0.
** Если в данном уравнении A) а12 = 0, то эту часть рассуждений,
относящихся к доказательству теоремы, следует опустить.
$ 141. ОБШЕЕ УРАВНЕНИЕ ВТОРОЙ СТЕПЕНИ 341
принимает вид
о12 (cos2 а — sin2 а) + (а22 — ап) sin a cos а = О,
откуда
Zal
При повороте на угол се, определяемый этим соотношением,
в преобразованном уравнении коэффициент а'19 обратится в нуль
и оно примет вид
* г 0. (8)
1 случай] апф0, а'2гф0.
Преобразуем уравнение (8) к виду
* ' --v- .£_£_«. ,n
Производя перенос осей x'Ot/' так, чтобы новым началом
координат стала точка
1 2l>
(координаты этой точки даны относительно системы х'Оу') и
обозначая новую систему координат через XO'Y, будем иметь
так что уравнение (8) примет вид
anX* + a'22Y* + D = 0, (I)
где
II случай: или а'22 = 0, а'2^0, или 0:^ = 0, а\ Ф 0.
Предположим, что а^2 = 0, а'2 =^0. Тогда уравнение (8) имеет вид
г / + а = 0, A")
или-
ц
342 Глава XI ЛИПНИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
ИЛИ
Производя перенос осей x'Otf так, чтобы новым началом коор-
/ ai~ \
а о I
динат стала точка О'\ Л, ~ I (координаты этой точки
даны относительно системы х'Оу'), и обозначая новую систему
через XO'Y, будем иметь
1 а ~
а, а,,
так что уравнение A") примет вид
(это уравнение параболы).
III случай: или а'22 = а'2 = 0, или 0^ = 0^ = 0. Предположим,
что я22 = а2 = 0- Тогда уравнение (8) имеет вид
или
+а~^- = 0. (V")
Перенося оси х'Оу' так, чтобы новым началом координат стала
точка
и обозначая новую систему координат через XO'Y, будем иметь
Х = х' + 3-, Y = y,
так что уравнение (Г") примет вид
где
141. ОБЩИЕ УРАВНЕНИЯ ВТОРОЙ СТПШНИ
343
Теорема 2. Общее уравнение линии второго порядка
апхг + 2аиху -\- а21у- -j- 2aLx -j- 2а,у -\- а — 0. (9)
заданное относительно общей декартовой системы координат,
определяет одну из следующих девяти линий (см. таблицу).
Т а б л и и а
Группа
I
11
III
Л»
1
2
3
4
5
6
7
8
9
Уравнение линии „
а2 ' V ~ 1
- §+§~°
а- б2
д:2 = а2(а 56 0)
*2=—а2 (а ?i 0)
Название линии
эллипс
мнимый эллипс
две мнимые пересекающиеся
прямые
гипербола
две пересекающиеся прямые
парабола
две параллельные прямые
две мнимые параллельные
прямые
две Совпадающие прямые
Доказательство. Перейдем от общей декартовой системы
координат к декартовой прямоугольной. Как было доказано в § 139,
п. 1, порядок линии при этом не изменится и данная линия в
декартовой прямоугольной системе координат будет определяться
уравнением того же вида (9) (но уже с другими значениями
коэффициентов aik, а,- и а). Но в предыдущей теореме доказано, что если
общее уравнение линии второго порядка задано относительно
декартовой прямоугольной системы координат, то оно при помощи
преобразования прямоугольной системы координат в
прямоугольную может быть приведено к одному из следующих простейших
видов*:
а'цХ2 -'-а'22у2 -\~ D = 0, а'и=^=0, а'22Ф0, (I)
а' х* -i• 2а' и — 0 а' =7^0 я' =^=0 (II)
a'^-^D^O, а'иФО. (III)
* Здесь через х и у мы обозначаем координаты точек в той системе
координат, в которой уравнение линии является простейшим.
344 Глава XI ЛИНИИ. ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Рассмотрим, какой вид могут принять простейшие уравнения
(П, (II) и (III) линии второго порядка в зависимости от знаков
коэффициентов этих уравнений
I. 1. Если аи и a2i одного знака, a D имеет
противоположный знак, то, деля обе части уравнения (I) на —D и полагая
—: ~т-= <г, — = »-, приведем уравнение (I) к виду
a п
это каноническое уравнение эллипса.
2. Если аи, а22 и D одного знака, то уравнение (I) приводится
к виду
Л L-L 1
а2 й2
и определяет мнимый эллипс (на мнимом эллипсе нет, очевидно,
ни одной точки (действительной), так как если х и
{/—действительные числа, то ~ + |г ^ 0) •
3. Если D = 0, a aXi и а22 одного знака, то уравнение (I)
приводится к виду
v-J <,2
_^ I У_ г\
Это уравнение удовлетворяется только при х = у — 0. Но так
как
то говорят, что это уравнение распадается на пару мнимых
прямых
пересекающихся в действительной точке О'@,0).
4. Если ац и а22 разных знаков, a D^=0, то уравнение (I)
приводится к 1иду
У2 _
D D
ьчитая, что
И полагая г~ —аъ, -r- = b%, получим каноническое уравнение
ахх «и
142 ТЕОРИЯ ИНВАРИАНТОВ 345
гиперболы
г меть
(если <0, -г-<0, то получим —~ л--^-=1 и, производя
поворот осей на угол 90°, т. е. полагая х —— у', у = х', будем
ь2 о» у
5. Если alt и а22 разных знаков, a D = 0, то уравнение
(^приводится к виду
х2 у2
"о2" ¥ ~°
и определяет две пересекающиеся прямые:
а ' b ' a 6
П. Уравнение (II) можно привести к виду
где р = Л =^0. Число р можно считать положительным, так
аи
как в противном случае достаточно изменить положительное
направление оси Оу на противоположное.
III. Уравнение (III) приводится к виду
х2 = — — , или х2 = а2, х2 = — а\ *2 = 0
в зависимости от того, будет
Я- >0, —?- <0 или же D = 0.
а,, а,.
§ 142. Теория инвариантов
В настоящем параграфе понадобятся следующие теоремы.
Теорема I. Произведем над переменными х и у квадратичной
формы
A)
линейное однородное преобразование
\12у ,
+спу'\
346 Гдаю XI ЛИНИИ. ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
квадратичная форма ц. примет вид
Ф' = а\ У + 2а\ „x'i/ + а\гу'\ C)
Тогда между матрицами
( (А,
21 а) \ а j/
квадратичных форм A) м C) ы матрицей
E,
преобразования B) имеет место соотношение
В^С'АС, F)
G)
1г с22/
матрица, полученная транспонированием матрицы С.
Теорема 2. Произведем над переменными к, v и г тадратичной
формы
ф = апх'г + a^if + аз3гг + 2altxy + 2a2syz + ш.А1гх F)
линейное однородное преобразование
y = c2lx' +ci2y' +ci3ze, (9)
г = cslx' + сягу' + сздг';
квадратичная форма q> примет вид
zV. A0)
Тогда между матрицами
/аи й12 огз\ / a'n a'ls a'18\
Л =f a21 a22 a23 1 a ^ = ( a}l a?2 а'г8 ) A1)
\a31 a32 as3/ \ a3l a8, a88/
й матрицей
(Cll C12 С1в\
c2i c22 c23 A2)
CS1 C32 CS8/
преобразования (9) имеет место то же самое соотношение F)!
Я = С'ЛС, A3)
где С'—матрица, t о лученная транспонированием матрицы С.
§ 142 ТЕОРИЯ ИНВАРИАНТОВ 347
Обе теоремы имеют место для квадратичных форм от любого
числа переменных*. Отметим некоторые следствия из этих теорем.
Следствие 1. Так как определитель произведения матриц
равен произведению определителей сомножителей и так как
определитель не меняется при транспонировании, то из соотношения F)
или A3) следует, что
DetB = Det /b(DetCJ. A4)
Следствие 2. Если над переменными хну целой
рациональной функции второй степени
f = апл;2 -f 2а12ху + <з22у2 + 2avx -f 2a2y + a A5)
производится линейное неоднородное преобразование
t/ = C21X -г- Сг%у т С2,
то функция / преобразуется в функцию
/' = а'11х'г-т2а12х'у' + а2гу'г + 2а'1х' -\-2а'2у' + а' A7)
с матрицей
/ ап а,2 а}\
A8)
\fl; a, a'J
причем
" """ A9)
где
/ап о12 аД
B0)
С= с21 с2а с2 (, B1)
\ 0 0 1
а С — матрица, полученная транспонированием матрицы С.
В самом деле, целая рациональная функция / может быть
получена из квадратичной формы
f = Й11л:2 + 2а12ху -f а22г/2 + 20^2 + 2а2г/г + аг2 A5')
при г=1, а неоднородное преобразование A6) получается из
однородного:
' ' ' '
A6')
z= г'
при г'= 1.
* См. А Г Курош Курс высшей алгебры М., «Наука», 1965, гл 6,
§ 26,' стр 160
348
Глава XI. ЛИНИИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Так как
>си с12 г,
DetC=Detl c21 c22 c2 j =
\ 0 0 1/
то из соотношения A9) следует
'21
a» a
a}
a2
r
«u
«21
«12
«22
a,
«2
Cll
C22
B2)
B3)
Следствие 3.
Так как при преобразовании A6) квадратичная форма
апх2 + 2а12ху + а22г/2, B4)
входящая в состав функции /, перейдет в квадратичную форму
a11x" + 2jltx'y'+dt,y'\ ' B5)
входящую в состав функции /', если над переменными х и у
произвести однородное преобразование
х = с11х' + с12г/') у = с21х'+сг2у', B6)
то
С22
B7)
В самом деле, подставляя в выражение A5) вместо х и у их
значения из формул A6), мы увидим, что коэффициенты при х'",
х'у' и у'2 не зависят от сх и с2 (a11=a11c\1+2a12cncil-\-a22cli и
т. д.).
Из соотношения B7) следует, что
2
«11 «12
22
-11
«11 «12
Определение. Целая рациональная функция
/(«11, «12. °22> «1. «2. «)
от коэффициентов целой рациональной функции
f = аг1хг + 2а12ху -)- а22г/2 + 20^ + 2а2г/ + а
B8)
B9)
C0)
называется ортогональным инвариантом, если имеет место
равенство
/(«п. «12. «гг. «1. «г. а)= /(a'u, a'12, a'iit a\, a\, а'), C1)
где аи, а12, а22> «j. «г» а'— коэффициенты целой рациональной
142 ТЕОРИЯ ИНВАРИАНТОВ
349
функции
f = а'их" -f 2altx'y' + 2а22у" -f 2а'гх' + 2а2у' + а', C2)
которую мы получим, производя ортогональное преобразование*
C3)
C4)
C5)
C6)
над переменными х и у целой рациональной функции /.
Теорема 3. Три функции **
агг а2
а, а
являются ортогональными инвариантами целой рациональной
функции
f = апл:2 + 2atixy + а22у2
+ 2а2у + а.
Доказательство. Так как определитель ортогонального
преобразования равен ± 1, то его квадрат равен 1 и
инвариантность /2 и Кц следует из соотношений B8) и B3).
Для доказательства того, что /i = flu + a22 также является
ортогональным инвариантом, заметим прежде всего, что коэффициенты
при к2, ху и у2 не меняются при преобразовании переноса
х = х' + сг, У = у'+с2. C7)
В самом деле, при этом преобразовании функция /
преобразуется в функцию
/' = ап (х + саJ + 2а12 (х' + сх) (у' + с2) + а22 (у' + с2J +
+ 2a1(x' + c1) + 2ai(y' + ci)+a,
и коэффициентами при х'\ х'у' и у'" будут соответственно ап,
2а12 и а22. Поэтому достаточно доказать, что /i = a11 + a22 —
инвариант однородного ортогонального преобразования
х = сг1х _+с1гу, ^щ
* См. формулы A0) § 99, п. 3.
** /2 называется дискриминантом квадратичной формы ап
(входящей в состав функции f).
350
Глава X/ ЛИНИИ ЗАДАННЫЕ ОБЩИМ
При преобразовании C8) функция f преобразуется в функцию
(г1
(спх' -
+ а22 {с21х' +1пу')г + 2а1 (сих' +сиу')
значит,
откуда
Но так- как
~аи ( Си +
матрица
ортогональная, то с2и-
потому
auci, -
2
■cj.) +
^а12 (С11С21
/ Ч
\С21 С22/
= 0 и
Теорема 4. Функция
а11а1
а, а
а22а2
аг а
является инвариантом однородного ортогонального преобразования;
если же функция
2агх + 2а2у + а
однородн <ш ортогональным преобразованием может быть приведена
к виду
то Къ является и ортогональным инвариантом.
Доказательство. Рассмотрим функцию
F = а1 lX* + 2а12ху + а22г/2 + 2avx + 2а2у + a — k(
производя однородное ортогональное преобразование
х = с11х'+с12у', у = Сцх' +сггу',
получим функцию*
F' = а„х'2 + 2а\гх'у' + а22у'* + 2ахх' + 2а2у' + а'—\ {х'г + у'г).
так как матрица (cltt) ортогональная.
142 ТЕОРИЯ ИНВАРИАНТОВ
351
По доказанному /(8 является ортогональным инвариантом.
Используя это по отношению к функции F, получим
,,—А а,„ а, !
fl22
■л а, г а.
а2
а'
Приравнивая коэффициенты при К первой степени в левой и
правой частях этого равенства, получим
о и
*1
а1
а
-1-
1
а22
«2
а
«и
а',
о'
а'22
«а
а'
Предположим теперь, что существует однородное ортогональное
преобразование со^ при котором функция / принимает вид
Докажем, что тогда функция К2 является ортогональным
инвариантом. В самом деле, пусть со—произвольное ортогональное
преобразование. Рассмотрим ортогональное преобразование
со' = сосоГ1". тогда co = co'g>j.
Далее, представим со' в виде произведения однородного
ортогонального преобразования соа на перенос со2; тогда
СО = С1KСО2СО1.
После однородного ортогонального преобразования <мх
функция f перейдет в функцию
J1 = alix 4-2axx +а
и по доказанному К2 не изменится. Произведем преобразование
переноса со2:
х — х -\-х0, у —у
Функция /х перейдет в функцию
llx02
Подсчитывая функцию /С2, для функций f1 и /2 будем иметь
0 0 I.
а\ а'
О а'
«И
a'nX0 + ai
и (
2alX()+a |
ау а
О
О
О a'11Xo-T-2a1xo-f a
352 Рлаге XI, ПИНИЙ ЗАДАН Н bIF ОБЩИМ ^ГДВНЕНИРМ
i\x'o + let, a'n\ + aufl —a^x\ — 2a\allxu — a/ = а'^а' — а'
a,
Гаким образом, функция К2 не меняется при переносе. I
Наконец, однородное орюгональное преобразование т8 опять!
не изменит К2. Значит, /<2 не изменится п в результате преобрази- :
ванпя frtgCOjfrt,, которое равно го.
§ 143. Определение канонического уравнения линии второго
порядка при помощи инвариантов Распадение линии второго
порядка на две прямые
Теорема I. Для того чтобы линия второго порядка, заданная
общим уравнением относительно декартовой прямоугольной
системы координат, относилась к первой группе, необходимо и
достаточно, чтобы 1.гф0, ко второй: /2 = 0, Кяф0, к третьей: /2 = 0,
Доказательство необходимости.
1. Предположим, что линия второго порядка принадлежит к
первой группе, т. е. ее общее уравнение
аих* + 2altxy -f a22y2 + 2ахх + 2а2у -f- a = 0,
заданное относительно прямоугольной системы координат,
преобразованием прямоугольной системы координат в прямоугольную
(т. е. ортогональным преобразованием) может быть приведено к
виду
> = i), где
В таком случае
аи О
/.=
0 а22
2. Предположим, что линия второго порядка принадлежит ко
второй группе, т. е. ее общее уравнение при помощи
преобразования прямоугольной системы координат может быть приведено к
виду
где aii =5^0, a'z^O.
В таком случае /2 = 0, Кг——а'иа.гФ0.
3. Предположим, что линия второго порядка принадлежит к
третьей группе, т. е. ее общее уравнение при помощи преобразо-
§ 143. ОПРЕДЕЛЕНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ ЛИНИИ
353
вания прямоугольной системы координат может быть приведено
к виду
п У2 ' Г) О
а1\л Т LJ = U,
где fli i^O.
В таком случае /2 = 0, Ks = 0, 11 = а'1хФО.
Доказательство достаточности получается сразу
методом от противного:
1) предположим, что /2^0; требуется доказать, что линия
второго порядка принадлежит к I группе. Предположим, что эта
линия принадлежит ко II или III группе; тогда (в силу
необходимости) /2 = 0, и мы приходим к противоречию.
Аналогично доказывается, что в случае /2 = 0, КгФ0 линия
принадлежит ко II группе, а в случае /2 = 0, К3 = 0 к III.
Теорема 2. Если линия второго порядка задана общим
уравнением относительно декартовой прямоугольной системы координат,
то ее простейшие уравнения имеют вид
V^ + ^2 + ^ = 0, -(I)
А^=о, (II)
/xA2 + 4f = 0, (III)
соответственно тому, является ли эта линия линией 1, II или III
группы, причем %х и К2 — корни уравнения
или
называемого характеристическим.
Доказательство. 1. Пусть линия второго порядка
принадлежит к I группе; тогда ее простейшее уравнение имеет вид
где
Находим
и
alt 0
О а'
11 = а\ 1 +#22.
так что а'ц и а'22 —корни Кх и Я2 уравнения
12 п, с. Моденов
354
Глава XI ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
и, далее,
откуда
Ко =
2Ы О О
О а\г О
О 6 D
A
'2
2. Пусть линия второго порядка является линией II группы
(т. е. является параболой). Тогда ее простейшее уравнение имеет вид
Находим
откуда
11 — аП) К3 = — /1
3. Пусть, наконец, линия второго порядка является линией III
группы, т. е. ее простейшее уравнение имеет вид
Находим
/2 = U, t\a — V, /1 = "щ
но так как для линий III группы и К2 является ортогональным
инвариантом, то
А2 О D "*" 0D -<*ии-'1и»
откуда
D =
К,
Теорема 3* S следующей таблице даны необходимые и
достаточные признаки каждого из девяти классов линии второго порядка:
Таблица
№
1
2
3
4
5
6
7
8
9
Название линии
Эллипс
Мнимый эллипс
Две мнимые пересекающиеся
прямые
Гипербола
Дне пересекающиеся прямые
Парабоча
Две параллельные прямые
Две мнимые параллельные прямые
.Чве совпадающие прямые
Признак
/2> 0 /!Я3<0
/2>0 hK3>0
/2>0 K3 = Q
/2<0 К.Лф0
/2<0 Я3 = 0
/2 = 0 Яз^О
/2 = 0 К3 = 0 Я2<0
/2 = 0 Я3 = 0 К2>0
/а = 0 Я8 = 0 Л2=0-
§ 143 ОПРЕДЕЛЕНИЕ КАНОПИЧЬСКОГО УРАВНЕНИЯ ЛИНИИ 355
Докажем сначала достаточность этих признаков.
1. Если /2> О, /Д3<0, то корни Ях и Я2 характеристического
уравнения Я2—11\-\-1г = $ имеют одинаковый знак (/2 = Я1Я2). Так
как /1 = Я1-}-Я2 и /1/(з<0> то знак /j одинаков со знаками Ях и Я2,
a K.s имеет знак, им противоположный. Отсюда следует, что
простейшее уравнение (I) приводится к виду:
X2 Уг
К К
и так как—т~ > 0, —т—f->0, то это уравнение является канониче-
Л-1'2 А2'2
ским уравнением эллипса с полуосями
2. Если /2>0, 1хКг> 0, то Ях, Яа и Я3 имеют одинаковые
знаки и, значит, простейшее уравнение, которое мы теперь
перепишем в виде
1
является уравнением мнимого эллипса (^-т->0, *—7->0-] .
\hil . Л2'2 У
3. Если /2> 0, /<з = 0, то простейшее уравнение принимает вид
причем Яг и Я2 в силу условия /2 = Я1Я2>0 имеют одинаковые
знаки; последнее уравнение можно переписать в виде
ИЛИ
а2 б2 '
где а2 = тгт. ^2 = ?п '. оно является уравнением двух мнимых пере-
1Л1| \Ы
секающихся прямых.
4. Если /2<0, КзфО, то Яг и Х2 разных знаков. Обозначим
через Ях тот из корней характеристического уравнения, который
имеет знак, противоположный знаку К3, и перепишем
простейшее уравнение (I) так:
х? у*_
12*
356 Глав_а_)и.
Здесь
и, полагая
получаем каноническое уравнение гиперболы:
а2 б2
5. Если /2<0, /С3 = 0, то простейшее уравнение имеет вид
V^ + ?l2K2=0.
Здесь Ях и А2 разных знаков (Я1Х1==/а<0); считая A.j>0,
Я2<0, перепишем это уравнение в виде
или
где «2=f-> 62= —Д- Последнее уравнение является уравнением
двух пересекающихся прямых.
6. Если /2 = 0, #3=^0, то простейшее уравнение
___ § у __ А
является уравнением параболы.
7. Если /2=^8 = 0, то простейшее уравнение имеет вид
Отсюда следует, что если /С3<0, то это уравнение является
уравнением двух параллельных прямых, если К2>0, то
уравнением двух мнимых параллельных прямых, а если /С2 = 0, то
уравнением двух совпадающих прямых.
Достатвчность всех признаков доказана. Необходимость
доказывается методом от противного. Пусть, например, общее уравнение
линии второго порядка, заданной относительно декартовой
прямоугольной системы координат, является уравнением эллипса;
требуется доказать, что /2>0, /iA8<°- Предполагая /?<0,
заключаем, что данное уравнение является уравнением одной из линий
4—9, указанных в таблице на стр. 354.
§ 144. ЦЕНТР ЛИНИЯ ВТОРОГО ПОРЯДКА 357
Итак, /2>0. Предполагая 1ХК^^, заключаем, что данное
уравнение является либо уравнением мнимого эллипса, либо
уравнением двух мнимых пересекающихся прямых. Значит, /1/^3<0.
Аналогично методом от противного с использованием
доказанной достаточности признаков, указанных в таблице на стр. 354,
доказывается необходимость всех этих признаков.
Следствие. Для того чтобы линия второго порядка,
заданная общим уравнением
а1гх2 -f 2аиху + a2iy2 -j- 2а1х -f 2а2у + a = 0
относительно аффинной системы координат, распадалась па две
прямые, необходимо и достаточно, чтобы выполнялось равенство
а21
= 0.
Доказательство. Из доказанной теоремы следует, что если
для линии первой группы /С3 == 0, то соответствующее уравнение
K1X2-irX2Y2 = 0 является уравнением двух прямых, а если АС3#0, то
уравнение линии первой группы не является уравнением двух
прямых. Для параболы (вторая группа) К3ф0, а для всех линий
второго порядка третьей группы, каждая из которых распадается
на две прямые, /С3 = 0. Следствие доказано для прямоугольной
системы. Однако при переходе к общей декартовой системе
координат в силу соотношения B3) § 142 условие К = 0 является
необходимым и достаточным условием распадения линии
второго ^.порядка на две прямые и в общей декартовой системе
координат. В самом деле, формулы A6) § 142 можно рассматривать как
формулы преобразования декартовой прямоугольной системы
координат в любую общую декартову, а потому
§ 144. Центр линии второго порядка
Определение. Центром линии второго порядка называется центр
симметрии этой линии, т. е. точка S, обладающая следующим
свойством: если на линии лежит точка* М, то на этой же
линии лежит точка М', симметричная точке М относительно S.
Теорема 1. Пусть относительно общей декартовой системы
координат задана линия второго порядка общим уравнением
-!г2а2у + а=0. A)
Для того чтобы начало координат являлось ее центром,
необходимо и достаточно, чтобы в уравнении A) отсутствовали члены с
* В этом определении мы имеем в виду и комплексные «точки», лежащие
на данной линии.
358 Глава XI ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
х и у в первой степени, т. е. чтобы
ai = а2— О,
иначе, чтобы уравнение линии имело вид
allX* + 2a12xy + a22y* + a = 0. B)
Доказательство достаточности. Если а1 = а2 = 0, то
уравнение линии имеет вид B), и если ему удовлетворяют
координаты х и у точки М, то ему удовлетворяют и координаты —х,
— у точки М', симметричной М относительно начала координат.
Доказательство необходимости. Пусть начало
координат является центром линии A). Предположим вопреки
утверждению теоремы, что по крайней мере одно из чисел а1 или а2
отлично от пуля. Возьмем на линии A) произвольную точку
М (х, у). Ее координаты удовлетворяют уравнению A), а так как
начало координат является центром симметрии линии A),то
уравнению A) удовлетворяют и координаты точки М'( — х, —у),
симметричной точке М относительно начала координат, т. е.
апх2 -f 2а12ху 4 а22у2—2ахх — 2а2у -f a = 0.
Из этого соотношения и из соотношения A) находим
Этому уравнению удовлетворяют координаты всех точек линии
На основании теоремы 2, п. 3, § 139 функция *
Ф = аХ1х2 + 2а12ху + а22у* + 2ахх + 2а2у + а
может быть представлена в виде произведения двух линейных
функций от х и у, одной из которых является форма
axxJr a2y.
Таким образом, данное уравнение распадается на два:
Но так как координаты всех точек линии A) удовлетворяют
уравнению агх-\-а2у = 0, то последние два уравнения являются
уравнениями одной и той же прямой, значит,
а уравнение ср = О или
апх2 + 2а12ху + а22у2 + 2ахх + 2а2у + а = 0
приводится к виду
= 0,
$ 144. ЦЕНТР ЛИНИИ ВТОРОГО ПОРЯДКА 359
т. е. не содержит членов с х и у в первой степени вопреки
предположению.
Теорема 2. Если относительно общей декартовой системы
координат задана линия второго порядка общим уравнением
а1Хх2 + 2апху + а22г/2 + Чахх + 2а2у + а=0,
то координаты х0, у0 ее центра определяются из системы
уравнений
0, C)
причем в случае несовместности этой системы линия не имеет
центра (т. е. является параболой).
Доказательство. Произведем перенос данной декартовой
'системы координат так, чтобы новым началом координат стала
точка О'(хо, у0). Обозначая координаты произвольной точки
М(х, у) в новой системе х'О'у' через к' и у', будем иметь
х=х' + х0, у=у'+у0,
и уравнение A) примет вид
а^х'" + 2а12х'у' + а22у'" + 2 (а^х0 + а12у0 + аг) х'+ 2 (а21х0 +
г) У' + fliA2 + 2а12-<оУо + аыУп2 + 2«i^o + 2«2Уо + а = °-
На основании предыдущей теоремы точка О'(х0, у0) является
центром данной линии тогда и только тогда, когда
«21% + «
Если
/s=
ana12
то система C) имеет единственное решение, т. е. линия A) имеет
единственный центр.
Если система C) неопределенная, т. е. имеет бесконечное
множество решений, то линия A) имеет бесконечное множество
центров—прямую центров, так как в случае неопределенности
системы множество всех ее решений есть множество всех решений
одного уравнения первой степени относительно х и у.
Замечание. Данное и этом параграфе определение центра
линии второго порядка носит геометрический характер лишь по
отношению к тем действительным линиям второго порядка,
которые имеют хотя бы одну точку; для мнимого эллипса и двух
мнимых параллельных прямых это определение иосит уже
аналитический характер, так как приходится привлекать понятие
мнимых точек. Кроме того, при доказательстве необходимости в
теореме 1 мы снова обращались к понятию мнимых точек. Поэтому
надо показать, что система уравнений C), из которой находятся
360 Глава XI, ЛИПЛИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
координаты центра, определяет всегда одну и ту же точку,
независимо от выбора системы координат*, или остается несовместной
прн любом выборе системы координат.
Можно изменить определение центра линии, чтобы оно стало
геометрическим на евклидовой плоскости, не зависящим от
выбора координатной системы. Это будет сделано ниже и по
отношению к понятию центра, и по отношению к асимптотическим
направлениям, и по отношению к направлениям, сопряженным
относительно линии второго порядка, Только после этого можно
утверждать, что данная в § 143 классификация линий второго
порядка по группам I, П, III является классификацией этих
линий по характеру их места центров: линии группы I имеют
единственный центр (начало координат в их простейшем уравнении);
линии группы II не имеют центра (парабола); линии группы III имеют
прямую центров (ось O'Y в простейшем уравнении). В этом можно
убедиться, составляя систему C) для каждого из уравнений:
0, au'#0,,fl22'#0, A)
= 0, flnV-0, а2'ф0, (II)
0, аХ1'ф0. (Ill)
§ 145. Пересечение линии второго порядка с прямой..
Асимптотические направления. Классификация линий по числу и
действительности асимптотических направлений
Предположим, что относительно общей декартовой системы
координат задана линия второго порядка общим уравнением
аих2 + 2а12ху + a22t/2 + 2atx + 2а2у + а = 0. A)
Будем исследовать пересечение этой линии с прямой,
уравнения которой возьмем в параметрической форме:
x = xo + lt, y = yo + mt. B)
Здесь (х0, у0)—некоторая точка прямой, а {/, т]—ее
направляющий вектор. Для нахождения координат точек пересечения
прямой B) с линией A) надо найти значения параметра t, при
которых точка прямой B) лежит на линии A). Подставляя в
уравнение A) вместо к и у их выражения из формул B), получим:
(ап12 + 2a12im + a22rn*)t2 -f- 2{l(anx0 -j- al2y0 -j- ax) + m(anx0 + a22y0 +
+ a2)]t -f aux02 + 2a12xoyo + a22y02 + 2axxu + 2a2y0 + a = 0. C)
♦Читателю предлагается проверить, что понятие середины С (х, у) отрезка
1+х'
А В с концами A {xlt yt) и В (хъ у2) как точки с координатами х= . >
у_ ;а+&2 не завнси1 от вь,бора системы координат, даже если точки А и
В—мнимые Для доказательства надо воспользоваться формулами преобразования об
щей декартовой системы координат (см, § 138, п. 1, формулы E)).
§ 145 ПЕРЕСЕЧЕНИЕ ЛИНИИ С ПРЯМОЙ 361
Если в этом уравнении коэффициент при t2 отличен от нуля,
то уравнение C) имеет два корня (действительных различных,
мнимых различных, или действительных совпадающих), и, значит,
прямая B) пересекает линию A) в двух точках (соответственно
действительных различных, комплексных сопряженных, или
действительных совпадающих).
Если же
апР±2а121т-)- a22tn2 = 0, D)
то прямая с направляющим вектором {/, т) либо пересекает
линию второго порядка только в одной точке (это будет тогда и
только тогда, когда коэффициент при t% а уравнении C) равен
нулю, а коэффициент при / не равен нулю), либо не пересекает
ее (это будет тогда и только тогда, когда коэффициенты при t* и t
в уравнении C) равны нулю, а свободный член не равен нулю),
либо входит в состав данной линии (это будет тогда и только
тогда, когда соотношение C) является тождеством относительно t).
Будем говорить, что прямая имеет асимптотическое направление по
отношению к данной линии второго порядка, если координаты \,т
ее направляющего вектора удовлетворяют уравнению D). Мы
будем говорить также, что вектор {/, т] имеет асимптотическое
направление.
По отношению к асимптотическим направлениям линии
второго порядка делятся на три группы.
A. Линии эллиптического типа; это линии второго порядка,
не имеющие действительных асимптотических направлений (эллипс,
мнимый эллипс, две мнимые пересекающиеся прямые).
B. Линии гиперболического типа; это линии второго порядка,
имеющие два действительных асимптотических направления
(гипербола, две пересекающиеся прямые).
C. Линии параболического типа; это линии второго порядка,
имеющие одно асимптотическое направление (парабола, две
параллельные прямые).
Теорема. Необходимым и достаточным условием того, что
линия второго порядка, заданная общим уравнением A)
относительно общей декартовой системы координат, не имеет
асимптотических направлений {действительных), т. е. является линией
эллиптического типа, является условие
/, =
'2
апа12
Необходимым и достаточным условием того, что эта линия
имеет два различных действительных асимптотических
направления, т. е. является линией гиперболического типа, является условие
362 Глава XI. ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
а необходимым и достаточным условием того, что эта линия
имеет только одно асимптотическое направление, т. е. является
линией параболического типа, является условие
/2 = 0.
Доказательство. Координаты вектора {/, т), имеющего
асимптотическое направление, определяются из уравнения
ап 12 + 2а121т + а22т2 = 0.
Так как вектор {/, т) непулевой, то имеет смысл
рассматривать по крайней мере одно из отношений
k = -r ИЛИ k'-=-.
I m
Уравнение
следовательно, эквивалентно одному из уравнений (или аг1Ф0 или
О)
n = 0, или ank'" + 2ank' -f a22 = Q.
Для того чтобы решения любого из этих уравнений были
комплексными (сопряженными), действительными различными, или
совпадающими, необходимо и достаточно, чтобы выполнялось
соответственно условие
/2>0, /2<0, /2 = 0.
В первом случае (/2> 0) линия не имеет действительных
асимптотических направлений и является линией эллиптического
типа; во втором случае (/2<0) линия имеет два различных
действительных асимптотических направления и является линией
гиперболического типа; в третьем случае (/2 = 0) линия имеет одно
(действительное) асимптотическое направление и является линией
параболического типа. В последнем случае угловой коэффициент
k = — единственного асимптотического направления определяется
одним из соотношений
если а12 — а22 = 0, то асимптотическим направлением является
направление оси Оу, так как уравнение, определяющее
координаты векторов, имеющих асимптотические направления, принимает
вид ап/2 = 0, откуда / = 0.
Остается рассмотреть случай аХ1 = а22 = 0.
Уравнение линии принимает вид
2а12ху + 2ахх + 2а.гу + а = 0,
§ 145 ПЕРЕСЕЧЕНИЕ ЛИГГИИ С ПРЯМОЙ • 363
а уравнение, из которого находятся координаты векторов,
имеющих асимптотическое направление:
2ап1т — О,
следовательно, либо / = 0, либо т = 0, т. е. линия имеет два
различных действительных асимптотических направления—
направления осей координат (заметим, что /2 =—а122<0, значит, линия
гиперболического типа).
Обратно, если оси координат имеют - асимптотические
направления, то уравнение
2a12/m + аг2т? = О
должно удовлетворяться и при 1 — 0, и при т — 0, т. е.
значит уравнение линии имеет вид
2а12ху + 2ахх -\- 2а2у + а = 0.
Для гиперболы
или для двух пересекающихся прямых
- — ^- = 0
а2 Ь2
координаты /, m векторов, имеющих асимптотическое
направление, определяются из уравнения
а2 б2 '
т. е. это соответственно или направления асимптот гиперболы, или
направления рассматриваемых прямых.
Для параболы
хг = 2ру
уравнение, определяющее координаты вектора {/, т]
асимптотического направления, имеет вид
/2 = 0, т. е. /=0,
значит, асимптотическое направление параболы есть
направление ее оси. Если, наконец, уравнение линии второго порядка
определяет две параллельные (или совпадающие) прямые, то
асимптотическим направлением является направление этих прямых.
364 Глава XI ЛИНИИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
§ 146. Диаметр, сопряженный данному неасимптотическому
направлению
1. Общая теория
Теорема 1. Геометрическим местом середин хорд линии
второго порядка, параллельных вектору неасимптотического
направления, является прямая линия; эта прямая линия называется
диаметром данной линии, сопряженным рассматриваемым
параллельным хордам. Если линия второго порядка задана относительно
общей декартовой системы координат общим уравнением
апх2 + 2а12ху + а^у2 + 2а^ + 2а2у + а = О, A)
а ее хорды параллельны ненулевому сектору {1,т}
{неасимптотического направления), то уравнение диаметра, сопряженного этим
хордам, имеет вид
Доказательство. Пусть прямая р, коллинеарная вектору
{I, т} неасимптотического направления по отношению к линии A),
пересекает эту линию в точках Мх(хг, yt) и М2 (х2, у2).
Обозначим через Мо середину отрезка МгМг. Уравнения указанной
прямой можно записать в виде
y^yo + mt. C)
Значения параметра t, соответствующие координатам точек Мх
и Мг, определяются из уравнения
(axll2 + 2al2lm -j- а.,2т*) Г2 + 2 [/ (аХ1х0 + а12у0 + a J +
+ т (а21х0 + а22у0 + а2)] t + аХ1х02 + 2а13зд0 + а22у02 +
которое получим, подставив в уравнение A) вместо х и у их
выражения из формул C).
Пусть t1 и /. — корни этого уравнения. Так как tt и /8 — это
координаты точек Мх и М2 па прямой р с началом координат в
точке М„ и масштабным вектором {/, »»}, а точка Мо- середина
Мг М2, то точка Мо на прямой р в указанной системе координат
имеет координату < = Цр*, а так как, с другой стороны, из
соотношений C) ясно, что / = 0 для точки М0(х0, у0), то ^ + ^ = 0 и
потому
/ (аах0 + а12у0 + а1) + т ((kixo + а22Уо + аг) = °-
Это соотношение, таким образом, является необходимым и
достаточным условием того, что хорда, имеющая направление векто-
ра {/, т), точкой М0{х0! у0) делится пополам.
§ 146, ДИАМЕ1РЫ ^ 365
С другой стороны, каждая прямая, параллельная вектору {I, т},
пересекает линию A) в двух точках (действительных различных,
мн <мых различных, или действительных совпадающих), а потому
геометрическим местом середин хорд линии A), параллельных
вектору {/, т}, является вся прямая, уравнение которой
В этом уравнении коэффициенты при хну одновременно
в нуль не обращаются, так как если бы мы имели
a11l-\-a12m = Q, a2ll + a2itn = О,
то было бы выполнено и соотношение
/ (ап1 -г апт) + т (а21/ + а22т) = О,
или
аи1г + 2 a12lm + а2%тг = О,
т. е. вектор {I, т] имел бы асимптотическое направление.
Из уравнения D) находим координаты /' и т1
направляющего вектора диаметра, сопряженного хордам, параллельным
ненулевому вектору {/, т}\
/'= — (а21/ + а22/п), т' =аа/ -\-а12т. E)
Умножая первое из этих соотношений на —т', второе на /' и
складывая, получим
ап//' + а12 {1т' + l'tn) + a2imm' = 0. F)
Таково необходимое условие, связывающее координаты
ненулевого вектора {/, т), параллельного хордам линии второго
порядка, заданной общим уравнением
аХ1л:2 -\- 2 а12ху + а22у2 + 2 агх + 2 а2у + а = 0
относительно аффинной системы координат, и координаты
ненулевого вектора {/', т'}, параллельного диаметру, сопряженному
этим хордам.
Условие F) и достаточно, так как из пего следует, что
I' :т'= — (a21l + а2гт): (au/ + а^т),
т. е. {/', т'} — ненулевой вектор, параллельный диаметру D).
Соотношение F) выполняется для асимптотического направления
линии второго порядка, если в нем положить 1 = 1' и т=>т' (так
как тогда мы получим a11li + 2a12lm + a22mi = 0), поэтому
асимптотическое направление линии второго порядка часто называют
самосопряженным.
Теорема 2. Если линия второго порядка является линией,
имеющей единственный центр, и если рассмотреть семейство
параллельных хорд этой линии, не имеющих асимптотического направ-
366 Рла»а XI. ЛИНИИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
ления, то диаметр, им сопряженный, также не имеет
асимптотического направления; если взять семейство хорд линии второго
порядка, параллельных этому диаметру, то диаметр, им
сопряженный, будет параллелен хордам первоначального семейства.
Доказательство. Пусть относительно общей декартовой
системы координат задана линия второго порядка общим
уравнением
апх2 + 2 а12ху + аг2уг -f 2 ахх + 2 а2у -f a — 0.
Предположим, что эта линия имеет единственный центр, т. е.
/ о
2' а,
а
12
Возьмем любой ненулевой вектор {/, т}, не имеющий
асимптотического направления, и рассмотрим уравнение диаметра
1(апх + а12у + аг) + т {а21х + а22у + а2) = 0,
=1т —I
сопряженного хордам, параллельным вектору {/, т}.
Направляющий вектор {/', т'\ этого диаметра имеет координаты
7'= — {аг11-\-а.12т), т' = а111-\-а12т.
Векторы {/, т) и {/', т'} неколлинеарны, так как
/ т
I' т'
■= / (ап/ + а12т) + т (а21/ -J- а22т) =
= anl-Jr2a12lmJt-a22m2 ФО.
Вектор {V, т'} не имеет асимптотического направления. В
самом деле, так как /2#=0, то числа ах11'-\-а12т' и а211' + а22т' не
обращаются в пуль одновременно. Поэтому уравнение
{ап1г + апт') I + (а21Г + а22т') т = 0, G)
в котором / и т рассматриваются как неизвестные, не может иметь
два линейно независимых решения. Но одним из его решений
является пара координат вектора {/, т], направлению которого
сопряжен диаметр с направляющим вектором {/', т'}, неколлинеар-
ным вектору {/, т}. Значит, координаты вектора {/', т'} не
удовлетворяют уравнению G), т. е.
(ап1' •+■ а12т') V + (а2/ + а22т') т' ф О,
или
a^l'^ + 2 a12l'm' + a22rn'z ■■
т. е. {V,т'\ — вектор, не имеющий асимптотического направления
линии A).
146 ДИАМЕТРЫ об/
Теперь из соотношения
ап1Г + aX2(ltn' -f- I'm) + аптт' = О
в силу его симметрии относительно пар чисел I, т и V, т'
следует, что если линия второго порядка имеет единственный центр,
то диаметр, сопряженный хордам, параллельным вектору {/', tn },
коллинеарен вектору {/, т).
Определение. Два диаметра линии, имеющей единственный центр,
из которых каждый делит пополам хорды, параллельные другому,
называются сопряженными.
Условие
anll' -f-a12Gm' + I'm) + ai2mm' —0
можно теперь интерпретировать как необходимое и достаточное
условие сопряженности двух диаметров линии второго порядка,
имеющей единственный центр и заданной уравнением
апх2 + 2апху + ai2y2 + 2ахх -f- 2а2г/ + а = О
относительно общей декартовой системы координат. Если 1-фО
и Г=^=0, то это необходимое и достаточное условие сопряженности
можно записать в виде
аи + а12 (k + k') + a2ikk' = О,
= уИ k'.=j,— угловые коэффициенты сопряженных
диаметров.
Теорема 3. Если линия второго порядка имеет единственный
центр, то любая прямая неасимптотического направления,
проходящая через ее центр, является диаметром этой линии.
Доказательство. Если линия, заданная уравнением
апх2 + 2a12xy-i-a22y2 + 2a1x-\-2а2у + а — 0, имеет единственный
центр, то прямые
пересекаются в ее центре A2ф0), но в таком случае урав-
ггение любой прямой р, проходящей через центр линии, можно
записать в виде
/ (апх + aV2y + агу) + т (а.п1 + а22т + с J = О,
где хотя бы одно из чисел / или т не равно 0.
Значит, прямая р является диаметром линии, сопряженным
хордам, параллельным вектору {/, т), если этот вектор
неасимптотического направления. Но из неасимптотичпости направления
прямой р вытекает неасимптотичность сопряженного ей направления
{/, т], следовательно, прямая р является диаметром.
368 Глава XU ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Теорема 4. Если линия второго порядка является линией
параболического типа, то диаметр, сопряженный хордам линии,
параллельным неасимптотическому направлению, имеет асимптотическое
направление
Доказательство. Вектор {/', т'}, коллннеарный диаметру,
сопряженному хордам, имеющим неасимптотическое направление
{I, т), имеет координаты
/' =—(а211-\-а22т), т' = au/ -f а12т
(см. доказательство теоремы 2). Отсюда в силу /2 = 0 находим
ап/' + а12т' = — 12т — О, a21l' + аггт' = 121 = О,
значит,
/' (ап1' -J- а12т') + т' (anl' -f а22т') = 0,
или
ап1'2 + 2а12Гт' + а^т'2 = 0.
Заметим, что векторы {— ап, оп} и {—с22, а21}, по крайней
мере один из которых ненулевой, имеют асимптотическое
направление для линии параболического типа.
Теорема 5. Если линия—парабола, то диаметром является
любая прямая, имеющая асимптотическое направление относительно
этой линии
Доказательство. Если линия является параболой, то на
основании теоремы 4 все ее диаметры имеют асимптотическое
направление. Докажем, что и обратно: любая прямая р, имеющая
асимптотическое направление параболы, является ее диаметром.
Возьмем на прямой р произвольную точку (х0, у0) и выберем
ненулевой вектор {/, т}, не имеющий асимптотического направления,
и такой, чтобы его координаты удовлетворяли соотношению
I (au*o + а12у0 + а1) + т (а21х0 + а22у0 + а2) = 0.
Для этого достаточно положить
/ = _ (а21дг0 -J- а22(/0 + а2), т = спдг0 + апу0 + ах.
Вектор {/, т] ненулевой, так как для параболы, заданной
общим уравнением, система anxJra12y-\ra1 = 0, a21x -f ai2y + a2 = 0
несовместна. Этот вектор не имеет асимптотического направления,
так как, предполагая обратное, из последних соотношений (в
силу /2 = 0) найдем
Яц* + «12^ = Q12ai — аПа2 ~ °. п211 + а22^ = а22«1 ~ «12Q2 = 0
и система
оказалась бы совместной.
146 ДИАМЕТрЫ 369
Значит, при указанном выборе / и т уравнение
/ (апх + al2y + a J 4- m (anx + аг2у + а,) = О
будет уравнением прямой р.
Замечание. Если линия имеет прямую центров, то каждая
точка этой прямой должна принадлежать каждому из диаметров
линии. Таким образом, прямая центров оказывается единственным
диаметром линии; так как в рассматриваемом случае линия
второго порядка есть пара параллельных (или совпадающих) прямых,
а линия центров есть прямая, лежащая посередине между ними,
то эта последняя прямая и будет единственным диаметром линии
(распадающейся на две параллельные или совпадающие прямые).
2. Диаметры линий второго порядка, заданных
каноническими уравнениями
Если эллипс задан каноническим уравнением
,,2
4- • - = 1
^ й2
то уравнение диаметра, сопряженного хордам, параллельным
ненулевому вектору {/, т\, имеет вид
1х .ту л
а уравнение диаметра, сопряженного с ним,
тх—1у—0.
На рис. 216 изображен эллипс,
два его сопряженных диаметра и
хорды, параллельные каждому из
них.
Если гипербола задана
каноническим уравнением
£! у1 — 1 Рис. 216
а2 Ьа
и ненулевой вектор {/, т) не имеет асимптотического направления
(т. е. не коллииеарен ни одному из векторов {а±Ь}), то уравнение
диаметра, сопряженного хордам, параллельным этому вектору,
имеет вид
а уравнение диаметра, ему сопряженного,
тх—1у—0.
На рис. 217 изображена гипербола, се сопряженные диаметры d
и 6! и хорды, параллельные каждому из них.
370
Глава XI, ЛИНИИ. ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Уравнение диаметра параболы
Рис. 217
сопряженного хордам, параллельным ненулевому вектору {I, т),
имеет вид
— /р-г/ш/ = 0, или t/ = y,
где k — угловой коэффициент
хбрд.
Все диаметры параболы
параллельны ее оси. На рис. 218
дано одно из семейств
параллельных хорд параболы и сопряжен-
х ный им диаметр.
§ 147. Касательная к линии
второго порядка
Пусть относительно общей
декартовой системы координат
на плоскости линия второго
порядка задана общим уравнением
-f 2ахх + 2агу + а = 0. A)
рис, 218
ахххг + ?.а12ху
Будем называть точку М0(х0, у0), лежащую на этой линии,
неособой, если среди чисел *
есть хотя бы одно, не равное нулю.
* Эти числа являются значениями в точке Мй {ха, у0) половин частных
производных первого порядка от левой части уравнения A).
§ 147 КАСАТЕЛЬНАЯ К ЛИНИИ ВТОРОГО ПОРЯДКА 371
Ясно, что точка Мо, лежащая па линии A), является особой
тогда и только тогда, когда она является центром линии A).
Таким образом, среди линий эллиптического типа только
линия, распадающаяся на две мнимые пересекающиеся прямые, имеет
особую точку (это точка их пересечения); среди линий
гиперболического типа особую точку имеет пара пересекающихся прямых
(это также точка их пересечения) и, наконец, среди линий
параболического типа особые точки имеет пара совпадающих прямых
(особыми точками являются все точки прямой, с которой
совпадают рассматриваемые прямые).
Определение. Касательной к линии второго порядка в неособой
точке, лежащей на этой линии, называется прямая, проходящая
через эту точку, пересекающая данную линию в двукратной точке
или сливающаяся с прямой, входящей в состав данной линии.
Теорема 1. Пусть М0{х0, у0) —неособая точка линии второго
порядка, заданной относительно общей декартовой системы
координат уравнением
аХ1х2 + 2а12ху + а22у* + 2ахх + 2а2у + а =■ 0. A)
Тогда уравнение касательной к этой линии в точке Мо имеет вид
{аххх0 + аХ2у0 + ах) х + (a21x0 + а22уй + <*2)у + ахх0 + а2у0 + a = 0. B)
Доказательство. Рассмотрим уравнения прямой
x = xo-\-lt, y^yo + mt, C)
проходящей через данную неособую точку М0(х0, у0) линии A).
Найдем точки пересечения прямой C) с линией A). Подставляя
в уравнение A) xo + lt и yo-\-mt вместо х и у, получим ♦
ахх (х0 + It)* -!- 2а1а (*0 + И) (у0 + mt) + а22 (у0 + mif +
+ 2а1 (х0 + It) + 2а2 (у0 + mt) + а = 0,
или
(anZ2 + 2a12/m-b a22m2) t% +
+ 2 [/ (axl*0 + а12г/0 -\-ax) + m (a21x0 + any0 + a2)] t +
+ altxl -f 2a12xoyo + a22yl + 2аххй + 2а2г/0 -J- a = 0.
Но по предположению точка MQ (x0, y0) лежит на данной
линии, поэтому
аХЛх\ + 2а12хоуо -f a22yl + 2а1х0 -\- 2а2у0 + а = 0,
и последнее уравнение принимает вид
(аи/2 -f 2a12/m + а22т2) f- +
+ 2 [/ (aux0 + «12^0 + ai) + m («2i«u + й22Уо + o2)] t = 0. D)
Одним из корней этого уравнения является £ = 0; при этом из
соотношений C) находим х = х0, у = у0, т. е. координаты точки Мо.
372 Глава XI ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Для того чтобы прямая C) являлась касательной к линии 1),
необходимо и достаточно, чтобы уравнение
(Яц/2 + 2al2lm -\- a22m-) t -f-
+ 2 [I (апх0 + а12у0 + ах) + т (а21ха + а22у0 + а2)} = 0 D')
имело и второй корень, равный нулю t = 0, а для этого
необходимо и достаточно, чтобы было выполнено условие
1КЛ -г а12у0 + al) + tn (а21л;0 + а22у0 + а2) = 0.
Таким образом, координаты направляющего вектора касательной
(этот вектор ненулевой, так как точка М0(х0, у0) по
предположению неособая).
Если вектор {I, т), координаты которого определяются
соотношениями E), неасимптотического направления, т. е.
ou/2 + 2al2ltn -f a22m2 = 0,
то уравнение D') имеет только корень ^ = 0, а если вектор {/, т)
имеет асимптотическое направление, т. е.
an/2 -f 2а1г1т -f а22т2 = 0,
то уравнение D') обращается в тождество, прямая C) входит в
состав данной линии A) и, значит, согласно принятому
определению является касательной к линии A) в точке УИ0(д:0, у0).
Итак, уравнения касательной к линии A) в ее неособой точке
Мо(*о> У о) имеют вид
х = хо — (а21хо + а22г/0 + а2) t,
y
или
ИЛИ
и так как
апд:о + 2а12х0у0 + о22г/о + 20^,, + 2а2г/0 + а = 0,
то окончательно
Теорема 2. Пусть относительно общей декартовой системы
координат линия второго порядка задана общим уравнением
aux2 -f 2a12xy -f a22j/2 -f 2axx -f 2а2г/ -f a = 0.
§ 148 ЧАСТНЫЕ ВИДЫ VpABHHHHfl ЛИНИИ 373
Пусть диаметр
(anx-\-aV2y i- aj I + (аг1х -\- as2y J,- а.г) m = 0 F)
этой линии, сопряженной хордам, имеющим неасимптотическое
направление {I, т], пересекает рассматриваемую линию в неособой
точке М0(х0, у0). Тогда касательная к этой линии в точке Мо
параллельна хордам, которым сопряжен диаметр F).
Доказательство. Так как диаметр F) проходит через
точку М0(х0, г/0), то
(апх0 + а12у0 + a1)l-{- (a21x0 -j- а22у0 + а2) т = О
и так как М0(х0, у0) — неособая точка рассматриваемой линии,
то можно считать, что
/ = — ("гА + а2г1/о -г 0%), т = аих0 + а12у0 -f аи
а это—координаты направляющего вектора касательной к
рассматриваемой линии второго порядка в неособой ее точке (см,
выше формулы E)).
Замечание. Данное в этом параграфе определение
касательной к линии второго порядка в се неособой точке М0(х0, у0)
совпадает с определением касательной и линии, которое дается в
курсах математического анализа. Здесь линия задана уравнением
вида F (х, у) — 0. Функция F(x, у) при х = х0, у = у0
обращается в нуль, а частные производные от нее по л; и у, т. е.
2(a1-1xJra12yJra1) и 2(a21x + a22t/-fa2) согласно условию теоремы 1
одновременно в нуль не обращаются. Функция F(x, y)~целая
рациональная функция от х и у. Значит, уравнение касательной
к линии можно записать в виде*
xo) + Fy(xo, уQ) {у—уо) = О,
или
(апх0 + а12у0 + aj (x—x0) + (а21х0 + a.i2y0 + а2) (у—у0) = 0.'
§ 148. Уравнение линии второго порядка, отнесенной к двум ег
сопряженным диаметрам; уравнение линии второго порядка,
отнесенной к касательной и сопряженному к ней диаметру
Теорема 1. Пусть относительно общей декартовой системы
координат линия второго порядка задана общим уравнением
а1гхг -у 2alzxy + аг„уг^г2а1х -j- 2o2j/-f- a = 0. A)
Для того чтобы одна из осей имела направление диаметра,
сопряженного хордам, параллельным другой оси, необходимо и до-
* См. Г. М. Фихтенгольц. Курс дифференциального и интегрально-:
го исчисления, т. I. M., Физматгиз, 1958, гл. VII, § 2, стр. 530.
374 Глава XI. ЛИНИИ, ЗАДАННЫЕ ОБЩИМ. УРАВНЕНИЕМ
статочно, чтобы а12 = 0, т. е. чтобы уравнение имело вид
аг1х2 -\~ аггу% -г 2а хх -г 2а2у -j- а = 0.
Доказательство. Пусть, например, ось Ох не имеет
асимптотического направления. Тогда координаты вектора,
параллельного диаметру, сопряженному хордам, параллельным оси Ох, будут
Но вектор {Г, т'} коллпнеарен оси Оу тогда и только тогда,
когда Г = а12 = 0.
Теорема ' 2. Пусть относительно общей декартовой системы
коорёинат задана линия второго порядка общим уравнением
ailx2 + 2а12ху + а22у* + 2а,х + 2а2у + а = 0 B)
и пусть она имеет единственный центр. Тогда, если оси
координат являются сопряженными диаметрами этой линии, а начало
координат—ее центром, то уравнение линии имеет вид
где an^0 и а22 Ф0. •
Обратно, если уравнение линии, имеющей единственный центр,
имеет относительно некоторой общей dei ар.повой системы
координат уравнение
где ап Ф 0, о22 Ф 0, то начало координат является центром линии,
а оси координат ее сопряженными диаметрами.
Доказательство. Если оси координат являются
сопряженными диаметрами линии B), то а12 = 0 (теорема 1 этого
параграфа); так как начало координат является центром линии, то в
уравнении B) отсутствуют х и у в первой степени.
Обратно, если уравнение линии второго порядка, заданное
относительно общей декартовой системы координат, имеет вид
а1гд;24-а22{/2 + а = 0, то начало координат является центром линии
(теорема 1, достаточность, § 144).
Линия имеет единственный центр, значит,
/,=
О а22
откуда а1Хф0 и а22ф0; наконец, так как в уравнении аг1х2 +
+ й22г/2 -]- а = 0 коэффициент при ху равен 0, то оси координат
являются свпряженными диаметрами этой линии (теорема 1,
достаточность).
Теорема 3. 1°. Если общая декартова система координат по
отношению к эллипсу расположена так, что:
S 148, ЧАСТНЫЕ ВИДЫ УРАВНЕНИЯ ЛИНИИ 375
1) оси координат являются сопряженными диаметрами
эллипса;
2) единичной точкой оси Ох является любая точка
пересечения одного из диаметров с эллипсом;
3) единичной точкой оси Оу является любая точка
пересечения другого диаметра с эллипсом,—то уравнение имеет вид
x2 + J/2=l-
Обратно, если относительно некоторой общей декартовой
системы координат дано уравнение
то это—уравнение эллипса, а система координат по отношению
к нему обладает свойствами EХ).
2°. Если общая декартова система координат по отношению
к гиперболе расположена так, что;
1) оси координат являются сопряженными диаметрами
гиперболы;
E,)
2) единичной точкой Е системы координат является
точка пересечения любой из асимптот гиперболы с касательной
в любой из точек пересечения одного из этих диаметров с
гиперболой, то уравнение гиперболы имеет вид
Обратно, если относительно некоторой общей декартовой
системы координат дано уравнение
то это уравнение гиперболы, а система координат по отношению
к ней обладает свойствами (S2).
3°. Если общая декартова система координат по отношению к
параболе расположена так, что:
1) осью Оу является касательная к параболе в любой
точке О, лежащей на этой параболе;
2) осью Ох является диаметр параболы, проходящей через
точку О;
3) единичная точка Е системы координат лежит на па-
раболе, то уравнение параболы имеет вид
Обратно, если относительно некоторой общей декартовой
системы координат дано уравнение
то это уравнение параболы, причем система координат по
отношению к этой параболе обладает свойствами (S3).
376 Глава XI. ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Доказательство. 1°. Так как оси координат являются
сопряженными диаметрами эллипса, то его уравнение имеет вид
(теорема 2 этого параграфа). Так как точки A, 0) и @, 1)
принадлежат эллипсу, то
и последнее уравнение принимает вид
— ах2— ау2 -{-а — О, или гЦ-г/а=1.
Обратно, линия х2-\- г/2=1 имеет единственный центр. f-ja
основании той же теоремы 2 для линии, заданной уравнением
оси координат являются сопряженными диаметрами линии и
пересекают ее в четырех точках (±1,0), @, ±1). Но этим свойством
по отношению к сопряженным диаметрам обладает только эллипс
2°. Так как оси координат являются сопряженными
Диаметрами гиперболы, то ее уравнение имеет вид
Точка A,0) должна лежать па этой гиперболе, а точка A 1)
на одной из ее асимптот '
Значит,
аи-\- а = 0, а.
и уравнение гиперболы принимает вид
— ах2 + aif + а = 0, или г2 — г/8=1.
Обратно, линия хг — if — \ имеет единственный центр, а на
основании теоремы 2 этого параграфа оси координат являются
ее сопряженными диаметрами. Один из этих диаметров @*сь qx\
пересекает линию в двух точках (±1, 0), а другой (ось Оц) ее
не пересекает. Этим свойством по отношению к сопряженным
диаметрам обладает только гипербола. Далее, точка A, 0) лежит на
гиперболе х2 — г/2=1, а точка (i, 1) — на ее асимптоте у=ях
3°. Диаметр параболы имеет направление, сопряженное по
отношению касательной к параболе в той точке, в которой он
пересекает эту параболу, поэтому в общем уравнении параболы
должно быть а12 = 0. Так как, кроме того, начало координат о
лежит на параболе, то а — О Уравнение параболы имеет вид
2,Ы = 0.
§ 148. ЧАСТНЫЕ ВИДЫ УРАВНЕНИЯ ЛИНИИ 377
Уравнение касательной к этой параболе в начале координат
имеет вид
а так как касательной в начале координат является ось Оу, то
это уравнение эквивалентно уравнению
значит,
последнее уравнение принимает вид
\-2a^x = Q, где
Здесь аг2^=0, так как в противном случае уравнение
определяло бы две прямые х = 0 и а11х-{-2а1 = 0. Если бы еще было
апф0, то линия имела бы центр (притом единственный), а
парабола центра не имеет. Значит, #п = 0, и уравнение параболы
принимает вид
Так как единичная точка лежит на этой параболе, то
а22 + 2ах = 0.
Значит, 2ах— — а22, и последнее уравнение принимает вид
а22г/2 — а22х=0, или уг~х.
Обратно, все диаметры линии у2 = х параллельны оси Ох.
В самом деле, координаты векторов, имеющих асимптотическое
направление относительно линии у2 = х, определяются из
уравнения /л2 = 0, т. е. ось Ох имеет асимптотическое направление.
Пусть {/, т), тфО, — любой вектор, не имеющий
асимптотического направления относительно линии у2 — х. Уравнение
диаметра, ему сопряженного,
— 2"/ + mf/ = 0, или у = ^,
все диаметры линии уг — х параллельны между собой; этим
свойством обладает только парабола. Далее, уравнение
касательной к линии у2—х = 0 в точке @, 0) имеет вид х — 0—это ось Оу.
Уравнение диаметра, сопряженного хордам, параллельным
вектору {0, 1}, имеет вид у = 0—это ось Ох. Наконец, единичная
точка A, 1), очевидно, лежит на линии у2 = х.
Теорема 4. Если неособую точку линии второго порядка
принять за начало координат, за ось Ох—диаметр, проходящий
через эту точку, а за ось Оу—касательную к линии второго поряд'
378 Глава XI ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
ка н этой точке, то уравнение линии примет вид
i 2 + 2a1x = 0, где
и обратно, всякое такое уравнение в случае а^О, аггф§
является уравнением линии второго порядка, по отношению к которой
система координат обладает сформулированными выше свойствами.
Доказательство. Так как касательная к линии второго
порядка в ее неособой точке имеет направление, которому
сопряжен диаметр, проходящий через эту точку, то в общем
уравнении линии коэффициент при ху равен нулю (теорема 1, § 148).
Далее, так как линия проходит через начало координат, то а = 0.
Уравнение линии имеет вид
в начале координат
и так как оно должно быть эквивалентно уравнению х — 0 оси
Оу, то а^О) а2 — 0, и последнее уравнение принимает вид
Уравнение
имеет вид
аих2-\-а2.
касательной
а
,у
к
1*
-f 2агх + 2а2у
этой линии
+ а„у = 0,
Обратно, если ахФ§~ то начало координат —неособая точка
линии. Уравнение касательной к этой линии в точке @, 0)
имеет вид х = 0 — ось Оу. Диаметр, сопряженный хордам,
параллельным вектору {0, 1} (не имеющему асимптотического направления
в силу а22 ф 0), имеет уравнение г/ = 0 —ось Ох.
Замечание к § 144—146. Как было указано в замечании
к §'144, а также, как ясно из содержания § 144—146,
определения, относящиеся к понятиям центра линии второго порядка,
асимптотических направлений и сопряженности диаметров, не для
всех линий второго порядка носили геометрический характер, а
потому нуждались в доказательстве инвариантности относительно
преобразования одной общей декартовой системы координат в
другую.
Однако этим определениям можно придать во всех случаях
геометрический характер (а следовательно, снять необходимость
в доказательстве инвариантности определений и ряда с ними
связанных результатов относительно преобразования декартовой
системы координат). Для этого вместо одной линии, заданной
общим уравнением
апх2 + 2а12ху + а22у2 + 1аЛх + 2а2г/ + а = 0,
или / = 0 (через / обозначена левая часть уравнения линии),
рассмотрим семейство линий [ = С где С принимает все
действительные значения.
148. ЧЛС1ПЫГ. ВИДЫ У РЛ В 11 Г. 111 i Я ЛИНИИ
379
Если уравнение f — О есть уравнение или действительного
эллипса, или мнимого эллипса, или уравнение двух мнимых
пересекающихся прямых, то в семейство / = С включаются все эллипсы
с общим центром* и гомотетичные друг другу, причем центром
гомотетии является их общий центр. В самом деле, после перепо-
Рис. 219
са начала координат в центр линии получим вместо f = 0
уравнение
а1Хх'2 + 2а12х'у' + a22j/'2 + а' = О,
а вместо уравнения / = С —уравнение
йпх'2 + 2а12х'у' -f й22г/'2 + а' — С = 0.
Если а'фО и а'~СфО, то одно из этих уравнений переходит
в другое заменой х и у на Хх и Ху (при подходящем выборе Я).
На рис. 219 изображено семейство действительных эллипсов,
входящих в семейство линий второго порядка / = С
эллиптического типа.
Если линия f = 0 гиперболического типа, то нет
необходимости включать ее в семейство / = С, но можно это и сделать
(рис. 220). Семейство f — C будет состоять из всех соасимптоти-
ческих гипербол, при этом гиперболы, лежащие в одной и той
же паре вертикальных углов, образованных их общими
асимптотами, гомотетичны друг другу относительно центра.
* Так как координаты центра определяются из системы
т. е. из системы уравнений, не содержащих свободного члена уравнения
линии второго порядка.
380
Г а аба XI ЛИПНИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Если / = 0—уравнение параболы, то f = C есть уравнения m
рабол, полученных из / = 0 параллельным переносом (рис. 221)
Если, наконец, / = 0 есть ^равнение нары параллельных пря
мых (действительных или мнимых, или уравнение пары совпадаю
щих прямых), то семейство f = C включает в еебя все пары па
раллельных прямых с общей линией центров.
Рис 220
Рис. 221
Теперь определения, данные в § 144—146, можно
модифицировать так:
центром линии второго порядка, заданной общим уравнением
/ = 0 относительно общей декартовой системы координат, назовем
центр симметрии любой действительной линии семейства
/ = С.
Направление называется неасимптотическим относительно
линии второго порядка, заданной общим уравнением / = 0 в
аффинной системе координат, если для действительной линии f = C, не
являющейся парой совпавших прямых, найдется прямая этого
направления, пересекающая линию f-C в двух действительных и
различных точках.
Направления, не обладающие этим свойством, назовем
асимптотическими.
Два диаметра второго порядка, заданной общим уравнением
/ = 0 относительно общей декартовой системы координат,
называются сопряженными, если каждый из них делит пополам хорды
действительной линии семейства f — C, параллельные
другому, и т. д.
149. ГЛАВНЫЕ НАПРАВЛЕНИЯ И ГЛАВНЫЕ ДИАМЕТРЫ 381
§ 149. Главные направления и главные диаметры
Определение. Неасимптотическое направление линии второго
порядка называется главным, если оно перпендикулярно диаметру,
сопряженному с хордами, имеющими это направление. Этот
диаметр называется главным диаметром линии второго порядка. Он
является осью симметрии линии.
Теорема 1. Координаты I, m вектора (ненулевого), имеющего
главное направление относительно линии второго порядка,
заданной общим уравнением
а1гхг + 2avixy -f- a2iy2 -f 2axx + 2a2y -f a = 0 A)
относительно декартовой прямоугольной системы координат,
определяются из системы
— U, B)
где К—отличный от нуля корень квадратного уравнения
аи — А а12
= 0,
или
^2_/1^_|_/2==о, C')
где
1 ~" ' V D)
•*12
^21 <
а„ E)
Доказательство. Пусть ненулевой вектор {/, т] не имеет
асимптотического направления относительно линии A). 'Тогда
уравнение диаметра, сопряженного с хордами линии A),
параллельными вектору {I, т), имеет вид (§ 146, п. 1)
(а и* + а12у + агI -f- (аг1х + а12у + аг)т = О,
или
(йи/ + aXim)x + (аг11 + аггт)у -f axl -f a2m = 0. F)
Так как система координат прямоугольная, то этот диаметр
перпендикулярен хордам, параллельным ненулевому вектору {/, т]
тогда и только тогда, когда ненулевые векторы
{au/ + a12m, a21l-{-a22m} и {/, т)
коллинеарны, т. е. тогда и только тогда, когда существует
такое число X, что
В этих соотношениях Я^О, так как в противном случае мы
имели бы
/j /.. . г* yyi — 1} at ~r~ a tn о
382 Глава XI ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
откуда
)/ (/ + ) = O, или
т. е. вектор {/, т} имел бы асимптотическое направление.
Далее, переписывая систему G) в виде
l' ' (,«22 h)m = U
и замечая, что она имеет ненулевое решение /, т, заключаем, что
ап —Я й12 ^q^ ^
«21 «22 Л
Обратно, уравнение (8) всегда имеет действительные корни ^
и Я2; в самом деле, переписывая его в виде
находим дискриминант:
Д = («и + аггJ — 4 (aua22 —- a?2) = («п — а2,J + 4а
Случай 1. ^=^0, Х2ф0 и Tij^A, (эллипс действительный
или мнимый, гипербола, две пересекающиеся прямые,
действительные или мнимые).
В этом случае система G) при к = к1 принимает вид
и в силу условия
П2
=-0
имеет ненулевое решение llt m1.
Из соотношений A0) для этого решения, которые принимают вид
a11l1 + a12mi = k1l1, ,,..
аг111 + а22т1 = Х1т1, К '
находим ,
{ап114- a^nij) lj_ + (й21^ + аггт^ т1 = X^ll + т\) Ф 0,
или
1\
аХ11\ + 2 a12l1m1 -f a22mi =^ 0.
Значит, это решение не имеет асимптотического направления
линии A), а в силу соотношений A0) ненулевой вектор {tlt тх}
имеет главное направление линии A).
Аналогично при %=)i из системы G) находим ненулевой
вектор {/2, т2}, такой, что
также имеющий главное направление относительно линии A).
149. ГЛАВНЫЕ НАПРАВЛЕНИЯ И ГЛАВНЫЕ ДИАМЕТРЫ 383
Докажем, что векторы {1г, т1} и {1%, т2} взаимно
перпендикулярны. Из соотношений (II) н A2) находим
(au/2 + а1гт2I^ -\- (я21/,, -|- й22т,)тг = Х2(/х/2 + тх
Левые части этих равенств одинаковы, значит, A1(/12
= Я2(/1/2-гт1/и2). или (Xj — Х2) (/Л Н-т^г,,) =■-(), откуда
т. е. векторы {1г, тх} и {/2, т2} взаимно перпендикулярны. Отсюда
также следует, что в случае кгф0, К2ф0, к^к2 система G)
при Х = Х1 имеет ненулевое решение, но не может иметь двух
линейно независимых решений (то же и при Х = Х2). Иначе
говоря, линяя имеет два и только два взаимно перпендикулярных и
главных диаметра.
Случай 2. кх — к2ф0 (окружность действительная, нулевая
или мнимая).
В этом случае асимптотических направлений нет и любое
направление является главным; уравнение F) диаметра,
сопряженного хордам, параллельным ненулевому вектору {/, т\, принимает
вид
=:0 A3)
и является уравнением прямой, перпендикулярной вектору
{/, т\ (аХ
Главным диаметром в этом случае является любая прямая A3),
проходящая через центр линии.
Случай 3. Х1 = 0, Х2=т^0 (парабола, две параллельные или
совпадающие прямые).
В этом случае /2 = 0. Система G) при Х = Х2 имеет ненулевое
решение /2, т2\ вектор {/,, т2} не имеет асимптотического
направления линии A) и имеет главное направление.
При k — kx = Q система G) принимает вид
anl-\-a12m — 0, a21l + a22m — Q;
эта система имеет ненулевое решение llt тъ однако вектор {/х, mj
имеет асимптотическое направление, так как из соотношений
следует, что
anll + 2aliliml + atiml = 0.
384 Глава XI. ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
пекторы [llt mL}, {1г, т2] и здесь ортогональны (в силу того
что kt Ф к2, доказательство дано выше). Отсюда следует, что
система
в этом случае имеет одно ненулевое решение, но не имеет двух
линейно независимых решений. Из последних соотношений следует,
что векторы
{—«12. «ц} и { — «2а- а21} A4)
имеют асимптотическое направление (в случае, если уравнение A)
является уравнением параболы, или двух параллельных или двух
совпадающих прямых); при этом по крайней мере один из этих
векторов ненулевой.
Так как вектор, имеющий главное направление,
перпендикулярен асимптотическому направлению, то главное направление
линии A) в случае ^ = 0, Я2=^0 определяется одним из векторов
или jau, a12}, или {а21, а22} (один из которых ненулевой).
Таким образом, в случае линии параболического типа имеется
только один главный диаметр; его уравнение
alt(anx + al2y -j- аг) + a12(a2lx + а22у + a2) = 0,
или '
a21(anx + a12y + aj + a22(a21x + a2iy -f a2) = 0.
При этом надо взять то из уравнений, в котором коэффициенты
при anx-\-al2y-\- at и o21x + a22(/ + a2 одновременно не равны нулю,
и любое из них, если оба вектора {alv a12} и {а21, а22} ненулевые.
В случае параболы — это ее ось симметрии; для двух
параллельных или совпадающих прямых главный диаметр совпадает с местом
центров линии.
Заметим, что в случае 1гф0 направление любого главного
диаметра является главным, а в случае /2 = 0 главным будет
направление, перпендикулярное к единственному главному диаметру.
§ !50. Определение расположения линии второго порядка по
отношению к прямоугольной системе координат
Для определения расположения линии второго порядка,
заданной общим уравнением
аих2 + 2а12ху + а22уг + 2агх + 2а2у + а = 0 A)
относительно прямоугольной системы координат, достаточно знать
параметры, характеризующие данную линию и ту систему
координат, в которой уравнение линии является каноническим.
Если уравнение A) является уравнением эллипса, то надо
найти его полуоси, центр и направление оси, на которой лежат его
фокусы (или оси, к ней перпендикулярной).
? 150 ОПРЕДЕЛЕНИЕ РАСПОЛОЖЕНИЯ ЛИНИИ 385
Если уравнение A) является уравнением гиперболы, то надо
найти ее полуоси, центр и направление действительной (или
мнимой) оси.
Если уравнение A) является уравнением параболы, то надо
найти ее параметр, вершину и направление одного из двух лучей
оси, например того, на котором лежит фокус.
Если линия сводится к одной точке, то надо найти ее
координаты.
Наконец, если линия распадается на две действительные
прямые, то надо найти (в данной системе координат) уравнение каждой
из них *.
Если в уравнении A) а12 = 0, то расположение линии
определяется при помощи одного переноса (см. примеры ниже). Пусть а12фО.
Как было доказано в § 141 (теорема 1), уравнение A) при помощи
поворота осей координат хОу на угол а и последующего переноса
можно привести к одному из следующих видов:
a'11^2 + fl'11V2-r£> = 0, где а'
а'11Х2 + 2а'2К = 0) где а',,^ 2
a\1X* + D = Q, где а'иФ0,
а в § 143 были найдены значения коэффициентов простейших
уравнений (с помощью теории инвариантов) и их мы записали в виде
—&-У = Ъ, (II) B)
0
Переписывая формулы B) и C) § 141 в виде
^i — аи cos2 а + 2а12 cos а sin a -f- а22 s'ln& а-
0 = о12 (cos2 а—sin2 а) + (а22—ахх) sin а cos а,
имеем
%.х cos a = au cos3 а + 2а12 sin a cos8 a + а22 sin2 а cos а,
0 = —sinaa12 (cos2 a—sin2 a) -f (au — a.i2) sin2 a cos a
и складывая, получим
Xt cos a =■ а1г cos a -|- a12 sin a,
откуда угловой коэффициент новой оси О'Х для каждого из
простейших уравнений B) линий второго порядка
tga-*-»^, C)
*• Вопрос о расположении мнимых линий мы не рассматриваем.
13 П. с Л.членов
386 Глава XI. ЛННйИ. ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
где ?.v —тот корень характеристического уравнения, который
является коэффициентом при X2 в каждом из простейших уравнений B).
1~. Если уравнение A) является уравнением эллипса, то
простейшее уравнение имеет вид
Считая, что через А,х обозначен меньший по абсолютной
величине корень характеристического уравнения (| kt\ <;| Я81), и
переписывая последнее уравнение в виде
X2 Г2 ,
ЧкГ (У:
или
где
заключаем, что а> //, так что по формуле C) определяется угловой
коэффициент большей оси эллипса.
Координаты цетра эллипса находятся из системы
аих + avly +■ а1 = 0, D)
а21х Jr a22y + a3 = 0.
2е. Если уравнение A) является уравнением гиперболы, то ее
простейшее уравнение имеет снова вид (I). Обозначая через Хг
корень характеристического уравнения, имеющий тот знак, что и
/С8, перепишем уравнение (I) в виде
X» V2 ,
1
или
X^ Y*__ .
a* *2 ~ '
а=/- К°
длина действительной полуоси, а
длина мнимой полуоси.
§150. ОПРЕДЕЛЕНИЕ Р\СПО ТОЖПП1Я ЛИНИИ
По формуле C) определяем теперь угловой коэЬфицнел!
действительной оси О'Х. Координаты центра находим по-ирежнем. >п
системы D).
3°. Если уравнение A) является уравнением параболы, то ее
простейшее уравнение имеет вид
откуда параметр параболы
Вершина параболы находится так: возьмем на параболе точку
(х, у). Координаты вектора п, нормального к касательной, к
параболе в этой точке таковы:
altx + а12у + alt а21х+ а2
Для того чтобы точка (х, у) являлась вершиной параболы,
необходимо и достаточно, чтобы вектор п имел направление диаметров
параболы (асимптотическое направление), т. е. чтобы выполнялось
условие
а1гх + а12у-\- ах = — atit, E)
(см. теорема 4, § 146). Умножая эти равенства соответственно на
—а12 и а1Х и складывая почленно, будем иметь
a2atl — аха12 = {а\х + aj2) t,
откуда
, _ а2ап
2
Переписывая уравнение параболы в виде
(anx + а12у + ax) x + {azlx + а22у + a2) у + агх -f a2y + a = 0,
в силу соотношений E) имеем
0. G)
Таким образом, для нахождения координат вершины параболы
надо решить линейную систему E), G), где t определяется
формулой F).
По формуле C) (^=£0) находим угловой коэффициент
касательной к параболе в ее вершине (а если ч формуле C) взяи>
?ч~0, то она определит угловой коэффициент диаметров парабо".м).
Для нахождения вектора, коллинеарного диаметрам параболы
и идущего в сторону ее вогнутости, заметим, что уравнение A) в
13*
3?8 Глава XI. ЛИНИИ. ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
силу /2 = 0 можно всегда переписать в виде
(ax+f>yJ + px + qy + r = Q. (8)
Точка {х0, у0) пересечения прямых
всегда лежит на данной параболе (эти прямые всегда пересекаются
в случае, если уравнение A) является уравнением параболы).
Уравнение
рх -f qy -f- r = О
является касательной к параболе в этой точке ЛТ0, а
уравнение диаметра,'проходящего через точку касания. Парабола,
уравнение которой записано в виде (8), лежит в отрицательной
полуплоскости от прямой pxJrqy~rr = 0, а главный вектор {р, q)
этой касательной направлен в положительную полуплоскость от
прямой рх-\- qy-\-r = Q. Поэтому если ненулевой вектор {— а12, аи}
(а12=^0), коллинеарный диаметрам параболы A), направлен в
отрицательную полуплоскость от прямой px-j--qyJrr = Q,T.e.—a12p-f-ang<0,
то вектор {— а12, au}, коллинеарный диаметрам параболы,
направлен в сторону ее вогнутости, а если — a12p + auq > 0, то в
сторону выпуклости.
В случае —a12p -j- axlq > 0 вектор {a12, —au} коллинеарен
оси параболы и направлен в сторону ее вогнутости.
Замечание. Последний вопрос определения направляющего
вектора диаметров параболы A) решен в предположении, что
уравнение A) параболы задано относительно общей декартовой
системы координат.
§ 151. Примеры и задачи к главе XI
1. Задачи с решениями
Пример I. Исследовать уравнение
Преобразуем гто уравнение так:
или
4 (х+1L-9 (у—2)а_36 = 0.
Производя перенос осей координат так, чтобы новым началом координат
была точка (—1, 2), т. е. полагая Х = х+1, Y = y — 2, получим
4Х2+9У2—36 = 0, или y+-qp=l (рис. 222).
5 151. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XI
389
Пример 2. Исследовать уравнение
х2+4х~- j/-f5 = 0, или 1/ =
Имеем
где Х = х+2, Y — y-~\. Уравнение выражает параболу {рис. 223).
Рис.
222
Y
1
V
у
0
4
\
V
0'
Y
/
I
0
у
_ у
1
Рис. 223
А
Рис. 224
О
Рис. 225
Пример 3. Исследовать уравнение
Преобразуем уравнение так:
или
где Х=х+3, К = ?/-~2 Уравнение выражает равностороннюю гиперболу
С центром в точке (—3, — 2) (рис. 224).
390 Г лапа XI .ЛИНИИ ЗАДАННЫЕ ОБЩИМ VPARHEIIHFM
Пример 4. Исследовать уравнение
х2+ху — 2у3
Так как /2 < О, Л = 0, го это уравнение выражает две действительные
пересекающиеся прямые Преобразуем левую часть этого уравнения так1
Данное уравнение определяет две прямые (рис 225):
х + 2у = 0, х-у +
Другой вариант решения Из уравнении
x + -iy+l=0, jX
находим координаты центра линии (в данном случае точку пересечения тех
прямых, на которые распадается эта линия)
4 2
Из уравнения
14-ft — 2fe2 = 0
находим угловые коэффициенты асимптотических направлений данно'1 линии
(т. е. угловые коэффициенты тех прямых, на которые распадается линия)
Уравнения прямых, на которые распадается линия:
2 ,4 2 1 / . 4
у~т^х+т и у-[х+
или
Пример 5. Исследовать уравнение
5х2 4- 2ху + 2//а 4- 1 4л; 4- 4(/ 4- 10 = 0.
Так как /С3 = 0, то эго уравнение выражает две прямые. Преобразуем
левую его часть гак!
- Ю-5
Данное уравнение выражает две мнимые пересекающиеся прямые
Единственную точку плоскости, координаты которой удовлетворяют данном)
уравнению, найдем, разрешая систему
* + 4^ = 0, 30+1=0,
<s 151 ПРИМЕРЫ И -!ЛД'\ЧН КГЯМ'Н XI
391
отсюда искомая точка
м ( —f. -4
Другой вариант решения. Так как /2 > 0, /C = 0, то данное уравнение
определяет две мнимые пересекающиеся прямые, т. е. удовлетворяется
координатами только одной точки, Эта точка является центром данной линии, поэтому
ее координаты получим, решив систему уравнений
Пример 6. Найти форму, размеры и расположение линии второго порядка
бху + 8у2 — 12х — 26</ + 11 = 0.
Находим
Рис. 226
следовательно, данное уравнение определяет гиперболу. Далее,
характеристическое уравнение
Vs —8Я —9 = 0;
его корни
Простейшее уравнение
каноническое уравнение
X2 К2
Координаты центра О'{—], 2) находим из системы
Зу—6 = 0, Эх-\-Ъу—13 = 0.
392
Рлава X/, ЛИНИИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Угловой коэффициент действительной оси гиперболы
k=Xi-au =3 (рис. 226).
«12
Пример 7, Исследовать уравнение
x2-f-2xi/ + i/2 —
Находим
данное уравнение является уравнением параболы. Простейшее уравнение
У
\
каноническое уравнение
Так как
то вектор {1, —1} направлен от
вершины параболы к ее фокусу.
Координаты вершины параболы найдем, решая
систему
или
= 8x—4,
Рис. 227
откуда х = 1, (/=1. Вершина О' A,1)
(рис. 227).
Пример 8. Составить уравнения асимптот гиперболы
6х{/ + 8//2— 12х — 26у+ 11=0.
Решение. Если изменять свободный член в уравнении гиперболы, то
получим уравнение семейства гипербол с общими асимптотами, причем в 'это
семейство войдет линия второго порядка, распадающаяся на пару асимптот
данной гиперболы. В самом деле, координаты векторов, имеющих
асимптотическое направление, и координаты центра гиперболы определяются из
уравнений, в которые не входит свободный член уравнения. Итак, уравнение пары
асимптот данной гиперболы можно записать в виде
6ху + 8</2 — 12* — 26г/ + С = 0,
число С находят из условия распадения этой линии на две прямые)
0 3-6
3 8—13 =0, С = 20;
— 6 —13 С
искомое уравнение (сокращаем на 2):
§ 151. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XI 393
Оно распадается на два:
Зх + 4у — 5 = 0, (/ — 2 = 0,
это и есть уравнения асимптот данной гиперболы.
Замечание 1. Можно решать задачу и так: из уравнения 6/ш-f-Зяг2 = 0
найти координаты векторов, имеющих асимптотическое направление: {1,0^
и | —4, 3}, а из системы
3(/—6 = 0, Зх + 8у — 13 = 0
=0,
найти координаты центра гиперболы: х = —1, у —2. ■
Искомые уравнения
1 0
= 0 и
х+\ у—2
— 4 3
или
у —2 = 0, Зх + 4г/ —5 = 0.
Замечание 2. После того как найдены векторы
{1, 0} и {-4, 3}
сами асимптоты можно найти как самосопряженные диаметры:
1-C(/ — 6) + 0-Cx + 8t/— 13) = 0,
— 4 (Зу - 6) + 3 (За: + 8у— 13) = 0,
или
у— 2 = 0, 3*4-40—5 = 0.
Пример 9. Найти фокусы и директрисы линии второго порядка
бху + 8(/2 — 12х — 26(/ +11 = 0.
Решение. Находим
/2=_9<0, К3 = 81^0,
следовательно, данное уравнение определяет гиперболу.
Находим /i."
Характеристическое уравнение
XZ—SI — 9 = 0;
его корни
/ti = 9, А.2 ^ — 1
(через ?ix здесь обозначен корень, имеющий тот же знак, что и /C).
Простейшее уравнение
QJ у 2 V''
*_К2-^- = 0, или -^ ^- = 1,
откуда а=1, 6 = 3, следовательно, с V
Координаты центра определяются из уравнений
Зу—6 = 0, Зх + 8у —13 = 0,
откуда
394 Г лава XI, ЛИНИИ. ЗА/HHHblF ОБП1ИМ VPAPHF.HHFM
центр
О'(-1. ")
Угловой 1 оэффиииепт действительной оси
On 3
Пусть а—угол наклона действительной оси гиперболы к оси Ох тогда
tga = 3,
следовательно,
3 1
sin a— cosn=s ,
а так как новое начало координат — центр гиперболы 0'(—1, 2), то формулы
преобразования координат примут вид
х~ Ую v~ j/ То
Так как координаты фокусов в новой системе XO'Y суть соответственно
то их координаты в начальной системе хОу получим, подставив i' последние
формулы вместо X и Y их значения:
Уравнения директрис в новой системе координат
т. е. в нашем случае
V ю
Выражая из формул (а) координаты X и У через хну, получим
©тсюда уравнения директрис будут
1 + 3(у-2) 1
y"To" /То"
или
или
? П РРПМГРЫ Ч ЗАДАЧИ К ГЛАВЕ X! 395
fit., ер !0 .iai'iTii координаты ркус я \р..|Шелия директрис линии
второго порядка
х* + 2ку+у*—8х 1-4=0
1'ачодим
/2 = 0, К3= —16=0,
данное уравнение определяет паработу Далее,
Далее, так как - a12p + au£/=--1 • — 8+1-0 > 0, то вектор \а12,—аи\ =
= {1, —1} направлен от вершины параболы к ее фокусу.
Обозначая через а угол от оси Ох до направления этого вектора, находим
1 1
cos а = , , sin а= г=>
Координаты вершин»! находим из системы уравнений
х*-\-2ху + у* — 8д + 4=0, х + у— 2 = 0,
или
{х-\-уУ — 8х + 4=0,
или
отсюда х=\, у=\. Вершина О'A, 1)
Формулы преобразования кооозннат
фокуса и новой системе
а в начальной
Решая уравнения (р) относительно X и К, получим
Yx—I—(t/—1)_л —г; }/>-—I J-1/--1 _.у + У—2
f/2" yT" -/" ]/~
Уравнение директрисы в новой системе
л— 2 '
а в начальной
ZlZJL— — l—-t или ж—(/+1=0
Гример 11, Дано общее уравнение линии второго порядка
a11xi-\-2a12xy-\-a22y2+2a1x-\ 2a2y-\-a—Q A)
396 Р л а о а XI ЛИНИИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
относительно декартовой прямоугольной системы координат. Дано /г Ф 0.
Составить уравнение линии второго порядка, распадающейся на пару главных
осей этой линии
Решение. Уравнения главных осей данной линии
2i* + a22f/+a2)=0, B)
(а21х-{-а22у->га2) = 0,
где kr и к%— угловые коэффициенты главных осей. Уравнение линии второго
порядка, распадающейся на две прямые B), запишется так:
(апх + а12у + atJ + {kx + ka)(aux + a12y -f at) (a21x-f- a22y + a2) —
так как kxk2——1
Угловые коэффициенты kx и ft2 определяются из уравнения
a12£2 + (on — a22) k—а12 = 0
(это уравнение получается из уравнения, приведенного на стр. 341, если
поделить левую часть последнего на cos2 а).
Из последнего уравнения следует, что
а значит, искомое уравнение
+ а2гу + а2J = 0.
Замечание Если данная линия распадается на две пересекающиеся
прямые, то последнее уравнение распадается на уравнения пары биссектрис
углов между ними.
Пример 12. Пусть общее уравнение линии второго порядка
2 + 2а12ху + а2гуг ■+ 1ахх + 1агу + о = 0, A)
заданное относительно общей декартовой системы координат, является
уравнением параболы Доказать, что тогда вектор ta=\Alt А2}, где Ах н А2 —
алгебраические дополнения элементов аг и о2 в определителе
К3 =
ап а12 ах
вы «22 О2
Oj a2 a
ненулевой, коллинеареп оси параболы и направлен в сторону вогнутости
параболы
Решение. Так как К3=а1Л14-а2Л2 Ф 0, то из двух чисел Аг или Ла
хотя бы одно не равно нулю и, значит, вектор w ненулевой. Далее,
<u — {Alt Аг\ = {аг1а2 — а1а2г, a12a1 — ana2\ = a1{~a.i2, а12\+а2\а1г, —ап\.
Из этого соотношения следует, что вектор « коллинеарен диаметрам
параболы A), так как он является линейной комбинацией векторов
■{—q22, a12} и {а12, ~ац\, каждый из которых коллинеарен диаметрам
параболы A)
Если ап > 0 или а22 > 0, то уравнение параболы A) можно записать
в виде
(Y"^i х + Y"^2 у? + 2а1х + 2а2у + а = 0
и на основании § 150 вектор {Аи Л2} направлен в сторону вогнутости пара-
S 151 ПРИМЕРЫ И ЗЛДЛЧП К ГЛ \ BE XI 397
Со"■>! ,i) тогда и тотько тогда, когда он направлен в отрицательную
полуплоскость от прямой
а это будет иметь место тогда и только тогда, когда
Но это условие выполняется, так как
a1A1~-atAi = K3—— («i Ya22 — a2 Va^Y-
Если же ап < 0 или а22 < 0, то уравнение A) можно переписать в виде
(х У—ап-\-у уг—а22J—2а1х—2а!1у — а = 0.
Парабола лежит теперь в положительной полуплоскости от прямой
и, значит, вектор « направлен в сторону ее вогнутости, если
а1А1-\-а2А2 > 0.
Но это выполняется, так как в случае ап < 0 или аш < 0 имеем
2 = Кв = {а1 Y~—a22—a2 У~~ апJ > 0.
Итак, вектор 0} = {Alt A2\ всегда направлен в сторону вогнутости
парабо ты.
Пример 13. Найти огибающую семейства прямых, рассекающих данный
треуго!ьник ABC на две равновеликие части
Решение. В данное семейство прямых входят, очевидно, медианы
данного треугольника Прямая Д, отличная от медиан и пересекающая,
например, отрезки АВ и АС соответственно в точках и и v, принадлежит данному
семейству, если площадь треугольника Auv равна половине площади тре-
\гольника ABC. Отсюда
Аи- Av = -^->
значит, прямая uv касается дуги ру гиперболы с асимптотами АВ п АС.
Концами р и у этой дуги гиперболы являются середины медиан ВВ' и СС'.
Между прочим, точкой М касания прямой uv с указанной дугой гиперболы
является середина отрезка uv.
Искомая огибающая состоит из указанной дуги fly и ДУГ Ра> аУ Двух
других гипербол, аналогичных дуге ру (сделать чертеж).
2. Задачи для самостоятельного решения
1. Доказать, что расстояние от центра эллипса до прямой, проходящей
через концы двух его взаимно перпендикулярных диаметров, есть величина
постоянная.
2. Найти сумму квадратов длин сопряженных радиусов эллипса с
полуосями а и Ь.
Отв. а2-}-Ь\
3. Вычислить площадь параллелограмма со сторонами ОМ и ОМ', где
ОМ и ОМ' — два сопряженных радиуса эллипса, полуоси которого равны а и Ь.
Ошв ab.
Г ion Л' ,i.| : 1 ?-ЧЧ- !:'* ii'LI'v !> "ABi! i lliIEVi
4. !!<1йтн cyvMj для» «вух хорд эллипса с полуосями (I и Ь, проходящих
j е> о фокус и параллельных двум его сопряженным диаметрам
Отв 2
5. Доказать, что сопряженные диаметры равносторонней гиперболы
одинаково наклонены к ее асимптотам.
6 Доказать, что сопряженные диаметры гиперболы кососимметричны
огласительно одной из ее асимптот по направлению другой асимптоты!
7. Назовем сопряжениями радиусами ОМ и ОМ' гиперболы
дна отрезка, лежащие на сопряженных диаметрах этой гиперболы, причем
концами этих отрезков явтяются центр симметрии данной гиперболы и точки
М и /И' пересечения сопряженных диаметров гиперболы с данной
гиперболой и с гиперболой
£ !!___!
сопряженной с данной.
Доказать, что если
М Гу
конеи oaiiOio из сопряженных радиусов, то конец другого
8. Найти геометрическое место точек пересечения касательных к эллипсу
проходящих через концы его сопряженных диаметров.
9. Концы сопряженных диаметров эллипса
х2 г/2_
соединены хордами Определить геометрическое место их середин
10. Доказать, что вершины ромба, описанного около эллипса, лежат на
его осях
И Определить эллипс наибольшей площади, вписанный в данный
параллелограмм
Опт Эллипс, касающийся сторон параллелограмма в их серединах
12. Определить геометрическое место середин хорд эллипса, отсекающих
от них сегменты постоянной площади
Сте. Эллипс.
§ 15! ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XI 399
13. Доказать, что диа1 опали параллелограмма, стороны которого каса
ются эллипса, являкися сопряженными .'иамеграми эюго эллипса
14. Доказать что произведение отрезков МР\ и /VI Р., касательно.*! 1'1МР2
к эллипсу {Л/—точка прикосновении), где Р, и Р2—точки, р которых 5>зс-
сматриваемая касательная пересекается с двумя произвольными параллеть-
ными, касательными к эллипсу, постоянно
16. Вычислить площадь эллипса с полуосями а и Ь.
Отв лаЬ
х^ и
16. На эллипсе —г--1--тг" = 1 саны две точки М1(х1, цх) и М?\х.;, d,i
Найти углозоа коэффициент прямой, проходящей чер.;з центр эллипса л дели
щий пополам площадь эллиптического сектора O,ViL,U2 (О — центр эллипса)
111 -j- W,
Отв J1 ', - .
17. Найти все аффинные преобразования (см § 175—179), переводящие эллипс
'о2" + "Ь2"==1
в себя.
^ i b . . , а ,
Отв. х —х cos ф——у sin ф, ^ х =xcos Ф т -г- У sin ф,
. или
о . Ь
У =-т- XSin ф-|-(/ СОБф, ! (/ =—ХЫПф—у COS ф
(ф — любое число),
18. Найти все афинпые преобразования, переводящие гиперболу
"о2 br==l
в себя.
Отв. х'^^1%+4-)х + ±^
1де Я — любое число, не равное нулю,
19. Рассмо1рим два радиуса гиперболы, таких, что площадь
гиперболического сектора, образованного этими радиусами и дугой гиперболы, имеет
данную величину.
Доказать, что:
1) хорды, соединяющие концы этих радиусов, касаются некоторой (ипер-
Солы, гомотети«пой данчой, причем точ;га^и касания служат середины хорд;
2) сегменты гиперболы, заключенные между этими хордами и дугой
гиперболы, имеют постоянную площадь;
3) треугольник, имеющий сторонами одну из хор.ч v. касательные к
гиперболе в ее концах, имеет постоянную площадь.
20. Определить аффинное преобразование, которое параболу у2 = 2рх
переводит в ту же параболу.
Отв. х'= -- С2рх — 2ту-\-т2), у' = К(у — т)
где %—любое число, не равное нулю, а .«—любое число
400 Глава XI. ЛИНИИ. ЗАДАННЫ^ ОБЩИМ УРАВНЕНИЕМ
21. Определить все унимодулярные, т. е. такие преобразования х' п
i-auy + av у' ■» а21х + а22у -f- о2, для которых anai2—а12а21 = 1, при
которых парабола у* = 2рх переходит в себя.
Отв.
х' = -~-Bрх
22. Определить геометрическое место середин хорд параболы г/2 = 2р*,
отсекающих от этой параболы сегменты постоянной площади.
Отв. уг = 2р(х—а), где а—расстояние от вершины данной параболы до
хорды, перпендикулярной к ее оси и отсекающей от данной параболы сегмент
данной площади.
23. При каком необходимом и достаточном условии две линии второго
порядка, заданные общими уравнениями
fl22y2-f 1агх-
+ 2bnxy + 622j/2 + 2blX + 2Ьъу + Ь = 0,
имеют одни и те же главные направления.
Отв. a^~a^^b~L
a12 "IS
Это условие эквивалентно следующему;
АВ = ВА, где А-.
24. Найти геометрическое место центров равносторонних гипербол,
проходящих через три фиксированные точки, не принадлежащие одной прямой,
Отв. Окружность,
25. Относительно прямоугольной системы координат линия второго
порядка задана уравнением
4ху+Зу2-И6;с+*2у — 36 = 0.
Доказать, что эта линия —гипербола. Найти длины ее полуосей,
координаты центра, уравнения действительной и мнимой осей, уравнения асимптот,
координаты фокусов, координаты вершин, уравнения касательных в вершинах.
Отв. /2== — 4 < 0, /Са= 144^0, гипербола; действительная полуось а = 3,
мнимая полуось 6 = 6; центр C, —4); действительная ось 2х—у—10 = 0,
мнимая ось х + 2г/ + 5 = 0; асимптоты (/ + 4=0, 4х + 3(/ = 0; фокусы F, 2), @,-10);
соответствующие им директрисы х + 2(/+2 = 0, х + 2у + 8 = 0; вершины
/з в д / з 6 _ л
касательные в вершинах х + 2(/ + 5 ± 3 \^5 =0.
26. Какая линия второго порядка определяется условием ^=0, Кз Ф 0?
Отв. Равносторонняя гипербола.
27. Линия второго порядка, заданная общим уравнением ер (х, (/)=0
второй степени, распадается на две параллельные прямые. При каком
необходимом и достаточном условии точка /И0(х0, у0) лежит между ними?
Рте. /хф (х01 г/0) < о.
ГЛАВА XII
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА, ЗАДАННЫЕ 0БЩШ1
УРАВНЕНИЕ!
§ 152. Теорема о том, что всяко*е уравнение второй степени
с тремя неизвестными определяет эллипсоид, гиперболоид,
параболоид, конус, цилиндр или две плоскости
Теорема I. Всякая квадратичная форма однородным
ортогональным преобразованием может быть приведена к такому -:иду
(каноническому) чтобы преобразованная форма не содержала ч генов с
произведением новых переменных, взятых попарно
Коэффициентами преобразованной формы будут корни
характеристического уравнения.
Общее доказательство этой теоремы дается в курсах высшей
алгебры*.
Здесь дадим геометрическое доказательство этой теоремы для
случая квадратичной формы от трех переменных:
Ф = ахххъ + а22 if + as3z2 + 2ai2xy -f 2a23yz + 2a31zx. A)
Доказательство. Введем в пространстве ортонормированный
базис /, у, к. Переменные х, у, z рассматриваем как координаты
вектора {х, у, z) в этом базисе. Введем новый ортонормированный
базис /', /", к', Координаты х, у, z произвольного вектора а в
базисе /, /, к через координаты х', у', z того же вектора а в
базисе Г, /', к' выражаются соотношениями A) § 100. Этими
соотношениями выражается ортогональное преобразование {ЛЪ
поскольку матрица А этого преобразования — ортогональная.
Подставляя в выражение A) вместо х, у, z их значения из
формул A) § 100, получим
ф'= an ix'cos ai + У' cos a2 + z'cos asf +
* См Л. Г. Курош Курс высшей а.чги&ры М., „Наука", 1965, гл 8,
§ 37, стр 226.
§152, ОБЩЕЕ ,/РЛ!
ЛГ ПОПГ.РХ НОС I И
403
Докажем сначала, что ортои-. фованный базис /'./', к' можно
выбрать так, что в выражении (]'; обратятся з нуль
коэффициенты при z'x' и y'z'. Выписывая кз соотношения (Г) половины
коэффициентов при z'x' н y'z' и приравнивая их пулю, получим
уравнения, которые можно записать в виде
(ои cos a.s + aVi cos Pg -f a13 cos y8) cos ax +
-}- (a, t cos as -j- й22 cos j33 -f <?23 cos y3) cos рг 4-
-f (я31 cos a3 -f- a32 cos \ia -f ass cos y3) cos Yi = 0,
(an cos cc8 + a12 cos [j8 -f a13 cos у8) cos a2 +
-f- (a.?1 cos a3 -f a22 cos рз Ц- a23 cos Уз)соэ Р2 +
+ (a,x cos a3 -|- a32 cos py -;- a33 cos Y3) cos y2 = 0.
Эти соотношения означают, что вектор
{an cos a3 -|- o12 cos r% -f g13 cos у3, c2] cos a3 -,L o22 cos p3 -f o23 cos у3.
«si cosa3 -i- a32 cos B3 -1- a33 cos y3)
должен быть ортогонален векторам
{1 cos >>!, cos
иначе коллипеареп вектору
т. е.
cosy2},
cosP3, cosy3},
или
au cos a3 + a12 cos рз + aln cos Ys = ^ cos аз>
a21cosa3-i-c22 cos P3-f a23cosY3 ==^cosp3, >
a31 cos a3 + a32 cos P3 + o33 cos y3 = К cos y?>, j
(ац —A.) cos a8 + c12 cos рз -|- a13 cos y3 = 0.
3
asl cos a3 + a32 cos {i3 + (a33 -1) cos y3 = 0.
B)
C)
Так как вектор &' должен быть единичным (cos2 a3 -f- cos2 p3 +
+ cos2y8=l) и так как система C) линейная, однородная
относительно cosa3, cosPg, cos уд, то она имеет ненулевое решение
тогда и только тогда, когда определитель системы равен нулю:
~ ^ a
i2
32
= 0.
D)
Это уравнение ргазывается характеристическим уравнением
формы ф. Оно третьей степени относительно Я. Но так как все числа
alk мы считаем действительными, то уравнение D) имеет по
крайней мере один действительный корень. Оставляя пока в стороне
Глава XI1, ПОВЕРХНОСТИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
случай, когда уравнение D) имеет трехкратный корень, можно
утверждать, что уравнение D) имеет простой действительный
корень, который обозначгм так: Я--=Я3. Подставляя это значение
^ = А3 в систему C), пслучим систему
(йп—Я3) cosa3 + a12 cos |33 j-fl13 cos у3 — О,
a21cosa3 ;-(a22 — А3) cos f>3 + агз cos Уз = 0. E)
u31costf3 + a32cos|33-f (a3J —A3)cosy3 = 0.
Система E) не может иметь относительно cosa3, cosp3, cos Уз
два линейно независимых решения. В самом деле, в противном
случае матрица
12
по
21
•♦is
\ 1 2 2"
имела бы ранг, меньший 2, и, значит, производная от
характеристического определителя
-А. а,
Д (>.)==
которая равна
fl22 ^ fl23
а,2 — Я
^32
*22
а
32
а
33
, —Л а,
а33 —Я
, —Я
при Я = Я3 обращалась бы в нуль, т. е. корень А = А3
характеристического уравнения имел бы кратность больше 1 вопреки
предположению.
Итак, существуют только два противоположных единичных
вектора
ft' = {cosa3, cosp3, cosy3} и #' = { — cosa3, — cosj?3, —cosy3},
координаты которых удовлетворяют системе E). Выбирая любой
из них
располагая векторы
i' = {cosa1, co
, cosp8, cosy3},
/ = {cosa2, cosp2, cosy2}
перпендикулярно вектору к' и друг другу, получим, что
форма (Г) примет вид
Теперь произведем поворот осей Ox'y'z' вокруг оси Oz'; этому
§ И7 ОБЩЕЕ УРАВНЕНИЕ ПОВЕРХНОСТИ 405
повороту соответствует ортогональное преобразование й2
x' = x"cosce — у" since,
у' = х" sin се -\- у" cos a,
F)
которое, как было показано в § 141, можно выбрать таким, что
форма а'цх'2-\-2а12х'у'-\-a2iy'2 преобразуется в форму ац.х"г +
;
При ортогональном преобразовании Q = Q2QX форма ср
преобразуется в форму
2 L/2- (П
Теорема доказана. Отметим (и это очень важно для
дальнейшего), что
+ (a21 cos a8 + a22 cos E3 + a23 cos ys) cos p3 +
+ (a8l cos a3 + a32 cos P3 + a83 cos ys) cos y3 ==
= A3 cos2 a3 + Я3 cos2 рз + Я3 cos2 y3 = ^3-
Так как форма ср" не содержит произведений координат х"у"
и x"z", то a11 = A.1, где А.х —также корень того же
характеристического уравнения D) отличный от Я3, и аналогично а22 = Я2, где
Я2—корень характеристического уравнения D).
Таким образом, канонический вид формы ф имеет вид
где Ах, к2, ks — корни характеристического уравнения формы ср.
Из доказанного следует также, что:
1) все корни характеристического уравнения действительны;
2) если все корни Я1; Х2, Xs прветые, то, подставляя в
систему C) Кг вместо Я, и заменяя а3, рз, у3 на av pt> Yi> получим
систему, из которой можно найти только два (взаимно
противоположных) единичных вектора новой оси Ох', а при Я = А.2 только
два (также взаимно противоположных) единичных вектора новой
оси Оу';
3) если %1 — %2ф %3, то форма ср" имеет вид
и при любом ортогональном преобразовании Q2 она не будет
менять этог© вида, так как из фермул F) следует, что х'2-\-у'2 =
~Х"% + У- Таким образом, уже при ортогональном
преобразовании Q-l форма ф перейдет в форму
406 Г лаво ХП ПОРСРЧНОСПП ЗАДАННЫЕ ОБЩИМ S РЛ (ШЕПНЕМ
Так как координаты вектора /' ортонормировании! о Сазпса /', /",
ft', в котором форма ф не содержит произведений х'у' и x'z',
находятся всегда из системы C), в которой надо положить Я = Я1(
то в случае Я.1-=Я2^=Я3 система C) (в которой Я заменено на Я1;
а аз> Рз> Уз ua ai> Pi> Yi) имеет два линейно независимых
решения. В качестве векторов /" и /", как мы уже указывали, можно
в этом случае взять два любых вектора, оотогональных вектору к'
и между собой.
4) Если, наконец, Я1 = Я2 = Яа, то форма ср' имеет вид
Но из соотношений A) § 100 следует, что для любого
однородного ортогонального преобразования
Назначит, форма ф с самого начала имеет канонический вид
Теорема 2. Общее уравнение
ацхг + а.г2уг + агзг2 + 2а12ху + 2a2zyz + 2azlzx +
+ 2atx + 2агу + 2asz + а = 0 G)
поверхности второго порядка, заданное относительно общей
декартовой системы координат, при помощи преобразования системы
координат в прямоугольную систему можно преобразовать к
одному из следующих пяти простейших уравнений *:
= 0. где Я^ 0, Я, ^ 0, Я3 =^0, (I)
= 0, где Я^О, А2=И=0, а'3ф0, (II)
= 0, где Я^О, Я2^=0, (III)
= 0, где Я1^=0, а^О, (IV)
^Q, где A,1?fc0. (V)
* Здесь, как и в § 141, по существу идет речь о том, что целую
рациональную функцию второй степени от трех аргументов:
аих- + a22y2 + aJ322 + 2апху + 2ai3yz + 2апгх
при помощи некоторого неоднородного ортогонального {см. ниже доказатель
ство теоремы) преобразования можно привести к одному из следующих пяти
видов:
где %г фЪ, %2 ф 0, 13 ф 0,
где Хх ф0, %г ф 0, а.й ф 0;
где %!ф0. Х2ф0,
2a2K, где Х1ф0,
2 + D, где Хх 56 0.
152 ОБЩЕЕ SPABHEHHF. ПОВЕРХНОСТИ
407
Доказательство. Перейдем сначала от общей декартовой
системы координат к декартовой прямоугольной. Так как при
преобразовании декартовой системы координат порядок
поверхности пе меняется (§ 140, п. 1), то при переходе к декартовой
прямоугольной системе координат уравнение G) перейдет в ура;не-
ние такого же вида . Поэтому с самого начала предполагаем, что
уравнение G) дано относительно декартовой прямоугольной
системы координат Oxyz,
В теореме 1 этого параграфа доказано, что можно от
прямоугольной системы координат Oxyz перейти к другой
прямоугольной системе Ox'y'z', такой, что в системе Ox'y'z' уравнение G)
преобразуется в следующее;
V'2 + Ку'2 + К*'2 + 2а>' + 2a'ty' -f 2asz' + а = 0, (8)
— корни характеристического уравнения
где
Х2 и
а,, —;
12
13
«33 ~
-0.
(9)
При этом координаты cosocj, cos p,-, cosy; единичных секторов
/ k' новых ' осей Ох', Оу', О г' находятся соответственно из
систем:
(йц - h)cos at + «i2 cos p, + als cos у, = 0,
a2l cos a,- + {a22 — %i) cos p. + a23 cos y,- = 0,
asl cos a; + a32 cos p, -f- (a3g — Kt) cos y,- = 0,
A0)
2,3.
Г.слп
12, 2^g 8^1, то получаем единственную
тройку новых осей Ох', Оу', О г' (с точностью до выбора на них
положительных направлений). Если К1 — К2ФКВ, то из системы A0)
при (=3 находим единственную ось Oz' (с точностью до выбора
на ней положительного направления), а оси Ох' и Оу'
располагаем перпендикулярно к оси Oz' и друг к другу. Если, наконец,
л 1 ..-К., — %3> то уже начальное уравнение G) не содержит членов
с ху, ijz и zx и квадратичная форма гр, входящая в левую часть
уравнения G), имеет вид X (х2-}-у2-{-z2).
I случай. Предположим, что в уравнении (8)
Тогда уравнение (8) можно переписать в виде
где
408 Глава X1U ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Производя перенос системы Ox'y'z' так, чтобы новым началом
координат была точка
о' (~ai i ^Л
где координаты точки О' даны относительно системы Ox'y'z', и
обозначая координаты точек в новой системе через X, Y, Z,
будем иметь
и уравнение A1) примет вид
%1X* + X2Y* + %3Z* + D = Q, (I)
где
^^=0, 12ф0, Х3ф0.
II случай. Предположим, что в уравнении (8)
Х^О, к2ф0, ^ = 0, а'3^0.
Тогда уравнение (8) преобразуем так:
где
П '2
Перенося систему Ox'y'z' так, чтобы новым началом
координат стала точка
0 [-ТГ' h ' 2a'J
(координаты точки О' даны относительно системы Ox'y'z'), т. е.
полагая
приведем уравнение (8) к виду
XlX2 + k2Y* + 2a3Z = Q, (II)
где
Хг #0, Я2 ф 0, а', ^ 0.
Ш случай. В уравнении (8)
Ач^О, ^^=0, А3 = 0, а3-0.
§ 152 ОБЩЕЕ УРАВНЕНИЕ ПОВЕРХНОСТИ 409
Тогда уравнение (8) имеет вид
h±x -\-K.^y -\- ZciiX -j- 2@2У '\~d==Ut
или
. 2
' + тг) +D = 0, A2)
где
Производя перенос системы координат Ox'y'z' так, чтобы новым
началом координат была точка
т. е. полагая
приведем уравнение A2) к виду
K^ + K^ + D^O, (III)
где
IV случай. В уравнении (8)Я2 = А3 = 0, но хотя бы один из
коэффициентов а2 или а3 отличен от нуля.
Если A2 = ?ig = 0, а8 ^=0, а3 = 0 или А,2 = Я3 = 0, ад ^0, а'2 = 0,
то при помощи одного только переноса осей уравнение (8) можно
преобразовать к виду
или (если а3 Ф 0, а2 = 0) к виду
Если же а2 =7^=0 и а3=7^0, то при помощи переноса осей Ox'i/z'
избавимся в уравнении (8) от первой степени х" и оно в
некоторой системе O'x"y"z" примет вид'
Производя затем поворот осей O'x"y"z" вокруг новой оси О'х"
приведем последнее уравнение к виду
410 Рлаво XI) ПОВЕРХНОСТИ, ЧЛЛАННЫГ ОБПШМ vpa
или, обозначая половину коэффициента при Y по-прежнему через а2'
>., \'2 + ?а'?У=0. (IV)
V случаи. Х2 ~'ks — а. =ач = 0,
Уравнение (8) имеет вид
и переносом осей координат приводится к виду
>.гХ* + О = 0, где 1нф0. (V)
Теорема 3. Общее уравнение
a33z2 + 2а12ху + 2a2syz + 2aslzx +
J,- 2a.sz + a = 0
поверхности второго порядка, заданное относительно общей
декартовой системы координат, выражает одну из следующих
семнадцати поверхностей'
ж2 и2 z2
1 эллипсоид — + |г + т5' ~ *'
2° мнимый эллипсоид —г + -fr + -г = — 1"'
О. О С
3° однополостный гиперболоид —+ -|г—Т5""''
4° двуполостный гиперболоид —5-+"тг—Т2^"— '
5° конус ^- + |1_|гв:0;
6° мнимый конус -г" +-fr + — — 0;
7° эллиптический параболоид — -f-— ~Ъ, р>0, q>0;
8° гиперболический параболоид = 2г, р > 0, ^ > 0;
9° эллиптический цилиндр ■—§■-{--jr— l!
л2 у2
10° мнимый эллиптический цилиндр -^- + ^ — — 1;
11° две мнимые пересекающиеся плоскости— +-^ = 0;
12° гиперболический цилиндр —^—~^- — 1;
13е две пересекающиеся плоскости —$ g^" = 0;
OliiUFF. VP.IBIIF.HIIF ПОВЕРХНОСТИ 4Ц
14е паралолическин цилиндр х2~2ру, р > I);
15° две параллельные плоскости х2 = а2, а Ф 0;
16° две мнимые параллельные плоскости х2 — — а2, афО;
17° две совпадающие плоскости х2 = 0.
Согласно двум предыдущим теоремам нужно рассмотреть
следующие случаи *.
I случай. Х1х2 + 'к2у2 + Х3г2 + О = 0,Х1ф0,12ф0, Х3ф0. (I)
1) Klt Х2, Я3 одного знака, а£> имеет знак, им противоположный.
В этом случае уравнение (I) можно переписать так:
D
j ^ j
т п г
и так как —-г— > О, —т— > О, —-т— > О, то можно положить
D. = a2 _^_ = 52 9. С2.
тогда получим уравнение 1°.
2) klt k2, ks и D одного знака. В этом случае уравнение (I)
перепишем в виде
А| Р*2 ">
или
где
„ D ,, D , D
Aj A2 А3
3) к1 и К2 одного знака, а 15 и D противоположного.
Перепишем уравнение (I) в виде
—^-=1.
D "•" D D
Так как —г- > 0, —j— > 0, у- > 0, то можно положить
D 9 D ,, D «
и мы приходим к уравнению 3°.
4) к1У Кг и D одного знака, а ^3 противоположного.
* В простейших уравнениях 1—V поверхностей второго порядка
относительно декартовой прямоугольной системы координат (см. условие теоремы 2
§ 152) снова будем обозначать координаты буквами х, у, г-
412 Г лава КН. ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Перепишем уравнение (I) в виде
X1 V2 2^ X2 У* Z2
где
а2 = — Ь2 = — c2__iL
5) Xt и К2 одного знака, Хя имеет знак, им противоположный,
В этом случае уравнение (I) можно переписать так;
или
где
х* , У2 г2 п х' , у2 г2 „
х+х~х= •или ^+^"^=0>
а2 — —5- Ь2 = ] с2 ?—
I Oi I > 111» — I \ I '
6) лг, л2, л3 одного знака, a D = 0. В этом случае уравнение (I)
можно переписать так:
1Ч*а + 1 W + l^|z2 = 0- или ^ + |l + il^0.
II случай. ^л:2 + X2^ + 2a',z = 0, ^=#0, Кг ф 0, а, ф 0. (II)
7) ?4 и Я,2 одного знака.
Выбором положительного направления оси Oz можно добиться
того, что коэффициент при z в уравнении (II) будет иметь знак,
противоположный знаку 1г и Кг. В таком случае уравнение (II)
можно переписать так:
х* ,_£ 2z
или, полагая
(р > 0 и 7 > 0. так как а^ имеет знак, противоположный знаку
и )t2), будем иметь:
153, ТЕОРИЯ ИНВАРИАНТОВ 413
8) Ki и Я2 разных знаков.
Положительное направление оси Oz всегда можно выбрать так,
чтобы знак а3 был противоположен знаку Хх. Переписывая тогда
уравнение (II) в виде
2 2
и замечая, что
получим уравнение 8°:
Аналогично исследуются случаи III, IV, V, приводящие к
уравнениям 9°—17°.
Рассмотрение поверхностей, определяемых уравнениями A11),
(IV) и (V), проводится так же, как в § 141 исследовались линии
второго порядка, простейшие уравнения которых мы обозначали
соответственно через (I), (II) и (III).
§ 153. Теория инвариантов
В настоящем параграфе будет использована теорема,
сформулированная в § 142, но для случая трех и четырех переменных.
Именно произведем над переменными х, у, г целой
рациональной функции F второй степени от этих переменных
F = апх* -f а22уг + assz2 + 2a12xy -f 2a23yz + 2aslzx -f-
A)
линейное неоднородное преобразование:
х = с1гх' + c12i/ +cnz' -\-
г/ = с21л:'4-с22у' + с2з2' + с2, B)
z = cslx' + cs2i/ + cS3z' + c3.
Пусть
F' = ацх'2 + a'i2t/z + a'3Sz'2 + 2a\2x'y' + 2а2лу'г' + 2a'siz'xr +
+ 2a'1x' + 2aiyr + 2a3z' + ar C)
функция, в которую при этом преобразуется функция F. Тогда
имеют место соотношения
с21 с3Л/йп
[I
I a21 a?2 a23 |= c12 c22 c32 [I a21
\ Й31 й32 a33/ \cl3 c23 cg3/ \a
31
414
Г л о 1 а XII, ПОР. !:Г \!ЮСТП, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
CUC21C3l 0\ /«U«12 «13 «1
с,, с,,с^ О
12 U22 C32
<-13 C23 <-33 "
C-i C.j Co i t
cl.2 i a2^ a<i% Ч2
«31 «32 «33 «3
\a1 a, a.
В самом деле, квадратичная форма, входящая в состав
функции F, преобразуется в квадратичную форму, входящую в состав
функции F' при однородном преобразовании
+ сУЗг\ F)
+ c2sz',
-, ,- v' \ г и' ' г ■у'
6 —(-31Л Т°32У "ГсЗЗ'г •
Отсюда следует формула D).
Далее, функция F может быть получена из квадратичной формы:
а1гх2 -\- ai2y2 -f a.]Sz2 + 2av,xy -\- 2a2syz -f 2a3lzx +
при ^=1, а неоднородное преобразование B) получается из
однородного;
' г Г , Г , ,1
V »" \' —J— »" // —J— Р у . >" /
л — t/-^^л ^^ ^ 12i/ l^ 13 I 1 *
у = с21х' -f с22г/' + с23г' + c2t',
^ _ jf'
при ? —\.
Из этих соображений получается формула E) *. Из
соотношений D) и E) следует, что при линейном преобразовании B) над
переменными х, у, z целой рациональной функции F, при котором
она переходит в функцию F', имеют место соотношения!
hi an «is " " " 2
p Й22 «23
31 «32 «33
аи а12 а,3 а^
«21 ^22 «23 «2
«31 G3 2 «3 3 «3
Й1 а2 а3 а'
«21 «22 «23
'21 «-22 "-23
'31
«11 «12 «13 «1
«31 ^32 «33 «3
'11
'21 ^22 ''гз
D')
E')
Определение. Целая рациональная функция от коэффициентов
многочлена второй степени называется ортогональным инвариантом
этого многочлена относительно ортогонального преобразования,
" См А. Г. К у р о ш. Курс высшей алгебры, изд. 6. М., Физматгиз, 1965,
§ 26, стр. 169.
1Г.0РИЯ ИНВАРИАНТОВ
415
если она сохраняет свое значение при неоднородных ортогональных
преобразованиях переменных.
Теорема 1. Функции *
G)
(8)
(9)
I1 = an + aii-\-a33 ПО)
являются ортогональными инвариантами целой рациональной
функции второй степени от трех аргументов:
F = апх2 + а22уг -+- «Ззг2 + 2al2xy -f- 2a23yz -f- 2a3lzx -j-
-f- 2аг.г + 2a2y -}- 2a3z + a.
Д
i \
«11
«21
s =
«12
«22
«
a
a
a
a
a
a
_L
T
1
1
21
31
11
21
31
1
«22
«32
«12
«22
«32
«2
a31 a
«13
«23
«ЗЯ
«13
«23
«33
a3
13
33
«1
«2
«3
a
L
«22
a
32
«23
«33
Доказательство. Так как определитель ортогонального
преобразования равен ± 1, то его квадрат равен 1 и
инвариантность /3 и /С4 следует из соотношений D') и E') настоящего
параграфа.
Для доказательства того, что /2 и /г также являются
ортогональными инвариантами, заметим прежде всего, что коэффициенты
ап, a22, a33, а12, а23, а31 являются инвариантами переноса:
х = х'-\-с и=ц' ' с z — z' А-с A1)
Это доказывается так же, как и в § 142. Поэтому достаточно
доказать, что /2 и 1г являются инвариантами однородного
ортогонального преобразования:
у' -'гс33г',
A2)
При этом преобразовании имеет место соотношение
(это доказывается так же, как и соответствующее равенство
+ *- х'2-:~у"' в теореме 4 § 142).
/3 называется дискриминантом формы ф.
416 Глава XII ПОВЕРХНОСТИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Рассмотрим вспомогательную квадратичную форму
22t/ + a33zl + 2а12ху + 2a,i3yz 4- 2aslzx —
A3)
При ортогональном преобразовании A2) она перейдет в форму
я|з' = а^х1'4-а\гу'1 -\-a33z'1'4-2а',%х'у'4-2a23y'z' 4-2a3lz'x' —
— 'k(x'ijry''i-\-z'2). A4)
По доказанному дискриминант квадратичной формы является
ортогональным инвариантом, значит,
L ^ «12 «13
й„, й.
И " «12 «13
«21 «22 ^ «23
«3 1 «3 2 «3 3 "
Это равенство верно при всех значениях X, следовательно,
равны соответствующие коэффициенты при А,2 и А, в левой и
правой частях, т. е.
«11 «12
«21 «2-2
«п
«13
«31 «33
«22
«32
Теорема 2. Функции
^3 =
«И «12 «1
«21 «22 «2
йа й2 а
2
«И
«1
«2
«зз
4-
аг
а
а;, а.
«13
«31 «33
!
г
«11 «13 «1
а31 «зз «з
йх а3 а
i
«22 «2
а
2 «
4"
«22 «23 «2
«32 «33 «3
а2 а3 а
«33 «3
!
h
а
1
«22 «23
«4 2 «3 3
A5)
A6)
являются инвариантами однородного ортогонального преобразования.
Эти функции K,s и К2 называются «семиинвариантами»
(полуинвариантами).
Если же функция
F = а1ххг + «22г/2 + «ззг2 + 2а12л:у + 2a23yz + 2a31zx +
4- 2агх 4- 2й2г/ 4- 2й8г + «
однородным ортогональным преобразованием может быть приведена
к виду
F = а'пх'2 + «;2у'2 4- 2а12х'у' + 2а[х' + 2а'2у' + а, A7)
то К3 является ортогональным инвариантом, а если F однородным
ортогональным преобразованием может быть приведена к виду
F'^=anx'1 +2а'хх' ^а, A8)
то К, (и Кз) является ортогональным инвариантом.
$ 163. ТЕОРИЯ ИНВАРИАНТОВ
417
Доказательство. Рассмотрим вспомогательную функцию
ф = а1гх2 + ai2y2 + as3z2 + 2а^ху + 2a23yz + 2aZxzx +
-f 2axx -г 2а2у + 2asz -f a — К (x2 + y2+z2).
Производя однородное ортогональное преобразование A2),
получим функцию
ф' = а11х' + а22у' + азяг' -\-2а12х'у' + 2а23у'г' +2a3lz'x' +
-\-2a\x' + 2а'2у'-\-2а3г' -\-а' — Х(х'г -{-у''+ г'*), где а' = а.
По доказанному /\4 — ортогональный инвариант. Используя это
по отношению к функции Ф, получим
«11-
«21
«31
аг
«22 —
«32
«2
«13
л а23
«33
а8
— Я,
а,
а2
«3
а
аи—К а12 а13 а2
«21 «2i ^ «23 «2
' ' ' 1 '
«3i «32 «зз—Л а3
ах а2 аъ а'
(тождество относительно ?.). Приравнивая коэффициенты при А. и
в левой и правой частях, получим
«22 «23 «2
а, а, а
«11
«31
«13
«33
«8
Я
а
о
1
3
«11
«21
«1
«12
а22
а2
ах
а2
а'
+
flu
«31
«1
«13
«38
а3
«8
а'
+
«22 «23 «2
«32 «за «з
Я2 «з «'
а, а
«33 «8
аи а,
Й1 а'
«2 2 «2
я а'
Предположим теперь, что существует однородное ортогональное
преобразование u)lt при котором функция F переходит , ^
A7). Для функции A7) семиинвариант Д'8 имеет значение
«И Й12 Й!
«21 «22 Я2
«i aa а'
09)
П. С. Моденов
418 Глава XII. ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
равное его значению, вычисленному по формуле A5). Определитель
ап й]2 й!
а21 а22 аг
аг а2 а'
не меняется, если над переменными х' и у'функции A7) совершить
преобразование переноса со2: х' = х" -\-cv у' — ц"-\-с2 (это следует
из теоремы 2 § 142, формула B3), где сп = с22 = 1, с12 = с21 = 0).
Пусть о) — произвольное ортогональное преобразование.
Рассмотрим ортогональное преобразование со'= cocoj; тогда © = ©'©!.
Далее, представим ортогональное преобразование со' в виде произ-
гедения однородного ортогонального преобразования со3 на перенос
сог; тогда
После однородного ортогонального преобразования coj функция F
перейдет в функцию A7) и по доказанному Ks не изменится и будет
равен его значению, вычисленному по формуле A9).
При преобразовании переноса м2 функция F' перейдет в функцию
и ко доказанному
x"y" + 2агх" + 2ау" + а"
А, = Аз — Аз =
Cl\ j Q-j 2 ^ 1
а\ а а"
наконец, после однородного ортогонального преобразования со8
функция F" перейдет в функцию
г = ацХ -+-аг2у -j-a33z
2х у -г...
= /С3 = а'3 = /(8
«23
и, следовательно,
Й]Л «12 fl
а21 «22 а
ai а» а'
Аналогично доказывается, что Кг является ортогональным
инвариантом если функция F однородным ортогональным
преобразованием может быть приведена к виду
+
а
а
а
и
з']
1
а
а
а
13
33
3
>' 1
а,
а'з"
о!"
по а
аъ
in
<} 154 ОПРЕДЕЛЕНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ
419
§ 154. Определение канонического уравнения поверхности
второго порядка при помощи инварианта
В таблице 1 указаны необходимые и достаточные признаки того,
что поверхность второго порядка является поверхностью 1, II,
III, IV или V групп:
Таблица !
Номер
группы
1
11
III
IV
V
0
/*=о л
/', = 0 К
I = 0 К
/3 = 0 К
Признак группы
• фО
4 = 0 12ф0
__q /2 = o КзфО
Доказательство. Если поверхность второго порядка задана
общим уравнением относительно декартовой прямоугольной системы
координат, то, как было показано и § 152, оно при преобразовании
данной декартовой прямоугольной системы координат Oxyz в другую
декартову прямоугольную систему Ох'у'г' может быть
преобразовано к виду
К^'* + К2у'г + X3z'* + 2alx' + 2а'гу' -f 2a8z + а == 0,
где Klt А,2, К3—корни характер!1стнческого уравнения.
Если все они отличны от нуля, то уравнение поверхности
переносом осей может быть приведено к простейшему уравнению
поверхностей первой группы. Если один из корней
характеристического уравнения, например К3, равен нулю, но а'3ф0, то —
к простейшему уравнению поверхностей второй группы.
Если один из корней равен 0, например Я3 = 0 и а3—0, то
к простейшему уравнению поверхностей третьей группы и т. д.
1. Пусть поверхность Еггорого порядка является поверхностью
1 группы. Тогда, как было показано в § 152, уравнение этой
поверхности при помощи преобразования прямоугольной системы
координат в прямоугольную систему можно привести к виду
где ^=7^=0,
2. Пусть поверхность второго порядка является поверхностью
I i группы. Тогда (§ 152) ее уравнение при помощи преобразования
14*
. В гаком случае
0
0
0
К
0
0
0
К
420 Глава til ПОВЕРХНОС1М ЗЛДАНЕ1ЫЕ ОБЩИМ iPABHFHHLM
прямоугольной системы координат в прямоугольную может быть
приведено к виду
где A,j п К2— отличные от нуля корни характеристического
уравнения (А,3 —0) и аяф0. Находим
/я =
К
0
0
0
К
0
0
0
0
= 0,
= — ^20;,
3, Пусть поверхность второго порядка является поверхностью
III группы. Тогда (§ 152) ее уравнение при помощи преобразования
прямоугольной системы координат в прямоугольную систему может
быть приведено к виду
К
0
0
0
0
К
о
0
0
0
0
а.
0
0
а„
0
где %! и К2 — отличные от нуля корни характеристического
уравнения. Отсюда находим
= 0,
К
0
0
0
К
о
0
0
0
^000
о к2 о о
0 0 0 0
0 0 0 D
= 0,
/2=
0
0
к
0
0
0
К
0
0
0
4. Пусть поверхность второго порядка является поверхностью
IV группы. Тогда ее уравнение при помощи преобразования
прямоугольной системы координат в прямоугольную систему координат
может быть приведено к виду
г—отличный от нуля корень характеристического уравнения
154. ОПРЕДЕЛЕНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ
■121
= А,3 = 0), причем а2=^=0. Отсюда находим
Х1 0
0 0
0 a't
/,=
0
0
0
0
0
0
0
0
= 0,
X, О
О О
Х1 0
а
о о
0 0
о о
о о
О 0 а2
00 0
' 0 0
0
0
0
0
а2
= 0,
0 0
о о
0 а',
0 0
0 0
= 0,
5. Пусть, наконец, поверхность второго порядка является
поверхностью V группы. Тогда ее уравнение при помощи
преобразования прямоугольной системы координат в прямоуГОЛЬНуЮ
систему координат может быть приведено к виду
где Хг—отличный от нуля корень характеристического уравнения
(Х2 = К3 = О). Отсюда
= 0,
К
0
0
0
0
0
0
0
0
к
0
0
к
а
:!0
0
0
0
'* =
1 °
0
о
0
D
1
■1
0
0
0
"*"
-\-
)
с
с
0
0
0
0
^1
0
)
)
0
0
0 0
0 0
0 D
0
0
0 0
0 0
0D
+
= 0,
0
0
0
- 0
Q
0
0
0
0
о
г
0
0
D
= 0,
Необходимость признаков доказана. Так как эти признаку попарно
несовместимы, то они и достаточны.
Теорема 2 i. Если поверхность второго порядка, заданная обм,ил',
относительно прямоугольной системы KOopdit,Hajn itii.
422 I л а -о XII ПОВЕРХНОСТИ, ЗАДАННЫЕ О1МПИМ VPABH V. Н НЕМ
ляется поверхностью I группы, то ее простейшее уравнение имеет
вид
где Klt К2, Х3 —корни характеристического уравнения
— к а
12
32
3
а33 — К
= 0,
II. Если поверхность второго порядка является поверхностью
II группы, то ее простейшее уравнение имеет вид
/2±21/ — ^Z = 0,
где %! и Х2 — отличные от нуля корни характеристического
уравнения.
III. Если поверхность второго порядка является поверхностью
III группы, то ее простейшее уравнение имеет вид
где Х,г и К2 —отличные от нуля корни характеристического
уравнения.
IV. Если поверхность второго порядка является поверхностью
IV группы, то ее простейшее уравнение имеет вид
V. Наконец, если поверхность второго порядка является
поверхностью V группы, то ее простейшее уравнение имеет вид *
Доказательство. 1. Если поверхность второго порядка
является поверхностью I группы, то ее каноническое уравнение
имеет вид
где
= 0,
* В случаях JV и V инвариант 1г равен отличному от нуля корню
характеристического уравнения
164 ОПРЬДЬЛЕНИГ. КАПОНИЧ1.СК.О1О УРАВНЕНИЯ
42J
Находим
яг о о о
о %г о о
о о х3 о
О О О D
к*
следовательно, D = у
II. Если поверхность второго порядка является поверхностью
II группы, то ее каноническое уравнение имеет вид
где ht н А.2 — отличные от пуля корЕШ характеристического
уравнения и а3ф0. Отсюда находим
\К1 О
О Зса
4 " о о
О
(У
0 0
о
о
О а,
а, О
следовательно, ад = ± 1/ — -р .
Аналогично доказываются остальные утверждения теоремы.
Теорема 3. В таблице 2 даны необходимые и достаточные
признаки каждого из семнадцати классов поверхностей второго порядка.
Доказательство необходимости. В этом параграфе
было доказано, что если относительно декартовой прямоугольной
системы координат Охуг поверхность второго порядка задана общим
уравнением, то преобразованием данной системы координат Охуг в
декартову прямоугольную О'XYZ данное уравнение можно
преобразовать к одному из следующих простейших уравнений:
если
A)
^Z = 0, если /3 = 0
'2
(И)
если /3 = 0 /С4 = 0 /2^=0 (Ш)
если /3 = 0 /С4 = 0 /2 = 0/C3^0(IV)
если /3 =
= 0/C =
. (V)
Во всех этих уравнениях А,,- — отличные от нуля корни
характеристического уравнения, а инварианты /,- и /(,- вычисляются но
формулам, указанным в § 153.
424 Г „о,а КН. ПОВЕРХНОСТИ, ЗАДАННЫГ ОБЩИМ УРАВНЕНИЕМ
Таблица 2
1
2
3
4
5
6
7
8
9
10
1!
12
и
14
15
16
17
Название поверхности
Эллипсоид
Мнимый эллипсоид
Мнимый конус
Однополостный
гиперболоид
Двуполостпый
гиперболоид
Конус второго' порядка
Эллиптический парабо
лоид
Гиперболический
параболоид
Эллиптический цилиндр
Мнимый эллиптический
цилиндр
Две мнимые пересекаю
щиеся плоскости
Гиперболически!: ци
Две пересекающиеся
плоскости
[ 1араболический цилиндр
Две параллельные
плоскости
Две мнимые
параллельные плоскости
Две совпадающие
плоскости
/s
Is
I3
l3
[л
/j
l3
h
/«
/3
Is
h
I*
и
Ф o>
Ф o,
Ф0,
= 0,
= 0,
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
K4
K4
Ki
к,
K4
к.
Ki
Ki
K*
K4
кй
Kt
* 2 *"
[ -^
^ -^
<o
= 0
<o
>o
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
= 0
.0
>D
>0
и
и
и
/2
/2
/2
/2
/2
/a
/2
/2
Признак
hh
/l/.
ИЛИ
или
или
>o
>o
>o
<o
<o
= 0
= 0
= 0
= 0
>
>
>
i
/x
к
к
к
к
к
0 К
0 К
0 К
Г2<(
8<(
Кз <
К3 >
3 = 0
зФО
з = 0
^о
= 0
= 0
4 <0
4>0
4 = 0
) или
или
или
0
0
К2<
к2 >
/]/3<;о
/х/3<0
/i/8<0
0
0
)
1°. Если уравнение (I) является уравнением эллипсоида, то
числа klt ^a и Яа одного знака, а число -р имеет знак, им
противоположный. Но так как /з = ^1^з> то К*<®> и далее,
U = ^2^3 + ^1 + ^1^2 > (). IJz = (^1 + ^2 + Ю ККК > 0.
'2 Если уравнение (I) является уравнением мнимого
эллипсоида, то все числа klt Я2, Х3, -р одного знака: так как /3 = Х1Я2Х3,
то /<4>0. Соотношения /2 > 0 и /1/8 > 0 доказываются так же,
как и в 1°.
3° Если уравнение (I) является уравнением мнимого конуса,
то А.,, К2, Х3 одного знака, а т1 = 0, откуда /D = 0; неравенства
3
1?.>Q> /i/b>0 получаются так же, как и в 1 .
§ 154. ОПРЕДЕЛЕНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ 125
4°. Если уравнение (I) является уравнением однополостного
гиперболоида, то из чисел klt Я2, Ks, -—■ два положительны, а два
К
отрицательны; если, например, Кх > О, Я2 > О, Х3<0, -~ < О,
то /3 < 0, /<4 > 0 и если, например, /2 = ^1Я24-Я2Х3-|-^3Я, > О,
то /i/3 = (^i + Я2 -г ^з) ^Дг^з имеет знак, противоположный знаку
b-i + K + K- Докажем, что Kl-\-K.2 + ks^l) (тогда IJS^^)-
В самом деле, если бы мы имели Х1 -f- Я2 -)- Я8 < 0, то —Ха >Xj + *-2,
вопреки предположению. Тот же результат (/3=^0, /D > 0, пли
/2<0, или /j/g^O) получим, предположив, что ^ < О, А,2 < О,
Я3!>0, -т1 > 0. Выкладки рекомендуется произвести читателю
самостоятельно.
5°. Если уравнение d) является уравнением двуполостного
гиперболоида, то два из корней hlt k2, Я8 имеют одинаковый ^нак
с -р, а третий корень—знак, им противоположный. Пусть, на-
пример, к1 > 0, Я2 > 0, у* > 0, Я3 < 0. Тогда К4 < 0, /, < 0, а го,
что или 12^.О, или IJg^.0, доказывается так же, как в
случае 4°.
6°. Если уравнение (I) является уравнением конуса второго
порядка, то -р —0> откуда Kt~0; 13=£O, и далее, два из корней
'я
Х^ Я2, Я3 имеют одинаковый знак, а третий—знак, им
противоположный. Отсюда, как и в случае 4°, доказывается, что или
/2<0, или V^O.
Перейдем к исследованию поверхностей второго порядка
[1 группы.
7°. Если уравнение (II) является уравнением эллиптического
параболоида, то 'к1 и К2 в уравнении (II) —числа одного знака,
а, значит, /2 = X.jA,2>0 и из уравнения (II) следует, что Kt < 0
число —р- под радикалом в уравнении (II) положительно).
>г )
8°. Если же уравнение (II) является
уравнением_гиперболического параболоида, то числа Я, и Я2 разных знаков, значит,
/2 = ^2 < 0, и из условия — y > 0 находим К4 > 0.
Рассмотрение остальных случаев по существу уже было сделано
в теореме 3 § 143.
Достаточность всех признаков доказывается методом от
противного (эти признаки взаимно исключают друг друга).
Результаты предыдущих исследований помещены в табл, .3,
Таблица 3
Каноническое
уравнение
Признак
класса
Оторолзст
ный
гиперболоид
Цвуполост-
ный
гиперболоид
Конус
второго
порядка
Эллиптиче
спий пара-
Питый эл-,
пиптичеюй
цчриндр
дрекнимья
пересекащ
плоскости
Гиперболи-
цит. Эр
Параболический
\ цилиндр
<t 154 ОПРЕДЕЛЕНИЕ КАНОНИЧЕСКОГО УРАВНЕНИЯ 427
Класс поверхности второго порядка I группы можно
определить и не решая характеристического уравнения,
воспользовавшись следующей теоремой Декарта: если все корни уравнения
с действительными коэффициентами являются вещественными
числами, то число положительных корней этого уравнения равно
числу перемен знаков в последовательности
коэффициентов этого уравнения.
Так как корни характеристического уравнения
Xя — /,Я,2 -|- /8Л. — /я =. О
всегда действительны, то этим правилом можно пользоваться для
определения знаков коэффициентов простейшего уравнения
поверхностей I группы.
Если поверхность принадлежит ко II и III группам, то один
из корней характеристического уравнения равен нулю, а два
других—корни квадратного уравнения. В случае, если поверхность
принадлежит к IV или V группе, ее простейшее уравнение
находится без решения характеристического уравнения. Поэтому
теорему Декарта естественно применять лишь по отношению к
поверхностям I группы. В соответствии с этой теоремой число
положительных корней характеристического уравнения равно числу
перемен знаков в последовательности
Замечание Если в n-мерном евклидовом пространстве * задана
поверхность второго порядка** >равнением
п п п
2 2 aikxixk + 2 2а'*Н-а = 0,
то ортогональным преобразованием это уравнение можно привести к одному
* л-мерным евклидовым пространством будем называть совокупность всех
конечных упорядоченных последовательностей чисел (хь х2 хп), каждую
такую упорядоченную последовательность будем называть «точкой», а числа
Х(— ее координации См В. А. Ильин и Э. Г Поз н як. Основы
математического анализа М., „Наука", 1965, гл. XIV, ■■$ 1, п 4
** То есть множество точек, координаты которых удовлетворяют этому
уравнению.
г лава XII I IOi' t- Г X HOC I И ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
из следующих 2л 4 1 простейших уравнений:
>.,Х* + Ь2Х^ . 4 >.„Х* + ^'±1=и, если
(П)
И 1 Д.
если /„=(>, К„
■tXl+ ... + K_lX*_l-\~/^~ = O, если /„ = П, К„ + , = 0, /„_, ,4 0 (III)
' П — i
М^+^ — О, если /„ = 0, К„+г = 0, /„_i = 0 /2 = 0, /С3 = 0,
-''j#0, Brt—1),
где ^,, в каждом случае — отличные от нуля корни характеристического
уравнения
— X Оц, ... а1п
1
«„„ —
= 0,
/,;—определитель матрицы {о,^1, /n_i — сумма диагональных миноров п—I
пепядка определителя /„ 1п-г — сумма диагональных миноров п — 2 порядка
определичечя 1п и т. д , наконец, /, = Оц + «22+ ■ • • +алл Далее,
а2,
oni
«1
а12
а28
ап1
а2
• • «in
.. О2„
... а„
h
°\
ап
а
а К„, К„_,, К„_2> ... получаются из выражений для /„_i, /я_2, /л_з. ...
окайм..опием определителей, входящих в выражения для /fr соответствующими
коэффициентами линейной формы
и свободным членом а уравнения по-
верхностн *.
§ 155. Центр поверхности второго порядка
Определение. Центром поверхности второго порядка называется
центр симметрии этой поверхности.
Теорема 1. Пусть относительно общей декартовой системы
координат задана поверхность второго порядка общим уравнением
Ф =
.is3z2
2a.slzx +
A)
* См Г. E, Шилов. Введение is теорию линейных пространств №., Гос-
телнздат, 1956, рл. II, § 77, стр. 218--233
<j 1о5 ЦЕНТР i OBEPXHOcIH ВТОРОЮ ПОРЯДЮ 429
Для того чтобы начало координат было центром этой
поверхности, необходимо и достаточно, чтобы в ее уравнении
отсутствовали члены с х, у и z в первой степени, т е чтобы
a1 = ai = as — О,
иначе, чтобы уравнение A) имело вид
а1гх2 + a22if + a33z* + 2а12ху + 2ai4yz + 2aslzx + а = 0. B)
Доказательство необходимости. Предположим, что
начало координат является центром поверхности A). Возьмем на
поверхности A) произвольную точку М(х, у, г). Ее координаты
будут удовлетворять уравнению A), а так как начало координат
является центром симметрии поверхности A), то уравнению A)
будут удовлетворять и координаты точки М' (—х, —у, —г),
симметричной точке М относительно начала координат, т. е.
аих2 + а22у2 + азгг2 -f 2а12ху + 2a2syz + 2a31zx—
— 2агх — 2а2у — 2а3г + а = 0. C)
Из этого соотношения и из соотношения A) находим
агх -f- a2y + asz = 0.
Этому уравнению удовлетворяют координаты всех точек
поверхности A) Предположим, что хотя бы одно из чисел а1( а2, аъ не
равно нулю Тогда все точки поверхности лежат в плоскости
a1x-}-a2y-{-asz = 0.
Это может быть тогда и только тогда, когда уравнение A)
определяет две плоскости, совпадающие с плоскостью
ахх -г а2у -f- aAz = 0.
На основании теоремы § 140, п. 3, левая часть уравнения A)
разлагается в произведение двух линейных относительно х, у, г
множителей, одним из которых является форма аух + а2у-J-аьг\
Ф == {ахх + а2у + a,z) (Ax + By + Cz +D).
Плоскость, заданная уравнением
на основании сделанного выше замечания должна совпадать с
плоскостью a1xJra2y-\-a3z = 0, значит,
А:В\С = a1:a2:as, D—Q
и потому
Мы приходим к противоречию с тем, что в уравнении A) хотя
бы один из коэффициентов при х, у или z в первой степени
отличен от нуля.
430 Глава XII ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Теорема 2. Есги относшлельно общей декартовой системы
координат поверхность второго порядка задана общим уравнением
аг1х2 + ai2if -f od3z2 + 2alixy -f- 2a2syz + 2а31гх +
+ 2а,л; + 2а2у + 2а3г + а = 0, D)
то координаты х0, у0, ^0 ее центра определяются из системы
апх + й12у + а1з? + ^ = 0,
о21ж -f а22у + а23г + а2 = 0, E)
а.пх + апу + а!8г + а, = 0,
причем в случае несовместности этой системы поверхность не имеет
центра.
Доказательство Произведем параллельный перенос дан
ной декартовой системы координат, при котором новым началом
координат будет точка О (х0 у0 г0) Обозначая старые координаты
проилзольной точки /11 через х, у, г, а новые ее координаты —
через х', у', г', будем иметь
х = х + х0, у = у -\-у0, z = z'
и уравнение A) примет вид
аих" + a22y'' + адз?'" + 2а12х у' +2ai4y'z' + 231г'х' +
+ 2(Qnx0 + a12(/t +alizt) + a1)x +2(a.21x0 + a2iy0 + а23г0 + а2)«/'
Уо +" аззго + a-i) г' + ф (-^о- Уо< го) = 0,
где Ф(х0, у0, г0) — результат подстановки координат х0, у0, г0
точки О' в левую часть уравнения A),
На основании теоремы 1 точка О' (х0, у0, г0) будет центром
поверхности A) тогда и только тогда, когда
а21х0 + a22yQ + о23г0 4- a2 — О,
а81х0 + а32у0 -4- аз320+ а3 = 0.
§ 156. Классификация поверхностей второго порядка
по характеру места центров
Пусть поверхность isTopoio порядка задана общим уравнением
ахгх2-\-а2гф^г Я) 24-2а12ху 4- 2агъуг \-2аъХгх-\-
етносителыю общей декартовой системы координат.
Рассмотрим матрицы
/ап av, a13>y
и Л* = |
156 КЛАССИФИКАЦИЯ ПО ХАРАКТЕРУ MEl.TA ЦЕНТРОВ
131
В таблице даны необходимые и достаточные признаки
характера места центров поверхности, заданной уравнением A)
Таблица
Ранг Л
3
2
2
1
1
Ранг А*
3
3
2
2
1
Характер месга цешров
ючка
нет цетра
прямая
нет цетра
ПЛОСКО'" I Ь
В самом деле, если каждое из уравнений E) § 155 является
уравнением первой степени, т, е. в каждом из уравнений E) хотя
бы один из коэффициентов при х, у или г не равен пулю, то
табл. 1 сразу следует из § 83 о взаимном расположении трех
плоскостей.
Впрочем, эта таблица следует и из общей теории систем
линейных уравнений*.
Теорема. Классификация поверхностей второго порядка по
группам (I)-(V) (теорема 2, § 152) совпадает с классификацией
поверхностей второго порядка по характеру их места центров, иначе
по рангам матриц:
.= а.
= а
Предполагается, что поверхность второго порядка задана общим
уравнением относительно общей декартовой системы координат.
Доказательство. Обозначим через В матрицу
квадратичной формы, входящей в левую часть каждого из простейших
уравнений (I)—(V) поверхности второго порядка (теорема*2, § 152)!
Тогда В = С'АС, где Г—матрица из коэффициентов при X,
Y, Z в преобразовании
с21Х + c22Y -f-c.MZ + с2
= с31Х
33
3,
* См Г. Е Шило в. Введение в leopnio .чиненных пространств М., I ос-
техиэдат, 1956, гл 3, § 22, стр 60.
432 Глава XII ПОВЕРХНОСТИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
выражающем координаты х, у, г точки в данной системе Охуг
через координаты X, Y, Z той же точки в системе O'XYZ (уже
прямоугольной), в которой уравнение поверхности имеет простейший
вид (I)-(V).
Так как
невырожденная матрица, то ранги матриц А и В равны между
собой.
Для поверхностей 1 группы RgB=--3, значит, и RgA = 3. Для
поверхностей II и III групп RgB = 2, значит, и 1^Л = 2. Для
поверхностей IV и V групп RgS=l, значит, и Rg Л = 1.
Далее, если Rg А = 3 (т. е. поверхность принадлежит к I группе),
то и Rg,4* = 3.
Если поверхность принадлежит к Ш или V группам, то,
составляя систему уравнений E) § 155, определяющую координаты
центра поверхности для простейших уравнений (HI) h(V), убедимся,
что эта система совместна (причем для поверхностей III группы
местом центров является ось O'Z, а для поверхностей V группы —
плоскость O'ZY). Значит, для поверхностей III и V групп система
E) также совместна, а потому на основании теоремы Кронекера —
Капелли* RgЛ = RgЛ*. Поэтому для поверхностей III группы
Rg/4 = Rg/4* = 2, а для поверхностей V группы RgA = Rg^* = l.
Наконец, для поверхностей II и IV групп система E),
составленная для их простейших уравнений, несовместна, т. е. эти
поверхности не имеют центра. Значит, несовместна и сама система E),
следовательно, Rgv4*>Rg^4. Но для поверхности II группы
RgЛ = 2, значит, Rg,4*=3. Для поверхности IV группы Rg Л = 1,
значит, Rg Л* = 2.
Поверхность второго порядка, имеющая единственный центр,
называется центральной. Центральными поверхностями являются
эллипсоиды —действительные и мнимые, гиперболоиды —однополо-
стные и двуполостные и конусы — действительные и мнимые. Для
того чтобы поверхность, заданная общим уравнением относительно
общей декартовой системы координат, была центральной,
необходимо и достаточно, чтобы определитель квадратичной формы,
входящей в левую часть уравнения этой поверхности, был отличен
от нуля!
«11 «12 fl13
= 0.
* См Г. Е. Шилов. В(зедеи!1е в теорию линейных пространств. М., Гос
техиздат, 1956, гл 3, § 22, стр 60.
§ 157 КОНИЧЕСКИЕ И ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ ;j,j
§ 157. Конические и цилиндрические поверхности второго
порядка, заданные общим уравнением
1. Конические поверхности
Определение конических и цилиндрических поверхностей было
дано в § 25. Мы перенесем эти определения и на поверхности
второго порядка. Если поверхность второго порядка является
конической, то ее вершина— центр этой поверхности, причем лежит
он на самой поверхности.
Теорема 1. Для того чтобы поверхность второго порядка,
заданная относительно общей декартовой системы координат общим
уравнением
аххх2 + а22у2 + assz2 + 2a12xy + 2a23yz + 2aslzx +
= 0, A)
являлась уравнением конической поверхности с вершиной в начале
координат, необходимо и достаточно, чтобы в этом уравнении
отсутствовали как члены с первыми степенями координат, так и
свободный член.
Доказательство необходимости. Пусть уравнение A)
является уравнением конической поверхности с вершиной в начале
координат. Так как вершина конической поверхности лежит на
этой поверхности, т. с. начало координат лежит на данной
поверхности, то из уравнения A) следует, что а — О. Далее,
уравнения E) § 155, определяющие координаты центра поверхности,
должны удовлетворяться при x = y = z~Q. Отсюда a1 = a2 = as = 0,
и уравнение A) принимает вид
а1гх2 + а22у2 + aS3z2 + 2а12ху + 2a23yz + 2аЯ1гх = 0. B)
Доказательство достаточности очевидно, так как
уравнение B) однородное относительно х, у, z. Уравнение B)
после приведения к простейшему виду таково;
аих +а22у 4-а33г =0,
значит, среди поверхностей второго порядка коническими
поверхностями являются следующие:
Г2 f/2 Z2
'~2 -гр + ^г = 0 (мнимый конус второго порядка)
X2 V2 22
~2+р"—^г = 0 (действительный конус второго порядка)
х— -)-1^ = 0 (две мнимые пересекающиеся плоскости)
„2 (,2
1—р*" (две Действительные пересекающиеся плоскости)
х2 = 0 (две совпадающие плоскости)
434 Глава XII, ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Остальные поверхности второго порядка не конические, так
как они либо не имеют центра, а если имеют его, то он не лежит
на рассматриваемой поверхности.
Теорема 2. Для того чтобы поверхность второго порядка,
заданная относительно общей декартовой системы координат общим
уравнением A), была конической, необходимо и достаточно, чтобы
ранги матриц
(аи Й12 fll,\ Г11 °п
А п п п '• и R I Q21 «22 «28 «2
Л = a2l a22 o23 i и В = \
равны между собой.
Доказательство необходимости. Пусть поверхность
второго порядка, заданная уравнением A) относительно общей
декартовой системы координат Охуг, является уравнением
конической поверхности. Пусть О'(сх, с2, с.,) — вершина этой поверхности.
Произведем перенос системы Охуг так, чтобы новым началом
координат стала вершина О' данной конической поверхности. Тогда
уравнение A) примет вид
О у' _!_ /у */'** -!— п у1 —1— с?п v'tj/ —1— ()п а'у' -I— Уп у' у — О
а матрица В преобразуется в следующую:
«11
«21
«31
0
а
а
а
0
12
22
3 2
а
а
а
0
1»
23
33
0
0
0
0
Но при преобразовании переноса
C)
ранг матрицы В не меняется; это следует из формулы E) § 153
и того обстоятельства, что матрица
фигурирующая в равенстве E) § 153, здесь, т. е. при переносе C),
принимает вид
1 0 0
0 t 0 „а
0 0 1 с,
0 0 0 1
Cl \
Со. \
§ 157. КОНИЧЕСКИЕ И ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ 435
а следовательно является невырожденной. Но ранги матриц А и
В' равны между собой, следовательно, равны и ранги матриц Л и В.
Доказательство достаточности. Предположим, что
ранги матриц А и В равны между собой. Тогда равны и ранги
матриц
аи aVi ala \ / аи а12 аи аг
«11
«21
«31
0
«12
«•22
«32
0
«13
«23
«33
0
F(x
0
0
0
0>
А = \ а.п а23 а28 | и Л*=| а2, а2г а23 а2
\ «31 аз2 азз / V «si й3, а33 а3
значит, поверхность имеет центр (или даже прямую центров,
или плоскость центров). Произведем перенос осей Oxyz так, чтобы
новым началом координат в новой системе координат О'х'у'г' стал
центр поверхности. Тогда коэффициенты при х', у', г' в
преобразованном уравнении обратятся в нуль и оно примет вид
аих" 4- а22у'2 4- ааяг'' -\- 2anx'y' + 2a.i3y'z' -г2ая1г'х' 4- F(x0, у0, г0) = О,
где F (х0, у0, г0) есть результат подстановки координат х0, у0, г0
центра О' поверхности в левую часть уравнения A) этой
поверхности Как мы уже указывали, ранг матрицы В при переносе не
изменится. Но В преобразуется при этом в матрицу:
В' =
Ранги матриц В' и В равны, значит, равны ранги матриц А
и В'. Но если F {х0, у0, го)фО, то ранг матрицы В' больше ранга
матрицы А. поэтому F(х0, у0, zo) = O. Значит, центр О'(х0, у0, г0)
поверхности второго порядка лежит на самой этой поверхности.
Но этим свойством обладают только конические поверхности
второго порядка.
2. Цилиндрические поверхности
В § 25 было доказано, что поверхность является
цилиндрической тогда и только тогда, когда существует система координат,
в которой уравнение поверхности имеет вид
F(x, y) = 0.
При этом образующие поверхности параллельны оси Ог, а ее
направляющей является, например, линия, определяемая
уравнениями
F[x, t/) = 0, г = 0
(см. теоремы 1 и 2 § 26).
Глава XII. ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИ»! УРЛВНГНИЕМ
Теорема 3. Для того чтоои поверхность второго порядка,
заданная общим уравнением
ху -(■- 2a.Z3yz + 2aslzx +
Q D)
относительно общей декартовой системы координат, была
цилиндрической, необходимо и достаточно, чтобы выполнялись равенства
flll
°21
fl..
fl12
fl22
floo
a
a
a
ЗЗ
-О, Я4 =
•'32
-*23
Я33
*з
= 0.
Доказательство необходимости. Если уравнение D)
является уравнением цилиндрической поверхности, то
преобразованием системы координат Oxyz в систему Ох'у'г' уравнение D)
может быть преобразовано к виду
atlx'2-\- a2iy'2 + 2а12х'у' + 2а1х' + 2а'2у' -f a = 0. E)
Но так как при преобразовании системы координат координаты
х, у, г точки М в системе Oxyz через координаты х', у', г' той
же точки М в системе Ох'у'г' выражаются соотношениями вида
13
+ c.Z3z
то, обозначая через А определитель
С11 С12 С13
с с с
Cpi С$9 Сг
будем иметь
L32
(см. соотношения D') и E') § 153). Вычисляя Is и К.\ по
уравнению E), получим
' г! г! п
п п П 1 2 и '
flll Й12 W , ,
a2i a22 0 i
/.=
a2i
0
«22
0
0
0
0
=о, /<;=
о о
о
о
0
a
= 0,
значит, и /3 = 0, и /<4 = 0.
Доказательство достаточности. Пусть /3 = 0 и /D = 0.
Преобразуя данное уравнение D) к простейшему виду, в силу
Соотношений /3=0, /D=0 заключаем, что и для простейшего
157. КОНИЧЕСКИЕ И ЦИЛИНДРИЧЕСКИЕ ПОВЕРХНОСТИ 4 V
уравнения поверхности будем иметь /3 = 0, /С4 = 0. Значит,
поверхность, заданная уравнением D), принадлежит к III, IV и V
группам, а все эти поверхности цилиндрические*.
Таким образом, цилиндрическими поверхностями второго
порядка являются все поверхности групп III, IV и V и только эти
поверхности:
^гт-гг—' (действительный эллиптический цилиндр)
- + -|г =— 1 (мнимый эллиптический цилиндр)
- + -—=0 (две мнимые пересекающиеся плоскости)
1^ = 1 (гиперболический цилиндр)
тг"~0 (Две Действительные пересекающиеся плоскости)
а*
х?_
а2
х2 = 2ру (параболический цилиндр)
х2 = а2 (две параллельные плоскости)
хг= —а2 (две мнимые параллельные плоскости)
Л'2 = О (две совпадающие плоскости).
3. Распадение поверхности второго порядка
Теорема 4. Для того чтобы поверхность второго порядка,
заданная уравнением
аг гхг -f а22у2 + a33z2 -f 2а12ху + 2a23yz + 2a31zx +
-f 2агх + 2a2y + 2asz + a = 0,
распадалась на две плоскости, необходимо и достаточно, чтобы
ранг матрицы
г31 a3i aS3 а3
2, а, а, а
меньше или равен 2.
Доказательство. Канонические уравнения поверхностей
второго порядка, распадающиеся на две плоскости, имеют вид:
х , У п _±_ У_ Л у2 пЧ Г) У2 п2 Л Г2 Г)
-^--Г Ьг ~и> ai b2 —и' " и- А « —и, * —и.
Составляя матрицу М для каждого из этих уравнений, убедимся
в том, что для четырех первых уравнений RgM = 2, а для
последнего RgM = l. Для канонических уравнений всех остальных
* Соотношения /3 •= Kt •=■ 0 инвариантны относительно преобразования
системы координат.
438 Глава XII ПОВ FP \НОС 111 ЗАДАННЫ!: ОБЩИМ УРАВНЕНИЕМ
поверхностей RgM>2. При переходе к любой общей системе
координат ранг матрицы М не изменяется, так как она
умножается слева и справа на невырожденную матрицу. Следовательно,
условие RgM^2 является необходимым и достаточным условием
распадения поверхности второго порядка па две плоскости в л
гобой общей декартовой системе координат (а не только в
канонической).
§ 158. Пересечение поверхности второго порядка с прямой.
Асимптотические направления, асимптотический конус
и конус асимптотических направлений
Предположим, что относительно общей декартовой системы
координат поверхность второго порядка задана общим уравнением
аих2 + аггу- -f a3sz2 + 2а12ху + 2агзуг -f 2a31zx +
+ 2о1х- + 2а2у +2а3г + а = 0. A)
Будем исследовать пересечение этой поверхности с прямой,
уравнения которой возьмем в параметрической форме:
x = xo + lt, y = yo + mt, z = zo-\-nt. B)
Здесь (х0, у0, г0) — некоторая точка прямой, а {/, т, п} — ее
направляющий вектор.
Подставляя в левую часть уравнения A) вместо х, у и z их
выражения из формул B), получим следующее уравнение
относительно t:
AP + 2Bt + C = 0, C)
где
Л=гап/2-| a22m2-\-assn2jr2a12lm-\- 2а2ятп-\-2aslnl, D)
В = / (аих0 + aJ2y0 + а1зг0 + ах) +
+ т{а21хо + а22уо + а23го + а2)+ E)
+ п («зЛ + «ззУо + «зз^о + аз).
C = F(x0, y0, г0) F)
(F (х0, у0, г0) — результат подстановки в левую часть уравнения
A) вместо х, у, z координат точки М0(х0, у0, г0)).
Координаты точек пересечения прямой B) с поверхностью A)
получим при тех значениях /, которые являются корнями
уравнения C).
Если и уравнении C) коэффициент при /2 отличен от нуля,
то уравнение C) имеет два корня, значит, прямая B) пересекает
поверхность A) в двух точках.
Если же
аг1Р + аг2т2 -\- а33п2 + 2a12/m -f 2a23mn + 2a.nnl = 0, G)
то прямая с направляющим вектором {/, т, п\ либо пересекает
поверхность A) только в одной точке, либо не пересекает ее,
§ 158 ПЕРЕСГ.ЧиШП- ПОВЕРХНОСТИ С ПРЯМОЙ 439
либо входит в состав поверхности A). В этом случае говорим,
что направляющий вектор {/, т, п) имеет асимптотическое
направление относительно поверхности A). Итак, координаты векторов,
имеющих асимптотическое направление, определяются из
соотношения G).
Уравнение
*- й33г2-;-2а1гл;у + 2а2ауг~!-2a31zA' = 0 (8)
как однородное уравнение относительно х, у, z определяет
коническую поверхность (действительную или мнимую), образованную
прямыми, проходящими через начало координат. Координаты х,
у, z точки М, лежащей на образующей конуса, являются
координатами вектора ОМ. Таким образом, образующие конуса (8) —
прямые, имеющие асимптотические направления поверхности A)
и обратно: любое асимптотическое направление является
направлением одной из образующих конуса (8). Конус, определяемый
уравнением (8), а также любой конус, полученный переносом этого
конуса, называется конусом асимптотических направлений
поверхности A) (вершина конуса, заданного уравнением (8), находится
в начале координат).
Асимптотическим конусом поверхностей второго порядка,
имеющих центр, называется конус асимптотических направлений,
вершина которого лежит в центре поверхности.
X2 if1
Таким образом, асимптотический конус эллипсоида —+ Та"~г
~^--=1; мнимого эллипсоида —г + — + 2= — 1; мнимого конуса
С Cl DC
V2 Н2 Z2
~г + "ьз~ "г — 0 имеет уравнение
т. е. является мнимым.
Асимптотический конус однополостного и двуполостного
гиперболоида
а2 "Т" V- с2 ~~ ±
имеет уравнение
а асимптотический конус конуса второго порядка совпадает с ним
самим. :
Далее, так как гиперболический параболоид
',' - ~ •-- 2г (р > 0, q > 0)
440 Глава XII ПОВЕРХНОСТИ, ЗАДЛННЫЕ ОБЩИМ УРАВНЕНИЕМ
не имеет центра, то у него согласно данному выше определению
нет асимптотического конуса. Один из конусов асимптотических
направлений выражается уравнением
1 JL-^o,
Р Я
и он распадается на две пересекающиеся плоскости
« + ^=-о и * -JL-
V Р Vq Vp V Q
Все конусы асимптотических направлений получаются всеми
переносами этой пары плоскостей.
Эллиптический параболоид
|L + iL = 2z (р>0, q>0)
также не имеет асимптотического конуса, а все его конусы
асимптотических направлений получаются всеми переносами двух
мнимых пересекающихся плоскостей
Р Ч Vp Vq Vp Vq
У эллиптического цилиндра (действительного или мнимого) и у
пары мнимых пересекающихся плоскостей
асимптотический конус состоит из двух мнимых пересекающихся
плоскостей
* L1 У П
У гиперболического цилиндра и пары пересекающихся
плоскостей
± У__ 1 ±_ У_ О
а2 2>а ~ ' а2 ~" fc2 ~
асимптотический конус распадается на две действительные
пересекающиеся плоскости
а ' b a b
У параболического цилиндра у2 = 2рх конусом асимптотических
направлений является плоскость у = 0 — плоскость симметрии этой
поверхности, проходящая через ось направляющей: у = 2рх, 2 = 0,
и любая из плоскостей, ей параллельная. Наконец, у пары
параллельных или пары совпадающих плоскостей асимптотический конус
совпадает с плоскостью центров поверхности,
_^ S 159. ДИАМЕТРАЛЬНАЯ ПЛОСКОСТЬ 441
Конус асимптотических направлений (для поверхностей,
имеющих центр) получается из асимптотического конуса любым
переносом.
Пусть поверхность, заданная общим уравнением
аых2 + а2гуг + a3sz2 -f- 2al2xy + 2a23yz + 2a31zx +
+ 2агх + 2a2y + 2a3z -f a = 0 (9)
относительно общей декартовой системы координат, имеет
единственный центр. Замечая, что /3 и /С4 —инварианты переноса общей
декартовой системы координат, заключаем, что уравнение данной
поверхности после параллельного переноса осей координат, при
котором новым началом координат будет центр поверхности,
примет вид
2yri + а33г>г + 2alzx'y' + 2a2Sy'z' + 2a31z'x' + ^ = 0.
22
Значит, уравнение
аих2 + а22у2 + а33г2 + 2а12ху + 2а23уг + 2a31zx +
+ 2а^х + 2а2у + 2а3г -f а = ~-
•3
является уравнением асимптотического конуса центральной
поверхности, заданной общим уравнением (9) относительно общей
декартовой системы координат.
§ 159. Диаметральная плоскость, сопряженная данному
неасимптотическому направлению. Особые направления
относительно поверхности второго порядка
Теорема 1. Геометрическим местом середин параллельных хорд
поверхности второго порядка является плоскость. Эта плоскость
называется диаметральной плоскостью данной поверхности,
сопряженной хордам данного направления. Если поверхность второго
порядка задана относительно общей декартовой системы координат
общим уравнением
2а12ху + 2a23yz + 2a3lzx +
A)
а ее хорды коллинеарны вектору {/, т, п) (не имеющему
асимптотического направления), то уравнение диаметральной плоскости,
сопряженной этим хордам, имеет вид
т (а21х -f ai2y + a28z + а2) -Н
0. B)
Доказательство этой теоремы такое ж«, как и теоремы 1 § 146.
442 Глава XII ИОВЕ'РХИОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Из уравнения B) следует, что все диаметральные плоскости
поверхностей второго порядка содержат геометрическое место ее
центров, ^сли оно не пусто, так как уравнение B)
удовлетворяется, если
0
а21х + а22у + a23z + a3 = О,
flsi^ + азгу + assz + a3 = 0.
Вектор а~{1,т,п} некомпланарен диаметральной плоскости,
сопряженной его направлению, так как главный вектор плоскости
B) имеет координаты
a* = {ou/ + fl1,m-a13tt, a21l +a22rn-\-a2sn, a31l + a32m-\-a3sn},
откуда
/ (au/ + аЛ2т + alsn) -f т (о21/ -|- аггт + a23n) -i- « (аях1 -f- аггт -j- a3sn) =
= оп/2 +-a^jri1 + a33«2 -f 1avilm -f 2a23mn - 2aslnl
Теорема 2. £су?« существует в. ктор Ь неасимптотического
направления, компланарный диаметральной плоскости, сопряженной
хордам поверхности второго порядка, коллинеарным вектору а, то
вектор а будет компланарен диаметральной плоскости,
сопряженной хордам этой поверхности, коллинеарным вектору Ь.
Доказательство. Пусть вектор Ь = {/^ т1, nY) компланарен
плоскости B) и не имеет асимптотического направления
поверхности A). Тогда
/i (an/ + а1гт -j- a13n) +- тг (a21/ + аг2т -\- ai3n) -f
+ пх (a31l + а32;: + а33п) = 0,
или
I(a-nl\ + fli2mi + ai3«i) -I-m (fl2i/i + a22m, -|-a23«!) +
+ n (asllx + a3im1 -f aggWi) = 0,
а это и означает, что вектор {/, т, п} компланарен
диаметральной плоскости, сопряженным хордам, коллинеарным вектору
{1и тъ nj.
Из доказанной теоремы следует, что если диаметральные
плоскости Sj и 62, сопряженные направлениям двух неколлинеарных
векторов ах и а, (не имеющих асимптотического направления)
пересекаются, и прямая их пересечения не имеет асимптотического
направления относительно поверхности второго порядка, то
диаметральная плоскость, сопряженная направлению хорд
поверхности, параллельных этой прямой, компланарна векторам ах и а2.
Мы получаем и этом случае три диаметральные плоскости,
обладающие тем свойством, что любая из них сопряжена с
направлением прямой, по которой пересекаются две другие.
Замечание. При определении центра поверхности второго
порядка, асимптотических направлений, диаметральной плоскости
<t 159 ДИ Л1Ы РЛ-ЧЫ1 \'Л П.'ЮСКОСГЬ 443
п при доказательстве ряда теорем, связанных с этими
определениями, предполагалось использование «мнимых» точек.
Как указывалось по отношению к линиям второго порядка,
можно включить и рассматриваемую поверхность второго порядка,
заданную общим уравнением Ф = 0 относительно общей декартовой
системы координат, в семейство поверхностей Ф = const. Для
эллипсоида и мнимого конуса такое семейство будет включать в
себя все эллипсоиды, гомотетичные друг другу, причем центром
гомотетии будет их общий центр. Для гиперболоидов и конуса
второго порядка семейство Ф = const будет состоять из всех
соаснмптотических гиперболоидов, т. е. гомотетичных между собой
однополостных и двуполостных гиперболоидов и их общего
асимптотического конуса. Для параболоидов семейство Ф = const будет
состоять из поверхностей, полученных параллельным переносом
данной поверхности вдоль ее оси симметрии. Для остальных
поверхностей семейства Ф — const будут характеризоваться их
сечениями плоскостью, не параллельной образующим (т. е. дело
сведется к аналогичному замечанию, сделанному выше для линий
второго порядка).
Все определения и доказательства теорем для семейств Ф = const
могут быть проведены с использованием только точек трехмерного
евклидова пространства и потому все они инвариантны
относительно преобразования системы координат, так как аналитические
выводы, относящиеся к центру, асимптотическим направлениям,
диаметральным плоскостям, не зависят от свободного члена общего
уравнения поверхности.
Определение. Особым направлением относительно поверхности
второго порядка называется направление прямой, параллельной всем
диаметральным плоскостям этой поверхности.
Теорема 3. Пусть относительно общей декартовой системы
координат задана поверхность второго порядка общим уравнением
ацХг + a2iy2 -f o3322 -f 2аыху + 2anyz + 2a31zx +
+ 2a1x + 2a2y + 2a3z~{-a = 0. C)
Тогда если это уравнение является уравнением центральной
поверхности (т. е. поверхности, имеющей единственный центр), то
у нее нет особых направлений. Все остальные поверхности имеют
особые направления. Для того чтобы ненулевой вектор {/„, т0, п0}
имел особое направление относительно поверхности C). необходимо
и достаточно, чтобы его координаты удовлетворяли соотношениям
01А + «12^0 + Q13«0 = 0.
«0 = 0, D)
444 Г ,aia XII nOBEPXHOCTVI ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Доказательство. Из уравнения B) следует, что вектор
{/0, т0, п0) имеет особое направление тогда и только тогда, когда
выполняется равенство
10 (аи1 + а1гт + а13п) + т0 (о21/ + а22т + а23п) -}-
-f n0 (a31l + а32т + а33п) = О,
или
(аи/0 + а12т0 + я13п0) !■ + (а2Л + «22то + «2з«о) m +
/ ^ / _|- q /72 -4— G П, t ft ==: U (^)
где {/, т, п) — любой вектор, не имеющий асимптотического
направления. Так как всегда можно выбрать три неколлинеарных
вектора {/,, тп л,}, имеющих относительно поверхности C)
неасимптотическое направление, то однородное относительно I, т, п
уравнение E) имеет три линейно независимых решения {/,, тп п,),
а это возможно тогда и только тогда, когда все коэффициенты при
I, m и п в уравнении E) обращаются в нуль; таким образом,
соотношения D) выполняются. Если поверхность имеет единственный
центр, то
«21 «22 «23
«31 «32 «33
и, значит, система D) не имеет ненулевых решений /0, т0, пп,
особых направлений нет.
Для всех остальных поверхностей /3 = 0 и система D) имеет
ненулевые решения.
Если ранг матрицы
/«11 «12 «13\
А= «21 «22 «23
\«31 «32 «33/
равен 2 (поверхности II и III групп), то система D) имеет
ненулевые решения /0, т0, п0, но не имеет двух линейно независимых
решений. Это значит, что поверхности II и III групп имеют лишь
одно особое направление. Составляя систему D) для простейших
уравнений этих поверхностей, убедимся, что особое направление —
это направление оси O'Z в простейших уравнениях этих
поверхностей.
Если Rg /1 = 1, то система D) имеет два линейно независимых
решения {/„, >п0, п0} и {/„, т0, «„}. Все решения системы D)
являются всеми линейными комбинациями этих двух. Это значит,
что для поверхностей IV и V групп существует плоскость, такая,
что любая прямая, параллельная этой плоскости, имеет особое
направление и этими направлениями исчерпываются все особые
направления этих поверхностей (это плоскость "O'Z в простейших
уравнениях (IV) и (V)).
160. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ 445
§ 160. Касательная плоскость
Точка Мо (х0, у0, г0), лежащая на поверхности второго
порядка, заданной относительно общей декартовой системы
координат уравнением
апх2 + а22у2 + о33г2 + 2а]2ху -\- 2а23уг + 2a3lzx +
+ 2a1x + 2a2y-{-2asz + a=-0, A)
называется неособой, если среди трех чисел:
г0 + а„ а21х0 + а22у0 + a23z0 + Ч,
есть хотя бы одно, не равное нулю*.
Таким образом, точка М0(х0, у0, г0), лежащая на поверхности
второго порядка, является особой тогда и только тогда, когда
является ее центром (см. § 155), иначе, когда поверхность
коническая, а точка 7И0—вершина этой поверхности (§ 157, п. 1).
Определение. Касательной прямой к поверхности второго
порядка в данной на ней неособой точке называется прямая,
проходящая через эту точку, пересекающая поверхность второго порядка
в двукратной точке или являющаяся прямолинейной образующей
поверхности.
Теорема. Касательные прямые к поверхности второго порядка
в данной на ней неособой точке (х0, у0, г0) лежат в одной
плоскости, называемой касательной плоскостью к поверхности в
рассматриваемой точке. Уравнение касательной плоскости имеет вид
F'x(x0, уо, zo)(x—xo)~F],(x0, y0, го)(у—уо) +
+ К(х0, j/o, z0)(z-zo) = 0. B)
Доказательство. Пусть
y = yo-\-mt, z =
параметрические уравнения прямой, проходящей через неособую
точку М0(х0, у0, zQ) поверхности второго порядка, заданной
уравнением A). Подставляя в уравнение A)
вместо х, у и z, получим
+ aS3n2 + 2aX9lm + 2а^тп + 2а?Лп1) Р
x0, у0, г0) I + Fy (х0, и0, zo)m + Fz(x0, y0,
x0, у0, го) = 0. D)
* Эти числа являются значениями в точке М0(х0, у0, г0) половин частых
производных по х, у и г от левой части уравнения A); в дальнейшем будем
обозначать их соответственно Fx (х0, у0, г0), Fу (х0, г/0> го)> ?г (Ч> У<* го)> а в
соответствии с этим левую часть уравнения A) будем обозначен через 2F.
446 Глава XII П0В1 РХМОСТИ, ЗАДАННЫЕ ОБЩИМ СРАВНЕНИЕМ
Так как точка М(,(хп, у0, г„) лежит на поверхности A), то
2F(x0, у0, го) = (), и из уравнения D) находим /==0 (это
значение t соответствует точке Мо). Для того чтобы точка пересечения
прямой C) с поверхностью A) была двойной, или чтобы прямая C)
целиком лежала па поверхности, необходимо и достаточно, чтобы
выполнялось равенство
Р'*{4, «/о. ?o)l + F'v(xo> !/о. Ч)т-\-РЛч, Уо. го)п = О; E)
если при этом а^Р+ а22т2-}-азяп2 + 2avjm + 2a23mn ~-2a31nl фО,
то точка пересечения прямой C) с поверхностью A) двойная, а если
alt/2 -f a22m2-f-a33n2-f 2а12//тг + 2a.23mn -j-2a31nl = 0, то прямая C)
целиком лежит на поверхности A).
Из соотношения E) и соотношений C) следует, что координаты
х, у, г любой точки М (х, у, г), лежащей на любой касательной
к поверхности A), удовлетворяют уравнению
Fx(x0, у0, zo)(x—xo) + F,(xo, yus го)(г/ — уо) +
+ Рг(х0, у0. го)(г —го) = О. F)
Обратно, если координаты какой-нибудь точки М(х, у, г)
отличной от Мо, удовлетворяют этому уравнению, то координаты
1 = х — х0, т = у—у0, n = z — z0 вектора М0М удовлетворяют
соотношению E), а значит, прямая М0М — касательная к
рассматриваемой поверхности.
Так как точка М0(х0, г/0, г0) — неособая точка поверхности A),
то среди чисел
Гг(хо' Уо> го)> ч \хо> Уо> го)> 'чг(-";о> Уо> го)
есть по крайней мере одно, не равное нулю; значит, F)
—уравнение первой степени относительно х, у, z — это уравнение плоскости,
касательной к поверхности A) в данной на ней неособой точке
Мо(*о. г/о, го)-
Замечание. Левая часть уравнения A) получается из
квадратичной формы от четырех аргументов!
2F = аихг + a22tf- -f- а33г2 + 2а12ху + 2а23уг -f 2aHzx +
+ 2a1xt + 2a2yt + 2a3zi + at2,
если считать, что /=1. Эту квадратичную форму можно записать
в виде
2F
или
2
+ (а31
IF^xF,
+ а12у +
х + а32у-]
Лх, У, г,
0,з? +
- а33г -
t) + l,
art)x-\
\-ач()г-
'^(*, «
/. • ')
|-а.ггу + й
го2у + а£
+ г/% (х,
!23г + й
,г + а/)
г/> г>
20у
0 +
, у, г, t), G)
t) 161 ППР^СГЧЬНИЕ КЛСА П:ЛЬ!1О;-! ПЛОСКОСТИ С ПОВЕРХНОСТЬЮ 4-17
г i i e
где Fx, F,,, Fz, Ft — половины частных производных по х, у, г и t
от функции 2F.
Так как точка М0(х0, у0, г0) лежит па поверхности A), то
2F (х0, {/„, го) = О, и из тождества G) находим
x0Fx(x0, Уо> гс '^о)-!-'/o^v (-^о. Fo. г0, to) + z0F2(x0, у0, г0, ?„) +
-г^'(^о> Ус го> /о) = 0
(fo=l). Отсюда следует, что уравнение F) касательной
плоскости к поверхности A) в данной на ней неособой точке можно
записать в виде
xF'x(x0, i/o, г0> to)-\-tjFh.(xo, г/0> г0, /0) -r ?K (х0, у0, г0, 10) +
■i-(F,(x0, у0, г0, to) = Q, (8)
где t = to=l.
Исходя из канонических уравнений поверхностей второго
порядка и уравнения (8) легко составить уравнения касательных
плоскостей к эллипсоиду, гиперболоидам, параболоидам и т. д.
в данной на них точке (х0> у0, г0): касательная плоскость к
эллипсоиду
а" т б2 ~|" с2
к однополостному и двуполостному гиперболоиду
к конусу в точке (х0, у0, г0), не являющейся его вершиной,
v j УоУ £о£_ _ q
а2 ' б2 с2 '
к эллиптическому и гиперболическому параболоиду
~±Jf=z + z0 и т. д.
§ 161. Пересечение касательной плоскости с поверхностью
■ второго порядка
Примем нсособую точку О поверхности второго порядка за
начало координат общей декартовой системы коврдинат, оси Ох
и Оу расположим в плоскости, касательной к поверхности в точке О.
Тогда в общем уравнении поверхности
ах vxl + а22у2 -,'- а33г* + 2а1гху -\- 2а23уг + 2a3lzx +
+ 2fl1.v-|-2o2j/ + 2ag2 + a = 0 A)
свободный член равен нулю: а = 0, а уравнение плоскости, каса-
448 Глава Xll ПОВЫ'ХНОСТИ ЛАДАННЫ, ObllUlM VPABliFHllEM
ющепся поьерхности в начале координат, должно иметь вид
Согласно уравнению F) § 160 уравнение плоскости,
касательной к поверхности A) в начале координат, имеет вид
и так как это уравнение должно быть эквивалентно уравнению
г —0. то а1 — а2 — 0, а3ф0.
Итак, в выбранной системе координат уравнение поверхности
A) шеет вид
аг1х2 -г а22у2 + assz2 + 2al2xy -j- 2а23уг + 2anzx -|- 2asz = 0. B)
Обратно, если o^^O, то это уравнение является уравнением
поверхности, проходящей через начало координат О, а плоскость
г = 0 —касательная к этой поверхности в точке О. Уравнения
линии, по которой касательная плоскость к поверхности в точке О
пересекает поверхность B), имеют вид
Если
"и Я12
21 Я22
то это две мнимые пересекающиеся прямые; если б < 0, то две
действительные прямые; если 6 = 0, но хотя бы один из
коэффициентов ап, о12, а22 не равен нулю, то линия пересечения — две
совпадающие прямые. Наконец, если оп = а12 = а22 = 0, то плоскость
г = 0 входит в состав данной поверхности, а сама поверхность
распадается, следовательно, на пару плоскостей.
§ J62. Эллиптические, гиперболические или параболические точки
поверхности второго порядка
В настоящем параграфе рассмотрим только действительные
и нераспадающиеся поверхности второго порядка.
Пусть О — неособая точка такой поверхности. Так как
поверхность мы предполагаем нераспадающейся, то касательная плоскость
к поверхности в точке О не может входить в состав самой
поверхности Могут представиться три случая.
1° Касательная плоскость к поверхности в точке О пересекает
ее по двум мнимым пересекающимся прямым. В этом случае точка О
называется эллиптической точкой поверхности.
2°. Касательная плоскость к поверхности в точке О пересекает
ее по двум действительным прямым, пересекающимся в точке
касания В этом случае точку О будем называть гиперболической.
162 ТИПЫ ТОЧЕК ПОВЕРХНОСТИ
419
3°. касательная плоскость к поверхности в точке О пересекает
ее по двум совпадающим прямым. В этом случае точку О будем
называть параболической.
Теорема. Пусть поверхность второго порядка задана общим
уравнением
а22у2
+ 2а12ху + 2а23уг + 2а31гх
A)
относительно общей декартовой системы координат Охуг и пусть
данное уравнение A) является уравнением действительной нераспп'
дающейся поверхности второго порядка. Тогда если
И
а.
.21
а,3 а2
t a2 a3 a
то все точки поверхности—эллиптические, если /С4 > 0, то все
точки поверхности—гиперболические, и если Kt = 0, то-
параболические.
Доказательство. Введем новую систему координатMx'y'z',
выбирая за начало координат любую неособую точку М данной
поверхности и располагая оси Мх' и My' в плоскости,
касательной к поверхности в точке М. Уравнение A) при переходе к
системе координат Mx'y'z' преобразуется в уравнение вида (см. § 161)
ацх'* + a22i/ + a3Sz'2 + 2а1гх'у' + 9a23i/z' + 2a3lz'x' + 2a,z = 0, B)
где a3=f^0. Вычислим определитель К* для этого уравнения:
a
2l
а31 аз
О 0
0
0
03
0
2
«11 012
Й2 1 02 2
013
023
033
03
Так как при переходе от одной общей декартовой системы
оди-
координат к другой знак /D не меняется, то знаки /D и
наковы, а, значит, знаки
КЛ и
ЙЦ
>0
противоположны. Поэтому если К4 < 0, то
«21 022
и, как следует из § 161, касательная плоскость к поверхности в
15 П. С. Моденов
Г л а о а XII. ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
точке М пересекает поверхность по двум мнимым пересекающимся
прямым, т. е. М — эллиптическая точка.
Если /D > 0, то Л < 0, касательная плоскость к поверхности
в точке М пересекает ее по двум прямым, пересекающимся в
точке М; точка М— гиперболическая.
Если, наконец, /D = 0, то и 6 = 0; касательная плоскость к
поверхности в точке М пересекает ее по паре совпадающих прямых;
точка М — параболическая.
Ограничиваясь, как уже было указано, действительными
нераспадающимися поверхностями вторего порядка и вычисляя /С4,
например, по каноническим уравнениям этих поверхностей,
убедимся в том, что;
1) эллипсоид, двуполостный гипербелоид и эллиптический
параболоид состоят из эллиптических точек;
2) двуполостный гиперболеид и гиперболический параболоид
состоят из гиперболических точек;
3) действительный конус второго порядка (вершина
исключается), эллиптический (действительный), гиперболический и
параболический цилиндры состоят из параболических точек.
§ 163= Простейшие уравнения поверхностей второго порядка
в общей декартовой системе координат
В настоящем параграфе мы рассмотрим некоторые общие ;.е-
крртовы системы координат, в которых уравнение поверхности
второго порядка имеет простейший вид.
1°. Эллипсоид. Примем за начало координат центр О
эллипсоида, за ось Ох — произвольную ось, проходящую через его
центр 0, за ось Оу—произвольную ось, проходящую через точку О
и лежащую в диаметральной плоскости, сопряженной
направлению оси Ох, и. наконец, за ось Oz—ось, являющуюся
пересечением диаметральной плоскости, сопряженной направлению оси Ох,
с диаметральной плоскостью, сопряженной направлению оси Оу.
Оси Ох и О у лежат в диаметральной плоскости, сопряженной
направлению оси Oz (теорема 2 § 159).
В выбранной системе координат в уравнении эллипсоида будут
отсутствовать члены с первыми степенями координат х, у, г (так
как центр поверхности является началом координат), а также
члены с произведениями ху, уг и гх. В самом деле, уравнение
диаметральной плоскости, сопряженной направлению оси Oz, т.е.
вектору {0, 0, 1}, имеет вид
(уравнение B) § 159), а с другой стороны, это уравнение должно
иметь вид
2=0 (плоскость хОу).
163. ПрОСГЕПШИП УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
Отсюда
«si = «32 = 0. aSs Ф °-
Аналогично доказывается, что fl12 = 0 (и что яп=^0, а22^=0).
Итак, уравнение эллипсоида в выбранной системе координат
Выберем теперь в качестве единичной точки оси Ох любую из
двух точек пересечения этой оси с эллипсоидом. Аналогично
произведем выбор единичных точек на осях Оу и Oz. Тогда
координаты точек A,0,0), @, 1,0) и @,0, 1) должны удовлетворять
уравнению A):
и уравнение A) принимает вид
—ах2—ау2—az2 -{-а — О,
или (а Ф 0)
Обратно, в любой общей декартовой системе координат
уравнение х2 + г/2-fz2 = 1 является уравнением эллипсоида, причем
начало координат—это центр поверхности, а каждая
координатная плоскость сопряжена к направлению координатной оси., не
лежащей в этой плоскости.
В самом деле, поверхность, заданная уравнением х2-\- у2-\-г2 —
— 1=0, действительная, имеет единственный центр (он совпадает
с началом координат) и /С4 < 0.
Но единственная поверхность, обладающая этими свойствами, —
эллипсоид.
2°. Однополостиый гиперболоид. Примем за начало
координат центр О поверхности, за ось Ог—произвольную ось,
проходящую через центр О, не имеющую асимптотического
направления и не пересекающую поверхность (из всех прямых,
проходящих через центр поверхности, таким свойством обладают
только прямые, проходящие внутри асимптотического конуса одно-
полостного гиперболоида).
Если принять за плоскость хОу диаметральную плоскость,
сопряженную оси Oz, то уравнение однополостного гиперболоида
в такой системе будет иметь вид
аххх2 + 2а12ху + а22у2 + a3Sz2 -f a = 0,
причем а33 и а—числа одного знака, так как Oz не пересекает
поверхность. Далее,
«11
о"
0
«12
Я, 2
0
0
0
0
«33
0
0
0
0
а
— п п
UUo--
Од
«И
«21
«12
«22
15*
452 Глава XII ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
и так как для однополостного гиперболоида К4 > 0, а аа33 > 0, то
6 =
Отсюда следует, что любой ненулевой вектор {/, т, 0},
компланарный плоскости хОу, не имеет асимптотического
направления, так как уравнение
аЛ 11г 4- 2а, Лт -4- а99т2 — 0
в силу того, что б > 0, имеет только нулевое решение.
Отсюда следует, что если ось Оу выбрать в диаметральной
плоскости, сопряженной оси Oz, за ось Ох—прямую, по которой
пересекаются диаметральные плоскости, сопряженные
направлениям осей Oz и Оу (а они пересекаются, так как первая из них
проходит через ось Оу, по в ней не лежит ось Oz, а вторая
проходит через ось Oz и в ней не лежит ось Оу), то, как и в случае
эллипсоида, получим систему координат, в которой начало
координат является центром поверхности, а каждая из плоскостей
yOz, zOx и хОу—диаметральной плоскостью, сопряженной
соответственно направлению оси Ох, Оу и Oz.
В такой системе координат уравнение однополостного
гиперболоида имеет вид
Здесь аяз и а — числа одного знака, а так как
то числа оп и о22 также одного знака, причем знак чисел ап и
а22 противоположен знаку чисел а33 и а, г противном случае B)
являлось бы уравнением мнимой поверхности. Отсюда сразу
следует, что ось Ох пересекает поверхность в двух точках £, и Е1 ,
а ось Оу также пересекает поверхность B) в двух точках Е2 и Е2 .
Прямая, по которой пересекаются плоскости
х =
касательные к поверхности B) в точках Ех и Е2, пересекает
поверхность B) в двух точках Е и Е', так как, подставляя эти
значения х и у в уравнение B), получим уравнение а38гг — а,
имеющее два действительных и различных корня. Выбирая любую
из точек Е или Е' за единичную точку системы координат,
заключаем, что точка Ех пересечения оси Ох с поверхностью имеет
координаты 1, 0, 0, т. е. является единичной точкой этой оси, а
точка Е2 пересечения оси Оу с поверхностью имеет координаты
0f 1,0, т.е. является единичной точкой оси Оу.
? 163 ПРОСТЕЙШИЙ УРМЗНЕНИЯ ПОВЕРХНОСТЕЙ 453
Таким образом, из уравнения B) имеем
Отсюда
аи = — а, ам = — а, a.J3 = a
и уравнение B) принимает вид
— ах2 — ay2 + az2 + a = 0,
или
x2-f у2—г2 = 1. (II)
Обратно, уравнение (II) в любой системе координат является
уравнением однополостного гиперболоида, центр которого
совпадает с началом координат, ось Oz не пересекает поверхность, оси
Ох и Оу пересекают ее (а плоскость хОу пересекает поверхность
по эллипсу х2-\-у2 = 1, 2 = 0) и, наконец, каждая из плоскостей
yOz, гОх и хОу является диаметральной плоскостью, сопряженной
соответственно направлениям осей Ох, Оу, Oz.
В самом деле, уравнение х2-^-у2— z2—1=0 является
уравнением действительной невырождающейся поверхности второго
порядка, имеющей единственный центр, для которой Кц > 0. Всеми
этими свойствами обладает только однополостный гиперболоид.
3°. Двуполостиый гиперболоид. Выберем за начало
координат центр поверхности, за ось Oz—любую прямую,
проходящую через центр поверхности и пересекающую ее (т. е.
идущую внутри асимптотического конуса), а за плоскость хОу —
диаметральную плоскость, сопряженную оси Oz. Так же, как в
случае однополостпого гиперболоида, доказывается, что в
плоскости хОу нет ни одного асимптотического направления,
следователь/го, всегда можно выбрать оси Ох и Оу, так что каждая
координатная плоскость является диаметральной плоскостью,
сопряженной направлению той оси, которая не лежит в этой
плоскости. Уравнение двуполостного гиперболоида в этой системе
координат будет иметь вид
+ а33гг + а = 0. C)
Однако теперь числа а33 и а разных знаков, а числа ап и а22
одинаковых знаков. Знак чисел а1г и а22 противоположен знаку
числа ais, так как если бы числа а1Х, ам и а33 имели одинаковый
знак, а а — знак, им противоположный, то уравнение C) было бы
уравнением эллипсоида. Таким образом, числа ап, а23 а одного
знака, а число ass имеет знак, им противоположный. Не нарушая
общности, можно считать, что
ап>0, аг2>0, а>0, аза<0.
Примем за единичную точку двуполостного гиперболоида C)
точку, в которой пересекаются следующие три плоскости:
454 Главе XII. ПОВЕРХНОСТИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
1) ПЛОСКОСТЬ
касательная к поверхности C) в одной из точек пересечения оси
Ог с этой поверхностью;
2) плоскость
касательная к асимптотическому конусу поверхности C) вдоль
образующей этого конуса, лежащей в плоскости yOz;
3) плоскость
Kaux—К—а332 = 0,
касательная к асимптотическому конусу поверхности C) вдоль
образующей этого конуса, лежащей в плоскости хОг. Тогда
откуда
и уравнение C) примет вид
или
** + {/* —z! = -l. (Ill)
Обратно, это уравнение является уравнением двуполостного
гиперболоида, центром поверхности является начало координат,
координатные плоскости yOz, гОх и хОу—диаметральные плоскости,
сопряженные соответственно направлениям осей Ох, Оу и Ог.
Ось Ог пересекает поверхность в двух точках, а плоскость хОу
поверхность (III) не пересекает. Единичная точка указана выше.
В самом деле, уравнение (III) является уравнением
действительной поверхности второго порядка, имеющей единственный
центр, причем существует плоскость, проходящая через этот центр
и не пересекающая поверхность. Этими свойствами из всех
поверхностей второго порядка обладает только двуполостный
гиперболоид.
Можно рассуждать иначе: поверхность (III) имеет
действительный асимптотический конус хг-\-уг — z2 = 0 и для нее /D<0.
Этими двумя свойствами обладает только двуполостный
гиперболоид.
4°. Эллиптический параболоид. Выберем любую
точку О поверхности за начало координат, за ось Ог—любую
ось, проходящую через точку О и имеющую особое направление
относительно поверхности, а за плоскость хОу плоскость,
касательную к поверхности в точке О.
1S3. ПРОвТЕЙШИЕ УРАВНЕНИЯ ПОВЕ1- X НОвТЕЙ
455
Заметим, что ни одна из касательных плоскостей к
эллиптическому параболоиду не содержит особого направления этой
поверхности. В самом деле, касательная плоскость к эллиптическому
параболоиду в любой его точке имеет с эллиптическим
параболоидом только одну общую точку О—точку касания. Любая
прямая, проходящая через точку О и лежащая в плоскости,
касающейся эллиптического параболоида в точке О, пересекает
поверхность эллиптического параболоида в двукратной точке О,
а прямая особого направления, проходящая через точку О,
пересекает эллиптический параболоид в одной (не кратной) точке О.
Отсюда следует, что выбранная нами ось Ог не лежит в
плоскости хОу, касающейся эллиптического параболоида в точке О
Так как уравнение касательной плоскости к поверхности,
заданной общим уравнением в ее неособой точке, в случае если
эта точка является началом координат, имеет вид
ахх-{- а2у -fa,,2 = 0,
и эта плоскость принята нами за плоскость хОу, то a1 — ai = 0,
а3ф0 Кроме того, а —0, так как начало координат лежит на
поверхности. Далее, так как вектор {О, G, 1} имеет особое
направление, то система
о21/
a3sn=Q
должна удовлетьоряться при / = 0 //г = 0, п=\ откуда
Уравнение поверхности в выбранной системе координат имеет
вид
|де
аихг + 2avzxy -f a22if -f 2a3z = 0,
Так как пЛЯ эллиптического нарлболодца А4<0 и Одт^О, го
°11 «12
«21 «22
Отсюда следует, что в касательной плоскости хОу к
поверхности эллиптического параболоида нет ненулевых векторов {/, "^Ог,
имеющих асимптотическое направление. Выберем за ось Оу
произвольную ось лежащую в касательной плоскости к поверхности.
Диаметральная плоскость сопряженная направлению оси Оу,
имеет уравнение
а
а
0
0
и
■г л
2
«22
0
0
0
0
0
«<,
0
0
«3
0
— -—о2
«11 A2
«21 °22
456 Г лага ХП, ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
значит, проходит через ось Oz. Примем за ось Ох прямую, по
которой пересекаются касательная плоскость к поверхности в
точке С с диаметральной плоскостью, сопряжешюй оси Оу.
(Плоскость ijOz будет тогда диаметральной плоскостью, сопряженной
направлению оси Ох.)
Так как плоскость хОг является диаметральной плоскостью,
сопряженной оси Оу то уравнение
a2lx -f й22г/ = 0
должно приводиться к уравнению </ = 0, т. е. а12 = 0, а22Ф0. Итак,
в выбранной системе координат уравнение эллиптического
параболоида имеет вид
oulx2 + a22^ + 2a3z = 0, D)
Из условия /<4 < 0 н того, что а3ф0, находим oua22 > 0, так
что ои и о22 — числа одного знака. Не нарушая общности, можно
считать, что знак а3 противоположен знаку au и а23 (в
противном случае достаточно изменить направление оси Ог на
противоположное).
Рассмотрим сечение эллиптического параболоида плоскостью
2= 1:
anx2 + a22*/2 + 2a3 = 0, 2=1.
Это уравнения эллипса. Пусть Р — одна из точек пересечения
зтого эллипса с его диаметром у —0, 2=1, а Q — одна из точек
пересечения с другим диаметром х = 0, 2=1. Принимая
параллельные проекции точек Р и Q на оси Ох и Оу по направлению
оси Ог за единичные точки осей Ох и Оу, получим
Теперь уравнение D) принимает вид
х* + у*—г = 0. (IV)
Обратно, уравнение (IV) является уравнением эллиптического
параболоида, так как поверхность (IV) не имеет центра и для
уравнения (IV) /<4 < 0. Плоскость хОу—касательная к
поверхности (IV) в начале координат. Ось Oz имеет особое направление.
Плоскости xOz и yOz — две диаметральные плоскости,
сопряженные соответственно направлениям осей Оу и Ох.
5°. Гиперболический параболоид. Как и в случае
эллиптического параболоида примем за начало координат любую
точку О поверхности, за ось Oz — ось, проходящую через эту
точку и имеющую особое направление относительно поверхности, а
за плоскость хОу— плоскость, касательную к гиперболическому
параболоиду в точке О.
1G3. ПРОСТЕЙШИЕ УРАВНЕНИЯ ПОВЕРХНОСТЕЙ 457
Как и в случае эллиптического параболоида, докажем, что
ось Oz не лежит в плоскости хОу (здесь любая прямая,
проходящая через точку О и лежащая в касательной плоскости к
гиперболическому параболоиду в точке О, либо пересекает его р
двукратной точке, либо лежит па поверхности; прямая же, проходящая
через точку О и имеющая особое направление, пересекает
поверхность в одной простой точке О).
Уравнение гиперболического параболоида в выбранной системе
координат имеет вид
ап*г + 2о12л;(/-\-а22у2-[-2а3г = 0, где а3ф0; (А)
однако здесь
п.А
6 =
ачл а
<0
и в плоскости хОу имеются асимптотические направления
относительно рассматриваемой поверхности. Отметим, что эти
асимптотические направления являются направлениями действительных
прямых
а1гх2-\-2а12ху ]-а2гу2, г = 0, (В)
по которым поверхность гиперболического параболоида
пересекается касательной плоскостью в точке О.
Выберем в качестве оси Оу ось, лежащую в касательной
плоскости к поверхности (А) в точке 0@, 0, 0) и не совпадающую
ни с одной из прямых (В), т. е. не имеющую асимптотического
направления относительно поверхности. Диаметральная плоскость,
сопряженная оси Оу относительно поверхности (А), будет иметь
уравнение
о21л; + о22г/ = 0,
и если ее принять за ось Ох. то будем иметь ari = 0, а22фО, и
уравнение (А) примет вид
Здесь (в силу условия К4 > 0) atl и о22 — числа разных знаков.
Выбором единичной точки системы координат последнее
уравнение можно привести к виду
x2 — y2 = z. (V)
Обратно, уравнение (V) является уравнением гиперболического
параболоида, так как эта поверхность не имеет центра, и для
уравнения (V) /С4 > 0. Начало координат лежит на поверхности.
Ось Oz имеет особое направление Плоскости хОг и уОz —
диаметральные плоскости, сопряженные соответственно осям Оу и Ох.
Плоскость хОу является плоскостью, касательной к поверхности
в начале координат.
458 Pnata XI), ПОВЕРХН@@ТИ 8АДАННЫВ 06ЩИМ УРАВНРНИЕМ
Читателю рекомендуется сформульровать и решить
аналогичные вопросы для следующих пове; хностей второго порядка:
х2+(/2-г2 = 0
— действительный невырождаюшийся кону*, гторого порядка;
2 i 2 1 ** 2 1 2
— действительные нераспадающиеся цилиндрические поверхности
второго порядка.
§ 164. Главные направления поверхности второго порядка
Определение. Главным направлением поверхноспш чторогс
порядка называется неасимптопшческое направление этой поверхно~
сти обладающее тем свойством, что диаметральная плоскость,
сопряженная этому направлению, перпендикулярна к нему.
Пусть поверхность второго порядка задана общим уравнением
аих* + а22.'/2 + «зз2Й Н~ 2я12а:£/ -f :)-а2яуг -j- 2aslzx -f 'ахх +
относительно декартовой прямоугольной системы координат.
Пусть сектор а—{1, т, п) имеет главное направление Тогда
он б)дет коллипеарен вектору
а* = \а-,Л14-аЛ9т-[- а-,чп, а9,1 + а?91п4-а„яп, а„,/ 4-а„,ш -{-а„»п\,
нормальному к диаметральной плоскости, сопряженной
направлению i ектора а (§ 159, теорема 1).
Следовательно,
aiXi -f a,2(. -j- а2,п = Хп, B)
.1ЛИ
(°11 — ^) ' "Г «12т + Я13П = ^>
а21/4-(а22 — К) т-\-а23п = 0, B')
о31/ + ая2т -f- (о83 — А.) я = О,
и так как вектор {/, т, п) ненулевой, то
<3ц —^ «12 «1;
•*21 2 /ь 3
331 «32 аЗЗ ^
= 0, C)
или
Я,з_/1Л2+ /8я,_/ =0, D)
где /j, /2, /,—1-нварианты ортогонального преобразования (§ 153).
Таким образом, если вектор а={/, иг, п} имеет главное
направление относительно поверхности A), то имеют место соотно-
§ 165 ЧИСЛО ГЛАВНЫХ НАПРАВЛЕНИИ 459
шенин B), где л—корень характеристического уравнения C).
Этот корень % характеристического уравнения не равен нулю,
так как в противном случае вектор а имел бы относительно
поверхности A) особое, следовательно и асимптотическое,
направление.
Обратно, любой ненулевой вектор а = {1, т, п], координаты
которого определены из системы B), где л, — отличный от нуля
корень характеристического уравнения, имеет главное
направление относительно поверхности A). В самом деле, при ХфО и
а — {1, т, п}фО из соотношении B) следует, что
/ (ап1 + а12т + а13п) + т (a2I/ -f а22т + а23п) -f n (aSil + аьгт + а33п) =
или
ап12 + а22т2 + а33п2 -(- 2a12lm -f 2а2ят,. -f 2ая1п1 Ф О,
т. е. вектор а ие имеет асимптотического направления.
Соотношения B) теперь выражают то, что этот вектор ортогонален
диаметральной плоскости, сопряженной его направлению.
§ 165. Число главных направлений поверхности второго порядка
Докажем следующие положения.
1°. Если Х — к1 — простой корень характеристического
уравнения то система B) § 164 имеет ненулевое решение, но не может
иметь два линейно независимых решения.
В самом деле, если бы система B) (при К^К^) имела два
линейно независимых решения, то ранг определителя А (к) был бы
ниже 2 и потому Л'(^1) = 0, т. е. ^ было бы корнем уравнения
Д(^) = 0, кратность больше i.
2°. Если Х1Ф%2, то ненулевые векторы а1 = {/1, mlt nx\ и
а2 = {/2, <п2, п2], которые мы получим из системы B) при X = Xj.
и % = Х2, ортогональны друг другу.
В самом деле, из соотношений
йц^ + ai2mi-Ь агз«1 = Mi.
а2 А -г a22mi + аггпг .= \хтъ
flu's + ai2m^ -M1312 = Мг.
а21/г + аг2т, -4- о23«г = КЩ,
находим
«2 («3 A + «32^1 + a38«l) = ^1 ([J-2 4" «1^2 + "l«2).
вц'г + «I2m2 + «1з"г) + mi («2 A + <W«2 "f »гз) +
"i(fljA r(ls,m2-l-ayin2)^Ki(lili \-тхтг-\-пхп.г).
460 Рлава XII. ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Левые части этих равенств тождественны, значит,
,) = \г (IJO_ -f mxm.2 + nLn.z),
или
(K1 — l2) AХ12 + тхт.г + и уЩ) = 0,
и так как \гФ А.2> то
1г1.2 + тгт2 + пхп2 = 0,
а это значит, что ах}_а2.
i-i3 доказанного, а также из предыдущего параграфа приходим
к следующим выводам.
I. Если Хгф\г, 12ф13, К^^и К¥=0, *-а=И=0» ^3=^°- то
поверхность имеет только три попарно перпендикулярных
главных направления.
II. Если к1 = к2ф'к3, Ххф0, Хяф0, то поверхность имеет
одно главное направление, соответствующее корню % = \3, и
всякое направление, к нему перпендикулярное, также будет главным.
В этом случае поверхность второго порядка является
поверхностью вращения.
III. Если Х1 = К2~Х3ф0, то любое направление является
главным (сфера).
IV. Если ^j^O, Х2ф0, к1фк2, л.3 = 0, то поверхность имеет
два главных взаимно перпендикулярных направления.
V. Если Х^^ — К^фО, л8 = 0, то любое направление,
перпендикулярное вектору, соответствующему корню Х3, будет главным
(поверхность вращения).
VI. Если К1ф0, ^2 = ?13 = 0, то имеется одно главное
направление, соответствующее корню кг.
Диаметральная плоскость, соответствующая главному
направлению, называется главной диаметральной плоскостью. Главные
диаметральные плоскости — это плоскости симметрии поверхности, а
главные направления — это направления прямых, не имеющих
асимптотического направления, перпендикулярных к этим
плоскостям симметрии.
Замечание. Все центральные поверхности, не являющиеся
поверхностями вращения, имеют по три плоскости симметрии,
попарно перпендикулярные друг другу, и по три оси симметрии,
имеющие главные направления, перпендикулярные к плоскостям
симметрии и проходящие через центр поверхности.
Каждая из центральных поверхностей вращения обладает
плоскостью симметрии, проходящей через ее центр и
перпендикулярной к оси вращения. Кроме того, плоскостями симметрии
будут все плоскости, проходящие через ось вращения. Осью
симметрии п этом случае будет ось вращения, а также всякая
прямая, проходящая через центр поверхности и перпендикулярная
к осп вращения. Все оси симметрии идут по главным направлениям.
166 ОПРЕДЕЛЕНИЕ РАСПОЛОЖЕНИЯ ПОВЕРХНОСТИ 461
Эллиптический параболоид, не являющийся параболоидом
вращения, и каждый гиперболический параболоид имеют по две
перпендикулярные друг к другу плоскости симметрии, являющиеся
главными диаметральными плоскостями. Линия их пересечения
является осью симметрии поверхности*. В отличие от осей
симметрии центральных поверхностей ось симметрии параболоида
имеет не главное, а особое направление, причем ось симметрии,
являющаяся линией пересечения плоскостей симметрии,
пересекает параболоид в одной точке—в его вершине.
Параболоид вращения имеет одну ось симметрии — ось
вращения. Всякая плоскость, проходящая через нее, является главной
диаметральной плоскостью.
Рассмотрение главных диаметральных плоскостей и осей
симметрии для остальных поверхностей второго порядка
предоставляется читателю.
§ 166. Определение расположения поверхности второго порядка
по отношению к декартовой прямоугольной системе координат
Постановка вопроса о расположении поверхности второго
порядка, заданной общим уравнением относительно прямоугольной
системы координат, аналогична постановке этого вопроса для
линий второго порядка, а именно, помимо канонического
уравнения поверхности второго порядка надо знать ту (каноническую)
систему координат, в которой уравнение поверхности имеет
канонический вид, а для этого необходимо знать повое начало
координат этой системы и направления ее осей.
Для центральных поверхностей достаточно найти координаты
центра из системы
Оц* + а1гу + a13z + а1 = 0,
a21x + a22(/ + a232 + aa = 0. 0)
a3ix + азгУ + азз2 + аз = °.
и координаты векторов, имеющих главные направления, из системы
(ап — 1I-\-а12т + а13п = 0,
a21/-f(a22 — k)m + a2Sn = 0, B)
asll + as2m + (a33 — \) n = 0,
где вместо к надо подставлять корни характеристического
уравнения.
В случае центральных поверхностей вращения достаточно
найти координаты центра и координаты направляющего вектора
* Гиперболический параболоид, который пересекается с касательной
плоскостью в его вершине по двум взаимно перпендикулярным
образующим, имеет эти прямые своими осями симметрии.
462 Рлавй XII. ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
оси вращения, соответствующего простому корню
характеристического уравнения. В случае сферы достаточно определить
координаты ее центра п радиус.
В случае, если общее уравнение поверхности второго порядка
является уравнением эллиптического или гиперболического
цилиндра, вопрос о расположении решается так: уравнения A)
являются уравнениями места центров (прямая); координаты
векторов главных направлений (если данная поверхность не является
круговым цилиндром) находятся из системы B), куда надо
подставлять вместо к отличные от нуля корни характеристического
уравнения.
Если рассматриваемое уравнение является уравнением прямого
кругового цилиндра, то для определения его расположения
достаточно знать уравнения его оси (уравнения A)) и радиус.
Для нахождения свободного члена D в простейшем уравнении
X^ + W+D^O C)
эллиптического или гиперболического цилиндра можно и не
пользоваться для вычисления D семиинвариантом К3, т. е. не
пользоваться формулой
'г
Число D в простейшем уравнении равно результату
подстановки координат любого из центров в левую часть данного
уравнения поверхности (это, между прочим, верно по отношению
к простейшему уравнению любой из поверхностей, имеющих центр).
Координаты же какого-нибудь центра (в случае эллиптического и
гиперболического цилиндра) находятся из уравнений A).
Для параболоидов надо определить координаты вершины О',
координаты векторов е\, е'2, имеющих главные направления,
координаты вектора е'3, к ним перпендикулярного, и каноническое
уравнение в системе O'XYZ, в которой за положительные
направления осей О'Х, O'Y и O'Z взяты соответственно направления
вектороа е , е[ и e's. Для параболоида вращения достаточно
определить координаты вершины и координаты вектора, коллинеар-
иого оси вращения.
В отличие от центральных поверхностей при определении
направления вектора ез нам нужно знать не только прямую,
направление которой этот вектор определяет, но и направление
того луча этой прямой, который проходит внутри параболы,
являющейся сечением параболоида плоскостью XOZ канонической
системы координат.
§ 166. ОПРЕДЕЛЕНИЕ РАСПОЛОЖЕНИЯ ПОВЕРХНОСТИ 463
Докажем что вектор е'3 = {/3, тя, п3}, координаты которого
определяются из системы (^8 = 0)
a21l + ai2m + a2Bn = 0, D)
asll + aZ2m + assti=*Q,
будет направлен внутрь сечения параболоида плоскостью XOZ
тогда и только тогда, когда
В самом деле, будем считать векторы
e\ = {h, mv nj), е'2^{12, m2, /?,}, e'3 = Rv '«3, «si
единичными. Не изменяя начала координат, направим новые оси
координат Ох', Оу', Oz' соответственно по этим векторам. Тогда
формулы преобразования координат будут иметь вид
а общее уравнение параболоида
апх2 + о22г/2 -Ь а3зг2 -г 2о12хг/ + 2а23г/2 + 2aslzx + 2ахх + 2а2
примет вид
^ " + 2а\х' + 2а/ + 2а'3г' + а = О,
где
Далее, при помощи переноса осей мы преобразуем последнее
уравнение к простейшему:
причем по-прежнему
а'а = а11з + а2>
Сечение параболоида
^Ха + ^Уа + 2с,2- О
плоскостью XOZ является параболой, уравнения которой
Значит, если Г'^о'з < 0, то ось O'Z направлена внутрь сечения,
а если %га3 > 0, то —во внешнюю сторону этого сечения. Для
464
Глава XII ПОВЕРХНОСТИ ЗАДАННЫЕ ОБЩИМ УРАВНРНИЕМ
определения знака произведения
%.ха\ = л-j (йх/3 + агтя+ a3ns)
несущественно, будет вектор e'a = {ls, т3> п3) единичный или нет.
Поэтому окончательно, если
л.1 (а ^з + а2т3 + a3ns) < О,
где координаты вектора е'3~{13, т3, пь} определены из системы D),
то вектор е3 направлен внутрь параболы, являющейся сечением
поверхности
плоскостью XO'Z, а если
то—в противоположную сторону.
Замечание. Обозначим через alk алгебраическое дополнение
элемента aik в определителе /3. Тогда каждый из векторов
p — {alv an, а13},
q = {a2V a22, а23},
г — {а31, а32, а33},
как это следует из системы D), будет коллинеарен вектору е3.
Значит, вектору ёъ будет коллинеарпа и следующая линейная
их комбинация:
а3г) = — {а^аи + а~а
23, ага13
о, а
12 3
;+«3«
Oil «1 «13
a2l a2 a28
а2а
2а23
Х + а3а31,
3а33} =
«31 «3 «33
«12 «1
*21
■*32
J
— j «2 °22 °23
I «3 «32 «33
где Av A2, Ag — алгебраические дополнения элементов alt a2, a3
в определителе КА.
Вектор {Alt A2, A3) ненулевой (так как в противном случае
мы получили бы, что /у 4 = 0).
Подставляя в выражение
вместо /8, т3 и ng соответственно Аъ А2, Ач и замечая, что
(так как алгебраическое дополнение элемента а в определителе /<4
равно /3 = 0), заключаем, что если
§ 166, ОПРЕДЕЛЕНИЕ РАСПОЛОЖЕНИЯ ПОВЕРХНОСТИ 465
то вектор
{Alt А2, А3}
направлен внутрь сечения параболоида
k1X* + KiY* + 2a'aZ = 0
плоскостью XO'Z, а если ^i/<4>0> то—в противоположном па-
правлении.
Для эллиптического параболоида /С4<0, а корни >., и К2
одного знака. Значит, если эти корни положительны, то вектор
{Alt А2, А3} направлен внутрь указанного сечения, а если
—отрицательны, то—наружу. Для гиперболического параболоида "kt и
%2 разных знаков, а /С4 > 0. Поэтому считая Ъг > 0, заключаем,
что вектор {Ах, А2, АЛ направлен внутрь сечения этой
поверхности плоскостью ХО Z. Вершина параболоида находится так.
Возьмем на поверхности параболоида точку (х, у, г).
Координаты вектора, нормального к касательной плоскости в этой точке
поверхности, таковы:
и, значит, точка (х, у, z) будет вершиной поверхности тогда и
только тогда, когда эти координаты пропорциональны
координатам вектора, коллинеарпого особому направлению, т. е.
= l3t,
= mat, F)
Умножая эти равенства соответственно на /3> тз> пз и
складывая почленно, в силу соотношений D) получим
3 +а3п3 =
Отсюда находим
Переписывая уравнение поверхности в виде
+ (аз1х -\- а32у + a33z + ая) z + atx + а2у +• a3z + a = 0, (8)
в силу соотношений F) получим
Q. (9)
Таким образом, для нахождения координат вершины надо
решить линейную систему F), (9).
466 ГАаю X// ПОВЕРХНОСТИ ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Предположим что общее уравнение поверхности второго
порядка является уравнением параболического цилиндра. Пусть С—
парабола, по которой плоскость перпендикулярная к образующим
параболического цилиндра, пересекает эту поверхность, а я —
плоскость, в которой расположена парабола С Обозначим через
e,—{llt mv и^ и е2 = {/2. m2. пг) векторы, лежащие в
плоскости л, первый из которых перпендикулярен к оси параболы С, а
второй ей коллппеарен. Обозначим через е3 — {'з- тз> ns\ вектор,
коллинеарный образующим цилиндра. Будем считать все векторы
е,. е2 б.ч единичными. Произведем преобразование системы
координат: не меняя качала координат О, направим новые оси Ох',
О у' О г' соответственно по векторам еи е2, е'а. Формулы
преобразования координат тогда имеют следующий вид:
г = пгх' + n2t/ + n8z',
а уравнение параболического цилиндра в системе Ox'y'z' таково!
V'2 + 2а[х' + 2агу' + а = 0, (А)
где
Переносом осей координат последнее уравнение приводится
к виду
причем по-прежнему a'2 = a1l2Jrct2m2+a3n2.
Таким образом, если ^ха2 < 0, или
/j(aj/2 + o2m2 + fl3«2)<0. (JO)
то вектор |/2. т2, п2) направлению оси параболы внутрь
параболы, а если
0, A1)
то — в противоположном направлении.
Остается доказать, как находятся векторы е,, е2. е3. Из
соотношения (А) следует, что [> начальной системе координат Охуг
уравнение всякого параболического цилиндра можно записать в виде
(ах + у-у + \zf -г 2аLx + 2a2y -j-2a3z-{-а — О.
Уравнения
0, 2a1x-\-2a2y-Jr2a3z-[-a = 0
167 ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XII 46?
являются уравнениями прямолинейной образующей этого цилиндра,
и из них мы находим координаты вектора е3, коллинеарного
образующим. Координаты вектора et, имеющего главное направление,
находим из системы B), где надо положить 'к = 11. Вектор е>
находим как вектор, перпендикулярный к е\ и е3. При
исследовании знака произведения
вектор е2 — {1%, щ, п2} можно считать не единичным (так же как
и векторы е1 и е3).
Зная вектор, имеющий главное направление, можно составить
уравнение главной диаметральной плоскости. Уравнение этой
плоскости совместно с уравнением самой поверхности определяет прямую,
по которой указанная главная диаметральная плоскость
пересекает поверхность. Из этих двух уравнений легко найти координаты
какой-нибудь одной точки этой прямой.
В заключение отметим, что если общее уравнение поверхности
определяет пару плоскостей, то вопрос о ее расположении
решается разложением на линейные множители левой части данного
уравнения.
§ 167. Примеры и задачи к главе XII
1. Задачи с решениями
Пример 1. Даны эллипсоид
и плоскость
Злг+4г/ + бг-12 = 0. B)
Установить, пересекает ли эта плоскость д-анный эллипсоид (по
действительно."j линии) и в утвердительном смысле найти центр линии сечени-'
Решение. Запишем уравнение плоскости B) в параметрической форме:
х = 6и, y^&v, г = 2 —Зи —4ь '3)
или
Г={6и, 6и, 2—Зи —4о} = {0, 0, 2} + и{6, 0, —3^-т г){0, 6, —4}.
Таким образом, и и и —общие декартовы координаты точки М плоскости
B) с началом координат в точке @, 0, 2) и масштабными векторами
ei = {6, 0, —3} и е2^{0, 6, —4},
Уравнение линии сечения на плоскости B) в этой системе координат
имеет вид
4и2 + 9и2+ B — Зи — 4иJ = 1,
или
25o2—i2a—i6y-[-3 = 0.
468 Глава ХП ПОВЕРХНОСТИ. ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Координаты и, v центра сечения определятся из системы
13и-г 12а—6 = 0,
12« + 25w —8 = 0;
_ 54 _ 32
U~"l8T' Р-~18Г-
Из соотношений C) находим координаты центра М сечення в данной
системе координат Охуг:
_ 324 192 72_
Х~ 181 ' У~ 181 ' Z~ 181 '
Далее, так как
324 N а / 192 \2 / 72 \г
181 / , V 1в1 У , V 181
■+—4—
то точка М лежит внутри данного эллипсоида, т. е. сечение является
действительной линией, именно —эллипсом в силу того, что
13 12 >о
12 25 >
Заметим, что систему координат Охуг можно считать общей декартовой
Пример 2. Даны двуполостный гиперболоид
х2+У2—г2=— 4 A)
и плоскость
Установить, пересекает ли плоскость гиперболоид (по действительной
линии) и в утвердительном случае определить вид линии пересечения. Система
координат общая декартова.
Решение. Запишем уравнение данной плоскости в параметрической форме
или
r = {u, v, ц + а + 3} = {0, 0, 3} + {1, 0, l}u + {0, I, l}v.
Значит, и и а —координаты точки М плоскости в общей декартовой
системе координат с началом в точке @,0,3) и масштабными векторами е, ==
= {1,0, 1} и е2 = {0, 1, 1}.
Уравнение линии сечения в этой системе координат на плоскости B)
имеет вид
или
Так как
/2 < 0, Кз Ф 0,
го это уравнение гиперболы.
Замечание. Здесь, как и в предыдущем примере, можно предполагать,
что система координат Охуг общая декартова. Если же система прямоугольная
и требуется определить не только тип линии, но и ее каноническое уравнение
и расположение, то вместо базиса ^={1,0, 1}, е2^\0, I, 1} на данной
плоскости можно перейти к ортоиормированиому базису. Сделать это можно так:
§ 167. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XIT 469
выберем k так, чтобы вектор ех-\-ке% был ортогонален вектору elt т е.
ех'в\ -)-/еег) = О, е\ -)-ке^вг = 0, 2-j-ft = 0, fe=—2, значит,
Теперь векторы
^ = {1,0,1} и А = {1, — 2, — If
ортогональны (и, конечно, компланарны данной плоскости). Нормируем их!
, i 1 1 I , i I 2 i
X \ Л/ С\
Уравнение плоскости B) можно теперь записать в виде
Г2 ' ' У
значит,
2v
х-
и в декартовой прямоугольной системе координат Muv уравнение линии
сечения:
EV+4-0
и т. д. (теперь применима вся теория ортогональных инвариантов).
Пример 3. Определить вид поверхности второго порядка:
х2 + 5{/2 + г2 + Чху + бхг -f 2(/г—
Решение.
Характеристическое уравнение: h,3 — +
Его коэффициенты: -f-1, —7, -f-36. Здесь имеются две перемены знака: при
переходе от +1 к —7 и от —7 к —(— 36; ьначит, уравнение имеет два
положительных корня и один отрицательный.
Кроме того, —- = —1<0; следовательно, данная поверхность —однопо-
'з
лостный гиперболоид.
Пример 4. Определить вид и расположение поверхности, заданной
относительно декартовой прямоугольной системы координат уравнением
ха + 5j/2 + z2 + 2ху + Ьхг + 2yz — 2х + &у+2г = 0.
Находим
/3=_36, Д = 36, /х = 7.
Так как /1/3<0, ^4>0, то данное уравнение выражает однополостный
гиперболоид. Далее,'/2 = 0.
Характеристическое уравнение
А.3 — 7X4-36 = 0
имеет корни
Afj ==- о, Л2 = и, Ау = ^— ^.
470 Глала XII ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Простейшее уравнение
2 — 2Z4^L
-36 '
или
I i L _1
! ' \2 / 1 \2
_LV7—
Координаты центра поверхности найдем, разрешая систему
x-\-y-\-2>z—1=0, x-f-
откуда
1_ _ __2 __2
3 3 3
Центр
' .1 _!. 1
Обозначая через /х, mb nx \ оординаты векгора, коллинеарного большей
оси горлового эллипса, находим эти координаты из системы
A—3)/!-
откуда
{k, тъ ni\ = {\, -1, 1}.
Аналогично находим векторы
\!2, т2, п2} = {\, '2, 1}, {13, т3, п3} = {\, 0, -1},
дающие направления осей: меньшей оси горлового эллипса и оси поверхности.
Тем самым расположение поверхности определено
Составим еще формулы преобразования координат Найдем сначала
единичные век горы /', /', ft', идущие в положительных направлениях осей О'Х,
O'Y, O'Z:
отсюда
X Y } Z 1
X , 2К 2
~Fi};
i; 167, llpHMFPhl l-i ЗАДАЧИ К ГЛАВЕ XII 471
"ЛИ
v Х—Ц + 2—1 v X+2l + >+[
Пример 5. Определить вил и расположение поверхности, заданной
относительно декартовой пря .оуюльной сивтемы координат уравнением
1х2 + ?/2 + 2z2 — -Zxy + 2у? + 4х — 2у = 0. < 1>
Первый способ решения Составляем систему уравнений
определяющих координаты центра:
—1=0,
Эти уравнения к в л я юте i уравнениями 1^е.ч плоскостей, прохоляших ^среч
одну прямую Полагая у = г = О, находим точку v — 1, 0, 0)j являющуюся с^"им
из центров поверхности, Направляющий вектор прямой центров {1 2, —U.
а сами уравнения прямом центров
x= — \ + t, 9 = 2f, г=—г
Перенося оси координа! так чтобы новым начало л координат стала точка
(—1 0, 0), получим что в новой системе координат уравнение поверхности
имеет вид
^'2 + i/'2 + 22'2-2xy + 2(/V+D = 0, '■>-)
где D — результат подстановки координат точки {— 1, 0, 0) в леву-ч часть
уравнения A), т е D=—2.
Уравнение B) принимает вид
2г'2— 2*У-i-2(/V — 2 = 0
Составляя и решая характеристическое vравнение
2-Х -1 1
— 1 1-Х 1 =0,
0 I 2-Х
или
получим
т, __ о Oi _— Q у __. Q
Поэтому, повернув оси О'х'у'г' вокруг точки О'( — 1, 0, 0) так чтобы
оси О'х' и О'у' пошли го главным направлениям, соответствующие корням
>»i = 2 и Х2 = 3, получим уравнение поверхности в виде (свободный член —2
не изменится)
2Х2 + ЗК'! —2 = 0
или
X2 . К2
/I)"
Координаты вектора, коллинеариого меньшей оси направляющего эллипса,
являющегося сечением поверхности плоскостью XO'Y найдем, решая систему
472 Глава XII ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
откуда
Аналогично из системы
B—2)/2— т2 + 0.д2 = 0, — /2+{1 — 2)m2 + n2 = 0, O./2 + m2+B—2) п2 =
находим вектор
{/2, т2, л2} = {1, 0, {},
коллинеарный большей оси указанного эллипса.
Уравнения плоскостей симметрии, проходящих через осы
г—1)+
или
х—у —z+l=O, х+г+\=О.
Второй способ. Находим
/2>0, liK3<0;
уравнение выражает эллиптический цилиндр Характеристическое уравнение
Его корни
Простейшее уравнение
12 „
каноническое!
.=1.
Уравнения оси;
г—1=0,
Отсюда находим вектор
{1,2, -1},
имеющий направление оси
Главные направления и главные диаметральные плоскости находим так,
как указано в первом способе.
Пример 6. Определить вид и расположение поверхности, заданной
относительно декартовой прямоугольной системы координат уравнением
Реше н и е.
/3=
0 1 2
1 1 1
=0,
2 1 О
0 12—2
1 11-1
2 10 0
— 2—10 0
= 0,
§ 167. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XII
473
/*=
О 1
1 1
О 2
2 О
1 1
1 О
= -6,
0
1
2
1
1
— 1
— 2
-1
0
/
+
0
2
-2
1 = 0+1
2
0
0
+
— 2
0
0
0=1
+
1 1
1 0
— 1 0
-1
0
0
=0,
так как /3 = ^ = 0, /2<0, /(з = 0, то данное уравнение определяет пару
пересекающихся плоскостей
Чтобы найти уравнения этих плоскостей, разложим левую часть данного
уравнения на линейьые относительно х, у, г множители*
у2 -г 2жJ/ + Ахг + 2j/2 — 4х — 2у = у2 + 2 (х + г — 1) у + te — 4л: =
= (/2 + 2(л: + 2— 1)(/+(* + г— iJ-}-te — 4л:— (х + г— 1J =
/-г г— 1J + 4л;2 —4л: —л:2 —2д:2 —г2—1+2л: + 22 =
г—IJ —х2+2лг —2л—г2+2г—1=(л:+(/ + г—1)а—
2-1J—[л:2+2A-2)л + A-2J] =
Отсюда находим уравнения плоскостей, на которые распадается данная
поверхность:
0, у + 2г —2 = 0
Пример 7. Определить вид и расположение поверхности, заданной
относительно декартовой прямоугольной системы координат уравнением
5х2 —{/2 + 22 + 4ху + б2х + 2л + 41/ + 6г —8 = 0
Находим
Данное уравнение выражает гиперболический параболоид
Далее
/1 = 5, У2= —14
Характеристическое уравнение
ХЗ_5А,2- 14Л. = 0;
его корни
Я,х = 7, L,= — 2, Х3 = 0
Координаты 1Ь тъ щ вектора, коллинеарного оси О'Х, находим из
системы
(о— 7)/i-| 2m1 + 3n1 = 0,
откуда
, тъ пх) = {4, 1, 2}
Аналогично из системы
(-I+2)m2-i-0-n2 = 0,
4?4 Peata XII. ПОВЕРХНОСТИ. ЗАДЛННЫР ОВШ.ИМ УРАВНЕНИЕМ
1 аходим р
{It, Щ, Ы = { — 1. 2> lh
колли неарный осп O'Y Вектор
{U, >и, n,} = {\ 2, -Ъ\,
холлу еарный оси певерхности находим из системы
как вектор, соответствующий значению 'к^
Простейшее уравнение
-2У--2 у ||Z =
а каноническое
Так как
ail$+ а^т.д-\ о„«3= 1-1+2-2— 3-3 < О,
то ве тор ^ 1, 2, —3^ направлен в положительной направлении оси па-
рабо ьи
Вершину
п, /617 _ИЗ 1011 \
\ 392' 196 392 У
находим из системы
Чх — ц +2 = 2*.
Зх +z+3 = —3*.
(х-\-2у — Zz)i + x-{-2y-\-3z—8 = 0.
Сначала находим
,_ail» + tyna + <hnt Ы + 2-2-3-3_ 2
~ ;;; 1+4+9 - 7 т-д-
Пример 8. Определить вид и расположение поверхности, заданной
относительно декартовой прямоугольной системы координат уравнением
х2 + У'1 + 4гг + 2*2/ + 4xz + 4yz — 6г + 1 = 0.
Находим
/3 = 0, /С4 = 0, /2 = 0, /С3 = — 18 5^ 0,
данное уравнение является уравнением параболического цилиндря Пере-
пишем его в виде
'х + у + 2гJ—
5 167 ПГИМЕрЫ И ЗАДАЧИ К ГЛАВЕ XII 475
Уравнения
x + y+2z = 0, —62+1=0
являются уравнениями прямолинейной образующей, из этих уравнений
находим вектор
«,H-i. 1. о},
коллинеарный образующим.
Координаты вектора e'v идущего яо единственному главному
направлению, находим из системы (/i = 6)
откуда
•;-{i. 1.2}
Наконец, вектор e't, коллияеарнмй оси сечения параболического цилиндра
плоскостью, перпендикулярной образующим.
Простейшее уравнение
6Х2-2 ]/-
а каног/ическое
Так как
то вектор { 1, 1, —1 } направлен по оси сечения
в сторону выпуклости этой параболы.
Уравнение главной диаметральной плоскости
x + J/ + 2z-)-x+(/-|-2z-f-2Bx + 2j/ + 4z —3) = 0,
или
Уравнения
(х + у-\-2г)*—6г+1 = 0, *-{-у-{-2г —1=0,
или
-32+1=0, х + у + 2г-1=0, (Я)
являются уравнениями прямолинейной образующей, по которой главная
диаметральная плоскость пересекает данный параболический цилиндр. На
авнение пло-
этой образующеи лежит, например, точка [0, -=•, -j-J. Ур
V d 6 I
скосги, касательной к параболическому цилиндру вдоль образующей X,
имеет вид
7 =0, или х + у — 2 = 0.
476 Глава XII. ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
Пример 9. Исследовать в зависимости от значений параметра т характер
поверхности, заданной уравнением
х2+B/я2 -J-1) (у2 + г2) — 2ху — 2хг—2уг — 2т2 + 3/п — 1 = 0.
Решение
= -4(m2+D(m— IJ Bm — l
/2 = 4m2(m2 + 2),
/C = _ 4m2 (m2 + 2) (m - 1) Bm - 1),
Инвариант /3 обращается в нуль при т=— 1 и т=1, инвариант /D—
при т = 1 и т——- Поэтому рассмотрим следующие интервалы изменения
параметра m и значения т: 1) т < — 1; /- > 0, /а > 0, /t > 0.
Последовательность коэффициентов
1. — /i. /2. — ^з
имеет три перемены знаков, значит, все корпи Xit Л2, %3 характеристического
уравнения положительны. Далее, /D < 0 при т< — 1, значит, данное
уравнение является при т < — 1 уравнением эллипсоида.
2) т = — 1 Тогда /3 = 0, /С4 = 0, /2 > 0, /С3 < °> /j > 0—эллиптический
цилиндр,
3) — 1 < m < — ; тогда /3 < 0, /2 > 0, 1г > 0, /D > 0. В
последовательности
Ь — /i» I2, — /3
две перемены знака. Два корня характеристического уравнения положительны,
один отрицателен, ■—■ < 0—однополостньш гиперболоид.
'3
4)т=у;тогда /3 < 0, /2 > 0, 11>0, /D = 0—конус (действительный).
5) у<т<1; тогда /3 < 0, /2 > 0, /, > 0, К4 < 0—двуполостным
гиперболоид.
6) т=1; тогда /8 = 0, /D = 0, /2 > 0, /C = 0—две мнимые пересекающиеся
плоскости.
7) m > 1; тогда /8 > 0, /2 > 0, /t > 0, К4 < 0 —эллипсоид.
2. Задачи для самостоятельного решения
1. При каком необходимом и достаточном условии эллипсоид
и плоскость
Ах+Ву + Сг + D—O
1) касаются, 2) пересекаются, 3) не пересекаются?
Ошв 1) а*А2 + Ь2В2-{-с*С* = О*,
2) а2Л2+ |,2S2 + C2C2 > D2. 3) а2Л2 + 62В2 + с2С2 < D2.
5 167. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XII 477
2. Составить уравнение диаметральной плоскости эллипсоида
v2 ifi г2
9 т 16 Т 4 '
делящей пополам хорды, коллинеарные вектору а = {2, 1, 2}.
Отв. 32x + 9(/ + 72z = 0.
3. Составить уравнение плоскости, пересекающей эллипсоид
о2 + &2 + с2 ~
по эллипсу, центр которого находится в точке (х0, у0, г0). Дано, что
4. Найти на эллипсоиде
геометрическое место точек, для каждой из которых расстояние от центра
эллипсоида до касательной плоскости в этой точке имеет одно и то же
значение, равное d (полодия).
Отв.
м2 ,2 v-2
у v-2 ,,2 ,2 I
а2 ' б2 "'"с2 ' а*"^ ' с4 da"
а2
5. Составить уравнения прямой, на которой расположены центры
сечений эллипсоида
плоскостями, параллельными плоскости Ах-\- By -\-Cz = 0.
х ц г
6. Пусть (ха, у0, го) — внешняя точка эллипсоида
> У1 ■ zl-i
~ Гс2 -1-
Составить уравнение конуса с вершиной в дайной точке (х0, у0, г0),
хг уг г2 ,
описанного около данного эллипсоида -jj + гг~ + "а •
— а-0) Уо(У-Уо) г0 (г—г0)
+ +
■178 Г/I а в а XI! ПОВЕРХНОСТИ, ЗЛДЛГ1Н ЫЕ О БЩИМ УРАВНЕНИЕМ
7. Найти геометрическое место точки пересечения трех взаимно
перпендикулярных плоскостей, каждая из когорлч касается эллипсоида
51 л. t • £ -\
а2 ' ft2 -rca --1
Отв. Сфера.
8. Какой вид будет иметь уравнение эллипсоида, если за плоскость хОу
принять плоскость кругового сечения, проходящего через центр эллипсоида,
а за ось Ог— диаметр, сопряженный этой плоскости
Отв, х2 + (/2 + /г222=1, где k > О
9. Определить геометрическое место точки пересечения трех взаимно
перпендикулярных плоскостей к параболоиду
■л ,л
Отв Плоскость
ГЛ. ~у™ 1J
10. Составить уравнение цилиндра с образующими, коллинеарными
вектору а=|/, ш, п \, описанного около однополостного или двуполостного
гиперболоида
*2 , У2 гЯ _ . I
11. Как запишется уравнение однополостного гиперболоида, если за
начало координат принять точку О этой поверхности, за оси Ох и Оу —
прямолинейные образующие, проходящие через эту точку, а за ось Ог —
диаметр, сопряженный плоскостям, параллельным плоскости хОу?
Отв. ху + Хг2 + 2цг = 0, Я, 96 0, ц ф 0.
12. Как запишется уравнение двуполостного гиперболоида, если за
начало координат принять произвольную точку О этой поверхности, за оси Ох
и Оу — две прямые, лежащие в касательных плоскости в точке О, имеющие
сопряженные направления относительно любого сечения плоскостью,
параллельной касательной, а за ось Ог — прямую, проходящую через центр
поверхности?
v2 ,л ,г
Отв. 22 = ^-1.* -L..
а2 б2 с2
13. Какой вид примет уравнение однополостного гиперболоида, если за
плоскость хОу принять плоскость кругового сечения, проходящего через
центр поверх-иости, за начало координат —центр поверхности, а за ось Ог
принять:
1) диаметр, сопряженный плоскости хОу,
2) нормаль к плоскости хОу, проходящую через центр поверхности?
Отв 1) я;2+(/2 — k2z2 = \i\ кфО, ц ф 0;
2) x2+(/2 + a22-f2px2 + 2Y(/z-fa==0, а<Р2 + у2, а < 0.
14. Ка.кой вид примет уравнение двуполостного гиперболоида, если
принять за плоскость хОу плоскость, проходящую через центр поверхности,
параллельную плоскости круговых сечеии";, а за ось Ог принять;
1) диаметр, сопряженный плоскости хОу,
■178 Г/I а в а XI! ПОВЕРХНОСТИ, ЗЛДЛГ1Н ЫЕ О БЩИМ УРАВНЕНИЕМ
7. Найти геометрическое место точки пересечения трех взаимно
перпендикулярных плоскостей, каждая из когорлч касается эллипсоида
51 л. t • £ -\
а2 ' ft2 -rca --1
Отв. Сфера.
8. Какой вид будет иметь уравнение эллипсоида, если за плоскость хОу
принять плоскость кругового сечения, проходящего через центр эллипсоида,
а за ось Ог— диаметр, сопряженный этой плоскости
Отв, х2 + (/2 + /г222=1, где k > О
9. Определить геометрическое место точки пересечения трех взаимно
перпендикулярных плоскостей к параболоиду
£L + -^ = 2z
Отв Плоскость
ГЛ. ~у™ £J
10. Составить уравнение цилиндра с образующими, коллинеарными
вектору а=|/, т, п \, описанного около однополостного или двуполостного
гиперболоида
Я2 I/2 22
Утв I О I УЧ о _И » I I ..I , n of I л 1" ,п " (Г I
11. Как запишется уравнение однополостпого гиперболоида, если за
начало координат принять точку О этой поверхности, за оси Ох и Оу —
прямолинейные образующие, проходящие через эту точку, а за ось Ог —
диаметр, сопряженный плоскостям, параллельным плоскости хОу?
Отв. ху + Хгг + 2цг = 0, X ф 0, ц ^ 0.
12. Как запишется уравнение двуполостного гиперболоида, если за
начало координат принять произвольную точку О этой поверхности, за оси Ох
и Оу — две прямые, лежащие в касательных плоскости в точке О, имеющие
сопряженные направления относительно любого сечения плоскостью,
параллельной касательной, а за ось Ог — прямую, проходящую через центр
поверхности?
х2 и2 гг
Отв. 2г = -2 -ГГ2- — -г .
а* сг с2
13. Какой вид примет уравнение однополостного гиперболоида, если за
плоскость хОу принять плоскость кругового сечения, проходящего через
центр поверх-пост», за начало координат —центр поверхности, а за ось Ог
принять:
1) диаметр, сопряженный плоскости хОу,
2) нормаль к плоскости хОу, проходящую через центр поверхности?
Отв 1) *2+(/2 — &222 = ji2, k Ф 0, (j, Ф 0;
2) я24-у*-\-а,г2-\-2$xz-\~2yyz-\-a — 0, a<P24-Y2, a < 0.
14. Ка.кой вид примет уравнение двуполостного гиперболоида, если
принять за плоскость хОу плоскость, проходящую через центр поверхности,
параллельную плоскости круговых сечеии";, а за ось Ог принять;
1) диаметр, сопряженный плоскости хОу,
480 Глава XII ПОВЕРХНОСТИ, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
двумя сопряженными диаметральными плоскостями, то
p'—q' = p-q.
23. Доказать, что касательная плоскость в вершине гиперболического
параболоида делит пополам отрезок прямолинейной образующей,
заключенный между двумя главными плоскостями этой поверхности.
24. Доказать, что параметрические уравнения
х= V~P (и + f). У= Y~Q (« — v), z = 2uv, где р > 0, q > 0,
суть уравнения гиперболического параболоида. Какие линии определяют
уравнения u = const, c = const'
25. Доказать, что если две плоскости касаются конуса второго порядка
вдоль его образующих, то хорды, параллельные линии пересечения этих
плоскостей, делятся пополам плоскостью, проходящей через указанные
образующие
26. Доказать, что геометрическое место центров поверхностей второго
порядка, проходящих через две пары противоположных ребер тетраэдра,
есть прямая, соединяющая середины ребер третьей пары,
27. Составить уравнение касательной плоскости к поверхности
2ху + Ъуг — Ах — у — 2г = 0,
которая (плоскость) проходит через прямую 4x — 5y — Q, г—1—0.
Отв 4^—5у — 2z-J-2 = 0.
28. Определить X и ji так, чтобы уравнение
х2 — j/H- Зг2 + (Кх + \iy J — 1 = 0
определяло круглый цилиндр
Отв Х=± 1, ц.= ± V2
29. Определить k так, чтобы конус л:2— 2xy~{-kz2 = 0 был конусом вращения
и найти ось вращения
Отв k=l ± У~5 (два конуса) Оси
— 2у = 0, 2) г = 0, (\—
30. Какой вид примет общее уравнение <р = 0 невырождающейся
действительной поверхности второго порядка, если за плоскость хОу принять
касательную плоскость, точку прикосновения — за начало координат, а оси Ох и
Оу направить по главным направлениям кривой, но которой данная
поверхность рассекается плоскостью, параллельной касательной?
Отв аих* + о22(/2 + амг2 + 2а13хг + 2a2ayz + 2a3z = 0.
31. Доказать, что, для того чтобы в конус второго порядка можно было
вписать трехгранный угол, ребра которого попарно перпендикулярны
(прямоугольный триэдр), необходимо и достаточно, чтобы /4 = 0
32. Общее уравнение <р = 0 поверхности второго порядка определяет
гиперболический цилиндр Что определяет уравнение
Отв. Две его асимптотические плоскости.
§ 167. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XI! 481
33. Пусть общее уравнение поверхности второго порядка определяет
гиперболоид. При каком необходимом и достаточном условии точка М„и0, г/0, г0!
лежит между поверхностью этого гиперболоида и поверхностью его аси'мшо-
тического конуса?
Отв Результат подстановки координат данной точки в левую часть
is
уравнения гиперболоида должен быть заключен между 0 и -— ■
34. Общее уравнение поверхности второго порядка определяет две
пересекающиеся плоскости. Найти котангенсы углов между ними.
Отв. ctgotii2=±
/i
2/-/,'
35. Общее уравнение поверхности второго порядка определяет
эллиптический цилиндр При каком необходимом и достаточном условии точка
(х0, уо> 2о) лежит внутри этого цилиндра?
Отв /jtp (х0 г/о. го) < 0.
36. Общее уравнение поверхности второго порядка определяет две
параллельные плоскости Найти расстояние между ними.
Отв. й^
l/il
37. Как запишется уравнение круглого конуса, касающегося плоскостей
хОг и уОг по прямым Ох и Оу? ^__
Отв. г2=±2ху.
38. Составить уравнение поверхности второго порядка, пересекающей
плоскости координат по гиперболам х~0, yz = a; у = 0, хг = Ь; г = 0, ху — с.
_ ху , уг , zx .
Отв. — + — -\-——\.
с ' а ' b
39. Составить уравнение поверхности второго порядка, пересекающей
плоскость хОу по двум прямым, а плоскости хОг и уОг — по окружностям
радиуса г, касающимся оси Oz в начале координат и расположенным в
положи 1ельпых полуплоскостях
Отв (х-\-у — г)~-\-г* = гг .'эллиптический иилиидр)
40. Составить уравнение параболоида вращения, проходящего через
окружность х — 2 = 0, х2+(/2 + 22 — 2х — 2z = 0 и точку A. 1, 0).
Указание Предварительно составить уравнение параболоида
относительно новой системы координат, координатная плоскость х'О'у' которой
совпадает с плоскостью х — г = 0.
Oms x2-f--2y2 + z2-f 2хг — Зх — 5г = 0-
41. Составить уравнения:
1; однополостного гиперболоида; 2) гиперболического параболоида,
принимая за начало координат какую-нибудь точку О поверхности, ■>.& оси Ох и
Oij — прямоаинейные образующие, проходящие через эту точку, а за ось Oz—
проходящий через эту точку диаметр,
Отв 1) а33г2 -\- 2апху -J-- 2«sz = 0, 2) auxy+a:iz =0.
16 П. С. Моденов
Г л а ь l, XII ilubEPXHOCTH. ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
\2. Найти геометрическое место вершин конусов второго порядка,
имеющих общую направляющую окружность, при условии, что на поверхности
каждого такого конуса имеются три попарно перпендикулярные образующие.
Отв х2-J- \f--\- 2г2= /2, где /-—радиус данной окружности.
43. Доказать, что для того чтобы главные оси двух поверхностей второго
порядка были соответственно параллельны, необходимо и достаточно, чтобы
матрицы квадратичных форм, входящих в состав левых частей уравнений
поверхностей, были перестаионочны
44. Найти геометрическое место вершин конусов вращения, проходящих
через эллипс
Отв Гипербола
ГЛАВА XIII
ОТОБРАЖЕНИЯ И ПРЕОБРАЗОВАНИЯ
§ 168. Отображение и преобразование
Если каждому элементу х множества * /И поставлен в
соответствие элемент у множества М', то говорят, что задано
отображение множества М во множество М'. Элемент у называется
образом элемента х, а элемент х — прообразом элемента у.
Если при отображении множества М во множество М' каждый
элемент у множества М' имеет прообраз х в множестве М, то
говорят, что множество М отображается на множество М'.
Отображение множества М на множество М' называется взаимно
однозначным, если:
1) каждый элемент х множества М имеет и притом только
один образ у из множества М' и
2) каждый элемент у из множества М' имеет и притом только
один прообраз х во множестве М.
Это определение эквивалентно такому:
1) каждый элемент х множества М имеет и притом только
один образ у из множества Мг;
2) каждый элемент у из множества М' имеет прообраз х из
множества М;
3) двум любым различным элементам х и х' из множ'ства М
соответствуют два различных образа у и у' из множества М'.
Если множество М отображается на множество М' взаимно
однозначно, то отображение, при котором любому элементу у из
множества М' ставится в соответствие прообраз х этого элемента у,
называется обратным данному; отображение, обратное взаимно
однозначному отображению, очевидно, также взаимно однозначно.
Отображение множества М в себя называется преобразованием
множества.
* Определения и понятия, введенные в $ 168—170, относятся к
произвольным множествам; для аналитической гоометрии эти множества суть
прямая, плоскость, пространство или какие-нибудь фигуры, лежащие на
плоскости или в пространстве.
16*
484 Г ,.авч XIIh ОТОБРАЖГ.ПИЯ И ПРЕОБРАЗОВАНИЯ
Взаимно однозначным преобразованием множества называется
взаимно однозначное отображение множества на себя,
Тождественным {или единичным) преобразованием Е множества
М называется преобразование, при котором каждому элементу х из
множества М ставится в соответствие этот же элемент.
Если А — какое-нибудь взаимно однозначное преобразование
множества М, то обратное преобразование обозначим А'1.
§ 169. Произведение преобразований
Пусть А и Б—два каких-нибудь преобразования множества М.
Возьмем произвольный элемент х во множестве М.
Пусть у—образ элемента х при преобразовании В, a z — образ
элемента у при преобразовании А. Тогда соответствие, при
котором элементу х соответствует элемент г, является преобразованием.
Это преобразование называется произведением
преобразования А на преобразование В и обозначается АВ.
Очевидно,
где А — любое взаимно однозначное преобразование множества,
А'1 — ему обратное, а Е — тождественное.
Докажем, что произведение преобразований ассоциативно,
т. е. если А, В и С—три любых преобразования множествам, го
А(ВС) = (АВ)С.
В самом деле, пусть х—любой элемент множества М, у — его
образ при преобразовании С, г — образ элемента у при
преобразовании В и t—образ элемента г ври преобразовании А.
На основании определения произведения преобразований
элементу х при преобразовании ВС соответствует элемент г, а
элементу у при преобразовании АВ — элемент t. Значит (опять на
основании определения
пронзав ведения преобразований),
элементу х при преобразовании
(АВ)С и при преобразовании
А(ВС) соответствует один и
тот же элемент t, а это и
означает, что (АВ) С = А (ВС).
Отметим еще, что
произведение двух взаимно однозначных преобразований есть взаимно
однозначное преобразование.
Пример. Пусть М — множество всех точек какой-нибудь прямой /.
Обозначим через В преобразование, при котором ючке х прямо!! / стявится г,
соответствие точка х'', симметричная точке к относительно точки О прямой Л
а через А обозначим преобразование, которое точке х прямой I ставит в соот-
§ 170. ГРУПП \ ПРЕОБРАЗОВАНИИ 485
ветствие точку х" той же прямом, такую, что хх" = а, где а —заданный вектор
на прямой /. На рис. 228 построены точки р и q, соответствующие точке х
при преобразованиях ВА и АВ. Эти точки различны, значит, различны и
преобразования ВА м АВ, иначе произведение преобразований (вообще говоря)
некоммутативно.
§ 170. Группа преобразований
Пусть Г есть множество, элементами которого являются взаимно
однозначные преобразования множества М. Тогда множество Г
называется группой преобразований (множества М), если выполнены
следующие два условия.
I. Если А и В—два любых преобразования из множества Г, то
преобразование АВ также входит во множество Г.
II. Если А — любое преобразование из множества Г, то
преобразование Л также входит во множество Г.
Из этого определения следует, что всякая группа
преобразований содержит тождественное преобразование; в самом деле,
пусть Л — какое-нибудь преобразование, входящее в группу Г. На
основании условия II Л также входит в группу Г, а на основании
условия I в группу Г входит произведение АА~1, которое есть
тождественное преобразование.
Подмножество Гх элементов группы Г называется подгруппой
группы Г, если 1\ само является группой,
Г Л 4 В 4 XIV
ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
§ 171. Линейные преобразования и линейные отображения
множества точек пространства, плоскости или прямой
В этом параграфе рассмотрим линейные преобразования
множества всех точек пространства. Для случая плоскости все
рассмотрения носят аналогичный характер.
Линейным преобразованием f множества всех точек
пространства называется отображение множества всех точек этого
пространства в себя, при котором трем любым точкам А, В и С,
принадлежащим одной прямой, соответствуют три точки А', В',
С, также принадлежащие одной прямой и притом так, что если
между направленными отрезками АС и АВ имеет место соотношение
то и направленные отрезки АС и А В' связаны соотношением
Образ А' точки А при линейном преобразовании / иногда
будем обозначать [А.
Аналогично определяется линейное преобразование множества
всех точек плоскости и линейное преобразование множества всех
точек прямой, а также линейное отображение одной плоскости на
другую и линейное отображение одной прямой на другую.
Примером линейного преобразования плоскости является
параллельное проектирование на плоскость и прямую. В самом деле,
если А, В, С —три точки, принадлежащие одной прямой, то их
параллельные проекции А', В', С' также принадлежат одной
прямой, причем если
то
§ 172. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ МНОЖЕСТВА ВЕКТОРОВ 487
так как при параллельном проектировании сохраняется порядок
точек, лежащих на одной прямой, и отношение отрезков, лежащих
на одной прямой.
Если даны два линейных преобразования / и « множества всех
точек пространства, то их произведением fg в соответствии с § 169
назовем преобразование, которое точке М ставит в соответствие
точку f (gM) (это преобразование, очевидно, линейное).
Произведение линейных преобразований (как и произведение любых
преобразований) ассоциативно:
Замечание. Данное здесь определение линейного
преобразования пространства переносится без изменения на комплексное
пространство, комплексную плоскость или комплексную прямую.
§ 172. Линейные преобразования множества векторов
пространства, плоскости или прямой
Рассмотрим множество Ш всех векторов пространства. Поставим
в соответствие каждому вектору а вектор fa. Если это
соответствие удовлетворяет двум условиям:
где а и Ь—любые векторы, ь К — любое число, то оно называется
линейным преобразованием множества всех векторов тр.хмерного
пространства.
Аналогично определяется линейное преобразование множества
всех векторов плоскости или прямой, линейное отображение
множества всех векторов одной плоскости в множество всех векторов другой
плоскости, а также линейное отображение множества всех
векторов, принадлежащих одной прямой, в множество всех векторов
другой прямой.
Примером линейного преобразования множества всех векторов
х трехмерного пространства может служить следующая функция
вектора х:
fx=-{ax),
где а—фиксированный вектор.
В самом деле,
f (kx) = [a (kx)] = Я [ад:] = Kfx.
Если даны два линейных преобразования fug множества всех
векторов пространства, то их произведением fg называется
преобразование, которое вектору а ставит в соответствие вектор / (ga)
483 Глава XIV. ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
(это преобразование, очевидно, линейное). Произведение линейных
преобразований ассоциативно: / (gh) = (fg) h. Суммой f-\-g линейных
преобразований множества всех векторов
пространства называется линейное преобразование, которое вектору а
ставит в соответствие вектор fa-rga (это преобразование, очевидно,
линейное).
Пусть, наконец, / — линейное преобразование множества всех
векторов пространства. Тогда линейное преобразование, которое
вектору а ставит в соответствие вектор kfa, называется
произведением числа К на линейное преобразование f,
§ 173. Свойства линейных преобразований множества точек
пространства, плоскости или прямой
Теорема 1. При линейном преобразовании равные направленные
отрезки переходят в равные.
Доказательство. Пусть / — линейное преобразование и
AB = CD. Требуется доказать, что fAB = fCD.
Обозначим образы точек А, В, С, D при линейном
преобразовании / соответственно через А', В', С, D'. Из равенства AB — CD
следует, что середина отрезка AD совпадаете серединой отрезка ВС.
В силу определения линейного преобразования образы середин
отрезков AD и ВС будут серединами отрезков A'D' n В'С, а так
как середины AD и ВС совпадают, то и середины отрезков
A'D' и В'С совпадают; но отсюда следует, что f (AB) = f (CD)
(A7fl' = C7D/).
Из доказанной теоремы следует, что всякое линейное
преобразование / множества всех точек пространства порождает
преобразование множества всех векторов пространства (его мы
будем также обозначать буквой /). В самом деле, пусть
/—линейное преобразование множества всех точек пространства, а а —
произвольный вектор. Пусть АВ — произвольный направленный
отрезок, входящий в класс равных между собой направленных
отрезков, образующих вектор а. Обозначим через А' и В' образы
точек А и В при преобразовании /. Поставим в соответствие
вектору а вектор fa, который является классом всех направленных
отрезков, равных направленному отрезку А'В'.
Из доказанной теоремы следует, что если задан свободный
вектор а, то указанное соответствие от а к fa однозначно
определено.
Теорема 2. При линейном преобразовании множества всех точек
пространства образ суммы двух векторов равен сумме образов
слагаемых, т. е.
? 173. СВОЙСТВА ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ 489
Доказательство. Отложим вектор а от точки А
а=АВ,
а от точки В отложим вектор b
b^BC,
Тогда
Пусть А', В' С — образы точек А, В, С при линейном
преобразовании /; тогда
А В' = fAB = /а,
АХ' = [АС = / (а + Ь).
Но аЪ' + вЪ'^аЪ', значит,
t{a + b) = fa + fb.
Теорема 3. При линейном преобразовании множества всех /почек
пространства образ произведения числа на вектор равен произв дв-
нию этого числа на образ рассматриваемого вектора, т. е.
Доказательство. Отложим векторы аи b = ka от одном
и той же точки А:
а=АВ: Ха = АС.
Тогда
и утверждение теоремы сразу следует из определения линейного
преобразования множества точек пространства,
Из теорем 1 и 2 следует, что линейное преобразование
множества всех точек пространства порождает линейное преобразование
множества всех векторов пространства.
Имея в дальнейшем дело с линейными преобразованиями
множества точек и множества векторов, будем различать эти понятия
терминами: линейное точечное преобразование и линейное
векторное преобразование.
Из теорем 2 и 3 вытекает теорема 4 о линейной комбинации
векторов.
Теорема 4. При линейном преобразовании образом линейной
комбинации векторов является линейная комбинация их образов
490 Глава XIV. ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
сссп.сипитвенно с теми же коэффициентами:
Teopewa 5. При линейном точечном преобразовании
пространства оно отображается или на пространство, или на плоскость,
или на прямую, ила в точку.
Доказательство. Введем в пространстве общую декартову
систему координат с началом в точке О и масштабными
векторами ег, ег, es. Пусть М (х, у, z)— произвольная точка пространства,
О' и Ж — образы точек О и М при линейном преобразовании /.
Так как
то
JOM = СУМ' = xfel + yfe2 -f zfes.
I случай. Векторы jev, fe2, fe3 линейно независимы,
следовательно, некомпланарны.
Тогда каждая точка М' пространства при преобразовании /
имеет прообраз. В самом деле, если векторы felt fe2, fes некомпла-
иарны, то вектор О'М' можно разложить по этим векторам:
О'М' —xfe1Jr yfe2 + г/е3 и мы видим, что точка М' является
образом точки М, определяемой радиусом-вектором
Таким образом, в этом случае пространство отображается на
пространство (а не в пространство). Это отображение к тому же
взаимно однозначно, так как разные прообразы М и N,
определяемые радиусами-векторами:
ОМ = хег + уе2 + ze3,
имеют разные образы М' и N', такие, что
(УМ' = х\ех + yfe2 -г zfe3,
+ zjea.
В самом деле, если предположить, что точки М' и N'
совпадают, то в силу того, что точки М (х, у, г) и N (xlt ylt zx) различны,
мы получили бы
xfeY + yfe2 -f zfe3 = xjet + y1fet
т. е. векторы \ех fe2, fes оказались бы линейно зависимыми (ибо
в силу различия точек М и N хотя бы одна из разностей х—х1г
у~ух, z-—zl отлична от нуля).
§ 173. СВОЙСТВА ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ 491
[1 случай. Векторы [еи \ег, fes линейно зависимы
(следовательно, компланарны), но среди них есть два линейно
независимых (следовательно, неколлииеарных).
Пусть /ех и fe2 — неколлипеарные кекторы. Так как
векторы fev fe2, fe3 компланарны, то из соотношения О'М' =xfe1 +
■\-yfet-\-zfe3 следует, что точка М' лежит й плоскости,
проходящей через точку О' компланарно векторам fet и \е2. Так как
векторы \ег и fe2 иеколлинеарны, то любая точка М' этой плоскости
имеет прообраз в рассматриваемом линейном преобразовании;
в самом деле, если М' —любая точка указанной плоскости, то вектор
О'М' можно разложить по векторам \е^ u fe2:
и прообразом точки М' при линейном преобразовании / является
точка М, определяемая радиусом-вектором
ОМ = хег + уе2.
Таким образом, в этом случае пространство отображается на
плоскость (а не в плоскость).
III случай. Векторы felt fe2, 'e3 попарно коллинеарны, но
среди них есть ненулевой вектор.
Пусть, например, [е1ф0. Так как векторы /e1; /e2, fe9 попарно
коллинеарны, то из соотношения О'М' = xfe1 + yfei-\-zfe3 следует,
что точка М' лежит на прямой, проходящей через точку О' кол-
линеарно вектору fe^
Вместе с тем любая точка М'(х,у,г) этой прямой имеет
прообраз; это будет, например, точка М, определяемая
радиусом-вектором ОМ = хех. __^
IV случай. /е1 = /е2 = /е3 = 0. В этом случае О'М' = 0 для
любой точки М' и все пространство отображается в одну точку О'.
Теорема 6 (обратная). Рассмотрим в пространстве две
произвольные точки О и О', три некомпланарных вектора ех, е2, £3 "
три произвольных вектора е\, ё2. е\ (они могут быть и
компланарными).
Пусть М—произвольная точка пространства и пусть
ОМ = хе1 + уе2 + гег.
поставим точке М в соответствие точку М', определяемую
относительно точки О' радиусом-вектором
Тогда такое соответствие есть линейное точечное
преобразование.
492 Глава XIV. ЛИНЕЙНЫЕ I! АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Доказательство. Пусть А, В, С — три коллииеарные точки,
связанные соотношением
АС^ХАВ. A)
Пусть х1г ylt Zy't х2, у2, г2; х3, у3, г3— соответственно координаты
точек А, В, С в общей декартовой системе координат с началом
координат в точке О и масштабными векторами ех, е2, е3, а А', В',
С, О' —образы точек А, В, С, О. Тогда
OA=xle1+yle2 + z1e3 |
67A' = xle\ +yle, -fzjg,,
075'=^', +//2е8 +zse',,
<7С' = х3е', + у3е'2 -f zae2.
Из соотношений A) и B) находим
(Xg—Xj) ег + (Уз—Ух) е2 + (г3—2L) e3 =
откуда в силу некомпланарностн векторов ех е2 е3
x?—x1='k{xi~xl), у3 — у1 = 'к(уг—у1) г3 — г1 = Х(гг — г1),
значит,
(*i—xi)e\ +(y3—yi) е* + (г3 —2i)e3 =
= ^ f(-^2 ~-^l) «i -f О/г ~ J/i) el + B2~2i) ej]>
или
AX' = ХЛ7^'.
Теорема 7. £сли пры линейном точечном преобразовании f
пространства два неколлинеарных вектора ег и е2 отображаются в два
нгколлинеарных вектора fet и ,е2, то всякая плоскость л,
компланарная векторам ег и е2, отображается и притом взаимно
однозначно на некоторую плоскость я', компланарную векторам fex и fe2.
Доказательство. Возьмем на плоскости я произвольную
течку О; пусть О' —образ точки О при преобразовании /.
Обозначим через п' плоскость, проходящую через точку О' компланарно
векторам fex и fez. Тогда плоскость я линейным преобразованием /
отображается взаимно однозначно на плоскость я'.
В самом деле, пусть М — произвольная точка плоскости п.
Вектор ОМ можно разложить по векторам ех и ег\'
хе1+уе2.
$ 173 СВОЙСТВА ЛИНЕЙНЫХ ПРГ-ОБРЛЗОВАНИ.1 493
Отсюда
где М' — образ точки М при преобразовании/. Из последнего
соотношения следует, что точка ЛГ лежит в плоскости я'.
Далее, если М' — любая точка плоскости л', то вектор О'М'
можно разложить по векторам fex и /е2 (эти векторы по условию
неколлинеарны):
и прообразом точки М' в плоскости л является точка М,
определяемая радиусом-вектором
Наконец две различные точки М я N плоскости л
отображаются при преобразовании / в две различные точки Mf и N',
так как из соотношений
ОМ ^х
следует
и точки М' и Л" различны, так как различны точки М и N, а
векторы fet и /е2 неколлинеарны.
Теорема 8. Если при линейном преобразовании / пространства
ненулевой вектор eL переходит в ненулевой вектор felt то всякая
прямая, коллинеарпая вектору ег, отображается и притом взаимно
однозначно на некоторую прямую, коллинеарную вектору je1.
Доказательство анало! ично доказательству предыдущей теоремы.
Следующие теоремы для плоскости доказываются аналогично
соответствующим теоремам для пространства.
Теорема 9. При линейном отображении плоскость отображается
или на плоскость, или на прямую, или в точку, причем в случае
отображения на плоскость оно будет взаимно однозначным.
Теорема 10 (обратная). Введем общую декартову систему
координат с началом в точке О и масштабными векторами et и е.г.
В той же или другой плоскости л' возьмем точку О' и два век-
тори ewe (может быть линейно зависимые). Поставим в
соответствие произвольной точке М (х, у) плоскости л, заданной
радиусом-вектором ОМ = хе^+уе.г, точку М', определяемую радиусом-
вектором О'М' = хв\ -\-ув2 ■ Гакое отображение будет линейным
отображением плоскости п в плоскость л' (если плоско, пш лил'
совпадают, то следует говорить о преобразовании плоскости л).
494 Глава XlVt ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Теорема 11. Если при линейном отображении / плоскости какой-
либо ненулевой вектор ег отображается на ненулевой вектор fe±, то
любая прямая \ плоскости я, коллингарная вектору ех,
отображается и притом взаимно однозначно на прямую Г плоскости я',
колшнеарную вектору \ех {если прямые I и /' совпадают, то
следует говорить о линейном преобразовании прямой I).
§ 174. Линейные преобразования в координатах
Введем в пространстве общую декартову систему координат
с началом в точке О и масштабными векторами ех, еъ, е3 и
обозначим через О' образ точки О, а через е^, е2, ез—образы
векторов ег, ег, е3 при каком-нибудь точечном линейном
преобразовании f. Пусть М(х, у, г) — произвольная точка пространства, а М'—■
ее образ при рассматриваемом линейном преобразовании /. Тогда
A)
и потому
4 B)
Разложим векторы Jev 'e2, fe3 и 00' по векторам еи е2, е3:
C)
a33e3,
00' = а1е1 + а2е2 + а3е3. D)
Из соотношений B), C), D) найдем
Отсюда находим координаты х', у', г' точки М' (как
коэффициенты при ev e2 е3):
х' = altx + al2y -f аиг -\- ах,
z = а31х -f а32у + а33г + а3.
Матрицу
/«И «12 «13'
А = I О21 «22 «23
\«31 «32 «33/
§ 174 ЛИНГ.ИПЫЕ ПРЕОБРАЗОВАНИЯ В КООРДИНАТАХ -J95
будем называть матрицей линейного преобразования /, а матрицу
/01Л «12 «13 «1
-1 = («21 «22 «23 «2
\«31 «82 «33 (■
расширенной матрицей линейного преобразования /.
При линейном преобразовании множества всех векторов
пространства координаты вектора fa —{х', у', z'} в любом базисе
еи е2, е8 через координаты сектора а = {х, у, z} в том же базисе
выражаются линейными однородными соотношениями. В самом деле,
разлагая а по базису eL, e2, ея
находим
и полагая
/е2 = {ап, а21, аь1}, /е2 = \а1г, а22, а32}, )'е3 = {а1з, а23, а33},
получим
Z, F)
г' = ая1х + ая2у + а33г.
Матрицу
/ои о12 о13\
Л = о21 ог2 а23 I
\«31 «32 «33/
будем называть матрицей, соответствующей линейному
преобразованию f множества всех векторов пространства.
Если даны два линейных преобразования f и g в координатах;
а12г/ + «13^ + ах л:' = й их + 6
' (g)
г' = ал1х + аму + aS3z + а,, г' = Ья хх + 6
то линейное преобразование )g в координатах запишется гак!
х' = ап Fпх + & к г/ + Ь1зг + bL) + «i2 (&2Ja; + b.i2y
у' = а21 (bnx + bl2y + blsz
+ «аз Ф31х + bs2y + 6S32 + bs) + a2,
г' = a81 (bnx + b^u + blsz + by) + a32 (/;2Ix + Лг2/у + b.i3z + &2) -f
г + ^з) + «3.
496 Г л л в и XIV ЛИНЕЙНЫЕ И АФФИННЫЕ [^ОБРАЗОВАНИЯ
или
X —
+
4,' = .
г'-
(о, А,--а
■ (<?[ А^з i <■
(a., Ai + <J;
(«8 Al "I" п
'12&21 + а13&81)*
J12&23 + ai3^i3)?
22^21 + a2Ai)*-
ft I /7 Л ) У
1
/
+ C#i A
-Х- in h
2 + Oi2^o
f a12624-
+ «22622
"Г «32^22
.,-ЬОгАг)//
■oJ3&g + ai,
— a 6 ) г/ -1
+
Отсюда видно, что линейному преобразованию /g соответствует
матрица АВ, где Л и S — матрицы, соответствующие линейным
преобразованиям / и g (это, конечно, верно и в том случае, если
рассматриваются линейные преобразования множества всех
векторов пространства). Если линейное преобразование /
невырожденное (взаимно однозначно), то линейное преобразование /~х,
обратное, дли f, в координатах выражается соотношениями
х= Аи(х' -aJ+Aviy' — at) + А1з(г' — ая),
У=А21(х' — а1) + А2г(у' — ал) + А2а(г' — а3),
z = AS1 (x'-aj + Ass (у' —а2) + AS3 (г' — аа),
которые мы получим, разрешив уравнения (/) относительно х, у и г.
В этих соотношениях (A{k) — матрица Л, обратная для матрицы А.
Таким образом, если линейному преобразованию f соответствует
матрица А и если / — невырожденное линейное преобразование, то
линейному преобразованию /"', обратному для /, соответствует
матрица Л, обратная для А (это верно и в том случае, если / —
преобразование множества всех векторов пространства).
Если / и g — линейные преобразования множества всех векторов
пространства, если ..м соответствуют матрицы А и В, го линейному
преобразованию / ■{-g соответствует матрица А-{-В. Наконец,
если f — линейное преобразование множества всех векторов
пространства, то преобразованию Xf соответствует матрица КА, где
А — матрица, соответствующая преобразованию /.
Мы показали, что при любом точечном линейном
преобразовании / координаты х', у', z образа А-Г точки М через
координаты х, у, z точки М выражаются линейными соотношениями.
Верно и обратное положение: если в пространстве введена общая
декартова система координат и каждой точке М(х,у,г) ставится
в соответствие точка М' (х1, у', г'), координаты которой через
координаты точки М выражаются линейными соотношениями E), то
такое соответствие есть точечное линейное преобразование.
В самом деле, рассмотрим точку О' и векторы 00' fel7 /ег, /еа,
определяемые соотношениями D) и C); тогда
Ш' = 00' \х\ех i-yle2 -|- г[еа,
174 ЛИНИИ ЫЦ ПРЕОБРАЗОВАНИЯ В КООРДИНАТАХ 497
ИЛИ
в то время как
Остается сослаться на теорему 6 предыдущего параграфа.
Таким образом, точечное линейное преобразование
пространства можно было определить линейными соотношениями E),
выражающими координаты образа М' через координаты
прообраза М, и такое определение было бы эквивалентно данному
выше.
Проще доказывается аналогичное положение для множества
векторов: линейное преобразование fa множества секторов
пространства можно определить как преобразование, при котором вектору
а = {х, у, z}, заданному своими координатами относительно общей
декартовой системы координат, ставится в соответствие вектор
fa = {x', у', г'}, координаты которого выражаются через х, у, z
соотношениями F). Для доказательства надо проверить выполнимость
соотношений
для любых двух векторов а и Ъ и любого числа К,
Если линейное преобразование множества всех точек
пространства в некоторой общей декартовой системе координат выражается
соотношениями E), то соответствующее ему линейное
преобразование множества всех векторов пространства в той же системе
координат выражается соотношениями F) с Теми же значениями aik
(это следует из того, что координаты вектора А В равны
разностям соответствующих координат конца В и начала А этого
вектора).
Аналогично доказывается, что линейное преобразование
плоскости в координатах записывается в виде
х' = аг1х + апу + аъ у' = a2lx + ai2y + a2,
где О' (аъ аг) — образ начала координат О, а /е1 = {а11, а21} и
/е2 = {а12, а22} —образы масштабных векторов ех и ег.
Линейное преобразование прямой в координатах имеет вид
X = пг1Х -f- flj,
где О'{аг) — образ начала координат, а яп — координата образа [et
масштабного вектора ev Если же речь идет о линейном
отображении плоскости я в плоскость я' или прямой / в прямую /' то
формулы остаются теми же, только надо предположить, что имеются
две общие декартовы системы координат: одна в плоскости л,
другая в плоскости п' (или одна на прямой /, другая на прямой /');
498 Глава XIV. ЛИНЕЙНЫЕ I] АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
при этом если за начало координат в плоскости л' (или на прямой /')
взять образ точки О, то формулы будут не только линейными, ею
и однородными (х' — allx + a12y. у' = a2lx + a2iy для
отображения плоскости в плоскость и x'=atlx для отображения прямой
в прямую).
Теорема. Введем в пространстве две системы координат:
О, ех, е2, ея и Q, slt s2, s3 (О и Q — начала координат).
Пусть
Ml 2 3 \ /1 2 з\
*21 2 3 I " ~~
J31 «32 «Зз/
соответственно матрица линейного преобразования * f в этих
базисах.
Рассмотрим матрицу
С32 С33/
элементы которой являются коэффициентами разложения векторов
slt s2> S3 по бамсу е{, е2, е3:
B2 "Г ''ЗЗ
Тогда
Доказательство. Рассмотрим линейное преобразование g
множества всех векторов пространства, которое векторы ех, е2, es
переводит соответственно в векторы slt s2, s8:
Матрицей этого преобразования в базисе ev e2, e3 будет С.
Согласно условию теоремы
} = Ь l
* f — линейное преобразование множества всех точек пространства или
множества всех векторов пространства (в последнем случае достаточно ввести
в рассмотрение ква базиса; eit e2, еъ и sx, s%, $4).
§ Е75 АФФИННЫЕ ПРЕОБРАЗОВАНИЯ 499
ИЛИ
fge2 = b12gex -|- &22^e2 + b32ges,
или
/g«i = g {buex + fr21e2 -f 6sle3),
/g^2 = g {bViet + bvle2 -!- &32e3),
fge., = g {bl3el -r biSe2 + bSiie3),
или
Таким образом, матрица линейного преобразования g~^fg (в
базисе ех, е2, е3) есть матрица Б. Но матрица линейного
преобразования g есть С, а матрица произведения линейных
преобразований равна произведению матриц сомножителей.
Значит,
Отсюда следует, что
Det В = Det С"' Det A Det С = ~ Det A Det C-Det Л,
т. е. определитель матрицы линейного преобразования не зависит
от выбора базиса.
Аналогичные положения имеют место на плоскости.
§ 175. Аффинные преобразования и аффинные отображения
Линейное точечное преобразование пространства (плоскости
или прямой) называется аффинным, если оно взаимно однозначно.
Линейное точечное отображение плоскости на плоскость или
прямой на прямую называется аффинным., если оно взаимно одно-
значно.
Из § 172 (теорема 5, I случай) следует, что линейное
преобразование пространства будет взаимно однозначным, т. е.
аффинным тогда и только тогда, когда при этом преобразовании какие-
нибудь три некомпланарных ьектора переходят снова в некомпла-
нарные векторы.
Замечание. Если преобразование пространства аффинное,
то оно любую тройку некомпланарных векторов переводит б
некомпланарную тройку. В самом деле, предположим, что какие-
нибудь три некомпланарных вектора а, Ь, с при аффинном
преобразовании / переходят в компланарные векторы а', Ь', с'.
500 Глава XIV ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Отложим секторы а. Ь, с от произвольной точки О пространства
Пусть Ог, А', В', С —образы точек О. А В, С при
преобразовании /. Тогда
ОГА' = а', О7В' = Ь', О'С'^с'.
Так как по предположению векторы а', Ь', с' компланарны,
то точки О', /Г, В', С лежат в одной плоскости и, значит,
преобразование f любую точку М пространства переводит в точку
этой плоскости. Значит, / — не взаимно однозначное
преобразование, что противоречит предположению. Отсюда также следует, что
при аффинном преобразовании два неколлинеарных вектора
переходят в два неколлинеарных вектора, а любой ненулевой сектор
переходит в ненулевой вектор.
Аналогичные положения имеют место для аффинных
отображений плоскости на плоскость и для аффинных преобразований
плоскости, а также для прямых.
Если точечное линейное преобразование пространства задано
в координатах
х' = аих + апу + alsz + av
у' = а21х + а22у + a2Sz -f a2, A)
г' = а31х + а32у -}- а3,г -f ая,
то оно будет взаимно однозначным, следовательно аффинным, тогда
и только тогда, когда
А=
22
так как при заданном образе М'(х', у', г') он будет иметь один
и только один прообраз М(х, у, z) тогда и только тогда, когда
система A) имеет при заданных х', у', г' одно и только одно
решение х, у, г, а необходимым и достаточным условием этого
является неравенство Д^О.
Аналогично точечное линейное отображение плоскости п в
плоскость л' или точечное линейное преобразование плоскости л будет
взаимно однозначным (т. е. аффинным) тогда н только тогда,
когда оно два неколлинеарных вектора ех и ег плоскости л
переводит в два неколлинеарных вектора.
Если точечное линейное отображение плоскости я на плоскость
л', или точечное линейное преобразование плоскости л, задано
в координатах
х' = altx + а12у + alt у' = а21х + а22у + а2,
$ 176. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ АФФИННЫХ ПРЕОБРАЗОВАНИЙ 501
то оно будет взаимно однозначным, следовательно аффинным, тогда
и только тогда, когда
11 «12
При аффинном преобразовании пространства любая плоскость
я отображается аффинно на некоторую плоскость я', которая,
в частности, может совпасть с плоскостью я. Говорят, что
аффинное преобразование пространства порождает аффинное
отображение плоскостей пространства.
Наконец, линейное отображение прямой р на прямую р или
преобразование прямой р будет взаимно однозначным тогда и только
тогда, когда оно непулевой вектор е1 прямой р переводит в
ненулевой вектор.
Аффинное преобразование пространства порождает аффинные
отображения прямых пространства. Аффинное отображение
плоскости на плоскость порождает аффинное отображение прямых,
лежащих в этих плоскостях.
Если линейное отображение прямой на прямую или
преобразование прямой задано в координатах
то оно будет взаимно однозначным, следовательно аффинным, тогда
и только тогда, когда ап^0.
§ 176. Геометрическая теория аффинных преобразований*
Аффинное отображение плоскости я на плоскость я' (и
аффинное преобразование пространства) можно определить как такое
взаимно однозначное отображение плоскости л на плоскость л',
при котором три любые точки плоскости л, принадлежащие одной
прямой, отображаются в три точки плоскости я', также
принадлежащие одной прямой.
Из этого определения следует, что такое отображение
линейное. Доказательство этого положения достаточно сложное, поэтому
разделим его на ряд теорем**.
* Все данные здесь определения и теоремы относятся к действительной
плоскости и действительному пространству. Данное здесь определение
аффинного отображения и аффинного преобразования в случае действительной
плоскости и действительного пространства не эквивалентно определению, данному
в предыдущем параграфе, которое можно отнести, со всеми вытекающими
из него свойствами, для комплексного пространства и комплексной
плоскости.
** Таким образом, аод аффинным отображением плоскости л на плоскость
я' во всех последующих теоремах мы подразумеваем взаимно однозначное
отображение, сохраняющее прямолинейное расположение точек.
Доказательство линейности взаимно однозначного преобразования пространства,
сохраняющего прямолинейное расположение точек, не содержит никаких
дополнительных трудностей
502 Глава XIV ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Теорема S. При аффинном отображении а плоскости я на
плоскость п' множество всех точек произвольной прямой I, лежащей
на плоскости л, отображается и притом взаимно однозначно на
множество всех точек некоторой прямой /', лежащей на
плоскости я'
Прямая [' называется образом прямой I, а прямая
I—прообразом прямой V при аффинном отображении а.
Доказательство. Возьмем на прямой / две различные точки
А и В. Пусть А' и В'— их образы при аффинном отображении а.
Тогда множество всех точек прямой I отображается во множество
всех точек прямой /', проходящей через точки А' и В'.
Обратно, прообраз С любой точки С' прямой А'В' лежит на
прямой АВ. В самом деле, допустим, что на прямой /' есть точка С,
прообраз С которой не лежит на прямой АВ. Возьмем любую
точку М, лежащую на плоскости л. Из трех пар прямых:
МА, ВС; MB, СА; МС, АВ
есть по крайней мере одна пара пересекающихся. Пусть,
например, МА и ВС пересекаются в точке Р. Так как точки В, Р и С
принадлежат одной прямой, то их образы В', Р', Сг также
принадлежат одной прямой, именно прямой /'. Далее, точки Р, М и А
принадлежат одной прямой, следовательно, их образы Р', М' и А'
также лежат на одной прямой, а так как точки Р' и А' лежат
на прямой /' и различны, то точка М' лежит на прямой /'.
Таким образом, образы всех точек М плоскости л лежат на
прямой /' и, значит, преобразование а не взаимно однозначное —
противоречие.
Итак, доказано, что прообраз С любой точки С прямой /'
лежит на прямой I. Значит, отображение а порождает
отображение множества всех точек прямой / на множество всех точек
прямой /'. Это отображение взаимно однозначное в силу взаимной
однозначности отображения а.
Замечание. В процессе доказательства установлено, что при
аффинном отображении а плоскости л па плоскость л' три точки
плоскости л, не принадлежащие одной прямой, отображаются в три
точки плоскости я', также не принадлежащие одной прямой.
Следовательно, отображение, обратное аффинному, снова
аффинное.
Теорема 2. При аффинном отображении а плоскости л на
плоскость л' образы р' и q' параллельных прямых р и q суть
параллельные прямые, а образы р' и q' пересекающихся прямых р и q
суть пересекающиеся прямые; при этом точка М' пересечения
прямых р' и q' является образом точки М пересечения прямых р и q.
Доказательство. Если прямые р и q параллельны, т. е.
не имеют ни одной общей точки, то их образы р и q' при аффинном
отображении а также ;<": имеют ни одной общей точки, т. е. p'\\q'.
176. ГЕОМЕТРИЧЕ-СКЛЯ ТЕОРИЯ АФФИННЫХ ПРЕОБРАЗОВАНИИ 503
Если прямые р и q пересекаются, т. е. имею г и притом только
одну общую точку М, то и прямые р' и q' имеют только одну
общую точку М', являющуюся образом точки М.
Теорема 3. При аффинном отображении а плоскости л на
плоскость л' середина О произвольного отрезка А В переходит в
середину О' отрезка А'В' (А' и В'— образы точек А и В при
отображении а).
Доказательство. Возьмем на плоскости к произвольную
точку С, не лежащую на прямой АВ, соединим ее с точками А
и Б и проведем через точку А прямую, параллельную ВС, а через
точку В — прямую, параллельную АС; точку пересечения
проведенных прямых обозначим через D. Прямые CD и АВ пересекаются
в точке О, являющейся серединой отрезка А В. После аффинного
отображения а точки А, В, С, D перейдут в точки А', В', С, D',
такие, что A'D'\\C'B' и Л'С'ЦВ'О', причем прямые А'В' и CD'
пересекаются в точке О', являющейся образом точки О. В силу
того' что A'D'WC'B' и A'C'\\B'D' точка О' является серединой
отрезка А'В'.
Теорема 4. Если разделить отрезок А В на п равных частей
AOl = OlOs=...=On_1B,
то
где А', О\, О'%, ... , On-i, В'—образы точек А, О1( О2, ...,Оп_1, В
при аффинном отображении а плоскости п на плоскость л'.
Эта теорема является следствием предыдущей.
Из этой теоремы следует, что если точка С делит
направленный отрезок А В в рациональном отношении к, то образ С
точки С при аффинном отображении а плоскости я на плоскость
п' делит отрезок А'В в том же отношении к.
Основная трудность, которую нам еще предстоит преодолеть,—
это доказательство того, что простое отношение (ABC) трех точек,
принадлежащих одной прямой плоскости я, инвариантно при
аффинном отображении плоскости я на плоскость я' и в том случае,
когда (ЛВС) —иррациональное число.
Теорема 5 (Дарбу), Рассмотрим аффинное отображение а
плоскости л на плоскость л'. Пусть АВ — произвольный отрезок,
лежащий на плоскости л, а С — какая-нибудь точка прямой АВ,
внешняя для отрезка АВ. Тогда образ С точки С при отображении
а является внешней точкой для отрезка А'В', где А' и В'-—образы
точек А и В при отображении ос.
Доказательство. Проведем через точки А и В две
параллельные прямые р и q и построим два неравных отрезка РгР2
и QxQ-4, лежащих соответственно на прямых р и q, таких, что
504 Глава XIV ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
точка А является серединой отрезка РгР2, а точка б—серединой
отрезка Q^^,. Прямые P1Q1 и P2Q2 пересекаются в точке М*
лежащей на прямой А В; прямые /\Q2 и P2Q1 также пересекаются
в точке Л', лежащей па прямой А В. Обозначим через С середину
отрезка MN и докажем, что:
1) точка С лежит вне отрезка АВ;
2) изменяя отрезки РХР2 и QxQ2, можно придать точке С
любое положение на прямой АВ вне отрезка АВ.
1. Введем на прямой АВ систему координат и пусть точки
Л и В во введенной системе имеют координаты хх и х2.
Так как
AN AM PJA^
NB MB q^q2
то координаты хм и xN точек М и N определяются соотношениями
а координата точки С
Г—1 (Г I 1- > _ *l—k**2
Отсюда следует, что точка С делит направленный отрезок АВ
в отношении —X2 и потому лежит вне отрезка АВ.
Р Р
2. Так как Х = -^-у, а выбор длин и направлений отрезков
РХР2 и QXQ2 произволен, то "К может принимать все
действительные значения кроме 0 и ±1 (так как мы считаем отрезки РгР2
и QiQ2 невырожденными и предполагаем, что РХР2 Ф QjQ2)-
Отсюда следует, что число —%? принимает все отрицательные
значения кроме —1, а это и означает, что точка С может занимать
на прямой АВ любое положение вне отрезка АВ.
Произведем теперь аффинное отображение а плоскости я па
плоскость л'. Пусть А', В' р\, Р2, Q[, Qit M', N', С-образы
точек А, В, Рх, Р2, Qlt Q2, M, N, С. В силу предыдущих теорем
P'lP's II Q\Q\ и точки А' и В' ссотнетствснно середины отрезков
Р\Р\ и Q-,Qi', точка М' пересечения прямых PtQi и P.2Q.Z лежит
на прямой А'В'\ точка Л'' пересечения прямых PiQ2 и P2Qi также
лежит на прямой А'В'. Наконец, точка С" середина отрезка А'В'
и внешняя точка для отрезка А'В' (это доказывается точно так же.
как выше было доказано, что точка С лежит вне отрезка АВ).
Из доказанной теоремы следует, что при аффинном
отображении а плоскости я на плоскость л' любая внутренняя точка С
отрезка АВ, лежащего на плоскости п, отображается во
внутреннюю точку С отрезка А'В'.
S 176. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ АФФИННЫХ ПРЕОБРАЗОВАНИЙ 505
В самом деле, в противном случае аффинное отображение а
плоскости л' на плоскость я, обратное для а, отображало бы
внешнюю точку С" отрезка А'В' во внутреннюю точку С отрезка АВ,
что противоречит теореме Дарбу.
Теорема 6. При аффинном отображении а. плоскости л на
плоскость п' сохраняется простое отношение трех точек,
принадлежащих одной прямой.
Доказательство. Возьмем на плоскости л три
произвольные попарно различные точки А, В и С и обозначим простое
отношение (ABC) через К:
— >■
А Г
~ = Х.
ев
Рассмотрим аффинное отображение а плоскости л на
плоскость л'. Пусть А', В', С—образы точек А, В и С при этом
отображении. Обозначим простое отношение (А'В'С) через X':
С'В'
требуется доказать, что К —К'. Предположим, что точка С —
внутренняя точка отрезка АВ (так что 1>0), тогда в силу следствия
из теоремы Дарбу точка С —внутренняя точка отрезка А'В' (так
что и X' > 0). Предположим, что X > К'. Разделим направленный
отрезок А'В' в отношении X:
D'B'
Разделим отрезок А'В' на п равных частей и выберем п столь
большим, чтобы одна из точек деления О' попала между точками
С" и D'. Так как (при X > %') точка D' лежит между точками С"
и В', то и точка О' лежит между С" и В', а следовательно,
прообраз О точки О' лежит между точками С и В. Теперь находим
6ч1' 0% О7? 1УВ' СВ Об
и мы пришли к противоречию.
Если точка С лежит вне отрезка АВ, например точка В лежит
между точками А и С, то
вс
506 Г л a tn XIV. ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
и прибавляя к обеим частям этого равенства по 1, получим
АС _ Л7?
СВ СЧЗ1
Аналогично доказывается инвариантность простого отношения
при аффинном отображении в случае когда точка А лежит между
точками й и С, Итак, доказано, что аффинное отображение
линейное.
§ 177. Свойства аффинных преобразований и отображений
Теорема 1 *. Произведение двух аффинных преобразований есть
снова аффинное преобразование.
Доказательство. Пусть f и g —два аффинных
преобразования. Рассмотрим три произвольные точки Л, В и С,
принадлежащие одной прямой, и пусть А', В С—образы точек А В, С при
аффинном преобразовании /, а А", В", С"—образы точек А', В', С
при аффинном преобразовании g.
Так как точки А, В, С принадлежат одной прямой, то
существует такое число к, что АС— "к А В но тогда в силу линейности
отображения / А'С = "КА'В , значит (в силу того, что g также
линейное преобразование) А"С" = 1.А"В". Таким образом,
произведение gf есть линейное преобразование, К тому же оно и взаимно
однозначно (ибо произведение двух любых взаимно однозначных
преобразований есть взаимно однозначное преобразование),
следовательно, gf— аффинное преобразование.
Теорема 2. Преобразование /~\ обратное к аффинному
преобразованию, также является аффинным.
Доказательство. Пусть А', В', С—три произвольные
точки, принадлежащие одной прямой и связанные соотношением
А'С = %А'В'\ докажем, что тем же соотношением будут связаны
их прообразы при аффинном преобразовании а.
R самом деле, пусть А « В — прообразы точек А' и В'.
Построим точку С, такую, что АС^кАВ. Пусть С*—образ точки
—-~* —■ —>
С при аффинном преобразовании f Тогда А С* = "КА'В'. Значит,
А'С = А'С*, т. е. точка С* совпадает с точкой С, поэтому С —
прообраз С'. Кроме того, ясно, что /~' взаимно однозначное пре-
* В георемах 1 и 1 имеются в виду аффинные преобразования
пространства, плоскости или прямой, причем в дальнейшем под аффинным
преобразованием будем понимать точечное линейное и взаимно однозначное
преобразование пространства, плоскости или прямой (§ 175).
§ 177 СВОЙСТВА АФФИННЫХ ПГ^ОБРАЗОВАНИЙ 507
образование (так как преобразование, обратное любому взаимно
однозначному преобразованию, снова взаимно однозначно).
Следствие. Из теорем 1 и 2 следует, что множество всех
аффинных преобразований пространства образует группу.
Точно так же доказывается, что множество всех аффинных
преобразований плоскости образует группу так же, как и множество
всех аффинных преобразований прямой образует группу.
Теорема 3. При аффинном преобразовании пространства
1) две параллельные плоскости переходят в две параллельные
плоскости;
2) две пересекающиеся плоскости ях и я2 переходят в две
пересекающиеся плоскости Я! и я2; образом прямой (пг, я2), по
которой пересекаются плоскости ях и <"т2, является прямая (ях, я2)
пересечения плоскостей к\ и я2; при этом отображение прямой
(я1; я<>) на прямую (п'и я2) — аффинное;
3) две параллельные прямые переходят в две параллельные прямые;
4) две пересекающиеся прямые р и q переходят в две
пересекающиеся прямые р' и q', причем образом точки М пересечения
прямых р и q является точка М' пересечения прямых р' и q';
5) две скрещивающиеся прямые переходят в две скрещивающиеся
прямые;
6) если прямая р параллельна плоскости я, то и прямая р\
являющаяся образом прямой р, параллельна плоскости я', в
которую переходит плоскость я при данном аффинном преобразовании;
7) если прямая р и плоскость я пересекаются, то пересекаются
прямая р' и плоскость я', являющиеся их образами, причем точка
пересечения М' является образом точки М пересечения прямой р
и плоскости я.
Доказательство. 1. Если бы образы двух параллельных
плоскостей имели хотя бы одну общую точку /И', то ее прообраз
М должен лежать на каждой из данных параллельных
плоскостей, что невозможно.
2. Если плоскости яг и я2 пересекаются, ях и
я2—соответственно образы плоскостей лх и яа> то образ любой точки прямой
(яь я2) должен лежать и на плоскости яь и на плоскости п2,
т. е. на линии (яи я2) их пересечения. Таким образом, прямая
(яъ я2) отображается в прямую (я,, л2). Так как преобразование,
обратное аффинному, снова аффинное, то и обратно, прямая
(я1( яа) аффинно отображается в прямую (дь я2). Поэтому прямая
(яь яа) отображается на прямую (ях, яа). Линейность и взаимная
однозначность этого отображения (т. е. аффинность) следуют из
того, что /—аффинное преобразование.
3. Две параллельные прямые р и q всегда лежат в одной
плоскости я. Их образы р' и q' при аффинном преобразовании / бу-
508 Глава XIV. ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВ \НИЯ
дут лежать на плоскости л', являющейся образом плоскости л
при аффинном преобразовании /. Прямые р' и д' параллельны, так
как если бы они имели общую точку ЛГ, то ее прообраз М
должен лежать и на прямой р, и на прямой q, что невозможно
Положения п, 4, 5, 6, 7 доказываются аналогично.
Теорема 4. Существует и притон только одно аффинное
преобразование пространства, которое любые четыре точки А, В, С,
D, не лежащие в одной плоскости, переводит в произвольные четыре
точки А', В', С", D', также не лежащие в одной плоскости.
Доказательство существования. Так как точки А,
В, С, D не лежат в одной плоскости, то векторы DA, DB, DC
некомпланарны. Точно также некомпланарны и векторы D'A', D'В
и D'C. Рассмотрим две системы координат: одну с началом в
точке D и масштабными векторами DA = elt DB — ez, DC — e3 и дру.
гую с началом в точке D' и масштабными векторами D'A' = ey,
Т)'~В' = ег, /Ге"' = ез.
Пусть М — произвольная точка пространства и х, у, г— ее
координаты в первой системе. Поставим в соответствие точке М
такую точку ЛГ, которая во второй системе имеет те же координаты
х, у, г, какие имеет точка М в первой системе. Это соответствие
является аффинным преобразованием, так как оно взаимно
однозначно и линейно. Это преобразование переводит точки A, B,C,D
соответственно в точки А', В', С', D', так как точки первой
четверки имеют в первой системе такие же координаты, какие точки
второй четверки имеют во второй системе.
Доказательство единственности. Предположим, что
существует другое аффинное преобразование, переводящее точки
А. В, С, D соответственно в точки А', В', С, D'. В силу
линейности преобразования любой точке М, имеющей в первой системе
координаты х, у, г, должна соответствовать точка ЛГ, которая имеет
во второй системе такие же координаты, какие точка М имеет
и первой системе. Следовательно, это преобразование совпадает
с тем, которое было построено при доказательстве
существования.
Следствие. Аффинное преобразование пространства,
которое оставляет неподвижными четыре точки, не лежащие в одной
плоскости, есть тождественное преобразование.
Замечание. Аналогично доказывается, что аффинное
отображение плоскости на плоскость или аффинное преобразование
плоскости определяется и притом однозначно соответствием двух не-
коллинеарных троек точек.
Аффинное отображение прямой на прямую или аффинное
преобразование прямой определяется и притом однозначно заданием
двух пар соответственных точек.
178, АФФИННЫЕ ПРЕОБРАЗОВАНИЯ "' КООРДИНЛ1ЛХ
509
§ 178. Аффинные преобразования е координатах
Пусть даны два аффинных преобразования пространства f и g
относительно общей декартовой системы координат:
х' = апх + а12у + a13z + аг,
г' =
Det A
+ а32у -\- а33г + а3,
а21
i2 а2
23
DetB =
b., b,9 b.
Преобразование^ переводит точку М(х, {/, г) в точку М' (х' у', г /,
определяемую формулами (g), а преобразование f точку М' (х', у' z )
переводит в точку М" (х", у", г") с координатами
х" = йцх' + а12у' + а13г' -К ах,
у" = а2хх' + а22у' -f о23г' 4- «2»
Значит, мы получим преобразование fg в координатах, если
в последние формулы вместо х', у', г' подставим их выражения
из формул (g); сделав это, получим
х" = (aubu + aiabtl + a13b31) x + (а1УЬи + a12bn + al3b32) у +
+ (aUbib + Gi2^23 + «13Ьзз) z + «ii&i + агФг + «1з&з + «1.
У" = («21&П + aMbtl+a23b31) x + (atlblt + a22bi2 + a23b32) у +
+ («2 А? "Г «22^23 + «23&3з) Z + G21&1 + Я22Ь2 + G23fc3 + «г»
г" = (я3 Ai + «32621 + a3Ai) * + («3i6i2 + а^22 + аззЬ32) У +
+ (fl3 Аз + G32^23 + «33&3з) 2 + «31*1 + а32^2 + G33^3 + «V
Отметим, что матрица С преобразования fg равна произведению
матрицы А преобразования f на матрицу В преобразования g:
Отсюда
Det С = Det A • Det В,
и так как DetA^O и Det В Ф 0, то и DetC^O. Мы еще раз
доказали теорему о том, что произведение двух аффинных
преобразований есть аффинное преобразование.
Заменяя в соотношениях (f)x,y,z соответственно на х', у', г',
а у.', у', z соответственно на х, у, z и разрешая затем полученные
соотношения относительно х , у', г', получим формулы, дающие
510
Г га еа XIV. ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
в координатах преобразование [~г, обратное /i
х' = at, х -f a! 2/у + о13г + ах,
+ «2.
+
A)
Матрица B = (aik) этого линейного преобразования есть матрица,
обратная для матрицы А аффинного преобразования /:
а потому
DetB =
1
Det A
Следовательно, формулами A) дается аффинное преобразование.
При аффинном преобразовании/, заданном формулами (/),
координаты вектора а' == {х', у', z'\, являющегося образом вектора а =
— {х,у, г}, выражаются теми же соотношениями (f), в которых
надо положить а1 = а2 = а3~0, т. е. координаты х', у', z образа а'
вектора а=[х, у, z} являются линейными однородными
функциями координат х, у, z:
где Д =
1Х
13
B)
Докажем теперь следующую теорему.
Теорема. Рассмотрим в ориентированном пространстве
произвольную упорядоченную тройку векторов а, Ь, с. Пусть а' ,Ь', с' —
образы этих векторов при аффинном преобразовании B). Тогда
объемы а'Ь'с' и аЬс ориентированных параллелепипедов,
построенных на этих тройках векторов, связаны соотношением
ah с =
где А=
ап
а21 а22 а
13
21 а22 а%ъ
а3
31
33
Доказательство. Пусть а — {хъ цх, гг], b~{x2, y2, z2
С—\Х3, ys, Z3), п ={Х|, ylt Zi\, О ={Х2, у2, 22}, С ={Хд, у3, Za\.
Тогда
ii' = ax-4-au--\-az i=\ 23 (
Теперь находим
а'Ь'с'■ =
£/l 2!
S irs. лффинньм; преобразования u координатах
511
Подставляя сюда вместо X/, yi,zt(i=l, 2, 3) их выражения из
формул C) и используя формулу для произведения двух
определителей третьего порядка, получим
*i «/1 г,
Й,1 «12 «13
ИЛИ
п' I у ,, у
* — 2 i/ 2 2
a'b'c' = abc A,
D)
так как
abc =
2г
Из доказанной теоремы следует, что при аффинном
преобразовании пространства отношение объемов ориентированных
тетраэдров (невырожденных) не меняется.
В самом деле, если р, q, г — три некомпланарных вектора, а
р', q', г' —их образы при аффинном преобразовании B), то
p'q'r'=pqr A.
Отсюда и из соотношения D) (в силу того что А^О) получим
a'b'c' abc
jFq7? ~ ~pq? ■
Отметим еще ряд следствий: если А > 0, то аффинное
преобразование (f) сохраняет ориентации ориентированных
параллелепипедов, а если А < 0, то меняет их ориентации на
противоположные.
Если |А| = 1, то объемы всех параллелепипедов при таком
аффинном преобразовании сохраняются.
Множество Г\ всех аффинных преобразований пространства,
сохраняющих объемы, образует группу, являющуюся подгруппой
группы Г всех аффинных преобразований.
Если А=1, то сохраняются и объемы, и ориентации
тетраэдров; множество всех аффинных преобразований пространства,
сохраняющих объемы и ориентацию, также образует группу Г2,
являющуюся подгруппой группы Гг аффинных преобразований,
сохраняющих объемы.
Если Det А~— 1, то объемы тетраэдров сохраняются, но
ориентации их меняются на противоположные (множество таких
преобразований не образует группы).
Если при аффинном преобразовании пространства имеется
неподвижная точка (т. е. точка О, образом которой является она
сама), то такое аффинное преобразование называется центроаффин-
ным. Если принять неподвижную точку центроаффинного преобра-
512 Глава XIV ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
зовапия за начало общей декартовой системы координат, то цен-
троаффинное преобразование в координатах запишется так:
Множество всех центроаффииных преобразований пространства
образует групп) Г3, являющуюся подгруппой группы Г всех
аффинных преобразований пространства. Множество всех центроаф-
финных преобразований, сохраняющих объемы, образует группу Г4,
являющуюся подгруппой группы Г1 и подгруппой Г3. Множество
всех центроаффииных преобразований, сохраняющих объемы и
ориентацию, является группой Г5; эта группа является
подгруппой групп Г, Г\, Г3, Г4.
Аналогичное положение имеет место и для аффинных
преобразований плоскости, только вместо объемов ориентированных
параллелепипедов надо говорить о площадях ориентированных
треугольников (или ориентированных параллелограммов).
§ 179. Примеры аффинных преобразований
Пример 1. Введем на плоскости декартову прямоугольную систему
координат и поставим в соответствие точке Л1 (а, у) точку А1'(х',у') с
координатами
х' = х, у' = ку, A)
где к > 0.
Матрица этого преобразования
Отсюда Det^ = fe^O, следовательно, преобразование A) — аффинное.
Пусть Р (х, 0) —проекция точки /И (х, у) на ось Ох Образом Р' точки Р бу-
де> она сама Далее, РМ' = {0, kij), ~Р*М = {0, у), значит, ~РМ'—кТм (рис 229)
Отсюда название этого преобразования, аффинное сжатие к оси Ох Это
преобразование мы уже использоналя выше (см § 105) и называли его
равномерным сжатием плоскости к прямой На рис 230 дан образ фигуры при сжатии
д. я fe = -g-. Для построения образа фигуры при сжатии заключаем фигуру
в прямоугольник и прямыми, параллельными его сторонам, делим этот
прямоугольник на равные прямоугольники Затем строим образы вершин
прямоугольника— это будут вершины параллелограмма. Делим этог параллелограмм
па равные парачлелограммы соответственно таким же числом ,каки для
прямоугольника) прямых, параллельных его сторонам, и врисовываем по клеткам
образ начального рисунка
Пример 2 Преобразование
х'=ж, y' = ky, к > 0,
заданное относительно общей декартовой системы координат, также является
аффинным. Оно называется косым сжатием к оси Ох по направлению оси Оу;
!79 ПРИМЕРЫ АФФИННЫХ ПРЕОБРАЗОВАНИЙ
513
если Р (х, 0) — проекция произвольной точки М (х, у) плоскости на ось Ох
параллельно оси Оу, а М' (х, ky) — образ точки М в рассматриваемом
преобразовании, то РМ'= k PM. Косое сжатие называется иногда родством (рис 231).
На рис. 232 дана фигура и ее образ при косо.; сжатии к оси Ох
Пример 3. Линейное преобразование, заданное относительно
прямоугольной (или общей декартопой)
системы координат соотношениями
x' = x-\-ky, y' = y, кфО,
называется сдвигом относительно
оси Ох
Сдвиг есть цептроаффинное
преобразование с детерминантом
k
0
—-1
так как образом точки 0@, 0)
является сама эта точка При
сдвиге сохраняются площади и
ориентация (Det Л = 1)
Если М (х, у) — произвольная
точка плоскости, а М'(х-\-ку, у)
— ее образ при сдвиге, то ММ' =
= {ky, 0^, т. е. каждая точка М
«сдвигается» по направлению оси
Ох на расстояние,
пропорциональное ее ординате (отсюда еле-
М(х,у)
М'(х',У)
Рис. 229
Рис. 230
дует, что точки, лежащие по разные стороны от оси Ох, сдвигаются в
противоположных направлениях) (рис. 233).
На рисунке 234 показан образ фигуры при
сдвиге.
Пример 4. Преобразование гомотетии с
центром гомотетии в начале координат и
коэффициентом гомотетии, равным к, выражается
соотношениями:
x' = kx, y' = ky (рис. 235).
Так как
М(х,у)
Рис. 231
Det A-.
k 0
0 k
то гомотетия—центроаффинное преобразование, сохраняющее ориентацию.
17 п. С. Моденов
514
Глава А IV. ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
На рисунке 236 дана фшура и ее образ при гомотетии с коэффициентом
k = 2.
Пример 5. Рассмотрим линейное преобразование плоскости, заданное
относительно общей декартовой системы координат соотношениями
РОДСТВО
\
\
1
\л
i
г)
(
)) L
Рис 232
Это преобразование—центроаффинное, так как данные соотношения
линейные однородные и детерминант
1»
О /<:
1
При этом преобразовании сохраняются площади и ориентация. Оно
представляет собой произведение двух косых сжатий: одно к оси Ох по
направлению оси Оу с коэффициентом k, другое к оси Оу по направлению оси Ох
с коэффициентом -г.
Так как х'у'<=ху, то при рассматриваемом преобразовании каждая гипер
бола «/ = С (С Ф 0) отображается на себя (рис 237 и 238); прообраз ikx, -£-
toiikj; (л, у) при этоу преобразовании также чежит на той же гиперболе ху=С>
на которой лежит точка (х, у) Любая точка оси Ох переходит н точку оси Ох;
лкбая точка оси Оу переходит в точку той же оси. Это преобразование на-
<S !79 ПРИМГ.РЫ АФФИННЫХ ПРПОБРЛЗОВАНИЙ
515
зывается гиперболическим поворотом, inn лоренисвым преобразованием Оно
рассматривается в теории относительности.
На рис 239 дан образ фигуры при гиперболическом повороте.
Пример 6. Рассмотрим семейство пара-
т _ _
где а—фиксированное отрицательное
"пело, а с —параметр (рис. 240) Пусть М
{х, (/) —произвольная точка плоскости.
Перенесем точку М в направлении вектора
а, перпендикулярного оси параболы, на
одно и то же расстояние h для всех точек
плоскости. Пусть точка М перейдет при
этом переносе в точку Р. Проведем через
точку Р прямую, параллельную оси
параболы, и пусть эта прямая пересечет ту
из парабол семейства у = ах2-\-с, на которой лежит точка М, в точке М'.
Поставим точке М в соответствие точку /И'. Докажем, что это соответствие теть
аффинное преобразование. В самом деле, пусть точка М (х, у) лежит на пара-
N
Рис. 233
Рис. 234
боле у = ах2-\-с. Точка М'(х',у') лежит на той же параболе, поэтому
у' = ах'2 + с.
Но по определению рассматриваемого преобразования имеем
поэтому
у' == а (х + ЛJ+о = ах2+2ahx + ah2 + с,
и так как
О
Отсюда
Рис. 235
— x-f-h, у =
1 0
lah 1
= 1.
17*
516
Рлава XIV. ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Значит, построенное аффинное преобразование сохраняет площади и
ориентацию; оно г{азывается параболическим поворотом. При параболическом
повороте каждая парабола семейства парабол
Рис. 236
переходит в себя. Параболическому повороту можно дать следующее
механическое истолкование. Пусть из различных точек вертикали в различные
моменты времени, но с одной и той же начальной скоростью выбрасываются
материальные точки. Тогда все они будут описывать параболы с общей осью
(если рассматривать движение в
пустоте) За произвольный про- гЦ
межуток времени в
горизонтальном направлении все точки
пройдут одно и то же расстояние и
каждая точка останется на своей
траектории, т. е. сила тяжести
над движущимися точками
произведет параболический поворот.
Таким образом, например,
площадь треугольника ABC,
образованного свободно летящими
точками, не будет меняться с
течением времени (если, конечно,
точки были вьгброшеныизточекод-
ной вертикали с одинаковыми
начальными скоростями (рис. 241)).
На рисунке 242 дан образ фигуры
при параболическом повороте.
Пример 7. Формулами
х' = х, у' = у, г'' = kz (k > 0)
определяется линейное преобразование пространства. Оно аффинное, так как
1 0 0
0 1 0 =кфЪ.
0 k
Рис. 237
Рис. 238
-9f X
Рис. 239
518
Г л а в о XIV. ЛИНЕЙНЫЕ 11 АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Если М (х, у, г) — произвольная точка, М' (х', у', г') —ее образ при этом
преобразовании, а Р (х, у, 0) — параллельная проекция точки М (х, у, г) в пло-
Рис. 240
Рис. 241
Рис. 242
скость хОу параллельно оси Ог, то РМ' =k PM. Это преобразование
называется аффинным сжатием пространства к плоскости хОу по направлению осп Ог
(рис. 243). На рис. 244 дана фигура и ее образ при аффинном сжатии к
плоскости хОу по направлению оси Ог.
174 примеры аффинных преобразований
519
Пример 8. Формулами
x'=x-\-kz, у' = (/, г'= г (k # 0)
определяется центроаффишюе преобразование, так как формулы линейные,
однородные и
1 0 k
0 1 0
0 0 1
= 1 >0.
г
,
М
М!
Р
м м
Рис. 245
244
Рис. 246
Это аффинное преобразование
называется сдвигом пространства
относительно плоскости хОу по
направлению оси Ох (рис 245) При
сдвиге сохраняются объемы и
ориентация. Если М—произвольная
точка пространства, а М'—ее
образ, то MM' = {kz, 0, 0}, т. е. все
точки пространства сдвигаются по
направлению оси Ох на величину,
пропорциональную аппликате; точки, лежащие по разные стороны от плоскости
хОу, сдвигаются в противоположные стороны. На рисунке 24S дана фигура и
ее образ при сдвиге относительно плоскости хОу по направлению оси Ох.
520 Глаео XIV ЛШ1Г I'lIlblF. П ЛФТПНШЛГ ПРЕО^4 1ЧОВА НИЯ
§ 180. Ортогональные преобразования и движения
Ортогональным преобразованием пространства называется
преобразование множества всех точен пространства, обладающее
следующим свойством: если А и В — две произвольные точки, а А' и
В'— их образы, то АВ = А'В'.
Иначе говоря, ортогональным преобразованием пространства
называется преобразование, при котором сохраняются длины от-
резкое.
Аналогичное определение дается для ортогонального
преобразования плоскости и для ортогонального отображения плоскости
на плоскость.
Теорема 1. Ортогональное преобразование есть линейное
преобразование.
Доказательство. Рассмотрим три попарно различные
точки А, В, С, принадлежащие одной прямой. Пусть точка В лежит
между точками А и С; тогда АВ + ВС = АС. Пусть А', В', С —
образы точек А, В, С при ортогональном преобразовании оз. Тогда
А'В'^АВ, В'С' = ВС, А'С' = АС,
значит,
следовательно, точки Л', В', С попарно различны, принадлежат
одной прямой и точка В' лежит между Л' и С'. Отсюда следует,
что если АС = кТв, то и Vc' = А,АЪ''.
И для плоскости, и для пространства имеют место следующие
утверждения, вытекающие непосредственно из определения
ортогонального преобразования: произведение двух ортогональных
преобразований есть ортогональное преобразование; преобразование,
обратное ортогональному, снова ортогональное.
Иначе говоря, множество всех ортогональных преобразований
пространства образует группу.
Эта группа является подгруппой группы аффинных
преобразований пространства.
Аналогичные положения имеют место и для плоскости.
Ортогональные преобразования пространства, сохраняющие
ориентацию, называются движениями, или ортогональными
преобразованиями первого рода.
Множество всех движений пространства также образует группу;
эта группа есть подгруппа группы всех ортогональных
преобразований пространства.
Аналогичные положения имеют место и для плоскости.
Ортогональные преобразования пространства, меняющие
ориентацию, иногда называют движениями второго рода.
Совокупность движений второго рода группы не образует (аналогично
и для плоскости).
§ 180. ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ И ДВИЖЕНИЯ 521
Теорема 2. Существует и притом только одно ортогональное
преобразование пространства первого рода, которое три неколли-
неарные точки А, В, С переводит соответственно в три неколли-
неарные точки А', В', С, такие, что В'С' = ВС, С'А' = СА,
А'В' = АВ.
Доказательство. Докажем существование и единственность
ортогонального преобразования, не меняющего ориентации
и переводящего точки А, В, С соответственно в точки А', В', С
Возьмем в пространстве две точки О и О', такие, чтобы тетраэдры
>■ _->
АВСО и А'В'С'О' были равны и имели одинаковую ориентацию.
Существует и притом только одно аффинное преобразование,
которое точки А, В, С, О переводит соответственно в точки А', Вг,
С, О'. При этом если М и N—две произвольные точки
пространства, то, разлагая векторы ОМ и ON по векторам
ОА = а, ОВ^Ь, ОС = с,
будем иметь
—►
ОМ =
где М' и //'—образы точек М н N при этом аффинном
преобразовании, a a' = 0'A't b' = O'B', с' = О'С'. Отсюда находим
+ 2 (*«—*i)(J/a~УдаЬ + 2 (у2—Уг) (га—гО be+ 2 (z2—zx) {x2—xx)ca,
,iy {y2yly + {2lY +
Ц21)(у2у1)' + 2(у2—yj)(zt—zjb'c' + 2(z2—zl)(x,—x1)c'a'.
Но так как тетраэдры АВСО и А'В'С'О' равны, то а2 = а , № = &'*,
c2 = c'z, ab^a'b', bc = b'c', ca = c'a' и, значит, MN = M'N'.
Значит, указанное выше аффинное преобразование—ортогональ-
. у
ное; при этом оно первого рода, так как тетраэдры АВСО и
А'В'С'О' имеют одинаковую ориентацию.
Единственность ортогонального преобразования первого рода,
переводящего точки А, В, С соответственно в точки А', В', С,
следует из того, что всякое ортогональное преобразование,
переводящее точки А, В, С в точки А', В', С, переводит точку О
в точку О*, такую, что О А = О*А',ОВ = О*В', ОС = О*С, и такую,
что тетраэдр А'В'С'О* имеет ориентацию, одинаковую с тетраэдром
522 Глава XIV ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
АВСО. Но тем же свойством обладает тетраэдр А'В'С'О' и
никакого другого тетраэдра, обладающего этими свойствами пет.
Значит, точка О* совпадает с 0'. Теперь единственность
ортогонального преобразования первого рода, переводящего точки А, В, С
соответственно в точки А' В', С", следует из теоремы 4 § 177.
Теорема, аналогичная доказанной, имеет место и па плоскости.
§ 181. Ортогональные преобразования в координатах
1. Ортогональные преобразования плоскости
Введем на плоскости прямоугольную систему координат хОу
с началом О и единичными векторами /, / Пусть О'—образ точки
О при ортогональном преобразовании со, а /' и /'—образы
векторов / и / при том же преобразовании. Векторы /' и/' — единичные
взаимно перпендикулярные.
В силу линейности ортогонального преобразования точке М,
имеющей в системе О, I, / координаты х и у, соответствует точка
М', имеющая те же координаты относительно системы О', /', /'.
Как и в общем случае, выводим
х' = anx+any + xQ, у = апх + а22у + у0,
где х', у' — координаты точки М' в системе хОу, {йи, а21} = /',
{а12, а22} =/' (координаты векторов /' и /" даны в системе хОу),
а х0 и у0 — координаты точки О' в системе хОу.
Но, как было показано выше (§ 99, п. 1 и 2), в случае, если
базисы /, / и /', /' имеют одинаковую ориентацию, то
/' = {cos a, sin а}, /' = {— sin а, cos а},
так что
x'=xcosa—у sina-j-A:0, .
у' =xsma-\-ycQsa+ y0, >
где a—угол от вектора / до вектора /' (ориентация определяется
системой хОу), а если базисы /, / и /', /"' имеют противоположную
ориентацию, то
/' = {cosa, sin a}, /' = {sina, — cos a},
значит,
У sin a + x0, y' = xsma—ycosa+y0. B)
В соотношениях A) и B) x0 и у0 — координаты образа О'
начала координат системы хОу при рассматриваемом ортогональном
преобразовании.
Определитель из коэффициентов при х и у в преобразовании
A) равен + 1, а в преобразовании B) равен —1.
§ 181 ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ В КООРДИНАТАХ 523
Обратно, формулами A) при любых а, х и у задается
относительно декартовой прямоугольной системы координат
ортогональное преобразование. В самом деле, если A(xv уг) и В(х2, у2) —
две произвольные точки, то
Обозначая через А'(х1г у,), В'(хг, уг) образы точек А я В,
при ортогональном преобразовании A) будем иметь
*! = A'1cosa—yls'ma-i-x0, уг ~xl sin а + y1cosa + y0;
х2 =х2 cos a—у2 sin a + xu, t/2 = x2 sin а + г/2 cosa-j-y0
и, далее,
А 'В' =
—f/i)cosaja
Вместе с тем ортогональное преобразование A) сохраняет
ориентации всех треугольников. Аналогично доказывается, что
формулами B) при любых а, х, у задается также ортогональное
преобразование, которое в отличие от ортогонального преобразования
A) меняет ориентацию любого треугольника на противоположную.
2. Ортогональные преобразования пространства
Введем в пространстве прямоугольную систему О, I, J, к с
началом О и единичными векторами /, /", к. Пусть О' — образ точки
О при ортогональном преобразовании со. а Г, /', ft' —образы
векторов г, /, ft при том же преобразовании. Векторы /', /', к' также
единичные и попарно ортогональные.
В силу линейности ортогонального преобразования точке М,
имеющей в системе О, i, j, к координаты х, у, г, соответствует
точка М', имеющая те же координаты х, у, z в системе О', V, /, к'.
Как и в общем случае, выводим
х' = ayix + alzy + a13z + х0,
У' = а21х + аг2у + а23г +у0,
где х',у', г' —координаты точки М' в системе Охуг, {ац,а21,азг} = 1г,
{а12, о22, а32}=/, {а1я, а23, а33}=й' (координаты векторов V, /',
k' даны в системе Охуг), а х0, у0, г0 — координаты точки О'в
системе Охуг (§ 100). Координаты единичного вектора /' в
прямоугольной системе Охуг равны cosaj, cosf^, cosYi, где аг, f>x, Yi —
углы между вектором /' и соответственно векторами i, j, ft; коор-
524
Глава XIV. ЛИИЬЛМЫЕ И АФФИННЫЕ nPFOBPA3ORАНИЯ
динаты единичного вектора /" i. той же системе равны cosa2,
cos62, cosYa. где ос2, р'2, у2 — углы между вектором /' и
соответственно векторами /, /, к, координаты единичного вектора к'
в системе Охуг равны cosa3, cos Рз> C0SY3> r&e a3i Рз> Уз — углы
между вектором к' и соответственно векторами /, j, к. Итак,
ортогональное преобразование в координатах запишется такз
0,
д;' = х cos cij -f- у cos >.г + г cos as + x
y' = x cos p, -J- 7 cos p2 + г cos [5S + y0,
z — x cos Yi + у cos Y2 -f z cos ys 4- z0,
C)
где х', г/', г' —координаты точки М' относительно системы Oxyz;
ха> Чо' го—координаты образа 0' точки О относительно той же
системы, а ос,, В.-, Y/. t = l, 2, 3, —углы между векторами /, /, к,
V, /', к'х
i'
1
fe'
/
а,
а.г
а,
J
Й,
Рз
к
Y2
Y»
Дстсрминанг матрицы преобразования C) равен ±1.
Матрица ортогонального преобразования —ортогональная.
Обратно, соотношениями
х' = аих 4- а12у + anz 4- alt
где (a,ft) — ортогональная матрица., определяется ортогональное
преобразование. В самом деле (аналогично тому, как это
делалось для плоскости) из условий
n 4
88 = 1, a2i3 + 023+033 =
a31«32 =
следует сохранение длины любого отрезка:
'- г,'J
__ уг {х x )
182. ПРИМЕРЫ ОРТОГОНАЛЬНЫХ ПР EORP <\"ЮПЛПИЙ
525
§ 182. Примеры ортогональных преобразований
Пример 1. Введем на плоскости прямоугольную систему координат и
поставим i; соответствие каждой точке М {х, у) плоскости точку М'(х', у')
М(х,у)
Рис. 247
СИММЕТРИЯ RNPT3MMN3
Рис. 248
симметричную точке М относительно оси Ох (рис. 247). Тогда
х' = х, у'=—у
Симметрия плоскости относительно прямой есть ортогональное
преобразование второго рода.
На рисунке 248 показано преобразование симметрии фигуры вместе с иад-
.писыо к ней «симметрия».
Рис. 249
526 Глава XIV ЛИНЕЙНЫЕ Н АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
'■-ормулами х'—х, у'=у г'=—г ошогителыю прямоуюлыюй системы
координат определяется ортогональное преобразование, называемое
симметрией пространства относительно плоскости (рис. 249)
Пример 2 Фиксируем вектор а Ф 0. Поставим в соответствие точке А
пространства точку А', такую, что АА' = а (рис 250). Это преобразование
называется переносом Если 8 — любая другая точка, а 8' — ее образ при пе-
репо-е, то ВВ'=а, и из равенства АА' — ВВ' следует, что АВ = А'В', т. е.
АВ = А'В', иначе перенос —ортогональное преобразование
Если ввести декартову прямоугольную систему координат и обозначить
координаты вектора а через а, Ь, с, через х, у, г обозначить координаты юч
ки Л, а через х', у', г' —координаты образа А' точки А при переносе, то из
равенства А А'=а найдем
х' = х-\-а, у' = у-\-Ь, г' = г+с.
Maipnua переноса есть
единичная матрица
1 0 0'
0 1 0
0 0 1
а
Рис. 250 Рис. 251
следовательно, перенос есть движение. Множество всех переносов
пространства образует группу. Эта группа переносов является подгруппоЛ группы
движения. На рисунке 251 дан образ фигуры при перенос.
§ 183. Подобные преобразования
Подобным преобразованием пространства называется
преобразование множества всех точек пространства, обладающее следующим
свойством: если А и В — две произвольные точки, а А' и В' — их
образы, то А'В' = kAB, где k—положительное число, одно и то
же для всех пар точек пространства, называемое коэффициентом
подобия.
То же определение подобного преобразования принимается и
для плоскости, и для прямой.
Так же как и для ортогональных преобразований,
доказывается, что подобное преобразование есть аффинное преобразование
и что в декартовой прямоугольной системе координат на плос-
$ 183. ПОДОБНЫЕ ПРЕОБРАЗОВАНИЯ 527
кости в случае сохранения ориентации оно выражается
соотношениями
х' — k (x cos а — у sin a) -J- х0, у =k(x sin а-f# cos а)-}-//„;
где О'(хп, у0) — образ начала координат, а а—угол от единичного
вектора / оси Ох до его образа ki'{V — также единичный вектор),
я в случае изменения ориентации на противоположную —
соотношениями
х' — k (x cos a -~ у sin а) + х0, у' = k (x sin а—у cos а) + (/0.
Для пространства
х' — k (xcosaj + г/cos a2-f г cos as) -\-x0,
у = k (x cos "*• t -f- у cos p* 2 -f- г cos fJ3) -f £/0>
z' ~k(x cos Yi +// cos y2 + г cosy3) -Ь г0,
где 0' (x0, y0, zQ) — образ начала О декартовой прямоугольной
системы координат, М(х, у, г) — произвольная точка пространства,
М' {х , у', г') — ее образ при подобном преобразовании, аъ ри
у± — углы между образом ki' вектора / и векторами /, J к; аг,
р2, Y2 — углы между образом kf вектора / и векторами I, j, k,
аз> Ps> Тз — углы между образом kk' вектора k и векторами /, j, k.
Подобные преобразования пространства (и плоскости) так же,
как и аффинные преобразования, делятся на подобные
преобразования первого и второго рода в зависимости от того, сохраняют
ли они ориентацию, или меняют ее на противоположную.
Множество всех подобных преобразований пространства
образует группу. Эта группа является подгруппой группы аффинных
преобразований пространства, а группа ортогональных
преобразований— подгруппой группы подобных преобразований.
Множество Г всех подобных преобразований пространства, не
меняющих ориентации, есть также группа, являющаяся
подгруппой группы всех подобных преобразований.
Множество движений пространства есть подгруппа группы Г.
Теорема 1. Существует и притом только одно подобное
преобразование пространства как первого, так и второго рода, которое
три точки А, В, С, не принадлежащие одной прямой, переводит
в три точки А', Вг, С, также не принадлежащие одной прямой,
и такие, что B'C'^kBC, C'A' = kCA, A'B' = kAB. Эту теорему
можно доказать аналогично соответствующей теореме для
ортогональных преобразований.
Отметим, в частности, формулировку для плоскости.
Теорема 2. Существует и притом только одно подобное
преобразование плоскости как первого, так и второго рода, которое две
различные точки А и В переводит соответственно в две различные
точки А' и В'. Коэффициент этого подобного преобразования
А'В'
равен -J5-.
528 Рлаза XIV ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
§ 184 Собственные векторы линейного преобразования
Назовем собственным вектором линейного преобразования
множества всех векторов пространства всякий ненулевой вектор е,
образ которого при линейном преобразовании f коллинеарен
вектору е:
[е = Ке A)
Число % назовем собственным значением, соответствующим
собственному вектору е
Очевидно, что если вектор е собственный, то и всякий вектор
ke{ky^0), ему коллинеарный, будет также собственным с тем же
собственным значением так как из равенства fe = le следует
B)
Пусть линейное преобразование f задано относительно базиса
х =
где а;, у, г—координаты произвольного вектора а, а х9, у', г' —
координаты его образа fa
Для того чтобы вектор е = {х, у, z\ был собственным,
необходимо и достаточно, чтобы fe — \x', у', г'} = К{х, у, г] т. е. чтобы
х'= кх, y' = ty, г'= lz,
или
- а23г = %у, C)
откуда
Относительно а;, у, z эта система однородная, значит, для того
чтобы она имела ненулевое решение х, у, г, необходимо и
достаточно, чтобы было выполнено условие
аи—X аи als
а21 а22 — 'к а23 =0, E)
и31 2
или
F)
184. СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
529
где
•41
i
Hi
ai
G32
'зз
•'22
G)
(8)
О)
Уравнение E) или F) называется характеристическим
уравнет ем линейного преобразования /; оно третьей степени,
поэтому если считать, что коэффициенты этого уравнения —
действительные числа, то оно имеет по крайней мере один
действительный корень K = XV Подставляя это значение ^ = ^, з систему D),
получим линейную однородную систему относительно х, у, г; тгк
как определитель этой системы равен нулю, то она имеет
ненулевое решение х, у, г. Это ненулевое решение будет удовлетворять
и соотношениям C), т. е. соотношениям
X —
Z —
или
Таким образом, в трехмерном пространстве всякое линейное
преобразование имеет по крайней мере один (с точностью до
множителя, не равного нулю) собственный вектор, и собственное
значение, соответствующее этому собственному вектору, является
корнем характеристического уравнения.
На плоскости это не так: уравнение, аналогичное уравнению
E), имеет вид
-*12
«21
= 0,
или
где
/, = 0,
/.=
«12
«22
E')
F')
G')
(8')
и уравнение E') может иметь мнимые корни (тогда собственных
векторов нет). Однако .■-л.: корпи характеристического уравнения
действительны, то и на плоскости имеется собственный вектор.
530
Глава XIV ЛКНСПНЫЕ 11 АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Теорема. Значения выражений
«ii au
3S
Ml
1з
а следовательно, и корни Х1, Я2, Х3 характеристического уравнения
!«,,—А а,, а,
■'is
«3
= 0
не зависят от вь'бора базиса еи е2, es декартовой системы
координат, в котором задано линейное преобразование f.
Доказательство. Пусть
/fill «12 СЦз"
А = \ а21 а22 о23
331 а32 «33 ,
матрица линейного преобразования / в базисе е1( е2, е3.
Рассмотрим наряду с преобразованием / линейное преобразование g с
матрицей
/«И—^ «12 «13 \
G = l o21 а22 — А, о23 1
\ «81 fl32 «33 — ^- /
(Е—единичная матрица). При переходе к другому базису
матрица А линейною преобразования / преобразуется в матрицу
(blk) = В = С~1АС, а матрица G линейного преобразования g
преобразуется в матрицу
/Ь
11"
Ь21 Ь.22 — % 623
^31 ^32 ^33 ~
(см. теорему в конце § 174).
На основании той же теоремы имеем
а29. — К а
13
23
— % Ь-
12
6, о
185 САМОСОПРЯЖЕННОЕ -ЛИПППНОЕ ПрЕОПР \ЗОПЛ ПИЕ
531
(тождество относительно К) Отсюда следует, что равны
коэффициенты при К в одинаковых степенях, т. е.
«П + «22 + «33 = ЬП + Ь1% + Ь33-
«22
«32
а
а
23
33
"Г
«п
«31
^13
«S3
«И
«21
«Я1
«11
«21
ап
«22
«32
«22
«23
«83
=
622 62а !
ft32 Ь831
bu b12 bl3
Ъ Ь b
bo, ba2 Ь3ч
Ьц bls I
•
Ьц
Ьгч
§ 185. Самосопряженное линейное преобразование и его
собственные векторы
Линейное преобразование \ множества всех векторов пространства
называется самосопряженным, (или симметрическим), если для двух
любых векторов а и b выполнено соотношение
afb — bfa.
Теорема 1. Для того чтобы линейное преобразование было
симметрическим, необходимо и достаточно, чтобы матрица этого
преобразования
заданного относительно ортонормированного базиса, была
симметрической.
Доказательство необходимости. Пусть / — спммет-
рическое линейное преобразование. Введем в пространстве орто-
нормированный базис i, j, k. Тогда координаты х , у', г' образа
вектора {х, у, г} через координаты этого последнего будут
выражаться соотношениями
as2y
{а
п
а.,
Отсюда находим // = /{1, О, С, , ±1, „±, „,,,
= {0, 1, 0} \ац, а21, ogl} = fl21. Аналогично найдем ijj=an
так как jfi — ifj, то a12 = a2i- Аналогично доказывается,
Доказательство достаточности. Если al2 = a.n, al6 =
значит, /7/ —
Но
что
д с al2 a.n, а1д
— аз2> то для ДВУХ произвольных векторов а = {хх, yv
532 Г да,а XIV. /IHHH'lllblF И ЛТФИННЫЕ ПРЕОБРАЗОВАНИЯ
и &=■ {х2, ij2, гг\ имеем
2 + аазг2} = хх
l («31^2 + й
a13z2) + ih (a2ix2 + a22y2
а88гх) =
а31л
a31Xi + Og.^! + 0332!) = x2x\ + y2y\ + г2г; =
= {x2, y2l г2}{х1 yv z[} = bfa.
Теорема 2. Если j'—симметрическое линейное преобразование,
то все корни его характеристического уравнения действительны.
Доказательство. Введем в пространстве ортонормиро-
ванный базис i, j, k.
Тогда матрица
/аи а12 а13
= 1 a2l a22 a23
\а31 й32 а33/
A)
симметрического преобразования / будет симметричной (aik — akl).
Характеристическое уравнение имеет вид
ап~% а
с1ь
— К а
23
= 0.
B)
Предположим, что оно имеет мнимый корень K1 — aJrpi, где
а и р —действительные числа и р^--0. Рассмотрим линейную
однородную систему
C)
Так как определитель этой системы равен нулю, то она имеет
ненулевое решение х, у, г. Таким образом, имеются три числа
х, у, г, не равные нулю одновременно, при которых будут
выполнены соотношения C) пли соотношения
г^к^, D)
z = %!!/, E)
a^x + a^y + a^z^X^. F)
Умножая обе части равенства D) на х, обе части равенства E)
на у и обе части равенства F) на г и складывая, получим (в силу
is 185 СЛМОСОПРЯЖППНОР Ml'-IlUHliUP. ПРЬиГП>л:-;ОВЛ!|ИЕ 533
anxx + a22yy + a^zz -h c?i 2 (xy + ,v^) ■
Если в левой части зтого равенства заменить все числа им
сопряженными, то получим число, сопряженное тому, которое
было в левой части;_с другой стороны, при замене х, у, г
соответственно на х, у, z, ах, у, z соответственно на х, у, z левая
часть не изменится (заметим, что al-k = atk)l значит, левая часть
есть действительное число; мы пришли к противоречию, так как
число мнимое. Теоремы, аналогичные теоремам 1 и 2, имеют место
и на плоскости и доказываются аналогично. В частности, отсюда
следует, что любое линейное симметрическое преобразование
плоскости имеет собственный вектор.
Теорема 3. Всякое симметрическое линейное преобразование
пространства имеет три попарно перпендикулярных собственных
вектора. Собственными значениями этих векторов являются корни
характеристического уравнения соответствующего преобразования /.
Доказательство. Как было показано выше, любое
линейное преобразование пространства, в частности и данное
симметрическое, имеет собственный вектор i (будем считать его
единичным):
Докажем, что симметрическое линейное преобразование /
каждый вектор, перпендикулярный вектору /, переводит в вектор,
перпендикулярный вектору /. В самом деле, если aj_/, то
la = 0.
Но тогда в силу симметрии линейного преобразования f
i]a — afl = alj = k^i = 0.
Значит, линейное преобразование / преобразует множество всех
векторов, компланарных плоскости, перпендикулярной вектору /,
в себя, а так как преобразование / симметрическое, то в этой
плоскости есть собственный вектор j (будем считать его единичным):
U=hJ-
Вектор k(\k\=l), перпендикулярный векторам /и/ также
будет собственным, так как из условий
534 Глава XIV. ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
следует
i]k = *// = UXJ --= О, jfk = kfj= kXJ= 0.
Значит, вектор fk ортогонален векторам / и / так же, как и
вектор к. Следовательно, векторы к и fk коллинеарны и потому
Введем в пространстве ортопормированный базис /, J, ft,
состоящий из собственных векторов, рассматриваемого
преобразования /, тогда координаты х', у', г' образа вектора {х, у, z} через
координаты этого последнего выражаются формулами
х = кхх, у'= кгу, z = X3z,
а матрицей преобразования / в такой системе будет матрица
v 0 0\
о К о
,0 0 к3)
Характеристическое уравнение этой матрицы будет иметь вид:
кх—к 0 0
0 Я2 —к 0 =0
0 0 кй — X
и его корни k = klt к = к2, к~к3. В силу инвариантности корней
к±, к2, к3 характеристического уравнения относительно
преобразования базиса числа kv к2, ks являются корнями
характеристического уравнения, соответствующего линейному симметрическому
преобразованию f в любом базисе (даже и не ортонормирован-
ном).
Замечание 1. 1) Если кхфкг, к.2Фкь, кьфкг, то линейное
симметрическое преобразование f имеет единственную тройку
(с точностью до постоянных множителей, отличных от нуля)
собственных векторов, так как любой вектор {х, у, z\ перейдет в
вектор {кух, к2у, k3z], пеколлинеарный вектору {х, у, z\, если
хотя бы две из координат вектора \х, у, г} не равны пулю.
2) Если к1 = к2фк3, то собственными векторами являются
вектор ft, соответствующий собственному значению к = к3, и все
векторы к нему перпендикулярные. В самом деле, векторы
{х, у, г} и {кгх, кгу, к3г)
в случае кг = к2фк3 коллинеарны тогда и только тогда, когда
или 2 — 0, или х = у = 0.
Если kL = k2 — ka, то любой (ненулевой) вектор является
собственным.
<S 185. САМОСОПРЯЖГ.ННОЕ ЛИНЕЙНОЕ ИРЕОБРАЗОВЛ НИР. 535
Замечание 2. Если относительно декартовой и р я м о у г о л fa-
ной сяочмы координат Oxijz задано общее уравнение
+ о33г2 + 2 aV2xy -f 2 a%3yz + 2 я31г* -+- 2 ахл -f 2
поверхности второго порядка, то этому уравнению в данной
системе координат можно поставить в соответствие симметрическое
линейное преобразование множества всех векторов пространства,
определяемое соотношениями
x'^a^x + a^y + a^z, у' = аг1х + а22у-\-а^г, г' = а31х + а^у + az3z.
Будем рассматривать векторы г={х, у, z} и }г={х', </, г'}
как радиусы-векторы точек М(х, у, г) и М'(х', у', г'). В таком
случае квадратичная форма, входящая в левую часть уравнения
поверхности, является скалярным произведением векторов г и /г:
+ aS3z2 + 2 а12ху + 2 aMyz + 2 azlzx = rfr.
Повернем оси координат Oxyz вокруг точки 0 так, чтобы
новые оси Ох', О у' и Ог' пошли по направлениям трех
единичных и попарно ортогональных собственных векторов /', /, к'
преобразования /. Тогда
rfr = (х'Г + у1 Г + г'к') / (хГ + у'/ + г'к') =
= (x'V + у'Г + г'к') (x'fi' + y'ff + z'fk') =
= (x'V + y7 + z'k') {x"kxi' + y'XJ + z\k') = llX'* + кгу'* + V'2.
Мы видим теперь, что в § 152 при преобразовании системы
координат новой оси Oz' сначала придавалось направление
собственного вектора линейного преобразования f, соответствующее
данному уравнению, а затем поворотом вокруг оси Ог' осям Ох'
и Оу' придавались также направления собственных векторов этого
преобразования. В § 164, 165 и 166 мы по существу имели дело
с собственными векторами линейного преобразования, которое
ставится в соответствие заданному уравнению поверхности.
Все сказанное относится к уравнению линии второго порядка,
заданной общим уравнением относительно декартовой
прямоугольной системы координат.
В действительном n-мерном евклидовом пространстве общую теорию
поверхностей второго порядка следует строить по такому плану: сначала
изложить теорию линейных преобразований множества иекторов этого
пространства, сформулировать определение собственного вектора и доказать, что
самосопряженное линейное преобразование имеет п попарно ортогональных
(и единичных) собственных векторов ik; квадратичная форма /, входящая в
левую часть общего уравнения поверхности в системе @,1^), примет иид
где ?\,А— корни характеристического уравнения и т.д. (см. сноску на стр. 428),
536 Глава XIV. ЛИНЕЙНЫЕ И АФФИННЫЕ nPF0BPA30BАНИЯ
§ 186. Представление аффинного преобразования в виде
произведения ортогонального преобразования и трех сжатий
к попарно перпендикулярным плоаиэстям
Теорема 1. Каково бы ни было аффинное преобразование
пространства, существуют три попарно перпендикулярных вектора,
образы которых также попарно перпендикулярны.
Доказательство. Достаточно рассмотреть случай цеатро-
аффинпого преобразования, так как всякое аффинное преобразование
можно представить в виде произведения переноса на центроаф-
финное преобразование, а при переносе всякий вектор переходит
в равный ему вектор.
Итак, рассмотрим какое-нибудь центроаффинное
преобразование /. Введем в пространстве декартову прямоугольную систему
координат Oxyz, принимая за начало координат О неподвижную
точку этого преобразования. Тогда в координатах
рассматриваемое преобразование будет иметь вид
х' = апх + апу + а1Ъг,
у' = а21х + а12у + а232, A)
причем этими же формулами определяются координаты х', у', г'
образа {x',i/,z'} вектора {х, у, г).
Обозначим через А матрицу преобразования A):
ап а12 als^
A = I Ugi U22
а через А'—матрицу, полученную транспонированием матрицы А\
А = I
\a13ai3as3/
Составим произведение
А'А =
I аД + а/, + аЙ\ апа12+а21аг2+а31а32 аиап+а21а23+а31а33\
= аиап+а21а22+а31а32 а^ + а2% + а£, a-rais 1-а22а2з+аз2азз I.
\я1за11+а23а21+а83а31а13а12+а23йг2+а.!3йз2 а,\ + аД + ai3 J
Будем обозначать образ любого вектора е при аффинном
преобразовании через Ае, где А — матрица этого аффинного
преобразования. Отметим, что для любых двух векторов
^i = K. 2/i. гг] и е% = {х%, yit г2]
$ 186. ОСНОВНАЯ ТЕОРЕМА 537
скалярные произведения е1Ае2 и eiA'el равны между собой:
+ ай2у2 + а,3г2} = х1 (аих2 -|-а1гу2 + а13г2) + у1 (а21хг -\- а22у2 +
( а33г2) = х2 {аихх + а.^ -f aslz t) -j-
2i) -f 22(oJ3x1 -f а23г
Так как матрица Л'Л симметрическая, то соответствующее
ей центроаффишюе преобразование (имеющее ту же неподвижную
точку О, что и преобразование А) также симметрическое и,
значит, имеет три попарно перпендикулярных собственных вектора
ev e2, е3, т. е.
Обозначим образы векторов ev ег, ей при аффинном
преобразовании А через е1у ег, е3:
Имеем
е\ег = е±Аег — егА'е± — е2А'Аех --- е2%1е1 — О
и аналогично e«es — 0, e3ei = 0, т. е. векторы ех, е2, е3
попарно перпендикулярны (все эти векторы, очевидно, ненулевые в силу
взаимной однозначности рассматриваемого центроаффинного
преобразования).
Теорема 2. Всякое аффинное преобразование f можно
представить в виде произведения ортогонального преобразования а и трех
аффинных сжатий k^ k2, k3 к трем попарно перпендикулярным
плоскостям:
Доказательство. Пусть ех, е2, е3 — три попарно
перпендикулярных вектора, которые при аффинном преобразовании /
снова переходят в перпендикулярные векторы
Отложим векторы ех, е2, е3 от какой-нибудь точки О:
l v 2 2 3 3
Пусть О' —образ точки О при аффинном преобразовании /.
Отложим векторы ёи е2, е3 от точки O'i
(УЁг - е\, О7!', = et, ОЕ', = е,.
538
Глава XIV ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Точки £j, £2, Es~образы точек Ev Е2, Еъ при аффинном
преобразовании /.
Рассмотрим сжатия кг, k%, ks к плоскостям ОЕ2Е9, ОЕъЕ1ь
0EtE2, при которых векторы 0Е1У 0£2, 0Е перейдут в
векторы ОЕХ , ОЬ , 0Es, имеющие длины, соотР!етственно равные
длинам векторов О'ЕХ ~ех , О'£2 = е2 и О'Е6 = е3
Существует ортогональное преобразование га, которое точки О,
Et Ег, El переводит соответственно в точки О', Elt E2, Es .
Произведение ^kxk2kn является аффинным преобразованием и оно
так же, как и аффинное преобразование /, переводит точки О,
Е1% Е2, Еь соответственно в точки О', Еи Е2, Е3.
Следовательно (§ 177, теорема 4),
§ 187. Применение аффинных преобразований к исследованию
свойств линий второго порядка
Аффинные преобразования могут быть использованы при исследовании
геометрических свойств линий второго порядка, причем это исследование
можно в ряде случаев проводить синтетически
Пример 1. Применим теорию аффинных преобразований к исследованию
некоторых свойств эллипса Для этого заметим, что всякий эллипс можно
рассматривать как образ окружности
при аффинном преобразовании.
Г Так как окружность С имеет
центр симметрии, и только один, то
и эллипс К имеет центр симметрии
(являющийся образом центра окружности
С), и притом только один
2° Так как середины
параллельных хорд окружиости лежат на одной
прямой, а при аффинном
преобразовании параллельные хорды окружности
С перейдут в параллельные хорды
эллипса К и середины хорд
окружности — в середины хорд эллипса, то и
середины ггараллельных хорд эллипса
лежат на одной прямой
3° Если через центр эллипса К
провести произвольную прямую d', то
найдется другая прямая d, проходя-
Рис 252 щая через центр эллипса К, такая,
что каждая из прямых d и d' делит
пополам хорды эллипса, параллельные
другой прямой Это свойство эллипса имеет место в силу того, что оно имеет
место для двух взаимно перпендикулярных диаметров окружности, и и силу
основных свойств аффинного преобразования (сохранение параллельности,
середины отрезка и т д.)
Пример 2. Пусть М —произвольная точка гиперболы, А и В — точки
пересечения с асимптотами касательной к гиперболе в точке М тогда
187. Ш'ПчГ-Ш-НИ!- АФФИННЫХ ПР ПОБРЛЗО15Л,ЧИП
530
1°. МА = МВ.
2°. Площадь ДОЛб имеет одну и ту же величину при любом положении
точки М на гиперболе (рис. 252),
В самом деле, если Мо—вершина гиперболы, а Ло и б0 — точки, в
которых касательная к гиперболе в точке А10 пересекает се асимптоты, то
МоАо = МаВо. Рассмотрим гиперболический поворот (§ 179, пример 5),
преобразующий данную гиперболу в себя и переводящий точку Мо в точку М.
При этом касательная к гиперболе в точке Мо перейдет в касательную
к гиперболе в точке М и точка М будет серединой отрезка АВ в силу того,
Рис. 253
что гиперболический поворот есть аффинное преобразование; а в силу того
что это преобразование сохраняет площади, имеем
пл. ДОЛ0В0 = пл. ДОЛВ.
Пример 3. Из § 123 вытекает следующий способ построения касательной
к параболе из точки М, лежащей на ее оси: строим Oi\' = OM, PQJ_MN,
тогда МР и MQ — касательные к параболе (рис. 253).
Пусть точка М не лежит на параболе (рис. 254). Проведем через точку М
прямую, параллельную оси параболы, и пусть эта прямая пересечет
параболу в точке S. Рассмотрим параболический поворот, переводящий точку S
в точку О. Строим образ Мо точки М при этом повороте. Далее,
Теперь сделаем параболический поворот, обратный рассмотренному.
Точка Мо вернется в точку /И, а касательные М0Р0 и /WoQo (эти прямы.1 на
рис. 254 не показаны) перейдут в касательные МР и MQ к параболе.
Аффинные преобразовании применяются в основном к тем свойстам
линий второго порядка, которые связаны с понятием параллельности,
отношения параллельных отрезков, отношения площадей, касательной к лиши/
второго порядка, диаметра, асимптоты.
540
Глава XIV /IHHRfiHUr И Д'ЬМШИЫЕ ПРПОБР ЛЗОВАНИЯ
§ 188. Аффинная классификация линий второго порядка
Определе
одному и тому
преобразование,
же одну линию
вести в другую,
классам (линии
Теорема Все
классов:
н и е. Две линии второго порядка принадлежат
же аффинному классу, если существует аффинное
переводящее одну из этих линий в другую. Если
никаким аффинным преобразованием нельзя пере-
то эти линии принадлежат различным аффинным
аффинно неэквивалентны),
линии второго порядка делятся на 9 аффинных
1°. Эллипсы.
2°. Мнимые эллипсы.
3°. Паря мнимых пересекающихся прямых.
4°. Гиперболы.
Пары пересекающихся прямых.
Параболы.
7°. Две параллельные прямые.
8°. Две мнимые параллельные прямые.
9°. Две совпадающие прямые.
5е.
6°.
Рис. 255
Доказательство. Докажем сначала, что всякие две линии,
принадлежащие одному классу, аффинно эквивалентны. Возьмем
два любых эллипса на плоскости, и пусть их канонические
уравнения (вообще говоря, в разных системах координат) будут
(рис. 255):
£1 j_*£— Kll j_ у2 —
а2 + £2 — I > 7^1 + у~2 — •
Производя аффинные сжатия,
1S8 ДФФИЩГЯ КЛАССИФИКАЦИЯ ЛИНИЙ
541
к осям О'у' и О'х', мы преобразуем эллипс
в эллипс
+
конгруэнтный эллипсу
Теперь эллипс ^- + ^-=1 совмещается с эллипсом ~ -J- — = 1
движением. Так как аффинные сжатия и движения—аффинные
преобразования, то и результирующее преобразование,
переводящее второй эллипс в первый, также аффинное.
О
Рис 256
Гипербола. Доказательство того, что любая гипербола
может быть аффинио преобразована в любую другую гиперболу,
проводится аналогично (рис. 256).
Парабола. Рассмотрим две параболы у2 — 2рх и у'2—2р'х'.
Произведем преобразование гомотетии х' = — Х, y' = — Y. Тогда
парабола у'2 = 2рх' перейдет в лилию ^-У2—2~ X, или Y2 =
= 2рХ, т. е. снова в параболу, параметр которой равен р.
Теперь парабола Уг~2рХ с параболой t/2 — 2p.x совмещается
движением (рис. 257). Таким образом, все параболы не только
аффинно эквивалентны, но даже подобны.
542 Г i a i a XIV ,'П'НЕПНЫВ И ЛФФИИНЫП ПРЕОБРАЗОВАНИЯ
Рассмотречие остальных случаев не представляет затруднении.
Перейдем к доказательству -торой части теоремы: всякие две
линии, принадлежащие разным классам, аффишго неэквивалентны.
Прежде всего заметим, что так как аффинное преобразование
выражается линейными соотношениями в координатах, то образ
любой линии второго порядка при любом аффинном
преобразовании есть линия второго
порядка.
Эллипс нельзя
преобразовать аффинно ни в одну из
других линий, указанных в
условии теоремы, так как среди
ч„ всех линий второго порядка
эллипс—единственная линия,
лежащая в ограниченной части
плоскости и содержащая
бесконечное множество точек
(действительных). Это свойство
Рис. 257 множества сохраняется при
любом аффинном преобразовании,
поэтому образом эллипса при любом аффинном преобразовании
будет снова эллине.
Гипербола от всех остальных линий второго порядка,
перечисленных в условии теоремы, отличается тем, что имеет две
ветви и не содержит трех точек, лежащих на одной прямой;
эти свойства сохраняются при аффинном преобразовании, поэтому
аффинным образом гиперболы будет гипербола.
Парабола от всех остальных линий второго порядка,
указанных в усложни теоремы, отличается тем, что является
неограниченной линией, имеющей одну вегвь, и не содержит трех точек,
принадлежащих одной прямой; это свойство сохраняется при
аффинном преобразовании.
Две пересекающиеся прямые при аффинном преобразовании
переходят в две пересекающиеся прямые, а две параллельные
прямые — в две параллельные прямые.
Если линия второго порядка распадается на две мнимые
пересекающиеся прямые, т. е. на плоскости есть только одна точка,
координаты которой удовлетворяют данному уравнению, то после
аффинного преобразования образом этой точки будет точка, т. е.
образом двух мнимых пересекающихся прямых будут снова две
мнимые пересекающиеся прямые.
Мнимый эллипс аффинно неэквивалентен двум мнимым
параллельным прямым, так как мнимый эллипс имеет единственный
центр, а две мнимые параллельные прямые — прямую центров,
а эти свойства сохраняются при любом аффинном
преобразовании.
§189. АФФИННАЯ КЛЛССИФИК ЛЦИЯ ПОВЕРХНОСТЕЙ 543
2)
3)
4)
5)
6)
7)
8)
9)
X2
X2
X2
X2
У2
X2
X2
X2
+ У2 = -1
+ У2 = 0
~f=\
у2 Q
= Х
j
= 0
Доказанная теорема позволяет назвать проведенную выше
классификацию линий второго порядка аффинной.
Таким образом, аффинной классификацией линий второго
порядка является разделение всех линий второго порядка на 9
аффинных классов, в каждый из которых включаются все линии
второго порядка, такие, что любые две из них могут быть
переведены одна в другую некоторым аффинным преобразованием;
если же линии второго порядка принадлежат разным аффинным
классам, то никаким аффинным преобразованием одна линия не
может быть переведена в другую.
Простейшие представители девяти аффинных классов линий
второго порядка таковы:
1) хг -{■ у2 — 1 эллипс
2 мнимый эллипс
две мнимые пересекающиеся прямые
гипербола
две действительные пересекающиеся прямые
парабола
две параллельные прямые
две мнимые параллельные прямые
две совпадающие прямые
§ 189. Аффинная классификация поверхностей второго порядка
Определение. Две поверхности второго порядка принадлежат
одному и тому же аффинному классу, если существует аффинное
преобразование, переводящее одну из поверхностей в другую. Если
же одна поверхность второго порядка никаким аффинным
преобразованием не может быть переведена в другую, то эти две
поверхности второго порядка принадлежат различным аффинным классам.
Теорема. Все поверхности второго порядка делятся на 17
аффинных классов, названия которых даны в теореме 3 § 152.
Доказательство теоремы состоит из двух частей.
1. Любые две поверхности второго порядка, принадлежащие
одному и тому же классу из числа семнадцати, указанных в
теореме 3 § 152, могут быть аффинным преобразованием переведены
друг в друга. Это доказывается совершенно так же, как для
линий второго порядка.
2. Любые две поверхности, принадлежащие к разным классам
из числа семнадцати, указанных выше, никаким аффинным
преобразованием нельзя преобразовать друг в друга. Принцип
доказательства этого положения состоит в том, что сравнивая две
поверхности, мы указываем такое свойство, инвариантное
относительно аффинного преобразования, которым обладает одна
поверхность и не обладает другая.
544 Глава XIV, ЛИНЕПНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Мнимый эллипсоид, мнимый эллиптический цилиндр и две
мнимые параллельные плоскости не содержат нн одной
действительной точки и, значит, аффинио не могут быть преобразованы
ни в одну из поверхностей остальных аффинных классов, так как
при аффинном преобразовании действительные точки переходят
в действительные.
Две пересекающиеся плоскости, две параллельные плоскости
и две совпадающие плоскости не могут быть аффинно
преобразованы пи в одну из поверхностей остальных аффинных классов,
так как только они состоят из плоскостей Параллельные
плоскости не могут быть преобразованы в пересекающиеся, а
различные— в совпадающие. Две мнимые пересекающиеся плоскости
содержат только одну действительною прямую, и никакая другая
поверхность ьгорого порядка не обладает этим свойством.
Среди поверхностей остальных аффинных классов эллипсоид,
двуполостнъш гиперболоид и эллиптический параболоид отличаются
от поверхностей остальных аффинных классов тем что не
содержат прямолинейных образующих, а между собой—тем, что
эллипсоид— поверхность ограниченная, тогда как двуполостный
гиперболоид и эллиптический параболоид — поверхности неограниченные;
при этом двуполостный гиперболоид состоит из двух кусков, а
эллиптический параболоид—из одного куска. Это различие
сохранится при любом аффинном преобразовании.
Среди остающихся линейчатых поверхностей конус отличается
от поверхностей остальных классов тем, что представляет собой
поверхность, образованную прямыми, проходящими через одну
точку и не лежащими в одной плоскости, а эллиптический,
гиперболический и параболический цилиндры—тем, что образовачы
параллельными прямыми. Друг от друга эти три поверхности
отличаются тем, что сечения их плоскостями, не параллельными
образующим, будут соответственно эллипсами, гиперболами,
параболами. Наконец, одиополостный гиперболоид от
гиперболического параболоида отличается тем, что первая поверхность имеет
центр симметрии, а вторая — нет.
Мнимый эллипсоид имеет единственный центр, мнимый
цилиндр— прямую центров, и две мнимые параллельные плоскости —
плоскость центров. Так как это свойство инвариантно по
отношению к любому аффинному преобразованию, то эти поверхности
принадлежат к трем различным (аффинным) классам.
§ 190. Примеры и задачи к главе XIV
1. Задачи с решениями
Пример 1. Докажем, что если ортогональное преобразование пространства
первого рода имеет одну неподвижную точку О, то существует прямая, про-
ходчщая через точку О, все точки которой неподвижны при этом
ортогональном преобразовании.
190. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВ!: XIV
545
В силу того что рассматриваемое преобразование ортогональное,
собственное значение, соответствующее собственному вектору, может быть равно или
-f- 1, или — 1 Если Х = + 1, то конец Л собственного ве тор,- ОА останется
неподвижным, значит, неподвижными будут все точки прямой ОА, т е.
данное ортогональное преобразование первюго рода оставляет на м;сте все точки
некоторой прямой, проходящей через неподвижную точку О.
Если Х = —1, а два других корпя характеристического уравнения —
комплексные (сопряженные), то Dei А < 0, т. е. данное ортогональное
преобразование второго рода. Если X —— 1, а два других корня
характеристического уравнения действительны, то один из них равен ~- \, а другой — 1
(ибо Det А — 1 и в силу ортогональности преобразования корни
характеристического уравнения по модулю равны 1), а значит, данное преобразование
является симметрией относительно прямой ОА (ОА — собственный
соответствующий корню +1).
Если однородное ортогональное преобразование первого рода задано в
базисе elt e2, е3 соотношениями
вектор,
то координаты вектора, дающего направление прямой, псе точки которой
неподвижны, находятся из системы (Х=1):
(аи—
—1) у-\ a2sz = 0, a3
—l) г = 0.
Эта система имеет ненулевое решение в силу того, что ее определитель
равен сумме (Х=1 — корень характеристического уравнения).
Пример 2. Докажем, что всякое подобное преобразование пространства
с коэффициентом подобия k Ф i имеет и притом только одну неподвижную
точку.
В самом деле, полагая х — х', у —у', г = г' в формулах подобного
преобразования ((я/j) — ортогональная матрица)
получим систему
x' = k (апх + a,2r/
г/=/г (а21х + а22/+ 23)+2>
г' — k (aslx -Ь aS2y -\- азэг) + а3,
— J
аи~-г)
к j
+fo2
Определитель этой системы
1
<*з\ ак a»-J
отличен от нуля, тач как ортогональное преобразование не может иметь
собственных значений, не равных по модулю единиие. Следовательно,
написанная выше система всегда имеет решение и притом только одно, т. е
рассматриваемое преобразование обладает единственной неподвижной точкой.
18 П. С. Моденов
546 Г лава X/V, ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Пример 3. Найти все линейные преобразования множества нсех векторов
плоскости и пространства, каждое иг которых всякий вектор а переводит
в вектор /а, ортогональный вектору а. Эти линейные преобразования
называются антисимметрическими.
Решение Пусть t—линейное преобразование, обладающее указанным
свойством, т. е.
afa = 0,
каков бы ни был вектор а. Отсюда следует, что для двух любых векторов а
и Ь будем иметь
или
ИЛИ
afft = -6fa.
Случай плоскости. Введем на плоскости ортонормированный
базис /, J. Пусть в этом базисе а= { х, у}, fa — {anx-\-alty, аах-\-см/ }■
Так как an — ili, О22=Д/, то au = c22 = 0. Так как a12 = ifj, аи—Д1 и
ifj—~jfi, то а81 = — а12. Таким образом, координаты х', у вектора fa,
являющегося образом вектора а — \х, у\, выражаются через координаты х
и у соотношениями (полагаем <з2, =*\)
*' = — \у, у'=%х,
где Я—любое число. Это преобразование заключается в повороте век-
зх
тора а па угол +-„- и умножении повернутого вектора на число К,
Случай пространства. Введем в пространстве ортонормировац-
ный базис i, j, к и пусть в этом базисе а = {х, у, г\, а вектор [а имеет
координаты
х' — аих-\-а1гу-{аиг, y'^aixx-\- а^у + а^г, г' = aslx-f aiay-f a8sz.
Рассуждая так же, как и выше, докажем, что
ап = а22 = о33 = 0, о12=— о21, а31=— ols, а23=—азг.
Полагая а12 = с, asi~b, a2s — a, получим
х' = су — Ъг, у' — —сх-\-аг, z' — bx—ay.
Таким образом, а-', у', г'—координаты векторного произведения вектора
а=\х, у, г) на вектор р={а, Ь, с}:
1а=[ар].
Очевидно и обратно: если р—фиксированный вектор, то преобразование,
которое вектору а ставит в соответствие вектор la, равный
линейное и afa = 0.
Матрица, соответствующая антисимметрическому линейному
преобразованию в ортонормированием базисе, антисимметрична: на плоскости
/О — АД
в пространстве
О с — Ъ-
1 = ( —с 0 а
Ь —а О,
§ 190. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XIV
547
Обратно, всякая антисимметрическая матрица соответствует в ортонорми-
рованном базисе некоторому антисимметрическому преобразованию.
2. Задачи для самостоятельного решения
1. Двойной прямой аффинного преобразования плоскости называется такая
прямая, которая при этом аффинном преобразовании переходит в себя (не
обязательно, чтобы точки этой прямой были неподвижными при этом аффинном
преобразовании). Найти двойные прямые аффинного преобразования
Отв. Если уравнение
1 Л
ап
021
Я,
«12
а22
= 0
ФО.
имеет мнимые корни, то двойных прямых нет.
Если корни уравнения A) действительны, различны и ни один из них не
равен 1, то существуют две и только две двойные прямые.
Если корни уравнения A) действительны, различны, один из корней не
равен 1, а другой равен 1, то имеется пучок параллельных между собой
двойных прямых и еще одна двойная прямая, их пересекающая.
Если уравнение A) имеет двойной корень %, не равный 1, и если хотя бы
одно из чисел аи—Я,, а12, аи, а22—Я, не равно нулю, то имеется только одн£
двойная прямая.
Если уравнение A) имеет двойной корень X, не равный 1, и если ап — X, =
= а12 = а21 = я22— Я, = 0, то двойной прямой является любая прямая, проходящая
/ а, а* \
через точку [-—*чс-, -.—=т- , и этим исчерпываются все двойные прямые.
\ 1 — К I — Л J
J-X ' 1- ,
Если оба корня уравнения A) равны 1, но среди чисел ап — X, <з12) ап,
а22—X, есть хотя бы одно, не равное нулю, то имеется пучок паралл льных
между собой двойных прямых.
Если оба корня Я, уравнения A) равны нулю и ап — Х = а12 = a2l = a22—Х, = 0,
то данное аффинное преобразование имеет вид х' = х-\-аь у' = у-\-а2; если щ и а-
не равны нулю одновременно, то двойной прямой является любая прямая,
параллельная вектору {аь а2}. Если ах = а2 = 0, то данное аффинное преобра
зование тождественное: х' = х, у' = у и двойной является любая прямая.
2. Относительно общей декартовой системы координат задано аффинное
преобразование
ап а12
Написать формулы этого аффинного преобразования в новой системе
* * * г, %>* *
координат Оху, если переход от системы Оху к системе Оху определяется
соотношениями
* #
= спх-\-спу-\-с1, у =
Отв. x' — bnx + bny + bi, if —2Х
где числа b;k, Ь{ определяются из следующего матричного равенства!
6 612 Ьа /cn cn ct\ ~yan a12 ад /сп с12
&22 &g ) = I c2i е22 с2 j a2, a22 a2 ) czi c22 c2
0 0 1/ \0 0 1/40 0 1/\0 0
в!
са
c2 ).
1/
18*
548 Г лае а XIV ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
3. Найти все аффинные преобразования плоскости, квадрат каждого из
которых равен единичному преобразованию
Отв 1) тождественное преобразование; 2) симметрия относительно любой
ючки плоскости, 3) «косая» симметрия относительно любой прямой в
направлении любой другой (ее пересекающей) прямой.
4, Дано ортогональное преобразование первого рода1
х'*=апх + а12у+а19г, у'^
Это преобразование может быть осуществлено поворотом на некоторый
угол ф вокруг неподвижной прямой. Найти этот угол.
О/по, (p
5. Найти ортогональное преобразование первого рода, эная направляющий
вектор а неподвижной прямой, определяющей это преобразование, и угол ф
поворота.
Отв. Выбирая начало радиусов-векторов в любой неподвижной точке
преобразования, обозначая через г радиус-вектор любой точки пространства,
а через г' радиус-вектор образа М' точки М при данном преобразовании,
будем иметь
г'**r cosq>-\-[ar] sin <$-\-a(ar) A — cosq>).
6. Доказать, что если линейное преобразование J множества всех векторов
пространства удовлетворяет соотношению
то оно вырожденное.
?. Пусть I и g—произвольные линейные преобразования множества всех
векторов пространства. Доказать, что преобразования [g н g| имеют одни
и те же собственные значения.
8. Доказать, что преобразование
х' — 2х~ у, у'=*Ъх—у
периодическое. Существует ли базис, в котором это преобразование является
вращением?
9. Пусть линейным преобразованиям £ и g множества всех векторов
пространства соответствуют матрицы А и В:
Доказать, что тогда
t±8—+A± В, Ц-+\А.
10. Линейное преобразование f/ множества всех векторов пространства (или
плоскости) называется сопряженным к линейному преобразованию f, (этого
множества), если для любых двух векторов а и Ъ выполняется соотношение
afb^bf/a.
Доказать, что для всякого линейного преобразования {, существует ему
сопряженное и притом только одно. Найти матрицу, соответствующую
линейному преобразованию /', если преобразованию [ в ортонормированием базисе
соответствует матрица А»
Отв. В ортонормированием базисе преобразованию /' соответствует
матрица А , подученная транспонированием матрицы А.
5) 190. ПРИМЕРЫ ii ЗАДАЧИ л Г.'ЛВЕ XIV n-19
11.n Доказать соотношения
a±gY=£'±g: (W)=u:. ag)'=s'f:
(см. предыдущую задачу).
12, Доказать, что если / и g— невырожденные линейные преобразования
множества всех векторов пространства, то
13. Доказать, что если ^—невырожденное линейное преобразовани:
множества всех векторов пространства, то
14. Назовем линейное преобразование со множества всех векторов
пространства ортогональным, если
0)Ш' = 1
A—тождественное преобразование). Доказать, что если и — ортогональное
преобразование, то
1) |а| = |(оя| для любого вектора а (сохранение длины вектора);
2) ab — <aaa>b (сохранение скалярного произведения);
3) ш'^ш;
4) матрица П, соответствующая со в орюпормированмом базисе,
ортогональная.
15. Доказать, что если линейное преобразование / множества всех векторов
плоскости обладает следующим свойством: l'——i (антисимметричность), то
ш=ш <»>
ортого!1алыюе преобразование первого рода. Обратно, если со —ортогональное
преобразование первого рода и —1 не является собственным значением этого
преобразования, то
>_1-м
антисимметрическое (т. е. f,'=—f,).
Замечание A—/5) A + £)~1 = U +/E) A—7) (доказать!), поэтому произ-
I—/
ведение это можно обозначать дробью ■ ..
Найти матрицу, соответствующую матрице со, исходя из cooiношения A)
и считая, что преобразованию f, соответствует в ортонормированием базисе
матрица
0 с — Ь\
—с 0 а
Ь —а 0у
16. Доказать, что всякое линейное преобразование f множества всех
векторов пространства тождественно удовлетворяет своему характеристическому
уравнению, т. е.
021 а22 — Ь
=о,
взятому в любом базисе в\,, е2, <?з
* Это тождество называют часто уравнением Гамильтона -•■ Кэли.
550
Глава XIV. ЛННЕЙНЫЬ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Замечание. В соотношении A) под о,й подразумевается линейное
преобразование, которое вектору а стгтеит в соответствие вектор а^а. Следует
еще заметить, что при перемножении целых рациональных функций от одного
и того же линейного преобразования ""
X = ada + adn-1+... + an, К = ЬоГ + ЬгГ "'+••■ + »«
порядок множителей не играет роли, т. е. XY = YX (в этом можно убедиться,
умножая один раз X на Y, другой раз Y на X —получится одна и та же целая
рациональная функция от линейного преобразования [: ao6ofra+" +
Таким образом, имеет смысл говорить об определителе Д, элементами
которого являются целые рациональные функции от одного и того же линейного
преобразования f.
Р П
ве
реобразования f.
Решение. Пусть в базисе еъ е2, еъ вектору а = {х, у, г\ соответствует
ектор fa = {x', у', г'\ с координатами
х' ^апх~-а12у->гапг, у' = аах+ а22у + а23г, г' = a31x-\-a32y-\-a3Sz.
Вектор е1 = \\, 0, 0} при преобразовании { переходит в вектор
Аналогично
Из последних трех соотношении следует
(«и — D
3 = а1гех + a2Se
B)
aSs—t) е3 = 0
(здесь aik рассматривается как линейное преобразование, при котором вектору а
ставится в соответствие вектор a;ka).
Из соотношении B) следует, что
а23
[(«и — I) <?i + О2хе2 + апе3] —
[а12<?х + (aM — t)
аг1
[a13«?x+ «23^2+ («зз— t) e»! =0.
или
где Д—линейное преобразование, определяемое формулой
А =
«и— I
asi
«12 «22 — I «3:
«ХЗ «23 аЗЗ- „
Аналогично получим Де2 = 0 и А#3 = 0. Отсюда следует, что Да = 0 для
любоТо вектора а. В самом деле, пуст>
согда
Аа = х{±е!-]-у£
Итак, Д —нулевое преобразование.
190. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XIV
551
Замечание 1. Так как сумме и произведению линейных
преобразований соответствуют сумма и произведение соответствующих им матриц, то матрица
аи A a2I a3i
где
Л 23 «33— А
ап а12 а13
= 0,
C)
(в определителе D числа aik рассматриваются как скалярные матрицы ац,Е,
где Е — единичная матрица).
Все доказанные положения верны и гля линейных преобразований >;но-
жества всех векторов плоскости.
Соотношение, аналогичное соотношению 1,3), имеет место для любой
квадратной матрицы я-го порядка:
Я]] — А а12 ••• ain
где
а22 — А... а2п
/ап а12 ..
Л _ а21 Ом ■ •
I ....
\Яп1 Qn2 ■ •
D)
а числа ад в соотношении D) рассматриваются как скалярные матрицы ^
Замечание 2. Из доказанного следует, что, например, для линейного
преобразования ft множества всех векторов плоскости всякая целая
рациональная функция от I л-й степени
сводите!: к линейной функции р)!+<? от преобразования /. В самом деле, 1ак
как преобразование | тождественно удовлетворяет соотношению
aai—f
или
где
то
= 0,
ап а12
«21 «22
и, далее,
-/,)£-/,/, и т. д.
Представим f" в виде p/ + <j, где п—целое положительное число, а (—линейное
преобразование множества всех векторов плоскости.
I я а в а XIV ЛИНЕГ-ШЫЬ И АФФННИЫЬ ПРЕОБРАЗОВАНИЯ
И;, соотнои'ения
/2-/х/ + /2-0
след* от что
f" -/,/""' + /Jn-2 = 0, E)
где /г — иелое положительное число, большее или равное 2.
Рда-мотрим скачала числовую последовательность х„, удовлетворяющую
соон'с,пению
хп— 1\*п-\Л- 1%Хп-2=* «5гЗ, F)
и предположим сначала, что /2 ?~ 1) *.
Л- калом, что существует геометрическая прогрессия хп = Хп~1 (где X, ^ 0),
удо!'."-; т»оряю1Ь.ая этому соотношению. Имеем
и li'K t<ai< }. ф 0. то
?.2-/,ХН~/2 = 0. G)
Так как /2 ^ 0, то это уравнение имеет корпи ^ и ).г, не равные нулю.
Если Я, ^ л-2, то уравнению F) удовлетворяют две прогрессии А," и ^j", a
текже произвольная их лнноппая комбинация Ci?v"~1 + C2^"~1, где Cj и С2—-
произвольные числа.
Если ^, = Яа(^0), то уравнению F) удовлетворяет помимо прогрессии
Я£~2 еще последовательность (п—\)%'\~1. В самом деле,
(я- 1)Ц~' - /х (л-2)Х?~2-I- /2 (я- 3)^~3 =
Так как it^X^, то /j = 2/\,, /s = ^,, и, значит,
Ясно, чю решением соогношення F) является также (в случае
линейная комбинацн:
указанных двух последовательностей.
Возвращаясь к соотношению E), видим, что последовательность линейных
преобразований
1 f f2 in
является возвратной последовательностью второго порядка.
Если /2 ф 0 и корни \х и ?i2 характеристического уравнения линейного
преобразования / не раины друг другу, то последовательность линейных
преобра joваннн
1. /. IS ■••> Iя, ••• (8)
и последовательность
(9)
* Последовательность, для которой каждый член, начиная с третьего, вы-
ражается одной и тон же линейной комбинацией двух предыдущих, называется
возвратной последовательностью второго порядка.
190. ПРИМЕРЫ И ЗАДАЧИ К ПЛВГ. XiV
где g и h — любые линейные преобразования множества всех векторо.;
плоскости, удовлетворяют одному и тому же реку ppeiii ному соотн.нтнию
Выберем g и ft так, чтобы два первых члена последова1елыюсти (9; оы ш
равны соответственно двум первым членам последовательности (8);
g-\-h~l,
Отсюда
и последовательность (9) принимает вид
Р^гК~1-гР1Ц-К-1- по)
Л| — Ag fv'2 """^l
Но так как последовательности (8) и A0) удовлеторяют к тому же еще одному
и тому же рекуррентному соотношению F), то
л^ — Ag ^2 — ^i
при всех натуральных п. Задача решена в случае A.i ф \2
Если ?ц = Х2 Ф 0, то последовательность '8) и последователы'ость
(И)
удовлетворяют одному и тому же рекуррентному соотношению F,1. Выбарем g
и h так, чтобы при /i=l и й = 2 соотаетственно <i=l, t2 = fi'.
Значит, искомая последовательность
* fill. 1) Л-~М ? '-1 и р._. fi i „ /■ —^i \ ?я
\ Л1 / \ я: /
при всех натуральных п.
Если, наконец, /3 = 0, го P — ht» i3 = /i/"J= /Jit' и вообще ;J" = /'J~1f!-
Читателю предлагается доказать, что если J лниейьое преобраЗна
множества всех векторов пространства, то
1) если собственные значения преобразования £ поаарио различны ах
Х2 ?i А3> л3 ?i Х1; то
где лилейные преобразования g, h и s определяются из системы
2) если Кх =Х2 ^ Х3, то
де линейные преобразования g, h и s определяются из системы
554
Глава XIV. ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
3) если Х1—К1 = Х3, то
где
В случае, если одно из собственных значений линейного преобразования ft
равно нулю, последовательность f" является возвратной последовательностью
первого порядка Исходя из применяемого здесь отображения множества
линейных преобразований на множество квадратных матриц, можно
сформулировать соответствующие предложения для матриц.
Рассмотрим числовой пример: дана матрица
/113
Л = ( 1 5 1
\3 1 1
Найти Ап.
Находим собственные значения:
— Я 1 3
1 5-1 1 1 = 0,
3 1 1-Х.|
Х.,=3, Х2 = 6, Х3=—2
Значит.
где Р, О, S—матрицы, определяемые из системы
Отсюда находим
15
l
l -1 Ь
I -I 1
2 4 2
1 2 1
0
0 0 0
1 0 -
Следовательно,
= (— 1
1
1 -1
—1
/12
3"-'+B 4 2
\1 2 \
10
00 0](-2)'!-1
1 0 -1
§ 190. ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XIV
17. Пусть /— линейно.-1 преобразование множеива всех векторов плоскости
(или пространства) Введем следующие определения:
/2 М
+
f2 /3 fn
Доказать, что sin2 f + cos2 /== 1 (I — единичное преобразование^
sin (/ + g) =sin I cos g ± cos I sin g,
cos (| i g) = cos|cosg T sin
Доказать, что если [—антисимметрическоо преобразование, то е/—ортого:
иальиое преобразование.
Замечание. Суммой ряда
элементами которого являются линейные преобразования множества всех век- •
торов пространства (или плоскости), называется предел последовательности
sn = h + h+-- +tn
частичных сумм этого рода.
Линейное преобразование s называется пределом последовательности sn
линейных преобразований, если для любого вектора л: и любого
положительного 8 существует такое число Л', что для всех п. > N выполняется
неравенство [ snx—sx | < 8.
Если (e£j5 ) — матрица, соответствующая линейному преобразованию sn
в любом базисе, то для того чтобы последовательность sn имела предел,
необходимо и достаточно, чтобы существовали пределы
lim a$ = atk
п. —>■ со
При этом линейное преобразование s, соответствующее матрице (а,-^),
и будет пределом последовательности sn.
Решение, Пусть, например, f есть линейное преобразование множества
всех векторов плоскости и пусть собственные значения %i и Х2 этого
преобразования отличны от нуля и не равны друг другу:
?м ф 0, Х2 ф 0, X, Ф \ц
Тогда
1 л л- t — ^i \n
1 * *> 1 а
'V2 ЛХ
(стр. 553).
55Ь Глава Xll JJUHLHHbJt И Л^ФННЛЫЬ ПРЕОБРАЗОВАНИЯ
Д<1 в силу принятых выше on,4Lue 1ечии
sin t — —3^~sm ^' ~'~^ Y~sin ^2'
сиъ f, =; ~~~ cos A, -f г ~ cos Яг
Отсюда
siii /n tcj , — ,г i 42 i ,- i {.; "Г
+ 2 sin %t sin X,2
sm2|;+cos2/ =
2 77 ^—2 1" i COS ky COS A2 7T ТГ-.r;
Ho //—(A.j-1 Л2) / + ?.,\2 = J2— У^+/2 = 0, значит, остается
: = 1 И Т. Д.
Г X А В А ХТ
ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
§ 191. Проективная плоскость
1. Первая модель проективной плоскости
Пусть дана плоскость л и принадлежащая ей прямая.
Присоединим к множеству точек прямой новый элемент, природа
которого для нас совершенно безразлична. Мы получим новое
множество, состоящее из точек рассматриваемой прямой и вновь
присоединенного элемента. Это новое множество называется
проективной прямой, соответствующей взятой обыкновенной
прямой. Элемент, вновь присоединенный к множеству точек
обыкновенной прямой, называется несобствен и ой, или бесконечно
удаленной, точкой проективной прямой.
Условимся в следующем: если на плоскости взять две
пересекающиеся прямые, то соответствующие им проективные прямые
имеют различные несобственные точки, т. е. эти проективные
прямые образуются присоединением двух различных элементов к
множествам точек обыкновенных прямых. Если же прямые
параллельны, то условимся, что соответствующие им проективные
прямые имеют одну и ту же несобственную точку, т. е. эти
проективные прямые получаем присоединением одного и того же элемента
к каждому из множеств точек взятых прямых.
Совокупность всех несобственных точек, т. е. совокупность
всех вновь присоединенных элементов, назовем несобственной,
или бесконечно удаленной, проективной прямой.
Множество, состоящее из всех точек рассматриваемой
евклидовой плоскости я и всех несобственных точек, называется
проективной плоскостью.
Условимся в следующей терминологии: точки и прямые
евклидовой плоскости и самою евклидову плоскость будем называть
558 Глава XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
обыкновенными точками, обыкновенными прямыми и обыкновенной
плоскостью. Обыкновенные точки, рассматриваемые как элементы
множества, являющегося проективной прямой, или проективной
плоскостью, будем называть собственными точками.
Все прямые проективной плоскости, кроме несобственной, будем
называть собственными прямыми проективной плоскости. Далее,
будем говорить, что точка (как собственная, так и несобственная),
которая принадлежит множеству, составляющему проективную
прямую, лежит на этой прямой, или что проективная прямая
проходит через эту точку.
Покажем следующее.
1. Через любые две различные точки проективной плоскости
проходит и притом только одна прямая.
В самом деле, если эти две точки собственные, то существует
и притом только одна обыкновенная прямая, проходящая через
эти точки, которой соответствует вполне определенная проективная
прямая, проходящая (по принятой нами терминологии) через две
эти точки.
Если одна из точек собственная, а другая — несобственная, то
из пучка обыкновенных параллельных прямых, к каждой из
которых присоединена эта несобственная точка, нужно выбрать ту,
которая проходит через данную собственную точку. Проективная
прямая, которую мы получим, присоединив к ней данную
несобственную точку, и будет той единственной собственной прямой,
которая проходит через две данные точки.
Если, наконец, обе данные точки несобственные, то они по
определению лежат на единственной несобственной прямой.
2. Любые две различные прямые проективной плоскости имеют
и притом только одну общую точку.
В самом деле, если обе прямые собственные, то они
соответствуют двум различным обыкновенным прямым; если эти прямые
пересекаются, то данные проективные прямые имеют различные
несобственные точки, значит, указанная выше обыкновенная точка
пересечения является единственной точкой, общей для двух данных
проективных прямых. Если же обыкновенные прямые, которым
соответствуют данные проективные прямые, параллельны, то
данные проективные прямые по определению имеют общую им обеим
несобственную точку, и эта точка является единственной точкой,
общей для данных прямых. Наконец, если одна из данных
проективных прямых несобственная, а другая собственная, то
единственной их общей точкой является несобственная точка данной
собственной прямой.
Мы видим, что на проективной плоскости нет параллельных
прямых: всякие две проективные прямые проективной плоскости
пересекаются.
191. ПРОЕКТИВНАЯ ПЛОСКОСТЬ 559
2. Вторая модель проективной плоскости
Назовем проективной плоскостью собственную связку прямых
и плоскостей трехмерного пространства с центром в точке О.
Каждую прямую связки будем называть «точкой» проективной
плоскости, а каждую плоскость связки «прямой» проективной
плоскости.
Ясно, что 1) через две любые «точки» проективной плоскости
проходит и притом только одна «прямая» (это означает, что через
две любые различные прямые связки проходит и притом только
одна плоскость этой связки) и 2) две любые «прямые» проективной
плоскости всегда пересекаются в одной «точке» (т. е. две любые
различные плоскости связки имеют и притом только одну общую
прямую).
Между двумя построенными моделями проективных плоскостей
можно установить взаимно однозначное соответствие, притом такое,
что трем любым точкам одной модели, лежащим на одной прямой,
будут во второй модели соответствовать три точки, лежащие также
на одной прямой.
В самом деле, пусть л— евклидова плоскость, пополнением
которой несобственными точками получена проективная плоскость
П (первая модель). Расположим плоскость л так, чтобы она
не проходила через центр О связки прямых и плоскостей, и
поставим в соответствие каждой прямой связки точку плоскости л,
в которой эта прямая пересекает плоскость я, а каждой плоскости
связки поставим в соответствие прямую, по которой эта плоскость
пересекает плоскость л.
Далее, прямой связки, параллельной плоскости л, поставим
в соответствие ту несобственную точку, которая присоединена к
прямым плоскости л, параллельным рассматриваемой прямой связки
и, наконец, плоскости связки, которая параллельна плоскости л,
поставим в соответствие несобственную прямую плоскости И. Это
соответствие удовлетворяет высказанным выше требованиям.
Замечание. Мы построили две модели проективной
плоскости. Изучение проективной геометрии можно производить на любой
из них. Первая модель имеет то преимущество, что связывает
понятие проективной плоскости с представлением об обыкновенной
евклидовой плоскости; построения, относящиеся к проективной
плоскости, могут быть при этом выполняемы на обыкновенной
плоскости (которой соответствует данная проективная),
Достоинством второй модели проективной плоскости является возможность
свести изучение свойств проективной плоскости к изучению
соответствующих свойств обыкновенного трехмерного евклидова
пространства.
Можно построить и другие модели проективной плоскости.
560 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
§ 192. Однородные координаты точки и прямой на проективной
плоскости
1 Первая модель проективной плоскости
Введем на евклидовой плоскости л общую декартову систему
координат. Дополним эту плоскость несобственными точками до
проективной плоскости П.
Возьмем на этой проективной плоскости собственную точку М.
Пусть X и У —ее координаты. Будем называть любую тройку
чисел х1% xit хъ однородными координатами точки М, если
х3 =^0 и если
Х1 __ у Х2 у
Из этого определения следует, что если хх, х2, х3 — однородные
координаты собственной точки М проективной плоскости, то три
числа kxx, kx2, kx3, где k — любое число, не равное нулю, также
будут однородными координатами точки М.
Таким образом, однородные координаты собственной точки —
это три любые числа из класса х1:х2:ха всех пропорциональных
между собой троек чисел, таких, что последнее число хаф0. Это
обстоятельство отмечают следующей записью:
Например, запись МA:2:—2) означает, что однородные
координаты точки М —это числа 1, 2,-2, или 2, 4—4, или —3,
— 6, бит. д., аффинные же декартовы координаты этой точки
Пусть теперь М —несобственная точка. Рассмотрим какой-нибудь
вектор а, не равный нулю и коллинеарный тем собственным
прямым проективной плоскости, на которых лежит точка М
Обозначим координаты вектора а через xv x2.
Вектор с координатами kxv kx2, где fe —любое число, не равное
нулю, также ненулевой, коллипеарен вектору а и собственным
прямым, на которых лежит несобственная точка М. Назовем любую
тройку чисел из класса троек kxv kx2, 0 однородными
координатами несобственной точки М и будем писать
M(x1ixi:0)
Итак, однородные координаты несобственной точки М — это
любая тройка чисел из класса пропорциональных между собой
троек x1:x.i:0, где xlt x2 —координаты какого-нибудь непулевого
вектора, коллннеариого собственным прямым на которых лежит
точка М.
§ Ш. ОДНОРОДНЫЕ КООРДИНАТЫ ТОЧКИ И ПРЯМОЙ С61
Так, например, несобственная точка оси Ох; A:0:0), так как
е1 = {1, 0} | Олг. Несобственная точка оси 0у:@:1:0), так как
е2 = {0, \}\ Оу. Отметим еще, что начало координат имеет
однородные координаты 0:0:1, а единичная точка Е— однородные
координаты 1:1:1.
Теорема. Всякая прямая на проективной плоскости выражается
однородным уравнением первой степени
и обратно, всякое такое уравнение является уравнением некоторой
прямой на проективной плоскости.
Доказательство. Пусть я — обыкновенная плоскость, а П —
соответствующая ей проективная плоскость. Введем на плоскости л
общую декартозу систему координат и возьмем па плоскости П
любую собственную прямую Л.
Пусть и±Х J;-u2Y -f и3 —0 — уравнение той обыкновенной прямой
К плоскости л, присоединением к которой несобственной точки
получена прямая Л. Если xv хг, *3 —однородные координаты
любой собственной точки М прямой Л, то
ч ч
и, значит,
или
:, = 0
Если же М — несобственная точка прямой Л и хх, хг, 0 —ее
однородные координаты, то вектор {xv х2\ коллннеареи npsiMofl К,
значит, u1x1-{-uixi = 0, или
Аналогично доказывается, что если точка (xl:xi:xs) (собственная
или несобственная) не лежит на прямой Л, то
иххх + u2xz + ияхя ф 0.
Если Л—несобственная прямая, то ее уравнение имеет вид
*3 = 0.
Обратно, всякое однородное уравнение
первой степени относительно xlt x2, хя является уравнением
собственной прямой, если хотя бы одно из чисел лх или и% не равно
нулю, и несобственной, если ы1 = ма = 0, иь^0.
562
Глава XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Любые три числа из класса и1:и2-ий троек чисел,
пропорциональных коэффициентам в уравнении проективной прямой,
называются координатами этой прямой.
Проективную прямую вместе с ее координатами будем
обозначать [и1:и2:ия].
Две прямые совпадают тогда и только тогда, когда их
координаты пропорциональны.
2. Вторая модель проективной плоскости
Покажем теперь, как можно ввести координаты точек и прямых
для второй модели проективной плоскости.
Введем в пространстве общую декартову систему координат
Oxyz, принимая за начало координат центр О связки, а за оси
координат три прямые Oxf Oy, Oz связки, не лежащие в одной
плоскости (рис. 258). Возьмем произвольную «точку», т. е. произ-
т
Рис. 258
Рис. 259
вольную прямую т. связки; выберем на этой прямой т
произвольную точку М, не совпадающую с центром О связки. Пусть х, у,
z — координаты точки М в системе Oxyz. Три числа х, у, г
называются проективными координатами выбранной точки М.
Если взять на прямой т другую точку М'{хе, у', г'), не
совпадающую с О, то
х:у:г = х' \у' :г'
и, обратно, если
to точка Af (%', у', г') лежит на прямой ОМ. Поэтому любые три
числа, пропорциональные числам х, у, г, также являются
проективными координатами выбранной точки М. Таким образом, каждой
«точке» проективной плоскости соответствует класс пропорциональ-
§ 192. ОДНОРОДНЫЕ КООРДИНАТЫ ТОЧКИ И ПРЯМОЙ 563
ных троек ее координат. Так как уравнение всякой плоскости,
проходящей через начало координат, имеет вид
их + vy + wz = О
и, обратно, всякое такое уравнение является уравнением
плоскости связки, то и для этой модели проективной плоскости верна
теорема: всякая «прямая» проективной плоскости выражается
линейным однородным уравнением ux + vy + wz = 0, где или иФО,
или v^O, или wj^O и, обратно, любое такое уравнение выражает
«прямую».
Любые три числа из класса u:v:w троек чисел,
пропорциональных коэффициентам в уравнении «прямой», называются
координатами этой «прямой» (во второй модели). Две «прямые» совпадают
тогда и только тогда, когда их координаты пропорциональны.
3. Связь проективных координат точки во второй
модели с однородными координатами точки
в первой модели
Проведем через точку Еа@, 0, 1) плоскость я, параллельную
плоскости хОу. Введем на плоскости я систему координат,
принимая за начало координат точку Е3, за оси координат прямые
ЕаХ и E3Y, соответственно параллельные прямым Ох и Оу и
одинаково с ними направленные; масштабные отрезки на осях Е3Х
и E3Y выберем соответственно равными масштабным отрезкам осей
Ох и Оу (рис. 259). Обозначим через II проективную плоскость,
которая соответствует плоскости я. Тогда проективные координаты
х, у, г «точки» т будут и однородными координатами точки М
(на плоскости П), соответствующей прямой т.
В самом деле, пусть «точке» т соответствует собственная точка
М плоскости П, т. е. прямая т пересекает плоскость я в точке М.
Тогда точка М в системе координат ESXY имеет координаты X, Y.
Но так как единичный вектор оси Е3Х равен единичному вектору
оси Ох, а единичный вектор оси EBY равен единичному вектору
оси Оу, то Х = х, Y = y. Значит, первые две координаты тройки
чисел х, у, 1, являющиеся проективными координатами «точки» /га,—
это декартовы координаты точки М, т. е. проективные
координаты х, у, z «точки» т являются однородными координатами
соответствующей ей собственной точки М плоскости П.
Если «точке» т соответствует несобственная точка плоскости II,
т. е. если прямая т параллельна плоскости я, то 2 = 0, а х и у—
координаты вектора, коллинеарного прямой т и лежащего в
плоскости я. Таким образом, и в этом случае проективные
координаты «точки» т есть однородные координаты соответствующей
несобственной точки плоскости П.
об 4
I лава XV ЗЛНЛ\1Л11Ь: ЛРОЕКТШШОЙ
§ 193. Уравнение прямой на проективной плоскости*,
проходящей через две точки; пучок прямых
Через две различные точки (а1:а2-а3) и (bx:b2:bs) проходит и
притом только одна прямая, уравнение которой можно записать
в виде
а1 а.г аг
Ьх Ьг Ья
0.
В самом деле, написанное уравнение является однородным
уравнением первой степени относительно хх, х2, хг (данные точки
предполагаются различными, следовательно, их координаты не
пропорциональны и, значит, среди коэффициентов при хх, хг, х3
в написанном уравнении по крайней мере один не равен нулю).
Координаты этой прямой:
аг а3
•
ЙЗ а1
'•
ах а2
Ьг Ь2
Если А (ах:а^:аь) и В фх'.Ьг:Ь3) — две различные точки
проективной плоскости, то при любых а и р\ не равных нулю
одновременно, точка М с координатами
лежит па прямой АВ и, обратно, координаты любой точки прямой
АВ могут быть представлены в таком виде.
В самом деле, прямая АВ выражается однородным уравнением
первой степени относительно хх, х„, х3; а1, а.2, а3 и 61; 62, Ь3 — два
линейно независимых решения этого уравнения; значит, все
решения будут линейными комбинациями этих двух.
Аналогично устанавливаются и следующие два предложения:
две различные прямые
+ + 0, v xxx + v2
и1х1 + «2*2
пересекаются в точке
= 0
\и3 их
прямая
а {ихх1
-\- р [vlx1 -f u2x2 + v3x3) = 0,
где а и р не равны нулю одновременно, входит в пучок прямых,
определяемых двумя данными, и, обратно, уравнение любой прямой
этого пучка можно записать в таком виде.
* В этом параграфе имеется в виду любая из двух моделей проективной
плоскости В случае первой модели x1:xi:x3 — однородные координаты точки,
в случае второй — проективные координаты,
§194 ГРУППл Ш-OIiKl HBIiblX ПРЕОЬРАЗОП МШП
§ 194. Группа проективных преобразований проективной плоскости.
Группа аффинных иреобразований как подгруппа группы
проективных преобразований
Проективным отображением проективной плоскости П на
проективную плоскость IV называется взаимно однозначное
отображение плоскости И на плоскость IV, при котором три любые точки
плоскости П, принадлежащие одной прямой, переходят в три точки
плоскости II', также принадлежащие одной прямой.
Проективное отображение проективной плоскости П на себя
называется проективным преобразованием проективной
плоскости .
Таким образом, определение проективного отображения
плоское ги II на плоскость II' и определение проективного
преобразования плоскости П точно такие же, как и определения аффинного
отображения и аффинного преобразования (§ 176), Следует, однако,
иметь в виду, что эти определения относятся к разным объектам:
определение аффинного отображения и аффинного преобразования
дается для евклидовой плоскости, а определение проективного
отображения н проективного преобразования—для проективной
плоскости. Этим и объясняется глубокое различие свойств
аффинных и проективных отображений и преобразований.
Рассмотрим множество всех проективных преобразований
проективной плоскости II. Пусть 3J и 23 — два любых проективных
преобразования плоскости П. Произведение ЗШ является взаимно
однозначным преобразованием и переводит три любые точки
плоскости П, принадлежащие одной прямой, в три точки плоскости П,
также принадлежащие одной прямой.
Следовательно, ШЗ — проективное преобразование.
Преобразование ЗС, обратное преобразованию 31,— взаимно однозначно.
Преобразование ЭД" три любые точки А', В', С плоскости IT,
принадлежащие одной прямой, переводит в точки А, В, С, также
принадлежащие одной прямой. В самом деле, предполагая, что
точки А', В', С принадлежат одной прямой и допуская, что их
прообразы А, В, С при преобразовании 2I" не лежат на одной
прямой докажем (так же, как в теореме 1 § 176), что при
преобразовании 31 все точки плоскости 11 отображаются в точки прямой
А'В'С, а значит, 31 — невзаимно однозначное преобразование.
Итак, ЗС— проективное преобразование. Таким образом,
множество всех проективных преобразований проективной плоскости
образует группу, называемую группой проективных преобразований
проективной плоскости.
При проективном отображении 31 проективной плоскости П на
проективную плоскость П' (и при проективном преобразовании
плоскости ТТ) множество всех точек прямой / отображается и
притом взаимно однозначно на множество всех точек некоторой прямой
566 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
/' (это следует из того что S4—также проективное отображение
плоскости II' па плоскость П)
Прямая I' называется образом прямой /, а прямая / прообразом
прямой /' при преобразовании 8(.
Множество всех проективных преобразований плоскости, каждое
из которых отображает па себя какую-нибудь фиксированную
прямую, образует подгруппу группы проективных преобразований
В самом деле, произведение Ш.Ч5 проективных преобразований,
каждое из которых отображает прямую / па себя, будет также
отображать прямую / на себя. Преобразование St будет
отображать прямую / на себя, если преобразование 3( отображает / на
себя
В частности, если проективная плоскость задана в виде первой
модели, то множество Т1 всех проективных преобразований
плоскости, отображающих на себя несобственную прямую, будет
подгруппой группы Г проективных преобразований плоскости
Каждое из проективных преобразований подгруппы 1\
переводит собственные точки плоскости П в собственные точки
плоскости П. В самом деле, если бы какая-нибудь собственная точка
плоскости П каким-нибудь проективным преобразованием из Гх
переводилась в несобственную, то три точки М и любые две
несобственные точки переводились бы в три несобственные точки,
а значит, при преобразовании, обратном рассматриваемому (также
проективном), три несобственные точки переходили бы в две
несобственные и в одну собственную. Это невозможно, ибо три
несобственные точки принадлежат одной прямой, а две несобственные
и одна собственная не принадлежат одной прямой.
Из сказанного следует, что любое преобразование из 1\
порождает в плоскости я, пополнением которой получается плоскость II,
аффинное преобразование Группе Т1 всех проективных
преобразований плоскости П соответствует в указанном смысле группа всех
аффинных преобразований плоскости я.
§ 195. Проективное преобразование плоскости в координатах.
Основная теорема
Теорема 1. Преобразование й проективной плоскости П, при
котором точке М{хх:х,1:хг) ставится в соответствие точка
М' (Xi:x2:x3) той же плоскости, и такая, что ее координаты
выражаются через координаты точки М линейными однородными
соотношениями
х\ = а11х1 + а12х2 + а13х3,
Xi = ailxl 4-o22-*2 "Ь^гз-^з» О)
§ 195. ОСНОВНАЯ ТЕОРЕМА
где
Д =
п
ач1 а.
13
за а,чз
является проективным.
Доказательство. В силу условия
взаимно однозначно.
Рассмотрим три произвольные точки
преобразование
С ({ахх + $ух) : (ах2 + Р«/а) : («*3 + рг/3))>
принадлежащие одной прямой. Пусть
А'(х\\х\:х3), В' (y'l'.y'i'.y's)
образы точек А и В при преобразовании S. Тогда в силу
соотношений A) образом точки С будет точка
С ((си, + рУл : (ох', + Ш х (ах3 + f>y'3)),
принадлежащая прямой А'В'.
Теорема 2 (обратная). Всякое проективное преобразование
проективной плоскости II в координатах выражается линейными
однородными соотношениями с определителем Д, не равным нулю.
Доказательство. Реализуем проективную плоскость первой
моделью.
1°. Рассмотрим сначала случай когда проективное
преобразование Ш. несобственную прямую переводит в несобственную
прямую.
Так как образом любой собственной точки является в этом
случае собственная точка, то на множестве собственных точек
проективное преобразование Ш. совпадает с некоторым аффинным
преобразованием А Аффинное преобразование А в однородных
координатах выражается соотношениями вида
= а11х1
al3x3,
B)
где
Соотношениями B) задается и некоторое проективное
преобразование А, которое несобственную точку (x1:x2:Q) переводит в
несобственную же точку ({a^x-L -J-а12х2) ■(а21х1 -\~а22х2) :Q), Проективные
преобразования SI и Л, как мы только отметили, совпадают на
множестве всех собственных точек плоскости П; докажем, что они
668 Глава XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ Г hO.WE I РИМ
производят одно и то же преобразование и над несобственными
точками. В самом деле, пусть С — несобственная точка прямой
АВ(А и В — собственные точки). Тогда и при преобразовании St,
и при преобразовании А точки А и В перейдут в собственные
точки А' и В', а точка С перейдет в несобственную точку С"
прямой А'В'. _
Итак, at-Л.
2°. Предположим теперь, что несобственная прямая / плоскости П
при проективном преобразовании 31 переходит ъ собственную
прямую /', уравнение которой в однородных координатах имеет вид
азА + аз2*2 + assx3 = 0.
Доказательство сведем к первому случаю. Для этого
рассмотрим проективное преобразование &, определяемое соотношениями
Х3 = 031*1 "Г ag2*2 T a33*3>
где числа а1и а12, а13, о21, а22, а23 выбраны произвольно, но так,
чтобы выполнялось неравенство
При преобразовании 2 прямая /' перейдет в прямую лг3 = 0, т.е.
в несобственную прямую плоскости П. Произведение £21,
являющееся проективным преобразованием, переводит несобственную
прямую в себя, а потому, по доказанному (случай 1°), в
однородных координатах выражается соотношениями вида
x1 = bljXl + bVix2 + b1,x.s.
Х2 = ^21*1 "Т" ^22*2 "Ь ^23*3>
Х3 = Xs.
Обозначим это преобразование через А. Из соотношения
ш=л
находим
31 = 2-4.
Но в координатах А и й выражаются линейными
однородными соотношениями с определителем, отличным от нуля,
следовательно, и проективное преобразование Ш, являющееся
произведением й-1 на А, в координатах также выражается линейными
однородными соотношениями с определителем, отличным от нуля,
$ 195. ОСНОВНАЯ ТЕОРЕМА 569
Из теорем 1 и 2 следует, что проективное преобразование
проективной плоскости П можно определить в однородных
координатах как линейное однородное преобразование с определителем,
отличным от нуля
Заметим, что если при проективном преобразовании 21
проективной плоскости П образом собственной точки М (х, у) является
собственная точка М'(х', у'), то координаты х', у' образа ЛГ
точки М через координаты х и у прообраза выражаются дробно-
лннойными соотношениями
X — 1 , у ="• —
где
a
Ct
a
11
21
31
a
a
a
12
22
34
°24
fl33
Обратно, отображение собственных точек проективной
плоскости II в собственные, заданные соотношениями C) при условии,
что А ф 0 совпадает на множестве собственных точек с
проективным преобразованием
Х1 = аПХ1 "Г а\2
Л*2 —~ ^2\Х1 "i ^22
хз — a-i\xi ~r аггхг 4" ^з
Отметим еще, что прообразом прямой
при проективном преобразовании §1 является прямая
«1 («11^1 + «12-^2 + «1.Л) + «2 @21^1 4-022*2 + 023
4- «з (а3Л 4- «32^2 4- а3Л) = О'
или
(auui +а21и2 ~а31и3) хг + (a12«i -f-a22
4- (Oi3"i 4- Чьа-2 4- a33«s) ^з = 0.
Таким образом,
их = аХ1и] + anii, + aalu's,
иг — а1ги1 4- аг%и'г 4- а32"з,
т. е. матрица проективного преобразования, выражающего
координаты ult ы2, и3 прообраза прямой через координаты ее образа,
является матрицей А', транспонированной по отношению к
матрице А проективного преобразования Ш,
570 I лава W ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Докажем следующую основную теорему о проективных
преобразованиях плоскости.
Теорема 3. Если на проективной плоскости заданы двг четверки
точек А, В, С, D и А', В', С, D' так, что никакие три точки
из первой четверки не лежат на одной прямой и никакие три
точки из второй четверки не лежат на одной прямой, то
существует и притом только одно проективное преобразование, которое
точки А, В, С, D переводит соответственно в точки А', В', С, D'.
Доказательство существования. Докажем сначала,
что существует проективное преобразование %, которое точки A:0:0),
@:1:0), @:0:1), A:1:1) переводит соответственно в точки
А(ах:а.2:а3), В (bx:b2:b3)T С (с 1:с2:с3), D {dx:d2:ds).
Искомое преобразование будем искать в виде
х! = ахрхх + bxqx2 + cxrx3,
х2 = а2рхх -j- b2qx2 -\- c2rxs,
х3 = а3рхг + bsqx2 + с3гхд,
где р-фО, q^O, гф-0 (эти числа определим ниже). Ясно, что
это проективное преобразование точки A:0:0), @:1:0) и @:0:1)
переводит соответственно в точки
А(ах:ай:а3), В (Ь^.Ь^.Ь^, С {сх:с^\съ).
Для того чтобы точка A:1:1) перешла в точку (dx:d2:d3),
достаточно р, q, r выбрать так, чтобы
Эта система имеет решение относительно р, q, r, так как ее
определитель не равен нулю. Ни одно из чисел р, q, r,
составляющих это решение, не равно 0, так как точки В, С, D не
лежат на одной прямой, точки С, A, D не лежат на одной прямой
и точки А, В, D не лежат на одной прямой«
Аналогично доказывается, что существует проективное
преобразование *}, которое точки A:0:0), @:1:0), @:0:1) и A:1:1)
переводит соответственно в точки Л', В', С, D'. Но тогда
преобразование ЗЗЗС точки Л, В, С, D переводит соответственно в
точки А', В', С, D'.
Доказательство единственности. Предположим, что
существует еще проективное преобразование 5E, которое точки
А, В, С, D переводит соответственно в точки А', В', С, D''.
Тогда преобразование Ъ~Щ${ каждую из точек
A:0:0), @:1:0), @:0:1), A:1:1)
§ 195. ОСНОВНАЯ ГЕОРЕМА 571
оставляет на месте. Докажем, что на месте останется и любая
точка плоскости, т. е. что 23~и|Ш есть единичное преобразование.
Пусть
хз = "зЛ
проективное преобразование 33~х$31. Так как оно точки
A:0:0), @:1:0), @:0:1), A:1:1)
оставляет неподвижными, то
1:0:0 = 611:6!1:631.
0:1:0 —Ь12\Ьгг:Ьзг,
0:0:1 =bls:b2a:b3s,
1:1:1 = (bxl + 612 + *18) : Фи + Ьы + Ь23) : (Ья1 + bs2 + bss),
откуда
^12 = ^21 = ^23 = ^32 = Ь31 = Ь13 == 0,
и, значит,
Таким образом,
где Е — единичное преобразование. Отсюда
1 — ^22 = 3'
т. е. проективное преобразование 9$ совпадает с тем, которое было
построено выше.
Следствие 1. Если проективное преобразование четыре точки
проективной плоскости, из которых никакие три не лежат на
одной прямой, оставляет неподвижными, то оно является
тождественным или единичным.
Следствие 2. Существует и притом только одно проективное
отображение проективной плоскости П на проективную плоскость
П', при котором четырем точкам А, В, С, D плоскости П, по три
не принадлежащим одной прямой, соответствуют четыре точки
А', В', С, D', также по три не принадлежащие одной прямой.
В самом деле, пусть §1 и 23—два проективных отображения
проективной плоскости П на проективную плоскость П', при
котором четыре точки Л, В, С, D плоскости П, из которых никакие
три пе принадлежат одной прямой, отображаются соответственно
в точки А', В', С, Dr плоскости П', из которых также никакие
три не лежат на одной прямой, Произведение ЗЗ^ есть преоб-
572
Главы XV. BJ1EMLH 1 Ы Ш Oh K'l 1 BliUFl 1L0ML1PI1H
разование плоскости J3, при котором точки А, В, С, D
неподвижны. Следовательно, 23" *Й— тождественное преобразование
%-*■% = Е,
откуда
венную точку
§ 196. Примеры проективных преобразований проективной
плоскости
Пример 1. Важным примером проективного отображения проективной члос-
кости II па проективную плоскость II' является перспектива
Рассмотрим в евклидовом пространстве две пересекающиеся плоскости л
и я', которым соответствуют проективные плоскости П и II'. Возьмем собст-
S, не лежащую ни на одной из плоскостей я, и я' (рис. 260).
Пусть М — произвольная точка плоскости II и пусть
SM пересекает плоскость II' в точке М'. Если
прямая SM параллельна плоскости я', то ючка М' — это
несобственная точка плоскости П', присоединяемая к
прямым плоскости л', параллельным прямой SM;
аналогично, если прямая, проходящая через S,
параллельна плоскости л, то прообразом точки М', в
которой она пересекает плоскость л', будет несобственная
точка плоскости П, присоединяемая к прямым
плоскости я, параллельным указанной прямой; наконец,
если прямая, проходяшая через S, параллельна
прямой р, по которой пересекаются плоскости л и я',
то несобственной точке прямой р мы стачим в
соответствие самое эту точку Такое сооизетстиие
плоскостей II и IP называется перспективным, Оно
взаимно однозначно и трем любым точкам проективной
плоскости II, принадлежащим одной прямо!!,
соответствуют три точки проективной плоскости П', также
принадлежащие одной прямой, следовательно,
перспектива — проективное отображение
Эти соображения находят простое приложение к
трансформированию аэрофотоснимков
с летящего самолета производится фотографирование
местности Если в момент экспозиции фотоаппарата его ось вертикальна, то
изображение плоского куска местности на фотопленке подобно
фотографируемому куску местности и фотография является хорошей картой местности.
Однако вследствие неизбежной качки самолета ось фотоаппарата меняет свое
направление и на фотопленке получаются различные перспективные
изображения частей местности (рис 261). Фотографирование обычно производится
столь часто, что каждый следующий фотоснимок захватывает часть местности,
заснятой на предыдущем снимке Полученные фотоснимки чуждаются в
исправлении от искажений, внесенных крепом самолета. Фотоснимки
исправляют фототрачсформатором (рис. 262) На негативе прокладывают какие-
нибудь че:ыре точки, из которых никакие три не лежат на одной прямой,
взаимное расположение которых на карте предварительно известно (например,
дерево, колодец, дом, фабричная труба), и поворачивают негатив так, чтобы
лучи, падающие от точе-ыого источника cBeia, находящегося над негативом,
проходя сквозь наколы, заняли те мое га, которые им соответствуют на карте
и которые нанесены на ''пениалыюм листе 5уча;н, лежачг.-м поч негативом
После того как совмещение известных четырех ориентиров (из коюрых ннка-
Рис
Предположим, что
196. ПРИМЕРЫ ПРОЕКТИВНЫХ HIT ОЬР ЛЗОВЛНИИ
573
кие три не лежат па одной прямой) достигнуто, мы можем утверждать,
что оптически осуществлена перспектива, которая дает проективное отбраже-
ннс фотоснимка и истинную каргу местности Лист б\маги заменяют
фотобумагой и изготовляют позитив н найденном положении негатива (освещая его
Рис 261
сверху тем же точечным источником снега). Полученные затем фотоснимки
склеивают друг с другом но границам общих частей
Пример 2. Покажем, как начертить образ ка,\опшгбуд!> фигуры,
лежащей па проективг.ой плоскости * при проективном преобразовании.
Пусть А', В', С", D'— образы вершин квадрата ЛВС!) (рис. 2G3) при
проективном преобразовании 9(. На рис. 264 показано, как тогда построить образ
* Имеется в виду первая модель
57 t
Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
О' центра О квадрата ABCD и образы Р', Л"', Q', /И' середин Р, N, Q, М
его сторон. Зная образ Р'А'У'О' квадрата PANO и образы аналогичных ему
квадратов, можно повторить построение, найти образы точек Ох, О2, О3, О., и
образы середин сторон квадратов PANO,
ONBQ, QCMO и УИОРО и т. д. Таким
образом, будет построен проективный
образ квадратной сети, покрывающей
квадрат ABCD, и если на нем
нарисована какая-нибудь фигура (рис. 265), то
приближенно по клеткам можно
нарисовать ее образ при рассматриваемом
проективном преобразовании.
Построение таких проективных сеток
было с успехом использовано проф.
М. В. Пентковским в номографии при
проективных преобразованиях.
На рис. 266 таким построением дан
проективный образ шестигранного паркета.
Пример 3. Рассмотрим проективное
преобразование проективной плоскости,
оставляющее на месте все точки некоторой
прямой / и еще одну точку S, не лежащую
на прямой /. Такое проективное
преобразование называется
гиперболической гомологией. Прямая /
называется осью гомологии, а точка S —
центром гомологии. Будем считать, что
проективная плоскость реализована первой
моделью и что S — собственная точка, а
/ — собственная пряма'я. Примем прямую /
за ось Ох, а точку S — за единичную точку
оси Оу общей декартовой системы
координат. Пусть п этой системе координат гипер-
соотиошениями
262
болическая гомология выражается
X1 = а11Х1 -f-
A)
X = пиХ1 + «32*2 + «33*3
«L
А1'
Рис. 263
Р' В'
Рис. 264
196 ПРИМЕРЫ ПРОЕКТИВНЫХ ПРЕОБРАЗОВАНИЙ
575
Так как три точки A:0:0), @:0:1), A:0:1), лежащие на прямой /,
неподвижны при рассматриваемой гомологии, то
откуда
23) : (asl-f «зз)>
= а31 = а13 — а23 = °. п.зз = йп.
Рис. 265
и соотношения A) принимают вид
х'1=а11х1-\-а12х!1,
Проективное преобразование (Г) оставляет на месте все точки прялшй /.
самом деле, если М (хг:0:хь) — произвольная точка прямой /, то ее образ
ф A) О М
д (гь) р
, как следует из формул A), имеет координаты х^.О-.х^, т. е. совпадаете М.
Потребуем еще, чтобы точка S @:1:1) оставалась неподвижной. Тогда
0:l:l=a12:a22: (a32-f-an),
откуда
0 a
Рис. 266
196. ПРИМЕРЫ ПРОЕКТИВНЫХ ПРГ.ОБР АЗОВ All ИЙ
577
и потому
хх=апкх, х2=<
Полагая зде^ь ап — \, а22 = /ь, будем иметь
B)
Этми формулами и определяется рассматриваемая гиперболическая
гомология Соответствие между собственными точками проективной плоскости при
гиперболической гомологии определится
соотношениями
(Х-\)у+\
Ху
У =;
Гиперболическую гомологию можно-
задать ее осью /, центром S и нарой
соответственных точек М и М' (лежащих,
конечно, на прямой, проходящей через
центр S гомологии). Тогда можно и гео- рИС- 267
метрически построить образ Р' любой точки
Р (рис. 267).
На рис. 268 выполнено построение образа рисунка и надписи к нему в
гиперболической гомологии, заданной осью /, центром и двумя
соответственными точками А и А'.
Отметим, что произведение Г^1\ гипер олических гомологии
у — у v ^^ I
Л1 Л], An f
= (jj,— 1)х2-\-х3
выражается формулами
C2=).U.V2,
■ 1) JC2 —X;, =(Х,Ч 1) Хг
е. снова является гиперболической гомологией ГХ|1 с той же осью и центром.
Отсюда следует, что множество всех гиперболических гомологии с данной
осью и центром образует подгруппу группы всех проективных преобразований
плоскости.
Если ?.-= — !, то гиперболическая гомология
т.
называется инволюционной. Квадрат инволюционной гиперболической
гомологии есть тождественное преобразование. Очевидно (см. соотношения (Гх^.)),
только тождественное преобразование и инволюционная гиперболическая
гомология обладают среди всех гомологии тем свойством, что Г2 = С где
£—тождественное проективное преобразование.
Если центр S гиперболической гомологии является несобственной точкой
и если М и Л'—две произвольные собственные точки, а ЛГ и N'— их образы,
то (рис. 269 и 270)
РМ' QN'
19 П. С. Моденов
ГЕОМЕТРИИ
с'осьюТ' над со3ствеиными гочками производится преобразование родства
Если ось гомологии —несобственная прямая, то над
производится преобразование гомотетии (рис 271). На
Рис 268
болическас гомология порождается аффинным сжатием трехмерного
пространства к плоскости («ось гомологии») по направлению некоторой прямой («центр
гомологии») (рис.272).
М
М
м',
/;
* /t
Примео 4. 1 :араболической гомологией называется проективное
преобразование проективной плоскости, при котором имеется такая прямая (называемая
огыо гомологии), что нее ее точки остаются неподвижными при этом
преобразовании, а па этой прямой есть точка S (центр гомологии), обладающая
следующим свойством; если М — любая точка проективной плоскости, а М' — ее
образ, то точки S, М и ^/'принадлежат одной прямой. Реализуем проективную
» 1ЧЯ ПРИМЕРЫ ПРОЕКТИВНЫХ ПРЕОБРАЗОВАНИЙ
579
плоскость р виде первой модели Примем ось 1О\тологии за ось Сх чффшшой
системы координат, а центр гомологии 5 — за начале координат и введем
однородные координаты, соответствующие этой аффинной системе. Как было
доказано в предыдущем примере, проективное преобразование оставляющее па
месте все точки прямой Ох, записывается так:
Образ несобственной точки (Oil:0) оси Оу будет (ai2--o22:332>), il так как
точки @:0:1), (OiliO) и (als:ais:ass) должны лежать на одной прямой то
0 0 I
0 I J
а12 а22 о32
= 0,
Рис. 272
т. е. а12 = 0, и, значит,
=anxu х\ =
= amxt + anxs.
Образом точки A:1:1) является ючка (ац:о22: (BB2 + Oii))> которая лежит
на одной прямой с точками @:0:1), A:1:1).
Поэтому
0 0 J
1 1 1
0,
т. е. а22 = а11( и, значит,
х1—апх1, xi=
Полагая ац = 1, ait = K. будем иметь
Теперь нетрудно проверить, что любая точка (Xi:x2'xs) я ее образ лежат
на одной прямой с точкой @:0:1), так как
0 0 1
х3
=0.
х, х2 Ах2 + Ч
Соответствие собственных точек рассматриваемой параболической гомологии
таково:
19»
580
XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Произиедениг двух параболических гомологии ПХП есть параболическая
гомология Пх+ Множество всех парабо ических гомологии с данной осью i
центром образует группу
Параболическая гомоло! и i пполне определяется заданием оси /, центра S и
пары соответственных точек № и /W (коллипеар
ных с S) По этим данным можно гостроить образ
Р' любой точки Р (рис. 273). На рнс>пке 274 пост
роен образ рисунка и надписи к нему при парабо
лической гомологии
Во второй модели параболическая гомология
порождается аффинным сдвигом пространства отно
сителыю некотором плоскости связки («ось гомо
логин») по направлению прямой связки, лежащей
в этой плоскости («центр гомологии») (рис 275),
Сели проективная плоскость реализована в ви
рис 273 Ае пеРВ0Й модели и ось гомологии—собственная
прямая, а центр — гесобствеииая точка (лежащая па
этой прямой), то параболическая гомология осуще
ствляет над собственными точками аффинное преобразование, являющееся сдвн
гом относительно оси гоыолопы (рис. 276.)
Рис 271
М'/
I / \
V
Рис. 275
Ль
Рис. 277
107 ПОНЯТИЕ О ПРОЕКТИВНОМ ПРОСТРАНСТВЕ 581
Если несобственными являются и центр, н ось параболической гомологии,
то над собственными точками она осуществляет преобразование переноса
(рис. 277).
§ 197. Понятие о проективном пространстве
Подобно тому как множество точек обыкновенной плоскости
присоединением несобственных элементов превращается в
проективную плоскость (точнее в ее первую модель), можно построить
модель трехмерного проективного пространства исходя из
трехмерного обыкновенного евклидова пространства.
Проективная прямая проективного пространства получается,
как и в случае .плоскости, из обыкновенной прямой
присоединением к множеству ее точек нового элемента, который
по-прежнему будем называть несобственной или бесконечно удаленной
точкой проективной прямой.
Условимся в следующем, если две прямые параллельны, то
соответствующие им проективные прямые имеют одну и ту же
несобственную точку. Если же две различные прямые не
параллельны, то соответствующие им проективные прямые имеют различные
несобственные точки.
Проективной плоскостью проективного пространства,
соответствующей данной обыкновенной плоскости евклидова пространства,
назовем множество точек, получаемое присоединением к
множеству точек обыкновенной плоскости всех тех несобственных точек,
которые присоединяются к прямым, лежащим на этой плоскости.
Несобственной или бесконечно удаленной прямой проективной
плоскости называется множество всех несобственных точек,
присоединенных к множеству точек той обыкновенной плоскости,
которой соответствует рассматриваемая проективная плоскость.
Наконец, множество всех несобственных точек назовем
несобственной или бесконечно удаленной плоскостью.
Точки, проективные прямые и проективные плоскости, которые
не являются несобственными, будем называть соответственно
собственными точками, собственными прямыми и собственными
плоскостями.
Множество, состоящее из всех обыкновенных и несобственных
точек, называется проективным пространством.
Условимся в следующей терминологии:
1) будем говорить, что точка (собственная или несобственная)
лежит на проективной прямой или что проективная прямая
проходит через рассматриваемую точку, если эта точка принадлежит
множеству точек, составляющему эту проективную прямую;
2) будем говорить, что проективная прямая (собственная или
несобственная) лежит на проективном плоскости (собственной или
несобственной) или что проективная плоскость проходит через проек-
582 P/iaea XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
тивную прямую, если множество точек проективной прямой входит
в множество точек рассматриваемой проективной плоскости;
3) будем говорить, что точка (собственная или несобственная)
лежит на проективной плоскости (собственной или несобственной),
если эта точка является элементом того множества, которое
составляет рассматриваемую плоскость;
4) вместо того чтобы говорить, что точка лежит па прямой (или
пр$!мая проходит через точку), точка лежит на плоскости (или
плоскость проходит через точку), прямая лежит на плоскости (или
плоскость проходит через прямую), говорят: точка и прямая
инцидентны, точка и плоскость инцидентны, прямая и плоскость
инцидентны.
Мы построили модель проективного пространства. Отметим
некоторые свойства проективного пространства исходя из этой
модели *
I Всяким ДВ}М различным точкам инцидентна прямая и
притом только одна.
II. Всякие две различные плоскости инцидентны прямой и
притом только одной.
III. Если точки А и В инцидентны плоскости П, то прямая
АВ ** инцидентна этой плоское! и.
IV. Если плоскости а и Ъ инцидентны точке /И, то прямая
ab *** 'инцидентна этой точке
V. Три точки, не инцидентные одной прямой, инцидентны и
притом только одной плоскости.
VI. Три плоскости, не инцидентные одной прямой
инцидентны и притом только одной точке.
Читателю рекомендуется провести подробные доказательства
этих свойств.
Мы потому особо выделили свойства I—VI проективного
пространства, что при аксиоматическом построении
проективной геометрии именно эти свойства включаются в аксиомы,
определяющие понятие проективного пространства.
' В качестве дополнительных предложений рекомендуем
доказать следующие свойства проективного пространства.
VII. Всякие две различные прямые, инцидентные одной
плоскости, инцидентны и притом только одной точке.
VIII. Всякие две различные прямые, инцидентные одной точке,
инцидентны и притом только одной плоскости.
IX. Точка и неинцидентная ей прямая инцидентны и
притом только одной плоскости
* Приводимые ниже свойства I—VI играют основную роль при
аксиоматическом построении проективного пространства
*"" АВ — прямая, инцидентная точкам Лий.
*** «6—прямая, инцидентная плоскостям чи |.
S 198. ПРИНЦИП ДВОЙСТВЕННОСТИ
583
X. Плоскость и неинцидентная ей прямая инцидентны и
притом только одной точке.
В проективном пространстве, как и на проективной плоскости,
нет параллельных прямых: две любые прямые, лежащие i- одной
плоскости, всегда пересекаются (VII). В проективном пространстве
нет и параллельных плоскостей: всякие две плоскости
проективного пространства пересекаются по прямой линии (II). Наконец,
любая прямая, не лежащая в проективной плоскости всегда
пересекает последнюю (X). Всем этим проективное пространство су-
щестленно отличается от евклидова."
§ 198. Принцип двойственности
Перепишем предложения 1 — X ь виде следующей таблицы:
I. Всяким двум различным
точкам инцидентна
прямая и притом только
одна
III Если точки А и 5
инцидентны плоскости П, то
прямая АВ инцидентна
этой плоскости
V, Три точки, не
инцидентные одной
прямой,инцидентны и притом только
одной плоскости
VII. Всякие две различные
прямые, инцидентные
■одной плоскости,
инцидентны и притом
только одной точке
IX. Точка и неинцидентная
ей прямая инцидентны
и притом только одной
плоскости
11. Всякие две различные
плоскости инцидентны'
прямой и притом
только одной
IV. Если плоскости а и Ъ
инцидентны точке /И,
то прямая ab
инцидентна этой точке
VI. Три плоскости, не
инцидентные одной
прямой, инцидентны и
притом только одной точке
VIII. Всякие две различные
прямые, инцидентные
одной точке,
инцидентны и притом только
одной плоскости
X. Плоскость и неинци-
дентпая ей прямая
инцидентны и притом
только одной точке
Сопоставляя предложения I—II, III —IV, V —VI, VII—VIII,
IX—X, видим, что каждое из них получается из другого
заменой в нем слова «точка», словом «плоскость» и, наоборот, слово
«плоскость» словом «точка», слово «прямая» остается без изменения.
Два предложения о точках, прямых и плоскостях,
сформулированные тслько в терминах инцидентности, называются
двойственными, если одно из них получается из другого заменой слова
«точка» словом «плоскость», слова «плоскость» словом «точка» с
сохранением слова «прямая»
584 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Таким образом, предложения I, III, V, VII, IX соответственно
двойственны предложениям II, IV, VI, VIII. X.
Оказывается, что если верна некоторая теорема А о точках,
прямых и плоскостях проективного пространства,
сформулированная только в терминах инцидентности между ними то будет
верил и двойственная теорема В.
Это предложение составляет содержание так называемого
принципа двойственности. Более полно этот принцип может быть
сформулирован и доказан лишь при аксиоматическом построении
проективного пространства.
Для проективной плоскости имеет месте так называемый
малый принцип двойственности: если г.ерна некоторая теорема А о
точках и прямых проективной плоскости, сформулированная только
в терминах инцидентности между ними, то будет верна теорема В,
двойственная теореме А, т. е. теорема, которая получается из А
заменой слова «точка» на слово «прямая», а слова «прямая» на
слово «точка». Например, утверждению: двум любым различным
точкам инцидентна прямая и притом только одна двойственно
утверждение: двум любым различным прямым инцидентна точка
и притом только одна.
Доказательство малого принципа двойственности так же, как и
сформулированного выше большого принципа двойственности,
получается лишь при аксиоматическом построении проективного
пространства.
§ 199. Однородные координаты точки и проективной плоскости в
проективном пространстве
Введем н пространстве сбщую декартову систему координат.
Если точка М собственная, то в выбранной системе координат она
имеет координаты X, Y, Z. Рассмотрим четыре числа X, Y, Z, 1
и возьмем класс х1:х2:х3:х4 tcex четверок чисел,
пропорциональных четверке чисел
X, Y, Z, 1,
т. е.
где k принимает псе действительные значения, кроме нуля. Так
как А'4=т^0, то
У=— У = — 7 == —
х4 х4 х4
Любые четыре числа построенного класса x1:xn:xs:xi
называются однородными координатами точки М.
Гели М —несобственная точка пространства, то через нее про-
ходиг связка параллельных между собой прямых. Возьмем какой-
§ 200. УРАВНЕНИЯ ПРЯМОЙ. ПУЧОК И СВЯЗКА 585
нибудь вектор а, коллинеариый этим прямым; пусть X Y, Z —
координаты этого вектора. Рассмотрим четверку чисел X, Y, Z. 0
II возьмем класс x1:x2:xs:0 всех четверок чисел,
пропорциональных четверке чисел X, Y, Z, 0:
x1:x2:xs:xi = X:Y :Z:Q,
т е.
х1 = kX, х2 = kY, xs = kZ, xA = 0,
где k принимает все действительные значения, кроме 0. Любые
четыре числа построенного класса x1:x2:x3:xi называются
однородными координатами несобственной точки М. В проективном
пространстве всякая проективная плоскость определяется в
однородных координатах линейным однородным уравнением
U1X1 -f «2*2 "Г USXS -f UiXi = 0
и, обратно, любое линейное уравнение такого вида определяет в
проективном пространстве плоскость.
Проективными координатами проективной плоскости в
проективном пространстве называется любая четверка чисел из класса
u1:u2:u3:ui четверок чисел, пропорциональных коэффициентам
уравнения этой плоскости. Самую проективную плоскость будем
обозначать так:
[«1:«2:«8:«41.
Две плоскости совпадают тогда и только тогда, когда их
координаты пропорциональны.
§ 200. Уравнения прямой, проходящей через две точки.
Пучок и связка плоскостей
Точка М (x1:x2:x3:xi) лежит на прямой, проходящей через
точки A(al:a2:a3:ai) и В(b1:bt:b3:bi) тогда и только тогда, когда
х1 = аа1-\-$Ь1, х2 = аа2 + Р&2, ха — аа3-\-$Ь3, х4 = с.а4 + Р&4,
где аир принимают любые значения, не равные нулю
одновременно.
Эти уравнения называются параметрическими уравнениями
прямой. Уравнение всякой плоскости пучка, определяемого двумя
различными плоскостями л1 и я2,
UXXX -г «2*2 "t" «3А'з + Ы4А'4 " 0 V\X\ + V2X2Jr VSX3 ~Г ViXi = 0.
может быть записано в виде
a(UlXl + «2*2 + *3 + *4) "I" P (V\Xl + У2*2 + VZXS "I" У4*4) = 0
и, обратно, если аир не равны нулю одновременно, то это
уравнение является уравнением плоскости, входящей в пучок,
заданный двумя плоскостями ях и ля.
586
Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Три ТОЧК1-1
В F, :b2:bs:b4) С |с,:с2:с3:с4)
не принадлежат одной прямой тогда и только тогда, когда ранг
матрицы
1аЛ а2 а3 it\
Ь, b, bs Ь
равен трем, ибо тогда строки этой матрицы будут линейно
независимы и значит, координаты ни одной из точек Л, В С не
могут быть представлены линейной комбинацией координат лвух дру
гих точек
При этом ураш.'егшс плоскости я проходящей через эти точки,
имеет вид
ах а2 а3 а4
Ьх Ьг Ьг bi
= 0.
Три плоскости, заданные уравнениями
игхх + игх2 + u3xs + «4л4 = 0,
vxxl + югх2 + usxz -Ь vixi = 0,
©jX, + ^2*2 + «Л3Х3 + ^4*4=°.
имеют одну и только одну общую точку тогда и только тогда,
когда ранг матрицы
ХЮ4
vx v2 of
является точкой их пересечения.
Если точки A (a1:a2:as:ai). В (bx:b2:bs:bl), С (с1:с2:с3:с4) не
лежат на одной прямой, то точка
М (Сад, -|- Р
равен трем При этом точка М
«4
щ
и.
w2
к
их
щ
и,и3
ш4 да3
их
«2
ш
+ ус.г): (aas
усх):
при любых а, р\ Yi не равных пулю одновременно, лежит в
плоскости ABC и обратно, координаты любой точки плоскости ABC
|5 ?01 ОСНОВНАЯ ТПОРЕМЛ
587
могут быть представлены линейными комбинациями координат
точек Д, В, С.
Если плоскости
3 + vixi = О,
да^! + w7x2 -f wsx3 -f гг-'4л:4 = О
имеют и притом только одну общую точку, то плоскость
a (uxx, •+■ u2a:2 -f «-3X3 + u4x4) -f
+ 6 (v tx x + о2л
проходит через эту точку и, обратно, уравнение плоскости,
проходящей через эту точку, может быть выражено в таком виде.
Правильность всех этих утверждений следует из теории
линейных однородных систем уравнений
§ 201. Группа проективных преобразований проективного
пространства. Основная теорема
Проективное преобразование Й проективного пространства
геометрически определяется аналогично проективному преобразованию
плоскости В координатах такое преобразование является
преобразованием, при котором точке М (x1:x2:x,^.xi) ставится в
соответствие точка М' (xl:x2:x3:xi) с координатами
Хх =
«12*2
«18*3
— «21-^1 4" «22*2 Т
«24*
24*4!
-3 = «31Х1
4 = ailx1
где
д_
Матрица
аи а
+ «33XS ~f Q3
Xo + ai3x3 + a4
/ q
12 «13 «14
!21 U22 3 4
«31 «32 «33 «34
«41 ai2 a*3 «44
А = (а/*)
называется матрицей проективного преобразования 91.
Множество всех проективных преобразований пространства
образует группу Группа аффинных преобразований пространства
изоморфна подгруппу группе всех проективных преобразованный
588 Г л а в а XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
пространства, которые отображают несобственную плоскость
на себя.
При проективном преобразовании пространства всякая плоскость
отображается на плоскость, причем координаты прообраза
выражаются через координаты'образа при помощи линейных
однородных соотношений с матрицей А', полученной транспонированием
матрицы А проективного преобразования 9(.
Если в проективном пространстве заданы две группы по пять
точек в каждой А В, С, D, Е и А', В', С, D', £', такие, что
никакие четыре точки первой группы не лежат в одной плоскости
и никакие четыре точки второй группы не лежат на одной
плоскости, то существует и притом только одно проективное
преобразование, которое точки А, В, С, D, Е переводит
соответственно в точки А', В\ С, D', Е'.
Доказательство этой теоремы аналогично доказательству
теоремы для проективной плоскости.
§ 202. Ангармоническое отношение. Гармонизм
Рассмотрим первую модель проективной плоскости. Возьмем на
этой плоскости собственную прямую, а па пей упорядоченную
четверку попарно различных собственных точек А, В, С, D.
Сложным, или ангармоническим, отношением (ABCD) точек А, В, CD,
взятых в этом порядке, называют число, определяемое равенством
Если точки Л и С совпадают или точки D и В совпадают, то
считаем (ABCD) = 0 Если точка D совпадает с точкой А или
точка С совпадает с точкой В, то (ABCD) не определяется.
Если одна из точек, например точка D, несобственная, то по
определению (ABCD) принимается равным пределу сложного
отношения (ABCDJ, где Dj—собственная точка, причем предел
берется в предположении, что точка D1 неограниченно удаляется по
прямой ABC.
Так как
lim ^
при этом условии равен — 1, то в случае, если D — несобственная
точка,
{ABCD)=— й£ = 4§.
СВ ВС
« 202 ЛНГЛРЛ'.ОИИЧПСКОЕ О1НОШЕПИЕ. ГЛРМОНИЗМ 589
Аналогично, если /. — несобственная точка, то
ев
если В — несобственная точка, то
(ABCD)=.~
DA
н, наконец, если С—несобственная точка, то
(ABCD) = ~
AD
Определение сложного отношения четырех несобственных точек
дано ниже.
Ьудем говорить, что ряд точек А, В, С, D, Е, ..., лежащих
па одной прямой /, перспективен ряду прямых а, Ь, с, d,
е, ... пучка с центром О, не лежащем на прямой /, если прямые
а, Ь, с, d, е, ... проходят соответственно через точки А, В, С,
D, В, ...
Сложным, или ангармоническим, отношением (abed) четырех
попарно различных прямых а, Ь, с, d одного пучка с центром О
назовем сложное отношение (ABCD) четырех точек А, В, С, D
лежащих на собственной прямой I, не проходящей через точку О,
и перспективных прямым а, Ь, с, d (в случае, если совпадают
прямые awe или d н Ь, считаем (abcd) = 0; если прямая d совпадает
с а или прямая с с Ь, то (abed) не определяется).
Это определение нуждается в обосновании, а именно: нужно
доказать, что если а, Ь, с, d—четыре попарно различные прямые,
принадлежащие одному пучку с центром О, и если / и /'—две
собственные прямые, не проходящие через О, то, обозначая через
А, В, С, D точки пересечения прямой / соответственно с прямыми
а, Ь, с, d, а через А', В', С, D' точки пересечения прямой /' с
прямыми а, Ь, с, d. будем иметь
(ABCD) = (A'B'C'Dr) A)
Для доказательства этого соотношения установим сначала
следующие положения.
1. Если т[ и собственные точки А, В, С попарно различны и
принадлежат одной прямой /, а О —произвольная точка, не
лежащая па прямой /, то*
Тс дТ
се осв
" Отношение площадей двух ориентированных треугольников есть число,
абсолютная величина которого равна отношению их площадей и которое
положительно, если эти треугольники имеют одинаковую ориентацию, и
отрицательно, если ориентация их различна.
690 Плача XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
В самом ]]еле, треугольники О АС и ОСВ имеют общую сер-
шину О, а остальные их вершины лежат на одной прямой.
Значит, отношение их площадей равно отношению оснований. Далее,
если направленные отрезка АС и СВ имеют одинаковое
направление, го треугольники ОАС и ОСВ имеют одинаковую
ориентацию, а если отрезки АС и СВ имеют противоположное
направление, то треугольники ОАС и ОСВ имеют противоположную
ориентацию. Значит, и знаки отношений
ЛС Ь~АС
СВ ~ОСВ
одинаковы. Таким образом равенство B) доказано.
2. Докажем, что
О~АС _ РАС
~св ЪсЪ'
C)
где С —любая точки, лежащая на прямой ОС (но отличная от
точки О). В самом деле, на основании уже доказанного
СО JCO WCO
ОС АОС' ВОС'
откуда и следует равенство C).
Теперь докажем равенство A).
I". Предположим, что О—собственная точка; точки Л, В, С,
D, А', В', С, D' также собственные.
Тогда
(ABCD) = ^ • ^^ °^ • в^ = ^' ^В D)
СВ DB ~ОСВ O~DB ~ОСВ-О~аЬ
Правая часть равенства D) не изменится, если точку А
заменить на точку А' прямой О А. В самом деле, на основании равен-
стиа C) имеем
ЪаЬ Ь~аЬ ЪКЪ ШЪ
Аналогично доказывается, что правая часть равенства D) не
меняется, если точку В заменить точкой В' прямой OS, точку С —
точкой С прямой ОС, а точку D—точкой D' прямой 0D. Значит,
(ABCD) = °ЛС'' °В1Щ = (А1 В'CD').
OC'B'-OA'D'
« 202 АНГАРМОНИЧЕСКОЕ ОТНОШЕНИЕ. ГЛРМОНИЗМ 591
2°. Точки А, В, С, D собственные, но среди точек А', В', С,
D' есть одна несобственная.
Пусть, например, D'—несобственная точка. В таком случае
по определению
(A'B'C'D')=— 4^.
С'В'
С другой стороны,
(ABLD)— ———p^;—.
OCB-OAD OCrB'-OA'D
Ho
=r=—=—;=— 1 (в силу того что Л'В' ||OD).
OA'D A'OD
Итак,
(ABCD) = —^^: = —4^ = (A'B'C'D1).
OC'B' C'B'
3°. Предположим, что точка О несобственная, т. е. прямые а,
Ь, с, d параллельны (и попарно различны) или три из них
параллельны (и попарно различны), а четвертая прямая несобственная.
В этом случае равенство A) следует из того соображения, что
если три параллельные и попарно различные собственные прямые,
например а, Ь, с, пересечены двумя собственными прямыми / и /'
соответственно в точках А, В, С и А', В\ С, то
Jc J'C
св ев'
Теперь равенство A) очевидно. В случае, если одна из
прямых а, Ь, с, d несобственная, следует еще заметить, что
собственная прямая, пересекающая прямые а, Ь, с, d, пересечет три из
них в собственных точках, а одну — в несобственной; кроме того,
в этом случае сложное отношение (ABCD) сводится к простому
отношению трех собственных точек.
Выше не было дано определения сложного отношения четырех
несобственных точек А, В, С, D Будем считать в этом случае
(ABCD) = (abcd),
где а, Ь, с, d—четыре собственные прямые собственного пучка,
перспективные точкам А, В, С, D.
Теорема 1. Ангармоническое отношение (ABCD) четырех точек
проективной плоскости, заданных своими однородными координа-
5Э2 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
тами
С((ахг
DUlXi
равно
L:»=%. E)
Доказательство. Предположим, что все четыре точки
собственные и попарно различные Параллельные проекции точек Л,
6, С, D или на ось Ох, или на ось Оу будут тогда попарно
различны. Пусть, например, попарно различны проекции А', В', С,
D' точек Л, В, С. D на ось Ох параллельно оси Оу. Тогда
В~ХС ХН~ХО
x\
oua + Pi/a
Уз а^з+Pi/s Уз
Если точка D несобственная, т. e. /aa-f- p-y3 — 0, то
CS SC B'C хс—*в
а^з+ РУз Уз
Но из соотношения ?а„ + цг/3 = 0 следует, что — = , так
что опять
Аналогично доказывается справедливость этой формулы, если
какая-либо из остальных точек А, В, С несобственная.
Если все четыре точки
A (Xi:x2-.O),
С ((ах, + Pih):(y.x2+ $у2):%
D ((Кх1 + nyj: (кхг + \1у2); 0)
202 АНГАРМОНИЧЕСКОЕ ОТНОШЕНИЕ I ЛРУЮНИЗМ
593
несобственные, го из определения сложного отношения (АВСО)
четырех несобственных точек А, В, С, D следует, что
где Л,, В,, С1; Dx — собственные точки прямых, проходящих
соответственно через точки А, В, С, D и через одну и ту же
собственную точку О. В качестве точек Лг, Вх, С\, Ох можно взять
точки
Л, (*!, х2),
С, (ал-, + Рг/!, ах2-|-рг/2),
так что
(Л BCD):
/а-2 + ur/2
Уг
ч
У1
*1
#1
.'/2
Иг
•
Xt
Hi
Ч
Уг
Ч
Уг
Ж
Если точки Л и С совпадают, то (ЛВСО) = 0, но и ~ = 0 (так
как если точки Л и С совпадают, то Р = 0). Если точки В и D
совпадают, то Х, = 0 и, значит,
Теорема 2. Сложное отношение четырех точек и сложное
отношение четырех прямых не меняются при проективном
преобразовании.
Доказательство. Достаточно, очевидно, доказать первую
часть теоремы. Рассмотрим две произвольные различные точки:
Возьмем на прямой АВ две точки:
С ((ах1 + Рг/Х): (ал:2 + Р#з): («т + Pi/a)),
D ((Х*! + jiir/i):(Ъс2 -|- (п/2): (Кх.х + ц;/,)),
такие, что точки С и В различны, точки D и А также различны,
594 Глава XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Тогда
аи.
Произведем проективное преобразование
^3, (б)
л;3 = ОдЛ + а32*2 + a33xs.
Пусть
Л'^:^:^), В'(у[:у[:у'3)
образы точек А а В при этом преобразовании. Тогда образами
точек С и D в силу соотношений F) будут точки:
С ((си, + Р^):(«*, + |3у2):(ах3 + р£/3)),
D'(
Отсюда
Следствие. При проективном отображении проективной
плоскости II на проективную плоскость II' сложное отношение
четырех прямых и сложное отношение четырех точек не меняются.
Доказательство. Пусть 91 — проективное отображение
проективной плоскости П на проективную плоскость П'.
Рассмотрим проективное отображение Q плоскости IV на плоскость П,
которое на множестве собственных точек плоскости П'
совпадает с ортогональным отображением плоскости л' на плоскость п.
Тогда £Ш есть проективное преобразование плоскости П:
QSl = $.
Отсюда
Так как и при преобразовании ^ плоскости П, и при
отображении Q плоскости П на плоскость ГГ сложное отношение
не меняется, то оно не меняется и при отображении St, равном
произведению отображения Q на преобразование ^3.
Если ангармоническое отношение (ABCD) четырех точек,
лежащих на одной прямой равно —1. то говорят, что пара точек Л
и В гармонически разделяет пару точек С и D, или что пара
точек С п D разделяет гармонически пару точек Л и В. Иначе
точки Л и В гармонически сопряжены относительно точек Си D,
или точки С и D гармонически сопряжены относительно точек
А и В.
$202. АНГАРМОНИЧЕСКОЕ ОТНОШЕНИЕ ГАРМОНИЗМ 595
Если (abcd) =— 1, то говорят что четыре прямые а, Ь. с, d
(взятые р этом порядке) образуют гармоничесьую четверку или
что прямые а и b гармонически разделяют прямые с и 'L или,
наконец, что прямые с nd гармонически сопряжены относительно
пары прямых а и b (и наоборот).
Из доказанной теоремы следует, что если заданы три точки
принадлежащие одной прямой, го точкой, гармонически
сопряженной с С относительно точек А и В, является точка
Примерами гармонических четверок точек могут служить:
1) концы А и В отрезка, его середина С и несобственная
точка D прямой АВ;
2) вершины А я В треугольника АОВ и основания С и D
биссектрис внутреннего и внешнего углов при вершине О;
3) центры А и В двух неконцеитричеа.их окружностей и
центры С и D положительной и отрицательной гомотетий
переводящих одну из этих окружностей в другую;
4) рассмотрим четыре точки Р, Q, R, S, из которых никакие
три не лежат на одной прямой (рис. 278). Обозначим через А
точку пересечения прямых PQ и /?S а через В—точку
пересечения прямых PS и QR. Через С и D обозначим точки пересечения
596
Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
прямых QS и PR с прямой АВ. Тогда
Рис 279
В самом деле, произведем проективное преобразование, при
котором точки А а В перейдут в несобственные точки. Тогда
четырехугольник PQRS перейдет в параллелограмм, а точка О пе
ресечения прямых PR и QS— в
точку О' пересечения диаго
налей этого параллело1раыча
(рис. 279).
Прямые О А ОВ, ОС и 0D
перейдут в прямые а', Ь', с ,
d', из которых первые две про
ходят через точку О' и парал
лельпы сторонам параллело
грамма, а прямые с' и д!
являются его диагоналями Так
как (a'b'c'd') = --\ (докажите'),
то четверка прямых а', Ь', с',
d' гармоническая. Значит, и
четверка прямых ОА ОВ, ОС, OD также гармоническая, а потому
(ABCD) = — l.
Замечание. Данное выше определение сложного отношения
упорядоченной четверки точек, принадлежащих одной прямой,
и упорядоченной четверки прямых, принадлежащих одному пучку,
без изменений переносятся па проективное пространство. Отметим
лишь одно обстоятельство, если А (х^.х^.х^.Хц) и В (г/1:г/2:(/3-.(/4)~Две
различные точки проективного пространства, заданные
однородными координатами, то точки
С {{<ххх -f р#х): (ах% -\- $у2): (ахч + pt/3): (ах* 4 $У*))
и
D ((Кх1 + nyj: (Lv2 -f- \iy2).(Kxs + \iys) :(%xi-{- \iyt))
лежат на прямо» АВ и (в случае а=^=0
аи,
В самом деле, пусть прямая АВ не параллельна оси Oz; тогда
проекции А' (хг:х2.0:х4) и В' (yl:y2:0:yi) точек Л и В на
плоскость хОу параллельно оси Oz различны; точки
D'
! 4-
): 0:
являющиеся проекциями точек С и D на плоскость хОу
параллельно оси Oz, лежат иа прямой АВ, и на основании теоремы 1
202. АНГАРМОНИЧЕСКОЕ ОТНОШЕНИЕ. ГЛРМОПИЗМ 597
Но {A'B'C'D') = (ABCD), значит, и
cqx
Если прямая АВ параллельна оси Ог, то, проектируя точки
А, В, С, D па ось Ог плоскостями, параллельными
плоскости хОу, получим в проекции точки
A'@:0:xa:xt) В' @:0://3://4), С (@:0:(аха + Руа
и проводя ту же выкладку, что и в теореме 1, получим
(Д'В'С'О') = М; и здесь ясно, что {ABCD) = {A'B'C'D'), так что
опять
{ABCD)=&.
Из доказанного следует, что если точки A (x1:x2:xs:xi) и
в(У1'Уъ'Уз'-У*) различны, то точка
где а=5&0 и $=£0, лежит на прямой АВ. При этом точка
D {(ах1 - pr/J: (ах2 - р#2): (ах3 - р^3
гармонически сопряжена с точкой С относительно точек А и В,
т. е. (ЛВСО) = — 1.
Замечание к § 191—202. Аналогично тому, как это было
сделано в главе X. можно ввести понятие комплексной
проективной плоскости (и комплексного проективного пространства).
Точкой комплексной проективной плоскости назовем класс М (х1:х2:хя)
всех пропорциональных упорядоченных троек комплексных чисел,
из которых по крайней мере одно отлично от нуля. Точно так же
определяется прямая т комплексной проективной плоскости,
которую в отличие от точки обозначим т[и1:и2:и3]. Будем говорить,
что точка М лежит на прямой пг, или что прям-ая т проходит
через точку М, если выполнено соотношение
Uj*! + U%X2 4-UgXg = 0.
Это уравнение при фиксированных иг, и2, и3 называется
уравнением прямой [и1:и2:и3]л а при фиксированных ,vlt x2, х8 —
уравнением точки (xl:x2:x3).
Аналогичное обобщение дается и для понятия комплексного
проективного пространства: точка (xl:x2:x3:xi), плоскость
[u1:ui:u3iui], условие их инцидентности и^х^-\-игхг-\-и3х3-f u4x4 = 0
и т. д.
598 Рлава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Аналитические определения проективного преобразования
плоскости и пространства (линейные,.взаимно однозначные)
переносятся и на случай комплексной проективной плоскости и
комплексного проективного пространства Результаты § 193—195, 200,
201 имеют место и для комплексной проективной плоскости, и для
комплексного проективного пространства. Однако некоторые
теоремы становятся теперь определениями (например, 1еорема 1 § 195).
Понятие линии и поверхности второго порядка,
касательной к ней, понятие ангармонического отношения четырех точек,
принадлежащих одной прямой понятие полюса и поляры
относительно линии и поверхности второго порядка переносятся
и на комплексную проективную плоскость, и комплексное
проективное пространство, причем здесь следует сохранить лишь
аналитические определения и выводы; основные уравнения при этом
сохранятся (уравнение касательной, поляры и т д ). Однако ха
рактер проективной классификации уже изменится, так как,
например, на комплексной проективной плоскости линия
х\ + Х1 + #з = 0 при проективном преобразовании xx—x'v х.2 = х'1>!
xs = ixs переходит в линию х* -\-х'* — х'* — 0 и т д Аналогичное
обстоятельство имеет место и в комплексном проективном
пространстве Мы не будем касаться тех вопросов (например, вопросов
проективной и проективно аффинной классификации линий и
поверхностей второго порядка) решение которых на комплексной
проективной плоскости и в комплексном проективном
пространстве принципиально отлично от их решения в действительном
проективном пространстве.
§ 203. Линии второго порядка на проективной плоскости.
Классификация линий второго порядка по характеру пересечения
с несобственной прямой
Линией второго порядка на проективной плоскости называется
геометрическое место точек проективной плоскости, однородные
координаты которых удовлетворяют однородному уравнению
второй степени
0ц*? + Чгх\ + аззх1 + 2ai2*i*2 + 2a23.»V3 + 2a3i*3*i = 0- A)
Так как при переходе к другой системе старые координаты
точки выражаются через новые координаты той же точки
линейными однородными соотношениями с определителем из
коэффициентов, отличным от нуля, то уравнение A) преобразуется снова
в однородное уравнение второй степени
Координаты собственных точек линии A) удовлетворяют
уравнению
а11х2+2а12ху + а22у°- + 2а13х + 2a2Sy + о33 = 0, B)
« 203 ЛИНИИ ВТОРОГО ПОРЯДКА 599
которое получается из уравнения A) целением всех его членов
на х-.
Множество всех собственных точек линии второго порядка на
проективной плоскости в случае, если xi тя бы один из коэффи
циентов а1Ъ o12v a22 не равен нулю, есть множество всех точек
одной из линий второго порядка, изученных в главе XI (эллипс,
гипербола, парабола, две пересекающиеся прямые и т. д.). Если
°и = ai2 — а22 = 0. но хотя ^'Ы одно из чисел о13 или а2з не равно
нулю, то множество собственных точек линии A) состоит из точек
прямой
Наконец, если в уравнении A) все коэффициенты, кроме аяа,
равны нулю, то на линии A) нет пи одной собственной точки;
линия A) в этом случае состоит ш пары прямых совпадающих
с несобственной прямой
Что касается несобственных течек, принадлежащих линии ьто-
рогь порядка, заданной уравнением A), то для них х8 = 0, а
координаты хх и х2 этих точек определяются из уравнения
апх\ + 2а1гхгх2 + avix\ = 0,
которое мы получим из уравнения A) положив в нем х3 = 0. Но
этому же уравнению удовлетворяют координаты векторов,
имеющих асимптотическое направление относительно линии B) (мы
сейчас предполагаем, что хотя бы одно из чисел яц о12, аг., не
равно нулю) Следовательно несобственные точки линии второго
порядка являются н то же время и несобственными точками тех
прямых, которые имеют асимптотическое направление по
отношению к данной линии B) В частности, если совокупность
собственных точек линии A) второго порядка есть гипербола, то
несобственные точки этой линии являются несобственными точками се
асимптот, а сами асимптоты касаются линии в этих несобственных
точках
Тип линии A) определяется но типу линии B) Таким образом,
линию A) мы будем называть линией эллиптического.,
гиперболического 1,ли параболического типа, если множество всех ее
собственных точек является соответственно линией эллиптического,
гиперболического или параболического типа, т е. если
уравнение B) эллиптического гиперболического или параболического
типа.
Линии эллиптического типа, т. е. эллипс мнимый эллипс лее
мнимые пересекающиеся прямые, не имеют несобственных точек;
линии гиперболического типа, т е гипербола, две пересекающиеся
прямые пересекаются с несобственной прямой в двух различных
точках
Линии параболического типа, т е. парабола, пара
параллельных прямых (действительных и мнимых), сдвоенная прямая, имеют
600 Глава XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
только одну несобственную точку и в случае параболы линия
касается в этой точке несобственной прямой (§ 207).
Таким образом, на проективной плоскости, полученной из
евклидовой плоскости пополнением несобственными элементам»,
линия второго порядка является одной из следующих линий.
1) Эллипс; у этой линии нет действительных несобственных
точек.
2) Гипербола, дополненная двумя несобственными точками ее
асимптот.
3) Парабола, дополненная несобственной точкой ее диаметров
(имеющих асимптотическое направление).
4) Две пересекающиеся в собственной точке прямые
дополненные их несобственными точками
5) Мнимый эллипс.
6) Две мнимые прямые, пересекающиеся в собственной точке.
7) Две параллельные прямые, дополненные их несобственной
точкой.
8) Две мнимые параллельные прямые, дополненные общей
действительной несобственной точкой.
9) Две совпадающие прямые, дополненные их несобственной
точкой.
10) Две прямые, из которых одна собственная, а другая
несобственная.
11) Дважды взятая несобственная прямая.
§ 204. Проективная классификация линий второго порядка.
Распадающиеся и нераспадающиеся линии
Разобьем множество всех линий второго порядка, лежащих на
проективной плоскости, па следующие пять классов
I. Линии второго порядка, которые не распадаются на две
прямые и содержат бесконечное множество действительных точек.
II. Линии второго порядка, не имеющие ни одной
действительной точки.
III. Линии второго порядка, распадающиеся на две различные
действительные прямые.
IV. Линии второго порядка, содержащие только одну
действительную точку (две мнимые пересекающиеся прямые).
V. Линии второго порядка, вырождающиеся в сдвоенные
прямые.
Определение. Две линии второго порядка принадлежат к одному
и тому же проективному классу, ^ если существует проективное
преобразование, переводящее одну из этих линий в другую. Если
жг не существует проективного преобразования, которое одну из
линий переводит в другую, то эти линии второго порядка
принадлежат к различным проективным классам.
■§ 204 ПРОЕКТИВНАЯ КЛАССИФИКАЦИЯ ЛИНИЙ 601
Докажем, что указанное разделение линий второго порядка
на пять классов и дает проективную классификацию этих линий.
Теорема. На проективной плоскости все линии второго порядка
разделяются на пять проективных классов.
Следующие уравнения
(II)
х?+*| = 0, (IV)
*! = 0 (V)
являются простейшими уравнениями линий второго порядка,
принадлежащими соответственно к этим пяти проективным классам.
Доказательство. Как известно из высшей алгебры,
квадратичную форму
Ф = а1Хх\ -f a.nx\ + азях1 -'- 2а12хгх% + 2а23х2хя + 2а3 ххахг
невырожденным линейным преобразованием
X1=CllXi + CnXz + C1SXS,
v — r x -L r *' -X- r x
Xg = £31-^1 ~T~ ^32-^2 "Г £33^3
можно привести к каноническому виду
°22 °23
^
где е;- равны +1, —1 или 0.
Геометрически это и означает, что существует проективное
преобразование, которое лю0ую линию второго порядка, заданную
уравнением
aiX + a.22x22 + aS3xl + 2al2xtx2 + 2a23x2x3 + 2a31xsxl = 0,
переводит в одну из следующих пяти линий:
xl + xl-xl = 0, (I)
*? + *;+*?-о, (и)
x\ — xl^0, (III)
*! + *!== о, (IV)
*! = о. (V)
602 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Линия (I) является нераспадающейся действительной линией
второго порядка, имеющей бесконечное множество действительных
точек (овальная линия).
Линия (II) не содержит ни однвй действительной шчки.
Линия (III) распадается на две прямые!
Линия (IV) распадается на две мнимые прямые!
На этой линии имеется только одна действительная точка
@:0:1)
Линия (V) является двойной прямой.
Таким образом, линии (I) — (V) являются представителями
указанных пяти классов
Указанные в начале параграфа признаки линий второго
порядка по которым мы провели их классификацию, таковы, что
они различны и инвариантны по отношению к проективным
преобразованиям Значит, никаким проективным преобразованием линию,
принадлежащую одному из этих классов, нельзя преобразовать
в линию другого класса.
С другой стороны, так как всякую линию второго порядка
можно проективно преобразовать в одну из линий (I) — (V), то
две любые линии, входящие в один класс, могут быть
преобразованы одна в другую некоторым проективным преобразованием
В самом деле, возьмем, например, две овальные линии Сг и С2.
Существует проективное Преобразование Ш, которое линию Сг
преобразует в линию (I), и существует проективное
преобразование 23 которое линию С2 преобразует в линию (I). Проективное
преобразование ЙЗ"Щ линию Сг преобразует в линию С2.
Аналогично доказывается, что две любые линии,
принадлежащие к одному и тому же из остальных классов, также проективно
эквивалентны.
Овальные линии, действительные и мнимые, называются невы-
рождающимися или нераспадающимися. Все остальные линии
распадаются на две прямые (действительные различные или мнимые,
или совпадающие) и называются вырождающимися или
распадающимися.
Для того чтобы линия второго порядка, заданная общим
уравнением
<р = аХ1х] + аг%х\ + aasxl + 2а12хгх2 + 2а23х2х3 + 2а31хях1 = 0
t ^05 ПР0ЕКТИВН0-ЛФФИН1ТЛЯ КЛАССИФИКАЦИЯ ЛИНИЙ 603
распадалась, необходимо и достаточно, чтобы дискриминант
квадратичной формы, входящий в левую часть уравнения этой
линии, был равен нулю'
Л =
аЛ
21 а22
= 0.
В самом деле, в этом и только в этом случае ранг матрицы
(aik) квадратичной формы ф равен 2 или 1, а значит, эта форма
разлагается в произведение двух линейных форм
Впрочем, условие Д = 0 сразу проверяется на простейших
уравнениях (III), (IV), (V) распадающихся линий. При
проективном преобразовании определитель А получает множитель, равный
квадрату определителя преобразования, и, значит, условия Д=0
и Д^О (для линий (I) и (II) класса) инвариантны относительно
проективного преобразования.
§ 205. Проективно-аффинная классификация линий
второго порядка
Пусть проективная плоскость реализовала в виде первой
модели.
1 Овальными линиями будут тогда все эллипсы, все
гиперболы, каждая из которых дополнена несобственными точками ее
асимптот, и все параболы, каждая из которых дополнена
несобственной точкой ее диаметров.
2. Второй проективный класс образуют все мнимые эллипсы.
3 Третий проективный класс образуют пары пересекающихся
прямых, пополненных их несобственными точками, а также пары
параллельных прямых (каждая такая пара дополняется одной
несобственной точкой, через которую они проходят).
4 Четвертый проективный класс образуют пары мнимых
пересекающихся прямых, а также пары мнимых параллельных
прямых, дополненных их общей (действительной) несобственной
точкой.
5 Пятый проективный класс образуют сдвоенные прямые,
дополненные их несобственной точкой
Проективно-аффинпой классификацией линий второго порядка
называется разбиение их на классы эквивалентности по отношению
к проективным преобразованиям проективной плоскости,
реализованной в виде первой модели, при которых несобственная прямая
переходит в себя.
Имеется одиннадцать проективно-аффинных классов линий
второго порядка. А именно это те классы, которые перечислены
в § 203.
601 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
§ 206. Необходимое и достаточное условие того, что два
однородных уравнения второй степени определяют
одну и ту же линию второго порядка
Теорема 1. Для того чтобы два уравнения
Ф = а пх? -Ь аггх\ + a.33xl + 2alix1x2 + 2а23х2х3 + 2а31х3х1 = 0 A)
и
4>=bnx* + bi2x* + b33xl + 2bl2x1x2 + 2Ь23х2х3 + 2Ь31хях1 = 0 B)
определяли одну и ту же линию второго порядка на комплексной
проективной плоскости, необходимо и достаточно, чтобы
соответствующие коэффициенты этих уравнений были пропорциональны.
Доказательство Достаточность условия очевидна.
Докажем необходимость.
Предположим сначала, что линии A) и B) распадаются на
пару прямых В этом случае левые части уравнений ср = О и -ф = 0
разлагаются в произведение двух линейных форм относительно
Так как уравнения «1 = 0, vt = 0 и и2 = 0, v2=0 являются
уравнениями одной и той же пары прямых, то коэффициенты
уравнения «1 = 0 пропорциональны коэффициентам уравнения
и2 = 0 (или у2 = 0), а коэффициенты уравнения их = 0
пропорциональны коэффициентам уравнения и2 = 0 (соответственно «2 = 0).
Значит, и коэффициенты aik произведения u1v1 = q>
пропорциональны соответствующим коэффициентам bih произведения u.zv2 = \lp.
Пусть линии A) и B) нераспадающиеся. Рассмотрим
пересечение их с прямой х3 = 0; для первой линии координаты точек
пересечения определяются из системы
ср j = а1гх\ + 2а12хххг + аггх\ = 0 х3 = 0;
для второй —из системы
ЧЧ = ^li^i -г 2blix1x2 + bi2x\ = 0, х3 = 0.
Уравнения cpj = O и ty1 = 0 являются уравнениями одной и
той же пары прямых, так как б противном случае точки
пересечения прямой х3 = 0 с линией, заданной уравнением A) или B),
были бы различны. Значит, коэффициенты форм cpj и ipx
пропорциональны all = kb11, ai2 = kbn, 022 = &Ь22.
Рассматривая пересечение линии, заданной уравнением A) или
B), с прямой х2 — 0, докажем что пропорциональны
коэффициенты форм
■ф2 = 6ii*i + ^lsxtx3 + b33xl;
(- 206 ДВЛ ОБМОРОЧНЫХ УР\ВППЦИЧ ВТОРОЙ СТЕПЕНИ 605
но так как ull — kbll го al3 — -cbli i 4'ss=kbS:i Рассматривая
пересечение линии, заданной уравнением A) или B) с прямой
Xj = O, докажем, что о23 = /гЬ2и
Теорема 2. Для того чтобо1 два уравнения
Ф = axlx\ + аггх\ -f а%.Лх1 + Га12х1лг + 2<?23*2*3 + 2035*3*! = 0, C)
л\> = bxlx\ + Ь22х22 + Ьязх1 + 2bl2x1x., -f 2Ь23л^*3 + 2bsixsx1 = 0 D)
определяли на действительной проективной плоскости одну и ту
же действительную линию второго порядка, имеющую бесконечное
множество действительных точек, необходимо, чтоб-л
соответствующие коэрфициентя этих уравнений были пропорциональны.
Доказательство. Если линии распадающиеся, то
доказательство такое же, как и в теореме 1 (необходимость)
Предположим, что уравнения C) н D) определяют линию
второго порядка: эллине, или гиперболу, дополненную
несобственными точками ее асимптот, или параболу, дополненную
несобственной точкой ее диаметров.
Во всех этих случаях можно перейти к такой системе
координат О'*1*2*з, что уравнения C) и D) преобразуются в
уравнения вида
Ф, —а(х\ +■ х2 ~х3 ) = 0, \|>!=&(*-, + *'2 — *3 ) = 0
(афО, ЬфО)
в случае эллипса; в уравнения вида
х\ — *, ) =
в случае гиперболы и в уравнения вида
в случае параболы. Для всех случаев коэффициенты уравнений
ф/ = 0 и яр, = 0 пропорциональны
Производя переход от системы О'ххх%х3 к системе О*1*2*3,
т. е. заменяя в уравнениях ф, = 0 и г|?, == 0 координаты*,, *2, x.s их
выражениями через xlt хг, *3 (эти выражения — линейные
функции от *ь *2> *3 с определителем, отличным от нуля), получим
уравнения C) и D), коэффициенты которых пропорциональны.
Замечание. Для мнимых линий теорема неверна.
Пример 1. Линии
имеют единственную действительную точку @:0:1) (начало координат), но
соответствующие коэффициенты их уравнений не пропорциональны.
606 Р1ава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Пример 2. Линии
имеют единственную действительную несобственную точку (OiliO), но eooTiei
ствуюшие коэффициенты их уравнений непропорциональны
§ 207. Касательная к линии второго порядка
Пусть линия второго порядка задана на проективной
плоскости уравнением
аг2х\ 4- а ^х\ + 2й1?х1х2 + ia^xtx + 2а.лхчхх = 0.
Особом гочкой М0(х]'.х\'.х1) этой линии будем называть
точку, координаты которой удовлетворяют соотношениям
аххх" + а12х" + ах ,xl = 0,
aiXx" + амх^ + aMx°s = 0,
aslx1 + a.i2Xa + о38^8 = 0.
Овальная и мнимая нераспадающаяся линии не имеют особых точек.
Две прямые (действительные или мнимые) имеют в качестве
особой точки только точку их пересечения. Наконец, если линия
второго порядка является парой совпавших прямых, то все ее
точки особые.
Определение. Касательной к линии второго порядка с заданной
на ней неособой точке называется прямая проходящая через эту
точку, пересекающая линию в двойной точке или целиком входящая
н состав рассматриваемой линии
Теорема. Уравнение касательной к линии второго порядка,
заданной уравнением
аггх\ 4- а22х22 + аъъх\ + 20,^^2 + 2а21х2хя + 203^.^! = 0, A)
в данной на ней неособой точке М0(х\:х1:х1) имеет вид
(аХ1х\ 4- ахгх\ 4- alsx") *i + №21*? + 2^2 + <V°) x2 -f
4- (а.пх°, 4- aS2^2 + aiSxl) хя = 0.
Доказательство. Проведем через точку Мо произвольную
прямую. Возьмем на этой прямой произвольную точку М (х1:ха:х8),
отличную от точки Мо Тогда координаты любой точки Р прямой
М0М можно представить в виде
ах" 4- P*i, а*2 + Р-^2> axl + 'iXz-
Прямая М0М будет касательной тогда и только тогда, когда
она или пересекает данную линию в двойной точке /Ио, или
входит в состав этой линии.
207. КАСАТЕЛЬНАЯ К ЛИНИИ ВТОРОГО ПОРЯДКА
Чтобы найти координаты точек пересечения прямой М0М
с данной линией, подставим координаты точки Р в уравнение
данной линии. Будем иметь
+ КJ + 2alt (ах\ + ^2) (аХ° + рхх) + я2а (ахЧ + КJ +
+ 2а13 (ах\ + PjCj) (ax? + ^г3) +
+ 2а23 (ах° + |3х2) (ах^ + р*3) + а3з (ал;з + Р*8J = 0'
или, обозначая левую часть уравнения данной линии через
(f(x1} хг. х3):
Ф(х?, х\, х,0)аг
где
Р = (йцД:? + а12хг + а13х°3) хх
Так как точка (x\\x\\xl) лежит на данной линии, то
Ф (х\, xl, xl) = 0 и, значит,
(х1, х2, х3)Р2 = 0.
Отсюда •
или \i — 0, или 2Pa-\-(f(xlt x%, xs)$ = Q.
При {4 = 0 из выражений для координат точки Р:
(cue? + Рхх): {ах\ + р^8): {ах\ + {4х3)
получаем координаты точки Мо:
(ax\):(axl):(axt) = х\:х\\х\.
Для того чтобы и вторая точка пересечения совпадала с Мо,
или чтобы прямая М0М целиком входила в состав данной линии,
необходимо и достаточно, чтобы
Р = 0,
так как тогда и только тогда из уравнения
(х1 хг, х3)Р = 0
мы получим, что Р = 0, или что (при ф(*!, х2, х3) = 0) это
последнее соотношение выполняется тождественно.
Условие Р = 0 подробно записывается так:
(axlx\ + ахгх\ + a13x30) xx +
+ (fl21x? 4- o-22x" + а23х") х2 4-
4- (аз1х0! 4- a3ixl + as&x°s) xs = 0.
608 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Таким образом, прямая М0М имеет с данной линией второго
порядка одну общую двойную точку тогда и только тогда, когда
координаты x1:xi:xs точки М удовлетворяют этому уравнению
первой степени. Это уравнение и есть уравнение касательной к
дайной линии в данной па ней точке Мо.
Пример. Пусть
-a22t/ + a,uzi-\~2a^yz \-'2aJlzx->s-2al2xy = 0 C)
уравнение в однородных координатах действительной овальной линии второго
порядка.
При каком необходимом и достаточном условии прямая
, их -j- vy + wz = 0 D)
касается данной линии.
Решение. Необходимость. Предположим, что прямая D) касается -
линии C) в точке (х0, i/0, г0). Тогда
uxo-\-vyo + wzo = O, (о)
причем координаты и, v, ~a этой касательной определяются соотношениями
(см. уравнение B) этого параграфа)
Разрешая эти соотношения относительно х0, у0, г0, получим
G)
где A,ft —алгебраическое дополнение элемента aik в патрице (a/ft). Из
соотношений E) и G) следует равенство
Аци*-\- A2iv2+ A.i3w'i + 2A23vw-r 2A3lwu + '2Al2uv = 0 (8)
Достаточность Предположим, что ранеиство (8) выполнено.
Докажем, что тогда прямая D) касается данной линии C). Рассмотрим точку
(А'о- Уо' го)> координаты которой определяются равенствами G).
Из соотношений G) и (8) следует, что
uxo-i-vyo + wzo=^Q; (9)
но из соотношений G) следуют соотношения F). Из соотношений (9) и F)
следует, что
Л ) г0 = 0,
или
а\ i*\ + «22.1» о + °зз2о "I" 2а2.-!Уо2о + 2а»1гохо "Г 2а12х0у0 = 0,
т. е. точка (.v0, y0, z0), координаты которой определяются соотношениями G),
лежит па данной линии C). В силу равенств F) уравнение D) можно
переписать так:
(апх0 + а12уа + alsz0) х + (а21х0 -f- a22y0 + я23г0) у + (апх0 + аЯ2уа + aSizQ)z — 0,
208. ПОЛЮС И ПОЛЯРА ЛИНИИ ВТОРОГО ПОРЯДКА 609
но это есть уравнение касательной к линии C) в точке (х0, у0, гд). Уравнение
(8), связывающее координаты и, v, w всех прямых, касающихся данной дейст-
нитеи.ной овальной линии второго порядка, называется тангенциальным
уравнением этой линии. Его можно записать и так:
аи
ам
и
а12
а22
0.12
V
3
аъз
а-зз
W
и
V
W
0
§ 208. Полюс и поляра линии второго порядка
Рассмотрим уравнение линии второго порядка на проективной
плоскости
апх] + a.2ixl + arixl -f 2а ихгх.2 + 2агяхгхл + 2а31х3х1 = 0. A)
Возьмем точку М(х\\х\:х\), пе лежащую на линии A), и
проведем через нее секущие к данной линии. Обозначим через Р и Q
точки пересечения одной из этих секущих с данной линией, а
через /7-— то-чку, гармонически сопряженную точке М
относительно точек Р и Q, т. е. такую точку, что точки Р, Q, М, N
образуют гармоническую четверку:
(PQMN)=-\.
Теорема 1. Точки-N, гармонически сопряженные с точкой М
относительно точек Р и Q пересечения с линией второго порядка
секущих, проходящих через точку Л4, лежат на одной прямой.
Доказательство. Обозначим координаты точки N через xlt
х'2, х3. Тогда координаты любой точки прямой MN:
\ + Р*х = axl 4-
х 1 = ах\ + Р*i, хг = axl 4- $х2, хя — ах", + $х3.
Подставляя координаты этих точек в уравнение линии,
получим уравнение, из которого найдем отношение а:р",
соответствующее точкам Р и Q:
«и (ах! + P*iJ + о22 {ах] + Рх2J + а33
+ 2а12 {ах0, + }х\ ){axl + р/2) +
+ 2о28 (ах,0 + pjCaKotjeS + fix's) +
+ 2а31 (oucj + $хй){ах\ + $х[) = О,
или, обозначая через ф(х,, х2, х3) левую часть данного
уравнения:
Ф(*!, 4, *S) ^ + 2Рар + ■,(/,, х2, x3)i32 = 0, BJ
где
Р = [а1Хх\ + alzx\ + al3xl) x\ +•
20 П. С. Моденов
6H
Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Обозначил! через a1:fi1 и ct2:p2 решения последнего уравнения.
Тогда координаты точек Р и Q будут соответственно
1, то на
оси
(а2х° + p2xi): (a2x\ + p1^) :(a2^ + $2x
и так как ангармоническое отношение (MNPQ) =
новании § 202 (теорема I) имеем
Pi . Ра 1
— :—= — 1,
a] a2
или
aij_a2_A
Pi ' Р2
Отсюда и из уравнения B) следует, что
Р = 0,
ИЛИ ПОДробНО!
Л-(аъ1х\ + a32xl + аъзх1)х'г = 0.
Мы видим, что координаты точек N удовлетворяют
следующему уравнению первой степени относительно xlt x2, хг\
{апх\ + aX2xl + alsxl) хг +
+ (a,i*J + ai2xl + а23х°3) х2 +
+ {aux01+aS2xl + a33xl)x3 = Q. C)
В этом уравнении коэффициенты при
xlt хг, х3 одновременно в нуль не
обращаются, так как в противном случае мы
имели бы
или
п
*? + аг2х\ + ai3xl)xl +
l + aS2xl + а33х°3)х03 = 0,
^J = 0,
т. е. точка М лежала бы на данной линии.
Значит, все точки /V лежат на прямой, определяемой
уравнением F) (рис 280)
Определение Прямая т, на которой лежат точки, гармонически
сопряженные точкой М относительно точек пересечения линии
второго порядка секущими, проходящими через точку М,
называется полярой точки М относительно рассматриваемой линии вто-
!> 208 ПОЛЮС И ПОЛЯРА ЛИНИИ ВТОРОГО ПОРЯДКА
Ы\
рпго порядка. Точка М называется полюсом прямой т
относительно этой линии.
Сопоставляя уравнение поляры с уравнением касательной к ли-
1 ии второго порядка, видим, что уравнение касательной к липни
второго порядка в неособой ее точке (x\:x\;xl) и уравнение
поляры точки {x\:x\:xl), i.e лежащей на этой линии, имеют один
и тот же г.ид. Поэтому данное определение поляры точки
относительно линии второго порядка обычно дополняют следующим если
М (xlixl'.xl) — неособая точка линии второго порядка, то ее
полярой относительно этой линии называется касательная к этой
линии в точке М.
Теорема 2, Если точка М лежит
на поляре > точки Т, то точка Т
лежит на поляре т точки М (рис. 281).
Доказательство. Пусть коор-
яииаты точек М и Т таковы.
Уравнение поляры m точки /И
имеет вид
(QjjX" -)- пцХ\ -\- О13Хз) Xt -(- РИС 281
.л j /j V1 —I— fj y I /> у- J у „_ {Л
Уравнение поляры t точки Т имеет вид
Условие того, что точка М лежит на поляре / точки Т, имеет
вид
(аих1+а-[гх2 -Ь
Это равенство можно переписать так:
+ (ап\° + aTlxl + ayix")xs =0,
а это значит, что точка Т лежит на поляре m точки М.
20*
612 Глава XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Доказанная теорема может быть сформулирована и так: если
поляра / точки Т проходит через точку М, то и поляра m точки
М проходит через точку Т.
Теорема 3. Если уравнение
а1Хх\ + аг2х\ -f о33х32 + 1аХ2кххг -f 2a23x2x3 + 2fl31x3x, = О
является уравнением действительной овальной линии второго
порядка и если из точки М{х\\ха2:х1), не лежащей на этой линии,
можно провести к ней две действительные касательные, то
полярой точки М является прямая ТгТ2, проходящая через точки
прикосновения 7\ и Т'2 этих касательных с данной линией (см. рис. 280).
Доказательство. Так как точки 7\ и Т2 лежат на прямой
TVT2, то полюс прямой 7\Г2 должен лежать па полярах точек
Т1 и Г2. Но поляры точек 7\ и Т2 — это касательные к овальной
линии в точках 7\ и Т2; эти касательные пересекаются в точке М.
Значит, точка М — полюс прямой 7\Т2.
§ 209. Сопряженные диаметры, центр и асимптоты в
проективной теории линий второго порядка
Если полюсом является несобственная точка проективной
плоскости, не лежащая на линии второго порядка, то прямые, к
которым присоединяется эта несобственная точка, параллельны
между собой и имеют пеасимптотическое направление. Точки,
гармонически сопряженные с рассматриваемой несобственной точкой
относительно точек пересечения этих прямых с данной линией,
будут серединами хорд линии, высекаемых на прямых данной
линией. Их геометрическим местом будет диаметр линии. Так»ш
образом, диаметр линии С, сопряженный параллельным хордам
этой линии, есть поляра несобственной точки, присоединяемой
к этим хордам, или иначе: полюсом диаметра линии С является
несобственная точка хорд, сопряженных этому диаметру Каждый
из сопряженных диаметров линии второго порядка делит пополам
хорды, параллельные другому диаметру. Это свойство вытекает
из теоремы 2 § 208. В самом деле, если диаметр d сопряжен
хордам, параллельным прямой /, т. е. является полярой
несобственной точки прямой /, то поляра несобственной точки диаметра d
должна проходить через несобственную точку прямой /, т. е.
диаметр, сопряженный хордам, параллельным d, должен быть
параллелен прямой /.
Центр линии второго порядка является полюсом несобственной
прямой.
В заключение параграфа отметим, что асимптоты гиперболы
являются касательными к гиперболе в ее несобственных точках.
$ 210 ОПРЕДЕЛЕНИЕ ЛИНИИ ПО ПЯТИ ТОЧКАМ E13
Запишем уравнение гиперболы
в однородных координатах
Решая это уравнение совместно с уравнением асимптоты
получим одну точку (а:Ь:0) — несобственную, в которой, асигш.тота
касается гиперболы. Другая асимптота
касается той же гиперболы в точке (а:—Ь:0).
Наконец, парабола
х\ — 2px1x.it
касается несобственной прямой х3 — 0 в точке A:0:0) —
несобственной точке ее диаметров.
§ 210. Определение линии второго порядка по пяти точкам
Теорема. Если на проективной плоскости заданы пять точек,
из которых никакие три не лежат на одной прямой, то
существует и притом только одна овальная линия второго порядка,
которая проходит через эти пять точек.
Доказательство. Пусть па плоскости заданы пять точек!
» ^2> ™3> > ^5
Предположим сначала, что точки А1г А2, А3 и Л4 совпадают
соответственное точками A:0:0), @:1:0), @:0:1) и A:1:1) и пусть
x{\x\\xl — координаты точки Аь
Пусть
= 0
— искомое уравнение. Из условия прохождения линии через точки
^A:0:0), А, @:1:0), А, @:0:1)
находим
так что искомое уравнение имеет вид
614 Глава XV ЭЛЕЛ\Е1ПЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Из условия прохождения этой линии через точки A:1:1) и
{x\:xl:xl) имеем
отсюда
ai2:aM:a3^\xl(xl-xl)}:\x1(xl-xl)\:[xl(xl-xl)].
Искомое уравнение:
■^•3 \ % 1 ^/ Х-^Х2 ~т~ %1 \ *^2 -^/ •^2*^3 I -^-2 \ -^3 -^-1 / ■^•3'^1 =^
Последнее уравнение определяет опальную линию второго
порядка, так как на линиях других проективных классов нет пяти
точек, из которых никакие три не лежат на одной прямой
Пусть теперь Av Л2, Л3, Л4, Аь — произвольные точки
проективной плоскости, из которых ник-акие три не лежат на одной
прямой. Произведем проективное преобразование %, которое точки
О1 A:0:0), О2 @:1:0), О8 @:0:1) и £A:1:1) переведет
соответственно в точки Аи А2, А3 и А4. Пусть Р(х\:х\:х..)— прообраз
точки Аъ при этом преобразовании. По доказанному существует
и притом только одна овальная линия С второго порядка,
проходящая через точки О1? 02, О3, Е и Р. Производя проективное
преобразование 91, получим овальную линию S образ линии 5
при этом преобразовании 21, которая будет проходить через пять
данных точек Alt A2, A3, Ait Аь. Другой линии второго
порядка, проходящей через эти пять точек, не существует, так как
если бы такая линия существовала, то существовали бы две
различные овальные линии второго порядка, проходящие через точки
Оь О2, О3, £ и Р.
Замечание. Имеет место более общая теорема: если
никакие четыре точки из пяти данных точек не принадлежат одной
прямой, то через эти пять точек проходит только одна линия
второго порядка *.
§ 211. Пучок линий второго порядка
Рассмотрим две линии второго порядка, заданные уравнениями
Ф = ах±х\ -|- а22л:2 + аяях1 + 2ах 2хгх2 + 2а23х2х3 -f 20,^^! = 0 A)
и
г|, = Ьпх\ + Ь22х\ + Ъ.АЗх\ -f ЪЪх%ххх2 + 2b23x2x3 -|- 2b31x3x1 = 0, B)
и линию второго порядка, заданную уравнением
ф + Ал|) = 0. C)
* См. Н. Н. Му сх е л ишв и л и. Курс аналитической геометрии. М.-Л.,
ОГИЗ, 1947, гл. VIII, § 212, стр. 404.
211 ПУЧОК ЛИНИЙ ВТОРОГО ПОРЯДКА
Уравнение C) определяет множество линий второго порядка,
проходящих через точки пересечения линий ф = 0 и ф = 0, так
как если удовлетворяются одновременно уравнения ф = 0 и ф = 0,
то будет удовлетворяться и уравнение C). В общем случае две
линии второго порядка пересекаются в четырех точках и, таким
образом, уравнение C) выражает линию второго порядка,
проходящую через эти четыре точки.
Уравнение C) называется уравнением пучка линий второго
порядка, заданного линиями ср = О и -ф = 0.
Докажем, что любая овальная линия С второго порядка,
проходящая через точки, общие линиям A) и B), может быть
выражена уравнением вида C), если только никакие три из точек
пересечения линий A) и B) не лежат па одной прямой. В самом
деле, возьмем на линии С точку, не лежащую ни на линии A),
ни на линии B), ни на одной из прямых, проходящих через
какие-нибудь две из точек пересечения линий A) и B).
Подставляя координаты этой точки в уравнение C), получим
где ф0 и ^„ — результаты подстановки координат взятой точки
в левые части уравнений A) и B).
Из последнего уравнения находим
и уравнение C) принимает вид
1\>Ф —ФоЧ> =
Это и есть уравнение линии С, так как овальная линия С
вполне определяется заданием на ней пяти точек, из которых
никакие три не лежат на одной прямой.
В частности, таким путем можно составить уравнение
овальной линии второго порядка, проходящей через пять точек, из
которых никакие три не лежат на одной прямой. В самом деле,
рассмотрим такие пять точек А, (а[:а12:а1)к /— 1, 2, 3, 4, 5;
уравнения прямых АГА2, А2А3, АгАц, AiA1 запишем так:
/13=0, fsa = 0, /31 = °. ^i = 0.
Рассмотрим линии второго порядка
Ф = /12/34 = 0, "Ф = /23/41 =0,
каждая из которых распадается па две прямые (первая на прямые
АхАг и A3Ait вторая ча прямые А2А3 и АХА^. Эти линии
пересекаются в точках Л1, Л2> /43, Л4.
j16 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Рассмотрим пучок линий второго порядка
/12/34 + л/гз/и ""О
Подставляя сюда координаты пятой точки Аъ, найдем %, и
подставляя это значение % в последнее уравнение, получим
уравнение линии второго порядка, проходящей через пять заданных
точек А;.
§ 212. Поверхность второго порядка в проективном пространстве.
Классификация поверхностей второго порядка по характеру
пересечения с несобственной плоскостью
Поверхностью второго порядка в проективном пространстве
называется геометрическое место всех точек проективного
пространства, однородные координаты которых удовлетворяют
однородному уравнению второй степени:
а1Хх\ + а2гх\ + a33xl + аих\ -\ 2al2xvx2 -'r 2alsx1x3 +
-\- 2alixlxi +• 2a23%2-*'3 + 2а24х2А'4 -|- 2а?Ах3хА = 0. A)
Так как при переходе от одной системы координат к другой
старые координаты через новые выражаются линейными
однородными соотношениями с определителем из коэффициентов, отличным
от нуля, то это уравнение A) преобразуется снова в однородное
уравнение второй степени.
Координаты х, у, z всех собственных точек поверхности A)
второго порядка удовлетворяют уравнению
«11*2 + а^У2 + я Ззг2 + 2а12ху + 2а2ъуг + 2a31zx +
44 = 0, B)
т. е множество всех собственных точек поверхности второго по-
оядка в случае, если по крайней мере один из коэффициентов
fllli fl22> °33' °12< Й23> °31
не равен нулю, есть множество всех точек какой-то поверхности
второго порядка, принадлежащей к одному из 17 аффинных
классов (эллипсоид, гиперболоид, параболоид, конус и т. д., см.§ 189).
Если ап = а22 = а33 = а12 = а23 = а31 = 0, но хотя бы один из
коэффициентов а14) a2i, aBi не равен пулю, то множество всех
собственных точек поверхности A) образует плоскость
2а,4* + 2a2iy + 2a3iz + a44 = 0.
Если, наконец, в уравнении A) все коэффициенты, кроме aiit
равны нулю, то поверхность A) вырождается в пару плоскостей,
совпавших с несобственной плоскостью; в этом случае на пей нет
ни одной собственной точки.
212. ПОВЕРХНОСТЬ ВТОРОГО ПОРЯДКА Q17
Что касается несобственных точек, принадлежащих поверхности
A), то их однородные координаты удовлетворяют уравнениям
xi = О,
аих\ + аг2х1 + ай3х\ -j- 2а^хххг -}- 2аГАх.гх3 + 2а3]хях} = 0. C)
В случае, если хотя бы один из коэффициентов уравнения C)
не равен нулю, это уравнение определяет координаты хи х2, х3
векторов, имеющих асимптотическое направление относительно
поверхности второго порядка, заданной уравнением A), или, что
то же, конус асимптотических направлений с вершиной в начале
координат
y2-|- а?>3гг — 2al2xy + 2a2syz~ 2a3lzx = 0 D)
для поверхности B).
Уравнение C) на несобственной плоскости л:4 = 0 определяет
в этом случае линию L второго порядка. Эта линия может быть
одной из следующих:
1° мнимая овальная линия второго порядка;
2° действительная нераспадающаяся (овальная) линия второго
порядка;
3° две действительные различные прямые;
4° две мнимые прямые, пересекающиеся в действительной точке;
5° две совпадающие (действительные прямые}«
В первом случае уравнение D) определяет мнимый конус, а
значит, уравнение B) может определять или эллипсоид, или
мнимый эллипсоид, или мнимый конус.
Во втором случае уравнение D) определяет действительный
конус. Тогда уравнение B) может определять или однополостный
гиперболоид, или двуполостпый гиперболоид, или конус второго
порядка. Таким образом, точками этой несобственной линии L
поверхность B) второго порядка евклидова пространства
дополняется до поверхности второго порядка A) в проективном
пространстве.
В третьем случае уравнение D) определяет две действительные
пересекающиеся плоскости, пересекающие несобственную плоскость
по двум различным прямым 1Х и /2 Уравнение B) в этом случае
определяет или гиперболический параболоид, пли гиперболический
цилиндр, или пару действительных плоскостей. Значит, в случае 3°
уравнение A) является уравнением одной из этих поверхностей,
дополненных всеми точками прямых 1Х и /2
В четвертом случае уравнение D) определяет две мнимые
плоскости, пересекающиеся по действительной прямой /, значит,
поверхность B) будет или эллиптическим параболоидом, или
эллиптическим цилиндром, или мнимым эллиптическим цилиндром, пли
парой мнимых пересекающихся плоскостей; уравнение A) является
618 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
уравнением одной и этих поверхностей, дополненной одной
несобственной точкой прямой /.
Наконец, в пятом случае уравнение D) является уравнением
двух совпадающих плоскостей (действительных), пересекающих
несобственную плоскость по двум совпадающим (несобственным)
прямым I Уравнение B) в этим случае является уравнением или
параболического цилиндра, или парой действительных
параллельных плоскостей, или парой мнимых параллельных плоскостей, или
парой совпадающих плоскостей; уравнение A) является уравнением
одной из этих поверхностей, дополненных всеми точками
действительной несобственной прямой /
§ 213. Проективная классификация поверхностей второго порядка
Определение. Две поверхности второго порядка в проективном
пространстве принадлежат одному и тому же проективному классу,
если существует такое проективное преобразование, которое одну
из поверхностей переводит в другую. Если же никаким проективным
преобразованием одну из поверхностей второго порядка нельзя
преобразовать в другую, то эти поверхности второго порядка
принадлежат различным проективным классам.
Теорема 1. Всякую поверхность второго порядка в проективном,
пространстве можно проективным преобразованием перевести в одну
из следующих восьми поверхностей:
4+4+4-4=0 (I)
4+4+4+4=0 (П)
4+4~4~4=0 (Ш)
4+4-4=0 (IV)
4+4+4=0 (V)
4-4 = 0 (VI)
4 + 4 = 0 (VII)
4 = 0 (Viii)
Доказательство. Как известно из высшей алгебры,
квадратичную форму
<р = ап4 + апх\ + а334 + аих\ + 2а12хгх2 + 2auxxxz +
+ 2аих1х4 + 2а23хгх3 + 2a2ixixi + 2аз4*3*4 A)
невырожденным линейным однородным преобразованием можно
привести к виду
<Р=-ч4 + е2л:;;+ьв4 + Ь44> B)
$ 213. ПРОЕКТИВНАЯ КЛАССИФИКАЦИЯ IIOBFPXHOCTEfi 619
|де t-'i, f.2) е3, е4 принимают значка;:;! -1-1, —1 или 0; при этом
доказывается, что число коэффициентов среди в,-, равных -f 1. число
коэффициентов е,-, равных — 1, и число коэффициентов е,-, равных
п^лю, всегда одно м то же независимо от того линейного
невырожденного преобразования, которое форму A) приводит к
каноническому виду B) (закон инерции квадратичных форм)*. Отсюда
следует, что не существует линейного невырожденного однородного
преобразования, преобразующего одну из поверхностей (I) — (VIII)
в другую.
Итак, всякую поверхность второго порядка можно
проективным преобразованием преобразовать в одну из поверхностей
(I)—(VIII), данных п условии теоремы, но не существует
проективного преобразования, которое любую из поверхностей (I)—(VIII)
переводит в другую.
Следствие. Из доказанной теоремы следует, что все
поверхности второго порядка в проективном пространстве делятся на
восемь проективных классов Поверхность, заданная уравнением-
(I), входит в первый проективный класс I, и все поверхности
этого класса получаются всеми проективными преобразованиями
поверхности (I). Поверхность, заданная уравнением (II), входит
во второй проективный класс II, и i.-ce поверхности второго
порядка этого класса получаются всеми проективными
преобразованиями поверхности (II) и т. д до поверхности, заданной
уравнением (VIII)
Сформулируем теперь геометрические свойства поверхностей
второго порядка, составляющих эти восемь классов, которые, во-
первых, инвариантны по отношению к проективным
преобразованиям и, во-вторых, характеризуют поверхности этого класса в том
смысле, что указанными свойствами обладают поверхности только
рассматриваемого класса.
I. Поверхность, заданная в однородных координатах уравне-.
нием A) относительно декартовой прямоугольной системы
координат, является сферой (единичная сфера), Сфера содержит
бесконечное множество точек и не имеет прямолинейных образующих
(действительных). Так как эти свойства инвариантны относительно
проективных преобразований, то теми же свойствами обладают
все поверхности второго порядка I проективного класса. Они
называются овальными поверхностями второго порядка.
П. Поверхность, заданная уравнением (II), не имеет пи одной
(действительной) точки. Значит, этим свойством обладают все
поверхности второго порядка, входящие во II проективный класс.
Они называются поэтому мнимыми.
III. Поверхность, заданная в однородных координатах
уравнением (Ш), является одноиолостным гиперболоидом (дополненным
* См. Г. Е. Шилов. Введение в теорию линейных пространств. М.,
Гостехиздат, 1956, гл. VI, § 43, стр 125.
620 Гчава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
несобственными точками всех образующих его асимптотического
конуса).
Через каждую точку этой поверхности (в том числе и через
каждую несобственную ее точку) проходят две прямолинейные
образующие разных серий, пересекающиеся в этой точке. Тем же
свойством обладают поверхности, полученные из поверхности (III)
всеми проективными преобразованиями, т.е. все поверхности
второго порядка III проективного класса.
Поверхности III класса называются линейчатыми
невырожденными поверхностями второго порядка (или торо-
и д а л ь н ы м и. или кольцевидным и).
IV. Поверхность, заданная уравнением (IV) в однородных
координатах, является действительной конической
поверхностью второго порядка. Вершиной конуса является точка
@:0:0:1), а его направляющей, например, действительная
овальная линия второго порядка, заданная на несобственной плоскости
уравнениями
v2 -L у2 у-2 — П V- — Л
Л| T*J Лд U, Хц = U.
Тем же свойством обладают, очевидно, все поверхности второго
порядка, входящие в IV проективный класс.
V Поверхность, заданная уравнением (V) в однородных
координатах, выражается однородным уравнением, следовательно,
является конической поверхностью. Однако па этой конической
поверхности есть только одна действительная точка @:0:0:1). Поэтому
все поверхности V класса также конические и все они имеют
только одну действительную точку (вершину конуса). Поверхности
V класса называются поэтому мнимыми коническими
поверхностями второго порядка.
VI. Поверхность, заданная уравнением (VI), распадается на
две различные действительные плоскости. Отсюда следует, что
каждая поверхность второго порядка VI проективного класса
является парой различных плоскостей.
VII. Поверхность, заданная уравнением (VII), распадается на
две различные мнимые плоскости. Множество всех
действительных точек поверхности (VII) состоит из множества всех
точек оси Ог, дополненного одной несобственной точкой этой оси.
Эти свойства инвариантны по отношению к проективным
преобразованиям, поэтому любая поверхность VII проективного класса
является парой мнимых плоскостей, имеющих общую
действительную прямую (проективную)
VIII. Класс VIII состоит и„ сдвоенных плоскостей.
Мнимые, овальные и тороидальные поверхности второго порядка
называются н ев ы рождающимися. Для того чтобы
поверхность, заданная уравнением (I), была иевырождающейся,
необходимо и достаточно, чтобы ранг квадратичной формы ф был равен 4.
§ 214 ПРОЕКТИВНО-АФФННПЛЯ КЛАССИФИКАЦИЯ ПОБЁРХНОСТЕЙ 621
Действительная и мнимая конические поверхности называются
вырождающимися.
Для того чтобы поверхность была конусом действительным или
мнимым, необходимо и достаточно, чтобы ранг квадратичной формы
<р был равен 3.
Поверхность второго порядка, являющаяся парой плоскостей,
называется распадающейся.
Для распадения поверхности второго порядка на пару
плоскостей (действительных или мнимых, различных или совпадающих)
необходимо и достаточно, чтобы ранг квадратичной формы ср был
меньше или равен 2.
§ 214. Проективно-аффинная классификация поверхностей
второго порядка в проективном пространстве
Определение. Проектиено-аффинной классификацией поверхностей
второго порядка называется разбиение их на классы эквивалентности
по отношению к проективным преобразованиям проективного
пространства, при которых несобственная плоскость переходит в себя.
Теорема 1. Все поверхности второго порядка в проективном
пространстве делятся на девятнадцать проективно-аффинных классов:
1°. Эллипсоиды
2°. Двуполостные гиперболоида
3°. Эллиптические параболоиды
4°. Мнимые эллипсоиды
5°. Однополостные гиперболоиды
6°. Гиперболические
параболоиды
Т. Действительные конусы
второго порядка
8°. Действительные
эллиптические цилиндры
(каждый из которых
дополняется несобственной точкой
любой образующей его
асимптотического конуса)
(каждый из них дополняется
одной несобственной точкой его
особого направления)
(каждая из этих поверхностей
дополняется несобственными
точками всех ее прямолинейных
образующих).
(каждая из этих поверхностей
дополняется несобственными
точками всех ее
прямолинейных образующих)
(каждая из этих поверхностей
дополняется несобственными
точками всех его образующих)
(каждый из них дополняется
одной несобственной точкой
его образующих)
Глава XV ЭЛЕМППЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
9 Гиперболические цилиндры
10 Параболические цилиндры
11е Мнимые конусы
\Т Мнимые эллиптические
цилиндры
13° Пары действительных
пересекающихся плоскостей
14' Пары действительных
параллельных плоскостей
15е Пары действительных
плоскостей, из которых одна
собственная, а другая
несобственная
16е. Пары мнимых
пересекающихся плоскостей
\Т. Пары мнимых
параллельных плоскостей
18е Пары сдвоенных
собственных плоскостей
19е, Пары сдвоенных
несобственных плоскостей
(каждая из этих поверхностей
дополняется одной
несобственной точкой ее образующих)
(каждая из этих поверхностен
дополняется одной
несобственной точкой ее образующих)
(на каждой такой поверхности
имеется только одна
действительная и притом
несобственная точка)
(каждая такая пара
дополняется прямыми, но которым
эти плоскости пересекаются
с несобственной плоскостью)
(каждая такая пара
дополняется прямой, по которой они
пересекают несобственную
плоскость)
(каждая такая пара плоскости
дополняется одной
действительной несобственной точкой той
действительной прямой, но
которой пересекаются плоскости)
(на каждой такой поверхности
имеется только одна
действительная прямая, притом
несобственная)
(каждая такая поверхность
дополняется прямой, по
которой сдвоенная плоскость
пересекает несобственную
плоскость)
Доказательство. Если проективное преобразование ?{
переводит несобственную плоскость в себя, то на множестве
собственных точек проективного пространства оно равно некоторому
$ 214 ПР0ЕКТНВ1Ю-ЛФФИННАЯ КЛАССИФИКАЦИЯ ПОВЕРХ HOC J КП (,2О
аффинному преобразованию А. При этом если это
аффинное-преобразование А прямую / переводит в прямую /', то проективное
преобразование \Н несобственную точку прямой / переводит в
несобственную точку прямой /'. Если аффинное преобразование Л
плоскость л переводит в плоскость я', то проективное
преобразование 21 несобственную прямую плоскости л переводит в
несобственную прямую плоскости л'.
Но так как па множестве собственных точек проективного
пространства указанное разбиение па классы Г—19° является
аффинной классификацией, то на множестве всех точек проективного
пространства указанная классификация — ироективно-аффинная.
Теорема 2. I проективный класс составляют эллипсоиды,
двуполостные гиперболоиды и эллиптические параболоиды.
II проективный класс составляют мнимые эллипсоиды.
I11 проективный класс составляют однополостные гиперболоиды
и гиперболические параболоиды.
IV проективный класс составляют действительные конусы
второго порядка и действительные цилиндры второго порядка
(эллиптический, гиперболический и параболический.)
V проективный класс составляют мнимые конусы и мнимые
эллиптические цилиндры.
VI проективный класс составляют пары действительных
пересекающихся плоскостей, пары действительных параллельных плоскостей
и пары действительных плоскостей, из которых одна собственная,
а другая несобственная.
VII проективный класс образуют пары мнимых пересекающихся
и пары мнимых параллельных плоскостей.
VIII проективный класс образуют сдвоенные собственные
плоскости и сдвоенные несобственные плоскости.
При этом указанные выше поверхности дополняются
несобственными точками так, как указано ч предыдущей теореме.
Доказательство. Для доказательства достаточно проверить'
проективпо-инварнаптпые характеристики каждого из восьми
классов поверхностей второго порядка в проективном пространстве.
•I. В самом деле, эллипсоиды, двуполостные гиперболоиды и
эллиптические параболоиды, имеют бесконечное множество
действительных точек и не имеют прямолинейных образующих.
II. На мнимых эллипсоидах нет ни одной действительной точки.
III. Однополостпый гиперболоид и гиперболический параболоид
обладают тем свойством, что через каждую точку их поверхности
(в том числе и через несобственную!) проходят две различные
прямолинейные образующие.
IV. Действительный конус второго порядка, эллиптический,
гиперболический и параболический цилиндр являются
действительными коническими поверхностями; для трех последних поверхностей
вершина — несобственная точка и т.д.
624 Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Замечание. Покажем, какие проективные преобразования
переводят друг в друга поверхности, входящие в один
проективный класс, но в различные проективно-аффинные классы.
I Однородные уравнения эллипсоида, двуполостного
гиперболоида и эллиптического параболоида *
+
+ 2x3x4 = 0 (р>0,9>0)
переводятся в уравнение сферы
<+<+<-<=0
соответственно следующими проективными преобразованиями:
xx = V~px\, x2 = V
B)
C)
Отсюда следует, что проективное преобразование ЭД^Г1^
переводит эллипсоид A) в двуполостный гиперболоид B); преобразо-
вание^Г1?^ Двуполостный гиперболоид B) переводит в эллипсоид A).
Преобразование З!^1?^ переводит эллипсоид A) в эллиптический
параболоид C), а преобразование 91Г]^3 эллиптический параболоид
C) переводит в эллипсоид A). Преобразование SfJT1^ переводит
двуполостный гиперболоид B) в эллиптический параболоид C),
а преобразование ЗХ^-313 эллиптический параболоид C) переводит
в двуполостный гиперболоид B).
II. Все мнимые поверхности второго порядка образуют один
проективный и один проективно-аффинный классы.
Однородное уравнение мнимой поверхности
*2 х2 х1
Э + "ИГ + -^2 + *4 = 0
переводится в уравнение
Все поверхности, о которых говорится здесь и ниже, предполагаются
дополненными несобственными точками так, как это указано выше.
§ 214. ПРОЕКТИЕНО-ЛФФИННАЯ КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ 625
следующим проективным преобразованием:
III. Уравненияоднополостного гиперболоида и гиперболического
параболоида
X2 У2 У2
__Lj_-— ■— г —О (А\
2 2
^- —^- -2V4 = 0 (р > 0, 9 > 0) E)
преобразуются в уравнение
-2
соответственно следующими проективными преобразованиями:
-2 '2 '2 /2
рх\, x2 = Vqx3, X3= y_l , x4 = ^i
Значит, преобразование 31Г'^4 переводит одиополостный
гиперболоид D) в гиперболический параболоид E), а преобразование
ЗХ^§15 вторую из этих поверхностей преобразует в первую.
IV. Уравнения конуса и цилиндров второго порядка
х2
х'1 х2
1 2 2 (\ ,о.
~~2 £2 Л* —U> \°1
а-2 — 2рх2х4 = 0, р>0 (9)
преобразуются в уравнение
/2 /2 '1
соответственно следующими проективными преобразованиями:
x1=axs, xa =
626 Глава XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Значит, преобразование -ЛГЦ<МЪ преобразует конус F) d
эллиптический цилиндр G), а преобразование ЙГ'^Ц, наоборот,
эллиптический цилиндр преобразует в конус F) Преобразование ^'1>(в
преобразует конус F) в гиперболический цилиндр (8), а
преобразование ?С^8 преобразует гиперболический цилиндр (8) в конус
F) и т. д. (всего 12 различных проективных преобразований,
преобразующих одну из поверхностей F) —(9) в другую)
V. Уравнения мнимого конуса и мнимого эллиптического
цилиндра
преобразуются в уравнение
,2 , ,2
соответственно следующими проективными преобразованиями;
Значит, преобразование 5MJY ЭД10 преобразует мнимый конус A0)
в мнимый эллиптический цилиндр (И), а преобразование 2(["о 9tu —
мнимый эллиптический цилиндр (II) в мнимый конус A0). -
Рассмотрение остальных случаев VI, VII, VIII предоставляется
читателю.
§ 215. Необходимое и достаточное условие того, что два
однородных уравнения второй степени определяют одну и ту же
поверхность второго порядка
Теорема 1. Для того чтобы два уравнения
\
апх1 + аггх\ + ai3xl + а^х\ + -^Чг* А + 2«i3^i^3 +
2a.23x^xs -f 2a24x2x4 + га^^ = 0 A)
bnxi + b22xl -|. b.i3xl + Ь^х\ -J- 2bux1x2 + 2buxtxs +
+ 2biix1xi + 2b2Sx2x3 +■ 2blixlxi -f- 2bZixzxi = 0 B)
выражали одну и ту же поверхность в комплексном проективном
пространстве, необходимо и достаточно, чтобы соответствующие
коэффициенты этих уравнений были пропорциональны.
Л о касательств о необходимости (достаточность
очевидна). Пусть уравнения A) и B) выражают одну и гу же поверх-
§ 215 ДВА ОДНОРОДНЫХ УРЛПП1ШИЯ BTOPOi! СГЕ1ШНИ 627
ность. Если зта поверхность распадается на две плоскости, то
теорема следует из того, что если два уравнения с однородных
координатах являются уравнениями одной и той же плоскости,
то соответствующие коэффициенты уравнений этих плоскостей
пропорциональны.
Предположим, что поверхность, заданная уравнением A) или
B), нераспадающаяся.
Рассмотрим сечение поверхности плоскостью х4 — 0; уравнения
линии сечения:
a11x'i -f a2ixl -j- азях1 -\- 2a12xlxi -)- 2aisx2x^ + 2a.nx3x1 — 0, xt = О, C)
или
bnx\ + bi2xl -f- 633X3 -f 2b1%x1xi -t- 2b2sx2x.< + 2Ья,хйх} = 0, x4 = 0. D)
Так как поверхности A) и B) совпадают, то уравнения C) и
D) выражают одну и ту же линию на плоскости л:4 = 0 и, значит,
на основании теоремы 1 § 206 коэффициенты уравнений C) и D)
пропорциональны
Рассматривая еще сечения данных поверхностей плоскостями
х3 — 0, х2 = 0, х1 — 0, докажем, что Есе коэффициенты уравнений
A) и B) пропорциональны
Теорема 2. Для того чтобы уравнения A) и B), заданные в
однородных координатах точек действительного проективного
пространства, являлись уравнениями одной и той же действительной
поверхности второго порядка, имеющей бесконечное множество
действительных точек, не принадлежащих одной прямой, необходимо,
чтобы соответствующие коэффициенты этих уравнений были
пропорциональны.
Доказательство. Теорема, очевидно, верна, если A) и B) —
уравнения одной и той же поверхности второго порядка,
распадающейся па две плоскости. Предположим, что уравнения A) и
B) являются уравнениями действительной нераспадающейся
поверхности второго порядка, имеющей бесконечное множество
действительных точек, не принадлежащих одной прямой. Это значит,
что поверхность может быть одной из следующих: эллипсоид, дву-
полостиый гиперболоид, эллиптический параболоид, однополостпый
гиперболоид, гиперболический параболоид, действительный конус
второго порядка и один из цилиндров: эллиптический,
гиперболический или параболический.
Во всех случаях можно перейти к такой специальной системе
координат, что уравнения A) и B) в однородных координатах
имеют одинаковый вид с точностью до числового множителя
левой части (отличного, конечно, от пуля).
Так, например," если уравнения A) и B) являются уравнениями
однополостного гиперболоида (дополненного несобственными
точками его образующих), то существует система координат O'x'y'z',
и'_>« Глава XV ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
такая, что в однородных координатах хи хг, х3, х4, введенных в
этой системе, уравнения A) и B) одпополостного гиперболоида
имеют вид
,2 /1 ,2 ,2 ,i /^ ,'L ,2
a{x, + x.2 — x3 — Xi ) = О и b (x, -f x2 — x3 — xt ) = 0. E)
Соответствующие коэффициенты этих уравнений
пропорциональны, значит, пропорциональны и соответствующие коэффициенты
уравнений A) и B), так как эти уравнения получаются из
уравнений E) при одном и том же преобразовании координат х1} х2,
■2 ,2 ,2 ,2
х3, xit при котором форма х\ -\-х2 —х3 —xt перейдет в одну и ту
же квадратичную форму.
Остальные случаи принципиально ничем не отличаются от
произвольно выбранного (одиополостный гиперболоид). Надо
воспользоваться результатом § 163.
§ 216. Касательная плоскость к поверхности второго порядка
Точка Мо (x\\xl:xl:x\) называется иеособоп точкой
поверхности второго порядка, заданной общим уравнением
anxi + a22xt -l a<iSxl + a^x\ -f 20^x^2 + 2аихгхь -\- 2alix1xi +
+ 2a2sx2xs + 2a2ix2xi + 2a3ixsxi = 0,
если хотя бы одно из чисел
ацх°1 + anxl + alsx°3 -f aux\, a21x\ -f a22xl + а,3х°3
отлично от пуля,
Невырождающиеся поверхности не имеют особых точек. Особой
точкой конуса является его вершина Особыми точками
распадающейся поверхности являются все точки линии пересечения тех
плоскостей, па которые распадается поверхность
Касательной прямой к поверхности второго порядка в данной
на ней неособой точке называется прямая, проходящая через эту
точку и пересекающая поверхность в двойной точке, либо целиком
принадлежащая этой поверхности. Все прямые, проходящие через
неособую точку поверхности и касающиеся ее, лежат в одной
плоскости. Эта плоскость называется касательной к данной поверхности
в данной на ней точке Если поверхность задана уравнением
аих\ + аггх1 + a33xl + аих\ + 2ахгхххг +- 2alsx1xs +
+ 2alixlxi + 2а2.йх2х3 -\- 2аых2х4 -f- 2a3ix.ixi — 0,
а неособая точка, лежащая на ней, имеет координаты x\:xl:xl:x\,
то уравнение касательной плоскости к поверхности в данной точке
217. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ КАСАТЕЛЬНО!'! ПЛОСКОСТЬЮ
имеет вид
(аих1-+аг2х1 +algx°3+alix°l)xl
1 ~\~®22Х2 "Т а2зХ3 ~\~ Q24 •*•<!/ Х
+ (a4i*? + ai2x°2 + aisx°3 + аих\) xt = 0.
Доказательство этой теоремы аналогично доказательству
теоремы § 207.
§ 217. Пересечение поверхности второго порядка
касательной плоскостью
Пусть О—неособая точка действительной поверхности второго
порядка. Ограничимся рассмотрением действительных овальных
поверхностей (I проективный класс), иевырождающихся линейчатых
поверхностей (III проективный класс) и действительных конусов
второго порядка (IV проективный класс). Поверхности I и III
проективных классов не имеют особых точек, поверхности IV
проективного класса имеют только одну особую точку (вершина
конуса).
Предположим сначала, что точка О — собственная. Примем ее
за начало общей декартовой системы координат, а за плоскость
хОу примем плоскость, касательную к поверхности в точке О.
Пусть в выбранной системе координат уравнение поверхности в
однородных координатах примет вид
аххх\ + a2ixt + assxt -f aiAxt -f 2a12x1x2 + ^a^x^.^ +
+ 2alixlxi + 2a23x2xs + 2о24х2д;4 + 2as4x3x4-= 0. A)
Так как уравнение плоскости, касательной к поверхности в
точке @:0:0:1), таково:
аых1
и оно должно быть эквивалентно уравнению
ха = 0 (уравнение плоскости хОу),
то
и уравнение A) принимает вид
.2 -f 2агзхгх3 + 2a13x1xs -f-
(Г)
630
Глава XV. ЭЛЕМЕНТЫ ПРОЕ.КТПВНОП ГЕОМЕТРИИ
Уравнения линии, по которой ее пересекает касательная к
этой поверхности плоскость хя — 0 в начале координат, имеют вид
"I | Л | ~\' *~fit 1 оА 1 а>) "~~f Li ^ Пш\ •) —- v/1
у Q
B)
В плоскости хОу первое из уравнений B) является уравнением
пары прямых. Это две мнимые пересекающиеся (в точке О
касания) прямые, если
i«2I °22
точка О в этом случае называется эллиптической точкой
поверхности Если 8<0, то линией пересечения являются две различные
действительные прямые; точка О в этом случае называется
гиперболической. Если, наконец 8 — 0, то линия пересечения
поверхности с касательной плоскостью является сдвоенной прямой, точка О
поверхности в этом случае называется параболической. Докажем,
что действительные овальные поверхности состоят из
эллиптических точек, действительные линейчатые невырождающиеся
поверхности состоят из гиперболических точек, а действительные конусы
вторе го порядка — из параболических точек.
Вычислим определитель Kt квадратичной формы <р:
Кло22
«81 «32
0 О
«13
«28
«S3
«34
0
0
«3J
0
2
«11 «12
- 34i«21 «22
C)
Отметим, что знак Кц не меняется при преобразовании
системы координат, так как при таком преобразовании /D умножается
на квадрат определителя из коэффициентов преобразования, т. е.
на положительное число.
Для действительных овальных поверхностей второго порядка
JD<0 (в этом можно убедиться, вычислив /С4 из уравнения
х\ -[ х\ -\-х.\— х\ = 0). Для линейчатых певырождающихся
поверхностей второго порядка (х\-\-х\ — х\ — х\ = §) КА>0, а для
действительных конусов второго порядка (х\-\-х\ — х\ = 0)/^4 = 0.Отсюда
и из равенства C) заключаем, что если /С4<0, то 8>0; если Kz>Q,
то б<0, и если /D = 0, то 8 — 0. Значит, касательная плоскость к
действительной овальной поверхности второго порядка пересекает
ее по двум мнимым прямым, пересекающимся в точке касания.
Касательная плоскость к невырожденной линейчатой поверхности
второго порядка пересекает ее по двум пересекающимся прямым
(прямолинейным образующим разных сер.ш). Наконец, касательная
плоскость к действительному конусу (вершина исключается!) не-
S 218. ПОЛЮС И ПОЛЯРНАЯ ПЛОСКОСТЬ 6'И
ресекает его по сдвоенной действительной прямой (по образующей
конуса, проходящей через точку касания).
Если О — несобственная точка, то существует проективное
преобразование %, которое переводит ее в собственную точку О'.
При проективном преобразовании Ш рассматриваемая поверхность
П перейдет в поверхность П' того же проективного класса
Касательная плоскость в точке О' к поверхности W пересекает ее
соответственно по двум мнимым, действительным различным или
совпадающим прямым в зависимости от того, принадлежит ли
поверхность II соответственно к I, III пли IV проективным классам.
При преобразовании 51"' поверхность II' перейдет в поверхность П,
а плоскость л', касательная к поверхности П' в точке О',
перейдет в плоскость л, касательную к поверхности П в точке О
(понятие касательной плоскости проективно инвариантно), поэтому
характер пересечения поверхности П с касательной плоскостью в
несобственной точке О таков же, как в случае, когда точка О
собственная.
Например, несобственная плоскость касается эллиптического
параболоида в его единственной несобственной точке; касательная
плоскость в несобственной точке однополостного гиперболоида
пересекает его по двум различным (параллельным!) прямолинейным
образующим, проходящим через эту несобственную точку, и т. д.
§ 218. Полюс и полярная плоскость поверхности второго порядка
Теорема 1. Рассмотрим уравнение
#11^1 ~Г'°22-"-2 ~Г ^ЗЗ-^З "Г Q44"*:4 "T" бй-цХ^Х^ -J- ^GjgXjXg -f- 2,a^iX^Xi -f-
-f 2a23*2*3 -i- 2aiixixi + 2a34x3*4 = 0 A)
поверхности второго порядка. Пусть M(x\:x\\xl:x\)— произвольная
точка, не лежащая на этой поверхности. Тогда все точки N,
четвертые гармонические к точке М относительно пары точек Р и Q
пересечения произвольной прямой, проходящей через точку М, с
данной поверхностью второго порядка, лежат в одной плоскости,
называемой полярной плоскостью точки М относительно данной
поверхности Уравнение полярной плоскости точки М(х\:х!2:х1:х\)
относительно поверхности A) имеет вид
{allx\Jra^xl + auxl^ralixl)xl -f-
+ (аг1х1 -f a224+ агъх\ + a^xl) хг +
х\ -1- ai3xl -|- ам4) х3 +
х1 + aisx°s +auxl) х4 = 0. B)
Доказательство этой теоремы вполне аналогично
доказательству соответствующей теоремы 1 для линии второго порядка (§ 208).
632* Глава XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Если точка М является пеособой точкой поверхности пторого
порядка, то полярной плоскостью ее относительно данной
поверхности назовем плоскость, касательную к поверхности в этой точке.
Отметим, что уравнение полярной плоскости для неособой точки
поверхности, имеет тот же вид B)
Из уравнения полярной плоскости следует
Теорема 2. Если из двух точек М и N первая лежит на поляре
второй, то и вторая лежит на поляре первой. Иначе, если из двух
плоскостей тип первая проходит через полюс второй, то и
вторая проходит через полюс первой.
§ 219. Примеры и задачи к главе XV
1. Задачи с решениями
Пример 1. Относительно декартовой прямоугольной системы координат
задано уравнение параболы:
=*0 (/2 = 0, К3Ф$). A)
Найти координаты ее фокуса и уравнение директрисы.
Решение Уравнение параболы относительно декартовой
прямоугольной системы координат п том случае, когда за начало координат
принимается фокус параболы, можно записать и виде
где x'cosa-j- (/sin a—р —О—уравнение директрисы (нормальное), а р—
параметр параболы
Преобразуя уравнение B), имеем
х'2 sin2 а — 2х'у'ьи\ a cosa + y'2cos2 a \-2px' cosa-{-2py' sin а —р2 = 0.
Это уравнение в тангенциальных координатах будет иметь вид
sii.2a —sinaccsa pcosa и
— sinacosa cos2 a p since v
pcosa psina —p2 w
и v w 0
= 0,
или
Перенесем данную систему координат так, чтобы новым началом
координат стал фокус данной параболы Тогда
и данное уравнение A) примет вид
аих' -Ь^°12*'у' "г" °22J/' 4" 2Fxox' -\-2Fy(sy' -\-2Fq = 0, D)
гае
= anxl + 2a12.v0(/0 -)- а^гу\ + 2axxQ + 2а2уп + а.
§ 219 ПРИМЕРЫ И ЗАДАЧИ К ГЛАВЕ XV
6'Й
Уравнение D) в тангенциальных координатах:
П «12 fjfo «
v ° и) О
Отнимая из элементов третьего столбца соответствующие, элементы
первого столбца, умноженные на х0, и элементы второго столбца, умноженные
на у0, получим
v' w — хои — yav
0
=0-
Отнимая из элементов третьей строки соответствующие элементы первой
строки, умноженные на х0, и элементы второй строки, умноженные на у0,
получим
ап ап Я]
q21 a22 a2
«! о2 а к.1 —
и v w—хои—yov
или
= 0,
(ю — a-ou — you) = O.
C)
Так как уравнение E) должно Сыть эквивалентно уравнению C), а
уравнении C) коэффициент при uv равен нулю и коэффициенты при и2 и
равны между собой, то
А 12 — у0А1 — х0А2 - 0, А и — 2.г0Л! = Л22—
Отсюда и находим координаты х0, (/о фокуса:
2 о" J (^22—
Иia + "о- ^2(^22 —
4Иia
1 '
Переписывая уравнение C) в виде
2-|-2 cosa uw-r-2 sin a vw = 0,
находим
откуда
coscx sin а >
— р cosa sin a '
и уравнение директрисы в системе х'О'у' имеет вид
или
?-0,
Глава XV ЭЛЕМЕНТЫ ПРОЬКТИВПОЙ ГЕОМЕТРИИ
a jpdHHi'iiHt директрису в начплиш < сы ie с
Пример 2 Найти огибающую общих касаюльяых а двум ортогональным
окружностям, проходящим через две фиксированные точки @, а) и @,—а)
Решение Центры окружностей (at, 0) и ( —Г'1I квадраш их
радиусов а2 (I-\-X2) н-% (I-{-12) Координаты и, v, w общей касательной
удовлетворяют тангенциальным уравнениям этих окружностей.
(aut-\- wJ = a2_ A -)-1*) (u2+ v2),
Отсюда
или
—уравнение огибающей вташенциальных координатах Уравнение же в точеч
ных координатах
—эллипс
Пример 3 Найти геометрическое
место полюсов М хорд параболы,
которые видны из фокуса под
прямым углом
Геометрическое
решение Рассмотрим поляритет* II отно
сительпо окружности С] с ценiром
в фокусе F параболы и радиусом
FS, где S—вершина параболы (рис.
282) При этом поляритете каждая
касательная I к паработс перейдет
I' точку Т луча, выходящего из
фокуса F и пересекающего касатель
ную t в точке М, такой, что FTx
XFM = FS2 Но так как проекции
/И фокуса на касательные к пара
боле описываю! касательную к
параболе в се вершине, то множеством
точек Т будет линия, получаемая
из касательной ь параболе в ее
вершине при инверсии центром F и
степенью инверсии, равной FS2
Но при такой инг.ерсии прямая SM перейде1 в окружность С2 с
диаметром FS Датее, точка А прикосновения касатетыюй X к данной
перейдет в прямую а, перпендикулярную FA и касающуюся
окружРис
парабол!
ности С2 Если В —другая юч^а параболы, такая, что
= -^-, то точка В
v касательная к параболе в точке В перейду! соотвектрепно в касательную Ь
к окружности С2 (причем касательные Ь ' и а взаимно перпендикулярны)
и в точку К прикосновения прямой Ь с окружностью С2 Значит полюс
* Т s отображение, при котором точке ставится в соответствие ее поляра
и наоборот.
§ 219. ПРИМЕРЫ И ЗЛДЛЧИ К ГЛАВЕ XV ' £35
хорды АВ перейдет в прямую ТК, геометрическое же место полюсов хорд АВ
перейдет в множество прямых ТК Но отрезок ТК есть сторона квадрата,
«писанного в окружность С2. Значит, геометрическое место полюсов хорд АВ
параболы, видимых из фокуса F под прямым углом, перейдет в множество
касательных к окружности С3, центром которой является середина отрезка FS,
а радиус равен , где р — параметр параболы. Геометрическим местом
I я \
полюсов хорд АВ (таких, что /_ AFB = ~^-\ будет образ множества
касательных к окружности Сп при рассматриваемом поляритете. Полярой фокуса F
относительно окружности С3 является прямая PQ, проходящая через точки
прикосновения касательных, проведенных из точ«и F к окружности С3.
Так как при поляритете II точка F переходит в бесконечно удаленную
прямую, то ее поляра PQ переходит в центр искомой кривой. Но гак как
расстояние от точки F до прямой PQ равно -^- , то прямая PQ перейдет в центр О
о
искомой линии, лежащий на луче FS на расстоянии 2р от точки F 1 ибо тогда
JL . 2р=-^—= FS2 ) . Далее, прямые FP и FQ перейдут в бесконечно удален-
8 4 /
пые точки соответственно прямых FQ и FP, значит, искомая линия имеет
две различные бесконечно удаленные точки и они лежат на двух взаимно
перпендикулярных прямых. Значит, искомая линия—равносторонняя
гипербола, асимптоты которой проходят через указанный выше центр О и
наклонены к прямой FS под углом 45°. Наконец, вершины гиперболы — образы
в поляритете П прямых, касательных к С3 и перпендикулярных к SF. Одна
из таких касательных отстоит от F на расстоянии FN=-~ -j — . Значит,
4 4 J/ 2
она перейдет в вершину А гиперболы, отстоящую от точки F на расстоянии
р ('2—У 2); полуоси гиперболы равны р У 2.
Аналитическое решение. Принимая за начало координат фокус F
параболы, можно записать ее уравнение в виде уг — 2рх — р2 = 0. Поляра
точки Р (X, Y) имеет уравнение рх — Уу-\-рХ-\-р2 — 0. Отсюда р=— ~-—-,
л -гр
значит, следующее уравнение будет следствием дяух предыдущих (уравнения
параболы и поляры точки относительно параболы):
„2 , oYPx—Yy (px—YyJ__n
или
x2_2x(/ XY-
Но это уравнение однородное относительно х и у и, значит, оно
определяет пару прямых, проходящих через начало координат и точки пересечения
поляры с параболой. Условие ортогональности этих прямых!
или
(X + 2р)«
и мы приходим к тому же результату.
6.36 Глава XV. ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
2. Задачи для самостоятельного решения
1. Опр делить общий вид проективных преобразований, при которых
гипербола
а2 й2
переходит в себя, а касательные в вершинах гиперболы переходят в ее
асимптоты
Ошв
Ь Ь2
х' = ± — (х ch ф + a sh ф), у' = ± — (х sh ф + a ch ф).
2. Доказать, что если уравнение
= О
определяет действительную овальную линию второго порядка, го условие
й31 a3s
ф (*i. «а.
является необходимым и достаточным условием того, что точка (хх:хг:х3)
внутренняя.
3. Определить поляру точки, лежащей на асимптоте гиперболы
■л и2
относительно' этой гиперболы
х у
Отв. Если точка М0(х0, у0) лежит на асимптоте ь~=^' н0 не совпа"
дает с центром гиперболы, то уравнение поляры имеет вид
£-*-•■
Где t — некоторое число Обратно, если t — любое действительное число,
не равное нулю, то на гиперболе A) найдется точка Мо, для которой при»
мая B) будет полярой Аиачогпчны выводы и для второй асимптоты.
4. Доказать, что необходимым и достаточным условием полярной
сопряженности двух прямых, проходящих через фокус линии второго порядка,
является их перпендикулярность Является ли это свойство фокуса линии
второго порядка его характеристическим свойством?
5. Пусть С —действительная овальная линия второго порядка, a F — ее
фокус Рассмотрим окружность S с центром в точке F Поставим в соответ-.
ствие каждой касательной к линии С ее полюс И относительно окружности 5'.
Доказать, что геометрическое место точек М есть окружность
6. Уравнение
^l^l ^ 0 A)
определяет действительную овальную линию второго порядка. Дана прямая
B)
1) При каком необходимом и дос1аточном условии прямая B) пересекает
линию A) в двух различных (и действительных) точках?
2) При каком необходимом и достаточном условии прямая B) не пересе-
кае! линию A)?
fc 219. ПРИМКРЫ И ЛЛДЛЧИ К ГЛАВЕ XV
637
Отв.
22 О 2» «2
u2 u3 О
> 0; 21 \ < 0.
7. Доказать, что если из внешней точки действительной овальной линии
провести касательные к ней, то прямая, соединяющая эту точку с серединой
хорды прикосновения, будет диаметром линии, сопряженным направлению
хорды
8. Найти огибающую семейства прямых, образующих вместе с двумя
данными прямыми треугольник постоянной площади.
S
Отв ху=у—. , где S —площадь треугольника, а со —угол между
данными прямыми (за оси коордипач принимаются данные прямые).
9. Дан треугольник АО В; из каждой точки его стороны А В опущены
перпендикуляры на стороны ОА и OS. Найти огибающую прямых,
соединяющих основания этих перпендикуляров.
Отв. Парабола.
10. Составить тангенциальное уравнение поверхности второго порядка:
Отв.
a12 а13 аи аг
Й22 а23 Q24 U2
«32 «33 «31
«42 °43 °44 «4
и2 ил ил О
= 0,
ИЛИ
где Aik— алгебраическое дополнение элемента a;k в матрице (a.-f,).
11. Найти геометрическое место точек пространства, из которых данная
точка и данная прямая проектируются на плоскость данной линии второго
порядка в ее полюс и поляру
Отв Линия второго порядка, лежащая в плоскости, проходящей через
данную точку и поляру точки пересечения данной прямой с плоскостью данной
кривой относительно этой кривой
ДОПОЛНЕНИЕ I
ОРИЕНТАЦИЯ
1 Ориентация плоскости
Определение 1. Ориентированным треугольником ABC называется упоря
доченная тройка точек, не принадлежащих одной прямой
При обозначении ориентированного треугольника порядок его вершин
определяется порядком их записи
Определение 2 Цепью, соединяющей ориентированные треугольники ABC
и А'В'С, называется' конечная упорядоченная последовательность
ориентированных треугольников первым ччекентом которой является ориентированный
треугольник ABC, последним — ориентированный треугольник А'В'С, такая,
что каждые два соседних ориентированных треугольника этой последователь
поста отличаются только одной вершиной, занимающей в обоих треугольниках
одно и то же место
Теорема I. ЛюСые сва ориен/?1ированных треугольника ABC и А'В'С
можно соединить цепью
Доказательство Такая цепь будет, например,
А~ВС. ABQ, APQ A^Tq, A'B^Q, А'ВХ',
где Q — любая ючка, ие лежащая ни на прямой АВ, ни на прямой А'В',
а Р— какая-нибудь точка, не лежащая ни па прямой AQ ни на прямой A'Q'
(рис 283).
Определение 3. Два ориентированных треугольника ABC и ABD имеют
одинаковый обход, если точки С и D лежат по одну сторону от прямой А В
(рис 284) Если же точки С и О лежат по разные стороны от прямой АВ,
то ориентированные треугольники ABC и ABD имеют противоположный обход
(рис. 285) Аналогично определяется одинаковый и противоположный обход
ориентированных треугольников, отличающихся только вторыми или только
первыми вершинами
Определение 4. Если в цепи, соединяющей ориентированные треуголь
ники ABC и А'В'С, число пар соседних треугольников, имеющих
противоположный обход, четное, то говорят, что ориентированные треугольники ЛВС
и А'В'С имеют одинаковую ориентацию, если же это число нечетное,
ОРИЕНТАЦИЯ
639
то ориентированные треугольники ABC и А'В'С имеют противоположную
ориентацию
На рис 286 изображены два ориентированных греугольника ABC и А'В'С\
В пени
А~ВС, ОВС, DEC, DEC, A'EC, А'В'С
В1
Рис 284
обход меняется два раза, значит, ориентированные треугольники ABC и А'В'С
имеют одинаковую ориентацию
Для того чтобы оправдать определение 4, надо еще доказать следующую
.теорему
Теорема 2. Во всех цепях, соединяющих ориентированные треуголь-
V
Рис 285
Рис 286
пики ABC и А'В'С, число пар соседних треугольников, имеющих
противоположный обход, или, всегда четное, или всегда нечетное.
Иными словами, надо показать, что свойство двух ориентированных
треугольников иметь одинаковую или противоположную ориентацию не зависит
от выбора цепи, соединяющей эти ориентированные треугольники
Теорема 2 является следствием следующей теоремы,
Теорема 3. Пусть относительно общей декартовой системы координат
заданы вершины
А (*!, ух), В (*2 </2), С (*„ yt)
А'(х[, у,), Я'(/2> у\), С'(х3 уг)
6-Ю
ДОПОЛНЕНИЕ 1
ориентированных треугольников ABC и А'В'С. Для того чтобы
ориентированные треугольники ABC и А'Я'С имели одинаковую ориентацию, необходимо
и достаточно, чтобы определители
х2
Ч
Ух
Уч.
Уз
1
1
1
Д' =
Х1
У*
Уз
1
1
1
л =
имели один и тот же знак.
Доказательство. Рассмотрим каких-нибудь два соседних треуголь.
ника цепи, соединяющей ориентированный треугольник ABC с
ориентированным треугольником А'В'С.
Пусть, например, это треугольники MNP и MNQ с вершинами
М. (хм, ум), Л' (xjv> Vn), P (хр> Ур), Q {xq, yQ).
Уравнение прямой M/V имеет вид
х у 1
хм Ум 1 =1-
х,\ <//v 1
Рассмотрим результаты бр и
вую часть этого уравнения:
Хр
подстановок координат точек Р и Q в
леУр
УМ
У!Я
1
1
1
И 6(j =
xq
хм
XN
Уд
Ум
Уи
1
1
1
XN
На основании § 62 числа бя и 6q одного знака, если точки Р и Q лежат
по одну сторону от прямой MN, и разного знака, если точки Р и Q лежат
по разные стороны от прямой МЛ' Иначе говоря, числа бр и 6q будут одного
знака тогда и только тогда, когда ориентированные треугольники MNP
и MNQ имеют одинаковый обход.
Отсюда следует, что число перемен знака в конечной последовательности
определителей, соответствующих треугольникам цепи, соединяющей
ориентированные треугольники ЛВС и А'В'С, равно числу пар соседних
треугольников этой цепи, имеющих противоположный обход. Но если определители Д
и Л' имеют одинаковый знак, то в последовательности определителей,
соответствующих ориентированным треугольникам цепи, знак меняется четное число
pai независимо от выбора цепи, а значит, независимо от выбора цепи,
соединяюще"! ориентированные треугольники ABC и А'В'С, число пар соседних
тре\голыгаков, имеющих противоположный обход, или всегда четное, или
все! да нечетное
Из доказанной теоремы следует, что два ориентированных треугольника,
имеющих одинаковый обход, имеют одинаковую ориентацию, а два
ориентированных треугольника, имеющих противоположный обход, имеют
противоположную ориентацию
Следствие 1. При круговой перестановке вершин ориентированного
треугольника ABC его ориентация не иечяется, а при нарушении кругового
ОРИЕНТМДИЯ
641
порядка вершин ориентация меняется и я противоположную, т. е. треугольники
А~ВС, ВС*А, С~АВ A)
имеют одинаковую ориентацию, треугольники
ВАС, А~С~В, СВА B)
Рис 287
Рис 288
Рис. 289
также имеют одинаковую ориентацию, а любой треугольник A) с любым
треугольником B) имеют: противоположную ориентацию.
Эго следует из того, что определитель
X,
Ч
Ч
.Ух
1
1
1
не меняет =пака при круговой перестановке его строк и меняет знак на
обратный при нарушении кругового порядка строк
Следе 1ние 2. При преобразовании симметрии очюси гельно прямой
^п_. 287) ориентация ориентированного греугольникл меняется на
противоположную 'для доказательства внести декартоку прямоугольную систему коор-
цинат, принимая ось симметрии за ось Ох)
Следствие 3 При симметрии относительно точки О (рис. 288) ориентация
ориентированного треугольника не меняется (для доказательства внести общую
декаргову систему координат,--приняв ючку О за начало координат)
Следствие 4 Ориентация ориентированного треугольника не меняется
—у —► —^
при переносе, т е если А А' = ВВ' — СС рис 289), то ориентированные
треугольники ABC ь А'В'С имеют одинаковую ориентацию
Определение 5 Плоскость на которой фиксирован ориентированный
треугольник £]£2О, называется ориентированной плоскостью. Если
ориентированны" треугольники ABC и FfE.,0 имеют одинаковую ориентацию, то будем
сварить, что треугольник ABC имеет положительную ориентацию, а если
ориентированные треугольники ABC и £[£2О имеют противоположную ориен-
■■ амию, то треугольник ABC имеет отрицательную ориентацию
Если на плоское™ ««едена общая декартова система координат, го ее
ориентируют треугольником £j£2O (базисный треугольник), где О —начало
координат, а £2 и £2 —соответственно единичные точки осей Ох и Оу.
21 п С. Моденов
642
ДОПОЛПГ.ИИЕ !
Все декартовы системы координат на плоскости делятся на два класса:
две системы принадлежат одному классу, если их базисные треугольники имеют
одинаковую ориентацию (рис 290), и разным классам, если базисные треуголь
пики имеют противоположную ориентацию (рис. 291).
Теорема 4. Если относительно обшей декартовой системы координат заданы
вершины треугольника
Рис 291
то ориентированный треугольник ABC имеет положительную ориентацию,
если
Д =
х2 у, I
Х2
к отрицательную, если Л < 0 (Хг Yx — координаты вектора СА; Х%, Y2 —
координаты вектора С В).
Доказательство Так как
то
£, = {1, 0}, О£2 = {0, 1},
1 0
А' =
0
= 1 >0,
И, значит, если А > 0, то оркенп<ров:.Ш1ые треугольники ABC и ЕХЕ2О имеют
одинтковую ориентацию, а если Д < 0, то — противоположную.
2. Ориентация пространства
Определение 1. Ориентированным тетраэдром ABCD называется
упорядоченная чеггверка точек, не принадлежащих одной плоскости
Определение 2. Цепью, соединяющей ориентированные тетраэдры A BCD
и A'B'C'D', называется квнтная упорядоченная последовательность
ориентированных тетраэдров, перши элементом которой является ориентированный
тетраэдр ABCD, песлеёним A'B'C'D', такая, что каждые два соседних
ориентированны' тетраэдра отличаются только одной вершиной, занимающей
в обоих ориентированных тетраэдрах одно и то же место
Теорема I. Любые два ориентированных тетраэдра ABCD и A'B'C'D'
можно соединить цепью.
ОРИЕНТАЦИЯ
61S
Доказательство Такой цепью будет, например, цепь
ABCD, А ВСЯ, Ab'qR, APQJt,
A'PQR, A'B'QR, A'B'C'R, А'В'CD',
где точки P, Q, R выбираются последовательно гак: R — точка, не лежащая
в плоскостях ABC и А'В'С, Q— т.очка, не лежащая в плоскостях А'В'R
и ABR, а Р — точка, не лежащая в плоскостях AQR и A'QR.
Определение 3. Два ориентированных тетраэдра A BCD и АВСЕ имеют
одинаковый обход, если точки D и Е лежат по одну сторону от плоскости
ABC, и противоположный обход, если точки D и Е лежат по разные стороны
от плоскости ABC.
Аналогично дается определение одинакового или противоположного обхода
для двух ориентированных тетраэдров, отличающихся только одними первыми,
или только одними вторыми, пли только одними третьими вершинами
Определение 4 Если в цепа, соединяющей ориентированные тетраэдры
ABCD и A'B'C'D', число пар соседних ориентированных тетраэдров, имеющих
противоположный обход, четное, то ориентированные тетраэдры ABCD
и A'B'C'D' имеют одинаковую ориентацию; если же это число нечетное, то
ориентированные тетраэдры ABCD и A'B'C'D' имеют противоположную
ориентацию,
Теорема 2. Во всех цепях, соединяющих ориентированные тетраэдры ABCD
и A'B'C'D', число пар соседних ориентированных тетраэдров, имеющих
противоположный обход, или всегда четное, или всегда нечетное.
Эта теорема является следствием следующей.
Теорема 3. Пусть относительно общей декартовой системы координат
заданы, вершины
A(xv Ух, гх), В(х2, у2, 2а), С (х3, у3, г3), D (x4, t/4, г4);^
А'(х\, у\, г\), B'(x't, у'2, г'2), С'(х'3, у'3, г'9), D' ( х\ у\, г\)
двух ориентированных тетраэдров ABCD и A'B'C'D'. Для того чтобы эти
ориентированные тетраэдры имели одинаковую ориентацию, необходимо и
достаточно, чтобы определители
Л =
Ч У\ Ч
Ч У2 ?2
Ч У-i za
x4 У* г4
и Д' =
имели один и тот же знак.
Эта теорема доказывается на основании § 85 о расположении точек по
одну и по разные стороны от плоскости аналогично тому, как доказывается
теорема предыдущего пункта на основании теоремы § 62.
Из этой теоремы следует, что, переставляя буквы А, В, С, D всеми
двадцатью четырьмя способами, получим 24 ориентированных тетраэдра, из которых
12 имеют одинаковую ориентацию, а 12—им противоположную.
Следует также заметить, что два ориентированных тетраэдра, имиллиих
одинаковый обход имеют ч одинаковую ориентацию, если же они имеют
противоположный обход, онн имеют и противоположную ориентацию.
21s
644
ДОПОЛНЕНИЕ 1
Из доказанной теоремы вытекают следствия
Следствие 1. При преобразовании симметрии относительно плоскости
ориентации ориентированного тетраэдра ARCD меняется па противоположную
(для доказательства достаточно принять плоскость симметрии за плоскость
хОу прямоугольной системы коордичат кОц и воспользоваться георемой 3)
Следствие 2. При преобразовании симметрии относит льно прямой
ориентация ориентированного тетраэдра A BCD не меняется 'для
доказательства цвести декартову прямоугольную систему «оориинат приняв за ось Ог
данную прямую)
Следствие 3 При преобразовании симметрии относительно точки
ориентация ориентированного тетраэдра меняется
Следствие 4 Ориентация ориентированною тетраэдра не меняется
при переносе т е если
AA' = ~BB'=~CC' = DD',
то ориентированные тетраэдры ABCD и А'В'CD' имеют одинаковую ориентацию
Определение 5 Если в пространстве фиксирован ориентированный
тетраэдр
(базисный тетраэдр) то пространс пво ориентировано. Если
ориентированные тетраэдры ABCD и E1E2ESO глеют одинаковую
ориентацию, то ориентированный тетраэдр ABCD имеет положительную ориентацию,
а если ориентированные тетраэдры ABCD и Е-^Е^Е/) имеют противоположную
ориентацию, то тетраэдр ABCD имеет отрицательную ориентацию
Если в пространстве введена общая декартова система координат то его
обычно ориентируют ори итированным тетраэдром £хЕ2Е30, где О —начало
координат, а £,, £2, £< —единичные точки осей Ох Оу, Ог
Таким образом все декартовы спстечы юлрдинат в пространстве можмо
рязбить на два класса две системы принадлежат h одному ктассу, ести их
базисные тетраэдры имею! одинаковую ориентацию и к разным классам если
базисные тетрлэдры имеют противоположную ор 1ентаиию
Теорема 4 Ориентированный тетраэдр ABCD с вершинами
А (х, (/!, 2i) В (х2 у2 г?) С кх<, у3, г,), D (x4, yt, г4),
заданными относительно общей декартовой системы координат, имеет
положительную ориентацию, если определитель
Д =
X,
Ч
Ч
х4
Vi
У?
Уз
г/4
ч
ч
ч
г4
1
1
1
1
Х2
Vi—Уа Ч — Ч
У 2 — У4 г2 — г4
1/3 — 1/4 г3 —г.
X, Y, Z,
Л-2 У 2 ^2
X, Y, Z8
и отрицательную, если А < О (ХХ К3, Zj — координаты вектора DA,
Xit У2, Z2 — координаты вектора DB Х3, У3, 7.д — координаты лектора DC)
Доказательство '! ai. как
1 = {1, 0, 0} ОЯ2 = {0, 1, 0},
Н=^{0, 0,
ОРИЕНТАЦИЯ
645
Л' =
I О О
О 1 О
О О I
= 1 >0,
то утверждение теоремы следует из определения 5 и теоремы 3.
Определение 6. Рассмотрим две упорядоченные тройки некомпланарных
векторов а, Ь, с и а', Ь'', с'.
Отложим векторы а, Ь, с от произвольной точки D:
DA = a DB — b, DC = c,
а векторы а', Ь', с' от произвольной точки D'.
ЪТА' = а', D7B'=b', D7? ==<?'.
■Упорядоченные тройки некомпланарных векторов а, Ь, с и а\ Ь', с' имеют
одинаковую ориентацию, если ориентированные тетраэдры ABCD и A'B'C'D'
имеют одинаковою ориентацию.
Если же эти ориентированные тетраэдры ABCD и A'B'C'D' имеют
противоположную ориентацию, то упорядоченные тройки векторов а, Ь, с и
а', Ь', с' имеют противоположную ориентацию
Заметим, что выбор точки D (и D') произвольный В самом деле, если
векторы а, &, с отложены от точки Р
РА2 = а, РВ2=Ь, РС^ — с,
то тетраэдры ABCD и A2B2C2D2 получаются один из другого переносом
и потому имеют одинаковую ориентацию
Если в пространстве греден базис е,, ё?2, ег, го мы будем говорить, что
упорядоченная тройка нскомп::апарных ректоров а, о, с имеет положительную
ориентацию, если эта упорядоченная тройка и;«еет ориентацию, одинаковую
с базисом Если же упорядоченная тройка некомплапарпых векторов а, Ъ, с
и базис имеют противоположную ориентацию, то будеч говорить, что она иуеет
отрицательную ориентацию
Ясно, что упорядоченная тройка пекомплаиарпых векторов
/у V 71 h } У V 7 \. *• I У V 7 К
{1 1 II > ** — B 2 2f> ~ t3 3 Sj*
заданных своими координатами относительно общей декартовой системы
координат, имеет положительную ориентацию тогда и только тогда, когда
X V 7
Л, Y 1 {-!
An Кл L>n
Д =
X, Yj Z,
> о
Если Д < 0, то упорядоченная тройка а, &, с векторов имеет
отрицательную ориентацию.
Замечай и е. Данные определения ориентации плоской и и пространства
опираются лишь на аксиомы соединения и порядка Значит, данные опредечония
одинаковой или противоположной ориентации двух ориентированных
треугольников или двух ориентированных тетраэдров можно перенести, например, на
плоскость и пространство Лобачевского (или в абсолютную геометрию).
ДОПОЛНЕНИЕ II
МЕТРИЧЕСКАЯ ТЕОРИЯ ИНВАРИАНТОВ МНОГОЧЛЕНА
ВТОРОЙ СТЕПЕНИ ОТ ДВУХ И ТРЕХ ПЕРЕМЕННЫХ
ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОБЩЕЙ ДЕКАРТОВОЙ
СИСТЕМЫ КООРДИНАТ
1. Контр авариантные и ковариантные координаты
точки и вектора на плоскости
Пусть на плоскости введена общая декартова система координат хОу
с масштабными векторами elt е2. Введем следующие обозначения для
скалярных квадратов масштабных векторов и для самого скалярного произведения е&г
Совокупность этих чисел g^ будем называть метрическим тензором в
базисе еъ е2.
Наряду с системой хОу рассмотрим систему хг0уг с тем же началом
координат и такую, что ось Охх перпендикулярна оси Оу и образует с осью Ох
острый угол, а ось Оух перпендикулярна оси Ох и образует с осью Оу острый
угол, масштабные векторы е1 и ег осей Ох1 и Ог/j выберем такими, чтобы
скалярные произведения е± ега е2е2
были равны 1 Итак,
в в^ = 1 в о2 = 0 в в^ = 0 р. ^2 |
или короче
где 6*=1, если i=k, и 6(* = 0, если
i фк
Систему хг0у^ будем называть
взаимной к системе хОу (рис,
292) Очевидно, что системой,
взаимной для хг0уи будет исходная
система хОу,
Упорядоченные пары векторов ег, е? и е1, е2 называются взаимными
базисами
Совокупность скалярных произведений glk=ele>1 называется метрическим
конгранариантным тензором базиса е1, е%
Рассмотрим вектор а. Разложим его но векторам^, е2 и по векторам е', еЬ
Рис 292
Коэффициенты а1, а% называются контравариантными координатами
вектора a, a au а2"~к0вариантными координатами вектора а в базисе eit ea
МЕТРИЧЕСКАЯ ТЕОРИЯ ИНВАРИАНТОВ МНОГОЧЛЕНА 647
Рассмотрим два вектора о и Ь, разложим их по векторам в\, е2, а хакже
по векторам е1 и ег\
Составим скалярное произведение ab в четырех видах!
ab =
Мы видим, что удобнее всего выполнять скалярное умножение двух
векторов, если один вектор задан ковариапгпы.чи, а другой кошравари.штными
координатами
Установим связь коптраиариантны . координат а1, а- с ковариаптными
координатами av а2 одного и того же вектора a
Из соотношения
a = a>e, + a2e2 = ахех + а2ег
находим
a1 = «l
или
ai =
или
если условиться, что по индексу а, который один раз является нижним, а
другой раз —верхним, производится суммирование от 1 до 2.
Аналогично находим
Отметим еще формулы
al = aet и а{ = аеь
выражающие коптрапариантные и ковариантные координаты вектора а через
скалярные произведения этого вектора на базисные векторы в; и е1. Наряду d
понятием контравариаптпых и ковариантных координат вектора вводится
понятие контравариантных и ковариантных координат точки М, как координат
ее радиуса-вектора ОМ. Точку М вместе с ее коптравариантными
координатами обозначим М (х, у), а точку М вместе с ее ковариаптными координатами
М[х,у]. Таким образом, контраварнаптиые координаты точки М— это ее
общие декартовы координаты, а коварпацтные координаты точки /И — это
скалярные произведения ее радиуса-вектора ОМ па базисные векторы ех и е2.
Таким образом, если в уравнении прямой
заданной относительно общей декартовой системы координат, х и у
рассматривать как кхгатравариантные координаты точек, а А и В как ковариаитные
координаты вектора, то вектор п = [А,В] является вектором, нормальным к
данной прямой. Вектор и через векторы е1,^2 базиса, взаимного к базису eit e2,
выражается соотношением
n=Ae1Jt-Be2.
Разложим векторы ех и е2 по векторам е{ и е2:
a- A)
648 ДОПО1НЕНИР TT
Умножая скалярьо обе частт первого из этих соотношений на ех и е'г,
по "учим
и аналогично из второго соотношения
g21=«2> g22 = pY
Формулы A) принимают вид
S-g"ea ' B)
Годобным же образом выводится соотношение
«/=*„«" <3>
Умножая скалярно обе части соотношения B) на е^, получим
e'ek = g'aeaek, или g1* g*k=> blk D)
Из соотношения D) следует, что матрицы (g,-j) и (glk) обратны друг другу
так что
ё g ' к В ' g 8 '
где
Отмстим также, что соотношение D) —то же самое, что и следующее
равенстве Nio/кду матрицами (g,^) и (g'*):
2. Контравар ii антные и коварна нт и ые координаты
вектора и точки в пространстве
Вес сказанное выше Сез существенных изменений переносится на случай
трехмерного евклидова пространства! базис ег, е2, е3 вместе с фиксированной
точкой О пространства определяет обш^ю декартову систему координат.
Координаты вектора и точки в этой системе будем называть контравариант-
н ы м и.
Взаимной тройкой е1, е2, е3 к базису ех е? е3 называется базис,
определяемый условием
р р"_х*_ /0 если / Ф /г,
е'е -Ь'-\\ если - = /г
т. е вектор е] перпендикулярен векторам е5 и е3 и образует с вектором ел
остры? j гол модуль вектора е] определяется условием е]е1=1 и т. д
Векторы е1, е2, еъ через векторы ел еч ,ег выражаются соотношениями
3
Коитрав.)риантные координаты вектора а выражаются в випе
а1 = аеК
МЕТРИЧЕСКАЯ ТЕОРИЯ ИНВАРИАНТОВ МНОГОЧЛЕНА 649
Метрические тензоры (ковариаптные и коитраварнашньш] и базисе ах, е%,
es определяются соотношениями
Векторы в/ и е1 связаны соотношениями
e! = g'*ea, */ = £/»«*•
Ковариаптные координаты а,- вектора а с его контравариацтными
координатами а1 связаны аналогичными соотношениями
Матрицы (g;ft) и (glk) симметричны и обратны друг другу.
Скалярное произведение аЬ двух векторов может быть выражено в одном
из следующих видов;
(по а и Р суммирование от I до 3).
Контравариантными координатами точки М в общей декартовой системе
координат @, ех, е2, е3) называются коптравариаитные координаты ее радиуса-
вектора ОМ. Следовательно, это общие декартовы координаты ючки Л).
Ковариантными координатами точки М в общей декартовой системе
координат (О, elt e2, е3) называются ковариантные координаты ее радиуса-векюра
ОМ, т. е. координаты этого вектора в базисе el, е*, es.
Так, например, если в уравнении плоскости
заданной относительно общей декартовой системы координат, рассматривать
х, у, г как контравариантпые координаты точек, то А, В, С — ковариаптные
координаты вектора, нормального к этой плоскости.
3. Теория инвариантов уравнения линии второго
порядка
Пусть относительно общей декартовой системы координат линия eiuporo
порядка задана уравнением
апх2~\- la^xy -\- а^у'1 + 2 ахх + 2а.гу + а — Ъ. A)
Постав! м задачу найти каноническое уравнение и расположение этой
линии. Преобразуя данную систему координат в прямоугольную, снова получим
уравнение второй степени относительно х и у, а потому уравнение A)
определяет одну из линий уже известных нам восьми аффинных классов. Однако при
переходе от общей декартовой системы координат к прямоугольной, фупкшш,
которые рассматривались в § 142, уже не будут инвариантными, так как
переход от общей декартовой системы к прямоугольное Не является ортогональным
преобразованием. Таким образом, теория инвариантов, а вместе с тем и
вопрос о расположении линии, нуждается ь обобщении, к которому мы и пере-
X 'ДИМ
Определение. Метрическим инвариантом называется такая рациональная
функция 1 от коэффициентов уравнения A) и от компонент f>th метрического
тензора данной общей декартовой системы координат, которая имеет одно и
то же значение в двух любых таких системах:
1 (а,к, a,-, a, gik) = 1 (alk, a'{, a', g'ik).
650
ДОПОЛНЕНИЕ II
Teopefaa 1. Следующие функции являются метрическими инвариантами:
1
а2
а2
а2
§21 t
+
а
>22
|;
а22
л =
Доказательство. Рассмотрим наряду с данной системой координат хОу
другую систему координат х'О'у'. Формулы преобразования координат имеют вид
x = cnx' + cls,y' + clt у=сг1х'+с22у'-\-с2, B)
где cn, c2i, и с12, с22—координаты новых масштабных векторов ех и е2 в
начальной системе хОу
После преобразования B) уравнение A) перейдет в следующее!
апх'*+;>а'12х'у' + а\ 2(/'а+ 2а\х' +
причем, как было указано в § 142!
а' = 0,
а21 а22
=
ап а12
а21 а22
Сц с12
«Sftl C22
°11 а12 а1
а21 а22 а2
а, а, а
Сц
С21
Докажем еще соотношение
£22
§22
«И
A')
C)
D)
E)
В ~амом деле, так как ег —с^ех-\-с2Хе2,
то
21 022
И далее, умножая обе части этого равенства на определитель Det (c,-^), получим
£12
g22
CU C12
C21 C22
МЕТРИЧЕСКАЯ ТЕОРИЯ ИНВАРИАНТОВ МНОГОЧЛЕНА
651
или
или
е
е
в'}1
8з1
е
е
в
§
Iе 2
12
22
1 gn
S21 #22
8ll
8 21
1
£22
Си
с21
С11 С
С
с12
с22
12
22
2
Теперь из равенств C) —E) находим
«21 S22
а, а„ a
«11 «12
а21 а22
!l §22
<j2i а2г а2
ffi а2 а
Таким образом доказано, что /2 и /<;|—метрические инварианты.
Остается доказать инвариантность /^ Рассмотрим функцию
где X—произвольный параметр. При переходе от системы хОу к системе х'Оу'
с тем же началом координат эта функция перейдет в функцию
так как
Применяя уже доказанную инвариантность /2 к вспомогательной функции ф,
получим
а11~"^1! «12—^1
a9i—kgai а22— ^8з
6 I 1 *> _] 2
grf
21 S22
Приравнивая коэффициенты при л в первой степени, получим
Я11 й
а21 й
12
22
!
§11 §
§21 8
8
11 а12
ёз\ а22
,12
22
£21^22
652
Зчпч док азач> м,'[ чпи г> 7, тпосительчо преобразования обшей
декартовой системы координат r оГпцую декартову систему с тем же началом
Но так как в выражение длп /j входят лишь коэффициенты при х2, ху и #2.
которые не меняютсл при переносе, то /s является инвариантом переноса
З Ф / К / б
Замечание Функции /2,
виде:
/,=
где
а; а
s р р
можно записать в более компактном
а* а] а,
а\ а\ а2
В самом деле.
Уг —
gu Sn
ai2
«lag"
ffj flfo
Sll gl2J
!
a12
U2ote
а„ «г11
g
я
0
11
21
а2
«а
g22
0
0
0
1
«2
=
«2
а1
а2
а2
а,
о2
а
«is
ai a
г
2»
а,
а\
0
Й
а1
1
*>?2
1 Si
1 fll
I
lgi2
0
<
taS
- a^a
Теорема 2. Функция
gn
Й21
0
al2
a2?
ai
a\
°2
а
|g
0,
Q2
0,
I glS
1 Й2
I ?2
0
a2
является инвариантом такого преобразования общей декартовой системы
координат, при котором сохраняется начало координат Если же линия A)
распадается на две параллельные или совпадающие прямые, то К2 —инвариант
общего преобразования декартовой системы координат хОу в любую другую
х'О'у'.
Доказательство Рассмотрим функцию
Ф — %гг,
где ф — левая часть уравнения A), а г = х
МЕТРИЧЕСКАЯ ТЕОРИЯ ИНВАРИАНТОВ МНОГОЧЛЕНА
653
Имеем <р —
При переходе к системе х'Оу' с тем же началом получим
Применяя к функции ф — кг2 уже доказанную инвариантность К3, будем
иметь
tflj
0-21
— ktr
u
— ?"g21
a,
gn
Й21
«22 ~
a2
gl2
g22
ig15 a,
kgi2 a2
a
812
?22
и приравнивая коэффициенты при X в первой степени, получим
ёп ai2 ai
S21 2 j
О а„ a' i
822 а2
О а'
О
а! О а
Ь 1 1 *» 1 2
Й2) 'j2 2
gl2
£22
При переходе от системы хОу к прямоугольной х'Оу' с тем же началом
п' меняется. » прямоугольной системе координат Кг принимает вид
a,., a,
22 U2
и, как было доказано в § 142 в случае распадения линии на две
параллельные прямые Кч не меняется при переносе Значит, Ks имеет одно и то же
значение во нее общих декартовых системах координат
Замечание Функцию К2 можно записать в более компактном виде!
Теперь так же, как это сделано в § 143, доказываем, что
линия A) принадлежит к I, II или III группе, если соответственно
и что простейшие уравнения соответственно имеют вид
2 + 7f=
(I)
(H)
(III)
654 ДОПОЛНЕНИЕ II
где Кх и ка — корни характеристического уравнения
L1—^8и а12 — ^12 _-0.
S1 ^21 Я22 ^§22
4. Определение расположения линии
второго порядка
Если уравнение
Ф = апх2 + 2а12ху + а22у2 -f 2агх -f 2а2у -\- а = О
является уравнением центральной линии второго порядка,
заданной относительно вбщей декартовой системы координат, то
координаты центра находятся из системы
Рассмотрим линейное преобразование, которое точке М(х, у)
ставит в соответствие точку М' [апх-\- а12у, й^х-\-a2iy\
(координаты точки М даны в системе хОу, а координаты точки М' — во
взаимной системе л^Огд). Это преобразование / самосопряженное,
так как для любых двух векторов а = {1, т) и Ь = {1', т'}
выполняется соотношение
afb = b\a
В самом деле,
a[b=*\l, т } \аи1' +а12т', аг11'+амт'] =
= ЯцМ'+ах2 (Im' -\-1'm)-\-a2imm' =
=■{ V, т' \ \a-ill-\-a12m, ог,/ + а22т] — bfa
Значит, имеются два взаимно перпендикулярных собственных вектора
и у (будем считать их единичными):
где ?ч и Х2—собственные значения, соответствующие этим собственным век-
торям Соотношение fa = Xa (а — собственный вектор I) подробно запишется так;
(ап1 + апт) ег-\ (a2I/ + a2im) e2 = 'k(lel-\-me2)
Умножая скалярно обе части этого равенства один раз на ev другой раз
на е2, получим
aill-ra!i2m = k(gsll+g22m),
или
.}- a12_Xg]2) m=0,
(a2! — Xg2l) I + (a22 — Xg21) in = 0,
и так как I и in не равны пулю одновременно, то собственные значения Кх и
^.g должны удовлетворять уравнению
МЕТРИЧЕСКАЯ ТЕОРИЯ ИНВАРИАНТОВ МНОГОЧЛЕНА 6">5
или
.,2
= 0, B'>
i\-K а;
fli °2
или
к2 — 7^ + /, = 0 B")
Обратно, если ^—корень этого уравнения, то система A1 имеет ненулевое
решение /, т. Но из уравнений A) следует
т. е. 1еу-\-те2—собственный вектор преобразования [, а ^ —соответствующее
ему собственное значение.
Так как линейное преобразование f — симметричное, то оно имеет два
взаимно перпендикулярных собственных вектора, причем соответствующие им
собственные значения, т. е. корни уравнения B\ или B'), или B")
действительны.
Перейдем от данной системы координат хОу к прямоугольной х'Оу',
направив осп Ох' и Оу' по собственным единичным и взаимно
перпендикулярным векторам /, J преобразования f. Тогда, полагая г—хв\-\-уег, имеем
= (x'i+y'J) f, (x'i + У'Л = {x'i + у'Л (x'tl + y'ff) =
= (x'i + y'f) .x'kj -i- y'bj) = XlX'2 + X2(/'2,
Таким образом, если направить оси Ох' и Оу' по взаимно
перпендикулярным собственным векторам линейного самосопряженного преобразования f,
то уравнение линии второго порядка примет вид
^х'2 + кйу" + 2а\х + 2а^ + а-=0 C)
Далее, при помощи переноса осей это \равнение приводят к одному из
простейших уравнений (I), (II), (III).
Если линия центральная ()п Ф 0, к% Ф 0), то координаты векторов,
дающих направления ее новых асей О'Х и О'У', в каноническом уравнении A)
находятся из системы ,
координаты направляющего вектора оси О'Х найдем, полагая здесь к = кь
а координаты направляющего вектора оси O'Y найдем, полагая %=-к2.
Если линия является параболой, го координаты направляющего вектора
оси находят из системы
anl + a12m = 0, a21/ + a22'n=0 * E)
Вершину параболы можно найти так. Уравнение касательной к параболе,
заданной общим уравнением, имеет вид
{аих0 + апу0-\-ai) (х—х0) -f (а21х0 -\-а22у0 + a2) (у — у0) =0
Значит, Оц^о+ а,2Уо + а1 и a21x0 + a22y0+a2— ковариантные координаты
нормального к пей вектора. Значит, точка (х0, j/o) будет вершиной параболы
тогда и только тогда, когда
(ац*0 Н- а12у0 + aL) e1 + (a2i^o + ^22^0 + ) е* = / (lex -\- те2),
656
ДОПОЛНЕНИЕ II
где I, •?; —контравариантные координаты направл юшего чектора оси
(т. е. / = а1г, т = —аи, или / = а22, т = —ап)
Умножая скалярно обе части последнего соотношения одни раз на ev
другой раз па е2> получим
= ' (Sll' + SW)' (К\
..„_,-- . . * W
'о -j- а2 = t
Умножая обе части первого соотношения на /, обе части второго па т и
складывая, в силу соотношений E) будем и verb
откуда
l -|- а2т = t (gn/" + 2gV
<= aLl-\-a,m
Но точка (x0, y0) лежит па параболе, значит,
aux\ + 2a l2x0(/0 + a22(/ = + :
а = 0,
или
или
и для отыскания координат вершины остается решить линейную систему F),
G) (t уже определено).
Вектор, коллинеарный оси и направленный в сторону вогнутости
параболы, определяется так же, как и в § 150, если 11(а11-\-агт) < 0 (здесь / = а12,
т — -~ап, или / = а22, т = — а12), то вектор \ I, т) направлен в сторону
вогнутости параболы, а если
/l (Ol' + a2ff!) > 0>
то в сторону выпуклости
Случаи мнимых линии и случаи распадения линии на две прямые не
представляют интереса.
5. Поверхности второго порядка
Предполггая, что поверхность второго порядка задана относительно обшей
декартовой системы координат (с метрическим тензором gtl}) уравнением
рассуждениями, вполне аналогичными предыдущим, устанавливаем, что
следующие функции являются инвариантами преобразования общей декартовой
системы координат в другую:
ап а12 а13
а21 °£2 а23
«31 «32 «33
IS
Sll gi2 gisj ' "*
Й21 Й22 ^23J
g'il g$2 gsS!
°ll a12 «13 L
^1 «22 «23 ^2
a31 я32 азй а3
а, а2 a.s a
?u Ч12 «\з
г?21 Й22 <=M
gsi gs2 g3Z
■V.EI РИЧГ'ЖАН ТЕОРИЯ Ч Н ВЛРП ЛНТ'.В '-'• НОГОЧ.П ;.Н Л
657
/а =
§11 «12 °1S
§21 °22 «23
s#l ^32 ^33
Si
«fit
§11
§21
§3,
§22
I'g2
§.2
§S2
§32
«23
«33
§1S
§23
§3S
+
«21 «2? §23
§11 §12 °13
§21 §2P «28
§11 at2 §13
?31 'г32 §33
Ни
tl 23
«11 §12 §13
«21 §2? .§23
«П §32 §33
и что функция
§u
§21
§31
0
«12
a22
«2
«IS
«23
«33
«.■!
«1
«2
«3
a
4-
1
a
11 §12
«21 §22
1 §35
a, 0
§u §
aVi
«53
«Bo
°3
12 §
I §
a
«2
a3
a
13
4.
1
«11
<4i
1
171
«12
«22
a-.it
a2
§13
g23
§38
0
«1
«2
«3
a
является инвариантом преобразования общей декартовой системы в общую
цекартову для поверхностей III IV и V групп, а функция
§11 §12
§21 §22
§81 §32
«13
«2 3
«33
«3
a1
«2
«3
a
а
11
«21
«31
«1
§12 Я
§22 §
§32 §
0 0
§11 §12
§2
g
1 §22
П §82
13 «1
23 «2
33 «3
a
§13
§23
§33
§11
§21
§31
0
«12
«22
«32
a2
gis
§23
§33
0
«1
a2
a3
a
является инвариантом указанного общего преобразования для поверхностей,
распадающихся на пару параллельных плоскостей, или совпадающих '■
лоск остей.
Все эти инварианты и семиинварианты могут быть записаны и более
компактном виде!
/3 =
1 2
L 1
2 2
Й1
«1
fll
«1
fll
«3
«I
<
a\
a\
a
a
2 «2
3 «3
1 a2 a3 a
658
ДОПОЛНЕНИЕ II
а
а
а
1
1
1
2
1
1 =
а
2
а\ а2
а2 а
а\с
а1 а
-1-
а
i
1
а1
j_
а
а
<
а3
2
2
а
Ч
а
«2
а
2
я2
а2
<
а3
а
3
2
а3
а3
«3
а
а2
а3
а
где
Простейшие уравнения поверхностей I—V групп записывают так же, как
и в случае прямоугольной системы:
._*«_п A)
(И)
(HI)
(IV)
(V)
где Ях, Я2, ^з—корни характеристического уравнения
2S =0.
1 — /w?,i aJ2—Agj2 a13-
В случае центральных поверхностей (группа 1) координаты центра
наводят из системы
-га|2.1/ + a13z + a, =0,
a232 + a2 = 0, (8)
0
(для поверхностей III группы этими уравнениями задается прямая центров,
а для поверхности V группы —плоскость центров). Координаты
направляющих векторов осей канонической системы координат для центральных
поверхностей (/j ф 0) находят из системы
(9)
— Xgw) n = 0,
—Xg3i) m-f (a3S —J
куда вместо X надо подставить поочередно корни характеристического
уравнения
1 —V?.-a «32—
= 0,
или
(Ю)
(Ю')
МЕТРИЧЕСКАЯ ТЕОРИЯ ИНВАРИАНТОВ МНОГОЧЛЕНА Q59
В случае параболоидов координаты векторов, имеющих главное
направление (оси О'Х и O'Y о каноническом уравнении (II)], находят из системы (9),
куда надо подставлять вместо X отличные от нуля корни характеристического
уравнения.
Из системы
а211-\-а22т-\-а23п=0,
находят координаты I, m, n вектора, имеющего особое направление Если
при этом
Х1 (/a,-)-ma2-l- па3) < О,
то вектор {/, т, п\ направлен я сторону вогнутости сечения поверхности (II)
плоскостью Y = 0, если же
Кг (idi -{- та^-\- паь) > 0,
то в сторону выпуклости
Наконец, координаты х0, у0, г0 вершины [[араболоида находят из системы
^ A2)
о + аввг0 + а3 = / (gail
где Z, т, п находят из системы A1) Из системы A2) находим
t_
и вопрос сводится к решению линейной системы относительно х0, уй, г0.
Исследование расположения эллиптического, гиперболического и
параболического цилиндров и рассмотрение остальных аффинных классов
представляется читателю.
ДОПОЛНЕНИЕ III
ПЛОСКИЕ СЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА.
КРУГОВЫЕ СЕЧЕНИЯ. ОМБИЛИЧЕСКИЕ ТОЧЖИ
1, Приведение к каноническому виду
плоского сечения поверхности второго порядка
Теорема 1. Если относительно прямоугольной системы координат заданы:
1) поверхность второго порядка своим общим уравнением
ацХ'Ч-а22у2 + азн22 + ','м12ху + 2а, >tjz + '< а31гх + 2а,*-]- 2а2у + '2ааг-\-а = 0, A)
2) плоскость своим нормальным уравнением:
2 = 1 B)
и если плоскость B) пересекает поверхность A) по линии второго порядка*,
то простейшее уравнение линии второго порядка, по которой плоскость B)
пересекает поверхность A), пишется в одном из следующих видов:
^ = 0 в случае /2 ф О,
где
± '■> V — ~V=0 в случа? /2 = 0. К3ф0,
К
-^=0 в случае /2=0, Л'з = 0, /j ^ 0,
«12 «13 А
а22 а23 В
а32 аЗЗ С
В С 0
ап а12 А
а21 а2% В
А В 0
'11 "!3
Л
Л С 0
а22 а23 В
SCO
C)
D)
* Случаи, когда плоскость B) пересекает поверхность A) по одной
прямой или когда плоскость B) входит в состав поверхности B), мы, таким
образом, исключаем.
ПЛОСКИЕ И КРУГОВЫЕ СЕЧЕНИЯ
К я— —
«и о-,: a\i °i A
ап о22 а28 а2 В
«si о32 я3з °в c
а] a? as a D
А В С О О
а21
«1
0,5
2
а2
В
а2
а
D
А
В
D
0
I
°31
al
А
«13
°33
«з
С
«1
а.6
а
п
А
С
D
0
а2 а3 а Л1
В С D С
661
E)
F)
а к} и Я2 — корни характеристического уравнения
X2—У,Л + У2 = 0
Доказательство ПреоОразуеч данную прямоугольную систему
координат в прямоугольную так, чтобы плоскость Ах-}■ By + Сг = О стала
плоскостью х-'Оу'. Тогда одна из формул преобразования координат будет
иметь следующий вид:
Уравнение A) в новой системе координат примет вид
W '' '' 'ix'y1+<2a'ssy'z' + 2a'slz'x' -f
П)
Линия пересечения поверхности A) плоскостью B) в ноной системе
координат выражается уравнениями
По условию теоремы это сечение является линией второго порядка, т. е.
среди чисел air a12, a22 хотя бы одно отлично от нуля. Поэтому
простейшее уравнение последней линии в плоскости г' = — D пишется в виде
К.
^-4 = Q. если /2 =
/к'
±Y = Q,
если /2=0,
662
ДОПОЛНЕНИЕ III
и в виде
причем
-4=0, если /2=0, К'3=0, l\*=c
a\-a'l3D
я„ — а„„Р о»
«'■-«'„0
а Xj и Х2 — корни характеристического уравнения
?/-/>'+ /2=0.
Рассмотрим уравнение
После указанного преобразования координатной системы это уравнение
примет следующий вид:
аих'2 -га22У'2 + a'33z'2 + 2a'12x'i/ +2а'23у'г' + 2а'31г'х' +2г' =0.
Сравнивая инвариант /<4 и семиинвариант К3 для двух последних
уравнений поверхности, получим
/. = ■
«11
ап
«31
А
«12
2
«32
В
«13
«23
«33
С
Л
В
с
0
«11 «12 «13 0
«2. «22 «23 0
«3! «32 «33 '
0 0 10
=/.
\ап а13 Л \а22 а23
— I a si ая* С
А С 0
— I «32 3 С
\ в с о
«11
«21
0
«12
«22
0
0
0
0
—
«11
«3,
0
а
а
13
33
1
0
1
0
—
222 «23 0
а32 «33 !
О 1 О
*11
Теперь рассмотрим уравнение
2 -;- я22у2 4- а33г2 -^ 2al2xy + 2a23yz + 2о31гх +
поверхности второго порядка в четырехмерном пространстве.
Произведем то же преобразование поворота осей Ox, Oy, Oz (сохраняя
ось Ot, т. е. полагая < = Г); тогда получим новое уравнение в виде
'2-f 2/
0.
ПЛОСКИЕ И КРУГОВЫЕ СЕЧЕНИЯ
663
Сравнивая определители пятого порядка, составленные из всех
коэффициентов двух последних уравнений, получим *
аи ai2 au ax A
а21 а22 а28 а2 ^
а31 а82 «33 аЗ С
аг аг at a D
А В С D О
a,—a,.D an—an,D a., —a,
•*13
11
О
«31 «82 «33 «3 '
«3 « D
1 D 0
аг О
fl; о
«; i
a—Da. 0
D 0
13
12
О
«з-«зз°
I
a.
D
Умножая элементы третьего столбца на D и вычитая из последнего столбца,
получим детерминант, равный к\- Если сечение представляет собой две
параллельные прямые, то, сравнивая семиинвариант К4 для двух последних
уравнений поверхности в четырехмерном пространстве (не выписаны слагаемые,
* Если над переменными многочлена второй степени Vajjj^j-1-2 "V а,-л:,- + я
производится линейное преобразование ^,- = 2j6(-^+6,-, то получается
функция вида "^la*kxixk-{-2 2 а* ** +а*, причем коэффициенты преобразованного
многочлена с коэффициентами начального многочлена связаны соотношениями
ai a*
Отсюда следует, что
b{
aik ai
ak a
0 1
где blk = l
Эти положения следуют из аналогичной теоремы для квадратичной формы
(см. подстрочное примечание на стр. 347).
ееи
ДОПОЛНЕНИЕ III
равные иулю), получим
К2=-
А В
а„
Oj A
п% В
a D
D О
Л
Я13
азз
аз
с
а1
as
а
D
А
С
D
0
^22 ^28 ^2 ^
а2 а3 a D
8 С D О
О О
°1
а
D
О
D
и
—
азз
0
а1
«3
0
Z)
0
1
D
О
0
О D О
Первый детерминант прапой части равен нулю в силу того, чго
а,, а.
#22
= 0
(мы предполагаем, что линия пересечения есть пара параллельных прямых).
Два остадьннх детерминанта преобразуются к виду!
а это выражение равно
2. Расположение в пространстве плоского сечения
поверхности второго порядка
Покажем, как определить расположение в пространстве плоского сечения
поверхности второго порядка в случае, если сечение является
нераспадающейся линией второго порядка
Случай I. Линия сечения является действительной центральной
нераспадающейся линией второго порядка (эллипс или гипербола). Пусть
(*о. Уч <а) — центр линии сечения.
При выводе уравнения диаметральной плоскости поверхности второго
порядка было показано что необходимым и достаточным условием того, чтобы
точка (х0, (/„, 20) была серединой хорды, имеющей направление вектора
\1, т, п), является равенство
A)
п = 0.
Но так как (хОч г/0, ?0)—иентр сечения, то для направляющих векторов
^1, т, п) хорд поверхностей, лежащих в плоскости, проходящих через эту
точку, соотьошение A) выполняется.
Кроме того, из условия компланарности некюра \1, т, п\ и плоскости
имеем
B)
Зто рааенство удовлетворяется при тех же значениях I, т, п, при кото
рых выполняется равенство A), поэтому соответствующие коэффициенты пр.
ПЛОСКИЕ И КРУГОВЫЕ ССЧЕНИЯ 665
/, т, п в ypai нениях A» и B) пропорциональны
а21х0-{ 9S!!//,,-| а21г0-{ а, = 1В, , C)
«siXo + o-jsVo+ajsZo-l- а3 = ^с-
Так как центр (лт0, г/0, г0() сечения лежит р еекушей плоскости,
Аха-\ 8t,0+O(,+./ =0. • D)
Итак, координаты *о>?А)>го иентря сечения, если линия сечения
центральная, находятся из системы C), D)
Для определения расположения сечения о случае, если оно эллипс или
гипербола, остается определить координаты аекгоров, имеющих главное
направление
Пусть
единичные векторы, коллинеарные соответственно осям (УХ и O'Y симметрии
линии сечения, причем в системе ХО'У пиния сечения выражается уравнением
%lX*+'k2Y2-\- JS± =0,
'а
где ^i и Х2 — корни харгктеристического уравнения
Введем в пространстве сисгему координат O'XYZ, принимая оси
симметрии линии сечения за оси координат О'X и O'Y, а за ось О'Z нормам, к
плоскости линии Единичные векторы осеП (УХ, O'Y, O'Z обозначим так:
Ei = \l1,ml,n1\, Е2 = \12,т^п^\ E-i = \A,B,C\.
Формулы преобразования координат имеют вид;
где х0, у0, г0— координаты центра О' линии сечения.
В указанной системе координат группа старших членов уравнения
поверхности имеет вид
причем матрица этой квадратичной формы выражается через матрицу
квадратичной формы
соотношением
О р,\ //, т, л,\ /аи ап aVi\ //, /2 А
О Я2 Во ) = ( k Щ % ^21 а25 °->3 I ( ml m2 В \.
f>2 у/ \А 1 С/ \a,,j a32 aS3/ ^«j i2 С
Тйк как матрица
«1 т2 В
п, пг С
ортогональная то обратная к пей совпадает с транспонированной Поэтому,
666 ДОПОЛНЕНИЕ III
умножая обе части последнего матричного равенства слева на матрицу
I tU\ tn% В I,
Vfi, fi2 c/
получим
Л»п a12 ova flx k A\ flx k A\ /К О Pi
a22 a2 l( «, m2 Bj=( mj m2 fl j( О
a32 O33/ \fi1 n2 C/ \ttj п2 С/ ЧЙ] B2
Перемножая матрицы и сравнивая соответствующие элементы
произведений, получим систему
(ап — К])(, + Qj2fni 4 Ois^j — A[5j=O,
а кроме того,
/!/, + ««! + Cn,=0.
отсюда найдем координаты вектора Еь имеющего направление оси
симметрии О'Х
Аналогично из уравнений
(ап — A.2)'2 + ai2«2+ai3«2— ЛВ2 = 0,
Oal'j + (a22 — ^2) «2 5P °
найдем координаты вектора £2, имеющего направление оси симметрии O'Y.
Впрочем, можно найти Е2, заметив, что £'2 = [£'3iS'1]; координаты £, найдены,
а £а равно {А, В, С\
Случай II Линия сечения —парабола Принимая за новое начало
координат вершину О' параболы, за ось О'Х—касательную к вершине, за ось
O'Y — ось симметрии, а за ось O'Z — нормаль к плоскости сечения, приведем
группу старших членов уравнения поверхности к виду
Z + 2p\,KZ 4- \Z2
и предыдущими рассуждениями установим, что координаты , вектора
Ei — {llt mi, n^, коллинеарного касательной к параболе в ее вершине,
определяются из системы
(an — ^i)
2 — ^1) m14-a23n1 —SP,=O,
+ (a33 — ?ч) nt — СВХ = 0,
где Яа т^ 0, а следовательно, уравнение плоскости, сопряженной направлению
касательной к параболе в ее вершине,
+ 33{3) = 0
вместе с уравнением плоскости сечения
Л*4-Вг/4-Cz 4-D=0
определиют ось параболы.
ПЛОСКИЕ И КРУГОВЫЕ СЕЧЕНИЯ 667
Вершину параболы найдем, разрешая систему трех уравилшй.
+ 2aYx -f 2a2y -f- 2a3z -\- a = 0-
Координаты вектора £12 = |/2, m2, n2}, коллинеарного оси параболы, проще
всего определить из соотношения Ё~г — [ЕЛЕХ] или из приведенной выше
системы уравнений при % = 0.
Если преобразовать данную прямоугольную систему координат Oxyz в
прямоугольную систему Ox'y'z' с тем же началом, направив оси Ох', Оу', Ог'
соответственно по векторам Еу, Е2, Еъ, то уравнение A) примет вид
так как при г'=0 это уравнение получается из канонического уравнения
сечения (парабола) в результате преобразования переноса.
Уравнения линии сечения:
a'llx'2+2a'1x'+2a';iy'+a = 0, г' = 0.
Здесь а11=Х15*0, а так как обе системы координат Oxyz и Ox'y'z'
имеют одно и то же начало, то а2—рЕ2, где p = {alt a2, а3[. Отсюда следует, что
если рЕ2 и %х имеют разные знаки, то вектор Е2 направлен в сторону
вогнутости параболы, а если одинаковые, то в сторону выпуклости.
3. Круговые сечения поверхностей второго
порядка
1. Эллипсоид!
Пусть
Ax+By + Cz + D=.O ~ B)
нормальное уравнение плоскости (т. е. Л2 + В2 + С2=1). Исходя из формул
C) — E) п. 1 настоящего дополнения находим
А2 В2 , С2
Для того чтобы сечение эллипсоида A) плоскостью B) было окружностью,
необходимо и достаточно, чтобы
/2_4/2 = 0, /х/Сз < 0.
Первое условие принимает вид
668 дополнение пг
или, так как Л2-+ S2-hС2= 1, го
или
и полагая, что а> b > с, находим
А__ с \ а*—Ь*
С ~ a Yb'1—^
Условие /Х/С, <0 принимает вид
Так как Л2 + С2=1, то
с2 (a2-ft2) а2 (б2-с2)
б2 (а2—с2) ' ' б2 (а2—с2)'
и, значит,
(а2_с2) '
ИЛИ
£
£
«■<£•
ИЛИ
Итак, плоскости, пересекающие эллипсоид A) по окружности,
выражаются урапнениям!!
, у L П ■? _1 > /7/4 Г)
У а2-с* Y
где | X, | < 1. Вместе с тем этими уравнениями выражаются плоскости веек
круговых сечений эллипсоида A).
I!. Эллиптический параболоид
^ + --22 = 0, р>0, 9>0.
Находим
ПЛОСКИЕ И КРУГОВЫЕ СЕЧЕНИЯ 669
К3 = — BDC
Условия
здесь принимают вид
/дне*
V Р Q J РЯ
2DC— В2</- А°-р <0: (Р)
заменяя С2 на 1 — Л2—б2, преобразуем соотношение (а) к виду
откуда
Лб = 0, (Л2—!
Если В = 0, то в предложении р> а приходив к противоречию: Л"
о — р
---—— < 0, значит, остается (в случае р > q) положить Л=0; гогда В2
--—- , следовательно,
Р
Р
Так как Л2+В2-|-С2= 1, А=0, то
Изменением знака левой части уравнения
можно всегда добиться того, что С
Взяв
из условия liKs < 0> т- е- условия
2DC—б2-, <0,
находим
Значит, плоскости кругопых сечений (притом всех круговых сечений)
выражаются уравнениями
где ^ — любое число, меньшее 1.
III. Однополостный гиперболоид:
670 ДОПОЛНЕНИЕ III
Находим
C2c2-/!2a2- S262).
Условие /j— 4/2=0 принимает вид
4 (C%2 — Л2а2
или
откуда (а > 6)
следовательно,
Условие /j/Сз < 0 дает
что выполняется при любом значении D.
Итак, плоскости
ила
где ^i— любое действительное число, пересекают однополостпьгй гиперболоид
по окружностям.
Вместе с тем указанными уравнениями выражаются плоскости всех
круговых сечений рассматриваемой поверхности.
IV. Днуполостный гиперболоид:
х2 u2 z2
_ 4-" — 4-1 —П
В этом случае выкладки несущественно опичаются от тех, которые
проведены при рассмотрении круговых сечений однополостного гиперболоида.
ПЛОСКИН И КРУГОВЫЕ СЕЧР.НИЯ 671
Однако условие /1Кз<0 здесь приме! вид
~ — D^<Q, т.е. |D|>^.
Плоскости всех круговых сечений двуполостного гиперболоида
у Ь^-Гс2 у b
где X—любое действительное число, по абсолютной величине большее 1.
4. Омбилические точки
Если плоскость параллельна плоскости кругового сечения эллипсоида,
эллиптического параболоида или двуполостного гиперболоида и имеет с
поверхностью только одну общую точку, то эта точка называется омбилической.
Таким образом, омбилическую точку одной из указанных выше поверхностей
можно определить как круговое сечение по окружности нулевого радиуса.
Так как условие, определяющее такое сечение, имеет вид
/2 > о, /* —4/2 = 0, К3 — 0
и так как координаты центра симметрии сечения определяются из системы
уравнений C), D) п. 2 настоящего дополнения, то
1) для эллипсоида
хг у2 г2
а2 Ь2 с2
координаты омбилических точек находятся из двух систем уравнений!
JL—ЯУ а2~~&2 *
о / —— *■*
== аУЬ-с
=zr- x ± —— z ±ac — 0,
где перед радикалами надо брать одновременно либо оба верхних, либо оба
нижних знака. Разрешая эти системы, находим четыре омбилические точки
трехосного эллипсоида:
2) для эллиптического параболоида 1- — = 2г, р > q >0, указанная
выше cvicieMa примет вид
-=0.
672
ДОПОППРННР Ш
Отсюда находим две омбилические точки:
(»•
p—q
2
3) дли двуполостного гиперболоида сказанная система принимает вид
4 = о,
г ± Ьг = О,
где, как и в случае эллипсоида, перед радикалами берутся либо
одновременно верхние, либо одновременно нижние знаки.
Решая эти системы, найдем четыре омбилические точки двуполостною
гиперболоида:
ДОПОЛНЕНИЕ IT
ПРОЕКТИВНЫЕ КООР;Ц1НА ГУ. ТЕОРЕМЫ ДЕЗАРГА,
ПАСКАЛЯ Н БРЛАИШОНА. А1ЛШ0.ТЯРНЫЙ ТРЕУГОЛЬНИК.
АВТОНО.1ЯРНЫЙ ТЕТРАЭДР
1. Проективные координаты на проективной
плоскости
Реализуем проективную плоскость в виде связки S прямых и плоскостей
трехмерного евклидова пространства (вторая модель',. Напомним, что прямые
св5 зкн являются «точками).' проективной плоскости, а плоскости связки
«прямыми» (рис. 293).
Выделим в связке S четыре
прямые Oj, о2, о,!, е, из которых никакие
три не принадлежат одной
плоскости. Возьмем па прямой е
произвольную точку, отличную от S, и
проведем через нее три плоскости, одна
Рис. 293
Рис 294
из которых параллельна прямым ot и о2, другая параллельна прямым о5 и о3,
а третья параллетьна о3 и oj (рис. 294)
Пусть проведенные плоскости пересекают прямые о,, о2, о3 соответственно
в точках Тг, 7'2, Т,
Пусть m — произвольная прямая связки Возьмем на ней произвольную
точку М, отличную от S. Тогда координаты *,, х2, jc3 точки М в общей
декартовой системе координат с началом .S и масштабными отрезками STt, S7'2, STa
называются проективными координатами «точчи» ш. Ясно, что если «точка» пг
имеет координаты xv x2, х3, то ее координатами будут также три числа kxv
kx2, kxit где k — любое действительное число, не равное нулю. Кроме того,
отметим, что если на прямой выбрать другую точку (для построения
вспомогательной обшей декартовой системы координат), то масштабные векторы новой
22 п. С. Моденов
674
ДОПОЛНЕНИЕ IV
общей декартовой системы координат будут пропорциональны векторам STV
ST2, S7\ и, значит, проективные координаты «точки» т образуют тот же
класс пропорциональных троек чисел д:1:х2:х3.
«Точки» olt о2, о3 называются фундаментальными, «точка» е — е д и-
н и ч I! о й; они имеют следующие проективные координаты: ох A:0:0), о2 @:1:0),
о3 @:0:1), еA:1:1).
Таким образом, проективная система координат на проективной плоскости
(в случае реализации ее в виде второй модели) определена, если па ней
выбрать произвольно четыре «точки» ov o2, о3, е, по три не принадлежащие
одной «прямой», и приписать им соответственно следующие координаты:
1:0:0, 0:1:0, 0:0:1, 1:1:1.
Уравнение произвольной плоскости связки (в указанной выше общей
декартовой системе координат) имеет вид
+ «2*2 + " А = 0
и, обратно, всякое однородное уравнение первой степени относительно xlt х2,
Xj является уравнением плоскости связки.
Таким образом, всякая «прямая» проективной плоскости выражается
однородным уравнением перпой степени и обратно.
Класс и1:и2:и3 пропорциональных троек чисел из коэффициентов в
уравнении «прямой» называют проективными координатами этой «прямой».
«Точку» т вместе с ео проективными координатами будем обозначать так:
т (х^.Хъ'Хь), а «прямую» Л таи.: 'k[u,i:u2:u3]
Покажем теперь, как вводятся проективные координаты точки в случае,
если проективная плоп-ость рассматривается как евклидова, пополненная
несобственными точками.
Возьмем в пространстве произвольную плоскость я и дополним ее до
проект кпиой гпогкости II Выбере-' в евклидовом пространстве произвольную
точку S, не лежащую на плоскости я, и
рассмотрим связку прямых и плоскостей с
центром S (рис 295). Поставим в соответствие
каждой прямой т связки точку М, в которой
прямая т пересекает проективную плоскость
11, если прямая т параллельна евклидовой
плоскости я, то точкой ее пересечения с
плоскостью II будем считать т\ несобственную
точку плоскости П, которая присоединена к
прямым плоскости я, параллельным прямой т.
Построенное соответствие между
множеством «точек» проективной плоскости,
реализованной в виде связки с центром S B-я
модель), и множеством точек проективной
плоскости, реализованной пополненной
несобственными точками евклидовой плоскости A-я
модель), называется перспективным.
Перспективное соответствие взаимно однозначно, и
при этом любым трем точкам, принадлежащим одной прямой (в первой
модели), оно станит в соответствие 1ри точки, также принадлежащие одной прямой
(во второй модели)
Внедем проективную систему коордкнат во второй модели проективной
плоскости. Тогда каждая «точка» будет иметь проективные координаты. Пусть
М — произвольная точка плоскости П, а т — «точка», ей соотпстсшующая в
указанной перспективе. Будем считать, что точка М имеет те же координаты
x1:x2'xt, какие имеет «точка» т, и называть их проективными координатами
точки М.
ТЕОРЕМЫ ДЕЗЛР1 А, П\СКАЛЯ И БРИЛНШОМЛ
67.1
Пусть прямые ох, с2> о3, е пересекают плоскость П в точках Olt О2, O;J, E.
Точки Ov О2, О3 называются фундаментальными, или базисными, точками
проективной системы координат на плоскости П, а точка £ — единичной точкой.
Если на плоскости П выбрать произвольно четыре точки О1, О2> О3, Е, из
которых никакие три не принадлежат одной прямой, то любая точка М
плоскости П получит вполне определенные проективные координаты. В самом деле,
выберем две произвольные точки S и S', не лежащие на плоскости д. Прямые
S0v SO2, SO:I, SE можно перевести в прямые S'OV S'O2, S'OS, S'E таким
аффинным преобразованием пространства, при котором все точки плоскости л
неподвижны, а точка S переходит в S' (косое сжатие к плоскости я).
При этом преобразовании прямая SM перейдет в прямую S'M. Отсюда
следует, что точка М плоскости П имеет одни и те же проективные
координаты, если реализовать проективную плоскость любой из связок S и S'■ Мы
видим, что проективные координаты точки М на плоскости П не зависят от
выбора центра S вспомогательной связки (при помощи которой на плоскости
П вводятся проективные координаты точки), если только на плоскости П
фиксированы фундаментальные точки 0^ О2, О3 и единичная точка Е,
которым приписаны соответственно координаты
A:0:0), @:1:0), @:0:1), A:1:1).
Предположим теперь, что на плоскости а введена общая декартова
система координат X0Y, а кроме того, на плоскости П введена проективная
система координат. Будем обозначать проективные координаты точки М через
х^:х2:х3, а однородные через x:y:z (так что для собственных точек плоскости
II отношения — и — являются общими декартовыми координатами в системе
XOY). Установим формулы, связывающие проективные координаты с
однородными.
Пусть на проективной плоскости П заданы базисные точки Оъ О2, О3 и
единичная точка Е своими однородными координатами (никакие три точки из
точек О1( О2, 03, и Е не принадлежат одной прямой):
Ох (au:a21 :a3i). O2 (a12:a22:aS2), O3 (а13:а23:азя), £(е1:еа:е3).
Пусть х:у\г — однородные координаты точки М плоскости 11, а х1:х2:х3—
проективные координаты той же точки М. Однородные координаты точки М
можно рассматривать как
проективные, если ввести их на плоскости
П при помощи общей декартовой
системы координат оси Sx' и Sy',
которой параллельны плоскости л.
(пополнением которой
несобственными точками получается
проективная плоскость II),а единичная прямая
SE' проходит через единичную точку
£' той системы координат XOY, при
помощи которой на плоскости П
вводятся однородные координаты
(рис. 296)
Таким образом, х, у, г (см. § 98)
являются линейными однородными Рис 296
функциями от xv x2, хг, причем
определитель из коэффициентов при хъ х2, хя в этих формулах отличен от
нуля. Докажем, что эти формулы можно записать в виде
* = allP 1*1 + а1
A)
22*
676
ДОПОЛНЕНИЕ IV
где а,£ имеют j казенный выше геометрический смысл (однородные координаты
точек Oi, Ог, О3), а р1э р2, Рз~ отличные от нуля чис.-а, которые мы сейчас
определив. В Cr<vo>! деле, из формул A) следхет, что однородные координаты
точки О], имеющей проективные координаты хх — \, х2 = 0, *3 = 0, будут
(«n Pi)'(Q2i Pi)"!<7.5i Pi) = au'a2i'an>
однородные координаты точки О„ проективные координаты которой % —О,
Jfa=l. Хз^0. бУДУт
наконец, однородные координаты точки 03
в соответствии с поставленной задачей. Что касается чисел plf p2, р3, то их
надо выбрать так, чтобы однородные координаты единичной точки Е,
проективные координаты которой 1:1:1, били равны e1:e2:ej, т. е
аи01
«21Р1
a:nPi
-Ь «2зРз=«2.
+ «.«Рз — ез-
Эта система имеет v притом только одно решение plt p2, р3, так как
Det (а,-^) Ф 0 (ючки Ov 02, 0^ не принадлежат одной нряуой). Это решение
Pi' Рг> Рз состоит из трех чисел, не равных нулю, гак как точка Е не лежит
на одной прямой с любыми друмя из трех точек Olt 02, Os.
Но так как общая декартова система координат определяется (с точностью
до выбора на единичной прямой единичной точки) выбором трех прямых olt
о2, о3 связки, не принадлежащих одной пря.гой и единичной прямой е (той же
связки), не компланарной ни с какими днумя из трех прямых olt o2, os, то
формулами (I) определяется преобразование одной из систем координат SOlt
SOz, SOV SE и Sx', Sy', Sz', SE' в другую
Из соотношений A) находим выражения для проективных координат
точки через однородные:
B)
Так как л;, у, г через хь х2, х6 вырал<аются линейными однородными
соотношениями с определителем, отличным от нуля, то прямая на проективной
плоскости в чроемивных координатам выражае1ся однородным уравнением
X
У
z
е,
Ч
е>
«12
°22
«32
«12
а22
а32
«13
«23
«33
«1.!
«2Й
a,s
Ч
«и
«21
«31
ап
«21
«31
X
У
г
Sl
е2
е3
«13
«23
«83
3
«23
«Ч!
. «3
«11
«21
«31
«11
«21
2
а22
«82
«12
«22
«3-
X
У
Й1
е2
а линия второго порядка на проективной плоскости выражается уравнением
второй степени относительно проективных координат:
«н*1 + Й22*2 + «аз*! + 2ai2XiX2 + 2а23х2л:з + 2a31«3«i = 0.
Теорема 1 § 202 имеет место н в том случае, когда точки заданы
проективными координатами.
Определение неособой точки линии второго i оря..ка 6e.s ичмененпя даеюя
и для того случая, когда лимия задача в проективных i оордипатах Не
меняется уравнение касательной к линии второго порядка, уравнение поляры
ТЕОРЕМЫ ДЕЗ.АРГА, ПЛСКЛЛЯ И БРИАИШОНЛ
677
точки относительно данной липни второго порядка, заданной уравнением в
проективных коордипаох, и т. д. .
Покажем, как строится точка М но ее проективным координатам в
первой модели проективной плоскости !1. Предполагая, что на плоскости П вве-
Рнс. 29?
дена проективная система координат (Oj, О2, О3, Е), заметим, что прямые
МО у, МОг, М0-й пересекаются с прямыми О2ОЯ, O-fly, О^О« соотнетственно в
точках /VI] @:г3:л;3), Мг(х\:й:хя), Ms(xl:x2:0),
Пусть £\ @:1:1), £2 A:0:1), lsA :1:0)-~ точки пересечения прямых £ОХ>
ЕО2, EOj соответстве!'ло с
прямыми О.^О3, OaO^Ofiz.
На рис. 297 и '298
изображены прямые Oj, o2, o3, e, elt e2, е3,
т, ти тг, т3, соответствующие
точкам О1; О2, Os, Е, £,, £2> Е3,
М, Мх, М%, М3 в
перспективном соответствии со связкой.
Прямую т1 легко построить, знуя
прямые о.2, о3, в плоскости
которых лежит эта прямая, и зная
«единичный луч» этой плоскости.
Для этого надо в системе
координат с началом S, осями о2, os и
единичной точкой, лежащей па
прямой e-i (отличной от S),
построить точку n^Xj, хь). Прямая
SjX] и буд:т прямой тх. Так как
(по доказанному выше) это
построение не зависит от выбора
центра связки, то в первой модели точку N[\ можно построить, выбирая общую
декартову систему координат с началом О', не лежащим на прямой Е,х020.^
оси si и 0'0„ н О'Оч и единичной точкой Ег ,'рис 299). Ча рис 300 построены
точки Mi @:1:2), Л42 ,— 1:0-2), М3{—\:\:п) и точка М (—1: | :^.
„
678
ДОПОЛНЕНИЬ. IV
Замечание. Предположим, чю проективная плоскость il реализована в
виде первой модели и что все точки О1? О2, 03, Е собственные Заметим, что,
приравнивая нулю числители формул B), выражающих проективные
координаты хъ х2, х~ точки /И через ее однородные координаты, мы получим
уравнеОО OO 00 З
2
ния прямых О2О3,
р др р у ур
и 0у02 в однородных координатах х, у, г.
ЗнаменатеB)
ли же упомянутых формул B) являются результатами подстановок однородных
координат единичной точки Е в левые части уравнений сторон О2О3, 0о0у, О{О^
базисного треугольника О^О^О^. Значит, |х,|, |хг|, \хг\ пропорциональны рассто-
0, Нг)
Рис 299
яниям dlt d2, ds от точки М ,,о сторон базисного треугольника, причем
коэффициентами пропорциональности служат расстояния ftj, k2, k3 от единичной
точки Е до сторон базисного треугольника:
а что касаетс;. знака хг, ю в формулах B) буд:т хг > 0, если точки Ej и М
лежат по одну сторону от прямой О2О?>, и х1<0, если —по разные. Аналогично
определяются знаки х2 н хя в формулах B). Выбором единичной точки можно
добиться различных интерпретаций Так, если Е — центр окружности,
вписанной в Д Oj_O2O,4 то l^], \x2\, \х3\ пропорциональны расстояниям от точки М до
сторон базисного треугольника, а знаки Х\, х2, х3 выбираются, как указано
Г5ыше.
Если точка Е совпадает с точкой пересечения медиан базисного
треугольника, то
Ху: хг: х% = МВС: А1С*А: /иТй;
такая система координат называется барицентрической. Специальные
проективные системы координат широко применялись в геометрии треугольника (а в
пространстве — и геометрии тетраэдра). Координаты точек на плоскости
называли при этом трилинейными (в пространстве —тетраэдрическими)
2. Автополярный треугольник
Пусть на проективном плоскости задана нераспадающаяся линия С нторо
го порядка.
Возьмем прои.-шо-тьпую точку Ох, не лежащую на линии С, и построим
поляру точки О, относительно линии С. Эта поляра не пройдет через точку Oi
Возьмем па этой поляре точку 02, не лежащую m линии С, и построим ее
поляру. Пусть O.j — точка пересечения поляр точек Ох и 02; тогда точка 03
будет полюсом прямой ОхОг. Примем точки Оь 02, Оа за базисные точки
проективной системы координат. Треугольник ОхОгОь обладает тем свойством, что
ТЕОРЕМЫ ДЕЗАРГЛ, ПАСКАЛЯ И ВРИАНПЮНА
679
каждая его вершина является полюсом противоположно"! стороны (рис. 301).
Такой треугольник называется ащополярным относительно линии второго
порядка С
Примем автополярный треугольвпк OiO2Oj линии С за базисный
треугольник проективной системы координат и пусть
= 0
аих\
2а23х2х3 -•-
A)
урлвпение линии С в этой системе
координат. Уравнение поляры точки
Oi A:0:0) имеет вид
и эквивалентно уравнению прямой О2О3,
т. е. уравнению xl = 0. Отсюда следует,
что аи = аи — 0. Аналогично
доказывается, что а2Я — 0 Итак, уравнение
линии С имеет вид
<Р =
х; -1- ai:t V* =0,
B)
Рис. 301
где ап ф 0, а2» ф 0, аяя Ф 0. Обратно,
для липни, заданной уравнением B),
при условии ап ф 0, ап ф 0, а;и ф 0,
каждая точка Oi A:0:0), О2 @:1:0),
О3 @".0:1) является полюсом прямой,
проходящей через две другие точки.
Таким образом, для того чтобы уравнение нераспадающейся линии второго
порядка в проективных координатах не содержало членов с произведениями
координат, необходимо и достаточно, чтобы базисный треугольник OiO2O3
проективной системы координат был автополярным.
Преобразуем проективную систему координат (О^^Е), сохраняя базисные
точки Oi, O2, О3 и принимая в качестве новой единичной точки любую из
четырех точек: Е' (± ]/" | ап \: ± ]/ | а22 |: ± V |а83 |) (набор знаков любой). Тогда
формулы преобразования системы координат будут иметь вид
*i = ± V\an
и, значит, уравнение B) примет вид
=0,
C)
B')
где е,- равны +L или —1. Если г,- все одного знака, то уравнение B') может
быть переписано в виде
v-2 J V2 i V1 r\ i л\
это мнимая нераспадающаяся линия второго порядка.
Если же линия B) — действительная овальная линия второго порядка, то,
считая аи > 0, а22 > 0, ass < 0, заключаем, что уравнение B) при
преобразовании C) системы координат принимает вид
-х3 =0.
E)
680
ДОПОЛНЕНИЕ !V
В этом случае фA, 0, 0) = аи>0, ф @, 1, 0) = а22>0, ф (О, О, l) = aw<0,
а так как **
аи О О
Д = О а„ О
О О а33
го для точек Oj и 02 имеем фД < 0, а для точки О3 фД > 0. Значит, для дей-
ствите;и ной овальной линии второго порядка вершина О3 автополярпого тре-
\го:ч,иика является внутренней точкой линии E), а вершины О1 и Оа—внеш-
Рис 302
Рис 203
ними точка11 и. Проведем из точек О1 и О2 касательные к линии E), Они
пересечется п четырех тс. лах Е Ft о стрический смысл выбора новой
единичной точки £ (формулы C)) ..аключаете/' н том, что за новую единичную точку Е
берстег любая из точек П (рис 302)
3 Теоремы Дезарга, Паскаля и Бриан шона
Теорема 1 (Дезарга), Если прямые А А', ВВ', СС, соединяющие
соответствен/ые вершины двух треугольников ABC и А'В'С, проходят через одну
точку О, то точки Р, Q и R пересечения соответствующих сторон ВС и В'С,
С А и СМ'( АВ и А'В' .ежат на одной прямой и обратно (рис 303)
Доказательство Введем на плоскости проективную систему коорди»
нат принимая точки Л, 8 С за базисные, а О — за единичную;
0A:1:1) /1A:0:0) В @:1:0), С@:0:1)
Тогда гички А', В', С имеют координаты
Л' (A 4-Х.): 1:1), В'A:A + Ц): 1), С A • 1 A + v)).
Попт ч АВ ВС и С А имеют координаты
ЛВ [0:0:1 Ь SC[l:0:0] СЛ |0:1:0],
а прямые А'В', В'С' и СМ':
А'В' [\1-.'К:(~-К—\х.
В'С [(-у —n-vu
С A' |v:(-X-v-X
ТЕОРЕМЫ ДЕЗАР1 Л, ПАСКА 1Я И БРИАИШОНА
631
Точки Р, Q, Я пересечения ВС и Н'С, СА и С А', АВ и А'В' будуп
Р@:-~ ц.-v), <?(A,fOi—v), Я(А,»-ц;0)
Так как
0 -1х v
к 0 -v
X -ц О
= 0,
то точки Р, Q, /? лежат на одной прямой Обратная теорема следует из
доказанной по малому принципу днойственности (она может быть доказана также
аналогично проведенному доказательству прямой теоремы),
Теорема 2. (Паскаля) Точки пересечения протиеипо южных сторон
шестиугольника, вписанного о действительную нераспадающуюся линию второго
порядка, лежат на одной прямой
Доказательство. Пусть Alt /12, А-й, At, Аъ, Лв—шесть произвольных
точек, лежащих па действительной нераспадающейся линии второго порядка.
Примем точки Av A2, Aa за вершины базисного треугольника!
Л! A:0:0), А2 @:1.0), А3 @:0:1),
а точку
за единичную;
Пусть п этой системе проективных координат точки Л$ и А„ имеют
координаты
A3(a:b:c), As(a':b':c').
Тогда уравнение линии второго порядка, проходящей через точки Аг, А2,
Л3. <44> Аъ (см. § 210), имеет вид
c(a — b) x^i + a (b — с) х2х-А-\-Ь (с—a) x^x^ — 0.
Так как эта линия проходит через точку Л6 (a'-.b''.с'), го
с (a — b) a'b' + a(b — c) b'c' -|- b (с— а) с'а' = 0.
Теперь найдем координаты сторон шестиугольника.
Сторона Л^г-' [0:0:1]
Сторона Л2Л3: [1:0:0].
Сторона
или
Сторона
или
Сторона
43Л
Л4Л
— 6
Л5Л
rfc')
4
11:
41
):(а
:(са
1?
—
1
&
—
1
1
1:01
1
с
с):(Ь
-а
■')
1 0
0 0
I I
1 1
с а
1 1
a b
-а)\
;(аЬ'
—
аЩ
и, наконец, сторона Л0Л!3
[О-.е':— (/].
Зная координаты прямых
их пересечения:
и А4А6, находим точку Р
682
ДОПОЛНЕНИЕ IV
Зная координаты прямых А*А% и Л^Ае„ находим точку Q их пересечения:
Q@:— (а// — а'Ь):(а'с~ ас')).
Наконец, зная координаты прямых Л3Л4и ЛвЛ,, находим координаты точки
R их пересечения:
Далее,
— (а—с) с-—Ь О
О —{ab' — а'Ь) а'с — ас'
V Ь' с '
в силу соотношения A), значит, точки Р, Q, R
лежат на одной прямой (ркс. 30J)
Рис 304
■ Рис. 305
Аналогично доказываются следующие теоремы (часто называемые частными
случаями теоремы Паскаля)
Теорема 3. Пусть Л,, Л2, Ая, А.„ Л-, — пять произвольных точек, лежащих
на действительной нераспадающейся линии второго порядка, I—касатегьная к
этой линии в точке А1 Тогда точки
пересечения прямых
I и АЯАЛ,
Л,/42 и АХЛЪ,
А2А3 и АгАъ
лежат на одной прямой (рис. 305).
Теорема 4. Пусть Л,, Д2> А3,
А>,—четыре произвольные точки,
лежащие на действительной
нераспадающейся линии второго порядка, /,,
h< '.). 1\—касательные к этой линии,
проведенные соответственно в точках
Л], Л2, Л3, Л4. Тогда четыре точки
пересечения прямых
АхАг и A3Ait
А2Аз и A-iAlt
1г и lit
1х и /3
лежат на одной прямой (рис. 306).
Рис 306
ТЕОРЕМЫ ДЕЗЛРГЛ, ПАСКАЛЯ И 1>РИАПШОН\
683
Теорема 5. Пусть Ль Л2, А3— три произвольные точка действительной
нераспадающейся линии второго порядка, a lx, l2, 13—касательные к этой
линии, проведенные к ней в этих точках. Тогда точки пересечения прямых
лежат на одной прямой (рис. 307).
Теорема 6 (Брнаншона). Прямые, соединяющие противоположные вершины
шестиугольника, олисанного около действительной невырождающейся линии
второго порядка, проходят через одну точку (рис. 308).
Доказательство. Пусть точки
касания сторон описанного
шестиугольника будут /И,, М2, Мл, Л1.„ Мъ, Мв.
Обозначим стороны вписанного шести-
'|-\ „/ | \ угольника
МйМг
Рис. 307
соответственно через fA, /2, /3, gt, g2, gs. Вершины Ft F2, F3, Glr G2, G3
шестиугольника, описанного около линии второго порядка, будут полюсами сторон
Л> /г> /з> 8г> Й2> Вз- На основании свойств поляр и полюсов прямая FtGi будет
полюсом точки (/ь ^|), прямая F2Gz—полюсом точки (/2, g2) и прямая F:lGs—
полюсом точки (/3, g--.). Так как точки (flt gt), (/2, g2) и (/3, g:l) лежат на одной
прямой, то прямые Ffi^, F2G2, F3G-j проходят через одну точку (полюс этой
прямой).
Теорему Врнаишопа можно доказать и аналитически, исходя, например, из
следующего уравнения овальной линии:
Частные случаи теоремы Брианшона:
1. Пусть A1A2A:!AiA5 — пятиугольник, описанный около действительной
нераспадающейся линии второго порядка, и Ав-—точка прикосновения
прямой А\АЪ к этой линии; тогда прямые A1A,i, A2A^, А3Аъ проходят через одну
точку (рис 309)
2. Пусть AiAzA-jAi — четырехугольник, описанный окою действительной
нераспадающейся линии второго порядка, а Л5, Л& Л7, Л8 — точки
прикосновения сторон Л,Л2, АгА3, Л3Л4, Л.,Л1- Тогда четыре прямые АХА3, A%AV АьАт, АвА9
проходят через одну точку (рис. 310).
68 i
ДОПОЛШ-ЛЖЬ IV
Рис 309
Рис 310
3. Пусть А,А2А.Л—треугольник, описанный около действительной
нераспадающейся линии второго порядка
Рис 311
точки прикосновения сторон
/1И», А2Л3, ASAX.
Тогда прямые АХАЪ> А2Ав, A3At
проходят через одну точку (рис 311).
Эти три положения могут быть
доказаны непосредственно
(аналогично приведенному выше
доказательству теоремы Паскаля) или выведены
из частных случаев теоремы Паскаля
с использованием сгойсти поляр и
полюсов (гак, как была выше
доказана теорема Брианшопа).
4. Проективные
координаты в проективном
пространстве
Введение проективных координат
точки (и прямой) на проективной
плоскости мы дали, исходя из второй
модели проективной плоскости И
здесь, конечно, можно было бы
следовать тому же пути, вводя в
рассмотрение четырехмерное евклидово
пространство. Однако ввиду
отсутствия геометрической наглядности
такого построения мы выберем другой
путь, по аналогии с формулами A),
которые были получены в п.1 этого
ТЕОРЕМЫ ДЕЗАРГЛ, ПАСКАЛЯ И БРИЛПШОНА
685
дополнения и которые устанавливали связь однородных координат точки с ее
проективными координатами
Именно назовем проективной системой координат (О^О^О^ьЕ) в
проективном пространстве совокупность пяти точек Oj, 0£, 03, 04, Е, из которых никакие
четыре не принадлежат одной плоскости. Точки 0\, 0г, 03, О4 будем называть
базисными, а точку Е— единичной. Тетраэдр OiO.JJ.iPn будем называть базисным.
Внедем в проективном пространстве общую декартову систему координат Охуг
и пусть в этой системе координат базисные точки и единичная точка
проективной системы координат имеют координаты Oi(Qn:a2i:«3i:a4i)> C(ai2:«22:«32:«42)'
03(ап:а23:аяя:ак), 0А{аи:а2^.ат:а^) и £(е, :ег:е3:е4).
Пусть М — произвольная точка проективного пространства, а </, '.Уг'-Уз'-У^ —
ее однородные координаты (в системе Охуг). Назовем проективными
координатами точки М четыре числа хи х2, х-г, х.г (а также любую четверку чисел
kxlt kx2, /«j, tixt, где к— любое число, не равное 0), определяемые из
соотношений
yiiiPii + i2p22 i
У 2 = «21pl*l+ «2Sp2*2 + «2
4. I
[
J
A)
где рх, р2, р3, р4 определяются из системы уравнений
al?p2+
°22Р2+
B)
В силу того, что точки Ov О2, О3, О4 не принадлежат одной плоскости,
i(ik)^0, значит, эта система имеет н притом только одно решение pj, рг,
р8> р4. Все числа рх, р2, р3, Р4> образующие это решение, отличны от нуля в
силу того, что точка £ не лежит в одной плоскости ни с одной из трех точек
из числа четырех базисных.
Из соотношений A) v B) следует, что проективные координаты xlt xit x3, xx
через однородные выражаются соотношениями
Уг
Уз
Ч*
«1
е2
е-з
е.
«12
2
«32
«42
а 12
«32
«42
аи
«83
«48
а13
а23
«3S
043
«14
«24
«84
а и
024
0.34
«14
«11
«21
а.п
«41
«11
«21
«41
{/1
Уг
Уз
?У4
Й1
г2
е8
е4
«15
Й23
«S3
«43
Ois
«23
«33
«43
«14
«21
«34
«44
«14
«24
«31
«44
IQ1)
«21
0,1
«41
«11
«21
«31
«41
«12
«22
0.32
Й42
«12
«22
«32
«42
г/i
</2
Ув
У4
«!
е2
«з
«4
«14
«24
«34
«44
«14
«24
«34
«44
х. —
«D
Q21
«31
«41
«И
«21
«31
«41
«12
«22
«32
«42
«12
«22
«32
«42
«13
«23
а3ь
«13
«13
«2Э
«33
«4Й
fl
г/г
Уз
г/4
*1
«2
е4
Из этих же формул следует, что проективные координаты базисных точек
02, 03, 04 и единичной точки Е проективной системы координат соответег-
bfc6 ДОПОЛНЕНИЕ IV
вон но гаковы!
С\ A:0:0.0),
О2 @:1:0:0),
О8 @:0:1:0),
О4 @:0:0:1),
£■A:1:1:1)
Рели все точки Оь О2, О3, О4, £ —собственные, то проективные
координаты *, х2, хд, х4 точки М пропорциональны произведениям
Mi. Мг. Мз> М«
расстояний ku k2, k3, fe4 от единичной точки Е до граней
OsAA, OiOaO*. О!О2О4, С^О-А
базисного тетраэдра, на расстояния dt, d2, ds, di от точки М соответственно
до тех же граней
Этим расстояниям приписывается знак: ki и dl — одного знака, если
точки О, я М лежат по одну сторону от грани O2O3Ot, n разного знака, если
точки Ог и М лежат по разные стороны от плоскости О2О3О^ (аналогично
приписываются знаки k2 и d2 ki и ds k4 и d.t) Выбором точки Е получаются
различные проективные системы координат относительно базисного тетраэдра.
Однородная система координат теперь сама может быть рассматриваема
как проективная Базисными точками однородной системы координат являются
несобственные точки осей коорлинат и начало координат; точкой Е будет
единичная гочка Е общей декартоной системы координат Покажем, какой
геометрический смысл имеют проективные координаты точки М. Рассмотрим две
плоскости, проходящие через прямую ОЛО^ и каждую из точек
M1(x1:xi:xB\xi) и £A:1:1:1).
Эти плоскости пересекают прямую OXOZ в точках
£и A:1:0:0) и М12 (х^.х^.О-.О)
Рассмотрим четыре точки
Ох A«0:0:0), О2 @:1:0:0), £i2 и М12
Координаты точек £12 и М12 через координаты точек Ох и Оа выражаются
соотношениями
1=а-1+Р-0,
и, далее (дл.-. координат точки М12):
где к=х1 и (х = д;2 Значит, сложное отношение
(О102£12/И12)=^н т д.,
т е отношение проек!ивных координат точки имеет чисто геометрический смысл.
Отсюда следует важный вывод: проективные координаты точки, лежащей
в проективном пространстве, вполне определяются заданием проективной систе-
ТЕОРЕМЫ ДЕЗЛРГЛ. ПАСКАЛЯ И ПРИАНШОНА
6S7
мы координат (ОхО^О^О^Е) (и не зависят от выбора той вспомогательной
общей декартовой системы координат, при помощи которой проективные
координаты определялись как линейные однородные функции однородных)
Вместе с тем из полученного соотношения
= — вытекает гсо-
2
метрический способ построения точки в проективном пространстве по ее
проективным координатам: «роим точку Е12, в которой плоскость ОАО±Е Пересе-
(иг)
Ри< 312
кает прямую ОгО2. Пусть S12 —произвольная точка, не лежащая на прямой 0,9а.
Проводим прямые Oj_S]2, O2S1S, и £"i2S12 На прямой El2Sl2 берем
произвольную точку, ситичную от точки Si2, и принимаем ее за единичную точку общей
декартовой системы координат с началом координат в точке Sl2 и осями
координат Sl2Oi и 5i202 [5 этой системе координат строим точку (xj, х<г) Тогда
прямая, проходящая через эту точку и точку 512, пересечет прямую 0\0г в
точке Мц Аналогично строим точки M3i, M2i, ,Й41 Точка М (х1:хг:ха:х4) является
точкой пересечения прямых МпМы и Mi3Miv
688 ДОПОЛНЕНИЕ IV
На рис 312 построена точка М (! :'2:4:'2) Отметим также, что х1:х^:хл —
проективные координаты проекции Л14 io"\h Л1 па плоскость О^О2О3 из точкн04,
если за бтзнсные точки принять coot ueic гленно 0L, O2, О., а за единичную
точку принять проекцию единичной точки £A:1:1:1) из точки О4 на
плоскость OjO2O3.
Аналогичный геометрический смысл имеют отношения х^.х^.х^ и т. д.
5. Автополяр и ы и тетраэдр
Рассмотрим певырождающуюся поверхность i торого порядка. Возьмем
произвольную точку Oj, не лежащую на рассматриваемой порерхности и
построим для нее : полярную плоскость <Bj ото ителыю данной поверхности.
В плоскости сох возьмем произвольную точку 02, не лощащую на данной
поверхности; ее полярная плоскость ш2 пройдет через точку О, На прямой, по
которой пересекаются плоскости м, и о>2, возьмем произвольную точку 03, не
лежащую на дайной поверхности, ее полярная плоскость го3 пройде! и через
точку О1; и через точку 02 Пу^ть, наконец, Ол— точка пересечения плоскостей
сох, ш2, со3. Тогда 04 — полюс плоскости Ofl^D.,
Тетраэдр OiO.fi.fin обладает тем свойством, что кьждая его грань является
полярной плоскостью противоположной вершины.
Такой тетраэдр называется антополярныч относительно данной говерх-
ности второго порядка.
Для того чтобы уравнение невырождающейся поверхности второго порядка
имело вид
ап х\ + а^х\ + а33 х\ + а„ х\ = О, (I)
необходимо и достаточно, чтобы базисный тетрлэдр О^^О^^ проективной
системы координат был антополярным. Это докаливается аналогично
соответствующей теореме для линий второю порядка (п 2 настоящего дополнения)
Сохраняя и качестве базисного тетраэдра антополярньш тетрлэдр
относительно поверхности второго порядка и принимая за новую единичную точку
любую из точек;
Е'{±У'Ы-±}ГЫ:±^^-±^\^\), B)
приведем уравнение A) к виду
^ | 83.t|-fe4x' = 0, где |е,| = 1 C)
Если все е,- одного знака, получаем мнимую поверхность. Если три из
коэффициентов в,- одного знака, а четвертый имеет противоположный чнпк, то
получаем действительную овальную поверхность второго порядка:
Если два из е,-равны +1, а два —1, то получаем тороидальную поверхность!
<p=x\i-xl — xl — xl=a E)
Выбор единичной точки для овальных и тороидальных поверхностей
второго порядка имеет следующий геометрический смысл
Если базисный тетраэдр 0^0./^ действительной невырождающейся
поверхности является автополярным, то уравнение поверхности имеет вид
«hi*? + а^х\ + a33xl + п1Мх\ = 0 F)
Будем считать, что в случае опа.г|ыюн поверхность
«и > 0. «22 > °. а» > °> аи < °
ТЕОРЕМЫ ДЕЗАРГА, ПАСКАЛЯ И БРИАНШОНА f,89
(тогда и только тогда точки Olt О2, Оа являются внешними точками
поверхности, а О4—внутренней), а в случае тороидальной поверхности
ап > 0, а22 > 0, а83 < 0, аи < 0.
В случае овальной действительной поверхности ребра OiOtl 020i, OBOi
пересекают поверхность F), каждое в двух действительных точках. Пусть Е14, £24,
£3]—точки пересечения прямых 0^0^, О2ОА и 0,0$ с овачыюй поверхностью
(из указанных двух точек пересечения берем по одной на каждой прямой ОХО^,
O2Ot, О3О±). Плоскости 020лЕц, О^Е^, OiOaESt имеют и притом только одну
общую точку £'. Примем се за единичную точку проективной системы
координат (OjOjOfiiE'). Пусть в этой системе координат уравнение F) имеет вид
Ьцх[ + &22х2' + bssXg + Ькхх\ = 0. ^ )
Точки Еи. £24, ES4 B системе (OiO2O3O4£') имеют координаты
Еи A:0:0:1) Ем @:1:0:1), £34 @:0:1:1),
и так как они лежат на поверхности G), то
и уравнение G) приводится к виду
©братно, для овальной поверхности (8), заданной уравнением вида (8),
базисный тетраэдр О1О2О8О4 —автополярный, а точка £ —точка пересечения
плоскостей OZO3EU, Q3OiE2i, ОхО^Ещ, где Еи, £24, EJt — соответственно точки
пересечения с поверхностью прямых 0i04, O^O^ ОЯО^.
Если поверхность F)—тороидальная (и ап > 0, azi > 0, а3з < 0, аи < 0),
то ребра OjO.1, 020$ и, например, Ох0з пересекают поверхность F) каждая в
двух действительных и различных точках. Выбирая соответственно по одной
из них Еи, £24 и Е31, примем за единичную точку Е' точку пересечения
плоскостей
O2OSEU, O&Eu, ОАЯц •
Гогда в системе (О^О^О^Е1) точки £14) E2i, £31 имеют координаты
£14 A:0:0:1), £24 @:1:0:1), £31 A:0:1:0),
а уравнение поверхности F) примет вид G). Но так как точки £14, Е24, £31
лежат на поверхности G), то
и уравнение (8) приводится к виду
/2 ,! ,1 ,!
х1 + х2 — х3 - *4 =0.
Заметим, что единичная точка лежит на поверхности. Обратно, уравнение (8)
является уравнением тороидальной поверхности в проективной системе
координат (OiO2O3O4£'), для которой базисный тетраэдр О^цО-зО^ является
автополярным, а единичная точка £ лежит на поверхности и является точкой
пересечения плоскостей OjjO3£14, Os^i, £24. О^О4Е13, где £14, £24, £13 — точки
пересечения прямых 0^^ О2Ой и Oj.O3 с поверхностью.
ОГЛАВЛЕНИЕ
Пргднсловне 3
Глава 1
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПРЯМОЙ
§ 1. Направленные отрезки 5
§ 2. Ось Координата направленного отрезка 5
§ 3. Ось координат. Координата точки 6
§ 4. Теорема Шаля. Координата направленного отрезка, заданного
двумя точками декартовой оси координат. Расстояние между двумя
точками, лежащими на оси координат 7
§ 5. Деление направленного отрезка в данном отношении 8
§ 6. Преобразование системы координат па прямой 10
§ 7. Векторы 10'
Глава II
ПРОСТЕЙШИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА
ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
I. Координаты точки и вектора на плоскости и в пространстве 15
§ 8. Параллельное проектирование 15
§ 9. Общая декартова и декартова прямоугольная системы координат
на плоскости 17
§ 10. Общая декартова и декартова прямоугольная системы координат
в пространстве 18
§ 11. Координаты вектора на плоскости и в пространстве 21
II. Расстояние между двумя точками, деление направленного отрезка
в данном отношении, площадь треугольника, объем тетраэдра ... 25
§ 12. Расстояние между двумя точками на плоскости и в простраистге 25
§ 13. Деление направленного отрезка в данном отношении 28
§ 14 Ориентированный треугольник. Ориентированная плоскость. Пло 25
щадь треугольника Ю
§ 15. Ориентированный тетраэдр. Ориентированное пространство
Объем тетраэдра 38
§ 16 Углы 43
1 Определение угла 43
2 Ориентированный угол. Его величина. Равенство, сумма и
разность величин ориентированных углов 43
3. Угол между двумя осями. Угол от одной оси до другой
и его величина 45
4. Углы ме;;сду двумя прямыми. Угол от одно:"] прямой до
другой и его величина 46
ОГЛАВЛЕНИЕ 691
§ 17. Теорема Шаля для ориентированных углов 48
III. Полярная система координат на плоскости и в пространстве .... 50
§ 18. Полярная система координат на плоскости 50
§ 19. Полярная система координат в пространстве. Полярные и
сферические координаты 52
§ 20, Задачи к главе II 54
1. Задачи с решениями 54
2. Задачи для самостоятельного решения 58
Глава III
ЛИНИИ, ПОВЕРХНОСТИ И ИХ УРАВНЕНИЯ
I. Линия и ее уравнения 61
§ 21. О понятии линии и ее уравнениях 61
§ 22. Примеры составления уравнений линии 62
П. Поверхности и линии в пространстве 69
§ 23. Поверхность и ее уравнение 69
§ 24. Примеры составления уравнений поверхностей 70
§ 25. Цилиндрические и конические поверхности 74
1. Цилиндрические поверхности 74
2. Конические поверхности 75
§ 26. Поверхности вращения 77
§ 27. Линия в пространстве и ее уравнения 80
§ 28. Примеры уравнений линий в пространстве 81
§ 29. Задачи к главе III для самостоятельного решения 83
Глава IV
ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
§ 30. Сумма векторов 90
§ 31. Разность векторов 92
§ 32. Произведение числа па вектор 93
§ 33. Теоремы о проекциях векторов 95
§ 34. Теоремы о координатах векторов 96
§ 35. Сумма, разность н произведение числа па вектор в координатах 97
§ 36. Линейная зависимость векторов Линейная комбинация векторов.
Коллинеарность векторов. Компланарность векторов 99
§ 37. Базис и координаты вектора 104
§ 38. Скалярное произведение двух векторов 107
§ 39, Выражение скалярного произведения в координатах 109
§ 40. Угол от одного вектора до другого на ориентированной
плоскости 112
§ 41. Объем ориентированного параллелепипеда 114
§ 42. Объем ориентированного параллелепипеда в координатах. Объем
тетраэдра , 119
§ 43. Векторное произведение ' 121
§ 44. Смешанное произведение трех векторов 123
§ 45. Координаты векторного произведения . 123
§ 46 Свойства векторного произведения , 124
§ 47. Двойное векторное произведение . 125
§ 48. Площадь параллелограмма и треугольника в пространстве . . . 125
§ 49. Примеры и задачи к главе IV 126
1. Задачи с решениями ' 126
2. Задачи для самостоятельного решения , . . 136
699 ОГЛАВЛЕНИИ
Глава V
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
§ 50 Уравнение прямой, проходящей через данную точку в данном
направлении 138
^ 51 Общее уравнение прямой 139
§ 52. Нанрарляющий вектор прямой 139
§ 53 Частные случаи расположения прямой относительно системы
координат 141
§ 54. Параметрические уравнения прямой . . 141
§ 55. Уравнение прямой, проходящей через две точки 141'
§ 56. Уравнение прямой в отрезках 143
§ 57. Угловой коэффициент прямой 143
§ 58. Уравнение прямой с угловым коэффициентом 144
§ 59. Взаимное расположение двух прямых 144
§ 60. Пучок прямых 146
§ 61. Взаимное расположение трех прямых 149
§ 62. Геометрический смысл неравенства первой степени с двумя
неизвестными 150
§ 63. Расстояние от точки до прямой 152
§ 64. Нормальное уравнение прямой 153
§ 65 Угол между двумя прямыми, условие перпендикулярности
двух прямых 153
§ 66. Угол от одной прямой до другой в ориентированной плоскости 156
§ 67. Примеры и задачи к главе V 158
1. Задачи с решениями 158
2. Задачи для самостоятельного решения •«. 168
Глава VI
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
§ 68. Уравнение плоскости, проходящей через данную точку
компланарно двум неколлинеарным вектора?-) , 170
§ 69. Общее уравнение плоскости 170
§ 70. Условие компланарности вектора и плоскости 173
§ 71. Частные случаи расположения плоскости относительно системы
координат 173
§ 72. Параметрические уравнения плоскости 174
§ 73. Уравнение плоскости, проходящей через две точки компланарно
данному вектору 175
§ 74. Уравнение плоскости, проходящей через три точки, не
принадлежащие одной прямой 175
§ 75. Уравнение плоскости в отрезках 176
§ 76. Взаимное расположение двух плоскостей 176
§ 77. Уравнения прямой, проходящей через данную точку в данном
направлении Параметрические уравнения прямой 179
§ 78. Уравнения прямой, проходящей через две точки 180
§ 79. Взаимное расположение двух прямых 180
§ 80. Взаимное расположение прямой и плоскости 181
§ 81. Прямая как линия пересечения двух плоскостей 182
§ 82. Пучок плоскостей 183
§ 83. Взаимное расположение трех плоскостей , 186
§ 84. Связка плоскостей 187
§ 85. Геометрический смысл неравенства первой степени с тремя
неизвестными 192
§ 86. Расстояние от точки до плоскости 193
§ 87. Нормальное уравнение плоскости 193
ОГЛАВЛЕНИЕ 593
§ 88 Угол между двумя плоскостями. Условие перпендикулярности
двух плоскостей 196
§ 89. Угол между двумя прямыми Условие перпендикулярности двух
прямых 197
§ 90. Угол между прямой и плоскостью. Условие
перпендикулярности прямой и плоскости 198
§ 91. Уравнения перпендикуляра, опущенного из данной точки на
данную прямую 199
§ 92. Уравнения общего перпендикуляра к двум неколлинеарным
прямым 199
§ 93. Расстояние от точки до прямой в пространстве 201
§ 94. Кратчайшее расстояние между двумя прямыми 201
§ 95. Примеры и задачи к главе VI 203
1. Задачи с решениями 203
2. Задачи для самостоятельного решения 210
Глава VII
ПРЕОБРАЗОВАНИЕ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ НА
ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
§ 96. Перенос декартовой системы координат 214
§ 97. Преобразование общей декартовой системы координат на
плоскости 216
§ 98. Преобразование общей декартовой системы координат в
пространстве 218
§ 99. Преобразование декартовой прямоугольной системы координат
на плоскости 219
1. Переход от одной декартовой прямоугольной системы
координат на плоскости к другой декартовой прямоугольной
системе с той же ориентацией и с тем же началом координат 219
2. Переход от одной декартовой прямоугольной системы
координат на плоскости к другой прямоугольной системе с
противоположной ориентацией и с тем же началом координат 221
3. Общее преобразование одной декартовой прямоугольной
системы координат на плоскости в другую прямоугольную
систему ... 222
§ 100. Переход от одной декартовой прямоугольной системы
координат к другой прямоугольной системе в пространстве 223
§ 101. Углы Эйлера 227
Глава VIII
ЛИНИИ ВТОРОГО ПОРЯДКА, ЗАДАННЫЕ КАНОНИЧЕСКИМИ
УРАВНЕНИЯМИ
§ 102. Эллипс и его каноническое уравнение 230
§ 103. Исследование формы эллипса 233
§ 104. Директрисы эллипса 235
§ 105, Эллипс как образ окружности при равномерном сжатии к ее
диаметру 238
§ 106. Параметрические уравнения эллипса 240
§ 107. Построение эллипса по точкам 241
§ 108. Вычерчивание эллипса непрерывным движением ........ 242
§ 109. Эллипс как ортогональная проекция окружности 243
§ ПО. Касательная к эллипсу 245
>: 111. Оптическое свойстпо эллипса 246
§ 112. Гипербола и ее каноническое уравнение 247
§ 113. Исследование формы гиперболы 250
§
§
§
§
§
§
§
§
§
§
§
ll'l.
115.
116
117
118
119
120.
121.
122.
123
124.
125
126
127
691 ОГЛАВЛЕНИЕ
Эксцентриситет н директрисы гиперболы 253
Параметрические уравнения гиперболы . , 256
Сопряженные гиперболы . . , , 257
Уравнение гиперболы, отнесенной к асимптотам 258
Касательная к тлерболе 259
Оптическое свойство гиперболы 259
Парабола и ее каноническое уравнение 261
Исследование формы параболы 262
Построение паработы по точкам 261
Касательная к параЗчле 265
(Этническое свойств) параболы 266
Полярное уравнение эллипса, гиперболы и параболы 267
Элпипс, гипербола и парабола как конические сечения .... 268
Примеры и задачи к глазе VIII 272
1. Задачи с решениями , 272
2. Задачи для самостоятельного решения 277
Глава IX
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА, ЗАДАННЫЕ
КАНОНИЧЕСКИМИ УРАВНЕНИЯМИ
§ 128. Эллипсоид 284
§ 129. Одпополостный гиперболоид 288
§ 130. Двуполостпый гиперболоид 291
§ 131. Конус второго порядка 293
§ 132. Асимптотический конус гиперболоидов 294
§ 133. Эллиптический параболоид 296
§ 134. Гиперболический параболоид 298
§ 135. Цилиндры второго порядка 301
§ 136 Прямолинейные образующие однополостиого гиперболоида и
гиперболического параболоида 302
1. Прямолинейные образующие одиополостпого гиперболоида 302
2. Прямолинейные образующие гиперболического параболоида 309
§ 137. Примеры и задачи к главе IX 313
1. Задачи с решениями 313
2. Задачи для самостоятельного решения 316
Глава X
КОМПЛЕКСНАЯ ПЛОСКОСТЬ И КОМПЛЕКСНОЕ ПРОСТРАНСТВО.
АЛГЕБРАИЧЕСКИЕ ЛИНИИ И АЛГЕБРАИЧЕСКИЕ ПОВЕРХНОСТИ
§ 138. Комплексная плоскость и комплексное пространство 320
1. Комплексная плоскость 320
2. Комплексное пространство 325
§ 139. Плоские алгебраические линии 329
1. Определение плоской алгебраической линии и ее порядка . . . 329
2. Пересечение алгебраических линий. Пересечение
алгебраической линии с прямой 331
3. Распадение алгебраических линий 333
§ 140. Алгебраические поверхности 334
1. Определение алгебраической поверхности 334
2. Пересечение алгебраической поверхности с прямой и
плоскостью 335
3. Распадение алгебраических поверхностей 337
ОГЛАВЛЕНИЕ 695
Глава XI
ЛИНИИ ВТОРОГО ПОРЯДКА, ЗАДАННЫЕ ОБЩИМ УРАВНЕНИЕМ
§ 141 Теорема о том, что всякое уравнение второй степени с двумя
неизвестными определяет эллипс, гиперболу, параболу пли "две
прямые 339
§ 142. Теория инвариантов 345
§ 143. Определение канонического уравнения линии второго порядка
при помощи инвариантов. Распадение линии второго порядка
на дв: прямые 352
§ 144. Центр линии второго порядка 357
§ 145. Пересечение липни второго порядка с прямой. Асимптотические
направления. Классификация линий по числу и
действительности асимптотических направлений 360
§ 146. Диаметр, сопряженный данному неасимптотическому
направлению ". 364
1. Общая теория 364
2. Диаметры линий второго порядка, заданных каноническими
уравнениями 369
§ 147. Касательная к линии второго порядка 370
§ 148. Уравнение линии второго порядка, отнесенной к двум ее
сопряженным диаметрам; уравнение линии второго порядка,
отнесенной к касательной и сопряженному к ней диаметру 373
§ 149. Главные направления и главные диаметры 381
§ 150. Определение расположения линии второго порядка по
отношению к прямоугольной системе координат 384
§ 151. Примеры и задачи к главе XI 383
1. Задачи с решениями 388
2. Задачи для самостоятельного решения . , . , 397
'Глава XII
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА, ЗАДАННЫЕ ОБЩИМ
УРАВНЕНИЕМ
§ 152. Теорема о том, что всякое уравнение второй степени с тремя
неизвестными определяет эллипсоид, гиперболоид, нграболоид,
конус, цилиндр или две плоскости 402
§ 153. Теория инвариантов 413
§ 154. Определение канонического уравнения поверхности второго
порядка при помощи инварианта 419
§ 155. Центр поверхности второго порядка 428
§ 156. Классификация поверхностей второго порядка по характеру
места центров 430
§ 157. Конические и цилиндрические поверхности второго порядка,
заданные общим уравнением 433
1. Конические поверхности 433
2. Цилиндрические поверхности 435
3. Распадение поверхности второго порядка 437
§ 158. Пересечение поверхности второго порядка с прямой.
Асимптотические направления, асимптотический конус и конус
асимптотических направлений 438
§ 159. Диаметральная плоскость, сопряженная данному леасимптоти-
ческому направлению. Особые направления относительно
поверхности второго порядка 441
§ 160. Касательная плоскость 445
§ 161. Пересечение касательной плоскости с поверхностью второго
порядка 447
696 ОГЛАВЛЕНИЕ
§ 162. Эллиптические, гиперболические или параболические точки
поверхности второго порядка 448
§ 163 Простейшие уравнения поверхностей второго порядка в общей
декартовой системе координат 150
§ 164. Главные направления поверхности второго порядка 458
§ 165. Число главных направлений поверхности второго поряпка . , . 439
§ 166 Определение расположения поверхности второго порядка по
отношению к декартовой прямоугольной системе координат . . . 461
§ 167, Примеры и задачи к главе XII 467
1. Задачи с решениями 467
2. Задачи для самостоятельного решения ,,,,.,.,.«, 47ft
Глава XIII
ОТОБРАЖЕНИЯ И ПРЕОБРАЗОВАНИЯ
§ 168. Отображение и преобразование 484
§ 169 Произведение преобразований 484
§ 170 Группа преобразований 485
Глава XIV
ЛИНЕЙНЫЕ И АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
§ 171 Линейные преобразования и линейные отображения множества
точек пространства, плоскости или прямой W)
§ 172 Линейные преобразования множества векторов пространства,
плоскости или прямой . 487
§ 173. Свойства линейных преобразований множества точек просгран
ства, плоскости или прямой 488
§ 174 Линейные преобразования в координатах 494
§ 175. Аффинные преобразования и аффинные отображения 499
§ 176. Геометрическая теория аффинных преобразований 501
§ 177. Свойства аффинных преобразований и отображении ИОЬ
§ 178. Аффинные преобразования в координатах 509
§ 179 Примеры аффинных преобразований 512
§ 180. Ортогональные преобразования и движения , 520
§ 181. Ортогональные преобразования в координатах 522
1. Ортогональные преобразования плоскости 522
2. Ортогональные преобразования пространства 523
§ 182. Примеры ортогональных преобразований 525
§ 183. Подобные преобразования 526
§ 184. Собственные векторы линейного преобразования 528
§ 185. Самосопряженное линейное преобразование и его собственные
векторы 531
§ 186. Представление аффинного преобразования в виде произведения
ортогонального преобразования и трех сжатий к попарно
перпендикулярным плоскостям . 536
§ 187. Применение аффинных преобразований к исследованию сгойств
линий второго порядка 538
§ 188. Аффинная клас ификация линий второго порядка 540
§ 189. Аффинная классификация поверхностей второго порядка . . . 543
§ 190 Примеры и задачи к главе XIV 544
1. Задачи с решениями 544
2. Задачи для самостоятельного решения 547
ОГЛАВЛЕНИИ 697
Г л j в а XV
ЭЛЕМЕНТЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
§ 191 Проективная плоскость 557
1 Первая модель проективной плоскости . 557
2. Вторая модель проективной плоскости 559
§ 192. Однородные координаты точки и прямой на проективной плос
кости 560
1 Первая модель проективной плоскости 560
2 Вторая модель проективной плоскости , . 562
3. Свлзь проектинпых координат точки во второй модели с
однородными координатами точки в первой модели 563
§ 193. Уравнение прямой на проективной плоскости*, проходящей
через две точки; пучок прямых 564
§ 194. Группа проективных преобразований проективной плоскости.
Группа аффинных преобразований как подгруппа группы
проективных преобразовании , . . . . 565
§ 195 Проективное преобразование плоскости в координатах
Основная теорема 566
§ 196 Примеры проективных преобразований проективной плоскости 572
§ 197 Понятие о проективном пространстве 581
§ 198 Принцип двойственности 583
§ 199 Однородные координаты точки и проективной плоскости в
проективном пространстве 584
j 2(И! Уравнение прямой, проходящей через две точки. Пучок и
связка плоскостей ... . . 585
§ 201 Группа проективных преобразований проективного
пространства Основная теорема ... 587
§ 202 Ангармоническое отношение. Гармоннзм 588
§ 203 Линии второго порядка на проективной плоскости.
Классификация линий второго порядка по характеру пересечения с
несобственной прямой 598
§ 204. Проективная классификация линий второго порядка
Распадающиеся и нераспадающиеся линии 600
S 205. Пооективпо-аффинная классификация линий второго порядка 603
§ 206. Необходимое и достаточное условие того, что два однородных
уравнения второй степени определяют одну и ту же линию
второго порядка 604
:) 207. Касательная к линии второго порядка 606
§ 208. Полюс и поляра линии второго порядка . 609
§ 209. Сопряженные диаметры, центр и асимптоты в проективной тео^
рпи линий второго порядка 612
§ 210. Определение линии второго порядка по пяти точкам 613
§ 211. Пучок линий второго порядка 614
§ 212. Поверхность второго порядка в проективном пространстве.
Классификация поверхностей второго порядка по характеру
пересечения с несобственной плоскостью 616
§ 213. Проективная классификация поверхностей второго порядка . . 618
§ 214. Проективно-аффииная классификация поверхностей второго
порядка п проективном пространстве 621
Ч 215, Необходимое и достаточное условие того, что два однородных
уравнения второй степени определяют одну и ту же поверхность
второго порядка 626
§ 216 Касательная плоскость к поверхности второго порядка .... 628
§ 217 Пересечение поверхности второго порядка касательной
плоскостью .......... 629
698 ОГЛАВЛЕНИЕ
S 218. Полюс и полярная плоскость поверхности второго порядка . . . 631
§ 219, Примеры и задачи к главе XV . 632
1. Задачи с решениями 632
2. Задачи для самостоятельного решения 636
Дополнение 1
ОРИЕНТАЦИЯ
1. Ориентация плоскости 638
2. Ориентация пространства 642
Д о п о л и : и и е 11
МЕТРИЧЕСКАЯ ТЕОРИЯ ИНВАРИАНТОВ МНОГОЧЛЕНА ВТОРОЙ
СТЕПЕНИ ОТ ДВУХ И ТРЕХ ПЕРЕМЕННЫХ ОТНОСИТЕЛЬНО
ПРЕОБРАЗОВАНИЯ ОБЩЕЙ ДЕКАРТОВОЙ СИСТЕМЫ КООРДИНАТ
1. Контраварнаитиые и ков;>рнаптные координаты точки и
вектора па плоскости 646
2 Кощравариантпые и ковариаптные координаты вектора и
точки в пространстве 648
3. Теория инвариантов уравнения линии второго порядка . . . 649
4. Определение расположения линии второго порядка 654
5. Поверхности второго порядка 656
Дополнение 111
ПЛОСКИЕ СЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА.
КРУГОВЫЕ СЕЧЕНИЯ. ОМБИЛИЧЕСКИЕ ТОЧКИ
1. Приведение к каноническому виду плоского сечения
поверхности второго порядка 660
2. Расположение в пространстве плоского сечения поверхности
второго порядка 664
3. Круговые сечения поверхностен второго порядка 667
4. Омбилические точки 671
Дополнение IV
ПРОЕКТИВНЫЕ КООРДИНАТЫ. ТЕОРЕМЫ ДЕЗАРГА, ПАСКАЛЯ
И БРИАНШОПА. АВТОПОЛЯРНЫЙ ТРЕУГОЛЬНИК.
АВТОПОЛЯРНЫЙ ТЕТРАЭДР
1. Проективные координаты на проективной плоскости .... 673
2. Автоиолярнуй треугольник 678
3. Теоремы Дезарга, Паскаля и Брианшона 680
4. Проективные координаты в проективном пространстве . . . 684
5. Ангополярный теграэдр 688
Петр Сергеевич Моденов
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
БЗ 79—1969—8
Редактор А. С, Пархоменко
Редактор изд-ва Т. Г. Батенина
Художественный редактор
К. И. Журинская
Переплет художника Л. #. Рубен
Технич. редактор К- С. Чистякова
Корректоры С. С. Мазурская,
Г. N. Куд'мови, Е. П. У танина
Сдано в набор—!4/VII — 19G6 г.
Подписано к печати — I8/VI1 — 19G7 г.
Л —95463. Формат 60х90/16. Физ. печ.
л. 44,0. Уч.-изд л. 51,33. Изд. Л» 71.
Зак. 400. Тираж 50 000 экз. Бум.
тип. Л» 2. Цена 1 р. 64 к.
Издательство
Московского университета
Москва, Ленинские горы
Административный корпус
Отпечатано с матриц
ордена Трудового Красного Знамени
Первой Образцовой типографии
имени А. А. Жданова Главнолиграф-
прома Комитета по печати при Совете
Министров СССР
Москва, М-54, Валовая, 28
в типографии изд-ва МГУ
Москва, Ленински-' горы