Текст
Б. 3. ВУЛИХ
ВВЕДЕНИЕ
В ФУНКЦИОНАЛЬНЫЙ
АНАЛИЗ
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1967
БИБЛИОТЕКА Колхоза
"Оскорка"
со вин выдачи
Пне №33
руки u2xg две
517.2
В 88
УДК 517.0
Введение в функциональный анализ. В у л и х Б. 3., 1967 г.
Книга содержит элементарное изложение основ функционального анали-
анализа. В первых двух главах изучается конечно-мерное эвклидово пространство,
и на этом примере читатель подготовляется к введению в последующих главах
общих абстрактных понятий функционального анализа. Далее рассматри-
рассматриваются метрические пространства и непрерывные операторы в них. Вводится
основной класс пространств, изучаемых в книге,— нормированные про-
пространства. Отдельная глава посвящена гильбертову пространству, которое
вводится как частный случай нормированного пространства. Даются обе
классические реализации бесконечно-мерного сепарабелыюго гильбертова
пространства — координатная и функциональная. Попутно указываются
два подхода к построению функциональной реализации гильбертова про-
пространства: обычная конструкция пространства функций, суммируемых
с квадратом, и построение пространства, составленного из функций промежут-
промежутка, иными словами, функций, задаваемых своими средними значениями.
В книге изучаются также линейные операторы и функционалы в нормиро-
нормированных пространствах, проводится специальное исследование самосопряжен-
самосопряженных, в частности, вполне непрерывных самосопряженных операторов в гиль-
гильбертовом пространстве. Даются краткие сведения о применении методов
функционального анализа к приближенному решению функциональных
уравнений. В конце книги приводятся краткие сведения о счетно-нормиро-
ванных и полуупорядоченных пространствах. Общая теория иллюстрируется
многими примерами из алгебры, анализа, теории функций, дифференциальных
и интегральных уравнений.
От читателя требуется знание лишь основ математического анализа,
и только в некоторых местах предполагается знакомство с интегралом Лебега.
Во втором издании включена новая глава о счетно-нормированных
пространствах, увеличено число примеров за счет привлечения пространств
суммируемых функций, дан геометрический подход к изучению линейных
функционалов (введено понятие гиперплоскости). Иллюстраций 21, библио-
библиографических ссылок 23.
2-2-3
78—67
ОГЛАВЛЕНИЕ
Из предисловия к первому изданию 7
Предисловие ко второму изданию 8
Глава I. Конечно-мерное эвклидово пространство 9
1.1. Понятие пространства в математике 9
1.2.. n-мерное векторное пространство 10
1.3. Норма вектора 12
1.4. Скалярное произведение векторов 15
1.5. Линейные преобразования 17
1.6. Матрицы 20
1.7. Норма оператора линейного преобразования 24
1.8. Непрерывность линейного преобразования 25
1.9. Линейные функционалы 27
1.10. Сопряженные и самосопряженные операторы 28
1.11. Подпространства в Rn 30
1.12. Ортогональный базис 35
1.13. Собственные числа и собственные векторы 39
1.14. Комплексное re-мерное эвклидово пространство 43
Глава II. Бесконечно-мерное эвклидово пространство 46
2.1. Векторы с бесконечным множеством координат 46
2.2. Пространство I2 47
2.3. Скалярное произведение векторов из г2 48
2.4. Сходимость последовательности векторов 49
2.5. Непрерывность нормы и скалярного произведения .... 53
2.6. Линейные функционалы 55
2.7. Лииейвые операторы 57
2.8. Подпространства в I2 59
2.9. Ортогональный базис 62
2.10. Комплексное бесконечно-мерпое эвклидово пространство 66
Глава III. Метрические пространства 68
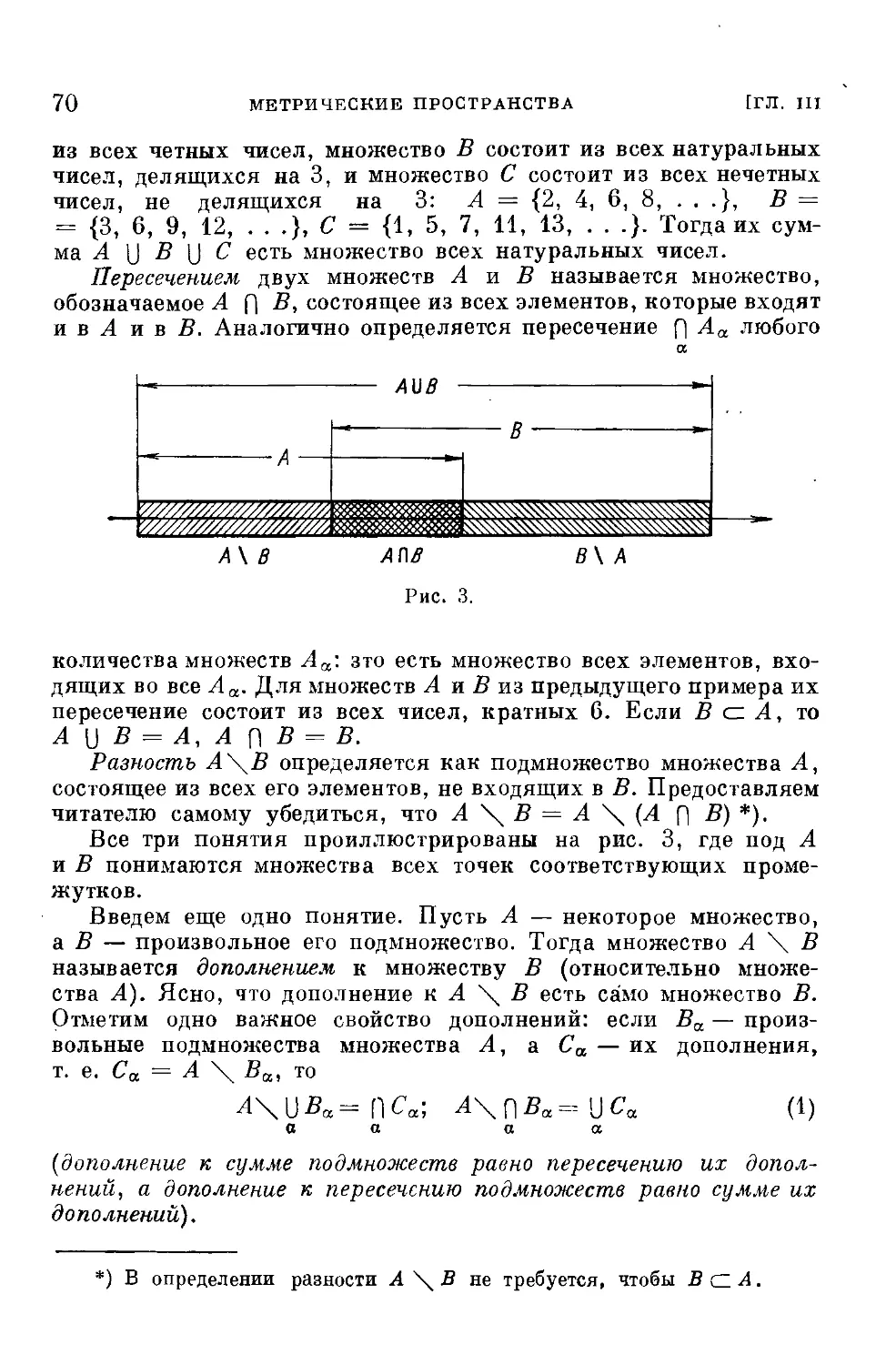
3.1. Некоторые понятия теории множеств 68
3.2. Определение метрического пространства 71
3.3. Сходимость- в метрическом пространстве 79
3.4. Замкнутые и открытые множества 83
3.5. Полные метрические пространства 87
3.6. Счетные множества 91
3.7. Сепарабельные пространства 96
3.8. Компактные множества 99
3.9. Критерий компактности в пространстве € 107
4 ОГЛАВЛЕНИЕ
Глава IV. Непрерывные операторы в метрических пространствах 111
4.1. Основные определения 111
4.2. Непрерывные операторы и функционалы 112
4.3. Неподвижные точки. Метод последовательных приближений 114
4.4. Операторы сжатия 115
4.5. Интегральные уравнения 123
4.6. Теорема Пеано 125
Глава V. Нормированные пространства 130
5.1. Линейные системы 130
5.2. Нормированные пространства 133
5.3. Конечно-мерные пространства 138
5.4. Подпространства 143
5.5. Задача о наилучшем приближении 145
5.6. Пространства со счетным базисом 148
Глава VI. Гильбертово пространство 151
6.1. Скалярное произведение 151
6.2. Определение гильбертова пространства 153
6.3. Понятие ортогональности 154
6.4. Проекция элемента на подпространство 156
6.5. Ортогональные разложения гильбертова пространства . . 159
6.6. Ортогональные системы элементов 161
6.7. Ортогонализация системы линейно независимых элементов 165
6.8. Задача о наилучшем приближении в гильбертовом простран-
пространстве 167
6.9. Изоморфизм произвольного сепарабельного гильбертова
пространства с пространством I2 168
6.10. Комплексное гильбертово пространство 170
Глава VII. Пространство L2 171
7.1. Основные свойства пространства L2 171
7.2. Скалярное произведение 173
7.3. Ортогональные ряды 175
7.4. Метод последовательных приближений для интегрального
уравнения Фредгольма 181
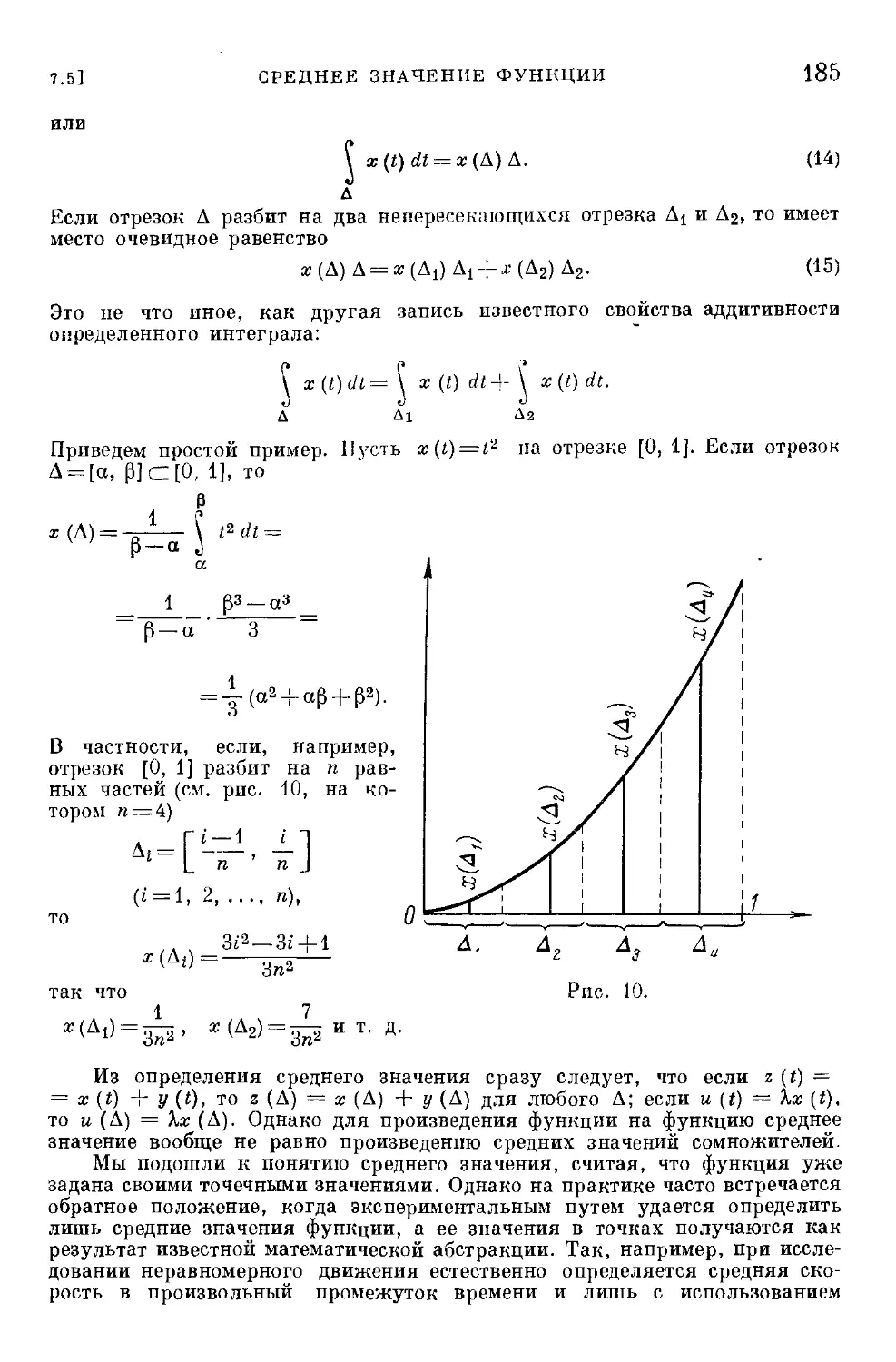
7.5. Среднее значение функции 184
7.6. Определение пространства L2 187
7.7. Плотность множества непрерывных функций в пространстве X2 193
7.8. Умножение функций из Is 197
7.9. Скалярное произведение в 1! 200
Глава VIII. Линейные операторы 203
8.1. Аддитивные операторы 203
8.2. Линейные операторы 205
8.3. Ограниченность линейных операторов 206
8.4. Распространение линейных операторов 211
8.5. Последовательности линейных операторов 213
8.6. Пространство линейных операторов 216
8.7. Обратные операторы 219
8.8. Матричные линейные операторы 224
8.9. Бесконечные системы линейных алгебраических уравнений 226
8.10. Некоторые интегральные операторы 229
8.11. Линейные дифференциальные операторы в пространстве
дифференцируемых функций 231
ОГЛАВЛЕНИЕ О
Глава IX. Линейные функционалы 234
9.1. Линейный функционал как частный случай линейного опе-
оператора 234
9.2. Общие формы линейных функционалов в некоторых про-
пространствах 235
9.3. Линейные функционалы в пространствах суммируемых
функций 238
9.4. Распространение линейных функционалов 244
9.5. Линейные функционалы в пространстве непрерывных
функций 248
9.6. Гиперплоскости 257
9.7. Сопряженное пространство 260
9.8. Второе сопряженное пространство 261
9.9. Слабая сходимость функционалов 264
9.10. Сходимость процесса механических квадратур 266
9.11. Линейные фупкционалы в пространстве сходящихся после-
последовательностей 271
9.12. Обобщенные методы суммирования рядов 273
9.13. Линейные функционалы в комплексном нормированном про-
пространстве 277
Глава X. Сопряженные и самосопряженные операторы в гильбер-
гильбертовом пространстве 278
10.1. Сопряженные операторы 278
10.2. Самосопряженные операторы 281
10.3. Инвариантные подпространства 285
10.4. Собственные числа и собственяые элементы самосопряжен-
самосопряженного оператора . 286
10.5. Неограниченные симметричные операторы 288
10.6. Спектр самосопряженного оператора 290
10.7. Интегральные самосопряженные операторы 298
10.8. Дифференциальные симметричные операторы 300
10.9. Самосопряженные операторы в комплексном гильбертовом
пространстве 303
Глава XI. Вполне непрерывные операторы 305
11.1. Определение и общие свойства 305
11.2. Вполне непрерывные операторы в гильбертовом простран-
пространстве 309
11.3. Спектр вполне непрерывного самосопряженного оператора 310
11.4. Разложение значений оператора по собственным элементам 313
11.5. Решение уравнения (А — X I) х — у 316
11.6. Интегральные уравнения с симметричным ядром 318
11.7. Применение интегральных операторов к краевым задачам для
уравнения Штурма — Лиувилля 322
/
Глава XII. Приближеннее решение функциональных уравнений 329
12.1. Замена точного уравнения «приближенным» 329
12.2. Замена произвольного интегрального уравнения на уравне-
уравнение с вырожденным ядром 331
12.3. Решение бесконечных систем линейных алгебраических
уравнений по методу редукции 335
12.4. Метод Рптца 337
12.5. Применепие метода Ритца к решению дифференциальных
уравнений Штурма — Лиувилля 342
6 ОГЛАВЛЕНИЕ
12.6. Применение метода Ритца к нахождению собственных
значений 346
12.7. Понятие о методе Бубнова — Галеркина 353
Глава ХШ. Счетно-нормированные пространства 355
13.1. Полунормы и определение счетно-нормированного простран-
пространства 355
13.2. Примеры счетно-нормированных пространств 358
13.3. Эквивалентные системы полунорм 361
13.4. Введение метрики в счетно-нормированном пространстве . 365
13.5. Ограниченные множества в счетно-нормированном про-
пространстве 368
13.6. Линейные операторы в счетно-нормированных пространствах 371
13.7. Линейные функционалы 375
13.8. Общие формы линейных функционалов в некоторых счетно-
нормпрованных пространствах 378
Глава XIV. Полуупорядоченные нормированные пространства . . 383
14.1. Линейные структуры 383
14.2. Положительная и отрицательная части элементов линейной
структуры 389
14.3. Полуупорядоченные банаховы пространства 392
14.4. Линейные функционалы в полуупорядоченных банаховых
пространствах 394
14.5. Другой вывод общей формы линейного функционала в про-
пространстве непрерывных функций 397
14.6. Монотонные самосопряженные операторы в гильбертовом
пространстве 400
14.7. Частичное упорядочение пространства L2 402
14.8. Сильно положительные линейные операторы 404
Литература по функциональному анализу 410
Предметный указатель 412
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Функциональный анализ — сравнительно молодая математи-
математическая дисциплина, возникшая в начале XX столетия. Однако,
несмотря на свой небольшой возраст, функциональный анализ,
развиваясь исключительно быстрыми темпами, превратился
к настоящему времени в весьма обширную область математики,
имеющую многочисленные приложения в целом ряде других ее
разделов.
Функциональный анализ сложился в результате обобщения
различных понятий и методов, использовавшихся в существовав-
существовавших ранее математических дисциплинах, в первую очередь мето-
методов классического математического анализа, алгебры и геометрии.
Это обобщение строилось за счет перехода на более высокую сту-
ступень математической абстракции, что весьма характерно для мето-
методов современной математики. Рассмотрение различных задач клас-
классической математики с более общей, более абстрактной точки зре-
зрения часто позволяет лучше выявить "их основные закономерности,
лучше вскрыть то общее, что присуще задачам, сходным по мето-
методам их решения, но различным по своему конкретному содержа-
содержанию. Построенные же общие теории затем с большим успехом
применяются при решении конкретных задач, вплоть до приклад-
прикладных вопросов математики. Не будет преувеличением сказать, что
в настоящее время трудно представить себе решение сколько-
нибудь серьезного вопроса из области дифференциальных уравне-
уравнений математической физики или приближенных вычислений без
применения методов функционального анализа. Этим объясняется
и тот факт, что методы функционального анализа проникают
и в техническую литературу, в той ее части, которая использует
серьезный математический аппарат.
Основную роль во всем функциональном анализе играет поня-
понятие оператора, представляющее обобщение понятия функции, изу-
изучаемого в математическом анализе. Исследование общей теории
операторов с точки зрения ее использования в математическом
анализе и есть главное содержание функционального анализа.
В настоящей книге излагаются лишь начальные сведения из
функционального анализа, и тут же дается целый ряд приложений
общей теории к задачам из различных областей математики. В то
же время ряд важных более сложных вопросов самого функцио-
функционального анализа совершенно не затрагивается. Для облегчения
изложения некоторые вопросы разобраны при дополнительных
предположениях, упрощающих исследование.
8 ПРЕДИСЛОВИЕ
В первых двух главах ряд основных понятий функционального
анализа, вводимых позднее в общем виде, рассматривается пред-
предварительно при более простых частных условиях — в эвклидовых
пространствах. Такое изложение должно облегчить читателю
переход, начиная с гл. III, к общей теории.
Для удобства ссылок параграфам даны номера, состоящие из
двух частей: первая часть — номер главы, а вторая — номер
данного параграфа внутри этой главы (например, 7.2—§ 2 гл. VII).
Теоремы и леммы имеют нумерацию внутри каждого параграфа
в отдельности. Например, теорема 3.5.2 означает — вторая тео-
теорема § 5 гл. III. Нумерация формул — сквозная в пределах
каждой главы; при ссылках на формулу из той же главы указы-
указывается только ее номер.
Считаю своим долгом поблагодарить редактора книги Г. П. Аки-
лова за ценные замечания, сделанные им при чтении рукописи.
Б. Byлих
Июнь 1957 г
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Наиболее существенные изменения, внесенные во второе изда-
издание этой книги, следующие: 1) добавлена глава о счетно-норми-
рованных пространствах; 2) в примерах, иллюстрирующих общую
теорию, широко используются пространства Lp, состоящие из функ-
функций, суммируемых с р-й степенью. Таким образом, в новом изда-
издании книги предполагается, что читатель имеет представление об
интеграле Лебега. Однако читатель, не знакомый с интегралом
Лебега, легко сможет пропустить при чтении книги те примеры,
где этот интеграл используется.
Кроме того, добавлены краткие сведения о геометрическом
подходе к изучению линейных функционалов (введено понятие
гиперплоскостей) и о втором сопряженном пространстве. Несколь-
Несколько полнее проведено изучение сильно положительных линейных
операторов. Внесены также небольшие изменения, касающиеся
деталей изложения.
Элементарный характер книги сохранен и во втором издании.
Книга по-прежнему рассчитана на довольно широкий круг чита-
читателей, не только математиков, механиков, физиков, но также
и инженеров. В новом издании сохранены те пояснения, которые
давались в этой книге при использовании сведений из математи-
математического анализа, обычно не включаемых в учебники для втузов.
Б. Byлих
Июнь 1966 г.
ГЛАВА I
КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО
1.1. Понятие пространства в математике
Понятие пространства имеет в науке различный смысл. Как
философская категория пространство есть одна из форм суще-
существования материи. Пространственные формы действительного
мира составляют вместе с количественными отношениями предмет
изучения математики, при этом именно пространственные формы
составляли главное содержание геометрии, во всяком случае,
на первых ступенях ее развития. В школьном курсе геометрии,
в элементарном курсе аналитической геометрии понятие простран-
пространства встречается в его простейшей форме; под пространством
понимается пространство трех измерений, удовлетворяющее опре-
определенной системе аксиом (так называемые аксиомы эвклидовой
геометрии). Однако уже методы аналитической геометрии позво-
позволяют подойти к понятию трехмерного пространства с несколько
иной, арифметической точки зрения. Именно, поскольку каждая
точка пространства определяется тремя координатами и, обратно,
каждая тройка чисел определяет некоторую точку пространства,
для которой заданные числа являются координатами, точки
трехмерного пространства можно отождествить с тройками веще-
вещественных чисел. Таким образом, трехмерное пространство можно
рассматривать как множество всех троек вещественных чисел
(х, у, z). При этом такое геометрическое понятие, как расстояние
между двумя точками, может быть тоже определено арифметиче-
ски по известной формуле из аналитической геометрии. Плоскость
может быть определена как совокупность всех троек чисел, удов-
удовлетворяющих одному и тому же уравнению 1-й степени.
При таком подходе к понятию пространства последнее есте-
естественно обобщается в математике и на случай более сложных обра-
образований. Коротко говоря, под пространством в современной мате-
математике понимается совокупность любых объектов (ими могут быть
наборы чисел, функции, наборы функций), между которыми уста-
устанавливаются соотношения, аналогичные тем или иным простран-
пространственным отношениям, изученным в элементарном трехмерном
10 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
пространстве. В пределах настоящей книги мы сможем просле-
проследить за несколькими стадиями обобщения понятия пространства,
первой ступенью которого является изучаемое в этой главе конеч-
конечно-мерное эвклидово пространство.
1.2. ?г-мерное векторное пространство
Понятие вектора является одним из основных понятий мате-
математики. Однако, если на более ранней ступени развития матема-
математики рассматривались лишь векторы в трехмерном пространстве,
то обобщение понятия пространства существенно связано со
значительным обобщением понятия вектора. Простейшим обобще-
обобщением является понятие вектора в га-мерном пространстве, к
рассмотрению которого мы и переходим.
В пределах этой главы мы будем пользоваться следующим опре-
определением.
Определение. Вектором называется совокупность п
вещественных чисел а,, а2, . . ., ап (п — любое натуральное
число), расположенных в определенном порядке. Будем обозна-
обозначать вектор одной буквой и записывать, например, так:
а==(аи а2, . . ., а„).
Числа аи а2, . . ., ап назовем координатами вектора а*).
Ниже мы встретимся также с более общим понятием вектора,
координаты которого будут комплексными числами.
В этой главе, как правило, векторы и их координаты обозна-
обозначаются латинскими буквами а, Ь, с, . . . (координаты — теми же
буквами с надлежащими индексами); греческие буквы а, |3, у, . . .
. . ., X, ц, ... будут обозначать числа.
Распространим на введенные нами векторы основные определе-
определения векторной алгебры, чем, в частности, будет вполне оправдано
и само название «вектор». При этом предполагается, что в даль-
дальнейшем п имеет одно и то же фиксированное значение.
Прежде всего условимся считать векторы: а — (аи а2, . . ., ап)
и b = (bu b2, . . ., bn), равными (и писать а -— Ь) тогда и толь-
только тогда, когда at = bt при всех i = 1, 2, . . ., п. Это опре-
определение равенства еще раз подчеркивает, что вектор определяет-
определяется не просто как множество п чисел, а как совокупность
п чисел, расположенных в определенном
порядке. Действительно, совокупность тех же п чисел, рас-
расположенных в каком-нибудь другом порядке, представляет, как
*) Имея в виду единообразие с обозначениями, употребляемыми
в функциональном анализе, мы отказываемся от принятого в геометрии того
или иного специального обозначения для векторов (жирный шрифт, черточка
наверху и др.)-
! 2] ге-МЕРНОЕ ВЕКТОРНОЕ ПРОСТРАНСТВО \\
правило, другой вектор. Такая трактовка понятия вектора вполне
согласуется с обычными определениями для векторов в трехмер-
трехмерном пространстве.
Вектор, все координаты которого равны 0, называется нулевым
и обозначается 9*).
Сложение двух векторов определяется покоординатно, т. е.
суммой векторов а и Ъ называется вектор а -\- Ь, определяемый
формулой
a-\-b^(ai-\-bi, аг-{-Ь2, . . ., ап-\-Ъп).
Аналогично определяется произведение ка вектора а на веще-
вещественное число к:
ка = (Xdi, ка2, . . ¦, кап).
Читатель без труда убедится, что при таких определениях для
векторов сохраняются следующие основные законы алгебры:
1)а+Ь = Ь + а (коммутативность сложения);
2) (а + Ъ) + с = а + (Ъ + с) (ассоциативность сложения);
3) к (a -f- b) = ка -f- Kb \ (дистрибутивность умножения отно-
4) (к + (х)а = ка + \иг ] сительно сложения);
5) к (ца) = (кц) а (ассоциативность умножения);
6) Оа = 9 (произведение любого вектора на число нуль есть
нулевой вектор);
7) la = а (произведение любого вектора на число единица
равно тому же вектору).
Эта группа свойств сложения и умножения будет играть суще-
существенную роль в последующих главах и мы назовем ее основной
группой алгебраических законов.
Вычитание векторов определяется посредством умножения
на —1 и сложения формулой
а — Ь=^а-Ь( — 1)Ь,
т. е.
a—b — (a1 — blla2 — b2, ..., an — bn),
и тогда само собою получается, что вычитание есть действие,
обратное сложению:
(a — b)-\-b = a.
Заметим еще, что нулевой вектор обладает тем свойством, что
а -\- 8 = а для любого а.
Множество всех векторов (при заданном значении п) называется
п-мерным векторным пространством. Будем обозначать его Rn.
В отличие от встречающегося в дальнейших главах более общего
*) Впрочем, часто нулевой вектор обозначается просто нулем. При этом
в каждом конкретном случае из контекста видно, в каком смысле употреблен
символ 0 — обозначает ли он число нуль или нулевой вектор.
12 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
понятия вектора, векторы, образующие пространство Лп, мы будем
иногда называть векторами га-мерного пространства. Если п = 3,
то получаем обычное трехмерное пространство векторов. При
п = 1 каждый вектор определяется всего лишь одной координа-
координатой; действия над такими векторами сводятся к тем же действиям
над числами, а потому одномерное векторное пространство Вч
можно отождествить с совокупностью вещественных чисел (или
векторов на прямой).
Все д-мерные векторные пространства (с любым п) называются
конечно-мерными.
Обобщим теперь на случай векторов из Лп формулу разложе-
разложения произвольного вектора по координатным ортам. Координат-
Координатными ортами в Лп называются векторы, у которых одна из коорди-
координат равна единице, а остальные равны нулю. Обозначим через et
тот координатный орт, у которого единице равна i-я координата.
Всего в Rn существует п координатных ортов et, е2, . . ., еп.
Из определения действий над векторами сразу вытекает, что век-
вектор а = (аь а2, . . ., ап) представим в виде
... +апеп; A)
действительно, это равенство при подробной записи входящих
в него векторов имеет вид:
(а„ а2,..., ап) = о1A, 0, . . ., 0)+а2@, 1, ... ,0) + ...+в„ @, 0, . . ., 1),
а в такой форме оно очевидно. Таким образом, координаты а,
играют роль проекций вектора а на орты et. Ниже эта аналогия
будет уточнена.
1.3. Норма вектора
По аналогии с выражением длины вектора в трехмерном про-
пространстве назовем длиной, или нормой, вектора а из Нп арифмети-
арифметический (положительный) квадратный корень из суммы квадратов
его координат; обозначим норму вектора а через || а ||. Таким
образом,
||a||=/a* + a22+••¦+«?• B)
Отметим следующие основные свойства нормы вектора:
1) || а || > 0 для любого а и || а \\ = 0 только для а = 6;
2) || Ь|| = 14-11 я II-
Эти свойства совершенно очевидны. Некоторые выкладки тре-
требуются для проверки
3) || а + Ь||<|| а || + || Ь||.
Это неравенство в трехмерном пространстве выражает тот элемен-
элементарный геометрический факт, что сумма двух сторон треугольника
1.3] НОРМА ВЕКТОРА 13
не меньше третьей стороны *), и потому называется неравенством
треугольника. Дадим его доказательство.
Предварительно докажем важное неравенство Коши
S.?X C)
i=l i=l г=1
справедливое для любых вещественных чисел аг и b-L **). Простое
доказательство этого неравенства основывается на следующем
замечании: если квадратный трехчлен с вещественными коэффи-
коэффициентами Ах* + 25а: + С неотрицателен при всех вещественных х,
то его дискриминант Вг — ЛС<0***). Составим вспомогатель-
вспомогательную функцию ф (х) от вещественной переменной х, сводящуюся
к квадратному трехчлену:
Здесь
Из определения ф (х) видно, что ф(г)>0 при всех х. Тогда, на
основании предыдущего замечания,
а это и есть иначе записанное неравенство Коши.
Теперь из неравенства Коши выведем неравенство треуголь-
треугольника, которое согласно определению нормы вектора в Rn можно
*) Знак равенства возможен для «вырождающегося» треугольника,
у которого все три вершины лежат на одной прямой.
**) О. Л. К о ш и A789—1857) — знаменитый французский математик,
с именем которого связаны многие основные результаты математического
анализа и теории функций комплексной переменной.
***) Действительно, если трехчлен Ах* + 2Вх + С > 0 при всех х
ж А Ф 0, то его график (парабола) не может пересекать ось абсцисс и, в край-
крайнем случае, может лишь касаться ее. Поэтому такой трехчлен не может иметь
двух различных вещественных корней. Но тогда из формулы для корней
квадратного уравнения Л
сразу видно, что В2 — АС -< 0. Если же А = 0, то трехчлен превращается
в линейную функцию 2Вх + С, а линейная функция может быть неотрица-
неотрицательной при всех х только, если она сводится к постоянной, т. е. если В = 0
(а С > 0). Но в этом случае В2— АС = 0.
14 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО
записать в виде
]
(а, -
[ГЛ. I
D)
Последнее неравенство тоже называют неравенством Коши.
Для доказательства неравенства D) извлечем квадратные
корни из обеих частей неравенства C)*), затем обе части полу-
полученного нового неравенства удвоим и прибавим к ним выражение
аг "Г
В результате получим
г=1
2
г=1
1=1
г=1
i^i
Это неравенство можно переписать и так:
п
ИЛИ
1=1
Извлекая теперь квадратные корни из обеих частей последнего
неравенства, получим неравенство треугольника.
Отметим очевидное свойство нормы вектора: если а Ф- 6, то
1
вектор
j—-,
a имеет норму, равную единице.
Существуют и другие определения нормы вектора в JS^, при
которых она также обладает тремя перечисленными выше свой-
свойствами. Например, иногда бывает полезно определение нормы по
ф || | | | | 1 | |) ** О
рр
формуле || о || = max (| а, |, | а2
ф 2)
| ап |) **)• Однако при определе-
определе|| || 1 |
нии нормы по формуле B) и-мерное пространство Rn оказывается
по своим свойствам ближе к трехмерному пространству, изу-
изучаемому в эвклидовой геометрии.
*) При этом в левой части мы берем то значение корня, которое
п
равно 2а'&ь
г—1
**) Символ max обозначает, что из написанных за ним чисел нужно взять
наибольшее. Аналогично, символ min употребляется для обозначения наи-
наименьшего из написанпых за ним чисел.
1.4] СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ 15
Определение, и-мерное векторное пространство Iin,
в котором по формуле B) определена норма вектора, называется
п-мерным эвклидовым пространством.
В дальнейшем пространство Нп всегда рассматривается как
эвклидово. Отметим, что в одномерном эвклидовом простран-
пространстве Mi, т. е. в совокупности вещественных чисел, норма совпадает
с абсолютной величиной числа.
1.4. Скалярное произведение векторов
Читателю известно, насколько широкое применение имеет
не только в математике, но и в механике, в физике, понятие ска-
скалярного произведения векторов. Распространим это понятие
на векторы из Iin, принимая в качестве определения ту формулу,
которая в трехмерном пространстве выводится на основе геомет-
геометрического определения скалярного произведения.
Определение. Скалярным произведением (а, Ъ) двух
векторов а и Ъ называется выражение, определяемое формулой
(а, Ь) - S atbi. E)
i=i
Легко видеть, что скалярное произведение обладает свойст-
свойствами коммутативности, т. е. (Ъ, а) = (а, Ъ), ассоциативности по
отношению к умножению на число, т. е. (Ха, Ъ) = X (а, Ъ); верен
также и распределительный закон:
(а, Ъ-\-с) =-(а, Ь) + (а, с).
Последние два свойства можно объединить в одной формуле:
(а, ХЪ + ис) = X (a, b) -f ц (а, с).
Эта формула, очевидно, обобщается и на случай любого конечного
числа слагаемых:
(a, S М*>)= SMe, аС>)
i=l i=l
(здесь а<*) — векторы, Xi — числа). Из определения скалярного
произведения также следует, что ,'
\\a\\ =У(а, а) .
Определение. Два вектора а и Ъ называются ортого-
ортогональными а _|_ Ь, если (а,Ь) = 0.
Это определение очевидным образом согласовано с признаком
перпендикулярности векторов в трехмерном пространстве. Из
него сразу следует, что координатные орты et попарно ортого-
16 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
нальны. Действительно, так как у орта et отлична от нуля только
i-я координата, а у орта eh — только к-я, то ясно, что
{ей е^ = 0 при 1фк.
Далее, если а — произвольный вектор, то
{a, ei) = ai,
следовательно, формуле A) разложения вектора по координат-
координатным ортам можно придать и такой вид:
а = 42(а,е,)е«. F)
Если учесть, что \\et || = 1, то можно, опять — по аналогии с трех-
трехмерным случаем, назвать скалярное произведение {a, et) проек-
проекцией вектора а на орт et. Таким образом, для получения разложе-
разложения A) или F) используются проекции вектора на координатные
орты.
Из ассоциативности умножения скалярного произведения
на число сразу следует, что если а ±_ 6, то и k I \ib при любых
% и \i. Действительно, {Ка, \ib) = %ц (а, Ь) = 0, если a _L Ъ.
Выведенное в предыдущем параграфе неравенство Коши C)
можно переписать в такой форме:
{а, Ъ)*<\\а\?\\Ъ\\\
Извлекая из обеих частей арифметические квадратные корни,
получаем новую форму неравенства Коши
G)
Неравенство G) выражает одно из основных свойств скалярного
произведения — скалярное произведение двух векторов по абсолют-
абсолютной величине не превосходит произведения их норм.
Отметим один факт, представляющий своеобразное обобщение
теоремы Пифагора: если вектор а представлен в виде суммы
V
нескольких попарно ортогональных векторов, а = ?j a(i\ то
il
т. е. квадрат нормы суммы ортогональных векторов равен
сумме квадратов норм всех слагаемых. Действительно, из свойств
скалярного произведения следует, что
|| а ||а = (а, а) = B а<*\ 2«(Л)= 2 («(i
i=l 7=1 ». j=l
1.5]
Но
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
ti) = 0 при i-ф], поэтому
17
p
v
г=1
а
1.5. Линейные преобразования
Чтобы подойти к основному в функциональном анализе поня-
понятию линейного преобразования, рассмотрим следующий простой
пример в пространстве В21 T- е- на плоскости." Представим себе
(рис. 1) два экземпляра плоскости в виде листов бумаги, наложен-
наложенных друг на друга, причем для верхнего листа взята прозрачная
бумага. Представим, что на нижнем листе изображены всевозмож-
всевозможные векторы, проведенные
из начала координат, и
перенесем их изображения
на верхний лист в виде
точной копии. Затем повер-
повернем верхний лист вокруг
начала координат на неко-
некоторый угол а, положитель-
положительный или отрицательный,
после чего для каждого
вектора а с нижнего листа
ого изображение на верх- '
нем листе будет находить-
находиться уже не против а, а
против некоторого другого
вектора а', отличающегося
от а направлением. Этот
вектор а' и назовем изображением вектора а после вращения.
Таким образом, у нас установлено правило, по которому каждому
яектору а из В% сопоставлен определенный вектор а', также из 2?2-
В этом случае говорят, что определен оператор, осуществляющий
преобразование В2 в i?2.
Найдем зависимость между координатами векторов a = (ab аг)
и а' — (а[, а',). Для этого рассмотрим сначала орт еь направлен-
направленный по оси ОХ. В результате преобразования орт е^ переходит
в вектор е[, имеющий ту же длину единица и составляющий угол а
с осью ОХ. Проекции вектора е[ на координатные оси будут,
в таком случае, равны, соответственно, cos a и sin a:
е\ = (cos a, sin a).
Аналогично находим, что орт е2 преобразуется в вектор
е'= (—sin a, cos а). Для произвольного вектора а вектора',
2 Б. 3. Вулих
О
Рис. 1.
18 КОНКЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. 1
полученный из а также вращением на угол а, должен иметь
те же проекции на е\ и ег, каковы проекции вектора а на et и е2.
Следовательно,
а' = ахе\ + а2е'2 = (at cos а — a2sln а, ajsin а ]-a2cos a).
Тем самым мы нашли координаты а'х и а'2 вектора а' и получили
формулы, которыми и описывается рассматриваемое преобразо-
преобразование:
а[ = a^cosa— a2sma, 1
, } (8)
a2 = а{ sin a + a2cos a. |
Читатель, конечно, заметит сходство между зтими формулами
и формулами преобразования прямоугольных координат на пло-
плоскости при повороте осей. Предлагаем читателю, чтобы лучше
понять причины этого сходства, самому получить формулы (8)
несколько иным способом, исходя из формул преобразования
координат.
Заменяя найденные коэффициенты при aj и а2 в формулах (8)
произвольными числами, напишем формулы более общего вида:
<¦'""- 1 (9)
Этими формулами определяется преобразование, которое при
произвольных коэффициентах может иметь гораздо более слож-
сложный характер, чем рассмотренное выше вращение. В результате
такого преобразования могут измениться и длины векторов и их
взаимное расположение.
Возвращаясь к n-мерному пространству, составим формулы,
аналогичные формулам (9):
а1 = ^Ual ~Ь ^12а2 ~Ь • • • 4~ t-lnani
а2 = t2iav + t22a2+ ... + t2nan,
A0)
- lnnO-п
Коротко эти формулы можно записать так:
п
"¦I = ?J '(ft"ft \l == *I ?•! • • . , П).
Все числа tih считаем вещественными. Формулами A0) каждому
вектору а = (аь а2, . . ., ап) из Rn сопоставляется вектор а' =
— (а[, а2, . . ., а'п) также из Вп, т. е. эти формулы определяют
оператор, преобразующий Нп в 2?„. Так как координаты вектора
а' линейно выражаются через координаты вектора а, то и само
преобразование назовем линейным.
1.5] ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ 19
Понятие оператора является непосредственным обобщением
понятия числовой функции. Можно сказать, что рассматриваемый
оператор есть функция, аргументом и значением которой являются
векторы из Rn. Обобщая обозначение функциона. ьного соотно-
соотношения, запишем тот факт, что вектор а' есть результат преобра-
преобразования, произведенного по формулам A0) над вектором а, в виде
а = Та. При этом мы считаем, что Т есть обозначение оператора
(или преобразования) *). Вектор а называется также образом
вектора а при преобразовании Т.
Отметим некоторые, почти очевидные свойства линейного пре-
преобразования Т:
1) Т (а + Ъ) = Та + ТЪ (аддитивность);
2) Т (Ха) = % (Та) (однородность);
3) 79 = 9.
Проверим, например, первое. Положим с = Т (а -\- Ь), а' = Та,
Ь' = ТЪ. Тогда при любом i = 1, 2, . . ., п имеем
п п п
С;= 2 tik(ak+bh)= 2 tihO-h+ 2 tihbh = a.i + b'i
fe=l ft=l fc=l
(здесь al, b\ — координаты векторов а' и Ь', соответственно).
Таким образом, с = а' + V.
Оказывается, что свойства аддитивности и однородности пол-
полностью характеризуют линейное преобразование, т. е. если каким
угодно способом задано преобразование Т, посредством которого
каждому вектору а из i?n сопоставляется некоторый вектор а'
также из Rn, и это преобразование аддитивно и однородно, то оно
может быть записано формулами A0) при надлежаще подобранных
коэффициентах.
Действительно, рассмотрим образы e'k координатных ортов
Ch {e'k = Те^)- Обозначим через tik (i = 1, 2, . . ., п) координаты
вектора e'k, т. е. e'k = (tik, t2k, ¦ ¦ ., tnk). Для произвольного
вектора а, благодаря аддитивности и однородности преобразова-
преобразования Т, имеем
П П 71
а' = Та = Т ( 2 O'tfih) = 2 ah (Teh) = 2
ft=i ft=i k=i
Отсюда для координат вектора а' получаем
п
а'г= 2 ahtih (i----l, 2, ..., п),
fe=l
*) В отличие от записи функции [например f (х)\, мы не заключаем
здесь аргумент а в скобки. Однако это не должно наводить читателя на
мысль о каком-то перемножении символов Т и а. Впрочем, иногда и здесь
заключают аргумент в скобки и пишут Т (а). Если же аргумент представ-
представляется выражением, составленным из нескольких векторов, например а + Ь,
то запись его без скобок просто неудобна.
2*
20 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
а это и есть формулы A0). Попутно мы выяснили и геометрический
смысл коэффициентов t^ (эти коэффициенты — координаты век-
векторов e'k).
1.6. Матрицы
Поскольку структура формул A0), определяющих линейное
преобразование в /?„, для всех преобразований одна и та же, раз-
различие может сказываться лишь в коэффициентах, следовательно,
каждое линейное преобразование полностью определяется коэф-
коэффициентами ttk. Выпишем эти коэффициенты в виде квадратной
таблицы:
Такая таблица называется матрицей п-то порядка и мы будем
обозначать ее той же буквой Т, что и преобразование *). Будем
также пользоваться краткой записью матрицы
Т = (tih)i, ft=l, 2, . . ., n-
Числа tih называются элементами матрицы Т. В обозначении
элементов первый индекс есть номер строки, а второй — столбца,
на пересечении которых находится данный элемент. Как мы виде-
видели в предыдущем параграфе, столбцы матрицы Т состоят из коор-
координат векторов e'k = Те^. Следовательно, изменение хотя бы одного
элемента матрицы уже влечет изменение образа одного из коор-
координатных ортов. Таким образом, не только каждой матрице п-то
порядка отвечает одно линейное преобразование, но и обратно,
каждое линейное преобразование описывается только
одной матрицей. В таком случае говорят, что соответствие
между матрицами и линейными преобразованиями взаимно
однозначное.
Приведем некоторые примеры.
1°. Единичная матрица
/1 0 0 ... 0\
О 1 0 ... О
I ~ 0 0 1 ... 0
V0 0 0 ... \)
*) Понятие матрицы не следует смешивать с понятием определителя.
¦Определитель есть число, составленное по определенному правилу из чисел
квадратной таблицы, матрица же есть сама таблица.
1.6]
МАТРИЦЫ
21
Если элементы этой матрицы обозначить через 6ik и записать
I = (Sik)i, k=i. 2 п. то ясно, что би = 1 и 6ik = 0 при i Ф к.
Из формул AС) сразу следует, что 1а — а для любого а, т. е. мат-
матрица / описывает тождественное преобразование.
2°. Матрица равномерного растяжения
Т = (kblk)^ k=u 2, ...,«, т. е.
Т =
ДОО ... O\
0X0 ... О
О О А, ... О
О 0 0 ... К)
Ясно, что Та = Ха.
3°. Матрица проектирования на орт et
/0 0 ... 0 ... 0\
0 0 ... 0 ... 0
О 0
1
О
\о о
— 1-я строка.
О ... О/
t-й столбец
В этой матрице все элементы равны нулю, кроме элемента, стоя-
стоящего на пересечении ?-й строки и ?-го столбца, который равен еди-
единице. Легко видеть, что Pta = а^е^
4°. Матрица круговой перестановки
ортов, т. е. такого линейного преобразования, при котором
орт ej переходит в е2, е2 в е3, . . ., en-i в е„, а еп в е^. На основа-
основании замечания о геометрическом смысле столбцов матрицы линей-
линейного преобразования мы сразу видим, что матрица круговой пере-
перестановки ортов имеет вид
/0 0 ... 0 1\
1 0 ... 0 0
0 1 ... 0 0
т
Vo о
о;
5°. Нулевая матрица в, у которой все элементы
равны нулю. Эта матрица преобразует все векторы пространства Л.п
в нулевой вектор.
22 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. 1
Определим некоторые действия над матрицами. При этом будем
рассматривать только матрицы одного и того же порядка. Пре-
Прежде всего условимся считать матрицы ЗП = (ljh)i, k=i, 2 п и
U = (Uihjith=i,2, ...,п равными (и писать Т = U) тогда и только
тогда, когда tih = ulh при всех i, к = 1, 2, . . ., и; иначе гово-
говоря, равными считаются матрицы, совпадающие по виду.
Сумма Т + U матриц Т и U определяется как матрица V, эле-
элементы которой vik = tik -\- uih. Произведение XT матрицы Т на
число X определяется как матрица с элементами Xtlh (i, к -
= 1,2,..., п). Таким образом, в отличие отправила умножения
определителя на число, при умножении матрицы на число следует
умножить на это число все элементы матрицы.
Сформулированные для матриц определения действий над ними
можно перенести и на операторы линейных преобразований в Вп.
Так, суммой V — Т -\- U двух операторов Т и U называется опе-
оператор, определяемый суммой матриц Т и U. Полагая для любого а
из Вп а' = Va, b = Та, с = Ua, имеем
п п п п
a'i= 2 Vikah= Ц (tih + Uih)dh= 2 tihak+ 2 uihah=bi + Ci,
т. e. a' = b -\-c или
Va = Ta + Ua. A1)
Рассуждая в обратном порядке, читатель легко убедится, что
из равенства A1) следует, что оператор V выражается суммой
матриц Т + U. Таким образом, равенство A1) полностью характе-
характеризует сумму операторов Т + U.
Аналогично, посредством матриц определяется произведение
U = XT оператора Т на число X и это произведение характери-
характеризуется равенством
Ua = X(Ta), A2)
справедливым для любого а из Вп.
Возвращаясь к приведенным выше примерам матриц, мы
можем теперь сказать, что матрица равномерного растяжения
имеет вид XI, а единичную матрицу можно представить в виде
суммы матриц проектирования на орты: /= Pi + Р2 + • . • + Рп-
Рассмотрим теперь вопрос о произведении линейных преобра-
преобразований (или произведении операторов). Произведением UT двух
линейных преобразований Т и U называется преобразование,
получающееся в результате последовательного применения пре-
преобразований Т и U:
(UT)a^U(Ta).
Правую часть этого равенства нужно понимать как «сложное»
преобразование (аналогично понятию сложной функции): сначала
1.6] МАТРИЦЫ 23
над вектором а производится преобразование Т, а затем над резуль-
результатом этого преобразования, т. е. над вектором Та, производится
преобразование U *).
Покажем, что произведение двух линейных преобразований
также является линейным преобразованием и найдем выражаю-
выражающую его матрицу. Положим Ъ = Та, с = Ub = (UT) а. Тогда
п
bJ = 2 hkdk (/ = 1,2, ..., п),
fti
п п п п п п
ct = 2 u-ijbj= 2 Utj 2 tjkak --- 2 UijtJkak= 2 ( 2 WijOft) «ft
;=1 j=l ft=l , j, ft=l ft=l i=l
(i = l, 2, ..., /г)
(последнее равенство получено за счет изменения порядка сумми-
суммирования, которое в конечных суммах всегда возможно). Теперь
введем матрицу V, элементы которой определяются формулой
A3)
Тогда мы имеем
C
п
i-= 2 vikak (?=1,2, . . ., тг),
А1
т. е. вектор с получается из а посредством линейного преобразова-
преобразования V, с = Va.
Согласно нашему определению, преобразование V и есть про-
произведение UT, а матрицу V, элементы которой определяются фор-
формулой A3), мы также назовем произведением матриц Т и U.
В отличие от произведения чисел или скалярного произведе-
произведения векторов произведение матриц (и соответствующих им опера-
операторов) зависит от порядка сомножителей. Покажем это на при-
примере матриц 2-го порядка. Пусть
Тогда
для V
"и
Т-
/0 1\
= (оо)
= UT имеем:
= Untn-.
Ь2<21 =
Ь^22<21Г
= 0,
= 0,
тт 1°
V12 = Unl
V22 = U2ii
о\
о)"
•12 +
fl2 +
= 0,
*) Вместо термина произведение для операторов употребляется также
термин суперпозиция.
24 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
Меняя местами Т и U, мы для W — TU имеем вместо A3) формулу
п
wik = 2 ttjUjh (i, к ---- 1, 2, . . ., и),
откуда
U>u = f иИц + t12U2i = 1, И>12 = <цИ12 + t12U22 = О,
= "? ^22 = ^21^12 Ч~ ^22W22 = ".
Таким образом,
^0 0\ /1 0\
и
Благодаря зависимости произведения матриц от порядка сомно-
сомножителей, их порядок необходимо указывать в определении произ-
произведения. Следовательно, формула A3) должна быть прочитана так:
элемент vih произведения матриц UТ равен сумме всех произведе-
произведений элементов ?-й строки левого сомножителя на соответствую-
соответствующие (т. е. взятые в том же порядке) элементы к-то столбца пра-
правого сомножителя.
Нетрудно указать некоторые частные случаи, когда произве-
произведение матриц не зависит от порядка сомножителей. Например,
читатель легко проверит, что если один из сомножителей — еди-
единичная матрица /, то для произвольной матрицы Т (того же поряд-
порядка) TI = IT = Т.
Предоставляем также читателю проверку того, что сложение
матриц и умножение матрицы на число подчиняются всей основной
группе алгебраических законов (см. 1.2).
1.7. Норма оператора линейного преобразования
До сих пор мы изучили некоторые свойства линейных преобра-
преобразований в Ип, связанные только с алгебраическими действиями над
векторами. Сейчас перейдем к сравнению вектора и его образа
по норме.
Пусть а' = Та, где Т — линейное преобразование. Тогда имеем
По неравенству Коши
B W
Подставляя в предыдущее равенство, находим
1КИ2<( 2 4) II «II2-
i, ft=l
1.8] НЕПРЕРЫВНОСТЬ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ 25
Введем постоянную
* ? 1 ^
Тогда
|К||<М||а||. A4)
Таким образом, для оператора Т существует такая постоянная М,
что норма образа любого вектора удовлетворяет неравенству A4).
Исключая случай а = 9, можно сказать, что отношение нормы
образа к норме исходного вектора не превосходит некоторой
постоянной М. Беря точную верхнюю границу С отношения *.а .
(а ф 6) *) мы получим, что || а'||-<С || а || при всех а из Цп иг
при этом С есть наименьшая из постоянных, которую можно поста-
поставить в неравенство A4) вместо М с сохранением этого неравенства
при всех а из Вп. Эта наименьшая постоянная называется нормой
оператора Т и обозначается || Т ||. Таким образом, для любого-
а из JRn
•га
|| Га |Г< || Г || || a IJ, A4а>
причем || Т || < М или | Т \ < "
V i,ft=i
1.8. Непрерывность линейного преобразования
В трехмерном эвклидовом пространстве расстояние между
двумя точками может быть выражено как длина разности радиу-
радиусов-векторов этих точек (рис. 2):
Поэтому сходимость некоторой последовательности точек Мп.
к предельной точке N-, т. е. стремление | MnN | —> 0, может быть
охарактеризована следующим условием | ОМп — ON \ —*¦ 0. Ана-
Аналогично, будем говорить, что последовательность векторов а,(т)
из Лп сходится (или стремится) к вектору а (пишем а<т> -*¦ а
или а = Нт а<т>), если
|| а(т) — а||-»0. A5)
*) Точной верхней границей ограниченного сверху множества чисел
называется наименьшая из его верхних границ. Существование точной
верхней границы доказывается в курсе математического анализа. Точна»
верхняя граница обозначается знаком sup, происходящим от латинского
слова supremum —«наивысшее».
26
КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО
[ГЛ. X
В этих обозначениях мы опускаем указание, что предел берется
при т—v оо, и будем поступать так же и в дальнейшем во всех
случаях, когда не будет опасности какой-нибудь путаницы.
Пусть заданные векторы имеют вид:
л а = [аи <22> • • ¦> ап)- Тогда условие A5) можно записать в форме
ft=l m-nx>
Если сумма неотрицательных слагаемых стремится к нулю, то и
каждое из них тоже стремится к нулю. Обратное верно (для конеч-
конечной суммы) независимо
от знака слагаемых. По-
Поэтому условие A5) рав-
М носильно такому:
N
*-Y
(Л = 1,2, ..., и),
т. е. определенная выше
сходимость последова-
последовательности векторов есть
сходимость по координа-
координатам. Читателю известен
аналогичный результат
для сходимости последо-
последовательности точек в трех-
трехмерном пространстве.
Теперь покажем, что линейное преобразование а' = Та в R^
обладает следующим свойством: если а(т) —*¦ а, то Га(т) —v Та. По
аналогии с соответствующим определением для функций это свой-
свойство называется непрерывностью оператора (или преобразования).
Действительно, по формулам A0) имеем для b(m) = Та<-т).
Рис. 2.
k=i
=l,2, .... n).
Но так как сходимость векторов в Jin есть покоординатная схо-
сходимость, то по A6)
ft=i
(t = l, 2, ..., /г),
. е. b(m) = {Ъ{™\ Ь[т\ ..., Ъ™) ~* а' = «, av ..., ап), где а' =-- Га.
1.93 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ 27
Непрерывность оператора Т можно доказать и иначе, исполь-
используя введенную в предыдущем параграфе норму оператора.
Именно,
fa(m) _ Та = f (a(m) _ a) (
следовательно,
|| ГоС») - Та ||< || Т || || а<»0 - а || -> 0.
В этом доказательстве мы не используем конкретного вида опе-
оператора Т, а опираемся лишь на его аддитивность, однородность
и тот факт, что для любого а выполнено неравенство A4)
[или A4а)].
1.9. Линейные функционалы
Понятие функционала является более простым, по сравнению
с оператором, обобщением понятия функции. Будем говорить,
что в Кп задан функционал /, если каждому вектору а из Цп сопо-
сопоставлено вещественное число / (а). Примером функционала может
служить скалярное произведение
/(«) = («, с), A7)
где с -заданный вектор из Вп- Развернутая запись формулы A7)
имеет вид
/ (а) = a^i + а2с2 + . . . + апсп
и потому этот функционал называется линейным.
Из свойств скалярного произведения сразу следует, что функ-
функционал / аддитивен и однороден в том смысле, как это было опре-
определено в 1.5 для операторов:
/ (а + Ь) = / (а) + / (Ь); / (Ка) = Xf (a).
Установим обратный результат. Для всякого аддитивного
м однородного функционала /, заданного в 1{п, существует такой
вектор с, что при любом а имеет место равенство A7).
Действительно, положим сг = / (ег) (? = 1, 2, . . ., п), где
е{ — координатные орты, и введем вектор с = (с1? с2, . . ., с„).
Тогда для любого а имеем, благодаря аддитивности и однород-
однородности /,
/(«)=/( 2 Wi) = S aif (ед = S Wi = (a. c)
i=i i=l t=i
и требуемое представление доказано.
Покажем еще, что по заданному функционалу / вектор с =
= (clt c2, • • •, с„), с помощью которого функционал записывает-
записывается в виде скалярного произведения, определяется единственным
28 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. 1
образом. Действительно, если дана формула A7), то для
а = et имеем (е;, с) = / (et). Но (ег, с) = сь следовательно, обяза-
обязательно должно быть ct = / (е;).
По неравенству G)
Таким образом, для / (а) выполнено неравенство вида A4):
\f(a)\<M\\a\\, A8)
причем в качестве одной из возможных постоянных М можно
взять ||с||. Оказывается, что ||с|| — наименьшая из всех возмож-
возможных постоянных. Чтобы убедиться в этом, положим а = с. Тогда
получаем
/ (с) = (с, с) НИ»-|| с || || с ||,
и поскольку здесь имеется точное равенство, знак ¦<; в формуле
A8) нарушится хотя бы для / (с) при попытке взять М < || с || *).
Так же как для операторов, наименьшую постоянную в нера-
неравенстве A8) назовем нормой функционала / (обозначаем ||/||).
Мы показали, что \\ / || = || с \\.
Предоставляем читателю самостоятельно проверить непрерыв-
непрерывность линейного функционала, т. е. что из а^т~> —*¦ а следует, что
/ (fl(">) -v / (a).
Если в скалярном произведении (ajb) оба сомножителя считать
переменными векторами, то получается обобщение функции двух
переменных — функционал с двумя аргументами, линейный по
отношению к каждому аргументу в отдельности. Этот функционал
называется билинейным.
1.10. Сопряженные и самосопряженные операторы
Во многих вопросах, связанных с матрицами, встречается опера-
операция перестановки их строк со столбцами. Например, в простей-
простейшем случае преобразования координат на плоскости при повороте
осей матрицы коэффициентов из выражений «старых» координат
через «новые» и «новых» через «старые» получаются друг из друга
перестановкой строк со столбцами. Введем общее определение.
Матрица Т* = (t*k)i, k=i, 2, ...,п, получающаяся из матрицы Т
перестановкой строк со столбцами, т. е. элементы которой t*^ = iA;,
*) Случай, когда с — 8, в Этом рассуждении исключается. Однако
в этом случае f (а) = 0. Следовательно, и в этом случае || с || (= 0) — наимень-
наименьшая из возможных постоянных в неравенстве A8).
1.10] СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 29
называется транспонированной (относительно Т). Например,
/ 1 2 3\ /1 0 — Г\
Т = I 0 12J, Г* = I 2 1 0 I .
\ —1 0 1/ \3 2 1/
Матрицы Г и Г*, как матрицы одного порядка, определяют
линейные преобразования в одном и том же эвклидовом простран-
пространстве Ип. Оператор Т* называется сопряженным по отношению
к оператору Т.
Основное свойство сопряженного оператора заключается
в равенстве
(Та,Ъ) = (а,Т*Ъ), A9)
имеющем место для любых а и b из Нп.
Для проверки этого равенства произведем следующий подсчет,
полагая а'= Та, Ъ' =Т*Ъ:
п п п п
(Та, Ь) = (а', Ь) = 2 «ifcj -2B ««АО») Ь* = 2 tlhahbu
i=i i=i ft=i *, ft=i
n n n n
(а, Г*6) = (a, b') = 2 flftbi= 2 a*( 2 *ft/bi) = 2 tikdkb.
ft=l /i=l /=1 ft, /=1
Полученные результаты различаются только обозначением одного
из индексов и, следовательно, A9) доказано.
Покажем, что оператор Г* — единственный линейный опера-
оператор в Нп, для которого при всех а и b выполнено A9). Пусть U —
линейный оператор и
(Та, b) = (a, Ub)
при всех а и Ъ. Положим а = et, b = eh. Тогда, как мы знаем из
1.5, Та и Ub выражаются соответствующими столбцами матриц Т
и U, именно
Ta=(tu, t2i, ..., tni), Ub=(uih, u2h, . . ., unk),
и предыдущее равенство дает thi = uih или uik = t*k. Таким обра-
образом, U = Т*.
Благодаря доказанным свойствам сопряженный оператор Т*
может быть определен как оператор, удовлетворяющий при любых
¦а и b из Вп условию A9).
Из формулы A9) следует, что скалярное произведение (Та, Ъ)
при фиксированном Ъ представляет линейный функционал от а.
Впрочем, в этом легко убедиться и непосредственно, опираясь
на результаты предыдущего параграфа.
30 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
Отметим очевидное соотношение Г** = Т, т. е. оператор, сопря-
сопряженный к сопряженному оператору, совпадает с исходным.
Оператор Т, совпадающий со своим сопряженным Т* (Т* = Т),
называется самосопряженным. Из определения транспонирован-
транспонированной матрицы Т* видно, что оператор Т будет самосопряженным
тогда и только тогда, когда thi = tih при всех i, к = i, 2, . . ., п.
Матрицы, удовлетворяющие этому условию, называются сим-
симметричными. Из равенства A9) вытекает следующее основное
свойство самосопряженного оператора: для любых а и b из Вп
(Та,Ь) = (а,ТЬ). B0)
Равенство B0)— частный случай равенства A9). Мы знаем, что
равенством A9) по заданному Т полностью определяется оператор
Т*; поэтому, если некоторый оператор Т удовлетворяет условию
B0), то для него Г* = Т. Таким образом, выполнение равенства
B0) при любых а и Ь является условием, необходимым и доста-
достаточным для самосопряженности оператора Т.
1.11. Подпространства в Вп
Линейной комбинацией заданных т векторов aiV, ai2\ . . ., а(№
называется всякий вектор, предетавимый в виде
Например, из формулы A) мы знаем, что любой вектор из Лп
является линейной комбинацией п координатных ортов.
Множество X всех векторов вида B1) называется подпростран-
подпространством пространства tfn, порожденным векторами ап\ а<2), . . .
. . ., а!т'. Легко видеть, что сумма любых двух векторов- из X
и произведение любого вектора из X на число также вкодят в X.
Среди векторов, образующих подпространство L, есть нулевой
вектор. Он получается из формулы B1) при kt = Х2 = ¦ • ¦ ~=
т
= Хт = 0. Может случиться, что 2j ^г#'!' = 9 и при некотором
другом наборе коэффициентов kt, среди которых имеется по край-
крайней мере один, отличный от нуля. В этом случае векторы аA\
а<2), . . ., а(т) называются линейно зависимыми. Если же равен-
т
ство 2 ^1а'г' — 9 имеет место только, когда Xi = Хг = • ¦ •
... = "кт = 0, векторы аа\ а<а), . . ., аШ) называются линейно
независимыми. Так, например, п координатных ортов линейно^
независимы, а векторы
1.111 ПОДПРОСТРАНСТВА В «п 31
линейно зависимы; между ними имеется зависимость
Линейная зависимость векторов означает, что, по крайней
мере, один из них является линейной комбинацией остальных.
т
Если 2 Ка^ = 9 и, например, Хтф0, то
г=1
Обратно, если, например, a<m) — А,,^1'-!-А,2яB) + • ¦ ¦ + ^m-ia(m~u»
то имеет место зависимость
m
VA) -h • • • + ^m-iaC"-1' — a<m> = Э или 2 ^«(i) = 9.
t=i
где A,m = —1.
Очевидно, что любые векторы, выделенные из некоторого набо-
набора линейно независимых векторов, также линейно независимы.
Заметим также, что среди линейно независимых векторов ни один
не может равняться" Э, так как, в противном случае, один из этих
векторов — нулевой ¦— можно было бы представить в виде ли-
линейной комбинации остальных (с коэффициентами, равными
нулю).
Возвращаемся к подпространству L, порождаемому векторами
аA), аB), . . ., а("°. Все эти векторы считаем отличными от нуле-
нулевого *). Допустим, что они линейно зависимы, например, а'' —
линейная комбинация остальных:
го-1
а(™>= 2 H-;«(i)-
г=1
Подставляя это выражение в формулу B1), получаем
т—1 т— 1 т—1 т— 1
i=l i = l г=1 1=1
Следовательно, каждый вектор B1) представляется также в виде-
линейной комбинации векторов аа\ аB), . . ., aim~x\ Обратно,
всякая линейная комбинация векторов аш, аB), . . ., а''может
быть записана и в форме B1), если положить Хт = 0. Таким об-
образом, если вектор а'' есть линейная комбинация векторов
*) Ясно, что нулевой вектор можно было бы выбросить из порождающей
системы и после этого порождаемое подпространство осталось бы прежним
32 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
«A), а<2), . . ., a'm~v, то подпространство, порождаемое векто-
векторами аA\ а<2), . . ., а'"", совпадает с подпространством, порож-
порождаемым векторами аа), а<2), . . ., а''. Следовательно, не изменяя
подпространства, можно исключить из системы порождающих его
векторов всякий вектор, являющийся линейной комбинацией
остальных. Произведя такое исключение последовательно надле-
надлежащее количество раз, можно добиться того, чтобы из заданной
системы векторов аA), а<2), . . ., а°п) остались только линейно
независимые, порождающие то же подпространство L. Таким обра-
образом, при определении подпространства всегда можно считать, что
порождающие его векторы линейно независимы.
Одно и то же подпространство может порождаться различными
системами линейно независимых векторов. Например, системы
иа) = е4, a'2) = ег и ba) = e4 -f- ez, fe'2> = ej — ez порождают
одно и то же подпространство. Если рассматривается трехмерное
эвклидово пространство, a et и ez — орты по осям ОХ и OY, то
порождаемое обеими указанными системами подпространство
состоит из всех векторов, лежащих в плоскости XY. Однако мы
докажем следующую важную теорему:
Теорема 1.11.1. Число *линейно независимых векторов,
порождающих заданное подпространство, при любом их выборе —
одно и то же.
Доказательство*). Пусть подпространство L порож-
порождается двумя системами линейно независимых векторов
аA), а<2), ..., а<т> и ЬA), Ь<2), ..., Ь(р).
Допустим, что р <; т, и рассмотрим векторы аA>, о'2
Как всякий вектор из L, аа\
комбинациями векторов второй системы:
Каждое из этих векторных равенств может быть заменено равно-
равносильной системой п координатных равенств
р _
B2а)
Покажем, что определитель D, составленный из коэффициентов у^
формул B2), отличен от нуля. Пусть Х1,Х2,--->^р удовлетворяют
*) В доказательстве мы используем общие теоремы о системах р линей-
линейных алгебраических уравнений с р неизвестными. Читатель, изучавший ранее
лишь системы из двух или трех уравнений, может для понимания идеи дока-
доказательства допустить, что р равно 2 или 3.
1.11] ПОДПРОСТРАНСТВА В Лп 33
однородной системе линейных алгебраических уравнений
v
2 \tk^i = О (/с = 1, 2, ..., р), B3)
или, в развернутом виде,
= 0,
= 0,
Yip^i -f ЪрК -г • • • + Ypp^p =-" °-
Из B3) следует, что
Но по B2)
= 2 *« 2 Y«*b(ft)= 2
il fel il
P
Следовательно, если Я,г удовлетворяют системе B3), то
i=i
= 0, а тогда, благодаря линейной независимости векторов
аа\ аB), . . ., а(Р), непременно ^ = Я,2 = ... = Хр = 0. Итак,
система B3) имеет только нулевое решение, а тогда ее определитель
отличен от нуля. Но матрица коэффициентов системы B3) полу-
получается из матрицы коэффициентов формул B2) транспонирова-
транспонированием, следовательно их определители равны и D Ф- 0.
Так как ?} =^= 0, из системы B2) можно получить выражение
векторов blh) через «'" (по известным формулам Крамера)
bW4iv (* = 1,2,...,р), B4)
i=l
где Dik — алгебраическое дополнение элемента у^*)- Но, ана-
аналогично формулам B2), векторы а<р+1), ..., а*"*) также
*) Чтобы убедиться в том, что правило Крамера применимо и к вектор-
векторным системам уравнений, достаточно решить по этому правилу каждую
из «координатных» систем B2а); тогда мы получим
БИБЛИОТЕКА Колхоз!
"Оскорка"
а эти равенства равносильны B4). Впрочем, правило Крамера можно вывести
обычным путем и непосредственно для векторных систем. |Ин
3 б. 3. Булих
34 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ.
представляются в виде линейных комбинаций векторов Ь( ':
a(i>= S yjkbih} (У-p-l-l, .... m).
ft=i
Подставляя сюда B4), получим
fe=l i=l i=l fc=i
откуда следует, что векторы а<р+1', . . ., а'т) суть линейные ком-
комбинации векторов аш, . . ., а<Р). Это противоречит линейной
независимости всех этих векторов. Полученное противоречие
доказывает невозможность неравенства р <^т. Аналогично, невоз-
невозможно и обратное неравенство т <С р, следовательно, непременно
должно быть т = р. Теорема доказана.
Доказанная теорема применима и ко всему Мп. Так как Кп
совпадает с подпространством, порождаемым п координатными
ортами (так что подпространством в частном случае может быть
и всё JRn), то и любая система линейно независимых векторов,
порождающих всё Rn, должна содержать п векторов. Подпро-
Подпространство, порождаемое одним вектором а, т. е. множество всех
векторов вида Ха (—оо <; % <; -(- оо), называется прямой, прохо-
проходящей через нулевой вектор.
Определение. Размерностью подпространства назы-
называется число порождающих его линейно независимых векторов.
Любая система линейно независимых векторов, порождающих
данное подпространство, называется его базисом.
Так, размерность всего Лп равна п, размерность прямой равна
единице. К подпространствам причисляется и множество, состоя-
состоящее из одного нулевого вектора, и его размерность считается рав-
равной нулю *). Из доказательства теоремы 1.11.1 следует, что в под-
подпространстве размерности т вообще не существует системы из
более чем т линейно независимых векторов.
Пусть Ъ — подпространство в Rn размерности т, векторы Ьп\
Ь'2\ . . ., Ъ{т — какой-нибудь его базис. Тогда L состоит из всех
векторов, имеющих вид
b=SP^(i). B5)
*) Если в соответствии с общим определением образовать подпростран-
подпространство, порождаемое нулевым вектором, то оно как раз и будет состоять из
одного этого вектора (так как а = Я,9 = 8). Однако нулевой вектор не
подходит под определение базиса, так как равенство Я-8 = 8 имеет место
при любом X. Таким образом, в подпространстве размерности нуль нет базиса .
1.12] ОРТОГОНАЛЬНЫЙ БАЗИС 35
При этом коэффициенты Р* в разложении B5) определяются
единственным образом. Действительно, если
то S (Pi — Уд ^<1> = ® и> благодаря линейной независимости
i=l
векторов b(l), P; = у, при всех i = 1, 2, . . .,.m.
Каждому вектору 6 из X сопоставим вектор а— (рь р2, . . ., Р™)
из m-мерного эвклидова пространства Вт. Тогда мы получим
взаимнооднозначное соответствие между векторами из ? и из Щп,
т. е. каждому Ъ из L соответствует только один а из Rm и, обратно,
каждый вектор а из Вт оказывается сопоставленным только одному
вектору Ъ из L. Можно сказать, что указанным соответствием опре-
определен оператор а = А Ь, отображающий L на Ит- Этот оператор А,
очевидно, аддитивен и однороден, т. е.
т т
Действительно, если, например, 6=2 Р^A). с= S уФ^К то
ii ii
Y2. •• •» Ут)
Таким образом, взаимнооднозначное соответствие, установлен-
установленное между L и Лт, обладает тем свойством, что алгебраическим
операциям (сложению и умножению на число) над векторами из
Tj соответствуют те же операции над их образами в Лт. Такое
взаимнооднозначное соответствие называется алгебраическим изо-
изоморфизмом, а подпространство L и m-мерное векторное простран-
пространство Rm называются алгебраически изоморфными. Однако при уста-
установленном алгебраическом изоморфизме в общем случае могут
не совпадать нормы векторов из I и их образов из Вт. В следую-
следующем параграфе мы увидим, каким условиям достаточно подчинить
базис в L для того, чтобы такое равенство норм имело место.
1.12. Ортогональный базис
Прежде всего докажем, что если векторы аA), а<2), . . ., а(т
попарно ортогональны и отличны от 6, то они линейно независимы.
771
Действительно, пусть имеет место равенство 2 ?ца<1) = 8.
Л=1
Умножим обе части равенства скалярно на а . Благодаря
3*
36 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
дистрибутивности скалярного произведения
и, таким образом, 2 Яг (a(i>, a(ft)) = F, а{к>) = 0. Но a(i) J. a""
при i Ф к, т. е. (a(l), а ) = 0, следовательно, из предыдущего
равенства получается A,h (aih\ а(к>) = 0, или Kh || а<'() ||2 = 0. Так
как а{к) Ф 0, то Kk = 0. Это рассуждение справедливо для любого
к = 1, 2, . . ., т, следовательно, ?ц = Я2 = ... = Ят = 0,
и вектоБЫ а<г) линейно независимы.
Определение. Базис подпространства, состоящий из
попарно ортогональных векторов, называется ортогональным. Если
нормы всех векторов, составляющих ортогональный базис, равны
единице, то базис называется ортонормированным.
Примером ортонормированного базиса в Лп может служить
совокупность всех координатных ортов.
Теорема 1.12.1. Если в подпространстве Ъ размерности т
выбран ортонормированный базис, то при алгебраическом изо-
изоморфизме между L и Вт, установленном в предыдущем параграфе
посредством оператора А, для любых векторов Ъ и с из Ъ
в частности, || АЪ || = || Ъ ||.
Доказательство. Пусть векторы 6A), ЬB\ . . .,
образуют ортонормированный базис в. L и пусть
Тогда АЪ = (рь р2, . . ., рт), Ас = (уи у2, ..., ут). Следовательно,
по определению скалярного произведения в Вт,
т
{АЪ, Ас)= 2 РФ-
С другой стороны,
mm m m
(b, с) = ( 2 P;&(i\ 2y^0))= 2 PiY.j(&<i). &Ш)= 2 PiYi(&(i), &(i)),
так как b(i) ± bm при i=fc/. Кроме того, (b(i), fe(i)) = || b(i) ||2 = 1,
а потому
1.12] ОРТОГОНАЛЬНЫЙ БАЗИС 37
В частности,
|| Ъ || = УЖЦ = V(Ab, АЪ) =--1| АЪ ||.
Теорема доказана.
Взаимнооднозначное соответствие а = АЪ между векторами
из Ъ и Rm, для которого || АЪ ||= || Ъ || при всех Ъ из Ь, называет-
называется изометричным.
Теперь покажем, что во всяком подпространстве (с размер-
размерностью, большей нуля) существует ортонормированный базис.
Именно, если аA\ а<2>, . . ., а<т) — произвольный базис под-
подпространства L, то в Ъ существует ортонормированный базис,
состоящий из векторов вида
Ъ(т) = |xmla<D + |хт2а<2> + ... -f |хттаС»).
Сначала построим ортогональный базис в Т, из векторов вида
2-1
сМ=.аМ, с(*> = а<*> — 2 ?wftc(ft) при i==2, 3, . .., m,
ft=i
которые определяются последовательно. Для этого нужно подо-
подобрать коэффициенты Х^ так, чтобы было соблюдено требование
ортогональности векторов са>, с<2), . . ., с''. Если коэффициен-
коэффициенты в выражениях векторов са), с<2>, . . ., cil'v, т. е. A,2i, Я31,
Я32, . . ., Vi, i> ^i-i, 2> • ¦ ¦. Vi, г-2 уже выбраны так, что сA),
с'21, . . ., с"' попарно ортогональны, то при к <С i имеем
г-1 г-1
, С(А)) = (а(О _ ^ J,O-C<J
3=1
Если последовательно подставить выражение сA) в с<2), сA)
и с ^ в сй и т. д., мы увидим, что каждый вектор с есть линейная
комбинация линейно независимых векторов аA), а<2), . . ., аа1,
причем коэффициент при а<1) равен единице. Поэтому, каждый
са) ф g *^_ Тогда из условия (с<г), с'к)) = 0 находим
. _ (а'{>, с(*>)
г^ 11^ II2 •
Итак, если все коэффициенты К^ определить по этой формуле,
векторы с^1), с<2>, ..., с<т> будут попарно ортогональны.
*) Все векторы а^ Ф.%, как линейно независимые. Поэтому, в част-
частности, сО Ф в.
38 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
Положим
Ясно, что эти векторы также попарно ортогональны, || Ь(г) || = 1
и каждый Ь(г) есть линейная комбинация векторов а'1', аB), .. ., a(i).
Из определения векторов с(*> видно, что
г-1 г-1
Так как каждый вектор из L есть линейная комбинация векторов
аA), аB), . . ., а(т), то, с помощью предыдущих формул, его
можно представить и как линейную комбинацию векторов
ЬA), 6B), . . ., Ь{т)*), следовательно, эти векторы образуют в L
ортонормированныи базис требуемого вида. Мы не останавливаем-
останавливаемся на составлении явных выражений для коэффициентов \iik-
Описанный процесс построения векторов сA), . . ., с("" или
Ьа\ . . ., ?т) называется ортогонализацией системы векторов
аа\ . . ., а(т).
Поясним изложенное на простом примере в трехмерном про-
пространстве. Пусть
о«> = A, 1, 0), а<2' = @, 1, 1), fl<3> = (l, 1, 1)
(читатель может непосредственно убедиться в линейной незави-
независимости этих векторов). Согласно общему методу полагаем
c<i> = aa) = (l, 1,0);
при этом || сA) || = У2. Далее
-<2) _ я<2)_ V rll)
— ( ! JL \\ II г<2) II — 1/ —
— ( ^ 'Уу' I' " — у 2 '
*) Мы пользуемся очевидным свойством линейных комбинаций: если
m
вектор а есть линейная комбинация векторов а' \ ..., а'', а= 2j ^ia >
а каждый а'г^ есть линейная комбинация векторов Ъ^\ ..., i>'p\ а'г^ =
= 2 Rft6(ft). то
следовательно, а —тоже линейная комбинация векторов б' *.
1.13] СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ВЕКТОРЫ 39
Наконец,
(а<3), с'1') , « (a<3), c<2>) 2
И
,,C) _ „C) 1 -<1) J. ^.B) — [ -i- — _^\ II /.C) II — _L_
с - а л31с л32с — ^ з ' 3 ' 3 у ' " " ~ уТ '
Теперь осталось нормировать построенные векторы, т. е. заменить
векторы c(i> векторами &(г\ Получим
1 ' о\ б<2>-
Уз" '
Эти векторы образуют ортонормированный базис в _R3, получен-
полученный методом ортогонализации первоначально заданных векторов.
Поскольку в любом подпространстве (с размерностью большей
нуля) существует ортонормированный базис, то алгебраический
изоморфизм между подпространством L размерности т и про-
пространством Rm всегда можно построить так, чтобы он был изомет-
ричным. В связи с этим подпространство Ъ и пространство Вт
тоже называются изометричными.
1.13. Собственные числа и собственные векторы
Для оператора Т = XI (где / — тождественный оператор,
определяемый единичной матрицей) любой вектор а из Rn удовле-
удовлетворяет соотношению
Та = \а. B6)
В то же время существуют операторы, для которых равенство B6)
с любым % не имеет места ни при одном а ф 0. Таков, например,
оператор вращения плоскости, рассмотренный в начале 1.5. Для
произвольного линейного преобразования Т ъ Rn вводим:
Определение. Всякое число к, для которого существует
вектор а^9, удовлетворяющий условию B6), называется соб-
собственным числом оператора Т, а упомянутый вектор а называется
собственным вектором оператора Т. Про этот вектор говорят, что
он соответствует собственному числу К.
Покажем, как находить собственные числа. Используя фор-
формулы A0), перепишем условие B6) в виде
t12a2 4- • . . -h tinan --= ),au
tn2a2 + ... 4- tnnan =
40
или
КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО
(tit — X) ai + t12az + . ..
ла^ + (t22 — X) a2 -b . . .
lnan = 0,
n = 0,
[ГЛ. I
B7)
Системой уравнений B7) определяются координаты ау, а2, . . ., ап
собственных векторов а. Но так как у собственного вектора по
крайней мере одна из координат отлична от нуля, то число X
будет собственным тогда и только тогда, когда система B7) имеет
ненулевое решение. А для этого необходимо и достаточно, чтобы
определитель системы B7) был равен нулю. Следовательно, соб-
собственные числа оператора Т находятся как корни уравнения
hi
¦X ..
tin
tin
t
rai
"
= 0.
B8)
Это уравнение называется характеристическим (или вековым)
уравнением оператора или матрицы Т *).
Уравнение B8)— алгебраическое уравнение п-й степени. Если
оно имеет вещественные корни, то оператор имеет собственные
числа; при этом различных собственных чисел оператор Т может
иметь не более п.
Матрица сопряженного оператора Т * получается из матрицы Т
транспонированием, а при транспонировании характеристическое
уравнение B8) не изменяется. Поэтому собственные числа опера-
операторов Г и Г* — одни и те же. Однако собственные векторы опера-
операторов Т и Т*, соответствующие одному и тому же собственному
числу, могут быть различными.
Если а — собственный вектор оператора Т, соответствующий
числу X, то, вследствие однородности Т, всякий вектор fia при
Р =?. 0 тоже — собственный вектор, соответствующий тому же X:
Полагая
—rr , мы получим собственный вектор —1| а || с нор-
мой, равной единице.
Если оператор Т самосопряжен, то его собственные векторы,
соответствующие различным собственным числам, ортогональны.
*) Название этого уравнения —«вековое» вошло в математику из астро-
астрономии.
1.13] СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ВЕКТОРЫ 41
Действительно, пусть Та = Ха, ТЪ = цЬ и X =/= ц. Тогда с помо-
помощью формулы B0) имеем
X (а, Ъ) = (Ха, Ъ) =- (Та, Ъ) = (а, ТЪ) = (а, цЬ) = ц (а, Ь)
или (X — fi) (а, Ъ) = 0. Но А, — fi Ф О, следовательно, (a, fr) =
= О*).
Докажем, что у самосопряженного оператора Т в Нп всегда
существует по крайней мере одно собственное число.
Характеристическое уравнение B8), как всякое алгебраиче-
алгебраическое уравнение, имеет по крайней мере один комплексный корень
X = [J. + iv. При подстановке этого значения X в систему B7)
последняя будет иметь ненулевое комплексное решение
ai = bi + icu a2=b2-\-ic2, ..., an = bn-\-icn,
т. е.
п
2 hh (bh -г геи) = (ц -Иv) (bj + iCj) (/ = 1, 2, . . ., re).
ft=i
Отделяя в этих равенствах вещественные и мнимые части, имеем
п п
S h = V-bj — vc}\ 2 hhCk --- цс; + vb7- B9)
ftl
h=l
(/ = 1,2 71).
Введем векторы Ь = (bu b2, . . ., bn) и с = (ct, c2, . . ., cn).
Так как хоть одно из чисел Ъи. Ъг, . . ., Ъп, си с2, . . ., сп отлично
от нуля, то по крайней мере один из векторов Ъ или с отличен от 0,
а потому || Ъ [|2 + || с ||2 >0.
Используя обозначение оператора Т, мы можем записать равен-
равенства B9) в виде
ТЬ--=цЬ—vc; Тс = цс + vb.
Вследствие самосопряженности оператора Т, (ТЬ, с) = (Ь, Тс). Но
(ТЪ, с) - (ц,Ь — vc, с) = ц (Ь, с) — v (с, с),
(Ь, Тс) = (b,nc + vb) = li (b, с) + v (Ь, Ь).
Приравнивая правые части, находим
— v(c, c)=-v(b, Ь),
или — v || с |j2 = v|| Ь ||2, откуда
*) В общем случае аналогично доказывается ортогональность собствен-
собственных векторов операторов Г и Г*, соответствующих различным собственным
числам.
42 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
Так как || Ъ ||2 + || с ||2 > 0, то непременно v = 0, а это и означает,
что рассматриваемый корень К характеристического уравнения —
вещественный и, следовательно, является собственным числом.
Фактически мы доказали, что для самосопряженного оператора
уравнение B8) имеет только вещественные корни.
Если характеристическое уравнение для самосопряженного
оператора имеет п различных (простых) корней, то оператор
имеет п попарно ортогональных собственных векторов и, следова-
следовательно, в Rn можно построить ортонормированный базис из соб-
собственных векторов. Можно доказать, что этот результат верен для
любого самосопряженного оператора в Rn, независимо от харак-
характера корней векового уравнения.
Приведем пример. Пусть все координатные орты еь е2, . . ., еп—
собственные векторы оператора Т, соответствующие собствен-
собственным числам Я,,, %2> . . ., %п (среди которых могут быть и равные).
Тогда для любого к = 1, 2, . . ., п будет Teh = Kheh, следова-
следовательно, в к-м столбце матрицы Т элемент thh — ^s> а прочие эле-
элементы равны нулю. Таким образом, матрица Т имеет диагональ-
диагональный вид:
, 0 ... О
Оператор Т в этом случае самосопряженный.
Рассмотрим теперь более общий случай. Именно, пусть в Rn
имеется ортонормированный базис из собственных векторов biV,
bB), . . . 6A) оператора Т, соответствующих собственным числам
%i, Х2, . . ., "кп. Каждый вектор Ъ из Rn представим в виде Ъ =
п
~- 2 Pjb(t). Исходя из этого представления, как показано в 1.11
и 1.12, можно построить изометрическое отображение простран-
пространства Вп на другой экземпляр Нп (обозначим его Н'п), полагая
АЪ = а, где а = (р„ р2, • • ¦. Р/0-
При этом отображении векторам ?1) из Rn соответствуют коорди-
координатные орты е% из R'n. Оператор Т порождает линейное преобразо-
преобразование Т' пространства R'n, если положить для всякого а из Rn
Т'а = А{ТЪ),
зделяемый соо
з Rn
Т'{АЪ) = А(ТЪ).
где Ъ — вектор из Rn, определяемый соотношением АЪ — а. Иными
словами, для любого Ъ из Rn
1.14] КОМПЛЕКСНОЕ n-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО 43
Аддитивность и однородность преобразования Т вытекает из
наличия этих свойств у операторов Т ж А.
Легко видеть, что координатные орты ei из В'п — собственные
векторы оператора Т'. Действительно,
T'et = A (Tb(i)) = А Aф{1)) = h (Ab(i)) = }чеь
На основании разобранного выше примера, матрица Т' — диаго-
диагональная, а оператор 7" — самосопряженный. Так как по теоре-
теореме 1.12.1 оператор А сохраняет без изменения"величину скаляр-
скалярного произведения, то и оператор Т — самосопряженный. В самом
деле, для любых Ъ и с из Лп имеем
(ТЬ, с) = (А (ТЬ), Ас) = (Г (АЬ), Ас) =
= (АЬ, Г (Ас)) = (АЬ, А (Тс)) = (Ъ, Тс),
т. е. (ТЬ, с) = (Ь, Тс), а этим свойством и характеризуются само-
самосопряженные операторы.
Таким образом, мы показали, что если линейный оператор
в Нп имеет п попарно ортогональных собственных векторов, то
он — самосопряженный. Кроме того, мы видим, что, используя
собственные векторы самосопряженного оператора для составле-
составления базиса, мы можем сводить изучение этого оператора к изуче-
изучению более простого оператора, записываемого матрицей диаго-
диагонального вида. Более подробно на вопросе о структуре матрицы Т'
при различных выборах базиса в Rn мы не останавливаемся.
1.14. Комплексное те-мерное эвклидово пространство
Изложенное в этой главе может быть обобщено на случай
векторов с комплексными координатами. Комплексным вектором на-
называется совокупность п комплексных чисел а = (at, а2, • • •, ап).
Алгебраические операции для комплексных векторов опреде-
определяются так же, как в 1.2, но произведение Ха теперь имеет
смысл для любого комплексного числа К. Сохраняется в силе
основная группа алгебраических законов. Множество всех ком-
комплексных векторов (при фиксированном п) называется п-мерным
комплексным векторным пространством. Обозначим его Нп.
Норма вектора в ,К„ определяется формулой
2
t=i
частным случаем которой является формула B), данная выше для
Вп. При таком определении нормы пространство Нп называется
п-мерным комплексным эвклидовым пространством.
44 КОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. I
Скалярное произведение векторов а и Ъ определяется в Цп
следующим обобщением формулы E):
(а, Ь) = 2а^*).
Норма и скалярное произведение в Бп обладают теми же свой-
свойствами, что и в Rn, включая неравенство треугольника для нормы
и неравенство Коши G) для скалярного произведения **), кроме
коммутативности скалярного произведения, которая заменяется
в Вп тем, что
т. е. при перестановке сомножителей скалярное произведение
принимает сопряженное значение. Ассоциативность по отношению
к умножению на число принимает вид:
(la, b)^X(a, Ъ); (а, Щ=Л(а, Ь).
Определение ортогональности векторов в Rn вводится так же,
как в Rn\ a _L Ъ, если (а, Ъ) — 0.
Теми же формулами A0), что ивйП! можно определить линей-
линейное преобразование в Rn, допуская, однако, при этом в качестве
коэффициентов tih любые комплексные числа. Таким образом,
линейные операторы в Sn описываются матрицами с комплексными
элементами. Установленные в 1.5—1.8 свойства линейных опера-
операторов сохраняются и в Iin. Для нормы оператора получается оценка
\\т\\<\/ 2 \tih\\
\ г,ь=1
Сопряженный оператор Т* определяется матрицей, элементы
которой t*k связаны с элементами исходной матрицы соотноше-
соотношениями
t*k = thi (г, к = 1, 2, . .., п).
*) Черта означает переход к сопряженному комплексному числу.
**) Для сумм комплексных чисел неравенство Коши имеет вид:
|2|C)C)
г=1 г=1 1=1
Это неравенство легко получается из неравенства Коши, установленного
для вещественных чисел, а именно:
1.1'i] КОМПЛЕКСНОЕ n-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО 45
При этом получается прежнее равенство A9), которым оператор Т*
полностью характеризуется. Оператор самосопряжен тогда
и только тогда, когда t^ = t^ при всех i, к = 1, 2, . . ., п.
В частности, диагональные элементы tH должны быть веществен-
вещественными.
Так же, как в 1.11, вводится понятие подпространства, причем
в определении линейной комбинации векторов по формуле B1)
коэффициенты могут быть любыми комплексными числами.
Собственные числа и собственные векторы определяются так
же, как в 1.13, посредством равенства B6), однако здесь допу-
допускается, что собственное значение может быть любым комплекс-
комплексным числом. Для нахождения собственных чисел по-прежнему
получается характеристическое уравнение B8). Но так как алге-
алгебраическое уравнение всегда имеет по крайней мере один комплекс-
комплексный корень, то всякий линейный оператор Т в Rn имеет по край-
крайней мере одно собственное число. Каждому собственному числу X
оператора Т отвечает сопряженное собственное число оператора Т*.
Хотя, в общем случае, собственными числами могут быть
любые комплексные числа, но все собственные числа самосопря-
самосопряженного оператора Т в Ип вещественны. Этот результат по суще-
существу уже доказан в 1.13 для того частного случая, когда все эле-
элементы матрицы Т вещественны. Проведем доказательство, приме-
применимое для любого самосопряженного оператора Т в Цп. Пусть
Я — собственное число на — соответствующий ему собственный
вектор. Тогда
% (а, а) = (%а, а) = (Та, а) = (а, Та) = (а, Ка) = Х(а, а).
Отсюда, так как а Ф Э, следует X = К, и, таким образом, Я —
вещественное *).
Для самосопряженного оператора собственные векторы, соот-
соответствующие различным собственным числам, ортогональны.
*) Значительное упрощение этого доказательства по сравнению с рас-
рассуждением из 1.13 объясняется переходом к рассмотрению пространства
комплексных векторов.
ГЛАВА II
БЕСКОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО
2.1. Векторы с бесконечным множеством координат
В настоящей главе мы будем изучать пространство более слож-
сложной структуры, чем конечно-мерное эвклидово, но все же во мно-
многом сходное с ним по своим свойствам. Это пространство состоит
из векторов, определяемых бесконечным множеством координат.
Как и в гл. I, основное изложение будем вести для векторов
с вещественными координатами.
Определение. Вектором с бесконечным множеством
координат (в дальнейшем часто будем говорить просто — вектор)
называется бесконечная последовательность вещественных чисел
(а.1, а2, . . ., аь . . .). Как и раньше, будем обозначать вектор
одной буквой и писать, например, так:
а — (аи а2, . . ., at, . ..).
Члены последовательности а^, а2, . . ., «;, ... назовем коор-
координатами вектора а-
Вектор, все координаты которого равны нулю, как и в гл. I,
называется нулевым и обозначается 0.
Равенство векторов, их сложение и умножение на веществен-
вещественное число определим по тому же принципу, что и в Rn. Именно,
если а = (аи а2, . . ., at, . . .) и Ъ = (Ьи Ь2, . .- ., Ьи . . .), то
а — Ь означает, что ai = bi при всех г = 1, 2, ...;
а-\-Ъ = (ai-rbi, а2-\-Ъ2, .. •, a.i-\-bu ...);
Ха = (Хаи Ха2, . .., XaL, .. .).
Как и в i?n, сложение векторов с бесконечным множеством
координат и их умножение на число удовлетворяют основной
группе алгебраических законов (см. 1.2). Так же, как в Rn, можно
определить вычитание векторов, и действие вычитания оказывает-
оказывается обратным сложению.
Множество всех векторов с бесконечным множеством коорди-
координат будем обозначать s. По аналогии с Rn его следовало бы назвать
2.2] ПРОСТРАНСТВО П 47
бесконечно-мерным векторным пространством. Однако, как мы
увидим дальше, представляет интерес не только всё s, но и некото-
некоторые его части, которые также могут быть названы бесконечномер-
бесконечномерными векторными пространствами и которые по своим свойствам
ближе к пространствам Rn. Поэтому мы будем называть s просто
пространством всех числовых последовательностей.
Координатными ортами в s назовем векторы, у которых одна
из координат равна единице, а все остальные равны нулю. Таким
образом, если, как в 1.6, Ьц = 1 и Ьи = О при i Ф /, то орт et
определяется как следующая числовая последовательность:
Однако в этом параграфе мы не имеем возможности дать формулу
разложения произвольного вектора по координатным ортам. Дей-
Действительно, если вектор имеет бесконечное множество отличных
от нуля координат, то он не представим никакой линейной комби-
комбинацией конечного числа ортов
Следовательно, формула разложения в прежнем виде невозможна.
Ниже мы установим ее обобщение.
2.2. Пространство Р
Выделим из s множество векторов более близкое по своим свой-
свойствам к конечно-мерному эвклидову пространству. Именно, обо-
обозначим через I2 множество всех векторов а из s, для которых
2 я? < + со
(т. е. ряд, составленный из квадратов координат, сходится).
Ясно, что если а входит в I2, то и "ка входит в I2 при любом X.
Менее очевидно, что и операция сложения векторов не выводит
из Р. Докажем это.
Пусть а и Ъ — два вектора из I2. При любом натуральном п по
неравенству треугольника, доказанному в 1.3,
i=
Тем более,
v, J°'+V,S«l-
48 БЕСКОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. II
Так как в правой части неравенства стоит постоянная, а для поло-
положительных рядов ограниченность частичных сумм влечет сходи-
сходимость ряда, то ряд
сходится и при этом
\/ .| (<Ч + Ьг)'< у Jj a\
a\ + уД Ь\.
Тем самым доказано, что вектор а + Ь входит в I2, а заодно
неравенство треугольника обобщено на бесконечные суммы.
Поскольку сложение векторов из I2 и умножение вектора из I2
на число не выводят из ?2,,в этом множестве также выполнены все
алгебраические законы основной группы, справедливые, как мы
отмечали, и во всем s.
Теперь для векторов из I2 определим норму по формуле
II a II =-
Эта норма, очевидно, обладает тремя основными свойствами, пере-
перечисленными в 1.3. Неравенство треугольника для нормы есть
другая запись только что доказанного неравенства треугольника
для бесконечных сумм.
Определение. Множество I2, в котором по формуле A)
определена норма вектора, называется бесконечно-мерным эвкли-
эвклидовым пространством.
В дальнейшем множество I2 всегда рассматривается как эвкли-
эвклидово пространство.
2.3. Скалярное произведение векторов из I2
По аналогии с понятием скалярного произведения векторов
из Нп определим скалярное произведение (а, Ъ) двух векторов
а и Ь из I2 по формуле
(а, Ь) = _2<М>{. B)
Чтобы это определение имело смысл, нужно показать, что ряд
в правой части B) сходится.
По неравенству Копти, установленному в 1.3, имеем при любом
натуральном п
2.4] СХОДИМОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ВЕКТОРОВ 49
Заменяя в правой части гена оо и рассуждая так же, как в преды-
предыдущем параграфе при обобщении неравенства треугольника на
00
случай бесконечных сумм, получим, что ряд 2 I ai I ! ^г | сходит-
ся и что
Тем самым доказана абсолютная сходимость ряда 2 aibu а нера-
i=i
венство Ноши также распространено и на бесконечные суммы:
Bа«Ь»J<B«!)BЬ?)- C)
t=i i=i t=i
Итак, скалярное произведение имеет смысл для любых двух
векторов из Р. При этом из неравенства Коши C), как и в Мп,
вытекает, что
\(а, й)|<||а||||Ь||. D)
Последнее соотношение также называют неравенством Коши.
Отмеченные в 1.4 свойства скалярного произведения в Лп:
коммутативность, ассоциативность по отношению к умножению
на число, дистрибутивность относительно сложения, очевидно,
сохраняются и в I2. Между нормой и скалярным произведением
существует прежняя зависимость
|| a || =/(a, а).
Так же, как в Вп, определяем понятие ортогональности век-
векторов:
a j_ b, если (a, b) = 0.
Это определение позволяет ив?2 дать то обобщение теоремы
Пифагора, которое было получено в 1.4.
Таким образом, нам уже удалось перенести в Р ряд основных
определений, введенных ранее в Цп, с сохранением многих основ-
основных свойств последнего.
2.4. Сходимость последовательности векторов
Как и в Нп, будем говорить, что последовательность векторов
а'"" из I2 сходится к вектору а из I2, (а"'" ->¦ а), если
||а(т)_а||_^0. E)
Вводя в рассмотрение координаты векторов a(m) и а, именно,
4 Б. 3. Вулих
50 БЕСКОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. II
записывая эти векторы в виде4
аЫ) = (a(m)i аоп)г . . . , в(т)| . . .) ' д = (в11 п2 в,, . . .),
можно представить условие E), в виде
Отсюда ясно, что если а^т^—>а, то
а\т) —> at при всех i = 1, 2, ... F)
Однако, в отличие от Rn, в I2 уже нельзя сделать обратного заклю-
заключения, т. е. сходимость последовательности векторов содержит
в себе более сильное требование, чем просто сходимость по коор-
координатам.
Поясним сказанное на примере. Пусть а'' = ет (ет — коорди-
координатный орт), а = 9. При каждом i будет а!™' = 6т1, следовательно,
а'т) = 0 при т > ?, а так как at = 0 при всех i, то F) выполнено.
Однако
||M
следовательно, а"п) не стремится к а *).
Для вещественных чисел известен следующий признак сходимо-
сходимости (Больцано — Коши): для того чтобы последовательность веще-
вещественных чисел хт имела конечный предел, необходимо и достаточ-
достаточно, чтобы
хт — Хр—>0 при т, р~->со.
Последнее означает, что для любого е > 0 существует такое М,
что \хт — хр | < е при т, р^М **). Покажем, что аналогичным
свойством обладает и сходимость в f2: для того чтобы последова-
последовательность векторов а('"' из Р сходиласък некоторому вектору (из V2),
необходимо и достаточно, чтобы
>o при т,
Пусть a(mJ—> а. Так как из равенства
а(т) _ а(р) ^ (a(m) _ a) ^ (д _
следует, что
|| a<m) _ д(р) || ,С J) д(т) _ в Ц + || в<М - в |
а при т, р—> оо правая часть стремится к нулю, то и
*) Из этого рассужценяя также сразу следует, что последовательность
ортов {ет} вообще не имеет никакого предела.
**) См., например, Г. М. Ф и х т е н г о л ь ц. Основы математического
а-нализа, т. I, стр. 107.
2.4] СХОДИМОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ВЕКТОРОВ 51
Несколько сложнее доказывается обратное. Пусть последова-
последовательность векторов aim) такова, что || aim) — air>) || -v 0 при
т, р -*¦ оо. Так как
а при каждом г
_ аи>) ||в = 2
S
то и a|m) — <4Р) -v 0 при каждом i = 1, 2, ... По признаку Боль-
цано — Коши для вещественных чисел отсюда следует, что при
каждом i существует конечное at = lim al'. Составим вектор
?n-voo
а = (a(, аг, . . ., аг, . . .) из пространства s. Докажем, что он
входит в Си что а = lim а("'\
Согласно данному условию, для любого е > 0 существует
такое М, что при т, р > М
у е2.
Оставляя в сумме лишь конечное число слагаемых, имеем тем
более при любом п и при т, р^-М
Фиксируя т и переходя к пределу при р—> оо, получаем
п
1=1
Так как это неравенство верно при любом натуральном п, то ряд
^ (а[т> —а,J сходится и
оо
2 (а<т'-а;J<уе2<е2.
Тем самым доказано, что вектор а(т> — а входит в Р и
Ц а<т> — а || < е при т>М. Но тогда, по доказанному в 2.2,.
и вектор а = аищ — (а() — а) входит в 1г и при этом а<т) -v 4„
4*.
52 БЕСКОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. 11
Таким образом, в указанном обобщенном виде признак Боль-
цано — Коши верен и в I2. Читатель, конечно, заметил, что прове-
проведенное рассуждение, с надлежащими упрощениями, справедливо
и в Вп, следовательно, признак Больцано — Коши верен также
и в В„.
Обратимся теперь к рассмотрению бесконечных рядов, состав-
составленных из векторов, входящих в I2:
оо
2 ь("\
л=1
где b{h) — векторы из I2.
Сумма такого ряда определяется, аналогично сумме числового
ряда, как предел последовательности частичных сумм: о =
т
= lim om, где ат = 2 Ь{к) (здесь ат и а — векторы из I2). Если
такой предел существует, то ряд называется сходящимся, в про-
противном случае говорят, что ряд расходится.
Рассмотрение рядов позволяет ив?2 дать формулу разложе-
разложения произвольного вектора по координатным ортам. Именно,
m
для произвольного вектора а положим ат = 2 aiei- Тогда
!=1
ат=(а,, аг, ..., ат, 0, 0, .. .),
а — от = @, 0, . . ., 0, йт+1, йт+2, . . .)
и
так как ряд 2 а* сходится. Таким образом, a=Iimom, или
i=i
оо
а= 2 «(«г- G)
i
Коэффициенты этого разложения имеют тот же вид, что и в
Д„ : ог = (а, е,).
Если векторный ряд 2 ^((" таков> что сходится числовой ряд
*=i
оо
2 II ^<;" ||, то и данный векторный ряд тоже сходится и называется
А=1
абсолютно сходящимся. Действительно, обозначим через ат и sm
частичные суммы указанных рядов, векторного и числового
2.5] НЕПРЕРЫВНОСТЬ НОРМЫ И СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ 53
(соответственно). Тогда, при т> р,
и так как sm — sp->0 при т, р -v оо, то и || от — ар || -v 0. Но
тогда существует о = lim am, т. е. данный векторный ряд схо-
сходится.
2.5. Непрерывность нормы и скалярного произведения
Покажем теперь, что норма вектора и скалярное произведение
двух векторов из I2 непрерывны в следующем смысле:
если а<т)—>а, то || а<т> ||-^-1| а ||;
если a<m>->a, b(m)-+b, то (а(т\ Ь(т)) -> (а, Ь).
Хотя первое утверждение получается из второго, если
положить 6(т) = а(т) при всех т, все же удобнее сначала доказать
первое.
Пусть а<т' —> а. Из равенств
а(т) = а + (а<т> — а), а = (а — а<т)) -(- а<т)
имеем
Решая второе неравенство также относительно || а<т) || и объеди-
объединяя с первым, получаем
Отсюда и видно, что || ат) || -> [| а ||. Так как сходящаяся число-
числовая последовательность ограничена, то из доказанной непрерыв-
непрерывности нормы вытекает, что нормы векторов, образующих сходя-
сходящуюся последовательность, в совокупности ограничены.
оо
Возвращаясь к абсолютно сходящемуся ряду 2 &""> рассмо-
тренному в конце предыдущего параграфа, запишем сначала
неравенство
Переходя к пределу при т->оо и используя непрерывность
*) Неравенство треугольника для нормы по индукции, очевидно, обоб-
обобщается на любое конечное число слагаемых.
54 БЕСКОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. II
нормы, получаем для суммы ряда неравенство
Таким образом, на абсолютно еходящиеся ряды расирвстраияется
неравенство треугольника:
II 2 ь(Л)|1< Sl|b(fc)l!-
Переходим к непрерывности скалярного произведения. Пусть
а^т)—>а, fc<m>—>ft. Имеем тождество
(«С»), Ыт))—(а, Ь)^ («С»), &("»)) — (а, Ыт))-±{а, 6<m>) — {а, Ъ) ^
= (а<т> — a, 6<m>) -f (а, Ыт) — Ъ).
По доказанному || Ыт)\\ <С при всех т, где С — некоторая постоян-
постоянная. С помощью неравенства Коши D) имеем:
_ а, Ыт) | < || а<т> - а || || b<m) || < С || а(») - а \\ -> О,
| (а, Ь(»>- Ь) | < || а || || 6(«)- Ь ||-> О,
откуда (a'm), b<m))-^ (а, 6).
Непрерывность скалярного произведения позволяет устано-
установить, что оно обладает свойством дистрибутивности и по отношению
к сложению бесконечного множества слагаемых. Именно, пусть а
и Ъ — два вектора, причем Ъ -- 2 Ь^, т. е. Ь—- lim om, где
7/1
ат = 2 Ь('°- Тогда
тп m оо
(а,- Ь) = lim (а, от) - Ит (а, 2 Ь<*>) = Нт j (а, &<*>)= 2 (а, Ь(*>)-
ft=i ft=i k=i
Отсюда, в частности, следует, что если вектор a _L b^ при
любом А; — 1, 2, . . ., то a J_ Ь.
Теперь мы можем дать и обобщение теоремы Пифагора для
бесконечных сумм. Пусть Ъ — 2 ^<ft) и векторы Ык) попарно орто-
тональны. Тогда
ць|,»-(ь, ъ)~(ь, §&(*))= 2 (М
Но так как Ы1> J_ fe<ft) при 1фк, то
= ( 2 b«'
2.6] ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ 55
следовательно,
Очевидно, что все сказанное в этом параграфе справедливо
и в пространстве Л„.
2.6. Линейные функционалы
Рассмотрим скалярное произведение (а, с), считая с заданным
вектором из Р, а — произвольным. Тем самым, каждому век-
вектору а из I2 сопоставляется вещественное число (а, с), и мы можем
сказать, что выражение (а, с) представляет функционал от а:
1 (а) =--- (а, с). (8)
В развернутом виде
Из свойств скалярного произведения вытекает, что функцио-
функционал / аддитивен, однороден и непрерывно зависит от а. Как
н в Еп, этот функционал / называют линейным.
Так же, как в 1.9, из неравенства Коши следует, что
1/ИК1М1И1
и что || с || — наименьшая из постоянных М, для которых при
любом а имеет место неравенство
\f(a)\<M\\a\\. (9)
Эта наименьшая из постоянных М называется нормой функциона-
функционала / (обозначается || / ||). Свойство, выраженное неравенством (9),
называется ограниченностью функционала /. Заметим, что это
свойство не означает, что множество всех значений функционала
/ (а) ограничено. Из неравенства (9) вытекает лишь то, что для
любого множества векторов а, нормы которых в совокупности огра-
ограничены, множество значений / (а) тоже ограничено.
При исследовании функционалов в Z2 свойство ограниченно-
ограниченности играет более существенную роль, чем в ffn. В отличие от функ-
функционалов в /?п, если в I2 задан произвольный аддитивный и одно-
однородный функционал, т. е. каждому вектору а из I1 сопоставлено
вещественное число / (а), причем
то нельзя утверждать, что этот функционал представим по
формуле (8). К формуле (8) сводятся лишь те аддитивные и однород-
56 БЕСКОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО ГГЛ. II
ные функционалы в Z2, которые удовлетворяют условию ограни-
ограниченности (9), а класс всех аддитивных и однородных функциона-
функционалов в I2 оказывается более широким.
Итак, пусть / — произвольный аддитивный и однородный функ-
функционал, заданный в Z2 и удовлетворяющий условию (9) *). Прежде
всего заметим, что из этих свойств функционала / вытекает его
непрерывность. Именно, если а(П" -+• а, то
/ (а<т>) — /.(а) | =- | / (д<т> — а),\<М\\ а<т> — а || —> О,
т. е. / (а<т>) —> / (а). Далее, положим сг = / {е{) (i = 1, 2, ...), где
е, — координатные орты. Используя формулу разложения G),
имеем для любого а из Р
оо т
/ (а) - / ( 2 ад) =.- / (lim 2 а<«г) =;
--¦ lim / ( 2j flj^j) = lim 2j a'd (eO -
и формула (8а) получена. Однако, чтобы записать f(a) в виде
скалярного произведения вектора а на постоянный вектор из Р,
нужно показать, что вектор с = (сь с2, . . ., си . . .) входит в Р.
С этой целью, при произвольном натуральном п возьмем век-
вектор а, у которого
ai =¦ ci Для i — 1, 2, . . ., п; й, — 0 для i > п.
п
Тогда по (8а) / (а) =-- 2 °Ь С другой стороны, по неравенству (9),
/п п Г п
2 с?. Следовательно, 2с?^-^1/ 2 сь откуда
V
/ п
2 с! < Л/, или
1=1
1 = 1
Так как это верно при любом натуральном п, то ряд 2 c'i сходит-
1=1
ся, а это и означает принадлежность вектора с к Р.
В точности так же, как в 1.9 для функционалов в простран-
пространстве Вп, доказывается, что вектор с, с помощью которого функцио-
функционал / (а) представляется по формуле (8),— единственный.
*) Можно показать, что однородность вытекает из аддитивности и огра-
ограниченности. Это будет сделано в более общем случае в гл. VIII.
2.7] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 57
2.7. Линейные операторы
С целью распространения на I2 понятия линейного преобразо-
преобразования, введенного в 1.5, составим бесконечную систему формул
а[ — tnax -f /12а2 -f ¦ ¦ ¦ -Г ti^k + • ¦ ¦ )
а'г = tuax + Z22a2 -J- . . . - I
а| — /иа, -r-/j2a2-f- • ¦ ¦
[краткая запись:
оо
a'i= 2 /,-ftaA (i = l, 2, ...)].
Как и раньше, коэффициенты ?ift предполагаются вещественными.
Однако, если аналогичными формулами A0) из 1.5 при любой
матрице Т коэффициентов tik определялось линейное преобразова-
преобразование пространства Iin в 2?„, то сейчас, чтобы формулы A0) опреде-
определяли преобразование пространства I2 в I2, на таблицу коэффициен-
коэффициентов, которую мы назовем бесконечной матрицей, нужно наложить
некоторые ограничения.
Если мы потребуем, чтобы все формулы A0) имели смысл для
любого вектора а из I2, то при каждом i ряд 2 *iftaft должен
ОО
быть сходящимся, как только 2 «|-< + оо. При этом условии
формулами A0) каждому вектору а из I2 сопоставляется вектор
а = (а[, а'2, . . ., щ, ...) из s, т. е. определен оператор а' = Та,
который, очевидно, аддитивен и однороден. Если же мы потре-
потребуем, чтобы для любого а из I2 его образ также входил в I2, т. е.
оо
имело место неравенство 2 Я{2<С+°о, то это накладывает еще
i = \
дополнительное ограничение на матрицу Т и получается, что для
любого вектора а из I2 должно выполняться неравенство
Мы не будем выяснять, каким более простым свойствам
матрицы Т равносильно это, не легко проверяемое условие A1)»
а ограничимся рассмотрением одного частного случая, когда
58 БЕСКОНЕЧНОМЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. 11
условие A1) заведомо будет выполнено. Именно, пусть матрица Т
такова, что
АЯ- 2 2 /?*<-f-oo. A2)
i=l k — l
Тогда, с помощью неравенства Коши, имеем
2S
Тем самым доказано, что A1) выполнено для любого а из 1г и,
ос
следовательно, а'—Та тоже входит в ?2. При этом || Та ||2— 2 а*2>
а потому
||. A3)
Как и для функционалов, мы назовем такое соотношение усло-
условием ограниченности оператора Т. Однако постоянная
/ оо оо
м = - ¦ ¦ ¦
может не быть наименьшей возможной постоянной в условии A3).
Если, как и в 1.7, наименьшую из таких постоянных обозна-
обозначить ЦТ11| (ее также называют нормой оператора Т), то
\Т\\<
/ОО ОО
2 2 4-
i=i *=1
Покажем теперь, что если каким угодно способом задан адди-
аддитивный и однородный оператор а' = Та, преобразующий I2 в I2,
удовлетворяющий условию ограниченности A3) (такие операторы
и называют линейными), то это преобразование может быть записа-
записано формулами A0). Но матрица Т при этом может и не удовлетво-
удовлетворять условию A2).
Так же, как в 2.6 для функционалов, проверяется, что из сде-
сделанных предположений вытекает непрерывность оператора Т,
т. е. а(т) -*- а влечет Та}"' -*- Та.
*) Как мы видели в-2.3, из сходимости рядов 2 'fft и 2 а^ вытекает
ft=l h=l
оо
сходимость ряда 2 Ukah-
2.J] ПОДПРОСТРАНСТВА В «2 59
Пусть, теперь, tik — i-я координата вектора Teh, т. е.
Teh = {tih, /,ft, ..., tik, ...). A4)
Тогда для любого а из Р
оо т т
а' = Та^Т{^ aheh)=T(Jim I' flfteft)- lim 7"( 2 afteft) =
fc=l ТП^*-Л. ti —1 7П- + ОО //= 1
7ГС ОО
= iim %ah(Teh) = ^ah{Teh). . A5)
т-кх> h = i ft = l
Благодаря дистрибутивности скалярного произведения,
оо оо
а; ----- (а, е,-) -^ ^ а& (?'ей. е;) -"=-" ^ tihah.
k=i ft=i
Представление преобразования 71 по формулам A0) получено. При
этом установлен тот же геометрический смысл элементов столбцов
матрицы Т, что и для линейных преобразований в У'„.
Рассмотрение сопряженных операторов, а также собственных
чисел и векторов мы отложим до гл. X, где эти вопросы будут изу-
изучены в более общем виде. Заметим лишь, что если непосредственно
искать числа К и векторы а, удовлетворяющие условию Та = ha,
то из A0) мы получим бесконечную систему уравнений с бесконеч-
бесконечным множеством неизвестных
(in —X) ai-rii2a2-r • ¦ ¦ - tih<*h— • • . = 0,
l2la, + (i22 — X) а2 -- . . . -г /где*-: • • • = ",
-, ...---О,
Решение таких систем представляет значительно большие трудно-
трудности, чем решение конечных систем линейных алгебраических урав-
уравнений. Некоторые результаты о бесконечных системах будут
установлены в гл. VIII.
2.8. Подпространства в I2
Вследствие того, что I2 состоит из векторов с бесконечным мно-
множеством координат, понятие подпространства в I2 формулируется
несколько сложнее, чем в Вп. Предварительно введем понятие
замыкания для произвольного множества Е векторов из I2. Именно
замыканием множества Е называется множество всех векторов из
I2, представимых в виде предела какой-нибудь последовательности
векторов из Е. В частности, само множество Е входит в свое
60 БЕСКОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. II
замыкание, так как если а — вектор из Е, то представляя его
в виде а = lim а('"\ где все а('"' = а, мы сразу заключаем, что а
входит и в замыкание множества Е.
Для векторов из I2 сохраняем то определение линейной комби-
комбинации конечного числа векторов, которое дано в 1.11. Рассмотрим
конечную или бесконечную систему векторов из Z2
), at2), ..., a<m>, ... A6)
Эти векторы называются линейно независимыми, если ни один из
них не является линейной комбинацией конечного числа других
векторов из данной системы. Рассуждения, проведенные в нача-
начале 1.11, справедливые и для векторов с бесконечным множеством
координат, показывают, что для конечных систем приведенное
здесь определение равносильно данному в 1.11.
Множество Е всех линейных комбинаций любого конечного
числа векторов из системы A6) называется линейной оболочкой
этой системы. Замыкание X линейной оболочки Е называется
подпространством пространства I2, порожденным системой век-
векторов A6). Итак, X состоит из всех векторов вида 'kia(-r"l) -(-
-f X2a<m^ + • • • + ^na<m7l) и пределов всех сходящихся последо-
последовательностей векторов такого вида.
Подпространство X обладает следующими свойствами:
а) если а и Ъ входят в X, то и а ~ Ь входит в X;
б) если а входит в X, то и la входит в X при любом %.
Действительно, для линейной оболочки Е эти свойства очевид-
очевидны. Переход же к X осуществляется так: имеем а = lim a<m'.
Ь = lim bim), где оAИ) и Ь(т> входят в Е. Тогда
(a -f й) || < || a<™) — а || + || Ыт) — Ъ \\ -» О,
а так как а°п] -f b(m и Ка°П) входят в Е, то а-\~ Ъ и Ка входят в X.
Приведем пример. Пусть задана система координатных ортов:
aim> ~ gm (/n = 1, 2, . . .). Тогда линейная оболочка Е состоит
из всех векторов, у которых имеется лишь конечное число отлич-
отличных от нуля координат, а подпространство X совпадает со всем 1г,
т
так как каждый вектор а из I2 имеет вид а = lim 2 «&?&•
m-*-oo h=t
Таким же рассуждением, что и в 1.11, легко показать, что если
в системе A6) есть вектор, представляющийся в виде линейной ком-
комбинации некоторых других векторов этой системы, и этот вектор
исключить из системы A6), то это не отразится на линейной оболоч-
оболочке Е, а следовательно, и на подпространстве X. Однако в случае,
если система A6)— бесконечная, повторяя последовательно такое
исключение конечное число раз, мы можем еще не получить системы
2.8] ПОДПРОСТРАНСТВА В П 61
линейно независимых векторов. Такую систему линейно независи-
независимых векторов можно выделить из A6) следующим путем.
Будем считать, что если в системе A6) встречались векторы,
равные 6, то мы их уже выбросили, и что теперь все а'' =?= 6.
Перебирая поочередно все векторы аа\ а<2), . . ., а'', . . ., мы
относительно каждого будем решать, сохраняется ли он в системе
или исключается. Именно, вектор аш мы непременно сохраним
и обозначим его теперь Ьа\ Далее действуем по индукции. Пусть
уже перебраны векторы a'v, ai2\ . . ., а(Ш) и из них оставлены
линейно независимые векторы bn\ bt2), . . ." b<n) (ясно, что
п^Ст); тогда вопрос относительно очередного вектора а<т+1)
решается так: если векторы 6"\ 6B\ . . ., Ып), а(Ш+1> линейно
независимы, то вектор а""+1) сохраняется и обозначается Ь(П+1),
если же векторы ba>, bi2), . . ., bln>, af'n+v линейно зависимы, то
а('"+1> исключается. Таким образом, по построению векторы
fed), б*2), ..., Ып\ ... A7)
линейно независимы. Чтобы доказать, что их линейная оболочка —
та же, что у системы A6) (а тогда совпадают и порождаемые под-
подпространства), достаточно показать, что любой исключенный век-
вектор — линейная комбинация конечного числа векторов из сис-
системы A7). Пусть вектор а<ш+1) был исключен. Это значит, что суще-
существует соотношение вида
в котором хоть один из коэффициентов отличен от нуля. Если бы
было ji = 0, то мы бы получили равенство
в котором тоже не все коэффициенты равны нулю, а это проти-
противоречит линейной независимости векторов 6<*), . . ., Ып). Следова-
Следовательно, ц фО и
Итак, при определении подпространства всегда можно счи-
считать, что порождающая его система состоит из линейно независи-
независимых векторов. Если эта система состоит из конечного числа векто-
векторов, то подпространство называется конечно-мерным,,а порождаю-
порождающая его система векторов называется базисом. При этом, точно
•гак же, как в Нп (см. 1.11), доказывается, что тлг
б
р
всех базисах данного подпространства — одно и то же. Е?о__назы-
вают размерностью подпространства. Если же порождающая
62 БЕСКОНЕЧНО-МКРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. II
система содержит бесконечное множество векторов, то подпро-
подпространство называется бесконечно-мерным.
В следующем параграфе мы покажем, что для конечно-мерных
подпространств линейная оболочка базиса совпадает с самим под-
подпространством, т. е. конечно-мерные подпространства в I2 можно
определять так же, как в Rn.
2.9. Ортогональный базис
Точно так же, как в 1.12 для Вп, доказывается, что если в I2
конечная или бесконечная система состоит из векторов, попарно
ортогональных и отличных от нуля, то эти векторы линейно неза-
независимы.
Если система векторов, порождающих подпространство X,
состоит из попарно ортогональных векторов (отличных от нуля),
то такая система называется ортогональным базисом подпростран-
подпространства Ъ *). Если все векторы, составляющие ортогональный базис,
имеют норму, равную единице, то базис называется ортонорми-
рованным.
Если в конечно-мерном или бесконечно-мерном подпростран-
подпространстве L пространства I2 задана произвольная порождающая L систе-
система линейно независимых векторов аа>, а<2>, . . ., а"", . . ., то
тем же процессом ортогонализации, который был изложен в 1.12
(для бесконечной системы он будет состоять из бесконечного мно-
множества последовательных шагов), можно построить в L ортонор-
мированный базис biV, bri\ . . ., b'"J\ . . . так, что каждый век-
вектор Ь(П) есть линейная комбинация первых т веиторов первой
системы. Одновременно векторы а0'' будут линейными комбина-
комбинациями векторов второй системы. Совпадение подпространств,
порождаемых обеими системами, вытекает из совпадения их линей-
линейных оболочек.
Ортонормированные (и вообще ортогональные) базисы обладают
некоторыми дополнительными свойствами, благодаря которым
они часто оказываются, при исследовании подпространств, более
удобными по сравнению с произвольными порождающими систе-
системами. В частности, удается установить формулу разложения про-
произвольного вектора из подпространства по векторам его ортонор-
мированного базиса.
Лемма 2.9.1. Пусть 1^ — подпространство, порождаемое
произвольной системой векторов b<v, 6<2', . . ., ЬAН\ . . . Если
некоторый вектор с из I2 ортогонален каждому из векторов 6'"',
то он ортогонален и любому вектору а из L.
*) Общее определение базиса, без требования ортогональности, для
бесконечно-мерных пространств будет дано в гл. V.
2-9] ОРТОГОНАЛЬНЫЙ БАЗИС 63
Доказательство. Если а входит в линейную оболоч-
п
ку Е заданной системы векторов, т. е. если а = 2 ^г^'*', то
i
Если же а—произвольный вектор из L, то o=limo'n', где а(">
входят в Е, и, по непрерывности скалярного произведения
и доказанной ортогональности с и а(п\
(с, a) — l\m(c, aW) -0.
Следствие. Если вектор a us L ортогонален каждому u-t
векторов 6*'"> порождающей система, то а — 0.
Действительно, вектор а должен быть ортогонален каждому
вектору из L, в частности самому себе, а тогда
Выведем теперь одно важное неравенство. Пусть 6(", ЬB\ .. .
..., Ь(т>, ... —любые попарно ортогональные векторы с нормой,
равной единице. Для произвольного вектора а из 1г положим.
К = (а, Ь<«>) (т-1, 2, ...)
и образуем векторы
Подсчитаем || а("> — а||2. Имеем
|| а<") — a ij2 =- (а<") — а, а<п> — а) =
- (а<">, а<")) — (а, а^) — (а<"\ а) -г (а, а) •-=
.¦=Ца(»)||8-2(о, о(»)) + ||а!1«. A9)
По обобщенной теореме Пифагора
!!«<"> li2- S |1М(га)Н2= S PS.||ft<in)li8- S Pm.
m = l m=l ?n = l
затем
(а, а'*)) = (а, J М(т)) ^ S Р«(а. ь(ж)) = 2 Р«-
т —1 m^^l m=l
Подставляя в A9), получим
64 БЕСКОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. II
Так как левая часть, очевидно, не отрицательна, то
m=i
Если данная система векторов fe(m> бесконечная, то в неравенстве
B1) п может быть любым натуральным числом. Тогда из B1)
оо
вытекает сходимость ряда 2 Рт и так называемое неравенство
Бесселя
2 Рт<||<42- B2)
т=1
Если же векторов b('n) конечное число п, то неравенством Бесселя
называют установленное выше неравенство B1).
Теперь переходим к основной теореме этого параграфа.
Теорема 2.9.1. Для того чтобы вектор а из I2 входил
в подпространство L с ортонормированным базисом Ьа\ Ъ{2\ . . .
. . ., ?(>, . . ., необходимо и достаточно, чтобы он был предста-
представим в виде
о- 2 Р^(т>; B3)
т=1
при таком представлении непременно p,n = (a, b°'L)) при всех т
и, следовательно, такое представление единственно.
Мы проведем все доказательство, предполагая базис бесконеч-
бесконечным. Но читатель легко проследит, что все рассуждения, с соответ-
соответствующими упрощениями, справедливы и при конечном базисе,
причем бесконечный ряд из формулы B3) в этом случае, естествен-
естественно, заменяется конечной суммой.
Доказательство, а) Достаточность. Пусть
представление B3) имеет место. Тогда, вследствие ортонормиро-
ванности базиса,
(а, 2
Кроме того, частичные суммы ряда B3) входят в линейную оболоч-
оболочку базиса, а тогда вектор а, как предел последовательности частич-
частичных сумм, входит в L.
б) Необходимость. Возьмем вектор а из X, положим
Р„, = (а, 6й"') при т = 1, 2, . . . и составим векторы а(п) по
формуле A8). Покажем, что для последовательности векторов ат>
выполнено условие Больцано — Коши.
2.9] ОРТОГОНАЛЬНЫЙ БАЗИС 65
Действительно, при р ~> п
m=n+l
а потому, вследствие сходимости ряда из B2),
р
||д(р) — а(")||2= V BL >0
Но тогда существует вектор из Р
П оо
который по доказанному в а) входит в X; при этом fim = (b, Ыт)).
По общим свойствам подпространства вектор а — b также вхо-
входит в подпространство X. При этом, при любом т=1, 2, ...
(а — Ь,
Отсюда с помощью доказанного выше следствия из леммы полу-
получаем, что а — 6 = 6, т. е.
m=l
Это и есть требуемая формула разложения. Теорема доказана.
По ходу доказательства мы установили, что если вектор а
входит в X, то а = lim a(">, а тогда из B0) следует, что
ИЛИ
И2= S P- B4)
m=l
Равенство B4) называют уравнением замкнутости.
Обратно, если B4) выполнено, то из B0) следует, что
|| а1п) — а || —^ 0 и, так как все а1п) входят в линейную оболочку
данного базиса, то а входит в подпространство X. Таким образом,
равенство B4) является условием, необходимым и достаточным для
того, чтобы вектор а входил в подпространство X. Значит, для
векторов, не входящих в X, в неравенстве Бесселя имеет место
строгое неравенство, т. е. стоит знак <.
Приведем пример. Пусть задана система, состоящая из всех
координатных ортов с четными номерами, Ъ{т) = е2т (т= 1, 2,...).
Подпространство X, порождаемое этим ортонормированным
5 Б. 3. Вулих
66 БЕСКОНЕЧНО-МЕРНОЕ ЭВКЛИДОВО ПРОСТРАНСТВО [ГЛ. II
базисом, состоит из всех векторов, допускающих разложение вида
т. е. векторов вида а = @, а2, 0, а4, ..-), у которых все коорди-
координаты с нечетными номерами равны нулю. При этом
Рт = (а, 6(т)) = (а, е2т) = а2т.
оо
Для векторов а из Z, очевидно ||а||2= 2 Р* Если же вектор
771=1
а = («1, а2> • • • > a»i • • •) из Z2 не входит в I, то у него, по край-
крайней мере одна из координат a2m-i (с нечетным номером) отлична
от нуля и
1И"= I «L+ 2 <-i>2 «L= 2 Р?-
m=l m=l m=l m=l
Читатель безусловно заметил большую аналогию между прове-
проведенными в этом параграфе построениями и теорией рядов Фурье.
В последующем, в гл. VI, мы специально остановимся на этой ана-
аналогии, рассмотрев теорию ортогональных разложений в более
общем виде.
Теперь докажем результат, упомянутый в предыдущем пара-
параграфе.
Теорема 2.9.2. Конечно-мерное подпространство L про-
пространства I2 (с размерностью, большей нуля) совпадает с линейной
оболочкой своего базиса.
Доказательство. Так как при ортогонализации про-
произвольного базиса получается базис, имеющий туже линейную обо-
оболочку, то мы сразу можем считать, что заданный в подпростран-
подпространстве X базис Ъа\ Ь<2\ . . ., Ъ<т> — ортонормированный. Тогда,
по теореме 2.9.1, каждый вектор а из X представим в виде
а = 2 Pft^(ft)i T- е- входит в линейную оболочку базиса.
2.10. Комплексное бесконечно-мерное
эвклидово пространство
Теория, изложенная в настоящей главе, распространяется и на
пространство, составленное из векторов с комплексными коорди-
координатами, подобно тому, как это намечено в 1.14 для конечно-мер-
конечно-мерных эвклидовых пространств. Комплексное бесконечно-мерное
эвклидово пространство I2 определяется как множество всех ком"
плексных векторов а = (аи а2, . . ., аг, . . .) с бесконечным мно-
БИБЛИОТЕКА Колхоз!
"Оскорка"
2.10] КОМПЛЕКСНОЕ БЕСКОНЕЧНО-МЕРНОЕ ПРОСТРАНСТВО 67
жеством координат, значениями которых могут быть любые ком-
оо
плексные числа, удовлетворяющие условию 2 | ai |2 < + °°! при
i=i
следующем определении нормы вектора:
Скалярное произведение двух векторов а и Ъ из Р опреде-
определяется формулой
(a, b)= |jaj6;.
Алгебраические операции вводятся так же, как и в I2, но в I2
имеет смысл умножение вектора на любое комплексное число.
Норма и скалярное произведение в I2 обладают свойствами,
отмеченными в ?„, а также свойствами непрерывности, установ-
установленными выше в I2. В большие подробности здесь мы входить
не будем.
5*
ГЛАВА III
МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
3.1. Некоторые понятия теории множеств
В настоящей главе мы перейдем к изучению значительно более
общего понятия пространства по сравнению с теми эвклидовыми
пространствами, которым были посвящены первые две главы.
В связи с этим нам будут полезны некоторые понятия и обозначе-
обозначения из общей теории множеств.
Само понятие множества является настолько общим, что было
бы затруднительно дать для него формальное определение. Но
в таком определении и нет необходимости. Мы и так совершенно
свободно оперируем понятием множества и в повседневных житей-
житейских разговорах и в научной литературе. Так, каждрму ясно, что
понимать под множеством тех или иных предметов, находящихся
в его квартире, например, под множеством книг, стоящих в книж-
книжном шкафу, или, что понимать под множеством людей, живущих
в данном городе. Также у нашего читателя, очевидно, не возни-
возникало никаких вопросов, когда мы определяли в предыдущих гла-
главах эвклидовы пространства как множества тех или иных векторов.
Часто вместо термина «множество» употребляется равносильный
термин «совокупность».
Говоря о некотором множестве, мы называем его элементами
те предметы или математические объекты, из которых оно состав-
составлено. Если множество обозначено буквой А, а общее обозначение
произвольного его элемента х, то пишут А = {х}. Далее, если
нужно указать, что какой-нибудь объект а есть один из элементов
множества А, то употребляют так называемый знак включения ?
и пишут а ? А [читается: а включается (входит) или содержится
в Л). Если же объект а не встречается среди элементов множе-
множества А, то пишут а\А [читается: а не включается (не входит)
или не Додержится в А ]. Например, пусть А — множество всех
четных (положительных) чисел. Так как общий вид любого чет-
четного числа 2га (га — натуральное), то можно записать А = {2га}.
Далее можно, например, записать, что 24 ? А, а 25 ? A.
3.1] НЕКОТОРЫЕ ПОНЯТИЯ ТЕОРИИ МНОЖЕСТВ 69
Пусть рассматриваются два множества А я В. Если каждый
элемент множества В входит также и в множество А, то говорят,
что В есть часть или подмножество множества А. Для обозначе-
обозначения этого факта употребляют несколько иной знак включения
сг и пишут В сг А (читается так же, как и запись со знаком Q.
Например, множество I2 есть подмножество множества s: 1г сг s.
Важно отметить, что соотношение В сг А не исключает и совпа-
совпадения В с А, т. е. само множество А включается в число его под-
подмножеств.
Иногда знаки включения записывают и так:
А Эя вместо а? А,
А^> В вместо В а А.
Равными (пишут А = В) называются одинаковые множества,
т. е. множества, состоящие из одних и тех же элементов. Заметим,
что если относительно двух множеств А и В установлено, что
одновременно В а А и А а В, то это и означает, что А = В.
Если х и у — элементы каких-нибудь множеств, то знак равен-
равенства между ними, х = у, также используется для обозначения их
совпадения.
Иногда, определяя какое-нибудь множество, мы можем еще не
знать, содержит ли это множество по крайней мере один элемент.
Например, нас может интересовать множество вещественных кор-
корней того или иного алгебраического уравнения, но дальнейшее
исследование может показать, что данное уравнение совсем не
имеет вещественных корней. В связи с этим вводится понятие
пустого множества. Так называется множество, не содержащее
ни одного элемента. Пустое множество обозначается Л и, следо-
следовательно, запись А = Л будет говорить, что А — пустое множество.
Определим некоторые операции, которые часто приходится
производить над множествами.
Суммой двух множеств А и В называется множество, обозна-
обозначаемое A U В, которое состоит из всех элементов, входящих, по
крайней мере, в одно из множеств А или В. Аналогично опреде-
определяется сумма любого количества множеств. При этом, если задан-
заданные множества обозначены Аа (значок а может при этом сам
пробегать какое угодно множество; это не обязательно — поряд-
порядковый номер), то их сумма обозначается \] Аа и, по определению,
а
эта сумма состоит из всех элементов, входящих по крайней мере
в одно из множеств Аа *). Пусть, например, множество А состоит
*) Мы будем считать, что если под знаком суммы не указана область
изменения значка а, то значит суммирование распространяется на все зна-
значения, которые а может принимать в рассматриваемой задаче. То же отно-
относится и к вводимому ниже знаку пересечения.
70
МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[ГЛ. III
из всех четных чисел, множество В состоит из всех натуральных
чисел, делящихся на 3, и множество С состоит из всех нечетных
чисел, не делящихся на 3: А = {2, 4, 6, 8, . . .}, В =
= {3, 6, 9, 12, . . .}, С = {1, 5, 7, 11, 13, . . .}. Тогда их сум-
сумма A U В U С есть множество всех натуральных чисел.
Пересечением двух множеств А и В называется множество,
обозначаемое А [\ В, состоящее из всех элементов, которые входят
и в А и в В. Аналогично определяется пересечение f| Aa любого
количества множеств Аа: зто есть множество всех элементов, вхо-
входящих во все Аа. Для множеств А и В из предыдущего примера их
пересечение состоит из всех чисел, кратных 6. Если В с А, то
А[}В = А, А[]В = В.
Разность А\В определяется как подмножество множества А,
состоящее из всех его элементов, не входящих в В. Предоставляем
читателю самому убедиться, что А \ В = А \ (А П В) *).
Все три понятия проиллюстрированы на рис. 3, где под А
и В понимаются множества всех точек соответствующих проме-
промежутков.
Введем еще одно понятие. Пусть А — некоторое множество,
а В — произвольное его подмножество. Тогда множество А \ В
называется дополнением к множеству В (относительно множе-
множества А). Ясно, что дополнение к А \ В есть само множество В.
Отметим одно важное свойство дополнений: если Ва — произ-
произвольные подмножества множества А, а Са — их дополнения,
т. е. Са = А \ Ва, то
Ba=[)Ca; A\[)Ba=[)Ca A)
(дополнение к сумме подмножеств равно пересечению их допол-
дополнений, а дополнение к пересечению подмножеств равно сумме их
дополнений).
*) В определении разности А \ В не требуется, чтобы В d A.
3.2] ОПРЕДЕЛЕНИЕ МЕТРИЧЕСКОГО ПРОСТРАНСТВА 71
Докажем первую формулу; вторая — доказывается аналогично.
Требуемое равенство мы установим с помощью двух противопо-
противоположных включений. Пусть х ?А~\{] Ва. Это значит, что х ?А, но
_ а
^6 U^a- Тогда, по определению суммы, х?Ва ни при одном а,
а
следовательно, х?Са при всех а и х?[)Са. Таким образом,
а а
Обратно, пусть х^{]Са. Это значит, что х?Са при всех а,
а
следовательно, х?А, но х?Ва ни при одном а. Тогда х?\]Ва
а
и, тем самым, х^А\[)Ва. Таким образом, П Са сг (А\ [) Ва).
а а а
Из двух доказанных включений и следует, что
Л\[]Ва= [\Са.
а
3.2. Определение метрического пространства
Пространства, рассмотренные нами в первых двух главах,
составлялись из некоторых конкретных математических объектов—
векторов с тем или иным множеством координат. Это уже было
обобщением того понятия пространства, которое изучалось в эле-
элементарной геометрии. Сейчас мы сделаем значительно больший шаг
в направлении обобщения понятия пространства. Именно, мы назо-
назовем пространством произвольное множество, состоящее из элемен-
элементов какой угодно природы, на которое накладывается только одно
требование: должно быть определено понятие расстояния между
его элементами, подчиненное некоторым условиям *). Дадим точ-
точное определение.
Определение. Метрическим пространством называет-
называется всякое множество Е, в котором для любых двух его элементов х
и у определено вещественное неотрицательное число, называемое
расстоянием между х и у, обозначаемое р (х, у), причем должны
выполняться следующие требования:
1) р (х, у) = 0 тогда и только тогда, когда х = у;
2) р (х, у) = р (у, х) (аксиома симметрии);
3) для любых трех элементов х, у и z
р (х, у) < р (х, z) + p (z, у) (аксиома треуголь-
треугольника).
Элементы метрического пространства чаще называют его
точками.
*) В пределах настоящей книги это будет наиболее общим понятием
пространства. Однако в математике изучаются и еще более общие понятия
пространства, например, топологические пространства.
72 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. Ш
Перечисленные требования вполне согласуются с нашими
житейскими представлениями о расстоянии: расстояние всегда неот-
неотрицательно; расстояние равно нулю только между совпадающими
точками; обе точки, между которыми определяется расстояние,
совершенно равноправны («расстояние от х до у» равно «расстоя-
«расстоянию от у до х»); наконец, аксиома треугольника выражает тот факт,
что, говоря образно, прямой путь из х в у не должен быть длиннее,
чем путь из х в у через третью точку z. Всеми этими свойствами
обладает, в частности, расстояние на плоскости и в трехмерном
эвклидовом пространстве. Однако при определении общего поня-
понятия метрического пространства все перечисленные требования
не выводятся из каких-то ранее установленных фактов, а форму-
формулируются в виде аксиом. В дальнейшем эту группу условий мы
и будем называть системой аксиом метрического пространства.
Приведем некоторые примеры.
1. В эвклидовом пространстве Вп расстояние между двумя век-
векторами определяем по формуле
р(х, у) = \\х — у\\.
Получаем, очевидно, метрическое пространство. В частности,
выполнение аксиомы треугольника вытекает из неравенства тре-
треугольника, установленного в 1.3 для нормы вектора, если записать
х — У = (х — z) + (z — у).
Заметим, что если при п = 3 элементы х = (х±, хг, х3) про-
пространства В3 изображать в виде точек в прямоугольной системе
координат, то для расстояния получится элементарная формула:
расстояние между двумя точками равно длине разности их радиу-
радиусов-векторов. То же имеем и при п = 2. А при п — 1 картина еще
проще: одномерное эвклидово пространство RY есть не что иное,
как совокупность вещественных чисел с расстоянием р (х, у) =
= \x-y\-
2. Бесконечно-мерное эвклидово пространство I2 при том же
определении расстояния, что в Rn, также будет метрическим про-
пространством.
3. Пусть множество / состоит из всех бесконечных числовых
последовательностей х = (?i? |2> • • -. ?ь • • •) (или векторов
с бесконечным множеством координат), удовлетворяющих уело-
вию 2 I ?г | <+°°* Положим для любых двух элементов х —
= {?*} и у = {г[г} из I:
Р( Т 7/^ ^1 fi , .. yi,
\шЛ^) if/ ^\ \ д? \l |*
t=i
Выполнение первых двух аксиом метрического пространства оче-
3.2] ОПРЕДЕЛЕНИЕ МЕТРИЧЕСКОГО ПРОСТРАНСТВА 7$
видно [р (х, у) —О равносильно ?; = т); при всех i, т. е. х-—у}..
Аксиома треугольника тоже почти очевидна: для x = {E,i}, J/ = {t];}
и 2 = {?;} имеем
Р(х, y)=2lb-Tn|<2(lb-S«l + |?«-Tii|) =
— 2 I ?• ы I + 2 I s« 'n» I — p (*>z)+p (z> 2/)-
1=1 i=l
Таким образом, I — метрическое пространство.
4. m — метрическое пространство, состоящее из всех ограни-
ограниченных бесконечных числовых последовательностей с расстоя-
расстоянием, определяемым для ? = {?;} и y = {'f\i} по формуле
Р (Х, у) = SUp I li — Tl; I *).
i
Проверим выполнение аксиомы треугольника. Берем х = {Ъ}г
y—{\\i}, z = {li}- При любом i = l, 2, ...
I h — "Пг I < I ii — Si I + lit — 4i | < sup \li — li | -f sup | li — tjj I =
i i
= P(Z, z) + p(Z, !/).
А тогда, по определению точной верхней границы,
р (х, y) = sxip\li — i\i\<p {x, z) + p (z, у).
5. В множестве в всех бесконечных числовых последователь-
последовательностей (рассмотренном уже в гл. II) определяем расстояние.,
полагая для х = {?;} и у = {т];}
оо
Сходимость последнего ряда обеспечена, так как его i-й член
меньше, чем —. Выполнение первых двух аксиом метрического-
пространства здесь очевидно. Несколько сложнее, чем в преды-
предыдущих примерах, проверяется аксиома треугольника.
Установим предварительно вспомогательное неравенство.
Пусть 0<а<р. Тогда a-faf}<p-j-aP- Деля обе части
*) Так как по условию ?,- в совокупности ограничены, | g; | <; К, и, ана-
аналогично, |t];|^;L, to | ?г—-T]j | < K-j-L, т. е. и разности |j — t]j в сово-
совокупности ограничены. А тогда среди верхних границ множества чисел
11; — t)i | существует наименьшая: sup | ?j — т); |
74 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
на A -{- а) A + р), получим
« < Р /о)
Теперь при любых я----{?г}, */={ili}, z = {?;} из s для каждого
i = l, 2, . . . \h — f\i\<\li — ?г|т|?г — "Пг 1, а потому с помощью
неравенства B) имеем
Ег-С«1
<¦
Умножая крайние члены на 2~г и суммируя по i, получим
р{х, у)<р{х, z)-j-p(z, у).
Итак, s — метрическое пространство.
Заметим, что во всех рассмотренных примерах можно ограни-
ограничиваться последовательностями, состоящими только из веществен-
вещественных чисел, а можно рассматривать и аналогичные комплексные
пространства последовательностей, допуская, что их членами
могут быть и не вещественные числа.
Рассмотрим еще примеры метрических пространств, состав-
составленных из непрерывных функций.
6. С — множество всех непрерывных функций х (t), задан-
заданных на отрезке а<<<6, причем для любых двух элементов
¦х> У 6 С расстояние определено по формуле
р(х, y) =
Таким образом, расстояние в С есть максимальное отклонение
одной функции от другой.
Ясно, что р (х, у) = 0 тогда и только тогда, когда х (t) = у (t)\
аксиома симметрии очевидна. Аксиома треугольника для любых
трех функций х (t), у (t) и z (f) из С проверяется так:
< max | х (t) — z (t) | -|- max | z (t) — у (t) \ —
= p(z, z)-f p(z, y).
Так как это верно при любом t ? [а, Ь], то, в частности, то же
неравенство получается и для р (х, у) = max | х (t) — у (t) |.
*) Из курса математического анализа известно, что функция, непре-
непрерывная на отрезке, имеет наибольшее и наименьшее значения (теорема
Вейерштрасса).
EHinjgKI
.3.2] ОПРЕДЕЛЕНШквЕТРИЧЕСКОГО ПРОСТРАНСТВА 75
Таким образом, С — метрическое пространство.
7. Рассмотрим то же множество функций, что и в предыдущем
примере, но расстояние определим иначе:
ь
р(х, y)=J \x{t)-y{t)\dt.
а
Предоставляем читателю самому убедиться, что все аксиомы
метрического пространства выполнены. Таким образом, мы имеем
метрическое пространство, составленное из тех же элементов, что
и С, но с другим определением расстояния. Так как определение
расстояния входит в качестве весьма существенной части в опре-
определение метрического пространства, то метрические пространства,
хотя и составленные из одних и тех же элементов, но с различ-
различными определениями расстояния, следует считать различными.
Пространство, определенное в настоящем примере, обозначим CL.
Если дано какое-нибудь множество, то сама операция опреде-
определения в этом множестве расстояния между элементами, удовлетво-
удовлетворяющего всем аксиомам метрического пространства, называется
введением метрики в данном множестве (или его метризацией).
Можно сказать, что в примерах 6 и 7 мы в одном и том же мно-
множестве непрерывных функций ввели метрику двумя способами.
8. В том же множестве непрерывных функций, что и в двух
предыдущих примерах, определим метрику еще одним способом,
полагая
У)=Л/ \ [x(t)-y(t)]>dt. C)
Из аксиом метрического пространства не очевидно только выпол-
выполнение аксиомы треугольника. Для ее проверки выведем сначала
интегральное неравенство Буняковского*), аналогичное нера-
неравенству Коши для сумм, которое было доказано в 1.3.
Пусть / (t) и g (t) — две функции, непрерывные на отрезке [а, Ь].
Вводим вспомогательную функцию ср (х) от вещественной пере-
переменной х:
ъ
0 0 О
= хг[ f (t) dt-\-2x\ f (t) g (t) dt+[ g% @ dt.
«3 t) t)
a a a
*)В. Я. Буняковский A804—1889) — выдающийся русский
математик
'ДВД^ВА
76 МЕТРИЧЕСКИЕ ПРОСТРДШртВА • [ГЛ. III
Так как ср(а;)>0 при всех х (как интеграл от неотрицательной
функции), то дискриминант квадратного трехчлена должен быть
неположительным, а потому
ъ ь ь
V <> J i J
а а а
Это и есть неравенство Буняковского.
Теперь, аналогично тому, как это сделано в 1.3, извлекая
из обеих частей неравенства Буняковского квадратные корни,
удваивая эти корни и прибавляя к ним
ь ь
[ p(t)dt+ [ g2(t)dt, .
а а
мы получим
ь
или
1/ \ [/W + ?@12^<l/ \p(t)dt+y \gz{t)dt. E)
Это — интегральная форма неравенства треугольника.
Аксиома треугольника для расстояния, определенного фор-
формулой C), проверяется теперь сразу, если при заданных x(t),
у (t) и z (t) положить в неравенстве E)
i = z@-«@. g(t) = *(t) — V(t)-
Построенное в этом примере метрическое пространство обо-
обозначим Ci2.
9. Используя понятие интеграла Лебега*), можно построить
еще некоторые функциональные метрические пространства. Имен-
Именно, зададим число р > 1 и обозначим через L'1 множество всех
*) Введенное французским математиком А.Лебегом A875—1941) поня-
понятие интеграла пмеет смысл для функций значительно бэлее широкого клас-
класса, чем интеграл Римана, т. е. интеграл, изучаемый обычно в общем курсе
математического анализа. Подробное изложение теории интеграла Ле-
Лебега можно найти, например, в книгах: И. П. Натансон, Теория
функций вещественной переменной пли Б. 3. В у л и х, Краткий курс теории
функций вещественной переменной. В частности, в этих книгах можно найти
и некоторые сведения о разбираемых ниже пространствах Ы>.
3.2] ОПРЕДЕЛЕНИЕ МЕТРИЧЕСКОГО ПРОСТРАНСТВА 77
функций х (t), заданных и измеримых на отрезке [а, Ь] и таких, что
ъ
\x(t)\p dt <+оо.
Про такие функции говорят, что они суммируемы с р-й степенью.
При этом условимся отождествлять друг с другом эквивалентные
между собой функции, т. е. считать их одним и тем же элементом
множества L11 *). Таким образом, каждый элемент множества Lp
изображается не одной определенной, а любой функцией из целого
класса эквивалентных между собой функций.
Введем метрику в множестве Lv, полагая
ь 1
р(х, y)=(\\x(t)-y(t)\»dty. (За)**)
Чтобы проверить, что введенное, таким способом расстояние
удовлетворяет всем аксиомам метрического пространства, следует
воспользоваться одним неравенством, которое называется нера-
неравенством Минковского и которое мы приведем без доказатель-
доказательства ***). Именно, для любых двух измеримых функций / (t) и g (t)
ъ L ь L ь 1
Из этого неравенства, в частности, следует, что если функции
х, у ? ?р, то и их сумма х + у 6 Ijp. Заменяя у на —у, мы полу-
получим, что и разность х — у ? Lp. А тогда расстояние, определенное
выше, имеет конечное значение для любых х, у ? V. Заметим,
что неравенство Минковского при р = 2 превращается в то нера-
неравенство E), которое уже встречалось выше.
Если р (х, у) = 0, то из свойств интеграла вытекает, что
х (t) = у (t) почти всюду, т. е. х и у равны, как элементы множе-
множества Lv. Выполнение аксиомы симметрии очевидно. Наконец,
аксиома треугольника — простое следствие из неравенства Мин-
Минковского и получается из него, если положить, как мы только что
делали в пространстве Оьг,
= x(t)-z(t), g(t) = z(t)-y(t).
*) Напомним, что две функции х (t) и у (t) называются эквивалентными,
если a; (t) = у (t) почти всюду, т. е. если множество тех точек, где а: (?) Ф- у (t),
имеет меру 0.
**) Формула (За) очевидным образом обобщает формулу C).
***) Г. М и н к о в с к и й A864—1909) — немецкий математик и физик.
Доказательство неравенства Минковского см., например, в только что цити-
цитированной книге автора, стр. 260—261.
78 ' МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЯ. 111
Таким образом, X2' при р>1 —метрические пространства.
Наиболее простым среди пространств Lp является то, которое-
получается при р = 1, т. е. пространство всех функций, сумми-
суммируемых на отрезке [а, Ь]. Его обозначают просто L. В этом про-
пространстве неравенство Минковского тривиально, а расстояние-
определяется по той же формуле, что и в пространстве Сь. Тем
самым, CL можно рассматривать как подмножество в X *). Анало-
Аналогично, пространство СЬ2 можно рассматривать как подмноже-
подмножество в L2 **).
Как мы увидим ниже, среди всех Lp наиболее широкие при-
применения находит пространство L2, и потому этим пространством
мы займемся подробно ниже (в гл. VII). В частности, там будет
более простым способом доказано, что сумма двух функций из L2
тоже принадлежит X2.
Можно доказать (ср. 9.3), что с возрастанием индекса р про-
пространство I/1' по своему составу убывает, т. е. что Lv id Lq, если
q > р. Таким образом, самым обширным среди Х!) по составу
элементов является пространство L, все прочие — его подмно-
подмножества.
Неравенство Минковского перестает выполняться, если р < 1.
Поэтому пространства Lp с метрикой, вводимой по формуле (За),
рассматриваются только прир>1.
10. По аналогии с пространством Lv можно рассмотреть про-
пространство V (р>1), состоящее из всех бесконечных последова-
последовательностей х = (?,, ?2! •••)?!>•• •)' Для которых справедливо
неравенство
В пространстве I" расстояние определяется по формуле
i
Р(ЪУ) = (У> \tt-r\t\*)p (здесь x={h}, У = Ы)
i i
Х1астным случаем таких пространств являются рассмотрен-
рассмотренные выше I и I2. При проверке неравенства треугольника в 1Р
*) Следует заметить, что если две непрерывные функции отличаются
друг от друга хотя бы в одной точке, то они отличаются и в некоторой окре-
окрестности этой точки, а потому не эквивалентны. Таким образом, две непрерыв-
непрерывные функции совпадают как элементы пространства L только в том случае,
если они тождественно равны друг другу.
**) Можно по аналогии с С ; определить и пространство С р (р > 1).
составив его только из непрерывных функций и введя в нем метрику из про-
пространства U>.
3.3] СХОДИМОСТЬ В МЕТРИЧЕСКОМ ПРОСТРАНСТВЕ 79
используется неравенство Минковского для последовательностей:
5§§
Понятие метрического пространства введено в науку в начале
XX столетия современным французским математиком М. Фреше-
3.3. Сходимость в метрическом пространстве
Наличие расстояния позволяет определить в метрическом про-
пространстве понятие предела.
Определение. Точка х метрического пространства Е назы-
называется пределом бесконечной последовательности точек хп ? Е
(пишем хп -> х или х = lim хп), если р (хп, х) ->¦ 0.
Определенную таким образом сходимость последовательности
точек будем иногда называть сходимостью по расстоянию (или
по метрике пространства Е).
Докажем, что у данной последовательности точек может
существовать только один предел. Пусть хп -> х и хп -> у.
По аксиоме треугольника р (х, у)<р {х, хп) + р (хп, у). Но пра-
правая часть стремится к нулю при ге-> оо, а левая неотрицательна,
следовательно, р (х, у) = 0 и х = у.
Установим еще одно неравенство, верное для любых четырех
точек х, у, z, и из Е:
\р{х, y) — p(z, и)\<р{х, z)+p(y, и). F)
Действительно, из аксиомы треугольника следует, что
Р (ж, у) < р (ж, z) + p (z, г/)< р (ж, z) -f p (z, ц) -f p (и, г/),
откуда
р(х, у) — p(z, и)<р(ж, г) + р(г/, и). G)
Но в этом неравенстве ? и i/ можно поменять местами с г и и (соот-
(соответственно), и потому
p(z, u) — p(x, y)<p(x, z)-f-p(i/, u). (8)
Так как для любого числа а имеет место или | а | = а или | а
= — а, то из неравенств G) и (8) и вытекает F).
В качестве следствия из неравенства F) сразу можно получить,
что расстояние р (х, у) — непрерывная функция от х и у в том
смысле, что если хп -> х и уп ->¦ у, то р (ж„, у„) -> р (ж, у).
Действительно с помощью F) имеем
| р (хп, уп) — р (х, у) | < р (хп, х)~р (уп, у) —> 0.
SO МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. Ill
Заметим также, что если хп —у х, то и любая частичная после-
последовательность точек Xnh (щ <С п2 < . . . < nh <;...), выделен-
выделенная из {хп}, тоже сходится к х. Это очевидно, так как из р (хп, х) ->
-> 0 следует, что и р (znft, x) -*¦ 0.
Если хп = х при всех п, то и Iim ?„ = х.
Выясним конкретный смысл сходимости в тех метрических
пространствах, которые приведены в качестве примеров в преды-
предыдущем параграфе.
В пространствах Rn и I2 определение сходимости по расстоянию
совпадает с тем, которое уже давалось в гл. I и П. Там же было
выяснено, что сходимость в 2$, есть сходимость по координатам,
а сходимость в I2 влечет сходимость по координатам, но не равно-
равносильна ей. Последнее справедливо и для пространства I, причем
установить, что в I сходимость по координатам не влечет сходи-
сходимости по расстоянию, можно с помощью того же примера, кото-
который рассмотрен с этой же целью в I2 (см. 2.4). В пространстве Лг
сходимость по расстоянию есть обычная сходимость числовой
последовательности к пределу.
Обратимся к пространству т. Пусть хп = {?{п)}, х = {?г}.
Тогда сходимость хп —>• х означает, что
sup |^п)-?; |-^0,
г п->оо
т. е. каково бы ни было е > 0, неравенство | ?;["* [ — |j | < е
выполнено, начиная с некоторого п, при всех i = 1,2, ... В этом
случае говорят, что ?fn) -> ?г равномерно относительно i. Итак,
сходимость в т означает равномерную сходимость по коорди-
координатам.
В связи с тем, что и в I2, и в I, и в т сходимость по расстоянию
содержит в себе более сильные требования, чем сходимость по
координатам, особый интерес представляет метрика простран-
пространства *. Именно, мы покажем, что в * сходимость по расстоянию
совпадает со сходимостью по координатам.
Предварительно отметим следующее вспомогательное предло-
предложение: если 6„ = г-— ?>-0 (ая>0), то и а„^0. Это сразу выте-
1~ГаП
кает из соотношения а„ = ^_ .
Пусть ?« = {& }, ? = {?;;} суть точки из s и х„—>а;. Из опре-
определения расстояния в * сразу следует, что
при каждом i. На основании отмеченного выше вспомогательного
3.3]
СХОДИМОСТЬ В МЕТРИЧЕСКОМ ПРОСТРАНСТВЕ
81
предложения отсюда вытекает, что | ^п) — ?j | -> 0, т. е. |jn) -»- |г
при каждом i. Следовательно, сходимость по расстоянию в s влечет
сходтаюсть по координатам.
Обратно, пусть ?in)—>|j при каждом i. Зададим число е>0
и подберем р так, что 2 ~ — ~2р
¦ Далее> Для конечного
i=p+l 2
числа индексов i = l, 2, ..., р подбираем общин номер ЛГ так,
что
in) — h | <у ПРИ n>N,
Тогда, при n>N, имеем
p (xn, x) = У -—
» = 1, 2, ...,p.
I e . е *)
г=1
г=р+1
значит, ?„, —»- а;. Таким образом, и сходимость по координатам
влечет в * сходимость по расстоянию, следовательно, эти две схо-
сходимости в * совпадают.
В С сходимость по расстоянию равносильна равномерной схо-
сходимости функций, т. е. хп -> х в С означает, что
max | хп (t) — х {t) | —> 0.
Сходимость в CL и CL2 накладывает значительно менее тяжелые
требования на функции; последовательность функций может даже
не сходиться ни в одной точке. Мы ограничимся более простым
примером, именно построим последовательность непрерывных
функций хп (t) на отрезке [0,1], сходящуюся по расстоянию
к х (t) s= 1 и в CL и в CL2, но не стремящуюся к единице при t = 0.
Для этого положим (рис. 4)
nt при
при —
*) Напоминаем, что
в Б. 3. Вулих
82 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. Ill
Тогда, например, в метрике пространства CL, при x(t) = l.
1 п
р (хп, х) = \ [х U) — хп (t)\ dt= \ A — nt) dt —
о о
= t-
nfi
Аналогично подсчитывается, что и в метрике пространства CLi
р{хп, х) =. —>0. В то же время хп @) = 0 при всех п.
у Otl
Определение расстояния в CL и CL2 связано с часто используемы-
используемыми в приближенных вычислениях мерами отклонения одной функции
от другой. Именно, для функций f (t) и
g (t), заданных на отрезке [а, Ъ ], следую-
следующие величины называются средними
11 * !л(с) отклонениями одной функции от другой:
среднее отклонение 1-го порядка
ь
среднее квадратическое отклонение
±i\ \i{t)-g{t)fdt.
Рис. 4.
Сходимость по расстоянию в CL и Сь2
равносильна стремлению к нулю последовательности соответству-
соответствующих средних отклонений. В связи с этим сходимость по рас-
расстоянию в Сх и CL2 называется сходимостью в среднем 1-го
или 2-го порядка (соответственно).
Для любых двух непрерывных функций / (t) и g (t) их средние
отклонения друг от друга не превосходят величины максимального
отклонения / (t) от g (t), т. е. max | / (t) — g (t) |.
Действительно, если М = max | / (t) — g (t) |, to
Л/ ъЬ\ ['<0-
3.1] ЗАМКНУТЫЕ И ОТКРЫТЫЕ МНОЖЕСТВА 83
Поэтому, .если последовательность непрерывных функций схо-
сходится к пределу по расстоянию в С, то она сходится к тому же
пределу и в CLu в CL2. Обратное неверно.
В пространстве Lp сходимость по расстоянию называется
сходимостью в среднем р-го порядка. В теории интеграла доказы-
доказывается, что если последовательность функций сходится к некото-
некоторой предельной функции в среднем того или иного порядка, то
предельная функция не единственна, а определяется лишь с точ-
точностью до значений на множестве меры 0. Таким образом, если
задана последовательность функций из Lv и функция х (t)
(из L1') — одна из предельных функций, то и любая ей эквивалент-
эквивалентная — тоже предельная для данной последовательности (в смысле
метрики того же пространства ?''). Это нисколько не противоречит
единственности предела в метрическом пространстве. Ведь все
эквивалентные между собой функции — это один и тот же элемент
пространства X'J.
3.4. Замкнутые и открытые множества
Введем некоторые определения, важные в теории метрических
пространств. Перенесем сначала из трехмерного эвклидова про-
пространства в произвольное метрическое пространство Е понятие
шара. Для этого заметим, что шар состоит из всех точек, рас-
расстояние которых от его центра не превосходит радиуса (или
меньше радиуса, если речь идет только о внутренних точках
шара).
Определение. Открытым шаром с центром а ? Е
и радиусом г > 0 называется множество S (а, г) всех точек х ? Е,
удовлетворяющих условию р (х, а) < г. Аналогично замкнутым
шаром S* (а, г) (г > 0) называется множество всех точек х ? Е,
удовлетворяющих условию р (х, а) < г.
В J?j, т. е. на числовой прямой, открытый шар будет интерва-
интервалом (а — г, а + г), а замкнутый — отрезком [а — г, а + г].
В С шар S (у, г) состоит из всех функций х (t), удовлетворяю-
удовлетворяющих условию | х (t) — у (t) | < г на всем отрезке [а, Ь], т. е. гра-
графики которых умещаются в полоске, показанной на рис. 5.
Понятие шара позволяет дать следующую характеристику
предела сходящейся последовательности точек: для того чтобы
х = lira хп, необходимо и достаточно, чтобы, каков бы ни был
шар S (открытый или замкнутый) с центром в точке х, существо-
существовало такое N, что хп ? S при n~>N.
Определение. Множество F, содержащееся в Е (F а Е),
называется замкнутым, если, какова бы ни была сходящаяся
к пределу последовательность точек хп ? F, ее предел тоже вхо-
входит в F. t
6*
84 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. 11J
Из определения следует, что всё Е замкнуто; пустое множе-
множество тоже считается замкнутым, так как из него вообще нельзя
выделить никакой последовательности точек. Конечное множе-
множество F = {г/!, . . ., yh) *) замкнуто, так как если последователь-
последовательность {хп} состоит из точек этого множества, то по крайней мере
одна из точек, пусть это будет yt, повторяется среди хп бесконечное
множество раз, а тогда и предел (если он существует) должен сов-
совпасть с г/;. (Читатель легко сообразит, что в таком случае, начиная
с некоторого п, все хп = г/г.)
Примерами замкнутых мно-
множеств в Hi могут также служить
любой отрезок а<ж< Ь, множе-
множества всех чисел х>а или всех
чисел х < Ъ.
Покажем, что в любом метри-
метрическом пространстве замкнутый
шар S* (а, г) всегда представляет
замкнутое множество. Действи-
Действительно, пусть хп ? S* (а, г);
тогда р (хп, а)<Сг. Если при
этом хп ->- х, то по непрерыв-
непрерывности расстояния
Рис- 5- p(i й)
0
1
1
1
.к
ri
а
i
i
1
1
1
1
Ъ
следовательно, и х ? S* (а, г).
С понятием замкнутого множества тесно связано понятие
предельной точки. Именно, пусть А — произвольное множество
точек из Е; точка х ? Е называется предельной точкой множе-
множества А, если существует такая последовательность точек хп?А,
среди которых имеется бесконечное множество различных, что
х == lim хп. Например, в В± точка х = 0 является предельной для
интервала 0 < х << 1, так как можно положить хотя бы хп = ^~,
ж тогда 0 < хп < 1 и хп ->- 0. Вообще предельными точками
интервала а -< х << b являются все его точки и два конца х = а
ш х = Ь.
Ясно, что замкнутое множество содержит все свои предельные
точки. Однако в определении замкнутого множества мы говорили
о любых сходящихся последовательностях, в которых допу-
допускаются какие угодно повторения точек. Предлагаем чита-
читателю проверить, что получится равносильное определение, если
замкнутым назвать множество, содержащее все свои предель-
предельные точки.
*) Эта запись означает, что множество F состоит из точек yit . . ., yk.
3.4] ЗАМКНУТЫЕ И ОТКРЫТЫЕ МНОЖЕСТВА 85
В следующих двух теоремах устанавливаются основные свой-
свойства замкнутых множеств. При этом рассматриваются мно-
множества, содержащиеся в одном и том же метрическом про-
пространстве JE.
Теорема 3.4.1. Сумма конечного числа замкнутых мно-
множеств также — замкнутое множество.
Доказательство. Так как сумму любого конечного
числа множеств можно образовать последовательным прибавле-
прибавлением по одному множеству, то достаточно доказать теорему для
суммы двух множеств.
Пусть Ft и F2 — замкнутые множества, F = Ft \j F2, xn ? F
(п = 1, 2, . . .) и хп ->- х. В последовательности {хп} существует
бесконечная частичная последовательность {^пд}> состоящая цели-
целиком из точек одного из данных множеств, например хПд ? Ft.
Но хп тоже стремится к х, и так как Fi замкнуто, то х ? Fu
а потому х ? F.
Теорема 3.4.2. Пересечение любого множества замкнутых
множеств замкнуто.
Доказательство. Пусть F = f| Fa и все Fa замкнуты.
а
Если хп ->- х и хп ?F (п = 1, 2, . . .), то все хп ? Fa при любом а,
а потому их ? Fa при любом а. Следовательно, х ? F,vlF замкнуто.
В дальнейшем важную роль будет играть операция замыкания
произвольного множества А с JE, заключающаяся в присоедине-
присоединении к множеству А пределов всех сходящихся последовательно-
последовательностей его точек. Получаемое таким способом множество обозна-
обозначается [А] и называется замыканием множества А *).
Таким образом, всегда А с [А]. Из определения замыкания
сразу следует, что множество А замкнуто тогда и только тогда,
когда А = [А ].
В Ht замыканием интервала (а, Ъ) будет отрезок [а, Ъ\. Однако
в произвольном метрическом пространстве для замыкания откры-
открытого шара имеет место лишь включение [S (а, г) ] с S* (а, г),
но равенство не обязательно.
Лемма 3.4.1. Всякая точка х ? [А ] представима в виде
х = lim xn, где хп ? А.
Доказательство. Если х ? А, то можно положить
хп = х при всех п. Если же х g A, то, по определению, включение
iE W1 означает, что х = lim xn, где хп g A.
Л _е м м а 3.4.2. Для того чтобы х g [А], необходимо и доста-
достаточно, чтобы, каково бы ни было е > 0, существовала такая
точка х ? А, что р (х , х) < е.
*) Определение замыкания получится равносильное, если говорить
о присоединении всех предельных точек множества А.
86 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
Доказательство. Необходимость условия доказана
в предыдущей лемме. Если, наоборот, условие выполнено, то при
каждом п существует такая точка хп ? А, что р (хп, х) < —;
тогда х = lim xn и х ? [А].
Теорема 3.4.3. Замыкание любого множества замкнуто.
Доказательство. Пусть хп ? [А] и хп —>¦ х. Согласно
лемме 3.4.2 для каждого п можно подобрать уп ? А так, что
Р (Уп, Хп) < ^. Тогда
р (уп, х)<р (уп, хп) + р (х„, х)< — + р (хп, х) —> 0.
Следовательно, уп -> х. Таким образом, х ? [А ] и [А] замкнуто.
Теорема 3.4.4. Замыкание [А ] есть наименьшее замкнутое
множество, содержащее А.
Доказательство. Всякое замкнутое множество F,
содержащее А, должно содержать и пределы всех сходящихся
последовательностей точек из А. Следовательно, [A] a F. Но так
как само [А ] замкнуто, то оно и есть наименьшее из всех замкну-
замкнутых F Г5 А.
Определение. Пусть А — произвольное множество точек
из Е. Точка х ? А называется внутренней точкой множества А,
если при некотором е > 0 шар S (х, е) с А. Множество G cz E.
все точки которого — внутренние, называется открытым.
Всё Е — открытое множество; пустое множество также при-
причисляется к открытым. В Hi примерами открытого множества
могут служить любой интервал а < х ¦< Ь, множества, определяе-
определяемые неравенствами а; > а или х < Ъ.
Покажем, что в любом метрическом пространстве всякий
открытый шар S (а, г) — открытое множество. Действительно,
пусть х ? S (а, г). Это значит, что р (х, а) << г. Положим е =
= г — р (х, а). Если у ? S (х, е), т. е. если р (у, х) << е, то
р (у, а)<р (у, х) + р (х, а) < г, откуда у 6 S (а, г). Таким обра-
образом, весь шар S (х, е) с S (а, г), т. е. х — внутренняя точка
множества S (а, г).
Связь между открытыми и замкнутыми множествами устанав-
устанавливается следующей важной теоремой:
Теорема 3.4.5. Для того чтобы множество G а Е было
открытым, необходимо и достаточно, чтобы его дополнение
F = Е\ G было замкнутым.
Доказательство, а) Необходимость. Пусть
G открыто, а хп ? F (п = 1, 2, . . .) и хп ->- х. Если бы х ? G,
то и некоторый шар S(x, e) входил быв Си не содержал точек
из F, что невозможно для предела последовательности точек
хп 6 Р. Следовательно, х ? F и F замкнуто.
3.5] ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 87
б) Достаточность. Пусть F замкнуто, а х ? G. Тогда
существует е > 0, при котором шар S (х, е) не содержит ни одной
точки множества F. В противном случае, по лемме 3.4.2, х входила
бы b[F], а так как [F]=F, тох входила бы ив/1. Таким образом, весь
шар S (x, e) d G, х—внутренняя точка множества G и G—открыто.
Теорема 3.4.6. Сумма любого множества открытых мно-
множеств и пересечение конечного числа открытых множеств —
также открытые множества.
Доказательство. Пусть G = [) Ga и все Ga открыты.
а
Тогда Fa = Е \ Ga замкнуты, а по свойству дополнений [см. фор-
формулу A) ] Е \ G = П Fа. Следовательно, по теореме 3.4.2, Е \ G
а
замкнуто, а по теореме 3.4.5 G открыто.
п
Аналогично, пусть G = (] Gt nGt открыты. Тогда Ft = Е \ Gt
п
замкнуты и F = |J Ft тоже замкнуто по теореме 3.4.1. Но G =
= Е\ F по свойству дополнений, следовательно, G открыто.
3.5. Полные метрические пространства
В математическом анализе весьма важную роль играет то, что
в совокупности вещественных чисел признак сходимости Боль-
Больцано — Коши является не только необходимым, но и достаточным
(зто — так называемое свойство полноты множества вещественных
чисел). В 2.4 мы видели, что этот признак в полном объеме верен
и в эвклидовых пространствах I2 и Вп. Однако в произвольном
метрическом пространстве признак Больцано — Коши может ока-
оказаться неприменимым в части достаточности. Например, если
в множестве всех рациональных чисел определить расстояние,
по той же формуле, что и в Ви т. е. положить р (х, у) = | х — у \,
то получится метрическое пространство. Но последовательность,
составленная из рациональных чисел, может и не иметь в этом
пространстве предела и, в то же время, удовлетворять условию
Больцано — Коши; так будет в том случае, если пределом зтой
последовательности в В^ является иррациональное число. В на-
настоящем параграфе мы выделим класс пространств, в которых
признак Больцано — Коши остается в силе.
Определение. Последовательность точек хп метриче-
метрического пространства Е называется фундаментальной (или сходя-
сходящейся в себе), если р (хп, хт) -*¦ 0 при п, т -> оо.
Следующая теорема устанавливает, что в части необходимо-
необходимости признак Больцано — Коши действует в любом метрическом
пространстве.
88 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. И)
Теорема 3.5.1. Если последовательность {хп} сходится
к пределу, то она фундаментальна.
Доказательство. Пусть хп -*¦ х. Тогда
р (хп, хт) < р (хп, х) -j- р {х, хт) > 0.
п т+оэ
п,
Определение. Множество точек метрического про-
пространства называется ограниченным по расстоянию (говорят
и просто — ограниченным), если оно содержится в каком-нибудь
шаре.
Для числовых множеств (т. е. множеств в i?j) это определение
ограниченности совпадает с обычным.
Теорема 3.5.2. Всякая фундаментальная последователь-
последовательность {хп} ограничена.
Доказательство. Зададим е > 0 и подберем N так,
что р (хп, хт) < е при п, m>N. В частности, р (хп, ariV) < e
при n^-N. Теперь положим
r = max[e, р(ж1, xN), p(x2, xN), ..., p(xN-t, xN)}.
Тогда уже при всех га = 1, 2, . . . р(хп, xN)*Cr, т. е. все
хп € S* (xN, r).
Заменяя г на г' > г, можно все хп заключить и в открытый шар
S (хя, г').
Дадим основное в теории метрических пространств определение.
Определение. Метрическое пространство называется пол-
полным, если в нем всякая фундаментальная последовательность имеет
предел.
Большинство пространств, приведенных в качестве примеров
в 3.2, полны. Относительно I2, а также и Вп, мы уже знаем это
из гл. II. Полнота I доказывается совершенно так же, как пол-
полнота I2 (см. 2.4), если вместо нормы разности векторов писать
расстояние между точками и учесть, что если I рассматривать как
подмножество множества s, то сумма двух векторов из I также
входит в I.
Проверим полноту С. Пусть хп (t) — функции из С и р (хп, хт) ->
-> 0. Так как р (хп, хт) = max | xn (t) — xm (t) |, то при каждом t
последовательность значений {хп (?)} — фундаментальная. Следо-
Следовательно, существует х (t) = lim xn (t).
Теперь, по заданному е > 0 находим N так, что р (хп, хт) < е
при п, m^N, т. е.
| хп (t) — xm(t)\<Ze при всех t и при га,
Переходя здесь к пределу при т—>оо, получим
\xn{t) — x(t) |<e при всех t и n>N,
3.5]
ПОЛНЫЕ МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
89
т. е. сходимость хп (t) к х (t) — равномерная. А тогда х (t) —
непрерывная функция*), т. е. принадлежит С, и р (хп, х) -»- 0.
По аналогичной схеме доказывается полнота т. Еще проще
доказывается полнота s. Если хп = {|'п)} образуют фундамен-
фундаментальную последовательность, то и координаты |[ при каждом i
образуют фундаментальную последовательность и, следовательно,
существуют |г = lim ?(п). Положим х = {|г}. Это — элемент из я.
А так как в s сходимость по расстоянию
совпадает со сходимостью по координатам,
то р (хп, х) ->¦ 0.
Упомянем без доказательства, что про-
пространства Lv и Z; при любом р > 1 полны**).
В терминах сходимости в среднем это
значит, что если последовательность функ-
функций хп (t) из Lp сходится в себе в среднем
р-го порядка, т. е. если
ь
J \xn(t)-xm(t)
dt
при n, m—> oo,
то существует функция из Lv, к кото-
которой данная последовательность сходит-
сходится (тоже в среднем р-го порядка).
Пространства Cl и (Зц. не полны. Приведем пример фундамен-
фундаментальной последовательности из Сь, не имеющей, однако, в С%
предела. Беря для простоты в качестве [а, Ь] отрезок [0. 1].
рассмотрим функции (рис. 6)
( 1
хп (t) = \ п 4 1 — 2nt при у <
при
1
1
2ге
при ~ + -^Г"
Легко проверить, что в пространстве L эта последовательность
сходится к функции
I 1 при 0 < t < у ,
[ 0 при -2-<г<1.
*) Известно! что предел равномерно сходящейся последовательности
непрерывных функций — непрерывная функция. См., например, Г. М. Ф и х-
тенгольц. Основы математического анализа, т. II, стр. 77.
**) По поводу полноты ЬР см., например, В. 3. В у л и х, Краткий курс
теории функций вещественной переменной стр. 262. Полнота I? доказы-
доказывается по той же схеме, что и полнота I2.
90 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
Действительно,
2п
xn{t)dt-
так как 0<х„ (*)<1, то р (хп, а;)<^ и потому хп -> х. Отсюда
уже следует, что последовательность {хп} — фундаментальная *).
Если бы она имела предел в пространстве Cl, to предельная
функция должна была бы быть эквивалентной с х (t), поскольку
предел в X — единственный. Однако непрерывной функции,
эквивалентной х (t), не существует **). Поэтому последователь-
последовательность {хп} предела в Сь не имеет.
Эта же последовательность {хп} оказывается фундаментальной
и в пространстве С/.2, но и в нем не имеет предела, что подтверж-
подтверждает неполноту Cl2.
В математическом анализе часто используется теорема о после-
последовательности вложенных друг в друга отрезков, доказательство
которой опирается на полноту множества вещественных чисел.
Покажем, как эта теорема переносится в любые полные метриче-
метрические пространства.
Теорема 3.5.3. Пусть {Sn} — последовательность замкну-
замкнутых шаров из полного метрического пространства Е, причем
Snn cr Sn при любом п, а радиус шара Sn стремится к нулю
при п -> оо. Тогда шары Sn имеют непустое пересечение, состоящее
из одной точки.
Доказательство. Пусть Sn -¦= S* (хп, гп) (хп — центр,
гп — радиус шара). По условию, гп ->- 0. Далее, хт ? SmdSn
при т > п, следовательно, р (хт, хп) <г„, а потому последова-
последовательность центров хп — фундаментальная. Вследствие полноты
в М существует х = lim хп. Так как при любом п и при т> п
будет хт ? Sn, то, вследствие замкнутости Sn, x 6 Sn. Таким обра-
образом, х — общая точка всех шаров Sn.
Пусть точка у также входит во все шары Sn. Тогда при
любом п:
р (х, у) <р (х, хп) +р(хп,У)<2г„
*) Так как г, -> г в I, последовательность {хп } фундаментальна в L.
Но р {хп, хт) имеет одно и то же значение и в L и в С1,, следовательно, после-
последовательность {хп} фундаментальна и в CL.
**) Если бы такая непрерывная функция существовала, она должна
была бы принимать значение 1 на промежутке 0, — и значение Она про-
промежутке ( —-, 1 , но это противоречит непрерывности.
3.6] СЧЕТНЫЕ МНОЖЕСТВА 91
и так как гп ->- 0, то р (х, у) = 0, т. е. х — i/. Таким образом,
пересечение f) ^л состоит только из одной точки х.
п
Всякое подмножество Ei метрического пространства Ж может
рассматриваться и как самостоятельное метрическое пространство,
если для любых двух точек из Е1 сохранить то определение рас-
расстояния, которое было введено в Е. В связи с этим отметим одну
полезную для дальнейшего теорему.
Теорема 3.5.4. Всякое замкнутое подмножество F пол-
полного метрического пространства Е само является полным метри-
метрическим пространством.
Доказательство. Пусть хп ? F и образуют фун-
фундаментальную последовательность. Так как Е полно, то в
Ж существует х = lim хп. Но, вследствие замкнутости F, х ? F.
Следовательно, всякая фундаментальная последовательность
точек из F сходится в F к пределу, что и означает пол-
полноту F.
В дальнейшем, когда какое-нибудь подмножество Е1 метриче-
метрического пространства Е рассматривается как пространство, то без
специальных оговорок всегда будем считать, что определение рас-
расстояния в Et индуцировано (т. е. перенесено) из Е.
3.6. Счетные мно;кества
Этот параграф посвящается еще одному из вопросов общей
теории множеств. Если какое-нибудь множество состоит из конеч-
конечного числа элементов (пусть их будет р), то мы всегда можем
перенумеровать различными способами эти элементы, используя
в качестве номеров натуральные числа 1,2, . . ., р. Однако пере-
перенумеровать все элементы какого-нибудь бесконечного множества,
даже с использованием в качестве номеров всевозможных чисел
натурального ряда, уже не всегда возможно. Не приводя доказа-
доказательства, отметим, например, что нельзя перенумеровать все
вещественные числа. При этом заметим, что если бы речь шла
о перенумеровании всех вещественных чисел, например, в порядке
их возрастания, то невозможность этого была бы совершенно оче-
очевидна, так как в совокупности всех вещественных чисел нет наи-
наименьшего, которое мы должны были бы считать первым. Мы же
утверждаем нечто более сильное, а именно, что вещественные числа
нельзя перенумеровать, каким бы сложным способом мы ни попы-
попытались это сделать.
Если же элементы бесконечного множества могут быть перену-
перенумерованы с помощью всех натуральных чисел, т. е. могут быть
расположены в виде некоторой бесконечной последовательности хи
х2, . . ., хп, . . ., то такое множество называется счетным. Среди
92 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
различных бесконечных множеств счетные оказываются во многих
отношениях наиболее простыми.
Приведем некоторые примеры счетных множеств.
1. Натуральный ряд чисел. Натуральные числа
можно перенумеровать, например в порядке возрастания: xL = 1,
х2 = 2, . . ., хп = п, ... Тогда номер каждого числа совпадает
с его величиной.
2. Множество всех четных чисел. Четные чис-
числа тоже можно перенумеровать в порядке возрастания: xt = 2,
х2 = 4, . . ., хп = 2п, . . .
3. Множество всех корней функции sin x.
Как известно, корни уравнения sin х = О имеют вид х = кп
(к = О, ±1, ±2, . . .). Их не удается перенумеровать ни в порядке
возрастания, ни в порядке убывания, но можно это сделать,
например, так:
а:1 = 0, х2=-п, х3=—л, а:4 = 2л,
Хь= —2Я, ..., Х2п = ПП, ?2n+i= —ПК, ...
Заметим, что таким же способом нумерации:
^ = 0, х2=1, х3= — 1, z4 = 2, x5= — 2, ...
доказывается счетность множества всех целых чисел.
Установим некоторые свойства счетных множеств.
Теорема 3.6.1. Из всякого бесконечного множества можно
выделить счетное подмножество.
Доказательство. Пусть А — бесконечное множество.
Возьмем любой его элемент и назовем его а^. Кроме а1: в А имеется
еще бесконечное множество элементов. Возьмем любой из них
и назовем его а2. Кроме ах и а2, в А опять имеется еще бесконеч-
бесконечное множество элементов. Любой из них назовем а3. Этот процесс
можно продолжить до бесконечности. В результате из А будет
выделено счетное подмножество элементов at, az, . . ., ап, . . .
Теорема 3.6.2. Всякое бесконечное подмножество счет-
счетного множества тоже счетно.
Доказательство. Пусть множество А счетно, хи
х2, . . ., хп, . . .— его элементы, а В — бесконечное подмноже-
подмножество множества А. Располагая в порядке возрастания номеров
все элементы, из которых состоит подмножество В,
Xiil< Х> • • • ' Tnft, ¦ ¦ • (П{ < По < ¦ • ¦ <Щ <•¦¦)'
мы можем перенумеровать их заново всеми натуральными числами,
взятыми по порядку. Следовательно, В счетно.
Теорема 3.6.3. Сумма конечного числа счетных мно-
множеств — тоже счетное множество.
3.6] СЧЕТНЫЕ МНОЖЕСТВА 93
Доказательство. Пусть множества Аи А2, . . ., Ар
р
счетны, А = U Лг. Выпишем элементы данных множеств At в виде
следующей таблицы:
(Ai) ап, а12, . . ., а1п, . . .
(А2) do,, azz, . . ., а2п, ...
(¦tip) U]>ll Up2> ¦ ¦ ¦ ! И,рП! ¦ ¦
Здесь в обозначении элементов а^п первый индекс — номер множе-
множества At, из которого взят этот элемент, а второй — номер этого
элемента внутри множества At. Теперь перенумеруем заново все
элементы таблицы (9), располагая их, например, в виде последова-
последовательности
Иными словами, сначала мы занумеруем все элементы первого
столбца таблицы (9), следующими натуральными числами зануме-
занумеруем элементы второго столбца и продолжаем далее в том же
порядке. Если множества At содержат некоторые общие элементы,
то один и тот же элемент может повториться в последователь-
последовательности A0) несколько раз. Однако мы нумеруем его, естественно,
только один раз, например тогда, когда этот элемент впервые
встретится в последовательности A0); при последующих же
встречах с этим элементом мы просто пропускаем его. Таким
образом, все элементы множества А могут быть перенумерованы,
т. е. А — счетно.
Обратим внимание читателя, что, доказывая счетность множе-
множества А, мы должны были найти такой «путь» для перенумерования
элементов таблицы(9), двигаясь по которому, мы можем ручаться,
что до любого элемента таблицы мы дойдем после конечного числа
шагов. Это и гарантирует, что каждый элемент получит номер.
Поэтому нельзя было нумеровать элементы таблицы (9), например,
по строкам, так как уже первая строка содержит бесконечное
множество элементов и за конечное число шагов мы никогда не
доберемся до элементов второй строки; все номера будут исполь-
использованы на одну первую строку.
Теорема 3.6.4. Сумма счетного множества счетных мно-
множеств — тоже счетное множество.
?о
Доказательство. Пусть А = {] At и каждое множе-
множество At — счетное. Возможность занумеровать сами множества At
и означает, что множество этих множеств — тоже счетное. Дока-
.жем, что и А счетно.
94 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. 111
Выпишем элементы множеств At в виде таблицы, которая отли-
отличается от (9) тем, что в ней бесконечное множество строк:
(At) аи, а12, . . ., atn,
(А2) а21, а22. . . ., а2п, . . .
A1)
al\.i ai2> ¦ • ¦ 1 ain,
Элементы таблицы A1) можно перенумеровать, но уже не по столб-
столбцам, так как каждый столбец содержит бесконечное множество
элементов, а, например, по диагоналям, т. е. в таком порядке:
ап, ai2, a2i, ai3, а22, a3i, . . . Повторяющиеся элементы нумеруем
по одному разу, так же, как и при перенумеровании элементов
таблицы (9). Таким образом, множество А счетно.
Ясно, что если из таблицы (9) или A1) некоторые элементы
вычеркнуть, например оставить в некоторых строках лишь конеч-
конечное число элементов, то это не помешает перенумеровать остальные
элементы в том же порядке, как это сделано выше. Поэтому
теоремы 3.6.3 и 3.6.4 остаются верными и в том случае, когда
некоторые из складываемых множеств (но не все) конечны. Если
же они все конечны, то сумма может быть или конечной или счет-
счетной. Объединяя все эти замечания с теоремами 3.6.3 и 3.6.4, мы
можем сформулировать следующий общий результат:
Теорема 3.6.5. Сумма конечного или счетного множества
множеств, каждое из которых конечно или счетно, есть конечное
или счетное множество.
Важную роль в функциональном анализе играет следующая
теорема:
Теорема 3.6.6. Множество всех рациональных чисел счетно.
Доказательство. Каждое рациональное число, отлич-
- т
ное от нуля, можно представить в виде несократимой дроби —, где
п — натуральное, am — целое, положительное или отрицатель-
отрицательное *). При заданном п множество всех дробей — (т — целое) —
счетно (см. замечание к примеру 3). Тогда и множество Ап несо-
несократимых дробей вида — также счетно по теореме 3.6.2 **).
*) Целые числа т Ф 0 для единообразия представляются в виде
дробей —
**) Несократимых дробей с заданным знаменателем — бесконечное
множество.
3.6] СЧЕТНЫЕ МНОЖЕСТВА 95
По теореме 3.6.4 множество А = [) Ап счетно. Но множество D
п=1
всех рациональных чисел получится сложением А с множеством,
состоящим из одного числа нуль. По теореме 3.6.5 ж D — счетно.
Из теорем 3.6.2 и 3.6.6 следует, что множество всех рацио-
рациональных чисел, содержащихся в любом заданном промежутке на
числовой оси ([а, Ь] или (а, Ь) при а < Ъ) также счетно.
Заметим, что рациональные числа, находящиеся в каком-
нибудь промежутке, конечно, нельзя перенумеровать в порядке
возрастания. Это следует хотя бы из того, что за любым рацио-
рациональным числом нет ближайшего большего. Способ нумерации
может быть найден из доказательств самой теоремы 3.6.6 и преды-
предыдущих, на которые опирается эта теорема.
Теорема 3.6.7. Пусть элементы множества А характе-
характеризуются конечным числом параметров, каждый из которых
независимо от остальных может принимать значения из неко-
некоторой счетной совокупности. Тогда множество А счетно.
Д оказательство. Запишем элементы множества А
в виде аГ1, . . ., pk, где рь рг, . . ., pk — параметры *). Пусть
все возможные значения каждого параметра pi перенумерованы:
Pu> Pi2, ¦ • ч Pirn • • • Будем вести доказательство индукцией
по к, т. е. по числу параметров.
Если к = 1, то элементы множества А могут быть перенуме-
перенумерованы в порядке значений единственного имеющегося пара-
параметра р^.
следовательно, А счетно.
Пусть теорема уже доказана, если число параметров к — 1.
Докажем, что она верна и для к параметров. Разобьем множе-
множество А на подмножества Ап, относя в Ап все элементы, для которых
параметр ph имеет фиксированное значение pkn. Тогда А — [} Ап.
п = 1
С другой стороны, внутри каждого из множеств Ап элементы раз-
различаются значениями параметров рь р2, ¦ . ., Pft-i, поскольку
значение параметра ри для элементов каждого из этих множеств
зафиксировано. По индуктивному предположению теорема спра-
справедлива для к — 1 параметров, а потому каждое из множеств Ап
счетно. Тогда и А, как их сумма, тоже счетно.
Дадим одно важное применение доказанной теоремы.
*) Хотя мы записываем параметры в виде индексов, но они могут
иметь какой угодно смысл; например, в следующей теореме это будут коэф-
коэффициенты в выражении полинома.
Ш МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
Теорема 3.6.8. Множество сР всех алгебраических поли-
полиномов с рациональными коэффициентами счетно.
Доказательство. Рассмотрим сначала множество сР„
всех полиномов фиксированной степени п с рациональными коэф-
коэффициентами:
Р (х) = соха + с1хп~1 +...+сп (с0 Ф 0).
Эти полиномы характеризуются п -\- 1 коэффициентами, каждый
из которых, по условию, может принимать только рациональные
значения. Таким образом, совокупность значений каждого из
коэффициентов — счетная. Коэффициенты и играют роль пара-
параметров из предыдущей теоремы, и по этой теореме множество <Рп
счетно. Но показатель степени п может принимать счетное множе-
множество различных значений: га = 0, 1, 2, . . . и аР = U сРп. Тогда
по теореме 3.6.4 и множество всех алгебраических полиномов
с рациональными коэффициентами счетно *).
3.7. Сепарабельные пространства
В множестве всех вещественных чисел 2?4 подмножество D всех
рациональных чисел обладает следующим важным свойством:
каждое вещественное число представимо как предел последователь-
последовательности рациональных чисел **). Таким образом, замыкание [D] =
= J?j. Это свойство называют плотностью множества рациональ-
рациональных чисел в J?j. Перенесем понятие плотности в произвольные
метрические пространства.
Определение. Множество А точек метрического про-
пространства JE называется всюду плотным (в Е), если [А ] = Е.
Согласно леммам 3.4.1 и 3.4.2, равенство [А ] = Е означает,
что каждый х ? Е представим в виде х = lim xn, где хп 6 А, или
что для каждого х ? Е по любому е > 0 можно найти х' ? А так,
что р (х, х') < е ***). Если же сказанное сейчас верно только для
тех х, которые принадлежат некоторому открытому или замкну-
замкнутому шару S cz E, то говорят, что А плотно в S.
*) Множество полиномов, коэффициентами которых могут быть любые
вещественные числа, уже не счетно.
**) Если данное число иррационально, то требуемые рациональныо
числа можно получить, взяв, например, десятичные приближения к нему
с недостатком или с избытком. Так, для }^2 можно положить г4 = 1,4; г.> =
= 1,41; г3 = 1,414; г4 = 1,4142 и т. д.
***) В этом условии, очевидно, строгое неравенство р (х, х') <Z e можно
заменить и таким: р (х, х') < е.
;!."] СЕПАРАБЕЛЬНЫЕ ПРОСТРАНСТВА 97
Определение. Метрическое пространство называется
сепарабелъным, если в нем существует счетное или конечное всюду
плотное подмножество.
Так как конечное множество замкнуто, то его замыкание совпа-
совпадает с ним самим (см. 3.4). Поэтому наличие в пространстве конеч-
конечного всюду плотного подмножества означает, что все пространство
состоит из конечного числа точек. Сепарабельность же простран-
пространства, содержащего бесконечное множество точек, означает, что
в этом пространстве существует именно счетное всюду плот-
плотное подмножество.
Большинство пространств, рассмотренных выше в качестве при-
примеров, сепарабельны.
В i?n каждый вектор представим в виде предела последователь-
последовательности векторов с рациональными координатами. А векторы с рацио-
ральными координатами образуют счетное множество по теореме
3.6.7 (координаты и представляют те параметры, о которых гово-
нится в этой теореме). Следовательно, _В„ — сепарабельно.
Установим сепарабельность Р. Рассмотрим х 6 I2, пусть х =
= (!,, 12, . . ., 1т, . . .). Положим хп = (\и12, . . ., 1п, 0, 0, . . .).
Тогда хп -*- х по определению сходимости в Р. Заменим каждый
вектор хп на х'п = (ги г2, . . ., гп, О, 0, . . .) с рациональными
координатами так, что
\П-Ы<4к (*• = !, 2, ...,#»)•);
тогда
Р(
Следовательно,
^,*»)=/|1с-.-ь)*</»-^=4--
р {х'п, х) < р (х'п, хп) -\- р (хп, х)<-^ + р (хп, х) -» О
И х'п —> X.
Множество Dn векторов вида (ги г2, . . ., гп, 0, 0, . . .)
с рациональными координатами по теореме 3.6.7 счетно при
?о
каждом фиксированном га = 1, 2, ... Сумма U Dn тоже счетна
п = 1
и, как мы уже показали,' всюду плотна в Р. Следовательно,
I2 сепарабельно.
Сепарабельность пространств V при любом р>1 и s уста-
устанавливается аналогично. Без доказательства отметим, что про-
пространство т не сепарабельно.
*) Каждое г; зависит, конечно, не только от i, но и от п. Однако мы
не отражаем этого в обозначениях.
7 Б. 3. Вулих
98 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
Пространство С сепарабельно. В нем счетным всюду плотным
множеством является, например, множество сР всех алгебраиче-
алгебраических полиномов с рациональными коэффициентами.
Действительно, по доказываемой в математическом анализе
теореме Вейерштрасса каждая непрерывная на отрезке функ-
функция х (t) представима как предел равномерно сходящейся после-
последовательности полиномов Qn (t) *). Равномерная сходимость и есть
сходимость в метрике пространства С, т. е. Qn —*- х. Заменяя все
коэффициенты каждого из полиномов Qn (t) достаточно близкими
рациональными, мы найдем полиномы Рп (t) из множества сР
так, что
на всем отрезке а< ?<6**). Тогда р (Рп, Qn) ¦< —, откуда
уже будет следовать, что Рп ->¦ х по расстоянию в С. Тем самым
доказано, что множество & всюду плотно в С.
Так как сходимость по расстоянию в С влечет сходимость
в Cl и Схг (см. 3.3), то множество оР всюду плотно и в CL и в С^г,
а потому и эти пространства сепарабельны.
Докажем две общие теоремы.
Теорема 3.7.1. Всякое подмножество Еу сепарабельного
метрического пространства JE само является сепарабельным про-
пространством.
Доказательство. Пусть {хп} (п = 1, 2, . . .) — счет-
счетное всюду плотное в Е множество его точек ***). Возьмем любые
дна натуральных числа пик. Если существуют такие точки х ? Еи
для которых р (х, хп) < -г, то выберем какую-нибудь одну из них
и обозначим ее х(к2'¦ Множество всех определенных таким образом
точек х{п обозначим через А; А с Е{. По теореме 3.6.7, если
бы точки х^п (с двумя параметрами кип) были определены и раз-
различны при всех п, к = 1, 2, . . ., то их множество было бы счетным.
Тем более счетно (или, может быть, конечно) множество А.
*) См., например, В. И. Смирнов, Курс высшей математики, т. II,
стр. 441.
**) Пусть i>(O = cotm-;-<^'n~1-f . ..-f cm, a Q(/) = rfo'm + rfi'm-1-b...
... +dm. Тогда
I P(t)-Q(t)\<\co-d0\\im\Jr\cl-dl\\^-i\Jr...+\Cm-dm\<:(m+l)M^
если | cj — tfj]<e при всех j = 0, 1, ..., m, a M—наибольшее нз чпеел
max I 1г I (*=¦--U, 1, ..., m).
o<feb
***) Если Е состоит из конечного числа точек, то теорема становится
тривиальной.
3.8] КОМПАКТНЫЕ МНОЖЕСТВА 99
Покажем, что А всюду плотно в ?",. Пусть х^Е%. Возьмем
1 е
е>0 и подберем натуральное к так, что -г<у- Так как мно-
множество {хп} всюду плотно в Е, то существует п0, при котором
р (хпд, х) <z-r- ¦ А раз при п — щ существует x?Et, удовлетво-
удовлетворяющий последнему неравенству, то существует и х^?А, при-
чем р (xw, хПй) <; -г-. Но тогда
Р (<>, *) < Р (<>. «п.) + Р (**.. *)< т < е.
Вследствие произвольности е отсюда следует, что А всюду плотно
в Еи и сепарабельность ? доказана.
Теорема 3.7.2. Если всюду плотное подмножество Ех
метрического пространства Е является сепарабелъным простран-
пространством, то и Е сепарабелъно.
Доказательство. Пусть А —¦ счетное (или конечное)
всюду плотное подмножество в Ех. Возьмем х 6 Е и зададим
е > 0. Так как Е1 всюду плотно в Е, то существует такой х ? Ei,
что п (х, х) < -s-; а так как Л всюду плотно в ZJj, то существует
такой ж" 6 Л, что р (я', а:") <С 4-. Отсюда следует, что р (х, х") <
< ей, вследствие произвольности е, зто означает, что А всюду
плотно в Е.
С помощью теоремы 3.7.2 легко доказывается сепарабельность
пространств Tjv. Именно, в теории интеграла устанавливается,
что множество непрерывных функций всюду плотно в любом из
пространств L1' (р > 1) *). Но это множество с метрикой из
любого L1' само представляет сепарабельное пространство (выше
это отмечено по отношению к Cl и Сх2, но это справедливо и при
любом р > 1). А тогда сепарабельность Ъу — прямое следствие
теоремы 3.7.2.
3.8. Компактные множества
Одной из важных теорем математического анализа является
теорема Больцано — Вейерштрасса: из всякой ограниченной бес-
бесконечной последовательности чисел хи х2, ¦ • ., хп, ... можно
выделить частичную хП1, хП2, . . ., тПд . . . (щ < п2 < . . .
... <С га& <•••)> сходящуюся к конечному пределу. Если А —
произвольное ограниченное множество чисел, то теорема Боль-
Больцано — Вейерштрасса применима к любой последовательности,
*) Для пространства L2 см., например, И. П. Натансон, Теория
функций вещественной переменной, стр. 188 (по изданию 1957 г.).
7*
100 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
составленной из чисел множества А. С другой стороны, если
А не ограничено, то из него можно выделить последовательность,
стремящуюся к со, а из такой последовательности нельзя выделить
никакой частичной, сходящейся к конечному пределу. Таким
образом, в пространстве Иг можно сформулировать следующий
результат. Пусть множество A cz Ri. Для того чтобы из любой
последовательности {х„}, все члены которой хп ? А, можно было
выделить частичную сходящуюся к конечному пределу, необходи-
необходимо и достаточно, чтобы множество А было ограничено. Однако
при переходе в произвольные метрические пространства мы уже
не получим такого простого результата и, чтобы выделить тот
класс множеств, в которых справедливо заключение теоремы
Больцано — Вейерштрасса, введем следующее определение:
Определение. Множество А, содержащееся в метриче-
метрическом пространстве Е, называется компактным, если из любой
бесконечной последовательности точек хп ? А можно выделить
частичную последовательность хП1, хП2, ¦ . ., хп , . . . (щ < п2 <
¦<...< nh •<...)> сходящуюся в JE к некоторому пределу *).
В частности, если само пространство Е обладает этим свойством,
то оно называется компактным пространством.
Из сказанного выше ясно, что в i?4 свойство компактности равно-
равносильно ограниченности множества.
Заметим, что всякое конечное множество точек метрического
пространства компактно. Действительно, пусть А = {уи . . .,ур},
а {хп} — любая последовательность, состоящая из точек множе-
множества А. Но тогда по крайней мере одна из точек yt повторяется
среди хп бесконечное множество раз, например при некотором i
и частичная последовательность лг„ —»- yt.
Отметим некоторые простые свойства компактных множеств.
Теорема 3.8.1. Компактное множество ограничено по
расстоянию (определение ограниченности множества дано в 3.5).
Доказательство. Пусть множество А не ограничено.
Возьмем любую его точку и назовем ее xt. Положим rt = 1. Так
как А не ограничено, то оно не может целиком содержаться в шаре
S (xlt rj). Возьмем любую точку из А, не входящую в этот шар,
и назовем ее х2. Тогда р (а^, х2) >rt. Положим г2 = р (#1, х2) + 1.
Так как А не может содержаться в S (хи г2), то можно найти
некоторую его точку х3, не входящую в этот шар; р (xt, x3)>r2-
Полагаем r3 = p (xt, x3) -\- 1 и продолжаем этот процесс до бес-
бесконечности. В результате строятся последовательность точек
хп ? А и возрастающая последовательность чисел гп так, что
*) Этот предел может и не принадлежать множеству А.
3.8] КОМПАКТНЫЕ МНОЖЕСТВА 101
при всех п = 2, 3, ...
Теперь при любых п > т > 2
Поэтому из неравенства
р(хи xn)<Cp(xi, хт)-\-р(хт, х'п)
вытекает, что г„,< (rm — 1) + р (хт, хп), откуда р (хт, хп) > 1.
Следовательно, никакая частичная последовательность, выделен-
выделенная из {#„}, не может быть фундаментальной и, тем более, не может
сходиться к пределу. Значит, А не компактно.
Обратное заключение неверно, например, в I2. Действительно,
в I2 все координатные орты ет находятся на расстоянии единица
от нулевого вектора, следовательно, образуют ограниченное мно-
множество. С другой стороны, р (ет, ер) = |/ при т Ф р, а потому
из последовательности {ет} нельзя выделить частичной сходя-
сходящейся.
Теперь покажем, что в пространстве Нп теорема Больцано —
Вейерштрасса сохраняет силу и, следовательно, получается сле-
следующий критерий компактности: для того чтобы множество
А с Ип было компактным, необходимо и достаточно, чтобы оно
было ограниченным по расстоянию.
Необходимость условия доказана в теореме 3.8.1 для любого
метрического пространства. Докажем его достаточность.
Каждый шар S (а, г) в пространстве h'n состоит из всех точек
z = (li, h, • ¦ •> in), для которых
(здесь а-ь суть координаты а). Таким образом, если х ? S (а, г), то
I; ~ ai I < г ПРИ каждом i или at — г <С \% < а-г + г. Следова-
Следовательно, координаты точек, образующих ограниченное множество
в Вп, в совокупности ограничены *).
Пусть A cr J?n и А ограничено. Берем любую последователь-
последовательность точек хт ? А: хт = (^(,т), ^1т', . . ., ?пт)). Так как числовая
последовательность f^,'} ограничена, то но теореме Больцано —
Вейерштрасса из нее можно выделить частичную, сходящуюся
к конечному пределу, \[тъ) -*- g,. Теперь из данной последователь-
последовательности точек хт сохраняем только точки Xmk с выделившимися
*) Предлагаем читателю проверить, что обратное заключение тоже верно.
102 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
выше номерами т^. Эта частичная последовательность точек
обладает тем свойством, что последовательность их первых коорди-
координат сходится. Рассматривая последовательность вторых координат
{Щ?;)} точек хт , мы можем выделить из последовательности
{xmk} новую частичную, еще более «редкую», для которой будет
сходиться к конечному пределу последовательность вторых коор-
координат. При этом свойство сходимости последовательности первых
координат не нарушится. Повторяя такое постепенное «просеива-
«просеивание» заданной последовательности точек п раз, мы получим частич-
частичную последовательность точек, для которых последовательности
всех координат сходятся к конечным пределам. А так как сходи-
сходимость в Rn есть сходимость по координатам, то выделенная частич-
частичная последовательность точек имеет предел в В^. Тем самым
компактность А доказана.
Заметим, что в пространстве s предыдущий критерий компакт-
компактности неверен. Действительно, в s расстояние между двумя точками
всегда меньше единицы, поэтому s совпадает с шаром S (я, 1)
каков бы ни был центр а; следовательно, s ограничено. С другой
стороны, в s легко указать последовательность точек, из которой
нельзя выделить сходящуюся частичную; например, можно взять
с этой целью хп = (п, 0, 0, . . .). Критерий компактности в s мы
выведем после доказательства еще некоторых общих теорем.
Сформулируем в явном виде то обобщение теоремы Больцано —
Вейерштрасса, которое мы фактически и вывели по ходу доказа-
доказательства критерия компактности в Вп: из всякой бесконечной
последовательности точек п-мерного векторного пространства,
все координаты которых в совокупности ограничены, можно выде-
выделить частичную последовательность, сходящуюся по координатам.
Определение. Пусть А с Е (Е — метрическое про-
пространство) и е > 0 — заданное число. Множество В а Е назы-
называется Е-сетъю множества А, если для любого х ? А существует
такая точка у ? В, что р (х, у) <. е.
Теорема 3.8.2. Всякое компактное множество при любом
е > 0 имеет содержащуюся в нем самом конечную е-сепгъ (т. е. е-сеть
состоящую из конечного числа точек).
Доказательство. Пусть А компактно, но допустим,
что при некотором е > 0 конечной е-сети в нем не существует.
Возьмем любую точку xL?A. Тогда существует такая точка
хг 6 А, для которой р (#!, х2) > е. В противном случае уже одна
точка xi образовывала бы е-сеть в А. Пусть уже определены точ-
точки хи х2, . . ., хп ? А так, что р (хи xh) > е при г, к = 1, 2, . . ., п
и г Ф к. Так как, по предположению, конечное множество точек
Xi, x2, . . ., хп не может составлять е-сеть для множества А,
то существует такая точка а^-н^Л, что р (хи xn+i) > e,
р (х2, хп+х) > е, ..., р (хп, хп-ц) > е. Продолжая этот процесс мы
3.8] КОМПАКТНЫЕ МНОЖЕСТВА 103
строим такую бесконечную последовательность точек хп?А, что
р (хп, хт)> г при любых пфт. Но из такой последователь-
последовательности нельзя выделить частичную сходящуюся, а это противоречит
компактности А.
Таким образом, при любом е > 0 в А существует конечная
е-сеть.
Следствие. Компактное пространство сепарабелъно.
Доказательство. Пусть Е.— компактное метрическое
пространство. Полагая е„ = — (га= 1, 2, . . .), мы найдем в Е
оо
конечные е„-сети Вп. Множество В = [} Вп конечно или счетно.
п=1
В то же время оно всюду плотно в Е. Действительно, для любого
х ? Е и любого числа е > 0 подбираем сначала натуральное п так,
I 1
что — < е, а затем у ? Вп так, что р (х, у) < еп = -- . Тем
самым у ? В, а р (х, у) < е; множество В всюду плотно в про-
пространстве Е.
Теперь докажем теорему, обратную по отношению к преды-
предыдущей, которая верна, однако, лишь в полных метрических про-
пространствах.
Теорема 3.8.3. Если для множества А, содержащегося
в полном метрическом пространстве Е, при любом е > 0 суще-
существует конечная г-сетъ, то А компактно.
Доказательство. Возьмем произвольную последова-
последовательность точек Хп ? А и покажем, что из нее можно выделить
частичную, сходящуюся в Е к некоторому пределу.
Зададим е± = 1 и по этому et выделим в Е конечную егсеть
для множества А. Пусть она состоит из точек at (i = 1, 2, . . ., k).
Около каждой из этих точек опишем шар радиуса единица.
По определению е-сети каждая точка множества А, в частности
каждая точка хп, отстоит по крайней мере от одной из точек аг
на расстоянии, меньшем единицы. Следовательно, каждая точка хп
попадает по крайней мере в один из построенных шаров. Но
так как этих шаров — конечное число, то по крайней мере
один из них, назовем его Su содержит бесконечное множество
членов последовательности {хп} *). В противном случае вся
последовательность {хп} состояла бы из конечного числа членов.
Те точки хп, которые входят в St, расположим в виде частичной
*) Когда мы говорим «бесконечное множество членов последовательно-
последовательности {хп}», мы имеем в виду члены с бесконечным множеством различных
номеров. Однако не исключено, что некоторые из этих членов могут пред-
представляться одинаковыми точками, т. е. не исключено, что хп = хт при неко-
некоторых пфт.
104 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
последовательности, но занумеруем их заново и обозначим
r(D r(i) „(и
¦^l > Л2 ' * • • > ^П 1 • • •
Л
Теперь зададим е2 = -у- Исходя из уже выделенной после-
последовательности {х*™} и рассуждая совершенно аналогично, мы
установим с помощью конечной е2-сети существование шара $2
радиуса у, в котором содержится бесконечная частичная после-
последовательность х[2\ xf\ . . ., х(п\ . . ., выделенная из первой
частичной последовательности.
Этот процесс постепенного «просеивания» частичных последо-
последовательностей, в отличие от похожего конечного процесса, приме-
примененного выше в Пп, продолжим до бесконечности. Именно, если
уже выделена частичная последовательность, содержащаяся
в шаре Ьп радиуса е„ = — , то, задавая е„+1 = -—т и используя
конечную 8п+1-сеть, мы сможем выделить из этой последователь-
последовательности новую частичную, содержащуюся в шаре Sn+i радиуса —г—,.
Запишем все эти последовательности в виде следующей таблицы:
A2)
af >, xf), xf), . . ., «(»),
В этой таблице каждая строка представляет частичную последова-
последовательность, выделенную из предыдущей строки. При этом п-я строка
обладает тем свойством, что все ее элементы содержатся в шаре Sn
(^радиуса —J.
Далее воспользуемся часто применяемым в математике диа-
диагональным методом. Именно, образуем последователь-
последовательность из всех точек, стоящих по диагонали таблицы A2):
По отношению к заданной вначале последовательности {хп}
это — частичная *). Далее, каково бы ни было п, если из диаго-
*) Здесь следует иметь в виду, что каждая точка уР?> стоит и в (ге — 1)-й
строке, причем находится там правее, чем х^~1К Поэтому номер точки ж'™',
который она имеет в исходной последовательности {хп}, больше, чем номер
точки s^~i' B той же последовательности.
3.8] КОМПАКТНЫЕ МНОЖЕСТВА 105
нальной последовательности A3) отбросить ж, ж!,2', . . ., .r("Zi\
то оставшиеся элементы будут входить в п-ю строку таблицы A2),
а потому будут содержаться в Sn. Следовательно, если а — центр
этого шара, то при любых т, р>п имеем
р (*?•>, а)<±, р (*(*, а)< 1 ,
а потому
р (*?\ 4Р)) < р № °) + р («
Таким образом, р (х^» ?рР)) -*¦ 0 при т, р -»- оо, т. е. диагональная
последовательность A3) фундаментальна. Вследствие полноты про-
пространства JE, последовательность A3) сходится к некоторому пре-
пределу. Тем самым, компактность множества А доказана.
Следствие. Если множество А, содержащееся в полном
метрическом пространстве Е, при любом е > 0 имеет компакт-
компактную г-сеть (т. е. г-сеть, являющуюся компактным множеством),
то само А также компактно.
Доказательство. Зададим произвольное е > 0 и пусть
множество В cz E является компактной у-сетью множества А.
Вследствие компактности В, по теореме 3.8.2, в нем существует
е
Т
е
конечная у-сеть. Пусть эта сеть состоит из точек аи . . ., ад.
Берем любой х ? А. Так как В есть у-сеть для А, то существует
такой у ? В, что р (х, у) < у. А так как точки е^, . . ., ah обра-
образуют у-сеть в В, то по крайней мере для одной из них, пусть это
будет аи р (у, at) < у. Но тогда р (х, at) < e. Таким образом,
каждая точка х ? А отстоит по крайней мере от одной из точек
аи . . ., ak на расстоянии, меньшем е, т. е. точки аь . . ., ah
образуют конечную е-сеть множества А. По теореме 3.8.3, вслед-
вследствие произвольности е, множество А компактно.
Теперь установим критерий компактности в пространстве s:
для того чтобы множество A cz s было компактным, необходимо
и достаточно, чтобы при каждом i = 1, 2, ... совокупность Ах
1-х координат \t точек х ? А была ограничена *).
а) Необходимость. Так как сходимость в s есть сходи-
сходимость по координатам, то из компактности множества А вытекает
компактность каждого из числовых множеств Аг. Но тогда все эти
множества ограничены.
*) Граница может зависеть от i: | |j | <; Сг.
106 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [ГЛ. III
б) Достаточность. Пусть множество А таково, что
все Аь ограничены. Зададим произвольное е>0и подберем р так,
оо
что 2 рГ = •>!'' ^ Е' Теперь каждой точке х = {?,} ? А сопо-
г=р+1
ставим точку у = {?ь |2, • - •, 1Р, 0, 0, . . .}, у которой первые
р координат — те же, что у х, а остальные равны нулю. Множество
всех полученных таким образом точек у (для всевозможных х ? Л)
обозначим через 5. Для каждого if 4я сопоставленного ему у d В
оо оо
i=p+l i=P+l
Следовательно, множество В составляет е-сеть множества А.
Проверим компактность множества В. Возьмем последователь-
последовательность точек уп ? В. По условию, их координаты в совокупности
ограничены. Если у каждого уп отбросить все координаты, начиная
с (Р + 1)-й (равные нулю), получится последовательность точек
{у'п} р-мерного векторного пространства. По обобщенной теореме
Больцано — Вейерштрасса из этой последовательности можно
выделить частичную {у'пк}, сходящуюся по координатам. Но так
как точки уПк отличаются от точек у'Пк только нулевыми коорди-
координатами, то и последовательность {уПк} будет сходиться по всем
координатам, т. е. в смысле сходимости по расстоянию в *.
Таким образом, множество В компактно.
Теперь компактность А получается сразу на основании след-
следствия из теоремы 3.8.3.
В пространстве I2 сходимость по расстоянию, как мы знаем, не равно-
равносильна сходимости по координатам. Поэтому критерии компактности, уста-
установленные выше для Вп и s, неверны в I2 *). Мы не будем выводить критерий
компактности в I2, а ограничимся кратким рассмотрением одного примера.
Основным параллелепипедом в I2 называется множество / всех точек
х = {?j} 6 12< для которых | %i | <! —¦ при всех i. Покажем, что / компактно
ОО
1
С этой целью зададим произвольное е > 0 и подберем р так, что ^ ~2i <^й-
i=p+l
Построив по / множество В так же, как это сделано по множеству А в пре-
предыдущем доказательстве, мы сразу увидим, что В — е-сеть множества /.
Компактность же В так же, как и выше, легко получается с помощью теоремы
Больцано—Вейерштрасса**). Отсюда и будет вытекать компактность /.
*) То же относится и к 1*> и к т.
**) Если отличные от нуля координаты встречаются только на первых
р местах, то из сходимости последовательности точек {уп } по координатам
легко следует сходимость {уп } по расстоянию в I2.
3.9] КРИТЕРИЙ КОМПАКТНОСТИ В ПРОСТРАНСТВЕ С 107
3.9. Критерий компактности в пространстве С
Ввиду большой важности для дальнейшего пространства С,
вопрос об условиях компактности в нем мы разберем полностью.
В математическом анализе доказывается следующая теорема
о равномерной непрерывности функций: если функция х (t)
непрерывна на отрезке [а, Ь], то по любому е>0 найдется
такое б > 0, что неравенство | х (^) — х (t2) | < е должно быть
выполнено в любых двух точках ti и t2 из [а, Ь], для которых
h — t2\ <^ Ь. Однако, если по одному и тому же е > 0 искать
соответствующее б для разных функций, то и значения б будут
получаться, вообще, различные. Поэтому, если рассматривается
бесконечное множество различных непрерывных функций, то
вполне возможно, что по некоторому в > 0 для них не удастся
подобрать общего б. В связи с этим введем
Определение. Пусть на отрезке [а, Ь] задано произ-
произвольное множество непрерывных функций х (t). Эти функции
называются равностепенно непрерывными, если по любому е > 0
найдется такое б > 0, что в любых двух точках ti и tz на отрезке
[а, Ь], для которых \ tt — t2 | < б, неравенство | х (^) — х (t2)\ <
< е выполнено для любой из заданных функций.
Если заданных непрерывных функций — конечное число, то
они обязательно равностепенно непрерывны, так как по любому
е > 0 сначала для каждой функции можно найти свое б, а затем
из всех этих б (их конечное число!) взять наименьшее. Это и будет
требуемое общее б.
Определение. Пусть задано некоторое множество функ-
функций х (t). Эти функции называются равноограниченными, если они
все удовлетворяют неравенству | х (t) \ ~-сМ с некоторой общей
постоянной М.
Критерий компактности множества в пространстве С дается
следующей теоремой итальянского математика Ч. Арцела
A847-1912):
Теорема 3.9.1. Для того чтобы множество A cz С было
компактным, необходимо и достаточно, чтобы функции множе-
множества А были равноограничены и равностепенно непрерывны.
Доказательство, а) Необходимость. Пусть
А компактно. По теореме 3.8.1 оно ограничено в метрике С,
т. е. A a S (у, г) при надлежаще подобранных у ? С и г > 0.
Это значит, что каждая функция х ? А удовлетворяет на всем
отрезке [а, Ь] неравенству
y(t)-r<x(t)<y (t) -J- г.
Положим l = iainy(t), L-= max г/(?). Тогда
l — r<x(t)<L + r,
108 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА 1ГЛ. Ill
а это и означает равноограниченность функций из множества А.
•Если, например, положить М = max (| L + г |, | I — г [), то
неравенство | х (t) ] <; М будет выполнено для любой функ-
функции х ? А.
Теперь докажем равностепенную непрерывность функций мно-
множества А. Зададим произвольное е > 0. По теореме 3.8.2 в про-
пространстве С существует конечная ir-сеть множества А. Пусть она
О
состоит из функций yt (t), у2 (t), . . ., yk (t). Так как этих функ-
функций — конечное число, то они равностепенно непрерывны, а пото-
потому существует такое б > 0, что при всех ? = 1,2, . . ., к
влечет
— yi{tz)\<~
(tu I2?[a, b\). Далее, для любой функции х?А по определению
8 F
-тг-сети можно найти такое i, что р (я, yt) <C-o-, т. е. при всех
*€[«, Ъ]
Тогда, используя это i, имеем при | ^—12\<С.Ь:
Таким образом, найденное б соответствует заданному е для всех
функций х (f) из множества А. Вследствие произвольности е, рав-
равностепенная непрерывность этих функций доказана.
б) Достаточность условия может быть выведена
с помощью теоремы 3.8.3; однако мы предпочитаем дать прямое
доказательство этой части теоремы Арцела.
Пусть функции множества А равноограничены и равностепенно
непрерывны. Возьмем любую последовательность функций хп ? А.
Выделим в [а, Ь] подмножество всех рациональных точек. Так как
это подмножество — счетное, то все входящие в него точки можно
перенумеровать: tu tz, . . ., tt, . . .
При каждом п рассмотрим последовательность значений функ-
функции {хп (?j))iLr Эти последовательности можно рассматривать
как точки из пространства *. Вследствие равноограниченности
функций из А последовательность i-x координат этих точек
ixn (^)}n=i ограничена при каждом i. Тогда, по признаку ком-
компактности в *, из {хп} можно выделить частичную последователь-
последовательность {хпк} так, что при каждом i существует конечныйПт хПк (ti).
Докажем, что частичная последовательность функций {хПк (t)}
сходится по расстоянию в С. Сначала установим, что xnh (t) стре-
стремится к конечному пределу в каждой точке t ? [а, Ь]. В рацио-
3.9] КРИТЕРИЙ КОМПАКТНОСТИ В ПРОСТРАНСТВЕ С 109
нальных точках это имеет место по построению. Пусть t иррацио-
иррационально и пусть задано е > 0. По числу -^- находим 6 из определе-
о
ния равностепенной непрерывности, общее для всех функций
из А, а затем находим рациональную точку т (это — одно из tt),
для которой \ t — т [ < б. Тогда при всех к = 1, 2, ...
Так как последовательность значений х„ (т) имеет конечный
предел по построению, то она — фундаментальная. Следовательно,
существует такое К, что
\хПк(т) — а;„г(т)|<у при к,
Отсюда и из A4) мы получаем, что при к,
i xnh @ - Xril (t) | < | ХПк (t) - Хч (Т) I +
+1 Xvk (t) -xni (r)\+) xni (x) - xH (t) |
т. е. последовательность {xn (t)} — фундаментальная. Следова-
Следовательно, конечный lim ж„А (t) = у (t) существует при всех t Е Ы, Ъ\.
Теперь докажем, что сходимость этой последовательности —
равномерная. Зададим е > 0 и воспользуемся тем общим б, кото-
которое было выше подобрано по -~-. Тогда при всех к
о
\t' — t"\<b влечет | х„к (t')-xnh (/") |<| . A5)
Переходя в последнем неравенстве к пределу, получим, что
\? -1" | < б влечет | у (*') - у (f) |< |- . A6)
Отсюда, в частности, вытекает непрерывность функции y(t).
Разобьем отрезок [а, Ъ] на конечное число частей с помощью
точек а — т0<т1<... <тр = Ь так, чтобы длина каждой части
была меньше б. Так как точек тг — конечное число, то для них
можно подобрать общее К таким образом, что
ХпкЫ — y(Ti)\<j при Л>Я, 1 = 0, 1, ..., р. A7)
Пусть, теперь, t — произвольная точка из отрезка [а, Ь]. Тогда
Tj<?<t;+i при некотором i. Если обозначить это тг через т, то
t-~ т|<1б. Используя A5) — A7), имеем при кК
xnk (t) - У @ |< I *пк (t)-Xnh (т) | +
110 МЕТРИЧЕСКИЕ ПРОСТРАНСТВА [.ГЛ. III
что и доказывает равномерную сходимость хПк (t) к у (t). Иными
словами, х„к -*¦ у по расстоянию в С. Компактность множества А
доказана, чем и завершается доказательство теоремы Арцела.
Укажем один достаточный признак равностепенной непрерыв-
непрерывности. Говорят, что функция х (t) (а<?<6) удовлетворяет на
отрезке [а, Ь] условию Липшица с постоянной К, если для любых
hi ^26 [я> Ъ\ выполнено неравенство
Л е м м а 3.9.1. Функции х (t), удовлетворяющие условию Лип-
Липшица с общей постоянной К, равностепенно непрерывны.
Доказательство. Зададим е > 0 и положим б = -гг
А
(не уменьшая общности, можно считать К>0). Тогда, если
\ h — h I < б, то для всех рассматриваемых функций
х (ti) - х (t2) \<K\t1 — t2\<:Kd = e
и их равностепенная непрерывность доказана.
В следующей главе мы дадим применение теоремы Арцела.
Г Л Л В А IV
НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
В МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ
4.1. Основные определения
Уже в первых главах мы вводили понятие оператора и функ-
функционала в конечно-мерном и бесконечно-мерном эвклидовых про-
пространствах.
В настоящей главе мы перенесем эти понятия в произволь-
произвольные метрические пространства и придем, таким образом, к весьма
широкому обобщению понятия функции. При этом мы будем рас-
рассматривать и такие операции, которые определяют преобразование
или, как часто говорят, отображение одного метрического про-
пространства не только в самого себя, но и в произвольное другое
метрическое пространство.
Определение. Пусть X и Т — метрические простран-
пространства, D — некоторое множество в пространстве X. Если каждой
точке х ? D по определенному правилу сопоставлена некоторая
точка у 6 Y, то говорят, что на множестве D задан оператор
со значениями в пространстве Y- Если этот оператор обозначен U,
то самое соответствие между точками х ? D и у ? У записыва тся
в виде у = Ux. Множество D называется областью задания (или
определения) оператора U. Символ х, обозначающий переменную
точку из множества D, называют аргументом оператора U.
Каждая точка у ? Y, представляющаяся в виде у = Ux, назы-
называется значением оператора U или образом соответствующей
точки х ? D. Относительно оператора U говорят, что он устана-
устанавливает отображение множества D в пространство Т*. Если сово-
совокупность значений оператора U совпадает со всем пространством Т,
то говорят также, что установлено отображение множества D на
пространство Т.
Пусть Е — некоторое подмножество множества D. Совокуп-
Совокупность всех значений у = Ux оператора U, которые он принимает,
когда х ? Е, называется образом множества Е и обозначается
U(E).
112 НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ ГГЛ. IV
Определение. Оператор, заданный на некотором множе-
множестве в метрическом пространстве, значения которого суть веще-
вещественные или комплексные числа, называется функционалом*).
В этой главе мы рассматриваем только функционалы с веществен-
вещественными значениями и в дальнейшем не будем это оговаривать
каждый раз.
Примером функционала в пространстве С может служить
ь
интеграл \ х (t) dt. Значение функции х (t0) в фиксированной
а
точке t0 также — функционал. Если каждой непрерывно-диффе-
непрерывно-дифференцируемой функции из С (так называют функцию, имеющую
непрерывную производную) сопоставить ее производную, то мы
получим оператор, отображающий подмножество непрерывно-
дифференцируемых функций из С на всё С **).
Иногда приходится рассматривать операторы с несколькими
аргументами. Не приводя точных определений, которые читатель
может сформулировать самостоятельно, укажем, например, что
на расстояние р (я, а;') в метрическом пространстве X можно смо-
смотреть как на функционал с двумя аргументами, mi', определен-
определенный для любой пары точек из пространства X.
4.2. Непрерывные операторы и функционалы
Изучая эвклидовы пространства, мы уже неоднократно поль-
пользовались термином ((непрерывность», вкладывая в него тот же
смысл, какой имеет это понятие для обычных функций. Дадим
теперь общее определение непрерывности для операторов в про-
произвольных метрических пространствах.
Определение. Оператор U, отображающий множество
D а X в пространство Y, называется непрерывным в точке х0 ? D,
если для любой последовательности точек xn?D, такой, что
хп ->- х0, имеет место соотношение Uxn ->- UxQ. Оператор назы-
называется просто непрерывным, если он непрерывен в каждой точке
того множества, на котором он задан.
Мы дали определение непрерывности оператора в точке х0 на
языке последовательностей. Можно сформулировать его и в других
терминах. Именно, оператор U непрерывен в точке xo?D, если
для любого е > О существует такое б > 0, что при всех х ? D,
удовлетворяющих условию р (а;, х0) < б, имеет место неравенство
р (Ux, UxQ) < e.
*) Впрочем, такой оператор называют и просто функцией.
**) Известно, что всякая непрерывная функция есть производная своего
интеграла, т. е. некоторой другой непрерывной фупкции.
1.2] НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ И ФУНКЦИОНАЛЫ ИЗ
Иными словами, последнее неравенство должно быть выполнено
для всех точек множества D, входящих в открытый шар S (х0, б)
радиуса б с центром в х0. Равносильность этого определения с пер-
первым, данным на языке последовательностей, «устанавливается
так же, как для обычных функций в математическом анализе *).
Мы не останавливаемся на этом и в дальнейшем будем пользо-
пользоваться первым определением.
Приведенные определения, конечно, имеют смысл и для функ-
функционалов как частного случая операторов.
Многие свойства вещественных непрерывных функций перено-
переносятся и на непрерывные операторы в произвольных метрических
пространствах или, по крайней мере, на непрерывные функцио-
функционалы. При этом те теоремы, где важную роль играет непрерыв-
непрерывность функции именно на отрезке, обладающем, как известно, свой-
свойствами замкнутости и компактности на числовой прямой, остают-
остаются, как правило, верными в общих метрических пространствах,
если область задания оператора — замкнутое компактное множе-
множество. Приведем одну такую теорему, обобщающую теорему Вейер-
штрасса о непрерывных функциях.
Теорема 4.2.1. Непрерывный функционал / (х), заданный
на замкнутом компактном множестве D си X, ограничен и среди
его значений есть наибольшее и наименьшее.
Доказательство. Докажем, что функционал / (я) огра-
ограничен снизу и имеет наименьшее значение. Аналогичным рассуж-
рассуждением устанавливается существование наибольшего значения.
Допустим, что/ (а;) не ограничен снизу. Тогда для любого нату-
натурального п существует по крайней мере одна точка хп ? D, в кото-
которой / (хп) < — п. Отсюда следует, что lim / (хп) = — оо. Вслед-
Вследствие компактности множества D из {хп} можно выделить частич-
частичную последовательность {хп.}, сходящуюся к некоторому пределу
х0 6 -X"- Так как D замкнуто, то х0 ? D и, по непрерывности функ-
функционала, / (хп.) -*- / (а;о). Но, с другой стороны, f (хп.)->-—оо
и, так как / (х0) — число, а не —оо, то мы пришли к противоречию.
Тем самым, доказана ограниченность / (я) снизу.
Теперь обозначим через т точную нижнюю границу значе-
значений / (я) **) и докажем, что / (х0) = т в некоторой точке х0 ? D.
Это и будет означать, что т — наименьшее значение / (х). Так как
при любом натуральном п число т 4-— уже не является нижней
*) См., например, Г. М. Фихтенгольц, Основы математического
анализа, т. I, стр. 70.
**) Точной нижней границей ограниченного снизу множества чисел
называется наибольшая из его нижних границ. Она обозначается inf (от
латинского слова infimum — «наинизшее»).
8 В. 3. Вулих
114 НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. IV
границей для / (х), то для каждого п можно подобрать точку
хп gZ), в которой / (хп) <С т -\ . Из последовательности {хп}
выделяем частичную подпоследовательность хп. ->- х0, где х0 ? D.
В неравенстве
переходим к пределу и получаем, что lim / (хп.) = т. Но тогда,
вследствие непрерывности функционала, / (х0) = т.
Заметим, что доказанная теорема верна, в частности, если
множество D совпадает со всем пространством X и это простран-
пространство компактно.
4.3. Неподвижные точки. Метод последовательных
приближений
Рассмотрим оператор U, отображающий метрическое про-
пространство X или некоторое его подмножество в метрическое про-
пространство Y. Если задать некоторый элемент у ? 1', то на соотно-
соотношение у = Ux можно смотреть как на уравнение с неизвестным х
и может быть поставлена задача, определить все те точки х,
в которых Ux принимает заданное значение у. В случае, когда
элементами пространств X и Y являются те или иные функции,
уравнение Ux = у называют функциональным.
С функциональными уравнениями вида Ux = у мы еще встре-
встретимся в последующих главах. Сейчас остановимся на уравнениях
несколько иного вида.
Если U — оператор, отображающий пространство X или неко-
некоторое его подмножество в то же пространство, то точки х?Х,
для которых Ux = х, называются неподвижными точками опера-
оператора U. На равенство Ux — x можно также смотреть как на урав-
уравнение и решение этого уравнения и сводится к отысканию непо-
неподвижных точек оператора U *).
Для нахождения неподвижных точек часто применяется метод
последовательных приближений. Мы изложим сейчас общую схему
этого метода, а в следующем параграфе будут указаны некоторые
условия, обеспечивающие его применимость.
Будем предполагать, что оператор U задан на некотором зам-
замкнутом подмножестве D пространства X и непрерывен и что все
*) Заметим, что оба указанных уравнения являются частными случаями
уравнения более общего вида: Ux = Vx, где U и V—два оператора, ото-
отображающих некоторое подмножество пространства X в одно и то же про-
пространство Y. В первом случае можно положить Vx = у, где у — постоянное,
во втором нужно считать, что пространства X и Y совпадают, a Vx = х,
т.е. V — тождественный оператор.
4.4] ОПЕРАТОРЫ СЖАТИЯ 115
его значения также принадлежат множеству D. Возьмем произ-
произвольную точку х0 ? D и положим Xi = Ux0. Если бы точка х0 была
неподвижной, то мы бы получили, что xt = х0; но при произволь-
произвольном выборе х0, как правило, будет х^ =^ х0. Далее, последовательно
полагаем х2 = Ux±, x3 = Ux2, ... и, в общем виде,
xn+i = Uxr. A)
При этом, по условию, если хп ? D, то и :г„+1 ? Z) и, следовательно,
построение следующей точки хп+2 возможно. Продолжая этот про-
процесс до бесконечности, строим последовательность точек хп ?D.
Если окажется, что существует х* = lim xn (в этом случае говорят,
что процесс сходится), то, вследствие замкнутости!), х* ? D. Пере-
Переходя к пределу в A) и пользуясь непрерывностью оператора U,
получим, что х* = Ux*, т. е. что х* — неподвижная точка.
Первый вопрос, который возникает в связи с описанным мето-
методом: будет ли процесс сходиться при произвольной начальной
точке х0 или начальную точку нужно подчинить каким-нибудь
ограничениям. Далее, метод последовательных приближений
может быть использован не только для доказательства существо-
существования неподвижной точки х*у но и для ее приближенного нахожде-
нахождения. Именно, точки хп, которые могут быть фактически найдены,
если оператор U задан в каком-нибудь конкретном пространстве,
и являются последовательными приближениями к х*. Если,
при этом, под погрешностью понимать расстояние р (хп, х*),
то сходимость процесса означает, что погрешность принципиально
может быть сделана сколь угодно малой. Однако может потребо-
потребоваться найти оценку погрешности, которая покажет, сколько
приближений нужно построить, чтобы достичь заданной точности.
Все эти вопросы могут быть решены, если будут известны надлежа-
надлежащие дополнительные сведения об операторе U.
4.4. Операторы сжатия
В настоящем параграфе мы рассмотрим операторы, для которых
расстояние между образами любых двух различных точек меньше
расстояния между самими этими точками, по крайней мере, в опре-
определенном отношении. Такие операторы будем называть операто-
операторами сжатия. Точнее, оператор If, заданный в метрическом про-
пространстве X или некотором его подмножестве, называется операто-
оператором сжатия, если существует такая положительная постоянная
а <! 1, что для любых х', х" из области задания оператора U
p(Ux', Ux")<ap(x', хЙ). B)
Легко видеть, что оператор сжатия U всегда непрерывен.
Действительно, если хп и х0 взяты из области задания оператора U
116 НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. IV
и хп -*¦ х0, то из неравенства р (Uxn, UxQ) <ctp (xn, x0) следует,
что и Uxn -> UxQ.
Теорема 4.4.1 (С. Банах) *). Если оператор сжатия U
отображает полное метрическое пространство X в самого себя, то
он имеет единственную неподвижную точку и эта точка может
быть получена методом последовательных приближений при
любой начальной точке х0 ? X.
Доказательство. Берем произвольно х0 ? X. Из фор-
формулы A) и условия сжатия B) получаем при любом п
р(хп+1, xn)=p(Uxn, Uxn-i)-Cap(xn, Xn-t).
В свою очередь, р(хп, xn.-1)-^.ap(xn-i, xn~2) и т. д. Повторяя
такую оценку п раз, находим
р(хт1, хп)*Сар(хп, zn_,)< а2р (хп-и хп-2)< ¦ ¦ ¦ <апр (хи х0).
Теперь покажем, что последовательность {хп} — фундаменталь-
фундаментальная. Пусть пг>га; тогда
m_1( хт-2) +. ..+р(хп+1, х„)
< (am"i + a7" + . . . + а") р (хи х0) <
) J?' хо)-
1=п
Отсюда видно, что р(хт, х„)—>0 при т, га^-оо. Так как про-
пространство X полно, то последовательность {хп} сходится к пре-
пределу х*, который, как мы знаем из предыдущего параграфа,
и является неподвижной точкой.
Единственность неподвижной точки вытекает из условия
сжатия: если х' и х" — неподвижные точки, то
р(х', x") = p(Ux', Ux")<ap(x', x"),
откуда р(х', х") = 0, т. е. х' = х".
Замечание 1. Если в неравенстве C) перейти к пределу
при т—^со, то получим
а™
р(х*, xn)<?j—^p(xu x0).
Это и есть оценка погрешности, получающейся при замене х* на
хп. Эта погрешность убывает со скоростью геометрической про-
прогрессии со знаменателем а. Кроме того, из найденной оценки видно,
что при одном и том же п точность приближения, как правило, тем
лучше, чем ближе ж4 к х0. Поэтому, если положение х* приблизи-
приблизительно известно, то для вычислений выгодно взять х0 где-то
*) С. Банах A892—1945) — выдающийся польский математик, один
из основателей функционального анализа.
4.4]
ОПЕРАТОРЫ СЖАТИЯ
117
вблизи х*. Тогда их, = Ux0 будет недалеко отх*, а следовательно,
и от х0.
Замечание 2. Так как замкнутое подмножество F пол-
полного метрического пространства X по теореме 3.5.4 само является
полным метрическим пространством, то теорема Банаха верна
и для оператора сжатия, заданного не на всем X, а только на его
замкнутом подмножестве F, если множество значений оператора
также содержится в F. При
этом за начальную точку
процесса последовательных
приближений можно принять
любую точку х0 ? F.
Приведем некоторые при-
примеры применения теоремы
Банаха.
1. Пусть / (х) — веществен-
вещественная дифференцируемая функ-
функция, заданная на отрезке
[а, Ь] числовой прямой, все
значения которой также за-
заключены в этом отрезке.
Пусть требуется решить урав-
уравнение / (х) = х, т. е. найти
точку пересечения графика
I (х) с прямой у = х (рис. 7).
Рассмотрим функцию / (х) как оператор, отображающий отре-
отрезок [а, Ь], являющийся замкнутым подмножеством полного про-
пространства Ви в самого себя. Если | /' (х) |<а < 1, то оператор
/ — оператор сжатия. Действительно, по формуле Лагранжа, для
любых х', х" ? [а, Ь]
| f (х')~ f (х")\= \ Г (I) (х: - х")\<а\х' -х"\
(?—точка между х' и х").
А тогда теорема Банаха применима, следовательно, оператор /
имеет единственную неподвижную точку, которая может быть
получена методом последовательных приближений, начиная с про-
произвольной точки х0 ?[а, Ъ]. Неподвижная точка оператора / и есть
решение уравнения / (х) = х.
2. Рассмотрим систему п линейных алгебраических уравнений
с п неизвестными:
Рис. 7.
ai2x2 -+-
... + а2пхп =
anlxi -f апгх2 + ... + annxn = bn.
118 НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. IV
Перенося все члены с неизвестными направо и прибавляя к обеим
частям первого уравнения по хи второго —по х2 и т. д., полу-
получим равносильную систему
ап) хх — ai2x2 — ... — alnxn + bu
— a22)x2— . . . — a2nxn + b2, v
xn= — anixl — an2x2 — . . . + A — ann) xn-\~bn.
Введем обозначения новых коэффициентов в правых частях
уравнений системы E); именно, положим
!1 при i = к,
О при 1фк,
и запишем систему E) в сжатой форме:
п
я* = 2 CjftZft f bs (i=^l, 2, ..., га). Ea)
Беря произвольную точку х = (xt, x2, ..., хп) из простран-
пространства _К„, определим отображение пространства Rn в самого
себя y=Ux, задавая координаты г/; точки у формулами
п
г/г=3 CikZh + bt (i = l, 2, .... га).
Решения системы D) или равносильной ей системы Eа) суть
неподвижные точки оператора U.
Укажем достаточное условие, при котором U — оператор
сжатия. Для этого сравним оператор U с оператором С линей-
линейного преобразования, определяемого матрицей (cih):
п
Vi= 2 clhxh (i=l, 2, . .., п).
Именно, Ux = Cx + b, где b = (bu b2, ...,bn). Для любых двух
точек х', х"?Цп имеем:
р (Ux', Ux") = || Ux' - Ux" || = || Cx' - Cx" || =-. || С (x' - x") ||.
Пользуясь нормой оператора линейного преобразования в Лп
[см. 1.7, формула A4а)], имеем
или
р (?/*', ^
Следовательно, если ||С||<;1, то U — оператор сжатия. Из оценки
'..4] ОПЕРАТОРЫ СЖАТИЯ Ц9
нормы оператора, данной в 1.7, видно, что последнее неравенство
имеет место, если, например,
2 c?fc<i. @)
Итак, при выполнении условия F) оператор U имеет единственную
неподвижную точку, которая может быть найдена методом после-
последовательных приближений.
Заметим, что условие F) требует, чтобы коэффициенты систе-
системы E) были не слишком большими по абсолютной величине,
в частности, это относится и к диагональным коэффициентам,
имеющим вид 1 — ан; следовательно, коэффициенты alt должны
быть (в среднем) близки к 1 *). Если бы оказалось, что все коэффи-
коэффициенты близки к —1, то следовало бы перед построением систе-
системы E) изменить знаки во всех членах уравнений системы D).
3. Аналогичный принцип может быть применен и к некото-
некоторым нелинейным системам. Рассмотрим следующую систему
уравнений:
п
xi--= 2 sin cikxk+bi (г'^1, 2, . . ., к), G)
и будем предполагать, что опять выполнено условие F). Как
и в предыдущем примере, обозначим через U тот оператор,
приводящий Л„ в Лп, который определяется правыми частями
уравнений системы G). Иными словами, y—Ux означает, что
!/,=•--- 2 smcihxk + bi (/ = 1, 2, ..., п)
(iji—координаты точки у).
Проверим, что U — оператор сжатия. Для любых двух точек
х = {x'h}, x" = {x"h}dBn положим y'=Ux', y" = Ux", и пусть
iji, у] — координаты точек у', у" (соответственно). Тогда
р (?/*', Ux") = p(y', у')=у 2 (y'i-ylJ- (8)
Но
П
ij'i — yl= 2 {sincikx'u—sincikx",,) (г = 1, 2, ..., п).
/i
*) Эти замечания, конечно, не имеют точного математического характера.
120
НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. IX
Применяя к каждому слагаемому формулу Лагранжа, мы
сразу найдем
п
У1 — У1 -"-¦ 2 cih (COS C,ft |г-й) (x'h — Xk)
h—l
(здесь ?;ft —некоторое промежуточное число, заключенное между
х'к и x'k). Отсюда сразу следует, что
п
fe=l
Применяя неравенство Коши (формулу C) из гл. I), получим
Т! ?1
п и
— \Zj Cib) \\Х — х \\ — \ Zi Cik) IP \x i x )\ ¦
С помощью этой оценки из (8) сразу вытекает, что
Г
p(Ux', Ux")<y i |) c?hp(x', x")
и благодаря условию F) U — оператор сжатия. А тогда теорема
Банаха обеспечивает существование и единственность решения
системы G), причем это решение может быть найдено методом
последовательных приближений.
4. Теперь покажем, как из теоремы Банаха можно получить
теорему о существовании и единственности решения дифферен-
дифференциального уравнения.
Рассмотрим уравнение 1-го порядка
V' = f{x, V) (9)
с начальным условием
У \х=х0 -= S/o- A0>
Пусть в прямоугольнике А (| х — л;0|<й> |{/—{/о|<&) Функ"
ция / (х, у) непрерывна и \f(x, y)\<M. Пусть, кроме тогог
существует такая постоянная К > 0, что
\j{x, yt)-f(x, yz)}<K\yi-y2\
при любом х из промежутка \х0 — а, х0 + а 1 и любых двух
значениях уи у2 из промежутка [у0 — Ъ, у0 + Ь]. Последнее
условие, как и для функций одной переменной, называется уело-
4.4] ОПЕРАТОРЫ СЖАТИЯ
вием Липшица *). Докажем, что при этих условиях найдется
такое достаточно малое положительное число h, что в промежутке-
\х0 — /г, х0 + /г] существует, и притом единственное, решение
уравнения (9), удовлетворяющее начальному условию A0).
Для доказательства придадим уравнению (9) другую — инте-
интегральную форму. Именно, считая у функцией от х, интегрируем
обе части (9) от х0 до переменного х. При этом благодаря началь-
х
ному условию A0) \ у' dx — у — у0, а потому мы приходим
х0
к уравнению
V)dx. A1)
Если уравнение A1) продифференцировать по х, то мы снова
вернемся к уравнению (9); кроме того, непосредственно видно,
что если функция у удовлетворяет уравнению A1), то у = у д.
при х = х0. Таким образом, уравнение A1) равносильно диффе-
дифференциальному уравнению (9), взятому вместе с начальным усло-
условием A0).
Примем за h любую положительную постоянную, меньшую,
чем у, ине превосходящую аи-^,и рассмотрим пространство С
непрерывных функций, заданных на отрезке б = [х0 — h, x0 -f h].
Обозначим через F подмножество пространства С, состоящее и»
всех функций у = у (х), для которых при всех х ? б
уо-Ь<у(х)<уо-'гЬ**). A2>
В пространстве С множество F — замкнутый шар радиуса Ьу.
центром которого является функция у = у0 (постоянная). Следова-
Следовательно, F — замкнутое множество.
Рассмотрим оператор, заданный на F посредством правой части,
уравнения A1), т. е. для каждого у ? F положим
[x, y(x)\dx (х?б) A3)
и запишем это соотношение коротко: z = Uy.
*) Условие Липшица, в частности, будет выполнено, если функция-
df
f (х, у) имеет в А ограниченную частную производпую по у:
**) Так как правая часть уравнения (9) задана в прямоугольнике А,
то решение можно искать только среди функций, удовлетворяющих усло-
условию A2).
122
НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
[ГЛ. IV
Проверим, что все значения оператора U входят в F и что
U — оператор сжатия.
Если y^F, то при любом :г?б точка (х, !/(#))? А, следо-
следовательно, правая часть A3) имеет смысл и z?C. Кроме того,
\f(x, у (х)) | <; М, а потому при всяком х ? б
\z(x)-yo\ = \f(x,y(x))dx <M\x-xo\<Mh.<M~=b,
следовательно, z?F.
Пусть у, y?F, z = Uy, z^Uy. Тогда при любом
мощью условия Липшица получим
z (*)-!(*) |- \f(x, y(x))dx-\f(x, y(x))dx
с по-
поx0
x, y(x))-f(x,y(x))\dx<K^ \y(x)~y(x)\dx
<Kmax\y (x) — y(x)\ \ x — x0 \
x-6
Kp (y,
^ap(y, y),
где a = Kh < 1.
Отсюда
p(z,
/, y).
Таким образом, теорема Банаха, согласно замечанию 2, при-
применима к оператору U и последний имеет единственную непо-
неподвижную точку, а это и есть единственное решение уравнения A1)
в промежутке б. Кроме того, теорема Банаха обеспечивает воз-
возможность получения этого решения методом последовательных
приближений. За начальную функцию можно принять, например,
У = г/о-
Аналогичную теорему о существовании и единственности реше-
решения можно получить из теоремы Банаха и для системы дифферен-
дифференциальных уравнений.
Метод последовательных приближений был применен фран-
французским математиком Э. Пикаром A856—1941) к уравнению (И)
для непосредственного доказательства теоремы о существовании
и единственности решения дифференциального уравнения, а также
и к системам дифференциальных уравнений. Доказательство Пикара
и послужило прототипом доказательства теоремы Банаха.
В следующем параграфе мы дадим еще некоторые применения
теоремы Банаха.
4.5] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 123
4.5. Интегральные уравнения
В предыдущем параграфе мы уже встретили уравнение, в кото-
котором неизвестная функция содержалась под знаком интеграла.
Это было уравнение (И), к которому привелось дифференциальное
уравнение (9). Вообще уравнения, содержащие неизвестную функ-
функцию под знаком интеграла, называются интегральными. Основы
теории интегральных уравнений были разработаны в конце
XIX и начале XX столетий итальянским математиком В. Воль-
терра A860—1940) и шведским математиком Э. Фредгольмом
A866—1927). К интегральным уравнениям сводятся многие задачи
математической физики. Развитие теории интегральных уравне-
уравнений послужило одним из толчков к созданию функционального
анализа, и некоторые важные результаты функционального
анализа являются прямым обобщением теорем, относящихся
к интегральным уравнениям.
Наиболее подробно изучены линейные интегральные урав-
уравнения, из которых мы остановимся на так называемых уравнениях
Фредголъма второго рода в их простейшем виде:
x(s) -=А, J К (s, t)x(l)dl-'rf(s). A4)
Здесь искомая функция х (s) должна быть определена на отрез-
отрезке fa, b], функция К (s, t), называемая ядром уравнения, пред-
предполагается заданной в квадрате А, определяемом неравенствами
u<s, t*cb, а свободный член / (s) задан на отрезке [а, Ь]\
Я — параметр с числовыми значениями. Для простоты ограничим-
ограничимся случаем, когда все функции, входящие в уравнение, предпола-
предполагаются вещественными и непрерывными, параметр к также считаем
вещественным.
Покажем, что при всех к, достаточно малых по абсолютной
величине, к уравнению A4) может быть применена теорема
Банаха. Правую часть уравнения A4) при каждом фиксирован-
фиксированном К можно рассматривать как оператор Ux, определенный
в пространстве С непрерывных функций, заданных на отрезке
Ja, b], со значениями в том же пространстве. Положим М —
¦— шах|К (s, t) | в квадрате А*) и покажем, что, при |Я|<
< тттг—т , U — оператор сжатия.
*) Непрерывная функция двух переменных, .заданная в прямоуголь-
прямоугольнике, ограничена и имеет наибольшее л наименьшее значения (теорема
13ейерштрасса).
124 НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. IV
Пусть х, х?С, y=Ux, y = Ux. Тогда
ъ
K(s, t)x(t)dt + f(s),
Ъ
y(s) = k \K(s, t)x(!)dt +f(s),
a
откуда
b
y(s)-y(s) = k \K(s, t)\x(t)-x(t)\dt.
a
Следовательно, при всяком s?[a, Ь\
b
I у (s) - у (s) I < IX | J | К (s, t)\ \x(t)-'x(t)\dt<
b — a) = \K\M(b — a)p(x, x),
а потому и
p (у, y)<ap(x, x), где a = | к | M (b — a)< 1.
Так как нахождение решения уравнения A4) сводится к оты-
отысканию неподвижных точек оператора U, то, следовательно,
при 1 ^ 1 < м iu_ уравнение A4) имеет единственное решение
при любом свободном члене и это решение может быть полу-
получено методом последовательных приближений. В гл. VII мы
увидим, что промежуток значений Я, для которых верен этот
результат, может быть расширен.
Остановимся еще на нелинейных интегральных уравнениях
вида
ъ
x(s) = X \ K(s, t, x(t))dt. A5)
Ядро K(s, t, x), рассматриваемое как функция трех перемен-
переменных, предполагается заданным и непрерывным при a*Cs, t*Cb
и |ж|</7, искомую функцию х (s) также считаем непрерывной
и пусть, кроме того, ядро удовлетворяет условию Липшица по
аргументу х:
\K(s, t, Xi)—K(s, t, x2)\<L\xi — x2 ¦
Положим M = max\K(s, t, x)\. Покажем, что если |Я|<
4.6] ТЕОРЕМА ПЕАНО 125
<С j ,, _ . и одновременно | Х\ <м,ь__ . то к уравнению A5)
теорема Банаха применима.
Для этого из пространства С непрерывных функций #(/),
заданных на отрезке [а, Ь\, выделим подмножество F, состоящее
из всех функций, удовлетворяющих неравенству | я: (/)]-<//.
Иными словами, F — замкнутый шар радиуса Н с центром
xA)slO. Оператор Ux, определяемый правой частью A5), ото-
отображает F в самого себя, так как для у — Ux,' x^F, имеем
ь
--1 X | | J К (s, I, х (*)) dt
о
Кроме того, С/ — оператор сжатия, так как для y--Ux,
у = Ux (x, x?F) имеем
ъ
I У (s) -y(s) | < | Я | J \K(s, t, х @) - К (s, t, x (t)) | dt <
\x (t) —"x (t)\dt < \k\ Lp (x, x)-(b
откуда
P (*/. y)<ap(x, x), где a = | X | L F — a)< 1.
Таким образом, уравнение A5) имеет при указанных условиях
единственное непрерывное решение, такое, что |я(?)|<Я\ и
процесс последовательных приближений сходится*). За начальную
можно взять любую функцию, ограниченную той же постоянной Н.
4.6. Теорема Пеано
В этом параграфе мы дадим одно приложение понятия ком-
компактности. Именно, мы приведем доказательство теоремы о суще-
существовании решения дифференциального уравнения (9) только
при одном предположении непрерывности правой части (без
требования выполнения условия Липшица). Такая теорема была
доказана итальянским математиком Д. Пеано A858—1932). Одна-
Однако, в отличие от теоремы, полученной в 4.4 методом последователь-
последовательных приближений, в теореме Пеано единственности решения,
удовлетворяющие заданному начальному условию, может не
быть, что подтверждается простыми примерами **).
Установим сначала лемму, используемую ниже.
*) Этот результат был установлен В. В. Немыцким.
**) Например, уравнение у' = Зу2'3 имеет два решения, удовлетворяю-
удовлетворяющих условию у\ ж=0 =0: у = 0 и у = х3.
126
НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
[ГЛ. IV
Л е м м а 4.6.1. Если функция у = <р (х) непрерывна на отрез-
отрезке [а, Ъ]и ее график — ломаная, все прямолинейные звенья которой
имеют угловые коэффициенты, заключенные между числами аи $
(а < Р), то для любых х', х" ? [а, Ь] при х' •< х"
а (х"-х') < ф (х") - ф (х') <р (х" — х'). A6)
Доказательство. Пусть абсциссы вершин ломаной
суть а = х0 < xv < . . . < хп = Ъ, а данные точки х' и х" рас-
расположены так, что Xi <Сх' < Хщ, Xj^Cx" •< х7+1 (;" > i). Если
/ = ?, то формула A6) очевидна, так как точки с абсциссами i'hi'
лежат на одном звене ломаной. Пусть теперь / > i. Обозначим
через Yr угловой коэффициент того отрезка ломаной, который
проектируется на [xr, xr+i] (г = 0, 1, . . ., п — 1). Тогда
— ф («') =
— Ф
Ф (^) — Ф ixi-\) = Yj-i
Ф (*") - Ф (*;) = \j(x"
Так как при всех г a<Yr<P. т
а (xi+i — ж'
г+1 — х'),
а (ж^- — ж,_,) <
а (х" - xs) < ф (х") - ф (*,) < р (х" - ж,).
Складывая почленно эти неравенства, получизи A6).
Теорема 4.6.1. Пусть правая часть уравнения (9) / (х, у)
непрерывна в прямоугольнике
А(|х — хо\ <</, \у — уо\<,Ь).
Тогда в промежутке [х0 —¦ h, х0 -\- А], гйе А — достаточно малое
положительное число, существует по крайней мере одно решение
уравнения (9), удовлетворяющее начальному условию A0).
Доказательство. Положим М = max | / (х, у) | в пря-
прямоугольнике А *) (рис. 8). Через точку (х0, у0) проведем две
прямые (Di) и (Dz) с угловыми коэффициентами М и —М (соот-
(соответственно). Затем возьмем любое h > 0, при котором прямые
x=xo-rh и х=х0 — А пересекаются с прямыми (Z)j) и (ZJ) внутри
или на контуре прямоугольника А. Построенные прямые ограничи-
ограничивают два треугольника ABC и АВ^С^ с общей вершиной А (х0, yQ).
*) Мы считаем дальше, что М > 0. Если М = 0, то теорема тривиальна.
4.6]
ТЕОРЕМА ПЕАНО
127
Далее строим так называемые ломаные Эйлера. Для этого
берем любое натуральное п и полагаем
h
a;i = х0 -|- — ,
Ль
_ , 2
Х2 — х0 — —
2h
—
7/
_ , rh
хт— х0 -p —
;n —: Xq -\- n;
h 2h _ гЛ _ ,
n n n
Затем из точки (x0, y0) проводим прямолинейный отрезок с угло-
угловым коэффициентом, равным / (х0, у0), до пересечения с прямой
х = xt. Пусть ух — ордината
точки пересечения. Тогда из \pz> Щ)/
точки (xit г/j) проводим пря-
прямолинейный отрезок с угло-
угловым коэффициентом, равным
/ (Ж1! У\), Д° пересечения о
прямой х = х2, и это построе- ^
ние продолжаем до пересече- *
ния с прямой х — ж0 + h.
В процессе этого построения
в каждой уже полученной
вершине ломаной (жг, уг) угло-
угловой коэффициент следующе-
следующего отрезка берется равным -
/ (хг, уг). Так как | / (х, у) \ < М
во всем прямоугольнике А,
то угловой коэффициент каж-
каждого отрезка заключен между
—М и М, а потому вся ломаная будет лежать между прямыми (Z)j)
и (D2) и, следовательно, не выйдет из треугольника ABC. Анало-
Аналогичное построение проделаем и налево от точки (х0, у0) в треуголь-
треугольнике ABiCi и объединяем обе ломаные в одну, которую обозна-
обозначим (Ln). Эту ломаную будем рассматривать как график некоторой
непрерывной функции ф„ (х), заданной на отрезке [х0 — h, ж0 + А].
Придавая п различные значения, получим бесконечную последо-
последовательность таких функций.
Функции фп (х) равноограничены, так как все их значения
удовлетворяют неравенству
h
Рис. 8.
2/о — Ъ.¦;;
Ъ.
Кроме того, по лемме, при любых х', х"?[х0 — /г, xo-^h] (x' < х")
— М (х" — x')<(fn (х") — ф„ (х') < М (х" — х'),
следовательно, при любых х', х"?[х0 — /г, xo-\-h]:
A7)
128 НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. IV
т. е. функции фп (я) удовлетворяют условию Липшица с постоян-
постоянной М. Тогда по лемме 3.9.1, функции фп (х) равностепенно непре-
непрерывны. По теореме Арцела C.9.1) множество функций <рп (х)
компактно в С, следовательно, некоторая частичная последова-
последовательность {ф„д(#)} равномерно сходится к какой-то непрерывной
•функции ф (х). При этом, по построению, все ф„(#о) = 2/о> следо-
следовательно, и ф (х0) — г/0, т. е. ф (х) удовлетворяет условию A0).
Докажем, что у = ф (х) — решение уравнения (9). Возьмем
любой а; из отрезка [х0 — h, х0 + h] и положим у = ф (х). Нужно
доказать, что ф' (х) = / (х, ф (х)), т. е. что
ИМ=_Ф_? = /6й. A8)
-Зададим е > 0. По непрерывности функции / (х, у) в прямоуголь-
прямоугольнике А, в частности в точке (х, у), существует такое tj > 0, что
A9)
•если \х — ж|<т|, \у—J/|<T) и точка (х, г/)?Д. Далее возьмем
б = штГ-Э-, -щ ] . Пользуясь сходимостью фп (х) к ф(ж), под-
под•берем N так, что при
|Фпа(г)-Й<4[- B0)
При этом мы будем считать, что JV>y. Тогда при n>iV раз-
разность между абсциссами соседних вершин ломаной (Ln) будет
— <-дГ<6. В частности, это имеет место при п = nhl если
(так как для частичной последовательности всегда щ > к).
•Следовательно, для каждой точки ломаной (Ln) (при n>iV),
абсцисса которой х удовлетворяет условию | х — х \ < 6, сосед-
соседние с ней вершины ломаной имеют абсциссы, удовлетворяющие
неравенству \ х — х \ < 26 <т]. Если же \ х — х \ < 26, то
по A7)
Тогда при k~>N вследствие B0) имеем
Таким образом, угловые коэффициенты всех тех звеньев ломаной
(Lnh) (A;>tV), которыми соединяются точки этой ломаной с абсцис-
абсциссами х я х, если | х — х \ < б, вычисляются в вершинах, коорди-
4.6] ТЕОРЕМА ПЕАНО 129
наты которых удовлетворяют условиям | х — ж | < Л> | У — 2/ I <
<т), а потому все эти угловые коэффициенты удовлетворяют
неравенству A9). Тогда, по лемме, считая для определенности
х > х, имеем
{f(x, у) —г] (x~x)<:(fnii(x) — (fnk(x)<[f(x, у)+г](х — х)
(при x<ix получим обратное неравенство). Переходя к пределу
при к—*¦ оо и деля на х — х, получаем, что при \х — х\<18
Тем самым равенство A8) доказано, а вместе с ним доказана и
теорема.
Уравнение (9) можно записать и с помощью операторов.
Для атого обозначим через U оператор, определяемый правой
частью уравнения (9), который каждой функции у (х) из С (на
отрезке [х0 — h, х0 + h]) со значениями, входящими в промежу-
промежуток [г/0 — Ь, г/о + Ь], сопоставляет функцию / (х, у (х)) тоже
из С. Если через D обозначить оператор дифференцирования,
сопоставляющий каждой непрерывно дифференцируемой функ-
функции у из С ее производную у', т. е. тоже точку из С (этот оператор
не непрерывен в метрике С), то уравнение (9) можно записать
в виде Dy = С/г/.
ГЛАВА V
НОРМИРОВАННЫЕ ПРОСТРАНСТВА
5.1. Линейные системы
В метрических пространствах мы занимались изучением вопро-
вопросов, связанных, главным образом, с понятиями расстояния,
сходимости, непрерывности. Уже эти вопросы, как мы имели воз-
возможность убедиться в предыдущей главе, находят важные приме-
применения в различных разделах математики. Однако, с другой
стороны, в гл. I—II мы видели, что в эвклидовых пространствах
весьма существенную роль играют и алгебраические операции,
которые можно производить над векторами. Те же алгебраические
операции сложения и умножения на число часто приходится
производить в математике и над другими объектами, например
над функциями. Поэтому представляет интерес изучить эти
операции с общей точки зрения, изучить те общие законы, которым
подчиняются эти операции во многих конкретных случаях. Есте-
Естественно ожидать, что для таких пространств, в которых, помимо
метрики, определены еще и алгебраические операции, в какой-то
степени согласованные с метрикой, можно построить более содер-
содержательную теорию, имеющую значительно более широкие при-
приложения по сравнению с общей теорией метрических пространств.
Начнем с введения некоторых алгебраических понятий. Будем
рассматривать множество Е, состоящее из произвольных элемен-
элементов, и предположим, что в этом множестве определены две опера-
операции: сложение элементов и умножение элемента на число. Именно,
мы считаем, что для любых двух элементов х, у ? Е однозначно
определен элемент из Е, называемый их суммой и обозначаемый
х + у; далее, для любого х 6 Е и любого числа к однозначно
определен элемент Хх ? Е, называемый произведением элемента х
на число X. При этом, возможно, что умножение определено
только на вещественные числа, но бывает также, что произведение
имеет смысл и при любых комплексных X.
Определение. Множество Е называется линейной систе-
системой, если в нем определены в том смысле, как указано выше,
5.1] ЛИНЕЙНЫЕ СИСТЕМЫ 131
операции сложения элементов и умножения элемента на число,
причем выполнены- следующие условия (здесь х, у, z обозначают
элементы, X, \i — числа):
1)х-\-у = у + х (коммутативность сложения);
2) (х + у) + z = х + (у + z) (ассоциативность сложения);
3) к (х + у) = Хх + Ху \ (дистрибутивность умножения отно-
4) (X + ц) х = Хх + [ix J сительно сложения);
5) к (\jlx) = (X\jl) x (ассоциативность умножения);
6) существует такой элемент 8 ? Е, называемый нулевым, что
Ох = 0 для любого х ?Е (произведение любого элемента на число
нуль равно нулевому элементу);
7) \х = х для любого х ? _Е (произведение любого элемента на
число единицу равно тому же элементу).
Таким образом, мы включили в определение линейной системы
всю ту основную группу алгебраических законов, выполнение
которых-мы уже отмечали в конечно-мерных эвклидовых про-
пространствах A.2), в * B.1) и в бесконечно-мерном эвклидовом про-
пространстве I2 B.2)*). Следовательно, Вп, s и I2—линейные
системы. Элементы линейных систем часто называют векторами.
Если умножение элементов линейной системы определено только
на вещественные числа, то система называется вещественной,
если же умножение определено на любые комплексные числа,
то система называется комплексной.
Установим некоторые следствия из аксиом линейной системы.
Введем одно общее понятие. Если в каком-нибудь множестве Е
определено коммутативное действие сложения, то говорят, что
некоторый элемент 04 6 Е есть нуль сложения, если х + 9i = x для
любого х ? Е.
а) В линейной системе Е нулевой элемент, и только он один,
является нулем сложения.
Действительно, для любого х?Е, по 6), 7) и 4), х -f- 0 ==
= lx + Ox = A + 0) х = lx = x, т. е. 8 — нуль сложения.
Если 64 — какой-то нуль сложения, то 8 + 04 = 0. Но так
как, по доказанному, 6 — тоже нуль сложения, то 0f + 6 = 04.
Отсюда, вследствие коммутативности сложения, 8! = 6, т. е. един-
единственность нуля сложения доказана.
Для каждого х из линейной системы Е определим элемент —х,
полагая — х = (—1) х. Тогда имеет место
б) х + (-х) = 8.
Действительно, по 7), 4) и 6)
х+ ( — х) = ix+ ( — 1) ж= A — 1) х = 0х = 8.
*) Некоторые авторы называют линейные системы линейными или
векторными пространствами. Мы предпочитаем сохранить термин «простран-
«пространство» для таких множеств, в которых определено понятие сходимости.
9*
132 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. V
Отметим также, что — (—х) = х [следует из 5) и 7)].
Теперь, исходя из действия сложения, определим в линейной
системе Е разность двух элементов, полагая
Тем самым мы определили в Е действие вычитания.
Из самого определения разности следует, что
Следующее предложение показывает, что вычитание есть действие,
обратное сложению.
в) При любых х, у 6 Е уравнение у + z = х с неизвестным z
имеет единственное решение z = х — у. Иными словами, слагае-
слагаемые можно переносить из одной части равенства в другую, заменяя
их при этом на элементы, противоположные по знаку.
Для доказательства в) заметим, что, с одной стороны, как мы
уже видели, z = х — у является решением данного уравнения.
С другой стороны, если какой-то элемент z удовлетворяет данному
уравнению, то, прибавляя к обеим его частям по —у, имеем
— J/ + J/ + 2 — х — у, т. е. Q+z = x — у или z — x — у.
Из б) следует, что х — х = 6. Верно и обратное, а именно:
г) если х — у = 8, то х = у.
Действительно, равенство х — у = 6 означает, что х — реше-
решение уравнения z + (—у) = 6. Тогда по в) х = 8 — (—у) —
= 8 +у = у.
Перейдем теперь к некоторым следствиям из аксиом линейной
системы, связанным с действием умножения.
Заметим, что законы дистрибутивности умножения 3) и 4)
справедливы и относительно вычитания. Действительно,
(к — ц)а;=|Я + ( — \i)]x = Xx+(— 1)ця = Ъ; — цх
Далее, отметим следующие свойства:
д) Я.0 = 0 при любом к;
е) если кх = 0, то или к = 0 или х = 0;
ж) если кх = ку, то или к = 0 или х = у;
з) если кх = [ix, то или к = \i или х = 6.
Доказательство, д) Имеем 06=9, а потому, по 5),
=(A,O) e=oe=e.
е) По 6) равенство Хг = Э выполняется для любого х?Е, если Х = 0.
Если же % Ф 0, то из равенства Хх = В имеем с помощью 7), 5) и д):
<Ь4е=е
5.2] НОРМИРОВАННЫЕ ПРОСТРАНСТВА 133
ж) Из равенства Хх — Ху, благодаря дистрибутивности умножения, сле-
следует, что X (х— у) = Хх—Xy — Q. А тогда, по е), или Я,=0 или х — ^ = 9,
т. е. х=у.
з) По дистрибутивности умножения
(X— \i) х = Хх— \1х = в,
а тогда, по е), или X—ц=0 или x=Q.
Таким образом, обе алгебраические операции, определенные
в линейных системах, обладают многими обычными свойствами
сложения и умножения чисел.
Все метрические пространства, рассмотренные в качестве при-
примеров в 3.2, легко превращаются в линейные системы. Мы уже
отмечали выше, что Лп, еж ?2при том определении сложения векто-
векторов и их умножения на число, которое уже было дано в гл. I—II,—
линейные системы. Если определение сложения и умножения из
пространства * перенести в I и т, то ясно, что последние также
будут линейными системами. Во всех этих пространствах нулевым
элементом является последовательность, все члены которой равны
нулю.
Наконец, в С, CL и CL2 и во всех пространствах Lp сумма
и произведение определяются, как обычно для функций:
z = z + y означает, что z{t) = x(t)+y{t),
z = Xx означает, что z{t) = Хх (t).
Булевым элементом является, очевидно, функция, тождественно
равная нулю *). Читатель легко убедится, что и здесь выполнены
все аксиомы линейной системы.
В дальнейшем все перечисленные пространства мы будем рас-
рассматривать как линейные системы, считая, что сложение и умно-
умножение определено в них так, как это было сейчас указано.
5.2. Нормированные пространства
Во многих линейных системах удается ввести метрику тем же
способом, как это было сделано в эвклидовых пространствах.
С этой целью, обобщая понятие нормы вектора в эвклидовых
пространствах, введем это понятие в произвольной линейной
системе.
Определение. Линейная система Е называется норми-
нормированным пространством, если для каждого элемента х ? Е опре-
*) В U> нулевой элемент изображается любой функцией, которая экви-
эквивалентна нулю (ср. 3.2).
134 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. V
делено вещественное число, называемое его нормой и обозначае-
обозначаемое || а; ||, причем выполнены следующие условия:
I. || х || >0 для любого х ? Е; \\ х || = 0 только для х = 9;
II. || Кх || = | X | || х || для любого х ? Е и любого числа 2,;
III. || х + у || < || х || + || у || для любых х, у ? Е (аксиома
треугольника).
\j Иными словами, норма есть функционал, заданный на линей-
линейной системе и удовлетворяющий перечисленным выше трем аксио-
аксиомам. Эти аксиомы совпадают с теми основными свойствами нормы
вектора в эвклидовых пространствах, которые отмечались в 1.3
и 2.2.
»| Элементы нормированного пространства называют как точ-
точками, так и векторами.
Нормированное пространство называется вещественным или
комплексным в зависимости от того, вещественной или комплекс-
комплексной является система Е.
Определим теперь расстояние в нормированном простран-
пространстве Е, полагая для любых х, у ? Е
р(х,у) = \\х-у\\ A)
— расстояние между двумя элементами равно норме их разности.
Из зтого определения следует, так как х—9= я, что
||х|| = ||х-е|| = р(х, 9),
т. е. норма любого элемента равна его расстоянию от 9.
Проверим, что в Е выполнены все аксиомы метрического про-
пространства.
Если х Ф у, то х — у Ф 9, а тогда, по аксиоме I из настоящего
параграфа, || х — у || > 0; если же х = у, то х — у = 9 и, следо-
следовательно, || х — у || = 0.
Далее, х — у — (—1) (у — х), а потому, на основании аксио-
аксиомы II, \\х — у\\ = \\у — х ||, т. е. р (х, у) = р (у, х).
Наконец, неравенство треугольника для расстояния вытекает
из аксиомы треугольника для нормы:
р (х, у) = \\х-у\\= \\ (x-z) + (z-y) || < || x-z || 4-1| z-y\\ =
= р(х, z) + p(z, у).
Таким образом, нормированные пространства — частный слу-
. чай метрических пространств.
В качестве примеров нормированных пространств приведем
все пространства, рассмотренные в 3.2 и в предыдущем пара-
параграфе кроме «. В В„ и I2 норма уже была определена в гл. I—II
5.2] НОРМИРОВАННЫЕ ПРОСТРАНСТВА 135
и там же были проверены основные свойства нормы. Используя
обозначения из 3.2, положим:
в I: ||*||= 2 \lt\,
в т: || х || = sup | ?г |,
в С: || х || = max | x (t) I,
в Сн и в Z2: II а; 11 =
в ?р при произвольном р>1: || я || = f \ \x(t)v\dtj
а
Пространства V при произвольном р > 1 также оказываются
линейными системами, если в них перенести определение сложе-
сложения и умножения из пространства *. Норму в Р можно ввести по
формуле
и тогда 1Р становится нормированным пространством. При зтом
во всех перечисленных пространствах норма и ранее определен-
определенное расстояние связаны формулой A).
Выполнение первых двух аксиом нормы во всех этих случаях
очевидно. Неравенство треугольника для нормы вытекает из
аксиомы треугольника для расстояния, уже проверенной для этих
пространств в гл. III. Именно, учитывая формулу A), получаем
, 9) =
О невозможности (в некотором смысле) превратить s в нормиро-
нормированное пространство мы скажем несколько слов ниже. Во всяком
случае заметим, что, в отличие от всех других рассмотренных про-
пространств, величина р (х, 0) не может быть принята в * за норму,
так как для нее нарушается аксиома II.]
*) Фактически в этом параграфе доказано, что если в линейной системе
определены расстояние и норма, связанные между собой формулой A),
то выполнение аксиомы треугольника для одного из них автоматически
влечет выполнение той же аксиомы для другого.
136 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. V
Отметим одно неравенство, вытекающее из аксиомы треуголь-
треугольника:
11* + 0||>И*|-||01!. B)
Чтобы получить его, достаточно представить х в виде х = (х + у)—
— у и записать, что по аксиоме треугольника, а также вследствие
аксиомы II,
После переноса \\y\\ в левую часть, получим B).
Если применить общее определение сходимости, данное в мет-
метрических пространствах, к нормированному пространству,
то получим:
хп-->х означает, что || хп — х\\—>0.
Эту сходимость мы будем иногда называть сходимостью по
норме. Далее, по общим свойствам расстояния в метрических
пространствах || х — у \\— непрерывная функция своих аргумен-
аргументов, т. е. если хп -+х,уп->- у, то || хп — уп || ->¦ || х — у || (см. 3.3).
В частности, полагая все уп = 8, получаем, что || хп || ->¦ || х \\
при хп ->¦ х (непрерывность нормы).
Теперь можно пояснить сказанное выше о пространстве «.
Именно, мы докажем, что в s никаким способом нельзя определить
норму так, чтобы сходимость по норме совпала с ранее определен-
определенной в * сходимостью по метрике, т. е. со сходимостью по коор-
координатам.
Рассуждая от противного, допустим, что такая норма в s суще-
существует. Пусть еп есть п-й координатный орт в в, т. е. вектор, у кото-
которого п-я координата равна 1, а все остальные равны 0. Так как
еп ф 6, то || еп || > 0.
Положим х„ = -—-еп(п=1, 2, ...). Тогда, по аксиоме II,
II еп II
II*. 11-^11*11=1.
При любом натуральном к последовательность к-х координат
элементов хп имеет вид
и тем самым стремится к 0. Таким образом, последовательность
{хп} сходится к 8 по координатам. С другой стороны, || агл|| -/* 0,
и мы приходим к противоречию с предположением, что сходимость
по введенной норме совпадает со сходимостью по координатам.
Покажем, что основные алгебраические операции в нормиро-
нормированном пространстве непрерывны.
5.2] НОРМИРОВАННЫЕ ПРОСТРАНСТВА 137
а) Если Хп ->¦ х, уп-+у, то хп + уп -> х + у.
Действительно,
б) Если хп ->¦ х, Х„ ->¦ X, то Х„я„ ->¦ Ях.
Действительно, учитывая, что Хп в совокупности ограничены
(поскольку {кп} стремится к конечному пределу), имеем
|| Кхп - Ад || = || кп (Хп - X) + (кп - I) X || <
Для ограниченности множества в нормированном простран-
пространстве можно дать более простое определение, равносильное тому
определению ограниченности по расстоянию, которое было введе-
введено в произвольных метрических пространствах (см. 3.5): множе-
множество А ограничено по норме (в дальнейшем мы часто говорим просто
ограничено), если нормы всех его элементов в совокупности огра-
ограничены. Действительно, если А ограничено по расстоянию, то оно
содержится в некотором шаре, A cz S* (а, г). Следовательног
\\ х — а ||<> для х ? А. А тогда
это и означает ограниченность норм || х ||, так как в правой части
стоит некоторая постоянная.
Обратно, если ||a;||<i? для всех х? А, то А сг S* (8, R}
и А ограничено по расстоянию.
Фундаментальные последовательности { хп } в нормирован-
нормированном пространстве в соответствии с определением расстояния харак-
характеризуются условием:
|| жп — ж,„||—>0 при п, т—>оо.
Так как, по теореме 3.5.2, фундаментальная последователь-
последовательность ограничена по расстоянию, то и нормы элементов всякой
фундаментальной последовательности в совокупности ограничены.
Применяя определение полноты, данное для произвольного-
метрического пространства, мы называем нормированное про-
пространство полным, если всякая фундаментальная последователь-
последовательность его элементов имеет предел.
Теория нормированных пространств построена, главным обра-
образом, С. Банахом в 20-х годах нашего столетия. Многие важные
результаты этой теории получены венгерским математиком
Ф. Риссом A880—1956). В связи с тем, что наибольшее внимание
Банах уделял полным нормированным пространствам, послед-
последние называют также банаховыми.
138 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. V
Как и для векторов в эвклидовом пространстве, можно рассмат-
рассматривать ряды, составленные из элементов произвольного нормиро-
оо
ванного пространства: ^ хп (ср. 2.4). При зтом сумма ряда опре-
деляется обычным способом, как предел последовательности частич-
частичных сумм, и если этот предел существует, то ряд называется сходя-
сходящимся. В 2.4 мы видели, что с помощью признака Больцано —
Копти, дающего в Р достаточное условие сходимости, можно было
из сходимости ряда норм V || хп || вывести сходимость ряда самих
п=1
оо
элементов ^хп. Тем самым в I2 было обосновано понятие абсолют-
п=1
оо
ной сходимости ряда 'S] хп. Так как признак Больцано — Коши
п=1
дает достаточное условие сходимости в любом полном простран-
пространстве, то проведенные в 2.4 рассуждения справедливы во всяком
полном нормированном пространстве. Таким образом, понятие
абсолютной сходимости ряда переносится и в любые банаховы
оо
пространства: если сходится ряд норм 2 II хп 1Ь то и Ряд элементов
п=1
оо
2 Хц тоже сходится и называется абсолютно сходящимся. При
71=1
этом Н2^||<211^11 (ср. 2.5).
П = 1 П=1
В дальнейшем мы будем рассматривать почти исключительно
вещественные нормированные пространства. По зтому поводу не
будем делать специальных указаний в каждом изучаемом вопросе.
В тех немногих случаях, когда будут рассматриваться комплекс-
комплексные пространства, это обстоятельство будет особо оговорено.
5.3. Конечно-мерные пространства •)
Понятие линейной независимости векторов эвклидова простран-
пространства, введенное в 1.11, может быть обобщено на элементы произ-
произвольного нормированного пространства^/. При этом, как и раньше,
линейной комбинацией элементов Х\, х2, . . ., хп называем всякий
п
элемент, представимый в виде х = V "Khxk.
ft=i
Определение. Элементы хь х2, . . ., хп ? Е называют-
называются линейно независимыми, если для линейной комбинации этих
*) Перед чтением этого параграфа особо рекомендуем читателю восста-
восстановить в памяти все содержание 1.11.
5.3] КОНЕЧНО-МЕРНЫЕ ПРОСТРАНСТВА 139
п
элементов равенство V Xhxh = 8 выполняется только когда
fe=i
Xi= К2= . . . = Х„= 0. В противном случае элементы х1; х2, ¦ ¦ ., хп
называются линейно зависимыми.
Совершенно так же, как в 1.11, можно установить, что:
а) элементы xif x2, . . ., хп линейно зависимы тогда и только
тогда, когда по крайней мере один из этих элементов представляет-
представляется в виде линейной комбинации остальных;
б) если элемент х ? Е представляется в виде линейной комбина-
п
ции линейно независимых элементов xi, х2, ¦ . •, хп, х = ^ Xkxk,
k=i
то коэффициенты %к в этой формуле определяются единственным
образом *).
Заметим также, что если элементы хи х2, . . ., хп линейно
независимы, то они все отличны от 8. Действительно, если бы,
например, хп = 6, то имелось бы представление хп = 0х^ + . . .
...-)- 0a;n-i, что, согласно а), противоречит линейной независи-
независимости Ху, Х2, . . ., Хп.
Нормированное пространство Е называется конечно-мерным,
если в нем существует конечное число элементов хи х2, . . ., хп,
через которые любой х ? Е выражается в виде их линейной комби-
комбинации. При этом если элементы хи х2, . . ., хп линейно зависимы,
то исключая из них последовательно, как в 1.11, те, которые пред-
представляются в виде линейной комбинации остальных, можно добить-
добиться, чтобы оставшаяся система состояла из линейно независимых
элементов, и при этом каждый х ?Е все же представлялся в виде
их линейной комбинации. Поэтому мы с самого начала будем
считать, что элементы ху, х2, . . ., хп уже линейно незави-
независимы. Тогда совокупность их называется базисом простран-
пространства Е**).
Если же в нормированном пространстве существует сколь
угодно большое число линейно независимых элементов, то про-
пространство называется бесконечно-мерным.
В конечно-мерном пространстве Е по заданному базису
хи х2, . . ., хп мы получаем для каждого х?Е единственное
представление вида
х= 2 А*хк. C)
*) Определение линейной независимости бесконечного множества век-
векторов, данное в 2.8, позднее E.6) тоже будет распространено и на элементы
произвольного нормированного пространства.
**) К конечно-мерным пространствам относится и нормированное про-
пространство, состоящее из одного нулевого элемента 0. В нем нет базиса
(ср. примечание в 1.11).
140 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. V
Обратно, по любым А,1? Я2, . . ., Х„ найдется х ? Е, имеющий вид
C) •).
По аналогии с координатами вектора назовем числа Kh
координатами элемента х. Сопоставляя каждому х ? Е вектор I
из -/?„ с координатами %и %2, • ¦ • > Ki> мы установим, как и в 1.11,
алгебраический изоморфизм между Е и Вп. При этом, так как эле-
элементу 8 ? Е соответствует нулевой вектор иэ Вп, а алгебраиче-
алгебраическим операциям над элементами из Е соответствуют те же опера-
операций над их образами в Вп и обратно, то линейно независимым
элементам из 2? соответствуют линейно независимые векторы из _Rn;
в частности, заданному базису ху, х2, . . ., хп соответствует в Jin
базис из координатных ортов.
Помимо заданного базиса в Е, можно найти и многие другие
базисы. При уже установленном по первому заданному базису
алгебраическом изоморфизме между Е и _В„ каждому базису из Е
будет соответствовать некоторый базис в Вп. По теореме 1.11
все базисы в Ип содержат п векторов. Следовательно, таково же
число элементов и в любом базисе в Е. Таким образом, число эле-
элементов во всех базисах конечно-мерного нормированного про-
пространства одно и то же **). Это число называется размерностью про-
пространства Е. Если размерность равна п, то пространство Е назы-
называется п-мерным ***).
Теперь мы исследуем изоморфизм, установленный выше между
и-мерным пространством Е и Вп по заданному в Е базису
Xi, х2, . . ., Хп, с другой, метрической, стороны. Именно, мы дока-
докажем, что сходимость по норме в Е равносильна сходимости по
координатам. Попутно докажем, что тот критерий компактности,
который был установлен в 3.8 для множеств в пространст-
пространстве Rn, верен в любом конечно-мерном нормированном прост-
пространстве.
Лемма 5.3.1. Сходимость по координатам влечет сходи-
сходимость по норме. Именно, пусть х(т~>^Е (т=1, 2, ...) и.
п
= 2 Xim)xft. Если ?i(fem) —> Xk при каждом k=l, 2, ...,п,
П
a i= 2 XfiXft, то
*) Так как xi, х%, . . ., хп (j Е, а Е — линейная система, то в Е опре-
п
делен элемент "SJ khxh.
fe=l
**) Этот результат можно установить и без ссылки на J2n, проведя дока-
доказательство теоремы 1.11.1 непосредственно для пространства JS.
***) Все сказанное до сих пор в этом параграфе может быть отнесено
не только к пространствам, но и к линейным системам.
5.3] КОНЕЧНО-МЕРНЫЕ ПРОСТРАНСТВА 141
Доказательство этой леммы вытекает сразу из непрерывности
суммы и произведения в нормированных пространствах:
ti^xu ->. \кхк (Л = 1, 2, .... и);
2 *(ГЧ-> 2***».
Лемма 5.3.2. Для любого х ? Е все его координаты kh удо-
удовлетворяют неравенству \ kk |<Н \\ х ||, где ~Н — постоянная,
зависящая только от выбора базиса в Е.
Доказательство. Обозначим через S множество всех
векторов I = (%1, Кг, . . ., Кп) из Rn с нормой, равной единице
(S можно назвать поверхностью единичного шара). Так как
S ограничено, то оно компактно (см. 3.8). Если Z(m> 6 S (т =
= 1,2,...) и Z(m> ->¦ I, то, благодаря непрерывности нормы,
|| 11| = 1, т. е. и I 6 S. Таким образом, S замкнуто.
Каждому I = (й,1, Х2, . . ., Х„) ? 5 сопоставляем элемент
п
-? = 2 hhxk, который обозначим х (I). Вследствие линейной неза-
п
висимости элементов xk и условия ^ Х% = 1, a; (Z) =^= Э. Будем
fe=i
рассматривать норму || х (I) || как функционал, заданный на S.
Пусть Z<m>?.S(m=l, 2, ...), l(m)^l. Так как сходимость
в i}n совпадает со сходимостью по координатам, а координаты
каждого l?S совпадают с координатами х{1), то по лемме 5.3.1
x(lim))-^ х (I). Отсюда, по непрерывности нормы, следует, что
\хA°п>) II—>||a;(Z) ||, т. е. IIх(I) II — непрерывный функционал
на S. Тогда по теореме 4.2.1 j|a;(Z)|| имеет на S наименьшее
значение т, причем, так как || х (I) || > 0 при всех I ? S, то
п п.
я т>0. Таким образом, ||х||>т, если х— J) Xkxk и У\ Х\= 1.
Положим Н = — . Пусть х=2 ^-hxk—произвольный элемент
из Е, отличный от 8. Возьмем элемент
I/ S ^
где
142 НОРМИРОВАННЫЕ ПРОСТРАНСТВА ' [ГЛ. V
п
Так как 2 Цй = 1, то ||а;'||>т. Тогда
1
11 = 1/ 2**И*'||>»»|/ 2 я*- (*)
2
н = 1
Отсюда, при любом к=1, 2, ..., и:
Теорема 5.3.1. В конечно-мерном нормированном про-
пространстве сходимость по норме совпадает со сходимостью по
координатам.
Доказательство. Благодаря лемме 5.3.1 осталось дока-
доказать, что сходимость по норме влечет сходимость по координа-
координатам. Пусть, по-прежнему, пространство Е и-мерно, а хи х2, ...
п
..., хп — его базис. Возьмем х(т> = 2 ^гГ'^й (»* = 1> 2, ...)
п
и допустим, что х(т)-^х= 2 ^-ft^ft- Из равенства
ft=i
следует, что разности Цт) — ?i& (A;=l, 2, ..., п) суть коорди-
координаты элемента х^т) — х. Тогда, по лемме 5.3.2,
следовательно, ?^т> -*¦ kk при всех к.
Теорема 5.3.2. В конечно-мерном нормированном про-
пространстве всякое ограниченное подмножество компактно.
Доказательство. Пусть М — ограниченное подмно-
подмножество и-мерного пространства Е, т. е. существует такая постоян-
постоянная С, что || х || < С для всех х 6 М. Как и выше, каждому х ? М
сопоставляем вектор I = (kit Х2, . . ., Л^) ? Д„, координаты кото-
которого Xh равны соответствующим координатам элемента х. Тогда,,
по неравенству D):
-\/Ii К <^1И = я
\\H\~ У Zj ^k ^"^"ll^ll= ^ ll^ll^-^^- (•>)
Возьмем любую последовательность элементов aKm> g M. Так
как по E) соответствующие этим элементам векторы Z(m> образуют
5.4] ПОДПРОСТРАНСТВА 143
ограниченное множество, а в Нп ограниченные множества ком-
компактны, то из последовательности {7<т>} можно выделить частич-
частичную {Z<m*>}, сходящуюся к некоторому пределу. Сходимость в Лп
есть сходимость по координатам, следовательно, и последователь-
последовательность {x'-mi'>} сходится по координатам. Но тогда, по лемме 5.3.1,
последовательность {я<т*>} сходится к некоторому пределу и по
норме: Тем самым компактность множества М доказана.
Теорема 5.3.3. Конечно-мерное нормированное простран-
пространство Е полно.
Доказательство. Возьмем фундаментальную последова-
п
тельность элементов z<m> = 2 ^т)я& € Е (те = 1, 2, ...), где
Xi, х2, ..., хп— базис пространства Е. По лемме 5.3.2 при
любом к= 1, 2, . .., п
и — о.
Следовательно, благодаря полноте множества вещественных чисел,
существуют конечные Х& = lim J\,<&m>. Тогда, по лемме 5.3.1,
ТО—юо
П
х(т) _^_ х _ vj Я&ж4, т. е. полнота 2? доказана.
А=1
Теорема 5.3.4. Конечно-мерное нормированное простран-
пространство сепарабелъно.
Доказывается в точности так же, как сепарабельность про-
пространства Rn (см. 3.7).
5.4. Подпространства
В линейных системах важную роль играют подмножества, обла-
обладающие тем свойством, что применение к элементам такого под-
подмножества основных алгебраических операций не выводит из
него. Именно, дадим следующее определение:
Определение. Подмножество Е1 элементов линейной
системы Е называется линейным, если из ж, у ? Ех следует, что
х + у ? Et, и из х ? Ei следует, что %х ? Е± при любом X.
Как следствие из этого определения вытекает, что если Et —
линейное подмножество и ж, у ? Ех, то 1.x + \*-У Е Eit при любых X
и \i. Распространяя зто свойство по индукции на любое конечное
число слагаемых, видим, что если хи х2, ¦ ¦ ., хп ? i?t, то и любая
их линейная комбинация входит в Et. Заметим также, что 6 ? Ех
(если Ei Ф Л), так как, взяв любой х ? Еи мы можем предста-
представить 8 в виде 8 = Ох.
Если в линейной системе Е задано произвольное подмно-
подмножество А, то легко видеть, что совокупность Е± всех элементов,
144 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. V
представимых в виде линейных комбинаций элементов из А,
п
Х^ 2 hhXk (XU Х2, ..., Хп?А),
представляет линейное множество. Действительно, если х^Е^,
то и
п
\лх = 2 №k)Xk?Eu
если же взять еще элемент
. р
У— 2j
ft=n+
TO
Такое множество Ег называется линейной оболочкой множества А
.(ср. 2.8).
Линейное подмножество Et линейной системы Е с теми алгеб-
алгебраическими операциями, которые определены во всей системе Е,
.само представляет линейную систему. Если линейное подмноже-
подмножество Ег выделено в нормированном пространстве Е, то и Et, с уже
определенной в нем нормой, представляет нормированное про-
пространство. Выделяя среди линейных подмножеств замкнутые,
введем следующее определение:
Определение. Подпространством нормированного про-
пространства называется всякое его замкнутое линейное подмноже-
подмножество.
Повторяя дословно рассуждение, проведенное в 2.8, мы увидим,
что замыкание линейной оболочки произвольного множества А
есть линейное множество; следовательно, будучи замкнутым, оно
является подпространством. Ясно, что это — наименьшее подпро-
подпространство, содержащее множество А (см. теорему 3.4.4). Мы будем
называть его подпространством, порожденным множеством А.
В частности, если само А — линейное множество, то его замыка-
замыкание и есть порождаемое им подпространство.
Теорема 5.4.1. Всякое конечно-мерное линейное подмно-
подмножество Et нормированного пространства Е — подпространство.
Доказательство. Пусть Et n-мерно. Возьмем я(т> ? Et
(т = 1, 2, . . .) и допустим, что х(т> -*¦ х (х ? Е). Тогда последо-
последовательность {#<"»>} является в Elt во всяком случае, фундаменталь-
фундаментальной. По теореме 5.3.3 существует такой х 6 Еи что х<-т) -*¦ х .
Но так как во всем пространстве Е предел сходящейся последова-
5.5 ЗАДАЧА О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ 145
тельности — единственный, то х = х и, следовательно, х ? Еи
и Et замкнуто.
В конечно-мерном пространстве всякое линейное подмножество
конечно-мерно, а следовательно, является подпространством.
Таким образом, чтобы в эвклидовом пространстве Кп получить
определение подпространства, равносильное данному в этом пара-
параграфе, достаточно было, как мы и сделали в гл. I A.11), брать
линейную оболочку заданной системы векторов.
Примеры подпространств, конечно-мерных и бесконечно-мер-
бесконечно-мерных, мы уже встречали в эвклидовых пространствах в гл. I—II.
Совокупность всех дифференцируемых функций из простран-
пространства С представляет, очевидно, линейное множество, но не замкну-
замкнутое, так как предел равномерно сходящейся последовательности
дифференцируемых функций может не быть дифференцируемой
функцией.
Определение. Пусть задано конечное или счетное мно-
множество подпространств Eh нормированного пространства Е. Если
для каждого х ? Е существует единственное представление
х = ^ xk, где xk ? Eh, то говорят, что подпространства 1?и обра-
h
зуют разложение пространства Е.
Приведем пока только один пример; другие будут позднее.
Если пространство Е и-мерно, а хи х2, . . ., х„, — его базис, то
одномерные пространства Ek, состоящие из всех элементов вида
"кхк *), образуют разложение пространства Е, так как каждый
п
х?Е имеет единственное представление вида х = "S\l.hxh,
a Xkxh ? Ek.
5.5. Задача о наилучшем приближении
Во многих вопросах математики приходится рассматривать
задачу о наилучшем в том или ином смысле приближенном пред-
представлении заданной функции с помощью функций определенного
класса. При этом обычно весьма полезно знать, что это наилучшее
приближение существует. Вопрос о существовании наилучшего
приближения может быть изложен в произвольном нормированном
пространстве в весьма общих терминах, а получаемые таким спо-
способом результаты находят применение в различных конкретных
задачах.
Пусть Е — нормированное пространство, Е± — его конечно-
конечномерное подпространство. Возьмем некоторый элемент х ? Е, не
*) Такое подпространство Е^ называют прямой, порожденной эле-
элементом Xk-
10 б. з. Вупих
146 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. V
входящий в JEi. Тогда для каждого у ? Et величину \\у — х \\
назовем отклонением элемента у от элемента х. Докажем, что
среди элементов у подпространства Et существует такой, для
которого отклонение \\ у — х || имеет наименьшее значение. Этот
элемент у называют элементом наилучшего приближения (в под-
подпространстве Ei) к элементу х. Впрочем, понятие элемента наилуч-
наилучшего приближения можно сформулировать и без требования,
чтобы Ei было конечно-мерным. Но тогда уже нельзя будет гаран-
гарантировать его существование. Можно распространить понятие эле-
элемента наилучшего приближения и на тот случай, когда х ? Et.
Тогда, очевидно, наименьшее отклонение \\ у — х || равно нулю
и оно достигается при у = х, т. е. сам х и будет элементом наилуч-
наилучшего приближения.
Теорема 5.5.1. Для любого х 6 Е в конечно-мерном под-
подпространстве Ei существует элемент наилучшего приближения.
Доказательство. Из сказанного выше видно, что
в доказательстве достаточно рассмотреть только случай, когда
х ? Ei. Будем считать х фиксированным. Возьмем любой у0 ? Ei
и обозначим через б его отклонение от х : б = || у0 — х ||. Ясно,
что элемент наилучшего приближения следует искать среди тех
элементов у ? Еи для которых \\у — х ||< б. Из этого неравенства
следует, что *
Положим М = || х || + б и обозначим через F множество всех
элементов у 6 -Ei, для которых || у ||<М. В F входят, в частности,
все у 6 Е\, для которых \\у — х ||< б, поэтому элемент наилучше-
наилучшего приближения достаточно искать во множестве F. Как замкнутый
шар в Ei (с центром0), множество F замкнуто, а будучи ограничен-
ограниченным, F компактно по теореме 5.3.2.
Теперь будем рассматривать отклонение \\ у — х || как функ-
функционал, определенный для всех у ? F, т. е. на замкнутом компакт-
компактном множестве в пространстве Et. Если ур ? F и ур ->- у (тогда
и у ? F), то ур — х¦-*• у — хв смысле сходимости по норме в Et (или
в Е) и по непрерывности нормы || ур — х || ~->- || у — х ||, т. е. функ-
функционал || у — х || непрерывен на F. По теореме 4.2.1 существует
такой у* 6 F, что \\ у — х \\ имеет наименьшее значение при
у = у*. Этот у* и есть элемент наилучшего приближения. Тео-
Теорема доказана.
Пусть подпространство Et порождено га линейно независимыми
элементами ?1,2:2,. - .,Хп, т. е. представляет их линейную оболоч-
оболочку; тогда задача о наилучшем приближении сводится к нахо-
нахождению таких коэффициентов %и Я2, . . ., Я„, при которых
п
— х\\ имеет наименьшее значение. Иными словами, разы-
6.5] ЗАДАЧА О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ 147
скивается та линейная комбинация элементов х1,х2,...,хп, откло-
отклонение которой от заданного элемента х — наименьшее. Доказан-
Доказанная теорема гарантирует существование такой комбинации. Ее
единственность может быть доказана лишь при некоторых допол-
дополнительных условиях, но на этом вопросе мы не останавливаемся.
Рассматривая конкретные функциональные пространства с раз-
различными определениями нормы в них, мы можем теперь устанавли-
устанавливать факт существования наилучшего приближения к заданной
функции при различных способах оценки точности приближения.
Остановимся на классической задаче о наилучшем равномерном
приближении полиномами (заданной степени) к произвольной
непрерывной функции. Эту задачу еще в середине XIX столетия
изучал знаменитый русский математик П. Л. Чебышев A821 —
1894) *).
Будем называть полиномом п-й степени всякий полином
п
P(t) = co-\-ett+ . . . +entn = 2 Crtr,
r=0
не требуя, чтобы непременно сп Ф 0, т. е. Р (t) может быть полино-
полиномом как точно п-й степени, так и более низкой. Коэффициенты сг
считаем вещественными. Если на отрезке [а, Ъ) задана вещественная
непрерывная функция f(t), то отклонением полинома Р (t) от функ-
функции / (t) назовем max \ P (t) — f (t) \, т. е. норму || Р — f || в про-
а<(<Ь
странстве С, построенном на отрезке [а, Ь]. В классе полиномов
заданной степени полиномом наилучшего приближения к функ-
функции / (t) называется тот, для которого отклонение \\ Р — /1| имеет
наименьшее значение.
Сам Чебышев не ставил вопроса о существовании полиномов
наилучшего приближения и занимался изучением их свойств,
считая эти полиномы уже данными. Существование полинома
наилучшего приближения любой степени для произвольной непре-
непрерывной функции было доказано позднее, в начале XX столетия,
французским математиком Э. Борелем A871 —1956).
Покажем, что теорема Бореля вытекает сразу из общей тео;
ремы 5.5.1.
В пространстве С множество всех полиномов п-й степени есть
линейная оболочка JEi следующего множества функций: постоян-
постоянной (например, f (t) = 1), t, t2, . . ., tn. Эти функции линейно
независимы, так как известно, что если их линейная комбинация
*) Работы П. Л. Чебышева о полиномах наилучшего приближения
послужили основой для развития в дальнейшем новой математической дис^
циплины — конструктивной теории функций.
10*
148 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. V
2 crtr, т. е. полином, равна тождественно нулю на некотором
г=0
отрезке, то все сг = 0 *). Таким образом, XJt — (п + 1)-мерное
подпространство пространства С. А тогда полином наилучшего
приближения n-й степени к заданной непрерывной функции / (t)
и есть элемент наилучшего приближения в подпространстве JEi
к элементу / ? С; существование же такого элемента наилучшего
приближения доказано в теореме 5.5.1.
Ниже, в гл. VII, мы увидим, как решается задача о наилучшем
среднем квадратическом приближении функций.
5.6. Пространства со счетным базисом
Теперь мы распространим понятие базиса, введенное в 5.3
только для конечно-мерных пространств, и на случай бесконечно-
бесконечномерных пространств. В этом случае базис уже не может быть конеч-
конечным, но мы ограничимся рассмотрением лишь таких пространств,
базис которых состоит из счетного множества элементов.
Определение. Счетное множество элементов хп (п =
= 1, 2, . . .) нормированного пространства JE называется его
базисом, если каждый х ? JE допускает единственное
представление вида
х= Б *.¦.*»••)• F)
п=1
При наличии такого базиса в пространстве Е последнее называют
пространством со счетным базисом.
Можно также сказать, что Е — пространство со счетным бази-
базисом {хп}, если одномерные подпространства, порождаемые эле-
элементами хп, образуют разложение пространства Е (определение
разложения дано в 5.4).
Распространяя определение линейной независимости, данное
в 5.3, на произвольное множество элементов нормированного про-
пространства, будем называть их линейно независимыми, если ни один
из них не выражается в виде линейной комбинации конечного
числа других элементов того же множества (ср. 2.8). Как и выше,
среди линейно независимых элементов ни один не может быть
нулевым.
Из определения базиса сразу следует, что образующие его
элементы линейно независимы. Действительно, если бы, например,
Хпо = CiXni + . . . -f СрХПр (Щ, . . . , Пр ф По),
*) Полином ге-й степени, у которого хоть один из коэффициентов отличен
от нуля, не может иметь более, чем п различных корней.
**) Эту сумму нужно понимать как сумму ряда (см. 5.2).
5.G] ПРОСТРАНСТВА СО СЧЕТНЫМ БАЗИСОМ 149
то для хпо мы бы получили два разных представления вида F):
хпо = 0х1 + . . . + 0гП0_1 -f 1хпо + Oxno+i + ...,
при п — щ (г = 1, 2, ..., р),
no ^i п «I м " ~ I 0 при прочих и (в частности, А.П0 = 0),
что невозможно.
Теорема 5.6.1. Всякое пространство со счетным базисом
сепарабелъно.
Доказательство. Покажем, что в пространстве JE
со счетным базисом {х„) существует счетное всюду плотное мно-
множество. Именно, таким множеством будет множество А всех
р
элементов вида V гпхп, где р — любое натуральное, а коэффи-
п=1
циенты гп — рациональные числа.
Действительно, обозначим через Ар множество всех элементов
р
вида ^j гпх„, где коэффициенты гп — любые рациональные числа,
п — 1
но число слагаемых р — фиксированное. Элементы множества Ар
определяются р параметрами ги г2, .. ., гр, каждый из которых
принимает значения из счетной совокупности (рациональных
оо
чисел). Тогда, по теореме 3.6.7, Ар счетно. Но А = \j Ap, сле-
p=i
довательно, по теореме 3.6.4, и А счетно.
Каждый х?Е представим по формуле F) в виде
р
х— lim 2j ^nXn- Для любого р подбираем рациональные числа
г^ (п = 1, 2, ..., р) так, что
\гТ-К\<
и полагаем
р
х(р1 = 2j
Тогда х^р) ? Ар с: А и
р р
п=1 п=1
150 НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. V
Следовательно,
1 1 —г|<у
п— 1 п—1
¦о,
откуда a; = lima;<p'. Тем самым доказано, что А всюду плотно,
a JE сепарабельно.
В пространствах 1% и I базисом является совокупность коор-
координатных ортов. Действительно, еслиа; = (|1, |2) •••» In, ...)??,
а еп — координатные орты, то положим
xW= S 6»e» = (Si, ?2, ...,?*, 0, 0, ...)•
п=1
Тогда
ОО
следовательно, а; = V Егаеп- Обратно, если для того же а; дано
п = 1
ОО
представление х — V А,ле„, то легко видеть, что Хп = \п при
п=1
всех п. Таким образом, каждый х ? I допускает единственное
разложение вида F) по координатным ортам, т. е. совокупность
ортов {еп} — базис. Аналогичное рассуждение справедливо и для
I2 (ср. 2.4).
Однако те же координатные орты в пространстве т уже не
образуют базиса. Это вытекает из того, что если для х ? т взять
построенные выше элементы х^к\ то
) — a; || = sup | In |
может не стремиться к нулю при к—>-оо, следовательно, ряд
V \п^п может не сходиться к г по норме в пространстве т. Так
п=1
как т не сепарабельно C.7), то оно вообще не может быть про-
пространством со счетным базисом.
В пространстве С базис строится сложнее, чем в I и I2, и мы
не будем останавливаться на его конструкции. О базисах в Сь
и Сха будет сказано в гл. VII. Заметим, что до сих пор не выяс-
выяснено, не будет ли вообще всякое сепарабельное банахово про-
пространство пространством со счетным базисом.
Г ЛАВ А VI
ГИЛЬБЕРТОВО ПРОСТРАНСТВО
6.1. Скалярное произведение
В предыдущих главах мы уже перенесли некоторые понятия,
установленные предварительно в эвклидовых пространствах, на
более общие образования и рассмотрели сначала весьма широкий
класс метрических пространств, а затем более узкий класс, но
зато состоящий из пространств, обладающих рядом алгебраи-
алгебраических свойств,— класс нормированных пространств. В этих
последних пространствах, помимо некоторых алгебраических
операций над элементами, было введено понятие нормы. Однако
мы еще не распространили на более общие пространства понятие
скалярного произведения векторов, определенное в эвклидовых
пространствах. Изучению нормированных пространств с опре-
определенным в них скалярным произведением и будет посвящена
настоящая глава. Как мы увидим в последующих главах, такие
пространства имеют весьма большое значение для многих при-
приложений функционального анализа. Как и выше, мы будем вести
основное изложение для вещественных пространств.
Определение. Пусть Е — вещественная линейная систе-
система и пусть любым двум ее элементам х и у (в частности, может
быть х = у) сопоставлено вещественное число, . обозначаемое
(х, у), причем выполнены следующие свойства:
а) {х, у) = {у, х);
б) (х + у, z) = {х, z) + (у, z);
в) (Кх, у) = К (х, у);
г) (х, х)|> 0 для любого х?Е, причем (х, х) = 0 тогда
и только тогда, когда х = 6.
При выполнении условий а) — г) число (х, у) называется
скалярным произведением элементов х и у; иными словами, ска-
скалярное произведение есть функционал с двумя аргументами
(х, у ? Е), обладающий перечисленными свойствами. При рас-
рассмотрении скалярного произведения (х, у) сами элементы х и
у часто будут называться его сомножителями.
152 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
Таким образом, в общее определение скалярного произведения
мы включили в виде аксиом ряд основных свойств, которые
в гл. I A.4) были отмечены для скалярного произведения в эвкли-
эвклидовом пространстве.
Выведем некоторые простейшие следствия из этой системы
аксиом. Благодаря своей коммутативности, скалярное произве-
произведение обладает свойствами б) и в) не только по отношению к пер-
первому сомножителю, но также и по отношению ко второму.
Проверим это, например, для свойства дистрибутивности (свой-
(свойства б).
Действительно, благодаря данным выше а) и б) имеем
(х, y + z) = {y+z, x) = (y, x) + (z, x) = (x, y) + (x, z).
Если один из сомножителей равен 8, то скалярное произве-
произведение равно нулю: @, х) = (Ох, х) = О (х, х) = 0.
Однако (как мы знаем, например, в эвклидовом пространстве)
обратное заключение неверно, т. е. скалярное произведение
может быть равно нулю и тогда, когда оба сомножителя отличны
от 9.
Теперь, используя скалярное произведение, определим норму
элемента в системе Е. Именно положим
\\x\\ = V^x), A)
где в правой части стоит арифметический корень из (х, х). Про-
Проверим, что при таком определении нормы система Е оказывается
нормированным пространством.
Из определения нормы и свойства г) скалярного произведения
следует, что || х ||>0 и что || х || = 0 тогда и только тогда, когда
х = 8. Далее,
|| Ъх || = У(Кх, %х) = jA2 (х, х) = 1111| х ||.
Прежде чем проверять неравенство треугольника, докажем,
что для любых х, у ? Е справедливо следующее неравенство,
которое уже было доказано в гл. I — II под названием неравен-
неравенства Коши для векторов в эвклидовом пространстве [см. 1.4,
формула G) и 2.3, формула D)]:
|(х,у)|<||х||||у|;. B)
Неравенство B) мы будем называть в общем случае неравен-
неравенством Коши — Буняковского, так как установленное в 3.2 [фор-
[формула D) ] интегральное неравенство Буняковского, как мы увидим
ниже (в гл. VII), также представляет частный случай неравен-
неравенства B).
«.2] ОПРЕДЕЛЕНИЕ ГИЛЬБЕРТОВА ПРОСТРАНСТВА
Для доказательства рассмотрим квадратный трехчлен от
вещественного аргумента А:
<р (X) = (Хх + у,Хх + у) = X2 (х, х) + 2Х (х, у) f (у, у) =
Так как ф {%) = \\кх + У || 2>0 при всех Я, то, как указано
в 1.3, дискриминант трехчлена не положителен, т. е. (х, у)* —
—-II х II 2 II У II 2<0. Отсюда и вытекает неравенство B).
Теперь для любых х, у ? Е имеем
\\*+У ||2 = <p(l) = |M|2 + 2(z
Поэтому, в силу неравенства Коши — Буняковского,
Извлекая корни из обеих частей неравенства, получаем нера-
неравенство треугольника
Отметим, что, как и в эвклидовом пространстве, скалярное
произведение непрерывно по 'обоим аргументам, т. е. если хп —*• х,
Уп -*• У (в смысле сходимости по норме), то (хп, уп) -*¦ (х, у).
Для доказательства нужно дословно повторить рассуждение,
проведенное с этой же целью в 2.5, сославшись при этом на нера-
неравенство Коши — Буняковского, а также на тот факт, что нормы
всякой сходящейся последовательности элементов ограничены
в совокупности.
Отсюда, так же как и в 2.5, вытекает, что скалярное произве-
произведение обладает свойством дистрибутивности и по отношению-
к сложению бесконечного множества слагаемых.
6.2. Определение гильбертова пространства
Будем говорить, что норма в нормированном пространстве-
порождена скалярным произведением, если в этом пространстве
задано скалярное произведение любых двух его элементов, а норма
выражается через скалярное произведение по формуле A).
Определение. Гильбертовым пространством (вещест-
(вещественным) называется ^п_олное , нормированное вещественное про-
пространство Ы, в котором норма порождена скалярным произве-
произведением.
Так как, по доказанному в 6.1, норма, определенная через
скалярное произведение по формуле A), удовлетворяет всем
аксиомам нормированного пространства, то можно дать и другое,.
равносильное определение: вещественная линейная система Н
54 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
со скалярным произведением называется гильбертовым простран-
пространством, если в отношении нормы, порождаемой этим скалярным
произведением, пространство Н оказывается полным. Заметим,
что это требование полноты является весьма существенным для
всей теории гильбертова пространства. Элементы гильбертова
пространства часто называют векторами.
Иногда в определение гильбертова пространства включается
еще требование, чтобы оно было бесконечно-мерным. Мы такого
требования не ставим и тем самым не исключаем случай конечно-
конечномерного гильбертова пространства. Примером конечно-мерных
гильбертовых пространств являются конечно-мерные эвклидовы
пространства. Бесконечно-мерное пространство I2 также гиль-
гильбертово. Действительно, в главе II B.3) определено скалярное
произведение в I2, норма в I2 порождается этим скалярным про-
произведением, а в 2.4 доказана полнота I2 (ср. также 3.5).
Гильбертово пространство получило свое название по имени
знаменитого немецкого математика Д. Гильберта A862—1943).
Гильберт в своих работах по теории интегральных уравнений
рассматривал некоторые конкретные пространства, составленные
из последовательностей (I2) и из функций, послужившие образцом
при построении в дальнейшем более общей теории пространств,
названных его именем. В нашем изложении мы сразу дали общее
аксиоматическое определение гильбертова пространства, не кон-
конкретизируя тех элементов, из которых оно может быть составлено.
Иногда, чтобы подчеркнуть отличие общего понятия гильбертова
пространства от тех конкретных пространств, которые рас-
рассматривал Гильберт, гильбертово пространство, определенное
аксиоматически, называют абстрактным.
6.3. Понятие ортогональности
Понятие ортогональности имеет исключительно важное зна-
значение для всей теории гильбертова пространства. Основное опре-
определение формулируется так же, как в эвклидовых пространствах.
Определение. Два элемента х и у гильбертова про-
пространства Н называются ортогональными (обозначается х JL у),
«ели (ж, у) = 0.
Из свойств скалярного произведения непосредственно вы-
вытекает:
1) нулевой элемент 0 ортогонален любому х ? Н;
2) х ±_ х только в том случае, когда х = 0;
п
3) если х jl i/i, J/2, . . ., з/„, то х j_ ^ \yi при любых %г;
t=i
иными словами, если х ортогонален каждому элементу некото-
6.3] ПОНЯТИЕ ОРТОГОНАЛЬНОСТИ 155
рого множества A cz Н, то х ортогонален и любому элементу
линейной оболочки множества А.
Отметим еще некоторые предложения.
4) Если х _|_ уп (га = 1, 2, . . .) и уп—>у, то х _|_ у. Это вытекает
из непрерывности скалярного произведения.
5) Если множество А всюду плотно в II, а х ортогонален каж-
каждому элементу из А, то x = Q. Действительно, по определению
плотности множества, х = lim хп, где хп ?А. Тар как, по условию,
х J. хп при всех га, то по предложению 4) х ± х, откуда и следует,
что х = 8.
В гильбертовом пространстве верна обобщенная теорема
Пифагора:
Если
(сумма может быть как конечной, так и бесконечной), м все
слагаемые попарно ортогональны, то
Действительно, благодаря дистрибутивности скалярного про-
произведения, справедливой по отношению и к конечным суммам
и к бесконечным рядам, имеем:
|| Х||2 = (X, X) = (х, 2 ХП) = 2 (X, ХП) = 2B *i». Ж») = 22 (*т, Хп).
п п п т п m
Но (zm, zn)=-0 при тфп, а потому
Теорема 6.3.1. Для того чтобы ряд 2 Ящ составленный
п = 1
из попарно ортогональных элементов, сходился (в смысле схо-
сходимости по норме, см. 5.2), необходимо, и достаточно, чтобы
оо
сходился числовой ряд 2 II хп ||2-
п = 1
оо
Доказательство. Если ряд 2 жл сходится, то и число-
п = 1
оо
вой ряд 2 llzn||2 сходится по теореме Пифагора.
1
156 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
Обратно, пусть сходится ряд 2 H^nll2- Положим sm= 2 хп-
п=1 п=1
При m > р
т
Sm Sp = 2j хп
и по теореме Пифагора
т
\\sm-sp\?= S II*™ II2-
7l=p+l
Л тогда из сходимости ряда квадратов норм хп следует, что
II sm— Sj, |j -—> 0 при т, р—>оо, т. е. что последовательность
{sm} — фундаментальная. Вследствие полноты пространства Н
оо
существует lim sm, т. е. ряд 2 хп сходится.
п = 1
Определение. Элемент у называется ортогональным
подпространству Hi a H (пишем у _L H^, если у ортогонален
каждому x?Hi. Два подпространства Hi и Hz гильбертова
пространства Н называются ортогональными (пишем Н i \_ H?),
если х _]_ у, каковы бы ни были х 6 Hi, у 6 Н%.
Из последнего определения сразу вытекает, что два ортого-
ортогональных подпространства имеют единственный общий элемент —
нулевой *).
6.4. Проекция элемента на подпространство
Если в трехмерном эвклидовом пространстве будут заданы
какое-нибудь подпространство, например плоскость Р (проходя-
(проходящая через начало координат О), и какой-нибудь вектор ОМ, не
лежащий в этой плоскости, то мы всегда можем представить
вектор ОМ в виде суммы ОМ = ON + NM, где вектор ON лежит
в плоскости Р, а вектор NM перпендикулярен этой плоскости.
При этом длина вектора NM есть кратчайшее расстояние от М
до точек плоскости Р, а точка N есть проекция точки М на плос-
плоскость Р. Аналогичную задачу можно решить в произвольном
гильбертовом пространстве Н.
Сначала выведем одно вспомогательное соотношение. Пусть
и, v ? Н. Тогда
| H"+у)-\-(и—vi и—v) = ("> и)-\~
(u, и)-2 (и, v) + (v, у) = 2 A1 иЦ« + Н12),
*) Нулевой элемент ортогонален любому подпространству
6.4]
ПРОЕКЦИЯ ЭЛЕМЕНТА НА ПОДПРОСТРАНСТВО
157
||« + У||» + ||и-У||« = 2A|«||» + ||У||«)*). C)
Теорема 6.4.1. Пусть Ъ — подпространство гильбертова
пространства Н. Тогда любой элемент х ? Н представим
единственным образом в виде х = у + z, где у ? L, г 1 I.
Доказательство. Если х ^ L, то требуемое пред-
представление мы получим, полагая у = х, z = 9. Если же if I,
то попытаемся определить у как такой элемент из L, для кото-
которого расстояние до х, т. е. норма || х — у ||, имеет наименьшее
значение; существование такого у нужно будет доказать.
Положим
d=inf||a;-y|j")
«б i-
(точная нижняя граница расстояния определяется здесь по всему
множеству элементов у ? L). Зададим числа d^ = d -\ (га =
= 1, 2, . . .). Из определения точной нижней границы следует,
что при каждом га существует yn^L, для которого
\\x-yn\\<dn. D)
Теперь, беря любые га и т, положим и=-х — уп, v — x — ут
и используем равенство C). Получим
\\2х-(уп+ут)\\* + \\ут-уп\\* = 2(\\х-Уп\\* + \\х-Ут\\2). E)
Так как у
то
\>d,
I
или
- 4 || х -1
|| 2х - (уп
Тогда из E), с помощью D), находим
||^-^||2<2№ +
Но dm, dn-^d, а потому \\ут — ул||
т, п
ность {у„} —фундаментальная. Вслед-
Вследствие полноты Н существует у = lira yn,
а так как множество L замкнуто (по
0, т. е. последователь-
*) Равенство C) является, очевидно,
обобщением элементарной геометрической тео-
теоремы: сумма квадратов диагоналей параллело-
параллелограмма равна сумме квадратов всех его сто-
сторон (рис. 9). Можно доказать, что если норма
в банаховом пространстве удовлетворяет
условию C), то такая норма порождается
скалярным произведением, т. е. данное
f б
яр
**
пространство — гильбертово,
й й
рд д рр р
) Напоминаем, что inf — обозначение точной нижней границы.
158 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
определению подпространства), тог/??. При этом {|д:—г/[[ =
= lim Цат—уп [|, и из D) следует, что \\х — y\\<d; но так как
знак < невозможен, то \\х — y\\ = d.
Теперь положим z = x— у и докажем, что z J_ JL, т. е. что z
ортогонален любому и??. При любом вещественном Я элемент
y-\-hi^Ij, а потому
\\x — y — Xu\\2>d2. F)
С другой стороны, имеем
следовательно, благодаря F), получаем Я2||и|]2 — 2к (z, и)>0.
Отсюда, при любом положительном X получаем (z, u)<-y-|l u II2
и, так как правая часть за счет X может быть сделана сколь угодно
малой, то (z, и)<0. Поскольку это верно при произвольном
u^L, то, в частности, неравенство сохраняется и после замены
и на —и, т. е. (z, — u)<0. Но (z, — ц) = — (z, u), а потому
(z, и)>0. Отсюда уже следует, что (z, ы) = 0, и тем самым
доказано, что z i I. Требуемое представление х = у -\- z, где
г/ 6 i, z _L X, получено.
Докажем единственность этого представления. Пусть имеем
еще одно равенство х = yt + z4, где у4 g I, Zj j. i. Тогда у +
-f z = yt + z, или у — ^! = Zj — z. Ho j-ji^I, a z4 — z
ортогонален любому элементу из i [см. 6.3, свойство 3) орто-
ортогональных элементов]; в частности, (zt — z) 1 (у — г/,), т. е.
(zt — z) _L (sj — z), а тогда zt — z = 8, или Zj = z; следова-
следовательно, и г/i = у. Теорема доказана.
Теперь мы можем дать следующее определение:
Определение. Для любого элемента х 6 BL и подпро-
подпространства L элемент у (^ L такой, что х — у ]_ L, называется
проекцией элемента х на подпространство L и обозначается PrLx.
Таким образом, х = PrLx + z, где г 1 I.
В теореме 6.4.1 доказаны существование и единственность
проекции. По ходу доказательства теоремы 6.4.1 установлено,
что PrLx есть элемент наилучшего приближения в подпростран-
подпространстве JD к элементу х. В подпространстве гильбертова пространства
можно доказать и единственность элемента наилучшего прибли-
приближения (фактически это сделано в доказательстве предыдущей
теоремы). Мы вернемся еще раз к этому вопросу в случае, когда
Ъ — конечно-мерно.
Из определения проекции следует, что PrLx = 0 тогда и только
тогда, когда х J_ L.
6.5] ОРТОГОНАЛЬНЫЕ РАЗЛОЖЕНИЯ 159
Возьмем в качестве Ъ одномерное подпространство, поро-
порождаемое элементом е ? Н с || е \\ = 1. Тогда L состоит из всех
элементов вида he, следовательно, и PrLx имеет такой же вид:
Prjjt — Кое, т. е. х — Хое + z, где z 1 Ь. Чтобы вычислить ХОг
умножим скалярно обе части последнего равенства на е. Так как
z _L е, то (х, е) — Хо (е, е) или Хо = (х, е). Аналогичным образом
вычисляется и проекция вектора на координатный орт в ана-
аналитической геометрии, с той лишь разницей,.что там принято
называть проекцией число, равное скалярному произведению
вектора на орт, а в гильбертовом пространстве проекция —
элемент:
PrLx=(x, e)e. (!)
6.5. Ортогональные разложения гильбертова пространства
В 5.4 мы определяли, что понимается под разложением
нормированного пространства на подпространства. Разложение
гильбертова пространства на подпространства, попарно ортого-
ортогональные, называется ортогональным. Начнем с построения орто-
ортогонального разложения гильбертова пространства на два под-
подпространства.
Определение. Если Ъ — подпространство гильбертова
пространства Н, то ортогональным дополнением к L называется
совокупность Ж всех элементов из Н, ортогональных к L.
Из определения проекции вытекает, что если X ф Н, то М
содержит элементы, отличные от 0.
Докажем, что М — также подпространство. Из 6.3 [свой-
[свойство 3) ] вытекает, что Ж — линейное подмножество простран-
пространства Н. Нужно проверить, что Ж замкнуто. Пусть zn ? Ж
и zn ->¦ z. Так как zn J_ у, каков бы ни был у ? L, то, по свойству
4) из 6.3, и z _[_ у, а потому z ? Ж.
Если теперь взять любой х ? Н, то по теореме 6.4.1 он пред-
представим единственным образом в виде х= у + z, где у ? L, z ? Жг
т. е. подпространства L и Ж образуют разложение простран-
пространства Н. Это разложение ортогонально.
Перейдем к рассмотрению более общих ортогональных разло-
разложений.
Лемма 6.5.1. Пусть задано конечное или счетное множество
попарно ортогональных подпространств Ъп и пусть некоторый
х ? Н представим в виде х — У] Ути ГД© Уп € ¦?»• Тогда такое
п
представление единственно и уп = PrL x.
Доказательство. Так как, каково бы ни было п,
ут 1. Ъп при т ф п, то и z = ^ Ут J- ^п [Для конечной суммы
160 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
это вытекает из предложения 3), 6.3, а для бесконечной — оттуда
же с учетом еще и 4)]. Таким образом, х = уп + z, где уп ?1П)
-г _L Х„, т. е. уп = Ргьпх, а
x = 1>PrLnx. (8)
п
Однако мы не можем утверждать, что любой х ? ЙГ пред-
представим по формуле (8), т. е. что подпространства Х„ образуют
ортогональное разложение пространства Н.
Выведем теперь одно важное неравенство. Возьмем любой
х 6 Н и положим уп = PrLnx, где 1>п, как и выше,— ортого-
ортогональные подпространства. Если подпространств Ln всего конеч-
конечное число, скажем, т, то представим х в виде
m
х= 2 yn + z (9)
и докажем, что z _L уп, при всех п = 1, 2, . . ., т.
Действительно, поскольку уп = PrLnx при любом п =
= 1, 2, . . ., т, то из равенства
х = Уп+( 2 J/ft + z)
вытекает, что у\ г/& + z J_ ?n. С другой стороны, каждый yh
при к Ф п ортогонален подпространству Х„, а потому V */fc -L Хп.
Следовательно, и z _L in (в частности, z J_ у„) при всех п =
= 1, 2, . . ., т.
Теперь из (9) по теореме Пифагора следует, что
1М1 2
п=1
откуда
Если же подпространств Ъп — счетное множество, то послед-
последнее неравенство справедливо при любом натуральном т, а тогда
оно справедливо и при замене т на оо. Итак, в обоих случаях
%\\Ргьпх\\*<\\х\\\ A0)
п
где суммирование распространяется на все номера данных под-
подпространств Ъп.
6.6] ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ЭЛЕМЕНТОВ 1G1
Из неравенства A0) по теореме 6.3.1 следует, что сумма
п
имеет смысл для любого х ? // и в том случае, когда слагаемых
бесконечное множество.
Определение. Система ортогональных подпространств Ъп
называется полной, если в Н не существует элемента, отличного
от 8, ортогонального всем Ln.
Теорема 6.5.1. Для того чтобы ортогональные подпро-
подпространства Ъп образовывали, разложение пространства Н, необхо-
необходимо и достаточно, чтобы система подпространств Ъп была
полной.
Доказательство, а) Необходимость. Пусть
подпространства Ъп образуют ортогональное разложение про-
пространства Н. Допустим, что система подпространств Ln не пол-
полна. Тогда существует х Ф 0, ортогональный всем Ln. При этом
по формуле (8) должно иметь место равенство х = V Рг^пх,
п
что, однако, невозможно, так как все Ргъпх = 0.
б) Достаточность. Пусть система подпространств Ln
полна. Возьмем любой х ? И и положим у = V Рг^пх. Как ука-
п.
зано выше, эта сумма имеет смысл. Далее, положим z = х — у.
При каждом п имеем х = PrLnx + zn, у = PrLny -\- zn, где
zn, z'n J_ Ъп. Но из определения элемента у по лемме 6.5.1 сле-
следует, что Prjj7lx = PrLny, а потому z = zn — z'n и, следователь-
следовательно, z X. Т^п- Вследствие полноты системы подпространств Ln,
z = 0, а х = у, т. е. х представим по формуле (8). Тем самым
доказано, что подпространства Ln образуют разложение про-
пространства Н.
6.6. Ортогональные системы элементов
Предыдущие построения приобретают весьма простой геомет-
геометрический смысл в случае, когда подпространства Ъп— одномерные.
В этом случае изучение ортогональных разложений приводит
к весьма общей теории рядов Фурье, содержащей, в частности,
те результаты, которые были получены для пространства I2 в 2.9.
Определения. Конечная или счетная система элемен-
элементов hn гильбертова пространства Н называется ортогональной,
если hn _|_ hm при пф т. Если, кроме того, || /г„ || = 1 при всех
п, то система называется ортонормированной. Ортогональная
система элементов называется полной, если в Л не существует
элемента, отличного от 0 и ортогонального всем элементам системы.
Рассуждая, как в 1.12, легко проверить, что элементы, всякой
ортогональной системы, если они отличны от 8, линейно неза-
независимы.
И В. 3. Вулпх
162 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
Примером полной ортонормированной системы в ?2 может слу-
служить система всех координатных ортов.
Заметим, что если все элементы ортогональной системы hn Ф- 0Г
то, изменяя данные элементы только за счет введения некоторых
числовых множителей, именно, полагая gn = , " *), мы полу-
чим ортонормированную систему. Будем дальше считать, что
уже сами элементы hn образуют ортонормированную систему.
Возьмем любую ортонормированнуго систему элементов hn.
Порождаемые элементами hn одномерные подпространства Ln
тоже ортогональны. По формуле G)
PrLnx = anhn, где ап = (х, /гп).
Числа ап = (х, hn) называются коэффициентами Фурье эле-
элемента х относительно системы элементов hn.
Из леммы 6.5.1 вытекает следующая теорема:
Теорема 6.6.1. Если элемент х ? Н представим в форме
х = V knhn, то это представление единственно и коэффициенты
п
Кп равны коэффициентам Фурье ап элемента х.
Действительно, если указанное представление имеет место,
то по лемме 6.5.1 'knhn = PrLnx = anhn, откуда Кп — ап и
* = 2<*Л. (И)
п
Формула A1) называется разложением Фурье (или ортогональ-
ортогональным разложением) элемента х по элементам h^.
Так как система подпространств Ъп, очевидно, полна тогда
и только тогда, когда полна ортонормированная система элемен-
элементов hn, то из теоремы 6.5.1 вытекает следующий основной
результат.
Теорема 6.6.2. Для того чтобы любой элемент х ? Н
был представим своим разложением Фурье по элементам hn орто-
ортонормированной системы, необходимо и достаточно, чтобы эта
система была полной.
Из этой теоремы, в частности, следует, что в га-мерном гиль-
гильбертовом пространстве полная ортонормированная система дол-
должна состоять из га элементов. С другой стороны, если в га-мерном
гильбертовом пространстве задан произвольный базис, состоя-
состоящий из попарно ортогональных элементов, то из теоремы
6.6.2 вытекает, что эта система полна.
Теперь для произвольного гильбертова пространства дадим
следующее определение:
х 1
*) Для краткости мы часто будем писать — вместо — х.
6.6] ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ЭЛЕМЕНТОВ 163
Определение. Полная ортонормированная система эле-
элементов называется ортонормированным базисом гильбертова про-
пространства.
Из возможности и единственности разложения любого х ? Н.
по элементам ортонормированного базиса вытекает, что и в слу-
случае, если этот базис — конечный, и тогда, когда он — счетный,
ортонормированный базис представляет частный случай того
общего понятия базиса, которое было введено^ в любых норми-
нормированных пространствах E.3 и 5.6).
Из теорем 5.3.4 и 5.6.1 следует, что ортонормированный базис
(конечный или счетный) может существовать только в сепарабель-
ном гильбертовом пространстве. Ниже будет установлено, что
такой базис в сепарабельном гильбертовом пространстве непре-
непременно существует. С другой стороны, можно доказать, что если
в гильбертовом пространстве И существует бесконечное, но не
счетное множество попарно ортогональных элементов, отличных
от 0, то Н. не сепарабельно. В этой книге мы не будем приводить
примеров не сепарабельных гильбертовых пространств.
Снова не предполагаем ортонормированную систему элемен-
элементов {hn} полной. Так как PrLnx = ctn4i и II Ki II = li то неравен-
неравенство A0), применительно к рассматриваемым подпространствам Хп,
принимает вид 2ап< II^Ц2 (ап> к&к и выше, — коэффициенты
п
Фурье элемента х). Последнее неравенство, как и неравенства
B1) и B2) в гл. II, называется неравенством Бесселя.
Из неравенства Бесселя следует, что даже если система {/г„ } —
бесконечная, все же ряд квадратов коэффициентов Фурье для
любого х ? И сходится. Соотношение
2<? = ||*11Я. A2)
п
получаемое иэ неравенства Бесселя, если в нем имеет место знак
равенства, называется уравнением замкнутости. Уравнение замк-
замкнутости и в общем случае играет ту же роль, что в пространстве I2.
Именно, мы установим следующую теорему:
Теорема 6.6.3. При произвольно заданной ортонорми-
рованной системе {/fo} следующие три утверждения относительно
элемента х ? Н равносильны:
1) для элемента х ? Л справедливо разложение Фурье (И);
2) элемент х ? Н входит в подпространство, порожденное
множеством элементов {/г„} *);
3) для элемента х ? Н выполнено уравнение замкнутости A2).
*) Понятие подпространства! порожденного некоторым множеством,
определено в 5.4.
11*
1G4 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
Доказательство. Если для х ? Н справедливо разло-
разложение A1), то по теореме Пифагора || х\\ 2 = ^ ||а„Л„||2 = ^ а«.
п п
т. е. для этого элемента выполнено уравнение A2).
Пусть теперь дано, что для некоторого х ? Н выполнено урав-
уравнение замкнутости. Обозначим через L подпространство, поро-
порожденное множеством элементов kn, и докажем, что х ? L. Пред-
Представим х в виде х = у + z, где у = PrLx, a zll, и потому
z L К. при всех га. Тогда (ж, hn)=(y, hn), т. е. элемент у имеет
те же коэффициенты Фурье ап, что и ж. По теореме Пифа-
Пифагора || х ||2 = || у ||2 + || z ||2, а с помощью неравенства Бесселя
для элемента у имеем
Так как для х выполнено уравнение замкнутости, то в последней
цепочке соотношений всюду должен стоять знак равенства,
в частности, ||'у ||2 = ||у||2 + II z Ц2, т. е. z = 8. А тогда х = у
и, следовательно, х ? L.
Пусть, наконец, дано, что ifl. Покажем, что тогда справед-
справедливо разложение A1). Положим у = ^ ап1гп, где ап — коэф-
п
фициенты Фурье элемента х. Как отмечено в 6.5 (для проекций
на любые ортогональные подпространства), такая сумма имеет
смысл и в том случае, когда слагаемых — бесконечное множе-
множество *). По теореме 6.6.1 коэффициенты Фурье элемента у рав-
равны ип, а потому
(х — у, hn) = (х, К) — (у, hn) = an — an = 0,
т. е. х — у !_ h^ при всех га. Отсюда следует, что х — у ортого-
ортогонален любой линейной комбинации элементов /г„, а значит, и все-
всему подпространству L. Но х ? L — по условию, а у ?L — вслед-
вследствие того, что он представляется как линейная комбинация
элементов hn или как предел таких линейных комбинаций. Сле-
Следовательно, их — у 6 -Ь, а тогда х — у ортогонален самому себе,
что возможно лишь при х — у = 8. Таким образом, х = у =
= у anhn, т. е. для х справедливо разложение Фурье по эле-
п
ментам /г„.
Таким образом, мы показали, что из трех утверждений, сфор-
сформулированных в теореме: 1) влечет 3), 3) влечет 2), а 2) снова
*) Впрочем, сходимость ряда ^] ап^п вытекает и непосредственно из
п
неравенства Бесселя и теоремы 6.3.1.
6.7] ОРТОГОНАЛИЗАЦИЯ СИСТЕМЫ ЭЛЕМЕНТОВ 165
влечет 1). Цепь рассуждений замыкается, что и доказывает равно-
равносильность всех этих трех утверждений.
Следствие. Сопоставляя теоремы 6.6.2 и 6.6.3, можно
сделать простой, но весьма важный вывод: для того чтобы ортонор-
мированная система была полной, необходимо и достаточно, чтобы
для любого х ? Н выполнялось уравнение замкнутости.
Следующая теорема представляет обобщение той части тео-
теоремы 6.6.3, где говорится, что из утверждения 1) вытекает 3).
Теорема 6.6.4. Если элемент х 6 Н представим своим
разложением Фурье A1) по элементам ортонормированной сис-
системы {/?„}, а у — произвольный элемент из Н, причем ап —
коэффициенты Фурье элемента х, а Р„ — коэффициенты Фурье
элемента у относительно системы {hn}, то
(х, у) = 2 а„Р„.
п
Действительно, по дистрибутивности скалярного произведе-
произведения из разложения A1) следует, что
(*. У) = 2 ап {К, У) = 2 апК •
п п
Если элементы /„ 6 Ч образуют полную ортогональную систе-
систему, но еще не нормированную, и если все /„ =^6, то, полагая
hn = " , мы построим полную ортонормированную систему.
II !П II
Тогда для любого х (Ц Н справедливо разложение A1). При этом
1 (х i )
«n = (x,hn)= jiy^jjO*! tn) откуда anhn =±^Mfni и разложению
A1) можно придать вид:
Это представление также называют ортогональным разложением
или разложением Фурье элемента х по элементам /п.
В гл. VII мы поясним, какой смысл приобретают установлен-
установленные результаты, если их применить к обычным функциональным
рядам Фурье.
6.7. Ортогонализация системы линейно независимых элементов
Пусть в гильбертовом пространстве Н задана конечная или
счетная система линейно независимых элементов gb g2, gs> • • •
Обобщая процесс ортогонализации, изложенный в 1.12, мы можем
по заданным элементам git g2, g3, • ¦ • построить ортонорми-
ортонормированную систему элементов hi, hi, h3, . . . так, что каждый hn
166 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
имеет вид:
К = Rnlgl + Rn2g2 +-...+ Pnngn A4)
и, обратно, каждый gn имеет вид:
gn = Vmhi-\-Vn2h2+ ¦• ¦ +vnnhn. A5)
Так как требуемые для этого построения выкладки ничем не
отличаются от проведенных в 1.12, то мы ограничимся кратким
повторением схемы процесса, пропуская промежуточные пре-
преобразования.
Сначала строим ортогональную систему элементов /4, /2, /3, ...,
п-1
полагая последовательно /4 = git fn = gn — 2 ^nhlh\ коэффи-
ft=i
циенты knk определяются из условий ортогональности: /„ _1_
-L /ь /2, • • •, fn-i- Произведя вычисления, мы найдем, что при
&< п
Так как из построения видно, что каждый fk представляет линей-
линейную комбинацию элементов glt gz, . . ., gk, причем коэффициент
при gk равен единице, то /ft =? 0. А тогда из условия (/„, /а) = О
находим
1 (gn, fk)
'"""~ || fk
Далее полагаем hn = -гг-т-п /„. Как и /п, каждый элемент hn есть
II In II
линейная комбинация элементов gt, g2, . . ., gn, т. е. имеет тре-
требуемый вид A4), и hn образуют ортонормированную систему.
Кроме того, из определения элементов /„ видно, что каждый gn
есть линейная комбинация элементов /i, /2, . . ., /п, а следова-
следовательно, и hi, hz, . . ., fin, т. е. имеет вид A5). Таким образом,
описанный процесс приводит к поставленной цели. При этом,
если исходная система была бесконечной, то и процесс состоит
из бесконечного множества шагов, а система элементов hn также
бесконечная. Если же элементов gn было конечное число, то
элементов fin будет столько же.
Заметим, что условия A4) и A5) влекут совпадение линейных
оболочек систем элементов {gn} и {hn}.
Если, например, L — конечно-мерное подпространство про-
пространства В, a gi, g2, . • •, gn — какой-нибудь его базис, то,
применяя к этой системе процесс ортогонализации, мы построим
ортонормированный базис подпространства L.
6.8] ЗАДАЧА О НАИЛУЧШЕМ ПРИБЛИЖЕНИИ 167
6.8. Задача о наилучшем приближении в гильбертовом
пространстве
Вернемся к той задаче о наилучшем приближении, которую
мы рассматривали выше E.5) в произвольных нормированных
пространствах. Если там мы могли лишь доказать существование
решения этой задачи, то в гильбертовом пространстве мы уста-
установим эффективный способ нахождения решения", который связан
с одним важным свойством коэффициентов Фурье.
Итак, пусть L — конечно-мерное подпространство гильбер-
гильбертова пространства Н. Учитывая замечание, сделанное в конце
предыдущего параграфа, мы можем считать, что в! нам известен
ортонормированный базис, состоящий из элементов А1? А2, . . .
n
. . ., hn. Следовательно, каждый у ? Ъ имеет вид у = V А^йд.
Пусть х — произвольный элемент из Н.
Теорема 6.8.1. Для любого х ? И в Ъ существует един-
п
ственный элемент наилучшего приближения, а именно у = J\ a^hk,
ft=i
где aft — коэффициенты Фурье элемента х относительно системы
элементов базиса А4, А2, . . ., А^.
п
Доказательство. Возьмем произвольный у = V hkhk ?Ъ
ft=i
и вычислим || у — х ||2. Имеем
II У-х ||2 = (у-х, у-х) = || у |,2-2 {у, х) + !| х !j2.
п
По теореме Пифагора ||у||2= 2 Д> кроме того,
(У, х) = ( 2 Mft, ж) = S h (hk, x) =
Следовательно,
Прибавляя к правой части и вычитая 2 aL получаем
Последние два члена правой части от у не зависят. Первый же
168 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
член, будучи неотрицательным, имеет очевидное наименьшее
значение нуль, которое достигается только при Х^ = а^. Следо-
Следовательно, элемент наилучшего приближения — только один и это
п
есть у = ^ ahhh.
k=i
6.9. Изоморфизм произвольного сепарабельного
гильбертова пространства с пространством Г1
В этом параграфе существенную роль играет требование, чтобы
рассматриваемое гильбертово пространство было сепарабельным.
Теорема 6.9.1. В сепарабелъном гильбертовом простран-
пространстве И, содержащем элементы, отличные от 9, существует конеч-
конечный или счетный ортонормированный базис.
Доказательство. По определению сепарабельности
в И существует счетное всюду плотное множество А. Перенуме-
Перенумеруем все элементы множества А. Повторяя построение, прове-
проведенное в 2.8, выделим из А конечную или счетную систему В
линейно независимых элементов, линейная оболочка которой
совпадает с линейной оболочкой множества А. При этом все
выброшенные из А элементы суть линейные комбинации эле-
элементов системы В. Систему В подвергнем процессу ортогонали-
зации и построим конечную или счетную ортонормированнуго
систему элементов hn. Докажем, что она полна.
Пусть х ? Н и х ортогонален всем hn. Так как элементы сис-
системы В суть линейные комбинации элементов hn, то х ортого-
ортогонален всем элементам системы В. Множество А отличается от В
тем, что оно содержит еще некоторые элементы, представляю-
представляющиеся в виде линейных комбинаций элементов системы В. Поэтому
х ортогонален всем элементам множества А. Но так как А всюду
плотно в Н, то х = 8 [см. 6.3, предложение 5)]. Тем самым пол-
полнота системы элементов /^ доказана.
Перенесем определения алгебраического изоморфизма и изо-
метрии, данные в 1.11 —12 для эвклидовых пространств, в любые
нормированные пространства. Именно, два нормированных про-
пространства Е и jE1] называются алгебраически изоморфными и изо-
метричными, если между их элементами можно установить
взаимнооднозначное соответствие так, что:
а) алгебраическим операциям над элементами из Е соответ-
соответствуют те же операции над их образами в Е{; б) нормы соот-
соответствующих друг другу элементов из Е и из Et равны.
Теперь сформулируем основную теорему этого параграфа.
Теорема 6.9.2. Всякое бесконечно-мерное сепарабелъное
гильбертово пространство И алгебраически изоморфно и изомет-
рично пространству Р.
6.9] ИЗОМОРФИЗМ ГИЛЬБЕРТОВА ПРОСТРАНСТВА С П 169
Доказательство. По теореме 6.9.1 в Н существует
счетный ортонормированный базис: ht, h2, . . ., hn, . . . По тео-
теореме 6.6.2 для любого х ? Н справедливо разложение в ряд
Фурье: х — ^ anhn- Теперь каждому х ? Н. сопоставим после-
71=1
довательность его коэффициентов Фурье {а„}, т. е. вектор с бес-
бесконечным множеством координат. Обозначим его через а. Как
мы знаем, благодаря неравенству Бесселя, а-? I2. Более того,
по следствию из теоремы 6.6.3 для любого х ? Н. выполнено урав-
уравнение замкнутости, а потому
II «11 = 1/ 2а« = И|. A6)
г п=1
Вектор а и будем называть образом элемента х.
Если а„ суть коэффициенты Фурье элемента х, а р„ — коэф-
коэффициенты Фурье элемента у, то для коэффициентов Фурье эле-
элемента х + у находим (х + у, hn) = (х, hn) + (у, К) = ап -у $п\ по-
поэтому образ элемента х -\- у равен сумме образов элементов
х и у. Аналогично проверяется, что если а — образ элемента х, то
Ка — образ элемента ах. Значит, алгебраическим операциям над эле-
элементами из Н соответствуют те же операции над их образами в I2.
Покажем, что каждый вектор а = {ап} ? I2 является образом
оо
некоторого х 6 Н. Для этого по заданному а составим ряд V anhn.
n = l
Так как члены ряда попарно ортогональны, а
S ||лп||2&<Ч,
п=1 п=1
то по теореме 6.3.1 ряд сходится. Если через х обозначить его
сумму, то по теореме 6.6.1 ап будут коэффициентами Фурье этого
х, следовательно, заданный вектор а будет его образом.
Теперь проверим, что установленное соответствие между эле-
элементами из if и векторами из I2 взаимнооднозначно. Действитель-
Действительно, если векторы а и Ъ — образы элементов х и у, соответственно,
то, по доказанному, а — Ъ есть образ элемента х — у и по A6)
\\а — Ъ \\ = \\х — у \\. Поэтому, если х фу, то и а ф Ъ *).
Таким образом, мы установили соответствие между элемен-
элементами из Я и векторами из ?2, которое представляет алгебраиче-
алгебраический изоморфизм и, по A6), изометрично. Теорема доказана.
Теперь докажем, что изоморфизм между Н и I2 установлен
также и с сохранением величины скалярного произведения.
*) Иными словами, если ортонормированная система полна, а два эле-
элемента xv. у имеют соответственно одинаковые коэффициенты Фурье, то х = у.
Для неполной системы это неверно.
470 ГИЛЬБЕРТОВО ПРОСТРАНСТВО [ГЛ. VI
Теорема 6.9.3. При, изоморфизме между пространствами
Н и I2, установленном в теореме 6.9.2, скалярное произведение
любых двух элементов из Н. равно скалярному произведению их
•образов в I2.
Доказательство. Пусть векторы а и Ъ суть образы
элементов хну, соответственно, а = {а„}, Ъ = {|3П}- Тогда
OQ со
х = ^ anhn, у = ^ Pnhn- Учитывая теорему 6.6.4 и определение
•скалярного произведения в I2, находим
со
(х, у)= %апрп=(а,Ь).
71=1
Благодаря установленному изоморфизму мы можем элементы
^произвольного абстрактного бесконечно-мерного, сепарабельного
гильбертова пространства изображать в виде точек простран-
пространства I2. При этом изображении сохраняются алгебраические
и метрические свойства элементов, а также свойство ортогональ-
ортогональности. Такое представление называют координатной реализацией
гильбертова пространства. Читатель легко сообразит, что для
конечно-мерного гильбертова пространства аналогичным обра-
образом устанавливается его алгебраический изоморфизм с конечно-
конечномерным эвклидовым пространством 2?„, также с сохранением
нормы и скалярного произведения.
6.10. Комплексное гильбертово пространство
В комплексной линейной системе Е скалярное произведение
'{х, у) определяется как комплексный функционал, обладающий
теми же свойствами б), в) и г), что и в вещественной системе
(см. 6.1), и свойством а) в измененной форме: (у, х) = (х, у).
Отсюда следует, что (х, Ху) = X (х, у). Норма в такой системе
¦определяется, как и в вещественной системе, по формуле A).
Остается в силе неравенство Коши — Буняковского, но его
доказательство становится немного сложнее; комплексная линей-
линейная система со скалярным произведением оказывается комплекс-
комплексным нормированным пространством. Если это пространство пол-
полно, то оно называется комплексным гильбертовым пространством.
Для комплексного сепарабельного гильбертова пространства
тем же способом, что и для вещественного, устанавливается его
изоморфизм с комплексным пространством I2 или Вп. При этом
следует учесть, что в комплексном гильбертовом пространстве
коэффициенты Фурье, определяемые той же формулой, что и в веще-
вещественном пространстве, могут иметь любые комплексные значения.
ГЛАВА VII
ПРОСТРАНСТВО Ь2
7.1. Основные свойства пространства Xя
Мы уже встречались в предыдущих главах с банаховыми
пространствами Lp (p > 1). Для многих приложений особый
интерес представляет случай, когда р = 2. Это объясняется тем,
что пространство L2 — единственное из пространства L", которое
оказывается гильбертовым. Таким образом, в пространстве L2
можно использовать весь тот специальный аппарат, который
был изучен в предыдущей главе. Ввиду особой важности про-
пространства L2 мы остановимся сначала несколько подробнее на
некоторых из тех элементарных фактов, которые уже упомина-
упоминались выше по отношению к любым пространствам ХЛ
Итак, пусть L2 означает совокупность всех вещественных
измеримых функций х (t), заданных и суммируемых с квадратом
на отрезке [а, Ь]. Суммируемость с квадратом означает, что
ь
\ х2 (t) dt<oo,
т. е. что функция a;2 (t) должна быть суммируемой. Эквива-
Эквивалентные функции отождествляются. Ясно, что в L2 входят,
в частности, все ограниченные • измеримые функции, заданные
на [а, Ь], тем более входят все непрерывные функции*).
Прежде всего проверим, что при естественном определении
алгебраических операций множество L2 — линейная система.
Действительно, сразу ясно, что если функция х (t) входит в Ъ2,
то и всякая функция вида ex (t), где с — любая постоянная,
тоже входит в L2. Менее очевидно, что если х (t) ж у (t) входят
в X/2, то и их сумма тоже входит в L2. Этот факт проверяется так.
*) Вместо отрезка [а, Ь] можно рассматривать любое измеримое множе-
множество с конечной мерой в любом эвклидовом пространстве Вп. Если же строить
пространство L2 из функций на множестве с бесконечной мерой, то в после-
последующем потребуются некоторые небольшие изменения.
172 ПРОСТРАНСТВО A3 [ГЛ. VII
Прежде всего замечаем, что сумма х (t) -f- у @ — измеримая
функция. Кроме того, справедливо очевидное неравенство
\x(t)y{t)\<x*{t)+y*{t).
Правая часть как сумма двух суммируемых функций тоже сум-
суммируема, а тогда и произведение x(t)y(t), будучи измеримым.,
суммируемо. Теперь из равенства
[х (/) + у {t)\2 = х2 (t) + 2х (t) у @ -f У2 (О
сразу следует, что функция (х (t) -f- у (ОJ суммируема, т. е.
x+y?L\
Попутно мы доказали, что произведение любых двух функ-
функций из L2 суммируемо. Беря, в частности, у (t) = 1, мы видим,
что любая функция х (t) из L2 суммируема, т. е. что Z2 cr L.
Этим включением оправдывается термин —«функции, суммируе-
суммируемые с квадратом».
Заметим, что произведение двух функций из L2, будучи всегда
суммируемым, может, однако, не входить в L2. Например,
пусть в качестве [а, Ь] взят отрезок [0, 1], a x (t) = t-1-'*. Тогда
о Vl
Таким образом, функция x?L2. Однако произведение ее самой
на себя, т. е. х2, уже не суммируемо с квадратом (так как х4 ? Z):
1
dl
= \ — =оо.
Дословно повторяя те рассуждения, которые были проведены
в 3.2, мы можем для любых двух функций из L2 получить
неравенство Буняковского
ь
I х (t) у @ dtj < I х* (t) dt ¦ I f- @ dt A)
tj
и вытекающее из него неравенство
Г \ Г
|/ \\x(t)-ry{t)?dt<y
-*/
ь
\y2(t)dt. B)
7.2] СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ 173
Как и раньше, норму в X2 вводим по формуле
х =
Мы уже знаем, что все аксиомы нормы при таком определении
выполнены; в частности, неравенство B) и есть неравенство тре-
треугольника. Таким образом, L2 — нормированное пространство.
Кроме того, мы знаем, что это пространство — банахово, и притом
сепарабелъное.
Для любого элемента х ? X2 можно одновременно рассматри-
рассматривать его нормы в пространствах L2 и Ъ: || х \\Li и || х Ц^ (значки
указывают те пространства, в которых вычислены эти нормы).
Заменяя в неравенстве A) х (f) на | х (t) | и полагая там у (t) = 1,
мы сразу получим
||я!к< V~b — а || x||L2.
Б частности, если за [а, Ь] принят отрезок [0, 1], то || х \\L <
<\\z\\i*-
Из неравенства Буняковского также следует: если |г/(?)|<
<М, то
ь
x{t)y{t)dt <M У~Ъ — а || х || C)
(здесь норма взята снова в пространстве Z2).
7.2. Скалярное произведение
Покажем, что в X2 можно определить скалярное произведе-
произведение так, что Z>2 оказывается гильбертовым пространством. С этой
щелью для любых х, у ? Z2 положим скалярное произведение
(г, у) равным интегралу от произведения этих функций по всему
отрезку [а, Ь]:
ь
(x,y)=\)x(t)y(t)dt. D)
а
В предыдущем параграфе было доказано, что этот интеграл имеет
конечное значение для любых х, у ? Z,2.
Формулу D) можно рассматривать как аналог тех формул,
по которым определялось скалярное произведение в 2?„ или
в I2, получаемый за счет замены конечного или счетного множе-
множества координат векторов несчетным множеством значений функ-
функций, а суммы — интегралом.
174 ПРОСТРАНСТВО L2 [ГЛ. VIE
Все требования, входящие в общее определение скалярного»
произведения (см. 6.1), очевидно, выполнены. Кроме того ясно,
что норма и скалярное произведение в Z>2 связаны соотношением
т. е. норма в Ъ2 порождена скалярным произведением. Следова-
Следовательно, поскольку пространство Ь2 полно и сепарабельно, оно-
является сепарабельным гильбертовым пространством. Кроме
того, оно бесконечно-мерно. Действительно, бесконечное мно-
множество линейно независимых элементов из Х>2 можно найти уже
среди непрерывных функций, взяв, например, функции вида
*»(п = 0, 1, 2, . . .)
Резюмируя все сказанное, мы приходим к следующему выводу:
L2 — вещественное, бесконечно-мерное, сепарабелъное, гильбер-
гильбертово пространство.
Можно рассматривать аналогичное пространство, составлен-
составленное из функций, суммируемых с квадратом и допускающих ком-
комплексные значения. Чтобы превратить такое пространство в комп-
комплексное гильбертово пространство, скалярное произведение
нужно ввести по формуле
ь
(х, у)= \x(t)y~(t)dt.
•• а
Заметим, что после введения в L2 скалярного произведения
неравенство A) становится частным случаем общего неравенства.
Коши — Буняковского (см. формулу B) из гл. VI).
К пространству Ъ2 применима теорема 6.9.2. По этой тео-
теореме L2 изоморфно и изометрично пространству I2, причем при
осуществлении этого изоморфизма можно исходить из любого
ортонормированного базиса в L2, сопоставляя его элементы
координатным ортам в I2. При этом по теореме 6.9.3 сохраняется
и величина скалярного произведения. Но так как любое абстракт-
абстрактное сепарабельное бесконечно-мерное гильбертово пространство
Н изоморфно ?2, то, сопоставляя каждому элементу h ? Н вместо'
надлежащего элемента из I2 соответствующий последнему эле-
элемент из L2, мы установим алгебраический изоморфизм между Н
и L2 с сохранением величины нормы и скалярного произведе-
произведения *). Таким образом, можно говорить, что пространство Z2
представляет функциональную реализацию абстрактного сепа-
рабелъного бесконечно-мерного гильбертова пространства.
*) Так как в абстрактном гильбертовом пространстве произведение эле-
элемента на элемент не определено, то, говоря об алгебраическом изоморфизм©
между Н и L2, мы имеем в виду, как и в 6.9, соответствие для элементов
из Н и их образов из Ьг лишь операций сложения и умножения на число.
7.3] ОРТОГОНАЛЬНЫЕ РЯДЫ 175
Обратим внимание читателя на то, что хотя и в простран-
пространстве Cl2 определено скалярное произведение (порождающее
норму, как и во всем X2), однако непосредственное применение
теории гильбертова пространства к Cj.2 невозможно, поскольку
последнее не полно. Этим и объясняется тот факт, что часто при
применении методов функционального анализа в таких задачах,
постановка которых возможна в пространстве См, для решения
задачи приходится привлекать пространство ГЛ
7.3. Ортогональные ряды
Понятие ортогональности элементов уже было введено в 6.3
в абстрактном гильбертовом пространстве. Если его применить
к элементам изL2, то ортогональность функций х (t) и у (t) будет
означать по D), что
ъ
J x(l)y(t)dt = O.
Таким образом, мы приходим к тому же понятию ортогональ-
ортогональности, которое уже известно читателю из математического ана-
анализа по крайней мере для непрерывных функций.
В случае, если в качестве [а, Ь] взят отрезок [—л, л], то
примером ортогональной системы элементов из L2 может слу-
служить известная тригонометрическая система функций
1, cos t, sin t, cos2i, sin It, ..., cosnt, sin nt, ... E)
Ее нормировка приводит к ортонормированной системе
j=cost, —^sin^ ..., —— cos nt, —-j^smnt, ... Ea)
У2л У я Уя У л У я
Приведем другой важный для приложений пример ортогональ-
ортогональной системы функций на отрезке [ — 1, 1]. Для этого возьмем
сначала систему линейно независимых функций
и применим к ней процесс ортогонализации, указанный в 6.7.
В результате получим ортогональную систему полиномов
hn (t) = Цпо + V-nit + }W2 + ¦ • • + JW"
(га = 0, 1, 2, ...),
в которой hn(t)—полином в точности п-п степени. Не требуя,
чтобы эта система была нормированной, примем /го(?) = 1 и по-
покажем, как последовательно могут быть вычислены hi (t), h2 (t)
и т. д.
176 ПРОСТРАНСТВО Li [ГЛ. VII
Полагая hl(t) = \il0-}-)illt, ставим условие: h{ JL h0, т. е.
требуем, чтобы
1
.-»
-1
Вычисляя интеграл, получим, что 2и.10 = 0, т. е. ^10 = 0, a \ilt
остается произвольным. Беря, например, ци = 1, найдем, что
h1(t) = t.
Теперь положим Л2 (t) = ^20 + ^21^ + ^22^ и поставим два
условия: Л2 _L h0, h2 J_ h, или
-1
Тем самым мы получим систему двух уравнений с тремя неиз-
неизвестными:
2 2
Выбирая, например, ц.22 = 1, находим ц2о=—т. (-i2i ~ 0 и тогда
1
Аналогично находим h3(t) = t3—^-t и т. д.
Полученная ортогональная система полиномов легко может
быть нормирована. Если же при указанном процессе построения
ортогональных полиномов мы вместо \inn = 1 будем выбирать \inn
так, чтобы все полиномы принимали значение 1 при t = \, то
получим так называемые полиномы Лежандра*):
отличающиеся от полиномов Л„ (t) лишь постоянными множи-
множителями.
*) А. М. Лежандр A752—1833) — крупный французский математик.
7.3] ОРТОГОНАЛЬНЫЕ РЯДЫ 177
Приведем без доказательства общую формулу, по которой
вычисляются полиномы Лежандра любой степени:
Теорема 7.3.1. Тригонометрическая система E) полна
в пространстве X2, построенном на отрезке [ — я, л].
Доказательство. Возьмем любой x?Ll, зададим произ-
произвольное б>0 и найдем у^Сы так, что IIа; — у||<т*)- Пусть
О
при этом \y{t)\<,M, где Л/>0. Возьмем положительное число
б •< „„..д и такое, что одновременно б «< 2е. Введем непрерывную
функцию z (?), полагая
z(t) = y(t) при — я<?<я — б,
г(я) = г( —я) = р( —л),
и определяя z(t) на промежутке я — 8<?<л по закону линей-
линейного интерполирования. Тогда и \z(t)\^M, a
/h
По теореме Вейерштрасса существует тригонометрический поли-
полином g(t), для которого \z(t) — g (^) 1 < /— на всем отрезке
[ — л, л]**). Тогда
= 1/ ^
1«-*|| = -' • -'" -'"¦"- - 8
3
Из полученных оценок следует, что || х — g || -< е, следователь-
следовательно, множество всех тригонометрических полиномов всюду плот-
плотно в L2.
Если некоторый х ? iz ортогонален всем функциям систе-
системы E), то он ортогонален и любой их линейной комбинации,
*) Это возможно, поскольку непрерывные функции образуют множе-
множество, всюду плотное в ?2 (ср. 3.7).
**) См. В.И.Смирнов, Курс высшей математики, т. II, п° 154. Бла-
Благодаря условию г (я) = г (—я) функция г (t) может быть распространена
на всю ось — oo<f< + oo по закону 2я-периодичности с сохранением
непрерывности, а потому к t(t) применима теорема Вейерштрасса на всей
оси, и в частности на промежутке [—я, я].
12 Б. 3. Вулих
178 пространство 1л [гл. vn
т. е. любому тригонометрическому полиному, а тогда, согласно
предложению 5) из 6.3, х = 9.
Теорема 7.3.2. Система полиномов Лежандра полна в пространст-
<е L2, построенном на отрезке [—1, 1].
Доказательство аналогично предыдущему. Пусть :r ? L!.
?
По произвольному 8 > 0 найдется такой у ? С/2, что || х — у || < -j . Далее,
по теореме Вейерштрасса о приближении алгебраическими полиномами,
найдется алгебраический полином g (?), для которого \ у (t) — g (t) \ О—-j=
при — 1 -4 t < 1, и потому |1 у — g || < — , а || х — g || < 8. Следовательно,
множество всех алгебраических полиномов всюду плотно в L2.
Из самого процесса ортогонализации (ср. 6.7) следует, что каждая из
функций tn (n^=0, 1, 2,...) представима в виде линейной комбинации не-
некоторых полиномов Лежандра, следовательно, и всякий алгебраический
полином есть линейная комбинация полиномов Лежандра. Поэтому, если
х ортогонален всем полиномам Лежандра, то он ортогонален вообще всем
алгебраическим полиномам, а тогда я =9 по тем же соображениям, что
и в доказательстве предыдущей теоремы.
Введем обозначения:
Фо(О-~1. (f'n(t) = cos nt, ip'n(t)~ sin nt
(n = i, 2, ...)•
Так как тригонометрическая система E) полна в L2 (на отрезке
[—я, я]), то, используя формулы A3) из 6.6, можно каждый
х ? L2 разложить в ряд Фурье по элементам этой системы. Запи-
Запишем это разложение в виде
оо
^-ЯоФо+ 2 (ап^п + Ьпц>п), F)
где
(п = 1, 2, ...).
Здесь
||ф0|,«=
—я
я я
n2
—л —я
(п = 1, 2, ...).
7.3] ОРТОГОНАЛЬНЫЕ РЯДЫ 179
Подставляя в G) вместо скалярных произведений их выражения
в виде интегралов, получаем
1С 1С
an=— \ x (t) cos ntdt, bn -----— \ x(t\sinnt dt
-Л —Я
(n=l, 2, ...),
т. е. коэффициенты разложения F) вычисляются по известным
формулам Эйлера-—Фурье. Заменяя в F) ф0, фп, фп их выраже-
выражениями, получим, что правая часть F) имеет вид
_ ~bn sin nt), (8)
n=l
и мы пришли к обычной форме тригонометрического ряда Фурье.
Однако даже в том случае, когда х есть непрерывная функ-
функция, равенство F) означает лишь сходимость ряда (8) к функ-
функции х (t) в смысле метрики пространства X2, т. е. в среднем.
Иными словами, если Sn(t) — частичная сумма ряда (8),
п
5п(/) = а0— 2 (flftCos kt -J- bfcSin kt),
ТО
{x(t)-Sn(t)fdt->0,
т. е. среднее квадратическое отклонение х (t) от Sn (t) стремится
к нулю. Известно, что точечная сходимость тригонометрического
ряда Фурье, т. е. равенство
х (t) = HmSn (t) при всех t,
даже и для непрерывной функции не всегда имеет место.
Так как полнота системы E) влечет полноту ортонормирован-
ной системы Eа), то из следствия из теоремы 6.6.3 вытекает,
что для любого х ? X2 по отношению к системе Eа) выполнено
уравнение замкнутости. Это значит, что
n=l
12*
180 ПРОСТРАНСТВО ?2 [ГЛ. VI]
Отсюда с помощью формул G) легко получаем
В такой форме обычно и записывается уравнение замкнутости
в теории тригонометрических рядов.
Теорема 6.8.1 о наилучшем приближении в гильбертовом
пространстве применительно к подпространству, состоящему из
всех тригонометрических полиномов не выше, чем п-ж степени,
где п — произвольно фиксированное число, означает, что для
любого х ? X2 наименьшее среднее квадратическое отклонение
дает тот полином, который совпадает с частичной суммой Sn (t)
ряда Фурье элемента х.
Аналогичные результаты можно установить и для разложепий но
полиномам Лежандра.
Обратимся к вопросу о существовании счетного базиса в про-
пространстве Cj,2. Этот вопрос был оставлен в 5.6 открытым. Для
простоты ограничимся случаем, когда за [а, Ь] принят отрезок
[—я, я]. Как мы видели, каждый х ? X2, в частности х ? Сьг,
единственным образом раскладывается (в смысле сходимости
в среднем) в тригонометрический ряд Фурье по функциям сис-
системы Eа). Но так как эти функции сами входят в С^г, то они и
составляют в нем счетный базис.
Можно доказать, что та же система функций Eа) представляет
базис и в пространстве CL-
Приведем еще некоторые следствия из общих результатов
гл. VI.
Теорема 7.3.3 (Ф. Рисе — Э. Фишер *)). Если {фь}~=1 —
произвольная ортоноржированная система функций из X2, а чис-
оо
ла Хп таковы, что 2 ^п < + °°1 то'-
оо
1) ряд 2 ^пфп сходится в среднем 1-го порядка к некоторой
п=1
функции ос из X2;
2) Хп суть коэффициенты Фурье этой функции;
3) для х выполнено уравнение замкнутости.
оо
Действительно, так как члены ряда 2 К.Чп попарно орто-
п=1
тональны, а || КУп II2 = К, то сходимость ряда вытекает из
*) Э. Фишер A875—1954) — немецкий математик. Им, в частности,
в начале XX столетия доказана полнота пространства L2.
7.4] МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ 181
теоремы 6.3.1; второе и третье утверждения вытекают из тео-
теорем 6.6.1 и 6.6.3.
Теорема 7.3.4. Пусть {ф„} — произвольная ортонорми-
рованная система функций из L2, а функция х ? L* представима
своим разложением Фурье по элементам этой системы, т. е.
х = 2 ^пфп в смысле сходимости по норме. Тогда для любого
п
измеримого множества е а [а, Ь]
lfn(t)dt. (9)
Таким образом, почленное интегрирование допустимо для
разложения функции из L2 в ряд Фурье даже при отсутствий
не только равномерной, но и просто точечной сходимости.
Доказательство. Пусть у (t) — характеристическая
функция множества е *). Тогда, как всякая ограниченная изме-
измеримая функция, у ? L2. По дистрибутивности скалярного про-
произведения
(х, y)-=SM<Pn. У)'
п
а это и есть иначе записанное равенство (9).
С доказанной теоремой интересно сопоставить тот факт, что,
как устанавливается в теории тригонометрических рядов, триго-
тригонометрический ряд Фурье любой суммируемой (например, на
промежутке [—я, я]) функции допускает почленное интегри-
интегрирование лишь по любому промежутку, содержащемуся в [—я, я],
но не произвольному измеримому множеству **).
1 Л. Метод последовательных приближений для интегрального
уравнения Фредгольма
Вернемся к интегральным уравнениям Фредгольма второго
рода
ь
^ , A0)
уже рассматривавшимся в 4.5. По-прежнему предполагаем ядро
К (s, t) и свободный член / (s) непрерывными. Пользуясь тео-
*) Это значит, что
fA f 1 при 1?е,
У ~ 1 0 при t$[a,b]\e.
**) См., например, И. П. Натансон, Теория функций вещественной
переменной, стр. 320 (по изданию 1957 г.).
182
ПРОСТРАНСТВО L1
[ГЛ. VII
ремой Банаха об операторах сжатия и исходя из метрики про-
пространства С, мы доказали в 4.5, что уравнение A0) имеет един-
единственное непрерывное решение при любом свободном члене,
Покажем теперь,
если I к I << тгг-т г , где М = max I К (s, t)
1 ' М (о — а) '
пользуясь метрикой пространства L2, что этот результат спра-
справедлив в более широком интервале значений параметра X.
Лемма 7.4.1. При любом x^TLP- функция
ъ
z (s) = \ К (s, /) х (t) dt
а
непрерывна.
Доказательство. Из равномерной непрерывности функ-
функции K(s,t) в квадрате a^.s,t,^b*) вытекает, что по любому
е > 0 можно подобрать такое б > 0, что при | Sj — s21 < б
| /С (Sj, t)~К (s2, i) | <C e для всех /1
А тогда с помощью неравенства C) имеем
|z(s,) —z(s2)| =
ь
^(s2, o]«(O й<
[а, Ь].
lt t)
(И)
Вследствие произвольности е отсюда вытекает непрерыв-
непрерывность z (s).
Из этой леммы видно, что правая часть уравнения A0) при
любом х ? L2 представляет непрерывную функцию; следователь-
следовательно, должна быть непрерывна и левая часть. Таким образом,
среди всех функций, входящих в L-\ решениями уравнения A0)
могут быть только непрерывные функции.
Будем рассматривать правую часть уравнения A0) как опе-
оператор Ux, заданный в пространстве 1? функций на отрезке fa, Ъ].
Значения Ux будем считать элементами того же пространства,
учитывая, что, по доказанному, они все входят в С^г. Положим
1
и проверим, что, при
/ ь ь
\ \ A'2 (s, 0 rfs с?/
а о
;—, Z7— оператор сжатия.
A2)
*) В курсе математического анализа доказывается и для функций двух
неременных, что если функция непрерывна в замкнутом прямоугольнике
(или в какой-нибудь другой замкнутой ограниченной области), то она равно-
равномерно непрерывна.
7.4] МЕТОД ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ 183
Используя те же обозначения, что и в [4.5, y = Ux, y~Ux
(х, x?L2) и полагая | = ж — х, имеем
ь
y(s)-y(s)=X\j K(s,t)t(t)dt.
а
Отсюда по неравенству Буняковского
ь
ly(s)-y(s)?<l"\ K*(s,t)dt\\l\\*,
а
а тогда
ь
}\У~У\\2=\ [y{s)-y{s)fds<
Ь Ь
K2(s,
о и
И
Таким образом,
\\у-у\\<\к\В\\х-х\\
л
и, при |Я[<<-р-, U — оператор сжатия. Тем самым доказывается
существование и единственность решения уравнения A0) при
| А, |«<-=-, причем решение автоматически оказывается непре-
непрерывным.
В то же время, очевидно, В<М(Ъ — а), причем равенство
возможно лишь только, если I К (s, 0 1= М. Поэтому интер-
вал | X | <; -у- вообще шире, чем интервал [ Я | <; .
Следует, однако, заметить, что если Я удовлетворяет усло-
условию .. , _ <; | X | <; —- и при таком X мы применим к урав-
уравнению A0) метод последовательных приближений, рассматривая
оператор U в пространстве L2, то вместо равномерной сходимости
процесса, установленной в 4.5 ( при | X | <; , _ J , можно гаран-
гарантировать лишь его сходимость в среднем.
Откажемся теперь от требования непрерывности ядра и свободного члена
и будем предполагать, что ядро К (s, t) измеримо в квадрате а <^ s, t ^ b,
причем
h 6
\ \ K*{s,
184 ПРОСТРАНСТВО JL2 [ГЛ. VIJ
и что ] ? ?2. В этих условиях от решения уравнения A0) естественно требо-
требовать, чтобы после его подстановки в уравнение левая часть была равна правой
при почти всех s из [а, Ь]. Будем искать решение среди функций из L2.
Точно так же, как и выше, мы сможем доказать, что, при | Я, | <; —, U — опе-
оператор сжатия, а потому уравнение A0) при | Я, | < — имеет в L2 единствен-
пое решение. Однако на этот раз решение уже совсем не обязано быть неире-
рывной функцией, а его единственность означает лишь единственность
«с точностью до перехода к эквивалентной функции». Конечно и выше, для
уравнения с непрерывным ядром, единственность решения в пространстве ?а
имела тот же смысл. Однако там нас интересовали непрерывные решения,
а непрерывных функций, удовлетворяющих уравнению A0), может быть
только одна *).
7.5. Среднее значение функции
В последующих параграфах этой главы мы укажем другой подход
к осуществлению функциональной реализации сепарабельного бесконечно-
бесконечномерного гильбертова пространства **). Основную роль в иоследующем
будут играть функции, задаваемые непривычным для читателя способом —
не своими значениями в каждой точке, точечными значениями, а посредством
средних значений.
Понятие среднего значения функции известно читателю из интегрального
исчисления. Если, например, функция х (t) непрерывна (или хотя бы инте-
интегрируема) ***) на отрезке [а, Ь], то ее среднее значение на этом отрезке опре-
определяется формулой
ъ
ц = г \ x(t) dt.
ь
При этом \ х (t) dt = ц (Ъ — а). Среднее значение функции можно опре-
а
делить пе только на всем отрезке [а, Ь], но и на любом отрезке Д, содержа-
содержащемся в [а, 6]. Будем обозначать среднее значение функции х (t) на отрез-
отрезке Д через х (Д). Той же буквой Д будем обозначать и длину отрезка Д.
Тогда
A3)
*) Следует заметить, что если две непрерывные функции равны между
собой почти всюду на отрезке [а, Ъ], то они тождественно совпадают на всем
отрезке.
**) При этом при самом построении мы не будем использовать понятие
интеграла Лебега. Лишь в заключительных абзацах последнего параграфа
интеграл Лебега будет привлечен для установления связи новой конструкции
с пространством ?2.
***) Напоминаем читателю, что всякая функция, непрерывная на от-
отрезке, ограничена и интегрируема.
****) \ обозначает интеграл по промежутку Д.
7.5]
ИЛИ
СРЕДНЕЕ ЗНАЧЕНИЕ ФУНКЦИИ
\ х (t) dt = х (А) А.
185
A4)
Если отрезок А разбит на два непересекающихся отрезка А4 и А2, то имеет
место очевидное равенство
2. A5)
Это не что иное, как другая запись известного свойства аддитивности
определенного интеграла:
\ x(t)dt=\ х (t) dt + \ x(t) dt.
Приведем простой пример. Пусть а:(?) = ?2 па отрезке [0, 1]. Если отрезок
Л = [а, Р]С[0, 1], то
Р-а
В частности, если, например,
отрезок [0, 1] разбит на п рав-
равных частей (см. рис. 10, на ко-
котором п = 4)
1 L п
то
так что
1
Зга2
> 2, •
i * (
.., ге)
t-a — 3t
Зге2
7
Зге2
т. д.
Из определения среднего значения сразу следует, что если z (t) =
= х (t) + у (t), то z (А) = х (А) + j/ (А) для любого А; если и (t) = Хя (<),
то и (А) = Хх (А). Однако для произведения функции на функцию среднее
значение вообще не равно произведению средних значений сомножителей.
Мы подошли к понятию среднего значения, считая, что функция уже
задана своими точечными значениями. Однако на практике часто встречается
обратное положение, когда экспериментальным путем удается определить
лишь средние значения функции, а ее значения в точках получаются как
результат известной математической абстракции. Так, например, При иссле-
исследовании неравномерного движения естественно определяется средняя ско-
скорость в произвольный промежуток времени и лишь с использованием
186 ПРОСТРАНСТВО /.2 [ГЛ. VII
математического понятия предела вводится определение скорости в тот или
иной момент. Поэтому представляет интерес изучение функций, заданных
своими средними значениями.
Будем говорить, что на отрезке {а, Ь] задана функция х (Д), называемая
функцией промежутка, если каждому отрезку Д CZ [а, Ь] сопоставлено
вещественное число х (Д), причем при разбиении Д на два непересекающихся
отрезка Д4 и Д2 выполнено условие A5). Для любого отрезка До С [а, Ь],
по аналогии с формулой A4), произведение х (До) До будем называть инте-
интегралом функции х (Д) по промежутку До. Тогда условие A5), как и выше,
выражает свойство аддитивности интеграла. Если какой-нибудь отрезок Д
имеет вид Д = [а, |3], то иногда вместо х (Д) будем писать х ([а, E]).
Суммой двух функций х (Д) и у (Д) назовем функцию
2(Д)==х(Д)+!/(Д).
Аналогично функцию и (Д) = %х (Д) назовем произведением функции х (Д)
на число %. Так как х (Д) и у (Д) удовлетворяют условию A5), то легко видеть,
что и z (Д) и и (Д) тоже удовлетворяют этому условию, что и дает нам право
называть их функциями.
В отличие от функций промежутка функции х (t), определяемые своими
точечными значениями, будем называть функциями точки.
Каждая непрерывная функция точки х (t), заданная на отрезке [а, Ь],
порождает по формуле A3) функцию промежутка х (Д). При этом х (t) может
быть восстановлена по своим средним значениям дифференцированием инте-
интеграла по верхнему пределу:
(
а
z(() = lim -г- [ x(t)dx= Mm x([t, t^-Al]). A6)
(
Тем же способом и любая ограниченная функция х (t) с конечным чис-
числом точек разрыва (а такая функция интегрируема) порождает функцию
промежутка х (Д) и может быть восстановлена по этой функции с
помощью формулы A6) во всяком случае в точках непрерывности.
В дальнейшем непрерывные функции и ограниченные функции с конеч-
конечным числом точек разрыва будем для краткости называть функциями
класса К.
Однако не всякая функция промежутка приводит предельным переходом
по формуле A6) к какой-нибудь функции точки, а тем более к ограниченной
интегрируемой функции. Например, если х (t) — неограниченная функция,
g
для которой \ х (t) it существует как несобственный, то имеет смысл
а
и \ х (t) dt по любому Д СЗ [а, Ь] и, следовательно, можно определить сред-
д
ние значения х (Д). Но тогда обратный переход по формуле A6)
приведет нас снова к функции х (t) в точках ее непрерывности, ai(t)
не ограничена.
7.6] ОПРЕДЕЛЕНИЕ ПРОСТРАНСТВА ?2 187
Примером функции такого типа может служить x(t) = —— на отрезке
[О, 1]*). Для любого [а, р1] d [0, 1]
а <х
В частности, если [а, $] = \t, t-f-At], то x(\t, t-j-At]) =
Отсюда в соответствии с формулой A6)
f 1 . А
I —р при t > О,
lim х ([/, г f Д/])=^ '|//
А(->0
V оэ при г = 0.
Можно построить и более сложные примеры функций промежутка х (Д),
для которых конечного lim x([t, t + Д?]) не существует ни при одном значе-
д<->0
нин f. Таким образом, рассматриваемый класс функций х (Д) содержит более
разнообразные функции, чем те, которые порождаются интегрируемыми
(в частности, непрерывными) функциями точки.
7.6. Определение пространства L2
Введем одно вспомогательное понятие. Пусть х (Д) — функция проме-
промежутка, заданная на отрезке [а, Ь]. Возьмем произвольное разбиение этого
отрезка на конечное число непересекающихся отрезков Дь Д2, . . -, Др
и составим неотрицательную сумму
Эту сумму назовем метрической суммой для функции х (Д).
Поясним смысл метрической суммы в частном случае, когда функция
х (Д) порождается непрерывной функцией точки х (I). Из теоремы о среднем
значении для определенного интеграла известно, что среднее значение непре-
непрерывной функции на любом отрезке совпадает с ее значением в некоторой точке
этого отрезка. Поэтому на каждом Д; найдется по крайней мере одна такая
р
точка t;, что х (Д;) = х {tj). Тогда а (х) = 2 х2 (*г) Д/> а это не что иное,
i=l
ь
как некоторая интегральная сумма для интеграла \ г2 (t) di.
а
\
*) В точке t = 0 выражение —— не имеет смысла. Поэтому можно считать
нашу функцию просто не определенной в точке t = 0, что не мешает рас-
1
сматривать несобственный интеграл \ , .
188 ПРОСТРАНСТВО 12 [ГЛ. VII
Теперь через ?,* обозначим множество всех тех функций промежутка
х (Д), заданных на отрезке [а, Ь], для каждой из которых метрические сум-
суммы, а (х), составленные при всевозможных разбиениях отрезка [а, Ь], в совокуп-
совокупности ограничены.
Покажем, что этим свойством обладают, в частности, вес функции х (Д),
порождаемые ограниченными интегрируемыми функциями точки х (t). Дей-
Действительно, если | х (t) | ^ М при всех t ? [а, Ь], то для любого Д d [а. Ь]
x (t) dt
а потому | x (Д) | <^ M. Тогда для любого разбиения
v v
i=i '' ' ^" i=i
Разобранная выше функция х (Д), порожденная на отрезке [0, 1] функ-
1
циеи точки —— , представляет пример функции, для которой метрические
суммы не ограничены и которая, следовательно, не входит в множество L2
(построенное из функций на отрезке [0, 1]). Однако мы не будем проводить
проверку этого утверждения, а рассмотрим похожий, но более легкий пример:
функцию х (Д), порожденную на том же отрезке [0, 1] функцией х (t) —
= Г3/*. Если взять отрезок Д = [0, б], то
¦(Л) =4- \
Так как в любой метрической сумме а (х) имеется слагаемое х2 (Д) Д, соот-
соответствующее отрезку Д, левый конец которого находится в точке 4=0,
то а (х) >16 6~3//2 б = —= . Следовательно, за счет уменьшения б сумма а (х),
может стать сколь угодно большой.
Аналогично можно убедиться, что функция промежутка, порождаемая
на отрезке [0, 1] функцией х (t) = t~P при любом р таком, что -=- < р < 1,
Li
1
не входит в L2. Если же р > 1, то \ — расходится и функция tr-P не порож-
0
дает функцию промежутка.
В множестве L2 определим операции сложения и умножения на веще-
вещественное число по правилу, введенному в 7.5 для произвольных функций
промежутка. Ясно, что при умножении на число функции, входящей в L2,
мы снова получим функцию из L2. Покажем, что и операция сложения не
выводит из L2.
7.6] ОПРЕДЕЛЕНИЕ ПРОСТРАНСТВА i2 189
Пусть г (Д) = х (Д) + у (Д), где ж, у ? ?2. Тогда для любого разбиения
имеем с помощью неравенства Коши
2
Л/ 2 [г(Л;)]2Л* + 1/ 2
* i=l У i=i
<
пли
o(z)<clYo~&)+Yo~(y)]2- ' A")
Так как а (х) я а (у) в совокупности ограничены, то ограничены и a (z).
Таким образом, jl* — линейное множество, в котором роль нулевого
элемента играет функция х (Д) =0 (порожденная непрерывной функцией
х (t) = 0). При этом мы считаем, что х = у, т. е. х и у совпадают как эле-
элементы из Ьг тогда и только тогда, когда х (Д) = у (Д) при всех Д С [а, Ь].
Отождествим функции точки х (t) класса К с порождаемыми ими функ-
функциями промежутка х (Д) и тем самым будем считать, что множество всех
функций класса К, заданных на [а, Ь], является подмножеством множе-
множества Z/2. При этом алгебраическим операциям — сложению и умпожешно
на число — над функциями х (t) (определяемым естественным образом, как,
например, в пространстве С) соответствуют те же операции над порождаемыми
функциями промежутка х (Д). Однако, если две функции класса К равны
между собой во всех точках, где они обе непрерывны, то они будут порождать
одну и ту же функцию промежутка *). Поэтому такие две функции мы считаем
совпадающими. Иными словами, функция с конечным числом точек разрыва
считается определяемой своими значениями в точках непрерывности, а еэ
значения в точках разрыва не принимаются во внимание.
Введем норму в ?2, полагая для любого х ? Jj2
|| х || = j/"sup a (x) = sup "|/а (х), A8)
где точная верхняя граница метрических сумм вычисляется по всевозможным
разбиениям отрезка [а, Ь]. Покажем, что при таком определении нормы в jJ
выполняются все аксиомы нормированного пространства.
Ясно, что всегда || х || > 0 и при этом || х || = 0 только для функции
х (Д) s 0. Далее, если и — %х, то для любого разбиения а (и) = Я20 (л),
а потому sup а (и) = X2 sup а (х) и || и || = | к | || х ||. Проверим аксиому
треугольника.
Если 2 = х + у, то из A7) следует, что
()<(\\\\ + \\y\\)
Так как это верно для любого разбиения отрезка [а, Ь], то и
,или || г || <; |] х и + ]| у ||.
*) Из интегрального исчисления известно, что изменение значений
интегрируемой функции в любом конечном числе точек не влияет на ее сред-
средние значения. В то же время если две интегрируемые функции х (t) и у (t)
отличны друг от друга в какой-нибудь точке t0, где они обе непрерывны,
то найдется окрестность точки t0, в которой между значениями х (t) и у (t)
можно вставить постоянную, например х (t) < М < у (f), а тогда средние
значепия х (Д) и у (Д) для Д, содержащихся в указанной окрестности,
различны.
190 ПРОСТРАНСТВО 1Л [ГЛ. VII
Итак, -L2 ¦— нормированное пространство. Множество непрерывных
функций точки на [а, Ь\ с нормой, определенной по формуле A8), будучи
линейным подмножеством пространства L2, само является нормированным
пространством. Покажем, что это и есть пространство CLi, т. е. что для непре-
непрерывных функций х (t) формула A8) сводится к равенству
A9)
С одной стороны, из неравенства Буняковского [см. 3.2, формула DI
сразу следует, что
( \ x
J
А Л
Поэтому для любого разбиения
v р
а (х) —- 2j [х (Д;)]2 А; = /, —г
г=1 г=1
р Ь
< 2 \ *2 @ dt = ^ г2 (<) <*<• B0)
Отсюда по формуле A8)
ь
Нт 1|2 ^ \ г2 ^Д tit Oi\
а
С другой стороны, мы уже видели, что если х (I) непрерывна, то каж-
каждая метрическая сумма а (х) есть интегральная сумма для интеграла
ь
\ x2(t)dt. Но известно, что интеграл есть предел интегральных сумм при
а
условии неограниченного дробления отрезка [а, Ъ]. Следовательно, среди
метрических сумм а (х) встречаются такие, которые сколько угодно
ь
мало отличаются от \ x2(t)dt, т. е. при любом е>0 найдется о (х) >
а
ъ
> \ x2(t)dt~s. Поэтому
п
Ь
II -г 112 — с|1П /т (~.\ "•>, V Т2 (f\ tli
a
Отсюда и из доказанного выше обратного неравенства B1) и вытекает фор-
формула A9).
*) Применяя здесь неравенство Буняковского, мы считаем второй мно-
множитель в подынтегральной функции равным единице.
7.6]
ОПРЕДЕЛЕНИЕ ПРОСТРАНСТВА f.2
191
Из формулы A9) следует, что если х ? С7 2 и | х (t) \ ^ М, то
'Ь-а *). ^ B2)
Как и в пространстве L2, сходимость по норме в пространстве L2 назы-
называется сходимостью в среднем 2-го порядка. Так как в этой главе сходимости
в среднем других порядков не рассматриваются, то мы будем называть сходи-
сходимость в L2 чросто сходимостью в среднем. В 3.3 уже было отмечено, что если
последовательность непрерывных функций {хп (<)} сходится равномер-
равномерно к непрерывной функции х (t) (max | хп (I) — х (I) \ -»- 0), то эта после-
последовательность сходится к той же предельной функции ji в среднем, т. е.
II х-п. —я II -*¦ 0. Впрочем, этот факт есть очевидное следствие неравенства B2).
а
,~$ с,+5
Сг-8
Рис. 11.
Покажем теперь, что формула A9) верна н для любой функции класса К.
Пусть | х (t) | < М на отрезке [а, Ь] и непрерывна всюду, за исключе-
исключением точек с4 < с2 < . . . < ст (рис. 11). Будем считать, что а и Ь ие входят
в число точек разрыва. Читатель поймет, как следует в противном случае
слегка изменить дальнейшие рассуждения. Так как при доказательстве нера-
неравенства B1) непрерывность х (t), по существу, не была использована **),
то оно справедливо и сейчас. Остается получить обратное неравенство.
Зададим е > 0 и подберем 6 > 0 так, чтобы интервалы (cj — 6, cj + 6)
(/ = 1,2, . . ., т) не налегали друг на друга и содержались в [а, Ъ] и что-
чтобы выполнялось неравенство б < '
ЫМ- '
ция
На каждом из отрезков функ
х (t) непрерывна. Поэтому по доказанному для такого случая равен-
ству A9) на каждом из этих отрезков Д^ интеграл \ х2 (t) dt равен точной
верхней границе множества метрических сумм. Следовательно, для каждого
из Д^ можно составить его разбиение на отрезки Д^ (i = 1, 2, . . ., pj), при
котором метрическая сумма
)=2{х
(m
(/=0, 1,
т).
*) Это неравенство вытекает, конечно, и из той оценки а (х), которая
была проведена в начале параграфа для ограниченной интегрируемой
функции.
**) Использованное по ходу доказательства неравенство Вуняковского
проверяется для функций класса К тем же элементарным рассуждением,
которое было проведено в 3.2 для непрерывных функций.
192 ПРОСТРАНСТВО ?2 [ГЛ. VII
Возьмем все отрезки Д^, и присоединим к ним отрезки [cj—б, j + ]
(/ = 1, 2, ...,т). Тогда получится некоторое разбиение отрезка [а, Ь].
Для соответствующей метрической суммы имеем
j=0 4=1 з' = 1
?Н 771
> У о^(т)>2 ^
3 = 0 3=0 д
Но
J=0 д . а з=
Прп каждом / = 1, 2, ..., т
Cj + 6
\ х*A)сПС2ЬМ*<
с.-О
а потому
Ь
a
Тем более,
Вследствие произвольности е отсюда и вытекает неравенство || х |,г >•
ь
> \ г2 (t) dt. Тем самым доказательство закончено.
a
Переходим к установлению полноты пространства L2.
Лемма 7.6.1. Если последовательность элементов xn?L2 (п = 1, 2, ...)
фундаментальна, то и для любого отрезка Д d [a, b] последовательность
значений {хп(А)\ тоже фундаментальна.
Доказательство. Любой Дс [а, Ь] можно рассматривать как один
из отрезков Д,- некоторого разбиения отрезка [а, Ъ]. Так как
р
2 [*» (Д»)-*т (Ai)]2 Aj = a (xn-xm) < И хп-хт |,2,
то, в частности, для 4{ = Д имеем
| хп (А)—хж (Д) |2 Д < |: х„-хт ||«
я, следовательно,
|х„(Д) — гто(Д);2->-0 при л, m->-oo,
7.7] ПЛОТНОСТЬ МНОЖЕСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ В 12 193
а вместе с тем п
хп (Д) — хт (Д) —>¦ 0 при п, т—)-оо.
Теорема 7.6.1. Пространство L2 полно.
Дока зательство. Возьмем фундаментальную последовательность
элементов хп?Ьг. Тогда || хп [|<С (л = 1, 2, ...), где С—постоянная
(см. 5.2). Положим х (Д) = Нтжп (Д) для любого Д С [а, 6]. Существование
этого предела доказано в лемме 7.6.1. Так как каждая функция хп(А) удо-
удовлетворяет условию A5), т. е.
хп (Д) Д = хп (Д4) Aj -\-xn (Д2) Д2,
то, переходя в этом равенстве к пределу, мы видим, что и х (Д) удовле-
удовлетворяет условию A5). Далее, для любого разбиения отрезка [а, Ъ]
о (хп) = 2 1*п (Л*)]2 А! < II хп i|2 < С2,
г = 1
а потому и
1=1 "-*00 i=i
следовательно, z?jL2. Покажем, что ж=Нтжл.
Зададим е>0 и подберем Л^ так, что ||жп — хт\Ке при л,
Тогда для любого разбиения отрезка [а, 6]
о(хп-хт)= 2 [xn(Ai)-xm(Ai)pAi^\\xn-xm\\2<E^
i=l
Переходя к пределу при т—»-оо, получим
р
а(хп-х)= ^ [*п(Л;)-*(Лг)]2Л1<е2
или ||жп —х||<8. Тем самым доказано, что хп—> х, а вместе с тем дока-
доказана и полнота L2.
Следствие. Из проведенного рассуждения как следствие полу-
получается теорема о предельном переходе для средних значений: если хп —*¦ х,
то хп (Д)—> х (Д) при любом Д CZ [а, 6].
7.7. Плотность множества непрерывных функций
в пространстве L2
Установим сначала некоторое вспомогательное предложение. Будем
говорить, что из двух разбиений отрезка [а, 6] второе мельче первого, если
второе получено из перзого дроблением некоторых из отрезков, составляющих
первое разбиение. На рис. 12 верхнее разбиение (II) получено из нижнего (I)
дроблением Дь Д3 и Д4. Имея любые два разбиения. (I) и (II) отрезка [а, Ь],
будем обозначать Oi (ж) и Оц (х) метрические суммы элемента ж, составленные
для (I) и (II) разбиений соответственно.
Лемма 7.7.1. Если разбиение (II) мельче разбиения (I), то оц (х) ^
>> Ох (х) для любого х 6 L*.
13 Б. 3. вулих
194 ПРОСТРАНСТВО 12 [ГЛ. VII
Доказательство. Достаточно рассмотреть случай, когда раз-
разбиение (II) получается из разбиения (I) делением только одного из его отрез-
отрезков Д на две части Д' и Д". Общий случай, очевидно, сводится к этому частно-
частному, если такое дробление только одного отрезка на две части повторить
надлежащее количество раз.-
_i_J liil i 1
А, ' Л? '. As ' Л4
Рис. 12.
Так как слагаемые в метрических суммах О\ (х) и (Гц (х), отвечающие
всем неделящимся отрезкам разбиения (I), одинаковы, то остается сравнить
слагаемые, отвечающие Д (в а\ (х)) и Д' и Д" (в оц (х)), и доказать, что
[х (Д)рД < [х (Д')]»Д' + [* (Д")Р Д».
- На основании условия A5) это неравенство равносильно
[X (Д') Д' + X (Д") Д"]2 ^ {[х (Д ')]2Д' _|_ [х (Д»)]2Д''} Д. B3)
Последнее неравенство проверяется совершенно элементарно, если рас-
рассмотреть разность между обеими его частями. Именно, так как Д = Д' +
+ Д", то
{[* (Д')РД' + [х (Д")]2А"} (А' + Д") - [х (Д') Д' + х (Д") Д']2 =
= [* (Д')]2А'2 + [* (Д")]2Д + {[х (Д')]2+ [* (Д"I2} Д'А" -
— [х (Д')]2Д'2— [х (Д")]2Д — 2х (Д') х (Д") Д'Д" =
= И* (А')]2 + [* (А")]2 — 2х (Д') х (А")} А'А" = [х (Д') — х (А")]2Д'Д" > 0.
Неравенство B3) доказано.
Теперь мы докажем две леммы о приближениях к элементам в простран-
пространстве L2.
Функция точки у (t), заданная на [а, Ь], называется кусочно-постоянной,
е'сли весь отрезок [о, Ъ\ разбивается на конечное число непересекающихся
промежутков А,-, на каждом из которых у (t) равна некоторой постоянной.
На концах промежутков Аг функцию у (t) можно считать неопределенной.
Кусочно-постоянные функции входят в класс К, а потому и в L2.
Лемма 7.7.2. Для любого х ? L2 и любого 8 > 0 существует такая
кусочно-постоянная функция у (t), для которой
Доказательство. Прежде всего подберем разбиение о =
<о1<...<оп = Ь отрезка [а, Ь] на отрезки Aj = [ai_1, a,] (i = l, 2, ...,п)
(обозначим дальше это разбиение (б), а соответствующую ему метрическую
сумму — ав (х)), так что
Тогда, по лемме 7.7.1, для любого разбиения, более мелкого, чем (б),
(х) < а(г)< || х||2, а потому
B4>
7.7] ПЛОТНОСТЬ МНОЖЕСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ В i2 195
Положим (рис. 13)
y(t) = x(At) при «,-_!<«<«! (? = 1, 2, ..., л).
Докажем, что для любого разбиения отрезка [а, Ь] на отрезки Д_,-
У о {х-у) < е.
Если задать произвольное разбиение, то, перемешивая его точки деления
с точками а;, мы получим разбиение более мелкое по-сраввению с данным
0
i rf ]
1 H 1
t 1
1 i
a a,\
I
1
i i i
U
i
j
i
i
i
i
b
Рис 13.
и с (б). По лемме 7.7.1 метрическая сумма при этом не может уменьшить-
уменьшиться, а потому достаточно доказать требуемое неравенство для метрических
сумм, составленных по разбиениям более мелким, чем (б).
Итак, пусть отрезки Д_,- составляют разбиение отрезка [а, Ь] более
мелкое, чем (б). Тогда
Так как у (I) равна постоянной на кажом Д^-, именно у (i) = x (Д{), если
Д./СД;, то п среднее значение у(Д^) = ж(Д;) и потому
lx—v\— V '
t=l л
*) Внутренняя сумма при каждом i распространяется на все те /, для
которых Д^С Д;. Так как взятое разбиение мельче (б), то каждый Д^ вхо-
входит целиком в один из Д;.
13*
196 ПРОСТРАНСТВО i2 [ГЛ. VII
Преобразуя правую часть и используя по ходу вычислений условие
A5) *) и неравенство B4), находим
n
n
= o(x)-2 2 [x _
= a (x) - 2a6 (x) + ae (z) = a (x) - a6 (z)< e*.
Таким образом, "l/ff^—i/Xe и> переходя в левой части неравенства
к точной верхней границе, получаем || х — i/|]<s.
Лемма 7.7.3. Для любой кусочно-постоянной функции у (t) (на отрезке
[о, 6]) и любого е>0 существует такая непрерывная функция z(t), что
\\у — г II < е (норма —в пространстве L2).
Доказательство. Пусть отрезок [а, Ь] (рис. 14) с помощью точек
a = a0<Cai<C — <Сап = & разбивается на такие промежутки Aj = (oj_i, щ),
на каждом из которых у (г) есть постоянная: y(t) = ct на Д^ (i = i, 2, ..., п).
Положим Af = max[c;[ и подберем т]>0 так, чтб т]<-у- при всех
* = 1, 2, ..., ге и т1<С"од72~ • Введем непрерывную функцию z (г), полагая
{с, при а <; t < aj — т),
с; при aj^ + TK' <ai — Ч (i = 2, 3, ..., га —1),
Сп При Яп-i -f- Т] ^ t «^ 6
и определяя z (г) в интервалах между этими промежутками по закону
линейного интерполирования. Тогда |z(t)[<^Af при всех t.
Теперь с помощью формулы A9) имеем
ь
ai oi+я
ai-T) ai
<12 an-l+Tl
[cn—г (OJ2 dt. B5)
02—Л an-i
*) Легко понять, что условие A5) распроираняется по индукции на
случай разбиения отрезка Д на любое конечное число непересекающихся
отрезков, так что, например,
**) Если бы оказалось М=0, то, считая у (а;) = 0 при всех i = 0, 1, ..., п,
мы получили бы у (t) = 0, т. е. уже у (t) была бы непрерывной функцией.
7.8]
УМНОЖЕНИЕ ФУНКЦИЙ ИЗ L2
197
В каждом из интегралов подынтегральная функция, очевидно, не превос-
превосходит 4М2 *), и потому каждый из интегралов не превосходит 4М*1\, а вся
сумма B5) не превосходит 2(л—1LМ2т]<8 (п — Vм2~g]tf2^ = —— е2<е2.
Таким образом, || у— z||<e.
Переходим к основной теореме этого параграфа.
О
Рис. 14.
Теорема 7.7.1. Множество С 2 всюду плотно в пространстве L2.
Иными словами, каждый элемент х ? L,2 может быть представлен как
предел сходящейся в среднем последовательности непрерывных функций.
Доказательство. Достаточно показать, что для любого х ? L2
и любого е > 0 существует непрерывная функция z (t), удовлетворяющая
неравенству || х — г Ц < е (см. 3.7). По лемме 7.7.2 существует такая кусоч-
но-постоянная функция у (t), что Ц х — У \\ <-тг, а по лемме 7.7.3 суще-
ствует непрерывная функция г (?), для которой || у— z || <—. Тогда
|| ж — г |[ < е, и теорема доказана.
Теорема 7.7.2. Пространство L2 сепарабельно.
Эта теорема вытекает сразу из теорем 3.7.2 и 7.7.1, поскольку в 3.7
мы уже установили сепарабельность пространства CLi.
7.8. Умножение функции из ?2
Введем определение произведения двух функций из L2 с таким расчетом,
чтобы для функций, сводящихся к функциям точки, произведение тгело бы
обычный смысл. Произведение будет определено как функция промежутка,
которая может и не входить в ZA
*) Можно доказать и более точную оценку: М2.
198
ПРОСТРАНСТВО Г2
[ГЛ. VII
Определение. Пусть х, у 6 ?а- Их произведением ху называется
функция промежутка z (Д), определяемая при любом Д с [я, Ь] равенством
-i- \ xn{t)yn{t)dt,
B6)
где *„, уп g Ci2 и хп -> ж, 1/л -> у.
Чтобы оправдать это определение, покажем, что предел B6) существует
и не зависит от выбора последовательностей {хп} и {уп} (стремящихся к х
и J/ соответственно) и что z (Д) удовлетворяет условию A5). Попутно мы
покажем, что в формуле B6) получится тот же предел, если в качестве хп (t)
и Уп @ взять любые функции класса К, сходящиеся в среднем к х н у соот-
соответственно.
Итак, пусть хп -4- х, уп -^ у ш хп (t), yn (t) — функции класса К. Суще-
Существование предела B6) будет следовать из того, что числовая последователь-
последовательность i \ хп @ уп @ dt > фундаментальна. Действительно, из сходимости
{хп} п {уп} вытекает, что |[ хп ]|, || уп || <; М, где М — некоторая постоянная.
Тогда, при любых пит с помощью неравенства Буняковского и формулы A9)
имеем
(t) [yn (t)-ym (/)] dt
t- \ ocm{l)ym(t)dt
A
n(t)-xm(t)]yn(t)dt
Vl @ '
а последнее выражение стремится к нулю npii n, m->co.
Теперь покажем, что предел B6) не зависит от выбора {хп} и {уп}-
Достаточно рассмотреть случай, когда изменяется одна из этих последо-
последовательностей. Пусть, например, дана другая последовательность х'п-+х
[х'п (t) — функции класса К]. Тогда, используя оценки, аналогичные только
что проведенпым, имеем
\ хп @ Уп @ dt—\^x'n (t) уп @ dt
А А
[*»(')-*;@1 yn(t)
<м||хп-ж;ц.
Но хп — х'п —>-9, а потому
lim \ хп («) у„ @ dt = lim \ х'п (г) Уп (t) dt.
7.8] УМНОЖЕНИЕ ФУНКЦИЙ_И32?2 * 199
Наконец, если отрезок Д разбит на два непересекающихся отрезка Д'
и Д", то
г(Д)Д=Ит \ xn(t)yn{t)dt =
ll-WO -J
Л
= lim \ xn(t)yn(t)dt+lim [ xn(t)yn(t)dt =
Д' Д"
= г(Д')Д'+г(Д")Д",
т. е. г (Д) удовлетворяет условию A5).
Остановимся на случае, когда один из сомножителей—непрерывная
функция.
Лемма 7.8.1. Если x?L2— произвольный, а у ? Сх2, то z = xy?L2
и || г ||< М \\x\\, где J»/ = max|j/ (i) |.
Доказательство. Возьмем хп g Ci2, так что хп —> х, а все у„
берем равными у. Для любого разбиения отрезка [а, 6] метрическая сумм?
Но по неравенству Буняковского, используя также формулу A9),
имеем
Переходя в полученном неравенстве к пределу и пользуясь непрерывно-
непрерывностью нормы, находим, что а (г) ^.Мг \\ х ||2. Таким образом, метрические
суммы а (л) в совокупности ограничены, т. е. г ? /А Кроме того, отсюда
же следует, что
Лемма доказана.
Если у (t) = 1 (тогда можно взять и уп (t) = 1), то из определения
произведения и из теоремы о предельном переходе для средних значений
{см. следствиеиз теоремы 7.6.1) сразу вытекает, что ху = х при любом х ? L2.
Вообще, если j A) ?j I есть постоянная, то ху = Хх, где правую часть нужно
понимать как произведение на число (так, как это было определено в 7.5).
Иными словами, умножение на функцию, равную постоянной, совпадает
с умножением на число. В частности, хВ = 0 при любом i f L2.
Из определения произведения сразу вытекает его коммутативность.
Проверим его дистрибутивность относительно сложения. Пусть у = у' + у",
а z=xy, z'=xy', z" = ху". Подберем хп, у'п, у"п 6 CLi так, что хп ->- х, у'я-*. у',
200 ПРОСТРАНСТВО Г2 [ГЛ. VII
у"п -*¦ у". Тогда у'п + у"п -*¦ У и, по определению,
* (Д) = lim 4" \ *п W [у'п @ + у'п @1 <** =
Д
= lim 4" \*п @ У'п @ Л + lim 4" \ хп @ Уп @ rfi = z' (Д)+** (А);
Л Л
т. е. ху = х(у' + у") = ху + у
Вопрос об ассоциативности произведения в полном объеме не имеет
смысла, так как произведение двух функций из L2 уже может не входить в Хг,
а тогда его произведение на третью функцию не определено. Ограничимся
некоторыми замечаниями по этому вопросу.
Если Я — число, то, очевидно, х (Ху) = Я (ху) при любых х, у б "*).
Покажем, что если q> ? CL2 — произвольная непрерывная функция, то
(ух) у = х (<ру).
Положим сначала z = (<px)y, 2^ = 2(9^). Подберем гп, ^п6Сх2 так' что
хп—> х, уп—> у. Тогда, по лемме 7.8.1,
II фг„ —фг || = || ф (хп — х) || < (max | ф (г) |) || хп—х ||,
следовательно, <рхп—> фг; аналогично, ууп—>ц>у. По определению произ-
произведения для любого Д С [а, 6]
(Д)= lim -i- [ [Ф (t) xn (t)} yn (i) dt,
Л
(Д) = lim -J- ^ хп @ [Ф (г) у„ (г)] Л,
и так как правые части одинаковы, то z = zt.
Легко видеть, что если х (t) и у (г) — функции класса К, то произве-
произведение ху, определенное по формуле B6), совпадает с обычным, т. е. при-
приводит к функции z(t) = x(t)y(t). Действительно, в этом случае можно при
всех п взять хп = х, уп = У- Тогда по формуле B6) для z = xy имеем
г (А) =4" \ *{t)y
Восстанавливая по функции промежутка z (Д) с помощью формулы A6)
функцию точки z (I), получим 2 (t) = x (t) у (t) во всяком случае во всех
точках, где х (t) ny (t) непрерывны.
7.9. Скалярное произведение в Ъг
Покажем, что в L2 можно определить скалярное произведение так, что
L2 оказывается гильбертовым пространством. С этой целью для любых
х> У 6 -Ь2 положим скалярное произведение (х, у) равным интегралу от произ-
произведения этих функций (определенного в 7.8) по всему отрезку [а, Ь]. Иными
*) Здесь следует учесть, что если уп 6 СГ2 и уп^-у, то \уп ?CL2 и
7.9] СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В А2 201
словами, если z = ху, то
(х, у) = z ([a, Ь])(Ь- а). B7>
Если *„, уп?С12 и хп-^х, уп—ь-у, то по формуле B6)
ь
(х, у)=Мш \ xn{t)yn{l)\dt.
а
В частности,
[х,х)=Мт \ xl(t)dt=\\m |]x»|
а
и вследствие непрерывности нормы
Проверим, что (х, у) удовлетворяет всем условиям, определяющим
скалярное произведение [условия а) — г) из 6.1]. Коммутативность выраже-
выражения (х, у), очевидно, вытекает из его определения. По формуле B8) (я, х) > О
для любого х ? L2 и отсюда же видно, что (х, х) = 0 только при а: = 9,
т. е. выполнено условие г).
Для проверки дистрибутивности выражения (г, у) положим при про-
произвольных х, у, z ? L?
ui = xz, u2 — yz,
Тогда благодаря дистрибутивности умножения функций и = щ^\-иг и
(х + у, z) = u([a, b])(b-a) = Ul(la,b])(b~a) + uz(la, b])(b-a) = (x, z) + (y, z).
Аналогично, если u = xy, a v = (Xx)y, то v = Xu и потому
(Ал, y) = v{[a, Ъ\){Ъ-а) = Ы{[а, Ь]) (Ъ-а) = \(х, у).
Итак, функционал (х, у), определяемый формулой B7),— скалярное про-
произведение. Кроме того, для любого х 6 L2 выполнено равенство B8). Таким
образом, норма в L2 порождается скалярным произведением, а потому L2,
будучи по теореме 7.6.1 полным,— гильбертово пространство.
Итак, мы построили еще одно функциональное сепарабельное гиль-
гильбертово пространство. Оно бесконечно-мерно, поскольку оно содержит
все непрерывные функции, заданные на отрезке [а, Ь]. Следовательно, оно
алгебраически изоморфно и изометрично пространству L2 функций, сумми-
суммируемых с квадратом. Как же установить этот изоморфизм наиболее есте-
естественным образом?
Используя теорию интеграла Лебега, можно доказать, что каждая функ-
функция промежутка х (Д) из L2 порождается по формуле A3) некоторой функ-
функцией точки х @ из L2 и притом единственной с точностью до значений на
множестве меры нуль. Обратно, каждая функция точки из L2 порождает
по формуле A3) функцию промежутка, входящую в L2. При этом алгебраиче-
алгебраическим операциям сложения функций точки и умножения функции на число
соответствуют те же операции над порожденными этими функциями точки
функциями промежутка. Кроме того, если взять две функции х (t) иг/ (г)
из L2 (им соответствуют функции промежутка х (Д) и у (Д)) и положить,
z (t) = х (t) у (t) (как известно, z 6 L), то z (t) по формуле A3) тоже будет
порождать некоторую функцию промежутка z (Д). Это и будет та функция
02 пространство Х2 [гл. vn
промежутка, которая была определена в предыдущем параграфе как произве-
произведение функций х (Д) и у (Д). Этим лишний раз подтверждается целесообраз-
целесообразность определения произведения, введенного в 7.8.
Формула B7), определяющая скалярное произведение в L2, может быть
теперь переписана так:
ь
(x,y)=\x(i)y(t)dt B9)
а
(здесь х, y?Z.2, a х {t) и у (I) — порождающие их функции точки). Отсюда,
в частности, вытекает, что для любого х ? L2
ъ
Таким образом, соответствие между элементами из L2 и L2, устанавливаемое
формулой A3), и есть алгебраический изоморфизм и оно изометрично. Соглас-
Согласно формуле B9), это соответствие сохраняет и скалярное произведение.
В тех приложениях, рассматриваемых в последующих главах, где встре-
встречается функциональное гильбертово пространство, мы будем пользоваться#
терминологией, связанной с пространством L2. При желании читатель легко
сможет сам перейти к пространству L2. При этом заметим, что в большинстве
разбираемых в книге приложений решение задачи оказывается непрерывной
функцией и потому для понимания постановки задачи достаточно пользо-
пользоваться классическим интегралом Римана. Однако для обоснования возмож-
возможности применения общих теорем функционального анализа встречающиеся
интегралы в ряде случаев следует понимать как интегралы Лебега или как
-значения функций промежутка, лишь записанные с помощью интегралов
-от функций точки.
ГЛАВА VIII
ЛИНЕЙНЫЕ ОПЕРАТОРЫ
8.1. Аддитивные операторы
При изучении операторов в нормированных пространствах
возникает ряд новых важных понятий и вопросов, которые свя-
связаны с алгебраическими операциями и с нормой и которые по этой
причине не могли быть рассмотрены в общих метрических про-
пространствах. В настоящей главе будет изучен наиболее важный
и весьма широкий класс операторов в нормированных простран-
пространствах — линейные операторы. Такие операторы мы уже рас-
рассматривали в первых двух главах в эвклидовых пространствах
и некоторые их свойства, установленные в гл. I — II, будут
теперь доказаны заново в более общем виде. Начнем с некоторых
понятий, относящихся к операторам в любых линейных системах.
Пусть X и Г— вещественные линейные системы, U — опера-
оператор, который каждому элементу х ? X сопоставляет элемент
уег.
Определения. 1) Оператор U называется аддитивным,
если
A)
для любых хи х2?Х.
2) Оператор U называется однородным, если
U (ах) = a (Ux) B)
для любого х ? X и любого числа а.
Отметим некоторые простые следствия из аддитивности опе-
оператора. Именно, если оператор U аддитивен, то:
а) т = 6 *);
б) U (—х) = — Ux для любого х ? X;
в) равенство B) выполнено для рациональных а.
*) Здесь одно п то же обозначение 6 употребляется для нулевых эле-
элементов обеих систем Хи Y. Это не приведет нас к каким-нибудь ошибкам,
так как из контекста всегда будет ясно, к какой системе относится тот или
иной знак 6. Точнее было бы писать, например, так: UQx = By, но мы не
хотим усложнять обозначений.
204 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
Доказательство, а) Для любого х?Х
а тогда С/0 = 0.
б) Так как х — x = Q, то, с помощью а), имеем
Ux + U ( — x) = U (х-х) = ?/0 = 0,
а тогда U ( — х)= — Ux.
в) Если и —натуральное, то
U (пх) = U (х + х + ... + х) = п {Ux).
п слагаемых
Если а == — , где п — натуральное, то
а отсюда
Если а = —, где т и п — натуральные, то, по предыдущему,
U (ах) = U (т ~ ж) = mU A х*) = т~ U (х) = -^ (С/ж) - a (Ux).
(
Наконец, если а — отрицательное рациональное число, т. е.
а= —г, где г имеет вид — (т, п — натуральные), то гпо уже
доказанному для положительных рациональных чисел с помощью
б) получаем:
U(ax) = U( — rx)= —U(rx)= —r(Ux) = a(Ux).
Если же а —0, то равенство B) очевидно благодаря а).
Можно показать, что даже в простейшем случае, когда X
и Y—множества вещественных чисел (а оператор U в этом случав
превращается в обычную функцию), из аддитивности U не вытекает
его однородность в полном объеме, т. е. выполнение равенства B)
при любых а.
Следующее предложение совершенно очевидно, но мы его
формулируем ввиду того, что в дальнейшем будем им постоянно
пользоваться.
г) Если оператор U аддитивен и однороден, то для любых
элементов хи х2, ..., хп?Х и чисел аи а2, ..., ап
j]() C)
Это свойство называют свойством дистрибутивности оператора.
8.2] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 205
8.2. Линейные операторы
Теперь будем считать X и Y — нормированными простран-
пространствами. Используя общее понятие непрерывности оператора
в метрических пространствах, данное в 4.2, введем следующее
определение:
Определение. Оператор у = Ux называется линейным,
если он аддитивен и непрерывен.
В отличие от операторов в общих метрических пространствах,
для которых мы сначала определяли непрерывность «в точке»,
а потом уже, «во всем пространстве», из класса аддитивных опера-
операторов в нормированных пространствах выделяются непрерывные
сразу во всем пространстве. Это объясняется следующей тео-
теоремой:
Теорема 8.2.1. Если аддитивный оператор U непрерывен
« какой-нибудь одной точке х0 ? X, то он непрерывен и в любой
точке пространства X, т. е. линеен.
Доказательство. Пусть хп ? X и хп ->- х. Тогда полу-
получим хп — х -\- х0 -*- х0. Вследствие непрерывности оператора U
в точке х0,
Uxn — Ux-\- Uxq = U (хп — х + х0) —> Uxc,
а тогда Uxn — Ux -> 8, или Uxn -> Ux.
Благодаря этой теореме при доказательстве линейности какого-
нибудь аддитивного оператора достаточно проверить его непре-
непрерывность, например, в точке 8. А так как для аддитивного опе-
оператора UQ = 0, то непрерывность U в точке 0 означает, что если
хп -> 0, то и Uxn -*¦ 0.
Теорема 8.2.2. Всякий линейный оператор однороден.
Доказательство. В предыдущем параграфе мы пока-
показали, что для всякого аддитивного оператора U равенство B)
выполнено при рациональных а. Если а — иррациональное, то,
как известно, всегда можно подобрать рациональные числа гп
так, что rn -v а. Тогда для любого х ? X будет гпх->- ах [см. 5.2,
пункт б)], следовательно, по непрерывности U и по доказанному
для рациональных множителей равенству B)
U (ах) = lim U (rnx) =iim rn (Ux) = a (Ux).
Таким образом, однородность оператора U доказана.
Теорема 8.2.3. В конечно-мерном нормированном про-
пространстве всякий аддитивный и однородный оператор линеен.
Доказательство. Пусть пространство X конечно-
конечномерно, xlt х2, . . ., Хр — его базис, а оператор U аддитивен
206 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
V
и однороден. Тогда всякий х ? X имеет вид х = 2 akxk, a
i
Ux=j]ak(Uxk).
ь1
Если теперь
то по теореме 5.3.1, а?п>—>а& при ге—>со (& = 1, 2, ..., р),
а потому
Ux(n) = 2 а(п) (?7жа) _^ 2 а, (Eteft) = Ux.
fc=i fe=i
Непрерывность оператора U доказана.
В частном случае, для эвклидова пространства 1?п, эта тео-
теорема была доказана в 1.8. Этой же теоремой объясняется и то, что-
в определение линейного оператора в Вп мы не включили тре-
требования непрерывности.
Для линейных операторов соотношение дистрибутидности C)
00
можно распространить и на бесконечные ряды: если ряд 2 °ажь
сходится, то, используя непрерывность и свойство «конечной»
дистрибутивности линейного оператора U, имеем
оо п П
U ( 2 akxk) = U (lim 2 «&ж&) = lim V ( 2
ft=l n->ooft=l П-+О0 k—i
П oo
-lim %ak(Uxk)= S a
n->oo ft=l ft=l
Понятия аддитивности, однородности и линейности, есте-
естественно, применяются и к функционалам как к частному случаю
операторов.
8.3. Ограниченность линейных операторов
Для аддитивных операторов в нормированных пространствах
свойство непрерывности оказывается равносильным другому
важному свойству — ограниченности, которое определяется сле-
следующим образом:
Определение. Оператор U, заданный в пространстве X,
называется ограниченным, если существует такая постоянная С, что
|| «7* || «711* || D)
для всех х g X.
8.с] ОГРАНИЧЕННОСТЬ ЛИНЕЙНЫХ ОПЕРАТОРОВ 207
Теорема 8.3.1. Для того чтобы аддитивный оператор U
был линейным, необходимо и достаточно, чтобы он был ограни-
ограниченным.
Доказательство, а) Необходимость. Пусть
оператор U линеен, но предположим, что он не ограничен, т. е. не-
несуществует такой постоянной С, чтобы неравенство D) было*
выполнено для всех х ? X. Следовательно, для любого нату-
натурального п существует элемент хп ? X, для которого
\\Uxn\\>n\\xn\\. E>
Так как из этого неравенства следует, что U хп -ф- 0, то и хпфВ.
Положим х'п= *" Ц . Тогда ||ж;|| = — -> 0, т. е. x'n->Q. С дру-
П || Хп || П
гой стороны, вследствие однородности линейного оператора
TJr' — * TTt-
п ~ л II г II "
" \\хп II
и из E) вытекает, что || Ux'n || > 1, а потому Ux'n не стремится
к 0, что противоречит непрерывности оператора U. Тем самым
доказано, что U ограничен.
б) Достаточность. Пусть аддитивный оператор U
ограничен, т. е. выполнено условие D). Если хп -> 8, т. е..
II хп II -*• 0, то из D) сразу следует, что и || Uxn || -> 0, т. е.
Uxn-*-Q. А раз оператор U непрерывен в точке 8, то по тео-
теореме 8.2.1 он линеен.
Из этой теоремы и теоремы 8.2.2 следует, что из аддитивности
и ограниченности оператора вытекает его однородность.
Теперь покажем, что для того чтобы аддитивный оператор U
удовлетворял во всем пространстве X неравенству D), необходима
и достаточно, чтобы неравенство || Ux \\ ¦< С (с той же постоян-
постоянной С) было выполнено для всех х с нормой || х \\ < 1. Множество-
таких х будем называть единичным шаром пространства Л".
Действительно, из неравенства D) сразу следует, что || Ux \\ <
< С при || ж || < 1. Обратно, пусть || Ux \\ < С при \\x\\ < 1.
Для любого х ? X можно подобрать рациональные числа гп >
> || х || так, что гп -> || х \\. Положим х'п — —. Тогда ||ж^|| <С 1,
а потому || Ux'n || < С. Но из аддитивности оператора вытекает
его «однородность» относительно рациональных множителей, сле-
следовательно,
Переходя в этом неравенстве к пределу, получим соотношение D).
Вследствие доказанного можно для аддитивного оператора
дать и другое определение ограниченности: аддитивный оператор
208 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
называется ограниченным, если ограничена совокупность его
значений на единичном шаре S* пространства X *). Из дока-
доказанного также следует, что точная верхняя граница множества
норм || Ux ||, соответствующих всевозможным х ? S*, есть наи-
наименьшая постоянная С, при которой неравенство D) выполняется
для всех х ? X.
ч Определение. Для линейного оператора U наимень-
наименьшая постоянная С, при которой неравенство D) выполняется
для всех х ? X, называется нормой оператора U и обозначается
II U ||.
Таким образом,
|| U||= sup \\Ux\\, ¦ F)
а
II Ux ]\<\\U |] || х || при всех х ? А'.
Вследствие однородности линейного оператора верна и такая
формула:
II U || = |( sup i \\Ux\\,
т. е. при определении нормы \\ U |] достаточно вычислить точную
верхнюю границу множества норм значений Ux только на «поверх-
«поверхности» шара S*. Проверку этой формулы предоставляем чита-
читателю.
Примеры линейных операторов и функционалов мы уже
встречали в первых двух главах. Приведем еще некоторые при-
примеры. Интегральный оператор из рассмотренного в 4.5 линейного
интегрального уравнения Фредгольма с непрерывным ядром
ь
y = Ux, где у (s) = % \ К (s, t) x (I) dt,
а
— линейный оператор, преобразующий пространство С в самого
себя. Действительно, его аддитивность очевидна**), а ограни-
ограниченность вытекает из оценки:
ь
\\y\\=max\y(s)\^M\%\ [ \x (t)\dt<M\X\(b-a)\\x\\,
а
где М = max | К (s, t) |. При этом \\U \\<М | X | (Ь — а). Впро-
чем, эта оценка нормы оператора U дана с большим запасом.
*) Ср. со сказанным в 2.6 об ограниченности линейного функционала в ?а.
**) Однако оператор, рассмотренный в 4.5 и включавший в себя свобод-
свободный член уравнения, не аддитивен.
8.3] ОГРАНИЧЕННОСТЬ ЛИНЕЙНЫХ ОПЕРАТОРОВ 209
Легко получить, например, такую более точную оценку:
ь
||?/||<|Я|шах^ \K(s, t)\df).
s v
а
Пусть Н — гильбертово пространство, L — его подпростран-
подпространство. Для каждого х ? Н полагаем у = PrLx. Тем самым мы
определяем на Н оператор со значениями в том же простран-
пространстве Н (обозначим его через Р), который называется проектором.
Проверим его линейность.
Пусть хи xze Н, г/! = Рхи у2 = Pxz, zt = x^ — г/,; z2 --=
== хг — У2- Тогда zu zz _L L. Сумму Xi -j- xz можно представить
в виде ж, + х2 = (j/i + у2) + 0ч + г2), причем j/, + y2 6 L,
a zi + z2 ± L. Следовательно, У\ + у2 = -Ро, (^i-l ^г), т- е.
Р (Xi -j- x2) = Pxi + Р^г- Оператор i3 аддитивен.
Для любого х g Н имеем х = Рх ^- z и по теореме Пифа-
Пифагора || x\f = ||Ра; || 2-L|j z (I2, откуда || Рх \\ < || х ||. Следователь-
Следовательно, оператор Р — линейный и ||Р||<1. С другой стороны,
Рх = х для х ? L. Значит, если только подпространство L не
нулевое, т. е. содержит элементы, отличные от 8, то существуют
такие х ф в, для которых || Рх || = || х ||. Таким образом, 1 —
наименьшая постоянная в условии ограниченности оператора Р,
т. е. || Р || = 1 **).
В качестве одного из применений теоремы 8.3.1 рассмотрим
вопрос об эквивалентности норм.
Определение. Пусть в одной и той же линейной сис-
системе Tj определены две нормы || х ||t и || х ||2, каждая из которых
превращает Е в нормированное пространство. Эти нормы назы-
называются эквивалентными, если сходимости по обеим нормам сов-
совпадают, т. е. из соотношения хп -*¦ х в смысле сходимости по
первой норме вытекает то же соотношение и по второй норме,
и обратно.
Обозначим через Х^ и Хг те нормированные пространства,
которые получаются из Е за счет введения первой и второй норм
соответственно. По составу элементов Xi и Xz совпадают.
Теорема 8.3.2. Для того чтобы нормы \\ х ||, и \\ х ||2,
заданные в линейной системе Е, были эквивалентными, необходимо
*) Можно доказать, что на самом деле в этом соотношении имеет место
точное равенство.
**) В теории операторов в гильбертовом пространстве обычно употреб-
употребляется несколько иная терминология. Линейным называется всякий адди-
аддитивный оператор. Линейные в нашем смысле операторы называются ограни-
ограниченными линейными, а кроме того, рассматриваются и неограниченные линей-
линейные операторы, т. е. аддитивные и однородные, но ие непрерывные. Однако
в дальнейшем мы и в гильбертовом пространстве будем придерживаться
определений, введенных в этой главе.
14 В. 3. Вулих
210 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
и достаточно, чтобы существовали такие постоянные М,т >0,
что
mWxW^WxW^MWxW, G)
для всех х ? Е.
Доказательство, а) Необходимость. Пусть
заданные нормы эквивалентны. Обозначим через А тождествен-
тождественный оператор, отображающий A'i на Х2 '• х = Ах. Ясно, что
этот оператор аддитивен, а из определения эквивалентности
норм следует, что если хп -> х в смысле сходимости по первой
норме, то Ахп —*¦ Ах по второй норме *). Таким образом, опера-
оператор А линеен, а тогда, по предыдущей теореме, он ограничен.
Следовательно, существует такая постоянная М > 0, что
|| Ах |12<М || х ||i для всех х ? Е **), а это и есть правая часть
неравенства G).
Аналогично, рассматривая тождественное отображение про-
пространства Х2 на Xi, мы получим неравенство || х \\i <C || х2 ||
(С > 0), и, полагая т ~ -w , мы придем к левой части неравен-
ства G).
б) Достаточность. Пусть выполнено условие G). Если
хп -> х по первой норме, т. е. || хп — х ||t -+¦ 0, то
и потому хп —>• х и по второй норме. Аналогично выводится обрат-
обратное утверждение и, таким образом, сходимости по обеим нормам
совпадают, т. е. нормы эквивалентны.
Пусть теперь нормы || х ||t и |[ х ||2 в Е таковы, что из соотно-
соотношения хп —v х в смысле сходимости по первой норме вытекает
то же соотношение и по второй норме, но обратное не предпола-
предполагается. Этот факт, как видно из доказательства предыдущей
теоремы, равносилен существованию такой постоянной М, для
которой при всех х ? Е выполнена правая часть неравенства G):
\\х12<М\\х\\,. (8)
При выполнении условия (8) будем говорить, что вторая норма
мажорируется первой. Таким образом, эквивалентность двух
норм означает, что каждая из них мажорирует другую.
Предлагаем читателю проверить, что норма в пространстве С,у
мажорируется нормой в пространстве С.
*) Ахп и Ах это — те же элементы, что и сами хп it x (соответственно),
но рассмотренные как элементы пространства Хг.
**) Постоянную в условии ограниченности D) всегда можно считать
большей нуля.
8.4] РАСПРОСТРАНЕНИЕ ЛИНЕЙНЫХ ОПЕРАТОРОВ 211
Интересно отметить, что если пространства Xt и Хг (полу-
(полученные, как указано выше, из системы Ж) полны и одна из
норм || a: ||i и\\х \\2 мажорирует другую, то эти нормы эквива-
эквивалентны *).
8.4. Распространение линейных операторов
Введем понятие о распространении операторов. Пусть X —
нормированное пространство, а Е — некоторое его подпростран-
подпространство или даже просто линейное подмножество. Тогда Е — тоже
нормированное пространство. Пусть на Е задан линейный опера-
оператор U со значениями в нормированном пространстве Y. Если
существует линейный оператор V со значениями в том же Г,
определенный на всем X и такой, что Vx — Ux для всех х ? Е,
то оператор V называется распространением оператора U с про-
пространства Е на пространство X.
Так как \\ U \\ — наименьшее значение постоянной С, при
котором неравенство D) выполнено для всех х ? Е, то ясно, что
при расширении области задания оператора норма не может
уменьшиться и || V ||, как наименьшая постоянная С, при которой
неравенство D) будет выполнено на всем X, должна удовлетворить
условию || V \\х>\\ U \\Е **). Если же || V \\х = || U \\Е, то гово-
говорят, что распространение осуществлено с сохранением
нормы.
Сначала рассмотрим один случай, когда распространение
с сохранением нормы всегда осуществимо.
Теорема 8.4.1. Пусть X — нормированное пространство\
TJ — всюду плотное в X линейное подмножество, у = Ux —
линейный оператор, заданный на Е, со значениями в банаховом
пространстве Y***). Тогда оператор U допускает единственное
распространение на всё X и притом с сохранением нормы.
Доказательство. Каждый х ? X представим в. виде
х = lim хп, где хп ? Е. Так как последовательность {хп} фунда-
фундаментальная, то || хп — хт || ->¦ 0 при п, т -> оо. Из ограничен-
ограниченности оператора U вытекает, что
|| Uxn-Uxm || = || U (хп-хт) ||< |! U || |! хп-хт ||,
а потому последовательность {Uxn} тоже фундаментальна. Вслед-
Вследствие полноты пространства Y существует у = lim Uxn. Покажем,
*) Cftf., например, Л.В.Канторович и Г. П. А к и л о в, Функ-
Функциональный анализ в нормированных пространствах, стр. 426.
**) Индексы при нормах поставлены, чтобы подчеркнуть, что опера-
оператор U задан только на Л, а оператор V — на всем X.
***) Напоминаем, что банаховыми называются полные нормированные
пространства E.2).
14*-
212 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. МП
что этот элемент у не зависит от выбора последовательности
элементов хп ? Е, стремящейся к х. Действительно, если дана
еще последовательность х'п -*- х, х'п ? Е, то х'п — хп -> 8, а тогда
и Ux'n — Uxn = U (х'п — хп) -> й по непрерывности операто-
оператора U; следовательно, lira Ux'n = lira Uxn.
Теперь мы определим оператор V на всем пространстве X,
полагая для любого х ? X
Vx--=YimUxn, (9)
где хп ? E и хп -> х. Покажем, что это и есть требуемое рас-
распространение оператора U.
Так как для х ? Е можно положить все хп = х, то по фор-
формуле (9) Vx = Ux. Аддитивность оператора V проверяется так.
Если х, z ? Л', хп ->- х, zn -> 2, где хп, zn ? Е, то жл -f zn -*-
—>- a; -f- 2 и
F (a: - z) ¦-¦- lim U (xn -f 2,,) --_. Jim (t/zn -f Z/z,,) ^
— lim Uxn-]- lim C/zn ~ Vx-\- Vz.
Наконец проверим, что оператор V — линейный и что || V \\ —
= || U ||. Пусть х ? Л", хп ? Е и хп ->¦ х. Переходя к пределу в
неравенстве || Uxn || -< || U \\ \\ хп \\ и учитывая непрерывность
.нормы, получим
|| Vx ]|< || U || || Ж||.
Таким образом, аддитивный оператор F ограничен, а следова-
следовательно, линеен, а так как || V || — наименьшая постоянная в усло-
условии ограниченности оператора V, то || F||<|| U \\. Но неравен-
неравенство в этом соотношении невозможно; тем самым доказано равен-
равенство норм.
Единственность распространения почти очевидна. Пусть
W — какой-нибудь линейный оператор, представляющий рас-
распространение оператора U на всё X. Если х ? X, хп ? Етл хп —>- х,
то, по непрерывности W,
Wx = lim Wxn = lim Uxn = Vx,
т. е. оператор W совпадает с V.
Замечание. Тем же рассуждением, которым доказана
в предыдущей теореме единственность распространения, уста-
устанавливается следующее предложение. Пусть в нормированном
пространстве X заданы два линейных оператора U и W со зна-
значениями в одном и том же нормированном (не обязательно бана-
банаховом) пространстве Y. Если Vx — Wx для любого х и-i некоторого
множества Е, всюду плотного в X, то Vx ¦-= Wx при всех х ? X *).
*) В этом предложении Е может не быть линейным множеством.
8.Г.] ПОСЛЕДОВАТЕЛЬНОСТИ ЛИНЕЙНЫХ ОПЕРАТОРОВ 21 3
В гильбертовом пространстве распространение линейного
оператора (с сохранением нормы) возможно с любого линейного
подмножества.
Теорема 8.4.2. Пусть Ы. — гильбертово пространство,
Е — его линейное подмножество, у = Ux — линейный оператор,
заданный на Е, со значениями в банаховом пространстве Y. Тогда
оператор U допускает распространение на всё Н с сохранением
нормы.
Доказательство. Обозначим через L замыкание мно-
множества Е; L — подпространство пространства Н. Так как Е
плотно в L, то распространение оператора U на Ъ с сохранением
нормы возможно по предыдущей теореме. Поэтому, не уменьшая
общности, можно с самого начала считать, что Е — подпро-
подпространство.
Обозначим через Р оператор проектирования пространства И
на подпространство L и положим для любого х ? Н
Vx=U (Рх).
Тогда аддитивность оператора V вытекает из аддитивности U
и Р, а
|!7*|!<||^||!|Лг||<||^||||Р||||:г|Н1^1!И1
(так как \\Р \\ = 1, см. 8.3). Отсюда, как и в доказательстве
предыдущей теоремы, следует, что оператор V линеен, а || F || =
--= |j U ||.
Благодаря тому, что в формулировке теоремы множество Е
не предполагается всюду плотным в Н, распространение опера-
оператора U в этой теореме может быть осуществимо не единственным
способом.
В следующей главе мы увидим, что для линейных функцио-
функционалов теорема 8.4.2 справедлива в любом нормированном про-
пространстве.
8.5. Последовательности линейных операторов
Для многих приложений весьма важную роль играет изуче-
изучение последовательностей линейных операторов, к которому мы
сейчас и переходим. Пространства I и Г считаем нормиро-
нормированными.
Определение. Пусть в пространстве X заданы опе-
операторы Un (п = 1, 2, . . .) и U, отображающие X в одно и то же-
пространство Y. Последовательность {Un} называется точечно
сходящейся к оператору U, если
Ux = lim Unx
для любого х ? X.
214 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
Лемма 8.5.1. Если последовательность линейных операто-
операторов {Un} точечно сходится к некоторому оператору U и нормы
\\ип II в совокупности ограничены, то предельный оператор U
тоже линейный.
Доказательство. Аддитивность U вытекает из сле-
следующих соотношений, верных для любых х, z ? X:
U(x + z)=^ lim Un (x + z) = lim (Unx + Unz) =
= lira Unx + lim Unz = Ux+Uz.
Далее, по условию, || Un \\<,C при всех п, где С — некоторая
постоянная. Переходя к пределу в неравенстве || Un x ||<С ||z||,
получим || Ux ||<C || х || для любого х 6 X. Следовательно,
оператор U линейный.
В полных пространствах ограниченность норм операторов
вытекает из точечной сходимости, и доказанный результат зна-
значительно усиливается. Предварительно введем следующее:
Определение. Последовательность {Un} операторов,
отображающих пространство X в одно и то же пространство Y,
называется точечно ограниченной, если в каждой точке х ? X
последовательность значений {Unx} ограничена.
Теорема 8.5.1. (С. Банах — Г. Штейнгауз). Если про-
пространство X полно, а последовательность линейных операторов Un,
отображающих X в Y, точечно ограничена, то нормы \\ Un \\
ограничены в совокупности. Если, в частности, последовательность
линейных операторов Un точечно сходится к оператору U *),
то оператор U линейный.
Доказательство. Достаточно доказать, что из точечной ограни-
ограниченности последовательности {?/„} вытекает ограниченность норм Ц Un \\.
Остальное будет следовать из леммы. Допустим, что || Un || не ограничены
в совокупности, и покажем прежде всего, что тогда, каков бы ни был замкну-
оо
тый шар S* С -?\ множество (J Un (S*) (сумма образов шара S*) не огра-
п=1
ничено. Действительно, если бы для некоторого шара S* = S* (х0, г) это
множество было бы ограничено, то имело бы место неравенство
|| Un х |К С при всех я ? .У* и л = 1, 2, ...,
где С — некоторая постоянная. Для любого х с нормой Ц х || < 1 положим
х' = х0 + гх. Так как || х' — х„ || = г || х || <г, то х' 6 S*, а тогда из
равенства
Unx= Un
вытекает, что для любого х с нормой || х \\ <; 1
II Unx ||<i- (|| Unx- 11 + Ц Unx0 || )< -21;
*) Ясно, что из точечной сходимости последовательности операторов
вытекает ее точечная ограниченность.
8.5] ПОСЛЕДОВАТЕЛЬНОСТИ ЛИНЕЙНЫХ ОПЕРАТОРОВ 215
1С
это же означает, что || Un || ^— (см. 8.3) вопреки предположению о не-
неограниченности норм || Un ||.
Возьмем произвольный замкнутый шар Sjf cz X радиуса г. Вследствие
неограниченности множества образов элементов этого шара найдутся номер щ
и элемент xt 6 Sjf, для которых |[ Un xt [| > 1. Не уменьшая общности,
можно считать #, внутренней точкой шара SJ, так как всегда можно сначала
взять шар с радиусом меньшим, чем радиус шара S$, а затем искать требуе-
требуемую точку xt в уменьшенном шаре *). Вследствие непрерывности оператора
Uni существует замкнутый шар Sf = S* (жь rt), во веех точках которого
Ц U х || !> 1 **). При этом, уменьшая rt в случае необходимости, мы можем
считать, что уже rt <^—- . Кроме того, так как xt — внутренняя точка шара
S*. то можно считать, что г, взято настолько малым, что Sf с S*.
Последовательность норм || Un |[, где п > щ, тоже не ограничена, а пото-
оо
му не ограничено множество |J Un (Sf). Следовательно, аналогично пре-
п=тц+1
дыдущему найдутся номер п2 > гц и внутренняя точка х2 шара 5f, для
которых || Un2x2 || > 2. После этого можно найти замкнутый шар S$ a Sf,
по всех точках которого || Un х [| !> 2, а радиус которого г2 -^ -— ^ -^ .
Продолжая этот процесс до бесконечности, мы получпм последователь-
последовательность вложенных друг в друга замкнутых шаров Sm с радиусами гт, причем
гт -*¦ 0, и последовательность индексов ni < n2 < • • • < пт < . . . таких,
что || Un х |1 > т для всех х ? Sm. Так как X полно, то, по теореме 3.5.3,
существует общая точка х* всехшаров Sm. В этой точке мы имеем || С/ х* || >
т
> т при любом т, т. е. последовательность {Unx*} оказывается неограни-
неограниченной, что противоречит точечной ограниченности последовательности
операторов Un.
Полученное противоречие и доказывает теорему.
В следующей теореме существенна полнота пространства Y.
Теорема 8.5.2. Если Un (п = 1, 2, . . .) — линейные опе-
операторы, отображающие пространство X в полное пространство Y,
причем:
*) Заметим, что если г' < г, то замкнутый шар S* (х0, г') содержится
и открытом шаре S (х0, г), а все точки открытого шара суть внутренние точки
последнего и потому они будут также внутренними точками замкнутого
шара S* (х0, г).
**) Это получается сразу из второго определения непрерывности опера-
оператора, приведенного в 4.2. Однако для линейного оператора это заключение
можно установить так. Положим а = || Ьг з^ || — 1 и п=тг-^—т- ¦ Тогда,
если || х — Xi |i <; гь то с помощью неравенства B) из 5.2 получаем
-|| Uni (х-х,) || > || ипщ 11-Ц t/nj II /-, = !!
216 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
1) для всех х из некоторого множества А, всюду плотного
в X, существует lim Unx;
2) ||?/„||<С при всех п, где С>0 — постоянная,
то lim Unx существует для всех х ? X, т. е. последовательность
{Un} точечно сходится к некоторому оператору.
При этом предельный оператор линеен по лемме 8.5.1.
Доказательство. Возьмем х ? X и зададим произ-
произвольное е > 0. Так как множество А всюду плотно в X, то най-
найдется такой х' ? А, что \\х' — х\\ < -=^-. По условию lim [/„я'
существует; следовательно, последовательность {Z7nz'} фундамен-
фундаментальная, а потому существует такое N, что при п, т>А'
\\Unx'-Um?'\\<±.
Теперь легко находим, что при п, m> N
- || Un (x-x') + Unx' - Umx' + Um (х' -х) || <
<\\Un(x-x')\\ + \\ Unx' - C7mx' \\ + \\Um(x'-x)\\<
< || f/n || || х-х' || +1] Unx' -Umx' |! + || Um || || ж' -ж|| <
Таким образом, последовательность {Unx} тоже фундаменталь-
фундаментальная, а тогда вследствие полноты Y существует lim Unx. Пре-
Предельный оператор U и определяется равенством
Ux = limUnx.
8.6. Пространство линейных операторов
Пусть X и Y — нормированные пространства. Обозначим
через X множество всех линейных операторов, отображающих X
в Y. Два оператора U и V (из X) считаем равными и пишем
U = V, если они совпадают на всем X, т. е. Ux = Vx для всех
х (; X. В этом же смысле мы будем понимать равенство между
операторами и в дальнейшем, когда будут встречаться и не линей-
линейные операторы.
Определим в X алгебраические операции, чтобы превра-
превратить X в линейную систему. Именно, для любых U, V ? X назо-
назовем суммой этих операторов и обозначим через U+V опера-
оператор W, определяемый формулой
8.6] пространство лишенных операторов 217
Аналогично произведением aU для любого оператора U ? X
и вещественного числа а называем оператор W, определяемый
формулой
\\'х --. a (Ux).
Легко видеть, что операторы U + V и a U оказываются линей-
линейными. Так, если W — U-\-V, то аддитивность и ограничен-
ограниченность W вытекает из следующих соотношений:
W (х^х2) = U (х, + х2) + V (х1-'гх2) =
- Ux, + Ux2 + Ух, + Fa:2
| = || Ux + Vx || < || Ux || -f || Vx || <
если же W — aU, то аналогично
W (xt 4- ;r2) "• at' (^j -|- ж2) — a (Uxt) a (Ux2) -- Wx^ -r И7'^;
,:!!"!^!!)^!!. (И)
Совершенно элементарно проверяется, что при введенных
определениях суммы и произведения множество X оказывается
линейной системой. Предоставляем эту проверку читателю.
Заметим лишь, что нулевым элементом в в X будет- «нулевой>>
оператор, определяемый формулой 6а; — 0 при всех х ? JC.
Для каждого оператора U, входящего в линейную систему X,
в 8.3 уже определена норма || U \\. Проверим, что она удовлет-
удовлетворяет трем аксиомам нормы из 5.2.
Действительно, если U = в, то || U || — 0; обратно, если,
|| С/ || — 0, то и || Ux || — 0 при всех х ? X, т. е. U = в. Аксио-
Аксиома II при a =- 0 очевидна. Если же а Ф 0, то, с одной стороны,
из неравенства A1) вытекает, что || a U ||< | a | || U \\; с другой
стороны, заменяя в этом последнем неравенстве U на at/, а a
1 1
на — , имеем || U \\ <.;— || a U \\, или || a U \\ > | a | || U ||. Сопо-
Сопоставляя оба неравенства, получим || aU \\ = | a | || U\\. Наконец,
неравенство треугольника || U + V || < || U || -j- || V \\ вытекает
из неравенства A0). Таким образом, X —¦ нормированное про-
пространство.
Как во всяком нормированном пространстве, в X имеет смысл
сходимость по норме, т. е. мы будем писать, как обычно, Un -*¦ U,
если \\Un — U || —v 0. В отличие от рассматривавшейся в пре-
предыдущем параграфе точечной сходимости последовательности
операторов, сходимость по норме называют также равномерной.
Подчеркиваем, что обозначение Un -*¦ U мы используем только
для сходимости по норме.
218 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
Ясно, что сходимость по норме влечет точечную. Действи-
Действительно, если Un -v U, то при любом х ? X
\\Unx-Ux\\ = \\{Vn-U)x\\<\\Un-U\\\\x\\->0,
и потому Uпх —*¦ Ux. Обратное заключение неверно даже для
функционалов. Пример, подтверждающий это замечание, мы
приведем ниже, в 9.9.
Сходимость по норме Un-+ U влечет также и равномерную
сходимость последовательности {Unx} к Ux на произвольном
ограниченном множестве Е d X. Этим и объясняется название
«равномерная» для сходимости по норме. Действительно, если
|| х ||<С для всех х ? Е, а || Un — U \\ < — при n>N, то из
приведенных выше оценок сразу следует, что || Unx — Ux || < е
при всех х ? Е (и ra>iV). Предлагаем читателю доказать обрат-
обратный результат: если операторы Un — линейные и последователь-
последовательность {Unx} равномерно сходится хотя бы на единичном шаре,
то точечная сходимость к некоторому оператору Unx —>- Ux
имеет место на всем X, предельный оператор U линеен и Un —*¦ U
по норме.
Следующая теорема дает условие, при котором простран-
пространство X оказывается банаховым.
Теорема 8.6.1. Если пространство Y полно, то и про-
пространство X полно.
Доказательство. Возьмем фундаментальную после-
последовательность операторов Un 6 X. Так как при любом х ? X
|| Unx - Umx || = || (Un - Um) х ||< || Ua - Um || || х ||,
•a \\Un — Um || -> 0 при п, т -»- со, то и последовательность
{Unx} фундаментальная. Вследствие полноты пространства Y
существует lim Unx. Кроме того, так как последовательность
{Un} фундаментальна, а всякая фундаментальная последова-
последовательность ограничена, то и последовательность норм || Un \\ огра-
ограничена, а тогда, по лемме 8.5.1, оператор U, определяемый фор-
формулой
Ux— lira Unx,
отображающий X в Y, тоже линейный, т. е. U 6 ?¦
Покажем, что Un-+ U но норме. По произвольно заданному
г >0 можно подобрать N так, что || Un — Um \\ <С е при п,
т > N. Это неравенство означает, что
\\Unx — Umx ||< е || х || при всех х?Х.
Переходя к пределу при то-^-оо, получим
\\Unx-Ux\\<?B\\x\\,
8.7] ОБРАТНЫЕ ОПЕРАТОРЫ 219
откуда следует, что || Un — U || <е при п>]у. Тем самым дока-
доказано, что Un -> С/, а вместе с этим доказана и полнота X.
Введем и операцию умножения (или суперпозиции) операто-
операторов, которую мы уже рассматривали в эвклидовых простран-
пространствах. Если U — оператор, отображающий пространство X
в пространство Y, & V — оператор, отображающий Y в про-
пространство Z, то через VU обозначается оператор, отображаю-
отображающий JC в Z, определяемый формулой
z = V(Ux).
Ясно, что если операторы U и V аддитивны, то и VU аддитивен.
Если же U и V линейны*), то и оператор VU линейный
и при этом
|!. A2)
Действительно, для любого х?Х
\\(VU)x\^-\\V(Ux)\\<\\V\\\\Ux\\<\\V\\\\U\\\\x\\.
Ясно, что операция умножения обладает свойствами ассоциа-
ассоциативности и дистрибутивности:
W (VU) = (WV) U;
Если пространства X и Y совпадают, то операция умножения
двух операторов из X приводит снова к оператору из X. При
этом, как мы уже видели в гл. I, операция умножения не ком-
коммутативна, т. е. может иметь место неравенство VU Ф UV. Опе-
Оператор VU, получаемый в результате умножения, называют произ-
произведением операторов V и U. Если операторы U и V равны между
собой, то их произведение UU обозначают U2. Аналогично опре-
определяют и более высокие «степени» оператора: Un = UU71'1 =
= UU...U. При этом из формулы A2) следует, что
п раз
И г/К И с/||п. A3)
8.7. Обратные операторы
Понятие обратного оператора связано с решением уравнений
вида Ux = у, где U — оператор, отображающий одно простран-
пространство в другое. Если решение оказывается единственным, то,
*) Пространства X, Y, Z предполагаются, конечно, нормированными.
220 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
сопоставляя каждому у, для которого уравнение разрешимо,
соответствующее ему решение х, мы определим некоторый опера-
оператор х = Vy, являющийся обратным по отношению к операто-
оператору U. Дадим точное определение.
Определение. Пусть у = Ux — оператор, заданный
в пространстве X, со значениями в пространстве Y, и пусть
Y\ = U (X) — совокупность его значений. Если каждому у ? Y \
соответствует только один х ? X, для которого Ux = у *), то
этим соответствием определяется оператор, заданный на мно-
множестве Y\ с областью значений X. Этот оператор называется
обратным для оператора U и обозначается С/.
Таким образом, для любого х 6 X
Если через / обозначить тождественный оператор в простран-
пространстве X, т. е. 1х — х для всех х ? X, то предыдущее соотношение
можно записать с помощью операции суперпозиции в виде
U~lU = /. Однако оператор f/ задан только на Yt; поэтому
если V — оператор, заданный на всем Г и отображающий Y
в X, и при этом VU = I, то отсюда не следует, что непременно V
совпадает с С/. Именно, если Yt ф Y то область определения
оператора V шире, чем область определения U'1.
Теорема 8.7.1. Если область значений Y\ оператора U
совпадает со всем пространством Y, а оператор V отображает Y
в X и при этом VU — /, то V = U'1.
Доказательство. Так как Yt = Y, то уравнение
Ux = у имеет решение при всяком у ? Y. Это решение легко
выразить через у, а именно:
х = Ix = (VU) х = V (Ux) = Vy.
Отсюда и вытекает, что вследствие однозначности оператора V
решение единственно и что U~l = V.
Изложенное до сих пор в этом параграфе имеет смысл в про-
произвольных метрических пространствах (и даже в множествах
без метрики). Теперь же будем считать X и Y нормированными
пространствами и установим сначала несколько простых пред-
предложений **).
а) Если оператор U аддитивен и однороден, то Yt = U (X) —
линейное множество.
Действительно, если уи у2 6 Yu то yt = Uxu y2 = Uxz, где
хи х2 6 X. Но тогда и yt + у2 = U (xt + х2) тоже входит в Yi.
*) В этом случае говорят, что оператор U устанавливает взаимно-одно-
взаимно-однозначное отображение пространства X на множество У4.
**) Предложения а) — г), в которых не используется понятие непрерыв-
непрерывности, верны, очевидно, и в любых линейных системах.
8.7] ОБРАТНЫЕ ОПЕРАТОРЫ 221
Так же, если у ? Yu т. е. у — Ux для некоторого а; ? X, то и ш/ =
= ^7 (ах) 6 F,.
б) /?слм оператор U аддитивен и однороден и существует
обратный оператор U~x, то он тоже аддитивен и однороден.
Действительно, пусть у,, уг 6 F,, xt = t/^,, х2 = U~1y2.
Тогда f/a:i = г/ь ?Лг2 = г/г и U (xt + xz) ---- yt + г/2. Но послед-
последнее и означает, что i, I i2 = U~* (yf + г/2), т. е. оператор С/
аддитивен. Аналогично доказывается, что если //? Fj и ж—'
~U~ly, то ах = t/ (аг/) при любом а.
в) Для того чтобы аддитивный оператор U имел обратный,
необходимо и достаточно, чтобы Ux = 6 только при х = 6.
Действительно, если Ux = 6 только при ж = 0, то имеем
# (^ — х2) Ф 6 при #! =jt x2, a тогда Uxr ф Ux2. Следовательно,
уравнение Ux — у имеет единственное решение при каждом
у 6 Y\. Обратно, если U~l существует, то уравнение Ux = 9
должно иметь только одно решение, которым и будет х — 6.
г) Если пространство X содержит элементы, отличные от 6,
а оператор U (не обязательно — аддитивный) имеет обратный,
то U~l не может совпасть с нулевым оператором 6.
Действительно, если х0 ф 6 и у0 = Ux0, то для обратного
оператора U~1y0 = х0.
Сопоставляя все сказанное, мы заключаем, что если U —
линейный оператор, отображающий нормированное простран-
пространство X в нормированное пространство У, то для существования
обратного оператора U~l необходимо и достаточно, чтобы равен-
равенство Ux = 9 выполнялось только при х = 9; при этом обрат-
обратный оператор оказывается аддитивным и однородным, отличным
от нулевого (если пространство X не состоит из одного элемен-
элемента 9), но может не быть линейным. В связи с этим представляет
интерес следующая теорема, справедливая в любых нормирован-
нормированных пространствах.
Теорема 8.7.2. Для того чтобы обратный оператор U'1
существовал и был линейным (как оператор в пространстве F4),
необходимо и достаточно, чтобы существовала такая постоянная
т > 0, что для всех х ? X .
\\Ux\\>m\\x\\. A4)
При этом || f/ || ¦-'. •—*).
Доказательство. Если оператор х = U~xy линейный,
то || х || < || г/ || || у |!, где y = Ux. При этом \\и~х\\ф0
(если бы пространство Л' состояло только из нулевого элемента,
*) В этой теореме U может быть любым аддитивным и однородным опе-
оператором.
222 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VI11
j
то теорема была бы тривиальной). Полагая т = . д, , мы
получим неравенство A4).
Обратно, если A4) выполнено, то из Ux = 9 следует, что
и х = 6, а тогда обратный оператор U~i существует. Полагая
у — Ux (тогда х — U~1y), мы получаем из A4) || и~лу || --.;
¦<—II У 11> следовательно, оператор U'1 линеен и || С/ ||<— .
В случае, когда пространства X и Гбанаховы, можно
доказать, что если линейный оператор у — Ux устанавливает
взаимно-однозначное отображение пространства X на все.
пространство Y, то обратный оператор U~x непременно линейный.
Определение. Линейный оператор U, отображающий
X в ? (X и Y — любые нормированные пространства), назы-
называется обратимым, если область его значений F4 = Y (т. е.
он отображает X н а ?) и существует линейный обратный
оператор U'1.
Укажем некоторые признаки обратимости линейных опера-
операторов в банаховых пространствах. При этом линейность обрат-
обратного оператора мы будем проверять непосредственно, не ссылаясь
на сделанное выше общее замечание.
Теорема 8.7.3. Если U — линейный оператор, отобра-
отображающий банахово пространство X в самого себя, с нормой \\ U || <С
< 1, а/ — тождественный оператор, заданный в пространстве X,
то оператор I — U обратим. Если при этом число q таково, что
i
T
Доказательство. Пусть || U || < 1. Возьмем любое
число q, удовлетворяющее неравенству || U ||< q <C 1. Тогда
для каждого х 6 X
\\{I-U)x\\--\\Ix-Ux\\ = \\x-Ux\\>
Следовательно, по теореме 8.7.2, обратный оператор (/ — U) l
существует и линеен, а || (/ — U)'11| < j^r.
Остается доказать, что совокупность значений оператора
/ — U совпадает с X. Для этого возьмем любой у 6 X и составим
оператор Vx = Ux -\- у (если у ф 6, то оператор V — нелиней-
нелинейный). Тогда для любых х', х" ? X
|| ух' - Vx" || = || Ux' - Ux" || =.-1| U (x' - x") |j < q || x' - x" \\,
следовательно, V — оператор сжатия. По теореме Банаха D.4.1)
оператор V имеет единственную неподвижную точку, т. е.
8.7] ОБРАТНЫЕ ОПЕРАТОРЫ 223.
существует х ? X, для которого х = Ux + У или
(I-U)x = y. A5)
Таким образом, произвольно взятый у ? X входит в совокуп-
совокупность значений оператора / — U. Теорема доказана.
Та же теорема Банаха гарантирует, что решение уравне-
уравнения A5), т. е. неподвижная точка оператора V, может быть най-
найдено методом последовательных приближений. Примем за началь-
начальное приближение х0 = у. Тогда
Полученные последовательные приближения суть частичные сум-
мы ряда 2 U"y *)¦ Из сходимости метода последовательных
п=0
приближений вытекает, что последовательность частичных сумм
этого ряда сходится к решению уравнения A5), т. е. сам ряд.
сходится и
A-и)-*у=%ипу. A6)
п=0
Предлагаем читателю непосредственными оценками проверить
абсолютную сходимость ряда A6) (учитывая, что \\Un\\<qn)
и подстановкой в уравнение A5) (не опираясь на метод после-
последовательных приближений) доказать, что сумма ряда есть
(/ - иу* у.
Теорема 8.7.4. Пусть линейный оператор U отображает
банахово пространство X (содержащее элементы х Ф 0) на бана-
банахово пространство Y и обратим. Тогда каждый линейный опе-
оператор V, отображающий X в. Y и удовлетворяющий условию
|| У — U || < . , тоже обратим. Если при этом число q
таково, что \\ V — U || || U'1 ||<дг<1,то|| ^ЧКг^- || С/!!**)-
1 —q
Доказательство. Возьмем оператор V, удовлетво-
удовлетворяющий указанному условию, и положим W = U — V. Если
*) Мы считаем 17° = /.
**) Если Y = X, а за U принять оператор /, то из этой теоремы как
частный случай получится теорема 8.7.3.
224 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
д таково, что || V -U\\\\ U^ || < <? < 1, то || W || < р^ .
К обеим частям равенства W — U — V применим оператор U'1.
Получим
где все три оператора U'1W, I и U'lV отображают X в X. При
этом из неравенства A2) следует, что || U~lW || < q. Тогда к опе-
оператору U~1V = / — U'1W применима теорема 8.7.3, т. е. суще-
существует линейный оператор Т — (U~1V)~1, определенный на всем
X, с нормой || Г||< ~.
Так как оператор U'1 устанавливает взаимно-однозначное
соответствие между элементами пространств Г и I, а совокуп-
совокупность значений оператора U~lV благодаря его обратимости есть
всё Л', то совокупность значений оператора V должна совпадать
с Y *). Введем линейный оператор S в пространстве Y со зна-
значениями в X, полагая S = TU~l. Тогда
SV = TU~W = (U^V)'1 (U'^V) =-¦ /
и по теореме 8.7.1 S = V'1. Тем самым доказана обратимость
оператора V. При этом
В гл. XII будет указано, каково значение последней тео-
теоремы для приближенных вычислений.
8.8. Матричные линейные операторы
Для многих приложений важную роль играют операторы,
задаваемые в пространствах числовых последовательностей посред-
посредством бесконечных матриц. Мы уже встречались с такими опера-
операторами в пространстве I2 B.7).
Итак, рассмотрим оператор у = Ux, сопоставляющий число-
числовой последовательности х = {х^} числовую последовательность
У ~ {Vi}- определяемый с помощью матрицы («;&);,й=1,2,. бес-
бесконечной системой равенств
?о
г/^ЕягЛ (г = 1,2, ...); A7)
ft=i
*) Если допустить, что некоторый г/0 6 Y не входит в совокупность
значений оператора V, то, полагая х0 = U~ly0, мы получим, что х0 по входит
в совокупность значений оператора ?"-' V, что невозможно.
Й.8] МАТРИЧНЫЕ ЛИНЕЙНЫЕ ОПЕРАТОРЫ 225
развернутая запись:
Уг = «2.^1 + «22^2 + • • • -Г a2kXk -f- • • • .
уi -— U-i[jC[ ^( 2 Г~ • • • т ^ih^k ~ ¦ • * ?
Такой оператор U мы и будем называть матричным. Область
задания этого оператора может содержать лишь те последова-
оо
тельности х — {xh}, для которых ряд 2 ага^а сходится при любом
i: = 1, 2, ... В дальнейшем нас часто будет интересовать слу-
случай, когда область задания матричного оператора U есть одно
из пространств т, I, I2. Значения оператора U всегда можно
считать элементами пространства s, но при определенных усло-
условиях они также могут попасть в одно из перечисленных выше
пространств.
Пусть JSC — любое пространство, элементами которого служат
числовые последовательности и в котором алгебраические опера-
операции определены так же, как bs (например, 8, т, 1,1г); матричный
оператор U, заданный в таком пространстве X. и отображающий
его в одно из таких же пространств, очевидно, всегда аддитивен
и однороден. Однако, для того чтобы он оказался непрерывным,
могут потребоваться некоторые дополнительные условия. Так,
оо
в 2.7 мы видели, что если 2 «1а < + °°, то оператор, определяе-
определяемый формулами A7), является линейным оператором, отобра-
отображающим 1г в 1г.
В 2.7 было также доказано, что любой линейный оператор,
отображающий I2 в 1г, представим в матричной форме A7). При
этом из свойства ограниченности линейного оператора вытекает
наличие такой постоянной С, что || у ||2 < С || х ||2, т. е.
оо оо оо
Ъ \ 2л O-ihXk) <C 2j xh
при любом х 6 I2- Ясно, что это последнее неравенство является
условием, необходимым и достаточным для того, чтобы матрич-
матричный оператор, заданный в I2 формулами A7), отображал 1г в 1г
и был линейным.
Приведем еще один пример. Пусть
2 <4<М A = 1,2,...). A8)
15 Б. 3. Вулих
226 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
оо
Тогда при любом x^V- все ряды 2 o-ikxh сходятся и при этом,
по неравенству Коши,
\У;
2 aikxh\<\/ S41/S xl-CVM\\x\.
Следовательно, у?т и из предыдущего неравенства получаем
| = sup|z/, |
Таким образом, матричный оператор U при условии A8) оказы-
оказывается линейным оператором, отображающим I2 в ж, и при этом
\\и\\< ум.
Другие примеры встретятся ниже.
8.9. Бесконечные системы линейных алгебраических
уравнений
В 4.4 мы рассматривали вопрос о решении конечной системы
линейных алгебраических уравнений и привели там достаточное
условие для разрешимости такой системы, полученное с помощью
метрики эвклидова пространства. Заметим, что тем же методом,
но используя другие возможные способы метризации или норми-
нормировки конечно-мерного пространства, можно получить и более
широкие условия разрешимости рассматривавшейся системы
уравнений. Сейчас же мы перейдем к рассмотрению бесконечных
систем линейных алгебраических уравнений с бесконечным мно-
множеством неизвестных.
Рассмотрим следующую систему уравнений:
1 OihXk-^bi (i = l. 2, ...). A9)
ft=i
Решением такой системы называется всякая последователь-
последовательность чисел {#*}, при подстановке которых в уравнения
системы A9) все ряды У\ aikxh оказываются сходящимися, а и.\
й1
суммы совпадают со свободными членами bt. Решение {х^} назы-
называется ограниченным, если числа xh образуют ограниченную
последовательность.
Проделав то же преобразование, что в 4.4, мы можем привести
систему A9) к виду
xi-^1elkxk = bl (i-1,2, ...) B0)
ft=i
(где с(ft = — aih + 6jft).
8.9] БЕСКОНЕЧНЫЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ 227
Укажем один класс систем B0), для которых можно с помощью
теоремы 8.7.3 дать простое условие их разрешимости.
Определение. Система B0) называется вполне регуляр-
регулярной, если существует такая положительная постоянная q < 1,
что лри всех i = l, 2, ...
Считая систему B0) вполне регулярной, определим с помощью
матрицы (см) матричный оператор y — Ux в пространстве т:
оо
y;=ljclhxh A=1,2,...)-
Тогда для любого х?т также и у?т и оператор U линеен.
Действительно, лри всяком i
Таким образом, последовательность {г/;} ограничена, т. е. у ? т, и
Тем самым установлена линейность оператора U и при этом
|!#||<?<1.
Будем считать, что свободные члены системы B0) в совокуп-
совокупности ограничены. Обозначим через / тождественный оператор
в пространстве т, а через Ь — элемент пространства т, опре-
определяемый свободными членами, b — {bt}. Тогда мы можем запи-
записать систему B0) в сжатом виде
(I~U)x=b.
Если искать только ограниченные решения системы B0), то ее
разрешимость при любых свободных членах (ограниченных
в совокупности) и единственность решения будут обеспечены,
если оператор / — U обратим. А так как \\ U || < 1, то приме-
применима теорема 8.7.3 и, следовательно, оператор / — U, действи-
действительно, обратим и при этом || (/ — U)'1 || <;г^. Таким образом,
получается следующая теорема:
Теорема 8.9.1. Вполне регулярная система B0) имеет
единственное ограниченное решение {xt} при любой ограниченной
совокупности свободных членов. При этом если | Ьг | <;2? при
всех i = l,2,..., то
Ы<т^г <*=-!, 2. ...)•
228 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
Решение, существование которого уже установлено, можно
получить из формулы A6) для обратного оператора, а именно
х=(/-С/)-16= 2 Unb. B1)
п=0
Вычисление по этой формуле равносильно применению метода
последовательных приближений к нашему уравнению, запи-
записанному в форме
, B2)
если за начальное приближение принять х0 = Ъ. Из теоремы
Банаха вытекает, что метод последовательных приближений
применим к уравнению B2) и при любом начальном приближе-
приближении х0 ? т.
Заметим, что если отказаться от требования, чтобы решение
системы B0) было ограниченным, то единственность решения
вполне регулярной системы уже не будет иметь места. Например,
система
очевидно, вполне регулярна ( за q можно принять -5- J , все сво-
свободные члены равны нулю, но она имеет бесконечное множество
решений: нулевое (xt = х2 = . . . = xt = . . . =0), которое
является ограниченным, и неограниченные решения вида xt =
= Х2\ где Я, — любое число, отличное от нуля.
Вернемся теперь к конечным системам
*4= S cihxk+bt (f=l,2, ...,n). B3)
Такую систему можно свести к бесконечной системе B0), если
принять;' что c~ih = 0, когда хоть один.из индексов г или к боль-
больше п, и bt ¦= 0 при i >• п. При этом все уравнения, начиная
ё (п + 1)-го, сводятся к равенствам xn+i = 0, жге+2 = 0, . . .
Таким образом, всякое решение построенной бесконечной
системы может содержать лишь конечное число неизвестных,
отличных от нуля, а потому будет ограниченным. Свободные
8.10] НЕКОТОРЫЕ ИНТЕГРАЛЬНЫЕ ОПЕРАТОРЫ 229
члены по той же причине образуют ограниченную последова-
последовательность. Условие вполне регулярности построенной бесконеч-
бесконечной системы сводится к неравенствам
п
2 \cik\<q<:l (S=l, 2, ..:, п).
Поскольку,это условие должно быть выполнено лишь для конеч-
конечного числа сумм, то оно может быть записано" в более простой
форме:
2 |с/й|<1 (i = l,2, ..., п) B4)
(так как при выполнении последнего условия за q можно при-
п
нять наибольшую из сумм 2j|cift|)- Следовательно, при усло-
й=1
вии B4) для системы B3) справедлив результат теоремы 8.9.1;
а так как неограниченные решения в нашем случае невозможны,
то получается, что при выполнении условия B4) система B3)
имеет единственное решение при любых свободных членах. Усло-
Условие B4) менее тяжелое, чем то условие F), которое было при-
приведено в 4.4.
8.10. Некоторые интегральные операторы
Среди простейших примеров линейных операторов, приведенных в 8.3,
мы уже встречались с интегральным оператором, преобразующим простран-
пространство С в самого себя. В этом параграфе мы рассмотрим интегральные опера-
операторы, задаваемые той же формулой, но при гораздо более слабых ограниче-
ограничениях, накладываемых нэ ядро.
Именно, будем предполагать, что функция К (s, t) измерима в квадрате
я <; s. (<^ii и для некоторого р > 1 удовлетворяет условию
ь
\ \K(s, t)\Vds^M при почти всех t B5)
а
(М — постоянная). Покажем, что при выполнении этого условия формула
ь
!/(s)=^ K(s,t)x(t)dt B6)
определяет линейный оператор, переводящий ? в U>. В частности, это верно
для интегрального оператора, у которого ядро — непрерывная или хотя
бы ограниченная почти всюду (в квадрате) измеримая функция.
Проверим, что для любого х 6 L при выполнении условия B5) функция
у (s), определяемая формулой B6), принадлежит LP. При этом нам придется
воспользоваться так называемым неравенством Гельдера, устанавливаемым
230 ЛИНЕЙНЫЕ ОПЕРАТОРЫ [ГЛ. VIII
в теории интеграла *). Именно, если <р ? Lp, а ф 6 Lq, причем р и q связана
соотношением
1 + 1=1, B7)
Р П Я
то произведение (рф суммируемо и при этом
± ь ±
Из B7) следует, что g = ¦ ¦ > 1. В частности, еслир = 2, то я g =2,
и неравенство Гельдера превращается в неравенство Буняковского.
Используя неравенство Гельдера, проводим при почти всех s следующую
оценку:
ь
\K(s,t)\[x(t)\dt =
a
Ь J b
a:(*, о lp 1 * (*) I *
a a
Ь J
Возводя обе части полученного неравенства в степень с показателем р,
а затем интегрируя почленно по s и изменяя при этом порядок интегрирова-
интегрирования в правой части **), мы получим:
ь _р_ . , р
x(t)\dt\ | К (s, t)\P ds || х || q < М || х || ч .
С помощью B7) легко по дочитывается, что 1 + — = р, следовательно,
*) О. Л. Гельде р A859—1937)— немецкий математик. Вывод неравен-
неравенства Гельдера см., например, в книге: Б. 3. В у л и х , Краткий курс теории
функций вещественной переменной, стр. 259—260.
**) Это делается на основании теоремы Фубини из теории интеграла
S.ilJ ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ 231
Тем самым доказано, что у ? М>. При этом для нормы элемента у в простран-
пространстве LP мы нашли оценку
j_
\\У\[<МР \\x\\.
Следовательно, оператор B6) ограничен, а вместе с тем и линеен.
Заметим, что доказанный результат верен и при р = 1, только прове-
проведенное нами рассуждение в этом случае значительно упрощается.
Рассмотрим теперь ядро специального вида
где А (», t) — функция, непрерывная в квадрате а <^ s, *-- Ь. Такого типа
ядра часто встречаются в математической физике и их называют ядрами
типа потенциала. Будем считать, что 0 < Я < 1. Покажем, что если р > 1
таково, что Хр < 1, то ядро B8) удовлетворяет условию B5).
Действительно, функция A (s, t), будучи непрерывной, ограничена на
всем квадрате: | A (s, t) | < С, а тогда
ь ь
Справа стоит сходящийся интеграл (так как показатель кр < 1), т. е. подын-
подынтегральная функция суммируема. Производя подстановку s— t = и,
получим
ь ь-t
ds ? du
J \s-t\x* i
a-t ' '
Отрезок [я —г, 6 — t] содержится в отрезке [ — 1, I], где I =Ь — а, не зави-
сящем от t, и мы получаем окончательную оценку:
Таким образом, условие B5) для ядра B8) выполнено.
Отметим, что весьма подробное исследование интегральных операторон
проведено в уже цитированной книге Л. В. Канторовича и Г. П. Акилова *).
8.11. Линейные дифференциальные операторы
в пространстве дифференцируемых функций
Рассмотрим множество Ci всех непрерывных функций х (t),
заданных на отрезке a^t<Cb и имеющих непрерывные про-
производные до 1-го порядка включительно, где I — заданное нату-
*) См. также недавно вышедшую книгу: М. А. Красносель-
Красносельский, П. П. 3 а б р е й к о, Е. И. П у с т ы л ь н и к и П. Е. С о б о-
.1 е в с к п и, Интегральные операторы в пространствах суммируемых функ-
функций, «Наука», 1966
232 ЛИНЕЙНЫЕ ОПЕРАТОРЫ • [ГЛ. VIII
ральное число. Ct является подмножеством пространства С всех
непрерывных функций, заданных на отрезке [а, Ь]. Ясно, что
С/. — линейное подмножество. При этом Сг всюду плотно в С,
так как в Ci входят все алгебраические полиномы, а полиномы
уже образуют в С всюду плотное множество. Однако если поль-
пользоваться в Ci той нормой, которая определена во всем С, то схо-
сходимость по норме будет означать лишь равномерную сходимость
последовательности самих функций, но ничего не будет давать
в отношении сходимости последовательности производных. Между
тем в некоторых задачах из области дифференциальных урав-
уравнений, например при приближенном решении последних, пред-
представляет интерес такая сходимость, которая означает не только
равномерную сходимость последовательности самих функций,
но и равномерную сходимость последовательностей некоторых
их производных. Такую сходимость можно представить как схо-
сходимость по норме, если Сг рассмотреть как самостоятельное
нормированное пространство с нормой, отличной от нормы в (\
Итак, определим норму в Ci по формуле
(здесь х<°) (t) = x(t)]. Легко проверить, что все аксиомы нормы
выполнены. Например, аксиома треугольника проверяется так.
Если х, у? Ci, то при любом к —0, 1, . . ., I
< max | ?<*> (t) | + max | y<ft> (t) \,
а тогда и
max\x^(t) + y(h>(t) |<max | x^ (t) \ + max \i/h> (t) \.
Следовательно,
|| x -f у || ¦--= 2 max \x <*> (t) + ylV (t) \ <
ft 0
max | @Ц S
h=0
Ясно, что в С/ сходимость по норме хп—>х означает, что
равномерно при ^ = 0, 1, ..., I.
Проверим, что пространство Ct банахово. Пусть последова-
последовательность элементов хп ? Ci фундаментальная. Так как при всяком
/г = 0, 1, ..., I
8.1 I ] ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ 233
то все последовательности {х^ (t)} равномерно сходятся к неко-
некоторым непрерывным предельным функциям q)fe (t) (к = 0, 1, ...
. . ., /). В математическом анализе доказывается, что если функ-
функции / n(t) имеют на некотором отрезке непрерывные производные
1-го порядка и если /„ (t) -> / (t), a f'n (t) -*- g (t) равномерно, то-
g (t) = /' (t) *). На основании этой теоремы
Ф, (t) = lim х'п (I)- -^- [ lim xn (t)] - ц>0A),
Фг (t) = lim 4° (/) - ¦¦-^¦ЩтхЦ-^(t)\ = Ф|_! (О ^ ф<0О (О-
Следовательно, ф0 € Ci и хп -*¦ ф0 по норме в пространстве Си
Приведем пример линейного оператора в пространстве Сг Рассмотрим
линейное дифференциальное уравнение J-го порядка:
а0 (г) х (I) -f Ч @ x'{t)+...+ai @ х<1> (I) = /(«), B9>
в котором все коэффициенты и свободный член предполагаются непрерыв-
непрерывными на отрезке [а, 6]. Левая часть уравнения определяет некоторый опера-
оператор L, имеющий смысл, во всяком случае, для любой функции х 6 Ct. Значе-
Значения оператора L суть функции из С, а само уравнение B9) может быть запи-
записано в форме
Lx = f
(где мы рассматриваем только x?Ci**)).
Проверим, что оператор L —линейный. Его аддитивность очевидна.
Чтобы доказать его ограниченность, положим М&=тах | ад, (*) | D=0, \, ..., 1)г
a M = max (Mo, Mt, ..., Mi). Тогда, если у — Lx, to
I I
fc=O
2
ft=0
откуда
*) См., например, В. И. Смирнов, Курс высшей математики, т. 1,
IV 145.
**) Если ai (I) Ф О, то, как легко ввдеть, всякая функция x(t), удовле-
удовлетворяющая уравнению B9), входит в С,.
ГЛАВА IX
ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
9.1. Линейный функционал как частный случай
линейного оператора
В этой главе, как и почти во всей книге, мы ограничиваемся
рассмотрением функционалов с вещественными значениями.
Некоторые замечания о комплексных функционалах будут сде-
сделаны в последнем параграфе главы. Как уже отмечалось в гл. VIII,
для функционалов / (х), заданных в произвольном нормирован-
нормированном пространстве X, имеют смысл определения аддитивности,
однородности, линейности. Так как множество вещественных
чисел _К4, в котором за норму принята абсолютная величина
числа, представляет нормированное пространство, то линейный
функционал в пространстве X представляет частный случай
линейного оператора, отображающего X в какое-то нормирован-
нормированное пространство Y.
Все общие теоремы, доказанные в предыдущей главе для
линейных операторов, верны и для линейных функционалов.
В настоящей главе мы рассмотрим некоторые специфические
вопросы, решение которых для функционалов оказывается зна-
значительно более простым, чем для произвольных линейных опе-
операторов.
Предварительно остановимся на формуле F) из гл. VIII для
нормы линейного оператора. Применительно к линейному функ-
функционалу / она может быть записана так:
Ц/11 =)(supj/(z)|. A)
Покажем, что для функционалов справедливо и следующее соот-
соотношение :
II/II- sup j{x) B)
(здесь в правой части отсутствует знак абсолютной величины).
=9.2 ОБЩИЕ ФОРМЫ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 235
Действительно, так как всегда f (х) <С \ f {x) |i то
sup f{x)< sup
11*11 Sl ||!!1
С другой стороны, согласно формуле A), по любому е>0
можно подобрать такой х из единичного шара, что
Но если ||а;0||<1, то и || —#0||<1, а одно из значений f(x0)
и f( — x0) совпадает с |/(а;0)|. Поэтому в единичном шаре суще-
-ствует такой элемент х (эго будет один из элементов х0
или — х0), что
Отсюда уже следует, что
sup /(
11111
а вследствие произвольности е
Из двух противоположных неравенств вытекает формула B).
В некоторых случаях формула B) оказывается более удобной,
чем формула A).
9.2. Общие формы линейных функционалов
в некоторых пространствах
Для линейных функционалов во многих пространствах доволь-
довольно просто решается следующая важная задача: найти общее
выражение линейных функционалов в заданном пространстве.
В 1.9 мы уже решили такую задачу в Вп. Именно, мы показали,
что если с — фиксированный элемент из Нп, то скалярное про-
произведение (х, с) представляет линейный функционал в Rn и,
обратно, для любого линейного функционала / (х) в Нп суще-
существует такой элемент с ? Нп и притом единственный, что / (х) =
= (х, с). При этом || / || = || с \\. Таким образом, формулой
п
/(Я) =2 Ct?h (?={ift}ft=l,!>,...,n),
где числа clf c2, . . . , сп могут быть любыми, и дается общее
выражение линейных функционалов в Ип *). Напомним, что в гл. 1
*) В частности, общий вид линейных функционалов в Rir т. е. аддитив-
аддитивных и непрерывных функций вещественной переменной, дается формулой
/ (аг) = сх. Этот результат был установлен еще Кошп.
236 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
A.5) мы также установили и общий вид линейных операторов,
отображающих Rn в /?„. Однако в бесконечно-мерных простран-
пространствах получение общих форм линейных операторов оказывается
значительно более сложной задачей и потому мы ограничимся
сейчас отысканием в таких пространствах общих форм линейных
функционалов.
В 2.6 была найдена общая форма линейного функционала
в ?2, также в виде скалярного произведения: / (х) = (х, с), при-
причем, как и в Вп, ||/ || = || с ||, а элемент с определяется един-
единственным образом. Иными словами, общий вид линейных функ-
функционалов в Р дается формулой
где x = {\h}, а числа ch должны удовлетворять условию V с"к'
<-j-oo. При этом ||/1| =
Если Н — произвольное бесконечно-мерное, сеп арабе льнов-
гильбертово пространство, то, как мы знаем из 6.9, оно изоморфно
пространству I2, причем изоморфизм может быть установлен
с сохранением нормы и скалярного произведения. Тогда каждый
линейный функционал в Н может быть интерпретирован как
линейный функционал (с той же нормой) в I2 и доказанная общая
форма линейных функционалов в I2 тем самым переносится
и в Н. Таким образом, формула
f(x) = (z, с)
дает общий вид линейных функционалов в И, причем || / || =
= || с ||. Этот результат может быть установлен и непосредствен-
непосредственно, без использования координатной реализации пространства Н
и без предположения о его сепарабельности *).
Напомним еще раз, что элемент с из пространства Н по задан-
заданному функционалу / определяется единственным образом, и пока-
покажем, как это можно установить, опираясь на общую аксиоматику
гильбертова пространства. Пусть / (х) = (х, с) = (х, с4) при всех
х, где с, Ci 6 Н. Тогда (а;, с ~ ct) ~ 0. Полагая, в частности,
х — с — сА, имеем (с — Cj, с — с,) = 0, следовательно, с — с, =
9, т. е. с = с(.
) Для пространства Ьг, представляющего функциональную реализацию
•ранства Н, общий вид линейных функционалов был установлен в 1907 г.
реше и Ф. Риссоы.
пространства .., .. . _
М. Фреше и Ф. Риссоы.
Э.2] ОБЩИЕ ФОРМЫ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 237
Перейдем к пространству 7. В I совокупность координатных
ортов eh образует базис. При этом каждый х = {?ft} ? I имеет
оо
вид х — 2 \i&h- Пусть / — линейный функционал в I. Положим
ft=i
cft = / (ek). Тогда по дистрибутивности линейного функционала,
имеющей место и для бесконечных рядов (см. 8.2),
При этом | cft |<||/|| ||еА||= || / |j, следовательно, числа eh обра-
образуют ограниченную последовательность и
sup|cft|<||/||. C)
Обратно, пусть задана произвольная ограниченная последо-
вательность чисел сА. Тогда для любого я = {?а}?? ряд ^ c^h
абсолютно сходится, и если в I определить функционал
то для него получится следующая оценка:
Таким образом, функционал D) имеет смысл для всех х?1
и ограничен. Аддитивность его очевидна, следовательно, он
линеен и
i<sup|Cft|. E)
Итак, формула D) при условии, что последовательность {сА}
ограничена, дает общий вид линейного функционала в I. Сопо-
Сопоставляя неравенства C) и E), мы заключаем, что
||/|| = eup|cft|.
Заметим, что в пространстве т, где координатные орты не
образуют базиса, общая форма линейного функционала оказы-
оказывается значительно более сложной. Легко видеть (см. также
оо
9.11), что если 2j I са | < ~Ь °°i to ряд D) представляет линей-
ный функционал в т; однако не всякий линейный функционал
в т представим в форме ряда D).
238 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
9.3. Линейные функционалы в пространствах
суммируемых функций
Применяя к пространству i2 сказанное в предыдущем парагра-
параграфе по поводу функционалов в гильбертовом пространстве, мы.
сразу увидим, что общий вид линейных функционалов в про-
пространстве L2 (на промежутке [а, Ь]) дается формулой
где у (t) —любая функция из ?2*), При этом
V
\ У2 (О
Далее мы увидим, что та же формула F) дает общий вид линей-
линейных функционалов и в любом из пространств Ъу (р>1), только»
в зависимости от р будут меняться условия, накладываемые на
функции у (t).
1°. Сначала будем рассматривать случай, когда р > 1. Суще-
Существенную роль в последующем будет играть неравенство Гель-
дера, уже использованное в 8.10. Именно, если ф ? Lp, г|) ? X''
и р и q связаны соотношением
то произведение фгр ? L и
Ь Ь
В пределах этого параграфа q все время будет обозначать число,
связанное с р равенством G). Иногда в этом случае q называют
показателем, сопряженным с р.
Из неравенства Гельдера выводится и тот факт, что если
1 О < s, то Ls cr Хг (это отмечалось в 3.2). Действительно,
положим р ¦— — . Тогда q = —— . Если х 6 Xs, то функция I a: (t)\
Р S — 7*
входит в ip **). Положим
ф @ = 1 *(*)!', *@ = i-
r
*) Варьируя фуш<цию у (t), мы будем получать различные функцио-
функционалы /.
**) (I х (t)\r)p = | х (t) |s, а последняя функция суммируема, поскольку
х 6 Ls
9.3] ФУНКЦИОНАЛЫ В ПРОСТРАНСТВАХ СУММИРУЕМЫХ ФУНКЦИЙ 239
Тогда 1|з 6 Ln, следовательно, произведение фгр, совпадающее
с | х (t) i7', суммируемо, т. е. функция х ? L1'. Таким образом,
?ч сз 1/.
Кроме самого включения, из неравенства Гельдера следует, что
Ь Ь 1 Ь J
s — r b
-(b-a)~
Отсюда, возводя обе части в степень с показателем—, полу-
получаем, что
Таким образом, если в пространстве Xs (с большим индексом)
рассмотреть две нормы — его основную ||х||?< и индуцированную
из I/, то первая будет мажорировать вторую (ср. 8.3).. Следова-
Следовательно, из сходимости в L* по его норме вытекает сходимость
по норме, индуцированной из Lr **).
Из неравенства Гельдера сразу следует, что функционал /,
определенный в пространстве Lp по формуле F) (такой функ-
функционал, очевидно, аддитивен) при любой функции у ? Lq будет
линейным, причем
Ь 1
\y{t)\4dt
т. е.
ь _i_
(9)
Заметим, что если две функции у, z ? Lq не эквивалентны,
то определяемые ими функционалы различны. Действительно,
пусть ел н е2 — множества тех точек, где y(t)>z(t) и
<.z{t) соответственно. Положим
( 1, если t?e\,
х (t) — \ —1, если t?e2,
I 0 в остальных точках.
*) Индекс при норме обозначает то пространство, в котором вычисляет-
вычисляется эта норма.
**) В частности, в пространстве L2 из сходимости в среднем 2-го порядка
вытекает сходимость в среднем 1-го порядка.
240 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
Тогда
6 b
x(t)y(t)dt— f х (t) z (t) dt-^
z(t)[y(t)-z(t))dt~
поскольку по крайней мере одно из множеств et или ег имеет
меру, большую 0. Таким образом, существует х? L1', для которого
ь ь
J x(t)y(t)dl^^ xA)z{t)dt.
а а
Ф. Рисе доказал в 1910 г., что формула F) при у ? L4 и дает
общий вид линейных функционалов в Lp, причем
ь _i
\y(l)\*dtj. A0)
а
Чтобы несколько упростить доказательство, мы ограничимся
значениями р < 2, т. е. будем дальше считать, что 1 < р < 2,
однако сформулированный сейчас результат верен при любом
Пусть / — произвольный линейный функционал, заданный
на L'1. Так как по сделанному выше замечанию ?2 ег L1', функ-
функционал / можно рассматривать и на ?2. Благодаря отмеченному
ранее соотношению между нормами в L2 и L" функционал / будет
также линейным и на L2, если это пространство рассматривать
с его обычной нормой. Но тогда существует такая функция
у 6 -Ь2, что для всех х ? L2 функционал / (а;) представим по фор-
формуле F). Нужно показать, что эта формула справедлива и на
всем Lv и что у ? Lq **).
Сначала проверим последнее включение. При этом естественно
ограничиться предположением, что у (f) не эквивалентна 0.
Введем обозначение, используемое здесь и в дальнейшем: для
произвольного вещественного числа а полагаем
( 1, если а > 0,
signa--{ — 1, если а < 0,
I 0, если а = 0***).
*) На случае, когда р = 2, мы остановились в начале параграфа.
**) Так как р < 2, то ? > 2 и включение у ? ?,« представляет более
тяжелое требование, чем включение у ? L2.
***) Обозначение sign происходит от латинского слова eignum — знак.
9.3] ФУНКЦИОНАЛЫ В ПРОСТРАНСТВАХ СУММИРУЕМЫХ ФУНКЦИЙ 241
Тогда при любом а имеем asigna = |a|. Теперь для любого
натурального п определим функцию
Упи) = \ если
| пsigny(t), если \y(t)\>n*).
Функции уп (I) измеримы, ограничены и
1М0|<И01 - (И)
при всех t. Далее положим
) (« = 1, 2, ...)•
Эти функции тоже ограничены и измеримы**), следовательно,
хп ? Ъ"9 и при этом
ь _i_
y (п=1, 2, ...)•
Поскольку xn(t) ограничена (а тогда zn?i2), / (хп) вычисляется
по формуле F), т. е.
I (хп) = J *„ @ у (<) dt = j | tfn @ |«-i | у @ | Л.
a a
Отсюда благодаря неравенству A1) вытекает, что
ь
Так как, с другой стороны, / (хп) < || /1| || хп ||, то
Ь Ъ 1
Раз мы предположили, что i/(f) не эквивалентна 0, yn'(t) тоже
не эквивалентна 0, а тогда, деля обе части последнего нера-
неравенства на интеграл, стоящий справа, мы находим
ь
*) Функции уп (t) называются срезками функции у (t).
**) Измеримость функции sign у (t) очевидным образом вытекает из
измеримости функции у {t).
16 Б. 3. Вулих
242 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
Переходя здесь к пределу при п—> оо, получим
ь 1
A2)
Тем самым доказано, что y?Lq.
Теперь уже нетрудно получить для функционала / фор-
формулу F) в полном объеме. С одной стороны, мы имеем линейный
функционал /, заданный на всем Lv и представимый по
формуле F) для х ? X2. С другой стороны, введем еще один
линейный функционал g, определенный на всем Lp формулой
ь
g (х) = J x (t) у (t) dt.
Эти два функционала совпадают на ?2, т. е. / (х) = g (x) при
х 6 L2. Но ?2 составляет множество, всюд\ плотное в L1' *).
Тогда по замечанию к теореме 8.4.1 / (х) = g (x) на всем L1'.
Представление функционала / по формуле F) на всем L" дока-
доказано, а из неравенств (9) и A2) вытекает формула A0) для нормы
функционала /.
2°. Случай, когда р = 1. На функционалах в пространстве L
остановимся короче. Используем следующее понятие, вводимое
в теории функций вещественной переменной. Говорят, что функ-
дия ф (t) ограничена почти всюду на промежутке [а, Ь], если
существует такая постоянная С, что | <р (t) |<C почти всюду
на [а, Ъ]. Легко доказывается, что если функция <р (t) ограни-
ограничена почти всюду, то среди постоянных С, обладающих указан-
указанным свойством, существует наименьшая **). Эта наименьшая
постоянная называется существенной точной верхней границей
функции ф (t) и обозначается
vrai sup | ф (t) | ***).
Ясно, что если х ? L, a функция у (t) измерима и ограничена
почти всюду на [а, Ь], то произведение ху суммируемо и фор-
формула F) определяет аддитивный функционал на L. Этот функ-
функционал линеен, что сразу вытекает из оценки:
| / (*) |< (vrai sup | у (t) |) [ | x (t) | dt = (vrai sup ] у (t) |) \\x\\.
*) L2 содержит все непрерывные на [а, Ь] функции, а уже множество
непрерывных функций всюду плотно в Lp.
**) См., например, Б. 3. В у л и х, Краткий курс теории функций
вещественной переменной, стр. 228.
***) vrai — французское слово, означающее «истинный».
9.3] ФУНКЦИОНАЛЫ В ПРОСТРАНСТВАХ СУММИРУЕМЫХ ФУНКЦИЙ 243
При этом ясно, что
A3)
Верно и обратное заключение, т. е. формула F) дает общий
вид линейного функционала в пространстве L, если в качестве
у (t) брать любую измеримую функцию, ограниченную почти
всюду на [а, Ъ\. При этом справедливо точное равенство:
||/||--vraisup|2/@|*). ' A4)
Обратный результат можно доказать по той же схеме, что
и для пространств Lv при 1 < р < 2. Сначала так же, как и там,
доказывается, что если / — линейный функционал, заданный
на Ъ, то / (я) представимо по формуле F) при х ? Z2. Далее сле-
следует проверить, что на этот раз у (t) ограничена почти всюду.
С этой целью зададим произвольное е > 0 и обозначим через е8
множество тех точек из [а, Ь], где | у (t) | > || / || + е. Затем
рассмотрим на [а, Ъ] функцию
^ ири '^
0 при t ^ е?.
Тогда, поскольку x
-J x(t)y(t)dt=
С другой стороны, || а; || =¦-теее и потому
/ (*)< || / || тее.
Одновременное выполнение обоих неравенств для / (х) возможно
лишь при пгее = 0. Таким образом, при любом e>0, \y(t)\<i
<С||/|| + е почти всюду на [а, Ь]. Вследствие произвольности е
отсюда сразу вытекает, что
|г/@|<|1/|1 почти всюду на [а, Ъ] ***).
Таким образом, y(t) ограничена почти всюду и
vraisup|y(*)|<||/||. A5)
Теперь представимость функционала / по формуле F) для всех
*) Общий вид линейных функционалов в L найден современным поль-
польским математиком Г. Штейнгаузом.
**) Буква т обозначает лебегову меру.
***) Чтобы прийти к этому выводу, достаточно задать последовательность
значений е„ -*¦ 0 и рассмотреть сумму множеств ее . Эта сумма имеет меру О,
а на дополнении | у (t) \ .< || / ||.
16*
244 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
х ? Ъ устанавливается совершенно так же, как в пространстве
Lp. Попутно из неравенств A3) и A5) вытекает формула A4).
В пространствах I" устанавливаются аналогичные результаты.
Общий вид линейного функционала в пространстве I уже найден
в 9.2 с помощью формулы D). Если же р > 1, то общий вид линей-
линейного функционала в 1Р дается той же формулой D), где после-
последовательность {ch} ? 1ч. При этом
f
9.4. Распространение линейных функционалов
В 8.4 мы установили некоторые общие результаты о распро-
распространении линейных операторов. Сейчас рассмотрим этот вопрос
специально для функционалов. Основным результатом здесь
является следующая теорема С. Банаха и Г. Гана *) о распро-
распространении линейного функционала с сохранением нормы с любого
линейного подмножества на все пространство:
Теорема 9.4.1. Пусть X — нормированное пространство,
Е — его линейное подмножество, / (х) — линейный функционал,
заданный на Е. Тогда функционал / допускает распространение
с сохранением нормы на все пространство X.
Доказательство. Мы ограничимся доказательством
этой теоремы для сепарабельного пространства X. Доказатель-
Доказательство для произвольного пространства требует привлечения идей,
выходящих за рамки настоящей книги.
Распространение функционала / осуществим постепенно.
Опишем подробно первый шаг. Возьмем некоторый фиксирован-
фиксированный у ? X, но не входящий в Е. Рассмотрим множество Е\,
состоящее из всех элементов вида х = х + о.у, где х ? Е. Ясно,
что JEi — линейное множество. Например, если х'± = х4 -f- aji/,
х'2 = х2 + а2у, х'±, х'2 ? Ei {хи х2, ? Е), то и их сумма
у A6)
имеет ту же структуру, а потому х[ + х'2 ? Ei. Аналогично про-
проверяется, что еслих' ? Еи то и Хх ? Ei при любом %..
Заметим также, что каждый х' из Е{ допускает единственное
представление вида х = х + он/, где х ? Е. Действительно,
если бы х = х + <ху = х, + a,i/, где х, х^ ? Е и а ф а,, то из
равенства х — xt = (a4 — а) у мы бы получили, что у = х _^1.
Тогда, вследствие линейности множества Е, у 6 Е, что неверно.
Таким образом, ai = а, а тогда и х4 = х.
*) Г. Ган A879—1934) — австрийский математик.
9.4] РАСПРОСТРАНЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 245
Множество Е cz Ei. Именно, каждый х ? Е может быть пред-
представлен в виде х = х + Щ, где а = О, а потому входит в М\.
Выведем теперь некоторое вспомогательное неравенство.
Возьмем любые два элемента xit xz?E. Тогда
f(x1)-f(x2) = f(xl-x2)<\f(xi~x2)\<\\f\\\\xl-x2%
Но
) - (Х2 + у) || < || Xt + у ||+ || Х2 + I/ ||,
а потому
/ (*i)-/ (*2)<|| /1| (||*, + у || + ||х2 + у ||).
Отсюда
Если, фиксируя сначала xlt взять точную верхнюю границу левой
части неравенства по всевозможным х2 ? Е (обозначим ее т),
а затем, рассматривая всевозможные ж, ? Е, взять точную ниж-
нижнюю границу правой части (обозначим ее М), мы получим
Так как х{ и х2 независимы друг от друга, то можно заменить
их произвольным х ? Е и записать, что
Наконец, приступим к распространению функционала / с Е
на Ei. С этой целью возьмем какое-нибудь число с, заключенное
между т и М, тга<с<М, и для любого х' = х -\- ш/ 6 Et
(х 6 JB) определим функционал <р (х1) по формуле
Ф (*')=/(*) + «•).
Вследствие единственности представления х' в указанном виде
функционал ф (ж') определяется для каждого х' 6 Et однозначно.
При этом для ж'6 Е, как мы знаем, а — 0 и из представления
х' = х'-{-0у следует, что ф (х') = / (ж').
Аддитивность ф проверяется с помощью формулы A6):
Ф (xi + xt) = / (ж, + аг2) + («1 + а2) с =
+ а,с] + [/ (*2) + а2с] = ф (*;) + ф (*;).
*) Если т < Л/, то числу с можно придать бесчисленное множество
различных значений и за счет этого получить бесчисленное множество раз-
различных распространений функционала / на Е±.
246
ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
[ГЛ. IX
Аналогично проверяется однородность: если х' — х-\- ау?Еи то
he' = he + (Ка) у и ср (he') = f {he) + (Яа) с = Я [/ (ж) + ас] = Яф (х1).
Теперь докажем, что функционал ф линейный. Пусть сна-
сначала x'^JEi таков, что для него <х^1, т. е. х'—х-{-у, где
х?Е. Тогда
Но по A7),
а потому
С другой стороны,
Ф (xr) = /(i) + c>/ (x) + т,
а по A7) т> —\\f\\\\z+y\\ — J(x) и потому
A8)
A9)
B0)
введем х[ = — =
хг
а тогда
Сопоставляя A8) и A9), получаем
|ф(*') КI
Для х' — x + ay^Ei с произвольным а
= ^- + у. По уже доказанному |ф (х[) |
вследствие однородности ф
|Ф (*')Нф(а*;)|Ча||ф(*;)|<|а|||/||
и мы также получаем неравенство B0).
Наконец, если х' ? Еи таков, что а = 0, то х' g E и ф (ж') =
= / (х'), и неравенство B0) сводится к условию ограниченности
функционала /. Следовательно, ф (х') удовлетворяет неравен-
неравенству B0) при всех х' ? Ех. Таким образом, функционал ф линей-
линейный и ||ф|к=Л/||в*).
Осталось показать, как осуществить распространение функ-
функционала / с Е на всё X. Так как мы предполагаем X сепарабель-
ным, то в нем существует всюду плотное счетное множество А,
элементы которого выпишем в виде последовательности хх, х2, ¦ ¦ ¦
. . ., хп, . . . Обозначим через у^ первый из элементов множе-
множества А, который не входит в Е. Полагая у = уи строим множе-
множество Еу. Затем принимаем за уг первый из остальных элементов
множества А, который не входит в Eit и, исходя из JEU строим
множество Е2, состоящее из всех элементов вида х ¦— х + Щг
(х ? Ei). Этот процесс продолжаем и далее. Если после
конечного числа шагов мы построим такое линейное множе-
множество Еп, что уже A czEn, то процесс остановится. В противном
*) В 8.4 мы видели, что при распространении норма не может умень-
уменьшиться .
9.4] РАСПРОСТРАНЕНИЕ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 247
случае процесс построения множеств Еп будет продолжаться
до бесконечности. По уже доказанному мы можем получить рас-
распространение заданного функционала / с сохранением нормы
с Е на Ei, затем продолжить распространение (тоже с сохра-
сохранением нормы) с Ei на Е2 и т. д. Если общее число шагов было
конечным (равным и), то в результате мы получим распростра-
распространение функционала / с сохранением нормы на множество Еп.
Если же процесс был бесконечным, то мы осуществим распро-
распространение функционала / с сохранением нормы на множество,
равное (J Еп *), которое, как легко видеть, линейно**). И в том
п=1
и в другом случае мы осуществим распространение функцио-
функционала / на линейное множество, содержащее в себе множество А
и, следовательно, всюду плотное в X ***). Тогда по теореме 8.4.1
(справедливой для функционалов, поскольку множество веще-
вещественных чисел полно) существует распространение функцио-
функционала / с сохранением нормы и на всё X.
Следствие. Каков бы ни был элемент х0 Ф 6 нормиро-
нормированного пространства X, на X существует такой линейный
функционал /, что
" а) Ц/11 =1; б) /(*„) = || аь || ••••).
Доказательство. Примем за Е множество всех эле-
элементов вида Кх0. Это множество — линейное. Зададим на нем
функционал / (Кх0) = к || х0 ||. Ясно, что этот функционал адди-
аддитивен, / (х0) = |1 х0 ||. а из равенства | / (кх0) \ = \\ Кх0 || выте-
вытекает, что / линеен и || / || = 1. По теореме Банаха — Гана суще-
существует распространение функционала / с сохранением нормы
на всё пространство X, а это распространение и будет линейным
функционалом на X, удовлетворяющим а) — б).
Итак, в нормированном пространстве для любого элемента
хи =?. 0 существует такой линейный функционал /. что / (х0) ^= 0.
Имея в виду этот факт, принято говорить, что во всяком норми-
нормированном пространстве существует достаточное множество
линейных функционалов.
*) Здесь следует иметь в виду, что при каждом следующем шаге
в построении распространения мы не меняем значений функционала, уже
определенных на предыдущем множестве. Поэтому если распространение все
оо
время обозначать через <р, то для каждого х' ? IJ Еп получается неравен-
стш) B0).
**) Например, если х"± ?ЕН1, щ ? Е'пг, то х[-\-х'2 ? Еп при ге = тах (щ, ng).
***) Если с самого начала в А не было ни одного элемента, не входя-
входящего в Е, то это значит, что уже Е всюду плотно в X.
****) Ясно, что если х0 = 9, то в X имеются элементы, отличные от нуле-
нулевого, то это предложение тоже справедливо, так как / F) = 0 для любого
.чиненного функционала /.
248 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
9.5, Линейные функционалы в пространстве
непрерывных функций
Общую форму линейного функционала в пространстве С
непрерывных функций х (t), заданных на отрезке [а, Ь], можно
получить с помощью теоремы 9.4.1 о распространении линейных
функционалов. Для распространения мы используем простран-
пространство J3, состоящее из всех ограниченных вещественных функ-
функций х (t), заданных на том же отрезке [а, Ь]. Алгебраические
операции в пространстве В мы считаем определенными по тем
же правилам, что и в С, а норму вводим по формуле
||*|| = sup|a:(/)|.
То, что В действительно является нормированным пространством
(и притом полным), проверяется так же, как и для С.
Если х ? С, то по теореме Вейерштрасса sup | x (t) | =
= max | х (t) I *), т. е. для х ? С нормы, заданные в С и в В, сов-
совпадают. Поэтому пространство С — линейное подмножество про-
пространства В **).
Дадим определение одного важного класса функций.
Определение. Функция g (t), заданная на [а, Ъ],
называется функцией ограниченной вариации, если существует
такая постоянная М, что для любого разбиения отрезка [а, Ъ\
на конечное число отрезков с помощью чисел а = t0 < ?4 < . . .
. . . <С tn = Ъ выполнено неравенство
S
Величина суммы, стоящей слева, зависит от способа разбие-
разбиения отрезка [а, Ь]. Но если множество всех таких сумм огра-
ограничено, то оно имеет конечную точную верхнюю границу, кото-
которая называется полной вариацией функции g (t) на отрезке [а, Ъ\
ь
и обозначается Var g (t).
а
Простейшим примером функции ограниченной вариация
является любая монотонная функция. Действительно, если,
например, g (t) — неубывающая функция на отрезке [а, Ъ\, то
*) Если среди чисел некоторого множества есть наибольшее, то оно
и является точной верхней границей этого множества.
**) Легко видеть, что С — подпространство пространства В.
9.5] ФУНКЦИОНАЛЫ В ПРОСТРАНСТВЕ НЕПРЕРЫВНЫХ ФУНКЦИЙ 249
для любого разбиения этого отрезка
i=0 i=0
= \g (h)-g(a)} + [g (*2)-*(*,)] +
Таким образом, все суммы, входящие в определение функции
ограниченной вариации, имеют для неубывающей функции одно
и то же значение g (b) — g (а) и тем самым в совокупности огра-
ь
ничены; при этом Var g (t) = g (b) — g (a).
a
Легко проверить, что сумма и разность двух функций огра-
ограниченной вариации тоже являются функциями ограниченной
вариации. Действительно, если g (t) = g{ (t) ± g2 (t), где gi (t)
и gi @" — функции ограниченной вариации, то для любого раз-
разбиения отрезка [а, Ъ]
%\g()g()\ S \[gl(t)gi
i=0 t=0
n—l
< S II gi (U+1) - gt (h) \+\gi ('«+!) - S2 (tt) \] -
i=0
n-1 n-1
= lj\gi(ti+1)-gi(ti)\+ S \g2(tm)-g2(ti)\<
i=0 i=0
т. е. требуемая ограниченность сумм для функции g (t) уста-
установлена.
Отсюда как следствие получается, что разность двух неубы-
неубывающих функций есть функция ограниченной вариации.
Несколько сложнее доказывается обратный результат: всякая
функция ограниченной вариации может быть представлена в виде
разности двух неубывающих функций. На доказательстве этого
предложения мы не останавливаемся.
Теперь переходим к отысканию общей формы линейного
функционала в пространстве С. Пусть / (х) — такой функционал.
По теореме 9.4.1 существует его распространение с сохранением
нормы на пространство В *). Обозначим зто распространение
*) Хотя мы ограничились доказательством теоремы 9.4.1 для сепара-
бельного пространства, однако пространство В не сепарабельно, и поэтому
здесь нам приходится использовать теорему 9.4.1 в полном объеме. В гл. XIV
A4.5) будет дан другой вывод общей формы линейного функционала в С,
который опирается на теорему Банаха — Гана лишь для сепарабельно го
пространства.
250 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
той же буквой /. Для любого т из промежутка а < т < 6 рас-
рассмотрим функцию
{1 при а < t < т,
0 при %<t<b.
Так как хх ?В, то / (хх) имеет смысл и представляет некоторую
функцию от т, которую мы обозначим g(i). Дополнительно опре-
определим функцию g (т) при х = а, полагая g(a) = 0. Таким обра-
образом,
(хх) при а < т < 6,
0 при т = а.
Докажем, что g(x) — функция ограниченной вариации. Возь-
Возьмем произвольное разбиение отрезка [а, Ь] на конечное число
частей с помощью чисел а = То<т1 <• • -<Тп = 6 и составим
кусочно-постоянную функцию
Ро при а<<<т15
Р; При Tj<7<T; + ,
где при каждом ? — 0, 1, .. ., га — 1
Pi = sign \g (xi+1) — g (т,-)] *).
Из определения функции а; (г) ясно, что в пространстве i* норма
|| х || < 1, следовательно, / (х) < | / (ж) | < || / ||- Из определения
же введенных выше функций хх следует, что если а< т' < т",
то разность хх« — a;t' есть функция, равная единице в проме-
промежутке т' < i<x" и равная нулю при прочих t из [а, 61. Поэто-
Поэтому из B1) вытекает, что
п-1
¦¦¦¦¦"¦ Ро Ti г ^Li Pt \ х • ~~ Х-^, 1 ^
а тогда
п-1
/ И = Ро/ (Zti) + 2 Pi[/(^t,+1) —/(«tj)] =
п-1
= Ро^ (Ti) + Д Р* I* (T*+i) ~ ^ (т'I-
Учитывая, что g (т0) = g (а) = 0, предыдущее выражение можно
*) См. обозначение, введенное в 9.3.
9.5] ФУНКЦИОНАЛЫ В ПРОСТРАНСТВЕ НЕПРЕРЫВНЫХ ФУНКЦИЙ 251
преобразовать так:
п-1
2 - У (xi)] =
п-1
= Ро 18 (т.) - g (То)] + 2 Pi
t=i
n-1
— У в г
i=0 - - - - - . . 4—-Q .
Последнее равенство вытекает из определения .чисел Р;. Следо-
Следовательно,
2
i=0
Тем самым благодаря произвольности разбиения отрезка [а, Ь\
доказано, что g (т) — функция ограниченной вариации и что
V6ar*(T)<||/||.
а
Теперь переходим уже непосредственно к получению ана-
аналитического выражения для функционала /. Возьмем произволь-
произвольный х ? С и зададим
е > 0. Благодаря свой-
свойству равномерной непре-
непрерывности функции х (t)
существует такое б >0,
что если взять любое
разбиение отрезка [а, Ь]
с помощью чисел а=то<
< Ti < . . . < т„ = b на
конечное число отрез-
отрезков, длины которых
меньше б, то
\x(t')-x(t")\<e
для любых двух точек
(', t", принадлежащих
одному и тому же от-
отрезку [Т;, Т;+1]. На КаЖДОМ ИЗ ОТреЗКОВ [Т;, Т;+1] (t—-0, 1, ...
...,п—1) берем произвольную точку Ц (t;<^<t!+i) и состав-
составляем кусочно-постоянную функцию у?В (рис. 15), полагая
x(t0)
y(t) =
Рис. 15.
при
при
A = 1, 2, . . ., П — 1).
Так как, каково бы ни было t ? la, b], у (t) = x (tt) при неко-
некотором i, причем t и tt входят в один и тот же из отрезков [т;, тг+1],
то из условия, которому мы подчинили разбиение отрезка [а, Ь],
252 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
вытекает, что
\x(t)-y(t)\ = \x(t)-x(ti)\<e.
Следовательно, \\х—г/||<е*) и
\f(x)-f(y)\<\\f\\s. ' B2)
Но
п-1
у = х (to) яТ1 + 2 х (h) (хх.+1 — хх.),
а потому
п-1
/ (у) - х (to) f (хХ1) + 2 х (h) [f (х,ш - f (хх.)] =
п-1
= X (to) g (Tj) + Д X (h) [g (T«+1) - g (T,)] =
n-1
t=0
[напоминаем, что g (т0) = g (a) = 0]. Таким образом, из неравен-
неравенства B2) вследствие произвольности е вытекает, что
п-1
f(x)= lim 2 я (г0 [#(тж) —g(fi)]- B3)
б-> 0 г=0
Сумма, стоящая в правой части, называется интегральной. Пре-
Предел нужно понимать в том смысле, что разность между / (х) и инте-
интегральной суммой оказывается по абсолютной величине меньше
произвольно малого заданного числа, если только сумма состав-
составлена для разбиения отрезка [а, Ь] на отрезки с длинами, мень-
меньшими надлежащим образом подобранного б > 0, причем про-
промежуточные точки tt на соответствующих участках взяты совер-
совершенно произвольно. Указанный предел называют интегралом
Стилтъеса от функции х (t) по функции g (t) и обозначают
ь
*)¦ B4)
Таким образом, формулу B3) можно переписать так:
ь
f(x)=\ix(t)dg(t). B5)
а
Итак, для каждого линейного функционала / в пространстве С
*) Легко проверить, что || х — у \\ < 8.
**) Т. И. Стилтьес A856—1894) — голландский математик.
9.5] ФУНКЦИОНАЛЫ В ПРОСТРАНСТВЕ НЕПРЕРЫВНЫХ ФУНКЦИЙ 253
можно подобрать функцию ограниченной вариации g (t) так, что
функционал / представим по формуле B5) в виде интеграла
Стилтьеса.
Перейдем теперь к установлению обратного результата: како-
какова бы ни была функция ограниченной вариации g (t), интеграл
Стилтьеса B4) существует для любой функции i^C и пред-
представляет линейный функционал в С. Основная трудность заклю-
заключается в доказательстве существования интеграла, т. е. в дока-
доказательстве существования предела интегральной суммы в том
смысле, как зто определено в связи с формулой B3). При этом,
если воспользоваться представлением функции ограниченной
вариации в виде разности двух неубывающих функций, то и инте-
интегральная сумма разобьется на две и, таким образом, достаточно
доказать существование интеграла Стилтьеса от непрерывной
функции по неубывающей функции. Это может быть сделано
почти дословно так же, как в курсе математического анализа
доказывается существование определенного интеграла от непре-
непрерывной функции. Однако, поскольку доказательство существо-
существования определенного интеграла проводится лишь в более под-
подробных курсах математического анализа *), мы даем ниже полное
ь
доказательство существования интеграла Стилтьеса \ х (t) dg (t),
а
считая сразу g (t) произвольной функцией ограниченной вариации.
Зададим произвольно б > 0 и подберем б > 0 так, что
|*A')-« (О |<—^ при \t'-f\<6**). B6)
2Varg@
а
Теперь возьмем любые два разбиения отрезка [а, Ь] на части с длинами,
меньшими б, и по ним с помощью произвольных точек составим интеграль-
интегральные суммы s' и s". Докажем, что \ s' — «" | < б. Пусть первое разбиение
получено с помощью чисел а = х0 < Tt < ... <, тп = Ъ и
п-1
«'=2 *('|>[*(*<+1>-*(т1>].
1=0
где Tj^tj^Tj+i. Если все точки, посредством которых получено второе
*) См., например, Г. М. Фихтенгольц, Основы математического
анализа, т. I, стр. 323—327.
6
**) Если Var g @ = 0, то g (t) есть постоянная, а тогда интеграл
а
Ь
\ х (t) dg (t) существует и равен нулю для любой х 6 С.
254
ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
[ГЛ. IX
разбиение, перемешать с точками деления первого разбиения, то получится
третье, «более мелкое», дробление отрезка [а, Ь]. Для точек деления этого
разбиения введем следующие обозначения:
A)
11
Выбирая на каждом из участков [x\i\
ставим новую интегральную сумму
произвольную точку t\'\ со-
со\'\
n-l mi~1
i=0 j=0
Оценим разность s—s'. Так как уже при первом разбиении длины
всех участков были меньше б, то при любых i и /
С помошыо этого неравенства имеем
п—1 mj—1
S—8' =
4=0 з=0
1 ^J — ^
г=0 э=0
п-1
г=0
—* (t,)
з=0
n-l
,•=0 з=0
n-l mt-l
ь Z. Zj
2Varg(«)i=0 j=0
<
2Varg(t)
р, д р умма s, поу р
шиванием точек деления первых двух разбиений, то оно является «более
Так как разбиение, для которого оставлена сумма s, получено переме-
перемебй бо
9.5] ФУНКЦИОНАЛЫ В ПРОСТРАНСТВЕ НЕПРЕРЫВНЫХ ФУНКЦИЙ 255
мелким» и по отношению ко второму из них, для которого составлена сумма s",
а потому совершенно аналогично \ s — s" | <^ — . Отсюда
Зададим убывающую последовательность чисел вп ->• 0. Для каждого еп
подбираем соответствующее ему б, обозначая его бл, так, чтобы при е = е„
и б = 6„ было выполнено B6). При этом, так как б, найденное по заданному е.
всегда можно уменьшить, не нарушая требуемого от неге свойства, мы можем
предполагать, что 6„ образуют тоже монотонную последовательность.
6п+1<6„. При каждом га берем какое-нибудь разбиение отрезка [а, 6]
на части с длинами, меньшими б„, и с его помощью составляем какую-нибудь
интегральную сумму, которую обозначим sn. Покажем, что последователь-
последовательность {sn} — фундаментальная. Если т^>п, то длины всех отрезков т-го
и га-го разбиений (для которых составлены суммы sm и sn соответственно)
меньше б„, а потому, по доказанному выше, \ sm — sn | < вп. Вследствие
полноты множества вещественных чисел отсюда следует, что существует
конечный Ijm sn.
Обозначим его через / и покажем, что
/=lims, B7)
6
где s обозначает произвольную интегральную сумму, а предел понимается
в том смысле, как указано выше.
о
Зададим произвольное е > 0 и подберем N так, что | «„ — / | <-=¦ при
п .^ N. Затем найдем некоторое щ > N так, что е„ ¦< -у . Возьмем любую
интегральную сумму s, составленную для разбиения на отрезки с длинами
меньшими Ьп . Так как и сумма sn составлена для некоторого разбиения.
о
удовлетворяющего тому же условию, то, по доказанному, | s—snQ | < 8По <; -^ .
Отсюда
Тем самым B7) доказано, т. е. доказано существование интеграла B4).
Ясно, что, как и все известные читателю интегралы, интеграл
Стилтьеса от суммы двух функций вычисляется почленно, т. е.
ь ь ъ
\ \Х[ (t) 4 xz @1 dg (t) = J xt (t) dg (t) + J x2 (t) dg (t),
если оба интеграла в правой части существуют. Поэтому если
фиксировать функцию ограниченной вариации g (t) и рассматри-
рассматривать интеграл B4) при х ? С как функционал, заданный на С.
то этот функционал аддитивен. Проверим его ограниченность.
256 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
Для любой интегральной суммы имеем очевидную оценку:
п-1 п-1
t=0 г=0
n-1 b
< (max | x (t) |) 2 Iff (Ti+i) - ff (ti) | < (Var g (*)) || z ||.
i=0 a
Переходя к пределу в этом неравенстве (при б—»0), получим
ту же оценку и для интеграла:
,* ь
\x(t)dg(t) <(Varff@)||af|!. B8)
а
Таким образом, интеграл B4) представляет линейный функционал
ь
в пространстве С и его норма не превосходит Var g (t).
а
Заметим, не входя в подробности, что по заданному в С линей-
линейному функционалу / функция ограниченной вариации g (t),
с помощью которой функционал / представляется по формуле B5),
определяется не единственным образом. Поэтому в общем случае,
ь
согласно B8), можно лишь утверждать, что || / || ¦< Var g (t).
а
Однако для функции g (t), построенной в начале этого параграфа,
мы имели и обратное неравенство и, следовательно, для этой
ь
функции ||/j| = Var g (t). Таким образом, мы доказали
а
теорему, впервые установленную в 1909 г. Ф. Риссом.
Теорема 9.5.1. Общая форма линейного функционала
f (x) в пространстве С дается формулой B5) в виде интеграла
Стилтьеса, где g (t) — функция ограниченной вариации, а \\f\\ <
ь
<Varg(f). При этом функция g (t) может быть подобрана
а
Ъ
а так, что \\f\\ = Var g (t).
а
В заключение настоящего параграфа укажем один случай,
когда интеграл Стилтьеса B4) сводится к определенному инте-
интегралу (Римана), изучаемому в курсе математического анализа.
Именно, пусть g (t) имеет на отрезке [а, Ь] непрерывную про-
производную. Положим М = max | g' (t) |. Для любого разбиения
отрезка [а, Ь] посредством чисел а = т0 ¦< т4 < . . • < т„ = Ъ
имеем по теореме Лагранжа при всех i — 0, 1, . . ., п — 1
g (Tj+i) — g (Т;) = g' (tt) (ТЖ — Т(),
9.6] ГИПЕРПЛОСКОСТИ 257
где т4 < it < Ti+1. Отсюда
SkMg()I = s \g'
i=0 i=0
n-i
S (Tj) = M(b —a),
i=0
следовательно, g (г)— функция ограниченной вариации*).
Используя именно те точки ti, которые получились по фор-
формуле Лагранжа, составим интегральную сумму s; получим
8 = So * (*,) fc (тЖ) - g (Ti)] = Д * (*,) g' (tt) (T|+1 - Tt).
Сумма, стоящая справа, стремится при неограниченном дробле-
ь
нии отрезка [а, Ь] (т. е. при S—>0) к \ x(t)g'(t)dt. С другой
а
стороны, интегральная сумма s стремится при том же условии
к интегралу B4) (здесь существенно, что интеграл есть предел
интегральной суммы, не зависящий от выбора точек /,)• Поэтому
ь ь
\ X A) dg (/.) = [ X (t) g' (t) dt.
a a
9.6. Гиперплоскости
В этом параграфе мы укажем некоторый геометрический под-
подход к изучению линейных функционалов.
Определение. Пусть X — нормированное пространство,
/ — аддитивный и однородный функционал, отличный от нуле-
нулевого (/ Ф 6)[ заданный на X, с — любая постоянная. Множе-
Множество Р всех элементов х ? А", где / (х) ~ с, называется гиперпло-
гиперплоскостью в X. Иначе можно сказать, что Р — множество, опре-
определяемое уравнением f (х) = с **).
Из аддитивности и однородности функционала / сразу сле-
следует, что гиперплоскость Ро, определяемая уравнением / (х) = О,—
линейное множество. Всякая другая гиперплоскость Р с урав-
уравнением / (о) = с (с Ф 0) получается из Ро переносом на какой-
нибудь из векторов у <Е Р (последнее включение означает, что
*) Заметим, что при доказательстве этого факта нам недостаточно было
опираться только на непрерывность самой g (t) и не всякая непрерывная
функция будет функцией ограниченной вариации.
**) В этом определении X может быть любой линейной системой.
17 б. 3. Булих
258 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
/ (у) = с), т. е. Р совпадает с совокупностью всех элементов
вида х = z -,- у, где z? Po.
Действительно, если х ? Р, то / (х) = с. Положим z = х — у.
Тогда / (z) = / {х) — / (у) = 0, т. е. z g Ро. Следовательно,
каждый х ? Р представим в виде а; = z + г/, где z ? Ро. Обратно,
всякий элемент х ? X, имеющий вид х = z + г/, где z ? Ро,
принадлежит Р, так как / (х) — f (z) + / (у) = с.
Лемм а 9.6.1. Если хоть одна из гиперплоскостей f (х) = с
(при некотором с) — замкнутое множество в X, то и все эти
гиперплоскости (при любом с) замкнуты.
Доказательство. Рассмотрим две гиперплоскости
Р : f (х) = с и Р' : / (х) = с' и допустим, что Р замкнута. Фик-
Фиксируем некоторые элементы у ? Р и у' ? Р'. Из предыдущего
замечания сразу следует, что гиперплоскость Ро получается из
Р переносом на вектор — у, а тогда Р' получается из Р пере-
переносом на вектор у' — у.
Пусть х'п ? Р' (п = 1, 2, . . .) и а;^ ->- а;'. Тогда существуют
такие хп ? Р, что а4 = хп + г/' — у. При этом
ж„ = а;;— у' + у—> х' — у'+у.
Но так как гиперплоскость Р замкнута, то х = х' — у' -\- у ? р,
следовательно, х' = х ~{- у' — г/ ? Р'. Тем самым, замкнутость
Р' доказана.
Теорема 9.6.1. Для того чтобы аддитивный и однородный
функционал /, отличный от нулевого, был линейным, необходимо
и достаточно, чтобы гиперплоскости f (х) = с были замкнутыми.
Доказательство, а) Необходимость. Пусть
функционал /, заданный на X, линеен, а Р — гиперплоскость
/ (х) = с. Если хп ? Р и хп —у х, то / (хп) = с при всех п, а потому
по непрерывности функционала / и / (х) = с, т. е. х ? Р. Таким
образом, гиперплоскость Р замкнута.
б) Достаточность. Пусть гиперплоскости / (,г) -.. с
замкнуты. Допустим, что функционал / не линеен, а тогда он
не может быть непрерывным ни в одной точке, в частности
в нулевой. Следовательно, существует такая последовательность
хп —у 8, что / (хп) ^ 0. Из последнего соотношения вытекает, что
при некотором е > 0 неравенство I / (хп) | > е выполнено для
бесконечного множества значений индекса п. Переходя в случае
необходимости к частичной последовательности, можно считать,
что это неравенство выполнено при всех п.
Положим х'п = тт^—. Тогда
т. е. х'п —*¦ 8. С другой стороны, / (х'п) = 1 при всех п, т. е. все
9.0]
ГИПЕРПЛОСКОСТИ
259
х'п принадлежат гиперплоскости Р с уравнением / (х) = 1. Но
тогда вследствие замкнутости этой гиперплоскости 0 6 Р, что
невозможно, так как / (8) = 0. Полученное противоречие дока-
доказывает теорему.
В следующей теореме вскрывается некоторый геометрический
смысл нормы линейного функционала.
Т е о р е и а 9.6.2. Пусть / — линейный функционал, задан-
заданный в нормированном пространстве X и отличный от нулевого,
а Р—гиперплоскость / (х) =1. Тогда
4, B9) -
где d = inf || x ]| *).
Для любого х ? X норма || х ||
есть его расстояние от нулевого
элемента 8. Тогда d можно рас-
рассматривать как «кратчайшее» рас-
расстояние от 8 до гиперплоско-
гиперплоскости Р **).
Проиллюстрируем сказанное на при-
примере пространства Л2. Всякий линей-
линейный функционал в й2 имеет вид
ч
ч
ч
Гиперплоскость Р превращается в
прямую cj?i + с2?2=1, d — длина пер- Рис. 16.
пендикуляра, опущенного из начала
координат на эту прямую, || / || — точ-
точная верхняя граница значений функционала / на единичном круге (в про-
пространстве И2 она достигается, и потому можно сказать «наибольшее значе-
значение»). Тогда 1 есть точная верхляя граница значений функционала / ва
1
круге радиуса —туг ¦ Из рис. 16 легко усмотреть, что радиус этого круга
как раз и должен быть равен d.
Доказательство. Из неравенства | / (х) | < || / [| || х ||
следует, что если х ? Р, то || / || || х \\ > 1, т. е. || х || > г-тт:.
Переходя в левой части к точной нижней границе, мы получим,
1 1
что d> тгттг (тем самым, d Ф 0) или ||/!|>-г.
*) Из формулы B9), в частности, видно, что d Ф 0. Предлагаем чита-
читателю вывести этот факт непосредственно из замкнутости гиперплоскости Р.
**) Однако в отличие от эвклидова пространства в общем случае это
кратчайшее расстояние может не достигаться, т. е. может не существовать
точка х 6 Р, для которой || х |] = d.
17*
260 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
Пусть, теперь S* обозначает замкнутый единичный шар в про-
пространстве X. Покажем, что
/(*)<-! C0)
для любого x?S*. Допустим, что / (х) >-т для некоторого х ?S*.
Положим х' = -тт-г-. Тогда
С другой стороны, / (х') = 1 и потому х ? Р, а тогда || х' || > d.
Полученное противоречие доказывает неравенство C0). Но тогда
по формуле B) ||/||<т-. Сопоставляя два противоположных
неравенства для нормы || / ||, приходим к равенству B9).
9.7. Сопряженное пространство
Множество всех линейных функционалов, заданных в нор-
нормированном пространстве X, можно рассматривать как частный
случай того пространства X линейных операторов, отображаю-
отображающих X в некоторое заданное пространство У, которое мы изучали
в 8.6. Тем самым будем считать, что алгебраические операции
в множестве линейных функционалов определены по тому пра-
правилу, как указано для X. По доказанному в 8.6, множество
всех линейных функционалов, заданных в пространстве X, само
представляет нормированное пространство. Это пространство
называется сопряженным к пространству X и обозначается X'*).
Теорема 9.7.1. Каково бы ни было нормированное про-
пространство X, сопряженное пространство X' полно.
Действительно, в теореме 8.6.1 была доказана полнота про-
пространства X в случае, если пространство У полно, а для X' роль
Y играет множество вещественных чисел, которое, как мы знаем,
полно.
Нахождение общей формы линейных функционалов в кон-
конкретных пространствах позволяет получить конкретную реализа-
реализацию их сопряженных пространств. Приведем некоторые примеры.
Из общей формы линейного функционала в Вп
f(x) = (x, с),
где с ? Rn и Ц/11 = || с ||, причем элемент с по заданному функ-
функционалу / определяется однозначно, следует, что между линей-
*) В литературе часто встречаются и такие обозначения сопряженного
пространства: X* или X.
9.8] # ВТОРОЕ СОПРЯЖЕННОЕ ПРОСТРАНСТВО 261
ными функционалами / в Вп и элементами с 6 Rn устанавли-
устанавливается взаимно-однозначное соответствие, представляющее алге-
алгебраический изоморфизм и сохраняющее норму. В связи с этим
говорят, что пространство Jttn реализуется в виде самого J}.n.
Аналогичный результат имеет место для пространства I2,
а следовательно, и для произвольного бесконечно-мерного сепа-
рабельного, гильбертова пространства //. Здесь мы также нашли
общую форму линейных функционалов в виде скалярного про-
произведения и между сопряженным пространством Ы' и самим Н
устанавливается алгебраический изоморфизм с сохранением нормы.
Впрочем, изоморфизм гильбертова пространства Н с сопря-
сопряженным пространством Н' может быть установлен и без пред-
предположения о сепарабельности И.
Из общей формы линейного функционала в пространстве I
следует, что сопряженное пространство V реализуется в виде
пространства in ограниченных последовательностей.
Наконец, из общей формы линейных функционалов в Lp
вытекает, что при р > 1 сопряженное пространство к ~LP реали-
реализуется в виде Lq, где q связано с р формулой G). Аналогично
сопряженное к пространству 1Р реализуется при р > 1 в виде Iя.
Пространство, сопряженное к L, реализуется в виде простран-
пространства измеримых, почти всюду ограниченных функций, в котором
норма функции у определяется по формуле
|jy|| = vraisup|y(*)|.
Последнее пространство обычно обозначается через 31. Есте-
Естественно, что эквивалентные между собой функции в Ж отожде-
отождествляются.
Заметим, что доказанная в 9.5 теорема Рисса об общей форме
линейного функционала в пространстве С еще не дает конкретной
реализации сопряженного пространства С' с помощью функций
ограниченной вариации, так как функция g (t) в формуле B5)
определяется по заданному функционалу не единственным обра-
образом. Чтобы получить реализацию пространства С посредством
функций ограниченной вариации, нужно сначала указать неко-
некоторое правило, по которому для каждого функционала будет
определяться единственная функция g (t), но на этом мы не оста-
останавливаемся.
9.8. Второе сопряженное пространство
Беря произвольное нормированное пространство X и его
сопряженное пространство X', мы можем рассмотреть в свою
очередь линейные функционалы, заданные на А". Эти линейные
функционалы в совокупности образуют пространство, сопря-
262 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ , [ГЛ. IX
женное к X'. Его обозначают X", и оно называется вторым
сопряженным пространством к пространсту X. По теореме 9.7.1,
как всякое сопряженное пространство, X" банахово.
Среди линейных функционалов, заданных на X', выделяются
некоторые функционалы специального вида. Именно, будем
в выражении / (х) считать х фиксированным элементом из X,
а / пробегающим все пространство X'. Тогда выражение / (х)
будет представлять функционал, заданный в пространстве X'.
Обозначим этот функционал через Fx, т. е. мы полагаем
Fx(f) = f(x). C1)
Теорема 9.8.1. При каждом фиксированном х ? X формула
C1) определяет линейный функционал Fx на X' и при этом
\\Fx\\=-\\x\\. C2)
Доказательство. Аддитивность Fx вытекает из равенств
Fx (/i + h) - (/i 4- h) (x) = /i (x) + h (x) = Fx (/,) + Fx (h).
Ограниченность Fx следует из оценки
Таким образом, Fx — линейный функционал и || Fx ||< || x \\.
Чтобы доказать, что здесь имеет место точное равенство, вос-
воспользуемся следствием из теоремы Банаха — Гана. Согласно
этому следствию по заданному х ф 0 (х 6 X) найдется / 6 X'
с || / || = 1, для которого
Таким образом, строгое неравенство || Fх \\ < || х \\ невозможно
и || Fx || = || х ||. Если же х = 6, то Fx (/) = 0 для всех / 6 X',
т. е. Fх = 6, и опять || Fх \\ = \\ х \\ ( = 0). Теорема доказана.
Рассмотрение функционалов вида C1) приводит к следующему
новому понятию. Если множество всех линейных функционалов,
заданных на X', исчерпывается функционалами Fx вида C1),
пространство X называется рефлексивным. В этом случае самой
формулой C1) устанавливается алгебраический изоморфизм с со-
сохранением нормы между множеством X" всех линейных функцио-
функционалов, заданных на X', и пространством X.
Примерами рефлексивных пространств могут служить про-
пространства L1' при р > 1. Действительно, общий вид линейных
функционалов в пространстве L1', даваемый формулой F) (где
у 6 f). позволяет, как было отмечено в предыдущем параграфе,
реализовать пространство, сопряженное к Lp, в виде JA При
этом q связано с р равенством G). Иными словами, линейные
9.8] ВТОРОЕ СОПРЯЖЕННОЕ ПРОСТРАНСТВО 263
функционалы /, заданные на Zp, можно отождествлять с функ-
функциями у ? Ъ1 (из формулы F)), а второе сопряженное к Lp можно
тем самым рассматривать как пространство линейных функцио-
функционалов на Ъч. Так как р и q входят в условие G) симметрично,
общий вид линейных функционалов F ? (L ')", будет даваться
формулой
где х ? Tjv. Следовательно, пространство (i)" исчерпывается
функционалами Fx вида C1), т. е. пространство I? рефлексивно.
Аналогичным способом проверяется рефлексивность про-
пространств I' при р > 1.
Нетрудно доказать рефлексивность произвольного гильбер-
гильбертова пространства, в том числе и не сепарабельного.
С другой стороны, пространства L и I не рефлексивны. Так, напри-
например, пространство, сопряженное к I, реализуется в виде пространства т,
а линейные функционалы в т не исчерпываются рядами D). Пространство
С тоже не рефлексивно.
Используем второе сопряженное пространство для вывода
одного важного признака ограниченности множества элементов
в произвольном нормированном пространстве.
Теорема 9.8.2. Пусть X — произвольное нормированное
пространство. Для того чтобы, множество Е ? X было ограни-
ограниченным (по норме), необходимо и достаточно, чтобы каждый
линейный функционал /, заданный на X, был ограничен на мно-
множестве Е, т. е. чтобы совокупность значений / (х) при х ? Е была
ограничена для каждого / 6 X'.
Доказательство, а) Необходимость почти
очевидна. Действительно, если множество Е ограничено по норме,
|| х || < А для всех х ? Е, то для любого / 6 X'
\f(x)\<\\f\\\\x\\<A\\f\\,
когда х ? Е.
б) Достаточность. Пусть выполнено условие теоремы,
но при этом предположим, что множество Е не ограничено. Тогда
из Е можно выделить последовательность элементов {хп} так, что
II %п II -*¦ + °°. Рассмотрим теперь функционалы Fx 6 -Ж"- Для
каждого / 6 X' имеем
F*n(f) = f(xn),
и по условию последовательность {/(^л)} ограничена. Таким
образом, последовательность функционалов Fx точечно огра-
ограничена. Так как сопряженное пространство X' полно, то к функ-
264 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
ционалам Fx применима теорема Банаха — Штейнгауза (тео-
(теорема 8.5.1). Следовательно, нормы || Fx \\ должны быть в сово-
совокупности ограничены. Однако по формуле C2) || FXn || = || хп ||,
и мы приходим к противоречию с нашим построением. Тем самым
ограниченность множества доказана.
9.9. Слабая сходимость функционалов
Рассматривавшаяся в 8.5 точечная сходимость последователь-
последовательности линейных операторов имеет специальное название слабой
сходимости в том случае, когда речь идет о функционалах. Имен-
Именно, введем следующее определение:
Определение. Последовательность линейных функцио-
функционалов {/п}, заданных в нормированном пространстве X, назы-
называется слабо сходящейся к линейному функционалу / (заданному
в том же X), если /„ (х) -> / (х) для любого х 6 X.
Для обозначения слабой сходимости будем употреблять сле-
следующую запись:
//
Общие теоремы о точечной сходимости, доказанные в 8.5,
дают применительно к функционалам следующие результаты.
1. В банаховом пространстве X всякая слабо сходящаяся
последовательность линейных функционалов ограничена, т. е.
ограничены в совокупности нормы этих функционалов (тео-
(теорема 8.5.1).
2. Если X — произвольное нормированное пространство и если
ограниченная (по норме) последовательность линейных функцио-
функционалов точечно сходится на некотором, множестве, всюду плотном
в пространстве X, то эта последовательность слабо сходится
к некоторому линейному функционалу (теорема 8.5.2).
Объединяя эти результаты, мы получим следующий критерий
слабой сходимости функционалов в банаховых пространствах:
Теорема 9.9.1. Пусть X — банахово пространство,
a fn (п = 1, 2, . . .) и / — линейные функционалы в X. Для того
С Л
чтобы /„ —#• /, необходимо и достаточно, чтобы:
1) нормы || fn || были ограничены в совокупности;
2) fn (х) -*¦ / (х) для всех х из некоторого множества А, всюду
плотного в X.
Действительно, необходимость условия 1) вытекает из тео-
теоремы 8.5.1, необходимость условия 2) тривиальна. Обратно,
из условий 1) — 2) по теорема 8.5.2 вытекает, что последователь-
последовательность {/„} слабо сходится к некоторому линейному функциона-
9.Я] СЛАБАЯ СХОДИМОСТЬ ФУНКЦИОНАЛОВ 265
лу ф и ф (х) = / (х) для х 6 А. Тогда по замечанию к теореме 8.4.1
СЛ.
ф (х) = f (х) для всех х 6 А", т. е. ф = / и /„ —-> /.
Мы уже знаем из 8.6, что равномерная сходимость последова-
последовательности линейных функционалов (т. е. сходимость по норме)
влечет слабую сходимость. Покажем на примере, что обратное
неверно.
Рассмотрим в пространстве I функционалы /п (х) = ?„, где
оо
Ъ,п — п-я координата элемента х. Из сходимости ряда 2 I %n I
71=1
вытекает, что Ъ,п -*¦ О, т. е. fn (x) -*¦ О для любого х 6 ?• Таким
образом, /„ —'-> 6*). Однако если представить функционал /„
по общей формуле D), доказанной для I (9.2), то нужно взять
е„ = 1 и cfe = 0 при к ф п. Следовательно, || /„ || = 1 и /„ не
стремится к 6 по норме.
Теперь укажем один случай, когда слабая сходимость совпа-
совпадает с равномерной.
Теорема 9.9.2. Для линейных функционалов в эвклидовом
пространстве Лт слабая сходимость совпадает с равномерной.
Доказательство. Нужно доказать лишь, что в Rm
С Л
из слабой сходимости вытекает равномерная. Пусть /„ —* /, причем
т
in (X) = (X, Сп) = 2 С^Ъь,
т
/ (х) =¦¦ (X, С) = 2 Cklk
[здесь х = (\и \z, . . ., \т), сп = (с\п\ cf\ . . ., cW), c = (cu ..., ст)\.
Беря х равным любому из координатных ортов eft, находим
<t> = fn (eh) —^ f(ek) = eh (k = 1, 2, ..., т).
Но в Rm сходимость по координатам равносильна сходимости по
норме, следовательно, сп—>с, а так как (fn — f) (x) — (х, сп — с).
т0 II fn — f || = У Сп — с || и /„--»/ по норме.
Понятие слабой сходимости приводит еще к одному виду понятия ком-
компактности.
Определение. Множество Е из пространства X' называется слабо-
компактным, если из всякой бесконечной последовательности функциона-
функционалов/„ ? Е можно выделить частичную {/п^}. слабо сходящуюся к некоторому
функционалу /6 X'.
*) В соответствии с обозначениями пз 8.6 здесь в — нулевой элемент
пространства V', т. е. функционал, тождественно равный нулю.
266 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ, IX
Теорема 9.9.3. Если пространство X сепарабелъно, то всякое ограни-
ограниченное подмножество Е пространства X' слабо компактно.
Доказательство. Вследствие сепарабельности X в нем суще-
существует счетное всюду плотное множество Л = {xi, х2, ¦ ¦ ., xj, ¦ ¦ .}. Так гак
Е ограничено, то существует такая постоянная М, что || / || <; М для всех
f ?Е.
Каждому / ? Е сопоставим элемент у пространства s, представляемый
следующей числовой последовательностью:
y = {1{xl), f(x2), ..., f(Xi), ...}.
Множество Е\ всех получаемых таким образом элементов у обладает тем
свойством, что при каждом i совокупность Е^р i-x координат элементов
у ? #1 ограничена:
Поэтому, согласно критерию компактности множества в пространстве s
C.8), Ei компактно. Следовательно, если взять любую последовательность
функционалов /„ ? Е, то из нее можно выделить частичную {/п^} так, что
¦соответствующие им элементы ynk образуют последовательность, сходя-
сходящуюся по расстоянию в s, т. е. так, что при всех i существует конечный
lim /nfc (xt)- Тогда по теореме 8.5.2 последователь гость {/л^} слабо сходится
к некоторому линейному функционалу. Тем самым слабая компактность
.множества Е доказана.
9.10. Сходимость процесса механических квадратур
В качестве приложения критерия слабой сходимости 9.9.1
рассмотрим вопрос о приближенном вычислении определенных
интегралов. Различные известные читателю способы приближен-
приближенного вычисления определенных интегралов — способы прямо-
прямоугольников, трапеций, параболический — и многие другие
заключаются в том, что интеграл приближенно заменяется суммой
произведений значений интегрируемой функции в некоторых
точках на некоторые коэффициенты, причем точки и коэффициенты
определяются по-разному в различных способах, но не зависят
от функции.
ь
Например, если \ х (t) dt вычисляется по способу трапеций,
а
то отрезок [а, Ъ] делится на п равных частей точками
it — t0 < ?j < . . . < tn = b и вычисление производится по при-
приближенной формуле
\ х (I) dt « ^- [±ХAО)+Х (/,)+• . . +Х
9.10] СХОДИМОСТЬ ПРОЦЕССА МЕХАНИЧЕСКИХ КВАДРАТУР 267
ИЛИ
Ь п-1
()^(o) + 2s x(h) + x(tn).
h=l
Формулы трапеций и другие упомянутые выше формулы при-
приближенного вычисления определенных интегралов или, как их
называют иначе, формулы механических квадратур выводятся
часто из геометрических соображений. Однако к составлению
таких формул можно подойти и с другой точки зрения. Пусть
для каждого натурального п заданы п + 1 точек
#<jfo <?( < . . . <С ln <С>
называемых узлами, и числа А^ (к = О, 1, . . ., п). Составим
приближенные формулы
Ъ п
\ я (/) d/ « 2 А^х (г<Л (я - 1, 2, . . . )• C3)
о h=0
Для того чтобы эти формулы представляли практический интерес,
нужно иметь какие-нибудь сведения об их точности. Например,
естественно требовать, чтобы точность улучшалась по мере уве-
увеличения п. Если для некоторой функции х (t) погрешность фор-
формулы C3) стремится к нулю при и-> оо, т. е.
\x(t)dt= Ит ^ ^in)zDn)),
а П - °° й=0
то говорят, что для этой функции процесс механических квадратур,
определяемый формулами C3), сходится. Мы выясним некоторые
условия, при которых формулы C3) определяют процесс, схо-
сходящийся для любой непрерывной функции.
Предварительно переведем поставленную задачу на язык
функционального анализа. Ограничиваемся рассмотрением на
I;
отрезке \а, Ь] непрерывных функций. Интеграл \х (t) dt пред-
а
ставляет линейный функционал в пространстве С; обозначим его
п
f {х). Сумма 2j ^ftn) x (*ftn)) также является функционалом в про-
странстве С, который обозначим /„ (х). Проверим, что и
268
функционал /„
U (*) = S 4П)
fe=0
ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
линейный. Действительно, если х = ж4 + х2, то
4П)) = 5]
ft0
Ограниченность /„ вытекает из следующей оценки:
fc=O
/1 = 0
=0
При этом || fn || <
Докажем, что здесь имеет место точное равенство. Для этого,
фиксируя п, построим следующую функцию х (t) (рис. 17): поло-
положим в узлах х Dn)) = sign А^. Затем будем считать х (а) = О,
Рис. 17.
если точка а не входит в число узлов, и х (Ь) = 0. если точка Ь
не входит в число узлов, а в промежутках (а, ?<,")), (t'J1), ?<n)), . . .
. . . , (tn , Ь) определяем х (t) по закону линейного интерпо-
интерполирования. Таким образом, график х (t) изображается ломаной
линией, a max \x (t) ] = 1 (мы исключаем не представляющий
интереса случай, когда все А? = 0). Для построенной функции
х (t) имеем
fc=0
2|
ft=0
C
й=0
«.10] СХОДИМОСТЬ ПРОЦЕССА МЕХАНИЧЕСКИХ КВАДРАТУР 269
п
откуда следует, что || /п II > 2 l-^i I • Вместе с обратным нера-
fe=0
венством, установленным выше, это дает равенство
||/, || = Jol^n)l- C4)
Сходимость процесса квадратур, определяемого формула-
формулами C3), для любой непрерывной функции означает, что в про-
пространстве С /„ —i /.
Теперь поставим требование, чтобы при каждом п формула C3)
оказывалась точной для всех алгебраических полиномов степени
не выше п, т. е. чтобы / (х) = /„ (х), если х (t) — полином сте-
степени не выше п. Для этого достаточно, чтобы формула C3) была
точной для функций xt(t) = tl (i = 0, 1, . . ., п), т. е. чтобы
f(Xi) = 1n{Xi) (i-0, 1, •••,«)• C5)
Действительно, если C5) выполнено, то для всякого полинома
вида
п п
х{1)=-- 2 с/= 2 etxt(l)
i=0 i = 0
имеем
/(*) = /(!] ClXi) = 2 Cif (X,) = 2 Cifn (Xt) = /„ ( S Wl) = fn (X).
i=0 i=0 i = 0 i=0
Таким образом, поставленное требование заключается в том,
что при каждом п должны быть выполнены (п + 1) условий C5).
В то же время в правую часть формулы C3) входят Bп + 2)
параметров А^ и 4™'. Следовательно, некоторые из них можно
задать произвольно. Зададим узлы 4П). Так как xt D™J) =
ь
= Dn))l> а функционал / (x) = \ x (t) dt, то условия C5) сво-
a
дятся к системе уравнений
$ C6)
й=0
из которых мы должны определить коэффициенты А^?\
Докажем, что определитель системы C6) отличен от нуля.
Для этого составим однородную систему уравнений
Зу«(#У = 0 (* = 0, 1, ...,л) C7)
г=0
270 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
с неизвестными у0, yt, . . ., уп. Если числа Y; удовлетворяют
всем уравнениям системы C7), то это означает, что полишпг
п
2! Уitl обращается в нуль при t =-- 4"\ *in) , • • •, 4"'- Но есл!г.
г=1
полином степени не выше п имеет более чем п различных корней,
то такой полином тождественно равен нулю, т. е. все его коэффи-
коэффициенты у; — 0- Таким образом, система C7) имеет только нуле-
нулевое решение. Тогда по известному свойству однородных систем
ее определитель должен быть отличен от нуля, а он лишь транс-
транспонированием отличается от определителя системы C6). Тем
самым доказано, что и определитель системы C6) отличен от
нуля.
Отсюда мы уже можем заключить, что система C6) имеет
(единственное) решение, т. е. требуемые коэффициенты А^ могуг
быть подобраны.
Теперь займемся исследованием сходимости процесса при
условии, что формулы C3) удовлетворяют поставленному выше
требованию.
Теорема 9.10.1 (Г. Пойа *)). Пусть при каждом п фор-
формула C3) точна для всех полиномов степени не выше п. Тогда для
того чтобы квадратурный процесс сходился для любой непрерывной
функции, необходимо и достаточно, чтобы существовала такая
постоянная М, что
п
2 I А{ъ1) | < М при всех п. C8)
Доказательство. Если х (t) — полином какой угодно»
степени р, то /„ (х) — / (х) при п>р. Поэтому /„ (х) -*- / (х)
для всех полиномов и, следовательно, точечная сходимость
in (х) -+- f (x) имеет место на множестве, всюду плотном в про-
пространстве С. Тогда по теореме 9.9.1 для слабой сходимости после-
последовательности {/„} к / необходимо и достаточно первое условие
этой теоремы, т. е. ограниченность норм || /„ ||. Остается применить
равенство C4).
Если узлы таковы, что все коэффициенты Ak^'^0, то схо-
сходимость квадратурного процесса обеспечивается без дополнитель-
дополнительных условий.
Теорема 9.10.2. (В. А. Стеклов **)). Пусть прикаждом и
формула C3) точна для всех полиномов степени не выше п и все-
*) Г. Пойя (Polya) — современный американский математик.
**) В. А. Стеклов A863—1926) — выдающийся русский математик,
работавший преимущественно в области дифференциальных уравнений
математической физики.
9.11] ПРОСТРАНСТВО СХОДЯЩИХСЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 271
коэффициенты А? >0. Тогда квадратурный процесс сходится
для любой непрерывной функции.
Доказательство. Проверим выполнение условия пре-
предыдущей теоремы. Если х (t) =:• 1, то формула C3) должна быть
п
точной при любом п *), следовательно, b — а = ^] А\ . Таким
образом, если положить М = b — а и учесть, что Аь >0,
мы видим, что C8) выполнено и тем самым сходимость процесса
доказана.
9.11. Линейные функционалы в пространстве
сходящихся последовательностей
Имея в виду приложения, даваемые в следующем параграфе,
рассмотрим еще одно пространство. Именно, обозначим через с
подмножество пространства т, состоящее из всех последователь-
последовательностей х = {?ft}, сходящихся к конечному пределу. Ясно, чта
с — линейное подмножество; докажем, что оно замкнуто.
Пусть последовательность элементов хп = {|ftn)}?c сходится
к некоторому я—•{?&}?/и-. Тогда по любому е>0 найдется
такое N, что \\хп— а;||-<-~- при n>N, в частности при п — N.
Следовательно, | ?йп)— ?й]<-|г при всех к. Далее, так как после-
последовательность {^й^} сходится, то, по признаку Больцано —
Коши, существует такое к0, что |?ftV) — ?i'V) <" при к, 1'^к0.
Тогда, при к, /<А-0
и, следовательно, по тому же признаку Больцано — Коши, после-
последовательность {?*} — сходящаяся, т. е. х ? с.
Таким образом, с — подпространство пространства т. Так
как пространство ш полно, то по теореме 3.5.4 и с как самостоя-
самостоятельное нормированное пространство также полно.
Мы не будем ставить вопроса об общей форме линейных функ-
функционалов в с и ограничимся рассмотрением функционалов вида
D), т. е.
7»=fjcftSft. D)
Предположим, что этот ряд сходится для любого х 6 с- Тогда
формулой D) в с определяется аддитивный функционал. Дока-
*) Постоянная — полином нулевой степени.
272 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
жем, что он линеен, и выясним, какому условию должны удовлет-
удовлетворять числа Cft.
Введем функционалы
h (х) = 2 chlk.
Так как
то функционалы fn — линейные. При этом вследствие сходимости
ряда D) /„ (х) -v / (х) для каждого х 6 с. По теореме 8.5.1 отсюда
следует, что функционал / — тоже линейный.
Теперь, беря произвольное п, положим
Efc = signcft при к=1, 2, .. ., п,
lh = 0 при к > п.
Тогда * = {?АКс и ||а;||<1*), а
/ {%) = 1j cft sign cA = ^] | cft |.
ft=i ft=i
71
Отсюда 2 I с*| = f (х) <|1/||> а вследствие произвольности п и
оо п
2 |с*|<[|/|[. Таким образом, ряд 2 1са| сходится.
оо
Легко видеть, что верно и обратное: если ряд 2 I ck I cxo-
ft=i
дится, то формула D) определяет линейный функционал / (х),
заданный во всем с (и даже в т). Действительно, для любого
X g С
ОО С» СО
2 ЫЫ<( 2 |e*|)suP|Eft| = ( 2
l Al
откуда и следует, что / (z) имеет конечное значение (т. е.ряд D)
сходится) для любого х ? с и что функционал / линеен.
Из сопоставления полученных неравенств следует также,
"О || / || = 2 I Ch |.
А = 1
В проведенном рассуждении содержится доказательство сле-
следующей теоремы, используемой ниже:
*) Если q = c2 = ... =с„ = 0, то и || ж ||=0. В противном случае, если
хоть одно из этих е? отлично от нуля, || z 11 = 1.
9.12] ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РЯДОВ 273
оо
Теорема 9.11.1. Для того чтобы ряд 2 са?а сходился для
любой последовательности {?&} ? с, необходимо и достаточно,
ОО
чтобы сходился ряд 2 I ch |-
А=1
9.12. Обобщенные методы суммирования рядов
Принятое в классическом анализе определение суммы беско-
бесконечного ряда применимо только к сходящимся рядам. Однако
и расходящиеся ряды оказываются полезными в различных вопро-
вопросах математики, например в теории рядов Фурье. Известно, что
ряд Фурье непрерывной функции может оказаться расходящимся.
В то же время венгерским математиком. Л. Фейером A880—1959)
в начале XX столетия установлен следующий замечательный
результат: если / (х) — любая непрерывная, 2я-периодическая
функция, a sn (x) — частичные суммы ее ряда Фурье
п
sn(x) = a0-)- 2 («aCos kx-}-bk sin кх),
то последовательность их средних арифметических
равномерно сходится к / (х) на всей оси. Таким образом, и в этом
случае можно говорить, что в некотором смысле ряд Фурье может
быть «просуммирован» и его «суммой» оказывается функция / (х).
Приведем некоторые общие определения. Пусть дан число-
числовой ряд
2 и» C9)
п=1
и sh — его частичные суммы (sh = ut + u2 + . . . + uk). Тогда
s = lim sft есть сумма ряда C9) в обычном смысле. Определение
каждого обобщенного метода суммирования заключается в ука-
указании правила, согласно которому lim sk заменяется некоторым
другим выражением, могущим иметь смысл и тогда, когда lim Sk
не существует, которое мы и называем обобщенной суммой. Ука-
Укажем весьма широкий класс обобщенных методов суммирования.
С этой целью зададим бесконечную матрицу А = (я;й) и положим
оо
Oi= 2j aiksk (l == * > '-¦< • • •)• (^")
18 Б. 3. Вулих
274
ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
[ГЛ. IX
Если ряд D0) сходится (в обычном смысле) при каждом i и если
существует конечный lim аг = а, то число а и называется обоб-
обобщенной суммой ряда C9), а ряд называется суммируемым данным
методом. Сам метод будет обозначаться той же буквой, что и опре-
определяющая его матрица — метод А.
Обычный метод суммирования получается из этой схемы,
если положить а,ц ~ 1 (i = 1, 2, . . .) и atk — 0 при i ф к. Тогда
О[ = S; при всех i и, следовательно, конечный lim 0; существует
тогда и только тогда, когда ряд C9) сходится в обычном смысле
и при зтом обобщенная сумма совпадает с обычной.
Использованный Фейером в теории рядов Фурье метод сред-
средних арифметических получается из той же общей схемы, если
взять матрицу
1, 0, 0, ... \
1 1 о
2 ' 2 ' и' - -
3 ' У' ~3 ' ' '
в которой ciih~— при i<i и а;й = 0 при
i
1 \Л
D1)
1. Тогда
т. е. 0; есть среднее арифметическое первых i частичных сумм sh-
Приведем пример расходящегося числового ряда, для кото-
которого методом средних арифметических можно получить обобщен-
обобщенную сумму. Возьмем ряд
1 —1 + 1 — 1+ .. -;
ТОГДа Si — S3 = S5 = . . . = 1, 52 = 8ь = 56— .
редно i =- 2га и i= 2га-)- 1, находим
2п
1 v 1
°-п ~ ~2п Zj $h — ~2r
k=l
2n+l
CT2i+i = 9„ I л /j sft =
=0. Полагая пооче-
поочеОтсюда ясно, что a = limaj = -2--
Обобщенный метод суммирования называется перманентным,
если всякий сходящийся ряд суммируем и зтим методом и при
этом обобщенная сумма совпадает с обычной. Естественно, что
перманентные методы и представляют наибольший интерес.
0.12] ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РЯДОВ 275
Используя понятие слабой сходимости функционалов, выведем
условия, при которых метод, определяемый матрицей А, перма-
перманентен.
Теорема 9.12.1 (О. Теплиц *)). Для того чтобы метод А
был перманентным, необходимо и достаточно, чтобы элементы
матрицы А удовлетворяли следующим условиям:
оо
1) S I aik < М (i = 1, 2, . . .) (М — постоянная, не зави-
сящая от i);
2) lim alk = 0 при каждом к = 1, 2, . . .;
3) I™ § ajft ^ 1.
Доказательство, а) Необходимость. Пусть
метод А перманентен. Любая сходящаяся числовая последова-
последовательность {sh} может быть представлена как последовательность
частичных сумм некоторого ряда C9). Для этого нужно положить
и{ — Si, u2 = sz — su . . ., un = sn — sn_4, . . . Так как конечный
оо
lim sA существует, то ряд 2 щ, сходится, а значит, он суммируем
71=1
и по методу А. Следовательно, все ряды D0) тоже сходятся, суще-
существует конечный lim a; = а и о = s = lim s^.
По теореме 9.11.1 из сходимости рядов D0) для любой схо-
сходящейся последовательности {s^} вытекает, что при каждом i
оо
ряд 2 I aik I сходится. Из 9.11 мы также знаем, что если после-
А1
довательности {s^} рассматривать как элементы пространства с,
х = {sk}, то формула D0) определяет при каждом г линейный
оо
функционал аг = /г (х) в пространстве с, причем || /г II = S la^l-
ft—1
Но мы уже видели, что для любого х 6 с существует конечное
a = lim /; (х), а тогда по теореме 8.5.1 все ||/г || < М, где М —
постоянная. Тем самым доказана необходимость условия 1).
Возьмем х равным координатному орту eh (т. е. полагаем Sk = 1,
si = 0 при I Ф к). Тогда s = lim st = 0 и, следовательно, о — 0.
Но о = lim a,-, а at = /; (eh) = aik, значит, должно быть выпол-
выполнено условие 2).
Наконец, возьмем х = {1, 1, 1, . . ., 1, . . .} (т. е. полагаем
оо
все sk -— 1). Тогда s = lim sk = 1, следовательно и ot = 2 aik~+-
-*-1, т. е. доказана необходимость условия 3).
О. Теплиц A881—1940) — немецкий математик.
18*
276 ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ [ГЛ. IX
б) Достаточность. Пусть условия 1) — 3) выполнены.
Из 1) вытекает, что формула D0) определяет при каждом i линей-
линейный функционал (X; = ft (х) (х = {sh}) в пространстве с с нормой
||/г ||<М. С другой стороны, если \sh} ? с, то s = lim sk также
представляет функционал s = / (х) в с, аддитивность и ограни-
ограниченность которого очевидны ( | / (х) \ -- | lim sh \ < sup | sk \ =
= II * ID-
Обозначим через Е множество всех элементов х = {|й} из с,
у которых все координаты, начиная с некоторой, равны между
собой:
= $n + i — §п+2 == • • • = S.
Если х?Е, то / (х) = s, a
ОО 71—1
n—1
и благодаря условиям 2) —3)
/г (я)->*=/(*).
Теперь покажем, что множество Е всюду плотно в простран-
пространстве с. Если T = {sft} — любой элемент из с, s —limsft, a e>0,
то подбираем п так, что \sh — s|<e при А>ге, а затем обра-
образуем элемент
х' = {sj, . . ., sn_l7 s, s, s, . . .}?E.
Тогда
a: — ж' = {0, . . ., 0, sn — s, sn+1 — s, . . .}
и || a: — i' || < e. Вследствие произвольности е отсюда и следует,
что Е всюду плотно в с.
Из точечной сходимости /г (х) к / (х) на множестве Е и огра-
ограниченности норм ||/jj| по теореме 9.9.1 вытекает, что /;—>/. Тем
самым доказано, что at -v s всегда, когда s = lim sh суще-
существует, а это и означает перманентность метода А. Теорема
доказана.
Легко видеть, что матрица D1) удовлетворяет всем условиям
доказанной теоремы, следовательно, метод средних арифмети-
арифметических перманентен.
9.13] КОМПЛЕКСНОЕ НОРМИРОВАННОЕ ПРОСТРАНСТВО 277
9.13. Линейные функционалы в комплексном
нормированном пространстве
Теория линейных операторов и функционалов, развитая
в двух последних главах, естественным образом переносится
и в комплексные нормированные пространства. Сделаем несколько
замечаний по поводу основных определений, относящихся к линей-
линейным функционалам.
В комплексном нормированном пространстве естественно рас-
рассматривать функционалы с комплексными значениями. Опреде-
Определение аддитивности и однородности функционала (и даже опера-
оператора), данное в 8.1, остается формально без изменения, однако
свойство однородности заключается теперь в возможности выно-
выносить из-под знака функционала любой комплексный множитель.
При этом оказывается, что теорема 8.2.2, в которой доказывается,
что однородность есть следствие аддитивности и непрерывности,
в комплексном пространстве уже не верна. Примером может
служить функционал в комплексном гильбертовом пространстве,
определяемый скалярным произведением / (х) = (с, х), где с —
постоянный элемент. Этот функционал аддитивен и непреры-
непрерывен, но
/(аж) = (с, аж) = а(с, x) = af(x).
В связи с указанным обстоятельством свойство однородности
включается в определение линейного функционала. Таким образом,
в комплексном нормированном пространстве линейный функцио-
функционал определяется как функционал аддитивный, однородный и не-
непрерывный. Учитывая, что в теореме 8.2.2. все же доказывается, что
из аддитивности и непрерывности функционала вытекает возмож-
возможность вынесепия из-под его знака вещественного множителя, пред-
предлагаем читателю проверить, что для того, чтобы аддитивный
и непрерывный функционал был однородным, необходимо и доста-
достаточно, чтобы / (га;) = if (х) для любого х (i — мнимая единица).
Сказанное о функционалах относится также и к понятию линей-
линейного оператора в комплексном пространстве.
Вещественность значений функционалов была существенно
использована в этой главе лишь в теореме о распространении,
где мы действовали с различными неравенствами, написанными
для значений функционала, взятых без модуля. Однако и эта
теорема переносится на линейные функционалы в комплексных
пространствах.
ГЛАВА X
СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ
В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ
10.1. Сопряженные операторы
Понятие сопряженного оператора, введенное в гл. I для линей-
линейных операторов в эвклидовых пространствах, ыы распространим
теперь на случай операторов в произвольном гильбертовом про-
пространстве. Это приведет нас естественным путем к выделению
класса самосопряженных операторов, т. е. таких, которые совпа-
совпадают со своими сопряженными. Изучение самосопряженных опера-
операторов и составит основное содержание настоящей главы. Понятие
сопряженного оператора в еще более общем виде — в произволь-
произвольных нормированных пространствах — в этой книге не рассмат-
рассматривается.
Пусть Н обозначает в дальнейшем вещественное, сепарабель-
ное, гильбертово пространство, а линейные операторы, рассмат-
рассматриваемые в Н, имеют значения в том же пространстве Н. Через /„
обозначим линейный функционал, определяемый на Н формулой
fv (х) = (х, у) (у — произвольный фиксированный элемент из Н).
Тогда || /„ || = || у || (см. 9.2).
Лемма 10.1.1. Для любого линейного оператора А, задан-
заданного на Н, и любого элемента у 6 Н существует единственный
элемент у* ? Н такой, что при всех х ? И.
(Ах, у) = (х, у*), A)
причем || у* || < || А ||-|| J/II-
Доказательство. При фиксированном у скалярное
произведение (Ах, у) можно представить как «сложный» функ-
функционал от х: (Ах, у) = fy (Ax). Опираясь на общие сведения
о суперпозиции операторов (8.6), мы сразу заключаем, что этот
функционал — линейный и что его норма не превосходит
II/у II IMII *)• Согласно общему представлению линейных функ-
*) Впрочем, аддитивность и ограниченность скалярного произведения
{Ах, у), как функционала от х, легко проверяется и непосредственно.
10.1] СОПРЯЖЕННЫЕ ОПЕРАТОРЫ 279
ционалов в Н в виде скалярного произведения существует един-
единственный элемент у* ? Н такой, что выполнено равенство A).
При этом норма || у* || равна норме функционала fu (Ах) и, сле-
следовательно, || у* || <. || fL, || || 4 || = || 4 || || у ||. Лемма доказана.
Если теперь каждому у ? Н сопоставить тот единственный
элемент у*, для которого равенство A) выполнено при всех х ? 17,
то мы определим на Н некоторый оператор: у* = А*у. С помощью
этого оператора равенство A) переписывается в виде
(Ах, у) = (х, А*у). ' B)
Последнее равенство и кладется в основу определения сопря-
сопряженного оператора.
Определение. Если А — линейный оператор, заданный
на Н, то оператор А *, также заданный на Ы, для которого при всех
х, у ? U выполнено равенство B), называется сопряженным
к оператору А.
В лемме 10.1.1 мы уже доказали, что сопряженный оператор
определен однозначно для всех у ? И.
Теорема 10.1.1. Сопряженный оператор А* — линейный
и || 4* || = || 4 ||.
Доказательство. Аддитивность оператора А* почти
•очевидна. Действительно, если у, z ? И, то по лемме существует
такой элемент (у + z)* и притом единственный, что
(Ах, у -f- z) = (х, (у + z)*) при всех х ? Н. Тогда, по опреде-
определению, (у -}- z)* = А* (у -j- г). С другой стороны, с помощью
¦формулы B) имеем
{Ах, yA-z) = (Ax, у)-V (Ах, z) = (х, А*у)+(х, A*z) =
= (*,
т. е.
¦откуда
Ограниченность Л* доказана в лемме: !| Л*у||'< || А \\ ¦ \\ у\\.
Таким образом, оператор А* — линейный и
!И*1КМ1!- C)
У оператора А*, в свою очередь, есть сопряженный — А**,
¦определяемый равенством, аналогичным B),
(А*у, х) = (у, А**х). D)
Но так как отсюда А**х определяется для каждого х однозначно,
то из сопоставления равенств D) и B) следует, что А**х = Ах,
т. е. А** = А. Применяя доказанное выше неравенство C) к А*
280 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
и А**, имеем || А || = || А** || <]| А* |], что вместе с C) и дает тре-
требуемое равенство
Отметим некоторые простые свойства сопряженных операторов.
Если А и В — линейные операторы на Н, то:
а) (А + В)* = A* -f #*;
б) (Ы)* = L4*;
в) (?Л)* = А*В*.
Доказательство вытекает из следующих соотношений;
а) ((А+В)х, у) = {Ах, у) + (Вх, у) = (х, А*у) + (х,
= (*, (Л* 4- В*) у);
б) ((Ы) х, у) = % (Ах, у) = Х (х, А*у) = (х, (Ы*) у);
в) ((ВА) х, у) = E (Ах), у) = (^ж, Д*у) = (х, А* (В*у)) =
= (х, (А*В*) у).
В 1.10 мы уже рассматривали сопряженные операторы в про-
пространстве Нп. При этом мы исходили из определения сопряженного
оператора, как оператора, задаваемого транспонированной матри-
матрицей, но показали, что сопряженный оператор полностью характе-
характеризуется соотношением B) [формулой A9) из гл. I]. Таким образом,
для операторов в Rn определение сопряженного оператора, данное
в 1.10, равносильно общему определению из этого параграфа.
Перейдем к пространству I2. Если z — Ах — произвольный
линейный оператор, отображающий I2 в I2, то, как мы знаем из 2.7,
он изображается с помощью некоторой бесконечной матрицы (aift)
по формулам
оо
2г= 2 aih^h (? = 1, 2, .. .)
(здесь x={xh}).
Пусть у = {уг} — произвольный элемент из I2. Тогда
оо оо оо
(Ах, у) = 2 Ziiji ¦= 2 2 aikxhyi.
i=i i=i ft=i
С другой стороны, пусть сопряженный оператор Л*, который,
как мы знаем, тоже линеен, изображается с помощью матрицы (bih).
Тогда
00 ОО
(х, А*у)= 2 xi 2 biftj/ft= 2 2 bihXiyh.
1 fel l ftl
2
г=1
Положим теперь a; = ej, y=em, где е^ и em—координатные орты.
Тогда
xi=~l, xk = 0 при А: Ф I,
r/m=l, г/; = 0 при 1фт.
10.2] САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 281
Следовательно,
(Аеь ет) = ат1, (еи Л*ет)~Ь1т
и, благодаря условию B), bim = апц. Таким образом, сопряжен-
сопряженный оператор А* определяется матрицей, транспонированной
относительно матрицы оператора А.
10.2. Самосопряженные операторы
Определение. Линейный оператор А в гильбертовом
пространстве Н называется самосопряженным, если он совпадает
со своим сопряженным: А* = А.
Иными словами, самосопряженный оператор А характери-
характеризуется условием
(Ах, у) = (х, Ау) E)
для любых х, у ? Н, т. е. самосопряженный оператор допускает
внутри скалярного произведения «перекидку» от одного сомно-
сомножителя к другому.
Из 10.1 сразу следует, что в I2 самосопряженные операторы
характеризуются симметричными матрицами, т. е. матрицами,
для которых aht = aih при всех i, к = 1, 2, . . .
Любая линейная комбинация самосопряженных операторов
А\, A-L, . . ., Ап
2+ .. . +ХпАп*)
также является самосопряженным оператором. Действительно,
при любых х,
п
(Ах, у) = ( 2 hAkx, у)=- Ц h (Akx, y)= J^ Xk (x, Aky) =¦--
k=if k=i k=i
2
ft—-i
= (x, Ay).
Таким образом, в линейном пространстве линейных операторов,
отображающих Н. в Н, самосопряженные операторы составляют
линейное подмножество. Кроме того, мы сейчас увидим, что это
подмножество замкнуто и, следовательно, является подпростран-
подпространством. Иными словами, если операторы Ап — самосопряженные
и Ап -> А (по норме), то и оператор А —самосопряженный.
Докажем даже более сильное утверждение: если операторы Ап —
самосопряженные и последовательность {Ап} точечно сходится
*) Так как мы рассматриваем вещественное гильбертово пространствоv
то и коэффициенты Ль Я^, . . ., А,„ нужно считать вещественными.
282 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
к оператору А, то А — тоже самосопряженный оператор *).
Действительно, благодаря непрерывности скалярного произве-
произведения при любых х, у 6 И
<Ах, у) = (lim А„х, у) = Jim (Апх, у) = Нт (х, Апу) = (х, limЛпу) ¦=
^(х, Ау).
Суперпозиция самосопряженных операторов может привести
и не к самосопряженному оператору. Если операторы А и В —
самосопряженные, то, как мы знаем из 10.1, {ВА)* —А*В* — АВ.
Следовательно, для того чтобы оператор В А был самосопряжен-
самосопряженным, необходимо и достаточно, чтобы, АВ = ВА, т. е. чтобы
¦операторы А и В были перестановочны между собой. В част-
частности, все степени Ап самосопряженного оператора А также —
самосопряженные операторы **).
Докажем одну важную формулу для нормы самосопряжен-
самосопряженного оператора.
Теорема 10.2.1. Если оператор А — самосопряженный,
то
|| А ||= sup \(Ax, х) |.
11*11=1
Доказательство. По неравенству Коши — Буняковского
имеем, при |j x || = 1,
\(Ах, *)|<||Аа:||||*||<||Л||.
Следовательно, если
С = sup | (Ах, х)\,
11*11=1
•то С < || А ||.
Докажем обратное неравенство. Прежде всего заметим, что
любой z? Н можно представить в виде z—\\ z\\ z', где || z' || = 1 ***).
Отсюда для любого z ? Н ф
\(Az, z)| = ||z|H(^z', z') |< С || z ||2. F)
Теперь для любых х, у?Н, учитывая равенство (Ау, х) =
- (Ах, у), имеем
(А(х + у), х + у) = (Ах, х) + 2(Ах, у) + (Ау, у),
(А(х—у), х — у) = (Ах, х)—2(Ах, у) + (Ау, у)
*) Точечную сходимость линейных операторов в гильбертовом про-
пространстве обычно называют сильной сходимостью.
**) Для А2 это очевидно. Для более высоких степеней равенство
А(Ап-1) = (А""-1) А доказывается по индукции.
***) Если z Ф Э, то %' = г.—г: ; если же z = 9, то за г' можно принять
I!z II
любой элемент с нормой, равной единице.
10.2J САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 283
и, вычитая, находим
4 (Ах, у) = (А(х + у), х-\-у) — (А(х — у), х — у).
Отсюда, по F),
(Ах, у)\<-^С(\\
и по формуле C) из гл. VI
\(Ах, г/)|<уС
Предполагая, что Ах ф 6 (а тогда ж х ф 6), положим в последнем
и х ||
неравенстве у = пЧ-,, Ах. Тогда || у || = || х ||, и мы получаем
A^-\\Axf<C\\xf
или || Ах || < С || х ||. Это же неравенство верно и при Ла; = 8.
Следовательно, \\А 1|<С и, тем самым, равенство || А || = 6'
доказано.
Следствие. Если для самосопряженного оператора А
(Ах, х ) = 0 при всех х ? /Г, то Л = 6.
Действительно, если (Лаг, х) = 0 при всех а; ? /Г, то, по тео-
теореме 10.2.1, || Л || = 0; а потому А = 0.
Для самосопряженного оператора Л вводится еще понятие его
границ — верхней и нижней:
МА — sup (Ах, х), тА— inf (Ax, х).
||х||=] 11*11=1
Из теоремы 10.2.1 следует, что
||Л|| = тах(|МА|, \тА\)*).
Из определения границ легко выводится, что для любого х? Н
тА || х |,2 < (Ах, х)<МА\\х\\2. G)
Действительно, для х = 0 это соотношение тривиально. Если
же х Ф Q, то вводим х' = й-^-тт . Тогда || х || = 1 и ffiA< (Ax , х') <
*) Мы пользуемся очевидной общей формулой: если какое-нибудь чис-
числовое множество Е ограничено, а Е^ — множество абсолютных величин всех
чисел из Е, то
| inf E |).
Предлагая читателю проверить эту формулу, рассматривая разные комби-
комбинации знаков sup E и inf E, приведем один поясняющий пример: если на
числовой прямой взять отрезок Е = [—5, 2], то Е\= [0, 5] и sup E = 2,
inf Е = — 5, sup Е{ = 5.
284 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
<МА. Подставляя вместо х' его выражение, получим
тл < j^i {А*, х) < Ма,
что равносильно G).
Самосопряженный оператор А называется положительным,
если (Ах, х ) > 0 для любого х 6 Н. Заметим, что квадрат всякого
самосопряженного оператора положителен. Действительно,
(А2х, х) = (А (Ах), х) = (Ах,
Важным примером положительного самосопряженного опе-
оператора является оператор проектирования. Действительно, пусть
Р — оператор проектирования (проектор) пространства II на
подпространство Ъ (см. 8.3), а М — ортогональное дополне-
дополнение к L. Возьмем произвольные х, у ? И и представим их в виде
х = Xi + х2, у = г/! + г/2, где xi = Рх, ух = Ру (хи j/j 6 L;
*z, Уг 6 J/). Тогда
(Рх, у) = (хи у)=(хи yi) + (xu y2) =¦¦=(*!, J/i);
(х, Ру) = (х, У\) = (хи yi)+(x2, yi) = (xu Vi);
следовательно, (Рх, у) = (х, Ру). При этом
(РХ, X) = (XU X) = (XU Xi) + (XU X2) = (XU ?,)>().
По доказанному выше любая линейная комбинация проекторов
также будет самосопряженным оператором, но уже не обяза-
обязательно положительным.
В начале этого параграфа мы определили самосопряженный
оператор как линейный оператор А, удовлетворяющий усло-
условию E). Однако на самом деле непрерывность самосопряженного
оператора может быть выведена из других его свойств, и, таким
образом, справедлива следующая теорема.
Теорема 10.2.2. Если аддитивный оператор А задан,
на всем пространстве Н и при любых х, у ? Н удовлетворяет
условию E), то он самосопряжен.
Доказательство. Чтобы доказать эту теорему, нужно
установить, что оператор А ограничен. Допустим, что это не так.
Тогда для любого натурального п существует такой хп ? Н, что
||*п||<1, \\Ахп\\>п. (8)
Рассмотрим последовательность функционалов, задаваемых на Н
формулой
fn(x) = (x, Axn).
Известно (см. 9.2), что эти функционалы линейны и что
II/4 = 11^11- (9)
-10.3] ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА 285
Из условия E) следует, что
fn(x) = (Ax, хп),
и потому по неравенству Коши—Буняковского
|М*)|<||Л*||||*п||<||Аг||.
Таким образом, последовательность функционалов {/„} точечно
ограничена, а тогда по теореме Банаха — Штейнгауза должны
быть ограничены в совокупности и нормы \\'fn ||. Однако это
последнее противоречит формулам (8) и (9). Полученное противо-
противоречие и доказывает теорему.
10.3. Инвариантные подпространства
Каждое подпространство X гильбертова пространства Н может
рассматриваться как самостоятельное гильбертово пространство*).
Однако, если на Н задан линейный оператор А, то, рассматривая
этот оператор только на подпространстве X, мы получим, вообще
говоря, линейный оператор, отображающий X не в самого себя,
¦а в более широкое пространство Н. Если же оператор А отобра-
отображает Ъ в X, то, рассматривая этот оператор только на X, мы отде-
отделим от А некоторую его «часть», представляющую линейный
оператор, заданный на X и имеющий значения в том же простран-
пространстве. В связи с этим вводится следующее определение:
Определение. Подпространство X называется инва-
инвариантным для оператора А, если Ах ? X при любом if I.
Перейдем к случаю, когда оператор А — самосопряженный.
Теорема 10.3.1. Если для самосопряженного оператора А
подпространство X инвариантно, то и его ортогональное допол-
дополнение М тоже инвариантно для А.
Доказательство. Пусть х ? М, ay — произвольный
элемент из X. Тогда (Ах, у) = (х, Ау) = 0, так как Ay ? X.
Следовательно, Ах J_ X, т. е. Ах ? 3/.
Эта теорема показывает, что понятие инвариантного подпро-
подпространства представляет особый интерес для самосопряженных
операторов. Именно, если X — инвариантное подпространство для
самосопряженного оператора А, то А как бы расщепляется на
две самостоятельные части: оператор в пространстве X и оператор
в пространстве М. При этом основное равенство E), характери-
характеризующее самосопряженные операторы, будучи выполнено для А во
всем Н, выполнено, в частности, в X и 31; следовательно «части»
оператора А, рассматриваемые на каждом из подпространств
X и М, также — самосопряженные операторы.
*) Так как Н полно, аЬ — ого замкнутое подмножество, то и как само-
самостоятельное пространство L тоже полно.
286 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 1.ГЛ. X
Приведем пример в пространстве i?n. Пусть матрица линей-
линейного преобразования А имеет вид
/аи ... alk О О \
(правый верхний и левый нижний квадраты сплошь заполнены
нулями). Тогда подпространство Z», порождаемое ортами еи е2,. . .
. . . eh — инвариантно. Действительно, если х ? X, т. е. а; —¦¦
ft
= ^] хге;, то Х/щ — . . . = хп = 0, а потому для у = Ах
имеем \)i = 0 при каждом г = к -|- 1, . . . , тг. Следовательно,
y^Jj. Аналогично, инвариантно подпространство Л/, порождае-
порождаемое ортами eft+1, . . ., еп. Впрочем, если матрица А — симметрич-
симметричная и, следовательно, оператор А — самосопряженный, то инва-
инвариантность Д/ вытекает из инвариантности Ъ.
10.4. Собственные числа и собственные элементы
самосопряженного оператора
Распространим на любые линейные операторы в гильбертовом
пространстве определение, введенное в 1.13 для линейных опера-
операторов в Вп. Впрочем, это определение имеет смысл для операторов
в любом линейном пространстве, если значения оператора при-
принадлежат тому же пространству.
Все время будем предполагать, что пространство Н. содержит
элементы, отличные от в.
Определение. Число А. называется собственным числом
линейного оператора А, если существует элемент х ^8, для
которого Ах = Хх *). Такой элемента; ф 8 называется собственным
элементом оператора А, соответствующим собственному числу А..
Из этого определения следует, что число Я = 0 — собственное
тогда и только тогда, когда существует х ф 8, для которого
Ах = Ох = 6, т. е. когда уравнение Ах -— 6 имеет решение, отлич-
отличное от 6.
К понятию собственных чисел и элементов оператора А можно-
подойти, поставив вопрос об одномерных инвариантных подпро-
подпространствах оператора А. Действительно, пусть подпростран-
подпространство L одномерно, т. е. состоит из элементов вида ох, где х ф 0 —
фиксированный элемент, и пусть L инвариантно для линейного-
*) Вместо «собственное число» часто говорят «собственное значение»..
10.',] СОБСТВЕННЫЕ ЧИСЛА САМОСОПРЯЖЕННОГО ОПЕРАТОРА 287
оператора А. Тогда Ах ?1 и, следовательно, Ах = ах при неко-
некотором X. Отсюда уже вытекает, что и при любом а будет А ( ах) =
= а (Ах) = аХх = X (ах), т. е. все отличные от 8 элементы под-
подпространства Ъ суть собственные, соответствующие собственному
числу X.
Теорема 10.4.1. Если X — собственное число линейного-
оператора А, то совокупность L, состоящая из всех собственных
элементов оператора А, соответствующих числу X, и ну левого-
элемента 8 — подпространство пространства Н'.
Доказательство. Условие Ах = Хх выполнено, по
определению, для всех собственных элементов оператора А, соот-
соответствующих числу X, а кроме них только для х =-- 8. Следова-
Следовательно, этим условием полностью характеризуются все элементы
х ? Ъ. Для любой линейной комбинации элементов хи х2, . . .
. . ., хп ? Ъ имеем
А
( 2
h=i
(Axk) =
2
2
n=l
a потому
2
й=1
Следовательно, Ъ — линейное подмно-
жество.
Если же xn(zL и хп —> х, то Ах = lim Ахп = lim Кхп — Хху
откуда х f L, т. е. Ъ замкнуто. Таким образом, L — подпро-
подпространство.
Определенное в теореме 10.4.1 подпространство L называется
собственным подпространством оператора А, соответствующим
числу X. Ясно, что это подпространство инвариантно для опера-
оператора А.
Заметим, что собственное подпространство даже и для само-
самосопряженного оператора может иметь любую размерность.
Например, для тождественного оператора 1х = х (/, очевидно,—
самосопряжен) собственное подпространство, соответствующее
числу "К = 1, есть всё Н.
Основное свойство собственных элементов самосопряженного
оператора устанавливается следующей теоремой:
Теорема 10.4.2. Для самосопряженного оператора А соб-
собственные подпространства L и М, соответствующие двум раз-
различным собственным числам X и и., ортогональны.
До казательство. Еслиа; ? L, у ? Ж, то Ах = Хх, Ау =
= \ку. Отсюда
X (х, у) = (Хх, у) = (Ах, у) = (х, Ау) = (х, цу) =• \i (x, у).
Но при X ф и. равенство X (х, у) = |я (х, у) возможно, только
если (х, у) = 0, т. е. если а; _|_ у. Тем самым доказано, что L ± М.
288 ОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
Теорема 10.4.3. Все собственные числа самосопряженного
оператора А заключены между его границами МЛ и тл.
Доказательство. Пусть К — собственное число, х —
соответствующий ему собственный элемент с нормой || х \\ = 1 *).
Тогда (Ах, х) = X (х, х) = X, следовательно, по определению
границ (см. 10.2), /nA<X -СМА.
Следствие. Собственные числа положительного само-
самосопряженного оператора А не отрицательны.
Действительно, в этом случае нижняя граница ттгА>0,
а потому и все собственные числа Я > 0.
Мы установили некоторые свойства, которыми обладают соб-
собственные числа и собственные элементы оператора в предположе-
предположении, что они существуют. Однако не всякий, даже самосопряжен-
самосопряженный, оператор имеет собственные числа и вопрос о существовании
собственных чисел представляет большой интерес и большие
трудности. В 1.13 мы доказали, что самосопряженный оператор
в Вп всегда имеет по крайней мере одно собственное число. В сле-
следующей главе мы рассмотрим важный класс самосопряженных
операторов в произвольном гильбертовом пространстве, для
которых существование собственного числа гарантировано.
10.5. Неограниченные симметричные операторы
В целях приложений к дифференциальным уравнениям рас-
распространим на более широкий класс операторов некоторые резуль-
результаты, только что установленные для самосопряженных операторов.
Определение. Аддитивный и однородный оператор А,
заданный на некотором линейном подмножестве D простран-
пространства Н., называется симметричным, если для любых х, у ? D
(Ах, у) = (х, Ау)**).
Самосопряженный оператор представляет частный случай
симметричного, именно, это — ограниченный симметричный опе-
оператор, для которого область задания D = Н ***). Более того, по
*) Такой элемент мы всегда можем найти, взяв произвольный собствен-
х
ный элемент х, соответствующий числу X, и заменив его на ^—г- .
II х II
**) Обычно в литературе по теории операторов в гильбертовом про-
пространстве в определение симметричного оператора включается требование,
чтобы множество D было всюду плотным в Н. Однако при том небольшом
использовании, которое имеет понятие симметричного оператора в этой
книге, в указанном требовании нет необходимости.
***) В общей теории операторов в гильбертовом пространстве рассматри-
рассматриваются и неограниченные самосопряженные операторы, которые также
представляют частный случай симметричных.
HI.5] НЕОГРАНИЧЕННЫЕ СИММЕТРИЧНЫЕ ОПЕРАТОРЫ 289
теореме 10.2.2 всякий симметричный оператор, у которогоD = Н,
самосопряжен. Но в общем случае симметричный оператор может
и не быть ограниченным, а у неограниченного симметричного
оператора область задания D обязательно отлична от Н.
Определение собственных чисел и собственных элементов,
данное в 10.4 для линейных операторов, можно распространить
и на любые аддитивные и однородные операторы, в частности
на симметричные. Собственные элементы симметричного опера-
оператора, естественно, должны принадлежать его области задания D.
Результаты, установленные в 10.4 для собственных элементов
самосопряженных операторов, переносятся на произвольные сим-
симметричные операторы в следующем виде:
Теорема 10.5.1. Если Я — собственное число симметричного
оператора А, то совокупность L, состоящая из всех собственных
элементов оператора А, соответствующих числу Я, и нулевого
элемента 9,— линейное подмножество множества D.
Для доказательства этой теоремы нужно дословно повторить
первую часть доказательства теоремы 10.4.1.
Теорема 10.5.2. Если х — собственный элемент симмет-
симметричного оператора А, соответствующий числу Я, а у — собствен-
собственный элемент, соответствующий числу |я, и Я ф |я, то х ± у.
Доказывается так же, как теорема 10.4.2.
Вместо теоремы 10.4.3 установим следующее более простое
предложение: если А — симметричный оператор и (Ах, а;)>0
при всех х ? D, то всякое собственное число оператора А не отри-
отрицательно. Действительно, если Я — собственное число, а х —
соответствующий ему собственный элемент, то
Я || х ||2 = % (х, х) = (%х, х) = (Ах, х)>0,
откуда и следует, что Я > 0.
Докажем еще одну лемму, используемую в дальнейшем.
Лемма 10.5.1. Если у симметричного оператора А суще-
существует обратный оператор А'1, то этот оператор А'1 тоже
симметричен.
Доказательство. Из общих свойств обратных опера-
операторов (см. 8.7, предложение б)) следует, что оператор А'1 адди-
аддитивен и однороден. Его областью задания служит линейное мно-
множество A (D) (см. 8.7, предложение а)). Возьмем произвольные
элементы х, у ? A (D). Тогда существует такой z ? D, что Az = у
(или 2 = А гу). Используя симметричность оператора А и вклю-
включение А'1 х 6-D, мы сразу находим
Тем самым* симметричность оператора А'1 доказана.
19 Б. 3. Вулпх
290 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
10.6. Спектр самосопряженного оператора
Понятие собственных чисел оператора А тесно связано с во-
вопросом разрешимости уравнения
(А-Х1)х = у, A0)
где / — тождественный оператор. При этом заметим, что если
оператор А — самосопряженный, то и оператор А — XI при любом
К — тоже самосопряженный как линейная комбинация двух
самосопряженных операторов.
Согласно предложению в) из 8.7 для того чтобы существовал
обратный оператор (А — Я/), необходимо и достаточно, чтобы
уравнение (А — XI) х = 9 или равносильное ему Ах = Хх имело
только нулевое решение ог = Э, т. е. чтобы X не было собственным
числом оператора А. В этом случае уравнение A0) имеет един-
единственное решение х при каждом у из совокупности значений опе-
оператора А — XI. Представляет интерес выяснить некоторые свой-
свойства этой совокупности. Будем обозначать ее через Fj,.
Лемма 10.6.1. Пусть оператор А — самосопряженный.
Если X не является его собственным числом, то совокупность F*
всюду плотна в Н. Если же X — собственное число оператора А,
то совокупность Vk не может быть всюду плотной в Н.
Доказательство. Пусть сначала А, — не собственное
число оператора А. Если допустить, что замыкание [FjJ фН,
то существует элемент h Ф Э, ортогональный к [F?J. Так как,
при любом а; ? Н, (А — XI) х 6 Vx, то ((А — XI) х, К) = 0. Вслед-
Вследствие самосопряженности оператора А — XI отсюда следует, что
(х, (А — XI) К) = 0, т. е. элемент (А— XI) h ортогонален любо-
любому х, следовательно, (А — XI) h = Э или Ah = Xh. Последнее
равенство невозможно, так как X — не собственное число.
Таким образом, [FjJ = Н, т. е. Vx всюду плотно.
Наоборот, если X — собственное число самосопряженного
оператора А, то совокупность V^ значений оператора А — XI
не может быть всюду плотной. Действительно, пусть L — соб-
собственное подпространство оператора А, соответствующее чис-
числу X. Тогда оператором А — XI оно отображается в нулевой
элемент и, следовательно, инвариантно для этого оператора. По
теореме 10.3.1 ортогональное дополнение М к подпространству L
тоже инвариантно для оператора А — XI. Любой х ? Н можно
представить в виде х = у + z, где у ? Z,, z ? М, а
отсюда
(А -Х1)х = (А —Х1)у + (А -XI) z = (А -XI) zt M.
Следовательно, Vh с М; тогда и [У*,] с М, а потому [^] ф Н.
10.6 СПЕКТР САМОСОПРЯЖЕННОГО ОПЕРАТОРА 291
Доказанную лемму можно переформулировать еще и так:
для того чтобы X было собственным числом самосопряженного
оператора А, необходимо и достаточно, чтобы совокупность V^
значений оператора А — XI не была всюду плотной в Н.
Введем некоторые важные определения. Пусть А — само-
самосопряженный оператор. Среди вещественных А, не являющихся
его собственными числами, выделим те, для которых совокупность
Vx значений оператора А — XI совпадает с if и .обратный опера-
оператор (А — XI)'1 линеен (иными словами, оператор А — XI обра-
обратим). Эти значения X называются регулярными. Множество всех
собственных чисел оператора А обозначим через S, множество
регулярных чисел — через R, множество остальных вещественных
чисел — через N. Сумма S\jN называется спектром оператора А.
Теорема 10.6.1. Для того чтобы число X было регулярным
для самосопряженного оператора А, необходимо и достаточно,
чтобы Vx = Н.
Доказательство. Необходимость условия вытекает
из определения регулярных чисел. Докажем его достаточ-
достаточность.
Если Vx = Н, то по предыдущей лемме А не может быть соб-
собственным числом. Тогда существует обратный оператор {А — а/)
и этот оператор по лемме 10.5.1 симметричен. Но так как Vx = H,
то область определения оператора (А — а/) совпадает с Н,
а тогда по теореме 10.2.2 оператор (А — XI)'1 линеен. Тем самым
число X регулярно.
Сопоставляя доказанную теорему с леммой, мы можем обра-
образовать следующую таблицу, показывающую, какому типу сово-
совокупности Vx соответствует включение числа А в множество R,
S или N:
ФН
УхфН, но
Дадим еще некоторые определения. Если множество S пусто,
то спектр называется чисто непрерывным. В случае же, когда
5 ф Л, рассмотрим множество всех собственных элементов опе-
оператора А и образуем порождаемое этим множеством подпростран-
подпространство Hi пространства Д. Если Hi = H, спектр оператора А назы-
называется чисто точечным. Ниже мы увидим, что при чисто точечном
спектре множество N не только не обязано быть пустым, но может
быть даже несчетным.
Теорема 10.6.2. Для любого самосопряженного операто-
оператора А существует такое разложение пространства Н на два инва-
инвариантных ортогональных подпространства Hi и Н2, что на Hi
19*
292 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
оператор А имеет чисто точечный спектр, а на Н2 — чисто
непрерывный *).
Доказательство. Как и выше, обозначим через Hf
подпространство, порождаемое множеством собственных элемен-
элементов оператора А, а через L — линейную оболочку того же множе-
множества **). Тогда [L] = Hi. Докажем, что /f4 инвариантно.
ft
Если х ? L, то х = 2 aixi, где xt — собственные элементы.
Пусть при этом xt соответствует собственному числу kt. Тогда
h k
Ах= 2 «; (Axi) = 2 VLiKxi ? L.
Для произвольного х ? Hi имеем a; = lim xn, где xn 6 L, a Ax —
= lim Axn. Ho Axn 6 L, а тогда yla; 6 /*i.
По определению оператор^ на Н4 имеет чисто точечный спектр.
Обозначим через/Гг ортогональное дополнение к Н\. B//j у опе-
оператора А нет ни одного собственного элемента (так как они все
входят в Hi), следовательно,на Hz оператор А имеет чисто непре-
непрерывный спектр.
Теорема 10.6.3. Спектр любого самосопряженного опе-
оператора — замкнутое множество.
Доказательство. Докажем, что дополнительное
к спектру множество R регулярных чисел — открытое. Пусть
%0 6 R. Применим теорему 8.7.4 и положим U = А — Х01,
V = А -XI. Тогда || V - U \\ = \Х - Ко | || / || = | к - к0 |, сле-
следовательно, если | X — Хо | < .jj2—. ГЧ-Щ1 то V = А — Ы обра-
|| (Л Ад 1) ||
тим, т. е. к 6 R. Таким образом, произвольная точка к0 из R
оказывается его внутренней точкой, а это и означает, что В
открыто.
Лемма 10.6.2. Для того чтобы число к было регулярным
для самосопряженного оператора А, необходимо и достаточно
существование такой постоянной к > 0, что при всех х ? Н
\\{А-к1)х\\>к\\х\\. A1)
Доказательство. Необходимость этого условия дока-
доказана в теореме 8.7.2. Докажем его достаточность, а для этого
по теореме 10.6.1 достаточно показать, что Vx = Н.
*) Мы говорим, «оператор А на подпространстве Нхъ, понимая под
этим тот оператор, который определится на Нх (со значениями в Ht), если
оператор А рассмотреть только на этом подпространстве.
**) Если собственных элементов у оператора А нет, то за Щ принимается
нулевое подпространство.
10.6) СПЕКТР САМОСОПРЯЖЕННОГО ОПЕРАТОРА 293
По той же теореме 8.7.2 из условия A1) вытекает, что обратный
оператор (А — XI)'1 существует и линеен на множестве V^ значе-
значений оператора А — XI. Следовательно, А, — не собственное число
и по лемме 10.6.1 Vx всюду плотно в Н. Докажем, что V\ = Н.
Возьмем произвольно у 6 Н. Тогда у = lim yn, где уп 6 F»,,
и, следовательно, существуют такие хп ? И, что
уп = (А-Х1)хп.
Из A1) вытекает, что
\\хп-хт\\<±\\(А-Х1)(хп-хт)\\ = ±\\уп-ут\\,
а так как || уп — ут || -*¦ 0 при га, т -*¦ оо, то и последовательность
{ хп }— фундаментальная. Вследствие полноты Н существует
х = lim xn, а вследствие непрерывности оператора А — XI
(А — KI) х = lim (А — KI) xn = \imyn = у,
и потому y?V},. Лемма доказана.
¦Теорема 10.6.4. Для того чтобы число X принадлежало
спектру самосопряженного оператора А , необходимо и достаточно,
чтобы существовала последовательность таких элементов хп ? Н
с нормой || хп || = 1, для которых
Axn — kxn-*Q*). A2)
Доказательство. Для того чтобы X принадлежало
спектру, необходимо и достаточно, чтобы не существовало постоян-
постоянной к >0, удовлетворяющей при всех х ? Н условию A1). Но
условие A1) равносильно
\\{А-Х1)х\\>к при ||я:|| = 1-). A3)
Нарушение же условия A3) и означает наличие такой последова-
последовательности элементов хп 6 Н с нормой || хп || = 1, для которой
|| (А — XI) хп || -> 0, что равносильно A2).
Следующая теорема является обобщением теоремы 10.4.3.
Теорема 10.6.5. Весь спектр самосопряженного опера-
оператора А заключен между его границами МА и тА.
*) Для собственных значений Я, это предельное соотвошение переходит
в равенство Ах — \х = 0, если все хп взять равными, например, одному
и тому же собственному элементу х.
**) A3) есть очевидное следствие из A1). Обратно, если A3) выполнено,
то для любого х Ф в
а это и дает A1). Для х = 0 неравенство A1) тривиально.
294 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
Доказательство. Докажем, что всякое число к, лежа-
лежащее вне отрезка [/гад, МА], регулярно. Пусть, например, к < тА.
Имеем при || х \\ = 1
(Ах, х) > тА, (КТх, х) = к (х, х) = к,
а потому
((А — KI) х, х)>пгА— к.
Но по неравенству Коши — Буняковского
\((A-kI)x, x)\<\\(A-kI)x\\\\x\\,
следовательно, при || х \\ = 1
\\(A-kI)x\\>mA-X,
т. е. выполнено A3) с постоянной к — пгА — Я. Условие A3)
равносильно A1) и по лемме 10.6.2 к регулярно. Аналогично
рассматривается случай, когда к > МА.
Следующая теорема обеспечивает непустоту спектра само-
самосопряженного оператора.
Теорема 10.6.6. Границы МА и тпА всякого самосопряжен-
самосопряженного оператора А входят в его спектр.
Доказательство. Проведем рассуждение для верх-
верхней границы МА. Аналогично доказывается, что и нижняя гра-
граница тА принадлежит спектру.
Допустим сначала, что || А || = МА. По определению МА
существуют элементы хп ? ?Г с нормой || х„ || = 1, для которых
(Ахп, Хп) -> МА. Проверим, что
Ахп-МАхп-+Ъ. A4)
Имеем
0<||Ахп-МАхп||2 = || (А-MJ)хп\\* =
= {{A-JlfA/) хп, (А-MJ) хп) = || Ахп ||2-2МА (Ахп, хп) + МА<
< 1М\-2МА (Ахп, хп) -*0,
откуда \\Axn — МАхп\\—>0, т. е. доказано A4). Теперь уже
из теоремы 10.6.4 сразу следует, что число МА принадлежит
спектру.
Переходим к общему случаю. Положим В = А — тА1. Тогда
при ||а;|| = 1
(Вх, х) = ((А — тА1) х, х) — (Ах, х) —тА,
следовательно,
Мв —. sup (Вх, х) = sup (Ax, х) — тА = МА — тА,
II х 11=1 || х 11=1
/гав= inf (Вх, х)— inf (Ax, х) — тА = тА — тА = 0.
Их 11=1 11*11=1
10.6] СПЕКТР САМОСОПРЯЖЕННОГО ОПЕРАТОРА 295
Таким образом, ||5|| = МВ (см. 10.2) и, по доказанному,
Мв входит в спектр оператора В, а тогда существует последо-
последовательность элементов хп ? М с нормой || хп \\ = 1, для которой
Вхп — Мвхп—>Э.
Но
п = (А — тА1) хп — (МА — тА) хп = Ахп — МАхп,
и поэтому Ахп — МАхп -*- 9, а тогда МА входит в спектр опера-
оператора А.
Обратим внимание читателя на то, что из доказанной теоремы
не следует существование собственных чисел. Спектр оператора
может быть не пуст за счет множества N, и мы лишь доказали, что
по крайней мере одно из множеств S или N не пусто.
Приведем некоторые примеры.
1°. Диагональный оператор в?2. Рассмотрим
линейный оператор А в 1г, определяемый матрицей, у которой
aih = 0 всегда, когда i ф к [см. формулы A7) из 8.8]. Такие
матрицы называют диагональными. Для элементов же аи, стоящих
по диагонали, введем другое обозначение: ан = %t. Предполо-
Предположим, что множество чисел Яг ограничено, и пусть М = supA,;,
in = inf А,;. Каждый элемент х = { xt } ? V переводится операто-
оператором А в элемент у с координатами
yi = liXi. A5)
При этом y^l1 и оператор А ограничен (а следовательно, и линеен),
что вытекает из элементарных оценок:
Кроме того, из симметричности матрицы вытекает, что опера-
оператор А — самосопряженный.
оо оо
Далее, при любом х ? Р, (Ах, х) — 2 У pi = 2 ^ixli откуда
il il
а при || х || = 1 имеем т^(Ах, х)*СМ. При этом (Aet, et) = %t
(et есть i-й координатный орт). Следовательно, существуют элемен-
элементы а; с нормой || а; || = 1, для которых (Ах, х) сколь угодно близко
к Мили к т, а потому
МА = sup (Ах, х) — М, тА= inf (Ax, х) = т.
II-* 11=1 11*11=1
296 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
Для х = ег имеем по A5) yt = Я.ь yj — 0 при / ф i, т. е. Аег =Я.гег.
Таким образом, каждое из чисел %г — собственное число опера-
оператора А, а координатные орты — собственные элементы. Из фор-
формулы A5) ясно, что никакое число, отличное от всех Я,г, не является
собственным. Таким образом, S = { Я.г }.
Так как спектр оператора А по теоремам 10.6.3 и 10.6.5—
замкнутое множество и содержится в отрезке [/га, М], то:
1) все предельные точки множества S входят в спектр;
2) все числа, лежащие вне отрезка [/га, М], регулярны.
Покажем, что в нашем примере спектр совпадает с замыка-
нием[5]. Пусть Я, ? [S]. Тогда существует такое число б > 0, что
в интервале (к — б, Я, + б) нет ни одного из чисел Я.г, т. е.
| Я, — %t | > б при всех i. Раскладывая любой х ? Р и Ах по коор-
координатным ортам, имеем
оо оо оо
\А —- К± ) X —^ АХ — КХ ::= /\ У\&1 — К /\ X(Gi == /1 (л*1 — Kj XiC\,
откуда
оо оо
II / Л 5 /"Ч -у 1|2 ^П It, 1 \2 -г? ^ Я2 ^ -г? Я2 II гг 112
| V ~— '^ / X N — ? yAf — Aj Х\ ^- и ?j Х\ — и || X ||
i=l i = l
и Я, по лемме 10.6.2 регулярно.
Так как все координатные орты — собственные элементы,
то линейная оболочка множества собственных элементов всюду
плотна в Р, а потому спектр оператора А — чисто точечный.
Однако не исключена возможность, что спектр оператора А,
будучи чисто точечным, заполняет весь отрезок [/га, М]. Дей-
Действительно, множество рациональных чисел, содержащихся
в [/га, М], счетно; поэтому их можно перенумеровать. Пусть
это и будут числа Я.г. В таком случае любая точка отрезка [т, М]
является предельной для множества S, следовательно, [S] =
= [/га, М]. Множество N состоит при этом из всех иррациональ-
иррациональных чисел отрезка [т, М].
2°. Оператор умножения на независимую пере-
переменную в пространстве ?А
Для простоты рассмотрим пространство ?2, составленное из функций,
заданных на отрезке [0, 1]. Пусть В есть оператор умножения на t, т. е. у =
= Вх означает, что у (t) = tx (t). Ясно, что оператор В аддитивен, а значе-
значения Вх 6 L? и || Вх || < || а; ||. Таким образом, оператор В — линейный
По определению скалярного произведения в L2 имеем при любых
х, z 6 L2
1 1
(Вх, *)=J [tx(t)]z(t)dt=^ x(t)[tz(t)]dt = (x, Bz),
О О
т. е. оператор В — самосопряженный. Кроме того, В — положительный
10.6] СПЕКТР САМОСОПРЯЖЕННОГО ОПЕРАТОРА
оператор. Действительно, для любого х ? ?2
1
(Вх, х)=\ tx*(t)dt>0.
По неравенству Коши — Буняковского (Вх, х)^ || Вх\\ || а: |
следовательно, при ||х|| = 1
откуда 0< mB <MB^ 1. Покажем, что пгв = 0, Мв = 1.
Зададим е > 0 (8 •< 1) и положим
( —^ при 0<г<е,
*№ = j У в
I 0 при е<г<!1.
г»
Тогда ||i|l = "|/ \ xz(t)dt = l. Значение Вх есть функция
,(„ = { ^ ПРИ °<i<e'
О при е</<1,
а потому
t 1 , /2
0~2 •
Вследствие произвольности е отсюда выгекает, что тв = 0.
Теперь положим
О при 0 < / < 1 — е,
1
—-=- при 1—е</<1.
Уе
Тогда опять, || ж || = 1, а
1
1 1 л — *2
\/1 ~\/1 ~~2&
e
2 '
1-е 2е 2
Снова вследствие произвольности е заключаем, что AfB = l.
Легко видеть, что оператор В не имеет собственных чисел, т. е. что
его спектр—чисто непрерывный. Действительно, если при некотором X
для элемента x?L2 выполнено соотношение Вх—"Кх, т. е.
tx (t) = \х (t)
для почти всех t ? [0, 1 ], то х (t) = 0 почти всюду, а это и значит, что х = 6
По теореме 10.6.5 спектр оператора В содержится в отрезке [тв, Мв] =
= [0,1]. Покажем, что он заполняет весь этот отрезок. Для этого нужно
установить, что если 0<;Я<^1, то число К не регулярно. Последнее же
будет вытекать из теоремы 10.6.1, если мы убедимся, что совокупность Vx
298 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
значений оператора В— Я./ не совпадает с -ЕЛ Проверим, что функция у (t) =
= 1 не входит в Fj,. Действительно, если бы существовал такой х ? ?а, для
которого {В — XI) х — у, т. е.
(t — X) х (t) = 1 почти всюду на [0, 1],
то мы имели бы
почти всюду, а эта функция не принадлежит L2 (она даже не суммируема).
Итак, X не регулярно, т. е. входит в спектр. Таким образом, для опера-
оператора В множество N = [0, 1] *).
10.7. Интегральные самосопряженные операторы
Обратимся снова к интегральному оператору вида
ь
K(8,t)x(t)dt, A6)
входящему в интегральное уравнение Фредгольма. Этот оператор
обозначим тоже буквой К, и тогда соотношение A6) примет вид
у = Кх. Сначала предполагаем ядро К (s, f) непрерывной функ^
цией, определенной в квадрате a*Cs, t<^b. Как и в 7.4, будем
считать оператор К заданным в пространстве X/2 функций, опре-
определенных на отрезке [а, Ь]. При этом по лемме 7.4.1 значения Кх
суть непрерывные функции, которые мы также можем считать
элементами пространства i2 (и тем самым Кх бСь^).
Оператор К аддитивен. Докажем его ограниченность в про-
пространстве X/2 **).' Пусть М = max \K (s, t) I. Тогда по неравен-
ству C) из гл. VII
b
K(s, t)x{t)dt <M]/T^^\\x\\ A7)
\y\\>=i
Следовательно, оператор К ограничен и || К ||<М (Ь — а).
•) В первом издании этой книги показано, как исследовать оператор
умножения на независимую переменную, если опираться на конструкцию
пространства L*.
•*) В 8.3 мы проверили линейность К как оператора, отображающего
С в С
10.7] ИНТЕГРАЛЬНЫЕ САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 299
Можно показать, что || К |] <; В, где В — постоянная, определенная
в 7.4 (см. формулуA2) из гл. VII). Действительно, по неравенству Коши—
Буняковского
а тогда
ь ь ь
Эта оценка справедлива не только для оператора A6) с непрерывным
ядром, но и при любом ядре, суммируемом с квадратом, т. е. таким, для
которого В < + оо. Таким образом, всякий оператор A6), ядро которого
суммируемо с квадратом,— линейный оператор, переводящий i2 в самого себя.
Ядро называется симметричным, если К (t, s) — К (s, t).
Покажем, что оператор К с симметричным ядром — самосопря-
самосопряженный *).
Для любых двух функций х, z?Ziz
ь ь ь ь
(Кх, z) = J ( J К (s, t) х (t) di\ z (s) ds = J J Я (s, *) a; @ z (s) ds d<f
a a a a
где справа стоит двойной интеграл по квадрату a<;s, t^.b.
С другой стороны, аналогично
ь ь
(х, Kz) = (tfz, ж) = J J K(s,t)z (t) x (s) ds dt.
a a
Меняя между собою в последнем интеграле обозначения пере-
переменных s и t и учитывая, что ЛГ (t, s) = К (s, t), получим
ь ь
(х, Kz)=^ ^K (s, t) z (s) x (t) ds dt,
a a
т. e. (Kx, z) = (x, Kz).
В следующей главе будет доказано, что оператор К с симмет-
симметричным ядром всегда имеет по крайней мере одно собственное
число. При этом для собственных чисел X ф 0 собственные эле-
менты удовлетворяют соотношению х = ~г^х' ^ случае, если
ядро К (s, t) непрерывно, элемент Кх есть непрерывная функция,
*) При этом достаточно потребовать выполнения равенства К (t, s) =
= К (s, t) почти всюду в квадрате а <! *, *<;Ь. Однако если ядро непре-
непрерывно, то из выполнения этого равенства почти всюду уже будет следовать,
что К (t, s) = К (*, t) во всех точках квадрата.
300 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
а тогда и х оказывается непрерывной функцией. Таким образом,
для оператора A6) с непрерывным ядром собственные элементы,
соответствующие числам К ф 0, суть непрерывные функции.
Приведем нашу терминологию в соответствие с той, которая
употребляется в теории интегральных уравнений. В этой теории
однородное уравнение Фредгольма обычно записывается в такой
форме:
ъ
х (s) = |д \ К (s, t) x (t) dt
a
((д. — параметр). Это уравнение в наших операторных обозначениях
имеет вид
х = цКх. A8)
При (д. = 0 уравнение A8) имеет, очевидно, только нулевое реше-
решение х = 9. Те значения (д (непременно отличные от нуля), при кото-
которых уравнение A8) имеет решения х ф 9, называются характери-
характеристическими числами уравнения A8). При (д ф 0 уравнение A8)
может быть записано в равносильной форме:
Кх = -х,
следовательно, каждому характеристическому числу (д уравне-
ния A8) отвечает собственное число — оператора К и, обратно,
каждому собственному числу К ф 0 оператора К отвечает харак-
теристическое число -г- уравнения A8). При этом собственные
к
элементы оператора К совпадают с ненулевыми решениями урав-
уравнения A8), которые и в теории интегральных уравнений тоже
называются собственными функциями.
10.8. Дифференциальные симметричные операторы
При решении многих задач математической физики важную
роль играют дифференциальные уравнения вида
-7й (р WS)-<* W*« = **(*). <19>
называемые уравнениями Штурма — Лиувилля. Функции р (t)
и q (f) мы считаем непрерывными на отрезке fa, b], причем р (t)
имеет непрерывную производную 1-го порядка, К — вещественный
параметр. Пусть искомая функция подчинена некоторым краевым
условиям. Для простоты ограничимся условиями
х{а) = х (Ь) = 0. B0)
10.8] ДИФФЕРЕНЦИАЛЬНЫЕ СИММЕТРИЧНЫЕ ОПЕРАТОРЫ 301
Однако дальнейшие выводы справедливы и при некоторых других
краевых условиях. Таким образом, решение уравнения A9) мы
ищем среди функций, непрерывных на отрезке [а, Ь] со своими
производными 1-го и 2-го порядка и удовлетворяющих усло-
условиям B0). Множество таких функций обозначим через D и рас-
рассмотрим его как подмножество в пространстве X2, построенном
на отрезке [а, Ь]. Ясно, что подмножество D — линейное.
Левая часть уравнения A9) представляет результат примене-
применения к функции х (t) некоторого дифференциального оператора.
Обозначим этот оператор буквой U и будем считать, что он задан
на множестве D. Значения оператора Ux — непрерывные функ-
функции, но мы будем считать их элементами пространства L2. Урав-
Уравнение A9) можно переписать в виде
Ux — %х.
Ясно, что оператор U аддитивен и однороден. В 8.11 мы рас-
рассматривали дифференциальный оператор более общего вида и дока-
доказали его линейность. Но там мы рассматривали этот оператор
« пространствах с другой нормировкой. В пространстве же D
¦с метрикой, перенесенной из X2, оператор U не обладает свой-
-ством непрерывности.
Покажем, что оператор U симметричен. При произвольных
ь ъ ь
(Ux,y)=-\ l(px'y + qx]ydt=-\ (pxr)'ydt-\ qxydt. B1)
Преобразуем первый интеграл посредством двукратного примене-
«ия формулы интегрирования по частям. Учитывая краевые усло-
условия B0), которым удовлетворяют х (t) и y(t), получим
Ь t=b Ъ Ъ
{ (рх')' ydt = (рх') у - \ (рх') y'dt=- [ х' (ру') dt =
a t=a a a
t=b Ь Ь
= -х (ру1) | + 5 * (РУ'У dt=^x (ру')' dt.
t=a a a
¦Отсюда
ъ ь ъ
{Ux, у) = — \ х (ру')' dt—\ qxydt= — \x
Будем считать теперь, что р (t) > 0, a q (t) < 0. Вычислим
{Ux, x) для произвольного x?D, используя формулу B1) и одно-
302 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
кратное преобразование первого интеграла по формуле интегри-
интегрирования по частям. Получим
b Ь Ь Ь
(Ux, *)= — { (px'Y xdt—\ qx* dt = [ рх'* dl—\ qx* dt. B2)
a a a a
Отсюда следует, что
(Ux, x)>0. B3)
Из установленных свойств оператора U вытекает, что для него
справедлива теорема 10.5.2, т. е. собственные элементы опера-
оператора U, соответствующие различным собственным числам, взаимно
ортогональны. Кроме того, при сделанных предположениях
относительно знаков функций р (t) и q (t), благодаря B3) можно
утверждать, как это показано в 10.5, что все собственные числа
оператора U не отрицательны. Но собственные числа оператора U
и являются теми значениями параметра К, при которых уравне-
уравнение A9) имеет решения, отличные от нулевого и удовлетворяющие
условиям B0), а собственные элементы суть эти решения. Таким
образом, мы получили некоторые важные для математической
физики свойства решений уравнения Штурма — Лиувилля.
В конце следующей главы, определив обратный оператор U'1, мы
проведем более полное исследование собственных функций этого
уравнения.
В качестве примера рассмотрим на отрезке 0 < t <; я урав-
уравнение
— х" = Кх B4)
с краевыми условиями х @) = х (п) = 0. Это уравнение получается
из A9), если положить />(Z) = 1, q (t) = 0. Так как все собст-
собственные числа Я>0, то, полагая Я = [х2, где (х>0, мы приведем
уравнение B4) к виду
При [х > 0 общий интеграл этого уравнения имеет вид:
х = Cj cos \x.t -\- C2 sin \it.
Так как х @) = Си то по первому краевому условию Ci = 0, сле-
следовательно, х (f) = С2 sin \it, а тогда х (я) = С2 sin \in, и по вто-
второму краевому условию С2 sin \in = 0. Но если положить С2 = 0,
то мы получим х (t) = 0. Чтобы найти ненулевое решение задачи,
оставим С2 произвольным и потребуем, чтобы sin \m — 0, а это
возможно только, если [х равно любому натуральному числу п.
Таким образом, собственные значения К суть Ki = п2 и каждому
10.9] САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 303
собственному числу можно сопоставить собственную функцию,
т. е. решение, хп (t) = sin nt (С2 полагаем равным единице).
Эти собственные функции образуют известную систему синусов,
ортогональную на отрезке [0, я].
Предоставляем читателю проверить, что Я —- 0 не является в рас-
рассматриваемом примере собственным числом, т. е. что при Я = 0
среди решений уравнения B4) только нулевое удовлетворяет
заданным краевым условиям.
Легко проверить, что оператор Ux = —х", соответствующий
уравнению B4), не ограничен. Действительно, для собственного
элемента хп имеем Uxn = п2хп, следовательно, || Uxn || = п2 \\ хп ||.
Поэтому не существует такой постоянной С, чтобы неравенство
|| Ux ||<С || х || было выполнено при всех х 6 D.
10.9. Самосопряженные операторы в комплексном
гильбертовом пространстве
В комплексном гильбертовом пространстве Н самосопряжен
ный оператор определяется так же, как и в вещественном; это —
линейный (т. е. аддитивный, однородный и непрерывный) опера-
оператор А, для которого при любых х, у 6 Н выполнено равенство
(Ах, у) = (х, Ау). В целом теория самосопряженных операторов
в комплексном гильбертовом пространстве сходна с их теорией
в вещественном пространстве, однако в комплексном гильберто-
гильбертовом пространстве в этой теории появляются и новые принципиаль-
принципиальные факты. Отметим некоторые из них.
Хотя в комплексном пространстве Н скалярное произведение
двух элементов может иметь любые комплексные значения, но
если А — самосопряженный оператор, то (Ах, х) имеет веществен-
вещественное значение при любом х ? Н. Действительно, с одной стороны,
по свойствам скалярного произведения (х, Ах) = (Ах, х), а, с дру-
другой, по определению самосопряженного оператора (х, Ах) =
= (Ах, х), откуда (Ах, х) — (Ах, х), следовательно, (Ах, х) —
вещественно. Более того, можно доказать, что вещественность
(Ах, х) при любом х 6 Н является не только необходимым, но
и достаточным условием для самосопряженности линейного опе-
оператора А.
В комплексном пространстве собственные числа линейного опе-
оператора могут быть любыми комплексными числами. Однако соб-
собственные числа самосопряженного оператора А непременно —
вещественны *). Действительно, пусть Ах = Хх и х ф 6. Тогда
*) В 1.14 это было доказано для самосопряженных операторов в комп-
комплексном пространстве Rn.
304 СОПРЯЖЕННЫЕ И САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ [ГЛ. X
(Ах, х) — (кс, х) = Я || х ||2 и так как {Ах, х) вещественно,
а || х || > 0, то К тоже вещественно.
Произведение КА самосопряженного оператора А (ф 0) на
число К остается самосопряженным только, если К — веществен-
вещественное. Действительно, при любых х, у ? Н имеем (КАх, y)=h (Ax, у),
а (х, Ыу) ='% (х, Ау), и так как (Ах, у) = (х, Ау), «^равен-
«^равенство (КАх, у) = (х, ХАу) выполняется только если К = Я, т. е.
если к вещественно. Следовательно, только относительно линей-
линейных комбинаций самосопряженных операторов с вещественными
коэффициентами можно утверждать, что они также будут само-
самосопряженными операторами.
Заметим еще, что если для любого линейного оператора А в Н
гак же, как в 10.1, определить понятие сопряженного опера-
гора Л*, то легко проверить формулу
(ХА)*=1а*.
ГЛАВА XI
ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
11.1. Определение и общие свойства
В ряде вопросов, относящихся к линейным операторам, наи-
наиболее законченные результаты удается получить в том случае,
когда оператор обладает некоторым дополнительным свойством —
полной непрерывности. Вполне непрерывные операторы пред-
представляют большой интерес и в произвольных нормированных
пространствах, но в этом общем случае мы ограничимся лишь
установлением некоторых основных фактов, а затем перейдем
к рассмотрению вполне непрерывных операторов, преимуществен-
преимущественно — самосопряженных, в гильбертовом пространстве.
Пусть X и Y — нормированные пространства, U — аддитив-
аддитивный оператор, отображающий X в Y.
Определение. Аддитивный оператор U называется
вполне непрерывным, если образ любого ограниченного множе-
множества из пространства X — компактное множество в простран-
пространстве Y.
Предлагаем читателю убедиться, что для полной непрерыв-
непрерывности аддитивного оператора достаточно, чтобы образ какого-
нибудь одного шара из X, например единичного S* (|| х ||<1),
был компактен.
Теорема 11.1.1. Всякий вполне непрерывный оператор
линеен.
Доказательство. По теореме 3.8.1 компактное мно-
множество всегда ограничено. Поэтому если аддитивный оператор U
вполне непрерывен, то образ единичного шара S* с= X ограни-
ограничен, что в свою очередь означает ограниченность оператора U
(см. 8.3). Таким образом, оператор U линеен.
Если у = Ux — произвольный линейный оператор, то из не-
неравенства D) гл. VIII следует, что образ любого ограниченного
множества тоже ограничен. Поэтому если пространство Y таково,
что в нем всякое ограниченное множество компактно, то и вся-
всякий линейный оператор, отображающий X в Y, вполне непре-
непрерывен. В частности, вполне непрерывными будут линейные функ-
20 Б. 3. By лих
306 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
ционалы, а также линейные операторы, совокупность значений
которых конечно-мерна (см. теорему 5.3.2)*). Однако в общем
случае при произвольных X и Г можно лишь утверждать, что
вполне непрерывные операторы составляют часть класса линей-
линейных операторов. Например, в пространстве I2 множество всех
координатных ортов ограничено, но из него нельзя выделить
сходящейся последовательности, так как расстояние между
любыми двумя различными ортами равно |/. Из этого следует,
что тождественный оператор в I2 не будет вполне непрерывным.
Теорема 11.1.2. Если Uit U2 — вполне непрерывные опе-
операторы, отображающие X в Y, а к и [х — любые числа, то и опе-
оператор U = Я?74 + \x.U2 вполне непрерывен.
Доказательство. Пусть множество Е а X ограничено.
В его образе U (Е) возьмем произвольную последовательность
элементов уп. Тогда существуют хп ? Е, при которых уп = Uxn (n^
= 1, 2, . . .). Положим г/п = UiXn, y'n = U2Xn. При этом уп =-
— ty'n + \*.у'п- Так как множество Ut (E) компактно, а у'п 6 #i (E),
то существует частичная последовательность {y'nk}, имеющая
предел. Вследствие же компактности множества U2 (E) из после-
последовательности {y'nh} тоже можно выделить частичную {упк },
имеющую предел. Но так как вместе с {у'Пк} сходится и после-
последовательность {ynk }, то существует lira yn , что и доказывает
компактность множества U (Е). Следовательно, оператор Uвполне
непрерывен.
Доказанная теорема означает, что в пространстве линейных
операторов, преобразующих X в Y', вполне непрерывные опера-
операторы составляют линейное подмножество. В следующей теореме
будет доказано, что, при условии полноты пространства Y, это
подмножество замкнуто, т. е. является подпространством.
Теорема 11.1.3. Если {Un} — последовательность вполне
непрерывных операторов, преобразующих X в Y, причем про-
пространство Y полно, и U = lim Un**), то и оператор U вполне
непрерывен.
Доказательство. Пусть множество Е cz X ограни-
ограничено. Как мы видели в 8.6, из определения сходимости по норме
вытекает, что Unx -> Ux равномерно на множестве Е. Следова-
Следовательно, по любому 8 > 0 найдется такое п, что || Unx — Ux || < е
для всех х g Е. Тем самым для каждого у ? U (Е) найдется такой
*) Совокупность значений линейного оператора, представляющую
линейное подмножество пространства Y, можно рассматривать и как само-
самостоятельное нормированное пространство, а потому, если эта совокупность
конечно-мерна, то применима теорема 5.3.2.
**) Как подчеркивалось в 8.6, эта запись обозначает равномерную схо-
сходимость {?/„} к U.
ll.i] ОПРЕДЕЛЕНИЕ И ОБЩИЕ СВОЙСТВА 307
у' е Un (Е), что || у - у' ||< е, т. е. Un (Е) - е-сеть для U (Е).
Но, благодаря полной непрерывности оператора Un, множество
Un (E) компактно, а тогда, вследствие произвольности е, по
следствию из теоремы 3.8.3 и U (Е) компактно. Тем самым дока-
доказано, что оператор U вполне непрерывен.
Мы уже отмечали, что если U — произвольный линейный
оператор, преобразующий X в Y, то образ всякого огра-
ограниченного множества из X ограничен в Y. Поэтому, если
V — вполне непрерывный оператор, преобразующий Y в про-
пространство Z, то и оператор VU вполне непрерывен. Предлагаем
читателю доказать и что если U вполне непрерывен, a F — про-
произвольный линейный оператор, то оператор VU также вполне
непрерывен.
Приведем два примера.
1. Матричный оператор. Рассмотрим оператор
у = Ах, преобразующий I2 в самого себя, задаваемый бесконеч-
бесконечной системой равенств
оо
yi= 2 aihXh (J---1, 2, . . .), A)
при условии, что 2 «ift <+оо*). Мы знаем, что такой оператор
линеен и что
/"S ¦
1И11<1/ 2 a}h B)
(см. 2.7). Докажем, что он вполне непрерывен.
Введем матричные линейные операторы А„(п — \, 2, ...)
в пространстве I2, определяемые матрицами (а\^),
W= 2 a\Vxk (i-1, 2, ...),
где
aih = a'ft ПРИ *^ге' я'"' —0 ПРИ
Иными словами, матрица (а^) получается из матрицы (а^), если
в последней элементы всех ее строк, начиная с (п + 1)-й, заменить
нулями. Отсюда вытекает, что если у = Апх, то, каков бы ни был
*) Как и выше, мы пишем ^ вместо ^] ^ однако можно иока-
i,h=l i = l ft=i
зать, что для положительных рядов порядок суммирования по i и к без-
безразличен.
20*
308 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
х ? 1г, yt= 0 при i > п. Следовательно, совокупность значений
каждого из операторов Ап конечно-мерна, a потому операторы Ап
вполне непрерывны. Представляя разность А — Ап с помощью
матрицы, мы сразу видим из оценки, аналогичной B), что
/ оо оо
УД, Л*
\\A-An\\<\/ 2j 2i ah -» 0,
а тогда оператор ^4 вполне непрерывен по теореме 11.1.3.
2. Интегральный оператор. Рассмотрим опера-
оператор К, определяемый равенством
ь
у (s) - \ К (s, 0 х (/) dt C)
а
с непрерывным ядром К (s, t). Как и в 10.7, будем считать этот
оператор заданным в пространстве X2 функций на отрезке [а, Ь].
Значения же оператора К, которые по лемме 7.4.1 являются непре-
непрерывными функциями, будем считать элементами пространства С-
Покажем, что оператор К вполне непрерывен.
Пусть множество Е cz X2 ограничено: || х \\ < N при х 6 Е.
Тогда, полагая М = max | К (s, t) \, имеем для любого х 6 Е
и при любом s [см. неравенство A7) из гл. X ]
| у (s) | < М УЬ — а \\ х || < MN \/~Ь — а,
следовательно, функции, составляющие множество К (Е), рав-
ноограничены. Из аналогичной оценки, проведенной в доказа-
доказательстве леммы 7.4.1 [см. неравенство A1) гл. VIII вытекает
их равностепенная непрерывность. А тогда по теореме 3.9.1
множество К (Е) компактно и оператор К вполне непрерывен.
Равномерная сходимость непрерывных функций влечет их
сходимость по норме в пространстве L2. Поэтому, если некоторое
множество непрерывных функций оказалось компактным в про-
пространстве С, то оно будет компактным и в пространстве ХЛ Отсюда
следует, что интегральный оператор К с непрерывным ядром,
рассмотренный как оператор из L2 в самого себя, также будет
вполне непрерывным.
Последний результат можно значительно усилить. Именно, пусть ядро
К (s, f) — любое, суммируемое с квадратом (ср. 10.7). Всякая функция,
суммируемая с квадратом, допускает сколь угодно хорошее приближение
в среднем 2-го порядка с помощью непрерывных функций *). Иными словами.
*) Множество непрерывных функций всюду плотно в пространстве ?2,
построенном из функций с любым (конечным) числом аргументов, в частности
из функций двух переменных.
11.2] ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ 309
существует такая последовательность функций Кп (s, t), непрерывных
в квадрате а ^ s, t <I b, что
\ \ [K(s, t)-Kn(s, t)]*dsdt -> 0.
Рассмотрим интегральные операторы КПУ определяемые в пространстве
равенствами
ь
у(*)=[ Kn(s, t)x(t)dt.
По доказанному выше эти операторы вполне непрерывны. Из оценки нормы
интегрального оператора, проведенной в 10.7, видно, что
Ь b
[K (s, t)— Kn(s, ()]2 dsdt.
a a
Следовательно, \\ К — Kn || -> 0, а тогда оператор К вполне непрерывен
по теореме 11.1.3.
11.2. Вполне непрерывные операторы в гильбертовом
пространстве
Для вполне непрерывных операторов, преобразующих гильбертово про-
пространство Н в самого себя, мы сможем дать другую характеристику. Для
простоты будем предполагать пространство Н сепарабельным. Однако все
сказанное ниже может быть распространено и на случай произвольного
гильбертова пространства.
Определение. Последовательность элементов хп ? Н называется
ел.
слабо сходящейся к элементу х ? Н (хп —> х), если
(хп, К) —> (х, h) при любом h g H. D)
ел.
Проверим единственность «слабого» предела. Действительно, если хп —* х
ел.
и хп —> у, то (х, h) = (у, h) при всех h ? Н', или (х — у, К) = 0. Но если
элемент х — у ортогонален всему Н, то х — у = 6 или х = у.
Из непрерывности скалярного произведения вытекает, что сходимость
по норме влечет слабую сходимость к тому же пределу.
Каждое из скалярных произведений (хп, h) и (х, h) есть линейный
функционал в Л" с аргументом h. В соответствии с определением из 9.9,
соотношение D) означает слабую сходимость последовательности линейных
функционалов (хп, К) к функционалу (х, h). А так как норма линейного
функционала в Н совпадает с нормой порождающего его элемента, то,
следовательно, всякая слабо сходящаяся последовательность элементов огра-
ограничена (см. 9.9, предложение 1).
Возьмем произвольную ограниченную последовательность элементов
а'„ 6 /Г Применение теоремы9.9.3к последовательности функционалов (хп, h)
показывает, что из всякой ограниченной последовательности элементов
пространства Н можно выделить частичную слабо сходящуюся. Иными
310 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
Словами, всякое ограниченное подмножество пространства И слабо ком-
компактно .
Лемма 11.2.1. Для любого линейного оператора А, преобразую-
сл. ел.
щего И в самого себя, из хп —* х вытекает, что Ахп —> Ах.
Доказательство. При любом h ? IT имеем (Ахп, h) = (xn, A*h),
СЛ.
где A* — сопряженный линейный оператор (см. 10.1). Так как х„ •—>х, то
(хп, A*h) —> (x, A*h) ¦= (Ах, А)
ел.
а потому и (Ахп, К) -*• (Ах, К), т. е. Ахп —* Ах.
Следующая теорема дает характеристику вполне непрерывных операто-
операторов в пространстве Н.
Теорема 11.2.1. Для того чтобы аддитивный оператор А, отобра-
отображающий И в самого себя, был вполне непрерывным, необходимо и доста-
достаточно, чтобы каждая слабо сходящаяся последовательность элементов
переводилась оператором А в сходящуюся по норме, точнее, чтобы из
ел.
хп —-> х следовало Ахп —*¦ Ах.
Доказательство, а) Необходимость. Пусть оператор А
ел. ел.
вполне непрерывен и пусть хп —> х. По лемме Ахп —> Ах. Допустим, что
Ахп у* Ах (по норме). Тогда существует такое е > 0, что
\\АхПк-Ах\\>е E)
для бесконечной последовательности индексов п^. С другой стороны, так как
последовательность {хп } ограничена, то множество {Ахп } компактно, а потому
из последовательности {Ахп } можно выделить частичную сходящуюся:
Ахп -*¦ у'. При этом, из неравенства E) следует, что у' Ф Ах. Из сходи-
^1 ел.
мости по норме вытекает слабая сходимость, а потому Axnfl —> у'. Таким
образом, последовательность {Axnlt } имеет два различных слабых предела,
что невозможно. Полученное противоречие доказывает, что Ахп -*¦ Ах.
б) Достаточность. Возьмем аддитивный оператор А, удовлетво-
удовлетворяющий условию теоремы. Пусть ЕсН—произвольное ограниченное
множество. Возьмем уп ? А (Е) (п = 1, 2, . . .) и подберем хп 6 Е так, что
уп = Ахп. Так как последовательность {хп} ограничена, а ограниченное
множество слабо компактно, то из {хп} можно выделить слабо сходящуюся
ел.
подпоследовательность: xn}t —> х, где х — некоторый элемент из И. Тогда,
по условию Axnk ->- Ах, т. е. последовательность {уп^} сходится, что н дока-
доказывает компактность множества А (Е) и, вместе с тем, полную непрерывность
оператора А .
11.3. Спектр вполне непрерывного самосопряженного
оператора
Перейдем к изучению вполне непрерывных самосопряженных
операторов в гильбертовом пространстве Н. При этом здесь мы
уже ни в какой мере не будем опираться на предположение о сепа-
сепарабельности И. Фундаментальным результатом всей теории вполне
И ,'|] СПЕКТР САМОСОПРЯЖЕННОГО ОПЕРАТОРА 311
непрерывных самосопряженных операторов является теорема
о существовании у таких операторов собственных чисел. В част-
частном случае, в пространстве Rn, эта теорема была доказана в 1.13*).
Предварительно докажем лемму.
Лемма 11.3.1. Всякое число, отличное от нуля и входящее в
спектр вполне непрерывного самосопряженного оператора
А (заданного в пространстве Л), является его собственным числом.
Доказательство. Пусть к ф 0 и принадлежит спектру
оператора А. Тогда по теореме 10.6.4 существуют элементы
хп ? Н с нормой \\ хп || — 1, для которых
Axn — kxn—>Q. F)
Так как множество {Ахп} компактно, то существует частичная
последовательность {жПд}, для которой {АхПк} сходится к неко-
некоторому пределу у ? Н. Тогда, благодаря F),
Хпк ~ Т ^АХпк ~ (АХпк ~~ ^Ч)] -* у у-
Следовательно,
или Ау = ку. Кроме того, так как ||a;nft|| = 1, то и -=- у
или || у || = | к | > 0. Таким образом, к — собственное число,
а у — соответствующий ему собственный элемент.
Теорема 11.3.1. Всякий вполне непрерывный самосопря-
самосопряженный оператор А, заданный в пространстве Н, имеет по край-
крайней мере одно собственное число**). При этом, если А ф в, то
он имеет собственное число, отличное от нуля.
Доказательство. Если А = в, то для любого h ? Н
будет Ah = 0/г, т. е. 0 — собственное число оператора А и при-
притом — единственное.
Если же А ф в, то по крайней мере одна из его границ МА
или тА отлична от нуля (см., например, теорему 10.2.1). По тео-
теореме 10.6.6 обе границы принадлежат спектру оператора А,
а тогда по лемме отличная от нуля граница — собственное число.
Чтобы лучше исследовать структуру спектра вполне непре-
непрерывного самосопряженного оператора, докажем еще одну лемму.
Лемма 11.3.2. Пусть число у > 0 и пусть {hn} — какая-ни-
какая-нибудь ортонормированная система, состоящая из собственных
*) Линейные операторы в Rn вполне непрерывны как операторы
в конечно-мерном пространстве.
**) Здесь, конечно, существенно, чтобы // содержало элементы, отлпч-
ние от 6.
312 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
элементов вполне непрерывного самосопряженного оператора А,
причем элемент Л„ соответствует собственному числу Хп и | Хп | >
>у*) при всех п. Тогда заданная система {А^} состоит только
из конечного числа элементов.
Доказательство. Допустим, что заданная система
} бесконечна. При любых п и т (п Ф т) по теореме Пифагора
имеем
|| Ahn - Ahm !| = ' | XJln ~ KJhn || = V^n+^m >
Следовательно, из последовательности {Af^} нельзя выделить
частичной сходящейся. Но это невозможно, так как благодаря
полной непрерывности оператора А множество {Ahn} должно
быть компактным.
Теорема 11.3.2. Собственное подпространство вполне
непрерывного самосопряженного оператора, соответствующее от-
отличному от нуля собственному числу, конечно-мерно.
Доказательство. Допустим, что собственное под-
подпространство i, соответствующее числу X ф О, бесконечно-мерно.
Тогда в нем существует бесконечная система линейно независи-
независимых собственных элементов hn, соответствующих числу X. При-
Применяя к системе {hn} общий процесс ортогонализации F.7), можно
построить бесконечную ортонормированную систему элементов
подпространства -С, т. е. бесконечную ортонормированную систему
собственных элементов, соответствующих числу X. Существова-
Существование же такой бесконечной системы невозможно по лемме 11.3.2.
Теорема 11.3.3. Пусть число у > 0. Для вполне непре-
непрерывного самосопряженного оператора А может существовать
лишь конечное множество собственных чисел X, для которых
Доказательство. Предположим, что существует бес-
бесконечное множество собственных чисел Хп оператора А, для
которых | Хп | > у. Каждому Х„, соответствует некоторый собствен-
собственный элемент hn с нормой ЦА^ || = 1. По теореме 10.4.2 эле-
элементы hn взаимно ортогональны, и мы снова получаем противоречие
с леммой 11.3.2.
Этой теореме можно придать другую форму, если ввести сле-
следующее определение: пусть 5 — произвольное множество точек
на вещественной оси и Хо 6 S; Хо называется изолированной точкой
множества S, если существует окрестность точки Хо, не содер-
содержащая других точек множества S. Пусть теперь Яо ф 0 — соб-
собственное число оператора А. По теореме 11.3.3 существует лишь
конечное множество собственных чисел X, имеющих тот же знак,
*) Среди чисел Хп могут быть, конечно, и одинаковые.
11.4] РАЗЛОЖЕНИЕ ЗНАЧЕНИЙ ОПЕРАТОРА 31 3
что и Хо, и для которых | X | >'—2°- ч Пусть е — расстояние от ^0
до ближайшего из этих X (если множество таких X пусто, то за е
можно взять любое положительное число). Если положить б =
= min { е, —^) (на рис. 18 б = е), то ясно, что в интервале
2
Рис. 18.
(Хо — б, А,о -{- б) нет ни одного собственного числа, отличного от
Хо, а следовательно, благодаря лемме 11.3.1, и вообще нет других
точек спектра оператора А. Таким образом, мы доказали, что все
отличные от нуля точки спектра вполне непрерывного самосо-
самосопряженного оператора суть его изолированные точки.
11.4. Разложение значений оператора по собственным элементам
Пусть А — вполне непрерывный самосопряженный оператор
в гильбертовом пространстве Н, причем А ф 0. Распо-
Расположим все отличные от нуля собственные числа X оператора
А в порядке убывания их абсолютных величин *). Это можно сде-
сделать, например, так. Сначала располагаем в указанном порядке
все собственные числа X, для которых | X \ > 1; таких чисел по тео-
теореме 11.3.3 может существовать лишь конечное число. Далее
помещаем те собственные X, для которых -тг<| X \ < 1, затем —
1 1
те, для которых -^- < | X | < у . и т. д. По теореме 11.3.1, хоть
одно отличное от нуля собственное число существует. Если встре-
встречаются сколь угодно большие п, при которых существуют соб-
1 .. л , ^ 1
ственные числа, удовлетворяющие неравенству ^^m^IM^TT -
то множество S всех собственных чисел счетно, а нуль — его
предельная точка. Но не исключена возможность, что собствен-
собственных чисел будет лишь конечное множество.
Каждому собственному числу X ф 0 соответствует конечно-мер-
конечно-мерное собственное подпространство. Выбирая в каждом из них
какой-нибудь ортонормированный базис и объединяя выбран-
*) Если встречаются два собственных числа, отличающихся друг от друга
только знаком, то порядок их следования для нас безразличен.
314 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
ные элементы в одну систему, получим некоторую счетную или
конечную ортонормированную систему собственных элементов,
которую назовем фундаментальной. По самому построению,
не существует собственного элемента, соответствующего числу
к ф 0, ортогонального всем элементам фундаментальной системы.
Всякий собственный элемент, соответствующий числу X ф О,
есть линейная комбинация некоторых элементов фундаменталь-
фундаментальной системы.
Перенумеруем элементы фундаментальной системы: сначала
занумеруем в любом порядке те собственные элементы, которые
соответствуют наибольшему по абсолютной величине собствен-
собственному числу, затем, продолжая нумерацию, занумеруем элементы,
соответствующие следующему по порядку собственному числу,
и т. д. Обозначим теперь элементы фундаментальной системы
через hn. Собственное число, которому соответствует элемент hn,
обозначим Кп. При этом, так как несколько элементов hn могут
соответствовать одному и тому же X, то возможно равенство
нескольких соседних чисел Кп между собой. Таким образом, фун-
фундаментальной системе собственных элементов {hn} соответствует
последовательность собственных чисел {кп}, для которой
| ?4 | > | Хг | > | h | > • • • > 0.
Эта последовательность содержит все собственные числа опе-
оператора А, отличные от нуля, причем каждое такое число встре-
встречается в этой последовательности столько раз, какова размер-
размерность соответствующего ему собственного подпространства.
Заметим, что построенная нами последовательность собствен-
собственных чисел {кп} определяется по данному оператору однозначно
с точностью до перестановки чисел, равных между собой по абсо-
абсолютной величине (если такие есть). В то же время фундаменталь-
фундаментальная последовательность собственных элементов {hn} зависит
от выбора базиса в каждом собственном подпространстве.
Обозначим через L подпространство пространства И, поро-
порождаемое фундаментальной системой {/г„}, а через М — его орто-
ортогональное дополнение.
Лемма НАЛ. Подпространства Ъ и М суть инвариант-
инвариантные подпространства оператора А.
Доказательство. По теореме 10.3.1 достаточно дока-
доказать инвариантность L. Пусть сначала элемент х ? L имеет вид
i
х= 2 akhnk. G)
Тогда
i i
Ах=-- 2 ahAhn = 2
ft=i ft
11.4] РАЗЛОЖЕНИЕ ЗНАЧЕНИИ ОПЕРАТОРА 315
Если же х — произвольный элемент из L, то х = lim xp, где
хр входят в линейную оболочку множества {/>„}, т- е. имеют вид
G). А тогда АхР ? L и Ах = lim Axp ? ?.
Следующая теорема так же, как 11.3.1, является основной
в теории вполне непрерывных самосопряженных операторов.
Теорема 11.4.1. Для. значений оператора Ах при любом
х ? Н справедливо разложение Фурье по собственным элементам
фундаментальной системы:
Ах = 2 СпК, где сп = (Ах, к„).
п
Доказательство Рассмотрим оператор А на подпро-
подпространстве М, которое по лемме инвариантно. Ясно, что и на М
оператор А — вполне непрерывный и самосопряженный. Если
допустить, что на М оператор А не сводится к нулевому, то по тео-
теореме 11.3.1 в М существует собственный элемент оператора А,
соответствующий отличному от нуля собственному числу. Но
такого собственного элемента, ортогонального к L и, в частности,
ко всем hn, быть не может. Следовательно, Ах = 8 при всех
х 6 М.
Любой х ? Н можно представить в виде х = у -j- z, где у ? L,
z ? М. Тогда Ах = Ay -\- Az = А у, а по лемме Ay ? L. Следова-
Следовательно, Ах ? Ъ при всех х ? Н. Теперь справедливость разложе-
разложения Ах по элементам /^ вытекает из теоремы 6.6.3.
Для коэффициентов сп, используя свойство самосопряжен-
самосопряженности оператора А, получаем следующие формулы:
с„ = (Ах, hn) = (х, А1гп) = (х, Xnhn) = Хп (х, hn). (8)
Теперь мы сможем закончить исследование структуры спектра
вполне непрерывного самосопряженного оператора А ф 0.
Попутно мы уже доказали, что А — оператор с чисто точеч-
точечным спектром.
Действительно, если L = И, то это и значит, что подпростран-
подпространство, порождаемое фундаментальной системой собственных эле-
элементов, совпадает с Н. Если же L ф Н, то М — собственное
подпространство оператора А, соответствующее числу К = 0.
Следовательно, и в этом случае подпространство, порождаемое
множеством всех собственных элементов, совпадает с Н*).
Теорема 11.4.2. Для того чтобы фундаментальная систе-
система собственных элементов {hn} была полна в И, необходимо и доста-
достаточно, чтобы X — 0 не было собственным числом оператора А.
*) В частности, если пространство Н сепарабельно, то из сказанного
легко следует, что в нем можно построить ортонормированный базис, состоя-
состоящий из собственных элементов оператора А. Этот результат отмечался в 1.13
для самосопряженных операторов в Вп.
316 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
Доказательство, а) Необходимость. Если
фундаментальная система {hn} полна, то Ъ = Л, а подпростран-
подпространство 31 состоит из одного нулевого элемента. Но если бы X = О
было собственным числом, то соответствующие ему собственные
элементы, будучи ортогональными всем hn, входили бы в 31,
что невозможно. Следовательно, число К = 0 — не собственное.
б) Достаточность. По ходу доказательства теоремы
11.4.1 мы видели, что Ах = 0 при всех х 6 31*). Следовательно,
если К = 0 — не собственное число, то 31 должно состоять только
из нулевого элемента, а тогда L = Л, и фундаментальная систе-
система полна.
Теперь, учитывая все сказанное в этом и предыдущем пара-
параграфах о спектре оператора А, легко сделать следующие заклю-
заключения:
1) если пространство Н бесконечно-мерно, а оператор А имеет
бесконечное множество собственных чисел, то X = 0, как пре-
предельная точка этого множества, входит в спектр; однако при этом
нуль может принадлежать множеству собственных чисел, а может
и не принадлежать;
2) если пространство Н бесконечно-мерно, но оператор А имеет
лишь конечное множество собственных чисел, то фундаменталь-
фундаментальная система, будучи конечной, не может оказаться полной, а сле-
следовательно, 0 — собственное число; спектр совпадает с множест-
множеством собственных чисел;
3) если пространство Н конечно-мерно, то оператор А имеет
лишь конечное множество собственных чисел. В этом случае легко
видеть, например, из матричного представления оператора в Кп>
что все числа %, отличные от собственных, регулярны, следова-
следовательно, спектр опять совпадает с множеством собственных чисел;
число 0 входит в спектр тогда и только тогда, когда оно является
собственным **).
11.5. Решение уравнения (А — %1)х = у
Считая по-прежнему оператор А вполне непрерывным и само-
самосопряженным в гильбертовом пространстве Н, рассмотрим урав-
уравнение
(А-кГ)х = у, (9)
где / — тождественный оператор. Параметр % будем считать
*) Впрочем, это вытекает и непосредственно из формулировки теоре-
теоремы 11.4.1 и из того, что подпространство М инвариантно.
**) Это будет в том случае, когда число элементов фундаментальной
системы меньше размерности пространства Н.
П..,] РЕШЕНИЕ УРАВНЕНИЯ (A—U)x=y 317
отличным от нуля. Тогда, по лемме 11.3.1, значения X могут
быть только регулярными или собственными числами оператора А.
Если X — регулярное, то, по определению, совокупность Vi
значений оператора А — XT совпадает с Н и существует обрат-
обратный линейный оператор (А — XI)'1. Таким образом, уравнение
(9) в этом случае имеет единственное решение при любом у ? Н.
В частности, однородное уравнение
(A — XI)x = Q A0)
имеет только очевидное нулевое решение.
Пусть X — собственное число оператора А, L% — соответ-
соответствующее ему собственное подпространство и М% — ортого-
ортогональное дополнение к L\. Подпространство Mi (вместе с Li) инва-
инвариантно для оператора А (см. 10.4). Но для оператора А,
рассматриваемого в Л1х, число X уже не будет собственным, а сле-
следовательно, будет регулярным. Поэтому оператор А — XI, рас-
рассмотренный на Мх, обратим и уравнение (9) имеет решение при
любом у ? М%. С другой стороны, для любого х ? Н имеем х = ж4 +
+ х2, где Xi ? Lx, x2 ? Mi, и так как (А — XI) я4 = Ах^ — Хх^ = 9,
то (А — XI) х = {А — XI) хг ? М%. Поэтому уравнение (9) имеет
решение только при у ? М\. При этом решение оказывается
не единственным. Именно, если х — какое-нибудь решение, соот-
соответствующее элементу у в правой части, то и при любом h ? L^
(А — ХТ)(х + И) = у, т. е. х + h — тоже является решением.
В частности, решением однородного уравнения A0) будет любой
Таким образом, мы получили следующие две теоремы:
Теорема 11.5.1. Для того чтобы уравнение (9) с X ф 0 име-
имело единственное решение при любом у ? Н, необходимо и достаточ-
достаточно, чтобы однородное уравнение A0) имело только нулевое решение.
Теорема 11.5.2. Если Я Ф 0—собственное число опера-
оператора А, то для разрешимости уравнения (9) необходимо и до-
достаточно, чтобы у был ортогонален собственному подпростран-
подпространству оператора А, соответствующему числу Я,
Это — абстрактная форма теорем, доказанных Фредгольмом
для интегральных уравнений.
Перейдем к самой технике решения уравнения (9) с помощью
фундаментальной системы {hn} собственных элементов оператора
А. Пусть, сначала, X — не собственное число оператора А.
По теореме 11.4.1 Ах = ^спПп, где коэффициенты сп = Я„ (х, hn)
п
являются пока неизвестными. Из уравнения (9) Ах = у + Хх
или
± ±(У Л A1)
318 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
Вследствие дистрибутивности скалярного произведения имеем при
любом т
Ст=к (х, ihn) - [ 2с (/г/г) (^ л) ] ¦=
откуда
т ~ 1 1 1 /•
Подставляя найденные выражения коэффициентов в формулу A1),
получим
Если же Я — собственное число, а у 1 !>., то, записывая
искомый а; по формуле A1), мы тем же способом, что и выше,
найдем коэффициенты сп при всех п, для которых Хп ф >.. Коэф-
Коэффициенты же сп при тех п, для которых Л„ = А., остаются про-
произвольными. Это согласуется с тем фактом, что, как показано
выше, при собственном Я решение не может быть единственным.
11.6. Интегральные уравнения с симметричным ядром
В этом параграфе мы сможем, в известном смысле, завершить
исследование интегрального уравнения Фредгольма второго рода
ь
;r(s) = |i [K(s, t)x(l)dt + f(s)._ A3)
г,
а
Ядро К (s, t) предполагаем непрерывными симметричным. Тогда, как
ь
мы знаем из 10.7 и 11.1, интегральный оператор \ К (s, t) x (t) dt,
а
который мы обозначаем буквой К, — самосопряженный и впол-
вполне непрерывный в гильбертовом пространстве L2. Уравнение A3)
перепишем в виде
Если ц Ф 0, то это уравнение равносильно
Кх х— /.
*) Заметим, что Хт — X Ф 0 при всех т, так как X не равно нп одному
из собственных чисел.
11.6] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С СИММЕТРИЧНЫМ ЯДРОМ 319
1 1
Полагая % = — , у =¦- /, получаем уравнение
(К-М)х^у,
которое и было исследовано в предыдущем параграфе.
Будем считать, что оператор К ф Э. Легко показать, что
для этого достаточно (и необходимо), чтобы функция К (s, t)
не была тождественно равна нулю во всем квадрате. Действи-
Действительно, пусть, например, К (s0, t0) > 0. Тогда, по непрерыв-
непрерывности ядра существует такое б > 0, что К (s0, t) > 0 при
t0— б < t <C to-]-d. Подберем непрерывную функцию х (t) так,
что х (t) > 0 при t0 — б < t <z t0 -\- б и а; (<) = 0 вне этого
интервала. Тогда, если у = Кх, то
f/(so)= J K_(s0, t)x(t)dt>0
to-6
и, следовательно, y^=Q.
В 10.7 мы специально останавливались на однородном интег-
интегральном уравнении Фредгольма. Там было показано, что харак-
характеристические числа интегрального уравнения с ядром К (s, t)
и собственные числа оператора К взаимно обратны, а собственные
функции интегрального уравнения и собственные элементы интег-
интегрального оператора одинаковы. Используя результаты 11.4, мож-
можно построить фундаментальную систему собственных функций
однородного интегрального уравнения {hn (t)}. Соответствую-
Соответствующие им характеристические числа интегрального уравнения суть
Р-п — г~ > гДе ^л — собственные числа оператора К. При этом,
Ал
так как Хп перенумерованы в порядке убывания абсолютной
величины, то
,ui ] < V21 < I М-з | < • • •
По теореме 10.4.3 все собственные числа Хп оператора К
заключены между его границами Мк и тк. Поэтому при всех п
Отсюда следует, что | \in | > rr^j, при всех п. Так как \i = 0 не
может быть характеристическим числом интегрального урав-
уравнения, то, таким образом, все характеристические числа интеграль-
, 1
ного уравнения удовлетворяют неравенству | ^г | ^ . .
Теоремы И.3.2, 11.5.1 и 11.5.2, переформулированные при-
применительно к интегральным уравнениям вида A3), носят название
320 ВПОЛНЕ НЕПРКРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
основных теорем Фредгольма. При этом следует заметить, что
хотя изложенные нами выше результаты применимы только
к уравнениям с симметричным ядром, однако Фредгольм построил
свою теорию для интегральных уравнений вида A3) с любым
ядром. Чтобы получить методом функционального анализа тео-
теоремы Фредгольма для уравнений с несимметричными ядрами,
нужно изучить собственные числа и собственные элементы вполне
непрерывных операторов в произвольных банаховых простран-
пространствах. Такой общий подход к теории Фредгольма был дан в рабо-
работах Ф. Рисса.
Так как по лемме 7.4.1 значения оператора Кх при всех х ? L2
суть непрерывные функции, то при непрерывном свободном члене
/ (s) уравнения A3) и всякое решение последнего непрерывно.
В частности, как мы знаем, все собственные функции непрерывны.
Теорема 11.4.1 означает, что всякая непрерывная функция
у (s), имеющая вид
ь
y(s)=^K(s,t)x(t)dt, A4)
а
раскладывается в ряд Фурье по собственным функциям /^ (<)
фундаментальной системы
г/=2с«л«. A5)
п
причем ряд сходится в среднем. Однако для интегральных опера-
операторов вида A4) этот результат может быть усилен, а именно имеет
место следующая теорема:
Теорема 11.6.1 (Д. Гильберт — Э. Шмидт) *). Для всякой не-
непрерывной функции у (s), представимой по формуле A4), где
х ? L2, справедливо разложение на отрезке [а, Ь] в абсолютно
и равномерно сходящийся ряд Фурье
У (S) = 2 Cnhn (S) A6)
п
по собственным функциям интегрального оператора К **).
Доказательство. Возьмем произвольное s на отрезке
[а, Ь] и докажем сходимость ряда
2 \cnhn(s)\. A7)
*) Э. Шмидт A876—1959) — немецкий математик.
**) Ясно, что эта теорема представляет усиление теоремы 11.4.1 только,
если фундаментальная система {hn (t)} бесконечна и именно этот случай
мы дальше п будем иметь в виду.
11.6] ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ С СИММЕТРИЧНЫМ ЯДРОМ 321
По формуле (8) сп = Хп (х, hn) или сп = Anan, где через ап
обозначены коэффициенты Фурье элемента х относительно систе-
системы {hn}. По определению собственных функций
h
Knhn (s) = J К (s, t) hn (t) dt,
a
т. e. %.nhn (s) при фиксированном s суть коэффициенты Фурье
функции К (s, t) как функции от аргумента I. По неравенству
Бесселя (см. 6.6)
ОО 00 Ь
2 о» < IIх iiz- S я»л» (s)
n=l n=l
Из сходимости двух последних рядов вытекает, как показано
в 2.3, сходимость ряда 2 | °л | | К \ \hn(s)\, т. е. ряда A7).
п=1
Теперь оценим остаток ряда A7). Если М = та.х\К (s, t)\, то
ь
K2(s, i)^<M2(fo — a).
По неравенству Коши имеем при любом р
Так как ряд 2 a« сходится, то
П=р р -> oo
При этом правая часть A8) не зависит от s. Следовательно,
остаток ряда A7), а вместе с ним и остаток ряда A6) равно-
мерно стремится к нулю. Остается доказать, что у (s) во всех
точках совпадает с суммой ряда A6).
Действительно, если положить
2 (S) = S
п=1
21 Б. 3. Вулих
322 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
то из равномерной сходимости ряда и непрерывности всех hn (s)
будет вытекать непрерывность z (s). Но так как равномерная
сходимость влечет сходимость в среднем, то z = 2 cnhn и в смысле
сходимости по норме в ?А Сопоставляя это с A5), видим, что
у = z, т. е. у (s) = z (s). Теорема доказана.
Теорема Гильберта — Шмидта вместе с теоремой 11.3.1 играет
основную роль в теории интегральных уравнений с симметрич-
симметричным ядром.
Легко понять, что ряды в формулах A1) и A2), полученных
в 11.5 для решения абстрактного уравнения (9), в случае построе-
построения их для интегрального уравнения A3) окажутся сходящимися
равномерно и абсолютно.
11.7. Применение интегральных операторов к краевым задачам
для уравнения Штурма — Лиувилля
На отрезке a^Ct^Cb рассмотрим неоднородное уравнение
Штурма — Лиувилля
(')'?)-? @*@-М0 = А0> A9)
отличающееся от уравнения A9) из 10.8 только наличием свободно-
свободного члена / (<). Будем предполагать, что в отношении непрерыв-
непрерывности и дифференцируемости р (t) и q (t) удовлетворяют усло-
условиям, указанным в начале 10.8, и что, кроме того, р (t) > 0 на
всем отрезке [а, Ь]. Свободный член f (t) также считаем непре-
непрерывным. Подчиним решения уравнения A9) тем же краевым
условиям, что и в 10.8:
х(а)^х (Ь) = 0. B0)
Используем обозначение оператора U, введенное в 10.8, считая
этот оператор заданным по-прежнему на множестве D функций
х (t), имеющих на отрезке \а, Ь] непрерывные производные 1-го
и 2-го порядка и удовлетворяющих краевым условиям B0) *). Тогда
уравнение A9) можно переписать в виде
Ux — Xx^.f. B1)
Напомним, что значения оператора U суть непрерывные функции.
*) Так как из A9) следует, что
р' (t) х' @+<7 @ х @ + U @ 4- / @
х (<)_ W
то на основании поставленных условий у всякой функции х (t), удовлетво-
удовлетворяющей уравнению A9), производная 2-го порядка х" (t) должна не только
существовать, но и быть непрерывной.
11.7] ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ 323
Поставим дополнительное условие, чтобы к — 0 не было
собственным числом оператора U. В этом случае оператор U
называют неособенным. Это значит, что на множестве D равен-
равенство 'Ux = 8 имеет место только при х = 8*). Займемся сначала
решением уравнения B1) при X = 0, т. е. уравнения
Ux -= /. B2)
Так как к = О — не собственное число оператора U, то на мно-
множестве значений последнего определен обратный оператор U
(см. 8.7, предложение в)). Следовательно, уравнение B2) при
любом свободном члене не может иметь более одного решения.
Мы покажем, что совокупность значений оператора U состоит
из всех непрерывных функций на отрезке [а, Ь] и, таким обра-
образом, уравнение B2) при любом непрерывном свободном члене
имеет единственное решение из множества D.
Обозначим через и (t) и v (t) решения однородного уравнения
?(О*(О = о. B3)
отличные от тождественного нуля и удовлетворяющие условиям
и (а) = 0 и v (Ь) = 0, соответственно **). Эти решения линейно
независимы, так как, в противном случае, они отличались бы
друг от друга постоянным множителем и мы имели бы, например,
и F) = 0. А тогда и ? D, и ф 8 и Uu = 6, что невозможно, так
как оператор U предположен неособенным. Вследствие линей-
линейной независимости и и v их вронскиан w (t) ф 0. Вычислим
w (t), пользуясь формулой Остроградского — Лиувилля:
w (t) =woe *р О = woe~^ p @ = ^ , B4)
где wn—некоторая постоянная. При этом, так как w (t) Ф 0, то и
0
*) Последнее условие выполняется, например, если g (t) <; 0. Действи-
Действительно, из формулы B2) в 10.8 следует, что при д (t) <; 0
ь
(Ux, z) > ^ px'z dt.
а
Но если х Ф 0, то из условий B0) следует, что х (t) не может быть постоян-
постоянной, а тогда х' (t) не может быть тождественным нулем. Поэтому, благодаря
ь
условию р (г) > 0, интеграл \ рх'2 dt > 0, следовательно, и (Ux, x) > 0,
а
а поэтому равенство Ux = 0 возможно только при х = 0.
**) Наличие таких решений гарантируется теоремой о существовании
решений для линейных дифференциальных уравнений 2-го порядка.
21*
324
ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
[ГЛ. XI
Теперь определим в квадрате a*Cs, t^Cb функцию двух пере-
переменных, называемую функцией Грина, полагая
Так как и и v суть непрерывные функции своих аргументов, а на
диагонали квадрата, т. е. при s = t, оба выражения функции G
совпадают, то функция Грина непрерывна во всем квадрате.
Кроме того, G (t, s) = G (s, t) при любых s и t. Действительно,
если, например, t<s, то G (t, s) вычисляется по первой формуле,
a G (s, t) — по второй (с перестановкой аргументов s и f), и в обоих
случаях получается одно и то же.
Составим интегральный оператор G] с функцией Грина в каче-
качестве ядра, полагая для любого / 6 ?2 (имеется в виду Г.2, пост-
построенное на [а, Ъ\)
*(«)= \ G(t, s)f(s)ds;
B5)
назовем оператор G оператором Грина. Это — вполне непрерыв-
непрерывный самосопряженный оператор того типа, который был иссле-
исследован в предыдущем параграфе. Покажем, что если / (s) — непре-
непрерывная функция, то х = Gf 6 D и удовлетворяет уравнению B2).
Таким образом оператор Грина, рассмотренный только на под-
подмножестве непрерывных функций из ?2, и есть обратный опера-
оператор U'1.
Так как, полагая поочередно t — а и t = Ъ, имеем за счет
условий для и ж v
G (a, s)= и (a) v Is) = 0,
«'о
G(b, s)=^ —-u(s)v(b) = 0,
то из B5) следует x (a) = x (b) = 0, т. е. x(t) удовлетворяет крае-
краевым условиям B0).
Далее подставляя в B5) выражения функции Грина, имеем
11.7] ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ 325
Дифференцируя по t, находим
х it) = - ± [ v' (t) J и (s) / (s) ds + v(t)u (t) f (I) +
a
Ь
+ u' (t) J p (s) / (s) ds~u(t) v (t) f (*)]*) =
t ь
^'®\ u(s)f(s)ds + u'(t)\ v (s) f (s) ds] .
a t
Так как и' (t.) и v' (l) непрерывны, то из полученного выраже-
выражения видно, что х (t) непрерывна. Далее, аналогичным образом
находим
t
(р @ х @I =-^{(P(t) V @)' \ и (s) / (s) ds +
а
Ь
+ (р (о и' @)' J у (s) / («) cZs + p @ / @1»' @ " @ -и' @ " @1} •
В частности, из этой формулы можно найти выражение для #"(?)>
из которого будет видно, что х" (t) непрерывна, а потому x^D.
Теперь, вычисляя Ux, мы получим
u(s)f(s)ds +
+ [(р @ и' (t))' + q(t)u(t)] ^v (s) f (s) ds +
+ p(t)f(t)[v'(t)u(t)-u'(t)v(t)]}
Так как и (t) и v (t) удовлетворяют уравнению B3), то выраже-
выражения в двух первых квадратных скобках обращаются в нуль.
*) Дифференцирование интеграла от непрерывной функции <р (s) по ниж-
нижнему пределу производится по формуле
ь
326 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
В последних же квадратных скобках стоит вронскиан
_ и (/) v (/)
W {t> - и' @ v' (О
и потому, благодаря формуле B4),
—¦уг(р(О*'(О)-?(О*(О =
т. е. Ux = /. Разрешимость уравнения B2) при любом непрерыв-
непрерывном свободном члене доказана.
Перейдем к уравнению A9) или B1) с произвольным А,. Пере-
Перенося член — Хх к свободному члену, запишем уравнение B1)
в виде
B6)
Если x?D есть решение уравнения B6), то, по доказанному,
U1(k f) т. е.
B7)
и обратно, если х удовлетворяет уравнению B7), то х ? D и являет-
является решением уравнения B6). Таким образом, отыскание решения
уравнения B6), т. е. отыскание решения краевой задачи для
уравнения A9) при условиях B0), равносильно нахождению
решения уравнения B7). Последнее же можно записать в инте-
интегральной форме:
ь
B8)
где
ь
\(t, s)f(s)ds
играет роль известного свободного члена. При этом уравнения
B6) и B8) оказываются однородными лишь одновременно. Имен-
Именно, если / = 9, то ясно, что q> = 0. Если же, при условии непре-
непрерывности функции / (s), ф = 8, а по доказанному выше из ф = Gf
вытекает, что / = СЛр, то и / = 8. Отсюда следует, что собствен-
собственные числа и соответствующие им собственные функции опера-
оператора Штурма — Лиувилля U совпадают с характеристическими
числами и соответствующими им собственными функциями инте-
интегрального уравнения B8). Отличные же от нуля собственные
числа оператора Грина получаются из собственных чисел опе-
оператора U переходом к обратным величинам. Впрочем, ниже будет
11.7] ПРИМЕНЕНИЕ ИНТЕГРАЛЬНЫХ ОПЕРАТОРОВ 327
установлено, что таким путем получаются все собственные числа
оператора Грина, так как к = 0 не является его собственным
числом.
Теперь докажем следующую теорему, установленную В. А. Стек-
ловым в конце XIX столетия более сложным путем:
Теорема 11.7.1. Всякая функция из множества D раскла-
раскладывается в абсолютно и равномерно сходящийся ряд по собствен-
собственным функциям оператора U.
Доказательство. Пусть х ? D. Положим Ux = /.
Тогда / (t) — непрерывная функция, а х = Gf. Следовательно,
по теореме Гильберта — Шмидта A1.6.1) функция х (I) раскла-
раскладывается в абсолютно и равномерно сходящийся ряд по собствен-
собственным функциям оператора G. Так как при этом используются
собственные функции, соответствующие отличным от нуля соб-
собственным числам, то, они совпадают с собственными функциями
оператора U, и теорема доказана.
Покажем, что множество D всюду плотно в пространстве
L2, построенном на отрезке [а, Ь]. Возьмем произвольный x2
и зададим е > 0. Найдется такой у ? С^г, что \\х — у || <
Пусть Af=max| у (t) | на отрезке [а, Ъ\. Подберем б > 0 ( б <—~ J
так что 6-М|/2б < е, и положим
z(t) = y(t.) при а + 6<г<Ь—б,
а в промежутках (а, а + б) и (Ь — б, Ь) определим z(t) по закону
линейного интерполирования. Тогда z (t) непрерывна, | z (t) | < М и
-__ _
Ь-6
Га
= l/
По теореме Вейерштрасса существует такой алгебраический
полином РA), что на всем отрезке а<?<&
\z{t)-P{t)\<- e
Так как z (a) = z F) = 0, то| Р (а) I, I Р (Ь) I < —-L= . Постро-
6/')а
1
им линейную функцию g (t) = at -\- р так, что g (а) = Р (а),
*) Мы снова опираемся на тот факт, что множество непрерывных функ-
функций всюду плотно в пространстве ?2.
328 ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ [ГЛ. XI
g (Ь) = Р (Ь). Тогда | g (t) |< I при всех t 6 [а, Ъ\. Если
о у о — а
теперь положить Q (t) = P (t) — g (t), то полином Q (t) будет
функцией из множества D и при этом
а тогда \\z — (?||<7г- Следовательно,
что и доказывает плотность множества D.
Из доказанной плотности множества D в пространстве L2 и из
теоремы 11.7.1 следует, что линейная оболочка фундаменталь-
фундаментальной системы собственных функций оператора G (или, что — то же
самое, оператора U) всюду плотна в L2. Тогда подпространство,
порождаемое фундаментальной системой, совпадает с L2. Поэтому
система собственных функций неособенного оператора Штурма —
Лиувилля полна в L2. Из этого же факта, по теореме 11.4.2, выте-
вытекает, что К = 0 — не является собственным числом оператора
Грина.
ГЛАВА XII
ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬНЫХ
УРАВНЕНИЙ
12.1. Замена точного уравнения «приближенным»
Одним из важных приложений функционального анализа
является исследование приближенных методов решения различ-
различных уравнений, в первую очередь — дифференциальных, инте-
интегральных, в которых искомыми объектами являются функции,
а также и других, например систем алгебраических уравнений,
В настоящей главе рассмотрим некоторые методы приближен-
приближенного решения функциональных уравнений. Для упрощения изло-
изложения мы в ряде теорем вводим дополнительные предположения,
от которых можно было бы освободиться. Однако, несмотря
на наличие таких дополнительных ограничений, мы все же смо-
сможем дать ряд интересных приложений общих теорем к конкрет-
конкретным уравнениям. Начнем с рассмотрения одного общего приема
решения уравнений в банаховых пространствах, основанного
на применении теоремы 8.7.4.
Пусть нам задано уравнение
(I-U)x = y, A)
где U — линейный оператор, отображающий банахово простран-
пространство X в самого себя, а / — тождественный оператор, заданный
в том же пространстве. Как известно, в технике часто приме-
применяется следующий прием приближенного решения уравнений.
Если данное уравнение слишком сложно, то его упрощают тем
или иным способом, затем решают полученное таким образом
«приближенное» уравнение, а решение последнего и принимают
за приближенное решение исходного уравнения. Чтобы обосно-
обосновать такой метод, рассмотрим второе уравнение
{I-V)x = y, B)
где V — тоже линейный оператор, отображающий X в X, кото-
которое и будет играть роль «приближенного» уравнения.
330 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛьН. УРАВНЕНИЙ [ГЛ. XII
Будем считать, что
\\У-Щ\<6,
где 6 — некоторая постоянная.
Теорема 12.1.1. Если оператор I — U обратим, а
8 || (/-?/)-* ||<1,
то оператор I — V также обратим. При этом, если х -= (/ — U)-1y,
a x — (I— V)~1y при одном и том же у, то
||z-z||<6||(/-V)-4IH|. C)
Доказательство. Первая часть этой теоремы является
почти дословным повторением теоремы 8.7.4 (с заменой U на
/ — U, V на I — V). Для доказательства неравенства C) заметим,
что
х = (I-V)-ly = (I— 7) (T — U)x ¦= (/- F) [(/— V) + G — 17I х =
= (/ — V)-1 (I — V) x+ {I— V)-1 G — U) x =
^x+{I-Vyl{V-U)x.
Отсйда
x-x={I-Vyl{V-U)x,
следовательно,
||x-x||<||(/-7)-4| \\V-U\\ \\x\\<b\W-V)-*\\ \\x\\.
Доказанная теорема гарантирует существование решения
уравнения B) при любом у, если оператор V «достаточно близок»
к U. Но эта теорема еще не дает возможности оценить погреш-
погрешность, получающуюся при замене х на х, так как в неравенство
C) входит норма ||а;|| неизвестного нам точного решения урав-
уравнения A). Такую оценку дает следующая теорема:
Теорема 12.1.2. При обозначениях, введенных в предыду-
предыдущей теореме, если б || (/ — V)'11|<<?< 1, то
IMi. D)
Доказательство. С помощью неравенства C) имеем
\\x-x\\<q\\x\\<q(\\x-x\\ + \\x\\)=.q\\x-x\\ + q\\x\\.
Отсюда A — q) \\ х — х || < q \\ x \\, что равносильно неравен-
неравенству D).
12.2] ЗАМЕНА ЯДРА НА ВЫРОЖДЕННОЕ 331
В следующих двух параграфах мы дадим приложения дока-
доказанных теорем.
Советским математиком Л. В. Канторовичем построена общая
теория замены данного уравнения «приближенным», которое
может быть задано и не в том же самом пространстве, где решается
данное уравнение *).
12.2. Замена произвольного интегрального- уравнения
на уравнение с вырожденным ядром
Рассмотрим интегральное уравнение Фредгольма
ь
х{з)= JiC(», t)x(l)dl + f(s) E)
а
с непрерывным ядром и непрерывным свободным членом. Ядро
К (s, t) называется вырожденным, если оно имеет вид
i=l
т. е. если оно представимо в виде суммы конечного числа слагае-
слагаемых, каждое из которых есть произведение функции от одной
переменной s на функцию от одной переменной t.
Решение уравнения с вырожденным ядром оказывается гораздо
более простой задачей, чем решение уравнения с произволь-
произвольным ядром. Именно, если функция х (s) — решения уравнения E),
то подставляя F) в E), мы получим
п Ъ
i=i a
ИЛИ
z @=2 aw (»)+/(»). (')
где
ь
щ = [ ifi (О Х @ dt (i ---1, 2, . .., re).
а
Формула G) определяет структуру искомой функции х (t), и зада-
задача сводится к отысканию п неизвестных коэффициентов at. Послед-
Последние же могут быть найдены из некоторой системы линейных алгеб-
алгебраических уравнений. Мы не будем выводить эту систему в общем
*) См. Л. В. Канторович. Функциональный анализ и прикладная
математика. Успехи матем. наук III A948), вып. 6. 89—185.
332 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬН. УРАВНЕНИЙ [ГЛ. XII
виде, а поясним ниже метод определения коэффициентов а,- на
примере. Поскольку решение уравнения с вырожденным ядром
сводится к алгебраической задаче, естественно использовать
для приближенного решения интегрального уравнения с про-
произвольным ядром метод его замены на уравнение с вырожден-
вырожденным ядром.
Пусть теперь ядро в уравнении F) — произвольное непре-
непрерывное, а К^ (s, t) — вырожденное ядро (тоже — непрерывное).
Обозначая через К и Kt интегральные операторы, определяемые
ядрами К (s, t) и Кх (s, t), соответственно, запишем уравнение E)
в виде
х — Кх = /
и заменим его на уравнение
х — Ktx = f.
В качестве пространства X, в котором будут рассматриваться
эти уравнения, берем С.
Если max \K(s, t) — Kv{s, 1)\<Ьи то (см. 8.3)
|| Ki -К ||< б, где б -б, (Ь -а). (8)
Следовательно, если 6j достаточно мало, то при условии обра-
обратимости оператора I—K мы сможем воспользоваться теоремами
12.1.1 и 12.1.2.
Возьмем в качестве примера уравнение
^V^ (9)
11 1
Так как 0< sin (si)<sin-т-<-т- при всех 0<s, t<; —, то для интег-
111
ралыюго оператора К с ядром sin (si) норма ||Х||<-7—^=т"- Тогда по
теореме 8.7.3 оператор I—K обратим. При этом || (/—К)~х \\ <
8
Разложим sin {st) в ряд Тейлора по степеням st:
sin (st) = st—1-S3j3 + _L S5<5_... A0)
1 / s ^
*) Так как lim — ( cos ——1 )=lim =0, то мы считаем,
,-»o s V г У s-»o s
что при s = 0 свободный член равен единице, что не нарушает его непре-
непрерывности.
12.2] ЗАМЕНА ЯДРА НА ВЫРОЖДЕННОЕ 333
и за приближенное представление ядра sin (st) примем первый член ряда,
т. е. st. Ядро TsTj (я, t) = st — вырожденное. Так как ряд A0) —знакочере-
—знакочередующийся с монотонпо убывающим по абсолютной величине общим чле-
членом, то
А тогда по (8)
1 18
Беря б = =^5 , имеем б II (/ —X) ||<=кз--=-< 1, а потому применима тео-
/DO /Do /
рема 12.1.1, и уравнение с вырожденным ядром Kt (s, t) = st
2
x(s) = ^ stx(t)dl f/(s) A1)
0
разрешимо при любом свободном члене.
Решаем уравнение A1). Переписывая его в виде
4
z («)•-=« \ tx{l)dt-Ui (s)
0
1
и полагая a= \ tx (t) dt, имеем
b
a:(s) = as + /(i). A2)
Для определения a подставим это выражение в уравнение A1). Получим
_1_
2
as-\-1 {s)--s \ t[at-\-i (t)] dt ~f (s),
b
откуда, после очевидных преобразований находим, что
J_
2
Формула A2) при найденном значении а и дает решение уравнения (И)
и тем самым определяет оператор (/ — ^i). Оценим его норму. Так как
! «/.(') I <J II /II ПРИ 0 < t <i-, то из A3) имеем
24 1 1 fi
l«!<ll/l! ^ll/ll
334 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬН. УРАВНЕНИЙ [ГЛ. XII
Поэтому, если ж = (/—AT,)/, то
т. е. || х || <; 2о II / II- Это и означает, что || (/—Kt)~x II <! «ч • Отсюда видно,
что при оценке погрешности можно пользоваться теоремой 12.1.2.
1 /" t \
При заданном свободном члене /(<) = l-j ( cos-^- —1 1 легко вычис-
лить, что а = 0,126 с точностью до 0,001. Тогда решение уравнения A1)
примет вид
1
Раскладывая cos -^- в ряд Тейлора, получим
Если сохранить только первые два члена, то искомое приближенное реше-
решение примет вид
ж~(«) «к 1+ 0,001s.
При этом погрешность, получаемая за счет отбрасывания остальных чле-
членов, не превосходит . , что < ^-- . Общая погрешность в выраже-
выражении х (s), с учетом округления а, меньше 0,001. Так как второй член 0,001s <;
«J 0,0005, т. е. меньше, чем уже допущенная погрешность, то, если мы отбро-
отбросим и этот член и положим х (s) гы 1, то можно будет ручаться, что погреш-
погрешность в последнем выражении х (s) меньше 0,0015. Отсюда следует, что |[ ж Ц <
< 1,0015.
Теперь по неравенству D) оценим отклонение приближенного решения
— 1 26
х (s) от точного х (s). В нашем примере можно взять д = :rS5 • ^ < 0.0015.
Тогда т^-^ТШ" II"» — ж I! < 0.002, т. е. | 7(«) — х (s) | < 0,002 при
всех s *). Отсюда следует, что точное решение х (s) уравнения (9) отличается
от найденного с округлением решения х (s) sss 1 уравнения с ядром si меньше
чем на 0,0035, т. е.
0,9965 < ж («)< 1,0035.
Предлагаем читателю проверить непосредственной подстановкой, что
х (s) = 1 является в действительности точным решением уравнения (9).
*) В этом неравенстве имеются в виду точные значения функции х (s),
удовлетворяющей уравнению A1), без учета произведенного округления.
12.3] РЕШЕНИЕ СИСТЕМ ПО МЕТОДУ РЕДУКЦИИ 335
12.3. Решение бесконечных систем линейных алгебраических
уравнений по методу редукции
Рассмотрим систему
&- 2 а**?А = тц (* = 1, 2, ...) A4)
с бесконечным множеством неизвестных Нг. Метод редукции
заключается в том, что решаются усеченные конечные системы
Sj-S «i*?* = 4« (i = i, 2, ..., п). A5)
Если при любом достаточно большом п система A5) имеет един-
единственное решение при заданных свободных членах т]г, а при
п -»- с» решение усеченной системы стремится по расстоянию
в некотором пространстве числовых последовательностей к реше-
решению системы A4), то говорят, что в этом пространстве метод
редукции для системы A4) сходится. В настоящем параграфе
мы докажем одну теорему о сходимости метода редукции.
Будем считать, что свободные члены цг образуют последо-
последовательность у = {4i} ? I2- Далее предположим, что матрица
(aik) удовлетворяет условию
Тогда, как мы знаем из 11.1, эта матрица определяет вполне
непрерывный матричный оператор А в Р. Ограничиваясь отыска-
отысканием решений х = {?,}, также принадлежащих I2, запишем
систему A4) в виде
A — А)х = у. A6)
Предположим еще, что матрица (а^) симметрична. Тогда опе-
оператор А самосопряжен. Впрочем, доказываемая ниже теорема
может быть установлена и без этого предположения.
Теорема 12.3.1. Если при сделанных предположениях
система A4) имеет в пространстве I2 единственное решение при
любом у = {t]j}6 I2, гпо метод редукции для системы A4) схо-
сходится в этом пространстве.
Доказательство. Так как по условию системы A4)
или, что то же самое, уравнение A6) имеет единственное решение
при всяком у ? I2, то число X = 1 не может быть собственным
числом оператора А (см., например, теорему 11.5.2). Тогда,
336 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬН. УРАВНЕНИЙ [ГЛ. XII
по лемме 11.3.1, оно регулярно, т. е. обратный оператор (/ — А)'1
задан на всем I2 и линеен *).
Введем в пространстве Р линейные операторы Ап (п = 1,
2, . . .), уже рассмотренные в 11.1, определяемые формулами
оо
?i= S aihlk При 1 = 1, 2, ..., П,
?; = 0 При 1^>П.
В 11.1 было доказано, что Ап^-А.
Если теперь задать любое 6 > 0, то при всех достаточно
¦больших п неравенство \\ Ап — А || < 6 будет выполнено. Поэто-
Поэтому, если 6 выбрано так, что 6 || (/— Л)1|<; g << 1, то к урав-
уравнению A6) можно применить теорему 12.1.1, приняв в качестве V
любой Ап с достаточно большим номером п. При этом по теоре-
теореме 8.7.4
Lyl)-i||. A7)
Тогда, если при любом у?12 положить х = A— А)'1 у, а 4 =
— (/ — An)'1 у, то по неравенству C)
при всех достаточно больших п, следовательно, ?*—>х.
Теперь по заданному у = {т],} составим у'п — {т](п)}, гдег]И = г];
при i = l, 2, ..., п, т](п'= 0 при i^>n. Затем положим х'п--
— (I — Ап)~х у'п. Тогда с помощью A7) имеем
Но у'п—*у, а следовательно, х'п — я*—>Э и х'п—>х.
Из определения хп следует, что его координаты получаются
как решение системы уравнений
00
Ь — 2 aiklk = Щ при i = l, 2, ...,п,
А = 1
Ь = 0 при 1 = п-'г1, п + 2, ...,
а эта система равносильна системе A5), дополненной уравнениями
I; = 0 при i > п.
*) Линейность оператора (Г— А)~1 может быть установлена более слож-
сложным путем и без предположения о самосопряженности оператора А. Поэтому
теорема и оказывается справедливой без требования симметричности
матрицы (а;;,).
12.4] МЕТОД РИТЦА 337
Таким образом, если решения (|ь ?2> ¦ • •, In) усеченных
систем A5) дополнить с помощью нулей до элементов
(?j, \i, . . ., \п, О, 0, . . .) из ?2, то получится последователь-
последовательность элементов х'п, сходящаяся по норме к решению системы A4).
Тем самым доказана сходимость метода редукции.
12.4. Метод Ритца
Вся остальная часть этой главы будет посвящена уравнениям
в гильбертовом пространстве //. В данном параграфе мы займемся
уравнениями вида
Ах-=у. A8)
Установим сначала предварительные результаты, позволяю-
позволяющие при определенных условиях сводить решение уравнения A8)
к отысканию минимума некоторого функционала.
Самосопряженный оператор А называется положительно опре-
определенным, если его нижняя граница тА > 0. По неравенству G)
из гл. X
(Лх,х)>тЛ\\х\\\ A9)
поэтому при тА > 0 равенство (Ах, х) = 0 (т. е. Ах !_ х) имеет
место только при х = Э. Кроме того, из того же соотношения A9)
с помощью неравенства Коптя — Буняковского следует, что
тА || х ||2 < || Ах || || х ||, откуда видно, что || Ах || > пгА || х \\
при всех х ? Н. Тогда из теоремы 10.6.5 следует, что для поло-
положительно определенного оператора А число К = 0 регулярно,
т. е. оператор А обратим, и при этом || А~1 \\ <— . В этом слу-
случае уравнение A8) имеет единственное решение при всяком у ? II.
Фиксируя элемент у, определим в Л функционал
F(x).-,(Ax,x)~2(x,y). B0)
Теорема 12.4.1. Пусть А — положительно определенный
самосопряженный оператор. Для того чтобы при заданном у ? И
элемент х0 ? Н был решением уравнения A8), необходимо и доста-
достаточно, чтобы функционал F (х) имел при х = х0 наименьшее
значение.
Доказательство. При любых х0, z ? Н и веществен-
вещественном а
F (хо-г az) — (А (хо~ ctz), х0 + ctz) — 2 (х0 -j- ctz, у) -----
= (Ах0, х0) + а (Az, х0) -f а (Ах0, z) 4 а2 (Az, z) — 2 (х0, у) — 2а (у, z).
Учитывая, что (Az, х0) --- (Ах0, z), имеем
F(xo + az)-.F(xo) + 2a(Axo-y, z)-ra*(Az, z). B1)
22 Б. 3. Вулих
338 ПРИБЛИЖКННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬН. УРАВНЕНИЙ [ГЛ. XII
Если х0—решение уравнения A8), то из B1) при а = 1 сле-
следует, что
F (х0 + z) = F (х0) -| ¦ (Az, z) > F (x0). B2)
Но так как любой х?Н можно представить в виде х -=xo^-z,
то, тем самым, F(х) > F (х0) при всех х^Н.
Обратно, если F (х) принимает наименьшее значение при
х=-х0, то F(xn^-az) > F (xQ) при любых а и z, т. е. при каждом
фиксированном z функционал F (хо-г az), как функция от и,
имеет минимум при а = 0. А тогда производная этой функции
равна нулю при а = 0. Но из B1) видно, что
-^F{x0 ¦- az) |а=ц -- 2 (Ах0 - у. z),
поэтому Ах0 — у _l z. Вследствие произвольности z отсюда выте-
вытекает, что Ах0 — у = 8, т. е. х0 — решение уравнения A8).
Итак, мы доказали, что единственным элементом, доставляю-
доставляющим функционалу B0) наименьшее значение, является решение
уравнения A8).
Назовем последовательность элементов {хп} минимизирующей
(для функционала /'), если F (хп) —*- min F (х).
Теорема 12.4.2. Если А — положительно определенный
самосопряженный оператор, то всякая минимизирующая последо-
последовательность {хп} сходится к решению уравнения A8).
Доказательство. Пусть х0 — решение уравнения A8).
Тогда, полагая в B2) z == хп — х0, имеем
F (хп) -= F (х0) -|- (А (хп — х0), хп — ,г0).
i!o F (х0) --- min F (х) и, так как последовательность {а;,,} —мини-
—минимизирующая, то F(хп)—>F(x0), т. е. (.4 (хп — хи), х,-,—хп)—>().
По неравенству A9)
|| ^п — Ч f < — (-1 {Хп — Ч), *п — Х0).
откуда и следует, что хп ->- х0.
Для приближенного решения задачи о минимуме функционала
F (х) воспользуемся методом, предложенным немецким мате-
математиком В. Ритцем A878—1909) *). В пространстве // выбираем
произвольную систему линейно независимых элементов {ф;}П=|,
полную в том смысле, что если х ? // и х 1 <р,- при всех i, то
х = 0 **). Далее фиксируем произвольное натуральное п и обра-
*) В. Ритц рассматривал более конкретные задачи на .минимум функцио-
функционалов. Абстрактное изложение метода и его теоретическое обоснованно были
дани позднее.
**) Мы считаем, что пространство Н бесконечно-мерно и сепарабелыш.
12./.] МЕТОД РПТЦА ¦ 339
зуем конечно-мерное подпространство tfn, порождаемое эле-
элементами фь ф2, . . ., фп. В подпространстве Нп находим эле-
элемент хп, на котором функционал F (х) в этом подпространстве
имеет наименьшее значение. Так как все элементы х ? Н„ имеют
вида: =--¦ 2а;Фг> то отыскание хп сводится к алгебраической задаче
нахождения п неизвестных коэффициентов at. Получаемый таким
образом элемент хп и принимается за приближенное решение
уравнения A8).
Проведем вычисления по изложенной схеме. Будем считать,
что оператор А — положительно определенный, самосопря-
самосопряженный.
Лемма 12.4.1. В подпространстве Нп функционал F (х)
имеет наименьшее значение.
Доказательство. Из определения F (х) вытекает
очевидная оценка:
F (х) >тА\\х j *- 2 |; х ;i Ij у \^\\х |, (тА ?х |; -2\}у\\).
Поэтому, если || х || > —^ , то /' (х) > 0. С другой стороны,
F @) =¦ 0. Следовательно, наименьшее значение функционала F
в Нп, если оно существует, должно приниматься на каком-нибудь
элементе замкнутого шара S* с Нп, определяемого условиями:
По теореме 5.3.2 этот шар компактен. В то же время из непрерыв-
непрерывности оператора А и непрерывности скалярного произведения
вытекает непрерывность функционала F'. А тогда существование
наименьшего значения F (х) на S*. а следовательно, и в Нп.
вытекает из теоремы 4.2.1. Лемма доказана.
31
Так как каждый элемент х?Нп имеет вид х= 2 «;(к,
то на Нп функционал F (х) принимает вид
п п п
фА)—2 2 аг(Ч/. ?/).
т. е. превращается в функцию Ф (а,, а2, . . -, а„) от «перемен-
«переменных аь а2, ¦ • ., ап. Тогда коэффициенты а,- того элемента х,
который доставляет функционалу ^наименьшее значение, должны
22*
340 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬН. УРАВНЕНИЙ [ГЛ. XII
удовлетворять п условиям:
Ц. = 0 (/ = 1,2,...,»)•).
Вычисляя эти производные и сокращая на 2, получим
оо П
2 ak(A(fi, щ) — (у, ер;) = 0**) или 2 <Мфм АЩ) = (у, Ф;)
((==1,2 в). B3)
Таким образом, для определения коэффициентов аи мы имеем
систему B3) п линейных алгебраических уравнений. Проверим,
что определитель системы B3) 6^0. Для этого достаточно пока-
показать, что соответствующая однородная система
п
2 aft (ф„ Ащ) = 0 (i=l,2 , п) B4)
п.:= 1
имеет только нулевое решение.
Действительно, переписывая каждое из уравнений системы B4)
в виде
- 0,
мы видим, что если сц представляют решение системы B4), то
п
А ( 2 °ьфь) i- ф; при любом г = 1, 2, .... п.
п
Но тогда Л ( 2 ctfetpfe) ортогонален и всему Нп, в частности,
п п
а B °йфь) 1 2
k=i k=l
*) Так как функция Ф (аь а2, . . ., а„) определена и имеет непрерывные
производные при любых значениях аргументов, то ее наименьшее значение
будет одновременно и минимумом, а потому мы можем воспользоваться
необходимым признаком экстремума функции нескольких переменных.
**) Поясним это дифференцирование на примере, когда п = 2. В этом
случае
Ф(а1? а2) = Иф1, tfJal + tAyi, <p2) а^г + (Лф2, ф1)а2а! +
+ Ифг. Фг) а? — 2 (ф„ у) а, - 2 (ф2, у) а2.
Тогда, учитывая, что (Лфг, ф1) = (Лф1, ф2), находим, например,
ЭФ
2Иф ф^^ + ^ф ф)а+(Лф ф^аг—2(ф1, у) =
ф1, Ф2)а, —(ф„ ,v)J.
1^.4] МЕТОД РИТЦА 341
По сделанному в начале параграфа замечанию отсюда следует, что
п
= 0, а тогда, вследствие линейной независимости ф&, все
ah — 0. Тем самым доказано, что 6 Ф 0.
Из доказанного следует, что система B3) имеет единственное
решение a(j0), ai,0), . . ., a^0). Поскольку это решение — единствен-
п
ное, то оно и должно определить элемент хп =j a* Ф*> Достав-
i=l
ляющий функционалу F в Нп наименьшее значение.
Придавая п всевозможные натуральные значения, мы построим
последовательность приближенных решений хп. Докажем сходи-
сходимость метода.
Теорема 12.4.3. При сделанных предположениях относи-
относительно оператора А последовательность элементов хп, полученных
по методу Ритца, сходится к решению х0 уравнения A8).
Доказательство. Согласно теореме 12.4.2, достаточ-
достаточно доказать, что последовательность {хп} — минимизирующая.
Ортогонализуя систему {<р,}, можно построить ортонормирован-
ный базис {hi }. Полнота системы {h-, } будет вытекать из полно-
полноты системы {фг}. Разложим решение х0 по элементам базиса,
00 П
х0 = 2 o-ihi-, и положим zn = 2 a,V Тогда zn ? Нп *)иг„^ а0;
i=i i=i
следовательно, F (zn) -*- F (х0). Но так как
F(xn) = min F(x), F (x0) = min F (x),
.x?Hn xeH
TO
F(xo)<F(xn)<F(zn),
а потому и F (xn) —> F(x0). Теорема доказана.
Дадим оценку погрешности, получаемой при замене х0 на хп.
Так как
хп — х0^- А~хАхп — А~ху = Л (Ахп — у),
то
\\xn-Xo\\K\\A-4\\\Axn-y\\KjL\\Axn-y\\. B5)
Рассмотрим в качестве первого примера бесконечную систему
линейных алгебраических уравнений
сю
2«1кБ* = Ч, (t = l, 2, ...) B6)
fti
*) Подпространство, порождаемое элементами h,, h2, . . ., hn, совпадает
с подпространством, порождаемым элементами ф4, <р2, ...,<$„ (см. 6.7).
342 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЫ!. УРАВНЕНИЙ [ГЛ. XII
и покажем, что для такой системы метод Ритца может быть сведен
к методу редукции. Мы будем считать, что допускаются только
последовательности {\^ } ? I2 и что оператор А, определяемый
матрицей (я,?,),— линейный, отображающий I2 в I2. Чтобы опе-
оператор А был самосопряженным, матрица должна быть симметрич-
симметричной, а положительная определенность оператора А обеспечи-
обеспечивается, если существует такая постоянная d > О, что для любой
последовательности {?; } 6 I2
оо ос
Функционал B0) F (а;) при x — {?,-} и #- {Л;} имеет вид
оо ос
F(x)-- 2 aikblk — 2 2 ^Л/-
г, ft = l i = l
I3. качестве {ф,} во.чьмем систему координатных ортов {г,}.
п
Тогда х? Н„ имеет вид х= J НгР; и роль а,- играют координаты %t.
i = l
Так как (е,-, ^4^й) — Я;й, (у, е;)---tj,, то система B3) совпадает
с усеченно!'! системой
п
2 aihlh=-i (i = l, 2, . . ., га),
получаемой из B6) отбрасыванием всех строк и столбцов с номе-
номерами, большими п.
12.5. Применение метода Ритца к решении» дифференциальных
уравнений Штурма — Лиувилля
Чтобы дать более важные применения метода Ритца, следует
несколько обобщить результаты предыдущего параграфа. Будем
считать, что оператор А в уравнении A8)— симметричный, может
быть и неограниченный, заданный на линейном множестве D,
всюду плотном в Н . Предположим, что он положительно опреде-
определенный в том же смысле, как это понималось в предыдущем пара-
параграфе. Иными словами, предположим, что существует такое чис-
число d > 0, что
{Ах, х) > d || х |j2 при всех x?D.
Отсюда следует, что если Ах = 9, то и х = 8, а потому существует
оператор А'1. Уравнение A8) имеет единственное решение при
всяком у из совокупности значений оператора А.
VI. л I
ПРИМЕНЕНИИ МЕТОДА РИТЦА
Функционал B0) F (х) будем считать определенным для всех
х ? D.
Теоремы 12.4.1 и 12.4.2 остаются в силе и при новых пред-
предположениях относительно оператора А, но min F (х) следует опре-
определять на множестве D. В доказательствах следует брать лишь
элементы х0, z, x из D, а вместо тпА использовать d.
При применении метода Ритца от выбираемой основной систе-
системы линейно независимых элементов { ф; } будем требовать, чтобы
все ф; 6 D и чтобы эта система была «полна» в D в следующем
усиленном смысле: для любого х ? D и любого е > 0 существуют п
и такой элемент х 6 Ип *), что
(.4 (х — х), х — х) < е.
Из последнего неравенства вытекает, что || х — х ||2 <Г -т , следо-
следовательно, благодаря произвольности е, каждый х ? D входит в под-
подпространство, порождаемое системой {фг}, а так как D всюду
плотно, то это подпространство должно совпасть с Н. Отсюда
уже следует, что система { ф; } полна и в прежнем смысле.
Лемма 12.4.1 остается в силе. Хотя мы в ее доказательстве .опи-
.опирались на непрерывность оператора А , а сейчас оператор А на мно-
множестве D может не быть непрерывным, но в конечно-мерном
пространстве Нп этот оператор все же непрерывен по теореме 8.2.3.
Таким образом, в каждом iui подпространств Нп мы можем решать
задачу на минимум функционала F, что опять приведет нас к реше-
решению системы B3). Теорема 12.4.3 о сходимости метода также сохра-
сохраняется, но несколько изменяется доказательство того, что после-
последовательность {хп}—минимизирующая. Дадим новое доказа-
доказательство этого факта.
Так как //, cz Н2 а И 3 а ... cz D, то
min F (х) > min F (х) > min F (х) - ... > min F (х).
т. е.
F (Xi) > F {х2) :;¦¦ ... .; F (хп) .-"-¦ ¦ ¦ ¦ > F (х0),
где х0 — решение уравнения A8). Зададим произвольное с > 0
п подберем .V и х?Нх так, что
(А (х — х0), x — xG)<:e.
Полагая в B2) z х — х0, мы находим, что
Тогда, тем более,
F(xs)<F(x0) :-f.
i/n iiMei'T здесь тот же смысл, что и в предыдущем параграфе.
344 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬН. УРАВНЕНИЙ [ГЛ. Ml
Следовательно, при всех n>iV
F(xo)^F(xh)<F(xo) + b,
откуда и вытекает, что F (xn)—> F(x0).
Следует заметить, что оценка погрешности по формуле B5)
теперь мало интересна, так как Ахп может не стремиться к у.
Рассмотрим дифференциальное уравнение Штурма — Лиувилля
~4 (*(')#)-?(')*(') =/(О B7)
с краевыми условиями
х (а) - х (Ь) = 0. B8)
По-прежнему предполагаем, что p(t), p' (t) и q(t) непрерывны
на [а, 6].
В 10.8 мы уже изучали симметричный дифференциальный опе-
оператор U, определяемый левой частью уравнения, считая его
заданным на множестве D функций, непрерывных на [а, Ъ ] со
своими производными 1-го и 2-го порядка и удовлетворяющих
краевым условиям B8). Считая, что/? (t) > 0, a q (t) <0, докажем,
что оператор U — положительно определенный.
Из формулы B2) гл. X следует, что для любого x^D
ь
(Ux, х)>*\ px'2dt.
а
Пусть /• = mmp(/); тогда г>0 и
ъ
(Ux, х) >/• \ х at,
а
откуда
ь
'2 ' Г7
Теперь, учитывая, что х(а) = 0, имеем
t
\x(t)\* =-\x (t)-x(a)\* == \ x'dt
а
b
' | dt У < (b — a) [x'2dt*)^ ^ (Ux, x). B9)
*) Здесь мы применяем неравенство Коши — Буняковского, считая вто-
второй сомножитель равным единице.
12.5] ПРИМЕНЕНИЕ МЕТОДА РИТЦА 345
Отсюда
\\x\\*~\x*dt<?=^-(Ux,x)
(I
или
(Ux,x)>-(T^p\\x\\*.
В конце 11.7 доказано, что множество D всюду плотно в про-
пространстве L2, построенном на отрезке [а, Ъ]. Таким образом, к урав-
уравнению B7) применима вся изложенная выше теория метода Ритца,
и сходимость метода обеспечена. Функционал B0) имеет в этом
случае вид
ь
F (х) -= \' (рх - цх2 — 2xf) dt
а
Icp. формулу B2) из гл. X].
Чтобы обеспечить усиленную «полноту» системы функций
Фг (х), которые сейчас нужно брать из множества D, достаточно
выбрать их так, чтобы для любого х ? D и любого е > 0 можно
было найти конечную линейную комбинацию функций ф> (t)
п
г=1
для которой на всем отрезке [а, Ь]
Х\1) — Х\1)\<^?, \Х \1) — X \1)\<^Ъ.
Действительно, в этом случае из формулы B2) гл. X имеем:
ь
(U(x — x),x—x)= \ [p(x'-x'J-q(x-x)*\dt <
V
а
< е2 (Ь — а) [max p (t) + max | q (t) \ ],
а за счет е правая часть может быть сделана сколь угодно
малой.
Не приводя доказательства, укажем два примера требуемых
систем функций фд(?):
1) (fh(t) = (b~t) (t — a)k\ 2) cpft (t) --¦-= sin кП^~а п) C0)
*) См. Л. В. Канторович и В. И. Крылов. Приближенны
методы высшего анализа. Гостехиздат, 1949, стр. 280—284.
346 ПРИБЛИЖЕННОЕ РЕШЕНИИ ФУНКЦИОНАЛЫ-!. УРАВНЕНИЙ [ГЛ.ХП
Заметим, что для уравнения Штурма — Лиувилля результат
теоремы 12.4.3 о сходимости метода Ритца может быть усилен.
Именно, покажем, что в этом случае минимизирующая последо-
последовательность {хп (t)} равномерно сходится к решению х„ (t) у/ши-
у/шипения B7).
Действительно, из B9) следует, что
| х„ (I) — х0 (/) |2 < -^- (U (хп — х0), хп — х0),
а последнее выражение стремится к нулю, как видно из дока-
доказательства теоремы 12.4.2.
Возьмем в качестве .примера уравнение
— х" ¦ х— — /,
заданное на отрезке [0, 1} при краевых условиях х @) —х A) — 0. Легко
найти точное решение
С другой стороны, применим метод Ритца, используя только одну фуик
цию nepBoii из систем C0)
Ф! (/)--=' (* —0 (ч.-^О, 6=1).
Иными слова.мн, будем искать первое приближение х^ к точному ]К'ше.ч:по
среди функций вида х =а/ A — /). В нашем примере
1
(я'2- х1 21 х) (П.
Подставляя x-ai(l—/), получим, что F (х) нрев]>атится в функцию
Ф (а) =.,т; а2- -х-а. Далее, из уравнения Ф' (а) —0 находим а= — ' - и, таким
.-К) о " 11
образом,
Д.Ч)| сравнения приведем значения решении л-'о (/) и первого приближе-
приближения х, (t) в середине промежутка:
¦М -т - -0,031), .г, - --0,0.37.
- у
12.6. Применение метода Ритца к нахождению
собственных значении
В этом параграфе мы рассмотрим другое применение метода
Ритца — к нахождению собственных значении самосопряженного
оператора. При этом ограничимся задачей отыскания наиболь-
наибольшего собственного числа.
12.0] НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИИ \\\l
Пусть А — вполне непрерывный самосопряженный оператор
в гильбертовом пространстве // и пусть его верхняя граница
МА Ф 0. Тогда по теореме 10.6.6 и лемме 11.3.1 МА является
собственным числом оператора А, а по теореме 10.6.5 это и есть
наибольшее собственное число *).
Введем функционал Е (х) = (Ах, х). С одной стороны, Е (х)^.
МА при || х || = 1. С другой, если х — собственный элемент
с нормой || ж || =¦ 1, соответствующий собственному числу Мл, то
Е (х) =-- МА (х, х) -•-- Мл. Следовательно,
М х ¦- max E (х).
'Задача отыскания М А сводится к нахождению наибольшего значе-
значения функционала Е (х) на «поверхности» единичного шара.
Для дальнейшего можно было бы использовать так же, как
и в 12.4, полную систему любых линейно независимых элементов.
Однако для некоторого упрощения выкладок будем исходить из
ортонормированпого базиса { Л; }. Как и раньше, через Нп обо-
обозначим подпространство, порождаемое элементами hit /ь, . . ., /'„.
п
Представляя х 6 Нп в виДе аг — У, агЛ;, мы можем свести функцио-
нал Е (х) в подпространстве Нп к функции п переменных:
-=Ф(«,, и, а„).
Множество (Л, тех элементов х из II п, для которых \\x\\ — 1,
замкнуто, как пересечение подпространства Нп с «поверхностью»
всего единичного шара (т. е. множеством всех х 6 Н с || х || — 1,
которое, очевидно, замкнуто). Кроме того, Q,, ограничено, а тогда
и компактно, так как оно содержится в конечно-мерном под-
подпространстве //„. Следовательно, непрерывный функционал Е (х)
достигает па множестве Qn наибольшего значения.
Пусть ц„ = max E (х), а хп — какой-нибудь элемент из Qn,
на котором реализуется значение и„, т. е. Е (хп) = и„. Если
взять любой х 6 Нп, отличный от 6, то Г|-^-7| 6 Qn, а тогда
— ^-—^—Dх х) -ц
*) Полная непрерывность оператора А использована только для этого
заключения. Если же уже известно, что наибольшее собственное число неко-
некоторого оператора А равно Л/д,то дальше достаточно предполагать А просто
самосопряженным оператором.
348 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛ!.Н. УРАВНЕНИЙ [ГЛ. XII
ИЛИ
Отсюда следует, что Е (аг)<|д.п \\х
Е{х) — рп(х,х)<0. C1)
Это же соотношение выполняется и при х—6, так как тогда
его левая часть равна нулю.
Возьмем теперь произвольный z?Hn и положим x = xn-\-yz,
где у —любое вещественное число. Подставляя в C1), получим
(.4 (хп + yz), хп - f- yz) — ц„ (хп + yz, хп + yz) < 0.
Раскрывая левую часть, используя самосопряженность опера-
оператора А, находим
(Ахп, хп) + 2у (Ахп, z)-[ry2(Az, z) — \in{xn, xn)—
— 2y\in (хп, z) — vV» (z' z) <"•
Так как (Ахп, хп) = Е (xn) =(in, a (xn, xn)=^i, то из предыдущего
неравенства получаем
2у[(Ахп, z)-]xn(xn, z)] + y*[(Az, z)-[kn(z, z)]<0.
Рассматривая левую часть как функцию / (у) от у, мы видим,
что при у = 0 она обращается в нуль, а следовательно, имеет
при у = 0 максимум. Тогда /' @) —- 0, что приводит нас
к равенству
(Ахп, z) — ц„ (xn, z) = 0, C2)
которое должно выполняться при произвольном z?Hn. Подстав-
Подставляя в C2) поочередно z = hit h2, . . ., hn, получим
(Axn,hi)-nn(xn, ht) = 0 (i = i, 2,...,«). C3)
n
Так как хп?Нп, то он имеет вид хп -- 2 ak^k- Подставляя
в уравнения C3), приведем их к виду
71
2 <*ftDAA, A?)-jinai = O (г -1,2, ...,n). C4)
fei
Если рассмотреть систему уравнений с неизвестными
l(Ahu hi) — \i\ax + (А/г2, hi)a2+ . . . +{Ahn, hl)an =
(Л/г,, h2)ai + [(Ah2, h2) — \i]a2^ .. . -\-(Ahn, h2)an =
. C5)
(Ahlt hn) ал + (Ah2, hn)a2 + ¦ ¦ ¦ +[(Ahn, hn) — \i] an = i
содержащую параметр (А, то равенства C4) означают, что коэф-
коэффициенты в выражении хп представляют решение этой системы
12.6] НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ 349
п
при \i — A„. Так как ]| хп ||2 - 2 а%~1, то, следовательно, систе-
система C5) имеет при [i = [j,n ненулевое решение. Л тогда ее опре-
определитель должен быть равен нулю. Иными словами. \in должно
быть корнем уравнения
(Ahuhi)~\i (Ah2, hi) ... (Ahn, hi)
(Ahuh2) (Ah2,h2) — [i ... (Ah,,,h2) q ,щ
(Aht, hn) (Ah2, hn) ... (Ahn, hn)~n
Так как матрица определителя из левой части C6) симметрична,
то, как установлено в 1.13, все корни уравнения C6)— веществен-
вещественные. Докажем, что \in ¦— наибольший из них *). Пусть |Л* —
какой-нибудь из корней этого уравнения. Подставим его вместо \i,
в уравнения системы C5) и найдем какое-нибудь не нулевое ее
решение: а*, а*, . . ., а?. Это решение всегда можно подобрать
так, что 2 а%2 = 1 **), а тогда элемент х* = 2 а5^А 6 Qn- Теперь
й=1 й=1
равенства
У al(Ahh, Л()-ц*а?-0 (U= 1, 2, ...,«),
fe=i
выражающие тот факт, что а? определены из системы C5),
запишем в равносильной форме
умножим каждое из них на соответствующее а* и сложим.
Получим
(Ах*, Saf^)-u*S af* -0,
i=l i = l
или (Ах*, х*) = \i*, т. е. Е (х*) = и*. Отсюда видно, что все кор-
корни уравнения C6) встречаются среди значений функционала Е (х)
на Qn. Поэтому ^п, как max E (х) на Qn, и должен равняться наи-
наибольшему из корней уравнения C6).
*) Если не ссылаться на 1.13, то из дальнейшего будет, во всяком случае,
вытекать, что ц„ — наибольший из вещественных корней уравнения C6).
**) Если первоначально взятое решение а*, а*, . . ., а% не удовлетворяет
такому условию, то это решение нужно заменить на paf, pajf pa^, где
Р=-
350 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬН. УРАВНЕНИЙ [ГЛ. XII
Числа и.,, мы и будем рассматривать как последовательные
приближения к искомому числу Мл. Докажем, что u.n -*¦ МА
при ге—>-оо. Пусть ха — собственный элемент с нормой || х0 ]] = 1,
соответствующей собственному числу Мл. Разложим х0 в ряд
Фурье но элементам базиса, х0 —¦ ^ Р;/«;. и положим уп -— 2 Р;/^.
/-¦1 ' i—")
Так как i/n -> ха, то || у„ || -> 1 и при достаточно больших п будет
уп ф 0. Тогда имеют смысл элементы zn = Уп. и zn ? Qn, При
I! .Vn II
этом zn -> х0, а потому и ? (zn)-> ?" (хо)—Мл. Если задать е > 0,
то найдется такое N, что ? (zn) > Л/л — е при п>Лг. Но-
Z? (г„) . ц„ = max E (х), а тогда и un > Л/ 4 — е. С другой
стороны, цп -^Л/А — max i? (я) при всех ге, следовательно,
:|.vii---i
ц„ —>¦ Л/д. Тем самым при сделанных предположениях доказана
сходимость метода Ритца в задаче отыскания наибольшего соб-
собственного значения.
Замечания. 1. К уравнениям C5) можно прийти и дру-
другим, более коротким путем, однако не дающим строгого обоснова-
п п
ния метода. Так как ^} af — 1 для любого х ~ V а;/г? ? Qn. то
отыскание [д„ есть задача на условный максимум для определенной
выше функции Ф (г<ь а2, .... с,,) при наличии связи между
и
аргументами: 2 af -'- !¦ Если решать эту задачу по методу неопре-
i=i
деленных множителей Лагранжа, то нужно составить вспомога-
вспомогательную функцию
п
Т («). и2, . . ., а,!) = Ф(а1) а2) . . ., и,,)— и. ^ а? =
V а;ал (ЛЛ;, ЛА) — |я V af,
i, /i = l i = 1
где и — неопределенный множитель. Вычисляя затем -;— и при-
равнивая их нулю, мы получим, после сокращения на 2,
п
2 ah(Ahi, hh) — \ia.i^0 (i=^l, 2, ..., га),
что совпадает с уравнениями C5).
2. Если мы будем исходить не из базиса {/',}. а из произволь-
произвольной полной системы линейно независимых элементов {ф;}, то
также может быть применен метод неопределенных множителей,
12.6J НАХОЖДЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИИ 351
но уравнение связи будет в этом случае сложнее:
2 а;а*(ср,-, щ)-- 1.
Вместо системы C5) получится система несколько более сложных
уравнений и наибольший из корней ее определителя будет, как
и выше, равен \хп.
3. Изложенный метод может быть применен н к нахождению
других собственных чисел. Например, если А — вполне непре-
непрерывный, положительный, самосопряженный оператор, а
Я. ко ?ХЯ.;: ...
— последовательность его собственных чисел, построенная по
фундаментальной системе { hn } собственных элементов, то чтобы
получить к2, нужно искать максимум функционала Е (х) на мно-
множестве тех элементов поверхности единичной сферы, которые орто-
ортогональны К })[.
Приведем пример. Рассмотрим интегральный оператор К
1
К (t, >)x(x)ds
с симметричным ядром
к и .*) - ^ i([~~s) пр" 1 -'*"''
I s A — () при I >- *¦.
Оператор Л —вполне непрерывямй и самосопряженный (см. 10.7 и 11 1).
Так как К (/, *•) >¦ 0 внутри всего квадрата 0<^;, s <^ 1. то
1 i .-
(Кг. х) -= \ \ К (t, s) x (s) x (I) ds dt > 0
0 b
для любой положительной функции (х (t) > 0). Следовательно, М h- >0и это
и есть наибольшее собственное число оператора К.
Чтобы получить приближенное значение для Мк, возьмем систему из
двух функций ф! (t) = 1, ф2 (t) = t. Хотя, согласпо замечанию 2, можно
решать задачу, пользуясь непосредственно этой системой функций, но
поскольку мы ограничились подробным изложением метода лишь для случая,
когда в основу положена ортонормнрованная система, ортогонализуем
систему функций Int. Получим h{ (t) = 1, h» (t) = 2 "] 3 ( t ¦
Теперь будем искать max E (x) — max (Кх. х) на множестве Q2 функций вида
x = a(/!i (t) + a2h2(t) при дополнительном условии aj + a| = 1.
Каждый х 6 Q2 есть линейная функция от t, x (I) = р" + yt. где |3 =
= at — a2 ~["А, у = 2а2 У.З. Поэтому функционал Е (х) = (Кг, х)- на Q2
352 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬН. УРАВНКНИЙ 1ГЛ. XI
можно представить в форме
1 1
E (x) = Ф (P, Y) = \ \ К (t, s) (P -]- ys) (P ~ yO rf.v ill ¦-=
О О
= 5 (Р rYO [(!-
о
В результате элементарных вычислений находим
Подставляя значения р и y> получим выражение Е (х) на Q2 через <Xj и а2:
Согласно замечанию 1, решаем задачу на условный максимум для
функции «Dfaj, a2), для чего составляем функцию
, a2) -tV o? + -^-a|-,^ (aj+aj).
12
Тогда
dat ' 6
и мы получим уравнения
da2 30
a2
Это и есть система C5) для данного примера. Приравнивая нулю ее опре-
определитель, составим уравнение C6)
1
о 4
О
- о.
которое имеет два корня: Ц = Г5 и 1х==г?;- Больший из них, ц--^, и есп,
искомое приближение к Mg.
Иначе можно было бы сразу составить уравнение C6) в виде
(Kht, Л±) — (х (Kh2, At)
^^ О,
{Kh±, h2) {Kh2, A2) — fx
Вычисляй элементы определителя, мы бы нашли, что
Однако эти выкладки были бы не короче, чем те, которые требуются
по схеме отыскания условного максимума.
12.7] ПОНЯТИЕ О МЕТОДЕ БУБНОВА - ГАЛЕРКИНА 353
Предлагаем читателю проверить, что мы пришли бы к тем же значе-
значениям (X, если бы решали задачу на условный максимум непосредственно
для функции Ф(р\ у) при уравнении связи р-|- Py + ~5- У2~ 1. которое
1
получается из условия ||z||2— \ ф-f- ylJ dt = 1.
О
Сравним найденное приближенное4 значение для наибольшего собствен-
собственного числа оператора К с точным. Легко проверить, что заданный опера-
оператор К есть оператор Грина для дифференциального оператора Штурма —
Лиувилля Ux = — ж", рассматриваемого при краевых условиях х @) =
= х A) = 0 (см. 11.7). Действительно, в этом случае функция Грина состав-
составляется с помощью двух решений и и у уравнения х" = 0, удовлетворяющих
условиям и @) = v A) = 0, а за такие решения можно принять и (t) = t,
v (t) = 1 — t. Собственные числа оператора Ux = — х" могут быть найдены
так же, как это сделано для промежутка [0, я] в 10.8. и мы получим, что
наименьшее из них равно я2. Так как собственные числа оператора Грина
получаются из собственных чисел оператора U переходом к обратным вели-
1 1
чинам, то наибольшее собственное число оператора К равно —^^ 0,101 яъ —^ .
Мы же получили приближенное значение -р- , используя систему всего лишь
из двух функций.
12.7. Цонятие о методе Бубнова—Галеркина
Метод Ритца решения уравнения A8) Ах — у был обобщен
в 1913—1915 гг. И. Г. Бубновым и Б. Г. Галеркиным *). Решая
по методу Ритца уравнение A8) с самосопряженным или симме-
симметричным оператором А, мы получили систему уравнений B3)
для определения га-го приближения хп к искомому решению.
Система B3) может быть записана в виде
п
{А ( Ц ВДй) — у, Фг) = 0 (?=1, 2, ..., ге),
fti
т. е. элемент хп = ^ aA(ps определяется из п условий ортого-
h=i
нальности
Ахп — y±q>i при /=1, 2, ...,п.
Вот это требование, вытекавшее в методе Ритца из других исход-
исходных соображений, положено в основу метода Бубнова — Галер-
Галеркина. При этом, поскольку указанные условия ортогональности
*) И. Г. Бубнов A872—1919) и Б. Г. Га л е р к и н A871—1945)—
крупные отечественные ученые. И. Г. Бубнов — специалист по строительной
механике корабля, Б. Г. Галеркнн— специалист по строительной механике и.
теэрни упругости.
23 Б. 3. Вулнх
354 ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬН. УРАВНЕНИЙ [ГЛ. XII
имеют смысл для произвольного оператора А, в методе Бубнова —•
Галеркина можно отказаться от требования самосопряженности
или симметричности оператора А. Таким образом, схема метода
Бубнова — Галеркина заключается в следующем.
Дано уравнение A8) с произвольным оператором А, заданным
на линейном множестве D, всюду плотном в гильбертовом про-
пространстве И. Выбираем систему линейно независимых элементов
{ф;} из D, удовлетворяющую требованию полноты в том или
ином смысле. Если потребовать, чтобы при заданном у элемент
Ах — у был ортогонален в с е м <р{, то благодаря условию полноты
отсюда будет следовать, что Ах — у = 8, т. е. что х — решение
уравнения A8). Вместо этого вводим подпространство Нп, порож-
порождаемое элементами q>i, <р2, . . ., <рп, и ищем тот элемент х ? Нп,
для которого
Ах — у J_ фг при с = 1, 2, . .., п.
Это и приводит к решению системы B3).
Сходимость метода Бубнова — Галеркина может быть дока-
доказана для уравнений с операторами более широкого класса, чем
это было сделано выше для метода Ритца. В частности, метод
Бубнова — Галеркина может быть применен к решению диффе-
дифференциальных уравнений более общего вида, чем уравнения
Штурма — Лиувилля. Однако мы не останавливаемся на иссле-
исследовании метода Бубнова — Галеркина. Такое исследование про-
проведено подробно в книге С. Г. Михлина «Вариационные методы
в математической физике».
ГЛАВА XIII
СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА
13.1. Полунормы и определение счетно-нормированного
пространства
Далеко не во всех пространствах, важных для приложений,
можно ввести норму так, чтобы сходимость по норме совпала
с интересующей нас конкретной сходимостью. В качестве примера
пространства, не допускающего нормировки, в 5.2 было указано *.
В этой главе мы встретим еще ряд таких пространств. Чтобы иметь
возможность изучить хотя бы некоторые из этих пространств
методами, близкими к теории нормированных пространств, вве-
введем понятие полунормы, обобщающее понятие нормы. Для полу-
полунормы сохраним то же обозначение, которое использовалось до
сих пор для нормы.
Определение. Вещественный функционал ||х||, задан-
заданный на линейной системе Е, называется полунормой, если он обла-
обладает следующими свойствами:
I. || х || > 0 для любого х 6 Е.
II. || Ад: || = | А, | || ж || для любого х ? Е и любого числа А.
III. || х + у || < || х || + II У II для любых х, у ? Е (неравен-
(неравенство треугольника).
Таким образом, по сравнению с определением нормы здесь
отсутствует требование, чтобы || х || = 0 только для х = 0, играв-
игравшее в теории нормированных пространств крайне существенную
роль. Ясно, что || 8 || = 0, но не исключено, что || х || = 0 и для
некоторого х Ф Q.
Заметим, что для полунормы справедливо неравенство B)
из гл. V, которое выводится так же, как для нормы.
В скрытом виде мы уже встречались с полунормами. Так,
например, если принять за Е совокупность всех суммируемых функ-
функций, заданных на отрезке [а, Ь], с естественным определением
сложения и умножения на число, но не производить при этом
никаких отождествлений, т. е. считать, что две функции из Е
различны, если они отличаются друг от друга хотя бы в одной
23*
356 счетно-нормированные пространства [гл. хш
точке, а затем положить
ь
|[*||= \* \x{t)\dt,
а
тго такой функционал будет полунормой в Е. Пространство L полу-
получается из Е за счет отождествления элементов, разности которых
имеют полунорму, равную 0. Нетрудно понять, что и в общем слу-
случае, если на линейной системе Е задана полунорма и мы отожде-
отождествим элементы, разность которых имеет полунорму, равную
нулю, то полунорма станет нормой, а Е превратится в нормиро-
нормированное пространство; обозначим его через Е°. При этом следует
учесть, что если х отождествляется с у, а у с z, т. е. если || х — у \\ =
= II У — z II = 0, то и || х — z || = 0, т. е. х отождествляется с z.
Таким образом, каждый элемент пространства Е° изображается
целым классом отождествляемых между собой элементов системы
Е. В частности, все элементы из Е, полунорма которых равна 0,
будут изображать нулевой элемент пространства Е\ Вообще ото-
отождествляемые элементы имеют одну и ту же полунорму, которая
и становится нормой после отождествления.
При определении суммы двух элементов из Е° нужно сложить
изображающие их элементы из Е (аналогично тому, как опреде-
определялась сумма в пространстве Ь). Легко видеть, что сумма как эле-
элемент из Е° не будет зависеть от выбора изображающих элементов
в пределах соответствующих классов *). То же замечание отно-
относится и к умножению на число.
Таким образом, линейная система с полунормой легко сводится
к нормированному пространству.
Существенное и далеко идущее обобщение получается тогда,
когда рассматриваются линейные системы, на которых задано
счетное множество полунорм **).
Определение. Линейная система Е называется счетно-
нормированным пространством, если на Е задано счетное множе-
множество полунорм
II -г II I! -г II II -г Г
X U, X Ч, . . . , \\Х\
\\Pi
(некоторые из них могут быть и нормами), причем если \\х \\р = 0
для некоторого х ? Е при всех р = 1, 2, . . ., то х = 0.
В счетно-нормированном пространстве определяется «сходи-
«сходимость по полунормам». Имепно, будем писать, что хп —*- х, если
*) Точно это значит, что если х отождествляется с у, a z с и, то х + z
¦отождествляется с у + и, т. е. || (х + г) — (у + и) \\ = 0.
**) Линейные системы с конечным множеством полунорм также не
представляют значительного интереса, поскольку и они сводятся к нормиро-
нормированным пространствам.
13.1] полунормы 357
II хп — х \\р -*- О при всех р = 1, 2, . . . В частности, хп ->¦ 9
означает, что || хп \\р —>- О при всех р.
Из определения сразу следует, что соотношения хп —*- х
и хп — х -*¦ 8 равносильны. Таким образом, для выяснения смысла
сходимости в конкретном счетно-нормированном пространстве
достаточно рассматривать сходимость к 8.
Нормированное пространство представляет частный случай
счетно-нормированного. Именно, это — такое счетно-нормирован-
ное, в котором все полунормы являются нормами и совпадают меж-
между собой. Тогда сходимость по полунормам превращается в схо-
сходимость по норме.
Проверим единственность предела в счетно-нормированном
пространстве. Пусть хп -+ х п одновременно хп ->¦ у. Тогда при
любом р '
Следовательно, || х — у \\р = 0, т. е. х — у = 8 по определению
счетно-нормированного пространства, а потому х = у.
Далее, || х — у \\р при каждом р — непрерывная функция
своих аргументов. Действительно, пусть хп -*¦ х, уп -*¦ у. Имеем
(см. неравенство B) из гл. V)
< || (Хп — х) + (у— уп) \\р < || Хп — X \\р + || У —
Аналогично
Таким образом,
\\\Хп — Уп\\р-\\у-х\\р\<С\\хп~х\\р+\\у-уп\\р->0.
Следовательно,
В частности, полагая все уп = 0 (а тогда и у = 8), получим,
что если хп ->- х, то || хп ||Р -*¦ \\ х \\р при всех р (непрерывность
полунорм). ,
Дословно повторяя рассуждения из 5.2, можно проверить
непрерывность алгебраических операций в счетно-нормирован-
счетно-нормированном пространстве.
Распространим на счетно-нормированные пространства еще
некоторые важные определения.
*) Этим рассуждением, в частности, проверяется непрерывность нормы
в нормированных пространствах без ссылки на непрерывность расстояния
в общих метрических пространствах.
358 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. ХЦ1
Определения. Последовательность элементов {хп} из
счетно-нормированного пространства называется фундаменталь-
фундаментальной (по полунормам), если для каждого р = 1, 2, . . .
I! %п — хт \\Р —> 0 при га, т—> оо.
Счетно-нормированное пространство называется полным, если
всякая фундаментальная последовательность его элементов имеет
предел.
Ясно, что банаховы пространства — частный случай полных
счетно-нормированных пространств.
Применим теперь к счетно-нормированным пространствам
соображения, развитые в начале этого параграфа в связи с поня-
понятием полунормы. Для каждого натурального р назовем р-экви-
валентными такие элементы х и у из счетно-нормированного про-
пространства Е, для которых || а; — у \\v — 0. Отождествляя jd-экви-
валентные элементы между собой, мы получим нормированное
пространство, которое обозначим через Е^ и в котором роль
нормы будет играть р-я полунорма || х ||р. Заметим, что если || х \\Р
было нормой уже ъЕ, то Е(р) по составу элементов совпадает с Е.
Но _Е(р) всегда рассматривается только с одной нормой || х \\р *).
Пусть теперь А — произвольное множество из Е. Обозначим
через Л<р> множество, которое получается из А за счет отождеств-
отождествления р-эквивалентных элементов. Л(р) можно рассматривать как
множество из Е^р). Будем называть А <р) образом множества А в про-
пространстве Е^К Это понятие будет неоднократно использовано
в дальнейшем.
13.2. Примеры счетно-нормированных пространств
В этом параграфе мы приведем ряд примеров счетно-нормиро-
счетно-нормированных пространств. Некоторые из них, именно — различные
пространства дифференцируемых функций, находят важные приме-
применения в теории дифференциальных уравнений.
1. Пространство s (определение см. в 2.1). Положим
для любого х — { \г } ? *
1Ир = |Е,| (Р = 1, 2, ...).
Легко видеть, что || х \\р — полунормы, а * становится счетно-
нормированным пространством. При этом соотношение
\\ХП ~ X \\р -> 0 (Хп = Щ">}, X = {?;})
*) Отметим, что из полноты пространства Е не вытекает полнота про-
пространств Е(РК Это может быть подтверждено примерами 4 и 5 из следующего
параграфа.
13.2] ПРИМЕРЫ СЧЕТНО-НОРМИРОВАННЫХ ПРОСТРАНСТВ 359
означает, что ?(рп)—>• ?Р, т. е. сходимость по полунормам в s совпадает
со сходимостью по координатам. Последовательность { хп } из *
фундаментальна по полунормам тогда и только тогда, когда она
фундаментальна по координатам. Тем самым пространство *
полно, как счетно-нормированное пространство, и его полнота
в этом смысле означает то же самое, что полнота s как метриче-
метрического пространства (ср. 3.5).
2. Пространство С (—оо, +°°) или, короче, О°°,
состоящее из всех непрерывных функций х (t), заданных на всей
оси —оо <; t <С оо. Алгебраические операции определяются в С°°
естественным образом, и С°° становится линейной системой. Нуле-
Нулевым элементом в Vх будет функция х (t) = 0. Полунормы опреде-
определим по формулам
||ж||Р= max |ж@| (р=1, 2, ...).
Ясно, что это, действительно,— полунормы, но не нормы. В самом
деле, если || х ||р = 0, то функция х (t) все же может быть отличной
от нуля вне отрезка [—р, р]. Однако если || х ||р = 0 при всех р,
то это уже будет означать, что х (?) = 0 на всей оси, т. е. х = 8.
Таким образом, С'°° — счетно-нормированное пространство.
Выясним смысл сходимости в этом пространстве. При каждом
фиксированном р соотношение || хп ||р —>- 0 означает, что хп (t) ->¦ 0
равномерно на отрезке [—р, р], а тогда хп —>¦ 0 означает в С°°,
что хп (t) —у- 0 равномерно на любом конечном отрезке.
Обратим внимание читателя на то, что из равномерной сходи-
сходимости на любом конечном отрезке не вытекает равномерная сходи-
сходимость на всей оси. Действительно, положим
0 при t < п — 1 и t > п -1- 1
и определим хп (t) в промежутках (п — 1, п) и (га, га + 1) по
закону линейной интерполяции. Тогда для любого натурального р
функции хп (t) = 0 на отрезке [—р, р], если п>р + 1. Таким
образом, хп (?) —>¦ 0 в каждой точке и равномерно на любом конеч-
конечном отрезке, но поскольку max xn (t) = 1, сходимость хп (t)
к 0 на всей оси не равномерна.
Проверим полноту пространства С°°. Пусть хп — хт —*- 8 по
полунормам. Это означает, что
хп @ — Хт @ —> 0 равномерно на каждом отрезке [ — р, р].
Так как каждое вещественное число попадает внутрь некоторого
из этих отрезков, последовательность { хп (t)} сходится в каждой
точке вещественной оси: хп (t) —>- х (t). Кроме того, сходимость
360 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XIH
в этом соотношении равномерна на каждом из отрезков [—р, р] *),
а тогда функция х (t) непрерывна на каждом из отрезков [—р, р]
и тем самым непрерывна в каждой точке вещественной оси. Таким
образом, х 6 С°°, а хп ->- х по полунормам в С'°°.
3. Пространство СТ, состоящее из всех функций х (t),
заданных на всей оси и имеющих непрерывные производные до
Z-ro порядка включительно (I — заданное натуральное число).
Алгебраические операции определяются в СГ естественным обра-
образом, а полунормы вводятся по формулам
ll*j|p=2 max
Получается счетно-нормированное пространство, представляющее
аналог пространства Ct непрерывно дифференцируемых функций,
рассмотренного в 8.11.
По аналогии с 8.11 и используя рассуждения, подробно прове-
проведенные при рассмотрении предыдущего примера, легко устано-
установить, что сходимость хп —>- х в СТ означает, что
xn (t) —> x^hi (t) равномерно на каждом отрезке f—р, р\
при к = 0, 1, . . ., I. Иными словами, эта сходимость равно-
равномерна на любом конечном отрезке. Как и С'ь пространство СТ
оказывается полным.
4. Пространство CZ, состоящее из всех функций
х (t), бесконечно дифференцируемых (т. е. имеющих непрерывные
производные любого порядка) на всей оси, с естественным опре-
определением алгебраических операций. По составу элементов С~
совпадает с пересечением всех пространств СТ A = 1, 2, . . .)
из предыдущего примера. Полунормы в CZ введем по формулам
К х ||р = § _гаах | а**> (/) | (р = 1, 2, . . .).
Таким образом, здесь при определении полунорм по мере уве-
увеличения номера р участвует все большее количество производ-
производных. Аналогично предыдущему примеру легко проверить, что
хп -*¦ х в CZ означает, что
равномерно на любом конечном отрезке при любом к = 0, 1, 2,...
Пространство CZ — полное.
*) Ср. с проверкой полноты пространства С в 3.5.
13.3] ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ПОЛУНОРМ 301
5. Пространство D бесконечно дифференцируемых
функций с равноограниченными носителями. Пусть [а, Ь] —
заданный отрезок, а через D обозначено множество (очевидно —
линейное) всех функций х (t) из С1^, которые обращаются в 0
вне отрезка [а, Ь] *). Из непрерывности самих этих функций
и их производных следует, что
(a) = XW (b) = 0 при А = 0,1,2,...
Ясно, что J), как подмножество из С™, замкнуто в том смысле,
что оно содержит пределы всех сходящихся последовательностей,
которые можно образовать из элементов множества 1). Ту же
сходимость, которая индуцируется в I) из С~, можно определить
как сходимость по полунормам, вводимым несколько проще,
чем в См, а именно:
||а;||р= |] max 11D @| (р=1, 2, ...).
При этом сходимость в D может быть охарактеризована как
равномерная сходимость функций и всех их производных на отрез-
отрезке [а, Ъ\ **). Полнота пространства Dвытекает уже из того, что D
замкнуто в полном пространстве Ссо-
Так как каждая функция из D обращается в 0 вне отрез-
отрезка [а, Ь], ясно, что если || х ||р= 0 при некотором р, то х (t) = О,
т. е. х = 6. Таким образом, каждая полунорма в 1) на самом
деле является нормой. Однако сходимость по каждой из этих
норм в отдельности отлична от той сходимости, которая описы-
описывается в I) всей совокупностью норм ||ж||Р. По отношению к каж-
каждой норме в отдельности D даже не будет полным.
13.3. Эквивалентные системы полунорм
Одна и та же линейная система может быть превращена в счет-
но-нормированное пространство многими способами. В связи
с этим введем следующее определение.
Определение. Пусть на одной и той же линейной сис-
системе Е заданы две счетные системы полунорм, превращающие Е
в счетно-нормированное пространство. Эти две системы назы-
называются эквивалентными, если они определяют в Е одну и ту же
*) Носителем непрерывной функции х (t) называют замыкание того
множества, где х (t) Ф 0. Таким образом, носители всех функций из D содер-
содержатся в [а, Ь].
**) Отсюда уже следует и равномерная сходимость на любом конечном
отрезке, поскольку носители всех функций из D содержатся в отрезке [а, Ь\.
•362 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XIII
сходимость (т. е. соотношение хп —*- х по полунормам одной сис-
системы влечет то же соотношение и по полунормам другой системы
и обратно).
Кроме того, систему полунорм || х \\р будем называть моно-
монотонной, если
для любого х ? Е.
Во всех примерах из 13.2, кроме первого (пространство s),
указанные там системы полунорм монотонны.
Теорема 13.3.1. В любом счетно-нормированном простран-
пространстве Е существует монотонная система полунорм, эквивалентная
первоначально заданной системе {||ж|]р}.
Доказательство. Для любого х ? Е положим
||*||p=max||s||f (p = l, 2, ...). A)
Легко видеть, что [| х \\'р — полунормы. Проверим, например,
неравенство треугольника. Действительно, для люых х, у ? Е
\\x-\- г/||р= max||o; + j/!!i<max (|| ж||г + || У \\i) <
l'iii.P iSii^P
< max \\x\\t+ max || у \\t = || x \\'p + \\y\\'p.
Если || x \\'p = 0 при всех р, то тем более || х \\р = 0 при всех р,
а тогда х = 0 по определению счетно-нормированного простран-
пространства. Таким образом, система Е с новыми полунормами также
является счетно-нормированным пространством. При этом сис-
система новых полунорм монотонна.
Теперь проверяем эквивалентность обеих систем полунорм.
Если хп -*¦ х по старым полунормам, т. е. || хп — х \\р —*- 0 при
любом р, то
р
l!^n — x\\p= max \\xn — x\\i< S\ \\xn — x\\t > О,
т. е. Хп —*- x по новым полунормам. Обратно, из неравенства
II х \\р < II х Hi» справедливого для любого х ? Е, сразу видно,
что из сходимости {хп} к i по новым полунормам вытекает схо-
сходимость к тому же пределу и по старым полунормам.
Замечание. Из доказательства теоремы легко видеть, что
•если в какой-нибудь системе полунорм любое конечное число их
заменить по формуле A) одной полунормой, то это не отразится
на сходимости.
Определение. Пусть || х \\ и || х \\' — две полунормы,
заданные на одной и той же линейной системе Е. Будем гово-
13.3] ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ПОЛУНОРМ 363
рить, что полунорма |[ х \\' мажорируется полунормой |[а;||,
если существует такая постоянная М, что || х ||'<M || x || для
любого х ? Е.
Теорема 13.3.2. Для того чтобы две монотонные системы
полунорм {||?||р} и {|| х \\'р} в счетно-нормированном простран-
пространстве Е были эквивалентными, необходимо и достаточно, чтобы
каждая полунорма из первой системы мажорировалась некоторой
полунормой из второй системы и обратно.
Доказательство, а) Необходим о" сть. Пусть
системы полунорм {||я||р} и {|| х \\'р} эквивалентны, и предполо-
предположим, например, что полунорма || х \\р не мажорируется ни одной
из полунорм второй системы. Тогда для любого натурального п
существует такой элемент хп ? Е, что
||*п||Ро>п||жп|Г„. B)
Заменяя хп на -г. г.— хп, можно сразу считать, что || хп \\Рп = 1,
II хп \\р0
следовательно, хп -f~ 9 по полунормам первой системы.
С другой стороны, проверим, что хп -*- 9 по полунормам вто-
второй системы. Действительно, для любого е > 0 и любого нату-
натурального р подбираем N > max (р, — ). Тогда при п >iV имеем
благодаря монотонности систем полунорм и неравенству B)
Таким образом, || хп \\'р-*- 0 при любом р, и мы приходим к про-
противоречию с условием эквивалентности данных систем полу-
полунорм.
б) Достаточность. Пусть выполнено условие теоре-
теоремы. Покажем, что если хп -*- х по полунормам первой системы, то
то же соотношение справедливо и по полунормам второй системы.
Для любой полунормы || х ||р найдем мажорирующую ее полу-
полунорму || х \\q из первой системы, а тогда существует такая пос-
постоянная М, что
Но || хп — х ||д ->¦ 0 благодаря сходимости по полунормам первой
системы, следовательно, и \\хп — х||Р->-0. Остается отметить,
что это рассуждение справедливо при любом р.
Аналогично из сходимости по полунормам второй системы
выводится сходимость по полунормам первой системы.
Заметим, что в доказательстве достаточности мы не опирались
на условие монотонности систем полунорм и, таким образом,
в части достаточности теорема верна для любых систем полунорм.
Я64 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XIII
Из определения эквивалентности систем полунорм сразу сле-
следует, что если из монотонной последовательности полунорм
отбросить любое конечное число их или перейти от нее к любой
ее частичной (бесконечной) подпоследовательности, то получится
система полунорм, эквивалентная первоначальной.
Поставим еще вопрос: в каком случае в счетно-нормированном простран-
пространстве Е можно ввести эквивалентную норму, т. е. такую, что сходимость
по этой норме совпадет со сходимостью по заданным полунормам? Для про-
простоты будем считать, что заданная в Е система полунорм {|| х \\р} монотонна.
Назовем полунорму |] х \\р существенной, если она не мажорируется ни одной
из предыдущих (т. е. с номерами, меньшими р). В частности, существенной
будет первая полунорма || х ||i.
Теорема 13.3.3. Для того чтобы, в счетно-нормированном простран-
пространстве Е с монотонной системой полунорм существовала эквивалентная норма,
необходимо и достаточно, чтобы в заданной системе полунорм было лишь
конечное число существенных.
Доказательство. От заданной системы полунорм сохраняем
лишь существенные полунормы, записывая их в том порядке, в каком они
входили в первоначальную систему. Из предыдущей теоремы сразу следует,
что полученная таким образом монотонная система полунорм (она может быть
как бесконечной, так и конечной) эквивалентна первоначальной. При этом
ясно, что если для некоторого х ? Е все существенные полунормы равны О,
то и любая полунорма (за счет условия мажорирования) тоже равна О,
т. е. х = 6 *).
Пусть {|| х \}р} — эта новая система, в которой существенные полунормы
перенумерованы заново натуральными числами, взятыми по порядку: р =
= 1, 2, ... Предположим, что эта система состоит из конечного числа г
полунорм. Благодаря монотонности системы ясно, что сходимость по всем г
полунормам равносильна сходимости по одной r-й полунорме. С другой
стороны, если || х \\г = 0, то и || х \\р = 0 при р < г, а потому х = Э. Таким
образом, r-п полунорма является на самом деле нормой, и эта норма экви-
эквивалентна первоначально заданной системе полунорм. Достаточность условия
теоремы доказана.
Обратно, пусть существует эквивалентная норма || х \\'. По теореме 13.3.2
она должна мажорироваться некоторой полунормой |] х ||г, т. е. существует
такая постоянная М, что
\\Т для любого х?Е.
Покажем, что г и есть число существенных полунорм.
Допустим, что в системе существенных полунорм есть полунорма с номе-
номером р > г. По теореме 13.3.2 она должна мажорироваться нормой || х [|',
т. е. существует такая постоянная N, что
II х Нр «С N \\ х ||' для любого х?Е.
Но тогда || х \\р <С NM || х \\ т для любого х ^E,i. е. полунорма || х ||р мажо-
мажорируется полунормой || х || г (с меньшим номером!) п потому не является
существенной. Таким образом, существенных полунорм лишь конечное число.
Теорема доказана.
*) Теорема 13.3.2, очевидно, остается в силе, если рассматриваемые
системы состоят из конечного числа полунорм, в частности, если одна из
систем сводится к одной норме. Заметим также, что если какая-нибудь полу-
полунорма мажорируется некоторой предыдущей, то она обязательно мажори-
мажорируется и одной из существенных.
13.4] ВВЕДЕНИЕ МЕТРИКИ 365
В 5.2 уже было доказано, что в пространстве s не существует нормы,
которая описывала бы сходимость по координатам, т. е. нормы, эквивалент-
эквивалентной заданной в «системе полунорм. Из теоремы 13.3.3 этот результат следует
мгновенно, поскольку совершенно очевидно, что все полунормы в s суще-
существенны. Можно доказать, что и во всех других'пространствах, приведенных
в качестве примеров в 13.2, все полунормы существенны, а потому ни в одном
из этих пространств нет эквивалентной нормы.
13.4. Введение метрики в счетно-нормированном
пространстве
В гл. V мы видели, что нормированные пространства — част-
частный случай метрических. Здесь мы покажем, что счетно-нор-
мированные пространства тоже представляют частный случай
метрических; однако на этот раз метрика вводится несколько
более сложным способом. Именно, образцом для введения метрики
в произвольном счетно-нормированном пространстве будет слу-
служить формула, по которой в 3.2 определялось расстояние в про-
пространстве s.
Итак, пусть Е — счетно-нормированное пространство с си-
системой полунорм {|| х \\р). Определим расстояние в Е, полагая
для любых двух элементов х, у ? Е
Проверка того, что при таком определении расстояния в Е будут
выполнены все аксиомы метрического пространства, произво-
производится совершенно так же, как это было сделано в 3.2 для про-
пространства s. Так же как для * (см. 3.3), проверяется, что сходи-
сходимость хп -*- х по расстоянию в s равносильна выполнению при
всех р = 1, 2, ... условий || хп — х \]р —*- 0, т. е. сходимость
по расстоянию совпадает со сходимостью по полунормам.
Остановимся на вопросе о полноте счетно-нормированного
пространства. Пусть Е — счетно-нормированное пространство
и по формуле C) в нем введена метрика. Выше (в 13.1) мы опре-
определили, что означает полнота счетно-нормированного простран-
пространства. С другой стороны, мы располагаем понятием полноты мет-
метрического пространства. Покажем, что в Е оба эти понятия равно-
равносильны.
Пусть Е полно как счетно-нормированное пространство,
а последовательность {хп} элементов из Е фундаментальна по
метрике, т. е. р (хп, жт)->-0 при п, щ->-оо. Из формулы C) сразу
следует, что
—¦—*• U при каждом р.
366 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. ХИН
Как и в &, отсюда следует, что
II хп — хт \\р - > 0 при каждом р,
т. е. последовательность {хп} фундаментальна по полунормам.
Но так как Е — полное счетно-нормированное пространство, то
{хп} сходится по полунормам к некоторому пределу х, а тогда
и р (хп, я) —*-0. Таким образом, Е полно как метрическое про-
пространство.
Обратно, пустьЕ полно как метрическое пространство, а после-
последовательность {хп} фундаментальна по полунормам. Проверим,
что тогда она фундаментальна и по метрике. Зададим е > О
°° . .
и подберем р0 так, что У\ оо = о»-<с4-. Затем подбираем ЛГ
р=ро+1 ге гРа 1
так, что
\\хп — хт\\р<.~ при п, m>N и р=1, 2, ..., р0.
Теперь ясно, что при п, т> N
. . vi 1 II хп хт \\р sr\ 1 \\хп. хт lip
sr\ 1
Z IP" 1
hi „, цр + Ц „ ||р
P=l p=po+1
Po °°
^2^-J2" ¦" 2P^2'2~r
p=l p=P0+l
т. е. последовательность {хп} фундаментальна по расстоянию,
и потому {Хп} сходится по расстоянию к некоторому пределу х.
Но тогда хп —*- х и по полунормам.
Если линейная система Е каким-то произвольным способом
метризована, то это еще не означает, что Е может быть превра-
превращено в счетно-нормированное пространство так, чтобы сходи-
сходимость по метрике совпала со сходимостью по полунормам. Это
следует хотя бы из того, что метрика, введенная с помощью фор-
формулы C) по полунормам, обладает рядом дополнительных свойств,
например свойством «инвариантности»: р (х, у) = р (х — у, 9),
из которого уже вытекает, что
р (хп, х)—>0 равносильно р (хп — х, 9) —> 0.
Тогда последним свойством должна обладать и всякая метрика,
описывающая ту же самую сходимость. Но и условия инвариант-
инвариантности метрики тоже недостаточно для счетной нормируемости
пространства Е. Приводить необходимые и достаточные условия,
при которых метрическое пространство, построенное на линей-
13.4] ВВЕДЕНИЕ МЕТРИКИ 3(J7
ной системе, может быть превращено в счетно-нормированное,
мы здесь не будем * ).
Рассмотрим счетно-нормированное пространство Ее моно-
монотонной системой полунорм. Будем считать, что Е метризо-
вано по формуле C). Если р — натуральное, а б > 0 — любое,
обозначим через F*,e множество всех х ? Е, для которых || х ||р ¦<
<б. Из непрерывности полунорм следует, что множества V*,,&
замкнуты. Действительно, если х„. ? F?,6 и хп ->- х, то
и потому х 6 Fp.e.
По аналогичным соображениям замкнуто и множество всех
тех х ? Е, для которых || х ||Р>6, а тогда его дополнение, обо-
обозначим это дополнение через VPin, т. е. множество всех х ? Е,
для которых || х ||р < б, открыто. Таким образом, 9 — внутрен-
внутренняя точка в Fp,e, тем более внутренняя точка в Fp.e (заметим,
что FP,6 с: V%,'i)-
Множества VP,s (соответственно F*,e) будем пазывать откры-
открытыми (соответственно замкнутыми) квазишарами с центром в 9.
Квазишары, для которых 6 = 1, будем называть единичными.
Лемма 13.4.1. Пусть U— Ь-окрестностъ нулевого элемента О,
т. е. открытый шар S (Э, 6) с центром в 0 и радиусом 6. Тогда существует
такое натуральное q, что квазишар V* i с U.
q 2 16
Доказательство. Пусть q > -т- . Тогда — < — и
О q ?
ZA 2v 29 5 2
Если x ? V* j, то || x ||p <^— природ. Следовательно,
9? «7
Zj 2P +||||p
р=1 Р=9+1
7
р=1 Р=9+1
Таким образом, V* i a U.
q
*) См., например, Л. В. Канторович и Г. П. Акилов,
Функциональный анализ в нормированных пространствах, стр. 368.
368
СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА
[ГЛ. Х1Ц
Замечание. Поскольку 0 — внутренняя точка в V* j , у нулевого
q'T
элемента существует некоторая шаровая окрестность W, которая содержится
в F* 4 . Взаимное расположение
множеств U, F* j n W проиллю-
проиллюстрировано на рис. 19.
-у* , 13.5. Ограниченные множества
*V в счетно-нормированном
пространстве
Пусть Е — снова произволь-
произвольное счетно-нормированное про-
пространство. По аналогии с опре-
определением ограниченности мно-
рнс ig жества в нормированном про-
пространстве можно ввести понятие
ограниченности по полунормам.
Определение. Множество A cz E называется ограничен-
ограниченным по полунормам, если существуют такие постоянные СР
(р = 1, 2, . . .), что || х ||р<-'Ср для каждого х ? А и любого р.
Заметим, что, например, всякая фундаментальная после-
последовательность {хп} ограничена по полунормам. Это сразу выте-
вытекает из неравенства
11 V II ^ II Г I1
в котором следует считать т фиксированным, а п пробегающим
все значения от 1 до оо (ср. с доказательством теоремы 3.5.2).
Теорема 13.5.1. Для того чтобы множество A cz E было
ограниченным по полунормам, необходимо и достаточно, чтобы
оно удовлетворяло следующему условию: для любых хп ? А и любой
последовательности чисел Кп —>¦ 0 последовательность кпхп —*- 0.
Доказательство. Необходимость условия очевидна,
так как при любом р
Проверяем его достаточность. Допустим, что условие тео-
теоремы выполнено, но при некотором р полунормы || х \\р (х 6 А)
в совокупности не ограничены, т. е. существуют такие хп 6 А, что
\\хп\\Р>п (п = 1, 2, ...).
1 1
Тогда положим Хп = — . По условию "кпхп -*- 0; однако —1| хп \\ р >
> 1. Мы пришли к противоречию и тем самым теорема доказана.
13.5] ОГРАНИЧЕННЫЕ МНОЖЕСТВА 369
Остановимся на одном из примеров, рассмотренных в 13.2,
именно на пространстве Х>, и покажем, что в этом пространстве
класс компактных множеств совпадает с классом множеств, огра-
ограниченных по полунормам *).
Если множество М с Ъ не ограничено по полунормам, то
оно не может быть компактным. Действительно, если некоторая
из полунорм, например р-я, принимает на элементах из М сколь
угодно большие значения, то в М существует последовательность
элементов {хп}, для которой ||?л||р -»- оо, а из такой последова-
последовательности нельзя выделить никакой сходящейся (по полунормам
или, что то же самое, по метрике). Остается показать, что если
М с D ограничено по полунормам, то оно компактно.
Пусть хп ? М (п = 1, 2, . . .) и тем самым || хп \\Р^СР при
каждом /7 = 1,2, ... Из ограниченности последовательности
|| Хп ||t вытекает, что сами функции хп (t) и их производные
х'п @ равноограничены на отрезке [а, Ь]:
\xn(t)\<Cu |av,(O|<Ci при a<t<b.
Из равноограниченности производных следует, что сами функ-
функции хп (t) удовлетворяют условию Липшица с общей постоян-
постоянной Ct **), а тогда по лемме 3.9.1 функции Хп (t) равностепенно
непрерывны. Следовательно, по теореме Арцела (теорема 3.9.1)
из последовательности {х„} можно выделить частичную, которая
сходится по метрике пространства С, т. е. равномерно сходится
на отрезке [а, Ь]. Запишем эту частичную последовательность
в виде:
Теперь из ограниченности вторых полунорм (\\ xin \\2 < С2)
следует, что у функций xin (t) равноограничены производные 1-го
и 2-го порядков:
kin@l<C2, \\x\n(t)\<C2 при а<<<Ь.
Тогда производные 1-го порядка х\п (t) оказываются равносте-
равностепенно непрерывными. Еще раз применяя теорему Арцела, мы
сможем выделить из D) новую частичную последовательность
^-21) 3-22» • • • i 3-2я» • • • i
для которой последовательность производных 1-го порядка будет
равномерно сходящейся на отрезке [а, Ь].
*) В то же время в бесконечно-мерном нормированном пространстве
совпадение классов компактных и ограниченных множеств невозможно.
**) Действительно, по формуле Лагранжа для любых tl и t2 из [а, Ъ]
I хп («,)-*„ (t2) | = | х'п (т) (*,-*2) К С, | *,-*2 I-
24 б. 3. Вулих
370 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XIII
Продолжая этот процесс до бесконечности, мы построим таб-
таблицу функций
3-22 -
так, что каждая ее строка (начиная со второй) представляет час-
частичную последовательность, выделенную из предыдущей строки,
а функции, стоящие в тг-й строке, обладают тем свойством, что
последовательности
№ п4 (*).¦¦•• 4п> @. ¦ ¦ • (А- - о, 1, .... п-1)
равномерно сходятся на отрезке [а, Ь]. Применяя известный
читателю диагональный метод, мы выделим диагональную после-
последовательность {хпп}, которая и будет сходиться по полунормам
в пространстве D, так как для этих функций производные любого
порядка образуют последовательность, равномерно сходящуюся
на отрезке [а, Ь]. Тем самым доказана компактность множе-
множества М.
Будем далее считать, что система полунорм в счетно-нормированном
пространстве Е монотонна. Докажем, что если пространство Е не сводится
к нормированному (т. е. если в нем не существует эквивалентной нормы),
то ни один квазишар не может быть ограниченным множеством.
Допустим, что квазишар V* 6 ограничен *). Это значит, что при любом
натуральном q существует такая постоянная Cq, что из неравенства |[ х ||р ^
^ б вытекает |[ х \\q <; Cq. Покажем, что тогда для любого х ? Е
Пусть сначала || х ||р Ф 0. Введем элемент х' = -,—-.— х. Ясно, что
II х \\р
|| х'р || = б, следовательно, х' ? F*_ e и потому || х' \\q < Cq, а тогда
Если же |1 х \\р = 0, то и || пх ||р = 0 при любом натуральном п и потому
пх ? F*e, а тогда || пх \\q < Cq, т. е. |] х \\q < — Cq при любом п = 1, 2, ...
Отсюда следует, что || х \q = 0 и тем самым неравенство E) выполнено.
*) Ясно, что наше рассуждение достаточно провести для замкнутых
квазишаров.
13.6] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 371
Неравенство E) означает, что g-я полунорма мажорируется р-й, и так
как это справедливо при любом q, средп полунорм в пространстве Л не может
быть бесконечного множества существенных *). Последнее противоречит
теореме 13.3.3, поскольку пространство Е, по предположению, пе сводится
к нормированному **).
13.6. Линейные операторы в счетно-нормированных
пространствах
Для упрощения ряда формулировок мы будем дальше, в этом
и следующем параграфах, считать, что в рассматриваемых счетно-
нормированных пространствах системы полунорм м о н о т о н-
н ы. Однако основные определения могут быть даны и в любых
счетно-нормированных пространствах.
Перенесем в счетно-нормированные пространства некоторые
понятия и результаты из гл. VIII.
Пусть X и Y — счетно-нормированные пространства. Как
и раньше, оператор U, отображающий X в У, называется линей-
линейным, если он аддитивен и непрерывен ***). Совершенно так же,
как в нормированных пространствах, доказываются теоремы
8.2.1 и 8.2.2 и для операторов в счетно-нормированных простран-
пространствах. Именно, можно установить, что если аддитивный оператор
непрерывен в какой-нибудь одной точке, то он линеен, и что
всякий линейный оператор однороден. Перенос в счетно-норми-
счетно-нормированные пространства теоремы 8.2.3 не представляет интереса,
так как можно показать, что во всяком конечно-мерном счетно-
пормированном пространстве существует эквивалентная норма.
Однако понятие ограниченности оператора при переносе в счетно-
нормированные пространства нуждается в изменении.
Определение. Оператор U, заданный в пространстве X,
называется ограниченным, если для любого натурального р суще-
существуют такое натуральное q и такая постоянная СР, что
\\Ux\\p<Cp\\x\\q F)
для всех х 6 X. В частности, если пространства X и Y норми-
нормированные, это определение ограниченности оператора сводится
к тому, которое было дано в 8.3.
*) Не будут существенными во всяком случае все полунормы с номе-
номерами, большими р.
**) Неограниченность квазишаров можно вывести еще и из того, что
если в счетно-нормированном пространстве существует хоть один ограни-
ограниченный квазишар, то Е должно быть нормируемо по одной теореме советского
математика А. Н. Колмогорова. Точную формулировку этой теоремы
А. Н. Колмогорова можно найти, например, в книге Л. В. К анторови-
ча и Г. П. А к и л о в а, стр. 365.
***) Непрерывность оператора U, как и выше, означает, что если хп -*¦ х,
то Uxn -*¦ Ux. Здесь, естественно, имеется в виду сходимость по полунормам.
24*
372 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XIII
Теорема 13.6.1. Для того чтобы аддитивный оператор U
был линейным, необходимо и достаточно, чтобы он был ограни-
ограниченным.
Доказательство*), а) Необходимость. Рас-
Рассуждая от противного, допустим, что оператор U линеен, но что
для некоторого р требуемой пары чисел q и Ср не существует.
Следовательно, для любого натурального п существует такой
элемент хп ? X, для которого
||Cten||p>n||*»IU G)
(в противном случае при некотором гс мы имели бы для всех
х?Х неравенство || Ux\\p<^n || x \\п, и мы могли бы взять q = n,
Ср = п). Из неравенства G) следует, что ||?/жп||р^0. Положим х'п =
— .. . " .,- . Тогда II Ux'n ||p = 1, следовательно, Ux'n не стремится
II ихп \\р ^
к 9. С другой стороны, из неравенства (/) вытекает, что
<— •
11 "||П II Uxn ||p ^ n
Тогда для любого е > 0 и любого натурального q имеем при
гс >> max ( q, — J
1
Таким образом, || ж^,||д->-0 при любом q, а зто означает, что
х'п-*- 6. Полученное противоречие с непрерывностью оператора U
и доказывает, что оператор U ограничен.
б) Достаточность. Пусть оператор U аддитивен и огра-
ограничен и пусть хп —*¦ 9. Возьмем любое натуральное р и восполь-
воспользуемся неравенством F). Так как || хп \\q -*¦ 0, то и || Uxn ||p -*¦ О,
следовательно, Uxn -*¦ 6. Тем самым непрерывность оператора U
в точке х — 9, а тогда и его линейность доказаны.
В точности так же, как в 8.3, доказывается, что для того,
чтобы аддитивный оператор U удовлетворял во всем простран-
пространстве X неравенству F), необходимо и достаточно, чтобы неравен-
неравенство || Uz\\p-*?.Cp (с той же постоянной Cv) было выполнено
для всех х из единичного квазишара Vqyi. Таким образом, огра-
ограниченность аддитивного оператора U означает, что для любого
натурального р найдется единичный квазишар в X, на котором
совокупность значений оператора U «ограничена по р-й полунорме».
*) Приводимое ниже доказательство — непосредственное обобщение дока-
доказательства теоремы 8.3.1.
13.6] ЛИНЕЙНЫЕ ОПЕРАТОРЫ 373
Из теоремы 13.6.1 легко выводится, что линейный оператор U
переводит всякое ограниченное (по полунормам) множество из X
в ограниченное (по полунормам) множество в пространстве Y.
Действительно, пусть множество А с X ограничено, т. е.
существуют такие постоянные Mq, что ||a;||g<Af9 для всех
х ? А. Возьмем у ? U (А), т. е. у = Ux, где х 6 А. Так как опе-
оператор U ограничен, то для любого р имеем по неравенству F)
\\y\\P<CP\\x\\q<CpMq.
Тем самым множество U (А) тоже ограничено.
Заметим без доказательства, что справедливо и, в известном
смысле, обратное заключение: если аддитивный оператор U
переводит всякое ограниченное (по полунормам) множество из X
в ограниченное (по полунормам) множество в пространстве Y,
то оператор U линеен. Приведем некоторые примеры.
В пространстве С°° рассмотрим оператор сдвига (со значе-
значениями в том же пространстве) : у = Ux означает, что у (t) =
= х (t -f- h), где h — фиксированное число, отличное от 0. Ясно,
что оператор U линеен. Его аддитивность очевидна, а непрерыв-
непрерывность означает, что если хп (t) ->- 0 равномерно на любом конеч-
конечном отрезке, то и хп (t + h) ->¦ 0 в том же смысле. Как линейный
оператор, U ограничен. Проверим его ограниченность непосредст-
непосредственно, причем для простоты остановимся лишь на случае, когда А=1.
'Имеем при любом р = 1, 2, . . .
\\Vx\\p= max |ж(/ + 1)[< max | х (?) | = || х ||р+1.
Таким образом, для любого р в условии ограниченности (в нера-
неравенстве F)) можно взять q = р-\-1, Ср = 1.
В пространстве D (бесконечно дифференцируемых функций
с равноограниченными носителями) рассмотрим оператор диф-
дифференцирования: Ux = х'. Линейность этого оператора очевидна.
Предлагаем читателю самостоятельно проверить для него условие
ограниченности.
Перейдем к последовательностям линейных операторов.
Прежде всего ясно, что если Ux = \\mUnx при всех х?Х,
где все операторы Un переводят X в Y и аддитивны, то и опе-
оператор U аддитивен.
Определение. Операторы Un (п = 1, 2, . . .), перево-
переводящие X в Y, называются равноограниченными, если для любо-
любого натурального р существуют такое натуральное q и такая по-
постоянная Ср, что
\\Unx\\p<Cp\\x\\q (8)
при всех х 6 X и при всех и = 1, 2, ...
374 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XIII
Совершенно так же, как лемма 8.5.1, доказывается, что если
последовательность линейных операторов {Un} точечно сходится
к оператору U и операторы Un равноограничены, то оператор U
тоже линеен. Мы покажем, что в полные счетно-нормированные
пространства переносится теорема Банаха — Штейнгауза.
Теорема 13.6.2. Пусть Un (и = 1, 2, . . .) — линейные
операторы, отображающие полное счетно-нормированное про-
пространство Ж в какое-нибудь счетно-нормированное простран-
пространство Y. Если в каждой точке х ? X совокупность значений {Unx}
ограничена (по полунормам в Y), то операторы Un равноогра-
равноограничены.
Доказательство. Чтобы доказать эту теорему, следует повто-
повторить с некоторыми изменениями доказательство теоремы 8.5.1. Мы покажем,
как это делается, пропуская некоторые подробности.
Рассуждая от противного, допустим, что для некоторого натурального р
пары чисел q и Ср, входящих в определение равноограниченности операто-
операторов Un, не существует. Покажем, что тогда, каков бы ни был замкнутый шар
оо
S* cz X, множество [j Un (S*) не ограничено по р-й полунорме *). Действи-
Действиям
тельло, иначе в некотором шаре S* = S* (х0, г) при всех х 6 S* и всех п =
= 1,2,... выполнялось бы неравенство
\\Vn*\\p<M
(М ¦— постоянная). Пусть теперь W— открытый шар с центром 6 и радиу-
радиусом г. Если х ? W, то, полагая х' = х0 + х, получим, что х' ? S*
ясно, что
II Unx ||Р<2М для всех x?W и п=1, 2, ...
По лемме 13.4.1 существует замкнутый квазишар V* i r~ w. Следова-
тельно,
если \\=c\\q<~, то \\Unx\\p*C2M (я = 1, 2, ...).
Повторяя то рассуждение, с помощью которого в 13.5 было выведено нера-
неравенство E), мы найдем, что для всех х 6 X
Ц^вг||р<2М'9||*||, (п = 1, 2, ...)•
Таким образом, для данного р нашлась такая пара чисел q и Ср — 2Mq,
что неравенство (8) выполнено, а это противоречит исходному предположе-
оо
нию. Тем самым доказана неограниченность множества U Un (S*) по р-й
п=1
полунорме.
Возьмем произвольный замкнутый шар S* d X радиуса г. Найдем
номер щ и элемент аг± ? S$, для которого || Uni xt \\p > 1 (р — то, о котором
идет речь в первой половине доказательства). Элемент xt можно считать
внутренней точкой в шаре 5J. Благодаря непрерывности оператора Uni
*) Мы пользуемся той метрикой, которая вводится в пространстве X
по формуле C).
13.7] ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ 375
существует замкнутый шар S* = S* (x±, rj), во всех точках которого
|| Un^x ||р > 1. Можно считать, что rt <; — и что Sf cz S$. Теперь снова
найдутся номер п2 и элементу 6 <Sf, для которого || ?/ xz \\p > 2, причем
х2 можно считать внутренней точкой в шаре S*. Продолжая это рассуждение,
мы построим такую последовательность вложенных замкнутых шаров 5т
с радиусами гт->Ои такую последовательность индексов пт, что \\Unmx \\p >
> «при всех х ? S^. В частности, эти неравенства будут выполнены в точ-
точке х*, общей для всех шаров 5^. Но тогда совокупность значений {Unx*}
не будет ограниченной по р-й полунорме, что противоречит условию теоремы.
Тем самым теорема доказана.
Аналогом теоремы 8.5.2 служит теорема, доказательства
которой мы не приводим ввиду его полного сходства с доказа-
доказательством теоремы 8.5.2.
Теорема 13.6.3. Если [/„(/1 = 1,2,...) — линейные
операторы, отображающие счетно-нормированное пространство X
в полное счетно-нормированное пространство Y, причем:
1) для всех х из некоторого множества А, всюду плотного в X,
существует lim Unx;
2) операторы Un равноограничены,
то последовательность {[/„} точечно сходится (на всем X) к неко-
некоторому линейному оператору.
13.7. Линейные функционалы
Все сказанное в предыдущем параграфе применимо, в част-
частности, к операторам, переводящим счетно-нормированное про-
пространство в нормированное и, в еще более частном случае, к функ-
функционалам. Однако для функционалов можно установить и неко-
некоторые дополнительные результаты и поэтому вопрос о линей-
линейных функционалах мы рассмотрим более подробно.
Итак, пусть X — счетно-нормированное пространство, а / —
функционал, заданный на X. Определение ограниченности, дан-
данное в 13.6 для оператора, применительно к функционалу озна-
означает, что существуют такие натуральное q и постоянная С, что
|/(*)|<С|И,- (9)
для всех х ? X. Это условие и является необходимым и достаточ-
достаточным для того, чтобы аддитивный функционал / был линейным.
При выполнении неравенства (9) будем говорить, что функцио-
функционал / ограничен по отношению к q-й полунорме.
В соответствии с 13.1 обозначим через Х^~> то нормированное
пространство, которое получается из X отождествлением #-зкви-
валентных между собой элементов *).
*) Напоминаем, что || х \\q принимаются за норму в
376 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XIII
Пусть на X задан линейный функционал /. Его ограничен-
ограниченность означает ограниченность по отношению к некоторой полу-
полунорме; q — номер этой полунормы. Тогда ясно, что если хну
^-эквивалентны, то / (х) = f (у). Действительно,
\f(x)-f(y)\ = \f(x-y)\<C\\x-y\\q = O.
Таким образом, функционал / можно рассматривать и как функ-
функционал на -ЛГ<9), причем и там он, очевидно, будет аддитивным,
а по условию (9) и ограниченным, следовательно, линейным.
Итак, каждый линейный функционал, заданный на X, есть
линейный функционал на некотором из пространств Х^.
Обратно, если на некотором XW задан линейный функцио-
функционал /, то / можно считать заданным и на всем X*). При этом
условие ограниченности функционала / в пространстве XW перей-
перейдет в условие его ограниченности в пространстве X, т. е. / будет
линейным функционалом и в X.
Таким образом, совокупность всех линейных функционалов на X
можно рассматривать как сумму (в том смысле, как это было
определено в 3.1 для множеств) пространств, сопряженных
(U (XW)').
q=l
На линейные функционалы в счетно-нормированных простран-
пространствах переносится теорема Банаха — Гана, а именно справед-
справедлива следующая теорема.
Теорема 13.7.1. Пусть X — счетно-нормированное про-
пространство, Е — его линейное подмножество, / — линейный функ-
функционал, заданный на Е **). Тогда функционал / допускает распро-
распространение с сохранением свойства линейности на всё X. При
этом если f ограничен на Е по отношению к q-й полунорме, то
и распространение можно осуществить так, что полученный
в результате распространения функционал оказывается огра-
ограниченным на X по отношению к той оке полунорме ***).
Доказательство. Пусть заданный на Е линейный
функционал / ограничен по отношению к q-й полунорме || х \\q.
Используем пространство -АГ<?> и обозначим (ср. 13.1) через E{q)
образ множества Е в пространстве Х^. Функционал / можно
рассматривать как линейный на множестве Е^~> и по теореме
*) При этом естественно следует считать, что на (/-эквивалентных
между собой элементах функционал / имеет одно и то же значение, а тогда
функционал /, очевидно, аддитивен.
**) Как линейное подмножество из X множество Е само является
счетно-нормированным пространством.
***) Кроме того, из доказательства будет видно, что если функционал /
удовлетворяет на множестве Е условию | / (х) | <^ С \\ х \\q, то распростране-
распространение можно осуществить с сохранением этого условия с той же постоянной С.
13.7] ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ 377
Банаха — Гана его можно распространить с сохранением линей-
линейности на Х^. Но тем самым получается функционал, ограничен-
ограниченный относительно q-й полунормы, который можно считать заданным
на всем X. Это и есть требуемое распространение функционала /.
В теории нормированных пространств чрезвычайно важную
роль играет полученное в гл. IX следствие из теоремы Банаха —
Гана о том, что во всяком нормированном пространстве суще-
существует достаточное множество линейных функционалов (см. след-
следствие из теоремы 9.4.1). Этим свойством обладают-и счетно-нор-
мированные пространства, именно и здесь можно установить
следующее следствие из доказанной теоремы.
Следствие. Каков бы ни был элемент х0 ф 6 счетно-нор-
мированного пространства X, на X существует такой линейный
функционал /, что / (х0) = 1 *).
Доказательство. Существует натуральное q, при
котором || xo\\q ф 0. Примем за Е множество всех элементов вида
hc0 и положим / (Кх0) = Я. Этот функционал ограничен по отно-
отношению к q-& полунорме. Действительно,
Тем самым функционал / линеен; кроме того, / (х0) = 1. Распро-
Распространяя его с сохранением линейности на всё X, мы и получим
функционал, существование которого требовалось доказать.
Покажем еще, что и критерий ограниченности множества, уста-
установленный в гл. IX для нормированных пространств, переносится
в счетно-нормированные пространства.
Теорема 13.7.2. Если А — произвольное подмножество
счетно-нормированного пространства X и для каждого линейного
функционала /, заданного на X, совокупность f (А) его значений
на множестве А ограничена, то множество А ограничено по полу-
полунормам.
Доказательство. Рассмотрим сначала все линейные
функционалы на X, ограниченные по отношению к некоторой
фиксированной полунорме || х \\я, т. е. функционалы, входящие
в (Х^)'. Вместо заданного множества А возьмем его образ А^
в пространстве Х^. Из условия теоремы следует, что совокуп-
совокупность значений каждого функционала из (XW)' ограничена на
А^К Поэтому по теореме 9.8.2 4W ограничено в Х^\ т. е. суще-
существует такая постоянная Cq, что || х \\q<^Cq для любого х ? А.
Поскольку это справедливо при любом q, множество А огра-
ограничено по полунормам в пространстве X.
*) За счет умножения функционала / на числовой множитель всегда
можно добиться, чтобы / (х0) имело любое значение, в частности, любое-
отличное от нуля (именно это и представляет основной интерес).
378 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XJJI
13.8. Общие формы линейных функционалов в некоторых
счетно-нормированных пространствах
Рассмотрим некоторые из пространств, приведенных в каче-
качестве примеров в 13.2.
1. Пространство *. При том способе введения в *
полунорм, который был указан в 13.2, система полунорм в *
не монотонна. Однако если воспользоваться доказательством
теоремы 13.3.1, то сразу видно, что эквивалентная монотонная
система полунорм может быть введена по формуле
|?i|, |?, |, .. ., \ЪР\).
Всякий линейный функционал /в * ограничен по отношению
к некоторой из полунорм || х ||р, например относительно полу-
полунормы с номером q:
\f(x)\^C\\x\[q A0)
для всех х ? *. Если элемент х ? * таков, что li = ?г = • • • =
= \q = 0, то || х \\q = О, а тогда из A0) следует, что и / (х) = 0.
Положим
аР = /(еР) (р=1. 2, ..., q),
где ер — тот элемент из *, у которого |р = 1, а все прочие коор-
координаты равны 0. Ясно, что любой х = {im} ? s можно предста-
представить в виде
причем первые q координат элемента у равны 0. Тогда / (у) =0
и потому
/ Н - Ы (е,) +---+tgf (eq) = S vptp-
p=l
С другой стороны, непосредственно ясно, что всякий функ-
функционал, заданный в * по формуле
/(*)=2«pSp. С11)
р=1
где q — любое заданное натуральное число, а ар — произвольно
заданные вещественные числа, линеен. Таким образом, фор-
формула A1) дает общий вид линейных функционалов в s.
2. Пространство С°°. Пусть / — линейный функ-
функционал в С°°, ограниченный относительно р-й полунормы. Будем
его рассматривать в пространстве (С°°)(р>, получающемся за
счет отождествления р-эквивалентных элементов из С°°. В про-
13.8] ОБЩИЕ ФОРМЫ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 379
странстве (Сто)(р) отождествляются любые две функции из С°°,
которые совпадают друг с другом на отрезке [—р, р]. Иными
словами, при рассмотрении элементов пространства (С°°)(р>
мы пренебрегаем значениями функций вне отрезка [—р, р].
Но это равносильно тому, что элементы пространства (С°°)(р)
можно интерпретировать как непрерывные функции на отрезке
[—р, р], т. е. пространство (С°°)<р) можно отождествить с про-
пространством С непрерывных функций на отрезке [—р, р]. Таким
образом, функционал / можно рассматривать как линейный
функционал в пространстве С на отрезке [—р, р], и согласно
теореме Рисса (теорема 9.5.1) об общей форме линейного функ-
функционала в пространстве непрерывных функций на отрезке функ-
функционал / представим в виде
/(*)= ^x(t)dg(t),
—р
где g (f) — функция ограниченной вариации.
С другой стороны, если g (t) — любая функция ограниченной
вариации, заданная на некотором отрезке [а, Ь], то функцио-
функционал /, определяемый формулой
ь
f(z)=\x(t)dg(t), A2)
а
— линейный функционал в пространстве С°°. Его аддитивность
очевидна, а ограниченность проверяется так: подбираем настоль-
настолько большое натуральное р, что [а, Ь] сг [—р, р]. Тогда по
неравенству B8) из гл. IX
| / (х) |< (Var g @) max | x (t) | < (Var g (*)) || х \\р.
Таким образом, формула A2), где [а, Ъ\—любой отрезок,
a g (t) — любая функция ограниченной вариации на этом отрезке,
дает общий вид линейных функционалов в пространстве С°°.
3. Пространство D. Как и в определении, данном
в 13.2, будем считать, что пространство D «построено на отрез-
отрезке [а, Ь]», т. е. что носители всех функций из D содержат-
содержатся в [а, 6].
Рассмотрим линейный функционал /, заданный на D и огра-
ограниченный по отношению к р-й норме (напоминаем, что полу-
полунормы в D суть нормы). Построим аддитивный и однородный
оператор А, отображающий пространство D на некоторое под-
подмножество из пространства С, составленного из всех непре-
380 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XIII
рывных функций на отрезке [а, Ь]. Именно, положим Ах =
т. е. каждой функции х ? X) сопоставим ее производную р-го
порядка, рассмотренную только на отрезке [а, Ь]. Легко видеть,
что отображение, устанавливаемое оператором А, взаимно-одно-
взаимно-однозначно. Действительно, пусть Ах = Ау, т. е.
xv(t) = yp(t) при а < t < Ъ.
Так как а^) (а) = у^-^) (а) = 0, то
ж<р-1) (t) = ^ ж<р) @ dt = [ г/(р) It) dt = yfr-U U)
а а
при любом t из [а, Ь]. Аналогично мы установим, что ?(р~2) (t) =
= j/(p-2) (^) и, таким образом, по индукции мы получим, что
х (t) = у (t) на отрезке [а, Ь]. Отсюда уже следует, поскольку
х, у ? D, что х (f) =ш у (t) на всей оси.
Обозначим через /? совокупность значений оператора 4 (Е с С).
По общим свойствам аддитивных и однородных операторов Е —
линейное множество (см. 8.7). Рассмотрим обратный опера-
оператор А'1, отображающий Е на X). Однако мы будем считать, что
значения оператора А'1 берутся из пространства D<p). Это про-
пространство по составу элементов не отличается от X), но оно —
нормированное и за норму в нем принята р-я норма из D : || х \\Р.
Докажем, что оператор А'1 как оператор, отображающий Е
на 1Iр\ линеен. С этой целью для любого х ? 1)<р) положим
ф (t) = ж<р) (f) на отрезке [а, Ь]. Тогда с помощью теоремы
Лагранжа сразу находим
@ — z(p-4) (a) | =
) | (*—а)< (max|<р (*) |) (й-а)<|] <р|| (Ь — а)
(здесь ||ф||= max ]ф(<)|, т. е. это—норма в пространстве С).
Аналогично
Продолжая дальше, мы найдем в конце концов, что
а отсюда уже вытекает, что
или
13.8] ОБЩИЕ ФОРМЫ ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ 381
(напоминаем, что ц> = Ах). Теперь линейность оператора А'1
вытекает из теоремы 8.7.2.
Функционал / можно рассматривать как линейный на про-
пространстве DQJ). Построим «сложный» функционал на множестве Е,
полагая
F(<?) = f(A-1<e) (ф?Я). A3)
Функционал F линеен как суперпозиция линейных операторов
(см. 8.6), а тогда его можно распространить с сохранением линей-
линейности с множества Е на всё пространство С. Следовательно,
существует такая функция ограниченной вариации g (t) на отрез-
отрезке [а, Ь], что
ъ
F (<р) = \ ф (t) dg (t) при всех ф?С
Но для любого :r?D<p> существует такая ф??\ что х=А\
(или ц> = хт). Тогда по формуле A3) f(x) = F(xW) и потому
A4)
Обратно, всякий функционал /, заданный в пространстве D
по формуле A4), где р — любое натуральное число, a g (t) —
любая функция ограниченной вариации, будет, очевидно, адди-
аддитивным и ограниченным по отношению к р-й норме. Следова-
Следовательно, / — линейный функционал в D. Таким образом, фор-
формула A4) дает общий вид линейных функционалов в простран-
пространстве I).
Заметим, что функционал, заданный по формуле A4) при
р = 0, также будет линейным в пространстве 2). Непосредствен-
Непосредственная проверка непрерывности такого функционала или проверка
его ограниченности по отношению к любой норме очевидны.
Таким образом, записывая по формуле A4) общий вид линей-
линейного функционала в пространстве D, можно считать р любым
целым неотрицательным числом.
Линейные функционалы в пространстве D называют также
обобщенными функциями. Чтобы объяснить происхождение этого
названия, рассмотрим линейный функционал, заданный в D
по формуле
/(*)= \x{i)Hp(t)dt,
где функция i|) (t) имеет непрерывную производную. Аддитивность
и ограниченность функционала / проверяются непосредственно.
382 СЧЕТНО-НОРМИРОВАННЫЕ ПРОСТРАНСТВА [ГЛ. XIII
Чтобы представить его по формуле A4), нужно положить р = О,
t
a g@ = \ ip @ dt (ср. 9.5). Рассмотрим также линейный функ-
а
ционал, заданный аналогичным образом с помощью функции
ь
h(x) ¦= \ x(t)ip' (l)dt.
а
Интегрируя по частям и учитывая, что х (а) — х (Ь) = 0, находим
ь ь
Теперь, беря любой линейный функционал / в простран-
пространстве D, положим по определению
и будем называть линейный функционал /' (его линейность оче-
очевидна), определяемый этой формулой, производной от функ-
функционала /, т. е. от обобщенной функции /. Опираясь на это опре-
определение, удается построить дифференциальное исчисление обоб-
обобщенных функций, которое включает в себя дифференциальное
исчисление обычных функций, но в некоторой степени оказы-
оказывается проще: например, всякая обобщенная функция имеет
производную! Можно построить также и обобщенные функции
нескольких переменных. В настоящее время обобщенные функ-
функции широко используются в теории дифференциальных уравне-
уравнений математической физики.
ГЛАВА XIV
ИОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАННЫЕ
ПРОСТРАНСТВА
14.1. Линейные структуры
Теория нормированных пространств опирается на общие
алгебраические и метрические свойства абстрактных линейных
множеств, обобщающие соответствующие свойства совокупности
вещественных чисел. Однако не все важные свойства веществен-
вещественных чисел были перенесены в нормированные пространства.
Именно, в теории этих пространств не нашло никакого обобще-
обобщения свойство сравнимости или упорядоченности
вещественных чисел, т. е. тот факт, что между любыми двумя
числами а и Ь имеет место одно из трех соотношений: а < Ь,
а> Ь или а = Ъ. В частности, не было обобщено понятие поло-
положительности. Между тем в классическом математическом анализе
имеется немало вопросов, где упорядоченность совокупности
вещественных чисел играет существенную роль: например, изуче-
изучение монотонной последовательности, монотонных функций, теория
рядов с положительными членами, различные оценки, даваемые
в виде неравенств, и др. В приложениях нередко представляет
интерес отыскание положительного решения той или иной задачи,
например положительной функции, удовлетворяющей заданному
уравнению.
Чтобы рассмотреть вопросы такого типа в общем виде, необхо-
необходимо ввести понятие упорядоченности в абстрактных множествах.
Однако, имея в виду использование упорядоченности в функцио-
функциональном анализе, было бы нецелесообразным требовать в абстракт-
абстрактном множестве сравнимости любых двух его элементов. Например,
при введении упорядочения в множество функций естественно
считать одну функцию большей или равной другой, если значения
первой функции во всех точках не меньше значений
второй. Но тогда не всякие две функции будут срав-
сравнимы, так как одна из них может быть в одних точках больше,
а в других — меньше, чем вторая. Поэтому для функционального
384 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
анализа более содержательной оказывается такая теория, кото-
которая вводит в абстрактном множестве лишь частичное
упорядочение, дающее возможность сравнивать лишь некоторые
пары элементов. Возникающая таким образом теория линейных
частично упорядоченных (или полуупорядоченных) пространств
с широкими применениями в функциональном анализе была
построена Л. В. Канторовичем в 1935—1937 гг. *). Эта теория
строилась совершенно независимо от теории нормированных
пространств и лишь в некоторых своих частях соприкасалась
с последней. Однако, ставя себе задачей дать в настоящей главе
лишь некоторое представление об использовании идеи порядка
в функциональном анализе, мы ограничимся здесь преимуще-
преимущественно частичным упорядочением в банаховых пространствах.
Такое направление функционального анализа развивалось в тече-
течение ряда лет в работах советского ученого М. Г. Крейна.
Начнем с введения некоторых общих понятий. Пусть Е —
вещественная линейная система (см. 5.1) и в Е указано, относи-
относительно каких именно элементов х ? Е мы будем говорить «х боль-
больше нуля», что записывается в виде неравенства х > 0. Все эле-
элементы, большие нуля, а также и нулевой элемент назовем поло-
положительными **). Множество всех положительных элементов
х ? Е обозначим JE7. Подчеркиваем, что самим характером эле-
элементов, из которых составлена система Е, смысл неравенства
х > 0 может быть еще не определен, и если мы хотим ввести в Е
частичное упорядочение, то и начинаем с того, что выделяем
в Е те элементы, которые будут считаться большими нуля.
Теперь вводим понятие неравенства между двумя элементами
х, у ? Е, полагая по определению х > у (х больше у), если
х — у > 0. Тем самым мы определили сравнимость для неко-
некоторых пар элементов х и у. Неравенство х > у будем записывать
и в виде у <с х. Как обычно, будем писать х^>у (у<Сх), если
известно, что или х > у или х = у. Тогда положительные эле-
элементы можно охарактеризовать соотношением а;>0. Неравен-
Неравенство х > у равносильно х — у > 0.
Элемепты х ? Е, удовлетворяющие соотношению а;<0, назо-
назовем отрицательными. Нулевой элемент удовлетворяет этому
соотношению и является, таким образом, одновременно и поло-
положительным и отрицательным элементом.
Теперь подчиним частичное упорядочение в системе Е некото-
некоторым аксиомам. Именно, введем следующее определение:
*) Некоторое применение идей частичного упорядочения в функцио-
функциональном анализе встречалось ранее в работах Ф. Рисса.
**) Здесь мы несколько расходимся с обычной терминологией, применяе-
применяемой для чисел, так как термин «неотрицательный» будет иметь у нас дру-
другой смысл.
14.1] ЛИНЕЙНЫЕ СТРУКТУРЫ 385
Определение. Вещественная линейная система Е назы-
называется линейной структурой, если в Е указано, какие элементы
считаются большими нуля, причем выполняются следующие
аксиомы:
I. Если х > 0, то х ф 0 *).
II. Если ?>0иг/>0, то и з; + у > 8,
III. Для любых двух элементов х, у ? Е существует эле-
элемент z ? Е, обладающий свойствами:
а) ж<г и у<г,
Р) если элемент и ? Е таков, что х<ми у <м, то и z <м.
IV. Если х > 0 и число А- > О, то и Аа; > 0.
Элемент z, вводимый в аксиоме III, обозначается х \J у. При
этом, свойство а) показывает, что, пользуясь обычной термино-
терминологией, элемент х \/ у можно назвать верхней границей мно-
множества из двух элементов х и у**), а свойство C) означает, что
это — наименьшая верхняя граница. Ее называют также супре-
супремумом (supremum). Заметим, что для множества из двух веще-
вещественных чисел, ввиду их сравнимости, супремумом будет боль-
большее из них. Однако в линейной структуре элемент х \J у, как
мы увидим ниже из примеров, может быть отличным и от ? и от у.
Если же, например, х>г/ (х и у сравнимы), то х V у = х.
Отметим некоторые простые следствия из аксиом линейной
структуры, обобщающие элементарные свойства числовых нера-
неравенств.
а) Если х > у, то х фу. Если же одновременно х >i/ и х < у,
то непременно х = у.
Действительно, если ? > у, то х — г/ > 0, следовательно, по
аксиоме I, х — у ф 0, т. е. х ф у. Если же допустить, что одно-
одновременно 1>уиг<у, тоа; — у > Q п у — х>9 и, по аксио-
аксиоме II, мы получим, что 0 = (х — у) + (у — х) > 0, что по
аксиоме I невозможно.
Из второй части предложения а) следует, что элемент z =
= х \J у, определяемый аксиомой III — единственный. Дей-
Действительно, если, кроме z, дан еще элемент zt ? Е, обладающий
теми же свойствами а) и C), то, с одной стороны, по C), будет
z<zlt a с другой, Z!<z, откуда zt = z.
Кроме того, из доказанного следует, что если одновременно
i>8 и i<9, то х = Q, т. е. в линейной структуре 0 — един-
*) Это свойство нельзя вывести из данных выше определений, так как,
пока на множество элементов х > 9 не накладывалось никаких ограничений,
можно было бы включить в это множество и сам элемент 9.
**) В линейной структуре определяется, как обычно, понятие верхней
границы и для произвольного множества: если множество М С-Е, а элемент
z ? Е обладает тем свойством, что х <! z для всех х 6 М, то г и называется
верхней границей множества М.
25 Б. 3. Вулих
386 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
ственный элемент, одновременно — положительный и отрица-
отрицательный.
б) Если х>у, a y>z, то и z > z (транзитивность
неравенства).
Действительно, х — z = (х — у) + (у — z), а тогда с помощью
аксиомы II сразу видно, что если х — y>Q и у — z>0, то
и х — z >0.
Теперь легко установить существование наименьшей верхней
границы для любого конечного множества элементов] Xi, х2, . . .
. . ., хп ? Е. Для этого доста-
достаточно положить
z = [...((xl\/x2)\Jx3)\J...}\Jxn.
Из транзитивности неравенства
сразу следует, что z — верхняя
граница множества элементов
Xi, хг, . . ., хп, и легко видеть,
что это — наименьшая верхняя
граница или супремум.
в) Если х^у, a z>«, то
х-\- z~^-y-\-u (в частности, если
?>г/, то х -f- z > г/ + z при
любом z ? Ж).
Действительно, (х -\- z) —
) () ()B
В
г) Если ?>г/, то—х-<—у.
частности, если х>0, то
Рис. 20. —x^.Q*). Действительно, —у—
— (—х) = х — y>Q.
д) Если х~>у, то Хх^-Ху при любом Я>0. Действительно,
Хх — Ху = X (х — у) > 0 благодаря аксиоме IV.
Простейшим примером линейной структуры является само
множество вещественных чисел. Приведем другой пример. Пусть
F — множество всех вещественных функций х (t), заданных на
отрезке [а, Ь]. Сложение элементов из F и их умножение на
число определим так же, как в пространстве С, а х ? .Fсчитаем
большим нуля, если x(t)>0 на всем отрезке и при этом хоть
в одной точке х (t) > 0. Легко видеть, что F — линейная струк-
структура. При этом супремум в F вычисляется по значениям функций
в каждой точке, т. е. равенство z = х \/ у означает, что z (t) =
= max [x (t), у (t)].
*) Таким образом, при умножении на (—1) положительные элементы
переходят в отрицательные и обратно.
14.1] ЛИНЕЙНЫЕ СТРУКТУРЫ 387
Например, если отрезок [а, Ъ] есть [0, 1], а х (t) = f, у (t) =
= 1- -|*, то (рис. 20)
--|г при 0<г<-1,
@ = 1 1
^ I2 при -j < t < 1.
Заметим, что в структуре jF1 аналогичным образом можно
было бы определить наименьшую верхнюю границу для любого
конечного и даже ограниченного сверху (т. е. имеющего верхнюю
границу) бесконечного множества ее элементов. Однако в произ-
произвольной линейной структуре супремум существует не для всякого
ограниченного бесконечного множества.
Функция х (t) из структуры F, которая принимает как поло-
положительные, так и отрицательные значения, представляет пример
не положительного, но и не отрицательного элемента. Таким
образом, в линейных структурах «неотрицательный элемент»
может в то же время не быть и положительным.
Возвращаясь к произвольной линейной структуре Е, назо-
назовем наибольшей нижней границей или инфимумом (infimum)
множества из двух элементов х,у ? Е элемент z, обладающий
свойствами:
а') х > z и y>z,
р') если элемент и ? JE таков, что я>ми1/>м, то и г>м.
Такой элемент z обозначается х Д у. Однако требование его
существования уже ненужно включать в аксиоматику линейной
структуры, так как существование инфимума может быть теперь
доказано.
Теорема 14.1.1. Для любых х, у ? Е элемент
z=-[{-x)\l {-у)\
является их инфимумом.
Доказательство. Так как — х<(— х) V (— у), то,
пог),х>г; аналогично, у > z. Если же и g E таков, чтох>м
и у>и, то — я< — м, — у<— и, а потому (— х) \J (— у) <
<—и, откуда, снова по г), z>m.
Как и для супремума, из предложения а) легко вытекает
единственность инфимума. Таким образом,
* Л */=-[(-*) V (-*/)]• A)
Если я>г/, то х/\у = у.
В структуре JF равенство z = x/\y означает, что
(t), y(t)].
25*
388 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
В примере, приведенном на рис. 20, х^у изображается
функцией, равной
при 0<<<1, 1-|-
при
Докажем еще две важные формулы, справедливые при любых
х, г/, z?E:
z = (x+z)\J(y + z), B)
z = (x + z)/\(y+z). C)
Действительно, пусть и = х \J у. Тогда я<и, а потому, по
в), х + z<w + z; аналогично, у -\- z*Cu -\- z, а потому
Положим теперь v = (z-f- z) V (?/ + z)- Тогда г;<м + 2.
Кроме того, х + г<!г> или, по в), х < v— z; аналогично,
у< v — z, следовательно, м< v — z, или м + z< v. Тем
самым доказано, что и-\-'z = v, т. е.
а это и есть равенство B).
Формула C) вытекает с помощью A) и B) иэ следующих соот-
соотношений:
Теперь докажем одну лемму, используемую в дальнейшем.
Лемма 14.1.1. Если 0<z<x + j/, где х, y>Q, то z
можно представить в виде z — zt + z2, г^е 9 < zi < ^> 9 ^
< z2 < у.
Доказательство. Положим Zj = z Д х. Тогда z^
удовлетворяет требуемым неравенствам. Затем положим z^ =
= z — z1# Тогда z2>0, z = Zj + 22 и остается доказать, что
z2<j/. Имеем
Но г/>9 и y>z — x, а потому
Приведем еще некоторые примеры линейных структур.
1) и-мерное векторное пространство Вп, в котором мы счи-
считаем х = (хи х2, . . ., хп) > 9, если все координаты xt>0
и, по крайней мере, одна из координат xt > 0;
14.2] ПОЛОЖИТЕЛЬНАЯ И ОТРИЦАТЕЛЬНАЯ ЧАСТИ ЭЛЕМЕНТОВ 389
2) пространства I, I2, m, s, в Которых частичное упорядоче-
упорядочение вводится по тому же правилу, что и в Jfn;
3) пространство С непрерывных функций, в котором частич-
частичное упорядочение вводится по тому же правилу, как зто сде-
сделано выше в линейной структуре F.
Проверка выполнения аксиом линейной структуры во всех
этих пространствах не представляет труда. Остановимся лишь
на проверке аксиомы III в пространстве С. Именно, нужно,
очевидно, доказать, что если функции х (t) и у (t) непрерывны,
то и z (t) = max [х (t), у (t)] — тоже непрерывна в любой точке.
Если в точке t0 будет х (t0) > у (t0), то и в некоторой окрестно-
окрестности этой точки х (t) > у (t), а тогда z (t) — x (t) в этой окрестно-
окрестности и, следовательно, z (t) вместе с х (t) непрерывна в точке t0.
Если же а; (@) = у (t0) (и равно z (t0)), то по е > 0 можно найти
окрестность точки t0, в которой обе функции х (t) и у (t) заклю-
заключены между z (t0) — е и z (t0) + e. Тогда в этой окрестности
что и доказывает непрерывность z (t) в точке t0.
В дальнейшем мы неоднократно будем рассматривать про-
пространство С как линейную структуру, подразумевая при этом,
что частичное упорядочение в С введено указанным здесь спо-
способом *).
14.2. Положительная и отрицательная части элементов
линейной структуры
В этом параграфе мы покажем, что всякий элемент линейной
структуры Е может быть представлен в виде разности двух поло-
положительных элементов.
Определение. Для любого х ? Е элемент х+ = х \/ 0
называется его положительной частью, элемент х_ = (— х) V 0 —
отрицательной частью и элемент | х \ — х+ + ?- — модулем
элемента х.
Из определения следует, что для любого х ? JE все три эле-
элемента х+, ?_ и | х [ положительны, причем |х|>а;+>а;. В част-
частности, если ?>0, то х+ = х, а так как в этом случае —?<9,
то Х- = 0, и потому | х | = х. Положительная часть элемента х
это — наименьший положительный элемент у, для которого
справедливо неравенство у>х.
*) Пространство С представляет пример линейной структуры, в которой
не всякое ограниченное сверху бесконечное множество имеет супремум.
[ГЛ. XIV
390 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА
В структурах F и С элементы х+, х- и | х | суть функции,
определяемые по х (t) следующим образом (рис. 21):
хA) в точках, где х (t) > 0,
0 в точках, где х (t) < 0;
0 в точках, где х (t) > О,
| х (t) I в точках, где а; (Л < 0;
*_(*) =
\x\(t) = \x(t)\ во всех точках.
В структурах, перечисленных в конце 14.1 и составленных
из последовательностей, чтобы получить из какого-нибудь х его
\x\{t)
Рис. 21.
положительную часть ж+, нужно все отрицательные координаты
нужно все координаты
заменить нулями, а чтобы получить | х ,
заменить их абсолютными величинами.
Теорема 14.2.1. Для любого х ? Е имеет место равен-
равенство х = х+ — ?_.
Доказательство. Вычислим х-\-х_. С помощью B) имеем
х + х- = х+ [(—x)\JQ] = 9\/z = х+, следовательно, х = х+~х-
14.2] ПОЛОЖИТЕЛЬНАЯ II ОТРИЦАТЕЛЬНАЯ ЧАСТИ ЭЛЕМЕНТОВ 391
Отметим очевидное следствие: если ж_ = 0, то
Представление любого х ? Е в виде разности двух положи-
положительных элементов не единственно. При этом справедлива
Л е м м а 14.2.1. Если х — у — z, где у, z>0, то х+^.у.
Доказательство. Так как у = х -\- г, то у>х.
Кроме того, y>Q, а потому у > х \/ 0 = ж+.
Следующие теоремы выражают важные свойства положитель-
положительной и отрицательной частей.
Теорема 14.2.2. х+ Д х- = 0 для любого х ? Е.
Доказательство. Пусть и = х+ Д ?-. Так как
х+, ?_>0, то и м>9. Положим у = х+ — и, z = х- — и. Тогда
из определения и сразу видно, что у, z > 0. При этом у — z =
= х+ — х_ = х, следовательно, по лемме х+ < у, а и = х+ — у < 0.
Из двух противоположных неравенств следует, что и = 0.
Теорема 14.2.3. \х\ = х \J (—х) для любого х ? Е.
Доказательство. Имеем с помощью формулы B)
и теорем 14.2.1 и 14.1.1:
x\l {-x) = \x\~\{x-\x\)\J {-х-\х\)] =
¦ =|z| + [(-2s_)V(-2s+)] = 1*1-1B*-) Д B*+)].
Положим у = Bх+) Д BxJ). Тогда 0<у у^.х+, х_ и из тео-
теоремы 14.2.2 вытекает, что -~-у = 0. Следовательно, и г/ = 0, и тре-
требуемое равенство доказано.
Из теоремы 14.2.3 моментально следует, что | — х \ = | х \
для любого х ? Е. Впрочем, это равенство легко вывести и из
определения модуля.
Доказанные теоремы читатель легко сможет проиллюстриро-
проиллюстрировать самостоятельно на примере структуры функций, с помо-
помощью рис. 21.
Теорема 14.2.4. Для любых х, у ? Е
Доказательство. Из равенства х = у+(х — у) и соотноше-
соотношений у < г/+ и х — у < | ж — у\ сразу следует, что
Тогда из определения положительной части видно, что
+ \х — у\ или
х+—у+<\х — у\.
Аналогично
у+ —ж+<|ж —у|,
392 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
а теперь с помощью теоремы 14.2.3 имеем
| х+ — г/+1 = (х+ — г/+) V (у+ — z+)< [ х — у \.
Теорема 14.2.5. Для любого х?Е и любого числа а>0
(ах-)—ах-, [ ctrc j = а j а; {. D)
Доказательство. Положим у —ах. Так как х<х+, то
a;f, а потому и г/+<аа;+. Аналогично, исходя из соотноше-
1 1
ния х = — у, мы получим, что z+<; — г/+ или ax+<Cy-i- Два
противоположных неравенства и дают равенство у+ = ах+. Совер-
Совершенно так же доказывается вторая из формул D), а тогда
IУ I = У++ У- = а (х+ + х-) = a | x |.
14.3. Полуупорядоченные банаховы пространства
Переходим к основному типу пространств, изучаемому в этой
главе.
Определение. Полное нормированное (вещественное)
пространство Е называется полуупорядоченным банаховым про-
пространством (или банаховой структурой), если Е одновременно
является линейной структурой и норма в Е удовлетворяет усло-
условию «монотонности»:
из j х | < | у | следует, что || х || < || у ||.
Из последнего условия вытекает, что если | х | = | у | , то
|| х || = || у \\. В частности, || х \\ = \\ \ х \ \\ (так как [ х\ > 0, то
модуль, составленный для | х \, равен | х | ), т. е. норма любого
элемента равна норме его модуля.
Пространства С, I, I2, Лп, **г с тем частичным упорядочением,
которое введено в них в конце 14.1, представляют примеры полу-
полуупорядоченных банаховых пространств.
В банаховых полуупорядоченных пространствах справедливо
следующее предложение, называемое принципом Архимеда:
Теорема 14.3.1. Если а; > 0, а числа Хп > 0 и %п ->- + оо
и при этом существует такой у, что Япж<г/ при всех п, то
х = 8.
Доказательство. Вследствие монотонности нормы
имеем ||Л„а:||<|| у ||, откуда || х \\ <т- у при любом п, что воз-
можно лишь при || а; || = 0.
Доказанная теорема означает, что если элемент х > 0 ^умно-
жать на неограниченно возрастающие числовые множители Я„,
то получаемая таким образом последовательность элементов
{Хпх} не может быть ограничена сверху каким-нибудь элемен-
14.3] ПОЛУУПОРЯДОЧЕННЫЕ БАНАХОВЫ ПРОСТРАНСТВА 393
том у пространства Е. В перечисленных выше конкретных про-
пространствах, например в С, это свойство совершенно очевидно.
Следствие. Если х — произвольный элемент из Е, а числа
А,„ > 0 м А,„ —>- + оо ц при этом существует такой у, что Хпх <
<3/ при всех п, то а:<0.
Это предложение называют принципом Архимеда в усилен-
усиленной форме.
Доказательство. Из данного неравенства следует, что
(Х„а;)+<г/+, а тогда по теореме 14.2.5 Я„а;+<г/+. при всех п.
Отсюда по теореме 14.3.1 вытекает, что х+ = 0, а это и означает,
что х = — х- < 0.
Основным результатом этого параграфа будет теорема о пре-
предельном переходе в неравенстве. Предварительно докажем лемму.
Лемма 14.3.1. Если хп -*- х, то Хп-*- х+ *)•
Доказательство. Из теоремы 14.2.4 и из монотон-
монотонности нормы следует, что
и потому xt. -*¦ х+-
Теорема 14.3.2. Если хп~>уп при всех п = 1, 2, . . ...
и хп-+х, уп-+У, то х>у.
Доказательство. Так как хп — уп > 0, то
С другой стороны, по предыдущей лемме
(Хп — Уп)+—>(х — у)+.
Таким образом, благодаря единственности предела, х — у =
= (х—у)+, а это и значит, что х — y>Q, т. е. я
оо
Следствие. Если х= 2 хп и все а;„>0, то #>хп при
всех п.
Доказательство. Фиксируя п, имеем при любом т>и
Переходя в этом неравенстве к пределу при т —>¦ оо, мы и полу-
ЧИМ, ЧТО ?>?„.
Заметим, что в этом параграфе мы не использовали полноты
пространства Е.
*) Как обычно, здесь имеется в виду сходимость по норме. Для удобства,
обозначений мы пишем х+ вместо (хп)+.
394 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
14.4. Линейные функционалы в полуупорядоченных банаховых
пространствах
Будем опять считать Е полуупорядоченным банаховым
пространством. Вещественный функционал / (х), заданный
на JE, называется положительным, если /(а:)>0 для любо-
любого я>0.
Для аддитивных функционалов положительность равносильна
следующему свойству монотонности: если а;>г/, то /(#)>/(г/).
Действительно, из а;>г/ следует, что x = y-\-z, где z>0.
Поэтому, если / положителен, то /(z)>0, a
Обратно, если / обладает свойством монотонности, тоиз:г>0
вытекает, что / (z)>/ @). Но из аддитивности следует, что
/ @) = 0, а потому / (х) > 0 при х > 0.
Для аддитивного положительного функционала имеем
таким образом, для любого х?~Е
\f(x)\<f(\x\). E)
Лемма 14.4.1. Всякий аддитивный положительный функ-
функционал f (x), заданный в Е, линеен.
Доказательство. Проверим непрерывность / (х) при
х = 0 (см. теорему 8.2.1). Пусть хп -*- 0, но при этом допустим,
что / (хп) не -уО. Тогда существует такое е > 0, что
|/(*nj|>e F)
для некоторой частичной последовательности индексов п^. Из
последовательности {хп \ выделяем новую частичную последова-
последовательность {хп } так, что \\хп ||<—а-. Положим ут = \хп, I.
°° оо
Так как числовой ряд ^ —г сходится, то и ряд ^ тУт схо-
7П=1
7П 1
дится (см. 5.2). Пусть у— его сумма. По следствию из теоремы
14.3.2 тг/т<г/ при любом т, откуда ут< — у [см. предложение д)
14.4] ФУНКЦИОНАЛЫ В ПОЛУУПОРЯДОЧЕННЫХ ПРОСТРАНСТВАХ 395
из 14.1]. Тогда вследствие монотонности функционала /
откуда вытекает, что / (ут) —>¦ 0. Следовательно, по неравен-
неравенству E) и / (хп ) ->-0, что противоречит F).
Теперь покажем, что для положительного линейного функцио-
функционала / норма может быть вычислена как точная верхняя граница
множества его значений только на положительных элементах
единичного шара, т. е.
|= sup f(x). G)
Действительно, для любого линейного функционала /
(см. 8.3). Поэтому если обозначить через М правую часть G),
то ясно, что М<||/||. С другой стороны, если ||а;||<1, то
и || | х 11| < 1, и по неравенству E) | / (х) | < / (| х |) < М, следова-
следовательно, и ||/||<ilf. Тем самым равенство G) доказано.
Следующая лемма о распространении аддитивного функцио-
функционала с множества Е+ положительных элементов на всё Е спра-
справедлива в любой линейной структуре.
Лемма 14.4.2. Если на Е+ задан функционал ср, обла-
обладающий свойством аддитивности, т. е. если ф (х + у) =
= ф (х) -f- ф (у) для любых х, у ? _Е+, то он может быть рас-
распространен на всё Е с сохранением свойства аддитивности.
Доказательство. Для любого х ? Е положим ф (х) =
= ф {х+) — ф (xJ). При этом, если х ? Е+, то х = х+, а х- = 0,
а потому на положительных элементах функционал ф (х) совпа-
совпадает с ф (х). Если х = у — z, где у, z^Q, то по лемме 14.2.1
= х+ + и, где и>9. Тогда из равенства х+ — х- — у — z
следует, что z = z_ + и. Теперь благодаря аддитивности ф имеем
ф (X) = ф (Х+) - Ср (Х-) =¦•
= [ф (х,) + ф (и)] - [ф (*_) f ф (и)] = ф (у) - ф (z). (8)
Наконец, если х = у + z, где у, z — любые элементы из _Е,
то а; = (г/+ + z+) — (у- + z_), и по (8)
ф (я) = ф (у+ + z+)— ф (г/_ + z_) = _ _
= [ф (у+) — ф (г/-I + Гф (z+) — Ф (z-)l = ф (у) + Ф (z)-
*) Возможность выносить рациональный множитель из-под знака адди-
аддитивного оператора установлена в 8.1.
396 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
Аддитивность функционала <р доказана *).
Теперь мы сможем получить некоторую новую характери-
характеристику класса линейных функционалов в полуупорядоченном
банаховом пространстве Е.
Теорема 14.4.1. Для того чтобы аддитивный функционал
в полуупорядоченном банаховом пространстве Е был линейным, не-
необходимо и достаточно, чтобы он был представим в виде разности
двух аддитивных положительных функционалов.
Доказательство. Достаточность условия вытекает сра-
сразу из леммы 14.4.1, так как разность двух линейных функцио-
функционалов представляет также линейный функционал (см. 8.6). Дока-
Докажем необходимость условия.
Пусть на Е задан линейный функционал /. Возьмем любой
x>Q. Если 0<а:'<:г, то \\х' || < || х ||, а потому | / (х')\ <
<Л1 / II II х II- Следовательно, множество значений / (х') при 9<.
<z'<:r ограничено. Положим
Ф(г)= sup f{x'). (9)
Докажем, что ср (х) обладает на Е+ свойством аддитивности.
Пусть x — y-r-z, где у, z^Q. Для любых у' и z', удовлетво-
удовлетворяющих условиям 0 < у' < у, Q^.z' *^z, имеем у' -j- z' < x и потому
/ (г/' + z') <ф (х) или f (у1) + /(z') <ф (х). Вследствие произволь-
произвольности у' и z' в левой части можно перейти к точным границам
и мы получим
ч> (у)+ ф(*Кф (*)••). (Ю)
Обратно, берем произвольный х', удовлетворяющий условию
' *Сх = у-\-г. По лемме 14.1.1 x' = y'-\z', где 0 <г/'<г/,
0<z' <z, а потому
/(*') = /(JO+ /(*').< ФЙО + Ф®.
Вследствие произвольности х' отсюда следует, что
4>(*)<<P(iO + 4>(z),
что вместе с A0) и дает равенство
*) Так как для аддитивного функционала / равенство / (х) = / (х^) —
— / (х_) всегда имеет место, то построенное в лемме распространение ф,
обладающее свойством аддитивности,— единственное возможное.
**) Подробно это делается так. Фиксируем сначала г' п из неравенства
((jKfW-fM получаем, что ф (г/)< ф (х) — f (г'). После этого из нера-
неравенства /(z')<<p (x) — ф(у), уже не считая г' фиксированныл1, находим
()<И(Л что и дает A0).
4.5] ФУНКЦИОНАЛЫ В ПРОСТРАНСТВЕ НЕПРЕРЫВНЫХ ФУНКЦИЙ 397
По лемме 14.4.2 функционал ф распространяется на всё Е
•е сохранением аддитивности. Пусть распространенный функцио-
функционал обозначен той же буквой ф.
Так как в формуле (9) х может совпасть с х или с 0, то при
я 6 -В+ имеем ф (х) >/ (х) и ф (х) >/ @) — 0. Последнее озна-
означает, что функционал ф положителен. Положим г|) (х) —
= ф (х) — / (х). Тогда tj> (a:)>0 при z>0 и, следовательно,
¦%\> (х) — тоже аддитивный положительный функционал, а / (х) =
= Ф (х) ~ г|> (х).
14.5. Другой вывод общей формы линейного функционала
в пространстве непрерывных функций
При выводе в 9.5 общей формы линейного функционала
в пространстве С в виде интеграла Стилтьеса мы использовали
в полном объеме теорему 9.4.1 о распространении линейных
«функционалов, которая была доказана нами лишь в частном
•случае (для сепарабельного пространства). Сейчас дадим другой
вывод общей формы линейного функционала в С, при котором
теорема 9.4.1 будет использована лишь в том объеме, в каком
•она была доказана.
Будем считать уже известным, что интеграл Стилтьеса
ь
\ х (t) dg (t) существует для любой непрерывной функции х (t)
а
и любой функции ограниченной вариации g (t). Это было уста-
установлено по ходу доказательства теоремы 9.5.1, но с распростра-
распространением функционалов это не связано. Заметим, что если g (t) —
= gi (t) ± gz (t) и каждая из функций gt (t) и gz (t) — ограни-
ограниченной вариации, то
ь ь ь
\ х (t) dg {l)=\x (t) dgi (t)± \x (t) dgz (t).
a a a
Это получится сразу, если перэйти к пределу в аналогичном
равенстве для интегральных сумм:
ti-i
2
.i=0
n-1 n-i
= 2 *('!)[*l(T!+1)-*i(T,)l± S
i=0 i=0
Из пространства В всех ограниченных вещественных функ-
функций, заданных на [а, Ь] (это пространство рассматривалось в
9.5), выделим некоторое линейное подмножество D, включающее
398 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
в себя пространство С. С этой целью перенумеруем вс&
рациональные числа, содержащиеся внутри интервала (а, Ь);
пусть это будут числа т%. Мы знаем, что множество рациональных
чисел счетно. Далее, рассмотрим функции хх (t), определенные
в 9.5, и положим т = Тр (р = 1, 2, . . .). Так как различные
функции хх* (t) имеют разрывы в различных точках т|, то они
линейно независимы между собой и линейно независимы с любой
непрерывной функцией, отличной от тождественного нуля.
Теперь примем за D линейную оболочку множества, состоящего
из всех х ? С и всех я-*, и будем дальше рассматривать D как
самостоятельное линейное нормированное пространство; С —
его подпространство. В то же время С, как мы знаем,— полу-
полуупорядоченное банахово пространство. В D мы по тому же пра-
правилу, что и в С, выделим класс положительных элементов; одна-
однако не будем проверять, что I) — линейная структура *).
Пусть / (х) — положительный линейный функционал, задан-
заданный в С. Обозначим через е (t) функцию, тождественно равную-
единице. Тогда для всякого положительного х ? С с нормой
||а;||<1 выполнено неравенство 0<а:<е, а потому / (х) <
</(е). Вследствие этого по формуле G) |] / || = / (е).
Теперь по теореме 9.4.1 распространим функционал / с сохра-
сохранением нормы с пространства С на пространство D. Так как
при этом мы можем поочередно присоединять к области опреде-
определения функционала элементы х%», то процесс распространения
потребует лишь счетной последовательности шагов, т. е. тео-
теорема 9.4.1 будет использована лишь в том виде, в каком она
была доказана.
Проверим, что распространенный функционал, который мы
обозначим той же буквой /, оказывается положительным в D.
Если х ? D и z>0, то 0<z(?)<M, где М — некоторая
постоянная (М > 0). Положим у = е — ^ . Тогда 0< у<е,
|| у || < 1 и | / (у) | < || / || = / (е). Следовательно, / (j^) =
= / (в) - / (У) > 0, а тогда и / (х) > 0.
Теперь положим
g(a) = 0, *(T*) = /(zt.) (p = l, 2, ...), g(b) = f{e).
Так как < х* <хг* <е при т$ < г*, то 0<g (t*)<g (r*) <
(b). Для прочих t из [а, Ъ] полагаем
g{t)= sup g(t*).
*) Заметим, что этот факт все же верен
14.5] ФУНКЦИОНАЛЫ В ПРОСТРАНСТВЕ НЕПРЕРЫВНЫХ ФУНКЦИЙ 399
Легко видеть, что функция g (t) оказывается монотонной (неубы-
(неубывающей) на всем отрезке [а, Ь]; всякая же монотонная функция,
как мы знаем (9.5), будет и функцией ограниченной вариации.
Далее, повторяя дословно рассуждение, проведенное в 9.5, мы
можем получить формулу B3) из гл. IX, выбирая точки деления
Т; среди т*, а так как предел, входящий в формулу B3) гл. IX,
и есть интеграл Стилтьеса, о существовании которого нам уже
известно, то приходим к равенству
ь
j{x)=\x{t)dg{t). A1)
а
При этом
\lvg(l)=-.g(b)-g(a) = \\f\\.
а
Если / (х) — произвольный линейный функционал в С, то
представим его на основании теоремы 14.4.1 в виде разности
двух положительных функционалов, / (х) = ф (х) — я|з (х). По до-
доказанному
ъ ъ
<р(х)=\х @ dgi (t), Ц(х)=\х @ dg2 (О,
гДе Si (О И Sz @ — неубывающие функции.
Положим g (t) = g4 (t) — g2 (t). В 9.5 показано, что разность
двух неубывающих функций есть функция ограниченной вариа-
вариации. Для любого х ? С
ь ь
x{t)dg(t)=^x{t)dgl(t)- J а:
и мы снова приходим к формуле (И).
Следуя этим же идеям, можно показать, что и для произ-
произвольного функционала / функция g (t) в формуле A1) может
ь
быть выбрана так, что ||/||=Var g (f)*).
*) Для этого нужно функционалы ф и \|) определить именно так, как
это сделано в доказательстве теоремы 14.4.1, а функции gl (t) и g2 (t) построить
по ф в t|) тем способом, каким выше для положительного функционала /
построена функция g (t).
400 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
14.6. Монотонные самосопряженные операторы
в гильбертовом пространстве *)
Для операторов, отображающих банахово полуупорядочен-
полуупорядоченное пространство X в пространство Y того же типа, так же как
для функционалов, можно ввести понятие положительности:
оператор U называется положительным, если Ux^-Q для любого
я>0. Для аддитивных операторов, как и для функционалов,
это свойство равносильно монотонности: Ux^Uxz, если xt >
> хг.
Если пространство Y = X, следовательно, имеют смысл сте-
степени Un, то ясно, что для положительного оператора U и все его
степени положительны.
Пусть теперь Н — гильбертово пространство, в котором
каким-нибудь способом введено частичное упорядочение так, что
Я одновременно — банахово полуупорядоченное пространство.
Примером таких пространств могут служить Р, Вп. Пусть А —
вполне непрерывный самосопряженный оператор, заданный в Н,
и А Ф 0. Так как для самосопряженных операторов термин
«положительный» уже употреблялся в другом смысле (см. 10.2),
то если оператор А является положительным в смысле только что
данного определения, мы будем называть его монотонным.
По теореме 10.4.3 все собственные числа оператора А заклю-
заключены между его границами МА и тА. При этом из теоремы 10.6.6
и леммы 11.3.1 следует, что каждая из границ, отличная от нуля,
является собственным числом. Тогда из формулы \\ А || =
= max (| МА [, |/Па|) (см. 10.2) вытекает, что та из границ,
абсолютная величина которой равна \\А ||, и есть наибольшее
по абсолютной величине собственное число К* оператора А.
Однако в общем случае нельзя утверждать, что это число Я,*
положительно. Мы знаем лишь, что по крайней мере одно из чисел
|| А || или — || А || — собственное. Если же даже А.* и будет поло-
положительным (как, например, для положительного в прежнем
смысле вполне непрерывного самосопряженного оператора А),
то нельзя утверждать, что среди соответствующих числу Я,*
¦собственных элементов оператора А найдется положительный.
В связи с этим представляет интерес следующая
Теорема 14.6.1. Если А — монотонный, вполне непре-
непрерывный, самосопряженный оператор (А ф Q), то \\ А \\ является
его (наибольшим) положительным собственным числом и этому
*) В этом параграфе и в 14.8 излагаются в сильно упрощенном виде
некоторые результаты, приведенные в обзорной статье М. Г. Крейна
и М. А. Рутмана «Линейные операторы, оставляющие инвариантным конус
в пространстве Банаха» [Успехи матем. наук III A948), вып. 1, 3—95].
11.6] МОНОТОННЫЕ САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ 401
числу соответствует по крайней мере один положительный соб-
собственный элемент.
Доказательство. Положим Яо = || А \\ и пусть уже
известно, что Яо — собственное число оператора А. Докажем
существование положительного собственного элемента, соответ-
соответствующего числу Яо.
Обозначим через L собственное подпространство оператора А,
соответствующее числу Яо, а через М — его ортогональное допол-
дополнение. Пусть Р — оператор проектирования пространства Н
на подпространство L. Покажем, что оператор Р — монотонный.
Всякое число Я, > Яо регулярно, т. е. на всем Н определен
линейный оператор Rx — (А — Я/). При этом если ifi, то
{А — XI) х = (Хо — X) х, а потому
на L-
С другой стороны, так как подпространство 31 инвариантно для
оператора А, то, рассматривая А только на Ж и учитывая регу-
регулярность Я,, мы видим, что оператор йя,, отображая всё Н на Н,
одновременно устанавливает отображение подпространства 31
на 31 *). Кроме того, для оператора А в подпространстве М число
Я,о уже не является собственным, следовательно, оно регуляр-
регулярно и на М определен линейный обратный оператор R^o =
= (А — Я-о/). Отсюда по теореме 8.7.4 следует, что при К,
достаточно близких к Яо, нормы операторов Rj,, вычисленные
в подпространстве 31, ограничены в совокупности. Поэтому в под-
подпространстве 31 оператор (А,о — X) R^ -*¦ в при Я, ->¦ Яо.
Для любого у 6 Н, полагая у' = Ру, у" = у — у' {у" 6 31),
имеем с помощью A2)
(Хо -1) RKy = (Хо - X) Rxy' + (Ко - Я) RKy" =
т. е.
Py=
х или — — у=(/——
Л \ К
как -г- <1> то по формуле A6) из гл. VIII
1 / А \
Если x = Rxy, то у = (А — Я,/)х или — — у=(/—— ) х, а так
Л \ К J
2Ап с 1
п=0
*) Если подпространство М — нулевое (а тогда L = Н), то утверждение
о наличии положительного собственного элемента тривиально.
26 Б. 3. Вулих
402 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
-n _ x ) У ЛПу
n=0
Если г/>9, то, благодаря монотонности оператора А (а вме-
вместе с ним и его степеней), по следствию из теоремы 14.3.2
(А.о — A.) Ri г/>9, а тогда из A3) и самой теоремы 14.3.2 выте-
вытекает, что Рг/>9, т. е. оператор Р — монотонный.
Если бы Ру = 9 при всех г/>9, то из формулы Ру =
= Ру+ — Ру- следовало бы, что Р = 6, а это невозможно, так
как Ъ содержит элементы, отличные от 0. Таким образом, суще-
существует у > 0, для которого Ру > 0. Но Ру ? ?, следовательно,
Ру является положительным собственным элементом оператора А,
соответствующим числу Ко.
Пусть теперь известно, что — Ло — собственное число опера-
оператора А. Тогда для любого собственного элемента х0, соответ-
соответствующего числу — Хо, имеем
АНй = А (Ах0) = А (.- XQx0) = - Ко (Ах0) = Х20х0,
т. е. Хг0 — собственное число оператора А2. Кроме того, опера-
оператор А2 — самосопряженный (см. 10.2), монотонный как квадрат
монотонного оператора, вполне непрерывен как результат супер-
суперпозиции двух вполне непрерывных операторов *) и
|| Л211= sup (А*х, х) = sup {Ах, Ах) — sup ||у1х||2 = || А ||2 = Х\.
11*11=1 11*11=1 ll*li=i
Следовательно, для оператора А2 и числа \\ справедлив резуль-
результат, установленный в первой части доказательства, и, таким
образом, существует xt > 0, для которого A2xt = Х\ху.
Положим х0 = Axt -f- X0Xi. Тогда хо>Аох1 >8 и
т. e. kQ — также собственное число оператора А. Но зтот случай
уже разобран в первой части доказательства.
14.7. Частичное упорядочение пространства ?2
Чтобы дать применение к интегральным операторам теоремы,
доказанной в предыдущем параграфе, введем частичное упорядо-
упорядочение в гильбертовом пространстве ХЛ Именно, будем считать
элемент х ? L2 большим нуля, если х (<)>0 почти всюду на от-
отрезке [а, Ь] **) и при этом на множестве положительной меры
*) См. предложение, отмеченное в 11.1.
**) Как и выше, мы рассматриваем пространство L*, составленное из
функций на отрезке [о, Ь],
14.7] ЧАСТИЧНОЕ УПОРЯДОЧЕНИЕ ПРОСТРАНСТВА Х2 403
выполняется неравенство х (t) > 0. Ясно, что для непрерывной
функции зто условие равносильно тому, что функция всюду неотри-
неотрицательна и по крайней мере в одной точке больше нуля. Поэтому
для непрерывных функций из L2 неравенство х > 0 имеет тот же
смысл, что и в пространстве С.
Покажем, что L2 — полуупорядоченное банахово пространство.
Выполнение в L2 аксиом I, II и IV линейной структуры оче-
очевидно. Проверяем выполнение аксиомы III (существование
супремума).
Если х, у ? L2, то положим
z(t) = max[x(t),y(t)]. A4)
Функция z (t) измерима. Действительно, если А — любое веще-
вещественное число, то множество тех точек, где z (t) > А, есть сумма
множеств, где х (t) > А и где у (t) > А, а потому оно измеримо.
Кроме того, из неравенства
\z(t)\<m&x[\x(t)\,\y(t)\]<\x(t)\
следует, что z 6 -Ь2-
Элемент z и есть искомый супремум: z = x \/ у. В самом деле,
из определения неравенства в пространстве Ъ2 следует, что z>a;
и 2>г/. Пусть еще задан такой элемент и ? i2, что ы>а; и ы>
>г/. Это означает, что u(t)~>x(t) и и {t)>y (t почти всюду
на [а, Ь], а тогда из A4) следует, что и u (<)>z (t) тоже почти
всюду, т. е. и >• z. Таким образом, z удовлетворяет требованиям
а) и Р) из аксиомы III, т. е. z = x \J у.
Итак, L2 — линейная структура. Из построения супремума
в L2 видно, что для любого х ? ?2 его положительная и отрица-
отрицательные части, а также модуль определяются по тем же форму-
формулам, что и в структурах F и С.
Монотонность нормы в i2 почти очевидна. Действительно,
если | х |< | у | , то | х (t) | < | у (t) \ почти всюду на [а, Ь]
и потому
/
\ y*(t)dt=-\\y\\.
Таким образом, X.2 — полуупорядоченное банахово простран-
пространство *).
Заметим, что хотя пространства i2 и I2, как гильбертовы,
изоморфны, однако частичное упорядочение мы ввели в зтих
*) В первом издании этой книги показано, как ввести частичное упорядо-
упорядочение в функциональном гильбертовом пространстве, если исходить из его
реализации с помощью функций промежутка, т. е. в пространстве ?2.
26»
404 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА |.ГЛ. X IV
пространствах по-разному и при изоморфизме между L2 и I2
классы положительных элементов этих пространств не будут
соответствовать друг другу.
Рассмотрим теперь интегральный оператор в L2
(s,t)x(t)dt A5)
с непрерывным ядром. Если это ядро К (s, t) > 0 во всем квад-
квадрате a<s, ?<fc, то у (s) > 0 для а;>0 при всех s. Таким
образом, оператор оказывается монотонным *). Если, кроме
того, ядро симметрично и отлично от тождественного нуля, то
к оператору A5) применима теорема 14.6.1, обеспечивающая,
в частности, сухцествование положительных собственных функций.
14.8. Сильно положительные линейные операторы
Имея в виду усилить предыдущий результат и доказать при
некоторых условиях единственность (с точностью до постоянного
сомножителя) положительной собственной функции интеграль-
интегрального оператора, введем еще один класс пространств.
Определение. Банахово полуупорядоченное простран-
пространство Ж называется банаховым пространством ограниченных эле-
элементов, если в Ж указан элемент е > 9, обладающий следующим
свойством: для каждого а;>0 существует такое число С, что
Будем дальше считать Ж банаховым пространством ограни-
ограниченных элементов. Элемент х ? Ж назовем сильно положитель-
положительным и записываем в этом случае х > 9, если существует число
6 > 0, при котором а;>6е.
Примером банахова пространства ограниченных элементов
может служить пространство С, в котором в качестве е выбрана
функция е (t) = 1. Тогда сильно положительными элементами
в С будут те функции, для которых min x (t) > 0.
Заметим, что если х — произвольный элемент из Ж, то для
него также при некотором С выполнено неравенство х^сСе.
Действительно, по определению пространства ограниченных эле-
элементов неравенство х+ < Се выполнено при некотором С, ai<i+.
Лемма 14.8.1. Если элемент х сильно положителен, а у —
произвольный элемент из Ж, то существует такое а > 0, что
у<ах.
*) Напоминаем, что значения оператора A5) входят в
I 1.8] СИЛЬНО ПОЛОЖИТЕЛЬНЫЕ ЛИНЕЙНЫЕ ОПЕРАТОРЫ 405
Доказательство. По определению пространства огра-
ограниченных элементов г/<Се при некотором С > 0 *). С другой
стороны, х>6е при некотором б > 0, т. е. е <-^ х. Отсюда мы
сразу заключаем, что
Q
у < Се <-ф-я,
С
т. е. -г и можно принять за а.
Лемма 14.8.2. Если х0, Х\ 6 X, яо> 8, а х{ ф 9, то суще-
существует число t*, при котором элемент х0 -\- t*xi положителен,
но не сильно положителен.
Доказательство. Обозначим через Т множество всех
чисел t, для которых
A6)
Это множество не пусто, так как, например, 0 ? Т. Докажем,
что Т ограничено по крайней мере с одной стороны (сверху или
снизу).
Допустим, что Т не ограничено сверху, т. е. в Т входят поло-
положительные, сколь угодно большие t. Тогда из неравенства A6)
мы бы получили, что t (— Xi)<Cx0 при сколь угодно больших t,
и по принципу Архимеда в его усиленной форме (см. следствие
из теоремы 14.3.1) отсюда следовало бы, что — Х!<9, т. е.
Xi > 9. Совершенно аналогично, допустив, что Т не ограничено
снизу, мы получим, что а;!<9. Следовательно, если Т не огра-
ограничено с обеих сторон, то Xi = 9, вопреки условию леммы. Таким
образом, Т ограничено с какой-нибудь стороны.
Предположим, для определенности, что Т ограничено сверху,
и пусть t* = sup Т. Докажем, что t* обладает требуемым свой-
свойством. Так как можно найти такие tn ? Т, что tn ->- t*, то, пере-
переходя к пределу в неравенстве х0 -f- <n?1>9, мы получим, что
х0 + t*x, > 9. Допустим, что х0 + t*xt > 9, т. е. что х0 -f- t*xt >
> бе при некотором 6 > 0. Так как —Xi^cCe при некото-
ром С > 0, то — -? х,<бе или — -^ xt < х0 + 1*х{. Тогда
хо-\- ( t* +— ) >0, т. е. число t* -f- тг 6 7\ что противоречит
—
определению <*.
Аналогично разбирается случай, когда Т ограничено снизу.
Лемма доказана.
Определение. Положительный линейный оператор А,
отображающий X в X, назовем сильно положительным, если
См. только что сделанное замечание.
406 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
для каждого х > 0 существует натуральное п, при котором
Апх > 9.
В частности, линейный оператор будет сильно положитель-
положительным, если он сам переводит всякий элемент х > 0 в сильно поло-
положительный элемент.
Заметим, что для сильно положительного оператора Ах > 0
при всяком х > 0. Действительно, если х > 0, то Л:г>0 вслед-
вследствие положительности оператора А. Однако если бы Ах = 0,
то и Апх = 0 при всех п.
Лемма 14.8.3. Если оператор А сильно положителен, то
Ах > 0 для любого х > 0.
Доказательство. Возьмем произвольный го>9и под-
подберем натуральное п так, что Апх0 > 0. Положим у0 = Ап~хха.
Тогда г/0 > 0, а Лг/0 » 0. Если а; » 0, то по лемме 14.8.1 уо<ах
при некотором а > 0. Тогда Лг/0<а (Ах), откуда сразу вид-
видно, что
уо>в
Таким образом, Ах > 6.
Лемма 14.8.4. Если оператор А сильно положителен, то
оператор А* тоже сильно положителен.
Доказательство. Берем произвольный х > 0. Тогда
у = Апх > 0 при некотором натуральном п. Применяя к у еще
п раз оператор А, получим на основании предыдущей леммы,
что и А21х » 0. Но А2а = (Л2I. Таким образом, (А2)ах » 0,
а это и означает, что оператор Л2 сильно положителен.
Лемма 14.8.5. Если оператор А сильно положителен,
аго>9 — его собственный элемент, соответствующий собствен-
собственному числу к, то х0 > 0, а X > 0. При этом собственное под-
подпространство, соответствующее числу К, одномерно.
Доказательство. Так как х0 > 0, то по сделанному
выше замечанию Ах0 > 0. Но Ах0 = %xQ, а потому Хх0 > 8,
откуда и видно, что % > 0.
Далее, Л%> > 0 при некотором п, т. е. Кпх0 > 0 или Кпх0>
>бе, где б > 0. Но тогда х0 > -^ е и z0 > 0.
Допустим, что #i — собственный элемент оператора А, соот-
соответствующий тому же числу Ко. Подберем число t*, обладающее
свойством, указанным в лемме 14.8.2. Тогда
А (х0 + Гц) = Ахо+ t* (Axt) = кохо + 1* (Vi) = ^о (*о+ t*xt).
Следовательно, если допустить, что х0 + t*Xi > 0, то х0 + t*xy
был бы собственным элементом оператора А, а тогда по уже дока-
доказанному х0 -f- ?*#i > Э, что противоречит определению числа t*.
14.8] СИЛЬНО ПОЛОЖИТЕЛЬНЫЕ ЛИНЕЙНЫЕ ОПЕРАТОРЫ 407
Таким образом, х0 -f- t*Xi = 0 и тем самым элементы х0 и xt
линейно зависимы.
Лемма 14.8.6. Если оператор А сильно положителен,
а х0 > 0 — его собственный элемент, соответствующий соб-
собственному числу А,о (при этом А,о> 0 по лемме 14.8.5), то у опе-
оператора А нет собственных чисел А. > А.о.
Доказательство. Допустим, что существует собствен-
собственное число А,4 > А.о, а у — соответствующий ему собственный эле-
элемент. По лемме 14.8.5 х0 > 0, а тогда по лемме_ 14.8.1 г/<ая0
при некотором а > 0. Отсюда следует, что Апу < аАпхй при
любом натуральном п, т. е.
или
Так как это неравенство справедливо при любом натуральном
п, а г*> 1, то по следствию иэ теоремы 14.3.1 г/<9.
С другой стороны, — у тоже собственный элемент, соответ-
соответствующий числу А,!, а потому для — у справедлив тот же вывод,
что и для у, т. е. —J/^0 или г/>0. Отсюда уже вытекает, что
у = 0, что противоречит понятию собственного элемента. Теи
самым доказано, что собственных чисел А. > А.о нет.
Теорема 14.8.1. Если линейный оператор А, отобра-
отображающий Ж в Ж, сильно положителен, а х0 > 0 — его собствен-
собственный элемент, соответствующий собственному числу А.о, то все
прочие собственные числа оператора А удовлетворяют неравен-
неравенству | А, | < А,о (А.о > 0 по лемме 14.8.5) и у оператора А нет
других положительных собственных элементов, линейно неза-
независимых с х0.
Доказательство. По лемме 14.8.6 у оператора А нет
собственных чисел А. > А.о. Остается доказать, что у оператора А
нет также и отрицательных собственных чисел А., для которых
А- | > А.о.
Пусть собственное число А. записано в виде А. = —ц,, где
pi > 0, и пусть у — собственный элемент оператора А, соответ-
соответствующий числу А.. Так как А. ф А.о, то у линейно независим
с х0 *). Из равенств
следует, что х0 — собственный элемент оператора А2, соответ-
соответствующий числу А.д, a |i! — тоже собственное число оператора
*) В противном случае хо должно было бы быть собственным элементом,
соответствующим одновременно собственным числам X и Яо, что невозможно.
408 ПОЛУУПОРЯДОЧЕННЫЕ НОРМИРОВАН. ПРОСТРАНСТВА [ГЛ. XIV
А2. При этом по условию теоремы х0 > 9, а тогда fi2 Ф А.*, так
как в противном случае собственному числу \\ оператора А2
соответствовали бы два линейно независимых собственных эле-
элемента х0 и у, что невозможно по лемме 14.8.5. Неравенство
ji2 > XI невозможно по лемме 14.8.6. Тем самым доказано, что
fi2 < А», т. е. что 1 А, | < К-
Теперь покажем, что у оператора А нет положительных соб-
собственных элементов, линейно независимых с х0. По лемме 14.8.5
собственное подпространство оператора А, соответствующее чис-
числу А,о, одномерно. Допустим, что у оператора А существует соб-
собственный элемент Х\ > G, соответствующий некоторому числу
Я( < Яо. (Неравенство A,j > А.о исключено по лемме 14.8.6.)
При этом Я4 > 0. Но тогда по той же лемме 14.8.6 невозможно
существование собственного числа Яо большего, чем ?ц. Полу-
Полученное противоречие завершает доказательство теоремы.
Вернемся к интегральному оператору К A5) с симметрич-
симметричным непрерывным ядром. Так как все его собственные функции,
соответствующие числам А. ф 0, непрерывны, то вывод, сделан-
сделанный относительно этого оператора в конце предыдущего пара-
параграфа, остается в силе, если оператор К рассматривать в про-
пространстве С, т. е. как отображение пространства С в С. Таким
образом, если К (s, t)~^>0, но не равно нулю тождественно, то
оператор К имеет наибольшее положительное собственное число,
которому соответствует по крайней мере одна положительная
собственная функция.
Укажем дополнительные условия, при которых оператор К
в пространстве С будет сильно положительным. Как мы отме-
отмечали в начале параграфа, С— банахово пространство ограни-
ограниченных элементов. Если, например, К (s, t) > 0 при всех s, t,
то для любого х> 9 иэ С будет у (s) > 0 при всех s, а тогда,
вследствие непрерывности у (s), min у (s) > 0 и у > 9.
Чтобы найти более общие условия сильной положительности
оператора К, выясним, какой вид имеет оператор К2. Если у =
= Кх, a z = Ку, т. е. если
ь ь
(г, I) х (/) dt, z{s)=\,K (s, г) у (г) dr,
а а
ТО
ь ь
z (s) -. '\ К (s, r)dr\K (г, /) х (t) dt ---¦
14.8] СИЛЬНО ПОЛОЖИТЕЛЬНЫЕ ЛИНЕЙНЫЕ ОПЕРАТОРЫ 409
таким образом, оператор К1 есть также интегральный оператор
с ядром
ъ
К2 (s, t)=^K (s, г) К (г, t) dr.
Пусть К (s, t) > 0 во всем квадрате и при этом К (s, t) > 0
в некоторой полоске вдоль диагонали квадрата, например при
\ s — t | < у. Тогда К2 (s, t) > 0, и легко видеть, что К2 (s, t) >
> 0 при | s — t |<2у. Аналогично, исходя из оператора/Р, мы
увидим, что оператор К* — интегральный оператор с неотрица-
неотрицательным ядром Kk (s, t), причем Kt (s, t) > 0 при \ s ¦— t |<C4y.
Если теперь натуральное п таково, что Ъ — а<2пу, то, пола-
полагая т = 2П, мы увидим, что для оператора Кт его ядро Кт (s, t) >
> 0 во всем квадрате, а тогда Ктх > 6 для любого х > 6 (х ? G).
Значит, и в этом случае оператор К сильно положителен.
Теперь на основании теоремы 14.8.1 можно утверждать, что
при указанных дополнительных условиях оператор A5) имеет
единственную с точностью до постоянного множителя положи-
положительную собственную функцию.
Заметим, что этот результат может быть обобщен и на урав-
уравнения с несимметричным ядром.
Различные приложения идеи частичного упорядочения к во-
вопросам функционального анализа без использования при этом
нормированных пространств можно найти в специальной литера-
литературе по теории полуупорядоченных пространств.
ЛИТЕРАТУРА ПО ФУНКЦИОНАЛЬНОМУ АНАЛИЗУ
Ахиезер Н. И. и Глазман И. М., Теория линейных операторов
в гильбертовом пространстве, изд. 2, перераб., «Наука», 1966.
Бурбаки Н., Топологические векторные пространства, ИЛ, 1959.
Виленкин Н. Я. и др., Функциональный анализ, под ред.
С. Г. Крейна (серия «Справочная математическая библиотека»), «Наука»,
1964.
В у лих В. 3., Введение в теорию полуупорядоченных пространств,
Физматгиз, 1961.
Гельфанд И. М., Райков Д. А. и Шилов Г. Е., Коммута-
Коммутативные нормированные кольца, Физматгиз, 1960.
Гельфанд И. М. и Шилов Г. Е., Пространства основных и
обобщенных функций (серия «Обобщенные функции», вып. 2), Физматгиз,
1958.
Данфорд Н. и Шварц Дж., Линейные операторы, ИЛ,
1962.
Д э й М. М., Нормированные линейные пространства, ИЛ, 1961.
Канторович Л. В. и Акилов Г. П., Функциональный анализ
в нормированных пространствах, Физматгиз, 1959.
Канторович Л. В., В у л и х Б. 3. и П и н с к е р А. Г., Функ-
Функциональный анализ в полуупорядоченных пространствах, Гостехиздат,
1950.
Колмогоров А. Н. и Фомин СВ., Элементы теории функций
и функционального анализа. Изд. МГУ, вып. I, 1954; вып. II, 1960.
Красносельский М. А., Положительные решения операторных
уравнений, Физматгиз, 1962.
Красносельский М. А. и Рутицкий Я. В., Выпуклые
функции и пространства Орлича, Физматгиз, 1958.
Л ю м и с Л., Введение в абстрактный гармонический анализ, ИЛ,
1956.
Люстерник Л. А. и Соболев В. И., Элементы функциональ-
функционального анализа, изд. 2, перераб., «Наука», 1965.
Морен К., Методы гильбертова пространства, «Мир», 1965.
Н а й м а р к М. А., Нормированные кольца, Гостехиздат, 1956.
ЛИТЕРАТУРА 411
Плеснер А. И., Спектральная теория линейных операторов,
«Наука», 1965.
Райков Д. А., Векторные пространства, Физматгиз, 1962.
Рисе Ф. и Секефальви-Надь Б., Лекции по функцио-
функциональному анализу, ИЛ, 1954.
Соболев С. Л., Некоторые применения функционального анализа
в математической физике, Изд. ЛГУ, 1950.
Хилле Э.и Филлипс Р., Функциональный анализ и полугруп-
полугруппы, ИЛ, 1962.
Шилов Г. Е., Введение в теорию линейных пространств, Гостех-
аздат, 1956.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксиома треугольника 71, 134
Алгебраически изоморфные простран-
пространства 35, 168
Алгебраический изоморфизм 35
Архимеда принцип 392
Арцела теорема 107
Базнс 34, 61
— конечно-мерного пространства 139
— ортогональный 36, 62
— ортонормнрованный 36, 62, 163
Банаха — Гана теорема 244
Банаха — Штейнгауза теорема 214
Бесселя неравенство 64, 163
Вольцаыо —• Вейерштрасса теорема
(обобщенная) 102
Больцано — Кошн признак 50
Бубнова — Галершша метод 353
Буняковского неравенство 76
Вектор 10
— комплексный 43
— нулевой 11
— с бесконечным множеством коор-
координат 46
Взаимно однозначное отображение
(соответствие) 20, 220
Вполне регулярная система урав-
уравнений 227
Гельдера неравенство 229
Гильберта — Шмидта теорема 320
Гиперплоскость 257
Границы самосопряженного опера-
оператора 283
Грпиа функция 324
Диагональный метод 104
Дистрибутивность оператора 204
Дополнение (множества) 70
Замыкание 59, 85
Изометричное соответствие 37
Изометричные пространства 39, 168
Интеграл Стилтьеса 252
— функции промежутка 186
Интегральное уравнение Фред
гольма B-го рода) 123
Инфимум 387
Квазишар 367
Координатная реализация гиль-
гильбертова пространства 170
Координаты элемента 140
Коши неравенство 13, 16, 49
Коши — Буняковского неравенство
152
Коэффициенты Фурье 162
Лежандра полиномы 176
Линейная комбинация 30, 138
— оболочка 60, 144
— система 130
вещественная 131
комплексная 131
— структура 385
Линейно зависимые векторы (эле-
(элементы) 30, 139
— независимые векторы (элементы)
30, 60, 138, 148
Линейное преобразование в Rn 18
Липшица условие 110
Мажорирующая норма 210
— полунорма 363
Матрица 20
— бесконечная 57
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
413
Матрица симметричная 30
— транспонированная 29
Метризация 75
Метрическая сумма 187
Минимизирующая последователь-
последовательность 338
Миыковского неравенство 77
Множество всюду плотное 96
— замкнутое 83
— компактное 100
— ограниченное по норме 137
— — по полунормам 368
по расстоянию 88
— открытое 86
— плотное 96
— пустое 69
— слабо компактное 265
— счетное 91
Модуль элемента 389
Монотонная система полунорм 362
Непрерывность нормы 136
— преобразования (оператора) в Rn
26
Норма вектора (элемента) 12, 133
— оператора 25, 208
— функционала в Rn 28
Нуль сложения 131
Область задания оператора 111
Образ множества 111
— точки 111
Ограниченность точечная 214
— функционала в lz 55
Оператор 17, 111
— аддитивный 203
— вполне непрерывный 305
— линейный 205
в счетно-нормированном про-
пространстве 371
в г2 58
— матричный 225
— монотонный 400
— неособенный (Штурма — Лиу-
вилля) 323
— непрерывный 112
— нулевой 217
— обратимый 222
— обратный 220
— ограниченный 206
в счетно-нормированном про-
пространстве 371
в г2 58
— однородный 203
Оператор положительный 400
— самосопряженный 30, 281
положительно определенный
337
положительный 284
— сжатия 115
— сильно положительный 405
— симметричный 288
— сопряженный 29, 279
Операторы равноограниченные 373
Ортогонализация 38, 165
Ортогональная система элементов 161
— полная 161
Ортогональное дополнение 159
— разложение пространства 159
Ортогональные векторы (элементы)
15, 154
— подпространства 156
Ортогональный базис 36, 62
Ортонормированная система эле-
элементов 161
Ортонормированный базис 36, 62,
163
Отрицательная часть элемента 389
Пеано теорема 125
Пересечение множеств 70
Перманентный метод суммирования
274
Пифагора теорема обобщенная 16,
54, 155
Подмножество 69
— линейное 143
Подпространство 30, 60, 144
— бесконечно-мерное 62
— инвариантное 285
— конечно-мерное 61
— собственное 287
Полином наилучшего приближения
147
Полная вариация функции 248
— система ортогональных подпро-
подпространств 161
Положительная часть элемента 389
Полунорма 355
— существенная 364
Предел в метрическом пространстве
79
Проектор 209
Проекция элемента на подпростран-
подпространство 158
Произведение матриц 23
— функций промежутка 198
Пространство банахово 137
• ограниченных элементов 404
414
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Пространство банахово полуупоря-
полуупорядоченное 392
— векторное и-мерное 11
— комплексное 43
— второе сопряженное 262
— гильбертово 153
комплексное 170
— компактное 100
— метрическое 71
полное 88
— нормированное 133
— — бесконечно-мерное 139
вещественное 134
комплексное 134
конечно-мерное 139
— рефлексивное 262
— сепарабельное 97
— со счетным базисом 148
— сопряженное 260
— счетно-нормированное 356
— эвклидово бесконечно-мерное 48
— комплексное 66
ге-мерное 15
комплексное 43
Прямая 34, 145
Равенство множеств 69
Разложение нормированного про-
пространства 145
— Фурье 162
Размерность (пространства, подпро-
подпространства) 34, 140
Разность множеств 70
Распространение оператора 211
Расстояние в метрическом простран-
пространстве 71
Регулярное число 291
Редукции метод 335
Ритца метод 337
Система полунорм монотонная 362
Скалярное произведение 15, 151
Собственная функция интегрально-
интегрального уравнения 300
Собственное подпространство 287
— число оператора 39, 286
Собственный вектор 39
— элемент 286
Спектр 291
— чисто непрерывный 291
точечный 291
Среднее значение функции 184
— отклонение 82
Степень оператора 219
Структура банахова 392
— линейная 385
Сумма матриц 22
— множеств 69
— ряда обобщенная 274
Суперпозиция операторов 219
Супремум 385
Существенная точная верхняя гра-
граница 242
Сходимость в себе 87
— в среднем 82, 83, 191
— по норме 136
— по полунормам 356
— по расстоянию 79
— последовательности векторов в Rn
25
— равномерная (последовательности
операторов) 217
— сильная 282
— слабая 264
в гильбертовом пространстве
309
— точечная 213
Точка внутренняя 86
— изолированная 312
— неподвижная 114
— предельная 84
Транзитивность неравенства 386
Умножение операторов 219
Уравнение замкнутости 65, 163
Фундаментальная последователь-
последовательность 87
по полунормам 358
— система собственных элементов
314
Функции равноограниченные 107
— равностепенно непрерывные 107
Функционал 27, 112
Функциональная реализация гиль-
гильбертова пространства 174
Функциональное уравнение 114
Функция кусочно-постоянная 194
— обобщенная 381
— ограниченной вариации 248
— промежутка 185
Характеристическое уравнение мат-
матрицы 40
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Характеристическое число
трального уравнения 300
пнте-
Шар единичный 207
— замкнутый 83
— открытый 83
Штурма — Лггувилля дифференци-
дифференциальное уравнение 300
Эквивалентные нормы 209
— системы полунорм 361
Элемент множества 68
наилучшего
415
приближе-
Элемент
ния 146
— нулевой 131
— отрицательный 384
— положительный 384
— сильно положительный 404
— собственный 286
Элементы р-эквивалентные 358
е-сеть 102
Ядро интегрального уравнения 123
вырожденное 331
симметричное 299
Борис Захарович Вулих
ВВЕДЕНИЕ В ФУНКЦИОНАЛЬНЫЙ
АНАЛИЗ
М., 1967 г., 416 стр. с илл.
Редактор В. М. Гринберг
Техн. редактор С. Я. Шкляр
Корректор А. С. Баку лова
Сдано в набор 11/Х 1966 г. Подписано
к печати 3/IV 1967 г. Бумага 60 X 9О'/1б- Физ.
печ. л. 26. Условн. печ. л. 26. Уч.-изд. л. 26,31.
Тираж 25 000 экз. Т-01864. Цена книги 1 р. 86 к.
Заказ М5 689.
Издательство «Наука».
Главная редакция
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15
Московская типография N«16
Главполиграфпрома Комитета по печати
при Совете Министров СССР
Москва, Трехпрудный пер., 9.