Автор: Люстерник Л.А. Соболев В.И.
Теги: анализ математический анализ функциональный анализ математика
Год: 1982
Текст
В. И. СОБОЛЕВ
КРАТКИЙ КУРС ФУНКЦИОНАЛЬНОГО АНАЛИЗА
Л. А. ЛЮСТЕРНИК, В. И. СОБОЛЕВ
КРАТКИЙ КУРС ФУНКЦИОНАЛЬНОГО АНАЛИЗА
Допущено
Министерством высшего и среднего специального образования СССР в качестве учебного пособия для студентов университетов, обучающихся по специальности «Математика»
МОСКВА «ВЫСШАЯ ШКОЛА» 1982
ББК 22.162 ЛИ
УДК 517.5(075)
Рецензенты:
кафедра теории функций и функционального анализа РГУ; д-р физ-мат. наук, проф. В. П. Михайлов
Люстерник Л. А., .Соболев В. И.
Л11 Краткий курс функционального анализа: Учеб, пособие.—М.: Высш, школа, 1982.—271 с., ил.
В пер.: 60 к.
Книга написана в соответствии с программой по курсу функционального анализа для университетов. Изложение материала ведется на высоком методическом и научном уровне, рассматривается широкий круг вопросов, имеется большое число интересных примеров и приложений.
Предназначается для студентов университетов.
„ 1702050000-032 Л' 001(51)' —82 38 82 ББК 22.162 517.2
© Издательство «Высшая школа», 1982
ОГЛАВЛЕНИЕ
Предисловие .................................................... • • • 5
Глава I, Необходимые сведения из анализа, алгебры и топологии .... g
§ 1. Функциональная зависимость. Пространство. Упорядоченность. 6
§ 2. Мера и интеграл Лебега....................................... 9
§ 3. Линейные пространства....................................... 16
§ 4. Метрические пространства ................................... 23
§ 5. Примеры метрических пространств............................. 27
§ 6. Полные пространства. Полнота некоторых конкретных пространств. Пополнение метрических пространств..................... 33
§ 7. Теоремы о полных пространствах. Принцип сжимающих отображений ....................................................... 40
§ 8. Сепарабельные пространства............................... 46
§ 9. Компактные множества в метрических пространствах...... 48
§ 10. Топологические пространства.............................. 54
Глава //. Линейные нормированные и линейные топологические пространства .......................................................... 63
§ 1. Линейные нормированные пространства ......................... 63
§ 2. Компактные множества в линейных нормированных пространствах 70
§ 3. Абстрактное гильбертово пространство......................... 77
§ 4. Линейные топологические пространства ........................ 85
Упражнения............................................................ 96
Г лава III, Линейные операторы........................................ 98
§ 1. Линейные операторы в линейных топологических пространствах 98
§ 2. Линейные операторы в линейных нормированных пространствах 105
§ 3. Линейные функционалы...................................... 111
§ 4. Пространство линейных непрерывных операторов................ 113
§ 5. Обратные операторы и теорема Банаха о гомеоморфизме .... 118
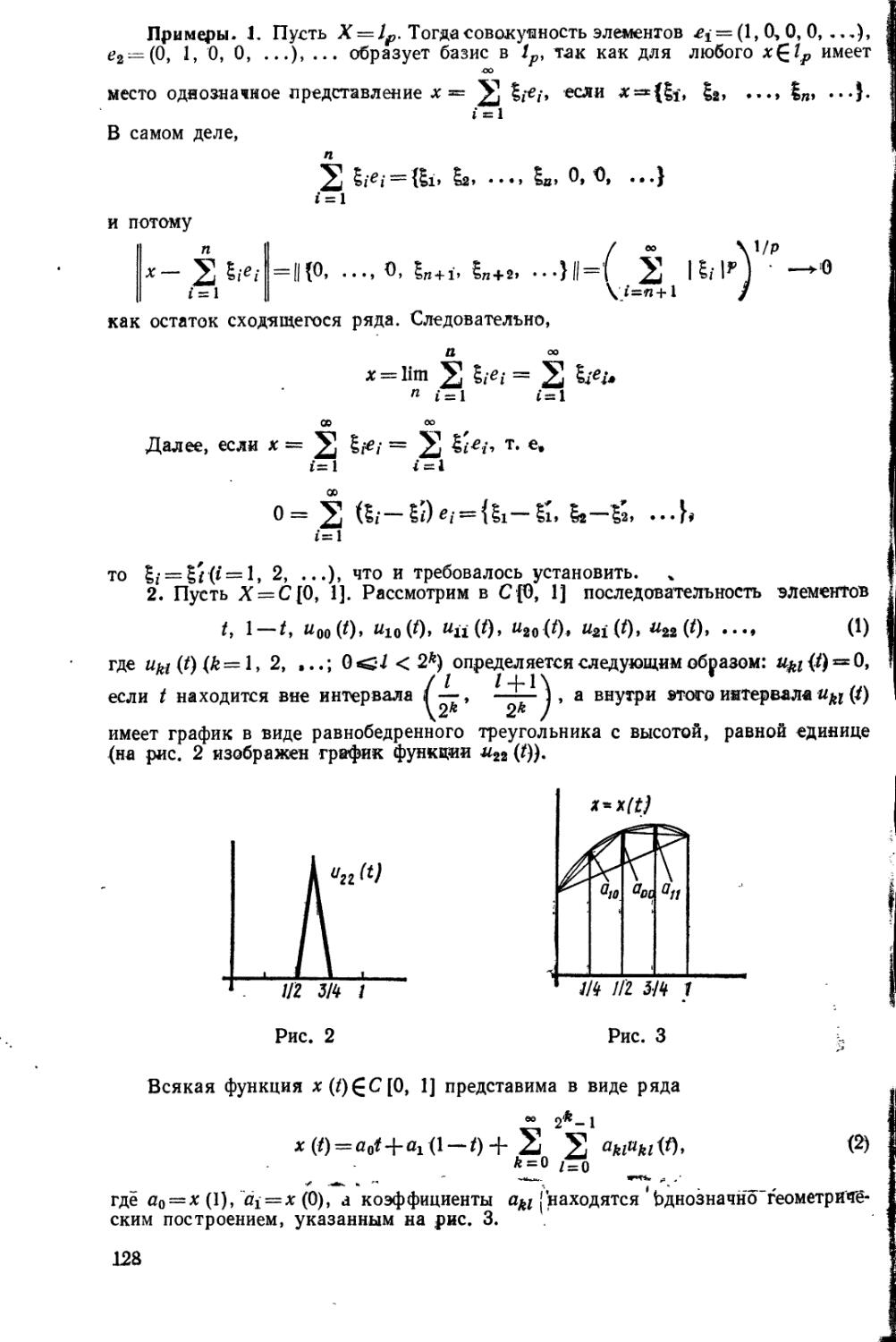
§ 6. Теоремы о замкнутом графике и об открытом отображении ... 125
§ 7. Пространство Банаха с базисом............................... 127
Упражнения........................................................... 133
Г лава IV, Линейные функционалы...................................... 134
§ 1. Теорема Банаха — Хана и ее следствия........................ 134
§ 2. Отделение выпуклых множеств................................. 140
§ 3. Общий вид линейных функционалов в некоторых функциональных пространствах ............................................... 144
§ 4. Сопряженные пространства и сопряженные операторы.......... 155
§ 5. Слабая сходимость .......................................... 165
§ 6. Универсальность пространства С [0, 1]....................... 172
Упражнения....................................................... . 176
3
Г лава V. Вполне непрерывные операторы и уравнения с ними......... 177
§ 1. Вполне непрерывные операторы............................. 177
§ 2. Линейные операторные уравнения с вполне непрерывными one-раторами......................................* ............. 182
§ 3. Принцип неподвижной точки Шаудера и его применения ...» 190
Упражнения........................................................ 195
Г лава VI. Элементы дифференциального и интегрального исчислений в линейных нормированных пространствах.............................. 196
§ 1. Дифференциал и производная Фреше......................... 196
§ 2. Производная Гато......................................... 201
§ 3. Теорема о локальном обращении дифференцируемого отображения. Метод Ньютона............................................ 207
§ 4. Производные высших порядков. Формула Тейлора............. 213
§ 5. Теорема о неявной функции и ее приложения................ 217
§ 6. Касательные многообразия и задачи на экстремум........... 221
§ 7. Интегрирование абстрактных функций....................... 227
Упражнения....................................................... 236
Глава VII. Элементы спектральной теории ограниченных самоспряжен-ных операторов в гильбертовом пространстве........................ 237
§ 1. Самосопряженные операторы...................*............ 237
§ 2. Унитарные и проекционные операторы.............ч . . . . . 240
§ 3. Положительные операторы. Квадратный корень из положительного оператора................................................ 244
§ 4. Спектр самосопряженного оператора........................ 247
§ 5. Спектральное разложение самосопряженного оператора ...... 253
Дополнения...................................................... 263
Литература ....................................................... 267
Предметный указатель.......................♦...................... 268
ПРЕДИСЛОВИЕ
Среди математических дисциплин, исследующих те или иные математические структуры, функциональный анализ наряду с абстрактной алгеброй и теоретикомножественной топологией играет важную роль. Его методы с успехом используются во многих разделах современной теоретической и прикладной математики. Более того, развитие таких дисциплин, как дифференциальные уравнения (обыкновенные и в частных производных), теория управления, методы вычислений и др., вряд ли было бы в последние годы столь успешным, если бы при этом не использовались идеи и методы функционального анализа. Поэтому функциональный анализ стал необходимым элементом серьезного математического образования и преподавание его основ включено в учебные планы математических специальностей университетов.
Настоящая книга явилась результатом обработки лекций, которые в течение ряда лет читались одним из авторов в Воронежском университете. При этом широко использовалась вышедшая ранее книга авторов «Элементы функционального анализа» (М., Наука, 1965). Меньшая по объему, чем предыдущая, настоящая книга тем не менее содержит весь материал, традиционно излагаемый в университетских курсах функционального анализа и указанный в программах, имеющихся по этой дисциплине.
Создание учебника или учебного пособия—достаточно сложная задача и, как правило, лишь совокупность нескольких книг дает весь материал, необходимый студенту, слушающему курс лекций по соответствующей дисциплине. Поэтому наличие книг различной степени полноты и сложности является необходимым условием для овладения предметом. Функциональному анализу посвящен ряд хороших учебных пособий и монографий, вышедших за последние годы в нашей стране. Достаточно назвать «Элементы теории функций и функционального анализа» А. Н. Колмогорова и С. В. Фомина, «Функциональный анализ» Л. В. Канторовича и Г. П. Акилова, а также вышедшие под тем же названием книги К. Иосиды и У. Рудина. Однако авторы надеются, что предлагаемая книга, не дублирующая названные монографии ни по материалу, ни по стилю изложения, может оказаться полезной для лиц, решивших овладеть основами функционального анализа.
Во многих местах и по содержанию, и по изложению настоящая книга близка к книге тех же авторов «Элементы функционального анализа». Вместе с тем ряд разделов функционального анализа изложен в ней по-иному, многие вопросы опущены, другие включены, что и побудило авторов дать книге новое название.
В книге имеется некоторое количество упражнений. Кроме того, в тексте сформулирован ряд утверждений, доказательство которых предоставляется читателю. Мы настоятельно рекомендуем читателям книги провести эти доказательства. Наконец, хорошим дополнением к нашей книге могут служить «Задачи и упражнения по функциональному анализу» А. Б. Антоневича, П. Н. Князева, Я. В. Радыно (Минск, Вышэйшая школа, 1978) и «Теоремы и задачи функционального анализа» А. А. Кириллова и А. Д. Гвишиани (М., Наука, 1979).
Для удобства пользования книгой в ней приняты следующие обозначения: начало и конец доказательства теоремы или утверждения отмечаются соответственно значками □ и
Авторы выражают искреннюю признательность Е. А. Лифшицу, А. И. Перову, В. П. Захарюте и В. Д. Ковальчуку за ряд полезных замечаний и предложений, способствовавших улучшению рукописи.
Авторы
ГЛАВ A I
НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ АНАЛИЗА, АЛГЕБРЫ И ТОПОЛОГИИ
§ 1. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ. ПРОСТРАНСТВО.
УПОРЯДОЧЕННОСТЬ
Одним из основных понятий математического анализа является понятие функциональной зависимости. Напомним определение функциональной зависимости, даваемое в анализе: пусть X и Y—два множества вещественных чисел; если каждому числу х£Х по некоторому закону (правилу) ставится в соответствие единственное число у £ Y, то говорят, что на множестве X определена однозначная функция y — f{x), область значений которой принадлежит множеству Y. Множество X называют также областью определения функции.
Легко видеть, что для идеи функциональной зависимости не является необходимым, чтобы X и Y были множествами вещественных чисел. Понимая под X и Y множества элементов различного характера, мы приходим к понятию более общей функциональной зависимости, примеры которой имеются в разных ветвях математического анализа.
I
Примеры. 1. Пусть y = f(xi, х2, хд)—вещественная функция п вещественных переменных. Тогда X есть множество упорядоченных систем из п вещественных чисел, У —множество вещественных чисел,
2. Пусть y = f (х)—вектор-функция, относящая вещественным числам х —>
n-мерные векторы у. Здесь X — множество вещественных чисел, Y—множество n-мерных векторов.
3. В вариационном исчислении рассматриваются функционалы
ь
I (?) = (xt U, У') dx, а
где у — кривая, заданная уравнением y=zf(x), в котором f (х) принадлежит классу Cj функций, обладающих непрерывной производной, и проходящая через две данные точки А (а; уа) и В (Ь; уь). В этом случае X — множество кривых с указанными свойствами, Y—множество вещественных чисел.
4. В теории интегральных уравнений рассматривается выражение вида
ь
y(t) = ^K (/, $) х (s) ds. a
Предполагается, что ядро ft (/, s) определено и непрерывно в квадрате a^t^b, a^s^b. Тогда написанное равенство можно рассматривать как некоторый закон, согласно которому каждой функции x(t), непрерывной на [а, Ь], соотносится другая функция, непрерывная на том же отрезке. Здесь X и Y—множества непрерывных функций.
6
Введем теперь общее определение функциональной зависимости.
Пусть даны два произвольных множества X и У и дан закон (правило), согласно которому каждому элементу х£Х ставится в соответствие единственный, вполне определенный элемент y£Y. Будем говорить тогда, что задан оператор у — f (х) (пишут также y = fx), определенный на множестве X, с областью значений, принадлежащей множеству У. Говорят также, что задано отображение множества X в* множество У и пишут f: X —► У. В том частном случае, когда значения оператора являются вещественными или комплесными числами, оператор называется функционалом.
Элемент y£Y, соответствующий при отображении f элементу xgX, называется образом элемента х, а х — прообразом элемента у. Отметим, что прообраз определяется, вообще говоря, неоднозначно.
Если отображение y~f(x) переводит X на У, то, очевидно, у каждого элемента y^Y существует по крайней мере один прообраз х. В том случае, если у каждого y£Y имеется только один прообраз х£Х, отображение X на У, устанавливаемое формулой y =zf(x), называется взаимно-однозначным.
Относительно свойств операторов, определенных таким весьма общим образом, почти ничего нельзя сказать. Поэтому введем дополнительные предположения.
Наряду с понятием функциональной зависимости другим основным понятием анализа является понятие предела и связанное с ним понятие непрерывности. Множество, в котором тем или иным способом определено понятие предела последовательности, обычно называется пространством.
Пространства, элементами которых являются функции или числовые последовательности, будем называть функциональными пространствами. Изучение некоторых классов операторов, определенных в функциональных пространствах, и составляет основное содержание функционального анализа.
Остановимся еще на некоторых понятиях, используемых в функциональном анализе.
Пусть в множестве X объектов некоторой природы для некоторых пар элементов a, b, с, d, ... этого множества введено отношение а < Ь. Множество X называется частично упорядоченным, если это отношение удовлетворяет следующим условиям:
Г. Из а < b и b < с следует а < с.
2°. а < а.
3°. Из а < b и b < а следует а = Ь.
Элементы а и Ь, для которых имеет место отношение а < b или Ь < а, называются сравнимыми.
Множество X называется упорядоченным (или линейно упорядоченным), если для любых двух различных элементов а и b этого множества либо а < Ь, либо b < а.
* Условимся говорить, что некоторое обстоятельство имеет место на мио-жестве, если оно имеет место для всех элементов этого множества, и в множестве, если оно имеет место, может быть, не для всех элементов множества.
7
Подмножество Y частично упорядоченного множества называется ограниченным сверху, если существует элемент b такой, что у <Ь для всех у £У. Элемент Ь называется верхней границей множества У. Наименьшая из всех верхних границ называется точной верхней границей (или верхней гранью) множества.
Аналогично определяются множество, ограниченное снизу, нижняя граница и точная нижняя граница (или нижняя грань) множества. Отметим, что точные границы могут и не существовать.
Наконец, элемент zQ^X называется максимальным, если в X не существует элемента х #= г0, удовлетворяющего соотношению z0 < х.
Имеет место следующее весьма важное утверждение.
Лемма Цорна. Если в частично упорядоченном множестве X для всякого линейно упорядоченного подмножества Y существует верхняя грань, то в X существует максимальный элемент z0.
Упорядоченное множество называется вполне упорядоченным, если любое его непустое подмножество имеет наименьший элемент, т.‘е. элемент, предшествующий всем элементам подмножества.
Теорема Цермело. Всякое множество путем введения некоторого соотношения порядка можно сделать вполне упорядоченным.
Доказательство теоремы Цермело опирается на так называемую аксиому произвольного выбора Цермело, утверждающую, что если дана любая система непустых попарнЪ не пересекающихся множеств, то существует новое множество, имеющее с каждым из множеств системы по одному и только одному общему элементу.
Можно показать, что лемма Цорна, аксиома ЦермелЬ и теорема Цермело —эквивалентные друг другу утверждения. Подробнее об этом см. [3] и [14].
Пример. Пусть М — некоторое непустое множество и T=\t)—совокупность всех его подмножеств t. Будем считать, что Ц < /2, если Ц CZ/2. Очевидно, что введенное таким образом отношение порядка удовлетворяет указанным выше трем условиям. Ясно также, что если М содержит более двух элементов, то при таком упорядочении множество Т не является упорядоченным (тем более вполне упорядоченным).
Если S — любое подмножество Т, то оно ограничено сверху и его точной верхней границей служит множество s= (J t- ВТ существует максимальный teS
элемент: это само множество М, рассматриваемое как подмножество, и лемма Цорна в этом случае очевидна. Теорема же Цермело утверждает, что Т можно сделать вполне упорядоченным, введя в нем иное отношение порядка, но как это сделать — из теоремы не вытекает, так как доказательство ее носит неконструктивный характер.
Подмножество А частично упорядоченного множества X называется направленным, если для двух любых элементов a, pg А существует элемент ygA такой, что у>а и у>р. Отображение f направленного множества А в произвольное множество Y называется обобщенной последовательностью или направлением, составленным из элементов множества У, и обозначается {уа}. Если А есть множество натуральных чисел, то направление является обычной последовательностью.
8
§ 2. МЕРА И ИНТЕГРАЛ ЛЕБЕГА
Во многих примерах, которые будут рассматриваться в этой книге, используются мера и интеграл Лебега. Напомним основные понятия и теоремы, относящиеся к теории Лебега; при этом предполагается знакомство с основными понятиями и теоремами теории множеств.
1. Абстрактные мера и интеграл. Пусть X —множество элементов некоторой природы. Совокупность А подмножеств множества X называется а-алгеброй, если выполняются следующие условия:
1°. Х£Х.
2°. Из А С А следует С А £ А.
3°. Если £ A (i== 1, 2, 3, ...), то и € А.
1=1
Из этих условий сразу вытекает, что пустое множество принадлежит А и что пересечение конечного или счетного числа множеств, принадлежащих о-алгебре, также принадлежит о-алгебре.
Тривиальным примером а-алгебры является система всех подмножеств множества X.
Другим примером о-алгебры могут служить так называемые борелевские множества на фиксированном отрезке числовой прямой. Возьмем на [а, Р]с(—оо, оо) последовательность открытых множеств {Gn}. Тогда U Gn есть открытое множество, но П Gn уже П=1 п-1
может быть и не открытым. Например, пересечение интервалов (a, b + e/ra), а > а, b + е < 0, есть полуинтервал (а, &]. Множества вида Г) G„ назовем множествами типа G&. Аналогично, п = 1
если {F„}—последовательность замкнутых множеств на [а, 0], то
Г) Fa замкнуто, а и Fn может быть ни замкнуто, ни открыто, лг = 1 п = 1
Множества вида и Fn назовем множествами типа Fa. Ясно, что п = 1
пересечение конечного или счетного числа множеств типа G& есть снова множество того же типа, но объединение счетного числа таких множеств может оказаться множеством ни замкнутым, ни открытым, ни типа G^, ни типа FG. В этом случае говорят, что это множество имеет тип G&g. Аналогично определяются множества типа и т. д.
Совокупность множеств, которая может быть получена из открытых и замкнутых множеств путем операций объединения и пересечения, повторенных в любом порядке конечное или счетное число раз, образует борелевс&ую систему В множеств на отрезке [а, Р]. Нетрудно проверить, что если М £ В, то также С[а> так что В является о-алгеброй.
Можно доказать, что существуют множества типа G^o... и Лгбаф.,, для любой конечной комбинации индексов а и 6, не сво
9
2°. и
дящиеся к множествам более простого типа, так что класс боре-левских множеств достаточно обширен.
С третьим примером о-алгебры мы познакомимся ниже.
Множества, принадлежащие о-алгебре А, будем называть А-оз-меримыми (или просто измеримыми).
Напомним, что последовательность {Л„} множеств называется сходящейся к множеству А, если
ОО/ОО Ч ОО » оо \
Г) ( и Aft)= U ( n ЛА) = А.
В этом случае А называют пределом последовательности {Л,} и пишут А = lira Ап. Ясно, что предел последовательности А-изме-римых множеств есть измеримое множество.
Числовая функция ц: А —> R называется мерой, если:
Г. р(Л)^О для любого Л^А.
U ЛЛ== 2ц(Л„), где Л„(=А(п=1,2, 3, ...), A^A^tf п=\ J ,7=1
при i=/= j.
Доказывав!ся, что мера есть монотонная функция, т. е. р (Л) ^р(В), при ЛсгВ; Л, ВС А; что р(0)=О; что для любых
Л,- с А (' = 1, 2, 3, ...) ц ( U Л,-) S И (А,) и что если Л = lim Ап, \i-1 / i=l
то рЛ = 1ппр.Л„.
Вещественная функция /(%), определенная на множестве ЕсХ, называется измеримой, если измеримо множество Е и при любом вещественном с измеримо множество Е (f > с) — {х £ Е \ [ (х) > с}.
Доказывается, что для измеримости f на измеримом множестве Е необходимо и достаточно измеримости при каждом с одного из трех множеств: E(f^c), E(f<c), E(fs^c).
Класс измеримых функций замкнут относительно алгебраических операций и относительно предельного перехода, даже если сходимость понимается как сходимость почти всюду, т. е. с точностью до множества с мерой, равной нулю.
Теорема 1 (Д. Ф. Егорова). Если f„(x) —>• f (х) почти всюду на Е, то для любого б > О можно найти измеримое подмножество Е'сЕ такое, что р(Е') > р(Е)—6 и на Е’ последовательность {fn(x)} 'сходится к f (х) равномерно.
Кроме сходимости почти всюду мы будем иметь дело и со сходимостью по мере: последовательность {/„(*)) измеримых на Е функций сходится по мере к измеримой функции f(x), если для любого а > О
при п —* ОО.
Нетрудно убедиться, что если последовательность {fn(x)} сходится к f (х) почти всюду, то она сходится к f (х) и по мере. Обратное утверждение, как показывают примеры, неверно, однако Ф. Рисе доказал, что из любой последовательности, сходящейся по 10
мере, можно выделить последовательность, сходящуюся почти всюду к тому же самому пределу.
Пусть Е — измеримое множество и / — неотрицательная измеримая на Е функция. Разобьем Е на конечное число непересека-ющихся измеримых частей £,•:
Е— и Eh £,Г|Д/ = 0 при i^j. i=i '
П
Пусть u; = inf/(x). Составим сумму Ум,рЕ,-. Конечная или беско-Ei i=l
нечная точная верхняя граница таких сумм по всевозможным разбиениям указанного вида множества Е называется интегралом Лебега от f(x) по множеству Е и обозначается J/(x)dp. Если
Е
J(x)dp<4-°o. то неотрицательная функция / (х) называется ин-Е тегрируемой (или суммируемой) на множестве Е.
Для функции /(х), принимающей на множестве Е значения разных знаков, по определению полагаем
$ / (х) dp = $ /+ (х) dp - $ /_ (х) dp, ЕЕ Е
если по крайней мере один интеграл справа конечен. Здесь
Если j/(x)dp^=±oo, то функция /(х) называется интегрируемой Е
(или суммируемой) на множестве Е.
Совокупность L (Е) интегрируемых на Е функций является линейной системой и
J [а/ (х) 4- pi (х)] dp = а $ / (х) dp 4-Р $ g (х) dp. Е ЕЕ
Имеют место также обычные свойства интеграла, выражаемые с помощью неравенств, и справедлива теорема о предельном переходе под знаком интеграла.
Теорема 2 (Лебега). Если fn(x)->-f(x) почти всюду на Е и I fn (х) | ф (х) для почти всех х£Е, причем J <p (х) dp < оо, то
Е
$ fn (х) dp —► ( / (х) dp.
Е Е
Весьма важным являются следующие два свойства интеграла Лебега.
11
Полная аддитивность: если Е — и где все Е, измери-i=* 1 1
МЫ U р. (Е{ Г) Ej) =0 (г =# /), то
J/(x)dp=2 $/(x)d,u. Е i =
Абсолютная непрерывность: для любого 8 > 0 найдется б > 0, зависящее лишь от функции f (х) и от & такое, что f (х) dp) < 8, каково бы ни было измеримое множество НаЕ с н
мерой [iH < б.
2. Мера и интеграл в евклидовом пространстве. Конкретной реализацией абстрактного интеграла Лебега является интеграл Лебега по множествам числовой прямой.
Пусть G —ограниченное открытое множество числовой прямой. Как известно, G = \J (ak, bk), где число интервалов является конечным или счетным, причем сами они попарно не пересекаются. Положим pG = ^(^—aj. Если F —ограниченное замкнутое множество и [а, Р]— наименьший отрезок, содержащий это множество, т. е. a = infF, р —supF, то множество открыто и полагаем
pF=s(£ —а)— рС[а, р]Г. Пусть теперь Е — произвольное ограниченное множество на числовой прямой. Внешней мерой Е называется число р*Е — infpG, где G открыто, а внутренней мерой Е —число
<?□ Е
p*E = suppF, где F замкнуто. Если р*Е = р*Е, то мнсЬкество Е FCE
называется измеримым по Лебегу и общее значение внешней и внутренней меры называется мерой множества Е:
[iE = р*Е — и^Е.
Доказывается, что совокупность всех измеримых множеств Е, лежащих в данном отрезке [а, Ь] или в конечном интервале (а, Ь), есть о-алгебра; что рЕ есть мера в смысле данного выше определения; вводятся понятия измеримой функции и интеграла Лебега $ f (х) dp, который чаще обозначают J / (х) dx; таким образом, все Е Е
факты, указанные выше для абстрактной меры и интеграла, остаются справедливыми для меры и интеграла на числовой прямой.
С понятием интеграла Лебега на числовой прямой связано понятие абсолютно непрерывной функции. Функция /(х), заданная на отрезке [а, 6], называется абсолютно непрерывной на этом отрезке, если для каждого 8 > 0 найдется такое б > 0, что из п и
V(xi, х, 4-й/) с [a, ft], (xi,xi+hi)f}(xJ-,x/+hj)= 0(i=£j) и^й/<6
следует
f(Xi 4-й/) -/(%,-)
8.
12
Ясно, что функция абсолютно непрерывная на [a, h], непрерывна на этом отрезке. Обратное утверждение, как показывают примеры, неверно.
Важное свойство абсолютно непрерывной функции выражает следующая теорема.
Теорема 3. Всякая функция fix), абсолютно непрерывная на Га, &J, имеет почти всюду на этом отрезке производную f (х), эта L X
производная суммируема и f — (t) dt + f (a),
a
Вещественная (комплексная) функция /(/), определенная и измеримая (такая, что Ref и Imf измеримы) на отрезке [а, &], называется принадлежащей классу Лебега L„ (а, Ь) или, иначе, ь
функцией с суммируемой р-й степенью, если J | f (t) dt < оо. а
Здесь интеграл понимается в смысле Лебега; р —некоторое положительное число. В дальнейшем мы всюду предполагаем, если не оговорено противное, что р 1. Можно доказать, что если f(t)€Lp(a, Ь) и g(t) £Lp(a, b), то f (t) + g(t) £ Lp{a, b) и kf (t)£Lp(a, b) для любого вещественного (комплексного) числа %. В теории лебеговских классов функций важную роль играют следующие два неравенства.
Неравенство Гельдера. Если f(f)£Lpia, b), р>1, и g(t)^.Lq(a, b), где —+ —= 1, то произведение f (/)git) — суммируемая на [а, &] функция и
b z Ъ \ 1/р / Ъ ч l/q
$lf(Og(O|d/<! sI/(ОГ dz) ( $ |g(0|«(И) а а / \ а /
(1)
Неравенство Минковского. Если fit), g (t) С Ер (а, Ь), то
Ъ \1/р /6 \ 1/р /Ь х I/P
$ |/(O + g(/)|?d/) <1 $)/(/) +( $|g(O|'d/) . (2)
а / \а / \а /
Отметим, что знак равенства в формулах (1) и (2) имеет место лишь если | f (t) \p — k | g(t) |« для (1) и соответственно f (t) = kg(t)t & > О, для (2) почти всюду на [а, 6].
Доказательство всех приведенных выше утверждений можно найти в подробных курсах математического анализа и в курсах теории функций вещественной переменной.
Приведем еще принадлежащую Н. Н. Лузину теорему, характеризующую строение функции, измеримой на отрезке.
Будем говорить, что заданная на отрезке [а, Ь] функция f (х) обладает С-свойством, если для любого в > 0 найдется совершенное (т. е. замкнутое и не содержащее изолированных точек) множество Рс[а, Ь] такое, что р (Р) > (Ь—а) — е и f (х) на Р непрерывна.
J3
Теорема 4 (Н. Н. Лузина). Для того чтобы функция f (х) была измерима на отрезке [а, 6], необходимо и достаточно, чтобы она обладала на этом отрезке С-свойством.
Аналогично строится мера и интеграл Лебега в пространстве R". При этом за меру открытого ограниченного множества принимается сумма ряда, составленного из объемов замкнутых параллелепипедов без общих внутренних точек, в виде счетного объединения которых может быть представлено открытое множество. Мера замкнутого ограниченного множества определяется как разность между объемом замкнутого параллелепипеда, содержащего это множество, и мерой дополнительного до параллелепипеда открытого множества. Затем, как и в одномерном случае, определяются внешняя и внутренняя меры ограниченного множества, измеримость и мера множества, измеримые функции и мы приходим к кратному интегралу Лебега.
Имеет место следующая важная теорема.
Теорема 5 (Фубини). Пусть функция f (х±,.. .,хп, yL, ..., ут) суммируема на параллелепипеде Р — {(хп ..., хп, уг, •••,«/„,)}, а^х^Ь^ Cj^.yj^.dj, евклидова (п + т)-мерного пространства. Тогда почти для всех (хг,...,х„), принадлежащих параллелепипеду Рх— {(Х1, . . ., Х„)}, G; X,- f^bt, функция
fx(yi, ...,х„, yt, ...,ут)'
суммируема на Ру = {(уи ..., ут)}, ct ^dj, интеграл
^ЛУх.......Ут)&Ух---&Ут
Ру
как функция от х*. ..., х„ суммируем на Рх и
..........хп, ylt ...,t/Jdx1...dxndz/1...dt/OT = р
= $ Л Нхх,---,хп, Ух, • • • ,ут) <$Ух-• .d^ldXx.. .dxn.
J
Переменные xt и yt можно поменять местами.
Если функция f (xu ..., х„, ylt ..., ут) задана на произвольном измеримом множестве Е, то надо заключить Е в параллелепипед Р и перейти к функции
н [f(x,y),ecmi(x,y)€E,
I {х, у) - 0> если е
3. Интеграл Стильтьеса. В некоторых вопросах функционального анализа используется понятие интеграла Стильтьеса. Мы ограничимся напоминанием определения и основных свойств интеграла Стильтьеса —Римана.
Функция f: [а, &] —► R называется функцией с ограниченной вариацией на отрезке [а, &], если существует постоянная с такая, что
14
для любого разбиения Т: а — х0 < xz < ... <хл_х < хп =i b этого п
отрезка 21 f (х,) —f (xz_r) | < с. i= 1
п
Число sup 2lf I называется при этом полной ва-
Т i = l
риацией функции f на [о, 6] и обозначается V^(f). Например, монотонная на [a, 6] функция имеет на этом отрезке ограниченную вариацию; функция / (х) = xsin (1/х) при х#=0 и f(0) = 0 не является функцией с ограниченной вариацией на отрезке [0, 1].
Пусть на отрезке [а, 6] заданы две функции f (х) и g(x). Разобьем отрезок на части точками а = х0 < хг <... < xn_j < х„ = Ь, выберем на каждом частичном отрезке [xz_n хг] точку gz и составим сумму п
2/&)[£(*/)-g^-i)]-
Если при неограниченном измельчении разбиения отрезка [а, на части эта сумма стремится к конечному пределу, не зависящему ни от характера разбиения отрезка, ни от выбора на частичных отрезках [xz_i, xz] точек то этот предел называется интегралом Стильтьеса от функции f (х) по функции g (х) и обозначается ь
$ f(x)dg(x). Если функция /(х) непрерывна на [а, 6], a g(x) имеет а
на этом отрезке ограниченную вариацию, то интеграл Стильтьеса существует. Интеграл Стильтьеса обладает свойством линейности как по отношению к интегрируемой функции /(х), так и по отношению к интегрирующей функции g(x), и имеют место следующие две теоремы о предельном переходе под знаком интеграла Стильтьеса.
Теорема 6. Если последовательность {/„(х)} непрерывных на [а, 6] функций равномерно сходится на этом отрезке к f(x), то для любой функции g (х) с ограниченной на [а, Ь] вариацией
ь ъ
lira J (х) dg (х) = J f (х) dg (х). п а а
Теорема 7. Пусть функция f (х) непрерывна на [a, &] и {g„ (х)} — последовательность функций с ограниченными на [а, Ь] вариациями, которая сходится в каждой точке этого отрезка к g(x). Если при этом Nba(g^^K (п = 1, 2, 3, ...), то g(x) также функция с ограниченной вариацией и ь ь
lim $ f (х) dgn (х) = $ f (х) dg (х). п а а
В заключение напомним следующие свойства функции g(t) с ограниченной на [а, Ь] вариацией и интеграла Стильтьеса; некоторые из них понадобятся нам в дальнейшем.
15
1. Функция g(t) есть разность двух монотонно возрастающих на [а,Ь] функций.
2. Функция g(t) имеет ограниченную вариацию на любом частичном отрезке [а', Ь'1 а.[а, 6].
3. Если а<с<Ь, то Уса (/) + V* (/) = V* (f).
4. Если g(t) непрерывна на [а, Ь], то V£(g) также непрерывна на этом отрезке.
5. Функция g(t) может иметь на [а, 6] не более счетного множества точек разрыва и притом только I рода.
ь
6. Величина интеграла J х (t) dg (t) для любой непрерывной функ-а
ции x(t) не изменится, если изменить значения g(t) на конечном или счетном множестве точек.
ь
7. Если J x(t) сЦт (/) = 0 для любой непрерывной функции x(t), а
то g(t)—g (а) во всякой внутренней точке непрерывности.
Функции с ограниченной вариацией называются также функциями с ограниченным изменением, а величина У£ (g) — полным изменением функции g (t) на отрезке [а, &].
§ 3. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
1. Определения и простейшие свойства. При рассмотрении многих конкретных множеств мы видим, что элементы этих, множеств (функции, числовые последовательности и др.) можно складывать друг с другом и умножать на числа, получая элементы того же множества. Исходя из таких конкретных примеров, мы приходим к общему определению линейного пространства.
Пусть X — множество элементов некоторой природы, удовлетворяющее следующим аксиомам:
I. X — абелева группа относительно групповой операции сложения.
Это значит, что. определена сумма х-\-у двух любых элементов х,у£Х, являющаяся элементом того же множества, причем операция сложения обладает свойствами:
1 °, х + у = у + х—закон коммутативности.
2°. х -|- (у + г) = (х + у) + г—закон ассоциативности.
3°. Существует однозначно определенный элемент 0 такой, что х + 0==х для любого х из X.
4°. Для каждого элемента х£Х существует однозначно определенный элемент —х того же пространства такой, что х + (—х) = 0. Вместо х + (—у) будем писать х — у.
Элемент 0 называется нулевым элементом (или нулем) группы X; элемент —х называется элементом, противоположным х.
II. Определено умножение элементов х, у, г, ... множества X на вещественные (комплексные) числа X, ц, v, ..., причем Хх является снова элементом множества X и выполнены условия:
16
1°. Л (цх) = (Хр) х — закон ассоциативности.
2°. X (х+у) = Хх4-Хг/, (Х + р) х — Хх + цх —закон дистрибутивности.
3°. \-х — х.
Множество X, удовлетворяющее аксиомам I и II, называется линейным (или векторным) пространством. В зависимости от того, на какие числа, вещественные или комплексные, допускается умножение элементов множества X, мы получаем вещественное или комплексное линейное пространство.
Примеры. 1. Совокупность R" вещественных «-мерных векторов образует вещественное линейное пространство.
2. Совокупность комплекснозначных решений обыкновенного однородного линейного дифференциального уравнения «-го порядка образует комплексное линейное пространство.
3. Совокупность элементов вещественного (комплексного) класса Lp (а, Ь) образует вещественное (комплексное) линейное пространство.
Приведем некоторые следствия из аксиом линейного пространства.
1. 0х = 0 при любом х£Х.
2. (—1)-х = — х.
3. Х-0 = 0 при любом X.
4. Если Ъх — рх и х=£0, то Х = ц.
Отметим, что если X— линейное пространство, то коммутативность сложения является следствием остальных аксиом. Действительно,
(х + у) — (у + х) = (х + у) + (—1) • (у + х) =
= х + у + (—1) •// + (—1)х = х + [у + (—!)• //] + (—1)*х = = х 4- 0 + (—1) • х = х + (—1) • х = 0.
Будем говорить, что два линейных пространства X и X' изоморфны, если между элементами этих пространств можно установить взаимно-однозначное соответствие, сохраняющее алгебраические операции, т. е. такое, что если х«->х' и у++у', то (х + у) <->х' +у' и Хх Хх'.
В линейном пространстве можно ввести понятия линейной зависимости и линейной независимости элементов. Элементы хп х2, ... ,х„ линейного пространства называются линейно независимыми, если из равенства
Н” ^2-^2 "Г • • • 4~ '+Хп = 0
следует, что Xt = Х2 = ... = Х„ = 0.
Если, наоборот, существуют такие не все равные нулю Хх, Х2, ..., Кг, что
XjXj 4- Х2х2 4-... 4- Хпх„ = 0,
то элементы хп х2, ..., хп называются линейно зависимыми.
Пусть в этом последнем случае, например, Х„=#0. Тогда
хц~ (К/^п) xl (Kfon) Xi • • • (Ч-Л) Хп-1>
17
или, полагая —%(Дп = р;, получим
х„ = НЛ + МЛ + • • • + Ня-Л-1.
В этом случае говорят, что элемент хп есть линейная комбинация элементов хп х2, ..., хп_^.
2. Линейные многообразия. Непустое множество L элементов линейного пространства X называется линейным многообразием, если вместе с элементами хп х2, ..., х„ множество L содержит любую линейную комбинацию
ад+ед+- • • +апхп этих элементов.
Отметим, что всякое линейное многообразие содержит нулевой элемент 0. В самом деле, так как L не пусто, то оно содержит некоторый элемент х. Поскольку L—-линейное многообразие, оно содержит и элемент — х = (—1)-х, а следовательно, и х + (—1)-х = 0.
Рассмотрим элементы хп х2, .... х„ линейного пространства. п
Совокупность всевозможных сумм У, а(-хг, очевидно, образует некоторое линейное многообразие Lo в X. В самом деле, если элементы п
yf имеют вид tjj- = У diXi (/ = 1,2, ..., k), то любая линейная ком-i = 1
бинация этих элементов в силу равенства
+ ~ S &txi »
i = 1
имеет тот же вид. Построенное линейное многообразие Lo есть, очевидно, наименьшее линейное многообразие, содержащее элементы хх, х2, ..., х„ (наименьшее в том смысле, что всякое другое линейное многообразие L, содержащее элементы хп х2, ..., х„, содержит Lo).
Определение наименьшего линейного многообразия, содержащего заданные элементы, нетрудно распространить и на случай бесконечного, например счетного, множества элементов. В самом деле, пусть {хъ х2, ..., х„, ...} —счетное множество элементов из X. Наименьшим линейным многообразием Lo, содержащим эти элементы, служит п
множество всевозможных сумм вида 2 Xzxz, где не только ^. — произвольные числа, но и п принимает произвольные натуральные значения. Наименьшее линейное многообразие, содержащее заданные элементы, называют также линейным многообразием, порожденным данными элементами, или линейной оболочкой этих элементов.
Если линейное многообразие L пространства X определяется конечным числом элементов, то оно называется конечномерным. Если L определяется элементами х2, ..., хп и эти элементы линейно независимы, то п называется числом измерений линейного многообразия L. В этом случае совокупность элементов хх, х2, хп назы
18
вается базисом* L. Если же элементы хп х2, ..., хп линейно зависимы, то числом измерений линейного многообразия L называется максимальное число линейно независимых элементов из совокупности Х2, Х2, • • •, Xrt.
Иными словами, многообразие L является п-мерным, если в L существуют п линейно независимых элементов, а всякий набор из п+1 элементов этого линейного многообразия линейно зависим.
Одномерное линейное многообразие, т. е. множество элементов вида Хх, где X пробегает R (или С, если пространство комплексное) и х—фиксированный ненулевой элемент пространства X, называется прямой.
Если в пространстве X (линейном многообразии L) для любого числа п существует п линейно независимых элементов, то пространство X (линейное многообразие L) называется бесконечномерным. Например, легко видеть, что пространство Lp (0, 1) бесконечномерно.
3. Прямые суммы. Введем понятие разложения линейного пространства в прямую сумму двух или нескольких линейных многообразий. Пусть X—-линейное пространство и Lt, L2, ...,Ln — принадлежащие ему линейные многообразия. Если каждый элемент х£Х можно однозначно представить в виде
x = x1 + x2-f-... + х„, x^Li (i = l, 2, ..., n), (1)
то говорят, что пространство X есть прямая сумма линейных многообразий Li, L2, ..., Ln, а выражение (I) называют разложением элемента х по элементам из Lit L2, ..., Ln. В этом случае будем писать
Легко видеть, что если X = У ©L{, a Lz= У то l' = l k = 1
п mi
х=2 2 ©4°.
i = 1 k = 1
В самом деле, тогда каждый элемент х G X можно представить в виде п п
x=£xt = 2 (х^ + х^ + .-.+х^.), x^Li, x^L$
и это представление однозначно, так как если
— другое такое представление, то в силу однозначности разложения
* Определение базиса для некоторых бесконечномерных пространств будет Дано ниже.
19
элемента х£Х по элементам линейных многообразий £; справедливы равенства
X; = хх (Д- Ха * Д- • • • Д- Xm*. = xV* Д- xl'* Д- ... Д- Хт. —xl (i = 1,2, ..., п), а в силу однозначности разложения элементов xz £ Lt по элементам линейных многообразий £1° — равенства
x{k =x<k> (i = l, 2, n; 6=1, 2, mt).
Нетрудно доказать, что если X = L±@L2, то и L2 имеют в качестве общего лишь нулевой элемент пространства.
□ В самом деле, если бы L, и £2 содержали другой общий элемент и, то для элемента х £ X, имеющего представление х = y + z, yfzLlt z£L2, было бы также справедливо представление
х= (у — и) + (г Д-w), у — u^Llt z + u$L2,
отличное от первого, что по условию невозможно. Ц
Обратно: если любой элемент х£Х может быть представлен в виде
x = y + z, y$Li, z£L2 (2)
и £1п£2={0}, то Х = £хф£2.
□ Для доказательства этого утверждения достаточно установить однозначность разложения (2). Но если х — уА-г = у + г\ у, y^L^, z, z£L2, to
У—y=~z — z, y — y^Lt, ~z — z£L2.
В силу сделанного предположения отсюда следует, что у—у = г — г= = 0, т. е. у —у, z = z. g|
Если Х = £хф£2, где £х —прямая, то £2 называется гиперподпространством (или гиперплоскостью, проходящей через нуль) пространства X.
В линейном пространстве X можно ввести операции сложения множеств и умножения множеств на число. Именно: если-Д и В— множества пространства X, то через 4+В обозначают множество всех элементов вида х-\-у, где х£А и у € В. Точно так же, если М множество чисел, то
df
МА = {Хх|X€М, х£А}.
Множество ХД, где X —число, называется гомотетией множества А.
Нетрудно проверить, что если А и В —линейные многообразия, то А + В также линейное многообразие и что для любых чисел а и р и любого АсХ справедливо соотношение аДД-рД э (а Д-Р) А.
Следующие понятия также будут использоваться в дальнейшем.
Множество АсХ называется уравновешенным (или центрированным), если из х£Д и |Х|^ 1 следует Хх£ Д. Ясно, что всякое центрированное множество содержит нуль.
20
Множество А с X называется поглощающим, если для любого х £ X найдется такое число а > 0, что х € при 101 а. Наконец, множество Аа:Х называется выпуклым, если вместе с точками хи у оно содержит весь отрезок [х, у], соединяющий эти точки, т. е. множество точек xt = ty + (l — t)x при
Нетрудно показать, что:
если А выпукло, xt, х2.......Хь$А и Х1, Х2, —неотри-
k k
цательные числа такие, что 2 \ = 1 > т0 S если А и В
1=1 i= 1
выпуклы, то А + В также выпукло.
4. Фактор-пространство. Рассмотрим линейное пространство X и некоторое линейное многообразие Lo cz X. Пространство X, как группа по сложению, распадается на классы смежности по отношению к подгруппе £0, а именно на множества L такие, что два элемента хх, х2 С X принадлежат одному и тому же множеству L тогда и только тогда, когда х1 — х2^Ь0.
Два класса смежности L± и Ь2 либо не пересекаются, либо совпадают. Если х — произвольный элемент из L, то всякий другой элемент х' класса L представим в виде х' =х-Ь*о, где *о€^о-Поэтому говорят, что L образован сдвигом на x£L линейного многообразия Lo. Элемент х называется представителем класса L, и класс L однозначно определяется выбором любого его представителя. Совокупность классов смежности L называется фактор-группой группы X по подгруппе Lo и обозначается XILQ.
Фактор-группу X/Lq можно наделить структурой линейного пространства. Именно: если классы и L2 имеют представителей хг и х2, то за сумму + Ц этих классов принимают класс, представителем которого является элемент х1 + х2. Таким способом сумма классов определяется однозначно, независимо от выбора представителей в классах слагаемых. Аналогично, произведение XL числа X на класс L определяется как класс, представителем которого является Хх, где х — представитель класса L.
Пространство X/Lo называется фактор-пространством пространства X по линейному многообразию Lo.
Пример. Рассмотрим в С [0, 1] линейное многообразие Со всех непрерывных функций, обращающихся в нуль при t = 1/2. Соответствующее фактор-пространство изоморфно вещественной прямой.
В самом деле, пусть х (/) и у (/) принадлежат одному классу смежности относительно Со. Это значит, что х (1/2) — у (1/2) = 0, т. е. х (1/2) = (/(1/2). Таким образом, в класс смежности объединяются функции, имеющие в точке t —1/2 одинаковое значение. Взяв в каждом классе смежности по представителю х (/) == = const, мы получим взаимно-однозначное соответствие между множеством констант и множеством классов смежности. Легко видеть, что это соответствие — изоморфизм.
Можно доказать, что если пространство Х = £1фЬ2, то X/Lf изоморфно 12.
5. Связь вещественных и комплексных пространств. Для комплексных чисел кроме алгебраических операций основной является также операция сопряжения: a-}-ib — a — ib. Естественно рассматривать
21
комплексное пространство, на котором определена аналогичная операция — инволюция.
Инволюцией называется операция, определенная для всех элементов х, у, г, ... линейного комплексного пространства X, относящая им элементы х, у, г, ... из X, причем*:
Г. х + у = х + у.
2°. Лх = Хх (X —комплексный множитель).
3°. (х) = х=х. _
Элементы xgX, для которых х = х, называются вещественными. Элементы х£Х, для которых х — —х, называются чисто мнимыми. Очевидно, что если х —вещественный, то ix — чисто мнимый элемент, и если (/—чисто мнимый, то у (/ — вещественный элемент. Таким образом, совокупность чисто мнимых элементов у совпадает с совокупностью элементов вида ix, где х — вещественный элемент.
Всякий элемент х£Х можно представить однозначно в виде x = u + iv, где и и V—вещественные элементы.
□ В самом деле, положим ы = у(х + х), и--^т-(х-х). Тогда x — u-j-iv, причем
«= у (х + х) = у(х + х) = у (х + х) = ы,
V = (х — х) = —(х—X) = -1- (X — х) = Ь,
т. е. и и у —вещественные элементы. Представление элемента х$Х в виде u + iv однозначно. Пусть x — u + iv = t-\- is. Тогда u — t = = i(s — v), где и, v, t, s — вещественные элементы. Далее,
u — t = u — t = u — t; i(s—v) = — i (s—v) = — i (s—v).
Поэтому и — t = — i (s—v) = — (u — t), t. e. u — t, а значит, ns = a. Однозначность представления доказана. В
Таким образом, мы показали, что для любого комплексного пространства X имеем X =Xl + iX2, где Хг и Х2 состоят из вещественных элементов и, следовательно, могут рассматриваться как вещественные пространства. Поэтому изучение многих вопросов, относящихся к комплексным пространствам, можно свести к изучению соответствующих вопросов в вещественных пространствах.
Обратно: каждому вещественному линейному пространству X можно однозначно сопоставить комплексное линейное пространство Z. В самом деле, рассмотрим формальные линейные комбинации х+ ((/, где х, у^Х и (—мнимая единица. Определим сумму
* Если в X определено понятие сходимости последовательности элементов, то вводится дополнительное требование:
4°. Из хп —► х0 следует хп —► ха.
22
таких линейных комбинаций с помощью равенства (*1 + iyi) + (х2 + i у2) = + х2) + i (yt + yt),
а произведение линейной комбинации x-\-iy на комплексное число Х = а-|-ф —с помощью равенства
X (х + iy) = (а + Ф) (х + iy) = (ах—fiy) + i (fix+ay).
Легко проверить, что множество Z всех таких линейных комбинаций удовлетворяет всем аксиомам комплексного линейного пространства и называется комплексификацией вещественного линейного пространства X.
Если теперь в пространстве Z определить инволюцию равенством x-^-iy = x—iy, то ясно, что х + »0 является вещественным элементом пространства Z, а О + iy— чисто мнимым. Взаимно-однозначное соответствие x<->x + i O показывает, что пространство X и множество вещественных элементов пространства Z изоморфны, а, значит, X можно рассматривать как множество вещественных элементов пространства Z. Но тогда в силу предыдущего Z — X-^-iX.
Комплексному пространству X можно соотнести вещественное пространство Xr и по-иному. Именно: положим, что Xr как множество совпадает с X, сумма в Xr определяется так же, как в X, но допускается умножение лишь на вещественные числа. Тогда элемент ix вместе с элементом х также входит в Xr, так как оба эти элемента принадлежат X, но в Xr эти элементы линейно независимы, в то время как в X они лежат на одной прямой. Пространство XR называют обычно вещественным пространством, ассоциированным с комплексным пространством X. Подробнее об этом см. § 1 гл. IV.
§ 4. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
В математическом анализе мы встречаемся с несколькими понятиями предела, причем в некоторых случаях для последовательности одних и тех же математических объектов в связи с разными задачами вводятся разные понятия предела. Прежде всего мы встречаемся с понятием предела последовательности вещественных чисел. Это понятие непосредственно обобщается на последовательности комплексных чисел и n-мерных векторов. Затем для последовательностей функций существует ряд понятий сходимости: простой (неравномерной), равномерной, в среднем и т. д.
Все эти понятия сходимости имеют большей частью то общее, что сходимость последовательности элементов х„ (являющихся числами, векторами или функциями) к элементу х означает неограниченное «сближение» х„ и х, неограниченное уменьшение «расстояния» между этими элементами при неограниченном увеличении номера п. В зависимости от того, как мы понимаем расстояние между элементами х„ и х, мы получаем различные определения предела. Но тогда представляется целесообразным для некоторых множеств
23
элементов дать общее определение расстояния между элементами, которое охватывало бы рассмотренные частные случаи, а затем с помощью этого расстояния ввести в таком множестве понятие предельного перехода и превратить множество в пространство.
1. Метрическое пространство. Множество X называется метрическим пространством, если каждой паре его элементов хи у поставлено в соответствие неотрицательно вещественное число рх(х, у), удовлетворяющее следующим условиям:
I. рх(х, #) = 0 тогда и только тогда, когда х = у (аксиома тождества).
II. рх(х, у) = Рх(/Л *) (аксиома симметрии).
III . рх(х, #) + pxQ/, ?)>ру(х, г) (аксиома треу гол ьни ка).
Это число рх(х, У) называется расстоянием между элементами х и у (или метрикой пространства X), а перечисленные три условия — аксиомами метрики. Очевидно, что аксиомы метрики представляют собой формулировку наиболее общих свойств расстояния между точками обычного трехмерного евклидова пространства.
В дальнейшем, если ясно, о каком метрическом пространстве X идет речь, вместо рх(х, У) будем писать просто р(х, у).
Из аксиом метрики легко получается так называемое обратное неравенство треугольника:
|p(x, г)—р(у, г)|<р(х, у).
□ В самом деле, р(х, г)^р(х, у) + р(у, ?), откуда р(х, г) — — р(у, г)^р(х, у). Меняя ролями х и у, получим
-[р(х, г) — р(у, г)]<р(г/, х) = р(х, у).
Но это означает, что
|р(х, г) — р(у, z) I <р(х, у).
Элементы метрического пространства будем называть также точками.
Наконец, отметим, что всякое множество У, лежащее в метрическом пространстве X и имеющее те же расстояния между элементами, что и X, само является метрическим пространством и называется подпространством пространства X.
2. Предел последовательности. Элемент х метрического пространства X называется пределом последовательности элементов хп х2, ..., х„, ... из X. если р(хп, х) —>0 при п-+со. В этом случае будем писать хп—>х или limx„ = x и говорить, что последовательность {xj сходится к х.
Относительно сходящихся последовательностей точек метрического пространства можно высказать несколько сбщих теорем.
Теорема 1. Если последовательность точек {хп} метрического пространства X сходится к точке х £ X. то любая подпоследовательность {x„ft} последовательности {хп} сходится к этой же точке. Доказательство очевидно.
24
Теорема 2. Последовательность точек {хп} метрического пространства может сходиться не более чем к одному пределу.
□ Пусть хп—+х и хп—>у. Тогда, каково бы ни было е > О, Р(х, у)<р(хя, х)+р(х„, у) <8
для достаточно больших п. Так как х и у — фиксированные точки, а 8 —произвольное положительное число, то это неравенство возможно лишь если р(х, у) = 0, т, е. х = у. g|
Теорема 3. Если последовательность {хл} точек из X сходится к точке х£Х, то числа р(х„, 0) ограничены для любой фиксированной точки 0 пространства X.
□ В самом деле, согласно аксиоме треугольника для любого п имеем
p(xn, 0)<pfo х) + р(х, 6)<L0 + p(^ 9)=^,
поскольку {р(хЛ, х)} как сходящаяся числовая последовательность ограничена и, следовательно, числа р (хп, х) не превосходят некоторой постоянной Lo. Ц
Назовем шаром (соответственно замкнутым шаром) с центром в точке а и радиусом г совокупность точек х пространства X, удовлетворяющих неравенству р (х, а) < г (соответственно неравенству р(х, а)^г). Ъудрм обозначать такой шар К (а, г) (соответственно К (а, г)). Назовем, далее, окрестностью точки х любой шар с центром в этой точке.
Легко видеть, что точка х является пределом последовательности {xj тогда и только логда, когда любая окрестность точки х содержит все точки рассматриваемой последовательности начиная с некоторого номера. Множество, лежащее целиком внутри некоторого шара, называется ограниченным.
Иногда бывает, что в некотором пространстве непосредственно задано понятие предела последовательности элементов. Если в этом пространстве можно ввести метрику так, что определяемое ею понятие предела последовательности будет совпадать с уже имеющимся понятием предела, то говорят, что данное пространство можно метризовать.
3. Замыкания. В метрическом пространстве могут быть введены многие важнейшие понятия, с которыми мы встречались в теории точечных множеств, расположенных на прямой. Так, для множества М с X точка а£Х называется предельной /почкой этого множества, если любая окрестность точки а содержит хотя бы одну точку множества 7И\о, т. е. если К (а, г) П (М\а) =4= 0 при любом г. Множество, полученное присоединением к А4 всех его предельных точек, называется замыканием множества М и обозначается М. Точки М называются точками прикосновения множества М.
Точка х£М называется внутренней точкой этого множества, если она входит в множество М вместе с некоторой окрестностью.
Нетрудно установить, что замыкания точечных множеств метрического пространства обладают теми же основными свойствами, что и замыкания числовых точечных множеств, а именно:
25
1) .иилг=милг;
2) Me М^_
3) (ЛТ) = Л4 = М;
4) замыкание пустого множества пусто.
Множество М называется замкнутым, если М. = М. Множество М называется открытым, если его дополнение Х\Л4 замкнуто. Можно показать, что множество М. открыто тогда и только тогда, когда все его точки внутренние. Множество М называется плотным в множестве N, если М о N. В частности, множество М называется всюду плотным в пространстве X или просто всюду плотным, если М = X. Наконец, множество М называется нигде не плотным в пространстве X, если каждый шар этого пространства содержит в себе некоторый шар, свободный от точек множества М. Подробное изложение свойств замкнутых и открытых множеств в метрических пространствах см. в [1].
4. Непрерывные функции. Гомеоморфизм. Пусть даны два метрических пространства X и У и функция y — f(x), определенная на некотором множестве М пространства и принимающая значения в пространстве У. Функция / называется непрерывной в точке х0£М, если для любого е>0 найдется 6>0 такое, что р(/(х), /(х0))<8для всякой точки х^М, удовлетворяющей неравенству р (х, х0) < 6.
Из определения непрерывности функции f (х) следует, что если х„ х0 (х„, х0 € М), то / (х„) f (х0). •
Верно и обратное утверждение: если f (х„) —> f (х0) для любой последовательности {х„}сЛ4, сходящейся к х0£М, то функция f (х) непрерывна в точке х0. Доказательство этих утверждений точно такое же, как и для вещественных функций вещественной переменной.
Можно рассматривать функции от двух (и более) точек метрического пространства со значениями в том же или в другом метрическом пространстве и вводить понятие непрерывности таких функций как по отдельным аргументам, так и по совокупности аргументов. Например, расстояние р(х, у) есть вещественная функция двух точек метрического пространства, непрерывная по совокупности аргументов. В самом деле, если х„ —> х0, уп —► yQ, то из обратного неравенства треугольника следует, что
IР (х„, у„)-р (х0, у0) К | р (х„, у„) -р (х0, у„) | +
+1Р (*о, Уп) — Р (*о, Л)|<Р (аг„, х0) + р («/„, i/0) —>0
при п —* ОО.
Пусть X, У— метрические пространства. Отображение /: X —> Y называется гомеоморфизмом, если f отображает X на Y взаимнооднозначно и если оба отображения f и /-1:У —>Х непрерывны. Пространства X и Y называются гомеоморфными, если существует гомеоморфизм /:Х —► У.
26
§ 5. ПРИМЕРЫ МЕТРИЧЕСКИХ ПРОСТРАНСТВ
1. Числовая прямая. Пусть X = R, где R-^множество всех вещественных чисел (числовая прямая). Если x, r/gR, то полагаем
Р(Х, г/) = |х-г/|.
Справедливость аксиом метрики очевидна. Сходимость в этом пространстве есть обычная сходимость числовых последовательностей.
2. Евклидово пространство. Пусть Хп — арифметическое п-мерное пространство, т. е. множество всех упорядоченных систем из вещественных чисел. Если х = (|1( £а, ..., £„) и у = (т^, т]2, ..., т]„), то полагаем
р (*•*/) = ]/ п<)а-
Справедливость аксиом метрики легко проверить. Пусть xk — = $Л........(* = 1,2,3, ...) и
/ Л
Р (**, х) = У 2 (&' — i,-)2 -* 0 при k оо.
Это равносильно условию Bp’ —> (I — 1, 2, ..., п) при k —> оо. Таким образом, сходимость в рассматриваемом пространстве есть сходимость по координатам. Л
Пространство Хп с такой метрикой называют п-мерным евклидовым пространством. Мы будем обозначать его
3. Пространство непрерывных функций с равномерной метрикой. Пусть X—множество всех непрерывных функций, заданных на отрезке* [0, 1]. Введем метрику, полагая
р (х, у) = шах | х (0 —у (t) |.
Проверим выполнение аксиом метрики. Очевидно, что р (х, у) О, причем р(х, z/) = 0 лишь если x(t) = y(t), а также что р (х, у) = = р(у, х). Остается проверить аксиому треугольника. Для любого € [0, 1] имеем
I х (/) — г (О К | х (0 — у (014- |у (0 — z (О К < шах | х (0 — у (0 | + шах | у (f) — г (i) | = р (х, у) + р (х, г).
Поэтому
р (X, г) = шах|х(О — у (t) |<р (х, у) + р (у, г).
Множество всех непрерывных функций, заданных на отрезке [О, 1], в котором метрика введена указанным образом,- называется пространством непрерывных функций и обозначается С [0, 1]. Мы
* Если отрезком изменения переменной t служит [а, &], то его можно преоб-
разовать в отрезок [0, 1], вводя новую независимую переменную т=(/—а)ЦЬ—а).
27
будем называть его также пространством непрерывных функций с чебышевской метрикой, так как расстояние между функциями совпадает с чебышевским уклонением.
Рассмотрим сходимость в пространстве С [0, 1]. Пусть дана последовательность {х„(0} элементов из С [0, 1], сходящаяся к х (t) (р (хп, х) —► 0 при п —» оо). Это значит, что
шах|хп (t)—x(t) | —> 0 при п —► оо, t
т. е. для любого числа е>0 найдется номер /г0 = п0(е) такой, что шах | xn(t) — х (/) | < е для п п0(е) и, следовательно, | xn(t) — х(/)| < е
для ni>n0(e) и для всех /£[0, 1]. Но это означает, что последовательность {х„(0} равномерно сходится к функции x(t).
Легко видеть, что и, обратно, если последовательность {х„(/)} равномерно сходится к x(f), то р (х„, х) —>0.
Таким образом, сходимость в пространстве С [О, 1] есть равномерная сходимость на отрезке [О, 1].
4. Пространство сграниченных числовых последовательностей. Пусть X — множество ограниченных числовых последовательностей х = {|1, £2, • • •> Это значит, что для каждого х существует
такая постоянная Кх, что для всех i.
Пусть х = {?Д и у={т](} принадлежат X. Введем расстояние с помощью равенства
. * р(х, z/) = sup|gz-Tiz|.
i
I
Очевидно, проверки требует лишь аксиома треугольника. Для гг-Чп.-Ь ? = &(} имеем
+ £,-|<
<sup|g,.-T1zH-sup|iii-^| = p(x, у) + р(у, г). I i
Следовательно, и
sup |— J;| = p (х, г) <р (х, г/)+р(г/, г). i
Полученное пространство называется пространством ограниченных числовых последовательностей и обозначается через т.
Пусть хп и х —элементы из т, хп = {^}, x = {gz} и р (хп, х) —>0 при п—> оо; это значит, что для любого 8>0 найдется такой номер По = по{8), ЧТО Р (xrt, х) = sup | —£z-1 < 8 при П^П0(8).
Следовательно, |^п)—gz|<e при п^п0(8) и любом i.
Легко видеть, что и, обратно, если | —-|z | < 8 при п^п0(8) и всех i, то р(х„, х) —>0 при п—>оо. Следовательно, сходимость в пространстве т есть сходимость по координатам, равномерная относительно номеров координат,
5. Пространство сходящихся числовых последовательностей. Пусть X—-множество сходящихся чйсловых последовательностей
28
x= {Si- •••-?«- • • • b т- e- существует lira Sz = g. Пусть
* = {Si-S2. •••>£„»•• •}» «/ = {П1,П2. •••}•
Полагаем
P(x, y) = sup|Ez—тп |.
Полученное пространство называется пространстзом с.
Очевидно, что пространство с сходящихся числовых последовательностей является подпространством пространства т ограниченных числовых последовательностей.
Отсюда следует выполнение аксиом метрики в с и то, что сходимость в с есть сходимость по координатам, равномерная относительно номеров координат.
6. Пространство ограниченных вещественных функций. Рассмотрим множество всех ограниченных функций х (/) вещественной переменной t, заданных на отрезке [0, 1]. Введем метрику, полагая р(х, t/) = sup|x(0— y(t)\.
t
Нетрудно проверить, что все аксиомы метрики выполняются. Множество всех вещественных ограниченных функций с такой метрикой называется пространством М [0, 1]. Легко видеть что сходимость в пространстве Л4[0, 1] есть равномерная сходимость на отрезке [О, 1]. Ясно также, что С[0, 1] а М [0, 1].
7. Пространство всех числовых последовательностей. Пусть X — множество всех последовательностей вещественных чисел. Введем в этом множестве понятие предельного перехода, полагая, что xn = {|Jn)} стремится к х=-{|(}, если В?’ —для всех i = 1,2, 3... (вообще говоря, неравномерно относительно i). Мы получаем, таким образом, некоторое неметрическое пространство, которое назовем пространством s.
Покажем, что пространство s можно метризовать.
□ Пусть х = {£(} и у = {т](} cs. Положим
p(x>g) = y ±. JjL-n/!,'
' 2< 1+1 li~П/1
i — 1
Аксиомы тождества и симметрии очевидны. Аксиома треугольника следует из неравенства
1 + |а+6| 1+|а| + 1+1И (
которое доказывается следующим образом. Рассмотрим функцию / (*) ' Имеем f (х) = так что f (*) — возрастающая
Функция. Значит,
Р+Н Iа|+|&| р| , |&|
1 + P+&I ^=1 + |а| + |г>|^ 1+|ар 1 + PI •
29
Возвращаясь к аксиоме треугольника, находим
р (х, г) = V 4- i j-Tt ^‘7 I lv ’ 4* 2‘ 1 + 1 Si—Sil
I = 1 1=1 1 = 1
Покажем, что сходимость в смысле введенной в метрики есть сходимость по координатам (вообще говоря, неравномерная относительно номеров координат).
□ Пусть хп = {?'"’}> * = {£J и хп~+х. Это означает, что
у * 1 * Ik”-Sil Гс
^2' 1+|йп’-5(.| 4
при п^л0(е). Но тогда для каждого фиксированного i тем более
_1_ Is^-Sil . е
2‘ 1 + 1 SP’-Sil
при п^п0(г), и так как е произвольно, a i фиксировано, то | | —> 0 при п оо.
Пусть, обратно, |^л> — gz | —>-0 при п —<- оо для каждого i. Возьмем произвольное число е > 0. Выберем сначала т так, чтобы
2 (1/2') <8/2. Тогда »
t=m+ 1
о(х х) = У-
Р( n> 1 £| 2f 1 + |g(«>_g.|
оо । m
у ±_Lk_zkL i=Tti * i+Ur-^-1
v 1 IS^-Sil
2-' l + IS^-Sil
1 IS^-Sil , 8
2i i + |g<«>_g(.| ф 2 *
Так как число слагаемых в оставшейся сумме конечно и фикси ровано, то можно выбрать такое na(s), что
У _L Ik’-S/I ^8 2'- l + l^-gj '2
при п^п0(е). Но тогда для п^и0(е) имеем р(хл, х) < в. g|
Из доказанного следует, что сходимость в смысле введенной метрики совпадает со сходимостью, ранее определенной в пространстве s, и, следовательно, введение этой метрики приводит к метризации пространства s.
8. Пространство сходимости по мере. Пусть X — множество всех измеримых функций х(/), определенных на отрезке [О, 1]. Две функции, совпадающие почти всюду, мы считаем тождественными.
30
Введем метрику с помощью равенства
р(х l*(O-HOI dt
р(,у) J 1 + |х (t)-y (0| at’
о
-рак же как и в предыдущем примере, убеждаемся, что аксиомы метрики выполняются.
Полученное пространство называется пространством S[0, 1]. Можно показать, что сходимость в S[0, 1] есть сходимость по мере.
9. Пространство функций с интегрируемой р-н степенью. Пусть / — множество всех функций x(t), принадлежащих £^[0, 1]. Две функции, отличающиеся ^лишь на множестве меры нуль, мы снова считаем тождественными. Если x(t)£Lp[Q, 1] и y\t)^Lp[Q, 1], то полагаем
/ 1 \ i/р
Р(*. «/)=($ lx(0—•
\о /
Выполнение аксиом тождества и симметрии легко проверяется; аксиома треугольника следует из неравенства Минковского для интегралов. Полученное пространство называется пространством Lp[0, 1], Пространство L2[0, 1] называется функциональным гильбертовым пространством.
Пусть x„(0€Lp[0, 1], п=1,2, .... и {%„(/)} сходится к x(f)£ е^[0, 1], т.е. 1
j I хп (0—х (01₽ а/ о о
при п—>00. Тогда говорят, что последовательность функций {%„(/)} сходится в среднем с показателем (индексом) р к функции x(t). При р = 2 говорят просто о сходимости в среднем.
10. Пространство числовых последовательностей lp(p^ 1). Пусть дано множество числовых последовательностей х={£(} таких, что
ОО
2 |1/1/’< со. Обозначим это множество через 1Р. Как и для функций с интегрируемой р-й степенью, можно показать, что если * = y= {^i}elp и 2 = {В/ + П/},то z£lp, и 4ToU = {Xy£/p. Снова имеют место неравенства Гельдера и Минковского с заменой интегралов на суммы, а именно:
со /оо \1/Р / 00 \1/<7
21S/п.-1( 2 II/) -(2h/l9) , i/p+1/^ = 1
i = I V = 1 / V = 1 /
и
/ 00 \1/р / 00 \1/р / 00 \ 1/р
( 2ll-+n;N С 2|1,-Н +(21п/1' •
V = 1 J \i = 1 / \t = l J
Пусть X —множество последовательностей вещественных чисел 12> •••> I», •••}> принадлежащих 1р. Если x={lt}^lp
31
и у= {v^} £lpl то определим расстояние по формуле
/ оо \1/Р
Р(Х, г/)= 2 I £/-Л/ lF )
Выполнение аксиом симметрии и тождества проверяется без труда Аксиома треугольника следует из неравенства Минковского дл$ сумм.
Полученное пространство называется пространством 1р. Прост ранство /2 называется координатным гильбертовым пространством Можно показать, что сходимость последовательности хп -к элементу в пространстве 1р означает, что:
1°. при п—> оо для всех i.
2°. Для любого е>0 найдется такое число /и0(е), чтс 00
У, 1|{-'!) < е.р для т т0 и всех п.
i =т+1
11. Пространство 1(рп). Пусть X— арифметическое n-мерное про-странство, т. е. множество всевозможных упорядоченных систем из п вещественных чисел, и пусть х--~ (?п £2> • • • и У — = {П1, П2, • • •, Пп}- Полагаем
. / п X 1/р
р(*. «/) = ( S •
м = 1 /
Полученное пространство называется пространством 1(рт. В частности, /а"’ есть n-мерное евклидово пространство R".
Можно считать *, что 1(рп> с 1р, если каждый элемент {£1( |2, ... отождествить с элементом ..., 0, 0, ...}€ 1р
Отсюда сразу следует выполнение аксиом метрики для Сходимость в пространстве 1рп> есть сходимость по координатам.
12. Комплексные пространства. Наряду с пространствам® С [О, 1], /-ДО, 1], с, 1р можно рассматривать содержащие их пространства, называемые соответственно комплексными пространствами С[0, 1], АДО, 1], с, 1р. Элементами комплексного пространства С [О, 1] являются комплекснозначные непрерывные функции вещественного переменного, пространства Lp[0, 1] — комплекснозначньк функции, p-я степень модуля которых суммируема. Элементами комплексного пространства с (соответственно 1р) являются последовательности комплексных чисел, которые сходятся (соответственнс ряд из р-х степеней модулей сходится).
Все определения, данные выше для вещественных пространств,
переносятся на соответствующие комплексные пространства.
В заключение отметим, что в одном и том же множестве X расстояния между элементами можно вводить по-разному, и мы получаем при этом, вообще говоря, разные метрические пространства. Поэтому часто метрическим пространством называют пару (X, р), состоящую из множества X и метрики р. Так, в пространстве X
* См. ниже об изометричных пространствах.
32
вСех измеримых и почти всюду ограниченных на [0, 1] функций помимо уже рассмотренной метрики
р(х м-f 1*(0-Н01 df р(,у) J 1 + 1И0-И01
о
мы можем ввести другое расстояние
Р*(х,у) = inf 1 sup I х (0-1/(011 , цЕ=0 ЦО, 1 ]\В f
где нижняя граница берется по всем множествам меры нуль. Получающиеся при этом пространства различны. Так, например, в пространстве (X, р*) сходимость есть равномерная сходимость почти всюду, в то время как в (X, р) сходимость есть сходимость по мере.
Если две метрики р и р*, введенные в одном и том же множестве X, таковы, что для любых х, у £ X
«Р (*> У) < Р* (х, у) < рр (х, у),
где а и р — положительные постоянные, то такие метрики называются эквивалентными. Ясно, что в этом случае пространства (X, р) и (X, р*) гомеоморфны.
§ 6. ПОЛНЫЕ ПРОСТРАНСТВА. ПОЛНОТА НЕКОТОРЫХ КОНКРЕТНЫХ ПРОСТРАНСТВ. ПОПОЛНЕНИЕ МЕТРИЧЕСКИХ ПРОСТРАНСТВ
1. Основные понятия. Последовательность {х„} элементов метрического пространства X называется сходящейся в себе (или фундаментальной), если для любого числа е > 0 найдется номер п0 (е) такой, что р (х„, хга) < е при п, т п0 (е).
Если последовательность {х„} сходится к пределу х0, то она сходится в себе.
□ В самом деле, пусть x0 = litnx„. Тогда для любого е>0 найдется номер п0(е) такой, что р(х„, х0) < 8/2 при п^п0(е). Следовательно,
Р (хп, хт) С р (х„, х0) + р (хт, х0) < е
ДЛЯ П, /П^П0(8). И
Обратное утверждение для произвольного метрического пространства неверно, так как существуют метрические пространства, В которых имеются последовательности, сходящиеся в себе, но не сходящиеся ни к какому пределу.
Примеры. 1. Пусть X—множество рациональных чисел, причем расстояние определяется по формуле р (ц, г2) = I ri—'al- Тогда X есть метрическое про-странство.
Возьмем последовательность гг = 1/2, г2 — 1/4,..., rn = 1/2", ... Эта последовательность сходится и в себе и к пределу го = О»
2 Nj 3054 33
Возьмем теперь последовательность rn~ 1• Эта последовательность сходится в себе, но не имеет предела в пространстве X, так как 11m (1-|—] =е не является рациональным числом.
2. Пусть X— пространство многочленов Р (/), с чебышевской
метрикой, т. е. если Р (/), Q(/)£X, то р (Р, Q) = max | Р (t) — Q (t) |. Пусть {Рп (/)} — последовательность многочленов, равномерно сходящаяся к непрерывной функции, не являющейся многочленом. Очевидно, что последовательность {Рп(0}—фундаментальная, но не имеет предела в пространстве X.
Если в метрическом пространстве X каждая сходящаяся в себе последовательность сходится к некоторому пределу, являющемуся элементом того же пространства, то пространство X называется полным.
Отметим, что замкнутое множество полного пространства есть само полное пространство.
2. Полнота некоторых конкретных метрических пространств.
Пространство R" — полное. Для случая евклидова «-мерного пространства R" полнота следует из критерия Коши существования предела последовательности точек этого пространства.
Пространстзо С [0, 1] — полное. Пусть дана последовательность {х„(0}, где х„(0€С[0,1], п=1,2, .... и пусть чр(х„, xJ-^-0 при п, Это означает, что для последовательности {х„(0}
выполняется условие Коши равномерной сходимости на [0, 1] и, следовательно, существует непрерывная на [0, 1] функция xg(f), к которой на [0, 1] равномерно сходится последовательность {х„(0}. Таким образом, х0 (Z) gС[0, 1] и р(хя, х0) = тах| х„(/)—
— хо(О|~*0, т- е- С[0. 1] —полное пространство.
Пространство т—полное. Пусть {хя} —последовательность элементов из т, сходящаяся в себе, и пусть хя — {I?’}. Так как хп£т, то | £(ги) | Кп для i = l,2, ... Так как, далее, {хя} сходится в себе, то для любого числа 8 > 0 найдется номер п0 (е) такой, что р (хя, xft) < 8 при п, k~^ пд (е), или, что то же,
sup —1У’| < 8 при n, k^n0(&).
i
Отсюда следует, что
ISr-^’Ke (1)
при п, п0(е) равномерно по i.
Фиксируем г. Тогда из неравенства (1) вытекает, что последовательность чисел ^2), ..., ...} удовлетворяет условию
Коши существования предела и, следовательно, сходится к некоторому числу L. Таким образом, получаем последовательность чисел
...Л,., ...}.
Если k-->-oo, то в пределе неравенство (1) дает
(2)
34
для п>«о(8) и Для всех *’• Отсюда
11,-1 =С | ~^| + 15/"о) 1 < 8 + Кп„
причем неравенство имеет место для всех I. Но это означает, что ограниченная последовательность, т. е. х = {Ц£т. Из (2) получаем sup |— |<е для п>п0(е), т. е. р(х„, х)<8 для п^По(е). Так как 8>0 произвольно, то отсюда следует, что х —+ х при п —»-оо. Полнота пространства т доказана.
” Пространство с — полное. Покажем, что пространство с, рассматриваемое как подмножество пространства т, замкнуто в т. Отсюда в силу замечания на с. 34 вытекает полнота с.
Пусть {хп}, где хп — {^'г), ^л>, ..., ^л), ...есть последовательность элементов из с и хп —>• х0, где х0 = {^0), ^0),. .., £(г0), ...}. Покажем, что —сходящаяся последовательность. В самом деле,
I %0)-5ГI < I zT |+1 IT-ir I+15/л) -5ГI <
<2р(х„, ХО) + ЩЛ)-£Г1-
Пусть задано произвольное число в > 0. Выберем сперва п настолько большим, чтобы р (х„, х0) < б/4, и зафиксируем такое п. Поскольку —сходящаяся последовательность, найдется номер
i0 такой, что | |<л> —IT I < 8/2 ПРИ А / го- Но тогда 11Т — &Т I < 8 при i, j^io, т. е. —сходящаяся последовательность. Итак,
х0£с и требуемое доказано.
Пространства /ДО, 1] и 1р —полные. В курсах теории функций вещественной переменной (см. [11]) доказывается, что L, [0, 1] и /2 —полные пространства. Аналогичными методами может быть доказана полнота Lp [0, 1] и 1р. Мы не будем проводить здесь этого доказательства и получим утверждение о полноте АДО, I] и 1р как следствие одной общей теоремы функционального анализа (см. ниже с. 156).
3. Пополнение метрических пространств. Известно, какую большую роль в математическом анализе играет свойство полноты числовой прямой. Только построение полной совокупности вещественных чисел позволило строго, в известных пределах, обосновать математический анализ. Большую роль играет свойство полноты метрических пространств и в функциональном анализе. Поэтому мы рассмотрим сейчас процесс пополнения произвольного неполного метрического пространства, аналогичный процессу пополнения множества рациональных чисел множеством всех иррациональных чисел. Предварительно, однако, введем одно понятие, которое нам понадобится и в дальнейшем.
Пусть даны два метрических пространства X и Y, причем расстояние между элементами Xj и х2 пространства X равно Рх(хъ х2), а расстояние между элементами уг и у2 пространства Y равно py(yit у,).
Если между элементами пространства X и Y можно установить взаимно-однозначное соответствие и притом таким образом, чтобы Расстояние между элементами одного пространства равнялось рас
2* 35
стоянию между соответствующими элементами другого пространства, то пространства X и Y называются изометричными.
Легко понять, что с точки зрения тех вопросов, которые связаны лишь с расстоянием между элементами, например с точки зрения вопросов сходимости, полноты и т. д., два изометричных пространства можно считать идентичными.
Можно говорить не только об изометричности пространств X и У, но и об изометричности множеств, расположенных в этих пространствах; результат, полученный для некоторого множества метрического пространства, верен для всех изометричных ему множеств.
Пусть дано метрическое пространство X. Предположим, что оно неполное, т. е. что в этом пространстве имеется последовательность, сходящаяся в себе, но не имеющая предела в X.
Покажем, что в этом случае существует другое метрическое пространство X — полное и такое, что в нем существует подмножество Хо, лежащее всюду плотно в X и изометричное пространству X. Пространство X называется пополнением пространства X.
Рассмотрим всевозможные последовательности {х„}, {«/„}, {?„}, ..., составленные из элементов пространства X и сходящиеся в себе, в том числе и последовательности, сходящиеся к пределу. Отнесем к одному классу две последовательности {х„} и {хА}, сходящиеся в себе и такие, что р (хп, х'п) —> 0 при п оо. Легко проверить, что два любых таких класса не пересекаются и что каждый класс однозначно определяется любой принадлежащей ему последовательностью. Эти классы х примем за элементы нового пространства X.
Пусть х, у£Х и {х„}, {//„} —соответственно последовательности из классов х и у. Из обратного неравенства треугольника следует, что существует предел lim р (х„,- г/„). В самом деле, п
|р(^«. Уп)-р(хт, IР (•*«» Уп) — р(хт, Уп)\ +
+1Р (х,„, уп) - р (х,я, ут)\ < р (х„, хт) +Р (уп, Ут) О при п, т—>-со. Таким образом, числовая последовательность {р (х„, уп)} удовлетворяет условию Коши и, следовательно, существует предел limp(x„, уп).
Введем теперь в X расстояние по формуле
р(х, «/) = lim р (х,„ уп).
п
Покажем, что такое определение расстояния р (х, у) корректно, т. е. limp(x„, z/n) не зависит от выбора представителей {х„} и {уп} п
в классах х и у. Пусть {х’п} и {«/А} — другие представители этих классов. Тогда
Р (х’а, у’п)^ Р (ХА, Х„) +р (х„, уп) +р {уп, Уп)
36
Л так как р (хп, х'п) —> 0, р (уп, у’п) О, то предыдущге неравенство в пределе дает limp(x', lim р (х„, уп). Аналогично получаем lim р (х„, Уп) < Чш р (х'п, у'п), откуда вытекает равенство Пт р (хп, уп) = =lim р (Хп, Уп)-
Проверим выполнение аксиом метрики.
I. Так как р (хп, уп)^0, то и р(х, г/) = lim р (хп, уп)>®-п.
Далее, равенство р (х, у) = lim р (хп, уп) = 0 означает по уело-п
вию, что последовательности {хп} и {уп} принадлежат одному классу.
Так как {х„} —любая последовательность класса х, а {«/„} —любая последовательность класса у, то х = у.
II. Равенство р (х, у) = р(у, х) очевидно.
III. Если {хп}£х, \уп}€у, {zn}€z, то очевидно, что
р (х, z) = limp (хп, z„) < limp (х„, у„) + п п
+ lim р (уп, гп) = р (х, у) +р (у, г), п
Докажем, что X — полное пространство. Возьмем последовательность {Xi, х2,..., хп,...} элементов пространства X, сходящуюся в себе, т. е. такую, что р (хп, хт) —>0 при п, т—*-оо. В каждом классе хп возьмем некоторую последовательность {х!л), х2л>, .... х*"*,...}. Так как эта последовательность сходится в себе, то можно выбрать такое kn, что р(ХрЛ>, x(kn)< Мп для p>ktt.
Рассмотрим теперь последовательность {х*1,’, х*/, ..., х*"*,...} и покажем, что она сходится в себе. Имеем
Р <’) < Р(х£>, <’) + р (х<,л>, х^) + р(хГ, хй). (3)
Пусть задано произвольное е > 0. Так как р (х„, хи) —*0 при п, /и—>оо, то найдется номер п0 такой, что при п, т~^пй
Р (хп, ~хт) = limp (х<р">, х(рт)) < е/2.
р
Поэтому при п, т~^па и достаточно больших р получим
Р (х<»л>, 4та>) < е/2. (4)
При этом мы можем считать п0 таким, что 1/п0<е/4. Фиксировав п и т, удовлетворяющие условиям п^п0, т~^пй, будем считать р настолько большим, что р > kn и p>km. Тогда в силу выбора чисел и km
xl">) < 1/п < 8/4, p(xg">, х^>) < \/т < е/4. (5)
Из неравенств (3), (4) и (5) следует, что р(х^’, х^) < е при п, % п0, т. е. что последовательность {х*"*} сходится в себе.
37
Обозначим класс, содержащий последовательность {х*"’}, через х.' Покажем, что х„—>х. Имеем, очевидно,
р (х„, х) = Нт р х$) <
р
< Пт р (х<рп >, x£>) + lim р (х^, х*/’) < -^ + И1П • (6)
р р р
Так как последовательность {х£п} сходится в себе, то для заданного 8 > 0 найдется п0 такое, что р (х^’, х1^) < 8/2 при п, р п9. Значит,
lim р (х^’, х^’) sC е/2 р
(7)
при п п9. При этом без ограничения общности можно предполагать, что 1/п0 < 8/2. Из неравенств (6) и (7) следует, что р (х„, х) < 8 при п п0, т. е. что последовательность {хп} сходится к элементу х и полнота пространства X доказана.
Введем в рассмотрение стационарные последовательности, т. е. последовательности вида {х, х, ..., х, ...}, которые, очевидно, сходятся в себе и, следовательно, относятся каждая к некоторому классу — элементу из X. Очевидно, что одному и тому же классу принадлежит лишь одна стационарная последовательность. Если теперь {х, х, . ..,х, . ..}£х, {у, у, -.-,у, .-.}€у, то, очевидно, р(х, у) = р(х, у). '
Покажем теперь, что X изометрично некоторому подмножеству Х9 пространства X, всюду плотному в X. Отнесем к Х9 все классы х, среди последовательностей которых имеется стационарная последовательность {х, х, ..., х, ...}. Между классами х£Х9 и элементами х, из которых составляется стационарная последовательность, вхоля ”ая в х, существует взаимно-однозначное соответствие, причем если {х}£х и {у}£у, то р(х, у) = р(х, у). Поэтому установленное вз; и и - днозначнэе соответствие между Х9 и X есть изометрия.
I -р\днт вид ть, что Х9 всюду плотно в X, т. е. что для любого числ > 0 и любого элемента х^Х найдется элемент хЕ£Х0 такой, ч'| р х, хе) < е. В самом деле, пусть х—класс, содержащий сходя ,?юся в с бе последовательность {хп х2, ..., х„, ...}. Возьмем так; п, чт бы р (х„, хт) < 8 для т > п. Построим стационарную пссл деятельность {хп, х„, ..., х„, ...} и обозначим через х8 класс, содержащий эту последовательность. Очевидно, хЕ£Х0. Далее, р (х, хе) - limp(x„, хт)^е и требуемое доказано.
Покажем, наконец, что пополнение пространства X определяется однозначно с точностью до изометрии, т. е. что существует лишь одно, с точностью до изометрии, полное пространство X, которое
38
содержит всюду плотное подмножество, изометричное X. В самом деле, пусть У—другое полное пространство, в котором X л?жит всюду плотно. Тогда каждая точка y^Y есть предел некоторой последовательности {х,, х2, ..., х„, ...}сХ. Так как эта последовательность сходится в себе, то она определяет некоторый элем ит х$Х. Этот элемент х поставим в соответствие элементу у. Пусть, обратно, дан элемент х' £ X и {х[, х’г...х'п...} — некоторая фунда-
ментальная последовательность из класса х'. Так как эта фундаментальная последовательность лежит в полном пространстве Y, то она определяет некоторый элемент у' £ Y. Этот элемент поставим в соответствие элементу х'. Таким образом, мы получаем соответ, ствие между элементами пространств X и Y, причем это соответствие, очевидно, взаимно-однозначно.. Так как, кроме того,
рх (х, х') = li.n р (х„, Хл) = рр (у, у'), п
то соответствие изометрично.
Примеры. I. Возьмем пространство /р, состоящее из всевозможных упорядоченных систем {51, |2, •••> 0* 0, ...}, где —любые вещественные числа,
ky—любое натуральное число. Если
X=U1, .... lkl, о, ...}, У = {г11, Т)а.Г1кг, 0, ...}
и то полагаем
/ kt kg Al/P
р(х, !/)=( у, | ^•-nrl/,+ 2 hil^) •
! \i=l iz=kt+\ ]
Пространство Гр— подпространство 1р, и притом неполное, так так, например, последовательность хп = {1, 1/2, ..., 1/2«”х, 0, 0, ...}, п = 1, 2, 3, ..., сходится в себе:
/ п J \ 1/р
Р (хп, хт) =( У, " " ) —> о при т < п, т, п —> оо,
\1=т+12 PJ
но в пространстве Гр не имеет предела.
Обозначим пополнение пространства 1Р через X. Так как, с другой стороны, очевидно, что 1Р лежит всюду плотно в полном пространстве 1р, то X изометрично 1р. Таким образом, пополнение пространства 1Р приводит к пространству, изометричному 1р.
2. Пусть Со[0, 1] — пространство многочленов, определенных на отрезке [0> 1], с метрикой р (р, 9) = тах |р (/) — q (0|, р, <у^Со[О, 1]. Пространство Со[О, 1], очевидно, не полно. Так как Со [0, 1] лежит всюду плотно в полном пространстве С [0, 1], то пополнение пространства Со [0, 1] приводит к пространству, изометричному С [0, 1].
3. Пусть Lp[0, 1]—совокупность всех непрерывных функций, определенных отрезке [0, 1] с метрикой
< 1 \1/р р(*. |x(0—.
39
Пространство Lp [0, 1] —неполное, так как последовательность непрерывных функций, сходящихся в среднем со степенью р к разрывной функции, есть последовательность, фундаментальная в Lp [0, 11, но не имеющая предела в этом пространстве. Пополняя Lp [0, 1], мы получим пространство, изометричное М°> ij.
§ 7. ТЕОРЕМЫ О ПОЛНЫХ ПРОСТРАНСТВАХ. ПРИНЦИП СЖИМАЮЩИХ ОТОБРАЖЕНИЙ
1. Свойства полных пространств. Следующая теорема является аналогом леммы Кантора о стягивающейся системе отрезков.
Теорема 1. Пусть в полном метрическом пространстве X дана последовательность замкнутых шаров, вложенных друг в друга (т. е. таких, что каждый последующий шар содержится снутри предыдущего), радиусы которых стремятся к нулю. Тогда существует одна и только одна точка, принадлежащая всем этим шарам.
□ Пусть К (щ, с,), К (аг, е2), .... К (ап, е„), ..., где 8„ -* О,— рассматриваемые шары. По условию теоремы, КхпК.о ... ...
(Кп — К (ап, 8„)). Рассмотрим последовательность а,, «2, .
центров этих шаров. Для р>0 имеем ап+р£ Кп+рс.Кп, откуда р (ап+р, ап) < г„ 0 при п —<- оо. В силу полноты X последовательность {ап} сходится к некоторому пределу а£Х. Так как {ап+;,}р=1.2, при любом п, ап+р->-а при р—> оо и шар К„ замкнут, то а£К„ при всех п= 1, 2, 3, ... .
Допустим, что существует точка Ь, принадлежащая всем шарам и отличная от точки а, так что р (а, Ь) = 6> 0. Так как а, Ь$Кп, п = 1, 2, ..., то мы должны иметь
6 = р (a, i)<p (а, а„) + р (ап, Ь) < 2еп,
что, однако, невозможно, так как гп~>0 при п —* оо. Ц
Замечание. Можно несколько обобщить доказанную теорему. Назовем диаметром ограниченного множества F метрического пространства число d(F)= sup р (х, у). Тогда имеет место следующая х, уЕ F
: теорема.
Теорема Г. Пусть в полном метрическом пространстве X дана последовательность замкнутых множеств, вложенных друг в друга, диаметры которых стремятся к нулю. Тогда существует одна и только одна точка, принадлежащая всем этим множествам.
Доказательство, по существу, то же, что и для теоремы 1.
Как известно, свойство числовой прямой, устанавливаемое леммой Кантора, можно принять за определение полноты или непрерывности множества вещественных чисел или числовой прямой. Аналогично, теорема о вложенных шарах характеризует полноту метрического пространства.
Теорема 2. Если в метрическом пространстве X любая последовательность вложенных друг в друга замкнутых шаров, диаметры
40
которых стремятся к нулю, имеет непустое пересечение, то пространство X —полное.
□ Пусть дана фундаментальная последовательность {х„}. Выберем пк таким образом, чтобы р (x„k+p, хП/1) < 1/2* для любого р > 0. Пусть Кк — замкнутый шар радиуса 1/2*”1 с центром в точке х„к. Тогда Кк+1сКк. В самом деле, если x£Kk+i, то
Р(х, x„ft)^p(x, Ч+х) + Р(Ч+1’ + i =
т. е. х£Кк. _
Радиусы шаров Кк стремятся к нулю. Следовательно, по предположению, существует точка х0, принадлежащая всем шарам Кк. Покажем, что точка х0 является пределом последовательности {хп}. Подпоследовательность {x„ft} сходится к х0, так как хПк, х0^Кка и, значит, р(х„Л, хв) <11/2*-1 ► 0. Но тогда и вся последовательность {хп} сходится к х0, поскольку р(х„, х0)<р(х„, x„ft) + p(x„ft, х0) и оба слагаемых можно сделать сколь угодно малыми, если выбрать п и пк достаточно большими. Ц
Множество М называется множеством первой категории, если оно может быть представлено в виде суммы не более чем счетного числа нигде не плотных множеств. Множество, не являющееся множеством первой категории, называется множеством второй категории. Например, множество рациональных точек прямой, очевидно, есть множество первой категории; множество всех иррациональных точек—множество второй категории, что легко вытекает из следующей теоремы.
Теорема 3 (Бэра). Полное пространство есть множество второй категории.
□ Предположим противное и допустим, что полное простран-00 .
ство X = U Мп, где множества Мп нигде не плотны. Возьмем шар __ П=1
К (а, 1) с центром в произвольной точке а и радиусом, равным единице. Так как множество Afi нигде не плотно, то внутри шара К (а, 1) найдется шар К(аь t\) радиуса ^<1/2, не содержащий точек множества Далее, так как М2 нигде не плотно, то внутри шара Г1) найдется шар К (ц2, г2) радиуса r2 < 1/22, не содержащий точек множества Мг, и т. д.
Таким образом, получим последовательность замкнутых шаров K(alt rj, К (а2, г2), ..., К(а„, гп), ..., каждый из которых вложен в предыдущий и радиусы которых стремятся к нулю. При этом шар К (а„, гп) не содержит точек множеств Mlt М2, ..., М„. По теореме 1, существует точка аа£Х, принадлежащая всем шарам. С другой стороны, эта точка а0 не принадлежит ни одному из множеств Мп\ поэтому ай 4 X = и Л1„. Мы получили противоречие, которое и до-/2 = 1
казывает теорему. Щ
41
I
2. Принцип сжимающих отображений. Хорошо известен метод | последовательных приближений (или итераций), широко применяю- ( щийся для доказательства теорем существования решений алгеб- , раических, дифференциальных, интегральных и других уравнений. ' Большое значение этого метода заключается кроме его широкой применимости также в том, что он может служить для получения приближенных решений уравнений. Метод последовательных приближений для различных типов уравнений укладывается в рамках функ: ионального анализа в общую схему и приводит к принципу сжимающих отображений (сформулированному польским математиком С. Банахом).
Теорема 4. Пусть в полном метрическом пространстве X дан оператор А, переводящий элементы пространства X сновав элементы этого пространства. Пусть, кроме того, для всех х и у из X
р(Ах, Л«/)<ар(х, у), (1) |
где а < 1 и не зависит от х и у. Тогда существует одна и только i одна точка х0 такая, что Лх0 = х0.
Течка х, называется неподвижной точкой оператора Л.
□ Возьмем произвольный фиксированный элемент х С X и положим хг~Ах, х3 — Ахг, .... хп = Лхл_п .... Покажем, что последователь- ! ность \хп} сходится в себе. Для этпго заметим, что
р (хх, х2) — р {Ах, Ах,) <1сер (х, xj — ар (х, Ах),
р (х2, х3) = р (Лхп Лх2) «Р (*i, х2) а2р (х, Ах),
р{хп, x„+i) <а”р (х, Ах).
Далее, |
Р Cvp •*•«+/>) Р (Хп> х„+]) 4- р (хл+1, хп+2) 4"... р (xn+p_i, хп+^) sei
< (а« 4-an+14-... 4-ап+л-1) p (x, Ax) = ~n~^n+pp (x, Ax). (2) 1 ОС
Так как, по условию, a< 1, то
Р(х„, хп+р) <i^p(x4 Ах), ;
откуда, в свою очередь, следует, что р(хл, хп+р) —>0 при п—►оо, р > 0 3 ачит, последовательность {хп\ сходится в себе. В силу ‘ п. ноты пространства X существует элемент х0£Х, являющийся пр д л >м этой последовательности: х0 Н;пхл.
Докажем, что Лх0 = х0. В самом деле, I
р (х0, Лхв) < р (х0, хй) + р (х„, Лх0) =
= р(хя, х0)4-р(Лх„_г, Лх0)<р(хл, х0)4-ар(х„_ъ х0).
Но при любом заданном 8 > 0 и достаточно большом п имеем р (хэ, хл) < 8/2, ap (х0, xn_J < 8/2. Следовательно, р (х0, Лх0) < е. Так как 8>0 произвольно, то р (х0, Лхо) = О, т. е. Лх0 = х0.
42
Предположим, что существуют два элемента х0, у0£Х такие, что Ах0 = х0, Ау0 = у0. Тогда р(х0, </0)=р(Ах0, Ау0) гаР г0, Если допустить, что р(х0, уаУ > 0, то из предыдущего следует, что 1 а, что невозможно в силу условия, Ц
Если в формуле (2) перейти к пределу при р—>оо, то придем' к оценке ошибки n-го приближения:
Р(хп, x0Xj^p(x, Ах). (3)
Замечания. 1. Построение последовательных приближений хп, сходящихся к неподвижной точке х0, можно производить, исходя из любого элемента х£Х. Выбор элемента х сказывается лишь на быстроте сходимости {х„} к своему пределу.
2. Иногда приходится рассматривать такое отображение А, что неравенство (1) выполняется не во всем пространстве, ди ть в некоторой замкнутой окрестности К. (х, г) какой-либо ег> т ч.:и х. Тогда принцип сжимающих отображений можно применять при дополнительном условии, что оператор А преобразует -т тир в себя и потому последовательные приближения не гь.х ят из рассматриваемой окрестности. Пусть, например, в дополнение к неравенству (1) удовлетворяется неравенство р (х, Ах) (1 —а) г. Если х£/С(х, г), то и Ах^К(х, г), так как
р (Ах, х) С Р (Ах, Ах) + р (Ах, х) ар (х, х) 4-
4- (1 — а) г < аг 4- (1 — а) г — г.
Поэтому можно рассматривать А как оператор, действующий в полном метрическом пространстве К. (х, г) (см. с. 34) и удовлетворяющий в этом пространстве условию (1). Но тогда согласно д: казанному оператор А имеет в Л (х, г) единственную неподвижную точку.
3. Примеры применения принципа сжимающих отображений.
Решение систем линейных алгебраических уравнений методом итераций. Рассмотрим арифметическое «-мерное пространство. Если х £2, .... £„}, </ = {111, Лг, • • •, Ли}, то положим р(х, у) = max | — tjz |. Легко доказать, что так опре-
деленное метрическое простр нство тп — полное. Рассм трич в этом пространстве оператор у-- Ах, заданный с помощью равенств
п
Л< = 2 (< = 1,2, ..., п).
/ = 1
Имеем
Р (</i, </2) = Р (Ахп Ах2) = шах | т)?’ — П<8> I = max
п
/
п
Стах У I у = 1 п п
С шах | В/1’ —1/2) | • max У | аи | = р (хп х2) • max 2 I I-/ i /=1 i / = 1
43
Если теперь предположить, что
п
2|й171<1 (4)
для всех i, то будут выполнены условия применимости принципа сжимающих отображений и, следовательно, оператор имеет единственную неподвижную точку. Таким образом, мы получили теорему.
п
Теорема 5. Если матрица (atA такова, что У |а/7|< 1 для i = i п
всех i, то система уравнений У а, Д7—(/ — 1,2, ..., п) имеет
/ = 1
единственное решение х0 = {^<10), Ba0*, . .-.Bn’}- 5/ио решение можно получить методом итераций, исходя из произвольного вектора х=
Условие (4) есть достаточное условие сходимости метода итераций для рассматриваемой системы. Если в n-мерном пространстве ввести другую метрику, то получим другое условие сходимости. Пусть, например, р (х, y) = j/~£ (В,- — Лх)2- При такой метрике
/п ( п ч А 2
2! а,-, (В/1*— в;-2,)| <
f' п I п п 2 А Г' п п
<1/ 2 2а?/2М”) =Р(^^)1/ Х24 '
Г 1 = 1 = 1 / = 1 } г i = l / = 1
Поэтому условием сходимости метода последовательных приближе-п п
ний в этом случае является выполнение неравенства 2 2 4' < !• i=i/=1
Существование и единственность решения интегрального уравнения. Пусть К (t, s) —действительная функция, определенная и измеримая в квадрате a^t^b, a^s^.b и такая, что
ь ь
$ s) d/ds< оо, (5)
а а
и пусть /(^)g£2[a, Ь]. Покажем, что тогда интегральное уравнение ъ
х = f (/) +Х J К. (t, s) х (s) ds, a
имеет при каждом достаточно малом значении параметра X единственное решение х(Г)£Ьг[а, &].
Рассмотрим оператор
ь
Ах = f (t) + £ U, s)х (s) ds-
44
Покажем, что он переводит каждую функцию х (/) £ L2 [а, ft] в функцию, принадлежащую снова тому же пространству. Так как /(/)£ £Ls[a, ft], то достаточно доказать, что оператор
ь
Аох = К (t, s) x(s) ds a
переводит каждую функцию x(/)€Z2[a, ft] в функцию из того же пространства.
Из условия (5) и теоремы Фубини следует, что № (/, s) интегрируема по s на [а, ft] для почти всех t из [а, ft]. Отсюда для почти ь
всех t из [а, Ь] вытекает существование интеграла J К (t, s) х (s) ds = а
= y(t). Тогда, согласно неравенству Буняковского,
/ b \4b ь
у2 (0 — ( $ К s) * (s) ds j J Л2 (/, s) ds x2 (s) ds. \o J a a
b b
Так как величина $ x2 (s) ds — постоянная, a ^K2(t, s) ds интегри-a a
руема no t на [a, ft] в силу условия (5) и теоремы Фубини, то у2 (/) также интегрируема по t на [а, ft], причем
ь ь ь ь
$ у2 (0 d/< J $ К2 (/, s) ds- $ х2 (s) ds. а а а а
Оценим теперь р (Ах, Ау). Имеем
р (Ах, Ау) =| П А. К (t, s)x(s)ds — 'k^K(t, s) у (s) ds J d/ }• = \ a ' a a / J
( Ь / b \ 2 \ 1/2
= IM s) [x (s) ~ У (s)] ds ) dt }•
V a \a /J
/ b b \l/2 / b \l/2
| A |H J № (/, s) dZ ds J M [x (s) — у (s)]2 ds J =
\a a / \a J
/ b b >1/2
= |A|H $№(/, s)d^dsl p(x, y).
\a a /
Если
IM<-T7---------1-----TTi- (6)
M № (t, s) di ds j \a a /
то выполняются условия применимости принципа сжимающих отоб
45
ражений. Поэтому существование и единственность решения рассматриваемого интегрального уравнения при значениях %, удовлетворяющих неравенству (6), доказаны.
§ 8. СЕПАРАБЕЛЬНЫЕ ПРОСТРАНСТВА
Пространство X называется сепарабельным, если в этом пространстве существует счетное всюду плотное множество, иными словами, если в пространстве X существует последовательность
xlt xt, хп, ... (1)
такая, что для любого х£Х найдется подпоследовательность хП1, хП2, •••, х„, ... последовательности (1), сходящаяся к х.
Если X — метрическое пространство, то определение сепарабельности можно сформулировать так: в пространстве X существует последовательность (1) такая, что для любого 8>0 и любого х£Х найдется элемент х„0 из (I) такой, что р(х, х„0) < е.
Установим сепарабельность некоторых конкретных пространств.
Евклидово п-мерное пространство R" сепарабельно. Действительно, множество К?, состоящее из всех точек пространства К" с рациональными координатами, счетно и всюду плотно в R".
Пространство С [0, 1] сепарабельно. Рассмотрим'в пространстве С [0, 1] множество Со, состоящее из всех многочленов с рациональными коэффициентами. Множество Со счетно. Легко убедиться, что С0 всюду плотно в С [0, 1]. В самом деле, возьмем любую функцию х(/)С^[0, 1]. По теореме Вейерштрасса, существует многочлен р (/) такой, что тах|х(/)—р (t) | < е/2, где е > 0 — заданное число. С другой стороны, очевидно, найдется другой многочлен р0 (/) с рациональными коэффициентами такой, что max | р (i) — р0 (01 < е/2. Отсюда следует, что р(х, р0) = max | х (t) — р0 (t) I < е, что и требова-t
лось доказать.
Пространство 1р сепарабельно. Пусть Еа—множество элементов х вида {гп г2, ..., гп, 0,0,...}, где г произвольные рациональные числа, а п — произвольное натуральное число. Множество Ео счетно. Легко показать, что £0 всюду плотно в 1р. В самом деле, пусть х — — любой элемент и пусть задано любое е > 0. Найдем сна-
ОО
чала такое натуральное число п, чтобы У |Вл|/?< е^/2. Возьмем затем A=n+ 1
п элемент х0 = {г12 гг, ..., гп, 0, 0,...} такой, что 2 I К < 8*72.
Тогда получим
[р (х, х0)р = 2 I Ik — rk К + 2 I h \р < 8F/2 + eZ72 = в*, k=l fc=n+l
откуда р (х, х0) < е, и требуемое доказано.
46
Пространство Lp [О, 1] сепарабельно. В самом деле, из свойства абсолютной непрерывности интеграла Лебега (см. с. 12) вытекает, что любая функция x(t) пространства Lp[0, 1J есть предел в среднем с показателем р последовательности ограниченных измеримых функций хп (t), определяемых условиями
f x(t), если |х(01 п;
хп (О — I Q, если | х (^) | > /г.
Далее, из С-свойства измеримых функций (см. с. 13) следует, что каждая ограниченная измеримая функция есть предел в среднем с показателем р последовательности непрерывных функций. Следовательно, множество непрерывных на [0, 1] функций всюду плотно в Lp [0, 1]. С другой стороны, счетное множество многочленов с рациональными коэффициентами всюду плотно в пространстве С [0, 1] в смысле метрики этого пространства, а тем более в смысле метрики пространства Lp[0, 1]. Но тогда рассматриваемое множество многочленов всюду плотно в Lp [0, 1] и сепарабельность пространства £Д0, 1] доказана.
Пространство s сепарабельно. Пусть £0—множество элементов х вида {rlt г2, ..., гп, 0, 0, ...}, где rt —произвольные рациональные числа, а п — любые натуральные числа. Множество £0 счетно. Покажем, что из Ео можно выделить подпоследовательность, сходящуюся к произвольно выбранному элементу х = {Bi, |2, 6
е s. Для каждого построим последовательность рациональных чисел а,...» сходящуюся при k —* оо к Рассмотрим последовательность {xk} элементов из Ео вида x(ft) = r^’, ..., л**’,
О, 0, ...}. Легко видеть, что xlft) —* х при k —>- оо. В самом деле, для доказательства этого утверждения надо показать, что п-я компонента хшсходится к n-й компоненте х при п—>- оо. Но это очевидно, так как если взять достаточно большое k > п, то —г{?’|<е.
Пространство т не сепарабельно. Рассмотрим множество элементов х= {£;•} из т, где = 0 или £( = 1. Множество этих элементов имеет мощность континуума. Возьмем два различных элемента х = {|(} и у = {т|г-} из этого множества. Тогда р (х, у) — sup | В,- — Л i I = 1 и мы имеем континуум элементов, находящихся друг от друга на расстоянии, равном единице. Отсюда легко вытекает, что т не сепарабельно.
В самом деле, допустим, что в т существует счетное всюду плотное множество £0. Опишем около каждого элемента из £0 шар радиуса е—1/3. Тогда все элементы пространства расположатся внутри этих шаров. Так как множество шаров —счетное, то по крайней мере в одном из них должно быть два разных элемента х и у из рассмотренного выше континуального множества. Пусть х0 — центр такого шара. Тогда
1 = р(х, Д<р(х, х0) + р(х0, {/)< 1/3+1/3 = 2/3, что невозможно. Следовательно, т не сепарабельно. Однако можно доказать, что пространство с, являющееся подпространством пространства т, сепарабельно.
47
§ 9. КОМПАКТНЫЕ МНОЖЕСТВА В МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ
1. Основные понятия. Более ста лет тому назад чешский математик Б. Больцано заметил, что всякое ограниченное бесконечное множество точек числовой прямой имеет хотя бы одну предельную точку, и обратил внимание на важность этого факта для строгого обоснования математического анализа. Идея выделения сходящейся последовательности из некоторых множеств, состоящих уже не из точек, а из функций или кривых, была использована при доказательстве теоремы существования решения обыкновенного дифференциального уравнения, в вариационном исчислении и т. д., что привело к общему определению компактности множества, расположенного в некотором пространстве.
Множество М метрического пространства X называется компактным, если из всякого бесконечного подмножества множества М можно выделить последовательность, сходящуюся к некоторой точке этого множества.
Из определения компактности и того факта, что в метрическом пространстве всякая подпоследовательность сходящейся последовательности сходится к тому же пределу, следует, что компактное множество замкнуто. Ясно, что замкнутое подмножество компактного множества является компактным.
Множество М метрического пространства X называется относительно компактным (или предкомпактным), если его замыкание М компактно.
Относительно компактное множество ограничено. ।
П В самом деле, предположим, что М относительно компактно, но не ограничено, и хх —произвольная точка М. Так как М не ограничено, то найдется точка х2$М, лежащая вне шара К (хх, 1). Положим г2 = р{х1, х2) + 1. Так как М не ограничено, то найдется такая точка х3£М, что х3^К(х19 г2). Положим r3 = p(Xi, *з) + 1 и т. д. Получим последовательность {xj cz М такую, что p(xz,x7-)^l при i Ф j, и, следовательно, не содержащую ни одной сходящейся подпоследовательности, что противоречит относительной компактности множества М. Ц
Если каждое бесконечное подмножество метрического пространства X содержит последовательность, сходящуюся к некоторому элементу из X, то пространство X называется компактным. Компактное метрическое пространство называют также компактом. Ясно, что компакт есть полное метрическое пространство.
Примеры. 1. Пусть Х = [0, 1] с метрикой, индуцированной пространством IR. В силу теоремы Больцано — Вейерштрасса X компактно. Пространство R не компактно, так как его подмножество М = {1, 2, 3, ...} не содержит ни одной сходящейся подпоследовательности. Однако всякое замкнутое ограниченное множество пространства R. компактно в силу той же теоремы Больцано — Вейерштрасса.
2. Пусть X есть n-мерное евклидово пространство IRrt. Аналогично предыдущему, X не компактно, но всякое замкнутое ограниченное множество элементов этого пространства компактно.
3. Пространство С всех комплексных чисел с метрикой р (z, z') — |z— z'| не компактно, но любое замкнутое ограниченное подмножество пространства С компактно, так как С изометрично пространству R2. Вообще, если два множества М 48
и М или два пространства X и X изометричны, то из компактности (относительной компактности) одного из них следует компактность (относительная компактность) другого.
4. Пусть Х = С[0, 1]. Это пространство некомпактно и, более того, в С [0, 1] существуют ограниченные замкнутые и некомпактные множества (см. с. 50).
5. Пусть Х = /2. Это пространство некомпактно. Более того, в этом пространстве имеются замкнутые ограниченные некомпактные множества. Таким множеством является, например, замкнутый единичный шар К (0, 1).
В самом деле, рассмотрим такую последовательность точек из К (0, 1): =
= {1, о, О, е2=={0, 1,0, Имеем ||е/—еу Ц = V2 при i j. Поэтому
последовательность {ej и любая ее подпоследовательность не сходятся, что и доказывает некомпактность К (0, 1).
Нетривиальным примером компактного множества в пространстве Z2 может служить так называемый основной параллелепипед координатного гильбертова пространства, представляющий собой совокупность U точекх = {£1, £2> • • •» • ••},
координаты которых удовлетворяют условию 0 1/л. Компактность множе-
ства U вытекает из общего признака компактности, который будет сформулирован ниже (см. с. 77).
Для компактных множеств можно доказать аналог теоремы о вложенных шарах полного метрического пространства, причем полнота X не предполагается. А именно справедлива следующая теорема.
Теорема 1 (Кантора). Пусть дана последовательность
Z) К2 Z)... Z) Z)... zd непустых компактных множеств метри-
ческого пространства X. Тогда пересечение 0 не пусто.
t = i
□ В самом деле, выбрав в каждом множестве по точке х{, получим последовательность {xj с Так как X, компактно, то из {х,} можно выбрать сходящуюся подпоследовательность {х.Д. Пусть x3 = limx,-.. Так как при любом фиксированном п начиная
/ 1
с номера ij~> п все члены этой последовательности принадлежат Кп
и Кп замкнуто, то х0£Кп. Но тогда х0€ Г) Xz. В
1= 1
2. Теоремы существования экстремумов. Доказательство основных теорем о непрерывных функциях, заданных на отрезке, опирается на свойство его компактности. Некоторые из этих теорем можно распространить на непрерывные функционалы, заданные на компактных множествах произвольного метрического пространства. Например, имеет место следующая теорема, являющаяся обобщением известных теорем Вейерштрасса.
Теорема 2. Пусть X и Y — метрические пространства. АсХ и функция f: A-+Y непрерывна на А. Тогда если А компактно, то f (А) также компактно.
П Пусть f(A) = B и {уп} — произвольная последовательность точек из В. Для каждой точки уп возьмем один из ее прообразов хп£А. f(x^ = yn. Так как А компактно, то из последовательности {*4 можно выделить подпоследовательность сходящуюся к точке х0$А. В силу непрерывности f на А и, в частности, в точке х0 имеем уп& = f (х„ J —> f (х0) = у^В и тем самым из по
49
следовательности {уп} с. В мы выделили подпоследовательность {уПк}-+Уо£В. Н
Если, в частности, У = К, т. е. f —функционал, заданный на компактном множестве А метрического пространства, то /(Л) является ограниченным и замкнутым множеством числовой прямой и, следовательно, содержит свою нижнюю границу а и свою верхнюю границу Р, т. е. / ограничен на Л и достигает на Л своей точной верхней и точной нижней границы.
Замечание. Следует отметить, что если непрерывный функционал /(х) задан на некомпактном множестве М, то sup /(х) и хеМ inf /(х) могут не достигаться.
хе М
Рассмотрим, например, в С[0, 1] множество М всех функций х(0 таких, что х(0) = 0, х(1) = 1 и тах|х(0|^1. Функционал 1 *
f (х) = х2 (0 (К непрерывен на М, но не достигает на нем своей о
нижней границы.
В самом деле, если х (0 = tn, то /(х) — 1/(2«+1). Значит, inf f (х) = м
= 0. Но очевидно, что для всякой непрерывной кривой х = х(0, соединяющей точки (0; 0) и (1; 1), /(х)>0 (отсюда, в частности, вытекает, что рассматриваемое множество кривых £ некомпактно, хотя оно и является ограниченным
/уч и замкнутым множеством в С[0, 1 ]). ,
/ \ X. Таким образом, прежде чем опираться на тео-
/ \ ч, рему 2, необходимо убедиться в компактности
/ \ X множества, на котором определен непрерывный
A в В функционал. Гипотеза о достижении точной Рис. 1 верхней или нижней границы функционала на некомпактном множестве может привести к неправильным выводам, как показывает рассмотренный пример.
В качестве другого примера того же рода приведем ложное доказательство пятого постулата Евклида. Известно, что пятый постулат Евклида равносилен гипотезе, что сумма углов хотя бы одного треугольника равна л. Можно совершенно строго доказать, что сумма углов треугольника не может быть большей. Докажем, что сумма углов некоторого треугольника равна л. Пусть а—точная верхняя граница суммы углов треугольника и пусть существует треугольник АВС (рис. 1), для которого сумма углов достигает максимальной величины а. Произвольную внутреннюю точку D стороны АВ соединим отрезком CD с вершиной С. Отрезок CD разбивает треугольник АВС на два треугольника ADC и DCB, сумма углов каждого из которых не превосходит а. С другой стороны, сумма углов обоих треугольников равна а+л. Следовательно, а4-+ л 2а. Но так как а не превосходит л, то отсюда следует, что а = л. Итак, существует треугольник, сумма углов которого равна л, и пятый постулат Евклида доказан.
50
В этом доказательстве ошибочным было предположение о существовании треугольника, у которого сумма углов достигает своей точной верхней границы (как мы видим, это равносильно пятому постулату Евклида). В геометрии Лобачевского разность между л и суммой углов треугольника пропорциональна площади последнего, и если эта разность стремится к нулю, то треугольник стягивается в точку.
Теорема 2 обобщается на случай так называемых полунепрерывных функционалов. Функционал f(x) называется полунепрерывным снизу (сверху), если из условия хп —► х следует, что f (х) lim f (хв) ________________________ п (соответственно f (x)>lim/(xB)) .
Для таких функционалов имеет место следующая теорема.
Теорема 3. Функционал /(х), полунепрерывный снизу (сверху) и определенный на компактном множестве, ограничен снизу (сверху) на этом множестве и достигает на нем своей точной нижней (верхней) границы.
Эта теорема имеет широкое применение в вариационном исчислении, так как важнейшие классы рассматриваемых в нем функционалов являются полунепрерывными.
3. Критерии компактности множеств в метрическом пространстве. Дадим общий критерий компактности множества, расположенного в метрическом пространстве. Для этого введем сначала следующее определение: множество N метрического пространства X называется е,-сетыо для множества М того же пространства, если для любой точки х^М найдется точка хе£М такая, что р(х, х£) < е (в частности, М может совпадать со всем пространством X).
Множество МсХ называется вполне ограниченным, если при любом е > 0 существует конечная е-сеть для множества М. Легко убедиться, что вполне ограниченное множество ограничено.
Теорема 4 (Хаусдорфа). Для того чтобы множество М с X было относительно компактным, необходимо, а в случае полноты пространства X и достаточно, чтобы М было вполне ограниченным.
□ Необходимость. Предположим, что М относительно компактно. Пусть Xi —любая точка из М. Если р (х, хг) < s для всех х£М, то конечная 8-сеть уже построена. Если же это не имеет места, то существует точка х2 £ М такая, что р (хп х2) 8. Если
для любой точки х£М либо р (х, хг) < е, либо р (х, х2) < е, то конечная 8-сеть уже построена. Если же это не имеет места, то найдется точка *х3£М такая, что р (хн х3)^8, р(х2, х3)^е.
Продолжая этот процесс, построим точки хп х2, ..., х„ такие, что р (х(, х7) ^8 при i #= /. Можно сделать два предположения: либо процесс построения точек после некоторого k-ro шага оборвется, либо указанный процесс можно продолжить неограниченно. Согласно первому предположению, для любого х£М будет выполнено одно из неравенств р (х, х() < е (i — 1, 2, ...,&) и в этом случае хп х2, ..., хк образуют конечную е-сеть* для М. Второе
* Полезно заметить, что эта е-сеть состоит из точек множества М.
51
же предположение исключается, так как если бы оно имело место, то мы получили бы бесконечную последовательность точек хп х3, ..., х„, ... такую, что р (xz, ху) > е для i /, и ни сама эта последовательность, ни любая ее подпоследовательность не были бы сходящимися, что противоречит предположению об относительной компактности множества М.
Достаточность. Предположим, что пространство X —полное и что для любого е > 0 существует конечная 8-сеть для М. Возьмем последовательность чисел {е„}, litne„ = 0 и для каждого е„ построим п
конечную ел-сеть {xi"), 4"’» • х^} для множества М. Возьмем
любое бесконечное подмножество Т а М. Около каждой из точек х^\ -41*, ..., Xi,1,’ опишем замкнутые шары радиуса 81. Тогда каждая точка из Т попадет в один из этих шаров. Так как число шаров конечное, то по крайней мере в одном из них окажется бесконечное множество точек из Т. Обозначим это подмножество множества Т через Т±. Возьмем точки х!2), х£2>, ..., х^ и опишем около каждой из этих точек замкнутые шары радиуса е2. Рассуждая так же, как и раньше, найдем бесконечное множество Тг cz 7\, расположенное целиком в одном из построенных шаров радиуса в2. Продолжая этот процесс, получим последовательность Т\:эТ2р.. .z>Tnzz>... бесконечных подмножеств множества Т, причем подмножество Тп содержится в замкнутом шаре радиуса е„ и, следовательно, расстояние между любыми двумя точками из Тп не превосходит 2е„.
Возьмем теперь точку li€7\, точку ВабТ'г» отличную от точку отличную от точек и |2, и т. д. Тогда получим
некоторую последовательность Та — |2, точек из Т.
Эта последовательность сходится в себе. В самом деле, £ Тп и %п+р £ С Тп+рсТп для-любого натурального р. Следовательно, р (1п+р, В„) < <2е„—*0 при п-^оо, р > 0. Так как, по условию, пространство X — полное, то последовательность Тш сходится к некоторой точке |£Х и, следовательно, относительная компактность множества М доказана. Ц
Следствие 1. Для того чтобы множество М полного метрического пространства X было относительно компактно, достаточно, чтобы для любого е < 0 существовала относительно компактная е-сеть для М.
П Пусть N — относительно компактная е/2-сеть для М. Применяя к N предыдущую теорему, получаем, что существует конечная е/2-сеть Хо для N. Тогда Хо —конечная е-сеть для М. В самом деле, для любой точки х£М существует точка такая, что р(х, |) < 8/2. В свою очередь, для точки существует точка € Хо такая, что р (?, х8) < 8/2. Следовательно, для любой точки х£/И найдется в такая точка хе, что
р(х, хе)<р(х, £)+р(£, Хе) < 8/2 + 8/2 = 8,
т. е. No является конечной s-сетью для М. Так как пространство 52
X — полное, то по предыдущей теореме заключаем, что М относительно компактно. Щ
Следствие 2. Компактное пространство X сепарабельно.
□ В самом деле, возьмем последовательность {е„}, 8„—> 0 и для каждого е„ построим конечную е„-сеть Nn= {x^’}i=i, 2..Пусть
/V = U К„. Очевидно, /V —счетное множество, всюду плотное в X. п= 1
Приведенное выше определение компактности есть обобщение свойства ограниченных замкнутых множеств числовой прямой, найденного Б. Больцано и К. Вейерштрассом и используемого при изучении непрерывных вещественных функций вещественной переменной. Однако известно, что эти же теоремы о непрерывных функциях можно доказать с помощью леммы Гейне —Бореля о покрытии. Это объясняется эквивалентностью свойств Больцано —Вейерштрасса и Гейне —Бореля, причем не только для числовых множеств, но и для множеств произвольного метрического пространства.
Система {Gg} открытых множеств метрического пространства X называется открытым покрытием множества M<z.X, если каждая точка х € X принадлежит хотя бы одному из множеств Gg этой системы.
Теорема 5. Для того чтобы множество МсХ было компактным, необходимо ^достаточно, чтобы из любого открытого покрытия {Gg} этого множества можно было выделить конечное подпокры-
тие.
□ Необходимость. Пусть Л4 компактно и М = {GJ — произвольное открытое покрытие М. Докажем, что тогда справедливо утверждение: существует е > О такое, что при любом х € М шар К. (х, е) входит целиком в некоторое множество Gg.
В самом деле, если это не так, то найдутся последовательности чисел е„ —> 0 и точек хп 6 М такие, что шары К (х„, е„) не войдут целиком ни в одно Gg. Вследствие компактности М из последовательности {х„} можно выделить подпоследовательность {хп/.}, сходящуюся к точке х0£М. Так как М —покрытие Л1, то найдется
Эх0. В силу того что Gg0 открыто, это множество содержит целиком шар К (х0, 6). Выберем теперь пк настолько большим, что
< 6/2 и р(хПк, х0) < 6/2. Тогда легко проверить, что К. (x„k, e„fc)c: сК (х0, 6)cGg0, хотя по построению К (х„А, 8„ft) не может входить целиком ни в одно Gg. Полученное противоречие доказывает спра-
ведливость высказанного утверждения.
Пусть е0 выбрано так, что это утверждение выполняется. Построим 80-сеть £(, = {%!, х2, ..., хр} для М, состоящую из точек этого множества. Так как расстояние от любой точки х£М до одной из точек xt меньше 80, то все множество М разместится целиком в объединении шаров £ (хп 80), К (х2, 80), .... К(хр, 80). В свою очередь, К (х(-, 80) входит целиком в некоторое Ggf. Но
р тогда Me (J Gg. 4 = 1 1
и необходимость доказана.
63
Достаточность. Предположим, что из всякого покрытия множества М можно выделить конечное подпокрытие; пусть/7 — подмножество множества М, не имеющее ни одной предельной точки. Тогда для каждой точки х^М найдется окрестность К (х, гх), не содержащая, кроме, может быть, самой точки х, ни одной точки из F. Эти окрестности образуют покрытие множества М. Выделим из него конечное покрытие К (xlt ех), К (х2, s2), ..., К (хт, ет). Так как все множество М, а следовательно, и F размещается в этих окрестностях и так как в каждой окрестности может содержаться не более одной точки из F, то множество F должно быть конечным. Следовательно, всякое бесконечное подмножество F а М дожно иметь предельные точки, а это означает, что М относительно компактно.
Покажем, что М замкнуто. Пусть а(£М. Тогда гх =р (х, а) > О для любой точки х£М. Открытые шары К (а, гх/3) и К (х, г^/З) не пересекаются и множество шаров К (х, гх/3), где х пробегает М, образуют открытое покрытие этого множества. Выделим из {К (х, гх/3)} конечное подпокрытие К (хх, rxj3), X (x2, rXi/3), ..., К(х„, гХп/3). Если r0 = minr^, то К(а,г1}!3') не пересекается ни с одним шаром К (х;, г^/3), (i = 1, 2, ..., п), а следовательно, и с /И. Но тогда а не может быть предельной точкой для М, т. е. М содержит все свои предельные точки.
Так как множество М замкнуто и относительно 'компактно, то оно является компактным, т. е. достаточность доказана. У
§ 10. ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА •
1. Основные понятия. При изучении множеств в метрических пространствах мы ввели понятие окрестности точки метрического пространства X и указали, что точка х£Х является пределом последовательности {х„} с X тогда и только тогда, когда для любой окрестности их этой точки найдется номер п0 такой, что хп£их при п^п0. Опираясь лишь на понятие окрестности, мы ввели понятия предельной точки множества, открытого множества и т. д. Нетрудно показать, что многие важные свойства предела последовательности, открытых и замкнутых множеств можно получить, используя лишь понятие окрестности и не прибегая к понятию расстояния. Так возникает идея топологического пространства, определение и основные свойства которого мы сейчас кратко напомним.
Определение 1. Множество X элементов какой-либо природы называется топологическим пространством, если в X выделена система т подмножеств, называемых открытыми, причем выполняются следующие аксиомы:
I. Все X и пустое множество—открытые множества.
II. Объединение любого, числа открытых множеств есть открытое множество.
III. Пересечение конечного числа открытых множеств есть открытое множество.
54
Рассматривая в качестве совокупности всех открытых множеств различные совокупности т подмножеств множества X, мы получаем, вообще говоря, различные топологические пространства. Поэтому часто топологическим пространством называют пару (X, т), состоящую из множества X и топологии т, которой наделено это множество.
Любое открытое множество, содержащее точку х g X, называется окрестностью этой точки. Обычно расширяют понятие окрестности, называя окрестностью точки х любое множество, содержащее открытую окрестность этой точки. С помощью понятия окрестности, так же как и в метрических пространствах, вводятся понятия предела последовательности, предельной и внутренней точки множества, замыкания и т. д. Однако в определенном таким образом общем топологическом пространстве X последовательность {хп} а. X не обязательно сходится к одному пределу. Так, если X = (— оо,оо), а в качестве открытых множеств берется X, 0 и любое множество, полученное из числовой прямой удалением конечного числа точек, то мы приходим к топологическому пространству, в котором для любой последовательности {хп} с X любая точка х£Х является пределом (рекомендуем доказать это самостоятельно). Чтобы избежать неоднозначности предела, к предыдущим аксиомам топологического пространства добавляются так называемые аксиомы отделимости Хаусдорфа.
Ограничимся формулировкой одной из четырех аксиом, а именно второй аксиомы отделимости: для двух любых точек х и у топологического пространства X найдутся такие окрестности их и иу этих точек, что их(]иу = 0.
Ясно, что при выполнении этой аксиомы предел последовательности определяется однозначно. Топологическое пространство, в котором имеет место вторая аксиома отделимости, называется хаусдорфовым (или отделимым).
Если мы рассмотрим совокупность {их, vx, wx, ...} всех окрестностей точки х, то очевидно, что имеют место следующие утверждения:
1. х$их для любой окрестности точки х.
2. Если их и vx—окрестности точки х, то существует окрестность этой точки wx с их П vx.
3. Если у£их, то существует окрестность точки у такая, что
Vy = Wx-
Это приводит ко второму определению топологического пространства, эквивалентному приведенному выше.
Определение Г. Множество X называется топологическим пространством, если каждой точке х £ X поставлено в соответствие непустое семейство Vx непустых подмножеств множества X, называемых окрестностями точки х, причем выполняются следующие аксиомы:
I. Каждая окрестность их точки х содержит эту точку.
II. Если их и vx—две окрестности точки х, то существует третья окрестность wx этой точки такая, что wx с ux(]vx.
55
III. Для любой точки у£их существует окрестность vy такая, ЧТО Vy с их.
Аксиомы I, II и III называются аксиомами Хаусдорфа топологического пространства. Далее, как и в случае метрического пространства, множество G сз X называется открытым, если для любой точки х С G существует окрестность их этой точки такая, что их с G. Пустое множество мы также считаем открытым.
Опираясь на аксиомы Хаусдорфа, нетрудно показать, что объединение любого числа и пересечение конечного числа открытых множеств есть открытое множество, после чего становится ясной эквивалентность приведенных определений.
Как и при первом определении топологического пространства, сразу же можно расширить понятие окрестности, понимая под окрестностью точки х £ X любое множество, содержащее их £ Vx. При этом семейство Vx называется фундаментальной системой (или базой) окрестностей точки х. Ясно, что метрическое пространство есть частный случай отделимого топологического пространства с базой окрестностей вида К (х, г).
В метрических пространствах важнейшее’топологическое понятие—замыкание М множества М—полностью определяется с помощью счетных процессов, а именно путем присоединения к М пределов всех сходящихся последовательностей {х„} сз М. В произвольном топологическом пространстве это не так. Пусть, например, X есть пространство F[0, 1] всех вещественных функций, определенных на [0, 1], и база Ух окрестностей точки х (*)€/•'[0, 1] состоит из множеств
о(х; tif t2, e)=-{y(t)£F\ \y (t^—x (/,•) | < e, i = 1, 2; ..., n}.
Легко проверить, что аксиомы I — III топологического пространства при этом выполняются.
Пусть А—множество всех тех функций пространства F[0, 1], каждая из которых всюду равна единице, за исключение*м конечного числа точек отрезка [0, 1], где она обращается в нуль. Ясно, что в топологическом пространстве F[0, 1] функция хо(/)н=О есть предельная точка множества А. Вместе с тем, какую бы последовательность (х„(/)} <зз А мы ни взяли, множество всех точек, где хотя бы одна из функций этой последовательности обращается в нуль, счетно. Поэтому существует точка ^€[0,1], в которой ни одна из функций последовательности {х„(/)| не равна нулю. Но тогда в окрестность нуля и(0; /0; 1/2) ие попадет ни одна функция этой последовательности, т. е. x„(t)-^-O. Таким образом, замыкание А множества А нельзя получить присоединением к А пределов всех последовательностей, составленных из точек множества А.
Топологическое пространство X называется метризуемым, если в нем можно ввести метрику так, что топология т (т. е. запас открытых множеств), порождаемая этой метрикой, совпадает с исходной топологией пространства X. Как только что показано, 56
f[0, 1] является примером неметризуемого топологического пространства.
Пусть (X, т)—топологическое пространство. Наделяя множество X другой топологией т', мы получим другое топологическое пространство (X, г'). Говорят, что топология т' сильнее (или тоньше), чем топология т, если каждое множество G с X, открытое в топологии т, открыто и в топологии т', или, что все равно, если каждая окрестность любой точки х£Х в топологии т является окрестностью точки х в топологии т'. Очевидно, что, для того чтобы топология т' была тоньше топологии т, необходимо и достаточно, чтобы для любой окрестности их из базы окрестностей Ух в топологии т нашлась окрестность и'х из базы окрестностей V' в топологии т' такая, что и'х а. их. Если, кроме того, для каждой v'x£Vx найдется vxcVx такая, что vx<zxx, то топологии т и т' эквивалентны в том смысле, что запас открытых множеств в пространствах (X, т) и (X, т') один и тот же.
Наконец, отметим, что если X—топологическое пространство и Хо—подмножество X, то Хо обращается в топологическое пространство при условии: в качестве открытых множеств в Хо надо принять «следы» в Хо открытых множеств из X, т. е. положить, что Н с Хо открыто тогда и только тогда, когда Я = ОПХо, где G—открытое множество пространства X. В этом случае говорят, что топология в Х9 индуцирована топологией пространства X.
Пусть X и Y—топологические пространства. Отображение f: X —» Y называется непрерывным в точке х € X, если для любой окрестности v,Mc.Y найдется окрестность их а. X такая, что f(ux) <zvf{xy Очевидно, что это определение есть абстрактный аналог «е, 6-определения» непрерывности Коши, в котором вместо числовых интервалов (/ (х)—е, /(х) + е) и (х—6, х + 6) фигурируют окрестности точек топологического пространства.
Теорема 1. Для того чтобы отображение f: X—было непрерывно на X, необходимо и достаточно, чтобы прообраз f~l (Н) любого множества Н, открытого в Y, был множеством, открытым в X.
2. Прямые произведения топологических пространств. Важным понятием является декартово (или прямое) произведение топологических пространств. Пусть {Хо},а£А,— семейство непустых множеств. Декартовым произведением (часто говорят просто произведением) множеств Ха называется совокупность всех систем вида х— {ха}, где ха£Ха и а пробегает множество А. Произведение множеств Ха обозначают Ц Ха. Множества Ха называются мно-
ае А
жителями произведения X = ГГ Ха, а элементы ха—координатами ае А
элемента х = {ха}.
Если все Ха тождественны между собой, Xa — Y для всех а£А, то пишут Ц Ха = УА. Так, например, если А = (1, 2....п}
ае А ,
п
и Х> = R для i = 1, 2, ..., п, то Ц R = R". Если дано произведе-i = i
57
ние X = УА, то, ставя в соответствие элементу а £ А координату уа элемента х = {уа}, мы получаем, что каждый элемент х$УА определяет отображение множества А на множество Y. Обратно: если дано отображение /: А—>У, то образуя систему {уа}, где Уа~?(а), мы получаем элемент множества УА. Таким образом, между множествами УА и F (А, У) всех отображений А на У устанавливается взаимно-однозначное соответствие, которое позволяет в ряде вопросов отождествить УА и F (А, У).
Пусть х — {ха}£ П Ха. Отображение х>—>ха множества Х = а€ А
— II Хл на множество Ха называется проекцией X на Ха и а € А
обозначается ла (х) = ха.
Если все Ха — топологические пространства, то X = Ц Ха а € А можно тоже наделить структурой топологического пространства. Это можно сделать различными способами. Наиболее удобным для дальнейшего является способ, предложенный А. Н. Тихоновым.
Пусть УХа—база окрестностей точки ха в пространстве Ха. Положим
их~ П «ха, 0)
а € А *
где «Аа.€^а. лишь для конечного числа значений индекса а=а1, ........ и нХа = Ха для всех остальных а. Совокупность Ух всех таких произведений примем за базу окрестностей точкй х = {ха}. Покажем, что Vx удовлетворяет аксиомам Хаусдорфа.
I. х£их, что очевидно.
II. Пусть их, vxgVx, причем у их лишь множители ыХар их„ , ..., их„ отличны от Ха и у vx лишь множители vx ,vx ,...
’ хап « J х XrS
. . ., 1)х отличны от Ха. Положим
ат
f если иЖа = 1»Ха = Ха;
^=4“^’ еСЛИ^аг = Ха’
I ох , если их =Ха.
( а/ а/
Если же и и ох„ отличны от Ха, то выберем wx„ с Vx так, чтобы wXa. с иХл, П vXa., что возможно. Положим wx— IT wxa-Ясно, что wx а. их A vx.
Рекомендуем самостоятельно проверить выполнение аксиомы III и доказать, что произведение отделимых пространств отделимо. Можно также доказать, что прямое произведение счетного числа метрических пространств есть метризуемое пространство.
В тихоновской топологии проекции ла являются непрерывными отображениями. В самом деле, если х = {ха}€ JJ Ха и «Хао—произ-а€ А
58
вольная окрестность точки ха„€Хао, то, полагая их = U иха, где
а е А
0*а,,=и«а. и v*a = Xo' для а=^ао> мы получим окрестность точки х такую, что л^ (их) с иХаг а это и означает непрерывность проекции ла„ в точке х. Наконец, отметим, что отображение f: У —X = Ц Ха непрерывно в тихоновской топологии простран-а € А
ства X тогда и только тогда, когда непрерывны все отображения fa==^‘a°f- Y Ха.
3. Компактные множества и теорема Тихонова. В метрических пространствах мы дали два эквивалентных определения компактного множества: с помощью последовательностей и с помощью покрытий. Так как в произвольном топологическом пространстве с помощью сходящихся последовательностей нельзя ввести многие основные топологические понятия, то естественно за опр°дзление компактности множества в топологическом пространстве принять его свойство, связанное с покрытиями.
Множество М топологического пространства X называется компактным, если из любого открытого покрытия этого множества можно выделить конечное подпокрытие.
Легко видеть, что замкнутое подмножество компактного множества компактно. В самом деле, пусть М компактно и F с М замкнуто. Если {Gg}— открытое покрытие F, то, присоединяя сюда CF, получим открытое покрытие М. Выделяя из него конечное подпокрытие и отбрасывая CF (если оно входит в это конечное подпокрытие), получим конечное покрытие F, выделенное из {Gg}.
Лемма. Всякое компактное множество отделимого пространства замкнуто.
□ Пусть М с X компактно и х(£М. Для любой точки у£М найдутся открытые окрестности иу и vy точек хну такие, что ыуПуу = 0. Семейство {vy} есть покрытие М и из него можно выделить конечное подпокрытие vy„ оУг, ..., vy . Тогда их=иу1(}
П иуг Л ... Л uyk есть окрестность точки х, не пересекающаяся
с
_и,Ч
о М, и, следовательно, СМ открыто. @
Известно, что непрерывный образ замкнутого множества может быть и не замкнут. Легко убедиться, что непрерывный образ компактного множества компактен. Предположим, что дано отображение f: X—>У, где X и У—топологические пространства, f непрерывно на X и М с X компактно. Пусть {Н^} — произвольное открытое покрытие f(M). Для каждого возьмем его пр образ Gg = /-1 (/7g). В СИЛУ непрерывности f все Gg—открытые множества и совокупность {Gg}, очевидно, покрывает М. Так как М компактно, то из {Gg} можно выделить конечное подпокрытие Gg,, <3^, ..., Ggft множества М. Но тогда 77g,, 77g,, ..., Нц покрывает f (М) и компактность этого множества доказана.
59
Система множеств топологического пространства называется центрированной, если любое конечное число множеств этой системы имеет непустое пересечение.
Следующий критерий компактности множества топологического пространства часто используется.
Теорема 2. Множество Н топологического пространства X компактно тогда и только тогда, когда замыкания множеств любой центрированной системы, состоящей из подмножеств Н, имеют в Н непустое пересечение.
□ Необходимость. Пусть Н а. X компактно и {Aцентрированная система подмножеств Н. Рассмотрим множества Эти множества открыты. Допустим, что они образуют покрытие И. Тогда в силу компактности Н из них можно выбрать конечное
__ п ___
покрытие ..п и СА%. =>Н. Переходя к дополнениям,
1=1 6
п _ п
получим U Ah с СН и тем более П А& с: СН. Но так как 1=1 i = 1
п
А^сН, то Л А% = 0, что противоречит центрированности системы {Л?!}. Таким образом,JCXg,} не покрывают Н и существуют точки х £ //такие, что х<^СА% при любом £, т. е. ПЛ^, и необходимость доказана.
Достаточность. Пусть для каждой центрированной системы {Л^} подмножеств Н имеется точка х£Н, принадлежащая замыканиям всех Л£. Рассмотрим произвольное открытое покрытое {Qg} множество Н. Так как и Q# z> Н, то Л CQ? с СН. Положим At —
1 _____ ?
= Н Л (CQg) с Н. Имеем Л5с:С’£^ = С£^ и потому Л Л& а лСЦс tzCH, т. е. замыкания множеств не имеют в Н общей точки. Отсюда следует, что Л^ не центрированная система и существуют
п п
At. (i = 1, 2, ..., ц) такие, что Л At. = 0, т. е. \J CAt. = X. Так ‘ i=i ' i=i'
как СА^.— С [//Л CQg.] = СН и Qg., то U СА^ = СН U^U и,
(п \ п
U Qg.) = X. Но это означает, что и Qg. э Н
i = 1 1' i = 1 1
и мы выделили из {Qg} конечное подпокрытие. Ц
Пусть даны различные центрированные системы, составленные из подмножеств некоторого фиксированного множества X. Центрированная система So называется максимальной, если она не является подсистемой (собственной) другой центрированной системы подмножеств того же множества X. С помощью леммы Цорна нетрудно показать, что всякая центрированная система содержится в некоторой максимальной центрированной системе.
60
□ В самом деле, если данная центрированная система S не является максимальной, то существует хотя бы одна центрированная система Sx, содержащая 5. Рассмотрим совокупность {Sx} всех таких систем и введем в ней частичное упорядочение по включению. Пусть {Sv}—произвольная линейно упорядоченная подсистема системы {S4- Положим Sx0 = U SK,. Ясно, что Sv^Sx0 для
f
любого X и, кроме того, Sx„—центрированная система. Действительно, пусть Alf А2, ..., Ak—любая конечная совокупность множеств из Sx0. Тогда с: для некоторого Х{-. Система Sv,
S,,, ..., S/ линейно упорядочена; пусть S,- —максимальная по 2 « «о
включению система. Имеем A- a. Sx- для всех i = l,2, Но k io
тогда П Дг- #= 0 и центрированность системы SKa доказана. i — 1
Таким образом, в совокупности {S^} всякое линейно упорядоченное подмножество имеет верхнюю грань и согласно лемме Цорна в системе существует максимальный элемент So. Это и есть максимальная центрированная система, содержащая S. Ц|
Замечания. 1. Если 5 = {Л^}—максимальная центрированная система, то, как легко видеть, пересечение любого конечного числа множеств Л^, Л^2, ..., Л| системы 5 принадлежит этой k системе. В противном случае, присоединяя к S множество Ло= п Л^., i=i 1 мы получили бы новую центрированную систему, большую S, что противоречит максимальности S.
2. Если 'S = {AJ—максимальная центрированная система В с X и Bn^j¥=0 при любом 5, то B£S, так как в противном случае, присоединяя В к S, мы получили бы, как легко видеть, снова центрированную систему, но более широкую, чем S, что невозможно.
Теорема 3 (А. Н. Тихонова). Пусть X = ЦХа — произве-ае А
дение топологических пространств. Для того чтобы множество Н с: X было компактным в тихоновской топологии пространства X, необходимо и достаточно, чтобы для любого а множества ла (Я) были компактны.
□ Необходимость условий следует из того, что непрерывный образ компактного множества есть компактное множество.
Для доказательства достаточности возьмем произвольную центрированную систему {Л^} подмножеств Н и докажем, что все множества Л^ имеют в Н общую точку прикосновения. Дополняя, если необходимо, {Л|} до максимальной центрированной системы, мы можем без ограничения общности считать, что {Л^} максимальна. Обозначим через Af проекцию А% на пространство Ха, т. е. Л^ = ла(Л^). Легко видеть, что для каждого фиксированного а система {Af}—центрированная.
61
Так как множества па(Н) компактны и А%сла(Н), то ЛЛ£#=0 сла(Н). Пусть ха£ ЛЛ^. Покажем, что {ха}€ ЛЛ5. S в
Рассмотрим сначала такую окрестность u0 = Циа точки {ха}, ае А
что иа=^Ха лишь для одного а = а0. Так как ua„ пА?°^ 0 для всех то ясно, что также иоЛЛ^#=0 при любом Но тогда в силу максимальности {Л^}, согласно замечанию 2 на с. 61, ыо€{^}- Так как любая окрестность и точки {ха} есть пересечение конечного числа окрестностей вида ы0, то в силу замечания 1 на с. 61 м€{Л^} и, следовательно, и Л А% Ф0 при любом Но это и означает, что {ха}с Л Л6. Ц
ГЛАВА II
ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ И ЛИЛЕЙНЫЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Если линейное пространство X является в то же время метрическим, причем метрика р инвариантна относительно сдвига, т. е.
Р(*, у) = р(х-\-г, у-\-г), х, у, z£X,
то оно называется линейным метрическим пространством. Важным классом линейных метрических пространств являются пространства Банаха или, как их иногда называют, пространства типа В.
§. 1. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА
1. Определения и простейшие свойства. Множество X называется линейным нормированным пространством (сокращенно ЛНП), если:
1°. X —линейное пространство с умножением на вещественные (комплексные) числа.
2°. Каждому элементу х линейного пространства X ставится в соответствие вещественное число, которое называется нормой этого элемента и обозначается ||х||, причем предполагается, что норма элемента удовлетворяет следующим условиям (аксиомам нормы):
I. ||х||^0, причем ||х|| = 0 лишь если х = 0.
II. 11ИНЧМ-
ш. h+i/Ki|x|l+M
В ЛНП можно ввести метрику с помощью равенства р (х, у) = —i'x — z/J. Легко проверить, что введенное расстояние удовлетворяет всем аксиомам метрики. После введения метрики определяется сходимость последовательности элементов {х„} к х, а именно х= = limxn, или хя—>х, если ||х„ —х||—>0 при п —>оо. Определенная таким образом сходимость в ЛНП называется сходимостью по норме. ,
Если ЛНП является полным в смысле сходимости по норме, то оно называется пространством Банаха (или банаховым пространством) .
Примеры. 1. «-мерное векторное пространство R" может быть сделано бана-ховым пространством. В самом деле, определяя норму с помощью равенства
’ х=&’ .......
М = 1 /
получим, что есть банахово пространство, причем метрика в этом пространстве совпадает с ранее введенной в R" метрикой.
63
2. С [О, 1] есть банахово пространство. Сложение функций и умножение функции на вещественное число определяем обычным образом. Далее, полагаем [I х [] = max | jv (/) |. Метрика полученного пространства совпадаете метрикой, ранее
введенной в С [0, 1].
3. 1р есть банахово пространство. В самом деле, определив сложение элементов и умножение элемента на вещественное число, как указано выше (см. с. 31), и полагая
/ оо \1/р
\Z = 1 J
получим пространство Банаха, метрика которого совпадает с прежней метрикой.
4. Lp [0, 1] есть банахово пространство. Здесь для x(/)£Lp[0, 1] положим / 1 \ i/р
lM = H |x(/)|Fd/ ) .
\о /
Метрика в полученном пространстве совпадаете прежней метрикой в Lp [0, 1].
5. т есть банахово пространство. Действительно, если для х = {£,-} положить || х |1 = sup {!/}. то получим банахово пространство, метрика в котором совпадает с метрикой в /и, введенной ранее.
6. Рассмотрим пространство функций х(/), определенных на [0, 1], непрерывных на этом отрезке и имеющих на нем непрерывные производные до Л-го порядка включительно. Введем в пространстве таких функций норму, полагая
|| х || = max /max | х (/)), шах|х'(0|, ...» max |х<*> (f)|V
I. t t t * /
Получим банахово пространство, которое обозначается Ck [0, 1]. Оно широко используется в вариационном исчислении.
Отметим, что из соотношений а
И(*«+уп) — (х+£)||< К—х ||+к» — у II.
1|1Л-^К1М-к„-хЛ+|Х„-х|.цх|
следует, что если хп —> х, уп-+ у, >X, то
х„ + уп-+х + у, Хпх„-^Кх.
Далее,
ИНк+(*-у)К1к11+11*-«/||, т. е. ||х||-к|К||х-у||.
Меняя местами х и у, получим
или Ikll—1к11Кк-«/И-
Отсюда следует, что если то ||х„||—Ч|х|| и, в частности, что
{||xj} есть ограниченная числовая последовательность.
Так как ЛНП есть метрическое пространство, то для такого пространства имеют смысл все понятия, введенные в метрических пространствах (шар, ограниченное множество, сепарабельность и т. д.), а также имеют место все теоремы, доказанные для таких пространств.
Для банаховых пространств оказывается справедливым все, что было ранее установлено для полных метрических пространств.
Легко видеть, что в ЛНП шар (замкнутый шар) есть выпуклое множество. В самом деле, пусть хп х2£К(а9 г), т. е. Цхд,—а|| < г,
64
|[t2—d||<r. Возьмем любой элемент вида у = (1 — t)xi + tx2, О < t < 1. Имеем
|| у—«|| = ||(1 — О х2 + tx2 — а|| = ||(1 — /) xt + tx2 — (1 — t) a — fa|| < < IK1 —О (*i ~«)|| + II t (х2 —«)|| = (1 - Oil *i — «11 +1II х8 <
< (1 — t) Г +tr = r.
Итак, fly—а||<г и, зйайит1, у£К{а, г).
Отметим два очевидных свойства шара й банаховом пространстве: для любой точки х=^0 шар с центром в Начале координат и радиусом г >||х|| содержит эту точку, а шар с цейтром в начале координат и радиусом г' <||х|| не содержит данной точки.
Так как ЛИП X есть частный случай линейного пространства, то для X имеют смысл все понятия, введенные в линейных пространствах, как, например, линейная зависимость и независимость элементов, линейное многообразие, разложение X в прямую сумму и т. д. .
Пусть L —линейное многообразие в ЛИП X. Если L является^ кроме того, замкнутым множеством, то L называется подпространством.
Если L — конечномерное линейное многообразие в ЛНП, то, как мы увидим ниже, L — L. Для бесконечномерных линейных многообразий это равенство может не иметь Места.
Пусть, например, Х = С[0, 1] и L—линейное многообразие, порождаемое элементами х0 = 1, xt— t, ..., xn — tn, .... Тогда L— множество всех многочленов, a L = C[O, 1]=£L.
Для подпространства ЛНП имеет место следующее важное предложение.
Лемма 1 (Ф. Рйсса). Пусть L —подпространство ЛНП X, не совпадающее с X. Тогда для любого заданного е. > 0 в X найдется такой элемент у с нормой, равной единице, Что ||х — у|| > 1—8 для всех x^L.
□ В самом деле, пусть у0—любой элёмейт из X, не принадлежащий L, и d — inf ||у9—х||. Тогда d > 0, так как иначе у0 был
XEL
бы предельным элементом для L и, следовательно, входил бы в L, что невозможно по условию. Для любого числа е > 0 найдется такой элемент x0^L, что d^||y0 — х0|] < d + de. Положим у = ~ 'fly0—хП|~‘ Элемент y&L (так как иначе у0 входил бы в L) и ||у||==1. Возьмем любой элемент х из L. Пусть г = х0 + ||у0—х01|х, z^L. Тогда
I’-г'>
>d + ds^°—z^d4-ed=* Т+;>|*’в' ®
2. Нормирование фактор-т^ространбТва. Изоморфизм нормированных пространств. Пусть X есть ЛНП, £0—его подпространство, X/Lq—соответствующее фактор-пространство. Легко убедиться,
3
№ 3054
65
что все классы L^X/L0—замкнутые множества. В самом деле, пусть x„£L и х„-+х0. Так как для любых п и т хп—xm£Lg, хп—Хт~^хп— Хо ПРИ т ~~* 00 И ^0 замкнуто, то хп—x0£Lg. Но это означает, что х0 входит в тот же класс, что хп, т. е. х0 С L, и требуемое доказано.
Фактор-пространство Х/L допускает следующее нормирование: ||L|| = inf ||х||. Проверим выполнение аксиом нормы.
xsL
I. Очевидно, что ||L||^0 и || Lo || = 0.
Пусть ||L || = 0. Тогда существует последовательность {xn}cL такая, что ||хп||—>0. Так как L замкнуто, то OgL, следовательно, L, —- Lq.
II. В силу определения Ц^Ц и |L2[|, для любого е>0 найдутся элементы хх £ и х2 € L2 такие, что ] Х{ || < || ||+е/2, || х21| < || L21|-|-е/2, откуда ||x1+x2||<||L1||+||L2|| + e. Тем более
inf ||х|| = inf hi + *2ll<llLill + IIM+6»
x€Li+L2 x2eL2
т. e.
||Lf-f-L2|| < ||Lj|| + ||L2||-f-e.
Вследствие произвольности e отсюда получаем
H1 + L2||<||L1|| + ||L2||.
III. Если X=0, то для любого L имеем
||UH||Lo|| = O=|X|.||L0.
Пусть X+=0. Тогда
||XL|| = inf||Xx||=|X|-inf||x|| = |X|-||L||.
xeL xeL !
Если X—полное, т. е. банахово, пространство, то X/Lo также банахово. Чтобы показать это, установим следующее: для того чтобы Ln—>~L в смысле сходимости по норме в пространстве X/Lg, необходимо и достаточно, чтобы существовала последовательность {х„}, xn£Ln такая, что хп->-х, x£L.
□ Пусть ||L„—L||-*0, т. е. ||L„—L|| = e„, где е„-> 0. Тогда в Ln— — L найдется элемент х'а—уп, х'п £ Ln,yn € L такой, что || х'п—уп || < 2е„. При этом вместо уп можно взять любой фиксированный (не зависящий от п) элемент x£L. В самом деле, из последнего неравенства следует ||(х^—уп + х)—х|| < 2е„, и так как х—yn£Lg, то х„=х;+(х—yn)£Ln и мы получим ||х„—х|| < 2е„-^0, xn£Ln, x^L.
Пусть, обратно, существует последовательность {х„}, xn^Ln такая, что хп—*-х, x£L. Так как ||L„—inf ||f/„—f/|K Уп е Ln, у 6 L
Теперь нетрудно доказать полноту X/Lo.
□ Пусть {£„}—сходящаяся в себе последовательность классов пространства X/L9. Выбирая в каждом классе Ln по элементу х„ так, чтобы || хп—xm||<2||Ln—LOT||, получим сходящуюся в себе по
66
следовательность элементов из X. Так как X—полное пространство, то существует элемент х£Х такой, что хп-+х. Но-тогда £ —►£, где L — класс, содержащий элемент х. Ц
" Наконец, отметим, что декартово произведение конечного числа нормированных пространств Хх, Х2, ..., Хп можно нормировать, если, например, для х = (хг, хг, .... х„) положить ||xj=|ki||+||х21| + + • • • + II Хп II-
Пусть Xf и Х2—ЛНП. Будем в дальнейшем называть эти пространства изоморфными, если существует взаимно-однозначное и взаимно-непрерывное изоморфное отображение Xt на Х2. Имеет место следующая важная теорема.
Теорема 1. Все конечномерные ЛНП данного числа измерений п изоморфны евклидову п-мерному пространству R" и, следовательно, изоморфны друг другу.
□ Пусть X есть n-мерное ЛНП и ап а2, ..., ап—базис этого пространства. Тогда любой элемент х£Х однозначно представим в виде
X—Ч” ^2^2 Ч” • • • ЧК0»*
Поставим элементу х 6 X в соответствие элемент х= & , В„) С R".
Очевидно, что установленное таким образом соответствие между элементами х и х является взаимно-однозначным. Кроме того, это соответствие есть изоморфизм линейных пространств X и R”. Покажем, что оно взаимно-непрерывно.
Для любого х £ X имеем
П / п Х1/2 f п Х1/2
i = 1 \i = 1 / v = 1 /
В частности,
Ik—
(1)
(2)
где р не зависит от х и у.
Установим теперь неравенство противоположного знака. На п
поверхности S единичного шара У =я 1 пространства R" рассмотрим функцию
f W — f (£1> ?2> • • • > ?л) — II х II —
п
I =1
Так как на S все не могут одновременно обращаться в нуль, то в силу линейной независимости а1У а2, аП имеем /(gx, g2, • • •, £„) > 0. Неравенство
1/(61, Ъ, --..U—112, Ч,)1 =
= I Ik II—Ik IIК Ik—у IK Р || х—у ||
показывает, что f (Blt |2, — непрерывная функция. По тео
3* 67
реме Вейерштрасса, эта функция достигает на S своего минимума а. Легко- видеть, что а > 0. Следовательно, для x^S имеем /(х) = =||х[|^а, откуда для любого x£R" находим
Из неравенств (1) и (3) следует взаимная непрерывность отображения X на R". Д
Из гомеоморфизма X и R" вытекает, что в конечномерном банаховом пространстве сходимость по норме сводится к покоординатной сходимости и поэтому такое пространство всегда полное.
3. Задача о наилучшем приближении. П. Л. Чебышев исследовал задачу о наилучших приближениях функций линейными комбинациями заданных функций. С учетом принятой здесь терминологии это были аппроксимации в прост* ранствах С [а, Ь], Ь2 и т. п.
Рассмотрим задачу о наилучшей аппроксимации произвольного элемента х нормированного пространства X линейными комбинациями заданной конечной системы линейно независимых элементов хъ х2, ..., Докажем, что задача о наилучшей аппроксимации разрешима. п
Лемма 2. При неограниченном возрастании 2 X? функция
i = l
□ Имеем <р (If, Х2, Хп)^ рывную функцию от параметров Xi,
п
^ixi t = l
Рассмотрим1 другую непре-
ф (Xi, Х2, Хл)—
п
На сфере 2 ^=1 пространства (являющейся компактным i = i
множеством) эта
функция достигает наименьшего значения р, которое положительно в си^у линейной независимости элементов xlt x2j .хп.
/п
2 $> (1/и)(й+||х||), то
величина ф (Хь Х2,
Теорема 2. Существуют вещественные числа X®, X®,
.., Х° такие, что при К; = K°i (t — 1,
п II
X — 2 Xi НМвет MUHUMyM
,, Хп) —
2, л).
68
□ Утверждение теоремы очевидно, если х линейно зависит от Xf, х$, ..., хп. Будем теперь считать, что х не лежит в подпространстве, порожденном элементами хх, х2, ...» хп. Прежде всего ясно, что ф (Хх, Х2, ...» Хд) есть непрерывная функция своих аргументов, что следует из неравенства
Iф(Л.1. •••. М—ф(м> Н2> •••> н»)1—
п
х ^ixi i = l
п
п
У Р-/) xi
i=l
я я
< 2 l^i—Rlh/||<max|%z~pH ||xz||.
i=1 1 i=l
л
В силу леммы ф (Хх, Х2, ...» IIхII вне некоторого шара Х?<г2. Так i=l
как этот шар компактен, то ф (Хх, Х2, ...» Хп) как непрерывная функция достигает на нем своего наименьшего значения v в некоторой точке (Хх, Х2, Хд). Но ¥«Сф(0, 0, 0) = ||х||. Поэтому v есть наименьшее значение функции
ф(Хх, Х2 Хл) во всем пространстве точек Хх, Х2, ХЛ. Ц
Линейная комбинация
Х?хх + Х2х2 + ... + Xrtxrt,
дающая наилучшую аппроксимацию элемента х, в общем случае не является однозначной. Для получения однозначности на аппроксимирующие выражения п
2 Х/х/ приходится налагать дополнительные условия. Так, в пространстве / = 1
С [0, 1] рассматривают системы функций, удовлетворяющие так называемому условию Чебышева. Однако можно указать некоторые пространства, в которых наилучшая аппроксимация всегда определяется однозначно.
Пространство X называется строго, нормированным, если при х Ф 0, у =£ О равенство ||* + #|| ==11*11 + 11 #11 возможно лишь при у=ах, где а > 0.
Нетрудно показать теперь, что в строго нормированном пространстве наилучшая аппроксимация определяется однозначно.
п
□ В самом деле, если существуют две динейные комбинации X?xz и
i
2 такие, что х— п= 1
п
я
У Х?Х/ = х— У р,?х/ =d, гдебЛ=ппп||х—У X/xz||>0,
i = 1 i= 1
то
Отсюда в силу строгой нормировацности пространства имеем
х— У fW = а(х— 2 )•
i=l \ i=1 /
Если бы а Ф 1, то х было бы линейной комбинацией элементов хх, xg, хд?
69
что, по предположению, исключается. Поэтому а—1, а тогда 2 М—Р?)х/ = 0, i = 1
откуда в силу линейной зависимости элементов xz- (t = 1, 2, ..., п) следует, что X? = |x? G=h 2,
Примерами строго нормированных пространств могут служить Lp [О, 1J и 1р для р > 1. Пространство С [0, 1] не является строго нормированным. Чтобы убедиться в этом, достаточно рассмотреть две неотрицательные линейно независимые функции х (/), у (t)£C [О, 1], имеющие максимальные значения в одной и той же точке отрезка [0, 1]. Для таких функций очевидно, что ||х+^|| = = 1И1 + 1Ы1> хотя у £ ах.
§ 2. КОМПАКТНЫЕ МНОЖЕСТВА В ЛИНЕЙНЫХ НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
1. Компактность и конечномерность. Так как линейное нормированное пространство является метрическим, то все утверждения, относящиеся к компактным множествам метрических пространств, остаются справедливыми для ЛНП. Наличие в ЛНП алгебраической структуры позволяет установить некоторые новые результаты.
Метрическое пространство X называется локально компактным. если всякое ограниченное и замкнутое множество этого пространства компактно.
Теорема 1. Для того чтобы ЛНП X было фокально компактным, необходимо и достаточно, чтобы оно было конечномерным.
□ Необходимость. Предположим, что каждое ограниченное и замкнутое множество элементов из X компактно. Возьмем в X произвольный элемент такой, что || || = 1. Обозначим через Li подпространство, порождаемое элементом хг. Если L1==X, то теорема доказана. Если же не совпадает с X, то согласно лемме Рисса в X найдется элемент х2 такой, что ||х2 —xill^ V2, ||х2||==1. Обозначим через £2 подпространство, порождаемое элементами хх и х2. Имеются две возможности: либо L2 — X и теорема доказана, либо L2 не совпадает с X. Тогда согласно лемме найдется элемент х3 такой, что ||х3—1/2, ||х3— х2||> 1/2, ||х3||= 1.
Продолжим этот процесс. Тогда можно сделать два предположения: либо Ln для некоторого п совпадает с X и теорема доказана, либо мы построим бесконечную последовательность {хД такую, что ||хд||==1 и Цх^—xJ|>l/2 при п^т для любых т и и. Но вторая возможность отпадает, так как она означала бы существование ограниченного замкнутого (||хл1| = 1) и некомпактного (||хя — 1/2 при п-=£т} множества, что противоречит условию
теоремы.
Достаточность. Пусть X есть м-мерное пространство. Тогда X гомеоморфно n-мерному евклидову пространству Ограниченное и замкнутое множество М с X взаимно-однозначно и взаимно-непрерывно преобразуется в ограниченное и замкнутое множество М cz и так как М в R" компактно, то М в X также компактно. ~ I
2. Критерий компактности в С{0, 1]. Функции из некоторого' множества М а: С [О, 1J называются равномерно ограниченными, если «
70
существует такая постоянная а, что | х (t) | а для всех x(f)£M при любом / С [0, 1], и называются равностепенно непрерывными, если для любого е > 0 существует 6 > 0, зависящее только от такое, что для любых и /2 из [0, 1], удовлетворяющих неравенству |^1 —/2|<б, и для любой функции х(0 из рассматриваемого множества имеет место соотношение {х (О—х(^2)|^е.
Теорема 2 (Арцела). Для того чтобы множество К cz С [0,1 ] было бы относительно компактным, необходимо и достаточно, чтобы функции х (/) были равномерно ограничены и равностепенно непрерывны.
□ Необходимость. Пусть К относительно компактно. Равномерная ограниченность функций х (/) С К вытекает из полной ограниченности, а следовательно, и ограниченности К в смысле нормы в пространстве С [0, 1]. Докажем равностепенную непрерывность функций х (/) С К- Построим для заданного е > 0 конечную е/3==сеть {хДО, х2 (t) ..., xk(t)} для К. Так как функции х{ (f) непрерывны на [0, 1], то они равномерно непрерывны на этом отрезке.
Для каждой функции х,- (Z) подберем число б,- так, чтобы | х(- (/г) — — х(-(Q | < е/3 при |/г —/2|<б;, каковы бы ни были tt, /2£[0, 1]. Пусть б —наименьшее из чисел 6(-(i = l, 2, ..., k). Если теперь Pi — /2| < б, то для любой функции х(0€/< имеем
| х (О - х (/2) | < max J х (0 -х,- (01 +1 х,. (tt) —Xi (Q | +
+ шах | Xi (t) — x (01 <2p (x, xz) + e/3. о < t < i
Если выбрать x, (0 так, чтобы p (x, x,) < e/3, to |x(^)—x(/2) | < e. Так как e > 0 произвольно и полученная оценка не зависит от положения точек tx и t2 на [0, 1] и от выбора функции x(t) в К, то равностепенная непрерывность функций, принадлежащих множеству К, доказана.
Достаточность. Включим пространство С[0, 1] в более широкое пространство М [0, 1] ограниченных на [0, 1] функций с метрикой р(х, у) = sup |х(/)— y(t) |. Сходимость в пространстве М[0, 1] является равномерной на [0, 1], и так как предел равномерно сходящейся последовательности непрерывных функций есть также непрерывная функция, то С[0, 1J —замкнутое подмножество пространства At [0, 1]. Поэтому если какое-либо множество КсС [0, 1] окажется относительно компактным в пространстве М [0, 1], то оно будет относительно компактным и в С [0, 1], поскольку пределы последовательностей функций этого множества не могут выйти из пространства С[0, 1].
Возьмем произвольное число е > 0; пусть б>0 — число, соответствующее данному е в условиях теоремы Арцела. Разобьем отрезок [0, 1] точками деления — G < t± < t2 < ... < tn_1 < tn= 1 на части так, чтобы выполнялось неравенство max | — 1 < б,
и зафиксируем эти точки деления.
71
Возьмем любую функцию х (/) € К и поставим ей в соответствие ступенчатую функцию x(t), определенную следующим образом:
- I *(^-1)при (i = l, 2, п-1),
Х I х (tn_^ при /„_!< t<t„. .
Так как на каждом отрезке [/;_$, f,] колебание функции х(0 меньше е, то р (х, х) = sup | x(t)- x(t) | < e и, следовательно, множе-
ство N, составленное из всех функций х (t), соответствующих х (0 € в пространстве Л4[0, 1] образует е-сеть для множества Д'.
Рассмотрим теперь множество N ступенчатых функций x(t). Каждая ступенчатая функция х (0 £ N однозначно определяется п числами — своими значениями в фиксированных точках ^,_i(t = l, 2, .... n). Принимая эти числа за координаты точки из п-мерного евклидова пространства R", установим взаимно-однозначное соответствие между множеством N и некоторым множеством Р с. Множество Р ограничено, так как для любой точки г £ Р
Р (г, 0) = "j/'.Z [* (h-1)]2 < a Vn=alt
где через а обозначена постоянная, ограничивающая модули функций х (/) £ К. Так как Р — ограниченное множество n-мерного евклидова пространства, то Р относительно компактно. Но тогда относительно компактно и N в смысле равномерной сходимости на [0, 1]. В самом деле, если {zn\аР и хп (0 6 М — функции, соответствующие г„, то
Р Схп, хт) = sup | хп (ti-J - хт | С i
/п
[Xn (^i-1) хт (^-1)]2 = Р (гл» Zm)'
Поэтому сходимость последовательности {z„}c:P влечет за собой равномерную сходимость соответствующей последовательности {x„(t)\ciN и относительная компактность множества NcM[0, 1] доказана.
Итак, для множества К. равномерно ограниченных и равностепенно непрерывных функций мы построили в М [0, 1 ] относительно компактную е-сеть. Но тогда Д также относительно компактно в М[0, 1], а следовательно, и в С[0, 1] и достаточность теоремы Арцела доказана. Н
Доказанная теорема допускает обобщение на случай отображений компактных множеств в компакты.
Пусть даны два метрических пространства X и У и множество F отображений f пространства X в пространство Y. Отображение f С F называется ограниченным, если для любого х € X справедливо неравенство р(/(х), 0)^Пу, где 0—некоторый фиксированный эле-72
мент пространства Y и af — постоянная, зависящая, вообще говоря, от отображения f.
Отображение f g F называется равномерно непрерывным, если для любого е > 0 найдется 6 > 0 такое, что р (/ (xj, f (х2)) < е для двух любых точек xt и х2 пространства X таких, что р (Xj-, х2)<б.
Пусть М (X, Y)—множество всех ограниченных отображений пространства X в пространство Y. Превратим М (X, Y) в метрическое пространство, полагая р(/, <р) = supp (/(х), <р(х)). Легко X
проверить, что все аксиомы метрики выполняются. Сходимость в пространстве М (X, Y) есть равномерная на X сходимость последовательности отображений {fn (х)} а М. (X, У) к отображению f (х) € М (X, У).
Если Y — полное пространство, то М (X, Y) также полное пространство.
□ В самом деле, если р (/„, fe) —* 0, когда п, т->- оо, то для любого е > 0 найдется номер п0 (е) такой, что
Р (fn (х), fm (х)) < в (1)
при п, т"^п0(ъ) и сразу для всех х£Х..Фиксируем х£ X. В силу полноты пространства Y последовательность {fn (х)}, сходящаяся в себе, сходится к некоторому элементу y£Y. Полагая f(x) = y= —lim/:„(x), получаем некоторое отображение пространства X в про-
странство Y.
Переходя в неравенстве (1) к пределу при т-^-оо, получим p(f„(x), /(х))<^8 при п^п0(е) и сразу для всех х£Х, откуда следует, что f£M(X, Y) и что fn(x) —> f (х) равномерно на X.
Ооозначим через С (X, Y) множество всех равномерно непрерывных отображений из М (X, Y). Легко убедиться, что предел равномерно сходящейся последовательности равномерно непрерывных отображений есть также равномерно непрерывное отображение, откуда вытекает, что множество С (X, Y) замкнуто в пространстве М(Х, У).
Введем, наконец, еще одно определение. Отображения f, входящие в некоторое семейство Q с С (X, У), называются равностепенно непрерывными, если для любого е > О найдется б > 0, зависящее лишь от 8, такое, что p(f(xi)> /(хг))<е ПРИ Р (*i. хг) < б сразу для всех f € Q и независимо от выбора точек хъ х2 £ X.
Теорема 3. Для того чтобы цз семейства Q непрерывных отображений компактного множества X в компакт У можно было выделить равномерно сходящуюся последовательность, необходимо и достаточно, чтобы отображения семейства Q были равностепенно непрерывны.
Мы докажем лишь достаточность сформулированного условия.
□ Прежде всего заметим, что У как компакт есть ограниченное множество и, следовательно, все отображения семейства Q равномерно ограничены. Поэтому Q с М (X, У). Так как С (X, У) замкнуто в М (X, У), то для доказательства относительной ком
73
пактности Q в С (X, Y) достаточно установить его относительную компактность в М. (X, Y).
Для произвольного е>0 выберем 6>0 так, чтобы
р(Ж), /(х"))<е/2 (2)
при р(х', х") < 6 сразу для всех / С что возможно в силу равностепенной непрерывности отображений. Возьмем затем конечную 6/2-сеть хь х2, ..., хп в множестве X. Введем множества
Х; = К(хь б/2)\ и К(х7, 6/2).
z < »'
Эти множества не пересекаются, дают в сумме все X, и диаметр каждого X,- не превосходит 6. Пусть, далее, у1( у2.......уп есть
е/2-сеть для компакта Y. Рассмотрим всевозможные функции g (х) € € М (X, Y), принимающие на множествах Х{ постоянные значения у,-. Эти функции образуют конечную е-сеть для множества Q. В самом деле, возьмем любое отображение Для произвольного х 6 X и любой функции g (х) имеем
Р (/(^). g(x))<ptf(x), Ж)) + Р(/(*Л g(xz)) + p(g(*/), g(X'j),
где х; выбрано так, что х £ Х{. Учитывая соотношение (2) и принадлежность х и х(- одному и тому же X,-, имеем р (/ (х), f (х^) < е/2, Р (£(*)» £(•*<•)) = 0, откуда * >
Р (/ СО, g СО) < е/2 + р (/ (х,-), g (х^). ,
Выберем теперь g(x) так, чтобы g(x^ = yf удовлетворяло неравенству p(/(xz), yj) < е/2. Тогда для любого х£Х имеем р(/(х), g (х)) < е и, следовательно, р (/, g) = sup р (f (х), g (х)) е. Так как
X
Q — подмножество полного метрического пространства имеющее конечную е-сеть, то Q относительно компактно. £|
3. Критерии компактности в Lp[0, 1]. Пусть x(f)£Lp[0, 1]. Продолжим функцию х (0 за пределы отрезка [0, 1 ], полагая х (0 = 0, если t лежит вне этого отрезка. Тогда для любого отрезка [а, />]
ь ь
числовой прямой интегралы J | х (0 | d/ и | х (0 d£ имеют смысл. а а
Теорема 4 (М. Рисса). Для того чтобы семейство функций К = {х (t)} с: Lp[0, 1] было относительно компактно, необходимо и достаточно, чтобы функции семейства были равномерно ограничены по норме и равностепенно непрерывны в среднем, т. е. чтобы:
1°) $|x(0|pd/ <с?-, о 1
2°) | х (t + h) — х (t) d/ < гР при 0 < h < 6 (е) сразу для всех
о
функций семейства.
74
□ Необходимость. Очевидно, что условие Г выполняется. Докажем выполнение условия 2°. Так как К— относительно компактное множество, то при любом е > 0 для этого множества существует конечная е/3-сеть хг (t), x2(f), .... xn(f). Поскольку каждая функция из Lp [0, 1] непрерывна в среднем, для любого i найдется б, такое, что
1
$ | х( (t + h)~ Xi (t) f d/ < (8/3)* о
при 0</г<6г. Пусть 6 = min6l-. Тогда
i
^\Xi(t + h)-Xi(t)\»dt< (e/3)* о
при 0 < h < 6 и для всех i = 1, 2, ..., n.
Возьмем произвольную функцию х (t) £ Д'. Найдется функция х{ (0 такая, что
1
$|х(0-хг(0|^/<(е/3)*. о
При 0 < h < б имеем
/ > \’/р / • \ i/р
( $\ХУ+Н)—x(0|*dM <( $|х(*4-Л)—x/(f4-/i)p’dH + / \о /
/1 \Vp /I \i/p
\о / \о /
/ 1 \ 1/р
< [\\x(t + h)-Xi(t+h)\Pdt} X О /
Но
1 1
J |х(/ + Л)—Xi(t + h) |*d/= $ |x(s)—x{(s) |pds 0 h
i
< $ | x (s) — X; (s) \p ds < (e/3)* о
(здесь мы воспользовались тем, что x(t) и х;(0 равны нулю вне [О, 1]). Из последних двух неравенств следует, что
/ 1 \ i/р
($|х(г+/О—x(Ofd/) <8 \0 /
при 0 < h < б, и так как х(0 —любая функция из К, то необходимость условия 2° доказана.
75
Достаточность. Рассмотрим средние функции СТекЛова /+й
хл (£) = JL J х (t) dt. Имеем t-h
!**(*+«)—*л(01=^
х (т + u) dr — у х (т) dr
t + h
J |x(r + u)-x(T)|dT<
7 Z-h
/ 1 \i/p %
<(b)1/P( J|*(t + «) — х(х)|'(1т) . (4)
\o /
Из условий Г и 2° и неравенств (3) и (4) следует, чтЪ при фиксированном h функции семейства {хЛ(0} для x(t)£K равномерно ограничены и равностепенно непрерЫЬны. Следовательно, семейство {хА(0} относительно компактно в смысле равномерной сходимости, а тем более в смысле сходимости в среднем с показателем р. С другой стороны,
t+h
|*(0—j |х(0—x(x)|dx«
Z-h
Л , h ' 1/р
= У |х(0—^(^ + T)|dx< Ш1/Р( J |*(0-*(* + t)|'dx\ .
-Л \-й /
Отсюда
1 1
yix(o-xA(o^d/<iJ о о
|х(/)-^х(^4-т) dr
h
dr < гР С dr =* е^, 2h J ’
-Л
1
так как (в силу условия 2°) $ | х(£ + т) — х(£) И* d£ < если |т| < 6. о
76
Тайим образом, семейство {Xh (0} образует е-сеТь для семейства К, и так как эта е-сеть относительно компактна, то согласно следствию из Теоремы Хаусдорфа относительно компактно и само множество К. Н
Приведем без доказательства еще два критерия компактности множеств в пространстве [0, 1].
Теорема 5 (А. Н. Колмогорова). Множество KcLp[Q, 1] относительно компактно тогда и только тогда, когда:
1°) нормы функций ограничены в совокупности;
2°) для любого е>0 найдется б>0 такое, что ||х—xh || < е при h<Z б сразу, для всех функций х (f) £ К.
Будем говорить, что семейство функций M=s{x(t)} имеет равностепенно абсолютно непрерывные нормы, если для каждого е > 0 можно указать 6>0 такое, что ||х(0%в(0||< 6 всякий раз, когда mesE < б (здесь Ха(0 ^-характеристическая функция множества £).
Теорема 6 (М. А. Красносельского). Пусть семейство KcLp[0, 1] имеет равностепенно абсолютно непрерывные нормы и относительно компактно в смысле сходимости по мере. Тогда это семейство относительно компактно в смысле сходимости в Среднем.
4. Критерий компактности в 1р.
Теорема 7. Для компактности замкнутого множества КаЛр необходимо и достаточно, чтобы множество К было ограничено и чтобы для любого 8 > 0 существовал номер п0, зависящий лишь от е,
00
такой, что У [gj? < е? для п^па и для любого x = {^it g2, ...
1 = П+1
.... •••}€/<.
□ Докажем достаточность этого условия; доказательство Необходимости рекомендуем провести самостоятельно.
е»;
Пусть 8 > 0 произвольно, выберем п так, чтобы 2 l = rt + 1
для всех х£/С, и зафиксируем такое п. Для х = {|1( ..., |й, ^„+1, •••}€# положим .....1п, о, О, ...}. Очевидно,
1!х—х»11<е и Кп = {х„|хСК} есть 8-сеть для К. Каждому х„£Кп поставим в соответствие элемент хп пространства /£”, имеющий те же координаты, что и первые п координат элемента х. Это соответствие взаимно-однозначно и взаимно-непрерывно. Пусть Кп=
Легко видеть, что Кп—ограниченное и замкнутое множество конечномерного пространства и, следовательно, компактно. Но тогда компактно и Дп. Таким образом, для произвольного 8 > 0 мы построили компактную е-сеть для К и компактность доказана. Ц
§ 3. АБСТРАКТНОЕ ГИЛЬБЕРТОВО ПРОСТРАНСТВО
1. Основные понятия. В n-мерном вещественном (комплексном) векторном пространстве R" (С") помимо операций сложения векторов и умножения вектора на вещественное (комплексное) число
77
определено скалярное (или внутреннее) произведение векторов этого пространства. Именно, скалярное произведение векторов х(|х, |2, £„) и y — (y\i, Лг- • ••, Ли) пространства R" есть число
И
<х, у> = 2 Вл1|- Норма (или длина) вектора х = (£х, g2, ..., g„) выражается через скалярное произведение следующей формулой:
2|^-12=/<х, х>.
В анализе широко применяется скалярное произведение функций. Поэтому естественно рассмотреть класс линейных пространств, в которых определено скалярное произведение элементов. Такие пространства называются гильбертовыми и задаются с помощью следующих аксиом.
Пусть Н—множество некоторых элементов х, у, г, ... . Предположим, что:
I. Н — комплексное линейное пространство.
II. Каждой паре х и у элементов из Н поставлено в соответствие комплексное число <х, «/>, называемое скалярным произведением этих элементов, удовлетворяющее условиям;
Г. <х, «/>=»<{/, х> (в частности, <х, х> —вещественное число).
2°. <хх + х2, г/>=<хх, #> + <х2, у>.
3°. <Хх, у~> = А <х, у> для любого комплексного числа А.
4°. <х, х> 0, причем <х, х> = 0 тогда и только» тогда, когда х = 0; число ||х|| = К<х, х> называется нормой элемента х. Ниже (см. с. 79) будет показано, что эта величина удовлетворяет всем требованиям нормы линейного нормированного пространства.
III. Н полно в смысле метрики р(х, у) в||х— г/||.
При выполнении этих трех аксиом множество Н будем называть унитарным пространством. Отметим, что n-мерное унитарное пространство есть комплексное евклидово пространство. Если пространство Н удовлетворяет, кроме того, следующей аксиоме:
IV. В Н для любого натурального числа п найдется п линейно независимых элементов, т. е. Н является бесконечномерным, то оно называется абстрактным гильбертовым пространством; в дальнейшем мы будем называть его просто гильбертовым пространством.
Примеры. 1. Комплексное пространство /2 становится гильбертовым, если для любых двух его элементов x = {gx, ...} и у = {г]х, т)2.•••}
ОО
положить <х, !/>= 2 Сходимость этого ряда для любых х и у из /2 выте-i = 1
кает из неравенства Буняковского для рядов.
2. Рассмотрим комплексное пространство L2, р [0, 1]- Это пространство комплексных функций, определенных и измеримых на отрезке [0, 1] и таких, что t
J р (0 | х (/) |2 d/ < оо, где р (/) вещественно и р (/) ^ О почти всюду на [О, 1], о
78
причем р(0>0 на множестве полной меры. Пространство L2t р [0, 1] станет гильбертовым, если для х, у£Ь2, р [0, 1] положить
1
<Х, о
Существование этого интеграла при любых x(t) и у (t) из р [0, 1] вытекает из неравенства Буняковского для интегралов. В частности, при р (/) = 1 получаем комплексное пространство L2 [0, 1] со скалярным произведением <х, i/> = 1
= Jx(07(0 dt.
о
Аналогично определяется вещественное гильбертово пространство. При этом скалярное произведение двух элементов должно быть вещественным.
Вещественные пространства Z2, L2, L2 р являются вещественными гильбертовыми пространствами.
Рассмотрим некоторые простейшие свойства гильбертовых пространств.
Прежде всего из аксиом I—III легко выводим, что
<Х, У1 + Уг>=<Х, У1> + <Х, у2У, <Х, КуУ = 1<Х, уУ.
Из последнего равенства следует, в частности, что 11МНМ-1И- (I)
Установим теперь для скалярного произведения неравенство Буняковского —Шварца. Для любых х, y<zH, любого ком-
плексного X имеем <х+Ху, х + ку'у^О, или
<х, хУ + К<х, уУ + Х<у, хУ + \\\г<у, yy^Q.
Полагая , получаем
или
|<+г/>К||х||-||г/||, (2)
что и представляет собой требуемое неравенство. Для случая y — Q неравенство (2)"тривиально.
Далее, получаем
II * + «/II2 =<* + #> х + уу = <х, ХУ + <х, УУ + + <У, ХУ + <у, УУ < Ц х ||а + 2II х j • II у 11 + II у II*, или h+z/IKM+kll- (3)
Из аксиомы II и формул (1) и (3) вытекает, что введенная с помощью скалярного произведения норма удовлетворяет всем аксио
79
мам нормы ЛНП, а следовательно, определяемое этой нормой расстояние удовлетворяет всем аксиомам метрического пространства.
Легко доказывается следующее предложение.
Лемма 1. Скалярное произведение есть непрерывная функция относительно сходимости по норме.
□ В самом деле, дусть хп —> х и уп -+ у. Тогда числа ||х„|| и || уп || ограничены; пусть М — их верхняя граница. Имеем
I <хп, упУ - <х, уУ К | <х„, упУ - <хп, уУ | +
+1 <х„, У>-<х,у>1 = 1<х„,у„-у>1 + '
+ \<хп -х, уУ | < || хп || • || уп — у|| + +K-M1.!/KM|!z/,,-t/||+||«/ii -h„-x||.
Так как ||х„—х||—>0 и ||уп —1/||—*0 при п—> оо, то и
I <•*„>{/„> — <х, г/>|—*0 при п—>оо. Л
2. Ортогональность. Два элемента х, у £Н называются ортогональными (в этом случае записывают х _]_«/), еели <х, г/> = 0. Элемент х называется ортогональном подпространству LcH, если х ортогонален любому элементу y£L. В этом случае записывают х J_L.
Имеет место следующая весьма важная теорема».
Теорема 1. Если X£Н U L—некоторое подпространство Пространства Н, то
х = у + г, f (4)
где y£L и г J_L. Указанное разложенце единственно.
□ Если х£А, то, очевидно, у = х, г = 0. Предположим поэтому, что x(£L. Пусть d— inf [|х — у||а и {«/„} —последовательность из L yeL
такая, что dn — || х — уп ||а —► d при п—*оо. Пусть, далее, /г —любой элемент из L, отличный от нуля. Тогда yn + sh£L для любого комплексного е и поэтому ||х —(r/„ + e/t)||a т. е.
к — УЛ* — е<х~уп, hy — s<Ji, х — yrt>-|-|e|a-||ft||a>d.
Полагая е = <х, подучаем
1х — уп ||а —1 <х > 4» или \<х^-уп, й>|а<кЛ3(^-<0,
откуда
\<х-уп, й>|<ЙА||/ап—d. (5)
При /г = 0 неравенство (5) также, очевидно, выполняется. Из этого неравенства для любого h^L следует
\<Уп — Ут, hy\^\<yn — x, hy\-\-\<yn-x, hy « ^(/d^d + /d7Id)k|l
ЭД
и, полагая, в частности, h=^yn—ут, получим
Я Уп—Ут II < Vdn—d + Vdm—d.
Поэтому последовательность {//„} сходится в себе, а значит, в силу полноты Н и к некоторому элементу у£Н. Так как L замкнуто, то у£L.
Переходя к пределу в неравенстве (5), получаем, что <х—у, h>=0, и так как Л —любой элемент подпространства L, то x—yJ_L. Полагая х — у = г, получаем требуемое равенство №t/ + z.
Остается доказать единственность этого представления. Пусть х=*уА-2 = у'+?', где у, y'eL, а г, z'J_L. Тогда у — у'—г'—г и
И«/— /112 = <2'— г, у—У> = 0, (6)
поскольку y—y'^L, a г'—z J_L. Но равенство (6) означает, что у = у', следовательно, также z=*z'. Н
Элемент у в разложении (4) называется проекцией элемента х на подпространство L. Легко видеть, что совокупность М всех элементов, ортогональных подпространству L, есть также подпространство; в самом деле, очевидно, что М—линейное многообразие, а его замкнутость следует из непрерывности скалярного произведения. Поэтому можно сказать, что элемент г разложения (4) есть проекция элемента х на подпространство М. Это подпространство М называется ортогональным дополнением к подпространству L и обозначается Н — L; говорят также, что Н есть ортогональная сумма подпространств L и М, и пишут H = L + M.
Очевидно, ортогональная сумма есть частный случай прямой суммы. Доказанная теорема дает, таким образом, разложение элемента на проекции на два взаимно дополнительных ортогональных подпространства.
Лемма 2. Для того чтобы линейное многообразие М было всюду плотно в Н, необходимо и достаточно, чтобы не существовало элемента, отличного от нулевого и ортогонального всем элементам многообразия М.
□ Необходимость. Прежде всего очевидно, что из х_|_2И следует #JLA4. Но, по условию, М = Н и, значит, х\_Ц, в частности xj_x, откуда следует, что х = 0.
__Достаточность. Пусть М не всюду плотно в Н. Тогда М -^=Н и существует элемент х(£М. По предыдущей теореме имеем х=;у-1-г, где у^М, z М, и так как х(£М, то z#=0, но это противоречит условию. Ц
3. Ортонормальные системы. Система е1; е2, ..., е„, ... элементов пространства Н называется ортонормальной, если <е„, ет> ffl, где 6„, т—известный символ Кронекера, равный единице при п = т и нулю при п^т.
Примером ортонормальной системы является система (п = 0, ±1, ±2, ...) в комплексном пространстве L2[0, 1].
81
Бесконечная система элементов линейного пространства называется линейно независимой, если любая конечная подсистема этой системы линейно независима.
Любую систему й1( й2, ..., hn, ... линейно независимых элементов можно превратить в ортонормальную с помощью следующего процесса ортогонализации Шмидта.
Полагаем е1 = Л1/ЦЛ1Ц. Пусть g2 ~h2—с21ек. Подберем число с21-так, чтобы g2 было ортогонально et. Очевидно, для этого следует взять с21 = </i2, 6j>. Полагаем ea=g2/|]g2||; при этом ||g2||#=0, так как в противном случае g2 = 0 и элементы /ц и й2 линейно зависимы, что противоречит условию. Пусть elt е2, ..., уже построены. Возьмем
fe-i gk -h-k S ckiei i = 1
и подберем числа cki так, чтобы £ьбыло ортогонально ef, е2, ek.if для чего следует взять cki = <_hk, е^. Полагаем eft = gfe/||g’ft||, причем снова ||g*|| у- 0, и т. д.
Пример. Если совокупность степеней 1, t, t2, .... tn ортогонализировать в вещественном пространстве L2f р [а, Ь] функций, суммируемых с квадратом с весом р (/), то мы придем к системе многочленов р0 (/) = const, pi(/), р2 (0> ••• ..., Рп (0> ••• ортогональных с весом р (/):
ь
J Р (0 Рп if) Рт (О d? = §пт*
а I
При р (/) = 1, а = —1, 6 = 1 мы придем с точностью до постоянных множителей к системе многочленов Лежандра; при р(/)=е-*2, а — —оо, 6 = 4-оо — к системе многочленов Чебышева—Эрмита; при р(/)_е~*, а = 0, 6 = оо—к системе многочленов Чебышева—Лагерра.
Пусть L—подпространство, порожденное ортонормальной системой е19 е2, ..., еп> ..., и x£L. Для любого г > 0 существует, сле-п II п II
довательно, линейная комбинация У a,et такая, что х — 2.<azez <6-
Но
где с,= <х, е;>.
Числа с, называются коэффициентами Фурье элемента х относительно ортонормальной системы {еД. Из последнего равенства получаем
х— 2 aie<
2 П П
=И2-2К12+2|«,—с.-12.
i = 1 i = 1
82
п
Отсюда следует, что норма разности х— У а(ег принимает наи-1 = 1
меньшее значение, когда коэффициенты az являются коэффициентами Фурье элемента х относительно системы {ez}. В этом случае имеем
2 П
=М2-£Ы2<8 i -1
(7)
и так как е можно выбрать сколь угодно малым, то п 00
х = lim 2 cfit — У с£о п -> оо i = 1 1=1
оо
Из формулы (7) следует также, что ряд У | ct |2 сходится, причем 1 = 1
S 1с-12==И2-
i = 1
Пусть теперь х—любой элемент пространства Н. Обозначим оо
через г проекцию х на L; тогда г = У с.е,-, где с; = <г, ez> =* <х, е .> 1 = 1
И У к||2 = [1г112’ Так как x = z/4-z, z£L, у то
И2=И2+Ы2>И2- . •
Следовательно, для любого элемента г из Н справедливо неравенство
ik.-pckh (8)
где с;- = <х, е,-> (t — 1, 2, ...). Это соотношение называется неравенством Бесселя.
4. Замкнутость в смысле Стеклова. В. А. Стеклов, исследуя вопрос о разложимости функций по ортогональным системам, ввел важное понятие замкнутости системы.
Пусть в пространстве Н дана ортонормальная система элементов {ej. Если не существует элемента х£Н, отличного от нулевого и ортогонального всем элементам системы {е(}, то эта система называется полной. Ортонормальная система {ej называется замкнутой, если подпространство L, порождаемое этой системой, совпадает с Н. Ряд Фурье по замкнутой системе, построенный для любого х^Н, сходится к этому элементу и для любого х£Н имеет место равенство Парсеваля—Стеклова
2^=м2. (9)
Замкнутая ортонормальная система называется также ортонормальным базисом гильбертова пространства.
83
Если ортонормальная система полная, то она замкнутая. В самом деле, в этом случае не существует элемента, отличного от нулевого и ортогонального линейному многообразию L, порождаемому системой. Но тогда в силу леммы 2 L = H и система замкнута.
Обратно: замкнутая ортонормальная система {ej полна, так как оо
дЛя такой системы ||х||а = 2 и если xj_e,-, т. е. с(-=0 (1=1,2,...), i = 1
то [|х|| = 0, что означает полноту системы (ej.
Примером полной ортонормальной системы является система тригонометрических функций Ltu , =-^sin/, —|=rcost,
f f ST Jr ST
-T~r sin 2t, ... в вещественном пространстве £2 [— л, л].
У л
Легко доказать существование полной ортонормальной системы в любом сепарабельном гильбертовом пространстве. Пусть О = = {gi, g2, ..., g„, ...} —любое счетное всюду плотное множество В пространстве Н, причем все gn (»—1, 2, ...) отличны от нуля. Полагаем ег = £i/||gi||. Пусть Lr—одномерное подпространство, порожденное элементом е1( И пусть gni — первый элемент множества G, не принадлежащий £1( а й2— проекция g„2 на Н — Lt. Полагаем е2 = й2/Ц й21|. ПусТь, далее, Lt—Подпространство, порожденное элементами et и ег, и пусть §Пз—первый элемент множества 6, не принадлежащий .£2, а й3—’проекция gnt на Н — Ь2. Полагаем е3 = й3/||h3[| и т. д. Получаем ортонормальную систему elt е2, ... ..., еп, ..., и Так как каждый элемент gn принадлежит некоторому Lm в силу построения этих подпространств, то подпространство, определяемое системой {е,}, совпадает с подпространством, определяемым системой (gj, т. е. с Н. При этом система (ej является счетной, поскольку если бы она содержала конечное число р элементов, то, как известно из линейной алгебры, в Н не существовали бы р 4-1 линейно независимых элементов, что противоречит аксиоме IV.
Если {е,}— полная ортонормальная система, ахи у—элементы из Н с коэффициентами Фурье, соответственно с{ и d{ (i = 1, 2, ...),
СО
то легко проверить, что <х, уУ = У сД.
5. Изоморфизм гильбертовых сепарабельных пространств. Пусть Я —сепарабельное гильбертово пространство, a (ej—полная ортонормальная система в этом пространстве. Если х —некоторый элемент из И, то этому элементу можно поставить в соответствие последовательность чисел {cz}, являющихся коэффициентами Фурье
оо элемента х по системе {еД. Как было показано выше, ряд У |cz|2 сходится и, следовательно, последовательность {с^, с2, ..., сп, ...} можно рассматривать как некоторый элемент х комплексного пространства Za. Таким образом, каждому элементу х^Н соответствует М
некоторый элемент х^/2, причем в силу условия полноты системы
IIх ||н — I ci I2 J — IIх llza,
(Ю)
где нижний значок показывает, в смысле какого пространства берется норма. Далее, очевидно, что если х£Н соответствует х£/2 и у соответствует у£12, то х ± у соответствует х ± у. Отсюда и из равенства (10) следует, что
11*-!/11я = 11*^-Й,-
(Н)
Пусть теперь г = {£(}—произвольный элемент иЗ /2. Рассмотрим
в Н элементы zn = У %,(ё{ (n = 1, 2, ...). При п> т имеем
l=m + 1
и потому ||гп—zm||—>0 при т, п—* оо. Таким образом, последо-вательноств {г„} сходится в себе в смысле метрики пространства Н и вследствие его полноты сходится к некоторому элементу г этого пространства. Так как
(г, е,.) = lim (г„, е;)^£;,
то коэффициентами Фурье элемента z по выбранной ортонормальной системе являются Как раз числа £(.. Таким образом, каждый элемент z£Z2 соответствует Некоторому элементу z£H. Тем самым мы имеем взаимно-однозйачное соответствие между элементами пространств Н и Z2.
Формула (11) показывает, Что это соответствие между пространствами Н и /2 есть изометрия. Кроме того, очевидно, что если х соответствует х, то Ах соответствует Ах; поэтому, учитывая ранее сказанное относительно сохранения операции сложения при рассматриваемом соответствии, получаем, что Н и /2 изоморфны. Таким образом, нами доказана следующая теорема.
Теорема 2. Всякое комплексное (вещественное) сепарабельное гильбертово пространство изометрично и изоморфно комплексному (вещественному) пространству 1г, и, следовательно, все комплексные (вещественные) сепарабельные гильбертовы пространства изомет-ричны и изоморфны между собой.
Отсюда, в частности, вытекает теорема.
Теорема 3 (Ф. Рисса —Фишера). Вещественные пространства L2 [0, 1] и 12 изометричны и изоморфны.
§ 4. ЛИНЕЙНЫЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
1. Определение и основные свойства линейных топологических пространств. Пусть X = {х, у, г, ..t, ..—множество элементов какой-либо природы.
85
Определение 1. Множество X называется линейным топологическим пространством (кратко ЛТГР, если:
I. X— линейное пространство.
II. X —топологическое пространство.
III. Структуры линейного пространства и топологического пространства согласованы в том смысле, что операции сложения элементов X и умножения элементов X на числа непрерывны в топологии пространства X.
Подробнее аксиома III означает следующее:
1°. Для любых двух элементов х, у£Х и любой окрестности их+у элемента x-j-y найдутся окрестности их и иу элементов х и у такие, что их + иу а их+у.
2° . Для любого числа а любого элемента х£Х и любой окрестности иах элемента ах найдутся число 6 > 0 и окрестность их элемента х такие, что ких с иах для всех X, удовлетворяющих неравенству |Х—а| < б.
Можно также сказать, что отображения (х, у)--+х + у и (X, х) —>Хх пространств ХхХ и АхХ, где Л —поле скаляров, в пространство X непрерывны в топологиях этих пространств.
В зависимости от того, является ли поле скаляров Л полем R вещественных чисел или полем С комплексных чисел, топологическое пространство X называется вещественным или комплексным.
Пусть х0 —фиксированный элемент ЛТП X h'G cz X —открытое множество. Тогда x0 + G также открытое множество. В самом деле, возьмем любую точку y£xQ-\-G так, что у==х0 + х, x£G. Тогда у—и так как множество G открыто, то оно является окрестностью точки у~~х0. В силу непрерывности сложения существуют окрестности иу и и{_Хо} точек у и —х0 соответственно такие, что иу + и(_Хо} с: G, в частности иу + (—xQ)a:G, т. е. uyc2X0+G. Это означает, что x0 + G открыто.
Аналогично, используя непрерывность умножения, можно доказать, что XG открыто для любого числа X^0 и любого открытого множества G.
Из доказанного следует, что если ^—окрестность точки х ЛТП X, то их—х есть окрестность нуля. Обратно: если и —окрестность нуля, то и + х есть окрестность точки х.
Таким образом, для того чтобы задать совокупность всех окрестностей всех точек ЛТП, а следовательно, и совокупность всех открытых множеств, т. е. топологию пространства X, достаточно задать совокупность всех окрестностей нуля этого пространства. Поэтому, по аналогии с заданием топологического пространства с помощью аксиом Хаусдорфа, можно наделить линейное пространство топологией путем задания совокупности окрестностей нуля. При этом, чтобы сложение элементов и умножение элемента на число оказались непрерывными, надо потребовать, чтобы окрестности нуля удовлетворяли некоторым дополнительным условиям.
Определение Г. Множество Х = {х, у, ..., /, ...} называется линейным топологическим пространством, если:
I. X —линейное пространство.
86
II. В X выделена непустая совокупность непустых подмножеств V = {u, v, ...}, удовлетворяющая следующим условиям:
1°. Каждое ugV—уравновешенное и поглощающее множество.
2°. Для любых и, и С V найдется wgV такое, что w с и пи.
3°. Для каждого и с V найдется v£V такое, что v-\-vcu.
Из того, что любое u£V — уравновешенное множество, следует, что 0 € и. Множества и, v, .. ,w, ... называются окрестностями нуля линейного топологического пространства X.
Сразу же расширим понятие окрестности нуля, называя окрестностью нуля в X любое непустое множество М а X, содержащее некоторое u£V. Ясно, что любая окрестность нуля —поглощающее множество.
Как и в произвольном топологическом пространстве, некоторая совокупность V окрестностей точки х называется фундаментальной системой (или базой) окрестностей этой точки, если для любой окрестности точки х найдется входящая в нее окрестность совокупности V. Из определения 1' ЛТП следует, что в нем существует база окрестностей нуля, состоящая из уравновешенных поглощающих множеств.
Окрестностью точки х ЛТП X называется всякое множество их вида и + х, где «—окрестность нуля пространства X.
Таким образом, окрестность точки х£Х—это сдвинутая на х окрестность нуля.
Прежде чем доказывать эквивалентность двух определений ЛТП, выведем некоторые следствия из аксиом определения Г.
Как обычно, непустое множество G ЛТП X будем называть открытым, если каждая точка xgG входит в это множество вместе с некоторой окрестностью. Отсюда следует, что открытое множество является окрестностью каждой своей точки.
Очевидно, что и при определении 1' объединение любого числа открытых множеств есть открытое множество, а с помощью аксиомы II легко проверяется, что пересечение конечного числа открытых множеств открыто.
Лемма 1. Всякая окрестность нуля содержит открытую окрестность нуля.
□ В самом деле, пусть и—окрестность нуля и и0—совокупность тех точек х£и, для которых и является окрестностью. Так как м0 содержит нуль, то и0 не пусто. Покажем, что «0 открыто. Возьмем произвольную точку х£ы0- Так как и—окрестность точки х, то u—x-j-u, где V — окрестность нуля. Пусть w — такая окрестность нуля, что w + wcv. Рассмотрим окрестность x+w точки х. Для любой точки y£x-}-w имеем y+w с х-)-ю + ш с x-)-v с и. Это означает, что и есть окрестность точки у, поэтому у^.и0, т. е. х + ®си0 и ы0—открытое множество. Так как ий содержит нуль и м0 с. и, то лемма доказана. Щ
Поскольку сдвиг открытого множества и при втором определении ЛТП есть открытое множество (докажите это), из леммы 1 вытекает такое следствие.
87
Следствие. Каждая окрестность любой точки х ЛТП X содержит открытую окрестность этой точки.
Лемма 2. Если и окрестность нуля, то любая ее гомотетия \и (X =/= 0) есть также окрестность нуля.
□ Возьмем v са и, v^V и выберем v2^V так, чтобы
Так как 2щсу1 + р1, то 2рх q: v. Далее, найдем v2$V такую, что 2пгс:п1 и, следовательно, 2го2 с v и т. Д, Пусть v„£V такова, что 2nvn с. о, где п выбрано таким образом, чтобы 2~" < |Х|. В силу уравновешенности vn имеем v„qр„, откуда vn<z№nvn<z'kvcz‘ku и, следовательно, Х« —окрестность нуля. £|
Назовем уравновешением множества М Э 0 множество М — — и ХМ. Если М уравновешено, то М — М. Если М от-о <|Х|< 1
крыто, то и М открыто, поскольку при каждом Х#=0 открыто ХМ. Так как и а и, то уравновешение любой окрестности нуля и есть снова окрестность нуля.
Теорема 1, В ЛТП существует фундаментальная система окрестностей нуля, состоящая из открытых, уравновешенных и поглощающих множеств.
□ Пусть V = (u, V, .... w, ...}—фундаментальная система окрестностей нуля, состоящая из уравновешенны^ поглощающих множеств. В каждой u£V возьмем открытую окрестность и2, пусть По-Уравновешение «0. Легко проверить, что совокупность V = = {«о, уо» • ••» wo> •••} удовлетворяет аксиоме II определения I'. Так как, далее, uoczu — u и й0 открыто, то система дкрестностей V удовлетворяет всем требованиям теоремы. ц
Можно доказать, что справедлива следующая теорема.
Теорема 1'. В ЛТП существует фундаментальная система окрестностей нуля, состоящая из замкнутых, уравновешенных и поглощающих множеств.
Из теоремы 1 следует, что ЛТП в смысле определения 1' есть действительно топологическое пространство, так как окрестности точек ЛТП, состоящие из открытых множеств, удовлетворяют всем аксиомам Хаусдорфа топологического пространства.
Теперь мы можем доказать следующую теорему.
Теорема 2. Оба определения ЛТП эквивалентны.
□ 1. Докажем, что из определения 1 следует Г. Пусть и — произвольная открытая окрестность нуля. Рассмотрим произведение
О .0=0. '-М-' '-Ч-'
чирлр элемент элемент
Вследствие непрерывности умножения найдутся 8 > 0 и открытая окрестность нуля v такие, что Xyczu при |Х| 6. Положим
= U Это снова открытое множество, содержащее нуль, т. е. О < | К |<6
окрестность нуля, но уже уравновешенная, причем иси. Докажем, что совокупность V всех таких множеств и удовлетворяет аксиомам I — III фундаментальной системы окрестностей нуля,
Пусть х£ Л —любое и и — произвольная окрестность нуля из совокупйосТи V. Из равенства
0-х =0
'-и-' '-V-'
число элемент элемент
на основании непрерывности умножения вытекает,* что существуют окрестности их точки х и число у>0 такие, что hux£tt при | X | у, в частности, Хх € « при | X | = у. Но это означает, что окрестность и поглощаетх. Таким образом, аксиома I для V выполнена.
Аксиома II, очевидно, выполняется, так как аг» = йПо открыто, содержит нуль и, следовательно, существует окрестность w£V такая, что wcwaHnv.
Наконец, из равенства
0+0=0 'Ы' элемент элемент элемент
и непрерывности сложения следует, что для окрестности и. С V найдутся открытые окрестности нуля и о2 такие, что t^ + i^ciu и тем более v + vcu, где Но тогда a-j-vcu и аксиома
III для V также выполняется.
2. Докажем, Что из определения Г следует определение 1. Как мы уже видели, из определения Г вытекает, что X есть топологическое пространство. Остается доказать, что операции сложения элементов и умйожения элемента на скаляр непрерывны при определений 1'.
1) Пусть «х+г, = (*+*/)+« и v такова, что v + vcu. Тогда если x'£x+v, tf £y-\-v, то x'+y'£x-\-v+y+v<z(x + y)+u и непрерывность сложения доказана.
2) Допустим сначала, что Х#=0. Если uu = Xx + u, то выберем w так, чтобы w-^-wj-wai. Для любого х’ £Х и любого скаляра X' имеем
Х'х' —Хх = (X' —X) (х' —х) +Х (х' — х) + (X' —X) х.
В силу поглощаемости w найдется е>0 такое, что (X'—Х)хСоу при |Х'—Х|<8. Пусть, далее, п^Х-1®. Если х’£x + vu то X (х' — х) Наконец, существует окрестность нуля э2такая,
что v2cs~1w. Тогда при x'Cx + v2 и |Х'—Х| < е имеем (X'—Х)х X (х' — x)cev2c:w. Положим v = o1nv2- Если теперь |Х'— Х| < е и х' £х + о, то
X'х' — Хх cz 8п2 + Xv2 + w a tso+w + w с и
и непрерывность умножения для случая Х+=0 доказана.
89
Случай Z = 0 рекомендуем рассмотреть самостоятельно. Щ
Каждая точка ЛТП имеет выпуклую окрестность. Чтобы убедиться в этом, достаточно рассмотреть выпуклую оболочку Со (и) окрестности нуля и и затем взять х +Со (и). Однако в произвольном ЛТП может и не существовать база окрестности нуля, состоящая из выпуклых множеств.
Если в ЛТП X существует фундаментальная система окрестностей нуля, состоящая из выпуклых, уравновешенных и поглощающих множеств, то пространство X называется локально выпуклым.
Большинство важных в приложениях пространств, в частности все ЛНП, являются локально выпуклыми.
С понятием поглощаемости связано понятие ограниченного множества в ЛТП. А именно: множество М ЛТП X называется ограниченным, если оно поглощается любой окрестностью нуля и, т. е. если существует а>0 такое, что МаХи при |Х|^а. Ясно, что в случае нормированной топологии (т. е. топологии, порождаемой нормой) новое определение ограниченности множества совпадает с данными ранее.
Лемма 3. Множество МсХ ограничено тогда и только тогда, когда для любой последовательности {хп}сМ и любой последовательности чисел {Х„}, сходящейся к нулю, Хпхп—>0.
□ В самом деле, пусть Ма.Х ограничено, {xn)>c:М, *0 и и — произвольная окрестность нуля, которую без ограничения общности можно считать уравновешенной. Так как {х„} —ограниченное множество, то существует |3 > 0 такое, что р,х„ £ и при любом п и при |р|^р. Так как >0, то |Х„| начиная с некоторого номера п0. Но тогда %пхп£и при п^п0,"а это и означает, что Хпхп—> 0.
Предположим, что М не ограничено и, следовательно, существует окрестность нуля и0, не содержащая целиком ни одной гомотетии pJW множества М. Пусть уп£(1/п)М такое, что у„£и0. Тогда хп = пу„£М, а (1/п)х„£и0 ни при одном п. Но это значит, что последовательность {(1/п) хп} не сходится к нулю, хотя {хп\с.М и 1/п—*0, т. е. условие леммы не выполняется...
Часто оказывается полезной следующая лемма.
Лемма 4. Для любого множества М ЛТП X имеет место равенство М— Г) (М+и), где V—фундаментальная система окрест-«€ V
ностей нуля. .___
□ Пусть х^М. Тогда (х + и) П М 0 для любой окрестности ugV (которую можно считать уравновешенной) и потому существует у£и такой, что х + у^М. Отсюда хС—у + Мси + М и, следовательно, х£ П (М + и).
UEV
Пусть, наоборот, х£ Л (М + м), т. е. х£М-\-и для всехи^У. ___________ ие V
Если бы х^М, то нашлась бы окрестность нуля uQ£V такая, что (х + и0) Г) М «0. Следовательно, x-j-y^M при любом у£и0, т. е. 90
х&—у + М и, значит, U (—у + М) — а0 + М. Это противоречит предположению, что х£ П (Л4 + и), и лемма доказана. Ц
В дальнейшем мы будем рассматривать лишь отделимые ЛТП. Поэтому представляет интерес следующая лемма.
Лемма 5. Для того чтобы ЛТП X было отделимым, необходимо и достаточно, чтобы для любой точки х^О существовала окрестность нуля и, не содержащая точки х, т. е. чтобы для любой фундаментальной системы V окрестностей нуля имело место равенство П ^ =; {0}.
□ Приведенное условие, очевидно, необходимо. Докажем его достаточность. Пусть г/#=х, т. е. х—у=Н=О, и v — окрестность нуля такая, что х—yffcv. Возьмем уравновешенную окрестность нуля ш, удовлетворяющую условию ш + шаи. Тогда x + w и y+w не пересекаются, поскольку иначе нашлись бы элементы z19 z2^w такие, что x+zt = y + z29 откуда х—у— z2 — ZiGw+wav, что невозможно. S
П римеры. 1. Рассмотренное в § 10 гл. I пространство всех определенных на [0, 1] вещественных функций с обычным определением сложения и умножения на число (вещественное) есть отделимое * ЛТП с базой окрестностей нуля
и (/1, /2, •••, е) = {х(/) | |x(/z) | < е, г = I, 2, ..., п}.
Более общо: F (S) — множество комплекснозначных функций, определенных на произвольном бесконечном множестве 5, с обычным определением суммы функций и умножением функции на число (комплексное). Если в качестве базы окрестностей нуля взять совокупность множеств вида
ц(«1, s2, ...» sn; 8) = {х (s) 11х (s/) | < 8, i=l, 2, ...,n},
то легко проверить, что аксиома II из определения 1' выполняется и что и (s1} s2, ..., s„; е) —выпуклые множества. Следовательно, F (S) есть комплексное локальное выпуклое пространство.
2. Пусть X—’Пространство бесконечно дифференцируемых на (а, Ь) функций х (/) с комплексными носителями Кх. Если в качестве базы окрестностей нуля принять совокупность всех множеств вида
vn (е) = {х (/) | max (max | xz (t) |) < g}, i=i, 2, п tzKx
то X есть локально выпуклое пространство.
3. Пусть X •— линейное и в то же время метрическое пространство. Если метрика этого пространства такова, что операции сложения элементов и умножения элемента на число непрерывны относительно сходимости, порождаемой метрикой, то X называется линейным метрическим пространством. Можно показать, что в линейном метрическом пространстве существует метрика, эквивалентная первоначальной и инвариантная относительно сдвига, т. е. такая, что (>(х, </) = р(х + г, у+г).
2. Полунормы. Нормируемость линейных топологических пространств. Как и произвольное топологическое пространство, ЛТП называется метризуемым, если в нем можно ввести метрику, порождающую исходную топологию. ЛТП называется нормируемым, если в нем можно определить норму элементов так, что топология,
* В дальнейшем слово «отделимое» мы будем, как правило, опускать.
91
порождаемая нормой, совпадает с исходной. Можно доказать, что для метризуемости ЛТП необходимо и достаточно, чтобы оно было отделимо и чтобы в нем существовала счетная фундаментальная система окрестностей нуля. Условия нормируемости ЛТП будут рассмотрены ниже.
Пусть Х~ локально выпуклое пространство и V—база окрестностей нуля этого пространства, состоящая из выпуклых множеств. Для каждой окрестности u$V построим так называемый функционал Минковского рц(х) = inf |Х|. Так как и —поглощающее мцо-
* € Ки
жество, то ра(х) конечен для любого х£Х. Функционалы Минковского выпуклых, уравновешенных и поглощающих множеств называются также полунормами. Таким образом, каждой выпуклой окрестности и локально выпуклого пространства X ставится в соответствие полунорма рв(х). Из определения полунормы непосредственно следует, что ри(х)5?0 для любого xgX.
Покажем, что:
р„(ах) = |а|рв(х); (1)
Ра (х + у) С ра (х) + ра (у). (2)
□ В самом деле, если у —0, то р№(у)==0 и равенство (1) при х = 0 или tj = O тривиально. Будем считать поэтому, что х=/=0 и а =^0. Тогда
Ра(^)= inf |Х|= inf |1|=?|а| inf |а"Ч| =
= l«l inf |р|^|«|рв(х), .
хе цц
и равенство (1) доказано.
Для доказательства неравенства (2) положим ра (х) — а, ра («/)==₽, откуда следует, что х€(а4-е)«, у ^(Р 4-е) и при любом 8 > 0. Поэтому х + уе (а 4-е) и + (Р4-?) и. В силу выпуклости и имеем
(а 4-е) и4- (Р 4- б) и = (а4-₽ + 2е) и
и, следовательно, х4-у£(а4-р4-28)н, Но тогда ри(х + у)^ а 4-р4-28, откуда в силу произвольности 8 получаем
Р« (х4-р)<а4-р = рв(х)4-рв(у),
и неравенство (2) доказано. Щ
Легко видеть, что если u/ciZg, то рв> (х) pttt (х) для всех х£ X. Отсюда следует, что совокупность полунорм {р„(х)}, соответствующих всем u^V, обладает тем свойством, что для двух любых полунорм рВ1 и рВа найдется третья полунорма р„3 такая, что для любого х^Х
Ри3 (X) > Р„, (х), Ри3 (х) > рВ1 (х). (3)
Система полунорм, обладающая этим свойством, называется фильтрующей. Ясно, что
ua{x€X|pa(x)< 1}. (4)
92
Так как из (4) следует, что ря(х)<8, если х£ги, то всякая полунорма непрерывна в нуле. Но тогда из неравенства
I Ри (х)~Ри (у) | < Ра (Х — у),
легко вытекающего из (1) и (2), следует, что ра (х) равномерно непрерывна на всем пространстве X.
Лемма 6. Пусть и—любая окрестность нуля. Тогда
{х £ X | ра (х) 1} = и, {х £ X | Ри (^) 1} и
и, следовательно, {х £ X | pa (х) = 1} — ди, где дц —граница и.
Докажем первое из этих утверждений, а остальные два рекомендуем доказать самостоятельно.
□ Положим {xg X | ра (х) < 1} — 5. Из определения функционала Минковского следует, что Веи. Кроме того, В открыто. В самом деле, если х£В, то ра (х) =а < 1; пусть е < 1 —а. Тогда для любого z£.x-\-&u имеем
Ра (г) = Ра (X + е t/X ра (х) + еря (z/)< а + е < 1, так что х + гисВ, т. е. В открыто. Но и--наибольшее открытое множество, содержащееся в и, и, следовательно, Веи. С другой стороны, если х£и, то, поскольку и открыто, найдется окрестность нуля v такая, что x + veu; так как и —поглощающее множество, то найдется 8 >0 такое, что ех£и, в частности x-f- ex € ие и. Поэтому ра (х + ex) 1, откуда
Ри (X) = Ра (X + 8Х)< -f-Ь- < 1.
Следовательно, иеВ и утверждение доказано. Щ
Предположим теперь, что в линейном пространстве X задана произвольная система полунорм, т. е. система {pgjatu функционалов, определенных на X, неотрицательных и удовлетворяющих условиям (1) и (2). Пусть, кроме того, эта система полунорм — фильтрующая, т. е. для любых а£ и а2 найдется а3 такое, что для ' всех х£Х имеем pa,(x) (х), р«3(х) > ра, (х). Положим в — = {х £ X | ра (х) < в}. Легко проверить, что совокупность {оа> Е} удовлетворяет аксиомам фундаментальной системы окрестностей нуля локально выпуклого пространства и, следовательно, порождает в X локально выпуклую топологию.
Из леммы 6 вытекает, что любая локально выпуклая топология может быть порождена фильтрующей системой полунорм. При этом легко видеть, что, для того чтобы пространство X с топологией, порожденной фильтрующей системой полунорм, было отделимым, необходимо и достаточно, чтобы для любого х=И=0 существовала полунорма- ра такая, что ра (х) 0.
Сравнение понятий нормы и полунормы показывает, что норма И есть такая полунорма р (•), для которой равенства х = 0 и р (х) = 0 эквивалентны. Поэтому ЛТП X является нормируемым, если его
99
топология может быть порождена одной-единственной полунормой, обращающейся в нуль лишь в нулевой точке пространства X. Условия этого дает нижеследующая теорема, принадлежащая А. Н. Колмогорову.
Теорема 3. Для того чтобы ЛТП X было нормируемым, необходимо и достаточно, чтобы оно было отделимым и в нем существовала выпуклая ограниченная окрестность нуля.
□ Пусть ы0—такая окрестность. Без ограничения общности можно считать ее уравновешенной. Положим || хЦ = рао(х). Соотношение Ц0j| = 0 выполнено. Пусть теперь х=/=0. Тогда" х(£(1/п0)и0 для некоторого п0. В самом деле, если х£ (1/п)ие для всех п, то у„=ях£и0 для всех п = 1, 2, 3, ... ив силу ограниченности ый получаем, что (1/л)уп—*0. Но это невозможно, так как (1/п)г/„ = = х=И=0 и в отделимом пространстве последовательность может сходится к одному пределу. Итак, х$(1/п0) ы0; поэтому Цх^ 1/п0 > 0 и аксиома I нормы выполняется.
Из равенств (1) и (2) для полунормы легко следует, что
1Ж1Ф1+Ы.
т. е. аксиомы II и III нормы также выполняются. Остается доказать, что топология, порождаемая нормой, совпадает с исходной топологией пространства X, т. е. что для любой Окрестности нуля и пространства X найдется шар [|х|<р, попадающий целиком в и, и, обратно, для любого шара ||х|| < г найдется окрестность нуля V, целиком входящая в этот шар.
Так как и0 ограничена, то для произвольной окрестности нуля и найдется число р>0 такое, что риоси. С другой стороны, единичный шар ||хЦ< 1 входит в и0, откуда следует, что шар ^х||<р войдет в рый, а тем самым ивы.
Пусть, обратно, дан шар ||xjl< г. Из определения нормы следует, что в этот шар войдет целиком окрестность нуля г'ы0, где г' —произвольное число, меньшее г.
Достаточность условий теоремы полностью доказана. Доказательство необходимости не вызывает затруднений. И
В нормированных пространствах (даже более общо—в произвольных метрических) два любых непересекающихся замкнутых множества можно заключить в непересекающиеся окрестности. При этом окрестностью множества М топологического пространства X называют любое открытое множество этого пространства, содержащее М, например им— П ых, где их — открытые окрестности точек хе м
х. В произвольном ЛТП такая отделимость не имеет места, однако можно доказать следующее.
Теорема 4. Пусть FczX —замкнутое множество и xffcF. Тогда существуют непересекающиеся окрестности uF и их множества F и точки х.
□ Пусть V = {u, v, ..., &у, ...}—фундаментальная система замкнутых окрестностей нуля в пространстве X. Поскольку G =* = X\F открыто и x^G, существует такая, что х + vgG»
94
Множество u = X\(x + t') открыто, содержит F и, следовательно, является окрестностью F. Ясно, что иП(х + о) — 0. Ц
Отделимое топологическое пространство, в котором верна доказанная теорема, называется регулярным. Таким образом, всякое отделимое ЛТП регулярно. Теорему о регулярности ЛТП мы доказали без предположения отделимости этого пространства и может показаться, что следствием теоремы 3, если взять в качестве F точку у^Х, является отделимость любого ЛТП. Однако это не так, поскольку замкнутость любого одноточечного множества в ЛТП эквивалентна отделимости этого пространства.
Выше было показано, что всякое конечномерное ЛНП изоморфно евклидову пространству того же числа измерений. Аналогичное утверждение имеет место и для ЛТП.
Теорема 5. В конечномерном ЛТП X имеется лишь одна отделимая топология, а именно евклидова топология, порождаемая нормой
/ П \1/2 П
|х|| = ( 2 5?) для х= где е1г е2, ..., е„ — базис в X. \ i =1 / i=l
□ Пусть т—некоторая отделимая топология в X и Хт—пространство с этой топологией. Пространство X с евклидовой топологией обозначим через Хп. Окрестности нуля в этих пространствах будем обозначать соответственно и(т) и и'"*.
Пусть ит—произвольная окрестность нуля в ХТ. Тогда найдется окрестность нуля vm такая, что и(Т)+ ... + v<T)c:u(T) (число слагаемых слева равно п) и для фиксированного ек найдется eft > О такое, чю при |gft|<eft. Положим e = mineft и и<п) =
k
~{х |)|х|| < е}. Тогда, как легко видеть, и<п)с:и(т). Отсюда, в частности, следует, что тождественное отображение Хп на ХТ непрерывно в топологиях этих пространств.
Пусть и'п)—произвольная окрестность нуля в Хп. Тогда ы(п) содержит некоторый шар К (0, e) = {x|jjx^< в}. Пусть S — граница этого шара, т. е. множество точек {x|j|x|i = e}; S — ограниченное замкнутое множество конечномерного нормированного пространства и, следовательно, компактно. Образ S при тождественном отображении Хп на Хт—также компактное множество отделимого пространства и потому замкнуто. Так как S не содержит нуля, то существует окрестность «(т) такая, что Sn«(T) = 0- Но тогда u(T)c:u(«>. В самом деле, если это не так, то существует точка х£и<*> такая, что х^и(п)=>Х (0, е), т. е. ||х||^е. Пусть Х = е./ЦхЦ и г/ = Хх. Так как то у£ит. С другой стороны, ЦуЦ — е,
т. е. y£S, что противоречит равенству umnS = 0. Итак,
В то время как декартово произведение метрических пространств является метризуемым лишь в случае конечного или счетного числа сомножителей, декартово произведение любого числа линейных топологических (локально выпуклых) пространств есть линейное топологическое (локально выпуклое) пространство.
95
□ Прежде всего для х=={ха} и у = {уа}, ха, уа£Ха полагаем х + у = {ха + уа}, Лх = {%ха} и убеждаемся, что X— Ц Ха является аё А
линейным пространством, если все Ха таковы. Пусть теперь все Ха являются ЛТП и V&—база окрестностей нуля пространства Ха. В тихоновской топологии окрестностями нуля пространства X служат множества и = Д va, где va = X«, за исклйочениём конечного (Х€ А
числа значений а — аи а2, .... и va{$Va. для 1 = 1, 2, ..., k. Легко проверить, что и—уравновешенные множества. Покажем, чтои—поглощающие Множества.- Пусть х = {ха} С X. Так как каждое v — поглощающее множество, то найдется число > 0 такое, что xai € Положим Х= шах %,-. Тогда xai £ Kuai при i = 1, 2, ..., k.
Так как, кроме того, XaGva = Ха=кХа при то
х€ П^«=хП9«в^-ае А аеА
В силу уравновешенности и имеем при т. е. и —
поглощающее множество.
Выполнение условия 2° аксиомы II было доказано выше (см. п. 2, § 10, гл. I). Рекомендуем проверить самостоятельно выполнение условия 3° аксиомы II.
Наконец, ясно, что X локально выпукло, если все таковы, у
Упражнейия
1. В пространстве С [0, 1] найдите бесконечномерное линейное многообразие L такое, что L £ С [0, 1].
2. Установите, чему равно (с точностью дог изоморфизма}:. а} С [—1, где Lo—подпространство четных функций; б) С/Со, где С, С9— пространства бхо-дящиЯся, соответственно сходящихся к нулю последовательностей.
3. В множестве непрерывных функций, ойрСДелёййШ йа (— оо, -f-oa) и равных нулю вне некоторого конечного (своего дЛя Каждой функции) отрезка, введена норма || х || sup | к (/). Является ли пространство этих функций полным в метрике р (х, у) = |fx — у$ Если нет, то что является пополнением этого пространства?
4. В множестве функций, определенных на (—6о‘, + оо} и измеримых" на каждом
т
конечном отрезке, рассматриваются *Ге, для которых lim -L f x2(f)dt< оо.
Т-*оо Т J
- т
Докажите, что эти функции образуют линейное нормированное пространство. Является ли оно полным?
5. Пусть Т — произвольное множество в банаховом пространстве X. Если шар К (о, то какой шар войдет в Т?
6. Пусть в банаховом пространстве X множество А замкнуто и В компактно. Докажите, что А-]-В замкнуто. Покажите, что только из замкнутости АъВ не следует замкнутость Л + В.
7. Докажите, что пространство m не является строго нормированным.
8. Пусть X—банахово пространство с нормой [|»||. Введена другая норма ||*||i так, что || х Цх < b || х ||, b > 0. ПокажйТе, ч^о если X полно в норКгё ||-(|, то эти нормы эквивалентны, т. е. а |] х |] [| х [|х b [| х || при некотором а > 0.
9. Докажите, что в ЛТП существует фундаментальная система окрестностей нуля, состоящая из замкнутых, уравновешенных и поглощающих множеств,
96
10. Докажите, что пространство s не нормируемо.
11. Являются ли в ЛТП: а) сдвиг и гомотетия замкнутых множеств замкнутыми; б) замыкание линейного многообразия линейным многообразием?
12. Нормируемо ли декартово произведение сметного множества нормируемых ЛТП?
13. Докажите, что если Л —выпуклое множество в ЛТП, А и, х£А, у£А, то [х, У)СЛ.
14. Докажите правило параллелограмма в гильбертовом пространстве: ||х + г/||24-+||х-^=2(М2+1Ы2)-
15. Покажите, что любое замкнутое выпуклое множество гильбертова пространства содержит элемент с минимальной нормой.
16. В гильбертовом пространстве Н определена проекция элемента х£Н на множество Л4сзЯ, как элемент из М, ближайший по норме к х. Покажите, что проекция любого элемента на любое замкнутое выпуклое множество существует и определяется однозначно.
17. Пространство X называется ровммернв выпуклым, если из ||х[| = || г/||= 1 и [|х —у||^8 > 0 следует || (х + у)/2 1 — 6, где 6 зависит лишь от 8. Пока-
жите, что гильбертово пространство равномерно выпукло. Является ли равномерно выпуклым пространство С [a, &J?
4
№ 3054
ГЛАВА HI
ЛИНЕЙНЫЕ ОПЕРАТОРЫ
Одним из важнейших и наиболее хорошо изученных классов операторов является класс линейных операторов, определенных в линейных пространствах.
§ 1. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЛИНЕЙНЫХ ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
1. Основные понятия. Пусть X и У —ЛТП, одновременно вещественные или комплексные. Оператор у — А(х), определенный на пространстве X и принимающий значения в пространстве Y, называется линейным, если этот оператор:
аддитивен, т. е. для всех xt и х2 из X
Л (х1 + хг) = Л(х1)4-Л (ха); (1)
однороден, т. е. для всех х £ X и любых вещественных (если X вещественно) или комплексных (если X комплексно) чисел %
Л(Хх) = М(х). (2)
Вместо Л (х) будем писать также Ах. ,
В дальнейшем, если не оговорено противное, мы будем рассматривать лишь непрерывные линейные операторы, действующие из X в Y, т. е. такие, что для любой точки х $ X и любой окрестности vax точки Ах найдется окрестность их точки такая, что Л (их) с: cvax- Очевидно, что для случая метрического пространства непрерывность оператора Л означает, что для любого е > 0 найдется б > 0 такое, что из х' С К (х, б) следует Ax' G /С (Ах, в).
Множество всех линейных непрерывных операторов, отображающих X в Y, будем-обозначать L (X, Y).
Легко видеть, что линейный оператор А:Х—>У, непрерывный в нулевой точке ЛТП X, равномерно непрерывен на всем X. В самом деле, если для окрестности нуля v пространства У существует окрестность нуля и пространства X такая, что Л (и) с о, то в силу линейности Л имеем Ах' — Лх" = Л (х' — x")£i> всякий раз, когда х'—х"£и; х', х"£Х.
Наконец отметим, что непрерывный оператор Л счетно непрерывен, т. е. из х„ —> х0 следует Лх„ —► Лх0. Обратное в общем случае неверно, но для операторов, действующих в ЛНП, из счетной непрерывности следует непрерывность (это нетрудно доказать).
Примеры. 1. Рассмотрим квадратную матрицу n-го порядка (aik); i, А>=1, п
2, л. Равенства т)/ = определяют, очевидно, оператор у = Ах, пере-
*=1
98
водящий элемент x = {Si, в элемент = Покажем,
что А—линейный непрерывный оператор. В самом деле, аддитивность и однородность оператора А очевидны. Его непрерывность следует из неравенства
I / п / п п / п
V 2 2 «?*•]/ S(u-U)\
' Г 1=1 г 1=1k=l г Л=1
I где х = {|/}, х' = {^}, г/ = Лх = {т]/}, 1/' = Лх' = {т]-}, получающегося очевидным образом с помощью неравенства Буняковского—Шварца для сумм.
1 С
2. Положим у (t)= \ К (/, s) х (s) ds, где # (/, s) —непрерывная в квадрате о
0<^1, функция. Если х [0, 1], то, очевидно, и у (t)£C [0, 1].
Следовательно, оператор у —Ах отображает пространство С [О, 1] в себя. Легко видеть, что А — линейный непрерывный оператор. В самом деле:
1
a) A (хх +х2) = J К (/, s) [xt (s) + х2 (s)] ds = о
1 1
= К (t, s) Xi(s)ds+ J К (/, s) x2 (s) ds = Лхт + Ax& о о
и условие аддитивности выполнено;
б) однородность оператора А очевидна;
в) пусть {хп (t)} сходится к х (/) в смысле сходимости в С [0, 1], т. е. равномерно на [0, 1]. Так как в случае равномерной сходимости можно перейти к пределу под знаком интеграла, то
lim \ К (t, s) хп (s) ds = \ # (/, s) х (s) ds^ n о о
t. e. lim Дхд— Ax, и непрерывность оператора А также доказана.
3. Пусть X — С [0, 1]. Рассмотрим в этом пространстве оператор у—Ах, определяемый равенством у (t) = J х (т) dr. Очевидно, что А—линейный непре-о
рывный оператор, определенный на всем X.
Рассмотрим в этом же пространстве другой оператор у — Вх, определенный равенством у (/) = -— х (/). Этот оператор определен уже не для всех х 1],
и если Вх существует, то не всегда у£С[0, 1]. Однако если за область определения оператора В принять линейное многообразие функций, имеющих непрерывную производную (лежащее всюду плотно в С [0, 1]), то область значений оператора В будет лежать также в С [0, 1].
Оператор В, очевидно, аддитивен и однороден. Но в области определения этот оператор не является непрерывным, так как производная от предела равномерно сходящейся последовательности функций может и не равняться пределу производных функций этой последовательности, если даже все эти производные существуют и непрерывны.
Пусть А — аддитивный оператор. Положим х = £ + откуда £ = х—Тогда Ах~ Al + Ai, = А1 + А (х—1), т. е.
А (х-& = Ах-А£.
(3)
99
Полагая в соотношении (3) х = £, имеем
А (0) = Лх-Лх = 0;
полагая, далее, х = 0, получим
Л(—£) = —Л£.
Теорема 1. Аддитивный оператор А, определенный на ЛТП X, принимающий значения в ЛТП Y и непрерывный в одной точке ха£Х, равномерно непрерывен на всем X.
Это утверждение следует из сказанного на с. 98.
Теорема 2. Аддитивный, и непрерывный оператор А, определенный на вещественном ЛТП X, однороден.
□ Пусть сначала t = n — целое положительное число. Тогда
А (пх) — Ах + Ах+ ... А-Ах — пАх.
Пусть теперь t = — /и —целое отрицательное число. Тогда
А (— тх) = — А (тх) — — тАх.
Пусть, далее, t — m/n—рациональное число. Имеем л(^-х)==тл(1х).
Положим— х = В. Тогда х = п£ и п
Ах = А («В) = nA (В) = nA x'j, т. е. А Ах.
Следовательно, л [ т \ т .
Л- —х = — Ах. \ п J п
Пусть, наконец, I — любое вещественное число. Необходимо рассмотреть лишь случай иррационального t. Найдется последовательность {/•„} рациональных чисел такая, что ги —* t. Поэтому rnx—+ tx, и так как Л непрерывен, то
Л (tx) = Л Him r„x\ — lim Л (rnx) = lim rnAx = tx. Ц \ п / п п
2. Пространство линейных операторов. В множестве линейных операторов, определенных на линейном пространстве X и принимающих значения в линейном пространстве У, можно ввести линейные операции. Пусть Л и В—такие операторы. Определим сумму этих операторов равенством
(Л + В) х = Ах + Вх
и умножение оператора на число—равенством
(ХЛ) х = ХЛх.
Очевидно, что при таких определениях все необходимые аксиомы выполнены и рассматриваемое множество линейных операторов
100
является линейным пространством. В частности, нулем этого пространства служит такой оператор О, что О (х) = 0 для любого х£Х. Если X и Y—ЛТП, то сумма непрерывных операторов и произведение непрерывного оператора на число также непрерывны. В самом деле, пусть о —произвольная окрестность нуля пространства Y, а аг)—такая окрестность нуля этого же пространства, что w-j-wczu. В силу непрерывности оператора А найдется окрестность нуля щ пространства X такая, что А (щ) <=w. Аналогично, существует окрестность нуля и2, для которой В(ы2)сау. Полагая и = ^Пи2, получим
(А 4-В) (а) = А (и) 4-В (и)сw4-wсv,
и непрерывность оператора А + В доказана.
Аналогично доказывается непрерывность оператора ХА.
В пространстве операторов можно определить предел последовательности операторов, полагая, например, что Ап—> А, если для любого х£Х имеем lim Апх = Ах. Возможны и другие определения п
предела последовательности операторов. Мы рассмотрим этот вопрос позже при некоторых дополнительных предположениях относительно пространств X и Y.
3. Кольцо линейных операторов. Возьмем линейное пространство X и рассмотрим множество всех линейных операторов, определенных на X и принимающих значения в этом же пространстве. Как только что показано, эти операторы образуют линейное пространство. Определим произведение операторов А и В из этого пространства, полагая (АВ)х = А (Вх). Легко видеть, что это снова линейный оператор.
По индукции определяется произведение любого конечного числа операторов. В частности, пишут
АА = А2, А2А = Аа
и т. д. Легко видеть, что
(АВ)С = А(ВС); (А + В)С = АС4-ВС; С (А +В)^СА + СВ,
а также что существует единичный оператор I, определяемый равенством 1х = х для любого х£Х и такой, что
1А-=А1 = А
для любого оператора А.
Если X есть ЛТП, то произведение непрерывных операторов есть непрерывный оператор. В самом деле, для любой окрестности нуля v найдется окрестность нуля w такая, что A(w)cv. В свою очередь, для w найдется окрестность нуля и, для которой В (и)си». Но тогда (АВ) («) = А (Вц)си и непрерывность оператора АВ доказана.
Таким образом, множество линейных непрерывных операторов L (X, X) образует кольцо с единицей, причем не коммутативное, так как в общем случае АВ В А.
101
Пример. Пусть Х = С[О, 1]. Рассмотрим операторы
1
Ах = J tsx (s) ds = t/(/); Вх = tx (t) = z (t). о
Имеем
t 1
ABx — J ts-sx (s) ds = t J s2x (s) ds, о о
1 i
В Ax = / tsx (s) ds = /2 J sx (s) ds. о о
Таким образом, AB BA.
Весьма важным является понятие обратного оператора. Согласно общему определению обратного элемента кольца, линейный непрерывный оператор В называется левым обратным для линейного оператора Л, если ВА = 1. Точно так же линейный непрерывный оператор С называется правым обратным для оператора Л, если ЛС —Если оператор Л имеет левый обратный В и правый обратный С, то они равны, так как
В = В(ЛС)-(ВЛ)С = С.
В этом случае говорят, что оператор Л имеет обратный оператор, который обозначают Л'1. Таким образом, если Л“х существует, то А"1 А = АА~1 = 1. К понятию обратного оператора мй вернемся снова несколько позже.
4. Функция оператора. Оператор
Л" = Л-Л- --Л
п раз
представляет собой простейший пример функции от оператора. Эта функция от оператора есть частный случай более общей функции, а именно многочлена от оператора
Рп (^) “ + • • • + апАп.
Определение функций от оператора f (Л) более сложных, чем многочлены, может быть осуществлено различными способами.
Пусть X есть n-мерное евклидово пространство и А — оператор, отображающий в К" в себя, заданный симметрической матрицей А. Приведем матрицу А к диагональному виду с помощью унитарного преобразования U такого, что
UAU~*=A,
где
/Xi 0 0 ... О \
д__I О А<2 о ... о ।
\о о о ... х„/
102
Пусть теперь f (t)— произвольная функция вещественной переменной tt определенная на отрезке [т, Af], где т — inf X;, Al = sup’%l-. Полагаем
i t
f (М 0 0 ... О
О f(X2) о ... о
/(A) —
О О О ... /(Х„)
и f(A) = U-4(A) и.
Таким образом, каждой функции f (t) вещественной переменной /, определенной на отрезке \т, Л4], ставится в соответствие функция от матрицы f(A). Очевидно, что функции / (0^0 ставится в соответствие нулевая матрица, функции /(/)=== 1—единичная матрица и функции f(t) — tm — матрица Ат. Далее, если Д0=Л(0 + М0, то /(Л) = Л(Л) + /2(Л), и если ф (0 = Л (0*М0> то <р (Л) = ~/1 (Л)-/г (Л). Эти равенства следуют из того, что для двух любых матриц В и С имеем
U(B + C) U-i^UBU-' + UCU-1, U (ВС) U-1=UBU'^-UCU‘\ и из того, что
f (А) = л (Л) + /2 (Л), Ф (Л) = Л (Л)./2 (Л).
Можно построить теорию функций от матриц и другим способом, перехбдя от матричных многочленов к матричным степенным рядам. Однако таким путем можно определить лишь аналитические функции от матриц. Построение же функций от матриц с помощью приведения матрицы к диагональному виду было обобщено на случай бесконечных матриц, а затем и на произвольные самосопряженные операторы в гильбертовом пространстве в спектральной теории этих операторов (см. [8], гл. VII).
В качестве второго примера рассмотрим функции от оператора дифференцирования. Пусть Х — С [0, 1] и D=-~ —оператор дифференцирования, относящий непрерывно дифференцируемой функции х (/) производную этой функции
z>x(/)=Ax(0=X' (0.
Для n-кратно непрерывно дифференцируемых функций имеют смысл выражения /а их । dx (/) . . dnx (t)
рп (D) х (ty — a^x (0+ai • • • +an •
где pn (s)~ любой многочлен n-й степени от аргумента s. Для неограниченно дифференцируемых функций имеет смысл выражение
п = 0 п=0
если только ряд, стоящий в правой части равенства, сходится и его сумма принадлежит С [0, 1]. В частности, это имеет место, если х (t) есть многочлен /п-й степени, так как тогда Dnx (/) = 0 для п > т и ряд обращается в конечную сумму.
Многочлены от оператора дифференцирования находят применение в теории линейных дифференциальных уравнений. Простейшим из этих применений является так называемый символический метод решения уравнений с постоянными коэффициентами. Более глубокие применения функций от оператора дифференцирования к линейным дифференциальным уравнениям —обыкновенным и в частных производных — содержатся в операционном исчислении.
Формальные операции с рядами и полученными с помощью рядов функциями от оператора дифференцирования широко применялись в первой половине XIX в» для получения некоторых формул в теории квадратур, интерполяции и т. д. Поясним сказанное примерами.
103
Прежде всего заметим, что оператор
/+w+^-2+^+ • • • +^+ • • • =еЛО
в применении к функции x{t), которую будем считать аналитической, дает х (t + h), В самом деле,
eADx (0 = х (0+hx' (/) + х\(0 + ... + х<«) (0 + ... = х (/ + ft).
Поэтому если через АЛ обозначить оператор взятия разности с шагом Л, т. е. х (Z) = х (t -\~h) — х (t), то
eW>x О) = х (/+ft) = х (0 + Д* х (/) = (/ + ДА) х (/),
или
/+Дй = е*°.
Производя формальное обращение степенного ряда, найдем
п
W = ln(/ + AA) = V „ tl
Мы получили формулу Грегори, ния через оператор взятия разности.
Рассмотрим далее операторы
п= 1
выражающую оператор дифференцирова-
Jx (0=^ х (?+т) dr, о
п
Sx(0= Ус/Х^ + Т;),
п
где 2 Q=l- Нетрудно убедиться в том, что i = i
вить как функции от оператора D, а именно:
с г. е° — I
J= \ eTDdT = —, S
о
операторы J и S можно предста-
Отсюда
п
гч xiD ср1 •
= 1
ctz
Ho 7 ег— 1
п
ci Г=1
J—S = J[l — J-iS] = J /-^2
Dex‘D j
•
является производящей функцией для многочленов Бернулли:
zeaz е^Т
fc = 0
Поэтому предыдущая формула примет вид
j_s==z =~4
i = l \fc=0 /J U = 1
п п
поскольку 2 с;во(Т|)= У с1 = 1« 1=1 1 = 1
Так как 1 /{№(/)] = tf+т) dT = x<*-i) (/ + 1)-х(^-1) (О, о
104
то мы приходим к обобщенной формуле Эйлера—Ма к л о рен а:
1 П со
J х (/ + т) dr =^с,х (/4-Tj) — О i=l k=l
&k fa)
Ze!
(X(A-1) (; + l)__x(*-l) (/)]e
В частности, при / — 0 получаем
1 Ч оо “ п
J х (т) dT = £Cfx (?,-)-£
[х(А-1> (1)_ (0)).
Приведенный вывод формул Грегори и Эйлера—Маклорена может считаться обоснованным, если функция х (I), к которой прилагаются эти формулы, является многочленом. В этом случае бесконечные ряды превращаются в конечные суммы и все проделанные нами формальные преобразования являются законными. Для произвольных же неограниченно дифференцируемых функций формулы Грегори и Эйлера—Маклорена нуждаются в дальнейшем обосновании, например с помощью оценки остаточных членов.
§ 2. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЛИНЕЙНЫХ НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
1. Непрерывность и ограниченность. Пусть X и У —ЛНП. Так как линейное нормированное пространство есть частный случай линейного топологического пространства, то для ЛНП сохраняется прежнее определение линейного оператора, заданного на X и принимающего значения в К, а также остаются в силе теоремы 1 и 2 § 1.
Отметим лишь, что так как сходимость в X и Y есть сходимость по норме, то непрерывность оператора А означает, что ЦАх„ — ЛхЦ-^О при ||х„—х|| —>• 0.
Операторы, рассмотренные в примерах 1 и 2 § 1, являются линейными непрерывными операторами, преобразующими сами в себя ЛНП R" и.С[0, 1].
Приведем еще один пример линейного оператора. Рассмотрим оо оо бесконечную матрицу i, k — 1,2, ..., такую, что 2 SI % |’<°°» q>1. Тогда система равенств
оо
= ~ 1 > 2,
k = 1
с помощью которой каждому элементу х = ставится в соответствие «/ = {»]<}> определяет линейный непрерывный оператор у = Ах, заданный на 1р и принимающий значения в lq, где — + — = 1, т. е. A£L(lp, lq).
Покажем прежде всего, что, действительно, y^.lq, если х£.1р. Имеем (пользуясь неравенством Гельдера для сумм)
п п
1=1 1 = 1
П оо ОО 00
I = 1fe=l I = 1fe=l
105
Так как это неравенство верно для любого п, то можно перейти к пределу при п—>-оо. Тогда получим
= 5) S 2 1«/k\4
t=l i=1k=1
И, значит, y£lq.
Докажем теперь, что Д —линейный непрерывный оператор. Пусть = {5-1*} € 1р и х2 = {%?у} £1р. Тогда из равенства
S aik = i aih®> + i aif№ k-\ fc=l fc==l
следует, что A (x1 + x2) = Лх1Ч~Лх2, т. e. аддитивность оператора A. Однородность этого оператора очевидна. Пусть теперь хп = С их = {Ц€/р Ахп = Уп = {»]'"’}> Ах = у = {-qj. Имеем
(оо \l/q / оо оо \ i/q
SK’-n/l’) <( 2 S|«zaI?) х
i = l / v = 1&=i /
/ 00 \l/p /оооо \ i/q
X==( s К-X».
\&=1 / \!=1Ы /
%
Отсюда ||#n—z/|] —>0 при ||x„—x|| —> 0 и непрерывность оператора Л доказана.
Оператор А называется ограниченным, если существует такая постоянная М, что || Лх||^ Л4||х|| для любого х£Х (Здесь норма ||Лх|| берется в смысле метрики пространства Y, которому принадлежит область значений оператора А, а ||х|| берется в смысле метрики пространства X).
Согласно этому определению, ограниченный оператор преобразует ограниченное множество элементов {х}сХ в ограниченное же множество элементов (Лх}аУ.
Теорема 1. Для того чтобы аддитивный и однородный оператор А был непрерывен, необходимо и достаточно, чтобы он был ограничен.
□ Необходимость. Пусть Л — непрерывный оператор. Допустим, что он не ограничен. Тогда найдется последовательность элементов {хп} такая, что || Лх„ || > п || х„ ||. Построим элементы = = -/--т . Очевидно, что £„ —► 0, так как
С другой стороны,
Значит, ДО = 0. Поэтому оператор А не непрерывен в нулевой точке, что противоречит предположению.
106
Достаточность. Пусть аддитивный оператор А ограничен, т. е. || ЛхК М ||х||. Пусть х„ —>х, т. е. ||х„—х||—>-0; тогда и
||Лхп-ЛхН||Л(хп-х)КМ||хв-х|НО,
т. е. Лх„-*Лх, и, следовательно, Л непрерывен. Ц
Докажем теперь лемму, которая иногда оказывается полезной.
Лемма. Пусть дан линейный (необязательно ограниченный) оператор А, отображающий банахово пространство X в банахово пространство Y. Обозначим через Хп множество тех х £ X, для которых || Лх||^и||х||. Тогда X = и Хп и по крайней мере одно из п = 1
множеств Хп всюду плотно.
□ Прежде всего каждое из множеств Хп не пусто, так как, например, 0£Х„ для любого п; кроме того, очевидно, что всякий х£Х, х=/=0 попадает в одно из множеств Х„; для этого достаточно взять в качестве п наименьшее целое число, превосходящее
|| Лх||/||х||. Поэтому можно написать X = (J Хп.
п= 1
Ввиду того что полное пространство X не может быть счетным объединением нигде не плотных множеств (см. теорему 3 § 7 гл. I), по крайней мере одно из множеств ХПо не является нигде не плотным. Следовательно, существует шар Д (х0, г0), в котором Д(х0, г0)ЛХПо всюду плотно.
Рассмотрим шар Д(хи rj, лежащий целиком внутри Д(х0, г0) и такой, что Xj СХ„о. Возьмем любой элемент х с нормой ||х|| = Г1. Элемент х + х1€Д(х1, Гх), так как ||(x + Xi) — [|=||х|| =
Поскольку Д (х1( г,) с Х„о, найдется последовательность элементов {zk} из Д(Xj, Г1)пХ„о такая, что zk —^x-j-x, при k—>оо (эта последовательность может быть стационарной, если x + Xj^X^). Следовательно, xk = zk — Xf —► х. При этом можно считать, что Гх/2^1 xft||, поскольку xft—*-х и ||х|| = гг; кроме того, ||xft|K
Так как zk, х^Х^, то
IIАЧII = IIАЧ—Лх, || < || Azk || +1] Axt || < п0 (|| zk || +1| Xi ||).
Далее,
IIЧII = кй + Xi || < II Xk II + II Xi IK G + II Xi ||.
Поэтому
11Axk IK «0 (G + 2II Xi II) и Xk ||.
Если обозначить через n наименьшее целое число, превосходящее 2п0(г1 + 2Цх1||)/Г1, то ||Xxft|K n||xft||, откуда следует, что всехА£Хи.
Итак, люоой элемент х с нормой, равной гх, можно аппроксимировать элементами из Х„. Пусть теперь х—любой элемент из X. Рассмотрим элемент £ = Г1Х/||х||. Имеем |Щ = гр По доказанному,
107
найдется последовательность {|ft}czX„, сходящаяся к |. Тогда
Отсюда следует, что хА£Х„. Значит, Х„ всюду плотно в X и лемма доказана. И
Если в произвольном банаховом пространстве линейный оператор может быть не непрерывным, то в конечномерном пространстве всякий линейный оператор непрерывен.
В самом деле, пусть е1( е2, ..., еп— базис в X и, следовательно,
п
любой элемент х этого пространства имеет вид х = У |(ez. В силу гомеоморфизма любого n-мерного банахова пространства евклидову «-мерному пространству, если
п п
Xk= S S 5 А,
1=1 i=1
то > £(- (» = 1, 2, ..., п). Но тогда
1 = 1 1=1
и требуемое доказано.
2. Норма оператора. Пусть А — линейный ограниченный оператор. Наименьшая из постоянных М, удовлетворяющих условию ||Лх||^С М. ||х|| при всех х£Х (а такие постоянные существуют в силу ограниченности А), называется нормой оператора А и обозначается || А ||. Таким образом, по определению, число ||Л|| обладает следующими двумя свойствами:
для любого х£Х справедливо неравенство
МхК||Л||.||х||, (1)
для любого е > 0 найдется такой элемент хе, что
IIЛxs II >(|| ЛII -8) II xs||. (2)
Покажем, что
IIЛ11--= sup II Ах II, (3)
11*1) < 1
или, что все равно, если х=/={0},
В самом деле, если ||х||^ 1, то
||Лх||<||Л||-||х||сМ||;
108
значит, и
sup ||Лх||^||Л||. (4)
0*11 < 1
С другой стороны, для любого е > 0 существует элемент хе такой, что
М*е11 >(И|-8)||хе||.
Возьмем 5eeMxe||- Тогда
||А я=таг ।А х* ii > таг{|1 А а ~е) 8 •
Так как j£e|| = l, то sup ||Лх||>||ЛВе||>||Л||-е. и *11 < 1
Следовательно, sup ЦЛхЦ^ЛЛ||. (5)
||*||< 1
Из неравенств (4) и (5) и вытекает равенство (3).
Пример. Найдем норму интегрального оператора с непрерывным ядром
1
1/(0 = J К (0 s) х (s) ds, о
рассматривая его как оператор, отображающий С (О, 1] в С [О, 1]. Полагая
1
Ах = К (/, s) х (s) ds, получим о
Ц Лх|=тах
1
К х (s) ds о
1
max \ | /< (/, s} [ ds*max | х ($) | =
1
= тах | s) | ds-||x J.
* о
Следовательно,
1
ЦЛ||<тах V |Я(/, $Hds.
* о
(6)
1
Так как | К (О s) | ds—непрерывная функция, то она достигает максимума о
в некоторой точке /0 отрезка [0, 1]. Положим z0 (s) =sign К (/0, s). Пусть хп (s) — непрерывная функция такая, что | хп (s) | 1 и хп (s) = г0 (s) всюду, кроме мно-
жества Еп меры, меньшей 1/(2Л1п), где Af = max|/( (/, s) |. На множестве Еп t, s
109
всюду | x„ (s) — z0 (s) | < 2. Имеем
1 « 1
С (/, s) z0 (s) ds— {t, s) xn (s) ds < J | К (t, s) 11 z0 (s) — xn (s) | ds = о о о
= C \K(t, s)| |x„(s) —z0(s)|ds<2max|K(/, s) | • 2^=-^-
En *’ s
Это неравенство справедливо для любого /£[0, 1].
Следовательно, для всех Z£[0, 1] имеем
1 1
Ck(/,s)z0 (s)ds< [к (t, s) xn(s) ds-Ь
J d и n
0 0
Полагая в этом неравенстве / = /0, получим
1
У И «О, S) |ds< IIА НМ+4-
О
Так как ||хЛ|К1, то предыдущее неравенство в пределе при п—> оо дает
1
$ |К(/0, s) | ds<|| А ||, о
т. е.
1
max С | К (t, s) | ds <|| A ||. (7)
z о 1
Из неравенств (6) и (7) получаем
1
|| Л || = max С |Я(/, s) | ds.
z о
Пусть в ЛНП X задано линейное многообразие L. Это линейное многообразие можно рассматривать как самостоятельное линейное пространство, может быть, неполное. Предположим, что на L определен аддитивный оператор А со значениями в некотором ЛНП У. Оператор А называется ограниченным на Л, если существует постоянная М такая, что || Лх||^ М||х|| для всех x^L. Наименьшая из таких постоянных называется нормой оператора А на линейном многообразии L и обозначается* ||Л||£.
Теорема 2. Линейный ограниченный оператор Ло, заданный на линейном многообразии L, всюду плотном в ЛНП X, и принимающий значения в полном ЛНП Y, может быть продолжен на все пространство без увеличения нормы.
Иными словами, на пространстве X можно определить оператор А такой, что Ах — Аох для x£L и ||Л||х = Molli-
* В соответствии с этим норму оператора на всем пространстве мы будем иногда обозначать || А ||х.
ПО
□ Пусть х—элемент пространства X, не принадлежащий L. Так как L всюду плотно в X, то найдется последовательность {xn}<=.L такая, что ||х„—х|| —*0 при п->оои, значит, ||х„—хт||—>0 при п, т^-со. Но тогда
II А(>Хп А0Хт II = II (Хп Хт) II II ^0 III'IIХп -^/вИ * ®
при п, т—>-оо, т. е. последовательность {Лох„} сходится в себе, а следовательно, в силу полноты У и к некоторому пределу. Обо-, значим этот предел через Ах. Пусть —другая последова-
тельность, сходящаяся к х. Имеем, очевидно, Цх„—1„||—>0, откуда || Дох„ —Л0|„Ц—>0. Следовательно, Л0В„—* Ах. Это означает, что оператор Л определен на элементах X однозначно. Если xgL, то берем х„ = х для всех п и тогда Ах = Ит Аох„ = Аох.
п
Построенный оператор Л аддитивен, так как
Л (Xj + х2) = Нт Л0 (х^ + х^2)) = lim ЛХП НтЛХ® = Ахг + Ахг, п п п
и ограничен, так как из неравенства || Л охп|К|| Л 0||£-||х„ || переходом к пределу получаем ||Лх||<||Л0||£-||х||. Из этого же неравенства следует, что ||Лх||х<|| Ло||£. Так как при продолжении оператора норма, очевидно, не может уменьшиться, то || Л ||х = || Л0||£ и теорема полностью доказана, g
Указанный процесс распространения оператора называется продолжением (или расширением) оператора по непрерывности.
§ 3. ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
Если значениями оператора являются числа, то, как сказано выше, оператор называется функционалом. Функционал f(x), определенный на линейном пространстве X, называется линейным, если:
О /(Xi + x2) = /:(x1) + h^);
2) f(Xx)==A/(x)
ДЛЯ Xj, X2gX, XgR (или С).
Линейные функционалы, определенные на ЛТП X, будем предполагать в дальнейшем непрерывными, не оговаривая этого каждый раз.
Так как R (или С) есть банахово пространство, то для линейных функционалов справедливы теоремы, установленные выше для линейных операторов (см. теоремы 1 и 2 § 1 и теорему 1 § 2).
Теорема 1. Аддитивный функционал, определенный на ЛТП X и непрерывный в одной точке х0 С X, равномерно непрерывен на всем X.
Теорема 2. Аддитивный и непрерывный функционал f, определенный на вещественном ЛТП X, однороден.
Теорема 3. Для того чтобы аддитивный и однородный функционал f, определенный на ЛНП X, был непрерывен, необходимо и достаточно, чтобы он был ограничен: |/(х)|^ А4||х||.
Наименьшая из постоянных М, удовлетворяющая этому неравенству, называется нормой функционала и обозначается ||/|]. Таким
111
образом, |f(x)K||flHI-v||. Кроме того, (|/|j= sup |/(х)|, или, что
И< 1 все равно,
Линейный ограниченный функционал, заданный на линейном многообразии Л, всюду плотном в ЛНП X, может быть однозначно продолжен на все пространство без увеличения нормы.
1
Примеры. 1. Пусть Х = £^[0, 1J; тогда / (х) = J х (/) (ft есть линейный функ-о ционал.
В самом* деле, f (х) имеет смысл для любого x£Lp{§, l что вытекает из неравенства Гельдера:
1
J х (/) (ft о
/ 1 \ 1/р / 1 \ 1/7
<( (/)|/’<1М •( У =|1*1Г-
\0 / \о /
Из этого же неравенства вытекает ограниченность f (х).; аддитивность f (х) очевидна.
2. Пусть X, есть R*, т. е. 6-мерное евклидова пространство. Для элемента х = {|/} этого пространства положим
f (х) = + C2I2 + • • • + ckifr*
%
где q, с*. — некоторые постоянные. Аддитивность функционала /(х) снова
очевидна. Так как х№—означает, что £<">—> для всех t=l„ 2, .6, то
k k
Um f (x^=lim J) ^>s= S e£i=i W • n n i = \ t=i
и непрерывность f (x) доказана.
Норме линейного функционала можно дать геометрическое истолкование. Так как в k- мерном евклидовом пространстве уравнение плоскости
СЛ1+^3 + • • • -|-Cfeife = C
можно записать в виде f (х) =с, то, по- аналогии, назовем гипер-плоскостью в произвольном линейном пространстве X множество точек этого пространства, удовлетворяющих уравнению /(х) = с, где f—линейный функционал на X. Гиперплоскости /(х) = с0 и /(x)=Ci естественно назвать параллельными.
Гиперплоскость /(х) = с делит пространство на два полупространства: множество точек х, в которых /(х)^е, и множество точек х, в которых f{x)^c. Назовем условно первое из этих полупространств лежащим влево, а второе—лежащим вправо от гиперплоскости f (х) = с.
Гиперплоскость /(х)=Ц/Ц обладает тем свойством, что весь единичный Шар | х | 1 лежит целиком слева от этой гиперплоскости (поскольку для точек такого шара f (х) ^||/|). С другой стороны, никакая из параллельных гиперплоскостей / (х)=»Ц/|| —е этим свойством уже не обладает.
112
По аналогии с теорией выпуклых тел ^-мерного евклидова пространства назовем гиперплоскость f (х) == ||f || опорной к шару
L
§ 4. ПРОСТРАНСТВО ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ ОПЕРАТОРОВ
1. Топологизация пространства операторов. Пусть X и Y — ЛТП. Как мы уже видели, пространство L(X, У) всех линейных непрерывных операторов, действующих из X, У, есть также линейное пространство. Пространство L(X, У) можно сделать топологическим, причем наделение L(X, У) топологией осуществляется обычно следующим образом.
Пусть М —некоторая совокупность ограниченных множеств М пространства X такая, что если 7И(£М (t = l, 2, ..., п), то п
U и W—фундаментальная система окрестностей нуля
1=1
пространства У, состоящая из уравновешенных и поглощающих множеств. Назовем окрестностью нуля пространства L (X, У) множество всех операторов A$L(X, У) таких, что Л(Л1)€йУ, где М и tog IF. Обозначим эту окрестность нуля v(M, w). Докажем, что совокупность V всевозможных таких окрестностей при всевозможных М£М и w£W удовлетворяет аксиоме II базы окрестностей нуля ЛТП.
1°. Множество v(M,w)— уравновешенное; проверку этого рекомендуем сделать самостоятельно. Покажем, что множество v(M,w) — поглощающее. Пусть A9£L(X, У). Так как М ограничено в X и Ло—непрерывный линейный оператор, то Л0(М) ограничено в У (докажите это). Поэтому найдется а>0 такое, что ХЛ0(Л1)сда при |Х|^а. Но это означает, что ХЛ0£о(Л1, ш) и поглощаемость v(M, ш) доказана.
2°. Пусть и(Mf, о(М2, w2)£V. Возьмем окрестность toczz^ria^, принадлежащую W, и М == М* и g М. Ясно, что v(M, w)a.v(Mit wt) П v (Мг, w2).
3°. Аналогично, еслиw'-i-w'cw, то u(M,w') + to')ao(M, да).
Далее, как обычно, за окрестность оператора A^L(X, У) примем A+v(M, w). Пространство, топологизированное таким образом, обозначают обычно через LM(X, У) и его топологию—через тм.
Наиболее важными среди топологий тм являются следующие три: 1) топология поточечной сходимости т5, которая получается, если в качестве М берутся все конечные множества пространства X;
2) топология ограниченной сходимости ть, если М—совокупность всех ограниченных множеств пространства X;
3) топология компактной сходимости хс, если М представляет собой совокупность всех компактных множеств пространства X.
В общем случае из этих топологий т6—самая 'сильная, — самая слабая и хс— промежуточная между ними. Иногда топологию т6 называют топологией равномерной сходимости, поскольку Л„—*Л? означает, что А„х—*-А,х равномерно на каждом ограни
113
ченном множестве МсХ, а топологию ts—топологией слабой сходимости .
В частном случае, когда У — множество вещественных (комплексных) чисел, т. е. когда мы рассматриваем множество непрерывных линейных функционалов /(х), определенных на ЛТП X, пространство L(X, У) называется пространством, сопряженным с X, и обозначается X*.
хь
Если X иУ—ЛНП, то сходимость Ап —-> Ао, где А„, AogL (X, У), означает, что || Л„ —Ло||—+0.
□ В самом деле, А„ —► Ло означает, что для любой окрестности нуля v(M, w) найдется номер п0 такой, что
An-Aoev(M, w) (1)
при п^п0. Положим Л1 = Х(0, 1)сХ и w — K(0, е)сУ. Тогда из (1) следует, что || Л„х—Лох|| < е при ||х||< 1 и п> п0. Следовательно, sup 1| Апх—Лох|Ке при п>п0, т. е., согласно равенству Цж||С 1
(2) § 2, ||Л„-Л0|]<е при п>л0. g|
Легко проверить с помощью равенства (2) § 2, что нормы операторов, отображающих ЛНП X в ЛНП У, удовлетворяют всем
аксиомам нормы, т. е.:
’I. | Л || = 0 эквивалентно Л = 0.
II. |М|]= Х|-||Л||.
III. ЦЛ + В1 <||Л|| + ||В||.
Таким образом, если X, У являются ЛНП, то и £(Х, У) есть ЛНП.
М||+||В||.
Теорема 1. Если У полно, то Lb (X, У) также полное и, следовательно, банахово пространство.
□ Пусть дана последовательность {Л„} линейных операторов, сходящаяся в себе по норме в пространстве линейных операторов, т. е. такая, что ||Л„ — Ли||—>0 при п, т—>оо. Тогда для любого х£Х
||Л„х-Лтх||<||Л„-Ли||-||х||—> 0
при п, т—+<х>. Поэтому для каждого фиксированного х последовательность {Лпх} элементов пространства У сходится в себе. В силу полноты пространства У последовательность {Л„г/} имеет некоторый предел у.
Итак, каждому х£Х ставится в соответствие у£У, и мы получаем некоторый оператор Л, определяемый равенством у = Ах. Этот оператор аддитивен:
Л (xj + х2) = Ига Л„ + х2) = Ига Апх1 + Ига Л„х2 = Лх! + Лх2. п п п
Покажем, что Л — ограниченный оператор. По условию, IM»—AJ-+0 при п, т-^оо. Значит, ||| Л„||—11Л J|при п, т—+оо, т. е. числовая последовательность {||ЛЛ||} сходится в себе и, следовательно, ограничена. Поэтому существует такая по
114
стоянная К, что ||Л„||<К для всех п. Отсюда ||Л„х||<К||х|| для всех п. Следовательно,
ЦЛх|] = Пт||Л„хК^кЯ п
и ограниченность оператора Л доказана. Так как А, кроме того, аддитивен и однороден, то Л—линейный ограниченный оператор.
Докажем, что Л есть предел последовательности {Л„} в смысле сходимости по норме в пространстве линейных операторов. Для любого е > 0 найдется номер п0 такой, что
||Лп+рх—А„х || < е (2)
для п > п0, р > 0 и всех х с нормой || х || 1. Переходя в нера-
венстве (2) к пределу при р-^оо, получим, что ||Ах—Л„х||^е для п п0 и всех х с нормой, не превосходящей единицы. Поэтому для /г п0 имеем
114 — ^11= sup ||Л„Х—Лх||<8.
11М< 1
Следовательно, Л = 1im Л„ в смысле сходимости по норме в прост-п
ранстве линейных ограниченных операторов и полнота этого пространства доказана.
Следствие. Пространство X*, сопряженное с ЛНП X, есть банахово пространство.
2. Принцип равномерной ограниченности и полнота пространства LS(X, К). Очевидно, что из равномерной сходимости, т. е. сходимости по норме, следует поточечная сходимость последовательности операторов. Обратное неверно, как показывает следующий пример.
Пусть X — гильбертово пространство Н с ортонормальным базисом {elf е2, ..., еп, ...} и Ап—оператор проектирования на подпространство Нп, порожденное элементами elf е29 ..., еп. Для любого х£Н имеем
П оо
Апх — S <х, et —> 2 <х, ег = х
i = 1 i = 1
и, следовательно, А„ —* I в смысле поточечной сходимости.
С другой стороны, для е0 < 1 любого п и р > 0 имеем
II ^п^п+1 ^п+р^п+1 II = II &п+11| ~ 1 > е0
и, следовательно, равномерная сходимость последовательности {Ап} в единичном шаре ||х|| 1 пространства Н не имеет места.
Теорема 2. Если пространства X и Y—банаховы, то пространство линейных ограниченных операторов, действующих из X в Y, также полно в смысле топологии поточечной сходимости пространства L(X, Y).
Так как для каждого х последовательность {Л„х} сходится в себе, то для каждого х существует у = Нш Апх и мы получаем п
115
оператор у = Ах, определенный на X и принимающий значения в Y. Как и выше, убеждаемся, что А—линейный оператор. Доказательство ограниченности оператора вытекает из следующей теоремы, называемой часто принципом равномерной ограниченности.
Теорема 3 (Б а н а х а—Шт ей н х а у са). Если последовательность {Л„} линейных непрерывных операторов ограничена в каждой точке банахова пространства X, т. е.
{II ^пх 11} n=i, г,... (3)
то последовательность {|| Лв||} норм этих операторов также ограничена.
□ Покажем сначала, что при выполнении условия (3) существует замкнутый шар К (а0, г0) такой, что множество {Anx}n-lt 2, ... ограничено, когда х пробегает К (а0, г0).
Предположим противное, т. е. что {A„x}n=i, 2,... не ограничено ни в одном замкнутом шаре. Возьмем произвольный шар Хо (х0, е0). Так как {Лпх} не ограничено в К (х0, е0/2), то найдутся элемент Xi€X(x0, е0/2) и номер nif для которых ||Л^хЛ^ 1. В силу непрерывности оператора Ani это неравенство будет выполнено и в некотором замкнутом шаре (хх, ех) с Хо. В шаре К (хп ех/2) множество {Л„х} снова не ограничено и потому найдутся элемент х2 € X (хх, ех/2) и номер л2, который можно считать большим, чем п1( такие, что ||ЛП2х2||^2. Снова это неравенство сохраняется в некотором шаре К2 (х2, 82) а Кх и т. д. Можно считать, что 8а—>0 при k—>00. Тогда будет существовать точка х, принадлежащая всем шарам Kk(Xnk, eft), k = 1,2........... В этой точке
|| АП)хЦk, что противоречит условию (3), и, следовательно, существование шара К (а0, г0), в котором множество {Л„х}й=1,2,... ограничено, доказано. Пусть||Л„х||^ Мо, л=1, 2, ..., для х£К (аи, г0).
Для произвольного хСХ(0, 1) положим х' = ГоХ + ао и, следовательно, х = -^-(х'—а0). Ясно, что х' СК (а0, г0) и потому || Лях'||С М0 для п = 1, 2, ... . Далее,
II4* Н 7; MX — К 7; (М о 4- II Апаа ||).
Но в силу (3) имеем ЦЛ„й0||^ Мо. Поэтому
и это верно для всех л = 1,2........ Следовательно, ЛЛ„|=
= sup М„хКМ-И
О X1} < 1
Следствие. Если последовательность линейных ограниченных операторов сходится в себе в каждой точке банахова пространства X, то последовательность норм этих операторов ограничена.
116
Это сразу вытекает из теоремы Банаха—Штейнхауса, если заметить, что последовательность таких операторов, сходящаяся в себе в каждой точке ЛНП, ограничена в каждой точке этого пространства.
Возвращаясь к оператору Ax = lim Апх, из неравенства || Ллх||^ п
М ||х|| (п = 1, 2, ...), вытекающего из следствия теоремы Банаха — Штейнхауза, в пределе при п —* оо получаем ||Лх||^ А4||х||, т. е. ограниченность оператора А.
Итак, существует предел любой поточечно сходящейся в себе последовательности линейных ограниченных операторов, который также является линейным ограниченным оператором, т. е. пространство операторов полно в смысле поточечной сходимости.
Часто оказывается полезной следующая теорема.
Теорема 4. Для того чтобы последовательность {Ап} операторов поточечно сходилась к оператору Ао, необходимо и достаточно, чтобы:
Г) последовательность {||ЛИ||} была ограничена-,
2°) Апх —> Лох для любого х из некоторого множества Хо, линейные комбинации элементов которого лежат всюду плотно в X.
□ Необходимость условия 1° есть не что иное, как доказанная выше теорема Банаха — Штейнхауса, необходимость условия 2° очевидна. Требуется доказать лишь достаточность этих условий.
Пусть /И = 8ир||Л„|| и пусть L(X0)—линейная оболочка мно-п
жества Хо. В силу линейности операторов А„ и Ло и условия 2° для любого x£L (Хо) имеем Апх —> Лох.
Возьмем теперь элемент х пространства X, не принадлежащий L (Хо). Для заданного е>0 найдется элемент x0£L(Xe) такой, что || х—х01| < еУ(4Л1). Тогда
II Ах КII Апх Л „х01| Л-1| Л„х0 Л охо || 4* || Л охо Л ох ||
II ^пхо Лохо || 4- (|| Ап || 4* || Ло j) || х х01| <С || Л„хв Л0хвЦ4-е/2.
Так как Л„х0 —+ Лохо, то найдется номер п0 такой, что || А„хв—ЛоХоЦ < 8/2 для п>п0. Поэтому для п>п0 имеем ||Л„х — — ЛоХ|| < 8. И
3. Применение к теории интерполирования. Доказанная выше теорема Банаха—Штейнхауса имеет многочисленные применения. В качестве примера такого применения приведем следующую теорему.
Теорема 5. Пусть на отрезке [0, 1] заданы точки, образующие бесконечную треугольную матрицу
dx> о о о о ...
d2) d2> о о о ...
A3’ dS) 4” о о ...
Для заданной функции х (t), определенной на отрезке [0, 1], строится интерполяционный многочлен Лагранжа Lax, узлами которого являются точки п-й
117
строки матрицы Т:
п
Lnx= 2 х№> #>(1), k= 1
где
'"м=^п£Ьй' ».и-П
Какова бы ни была матрица Т, существует непрерывная функция х (/), для которой интерполяционный многочлен Lnx не стремится равномерно к х (/) при п —> оо.
Будем рассматривать Lnx как оператор, преобразующий функцию х (/) £ ЕС [О, 1] в элемент того же пространства. Введем, кроме того, в рассмотрение п
величину А,л = тах Кп (t), где | (/) | . Тогда нетрудно доказать [10],
z k= 1
что || Ln[| = Xn. С другой стороны, имеет место неравенство С. Н. Бернштейна .
> 8 ]/^л ’ Следовательно, || [|—> оо, при п—>со. Отсюда сразу следует * сформулированная теорема, так как если бы Lnx—>х для всех х g С [0, 1], то нормы ||Ln|| были бы ограничены.
§ 5. ОБРАТНЫЕ ОПЕРАТОРЫ И ТЕОРЕМА БАНАХА О ГОМЕОМОРФИЗМЕ
1. Основные понятия. Ранее было уже введено понятие обратного оператора. С ним связаны, как мы сейчас увидим, вопросы о существовании и единственности решения операторных уравнений вида
Ах = у, * (1)
где у—известный элемент линейного пространства X, а х—искомый элемент того же пространства. Так как к уравнениям вида (1) относятся линейные алгебраические системы, линейные дифференциальные, линейные интегральные и другие уравнения, то очевидно, что нахождение оператора, обратного данному, является весьма важным.
Итак, рассмотрим уравнение (1) и предположим, что оператор А имеет обратный оператор Л-1. Полагая х — А~гу и подставляя это значение в равенство (1), получим тождество АА~гу = у, т. е. у = у- Следовательно, х—А~1у есть решение уравнения (1).
Допустим, что существует другое решение хх уравнения (1), т. е. Ахг=у. Действуя на обе части этого равенства оператором А'1, получим х1 = А~1у — х. Следовательно, решение х = А~*у единственно.
Если оператор А имеет правый обратный оператор С, то, как легко убедиться, х = Су есть решение уравнения (1), однако вопрос о единственности остается открытым.
Допустим, что для оператора А существует левый обратный оператор В. Тогда если уравнение (1) имеет решение х, т. е. Ах=у, то, применяя слева к обеим частям этого равенства оператор В, получим х — Ву, т. е. решение единственно. Однако вопрос о существовании решения остается открытым.
118
Анализ предыдущих рассуждений показывает, что обратный оператор (двусторонний, левый или правый) мы применяем не к любому х£Х, а лишь к элементам вида Ах, т. е. к образам элементов пространства X. Совокупность этих образов есть некоторое линейное многообразие (часть пространства X). Обобщая указанную ситуацию, мы приходим к следующему более общему определению обратного оператора.
Пусть даны два линейных пространства X и У и оператор А, отображающий X на Y. Если существует оператор А-1, определенный на У и принимающий значения в X, такой, что
А~1Ах = х (2)
для любого х X и
АА~гу = у (2')
для любого у £ Y, то операторы Л и Л’1 называются взаимнообратными. Из этого определения следует, в частности, что
(А~1)~1=А. Если оператор А-1 удовлетворяет лишь одному из предыдущих условий, то он называется левым (соответственно правым) обратным для оператора А.
Легко показать, что оператор, обратный линейному, также линеен. В самом деле, пусть */i,y2€K и А~1у1 = х1, A-1i/2 = x2. Тогда у2 — АА~1у1 — Ах2 и у2 = АА~1у2 = Ах2. Отсюда
А'1 (у1+уг)=А~1 (Ах1+Ах2) = А~1А (x1+x2)—xiA-x2 — A~1y1-)-A~1y2.
Аналогично доказывается, что А-1 (Хг/) — \А~1у.
Однако из непрерывности оператора А в некоторой топологии, вообще говоря, не следует непрерывность обратного оператора в той же или другой топологии, т. е. оператор, обратный линейному ограниченному, может не быть линейным ограниченным оператором.
2. Теоремы об обратном операторе. Приведем несколько теорем, дающих достаточные условия существования обратного линейного ограниченного оператора в ЛНП. Предварительно сделаем одно замечание. Пусть линейный ограниченный оператор А отображает X на У взаимно-однозначно. Тогда существует обратный оператор А-1, который является линейным. В самом деле, для любого у£Х существует лишь один прообраз х£Х. Ставя в соответствие каждому элементу y£Y его прообраз х£Х, мы получаем оператор А-1, который по смыслу своего определения удовлетворяет условиям (2), а из этих условий вытекает линейность оператора А-1.
Теорема 1. Пусть линейный оператор А, отображающий ЛНП X на ЛНП Y, для любого х£Х удовлетворяет условию
||Ах||>т||х||, (3)
где т ;>0 — некоторая постоянная. Тогда существует обратный линейный ограниченный оператор А-1.
□ Из условия (3) следует, что А отображает X на Y взаимнооднозначно: если Ах2 = у и Ах2 = у, то А (хх—х2) = 0 и, учитывая
119
неравенство (3), имеем
т||Xi—х2||< || A (х2—х2) |=»О,
откуда хх = х2. Поэтому, как показано выше, существует линейный оператор Л-1. Этот оператор ограничен, что сразу же следует из (3):
для любого y£Y. В
Рассмотрим два линейных ограниченных оператора А и В, отображающих ЛНП X в себя. Тогда имеет смысл произведение АВ. Покажем, что
||ЛВ||<||Л||-||В||. (4)
Для любого х£Х имеем
откуда и следует неравенство (4).
Пусть теперь А„, А, В„, BgL(X, X) и Л„ —- Л, В„—>В в смысле равномерной сходимости. Тогда АпВп->- АВ. В самом деле,
цл„в„—лвц<цлпвп—л„в||4-цляв—лвк <|MJ.||Bn-В||+|]В||-||Л„—Л ||.
Последовательность {|| А„ ||} есть сходящаяся числовая последовательность и потому ограничена, а ЦЛ„—Л|| —*0 и |(В„—ВЦ—+0. Поэтому ||Л„В„—ЛВЦ—>0, и требуемое доказано.
Теорема 2. Пусть линейный ограниченный оператор А отображает X в X и | Л q < 1. Тогда оператор 14- Л имеет обратный линейный ограниченный оператор.
□ В пространстве операторов, определенных на X и принимающих значения в том же пространстве, рассмотрим ряд
/ — Л + Лг—Л34-...+(—1)ЯЛЛ+... . (5)
Так как ЦЛ2|^Ц Л ||'2 и, аналогично, || Л" || ^ || Л ||", то для частичных сумм S„ ряда (5) имеем
1|5я+/,-5„Ы(-1)п+1Лп+1 + (—1)"+2Л"+2 + ... +
<|Л Ц"+14-ЦЛ|"+2 4- ... 4- || ЛЦя+Р<?"+14-^"+24- ... +уп+Р — 0
при я—>со, р > 0. Поэтому последовательность частичных сумм ряда (5) сходится в себе, а значит, в силу полноты пространства операторов, и к некоторому пределу, т. е. ряд (5) сходится.
Пусть S—сумма ряда (5). Имеем
S (/4-Л) =s lim Sn (/4-Л) =
= lim (/4-Л4-Л2 4- • • • 4-Л"—Л - Л2—...—Л"+1)=Нт (/ —Л"+1)=/. п п
120
Аналогично доказывается, что {I + A)S=I. Таким образом, S = (/ + 4)’1. Легко видеть, что S—линейный оператор. Кроме того, он ограничен, так как м оо
п= 0 п=0
Таким образом, (Z4-A)-1— линейный ограниченный оператор. Н Теорема 3. Пусть оператор A^L{X,¥) имеет обратный А~* и оператор ДА таков, что || ДАЦ < || А-1|| -1. Тогда оператор В = А-г&А имеет обратный В-1, причем
|В--Л->К ,_,‘^||,дл,1-4-‘|-. (6)
J □ В самом деле,
А4-ДА = А(Л-А-*ДА).
Так как || А~1 ДА|| < 1, то оператор / + А~1ДА имеет обратный
(7-J-А-1 ДА)-1 = 2 (—1)П(А-*ДА)П. п=0
Тогда, очевидно, (/ +А-1 ДА)-1 А-1 есть оператор, обратный оператору А (7 +А-1 ДА) = А 4-ДА. Далее, имеем
1|А+дд)-‘-а-1кИ-111-К/ + ^"1А^)"1-/К
^2ца-^да||«.||А-н
__ , у л-i I) <•_IIII________ц j-ip ~ 1—||А-^АЛ|| 11/1 1'^ 1—1| A-M-IIAAII_II
Пример. Рассмотрим интегральный оператор
1
Ах = х (/) + К {t, s) х (s) ds (7)
о
с непрерывным ядром К (t, s), отображающий пространство С [0, 1] в себя. Пусть Ко (Л s) —вырожденное ядро, близкое к ядру К (/, s), а Ао—интегральный оператор, соответствующий ядру Ко (/, s):
1
AqX = х (t) + J Ко (t> s) x (s) ds. (8)
I 0
Рассмотрим уравнения
Ах = У Ю
Лох = 1/. (8')
Положим (o = max | К (^, s)~Ко (/, s) ( . Если ДЛ = Л —Ло, то легко видеть, /, S
что ЦДЛ Как известно*, решение уравнения (8) с вырожденным ядром
* Смм например, [9].
121
сводится к решению линейной алгебраической системы. Предположим, что система имеет решение, которое запишем в виде xQ(t) = Ry, где R—оператор, определенный матрицей (rzy), обратной матрице вышеуказанной линейной алгебраической системы. Пусть г—норма оператора R. Тогда если со < 1/г, то в силу доказанной теоремы интегральное уравнение (7) с невырожденным ядром имеет решение х (/), причем
|)Х(О—хо(О II <1'2^7 гг.
Если, наоборот, известно, что уравнение (7) разрешимо, то теорема 3 может быть использована для доказательства существования решения у аппроксимирующего уравнения с вырожденным ядром и для оценки погрешности приближенного решения.
В заключение докажем следующую теорему, часто называемую теоремой Банаха о гомеоморфизме.
Теорема 4. Если линейный непрерывный оператор А отображает все банахово пространство X на все банахово пространство У взаимно-однозначно, то существует линейный непрерывный оператор Л-1, обратный оператору А, отображающий У на X.
□ Необходимо доказать лишь ограниченность оператора Л”1.
В силу леммы § 2 настоящей главы пространство У может быть
представлено в виде U Ук, где —совокупность таких эле-
fe=i
ментов у£У, для которых ||Л’^И^^ИИ и по крайней мере одно из множеств Ук всюду плотно в У. Пусть таким является множество У„.
Возьмем любой элемент у£У. Пусть ||/,||=»/; найдем yi£Yn такой, что •
k-^KZ/2, Ш1</
(это можно сделать, так как К (О, Z) Г) У„ всюду плотно в К (0, /) и J/€K(O, /)). Найдем далее элемент у2^Уп такой, что
Продолжая этот процесс, построим элементы ук£Уп такие, что
\\У—(У1 + Уг + •.. +ук)\\<1/2к,
k
Таким образом, получим у = lim 2 Уе Положим xk — A~lyk\ тогда k i = 1
К
Последовательность sk= У х{ при k—->оо сходится к не-i = 1
которому пределу х£Х, так как
II II
.S < nZ/2*-*
llt = fc+l II
и X — полное пространство. Следовательно,
k оо
x = 2 xi= xi'
k i = 1 i = i
122
Далее, имеем / k \ k k
Ах =s А (lim У X/ ) = lim T Ax.- = lim У у,- — у. к k i=i 7 k i=i ‘ k i=i a
Отсюда
М_1г/|1=к11=нт k
= 2n/ = 2n||z/||.
nl
Так как у—любой элемент из Y, то ограниченность, а следовательно, и непрерывность оператора А~1 доказана. В
Мы указывали, что имеют место случаи, когда оператор, обратный ограниченному линейному оператору, оказывается хотя и линейным, но определенным не на всем пространсте Y, а лишь на некотором линейном многообразии, и неограниченным на этом многообразии. Точно так же операторы, обратные неограниченному линейному оператору, определенному на некотором линейном многообразии, всюду плотном в X, могут оказаться ограниченными линейными операторами, определенными на всем Y. Детальное рассмотрение подобных случаев в произвольном банаховом пространстве выходит за рамки настоящей книги, и мы ограничимся тем, что приведем два простых примера, подтверждающих сказанное.
t
Примеры. 1. Пусть Х = С[0,1] и Дх=^х(т)с1т. Тогда А—ограниченный о
линейный оператор, но А ~ 1у = — у (t),— неограниченный оператор, определенный на линейном многообразии непрерывно дифференцируемых функций таких, что г/(0) = 0.
2. Пусть Х=С [0, 1], q(t)£C [0, 1], р (/) € Q [0, 1], р (/) # 0 и , d ( .,, dx ] . ...
Ax=di \p (Z)’d7f+9(/)x
— неограниченный оператор Штурма—Лиувилля, определенный на линейном многообразии дважды непрерывно дифференцируемых функций таких, что х(0) = = х(1) = 0. Обратный оператор
А~гу=^ °(*> т) У W dT> о
где G (t, т)—функция Грина, есть ограниченный линейный оператор, определенный на всем пространстве С [0, 1].
3« Операторы, зависящие от параметра. Часто в различных разделах математики встречаются уравнения вида
Ах—Хх = у, или (А—XI) х —у, (9)
где А—линейный оператор и %—некоторый параметр, с уравнением (9) рассмотрим уравнение
Ах—Хх — 0, или (Л—Х./)х = 0,
Наряду
(Ю)
123
которое называется однородным уравнением, соответствующим уравнению (9). Это уравнение всегда имеет решение х = 0, которое называется тривиальным.
Допустим, что для некоторого X оператор А—X/ имеет обратный (А—X/)"1 = Оператор называется резольвентным оператором (или резольвентой) для уравнения (9). Тогда для этого X уравнение (9) имеет при любом у единственное решение x = Ry.y. Однородное уравнение (10) имеет в этом случае только тривиальное решение х = 0.
Такие значения X, при которых уравнение (9) имеет единственное решение при любом у, а оператор R^ ограничен, называются регулярными значениями для уравнения (9) или для оператора А. Если уравнение (10) при данном X имеет кроме тривиального некоторое другое решение, то такое значение X называется собственным значением (или характеристическим числом) для уравнения (9) или оператора А, а нетривиальное решение называется собственным элементом уравнения (9) или оператора А, соответствующим данному собственному значению X.
Если X—собственное значение оператора А и уравнение (9) имеет решение при некотором у, то решение не является единственным. Действительно, пусть х0—решение уравнения (9), т. е. Ах0—kxg = y, и х—собственный элемент оператора А, соответствующий собственному значению X, т. е. Ах—Хх = 0. Тогда
А (х0 + х)—X (х0 + х)=>у ,
и, значит, х0 + х также является решением уравнения (9).
Совокупность всех значений X, не являющихся регулярными, называется спектром оператора А. В частности, все собственные значения принадлежат спектру.
Из теорем 2 и 3 вытекают следующие предложения:
Если X таково, что -уц-||Л || = <7 < 1, то оператор А—kl имеет обратный-, при этом
х + х2 + Xs +•••;•
Если X—регулярное значение, то и X + ДХ при | ДХ | < [ (А—X/) ~11|-1 также есть регулярное значение.
Отсюда следует, что совокупность регулярных значений есть открытое множество и, значит, спектр—замкнутое множество.
Пример. Рассмотрим в пространстве С [0, 1] интегральное уравнение
1
X (t)=y (0 + Х J к (t, s) X (s) ds, (11)
о
где Я (f, s) — непрерывная в квадрате O^s^l функция. Положим
1Д= и перепишем уравнение в том виде, в котором мы рассматривали выше
124
операторное уравнение; получим
1
К s) х (s) ds—рх (/) = — fiy (0, или Ax—px = — p# о
/ 1 \
f мы ввели обозначение Лх = J /С (tf, s) x (s) ds L Далее, находим к о /
1 / Д Л2 ДЗ \
/?g = /?1/x=-7(/ + y+-F+-F+--J=-M/+M+XM2+^ + ...).
Заметим, что
1
APz = J KP(t, s) z (s) ds, о
где Kp (t, s) есть p-я итерация ядра* К (/, s). Следовательно,
1 1
Я 1Лг = — Хг (0 —X2 У К (t, s) z (s) ds—Xs j K2 (t, s) г (s) ds — о о
1
— X4 J Кз(/, s) z(s)ds—... . о
Поэтому решение уравнения (11) имеет вид
1
* (0 = ЛIА ( - у У) = У (0 + j к a, S) У (S) ds+ о
1 1
Ч~Х2 /С 2 (Л а) х (s) ds-|-X3 Кз s) * (s) ds+ ... » о Oj
Таким образом, мы получили то же решение, что и в теории интегральных уравнений, а именно
1
х (t) = у (/) 4-Х J R (/, s; X) у (s) ds, о
где
/?(/, s; X) = /<(/, s)+KK2(tt s)4-X2K3(/, s)4-...
— резольвента ядра К (t, s).
Уравнения для резольвенты R (/, s; X), выводимые в теории интегральных Уравнений, выражают условия того, что R есть обратный справа и слева оператор для оператора ХЛ —/.
§ 6. ТЕОРЕМА О ЗАМКНУТОМ ГРАФИКЕ И ОБ ОТКРЫТОМ ОТОБРАЖЕНИИ
Теоремы этого параграфа вытекают из теоремы Банаха о гомеоморфизме. Однако их можно доказать и независимо от нее и тогда теорема о гомеоморфизме окажется следствием указанных теорем.
* См. [9J.
125
Для отображений банаховых пространств можно ввести понятие графика такого отображения, аналогичное графику вещественной функции вещественного аргумента.
Рассмотрим отображение f: M^-Y, где X и Y—банаховы пространства, ;ИсХ. Множество {(х, Ax)}aXxY, где х пробегает М, называется графиком отображения А и обозначается ОгЛ.
Мы ограничимся рассмотрением лишь графиков линейных операторов А: X—>-Y. Легко проверить, что в этом случае Gr А есть линейное многообразие в пространстве XxY, однозначно определяемое оператором А. Если оператор А непрерывен, то линейное многообразие ОгЛ замкнуто, т. е. является подпространством в XxY. В самом деле, пусть (х0, у0)—предельная точка множества Gr Л и {(х„, Ах„)} — последовательность точек этого множества, сходящаяся к (х0, у0). Это значит, что хп—<-хй, Ахп—>- z/0. Но в силу непрерывности оператора Л имеем Ахп—*Лх0, откуда z/0 = Ах0 и, следовательно, (х0, уо)=я(л;о> Лх0)$Ог Л.
Справедливо и обратное утверждение.
Теорема 1 (о замкнутом графике). Если линейный оператор А, отображающий банахово пространство X в банахово пространство Y, имеет замкнутый график, то этот оператор непрерывен .
□ На подпространстве Gr Л a XxY, рассматриваемом как самостоятельное банахово пространство, введем оператор проектирования Pt: ОгЛ—определяемый равенством Рх(х, Ах) = х. Это линейный непрерывный оператор, отображающий взаимно-однозначно ОгЛ на все X. По теореме Банаха о гомеоморфизме, существует обратный оператор Рг1: X —>Gr А, являющийся линейным и непрерывным. Далее, оператор Р2 (х, Ах) = Ах, действующий из ОгЛ в У, также линеен и непрерывен. Но тогда и А = Р^Р^1 является линейным непрерывным оператором. Ц
С понятием графика связано понятие о замкнутом линейном операторе. Линейный оператор Л: L—>-Y, где L—линейное многообразие пространства X, называется замкнутым, если замкнут график ОгЛ этого оператора. Иными словами, Л—замкнутый оператор, если из xn£L, хп->-х0, Ахп—^уа следует, что x0CL и Лх0 —£/о-
Согласно теореме о замкнутом графике, замкнутый линейный оператор, определенный на замкнутом линейном многообразии, т. е. на подпространстве банахова пространства, непрерывен, так что для таких операторов понятие замкнутого оператора ничего нового не дает. Однако для линейных операторов, определенных на незамкнутых линейных многообразиях, свойство замкнутости часто оказывается полезным для установления тех или иных свойств оператора.
Приведем пример замкнутого не непрерывного оператора. В пространстве С [а, 6] рассмотрим оператор Л = , определенный на
линейном многообразии С'fa, &]сС[а, 6]. Этот оператор, как мы видели, не является непрерывным, но является замкнутым. В са-126
мом деле, пусть хп (t) —> х0 (/) и х'п (t) —> у0 (t) в смысле сходимости по норме пространства С [а, б], т. е. равномерно на [a, ft], Тогда по известной теореме математического анализа ха (/) есть дифференцируемая функция и ya(t) = x'0(t), что и означает замкнутость рассматриваемого оператора.
Другой теоремой, примыкающей к только что доказанной, является теорема об открытом отображении.
Отображение f топологического пространства X в топологическое пространство Y называется открытым, если образ любого открытого множества из X есть открытое множество в Y.
Теорема 2 (об открытом отображении). Всякое линейное непрерывное отображение А банахова пространства X на банахово пространство Y является открытым.
□ Пусть N- ker А = {х| Лх = 0}. Так как А непрерывно, то N — замкнутое подпространство в X и, как мы установили выше (см. п. 2, § 1, гл. II) фактор-пространство Х/N есть банахово пространство. Введем оператор Л: X/N-—> У; для x^X/N полагаем Ах — Ах = А (х-\-и), где и —любой элемент из N.
Очевидно, что Л —линейный оператор. Более того, Л непрерывен, так как если хп—>х0, то в классах хп и х0 существуют элементы хп и х0 такие, что хп—>х0 (см. с. 66). Но тогда в силу непрерывности Л также уп = Ах„ —>у0 = Ах0, т. е. Ахп-^Ах„.
Наконец, ясно, что так как Л отображает X на все Y, то и Л отображает Х/N на все Y, причем взаимно-однозначно. По теореме Банаха о гомеоморфизме, существует обратный оператор Л-1, являющийся линейным непрерывным и отображающим Y на Х/N.
Пусть G—произвольное открытое множество пространства X и GaX/N — его образ при естественном гомеоморфизме X naX/N. Тогда G также открыто. В силу непрерывности оператора Л-1 прообраз HcY множества G тоже открыт. Но H — A(G) и теорема доказана. Я
§ 7. ПРОСТРАНСТВО БАНАХА С БАЗИСОМ
1. Основные понятия. Пусть X—бесконечномерное банахово пространство. Последовательность элементов е,, е2, ..., еп, ... из X называется базисом этого пространства, если любой элемент
ОО
х£Х можно однозначно представить в виде х= £zez, где gz— i = 1
вещественные или комплексные числа (соответственно для случая вещественного или комплексного пространства X). Однозначность
00
представления, очевидно, равносильна условию, что У 1^,- = 0
i = 1
тогда и только тогда, когда |; = 0 для всех i.
127
Примеры. 1, Пусть Х = 1р. Тогда совокупность элементов ^ = (1, О, 0, 0, .
е2 = (0, 1, 0, 0, образует базис в 1р, так как для любого х£1р имеет
-ОО
место однозначное представление х = У если #=*{51, 5а, • ••» 1п> •••}• i = 1
В самом деле,
2 ^ = {51, 52........U о,о, ...}
i = i
и потому
п
х 2
1 = 1
/ °° \1/Р
=||{0, о, 5n+i, 5w+2, 2 l^lpJ
\i=«+i у
как остаток сходящегося
ряда. Следовательно,
а оо
x = lim У 5/^i = У « i=i t=i
С© ОО
Далее, если * = 2 = У т* е#
i=i /=1
0= 2 52-5*2, -Ь
1=1
то 5f = ?r(J* = h 2, ...), что и требовалось установить.
2. Пусть Х = С{0, 1]. Рассмотрим в С [0, 1] последовательность элементов
/, 1—/, «00 (О» W10 (0> Wll(O» М20 (О* W21(0> W22 (0> •••♦ U)
где (t) (k=l> 2, 0^1 <2k) определяется следующим образом: х^/(/)==0,
если t находится вне интервала /—, , а внутри этого интервала (/)
\2k 2k )
имеет график в виде равнобедренного треугольника с высотой, равной единице (на рис. 2 изображен график функции (/))•
Рис. 3
Всякая функция *(/)£С[0, 1] представима в виде ряда
ео 2^— 1
X (/) = aof+Й! (1 — О + S 2 W
*=о zfo
где aQ — x (1), ai = x (0), а коэффициенты ам [находятся Ьднозначно геометрическим построением, указанным на рис. 3.
128
График частичной суммы ряда (2)
s-12ft-l
+ —О + 2 akiuki (О
Л=0 /=о
есть, очевидно, ломаная линия с 2^ +1 вершинами, лежащими нд кривой х==х (t) в точках с равноотстоящими абсциссами. Совокупность функций (1) образует базис в С [0, 1].
Если пространство X имеет базис, то оно, очевидно, сепарабельно. Счетным всюду плотным множеством в пространстве с ба-п
зисом является множество линейных комбинаций вида У] г{в[ с ра-1=1
циональными коэффициентами г,-. Однако обратное утверждение не верно; не всякое сепарабельное банахово пространство имеет базис. Итак, пусть X—банахово пространство с базисом ег,
..., еп, ... Рассмотрим линейное пространство Y, элементами которого являются всевозможные числовые последовательности у = ОО
= {Ль Ла, • • •. Л«» • • •} такие, что ряд 2 ЛА сходится.
п
Введем в Y норму, полагая ||y|| = sup У П 1=1
. Покажем, что
Y—банахово пространство. Прежде всего выполнение аксиом нормы легко проверяется. Пусть теперь дана последовательность {i/A} £ У, 2, ..., сходящаяся в себе. Тогда для заданного е>0 имеем
II У»—& Il «sup п
п
2 (лГ’-Л^) е{
1 = 1
< е при т, k^m0 (е)
и, следовательно,
(3)
при т, к~^--тй (в) и любом п. Отсюда
и потому | Лп"” — Лп*’| <2е/[|ел|| при tn, k^m0(e.) и любом п. Следовательно, числовая последовательность {лА'п>}т=1,2,... сходится к некоторому пределу т^0’ и это имеет место для любого п.
Перейдем в неравенстве (3) к пределу при k—> оо; получим
.21 (Л’™— ЛГ) е/|<в
(4)
5 № 3054
129
при m m0 (е) и любом п. Положим
sAm) = 2 лГЧ, s«” = S i\Tet. i=l i = l
Учитывая неравенство (4), имеем
11 + 28
при т^т9 (s) и любых п > 0, р > 0.
Пусть теперь задано произвольное число 6 > 0. Выберем сначала е, а тем самым и т0 (е) так, чтобы 2е < 6/2, а затем, фиксировав /п^/п0(е), возьмем па так, чтобы Цs«+p—при n^Ss п0 и любом р>0 (это возможно в силу сходимости ряда 2 лГ’е,-)- Тогда [|Sn+P— при n>n0 и любых р>'0, т. е. 1= 1 00
ряд 2 Лг°Ч сходится и, следовательно, уа = {т){0), т]£0),iff”,•..} £ У.
Так как, кроме того, из неравенства (4) получаем, что
In II
2 (if/"’— T]/0))eiIIС8 при 'т^'т0,
1=1 II
т. е. §ут—#01|при тй, то полнота пространства Y доказана. •
00
Очевидно, каждому х = У € X соответствует единственный 1 = 1
элемент yx = {lt, |2, . . ..}£У. Обратно: каждому элементу
у = {т(\{}£У соответствует единственный элемент xyf-X, а именно
00
Ху ~ ^iei’
Таким образом, можно считать, что определен оператор х = Ау, взаимно-однозначно отображающий Y на X. Легко видеть, что оператор А линеен. Кроме того, оператор А ограничен. В самом деле,
IMz/ll=M =
Следовательно, мы имеем линейный непрерывный оператор А, отображающий Y на X взаимно-однозначно. По теореме Банаха о гомеоморфизме, существует обратный оператор у—А-1х, который также является линейным ограниченным оператором.
оо
2. Биортогональные последовательности. Пусть х = 2 %iet — •
1 = 1 "
любой элемент из X. Определим функционал fk, полагая(х) = ^А.
130
Очевидно, функционал fft аддитивен. Далее,
k 6=1
. . . 2 ^>iei 2
lEfcVlkfell <=i t= i
1/л(*)1 l£J- ii^n “ hft||
1 __2Ь1|_2||Л-1х|| 2(|Л-1«
1ЫГ“ИЙ~ 1Ы1 1Ы1
п
откуда следует ограниченность и, следовательно, линейность fk, а также что [| fk||< 21| Л-1 [|/||ек||.
Построив для каждого k функционал fk, получим бесконечную последовательность линейных функционалов {Д, /2,.. .,fk, .. .}сХ‘, причем любой элемент х£Х можно записать в виде
х=
Положим, в частности, х = е,-. Тогда
е _ I 1 при i = /;
~ \ 0 при i Ф j, т. е.
f (p\=J 1 при i=t'r' га
'{( 0 при i Ф j. (5'
Таким образом, мы получили две последовательности: элементов {в(\ и функционалов {/J, удовлетворяющих равенствам (5). Такие две последовательности называются биортогональными.
Возьмем теперь любой линейный функционал [£Х*. Так как
х = 2 ft (х) et = lim 2 ft (x) eit 1=1 n i= 1
TO
n П 00
f (x) = lim 2 f \fi (x) ez] = lim 2 ft (x) f (&) = 2 ft (x) f n i- 1 n 1 = 1 i= 1
Обозначим f(ei) = Ci. Тогда получим, что для любого линейного функционала f^X* имеет место представление
/ (х) = 2 Cifi (х), или / = 2 с-ft, (6)
i—l i—1
где ряд справа сходится в смысле топологии поточечной сходимости.
Представление (6), очевидно, однозначно.
3. Разбиение единичного оператора. Пусть х—любой элемент ИЗ X; тогда
00 п 00
х= 2 = 2 Ва + 2 ifii
1 i= 1 i=n+ 1
5*
131
и каждому элементу х£Х можно поставить в соответствие два h оо
однозначно определённых элемента уп = S и zn = 3 et. t= 1 i=n +1
Этими равенствами задаются два оператора уп = Snx и zn = Rnx, определенные на X и принимающие значения в том же пространстве, так что
Ix = S„x + Rnx.
Очевидно, S„ и —линейные ограниченные операторы при каждом фиксированном п. В самом деле их линейность очевидна, а ограниченность следует из неравенства
IIVIlCsUp з |ге1.| = Ц-^КМ-1||.||х|| т i = 1 Ц
и аналогично ||/?„х|К 2|| А-1||-||х||.
4. Критерий компактности в пространстве с базисом.'
Теорема. Для относительной компактности Множества М банахова пространства X с базисом необходимо и достаточно, чтобы М было ограниченным и Чтобы для любого числа е > 0 существовал номер п0 такой, что || /?„х|| < е при и любом х£М.
□ Необходимость. Ограниченность множества М вытекает из его относительной компактности (см. § 9 гл. I). Докажем выполнение второго условия.
Возьмем некоторое число т) > 0 и построим конечную трсеть {xi, х2, ...» xft} для М. Для любого х£М найдем'хг, принадлежащий т)-сети, такой, что ||х—хг|| < т]. Тогда
II II =« II х—S„x|| || х—xt || +1| х^ Snx || <
< || х - Х; || +1| S„Xi - Snx || +1| RaXi |( <
<•(1 +p-i||)||x-xz|| + ||7?„x1.||< (1 +ЦД-1||)т1+||/?„х1.||.
Для каждого фиксированного x Rn(x)—>0 при n—>oo. Поэтому найдется такое n0, что || /?„хг || < т| при п п0 (1 = 1, 2, ...,£). Но тогда ||7?„х|| < (2 + || Д-1 ||)т] при п^ п0. {Теперь достаточно взять т] =«8/(2 + ||А-11|), чтобы получить требуемое неравенство, так как номер п0 не зависит от того, какой элемент х взят в множестве М.
Достаточность. Покажем, что при выполнении условий теоремы для любого е > 0 существует конечная е-сеть для множества М. Для этого по заданному е выберем пй так, чтобы || Rnax || < е/2 при всех х£М. Рассмотрим затем множество /ИПо, состоящее из элементов вида Snox, где х£М. Его можно рассматривать как множество, расположенное в и0-мерном пространстве Хп„ cz X, определенном базисными элементами е1( es, ..., еп. Так как, кроме того, в силу неравенства ||Sn„x||^||А-1||-||х|] и предположения об ограниченности множества М множество Л4Яо ограничено, то оно относительно компактно, поэтому в Мп„ существует конечная е/2-сеть для Л1Яо. Но эта же сеть служит, очевидно, е-сетью для множества М, и требуемое доказано. Ц
| 132
Из доказанной теоремы сразу вытекает установленный ранее критерий компактности в пространстве 1р (см. с. 77). Для этого достаточно заметить, что в 1р справедливо соотношение
/ ОО \1/р
11ад= 2 |Ы . \i=n+l /
Пример. Рассмотрим в 12 множество элементов х — {£/} таких, чтоО«с|п«^ 1/л,—основной параллелепипед кооординатного гильбертова пространства. Этот параллелепипед есть компактное множество. П. С. Урысон доказал, что всякое сепарабельное метрическое пространство гомеоморфно некоторому подмножеству основного параллелепипеда пространства /2.
Упражнения
1. Докажите непрерывность и найдите норму операторов Лхх = /х(/), Л2х={|2> 1з, ...}, х = {|х, g2, Вз, •••} соответственно в пространствах С [a, b] и
2. Докажите непрерывность и найдите норму функционалов (х)=ах (0)-]-bx (I), оо
в пространствах С [0, 1] и /2. i= 1
3. Докажите, что || Л [|= sup ЦЛх|].
4. Докажите, что функционал f (х), вообще говоря, нелинейный, определенный на плотном подмножестве Хо банахова пространства X и равномерно непрерывный на нем, мод<нр однозначно продолжить на все пространство.
5. Докажите, что для любого линейного оператора Л, действующего в банаховом пространстве X, существует p = lim 1| Л* || == inf ^/|] Л"]|, и если р > О, п v п у
то весь спектр оператора Л лежит внутри круга | к | «Ср. (Число р называется спектральным радиусом оператора Л.)
6. Выведите теорему Банаха о гомеоморфизме как следствие теоремы об открытом отображении.
7. Постройте базисы в пространствах с0 и с,
8. Всякий линейный оператор Л, действующий из ЛТП X в ЛТП У, ограничен, т. е. Л (М) ограничено в У, если М ограничено в X. Верно ли обратное?
9. Покажите, что линейный функционал, определенный на ЛТП, непрерывен тогда и тРДько тогда, когда он ограничен в некоторой окрестности нуля.
10. Пусть К (t, s)£L2(a, b; a, b), ап^а, bn\ b (n=l, 2, 3, ...) и
d bn
Лх — J К (6 s) x (s) ds, Anx = К (Z, s) x (s) ds; x (s)£L2 (a, b). a an
В какой топологии пространства операторов Ап сходятся к Л?
11. Покажите, что топология пространства L(X, Y) является локально выпуклой, если Y есть локально выпуклое пространство, и отделимой, если Y отделимо и М образует покрытие пространства X.
12. Пусть X, У—ЛТП и Х = Х/Хо» где Хо—замкнутое подпространство в X. В X введена трпология, причем окрестностями нуля в X считаются образы окрестностей нули в X при естественном отображении хь—>х, Пусть, далее, А:Х—>У и Лх = Лх, где х—представитель класса х. При каком условии оператор А однозначно определен и является ли он непрерывным, если непрерывен Л?
13. Найдите необходимые и достаточные условия того, что множество МсХхУ есть график линейного оператора A:L—> У, L CZ X.
14. Графиком какого отображения является «диагональ» 7И = {(х, х)|х^Х}?
15. Опишите характеристические свойства множества МсХхЯ> являющегося графиком полунормы Р (*)♦
ГЛАВА IV
ЛИНЕЙНЫЕ ФУНКЦИОНАЛЫ
В этой главе мы рассмотрим подробно простейшие свойства линейных непрерывных функционалов*, определенных в ЛНП.
Напомним прежде всего несколько теорем, доказанных выше и имеющих место как для операторов, так и для функционалов, и которые мы здесь сформулируем применительно к функционалам.
Теорема 1 (Банаха—Штейнхауса). Если последовательность {f„} линейных функционалов, определенных на банаховом пространстве X, ограничена в каждой точке х^Х, то последовательность норм {||/„||} этих функционалов также ограничена.
Теорема 2. Если последовательность линейных функционалов {/„} сходится в себе в каждой точке банахова пространства X, то существует линейный функционал f такой, что fn(x)-»-f(x) для любого х£Х.
Теорема 3. Для того чтобы последовательность {fn} линейных функционалов сходилась в каждой точке х банахова пространства X к функционалу f0, необходимо и достаточно, чтобы:
Г) последовательность была ограничена-,
2°) fn W fo (х) для любого х из некоторого множества М с X, линейные комбинации элементов которого лежат всюду плотно в X.
Теорема 4. Линейный функционал f, заданный на линейном многообразии L, всюду плотном в ЛНП X, и ограниченный на нем, может быть продолжен на все пространство без увеличения нормы и притом однозначно.
§ 1. ТЕОРЕМА—БАНАХА-ХАНА И ЕЕ СЛЕДСТВИЯ
1. Теорема Банаха — Хана в линейных топологических пространствах. Выше было показано, что линейный оператор, в частности, линейный функционал, заданный и ограниченный на линейном многообразии L, всюду плотном в ЛНП X, может быть продолжен по непрерывности на все пространство без увеличения нормы. Нижеследующие теоремы показывают возможность продолжения на все пространство с сохранением некоторых оценок линейных функционалов, заданных первоначально на линейном многообразии, не обязательно всюду плотном в пространстве X.
Пусть X — вещественное или комплексное линейное пространство, наделение которого топологией не предполагается. Функционал р, определенный на X, называется однородно выпуклым, если
* Так как в дальнейшем мы будем рассматривать лишь непрерывные линейные функционалы, то слово «непрерывный» обычно опускается.
134
он удовлетворяет условиям:
Р (х + у) Р (х) + р (у) для любых х, у£Х\
р (ах) = ар (х) для любого х £ X и любого а 0.
Если р —однородно выпуклый функционал, то
Ptty+U-OxK^GO+U -0р(х)
для любых х, у£Х и О< /< 1 и легко проверить, что множество
Л == {х£ X |р (х) < а}
является выпуклым поглощающим множеством, содержащим нуль.
Обратно: если дано выпуклое поглощающее множество А а X, содержащее нуль, то функционал Минковского рА (х) = inf %
X > 0, хеХЛ этого множества является однородно выпуклым функционалом, но в общем случае не полунормой (если А не является уравновешенным). Для однородно выпуклых функционалов, как и для полунорм, получаем, что
I Ра (х)-рА (у) | < max {рА (х-у), рА {у-х)},
и если и — окрестность нуля ЛТП X, не обязательно уравновешенная, то ри(х) равномерно непрерывен на X.
Пусть L—подпространство пространства X. Линейный функционал F, определенный на X, называется продолжением линейного функционала /, определенного на L, если F(x)=/(x) для всех x£L.
Теорема 1 (Банаха — Хана). Пусть на подпространстве L вещественного линейного пространства X задан линейный функционал f. Если существует определенный на X однородно выпуклый функционал р такой, что f(x)^p (х) для x£L, то функционал f можно продолжить на все пространство и притом так, что для продолжения F будет выполнено неравенство F (х) р (х) при всех х Е X.
□ Возьмем произвольный элемент z£X\L и рассмотрим подпространство L1 = L-\-tz, —ao<t <4- оо. Ясно, что Lf = L и каждый элемент у Е Li можно однозначно представить в виде у = х -f- tz, x£L, —оо</< + оо. Определим А (у) на Lit полагая
fi(y) = fi(,x+tz) = f(x) + ct,ceR. (1)
Легко проверить, что при любом выборе с (у)—линейный функционал, что fi(x)=/(x) для x£L, и остается подобрать с таким образом, чтобы A (у)=Ср(у) для всех y£Lt.
Неравенство
fi (х + /г)=/(х) + /с<р(х + ^г)
135
эквивалентно следующим двум:
/(7)+с<р(т+г) ПРИ z>0’
2) ПРИ *<°
(при t = 0 неравенство (х) = f (х) р (х) автоматически выполняется). Перепишем эти два неравенства так:
С<р (т + г)— f (т) ПРИ *>°-
Неравенства (2) будут, очевидно, выполнены, если удастся выбрать с так, чтобы для любых двух элементов х' и х" подпространства L имели место неравенства
f (х') — р (х' — г) С с < р (х" + г) — f <х"). (3)
Такой выбор возможен. В самом деле, для х', x"gL имеем
/ (х') + f (х") = f (х' 4- х") С Р (/ — г + х" + г)^ р (х' — z) + р (х" + г),
откуда
f (х') — р (х' — г) р (х" + г) — / (х").
Так как х' и х" можно брать независимыми дру^ от друга, то из (4) следует, что
sup {А(х') — p(x'-z)}<inf {p(x"-f-z) —f (х")}. х' 6 L x"eL
Но тогда, если выбрать с так, чтобы
sup {f(x')—р(х' —z)}^c< inf {p(x" + z) —f(x")}, x'eL x"eLt
то такое с удовлетворяет неравенствам (3), а следовательно, и неравенствам (2) и функционал Д, определенный равенством (1), окажется продолжением f на подпространство таким, что ft (х) ^р(х) для x^Lt.
Итак, мы получили требуемое продолжение линейного функционала f с подпространства L на более широкое подпространство Lp Если Ц = Х, то теорема доказана. Если Lj#=X, то для завершения доказательства теоремы воспользуемся леммой Цорна.
В совокупности Ф всевозможных продолжений Д функционала f таких, что (х) р (х) в своей области определения L^, введем упорядочение, полагая < /ц, если является продолжением Д. Ясно, что не все продолжения функционала / сравнимы между собой в указанном смысле*, так что Ф—частично упорядоченное
* Например, определенные на Li функционалы fi (х) (x)-f-c/ и f’i (х) =
— f (х)+с'Л где сие' удовлетворяют неравенствам (3) и с 56 с', не сравнимы.
136
множество. Пусть {/л}, Л>€ А,—произвольное линейно упорядоченное подмножество Ф. Тогда функционал fm, определяемый на £w== и/-а равенством /»(х) =/аДх>, если хё£а„, является, как a € А
легко проверить, линейным и служит верхней гранью для {Д4, a С А. Таким образом, выполнены все условия леммы Цорна и Ф имеет максимальный элемент F. Этот линейный функционал F определен на X, так как в противном случае его можно было бы продолжить и F не был бы максимальным элементом Ф. Теорема полностью доказана. В
Замечание. Так как число с, удовлетворяющее неравенствам (3), можно выбирать в общем случае по-разному и максимальный элемент в множестве Ф может быть не один, то продолжение линейного функционала по теореме Банаха —Хана, вообще говоря, не однозначно.
Теорема 2. Пусть X — вещественное ЛТП и р(х) —полунорма на X. Если на подпространстве L пространства X задан линейный функционал f (х) такой, что |/ (х)| 'С р (х), то If (х) можно продолжить на все пространство с сохранением указанного неравенства.
□ Так как f(x)^p(x) для всех х$А, то, по теореме 1, существует линейный функционал F (х), определенный на всем X, совпадающий f (х) на L и такой, что F (х)^р(х) для всех х£Х. Но тогда — F(x) — F (—x)s^p(—х)<р(х), т.е. | F (х) | < р (х). Ц
Для того чтобы распространить теорему 2 на случай комплексного пространства, приведем некоторые предварительные рассуждения. Пусть X — комплексное линейное пространство. Если ограничиться умножением элементов множества X лишь на вещественные числа, то мы получим вещественное линейное пространство Xr, которое назовем ассоциированным- с X. Таким образом, и комплексное пространство X, и ассоциированное с ним вещественное пространство Xr как множества совпадают, но как линейные пространства различны. Так, например, элементы х и ix принадлежат как пространству X, так и пространству Xr, но в то время, как в X элемент ix пропорционален х, в пространстве XR эти элементы при х=#0 линейно независимы. В самом деле, предположим, что для некоторого х=#0 найдутся вещественные числа аи₽ такие, что ax + pix = 0. Но тогда и в пространстве X имеем ах+ +Pix = 0, или (а + ф)х = 0, откуда а + ф = 0, т.е. а = р = 0.
Если f:X —>С, то f (x) = g(x) + ift(x), где g и h — функционалы, принимающие вещественные значения. Как линейные функционалы на X они аддитивны и однородны, в частности вещественно однородны. Поэтому их можно рассматривать как линейные функционалы на XR. Кроме того, так как
g (ix) + ih (ix) = f (ix) = if (x) = i [g (x) + ih (x)], to h (x) = — g(ix), откуда f (x) = g (x) — ig (ix), Обратно: если в пространстве Xr дан аддитивный и вещественно однородный функцио
137
нал g(x), то f (х) = g (х) — ig (ix) является линейным функционалом в X. В самом деле, аддитивность f очевидна и для доказательства комплексной однородности f достаточно убедиться, что f (ix) —i/(x). Но это верно, поскольку
f (ix) = g (ix) — ig (—x) = g (ix) + ig (x) = i [g (x) — ig (ix)] = if (x).
Если X есть ЛТП с базой окрестностей нуля V, то, принимая V за базу окрестностей нуля ив Xr, мы наделяем Xr структурой топологического пространства. Так как в определении выпуклости фигурируют лишь вещественные множители, то всякое множество, выпуклое в X, выпукло и в Xr; в частности, если пространство X локально выпукло, то и Xr локально выпукло.
Наконец, легко видеть, что если линейный функционал /:Х—»С представлен в виде f(x)=g(x) — ig(ix), то f непрерывен тогда и только тогда, когда непрерывен g.
Теорема 3. Пусть X — комплексное локально выпуклое пространство, L — линейное многообразие в X и f—линейный функционал, определенный на L, такой, что \f (х) | Р (х), x£L для некоторой полунормы р. Тогда f можно продолжить на все X с сохранением указанного неравенства.
□ Пусть f (х) = g (х) — ig (ix). Т огда | g (х) |< | f (х) |< р (х). Рассматривая g(x) как линейный функционал на линейном многообразии L вещественного пространства Xr, ассоциированного с X, продолжим его по теореме 2 до линейного функционала G (х), определенного на всем Xr. Положим F(x) = G(x)—iG(ix). Тогда F (х) — линейный функционал на X, являющийся, очевидно, продолжением /(х)|. Пусть F(x) — r (x)ei9(r>. Тогда
| F (х) | = F (х) е-‘е& = F (е-й & х) q (e~i9 <*> х) < р (е_,'е <*>х) ₽= | е~‘е w | р (х) = р (х).
При этом мы воспользовались тем, что если F (х) — вещественное число, то F (х) = G (х). Н
2. Теорема Банаха — Хана в линейных нормированных пространствах.
Теорема 4. Пусть X есть ЛНП (безразлично, вещественное или комплексное), L — линейное многообразие в X и f—линейный функционал, определенный на L. Тогда f можно продолжить до линейного функционала F, определенного на X, и притом так, что тина-
□ Положим р(х) = ]]f|L IIхИ- Очевидно, что р(х) —полунорма и | f (х) | С р (х). По теореме 3 продолжим f(x) до F (х), определенного на всем X. Так как |F (х) | р(х) = ||f ||£• ||х||, то ||F||x <||/|^. Но при продолжении линейного функционала его норма не может уменьшиться. Следовательно, ||F||x = ||/:||i. И
Следствие 1. Пусть X есть ЛНП и хо=/=О — любой фиксированный элемент из X. Тогда существует линейный функционал f, определенный на всем X и такой, что: 1°) ||Д=1; 2°) f (х0) = ||х01|.
□ Рассмотрим множество элементов L — {txa}, где / — пробегает всевозможные вещественные числа (или комплексные, если X—комп-138
лексное пространство). Множество L является подпространством пространства X, определяемым элементом х0. На L определим функционал ф следующим образом: еслих=/х0, то <р (х) = 11| х0||. Очевидно, что: 1) ф (х0) = ||х0||; 2) |<р(х)| =|/|.||х0|| = ||х||, откуда || <р||£ = 1. Продолжая функционал ср на все пространство без увеличения нормы, получим функционал f, имеющий требуемые свойства. В
Следствие 2. Пусть в ЛНП X заданы линейное многообразие L и элемент xg(£L, находящийся на расстоянии d>0 от L (d*= inf||х—x0|h. Тогда существует линейный функционал f, опре-\ xeL J
деленный всюду на X и такой, что: 1 °) f (х) = 0 для x£L; 2°) / (х0)=1; з°) ||f||=i/d.
□ Рассмотрим множество Л=£-Мх0. Любой его элемент можно однозначно представить в виде y = x+txg, где x£L и t — вещественное число (или комплексное, если X — комплексное пространство). Построим функционал ф(у) по следующему закону: если y = x-|-fx0, то y(y) = t. Очевидно, что ф линеен, <р(х) = 0 при х == L и <р (х0) = 1.
Найдем ||q>||f. Для y£L имеем
II4PWII-I4- у| ||х + /Хо||
= hll e IIУII IIУII
ННГКЮГ " '
откуда h||f<l/d. (5)
Далее, существует последовательность {х„} cz L такая, что lim |] х„ — — x0|| = d. Имеем |ф(х„—х0)]<||ф||г-||х„—хф||. Так как |ф(х„—х0)|= =|ф(х„) —ф(х0)|=1, то 1 ^||ф||£--|]хп —х0||. Переходя к пределу, находим 1 С||ф||£ • d, откуда
(6)
Из неравенств (5) и (6) получаем || ф Jf = 1 /d. Продолжив ф на все пространство с сохранением нормы, получим функционал f, имеющий требуемые свойства. В
Следствие 1 утверждает существование в любом нетривиальном ЛНП линейного непрерывного функционала, не равного тождественно нулю. С другой стороны, из этого следствия вытекает, что если для некоторого элемента х ЛНП X выполняется равенство f (х) = 0 для любого линейного функционала из сопряженного пространства X*, то х = 0. Отсюда следует, что если хп хг£Х, *i=Ax2, то существует линейный функционал f£X* такой, что f (xi) f (х2). В этом случае говорят, что функционалы совокупности X* разделяют точки пространства X или что на X существует достаточное число непрерывных линейных функционалов.
139
Следствию 1 можно дать также геометрическое истолкование, заключающееся в следующем: через всякую точку х0, расположенную на поверхности шара J х|| г, т. е. такую, что ||х0|| = г, можно провести опорную плоскость к этому шару.
Эта теорема есть обобщение предложения, доказанного для «-мерного пространства Г. Минковским.
В самом деле, уравнение опорной плоскости к такому шару должно иметь вид / (х) = г ||/||. Но для точки х0 можно построить функционал /0 с нормой 1, для которого Д (х0) = ||х0|| = г. Из этого равенства вытекает, что плоскость f9(x) = r является опорной и проходит через точку х0.
Следствие 2 имеет значение для выяснения вопроса о возможности аппроксимирования заданного элемента х0 линейными комбинациями других заданных элементов {хп х2, ..., хп, Именно: из этого следствия вытекает, что, для того чтобы ха был пределом некоторой последовательности линейных комбинаций вида п
2 срсь необходимо и достаточно, чтобы f (х0) = 0 для всех линей-1 = 1
ных функционалов f, обращающихся в нуль на элементах хп х2, ... ..., хп, ... .
□ Действительно, пусть из f(xf) = O (f = l, 2, ...) следует f(xoj = O. Тогда х0 не может находиться на расстоянии d>0 от линейного многообразия L, порождаемого элементами {xz}, поскольку в противном случае на основании следствия 2 существовал бы* функционал Д такой, что f0 (xz) = 0 (/ = 1,2, ...), а /0 (х0)=1. Но если d = 0, то либо х0 есть предельная точка линейного многообразия L, либо xogL и, следовательно, х0 может быть аппрокси-
п
мирован элементами вида У ср^.
i = 1
Обратно: пусть х0—предел последовательности элементов из L и пусть f(Xj) — O для некоторого функционала /. Тогда, полагая
x„ = limz/„, уп~ 2 c?'xt, П 1 = 1
найдем, что
kn
f(F„)=S<f№)=0,
i = 1
и, следовательно,
f (-^о) = / <’im == lim / (z/„) = 0. fl \ п ) п
§ 2. ОТДЕЛЕНИЕ ВЫПУКЛЫХ МНОЖЕСТВ
В этом параграфе, если не оговорено противное, пространство X считается вещественным.
1. Линейные функционалы и гиперплоскости. Напомним, что подпространство L линейного пространства X, дополнительное к
140
прямой О, называется гцперпадпространством. Если прямая D определяется точкой г0, то для любого х£Х имеет место однозначное разложение
x = y + tza, y£L, /£(—оо, —|—оо).
Сдвиг L + xa гиперподпространства L на элемент х0 называется гиперплоскостью, проходящей через точку х0. Само гиперподпро-странство L часто называют гиперплоскостью, проходящей через нуль.
Лемма 1. Любой гиперплоскости La, проходяще# через нуль, соответствует линейный (возможна, не непрерывный) функционал / =# О такой, что x£La тогда и только тогда, когда f(x) — O. Обратно: любой линейный функционал / =# 0 уравнением / (х) = О определяет некоторую гиперплоскость, проходящую через нуль.
□ Пусть Е)0 = {£г0}, —оо<^<-|-оо— прямая, дополнительная к Lo. Для x — y-\-tza положим f(x} = t. Ясно, что f(x) = O тогда и только тогда, когда х £ La, и из однозначности разложения любого элемента пространства X на сумму элементов из La и Da легко следует линейность функционала /. Очевидно также, что / (г0) == 1 и, значит, /=/=0.
Пусть, наоборот, дан линейный функционал /#=0. Рассмотрим множество 4о = {хСХ|/(х) = 0}. Очевидно, L—-линейное многообразие; покажем, что дополнение La до пространства X есть некоторая прямая. Поскольку /=^0, найдется элемент zogX такой, что /(z0)=l. Если теперь х—-любой элемент пространства X и /(х)=а, то /(х—<&го) = 0, т. е. x—axa = y£La, или х = у + сь?а. Это представление однозначно, так как если x = yl + alza = ya-[-a2za, то + =/О/г+з^о). откуда «! = а2 и, следовательно, уг=у2.
Таким образом, если D0 — {tza\, —<эе</< + <50, то X = La®Da. S
Замечание. Нетрудно проверить, что гиперплоскость, проходящая через нуль, однозначно (с точностью до скалярного множителя) определяет соответствующий ей функционал.
Следствие. Для любой гиперплоскости L существуют ненулевой линейный функционал f и число а такие, что
L = {x€X|f(x) = a}. (1)
Обратно: любой линейный функционал f, отличный от тождественного нуля, с помощью равенства (1) определяет гиперплоскость.
□ В самом деле, пусть L — La-\-xa, где La — гиперплоскость, проходящая через нуль, и [—функционал, соответствующий этой гиперплоскости. Если хо = О, т. е. L = La, то равенство (1) сразу же следует из леммы 1. Пусть хо=/=О. Так как xa£L0 и /(х)^0, то f (х0) = а =# 0. Для любого xgL имеем х = у-\-ха, где’г/££0, и потому f (х) = f (у) + f (х0) = а. Следовательно, Lc{x\f(x) = a}. Пусть, наоборот, /(х)=а. Тогда, f (х—х0) = 0, т.е. х—xa£La, или х^£04-х0, и мы доказали обратное включение.
Предположим теперь, что задан нетривиальный линейный функционал f, и построим с помощью равенства (1) множество L. Вы-
141
берем элемент х'9&Х так, чтобы и положим хо~-^х’о.
f w Для любого х$Ь имеем f(x —х0) =а—а = 0, т.е. у — х —х0 принадлежит гиперплоскости £0, проходящей через нуль и соответствующей функционалу f. Таким образом, х = у+х0) т.е. £с£0-|-х0. Обратно: если х^£0 + х0, то /(х) = а, так что £о + хос£. Следовательно, £ = £04-х0 есть гиперплоскость и обратное утверждение доказано, fl
Лемма 2. Для того чтобы гиперплоскость H—{x\f (х)=а) была замкнута, необходимо и достаточно, чтобы линейный функционал f был непрерывен.
□ Необходимость. Так как сдвиг замкнутого множества замкнут, то вместе с H& = {x\f (х) — а} замкнута и любая другая гиперплоскость Яр = {х]/(х) = Р}.
Предположим, что f не непрерывен и, следовательно, не непрерывен в нуле. Тогда существует е0 > 0 такое, что в любой окрестности нуля и, которую можно считать уравновешенной, найдется точка ха, для которой f (х„)^80. В силу уравновешенности и имеем
Ж) = е0. (2)
Пусть /78о = {х|/ (х) = 80}. Гиперплоскость Не„ не содержит нуля, но в силу (2) пересекается с любой уравновешенной окрестностью нуля, так что нуль есть предельная точка этой гиперплоскости и, следовательно, He„ не замкнута. Но это противоречит условию, и непрерывность f доказана.
Достаточность. Пусть / — непрерывный линейный функционал. Так как точка а есть замкнутое множество числовой прямой, то гиперплоскость На = /-1 (а) замкнута как прообраз замкнутого множества при непрерывном отображении, fl
2. Отделение выпуклых множеств.
Теорема 1. Пусть X —вещественное ЛТП, A tzX —открытое выпуклое множество и М— плоскость в X, не пересекающая А. Тогда в X существует замкнутая гиперплоскость И, проходящая через М и не пересекающая А.
□ Поскольку сдвиг открытого выпуклого множества есть также открытое выпуклое множество, без ограничения общности можно считать, что М — подпространство. Далее заметим, что если В — выпуклое открытое поглощающее множество, содержащее нуль, то В=={х\рв(х) < 1}. В самом деле, в первом утверждении леммы 6 § 4 гл. II можно положить и —В, так как в доказательстве этого утверждения уравновешенность и не используется.
Пусть хв — внутренняя точка множества А. Тогда А— х0 есть открытая выпуклая окрестность нуля и, следовательно, поглощающее множество. Если • рА —функционал Минковского множества А — х0, то, согласно только что показанному А — {у | рА (у—х„) < 1}. Так как МпА — 0, то рА (у—х0) 1 для у£М. Рассмотрим под-
пространство L = М + tx0 (— оо < t < + оо) и определим на L линейный функционал /, полагая f (у4-tx0) = — t. Если ^0, то f(y+tx0)^ 142
< 0 < рА (у + tx0)-, если же t < 0, то
f (У + ^о) = — t < (— О Ра =Рл(У+ ^о).
так как рА —х0) 1. Следовательно, / (г) ^рл (г) для любого
z£L.
По теореме Банаха—Хана можно продолжить f (г) до линейного функционала F (г), определенного на всем X и такого, что р(г)<рл(г). Так как в некоторой окрестности нуля о, которая содержится в А— х0 и которую можно считать уравновешенной, рл(г)< 1, то F (г) ограничен в этой окрестности нуля и, следовательно, непрерывен. Пусть /7 = {х| F(x) = 0}. Это замкнутая гиперплоскость, содержащая М. Далее, для г имеем
О = F (z) = F (г—х0) + F (х0) <рл (г—xj + f (х0) = рА (г - х0) — 1,
откуда рА (г—х0) > 1 для г С Н и потому Н л А = 0. Ц
Отображение f ЛТП X в ЛТП Y называется открытым, если образ при отображении f любого открытого множества пространства X есть открытое множество пространства Y.
Лемма 3. Всякий непрерывный линейный функционал f, отличный от тождественного нуля, есть открытое отображение.
□ Пусть ОсХ открыто, ag/(Q) и а = /(х0), х0£й. Так как f (х) ф 0, то найдется элемент хх 6 X такой, что f (xj = 1. Какова бы ни была окрестность нуля и, в силу непрерывности умножения в ЛТП существует е >0 такое, что из |Х—а| <е следует Axt £ axj+u. Выберем и так, чтобы хДисй, что возможно, поскольку О открыто. Тогда х0+А,Х1—aXjCXo + McQ и, следовательно, /(Xo + ^-Xj — — axj)^/^). Но f (Хо + Xxj—axj = a-f-A —a = X, так что X£/(Q), т. e. f (й) открыто. Ц
Теорема 2. Пусть X—вещественное ЛТП, А—выпуклое открытое и В—выпуклое множество, причем А ПВ = 0. Тогда существует непрерывный линейный функционал f и число а такие, что f (х) < а при х £ А и f (х) а при х£В.
□ Пусть С= А— В. Множество С выпукло, открыто и не содержит нуля. По теореме 1, существует замкнутая гиперплоскость, проходящая через линейное подпространство {0} и не пересекающая С. Пусть f (х) = 0—уравнение этой гиперплоскости. Тогда f — линейный непрерывный функционал, не обращающийся в нуль на С. Легко видеть, что f (х) сохраняет знак на С. В самом деле, если / (xj > 0 и /(х2) < 0, хп х2^С, то, полагая xz = /x2 + (l — t)xu имеем f (xt) = tf (x2) + (1 —t)f (xj и, следовательно, f (xZo) = 0 при t0 ~T(xi)—f (хг) ‘ T*K как a С выпукло, то xta£C и ра-
венство f(x/„)=O невозможно.
Изменяя, если необходимо, знак функционала f, можно считать, что /(С)<0, т. е. /(х) < f (у) для любых х£ А и у£В. Поэтому существует inf/(у) = а и /(x)^a, f(y)~^a для всех х£А, у£,В.
IZ6 в
по так как f непрерывен и А открыто, то / (Л) также открытое
143
множество числовой прямой и потому не может содержать своей верхней границы. Следовательно, /(х)<а для х£А. Щ
Теоремы 1 и 2 можно распространить на случай комплексного ЛТП. Для этого заметим, что в комплексном линейном пространстве уравнение гиперплоскости, проходящей через нуль, записывается в виде
g(x) + ih(x)*=0, (3)
где g(x) и h(x)—функционалы, принимающие вещественные значения, или, учитывая связь между g (х) и h (х),— в виде
g(x)-ig(ix)~0. (3')
Если Но — вещественная гиперплоскость, заданная уравнением
gW = 0, (4)
то iH0 = {ix\x^H0} также вещественная гиперплоскость с уравнением g'i(ix) — 0, или
h (х) = 0. (5)
Так как уравнение (3) эквивалентно паре уравнений (4) и (5), то всякая комплексная гиперплоскость Н, проходящая через нуль, есть пересечение проходящих через нуль вещественных гиперплоскостей Нл и iHb, т. е. Н = Я0ПгЯ0.
Верно и обратное утверждение.
Теорема 3. Пусть X—комплексное ЛТП, М — комплексная плоскость в X и А—открытое выпуклое множество, не пересекаю-щге М. Тогда существует замкнутая комплексная гиперплоскость Н, содержащая М и не пересекающая А.
□ Как и в теореме 1, не ограничивая общности, можно считать, что М проходит через нуль. Но тогда М вместе с х содержит и ix, т. е.
Рассмотрим вещественное пространство Xr, ассоциированное с X. Очевидно, что М в Xr по-прежнему является подпространством, Л —открытым выпуклым множеством и, по теореме I, существует вещественная замкнутая и проходящая через нуль гиперплоскость Яо, содержащая М и не пересекающаяся с А. Пусть Н = Яо П iH9 — комплексная гиперплоскость, проходящая через нуль. Очевидно, И замкнута, не пересекает А и так как М =*iMcziHe, то МсН, н
Рекомендуем самостоятельно перенести теорему 2 на комплексные ЛТП.
§ 3. ОБЩИЙ ВИД ЛИНЕЙНЫХ ФУНКЦИОНАЛОВ В НЕКОТОРЫХ ФУНКЦИОНАЛЬНЫХ ПРОСТРАНСТВАХ
Для многих конкретных функциональных пространств можно указать общий вид линейных функционалов, определенных на этих пространствах. Знание общего вида линейных функционалов может 144
оказаться полезным при различных исследованиях функциональных пространств.
1. Линейные функционалы в «-мерном пространстве R". Пусть
п
/ — линейный функционал, определенный на R". Длях =
i= 1
где {eit е2, ..базис в имеем
/ п А п п
= 2LZ(С,) = 2 Ui-, f^).
\ I = 1 / 1 = 1 1 = 1
Обратно: выражение вида
п
i -1
(1)
где fi—произвольные числа, есть, очевидно, линейный функционал на R”. Таким образом, выражение (I) дает общий вид линейного функционала, определенного на «-мерном пространстве. Так как fi можно рассматривать как компоненты «-мерного вектора f, то пространство (R")*, сопряженное с R", также есть «-мерное пространство с метрикой, вообще говоря, отличной от метрики R".
Пусть, например, ||хЦ = тах|^|. Тогда
l/W| =
откуда
1Л<Д|Л-|. (2)
I ® 1
п
С другой стороны, если взять элемент х,= 2 assignf/CR", то ||х0|| = 1 и л / п \
f ho) - ,S fi sign fI-( X \fi () ho II» i=l \i=l /
а потому
n
(3)
n
Из неравенств (2) и (3) следует, что || f Ц =* 2 I f 11 • t= 1
Если в R" ввести евклидову метрику, то легко убедиться, что в (R«)* метрика также является евклидовой.
Согласно терминологии, принятой в тензорной алгебре, элементы пространства R" называются контравариантными, а элементы пространства (R”)* — ковариантными. Линейный функционал f (х) представляется в виде скалярного произведения /(х) = <х, />, гдех^К", f € (Rn)*.
145
2. Общий вид линейных функционалов в пространстве s. Пусть j f (х) — линейный функционал, заданный на s (см. с. 00). Положим j
где Впп> = 1 и g'-'” = 0 для t#=n; пусть f(e^=an. Так как | сходимость в пространстве s есть сходимость по координатам, то | для элемента х = {^1, |2, ...} имеет место равенство
п ОО
x = lim 2 2
П 1=1 1=1
Отсюда в силу непрерывности функционала f (х) получаем
1 = 1 1=1
Так как этот ряд должен сходиться для любой числовой последовательности то начиная с некоторого номера а, должны быть п
равны нулю и, следовательно, f (х) = У
Обратно: такое выражение для любых вещественных чисел а(. ) и любого натурального п есть линейный функционал в пространстве s, поэтому общий вид линейных функционалов, определенных на пространстве s, дается равенством
п
/ (*) = 2
z=i ।
Числа п и at (t = 1, ..., и) однозначно определяются функционалом f.
3. Общий вид линейных функционалов в пространстве С[0, 1]. Теорема Рисса. Пусть на С[0, 1] задан линейный функционал f(x). Так как каждая непрерывная функция, заданная на С [0, 1], ограничена и так как для непрерывной функции sup I х (01 = max I х (/) I,
то, как уже указывалось выше, пространство С [0, 1] можно рассматривать как подпространство пространства М {0, 1], где ||х||=«р(х, 0) = sup | x(f) |. Функционал /(х), заданный в простран-о</< 1
стве С [0, 1], продолжим с сохранением нормы на все пространство Л4[0, I]; продолженный функционал обозначим через F (х).
Рассмотрим функции
( 1 при 0 5 < t, Ыо(5)=О, = 0 при /^^1.
Очевидно, «#(£)€Л1[0, 1J. Пусть F[ut (g)] = g(t). Докажем, что g (t)— функция с ограниченным изменением.
Разобьем отрезок [0, 1] на части точками ta =0 < tt < /2<... <
п
<^п-1<^ = 1. Составим сумму 2[g(O— £(^-i)] и положим
146
e, -sign[g'(O-g,(^-i)]- Тогда n п '
S Ig(Q-g('.--J 1= S e,[g(O-g(^-1)] = i=l i=I
n Г n
= 2 ez [F (ut) —F (ut _ )] = F e; (ut — ut )].
1 = 1 * 1 U = 1 1 1
Отсюда получаем
так как ||F|| = ||/|| и
Итак’
2 ig(o-
и, следовательно, g (t) — функция с ограниченным изменением.
Возьмем любую непрерывную функцию x(f), заданную на [0, 1], и построим функцию п
гп (О х [%/п (О ^-1)/п (0]>
Л=1 '
гЛ(0—ступенчатая функция. Имеем
п
Поэтому п 1
lim F (?„)=« lim £ х [g (^г)]=Й(^
k= 1 о
С другой стороны, при п—* оо последовательность {zn(t)\ равномерно сходится к x(t), т. е. ||г„—х||—>0, а так как функционал
F (х) непрерывен, то F (z„) —> F (х). Поэтому F (х) = J х (t) dg (t). Но о
F(x)=sf(x) для непрерывной функции x(t) и, следовательно,
1
f (x)=»$x(0dg(0. (4)
о
Итак, получаем следующую теорему.
Теорема (Ф. Рисе а). Всякий линейный функционал, задан-нЬ1й в пространстве С[0, 1], выражается с помощью интеграла Стильтьеса по формуле (4), где g(t)—функция с ограниченным изменением, определяемая по функционалу f (х).
147
1
Легко видеть, что и, обратно, функционал <р (х) = х (/) d/i (t), о
где h(t)—любая функция с ограниченным изменением, является линейным функционалом в пространстве С [0, 1].
В самом деле, аддитивность <р (х) очевидна, а непрерывность следует из того, что при равномерной сходимости последовательности функций можно переходить к пределу под знаком интеграла Стильтьеса.
Таким образом, убеждаемся, что формула (4) дает общий вид линейных функционалов в пространстве С [0, 1] в том смысле, что этой формулой при всевозможных функциях с ограниченным изменением g(t) выражаются все линейные функционалы в С [0, 1].
Найдем норму функционала /(х). Имеем
п
I = 1
откуда полное изменение
W) <11/11- (5)
С другой стороны, из равенства (4) получаем 1
/(*) = $x(/)dg(0 < max |x(O|VJ(g)=VJ(g)-||x||. о
Отсюда 1
|/|l<VJ(g). (6)
Из неравенств (5) и (6) следует, что ||/|| = VJ (g).
Необходимо заметить следующее. Так как величина интеграла 1
Стильтьеса Jx(^)dg(O для любой непрерывной функции x(t) не о
зависит от значений g (t) на конечном или счетном множестве точек и, очевидно, не меняется при замене g(t) на g(/) + const, то соответствие между fix) и g(x) не однозначно. Однако из равенства
1 1
о о
для любой непрерывной функции x(t) следует, что gtiD^gzit) во всех общих точках непрерывности этих функций. Поэтому если в соотношении (4) заменить g(t) на g(t), совпадающую с g(t) во всех точках непрерывности, и такую, что: 1°) g (0) — 0; 2°) g(c) — = g(c — 0), если с—точка разрыва g(t), то соответствие / (x/og (О окажется взаимно-однозначным. При этом не только не изменится величина интеграла $x(0dg(0» но и сохранится равенство Ц/j =» о
148
= VJ(g), так как при переходе от g(t) к g(t) неравенство (6), очевидно, не нарушится, а неравенство (5) может лишь усилиться, если, например, g(c) не лежит между g(c—0) и g(c + 0). Поэтому в дальнейшем мы будем предполагать, что функция g(t) в равенстве (4) удовлетворяет условиям 1° и 2°.
А. А. Марков обобщил теорему Рисса на случай функционалов в пространстве С (Q) функций, непрерывных на компакте Q.
4. Общий вид линейных функционалов в 1р. Пусть f (х) — линейный функционал, определенный на 1р. Так как элементы = образуют базис в 1р, то любой элемент х С 1р можно записать оо СП
в виде х=* 2 lkek< 2 °0- В силу линейности функционала
k—i /?=1
оо
/(х) имеем / (х) =* 2 W (£*)• Положим f(ek)=ck. Тогда числа ск k— 1
однозначно определяются функционалом f и мы получаем
/(х)=2сЛ. (7)
1
Выясним свойства чисел ск. Положим хл = {^"*}, где Insigne* ПРИ k^n’ ( 0 при k > п
п
и 4- + ~- = 1- Тогда f(x„)=£ С другой стороны, 4 р k=l
/ п \1/р / п \1/р
2КГН -ИИ( 2Ы’) •
/ \fes=l /
Таким образом, П / п \1/р
2Ы4<11Л( 2Ы’ .
k=\ \k~l J
(П \l/q
2 I ck |4 ) СИЛ- Это неравенство справедливо для любого п. Поэтому
(8)
Итак, {ck}<=lq.
Обратно: возьмем произвольную последовательность {dft}czZe.
оо
Тогца ф(х)=1 2 d£k является линейным функционалом в простран-/?=1
стве 1р. В самом деле, аддитивность этого функционала очевидна, а ограниченность легко доказывается с помощью неравенства Гель* Дера.
149
Таким образом, формула (7) дает общий вид линейных функционалов в пространстве 1р.
Вычислим норму функционала f. Из формулы (7) с помощью неравенства Гельдера получаем
l/Wi =
Следовательно,
i/А
Сравнивая неравенства (8) и (9), заключаем, что \\f || = 1 2Iе* I’ ) • \&= 1 / Из доказанного, в частности, следует, что общий вид линейного функционала, определенного на /2, таков:
,/(х)=2^й,
k= 1 оо / оо \ 1 /2
где 2 1<Д2< + °° и цл=( 2 Ы2) • •
fc=l \fc=l /
В функциональном анализе кроме пространства 1р рассматривают еще пространство I, элементами которого являются всевозможные последовательности чисел x = {£i, £2, . ...} такие,
00 оо
что 2 II < °°» причем = 2 |£fel- Можно доказать, что всякий /г=1 &=1
оо линейный функционал в пространстве I имеет вид /(х)=2са?й> *=i
где —ограниченная последовательность вещественных чисел.
Норма функционала f дается равенством J|/1| — sup |сА|.
5. Общий вид линейных функционалов в пространстве £Д0, 1]. Рассмотрим произвольный линейный функционал f(x), заданный на £Д0, 1] (р > 1). Положим
_ ( 1 при 0 < t,
u.©-0, М1)=|Опри(<Е<1;
пусть =
Докажем, что g(f)—абсолютно непрерывная функция. Пусть б;== (т;, t.) (i = l, 2, ..., и) —произвольная система неперекрываю-щихся интервалов, расположенных на отрезке [0,1]. Введем числа eif
150
определенные, как и выше (см. с. 147). Имеем
п п ( п Ч
21 g -g fr)I = 2 ъ ('<)-g (Ti)] “ f ( 2 [«/,- (5) ~«L- ©1 / <
<11/II-1.2
(П Л \1/P / П \l/p
2 $<£.•) =Ш 2mes6z. .
i = i6 J M = i /
Из полученного неравенства следует абсолютная непрерывность функции g(f) и, следовательно, функция g(t) является интегралом Лебега от своей производной. Положим g' (t) Тогда
t
g (0 ~g (0) = $ а (т) dt. 0
Ho g (0) = f [m0 (£)] = 0, так как и0 (g) == 0 есть нулевой элемент t
пространства ЬДО, 1]. Следовательно, g (t) = а (т) dt. о
Пользуясь функцией ит(0» имеем t 1
/ [«Т (0] = g (0 = $ a (т) dr =« $ ut (т) a (т) dt. 0 0
Так как /—линейный функционал, то, полагая
п
Zn (Т) =« S Ck [“*/» СО - Щк- 1)/п (0], k= 1
1
получим / (z„) — J z„'(t) а (т) dr. о
Пусть х(0 —произвольная ограниченная измеримая функция. Тогда найдется такая последовательность ступенчатых функций
(0}> что почти всюду при п—>-оо. При этом можно
считать, что последовательность {£„(/)} равномерно ограничена.
По теореме Лебега об интегрировании ограниченной последовательности получаем
1 1 1
lim / (z„) = lim$ zn (t) a (/) d/ = $ lim zn (t) a (t) df = J x {t) a (t) dt n n о о n 0
Так как, с другой стороны, zn(t)— x(t)—*0 почти всюду и zn(t) — ~~ х (t) равномерно ограничены, то
/ 1 \ i/р
-о
Хо /
151
при п—>ОО. Поэтому f (г„) -> f (х) и, следовательно, 1
f (х) = х (0 а (0 At. о
Рассмотрим теперь функцию xn(t), определенную следующим образом:
( | а (О I’’1-sign а (0 при | а (0 | < п,
I 0 при |a(f)[>n,
где q —число, сопряженное с р, т. е. = 1. функция xn(t)
ограничена и измерима. Следовательно, f (хп) xn(t)a(t)At и о
/ J \ i/р
1Ж)К11ЛНКМЛ $ IMOW . \о /
С другой стороны, 1 1 1Ж)1 = Ж) = $*Л0 «(0d* = $ |хя(0|- |a(0|d/> О 0 *
1 1 1
> $ I хп (О I • \ХП (011 /<«-') At = $ I хп (/) 1^-» (k = $ I хп (t) |р At. О 0 0
I Следовательно,
1 / 1 \ i/р
$\Хп (о г At < । л- кк и л 5\*п (t) г . о \0 /
Отсюда / 1 \ 1/<7
$K(0|'d/ <|Л.
\0 /
Но, очевидно, | хп (01 —► | a (/) |9-1 при п —> оо почти всюду на [0,1 ], так как a(/)—суммируемая функция и, следовательно, обращается в бесконечность лишь на множестве точек меры нуль. Переходя к пределу при п—>оо, получаем / 1 \ 1/<7
S|a(Ol(’’1)PdH СЦЛ1, \о /
или / 1 \ 1/q
J|a(OI’dH <И||. (Ю)
\о /
Отсюда следует, что a(t)^Lp\Qt 1]. 152
Пусть теперь x(Z)—любая функция из Lp [О, 1]. Тогда существует J x(t) a Далее, найдется последовательность ограни-о 1
ценных функций {xm(Z)| такая, что J | х (Z) — хт (t) f dZ —> 0 при о
т—> оо. В силу неравенства Гельдера 1 1 $ хт (t) a (i) dt —» $ х (i) a (Z) dZ о о
при tn —>оо. Так как хт (Z) —ограниченные измеримые функции, то j ха (/) a (Z) dZ = f (xm). Следовательно, f (хт) —-> j х (Z) a (Z) dZ при о о
т —> оо. С другой стороны, f (хв) —(х). Но тогда получаем, что 1
/(х) = jjx(Z)a(Z)dZ. (11)
о
Итак, всякий функционал, определенный на Lp [0, 1], можно представить с помощью равенства вида (11). Обратно: если 0 (Z) — произвольная функция, принадлежащая Ья [0, 1], то <р (х) = 1
= J х (Z) 0 (Z) dZ есть линейный функционал, определенный на Lp [0,1]. о
В самом деле, аддитивность функционала очевидна, а ограниченность легко следует из неравенства Гельдера.
Таким образом, формула (11) при произвольной фиксированной функции a (Z) £ Л, [0,1 ] дает общий вид линейного функционала, определенного на Lp [0,1].
Нетрудно найти норму этого линейного функционала. Из соотношения (И) получаем
Следовательно,
/ ' \ i/<?
|a(Z)|«dZ ) ||х||.
\о /
/ 1 \ 1/4
IIлк •
\0 /
(12)
Из неравенств (10) и (12) следует, что
/ 1 \ i/<
||Л1 = ( $|a(OI"dZ .
ХО /
153
Часто рассматривают пространство L[0,1] функций, суммируемых по Лебегу, в котором ||х|| = J |х(/) | At. Общий вид линейных о
функционалов, определенных на А [О,1], дается формулой
1
f (х) = J х (0 а (0 At, о
где а (/) — почти всюду ограниченная функция и
||/||= inf / sup |а (0|1.
mes£=0 l[0,l]\E /
6. Общий вид линейных функционалов в гильбертовом пространстве. В гильбертовом пространстве Н рассмотрим линейный функционал fix). Так как Я —комплексное линейное пространство, то естественно предполагать, что / (х) может принимать комплексные значения.
Пусть / (х)— произвольный линейный функционал, определенный в гильбертовом пространстве Н. Обозначим через L множество нулей этого функционала, т. е. совокупность элементов х£ Н таких, что /(х) = 0. Легко видеть, что L — подпространство. В самом деле, L— линейное многообразие, что следует из аддитивности и однородности функционала /(х), а замкнутость L вытекает из непрерывности /(х).
Возьмем произвольный элемент пространства Н,, не принадлежащий L, и обозначим через х0 проекцию этого элемента на подпространство H — L. Пусть /(ха) = а, причем, очевидно, а=^=0. Полагая Xj =х0/а, получим / (xj = 1. Если теперь х—любой элемент пространства Н и / (х) = 0, то
/ (х) —0/ (хх) = 0, или / (х—0Xj) — О,
откуда х—0xx = z, где z^L, т. е. x = fix1-)-z. Это равенство показывает, что пространство Н есть ортогональная сумма подпространства L и одномерного подпространства, порожденного элементом хх.
Так как хх | z, то <х, xt> = 0||х1||2, откуда, учитывая, что 0 = / (х), имеем / (х) = <х, Xj/Ц хх ||2>. Обозначив элемент х^Ц хг ||2 через и, получаем равенство
/(х) = <х, w>, (13)
т. е. выражение произвольного линейного функционала / (х) в виде скалярного произведения элемента х на фиксированный элемент и.
Элемент и определяется по функционалу / однозначно, поскольку если также /(х) = <х, к>, имеем <х, и — и> = 0 для любого х£Н, откуда следует, что u — v. Далее, из равенства (13) получаем
|/(х) | = |<х, и>|<||х|Н1Ч
откуда вытекает, что Ц/||<||ы||.
154
Так как, с другой стороны, /(u) = <u, u> = || и ||®, то отсюда следует, что J/II не может быть меньше, чем ||и||. Поэтому
Й/М«11- (14)
Итак, всякий линейный функционал / (х), определенный в гильбертовом пространстве, имеет вид / (х) = <х, и>, где [элемент и однозначно определяется функционалом /, а норма функционала дается равенством (14).
Легко видеть, что и, обратно, при любом и£Н соотношение (13) определяет линейный функционал / (х) с нормой (14).
Таким образом, формула (13) дает общий вид линейного функционала в гильбертовом пространстве.
§ 4. СОПРЯЖЕННЫЕ ПРОСТРАНСТВА И СОПРЯЖЕННЫЕ ОПЕРАТОРЫ
1. Примеры сопряженных пространств. Как уже было указано, совокупность всех линейных функционалов / (х), определенных на ЛНП X, образует банахово пространство X*, называемое пространством, сопряженным с пространством X. Пользуясь общим видом линейных функционалов, в некоторых случаях можно указать реализацию пространства X* с точностью до изоморфизма.
1. Пусть Х = С[0,1]. Рассмотрим множество функций g(t) с ограниченным изменением, определенных на [0,1] и обращающихся в нуль в точке / = 0. Будем считать, что в точках разрыва g(t) = = g(t—O). Очевидно, это множество есть линейное пространство при обычном определении операций сложения двух функций и умножения функции на вещественное число. Введем норму для функций с ограниченным изменением, полагая ||g|| = VJ (g). Нетрудно видеть, что все аксиомы нормы выполняются.
Полученное линейное нормированное пространство называется пространством функций с ограниченным изменением и обозначается через V.
Рассмотрим, с другой стороны, пространство Х* = С*[0,1] всех линейных функционалов, определенных на С[0,1]. Как доказано выше, каждый линейный функционал /£С*[0,1] определяет однозначно некоторую функцию g(t), g(0) = 0, с ограниченным изменением и, обратно, каждой такой функции соответствует функционал /£С*[0, 1]. Поэтому между множеством всех линейных функционалов из С* [0,1] и множеством всех элементов пространства функций с ограниченным изменением существует взаимно-однозначное соответствие. Так как очевидно, что сумме функционалов + отвечает сумма gi + g2 функций, а функционалу А/—функция kg, то соответствие между С* [0,1] и пространством функций с ограниченным изменением есть изоморфизм. Далее, так как ||/||-||g||, то это соответствие является также изометрическим.
С точки зрения многих вопросов функционального анализа эти два пространства неразличимы; поэтому часто говорят, что пространство, сопряженное с пространством непрерывных функций, есть пространство функций с ограниченным изменением.
155
2. Пусть Х = £ДО, 1]. Рассмотрим, кроме того, пространство [0,1], где у+у=1. Так как каждому функционалу f€Lp[0,1] однозначно соответствует функция g(0€£<?[0,1] и обратно, то между пространствами £^[0,1] и £ч[0,1] устанавливается взаимнооднозначное соответствие. Как и раньше, убеждаемся в том, что это соответствие изоморфно и изометрично, т. е. L*P[Q, 1] =»= £а[0,1], понимая это равенство с точностью до изометрии и изоморфизма. В частности, при р=2 имеем Ц [0,1]—£г[0,1]. Поэтому пространство £2[0,1] называется самосопряженным пространством.
3. Легко видеть, что Гр = 1ч и, в частности, /2₽/2. В § 4 гл. III мы установили, что пространство, сопряженное с линейным нормированным, не обязательно полным пространством, есть банахово, т. е. полное ЛНП. Так как £Д0,1] есть пространство, сопряженное с £Д0,1] (где у+-у= , и 1р — пространство, сопряженное
с 1а, то мы получаем новое доказательство полноты пространств £,[0,1] и I
4. Линейный функционал в гильбертовом пространстве порождается элементом того же пространства и, значит, гильбертово пространство является самосопряженным. По той же причине является самосопряженным и n-мерное евклидово пространство.
2. Рефлексивные пространства. Пусть X есть ЛНП и ^ — сопряженное пространство. Поскольку X* также есть ЛНП, можно построить Х** = (Х*)* и т. д.
Рассмотрим подробнее X**. Это —пространство лилейных функционалов F, определенных на пространстве X*, элементами которого являются линейные функционалы, определенные на X. Рассмотрим линейный функционал f (х), определенный на X. Здесь функционал f фиксирован, а х—переменный элемент из X.
Подойдем к выражению f(x) с другой точки зрения. Будем считать, что X—фиксированный элемент, а / — переменный элемент из X*. Пусть, например, /(х) = j x(t)dg(t). Фиксируя g(t) и меняя x(f), получаем первый случай; фиксируя x(t) и меняя g(t), получаем второй случай.
При фиксированном х и переменном f каждому элементу f£X* ставится в соответствие некоторое вещественное число; следовательно, выражение f (х) при фиксированном х и переменном f можно рассматривать как функционал Fx, определенный на пространстве X*. Поэтому можно написать f (х) = Fx(f). Нетрудно видеть, что Рх— линейный непрерывный функционал и, следовательно, Fx£,X**. В самом деле,
Fx fa+/»)»(f, + /8) (х) == fi (х) + h (х) = Fx (А) + Fx fa)
и
|Fx(/)l = l/(x)|<||x||-»fll.
156
Отсюда следует, в частности, что
HJCW- О)
Так как, далее, согласно следствию 1 из теоремы Банаха —Хана для каждого х существует линейный функционал fx с нормой, равной единице, такой, что fx (х) = || х ||, и для такого функционала
или, что все равно, то
ИЛ>И- (2)
Сравнивая неравенства (1) и (2), заключаем, что
(3)
Легко также видеть, что
FXi^ = FXi(f)+FX2(f} и Fu(f) = \Fx(j).
Таким образом, всякому х£Х естественным образом ставится в соответствие вполне определенный функционал Fx$X**, причем это соответствие между пространством X и множеством {FJczX** изоморфно и изометрично (взаимная однозначность соответствия между X и {Fx\ следует из равенства (3)), т. е. XczX**> В том случае, когда при таком соответствии X = X**, пространство X называется рефлексивным.
Примеры. 1. Евклидово n-мерное пространство рефлексивно. В самом деле, если X есть n-мерное евклидово пространство, то X* также n-мерное евклидово пространство, следовательно, и X** есть л-мерное евклидово пространство. Но если одно n-мерное пространство является частью другого, то они совпадают. Поэтому из X с X** следует X = X**.
2. Пространство Lp [0,1] (р > 1) рефлексивно. В самом деле, Ср* (0, и=(Жо, l])*=(L?[0, 1])*=Lf[0, 1].
3. Пространство ln(p> 1) рефлексивно; это доказывается аналогично.
4. Пространство с[0, 1] нерефлексивно. Предположим, напротив, что С [0, 1] рефлексивно. Тогда любой линейный функционал F (/), определенный на пространстве V функций с ограниченным изменением, должен иметь вид Fx(f)^f(x) при выбранном подходящим образом элементе х£С[0, 1]. Принимая во внимание общий вид линейных функционалов f (х), определенных на С [0, 1], получаем, что любой линейный функционал F (/) имеет вид
1
(/)=/(х) = J х(0 dZ (X) (4)
о
(через f (/) мы обозначили функцию с ограниченным изменением, соответствующую Функционалу f (х) из С* [0, 1]). Рассмотрим функционал
^(Л=/(^+0)ЧЙ-0),
Который каждой функции f (t) с ограниченным изменением ставит в соответствие скачок этой функции в точке Аддитивность этого функционала очевидна.
157
Далее,
Ио (/) I=I f (*о+о)-/ (/о-О) I < Vi (Л =|| f ||.
Следовательно, Fo (/) ограничен и имеет норму, не превосходящую единицы. Кроме того, очевидно, что Fo(f)^O. В самом деле, достаточно рассмотреть fo (Л), W
J 0 при /i ( ) — j ПрИ /0 < / 1.
Из равенства (4) следует, что должна существовать непрерывная функция х0 (t) такая, что
1
= (5)
о
t
Рассмотрим теперь функцию f0 (t) = J х0 (т) dr. Имеем FXo(fo)=O, так как /0 (0 о
непрерывна на [0, 1]. Но, с другой стороны, из F0(f)^Q следует хо(/)^О и
1 1
FXt (fo) = р0 (0 <Vo (0 = J 4 (Л df > 0. о о
Итак, мы получили противоречие, которое возникло в силу предположения, что всякий линейный функционал F£C*[0, 1] имеет вид Fx, т. е. что пространство С [0, 1] рефлексивно. Следовательно, пространство С [О, 1] нерефлексивно,
3. Сопряженные операторы. Рассмотрим линейный ограниченный оператор у = Ах, отображающий ЛНПХ в ЛНП У. Пусть <р (у) — линейный функционал, определенный на Y. Тогда <р (</) определен для у = Ах, где х— любой элемент из X, и для у —Ах имеем
<р(г/)=<р(4х) = /:(х),
где f(x)—функционал, определенный на X. Очевидно, что f(x) линеен. Тем самым мы получили, что каждому функционалу <р £ Y* ставится в соответствие функционал f € X*.
Таким образом, построен некоторый оператор, определенный на Y* и принимающий значения в X* Этот оператор обозначается через А* и называется оператором, сопряженным с оператором А. Равенство <р({/) = /(х) записывается в виде f — A*q>.
Примеры. 1. Рассмотрим n-мерное пространство R" и оператор А из L (Rn, R«). Тогда оператор А определяется матрицей n-го порядка (а,у) и равенство у = Ах, где х = П1, g2, .... У = {П1. Ла. записывается в виде Г],- = У в,Ду.
/=1
Рассмотрим линейный функционал f £ (R")*. Имеем
/ = {А, .....fn}, f (х) = 2 fiii-
i = l
Поэтому n \ n 2 aijfi 2 i = 1 / / = 1
n n / n \ n /
f (Лх) — 2 i 2 ) — 2 (
i = 1 1 = 1 v = 1 / j = 1 \
158
п
где^7= S Вектор g = {gi, g2, . gn} есть элемент пространства (R«)* 1 = 1
и получается из вектора / = {/ь Л>, •••> fn} того же пространства линейным преобразованием g = A*f, где А* порождается матрицей, транспонированной к матрице А. Следовательно, переход к сопряженному оператору в п-мерном пространстве означает переход к транспонированной матрице.
2. Рассмотрим bL2[0, 1] оператор
1
Ах = у (/) = J К (/, s) х (s) ds, о
где К (t, s)~— непрерывное ядро. Произвольный линейный функционал f (у) в [О, 1] имеет вид
1
Поэтому / (</) = <</. />=^(0/(0^; [0, 1]. 0 f (Ах) = f f (0 Н K(i, s)x (s) ds| d/ = о lo J = f x (s) / C /< (/, s) f (/) dA ds = С X (s) g (s) ds; о lo Jo 1 g(0=^(s, 0/(s)ds. 0
Таким образом, переход к сопряженному оператору в данном случае означает перестановку переменных в ядре (ядро К (s, I) называется транспонированным по отношению к ядру /< (/, s)).
Теорема 1. Оператор Л*, сопряженный с линейным ограниченным оператором Л, отображающим ЛНП X в ЛНП У, есть также линейный ограниченный оператор, причем || Л* [| = || Л [I.
□ Прежде всего очевидно, что оператор Л* аддитивен. Далее, имеем
|(Л‘ф) (х)| = |/(х)| = |Ф(Лх) |<||фНЛх||<11фНЛ||-||х||, откуда [ Л*ф||<|| Л||-||ф||. Следовательно, Л* —ограниченный оператор, причем
М*||<||Л||. (6)
Пусть х0—какой-нибудь элемент из X. Согласно следствию 1 из теоремы Банаха — Хана, существует такой функционал ф0 £ Y* с нормой ||фо11=1, что ф0 (Лх0) = Ц Лх01|. Отсюда получаем
II Ах0 У = Фо (Лхо) — fo (*о) < || /о II II %0 II =
= 1|Л*ф0||-||ХоКУЛ*||.уфо|Цх„У = ||Л*||.||х„у.
Следовательно,
IIА || <|| Л* ||. (7)
Из неравенств (6) и (7) вытекает, что || Л || = || Л* ||. у
159
Понятие сопряженного оператора можно ввести и в том случае, когда исходный оператор А является линейным неограниченным оператором, определенным на линейном многообразии L, всюду плотном в ЛНП X и принимающим значения в пространстве Y. Пусть А —такой оператор и ф € У*. Рассмотрим ф (Ах) = f0 (х), x£L. Тогда f0(x), очевидно, аддитивный и однородный функционал, i определенный на L. Для произвольного функционала ф из У* функ- ционал /0 не является, вообще говоря, ограниченным. Но если j для некоторого <р С У* функционал ограничен, то его можно про- , должить по непрерывности до линейного функционала f, опреде- | ленного на всем X. j
Таким образом, получаем, что на некотором многообразии М с У* определен оператор А*, ставящий в соответствие линейным функционалам <р £ У* линейные функционалы f £ X*. Этот оператор и называется оператором, сопряженным с линейным неограниченным one- 1 ратором А. Нетрудно проверить, что М — линейное многообразие и что А* — линейный оператор на этом многообразии, вообще говоря, не ограниченный на нем.
Пример. В пространстве Lq (G), где G—ограниченная измеримая область на плоскости, рассмотрим оператор дифференцирования
Л = Л 1 Д 7 (^1 ^2 ~ 0’ *
дх1\ ду12 v 1 1 7
определенный на линейном многообразии Lo ci Lq (G) непрерывно дифференцируемых I раз функций, обращающихся в нуль в некоторой граничной полосе области G. Многообразие Lo всюду плотно в Lq (G) и оператор А на нем дистрибутивен и не ограничен. Значения оператора будем считать принадлежащими тому же пространству Lq (G).
Пусть для некоторой функции и (х, y)£Lp(G) имеет место ра-
венство
G G G
при любой функции и (х, y)£LQ, где w (х, y)£Lp (G).
Так как функционал
/(“)=$$“ У) W (х, у) dx dy О
определен на LoCzL^t'G), то он, очевидно, дистрибутивен и, кроме того, ограничен вследствие того, что
|/(«)|= JJuaKkd# •|Ньх
G
и мы можем продолжить его на все Lq(G). Тем самым мы получаем оператор A*v = w, сопряженный оператору Л, определенный на некотором множестве функций v (х, y)£L0(G) и принимающий значения в том же пространстве. Функция (—называется обобщенной производной функции v (х, у) и обозначается, dlv т к х
как и обычная производная, символом ---------—. Таким образом, операцию обоб-
dxh ду1^
щенного дифференцирования можно рассматривать также как оператор, сопряженный оператору дифференцирования, определенному на множестве непрерывно
160
дифференцируемых I раз функций, обращающихся в нуль в граничной полосе области G.
4. Матричная форма оператора в пространстве с базисом. Пусть в банаховом пространстве X с базисом задан линейный ограниченный оператор А, отображающий X в это же пространство. Возь-п
мем х£ X. Тогда x=lim хп, гдех„= У] Следовательно, п i = 1
п
i/ = Ах — A /lim х„\ = lim У В,-Ле;.
\ п ) п i—\
Так как Ле,—снова элемент из X, то он может быть разложен
оо
по элементам базиса: Ле,- — У akiek, тогда /?=1
п / ОО \
У = Ах = lim 2 В,- ( У akiek ). (8)
п 1=1 \£=1 /
Но у£Х и, следовательно, также может быть разложен по элементам базиса:
00
(9) k —" 1
Пусть теперь {Д-} — последовательность функционалов, биортого-нальная к последовательности {ej. Тогда из соотношений (8) и (9) получаем
{п / 00 X)
Нт 2 М 2
п I =1 \Ai=l /}
{п f °° 1
i =1 \fe=l / )
П °® П оо
= lim У U akifm (еА) = lim 21 am£i = 2 “m&i- (Ю)
n i=l Л=1 п i= 1 1=1
Равенство (10) показывает, что оператор Л однозначно определяется бесконечной матрицей (с помощью этой матрицы по компонентам элемента х однозначно определяются компоненты элемента у—Ах).
Рассмотрим теперь сопряженный оператор А*, отображающий X* само в себя. Пусть /==Л*<р, т. е. <р(Дх) = /(х) для любого оо оо
х^Х. Пусть, далее, <р= У ctft и /= У djf{. Имеем
( оо / ОО X Л ( п / оо \
<р(Лх) = ф< У ( У a*&)e4 = lim<p{ У ( У akilAek \k=\ \i= 1 / j n \fc=l \i= 1 /
П / оо X
= lim У ( У akili]q(ek)^.
п Л = 1 \ i= 1 J n / ОО X оо / п Л
= lim У ( У akilt )ck= lim У ( У akick )gz. n /2=1 V= 1 / n j= 1 \/2=l /
6 N» 3054
161
С другой стороны,
Ф (Ax) = /(*)= 2 dtfi (x) = 2 dfci. 1=1 1=1
Следовательно,
оо оо / п \
2 d^i= lim 2 ( S
1 n i= 1 \/г = 1 J
(11)
Пусть x — em, t. e. £m=l, l, = 0, для i#=m. Тогда формула (11) дает fl 00
4 = lim 2 aknck= 2 akmck. n k=\ Л=1
Полученное равенство показывает, что матрица, соответствующая сопряженному оператору, является транспонированной матрицей по отношению к матрице, соответствующей исходному оператору. Такое представление операторов и им сопряженных имеет место, например, в пространстве /2.
Из матричного представления операторов легко получаем, что
1) (Л4-В)* = Л* + В*; 2) (ЛБ)* = В*Л*;
3) (Л-1)* = (Л*)"1, если Л-1 существует. I
Впрочем, эти формулы легко установить и без предположения, что пространство обладает базисом.
5. Скалярное произведение, ортогональные элементы, биортого-нальные системы. Пусть х£Х и f—линейный функциойал на X, т. е. f£X*. Рассмотрим выражение 4
/(х) = <х, />. (12)
Это выражение при переменных хи/ является билинейным функционалом относительно обеих переменных, т. е. линейным относительно каждого переменного. Этот билинейный функционал для J случая, когда X есть гильбертово пространство и, значит, Х* = Х, 1
превращается в скалярное произведение элементов хи/ (см. фор- I
мулу (13) § 3). Принято и в общем случае, когда Х^Х*, назы- ’ вать выражение (12) скалярным (или внутренним) произведением х^хи/ех*. ;
Элементы х£Х и /£Х* называются ортогональными, если i <х, /> = 0.
Теор'ема 2. Пусть ^—собственное значение линейного опера- *| тора A$.L(X, X); х0—соответствующий собственный элемент; «
р0— собственное значение сопряженного оператора Л*; /0—соответ- |
ствующий собственный элемент. Если Х0=#р0, то собственные эле- i менты х0 и fa ортогональны. 1
Эта теорема является обобщением теоремы об ортогональности I собственных функций союзных интегральных уравнений*. •'
* См., например, [9].
1G2
□ Пользуясь обозначением скалярного произведения, запишем связь между операторами Л и Л* в виде равенства <Ах, /> = = <х, Л*/>» справедливого при любых х£Х, X*. Согласно условию теоремы, имеем Лхо = Хохо, Л*/о = Ро/о- Отсюда и из приведенного выше равенства получаем
^0<*0, /о> = Ио<*о, fo>, ИЛИ (Хо — |10)<Х0, /о> = О-
Но, по предположению, k0^|i0; следовательно, <х0, f0> = 0. Ц
Как мы уже говорили ранее, последовательности {хп}<=.Х и {fn}cX* называются биортогональными, если
= (13)
Тем самым х,- и fj ортогональны при i =/= j.
В § 7 гл. III мы рассмотрели пример биортогональных последовательностей. Это элементы базиса Х, е2, ..., е„, ... и функционалы fit f2, ..., fn, .. •, определяемые равенством fk (х) =
оо
ДЛЯ Х= 2 ^iei-
i— 1
В самосопряженном пространстве, например гильбертовом, обе биортогональные последовательности лежат в одном и том же пространстве. Если fn — хп, то биортогональность переходит в обычную ортогональность.
Пусть последовательности {х„} и {fn} биортогональны и элемент х представлен в виде ряда
2 liXt, (14)
i= 1
Имеем
п п
<х, Z*> = lim (2 liXh f^ = lim 2 Л>.
п i— 1 п i= 1
п
В силу равенства (13) при n~^k имеем 2 %k, поскольку
i= 1
в этой сумме все члены обращаются в нуль, кроме члена §*<хА, — Значит, |ft=<x, и равенство (14) примет вид
Х= 2 <Х, fi>xb (15)
i= 1
Аналогично, если
(16)
TOd„=<X„, />.
Ряды (15) и (16) называются рядами Фурье по соответствующим биортогональным последовательностям.
Первые нетривиальные примеры биортогональных последовательностей t функций были рассмотрены П. Л. Чебышевым и А. А. Марковым в связи с задачами интерполирования.
6*
163
Покажем, что для любой линейно независимой системы элементов {хп х2, .хп}сХ существует биортогональная ей система линейных функционалов {fu f.2, ..., fn}<=X*.
□ Пусть L1 = L(x2, х3, хп) — линейное многообразие, порожденное элементами х2, х3, ..., х„. Так как хг лежит на расстоянии d > 0 от Li (в силу линейной независимости элементов xf, х2, ..., х„ и замкнутости Ьг), то существует линейный функционал А(х) (такой, что Л(х) = 0 на в частности на элементах Х2, Х3, ..., Х„, И
Повторяя эту операцию для многообразия Л2 = £(х1,х3, . ..,х„) и элемента х2 и т. д., получим требуемую систему функционалов.
Пусть, наоборот, дана система {fu f2, ..., fn}ccX* линейно независимых линейных функционалов, т. е. таких, что из соотношения
Wi (•*)+W2 (*) + ••• + Ktfn (х)= о
для произвольных х € X следует = Х2 = ... = = 0. Тогда существует система элементов {х1( х2, ..., х„}сХ, биортогональная этой системе функционалов.
Положим сначала п—1. Так как /1(х)^0, то существует элемент х0 такой, что fi (х0) = а #= 0. Тогда элемент xl = xQ/a обладает требуемым свойством.
Предположим, что утверждение доказано для п—1 линейно независимых функционалов. Докажем его для случая п функционалов. Пусть {х2, х3, ..., х„}~система элементов, биортогональная функционалам f2, f3, ..., fn. Обозначим через ЛА линейное многообразие, определяемое системой уравнений /3 (х) = 0, А (х) = 0, ..., fn (х) = 0. Для любого х € X элемент
п
и = х-% срсь где cz = /z(x), 1= 2
принадлежит этому многообразию. В М2 существует элемент х0 такой, что (х„' = а =И= 0. В противном случае А (и) равнялось бы нулю для всех и:
п п
/1 (*) — У cji (xz) - 0, или fi (х) = 3 A (xz) fi (х) i~ 2 t = 2
для любого х£Х. Это означало бы, что А есть линейная комбинация функционалов А, А> • • •, fn* что невозможно [по условию.
Итак, существует элемент х0 такой, что А (х0) = а 0, А(х0)= = А (*о) — ... = fn (х0) = 0. Полагая хг — х0/а, получаем первый элемент биортогональной системы.
Повторяя то же рассуждение для многообразия
М2= {х| А (х) = 0, А (*) = 0. • • •. fn (х) = 0}
и функционала А» получим элемент х2 и т. д. Н
6. Сопряженное пространство к линейному комплексному пространству. Все понятия, введенные в этом параграфе, переносятся и 164
на комплексные линейные пространства X. Сопряженным пространством X* мы назовем совокупность линейных комплексных функционалов на X.
Скалярным произведением <х, f>, где х£.Х, f£X*, по-прежнему будем называть число f(x). Для того чтобы сохранить при этом свойства скалярного произведения в комплексном гильбертовом пространстве, следует считать <х, /> линейным функционалом относительно х и сопряженно-линейным относительно f:
<Хх, /> = Х<х, />, <х, X/> = Z<x, />.
Тем самым определяется умножение на комплексное число X в X*; X/ есть такой линейный функционал <р на X, что <р (х) = (х).
Понятие сопряженного оператора А* к оператору А из L (X, X) переносится и на случай комплексных пространств: А* есть оператор из L(X*, X*) такой, что <Лх, /> = <х, Л*/> при любых х£Х и f£X*.
Все свойства сопряженных операторов переносятся непосредственно на комплексный случай с одним изменением: теорема об ортогональности собственных элементов х0 и f0 операторов Л и Л*, где Лх0 = Хх0, Л*/о = ро/о, имеет место, если Хоу=ро.
§ 5. СЛАБАЯ СХОДИМОСТЬ
1. Слабая сходимость последовательности функционалов. Мы видели, что в пространстве X* = L (X, R), где X есть ЛНП, можно ввести две топологии: топологию хь, совпадающую с топологией, определяемой нормой функционалов, и топологию поточечной сходимости т^. Сходимость последовательности функционалов в смысле топологии т, называется слабой сходимостью. Таким образом, последовательность {fn}czX* называется слабо сходящейся к функционалу f0£X* (символически если /„(х) —>/0(х)
для любого х£Х. Сходимость по норме часто называют сильной сходимостью последовательности функционалов.
Из предыдущего следует, что если */0, то ?„—<?<> Впрочем, это легко проверить и непосредственно. Обратное неверно. Так, если Х = 1р и, следовательно, X* = lq + y = 0 ’ то П0СлеД°ва' тельность функционалов {fn}, где f„ = {0, 0, ..., 0, 1, 0, ...} (1 стоит на n-м месте), слабо сходится к нулю. В самом деле, для любого x = {ln}£lp имеем fn (х) — ► 0, но {fn} не сходится
к нулю по норме, поскольку ||f„||=l (п=1, 2, 3, ...). Если же пространство X* конечномерно, то в таком пространстве сильная и слабая сходимости совпадают, так как в конечномерном отделимом ЛТП, а X* является таковым, все топологии эквивалентны.
Теоремы о сходимости последовательности линейных функционалов (см. теоремы 2 и 3 на с. 134) могут быть сформулированы теперь так.
165
Теорема 1. Последовательность линейных функционалов {/„}, слабо сходящаяся в себе, слабо сходится к некоторому линейному функционалу fQ.
Теорема 2. Для того чтобы последовательность {fn} линейных функционалов слабо сходилась к линейному функционалу необходимо и достаточно, чтобы:
Г) последовательность {|]/„||} была ограничена',
2°) fn (*) /о (*) для любого х из некоторого множества М, линейные комбинации элементов которого лежат всюду плотно в X,
Отметим еще, что из теоремы 1 вытекает слабая полнота пространства X*, сопряженного с банаховым пространством X.
2. Применение [к теории квадратурных формул. Рассмотрим в пространстве С [0, 1] функционал
1
f (х) = J X (/) do (/), о
где о (7) — некоторая неубывающая функция. Наряду с f (х) рассмотрим последовательность функционалов
kn fn{x)=^ c^>x(tW) (п=1, 2........),
k=z\
где выбраны так. что f (х) и fn (х) совпадают для всех многочленов степени^ п
не превосходящей п, т. е. f (x) = fn(x), если х (/) = 2 ар1р- Построенные таким р = 0
образом функционалы fn применяются для приближенного вычисления ] функционала f. Приближенное равенство f (х) & являющееся точным для всех многочленов степени ^п, называется квадратурной формулой.
Пусть имеется последовательность квадратурных формул f (х) « fn (х) (n = 1, 2, ...). Естественно поставить вопрос: сходится ли последовательность выражений fn (х) при п —> оо к значению f (х) для произвольной функции х (/) £ С [0, 1]; другими словами, является ли последовательность функционалов {fn} слабо сходящейся к функционалу /?
Теорема 3. Для того чтобы имела место сходимость последовательности квадратурных формул, т. е, чтобы
kn *
lira У] x (/<*)) — I x (0 do (t) n о
для любой непрерывной "функции x(t), необходимо и достаточно, чтобы &П
2 с(£У I/С = const для всех п.
/г=1
П По определению функционалов fn для всякого многочлена х (/) степени п kn
имеем /w(x)=/(x) при т^п. Далее, очевидно, ||/п||= У | с<£> |<Д, Таким 6=1
образом, последовательность функционалов {/„} сходится к функционалу f на множестве всех многочленов, всюду плотном в пространстве С [0, 1], и нормы функционалов fn ограничены. Но тогда доказываемая теорема непосредственно следует из теоремы 2 настоящего параграфа. Ц
Теорема 4 (В. А. Стеклова). Если все коэффициенты с^ квадратурных формул положительны, Imo последовательность квадратурных формул f (X) ~ fn{x) (л = L 2, ...) сходится для любой непрерывной функции х (t), 166
□ В самом деле, для любого п и х0(О^1 имеем fn (x0) = f (х0). Поэтому
Л
2 । W1= 2 Ъп> = \ (i)-o (0),
fe=l fe=l о
й теперь можно применить предыдущую теорему. В
3. Слабая сходимость последовательности элементов пространства ЛНП. Пусть X есть ЛНП и X** — второе сопряженное с X пространство. Если X** наделено топологией ть сходимости по норме, то, как мы видели, ХсХ**. Если же X** наделить слабой топологией т,, то эта топология индуцирует на X, как на линейном подмножестве линейного пространства X**, некоторую топологию xw. Так как на X** топология т, слабее топологии хь, то и на X топология xw слабее первоначальной топологии сходимости по норме пространства X. Поэтому топологию xw называют ослабленной (или слабой) топологией пространства X.
Если {хп}сХ и хп —*%0СХ, то это означает (см. с. 157), что FXn(f)-+FXo(f) для любого f$X* или, так как Fx (/) = f (х), что f (х„) —► f (х0) для любого f € X*.
Как и для функционалов, в этом случае будем писать х„-^-х0 и говорить, что последовательность элементов {хп} слабо сходится к элементу х0.
Снова, если X конечномерно, то xb = xw. В общем случае из х„ —> х0 не следует х„ —> х0, но существуют бесконечномерные ЛНП, в которых сильная и слабая сходимости последовательности элементов совпадают. Примером может служить пространство I по-00
следовательностей х={|Д таких, что ряд У |£;| сходится.
i- 1
Для елабо сходящихся последовательностей элементов имеет место следующая теорема.
Теорема 5. Для того чтобы последовательность {хп} слабо сходилась к х0, необходимо и достаточно, чтобы:
1°) последовательность {||хп||} была ограничена',
2°) f (х„) —f (х0) для любого f из некоторого множества Г линейных функционалов, линейные комбинации элементов которого лежат всюду плотно в X*.
□ Эта теорема представляет собой частный случай теоремы 2 настоящего параграфа. Чтобы убедиться в этом, следует только заметить, что слабая сходимость последовательности {х„}сХ к элементу х0£Х, очевидно, равносильна слабой сходимости этой же последовательности, но рассматриваемой как последовательность линейных функционалов {х„}, определенных на X*, к х0, также рассматриваемому как линейный функционал на X*. £
Заметим, что теорема 1 настоящего параграфа не переносится на случай слабой сходимости элементов, так как множество ХсХ** в общем случае не замкнуто в X** в топологии rs и последовательность {х„} элементов пространства X, слабо сходящаяся
167
в себе, сходится к функционалу Fo С X**, не обязательно имеющему вид Л (/) = /(*»)•
Так как всякая окрестность нуля в ослабленной топологии есть в то же время окрестность нуля в топологии то точка х, являющаяся предельной точкой множества МсХ в топологии сходимости по норме, служит в то же время предельной точкой этого множества в ослабленной топологии. Поэтому MczMw. Обратное включение в общем случае не имеет места, однако справедлива следующая теорема.
Теорема 6. Если М—выпуклое множество ЛНП X, то M = MW. _ _
□ Достаточно доказать лишь включение Mwс М. Пусть х0(£М. Если М выпукло, то М также выпукло и Х\М есть открытое множество, которое содержит некоторое открытое выпуклое множество, содержащее х0 и не пересекающееся с выпуклым множеством М. Поэтому (см. § 2 настоящей главы) найдется функционал такой, что для всех х из этого множества /0 (х) < inf /„ (у)
уьМ
и, в частности, /0 (х0) < inf /0 (у) = 0.
уем
Пусть /(хс) = а, е —любое число, меньшее (0 — а)/2 и = {х|/о(х) < е}. Это окрестность нуля в ослабленной типологии и, следовательно, х0 + и“ есть ослабленная окрестность точки х0. Для любой точки х^х0 + «“ имеем
/о (х) = (х0 + г) = f0 (х0) + /„ (г) < а + е < а + =т < 0,
откуда вытекает, что (хо + ио)ПМ—0. Следовательно, xef£Mw. Щ сл
Следствие 1. Если хп —>х0, то существует последователь-
ноешь выпуклых комбинаций <[ 2
тп
тп
, 2а'п) = 1 та-
1= 1
кая, что
0.
□ В самом деле, пусть М — совокупность всех выпуклых комбинаций точек последовательности {х„}. Тогда М — выпуклое множество и х0 принадлежит ослабленному замыканию множества М. В силу предыдущей теоремы хй£М, откуда и следует существование последовательности элементов М, сходящейся по норме к х0. И
Следствие 2. Если х0 есть слабый предел последовательности {х„}, то ||х„К И1п||х„ ||.
□ Допустим, что || х01| > lim || х„ ||. Тогда существует число с такое, что ||х0|| > с > lim ||х„||. Следовательно, найдется подпоследовательность {x„(.}, для которой || х0|| > с > ||х„.||. Построим функционал
такой, что || ДИ =1 и f„ (х0) = Цх0|| >с. Тогда
/о (хп.) || /о II II хП{|| — Ц хп. || < с
168
для всех I. Поэтому [а(х„.)[0(хл), что противоречит условию
хя * х9. Щ
Примеры показывают, что возможны случаи, когда осуществляется строгое неравенство ||х0|| < lim||x„||. Пусть X = L2[0, 1] и хп (0 = V2 sin nnt- Тогда ||х„||—1, так что lim||хпЦ = 1. С другой п
стороны, для любого линейного функционала f£X* имеем
1
f (хя) = У 2 $ х (0 sin nnt di = К2 с„, о
где ^ — коэффициенты Фурье функции x(i)£L3[0, I], и, следовательно, сп —>0. Таким образом, хп^- хо = О и || х01| = 0 < 1 = lim || х„ ||.
п
Лемма. Пусть А—линейный ограниченный оператор, действующий из ЛНП X в ЛНП Y. Если последовательность {хя}с:Х слабо сходится к х„£Х, то Ахп-^Ах0.
□ Возьмем любой функционал ф£У*. Тогда фИхя)=/(х„), где f^X*. Аналогично, ф (Ах0) = f (х0). Так как хп^-ха, то f(xn) —>/(х0), т. е. <р (Ах„)-> <р(Ах0). Но ф —произвольный функционал из Y* и, значит, Ахп -X Аха. Ц
Таким образом, всякий линейный ограниченный оператор не только сильно, но и слабо непрерывен.
3. Слабая сходимость в конкретных пространствах.
Теорема 7. Для того чтобы последовательность {х„} элементов хп = {1\п'}£1р (р>1) слабо сходилась к x0 = {|<i“,}^//), необходимо и достаточно, чтобы:
1°) последовательность {||х„||} была ограничена',
2°) I'-'0 —> ^0) при п—> оо для всех i (вообще говоря, неравномерно ).
□ Для доказательства заметим, что линейные комбинации элементов Д = (0, 0, ..., 0, 1, 0, ...) (i=l, 2, ...) лежат всюду । плотно в lq — l*p. Поэтому в силу общего критерия, для того чтобы хп —* х0, необходимо и достаточно, чтобы выполнялось условие 1° и чтобы Л (х„) = ^л)—>^0,=Д (х0) для любого i.
Таким образом, можно сказать, что слабая сходимость в 1р означает сходимость по координатам в соединении с ограниченностью норм. В
I Теорема 8. Для того чтобы последовательность с£Д0, 1], (р>1) слабо сходилась к элементу x0(t) £L?[0, 1] необходимо и достаточно, чтобы:
1°) последовательность {||х„||} была ограничена-,
2°) J xn(t) dt —> $ x0(t)dt для любого т£ [0, 1]. о о
169
□ Условие 1° совпадает с условием 1° общего критерия. Проверим выполнение условия 2°. Положим
I при 0^ t < т,
0 при t 1.
«г (0 =
Тогда линейные комбинации функций aT(Z), т. е. суммы
ci [аг/ (0 (0]>
где 0 = то < <... < т„_х < т„ = 1, лежат всюду плотно в ЬДО, 1]= =Лр[0. 1]. Следовательно, для того чтобы хп (/) х0 (/), необходимо и достаточно, чтобы выполнялось условие Г и чтобы при П —► оо
1 1 т т
J х„ (0 аг (/) d/ —► $ х0 (/) ах (/) d/, или $ хп (1) dt —► $ х0 (t) dt о о оо
для любого т С [0, 1]. Ц
Теорема 9. Для того чтобы последовательность {хп}с:С [а, &] слабо сходилась к х0£С[а, 6], необходимо и достаточно, чтобы:
Г) | хп (t) | М при всех t £ [а, b], п = 1, 2, 3, ...;
2°) xn(t)—>x0(t) для любого Ь].
□ Необходимость условий очевидна, так как ft[x)=x(t) есть непрерывный линейный функционал в пространстве С [а, Ь]. Докажем их достаточность.
Всякий линейный функционал в пространстве С]а, Z?] имеет ь
вид / (х) = J х (/) dg(O, где g(t)— функция с ограниченной вариа-а
цией. Так как всякая функция с ограниченной вариацией есть разность двух монотонно возрастающих функций, которые без ограничения общности можно считать строго возрастающими, то достаточно доказать, что при выполнении предыдущих условий ь ь
J хп (/) dq> (/) —> J х0 (0 dtp (/), где <р (/) — строго возрастающая
а а
функция.
Пусть ф(/) = г и / = ф(г)—функция, обратная к <р(0. причем если t—точка разрыва функции <р (t), то на отрезке [<р (i —0), <p(^ + 0)] функцию ф(г) мы полагаем постоянной и равной/. Тогда
Ь 4 (6)
$x„(/)d<p(O= $ x„[i|?(z)]dz.
а -ф (а)
Функции х„[ф(г)] измеримы, ограничены и всюду на [ф(а), Ф(&)]
170
сходятся к ХорФСЮ]. Поэтому, по теореме Лебега,
Ф (Ь) ф (Ь)
$ x„[i|)(z)]dz—> J x0[\p(z)]dz, Ф (а) ф (а)
Ъ Ъ
Т. е. $ хп (/) dtp (/) —► $ х0 (0 d<P (0- а а
В заключение этого пункта рассмотрим вопрос о слабой сходимости в гильбертовом пространстве. Так как в гильбертовом пространстве Н всякий линейный функционал f (t) есть скалярное произведение, то в этом пространстве xn^xQ означает, что <х„, у)—* —><х0, У> Для любого у^Н.
Ранее мы видели, что если хп—>х0, уп—^уь, то <хл, упУ —><х0 у0>, т. е. скалярное произведение непрерывно по совокупности обоих аргументов относительно сильной сходимости. Если же Уп—+Уо, т°, вообще говоря, <х„, уп>-^<х0, yQ>. Так, например, если хп = уп = еп, где {еп}—произвольная ортонормальная последовательность, то еп —> 0, поскольку для любого у^Н в силу неравенства Бесселя <у, е„>^0, но <еи, е„> = || е„ |j2 = 1 -^4-0 = <0, 0>. Однако если х„—>х0, уп^уп, то <х„, у„>-><х0, у0>.
В самом деле, в этом случае нормы ||ynj ограничены в совокупности. Пусть М = sup ||z/„||. Тогда
|<*и. Уп>~<Хо, «/e>K|<x„-x0. у„>| + |<х0, уп—у0> К М || хп XQ || Уп Уо>|
и оба слагаемых справа стремятся к нулю.
Наконец, отметим, что если хп —>х0 и ||хп || —>|]х01|, то хп —>х0, так как
II Хп IP ~ ^о> Х'п =
~ [Ц хп ||2 || 1|2] -|- [<х0, х$у <д0, •£«/’] 4~ [<^0, х$у <\ХП1 Яс/*] и все слагаемые справа стремятся к нулю.
Последнее утверждение справедливо и в пространстве Lp [0, 1]: СЛ
если {х„(0}<=М°> 1Ь МО —МО и ||х„ (011 — 11 МО II. то II хп (/)— хо(0||—*0. Доказательство этого мы опускаем.
4. Слабая компактность. Нижеследующая теорема является весьма важной и часто используется в приложениях функционального анализа. Ограничимся случаем вещественного пространства.
Теорема 10. Замкнутый единичный шар К* (0, 1) пространства X*, сопряженного с ЛНП X, слабо компактен.
□ Каждому х^Х сопоставим числовую прямую = (—оо, оо) и в декартовом произведении Т ~ JJ Rx, наделенном тихоновской хеХ
топологией, рассмотрим множество Л4= Ц [—[|х||, |]х||]. По тео-
171
реме Тихонова, множество М компактно. Отобразим X* в Т, поставив в соответствие каждому f£X* точку с координа-
тами tx(f) = f(x). Пусть У— множество всех таких точек t(f). Если К — образ Х*(0, 1) при таком отображении, то ХаМ.
Покажем, что множество К замкнуто в тихоновской топологии пространства Т. В самом деле, пусть /0 = ^ — предельная точка К. Определим на X функционал /0, полагая /0 (х) — Покажем, что /о€Х‘(О, 1). Для любых хп х2€Х и произвольного 8 > 0 рассмотрим окрестность и точки t, в которой лишь uXl, иХг, uXl +Хг отличны от всей прямой и равны соответственно (/“,—е, /°,4-е), {tX2 — е, С + в); (tXl+X2 — 8, /“l+X2 + e). Тогда найдется точка t£K такая, что Это значит, что — /“, | < е, |G,— /°г|<8,
К+х, — *“,+*, | < 8. Так как t£K, то ^, = f(Xi), tx, = )(xi), tXi+Xs = f(Xi + x2) = f(x1) + f(x2) = tXt + tX2 для некоторого функцио-нала f£K* (0, 1). Но тогда
I /о (*1 + fo (%1) /о (^2) | “ txx + х2 txx tx? I
I txx+x2 — ixx+x21 +] txx — ^xt +1 tx2 — tXi I < 3e, и так как г произвольно, то последнее неравенство означает, что /о (-^1 4“ ^2) ~ f 0 (-^1) + /о (^2) •
Аналогично доказываются равенство fQ (Хх) = Х/о (х) и неравенство | fQ (х) КII х||. Следовательно, /0С К* (0, 1), т.е. =
Так как А есть замкнутое подмножесто компактного множества М, то множество К компактно в Т. Но легко видеть, что тихоновская топология на YzdK есть в то же время слабая топология пространства X*, и, значит, слабая компактность К* (0, 1) доказана.
Следствие. В пространствах 1р и АДО, 1], р>1 всякий шар слабо компактен.
Это вытекает из того, что lp~l*q и АДО, 1] = АД0, 1].
§ 6. УНИВЕРСАЛЬНОСТЬ ПРОСТРАНСТВА С[0, 1]
В 1923 г. советский математик П. С. Урысон доказал, что существует «универсальное сепарабельное метрическое пространство», т. е. такое, которое содержит части, изометричные любому сепарабельному метрическому пространству. Впоследствии польские математики, С. Банах и С. Мазур показали, что одним из таких универсальных пространств является пространство С [0, 1].
Доказательство теоремы Банаха—Мазура связано со свойством слабой компактности сопряженных пространств.
Лемма. Всякое компактное множество метрического пространства есть непрерывный образ канторова совершенного множества.
□ Пусть М — компактное множество метрического пространства X. Рассмотрим последовательность {еп}, сходящуюся к нулю, и для каждого п=1, 2, 3, ... построим конечную еи-сеть 172
{х)я>}<=1, 2.mn Для M. Добавляя в случае необходимости допол-
нительные точки, мы можем всегда считать, что тп = 2к". Рассмотрим шары К)1* радиуса ех с центрами в точках х)1’. Множество М расположится целиком в этих шарах, а тем более в замкнутых шарах К?*. Пусть Mit = М П (ix — 1, 2, ..., т^. Мы получили, что множество М представлено в виде объединения т1 замкнутых множеств диаметра, не превосходящего 2вх. Как замкнутая часть компактного множества каждое есть снова компактное множество. Повторяя предыдущее построение, представим каждое М,-, в виде объединения т2 замкнутых множеств (t2= 1, 2, ..., m2) диаметра, не превосходящего 2еа, и т. д. Все эти множества можно считать непустыми.
Рассмотрим теперь канторово совершенное множество Ро. Это множество лежит целиком на отрезках &х-го ранга A/,/,.../ (/, = 0, 1), а также целиком на отрезках (Лх + ^2)-го ранга ит.д.
Перенумеруем отрезки #х-го ранга слева направо и обозначим их A(1(tx=I, 2, ..., т1 = 2к>). На каждом отрезке &х-го ранга А,, лежат 2кг = т2 отрезков (£х + &2)-го ранга. Перенумеруем их также слева направо и обозначим Д(11-2 (i2 = 1, 2, ..., m2) и т. д. Мы получим взаимно-однозначное соответствие между замкнутыми множествами Milia...is пространства X и отрезками А,-,;,..., отрезка [0, 1].
Возьмем произвольную точку t £ Ро. Она однозначно определяет систему отрезков Atl, А^, A,1(-2l-3, ..., содержащих ее и стягивающихся к ней. Рассмотрим соответствующую систему замкнутых множеств Mtl, Мцц, ... (с теми же индексами, что и от-
резки). Так как каждое следующее множество вложено в предыдущее и диаметры множеств стремятся к нулю, то существует единственная точка х£М, принадлежащая всем этим множествам, которую и поставим в соответствие точке t g Ро.
Покажем, что каждая точка х С М является образом некоторой точки t£P0. В самом деле, х € Л4(1 для некоторого значения индекса ix (этот индекс определяется, вообще говоря, неоднозначно, так как множества могут пересекаться), аналогично xgM^^ и т. д. Множествам М^, ... соответствуют отрезки Д/,, Д,,^,
... . Точка t, принадлежащая всем этим отрезкам, имеет образом рассматриваемую точку х. Итак, определено однозначное отображение х— <р (0 канторова совершенного множества Ро на компактное множество М. Покажем, что это отображение непрерывно.
Пусть x0 = <p(Q и К (х0, е)—окрестность точки х0. Возьмем такое множество из системы, стягивающейся к х0, диаметр
которого меньше е. Тогда (х0, е). Обозначим через 6 рас-
стояние от/0 до ближайшего конца отрезка соответствующего множеству Mt^ ,,сп. Если |/ — /0|< 6, тоД(1,следовательно, x~(f>(t)^MiIia...inc:K(x0, е) и потому р(х, х0) < е. Ц
Теорема 1. Всякое сепарабельное банахово пространство X изометрично и изоморфно подпространству пространства С[0, 1].
173
□ Пусть К*—-шар в пространстве X*, причем за схо-
димость в К* принимается слабая сходимость линейных функционалов. В силу теоремы 10 § 5 множество К*—компактное. Пусть alt а2, ..., ап, ... —счетное всюду плотное множество в единичном шаре 1 пространства X. Для любого функционала положим f(ak) = lh, |^|<1, k=\, 2,... . Если fn, f0 € К*, то (ak) —(a*) = Bfe0>- Таким образом, каждому f£K* соот-
ветствует элемент y={lk}, lk = f(flk) пространства s и fn-^+f0 влечет за собой уп —► у0 для соответствующих элементов пространства s.
Пусть N — множество точек пространства $, соответствующих функционалам /£№. Тогда JV есть непрерывный образ компактного множества и, следовательно, также компактное множество. Легко видеть, что обратное отображение N на X* также однозначно и непрерывно. В самом деле, пусть /(а*) = ф(аА), 2, ... . Для любого х£Х, такого, что ||х||^1 и 8 > 0, выберем а*0 так, чтобы ||х—a*J| < 8. Тогда
I f (х) — ф (х) | < | / (х—aft„) | +1 f (ak^ -ф (ako) | +1 ф (x-afto) | < 2в, откуда в силу произвольности 8 имеем /(х) = ф(х), т. е. / = ф.
Далее, если fn(ak)—^f0(ak), k=l, 2, ..., то в силу ограниченности норм функционалов (|]/„||^1; п — 0, 1, 2, . ..) отсюда сле-дует f„ —и взаимная однозначность и непрерывность соответствия доказана.
Согласно лемме, N как компактное множество метрического пространства есть непрерывный образ канторова совершенного множества До. Таким образом, каждому t £ Ро отвечает функционал ft € К*, совокупность всех ft совпадает с К* и ftn —► ft при tn —► t.
Выберем произвольный элемент х£Х. По определению слабой сходимости функционалов, ftn (х) —► ft (х) при При фикси-
рованном х ft (х) есть, следовательно, непрерывная функция от t £ Ро, которую обозначим
ф,(0=А(х). (1)
Функцию фх(0, определенную на Ро, доопределим линейно и непрерывно на смежных к Ро интервалах. Тем самым получим непрерывную функцию ф* (0, определенную на отрезке [0, 1], т. е. принадлежащую С[0, 1]. По определению нормы в С[0, 1] имеем В Фх lie — max I Фх (01- Но вследствие линейности ф* (t) на интервалах, о < t < 1
смежных к Ро, максимум фДО на [0, 1] совпадает с максимумом Фх(0 на Ро. Поэтому ||фх||с = тах | фд. (/) |,
С другой стороны, для t£P0 в силу (1) имеем
|фх(01 = 1А«|<|1А|М1хК||х||
и, следовательно,
174
Далее, для данного х можно построить функционал с нормой, равной единице, для которого /»(*) = II *11- Так как то су-
ществует t0€P0, для которого = Следовательно, М(х) = ||х||, т. е. <рхЛ) = И, и потому
* max 1^(01 >11* II- • (3)
teP„
Из неравенств (2) и (3) следует, что
II Фх 11с = 11 *11- (4)
Из построения функции <рх (0 видно, что если £ X и х2 С X соответствуют <рХ1 (/) и q>xs (0, то х1 + х2 соответствует <рЛ1 (/) + фЖг (0 и Хх соответствует Хфх (t). Следовательно, мы имеем изоморфное отображение пространства X на часть пространства С[0, 1]. Так как в силу изоморфизма элементу х2—х2 соответствует функция фх, (0—фх,(0» то по формуле (4) получаем |)*i—*2|| = ||фх, — Фх2||с. т. е. соответствие пространства X части пространства С[0, 1] не только изоморфно, но и изометрично. Ц
Теорема 2 (Фреше). Всякое метрическое сепарабельное пространство X изометрично части некоторого сепарабельного банахова пространства.
□ Пусть Л4 = {х0, хп ..., х„, ...} —счетное всюду плотное множество в пространстве X. Отнесем каждому элементу х£Х точку </=={'П|} пространства т, где т], = р(х, х()—р(х0, xz); i = 1, 2, 3, ... .В силу обратного неравенства треугольника
|П/1 = |Р(*. *<)-Р(*о. *;)1<Р(х, *0)
и, следовательно, {ц,} —ограниченная последовательность, т. е., действительно, у—точка пространства т.
Пусть элементам х и х' из X отвечают элементы у = {т| t} и у' = {т]J} из т. Имеем
k-/U = suphi—4i'l =
= sup | [р (х, х,) — р (х0, xz)] - [р (х', xz) — р (х0, х;)] | =
= sup |р (х, xz) — р (х', xz) |<р (х, х'). (5)
i
Пусть теперь s—произвольное положительное число, меньшее Р (х, х'). Существует точка х„ счетного всюду плотного множества М такая, что р(х, х„)< е/2. Следовательно,
р(х', х„)>р(х', х) — р(х, х„)>р(х', х)—у>0 и потому
1пв-п«1 = |р(*л. х)-р(х, х')|>р(х', Х„)~|->
>р(х', х)--1—|- = р(х, х')~8.
Отсюда
11У-/|1>Р(*> *')-е. (6)
175
Так как е> 0 —любое, то из (6) следует, что
х'). (7)
Сравнивая неравенства (5) и (7), получаем ||z/ — t/'|| = p(x, х').
Итак, расстояние между точками х и х' в X равно расстоянию между соответствующими точками у и у' в т и, следовательно, пространство X изометрично некоторой части L пространства т. Очевидно, эта часть пространства tn сепарабельна.
Пусть Хо —подпространство пространства т, порожденное элементами множества L. Тогда Хо есть некоторое сепарабельное банахово пространство, причем X изометрично части этого пространства. в
Теорема 3 (Б ан а ха —Маз ура). Всякое метрическое сепарабельное пространство изометрично некоторой части пространства С [0, 1].
Доказательство непосредственно следует из теорем 1 и 2.
Упражнения
1. Покажите, что если линейные функционалы ft и /2 совпадают на некоторой гиперплоскости, не проходящей через нуль, то они совпадают всюду.
2. Докажите, что любая гиперплоскость либо замкнута, либо всюду плотна в ЛТП X.
3. Найдите общий вид линейного функционала в пространстве [a, Z?].
4. Найдите пространства, сопряженные с сис0.
5. .Пусть Z = X-j-Y—прямая сумма банаховых пространств X и К. Чему равно Z*? t
6. Постройте примеры функционалов /, непрерывных на единичном шаре пространства /2 и таких, что: a) f не ограничен на этом шаре; б) f ограничен, но не достигает своих точных границ на этом шаре.
7. Докажите, что {f£X* ] | f (х) ] компактно в слабой топологии пространства X*.
8. Докажите, что ||х (| = sup | f (х) |, f£X*,
9. Докажите, что | А ||= sup | f (Ах) |.
|| f IIС 1, П х || < 1
10. Докажите, что {х£Х 11 f (х) | <; 1, где 7И° = {/ 11 f (х) 1, х^ТИ},
есть наименьшее замкнутое выпуклое множество, содержащее М. (Это множество называется биполярой множества Л1.)
11. Докажите, что если Хо не полно и X — пополнение Хо, то Хо =Х .
12. Следует ли из равенства X* — Y*> что банаховы пространства X и Y совпадают?
13. Покажите, что если X сепарабельно и X** —X, то X* также сепарабельно.
14. Всякий непрерывный линейный функционал ограничен на компактном множестве банахова пространства. Верно ли обратное, т. е. является ли множество компактным, если на нем любой непрерывный линейный функционал ограничен?
15. Являются ли единичные шары в пространствах /п, с, с0 слабо компактными?
ГЛАВА V
ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ И УРАВНЕНИЯ С НИМИ
§ 1. ВПОЛНЕ НЕПРЕРЫВНЫЕ ОПЕРАТОРЫ
1. Определение и простейшие свойства. Линейный оператор Л, определенный на ЛНП X и принимающий значения в ЛНП У, называется вполне непрерывным, если он отображает всякое огра» ниченное множество пространства X в относительно компактное множество пространства Y.
Очевидно, всякий вполне непрерывный оператор является ограниченным. Далее, легко проверить, что всякий линейный ограниченный оператор Л отображает относительно компактное множество в относительно компактное. Свойство полной непрерывности является, вообще говоря, более сильным по сравнению с простой непрерывностью. Так, например, единичный оператор в бесконечномерном пространстве X не является вполне непрерывным, поскольку он отображает единичный шар на себя, а последний не является компактным.
Пример. Пусть X — Y ==С [0, 1] и
t
Ах —у (/) = К (t, s) х (s) ds, о
где К (t, s) — непрерывное в квадрате O^s^l ядро. Докажем, что
оператор А вполне непрерывен. Пусть {х (/)} — ограниченное множество функций из С [0, 1], (| х||^г. Очевидно, что функции у (t) — J К (t, s)x(s)ds, где х (/)— о
функция из рассматриваемого множества, равномерно ограничены. Действительно, если /C = inax |/<(/,$) |, то \y (t)\^Kr. Далее, функции у(1) равностепенно t, s
непрерывны. В самом деле, пусть задано е > 0. В силу равномерной непрерывности ядра К (t, s) найдется такое 6 > 0, что \К Gi, s) — К (t2, s) I < s/r при I M < б и любых sg[0, 1]. Но тогда
1
IУ (*2) I < $ I к (h, s)-K (t2, s) VIX (s) 1 ds < e 0
всякий раз, когда | tf—t21 <6 для всех рассматриваемых функций у (I) сразу, что и означает равностепенную непрерывность функций у (t).
В силу теоремы Арцела множество функций {у (^)} относительно компактно в смысле метрики пространства С [0, 1] и полная непрерывность оператора А доказана.
Лемма. Если последовательность {хп\ слабо сходится к х0 и относительно компактна, то она сильно сходится к xQ.
□ Предположим, что это утверждение неверно. Тогда найдутся число 80 > 0 и неограниченно возрастающая последовательность
177
индексов n1( n2, .nk, ... такие, что ||x„fe — х0|]>е0. Поскольку последовательность {хя.} относительно компактна, она содержит подпоследовательность {Хп..сильно сходящуюся к некоторому элементу и0, тем более хп. -^>ы0. Так как в то же время хп. ~^+х0,то ы0 = х.
Итак, мы получили, что, с одной стороны, (|хя. — Х0||>80,
—х0||—>-0. Это противоречие доказывает лемму.
а с другой—1|хп.
Ч
Теорема 1. Вполне непрерывный оператор А отображает слабо сходящуюся последовательность в сильно сходящуюся.
□ Пусть последовательность {х„} слабо сходится к х0. Тогда нормы элементов этой последовательности ограничены и {хп\ как ограниченная последовательность переводится оператором А в относительно компактную последовательность {*/„}, где уп — Ахп.
С другой стороны, по лемме § 5 гл. IV имеем у„—Ах„ -X Аха—уп. Но тогда в силу леммы уп->-у0. Ц
Пусть А — вполне непрерывный оператор, отображающий бесконечномерное банахово пространство X в себя и В —произвольный линейный оператор, действующий в том же пространстве. Тогда АВ и ВЛ —вполне непрерывные операторы.
В самом деле, оператор В преобразует произвольное ограниченное множество МсХ в ограниченное множество В(М) и последнее оператор А преобразует в относительно компактное множество Л(В(М)). Следовательно, оператор АВ переводит любое ограниченное множество в относительно компактное и потому вполне непрерывен. Аналогично показывается, что и оператор В А вполне непрерывен.
Так как в бесконечномерном пространстве единичный оператор / не вполне непрерывен, то отсюда, в частности, следует, что в таком пространстве вполне непрерывный оператор А не может иметь ограниченного обратного оператора Л-1.
Наконец, очевидно, что если операторы Л и В вполне непрерывны, то аЛ-НрВ также вполне непрерывный оператор.
Теорема 2. Если последовательность вполне непрерывных операторов {Л„}, отображающих пространство X в полное пространство Y, равномерно сходится к оператору А, т. е. ||Л„ —Л||—>0, то Л также вполне непрерывный оператор.
□ Требуется доказать, что Л отображает всякое ограниченное множество пространства X в относительно компактное множество пространства У. Пусть М — ограниченное множество пространства X и г—такая постоянная, что ||х||^г для любого х£ М. Для заданного е>0 найдем номер п0 такой, что || АПо — А || < е/r. Пусть A(M) = N и An„(M) = N0. Множество Na есть е-сеть для V. В самом деле, взяв для любого y£N один из его прообразов х £ М и
178
полагая уа = АПах € ЛГ0, получим
II У~Уо 11 = || Ах - Лп„х|| < || А - А„о ||-1| х|| < (s/г) г = е.
Так как, с другой стороны, в силу полной непрерывности Л„о и ограниченности М множество Л?о относительно компактно, то мы получаем, что N при любом е > 0 имеет относительно компактную 8-сеть и потому само относительно компактно. Итак, оператор А отображает произвольное ограниченное множество в относительно компактное и, следовательно, вполне непрерывен, у
Пример. Покажем, что если X = Y = L2[0, 1], то оператор
1
Ах = у (t) = К (/, s) х (s) ds, о 1 1
где J J /<2(/, s) df ds < оо, вполне непрерывен, о о
Предположим сначала, что К (t, s) — непрерывное ядро. Пусть —ограни-1
ченное множество из L2 [0, 1] и J х2 (t) dt«Сг2 для всех x(t)£M. Рассмотрим о
1
множество функций у (t) = J Л (t, s) х (s) ds, х (t) £ М. Докажем, что функции о
y(t) равномерно ограничены и равностепенно непрерывны. Отсюда будет следовать относительная компактность множества {у (/)} в смысле равномерной сходимости и тем более в смысле, сходимости в среднем квадратичном.
Имеем
1
J К (t, s) х (s) ds о
\У«)\ =
/ 1 \l/2 / 1 \ 1/2
И я2(*, s) ds ) . Hx2(s)dsj
\o / \o /
где Д'== max |/< (/, s) |, и, следовательно, функции y(t) равномерно ограничены. tt s
Далее, / 1 \ 1/2 / 1 ч 1/2
s)]2dsj . I Jx2(s)dsj <e \o / \o /
при | tr—/2| < 6, где 6 выбрано так, чтобы при | tf — /2| < 8 было | К (ti, s)— — # (/2, s) | < 8/r, s£ [0, 1]. Оценка | у (/х) — у (t2) | < е не зависит от положения ti и t2 на [0, 1] и от выбора функции y(t)£M‘, следовательно, функции {у (/)} равностепенно непрерывны. Итак, в случае непрерывного ядра оператор А вполне непрерывен.
Предположим теперь, что /С (/, s) — произвольное ядро с суммируемым квадратом. Возьмем последовательность непрерывных ядер {Kn(t, $)}, сходящуюся в среднем к К (Л s), т. е. такую, что
1 1
{К (t> s)—Kn (/, s)P d/ ds —> 0 при n —> oot
о о
179
1
Полагая Ап х = Кп (/, s) х (s) ds, имеем о
1 П* 1/2
К (t, s) х (s) ds— J Kn (t, s) x (s) ds d/ I о J /
1 1 v/a
(K (/, S) -/<„ (/, s))2 ds. $ x2 (s) ds d/ I 0 J J
/11 * \ 1/2
Ш(О,5)~Кп(М)2^ [ -||x||.
Следовательно, pl V/2
М-ДЛ|)< j $ $ (O,s)-/<n(M)2d/ds I , too )
откуда вытекает, что (|Л —Лп||—>0 при п—>оо. Так как все операторы Ап вполне непрерывны, то по теореме 2 оператор Л также вполне непрерывен.
Замечание. Предел поточечно сходящейся последовательности {Лга} вполне непрерывных операторов может и не быть вполне непрерывным. В самом деле, в бесконечномерном пространстве Банаха X с базисом {ej рассмотрим операторы заданные равен-
П 00
ством S„x= Для = - Оператор S„ отображает X в ко-
1=1 Г=1
нечномерное пространство Хп и потому вполне непрерывен. При п —> оо последовательность операторов S„ поточечно сходится к единичному оператору 7, который не является вполне непрерывным.
Теорема 3. Область значений вполне непрерывного оператора А сепарабельна.
□ В самом деле, пусть множество Кп является образом шара Так как А вполне непрерывен, то Кп—относительно компактное, а следовательно, и сепарабельное множество (см. § 9 гл. I). Пусть Тп — счетное множество, всюду плотное в Кп. Так как область значений оператора А есть К — U Кп, то Т — и Тп п=1 п-1
является счетным множеством, всюду плотным в К. Ц
Теорема 4.* Если А—вполне непрерывный оператор, отображающий X в Y, то сопряженный оператор А*, отображающий Y* в X*, также вполне непрерывен.
□ Достаточно доказать, что образ А* (Л?) единичного шара К* пространства Y* относительно компактен.
Рассмотрим образ А (К) замкнутого единичного шара пространства X. Так как А — вполне непрерывный оператор, то А (К) — относительно компактное множество. Будем рассматривать на этом
180
множестве линейные функционалы, принадлежащие К*. Если f(zK*, У$А(К), то
l/(y)ICII/ll-lhll==ll/IHMxKII/ll-MII-hKMII.
так как ||/||^1, || х || 1. Следовательно, функционалы из К* на
множестве А (/С) равномерно ограничены. Далее, для уи уг£А (А), /£А* имеем
I / (У1) -f (Уа) I = I f (У1 —у2) I < hi ~УгII
и, следовательно, на А (К) функционалы из К.* равностепенно непрерывны. В силу обобщения теоремы Арцела (см. § 2 гл. II) множество К* относительно компактно в смысле равномерной сходимости на А (К).
Рассмотрим теперь произвольную последовательность {A*f„}cz сЛ’(^). Так как множество К* относительно компактно, то из последовательности {/„} можно выделить подпоследовательность {fn.}, равномерно сходящуюся на А (А):
sup |/„.(Ах) — fn (Ах)|—>0 при п,-, nz-*oo. хеК J
Но
sup I fn, (Ах) -fn. (Ах) I = sup I A* (fn —fn} X] = II A* fn. — A* fn J.
хек 1 хек 7 1
Поэтому последовательность {A*fnj\ сходится по норме в пространстве X* и относительная компактность А* (К*) доказана. И
2. Аппроксимация вполне непрерывного оператора в банаховом пространстве с базисом конечномерными операторами. Рассмотрим вполне непрерывный оператор А, отображающий банахово пространство X с базисом само в себя. Пусть А —единичный шар этого пространства. Так как А вполне непрерывен, то А (К)—относительно компактное множество. Тогда по теореме § 7 гл. III для любого числа е>0 найдется номер п — п(е) такой, что ||А„(у)||<е для всех у£А(К). Фиксируя это п, получаем
Ах = у = Sny + Rny = S„ (Ах) + Rn (Ах) = Atx 4- А2х,
где Ах и А2, очевидно, линейные операторы. При этом, полагая у = имеем 1=1
AiX = S„y — 5 Л,<-, i = 1
откуда видно, что оператор Ai —конечномерный в том смысле, что для любого х элемент Ах принадлежит конечномерному подпрост-
181
ранству, определяемому базисными элементами eit е2,..., еп. Далее, SUp||A%||= SUp_||/?„y||< 8, хеК уеА(К)
откуда следует, что || А2|| < е.
Итак, вполне непрерывный оператор А мы разложили на сумму двух операторов, из которых один конечномерный, а норма второго не превосходит наперед заданного числа, которое можно выбрать сколь угодно малым. Поэтому иногда говорят, что вполне непрерывные операторы в пространстве с базисом почти конечномерны.
§ 2. ЛИНЕЙНЫЕ ОПЕРАТОРНЫЕ УРАВНЕНИЯ С ВПОЛНЕ НЕПРЕРЫВНЫМИ ОПЕРАТОРАМИ
В этом параграфе мы рассмотрим линейные операторные уравнения с вполне непрерывными операторами. Как было показано Ф. Риссом, на такие уравнения переносятся основные результаты теории линейных интегральных уравнений Фредгольма.
1. Две леммы. Пусть А—вполне непрерывный оператор, отображающий банахово пространство X в себя. Рассмотрим уравнение
Ах—х — у, . (1)
или
Тх = у, (Г)
где Т — A — I. Одновременно с уравнением (1) будем* рассматривать уравнение
= (2)
или
T*f = g, (2')
где А* — оператор, сопряженный с Л и действующий в пространстве X*. Как было показано, А* также вполне непрерывный оператор.
Лемма 1. Пусть N—подпространство нулей оператора Т, т. е. совокупность элементов х таких, что Тх = 0. Тогда N—конечномерное подпространство пространства X.
□ Пусть М — произвольное ограниченное множество из N. Для любого x£N имеем Ах=х, т. е. оператор А оставляет инвариантными элементы подпространства N и, в частности, множество М. переводит само в себя. С другой стороны, А как вполне непрерывный оператор переводит М в относительно компактное множество. Следовательно, всякое ограниченное множество McN относительно компактно, откуда в силу теоремы 1 § 2 гл. II следует конечномерность подпространства N.
Замечание. Элементы подпространств X являются собственными элементами оператора А, соответствующими собственному значению Хо=1. Формулировка леммы и ее доказательство оста-182
ются справедливыми, если единицу заменить любым другим собственным значением %, отличным от нуля. Таким образом, мы доказали, что вполне непрерывный оператор А может иметь лишь конечное число линейно независимых собственных элементов, соответствующих одному и тому же собственному значению.
Лемма 2. Пусть L — T(X), т.е. L есть совокупность элементов у^Х, которые могут быть представлены в виде у—Ах—х. Тогда L—подпространство.
□ Очевидно, что L — линейное многообразие. Необходимо доказать лишь замкнутость L.
Сначала покажем, что существует постоянная а, зависящая лишь от Л, такая, что всякий раз, когда уравнение (Г), т. е. Тх=±у, разрешимо, по крайней мере для одного из его решений выполняется равенство
И<«Ы- (3)
Пусть х0 — одно из решений уравнения (Г). Тогда любое другое решение этого уравнения имеет вид x = x0H-z, где г —решение однородного уравнения Tx = Q. Рассмотрим функционал ф (z) = ||x0+z||, который является ограниченным снизу и непрерывным. Пусть d= inf <p(z) и {zn} <zN — минимизирующая последовательность, т. е.
ф(2„)==Ьо + 2п11~*^- (4)
Так как последовательность {||х0-|-гп||} имеет предел, то она ограничена. Но тогда ограничена и последовательность {||zn||}, поскольку
IIII = II (2„ + *о) ~ Хо II < IIХО + гп II + II хй ||.
Таким образом, {?„} есть ограниченная последовательность конечномерного пространства и, следовательно, из нее можно выделить сходящуюся подпоследовательность. Отбрасывая, если необходимо, лишние члены в последовательности {г„}, мы можем без ограничения общности считать, что zn—> z0. Тогда
ф(2«)-*ф(г0)- (5)
Из (4) и (5) следует, что ф (г0) = || х0 + z01| = d. Следовательно, в случае разрешимости уравнения (1') оно всегда имеет решение x = x0 + z0 с минимальной нормой.
Покажем, что для этого элемента справедливо неравенство (3). Рассмотрим отношение ||х||/||г/|| для y£L и предположим, что оно не ограничено. Тогда существуют последовательности уп и х„ такие, что ||хи||/||г/„ || —► оо. Поскольку 'Куп соответствует, очевидно, минимальное решение Хх„, без ограничения общности можно считать, что ||х„[|= 1; тогда ||уп|| —> 0. Так как последовательность {х„} ограничена и оператор А вполне непрерывен, то последовательность {Ах„} относительно компактна и, следовательно, содержит схо
183
/ n '
Tx=T[ lim 2** _
\ n £=0 J n ft=0 ” n
п.
п
=limS TxA=lim 2 (yk+i— yk)
fes= 1
дящуюся подпоследовательность. Снова без ограничения общности можно считать, что
Ахп -+ х0. (6)
Но тогда так как хп — Ахп — уп, то х„—>х0 и, следовательно,
Ахп —> Лх0. (7)
Из (6) и (7) следует, что Лх0 = х0, т. е. v0£N. Поэтому в силу минимальности нормы решения получим ||х„—х0||->||х„||== 1, что противоречит сходимости {х„} к х0.
Итак, отношение ||х||/||у|| ограничено, и если а = sup (||х||/||г/||), то требуемое неравенство доказано.
Пусть теперь дана последовательность {yn\c.L, сходящаяся у к у9. Переходя, если необходимо, к подпоследовательности, можно считать, что ||z/„ — z/0||< l/2n+1, откуда Цу„+1 — t/J< 1/2". Пусть х0—минимальное решение уравнения Тх—ух и хп (п=1, 2, ...) — минимальное решение уравнения Тх = уп+Г~уп. Тогда
К1| < “ II Уп+1 ~ У Л < а/2п-
ОО
Из этой оценки вытекает, что ряд ~£хп сходится^ причем если п=0
х —сумма этого ряда, то
= lim «/„+! = «/<> п
и мы получили, ЧТО y9€,L. И
2. Условия разрешимости и альтернатива Фредгольма.
Теорема 1. Для того чтобы при данном у£Х уравнение (Г) было разрешимо, необходимо и достаточно, чтобы f(y) = Q для любого линейного функционала f такого, что
A*f — f = O. (2")
□ Необходимость. Пусть уравнение Лх —х = у разрешимо, т. е. у может быть представлен в виде у— Лх0—х0 для некоторого ха£Х. Возьмем произвольный линейный функционал f такой, что A*f — f — Q. Тогда
/ (y)=f (Лх0 —х0)=/ (Лх0) -f (х0)=(Л*/) (х0) -f (х0) = (Л*/-/) W=0.
Достаточность. Покажем, что при выполнении условий теоремы справедливо включение y£L = T(X). Предположим противное, т. е. что y^L. Так как L замкнуто, то у находится от L на расстоянии d > 0 и согласно следствию из теоремы Банаха — Хана существует линейный функционал [0 такой, что f0 (у) = 1 и /o(z) = O для любого x£L. Последнее равенство означает, что
fo (Лх—х) = (A*f0—f9) (х) = О
184
для всех х£Х, т. е. что A*f0—/0 = 0. Мы пришли к противоречию, так как, с одной стороны, по построению, f0(y)— 1, а с другой стороны, по условию, /о(*/) = О- Следовательно, y^L. Q
Замечание. Уравнение Тх = у, обладающее тем свойством, что оно имеет решение, если f (у) — 0 для любого /, удовлетворяющего равенству T*f — O, называется нормально разрешимым. В предыдущей теореме, по сути дела, доказано, что для нормальной разрешимости уравнения Тх = у достаточно, чтобы £ = Т(Х) было замкнуто. Можно доказать, что это условие является и необходимым (см. [13]).
Следствие. Если сопряженное однородное уравнение A*f—f=O имеет лишь нулевое решение f = 0, то уравнение Ах—х — у разрешимо при любой правой части.
Теорема 2. Для того чтобы уравнение (2) при данном g£X* было разрешимо, необходимо и достаточно, чтобы g(x) = Q для любого элемента х € X такого, что
Ах—х — 0. (1")
□ Необходимость очевидным образом следует из равенства g (х) = (A*f—/) (х) = / (Ах—х) = 0.
Докажем достаточность. На подпространстве L определим функционал f0(y) с помощью равенства /0 (у) = g(x), где х —один из прообразов элемента у при отображении Т (т. е. Ах — х = у). При выполнении условий теоремы определение функционала f0 однозначно, так как если и — другой прообраз того же элемента у, т. е. Ах—х=Аи—и, то получаем, что
А (х — и) — (х—и) = 0, или g(x —и) = 0, или g(x) = g(u).
Аддитивность и однородность функционала /0 проверяются без труда, а его ограниченность доказывается следующим образом. Как было установлено при доказательстве леммы 2, по крайней мере для одного из прообразов х элемента у имеет место неравенство || х || d а || у ||. Но тогда
l/o (0l=I^WKkll-kKkll-«-IIMI
и ограниченность /0 доказана. Продолжая /0 по теореме Банаха — Хана на все пространство X, мы получим линейный функционал f такой, что
f (Ax — x) — f(y)=f0(y)=g(x), или (A*f —f)(x) = g(x),
т. е. решение уравнения (2). Q
Следствие. Если уравнение Ах—х = 0 имеет лишь нулевое решение х = 0, то уравнение A*f—f = g разрешимо при любой правой части g.
До сих пор мы исследовали связь между данным и сопряженным уравнениями. Теперь покажем, что между разрешимостью
185
однородного и неоднородного уравнений в одном и том же пространстве также существует тесная связь.
Теорема 3. Для того чтобы уравнение Ах—х — у (1), где А — вполне непрерывный оператор, отображающий банахово пространство X в себя, было разрешимо при любом у, необходимо и достаточно, чтобы соответствующее однородное уравнение Ах—х = 0 (1") имело лишь тривиальное решение х = 0. В этом случае решение уравнения (1) определяется однозначно и оператор Т = А — 1 имеет ограниченный обратный.
□ Необходимость. Обозначим через Nk подпространство нулей оператора Тк. Ясно, что из Ткх = 0 следует Тк+1х — 0, т.е. NkcNk+i.
Пусть уравнение Ах — х — у разрешимо при любом у, предположим, что однородное уравнение Ах—х — 0 имеет ненулевое решение хк. Пусть х2 — решение уравнения Ах—х = хк и вообще xk+i — решение уравнения Ах — х~хк (6=1,2, 3,...). Имеем
Тхк — хк_1, Т^хк — хк~2, ..., Тк гхк — Xi 0,
в то время как Ткхк = Тхг = 0. Поэтому xk£Nk и т. е.
каждое подпространство Nk_i служит правильной частью следующего подпространства Nk. Тогда по лемме Рисса (см. § 1 гл. II) в подпространстве Nk найдется элемент ук с нормой, равной единице, такой, что х||^ 1/2 для любого x£Nk_i. Последовательность {Аук} относительно компактна, так как ||«/J=1 и А — вполне непрерывный оператор. С другой стороны, пуст^ь ур и yq — два таких элемента и р > q. Так как
TP'1 (У9 + Тур - ТУ(]) = TP~iyq + ТРур - ТРу9 = 0,
то yq — Тур — Ty9eNp_i и потому
ИУР - ^11 = \\УР ~ + ТуР - TyJ II > 1 /2 •
Это противоречие возникло из предположения, что разрешимость уравнения (1) совместима с наличием у уравнения (1") ненулевого решения.
Достаточность. Пусть уравнение (1") имеет лишь тривиальное решение. Тогда, согласно следствию из теоремы 2, уравнение (2), т. е. A*f—f — g, разрешимо при любой правой части. Так как А* также вполне непрерывный оператор и X*—-банахово пространство, то в силу необходимости условия доказываемой теоремы уравнение (2"), т. е. A*f—f = O, имеет лишь нулевое решение. Но тогда уравнение (1), согласно следствию из теоремы 1, разрешимо при любом у и достаточность доказана.
Так как при выполнении условий теоремы уравнение (1) однозначно разрешимо, то существует оператор 7,-1 = (Л— 7)-1, обратный оператору А — I. В силу однозначности единственное решение в то же время является и минимальным и поэтому ||(Л —/)-1 г/||^а||у||. Теорема полностью доказана. Н
186
Теорема 4. Уравнения А х — х = О (Г) u A*f—f—O (2") с вполне непрерывными операторами А и А*, отображающими банахово пространство X (соответственно X*) в себя, имеют одинаковое число линейно независимых решений.
□ Пусть xit х2, хп —базис подпространства N решений
уравнения (1") и ft, f2, /„—базис подпространства решений уравнения (2"). Построим систему функционалов <р1Ч <ра, <р„, биортогональных х1( х2, ..., х„, т. е. таких, что <pz (ху) = (г, j—l, 2, ..., п), и систему элементов zt, z2, ..., zm, биортогональных fi, f2, ..., fm. Предположим, что n < m. Рассмотрим оператор
п
Ux = Ах 4- 2 Ф/ (*) z{.
i- 1
Этот оператор вполне непрерывен как сумма вполне непрерывного и конечномерного операторов. Покажем, что уравнение Ux—х = 0 имеет лишь нулевое решение. Пусть х0 — решение этого уравнения. Тогда fk(Ux(>— хо) = О (£=1, 2, ...,т), или
/ п \
fk ( 4*0 — хо + 2 Ф/ (*о) Zi ) = О,
откуда
п
(A*fk -fk) Хо + 2 Ф< (Хо) fk (Zi) = О, 1= 1
и, следовательно, с учетом биортогональности {/,•} и {г{} имеем q>ft(xo) = O, £=1, 2, ..., п (п<т). Поэтому (7х0 = Лх0 и, значит, х0 удовлетворяет уравнению Ах0—хо = О. Так как x0£N и {х;} — п
базис в N, то х0= 2Вл.. Но £,-= ф,-(х0) = 0. Поэтому хо = О, что i = 1
и требовалось доказать.
Так как уравнение Ux — х = 0 имеет лишь нулевое решение, то уравнение Ux — x = y разрешимо при любой правой части, в частности при y = zn+i.
Пусть х' — решение этого уравнения. Тогда, с одной стороны, как и выше,
(п \
Ax’-х' A-'^i^i(x')zi\-
п
= (A*fn+i — /и+х) х' + 2 Ф,- (х) /„+i (z^ = 0, i = 1
а с другой стороны, по построению fn+1 (zn+i) = 1. Полученное противоречие доказывает невозможность неравенства п < т.
Предположим, что, наоборот, т < п. Рассмотрим в пространстве X* оператор
т
и^ = АЧ + ^1(г^{.
187
Легко проверить (учитывая, что т < п), что этот оператор сопряжен с оператором U, в котором п заменено на т.
Покажем, что и для оператора U* уравнение U*f — f = Q имеет лишь тривиальное решение. Для всех k = 1, 2, ..., п имеем
т
(U*f — f)xk = (A*f —f) хк + 2 f (г,) <р,- (xft) =
= f (Aхк - хк) + f (zk) = f (zk). (8)
Поэтому если /0 —решение уравнения U*f — f = 0, то из равенства (8) получаем, что fQ (zk) = 0 (& = l,f2, ..., т). Следовательно, U*fa~A*fa и f0 — решение уравнения Л*/ —/ = 0. Но тогда
т т
= = 0.
i=l i=\
Так как U* — вполне непрерывный оператор, то по теореме 3 уравнение U*f~f = g разрешимо при любом g, в частности при £ = Ф»>+1- Тогда, с одной стороны, если /'—решение такого уравнения, то
фя+1 C^+i) = —П xm+i = (A*f —f) xm+i +
+ 2 f (Zi) Ф,- (xm+1) = /' (Axm+l — xm+1)= 0, i= 1
а с другой стороны, фт+1 (xm+i) — 1. Полученное противоречие доказывает невозможность неравенства т < п. Итак, m = n и теорема доказана. Щ
Объединяя результаты теорем 1—4, мы можем сформулировать следующее предложение, являющееся обобщением на произвольные уравнения с вполне непрерывными операторами известных теорем Фредгольма из теории линейных интегральных уравнений.
Даны уравнения Ах—х — у (1) и A*f — f = g (2), где А—вполне непрерывный линейный оператор, действующий в банаховом пространстве X, а А*—сопряженный оператор, действующий в сопряженном пространстве X*. Тогда:
либо уравнения (1) и (2) разрешимы при любых правых частях и в этом случае однородные уравнения Ах—х=0 (1") и A*f—f—O (2") имеют лишь нулевые решения;
либо однородные уравнения имеют одинаковое конечное число линейно независимых решений xlt х2, ..., хп; flt f2, ..., /„ и в этом случае, чтобы уравнение (1) (соответственно (2)) имело решение, необходимо и достаточно, чтобы Ь(у) = ®', i=l,2, ...,п (соответственно g (Xj) = 0; i = l,2,..., п).
Общие решения уравнений (1) и (2) соответственно имеют вид
п п
х = хо + 2 <Х{ХЬ / = /о + S Wi, 1=1 1=1
где xQ и /0—соответственно какие-нибудь решения уравнений (1) и (2), а ап а2, ..аЛ; Х2, ..^—произвольные постоянные.
188
3. Спектр вполне непрерывного оператора. Рассмотрим уравнения, содержащие параметр. Так как уравнение
Ах —кх = у (Х=#0) (!"')
может быть записано в виде
1 л 1
т- Ах — х =тУ К л а
и уЛ вполне непрерывен вместе с А, то теоремы, доказанные для уравнения (1), остаются справедливыми для уравнения (1"').
Из теоремы 3 следует, что при данном Х=Н=О либо уравнение Ах—Кх = у разрешимо при любой правой части, либо однородное уравнение Ах—кх — 0 имеет ненулевые решения. Поэтому каждое значение параметра либо регулярно, либо является собственным значением и других ненулевых точек спектра, кроме собственных значений, у оператора нет*.
Теорема 5. Если А — вполне непрерывный оператор, то его спектр содержит конечное или счетное множество точек. Все собственные значения расположены на отрезке [—1| А |], || А Ц] и в случае счетного спектра имеют единственную предельную точку Х=0.
□ Рассмотрим оператор 7\= А—X/. Преобразовав его к виду 7\ = — 1
видим, что в силу результатов § 5 гл. III при -^-||Л||< 1 оператор I—у Л, а следовательно, и оператор Т\ имеет обратный, т. е., действительно, спектр оператора А лежит на отрезке [—1| А ||, || А ||]. Пусть 0 < а < || Л ||. Чтобы завершить доказательство, достаточно показать, что может существовать лишь конечное число собственных значений X таких, что |Х|^а.
Предположим противное. Тогда можно выделить последовательность Xj, Х8, ..., Х„ различных собственных значений, причем |Х;|>а. Пусть xit х2, ..., хп, .. .—последовательность собственных элементов, соответствующих этим собственным значениям Ах„=к„х„.
Докажем, что элементы хх-, х2, ..., xk при любом k линейно независимы. Для k—\ это тривиально. Пусть xlt х2, ..., хк линейно независимы. Если предположить, что
k
^A+i = (9)
то, действуя на обе части этого равенства оператором Л, получим k
^+Л+1 = Xj-CjX;. (10)
1=1
* Размерность подпространств нулей оператора А—X/ называется кратностью собственного значения X. Из леммы 1 следует, что все ненулевые собственные значения вполне непрерывного оператора имеют конечную кратность.
189
Из равенств (9) и (10) следует (так как ^А+1=И=0), что k 1= 1
Но это невозможно в силу неравенств 1 — А,(.ДЛ+1- #= 0 (t = 1,2, ...,£) и линейной независимости х1? х2, xk.
Пусть Lk—подпространство, порожденное элементами хп х2, ... ..., х/(; Lk есть собственное подпространство пространства Lk+1. Поэтому найдется элемент ук+1 £ Lk+1, ||«/А+1|| = 1 такой, что ||г/А+1—х||^ ^1/2 для любого x$Lk. Оценим ||Аут — Лг/Я||, полагая, например, что т > п. Имеем
АУт Ауп ^тУт “Ь ^^т Ут ^пУп ^^пУп= ^тУт %*
где х = \пу„А-Тх„уп — Тхтут. Заметим теперь, что
ТХт Ут 3 АУт ^тУт 3 \ .2 2 3
J l—l
3 2 - 2 CzVz = 2 ^i — ^m) C(Xi-
i = 1 i = 1 i = 1
Поэтому Тляг/я€Ьи_1._Так как yn cLna Lm_it TKnyneLn_i c Lm_it to xПолагая x = Kmy, y£Lm_it получим
\\ Aym- Ayn || = || Kmym - \my || = | | • || ym - у || > a,/2
и, следовательно, ни {Ay„}, ни любая ее подпоследовательность не сходятся. С другой стороны, так как {уп}~ограниченное множество, то {Ау„} относительно компактно и, следовательно, содержит сходящуюся подпоследовательность. Полученное противоречие доказывает теорему. Щ
Теорема 5 характеризует так называемую дискретность спектра вполне непрерывного оператора.
§ 3. ПРИНЦИП НЕПОДВИЖНОЙ ТОЧКИ ШАУДЕРА И ЕГО ПРИМЕНЕНИЯ
Оператор А, вобще говоря, нелинейный, отображающий множество М банахова пространства X в банахово пространство Y, называется компактным на множестве М, если он переводит всякое ограниченное подмножество множества М в относительно компактное множество пространства У. Если, кроме того, оператор А непрерывен на М, то будем называть его вполне непрерывным на этом множестве (если А линеен, то это определение совпадает с прежним). Не уменьшая общности, множество М можно предположить в дальнейшем ограниченным.
Для вполне непрерывных операторов, которые отображают выпуклые тела банахова пространства в себя, Ю. Шаудером уста
190
новлена теорема, обобщающая известную теорему Брауэра о существовании неподвижной точки при непрерывном отображении выпуклого тела n-мерного евклидова пространства в свою часть. Эта теорема Шаудера имеет многочисленные применения для доказательства существования решения различных уравнений.
1. Леммы о вполне непрерывных операторах. Для доказательства теоремы Шаудера рассмотрим предварительно три вспомогательные леммы. Пусть М — множество элементов банахова пространства и {Л„} —последовательность операторов, вообще говоря, нелинейных, определенных на М. Будем говорить, что эта последовательность равномерно на М сходится к оператору Ло, если для любого числа е > 0 найдется номер п0, зависящий лишь от 8, такой, что || Л„х —Лох|| < 8 при п^п0 и любых х£М.
Лемма 1. Если последовательность {Л„} вполне непрерывных на М операторов равномерно сходится на этом множестве к оператору Л 0, то Л о также вполне непрерывен на М.
□ Докажем сначала непрерывность оператора Ло на М. Пусть {х„} а М сходится к xQ£M. Имеем
II ^охт Лохо || [I Аохт Апхт || 1| Апхт А„х01| 1| Апх0 Лохо ||.
В силу того что последовательность операторов {Л„) равномерно на М сходится к оператору Ло, для заданного 8 > 0 найдется номер п0 такой, что при п^п0
II Аохт А„хт || < 8/3, || Л„х0 Аохо |] < 8/3.
Фиксируем такое п. Так как оператор А„ непрерывен, то найдется номер т„ такой, что при имеем || Апхт — Л„х0|] < 8/3.
Но тогда при т^тй получим [| Аохт — Лохо|| < 8, т. е. оператор Ло непрерывен.
Докажем теперь компактность оператора Ло, для чего покажем, что множество Ло (/И) относительно компактно. Для заданного 8 > О выберем п0 так, чтобы |]ЛПох —Лох|| < 8 при всех х$М. Это можно сделать в силу равномерной сходимости последовательности {Ап} к Ло. Пусть N = АПа(М). Множество N относительно компактно и является s-сетью для множества Ло (/И) (см. доказательство теоремы 2 § 1). Отсюда следует, что и Л0(Л1) относительно компактно. Итак, Ло —непрерывный и компактный оператор. Ц
Лемма 2 (Шаудера). Всякий оператор А, вполне непрерывный на множестве М, есть равномерный предел на этом множестве последовательности {ЛА} непрерывных конечномерных операторов (отображающих М в конечномерное подпространство пространства X).
□ Так как Л —вполне непрерывный оператор, то Л (/И) —относительно компактное множество. Возьмем последовательность положительных чисел {ей}, сходящуюся к нулю, и для каждого k построим 8А-сеть Nk — {y[k>, у^'>.....у^\ для множества Л (/И),
состоящую из -точек этого множества. Определим на Л (/И) опера-
191
тор Рк, полагая для у £ А (М)
mk I mk
pM= и 9‘,ч/х
1 = 1 1 = 1
(1)
где
w.. I еь-Цу-Л если Ь-«/*Л)11<е/.
1 о, если II у — «/}•*’II >8ft.
Равенство (1) имеет смысл для любого у$А(М), так как все P*tS) (у) 0 и pj*’ (у) > 0 по крайней мере для одного i.
Оператор Рк(у) непрерывен на Л(Л4). Это следует из того, что ть
все (у)—непрерывные функции, а значит, 2р!Л>(у) также не-1 = 1
mk
прерывная функция от у. Кроме того, 2 (у) > 0 для каждого
1=1
mk
у£А (М), откуда вытекает непрерывность частного р**’ (у)/ Л p,’ft> (у),
тй k ,mk k
а следовательно, и выражения 2 Р^’ (у) / S Р^’ (у), т.е. опера-
1=1 1=1 *
тора Рк{у). Далее,
\\у-РкШ =
mk
1=1
у—~ь—
2 ’ (</)
1=1
mk
mk
i=l •
mk
2рИ(Ю
i = 1
2 p'*’ (у)
zk~k ~8*»
i = 1
так как если для некоторого i имеем ||у —у<?)||^ еА, то соответствующий коэффициент p.*ft) (у) равен нулю.
Полагая теперь Акх = Рк (Ах) для х £ М, получим последовательность конечномерных операторов {Ак} таких, что
|| Л х - Акх J = || Ах—Рк (Ах) || < ък
для любого х^.М, и лемма доказана. В
Замечание. Так как элементы у*?’ принадлежат множеству Л (А4), то значения операторов, построенных в лемме 2, принадлежат выпуклой оболочке множества Л (М).
Лемма 3. Пусть последовательность (Ап) операторов, вполне непрерывных на множестве М, равномерно сходится на этом мно
192
жестве к оператору Ло. Пусть, далее, Кп — Ап(М) (n=0, 1, 2, ...).
Тогда множество К = и К„ относительно компактно.
п=О
□ Согласно лемме 1, оператор Ло вполне непрерывен. Так как последовательность {Ап} равномерно сходится к оператору Лв, то для любого е > 0 и любого у€Кп при п п0 (е) найдется и £ такой, что ||у—ы|| <в. Это возможно в силу того, что если у — произвольный элемент из Кп и х—один из прообразов у при отображении А„, то в качестве и достаточно взять Аох.
Построим множество N = U К„. Легко видеть, что оно отно-п=0
сительно компактно. Покажем, что это множество есть s-сеть для К-«о
Пусть у£,К. Если у£ U К„, то доказываемое утверждение три-п=0
виально. Если же у£Кп при и> п0, то, как показано выше, существует такой, что ||I/—и||<8. Следовательно, N является относительно компактной 8-сетью для множества К и потому множество К относительно компактно. Ц
2. Принцип неподвижной точки.
Теорема 1 (Шаудера). Если вполне непрерывный оператор А отображает ограниченное замкнутое выпуклое множество М банахова пространства X на свою часть, то существует неподвижная точка этого отображения, т.е. такая точка х£М, что Лх = х.
□ Возьмем последовательность положительных чисел {8„}, сходящуюся к нулю, и построим, как и в лемме 2, последовательность непрерывных конечномерных операторов Ап, равномерно сходящихся на множестве М к оператору А.
В силу замечания к лемме 2 и того, что М выпукло, Апх € М для любого х£М. Пусть Х„ —конечномерное подпространство, в котором расположено множество Л„(А4). Рассмотрим оператор А„ на множестве Мп=М П Х„ подпространства Х„. Ясно, что М„ также выпуклое замкнутое множество. Так как А„ (М) с М и А„ (М) с Х„, то А„ (М) с Мп и тем более А„ (М„) <= Мп.
Таким образом, оператор А„, рассматриваемый на конечномерном пространстве Х„, отображает замкнутое выпуклое множество М„ этого пространства в себя и потому по известной теореме Боля — Брауэра существует неподвижная точка этого отображения, т. е. такая точка х„£М„, что Ллхв = х„. Но так как М„ с М, то х„ является неподвижной точкой оператора А„ и при отображении этим оператором множества М. Поскольку х„£ А„(М), последователь-
ность {хп} принадлежит множеству М= U Ап(М)сМ. В силу п — 1
леммы 3 множество М относительно компактно. Тогда из последовательности {хп} можно выделить сходящуюся подпоследовательность {ХиД и предел х0 этой подпоследовательности принадлежит М вследствие замкнутости М.
7 № 3054 193
Покажем, что х0 есть неподвижная точка оператора А. Имеем J Ах0 — х0 J < | Ах0 — АхП{ |+1| АхП{ — ЛЛ/ хп. || +1 Ап. хП{ — х01 = = || Лхв — Ах„. ||+1| Ахп. — Ап.хП{ || +1| хп. — х0 Ц.
Для заданного е > 0 выберем сначала п' настолько большим, что при nz>n' имеем ||х„. — х0| < е/З и || Лх0 — Ахп. Ц < 8/3. Затем выберем п" настолько большим, что при п,- п" имеем [ Ах—Ап х|| < <в/3 равномерно на /И и, в частности, для всех хП{. Тогда для п{ n0 = max (п', п") получим J Лх0—х0|| < 8. Так как в>0 произвольно, то это возможно лишь если Лх0 = х0, т. е. если хв есть неподвижная точка оператора Л. И
В качестве примера применения принципа Шаудера докажем известную теорему Пеано о существовании решения обыкновенного дифференциального уравнения.
Теорема 2. Пусть функция f (t, х) непрерывна по совокупности переменных в области 11—to ] < а, | х—х01 < 6 и Р—максимум | f (t, х) | в этой области. Если ft = min(a, 6/0), то на отрезке [/0—Л, <о+Л] существует хотя бы одно решение уравнения
= (2)
удовлетворяющее условию
x(h)=xQ. (3)
□ Уравнение (2) вместе с начальным условием (3) эквивалентно интегральному уравнению
t •
х(Л==х0+р(т, x(T))dT. (4)
Рассмотрим оператор Л, определенный равенством
t
Ах «=х0+ J f (т, х (т)) dr
на шаре ||х—х0||^6 пространства С[/о—Л, /0+^]. Покажем, что оператор А вполне непрерывен на этом шаре.
Прежде всего если последовательность {хп(/)}, принадлежащая шару |]х—х0[|^&, равномерно сходится к функции х (/), очевидно, принадлежащей тому же шару, то в силу непрерывности функции f (t, х) имеем f (t, хп (t)) —► —равномерно на [/0—Л, ^о+Л]. Отсюда вследствие возможности предельного перехода под знаком интеграла при равномерной сходимости получаем, что Ахп—► Лх, т. е. оператор Л непрерывен на шаре || х—х0 J < Ь.
Далее, для любого элемента х (/) шара || х—х01| < b имеем
Мх (0 |<|х0 | +
t
р (т, X (т)) dT
io
< I хо I +
(б)
Если tx и t2—две любые точки отрезка [/0—й, /0+Л], то
|Лх(Г^—4x(G)|< р(т, x(T))dT <₽IG—GI-
194
Неравенства (5) и (6) в силу теоремы Арцела показывают, что оператор А преобразует шар [| х—х0 II & в относительно компактное множество.
Покажем, наконец, что оператор А преобразует этот шар в себя. В самом деле,
| Ах (t)—xQ | =шах
/ (т, х (т)) dr
Таким образом, оператор А удовлетворяет всей условиям теоремы 1. Поэтому существует неподвижная точка этого оператора, т. е. такая функция х (/), что
t
* (Оэ*о+р(т, X (т)) dT.
Это равенство равносильно двум равенствам:
^=/(Л *(0), *Оо)=*о,
чем и завершается доказательство теоремы. |
При доказательстве теоремы Пеано мы применили принцип Шаудера к установлению существования решения интегрального уравнения (4). Этот же принцип позволяет установить существование решений у более сложных нелинейных интегральных и интегро-дифференциальных уравнений.
Упражнения
1. Для случая банаховых пространств с базисом докажите, не прибегая к обобщенной теореме Арцела, что если А:Х—► У—вполне непрерывный оператор, то А*:У—также вполне непрерывен.
2. Для банаховых пространств с базисом получите теоремы 1—4 § 2 как следствие соответствующих теорем для линейных алгебраических систем с конечным числом неизвестных.
3. Докажите, что если А —самосопряженный оператор, действующий в гильбертовом пространстве Я, то sup | <Ах, х> | достигается и реализующий его
IIX 11= 1
элемент есть нормированный собственный элемент оператора А.
°° В-
4. Докажите, что оператор Ах = У вполне непрерывен в пространстве I*.
i=i 21
5. Докажите, что линейный оператор А, действующий в гильбертовом простран-„ СЛ
стве Я, вполне непрерывен тогда и только тогда, когда из хп—>х0 следует Ахп —► Ах0.
/ оо \1/2
6. Пусть ел = {д/л}—стандартный базис в Z2, А: /2—► и Я(А) = 1 2Меп11* ) \л»1 /
(Число N (А) называется абсолютной нормой оператора А.) Докажите, что если N (А) < со, то А вполне непрерывен.
7. Пусть Ап*.Х—сходятся поточечно к А:Х—> У. Покажите, что на компактном множестве М а: X сходимость Ап к А равномерная.
8. Оператор А:Х—>У называется ядерным, если существуют ограниченные последовательности {уп} С У, {fn} С X* и числовая последовательность {cw} с I
оо
такие, что Ах= 2 сп1п(*)Уп- Докажите, что ядерный оператор вполне не-«=1
прерывен.
7
ГЛАВА VI
ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЙ В ЛИНЕЙНЫХ НОРМИРОВАННЫХ ПРОСТРАНСТВАХ
В этой главе мы рассмотрим различные определения производной и интеграла отображений линейных нормированных пространств и некоторые их применения.
§ 1. ДИФФЕРЕНЦИАЛ И ПРОИЗВОДНАЯ ФРЕШЕ
1. Основные понятия. Пусть X и У—ЛНП, a G—открытое множество пространства X. Отображение (функция, оператор) f:G—> —►У называется дифференцируемым по Фреше в точке х$С, если существует непрерывный линейный оператор Lx'.X —»-У, такой, что для любого h^X, удовлетворяющего условию x-f-Ji^G,
Д/=/(x + h)— f (x) = Ljeft+®(x, Л),
где № —> 0 при h —> 0 в смысле сходимости по норме в пространстве У. ’
Главная, линейно зависящая от h часть LJi приращения Д/ называется дифференциалом Фреше отображения f в точке х и обозначается df (х, Л), а выражение со (х, h) называется остатком приращения.
Итак, df (х, h) = LJi и приращение Д/ оператора записывается в виде
/(х+Л)—/(x) = d/(x, Л)+<о(х, Л), где
Иш Нш if(«+>)-/w-d/<«. »| _0
л-о П«П h-о 1|Л«
Линейный оператор Lx называется производной Фреше отображения / в точке х и обозначается f (х). Таким образом, df (х, h) = = f' (x)h.
Отображение, дифференцируемое в каждой точке множества G, называется дифференцируемым на G.
Покажем, что производная дифференцируемого отображения определяется однозначно. Пусть Лх:Х —* У — другой непрерывный линейный оператор такой, что
||/(х-|-Л)—/(х)—Л^ЛЦ п
ОЯЦ
196
при Л —»• 0. Тогда
|f (х)Л-А<А|
IIЛ ||
|/(*4-Л)—/(*)—/*(*) Л R
ИЛИ
||/(х+А)-/(х) ИГ"
-л«лд
—О
при h—► 0. Положим ft = /ft0, где Ад—произвольный ненулевой элемент пространства X. При I —»-0 также h—<-0 и мы получаем
II/' (*)(/Ло)-Лж((Ао)|| п
ет и-
В силу линейности f (х) и Лх это означает, что
Ilf (x)he-AAII=n га •
т. е. f (х)Л0 = ЛхЛ0. Так как в нуле оба оператора f (х) и Лх равны нулю, то f (х) h => XJi при любых ft и однозначность определения производной доказана.
Примеры. 1. Пусть дано отображение fr:G—► R'®, где GcR" и G открыто. Тогда приведенные выше определения дифференцируемости отображения и производной совпадают с определениями дифференцируемости и производной векторной функции векторного аргумента, которые даются в курсах математического анализа. В этом случае f (х) есть линейный оператор, определяемый матрице. (\-=i 2 ... т > где f (xl, Xs, .... х”)—координатные функции отображения f \ dxJ /1=1, 2:.... л
(см., например: Ильин В. А.. Садовничий В. Л., Сендов Б. X. Математический анализ, 1979, с. 629).
2. Пусть Х=Я—гильбертово пространство, K = R и f(x)=||x||. Предположим сначала, что х 0. Тогда
f (х+А)—/(х)____Их I АН ИхИ-Д'*И2 ________________2Re<x, А>-|-||А||г ц
Н*+п) /(х)—||х-|-Л|| их» ||х+Л|1+Цх| йх+Л|1+1|х|| 1
Так как -в—, -Д-/ „—т —► при h —► 0, то
11*4-А й+1| х || 2||х||
11*4-А|| 4-11*11 =‘ЩТ+“’ (2)
где а—>0 при h—>0. Из равенств (1) и (2) следует, что
г, . , х г , ч Re<x, Л> .
f (*4-А)—f (х) = —j—ц--Ьш,
Re <х, Л> v « . ,
где —линейный по п функционал и
<0 = 2Re<x, А>«4-^-4-а||А||».
Так как 2| Re<x, Л> | ^2||x||*||/i[|, то ясно, что <о/[|h ||—>0 при h—►О. Следовательно, f (х) = |]х|| дифференцируема в любой ненулевой точке х пространства h и
df (х = } |к II ’
Пусть теперь х = 0. Тогда f (h)—f (0) = ||Л||. Покажем, что не существует элемента и £ И такого, что при всех достаточно малых h
||Л|| = <Л, , , (3)
197
где <о/|| h, ||—>0 при h—► 0. Если бы это было так, то также
Ц — А|| = <— h, «>+<01, или ||Л|| = —</!, «>+<01, (4)
где <01/|| h || —> 0 при h —► 0. Но тогда из равенств (3) и (4) следует 1 — —* ®
при h —> 0, что невозможно.
Итак, отображение f (x) = [|x(j не дифференцируемо по Фреше в точке х«0.
8. Пусть Х = Г = С[а, д] и
ь
Ах= J К (t, s) g (s, x (s)) ds, a
где ядро К (t, s) непрерывно в квадрате a<t^bt g(u, 0—функция
двух переменных, определенная в полосе а^и^Ь, — оо < и < + оо и непрерывная в этой области. Тогда Ах есть функция, определенная на С [а, Ь] и принимающая значения в том же пространстве.
Допустим, что функция g(ut и) не только непрерывна, но и имеет частную производную gv («, о), равномерно непрерывную в полосе —со <v<
< -|- оо. Тогда Ах—дифференцируемая функция. В самом деле, для любой функции h (s) £ С (а, имеем
ь ь
A(x-f-A)—Ах== J/<(/, s)g(s, х («)+Л (s)) ds—J К (t, s)#(s, x(s))ds« а a
b
«= J К (t ») [«(«. «(«)+Л (»)) — g («. x (s))J d$. a
По теореме Лагранжа,
g(s, x(s)+A(s))—g(s, x(s))=gj(s, x(s)+0(s)A(s))A(s),
где O<0(s)<l. Далее, имеем
gi(s, x (s) + 0 (s) A (s)) =&,(«. x(s))+a(s, x(s), 0(s)A(s)).
При ||A||—>0, т. e. при h (s)—>0 равномерно на [a, 6], также a(s, x(s), 0(s)/i(s))—.0 равномерно на [a, d], поскольку функция, непрерывная в замкнутой ограниченной области а < s Ь, | х К cj, | h | < с2, равномерно непрерывна в этой области. Поэтому
ь
А (х+Л) — Ах s= J К (t, s) g'v (s, x (s)) h (s) ds-f-a b
+ J К (t, S) a (s, x (s), 0 (s) h (s)) A (s) ds-LA + ®, a
где b b
Lh — ^K (f, s) gv (s, x (s)) h (s) ds и co = J К (t, s) a (s, x (s), 9 (s) h ($)) h (s) d«. a a
При этом
|)ш (x, Л)|| = тах
b
J К (/, s) a (s, x (s), 0 (s) h (s)) h (s) ds a
<max|K(t s)||a(s, x(s), 0 (s) h (s)) || (b^-a) ЦЛ || = M [la (s, x (s), 0 (s) h (s)) || • t, s
и потому Ц G) [|/||h [|< M [j a (s, x (s), 0 (s) h (s)) || —► 0 при h —> 0,
198
Следовательно, Ах дифференцируема по Фреше и
ь
dA (х, Л) = J К (t, s) gv (s, x (s)) h (s) ds. a
4. Если <p:(0, 1)—► ? и предел <p'(0= Игл существует, to
А/-> o A*
ф дифференцируемо в точке t и d<p (/, Д0=ф' (!) Ы. В самом деле, в этом случае У - = ф' (0+а> где а—►О при М —>0, и дифференцируемостьф
очевидна.
Легко проверить, что множество отображений, определенных в окрестности точки х0£Х, принимающих значения в У и дифференцируемых в точке х0, есть линейная система и оператор дифференцирования является линейным, т. е.
d[a/(x0, A)+Pg(x0, ft)] = ad/(x0, ft)+Pdg(xc, Л), или иначе
(а/ (х) +0g (х));о = a/' (ха) +0g' (х,).
Далее, из равенства
f(x+h)—f(x) = f (x)ft+©
следует, что функция /, дифференцируемая в точке х0, непрерывна в этой точке. Обратное утверждение не верно, как показывает пример 2 (см. с. 197, 198).
Наконец, отметим, что если / — линейный непрерывный оператор, действующий из X в У, то для любого х£Х имеем/'(х) =/. В самом деле, тогда при всех h £ X
/ (х+Л) -/ (х) = /(х) + / (Л) -/ (х) = / (Л), откуда и следует приведенное утверждение.
Подчеркнем, что отображения / и /', имеющие область определения в одном и том же пространстве, действуют в различные пространства, а именно /(х)£У, a f (x) £L (X, У), так что если / дифференцируемо всюду на G, то /:О—*У, f :G ->-L(X, У).
2. Основные теоремы.
Теорема 1 (о дифференцируемости композиции отображений). Пусть X, У, Z—ЛНП и даны отображения f'.G —+Y, где GcX и G открыто; g:H —► Z, где Ha.Y и Н открыто. Если f~Y (Н) П G не пусто, отображение f дифференцируемо в точке Хо € /”1 (Н) Г) G, a g дифференцируемо в точке yt = f (х0) £Н, то сложное отображение F =g of дифференцируемо в точке х0 и
^'(x0)=gr'[/(x9)]o/'(Xo)-
□ Прежде всего заметим, что если h достаточно мало, то в силу открытости множеств G и Н и непрерывности отображений fag соответственно в точках х0 и г/0 = /(хв), точки х0 + й и у04-& = = / (х0 + Л) не выйдут за пределы множеств f~l(H)()G и Я. Далее,
199
имеем
F (х0 + h) — F (x0) = g [/ (x0 + h)]—g(ft) = g (yt + k) —g (yt).
Так как g дифференцируемо в точке у0, то
g (У o + k)—g (у о) = g' (Уч) k + <ох,
где ®Х/||А||-О при 6 — 0. В свою очередь,
k = f (х9 + h) — f (х0) = f (х0) h + со2,
где <о2/|]А||—*0 при 6 — 0. Поэтому
F (х0 + h) — F (х0) = g' (z/0) [/' (х0) А + <о8 ]+юх = = (g' (Уч) ° f (Хч)> h+g’ (у„) ©, + <»!.
Выражение (g' (у0) ° f (xt)) h кгъ линейный по А оператор, и остается доказать, что
0 ПРИ /г-^°-1|Л|| н
Имеем
№' (УоНг + йиП II g' (Уо)Н<М , 11<М
ИМ ИЛИ ||Л|| •
Первое слагаемое справа стремится к нулю, так'как ®2/||6|| — 0 при 6 — 0. Стремление к нулю второго слагаемого можно доказать следующим образом. Так как g дифференцируемо в точке у„, то (ох^6|| —0 ПРИ 6 — 0. Поэтому для любого е>0 наймется г] > 0, такое, что J<»хII < е IIАII при ||6||<т]. В свою очередь, в силу непрерывности / в точке х0 для данного t| > 0 найдется 6Х > 0 такое, что ||А || < г| при || h || < бх. Далее, так как f дифференцируемо в точке х0, то найдется 68 > 0 такое, что || <о21|/|| h || < 1 при ||А|| < в8. Пусть 6 = min(6x, 68). При || 61| <6 имеем
||®1 II < 8 IIА II = в II/' (Хо) 6 + (О81|С < 8 (К f (ХО) || || h || +1| (02 fl) < 8 (|| f (Хо) | + 1) || h |,
и так как s>0 произвольно, то это означает, что о^/ЦбЦ—*0 при 6 — 0. в
Примеры. 1. Рассмотрим отображение f:G—► У, дифференцируемое* на G, и точки a, b£G такие, что (a, с: G. Тогда функция <р:(0, I)—> У, определяемая равенством
Ф(0 = /[/Ь + (1-0 а], дифференцируема на (0, 1) и
<р' = (/*+(1-0 «I (^-fl).
2. Пусть отображение f:G —► X дифференцируемо на Gcz | R и А:Х —> Y — линейный непрерывный оператор. Тогда ф —До/—отображение, дифференцируемое на G, и ф' (х) = А [/' (х)].
Доказательства обоих утверждений получаются без труда.
♦ Здесь и далее в этой главе множества G, А/, на которых рассматриваются дифференцируемые функции, мы считаем открытыми, не оговаривая этого каждый раз.
200
Следующая теорема является аналогом теоремы Лагранжа о конечных приращениях вещественных функций вещественного аргумента.
Теорема 2 (о конечных приращениях). Пусть отображение f-.G—^Y дифференцируемо на G и отрезок [а, Ь] целиком входит в G. Тогда
17(b) sup ||f (х)||-||&—а||.
хе [а, 6]
□ Рассмотрим отображение g(t)—f(xt), где xt — //> + (1 — t) а-Это отображение непрерывно на [0, 1] как композиция непрерывных отображений f (х) и xt и в силу теоремы 1 дифференцируемо внутри (0, 1), причем
g' (0 = f (xt) x't = f'\tb + (l—t) a] (b—а).
Поэтому для любого линейного функционала l£Y* вещественная функция ф (/) = I [g (0] вещественного аргумента t непрерывна на [0, 1] и дифференцируема по крайней мере внутри (0, 1). Следовательно, по теореме Лагранжа,
Ф(1)-<р(О) = <р' (0), О<0<1. (5)
Но Ф (1) = /[/(Ь)], Ф (0) = / [/(а)] и
Ф' (/)-/{/' [й>+(1-/)<*] (Ь-а)}.
Поэтому равенство (5) примет вид
I 7 (b) -/ (а)] = I {Г [Ob + (1 -0)а] (Ь -а)}. (6)
Пусть 10—функционал с нормой, равной единице, и такой, что /«7(b)-/(«)] = 17(b)-Ж II- Тогда
II f(b)-f (а) || = /. {f [0b + (1 -0)а](Ь—а)} <
<11/'[0Ь + (1-0)а]||-||Ь-а||< sup ||/' (х)||-||&-а||. В х€[а, Ь]
§ 2. ПРОИЗВОДНАЯ ГАТО
1. Основные понятия. Для отображений ЛНП кроме производной Фреше можно ввести еще одно понятие производной. Пусть дано отображение /:О—х£(? и /—единичный вектор пространства X, определяющий некоторое направление. Предел
lim
t +0 *
если он существует, называется производной отображения f по направлению I (или производной Гато) и обозначается fj (х).
оо / оо \ 2
Пример. Пусть Х — У — 12 и f (х) = 2 2 j ei, где {е,} —стандарт-
z = i\/ = i /
00 00
ный базис в /2. Если 2 2 < 00» то f отображает в /2. В самом деле,
/=1/=1
2<М
/ оо \ 2
полагая тц- = ( 2а//£/ » с помощью неравенства Буняковского—Шварца убе-\/ = 1 /
оо 00
«даемся, что ряд 2 Лх сходится. Но тогда сходится и ряд V т$, так что
i = 1 i = 1
Для любого х£/2.
Выбрав в качестве единичного вектора направления орт ej, получим
f (x-J-tei) — f (х)= У
00 2 ' oo
2 a//(§/ + <«!/) - 2М/
21
Отсюда
2)2 aU^J 2iaikffik + tbik) \ei=*
1 = 1 U = 1 fc=i J
CO ( 00 \
= 2 2 [el.
t=l I k=\ J
f (x + <et)—f(x) t
i = l \ fe = l /
oo CO / 00 \
+ t 2 —* 2 2 ( aZl 2 ai*£* )
X=1 1 = 1 \ k=\ /
Следовательно, f'et (x) существует и оо ✓ 00 \
/«I W 2 ( 2 ) еь
( = 1 \ Л=1 /
Если фиксирован произвольный ненулевой вектор h£X, то часто говорят о производной по направлению h, понимая под f(x-4-th) —fix)
этим предел отношения lim ——1—/—при условии, что он суще-t + о
ствует; этот предел обозначается %(х). Ясно, что f'h (х) = || h || f b (х), где h± — единичный вектор направления й, т. е. й1 = й/|й||.
Замечание. Производная Фреше f (я) и производная по направлению f'h (х) являются элементами разной природы: f (х) есть линейный оператор из X в Y, в то время как fb (х) есть элемент пространства Y.
Легко убедиться, что если отображение / дифференцируемо в точке х по Фреше, то оно дифференцируемо в этой точке по любому направлению й:
(х) = df (х, й) = /'(х)й.
Обратное утверждение неверно, как показывает отображение / (х)=|| х Ц (см. с. 197, 198). Это отображение дифференцируемо в нуле по любому направлению, так как при t > 0 имеем
(0) || Н||
t t t ’
откуда следует, что f't (0) существует и равна 1. В то же время отображение /(х) =||х||, как мы видели выше, не дифференцируемо по Фреше при х = 0.
Условия, когда из дифференцируемости по направлению следует дифференцируемость по Фреше, мы рассмотрим ниже.
2. Основные теоремы. Для отображений, имеющих производные по направлениям, также имеет место аналог теоремы Лагранжа. Однако прежде чем формулировать и доказывать эту теорему, приведем одну лемму из теории функций действительного переменного.
Лемма* 1. Пусть вещественная функция <р (0 вещественной переменной t определена и непрерывна на отрезке [а, Ь] и имеет внутри промежутка [а, Ь) правую производную <р+ (0- Если т~ = inf <р+ (О, Af = supq>+(f), то
[а, Ь) [я, Ь)
Ь—а
□ Докажем правое неравенство. Допустим, что оно не верно, т. е > М. Тогда найдется достаточно малое в > 0 такое,
что все еще выполняется неравенство
4-е, или Ф (&) “Ф (а) ~(М + е) (Ь—а) > 0. (7)
Рассмотрим функцию ф(0 = <р (0 — ф (a) —(M-f-s) (t—а). Эта функция непрерывна на [а, 6] и ф(Ь) > 0 в силу (7). Так как
Ф (0 = (t —a) _ (м + е)]
и (а) М < М 4*8, то ф(0 < 0 при t, достаточно близких к а. Поэтому на интервале (а, Ь) найдутся точки, в которых ф (t) обращается в нуль. Пусть с—наибольший из корней уравнения ф(0==О. Ясно, что с<_Ь. Тогда ф(0>ф(с) = О для />с, откуда для всех таких t имеем
Ф (0 — <р (с) — (М + е) (t —с) > 0, или > Л1 + 8.
Таким образом, ф+ (с)^Л4-|-8, что противоречит определению числа М, и лемма доказана. (
Следствие 1. Если в условиях леммы max{|m|, |М|}=Л, то
|Ф(Ь)— ф(а)|<£(Ь-а).
Доказательство очевидно.
Следствие 2. Если при выполнении условий леммы дополнительно предположить, что непрерывна на интервале [0, 1), то Ф(0 непрерывно дифференцируема на (0, 1).
□ В самом деле, пусть /£(0, 1) и Д/ настолько мало, что
1). Положим /пд/= inf ф+(0, Мд/= sup ф^(0.
a, t+&t) (/, t+ы)
* На самом деле, имеет место несколько более общая лемма (см., например: Валле Пуссен. Курс анализа бесконечно малых, т. 1, п. 112).
203
Согласно лемме,
ША,<Т<'+«>-ФИ<д4й[.
Так как mAt и Л1д, стремятся к <р; (/) при А/-* О, то из предыдущего неравенства следует, что производная
Ф<0 = Цш <’<'+'“>-?«> _ф;(<)
существует и непрерывна по t, поскольку такова правая производная <?; (/). и
Теорема 1. Пусть отображение f:G — У непрерывно наб, x£G, h£X и отрезок [х, x-j-Л] целиком принадлежит G. Если f дифференцируемо по направлению h во всех точках отрезка [х, х+Л], то
M(x + h)-f (х)||< sup х€(Х, Х + Л]
□ Как и при доказательстве теоремы 2, введем функцию
ф(0 = Ф(х + «0], 0</< 1,
где /—произвольный непрерывный линейный функционал на пространстве Y. Очевидно, что <р (0 непрерывна на [0, 1], и легко видеть, что <р(/) имеет на [0, 1) правую производную ф+(0> равную [Гь (х+th)]. В самом деле, пусть t £ [0, 1) и А/> 0. Имеем
ФК+ДО—<р(/) _ . Г f (x+th+Mh)—f(x+th)] __ Д/ I Д/ J Г
= I [fh (*+ th) +a] = /[ft (x + /Л)] + / (a),
где a —► 0 при Д/ —* 0. Но тогда I (a) —* 0 и, следовательно, существует
Ф; (х)=jimo ф«+Д0-<р(0 = i {х+th)].
В силу следствия 1 из леммы 1 имеем
|Ф(1)—Ф(0)|С sup |ф;(01-о <t< I
Так как ф(1) = /[/(х-4-/1)], ф (0) = I[f (х)], то это неравенство дает
\l[f(x + h)-f(x)]\^ sup |/[/ИВ)]1-
£€[х, х+Л]
Пусть функционал I таков, что J/||=l, /[/ (х + Л) — f(x)] = = U(x + h)— f (х)||. Тогда
И(х + Л)-/(х)||< sup ||/ИВ)II- в
£€ [х, х + П]
Теорема 2. Если отображение f\X—+Y непрерывно в G и дифференцируемо в каждой точке этого множества по любому направлению й, а производная f'h(x} непрерывна по h и равномерно отно-204
сительно h непрерывна по х, то f дифференцируемо в G по Фреше и d/(x, ft)-ft(x).
□ Покажем прежде всего, что в условиях теоремы f'h (х) линейно зависит от h. Фиксируя точку xgG, при произвольных достаточно малых ft, k £ X и произвольном / £ X* рассмотрим функцию
Ф (/, т) = /[/ (х + th Ч-xfe)]
двух вещественных переменных t и т. Используя условия теоремы и следствие 2 из леммы 1, легко показать, что в достаточно малой окрестности точки (0, 0) функция ф (t, т) имеет непрерывные частные производные
x) = l [f'h(x + th + xk)], ф;(/, т)»/[/* (х-НЛ-W)]. (8)
Введем еще функцию
1 ф (0 = Ф (at, Р0, а, Р € R.
В силу теоремы о дифференцировании сложной функции имеем
Ф'(0)==оф;(0, О)+Рф;(О, 0). (9)
Но ф' (0) = /[/ай+з*(х)], откуда с учетом равенств (8) и (9) получаем I [fah+Qk (*)] = O-l [fh (*)] + ₽* [fk (X)].
Вследствие произвольности I £ X* это означает, что
Гаы-fik (х) = aft (х) +P/fe (х)
и линейность ft(x) по h доказана.
Остается доказать, что
|| f (х+ft) — f (х)—f (х) J - о (J h 0.
На этот раз положим
Ф (т) = / [/ (х + тЛ) — xfh (х)].
Снова легко убеждаемся, что ф(т) непрерывна на [0, 1) и имеет на [0, 1) непрерывную производную
ф' (т) = I [Гt (х + xh)—f'h (х)].
По теореме Лагранжа, ф (1) — ф (0) = ф' (6), т. е.
I [f (х + Л) - f (х) - f'h (х)] = I [ft (x + 0Л) - f'h (x)].
Для произвольного, но фиксированного h£X выберем l£X* так, чтобы || IИ = 1 и
/ [/ (x + h)-f (X) -f'h (х)] =11/ (x+ft)-/ (х) -ft (X) ||.
Тогда получим
II/ (х+Л) -f (х)-Г(x) || f'h (x + 6ft) -ft (x) ||.
205
Так как fj, (х) есть линейный (что доказано выше) и непрерывный (по условию) относительно h оператор, то f'h(x)—Lxh, где Lx£L(X, Y). Далее, в силу непрерывности f'h (х) по х равномерно относительно h получаем
ЦД»+д* Ех|| = sup || (Lх+дЛ Lx) h| ► О
II h II < 1
при Лх —► 0. Поэтому
||f(x + ft)-f(x)-fft(x)K
< || (Lx+eft - Lx) h || < J Lx +0Л - Lx || • || h || = о (J h |)
и теорема полностью доказана. Ц
3. Производные по подпространству. Понятием, промежуточным между производной Фреше и производной по направлению, является производная по подпространству. Пусть дано отображение f: G —► Y, GcX и Хо — подпространство X. Если для x£G существует непрерывный линейный оператор lx-.X0—>Y такой, что для любого /г£Х0, удовлетворяющего условию x + h^G,
f(x + h)-f(x)-lxh = o^h^),
то отображение f называется дифференцируемым в точке х по подпространству Хо, а линейный оператор 1Х называется производной по подпространству Хо и обозначается fx„(x). * Если X — прямая сумма подпространств Xt и Х2 и производные отображения f по подпространствам Х1 и Х2 в точке xgG существуют, то они называются частными производными отображения f в этрй точке и обозначаются f'Xi(x) и f'x,(x) (или и .
Лемма 2. Если X = Xi®X2 и отображение f:G—+Y имеет в окрестности точки x£G частные производные f'Xt(x) и /ха(х), непрерывные в этой точке, то отображение f дифференцируемо в точке х по Фреше и
f (х) h = f'Xi (х) ht + f'x, (x) ft2, h =. + ht.
□ В самом деле,
U(х + Л) -f (x)-[fXi (х) + f'Xa (x) Л2]||<
< j f (x+/11+ft2) — f (x+ft2) — f'Xi (x) hi II
+1| f (x + /i2)—f (x) — fXt (x) h21| = || f x, (x + й2) /if + oh — fx, (x) || + + ||<o2||<||MllfMx + /4)-fx, WII+W+K||),
так как Ц fx (x + /i2) — f x (x).|| — 0 при h -* 0, o>i = о (|| ht ||), w2=o (|| h2 )| и (/’I. 2).
Утверждение, обратное этой лемме, очевидно, причем
11.1. 2).
Понятия частных производных и предыдущие результаты непосредственно обобщаются на случай, когда X есть прямая сумма любого конечного числа подпространств.
206
Замечание. Так как в силу соответствия х14-х2<->(х1, х2) пространства Xj ф X, и Xj х Х2 изоморфны, а с метриками, порожденными нормами
hi+и=hi в+II II=II hi. xt) и,
и изометричны, то все сказанное выше о частных производных переносится на отображения вида f: Н—-Y, где НсХ{хХг.
Пусть теперь /: G—►У\хУ», G с X и, как всегда, G открыто, так что f(x) = (fi(x), где G-+Yt и ft: G->-Yt. Если «координатные функции» ft и f3 дифференцируемы в точке x£G, то f дифференцируемо в этой точке и f (х) h = (f (х) ft, f't (х) h). В самом деле,
/(х+Л)-/(х) = (/Дх + Л), /а(х+Л))-~Ш А(х)) = (/1(х + Л)-/1(х), /,(х+Л)-/.(х)) = = (/ih)A+©1, /;(x)ft+©2)=(fi(x)ft, f;h)A)+(®i. ®а).
причем
й(а>т, <о2)Я Hd 1^1 о h 0 IIM ИМ + ЦАЦ ипРи«-*и.
Эти результаты очевидным образом распространяются на случай отображений, принимающих значения в декартовом произведении любого конечного числа пространств.
§ 3. ТЕОРЕМА О ЛОКАЛЬНОМ ОБРАЩЕНИИ ДИФФЕРЕНЦИРУЕМОГО ОТОБРАЖЕНИЯ. МЕТОД НЬЮТОНА
1. Теорема о локальном обращении. Используя понятие производной отображения, можно доказать локальную теорему о существовании обратного отображения, аналогичную теореме о существовании функции, обратной монотонной функции, имеющей производную, не обращающуюся в нуль.
Теорема 1. Пусть отображение f: G —►У непрерывно дифференцируемо в некоторой окрестности точки х0 € G. Если f (х0) — непрерывно обратимый линейный оператор, то существуют открытая окрестность и точки х0 и открытая окрестность v точки Уо = [(хе) такие, что f отображает и на о взаимно-однозначно, т. е. существует обратное отображение f~l: о—-и. Это отображение непрерывно дифференцируемо, причем
(Г1Уу = {Г [/’Чу)]}’1.
□ Прежде всего заметим, что если L —непрерывно обратимый линейный оператор из Y в X, то f непрерывно дифференцируемо в некоторой окрестности точки x0£G тогда и только тогда, когда f1 = Lof: G —> X непрерывно дифференцируемо в этой точке. Далее ясно, что f взаимно-однозначно отображает и на v тогда и только тогда, когда Д взаимно-однозначно отображает и на Lv, причем fi1 = о L”1 непрерывно дифференцируемо на Lv тогда и только
207
тогда, когда f~l непрерывно дифференцируемо на v. Отсюда следует, что если теорема верна для /, то она верна для fu и обратно. Положим £ = [/'(х0)]-1. Тогда
К (*«) = Я/' (*о)]_ 1 ° f}' М = [Г (х,)]"1 о f (х0) = /.
Поэтому без ограничения общности можно считать, что /: G —X, G с X и f (х0) = 7.
Наконец, введем новую переменную г = х—х0 и новую функцию Ф (г) = f (z + х0) — f (х0), откуда х = г + xe, f (х) = <р(х—х0)—<р(0); аналогично предыдущему, убеждаемся, что если теорема верна для /(х), то она верна для ф(г), и обратно. Но ф отображает окрестность нуля в окрестность нуля и ф' (0) = /' (х0) = 1. Поэтому мы будем с самого начала предполагать f: G —► X, G с X, 0£G, хо = О, f (0) = 0, /'(0) =/.
Положим g(x) = x—/(х). Тогда g (0) = 0 и в силу непрерывности производной g' (х) найдется такое г > 0, что при х € X (0, г) имеем || g' (х) ||С 1/2. Тогда из аналога теорема Лагранжа следует
sup k4l)ll-W<(V2)hll [0. X]
для любого х из замкнутого шара X (0, г), т. е. g отображает этот шар в замкнутый шар X (0, г/2). Покажем', что для любого у£Х(0, г/2) найдется_единственный х£Х(0, г) такой, что f (х) = у и, следовательно, в X (0, г/2) будет определено обратное отображение /-1. •
Введем отображение h (х) = g (х) + у. Если || х || С г и || у || С г/2, то
ЛМх) II < № (*) НИК'/2 + г/2 = г
и потому h отображает шар X (0, г) в себя. Далее, имеем j h (xj — h (х2) J = || g (xf) — g (x2) || C (1 /2) || x, - x21|
для любых хъ x2 € X (0, г), так что й_(х) есть отображение сжатия полного метрического пространства X (0, г) в себя. Поэтому при любом фиксированном у € X (0, г/2) существует единственная неподвижная точка х £ К (0, г) отображения /г, т. е. такая, что h (х) = х, или g(x) + g = x—f (x) + g = x, или f(x) = y. Таким образом, мы получили обратное отображение f~l, определенное на шаре X (0, г/2) и принимающее значения в шаре X (0, г).
Это отображение непрерывно, так как
И Г1 (Ух) - f "г (yj II = II *1 - х2 II = И (xt)—h (х2) В -
*= И [£ (-«1) + У11 — [£ (х2—g2)] IK II g (xj — g (х2) И +
+ki— у2 IK ~Xz 1!°“
=|ll/-1(//1)-ri(i/2)ll+k1-^ll,
208
откуда
ll/-1 G/x)-IK 2 hi— ya|i (i)
для любых y1( y2.
Для доказательства дифференцируемости /-1 в шаре К (0, г/2) возьмем у, уо€К(0, г/2); пусть х = }~г(у), xe = f~1(yl>). Имеем
/-1 (у) -/“* (Уо) -{Г [Г1 (Уо)]Г1 (У-Уо) =
= х—хй - [f (х#)]-х (/ (х)—f (х0)) =
= [Г (*о)]-1 {/' (Хо) (X — Хо) — (f (х) -/ (х0))}.
Поэтому
II/-1 (У) -/“ (Уо) -{/' [Г1 (Уо)]}-1 (У-Уо) II <
<II[/' (Хо)]-1 III)/(х) -/(Хо)-/' (х„) (Х-Х0)Ц
и надо показать, что
Из неравенства (1) следует, что ||х—x0||<2h—Уо|| и, значит,
||/(х)~f (Хо) —f' (xn) (х—Хв)|| g ||f (х) — f(x0) — f (х0) (X — Хр)||
II//—//oil IIX— Хр||
Пусть у—*у9. Так как отображение х = /-1(У) непрерывно, то х —* х0. Но тогда в силу дифференцируемости f в точке х9 выражение в правой части последнего неравенства, а тем более в левой его части, стремится к нулю и равенство (2), а вместе с тем и дифференцируемость f~l в шаре К (0, г/2) доказана.
Попутно мы установили, что
[/^^'^{/'[/-/(Уо)]}-1.
Замечание. Согласно принципу сжимающих отображений, значение обратного оператора x = f~1(y) может быть получено как предел последовательных приближений, определяемых по формуле
хл = h (x„_i) = x„_i -/ (x„_!)+у.
Значение хв может быть выбрано произвольно в шаре К (0, г).
Пример. В пространстве С [О, 1J рассмотрим нелинейное интегральное уравнение
1
х(0- J K(t, S, x(s))ds = z/(O, (3)
О
где ядро /< (/, s, и) непрерывно в области О «С s 1, —оо <н< + оо
и имеет в этой области непрерывную производную Ki (t> s, и). Пусть, кроме того:
а> К(/, s, 0) = 0, K'u(tt s, 0) #0;
В № 3054 209
б) единица не является собственным значением ядра Ku (t. $, 0), т. е. линей-нейное интегральное уравнение
1
г(0~ s> °)2(s) ds===0 о
не имеет ненулевых решений.
Записав уравнение (3) в форме f(x)=y, легко проверить, что:
1) /(0) =0;
2) производная /' (х) существует в окрестности нуля и имеет вид
1
/' (х) h = h (/) — Ku (t, s, х (s)) h (s) ds;
0
поэтому она ограничена и непрерывна в этой окрестности;
3) [/' (О)]-”1 существует в силу условия б).
Тогда согласно только что доказанной теореме уравнение (3) для всех достаточно малых правых частей у (t) имеет единственное решение, которое может быть получено методом последовательных приближений.
2. Метод Ньютона. В качестве еще одного примера использования понятия производной отображения рассмотрим метод Ньютона решения операторных уравнений. Как известно, для случая скалярного уравнения f(x)--=O метод Ньюгона состоит в нахождении последовательности приближенных решений по формуле
г _ у /fa)
При выполнении некоторых условий, налагаемых на функцию f (х) и ее производные, доказывается, что приближенные решения хп сходятся к конечному пределу и этот предел является решением уравнения.
Л. В. Канторовичем было показано, что метод Ньютона может быть перенесен на операторные уравнения. Мы рассмотрим здесь этот метод, причем с целью упрощения доказательств будем предполагать выполнение довольно жестких ограничений.
Итак, пусть дано отображение /: G —>У, где G с: X и G открыто. Рассмотрим уравнение
/(х) = 0. (4)
Предположим, что в некотором шаре К (х0, г), центр х0 которого мы принимаем за приближенное значение решения уравнения (4), отображение f (х) дифференцируемо и его производная f (х) удовлетворяет условию Липшица (х)—/'(х)||^£||х—х||.
Если, кроме того, существует [/' (х)]-1, то по аналогии со скалярным случаем можно строить последовательные приближения по формуле
(х»)]"1/(*»)•
Эта формула имеет, однако, то, неудобство, что необходимо последовательно находить обратные операторы [/' (х„)]-1, т. е., по сути
210
дела, решать линейные операторные уравнения /' (x„) h = g. Чтобы, избежать указанного неудобства, Л. В. Канторовичем был предложен мо ди ф и ци р о в а н н ый метод Н ьютона, в котором последовательность приближений ^аходят по формуле
Хп+1 = Ха — [/' (х„)] -1 f (х„), (5)
где для любого п фигурирует один и тот же обратный оператор. Введем следующие постоянные:
= (Хо)ГЧ По = 11Г (Хо)]-1/ (х0)||.
Теорема 2. Если hQ = Mor]oL 1/4 ы t0—меныиий корень уравнения hff2 — /-{-1 = 0, то в шаре Цх—х0||^ /от]о уравнение /(х) = 0 имеет единственное решение х* и последовательные приближения хп, определяемые по формуле (5), сходятся к этому решению.
□ Рассмотрим оператор
Ах = х—[/' (х0)]~1/(х).
Этот оператор преобразует шар || х—х0|| /„По в себя. В самом деле, Ах—х0 = х — х0 — [/' (х0)]~1 / (х) =
= [Г (х0)]-1 {/' (х0) (x-xt)-f(x)+f (х0)}-[/' (х0)]"7(х0).
Отсюда
II Лх -х01| < || [/' (x0)]-i ||• || f (х) -f М --f (Хо) (X-х0)|| 4-11 [/' (х0)]-7(х„)||,
II Ах -х0 IK Мо || f (X) - f (Хо) - f (Хо) (х - Хо) || 4- По-
Рассмотрим функцию ср (х) = f (x)—f (х0) —f (х0) (х—х0). Имеем ф' (х) = /' (X) — f (х0). Пусть х€К (х0, /ОТ]О). Тогда
II ф' (*) II = II f (х) — Г (Хо) II < LII х—х0 II < L/оЛо.
Поэтому
IIФ (х) || = || ф (X) -<Р (х0) II < L/0T]o IIX- х0 (К L (/от]о)г-
Таким образом, если х € К (х0, ^оПо)> то
IIАX—х0 II < + Но = По (ДАVo +1) = По М +1) = г'о'По,
т. е. оператор А переводит шар (|х—х0||/оПо в себя.
Покажем, что в этом шаре А является оператором сжатия. Для х € К (х0, ^оПо) имеем
A' {x) = I-[f (Хо)]"1 Г (х) = [/' (Хо)]"1 (/' (Хо)-Г (х))
и потому
II Д' (х)К Мо||/' (х)-/' (Xo)KMoL||x-^oKM0LVo.
8*
211
Так как /0—меныпий корень уравнения Ло<2 —< + 1=0, то <0 — = (1 — j/1 —4h0)l (2й0). Следовательно,
|| А' (х) || < М М = h0 < q < 1,
откуда
||Лх' —Лх"||<<7||х'—x"||, х’, x"£K(xQ, <от]о), (6)
и требуемое доказано.
Итак, оператор Л осуществляет сжатые отображения шара К (х0, <o,tlo) в себя и потому имеет в этом шаре единственную неподвижную точку х*. Для этой точки
x* = x*-[f (х0)]-1 / (я*),
т.е. х* есть решение уравнения /(х*) = 0. Точка х* есть предел последовательных приближений
xn+i = Axn = xn-[f (х0)]-7 (х„),
и теорема полностью доказана. Ц
Замечания 1. Выполнение условия й01/4 может быть достигнуто за счет достаточной близости к решению начального приближения х0. '
2. Скорость сходимости последовательных приближений для модифицированного метода Ньютона определяется неравенством
к-х*к-А-ц[Г (хо)]-1/(хо)||,
* ч
которое легко может быть получено из (6). Если же рассмотреть основной (немодифицированный) метод Ньютона, то для него скорость сходимости оказывается более высокой, а именно:
kn-**»<2^r(2M2B-xno.
Подробнее об этом см. [6]. ,
Пример. Рассмотрим нелинейное интегральное уравнение Гаммерштейна
1
х (0 — J К (t s) g (s, х (s)) ds = 0, (7)
0
где ядро К (/, s) непрерывно по совокупности переменных в квадрате
0^s«Cl, функция g(s, и) непрерывна по совокупности переменных в полосе 1, — оо <^<~|-оо и имеет непрерывную производную g'u (s, и), удовлетворяющую по второй переменной условию Липшица |g’u (s, Ui)—gu(s, w2)I^Mui—w2|< Тогда оператор
1
f (x) =x (/) — J К (*, s)g(s, x(s))ds
0
212
преобразует пространство С [0, 1] в себя й является дифференцируемым. При этом
1
/' (х) h = h (/) — к (£, s) gu (s, X (s)) h (s) ds о
и производная также удовлетворяет условию Липшица || f' (х) — f' (х) (| ак || х—"х||,
где а = sup | /С (/, $) |.
t, S
Пусть единица не является собственным значением линейного интегрального уравнения
i
/<(/, s)g'u(s, x(s))h(s))ds (8)
о
i
и M0 = sup J | R0(t, s, 1) ds, где RQ(t, s, X)—рйольвента уравнения (8). Тогда при выполнении условия Яо = ЛЛ1о'По^ 1/4, где
1 1
Ло = sup f I Яо (t, s, 1) I x0 (s)— С к (s, o) g (o, x0 (ст)) do I ds,
* о 0
процесс последовательных приближений для метода Ньютона, примененный к уравнению (7) при начальном приближении х0(/), сходится к решению этого уравнения.
§ 4. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ. ФОРМУЛА ТЕЙЛОРА
1. Основные понятия. Пусть отображение /: G—>-У, где G с: X и G открыто, дифференцируемо на G. Если df(x, Л) как функция от х при любом фиксированном h, в свою очереди, дифференцируема в точке х£ G, т. е.
df(x + k, h) — df(x, h) — d [d/ (x, h), + т), (1)
где >0 при k—+ 0, то отображение f называется дважды дифференцируемым в точке х, а дифференциал d[d/(x, h), k] от первого дифференциала d/ (х, й) при k = h называется дифференциалом второго порядка (или вторым дифференциалом) отображения f и обозначается d*f(x, h). Таким образом, в рассматриваемом случае
б/(х+й, h) — d/(x, ft) = d*/(*> й)4-т]. (2)
Покажем, что d [d/ (х, h), й] есть симметричная билинейная форма, относительно h и k и, следовательно, d2/(x, h) есть квадратичная форма от h.
□ Так как, согласно определению дифференциала, d[d/(x, h), й] линейно зависит от k, то для доказательства билинейности этой формы достаточно показать, что d[d/(x, h), k] линейно зависит и от h.
Обозначая для краткости d[d/(x, h), й] через b(h)k, имеем
&f(x + k, h1)—df(x, hj) = b (hj) k + xii, df (x+k, h2)— d/(x, /12) = Ь(й2)й + т]2, df(x + k, hl + h2) — d/(x, hl + h2) = b(h1 + h2)k + x\3.
213
Вычитая из третьего равенства два первых, в силу линейности d/(x, ft) по h получим
b (ftt + ft2) k —b (fa) k — b (ft2) k Н-Яз —Л1~ Лг = 0.
Пусть k=tk0, fto=/=O. Тогда
b fa + ft2)ft0—b(AJka-bfa) k0 + sign t||ft01| (Д- Д- Д) = 0. (3) При /—>0 также ||й||—<-0; следовательно, -Д(л3 — Л1 —Ла) —”0 и равенство (3) в пределе дает
b (Л1 + Л2) k0 — b fa) k0 — b (fa ft0 = 0.
Так как при fto = O все три оператора последнего равенства обращаются в нуль, то для всех k С X получаем
bfafalfak^b fa)k + bfa)k. .
Аналогично показывается, что b (ah.) k — ab (h) k, и билинейность d[d/(x, ft), ft] доказана. H
Билинейное отображение, ставящее в соответствие паре (ft, ft) элемент d[d/(x, ft), ft], называется второй производной (или производной второго порядка)отображения f и обозначается f"(x). Таким образом,
d[df(x, ft), ft] —(х) (ft, ft) (4)
и
d2/(x, ft) = /"(x)(ft, ft). , (5)
Для сокращения вместо f" (x) (ft, ft) часто пишут f (x) ft2.
Покажем, что билинейное отображение f" (х) является симметрическим.
□ Введем функцию ф(/, x) = l[f (х4-th4-rft)], где/ — произвольный линейный функционал из Y*. Если t и т достаточно малы, то ф(/, т) дважды дифференцируема в окрестности нуля, причем
£ =, I [/' (X + th + ТЙ) ft], = I [Г (X + th + xk) ft],
^ = /[r(x + /ft + Tft)(ft, ft)], -^ = l[f"(x + th+xk)(k, ft)], и, следовательно,
Но если <р (/, т) дважды дифференцируема в окрестности нуля, то, как известно,
д2<р I ____ д2ф I
dt дх |/=т=о дх dt |/=т=о ’
т. е. l[f" (х) (h, ft)] = I [/" (х) (ft, ft)]. Так как линейный функционал l$Y* произволен, то f" (х) (п, k) = f"(x)(k, ft) и симметричность второй производной доказана. Ц
214
Если f дважды дифференцируема в точке х, то, записав для любого фиксированного h равенство (1) в виде
[f (x + k)-f (X)-f(x)k]h _ Т)
11*11 11*11
и учитывая, что т]/||А||—>0 при *0, получаем, что f как отображение G в L (X, У) дифференцируемо в точке х в топологии пото-
чечной сходимости пространства Л (X, У). Если же предположить, что d/(x, h) дифференцируемо по х в данной точке с равномерно малым остатком, т.е. если в равенстве (1) т]/||£|| —>0 при k—>0 равномерно по h в шаре ||/i||^l, то f (х) окажется дифференцируемым в рассматриваемой точке и в топологии равномерной сходимости, т. е. по норме пространства L (X, У). В самом деле, в этом случае согласно (1) для любого е>0 найдется 6>0 такое, что ।.т]/Н1111 < 8 ПРИ и при любом h, откуда
sup
IIM< 1
hll . . _11П ПЛ(х+*)-Л(х)-Г(х)*
11*11 “imI, IIL и *«
e,
t. e.
|1Г(х + *)-Л(х)-Г(х)*||
0*11
(6)
при P||< б, а это и означает, что f' (х) как отображение G в линейное нормированное пространство L (X, Y) дифференцируемо и (Г (*))' = ГМ-
Верно и обратное: из дифференцируемости f : G—+L(X, У) по Фреше вытекает дифференцируемость d/ (х, h) с равномерным остатком, так как тогда
||df(x + fe, h) — df(x, h)-r(x)(k, ft) II \\f(x + k)-f'(x)-r (X) *1)
11*11 11*11
если 6 выбрано так, что для любого h такого, что ||ft||^I, выполняется неравенство (6).
Определим теперь по индукции дифференциалы и производные любого порядка.
Пусть отображение /: G—>У дифференцируемо р — 1 раз на G, так что для всех x£G существует &p~'f(x, Л) =^. (х) hP"1, где
f{p~iy(x) есть (р — 1)-линейная форма на ХхХх ... хХ, зависящая также от х. Если d₽-1/(x, h) как функция от х для некоторого x£G и при любом ZigX дифференцируема, т. е.
Ар~Ч(х + 1г, /i)-d₽-7(x, /i) = d[d/”7(x, h),
где т|/|] k || —> 0 при k —> 0, то отображение f называется дифференцируемым р раз в точке х, а значение d [d^-1/(x, h), А] при k = h называется дифференциалом р-го порядка отображения f и обозначается dpf(x, h,). Дифференциал dpf (х, h) есть значение р-линейного отображения [{ру (х) в точке (h, h, ..., Л), а само р-линейное отображение f{Py (х) называется производной р-го порядка отображения f. Можно доказать, что /(*’(х) есть симметрическое р-линейное ото-
215
бражение и, следовательно, (Р/(х, h) есть однородная форма степени р.
Пример. Если в примере 3 § 1 функция g (и, v) дважды равномерно непрерывно дифференцируема в полосе а^и^Ь, —оо<Ь< + оо, то оператор Ах = J К (t, s) g (s, x (s)) ds дважды дифференцируем и о
t
d2/ (x, h) = К (/, s) g”v (s, x (s)) h2 (s) ds.
о
Аналогично при выполнении соответствующих условий выражаются дифференциалы высших порядков оператора А.
На случай производных высшего порядка обобщается теорема о дифференцировании сложной функции.
Теорема. Пусть даны отображения f: G —> У, где GaX и G открыто] g: H—+Z, где HaY и Н открыто. Если f"1 (H)ftG =#0, отображение f дифференцируемо р раз в точке х0 £ {//) П G, а
g дифференцируемо р раз в точке yQ^f(xQ)^H, то композиция отображений F~gof дифференцируема р раз в точке х0.
□ Для р — 1 теорема верна и имеет место равенство
р' = g' р (x0)]of (х0). (7)
Предположим, что теорема верна для дифференцируемых р — 1 раз функций. Так как f и g дифференцируемы р раз, то f и g' дифференцируемы р — 1 раз, а тогда в силу предположения индукции и формулы (7) отображение F' также дифференцируемо р —1 раз, т. е. F дифференцируемо р раз. g
2. Формула Тейлора. Пусть отображение f: G —> У имеет на G все производные до (n+l)-aj порядка включительно и х, x-\-h таковы, что [х, x + h]<=G. Тогда
Нх + /.) = ,« + ^ + ^+...+'-^ + Л,.
причем
SUP
\п -f- ! 2€ Х + Л]
□ Рассмотрим функцию <p (t) = I [f (х + /Л)], 0 t 1, где I — произвольный непрерывный линейный функционал на Y. Легко проверить, что <р (t) непрерывна на отрезке [0, 1 ] и имеет на нем производные до (п+1)-го порядка включительно, причем <j>(*>(0 = = I [f(*‘ (х + th) ft*]. Поэтому q> (I) может быть разложена по формуле Тейлора
216
где 0, в общем случае зависит от I. Так как <р<А) (0) = I [/<А) (х) Л*], то предыдущая формула принимает вид
/{/(х + Л)-/(х)-Ц^ + ^-...-^} = (х+е1Л)Л'»+ч’ nfl .
-1 ( ОНИ)! J ’ и < < ь
Обозначим выражение, стоящее в левой части этого равенства под знаком функционала, через /?„. Тогда
/ {п ч _ , ^Hx+Qih)h^\
l\Rn)-l\ (п+1)! р
Выбрав I так, чтобы Ц/||=1 и l(Rn) = || Rn Ц, получим
<rn-hv sup ^(л+п«нг1. I) . 2€ [Xt х + й]
Выше мы определили последовательно производные высших порядков и с их помощью получили формулу Тейлора. Однако можно идти и обратным путем. п
Назовем многочленом выражение вида Рп (h) = У akhk, где аД*— fe = о
однородные формы степени k, определенные на ХхХх ..хХ и принимающие значения в одном и том же пространстве Y. Если для отображения f: X —► Y существует многочлен Р„ (Л) такой, что
/(х + Л)-Нх) = РДЛ)4-(о,
где ®/|| ft Ц" —► 0 при h—>0 равномерно в некоторой окрестности точки а, то можно доказать, что f (х) имеет в точке а производные до n-го порядка и /(Л) (а) hk = k\ akhk. Доказательство этого опускаем (см., например, [8], гл. VIII, § 6).
§ 5. ТЕОРЕМА О НЕЯВНОЙ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
1. Основные теоремы. Теорема о локальном обращении дифференцируемого отображения и понятие частных производных отображения позволяют доказать теорему о существовании операторной неявной функции.
Теорема 1 (о неявной функции). Пусть X, Y — ЛНП и дано отображение F: Н —+Y, где НаXxY и Н открыто, причем F (а, Ь) — О' в некоторой точке (а, Ь)£Н. Если F непрерывно дифференцируемо в Н и Fy{a, b)—непрерывно обратимый линейный оператор, то в некоторой окрестности Ganx(H) точки а существует отображение f: G —» Y такое, что: 1°) f(a) = b\ 2°) F (х, f(x)) = O в G; 3°) f дифференцируемо в G.
217
□ Введем отображение Ф: Н —► X х Y, полагая Ф (х, у) — = (х, F (х, у)). Так как координатные функции Фх(х, у) = х и Фг(х, y) = F(x, у) отображения Ф дифференцируемы в Н, то и Ф дифференцируемо на этом множестве, причем
Ф' (х, y)(h, k) = (h, F' (х, y)(h, k)) = (h, F'x(x, y)h + FY(x, y)k).
В частности, в точке (а, Ь) имеем
Ф' {a, b)(h, k) — (h, F'x(a, b)h + FY(a, b)k).
Покажем, что оператор [Ф' (а, Ь)]-1 существует и непрерывен. В самом деле, пусть (h, ^ — произвольная точка пространства XxY и Ф' (a, b)(h, k) — (h, k). Это значит, что h = h, F'x(a, b)h-\-+FY(a, b)k = k. Отсюда FY(a, b}k — k — F'x(a, b)h, и так как [Fy(a, &)]~l существует, то
k=[Fy(a, b)]'1 (k—F'x (a, b)h).
Таким образом, точка (h, k) однозначно определяет точку (h, k), причем ясно, что (h, k) зависит от (h, k) непрерывно. Это означает, что существует [Ф' (а, Ь)]-1, являющийся непрерывным линейным оператором.
По теореме об обратном операторе найдутся окрестность и точки (а, Ь) и окрестность v точки Ф (а, b) = (a, F (а, &)) = (а, 0) такие, что Ф взаимно-однозначно отображает и на v, причем обратный оператор Ф-1 дифференцируем на v. ,
Так как отображение Ф не меняет первой координаты, то обратное отображение также ее не меняет и, следовательно, Ф-1 (х, «/) = = (х, ф (х, г/)), причем функция ф (х, у) дифференцируема на v. Для (*, у) € v имеем
(х, z/) = (Фоф-i (х, «/)) = Ф(х, ф(х, z/)) = (x, F[x, ф(х, I/)]),
откуда F[x, ф(х, у)\ — у. Полагая в последнем равенстве z/ = 0, что возможно, поскольку v есть окрестность (а, 0), получим
F[x, ф(х, 0)] = 0, х£л,х(у).
Поэтому, положив G = jix(v), в качестве /(х) можно взять ф(х, 0). Так как ф(х, 0) дифференцируема, то и /(х) дифференцируема. Наконец, поскольку Ф-1(а, 0) = (а, Ь), имеем /(а) = ф(а, 0) = &. Ц
Теорема 2. Пусть в условцях теоремы 1 отображение F дифференцируемо р раз в Н. Тогда f(x) дифференцируемо также р раз в G.
Доказательство теоремы опускается.
2. Приложения теоремы о неявной функции.
Изменение решения при изменении уравнения. Рассмотрим пространство C'[G, X] функций /(х), определенных на некоторой области G пространства X и принимающих значения из этого же пространства, причем функции / (х) дифференцируемы 218
и f(x), У (х) непрерывны и ограничены по норме. Положим ||/Ц = = sup (II/(X)II+ 11/' (х)||). Тогда C'[G, X] есть ЛНП.
G
Рассмотрим уравнение / (х) = 0, xgG, /£[G, X]. Предположим, что /о(хо) = О для некоторого x0£G, f0£C'[G, X] и оператор /о (х0): X —> X имеет обратный. Тогда справедлива следующая теорема.
Tte о р е м а 3. Существуют такие постоянные б > 0, е > 0, что для любого f£C'[G, X] такого, что ||/ — /0||< б, уравнение /(х) = 0 имеет решение х—х0 + ^.х, где ||Дх||< е, причем если то Дх—> 0.
П Будем рассматривать / (х) как функцию х € G и / g С [G, X], т. е. / (х) = Ф (/, х). Из построения функции Ф следует, что Ф(/, х) и ФД/, х) = /'(х) непрерывны.
По предположению, /о(хо) = О и [У (х0)]-1 существует. Это значит, что Ф(/о, хо) = 0 и [ФД/о, Хо)]"1 существует. В силу теоремы о неявной функции для некоторых б > 0 и е > 0 уравнение
Ф(/о + Д/, хо + Дх) = О
при ||Д/||< б имеет решение х„ + Дх, т. е. /(х) = 0, / = /0 + Д/, х = х0 + Дх, где ||Дх|| < е; при этом если б—>0, то ||Дх||—>0. Ц
Применение к собственным элементам. Рассмотрим прямую сумму //1 = Н@R, где Н — вещественное гильбертово пространство, R—числовая прямая; каждый элемент из имеет вид (х, t), х£Н, t£ R.
Пусть / — нелинейный оператор, определенный на Hit принимающий значения в том же пространстве и заданный равенством
/(Л; х, /) = (г/, »,
где у = Ах—tx£H, т=<х, х> —1CR, и Л —вполне непрерывный, самосопряженный линейный оператор из L(H, Н).
Уравнение / (Л; х, t) — 0 имеет вид
Ах — tx — 0, <х, х> — 1,
т. е. t — собственное значение, а х —соответствующий нормированный собственный элемент оператора Л. Если (х, t) получает приращение (Дх, ДО, то / (Л; х, /) получает приращение
(ЛДх —/Дх—хД/ —Д/Дх, 2<х, Дх> + <Дх, Дх>).
Главная линейная часть этого приращения есть
6/Я1 (Л; х, t, Ах, Д/) = (ЛДх —/Дх—хД/, 2<х, Дх».
Следовательно, /нДЛ; х, /) есть линейный оператор из L(Hit Н^, переводящий (Дх, Д/) в (ЛДх— /Дх—хД/, 2<х, Дх».
Если /„ — простое собственное значение оператора Ло и х0 — соответствующий собственный элемент, то существует обратный
219
оператор /н,(А0- х0, О)-1, т. e. для любого (у, х)^Нх уравнение А0Ах — t0Ax —x0At = у, 2<х0, Ах> = т (1)
имеет решение (Лх, А/) и это решение единственно.
В самом деле, Ах = ах0 + (Ах)1, где а + <Ах, х0> и <(Ax\ хо> = 0. Аналогично, у = Ьха + уц где Ь=(у, х0> и <z/n х0> —0. Далее, так как (Ао —/о/)хо = О, то ’
(Ао Ах — 0 Ах) — х0 А/ = (Ао —Л /) (Ах)г — ха Д t и
<(А0 (Ах)х, Хо> = <(А0 /0/) (Дх)1> = 0,
откуда и из уравнения (1) получаем
Ио ^/) (Д*)1= Уг> (2)
AZ =— Ь —— (у, х0>, 2а —х. (3)
Так как правая часть уравнения (2) ортогональна х0 (т. е. ортогональна всем собственным элементам, отвечающим собственному значению /0), то это уравнение имеет единственное решение, ортогональное х0:
(Ах)1 = (А0 Ш1У1= Ио ^o^)i1 [у <У> Х<Ф х0],
где через (Ао—V)i обозначен оператор А0 — taI на'подпространстве элементов, ортогональных х0.
Итак, уравнение (1) при любом, (у, х)^Нг имеет решение
Ах = у х0 + (Аа — [t/ — <z/, х0> х0], •
А< = — <у, х0>.
Отсюда следует существование оператора У'н,(А0; х0, О)]”1-
В силу теоремы 3 найдутся постоянные б > 0 и е > 0 такие, что при || ДА || <6 существуют собственное значение/0 4-А/и нормированный собственный элемент х0 + &х оператора А — А04-АА, т. е.
[(Ао 4- А А) — (t„ 4- AZ) I] (х0 4- Дх) = 0, <х0 4- Дх, х0 4- Лх> = 1, причем при jx||4-|A^| < е такое собственное значение и собственный элемент единственны.
У равнение, зависящее от параметра.
Теорема 4. Пусть у — у(t, х) есть функция элемента х£Х и числового параметра t с областью значений в том же пространстве X; далее, функция y(t, х) дифференцируема п раз по t и х и при t = t0 уравнение y(t0, х) = 0 имеет решение х = х0, причем существует оператор [y'x(t0, х0)]-1. Тогда существуют постоянные б > 0 и е > 0 такие, что при j t —101 < б уравнение
У У, х) = 0 (4)
имеет, и притом единственное, решение x — x(t) такое, что || х (0 — х0||< е. Это решение x(t) как функция t дифференцируемо п раз.
220
Сформулированная теорема есть непосредственное следствие теоремы о неявной функции.
Пример. Пусть А (/) — вполне непрерывный линейный оператор из L (Я, Я), причем А (/) как функция t дифференцируема п раз и оператор Л (/0) имеет простое собственное значение Хо с соответствующим нормированным собственным значением х0:
Л (/о) *о—Хохо = 0.
Рассмотрим прямую сумму = и определим функцию Ф (/; xf X), где (х, Х)£/7ф1К, Ф (t\ х, Х)£Яф&, с помощью равенства
Ф G; х, X) = (A(Z)x—Хх, <х, х>— 1).
Уравнение для* нормированного собственного элемента х (t) и собственного значения X (?) оператора A (t) имеет вид Ф (/; х, Х) = 0. Так как функция А (/) дифференцируема п раз по t, то Ф (/; х, X) также и раз дифференцируема по Как и выше, убеждаемся, что существует Ф (Zo; х0, Хо)1 . Но тогда
|_О (X, Л) J
применима теорема 4 и, следовательно, уравнение Ф (/; х, Х) = 0, т. е. уравнение
Л(/)х—Хх = 0, <х, х>=1, (5)
имеет решение (х(/), X (/)), которое является дифференцируемой п раз функцией параметра /.
У равнение в вариациях. При соблюдении условий теоремы 4 решение х(<) уравнения (4) есть дифференцируемая по t функция параметра t. Назовем вариацией 6х функции x(t) ее производную х' (t) по t при / = /0, т. е. = . Соответственно
для у~у(1, х) имеем =
Уравнение y(t, х(/)) = 0 есть тождество, и дифференцированием его по t получаем
^У<1, x(t)) + fxy(t, x(0)x'(0“0.
При i = t0 имеем
Ьу + у'Лв, хо)бх = О. (6)
Это уравнение называется уравнением в вариациях для исходного уравнения y(t, х) = 0.
Так как [y'x(ta, х0)]-1 существует, то
8х= — [y’x(ta, Хо)]-1^. (7)
Уравнение
(Л —%/) Ах + АЛх — АХх = 0 можно, например, считать уравнением в вариациях для уравнения (5), если заменить АЛ, Ах, АХ соответственно на 6Л, 6х, 6%:
8х — — (А — АЦг1 (бЛх — бХх), 6Х = <бЛх, х>.
§ 6. КАСАТЕЛЬНЫЕ МНОГООБРАЗИЯ И ЗАДАЧИ НА ЭКСТРЕМУМ
1. Касательные многообразия. Рассмотрим отображение <р: X—>У, где X и Y—банаховы пространства. Пусть М—множество точек х € X, удовлетворяющих уравнению ф (х) = 0. Если отобра
221
жение <р непрерывно дифференцируемо в некоторой окрестности точки х0 б М, то многообразие М называется гладким в окрестности точки ха. Многообразие, гладкое в окрестности каждой своей точки, называется просто гладким. Если оператор ф' (х0) отображает X на все Y, точка хй называется правильной. В дальнейшем будем считать, что х0 — правильная точка. Пусть
Т„ = кег ф' (х0) = {h £ X | ф' (х0) h = 0};
То —подпространство пространства X. Множество Тх<> = х0 + То назовем касательным многообразием к множеству М в точке х0. Это замкнутое линейное многообразие, проходящее через точку х0.
Рассмотрим фактор-пространство Х/То. Если элементы и й2 принадлежат одному классу Т £ Х/То, то ф' (х0) hr = ф' (х0) h2. Поэтому оператор ф' (х0) с помощью равенства
АТ — ф' (х0)h, h£T
порождает линейный оператор A: X/T0—>Y, причем легко видеть, что А отображает XlTa снова на все Y и притом взаимно-однозначно. Кроме того, А—непрерывный оператор. В самом деле, пусть Т„-+Т. Тогда существуют последовательность {hn}, hn£Tn и элемент h£Т такие, что hn->-h (см. § 1 гл. II), откуда
ЛТ„ = ф' (х0) h„ ф' (х0) h = АТ. '
По теореме Банаха о гомеоморфизме оператор A-1: Y—>Х/Тй, обратный оператору А, также является линейным,непрерывным оператором.
Теорема 1. Всякой точке х гладкого многообразия М, имеющего правильную точку х0, можно отнести точку х касательного многообразия Тх0 и, обратно, всякой достаточно близкой к х0 точке x£TXli можно отнести точку х£М так, что расстояние ||х—х|| между соответствующими точками есть величина высшего порядка малости по сравнению с расстоянием точек х и х до точки касания х0. Это соответствие, вообще говоря, неоднозначно.
□ Пусть xgM. Положим х = х0 + «. Имеем ф (х0 + «) = ф (х0) = 0, откуда
О = ф(хо + ы)—ф(х0) = ф' (х0)« + е(ы)
и, следовательно, ф' (х0) м=— е (и), где Це (и) || = о (|| и ||). ПустьТ—класс фактор-пространства Х/Т^, которому принадлежит и. Тогда АТ — = ф'(х0)ы = —е(ы) и Т = — А-*е(и), откуда ||7,|К||А~1||-||е(м)||. Поскольку ЦТ||= inf||^[|, найдется элемент |£Т такой, что
||М<2||Т||<2|| А-1 Ц-|]е (u)||. (1)
Так как и£Т и £€_Т, то и—%£Т0 и, следовательно, х = х0 + +(«—1)$ТХо. Точку х мы и поставим в соответствие точкех. При
222
этом в силу (1) имеем
||х-х|| = ||^|| = о(||и||) = о(||х-х0||).
Пусть теперь х= хй-\-Ь£ТХо. Будем искать соответствующую точку х£М в виде х=лг0 + й + ?; и, следовательно, £ должно удовлетворять уравнению ф(хо4-Л + £) = О, или эквивалентному уравнению
Т = Т-Л-1ф(х0 + Л + ^). (2)
Это уравнение для пары (|, Т), где %£Х, Т£ Х/Тв, будем решать методом последовательных приближений. За начальные приближения примем |о = О и То. Тогда 7\ = — Л-1ф (х0 + й) (То —нулевой элемент пространства Х1Т^. Выберем BiST’i так, чтобы
|1М<2||ТЛ<2М-1||.||ф(хо + /0[|.
Но
ф (х0 + h) = ф (х0) +.ф' (х0) h + ех (/г) = ех (й),
где Цех(/i)||=o(||h||), так как ф (х0) = ф' (ха)h = 0 (ведь ха€М и h £ То). Таким образом,
||В1||<2||Л-1||.(|е1(Л)||.
Возьмем г>0 настолько малым, чтобы ||e£ (й)|| < 4д^з£д • ДМ при ||/i||^r. Тогда ДВ11К г/2.
Пусть Th (/ = 0, 1, ..., п — 1) уже построены. Положим
T^T^-A-^X'+h H-Ux) (3)
и выберем так, чтобы ||ln —< 2||Т„ —Т„_1||. Уравнение (3) преобразуется к виду
. Т„ = Л-1(ЛТ„_1)-Л-1ф(х0+/г + ^_1) или к виду
Тп = - Л-1 [ф (ХО + h + Vi) ~ф' (ха) Vi],
так как ЛТ„_1 = ф'(ха)^„_£ в силу определения оператора Л.
Аналогично,
Tn-i = — А-1[ф(х0 + /г + ^_г)-ф' (ха)В„_2], откуда
тп—тп _ 1 = — Л -1 [ф (х0 + h + ln _ i) — ф (х0 + h +_ а) — Ф (Хо) (Ви-1 5л-г)]
и, следовательно,
11^-^-1й<2||Тп-Т„_£К2||Л-1||||ф(х04-/г + и1)-- ф (Хо + h +_ а) — ф' (Хо) (|„ _ i — 1п _ а )||.
223
Но
Ф (х0+Л +1„_1) — ф (х0 + h 4- ?я_2)—ф' (х0) Й„-1 —5„-») = = ф' (x0 + /i + E„_2)(?n_i— ?п_2) + ег g„_2) —
-ф' (х0) (£и-1 -Л-2) = [ф' (xj + Л+1„-2)—Ф' (*<,)] (£„_f—£„_,) +
+ e2(^-i-ln-2),
где J e2(5n_i-5n_2)|| = o(||5„_I-gn_2||). Если
и, следовательно, £Л-2||^2г, то при достаточно малом г : имеем
Йе2 (£»-1 £»-«) II < § || Л “11| ’ Я>л-4 !•
Будем считать также г настолько малым, чтобы в силу непрерывности ф' (х) было выполнено неравенство
||ф (х0-|-Л + Вп-2) ф (х#)|| < s||л~1 и *
Тогда
IH,-Uill<2M-i||(h' (хо+л+1„_2)-ф' (х0)||х хП„_1-UsIl+llM^-i-Ua)ll) CylUx-Я.
откуда
ИМ=11^+&-Л)+ • • • +(L-U!)K
<11М(и4-•• <2||^||<2Х.«г,.
Итак, для всех п имеем
Я5„||<Г, ll^-UiKlllUx-Ud-
Поэтому последовательность {О удовлетворяет условиям Коши и, следовательно, существует Пш|я = ^Х. Соответственно Тп—>
—> Т € Х/То и, переходя к пределу в равенстве (3) получаем
Т = 7’-Л-1ф(Хо + Л + ^),.т. е. ф(хо + /г + ?)=О.
Положим х = х04-/г + £- Так как
||х —х|| = Я(х04-Л+В) —(х0 + М=11В|1=я = IimHnK2g1||<2||4-4.||ei(ft)||,
IIX — X Я = О (II h II) = о (II х — «о II) •
Теорема полностью доказана.
Замечание. Предположим, что X есть прямая сумма Т0@Хв подпространства То и некоторого дополнительного подпространства Хо. Тогда теорема 1 допускает следующее усиление.
Теорема Г. Если в условиях теоремы 1 дополнительно предположить, что Х = 7’офХо, то при достаточно малых h существует
224
гомеоморфное отображение х04-й—*х0Ч-й + ?(Л). некоторой окрестности точки хе в касательном многообразии Тх„ на некоторую окрестность этой же точки в многообразии М, причем 1(h)— непрерывно дифференцируемая функция и I (0) = £'(0) =0.
Доказательство, легко получающееся с помощью теоремы о неявной функции, рекомендуется провести самостоятельно.
2. Пространства, линейные в малом. С понятием касательного многообразия связано понятие линейного в малом пространства, важное для некоторых исследований.
Пусть X, У— метрические пространства; ф: X —> Y — гомеоморфизм X на Y. Отображение ф называется почти изометрическим в точке х0 £ X, если для любых двух точек xt и х2 из некоторой окрестности точки х0
P(Xi, х2)(1-е)<р(ф(х1), ф(хг)Хр(х1( х2)(1 +е), где 8—+0 при р(хп х0)+р(х2, хв)—*0.
Пример. Пусть М —гладкое многообразие в X, заданное уравнением ф(х)=0, и ТХо—касательное многообразие к М в правильной точке х0£М. Предположим, что Х = ТвфХ0. Тогда для достаточно малых h отображение 'ф(хо+^)=хо+й+£(й), фигурирующее в теореме Г, является почти изометрическим в точке х0.
В самом деле, пусть х^, x2gTXo, х^х^-^Н;, где г достаточно
мало. Тогда
Ф (х2)—ф (*!) =ft2—Л1-Н1 (М—В (ML откуда
II II -II5 (h2) - g (MKII ф (х2) -ф (хх)|1 <|Л8-М+5 (h%) - g (М‘ (4)
В силу теоремы Г g' (А) непрерывно зависит от h и g' (0) ^=0. Поэтому || g' (Л)1К < 81 (г)» где 8Х (г) —> 0 при г —> 0. Далее, имеем
III (hz) -g (М = 11 Г (hl) (hz-hj 4-0 (h2 <
<111' (MII-l!^-^ll+H(/i2-/i1)||<8l(r)||^-/r1|i+ _|_8з (г)ЦЛ2—Лх|| = е(г)Ц ^H,
так как || co (h2 — /и)[| = о (|| h2 — &i||). Но тогда из (4) следует
II h2-ht ||(1 -г (г)) ^[| ф (Л2) — ф (Лх)|| <11^-^ Ц<1 + е (г)),
и так как ||Л2—Л1В=||х2—хх Ц, то отображение ф является почти изометрическим.
Если каждая достаточно малая окрестность произвольной точки х метрического пространства X допускает почти изометрическое отображение на окрестность нуля некоторого банахова пространства У, то пространство X называется линейным в малом.
Рассмотренный пример показывает, что в банаховом пространстве всякое гладкое многообразие, все точки которого правильные, является линейным в малом.
Понятие дифференциала распространяется на отображения линейных в малом пространстве. Пространства допустимых линий в ряде задач вариационного исчисления являются пространствами, линейными в малом, и вариации рассматриваемых в них функционалов дают примеры дифференциалов функций, определенных на множествах линейных в малом пространств.
225
3. Задачи на экстремум. Применим некоторые из введенных выше понятий к вариационным задачам. Рассмотрим отображение f: X —* R, где X — вещественное банахово пространство. Точка х0£Х называется точкой локального минимума (максимума) функции f(x), если найдется окрестность их> точки х0 такая, что f(x)~^f (х0) (соответственно / (х) f (*о)) Для всех х£иХо. Точки локальных минимумов и максимумов называются точками экстремумов.
Теорема 2. Если х0—точка локального экстремума функционала f, дифференцируемого в этой точке, то f (х0)=яб.
□ В самом деле, f (x0)h — -^-tf(x0-\-th)^ ^ Но f(x0 + th) есть числовая функция вещественного аргумента, достигающая экстремума при / = 0. Поэтому f (х0 + /й)| = /' (х0) Л = 0 при любом й и
at i=o
требуемое доказано, у
Рассмотрим теперь задачу на условный экстремум. Пусть дано отображение q>: X ->-Y и /—функционал, определенный на X. (Тогда х0 £ М = {х|<р (х) = 0} называется точкой условного минимума максимума) функционала f при условии ср (х) = 0, если найдется окрестность иХо точки х0 такая, что / (х) f (х0) (соответственно Для всех х£МГ|ил0.
Теорема 3. Если в правильной точке х0 гладкого многообразия М функционал f, дифференцируемый в окрестности этой точки, имеет условный экстремум, то существует линейный функционал l£Y* такой, что F' (х)=0 для функционала F = f—Хер.
□ Покажем сначала, что /'(х0)й —0 для й£Т0=»=кегср' (х0). В самом деле, пусть h£Ta и f (х0) й = с=И=0. По теореме 1, при достаточно малых |/| точкех0+#1 соответствует точка хо-Нй+п(О £М такая, что ||ц(/)|| = о (РI)- Тогда
f (Хо + th + V (t)) - f (Х0) == f (Х0) (th + V (t)) + CO (t) = = tc + f (X0)o(/)+® (t).
При t—>-0 сумма f (x0) v (t) 4- co (t) есть величина высшего порядка малости по сравнению с t и поэтому знак разности /(xo + ^/i + v(O)—/(х0) совпадает со знаком ct, так что при перемене знака t эта разность меняет знак. Но тогда точка х0 не может быть точкой локального экстремума. Следовательно, с=0, т. е. f (х)й = 0 для всех h£T0. Если ht и й2 принадлежат одному классу Т СХ/Т0, то f (х) hy — f (х0) h2 и однозначно определен функционал Х(Т)=Г(х0)й, h£T.
Для любого h$T имеем
1х(П1 = 1/' (Хо)й|<цг (x0)HM, откуда
1х(П|<|1/' Wll-inf \\h\\ = \\f (х0)||• ||Т.
Лет
Следовательно / (Г) —непрерывный линейный функционал, определенный на Х/То. Пусть h — произвольный элемент пространства X и Т — класс, содержащий h. Как мы видели выше, Т=Д’Чр' (х0)Л. 226
Поэтому
f (х0)/г = хСО = х[Л"1ф' (хв)Л] = (% о Л-Х)ср' (x0)/i.
Так как Л-1: Y —>Х/Тй и %: Х/Та —>R, то хоЛ-1 = /^У* и предыдущее равенство можно записать в виде
{f (*0) —Цф' (хо)]}й«=О
или в силу произвольности h в виде
Г (*о) —Цф' (*«)] = 0-
Пример. (Изопериметрическая задача.) Будем искать экстремум функционала f (х) при условиях ф,(х) = 0 (4=1,2, ..., л), где f и ф/ — непрерывно дифференцируемые функционалы, определенные на X. Пусть экстремум достигается в точке х0, правильной относительно отображения ф: X —> IRn с координатными фУнкЦиями Фг По теореме 3, существует линейный функционал такой, что
Г («о) —1 [ф' («о)] = о, или f (х0) — 2 <хо) = 0. i = i п
так как I [<р' (х0)] = У, 1/ф; (х0). Мы пришли к правилу множителей Лагранжа. ; = 1
§ 7. ИНТЕГРИРОВАНИЕ АБСТРАКТНЫХ ФУНКЦИЙ
Для того чтобы определить понятие интеграла от отображения f: E—+Y, где X и У—некоторые множества и ЕсХ, на X приходится налагать иные ограничения, чем при введении понятия дифференциала и производной отображения f. В частности, линейность множества X не играет при этом роли.
Интегралы J f dx можно вводить по-разному. Мы рассмотрим Е
здесь метод введения интеграла от функции со значениями в банаховом пространстве, принадлежащий С. Бохнеру и являющийся естественным распространением на векторнозначные функции метода Лебега построения интеграла от вещественной функции вещественного аргумента.
1. Измеримые функции. Пусть X — множество элементов некоторой природы и Y—банахово пространство. Отображение /: Е —>У, где Ес.Х, будем называть абстрактной векторной функцией. Если же Y = L(X, У), где X и У —банаховы пространства, то отображение f будем называть абстрактной операторной функцией.
Предположим, что на X задана а-алгебра А и на А —мера ц, причем не обязательно р(Х)<оо (см. §2, гл. I). Если р(Х) = оо, то будем предполагать, что существует последовательность множеств
{AfB}cA такая, что Х = и Мп и р (2И„) <оо для любого и. Будем 1
называть тройку (X, А, р) пространством с мерой, а множество Е С А — измеримым. Примером пространства с мерой может служить числовая прямая R, где А—совокупность всех измеримых по Лебегу
227
множеств конечной или бесконечной меры и роль Мп играют ОТ' резки [—п, и]. В дальнейшем для сокращения, если не возникает двусмысленности, пространство с мерой будем обозначать просто X.
Абстрактную функцию f: E-^-Y (векторную или операторную) назовем ступенчатой (или простой) на Е, если
f (х) —
Ci при х£Е; (i=sl, 2........п),
О при х£Е\ U Е;, i = 1
(1)
где все Е( измеримы, имеют конечную меру и E^Ej =0 при i^= j• Легко убедиться, что ||/(х)||—измеримая скалярная функция для любой ступенчатой функции f (х).
Абстрактная функция /(х), определенная на измеримом множестве Е, называется сильно измеримой, если существует последовательность {fn (х)} ступенчатых на Е функций такая, что при п—> оо ||/ (х) — f„ (х)|| —> 0 для почти всех х£Е. Из неравенства |||/(х)||—Ип(х)|||<||/(х)-/п(х)||, справедливого при любом х$Е, следует, что норма ||/(х)|| для сильно измеримой функции /(х) измерима как предел почти всюду сходящейся последовательности (|| fn (х)||} измеримых функций. Легко проверить, что линейная комбинация сильно измеримых на Е функций также сильно измерима.
2. Интеграл Бохнера. Пусть / (х) — ступенчатая- функция, определенная равенством (1). Полагаем по определению*
п
(x)dx= S , (2)
Без труда проверяется, что
$ [а/ (х) + Pg (х)] dx = a J f (x) dx4- 0 J g (x) dx
E EE
для любой линейной комбинации a/(x)+0g(x) ступенчатых на Е функций / и g. Так же легко получаем, что
$/(x)dx <J||/(x)||dx
Е Е
для любой ступенчатой на Е функции /(х).
Пусть теперь /(х) — произвольная сильно измеримая на Е функция и {/„(х)}— последовательность простых функций, сходящаяся почти всюду на Е к /(х). Тогда |/(х)—/„(х)||—измеримая функция н имеют смысл интегралы $llf(x)-/„(x)||dx, конечные или равные Е
-f-оо. Предположим, что Ц/(х) —/n(x)Jdx—>0 при п—«-оо. Тогда Е
* Если надо подчеркнуть, относительно какой меры определяется интеграл, то будем писать / (х) dp (х).
Е
22В
последовательность J J Д- (x) dx l сходится в себе в смысле сходимости ( е J
по норме пространства У. В самом деле,
II $ fn(x) dx — J fm (x) dx = | J [/„ (x) - fm (x)] dx||<
< $ II fn (x) —fm (x)|| dx sc J II fn (x) — f (x)|| dx + E E
E
при n, tn—► oo. Так как пространство Y полное, то существует lim J f„(x) dx.
n E
Абстрактная функция f(x) называется интегрируемой no Бохнеру на Е, если она сильно измерима на этом множестве и если для любой последовательности простых на Е функций {ДДх)}, сходящейся почти всюду на Е к f (х),
JlfW- fn (x)|| dx —> 0. (3)
Е
В этом случае предел ,
lim$f„(x)dx, (4)
« Е
который, как показано выше, существует, называется интегралом Бохнера от f (х) на Е и обозначается j f (х) dx или J f (х) dp.
Е Е
Покажем, что интеграл Бохнера определяется однозначно, т. е. что предел (4) не зависит от выбора аппроксимирующей последовательности простых функций, удовлетворяющих условию (3). Пусть {/„(х)}и {/„(х)}—две последовательности простых функций, удовлетворяющих условию (3), и I — lim \ fn (х) dx, 7 = lim \ fn (х) dx.
п Е Е
Последовательность
/1 (х), А(х), /2(х), f‘(x), ..., f„(x), f„(x),...
также удовлетворяет условию (3) и потому последовательность $ Л(х) dx, $ Л(х) dx, J fa(x) dx, $ f2 (х) dx.$f„(x) dx, $ fn (x) dx, ...
E E E E EE
сходится к некоторому пределу /0. Но тогда 1 = 1 =1а и требуемое доказано.
Теорема 1. Для того чтобы f (х) была интегрируема на Е по Бохнеру, необходимо и достаточно, чтобы f (х) была сильно измерима на Е и ||/ (х)|| dx < оо.
Е
229
□ Необходимость. Пусть f (х) интегрируема на Е по Бохнеру. Тогда в силу самого определения интеграла Бохнера f(x) сильно измерима, и если fn(x) — любая простая функция из любой аппроксимирующей последовательности, то
$ II f (х)II dx < $ II t (X) (X)II dx + $ II fn (x)|| dx.
EE E
Так как ^ [|/(%) — /„ (x)||dx—> О и, следовательно, величина ограни-Е
ченная, a J \\f„ (x)||dx <о°, то и J ||/(х)|| dx < оо. Е Е
Достаточность. Пусть f (х) сильно измерима на Е и {fn (х)} — произвольная последовательность ступенчатых на Е функций такая, что ||/ (х) — /„ (х)|| —► 0 почти всюду на Е. Так как
то без ограничения общности можно считать, что \\fn (х)[|^||/(х)|| + 1, а следовательно, \\fn (х) —f(x)||^ 2||/ (х)|| +1. Но тогда по теореме Лебега J \\fn (х) —f (х)|| dx —> 0 при п~>оо, а это и означает инте-Е
грируемость на-£ по Бохнеру f(x). Q
Пример. Пусть X = R, р—мера Лебега линейных точечных множеств и /: [0, 1]—>Г—непрерывное отображение [0, 1] в банахово пространство V. Тогда / (х) интегрируема по Бохнеру на [0, 1]. i
В самом деле, во-первых, f (х) сильно измерима, причем в качестве аппроксимирующей последовательности ступенчатых функций можно взять
для х€[х(?>, хЭД,
где Хоп) = О < *1° < х(2л) < ... < х^ = 1 — любое разбиение отрезка [0, 1] такое, что A,„ = max (xJ+i—х<л))-^0 при п—>оо и х#1]. Очевидно,
11 f (x) — fn Wil—^0 при п—>оо всюду на [0, 1], что легко следует из равномерной непрерывности f (х) на этом отрезке, которая доказывается для векторных функций точно так же, как и для скалярных. Во-вторых, \\f (х)|| — непрерывная, а следовательно, измеримая и ограниченная на [0, 1] скалярная функция, так
что || f (х) || dx <оо. Поэтому в силу теоремы 1 /(х) интегрируема по Бохнеру, о
1
Заметим, что в рассматриваемом случае интеграл Бохнера J f (х) dx есть силь-о kn
ный предел интегральных сумм вида f (gjrt)) Дх^ и является, таким образом, * f=i
интегралом римановского типа.
Интеграл Бохнера обладает следующими свойствами:
1. Если f: Е —и g: Е —>У интегрируема по Бохнеру на Е, то и линейная комбинация af + $g также интегрируема на Е,
230
причем
2. Если на Е, то
J [а/ (х) + pcf (х)]dx= а J / (х) dx + р $ g(х) dx.
Е Е
т
Е = U Е;, |л (Е,- П Ej) = 0 при i=£j и f интегрируема
Е
Sn /(x)dx= 2 $ /(x)dx.
/ = 1£.
3. Справедливо неравенство J/(x)dx J||/(x)||d*-Е
Эти свойства, очевидные для конечнозначных функций, получаются в общем случае путем предельного перехода.
4. Интеграл Бохнера f (х) dx есть абсолютно непрерывная функ-
Е
ция множества, т. е. для любого е > 0 существует 6 > 0, зависящее лишь от е, такое, что |\/-(x)dx <е всякий раз, когда HczE
н
Это сразу следует из неравенства
солютной непрерывности интеграла Лебега от суммируемой на Е скалярной функции ||/(х)||.
5. Интеграл Бохнера f (х) dx есть счетно аддитивная функ-
Е
ция множества, т. е. если Е = и Е(, где все измеримы и ц (Ei П Ej) =. О при i =f= j, то
J f (х) dx = 2 J f (*) dx.
е i=lEi
В самом деле,
J f (х) dx— 5 $ / (•*) Ах
Е i=lEi
J f (х) dx tl
Е\ U Е. t — 1 1
< $ ||/(x)[|dx—»-О,
п
Е\ и Е; 1=1 1
[ п 1
так как р( Е\ U Е; —> 0.
Теорема 2 (Лебега). Пусть {fn (х)} — последовательность интегрируемых на Е функций, сходящаяся по норме к f (х) почти всюду на Е. Если почти всюду на Е выполнено неравенство ||/л(х)|]^ <||ф(х)||, где ф (х) — интегрируемая на Е функция, то f(x) также интегрируема на Е и lim J fn (х) dx = J f (*) dx.
n E E
231
□ Переходя, если необходимо, к подпоследовательности, можно считать, что ||/„ (х)—/ (х)]| < 1/2л+1; Пусть gn (х) — простые функции такие, что ||f„ (х) —gn (x)J < l/2n+1, и, следовательно, jg„(x) — f (х)|| < < 1/2", так что последовательность {g„(x)J- простых функций сходится почти всюду к f (х). Это означает, что f (х) сильно измерима. Далее, имеем
[If (x)||=litn||fn(x)|K<p(x)|| п
и потому
$||f (x)||dx<$||<p(x)||dx
ОО.
Е Е
Следовательно, по теореме 1, f (х) интегрируема на £. Наконец,
К / (х) dx— $ f„ (х) dx|< J Ilf (х) — fn (х)II dx, е е
итак как |f(х)—/„(х)||<2||ф(х)||, то $||f(х)—f„(x)||dx-+0 при
Е
п->- оо в силу теоремы Лебега для скалярных функций. Ц
Теорема 3. Пусть функция f: Е —*X интегрируема на Е и А^.Иу, Z), где Z—банахово пространство. Тогда *Af(x) интегрируема на Е и
J Af (х) dx= А ( J f (х) dx\ (5)
е \Е / (
Теорема 4. Пусть операторная функция A: E—^L(Y, Z) интегрируема на Е. Тогда для любого y£Y векторная функция g (х) = (Л (х)) у интегрируема на Е и
J (Л (х)) убх — ( J Л (х) dx j у. е \е J
(6)
□ Докажем теорему 4 (теорема 3 доказывается аналогично). Так как Л (х) интегрируема на Е, то она сильно измерима на этом множестве. Пусть {Л„(х)} —последовательность простых операторных функций, сходящаяся по норме к Л (х) почти всюду на Е. Тогда Ап(х)у есть, очевидно, ступенчатая векторная функция для любого y^Y и
|| Л (х) у - Л „ (х) у |К || Л (х) - Л „ (х) j J у || О
почти всюду на Е. Следовательно, Л (х) у сильно измерима на Е при любом у € Y. Далее, из интегрируемости Л (х) на Е следует, что
J Л (х) || dx < оо. Но тогда для у £ Y имеем
$ М (x)«/[|dx< $ Ц Л (x)||dx|| у|| < оо
Е Е
232
и в силу теоремы 1 А(х)у интегрируема на Е. Равенство (6), очевидное для простых функций, получается в общем случае путем предельного перехода. Ц
Обозначим через L(E, р, У) множество функций /: Е—>У, интегрируемых по Бохнеру на Е. Как мы отметили выше, L(E, р, Y) есть линейное пространство. Для функции f(x)£L(E, р, У) положим || /||= ||/ (х) || dp. Легко проверить, что так определенная норма Е
удовлетворяет всем аксиомам нормы, если отождествить две функции fug, совпадающие на Е почти всюду.
Теорема 5. Пространство L(E, р, У)—полное в смысле сходимости по норме и, следовательно, банахово пространство.
Доказательство этой теоремы почти такое же, как и в скалярном случае (см., например, [5] или [9]), и мы его опускаем.
Предположим теперь, что Х — [а, &], р—мера Лебега на числовой прямой и /(х) непрерывна на [а, Ь]. Тогда справедлива в обычной формулировке теорема о дифференцировании интеграла по верхнему пределу.
Теорема 6. Если функция f: [а, 6]—* У непрерывна, то
(7)
H/®d? = /(х). 'х х х+Ьх
□ Полагая g (х) = $ / (?) d?, имеем g (х + Дх) — g (х) = $ / (?) d?, а х
х + &х 1
и так как / (х) = $ / (х) d?, то отсюда следует, что
X Х + &Х
Пусть задано произвольное 8 > 0. Найдется такое 6 > 0, что ||/(х')—/(х")||<е при |х'—х*|<б. Но тогда, если | Дх| < 6, имеем
|g(x-|-Ax)—g(x)
Х + &Х
$ !!/(£)—/(*) II d?
1
Х + &Х
8.
lim d5.±Ax)-g(±)
Дх -> О
< |Дх\
Последнее неравенство означает, что g' (х) =
существует и что g' (x) = f (х). Н
Теорема 7. Если функция f: [а, Ь] —► У непрерывна и имеет непрерывную производную f (х), то ь
J /'(x)dx =/(/?)—/(а).
(8)
233
□ В самом деле, для любого линейного функционала IС Y* имеем
* ь
I § f' (х) dx _а
b b
= ^[Г (x)]dx=$A/[/(x)]dx.
а а
Но I [/ (х)] есть вещественная функция вещественной переменной с непрерывной производной и для нее
ь
а
Поэтому
- Ъ
I $f'(x)dx =/[/(b)]-/[/(fl)] = /[/(&)-M«)].
а так как это равенство верно для любого l^Y*, то ь
$r(x)dx=/(6)-/(a). а
3. Решение дифференциальных уравнений. Рассмотрим дифференциальное уравнение
Д ‘ (9)
где х и f(t, х)—элементы банахова пространства X и Ь}. Будем предполагать, что f (t, х) непрерывна по t и к^к функция х удовлетворяет условию Липшица
Utf, х2)[|<L||Xi-U (Ю)
Обозначим через Сх [а, &] пространство всех непрерывных функций х(0, где /£[а, Ь], a Введем в пространстве
Сх[а, Z>] норму, полагая ||х||с — max||х (t) ||. Вместе с X и Сх[а, 6] есть полное пространство. Это предложение доказывается совершенно так же, как оно было доказано для частного случая, когда X = R.
Рассмотрим наряду с уравнением (9) уравнение t
х (0 — х0 + / (т, x(T))dT, (11)
^0
Правая часть At(х) этого уравнения есть оператор, переводящий х==х(0 из Сх|70, ta4-6] в некоторый новый элемент того же пространства. Имеем
t
11Л[х(0]-4[!/(0]||= х(т)1 —
1Л.+ 6
5 *(т)]—Ж у СО] II dr.
234
Отсюда с учетом неравенства (10) получаем
to + b
Mt W — At(y) $ k(T)-t/(T)||dT<
<L6maxJx(0-!/(0ll = b6||x-t/||. (12)
Если L6<1, то согласно (12) оператор At дает сжатое отображение пространства Сх[£о, /04-6] в себя и, следовательно, существует, и притом единственное, решение уравнения (11).
Уравнение (11) равносильно уравнению (9) при начальном значении х (/0) = хи. Следовательно, уравнение (9) имеет единственное решение на отрезке |70, ^4-6] такое, что x(Q = x0.
В частности, при любом начальном значении х (а) — х0 это урав-нение имеет единственное решение x(t) на отрезке [а, а4-6]. Это решение можно продолжить на весь отрезок [а, 6]. В самом деле, если а4-й<6 и х(а4-6) = х1, то, повторяя тот же процесс, построим решение на отрезке [а 4- 6, а 4- 26] с начальным значением xt и т. д.
Примеры. 1. Если X есть «-мерное линейное пространство, то получаем обычную теорему существования для системы из «дифференцированных уравнений.
2. Если X—одно из пространств 1р, с, ти т. д., то получим доказательство существования решения соответствующих классов бесконечных систем дифференциальных уравнений.
Вернемся к дифференциальному уравнению с начальным условием
£=/(Л х), х(О) = хо
и равносильному ему интегральному уравнению (11)
t
х (t)—х0 — f (т, х (т)) dr = 0.
о
Обозначим левую часть уравнения (11) через F (х0, х(/)). Пусть функция x(t)£C? [0, 1]. Тогда F(х0, х(?))—оператор, отображающий прямую сумму [0, 1] в С*[0, 1]. Если f(t, х) есть dnf (t х)
дифференцируемая п раз функция от х, причем —-Л2—- непрерывна дхп
t
по (t, х), то х (/) —- $ / (т, х (т)) dr есть дифференцируемый п раз о
оператор из С^[0, Г] вС^[0, 1]. Отсюда следует, что F (х0, х(0) есть дифференцируемый п раз по x(t) оператор. Поскольку х0 входит в F в виде отдельного слагаемого, F есть дифференцируемая п раз функция в ХфС^[0, 1].
Если х—х(/) получает приращение Дх=Лх(0, то главная линейная относительно Дх часть приращения F (х0, х) имеет вид
t
F'x\x — Ах (f) — fx (т, х (т)) (т) dx. (13)
о
235
Правая часть равенства (13) есть оператор из С^[0, 1] в [0, 1].
Этот оператор имеет обратный. В самом деле, для любой y(t) из С? [О, 1] уравнение Fx&x — y(t), или
t
Ьх (0 — $ fx (т, X (т)) Дх (т1<1т = у (О
о
равносильно дифференциальному уравнению относительно &x(t): x(t))^x(t)+y(t) и Дх(0) = //(0).
Последнее уравнение имеет единственное решение в силу теоремы существования (правая часть линейна относительно Дх(0, и, следовательно условие Липшица относительно Дх(0 автоматически удовлетворяется). Это решение реализует обратный оператор Дх (/) — = Дх—[Я*]”1 y(t). Теперь к рассматриваемому уравнению можно применить теорему о неявной функции.
Решение х = х(/) уравнения (9) может рассматриваться как функция начального значения х0: х=х(/, х0), причем х(^,х0) дифференцируема п раз по х0.
В частности, если X есть n-мерное пространство, то получаем теорему о непрерывно дифференцируемой зависимости решения от начальных данных.
Упражнения
1. Пусть fx(x) и f2 (х)—функционалы, вообще говоря, нелинейные, определенные на открытом множестве G банахова пространства X и дифференцируемые nd Фреше в точке x0£G. Покажите, что g (х) = (х) /2 (х), а еЬли /2 (х0) О, то и й(х) = /1(х)//2(х) дифференцируемы в точке х0, и найдите выражения для производных функционалов g(x) и h (х).
2. Пусть {^ — стандартный базис пространства /2 и отображение f: 1±—► 12 за-1
1 + —
дается равенствами f (кеп) = X п еп (п = 1, 2, ...),/ (х) = 0 при х £ кеп.
Покажите, что f дифференцируемо в нуле по Гато, но не дифференцируемо в этой точке по Фреше.
3. Найдите d2f (х, Л), если /(х) = |]х[|, х£Я\{0}, где Я—вещественное гильбертово пространство.
4. Докажите симметричность трилинейной формы d {d [/ (х, Л), &], /}.
5. Пусть отображение f: G—> Я, где G—открытое множество сепарабельного гильбертова пространства Я, дифференцируемое по Фреше в точке x0^G. Покажите, ЧТО оо
d/(Xo. А)= 3 <Л. «<>
i =1 1
где f' (х0) — производная Гато по направлению орта е/.
6. Пусть X, У—ЛТП и G—открытое множество пространства X. Отображение f: G —> Y называется Ь-дифференцируемым (s-дифференцируемым) в точке x0£G, если существует линейный непрерывный оператор Lx : X—>У такой, чт0 /(xq + ^)-/(x0)-/LXo/i о
при t —>0 равномерно по/г£Л4, гдеЛ!—произвольное, но фиксированное, ограниченное (конечное) множество пространства X. Покажите, что если X, Y — ЛНП, то 6-дифференцируемость совпадает с дифференцируемостью по Фреше, a s-дифференцируемость—с дифференцируемостью по Гато.
ГЛАВА VII
ЭЛЕМЕНТЫ СПЕКТРАЛЬНОЙ ТЕОРИИ ОГРАНИЧЕННЫХ САМОСОПРЯЖЕННЫХ ОПЕРАТОРОВ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ
§ 1. САМОСОПРЯЖЕННЫЕ ОПЕРАТОРЫ
Если рассматривать линейные операторы, определенные в гильбертовом пространстве, то благодаря самосопряженности этого пространства и наличию в нем скалярного произведения элементов можно выделить класс операторов, обладающих особым свойством симметрии (или самосопряженности), и изучить операторы этого класса глубже, чем произвольные линейные операторы в произвольном банаховом пространстве. Эти операторы играют особо важную роль в анализе и теоретической физике, и их теории посвящена обширная литература.
1. Сопряженный оператор. Пусть Я —гильбертово Пространство и А—ограниченный линейный оператор, определенный на Я и принимающий значения в том же пространстве. Рассмотрим линейный функционал
/у(х) = <Ах, у>. (1)
Так как fy(x)~-линейный функционал в гильбертовом пространстве, то он имеет вид (%) = <%, у*>, где у* — некоторый элемент пространства Я, однозначно определяемый функционалом fy. Очевидно, что с изменением у меняется функционал fy, а тем самым и элемент у*, и мы получаем оператор у* = А*у, [определенный на Я и принимающий значения в том же пространстве. Этот .оператор А* связан с оператором А равенством
<Ах, у> = <х, А*у> (2)
и называется оператором, сопряженным с оператором А. Оператор А* однозначно определяется формулой (2). В самом деле, если для всех хну имеют место равенства
<Ах, у> = <х, А*уУ — {х, АЧуУ, то отсюда следует, что А*у = А{у для всех у, а это и означает, что А*= а;.
Легко видеть, что приведенное здесь определение сопряженного оператора формально совпадает с определением, данным в гл. IV для случая банаховых пространств, но там мы предполагали банахово пространство вещественным, в то время как гильбертово пространство является комплексным. Однако легко убедиться, что в комплексных пространствах остаются справедливыми теоремы о сопряженных
237
операторах, доказанные в гл. IV. В частности, Л* —ограниченный | оператор, причем I
||Л*|Н||Л||. ' (3) |
Найдем оператор, сопряженный с Л*; обозначим его Л**.
В силу равенства (2) для любых х, у £Н имеем
<А*х, у) = <у, Л*х> = <Лг/, х> = <х, Ау>,
откуда следует, что Л** = Л. Аналогично Л***=Л* и т. д.
Легко видеть, что:
(Л+ В)* = Л* + В*; (А,Л)* = ХЛ*; (ЛВ)* = В*Л*. •
2. Самосопряженные операторы. Линейный ограниченный оператор Л называется ограниченным самосопряженным (или эрмитовым) оператором, если А* = А.
Примеры. 1. В n-мерном унитарном пространстве, которое можно рассматри-вать как конечномерный аналог гильбертова пространства, линейные операторы можно отождествлять с матрицами (а^), элементами которых служат комплексные числа. Оператором, сопряженным с (а;#), служит (aki). Самосопряженный оператор есть эрмитова матрица, т. е. матрица, для которой = а^. В случае вещественной матрицы (а/&) условие самосопряженности сводится к ее симметричности. ।
2. Для оператора Фредгольма в L2 [0, 1] с ядром К (/, s) сопряженным one- ; ратором является оператор Фредгольма с ядром К (s, 0- Условие самосопряженности имеет вид К (/, s)=K (s, /). В случае вещественного ядра это условие переходит в условие симметричности. г
3. Рассмотрим в L2 [0, 1] оператор Л, относящий каждой функции х [0,1] функцию Ах = tx (t)£L2 [0, 1]. Легко убедиться в том, что этот оператор самосопряженный.
В дальнейшем слово «ограниченный» мы будем опускать. Из предыдущего следует, что если А —самосопряженный оператор и % —вещественное число, то ХЛ также самосопряженный оператор, и если А и В —самосопряженные операторы, то Л + В самосопряженный, । а ЛВ— самосопряженный оператор тогда и только тогда, когда one-раторы Л и В перестановочны. Наконец, легко показать, что если \ Ап Л в смысле сходимости по норме в пространстве операторов или в смысле точечной сходимости и все Л и —самосопряженные операторы, то Л также самосопряженный оператор.
Если мы рассмотрим <Лх, у>, где Л—самосопряженный опера- , тор, как функционал и от х и от у, то этот функционал, который мы обозначим Л (х, у), как легко видеть, удовлетворяет условиям
Л(ахх + Рх2, у) = аА(х11 у)+М(*2> У)> (х, у)=Л(у, х).
Такой функционал мы будем называть билинейной эрмитовой формой. Эта форма ограничена в том смысле, что I
|А(х, у)|<Сл|И1Ы. ]
где СЛ — некоторая постоянная (в рассматриваемом случае Сл = || Л ||).
Таким образом, каждый самосопряженный оператор Л порождает некоторую ограниченную билинейную эрмитову форму
А(х, у) = <Ах, у> = <х, Ау>.
238
Обратно, если дана ограниченная билинейная эрмитова форма А (х, у), то она порождает некоторый самосопряженный оператор А, удовлетворяющий равенству А (х, у) = <_Ах, у>.
В самом деле, зафиксировав в форме А (х, у) элемент у, мы получим линейный функционал отх. Следовательно, Л(х, у) = <х, у*>, где элемент у* определяется однозначно. Таким образом, мы получаем оператор А, определяемый равенством Ау = у* и такой, что <х, Ау> = А(х, у). Очевидно, Л—линейный оператор. Легко убедиться, что Л—ограниченный оператор. Действительно,
I <х, Лу>| = |Л(х, у)|^Сл||х||||у||.
Полагая х = Ау и сокращая на || Лу||, находим || Лу||^Сл||у||. Покажем, что Л — самосопряженный оператор. Для любых х, у имеем
<х, Лi/> == Л (г/, х) = (у, Лх) = <Лх, у>, откуда и следует, что А—А* и Л (х, у) —<Лх, у>.
3. Квадратичные формы. Рассмотрим билинейную эрмитову форму Л (х, у) и положим в ней у — х. Получим квадратичную форму Л (х, х), принимающую для всех х вещественные значения и такую, что
Л (ах+Ру, ах+Ру) =
= ааЛ (х, х) + ар Л (х, у) +арЛ (у, х) + ррЛ (у, у).
Такую форму Л (х, х) будем называть квадратичной эрмитовой формой, соответствующей билинейной эрмитовой форме Л (х, у). Если задана билинейная эрмитова форма Л (х, у), то тем самым задана и соответствующая квадратичная эрмитова форма Л (х, х). Верно и обратное: задание квадратичной формы Л (х, х) однозначно определяет билинейную эрмитову форму Л (х, у), соответствующую квадратичной форме Л (х, х). Эта билинейная форма определяется равенством
^(х,'у) = ~{[А(х1, xj —Л(х2, х2)] + i [Л (х3, х3) —Л(х4, х4)]},
где Xi — x + y, х2 — х—у и x3 = x + iy, х4 = х — iy.
Нетрудно показать, что квадратичная эрмитова форма Л (х, х) является ограниченной, т.е. | Л (х, х) | Сл || х |]2, в том и только в том случае, когда соответствующая билинейная эрмитова форма ограничена.
Пусть m=i inf <Лх, х> и М = sup <Лх, х>. Числа т и
И*н = 1
М называются нижней и верхней границами самосопряженного оператора Л. Покажем, что
|| Л || = max (| т |, | М |) == sup |<Лх, х>|.
*ц = 1
В самом деле, пусть ||х||= 1. Тогда
|<Лх, х>|<||Лх||||х||С||Л||||х|М1Л||
239
и, следовательно,
Аг[|у/« 1 .
уЛ) и м = у-Лг, получим
лагая А =
Сл= sup \<Ах, х> К || Л||.
11*11»»
С другой стороны, для любого у£,Н имеем <Ау, 1/>^Сл||р||2. Поэтому если г—любой элемент из Н, отличный от нуля, то, по-
1
|| Лг||2 = <Л (Аг), и> = -^-[<Л (Аг4-и), А?4-ы> —<Л (Аг — и), Аг—и>]< < 4 СА [|| Аг + и |Г +1| Аг - и ||2]=± СА [|| Аг ||2 +|| и ||2] =
=4СЛ [А2Ь112 + ^-ЦЛгГ]^Сл||г||||Лг||,
откуда || Лг||^Сл||г||, и, следовательно,
= SUP \<Ах> *>[• (5)
il*ll = i
Из неравенств (4) и (5) получаем требуемое равенство.
Из доказанного, в частности, следует, что если для самосопряженных операторов А и В при всех х С Н выполняется равенство <Лх, х> = <Вх, х>, то Л = В.
§ 2. УНИТАРНЫЕ И ПРОЕКЦИОННЫЕ ОПЕРАТОРЫ
Рассмотрим два специальных класса операторов в гильбертовом пространстве.
1. Унитарные операторы. Линейный оператор •{/ называется унитарным, если он отображает пространство Н на все Н с сохранением нормы, т. е. если
11^|| = ||х||. (1)
Легко видеть, что это отображение взаимно-однозначно, так как если t/xi=t/x2, т. е. U (хг — х2) = 0, то ||xi— х21| —1| (хг —х2)|| = 0, и, значит, Х1 = х2. Поэтому существует обратный оператор U~\ который, очевидно, также унитарен.
Далее, из равенства (1) имеем
<Ux, Ux> = Ц (7х||2 = ||х||2 = <х, х>, откуда
<U*Ux, х> = <х, х> = <£х, х>, где через Е здесь и в дальнейшем обозначен единичный оператор. Так как квадратичные формы операторов U*U и Е равны, то эти операторы совпадают*:
U*U = Е. (2)
Умножая это равенство слева на U и справа на £/-1, имеем
UU*^E. (3)
* Отметим, что для любого линейного оператора А оператор А* А является самосопряженным.
240
Отсюда получаем, что U* — U~1. Из равенства (2) также следует, что <£/х, Uyy=?<pc, уУ. Обратно, из условий (2) и (3) вытекает, что [/ — унитарный оператор, так как из них следует существование U'1 — U*, т. е. отображение Н на Н взаимно-однозначно, а также выполнение равенства
||t/x||2 = <t/x, Ux> = <U*Ux, х> = <х, х> = ||х||2,
т. е. U сохраняет норму элемента.
Примером унитарного оператора в координатном гильбертовом пространстве 1г может служить бесконечная унитарная матрица (и,-/), т. е. такая, элементы которой удовлетворяют соотношениям
оо оо
2 «,z^ = 6z/. (4)
«=1 1=1
Пусть даны линейный оператор А, действующий в гильбертовом пространстве, и унитарный оператор U. Оператор
B = U AU~X = U AU* (5)
называют оператором, унитарно эквивалентным оператору А. Из равенства (5) видно, что оператор, унитарно эквивалентный самосопряженному, также самосопряженный.
Легко проверить, что нормы унитарно эквивалентных операторов равны.
2. Проекционные операторы. Пусть L — подпространство пространства Н. Любой элемент х£Я можно однозначно представить в риде х = у + г, где y£.L, z_|_L. Полагая Рх=у, получим некоторый оператор, определенный на всем Н, область значений которого есть подпространство L. Этот оператор называется проекционным оператором (или оператором ортогонального проектирования на подпространство L) и обозначается также через PL. Докажем, что оператор Р есть самосопряженный оператор с нормой, равной единице, и удовлетворяет условию Р2 = Р.
Прежде всего Р — линейный оператор. В самом деле, если х, — = !/i + и х2-уг + z2, где ylt y^L, a z2 J.L, то
axj +0x2 = (az/x +pz/2) + (azf +₽z2),
где ayi+$y2£L, аз1+рг2 L, откуда
P (axi +Px2)— az/i A-^yt-ctPxi +₽Px2.
уТя.прр
hll2 = h + M2=<// + z, у + гу = |Ы2 + 1И1а
в силу ортогональности yn z. Следовательно, ||у||^||х||, т. е. ||Рх|| ^ЦхЦ для любого х. Отсюда ||Р||1. Так как для x£L имеем Рх = х и,- следовательно, ||Рх|| = ||х||, то ||Р||=1.
Покажем, что Р— самосопряженный оператор. Пусть х2 и х2— любые два элемента из Н, уг и у2—их проекции на L. Имеем <PXf, х2> = < z/±, х2> =-- <i/i, УъУ. Аналогично <xi, Рх2> = <Xi, у2У = = <#,, yty. Следовательно, <Pxi, х2> = <х1, Рх2>.
? № 3054
241
Наконец, Px$L для любого Поэтому Р2х — Р (Рх) = Рх для любого х£Н, т. е. Р2 — Р.
Покажем, что верно и обратное утверждение, а именно, что всякий самосопряженный оператор Р, удовлетворяющий условию Р2 — Р, есть оператор ортогонального проектирования на некоторое пространство L.
Рассмотрим множество L элементов вида у = Рх, где х пробегает все Н. В силу аддитивности и однородности оператора Р множество L есть линейное многообразие. Легко показать, что L замкнуто. В самом деле, пусть уп-+у0, yn£L. Так как yn£L, то уп = Рхп для некоторого хп£Н. Поэтому
Рув = Р'ха=>Рхп~уп.
В силу непрерывности оператора Р из уп —► г/0 следует Руп —+ Руй. Учитывая равенство Руп — уп, получаем уп-+Ру0. Следовательно, Уо — Руо и y9£L.
Из самосопряженности оператора Р и условия Р2 — Р имеем
<х —Рх, РхУ = <Рх-Р2х, х> = 0,
т. е. х—Рх | Рх. Теперь из самого определения подпространства L следует, что Р есть оператор проектирования на это подпространство, и требуемое доказано. Заметим также, что L состоит из тех и только тех точек х£.Н, для которых Рх = х.
Из доказанного, в частности, следует, что вместе с Р и 1 — Р также проекционный оператор.
Отметим несколько простых свойств проекционных операторов.. Два проекционных оператора Pt и Р2 называются ортогональными, если P1Pi = Q. Это условие равносильно условию P2Pi = 0, так как если РхР2 = 0, то (PjP2)* = P2Pi = 0, и обратно.
Для того чтобы проекционные операторы Р± и Р2 были ортогональны, необходимо и достаточно, чтобы были ортогональны соответствующие подпространства Lx и L2.
В самом деле, если PjP2 = 0, то для имеем
(х±, х2> —- <^РjXj, Р2х2> = <Р2РiXj, х2> — <0, х2> = 0.
Обратно, если Lf_]_£2, то P2x£L2 для любого и, следовательно, PiP2x = 0, т.е. PiP2==0.
Лемма 1. Для того чтобы сумма двух проекционных операторов PLi и PLi была проекционным оператором, необходимо и.достаточно, чтобы эти операторы были ортогональны. Если это условие выполнено, то
Р4, + Р1, = РL,+L,’
□ Необходимость. Пусть P = P£i4-Pia— проекционный оператор. Тогда
(Pl, + Pl»)* = Pl, + Р L? или = 0-
Умножая слева на Р£1, получим P^P^+Pl,Pl,Pl,~^ умножая теперь справа на PLl, имеем PlPl,Pl, ~ 0» откуда Р£аР£, = 0.
242
Достаточность. Пусть PLPla=PLPL=§. Тогда (Рц+Рцр— = Рц+Р1.2. Следовательно, Р^ + Р^ — проекционный оператор.
В силу условия РцР^—Ъ подпространства Lt и £2 ортогональны. Если х$Н, то
Px = PIx+Pix = x1 + x2CL1+^. (6)
Если, далее, х = х1 + *2 — элемент из L1 + ^2> то, учитывая равенства P£x2 = 0, PLX! — 0, получим
х - Xj + х2 — PtX! + PL хг =
= Р^ (Xi + х2) + РЛа (Xj + х2) = (PL, + Р£а) х. (7)
Из равенств (6) и (7) следует, что Р есть оператор проектирования на Lf + L2. И
Лемма 2. Для того чтобы произведение двух проекционных операторов PLi и PLa было проекционным оператором, необходимо и достаточно, чтобы операторы PLi и PL1 были перестановочны. Если это условие выполнено, то
Р i.tP 1.2 — Plihl,-
□ Необходимость. Так как P = Pr Р, —самосопряженный оператор, то ‘ ’
PlSl, ~ (РцРЛ* - P^Pi ~ Рг2рц-
Достаточность. Если РLPLi — Р\Р£|, то Р — Р^Р^—самосопряженный оператор. Кроме того,
(Р Р \^-^р р р р -Pl Pl ~р р \ L\ Li' /-i L\ Li L\ Li
и, следовательно, Р —проекционный оператор.
Пусть х—любой элемент из Н. Тогда
Рх = Р£1РЛах==Р£Р£1х
принадлежит и Lf и L2, т. е. принадлежит ("|L2.
Пусть теперь y^Lj^oL^. Тогда
ру^р^р^^р^у^у-
Все это означает, что Р есть оператор проектирования на Pi П Р2* ^1
Проекционный оператор Р2 называется частью проекционного оператора Pit если Р1Р2==Р2. Переходя к сопряженным операторам, убеждаемся, что это определение равносильно определению Р2Р1 — Р2. Из определения непосредственно следует, что оператор Pia является частью оператора PLi тогда и только тогда, когда подпространство Р2 есть часть подпространства Lv
Для того чтобы проекционный оператор РДа был частью проекционного оператора PLi, необходимо и достаточно, чтобы для всех х$Н выполнялось неравенство ||PLax||||PLtx||.
В самом деле, из Р£аР£х=;Р£ах следует
9*
243
Обратно, если это условие выполнено, то для любого xgLs имеем
и так как верно также неравенство ЦВ^хЦ^||х||, то ||PLlx|| = Цх||.
Отсюда
Кни/МИ2-и£1х||2-°,
и, следовательно, xZ.Lt. Поэтому PLaxZLt для любого х£/7 и, значит, PL,PLlx^PLx, т. е. PlPl^Pl^ что и требовалось доказать.
Лемма 3. Разность Pt—Р2 двух проекционных операторов есть проекционный оператор тогда и только тогда, когда Р2 есть часть Pt. Если это условие выполнено, то LPi_Pa есть ортогональное дополнение к LPa в LPi.
□ Необходимость. Если Pt — P2 есть проекционный оператор, то E — (Pt — Р2)=*(Е—Pi)4-Pa также проекционный оператор. Но тогда в силу леммы 1 имеем (Е — Р1)Р2 = 0, т. е. PtP2 = P2.
Достаточность. Пусть Рг есть часть Р4. Тогда Е — Pf и Р2 ортогональны и в силу леммы 1 оператор (E-P^-j-Pa —проекционный и, следовательно, оператор Рг — Р2 также проекционный. Из условия PjP2 = P3 следует, наконец, что Pf —Р2 и Р2 ортогональны. Но тогда в силу той же леммы 1 LPi^LPi_PiA-LPa. g|
§ 3. ПОЛОЖИТЕЛЬНЫЕ ОПЕРАТОРЫ. КВАДРАТНЫЙ КОРЕНЬ ИЗ ПОЛОЖИТЕЛЬНОГО ОПЕРАТОРА •
Самосопряженный оператор А называется положительным (Д>0), если он отличен от нулевого и его нижняя граница не отрицательна, т. е. если <_Ах, х> О для любого х£ Н и <Дх, х> > 0 хотя бы для одного х£Е. Говорят, что самосопряженный оператор А больше самосопряженного оператора В(Д>В), если А — В > 0. В этом случае говорят также, что оператор В меньше оператора А. Легко проверить, что введенное в множестве самосопряженных one -раторов отношение неравенства обладает следующими свойствами *.
1) из Л>Ви C~^D следует Д-f-C^B + D;
2) из 0 и а>0 следует аА 0;
3) из Д В и В^С следует А С;
4) если Д > 0 и Д-1 существует, то Д-1 > 0.
Далее очевидно, что А А* и Д*Д —положительные операторы для любого линейного оператора А, отличного от нулевого. В частности, Д2 > 0 для любого самосопряженного оператора А (Д =^= 0). Из последнего следует, что примером положительного оператора может служить оператор проектирования на подпространство положительной размерности.
* Неравенство А 5= В означает либо А > В, либо А = В.
244
Теорема 1. Произведение двух перестановочных положительных самосопряженных операторов А и В есть также положительный оператор.
А
□ Положим A = А2=^А1 — А1, Л„+1 = Л„ — А2п, ....
Покажем, что для любого п
0^Ап^Е. (1)
Для п = 1 это очевидно. Пусть неравенство (I) верно для n — k. Тогда
<Л|(Е —ЛЛ)х, х> = <(Е — ЛА) Акх, ЛАх>>0,
т. е. Ак (Е — Лй) 0, и аналогично Ак (Е — Лл)а 0. Поэтому
Ак+ г^АЦЕ- Ак} + Лл (E - ЛА)а > 0 и
Е-Ла+1 = (Е-Ла)+Л|>0.
Следовательно, неравенство (-1) верно для п = &4-Ь
Далее, имеем
At — Л1 + Л2 — Af + Al + А3 — ... = А} + Л] 4*... + Л„ 4~ Ля+$,
откуда 2 = Л^ —Л„+1< Л1 (так как Л„+1>0), т. е.
k=i
У <Акх, ЛАхХ<Лгх, х>. k- 1
оо
Следовательно, ряд 2 Млх112 сходится и ||ЛАх||—>0 при k—*оо. Поэтому
( Ак ~Ап+1х ► AjX.
M=i /
Так как В, очевидно, перестановочен со всеми Ак, то
<ЛВх, х> = ||Л||<ВЛ1х, х> = || Л || lim У <ВАкх, х> =
Л k=l
= || Л || lim 2 <ВАкх, Ллх>=^0. п k= 1
Из этой теоремы легко следует, что если {Лл}—монотонно возрастающая последовательность самосопряженных перестановочных между собой операторов, не превосходящих самосопряженного перестановочного со всеми Ап оператора В, т. е. Лх Л2 Ап .
то последовательность {Ли} сходится к самосопряженному оператору Л и Л В. Аналогичное утверждение имеет место и для монотонно убывающей последовательности.
В самом деле, рассмотрим самосопряженные операторы Сп=В — Ап. Эти операторы положительны, перестановочны и образуют моно
245
тонно убывающую последовательность. Следовательно, для т < п 5 операторы (Ст— Сп)Ст и Сп(Ст — Сп) также положительны, откуда 1
<С^х, ху (С тС пх, х> <(Сйх, х>.
Монотонно убывающая положительная числовая последовательность {<С„х, х>} имеет предел. К этому же пределу в силу полученных неравенств при п, т —» оо стремится и <.СтСпх, х>. Поэтому 1 при п, т—-> оо
ЦСдаХ C„x||2 = <(Cm Сп)2х, х> =
= <С^х, х> —2<СЛС„х, х> + <С2пх, х>—>0. <
Таким образом, последовательность {Спх}, а значит и последо- i вательность {Лпх}, для любого х сходится к некоторому пределу; j обозначим последний через Ах: Ах— lim Апх. Очевидно, что А — само- !
п
сопряженный оператор, удовлетворяющий неравенству А В, что и требовалось доказать.
Самосопряженный оператор В называется квадратным корнем из положительного оператора А, если В2 = А.
Теорема 2. Существует единственный положительный квадратный корень В из любого положительного самосопряженного оператора А, перестановочный со всяким оператором, перестановочным с А.
□ Не нарушая общности, мы можем считать, что А Е. Положим Во = О и ,
В„+1 = ВЙ+|(Л-В*), п — 0, 1, ... . (2)
Все операторы Вп, очевидно, самосопряженные и перестановочные с любым оператором, перестановочным с Л. В частности, ВпВт = — ВтВ„. Нетрудно проверить, что
Е - Вп+1 = ±(Е- Вп)2+4 (£ - Л) (3)
И
Bn+i - вп = 1 [(£ - В„_х) + (Е - В„)] (Вп - Bn.t). (4)
Из равенства (3) следует, что В„^Е для всех п. Легко убедиться и в том, что Вп^.Вп+1. В самом деле, для п=?0 это очевидно в силу неравенства Вг = А/2 ^>0 = В9. Далее, равенство (4) показывает, что Вп+1 — Вп > 0, если Вп — Вп_г 0. Следовательно, Вп < Вп+1 для всех п. Таким образом, {Вп} — монотонно возрастающая ограниченная последовательность самосопряженных положительных операторов. Согласно предыдущему, эта последовательность сходится к некоторому самосопряженному положительному оператору В.
Равенство (2) в пределе дает
В = В+ 4(Л-В2), т. е. В2 = Л.
24G
Наконец, перестановочность В с любым оператором, перестановочным с А, следует из того, что этим свойством обладают операторы В„. Таким образом, оператор В обладает всеми требуемыми свойствами, и существование положительного квадратного корня из оператора А доказано.
Пусть Bi—другой положительный квадратный корень из А, который перестановочен с А. Тогда В1В = ВВ1. Поэтому если х — любой элемент из Н и у — (В — Bj х, то
<Ву, у> + <В1у, у>~<(В A-BJ у, у> =
= <(В + В1)(В — В1)х, у> = <(В2 — В1) х, г/> = 0.
Поскольку В и Bj — положительные операторы, отсюда следует, что <Ву, у> = <В1у, у>=0. Так как В > 0, то В=»С2, где С —самосопряженный оператор, и, значит, ||Сг/||2 = <С2у, уу — <^Ву, у> = 0, откуда Су = 0. Следовательно, и Ву = С (Су) — 0. Аналогично Bji/=0. Но тогда
ЦВрс — Вх||2 = <(В — Btf х, х> = <(В —BJу, х> = 0, т. е. для любого х^Н имеем Вх = Вгх, и единственность квадратного корня доказана.
Пример. В пространстве Z-s [0, 1] для оператора А, где Ах (t) = tx (t), положительным квадратным корнем является оператор В, где Вх (0 = + V tx(t).
§ 4. СПЕКТР САМОСОПРЯЖЕННОГО ОПЕРАТОРА
1. Основные теоремы. Рассмотрим семейство операторов А% = = А—А£, где А —самосопряженный оператор и Л —комплексное число.
Из теоремы 2 § 5 гл. III следует, что если ||у а|< 1 (т. е. если |Х|>||А||), то к — регулярное значение оператора А и, следовательно, весь спектр оператора А расположен внутри и на границе круга | к | || А ||. Это верно для произвольного линейного
оператора, действующего в банаховом пространстве. Для случая самосопряженного оператора, заданного на гильбертовом пространстве, ниже мы более точно укажем область, в которой расположен спектр оператора.
Если А —самосопряженный оператор, то все собственные значения его вещественны, так как из равенства Ах=кх следует, что <Ах, х> = Л<х, х>, где оба скалярных произведения <Ах, х> и <х, х> вещественны. Далее, из условия А = А*, вещественности собственных значений и теоремы 2 § 4 гл. IV следует, что собственные элементы, отвечающие различным собственным значениям самосопряженного оператора, ортогональны.
Теорема 1. Для того чтобы точка к была регулярным значением самосопряженного оператора А, необходимо и достаточно существование положительной постоянной с такой, что для любого х^Н
||Ахх|| = || Ах —Хх||>с||х||. (1)
247
□ Необходимость. Пусть существует ограниченный оператор 7?х=Лх1 и ||/?jJ| = d. Для любого х£Н имеем
H = RvM<d||Лхх||, т. е. ИЛххД>=4-||х||, и необходимость доказана.
Достаточность. Пусть у = Ах—кх и х пробегает пространство Н. Тогда у пробегает некоторое линейное многообразие L. В силу (1) соответствие между х и у взаимно-однозначно, так как если Xt и х2 переходят в один и тот же элемент у, то Л (х£—х2)— — X (хх — х2) — О, откуда
ll*i-*2 К у IIA (*1-х2) II = 0.
Покажем, что L всюду плотно в Н. В самом деле, если это не так, то существует элемент х9$Н, отличный от нуля и такой, что <х0, */> = 0 Для любого y£L. Это значит, что <х0, Ах — кху = 0, откуда в силу самосопряженности А имеем <Лх0—Хх0, х> = 0, и так как это верно для любого х£Я, то Лха—Ххо = О. Но это равенство при х0, отличном от нуля, невозможно ни при комплексном к (тогда у самосопряженного оператора были бы комплексные собственные значения), ни при вещественном к тогда к —к и ||х0||^
7 || ^ХС ^*0 II — •
Покажем, наконец, что L замкнуто. Пусть {yn}cL, уп = А^х„ и Уп~* Уо- В силу (1) ,
II *« *тя II 7II II= 7II У» Ут 11-
Пос ле довательность {уп} сходится в себе и потому ||*/п —УтЦ—*0 при п, т —► + оо. Но тогда ||х„ — хя|р—*0 при п, т->-<х>. Из полноты пространства Н следует существование предельного элемента для последовательности {xn}: x = limxn. При этом Лхх —lim Лхх„=
= Нтг/„ = г/, т. е. y^L. п
Итак, L — замкнутое всюду плотное в Н линейное многообразие, т. е. L = H. Так как, кроме того, соответствие у = Л^х взаимнооднозначно, то существует обратный оператор х = Anly — R^, определенный на всем Н. Неравенство (1) дает
11адЧ*К||1А*||=7М
т. е. является ограниченным оператором и
Следствие. Точка к принадлежит спектру самосопряженного оператора А тогда и только тогда, когда существует последовательность {х„} такая, что
1|Лх„-Ьх„||<с„||х„||, с„ — 0 при п-*<х>. (2)
248
В неравенстве (2) можно положить ||х„||=1, тогда
|Лх„-Хх„ц^о, kJ=i. (3)
Теорема 2. Комплексные числа X = а + i0 (где 0 =/= 0) являются регулярными значениями самосопряженного оператора А.
□ В самом деле, если у = А^х = Ах—Хх, то
(у, х> = <Лх, х>—Х<х, х>, <х, у> — (у, х> — (Ах, х>—Х(х, х>. Отсюда
<х, у> — <у, х> = (Х — Х)<х, х> = 2t0Jx||», или
2|0|||х||2 = |<х, у> — <у, *>|<|<х, У>\ + \<У, х> | < 2||г/Ц||х|| и, значит,
Ы>101Й4 т. е. ЦЛхх||>|0|||х||. (4)
Чтобы завершить доказательство, достаточно использовать теоре-му 1. Н
Теорема 3. Спектр самосопряженного оператора А лежит целиком на отрезке \т, Af] числовой прямой, где т= inf (Ах, х>, и «il=i
М — sup (Ах, х>.
и «н=1
□ Из предыдущей теоремы следует, что спектр может лежать лишь на вещественной оси. Покажем сейчас, что вещественные X, лежащие вне отрезка \т, Afj, являются регулярными значениями. Пусть, например, X > М, d>0. Имеем
(Акх, х> — (Ах, х>—Х<х, х><Л1<х, х>—Х<х, х> = —-d||x||2, т. е. |<ЛдЛ, х> | > d|| х||2. С другой стороны, | (Акх, х> |<|| ЛЛх||||х||. Следовательно, || Лд,х||> J||x||. Огсюда следует регулярность значения X.
Аналогично рассматривается случай X < т.
Теорема 4. Числа т и М—точки спектра.
□ Докажем это, например, для числа М. Заметим, что если оператор Л заменить оператором Лд, то спектр сдвинется влево на р, а числа М и т заменятся на М— р и т —р. Мы можем поэтому, не нарушая общности рассуждения, считать, что 0^.т^. М. В таком случае (см. с. 239) А1 = || Л||. Докажем, что М есть точка спектра.
В самом деле, в силу определения числа М = || Л || существует последовательность элементов хп, || хп || = 1, такая, что (Ахп, хн> = = М —6„, 6„ —0 при п-^оо. Далее, || Лх„||^|| Л ||||хя|| —1| Л || —М. Поэтому
ЦЛхя-Мхя||2 = <Лхя-Мхя, Ахп — Мха> —
=Ц Лхя ||2 -2М (Ах„, хп> + Л421| х„ ||2 < М2 - 2М (М - 6„) + М2= 2Л16„, или
||Ax,-MxJ|<J/2M6„;
249
Следовательно, || Ахп — Л1х^ —* 0, || хп || =* 1. Остается использовать следствие из теоремы 1.
Следствие. Каждый самосопряженный оператор имеет непустой спектр.
Примеры. 1. Если оператор А есть единичный оператор Е, то его спектр состоит из одного собственного значения 1, для которого соответствующее пространство собственных элементов 1Ц — Н. При X 5^ 1 оператор = г£ есть Л~~ 1 ограниченный оператор.
2. Определим оператор A: L2 [0, 1]—> L2 [0, 1] следующим образом: Ах (/) = —tx (t), ОяС t 1. Очевидно, /п = 0, М «С 1. Покажем, что все точки отрезка [0, 1] принадлежат спектру оператора А (откуда будет следовать, что 2И=1).
В самом деле, пусть Рассмотрим отрезок [X, Х+е](или[Х—еД]),
лежащий в отрезке [0, 1]. Пусть
хе(0=/ при * [Х> X-f-e],
I 0 при t ClM Х+е], Так как
1 X+S
Jxl(Od/= у -|-d/=l, о X
то хе (/)g£а [0, 1], ||хер= 1. Далее, Акхе (t) = (/—X) х6(<), откуда
Л + 8
1 р р2
IMxXe(0||2=-i- j (/-X)2d<=-^-.
X
I
При 8 —s- 0 имеем || A^xs || —> 0. Следовательно, X есть точка спектра при 0 X «С 1,
В то же время оператор А не имеет собственных значений. В самом деле, Afx (t) = (t—Х)х(0- Если Адх(0 = 0, то (t—Х)х(<) = 0 почти всюду на [0, 1], а значит, и x(t) почти всюду равно нулю.
2. Инвариантные подпространства. Подпространство L пространства Н называется инвариантным подпространством оператора А, если из x£L следует Ax£L. Приведем пример инвариантного подпространства. Пусть %—собственное значение оператора Ди — совокупность собственных элементов, соответствующих этому собственному значению, к которой присоединен нулевой элемент. Тогда Nt,— инвариантное подпространство, так как в силу равенства Ах==Кх из х^Ух следует Ax^N^.
Если L — инвариантное подпространство оператора А, то говорят также, что L приводит А. Установим следующие свойства инвариантных подпространств самосопряженных операторов.
1. Из инвариантности L следует инвариантность его ортогонального дополнения М = Н — L.
П Пусть х£М. Это значит, что <х, у> = 0 для любого y£L. Но Ау также принадлежит L для y^L и потому <х, Ау> — 0. Отсюда в силу самосопряженности А получаем <Дх, z/> = 0 для любого y^L. Следовательно, Ах£М.
Обозначим через GK область значений оператора А^, т. е. совокупность элементов вида у = Ах—Хх, где X—собственное значение.
250
Легко проверить, что Н — G^A-N^. В самом деле, если u^NK, то
<z/, «> = <Лх —Хх, и> = <х, Аи —Хм> = <х, 0> = 0.
Следовательно, GK_\_NK. Если y€.GK и y^G^, то y = limy„, где п
yn^.Gi. Из равенства <//„, и> = 0 получаем <у, и> — 'лт<.уп, и> — 0. п
Поэтому Gk_[_Nk.
Пусть теперь (у, и> = 0 для любого y^G^. Для произвольного х£Н получаем
0=<Лх—Хх, и> = <х, Аи — Хы>,
откуда Аи—Ум = 0, т. е. u£NK. Следовательно, NK — Н — G\ — =Н — G}..
Из свойства 1 и только что доказанного предложения следует, что Од, является инвариантным подпространством самосопряженного оператора А.
Обозначим через N ортогональную сумму всех подпространств NK, или, что то же самое, замкнутую линейную оболочку всех собственных элементов оператора А. Это также инвариантное подпространство данного оператора. Если Н сепарабельно, то в каждом А\ можно построить полную конечную или счетную ортонормальную систему собственных элементов. Так как собственные элементы из различных ортогональны, то, объединив эти системы, мы получим ортонормальную систему собственных элементов {хп}, полную в пространстве N.
Оператор А определяет в инвариантном подпространстве L оператор Al‘. L—^L', именно, ALx = Ax для x$L. Нетрудно проверить, что Лл есть также самосопряженный оператор.
2. Если инвариантные подпространства L и М образуют ортогональные дополнения друг к другу, то спектр оператора А есть теоретико-множественная сумма спектров операторов А{ и АЛ1.
□ Пусть X —точка спектра оператора AL или Ам. Тогда существует последовательность элементов {x„}<=L (соответственно М) такая, что ||х„||= 1, || Л£дхп ||->0. Но || Л£>хх„ || = ||Лд,х„ ||, поэтому X принадлежит спектру оператора Л.
Пусть теперь X не принадлежит ни спектру оператора Л£, ни спектру оператора Ам. Тогда существует положительное число такое, что для любых у £ L и г € М
||Лхг||>ф||.
Но любой элемент х£Н имеет вид x — y + z, y$L, z£M, ||х||2 = = ||y||2+hli2- Отсюда
IIЛ|| = || Аку + Акг || = (|| Аку ||2 +1| А>г ||2)
>с(Ь112 + 1И12)1/2 =с||х||.
Итак, X не есть точка спектра.
251
3. Операторы с чисто точечным спектром. Как мы видели, пространство Н представимо в виде ортогональной суммы двух пространств: пространства N— замкнутой линейной оболочки множества всех собственных векторов самосопряженного оператора А и его ортогонального дополнения G. Пространство N есть инвариантное подпространство оператора А; значит, спектр оператора А есть теоретико-множественная сумма спектров операторов AN и Ао. Спектр оператора AN называется точечным спектром * оператора А, спектр оператора Ао — непрерывным спектром оператора А. Если N — H, то непрерывный спектр отсутствует и оператор А имеет чисто точечный спектр; такой спектр, как мы видели в гл. V, имеют вполне непрерывные операторы. Если оператор не имеет собственных элементов, то подпространство N пусто, И — G и спектр оператора А — чисто непрерывный; примером может служить спектр оператора А в примере 2.
Если оператор А имеет чисто точечный спектр и {хп}—ортонормальная система собственных элементов, соответствующих собственным значениям Л„, то можно доказать, что
А^Р,, (5)
п
Л„—X ?п' ч (6)
п
где Рп — проекционный оператор, определяемый равенством Рпх = = <х, x„>x„ = c„x„.
Приведем теперь независимое от общих результатов r^i. V доказательство дискретности спектра вполне непрерывного оператора.
Теорема 5. Каждая отличная от нуля точка спектра самосопряженного вполне непрерывного оператора А есть его собственное значение.
□ Если X#:0 —точка спектра оператора А, то существует последовательность элементов {хп}сН такая, что ||х„|| = 1, || Ахп—Хх„|| —>0, откуда, полагая Ахп—кхп = уп, || уп || —> 0, имеем хп = у (Ахп — уп).
Оператор А преобразует последовательность {хч} в компактную последовательность {Лх„}. Поэтому существует сходящаяся подпоследовательность {Axn/J; вместе с ней сходится и подпоследовательность
Xnk = Т (AXnk ~Unk)‘
Пусть хп —> х. Тогда Ахп. —* Ах; далее, уп. —>-0, поэтому из равен-
Л 1 Л к
ства (7) следует х = -г-Дх, или Ах—кх. При этом || хЦ = lim|[|| = I.
Л п
Следовательно, х —собственный элемент, а X —собственное значение оператора А.
* Часто точечным спектром оператора А называют совокупность всех его собственных значений. Согласно определению, данному в тексте, к точечному спектру оператора относятся и предельные точки множества его собственных значений.
252
Следствие 1. Каждый самосопряженный вполне непрерывный оператор имеет по крайней мере одно собственное значение.
Это предложение вытекает из только что доказанной теоремы и следствия теоремы 4.
Следствие 2. Каждое ненулевое инвариантное подпространство L самосопряженного вполне непрерывного оператора А содержит его собственный элемент.
□ Вместе с А вполне непрерывным является и оператор Al£(L —► L). Этот оператор в силу следствия 1 обладает собственным значением X; следовательно, в L существует собственный элемент оператора ДЛ, а тем самым и оператора 4.
Следствие 3. Самосопряженный вполне непрерывный оператор обладает чисто точечным спектром.
□ В самом деле, инвариантное подпространство G, ортогональное всем собственным элементам,— нулевое. В противном случае оно в силу следствия 2 должно было бы содержать собственный элемент, в противоречие со своим определением.
Теорема 6. Множество собственных значений самосопряженного вполне непрерывного оператора А может иметь лишь одну предельную точку А=0.
Эта теорема является частным случаем теоремы 5 § 2 гл. V, но ей можно дать простое независимое доказательство.
□ Если бы существовала бесконечная последовательность различных собственных значений {%„} такая, что | 'кп | с > 0, то для соответствующих собственных элементов хп, ||хп|| = 1, в силу их ортогональности выполнялось бы соотношение
|М*„ ~ II2 = II М» ~ If = + Кп > 2С2
при п^т. Но в таком случае последовательность {4хп} не была бы компактной, в противоречие с полной непрерывностью оператора А.
§ 5. СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ САМОСОПРЯЖЕННОГО ОПЕРАТОРА
1. Разложение единицы. Обобщим формулы (5) и (6) § 4 на произвольные самосопряженные операторы.
Лемма. Пусть А и В—самосопряженные перестановочные операторы и А2 — Вг. Обозначим через Р оператор проектирования на подпространство нулей оператора А—В. Тогда:
1°) всякий ограниченный линейный оператор С, перестановочный с А — В, перестановочен с Р;
2е) из Ах = 0 следует Рх = х\
3°) А^(2Р-Е)В.
□ Пусть L — подпространство нулей оператора А — В и Р—оператор проектирования на это подпространство. Тогда если y£.L и оператор С перестановочен с А — В, то Су также принадлежит L, поскольку
(4-B)Q/ = C(4-B)«/ = 0.
253
Поэтому СРх С L для любого х С Н и, значит, РСРх — СРх, т. е. РСР = СР.
Аналогично С*Р = РС*Р, откуда
PC = (С*Р)* = (РС*Р)* == РСР.
Следовательно, СР —PC и утверждение Г доказано. В частности, АР = РА и ВР^РВ.
Далее, пусть Лх = 0. Тогда
||Вх||2 = <Вх, Вх> = <В2х, х> = <Л2х, х>=||Лх||2 = 0,
т. е. Вх = 0, Поэтому (Л —В)х=0; следовательно, Рх = хи утверждение 2° также доказано.
Наконец, (Л — В) (Л 4- В) — Л? — В2 = 0. Поэтому для любого х имеем (Л+В)хС£, и, следовательно,
Р(Л + В)х = (Л + В)х, т. е. Р(Л + В) = Л+В,
Так как, кроме того, Р (Л—В) = (Л —В)Р = 0, то Р(Л + В) — — Р(Л-В) = Л+В, откуда Л = (2Р-£)В.
Теорема 1. Для каждого самосопряженного оператора А существует проекционный оператор Е+ такой, что:
1°) любой ограниченный линейный оператор С, перестановочный с А, перестановочен с Е+\
2°) Л£+>0, Л (£-£+)<0;
3°) если Ах —0, то Е+х=^х.
□ Пусть Е+ — проекционный оператор, проектирующий все Н на подпространство нулей оператора Л —В, где В —положительный квадратный корень из Л2. Из леммы сразу следует, что утверждения 1° и 3° выполняются; в частности, АЕ+ = Е+А и В£+ = =Е+В. В силу этой же леммы Л = (2£+ — Е)В. Следовательно,
Л£+ = В£+>0, Л(£ —£+) = — (£-£+)В<0,
так как произведение двух перестановочных положительных операторов есть снова положительный оператор. Ц
Отметим, что из равенства Л^(2£+—£)В следует ВЕ+—
= Y(A-\-B), откуда
Л£+=|(Л + В), Л(£-£+) = 1(Л-В).
Оператор АЕ+ обозначают Л+ и называют положительной частью оператора Л, а оператор Л(£ — Е+) обозначают Л_ и называют отрицательной частью А. При этом Л = Л+ + Л_.
Примеры. 1. Пусть А есть n-мерная симметрическая матрица с собственными значениями Хх, Х2, ..., Хй, где Хь Х2, ..., X* < 0, X^ + f, Хй+2, ..., Хй > 0. Из линейной алгебры известно, что А унитарно эквивалентна диагональной матрице
(Xj, Х2, ...» Х^, Х^+1, ...» Хл) —-
Xi 0 0 ... 0
0 Х2 0 ... 0
0 0 0 ... Хй
254
т. е.
Д = [/ (Xj, %2, ..., Х^, X^+f, ...» lw) С/’1; тогда
Д+ = £У(0, О, ..., О, X*+i, ..., х^су-1, A^ = U (kit Х2, ..., Хл, О, ..., О) (У-1.
2. Пусть Л —оператор в L2 [—1, 1], определяемый равенством Ах (t) = tx (t). Тогда
Л+х(0= <-21 —х(0, 4 _х (0 ==-^-^-МО-
Теорема 2. Каждый сопряженный оператор А порождает семейство {Ед} проекционных операторов, зависящих от вещественного параметра X, —оо<Х< + оо, и удовлетворяющих условиям'.
1°) из АС —С А следует ЕуС — СЕ^ для любого X;
2°) Ех Ец, если X < р;
3°) Ед сильно непрерывен слева, т. е. Е^9 — Ек;
4°) Ед = 0 для—oo<i'k^.m, Е^ — Е для М < -j-оо, где т
и М —нижняя и верхняя границы оператора А.
Семейство {Ед} называется разложением единицы, порожденным оператором А.
Прежде чем доказывать эту теорему, приведем примеры.
1. Пусть А — U (Хх, Х2, Х„) (У"1 — симметрическая матрица n-го порядка,
где Хх < Х2 < ... < Хп, и в;—собственный вектор, отвечающий собственному значению X/. Тогда при Xf<X<X/ + 1 оператор есть оператор проектирования на t-мерное подпространство, порождаемое векторами ех, е2, ..., При X < Хх имеем £^~0; при X > Хп имеем Е^ = Е.
2. Пусть оператор А в L2 [—1, 1] определяется равенством Дх(0 = £х(0. Тогда Екх (0 = (0 х (/), где фЛ (0 = 0 при t > X, фх (0 = 1 при t < X. Очевидно, при X < —— 1 имеем £^ = 0, а при X > 1 имеем ЕК=Е.
□ Пусть % —произвольное вещественное число и Лд = Л—ХЕ. Обозначим через Ед проекционный оператор Е — Е+ (X), где Е+ (X) — проекционный оператор, построенный согласно теореме 1 для оператора Л—ХЕ.
Условие Г, очевидно, выполняется, откуда, в частности, следует, что Ед и Ен перестановочны для любых X и р.
Переходя к условию 2°, рассмотрим проекционный оператор Р = Ек(Е — Ер), где X < р. Имеем
ЕдР ~ Е\ {Е-Е^Е^Е-Е^Р (1)
и аналогично
(Е —ЕЦ)Р = Р. (2)
Далее, по определению Ек имеем
(Л - ХЕ) Ед < 0, (3)
(Л-рЕ)(Е-Ец)>0. (4)
Положим Рх = у для произвольного х£Н. В силу равенств (1) и (2) имеем Еку —E}liPx = Рх= у и аналогично (Е —Eg)z/=±у. Из неравенств (3) и (4) получаем
<(Л—ХЕ)#, #> = <(Л — ХЕ)Ед#, #><0,
<(Л—рЕ)#, у> = <(Л —рЕ)(Е—Ер)«/, z/>>0.
255
Вычтя из первого равенства второе, имеем
<G*—У><Л или (р —Mh)Ha<o.
Отсюда, учитывая неравенство X < р, заключаем, что у = Рх=0, где х — любой элемент из Н. Следовательно, Р = 0, или
Ех (Е — Е^) = Ех — ЕКЕ* = О,
и выполнение условия 2° доказано.
Рассмотрим полуинтервал Д = [Х, р) числовой прямой. Для проекционного оператора Е(Д) = ЕЦ —Ех имеем
ЕЦЕ(Д) = Е(Д), (Е-ЕХ)Е(Д) = Е(Д).
Поэтому
(Л - рЕ) Е (Д) = (Л - рЕ) ЕЦЕ (Д) С О,
(Л—ХЕ) Е (Д) = (Л —ХЕ) (Е-Ех) Е (Д) > О,
и, следовательно,
. ХЕ(Д)< ЛЕ(Д)<рЕ(Д). (5)
Обратимся теперь к условию 3°. Для любого х£Н выражение <.Екх, ху есть неубывающая функция от X. Поэтому существует lira <Е»,х, х>. Отсюда получаем, что
||Evx — Exx||2 = <(Ev — Ех) х, x> — <.Evx, х> — <Екх, x>—>0
при X < v < p и X, v —► p. Следовательно, для любого х С Н существует lim Ехх = Ец_ох. .
Легко проверить, что Е^.о — проекционный оператор. Докажем, что Е(1_0 = Е(1. Пусть Е(Д0) = Ец —Ер,_0. Имеем
Е(Д) = Ер, —Ех-*Е(Д0) при Х-*->р —0
в смысле точечной сходимости операторов. Переходя к пределу в неравенстве (5), что, очевидно, возможно, получаем рЕ (До) = = АЕ(До). Пусть теперь х —любой элемент из Н и у = Е(Д0)х. В силу предыдущего равенства имеем (Л —pE)z/ = O, откуда согласно условию 3° теоремы 1 получаем Ецу — 0. Далее, ЕцЕ (Д) = Е (Д). откуда, переходя к пределу, имеем ЕЦЕ (До) — Е (До). Следовательно, Е (До) х = ЕцЕ (До) х — Е^у = 0.
Так как х —любой элемент из Н, то это означает, что Е(До) = О, и выполнение условия 3° доказано*.
Выполнение условия 4° доказывается без труда. Пусть X < т и Ех=#0. Тогда существует элемент х такой, что Е^х^О. Полагая Екх=у, имеем E}jy=y, причем можно считать, что 1.
* Согласно определению Е^, нули оператора А — КЕ принадлежат ортогональному дополнению подпространства ЬЕ^. Если же оператор Е^ определить так, чтобы нули оператора А—КЕ входили в что можно сделать, не нарушая свойств Г, 2° и 4°, то Е^ будет непрерывен справа.
256
Тогда
<Лг/, у> — к = <Ау, у> — к<у, у> = <_(А—кЕ)у, у> —
= <(Л —ХЕ)Еку, (/><0,
т.е. <Ау, уУ^К^т, что противоречит определению числа т. Следовательно, Е^ = 0 для X </и. Вследствие непрерывности слева и Еи = 0. Аналогично показывается, что Ек = Е для X > М.
2. Спектральное разложение самосопряженного оператора. Теорема 3. Имеет место равенство
М +8
Л= $ XdEx, (6)
т
где интеграл понимается как предел интегральных сумм в смысле равномерной сходимости в пространстве операторов, а в—любое положительное число.
□ Пусть полуинтервал [т, ЛЦ-е), где 8 > 0, разбит на полуинтервалы Aj, Д2, ..., Д„, где ДЙ = [ХА, щ). Для каждого полуинтервала ДА в силу (5) имеем
ХАЕ(ДА)<ЛЕ(Д*)<щЕ(ДД
п
Суммируя по всем k— 1, 2, ..., п и замечая, что 2 Е^к) = Е,
получаем
п п
ЪКЕ^<А^ Ъ»кЕ^к\ £ = 1 £ = 1
Пусть vk — какое-нибудь число из [ХА, p.ft). Тогда п п п
2 (Ч - vA) Е (ДА) < Л - X vkE (А*) < У ~ Е (ДД 6=1 /г = 1 k-\
Положим max(pA—Xft) = 6. Тогда из этих неравенств получим k п
-6Е<Л - 2?*Е(ДА)<6Е, /г=1
т. е. if п \
— 6 <х, х> Л — У vkE (ДА) ]х, 6<х, х>.
\ л = 1 /
Отсюда следует, что п II п М+в
А — 5 vkE (ДА) <б, т. е. Л= lim S vkE (Дй) = $ XdEx, А=1 II 6 -> 0 6 = 1 Г.
что и требовалось доказать. Для вполне непрерывного оператора эта формула переходит в формулу (5) § 4. Д
Замечание. Так как сходимость последовательности операторов {Лп} к оператору А в смысле равномерной сходимости в пространстве операторов влечет за собой точечную сходимость {Л„}
257
к А, а также сходимость квадратичных форм <Лдх, х> к квадратичной форме <Лх, х>, то из теоремы 3 следует:
п М+8
1) Лх=1ш1 S vkE(Aii)x= J kdEKx-, k-i т
п М+8
2) <Лх, x> = lim 2 '’л<Е(ДА)х, *>= $ М < Е%х, х > для любого Л=1 т
х^Н.
3. Функции от оператора. Резольвента. Спектр. Определим
М +8
теперь интегралы вида J FQC)dEK, где F (%) — произвольная ком-т
плекснозначная ступенчатая на отрезке [т, М] функция, а {Е\}— разложение единицы, порожденное самосопряженным оператором Л. Если Хо —точка разрыва этой функции, то условимся считать, что F(Xo) = F(Xo+O). Продолжим F (%) на полуинтервал [т, Al-f-e), полагая в нем F (X) = F (М). Пусть F(Xft) = vfc на,ДА = [ХА, pft), k —
п
= 1,2, ..., п, причем U ДА = [/п, Л1 + е).
Полагаем по определению
М + 8 п
$ F(X)dEx=S^(A*).
т fe= 1 •
Легко видеть, что справедливо также равенство
M+S р
$ F(K)dEK = ZvtEfa, т * 1
где Дй—любые частичные полуинтервалы, на которых F (X) посто-М +8
янна и которые в сумме дают [т, М+&). Оператор § F(X)d£x
обозначим £(Л) и назовем функцией оператора А, соответствующей функции F(X) вещественной переменной X. Таким образом, мы получаем соответствие между ступенчатыми функциями вещественной переменной и функциями оператора Л.
Это соответствие обладает следующими свойствами:
1) аддитив ность: если F(X) = aFj (X) + pF2(X), то £(Л) = = а£1(Л)+₽£2(Л);
2) мультипликативность: если F(%) = Fx(X)F2(X), то F^mA);
3) £(Л) = [£(Л)]*, где черта над функцией означает переход к комплексно сопряженной функции;
4) ||F (Л)Ц^ max |F (X) |;
5) для любого ограниченного линейного оператора В из АВ = ВА следует F(A)B = BF(A).
258
Для доказательства свойств 1 и 2 разобьем полуинтервал [т, М + е) на части Дй, на которых обе функции Fx(X) и Fa(X) постоянны. Тогда для F (X) = aFj (X) +PF2 (^) имеем
п
F(A) = S(a^’+m£(Aft) = п п
2 2 с£’£(Дд) = аЛ(Л)+рР8(Л),
*=1 *=i
а для F (X) — Ft (X) F2 (X) вследствие ортогональности Е (ДА) и Е (Д,) при k^= l получаем
п
2^W») =
k— 1
= ^2/V’f(a*))(z2 (A)f2(A).
Далее,
<F (А) х, у> = ( 2 скЕ (ДА) х, у) = /г— 1 п —
= (х, 2 скЕ (ДА) у) = <х, F (А) у>, k — 1
откуда следует, что [F (А)]* = F (А). Наконец,
j п
|<F(A)x, х> | - (2 сЛ£(Д*)х, х)
I k — 1
п
2 | с* | <£ (Дй) х, х> max | F (X) | <х, х>. /? = 1
Отсюда IIF (А) ||= sup |<F(A)x, х> | max IF (X) I.
И * n=i
Свойство 5 очевидно.
Из определения F (А) следует, в частности, что £(Д) = Хд(А), где Хд(Х) —характеристическая функция полуинтервала Д. Пусть теперь F(X) —произвольная непрерывная на [т, М] функция. Продолжим ее на полуинтервал [т, Л4 + е), полагая F(X) = F(M) для Х$(Л1, М+е). Существует последовательность ступенчатых функций F„(X), равномерно сходящаяся к F (X) на [т, Л! 4-е). Рассмотрим соответствующие функции от оператора Fn(A). Имеем Hn(A)-Fra(A)|Kmax|F„(X)-Fm(X)|->0 при п, т^со.
В силу полноты пространства операторов существует оператор
М + 8
B = limFn(A). Положим по определению В = FltydEb- Вдаль-п т
нейшем будем обозначать В также через F (А) и называть функцией от оператора А, соответствующей непрерывной функции F (X) вещественной переменной X. Легко убедиться в том, что определе
259
ние F (Л) не зависит от выбора последовательности {Fn(k)}, сходящейся к F (X), и что свойства 1—5 сохраняются и для случая непрерывных функций. В частности, имеем
М + 8
Ап — n = 0, 1, 2 ... .
т
Полученное соответствие между функциями вещественной переменной и функциями от операторов может быть широко использовано для выяснения ряда свойств самосопряженного оператора, в частности спектральных свойств. Мы ограничимся здесь следующими тремя теоремами.
Теорема 4. Для того чтобы для данного Хо существовала резольвента = достаточно выполнения одного из сле-
дующих условий-
1°) Хо не вещественно-,
2°) лежит вне отрезка [т, М];
3е) если Хо £ [т, М], то существует полуинтервал [а, 0), а < Хо<0, внутри которого Ек постоянно.
Во всех этих случаях
~ J %-Х0 • т
□ В самом деле, в первых двух случаях функция f (A.)=1/(Z — Хо) непрерывна в [т, М + е) при достаточно малом е. Поэтому
М + 8 М+е М + 8 »
г г 1
$ (X-%0)dFx= $ =
m 0 т ' т
М+г М+е
и так как (X — Х„)d£\= А — Х0Е, то -j—t— = Rk„.
v Л — Лп
т т
В третьем случае разобьем полуинтервал [т, М + е) на три полуинтервала [т, а)' [а, 0) и [0, М+е). Пусть <р(%)= 1/(%—Хо) на [т, а) и [0, М + е) и линейна на [а, 0), причем ф (а) = 1 /(а— Хо), Ф (0)= 1/(0 —Хо).
₽
В силу постоянства в полуинтервале [а, 0) имеем J ф (X) dEK = О а для любой функции ф(^). Поэтому можно записать
М+8 М+8
J Ф(Х)6Е%= J ЗГТ--т т
Следовательно,
М +8 , „ М +8
SdE 4 г
т m
dE Отсюда вытекает, что R^o существует и равна \ 5—7-. В
260
Теорема 5. Если для вещественного Хо существует то Ао лежит внутри некоторого полуинтервала [а, 0), А0^а, в котором Ек постоянно.
□ Для произвольного х£Н рассмотрим равенство
М+е
(Д—Х0£)х = 5 (A — A0)d£xx т
и применим к обеим Частям его оператор где А = [а, Р)—
некоторый полуинтервал, содержащий внутри себя точку Хо. Получим
/ з £(Д)х-/?Ц $ (Х-Хо) d£zx \ct
Отсюда
Но, как ле'гко проверить,
3
5 (^~М d£xx а
<с||£(А)х||,
где с= шах(РХо, Хо—-а). Следовательно,
||£(Д)х||^с||/?х,,||[|£ (Д)х||.
Выберем теперь полуинтервал [а, 0) настолько малым, чтобы с[|7?х,|| < 1/2. Получим || Е (Д) х|| (1 /2) Ц£ (А) хЦ. Но это возможно, лишь если £(Д)х = 0, и так как х — любой элемент из И, то £(Д) = 0. Тем более £(Д) = 0 для любого полуинтервала ДсД, а это означает, что £х постоянно в [а, 0). Q
Из теоремы 4 непосредственно вытекает, что множество регулярных точек самосопряженного оператора А есть открытое множество, а следовательно, спектр самосопряженного оператора А представляет собой замкнутое множество, расположенное на вещественной оси (замкнутость спектра произвольного ограниченного линейного оператора в вещественном банаховом пространстве была установлена в гл. III).
4. Собственные значения самосопряженного оператора.
Теорема 6. Для того чтобы Ао было собственным значением самосопряженного оператора А, необходимо и достаточно, чтобы Ао было точкой разрыва для Е}_.
□ Необходимость. Пусть Дх0 —Аохо = 0 для некоторого хо^=О. Тогда <(Д — А0£)2х0, х0> = 0, и, следовательно,
М + е
$ (А—Ао)2 d <£лх0, хо> = 0. т
261
Так как подынтегральная функция неотрицательна, а интегрирующая функция монотонно возрастает, то и
3
J V d <£\х0, х0> = О а
для любого полуинтервала [а, 0). В частности, для любого 8>0
М + 8
J Vd<^x0, х0> — О,
Хо + 8
и так как на интервале интегрирования (X—%0)2>82, то тем более
М + 8
82 d^Z?%Xo, Xq/* ==х е2 (^%о, ^^Хо+бХо, хо» = О.
Хо + £
Следовательно, <х0, х0>—<ЕХо+ехо, х0> =0, т. е.
Е^Ло+e-^o = Хв. (7)
Аналогично
Х© —8
$ (X—X0)2d<Exx0, т
откуда с учетом того, что Ет = 0, получаем
Еко-ех0 = 0. * (8)
Из равенств (7) и (8) следует (Ехо+8—Ех0_е) х0 = х0, и так как 8 произвольно, то
(Ex0-f- 0 Xq Xg.
Следовательно, Хо есть действительно точка разрыва для Е^, причем собственный элемент х„ принадлежит подпространству, соответствующему проекционному оператору Ело+о — Ек„.
Достаточность. Пусть Е^+о^ Е-,.о и х0 —любой элемент из подпространства, соответствующего оператору Ел,0+о — Е^. Тогда (Е’хо+о — Ец) х0 = х0, т. е. х0 принадлежит ортогональному дополнению пространства Le>o в пространстве Поэтому Ехо+ох0 =
= х0, Елох0 = 0. Тем более Ехх0 = х0 для X > Хо и, значит, Е (Д) х0= = х0 для Д = [Х0, Х0 + е). Но тогда
Хо + 8 Хо + 8
Ах0 — АЕ (Д) х0 = J X dExx0, Хохо = Х0Е (Д) х0 = J Хо dExx0, и, следовательно,
Xq + 8
Лх0 (X Хо) d£\x0.
Хо
Отсюда
II Ахв ХохоЦ8ЦЕ(Д) х0Ц<81|х0Ц,
и так как 8 произвольно, то || Ах0 — Хохо||= 0. Попутно получено, что все подпространство, на которое проектирует оператор Ехо+о — Ех0, состоит из собственных элементов оператора А, соответствующих собственному значению Ао.
ДОПОЛНЕНИЯ
1. Теорема Боля — Брауэра
Докажем известную теорему Боля — Брауэра о существовании неподвижной точки при непрерывном отображении замкнутого выпуклого тела n-мерного евклидова пространства в себя. Эта теорема широко используется в функциональном анализе при доказательстве существования решений операторных уравнений. Так как все замкнутые выпуклые тела n-мерного евклидова пространства гомеоморфны друг другу, то достаточно доказать теорему Боля—Брауэра для непрерывного отображения n-мерного симплекса в себя.* Мы приведем замечательное доказательство этой теоремы, принадлежащее Кнастеру, Куратовскому и Мазуркевичу.
Рассмотрим n-мерный симплекс s0 и обозначим через х0, х19 ..., хп его вершины. Любую ^-мерную грань симплекса (0<:&^п) будем обозначать через (х/0, хц, ..., х/л), где Xim(tn = 0, 1, ..., k) образуют совокупность вершин этой грани. Пусть симплекс s0 симплициально разбит на некоторые симплексы s. Каждой вершине х симплексов s отнесем число ср (х) следующим образом.
Рассмотрим грань наименьшего числа измерений основного симплекса $0, содержащую точку х. Пусть это грань (х/0, х/р ...,х/л). Число (р (х) полагаем равным одному из индексов ..., ik. Например, если х совпадает с вершиной xi симплекса s0, то <p(x) = t; если х лежит на одномерной грани (х/, х/), не совпадая ни с одной из ее вершин, то мы можем положить ср (х) равным одному из чисел i или /, и т. д. Наконец, если х лежит внутри s0 (не принадлежит ни одной ^-мерной грани, & = 0, 1, ..., п—1, то (р (х) может равняться любому из п+1 чисел 0, 1, 2, ..., п. Назовем <р(х) нормальной функцией вершин.
Симплекс s разбиения назовем репрезентативным, если его вершинам отнесены п+1 различных чисел 0, 1, 2, ..., п.
На рис. 4 приведено разбиение двумерного симплекса с указанным отнесением вершинам симплексов разбиений чисел 0, 1,2. Заштрихованный треугольник есть репрезентативный симплекс.
Лемма 1 (Шпернера). Каково бы ни было симплициальное разбиение симплекса s0 я какова бы ни была нормальная функция вершин (р (х), заданная на вершинах симплексов разбиений, всегда существуют репрезентативные симплексы, и притом в нечетном числе.
□ Доказательство проведем по индукции. Для случая п = 0, когда симплекс сводится к точке, теорема тривиальна. Считая теорему верной для симплексов П—1 измерений, докажем ее для симплексов п измерений.
Пусть дано симплициальное разбиение n-мерного симплекса s0 и на вершинах х симплексов s разбиения определена нормальная функция вершин <р (х). Назовем (п—1)-мерной репрезентативной гранью (п—1)-мерную j х
грань симплексов разбиения, на п вершинах которой / \
функция ф (х) принимает значения 0, 1, ..., п—1. / \
Число (п—1)-мерных репрезентативных граней симп- г/ -—Af
лекса s разбиения обозначим через a (s). /I /\
Возможны три случая. / \
1. Функция (р (х) на вершинах симплекса при-
нимает все п+1 значений 0, 1, 2, ..., п, т. е. sT— п
репрезентативный симплекс и содержит единственную хо ° 2
репрезентативную (п—1)-мерную грань, а именно
противоположную вершине х, Хля которой (р (х) = п. Рис* 4
Отсюда a (sj) = 1 и
Sa(si) = pn, (1)
* Встречающиеся здесь топологические понятия можно найти в любом курсе алгебраической топологии (см., например: Понтрягин Л. С. Основы комбинаторной топологии. М., 1947).
263
где рп—число репрезентативных «-мерных симплексов; сумма в левой части равенства берется по всем репрезентативным симплексам.
2. Функция (р (х) на вершинах нерепрезентативного симплекса s2 принимает п значений 0, 1, 2, п—1. Одно из этих значений она должна принимать два раза. Следовательно, s2 имеет две репрезентативные (п—1)-мерные грани, т. е. a (s2) =2.
3. Функция ф (х) на вершинах симплекса $3 пропускает одно из значений О, 1, 2 п—1; следовательно, a(s3) = 0. Отсюда
2 a (s) ss 2 a (sx) (mod 2). (2)
Левая сумма берется по всем «-мерным симплексам s разбиения, правая—по репрезентативным «-мерным симплексам sx этого разбиения.
Произведем другой подсчет (я— 1)-мерных репрезентативных граней. Возможны два случая.
1. Репрезентативная грань попадает внутрь основного симплекса s0; она есть общая грань двух симплексов разбиений, и в сумме 2 a(s) мы ее считали два раза.
2. Репрезентативная грань попадает на границу s0. Из определения такой грани и функции ф(х) следует, что эта грань может находиться только на (лг— 1)-мерной грани (х0, хх, ..., xrt-x) основного симплекса. Обозначим через р„_х число («—-1)-мерных репрезентативных граней, попавших на (х0, хх....хп^. Имеем
Sa(s)sPn-i(mod 2). (3)
Из равенств (1), (2), (3) следует
(mod 2).
Но для (я— 1)-мерных симплексов мы считаем лемму доказанной, p^-i нечетно и, следовательно, рп нечетно и поэтому отлично от нуля. Ц
Лемма 2. Пусть симплекс s0 покрыт «+1 замкнутыми множествами Fo,
• ••> Fn таким образом, что каждая его k-мерная грань (х^,#^, ..., xz^) покрыта множествами F^, F^, ..., F(k. При этих условиях в s0 существует точка, принадлежащая всем «+1 множествам F[, i = 0, 1, ..., я.
□ Разобьем s0 симплициально и на вершинах х симплексов разбиений определим следующую функцию ф(х). Рассмотрим грань (xZe, х^.....xz-^j, Q^k^n,
наименьшего числа измерений, заключающую точку х. Эта точка попадает в одно из множеств Fz-0, F[t, ..., F;k, покрывающих (xz-0, xz-p ..., х^). Примем ф (х) равным индексу того из этих множеств, которое содержит х (или любому из таких индексов, если точка попала в несколько из множеств FZo, Fz-, ..., Fz-^). Ясно, что ф (х) есть нормальная функция вершин.
В силу -леммы Шпернера среди симплексов такого разбиения должен существовать репрезентативный симплекс $х. На .его вершинах х функция ф (х) принимает все «+1 значений 0, 1, я, т. е. вершины $х принадлежит я+1 раз-
личным множествам Fz*.
Будем производить симплициальное разбиение s0 на все более и более мелкие симплексы. Пусть диаметры симплексов т-го разбиения не превосходят Ьт, где bn—при т—>оо. Рассмотрим последовательность репрезентативных симплексов Sx, s2, sm, ... 1-го, 2-го, ..., m-го, ... разбиений. Вследствие компактности Sq множество вершин симплексов {sm } имеет предельную точку х*. Выбрав произвольное 6 > 0, рассмотрим те симплексы sm, для которых < 6/2. В шар радиуса 6/2 с центром х* попадает по крайней мере одна вершина одного из симплексов smi а следовательно, в шар радиуса 6 с центром х*—все я+1 вершин такого симплекса. Так как вершины sm принадлежит «+1 различным множествам Fo, Ft, ..., Fn, то в любой 6-окрестности х* найдутся точки всех множеств F;, i = 0, 1, ..., я. Следовательно, х* есть предельная точка для всех Fz, а так как F[ замкнуты, то х* принадлежит всем F;, i — 0, 1, ..., я. Ц
Теорема Боля — Брауэра. При всяком непрерывном отображении f (х) п-мерного симплекса s в себя существует неподвижная точка этого отображения, т. е. точка x*£s такая, что f(x*)=x*t
264
□ Введем на s барицентрические координаты р0, рь ..., р„, так, что п
2 Для точек s все р/^0. Пусть точка х (ро, р19 ...» p„)£s перейдет »=о
п
при преобразовании f в точку у (v0, Vi, ..., vn)£s, y = f(x). Снова 2 vz==l,.
i= о
vz^0, t = l, 2, ..., n. Пусть точка x (p0, pi, ..., рп) лежит на грани (xz-0, xz-t, •••, xik)y 0<:&sCn. Координаты py точки при j Ф t0, i19 ..., ik равны нулю.
n
Так как 1 =Hf.+H/i+• • •+Ra= 2 v<5sv<o+'Wi+• • •+v/ft> T0 невозмож-t= о
ное одновременное выполнение неравенств pz-0 < vZe, pZ1 < vZ1, ..pz-^ < vik и no крайней мере для одной из этих координат получим Pzr^vZ/t. Поэтому если обозначить [через Fz- множество точек, у которых координата pz- не возрастает при преобразовании Д то всякая точка х грани (xz-0, xz-t, ..., X(k) покроется одним из множеств Fz-0, Fz-t, ...» Fz-^.
Множества Г/ удовлетворяют всем условиям предыдущей леммы*. Поэтому на s существует точка х*(ро, pi, ...» рп), принадлежащая всем этим множествам. Ни одна из координат р* при преобразовании f не возрастает, и если f (х*) = — у* (vo, vj, ..., Vn), то
p*^vj, t~0, 1, ..., n. (4)
Из неравенств (4) и свойств барицентрических координат вытекает, что п п
i = 2^2v‘=1- <5)
i=0 ‘=0
Теперь из неравенств (4) и (5) следует, что p*=v*, t = 0, 1, ..., л, т. е. /(х*)=х* и, следовательно, х* есть неподвижная точка преобразования. |
Следствие. При непрерывном отображении ограниченного замкнутого выпуклого тела S п-мерного банахова пространства X в себя существует непод^ важная точка.
□ Пусть е^ е2, ...» еп—базис в X. Элементу х = + |2е2 + ... + 1пеп отнесем точку х = {If, |2, ...» гДе есть я-мер ное евклидово пространство.
Это соответствие ф изометрично и изоморфно и переводит замкнутое выпуклое множество SczX в замкнутое выпуклое множество ScziR". Пусть f—непрерывное отображение S в себя.
Тогда / =ф/ф“-1 есть непрерывное отображение.S в себя. По теореме Боля — Брауэра, существует неподвижная точка х* этого отображения, т. е. ф/ф~х(х*) = = х*, или /ср-J (х*) =ф”х (х*), и х* = ф“х(х*) есть неподвижная точка отображения Д |
Ik Принцип неподвижной точки Биркгофа — Тарского
При решении нелинейных уравнений помимо широко используемых принципов сжимающих отображений и Шаудера используется также принцип Биркгофа — Тарского. Он применяется при исследовании операторных уравнений в частично упорядоченных пространствах, причем можно обойтись без использования метрических или топологических свойств этих пространств.
Рассмотрим частично упорядоченное множество X, в котором каждое ограниченное сверху (снизу) подмножество МаХ имеет точную верхнюю границу sup М (точную нижнюю границу inf М). Такое множество называется условно
* Замкнутость Ft следует из непрерывности Д
265
полной решеткой. Множество точек х^Х таких, что где а и b фик-
сированные точки X, будем называть порядковым отрезком и обозначать [zz, &]» Оператор Л:Х—>Х называется изотопным, если из х, у^Х и х^у следует Ах «С Ау.
Теорема Биркго ф а — Т а р с к о г о. Пусть X—условно полная решетка и А—изотопный оператор, отображающий порядковый отрезок [a, 6]czX в себя. Тогда А имеет на [а, /?] хотя бы одну неподвижную точку.
□ Рассмотрим множество М~ {х£[а, д]| Лх^х}. Это множество не пусто, так как а^М, и ограничено сверху элементом Ь. Пусть x0 = supM. Для любого х£М имеем х^ Ах^ Ах0, откуда
Xq^AXq. (1)
Из неравенства (1) следует, что AxQ^A (Лх0). Это означает, что Axq£M и, следовательно,
Лх0 < х0, (2)
что в сочетании с неравенством (1) дает Лх0 = х0.
Пример. Пусть X = /2 с покоординатным упорядочением, т. е. х = ?2, • •
(оо \
2 Qijfj (*) ), /= 1 J
(=1, 2, ..., где aij—матрица с неотрицательными коэффициентами, причем
00
ац 1/Р и /у (х), / = 1, 2,.. .—функционалы, определенные на /2 и такие, что: /=1
для любых /= 1, 2, ... из х'^х" следует /.• (х') / .• (х"); ч
|/у(х) |</И I gyl, если x = (gb g2,...). 7
00 оо
Тогда прежде всего 2 2 < 00 и» как легко проверить, оператор Л
Z = 1/=1
действует из Z2 в £2. Далее, если (1/6) А!л2<г. 1, то оператор Л отображает отрезок [—х^_х], где х = (1, 1/2, 1/3, ...), в себя. В самом деле, если х = (|г-)£ £[—х, х] и У = = то |£;|<1/* и поэтому
И* 12 =
оо
S akifi (х) i=l
<«(i ««IblY<м±4,ti<Мi. 4 ' 1=1 1 = 1
т. е. у£.[—х, х]. Наконец, ясно, что А — изотопный оператор. Таким образом, все условия теоремы Биркгофа—Тарского выполнены и Л имеет на [ — х, х] неподвижную точку.
Отметим, что требование изотонности оператора Л в теореме Биркгофа — Тарского является весьма существенным. Без него теорема становится неверной,
266
как показывает следующий пример. Пусть Х==[0, 1] и
лу_ / 1 при 0<х < 1/2, я \ 1/3 при 1/2^х<:1
(рис. 5). Ясно, что графики функций у—Ах и у = х не имеют общей точки, а это означает, что на отрезке [0, 1] не существует такой точки х0, что х0=Ах0, хотя все условия теоремы Биркгофа — Тарского, кроме изотонности Л, выполнены. В то же время наглядно ясно, что возрастающая на [0, 1] и отображающая этот отрезок в себя функция у = Ах всегда пересекается с прямой у = х по крайней мере в одной точке, так как «проскочить сквозь разрыв» графика функции у —Ах прямая у = х не может (рис. 6). Строгим^ обоснованием этого и является теорема Биркгофа—Тарского.
ЛИТЕРАТУРА
1. Александров П. С, Введение в теорию множеств и общую топологию. М., 1977.
2. Биркгоф Г» Теория структур. М., 1952.
3. Булах Б. 3. Введение в теорию полуупорядоченных пространств. М., 1961.
4. Данфорд П. и Шварц Дж. Линейные операторы. Общая теория. М., 1962.
5. Канторович Л. В. и Акилов Г. П. Функциональный анализ. М., 1977.
6. Колмогоров А. Н. и Фомин С. В. Элементы теории функций и функционального анализа. М., 1968.
7. Красносельский М. А. Положительные решения операторных уравнений. М., 1962.
8. Люстерник Л. А. и Соболев В. И. Элементы функционального анализа. М., 1965.
9. Михлин С. Г. Лекции по линейным интегральным уравнениям. М., 1959.
10. Натансон И. П. Конструктивная теория функций. М., 1949.
11. Натансон И. П. Теория функций вещественной переменной. М., 1974.
12. РудинУ. Функциональный анализ. М., 1975.
13. Урысон П. С. Труды по топологии и другим областям математики. М., 1951.
14. Хаусдорф Ф. Теория множеств. М., 1937.
15. Шефер. X. Топологические векторные пространства. М., 1971.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная непрерывность 12
Абсолютно непрерывная функция 12, 13
Абстрактная векторная функция 227
— операторная функция 227
Аксиома отделимости 55
— произвольного выбора Цермело 8
— тождества 24
— треугольника 24
— симметрии 24
Аксиомы гильбертова пространства 78
— метрики 24
— нормы 63
— Хаусдорфа 55, 56
Ассоциированное пространство 23, 137
База окрестностей 56, 87
Базис 18, 19, 127
Банахово пространство 63
Бесконечномерное многообразие 19
Билинейная эрмитова форма 238 Биортогональные последовательности 131, 163
Борелевская система множеств 9
Вариация 221
Векторное пространство 17
Верхняя граница множества 8 ---самосопряженного оператора 239 — грань 8
Вещественное линейное пространство 17
Вещественный элемент 22
Взаимно-обратные операторы 119
Взаимно-однозначное отображение 7
Внешняя мера 12
Внутреннее произведение 78, 162
Внутренняя мера 12
— точка 25
Вполне непрерывный оператор 177, 190
— ограниченное множество 51
— упорядоченное множество 8
Всюду плотное множество 26
Выпуклое множество 21 ’
Гильбертово пространство 78,154—156, 171
Гиперплоскость 112
— , опорная к шару 113
— , проходящая через нуль 20, 141
Гиперподпространство 20, 141
Гладкое многообразие 222
Гомеоморфизм 26
Гомеоморфные пространства 26
Гомотетия 20
График отображения 126
Декартово произведение 57
Диаметр множества 40
Дифференциал второго порядка 213
— высшего порядка 215
— Фреше 196
Дифференцируемое отображение 196,
206
Дифференцируемость по подпространству 206 ---Фреше 196
Длина вектора 78
Евклидово n-мерное пространство 27, 34, 46, 48, 63, 145, 156—159
Единичный оператор 101
8-сеть 51
Задача о наилучшем приближении 68-
Замыкание 25
Замкнутая ортонормальная система 83
Замкнутое множество 26
Замкнутый линейный оператор 126
— шар 25
Измеримая функция 10
Измеримое множествб 10, 227
— по Лебегу множество 12
Изометричные пространства 35, 36
Изоморфные пространства 17, 67
Изопериметрическая задала 227
Изотонный оператор 266
Инвариантное подпространство 250
Инволюция 22
Индуцированная топология 57
Интеграл Бохнера 229—231
— Лебега И, 12
— Стильтьеса 15, 16
Интегрируемая функция 11
— по Бохнеру функция 229
Касательное многообразие 222
Квадратичная эрмитова форма 239
Квадратный корень из положительного оператора 246
Квадратурная формула 166
Ковариантный элемент 145
Кольцо линейных операторов 101, 102
Компакт 48
Компактное множество 48, 59
— пространство 48
Компактный оператор 190
Комплексное линейное пространство 17
— пространство 32
Комплексификация 23
Конечномерное многообразие 18
Контравариантный элемент 145
Координатное гильбертово пространство 32, 35, 49, 79, 85, 150, 156
Коэффициенты Фурье 82
268
Кратность собственного значения 189 Критерии компактности в конкретных ЛНП 71, 74, 77 ---общие 51, 53, 60, 61
Левый обратный оператор 102, 119
Лемма Ф. Рисса 65
— Цорна 8
— Шаудера 191, 192
— Шпернера 263, 264
Линейная зависимость 17
— комбинация 18
— независимость 17, 82
— оболочка 18
Линейно упорядоченное множество 7
Линейное в малом пространство 225
— метрическое пространство 63
— многообразие 18
---, порожденное данными элементами 18
— нормированное пространство 63
— пространство 17
— топологическое пространство 86, 87
Линейный оператор 98
— функционал 111
---, общий вид в некоторых функциональных пространствах 145—155
Локально выпуклое пространство 90 — компактное пространство 70
Максимальная центрированная система множеств 60
Максимальный элемент 8
Матричная форма оператора 161, 162
Мера 10 I
— множества 12
Метод Ньютона 210
---модифицированный 211, 212
Метризуемое пространство 56, 91
Метрика 24
Метрическое пространство 24, 32
Многочлен 217
Множество второй категории 41
— первой категории 41
— типа Fa 9
---Об 9
См. также соотв. названия
Направление 8
Направленное подмножество 8
Неподвижная точка 42
Непрерывная функция 26
Непрерывное отображение 57
Непрерывный спектр 252
Неравенство Бесселя 83
— Гельдера 13
— Минковского 13
Нигде не плотное множество 26
Нижняя граница множества 8 ---самосопряженного оператора 239
— грань 8
Норма вектора 78
— оператора 108, НО
— функционала 111
— элемента 63, 78
Нормальная функция вершин 263
Нормально разрешимое уравнение 185 Нормируемое пространство 91, 92 Нулевой элемент (нуль) группы 16
Область определения функции 6 Обобщенная последовательность 8 — производная 160
Образ 7
Обратное неравенство треугольника 24 Обратный оператор 102, 119 Ограниченное множество 25, 90 — отображение 72, 73 — сверху, снизу множество 8 Ограниченный оператор-106, ПО
Однородно выпуклый функционал 134, Однородное уравнение 123, 124 Окрестность нуля 87, 113 — точки 25, 55, 87 Оператор 7
— ортогонального проектирования 241 См. также соотв. названия Ортогональная сумма 81 Ортогональное дополнение 81 Ортогональные проекционные операторы 242
— элементы 80, 162
Ортонормальная система 81
Ортонормальный базис 83 Ослабленная топология 167 Основной параллелепипед 49 Остаток приращения 196 Отделимое пространство 55 Открытое множество 26, 56, 87 — отображение 127, 143 — покрытие 53
Относительно компактное множество 48
Отображение 7
Отрезок 21
Отрицательная часть оператора 254
Параллельные гиперплоскости 112 Плотное множество 26
Поглощающее множество 21 Подпространство 24, 65
Полная аддитивность 12
— вариация 15
— ортонормальная система 83
Полное изменение 16
— пространство 34
Положительная часть оператора 254 Положительный самосопряженный оператор 244
Полунепрерывный сверху, снизу функционал 51
Полунорма 92
269
Пополнение пространства 36
Порядковый отрезок 266
Почти изометрическое отображение 225
— конечномерный оператор 182
Правильная точка 222
Правый обратный оператор 102, 119
Предел последовательности 10, 24
Предельная точка 25
Предкомпактное множество 48
Представитель класса 21
Принцип неподвижной точки Биркгофа—Тарского 266
-------Шаудера 193, 194
— равномерной ограниченности 116
— сжимающих отображений 42
-------, примеры применения 43—46
Продолжение оператора 111
— функционала 135
Проекционный оператор 241
Проекция 58, 81
Производная второго порядка 214
— высшего порядка 215
— Гато 201
— по направлению 201
---подпространству 206
— Фреше 196
Прообраз 7
Простая функция 228
Пространство 7
— Банаха 63
— всех числовых последовательностей
29, 30, 47, 146
— непрерывных функций 27, 34, 46, 49, 64, 70, 71, 128, 129, 146—148, 155, 157, 158, 172—176
— ограниченных вещественных функций 29
— — числовых последовательностей 28, 34, 35, 47, 64
— с мерой 227
— сходимости по мере 30, 31
— сходящихся числовых последовательностей 28, 29, 35, 47
— функций с интегрируемой р-й степенью 31, 35, 47, 64, 70, 74, 77, 150— 153, 156, 157, 169, 170, 172
-------ограниченным изменением 155
— с 28, 29, 35, 47
— СГО, 1] 27, 34, 46, 49, 64, 70, 71, 128, 129, 146—148, 155, 157, 158,172— 176
— Ck [0, 1] 64
— С 48
— Н 78, 154—156, 171
— I 150
— 12 32, 35, 49, 79, 85, 150, 156
— 1Р 31, 32, 35, 46, 64, 70, 77, 128, 133, 149, 150, 156, 157, 169, 172
— 32
— £[0, 1] 154
— L2 [0, 1] 31, 35, 79, 85, 156, 159
270
— £2,р[0, 1] 78, 79
— L ’[0, 1] 31, 35, 47, 64, 70, 74, 77, 150—153, 156, 157, 169, 170, 172 — т 28, 34, 35, 47, 64
— М[0, 1] 29
— s 29, 30, 47, 146
— S [0, 1] 30, 31
— IR 27, 48
— IR" 27, 34, 46, 48, 63, 145, 156—159
— V 155
Противоположный элемент 16
Процесс ортогонализации Шмидта 82
Прямая 19
— сумма 19
Равенство Парсеваля—Стеклова 83 Равномерно непрерывное отображение 73
— ограниченные функции 70, 71
— сходящаяся последовательность 191
Равностепенно абсолютно непрерывные нормы 77 — непрерывное отображение 73 — непрерывные функции 71 Разложение единицы 255 — элемента 19
Расстояние 24 *
Расширение оператора 111
Регулярное значение 124
— топологическое пространство 95 Резольвентный оператор ^резольвента)
Репрезентативная грань 263
Репрезентативный симплекс 263
Рефлексивное пространство 157
Ряд Фурье 163
Самосопряженное пространство 156
Самосопряженный оператор 238
Сдвиг 21
Сепарабельное пространство 46 а-Алгебра 9
Сильная сходимость 165
Сильно измеримая функция 228
Скалярное произведение 78, 162, 165
Слабая компактность 171, 172
— сходимость 165
— топология 167
Собственное значение 124
Собственный элемент 124
Сопряженное пространство 114,155,165
Сопряженный оператор 158, 160, 165, 237
Спектр 124
Сравнимые элементы 7
С-свойство 13
Стационарная последовательность 38
Строго нормированное пространство 69
Ступенчатая функция 228
Суммируемая функция 11
Сходимость в среднем 31
--------с показателем р 31
— по мере 10
--- норме 63
— почти всюду 10
Сходящаяся в себе последовательность 33
— последовательность 10, 24
Теорема Арцела 71, 72
— Банаха 122
— Банаха—Мазура 176
— Банаха—Хана 135—139
— Банаха — Штейнхауса 116, 134
— Биркгофа —Тарского 266
— Боля — Брауэра 264, 265
— Бэра 41
— Егорова 10
— Кантора 49
— Колмогорова 77, 94
— Красносельского 77
— Лебега 11, 231, 232
— Лузина 14
— о дифференцируемости композиции отображений 199, 200, 216
---замкнутом графике 126
---конечных приращениях 201
---локальном обращении 207—209
---неявной функции 217, 218
— об открытом отображении 127
— Пеано 194, 195
— М. Рисса 74—77
— Ф. Рисса 147
— Ф. Рисса—Фишера 85
— Стеклова 166, 167
— Тихонова 61, 62
— Фреше 175, 176
— Фубини 14
— Хаусдорфа 51, 52
— Цермело 8
— Шаудера 193
Топологическое пространство 54—56
Топология компактной сходимости 113 — ограниченной (равномерной) сходимости 113, 114
— поточечной (слабой) сходимости 113, 114
Точечный спектр 252
Точка локального минимума, максимума 226
— метрического пространства 24
— прикосновения 25
— условного минимума, максимума 226
— экстремума 226
Точная верхняя, нижняя граница 8
Транспонированное ядро 159
Унитарная матрица 241
Унитарно эквивалентный оператор 241
Унитарное пространство 78
Унитарный оператор 240
Упорядоченное множество 7
Уравнение в вариациях 221
—, зависящее от параметра 220
Уравновешение множества 88
Уравновешенное множество 20
Условно полная решетка 265, 266
Фактор-группа 21
Фактор-пространство 21
Фильтрующая система полунорм 92
Формула Грегори 104
— Тейлора 216
— Эйлера — Маклорена 105
Фундаментальная последовательность 33 — система окрестностей 56, 87 Функционал 7, 111 — Минковского 92
Функциональное гильбертово пространство 31, 35, 79, 85, 156, 159 — пространство 7
Функция 6
— оператора 102, 258, 259
—, принадлежащая классу Лебега 13 — с ограниченной вариацией 14, 15
Характеристическое число 124
Хаусдорфово пространство 55
Центрированная система множеств 60
Центрированное множество 20
Частично упорядоченное множество 7
Частная производная 206
Часть проекционного оператора 243
Числовая прямая 27, 48
Число измерений многообразия 18, 19
Чисто мнимый элемент 22
— непрерывный спектр 252
— точечный спектр 252
Шар 25
Эквивалентные метрики 33
Эрмитов оператор 238
Лазарь Аронович Люстерник Владимир Иванович Соболев
КРАТКИЙ КУРС ФУНКЦИОНАЛЬНОГО АНАЛИЗА
Зав. редакцией литературы по физике и математике Е. С. Гридасова. Редактор А. М. Суходский. Мл. редакторы Н. П. Майкова, С. А. Доровских. Художественный редактор В. И. Пономаренко. Технический редактор
Э. М. Чижевский. Корректор Г, И. Кострикова
ИБ №3589
Изд. № ФМ-687. Сдано в набор 24.06.81. Подп. к печати 30.11.81.
Формат 60x90/16. Бум. тип. №1. Гарнитура литературная Печать высокая. Объем 17 усл. печ. л. Усл. кр.-отт. 17,25. Уч.-изд. л. 17,73. Тираж 25.000 экз. Зак. № 3054. Цена 60 коп..
Издательство «Высшая школа», Москва, К-51, Неглинная ул., д.29/14
Ордена Октябрьской Революции и ордена Трудового Красного Знамени Первая Образцовая типография имени А. А. Жданова Союзполиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли. Москва, М-54, Валовая, 28
60 коп