Автор: Гашников М.В. Глумов Н.И. Ильясова Н.Ю. Мясников В.В.
Теги: компьютерные технологии физика математика информатика компьютерные науки
ISBN: 5-9221-0270-2
Год: 2003
Текст
МЕТОДЫ
КОМПЬЮТЕРНОЙ
ОБРАБОТКИ
ИЗОБРАЖЕНИЙ
Под редакцией В.А.Сойфера
МЕТОДЫ
КОМПЬЮТЕРНОЙ
ОБРАБОТКИ
ИЗОБРАЖЕНИЙ
Под редакцией В.А.Сойфера
ИЗДАНИЕ ВТОРОЕ, ИСПРАВЛЕННОЕ
Допущено Министерством образования
Российской Федерации в качестве учебного пособия
для студентов высших учебных заведений,
обучающихся по направлению подготовки
дипломированных специалистов
“Прикладная математика”
МОСКВА
ФИЗМАТЛИТ
2003
УДК 681.3, 621.372.542
БЕК 22.343
М47
Коллектив авторов:
Гашников М.В., Глумов Н.И., Ильясова Н.Ю., Мясников В.В., Попов С.Б., Сергеев В.В.,
Сойфер В.А., Храмов А.Г., Чернов А.В., Чернов В.М., Чичева М.А., Фурсов В.А.
Методы компьютерной обработки изображений / Под род. В.А. Сойфера. —
2-е изд., испр. - М.: ФИЗМАТЛИТ, 2003. - 784 с. - ISBN 5-9221-0270-2.
В книге излагаются теоретические основы цифровой обработки изображений: матема-
тические модели, критерии качества и погрешности дискретного представления, методы
повышения качества и оценки геометрических параметров изображений, элементы теории
распознавания изображений. Рассматриваются новые методы, алгоритмы и информаци-
онные технологии: алгебро-арифметического синтеза быстрых алгоритмов дискретных ор-
тогональных преобразований, компрессии изображений, анализа изображений с помощью
поля направлений, параллельно-рекурсивной локальной обработки изображений, обнаруже-
ния и распознавания объектов на изображениях, оценки параметров моделей изображений
по малому числу наблюдений.
Для специалистов, работающих в области прикладной математики и информатики, а
также аспирантов и студентов старших курсов.
Табл. 46. Ил. 364.
Рецензенты
академик РАН Ю.И. Журавлев
академик РАО, чл.-кор. РАН В.Л. Матросов
ISBN 5-9221-0270-2
© ФИЗМАТЛИТ, 2003
© Коллектив авторов, 2003
ОГЛАВЛЕНИЕ
Предисловие ....................................................................9
Часть I
Теоретические основы цифровой обработки изображений
Глава 1. Математические модели изображений ....................................13
1.1. Модели непрерывных изображений ........................................13
1.1.1. Функция яркости.................................................13
1.1.2. Оптический сигнал ..............................................14
1.1.3. Двумерные линейные системы......................................17
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы ..............22
1.2.1. Спектр периодического сигнала...................................22
1.2.2. Спектр непериодического сигнала.................................24
1.2.3. Спектры импульсов ..............................................28
1.2.4. Спектры обобщенных функций .....................................35
1.2.5. Двумерное преобразование Фурье .................................37
1.2.6. Оптические линейные системы в частотной области.................39
1.3. Представление изображений в компьютере.................................40
1.3.1. Средства ввода изображения .....................................40
1.3.2. Дискретизация изображений ......................................40
1.4. Последовательности и линейные системы с постоянными параметрами . . 42
1.4.1. Последовательности..............................................42
1.4.2. Дискретные ЛПП-системы .........................................45
1.4.3. Физическая реализуемость и устойчивость ЛПП-систем .............47
1.4.4. Разностные уравнения ...........................................49
1.4.5. Двумерные последовательности ...................................52
1.4.6. Двумерные дискретные ЛПП-системы................................55
1.4.7. Физическая реализуемость двумерных систем ......................57
1.4.8. Двумерные разностные уравнения..................................60
1.5. Описание дискретных сигналов и систем в частотной области..............63
1.5.1. Частотная характеристика ЛПП-систем и спектры дискретных сигналов . . 63
1.5.2. Основные свойства спектров последовательности ..................65
1.5.3. Соотношение между спектрами непрерывных и дискретных сигналов .... 70
1.5.4. Описание двумерных дискретных сигналов и систем в частотной области . . 73
1.6. Описание дискретных сигналов и систем с помощью г-преобразования . . 78
1.6.1. Прямое ^-преобразование ........................................78
1.6.2. Основные свойства г-преобразования .............................84
1.6.3. Обратное ^-преобразование ......................................88
1.6.4. Анализ и синтез ЛПП-систем с использованием ^-преобразования....93
1.6.5. Двумерное г-преобразование .....................................99
1.6.6. Основные свойства двумерного ^-преобразования..................109
1.6.7. Анализ и синтез двумерных ЛПП-систем с использованием
^-преобразования................................................Ill
1.7. Спектральный анализ дискретных сигналов ..............................116
1.7.1. Дискретное преобразование Фурье ...............................116
1.7.2. Связь ДПФ с ^-преобразованием и непрерывным
спектром последовательности .......................'............119
4
ОГЛАВЛЕНИЕ
1.7.3. Использование ДПФ для вычисления отсчетов непрерывного спектра ... 121
1.7.4. Использование ДПФ для вычисления последовательности по ее спектру ... 122
1.7.5. Основные свойства ДПФ..........................................124
1.7.6. Вычисление линейной свертки при помощи ДПФ ....................127
1.7.7. Быстрое преобразование Фурье ..................................128
1.8. Вероятностные модели изображений .....................................135
1.8.1. Случайные процессы ............................................135
1.8.2. Случайные последовательности и их характеристики ..............139
1.8.3. Преобразование случайных последовательностей в ЛПП-системах.....143
1.8.4. Факторизация энергетического спектра...........................145
Глава 2. Критерии качества изображений и погрешности
их дискретного представления..................................................151
2.1. Критерии качества изображений.........................................151
2.1.1. Критерий визуального восприятия................................151
2.1.2. Среднеквадратичный критерий ...................................152
2.1.3. Критерий максимальной ошибки (равномерного приближения)........153
2.1.4. Вероятностно-зональный критерий ...............................153
2.1.5. Критерий пространственного разрешения .........................154
2.2. Погрешности дискретного представления изображений ....................158
2.2.1. Оценка погрешностей квантования параметра по уровню............159
2.2.2. Восстановление непрерывных изображений по их дискретному
представлению.........................................................161
2.2.3. Оценка среднеквадратичной погрешности дискретизации............164
2.2.4. Оценка максимальной погрешности дискретизации .................170
2.2.5. Обшая погрешность цифрового представления изображений .........173
Глава 3. Повышение качества изображений и оценка их геометрических
параметров ...................................................................175
3.1. Преобразования яркости изображений ...................................175
3.1.1. Коррекция амплитудных характеристик............................175
3.1.2. Линейное повышение контраста ..................................176
3.1.3. Преобразование гистограмм......................................178
3.1.4. Пороговая обработка ...........................................180
3.1.5. Препарирование.................................................182
3.1.6. Адаптивные преобразования яркости..............................184
3.2. Повышение резкости изображений........................................187
3.3. Выделение контуров ...................................................192
3.3.1. Определение контура............................................192
3.3.2. Дифференциальные методы........................................196
3.3.3. Методы выделения перепадов яркости с согласованием ............201
3.4. Линейная фильтрация и восстановление изображений......................204
3.4.1. Восстановление дискретного сигнала ЛПП-системой ...............204
3.4.2. Оптимальное линейное восстановление сигнала ...................208
3.4.3. Реализация оптимального фильтра обработкой «в прямом
и обратном времени»...................................................215
3.4.4. Реализация оптимального фильтра при помощи ДПФ ................218
3.4.5. Восстановление сигнала КИХ-фильтром............................221
3.4.6. Двумерная оптимальная линейная фильтрация .....................223
3.4.7. Двумерные линейные субоптимальные КИХ-фильтры .................231
3.5. Нелинейная фильтрация.................................................234
3.5.1. Медианная фильтрация ..........................................234
3.5.2. Адаптивные фильтры.............................................236
3.5.3. Ранговая обработка изображений.................................238
3.6. Оценка геометрических характеристик объектов на изображениях...........245
Оглавление
5
Глава 4. Распознавание изображений ..........................................251
4.1. Постановка задачи ..................................................251
4.2. Вероятностный критерий качества классификации.......................254
4.3. Оптимальные стратегии статистической классификации .................255
4.3.1. Классификатор Байеса.........................................256
4.3.2. Минимаксный классификатор....................................258
4.3.3. Классификатор Неймана-Пирсона ...............................259
4.4. Классификатор Байеса для нормально распределенных векторов
признаков .............................................................. 260
4.4.1. Алгоритмы классификации .....................................260
4.4.2. Вычисление вероятностей ошибочной классификации для нормально
распределенных векторов признаков ..................................263
4.5. Основные группы признаков, используемых при распознавании
изображений..............................................................265
4.5.1. Геометрические признаки .....................................266
4.5.2. Топологические признаки .....................................269
4.5.3. Вероятностные признаки.......................................270
4.5.4. Спектральные признаки........................................271
4.6. Некоторые алгебраические методы в задачах распознавания
изображений..............................................................275
4.6.1. О статистическом и детерминированном подходах к задачам анализа
изображений ..................................................275
4.6.2. Резонансный метод выделения геометрических примитивов........278
4.6.3. Линейная разделимость классов в пространствах с р-адической метрикой . . . 285
4.6.4. Рациональные приближения иррациональных алгебраических чисел
и теоремы устойчивости полиномиальных решающих правил...............291
Литература к части 1 .......................................................297
Часть II
Алгоритмы и информационные технологии обработки изображений
Глава 5. Алгебро-арифметические методы синтеза быстрых алгоритмов дискретных
ортогональных преобразований ...............................................301
5.1. Предварительные сведения............................................301
5.1.1. О проблеме синтеза быстрых алгоритмов дискретных ортогональных
преобразований .....................................................301
5.1.2. Конечномерные ассоциативные алгебры .........................304
5.1.3. Основные схемы редукции......................................306
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований . . . 309
5.2.1. Двумерный БА ДПФ с совмещением в алгебре кватернионов........311
5.2.2. БПФ с представлением данных в алгебре (2х2)-матриц...........313
5.2.3. Кватернионное двумерное ДПФ .................................315
5.2.4. Совмещенные алгоритмы дискретного косинусного преобразования .... 322
5.3. Быстрые алгоритмы ДОП при специальном представлении данных .... 330
5.3.1. Представление данных в круговых кодах.........................330
5.3.2. Алгоритмы одномерного ДПФ при длине преобразования /V—3*......332
5.3.3. Алгоритмы дискретного косинусного преобразования длиной Л=3* .... 333
5.3.4. Алгоритмы дискретных ортогональных преобразований,
реализуемые в кодах Гамильтона-Эйзенштейна..........................336
5.3.5. Алгоритмы дискретного косинусного преобразования коротких длин .... 343
6
ОГЛАВЛЕНИЕ
5.4. Унифицированный метрический подход к синтезу быстрых алгоритмов
многомерного ДПФ ........................................................356
5.4.1. Альтернативная интерпретация редукции Кули-Тьюки.............357
5.4.2. Алгоритмы двумерного ДПФ с покоординатным прореживанием
области суммирования..........................................359
5.4.3. «Чесс-алгоритмы» двумерного ДПФ для N- 2Г ...................362
5.4.4. Алгоритмы двумерного ДПФ — алгоритмы с расщеплением основания
нецелого порядка....................................................368
5.4.5. Алгоритмы двумерного ДПФ с «мультипокрытиями» области
суммирования .......................................................371
5.5. Некоторые приложения ...............................................373
5.5.1. Задача вычисления ДПФ последовательности произвольной длины .373
5.5.2 Исследование алгоритмов ДКП в методе блочного кодирования
с преобразованием.............................................378
Литература к главе 5 .....................................................383
Глава 6. Компрессия изображений.............................................385
6.1. Показатели качества методов компрессии..............................385
6.1.1. Показатели эффективности ....................................386
6.1.2. Показатели точности .........................................387
6.1.3. Системотехнические показатели ...............................389
6.2. Статистическое кодирование .........................................389
6.2.1. Код Шеннона-Фано ............................................391
6.2.2. Код Хаффмена.................................................392
6.2.3. Кодирование длин серий.......................................392
6.3. Оптимизация регулярного цифрового представления изображений .... 396
6.4. Метод дифференциального кодирования ................................400
6.4.1. Общее описание метода........................................400
6.4.2. Выбор квантователя для разностного сигнала ..................402
6.4.3. Алгоритмы предсказания отсчетов..............................406
6.4.4. Оптимизация дифференциального кодера изображений ............415
6.4.5. Дифференциальное кодирование бинарных изображений ...........418
6.5. Методы кодирования с преобразованием ...............................420
6.5.1. Общая схема методов кодирования с преобразованием ...........420
6.5.2. Выбор преобразования.........................................423
6.5.3. Кодирование трансформант.....................................426
6.5.4. Оптимизация процедуры кодирования с преобразованием .........427
6.6. Метод адаптивных выборок ...........................................434
6.6.1. Общая схема и примеры метода адаптивных выборок..............434
6.6.2. Метод выделения областей и кодирования контуров..............439
6.7. Другие методы компрессии изображений ...............................443
6.7.1. Гибридные методы кодирования ................................444
6.7.2. Стандарт компрессии изображений JPEG ........................446
6.7.3. Метод иерархической сеточной интерполяции ...................450
6.7.4. Экспериментальные исследования методов компрессии изображений . . . 453
Литература к главе 6 .......................................................456
Глава 7. Метод поля направлений.............................................459
7.1. Изображения со структурной избыточностью............................459
7.2. Математическое описание поля направлений............................461
Оглавление
7
7.3. Математическая модель изображений со структурной избыточностью . . 462
7.4. Нелинейная фильтрация полей направлений .............................467
7.5. Цифровые методы построения поля направлений .........................468
7.5.1. Методы параметрической аппроксимации..........................468
7.5.2. Методы локальных градиентов...................................476
7.5.3. Дифференциальные методы.......................................485
7.5.4. Проекционно-дисперсионные методы .............................487
7.5.5. Спектральные методы ..........................................49!
7.5.6. Экспериментальные исследования методов построения
поля направлений ..............................................495
7.6. Обработка и интерпретация дактилоскопических изображений ............498
7.6.1. Геометрические характристики глобальных особенностей дактилограмм . . . 500
7.6.2. Оценка геометрических характеристик глобальных особенностей...502
7.6.3. Обнаружение мелких нерегулярностей отпечатка пальца...........504
7.7. Обработка и интерпретация кристаллограмм слезной жидкости............509
7.7.1. Медико-диагностические признаки кристаллограмм ...............511
7.7.2. Оценка геометрических параметров кристаллограмм...............511
7.7.3. Классификация кристаллограмм на основе объединения
диагностических признаков......................................516
7.7.4. Экспериментальное исследование методов анализа кристаллограмм.517
7.8. Обработка и интерпретация кристаллограмм плазмы крови ...............520
7.9. Обсуждение результатов ..............................................524
Литература к главе 7 ........................................................525
Глава 8. Параллельно-рекурсивные методы локальной обработки изображений . . . 527
8.1. Цифровые параллельно-рекурсивные фильтры с конечной импульсной
характеристикой .........................................................527
8.1.1. Обработка изображений в скользящем окне ......................527
8.1.2. Принципы построения параллельно-рекурсивных КИХ-фильтров .....529
8.1.3. Рекурсивно реализуемые базисные функции ......................532
8.1.4. Секционирование импульсной характеристики КИХ-фильтров .......540
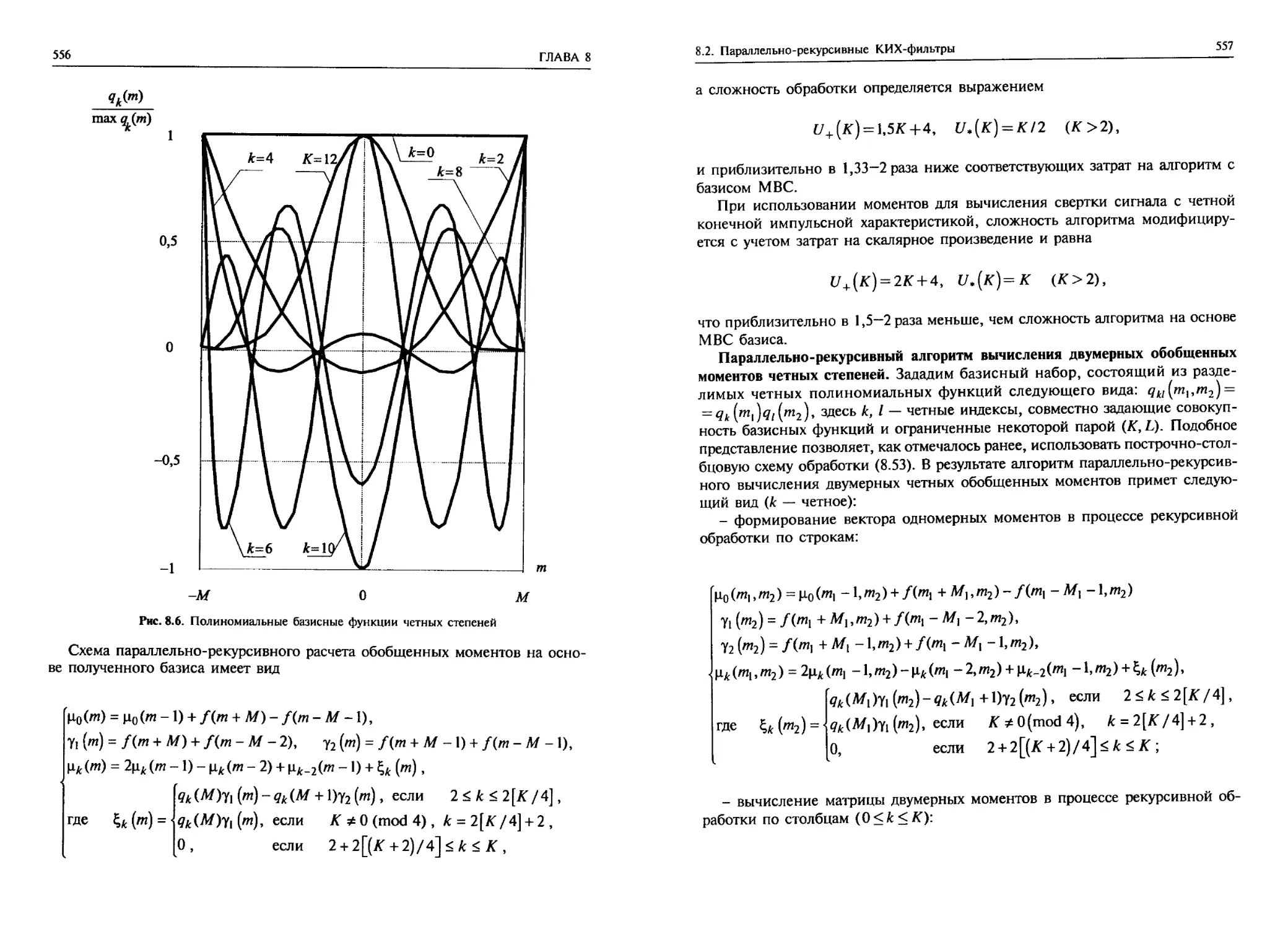
8.2. Параллельно-рекурсивные КИХ-фильтры с полиномиальными
импульсными характеристиками.............................................541
8.2.1. Полиномиальные базисы и обобщенные моменты ...................541
8.2.2. Параллельно-рекурсивные алгоритмы вычисления обобщенных моментов . . 543
8.2.3. Алгоритмы формирования МВС и МВС-подобных базисов ............546
8.2.4. Параллельно-рекурсивный алгоритм на основе полиномиальных базисов
четных степеней......................................................552
8.2.5. Параллельно-рекурсивной алгоритм фильтрации сигналов при нечетной
полиномиальной импульсной характеристике ............................558
8.2.6. Оценка качества полиномиальных базисов по различным критериям .... 562
8.3. Расчет и применение параллельно-рекурсивных КИХ-фильтров в задачах
обработки изображений ...................................................565
8.3.1. Общая схема расчета параллельно-рекурсивных КИХ-фильтров......565
8.3.2. Среднеквадратичная аппроксимация импульсной характеристики ...566
8.3.3. Среднеквадратичная аппроксимация частотной характеристики ....568
8.3.4. Моделирование ЛПП-системы.....................................571
8.3.5. Преобразование стационарных случайных процессов ..............573
8.3.6. Восстановление сигналов.......................................575
8.3.7. Обнаружение объектов..........................................577
8.3.8. Анализ эффективности параллельно-рекурсивных КИХ-фильтров
в задачах обработки изображений ...............................579
8.4. Применение методологии распознавания образов в задачах цифровой
обработки изображений ....................................................581
8.4.1. Общее описание преобразования данных .........................583
8
ОГЛАВЛЕНИЕ
8.4.2. Классификация отсчетов изображения .......................584
8.4.3. Вычислительные эксперименты по исследованию эффективности
алгоритмов локальной обработки изображений.......................587
8.5. Заключение.......................................................597
Литература к главе 8 ....................................................598
Глава 9. Обнаружение и распознавание объектов на изображениях ...........601
9.1. Задачи распознавания на изображениях ............................601
9.2. Формирование признаков по изображению ...........................603
9.2.1. Основные требования к признакам, вычисляемым по изображениям .... 604
9 2.2. Нормализация изображений при вычислении признаков ...605
9.2.3. Моментные инварианты как признаки изображения.............624
9.3. Обнаружение и локализация объектов на изображении ...............634
9.3.1. Постановка задачи и анализ современного состояния.........634
9.3.2. Критерии локализации объектов ............................636
9.3.3. Совместное обнаружение и локализация объектов ............644
9.3.4. Распознавание объектов двух классов ......................651
9.4. Совместная классификация ........................................662
9.4.1. Стратегии совместной классификации .......................663
9.4.2. Параллельная схема совместной классификации с минимальной
информацией о решениях экспертов ................................666
9.4.3. Двухэтапная последовательная процедура классификации......673
Литература к главе 9 ....................................................687
Глава 10. Построение оценок по малому числу наблюдений в задачах
обработки изображений....................................................692
10.1. Примеры и формулировка задачи...................................692
10.2. Проблема оценки по малому числу наблюдений......................698
10.3. Формы представления и ортогональные разложения ошибок...........703
10.4. Оценки достижимой точности .....................................707
10.5. Меры обусловленности и мультиколлинеарности.....................714
10.6. Связь и сравнительная характеристика мер обусловленности
и мультиколлинеарности............................................... 718
10.7. Построение проверочных неравенств для достижимой точности ......727
10.8. Общие принципы и схема построения оценок по малому числу
наблюдений ...........................................................734
10.9. Построение оценок путем непосредственной корректировки вектора
выхода модели ........................................................737
10.10. Построение алгоритмов оценки по методу взвешивания.............744
10.11. Идентификация моделей восстанавливающих фильтров ..............751
10.12. Идентификация кусочно-постоянных моделей в случае
пространственно-зависимых искажений...................................759
10.13. Оценка разрешающей способности видеотракта ....................763
10.14. Информационная технология совмещения изображений
по информативным фрагментам ..........................................768
10.14. Оценка по малому числу наблюдений в задачах обучения
распознаванию образов.................................................776
Литература к главе 10 ...................................................779
ПРЕДИСЛОВИЕ
Зрительные образы являются для человека основой восприятия окружаю-
щего мира. Изображение несет в себе информацию об объекте и в этом смыс-
ле может рассматриваться как многомерный сигнал, описываемый функцией
двух или большего числа переменных.
Обработка изображений означает выполнение над ними различных опера-
ций с заданной целью. Классическая цель и задача обработки изображений —
улучшение их качества — впервые возникла в оптике и традиционно решалась
путем создания более совершенных оптических систем, то есть с помощью
оптической обработки изображений. С момента появления компьютеров в
оптике произошла настоящая революция, связанная с проникновением в нее
цифровых методов.
Первые публикации по цифровой обработке изображений появились в
60-х годах применительно к задачам астрономии, ядерной физики, биофи-
зики, радиофизики и в практической части опирались на созданные в то
время устройства ввода-вывода изображений. В 1965 году Кули и Тьюки
опубликовали реализованный ими на компьютере алгоритм быстрого пре-
образования Фурье (БПФ), ранее известный только узкому кругу математи-
ков, и это стало мощным импульсом в продвижении идей и методов обра-
ботки изображений. К БПФ примыкает целый ряд других дискретных орто-
гональных преобразований.
В данном учебном пособии рассматриваются оптические изображения, хотя
в силу общности математических моделей, предлагаемые методы обработки
изображений являются достаточно универсальными и могут применяться для
обработки широкого класса многомерных сигналов различной физической
природы.
Многообразие целей и задач обработки изображений можно классифици-
ровать следующим образом:
— улучшение качества изображений;
- измерения на изображениях;
— спектральный анализ многомерных сигналов;
— распознавание изображений;
— компрессия изображений.
Книга состоит из двух частей. Первая часть монографии, состоящая из
четырех глав, может служить учебным пособием для знакомства с проблема-
ми, классическими методами и алгоритмами цифровой обработки изображе-
ний. В тексте первой части отсутствуют библиографические ссылки, однако в
10
ПРЕДИСЛОВИЕ
соответствующем списке литературы содержатся основные источники, ис-
пользованные при ее написании.
Вторая часть книги, состоящая из шести глав, написана в существенно
более лаконичном стиле и ориентирована на подготовленного читателя. В
этой части нашли свое отражение результаты многолетней работы коллектива
авторов — сотрудников Института систем обработки изображений РАН в дан-
ной области. В связи с этим, направленность содержания глав второй части
определяется, в первую очередь, научными интересами авторов. Излагаемые
результаты можно рекомендовать как базу для дальнейшей самостоятельной
работы.
Книга написана сотрудниками Института систем обработки изображений
РАН.
главы 1-4 — В.В. Мясниковым, С.Б. Поповым, В.В. Сергеевым, В.А. Сой-
фером, кроме п. 4.6, написанного В.М. Черновым,
глава 5 — В.М. Черновым, М.А. Чичевой,
глава 6 — М.В. Гашниковым, Н.И. Глумовым, С.Б. Поповым, В.В. Сер-
геевым,
глава 7 — Н.Ю. Ильясовой, В.А. Сойфером, А.Г. Храмовым,
глава 8 — Н.И. Глумовым, В.В. Мясниковым, В.В. Сергеевым, А.В. Чер-
новым,
глава 9 — Н.И. Глумовым, В.В. Мясниковым, В.В. Сергеевым,
глава 10 — В.А. Фурсовым.
Авторы выражают благодарность:
— академику Ю.И. Журавлеву за постоянное внимание и помощь в рабо-
те авторского коллектива;
— российско-американской программе «Фундаментальные исследования
и высшее образование» («BRHE»);
— российской общественной организации «Ассоциация распознавания
образов и анализа изображений» за плодотворное сотрудничество;
- доктору физико-математических наук Н.Л. Казанскому за организаци-
онно-методическую помощь;
— сотрудникам лабораторий математических методов обработки изобра-
жений и лазерных измерений Института систем обработки изображений РАН
за проведение большого количества компьютерных экспериментов;
- Е.В. Золотухиной, Е.В. Клевцовой, Л.В. Потаповой, С.В. Смагину,
Я.Е. Тахтарову и И.И. Успленьевой за оформительскую работу;
— Волгоградской медицинской академии за предоставленные диагности-
ческие изображения, Государственному научно-производственному ракетно-
космическому центру «ЦСКБ-ПРОГРЕСС» и предприятию «Совинформспут-
ник» за предоставленные натурные изображения.
Книга базируется на оригинальных научных работах, опубликованных за
последние 25 лет членами авторского коллектива; соавторами ряда работ были:
Э.И. Коломиец, М.В. Максимов, С.И. Парфенов, М.В. Першина, А.В. Ус-
тинов, Л.Г. Фролова, А.В. Шабашев, В.А. Шустов.
ЧАСТЬ I
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ЦИФРОВОЙ ОБРАБОТКИ
ИЗОБРАЖЕНИЙ
ГЛАВА 1
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ИЗОБРАЖЕНИЙ
1.1. Модели непрерывных изображений
1.1.1. Функция яркости
Необходимость построения математической модели возникает сразу же при
необходимости использовать компьютер для обработки изображений. Оцени-
вая «на глаз» расстояние между двумя предметами, мы не задумываемся о
том, как это делается. Поручив эти задачи компьютеру, мы обязаны научить
его выполнять подобные действия, то есть заложить в него соответствующие
данные и алгоритмы. Хорошо известно, что компьютер в качестве данных
имеет дело с массивами чисел. Таким образом, первой задачей компьютерной
обработки изображений является перевод изображений в числовую форму.
Это требует конкретизации самого понятия «изображение».
Рассмотрим объект, освещенный источником света, как показано на
рис. 1.1. На некотором расстоянии от объекта распределение энергии источ-
ника светового излучения, отраженного объектом, по пространственным ко-
ординатам х2 и по длинам волн X описывается функцией С(х(,х2,Х). Эта
величина является неотрицательной. Ее максимальное значение в изобража-
ющих системах ограничено предельной величиной светочувствительности
регистрирующих сред:
o<c(x„^A)<c,mjl, (i.i)
где Стах — максимальная яркость изображения.
Геометрические размеры ограничены характеристиками формирующей
системы и размерами фоторегистрирующей среды. Будем полагать, что все
изображения отличны от нуля в прямоугольной области
—Г] <%[</>!, — L1<x2<L2. (1.2)
Человеческое зрение и видеодатчики обладают спектральной чувстви-
тельностью, описываемой функцией ^(Х). Как известно, человеческий глаз
обладает чувствительностью к свету в диапазоне волн от Xmin =0.35 мкм до
14
ГЛАВА 1
Рис. 1.1. Формирование изображения объекта, ос-
вещенного источником света
Хтах = 0,78 мкм. При этом функ-
ция спектральной чувствитель-
ности достигает своего макси-
мума приблизительно в середи-
не этого диапазона и спадает к
его краям.
Каждый видеодатчик облада-
ет индивидуальной характеристи-
кой спектральной чувствительно-
сти, обусловленной физикой
прибора. Имеются видеодатчики
ультрафиолетового и инфракрас-
ного диапазонов, которые широко используются, например, при проведении
спектрозональных съемок Земли из космоса.
Как в случае наблюдения объекта человеком, так и в случае использования
видеодатчика, наблюдаемое изображение является результатом усреднения
функции С(л1,х2Д) по диапазону длин волн с весовой функцией s(X) и
описывается выражением
^|ПаХ
/(х|,х2) = f C(xi,x2,^)s(X]dX.
^•min
(1.3)
Функцию /(^],x2) в дальнейшем будем называть изображением. Таким
образом изображение — это ограниченная функция двух пространственных
переменных, заданная на ограниченной прямоугольной области.
1,1.2. Оптический сигнал
В целом ряде ситуаций необходимо рассматривать не только интенсив-
ность, но и фазу световой волны. Положим для простоты, что свет линейно
поляризован. Электрическое поле в момент времени t в точке с координата-
ми х = (x,,x2,x3), возбуждаемое монохроматическим источником света, мо-
жет быть записано в комплексном виде:
E(x,r) = (/(x)^w',
где (и = 2лс/'К — частота источника света, с — скорость света,
У(х) = Л(х)Л(’>
(1-4)
(1-5)
— оптический сигнал, имеющий амплитуду Д(х) и фазу ср(х).
1.1. Модели непрерывных изображений
15
Выражение (1.4), в котором пространственная и временная переменные
разделены, может быть использовано и для квазимонохроматического источ-
ника света, ширина полосы частот Асо которого существенно меньше сред-
ней частоты излучаемого света:
Асу/ <<; 1
/ со
(1-6)
Фотодетектор регистрирует среднюю интенсивность света на достаточно
большом интервале времени (-Т, Т), существенно превышающем период
Т » 2л/со:
(1.7)
г
В двумерном случае фотодетектор регистрирует изображение /(х|,х2).
Отметим, что голографическая запись позволяет регистрировать как амп-
литуду, так и фазу оптического сигнала через его квадратурные компонен-
ты — синусную и косинусную составляющие, каждая из которых может быть
представлена как изображение.
Рассмотрим примеры оптических сигналов.
Пример 1.1. Сферическая волна описывается выражением
1 '—х
(/(х) =—2 е х , |x|2 = xf+x2+x3. (1.8)
1Х1
Поверхность постоянной фазы — сфера.
Пример 1.2. Плоская монохроматическая волна, распространяющаяся вдоль
оси х3, описывается выражением
Е(х1,х2,л3,г)е-(О)^_Аз^\ (1.9)
Поверхность постоянной фазы — плоскость.
Отметим, что сферическая линза преобразует сферическую волну в плос-
кую и наоборот, как изображено на рис. 1.2.
Интерферограмма. Явление интерференции заключается в усилении или
ослаблении поля двух световых волн в зависимости от разности их фаз. Заре-
гистрированное изображение интерференционной картинки называется ин-
терферограммой. Интерференционные методы исследования часто применя-
ются в физике и технике.
Рассмотрим интерферометр Ллойда, изображенный на рис. 1.3.
16
ГЛАВА 1
Сферическая
волна
Плоская
волна
Рис. 1.2. Преобразование сферической волны в плоскую
На некотором расстоянии от зеркала находится источник монохромати-
ческого света 5, в зеркале появляется мнимый источник света S'. Рассмот-
рим интерференцию волн от этих двух источников в точке х, учитывая что
оптический сигнал, идущий от мнимого источника S', отличается только за-
паздыванием на время т, запишем
E(t) = U(t)+U(t-T).
(1.10)
Приемник света в точке х регистрирует интенсивность
1 -т 1 -Т
(111)
Рис. 1.3. Интерферометр Ллойда
Вводя в рассмотрение автокорреляцион-
ную функцию оптического сигнала
1 р-
Я(т)=1ш1 — , (1,12)
т-оо 2/ JT
из (1.11) при Т > оо получаем
/(т) = 2К(0) + 2Я(т).
(1.13)
1.1. Модели непрерывных изображений
17
Отметим, что использовать понятие «автокорреляция» для детерминиро-
ванного оптического сигнала не вполне корректно, так как оно изначально
введено для случайных сигналов, однако этот термин укоренился и широко
используется в оптике и смежных науках.
Пример 1.3. Рассмотрим точечный монохроматический источник.
<7 (г) = Acosco/. (1.14)
Автокорреляционная функция вычисляется в виде
1 г о А2
/?(т) = lim— I A2coscDf cosf(o(z-т)р/= —coscor, (1-15)
т -»оо 2Т JT J 2(0
и интерференционная картина описывается выражением
/(т) =—(1 +cos сот
2(0
(1-16)
График функции (1.16) приведен на рис. 1.4.
В двумерном случае интерференционная картина будет представлять со-
бой чередование темных и светлых полос с плавным переходом от темного к
светлому. Измерив расстояние между максимумами, можно определить час-
тоту излучения со.
1.1.3. Двумерные линейные системы
Из курса физики хорошо известно понятие оптической системы, осуще-
ствляющей преобразование изображений по правилам, определяемым сово-
купностью используемых в ней оптических элементов и их взаимосвязью.
С математической точки зрения под системой будем понимать правило £,
ставящее в соответствие входной функции / выходную функцию g. Различа-
ют одномерные (I-D) и двумерные (2-D) системы. Одномерные системы преоб-
разуют функции одной переменной:
(1-17)
g(x) = £[/(*)].
Рис. 1.4. Интерференционная картина для монохроматического источника
18
ГЛАВА 1
Соответственно двумерные системы преобразуют функции двух переменных:
я(л|,х2) = £[/(х1,.х2)].
(1.18)
Оптические системы по сути своей являются двумерными, но в некоторых
случаях могут рассматриваться как одномерные.
Особое место среди всевозможных систем занимают линейные системы.
Система называется линейной, если для нее справедлив принцип суперпози-
ции (наложения), который заключается в том, что отклик системы на взвеше-
ную сумму двух входных воздействий равен взвешеной сумме откликов на
каждое из воздействий, то есть
/| (х,, х2) 4- a2f2 (%!, х2)] = £[f (%|, х2)] 4- a2£[f2 (xj, х2)].
(1-19)
Принцип суперпозиции можно выразить в более общем виде, рассматри-
вая произвольное число К входных воздействий:
к к
л=1 *=1
(1.20)
В изучении оптических систем фундаментальную роль играет понятие то-
чечного источника света. Точечный источник обладает бесконечно большой
плотностью вероятностей распределения яркости в бесконечно малой про-
странственной области — в точке:
5(хрх2) =
ос, х, = 0 и х2 = 0,
0, в других случаях.
(1-21)
Такое представление исключительно полезно и допускает ясную физичес-
кую трактовку: дельта-функция может быть определена как предел обычной
функции, например
б(х],х2)= lim <а2ехр — сГл
а—»оо
(1.22)
Согласно (1.22) дельта-функция может рассматриваться как бесконечно
узкая колоколообразная функция, одномерный вариант которой приведен на
рис. 1.5.
Можно также ввести дельта-функцию, расположенную не в начале коор-
динат, а в произвольной точке с координатами (£,£2) по формуле
— £2) — '
ОО, X, и х2=£2,
0, в других случаях.
(1.23)
1.1. Модели непрерывных изображений
19
Дельта-функция обладает следующими важными свойствами:
Свойство нормировки:
ОС 30
J* J ,*2)^*1 ^х2 ~ 1
(1-24)
Физически это означает, что, хотя плотность вероятностей распределения
яркости точечного источника бесконечна, энергия его ограничена и равна
единице.
Фильтрующее свойство:
эс сю
f f f (*!, *2 )S(Xj - £1, X2 - £2 И*1 dx2 = /(£1Л2 ),
-сю —сю
(1-25)
где — произвольная функция двух переменных. Доказательство при-
веденных свойств выполняются с помощью подстановки в (1.24) и (1.25) вы-
ражения (1.22) и раскрытия предела.
Рассмотрим 2-D линейную систему, на вход которой подан сигнал в виде
дельта-функции. Реакция системы на дельта-функцию будет разной для раз-
личных систем. Она называется импульсным откликом и служит характеристи-
кой 2-D системы. Систему называют пространственно-инвариантной, если ее
импульсный отклик зависит от разности координат входной (xj,x2) и выход-
ной плоскостей. Для оптической системы, показанной на рис. 1.6,
это означает, что при перемещении точечного источника во входной (пред-
метной) области изображение этого предмета в плоскости наблюдения будет
также изменять положение, но сохранять форму.
Рис. 1.5. Физическая трактовка дельта-функции Дирака
20
ГЛАВА i
Для пространственно-инвариантных систем импульсный отклик описыва-
ется функцией
h(xt-^-b)=h^2),
(1.26)
где X] , х2 ^2 — ^2 ’
h(x},x2) = £[8(х|,х2)|. (1-27)
Используя функцию импульсного отклика, можно записать уравнение,
связывающее изображения на входе и выходе 2-D линейной оптической сис-
темы. Для этого представим входной сигнал /(х1,х2) в виде (1.25) и подадим
его на вход 2-D системы с характеристикой /г(^,,^2). Выходной сигнал запи-
шем в виде
£(Х|,Х2)=£[/(Х|,Х2)| =
ос оо
= £ / f
(1.28)
.—ос—ОС
Поскольку операция £ линейна, и операция интегрирования в фигурных
скобках (1.28) также линейна, их можно поменять местами и записать, что
ОО 00
g(x„x2)= J J
—ос—оо
Учитывая, что по определению
£{5(Х| -^1,x2-^2)} = /z(x1 -^,х2-С2),
1.1. Модели непрерывных изображений
21
окончательно получаем выражение, устанавливающее связь между изображе-
ниями во входной и выходной плоскостях линейной системы:
ОС ОС
g(x,.x2)= f f f^2)h{xt-^,x2-^d^d^.
—ос -оо
(1.29)
Уравнение (1.29) называется интегралом свертки. Из этого уравнения сле-
дует, что, зная импульсный отклик оптической системы h(xvx2), можно рас-
считать выходное изображение по входному.
Процесс свертки иллюстрирует рис. 1.7. На рис. 1.7д и 1.76 изображены
функция /(Л(,х2) на входе и импульсный отклик. На рис. 1.7в показан им-
пульсный отклик при обращении координат, а на рис. 1.7г — со сдвигом на
величину X], х2 . На рис. 1.76 заштрихована область, в которой произведение
/(С1Л2)Л(Х1 — — С2)> входящее в подынтегральное выражение (1.29), не
равно нулю. Интегрирование по этой области дает величину g(x,,x2) для
заданных значений координат х},х2. Таким образом, функция g(x1(x2) на
выходе может быть найдена сканированием входной функции скользящим
«окном» — обращенным импульсным откликом, и интегрированием по обла-
сти, в которой эти функции перекрываются.
Рис. 1.7. Пример двумерной свертки
22
ГЛАВА I
1.2. Спектры сигналов. Преобразование Фурье.
Линейные системы
1.2.1. Спектр периодического сигнала
Периодический сигнал — это полезная математическая модель, позволяю-
щая описывать некоторые существующие в природе процессы и их преобра-
зования.
Периодический сигнал — это сигнал, определяемый выражением
(1.30)
где L — период; / — любое целое число, принимающее положительные и
отрицательные значения.
Как и всякая периодическая функция, он может быть разложен в ряд Фу-
рье по тригонометрическим функциям:
/М^о+Eqcos 2т^--(рА
(1-31)
При этом периодический сигнал представляется суммой синусоидальных
колебаний, частоты которых кратны основной частоте \/L. Колебание с час-
тотой 1/L называется первой гармоникой (k = 1), с частотой 2/L — второй
гармоникой (к = 2) и т.д.
Выражение (1.31) часто записывают в форме
/(х) = с0 + 12
2л£ , . 2пк
at. cos--x+b,. sm----х
L L \
(1-32)
где
ак. = ск cos<pA.; Ьк = скsincp*, к>\,
так что
Ьк I-..
(р* =arctg—, к >1.
ак
Коэффициенты ак и Ьк вычисляют по формулам
/(x)cos
(2пк
х dx, Ьк=— J /(x)si
L -L/2
(2пк
— X dx, к>1. (1.33)
L
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы
23
При этом постоянную составляющую с0 определяют по формуле
с
(1-34)
Ряд Фурье может быть также записан в комплексной форме:
00
/W= Е • <135)
А=—оо
где
2dk =ске^к =ak~ibk^
Q =2К1’со (1.36)
Величина dk называется комплексной амплитудой и может быть вычислена
по формуле
Г/2 _.2nk v
=7 J L dx‘ (L37>
L^L/2
Как видим из формул (1.35), (1.36), функция f(x) полностью определяет-
ся совокупностью величин ск и (рА.. Совокупность величин ск называется
спектром амплитуд. Совокупность величин (рА. называется спектром фаз. Во-
обще говоря, спектром называют совокупность всех значений какой-либо
величины, характеризующей систему или процесс. В физике изучают опти-
ческие спектры-разложения света по длинам волн, акустические спектры —
характеристики звука, выражающие его частотный состав, и т.д. В теории сиг-
налов изучаются спектры сигналов и систем вне зависимости от их физичес-
кой природы. Заметим, что из общего определения спектра не следует, что в
качестве спектральных компонент обязательно должны быть коэффициенты
функции по тригонометрическому базису.
Введение рядов Фурье позволяет описывать периодические сигналы по всей
оси -ос < х < ос . Они же широко применяются для описания сигналов, за-
данных на ограниченных временных или пространственных интервалах (фи-
нитных во времени или пространстве).
Например, пусть сигнал /(х) отличен от нуля на отрезке —L/2 <х< L/2,
а вне этого отрезка равен нулю. Используем прием периодического продол-
жения и рассмотрим сигнал Д(х), заданный на всей оси (рис. 1.8). Сигнал
ft (х) является периодическим и может быть разложен в ряд Фурье в любой
24
ГЛАВА 1
из введенных выше форм записи. В то же время на отрезке [—L/2,L/2] сигнал
fL(x) совпадает с сигналом f(x), поэтому из формулы (1.35) получим
к=—оо
(1.38)
где
. Г/2
dk=~ f f(X)e L dx-
L-L/2
(1.39)
Подчеркнем, что формулы (1.38) и (1.39) дают спектральное представле-
ние финитного сигнала на ограниченном отрезке времени. Для решения
целого ряда задач такое представление является достаточным, однако не
следует забывать, что оно является в значительной мере формальным и не
позволяет описывать сигнал /(х) полностью (на всей оси времени). Для
полного описания непериодической функции следует использовать интег-
рал Фурье.
1.2.2. Спектр непериодического сигнала
Будем рассматривать непериодическую функцию как предельный случай
периодической при неограниченно возрастающем периоде.
Возьмем формулу (1.35) и, подставив в нее значение dk из выражения
(1.37), получим
Г/2 ,2тгк
J f(x)e L dx.
-Ц2
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы
25
Перейдем к пределу при L —+ оо . Вместо 1/L введем основную круговую
частоту co . Эта величина есть частотный интервал между соседними гармони-
ками, частота которых равна 2nk/L. При предельном переходе сделаем заме-
ну по следующей схеме:
L—юс, (Ь-2л------>со,
где (О — текущая частота, изменяющаяся непрерывно, dm — ее приращение.
Сумма перейдет в интеграл и мы получим
t}e~iio,dt dm
2л
(1-40)
или
где
/(*) = — f F^e^dw,
(1-41)
F(to) = J f(t)e~'™dt.
(1-42)
Формулы (1.41) и (1.42) являются основными в теории спектров сигналов.
Они представляют собой пару преобразований Фурье, связывающих между со-
бой вещественную функцию времени /(л) и комплексную функцию частоты
F(cd). Для обозначения этой связи будем использовать в дальнейшем симво-
лическую запись:
F(w), F(w)
При этом функция f(x) описывается суммой бесконечно большого числа
бесконечно малых колебаний бесконечно близких частот. Комплексная амп-
литуда каждого такого колебания составляет величину
dc = — F(m)dm.
(1-43)
Частотный интервал между двумя соседними колебаниями бесконечно мал
и равен dm. Величина
dm
(1.44)
26
ГЛАВА I
выражает не непосредственно спектр, а так называемую спектральную плот-
ность, то есть распределение сигнала по спектру. Однако эту деталь обычно
опускают и называют F(co) комплексным спектром непериодического сигнала, а
абсолютное значение (модуль) этой величины называют просто спектром.
Рассмотрим некоторые свойства спектров, основанные на свойствах пре-
образования Фурье.
Линейность. Если Fjco) и F2(co) — спектры функций /, (х) и /2(х),а а,,
ос2 — произвольные комплексные числа, то спектр функции /(х) = сс1У1 (х) +
+ а2/2(х) равен F(w) = a1F1 (со)+ a2F2(со), или в символической записи
/(х) = а1/|(х) + а2/2(х)
>F(co) = a|F, (co) + a2F2(co) .
(1.45)
Смысл соотношения (1.45) кратко выражается так: спектр суммы равен
сумме спектров.
Изменение масштаба. Если a — действительное число, то
(1-46)
Особый интерес представляет случай при a = — 1, тогда
(1-47)
Свойство запаздывания. Если функцию /(х) сдвинуть на величину то
спектр функции /(х-Q будет иметь вид
(1.48)
Таким образом, при сдвиге функции /(х) на величину ее фурье-образ
умножается на при этом изменяется только фаза, а модуль остается без
изменения.
Перенос спектра. Если со — действительное число, то
Г(©-ш) = 5Г[/(л)]е,й\
(149)
то есть перенос спектра по частоте на со приводит к появлению дополнитель-
ного множителя eliax перед функцией исходного сигнала.
Спектр производной. Выполняя дифференцирование обеих сторон соотно-
шения (1.41) j раз по х, получаем
dxs
= Л 1 (ко)' F(co)
(1.50)
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы
27
то есть дифференцирование функции соответствует умножению ее спектра на
(/со). При этом, конечно, полагается, что производная в левой части (1.41)
существует.
Все перечисленные свойства можно получить из соотношений (1.41) и (1.42).
Теорема о свертке. Сверткой двух функций /j (х) и /2 (х) будем называть
функцию /(х) у определяемую соотношением
ос
/W= J
-оо
(1.51)
Вычислим спектр этой функции:
ОС ОС ОС 00
F(<o)= f e^dxf f /,(?И f
-оо -ос —оо —ос
оо ОС
—ос -ос
Здесь после перемены порядка интегрирования сделана замена перемен-
ной по формуле £, = х — .
Итак, спектр функции /(х) есть
F(a») = F](co)F2((o).
(1.52)
Теорема Парсеваля. Рассматривая интеграл от произведения двух функций
/1(х) и /2(х), нетрудно получить соотношение
ОС | ОС
J fiW/2W^=—
Z7C
-оо -оо
(1-53)
или, с учетом того, что F(<o) = F(-co),
(1.54)
Для частного случая = f2 получаем соотношение
известное как формула Парсеваля.
(1.55)
28
ГЛАВА I
1.2.3. Спектры импульсов
Рассмотрим спектры импульсных сигналов, наиболее часто встречающих-
ся в практике.
Прямоугольный импульс (рис. 1.9) выражается формулой
1
2L*
Фурье-образ этой функции равен
г/ \ сгГгг / fl —«сих > sin coL . (aL
= <? = J —e dx =---------— sine------
, 2L ($L л
(1.56)
(1.57)
где sine x = sin tlx/tix называется функцией отсчетов.
Если прямоугольный импульс сдвинуть на величину , то, согласно свой-
ству запаздывания, получим
Рис. 1.9. Прямоугольный импульс и его спектр
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы
29
F [Пл (х - О] = е~**- = е-^ sine—.
L (0L л
Графики функции и ее спектр приведены на рис. 1.10.
Функция отсчетов произвольной частоты б) имеет вид
(1.58)
,/ \ бх sindix
Дх) —sine— =-------. (1-59)
л шх
Спектр ее вычислим из соотношения взаимности. Если f(cd) — фу-
рье-образ функции /(л) , то в результате прямого преобразования Фурье
получим
F(x)-
(1.60)
Это соотношение вытекает из равенства
ос
2я/(-х)= J F(co)e
—ос
da.
(1.61)
Рис. 1.10. Сдвинутый прямоугольный импульс и его спектр
30
ГЛАВА 1
В соответствии с формулами (1.57) и (1.60) получим
. СОХ
sine—
л
= 2лПй)(со) =
л । г- ~
со<со,
со
0, |со|>со.
График функции отсчетов и ее спектр изображены на рис. 1.11. Отметим,
что спектр функции отсчетов вещественен и лежит в ограниченной полосе
частот.
Два прямоугольных импульса разной полярности («меандр») имеют анали-
тическое выражение
г(л) = П£.(л + Л)-Щ(л-Ь). (1.62)
Фурье-образ такой функции вычисляем, используя свойства линейности и
запаздывания:
• • 2
F (о)=2,-^^
v ' (OL ' ' ml.
Графики меандра и его спектра приведены на рис. 1.12.
Треугольный импульс (рис. 1.13) можно записать в виде формулы
Рис. 1.11. Функция отсчетов и ее спектр
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы
31
Рис. 1.12. Два прямоугольных импульса разной полярности и спектр их суммы
Рис. 1.13. Треугольный импульс и его спектр
32
ГЛАВА 1
Легко убедиться, что функция (1.64) представляет собой интеграл от функ-
ции (1.62), деленный на 2L, то есть спектр функции (1.64) связан со спектром
функции (1.62) соотношением
откуда искомый спектр
(1.65)
Используя выражение (1.63), получаем
,sin2co£ 11 2 со£
i--------------= sine" —
(OL i(f)2L л
(1.66)
Замечаем, что спектр в данном случае — вещественная неотрицательная
функция (см. рис. 1.14).
Экспоненциальный спад описывается функцией, отличной от нуля, только
при х > 0:
Рис. 1.14. Спектр экспоненциального импульса
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы
33
Спектр функции вычисляется по формуле
Г(ю)=7е “е ,wcdx =—-—, (1.68)
J а + /со
или через амплитуду и фазу:
CD
] —rarctg—
F <0 = , е °. (1.69)
л/аЧш2
График амплитуды и фазы экспоненциального импульса приведен на
рис. 1.14.
Двусторонний экспоненциальный спад выражается как
/(x) = e“W. (1.70)
Спектр такого сигнала имеет вид
О ос
F(to) = f e‘“e-la“dt + J e^e^dx
-ос О
а — /СО а + /СО а2 -Ь со2
и является вещественной функцией.
Функция Гаусса имеет вид
/(х) = е"''2/“!. (1.72)
Спектр ее вычисляется с помощью таблиц интегралов и имеет вид
F^ — ayRe
(1-73)
то есть также описывается гауссовой функцией, в чем и состоит двойствен-
ность рассматриваемого сигнала. Функция (1.72) представлена на рис. 1.15а,
а функция (1.73) — на рис. 1.156.
Связь между длительностью импульса и шириной его спектра. Результаты
этого параграфа показывают, что у прямоугольного импульса длительности L
ширина основного лепестка спектра пропорциональна величине 1/L. Чем
больше крутизна спада экспоненциального импульса (чем больше а), тем шире
его спектр; аналогичным свойством обладает гауссов импульс. Представление
о связи длительности импульса с шириной его спектра вытекает из свойства
2 - 9044
34
ГЛАВА 1
изменения масштаба в преобразовании Фурье (1.46): если длительность функ-
ции уменьшена в а раз, то во сколько же раз возрастает ширина спектра функ-
ции. При этом полагается, что определения длительности импульса А и шири-
ны спектра Асо остаются неизменными. К практическому их определению
можно подходить из энергетических соображений. В частности, под длитель-
ностью импульса следует понимать промежуток времени, в котором сосредо-
точена подавляющая часть энергии импульса:
х+Д/2
х-Д/2 —ос
(1-74)
где х — характерная точка, определяющая местоположение импульса на оси вре-
мени; т) — доля полной энергии импульса, приходящаяся на промежуток А.
Аналогичным образом можно определить и ширину спектра:
J |f((o)|2 d(a=T| J* |f(co)|2 d(a.
о 0
(1.75)
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы
35
Из уравнений (1.74) и (1.75) при заданном h определяют Д и Дсо. Например,
при q = 0,9 говорят, что длительность импульса и ширина спектра определены
на уровне 0,9 по энергии. Так, для экспоненциального импульса (1.67) при
т] — 0,9 имеем Д = 1,155 л-1, Д<о — 6,16 а, Дсо измеряется в радианах в секунду.
1.2.4. Спектры обобщенных функций
Теория обобщенных функций разрешает много неясных вопросов о преоб-
разовании Фурье физических сигналов и создает удобный аппарат целого ряда
прикладных задач. Рассмотрим наиболее важные обобщенные функции.
Дельта-функция 8(х) введена Дираком. Значение ее равно нулю всюду, кроме
одной точки, где оно равно бесконечности, но интеграл от дельта-функции
равен единице (см. 1.21-1.25).
Вместо того, чтобы точно определить дельта-функцию, достаточно указать
ее основное, фильтрующее свойство:
(1.76)
—оо
где /(х) — любая достаточно «хорошая» функция, которая имеет непрерыв-
ные производные всех порядков. При х = 0 имеем соотношение
оо
/8(У/(?И = /(0).
-оо
(1.77)
Функция единичного скачка (Хэвисайда) (рис. 1.16) задается выражением
и
1,
0,
х > О,
х<0.
(1.78)
Легко заметить, что введенные функции связаны соотношением
dx
(1.79)
Можно также ввести функцию м(х — Q, описывающую единичный скачок
в момент времени £.
Из дальнейших рассуждений увидим, что введенные здесь обобщенные
функции являются очень полезными при решении задач преобразования сиг-
налов в линейных системах, однако встречаются лишь на промежуточных
этапах преобразований, а в окончательных результатах отсутствуют.
2*
36
ГЛАВА 1
Рассмотрим спектры обобщенных функций.
Спектр дельта-функции определяется на основании ее фильтрующего свой-
ства (1.77):
ос
у[б(х)]= f =
-ОО
(1.80)
где 1(со) — функция, принимающая значение 1 при -оо<со<оо (рис. 1.17).
Отсюда видим, что дельта функция обладает бесконечно широким равно-
мерным спектром. С точки зрения связи длительности импульса и ширины
его спектра здесь имеет место предельный случай: бесконечно узкий импульс
имеет бесконечно широкий спектр.
Спектр функции — имеет вид
оо
-ос
Модуль его равен 1(со), а фаза линейна (рис. 1.18).
Рис. 1.17. Дельта-функция и ее спектр
Рис. 1.18. Сдвинутая дельта-функция и ее спектр
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы
37
Спектр функции может быть вычислен с учетом соотношения (1.79)
на основании свойств преобразования Фурье:
откуда
(1-81)
Теперь рассмотрим сигналы, спектры которых выражаются через обобщен-
ные сигналы.
Спектры гармонических функций cos сох и sin сох:
cos йг = [е+ е-‘йх ] —. л [8(<о - й)+8 (со+6)] (1.82)
и
sin сох =— -е '<0А
—-—♦ in [5 (со+со) - 5 (со - со)].
(1-83)
1.2.5. Двумерное преобразование Фурье
Пусть /(х,,х2) — функция двух переменных. По аналогии с одномерным
преобразованием Фурье, определенным формулами (1.41) и (1.42), можно
ввести двумерное преобразование Фурье:
Г(со,,со2) = J f f(xl,x2)e"i(3),x,~^dx1(/x2. (1.84)
- ОС
Функция С'(Ш,Х|+Ш2Х2) при фиксированных значениях со,, со2 описывает
плоскую волну В ПЛОСКОСТИ (х],Х2) (рис. 1.19).
Величины со,, со2 имеют смысл пространственных частот и размерность
мм~1, а функция f(cO|,co2) определяет спектр пространственных частот.
Сферическая линза способна вычислять спектр оптического сигнала
(рис. 1.20). На рис. 1.20 введены обозначения: ф — фокусное расстояние,
2пх, 2пх
(0. =-—L, w, = —
(1-85)
38
ГЛАВА 1
Двумерное преобразование Фурье обладает всеми свойствами одномерно-
го преобразования, кроме того отметим два дополнительных свойства, дока-
Рис. 1.19. Иллюстрация к определению про-
странственных частот
зательство которых легко следует из оп-
ределения двумерного преобразования
Фурье.
Факторизация. Если двумерный сиг-
нал факторизуется,
(1.86)
то факторизуется и его спектр:
F(cO| ,(й2)—F] ((Oj) • F2 (со2) • (1-87)
Пример. 1.4. Прямоугольная аперту-
ра (рис. 1.21) описывается факторизуе-
мой функцией
/(xi^2) = /i (*i)/2(*2)> гДе /i(jri) = nL1(x1), /2(^2) = riL2(x2).
Используя результат (1.57), получаем выражение для двумерного спектра:
Рис. 1.20. Вычисление спектра оптического сигнала с использованием сферической линзы
1.2. Спектры сигналов. Преобразование Фурье. Линейные системы
39
Радиальная симметрия. Если двумерный сигнал радиально-симметричен,
то есть
(1.89)
то из (1.84) следует, что
•оо
f(r) = f PF(p)^o(Pr)^P>
О
•DC
F(p) = f <f(r)S0(pr)rfr, (1.90)
0
где Go (pr) — функция Бесселя нуле-
вого порядка.
Формулу (1.90), определяющую
связь между радиально-симметричным
двумерным сигналом и его простран-
ственным спектром называют преоб-
разованием Ганкеля.
Рис. 1.21. Прямоугольная апертура
1.2.6. Оптические линейные системы в частотной области
Введем понятие частотной характеристики линейной системы, определив
ее как преобразование Фурье импульсного отклика (1.27):
ОС оо
Н (о>|,со2) = J* h[xvx2}e~lVi'x' ^2X1dxxdx2.
-оо-оо
(1.91)
Тогда спектры сигналов /(хрХо) и #(*1*^) во входной и выходной плос-
костях, соответственно, связаны соотношением
G(co1,co2)=H(co1,(o2)-f(co},(o2) .
(1-92)
При этом импульсный отклик может быть вычислен через частотную ха-
рактеристику с использованием обратного преобразования Фурье:
/1(х,,х2)
-!у Г 7
4л -00-00
(1.93)
40
ГЛАВА 1
1.3. Представление изображений в компьютере
1.3.1. Средства ввода изображения
Техническая задача, которую необходимо решить в компьютерной обра-
ботке изображений, это ввод оптических изображений в память компьютера
и вывод (визуализация) изображений. К счастью, в современных компьюте-
рах задача визуализации решена. Для этих целей используется высокоразре-
шающие цветные дисплеи и другая техника отображения информации.
Ввод изображений в память компьютера осуществляется с помощью ви-
деодатчиков. Видеодатчик переводит оптическое распределение яркости изоб-
ражения в электрические сигналы и далее в цифровые коды. Поскольку изоб-
ражение является функцией двух пространственных переменных, а электри-
ческий сигнал является функцией одной переменной — времени, то для
преобразования используется развертка. Например, при использовании теле-
визионной камеры, изображение считывается по строкам: строка за строкой.
При этом в пределах каждой строки зависимость яркости от пространствен-
ной координаты х преобразуется в пропорциональную зависимость амплиту-
ды электрического сигнала от времени /. Переход от конца предыдущей стро-
Рис. 1.22. Фрагмент матричного видео-
датчика
ки к началу следующей осуществляется прак-
тически мгновенно. Широкое применение
в качестве видеодатчиков находят также
матрицы фотодиодов и матрицы приборов
с зарядовой связью. При использовании
матричных видеодатчиков изображение как
бы наблюдается сквозь экран с множеством
прозрачных ячеек. Число таких ячеек для
современных видеодатчиков весьма велико
и составляет величину 1024x1024 и более (см.
рис. 1.22).
Исходное изображение, как уже отмеча-
лось, представляет собой функцию двух не-
прерывных аргументов. В то же время циф-
ровая память компьютера способна хранить только массивы данных. Поэтому
ввод изображения в компьютер неизбежно связан с дискретизацией изобра-
жений по пространственным координатам и по яркости.
1.3.2. Дискретизация изображений
Рассмотрим непрерывное изображение — функцию двух пространствен-
ных переменных jq и х2 /(х(,х2) на ограниченной прямоугольной области
(рис. 1.23).
Введем понятие шага дискретизации Ai по пространственной переменной
X] и А2 по переменной х2. Например, можно представить, что в точках, уда-
1.3. Представление изображений в компьютере
41
Рис. 1.23. Переход от непрерывного изображения к дискретному
ленных друг от друга на расстояние Д| по оси Л] расположены точечные
видеодатчики. Если такие видеодатчики установить по всей прямоугольной
области, то изображение окажется заданным на двумерной решетке
/(П|Д„п2Д2) = /(х„х2)|х=пАл2=^
(1.94)
Для сокращения записи обозначим
/(п1Д1,п2Д2) = /(п|,п2).
(1-95)
Функция /(н]Л2) является функцией двух дискретных переменных и на-
зывается двумерной последовательностью. То есть дискретизация изображе-
ния по пространственным переменным переводит его в таблицу выборочных
значений. Размерность таблицы (число строк и столбцов) определяется гео-
метрическими размерами исходной прямоугольной области и выбором шага
дискретизации по формуле
(1.96)
где [...] обозначает целую часть числа.
Если область определения непрерывного изображения — квадрат Ly-l^L,
и шаг дискретизации выбран одинаковым по осям х, и х2 (^i=^2=2^)» то
(1.97)
и размерность таблицы составляет N2.
Элемент таблицы, полученной путем дискретизации изображения, назы-
вают «пиксел» или «отсчет». Рассмотрим пиксел f(n},n2). Это число прини-
мает непрерывные значения.
Память компьютера способна хранить только дискретные числа. Поэтому
для записи в памяти непрерывная величина/должна быть подвергнута анало-
гово-цифровому преобразованию с шагом Д/ (см. рис. 1.24).
42
ГЛАВА I
Операцию аналого-цифрового преобразования (дискретизации непрерыв-
ной величины по уровню) часто называют квантованием. Число уровней кван-
тования, при условии, что значения функции яркости лежат в интервале
[./min’ /min + » раВНО
Q-\AAf
(1.98)
номер уровня
4
3
2
1
Рис. 1.24. Квантование не-
прерывной величины
В практических задачах обработки изображений величина Q варьируется в
широких пределах от Q — 2 («бинарные» или «черно-белые» изображения) до
Q— 210 и более (практически непрерывные значения яркости). Наиболее час-
то выбираются Q ~ 28, при этом пиксел изображения
кодируется одним байтом цифровых данных. Из всего
вышеуказанного делаем вывод, что пикселы, храня-
щиеся в памяти компьютера, представляют собой ре-
зультат дискретизации исходного непрерывного изоб-
ражения по аргументам и по уровням. Ясно, что шаги
дискретизации Аь Д2 должны выбираться достаточно
малыми, для того, чтобы погрешность дискретизации
была незначительна, и цифровое представление со-
храняло основную информацию об изображении.
При этом следует помнить, что чем меньше шаг
дискретизации и квантования, тем больший объем
данных об изображении должен быть записан в память компьютера. Рас-
смотрим в качестве иллюстрации этого утверждения изображение на слайде
размером 50x50 мм, которое вводится в память с помощью цифрового изме-
рителя оптической плотности (микроденситометра). Если при вводе линей-
ное разрешение микроденситометра (шаг дискретизации по пространствен-
ным переменным) составляет 100 микрон, то в память записывается двумер-
ный массив пикселов размерности № = 500x500 = 25х104. Если же шаг
уменьшить до 25 микрон, то размеры массива возрастут в 16 раз и составят
/V2 = 2000x2000 = 4x10 . Используя квантование по 256 уровням, то есть ко-
дируя найденный пиксел байтом, получаем, что в первом случае для записи
необходим объем 0,25 мегабайт памяти, а во втором случае 4 мегабайта.
/uin А 2Д ЗД
1.4. Последовательности и линейные системы с постоянными
параметрами
1.4.1. Последовательности
При цифровой обработке непрерывный сигнал /(г) представляется по-
следовательностью — набором значений (отсчетов) в дискретные моменты
времени. Мы ограничимся рассмотрением наиболее распространенного на
практике случая, когда интервал между отсчетами (шаг дискретизации во вре-
мени) постоянен и равен А.
1.4. Последовательности и линейные системы с постоянными параметрами
43
Для записи последовательности будем пользоваться одним из двух обозна-
чений: / = {/(лД)} или / = В обоих случаях п — целое. Первая
запись определяет значения элементов последовательности как значения не-
прерывного сигнала в дискретные моменты физической шкалы времени, то
есть непосредственно отражает процесс дискретизации сигнала:
(1.99)
Во второй записи в качестве аргумента дискретного сигнала используется
просто порядковый номер отсчета п, которому в этом случае придается смысл
дискретного безразмерного времени. Второе обозначение короче и поэтому
предпочтительнее, однако в случаях, когда требуется учитывать реальный
масштаб времени, применяется первое.
Интервал определения последовательности может быть конечным, полу-
бесконечным или бесконечным. При где ~ иель1е, имеем
последовательность конечной длины, при пЕ(—оо, ДО2] левостороннюю, а при
правостороннюю последовательность. При оо, оо) последо-
вательность является двусторонней (бесконечной, неограниченной по аргу-
менту). Для унификации рассмотрения всякую последовательность обычно
приводят к бесконечной, полагая отсчеты, лежащие вне интервала определе-
ния, тождественно равными нулю. При этом данная классификация по суще-
ству относится не к области определения, а к области, в которой значения
последовательности могут отличаться от нуля.
Последовательность называется детерминированной, если можно точно ука-
зать ее значения для любого момента дискретного времени п. Последователь-
ность — случайная, если ее элементы — случайные величины.
Приведем примеры важнейших детерминированных последовательностей.
Единичный импульс:
Изображение единичного импульса приведено на рис. 1.25.
|5(м)
(i 5(и-«о)
О 1
л0 п
Рис. 1.25. Единичный импульс
44
ГЛАВА 1
Аналогично определяется и единичный
импульс, сдвинутый на и0 отсчетов:
S(w-«o)
1, п = п0
О, п^п0
Единичный скачок:
(") =
I, п>0
0, п < 0.
(1.102)
(1.101)
и
График единичного скачка показан на рис. 1.26. Единичный скачок можно
выразить через единичный импульс:
п со
«(«)= Ё 8И= Ё6^-*)-
Л——со Л=0
Приведенные обозначения единичного импульса и единичного скачка яв-
ляются стандартными и используются далее везде.
Дискретный прямоугольный импульс длиной N:
f(.n)=
1, 0<n>N — l
0, и < 0 или п > N.
(1.103)
Эта последовательность (рис. 1.27) очевидным образом выражается через
функции единичного импульса или единичного скачка:
/V-I
= 22б(л-&)=ф)-ф- А).
к=0
Дискретная правосторонняя экспонента:
f{n} =
а\ п>0
0, и <0
= апи(п).
(1.104)
и(л)- и(п -N)
График последователь-
ности при 0 < а < 1 показан
на рис. 1.28.
-1 0 1 2 ... 7V-1 W
Рис. 1.27. Дискретный прямо-
п угольный импульс
1.4. Последовательности и линейные системы с постоянными параметрами
45
Дискретная комплексная экспонен-
та задается выражением
f(n) = et<an = cos сом -Иsin ton ,
(1.105)
где i — мнимая единица, о — кон-
станта, имеющая смысл безразмерной
частоты. Последовательность (1.105)
играет исключительно важную роль
при анализе сигналов и систем в част-
ной области (см. п.1.5).
Рис. 1.28. Дискретная правосторонняя экспо-
нента
1.4.2. Дискретные ЛПП-системы
Будем называть дискретной системой £ правило преобразования одной
последовательности f , называемой входной, в другую последовательность g,
называемую выходной.
В общем виде это преобразование обозначается следующим образом:
{«(«)}=ф(«)}|- дюб)
Дискретная система £ называется линейной, если для нее соблюдается прин-
цип суперпозиции, то есть для любых /2 и постоянных а,Ь
(1.107)
Дискретная система с постоянными параметрами характеризуется тем, что,
если справедливо соотношение (1.106), то справедливо и соотношение
{<? (л-«о )} = £[{/(и-"о)}]
(1.108)
при любом целом м0. Иными словами, такая система обладает свойством
инвариантности к сдвигу во времени: задержка входного сигнала приводит к
равной задержке выходного сигнала без изменения самого закона преобразо-
вания входа в выход.
Дискретные системы, обладающие одновременно свойствами линейности
и инвариантности к сдвигу, называются дискретными линейными системами с
постоянными параметрами (ЛПП-системами). Классу ЛПП-систем принадле-
жат многие алгоритмы цифровой обработки сигналов и дискретные модели
реальных динамических объектов. Для таких систем наиболее глубоко разра-
ботаны математические методы анализа и синтеза. Мы ограничимся рассмот-
рением именно этого класса дискретных систем.
46
ГЛАВА I
Чтобы описать систему, нужно указать конкретное правило преобразова-
ния входного сигнала в выходной. ЛПП-систему можно описать с помощью
ее импульсной характеристики.
Импульсная характеристика h дискретной ЛПП-системы определяется как
реакция системы на выходное воздействие в форме единичного импульса:
{й(л)} = £[{5(л)}]. (1.109)
Импульсная характеристика исчерпывающим образом описывает ЛПП-
систему с точки зрения преобразования сигналов. Действительно, любую пос-
ледовательность на входе ЛПП-системы можно представить в виде бесконеч-
ной суммы
ОС
f(n)= 52 f(k)b(n-k). (1.110)
к——оо
В силу соотношения (1.107) преобразование суммы равно сумме преобра-
зований слагаемых. Каждое слагаемое в (1.110) есть сдвинутый единичный
импульс с коэффициентом — значением соответствующего отсчета входной
последовательности. Согласно (1.108) и (1.109) каждый такой импульс дает на
выходе отклик в виде сдвинутой импульсной характеристики с тем же коэф-
фициентом. Полная выходная последовательность записывается в виде1
оо
#(«)= 52 /(*) h(n-k).
k—~OQ
(1.111)
Таким образом, знания импульсной характеристики достаточно, чтобы по
входной последовательности вычислить выходную.
Выражение (1.111) задает свертку последовательностей f и h. Часто ис-
пользуется его краткая символическая запись:
£(п) = /(и)*й(л). (1.112)
Отметим некоторые легко доказываемые свойства свертки (пусть а, b и
с — произвольные последовательности):
коммутативность:
(1-ПЗ)
ассоциативность:
a(n)*b(n) — b(n)*a(n);
а
(1.Н4)
дистрибутивность:
(1.115)
’Здесь и далее полагаем, что последовательности, входящие в выражения вида (1.111) таковы,
что эта сумма ряда сходится при любом конечном л.
1.4. Последовательности и линейные системы с постоянными параметрами
47
Для любой последовательности а(п)
можно записать, что
а(п)*Ъ(п — п0) — а(п — л0)
(1.116)
при любом целом п0. (Формула (1.116) выражает так называемое фильтрую-
щее свойство единичного импульса.)
Легко показать, что, если ЛПП-система состоит из /V последовательно
соединенных звеньев с импульсными характеристиками h{, h2, ..., hN, то ее
импульсная характеристика h равна свертке импульсных характеристик
звеньев:
h(nj = /г, (л)*й2 (и)* ...
(1.И7)
При параллельном соединении звеньев их импульсные характеристики сум-
мируются, то есть для системы в целом
/г(п) = /г, (n) + /i2(п)-Ь...
+hN (п).
(1.118)
1.4.3. Физическая реализуемость и устойчивость ЛПП-систем
Дискретная система называется физически реализуемой, если значение вы-
ходной последовательности в произвольный момент и0 зависит только от
значений входной последовательности при n<nQ. Иначе говоря, для физи-
чески реализуемой системы отклик не опережает входное воздействие.
Для независимости выхода физически реализуемой дискретной ЛПП-сис-
темы от «будущих» значений входной последовательности требуется, чтобы в
свертку (1.111) все значения /(&) при к>п входили с нулевыми коэффици-
ентами. Очевидно, это выполняется, если
/г(п) = О при и<0. (1-119)
Это условие является необходимым и достаточным для физической реали-
зуемости ЛПП-системы.
Дискретная система называется устойчивой, если любому ограниченному
входному воздействию соответствует ограниченный отклик, то есть при
|/(n)|<My Vai
|#(л)|<Мк Vn,
из (1.110) следует, что
(1.120)
(1.121)
где М f, — некоторые положительные константы.
Необходимым и достаточным условием устойчивости дискретной ЛПП-сис-
темы является абсолютная суммируемость импульсной характеристики:
00
|Аг(лг)| <00.
(1.122)
п——оо
48
ГЛАВА 1
Докажем это. Сначала докажем необходимость, используя контрпример.
Рассмотрим ограниченную входную последовательность
1 при
— 1 при
h(—n)>0,
/г(—и) <0.
(1.123)
Определим значение последовательности на выходе системы при п = 0. В
соответствии с формулами (1.111) и (1.123)
оо оо оо
?(о)= Е /(*)*(-*)= Е |ЛЮ|= Е 1Л(*)|-
к—— оо к——оо к=—оо
Если условие (1.122) не выполняется, то не выполняется и условие устой-
чивости (1.121). Следовательно, выполнение условия (1.122) является необхо-
димым условием устойчивости системы. Для доказательства достаточности
предположим, что условие (1.122) выполняется, и на вход системы поступает
ограниченная последовательность, то есть справедливо неравенство (1.120).
Тогда, используя свойство коммутативности свертки (1.111), получаем, что
|«(")| =
00 00
Е < £ |A(*)| |Z('»—*)|<
к——оо к=—оо
оо
<A/Z Y. |/>W| = Ms<00>
к=—оо
то есть всегда выполняется соотношение (1.121), выходная последователь-
ность ограничена, и система устойчива.
Теперь, после введения понятий физической реализуемости и устойчивос-
ти можно дать простую, но важную классификацию ЛПП-систем по форме
импульсной характеристики. У ЛПП-систем с конечной импульсной характе-
ристикой (КИХ-систем), как следует из самого названия, импульсная харак-
теристика представляет собой последовательность конечной длины, то есть
/цп) = О при nGpVj, N2]. КИХ-системы всегда устойчивы, так как для них
сумма (1.122) конечна. При N] > 0 такие системы являются физически реали-
зуемыми.
ЛПП-системы с бесконечной импульсной характеристикой (БИХ-системы)
имеют в качестве импульсной характеристики правостороннюю, левосторон-
нюю или двустороннюю последовательность, то есть h(n) — 0 при n<Ni или
h(n) = O при п>ТУ2,или /г(п)^Опри п £(—оо,оо). Такие системы могут быть
неустойчивыми. Требование физической реализуемости здесь выполняется
только в первом случае при УУ, >0.
Если у КИХ- или БИХ-системы импульсная характеристика равна нулю
при п < /V] < 0, то такая система тоже может быть реализована, если допус-
1.4. Последовательности и линейные системы с постоянными параметрами
49
тить задержку в получении сигнала на выходе. Величина этой задержки долж-
на быть достаточной, чтобы «сдвинуть» импульсную характеристику вправо в
область неотрицательных значений аргумента на число отсчетов не мень-
ше (—ДО,). Строго говоря, при этом реализуется не исходная система, а дру-
гая, эквивалентная последовательному соединению системы и звена задерж-
ки. Однако в большинстве практических приложений такая замена вполне
допустима.
1.4.4. Разностные уравнения
Как следует из выражений (1.111) и (1.119), для физически реализуемой
БИХ-системы значение последовательности на выходе зависит от текущего и
всех предыдущих значений входной последовательности. Описание (1.111) не
является конструктивным в том смысле, что не позволяет практически по-
строить БИХ-систему: для получения каждого значения выходной последова-
тельности требуется выполнить бесконечное число операций сложения и ум-
ножения. Число операций можно сделать конечным, если выразить текущее
значение выходной последовательности не только через входные, но и через
предыдущие выходные значения, иначе говоря, записать уравнение ЛПП-си-
стемы в рекурсивной форме. При этом получаем описание ЛПП-системы в
виде линейного разностного уравнения с постоянными коэффициентами'.
М N
g(n) = Yw(n4)+Yj>jf(n-j), (1.124)
7=1 7=0
где {(2у — коэффициенты уравнения, М,N — целые константы, ха-
рактеризующие сложность системы.
Величина М при ам *0 определяет порядок разностного уравнения (ЛПП-
системы). БИХ-системы всегда имеют ненулевой порядок и являются рекур-
сивными'. для них каждое следующее значение выходной последовательности
вычисляется через М предыдущих. В частном случае, когда все коэффициен-
ты J равны нулю, уравнение (1.124) описывает нерекурсивную КИХ-систе-
му, имеющую нулевой порядок.
Заметим, что разностное уравнение (1.124) при конечных M,N описывает
более узкий класс физически реализуемых ЛПП-систем, нежели свертка (1.111).
Для некоторых форм импульсной характеристики переход от свертки к разно-
стному уравнению осуществить не удается. Впрочем, такие «неприводимые»
случаи на практике не встречаются и поэтому ниже не рассматриваются.
Обратный переход от разностного уравнения (1.124) к свертке (1.111) воз-
можен всегда, его осуществление означает выражение выходной последова-
тельности через входную в явной форме, то есть решение разностного урав-
нения. Методы решения разностных уравнений хорошо разработаны. В про-
стейших случаях продуктивным является последовательное отыскание отсчетов
50
ГЛАВА t
выходного сигнала путем прямой подстановки в уравнение с дальнейшим
обобщением результата методом математической индукции.
Пример 1.5. Пусть физически реализуемая ЛПП-система первого порядка
описывается разностным уравнением
g(n) = ag(n-l) + f(n),
(1.125)
где а — постоянный коэффициент. Требуется получить описание системы в
виде свертки. Найдем вначале импульсную характеристику системы. В соот-
ветствии с определением импульсной характеристики (1.109) уравнение (1.125)
можно переписать в виде
/i(n) = ah(n — 1) + 8(и).
(1.126)
Рассматриваемая система физически реализуема, поэтому все значения
импульсной характеристики при и<0 равны нулю (см. формулу (1.119)).
При п > 0 значения импульсной характеристики определяются прямой под-
становкой в уравнение (1.126) предыдущих значений с учетом формулы (1.100):
Л(о) = а/1(—1)+8(о) = п 0+1 = 1;
h(l) = a/i(o) + 8(l) = а 4 + 0 = а;
/1(2) = ah(l) + 8(2) = а • а + 0 = а2;
Анализируя этот результат, нетрудно заметить, что импульсная характери-
стика имеет аналитическое выражение в виде правосторонней экспоненты
(1.104):
/1(л) — апи(п).
(1.127)
С учетом свойства коммутативности свертки (1.111), а также выражения
(1.102) для единичного скачка получаем окончательный результат:
g(n)= lb h(k)f(n~k)= 22 aku(k)f(n- к) =
А=—ос к=—ос
ос
= 1>2akf(n-k).
(1.128)
Заметим, что при решении разностного уравнения (1.124) прямой под-
становкой необходимо задавать начальные условия, число которых зависит
от сложности уравнения. Так, для получения решения при п>0 нужно
задать у(-1) , у(-2) , ...,у(-М), атакже /(-1) , /(-2) /(-/V), тоесть
всего (М +N) величин.
1.4. Последовательности и линейные системы с постоянными параметрами
51
Метод прямой подстановки, будучи громоздким, имеет весьма ограничен-
ное применение. Существуют другие, более мощные аналитические методы
решения разностных уравнений, позволяющие сразу получить результат в
общем виде. Один из таких методов, основанный на применении z-преобра-
зования, мы рассмотрим ниже.
Описание ЛПП-системы с помощью разностного уравнения имеет важное
практическое значение, поскольку непосредственно определяет алгоритм пре-
образования входной последовательности в выходную. По разностному уравне-
нию легко строится структурная схема ЛПП-системы, состоящая из комбина-
ции типовых элементов, осуществляющих операции суммирования (рис. 1.29а),
умножения на коэффициент (рис. 1.296) и задержки (сдвига) последователь-
ности (рис. 1.29в).
На рис. 1.30 представлена структурная схема, соответствующая прямой ре-
ализации ЛПП-системы по разностному уравнению (1.124).
Рис. 1.29. Типовые элементы структурных схем ЛПП-систем: а — элемент суммирования; б —
элемент умножения; в — элемент задержки
Рис. 1.30. Пример структурной схемы для прямой реализации ЛПП-системы по разностному
уравнению
52
ГЛАВА I
1.4.5. Двумерные последовательности
Обобщим изложенное выше на случай двумерных сигналов.
Двумерный дискретный сигнал (последовательность) может быть получен
из двумерного непрерывного сигнала путем его дискретизации по
аргументам. Пусть интервалы между отсчетами сигнала (шаги дискретиза-
ции) по каждой координате плоскости аргументов постоянны и равны Др Д2,
то есть двумерная последовательность задается выражением
/(Мь и2Д2) = /(х„х2)
X, =А?[Д]
Х2 ~ П2^ 2
(1.129)
при целочисленных пх, п2. Формула (1.129) определяет последовательность
/={/(
njАI,через значения непрерывного сигнала в дискретных точ-
ках плоскости аргументов, то есть непосредственно отражает процесс дискре-
тизации сигнала. В тех случаях, когда «привязка» отсчетов к физической шка-
ле непрерывных координат не играет роли, можно воспользоваться более крат-
ким и удобным обозначением последовательности: / = n2)}, 1де п2
приобретают смысл порядковых номеров отсчетов по координатам.
Следует заметить, что термин «последовательность» формально перенесен
сюда из теории одномерных сигналов и в данном контексте не вполне кор-
ректен. Действительно, для отсчетов на плоскости нет объективно существу-
ющего «следования» (то есть отношения порядка, описываемого понятиями
«раньше» — «позже»), а имеется просто их двумерная совокупность или, как
говорят, решетка отсчетов.
Заметим также, что, если в одномерном случае существовал единственный
способ дискретизации с постоянным шагом, то для двумерного мы имеем
бесконечное множество ее вариантов, отличающихся наклоном прямых, «вдоль»
которых берутся отсчеты сигнала. Записанная выше процедура формирова-
ния двумерной последовательности соответствует так называемой прямоуголь-
ной решетке (см. рис. 1.31д)- В некоторых системах ввода изображений ис-
пользуется дискретизация по треугольной решетке (см. рис. 1.316), которая,
как показывают исследования, обеспечивает определенные преимущества при
обработке двумерных сигналов. Ниже мы будем рассматривать только дву-
мерные последовательности, заданные на прямоугольной решетке, поскольку
этот случай наиболее распространен на практике.
Рассмотрим некоторые важнейшие двумерные последовательности.
Двумерный единичный импульс:
5(nltn2) = -
1 при и, = п2 = О
О при Л] 0 или п2 0.
Изображение единичного импульса представлено на рис. 1.32.
(1.130)
1.4. Последовательности и линейные системы с постоянными параметрами
53
Рис. 1.31. Положение отсчетов двумерной последовательности на плоскости аргументов непре-
рывного сигнала: а — прямоугольная решетка; б — треугольная решетка
Двумерный единичный скачок'.
и(п},п2)=:
1 при
О при
п, > 0 и п2 > О,
и, < 0 и п2 < 0.
(1.131)
Эта последовательность изображена на рис. 1.33. Приведенные обозначе-
ния двумерных единичных импульса и скачка будем использовать далее везде.
Двумерная экспоненциальная функция первого квадранта'.
/(п^п^ — а^Ь^и^п^п^. (1.132)
Изображение этой последовательности для 0<п, Ь<1 дано на рис. 1.34.
Двумерная дискретная комплексная экспонента задается выражением
/(П|,П2) = И“'Л|+Шг"2),
(1133)
где I — мнимая единица, (Oj, со2 — вещественные константы, имеющие смысл
безразмерных пространственных частот (см. п.1.5).
Важный класс двумерных
последовательностей состав-
ляют разделимые (фактори-
зуемые) последовательности,
которые можно представить
в виде
(1.134)
Рис. 1.32. Двумерный единичный
импульс
54
ГЛАВА I
Рис. 1.33. Двумерный единичный скачок
Для разделимых последо-
вательностей многие задачи
анализа и синтеза двумерных
сигналов и систем решают-
ся наиболее просто, так как
сводятся к решению соот-
ветствующих «одномерных»
задач. Все рассмотренные
выше двумерные последова-
тельности являются раздели-
мыми. Например,
8(n1,n2) = 6(nl)5(n2),
и(п},П2) — и(л1)ы(л2),
где §(«,), S(zi2), «(nJ, м(п2) — одномерные единичные импульсы и скачки.
Как и в одномерном случае, можно дать классификацию двумерных по-
следовательностей по форме области ненулевых значений отсчетов. Правда,
здесь вместо четырех классов последовательностей (конечной длины, беско-
нечных, право- и левосторонних) мы будем иметь гораздо большее многооб-
разие. Так, только для разделимых последовательностей, опираясь на класси-
фикацию одномерных последовательностей, входящих в (1.134), можно ука-
зать 16 классов. Столь громоздкая классификация не очень удобна для анализа,
поэтому мы ограничимся разделением двумерных последовательностей всего
на два класса — на последовательности конечной длины'.
f(n},n2) = O
при и, ^[М|,Л/|]
или п2 [М2,N2],
(1.135)
где Mj, М2, N2 — це-
лые константы (Л/, <N(,
M2<TV2), и на последова-
тельности бесконечной длины,
для которых записанное ус-
ловие не выполняется. Дета-
лизацию второго класса бу-
дем вводить по мере необхо-
димости.
Рис. 1.34. Двумерная экспоненци-
альная функция первого квадранта
1.4. Последовательности и линейные системы с постоянными параметрами
55
1.4.6. Двумерные дискретные ЛПП-системы
Двумерной дискретной системой £ будем называть правило, ставящее в со-
ответствие входной двумерной последовательности f выходную двумерную пос-
ледовательность g. В общем виде это соответствие (преобразование) записы-
вается в виде
{# (П1 »П2)} = £[{f (ирЛ?)}
(1.136)
Определение двумерных дискретных линейных систем с постоянными па-
раметрами (ЛПП-систем) аналогично определению одномерных, то есть для
них должен соблюдаться принцип суперпозиции:
^[{«/[ («!
"г)}
= а £ [{/, (л,, п2 )}]+&£ [{f2 («I * ”2)}] (1 137)
для любых /j, f2 и постоянных а, Ь, и они должны обладать свойством инва-
риантности к сдвигу сигнала по каждой координате, то есть
{#(«,— т{, п2— т2)} = £?[{/(«!-т{, «2-wh)}] (1.138)
при любых целых тх, т2. Двумерные системы, для которых выполняется ус-
ловие (1.138), называются также пространственно-инвариантными или изо-
план атичными.
Импульсная характеристика h двумерной дискретной ЛПП-системы опре-
деляется как реакция системы на входное воздействие в форме двумерного
единичного импульса:
,и2)} = £ [{5 (wi» п2)}] • (1 •139)
Импульсная характеристика исчерпывающим образом описывает двумер-
ную ЛПП-систему с точки зрения преобразования сигналов. Выходная по-
следовательность определяется через двумерную дискретную свертку импульс-
ной характеристики и входной последовательности :
g(H|,n2)= 52 52 Л(т1,/и2)/(п1-лтз). (1.140)
mi - — ост2——оо
Ниже наряду с (1.140) будем использовать краткую символическую запись
двумерной свертки:
g(n1,n2) = /i(n1,n2)**/(n1,n2). (1-141)
'Здесь и далее полагаем, что последовательность, входящая в выражения вида (1.140) таковы,
что эта сумма сходится при любых конечных п2.
56
ГЛАВА 1
Двумерная свертка обладает всеми свойствами одномерной свертки: ком-
мутативностью, дистрибутивностью (см. п. 1.4.2) и, кроме того, рядом допол-
нительных свойств, вытекающих именно из двумерности рассматриваемых
последовательностей. Так, если hw f — разделимые последовательности, то и
выходная последовательность также разделима. Действительно, при выполне-
нии соотношений (1.134) и
А(П],Лг2) = («] )^2
(1.142)
из (1.140) получаем
<?(П1’П2)= £ 52 т1) =
т{ =—оо zn2 ——ос
= £ £ h2(m2)f2(n2-m2)= g}(n})g2(n2),
W|——ос ni2- ос
где обозначено
00
^i(wi)= Е hAmMn\-^i)’
/и1 —- сю
00
«г(”г)= 52 Л2(т2)Л(«2 ~тг\
—ос
Иначе говоря,
(1.МЗ)
то есть для разделимых последовательностей двумерная свертка вычисляется
через произведение одномерных.
Если импульсная характеристика двумерной ЛПП-системы факторизуема,
то для произвольного входного сигнала получаем
00 оо
g(nj,n2) = Е Е лг(т2)/(«1 -”\,п2 -т2) =
mt——oo m2=—оо
= /i] (п1)*Л2(п2) + /(п1,п2),
(1.144)
то есть операция двумерной свертки сводится к последовательному выполне-
нию двух одномерных сверток. Это означает, что преобразование сигнала дву-
мерной ЛПП-системой с разделимой импульсной характеристикой эквива-
лентно его последовательному преобразованию двумя одномерными система-
ми: с импульсной характеристикой А|(п|) по координате П] и с импульсной
характеристикой /г2(и2) по координате п2.
1.4. Последовательности и линейные системы с постоянными параметрами
57
Развивая аналогию между одномерными и двумерными системами, отме-
тим, что, как и в одномерном случае, двумерные ЛПП-системы могут ха-
рактеризоваться фундаментальными свойствами физической реализуемости и
устойчивости. Двумерная система называется устойчивой, если любому огра-
ниченному входному сигналу соответствует ограниченный выходной сигнал,
то есть при
|/(п|,и2)|<М/
выполняется
|«(n„n2)|<Wx,
где М f, Мк — некоторые положительные константы. Необходимым и дос-
таточным условием устойчивости двумерной дискретной ЛПП-системы явля-
ется абсолютная суммируемость импульсной характеристики:
со
|A(nt,A22)| <ОО.
(1.145)
И) —- ос
п2—-оо
Доказательство этого факта — такое же, как и в одномерном случае. С
понятием физической реализуемости двумерных систем дело обстоит слож-
нее, этот вопрос требует отдельного рассмотрения.
1.4.7. Физическая реализуемость двумерных систем
Вспомним, что мы называли физически реализуемой такую одномерную
систему, у которой выходной сигнал не зависел от входного сигнала в опере-
жающие моменты времени, то есть от его «будущих» значений. Однако, как
уже отмечалось, в двумерной последовательности аргументы являются не вре-
менными, а пространственными, для ее отсчетов не определено отношение
порядка типа «прошлое» — «будущее», и поэтому, строго говоря, понятие
физической реализуемости системы не имеет смысла. Тем не менее на прак-
тике обычно приходится искусственно вводить указанное отношение для дву-
мерного сигнала, задавая некоторое правило его развертки (упорядочения
отсчетов) в одномерную последовательность. При этом понятие физической
реализуемости вновь приобретает смысл, но оказывается жестко связанным с
конкретным видом развертки.
Известны различные, в том числе и довольно сложные способы развертки,
используемые в устройствах ввода и обработки двумерных сигналов. Наи-
большее распространение получила развертка телевизионного типа. Пусть
имеется двумерная последовательность конечной длины, отвечающая усло-
вию (1.135). Представим прямоугольную область ее ненулевых отсчетов в виде
матрицы размерами + 1)x(N2 -М2 +1):
58
ГЛАВА I
{/(«I.«2)}
7(m„w2)
/(m,+i,m2)
/(M„M2+1)
7(m,+i,m2+i)
/(М2)
/(W„W2+1)
/(«!• N2y
f(M,+l,N2)
f(N„N2) ,
Развертка телевизионного типа заключается в последовательном упорядо-
чении строк или столбцов этой матрицы. Очевидно, существует восемь вари-
антов такой развертки: начиная с каждого из четырех углов матрицы, по ее
строкам и столбцам. Мы ограничимся рассмотрением лишь одного, наиболее
часто используемого варианта — строчной развертки в направлении возраста-
ния аргументов. В этом случае осуществляется так называемое лексикографи-
ческое упорядочение отсчетов, в результате которого они выстраиваются в од-
номерную последовательность вида
+ К, /(M„W2).
/(М,+1,Л/2), /(м1+1,мг+1), к, Дм,+i,w2), К, /(W„W2).
Для простоты изложения далее будем считать, что размеры матрицы отсче-
тов достаточно велики, чтобы не обращать внимание на нерегулярность строч-
ной развертки, то есть на ее скачки с конца каждой строки на начало следу-
ющей. С учетом этой оговорки, для строчной развертки области «прошлого»
и «будущего», заданные относительно некоторого отсчета на плос-
кости аргументов выглядят так, как показано на рис. 1.35. При этом из соот-
ношения свертки (1.130) следует, что независимость выходных отсчетов
g(rt],n2) от будущих (в принятом смысле) значений входного сигнала обес-
печивается, если
Рис. 1.35. Области «прошлого» и «будущего» при строчной развертке
1.4. Последовательности и линейные системы с постоянными параметрами
59
при Ш| -0, т2 <0
и при «i,<0 и любых т2
(1.146)
Условие (1.146) является необходимым и достаточным для физической ре-
ализуемости двумерной ЛПП-системы при строчной развертке сигнала, см.
рис. 1.36п.
Часто к двумерной системе предъявляется более жесткое требование физи-
ческой реализуемости при любом порядке возрастания аргументов nt, п2 вы-
ходного сигнала, то есть и при строчной развертке, и при ее транспониро-
ванном варианте — развертке по столбцам. В этом случае приходим к следу-
ющему необходимому и достаточному условию реализуемости:
= 0
при < 0 и любом zn2,
и при любом т1 и т2 < 0.
(1.147)
Двумерная ЛПП-система, для которой выполняется это условие, называ-
ется каузальной, иллюстрация для ее импульсной характеристики дана на
рис. 1.366.
б
Рис. 1.36, Области потенциально ненулевых значений импульсных характеристик двумерных
ЛПП-систем (отмечены крестиками): а — система, физически реализуемая при строчной раз-
вертке; б — каузальная система; в, г — полукаузальные системы
60
ГЛАВА 1
Наряду с каузальными системами иногда приходится рассматривать и по-
лукаузалъные ЛПП-системы, для которых
Л(т|,т2) = 0 при т1 <0 или т2<0
(1.148)
(см. рис. 1.36<з, г). Для таких двумерных систем считается, что вся строка (или
столбец) матрицы отсчетов сигнала соответствует одному и тому же моменту
времени. Соответственно, есть «прошлые» и «будущие» строки (столбцы), но
отсчеты внутри каждой строки (столбца) поступают на обработку одновре-
менно (параллельно).
И, наконец, существуют некаузальные двумерные ЛПП-системы, то есть
такие, для которых не налагается никаких ограничений на область ненулевых
значений импульсной характеристики. Их одномерными аналогами являются
физически нереализуемые ЛПП-системы.
Заметим, что, если импульсная характеристика двумерной системы явля-
ется факторизуемой (см. (1.132)), то прослеживается простая связь между
физической реализуемостью составляющих ее одномерных систем и каузаль-
ностью. Если одномерные ЛПП-системы с импульсными характеристиками
h2 обе физически реализуемы, то двумерная система является каузальной,
если физически реализуема лишь одна из одномерных систем, то двумерная
система полукаузальна, если обе одномерные физически нереализуемы, то
двумерная некаузальна.
В заключение отметим, что, как и в одномерном случае, можно выделить
двумерные ЛПП-системы с конечной и бесконечной импульсной характерис-
тикой (КИХ- и БИХ-системы). У двумерной КИХ-системы импульсная харак-
теристика — двумерная последовательность конечной длины. Такая система
либо является каузальной, либо может быть приведена к каузальной системе
введением задержки по строкам и столбцам при получении выходного отсчета.
Как следует из (1.145), двумерная КИХ-система всегда устойчива.
Двумерная БИХ-система, как и ее одномерный аналог, в общем случае
может быть и физически нереализуемой (некаузальной), и неустойчивой.
1.4.8. Двумерные разностные уравнения
Двумерные системы, обладающие свойством физической реализуемости
при заданной развертке сигнала, во многих случаях можно описать, указав
способ рекурсивного вычисления отсчетов выходной последовательности. Для
двумерной ЛПП-системы такое описание дается в форме двумерного линей-
ного разностного уравнения с постоянными коэффициентами:
s(ni’n2) = Е ^аГПит^(п[-т1>п2-т2) +
(m^nhjeQg
+ Е Е^т|1т2/(П1
(mhm2)eQf
(1.149)
1.4. Последовательности и линейные системы с постоянными параметрами
61
где — коэффициенты уравнения, Qf, Qg — конечные
множества индексов, по которым производится суммирование отсчетов вход-
ной (/) и выходной (g) последовательностей.
Множества Qf и Q* должны выбираться так, чтобы при заданном спо-
собе развертки двумерных сигналов используемые в (1.149) отсчеты входной
последовательности не были «будущими» по отношению к текущему моменту
(точке (и|,и2) на плоскости аргументов), а отсчеты выходной последователь-
ности были строго «прошлыми». Так, например, для каузальной двумерной
ЛПП-системы уравнение (1.149) записывается в виде
м} м2
g(n^n2)= Е Е ат1,т28(щ-т\’п2-т2) +
т} =0 т2 — О
(mi
/V, /v2
+ Е Е -тх>п2-т2),
m{=Q ш2—О
(1.150)
где А/,, М2, W|, N2 ~ UejIbie константы, характеризующие сложность системы.
Пара значений (М,,М2) при
max
0<m2< М 2
® М\гп2
max
0 и
|°miM2 ।
0
определяет порядок разностного уравнения (1.150) (каузальной ЛПП-систе-
мы) по каждой из координат. Для БИХ-систем хотя бы одна из величин А/, и
М2 положительна. Такие системы являются рекурсивными: в них каждый
следующий отсчет выходной двумерной последовательности вычисляется че-
рез (М|+1)(М2+1) —1 предыдущих. В частном случае, когда все {пОТ1,^2}
равны нулю, уравнения (1.149) и (1.150) описывают нерекурсивную КИХ-сис-
тему порядка (0,0). Для нее, очевидно, имеет место совпадение разностного
уравнения со сверткой (1.140) при конечной импульсной характеристике:
/г(лП],т2) =
mtm2
при
при
Как средство описания ЛПП-системы разностное уравнение имеет оче-
видное преимущество перед сверткой: в нем каждый отсчет выходной после-
довательности может вычисляться за конечное число операций сложения и
умножения. В то же время следует иметь ввиду, что представление в виде
разностного уравнения удается применить далеко не к каждой двумерной
ЛПП -системе. Во-первых, еще раз напомним, что такое представление имеет
практический смысл, только если ЛПП-система физически реализуема, и,
следовательно, ее импульсная характеристика удовлетворяет рассмотренным
62
ГЛАВА 1
ограничениям. Во-вторых, импульсная характеристика даже физически реа-
лизуемой системы может быть такова, что в разностном уравнении (1.149)
потребуется использовать бесконечные множества Qf, Q (для каузальной
системы уравнение (1.150) будет иметь бесконечный порядок). На вопросах
переходов от импульсной характеристики двумерной ЛПП-системы к разност-
ному уравнению (в случае, когда это возможно) и обратно мы остановимся
ниже в п.1.6.
Разностное уравнение (1.149) непосредственно определяет алгоритм преоб-
разования двумерного сигнала дискретной физически реализуемой ЛПП-сис-
темой. Для иллюстрации такого преобразования часто используется условная
схема вычисления отсчетов выходной последовательности, общий вид которой
представлен на рис. 1.37. Для осуществления рекурсивных вычислений по раз-
ностному уравнению необходимо задать довольно много начальных условий. Так,
в случае каузальной ЛПП-системы, описываемой разностным уравнением
(1.150), для получения отсчетов выходной последовательности в первом квад-
ранте (при п,>0 и п2 >0) требуется указать значения #(и],и2) при
—и п2>~М2,
К] >0 и — М2 <п2<0,
а также рассматривать входной сигнал f(n},n2] не только в первом квадран-
те, но и при
—Wj < < 0 и п2 > —N2,
И] > 0 и — N2 <п2 < 0.
Рис. 1.37. Схемы вычисления отсчетов двумерной выходной последовательности по разностно-
му уравнению (1.149)
1.5. Описание дискретных сигналов и систем в частотной области
63
Ниже при использовании разностных уравнений мы будем считать, что
входные и выходные сигналы заданы на всей плоскости аргументов, поэтому
указывать начальные условия нам не потребуется.
1.5. Описание дискретных сигналов и систем в частотной
области
1.5.1. Частотная характеристика ЛПП-систем и спектры дискретных
сигналов
Весьма ценным для анализа ЛПП-системы является ее описание с помо-
щью отклика на синусоидальный входной сигнал. В теоретических исследо-
ваниях вместо синусоидального сигнала обычно берется комплексная экспо-
нента (1.105). Обратим внимание на использование в выражении (1.105) без-
размерной частоты
(0 = £2Д, (1.151)
использование которой является традиционным при описании дискретных
сигналов и систем вне связи с масштабом времени. В (1.151) Q — угловая
частота, имеющая размерность радиан/единица времени (см. п. 1.5.3).
Итак, пусть на вход дискретной ЛПП-системы поступает последователь-
ность (1.105). Тогда выходная последовательность запишется в виде
ОО 00 , . оо
«(*)= Е *(*)z(*-*)= Е "-*’=?“ £ h(k)e~‘^.
к——ос к=—оо к——ос
Мы получили выходную последовательность, совпадающую с входной с
точностью до множителя, зависящего от частоты. Этот множитель
. . 00
H(eitS)}= £ h(k)e~i(ok (1.152)
к=-ос
называется частотной характеристикой дискретной ЛПП-системы. Частот-
ная характеристика задает «коэффициент передачи» ЛПП-системой с ее вхо-
да на выход эталонного сигнала — комплексной экспоненты для каждого зна-
чения ее частоты (0.
Частотная характеристика определена тогда, когда ряд (1.152) сходится.
Условие устойчивости ЛПП-системы (1.122) одновременно является и усло-
вием абсолютной сходимости этого ряда. Таким образом, для устойчивой си-
стемы частотная характеристика определена всегда1.
1 Отметим, что ряд (1.152) можно рассматривать как степенной от комплексной переменной
г = е'“. Известно, что степенной ряд, абсолютно сходящийся на некотором множестве точек (в
нашем случае — на единичной окружности в плоскости z или, что одно и то же, на всей число-
вой оси вещественной переменной со), на том же множестве сходится равномерно. Этот факт
равномерной сходимости нам понадобится ниже.
64
ГЛАВА 1
Выражение (1.152) позволяет вычислить частотную характеристику по им-
пульсной. Установим и правило обратного перехода, для чего умножим обе
части выражения (1.152) на е,Ь}" и проинтегрируем по интервалу изменения
частоты (—л, л) (учтем при этом, что равномерно сходящийся ряд можно
интегрировать почленно):
л л оо
—п -п ~ °°
~i<’*d(0 = §Xk)Jе^п (1.153)
-00 -л
Вычисление интегралов под суммой с учетом формулы (1.101) дает
л
2л, п — к
О, п * к
= 2л5(п — &),
выражение (1.153) приводится к свертке и, в соответствии со свойством свертки
(1.116), упрощается:
* . . 00
J H^eia>)el0)nda = £ к(к)2я8(п-к)= 2nh(n)5(n)= 2лА(м).
-я к=-ос
Таким образом, окончательно будем иметь
da.
(1.154)
Выражения (1.152) и (1.154) определяют соответственно прямое и обратное
преобразование Фурье функции дискретного аргумента (последовательности).
Преобразование Фурье функции иначе называется ее спектром. Частотная
характеристика ЛПП-системы — это спектр ее импульсной характеристики.
Преобразование Фурье можно записать и для произвольной последова-
тельности /:
. . оо
fp“)= Е /(*)*’“
к=-<х>
(1155)
(1.156)
Выражение (1.155) определяет спектр последовательности, а выражение
(1.156) представляет последовательность через спектр. Будем считать, что
ряд (1.155) сходится (на условиях сходимости ряда и, следовательно, суще-
ствования спектра мы еще остановимся в следующем разделе).
1,5. Описание дискретных сигналов и систем в частотной области
65
Спектральное представление сигналов и систем широко применяется
при анализе измерительной информации, синтезе фильтров и т.д. Описа-
ние ЛПП-системы посредством частотной характеристики во многих слу-
чаях проще и удобнее описания во временной области. Убедимся в этом,
установив связь спектров последовательностей на входе и выходе системы.
Спектр выходной последовательности с учетом ее выражения через сверт-
ку (1.111) будет иметь вид
ОС оо оо
Е Е Е fWm-k)
т——х т=—ос к=~ос
е-^
OG ОС
= Е /(*) Е h{m-k)e^.
к——оо т——оо
Заметим, что допустимость перестановки сумм можно обосновать при ус-
ловии ограниченности последовательности f и абсолютной суммируемости h.
Заменим переменную для внутренней суммы j — m — k. Тогда
ОО 00 00 ОС
G(e'“)= Е /(*) Е h(j)e~M^= £ f(k)e-M £
к=—оо j——оо Jt=-oo j—-<x>
Принимая во внимание выражения (1.152) и (1.155), получаем алгебраи-
ческое соотношение
С[е'1^ = р[е^н{е^, (1.157)
которое однозначно связывает спектры входной и выходной последователь-
ностей.
Сопоставление формул (1.111) и (1.157) показывает, что свертка последо-
вательностей преобразуется в произведение спектров. Этот факт часто ис-
пользуют при анализе прохождения сигналов через ЛПП-систему и вообще
при вычислении сверток: применение прямого и обратного преобразования
Фурье и соотношения (1.157) по сложности вычислений иногда оказывается
проще непосредственного использования формулы (1.111).
1.5.2. Основные свойства спектров последовательности
Перечислим некоторые наиболее существенные свойства спектров пос-
ледовательностей. Для определенности будем в основном говорить о спект-
рах дискретных сигналов, хотя все сказанное, с точностью до обозначений,
остается справедливым и для частотной характеристики дискретной ЛПП-
системы. Вначале приведем несколько свойств, качественно характеризую-
щих спектры.
3 — 9044
66
ГЛАВА 1
Свойство 1. Достаточным (но не необходимым!) условием существования
спектра последовательности f является абсолютная сходимость ряда (1.155):
оо
52 |/(м)|<ОО.
Л—— ОО
(1.158)
При выполнении условия (1.158) спектр (1.155) есть непрерывная функ-
ция частоты со. Соответственно, как уже отмечалось, частотная характеристи-
ка ЛПП-системы определена и непрерывна в случае, если система устойчива
(см. формулу (1.122)). Если условие (1.158) не выполняется, то ряд (1.155)
либо расходится (при этом, естественно, спектр не определен), либо сходится
условно (не абсолютно). В последнем случае спектр существует, хотя возмож-
но не для всех значений частот, и может иметь разрывы.
Свойство 2. Спектр последовательности — периодическая функция часто-
ты. Его период равен 2л, то есть f(2'“) = F^W'27L^ j для любого целого к.
Это очевидным образом вытекает из периодичности по частоте дискретной
комплексной экспоненты, используемой в выражениях (1.155) и (1.156):
^г[иН-2лЛ]л _ iwn 12пкп_ib)n
В силу этого свойства для полного описания спектра достаточно задать его
на любом интервале частот длиной в период. Обычно используется интервал
сое[0, 2л).
В общем случае спектр — комплексная функция, которую можно предста-
вить через вещественную и мнимую части или через модуль и фазу:
F(e‘“) = ReF(ez“) + zImF(e,(0)= F(e‘“)
i arg
Указанные компоненты спектра обладают следующим свойством.
Свойство 3. Если f — вещественная последовательность, то модуль и ве-
щественная часть ее спектра являются четными функциями частоты, а фаза и
мнимая часть — нечетными. Это свойство несложно доказать.
Принимая во внимание периодичность спектра и рассматривая его на ин-
тервале сое[О, 2л), данное свойство можно сформулировать иначе: модуль и
вещественная часть спектра симметричны, а фаза и мнимая часть антисим-
метричны относительно середины интервала (точки С0 = Л). Такая симметрия
позволяет полностью описать спектр вещественной последовательности, за-
дав его лишь на половине периода, то есть при сое[0, л). Рассмотрим приме-
ры, иллюстрирующие указанные свойства.
Пример 1. Определим частотную характеристику ЛПП-системы первого
порядка из (1.125). Импульсная характеристика системы задается выражени-
ем (1.127). Частотную характеристику — спектр импульсной характеристи-
ки — получим, подставив выражение (1.127) в (1.152):
1.5. Описание дискретных сигналов и систем в частотной области
67
Н
ОО 00 ОО . , ь
= Г; = = •
1=—оо 1=0 1=0
(1.159)
Полученная сумма геометрической прогрессии сходится, и притом абсо-
лютно, если
ае
-103
= | а | < 1. Одновременно обеспечивается и сходимость ряда
(1.122), то есть устойчивость системы. Пусть система устойчива. Тогда после
суммирования ряда (1.159) получаем
_________1_________
I — a cos(o-H a sin со
Модуль и фаза частотной характеристики определяются, соответственно,
но формулам
—arctg
a sin (О
1 — a cos (О
Частотная характеристика зависит от синуса и косинуса частоты, то есть
является периодической (см. свойство 2). Семейства графиков для ее модуля
и фазы при различных значениях параметра а приведены на рис. 1.38. Видно,
что частотная характеристика — непрерывная функция частоты. Так как им-
пульсная характеристика системы вещественна, частотная характеристика
обладает симметрией на рассмотренном интервале (см. свойство 3).
Если | а | > 1, то ряды (1.122) и (1.152) не сходятся, система неустойчива, и
ее частотная характеристика не существует.
Пример 2. Последовательность
(1.160)
пп
не удовлетворяет условию (1.158), но ее спектр существует на интервале час-
тот [0,тс] всюду, кроме точки со=соо, и равен
1,
о,
О<со<со0,
С00 <С0<7С,
(1.161)
что легко проверяется подстановкой выражения (1.161) в (1.156) с учетом
симметрии спектра. Для данной последовательности ряд (1.155) является ус-
ловно сходящимся, и ее спектр имеет разрыв в точке со = со0.
68
ГЛАВА 1
Рис. 1.38. Модуль и фаза частотной характеристики ЛПП-системы первого порядка
Л ПП-система с импульсной характеристикой вида (1.160) называется идеаль-
ным фильтром низких частот дискретного времени. Этот фильтр удаляет из вход-
ного сигнала все спектральные составляющие в диапазоне частот соо < со < я.
Такая система не является ни физически реализуемой, ни устойчивой, но
тем не менее играет важную теоретическую роль в задачах синтеза цифро-
вых фильтров.
Следующие свойства спектров касаются различных действий с ними.
Свойство 4. Преобразование Фурье линейно. Это означает, что для любых
последовательностей /2 и постоянных а, b из соотношения
f3(n) = af\n)+bf2(n)
(1.162)
следует, что
F3 (е'“) = aF{ [e™}+bF2 {е™}.
(1.163)
1.5. Описание дискретных сигналов и систем в частотной области
69
Свойство 5. Сдвиг последовательности соответствует умножению ее спект-
ра на комплексную экспоненту, а именно, если
Л(п)-/1(п-по)> (1.164)
то
F2(e,co) = F] (1.165)
Такое преобразование спектра оставляет неизменным его модуль, но при-
бавляет к фазе слагаемое (—соио), линейно зависящее от частоты.
Свойство 6. Инверсия (изменение знака аргумента последовательности)
соответствует инверсии частоты в спектре, то есть если
Л(л) = /1(-л)> (1.166)
то
F2(eft0) = F1(e"iw). (1.167)
Если инверсии подвергается вещественная последовательность, то с уче-
том 4-го свойства модуль и вещественная часть ее спектра остаются без изме-
нения, а фаза и мнимая часть меняют знак, то есть получаем спектр, комп-
лексно-сопряженный исходному.
Справедливость выражений (1.163), (1.165) и (1.167) легко проверяется
подстановкой последовательностей (1.162), (1.164) и (1.166) в формулу (1.155).
Свойство 7. Свертка последовательностей соответствует произведению их
спектров, то есть последовательность
/з(Л) = /1(п)*/2(п) (1.168)
имеет спектр
F3 (е) = Ft [еiw) F2 (е. (1.169)
Это важное свойство в других обозначениях уже доказывалось и обсужда-
лось в предыдущем параграфе.
Свойство 8. Произведение последовательностей соответствует свертке их
спектров, а именно, если
/э(«) = Л(«)Л("). (1.170)
ТО
Формула (1.171) определяет так называемую круговую (циклическую) сверт-
ку периодических функций и F2. Для доказательства свойства 8 покажем,
70
ГЛАВА 1
что из соотношения (1.171) следует соотношение (1.170). Подставим формулу
(1.171) в выражение обратного преобразования Фурье (1.156) и далее переме-
ним порядок интегрирования:
Заметим, что для допустимости перемены порядка интегрирования доста-
точно, чтобы подынтегральное выражение (то есть спектр Г3) было ограни-
ченным. Введем новую переменную для внутреннего интеграла: в — со — <р ,
тогда получим, что
Все подынтегральные выражения — периодические, интегрирование идет
по периоду, поэтому можно сдвинуть пределы интегрирования для внутрен-
него интеграла, тогда
что и требовалось доказать.
1.5.3. Соотношение между спектрами непрерывных и дискретных сигналов
Как уже отмечалось, дискретный сигнал — последовательность — обычно
получают посредством дискретизации непрерывного сигнала. Дискретизация
оказывает влияние на характеристики сигнала и, в частности, изменяет его
спектр. Определим, как соотносятся между собой спектр исходной непрерыв-
ной функции времени и спектр полученной из нее последовательности.
Известно, что непрерывный сигнал /(f) и его спектр FH(Q) связаны меж-
ду собой преобразованиями Фурье:
ОС
—ос
Z7t
—ос
eiQ'd£l,
(1.172)
(1.173)
1.5. Описание дискретных сигналов и систем в частотной области
71
где П — угловая частота. Выражение (1.172) определяет спектр непрерыв-
ного сигнала (прямое преобразование Фурье), а выражение (1.173) дает пред-
ставление сигнала через спектр (обратное преобразование). Для взаимно од-
нозначного соответствия непрерывного сигнала и его спектра достаточно, чтобы
тот и другой были абсолютно интегрируемыми на (—оо ,оо), кусочно-непре-
рывными и кусочно-монотонными.
Чтобы сравнить спектр (1.172) со спектром последовательности (1.155),
нужно выразить последний в сопоставимых координатах, то есть задать спектр
последовательности в виде функции размерной частоты. Подставляя выраже-
ние для частоты (1.151) в формулы (1.155) и (1.156), получаем
, . 00
к—-оо
e^dQ..
(1.174)
(1175)
В выражениях (1.174) и (1.175) использовано обозначение последователь-
ности, отражающее процесс дискретизации непрерывного сигнала (см. фор-
мулу (1.99)). Спектр последовательности в формуле (1.174), в отличие от фор-
мулы (1.175), зависит от шага дискретизации Д и является периодическим по
частоте Q с периодом 2л/Д.
Установим связь выражений (1.174) и (1.172). Дальнейшие преобразования
ведутся в предложении, что функция FH ограничена и абсолютно интегри-
руема на (-оо, оо). С учетом формулы (1.99), перейдем от непрерывного
сигнала (1.173) к последовательности
(2/н—1)л/Л
Здесь на втором шаге произведена тождественная замена несобственного
интеграла бесконечной суммой интегралов по смежным интервалам длиной
2л/Д. После введения для каждого слагаемого новой переменной интегриро-
вания Q7 = £2 —2лдп/Д получаем
Изменим порядок суммирования и интегрирования, отбросим ненужный
штрих в обозначении частоты и учтем, что е,2ят" =1. Тогда
72
ГЛАВА I
Сравнение полученного выражения с выражением (1.175) выявляет иско-
мое соотношение между спектрами:
2л
—т
(1.176)
т=—оо
Таким образом, спектр последовательности состоит из суммы бесконечного
числа спектров непрерывного сигнала, сдвинутых друг относительно друга на
2 л/Д.
Если спектр непрерывного сигнала ограничен по полосе частот, то есть
FH (Q) = 0 при | О. | > л/Д ,
(1.177)
то в диапазоне £16 (—л/Д, л/Д), определяющем один период спектра после-
довательности,
F(?ni) = lFH(n).
Этот факт иллюстрирует рис. 1.39. Очевидно, что в данном случае можно
однозначно восстановить спектр непрерывного сигнала по спектру последо-
вательности, а следовательно, и сам непрерывный сигнал по дискретному.
Если ограничение (1.177) не выполняется, то возникает эффект наложе-
ния спектров, выражающийся в том, что высокочастотные составляющие
спектра непрерывного сигнала попадают в область более низких частот в
спектре последовательности (рис. 1.40). Этот эффект всегда нежелателен,
поскольку из-за него теряется взаимно однозначная связь спектров; часть
-2л/Д -л/Д 0 л/Д 2 л/Д
Г(е'пд)
1/Д
-Зл/Д —2л/Д 0 л/Д 2 л/Д Зл/Д
Рис. 1.39. Пример спектров непрерывного и дискретного сигналов
1.5. Описание дискретных сигналов и систем в частотной области
73
Р(е'пЛ)
Рис. 1.40. Пример спектра непрерывного сигнала и дискретного с наложением спектров
информации, содержащейся в непрерывном сигнале, необратимо теряется
при дискретизации.
Эффекта наложения можно избежать, если дискретизировать непрерыв-
ный сигнал с достаточно высокой скоростью: для выполнения неравенства
(1.177) нужно, чтобы верхняя частота Qbb спектре непрерывного сигнала
была меньше л/Д, или, соответственно, шаг дискретизации
Д < л/£2в.
(1.178)
Неравенство (1.178) представляет собой ограничение, налагаемое на шаг
дискретизации непрерывного сигнала известной теоремой Котельникова.
1.5.4. Описание двумерных дискретных сигналов и систем
в частотной области
Пусть на вход двумерной ЛПП-системы подается двумерная дискретная эк-
спонента (1.133). При условии сходимости суммы (1.140) для данного входного
сигнала на выходе системы имеем выходную двумерную последовательность
g(«i.«2)= Ё Ё л(т1.т2)Л(”,’и'и“*(”2’'”г)|=
mt——оо т2——оо
. . ос ОО . .
«||=—оо т2——оо
74
ГЛАВА 1
совпадающую с входной с точностью до множителя, зависящего от простран-
ственных частот <х>[, со2. Этот множитель
н(е'“',?“2) = £ £ й(т1,т2)е-(“'"|+Ш!"г)
/И|-=—ос —эс
(1.179)
называется частотной характеристикой двумерной дискретной ЛПП-систе-
мы. Частотная характеристика задает коэффициент передачи ЛПП системы
при входном сигнале — двумерной комплексной экспоненте для каждого
значения параметров со( и <о2. Выражение (1.179) задает прямое преобразо-
вание Фурье двумерной последовательности, которое также называется дву-
мерным (пространственным) спектром. Частотная характеристика двумер-
ной ЛПП-системы есть пространственный спектр ее импульсной характе-
ристики.
По формуле (1.179) можно установить и правило обратного перехода, то есть
выразить импульсную характеристику двумерной системы через частотную:
f И (е'“' ) е'(ш'л'+“’"’)</<0|аю2,
-Л
(1.180)
данное соотношение определяет обратное преобразование Фурье двумерной
последовательности А.
Преобразования Фурье по аналогии с (1.179) можно записать для произ-
вольного двумерного дискретного сигнала /:
(1.181)
П| ——ос п2 ——ОС
(1.182)
Выражение (1.181) определяет пространственный спектр двумерной по-
следовательности, а выражение (1.182) — представление двумерной последо-
вательности через пространственный спектр.
Представления двумерных дискретных сигналов и ЛПП-систем в час-
тотной области (то есть с помощью преобразования Фурье) широко при-
меняются при их анализе и синтезе, поскольку во многих случаях проще и
удобнее соответствующих представлений в области пространственных ар-
гументов.
Перечислим некоторые важнейшие свойства спектров последовательнос-
тей (их более простые «одномерные» аналоги изложены в п.1.5.2).
1.5. Описание дискретных сигналов и систем в частотной области
75
Свойство 1. Достаточным условием существования спектра двумерной
последовательности / является ее абсолютная суммируемость:
Е Е |/(П1>"2)| <ОО.
Л|= —ос /ь=—ос
(1.183)
Из сопоставления условий (1.145) и (1.183) следует, что для существования
частотной характеристики двумерной ЛПП-системы достаточно, чтобы сис-
тема была устойчивой.
Свойство 2. Двумерное преобразование Фурье линейно. Это означает, что
для любых последовательностей /, /2 и постоянных о, b из соотношения
/ (п,, я2) = а / («! ,п2) + b /2 (и,, и2)
следует
F^,0)| ,е'“2 )= a F( ,е'“2 ) + bF2 ,ez<t>2).
Свойство 3. Если двумерная последовательность разделима, то есть для нее
выполняется соотношение (1.134), то ее спектр также является разделимым:
(1.184)
Свойство 4. Спектр двумерной последовательности / — периодическая
функция пространственных частот со1, со2. Его период по этим переменным
равен 2л, то есть
|(®|4-2лА|) i{(i>2+2nk2)
при любых целых , к2.
Свойство 5. Если двумерная последовательность / вещественна, то ее спектр
обладает следующими свойствами центральной симметрии:
RcFj= ReF^e
Im , ez“2 ) = -1т?’(е^' ,<Tf°2),
F(eZw,,eZa>2
Fl<?~z®,,e'z“2
argF^z"l,ez<°2)= -argF^’^.e-'102).
В соответствии co свойствами 4 и 5, линии равных значений вещественной
части (или модуля) и мнимой части (или аргумента) спектра двумерной
76
ГЛАВА 1
последовательности в плоскости переменных <х>1я (02 могут выглядеть, на-
пример, так, как показано на рис. 1.41. Очевидно, чтобы полностью описать
такой спектр, достаточно задать его на периоде по одной пространственной
частоте и на половине периода по другой, то есть, например, на двумерном
«прямоугольном» интервале:
-Я, < CD] < л, 0 < со2 < п.
Если вещественная последовательность разделима, то свойства симметрии
ее спектра усиливаются, поскольку симметричным является каждый из двух
одномерных спектров, входящих как сомножители в (1.184). При этом доста-
точно рассматривать двумерный спектр на одном квадрате шириной в поло-
вину периода, то есть, например, при
О < CD, <71, 0<со2 <л.
Свойство 6. Свертка двумерных последовательностей соответствует произ-
ведению их спектров, то есть последовательность (1.141) имеет спектр
Из последнего свойства следует, что, как и в одномерном случае, частот-
ная характеристика Н е'“2j полностью определяет Л ПП-систему, то есть
однозначно задает правило преобразования входной двумерной последова-
тельности в выходную (при их описании в частотной области).
Рис. 1.41. Линии равных уровней спектров двумерной вещественной последовательности
1.5. Описание дискретных сигналов и систем в частотной области
77
Остановимся на важном вопросе соответствия между спектром двумерной
последовательности и спектром непрерывной двумерной функции, из которой
эта последовательность получена. Прямое и обратное преобразования Фурье
(переход к спектру и обратно) для непрерывной функции f пространствен-
ных переменных хр х2 задается соотношением
00 00
FH(D],n2)= J f f(xl,x2)e~‘^'X]+il2X^dxldx2,
-00 -оо
. оо 00
/(W2)=A J f
-ос -оо
(1.185)
(1.186)
где И, ,£12 — угловые пространственные частоты, имеющие размерность ра-
диан/единица длины. Из (1.129) и (1.186) выразим двумерную последователь-
ность, полученную в результате пространственной дискретизации непрерыв-
ной функции, через спектр FH этой функции:
. ос ос
/(П„П2)=/(П1Д„П2Д2) = -Ц- J J fH(S2l,n2)e,<n'4''"+n2Aj,'1’dnldn2.(1.187)
-00 -оо
С учетом значений шагов дискретизации произведем замену размерных про-
странственных частот на безразмерные, со, =<2^,, co2=Q2A2, и выполним
несложные преобразования выражения (1.187), заключающиеся в разбиении
интегрирования, замене переменных и порядка суммирования:
-----Fh
д,д2
СО] со2
А, Д2 2
/<о,л,+“2'12)с7со1 d(02
| оо оо
f («Н«2)^/(«1Д1>«2А2) = -^- J J
4тс"
-ос -оо
(2*2+1)л j
(2‘г-'>д'д2
<*>|
А
e^'^^d^dW^
и
со2
Д2 ,
1 [со. + 2тгС <02 + 2л£2
а1л2*1=-оо кг=-оо А1 А2
^((о|П|+ш2л2)^
Сопоставление последнего выражения с формулой (1.182) выявляет иско-
мое соотношение между спектрами:
Fp,^)=_l_ £ £ Fh+^,«g2±2^ (] |g8)
А1А2 *,=-оо t2=-oc А1 A j
78
ГЛАВА I
Таким образом, спектр двумерной последовательности формируется как
сумма бесконечного числа спектров исходной непрерывной функции, сдви-
нутых друг относительно друга по переменным <0j, со2 на интервалы, крат-
ные 2ти. Данное суммирование и определяет периодичность спектра последо-
вательности (см. свойство 4).
Если спектр непрерывной функции ограничен, а именно,
то на интервале |cOj | < л, | (02 | < тс, определяющем период спектра последова-
тельности,
Fl iсо. iсо,
И
<Л>! (02
В этом случае можно однозначно восстановить спектр непрерывного дву-
мерного сигнала по спектру последовательности, а сам непрерывный сиг-
нал — по дискретному.
Если ограничение (1.189) не выполняется, то наблюдается эффект наложе-
ния спектров, выражающийся в том, что высокочастотные составляющие спект-
ра непрерывной функции попадают в область более низких частот в спектре
последовательности. Такое наложение нарушает взаимно однозначное соот-
ветствие спектров непрерывного и дискретного двумерных сигналов и ис-
ключает возможность безошибочного восстановления непрерывной функции
по ее отсчетам. Чтобы не допустить эффекта наложения нужно выбрать шаги
дискретизации из условий
где Hlmax,Q2max — максимальные (граничные) пространственные частоты
спектра непрерывного двумерного сигнала:
Fh(Q„Q2) = O при |^1 |>^1тах ИЛИ |^2|>^
2 max
1.6. Описание дискретных сигналов и систем с помощью
z-преобразования
1.6.1. Прямое ^-преобразование
При изучении дискретных сигналов и систем чрезвычайно полезным ока-
зывается представление последовательностей при помощи z-преобразования.
1.6. Описание дискретных сигналов и систем с помощью ^-преобразования
79
Прямым ^-преобразованием последовательности f называется комплексная
функция
00
f(z)= Е /(«)*“"• (1.190)
п=—ОС
где z — комплексная переменная. Ниже иногда будем использовать сокра-
щенную запись (1.190) в форме /(«)-^ F(z). Множество значений z, для ко-
торых ряд (1.190) сходится, и, следовательно, z-преобразование существует и
является конечным, называется областью сходимости z-преобразования. Об-
ласть сходимости зависит от формы преобразуемой последовательности.
оо
Часто в литературе z-преобразование вводится в форме F(z) — •
л—0
Это так называемое одностороннее z-преобразование, которое применяется
для последовательностей, заданных только при п >0. Выражение (1.190) за-
дает более общее двустороннее z-преобразование. С математической точки
зрения оно определяет разложение комплексной функции F(z) в степенной
ряд Лорана.
Если f — последовательность конечной длины, то есть /(п) = 0при
[W,,W2], то z-преобразование вычисляется как сумма конечного числа
слагаемых:
Г(г)= (1.19D
k=Nt
Очевидно, что его область сходимости включает те значения z, при кото-
рых все слагаемые в сумме (1.191) конечны, то есть всю комплексную z-плос-
кость за исключением точки z = 0, если N2 >0, и точки z = oo, если 7V, <0.
Этот факт иллюстрирует рис. 1.42а, на котором область сходимости z-преоб-
разования отмечена штриховкой (такой способ изображения областей сходи-
мости будем использовать и в дальнейшем).
Для полубесконечной левосторонней последовательности при
n>w2)
«2
F(z) = Е (1.192)
л=—оо
В данном случае степенной ряд бесконечен по положительным степеням
z. Известно, что такой ряд сходится в круге с центром в начале координат
(рис. 1.426), то есть при
|z|</?+, (1.193)
где /?+ — внешний радиус сходимости, некоторая постоянная. Вопрос о схо-
димости на границе области, то есть при z =/?+ должен исследоваться до-
полнительно для каждого конкретного ряда. Следует заметить, что, если
80
ГЛАВА 1
Рис. 1.42. Примеры различных областей сходимости для ^-преобразования
N2 >0 » т0 РЯЦ (Ы92) содержит и конечное число членов с отрицательными
степенями z, в этом случае, очевидно, из области сходимости исключается
точка 2 = 0.
Для полубесконечной правосторонней последовательности (/(л) = 0 при
п < ) имеем бесконечный ряд по отрицательным степеням z.
оо
F (4= Е /(«)
n—N\
Z "
(1.194)
Опираясь на предыдущий случай, легко показать, что ряд (1.194) сходится
во внешней части круга (рис. 1.42в):
14>«- •
(1195)
где R_ — внутренний радиус сходимости, а также, возможно, на самой гра-
нице области (то есть при |z| —/?_). Если 1У<0, то из области сходимости
исключается точка z — оо.
В общем случае, когда / — бесконечная двусторонняя последователь-
ность, ее z-преобразование можно представить как сумму z-преобразований
левосторонней и правосторонней последовательностей:
оо JV оо
F(z)= £ f(n)z~n = Е f(n)z~n+ Е f(.n)z~n, (1-196)
п--оо п=-оо n=N+\
где /V — произвольное целое число. Первое слагаемое в выражении (1.196)
имеет область сходимости вида (1.193), второе слагаемое — область сходимо-
сти вида (1.195). Если то получаем, что полное z-преобразование
сходится внутри кольца (рис. 1.42г):
К_<ф|</?+, (1.197)
и, возможно, на его границах. Если R_ > R+ , то области сходимости слага-
емых в выражении (1.196) не пересекаются, и z-преобразование двусторон-
ней последовательности не существует. Если R_ = /?+ , то z-преобразование
определено лишь тогда, когда оба слагаемых в выражении (1.196) сходятся на
1.6. Описание дискретных сигналов и систем с помощью z-преобразования
81
границах своих областей сходимости. Примером такого «экзотического» слу-
чая может служить z-преобразование последовательности sincoon/7cn , сходя-
щееся только на единичной окружности (см. табл. 1.1, строка 14).
Следует заметить, что функция F (?), если ее задать не через ряд, а в
явном виде, может иметь смысл не только в области сходимости, но и на
Таблица 1.1. г-Преобразования некоторых последовательностей
№ п/п Последовательность z-преобразование Область сходимости z-преобразования
1 Единичн 5(/т) = ый импульс 1, л=0, 0 , п *0 1 Вся z-плоскость
2 „г \ 1 , П 0, о! и —п.. 1 = V 1,7 |о , п^О z^' Z^O (при n0>0) или z * оо (при n() < 0)
3 Единиц и(л) = ный скачок 1, п>0, 0 , л<0 1 |z|>l
1-Z’1
4 Прямоугольный импульс 1+г-'+г-Ч...+г-("-'1 = _l-z"
и п)—и(п —Л/), N >0
1-г~’
5 апи[п) 1 l-az-1 И>1°1
6 —али(—п — 1) 1 \-az~1 kl<hl
7 папи(п] az~l H>l“l
8 {и + 1)а"и(п) (1-аг-1)1 г|>Н
9 —(n + l)a"u (—и —1) 1 (1-аг-')г N<l°l
10 а" ст а я 1 3 .в = = i Л IV • а о с _ ' 1 в 3 -S1 | Л II 1 — ab (1— az 1 j(l— bz) Ci Л м Л
11 1 1 7^ l-Vl-д2 а L 1 l—y/l—a2 <|z|< I+Vl-a2
h 1-<Г <1 1— 0,5a(z + z a a
12 а п cos (ton + <р)и (п) costp — acos(tp — to)z’1 1 —2а (cos to) z 1 + a2z2 |z|>|a|
82
ГЛАВА 1
Продолжение табл. 1.1
№ п/п Последовательность ^-преобразование Область сходимости z-преобразования
13 1П 1 U-z |z|>l. Z*1
14 sin<D()7T л —, 0<(0<я пп [1 . |argz|<(0 [0 , соо < |arg 0 :|<л |z| = l, |arg z| * (Oo
15 аП ( X —и(п) п! V ' схр(-«г~^ z *0
всей комплексной плоскости. Область сходимости начинает играть роль лишь
тогда, когда мы связываем эту функцию с определенной последовательнос-
тью /, то есть пытаемся получить ее, суммируя ряд (1.190). Только при указании
области сходимости соответствие последовательности и ее ^-преобразования
является взаимно однозначным. Одно и то же z-преобразование, но с различ-
ными областями сходимости, соответствует разным последовательностям (см.
табл. 1.1, строки 5, 6 и 8, 9), поэтому при вычислении z-преобразований и
манипуляциях с ними указание областей сходимости является обязательным.
Как следует из свойств степенных рядов, внутри области сходимости функ-
ция F (z) является аналитической. Особые точки функции, в которых она
теряет аналитичность, определяют границу области.
Важнейший класс z-преобразований представляют дробно-рациональные
функции, то есть отношения полиномов от z или, что эквивалентно, от z~*:
j=0
м ’
(1.198)
где — постоянные коэффициенты.
Особыми точками дробно-рациональной функции, которые могут ограни-
чить область сходимости z-преобразования, являются полюсы, то есть те зна-
чения z, при которых она обращается в бесконечность. Очевидно, полюсы —
это корни полинома в знаменателе F (z). Введем в рассмотрение и нули дроб-
но-рациональной функции — корни полинома в числителе. Разлагая полино-
мы на множители, можно привести формулу (1.198) к виду
(1.199)
где > — нули, 1 pj j- - полюсы.
1.6. Описание дискретных сигналов и систем с помощью ^-преобразования
83
При получении (1.199) предполагается, что коэффициенты Ьо и с0 не
равны нулю. В более общем случае, когда Ьй bt , ...,Zfy и с0 с, , ..., cMf все
равны нулю, выражение (1.199) принимает вид
CMt +1
здесь кроме нулей {<7,} и полюсов (рД имеется еще (Л/, — /vj-кратный
нуль (если Af, > TVj) или (А, — Мf )-кратный полюс (если А, >Л/,) в начале
координат.
Как следует из формулы (1.199), дробно-рациональное ^-преобразование
с точностью до константы описывается расположением нулей и полюсов в
z-плоскости. Диаграмма нулей и полюсов в сопоставлении с областью сходи-
мости z-преобразования наглядно отражает основные качественные характе-
ристики последовательности. Отметим, что область сходимости дробно-раци-
онального z-преобразования никогда не включает границы, то есть соответ-
ствует строгим неравенствам (1.193), (1.195) или (1.197).
Пример 1.6. Вычислим z-преобразование правосторонней экспоненты
f(n) = апи(п). В соответствии с формулой (1.190), имеем
F(z) = 52 artH(n)z
п—-оо
Этот ряд (геометрическая прогрессия) сходится, если az 1 или |z|>|fl|.
При этом
Данное дробно-рациональное z-преоб-
разование имеет единственный полюс в
точке z — a и единственный нуль в нача-
ле координат. Соответствующая ему диа-
грамма нулей и полюсов для веществен-
ного положительного а приведена на
рис. 1.43 (на этом и следующих рисунках
полюсы обозначаются крестиком, а ну-
ли — кружочком).
Рис. 1.43. Диаграмма нулей и полюсов для правосто-
ронней экспоненты ^-преобразования
84
ГЛАВА 1
Еще раз обратимся к выражению (1.190). Если комплексную переменную
представить через модуль и фазу: z = re‘w, то
. . оо
П--ОО
(1.200)
При г = 1 выражение (1.200) совпадает с (1.155), то есть z-преобразова-
ние превращается в спектр последовательности. Таким образом, спектр пос-
ледовательности — это ее z-преобразование, вычисленное на единичной ок-
ружности (рис. 1.44):
f(eto) = F(z)
1(0 •
(1.201)
z-e
Разумеется, выражение (1.201) имеет смысл только тогда, когда единич-
ная окружность принадлежит области сходимости z-преобразования, то есть
Рис. 1.44. Интерпретация спектра последова-
тельности
когда R_ < 1, и 7?+ > 1, (см. форму-
лы (1.193), (1.195), (1.197)). Если об-
ласть сходимости не включает еди-
ничную окружность, то спектр по-
следовательности не определен,
однако z-преобразование существу-
ет. Следовательно, z-преобразование
является более общим средством
описания последовательностей, чем
спектр Фурье. Класс последователь-
ностей, описываемых при помощи
z-преобразования, включает не толь-
ко затухающие в обе стороны после-
довательности, для которых сходит-
ся ряд (1.155), но и многие другие,
не являющиеся ограниченными при
устремлении аргумента к плюс или
минус бесконечности.
1.6.2. Основные свойства z-преобразования
Для работы с z-преобразованиями и, в частности, для вычисления z-npe-
образований последовательностей, не вошедших в приведенную выше табли-
цу, могут оказаться полезными следующие их свойства.
Свойство 1. z-преобразование последовательности f существует, и ряд (1.190)
сходится в кольце:
К_<|г|<Я+>
(1.202)
1.6. Описание дискретных сигналов и систем с помощью z-преобразования
85
где R_ — неотрицательная, a R+ — положительная константы (R_<R+),
если
lim
л—» оо
у) |/(-n)| = К+,
(1.203)
где lim означает верхний предел последовательности.
л—юс
Напомним, что верхним пределом действительной последовательности а(п)
называется число А такое, что:
1) существует подпоследовательность данной последовательности, стремя-
щаяся к Л;
2) каково бы ни было е > 0, найдется такое 7V, что сг(н) < А 4-е при п > N.
Всякая последовательность имеет единственный (конечный или бесконеч-
ный) верхний предел. Верхний предел совпадает с пределом в обычном смыс-
ле, если последний существует.
На границах кольца, то есть, при |z| = R_ и |z| = R,z-преобразование мо-
жет как сходиться, так и расходиться. Примем этот результат без доказатель-
ства, ограничившись его простой интерпретацией. Пределы (1.203) означают,
что абсолютные значения элементов последовательности могут, например,
иметь экспоненциальную асимптотику:
|/(и)| ~ A'R” при
п —* оо ,
|/(п)|~А2/?+ при п—>— 00,
где А,, А2 — некоторые положительные числа.
Если R+ >R_ >1, то последовательность |/(«)|, является расходящейся, то
есть lim |/(и)| = 0, lim |/*(n)| = OQ. Если R_<R+<1, то она сходится к
Л — ОС Л—*ОС
нулю: lim I/'(/?)| — ос, lim = 0. При R_ < 1 имеем затухающую в обе
стороны последовательность, lim |/(л?)г—0, для которой выполняется ус-
ловие абсолютной суммируемости (1.158).
Свойство!, z-преобразование линейно, то есть если /j(n)—-—>F((z),
/2(п)—>F2(z)» т0 Дян любых постоянных а, b
af}(n)+bf2(n}
——> a Fj (z) 4- bF2 (z).
(1.204)
Справедливость соотношения (1.204) вытекает из самого определения
z-преобразования (1.190). Областью сходимости суммы (1.204) является
86
ГЛАВА 1
пересечение областей сходимости слагаемых. Исключение составляют си-
туации, когда, например, при линейной комбинации дробно-рациональ-
ных г-преобразований появившиеся нули компенсируют некоторые полюсы;
в этом случае область сходимости может расшириться (такой эффект имел
место при переходе от г-преобразования единичного скачка к z-преобразова-
нию прямоугольного импульса, см. табл., поз. Зи 4).
Свойство 3. Сдвиг последовательности соответствует умножению ее z-пре-
образования на целую степень z, а именно, если
А («) = />
(1.205)
то
F2(z) = z (г).
(1.206)
Для доказательства достаточно подставить последовательность (1.205) в
формулу (1.190) и заменить переменную при суммировании:
оо оо
F>(z) = £ fl(n-nQ)z~n = 52
Л—-ОО Л1--00
z“"'“"°=
ОС
= £ fl и
АН——ОС
z^z^Fjz).
При сдвиге последовательности область сходимости z-преобразования не
изменяется за исключением, возможно, точек z=Q и z~oo.
Свойство 4. Умножение последовательности на аргумент соответствует
дифференцированию ее z-преобразования, т.е. если
Л(«) = «/1("). <1.207)
ТО
F2(z) = -z^^. (1.208)
az
Для доказательства запишем сумму (1.190) относительно последовательно-
сти /] и продифференцируем:
п——ОС
z п
1.6. Описание дискретных сигналов и систем с помощью ^-преобразования
87
Внутри области сходимости степенной ряд можно дифференцировать по-
членно, поэтому
ЛГ (оо ос
л=-оо л—-оо
00
= -г"' Е Л(п)г-" = -г-|Г2(г),
п——ос
что эквивалентно соотношению (1.208). При умножении последовательности
на аргумент область сходимости z-преобразования не меняется за исключе-
нием, возможно, точек границ области, на которых функция F, (?) теряет
аналитичность.
Свойство 5. Умножение последовательности на экспоненту изменяет мас-
штаб аргумента в z-преобразовании. Если /Дя)—>F, (?) с областью сходи-
мости R_ < |z| < F+ и
/2(n) = «Vi(«), (1.209)
то
F2(z)=F,(z/a), (1.210)
с областью сходимости |п| R_ < zl < |а| /?+ . Для доказательства этого свойства
подставим последовательность (1.209) в формулу (1.190):
оо оо
^2(^) = Е anf^n)z~n - Е /](«)(?/а)’" = F^z/a),
Л——оо и—-ос
что и требуется получить. Область сходимости для F2 (?) получается подста-
новкой z/л вместо z в неравенство для области сходимости F,(z).
Свойство 6. Инверсия (изменение знака) времени последовательности при-
водит к замене переменной z на z-1 в выражении z-преобразования, то есть,
если /1(л)—-—>F((z) с областью сходимости R_ <|z|<F+ и
(1-211)
то
F2(z) = F1(z“I) (1.212)
с областью сходимости (1/F+) <|z| <(1/F_). Доказательство этого свойства
сводится к подстановке последовательности (1.211) в формулу (1.190) и заме-
не переменной при суммировании:
ос
F2(z)= Е /|(-«)г~"
II — — ос
оо
= Е лМ
т=—ос
88
ГЛАВА 1
Область сходимости F2(z) получим, подставив z~l вместо z в неравенство
для области сходимости F](z).
Свойство 7. Свертка последовательностей соответствует произведению их
z-преобразований. Если
Л(Л) = Л(л)*Л(л),
то
^(z) = ^(z)F2(z).
(1.213)
(1.214)
Нетрудно провести доказательство этого свойства, с точностью до обозна-
чений совпадающее с доказательством аналогичного свойства для спектров
(см. п. 1.5.1). Областью сходимости F3(z) является пересечение областей схо-
димости F](z) и F2(z). Исключение составляют случаи компенсации полю-
сов Fj(z) нулями F2(z) или наоборот, при которых область сходимости мо-
жет расшириться.
1.6.3. Обратное z-преобразование
Установим правило перехода от z-преобразования к исходной последова-
тельности. Соотношение для такого обратного z-преобразования можно вы-
вести из интегральной теоремы Коши, из которой следует, что
(fz*~ldz = 2ni8[k), (1.215)
с
где интеграл берется против часовой стрелки по замкнутому контуру С, охва-
тывающему начало координат комплексной z-плоскости. Умножим обе части
выражения (1.190) на z*-1 и проинтегрируем по С, выбрав контур так, чтобы
он полностью лежал внутри области сходимости z-преобразования:
п п 00
<p(z)z‘-'<fc = fz‘-' £ f(n)z~"dz.
С С п=—ос
Равномерно сходящийся на С ряд можно интегрировать почленно, поэто-
му с учетом формул (1.215) и (1.116) имеем
(fF(z)zk 'dz = f(n)$zk n ldz = 27ti -n) =2nif[k).
Q n=—OO (J П——О0
Отсюда следует окончательное соотношение для обратного z-преобразования:
= /F(z)z" ldz,
2ти Jc
(1.216)
1.6. Описание дискретных сигналов и систем с помощью ^-преобразования
89
где С — контур, окружающий начало координат с направлением обхода про-
тив часовой стрелки и расположенный в области сходимости F (z).
Практически взять интеграл (1.216) можно несколькими способами. Если
подынтегральная функция
U'(z) = F(z)z',“1 (1.217)
является аналитической во всей внутренней области контура, за исключени-
ем конечного числа особых точек, то универсальный способ вычисления дает
теорема о вычетах. В соответствии с ней, интеграл (1.216) определяется через
сумму вычетов:
W(z),
Z = Pj ,
(1.218)
где N — число особых точек внутри контура С, — особые точки,
Res[iv(z), z = pj\ — вычет функции W (z) в точке z = Pj.
Для функции W (z), имеющих своими особыми точками полюсы, вычеты
вычисляются следующим образом. Если полюс в точке z = Pj простой, то
есть W (z) можно представить в виде
z~Pj
где U (z) — функция, не имеющая особенностей (аналитическая) в точке z = р}, то
Res[w(z),
z = рj = lirn (z
(1.219)
Если полюс в точке z = Pj I-кратный, то есть
то
Res[w(z),
/~1
z = Pj\ =
lim
.(1.220)
Выражения (1.217)-(1.220) позволяют находить, в частности, обратные
z-преобразования для дробно-рациональных функций F (z).
90
ГЛАВА 1
Пример 1.7. Вычислим последовательность, соответствующую z-преобра-
зованию,
I — az
с областью сходимости |z|>|a|. Согласно соотношению (1.216), в данном случае
2тп £ 1 - az 'litiJcz-a
Рис. 1.45. Взаимное расположение области схо-
димости, контура интегрирования и полюсов:
иллюстрация к примеру
Контур интегрирования С должен
располагаться в области сходимости, то
есть вне круга радиуса |л| с центром в
начале координат. При п > 0 подын-
тегральная функция W(z)=Zn/z-a
имеет один простой полюс в точке
z = a. При п < 0 появляется второй
полюс кратности (-л) в начале коор-
динат. Взаимное расположение обла-
сти сходимости, контура интегриро-
вания и обоих полюсов показано на
рис. 1.45. Как видно, оба полюса ох-
ватываются контуром. В соответствии
с выражениями (1.218) и (1.219) при
/(n) = Res
При п < 0 последовательность опреде-
ляется как сумма двух вычетов, значе-
ние первого из которых уже найдено:
/(л) —Res
zn
----, z = a
z-a
[Res
zn
, z = 0 — an +Res
z-a
(1.221)
—, z = 0
z - a
При л = —1 полюс в
простои, и поэтому
z = 0
1
Res
, z ~0 =~a 1
При n — — 2 полюс двукратный. В соответствии с выражением (1.220)
1.6. Описание дискретных сигналов и систем с помощью z-преобразования
91
Для произвольного отрицательного п получается
(1.222) в формулу (1.221), при
Таким образом, подставив выражение
п < 0 имеем f(n} = an — ап =0.
Окончательный результат: /(«) =
п >0
п <0
Непосредственное вычисление обратного z-преобразования методом вы-
четов может оказаться весьма трудоемким, особенно если у функции F (z)
имеется много особых точек. На практике чаще используют обходной путь,
приводя F (z) к представлению в виде суммы простых функций, обратные
z-преобразования которых известны. Так, для дробно-рациональной функ-
ции F (z) общего вида (1.198) применяется ее разложение на простые дроби:
Р (Z 11 \ М lj г'
F(z)=-'—1= a(z-1 +Е Е,-----------т, (1-223)
e(r') v 1 м
где /’(z-1), e(z-1), a(z-1) — полиномы от z”1, M — общее число полюсов,
/ • — кратность полюса р^, С jk — постоянные коэффициенты. Слагаемое А
в разложении (1.223) присутствует, если степень полинома Р не меньше сте-
пени полинома Q, и определяется алгебраическим делением Р на Q. Значения
постоянных С можно найти методом неопределенных коэффициентов (см.
пример ниже). Выражение (1.223) позволяет представить произвольную дроб-
но-рациональную функцию через сумму табличных z-преобразований.
При переходе от выражения (1.223) к самой последовательности следует
обращать особое внимание на взаимное расположение полюсов z-преобразо-
вания и его области сходимости вида (1.197). Как уже отмечалось, именно
полюсы определяют радиусы области сходимости. Простая дробь
jk_____
-i\k
, и левосто-
соответствует последовательности правосторонней, если
ронней, если Область сходимости такого элементарного z-преобрг-
зования будет определяться соответственно неравенством |z| > р7|или |z|< pj .
92
ГЛАВА 1
Пример 1.8. Определим последовательность, соответствующую z-преобра-
зованию,
(1.224)
с областью сходимости
(1.225)
Для этого запишем выражение (1.224) в виде отношения полиномов по
отрицательным степеням z‘.
a- z
Ь,
-1
1
bZ
(1.226)
а затем, учитывая наличие полюсов в точках
ложение на простые дроби:
z = а и z = \/Ь, произведем раз-
_hJ +—L2.
’~az ' l-lz
b
(1.227)
где Cb C2 — неопределенные коэффициенты. Для отыскания С, и С2 при-
ведем (1.227) к общему знаменателю и сравним его с записью (1.226):
Cl— — C2z 1 + С2 — аС2 z 1
Н<|г|<1/И.
Приравнивая в числителях коэффициенты при одинаковых степенях z,
получаем систему линейных уравнений
С] С2 — О,
1 1
fe ь
решение которой дает: С, =1, С2 = — 1, то есть
1,6. Описание дискретных сигналов и систем с помощью г-преобразования
93
Первое слагаемое
1
1 — az~l
1
1 — az~l
L—= F1(z) + F2(z).
(1.228)
имеет полюс в точке z = a, располо-
женной на внутренней границе коль-
ца сходимости (1.225), как показано
на рис. 1.46. Следовательно, оно со-
ответствует правосторонней последо-
вательности и имеет область сходи-
мости |z|>|a|. Из таблицы ^-преоб-
разований получаем, что
Второе слагаемое в сумме (1.228),
Рис. 1.46. Расположение полюсов
f2(z) =
_1 -• ’
а bz
f|(z) =
/|(и) = Л(л).
имеет полюс в точке z = l/by расположенной на внешней границе кольца схо-
димости (1.225). Следовательно, оно соответствует левосторонней последова-
тельности и имеет область сходимости |z| < l/|b|. Из таблицы ^-преобразований
находим, что /2(л) = Ь~пи(-п-1). В силу линейности z-преобразования, окон-
чательный результат получаем в виде
л>0,
п < 0.
1.6.4. Анализ и синтез ЛПП-систем с использованием z-преобразования
Определим передаточную функцию дискретной ЛПП-системы как z-преоб-
разование ее импульсной характеристики:
сю
w(z) = £ h(n}z~".
п=—ОО
(1.229)
94
ГЛАВА 1
Передаточная функция является еще одной формой описания ЛПП-систе-
мы, она однозначно определяет закон преобразования входной последова-
тельности в выходную. Действительно, учитывая соответствие формул (1.213)
и (1.214), свертку (1.112) можно записать в z-области в виде
G(z) = F(z)»(z).
(1.230)
где G(z),F(z) — z-преобразования выходной и входной последовательнос-
тей. Область сходимости G (z) состоит как минимум из пересечения областей
сходимости F (z) и Н (z).
Выражение, аналогичное (1.230), мы имели и раньше при описании ЛПП-сис-
темы в частотной области (см. формулу (1.157)). Это естественно, ведь в соот-
ветствии с соотношением (1.201) частотная характеристика системы есть ее
передаточная функция (а спектр дискретного сигнала — его z-преобразова-
ние) при значениях переменной z, взятых на единичной окружности в комп-
лексной z-плоскости. Однако понятие передаточной функции существенно
шире понятия частотной характеристики, поскольку применимо и к систе-
мам, для которых ряд (1.229) не сходится на единичной окружности.
Передаточную функцию нетрудно получить непосредственно из разностного
уравнения ЛПП-системы. Покажем это на примере физически реализуемой
системы, описываемой разностным уравнением (1.124). Используя сформу-
лированные в п. 1.6.2 свойства 2 и 3 z-преобразования (линейность и сдвиг
последовательности), уравнение (1.124) можно записать в преобразованной
форме:
М N М N
G(z)=E>;G(z)z'y =G(z)'Eajz~J + f(z)EM~'-
j-o j=i ;=o
Отсюда легко выражается
в явном виде:
E*y Z’J
(1.231)
Сопоставив выражения (1.231) и (1.230), видим, что
ЕМ’'
"(0 = ^-------•
i- E«>z->
7=1
(1.232)
1.6. Описание дискретных сигналов и систем с помощью z-преобразования
95
Полученная передаточная функция Н(г) отличается от записи (1.198) только
обозначениями коэффициентов в знаменателе, то есть является дробно-рацио-
нальной. Нетрудно показать, что ЛПП-системы, допускающие представление
в виде разностных уравнений конечного порядка, всегда имеют дробно-рацио-
нальные передаточные функции.
Заметим, что переход от уравнения (1.124) к (1.231) по существу определя-
ет метод решения линейных разностных уравнений с помощью z-преобразо-
вания. В отличие от громоздкого и неуниверсального метода прямой подста-
новки, рассмотренного в п.1.4, в данном случае можно получить результат в
общем виде и не указывать начальные значения для участвующих в решении
последовательностей (предполагается, что они являются бесконечными, то
есть заданы для всех значений дискретного времени).
Пример 1.9. На вход ЛПП-системы, описываемой разностным уравнением
(1.125), поступает сигнал — правосторонняя экспонента:
/(п) — bnu(n)t b^a .
(1.233)
Определим последовательность на выходе системы. Для этого перейдем от
разностного уравнения к передаточной функции:
G(z) = oG(z)z"i+F(z), G(z) = F(z)-Цу, (1.234)
1—az
\-az 1
(1.235)
Передаточная функция имеет один полюс в точке z = а и соответствует
правосторонней импульсной характеристике (так как система физически ре-
ализуема). Следовательно, область сходимости Н (z) — внешняя часть кру-
га: |z|>|a|. Определив по таблице z-преобразований соответствующую пе-
редаточной функции (1.235) импульсную характеристику й(и) = апи(п), мож-
но записать решение разностного уравнения во временной области в виде
оо
свертки: g (n)=Y^atf(n-k), что совпадает с выражением (1.128). Однако в
данном случае нам известна входная последовательность, поэтому можно
конкретизировать результат. Для последовательности (1.233) из таблицы
находим, что
f(z)= *. И >1*1-
l—bz
(1.236)
96
ГЛАВА 1
Подставив формулы (1.225) и (1.236) в (1.230), получим
После разложения G (z) на простые дроби имеем
a~b l-az 1 a—b \-bz 1
(1.237)
Сопоставление полюсов функции G(z) с ее областью сходимости показы-
вает, что оба слагаемых в выражении (1.237) соответствуют правосторонним
последовательностям. После перехода от (1.237) к последовательности полу-
чаем окончательный результат:
---а и
а—Ь
an+l-bn+l
----------и
а — Ь
(”)
Выполняя последовательность преобразований (1.124) в (1.232) в обратном
порядке, можно перейти от дробно-рациональной передаточной функции к
разностному уравнению. Это открывает простую возможность синтеза струк-
туры ЛПП-системы с заданной импульсной характеристикой.
Пример 1.10. Построим структурную схему ЛПП-системы с импульсной
характеристикой
h(n) = an
л
cos—п и
2
(1.238)
С помощью таблицы z-преобразований перейдем от характеристики (1.238)
к передаточной функции системы:
1+Л-2’
В соответствии с выражением (1.230)
или
G(z) = F(z)H(z) = F(z)—
1 + a z
G(z)(l+a2z-2) = F(z), G(z) = ~a2G(z)z~2 + F(z).
1.6. Описание дискретных сигналов и систем с помощью z-преобразования
97
Последнему соотношению во временной области соответствует разностное
уравнение:
g(n) = -a2g(n-2) + ^(n). (1.239)
Структурная схема системы, описываемой (1.239), представлена на рис. 1.47.
Формулу (1.230) можно использовать и для определения передаточной функ-
ции ЛПП-системы по известным сигналам на входе и выходе, то есть для
синтеза системы, осуществляющей заданное преобразование
(1.240)
F(z)
а также для определения входного сигнала по известным выходному сигналу
и передаточной функции:
ГЫ-^. »
При этом однако следует учитывать, что соотношения (1.240) и (1.241) не
всегда позволяют однозначно определить последовательность h и f соответ-
ственно, так как во многих случаях можно произвольно назначать область
сходимости и, следовательно, получать правосторонние, левосторонние или
двусторонние последовательности.
Пример 1.11. Определим, какую последовательность f нужно подать на вход
ЛПП-системы с импульсной характеристикой /?(и) = 8(п) + 25(п — 1), чтобы
получить на выходе g (п) = Зи (п).
Перейдем к ^-преобразованиям:
H(z)=l+2z‘‘, г»0; G(z) = —|г|>1.
1 — Z
В соответствии с формулой (1.241) z-преобразование входной последова-
тельности имеет вид
= G{z'l^=
3 1
1-z'1 l+2z“l '
Для первого сомножителя в вы-
ражении (1.242) область сходимос-
ти известна (z|>l) . Для второ-
го — ее можно назначить либо внут-
ри окружности, проходящей через
Рис. 1.47. Структурная схема, описываемая
разностным уравнением (1.239)
4 — 9044
98
ГЛАВА I
полюс в точке z — — 2, либо вне ее. В первом случае область сходимости
F(z) — кольцо: 1< |z|<2, то есть f будет двусторонней последовательнос-
тью. Во втором случае область сходимости F (z) — внешняя часть круга:
jz| > 2, то есть f — правосторонняя последовательность. Таким образом, за-
дача имеет два решения:
f — двусторонняя последовательность:
( ) = 3 1 2
(l-z"‘)(l + 2z'') l-z“' l + 2z-1’
l<|z|<2 |z|>l |z|<2,
f(n) = u (n) - 2(-2)n и (-П -1) ;
f — правосторонняя последовательность:
Ранее было сформулировано условие устойчивости ЛПП-системы, выра-
женное как требование абсолютной суммируемости ее импульсной характе-
ристики (см. неравенство (1.122). То же условие можно выразить и как требо-
вание к передаточной функции системы. Имеется простая взаимосвязь между
расположением полюсов на z-плоскости, областью сходимости передаточной
функции и такими свойствами системы, как устойчивость и физическая реа-
лизуемость. Неравенство (1.122) означает, что ряд (1.229) абсолютно сходится
на единичной окружности, а такое возможно, если единичная окружность
расположена в области сходимости ряда. Следовательно, ЛПП-система явля-
ется устойчивой, если область сходимости передаточной функции содержит
внутри себя окружность единичного радиуса на z-плоскости.
Как уже говорилось, область сходимости дробно-рационального z-преоб-
разования ограничена полюсами. Если ЛПП-система физически реализуе-
ма, то есть ее импульсная характеристика является правосторонней после-
довательностью, удовлетворяющей условию (1.119), то область сходимости
передаточной функции — внешняя часть круга, проходящего через наиболее
удаленный от начала координат полюс. Такая система устойчива, если все
полюсы ее передаточной функции лежат внутри единичной окружности. При-
мер диаграммы полюсов для устойчивой физически реализуемой системы
дан на рис. 1.48.
1.6. Описание дискретных сигналов и систем с помощью z-преобразования
99
Рис. 1.48. Диаграмма полюсов для устойчивой физически реализуемой ЛПП-системы
Отметим, наконец, следующее: в соответствии с формулами (1.117), (1.118) и
свойствами z-преобразования, при последовательном соединении N ЛПП-систем
(звеньев) передаточная функция объединенной системы имеет вид
»Й=1ВД.
>1
(1.243)
где Hj(z) — передаточная функция j-го звена. При параллельном соединении
(1.244)
J=l
Соотношение (1.243) используется при реализации системы в последова-
тельной (каскадной) форме, а соотношение (1.244) — в параллельной. Пред-
ставление дробно-рациональной передаточной функции в виде (1.243) легко
получить, выразив ее через нули и полюсы (см. (1.199)), а представление в виде
суммы (1.244) — разложив ее на простые дроби (см. (1.223)).
1.6.5. Двумерное z-преобразование
Прямым z-преобразованием двумерной последовательности f называется
комплексная функция
4*
100
ГЛАВА 1
оо ОС
F(z^Z2) = Е Е
Л|=—ос л2=—ос
(1.245)
где Zj, z2 — комплексные переменные. Ниже иногда будем использовать
сокращенную запись (1.245) в форме
/(п1,и2)—^->F(zj,z2).
Естественно, данное «двумерное» z-преобразование имеет смысл только в
своей области сходимости, то есть на множестве таких значений Z| и z2, при
которых сумма (1.245) существует и является конечной. Достаточным услови-
ем этого является абсолютная сходимость записанного двойного ряда:
СО 00 .
Б Б |/(«|."2)гГ'гГ| =
П|- СО п2=—оо
оо оо
= Е Е |/(л1»"2)|к|Гй* |z2r"2 < 00. (1.246)
rt] =—оо л2=—оо
Из этой формулы следует важный вывод о том, что область сходимости
определяется только абсолютными значениями комплексных переменных Z|,
z2 , а значит, может быть задана на плоскости в координатах (|zi|, |z21). Речь
идет о внутренних точках области сходимости z-преобразования. На границах
области условие (1.246) может не выполняться, но ряд (1.245) сходится не
абсолютно (условно). Вопрос о существовании z-преобразования в каждой
точке границы области должен исследоваться дополнительно для конкретно-
го ряда. Рассмотрим частные случаи.
Пусть f — двумерная последовательность конечной длины, удовлетворяю-
щая условию (1.135). Тогда ее z-преобразование будет вычисляться как сумма
конечного числа слагаемых:
w, n2
F(^,Z2) = Е Е Л,г2"2-
rt I —~М । М 2 2
(1.247)
Очевидно, что область сходимости такого z-преобразования включает в
себя те значения переменных zls z2, при которых все слагаемые в сумме
(1.247) конечны, то есть все точки плоскости (|zj, |z2 ) за исключением,
возможно, некоторых: точки =0, если >0, точки |zj =оо, если М} <0,
точки г2=0,если TV2>0 и точки |z2==oo, если Л/2<0.
Этот факт иллюстрирует рис. 1.49а, на котором область сходимости z-пре-
образования отмечена штриховкой.
1.6. Описание дискретных сигналов и систем с помощью ^-преобразования
101
Рис. 1.49. Формы области сходимости двумерного z-преобразования: а — последовательность
конечной длины, б — разделимая бесконечная последовательность (общий случай), в — разде-
лимая бесконечная последовательность (правосторонние составляющие), г — произвольная бес-
конечная последовательность первого квадранта, д — произвольная бесконечная последователь-
ность второго квадранта, е — произвольная бесконечная последовательность третьего квадранта,
ж — произвольная бесконечная последовательность четвертого квадранта, з — последователь-
ность, отличная от нуля на всей плоскости аргументов
102
ГЛАВА 1
Пусть двумерная последовательность f разделима (для нее выполняется
условие (1.144)). При этом ее двумерное z-преобразование также является
разделимым:
оо ОС
F(z„z2) = £ /|(«|)гГ' £ f2(«2)z2’"!=F1(zl)F2(z2), (1.248)
П|=—ос п2=—ОС
и, следовательно, область сходимости можно определить по каждой перемен-
ной. Известно что одномерное z-преобразование общего вида сходится в коль-
це, то есть для и F2(z2) области сходимости записываются соответ-
ственно в форме двойных неравенств:
. <lzi| (1.249)
|л£2)<|г2| </??’
где R±\ , R^ — некоторые постоянные, характеризующие грани-
цы области сходимости. Система неравенств (1.249) определяет область схо-
димости разделимого двумерного z-преобразования (1.248). В общем случае
эта область имеет прямоугольную форму, (см. рис. 1.496). С конкретизацией
одномерных последовательностей, входящих в (1.144), конкретизируется и
форма области сходимости z-преобразования. Так, если f} и /2 — правосто-
ронние последовательности (в частности, если ненулевые отсчеты f лежат в
первом квадранте), то область сходимости двумерного z-преобразования (1.248)
определяется системой неравенств
|Z|| ж’0.
|z2| > R?1
(1.250)
и, следовательно, имеет вид, показанный на рис. 1.49в.
Если f— двумерная неразделимая бесконечная последовательность, то об-
ласть сходимости ее z-преобразования уже не выражается независимо по пе-
ременным |z)| и |z2|. Так, можно показать, что, если ненулевые отсчеты по-
следовательности сосредоточены только в первом квадранте плоскости аргу-
ментов (то есть при > 0 и п2 > 0), то область сходимости z-преобразования
опять задается системой неравенств типа (1.250), однако граница области по
каждой переменной зависит от другой переменной:
1Ф*г)(14
(1.251)
Функции и /??(•) здесь являются взаимообратными, они опреде-
ляют границу области сходимости в плоскости (|zj|, |z2[). В соответствии с
1.6. Описание дискретных сигналов и систем с помощью ^-преобразования
103
(1.251) эта граница не может иметь участков с положительным наклоном, то
есть ограничивает область сходимости снизу и слева (см. рис. 1.49г). Здесь и
далее условие взаимообратности позволяет на практике ограничиться исполь-
зованием любого одного из двух записанных неравенств.
Аналогично, для бесконечной последовательности с ненулевыми отсчета-
ми во втором квадранте (при п} <0, п2 >0) область сходимости определяет-
ся системой неравенств
Ы<Л+ (|z2|).
|z2|>«<2)(|z,|).
(1.252)
при взаимообратных функциях и Здесь граница области схо-
димости имеет неотрицательный наклон и ограничивает область снизу и справа
(см. рис. 1.49Э).
Для последовательности, расположенной в третьем квадранте (при д, <0,
п2 < 0) имеем
|zl|<41)(|z2|),
Iz2|<#5?(|zi|),
(1.253)
при взаимообратных /?+ (•) и область сходимости ограничена сверху
и справа (см. рис. 1.49е).
Для последовательности в четвертом квадранте (при п{ > 0, п2 < 0)
|zi|>«9(|z2|). (1.254)
|z,|<42)(hl).
при взаимообратных и область сходимости ограничена сверху
и слева (см. рис. 1.49ж).
В самом общем случае, когда двумерная последовательность f рассматри-
вается как отличная от нуля на всей плоскости аргументов, ее всегда можно
представить в виде четырех составляющих:
/(П]>П2)=/|('11’«2) + /2('г1>«2) + Л(лг1’П2)+Л('г1Л2)> (1.255)
где / — последовательности с ненулевыми отсчетами только в /-м квадранте
(i = 1, 2, 3, 4). Слагаемые в (1.255) имеют z-преобразования с областями схо-
димости (1.251)—(1.254). Если эти области имеют общее пересечение, то
существует и z-преобразование всей последовательности /, область сходимо-
сти которого может быть записана в виде обобщения системы двойных не-
равенств (1.249):
104
ГЛАВА 1
r-)(|z2|)<|z1|<4')(|z2|).
2??,(|z1|)<|z2|<42|(|zi|)-
(1.256)
В соответствии с (1.256), любое сечение области сходимости при |z[| = const
или z2- = const является односвязным, граница области в общем случае замк-
нута и состоит из четырех сегментов, два из которых имеют неотрицательный
наклон, а два — неположительный. Возможный вид такой области дан на
рис. 1.49з. Для иллюстрации рассмотрим несколько простых примеров.
Пример 1.12. Вычислим z-преобразование двумерной последовательности
первого квадранта (1.132):
/(П|,П2) = аЛ|/7"гм(п1,И2).
Данная двумерная последовательность является разделимой, соотношение
(1.134) для нее выполняется при
fl(ni) = an'u(ni)
Z-преобразования и области сходимости приведенных одновременных пос-
ледовательностей записываются в виде (см. таблицу в п. 1.6.1)
Ы>14
В соответствии с (1.248), для рассматриваемой двумерной последователь-
ности получаем, что
Область сходимости этого двумерного z-преобразования,
|Z||>I«|.
ы>и.
имеет вид, показанный на рис. 1.49е.
1.6. Описание дискретных сигналов и систем с помощью ^-преобразования
105
Пример 1.13. Вычислим z-преобразование двумерной последовательности
/(и1,л2) = йЯ|и(п1)5(п1 -л2),
(а — постоянная), представляющей собой «одномерную» экспоненту, распо-
ложенную на биссектрисе первого квадранта (см. рис. 1.50п). Очевидно, дан-
ная последовательность не является разделимой, поэтому произведем вычис-
ления по общей формуле (1.245):
оо оо
^(zi,z2)= £ Е аП1ф1)5(«|-п2)гГ’,?Г2 =
Л,=—ОО Л2=—ОО
ОО ОС , . ,,
= Е аЛ|и(и1)гГ/1,г2’"2 = Е^г’^г') '•
л,——со Л|— О
Если полученный ряд (сумма геометрической прогрессии) сходится, то
^(zi,z2) =
1
1-nzj-1 z21
Условие сходимости ряда,
az{ 1 z21 < 1, можно переписать в форме нера-
венств (1.251):
Рис. 1.50. Импульсная характеристика и область сходимости ее двумерного z-преобразования:
а — одномерная экспонента, расположенная по биссектрисе первого квадранта; б — область
сходимости двумерного z-преобразования одномерной экспоненты
106
ГЛАВА 1
Вид этой области сходимости в плоскости (|z|| , |z2|) показан на рис. 1.506.
Пример 1.14. Вычислим z-преобразование двумерной последовательности
при
при
|”1| = |«2|-
где а — постоянная (|«| < 1). Данная неразделимая последовательность пред-
ставляет собой «крест» из одинаковых экспонент, «разбегающихся» по бис-
сектрисам четырех квадрантов (рис. 1.51а). Запишем ее через функции еди-
ничных импульсов и скачков в виде четырех составляющих по квадрантам:
/(я|,Л2) = ^Я1^(«1)3(л1 -п2) + а "'«(-л, -1)5(л| + л2) +
+а~П1и(-п} -1)6(л| - л2)+аЛ|м(л1 - 1)5(л( + л2).
Для первой составляющей мы уже вычислили z-преобразование в преды-
дущем примере:
аЛ1м(п, )§(n, — n2)-^» ------q-rr*
1- az, z2
Производя аналогичные вычисления для остальных слагаемых, получаем,
что
z
а П|м(—л, — 1)б(п, +и2)
l-az,z2
а п,м(—и, — 1)5(п, — n2)—
1 — az,z2
|г,|<НЫ’
|г2|<ш;
1.6. Описание дискретных сигналов и систем с помощью ^-преобразования
107
hl >Hh|.
/ \ / \ 7 u* С С'У
atI'u(^n[ — l)S(/2j + w2)^---------!~zr—»
1-flZj z2
Для точек пересечения областей сходимости этих z-преобразований по-
лучаем
f(z„z2)=---------
1 — azx z2 1—flZ|Z2 l-flZ|Z2 1— az} z2
(l + a2^l — 3^2) + 2a3(z1-1 + zt )(z7’ + z2j — a2(z]-2 +zf + z22 + z2)
/ 9 \ “ / Э \ / —I \ / . i \ 9 / _n 9 _9 9 \
^l+o J — -|-a" Д£| +Z| Д^2 ~t~Z2j~l~a "b^l 4” Z-2 4”Z2J
Указанное пересечение (область сходимости искомого z-преобразования)
существует при |а| < 1 и может быть представлено в виде системы неравенств
(1.256), в которой
при
при
при
при
при
при
R
при
при
Вид данной области показан на рис. 1.5И.
Если двумерное z-преобразование сходится при |^| = |z2| = 1, то, положив
1<о. /Ют
Z| ~е 1, z2 —е 2,
при вещественных со2, из формулы (1.245) получаем спектр Фурье (1.181)
двумерной последовательности. Таким образом, как и в одномерном случае,
преобразование Фурье есть частный случай z-преобразования, который нахо-
дит применение при анализе двумерных абсолютно суммируемых сигналов и
устойчивых ЛПП-систем (при выполнении условий (1.183) и (1.145)). Само
108
ГЛАВА 1
Рис. 1.51. Импульсная характеристика и область сходимости ее двумерного z-преобразования:
а — вид «креста» из экспонент по биссектрисам квадрантов; б — область сходимости двумер-
ного z-преобразования
же z-преобразование является более общим средством двумерных последова-
тельностей и применяется значительно шире.
Важный класс двумерных z-преобразований образуют дробно-рациональ-
ные функции двух переменных, представляющие собой отношения полино-
мов от Zj и z2. Если использовать запись полиномов по отрицательным сте-
пеням переменных, то двумерное дробно-рациональное z-преобразование имеет
общий вид
F{Z^Z1) =
Е Еч^ГЧ"'
mpO m2=0
Л£| М 2
Е Е ^-'mlm2zl 'Z2
«1=0
(1.257)
В одномерном случае подобные z-преобразования было удобно описывать
своими нулями и полюсами, которые определялись в результате разложения
полиномов числителя и знаменателя на простые множители. Такое разложе-
ние опиралось на основную теорему алгебры, согласно которой степенной
полином одной переменной всегда может быть представлен через свои корни.
Однако для полинома от нескольких переменных аналогичной теоремы в об-
щем случае не существует, и подобное разложение невыполнимо. Многомер-
ный полином, как правило, не имеет конечного числа корней, он равен нулю
на непрерывных множествах значений переменных. В этом заключается глав-
ное качественное отличие одномерных и многомерных (в частности, двумер-
ных) сигналов и систем, серьезно усложняющее их анализ.
1.6. Описание дискретных сигналов и систем с помощью г-преобразования
109
1.6.6. Основные свойства двумерного z-преобразования
При работе с двумерным ^-преобразованием полезно учитывать его свой-
ства, которые перечисляются ниже. Некоторые из них достаточно очевидны
или легко доказываются, другие — уже обсуждались в предыдущем разделе.
Свойство 1. Если z-преобразование двумерной последовательности f су-
ществует, то ряд (1.245) абсолютно сходится во внутренних точках области
сходимости, в общем случае определяемой системой двойных неравенств
(1.256). В точках границы области ряд, соответствующий z-преобразова-
нию, может как сходиться, так и расходиться. Область дробно-рациональ-
ного двумерного z-преобразования всегда является открытой (не включает
границы).
Свойство 2. Двумерное z-преобразование линейно, то есть если
то при любых постоянных а, b
а /1 («I. п2)+bf2 («!, п2(zr z2) +bF2 (z,, z2).
Областью сходимости этого суммарного z-преобразования в общем случае
является пересечение областей сходимости слагаемых.
Свойство 3. Если двумерная последовательность разделима, то ее z-преоб-
разование также является разделимым, то есть из соотношения
/(«НЛ2) = /1(”1)/2(Л2)
следует
F(zi,z2) = F1(z1)F2(z2).
Свойство 4. Сдвиг двумерной последовательности по каждой координате
выражается в умножении ее z-преобразования на целую степень соответству-
ющей переменной, а именно, если
/2 (и, ,п2) = /] (Л] - к} ,п2 - к2),
при целых к{, к2, то
F2 (z, , z2) = гг*' & г. (z,. z2). (1.258)
При сдвиге последовательности область сходимости двумерного z-преоб-
разования не меняется, за исключением, возможно, точек
z(=0, z2 =0, |z,| = cxd и |z2| = oo.
но
ГЛАВА 1
Свойство 5. Умножение двумерной последовательности на аргумент выра-
жается в дифференцировании ее z-преобразования по соответствующей пере-
менной, если, например,
то
^'2(^|,z2)== —
dFi(zi,z2)
(1.259)
При умножении последовательности на аргумент область сходимости дву-
мерного z-преобразования не меняется за исключением, возможно, точек гра-
ниц области.
Свойство 6. Умножение двумерной последовательности на экспоненту из-
меняет масштаб аргумента в z-преобразовании. Если
с областью сходимости общего вида (1.256), и
/2(п1,н2) = ая,/?Я2/1(”|.«2),
где а, b — произвольные постоянные, то
F2(z„z2) = F, -Л
(1.260)
область сходимости определяется системой неравенств
IН J и
Свойство?. Инверсия (изменение знака) аргумента последовательности
приводит к замене соответствующей переменной в z-преобразовании на об-
ратную величину, если, например,
Л («1*^)
с областью сходимости общего вида (1.256), и
/2(/г1»П2) = /|(-«]»'г2),
1.6. Описание дискретных сигналов и систем с помощью z-преобразования
111
ТО
F2^\^2) = F\
(1.261)
область сходимости определяется системой неравенств
Свойство 8. Свертка двумерных последовательностей соответствует произ-
ведению их ^-преобразований. Если
то
g (п,, п2) = , п2) * */ (и,, п2),
G(z1,z2) = H(z1,z2)f(z1,z2).
(1.262)
Областью сходимости двумерного z-преобразования G(z,, z2 ) является, как
правило, пересечение областей сходимости Н(z),z2) и F{z.[,z2')-
1.6.7. Анализ и синтез двумерных ЛПП-систем с использованием
z-преобразования
Введем понятие передаточной функции двумерной дискретной ЛПП-систе-
мы Z/(z|,z2) — z-преобразования ее импульсной характеристики /г(п|,и2)-
Передаточная функция исчерпывающим образом описывает систему, так как
с учетом соответствия (1.141) и (1.262) однозначно определяет преобразова-
ние входной двумерной последовательности в выходную.
Передаточная функция может быть получена непосредственно из разно-
стного уравнения, описывающего двумерную ЛПП-систему. Действительно,
используя сформулированные в предыдущем параграфе свойства z-преобра-
зования, уравнение (1.149) можно записать в преобразованной форме:
G(z!,z2)= £ E«m1,m2c(zi^2)z1 m,z2m2 + £ £bm} tniF(zt,z2)zj m'z2m2.
Отсюда
G(z(,z2)
E
i- £ £«M1m2zrw,zr2
еея
F(zt,z2).
(1.263)
112
ГЛАВА 1
Сопоставляя выражения (1.263) и (1.262) видим, что
(1.264)
Аналогично, для каузальной ЛПП-системы, описываемой разностным урав-
нением (1.150), имеем
n2
Е Ew"^"2
о/Е „ /П|—0 ffl2~0_______
М] М2
Е Е ^ГЧ”"2
nt] —0 т2 =0
(wi .Wj) * (0,0)
(1.265)
Передаточные функции (1.264), (1.265) представляют собой частные слу-
чаи выражения вида (1.257), то есть являются дробно-рациональные. Несложно
показать, что двумерные ЛПП-системы, представляемые разностными урав-
нениями конечного порядка, всегда имеют дробно-рациональные передаточ-
ные функции.
Важной для практики является и возможность обратного перехода от переда-
точных функций (1.264), (1.265) через соотношение (1.263) к разностным урав-
нениям (1.149), (1.150). Такой переход позволяет решить задачу синтеза и реали-
зации двумерной ЛПП-системы с требуемой импульсной характеристикой.
Пример 1.15. Построим разностное уравнение для каузальной ЛПП-систе-
мы с импульсной характеристикой:
/1(и1,п2) = — м(п| —1, п2— 1).
Изображение этой импульсной характеристики дано на рис. 1.52а. Вычис-
ление z-преобразования от представленной двумерной последовательности
(переход к передаточной функции) приводит к выражению
H(z1,z2) =
Связь z-преобразований входного и выходного сигналов имеет вид
1.6. Описание дискретных сигналов и систем с помощью г-преобразования
113
Отсюда получаем, что
(1-Z1 1 —z21 +?! 1z21)g(z1,z2)=(1-z1 iz2‘)f(z1,z2),
или
C(Z1’Z2) = Z| 1g(^2) + z2 'g(z|,z2)-
-zi-1z2',G(z1,z2)+F(z1,z2)- zr1z21F(z1,z2).
Последнему соотношению в области пространственных аргументов соот-
ветствует двумерное разностное уравнение:
g(ni>n2) = g(ni “ ) + g(П1 ’«2 -0-
Построенная на базе этого уравнения схема вычисления отсчетов двумер-
ного выходного сигнала представлена на рис. 1.526.
Аппарат z-преобразования весьма
эффективен при решении задачи син-
теза двумерной ЛПП-системы, осуще-
ствляющей заданное преобразование
сигналов, то есть при конструирова-
нии передаточной функции системы
по соотношению
(1.266)
h («p^)
Рис. 1.52. Импульсная характеристика и соответствующая ей схема вычисления выходных от-
счетов: а — импульсная характеристика двумерной ЛПП-системы; б — схема вычисления вы-
ходных отсчетов
114
ГЛАВА 1
Следует однако иметь в виду, что результатами такого синтеза удается вос-
пользоваться на практике только тогда, когда z-преобразования входного и
выходного сигналов являются дробно-рациональными, поскольку только в этом
случае ЛПП-системе соответствует разностное уравнение конечного порядка.
Пример 1.16. Построим разностное уравнение для каузальной ЛПП-систе-
мы, преобразующей последовательность f(n]fn2) = u(nlfn2) — м(п] — 1,и2 — 1) в
единичный импульс:
^(wl,n2)=:8(n],n2).
Для z-преобразования входного сигнала имеем (см. предыдущий пример)
а для выходного сигнала
G(zi,z2) = 1 при любых |zj, |г2|.
Следовательно, по (1.266) можно получить, что
Н(г„гг) =
1-Z|1 - г2' + г, 'z21
1 Zj Z2
и далее перейти от передаточной функции к искомому разностному уравне-
нию (см. также рис. 1.53):
g(nl,n2) = g(n1 -h«2 -0 + /(nl’n2)“
+ -1,«2 “О-
Рис. 1.53. Схема вычисления выходных отсчетов для ЛПП-системы, преобразующей последова-
тельность вида м(п|,л2)—и(п} — 1,п2 — 1) в единичный импульс
1.6. Описание дискретных сигналов и систем с помощью z-преобразования
115
При решении подобных задач, когда числитель и знаменатель дробно-ра-
циональной функции меняются местами, возникает вопрос определения об-
ласти сходимости z-преобразования. В рассмотренном примере ответ на него
достаточно прост и однозначен. Область сходимости записанной дробно-ра-
циональной передаточной функции ограничивается такими значениями z,,
z2, при которых ее знаменатель обращается в нуль, то есть выполняется ра-
венство
“0, или Z|=l/z2.
Соответственно, для абсолютных значений комплексных переменных имеем
kil=i/|z2|-
Последнее соотношение задает гиперболическую границу области сходи-
мости в координатах (|zj |, |z21)- Форма границы позволяет рассматривать два
варианта самой области:
Поскольку ЛПП-система полагается каузальной (с импульсной характери-
стикой в первом квадранте), то необходимо принять первый вариант. Для
нашего примера решение оказалось очевидным, однако в общем случае на-
значение области сходимости «синтезированному» двумерному z-преобразо-
ванию может оказаться сложной процедурой с неоднозначным ответом.
Еще более сложным (а иногда и невозможным) является обратный пере-
ход от z-преобразования к исходной двумерной последовательности. Суще-
ствует общий метод вычисления обратного двумерного z-преобразования,
но он имеет весьма ограниченное применение из-за громоздкости вычисле-
ний, связанной, в частности, с невозможностью представления произволь-
ных двумерных дробно-рациональных функций в виде суммы простых со-
ставляющих. Обычно реконструкция двумерной последовательности осуще-
ствима лишь тогда, когда z-преобразование с учетом его свойств удается
свести к совокупности «табличных» формул, для которых указанный пере-
ход заранее известен.
Как и в одномерном случае, важным применением z-преобразования к
анализу двумерных ЛПП-систем является проверка устойчивости системы
по передаточной функции. Из сравнения основного критерия устойчивости
(1.145) с условием сходимости z-преобразования (1.246) следует, что для
116
ГЛАВА 1
устойчивости двумерной ЛПП-системы необходимо и достаточно, чтобы об-
ласть сходимости передаточной функции включала в себя значения ее ком-
плексных аргументов, для которых |z,| = 1, |z2| = 1- Это условие выглядит
простым, однако его выполнение обычно трудно проверить на практике.
Для анализируемой ЛПП-системы, как правило, известно разностное урав-
нение, по которому можно легко построить саму дробно-рациональную пе-
редаточную функцию, но чрезвычайно сложно в явном виде выразить ее
область сходимости. По этой причине находят применение косвенные тесты
устойчивости, не требующие определения всей области сходимости и про-
верки охвата ею точки |Z|| = 1, |z2| — 1. Более подробное рассмотрение воп-
росов анализа устойчивости двумерных ЛПП-систем выходит за рамки дан-
ного учебного пособия.
1.7. Спектральный анализ дискретных сигналов
Анализ спектров — это одна из основных задач цифровой обработки сиг-
налов. Основой цифрового спектрального анализа является дискретное пре-
образование Фурье (ДПФ), которое переводит последовательность, заданную
во временной области, в последовательность, соответствующую компонентам
спектра. Связь между непрерывным и дискретным преобразованиями Фурье
является одним из вопросов, рассматриваемых в данном разделе.
Практическая ценность ДПФ заключается в том, что для него разработаны
чрезвычайно эффективные алгоритмы вычисления, называемые алгоритмами
быстрого преобразования Фурье (БПФ).
1.7.1. Дискретное преобразование Фурье
Пусть /н(г) — непрерывная периодическая функция времени (см.
рис. 1.54):
/н(') = /н ('+*Г).
(1.267)
где Т — период, к — любое целое число.
Такую функцию можно разложить в ряд Фурье (см. п. 1.2.1), то есть пред-
ставить в спектральной области. Этот ряд (спектр) будет содержать гармони-
ческие (синусоидальные) составляющие с периодами Т, Т/2 , Т/3,...» Т/т,...
В комплексной форме представление периодической функции через ряд Фу-
рье записывается в виде
/н(')= £
(1.268)
m=—оо
1.7. Спектральный анализ дискретных сигналов
117
Здесь
00
т——ос
— набор функций, образующих базис, по которому производится разложение
/н (г) в ряд, FH (т) — коэффициенты этого разложения — спектральные
компоненты сигнала. Эти компоненты образуют последовательность — диск-
ретный спектр (см. рис. 1.55). Заметим, что дискретность спектра связана с
тем, что функция fH(t) периодична.
Пусть теперь f \n) — последовательность, периодическая с периодом N,
f(n) = f(n+kN), (1.269)
которую можно получить дискретизацией периодической функции непрерыв-
ного аргумента, удовлетворяющей условию (1.267). Такая последовательность
есть частный случай периодической функции общего вида, поэтому для нее
все сказанное выше остается в силе. При переходе от (1.267) к (1.269) мы
просто заменили t на л, а Т на N. В новых обозначениях можно записать и ряд
(1.268):
то -2п
-AJ ц
f(n)= У? F(m)e N . (1.270)
tn——ос
To, что теперь функция рассматривается при целочисленных значениях
аргумента, дает основание не удовлетворяться такой записью. Действительно,
в данной ситуации базис разложения содержит только N различных функций
Рис. 1.54. Пример непрерывной периоди-
ческой функции времени
(0)(2л/7)(4л/7) ... (Q)
Рис. 1.55. Дискретный спектр функции
118
ГЛАВА 1
а остальные базисные функции совпадают с ними. Это связано со свойством
периодичности дискретной комплексной экспоненты:
.2лтл ,2tcz ,
I--- t----(Д'
е N = е N
Естественно, одинаковые базисные функции дают и одинаковые коэффи-
циенты разложения. Поэтому представление последовательности через ряд
вида (1.270) является избыточным.
Для устранения избыточности предлагается усечь ряд (1.270), ограничива-
ясь базисом только из 7V различных комплексных экспонент. Разложение по
такому базису принято записывать в виде
,2лтл
е~
(1.271)
। N-1
^=о
где последовательность коэффициентов F(m) называется дискретным спект-
ром исходной последовательности. Появившийся множитель перед суммой
не меняет характера представления, он вводится исходя из некоторых допол-
нительных соображений.
Определим коэффициенты разложения (1.271). Умножим обе части выра-
.2л,
~1—кп
жения (1.271) на е N при 0<k<N— 1 и просуммируем по периоду:
N-l
E/W
м-0
,2я ,
—(—кп
е "
n=0 т~0
i— n(m—k)
N V '
(1.272)
После замены порядка суммирования выражение (1.272) преобразуется к
виду
/V-] -i—kn 1 AM AM i 2ZE n(m_k\
ZfW “I
n=0 m—0 л=0
(1.273)
Будем рассматривать интервал значений индексов длиной в период: 0<т,
k<N — \. Нетрудно показать, что для этого интервала внутренняя сумма
л=0
i— n(m—k)
т = k
m^k
= Nb[m— Л).
(1.274)
N
0
Подставив (1.274) в (1.273), после замены индекса получим:
,2я
I— тп
N
(1.275)
м-0
1.7. Спектральный анализ дискретных сигналов
119
Л«) а
Рис. 1.56. Иллюстрация периодичности последовательности и ее дискретного спектра
Пара соотношений (1.275), (1.271) определяют дискретное преобразование
Фурье последовательности: (1.275) — прямое ДПФ, (1.271) — обратное.
Заметим, что, в отличие от «классического» преобразования Фурье, здесь и
f(n), и F(m) — последовательности. Как следствие, и в этом легко убедить-
ся, и F(m), и /(л) — периодичны с периодом /V (условная иллюстрация
этого факта дана на рис. 1.56).
Из соотношений (1.271), (1.275) видно, что для вычисления и прямого, и
обратного ДПФ берутся отсчеты последовательностей только в N точках одно-
го периода. Это позволяет формально использовать ДПФ и для последователь-
ностей /(л) и F(т), заданных только на интервале [О,?/— 1], то есть непери-
одических (имеющих конечную длину). Однако при этом всегда неявно пред-
полагается периодическая продолженность преобразуемых последовательностей
на всю бесконечную числовую ось аргумента, как это показано на рис. 1.56.
1.7.2. Связь ДПФ с ^-преобразованием и непрерывным спектром
последовательности
ДПФ это третье функциональное преобразование последовательностей, ко-
торое мы определяем в данном учебном пособии. До этого были введены в
рассмотрение преобразование Фурье последовательности (см. п.1.5) и z-npe-
образование (п.1.6). Выясним, как связано ДПФ с введенными ранее преоб-
разованиями.
Пусть имеется последовательность конечной длины:
/(л) = 0 при w^[O,N — lj.
120
ГЛАВА 1
Вычислим ее z-преобразование (чтобы не было путаницы в обозначениях,
будем индексировать его буквой z):
оо
Fz(z)= £ /(«)
п=—00
N—\
п—0
(1.276)
z п
Сравнение выражений (1.275) и (1.276) показывает, что коэффициенты ДПФ
последовательности конечной длины N равны значениям ее z-преобразова-
ния в 7V точках, равномерно распределенных по единичной окружности в
комплексной z-плоскости (см. рис. 1.57):
F(m\ = F (z)l m
V ) z\c)\z=eN
(1.277)
Формула (1.277) задает простой способ определения ДПФ по z-преобразо-
ванию. Возможен и обратный переход, то есть определение z-преобразования
по ДПФ:
N-l N-i
fZ(z) = S/(n)z'”=E
п-0 п=0
TV—I
,2л
i— т п
е N
Z "
N щ=0
N
N-1
Нт=о
N-1
( .2л
I— т
е N z
-1
N-1
.2л
т
е N z
(1.278)
и=0
т—0
.2л
т
1 — е N z
п
N ш=0
Im z
Выражение (1.278) интерполируют зна-
чения коэффициентов ДПФ на всю комп-
лексную z-плоскость.
Теперь определим связь ДПФ и непре-
рывного спектра. Ранее мы уже получали,
что преобразование Фурье последователь-
ности есть ее z-преобразование, вычислен-
ное на единичной окружности, то есть при
Рис. 1.57. Связь ДПФ и z-преобразования
1.7. Спектральный анализ дискретных сигналов
121
Рис. 1.58. Иллюстрация связи непрерывного спектра и ДПФ
Z = etta (см. формулу (1.201)). Поэтому здесь можно воспользоваться только
что полученными результатами. Переход от непрерывного спектра к ДПФ
задается выражением
F(m) = Fz(ei“)
Ь3=—-т, O<zn</V—1
N ~ ~
(1.279)
Иными словами, коэффициенты ДПФ есть равноотстоящие отсчеты не-
прерывного спектра последовательности конечной длины на интервале час-
тот [0,2тг] (см. рис. 1.58).
Нетрудно выполнить и обратный переход, то есть вычислить непрерывный
спектр по ДПФ. Для этого нужно в формулу (1.268) для z-преобразования
подставить z = e,w. Поскольку получающееся при такой подстановке соотно-
шение нам далее не понадобится, мы его не приводим.
1.7.3. Использование ДПФ для вычисления отсчетов непрерывного спектра
При цифровом спектральном анализе прикладной интерес представляют
отсчеты непрерывного спектра. Если требуемое число отсчетов равно /V —
длине исходной последовательности, то они непосредственно определяются
через ДПФ в соответствии с формулой (1.279). Однако часто требуется более
«детальный» анализ спектра, то есть получение большего чем N, числа отсче-
тов. Дадим решение этой задачи.
Пусть имеется последовательность конечной длины:
у(л) = 0 при n^[0,/V —1],
122
ГЛАВА 1
и требуется определить L отсчетов ее непрерывного спектра равно-
мерно распределенных на интервале [0,2л], то есть на периоде спектра
(L>N).
Преобразование Фурье (спектр) последовательности задается выражением
(1.155), которое в данном случае записывается в виде
е1Ш
= Е /(и)е-'“"
оо
/V-I
= Е/(«)«-'“
п=0
(1.280)
Определим отсчеты спектра в L точках спектра (1.280), а именно, при зна-
чениях частоты o)/=2jc//L, 0 <1 < L-\:
N~l -“л I
fz(^)=E/W<Et
п=0
(1.281)
С другой стороны, введем в рассмотрение новую последовательность дли-
ной в L отсчетов,
/•(")=
/(и) 0<n</V~l,
О N<n<L~\,
(1.282)
и вычислим ее L-точечное ДПФ:
L-] -i^nl N-l -i—nl
f,W=E/,(«> L = Е/(Ф L (1.283)
л-0 n=0
На последнем шаге преобразований здесь учтено, что, поскольку при
/V <п< L — 1 последовательность (1.282) равна нулю, то пределы суммирова-
ния в (1.283) сужаются. Сравнивая выражения (1.281) и (1.283) видим, что
Fz[eib3l} = F'(l).
Таким образом, простое дополнение последовательности конечной длины
нулями позволяет получить сколь угодно большое число отсчетов ее спектра
при помощи ДПФ. На практике ограничениями при этом выступают конеч-
ность компьютерного представления чисел и шумы вычислений.
1.7.4. Использование ДПФ для вычисления последовательности
по ее спектру
Спектральный анализ дискретного сигнала основан на переходе от после-
довательности к ее спектру. Выше мы видели, что для вычисления любого
числа отсчетов спектра можно использовать ДПФ. Однако в практических
1.7. Спектральный анализ дискретных сигналов
123
приложениях встречается и обратная задача, когда спектр задан, а требуется
получить саму последовательность. Оказывается, для получения последова-
тельности по спектру также можно использовать ДПФ (точнее, обратное ДПФ).
Для вычисления обратного ДПФ нужен не сам непрерывный спектр после-
довательности, а лишь его отсчеты, то есть дискретный спектр F(m). Переход
от непрерывного спектра к отсчетам («дискретизация» спектра) может повли-
ять на форму получаемой последовательности. Поэтому, чтобы получить иско-
мый результат, нужно правильно выбирать значение N — длину ДПФ (число
отсчетов непрерывного спектра). Рассмотрим эти вопросы детально.
Пусть /(и) — произвольная последовательность (не обязательно конеч-
ной длины). Будем предполагать, что z-преобразование
оо
^(г)= Ё /(«)
и—-оо
Z "
сходится в области, включающей в себя единичную окружность. В этом слу-
чае можно положить z = el(a и перейти к непрерывному спектру последова-
тельности:
OG
= Е
П=—ОО
И теперь, имея мы должны при помощи обратного ДПФ полу-
чить исходную последовательность /(«)-
В первую очередь произведем дискретизацию спектра. Для этого на интер-
вале частот [0,2л) возьмем /V равномерно расположенных отсчетов спектра,
которые будем считать коэффициентами ДПФ:
F(m) = F2(?“)
~ ,2л
= 12 f(n)e N ’ (1-284)
От дискретного спектра F(rn) при помощи обратного ДПФ (1.271) можно
перейти к самой последовательности. Но, как уже говорилось, при этом полу-
чается не исходная (произвольная) последовательность, а периодическая с
периодом N:
, N—1 -2л
/Л«) = ^Е^Р
yV т—0
(1.285)
Выясним, как связаны между собой /(п) и fN(n) . Для этого подставим
в выражение (1.285) значения коэффициентов ДПФ (1.284) (при этом заме-
ним индекс внутреннего суммирования):
124
ГЛАВА 1
ПС .2п ,
. -I—тк
Е /(*к "
к ——ос
,2л
i— т п
е N
1 / \ v~л i—т(л-А)
=Т7 Е Л*)Е* N <1-286)
2* к=—оо т—0
Заметим, что в (1.286) внутренняя сумма, при произвольных й, к,
N—\
E*"
m=0
W при
О при
п - к 4- rN = О
п — к 4- rN О
= N 22 S(n— k+rN},
Г——СУС
где г — любое целое. Поэтому, продолжая цепочку преобразований (1.286),
получаем:
1 00 ОО
^(и) = ™ £ f(k)N £ S(n-k+rN)=
* к=—оо г—— оо
ОО 00 00
= Е Е /(*)8(л-*+riV)= Е f(n+rN). (1.287)
г=—оо к——оо г——оо
Таким образом, периодическая последовательность, полученная при по-
мощи обратного ДПФ из дискретизированного спектра непериодической по-
следовательности, состоит из бесконечной суммы сдвинутых копий исходной
последовательности.
Если длина последовательности /(п) превышает N, то слагаемые в (1.287)
имеют пересекающиеся области ненулевых значений, то есть возникает «эф-
фект наложения». Для бесконечной последовательности эффект наложения
есть всегда.
В случае последовательности конечной длины, чтобы эффекта наложения
не было, следует выбирать N больше длины последовательности.
1.7.5. Основные свойства ДПФ
Дадим сводку некоторых свойств ДПФ, которые могут быть полезны в
дальнейшем.
Свойство 1. Линейность. Если f} (и) —> F} (т), f2 (п) —> Г2 (те), то а (п) 4-
+ £ Л (п) ~*а (т) + bF2 (т) при любых постоянных а, Ь. Здесь предполагает-
ся, что последовательности и f2 имеют одинаковую длину.
Свойство 2. Периодичность (уже упоминалось выше). Последовательности,
удовлетворяющие прямому ДПФ,
1.7. Спектральный анализ дискретных сигналов
125
ЛМ
F(m)=12f(n)e N
тп
п—0
и, соответственно, обратному ДПФ,
т—0
.2л
I— тп
N
являются периодическими с периодом N. Такие последовательности удобно
представлять не на числовой прямой, а на окружности, как показано на
рис. 1.59.
При таком представлении их можно рассматривать одновременно и как
периодические, и как последовательности конечной длины на интервале
[О,ЛГ-1] .
Свойство 3. Сдвиг. Если последовательность /(п) — периодична с перио-
дом N, и ее ДПФ — F(/n), то последовательность f(n — п0) имеет ДПФ
Следует учитывать особенности сдвига, если ДПФ применяется к последо-
вательности конечной длины. В этом случае последовательность дополняется
до периодической и осуществляется так на-
зываемый круговой («циклический») сдвиг.
Если представить такую последовательность
на окружности, то циклической сдвиг соот-
ветствует повороту окружности на п0 точек.
Эффект циклического сдвига для последо-
вательности конечной длины, представленной
на числовой оси, иллюстрирует рис. 1.60. На
рис. 1.60а показана последовательность конеч-
ной длины, заданная на [0, — 1]. При ДПФ
последовательность считается периодически
продолженной (см. рис. 1.606). При умноже-
нии ДПФ на экспоненту сдвигается именно
периодическая последовательность, то есть мы
получаем последовательность, показанную на
рис. 1.60в. И сдвинутая последовательность
снова рассматривается на интервале [О, N -1],
то есть в результате имеем последовательность
Рис. 1.59. Представление конечных
последовательностей, удовлетворяю-
щих ДПФ
конечной длины, показанную на рис. 1.60г, в которой отсчеты, вышедшие в
результате сдвига за пределы интервала [0,7V — 1], например, как в данной
иллюстрации, вправо, опять появляются на этом же интервале слева.
126
ГЛАВА 1
/(«)
Рис. 1.60. Эффект циклического сдвига
Свойство 4. Циклическая свертка последовательностей. Пусть /(и) и Л (и) —
периодические последовательности с периодом и их ДПФ равны соответ-
ственно F[m} и Н{т\. Сформируем новое ДПФ, перемножив два имею-
щихся, G(mi) = F{m)H\in}, и вычислим обратное ДПФ от произведения. По-
лученная в результате этих действий последовательность g (и) будет связана с
исходными последовательностями следующим соотношением:
/V—1
к-О
(1.288)
Это соотношение определяет так называемую круговую (циклическую) свертку
периодических последовательностей. Такое название становится понятным, если
рассмотреть последовательности на окружностях (см. рис. 1.61). Значения
циклической свертки получаются поэлементным перемножением соответствен-
ных отсчетов на окружностях и последующим суммированием произведений.
На рис. 1.61а показан метод вычисления g(0):
/V-1
Н°)=
k—Q
Различные значения отсчетов круговой свертки получаются при смещении
одной окружности относительно другой (см. рис. 1.61 б' и в):
А-1 А-1
к(1)= 52/(*)й(1-*),.... «(Af-1)=
Л=0 А-0
1.7. Спектральный анализ дискретных сигналов
127
Рис. 1.61. Циклическая свертка последовательностей
Очевидно, последовательность g(n) также является периодичной с перио-
дом 7V. Рассматривается она на том же интервале [0, tV — | , что и сворачивае-
мые последовательности.
1.7.6. Вычисление линейной свертки при помощи ДПФ
Практический интерес при обработке сигналов представляет линейная (апе-
риодическая) свертка последовательностей вида (1.111), которая не совпадает
с циклической сверткой (1.288). Тем не менее хотелось бы для получения
линейной свертки применить ДПФ, поскольку это преобразование имеет очень
эффективный алгоритм вычисления (см. далее п. 1.7.7). Возникает задача, как,
производя вычисление циклической свертки последовательностей, получить
результат, совпадающий с линейной сверткой. Рассмотрим ее решение.
Пусть имеются две последовательности конечной (и, возможно, разной)
длины:
/(«)=0
/г(и) = 0
при
при
и ^[0,^-1],
и<[0Л2-1].
128
ГЛАВА 1
Требуется вычислить их линейную свертку (см. также (1.111)):
00
s(n)= Е f(k)h(n-k).
к——<х
(1.289)
Нетрудно убедиться, что последовательность (1.289) также имеет конеч-
ную длину в (/Vj + N2 ~ 1) отсчетов:
#(л) = 0 при п ^[0,/V, +W2 _2|-
С учетом этого согласимся получать вместо конечной последовательнос-
ти — линейной свертки периодическую последовательность — циклическую
свертку с тем условием, что на основном периоде (начинающемся с точки
и=0) они совпадут. Такое совпадение возможно, если период циклической
свертки будет не меньше, чем длина линейной (то есть не меньше 7V, 4- N2 — 1).
Но для того, чтобы циклическая свертка имела заданный период, такой же
период должны иметь сворачиваемые последовательности, и такую же длину
должно иметь ДПФ, применяемое здесь по схеме, изложенной в свойстве 4
(см. предыдущий параграф). Поэтому исходные последовательности нужно
дополнить нулями, как минимум до длины в (TVj + N2 — 1) отсчетов и приме-
нять ДПФ такой же длины.
Благодаря дополнению нулями, при циклической свертке, ненулевые зна-
чения периода одной последовательности f (л) будут взаимодействовать с не-
нулевыми значениями только одного периода второй последовательности h(и).
При этом полностью исключатся круговые наложения, характерные для цик-
лической свертки.
Метод вычисления линейной свертки при помощи ДПФ (см. схему на рис. 1.62)
получил название «быстрой свертки» в отличие от непосредственного сумми-
рования произведений в соответствии с (1.289) («прямая» свертка). Термин
«быстрая» здесь употреблен потому, что вычисление свертки через ДПФ бо-
лее эффективно с точки зрения числа выполняемых арифметических опера-
ций. Выигрыш в эффективности начинает ощущаться при длинах сворачива-
емых последовательностей в несколько десятков отсчетов и быстро растет с
увеличением и N2.
1.7.7. Быстрое преобразование Фурье
Рассмотрим принцип построения алгоритмов вычисления ДПФ, обладаю-
щих малой вычислительной сложностью и называемых алгоритмами быстро-
го преобразования Фурье (БПФ).
Построим здесь так называемый алгоритм БПФ с прореживанием во вре-
мени, как наиболее простой и наглядный. Вопрос построения быстрых алго-
1.7. Спектральный анализ дискретных сигналов
129
/(и): 0<n <Afj — 1 h^n): 0<n < N2 — 1
g (и): 0 < п < Nj + N2 — 2
Рис. 1.62. Схема вычисления линейной свертки при помощи ДПФ
ритмов дискретных ортогональных преобразований подробно рассмотрим в
главе 5.
Дискретное преобразование Фурье (прямое) имеет вид
N-]
F (т)= 12 f (n)wNn ,
n=0
(1.290)
где wN = e 't2^N — так называемый фазовый (поворачивающий) множитель.
Если использовать векторное представление комплексного числа на комп-
лексной плоскости, то умножение этого числа на wN поворачивает вектор
вокруг начала координат по часовой стрелке на угол Тк/М (см. рис. 1.63).
Сформулируем некоторые очевидные свойства фазового множителя, кото-
рые нам будут нужны:
1) = wfi при произвольном целом I, то есть степень wN , рассмат-
риваемая как показательная функция, периодична с периодом N;
5 — 9044
130
ГЛАВА 1
2) < =1;
3) <2=-1;
4) wN — WN 2
Поскольку дискретный спектр (1.290) рассматривается в N точках
(0<zn</V—1), то если вычислять его непосредственно по формуле (1.290),
считая, что фазовые множители получены заранее, потребуется N раз вы-
полнить по N операций умножения и по (TV- 1) операций сложения комп-
Рис. 1.63. Умножение комп-
лексного числа на фазовый
множитель
лексных чисел. Так как преобразование вычисля-
ется на ЭВМ, то общее время его выполнения (без
учета служебных операций) равно
7'дпф=№Ту+^-1)Гс
й№(г,+гс),
где Ту — время выполнения операции комплекс-
ного умножения, Тс — время выполнения опера-
ции комплексного сложения. Квадратичный харак-
тер возрастания вычислительной сложности ДПФ
и вызывает необходимость разработки алгоритмов
БПФ.
Одна из основных идей БПФ заключается в том,
что исходная ^точечная последовательность разбивается на несколько более
коротких последовательностей, дискретные спектры которых могут быть ском-
бинированы таким образом, чтобы в итоге получилось ДПФ полной последо-
вательности. В частности, можно разбить последовательность на две равные
части по N/2 отсчетов. Тогда, если пренебречь затратами времени на объеди-
нение (комбинирование) частей, то
2
ДПФ
12
то есть имеем двукратный выигрыш во времени по сравнению с (1.291). При-
чем операцию разбиения можно повторять многократно, при этом выигрыш
будет еще более значительным.
Реализуем идею разбиения для частного, но широко рассматриваемого слу-
чая, когда длина ДПФ равна целой степени двойки: N — 2м. Напомним, что
преобразованию подлежит последовательность f (и), 0 < п < N — 1. Введем в
рассмотрение две 7V. 2 -точечные последовательности, состоящие из четных и
нечетных членов исходной последовательности:
/1(0 = /(2/), f2(/) = f(2/+l) ,0</<у-1.
1.7. Спектральный анализ дискретных сигналов
131
Тогда Л-точечное ДПФ разбивается на два слагаемых:
N—i
N-\
Л’-1
п=0
окончательно
wmzi
WN
тп__
n—О
(по четным)
п=0
(по нечетным)
"-1 "-1
2 2
= Е/(2/)и'«”'
1=0
1=0
Ш.-1
2
F(m)=E/i
1=0
*-1
Л/-1 Л-1
2 2
= Е /1 (') WN/Im +wNY,fl (l)wN/2 = F> (">) + WNF2 M •
1=0 /-0
(1.292)
где F^m), F2 (n?) — 7V/2 -точечные ДПФ последовательностей /Дп) и f2(n).
Дискретные спектры F] (ли) и F2 (т) определены при 0 < т < — 1, од-
нако нам нужно знать F(rn) при 0<m<N — 1. Поэтому нужно доопреде-
лить формулу (1.292) для интервала N/2<m< N — 1, используя свойство пе-
риодичности спектров:
ЛИ
т----
2)
+ w™F2 т
/V
2
при 0 < т < — — 1,
/V ,
— < т < N — 1.
2 ~ “
(1.293)
при
Заметим, что из свойств фазового множителя следует, что
N
т--
это позволяет в два раза сократить в (1.293) число используемых значений
фазового множителя:
при
N
2
/’(w) =
N
т--
~WN 2
(1.294)
при
2
2
2
2 “
5*
132
ГЛАВА I
В этой формуле в обеих строках содержатся одинаковые значения дискрет-
значения фазовых множителей.
Полученное соотношение оп-
ределяет операцию объединения
«половинных» ДПФ в целое,
которую часто изображают гра-
фически. Для этого приняты
специальные обозначения. Вы-
числения по (1.294) требуют вы-
полнения двух типов «элемен-
тарных» операций: сложение-
«бабочки»): и умножения на
ных спектров F, (ли)
и одинаковые
ка
а
операции, используемые в
Рис. 1.64. Элементарные
ДПФ
вычитание пары чисел (так называемой
постоянный множитель, который мы уже использовали ранее (см. рис. 1.64).
На рис. 1.65 изображена схема формирования 8-точечного ДПФ из двух
ДПФ длиной 4.
Используя аналогичную операцию разбиения (прореживания) вычислим
каждое 4-точечное ДПФ через пару двухточечных. При этом обозначим:
] (и) — четные члены j\ (п),
/)2W — нечетные члены /|(м),
/2|(и) — четные члены f2\n),
f22\n} — нечетные члены /2(л)-
Схема, соответствующая предпоследнему шагу преобразований (рис. 1.65),
имеет вид, изображенный на рис. 1.66.
И, наконец, двухточечное ДПФ может быть вычислено несредственно, так
как показано на рис. 1.67 для первого блока приведенной схемы. Здесь учте-
но, что w2 ~ 1 ’ поэтому преобразование выполняется без умножений:
На рис. 1.68 изображена схема 8-точечного ДПФ полностью, в ней учтено
известное свойство фазового множителя wNj2 = , а также ради регулярности
Л (0)=Л0) —
/(1)=Л2) —
Л(2)=Я4) —
.4(3)=лб)—
Л>(0)=/(1) —
/2(1)=ЛЗ)—
Л>(2>/5) —
Z>(3)=/(7) —
-F((0)
4x-
точечное
ДПФ
4x-
точечное
ДПФ
F(0)
F(l)
F(2)
F(3)
F(4)
F(5)
F(6)
F(7)
-f2(0)
-f2(1)
КС»
Рис. 1.65. Схема формирования 8-точечного ДПФ из двух 4-точечных
1.7. Спектральный анализ дискретных сигналов
133
./jYOH, (2)=У(4)
.^2(0)=/j (1)=У(4)
jf2(0)=/, (3)=/(6)
4j(O)%(O)=/(1)
^(1)=/2(2)=/(5)
^0)=/2(1)=ДЗ)
42(1)=/2(3)=/(7)
Рис. 1.66. Предпоследний шаг преобразования 8-точечной последовательности в ДПФ
структуры показаны и тривиальные умножения. Аналогичную структуру имеет
и схема БПФ для большего числа точек (равного целой степени двойки).
Произведем оценку вычислительной эффективности алгоритма БПФ. Пре-
образование выполняется за lg2 N шагов. На каждом шаге, очевидно, нужно
выполнить W сложений (или вычитаний) и N/2 умножений. Поэтому время
выполнения БПФ
То есть ТБПФ пропорционально N 1g 2 А , что существенно меньше оцен-
ки (1.291). Относительный выигрыш от применения БПФ: ТДПФ/ТБПФ про-
порционален /V/lg2 N и растет с увеличением N.
В завершение параграфа сделаем не-
сколько замечаний.
Во-первых, из схемы БПФ видно, что
дискретный спектр получается из последо-
вательности с перестановленными элемен-
тами. Перестановка (переупорядочение)
данных — характерная особенность боль-
шинства алгоритмов БПФ. При N = 2М
закон перестановки весьма прост: отсчеты
входной последовательности должны быть
расположены в двоично-инверсном поряд-
Рис. 1.67. Вычисление двухточечного
ДПФ
ке. Такой порядок определяется следующим образом. Нужно записать аргу-
менты (номера) отсчетов последовательности в двоичном коде, используя М
134
ГЛАВА 1
Рис. 1.68. Полная схема 8-точечного ДПФ
двоичных разрядов. Затем порядок следования разрядов инвертируется (заме-
няется на обратный). Получаемые после этого числа и будут является поряд-
ковыми номерами отсчетов после перестановки.
На рис. 1.69 показана схема двоично-инверсионного переупорядочения
отсчетов для N= 8, на нем же приведено двоичное представление номеров
отсчетов до и после инверсии.
Если требуется обрабатывать последовательность, представленную в есте-
ственном порядке, нужно граф двоичной инверсии присоединить слева к рас-
смотренной ранее схеме БПФ.
Во-вторых, при использовании рас-
смотренного алгоритма не требуется до-
полнительной памяти ЭВМ кроме той,
которая отведена под исходные данные
(обрабатываемый массив). Результаты
всех промежуточных шагов вычисле-
ний, а также сам дискретный спектр
можно размещать в той же памяти, что
и входную последовательность. Подоб-
ные алгоритмы БПФ, в которых для
входной и выходной последовательно-
сти, а также для промежуточных дан-
ных используется одна и та же область
памяти, называются алгоритмами БПФ
Рис. 1.69. Схема двоично-инверсионного пе- С замещением.
реупорядочения отсчетов, используемая в В-третьих, ХОТЯ МЫ рассмотрели ЗЛ-
ДПФ длиной 8 горитм прямого ДПФ, заданного выра-
жениями (1.275) и (1.290), все сказанное остается в силе и для обратного
преобразования (1.271):
N-I
-тп
N /п=0
(1.296)
1.8. Вероятностные модели изображений
135
Обратное ДПФ вычисляется по тому же самому алгоритму БПФ, если в
нем заменить wN на а в конце вычислений разделить результат на N. То
есть рассмотренный алгоритм БПФ обеспечивает вычисление как прямого,
так и обратного преобразований.
1.8. Вероятностные модели изображений
1.8.1. Случайные процессы
В отличие от детерминированных процессов, течение которых определено
однозначно, случайный процесс (сигнал) представляет такие изменения физи-
ческой системы во времени и в пространстве, которые заранее в точности
предсказать невозможно.
Понятие случайного процесса хорошо знакомо. Каждый раз, когда прово-
дится эксперимент (опыт), итогом его является функция, определенная на
интервале времени, а не какое-либо одно число. Если f — функция одной
переменной, то говорят о случайном процессе, если f — функция двух или
большего числа переменных, то говорят о случайном поле.
Аргумент функции f может быть непрерывным и дискретным. В последнем
случае используют термин «случайная последовательность» — одномерная
(случайный процесс) или многомерная (случайное поле).
Для описания изображений широко используются математические модели
случайных двумерных последовательностей. На рис. 1.70 показаны примеры
синтезированных случайных полей, полученные при использовании различ-
ных моделей. На рис. 1.71 приведены примеры текстурных изображений, по-
лученные в электронном микроскопе при исследовании кровяной плазмы.
На рис. 1.72 приведены аэрофотоснимки различных участков поверхности
земли. При всем внешнем различии этих изображений, они могут быть опи-
саны моделями двухмерных случайных последовательностей. В этой общнос-
ти — достоинства и недостатки вероятностных моделей изображений.
Заметим следующее: каждая отдельная реализация случайного сигнала явля-
ется функцией детерминированной. Поэтому для описания индивидуальных
свойств реализаций случайного процесса следует использовать методы, изло-
женные в предыдущих разделах. Особенности случайного процесса проявля-
ются при изучении свойств совокупности реализаций или всего ансамбля.
Поскольку этот ансамбль — вероятностный, то и характеристики случайного
процесса оказываются вероятностными.
Одномерная функция распределения вероятностей
= /•{/(«) <п} (1.297)
связана с одномерной плотностью вероятностей'.
(1.298)
136
ГЛАВА I
Рис. 1.70. Синтезированные случайные поля
Рис. 1.71. Изображения кристаллограмм кровяной плазмы
Соответственно, г-мерная плотность вероятностей
(1.299)
где t = П = (ПрП2--Пг)-
В одномерном случае плотность вероятностей удовлетворяет условию нор-
мировки:
оо
J Prtn)dn = l-
(1.300)
-00
1.8. Вероятностные модели изображений
137
Рис. 1.72. Снимки различных участков поверхности земли
В r-мерном случае условие нормировки имеет вид
ОО 00
J...J Р,(П)<Й1 = 1. (1.301)
-оо -оо
Последовательности функций р;(Л)> Р/„/2(Л1» Л2) Р^г-г,(Л1> Л2 —Лг)
представляют своеобразную лестницу, поднимаясь по которой, удается все
более и более подробно характеризовать случайный процесс. В прикладных
задачах часто достаточно знать о случайном процессе меньше, чем дают функ-
ции распределения: можно ограничиться числовыми характеристиками слу-
чайного процесса.
138
ГЛАВА 1
Среди числовых характеристик случайного процесса наиболее важными яв-
ляются среднее значение Ц f (f), дисперсия (г) и корреляционная функция Bf (/, т):
Hz (z) = Е{/ (/)}, о} (/) = E{(/(г) - ц z (г))2},
Bf (/л) = е{(/ (г) -gz (т) - Hz (т))},
где (как и везде далее) £{•} —- оператор математического ожидания.
Очевидно, значения корреляционной функции зависят не только от степе-
ни взаимосвязи, но и от абсолютных значений характеристик процесса. Эта
зависимость устраняется введением нормировки:
величину р f (/,т) называют коэффициентом корреляции между сечениями про-
цесса, и она показывает меру их линейной зависимости.
Для определения меры статистической зависимости между двумя случай-
ными процессами f и g рассматривают взаимную корреляционную функцию
('•') = £ {(/(') -Н/ ('))(« w - J1S (т))} •
Если описание случайного процесса не выходит за рамки введенных ста-
тистических моментов, говорят, что оно выполнено в рамках корреляцион-
ной теории или на уровне статистики второго порядка.
Случайный процесс f(t) называется стационарным в узком смысле (строго),
если аналитическое выражение плотности вероятности не зависит от выбора
точки начала отсчета времени. Из приведенного определения стационарного
процесса следует, что одномерная плотность вероятностей не зависит от вре-
мени, а для числовых характеристик стационарного процесса справедливы
следующие свойства.
Среднее значение и дисперсия не зависят от времени:
= <у}(г) = <у* . (1.302)
Корреляционная функция зависит только от разности t = t' - т:
Bf (tf,т) = B f [t’ - т) = B f (t). (1.303)
При этом
|Bz(t)|<Bz(O) = 4 , BZ(/) = BZ(-»). (1.304)
Кроме того, обычно выполняется условие
Бу (г) —* 0 при t —> оо.
(1.305)
1.8. Вероятностные модели изображений
139
Случайные процессы, удовлетворяющие условиям (1.302), (1.303) называ-
ют стационарными в широком смысле (по А.Я. Хинчину). Случайные процес-
сы, стационарные в узком смысле (строго), являются стационарными в ши-
роком смысле, но не наоборот.
Вместо термина «стационарный процесс» в двумерном случае использует-
ся термин «однородное поле», корреляционная функция которого зависит от
двух аргументов:
В f & j (^1 ~Tl’z2
Стационарный случайный процесс называется эргодическим, если любая
его вероятностная характеристика может быть получена из одной достаточно
длинной его реализации путем усреднения во времени: среднее во времени
равно среднему по ансамблю. На практике, как правило, мы не располагаем
множеством реализаций случайного процесса, но имеем возможность наблю-
дать его в течении большого промежутка времени Т или на большем про-
странственном интервале. В этом случае выражения для оценок математичес-
кого ожидания и корреляционной функции выглядят следующим образом:
(1.306)
1 о
В двумерном случае
j Ъ т2
7i72 о о
Н/)(/(Г] +Т1»?2+^2)
У1У2 о 0
(1.307)
(1.308)
Свойство эргодичности стационарных случайных процессов создает кон-
структивную основу для экспериментального определения требуемых вероят-
ностных характеристик.
1.8.2. Случайные последовательности и их характеристики
Произвольная случайная последовательность f(n) может быть описана
посредством указания тех или иных ее статистических характеристик. В даль-
нейшем ограничимся рассмотрением статистик второго порядка. Для средне-
го и дисперсии выражения имеют вид
140
ГЛАВА 1
g f(n) = E {/(«)},
(1.309)
Корреляционная функция последовательности f называемая также автокор-
реляционной функцией, и взаимная корреляционная функция последователь-
ностей f и g определяются следующим образом:
Bf М = £{(/ W -И/ И)-(/ (/)-И, (/))}, (1.310)
(*.')=Е {(/(*)- М/ W) («(0 - К. ('))} • (1-ЗИ)
Коэффициент корреляции для случайных последовательностей
Р/М=
я, (А,/)
°/Wa/W ’
при этом во многих практических приложениях важную роль играет средний
коэффициент корреляции между соседними отсчетами ру = E|pz (n,n + l)}.
Условия стационарности (в широком смысле) случайной последователь-
ности аналогичны условиям для случайных процессов:
g/(n) = g/, о}
Bf(k,l) = Bf (к-1). (1.312)
Для корреляционных функций стационарных последовательностей спра-
ведливы следующие свойства:
В/(0) = О/. = В^к^В^-к), (1.313)
lim Bf(k) = 0, lim Bfe(k) = Q. (1-314)
А—>оо >ос
Везде далее мы ограничимся рассмотрением именно стационарных после-
довательностей.
Используя свойство эргодичности применительно к случайной последова-
тельности, можно получить оценки ее числовых характеристик. Действитель-
но, пусть число элементов последовательности 1 < п < N, тогда дискретные
аналоги выражений (1.306)-(1.308) определяются следующим образом:
1 N
W к=\
1.8. Вероятностные модели изображений
141
1 Л'—л
7V П к==}
В двумерном случае (1 < п} < /V], 1 < п2 < N2)
1
/v, n2
-Е ЕЖа),
2 *,=1*2=1
В f (nl’n2)~
______1______
(^1 -«0(^2-«?)
X
W|— n( N2 — n2
xE E (/(^i*^2)~+^i>n2^2)~M/)-
*|=1 *2=1
(1.315)
(1.316)
Для одномерной стационарной случайной последовательности /(и) кор-
реляционная функция Bf (т) представляет собой одномерную детерминиро-
ванную последовательность. Введем преобразование Фурье последовательно-
сти Bf (w), которое называется спектральной плотностью мощности {энерге-
тическим спектром) последовательности /(п):
ОС
Ф/(е,“) = Е (1.317)
п—-оо
При этом отсчеты корреляционной функции могут быть вычислены через
спектральную плотность Ф Де'“) через обратное преобразование Фурье:
(1.318)
Соответственно, в двумерном случае связь корреляционной функции и
спектральной плотности мощности определяется уравнением
фДе/ш,,?Ю2)= Е Ё 5z(«i,n2) в"'И|"'"'й)2"2, (1.319)
п,=—ос л2=—ОС
B/(n,,n2) = -L-J j'<P/le‘u'eMAe“>'"'+“,^da>lda>2. (1.320)
4,1 -1.-Я
Отметим некоторые свойства энергетических спектров:
- энергетический спектр фДе j — вещественная функция частоты;
- энергетический спектр всегда неотрицателен: фДег(О)>0;
- энергетический и взаимный энергетический спектры обладают свойства-
ми симметрии:
142
ГЛАВА 1
ф/И=ф/М. фА И=ф«/ М-
Рассмотрим примеры.
Пример 1.19. Белый шум (последовательность независимых случайных ве-
личин). Его корреляционная функция имеет вид
ВДи) = о^5(п).
Из (1.317) следует, что
Фу = Оу , -тс<со<тс,
то есть спектральная плотность белого шума постоянна на всех частотах (см.
рис. 1.73).
В двумерном случае
Bf (п1»пг) = <J/S(n1,n2), Фу (е'ш, е‘“2 j = Op -л<со, <тс, —тс<со2 <тс.
Пример 1.20. Последовательность с биэкспоненциальной корреляционной
функцией
hl
(1.321)
имеет энергетический спектр следующего вида (см. рис. 1.74):
1-Р / /
Фук =-----J-7С<СО<-7С,
v ' 1 + p -2pcos(co)
где р — коэффициент корреляции между соседними отсчетами последова-
тельности.
В двумерном случае
В/(п1,л2) = о} -Р^Рг21.
। _ 2 . 2
Ф fе, е'“2) = 1 Р1________________1 р2________,
' ’ ' 1 + р?-2p]COs((O]) 1 + р2-2p2cos((0]) ’
—ТС < СО, < тс, - тс < со2 < тс.
Ф(е'“)
со
Рис. 1.73. Спектральная плотность мощности последо-
вательности типа «белый шум»
1.8. Вероятностные модели изображений
143
р = 0,1 ; /9 = 0,5.
Рис. 1.74. Спектральная плотность мощности случайной последовательности с биэкспоненци-
альной корреляционной функцией
1.8.3. Преобразование случайных последовательностей в ЛПП-системах
Пусть известны характеристики входного сигнала — стационарной случай-
ной последовательности /(и): среднее значение Цу, автокорреляционная
функция Bf и энергетический спектр Ф /. Требуется получить соответствую-
щие характеристики для последовательности g(n) на выходе устойчивой
ЛПП-системы с импульсной характеристикой h(n), а также взаимные стати-
стические характеристики входной и выходной последовательностей.
Среднее значение для выходной последовательности с учетом стационарнос-
ти сигналов и известной формулы свертки определяется следующим образом:
нг = £{«(«)}=£
ОС
Е h(k)f(n-k)
,к~~<х
СО 00
= Е А(Л)Е{/(л-Л)} = Цу £ ОД. (1.322)
к=—оа к~-<х>
Если ЛПП-система описана не импульсной характеристикой, а частотной
Н или передаточной функцией H(z), то для вычисления среднего значе-
ния выходной последовательности можно воспользоваться соотношениями
<о=0
=И/ОД)|г=,,
(1.323)
которые вытекают из сравнения (1.322) с формулами (1.152) и (1.229), опреде-
ляющими указанные характеристики системы.
В дальнейшем для сокращения изложения будем полагать ц* =Н/ — О-
При невыполнении этого равенства всегда можно учесть математическое ожи-
дание и его преобразование отдельно на основании формул (1.322) и (1.323).
144
ГЛАВА 1
Корреляционная функция выходной последовательности
определяется следующим образом:
эо эо
М")= Е 52 А(/)л(л-л)
к~-ос 1——ОО
Bf (n-k).
(1.324)
Выражение (1.324), записанное с использованием оператора свертки, вы-
глядит следующим образом:
В* («) = h(n)* h(—n)* (и).
(1.325)
Взаимная корреляционная функция входной и выходной последовательнос-
тей вычисляется в виде
= 52 h(k^Bj(n-k} = h(n)*Bf(ri).
k=—<x>
(1.326)
То есть искомая характеристика является сверткой импульсной характери-
стики ЛПП-системы и автокорреляционной функции входного сигнала.
Энергетический спектр последовательности на выходе системы легко вы-
водится из уже полученного соотношения (1.325). Действительно, с учетом
свойств z-преобразования (см. п. 1.6.2) имеем
ф8(г) = н(г)//(г-')ф/(г),
(1.327)
и далее, положив г~е,ш, получаем собственно энергетический спектр:
Ф8(гй,) = н(е'“)н(е“'ш)ф/(е,ш).
(1.328)
Частотная характеристика обладает известной симметрией, и выражение
(1.328) может быть записано в более компактной форме:
(1.329)
Получаем, что энергетический спектр последовательности на выходе ЛПП-
системы равен энергетическому спектру входной последовательности, умно-
женному на квадрат модуля частотной характеристики системы.
1.8. Вероятностные модели изображений
145
Взаимный энергетический спектр входной и выходной последовательности
вычисляется аналогично:
/со
и далее при z = e ,
флй)=нй)фгй)’
(1.330)
(1.331)
1.8.4. Факторизация энергетического спектра
В развитие полученных результатов рассмотрим один важный методичес-
кий прием, который часто используется при синтезе алгоритмов цифровой
обработки сигналов.
Поставим следующую задачу: синтезировать физически реализуемую ус-
тойчивую ЛПП-систему, которая при поступлении на вход дискретного ста-
ционарного белого шума дает на выходе сигнал с заданной корреляционной
функцией В^п). Такую систему иногда называют «формирующим фильт-
ром». Для простоты изложения будем считать что входной белый шум имеет
единичную дисперсию, то есть его корреляционная функция
Bz(n) = 8(n).
Нам известно выражение (1.327), связывающее энергетические спектры на
входе и выходе ЛПП-системы. В данном случае Фу (z) = 1, а энергетический
спектр выходного сигнала Фк (z) — вычисляется по заданной последователь-
ности При этом вытекающее из (1.327) соотношение
Ф(,(г) = н(г)н(г-1) (1.332)
можно рассматривать как уравнение относительно передаточной функции
7/(z) искомого формирующего фильтра. Процедура нахождения #(z) пред-
полагает разложение Ф (z) на пару «симметричных» (в смысле (1.332)) мно-
жителей. Осуществление такого разложения будем называть факторизацией
энергетического спектра.
Решение задачи факторизации не является единственным. Для того, чтобы
оно имело практический смысл, необходимо выполнить следующие два тре-
бования.
1. Найденная передаточная функция H(z) должна соответствовать физи-
чески реализуемой ЛПП-системе конечного порядка, то есть допускать пред-
ставление в дробно-рациональной форме (в виде отношения полиномов по
отрицательным степеням г).
146
ГЛАВА 1
2. Передаточная функция //(г) должна соответствовать устойчивой
ЛПП-системе, то есть иметь полюсы, лежащие внутри единичной окружно-
сти в комплексной z-плоскости.
Если энергетический спектр ФДг) является дробно-рациональным, то
среди решений задачи факторизации всегда найдется такое, которое удовлет-
воряет выдвинутым требованиям. Рассмотрим детально процедуру построе-
ния этого решения.
В силу четности автокорреляционной функции Bf, (л) ее z-преобразова-
ние — энергетический спектр Фл, (г) обладает свойством симметрии:
фДг)=ф«(г'')-
и, следовательно, если он является дробно-рациональным, то может быть пред-
ставлен в виде
(1.333)
где
J--M
B(z)= £ b^~J
j=-N
(1.334)
(1.335)
— полиномы из положительных и отрицательных степеней z с коэффициен-
тами, удовлетворяющими условиям = а_ д, bj =b_j.
Рассмотрим сначала полином (1.334), стоящий в знаменателе дробно-ра-
ционального энергетического спектра (1.333). Уравнение A(z) = 0 имеет 2М
(то есть четное) число корней. Причем, благодаря симметрии коэффициен-
тов, если комплексное число р — корень этого уравнения (полюс функции
(z)), то и 1/р также является корнем (полюсом). Если |/?[ < 1, то |1/р|> 1,
то есть половина корней будет лежать внутри единичной окружности комп-
лексной z-плоскости, а другая половина — вне единичной окружности комп-
лексной окружности. На самой единичной окружности корней нет, так как
наличие таковых противоречило бы условиям сходимости рассматриваемого
дробно-рационального z-преобразования при |z| = 1. Обозначим через pj
корни, лежащие внутри единичной окружности. Несложно пока-
зать, что при этом степенной полином (1.334) может быть представлен через
свои корни в виде
1.8. Вероятностные модели изображений
147
= А)П(1~ Pjt />/),
7=1 7=1
(1.336)
где Aq — некоторая постоянная. Введем обозначение
м
7=1
(1.337)
с учетом которого выражение (1.336) принимает вид
A(z) = A+(z)A+(z
(1.338)
то есть требуемая факторизация полинома A(z) произведена.
Аналогичным образом осуществляется и факторизация полинома (1.335):
где
B(z) = Bh(z)B'(z '),
7=1
(1.339)
(1.340)
— полином по отрицательным степеням z, Во — некоторая постоянная,
Qj (l<j<А) — корни Z?+(z).
Следует остановиться на особенностях выбора корней полинома (1.340).
Во-первых, уравнение Z?(z) = O может иметь решение, лежащее на единич-
ной окружности комплексной Z-плоскости, (это всего лишь означает, что для
некоторых частот со энергетический спектр Ф^, равен нулю. Во-вторых,
к корням (1 < j < А) нет необходимости предъявлять требование qj < 1,
поскольку, как мы увидим ниже, они будут определять положение нулей пе-
редаточной функции искомой ЛПП-системы, не влияющей на ее устойчи-
вость. Основное условие формирования полинома (1.340) заключается в том,
что из всех 2 N корней указанного уравнения должно быть использовано по
одному корню из каждой пары взаимообратных.
Полученные факторизованные представления (1.338) и (1.339) полиномов
(1.334) и (1.335) позволяют произвести факторизацию и энергетического спект-
ра (1.333) в целом:
(1-341)
148
ГЛАВА 1
где
+ / \ в+(г)
фДг) = 7тН <1342>
Л (г)
— дробно-рациональная функция от г-1, не имеющая полюсов вне единим-
ной окружности в z-плоскости. Из сравнения (1.341) с (1.332) видно, что в
качестве искомой передаточной функции физически реализуемого и устой-
чивого формирующего фильтра можно принять, что
//(z) = O^(z)z“£,
при любом целом L > 0. Для простоты везде далее будем полагать L = 0, то
есть брать
н(г) = фЯг) = ;Ш- (1-343)
A (z)
Пример 1.21. Определим передаточную функцию и построим разностное
уравнение физически реализуемой и устойчивой ЛПП-системы, преобразую-
щей белый шум с единичной дисперсией в стационарную случайную после-
довательность с автокорреляционной функцией
Ву (fc) = - йр^+11 |р| < 1, |д| < 0,5.
С помощью таблицы в п. 1.6.1 и свойств z-преобразования (п.1.6.2) вычис-
ляем энергетический спектр выходной последовательности:
Полином в знаменателе сразу записан в требуемой факторизованной форме:
A(z)~ (l-pz-1)(l-pz) = 4+(z)/l+(z_i),
где
Л+(г) = 1 - pz"1.
Произведем факторизацию полинома в числителе, для чего решим уравнение
2?(z) = (l —р2)(1—az-1 — az)=0,
или
az2 -z + a =0.
1.8. Вероятностные модели изображений
149
Корни этого уравнения
Z] 2 = ± V1 — 4а2
’ 2а \
Легко проверить, что они являются взаимообратными: — ^/z^- В зависи-
мости от выбора одного из этих корней, используемого в качестве qx в (1.340),
имеем два варианта факторизации
В+(г) = л/^
, 1±71-4<Г .
1-—--------Z
2а
где значения множителя
найдены подстановкой (1.340) в (1.339), раскрытием скобок и приравнивани-
ем коэффициента при любом из имеющихся степеней z к соответствующему
коэффициенту в первоначальном представлении B(z).
Итак, согласно (1.343), получаем две различные передаточные функции
искомой ЛПП-системы:
1-pz 1
liVl —4а2 _1
---------z
2а
по которым легко строятся два варианта
уравнений:
описывающих систему разностных
Процедуру факторизации, очевидно, можно использовать и для решения
более общей задачи, чем та, которая была поставлена в начале данного раздела,
а именно для синтеза физически реализуемой устойчивой ЛПП-системы, пре-
образующей стационарную случайную последовательность с одной автокорре-
ляционной функцией В? (и) в последовательность с другой автокорреляцион-
ной функцией В (и). Действительно, непосредственно из (1.327) следует, что
ф8(г)
ф/(г)
= Н(г)н(г"');
150
ГЛАВА 1
дробно-рациональные энергетические спектры входного и выходного сигна-
лов могут быть факторизованы:
ф/(г)=фЯг)ф/(г')’
ф8(г)=ф:(г)фЯИ-
где
фЯг)
4^ (z), (z), Д*(г), B*(z) — полиномы, определяемые в процессе фак-
торизации. Следовательно, в качестве передаточной функции ЛПП-системы
можно принять
ф?(4
ф;м
(1.344)
Причем, здесь нужно более строго, чем раньше, подходить к выбору кор-
ней при факторизации числителя выражения для энергетического спектра
входного сигнала — ФДг), то есть при конструировании полинома Bj'(z);
в соответствии с (1.344) корни этого полинома оказываются полюсами пере-
даточной функции и для того, чтобы система была устойчивой, они должны
обязательно выбираться внутри единичной окружности z-плоскости. Задача
не будет иметь решения (система не получится устойчивой), если у B'f (z)
будут иметься корни, лежащие на единичной окружности, и эти корни не
будут скомпенсированы соответствующими корнями B^(z).
Заметим, что в двумерном случае общего подхода к факторизации энерге-
тического спектра не существует.
ГЛАВА 2
КРИТЕРИИ КАЧЕСТВА ИЗОБРАЖЕНИЙ
И ПОГРЕШНОСТИ ИХ ДИСКРЕТНОГО
ПРЕДСТАВЛЕНИЯ
2.1. Критерии качества изображений
При обработке и анализе изображений всегда приходится задаваться воп-
росом об их качестве. Качество столь сложного объекта как изображение яв-
ляется очень важным, но одновременно и довольно нечетким понятием. Оно
оценивается разными способами и в связи с различными задачами.
Иногда качество рассматривается как характеристика самого изображения
и определяется его собственными свойствами (статистическими, структурны-
ми, семантическими). Соответствующие критерии либо являются субъектив-
ными, либо опираются на объективные характеристики изображения: форму
и параметры распределения яркости, ширину пространственного спектра и
т.п. Такие безотносительные критерии имеют довольно ограниченное приме-
нение и почти нигде не используются.
При другом подходе качество рассматривается как мера близости двух изоб-
ражений: реального и некоторого идеального, или исходного и преобразован-
ного. Такой подход более конструктивен, он позволяет оценивать количе-
ственные изменения значений яркости, уровень искажений изображений при
их преобразованиях (фильтрации, сжатии данных и т.д.), то есть, по суще-
ству, качество самого средства преобразования — алгоритма или системы.
Именно это очень важно при построении алгоритмов и систем обработки
изображений и оценке качества алгоритмов.
Рассмотрим наиболее часто используемые показатели качества изображений.
2.1.1. Критерий визуального восприятия
Он базируется на результатах экспертизы. Обычная процедура оценки ка-
чества заключается в предъявлении набора пар изображений (анализируемые
и идеальные) экспертам-наблюдателям, которые высказывают суждения на
уровне: «искажения незаметны», «заметны, но не ухудшают», «ухудшают, но
152
ГЛАВА 2
не мешают», «немного мешают» и т.п. Индивидуальные оценки обрабатыва-
ются и усредняются. Существуют специальные приемы, исключающие «при-
выкание» экспертов в процессе экспериментов, их пристрастия к конкрет-
ным сюжетам и т.д.
Проведение подобной экспертизы — всегда сложная задача, и ее результа-
ты весьма приблизительны. Для специальных изображений (которые, напри-
мер, получаются при дистанционном зондировании) эксперты должны быть
специалистами по решению соответствующих прикладных задач анализа ви-
деоинформации.
Но главный недостаток субъективного критерия — отсутствие количествен-
ных оценок. Он не позволяет решать задачи оптимизации систем обработки
изображений в пространстве непрерывно изменяющихся параметров. Здесь
возможен только перебор вариантов и то не очень большой.
Желательно, чтобы критерий имел простую аналитическую форму и про-
сто вычислялся по предъявляемым изображениям. Этому требованию удов-
летворяет ряд критериев, рассматриваемых ниже.
2.1.2. Среднеквадратичный критерий
Пусть изображения f(n},n2) и g(nt,n2) описываются моделями однород-
ных случайных полей. Мерой соответствия реального изображения идеально-
му может служить среднее значение квадрата их разности:
эта величина будет постоянной по всему полю аргументов, поэтому аргумен-
ты (одинаковые для /, g) для краткости не указываем.
Если математические ожидания f и g равны, то разность имеет нулевое
среднее и величина евв приобретает смысл дисперсии разности (а значение
екв — среднеквадратичного отклонения g от /) двух изображений.
Для стационарной модели обычно считается выполненным условие эрго-
дичности, при котором усреднение по ансамблю реализаций может быть за-
менено на усреднение по одной реализации. Тогда для непрерывных изобра-
жений, заданных при | jq | < £,, | х2| < 1^, имеем
£кв~ТТТ-J /[/(*!,*2)- gCw2)] d*\dx2,
^4L2-Li
(2.1)
а для дискретных, заданных при 0 < «j < TVj — 1, 0 < п2 < N2 — 1, имеем
. Л/,-1 /V2-l
екв £[/'(«1>«2)“^(П1’П2)]2-
^1^2 н,=0 п2=0
(2-2)
2.1. Критерии качества изображений
153
Заметим, что в задачах сравнительного анализа вариантов и оптимизации
постоянные коэффициенты в (2.1) и (2.2) могут быть отброшены.
Выражения (2.1) и (2.2) позволяют вычислять среднеквадратичную ошибку
и для пары произвольных изображений, не обязательно описываемых стацио-
нарными полями. Так часто и делается. Однако в этом случае следует иметь в
виду, что значение е^в будет характеризовать «среднее» качество изображе-
ния в целом, а на различных его фрагментах ошибки, в принципе, могут
различаться.
Достоинство среднеквадратичного критерия — его простота. При его
использовании многие задачи анализа и оптимизации алгоритмов обра-
ботки изображений легко решаются аналитически. Поэтому он очень час-
то применяется.
При обработке изображений следует учитывать, что данный критерий пло-
хо согласуется с критерием субъективного восприятия.
2.1.3. Критерий максимальной ошибки (равномерного приближения)
В непрерывном случае
и в дискретном
emax = max |/(x1,x2)-g(x1,x2)|,
(*>, х2)
£
'-max
= max
(«1» п2)
|/(n1,n2)-g(n1,n2)|.
(2.3)
(2.4)
Это очень строгий критерий. Он используется в тех случаях, когда выдви-
гается требование высокой точности представления не изображения в целом,
а каждой его точки (отсчета). Это необходимо в ответственных случаях, при
получении ценных, уникальных изображений.
Однако данный показатель имеет серьезный недостаток — сложность тео-
ретической оценки и, соответственно, использования его в процедурах опти-
мизации (по крайней мере для общепринятых моделей изображения).
2.1.4. Вероятностно-зональный критерий
Этот критерий является модификацией (и обобщением) предыдущего.
В случае использования критерия максимальной ошибки считается, что все
значения разностного сигнала (текущей ошибки) Е — f — g лежат в диапазоне
[— Ещах» Етах], то есть распределение вероятностей для е имеет, например,
вид, показанный на рис. 2.1.
Однако на практике во многих случаях это не выполняется. Простейшим
примером является ситуация, когда изображение искажено аддитивным
154
ГЛАВА 2
гауссовым шумом g = f + v, имеющим плотность распределения, которая ниг-
де не обращается в нуль (см. рис. 2.2):
P„(v) =
-----е
2nov
Разность е = / — g = — v — имеет такое же распределение. Здесь можно
оценить максимальную ошибку только с некоторой доверительной вероятно-
стью р. Вероятностно-зональный критерий определяется парой чисел (£тах,р).
Смысл этого критерия выражается формулой
£|пах
f Pe(E)Je = p
-®та»
(2.5)
и иллюстрируется на рис. 2.3.
Здесь, как и в предыдущем случае, часто возникают сложности при теоре-
тической оценке. Значение такого показателя качества получают экспери-
ментально, в результате анализа гистограммы распределения ошибки £.
2.1.5. Критерий пространственного разрешения
В ряду показателей качества изображения, особую роль играет показатель
пространственного (линейного) разрешения или разрешающей способности.
Этот критерий положен в основу стандартных методик определения качества
изображений, получаемых фотографическими системами дистанционного зон-
дирования. Обычный способ экспериментальной оценки значения этого по-
казателя заключается в следующем. На вход системы подается тестовое изоб-
ражение — мира, состоящая из набора штриховых объектов различных разме-
ров. Здесь и ниже для определенности будем полагать, что каждый такой
объект представляет собой «трехшпальную миру», т.е. имеет вид квадрата,
составленного из пяти чередующихся полос постоянной яркости, имеющих
Рис. 2.1. Пример распределения вероятнос-
тей разностного сигнала
Рис. 2.2. Плотность распределения гауссова
шума
2.1. Критерии качества изображений
155
Рис. 2.3. Вероятностно-зональный критерий
затрудняет проведение эксперимен-
ширину / (см. рис. 2.4я). Изображение, прошедшее через информационный
тракт, предъявляется наблюдателю (оператору-дешифровщику). Перед наблю-
дателем ставится задача указать самый
малый объект с еще различимыми поло-
сами (штрихами). Минимальная шири-
на различимого штриха — /0 и являет-
ся искомым значением показателя ли-
нейного разрешения.
Однако при тестировании аппарату-
ры (при «апостериорной» оценке каче-
ства изображений) возможности исполь-
зования детерминированных тестовых
полей яркости крайне ограничены. Кро-
ме того, наличие человека-наблюдателя
тов и порождает субъективные ошибки оценивания. Очевидно, что совер-
шенствование процедуры оценки качества изображений должно идти по пути
формализации показателя линейного разрешения (т.е. замены наблюдателя
его математической моделью), а также выражения данного критерия через
такие характеристики изображения и сквозного тракта, которые могут быть
измерены по достаточно произвольным реальным яркостным полям.
Произведем формализацию показателя линейного разрешения примени-
тельно к оптико-электронным системам формирования изображений с циф-
ровым представлением данных. Пусть информационный тракт описывается
линейной моделью наблюдения двумерного сигнала с шумом и последующей
равномерной дискретизацией сигнала по координатам:
оо оо
g(xl’x2)= f / Л(^1Л2)/(Х|-^1*Х2_^2)^1^2+V(X1’X2)> (2-6)
—оо—оо
а б
Рис. 2.4. Трехшпальная квадратная мира
156
ГЛАВА 2
) = #(*Р*2)
Ми1’и2
Х|=П|Д ,
(2.7)
где /(хих2) — полезный непрерывный сигнал на входе сквозного видео-
информационного тракта (истинное поле яркости); ^(хрХг) — выходной
искаженный сигнал, представленный в том же масштабе, что и поле на вхо-
де; ^(^,^2) — импульсная характеристика искажающей двумерной непре-
рывной линейной системы с постоянными параметрами (ЛПП-системы);
v(x.,x2) — аддитивный шум наблюдения, пространственно однородное поле;
#о(х|,х2) — выходной сигнал после дискретизации; Д — шаг равномерной
дискретизации двумерного сигнала. И пусть в качестве входного сигнала ис-
пользуется тестовый объект, показанный на рис. 2.4а. Рассмотрим сечение
поля яркости объекта вдоль оси х, (в направлении, перпендикулярным штри-
хам). Соответствующая этому сечению одномерная функция изображена на
рис. 2.46. На этом рисунке введен параметр А — амплитуда яркостных им-
пульсов («контраст» объекта). Периодически продолжив данную функцию на
всю числовую ось (см. пунктир на рис. 2.46), разложим ее в ряд Фурье на
периоде, т.е. на интервале [-/, /]. Несложно показать, что основная, первая
гармоника этого разложения записывается в виде
т.е. имеет амплитуду
(2.9)
и пространственную частоту (измеряемую в радианах на единицу длины)
Q, = ti/1.
(2.10)
Частотная характеристика ЛПП-системы, определяемая как преобразова-
ние Фурье от импульсной характеристики (см. (1.91)), задает значения коэф-
фициента передачи пространственных гармоник двумерного входного сигна-
ла при любых частотах £2],£22. Рассматриваемая гармоника (2.8) после про-
хождения сквозного тракта (ЛПП-системы) будет иметь в выходном сигнале
(2.6) амплитуду, равную уже не (2.9), а
(2-Н)
Теперь обратимся ко второму слагаемому в модели наблюдения (2.6). Шум
наблюдения v(x,,x2) обычно является слабокоррелированным и после дис-
2.1. Критерии качества изображений
157
кретизации сигнала по правилу (2.7) его можно считать дискретным белым
шумом (полем со статистически независимыми пикселами). Пусть ov — сред-
неквадратичное отклонение отсчетов шума. Известно, что зрительный анали-
затор человека обладает способностью усреднять такой шум в пределах наблю-
даемых штрихов постоянной яркости, если только эти штрихи не слишком
вытянуты (отношение длины к ширине не превышает 9. Для рассматриваемо-
го тестового объекта сформулированное требование выполняется. На каждом
штрихе размещается приблизительно
независимых шумовых пикселов, поэтому «кажущееся» среднеквадратичное
отклонение шума (после его субъективного усреднения) будет равно
Типичная частотная характеристика линейной модели сквозного тракта
убывает (к нулю) с ростом частотных аргументов. Это означает, что при умень-
шении размеров объекта (параметра /) амплитуда (2.11) первой гармоники
полезного сигнала на выходе тракта будет также уменьшаться. Одновремен-
но, в соответствии с (2.13), будет наблюдаться рост кажущегося среднеквад-
ратичного отклонения шума. Следовательно, с уменьшением ширины / штриха
тестового объекта отношение «сигнал/шум»
(2.14)
монотонно убывает и при ширине, равной значению искомого показателя
линейного разрешения (/=/0), достигает некоторого нижнего порогового
значения
(2-15)
где К — безразмерный параметр (порог), зависящий от требуемого уровня
вероятности ошибок различения штрихов и, как правило, выбираемый в диа-
пазоне 2 < К< 5 . Из (2.15) с учетом (2.11), (2.13) и (2.14) получаем
d =
= К,
(2.16)
158
ГЛАВА 2
где в предпоследней записи введено обозначение для пространственной час-
тоты, соответствующей значению показателя линейного разрешения:
П = л//0. (2.17)
Из (2.16) следует уравнение относительно неизвестной частоты О.-.
H(£i,O)=Q£l, (2.18)
где
(219)
— параметр, совокупно характеризующий надежность различения штрихов
(через величину К), шаг дискретизации (Д) и относительное превышение конт-
раста над шумом (A/gv).
Формулы (2.17)—(2.19) позволяют определить величину показателя линей-
ного разрешения расчетным путем, без привлечения наблюдателя и без ис-
пользования тестового изображения. При заданных значениях Д и А для тако-
го расчета необходимо знать уровень шума на изображении и сечение частот-
ной характеристики искажающей ЛПП-системы. Используя несколько сечений
частотной характеристики, можно найти значения рассматриваемого показа-
теля по разным направлениям (при различных ориентациях штрихов на плос-
кости изображения), что актуально в случае неизотропных искажений поля
яркости.
2.2. Погрешности дискретного представления изображений
Реальное «физическое» изображение является функцией непрерывных про-
странственных координат — /(Х],х2). В компьютере обрабатывается его дис-
кретный аналог, матрица f(n},n2) — цифровое изображение. Оно лишь при-
ближенно соответствует непрерывному. Несоответствие обусловлено погреш-
ностями, которые вносятся в данные в процессе преобразования в цифровую
форму.
Все результаты цифровой обработки относятся именно к цифровому изоб-
ражению. Понятно, что такая обработка имеет смысл лишь в том случае,
если цифровые изображения достаточно точно описывают первичные, то
есть погрешность цифрового представления мала. Надо уметь оценивать эту
погрешность.
Такая оценка важна еще и потому, что позволяет определить потенциаль-
ные возможности процедур цифровой обработки (фильтрации, кодирования
и т.п.) с точки зрения точности.
2.2. Погрешности дискретного представления изображений
159
Определим погрешность двух основных процедур преобразования изоб-
ражений в цифровую форму — дискретизации (по пространственным коор-
динатам) и квантования по уровню (яркости). При решении этих задач при-
мем описание изображения моделью стационарного случайного поля. Начнем
с квантования.
2.2.1. Оценка погрешностей квантования параметра по уровню
Пусть преобразуемая величина (параметр) у может принимать любые зна-
чения из диапазона [/min, /тах ], который называется шкалой параметра.
При представлении параметра в цифровой форме в пределах шкалы фик-
сируется (назначается) Q квантовых уровней'. Текущее (фак-
тическое) значение параметра отождествляется с одним из квантовых уров-
ней и далее вместо значения параметра используется просто номер выб-
ранного уровня, кодируемый двоичным кодом. Если используется b —
разрядный код, то имеется возможность пронумеровать Q = 2Ь квантован-
ных уровней.
Расположение квантовых уровней на шкале параметров может быть раз-
личным. На практике интервалы между квантовыми уровнями обычно берут-
ся одинаковыми. При этом шаг квантования по уровню: &f=fq — fq.x для
любых 1 < q < Q — 1 есть величина постоянная.
Равномерное расположение Q уровней на шкале параметра показано на
рис. 2.5. Здесь шаг квантования
В данном случае текущее значение параметра отождеств-
ляется с ближайшим квантовым уровнем. Будем рассматри-
вать именно такой вариант квантования.
Для каждого конкретного значения параметра f выбира-
ется свой квантовый уровень — f4, при этом ошибка циф-
рового представления параметра (ошибка квантования по
уровню)
8/ = /-Л-
Поскольку f — случайная величина, то и тоже случайна.
Но можно определить максимальное и среднеквадратичное
значения ошибки.
Рис. 2.5. Равномерное расположение уровней квантования на шкале пара-
метра
160
ГЛАВА 2
Максимальная ошибка квантования по уровню (для нашего варианта кван-
тования):
max ШаХ I £у I Ду /2 .
(2.20)
Обычно шаг квантования Ду значительно меньше шкалы параметра (то
есть b>\, Q >> 1, Ду « /тах — /min). При этом логично допустить, что ошиб-
ка Су
зоне
— случайная и имеет практически равномерное распределение в диапа-
—Ду/2, Ду/2 (см. рис. 2.6.).
Дисперсия ошибки
А//2 д2
-Л/12 1Z
(2.21)
среднеквадратичное отклонение (корень из дисперсии)
_ £/max
— 2-Д — >/з
(2.22)
Рис. 2.6. Распределение ошибки
Учтем далее следующее. Если параметр
f имеет нормальное (или близкое к нор-
мальному) распределение с дисперсией Оу
и математическим ожиданием |1у , то обыч-
но стремятся выбрать шкалу так, чтобы она
совпадала с «доверительным интервалом»
— Зау, jLty + Зау (все значения f лежат в
этом интервале с вероятностью «0,997).
Тогда
6а у
Утах У min бПу , Ду ,
и получаем, что
За f >/з а f
с — ___________- с ----------------
/max yb ’ *-'/кв
(2.23)
Пример 2.1. Пусть Ь = 8 (очень популярный случай — байт на отсчет). Тог-
да относительная максимальная погрешность квантования (по отношению к
среднеквадратичному отклонению параметра):
= = —ks0,012, то есть 1,2%.
2Ь 256
2.2. Погрешности дискретного представления изображений
161
Относительная среднеквадратичная ошибка — в \/з раз меньше:
£ /Ч /Ч
= \ = — к 0,007, то есть 0,7%.
2Ь 256
Отношение средней мощности сигнала к средней мощности шума кванто-
вания составляет
£ f кв
d
q 26 г\ 16
= —= —«2-104,
3 3
то есть погрешностью квантования в данном случае можно пренебречь.
2.2.2. Восстановление непрерывных изображений
по их дискретному представлению
Перейдем к анализу второй процедуры преобразования изображения в
цифровую форму — дискретизации по пространственным координатам (см.
п. 1.3.2, формулы (1.94) и (1.95)). Чтобы оценить погрешность, с которой не-
прерывное изображение описывается своими дискретными отсчетами, нужно
восстановить непрерывную функцию по этим отсчетам и сравнить ее с той,
которая была до дискретизации.
Погрешность дискретизации изображения (она же — погрешность восста-
новления непрерывного поля по отсчетам) зависит от следующих факторов:
- величины шагов дискретизации Др Д2;
- статистических свойств изображения;
- способа восстановления непрерывного изображения (или вида интерпо-
лирующей функции).
С физической точки зрения выбор шага дискретизации диктуется шири-
ной пространственного спектра изображения. Чем больше ширина спектра
Д£1, тем меньше шаг дискретизации Д. Практически при дискретизации стре-
мятся удовлетворить соотношению
Д«2я/£1 (2.24)
К сожалению, реальные сигналы и изображения обычно не удовлетворяют
требованиям ограниченности спектра, поэтому процедура восстановления при
помощи идеального фильтра низких частот (ФНЧ) дает лишь приближенный
результат. В связи с этим обычно используют простые в реализации способы
восстановления, которые являются приближенными при любых характерис-
тиках сигнала, то есть восстанавливают не функцию f(xvx2), а некоторую ее
оценку — /(xj,x2).
6 — 9044
162
ГЛАВА 2
Чаще всего используется восстановление при помощи полиномиальной ин-
терполяции, при которой f и f совпадают в узлах интерполяции (отсче-
тах) и, возможно, различаются при всех других значениях непрерывных ар-
гументов.
Рассмотрим некоторые интерполирующие функции, которые используют
при оценке погрешности дискретного представления изображений.
Для прямоугольной (ступенчатой) несимметричной интерполяции
f(xl,x2) = f(nl^l,n2^2) ДЛЯ Mi <*1 <(И1+1)А1
и п2Д2 <х2<(и2+1)Д2.
(2.25)
Иллюстрация приведена на рис. 2.7а. Это самый простой способ восстанов-
ления. Как мы увидим, он дает самую большую погрешность восстановления.
Для прямоугольной (ступенчатой) симметричной интерполяции
/(Х1,х2) = /(п1Д1,и2Д2) для WjAi
^-<Х! <М1 +^-,
И
(2.26)
Иллюстрация приведена на рис. 2.76.
Этот способ восстановления почти столь же прост, как и предыдущий, но
является более точным. Нетрудно показать, что для полей с изотропными
статистическими характеристиками погрешность восстановления при шагах
ДРД2 здесь равна погрешности несимметричной ступенчатой интерполяции
при половинный шагах (то есть при Д1/2, Д2/2).
а
Рис. 2.7. Ступенчатая интерполяция
б
2.2. Погрешности дискретного представления изображений
163
Несмотря на указанное преимущество, данная интерполяция также явля-
ется довольно грубой. В обоих случаях функция яркости восстановленного
непрерывного изображения получается ступенчатой. Имеющиеся на ней скачки
ухудшают визуальное качество изображений.
Билинейная интерполяция. При восстановлении непрерывного изображе-
ния данным способом строится поверхность, проходящая через четыре сосед-
них отсчета. Интерполирующая функция
/(х1,х2) = Ах|х2+Вх1 +Cx2+D
(2.27)
является линейной по каждой коор-
динате. Коэффициенты A,B,C,D вы-
бираются из условия прохождения ин-
терполирующей функции через отсче-
ты. Определим их для случая, когда
интерполяция производится на пря-
моугольнике
0<Х]<Д|, 0<х2<^2>
как представлено на рис. 2.8. Это эк-
вивалентно выбору «локальной» сис-
темы координат для каждой четвер-
ки отсчетов, образующей подобный
прямоугольник.
Имеем систему уравнений:
/(0,0) = £>,
/(Д1,0) = ВД1+£>,
/(0,Д2) = СД2+О,
/(Д1,Д2) = АД1Д2+ВД1+СД2+О.
Ее решением являются следующие значения:
D = /(0,0), B = /(Al,0W(0,0)
/(0,Д2) —/(0,0)
д2
А = —[(/(Д1,Д2)-/(0,0))-(/(Д|,0)-/(0,0))-(/(0,Д2)-/(0,0))] =
/(Д„Дг)-/(Д„0)-/(0,Д2)+/(0,0)
Д1Д2
6*
164
ГЛАВА 2
То есть для 0 < л, < Д]; 0 < х2 < Д2
/(Д1,А2)-/(Д1,О)-/(О,Д2) + /(О,О)
। ’ *2; — —------------------xi х2 +
+ /(Д.,0)-/(О.О) + /(О, Д2)-/(0,0) + /(0 0) (2 28)
Д1 д2
или в другой форме
/(Х1,Х2) = /(Д1,А2)
Д]Д2 Д1 к
Д2;
+ /(0,Д2) 1
х2
-^ + /(0,0) 1
Д] J^2
1-2L
д. Л д
(2.29)
2
Существуют и другие более сложные интерполирующие функции, но они
не всегда дают выигрыш в точности. Показано, например, что для экспонен-
циально спадающих автокорреляционных функций (АКФ) поля билинейная
интерполяция близка к оптимальной. Поэтому ее используют наиболее часто.
Там, где налагаются жесткие ограничения на сложность, обычно берется прямо-
угольная интерполяция.
Следует сказать, что введенные интерполирующие функции важны не только
для оценки погрешности восстановления непрерывного изображения по от-
счетам. Они широко применяются при геометрических преобразованиях циф-
рового изображения.
2.2.3. Оценка среднеквадратичной погрешности дискретизации
Пусть интерполяция между отсчетами на каждом двумерном интервале
производится одинаковым способом. Тогда все интервалы со статической точки
зрения эквивалентны, и при анализе достаточно рассмотреть один из них.
Возьмем интервал {0<^ < А,; 0<х2 <Д2}.
Если /(х1,х2)— исходное изображение, a f(xitx2) — восстановленное, то
в каждой точке изображения имеем ошибку £Jt(x1,jr2) = /(jc1,x2) —/(jcj,x2)-
Это случайная величина.
Дисперсия ошибки в каждой точке
о2(Х],х2) = Е{е2(.Г1,Х2)}-
Среднеквадратичная погрешность по всему полю определяется через
усредненную дисперсию. Так как поле стационарно, усреднение достаточно
2.2. Погрешности дискретного представления изображений
165
выполнить по одному интервалу. Получаем квадрат среднеквадратичной по-
грешности:
£
X КВ
J Д1 Д2
—— J J* ol(x[,x2)dx]dx2
о О
Проведем указанные преобразования для конкретного случая. Далее будем
считать выполненными два упрощающих условия.
1. Шаги дискретизации по пространственным координатам равны:
Д, - Д2 ~ А •
2. АКФ поля обладает следующими свойствами симметрии:
Bf (х},x2) = Bf (±х,, ±х2), Bf (Xj,х2) = Bf (х2,х,)
при любых сочетаниях знаков.
Такая симметрия имеет место либо для изотропного поля, либо для поля
изотропного в перпендикулярных направлениях с линиями равных значений
АКФ, имеющими вид, показанный на рис. 2.9.
Возьмем простейшую интерполирующую функцию — прямоугольную не-
симметричную. Для нее на интервале 0<(Х],х2)<Д, /(xj,x2) = /(0,0).
То есть ел(х|,х2) = /(х|,л2)-/(0,0),
о2 (х, ,х2) = е|(/(Х] ,х2) - /(0,0))2| = e|/(xj ,х2)2} - 2Е{/(Х] ,х2)/(0,0)} +
+ е{/2(0,0)} -2^Bf (xj,x2) + p.J +g2 +Ц2 =2 g2 -Bz(X],x2)
Для дальнейших преобразований удобно ввести нормированную АКФ —
Ez(xi,x2) . Для нее /?z(0,0) = l, Е/(х1,х2) = Оу/?/(х|,х2).
Рис. 2.9. Линии равных уровней для АКФ специального вида
166
ГЛАВА 2
Тогда
(^(хрл^) — 2Оу[1 Rf (%],х2)], (2.30)
Квадрат среднеквадратичной погрешности
2о^ & &
ехкв = ~~2~ f f [i-^f(xl,x2)]dxldx2 =
& 0 0
А А
i-Л Li
= 2°/ '"ТУ Л(xl,x2)dvldx2 .
А л л
(2.31)
о о
Выражение (2.31) связывает среднеквадратичную погрешность с величиной
шага дискретизации А и корреляционной функцией изображения. Но оно не
всегда удобно для практического использования. Можно упростить вычисле-
ния, приняв во внимание следующее. Нормированную АКФ при xt,x2 >0 мож-
но разложить в степенной ряд (он всегда оказывается сходящимся):
здесь а- — коэффициенты разложения. Нам будет удобнее использовать этот
ряд в следующем виде (с учетом того, что «()0 — 1):
яДхр^^+ЕХо*/ + EXjV +^12aijx\x2J (2.32)
«=| ;=1
Подставляем этот ряд в выражение (2.31). И для рассматриваемой прямо-
угольной интерполяции получаем
Учитывая принятую симметрию АКФ: а1} — а^ (и в частности ai0 — aOi),
можно окончательно получить, что
2 « о
О кв ~ — 2Оу
ОО Д< ОО X
2£чо—+ЁЕХ
i=l Z+l *=17=1
А/+7
a+i)(j+D
(2.33)
2.2. Погрешности дискретного представления изображений
167
2
Практическим интерес представляют случаи, когда значение ЕЛ кв мало по
сравнению с дисперсией. Это соответствует ситуации, когда шаг Д мал, и ряд
сходится очень быстро. Поэтому при оценке погрешности в полученном вы-
ражении можно ограничиться только первым ненулевым членом, отбросив
слагаемые высших порядков малости.
Пример 2.2. Пусть изображение имеет биэкспоненциальную АКФ:
(x],x2) = e-a(lx,l+1X2l>.
Известно разложение экспоненты в ряд:
-X , . X2 JC х4
е = 1-х4
2 6 24
Следовательно, при Xj,x2 >0
э 2
R. (Х[,хэ) = 1 - а(х, + х,) + а + ~*2 — + -...=
“ "2
= 1 -ах, ~ах? +а2х,х? +—а2х.2 + —а2х2 + ...
2 2"
То есть а0) = аю = -а; а} , = а2; а02 — а2о — а2Д и Т-Д-
Квадрат среднеквадратичной погрешности дискретизации
(2.34)
Можно выразить эту величину через коэффициент корреляции между со-
седними отсчетами (в строке или столбце матрицы отсчетов). Этот коэффи-
циент
= R f(x.,х2)1 = е ал ~ 1- аД+ ... ,
2/L1=0;x2=A
то есть аД^1— р, и выражение (2.34) получит вид
eL^a^l-p).
(2.35)
Произведем численный расчет. Обычно 0,8<р<0,95. Возьмем р = 0,9.
Тогда е2 кв « 2с2 (1 - 0,9) = 0,2а2 .
168
ГЛАВА 2
Соотношение сигнал/шум дискретизации по мощности имеет вид
d2 =
е’„ 0,2
Относительная погрешность равна
£
X кв
1
5
0,45,
т.е. 45% от среднеквадратичного отклонения.
Не будем повторять выкладки для других интерполирующих и автокорре-
ляционных функций, а сразу дадим сводку результатов. По-прежнему счита-
ем шаги равными, а АКФ — симметричной.
Для прямоугольной симметричной интерполяции
А
2 ’
А
2 ’
(2.36)
£^кв = 2о)
А А
АЦЛ/(Х1>Х2)^1^2 =
А о о
А'
ЕХо——
>i-i
ОС 00
1=1 7=1
(2.37)
Для билинейной интерполяции
AJ
1-2^- 1
А
х2
"а.
+2КДА.0)
А( А)
х2
4 х}х2
х2
х2
АД
1
AJ
АД
-2Яг(А-х,,А-х2)^
J Д2
—27?^(А — XpXj)-^- 1
х2
"а
х2
-2/?а(Х],А-х2) 1
А) А
Х2У
— 2Rf(xitx2) 1
АД
(2.38)
2 ?
(^| , %2 ) & I
А
А
т
А
*1
А
1
*1
А
А
2.2. Погрешности дискретного представления изображений
169
при 0 < Л', < Д, 0 < х2 < Д ,
2 2
£хкв = Gf
13 4 1 R г
-+-r/(4,0)+-R/(A.A)-^/Jr/(x1.x2)(1-J-)(1
—) dx,dx2
Д 1 2
________8_______
(z+DG+2)0+1)0+2)
(2.39)
Составим таблицу оценок среднеквадратичных погрешностей для разных
интерполирующих и автокорреляционных функций (табл. 2.1). Для удобства
в таблицу сведем средние значения квадрата относительных погрешностей
£л кв _ 1
„2 ~ ~j2 "
CF!' и-
Как видно из таблицы, самой точной интерполяцией из рассмотренных
является билинейная. Выигрыш от ее применения особенно значителен для
«гладких» изображений, имеющих гауссову АКФ. Погрешности дискретиза-
ции для биэкспоненциальной и экспоненциальной изотропной АКФ при-
мерно равны. Для них билинейная интерполяция всего в 3 раза (по мощно-
сти) точнее простейшей прямоугольной несимметричной интерполяции.
Пример 2.3. Для экспоненциальной АКФ, р = 0,9 и билинейной интерпо-
ляции
X кв
Таблица 2.1. Оценки относительных среднеквадратичных погрешностей
АКФ Интерполяция
Прямоугольная несимметричная Прямоугольная симметричная Билинейная
Биэкспоненциальная: Rf(x],x2) = e Rf(nlt n2) = pl"1,+K ~2аД ~2(1-р) ~CtA~(l-p) ~ -аД ~ -(1 - р) 3 3V '
Экспоненциальная неразделимая (изотропная): Rf(x],x2) = e~a'^Xl+X1, Rf(ni,n2) = pn'+^.
Гауссова изотропная: Rf(x},x2)-e Rf(nltn2) = pn'+п-. и|аУ=Л(1-р) «|а2Д2«|(1-р) ~ 4 л 4 23 z \2 ~—а Д ~—(1-р) 90 90' '
г
170
ГЛАВА 2
То есть кв/Оу ~ 0,26, что также достаточно много.
2.2.4. Оценка максимальной погрешности дискретизации
Теперь оценим погрешность дискретизации по критерию максимальной
ошибки.
Полагаем, что на двумерном интервале интерполяции текущая ошибка,
£х(х,,х2 ) = /(х,,X,) - /(х,,х2) ,
есть случайная величина с дисперсией одх^х,). В некоторой точке двумер-
ного интервала (обозначим ее координаты (xlmax, *2та*)) эта дисперсия при-
нимает наибольшее значение:
2 2 Г 2 1
= max
0<х|<Д1,0<х2<Д2 1 J
Обычно точка (x)max, х2 max) является наиболее удаленной от узлов интер-
поляции. Так, для прямоугольной интерполяции (см. рис. 2.10^)
Xi = А.; Хп = До.
• max I * 2 max 2
Для прямоугольной симметричной и билинейной (рис. 2.106) интерпо-
ляции
Л1тах ~А1/2; %2max “^2/2-
Поскольку мы не знаем границ измерений текущей ошибки ех (известна
лишь ее дисперсия), можно говорить о максимальной ошибке лишь с некото-
рой доверительной вероятностью. Самый широкий «размах» ошибки наблю-
дается в точке с максимальной дисперсией. Эту точку и рассмотрим.
Рис. 2.10. Погрешность дискретизации
I
2.2. Погрешности дискретного представления изображений
171
Зададимся доверительной вероятностью р того, что значения ex(Xj,x2) в
точке с максимальной дисперсией лежат в интервале [—Ехтах, £АтахЬ Нера-
венство Чебышева для нашего случая (в наших обозначениях) запишется в
виде
2
Р{К<Л1.пах- = (2-40)
£хтах
Отсюда получаем
О
_ I .max (2.41)
V~P
В частности, при р = 0,99
/ 2
^х max < 1 у ®тах •
Неравенство Чебышева справедливо для любой функции распределения
случайной величины. Если распределение £х — нормальное (это будет вы-
полняться, если и поле f распределено нормально), то можно воспользо-
ваться более строгим соотношением:
(2.42)
2 ус _ 2
Здесь erf(y) = -y= е и du — интеграл вероятностей. Из последнего соот-
о
ношения следует известное «правило трех сигм»:
при р^ 0,997 , или
£ = 3\/о
’'хтах -'у'-'max
£2 = 9 су 2
‘-л max >'-'тах
(2.43)
(2.44)
Используя последнюю формулу, определим выражения для максималь-
ной ошибки при разных видах интерполяции. Как и при оценке среднеквад-
ратичной ошибки, ограничимся случаем, когда Л, =Д2 =А и автокорреля-
ционная функция (АКФ) обладает указанными в предыдущем параграфе свой-
ствами симметрии.
Опять рассмотрим простейшую прямоугольную несимметричную интерполя-
цию. Для нее, используя формулу (2.30) при х. ¥ =Д;х2тя¥ = Д, получаем
^11 Id А. “ 11 IdA
х,=д
х2—Д
[1- /?Z(A,A)],
(2.45)
172
ГЛАВА 2
ИЛИ
7
£“
х max
= 18а} [1 - Яа(Д,А)] .
(2.46)
Используя представление автокорреляционной функции в виде степенно-
го ряда (2.32), получаем
ОО ОС ОС ОО
। -1 -Е«юД' -ЕлА -££v'+'
1=1 j=\ 1=1 j=\
И, уже учитывая симметрию АКФ, (al0 =aoj
max * &
ОО 00 оо
25Z^oa' +Е£ХД,+/
i-i i=l ./=1
(2.47)
Как и раньше, здесь можно оставить только слагаемые первого порядка
малости и получить при этом приближенную оценку погрешности. Приведем
аналогичные соотношения для других интерполирующих функций.
Для ступенчатой симметричной интерполяции (прямоугольной)
^Imax Д/2» -*2тах Д/2»
Е2
х max
= 1807 1-/?
= -18а/ £
ос л» оо оо */+7
2 ,=i Z
(2.48)
д д
2 2
Для билинейной интерполяции
1тах
2 max
£2
^х max
.2 5
(д д
(2.49)
1
2
4
2 2
О I
В табл. 2.2 укажем приближенные оценки для Е~тах .
2.2. Погрешности дискретного представления изображений
173
Таблица 2.2. Оценки относительных максимальных погрешностей
АКФ Интерполяция
Прямоугольная несимметричная Прямоугольная симметричная Билинейная
Биэкспоненциальная, экспоненциальная изотропная «36аД»Зб{1-р) «18аД«18(1-р) «9аД«9(1 -р)
Гауссова изотропная «36а2Д2 *3б(1-р) «9(Г А2 «9(1 -р) 9 4.4 9/, \2 гз-аДй-1-р 2 2^ '
Пример 2.4. Для экспоненциальной АКФ при р = 0,9 и билинейной ин-
терполяции
£ /--------------------------------
летах „ п Л /? _
2 ~0,9 или £лтах ~ &/’
Для получения высокой точности описания непрерывного поля отсчетами
нужно брать шаги дискретизации очень малыми, чтобы коэффициент корре-
ляции между отсчетами р —> 1. Работая с цифровым изображением, всегда
можно по нему оценить коэффициент корреляции р, а затем вычислить, с
какой погрешностью оно описывает непрерывное изображение.
2.2.5. Общая погрешность цифрового представления изображений
Мы рассмотрели отдельно погрешность квантования отсчетов по уровню и
погрешность дискретизации изображения по пространственным координа-
там. Обе они входят как составляющие в общую погрешность цифрового пред-
ставления изображений.
Если изображение квантовано по уровню, то его восстановление (интер-
поляция) производится не по истинным значениям отсчетов поля яркости, а
по искаженным на случайную величину е,.
Возьмем ступенчатую (прямоугольную) интерполяцию и оценим средне-
квадратичную погрешность интерполяции (теперь это будет полная погреш-
ность, так как в ней учтем и квантование по уровню).
Дисперсия ошибки в каждой точке интервала интерполяции имеет вид
Х2
)-(/(0.0)+ez)
= £-{(/(л|,х2)-/(0,0))2|-2£{/(х|,х2) ej +2Е{/(0,0) ej+fife}}.
Если уровней квантования много (шаг квантования намного меньше шка-
лы параметра), то можно считать, что ошибки квантования Еу и само изобра-
жение статистически независимы. Тогда в полученном выражении останутся
только первое и последнее слагаемые, которые с учетом приведенных ранее
выкладок запишутся более компактно:
174
ГЛАВА 2
После усреднения по интервалу интерполяции получим, что
Е«=<+е/„- (2-50)
То есть квадрат полной среднеквадратичной ошибки определяется сумми-
рованием квадратов составляющих ошибок.
Такую же формулу можно использовать (и обычно используют) и для би-
линейной интерполяции, однако здесь она уже будет приближенной и даст
для среднеквадратичной погрешности оценку сверху. (Более детальный ана-
лиз, который мы опускаем, в этом случае показывает, что
(2.51)
причем при EJ —>0 значение полной погрешности смещается к нижней
границе.)
При оценке максимальной погрешности обычно ориентируются на самый
«неблагоприятный» случай, то есть считают, что ошибки суммируются:
^max max max ’ (2.52)
эта формула справедлива для всех способов интерполяции, которые мы рас-
сматривали.
Отметим, наконец, следующее. Мы рассмотрели «первичную» погрешность
цифрового представления изображения, которая возникает при квантовании
и дискретизации. В процессе формирования и преобразований изображение
подвергается действию еще многих искажающих факторов (шумов, линейных
искажений и т.п.). Это действие может быть выражено введением дополни-
тельной погрешности - еисккв, £ИС1стах.
Кроме того, дополнительную погрешность в данные вносят некоторые
процедуры обработки изображений (в первую очередь — процедуры сжатия
данных, то есть кодирования с возможностью последующего приближенного
декодирования). Обозначим соответствующие погрешности — еобркв, £ОбРтах •
Если считать, что все искажающие факторы статистически независимы, то
е
2
кв
= £*
(2.53)
^тах ^хтах +^/тах + ^иск.тах + ^обр.max (2-54)
Требования к точности цифровой обработки должны быть согласованы с
точностью описания исходного непрерывного изображения цифровым изоб-
ражением.
ГЛАВА 3
ПОВЫШЕНИЕ КАЧЕСТВА ИЗОБРАЖЕНИЙ
И ОЦЕНКА ИХ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
3.1. Преобразования яркости изображений
Рассмотрим довольно широкий класс операций, осуществляемых в про-
странственной области над отсчетами цифрового изображения — пикселами,
которые условно можно разделить на две основные группы.
1. Улучшение зрительных характеристик: повышение контраста, четкости,
выравнивание яркости по полю и т.д. Важно отметить, что речь здесь идет о
качестве как о характеристике самого изображения (а не о мере близости к
некоторому «эталону»), то есть цель обработки — получение в каком-то смысле
«удобного для наблюдения», «хорошего» изображения.
2. Препарирование: обработка изображения с целью выделения (подчерки-
вания) на нем некоторых существенных деталей или особенностей и, соот-
ветственно, подавления несущественных. В этом случае мы получаем изобра-
жение, возможно сильно отличающееся от исходного (естественного), но бо-
лее удобное для последующего анализа или визуальной интерпретации.
Четких границ между двумя этими задачами нет, во многих случаях одно-
временно преследуются обе цели. Рассмотрим основные задачи, решаемые с
помощью поэлементных преобразований.
3.1.1. Коррекция амплитудных характеристик
Коррекция амплитудных характеристик выполняется для устройств ввода-
вывода изображений. Реальные устройства ввода изображений в компьютер
(видеодатчики) обычно имеют нелинейную характеристику передачи уровней
яркости. Если £ — измеряемый физический параметр на входе видеодатчика,
то на его выходе (то есть в компьютере) получим значение f = U(fy, где U —
нелинейная функция преобразования (амплитудная характеристика) видео-
датчика (рис. 3.1а).
Нужно скомпенсировать нелинейные искажения при вводе, то есть найти
и использовать при_ обработке такую функцию поэлементного преобразова-
НИЯ U(f), чтобы (/(/) = £/[(/©] = t
176
ГЛАВА 3
Рис. 3.1. Функция преобразования яркости видеодатчиком и обратная функция
Это достигается, если функция U(f) является обратной по отношению к
амплитудной характеристике (рис. 3.16): U(f) = t/-1(/).
Такой операции поэлементного преобразования предшествует процедура
калибровки, то есть экспериментального определения амплитудной характе-
ристики при помощи детерминированных изображений известной яркости
(испытательных таблиц, «оптического клина» и т.д.). По данным калибровки
строится либо аналитическая зависимость (и далее С/-1(/)), либо не-
посредственно соответствующая таблица преобразования.
Аналогичная задача возникает и при выводе изображений. Только здесь
производится не компенсация уже внесенной нелинейности, а предыскаже-
ние отсчетов перед их выводом, чтобы точно воспроизвести требуемую яр-
кость на твердом носителе (фотопленке, бумаге), на экране дисплея, а точ-
нее — в глазу. Функция предыскажения должна быть обратной по отноше-
нию ко всему комплексу факторов, обуславливающих нелинейность вывода:
нелинейной амплитудной характеристике устройства, нелинейности фотогра-
фической (или какой-либо другой) записи поля яркости, нелинейной харак-
теристике зрительной системы человека и т.д.
В этом случае также проводятся предварительные эксперименты по опре-
делению амплитудной характеристики системы вывода. При этом использу-
ются синтезированные изображения с известными значениями яркости.
3.1.2. Линейное повышение контраста
Изображения, вводимые в компьютер, часто оказываются малоконтраст-
ными, то есть у них изменения яркости малы по сравнению с ее средним
значением (рис. 3.2д). При этом яркость меняется не от черного до белого, а
от серого до чуть более светлого серого. То есть реальный диапазон яркости
оказывается намного меньше допустимого (шкалы яркости). Задача повыше-
ния контраста заключается в «растягивании» диапазона яркости изображения
на всю шкалу (рис. 3.26).
3.1. Преобразования яркости изображений
177
а б
Рис. 3.2. Линейное повышение контраста изображения
Эту задачу можно решить при помощи поэлементного преобразования —
линейного контрастирования'.
(3-1)
где а, b — постоянные. Параметры этого преобразования можно определить
двумя простыми способами.
Первый способ заключается в том, что диапазон [/min,/тах ] преобразуется в
диапазон [gmin,gmax]. То есть имеет место система
откуда определяются
8 min min
8 max f max
8 max 8 min
max J mm
(3.2)
а =
Очевидно, здесь нужно предварительно оценить /min, /тах.
Второй способ заключается в том, что берутся такие а и Ь, которые приво-
дят математическое ожидание и дисперсию поля яркости к некоторым «стан-
дартным» величинам. Здесь предварительно оцениваются математическое
ожидание и дисперсия входного поля — и коэффициенты а, b выби-
раются так, чтобы для выходного поля получить «стандартные» LL., ,(5^:
Л г»
/ х f в., / X СГ
g[nl,n2) =-----------J-a +Ц =--------/(п,,Л2)+Ц -Ц,-----,
а/
178
ГЛАВА 3
то есть
а=--; = Ц
(3.3)
3.1.3. Преобразование гистограмм
Еще одна процедура повышения контраста заключается в приведении плот-
ности распределения вероятностей яркости к некоторому «стандартному» виду.
Она реализуется при помощи нелинейного поэлементного преобразования,
которое строится по экспериментально полученной гистограмме исходного
распределения вероятностей яркости (поэтому эта процедура и называется
преобразованием гистограмм).
Построим функцию, осуществляющую данное преобразование. Пусть случай-
ная величина f имеет плотность распределения Pj\f). И пусть преобразованная
величина g = g (f) (тоже случайная) должна иметь плотность распределения веро-
ятностей pg(g). Будем предполагать, 4rog(f) — монотонно возрастающая функция.
Введем в рассмотрение интегральные функции распределения:
/ S
Pf(f) = J J р/пМп.
—оо —ОС
Если случайная величина f принимает значение f <f0, то вероятность это-
го события
P[f<fo] = PfW-
В силу монотонности функции поэлементного преобразования, одновре-
менно с указанным неравенством, будет выполняться и другое соотношение:
S < £о = g(fo)-
Вероятность этого события
< Яо] = (#о) •
Указанные события жестко связаны (являясь следствием друг друга, они
наступают одновременно), их вероятности, естественно, равны:
Ф</о] = Ф<8(/о)]-
Отсюда, отбрасывая ненужный индекс, получаем
W) = PS [«</)]•
Зная требуемый вид плотности распределения вероятностей pg(g), а зна-
чит и Pg(g), изданного соотношения можно выразить функцию поэлемент-
ного преобразования.
3.1. Преобразования яркости изображений
179
Покажем, как это делается на примере очень популярной процедуры ~
эквализации (выравнивания) гистограммы. В данном случае требуется полу-
чить такое изображение, у которого все значения яркости в пределах заданно-
го динамического диапазона [#iriin , £max] равновероятны (рис. 3.3а):
Pg (£>) > ДЛЯ g mjn — g — gmax.
8 max 8 min
Интегральная функция распределения на указанном интервале линейна
(рис. 3.36):
p,(g)= 8
S max S min
Отсюда
p (y) g(f)-g min
8 max 8 min
и, следовательно,
8(f) (&тах 5min ) (f) 8 min •
(3-4)
Следует сделать одно замечание, касающееся практического применения
метода преобразования гистограмм для контрастирования: получаемые гис-
тограммы оказываются очень неровными, с большим числом пиков и впадин.
Для тех значений яркости, которые наиболее вероятны, будет пик Pf(f), и
интегральная функция Pf(f) будет резко возрастать (рис. 3.4).
пределения вероятностей яркости изображения
180
ГЛАВА 3
В результате участок яркости с большой вероятностью отсчетов сильно рас-
тянется, что, вследствие роста ошибок квантования по уровню, может привес-
ти к нежелательным эффектам (например, эффект «небритости» на портрете).
И, наоборот, интервалы с малой вероятностью отсчетов будут сжиматься, то
есть детали, имеющие «нетипичную» яркость будут терять контрастность.
Чтобы избежать этих нежелательных эффектов, функцию преобразования
строят не по истинной, а по сглаженной гистограмме. При этом само преоб-
разование гистограмм становится приближенным.
3.1.4. Пороговая обработка
Многие задачи обработки изображений связаны с преобразованием по-
лутонового изображения в бинарное (двухградационное) или, по-другому,
в графический препарат. Такое преобразование осуществляется для того,
чтобы сократить информационную избыточность изображения, оставив в
нем только ту информацию, которая нужна для решения конкретной зада-
чи (например, очертания объектов), и исключив несущественные особен-
ности (фон).
В ряде случаев требуемый графический препарат удается получить в ре-
зультате пороговой обработки полутонового изображения. Она заключается
в разделении всех отсчетов изображения на два класса по признаку яркости:
объект и фон. Например, выполняется поэлементное преобразование вида
g(nt,n2) =
1 при f(nt,n2)>f0,
О при /(п1,п2)</0,
(3.5)
где То — некоторое «пороговое» значение яркости (рис. 3.5).
Основной проблемой здесь является выбор порога. Пусть исходное полу-
тоновое изображение содержит интересующие нас объекты одной яркости
на фоне другой яркости (типичные
* примеры: машинописный текст, чер-
'1 тежи, медицинские пробы под микро-
скопом и т.д.). Тогда плотность распре-
1 деления вероятностей яркости должна
• выглядеть как два узких пика (в идеа-
! ле два дельта-импульса); то есть так,
i как показано на рис. 3.6а. В таком слу-
L чае задача установления порога три-
0 виальна: в качестве fQ можно взять лю-
Рис. 3.5. Пример порогового преобразования бое значение между «пиками». На
яркости изображения практике, однако, имеет место более
сложный случай: изображение зашумлено, кроме того, как для объектов, так
и для фона характерен некоторый разброс яркостей. В результате функция
плотности распределения вероятностей размывается (рис. 3.66).
3.1. Преобразования яркости изображений
181
Рис. 3.6. К вопросу выбора порога при поро-
говой обработке
Часто бимодальность распределения тем не менее сохраняется. В такой
ситуации можно выбрать порог соответствующий положению минимума
между максимумами (модами).
В общем случае гистограммы рас-
пределения вероятностей яркостей,
измеренные по реальным изображени-
ям, могут оказаться унимодальными
или, наоборот, иметь «изрезанный»,
полимодальный характер (рис. 3.7).
Укажем некоторые методики опреде-
ления порога в этих ситуациях.
Методика 1 заключается в апп-
роксимации участка гистограммы
между пиками какой-либо гладкой
функцией, например, параболой, и
нахождении ее минимума через про-
изводную (рис. 3.7д). По существу
такая аппроксимация реализует сгла-
живание гистограммы. Для этого
сглаживания можно построить спе-
циальный фильтр низких частот.
Методика 2 основана на том, что
иногда удается подобрать хорошие модели отдельно для плотностей распреде-
ления вероятностей яркости объекта и фона. Тогда можно произвести аппрок-
симацию гистограммы суммой этих плотностей вероятностей (рис. 3.76):
Рf(f) = Р'Pi(/) + (l-Р)-P2(f) >
где Р](/), р2(/) ~~ аналитически заданные функции плотности вероятнос-
тей для объекта и фона, р — вероятность объекта (точнее, доля площади изоб-
ражения, занимаемая объектом). Эта вероятность и параметры указанных плот-
ностей распределения вероятностей яркости, как правило, подлежат оценке.
объект
Рис. 3.7. Методики определения порога при пороговой обработке
Ml
фон
б
182
ГЛАВА 3
После оценки параметров можно выбрать порог f0 в соответствии с принци-
пом максимального правдоподобия, то есть из соотношения
Р ’ Р\ (/о) = 0 ~ Р}‘ Рг (/о)- (3.6)
Отметим, что данный способ определения порога сохраняет работоспособ-
ность и тогда, когда бимодальность гистограммы скрыта из-за большого раз-
броса яркостей и малой вероятности р. Основным недостатком метода явля-
ется сложность аппроксимации.
3.1.5. Препарирование
Широкий класс процедур обработки называется препарированием изобра-
жений. Оно заключается в приведении изображения к такому виду, который,
возможно, весьма далек от естественного, но удобен для визуальной интер-
претации или дальнейшего машинного анализа. Многие операции препари-
рования могут осуществляться при помощи поэлементных преобразований
специальных видов. Так, частным случаем препарирования является порого-
вая обработка, рассмотренная выше.
Используется и много других функций поэлементного преобразования
для препарирования. Их основные особенности заключаются в следующем.
Во-первых, им трудно дать физическую интерпретацию, скорее речь здесь идет
просто об эмпирическом подборе функции преобразования в интересах ре-
шения конкретной задачи. Во-вторых, препарирование обычно производится
в диалоговом режиме обработки изображений, поэтому соответствующие функ-
ции преобразования должны быть легко «управляемыми», то есть определены
с точностью до небольшого числа параметров, смысл которых понятен пользо-
вателю (оператору) системы.
Приведем некоторые примеры функций поэлементных преобразований,
используемых для препарирования.
Очевидным обобщением пороговой обработки является преобразование
яркостного среза (рис. 3.8а). Оно позволяет выделить определенный интервал
диапазона яркостей входного изображения. Перемещая «рабочий» интервал
по шкале и меняя его ширину, можно определить какие значения яркости
есть на изображении (и в каких точках), а каких нет, произвести визуальный
анализ отдельных объектов на изображении, различающихся по яркости. Де-
тали, не попадающие в указанный интервал, то есть относящиеся к «фону»,
будут подавлены. В данном примере фон черный (подавление фона). На
рис. 3.86 приведен вариант яркостного среза с сохранением фона. В данном
случае изображение в целом сохраняется, но на нем «высвечиваются» участ-
ки, попавшие в заданный интервал значений яркости. Если этот интервал
примыкает к границе шкалы яркости, то получаем преобразование так назы-
ваемой неполной пороговой обработки (рис. 3.8в).
3.1. Преобразования яркости изображений
183
Контрастное масштабирование в своем простейшем варианте совпадает по
смыслу с линейным контрастированием, только без опоры на статистику (или
экстремальные значения) входного изображения. С помощью этой функции
определенный участок диапазона значений яркости растягивается на всю шкалу
(рис. 3.8г). При этом возрастает контраст деталей, попавших в этот участок.
Детали, имеющие значения яркости за пределами участка, заменяются на
однородный фон: черный (рис. 3.8е), белый (рис. 3.8ая?) или серый (рис. 3.8з).
В других случаях контрастное масштабирование может быть связано с обра-
щением значений яркости, то есть получением «негатива» (рис. 3.8д).
Еще один вариант — пилообразное контрастное масштабирование иллюст-
рируется на рис. 3.8w. Как показывает практика, если изображение состоит из
нескольких крупных областей с медленно меняющимися (по плоскости) зна-
чениями яркости, то такое преобразование почти не разрушает целостности
а
Рис. 3.8. Примеры поэлементных преобразований
184
ГЛАВА 3
его восприятия, но, в то же время, резко увеличивает контрастность плохо
различимых мелких деталей.
К поэлементному препарированию можно отнести и преобразование изоб-
ражения в псевдоцвета. В данном случае каждому числовому значению ярко-
сти ставится в соответствие определенный цвет на экране дисплея. В принци-
пе, закон соответствия может быть любым, хотя на практике стараются, что-
бы функция преобразования была гладкой в том смысле, что плавному
изменению яркости исходного изображения соответствовало бы плавное из-
менение цвета препарированного. Представление изображения в псевдоцве-
тах сильно повышает визуальную читаемость изображенных объектов, по-
скольку глаз человека более чувствителен к малым изменениям цветового
тона, нежели к малым изменениям яркости, и широко используется, в част-
ности, в медицинских диагностических системах.
3.1.6. Адаптивные преобразования яркости
Статистические характеристики, необходимые для построения алгоритмов
обработки, могут быть оценены только по самому изображению. До сих пор
мы считали их неизменными по всему полю, то есть неявно предполагали,
что изображения описываются моделью однородного случайного поля. Одна-
ко во многих практически важных случаях яркость не является однородной.
При этом многие из рассмотренных выше процедур оказываются неработо-
способными или не обеспечивают требуемое качество обработки. Для неста-
ционарных полей используются адаптивные (то есть, подстраивающиеся под
локальные статистические характеристики) методы.
Простейший подход к построению адаптивных процедур заключается в
том, что все изображение разбивается на небольшие фрагменты, на каждом
из которых оцениваются (и используются при об-
работке) «локальные» характеристики изображения.
Каждый фрагмент обрабатывается независимо, как
отдельное изображение с однородными свойства-
ми. Достоинство такого подхода — простота, недо-
статок — плохая стыковка обработанных фрагмен-
тов: на полученном изображении образуются замет-
ные скачки яркости (контуры) по линиям «швов».
Рис. 3.9. К локальному преоб-
разованию изображения
Чтобы устранить этот недостаток, оценку ло-
кальных характеристик делают зависимой от со-
седних фрагментов. В этом случае фрагменты, на
которых используются локальные характеристики, и участки, по которым
они определяются, становятся несовпадающими по размерам: первые по-
прежнему стыкуются, а вторые — перекрываются (рис. 3.9).
В предельном случае оценка характеристик, полученная по некоторому
фрагменту, используется для обработки единственного отсчета в центре этого
3.1. Преобразования яркости изображений
185
фрагмента. Здесь мы приходим к довольно распространенной процедуре об-
работки изображений «скользящим окном», центр которого последовательно
(отсчет за отсчетом) пробегает все возможные положения на изображении.
Такие адаптивные преобразования яркости уже не являются, строго гово-
ря, поэлементными, так как теперь функция преобразования каждого отсчета
зависит от значений отсчетов в некоторой области.
Кратко остановимся на свойствах и особенностях реализации адаптивных
алгоритмов поэлементных преобразований.
Адаптивное повышение контраста. Здесь, как и в ранее рассмотренном
методе линейного контрастирования, вычисляется функция (3.1), но ко-
эффициенты преобразования меняются по полю изображения: а = а(п},п2),
b = b(nl,n2), то есть g(n],n2) = a(ni,n2)-f(n],n2) + b(nltn2).
Эти коэффициенты строятся на базе локальных оценок статистических
характеристик. Чаще всего (потому что это проще) оцениваются локальные
средние и дисперсии ц^(П],л2), Пу (п^п2), а далее рассчитываются коэффи-
циенты преобразования, обеспечивающего требуемые р,,, Стр (см. (3.3)):
О о
а(п^п2)~--—Z?(n1,n2) = |i -цДи,,^)--—*—-
О/(«1,м2) С/(П1,п2)
Так как изменения яркости на малом фрагменте обычно невелики (то есть
аДи],и2) мало), то в результате преобразования именно эти небольшие из-
менения растягиваются на всю шкалу. Эффект повышения контраста здесь
существенно выше, чем при использовании неадаптивного метода с глобаль-
ной оценкой дисперсии.
Еще один полезный эффект — «вытягивание» темных участков изображе-
ния и вообще выравнивание его по яркости. Это получается потому, что на
каждом участке (фрагменте) среднее значение яркости приводится к стандарт-
ному
Адаптивное преобразование гистограмм. В данном случае сохраняется вся
методика из п.3.1.3, но только теперь преобразуются гистограммы, опреде-
ленные по локальным фрагментам. Очень распространенная процедура об-
работки — скользящая эквализация. Внешний эффект от обработки при-
мерно такой же, как и при адаптивном контрастировании, только здесь «стан-
дартизируются» не только числовые характеристики распределения, но и
его вид.
Адаптивная пороговая обработка. Основной причиной введения адаптивно-
сти при пороговой обработке является нестационарность фона изображения.
Из-за этого становится невозможным подобрать единый «порог», обеспечи-
вающий хорошее разделение по всему изображению. Рассмотрим одномер-
ную иллюстрацию, приведенную на рис. 3.10: изображение постепенно свет-
леет по строке. Любой единый для всей строки «порог» разделит изображение
186
ГЛАВА 3
неправильно: часть фона (светлого) будет отнесена к объектам, а часть объек-
тов (темных) пропадет. Гистограмма не является бимодальной из-за широко-
го диапазона изменения яркости фона (рис. 3.10а).
Если применить адаптивный подход, то локальные гистограммы
p2(f) и определенные по участкам 1, 2, 3, будут иметь более удобный
вид для обработки. В случае, когда фрагмент захватывает и объект, и фон,
его гистограмма будет бимодальной, и несложно выбрать некоторое локаль-
ное пороговое значение. Некоторую сложность представляет обработка фраг-
ментов, содержащих только объект или только фон. Здесь гистограмма не
является бимодальной, и выбрать «порог» без привлечения дополнительных
соображений нельзя (см. участок 2 на рис. З.Юв). Обычно для разрешения
этой ситуации используется информация о локальных порогах с соседних
фрагментов.
Основная сложность при реализации адаптивных методов состоит в рез-
ком увеличении объема вычислений, необходимых для оценки локальных ста-
тистических характеристик. Это особенно ощущается при скользящей обра-
ботке окном, когда статистику приходится набирать для каждого выходного
отсчета. Выход из положения — применение рекурсивных процедур оценки,
при использовании которых статистические характеристики не пересчитыва-
ются заново на каждом фрагменте, а определяются через поправки к вычис-
ленным на предыдущем шаге.
Рис. 3.10. Иллюстрация пороговой обработки: а — пример фрагмента изображения; б~г —
локальные гистограммы яркости
3.2. Повышение резкости изображений
187
3.2. Повышение резкости изображений
При вводе в компьютер изображения подвергаются действию нескольких
искажающих факторов. Искажения, вызванные нелинейностью амплитудной
характеристики видеодатчика были рассмотрены в п.3.1.1.
Из-за неточной настройки оптической части системы, ненулевой площади
видеодатчика и других причин частотная характеристика системы формиро-
вания изображений отличается от идеальной. То есть в изображения вносятся
линейные искажения. Обычно эти искажения заключаются в ослаблении верх-
них пространственных частот спектра изображения. Визуально они воспри-
нимаются как расфокусировка, ухудшение резкости изображения, при которых
становятся плохо видимыми мелкие детали.
Следовательно, повышение резкости должно заключаться в подъеме уров-
ня высоких частот спектра изображения или, как говорят, в его высокочас-
тотной фильтрации. В результате этой фильтрации происходит подчеркива-
ние границ объектов, улучшается различимость мелких деталей (ранее размы-
тых), а также «текстуры», то есть небольших регулярных или случайных
колебаний яркости на участках без контуров.
Следует отметить, что здесь не ставится задача восстановления изображе-
ния, то есть возврата к «оригиналу». При повышении резкости иногда следует
произвести перекомпенсацию искажений, то есть избыточно поднять уровень
высокочастотных составляющих пространственного спектра. Эксперименты
по психовизуальному оцениванию качества изображений показывают, что
объекты с «неестественно» подчеркнутыми границами на глаз воспринима-
ются лучше, чем идеальные с точки зрения фотометрии. Таким образом, зада-
ча повышения резкости в равной степени относится и к улучшению качества,
и к препарированию изображений.
Итак, повышение резкости заключается в усилении высокочастотных со-
ставляющих пространственного спектра изображения.
Конкретных методов повышения резкости (и вариантов их реализации)
очень много. Рассмотрим простой (и довольно эффективный) метод, который
основан на пространственной линейной обработке изображения «скользящим
окном» небольшого размера. Это окно перемещается по изображению, и при
каждом его положении формируется один отсчет выходного поля яркости
(обычно этот отсчет соответствует центру окна). В данном случае алгоритм
повышения резкости реализуется как двумерный фильтр с конечной импульс-
ной характеристикой. Размеры и форма окна определяют область ненулевых
значений импульсной характеристики КИХ-фильтра.
Вначале покажем качественно, как строится фильтр, подчеркивающий гра-
ницы. Воспользуемся для этого рядом «одномерных» иллюстраций.
Пусть /(л) — произвольная строка исходного нерезкого изображения. На
рис. 3.11 кривая 1 представляет собой строку изображения с расфокусирован-
ной границей объекта.
188
ГЛАВА 3
Рис. 3.11. Пример подчеркивания границ с исполь-
зованием низкочастотной фильтрации
Процедуру обработки можно разбить на несколько шагов.
Сначала осуществляется низкочастотная фильтрация, то есть дополнитель-
ное сглаживание сигнала (обозначим сглаженный сигнал — f(n), рис. 3.11,
кривая 2). Далее из исходного сиг-
нала вычитается сглаженный. В ре-
зультате чего формируется разно-
стный сигнал — высокочастотное
изображение (рис. 3.11, кривая 3):
Затем этот разностный сигнал
прибавляется (с некоторым коэф-
фициентом) к исходному. Получен-
ный результат g (л) — изображение
с повышенной резкостью (рис. 3.11,
кривая 4). В спектре этого изобра-
жения низкочастотные компоненты
не изменились (то есть, общий уро-
вень яркости остался прежним), а
высокочастотные усилились (то есть, подчеркнуты локальные особенности —
границы, мелкие детали).
Теперь рассмотрим эту процедуру подробнее для двумерного случая. Низ-
кочастотная фильтрация (сглаживание) осуществляется усреднением отсче-
тов поля яркости в окне:
/(М|,«2)= 52 ЕХ*1’*2)/(П1 ~Л’П2 ~*2)>
где D — некоторая конечная область в пространстве аргументов, определяю-
щая окно ((fcj,fc2) ED). Видно, что записанное выражение задает двумерную
свертку сигнала с импульсной характеристикой а(кг,к2) сглаживающего
КИХ-фильтра.
Значения \а(к,,к2)г,, , выбираются так, чтобы получить действительно
сглаживание (то есть усреднение) отсчетов. Обычно берутся а[к1,к2)>0.
Кроме того, к процедуре сглаживания предъявляется следующее требова-
ние: она не должна изменять среднее значение (постоянную составляющую)
изображения, то есть необходимо выполнение условия
(л,.л2)ео
(3.7)
Часто все коэффициенты импульсной характеристики берутся одинаковы-
ми, при этом получается простое усреднение отсчетов изображения по окну.
3.2. Повышение резкости изображений
189
Далее вычисляются высокочастотное изображение
/'(л],И2) = /(Л1,Л2)-/(П1,П2)
и изображение с повышенной резкостью
g(n,,и2) =/(при2)+ <7/'(п),и2),
где q — коэффициент усиления разностного (высокочастотного) сигнала (q > 0).
Раскрывая обозначения, получаем
^(м1,И2) = /(л|,П2) + ^ f(nvn2)~ ~к\^2 “*2>
(^,*2)60
Если привести подобные члены, то можно получить это выражение в виде
свертки:
g(n],n2)_ 52 ~k\^n2“М»
{k^k^D
(3.8)
где h(k^k2} — импульсная характеристика КИХ-фильтра, осуществляющего
подчеркивание границ (повышение резкости);
h(0,0) = 1 + q — q а(0,0),
h(kl,k2) = -qa(k[,k2), (M2)eD, (Аг,,Аг2) (0,0). (3.9)
На практике из соображений простоты берут обычно центрированное квад-
ратное окно малого размера (3x3 или 5x5). При этом h^klfk2) имеет всего
несколько ненулевых отсчетов. Значения этих отсчетов удобно задавать в форме
так называемой «маски».
Рассмотрим примеры типичных масок размером 3x3 для повышения резко-
сти изображений. Маска
0 -1 О'
-1 5 -1
0-10
/
(3.10)
соответствует случаю, когда сглаживание производится усреднением по пяти
отсчетам,
«(0,0) = «(1,0) = «(-1,0) = «(0,1) = «(0,-1) = 1/5,
190
ГЛАВА 3
с коэффициентом q = 5. Маска
-1 -1 -Г
-1 9 -1
(3.11)
получается при сглаживании усреднением по девяти точкам:
a(kitk2) = 1/9 при -1<&ь к2<\ и при д=9.
Меняя размеры окна, значения {а(Л,,Л2)} и q, можно получить и другие
маски. Возникает вопрос, какие маски считать хорошими, а какие нет. Од-
нозначно ответить на него невозможно, так как мы не определили строго
показатель качества обработки. Но некоторые общие требования к маске (то
есть к импульсной характеристике КИХ-фильтра) сформулировать можно.
Два первых требования относятся к частотной характеристике КИХ-фильт-
ра, которая в общем случае определяется соотношением
Н(е'“’,е'"2) = (3.12)
Если импульсная характеристика является четной по обоим аргументам
(как в приведенных примерах масок), то частотная характеристика будет ве-
щественной и симметричной так, что достаточно ее рассматривать на двумер-
ном интервале 0 < СО] < л; 0 < со2 < л.
Итак, во-первых нужно, чтобы КИХ-фильтр действительно повышал рез-
кость, то есть его частотная характеристика имела бы подъем в области высо-
ких частот (при ©j —>л; <о2 ~*л)- Убедимся, что это так, на примере маски
(3.10). Соответствующий КИХ-фильтр имеет следующую частотную характе-
ристику:
,е‘Ыг) = 5 —eia' - е'“2- е-й°2 = 5- 2coscor 2cosco2.
Найдем и покажем на координатной сетке некоторые значения частотной
характеристики (см. рис. 3.12).
При С0],С02—»л косинусы стремятся к (-1), и частотная характеристика
достигает своего максимума. То есть действительно это фильтр высоких час-
тот. При СО], со2 —>0 частотная характеристика стремится к единице, то есть
низкочастотные составляющие двумерного спектра сигнала (изображения) не
искажаются.
Второе требование — частотная характеристика должна быть близка к изот-
ропной, то есть, в идеале, иметь линиями равных значений окружности. Это
3.2. Повышение резкости изображений
191
нужно, чтобы границы объектов на изображении с любой ориентацией под-
черкивались одинаково. В действительности это требование не всегда выпол-
няется. Например, для маски (3.10), при 0), = л, со2 — О, значение частотной
характеристики H(e'\e,Q) = 5, а в точке на окружности радиусом и, лежащей
в направлении диагонали, то есть
при Wj = лД/2 ; со2 = л/л/2 , зна-
чение частотной характеристики
. п .п
Н(е ,е то есть в 1,5
раза больше.
Видим, что в рассматриваемом
примере в диагональном направ-
лении на плоскости частот час-
тотная характеристика растет при-
мерно в полтора раза быстрее. Из-
за этого наклонные границы на
изображении будут подчеркивать-
ся сильнее, чем горизонтальны и
вертикальные.
Третье требование. Повышение
резкости не должно сопровождать-
ся чрезмерным повышением шума.
Подчеркивание полезных свойств
(границ) линейной системой все-
гда сопровождается увеличением
Рис. 3.12. Пример частотной характеристики высо-
кочастотного фильтра
шумовой составляющей на изображении,
поскольку шум является высокочастотным.
Рассмотрим этот вопрос подробнее. Если на изображении присутствует
шум, то это означает, что каждый отсчет искажен, и на вход высокочастотно-
го КИХ-фильтра поступает не > а /(прл2) = /(n1,n2) + v(«|,n2), где
v —- аддитивный шум.
Тогда и на выходе фильтра имеем смесь: g(m,n) = у(лг|,м2) + и’(п1,п2), где
w — шумовая составляющая на обработанном изображении,
w(nltn2)= E^i,^2)v(n1-^I,n2-^2)-
(kt,k2 )ео
Для простоты рассуждений будем считать, что исходный шум v — белый.
Тогда для дисперсии выходного шума имеем
<=°2 Е E'>2^i^2) = 2°v.
(*|ДО
(3.13)
192
ГЛАВА 3
где Q — коэффициент увеличения мощности (дисперсии) шума после под-
черкивания границ линейным фильтром:
Q= Е E*2(*i.M- 0-14)
(^1 Л2
Для рассмотренных выше масок этот коэффициент очень велик: для маски
(3.10) 0=29, для маски (3.11) 0=89.
Добиться уменьшения коэффициента Q можно путем уменьшения коэф-
фициента высокочастотной составляющей q. Однако это означает ослабление
«подчеркивающей» способности фильтра. Путем увеличения числа отсчетов в
окне обработки также можно уменьшить коэффициент Q (сохранив при этом
«подчеркивающие» свойства), для этого следует перейти к маскам 5x5, 7x7 и
так далее — это второй путь. Но он находится в противоречии с еще одним
требованием.
Четвертое требование', процедура обработки окном должна быть достаточ-
но простой, то есть желательно выбирать маску небольшого размера.
Сформулированные требования, как видим, довольно противоречивы, по-
этому всегда приходится искать не оптимальное, а компромиссное решение.
Поиски «масок» для алгоритмов обработки отсчетов в окне — предмет про-
должающихся исследований.
3.3. Выделение контуров
3.3.1. Определение контура
Задача пороговой обработки — выделение областей, одинаковых (одно-
родных) по яркости. В результате пороговой обработки получается бинарное
изображение с выделенными областями (рис. 3.13). Геометрические характе-
ристики этих областей служат важными признаками для классификации изоб-
раженных объектов и восприятия изображения в целом.
Во многих случаях наиболее информативными являются характеристики
границ областей — контуров. Биологические системы зрительного восприя-
тия, как показывают исследования, используют главным образом очертания
контуров, а не разделение объектов по яркости.
Задача выделения контуров состоит в построении бинарного изображения,
содержащего эти очертания — графического препарата.
Прежде чем приступить к изложению методов решения этой задачи уточ-
ним ее содержание.
Что такое контур? Возможны различные трактовки этого интуитивно яс-
ного понятия. Будем использовать наиболее распространенную. Назовем кон-
туром изображения пространственно протяженный разрыв (перепад, скачко-
3.3. Выделение контуров
193
Рис. 3.13. Пороговая обработка и выделение контуров
образное изменение) значений яркости. Рассмотрим участок изображения с
контуром. Одномерный случай представлен на рис. 3.14.
Изображенное изменение яркости характеризуется высотой скачка — /0,
углом наклона — 0 и координатой центра наклонного участка — х^. Перепад
яркости считается контуром, если его высота и угол наклона превосходят
некоторые пороговые значения. Идеальный детектор контура должен указать
на его наличие в единственной точке, расположенной в центре наклонного
участка (рис. 3.146).
В двумерном случае у перепада яркости появляется еще одна важная ха-
рактеристика — его ориентация (угол на плоскости). На рис. 3.15а изображен
локальный участок, на котором контур прямолинеен. Идеальный детектор
контура должен дать бесконечно тонкую непрерывную линию по центру об-
ласти изменяющейся яркости (рис. 3.156).
Рис. 3.14. Контур и его определение: а — пример контура; б — результат идеального определе-
ния контура
7 — 9044
194
ГЛАВА 3
Рис. 3.15. Определение контура на изображении: а — изображение с контуром; б — результат
идеального определения контура
Отметим некоторые проблемы, связанные с принятым определением кон-
тура.
Во-первых, введенное определение не гарантирует замкнутости контурных
линий. В процессе выделения контура могут быть его разрывы в тех местах,
где яркость меняется недостаточно быстро. Пример такой ситуации дан на
рис. 3.16.
Кроме того, из-за наличия шума на изображении могут ошибочно обнару-
живаться контуры там, где границ объектов нет. Все это требует специальной
дополнительной обработки изображений: прослеживания границ, интерпо-
ляции, обнаружения связных кривых в множестве выделенных «обломков»
контурных линий и т.п.
Во-вторых, при выделении контуров, из-за их размытости, шума или из-за
недостатков используемого алгоритма, могут получаться не только разрыв-
ные, но и излишне широкие контурные линии. В этих случаях опять прихо-
дится применять специальные процедуры обработки бинарного изображения
для «утончения» линий («скелетизации» графического препарата) (рис. 3.17).
В-третьих, на изображении иногда присутствуют (и подлежат выделению)
границы областей, не попадающие под введенное определение: объекты в
виде узких линий (рис. 3.18а), или изменения яркости в виде «излома»
(рис. 3.186). Узкая линия сама для себя контур, и ее легко можно выделить
пороговой обработкой. Что касается излома, то его можно «подогнать» под
данное определение контура, предварительно
продифференцировав функ-
цию/ (рис. 3.18<?).
В-четвертых, нужно учи-
тывать, что изображения
представлены в цифровом
Рис. 3.16. Пример незамкнутого
контура
3.3. Выделение контуров
195
виде — пикселами. Из-за дис-
кретности аргумента на гра-
фическом препарате контуры
представляют собой линии
единичной (а не нулевой) ши-
рины, то есть не являются бес-
конечно тонкими (рис. 3.19я,
скелетизация
Рис. 3.17. Пример широкого контура и его «скелет»
рис. 3.196). Имеется неоднозначность в положении контура величиной плюс-
минус один пиксел. Было бы корректнее определить контур не как линию
пикселов, а как границу между пикселами (рис. 3.19в). Однако по ряду при-
чин такое представление используется редко.
Теперь обратимся к самой процедуре выделения контуров. Наиболее ча-
сто используемый подход к решению задачи обнаружения перепадов (выде-
ления контуров) на одноцветном изображении схематически показан на
рис. 3.20.
дх
Рис. 3.18. Примеры контуров, не подходящих под определение
ооо ©•©
«ООО®;®
О О Oz6 О
о о о
Рис. 3.19. Особенности выделения границ на цифровом изображении
• • • • О
о о © © о
о ® ® о о
Рис. 3.20. Общий вид процедуры выделения контуров
7*
196
ГЛАВА 3
Исходное изображение /] подвергается линейной или нелинейной обра-
ботке для того, чтобы выделить перепады яркости. В результате этой опера-
ции формируется изображение f2, яркость которого существенно отличается
от нуля только в областях резких изменений значений яркости исходного
изображения. Затем после пороговой обработки из этого изображения фор-
мируется искомый графический (контурный) препарат — /3.
Вторую операцию — пороговую обработку — мы уже рассматривали.
Поэтому все внимание перенесем на первую операцию — выделение пере-
падов яркости. Рассмотрим две наиболее важные группы методов выделе-
ния контуров.
3.3.2. Дифференциальные методы
Одним из наиболее очевидных и простых способов обнаружения границ
является дифференцирование яркости, рассматриваемой как функция про-
странственных координат. То, что дифференцирование дает желаемый эф-
фект, видно из простого «одномерного» примера. До дифференцирования
сигнал имеет вид, представленный на рис. 3.21а. После дифференцирования —
вид на рис. 3.216, и теперь контур легко выделяется пороговой обработкой
(рис. 3.216).
Очевидно, в двумерном случае, если мы имеем изображение со значения-
ми яркости /(xi,x2), то обнаружение контуров, перпендикулярных оси х,,
обеспечивает взятие частной производной df /дх}, а перпендикулярных оси
х2 — частной производной df 'dx2 (рис. 3.22). Эти производные характери-
зуют скорости изменения яркости в направлениях Xj и х2 соответственно.
Можно вычислить производную и по произвольному направлению. Нам од-
нако необходимо найти характеристику, позволяющую обнаружить контур
независимо от его ориентации. В качестве такой характеристики, являющейся
признаком наличия контура в локальной области, можно использовать гради-
ент яркости: grad/Xx], x2) = V/(Xj, х2).
Рис. 3.21. Дифференциальный метод выделения контура
3.3. Выделение контуров
197
Рис. 3.22. Дифференциальный метод выделения контура на изображении
Градиент — это вектор (в нашем случае в двумерном пространстве), ориен-
тированный по направлению наиболее быстрого возрастания функции
/(л,, х2) и имеющий длину, пропорциональ-
ную этой максимальной скорости (максималь-
ному значению частной производной по направ-
лению), (рис. 3.23).
Так как направление нас не интересует, огра-
ничимся рассмотрением модуля градиента (дли-
ны вектора):
Рис. 3.23. К определению градиен-
та функции
Отметим, что для вычисления модуля градиента вместо производных д/дху
и д/дх2 можно брать производные по любой паре перпендикулярных на-
правлений. Итак, для выделения контура произвольного направления можно ис-
пользовать модуль градиента поля яркости.
В случае цифровых изображений, представленных матрицей отсчетов, вместо
производных берутся дискретные разности:
^/Ui?x2) 5)(„1>П2) = у(П) „2)_у(П1 -1,п2), (3.16)
дху
~ з2(щ,п2) = f(nx,n2)-f(nx, n2~l). (3.17)
ох2
Тогда преобразование, выделяющее перепады яркости, будет заключаться
в вычислении модуля «дискретного градиента изображения» f(ny,n2):
g(ny ,пг) = ^[5](И],П2)]2 +[52(П],п2)]2 =
= +[/(nl>n2)_/(nl’n2-1)]2 • (3.18)
198
ГЛАВА 3
Видно, что это вычисление производится в два этапа. Сначала изображе-
ние обрабатывается двумя двумерными КИХ-фильтрами для получения дис-
кретных разностей. Импульсные характеристики этих систем соответствуют
«маскам» размерами 2x1 и 1x2:
(3-19)
На втором шаге вычисленные разности нелинейным образом комбиниру-
ются для получения #(л|, и2).
При реализации процедуры детектирования контуров стараются избе-
гать трудоемких операций типа умножения и извлечения квадратного кор-
ня. Поэтому используют выражения, вычисляемые проще, «аппроксими-
рующие» дискретный градиент. Чаще всего модуль градиента заменяют
выражениями
«2)
= |5|(и1,П2)|+|у2(П1,П2)|
(3.20)
или
^(мрПо) —тах||
51(И1,Л2)|,| S2(rt],H2)|}.
(3.21)
Следует заметить, что такие приближения градиента уже не являются оди-
наково чувствительными к границам с любой ориентацией. Действительно,
для строго вертикальных или горизонтальных границ все три формулы (3.18),
(3.20) и (3.21) дают одинаковые результаты. Но для границы с наклоном 45°,
при котором л,1(Я|,и2) = s2(nlyn2), имеем:
7[^1(п1,Л2)]2 +[>2(П],П2)]2 = V2 | (И,, п 2 ) | ,
1(п,,п2)I-ь| ЛГ2(Л|,/?2)| = 2|5i(ni,zz2)I»
max||51(я],н2)|, js2(nlyn2)|} = |s](nI,n2)|.
Приближенные значения градиента отличаются от точного в л/2 раз. Од-
нако такие вариации на практике считаются приемлемыми.
Другой простой вариант вычисления дискретного градиента дает оператор
Робертса. При его построении используется тот факт, что для вычисления
модуля градиента можно использовать производные (разности) в любых двух
взаимно перпендикулярных направлениях. В операторе Робертса берутся ди-
агональные разности:
g(H|,п2) = 7[^i(«i,«2)]2 +[s2(«i,«2)]2 > (3-22)
3.3. Выделение контуров
199
где
sl(n1,n2) = /(n1,n2)-/(rt| -l,n2 -1), (3.23)
52(п1,л2) = /(л1,п2 -!)-/(«! -1,и2) • (3.24)
То есть здесь отдельные разности формируются двумя КИХ-фильтрами,
импульсные характеристики которых соответствуют маскам 2x2:
(-1 О) (0 -11
и
0 ') (1 о)
(3.25)
Очевидно, здесь тоже при комбинировании разностей можно использовать
вместо (3.22) приближения (3.20) или (3.21).
Еще один вариант — оператор Собела. В нем обработанное (промежуточ-
ное) изображение и2) формируется так же, как в операторе Робертса
(и обычном градиенте), но величины и s2 вычисляются линейной обра-
боткой масками 3x3:
Г
2
1,
(3.26)
Существуют и другие приближения градиента. Следует отметить, что при-
менение любых градиентных операторов дает обычно сходные результаты.
Различия наблюдаются только в их устойчивости к шуму.
Для решения задачи выделения перепадов яркости можно применять диф-
ференциальные операторы более высокого порядка, например оператор Лап-
ласа. В непрерывном случае
(3.27)
Значение лапласиана является нечувствительным к ориентации границ
областей, что и позволяет использовать его при детектировании контуров.
В дискретном случае оператор Лапласа можно реализовать в виде процеду-
ры линейной обработки изображения окном 3x3. Действительно, вторые
производные можно аппроксимировать вторыми разностями:
8 /<х1 , д„, +1>„2)-2/(п1,л2) + /(п1 -1,„2), (3.28)
дх{
200
ГЛАВА 3
f (jc х
---а V 2 ~/(П|,/г2 +1)-2/(П|,и2) + /(п1,и2 -1). (3.29)
ох2
Суммируя вторые разности, получаем маску
О 1 О'
1 —4 1
0 1 О
(3.30)
Это импульсная характеристика КИХ-фильтра, вычисляющего лапласиан.
Лапласиан может принимать как положительные, так и отрицательные значе-
ния, поэтому, в операторе выделения контуров следует взять его абсолютное
значение. Таким образом, получаем процедуру выделения границ, нечувстви-
тельную к их ориентации:
5(м1,п2) = |/(и1 + 1,п2) + У(и] -1,и2) +
+ /(И|,п2 +1) + /(И|,н2 -1)-4/(п|,п2)|.
(3.31)
У оператора Лапласа есть и достоинства, и недостатки по сравнению с
градиентными операторами. При обработке изображения он дает несколько
иные результаты, нежели градиент. Дело в том, что вторая производная по-
зволяет выделить не участки наклона функции, а участки ее изгибов. Одно-
мерный случай представлен на рис. 3.24.
Если граница размыта, то после обработки лапласианом она раздваивается
(рис. 3.24е). Это недостаток лапласиана, для его устранения приходиться ис-
пользовать дополнительную обработку полученного графического препарата.
Еще один недостаток лапласиана — сильное влияние шумов. В то же время
вычисление второй (а не первой) производной позволяет легко выделять гра-
ницы типа излома — это достоинство данного метода.
Рис. 3.24. Особенности применения оператора Лапласа:
а — контур; б — модуль градиента; в — модуль лапласиана
3.3. Выделение контуров
201
3.3.3. Методы выделения перепадов яркости с согласованием
Общим недостатком рассмотренных выше методов выделения перепадов
яркости является высокая чувствительность к шуму. Это объясняется тем, что
действие разностных операторов состоит в вычислении и комбинировании
разностей отсчетов в пределах «окна» малых размеров. Каждая разность вы-
числяется непосредственно по отсчетам, поэтому шум на изображении попа-
дает в результат преобразования с усилением.
В то же время сам подход к выделению контуров с помощью локальных
преобразований изображения скользящим окном представляется довольно
естественным и очень удобным для реализации. Можно, сохранив достоин-
ство дифференциальных методов, повысить их помехоустойчивость, если пе-
ред применением дифференциального оператора применить сглаживание зна-
чений яркости в пределах окна, то есть согласовать с ними некоторую поверх-
ность первого или второго порядка. Такой подход реализуется дифференциальными
методами с согласованием.
Рассмотрим метод согласования на примере обработки изображения ок-
ном 2x2. Учтем, что дискретное изображение получено из непрерывного:
/(п1,п2) = /(л1,х2)|л1=дл| .
Л2—Дл2
По наблюдаемым значениям яркости в пределах выбранного «окна»
7(п,-1,и2-1) — 1,л2)'
f(n^n2-\) /(П1,Л2) ,
построим на нем аппроксимирующую плоскость:
/(л, ,х2) = ах1 +Ьх2 +с. (3.32)
Если плоскость построена, то есть определены коэффициенты о, Л, и с, а
значит известны частные производные
0/(x„x2) = а df(x{,x2) = ь
дх) дх2
то можно вычислить искомый модуль градиента, который служит признаком
локального перепада яркости:
|v/(x,,x2) -y]a2+b2.
(3.33)
202
ГЛАВА 3
При построении плоскости удобнее всего воспользоваться методом наи-
меньших квадратов. При поиске коэффициентов будем минимизировать ве-
личину
Для любого положения окна коэффициенты будут определятся одинако-
выми функциями отсчетов, поэтому возьмем окно при п1 =п2 =1, для кото-
рого все выкладки будут более компактными. Итак, на рассматриваемом окне
e2=[a+ft+c-/(l, 1)]2+[* + с-/(0, 1)]2+[а+с-/(1, О)]2+[с-/(0, О)]2.
В точке минимума все производные погрешности аппроксимации по ко-
эффициентам равны нулю:
откуда
2a+fe + 2c = /(l,l) + /(l,0),
a + 2fc + 2c = /(l,l) + /(l,0),
a+6 + 2C = l(/(l,l)+/(0,l) + /(l,0) + /(0,0)).
Окончательно выражения для коэффициентов будет иметь вид
о = |(/(1,1)+/(1.0)-/(0,1)-/(0,0)),
(3.34)
Коэффициенты й, b могут быть вычислены путем линейной обработки изоб-
ражения масками 2x2, что равнозначно усреднению дискретных разностей по
окну 2x2. При этом градиент менее чувствителен к шуму.
Теперь сделаем очевидное обобщение. В общем случае построение проце-
дуры, использующей дифференциальный метод с согласованием, заключает-
ся в следующем. Вокруг обрабатываемой точки на изображении задается не-
которая область — «окно обработки». По отсчетом окна строится аппрокси-
мирующая полиномиальная поверхность. Естественно, нужно выбирать такой
3.3. Выделение контуров
203
порядок поверхности, чтобы число коэффициентов было меньше числа пик-
селов в окне. Для получения изображения с подчеркнутыми перепадами вы-
числяется дифференциальная характеристика (градиент или лапласиан) апп-
роксимирующей поверхности в центре окна.
Приведем еще некоторые варианты реализации дифференциального мето-
да с согласованием.
При аппроксимации плоскостью (3.32) функцию яркости в окне 3x3 полу-
чается, что коэффициенты а и b формируются в результате линейной обра-
ботки масками
[-1 -1 -I) [-1 0 1'
-О 0 0 и - -101
6 6
111 -101
(3.35)
соответствен но.
Множитель 1/6 можно отбросить, он влияет только на масштаб результата
и может быть учтен при установке порога. В этом случае модуль градиента
(3.33) определяет оператор Превитт, который довольно часто используется
на практике.
Если функцию яркости в окне 3x3 аппроксимировать поверхностью второ-
го порядка,
/(л|, x2) = axf +bx^ 4-cXjX2 4-OXj 4-P-X2 + Y, (3.36)
то лапласиан в окне равен
о2 7 о2 г
V2f{xl,x2) = -^+-4- = 2a+2b. (3.37)
oxi дх2
Коэффициенты а и b формируются масками
£
6
1
-2
1
-2 Г
-2 1
1 I
а поскольку лапласиан вычисляется как линейная комбинация этих коэффи-
циентов, то можно построить общую маску для «согласованного» лапласиана:
(2 -1 2)
1 .
(3.38)
Методы выделения перепадов яркости с согласованием обеспечивают суще-
ственно большую помехоустойчивость выделения контуров, чем «чисто» диффе-
ренциальные методы, при тех же характеристиках вычислительной сложности.
204
ГЛАВА 3
3.4. Линейная фильтрация и восстановление изображений
3.4.1. Восстановление дискретного сигнала ЛПП-системой
Пусть имеется полезный сигнал — последовательность f (и). Однако не-
посредственному наблюдению (измерению) он недоступен. В нашем распо-
ряжении имеется лишь сигнал (результат прохождения сигнала через
некоторую «искажающую» систему), дополнительно искаженный шумом v(n)
(см. рис. 3.25).
Требуется восстановить полезный сигнал по наблюдаемому. Для этого не-
обходимо синтезировать такую восстанавливающую систему (фильтр), чтобы
при подаче на ее вход наблюдаемого сигнала на выходе получалась бы оценка
/(л) полезного сигнала (см. рис. 3.26).
Далее мы сузим класс рассматриваемых сигналов и систем.
Во-первых, в большинстве практически важных случаев искажения сигна-
ла удается описать моделью ЛПП-системы, рассмотрением которой мы и огра-
ничимся. Будем считать, что известна ее импульсная характеристика h(n).
Тогда наблюдаемая последовательность запишется в виде
g(n) = f(n)*h(n) + v(n). (3.39)
Соотношение (3.39) задает так называемую линейную модель наблюдения в
дискретном времени.
Во-вторых, восстанавливать сигнал будем также при помощи ЛПП-системы:
/(и) = «(п)*йвмст(л), <3-40)
где ЛВОсст(л) — импульсная характеристика восстанавливающей ЛПП-системы.
В-третьих, и полезный сигнал /(«), и шум v(n) будем считать стационар-
ными случайными последовательностями, статистические характеристики
которых известны.
Заметим, что, поскольку все преобразуемые последовательности случай-
ны, то и ошибка восстановления в каждый момент времени случайна:
е(л) = /(л)-/(п). (3.41)
Рис. 3.25. Модель наблюдения полезного сигнала
3,4. Линейная фильтрация и восстановление изображений
205
Мы будем строить такой восстанав-
ливающий фильтр, который обеспе-
чивает минимум ошибки в средне-
квадратичном смысле, то есть мини-
мизирует ее дисперсию:
g Восстанавливающая система (фильтр) 7г
Рис. 3.26. Схема восстанавливающей системы
Е2 е2(и)} = е|j/(n) —/(л)] 1—>min.
(3-42)
Из всего сказанного наиболее существенным является ограничение, за-
ключающееся в требовании линейности восстанавливающей системы. Одна-
ко для нелинейных систем получить конкретные результаты их синтеза гораз-
до сложнее. Кроме того, из теории информации известно, что для важного
класса сигналов — гауссовых — оптимальное (наилучшее) в среднеквадратич-
ном смысле восстановление обеспечивается именно линейной системой.
ЛПП-система, реализующая преобразование (3.40) и обеспечивающая при
этом выполнение условия (3.42), называется «оптимальным линейным восста-
навливающим фильтром», А ее применение реализует процедуру оптимального
линейного восстановления.
Очень часто, однако, на импульсную характеристику восстанавливающей
ЛПП-системы налагаются дополнительные ограничения, связанные с удоб-
ством реализации. Например, требуется, чтобы она была КИХ-системой или
физически реализуемой БИХ-системой (см. п. 1.4.3). В таких ситуациях ошибка
восстановления несколько возрастет, то есть мы получим квазиоптималъные
процедуры восстановления.
Мы объединим рассмотрение оптимального и квазиоптимального восста-
новления следующим образом: будем считать, что импульсная характеристи-
ка восстанавливающей ЛПП-системы отлична от нуля для значений аргумен-
тов из некоторого множества D (интервала наблюдения):
ЛвосСТ(п) = ° ПРИ n^D. (3.43)
Определим при этом ограничении параметры системы, минимизирующие
ошибку восстановления. С учетом сказанного выше конкретизируется фор-
мула (3.40):
ОО
Е hWXcAkMn~k)= ЕХосст(*)Ил~ *)» <3-44)
к——оо keD
и условие минимизации ошибки (3.42):
е2=е| [/(«)-/(«)]2 =Е
£АВоет(*)«(п_*)~/(")
k(D
—>min. (3.45)
206
ГЛАВА 3
Минимизация ошибки осуществляется, путем варьирования ненулевых
отсчетов импульсной характеристики восстанавливающей системы. В точке
минимума обеспечивается равенство нулю всех частных производных:
дг2
^^ВОССТ (^)
= 0, те D .
(3.46)
Подставив (3.45) в (3.46), получаем
= Е
dhB0CcArn)
£h^(k)g(n-k)-f(n)
keD
g(n-m)
= 0, me D. (3.47)
Из последнего выражения следуют два важных соотношения.
Во-первых, это выражение можно записать в виде
е{ —т) } = 0, meD,
(3.48)
то есть взаимная корреляционная функция = ошибка оптимально-
го восстановления некоррелирована с наблюдаемым сигналом. Это утвержде-
ние известно как «лемма об ортогональном проецировании», которая будет нам
полезна в дальнейшем.
Во-вторых, перенеся в (3.47) вычитаемое в правую часть, после примене-
ния оператора математического ожидания, получим
5S ^BOCCT (^)^g
k€D
(3.49)
— уравнение Винера-Хопфа для дискретных систем.
Таким образом, импульсная характеристика оптимального линейного вос-
станавливающего (или квазиоптимального) фильтра определяется из систе-
мы, состоящей из уравнения Винера-Хопфа и ограничений, налагаемых на
импульсную характеристику:
k£D
Косст W = °* m$D. (3.50)
Различный вид области D приводит к существенно различным методам
решения системы (3.50). Определим ошибку восстановления сигнала опти-
мальным линейным фильтром, продолжив преобразования, входящие в (3.45),
с учетом (3.41) и (3.48):
3.4. Линейная фильтрация и восстановление изображений
207
е2
k€D
= £е(м)ЕЛвОсСТ(^)^(л-^)-£[еМ/(л)] =
(ten
/ J ‘'ВОССТ
кеО
/. j ‘восст
лео
(3.51)
Z j восст
k€-L>
2
kED
Рассмотрим важный частный случай, когда имеет место упрощенная мо-
дель наблюдения с белым шумом, независимым от сигнала, и нулевой отсчет
импульсной характеристики Лвосст(0) не равен нулю, ({o}gD):
g(n) = /(n) + v(«), fiv(fc) = <J2S(£). (3.52)
В этом случае
В, (к) = Bf (k) + Bv (к) ~ Bf (k) + o2vS(k),
вМ = Е{Лп) s(n+*)} = ^{/(«)[/(«+k)]+v(/2+*)}=
= E{f(n)f(n + fc)} + E{f(n)v(n + k)} = Bf (k) = Bf (-k).
Из уравнения Винера-Хопфа (3.49) получаем, что
£ ''мест W[B/ (т ~ <:)+Ог8(т -*)] = В1 (ш).
к^О
Е ^восег (*)в/ («1 - *) + а2 /2ВОССТ (т) = Вf (т),
kGD
и при т = 0
£ B«ocer W Bf Н)+о2, (0) = а? . (3.53)
kCD
208
ГЛАВА 3
При этих же условиях выражение (3.51) приобретает вид
Е2 = a2f - £ (k)Bf (-к) = a2 (О),
kED
а после подстановки в него выражения (3.53) получим, что
ё2 =а^в„сСТ(0). (3.54)
Это очень простое соотношение нам будет полезно в дальнейшем.
3.4.2. Оптимальное линейное восстановление сигнала
Пусть на отсчеты импульсной характеристики восстанавливающей ЛПП-сис-
темы не наложено никаких ограничений, то есть она может быть отлична от
нуля в любой точке. Это значит, что в оценке полезного сигнала будут учтены
все наблюдаемые отсчеты (как «прошлые», так и «будущие»). При этом вос-
становление, очевидно, будет наилучшим (оптимальным).
Так как ограничений на йвосст (и) в данном случае нет, то из введенной в
предыдущем параграфе системы уравнений (3.50) остается только уравнение
Винера-Хопфа, записываемое в виде
оо
Eh
восст
(3.55)
—ос
Выражение (3.55) можно интерпретировать как свертку последовательнос-
тей, поэтому, переходя к их ^-преобразованиям, получаем
° восст
(3.56)
Формула (3.56) задает передаточную функцию искомого оптимального
фильтра. Его импульсная характеристика может быть определена отсюда обыч-
ным путем через обратное z-преобразование.
Определим, какую минимальную ошибку восстановления обеспечивает
оптимальный фильтр. Для этого можно было бы, конечно, воспользоваться
формулой (3.51), полученной в предыдущем параграфе, но в данном случае
удобнее и полезнее для анализа сделать иначе. Определим сначала корреля-
ционную функцию и энергетический спектр ошибки восстановления:
3.4. Линейная фильтрация и восстановление изображений
209
Ве (ли ) = Е { е( п )е( и + ли) J =
~Е
оо
к=—оо
оо
УТ ^B0CCT(/)g(n + m-/)-/(n+m)
/=—оо
оо оо
У -/ У Т ^ВОССТ ( ^ ) ^ВОССТ ( ^ ) Вg ( т 1Л~
к——со {——оо
оо оо
- Е ЛвосстС* (-* —т) - Е Л«хст(/)Вл(т-/)+В/('л)-
Л=—оо /=—оо
Запишем это же выражение в сокращенной форме, используя оператор
свертки:
Ве (т) = /гвосст (ли) * /гвосст (-m) * Bg (т) ~
- Лвосст (-т) * Вfg (-т) - hB0CCT (m) * Вfg (m) + Bf (m). (3.57)
Далее перейдем к z-преобразованиям последовательностей, входящих в (3.57):
Фе(^) ВОССТ (z) kl восст
- н«»я(г"')фл (г~')~ нк»ст(г)Фл(z)+ фf (4 <3.58)
Выражения (3.57) и (3.58) справедливы для любой восстанавливающей си-
стемы, а не только для оптимальной (поскольку при их получении мы не
налагали ограничений на Лвосст(м))- Для оптимального фильтра учтем соот-
ношение (3.56) и получим, что
Ф. (z-1)
Ф£(г) = Ф/«-^у2Ф/к(4
или, что удобнее,
ФЕ W = ф/ (г) - (г)ФА (г). (3.59)
Из последней формулы искомую среднеквадратичную ошибку можно вы-
числить двумя путями.
1. Перейти от ^-преобразования (3.59) к самой последовательности (корре-
ляционной функции ошибки):
(^) = ~ УЗ ^ВОССТ (^") B fg — к} ,
к=—оо
210
ГЛАВА 3
и далее при т = 0 получить, что
00
ё2 = О/- £
к=—<х>
(последняя формула, кстати, является частным случаем формулы (3.51)).
2. Перейти от ^-преобразования к энергетическому спектру ошибки вос-
становления и вычислить ошибку по формуле
1 л
Ё2 =— f ФЕ
2лJ '
-л
В общей постановке решение задачи на этом завершается. Более продви-
нутый результат можно получить, введя дополнительные упрощения.
Рассмотрим частный, но очень распространенный случай восстановления
сигнала при линейной модели наблюдения (3.39), когда полезный сигнал и шум
статистически независимы. Оптимальный линейный восстанавливающий фильтр
для этого случая называется фильтром Винера-Колмогорова. Определим его пе-
редаточную функцию. Для начала подсчитаем корреляционные функции, вхо-
дящие в (3.55). Корреляционные функции наблюдаемого сигнала имеют вид
Bg Н = Е{s(w)s(w+'”)} =
00
Ё h(k)f(n-k)+v{n)
к—-со
= Е
00
52 Л(/)/(л + /и-/) + и{л + /и)
I——оо
ОО 00
= 52 52 h(k)h(l)E{f(n-k)f(n+m-l)} +
к=—со /——оо
+ 52 h(k)E[f(n-k)v(n + m)} +
к=—со
4- 52 А(/)£{/(л+/л-/)и(л)} + £’{у(и)у(и + /и)} =
I——оо
ОО 00
= 52 52 h(k)h(l)Bf(n + m-l)+Bv(m) =
к—-со 1—-оо
- Bj(m)+Bv(m).
Соответственно, для z-преобразований записанных последовательностей
Ф,(г)=я(г)н(г-')Ф/(г)+ФДг).
(3.60)
3.4. Линейная фильтрация и восстановление изображений
211
Взаимная корреляционная функция полезного и наблюдаемого сигнала
получается в результате аналогичных, но более простых преобразований:
00
Bfg(m) = E{f(n)g(n + m)} = £ h(k)Bf(m-k) = h(m)*Bf(m),
k——oo
то есть
фл(г) = Н(г)Ф/(г).
(3.61)
Подставив (3.60) и (3.61) в (3.56), получаем передаточную функцию фильт-
ра Винера-Колмогорова:
«(г-'^Дг)
LJ
П ВОССТ
й(г)и(г-')ф/(г) + фЛг)
(3.62)
(в этой формуле дополнительно учтено, что Ф f (г-1) = Фу (г)).
Фильтр Винера-Колмогорова обеспечивает минимальную среднеквадра-
тичную ошибку восстановления сигнала при линейной модели наблюдения и
отсутствии корреляции между полезным сигналом и шумом. Энергетический
спектр этой ошибки можно найти подстановкой (3.61) и (3.62) в (3.59):
фу(г)Фу(г)
Н(г)н(г"1)ф/(г)+Ф1,(г)’
(3.63)
а сама ошибка определяется отсюда известными двумя путями, описанными
выше.
Рассмотрим некоторые частные случаи применения фильтра Винера-Кол-
могорова.
1. Пусть имеется упрощенная модель наблюдения без «линейных» иска-
жений:
g(n)^/(n) + v(n). (3.64)
Здесь —5(п), H(z) = l, и поэтому из (3.62), (3.63) получаем, что
^воссг W =-----.......7~Х , (3.65)
7 ФуИ + ФДг)
Фе^)=:ф/(г)-|_ф • О-66)
Нетрудно заметить, что в данном случае, поскольку ФДг) = фДг-1),
Ф.,Ы = Фг1^ , то и ^B0CCT(z) = HBOCC_(z'1), а это означает, что
> \ / V I ] * dUCV I у f DUVLJ \ /
212
ГЛАВА 3
^восст (n) — ^восст (~n)> т-е- импульсная характеристика фильтра является чет-
ной последовательностью. Такой фильтр является физически нереализуемым
за исключением единственного вырожденного случая, рассматриваемого ниже.
2. Пусть кроме того шум — белый, то есть Bv(m) = aj5(m); =
Тогда из (3.65), (3.66) имеем
«воес,(г) = —Т' <367>
фе(г)
Ф, (z) + <3* ’
(3.68)
3. Пусть, наконец, и полезный сигнал также является белым шумом (этот
случай, как мы увидим ниже, имеет определенный практический смысл). Теперь
Вf (/и) = о)&(т); ф/(г) = о} (3.69)
и, следовательно,
Нвосст (г) ~ 2 , 2 ’ Фг(г)— 2 . 2' (3.70)
az+av °/+Gv
От (3.69) можно очень просто перейти во временную область:
восст (^) 2 i
и далее получить, что
то есть фильтрация заключается в простом умножении наблюдаемого сигнала
на коэффициент (это так называемая «точечная» оценка сигнала).
Ошибки восстановления в соответствии с (3.70) имеют вид
2 2 2 2
ё2=йе(о) = -^,
то есть дисперсия входного шума здесь умножается на коэффициент
т.е. шум убывает в максимально достижимой степени.
3.4. Линейная фильтрация и восстановление изображений
213
4. Еще один частный случай — отсутствие шума. При этом из (3.62) полу-
чаем
„ п_ _ 1
,occtW н(г)н(г-')ФДг)
так называемый обратный (инверсный) фильтр. В идеале такой фильтр обеспе-
чивает абсолютно точное восстановление сигнала. Однако в большинстве
практически интересных случаев он оказывается неустойчивым: бесконечно
малым отклонением входного сигнала обратного фильтра могут соответство-
вать бесконечно большие отклонения выходного сигнала, то есть задача вос-
становления относится к числу некорректных. Для получения устойчивого
фильтра используются различные методы регуляризации.
Пример 3.1. Пусть модель наблюдения сигнала имеет вид (3.64), полезный
сигнал имеет корреляционную функцию
Bf (m) = <j)pW,
где р — коэффициент корреляции между соседними отсчетами и наблюда-
ется на фоне белого шума:
Я„(т) = С^8(т).
Определим передаточную функцию фильтра Винера. В данном случае
°И'~р2)
(l-pz^^-pz) ’
♦/(*) =
Ф.(г) = а2.
Подставив эти величины в (3.65), после преобразований получаем
</2(1-р2)
^восст \Z) ” ’ 9 7 т\ 7 ’
J2(l-p2j+(l + p2J“p^ + z j
(3.71)
где обозначено d2 =а2/а2 — отношение сигнал/шум по мощности.
Поскольку фильтр должен быть устойчивым, область сходимости данного
^-преобразования должна включать в себя единичную окружность.
Из (3.71), основываясь на свойствах z-преобразования, можно определить
импульсную характеристику фильтра Винера-Колмогорова:
^восстИ^а1"1.
(3-72)
214
ГЛАВА 3
где
“~2
I .2
—bp +d
Ip
1
Можно показать, что всегда А>0; loci < 1. Фильтр с импульсной характери-
стикой вида (3.72), очевидно является физически нереализуемым. Поэтому
вопрос его практического использования пока остается открытым. Ответ на
него мы получим позже. А пока определим ошибку восстановления. В нашем
случае линейных искажений сигнала нет, и шум белый, поэтому сразу можно
воспользоваться формулой (3.54):
(3.73)
Проанализируем выражение (3.73). При р —> 1, то есть при увеличении кор-
релированное™ полезного сигнала ё2 —> О, и возможность фильтрации шума
возрастает. При увеличении отношения сигнал/шум (d2 —> оо) отношение
и относительная эффективность
фильтрации (коэффициент по-
давления шума) стремится к
единице (см. рис. 3.27).
Рис. 3.27. Зависимость качества восста-
новления от параметров искажения
3.4. Линейная фильтрация и восстановление изображений
215
3.4.3. Реализация оптимального фильтра обработкой «в прямом
и обратном времени»
Im Z
Re Z.
Рис. 3.28. Расположение полюсов в устой-
чивой физически реализуемой системе
Оптимальный линейный восстанавливающий фильтр, как правило, не от-
вечает требованию физической реализуемости. Поэтому оценка сигнала (3.40)
не может быть вычислена впрямую. Для того, чтобы практически воспользо-
ваться процедурой оптимального восстановления есть два основных способа.
В данном параграфе мы рассмотрим один из них, заключающийся в обработ-
ке сигнала «в прямом и обратном времени».
Этот способ обработки применяется в тех случаях, когда есть возмож-
ность сразу ввести в компьютер достаточно длинную реализацию сигнала.
Когда отсчеты последовательности запи-
саны в память компьютера, понятия «про-
шлого» и «будущего» становятся услов-
ными: по сигналу (то есть по массиву
отсчетов) можно двигаться как в направ-
лении возрастания аргумента (индекса),
то есть в «прямом времени», так и в на-
правлении убывания — «в обратном вре-
мени». Этот факт и позволяет реализовать
оптимальный фильтр.
Ниже будем считать, что характеристи-
ки обрабатываемых сигналов таковы, что
передаточная функция оптимального филь-
тра HBOCCT(z) является дробно-рацио-
нальной. Она соответствует устойчивой, но
физически нереализуемой системе, то есть
взаимное расположение полюсов и области
примерно такой вид, как на рис. 3.28.
Областью сходимости 77BOCCT(z) является кольцо, включающее единичную
окружность:
сходимости на ^-плоскости имеет
при R_ <1; /?+ > 1.
Дробно-рациональную передаточную функцию согласно формуле (1.199)
можно записать через нули и полюсы:
восст
7=1
(3.74)
к
'Z ,
где А, к — некоторые константы (к — целое). Часть полюсов в (3.74) имеет
модуль меньше единицы, а часть — больше единицы. Представим передаточ-
ную функцию в следующей форме:
216
ГЛАВА 3
восст (^) ВОССТ (^)^ВОССТ (^) ’ (3-75)
где к сомножителю H^ccr(z) отнесем часть знаменателя с полюсами, лежа-
щими внутри единичной окружности, а к — с полюсами вне еди-
ничной окружности. Распределение нулей и коэффициента А, в принципе,
произвольно. Очевидно, что здесь мы снова решаем задачу факторизации (см.
п. 1.8.4), но уже в более общей, «несимметричной» постановке.
Составляющая H+T(z} будет иметь область сходимости
|г|>Я_ («_<!),
то есть соответствовать передаточной функции некоторой устойчивой систе-
мы. Эта система физически реализуема, так как ее импульсная характеристи-
ка /*iccr(n)> соответствующая г-преобразованию H^CCT(z), является право-
сторонней последовательностью.
Аналогично, сомножитель H~0CCT(z) в (3.75) имеет область сходимости
|z|</?+ (Я+>1)
и соответствует передаточной функции устойчивой системы, реализуемой в
обратном времени (ее импульсная характеристика будет левосто-
ронней последовательностью).
Произведение передаточных функций соответствует каскадному (последо-
вательному) соединению систем. То есть мы имеем здесь «двухпроходную»
процедуру восстановления, заключающуюся в последовательной обработке
сигнала в прямом, и затем в обратном времени.
С другой стороны, можно представить передаточную функцию HB0CCT(z) в
виде суммы, используя разложение (3.74) на простые дроби:
м С
= ----Чт <3-76)
J=|l-P; z
(выражение (3.76) записано для случая правильной дроби и простых полюсов,
более общей формулой является (1.223)).
В данном случае получаем
н восст (г) = Нв+осст (г) + Н“сст (z), (3.77)
где слагаемые формируются по тому же принципу, что и раньше (см. формулу
(1.223)). Формула (3.77) задает двухпроходную процедуру параллельной обра-
ботки сигнала.
Пример 3.2. В предыдущем параграфе мы получили, что для восстановле-
ния сигнала с экспоненциальной автокорреляционной функцией из его сме-
3.4. Линейная фильтрация и восстановление изображений
217
Нвосст (^)
си с независимым белым шумом импульсная характеристика оптимального
(винеровского) фильтра имеет вид Авосст(м) = А а'"', где А>0, |а| < 1 — ве-
личины рассчитываемые через характеристики сигнала и шума.
Передаточная функция этого фильтра
а(1 - а2)
(l-az-l)(l-az)
с полюсами /?, = a, р2 = la. Построим двухпроходный последовательный
алгоритм обработки. В данном случае передаточная функция легко фактори-
зуется к виду (3.75), где
1 д[1-а2)
гт+ ( 1 fj- (7\ = _л_____L
п восст\~) , _1 ’ п восст\^) .
1—az 1—az
По этим передаточным функциям строятся разностные уравнения. На пер-
вом шаге обработки (в прямом времени) из искаженного сигнала g (и) полу-
чаем промежуточную последовательность w(n):
w(n) = aw(n — l) + g(n).
На втором шаге обработки (в обратном времени) получаем искомую оцен-
ку сигнала:
7(n) = a/(n+l)+w(n)A{l -a2).
Можно построить и двухпроходный параллельный алгоритм. Для этого,
вообще говоря, нужно разложить передаточную функцию HBOCCT(z) на про-
стые дроби. Но в данном конкретном случае поступим проще и представим
импульсную характеристику фильтра в следующем виде:
^восст (”) = Аа1"1 = А|а”м W + а~”м (~и) ”5 W] ’
то есть
Нвосст (^) А
1
1-az-1
1-az
восст восст
+
218
ГЛАВА 3
где
Aaz ]
1-az”1 ’
Нвосст (^)
ГТ — f \ _
п восст \ .
] — az
В соответствии с полученными соотношениями, при обработке в прямом
времени, формируется последовательность / + (л):
/+(и) = а/ + (п-1) +Aag(n-l),
а при обработке в обратном времени — f~(n):
f~(n) = af~(n + l)+g(n).
Далее для получения результата восстановления эти последовательности
суммируются:
3.4.4. Реализация оптимального фильтра при помощи ДПФ
Оптимальный линейный фильтр физически реализуем и притом чрезвы-
чайно прост в ситуации восстановления белого шума на фоне белого шума,
сводящегося, как мы видели, к точечной оценке (3.70). В общем случае сиг-
налы не являются белым шумом, в них наблюдается статистическая связь
между отсчетами, и при решении задачи восстановления мы приходим к урав-
нению Винера-Хопфа. Однако есть и другая возможность построения проце-
дуры оптимального восстановления. Можно произвести над сигналом неко-
торое обратимое преобразование, которое произвело бы декорреляцию сиг-
нала. К декоррелированному сигналу можно применить процедуру точечной
оценки, которая для такой ситуации является оптимальной. Затем после об-
ратного преобразования получим искомую оценку сигнала.
Требуемым декоррелирующим свойством при определенных условиях об-
ладает ДПФ, задаваемое соотношениями (1.290) и (1.296). Рассмотрим более
подробно процедуру оптимального восстановления в спектральной области
на примере, когда имеется модель наблюдения без динамических искажений,
заданная соотношением (3.64).
Поскольку ДПФ предполагает работу с последовательностями конечной
длины, наблюдаемый сигнал разбивается на отрезки длиной по N отсчетов.
3.4. Линейная фильтрация и восстановление изображений
219
Рассмотрим один из таких отрезков при 0<n<7V —1. После применения
ДПФ к (3.64) получаем уравнение наблюдения для дискретных спектров:
G(m) = F(m)+v(m), 0<m<N-l. (3.78)
Поскольку последовательности в исходной модели наблюдения считаются
случайными, их ДПФ тоже являются случайными последовательностями. И для
восстановления сигнала нам нужно знать их статистические характеристики.
Далее все количественные соотношения и формулы получим для нашего
сквозного примера из п.3.4.2 и п.3.4.3: будем считать, что экспоненциально
коррелированный сигнал наблюдается на фоне белого шума, то есть
В/(/:) = о}р|‘|, (3.79)
(3.80)
Определим корреляционную функцию ДПФ полезного сигнала. По опре-
делению, для нестационарной комплексной случайной последовательности
(0<£, Z < Л7 —1)
BF (kj} = E\F(k)F* (/)}, (3.81)
где * — знак комплексного сопряжения. Подставив в (3.81) сначала (1.290), а
затем (3.79), после выполнения ряда преобразований получаем
BF (k,l)= Е
N-\ N—l
p—0 r=0
/V-l /V—I . , N-\ N-l । । . , .
= E ^Bf{r-P)w^=X
p=0 r=0 p=0 r=0
= a2f N8(k- l)
p~45 _ i
i-p-'и^ i-p-'wtf
(3.82)
+ (j2
(1 -p-1 Wk)(l-pWtf) (1 - p JW? )(1 - pW*)
Первое слагаемое в (3.82) отлично от нуля только при к = /, то есть тогда,
когда АКФ превращается в дисперсию. По сравнению с этой дисперсией при
N »1 вторым слагаемым можно пренебречь, то есть
G2fN8(k-l)
1
1-р”1и^
(3.83)
1-р-'и^
220
ГЛАВА 3
— единичный импульс с коэффициентом. Таким образом, ДПФ сигнала яв-
ляется дискретным «почти» белым шумом. Положив в (3.83) к =1 — т, опре-
делим его дисперсию в каждой точке:
о2 (т) ~ &F = о2 А
р-'w»
l-p-'w™
1
l-p’lV¥Z
N----—P 1-----++ = °f N---------5
1+p — p + Ww j 1 + p2 — 2pcos-^/n
(3-84)
Видно, что дисперсия каждого спектрального компонента F(m) зависит от его
номера т, длины последовательности N и корреляционных свойств сигнала — р.
Аналогичным путем можно вычислить и дисперсии ДПФ шума. Однако в
нашем случае нет необходимости повторять весь ход преобразований. С уче-
том (3.80) можно, положив в (3.82) р = 0 и заменив индексы сигнала на ин-
дексы шума, сразу получить, что
Bv (kj) = N<52S(k-l),
т.е. белый шум во временной области переходит в белый же шум в спектраль-
ной области. В отличие от дисперсии (3.78), дисперсия спектральных компо-
нентов шума не зависит от т:
nJ (т) = Оу = Na2. (3.85)
Таким образом, для модели наблюдения в спектральной области задача
сводится к оценке белого шума с дисперсией (3.84) на фоне белого шума с
дисперсией (3.85). Восстановление заключается в точечной оценке, то есть в
умножении каждого спектрального отсчета на коэффициент
F(w) = XmG(/n), 0</л<А-1, (3.86)
где
d2(l-p2)+(l + p2)-2pcoS^m’
Далее полученная по (3.86) оценка F(m) переводится во временную об-
ласть при помощи обратного ДПФ (1.296). Схема всей процедуры восстанов-
ления показана на рис. 3.29.
Такая процедура восстановления является асимптотически оптимальной
при А —> ос .
3.4. Линейная фильтрация и восстановление изображений
221
Рис. 3.29. Схема процедуры восстановления сигнала с использованием ДПФ
3.4.5. Восстановление сигнала КИХ-фильтром
Построим теперь субоптимальный восстанавливающий КИХ-фильтр. В этом
случае за оценку сигнала Дп) принимается взвешенная сумма конечного
числа отсчетов наблюдаемого сигнала g (и), то есть здесь оценка строится
нерекурсивно, как результат непосредственного вычисления свертки:
f^^h^^n-k), (3.88)
kED
где D — конечное множество отсчетов, задающее «окно» обработки.
Выбрав область D вокруг восстанавливаемого отсчета достаточно большого
размера и рассчитав оптимальные коэффициенты КИХ-фильтра, можно по-
лучить среднеквадратичную погрешность восстановления, очень близкую к
минимально достижимой, обеспечиваемой оптимальным физически нереа-
лизуемым линейным фильтром. Более того, даже при относительно неболь-
ших размерах окна обработки ошибка получается, как правило, меньше, чем
у физически реализуемого восстанавливающего БИХ-фильтра. Это происхо-
дит благодаря тому, что в данном случае формируется «двусторонняя» (интер-
поляционная) оценка, в которой учтены не только «прошлые», но и некото-
рое число «будущих» отсчетов наблюдаемого сигнала. Естественно, в этом
случае восстановление реализуется с некоторой задержкой.
Задача синтеза субоптимального восстанавливающего КИХ-фильтра за-
ключается в определении значений Лвосст (и) в пределах окна обработки, обес-
печивающих минимум среднеквадратичной ошибки восстановления. Как и
ранее, они определяются из системы уравнений (3.50). Отличие от предыду-
щих случаев состоит в том, что теперь область D содержит конечное число
элементов — . Поэтому уравнение Винера-Хопфа (первая строка системы
(3.50)) определяет систему из ND линейных алгебраических уравнений с
таким же числом неизвестных — значений искомой импульсной характерис-
тики. Методы решений таких систем хорошо известны.
222
ГЛАВА 3
Пример 3.3. Построим простейший КИХ-фильтр вида (3.88) — процедуру
восстановления сигнала по трем точкам для экспоненциально коррелирован-
ного сигнала, искаженного статически независимым белым шумом (для мо-
дели наблюдения (3.64)):
/(«)= Е K0CCr(k)g(n-k)^
Ваоест ( Ой0"^" Ввосст (®)й ^восст (Ой (и О'
Здесь £> = {— 1, 0, 1}. Из уравнения Винера-Хопфа получаем:
при т=-1 В,,(0)Л,11с„(-0+В8(-0Лво<;„(0)+В8(-2)Лвоот(0 = Ва(0>
при т = 0 вД0л«ххт(-0 + в8(0)Л.оеСТ(0) + В8(-0лю^(0 = вл(°)'
при т=1 ^Ве(2)йюсс1(-0 + ВД0^(о)+Ве(О>^ст(0 = Вл(-0.
В данном случае
ВЯ (т) = В/ W + Вв (т) = Р^ + 8(т) >
в л (~т) = By (-т) = By (т) = о J ,
поэтому записанная система уравнений конкретизируется:
(а2+^)Л,осст(-0 + О/РЛ,осег(0) + О/р2Лккст(0 = °/Р-
О/РЛ№СТ(-0+(а/ +<’*)ЧТССТ(О):4-СГ/ рЛ.0ССТ(1) = ст?, (3.89)
О/ р2 Ввосе, (0+Р (о)+(а2 + о2 )hKCC, (0 = а} р.
Решение системы (3.89) имеет вид
-2р2
1
ВОССТ ( 1) ^ВОССТ (0 7 . Y7 . ’
1+^ 1+^+р2 -2р2
а Д а
где, как и раньше, использовано обозначение d2 =a2j/erf .
3.4. Линейная фильтрация и восстановление изображений
223
Полученный КИХ-фильтр может быть реализован с задержкой на один
шаг в форме прямой свертки так, как показано на рис. 3.30.
Ошибка восстановления сигнала здесь опять определяется по формуле
(3.54):
Е2
<*v восст (о) Ор
Достоинство нерекурсивных про-
цедур восстановления состоит в про-
стоте их расчета. Для построения
восстанавливающего КИХ-фильтра
достаточно решить систему линей-
ных уравнений, а не решать слож-
ную задачу факторизации энергети-
ческих спектров. Кроме того, как
уже отмечалось, КИХ-фильтр может
обеспечить качество восстановления
более близкое к оптимальному, чем
физически реализуемый винеровс-
кий фильтр.
Еще одно достоинство заключа-
ется в том, что данная методика рас-
чета процедур восстановления лег-
ко обобщается на случай обработки
Рис. 3.30. КИХ-фильтр, реализованный в форме
прямой свертки с задержками
двумерных сигналов.
3.4.6. Двумерная оптимальная линейная фильтрация
На двумерный случай переносятся все основные результаты теории опти-
мальной линейной фильтрации одномерных сигналов.
Пусть имеется линейная дискретная модель наблюдения двумерного сигнала:
g(ni,M2)-/(nl»W2)**^(/1l’/12) + V(”l>n2)> (3.90)
где /г(д|,п2) — импульсная характеристика искажающей двумерной линей-
ной системы с постоянными параметрами; /(п),п2) — полезный сигнал —
стационарное случайное поле; г(м,,л2) — помеха — тоже стационарное слу-
чайное поле.
224
ГЛАВА 3
Пусть восстановление двумерного сигнала осуществляется при помощи
ЛПП-системы с импульсной характеристикой ^ВОсст(п1’п2)>
/(ПР«2) = ^(«Ь«2)**ЛВОССТ(«1»«2)> (3.91)
которая отлична от нуля только в некоторой двумерной области Z):
h^(n\>n2) = G для всех (nltn2)^D.
Требуется найти восстанавливающую систему, которая при сформулиро-
ванных ограничениях на импульсную характеристику обеспечивает минимум
среднеквадратичной ошибки восстановления:
Тогда параметры восстанавливающей ЛПП-системы (значения ее импуль-
сной характеристики ^BOCCT(nj,n2)) определяются из двумерного аналога сис-
темы уравнений (3.50):
12 52 ^оаЛ*1А)А(И1-*1’П2-*2) = Вл(-И1’-П2)’ («П«2)ёО.
(Мг)® (3.92)
Лво<хт(п|.«2) = 0. (nt,n2)^D.
Дисперсия погрешности восстановления, осуществленного ЛПП-фильт-
ром с параметрами, определенными из этой системы, задается выражением
ё2=а^- £ -к2). (3.93)
(*i»*2)eD
Передаточная функция оптимальной восстанавливающей системы в об-
щем случае (см. формулу (3.56)) имеет вид
/ \,г2 )
фДг|>г2)
(3.94)
Если сигнал и шум статистически независимы, то передаточная функция
оптимальной восстанавливающей системы определяется аналогично формуле
(3.62):
LJ
п восст
(3.95)
3.4. Линейная фильтрация и восстановление изображений
225
Принципиальным отличием двумерного случая от одномерного является
невозможность выполнения факторизации. Наиболее успешно решение зада-
чи двумерной фильтрации осуществляется в спектральной области. Такая
процедура включает в себя три этапа.
На первом шаге обработки матрица отсчетов наблюдаемого поля #(п],и2)
(0 < и, < N| — 1; 0 < n2 < N2 -1) подвергается двумерному ДПФ, в результате
чего вычисляется дискретный спектр (трансформанты) — G(k]tk2)
(0<£]<Nj—1; Q<k2<N2—}). Эти трансформанты при достаточно боль-
ших оказываются практически некоррелированными, и поэтому оп-
тимальной является их точечная оценка.
Процедура точечного оценивания — второй шаг обработки:
F(^A) = XtlAxG(<:l,<:2), (3.96)
где — коэффициенты точечной оценки, F(k\,k2} — трансформанты
оценки полезного сигнала.
На третьем шаге при помощи обратного двумерного ДПФ переходим от
трансформант F^k^k^ в пространственную область, то есть получаем иско-
мую оценку полезного сигнала — /(п|,п2)-
Для получения значений коэффициентов точечной оценки воспользуемся
следующим подходом. Процедура оптимального восстановления, описывае-
мая сверткой (3.91), в ^-преобразованиях записывается в виде
^’(z1,z2) = G(z1,z2)-WB0CCT(zi,z2). (3.97)
Положив Z| = e'W|; г2=е'“2 можно записать аналогичное соотношение для
спектров и частотной характеристики оптимального фильтра:
) Явосст ,е'“2).
Восстановленный сигнал /(nItn2) в используемом подходе к реализации
восстанавливающего фильтра через ДПФ рассматривается на ограниченном
двумерном интервале (0<Hj <N, — 1; 0<n2 <TV2 — 1), т.е. это двумерная по-
следовательность конечной длины. Для такой последовательности известна связь
непрерывного спектра с дискретным (с ДПФ):
Г(£р£2) = #(?Ш|,£/Ш2)
То есть, взяв дискретный ряд частот, можно получить, что
F^.k^Gik^-H^k^, (3.98)
где (?(&,,&2) — ДПФ сигнала; Нъоссг(к{,к2>) — отсчеты частотной характери-
стики оптимального фильтра.
8 — 9044
226
ГЛАВА 3
Строго говоря, эти отсчеты не совсем являются ДПФ импульсной характе-
ристики /iBOCCT (и| ,л2), получаемой из решения (3.92), которая в общем случае
оказывается последовательностью бесконечной длины. Однако при TVj, TV2 >> 1
это несоответствие оказывается небольшим, а решение — близким к опти-
мальному.
Сравнивая выражение (3.98) с (3.96), видим, что коэффициенты точечной
оценки
Кк к =^воСст^1^2)=^ВосСт(е,С,|^'“2)
К] ВОССТ \ 1 ’ £. j ВОССТ I 7 I
(3.99)
или
^“к1,к2 восст (^1’^2) ^восст (^1 ’ ^2)
. 2я
I—*1
I---к2
. №
(3.100)
Пример 3.4. Пусть имеется модель наблюдения:
#(прЛ2) = /(>!,,П2) + у(П|,Л2), (3.101)
где /(^1,^2) ~ стационарное поле с АКФ
(3.102)
у(и|,п2) — стационарный дискретный белый шум, статистически независи-
мый от сигнала,
(3.103)
Определим коэффициенты ^к{.к2 Для двумерного оптимального фильтра.
Энергетические спектры сигнала и шума имеют вид
(3.104)
Ф р ( ZI, Z 2 ) — О~.
(3.105)
3.4. Линейная фильтрация и восстановление изображений
227
Передаточная функция оптимального фильтра имеет вид
(3.106)
где б/2=о2/о2.
Коэффициенты фильтра определяются соотношением
Нвосст (^1 ’ ^2 )
2 ~ 2л.
— 2p-cos—к,
w, ‘J
, ? „ 2л ,
1 +р~ — 2p-cos-^-K2
0<fcj <А7, —1,
0<к2 <N2 -1.
(3.107)
Основным достоинством такого спектрального алгоритма восстановления
с помощью ДПФ является его универсальность, т.е. применимость для любых
линейных моделей наблюдения. Этот алгоритм является асимптотически оп-
тимальным с ростом размера обрабатываемых матриц.
Очень серьезный недостаток алгоритма — большие требования к объему
оперативной памяти, трудоемкость и невозможность обработки в темпе по-
ступления информации.
Двумерность обрабатываемых сигналов дает возможность преодолеть не-
которые из указанных недостатков при построении спектрально-рекуррентно-
го алгоритма восстановления. Общая схема спектрально-рекуррентного алго-
ритма такова.
Пусть в матрице g(n^n2) первый индекс, n, g[0,N, —1], означает номер
строки, а второй — «2 £ [®»^2 — 1] — номер отсчета в строке.
8*
228
ГЛАВА 3
Сначала вычисляется одномерное ДПФ для строк /V] х Л\ -матрицы на-
блюдаемого (т.е. искаженного) поля:
-I— к2п2
8*("1.*г)= Esfo^)* • 0<t2<W2-|. (3.108)
«2=0
При этом получается дискретный полуспектр g*— двумерная по-
следовательность, один из аргументов которой (n{) соответствует простран-
ственной координате, а другой (^) — частотной. В силу де коррелирующего
свойства ДПФ при N2»\ элементы полуспектра в каждой строке будут
практически независимы друг от друга. Это означает, что поле в полуспект-
ральной области распадается на N2 независимых последовательностей, соот-
ветствующих столбцам. То есть полуспектр £*(п|,£2) можно рассматривать
как совокупность одномерных сигналов с аргументом nlt а к2 — принимает
смысл просто параметра, порядкового номера последовательности. Для того,
чтобы получить оценку полезного сигнала, осуществляется одномерная опти-
мальная фильтрация каждого столбца полуспектра (для этого строится двух-
проходный алгоритм).. После такой фильтрации получаем оценку в полуспект-
ральной области — j(nuk2\ На заключительном этапе эта оценка перево-
дится в пространственную область при помощи одномерного обратного ДПФ,
выполняемого по строкам:
л ] л2-1 л I—к2п2
f(nl,n2) = —-'^f4n\^2)’eN2 » 0<n2<7V2-l. (3.109)
k2=Q
Теперь рассмотрим, как рассчитывается алгоритм восстановления в полу-
спектральной области. Опять воспользуемся соотношением (3.97). Положим
,2л
I—к2
здесь z2~e 2 , 0<&2 < N2 — 1-Тогда
,2л, ,2л, .2л,
I «2 i к2 i к2
F(zt,e N1 ) = G(z„e"2 )-HBoccr(zl,e )’
Или, используя обозначения для дискретного полуспектра, получаем, что
i—к2
F (z„A:2) = G,(z„t2)-H,OCCT(zl,eN2 ). (3.110)
Здесь к2 является параметром. Задача состоит в построении алгоритма фильт-
рации одномерного сигнала, т.е. в построении ЛПП-системы с передаточной
,2л,
।—к2
функцией HBOCCT(Z|,e ). Здесь уже можно произвести факторизацию:
3.4. Линейная фильтрация и восстановление изображений
229
,2л. ,2л, .2л.
। к2 i к2 • «2
"2 ) = Нв+оот(г„ел'* 1 ) Н^(г„е ), (3.111)
i— к2
где H^CCT(zi,^ N1 ) — передаточная функция системы, реализуемой в «пря-
.2л
1—к2
мом времени» (т.е. при движении вниз по столбцам), N1 ) — пере-
даточная функция системы, реализуемой в «обратном времени» (т.е. при дви-
жении вверх по столбцам).
Пример 3.5. Пусть имеется модель наблюдения (3.101), где полезный сиг-
нал — стационарное поле с изотропной АКФ (3.102), шум — стационарный,
дискретный, белый, статистически независимый от сигнала, с дисперсией
Построим двухпроходную процедуру оптимальной оценки в полуспект-
ральной области. Передаточная функция оптимального фильтра (см. (3.106))
О / „ ' : ф/(г1-гг)
п восст \zl ’ ^2) ( \|А / А ~~
Ф/(г1,г2)-1-ФДг1,г2)
_____________________Л2(1-Р2)2________________________
d2(1 -р2)2 +[1 + р2 -p(zj +гГ’)][1 +р2 -p(z2 +^2 9]
J2(l-p2)2+(l+p2)2-p(i+p2)(zi+z,’)—p(n-p2)(z2 4-z7')+P2(z' "Fzi')(г2+г2')
.2л .
I--к2
Положим z2 =е N2 . Тогда
12я*2
«=ocCT(Z1.« "2 ) =
______________________________________tf2(l-p2)2_______________________________________
d!(l -р2)2 + (1+р2)2 -2р(1 + p2)cos^-t2 - р(1 +p2)(z, + zf') + 2p!(z, + г.'1 )cos^*2
/V 7 IN ?
___________А____________
+ zt )
(3.113)
230
ГЛАВА 3
где А = d2(l — р2) ,
B(/:2) = d2(l-р
2\^ / 2\“ _ ( 1\ 2 ТС
j + ^1 + р_) —2р^1+ р“ jcos——&•>,
С(Аг2) — р(1 + р2)- 2p2cos-^-A2 -
^2
Полученное выражение для одномерной передаточной функции всегда
можно факторизовать, т.е. представить в виде произведения:
-2л
Н (г eN1 2) =_____________-__________~
П BOCCTV^l ' /, \ f \{
_ ₽(^г) х ₽(^г) _г+/ \ г~(7 1
------;—;—г*-------лг~\---С (Zi)-G Izil, (3.114)
1-а(*2)г-’ 1-а(/с2)г, k 17 k
где а(Л2), Р(^г) — коэффициенты, определяемые в процессе факторизации;
G+(zj) — передаточная функция ЛПП-системы, реализуемой в прямом вре-
мени; G (z|) — передаточная функция ЛПП-системы, реализуемой в обрат-
ном времени.
Таким образом, получаем следующую спектрально-рекуррентную проце-
дуру фильтрации.
1. Из исходного поля вычисляется полуспектр по строкам
£*(и],£2) (2V, раз выполняется N2 -точечное ДПФ (3.108)).
2. Производится фильтрация в полуспектральной области «в прямом вре-
мени»:
/*(д[Д2) = а(*2)7*('21 + (3.115)
3. То, что получилось, фильтруется «в обратном времени»:
7*(П1’Л2) = а(Л2)7 *(«1+1А) + Р(*2)/*(П1А)- (3.116)
4. Результат переводится в пространственную область (см. (3.109), опять
/V, раз выполняется /V2 -точечное обратное ДПФ).
Спектрально-рекуррентная реализация оптимального фильтра оказывает-
ся проще, чем реализация с использованием двумерного ДПФ (примерно в
два раза). И, что очень существенно, здесь нет транспонирования. К недо-
статку можно отнести то, что, для простоты расчета фильтра крайне жела-
тельна разделимость всех АКФ и импульсной характеристики искажающей
системы (передаточная функция фильтра должна быть дробно-рациональной).
Данный алгоритм является тоже асимптотически оптимальным при /У2 —> оо
(по вертикали матрица может считаться бесконечной).
3.4. Линейная фильтрация и восстановление изображений
231
3.4.7. Двумерные линейные субоптимальные КИХ-фильтры
Рассмотрим построение субоптимального двумерного линейного КИХ-фильт-
ра путем переноса методики расчета для одномерного случая. Значения им-
пульсной характеристики непосредственно определяются из
системы уравнений (3.92), включающей в себя уравнение Ви-
нера-Хопфа и ограничения на импульсную характеристику.
В данном случае область D представляет собой двумерное
«окно», содержащее конечное (обычно небольшое) число от-
счетов. Поэтому процедура расчета КИХ-фильтра оказыва-
ется достаточно простой.
Рис. 3.31. Симмет-
ричная маска
Пример 3.6. Пусть имеет место модель наблюдения (3.101), полезный сиг-
нал имеет биэкспоненциальную изотропную АКФ (3.102), шум — белый, ста-
тистически независимым от сигнала, с дисперсией .
Рассчитаем КИХ-фильтр для окна из пяти точек:
D = {(0,0),(0,1),(1,0),(-1,0),(0,-1)} . (3.117)
Учтем предварительно, что в нашем примере
Bg(kl,k2) = Bf(kl,k2)iBv(kltk2), (3.118)
— ^/(^1*^2) (3.119)
Учтем также, что функция яркости обладает изотропными статистичес-
кими свойствами в перпендикулярных направлениях, и поэтому, очевидно,
что импульсная характеристика искомого КИХ-фильтра будет соответство-
вать симметричной «маске» (рис. 3.31) всего с двумя различными числовы-
ми значениями:
°=лк.Кт(°-0);
b = (0,-1) = h^-1,0). (3.120)
Строим систему для определения коэффициентов фильтра. Из уравнения
Винера-Хопфа, при п} = 0, п2 — 0, получаем
ft„CCT(0,0)Bg(0,0)+BMCCI(0,l)B!,(0,-l) + ftKCCT(l,0)Bs(-l,0) +
+лвос„(0,- 1)ВЛ, (0,1)+i,0)Bs (1,0)=в/К (0,0), (3.121)
или, принимая во внимание новые обозначения,
а(<4 +<j2) + 4b(jJ.p = c^.
(3.122)
232
ГЛАВА 3
Из уравнения Винера-Хопфа, при Л] = 1, л2 = 0, получаем, что
Лвосст (0,0)В/1,0) + Лвосст(0,1)В ?(1, -1) + Лвосст (1,0)BJ0,0) +
+лвосст (0, - 1)ВХ (1,1) + Авосст (- 1,0)В* (2,0) = Вff( (-1,0), (3.123)
или, в новых обозначениях,
aa}p + b[o2zp2+(G2/-+0j)+Gj.p2+0}p2 (3.124)
Остальные уравнения будут это повторять. Итак, вводя обозначение d2 для
отношения сигнал/шум по мощности, получаем систему:
а
( 1
—+ 1 +4£р = 1,
U2 J
1 ?
ар + b — + 1 + Зр =р.
\d
(3.125)
Решая систему, получаем
(3.126)
|1+~т 1 d2) 1+++ЗР2 ( d2 J -4р2
(3.127)
Удобство восстановления изображения КИХ-фильтром заключается в ис-
пользовании универсальной процедуры линейной обработки изображения
скользящим окном («маской»). Как уже отмечалось, для того, чтобы эта про-
цедура была достаточно простой, нужно брать маску небольшого размера: 3x3
или 5x5. При этом для определения оптимальных коэффициентов маски нуж-
но решить систему уравнений соответственно 9-го или 25-го порядка. Если
окно симметрично, а изображение обладает изотропными статистическими
свойствами, то расчет резко упрощается, при таких условиях для окна 3x3
имеем только 3 различных коэффициента, а для окна 5x5 — шесть. Простота
расчета — это тоже достоинство КИХ-фильтра.
3.4. Линейная фильтрация и восстановление изображений
233
На практике измерение или теоретический расчет корреляционных функ-
ций не всегда возможны. Поэтому часто используют непараметрический под-
ход к фильтрации. При этом учитывается тот факт, что спектр шума содержит
более высокие пространственные частоты, чем спектр идеального изображе-
ния. При этом любая низкочастотная фильтрация может служить эффектив-
ным средством подавления шумов. Приведем типичные примеры сглаживаю-
щих масок размером 3x3:
3 1 Г (1 1 Г 1 1 2 1
л =1 1 1 1 , Л2= — 1 2 1 , л3= — 2 4 2
1 9 J 1 2 10 J > 1. 3 16 1 \ 2 1
(3.128)
Коэффициенты данных масок нормированы ( Д’2) “ 1) так, что-
(*.А)е d
бы процедура подавления помех не вызывала смещения средней яркости об-
работанного изображения относительно исходного.
Маски (3.128) отличаются степенью сглаживания высокочастотных шумов
(у маски Aj она максимальная, у А3 — минимальная). Выбор коэффициентов
маски должен производиться экспериментально. При увеличении степени сгла-
живания шумов происходит также подавление высокочастотной составляю-
щей полезного изображения, что вызывает исчезновение мелких деталей и
размазывание контуров.
Если требуемая степень сглаживания с применением маски размера 3x3 не
достигается, то следует использовать сглаживающие маски больших размеров
(5x5, 7x7,...), хотя они используются редко, т.к. для них прямая свертка вы-
полняется достаточно долго. Исключение составляет простое усреднение по
окну КхК, которое и в случае больших окон может быть реализовано в рекур-
сивной форме.
Завершая краткий обзор «классических» линейных методов восстановле-
ния, следует отметить, что они не полностью решают проблему восстановле-
ния изображений. Это связано с несколькими причинами.
Во-первых, как известно, методы оптимальной линейной фильтрации яв-
ляются оптимальными вообще только для гауссовых сигналов и шумов. Изоб-
ражения и шумы таковыми чаще всего не являются.
Во-вторых, традиционно используемый в таких методах среднеквадратич-
ный критерий качества восстановления плохо согласован со свойствами зре-
ния, а также со многими целевыми функциями обработки изображений.
В-третьих, не всякие искажения описываются введенной выше линейной
моделью наблюдения.
И, в-четвертых, не всегда известны те характеристики сигналов и искаже-
ний, которые нужны для построения фильтра.
234
ГЛАВА 3
3.5. Нелинейная фильтрация
Линейная фильтрация очень широко используется при устранении шумов
на изображениях. Линейные КИХ-фильтры достаточно эффективны в вычис-
лительном отношении и просты в реализации. Однако в приложении к циф-
ровым изображениям они обладают рядом существенных недостатков: раз-
мывают очертания объектов и могут уничтожать мелкодетальные особеннос-
ти изображения.
Эффект размывания контуров может быть существенно снижен при ис-
пользовании нелинейных фильтров. Наиболее простым примером является
метод медианной фильтрации.
3.5.1. Медианная фильтрация
Этот метод нелинейной обработки сигналов, разработанный Тьюки оказы-
вается очень полезным при подавлении аддитивного шума, причем, он осо-
бенно эффективен, если шум v — импульсный и представляет собой ограни-
ченный набор пиковых значений на фоне нулей.
Метод очень прост, не требует настройки (является непараметрическим) и
поэтому получил широкое распространение. Медианный фильтр реализуется
как процедура локальной обработки скользящим окном различной формы
(рис. 3.32), которое включает нечетное число отсчетов изображения (обозна-
чим количество пикселов в скользящем окне через N).
Процедура обработки заключается в том, что для каждого положения окна
попавшие в него отсчеты упорядочиваются по возрастанию (или убыванию)
значений. Средний отсчет в этом упорядоченном списке называется медиа-
ной рассматриваемой группы из N отсчетов, для него существует (N —1)/2
отсчетов, меньших или равных ему по величине и столько же больших или
равных. Эта медиана заменяет центральный отсчет в окне для обработанно-
го сигнала.
Рис. 3.32. Примеры скользящих окон медианного фильтра
3.5. Нелинейная фильтрация
235
В результате применения медианного фильтра наклонные участки и рез-
кие перепады (скачки) значений яркости на изображениях не изменяются,
это очень полезное свойство именно для изображений, на которых, как изве-
стно, много контуров (ступенчатых границ функции яркости). В то же время
импульсные помехи, длительность которых составляет менее половины окна
будут подавлены. Чем больше окно, тем более крупные детали будут стирать-
ся (рис. 3.33).
Возможны различные стратегии медианной фильтрации для подавления
помех. Одна из них рекомендует начинать с минимального окна. Если изме-
нение изображения незначительно, то окно расширяется, и так до тех пор,
пока фильтрация не начнет приносить больше вреда, чем пользы («съедать»
заведомо полезные детали). Другая возможность заключается в каскадной
обработке изображения одним и тем же фильтром. Следует заметить, что те
области, которые остались без изменения на данном шаге каскадной обра-
ботки, не будут меняться и в дальнейшем, то есть в процессе фильтрации
изображение постепенно стабилизируется.
Существует много модификаций медианных фильтров, как одномерных,
так и двумерных. Отметим одну из них. Взвешеный медианный фильтр отлича-
ется тем, что при построении таблицы упорядоченных отсчетов каждый от-
счет берется не один раз, а столько, сколько указано его «весом» в окне.
Например, для окна 3x3 можно задать веса
1 1 1'
1 3 1
1 1 1
(3.129)
— теперь таблица будет составляться из 11 чисел.
Результат обработки таким фильтром изображения из предыдущего при-
мера выглядит так, как показано на рис. 3.34, то есть представляет собой не-
что среднее между полученными ранее результатами.
Целочисленные веса должны удовлетворять двум условиям:
- их сумма должна быть нечетной (для возможности выбора медианы);
Рис. 3.33. Примеры обработки медианным фильтром с различными окнами
236
ГЛАВА 3
- каждый вес должен быть меньше половины суммы (иначе применение
фильтра бессмысленно).
Очевидно, метод медианной фильтрации является эвристическим. Он пред-
полагает использование интерактивных систем обработки изображений, ког-
Рис. 3.34. Результат реали-
зации взвешенного медиан-
ного фильтра
ше, чем изображение,
да пользователь осуществляет экспериментальный
подбор окна и текущий контроль за результатами об-
работки.
Что касается качества их работы, то экспери-
ментально установлена их относительно слабая эф-
фективность при фильтрации флуктуационного
шума. Гораздо лучший эффект они дают при об-
работке изображений, искаженных импульсными
помехами, помехами типа «царапин», сбойных
строк, «штрихов» и т.п.
При равной среднеквадратичной погрешности
восстановления изображение, обработанное меди-
анным фильтром, визуально воспринимается луч-
отфильтрованное линейными методами, так как в
данном случае сохраняются контуры и границы областей.
3.5.2. Адаптивные фильтры
Для сохранения контуров и границ объектов на изображении при фильт-
рации флуктуационного шума широко используют адаптивные фильтры с
конечной импульсной характеристикой. Термин «адаптивный» означает то,
что коэффициенты импульсной характеристики фильтра изменяются в соот-
ветствии со структурой обрабатываемого изображения. В общем случае боль-
шинство адаптивных фильтров реализуют локальную обработку вида
7(П],П2) = -^- h(nl,n2\khk2)-g(ni+k],n2 + k2), (3.130)
И (kMeD
где Н — нормализующий коэффициент фильтра, обеспечивающий несме-
щенность средней яркости обработанного изображения относительно исход-
ного. Коэффициенты фильтра h[nl,n2,ki,k2) зависят от значений функции
яркости изображения в «скользящем окне» D. Для каждого положения окна
выполняется либо пересчет отсчетов маски фильтра, либо отбор обрабатыва-
емых в окне пикселов изображения, то есть изменение конфигурации окна.
Поэтому, несмотря на использование линейной обработки отсчетов в окне,
процедура адаптивной фильтрации в целом является нелинейной.
Например, коэффициенты фильтра можно определить как
h(nl,«2;^1,/c2) = l-|g(n1,n2)-<g(nl + к},п2 + *2)|,
(3.131)
3.5. Нелинейная фильтрация
237
при этом нормализующий коэффициент
н= l-|g(n|,n2)~^(ni + £|,и2+*2)|. (3.132)
(МгН*
Более простой вариант формирует маску фильтра следующим образом:
1,
О,
,n2; Acj, Ас2) =
если |g(nj,п2)-g(п} +*i,n2+fc2)|<Y,
(3.133)
иначе,
где у — константа, выбираемая пользователем, или среднеквадратичное от-
клонение значений яркости в скользящем окне, или на всем изображении.
Это очень напоминает другую распространенную процедуру, реализующую
о -фильтр, которая выполняет взвешенное усреднение только тех отсчетов в
окне, чьи значения не слишком сильно отличаются от значения яркости цент-
рального пиксела обрабатываемого окна,
/(nt,n2) = 12 Л(^]Л2)-^(«1+А:],п2+А:2), (3.134)
где обрабатываемая окрестность формируется следующим образом:
£> = {(Лс|,Л2);|^(п1 +*1Л2+*2)-£(л1,л2)|<а},
(3.135)
а коэффициенты фильтра реализуют простое или взвешенное усреднение (см.,
например, сглаживающие маски (3.128)).
Другой пример — фильтр Ли. При его реализации выполняется оценка
локального среднего р.Дл],л2) и дисперсии а2^,^} значений яркости изоб-
ражения, расположенных в текущем окне D. Выходное значение фильтра
формируется следующим образом:
7(п]Л2) = £(и],Л2) + [1-а(п]Л2)],
a(n1,n2) = max
оДи|,и2) av
^(П|,П2)
(3.136)
где а2 — оценка дисперсии шума на обрабатываемом изображении. Если
о (л|,п2)»а,,, то а(м1,п2)^1 и /(«j,«2) = g(nhп2), то есть никаких из-
менений не происходит, но если g^^nl,n2)«Gv, то а(п1,л2) = 0 и
/(п[,п2) = |1х, (и|,п2). Таким образом, фильтр выполняет сглаживание лишь
тогда, когда сигнал слабо отличается от шума, и оставляет значения яркости
неизменными, когда обнаруживается наличие сильного сигнала. Основным
недостатком этого фильтра является то, что в окрестностях контуров, границ
объектов и других деталей изображения шум не устраняется.
238
ГЛАВА 3
3.5.3. Ранговая обработка изображений
После обсуждения медианных и адаптивных фильтров совсем несложно
понять принцип действия ранговых алгоритмов. Это существенно более ши-
рокий класс процедур, куда медианная и адаптивная фильтрации входят как
частный случай. Понятие ранговой обработки введено в 80-х годах, хотя мно-
гие давно известные алгоритмы можно интерпретировать как ранговые. При-
чем фильтрация и восстановление сигналов это лишь одна из задач, которые
решаются при помощи ранговой обработки. Среди других можно назвать пре-
парирование изображений, выделение областей заданной геометрии, анализ
статистических характеристик изображений и т.д. Тем не менее, фильтрация —
важнейшее приложение ранговых фильтров, поэтому они и рассматриваются
в данной главе.
Чтобы не быть жестко привязанными к задаче восстановления, вернемся к
понятию системы и будем считать, что f — входной сигнал, g — выходной —
результат обработки.
Также как медианные фильтры и многие другие известные нам процедуры
обработки изображений, ранговые фильтры реализуют обработку «скользя-
щим окном»:
§(и1,и2) = ф[{/(п1 +kitn2 + fc2)}, (Л]Л2)с£)], (3.137)
где Ф — оператор преобразования отсчетов входного сигнала D— «окно»,
определенное относительно начала координат.
Принцип действия (и идея) ранговой обработки заключается в том, что
для каждого положения окна (то есть для фиксированных значений (п,,и2))
строится и анализируется вариационный ряд по отсчетам, попадающим в окно.
Вариационным рядом совокупности из N чисел {/} называется последова-
тельность {/г}, в которой эти числа упорядочены по неубыванию:
/1 < /2 < /з — • • • — /а •
Значение индекса г (порядковый номер числа fr в вариационном ряду)
называется рангом, а само это число г — порядковой статистикой (или стати-
стикой порядка г).
Итак, для ранговых алгоритмов нелинейный оператор преобразования Ф
строится через вариационный ряд отсчетов в окне D\
я(п|,п2) = Ф {/Г(П|,П2)},=1
(3.138)
где {fr (и1,и2)} — вариационный ряд для положения окна с центром в точке
(п],и2), при котором формируется выходное значение g(n},n2) , TV — число
отсчетов в окне D.
Ниже, учитывая, что для всех (nj,n2) обработка ведется одинаково, аргу-
менты (п],и2) мы писать не будем. Пределы индексации вариационного ряда
3.5. Нелинейная фильтрация
239
тоже очевидны (l<r<N ), поэтому опустим и их. Таким образом, будем
использовать краткую запись:
« = *[{/,}]• (3.139)
Приведем примеры простейших ранговых фильтров.
Пример 3.7. Медианный фильтр в терминах ранговой обработки записыва-
ется в виде
g = fN+l, при N нечетном. (3.140)
~2~
Пример 3.8. Пусть обрабатываются бинарные изображения. В вариацион-
ном ряду будут только два значения порядковых статистик 0 и 1. Тогда могут
быть определены следующие операции:
эрозия- g — /|, дилатация: g =fN .
Те же операции на полутоновом изображении дадут выделение, соответ-
ственно, наименьшего и наибольшего отсчета в окне (эта операция тоже мо-
жет быть полезна).
Очевидно, для приведенных примеров можно построить один универсаль-
ный фильтр
g = fr. (3-141)
где ранг г задается в виде параметра.
Пример 3.9. Подчеркивание контуров.
На участках без контуров (с малыми вариациями яркости) значение g,
g — fN — /], будет близко к нулю, а на участках со скачком яркости про-
изойдет выделение перепада (рис. 3.35).
Из других видов формирования отсчета выходного сигнала по вариацион-
ному ряду отметим усреднение:
ный сигнал; b — выделенный контур
240
ГЛАВА 3
Пока это не имеет явного смысла (усреднение по вариационному ряду дает
тот же результат, что и простое усреднение отсчетов по окну), но при даль-
нейшем изложении мы увидим ситуацию, когда выполнение этой операции
будет оправдано.
Далее, во многих случаях полезно принимать во внимание и значение цен-
трального отсчета входного сигнала — Мы его для кратности обо-
значим /0, тогда ранговый фильтр запишется в общем виде:
«=*[{Л}. /о]-
(3.143)
Указание значения центрального отсчета дает возможность построить мно-
гочисленные новые процедуры обработки (или переосмыслить известные с
точки зрения «ранговости»).
Пример 3.10. Экстремальный фильтр:
/1 при
fN при
(3.144)
Выходной отсчет будет максимальным или минимальным в окне в зависи-
мости от того, к чему ближе центральный отсчет в окне. Такой фильтр поле-
зен при выделении контуров (рис. 3.36). Вспомним, что при пороговой обра-
ботке была проблема с выбором порога из-за размытости мод вероятностного
распределения (рис. 3.37о). После многократной экстремальной фильтрации
«промежуточные» значения исчезнут, моды станут четче (рис. 3.376), и порог
выбрать легче.
Кроме того, при многократной экстремальной фильтрации изображение
стремится к кусочно-постоянному, на нем выделяются однородные области.
А это решение задачи сегментации, которая часто возникает при распознава-
нии объектов и анализе сцен.
И, наконец, приведенный пример показывает, что такой обработкой мож-
но повысить резкость и улучшить качество изображений, так как компенси-
руются динамические искажения функции яркости — происходит восстанов-
ление исходного кусочнопостоянного изображения из расфокусированного.
Рис. 3.36. Иллюстрация работы экстремального фильтра
3.5. Нелинейная фильтрация
241
Рис. 3.37. Пример использования экстремального фильтра: а — распределение значений исход-
ного сигнала; б — распределение значений преобразованного сигнала
Необходимо отметить, что на работу экстремального фильтра в описанном
варианте сильно влияют флуктуационные шумы. Его несомненное достоин-
ство — простота.
Прежде чем двигаться дальше, сделаем одно важное отступление. Построение
вариационного ряда для большого размера окна /V является трудоемкой проце-
дурой. Тем более, что ее надо выполнять для каждого положения окна (то есть
для каждого отсчета выходного сигнала). Если делать обычную сортировку,
то сложность вычислений будет примерно пропорциональна 7V2. Однако
есть другой путь реализации рангового алгоритма, обходящий указанную
трудность. Он основан на следующем факте: вариационный ряд целочисленных
(квантовых по уровню) отсчетов взаимно-однозначно связан с локальной гис-
тограммой отсчетов в окне, см. рис. 3.38.
Гистограмму при движении окна можно вычислять рекурсивно. При этом
сложность вычислений не зависит от размеров окна N.
Рис. 3.38. Пример соответствия вариационного ряда и гистограммы
242
ГЛАВА 3
Связь вариационного ряда и гистограммы полезна не только в «технологи-
ческом» смысле, то есть для упрощения вычислений. Не менее важно то, что,
имея в виду эту связь, можно интерпретировать в ранговой форме те процеду-
ры обработки изображения, которые основаны на анализе распределения яр-
кости. Продолжим примеры.
Пример 3.11. Скользящая эквализация изображений.
В поэлементных преобразованиях обсуждалась (п.3.1.3) эквализация изоб-
ражений, когда значения яркости делались равномерными в некотором ди-
апазоне [&min,gmax]• Ранее отмечалось, что такая эквализация может быть
адаптивной и, в частности, скользящей. Оказывается, это тоже ранговая про-
цедура. Действительно, для эквализации выполняется поэлементное преоб-
разование вида
8 (<?тах 5min )^>(/о) linin’
где P(fo) — интегральная функция распределения отсчетов в окне.
Интегральная функция, будучи умноженной на 7V, показывает число от-
счетов, не превышающих /0 , то есть ранг отсчета /0 , его положение в вари-
ационном ряду: /У-Р(/о) = г/о, где гх — функция, обратная fr.
То есть
g^g^-g^rh+gl!ia (3.145)
Вернемся к задаче фильтрации. Пусть обрабатываемое изображение иска-
жено шумом. Можно предположить, что наиболее искаженные отсчеты (то
есть отсчеты, наиболее отличающиеся от среднего), будут располагаться по
краям вариационного ряда, полученного по окну. Средняя часть ряда будет
характеризовать полезный (медленно и слабо меняющейся) сигнал. Для дос-
тижения эффекта фильтрации, прежде чем формировать выходное значение
из вариационного ряда, полезно отбросить в нем шумовые «хвосты». Или, что
эквивалентно, выделить в нем центральную часть. Обычно выделяемая часть
вариационного ряда строится как некоторая окрестность вокруг отсчета с за-
данным значением с. В качестве центра окрестности обычно берут:
входной центральный отсчет — с = /0,
медиану — с = fN+i,
среднее значение — с — £[{/г}] и т.п.
Причем, выделяется три основных типа окрестностей. Для их пояснения
воспользуемся рис. 3.39 (на рисунке окрестность строится строго вокруг не-
которого отсчета со значением с).
1. Окрестность по значениям определяется неравенством
c-Ez</r <с + е7.
(3.146)
3.5. Нелинейная фильтрация
243
Здесь
еГ2
е -4
к = 5
Рис. 3.39. Основные типы окрестностей в вариационном ряду
2. Окрестность по рангам определяется неравенством
гс ~~£г < г < г( . (3.147)
3. Окрестность по К ближайшим «соседям» определяется выражением
min
Г, —к<д<гс
max к — / I
q<r<q+k
(3.148)
т.е. отбираются k + 1 отсчетов в вариационном ряде начиная с номера q.
Обозначим операторы выделения окрестностей (то есть формирования «уко-
роченного» вариационного ряда {//}) следующим образом:
для окрестности по значениям
для окрестности по рангам
{/;}=о.[{л}. ег. 4
(3.149)
(3.150)
для окрестности по К ближайшим «соседям»
к, 4
(3.151)
(причем будем считать, что у усеченного ряда ранги уже перенумерованы:
l<r</V*, N*<N).
244
ГЛАВА 3
В различных ситуациях предпочтителен разный тип окрестности. Выбор
окрестности по значениям позволяет учесть при обработке априорную ин-
формацию о величинах скачков на изображении, дисперсии шума и, напри-
мер, отбросить отсчеты слишком далекие от /0. Окрестность по рангам по-
лезна при фильтрации импульсных помех. Окрестность по К «соседям» по-
зволяет использовать при обработке фиксированное число отсчетов (то есть
ориентироваться на детали определенной площади). Есть и реализационные
различия. Окрестность по значениям проще всего определяется по гистограмме.
Окрестность по рангам — по вариационному ряду. Окрестность по К ближай-
шим «соседям» в любом случае определяется наименее удобно.
После выделения окрестности получаем более короткий вариационный ряд.
С ним можно проделывать те же операции, что и с полным вариационным
рядом: формировать выходное значение, еще раз выделять окрестность друго-
го типа и т.д.
Пример 3.12. А. Розенфельд (1978) описал алгоритм сглаживания по К «со-
седям», который в наших обозначениях запишется в виде
g = E{DK[{/r}, к, /0]}, (3.152)
то есть за центр окрестности принимается значение центрального отсчета в
окне.
Такой фильтр оказался очень эффективен для сглаживания шума на ку-
сочно-постоянных изображениях, т.к. он усредняет шум по близким (&+1)
отсчетам и при этом не искажает перепады (скачки) яркости.
Пример 3.13. Упомянутый в п.3.5.2 сигма-фильтр работает по правилу
g = E{Dz[{/,}, G, /0]}. (3.153)
При надлежащем выборе ширины окрестности сигма-фильтр хорошо фильт-
рует шумы и, кроме того, подобно экстремальному фильтру, приближает изоб-
ражение к кусочно-постоянному.
Описанные фильтры могут быть применены многократно до получения
требуемого результата.
Существует много других процедур ранговой обработки, на которых мы
не останавливаемся. В завершение краткого изложения ранговых алгорит-
мов можно сказать следующее. Каждый конкретный ранговый фильтр, мог
бы быть построен с упрощением. Например, для экстремального можно было
бы сразу находить максимум и минимум из отсчетов в окне. Для сигма-
фильтра можно проводить усреднение непосредственно по отсчетам (с от-
брасыванием данных по значениям). Однако унификация подхода полезна
тем, что позволяет создать небольшое число модулей обработки и составить
3.6. Оценка геометрических характеристик объектов на изображениях
245
процедуры сочетанием этих модулей. Для этого необходимо реализовать сле-
дующие модули:
- построение вариационного ряда;
- выделение окрестности одного из типов;
- извлечение характеристик вариационного ряда: порядковой статистики,
ранга /у;
- усреднение.
Все остальные процедуры обработки достигаются их сочетаниями. Если
учесть возможность исследования разных окон и комбинирование ранговых
фильтров с линейными и с поэлементными преобразованиями, то очевидны
большие возможности ранговых алгоритмов при решении самых разных за-
дач обработки изображений.
3.6. Оценка геометрических характеристик объектов
на изображениях
Задача измерений на изображениях заключается в получении по имею-
щимся видеоданным количественных значений параметров, характеризую-
щих либо изображение в целом, либо отдельные объекты на нем.
Класс таких задач очень широк:
- оценка статистических характеристик изображений, то есть построение
и уточнение математической модели двумерного сигнала;
- обнаружение объектов и определение их координат;
- оценка геометрических параметров объектов и т.д.
Рассмотрим последнюю из перечисленных задач, представляющую наи-
больший интерес в практических приложениях. Она заключается в определе-
нии тех или иных параметров, характеризующих «геометрию» изображенных
объектов: размеры, площадь, положение, ориентацию и т.д.
Пусть имеется изображение, содержащее некоторую совокупность объек-
тов на однородном фоне. Без потери общности можно считать, что изображе-
ние бинарное, то есть значения отсчетов, соответствующих объектам, равны
единице, а отсчеты фона имеют нулевые значения. Полутоновое изображение
всегда может быть приведено к бинарному в результате пороговой обработки.
Требуется определить общее число объектов, например, частиц, их пло-
щадь, центры тяжести, поперечные размеры и т.д. Эти параметры объектов
могут представлять самостоятельный интерес и использоваться в виде списка
значений или гистограммы распределения, а могут служить признаками (или
«сырьем» для формирования признаков) для автоматической классификации
(распознавания) объектов.
Анализ поставленной задачи показывает, что многие геометрические пара-
метры объектов могут быть определены с помощью одного и того же универ-
сального алгоритма обработки бинарного изображения. При использовании
этого алгоритма все искомые параметры определяются за один проход по
изображению, например, при его построчной развертке.
246
ГЛАВА 3
Рассмотрим данный алгоритм измерения геометрических характеристик объек-
тов на примере определения площадей объектов. Будем считать, что площадь —
это число отсчетов, принадлежащих объекту, то есть каждый отсчет представляет
ределению площади объекта
собой квадрат единичной площади (рис. 3.40). Объект
определяется по критерию четырехсвязности.
Пусть прямоугольная матрица отсчетов обрабаты-
вается в порядке построчной развертки, то есть слева
направо в строке и сверху вниз по строкам. Рассмот-
рим произвольный отсчет /(«i,n2), не принадлежа-
щей первой строке и левому столбцу матрицы. Обра-
ботку граничных отсчетов рассмотрим отдельно.
Если /(п1,п2) = 0» то есть отсчет принадлежит
фону, то осуществляется переход к следующему от-
счету.
Если /(«j,^2) = 1, то выполняется анализ при-
надлежности текущего отсчета к какому-либо объек-
ту. Для этого дополнительно рассматриваются два соседних уже обработанных
отсчета: f(n}— 1,и21 и f(nltn2 — 1).
Если f[nl — 1,п2) = у(п],и2 —1) = 0, то текущий отсчет /(п|,л2) представ-
ляет собой начальную точку новой области (новый объект). К таблице харак-
теристик областей (в рассматриваемом примере — площадей) добавляется
строка этой области, и в нее заносится начальное значение характеристики
(для площади — единица).
Если /(«! ,м2 — 1) = 1 и f (fl] — 1,и2) = 0, то отсчет присоединяется к облас-
ти, к которой принадлежит соседний по горизонтали единичный отсчет
(/(и|,и2 — 1)), пересчитывается характеристика этой области (прибавляется
единица к площади).
Если f(n},n2 —1) = 0 и /(и, — 1,и2)=1, тр такое же действие выполняется
по отношению к области, к которой принадлежит отсчет /(гц — 1,и2).
Если /(пип2-1) = /(п1 - 1,и2) — I, то анализируются области принадлеж-
ности этих отсчетов.
В случае если оба соседних отсчета принадлежат одной области, то выпол-
няется присоединение к ней, как в двух предыдущих случаях.
В случае если эти отсчеты принадлежат разным областям, то эти области,
а также текущей отсчет объединяются в одну область, характеристики облас-
тей пересчитываются в общую характеристику (площади суммируются и при-
бавляется единица, чтобы учесть и текущий отсчет). Схема алгоритма расчета
представлена на рис. 3.41.
Обработка по приведенной схеме выполняется для всех отсчетов, не при-
надлежащих верхней строке и левому столбцу изображения. Обработка гра-
ничных отсчетов ведется по упрощенному алгоритму: для первой строки не
рассматриваются отсчеты /(пх,п2 — 1), для левого столбца не рассматривают-
ся отсчеты /(п],п2 "1) (они полагаются нулевыми), а при анализе углового
отсчета /(0, 0) либо ничего не делается (если /(0, 0) = 0), либо заводится
строка в таблице характеристик (ДО, 0) = 1).
" 3.6. Оценка геометрических характеристик объектов на изображениях
247
Рис. 3.41. Схема алгоритма расчета геометрических характеристик на изображении
Для окончательной ясности рассмотрим пример. Будем измерять площади
объектов на фрагменте 5x5 (рис. 3.42а). Составим таблицу площадей объек-
тов и покажем, как она модифицируется и наращивается в процессе построч-
ного просмотра отсчетов.
Для краткости в таблице показаны только те строчки, для которых
У(и1,н2) = 1 (то есть отсчеты соответствуют объектам, и таблица изменяется).
Текущий отсчет Характеристика (площадь) области
обл. 1 обл. 2 обл. 3
/(0,1) 1 — —
/(0,2) 1 + 1=2 — —
/(1,0) 2 1 —
/(1,2) 2+1=3 1 —
/(2,0) 3 1+1=2 —
/(2,1) 3 2+1=3 —
/(2,2) 3+3+1=7 объединена с обл. 1 —
/(3,3) 7 — 1
/(3,4) 7 — 1 + 1=2
248
ГЛАВА 3
Рис. 3.42. Измерение площади объекта на изображении: а — пример фрагмента изображения;
б — пример разметки областей алгоритмом
Разметка областей приведена на рис. 3.426 В итоге получим две области:
площадь первой — 7 отсчетов, второй — 2 отсчета.
Аналогично считаются и многие другие характеристики объектов. Един-
ственным требованием к характеристикам, измеряемым по описанному алго-
ритму, является следующее: должно существовать правило вычисления харак-
теристики объединенной области по характеристикам объединяемых областей.
Конкретнее, пусть F(D) — характеристика, вычисленная по области (множе-
ству отсчетов) D. Тогда должно существовать правило Ф такое, что
f(d1ud2)=®[f(di),f(d2)],
(D, А £>2 =0 — области не пересекаются). (3.154)
Это не очень жесткое ограничение. В частности, ему удовлетворяют про-
извольные характеристики следующих видов:
в f(D)= 53 (<р(« j,n2)) — «аддитивные» характеристики,
(л|,л2)ео
/ч / \ тих г . < ч
2) F(D)= ш(п1 ) г — «экстремальные» характеристики,
min 1 у
(ni,n2)ED
где <р(м1> n2), v(hj, и2) — произвольные функции координат и,, и2.
Примеры:
а) площадь F(d)= 1, то есть F(D)— аддитивная характеристика с
ф(п1,п2) = !; (л1«л2)ео
б) координаты «краев» изображения по вертикали и горизонтали (рис. 3.43а).
3.6. Оценка геометрических характеристик объектов на изображениях
249
Рис. 3.43. Измерение геометрических характеристик объектов: а — координаты краев области на
изображении; б — область изображения и ее центр тяжести; в — максимальные линейные разме-
ры объекта на изображении
Здесь
F,(D)= max ta}; F2(D) = min {n,
(Л|,Л2)бО
F3(D)= max {n2}; F3(D)= min {n2}
(ni,n2)€D (ni,n2)ED
— экстремальные характеристики c Vi(ni> л2) = и, и V2(ni> n2) = n2.
Подобные «объединяемые» характеристики можно назвать первичными (ба-
зовыми). По ним можно вычислять некоторые вторичные (производные) ха-
рактеристики, которые сами по себе не удовлетворяют сформированному тре-
бованию. Рассмотрим, например, следующие.
1. Центр тяжести объекта или области D (рис. 3.436) для случая непре-
рывных аргументов вычисляется по формулам
J* J x2dx{dx2
D
J J x}dx}dx2
1 ~ -’ Т2 ”---------------------------•
J J dx{dx2 f J dx{dx2
D D
(3.155)
Для цифрового изображения приведенные выражения запишутся в виде
Е п\
_ {пх,п2)ео .
1 El’
(л|,л2)ео
52 п2
(лрл2)ео
Е г
(л!.л2)€О
(3.156)
250
ГЛАВА 3
то есть
Ноо ~ 1
(лр л2)ео
W2=hoi5 где gjo= 22 «1
ИОО ИОО (n,,n2)CD
Hoi ~ XZ П2
("г п1№
(3.157)
— три аддитивные первичные характеристики.
2. Размеры объекта по вертикали и горизонтали (рис. 3.43в),
Дл, = max{n,} — minln,}, Ди2 — max{n2} — min{n2}, (3.158)
(rt|,n2)GD (лрл^ея (n,,n2)eD (rii,n2)eD
вычисляются через четыре экстремальные характеристики, рассматриваемые
выше.
Подобная методика измерений параметров объектов (и, соответственно,
понятие первичных и вторичных характеристик областей) могут быть обоб-
щены на случай обработки полутоновых изображений.
ГЛАВА 4
РАСПОЗНАВАНИЕ ИЗОБРАЖЕНИЙ
4.1. Постановка задачи
Существует широкий круг задач, в которых изображения рассматриваются
как источник информации, на основе которой необходимо вынести некото-
рое решение. Например, такого рода задачи возникают в медицинской диа-
гностике, где изображение того или иного человеческого органа анализирует-
ся с целью определения возможного заболевания. В криминалистике для уста-
новления личности человека сравнивают изображения отпечатков пальцев —
дактилограммы. С помощью средств спектрозонального дистанционного зон-
дирования получают изображения, по которым с высокой достоверностью
находят области, содержащие залежи полезных ископаемых. Этот список,
несомненно, может быть продолжен.
Основой для решения такого круга задач является теория распознавания
образов, которая особенно активно развивается в связи с созданием систем
искусственного интеллекта.
В рассматриваемом нами случае, носящем с точки зрения теории распоз-
навания образов прикладной характер, образом является изображение.
Задача распознавания образов заключается в классификации изображений
на основе определенных требований, причем изображения, относящиеся к
одному классу образов, обладают относительно высокой степенью близости.
Принятый подход к распознаванию образов заключается в классификации
на множестве признаков, вычисляемых по наблюдаемому изображению. Мож-
но также сказать, что классификация образов заключается в отображении
пространства признаков в пространство решений. При таком подходе распоз-
навание образов включает две задачи:
- отбор и упорядочивание признаков;
- собственно классификация.
Задача отбора и упорядочивания признаков трудно формализуема. Крите-
рием отбора и упорядочения является степень важности признаков для харак-
теристики образов.
Задача классификации — принятия решения о принадлежности образа тому
или иному классу на основе анализа вычисленных признаков — имеет целый
ряд строгих математических решений в рамках детерминистического и веро-
ятностного подходов.
252
ГЛАВА 4
Рассмотрим для примера классическую задачу распознавания печатных букв
латинского алфавита, соответствующую задаче классификации изображений
геометрических фигур (рис. 4.1).
На рис. 4.1а и рис. 4.Id показаны две первые буквы алфавита в их доступ-
ном для наблюдения виде, на рис. 4.1 в и рис. 4.1г — результат скелетизации
исходных изображений.
Для того, чтобы осуществить классификацию, необходимо отобрать при-
знаки. Здесь возможны самые различные подходы.
Примитивный подход заключается в использовании в качестве признаков всего
неупорядоченного набора пикселов, однако такой подход является неконструк-
тивным в силу огромной вычислительной сложности.
Можно предложить использовать в качестве признаков модули коэффици-
ентов ДПФ или любого другого дискретного ортогонального преобразования.
Рассматривая изображение
буквы рис. 4.1а как дву-
мерную последовательность,
содержащую N2 пикселов,
можно вычислить ее двумер-
ное ДПФ и отобрать из N2 —
пикселов спектра К наиболее
интенсивных. К. Фукунага
[20] для решения задачи от-
бора признаков предлагает
разбить изображение на К
клеток (на рис. 4.1 К = 36) и
использовать в качестве при-
знаков степень заштрихован-
ное™ клеток. К. Фу [19] пред-
лагает работать со скелетизи-
рованными изображениями и
выбирать в качестве призна-
ков расстояние, измеренное
в заранее заданном направ-
лении от края квадрата до
края буквы (см. рис. 4.1 в и
рис. 4.1г, ^=8).
При использовании любо-
го из трех рассмотренных под-
ходов мы получаем в качестве
Рис. 4.1. Иллюстрация отбора признаков в задаче рас-
познавания печатных букв латинского алфавита
признаков упорядоченный
набор числовых данных, обозначающих вектор признаков у=(у0, ун ..., ,
который можно рассматривать как точку в /^-мерном пространстве признаков D.
С геометрической точки зрения задача классификации заключается в разби-
ении пространства признаков D на L взаимно непересекающихся областей
Dt f/ = O,L —1), каждая из которых соответствует некоторому классу обра-
зов. В рассмотренном примере распознавания букв латинского алфавита L = 26 .
4.1. Постановка задачи
253
Задача классификации может быть решена с помощью разделяющей (диск-
риминантной) функции. Пусть По, Q,» ..., означают L возможных клас-
сов образов, и пусть
У=(Уо- Ун Ук-iY (4-1)
есть вектор вычисленных признаков. Тогда разделяющие функции dt(y) та-
ковы, что если наблюдаемый и представленный вектором признаков у образ
принадлежит классу Clj l/ = 0,L —11 , то величина dz(y) должна быть наи-
большей:
d,(y)>d;(y). I. 7 = 0, L-l. (4.2)
Таким образом в пространстве признаков D граница разбиений, называе-
мая решающей или разделяющей границей, между областями, относящимися
соответственно к классу Q.t и к классу Q.j, выражается уравнением
<;(y)=J/(y)-d;(y)=°- <4-3>
Пример разбиения двумерного пространства признаков на области, соот-
ветствующие двум разным классам, показан на рис. 4.2.
Имеется много различных подходов к построению разделяющей функции
d[ (у), удовлетворяющей условию (4.2). Рассмотрим линейную разделяющую
функцию:
/ \Т К—1 _____
<*/(у)= W' y+W^ZX'^+lv;,/=0,£—1, (4.4)
k=0
где Wl — — вектор весовых коэффициентов. Тогда разделя-
ющая граница между областями Dt и Dj в пространстве D имеет вид
Л--1 _____
dM-dAy)=^W«yt+wH=<. k—0 t А А 'k °'-'>,А В\ А [А А В v А область/)/ / _ V ’' . в в д в ), l,j=O,L-l, (4.5) область Д — V разделяющая У граница
Рис. 4.2. Пример разбиения двумерного пространства признаков
254
ГЛАВА 4
где
W* = Wlk -Wkj, l = O,L — \, к = (£к.
Уравнению (4.5) соответствует гиперплоскость в пространстве D. При
К = 2 выражение (4.5) соответствует уравнению прямой.
При построении разделяющей функции (4.5) основной вопрос заключает-
ся в выборе весовых коэффициентов Wk . От этого выбора зависит качество
классификации. Для решения этого вопроса можно предложить различные
процедуры обучения классификатора.
Обычно различают процедуры обучения двух типов: с предварительным обу-
чением и с совмещением процессов обучения и распознавания. В случае пред-
варительного обучения до начала распознавания для настройки классификато-
ра предъявляются ряд объектов известных классов. На основе этой информа-
ции определяются параметры классификатора, и в дальнейшем именно такой
классификатор применяется для распознавания всех остальных образов.
При распознавании образов с использованием процедуры совмещенного
обучения и распознавания информация, доставляемая первоначальной груп-
пой образов, учитывается при построении первоначального правила класси-
фикации. После этого берется следующая группа образов, к которой приме-
няется имеющееся правило классификации. Оценивается результат класси-
фикации и, при необходимости, правило корректируется с учетом новой
информации. Первоначальное правило может быть достаточно произволь-
ным — в результате подобного последовательного обучения достигается ка-
чественная классификация всех возможных образов.
К настоящему моменту разработан целый ряд процедур обучения, ориен-
тированных на решение задачи распознавания. Однако наиболее наглядной в
рамках статистического подхода является задача построения оптимального
классификатора, которая рассмотрена ниже.
4.2. Вероятностный критерий качества классификации
В идеале классификатор должен быть таким, чтобы области, выделяемые в
пространстве признаков, соответствовали классам, то есть должно выполняться
следующее условие: объект со принадлежит классу Q, тогда и только тогда, когда
соответствующий объекту вектор признаков у (со) принадлежит области £)z:
V coeQ: cogQz <^у(со)gDz, Z=O,L-1. (4.6)
Как правило, на практике данное условие выполняется не всегда и суще-
ствует вероятность неверно классифицировать объект и допустить ошибку
при распознавании. _________
Обозначим ру [l, j = 0,L -1) вероятность того, что классификатор прини-
мает решение об отнесении вектора признаков некоторого объекта к области
Dj, в то время как сам объект принадлежит классу Q.t:
4.2. Вероятностный критерий качества классификации
255
P(,.=P(YeD;/n,). (4.7)
При / j вероятности характеризуют ошибки распознавания и назы-
ваются вероятностями неверной или ошибочной классификации, а при I = j ве-
роятности рн задают вероятности верной (правильной) классификации пред-
ставителей соответствующего класса. Уменьшение вероятностей ошибочной
классификации — это основная задача, которая возникает при построении
классификатора.
Качество классификатора характеризуется величиной, называемой в тео-
рии статистических решений условным средним риском. Она задает среднюю
величину потерь, связанных с принятием классификатором решения об отне-
сении данного вектора признаков у к классу с номером j:
Ку(У) = ^-£с«ЛН/)Р(у/П/). (4.8)
Р(У)/-о
В данном выражении:
- P(OZ) — априорная вероятность появления объектов из класса Oz,
L-1
причем 1;
/-о
- p(y/Qz) — условная плотность вероятностей случайного вектора при-
знаков Y для объектов класса (в теории распознавания образов ее назы-
вают функцией правдоподобия для соответствующего класса);
- р(у) — безусловная плотность вероятностей случайного вектора Y;
- элементы квадратной матрицы
c=llcdXo (4-9)
характеризуют величины штрафов или потерь за ошибки классификатора.
Матрица С может быть достаточно произвольной. Единственным ограни-
чением на ее элементы является то, что штраф за ошибочное решение должен
быть больше, чем штраф за решение правильное, то есть: cZ/ >си.
Интегральной величиной, характеризующей качество классификатора, яв-
ляется математическое ожидание потерь или общий риск, который с учетом
(4.7) и (4.8) имеет вид
R = Ё J Ri (у)р (у И = Ё Ёс«р(п1) Рц • <4-10)
j=0Dj j—01—Q
4.3. Оптимальные стратегии статистической классификации
Процесс классификации аналогичен игре двух лиц, в которой выигрыш
(проигрыш) одного из участников равен проигрышу (выигрышу) другого. Выбор
оптимальной стратегии в игре зависит от количества исходной информации.
256
ГЛАВА 4
Могут использоваться байесова, минимаксная стратегии или стратегия Ней-
мана-Пирсона. В зависимости от того, какая из стратегий используется для
построения классификатора, последний называют, соответственно, класси-
фикатором Байеса, минимаксным классификатором или классификатором Ней-
мана —Пирсона.
4.3.1. Классификатор Байеса
Стратегия Байеса используется при наличии полной априорной информа-
ции о классах, то есть когда известны:
- функции правдоподобия для каждого из классов;
- матрица штрафов;
- априорные вероятности для каждого
Стратегия решения выбирается таким
мум общего риска (4.10). Минимальный
из классов.
образом, чтобы обеспечить мини-
общий риск при этом называется
риском Байеса. В соответствии с
выражениями (4.8) и (4.10), ми-
нимум общего риска R будет обес-
печен, если разбиение простран-
ства признаков D будет осуществ-
ляться по следующему правилу:
вектор у € D относится к облас-
ти D; только тогда, когда соот-
ветствующий условный средний
риск Я/(у) минимален:
V j*l К/(У)<
<лу(у) => уег>,. (4.11)
Иллюстрация страте-
гии Байеса приведена на
рис. 4.3а.
Если матрица потерь (4.9)
является простейшей, то
есть, если ее элементы удов-
летворяют равенству
0, i = j
1, i^j’
Рис. 4.3. Построение классифика-
тора Байеса для простейшей мат-
рицы штрафов: а — байесова стра-
тегия минимизации общего риска;
б — классификатор Байеса
4.3. Оптимальные стратегии статистической классификации
257
то после подстановки в (4.11) выражения для условного среднего риска (4.8)
имеем следующий явный вид классификатора Байеса (см. рис. 4.3о, б):
VjXlP(Sll)p(y/nl)>P(£lJ)p(y/£lj)^yeDl.
(4.12)
Из (4.12), в частности, видно, что решающими функциями классификатора
Байеса являются функции
dt(y) = P(Q.l)p(y/Q.l), l=O,L-\.
(4.13)
Часто используют также следующую форму записи классификатора Байеса:
=> у е D,.
(4.14)
При этом функция
Л/;(у) =
р(у/яу)
р(у/о>)_ ло,)
называется отношением правдоподобия, а величина
' P(&l)
— пороговым значением. Таким образом, классификатор Байеса основан на
сравнении отношения правдоподобия с пороговым значением
v j * I Лу(у) > Xjt => у ЕDj
и называется поэтому классификатором отношения правдоподобия.
Легко показать, что при произвольном виде матрицы штрафов в случае
двух классов классификатор Байеса имеет вид
p(y/^i) > ^(Qq)(coi соо)
р(у/П0) < Р(<21)(с1о-сц) Ро
с дискриминантными функциями:
dj(y)=-сл)р(у/а;), j=o,i.
9 — 9044
258
ГЛАВА 4
4.3.2. Минимаксный классификатор
Классификатор, основанный на минимаксной стратегии, используется для
случая двух классов и если известны:
- функции правдоподобия для каждого из классов;
- матрица штрафов.
Минимизировать величину общего риска при отсутствии информации об
априорных вероятностях классов, очевидно, невозможно. В то же время,
предполагая возможность произвольного изменения значений априорных ве-
роятностей классов, можно минимизировать максимально возможное значе-
ние риска. Действительно, общий риск (4.10) в случае двух классов может
быть представлен в следующем виде:
Я = (си +Р1о(<чо-Сн)) +
+ Д(^о)‘[(СОО + Poi (с01 — соо))~ (с11 + Рю (сю ~сп))]- (4.15)
При фиксированном классификаторе изменение априорной вероятности
приводит к изменению величины общего риска, причем характер зависимос-
ти в (4.15) линейный (рис. 4.4). Поэтому поиск классификатора, минимизи-
рующего максимально возможную величину общего риска, эквивалентен по-
иску такого байесовского классификатора, для которого величина (4.15) яв-
ляется постоянной, не зависящей от значения априорной вероятности P(Q0)
величиной. Таким классификатором, очевидно, является классификатор Байе-
са, удовлетворяющий следующему дополнительному условию:
(соо 4" Poi (coi ~ соо))_ (си + Рю (сю — сн))~0 • (4.16)
Рис. 4.4. Иллюстрация минимаксной стратегии построения классификатора
4.3. Оптимальные стратегии статистической классификации
259
Из рис. 4.4 видно, что значение величины общего риска для минимаксного
классификатора равно максимальному значению (минимального) риска Байеса.
Пара априорных вероятностей (Р*(£20),1 —P*(Q0)j, при которых риск Байе-
са принимает максимальное значение, называется наименее благоприятным
распределением априорных вероятностей. Таким образом, минимаксный клас-
сификатор — это классификатор Байеса, полученный для пары наименее бла-
гоприятных априорных вероятностей.
В более простой ситуации, когда элементы матрицы штрафов таковы, что
соо =сп сю — ci» с01 =со»
условие (4.13) преобразуется в следующее:
Poico = Piocr (417>
Последнее выражение представляет собой условие выбора областей £>0, £),
в классификаторе Байеса.
4.3.3. Классификатор Неймана—Пирсона
Критерий Неймана—Пирсона в теории статистических решений использу-
ется для проверки гипотез. В классической постановке задачи используется
только две возможные гипотезы и различают два типа ошибок:
ошибку первого рода р0 — в контексте настоящего изложения р0 = р01;
ошибку второго рода рх — в контексте настоящего изложения рх = р10.
Заметим, что в общем случае pt + р0 1.
Классификатор, основанный на стратегии Неймана—Пирсона, использу-
ется для случая двух классов, и если известны только функции правдоподо-
бия для каждого из классов. Суть стратегии Неймана—Пирсона состоит в сле-
дующем: задается допустимое значение вероятности ошибки первого рода р0,
а затем классификатор строится таким образом, чтобы обеспечить минимум
вероятности ошибки второго рода р,:
л, —> min
Ро =Ро-
(4-18)
Решением задачи Неймана—Пирсона является классификатор вида
Л(у) =
p(y/Qi)
р(у/й0)
уеО]
у е о0 ’
(4.19)
где значение пороговой величины X определяется, исходя из условия р0 — рц
(рис. 4.4). Из выражения (4.19) следует, что классификатор Неймана—Пирсо-
на — это классификатор отношения правдоподобия.
9*
260
ГЛАВА 4
4.4. Классификатор Байеса для нормально
распределенных векторов признаков
4.4.1. Алгоритмы классификации
На практике часто возникает задача распознавания детерминированных
объектов в условиях случайных помех. Ниже приведен достаточно типичный
пример постановки подобной задачи и ее решения с использованием страте-
гии Байеса.
Пусть входной сигнал, задаваемый вектором у = (у0,) и подлежа-
щий распознаванию, представляет собой аддитивную смесь детерминирован-
ной и шумовой составляющих. Будем считать, что наблюдаемые векторы имеют
нормальный закон распределения в каждом из L классов, то есть имеют плот-
ность вероятностей вида
р(уЛМ = ,к/2 Jj-iexp-|(y-M))rB,-|(y-M,). Z=O,L—1. (4.20)
(2я) 7|В,| 2
Здесь
М, =£{Y/n,}, В, =E,|(Y-M/)(Y-M,)r/n,}
— математическое ожидание и ковариационная матрица вектора признаков из
класса , соответственно. Математические ожидания или средние характе-
ризуют детерминированные составляющие распознаваемых сигналов, а кова-
риационные матрицы — характер шумовой составляющей. Считаются также
известными априорные вероятности Р(Пу) появления векторов из каждого
класса. Требуется по реализации у случайного вектора Y определить класс,
к которому данный вектор принадлежит.
Рис. 4.5. Иллюстрация стратегии Неймана—Пирсона построения классификатора
4.4. Классификатор Байеса для нормально распределенных векторов признаков
261
Решением данной задачи является классификатор Байеса с дискриминант-
ными функциями следующего вида:
d,(y) = lnP(n()-ln7iBj-|(y-M/)4’'(y-M/)- (4-21)
Выражение (4.21) может быть существенно упрощено в некоторых частных
случаях.
Случай 1. Предположим, что компоненты наблюдаемого вектора Y явля-
ются независимыми и имеют одинаковую дисперсию ву, то есть Bz ,
где I — единичная К хК-матрица. Тогда законы распределения (4.17) отли-
чаются только средними значениями, а решающие функции классификатора
Байеса преобразуются к следующему виду:
d/(y) = 2а} 1пР(О,)-||у - Ц,||2, Z = O,L-1, (4.22)
здесь Ц...Ц — евклидова норма. При равных априорных вероятностях данное
решающее правило приобретает очевидную трактовку: вектор признаков у
относится к тому классу, расстояние до центра которого минимально.
Классификатор в этом случае называют классификатором по минимуму ев-
клидова расстояния. Пример разбиения пространства признаков при исполь-
зовании подобного классификатора для случая трех классов приведен на
рис. 4.6а.
Нетрудно видеть, что решающие функции (4.22) можно преобразовать к
линейной форме:
^/(у) = М[у-|м[М/ +о* lnP(Qz), Z = O,L—1.
В этом случае разделяющие границы между различными областями Dt, за-
даваемые соотношениями вида:
de(y) = d,(y)-rf;(y) = O, 0<l<j<L-l,
также являются линейными:
d,(y) = (M, -М,)гу-1(М, +МУ)Г(М, -Mj+aJln 4^
0<Z< j<L-\,
и говорят о линейном классификаторе.
262
ГЛАВА 4
Случай 2. Предположим, что все корреляционные матрицы одинаковы:
В, = В. Тогда решающие функции классификатора Байеса представляются в
виде
<(у) = 21п Р(П,)-(у - М,)ГВ-' (у-М,), l=^L=~}.
Величина
Р(У.М,) = (у-М,)7'в-'(у-М,) (4.23)
называется расстоянием Махаланобиса между векторами у и Му и является
мерой близости вектора у к центру класса П,, учитывающей как дисперсии
компонентов вектора Y, так и их взаимную корреляцию. Очевидно, что в
данной ситуации классификатор снова оказывается классификатором по ми-
нимуму расстояния Махаланобиса (см. рис. 4.66). Кроме того, и решающие
функции, и разделяющие границы снова являются линейными:
^/(у) = М/гВ-,у-^М^В“1М/ +1пР(Ц), /=0,А-1, (4.24)
rf„(y) = (M,-MJfB-'y-l(M,+ M,)rB-|(M,-MJ)+ln-^
0</<j<L-l
а, следовательно, линейным явля-
ется и классификатор.
Рис. 4.6. Классификатор Байеса в случае нормально распределенных векторов признаков: а —
признаки статистически независимы и одинаково распределены; б — корреляционные матрицы
одинаковы; в — корреляционные матрицы различны
4.4. Классификатор Байеса для нормально распределенных векторов признаков
263
Случай 3. В ситуации, когда все корреляционные матрицы различны, не-
обходимо пользоваться выражением (4.21) для дискриминантных функций.
Разделяющие границы в этом случае представляются в следующем виде:
^(у) = уг(в;'-в,-')у + 2(м/7'в,-'-м/в;') у +
В,
In ‘ +21п
. В/
Р(П,)
0</<J<L-l, (4.25)
и являются, очевидно, квадратичными функциями. Такие границы называ-
ются гиперквадриками (гиперсферы, гиперпараболы и т.д., пример их приве-
ден на рис. 4.6в), а сам классификатор называется квадратичным.
4.4.2. Вычисление вероятностей ошибочной классификации для нормально
распределенных векторов признаков
Эффективность любого классификатора характеризуется вероятностями
ошибок. Однако их нахождение в общем случае оказывается достаточно слож-
ной задачей, поскольку требует вычисления многомерных интегралов:
Pij = f p(y/Qt)dy, = (4.26)
D,
При использовании классификатора Байеса, который является классифи-
катором отношения правдоподобия, многомерный интеграл (4.26) может быть
заменен одномерным от плотности вероятностей отношения правдоподобия
Лу в каждом из классов. В частности, в случае двух классов для вероятностей
ошибок имеем следующие выражения:
+оо X
Ро = f Pa(u/qo)^ Pl = f PA^/^du,
X -oo
(4.27)
где
1 ' rtva.)
— пороговое значение. Плотность вероятностей отношения правдоподобия
удается найти далеко не всегда. Однако, когда случайный вектор Y имеет
нормальный закон распределения, это может быть сделано.
264
ГЛАВА 4
Пусть вектор признаков в каждом из двух классов характеризуется нор-
мальным законом распределения, причем все корреляционные матрицы яв-
ляются равными В/=В (/ = 0,1). Тогда случайная величина А = 1п(Л(У))
имеет нормальный закон распределения с параметрами:
£{л/П0} = Е{1п(л(У))/П0} = -1р(М0,М,),
Е{л/П|} = Е{1П(л(¥))/П,} = 1р(М0,М1),
Е 1((Л/П,) - Е{Л/П, })21= р(М0,М,), I = 0J,
(4.28)
где р(м0,м,) — расстояние Махаланобиса между векторами средних Мо и
М,. Таким образом законы распределения Л в каждом из классов отличают-
ся лишь математическими ожиданиями, причем Е{a/Q, } = —Е{a/Q0} . В этом
случае плотности вероятностей искомой случайной величины выглядит так,
как показано на рис. 4.7.
Выражения для вероятностей ошибок (4.27) преобразуются к следующему
виду:
— 1 — £+1р(м0.м,) п — <Ь Х-|р(М0,М,) (Л
ко 1 w 7р(М0,М,) ’ Р\ 7р(М0,М,)
где Ф(...) — функция Лапласа, а
Л, = In А. = In
Р(П0)(с01 —Срр)
k ^*(^1)(с10 ~ с11) ,
— новая пороговая величина (рис. 4.7). В частном случае, когда матрица штра-
фов является простейшей, и априорные вероятности классов совпадают, имеем
2
Х = 1, Х = 0, Ро = 1-ф |7р(Мо-М|) • Р|=ф ~Vp(mo.mi) •
Общий риск при этом определяется формулой
/? = 1-Ф-7р(М0,М,)
12
(4.29)
и монотонно убывает с ростом расстояния Махаланобиса между векторами
средних.
4.4. Классификатор Байеса для нормально распределенных векторов признаков
265
Рис. 4.7. Плотности вероятностей логарифма отношения правдоподобия для нормально распре-
деленных векторов признаков с равными корреляционными матрицами
Минимаксный классификатор. Предположим, что матрица штрафов имеет
следующие элементы: с0! = cl0 =с, cw = сп =0. Тогда соотношение (4.17) для
выбора разделяющей границы классификатора Байеса, соответствующего ми-
нимаксной стратегии, превращается в равенство вероятностей ошибочной клас-
сификации: р0 = р{. С учетом выражений (4.28) получаем, что пороговое зна-
чение для минимаксного классификатора 1 = 1, 1 = 0.
Классификатор Неймана—Пирсона. Используя условие (4.18) и равенства
(4.28), получаем, что пороговое значение классификатора Неймана—Пирсона
определяется по формуле
Х = е\ Х = -1р(М0,М,)+7р(М0,М|)ф-|(1-р;), (4.30)
где pl — заданная величина вероятности ошибки первого рода.
4.5. Основные группы признаков, используемых
при распознавании изображений
Построение описания изображения на основе его представления с исполь-
зованием признаков — едва ли не самая сложная задача в процессе построе-
ния любой системы распознавания. При этом, если в рамках некоторых мате-
матических моделей удалось формализовать процесс классификации, то про-
цесс выбора признаков до сих пор остался процедурой эвристической и
зависимой как от предметной области, так и от разработчика. В то же время
определенный опыт, накопленный за годы использования средств распоз-
навания образов и обработки изображений для решения практических за-
дач, позволяет выделить ряд основных групп признаков, которые успешно
266
ГЛАВА 4
используются для описания и распознавания изображений. Принятая ниже
классификация признаков на группы отражает специфику подходов, на осно-
вании которых производится их построение.
4.5.1. Геометрические признаки
К этой группе относятся те признаки, расчет которых основан на использо-
вании геометрических характеристик представленных на изображении объек-
тов. Это могут быть, например, следующие признаки:
- геометрические размеры изображенного объекта по вертикали или гори-
зонтали,
- расстояние между наиболее удаленными точками на изображенном объекте,
- периметр и площадь изображенного объекта,
- компактность объекта (как соотношение между его площадью и пери-
метром),
- числовые характеристики описанных или вписанных в изображение объек-
та геометрических фигур, таких как окружности, многоугольники, и т.д.
Достаточно специфическими, но широко используемыми в геометричес-
кой группе являются признаки, связанные с представлением геометрии кон-
тура объекта. Как известно контур — одна из наиболее важных характерис-
тик изображенного объекта при его восприятии человеком. Поэтому описа-
ние контура — одна из распространенных задач, решаемых в обработке
изображений. К наиболее типичным методам описания контура, используе-
мым также и для решения задач распознавания, относятся следующие.
Цепные коды. Метод цепного кодирования для представления контура объек-
та был предложен Фриманом. Он заключается в том, чтобы границу объекта,
расположенного на дискретной сетке, представить в виде набора элементар-
ных отрезков. Тогда полной характеристикой границы в каждой точке явля-
ется направление требуемого отрезка (см. рис. 4.8а). В данном случае предпо-
лагается, что точки на границе являются только 4-х связными (отрезок откла-
дывается лишь в 4-х направлениях). Иногда применяют модификацию данного
метода, использующую 8-связную модель, как на рис. 4.86
Несомненным достоинством представления границы изображаемого объекта
цепным кодом является простота реализации алгоритма его описания, про-
стота получения на основе этого описания некоторых других геометрических
характеристик объекта (например: периметр, площадь, линейные размеры по
вертикали и горизонтали), возможность достижения инвариантности описа-
ния к преобразованиям подобия — масштабированию изображения, его пере-
носу и повороту. Основным недостатком является высокая неустойчивость
получаемых описаний к искажениям в изображениях.
Приложение непрерывных моделей к задаче представления дискретного
контура позволило получить ряд практически полезных описаний.
Ортогональные представления функции кривизны. Рассматривая угол накло-
на к касательной контура как периодическую функцию некоторой перемен-
4.5. Основные группы признаков, используемых при распознавании изображений
267
Рис. 4.8. Примеры построения цепного кода: а — 4-связная модель границы; б — 8-связная
модель границы
цепной код: 1023245577
ной, k(s) = k(*i (л), х2(л)), можно получить представление контура в виде
ряда, коэффициенты которого вычисляются:
cK=-J
L о
(4.31)
где {ф* (л )} набор ортонормированных или ортогональных функций на [0, L],
1 L
L о
L — периметр объекта. В качестве функций <p*(s) чаще всего используют
комплексную экспоненциальную функцию:
<рДл) = ехр
.2л
—I—sk
L
В этом случае говорят о представлении контура в виде ряда Фурье, а коэффи-
циенты Хк называют фурье-дескрипторами данного контура.
Описание (4.31) обладает свойствами инвариантности к преобразованиям
подобия. Однако для его использования необходимо получить промежуточ-
ное представление контура в виде функции к(а), которое само по себе явля-
ется его характеристикой. Это может быть сделано различными способами, в
частности с помощью у-кривых.
у-кривые. Представление контура объекта с использованием у-кривой ос-
новано на аппроксимации прямолинейных участков границы объекта в виде
отрезков ломаных, а области изменения направления границы — в виде дуг
окружностей (см. рис. 4.9).
В этом случае периодическая функция к(^) оказывается представлена пря-
молинейными горизонтальными участками и короткими кривыми, соответ-
ствующими областям изменения направления границы. При надлежащем по-
строении у-кривых можно также добиться инвариантности к преобразованиям
268
ГЛАВА 4
Рис. 4.9. Представление контура объекта у-кривой
подобия (например, выби-
рая в качестве начального
отрезка самый длинный или
самый короткий ит.д.).
Сплайн-аппроксимация
границы. Аппарат сплайнов
достаточно широко исполь-
зуется для практических
приложений, в частности,
для решения задачи описа-
ния границы. Суть метода
сплайн аппроксимации —
представления границы
объекта в виде кусочно-по-
линомиальной функции ча-
сто с выполнением ряда ог-
раничений, накладываемых
на ее гладкость. Наиболее
популярными являются сплайны третьего порядка, поскольку обладают наи-
меньшей степенью, при которой полиномиальная функция может менять знак
кривизны. Последнее позволяет добиться определенной гладкости в точках
соединения сплайнов за счет равенства первых производных в этих точках.
При использовании наиболее простого задания к(л) в виде горизонталь-
ных прямых с разрывом в точках изменения направления границы, получаем
представление контура в виде полилиний — соединяющихся между собой от-
резков прямых, см. рис. 4.10. Точки разбиения полилинии выбираются, исхо-
дя из соображений наилучшего представления контура.
Надо отметить, что изложенные методы и алгоритмы далеко не исчерпывают
весь комплекс методов представления контура объекта для его расположения, но
являются наиболее часто используемыми в практических приложениях.
В заключении рассмотрения группы геометрических признаков укажем их
основные свойства применительно к задаче распознавания. К ним относятся:
- возможность обеспечения инвариантности к преобразованиям подобия
изображенного объекта;
- низкая помехоустойчивость.
Рис. 4.10. Представление контура объекта полилинией
4.5. Основные группы признаков, используемых при распознавании изображений
269
Эти два основных свойства позволяют говорить о том, что геометрические
признаки могут использоваться в задачах распознавания, которые характери-
зуются:
- объектами с ярко выраженной геометрической структурой (границей);
- малым уровнем шумов и динамических искажений.
4.5.2. Топологические признаки
К данной группе относятся те признаки, которые характеризуют топологи-
ческие свойства изображенного объекта. Под топологическими свойствами
понимают те свойства, которые остаются инвариантными относительно то-
пологических или гомеоморфных отображений. Последние подразумевают под
собой взаимнооднозначные непрерывные (прямые и обратные) отображения.
В связи с этим топологические признаки оказываются априорно инвариант-
ными к широкому спектру геометрических преобразований: преобразовани-
ям подобия, аффинным преобразованиям и многим другим. В то же время
подобная общность признаков делает их достаточно неинформативными, так
как многие обладающие различной геометрией объекты оказываются нераз-
личимыми в рамках топологического описания. Такими, например, являются
объекты, изображенные на рис. 4.11.
Кроме того, топологических признаков относительно немного, и их рас-
чет, как правило, достаточно сложен. Приведем некоторые из них.
Число связных компонентов объекта — это такое минимальное число ком-
понентов, составляющих объект, в каждом из которых любые две точки мо-
гут быть соединены линией, полностью содержащейся в том же компонен-
те. Примеры объектов, состоящих из различного числа компонентов, при-
ведены на рис. 4.12.
Число «дыр» в объекте — характеризует число связных компонентов, не
принадлежащих объекту, но находящихся внутри него. Так на рис. 4.12л чис-
ло «дыр» равно трем.
Число Эйлера — вычисляется как разность между числом связных компо-
нентов объекта и числом «дыр» на нем. Для объекта на рис. 4.12в число Эйле-
ра равно (—2).
Рис. 4.11. Пример топологически неразличимых объектов
270
ГЛАВА 4
Рис. 4.12. Примеры топологически различимых объектов: а — однокомпонентный объект, б —
трехкомпонентный объект, в — двухкомпонентный объект
Суммируя все вышесказанное, можно утверждать о том, что топологичес-
кие признаки применительно к задаче распознавания на изображениях могут
быть использованы лишь в редких случаях и лишь при малом уровне искаже-
ний, связанных с исчезновением или появлением частей объектов.
4.5.3. Вероятностные признаки
Название этой группы признаков отражает характер модели, используемой
для описания функции яркости на изображении. А именно, на функцию яр-
кости смотрят как на реализацию (стационарного) случайного процесса или
процессов (для цветных изображений) (см. п.1.8). В этом случае признаками
изображения являются числовые характеристики случайного процесса. К наи-
более часто используемым относятся (для справки см. п.1.8):
- яркостные характеристики, такие как гистограмма распределения зна-
чений яркости на изображении, начальные щ и центральные тц моменты
функции яркости
Мд = *{/*(")}> Пд =£{(/(»)-Hi)‘}.
где gj =Н/ — среднее значение функции яркости на изображении;
- текстурные характеристики изображения, к которым относятся характе-
ристики случайного процесса, определяющие его корреляционные свойства,
такие как коэффициент корреляции на изображении, корреляционная функ-
ция изображения и др.;
- энергетические характеристики изображения, к которым относятся от-
счеты его энергетического спектра;
- признаки стохастической геометрии. Данные признаки характеризуют
случайные величины, связанные с наступлением каких-либо геометричес-
ких событий. Наиболее часто используемой схемой их генерации является
случайное бросание прямой линии на плоскость изображения и вычисле-
ние некоторых характеристик, связанных с событием пересечения этой
4.5. Основные группы признаков, используемых при распознавании изображений
271
линией области объекта. Например, это
может быть число пересечений объекта ли-
нией, максимальная или минимальная дли-
на отрезка линии, содержащейся в объек-
те, суммарная длина отрезков линии, на-
ходящихся в области объекта, и т.д. (см.
рис. 4.13). Вероятностные характеристики
таких случайных величин некоторым обра-
зом описывают форму объекта. Причем, в
силу случайности положения линии, дос-
тигается инвариантность к смещениям и
поворотам изображения. Более того, при
Рис. 4.13. Схема генерации признаков
стохастической геометрии
их помехоустойчивость и воз-
надлежащем построении характеристик мо-
жет быть достигнута инвариантность к мас-
штабу. Несомненным достоинством таких
признаков являются относительно высокая
можность достаточно простой автоматизации процесса наращивания числа
таких признаков.
В то же время, несмотря на целый ряд преимуществ, признаки стохасти-
ческой геометрии редко используются в распознавании изображений. Связа-
но это, в основном, с двумя причинами:
- высокой вычислительной сложностью расчета признаков;
- отсутствием явной геометрической интерпретации получаемых значений
признаков.
4.5.4. Спектральные признаки
К данной группе относятся те признаки, процесс получения которых ис-
пользует спектральную модель преобразования изображения:
Л^—I Л/2—1
g(/ni, т2) = 22 £ 7(ni’ n2> wi’
Л|=0 л2=0
Характер функций W (•), называемых ядрами преобразования, может быть
достаточно произвольным. Наиболее типичными являются следующие ядра и
соответствующие им преобразования.
Разложение Карунена—Лоэва (в форме Хотеллинга). Пусть для описания
функции яркости исходного изображения используется модель дискретного
случайного поля /(л],л2) с нулевым математическим ожиданием и извест-
ной корреляционной функцией
/?(zn1,m2,ni,n2) = A/[/(m|,m2)/(n1,n2)]
272
ГЛАВА 4
Тогда ядро преобразования Карунена—Лоэва имеет следующий вид:
W («j, п2, тщ, т2 ) = >m2 (Л), п2),
где т (пьп2) — собственные векторы корреляционной матрицы
R(mitm2tnitn2), вычисляемые из соотношения
А,-1А2-1
П|=0л2=0
т2 — собственные значения корреляционной матрицы R(mi,m2,ni,n2),
равные дисперсиям соответствующих признаков.
Основным достоинством разложения Карунена—Лоэва является наличие
ряда свойств оптимальности рассчитываемых признаков. А именно:
- концентрация мощности (дисперсии) в минимально возможном числе
признаков,
- минимальная среднеквадратичная погрешность восстановления исход-
ного изображения при заданном числе признаков,
- некоррелированность, а в случае нормального распределения яркости
исходного изображения и независимость, рассчитываемых признаков.
Отмеченные свойства позволяют решить задачу выбора минимального на-
бора признаков при заданной погрешности распознавания/классификации.
Главным недостатком признаков Карунена—Лоэва является отсутствие
быстрых алгоритмов их формирования. Кроме того, для получения оптималь-
ных результатов необходимо точное знание корреляционной функции исход-
ного изображения.
Определенную сложность представляет также проблема нахождения соб-
ственных векторов и собственных значений корреляционных матриц боль-
ших размеров. Так при размерах исходного изображения AjXN2 в общем
случае необходимо решать проблему собственных значений для матрицы раз-
мером
Однако известно, что для стационарных, в широком смысле, полей изоб-
ражений асимптотически (при увеличении размеров исходного изображения)
оптимальной аппроксимацией преобразования Карунена—Лоэва являются
преобразование Фурье и косинусное преобразование, рассмотренные ниже.
Фурье-преобразование (фурье-признаки изображения) имеет вид
;2Л[Я|т' | П2ОТ2 1
W(nj, и2,/Ир m2) = e N' N1. \
Данное преобразование позволяет получить спектр изображения, характе-
ризующий его на различных пространственных частотах. К достоинствам фу-
рье-признаков относятся существование быстрых алгоритмов их формирова-
4.5. Основные группы признаков, используемых при распознавании изображений
273
ния — БПФ (см. п. 1.7.7), полноту описания изображения (преобразование
обратимо), помехоустойчивость. К недостаткам — отсутствие инвариантнос-
ти к целому ряду геометрических преобразований, в том числе к преобразова-
ниям подобия.
Косинусное преобразование (косинусные признаки) имеет вид
, х (2/?, Н-1)/г/.) (2л, -Ь1)?и,
V I ^1 I N2 j
Достоинства и недостатки данного представления те же, что и для фурье-
признаков.
Преобразование Радона — наиболее часто встречающийся вид преобразо-
вания:
W(n|, п2, тх, —— Л]СО5Л1| — л28тлП]).
Суть преобразования — перевести линейные объекты, присутствующие на
изображении /(«,, п2), в точечные объекты в пространстве признаков — в
образ . Действительно, для непрерывного аналога преобразования
J f /(^,x2)8(^2“X1cos^1-x2sin^l)dr1Jx2 (4.32)
—оо—оа
линия, задаваемая в координатах входного изображения (х,,х2) уравнением
^2 =А', COS^] + х2 sin^],
перейдет в точку ^2) на изображении образа. При этом параметры и
^2 играют роль угла наклона прямой и расстояния от начала координат
(£2), как показано на рис. 4.14.
Легко заметить, что преобразование (4.32) эквивалентно интегрированию
изображения вдоль соответствующей прямой:
ос
X], -^-^Ctg^ dxx.
< cosSi
Иллюстрация преобразования Радона для изображения представлена на
рис. 4.15.
Признаки, вычисляемые с использованием преобразования Радона, за счет
нескольких дополнительных несложных преобразований над образом g(m{,m2}
могут быть сделаны инвариантными к преобразованиям подобия. Более того,
они достаточно помехоустойчивы и существуют алгоритмы их быстрого вы-
числения, базирующиеся на алгоритме БПФ. Все это позволяет утверждать о
274
ГЛАВА 4
Рис. 4.14. Соответствие изображения линии и ее образа в преобразовании Радона: а — изобра-
жение линии; б — образ линии
достаточной перспективности их использования в задачах распознавания изоб-
ражений.
Полиномиальные моменты имеют вид
/Л| /л2
№(т1э m2,nit n2) = 5252aijn'\n2 .
i-0j=0
Здесь а- — некоторые коэффициенты полиномиального ядра. Чаще всего
при распознавании на изображениях ограничиваются степенными моментами
Нт,т2» для которых
О, i или j ^т2,
1, i = mx и j = m2.
Они рассчитывается по формуле
/V|/2 N2/2
Pij= 52 52 n[nif(nlt п2).
(4.33)
nl=—Nl/2 n2=-N2/2
Популярность степенных моментов обусловлена тем, что на их основе
формируются так называемые моментные инварианты, имеющие вполне опре-
деленный физический смысл. К ним, например, относятся следующие:
Ф| =Н2О+НО2 . *2=(H2O-MO2)2+4U?|.
Фз—(Изо Зц12) +(3р.2| Моз) > Ф4 — (Изо +М12) "Ь(М21 "ЬИоз) •
4.6. Некоторые алгебраические методы в задачах распознавания изображений
275
Рис. 4.15. Преобразование Радона: а — исходное изображение; б — результат преобразования
В частности задает момент инерции двумерного объекта, Ф2 с точно-
стью до масштабного множителя (1/Ноо) определяет эксцентриситет (удлине-
ние) объекта ит.д.
Инвариантность указанных характеристик распространяется на преобра-
зования типа поворота. Также можно добиться инвариантности моментных
характеристик к более общим преобразованиям, в частности к аффинным
преобразованиям. Более подробно эти вопросы рассмотрены в главе 9.
4.6. Некоторые алгебраические методы в задачах
распознавания изображений
4.6.1.0 статистическом и детерминированном подходах к задачам анализа
изображений
Использование непрерывных моделей с необходимостью вынуждает ис-
следователя использовать теоретико-вероятностный или статистический ап-
парат для оценки качества алгоритмов, степени адекватности модели и т.д.
Первопричина этого достаточно ясна: для множества действительных или
комплексных чисел не существует, по всей видимости, математических
средств «индивидуализации» свойств (не величины!) этих чисел и можно
говорить только о «мере типичности» тех или иных вещественных или ком-
плексных атрибутов изучаемого объекта, то есть, о его вероятностных ха-
рактеристиках. Последовательное применение вероятностного подхода с не-
обходимостью приводит к представлению о часто уникальном объекте как о
рядовом представителе некоторого гипотетического (бесконечного) множе-
ства ему подобных, но не заданных реально. В этом случае «уникальность»
276
ГЛАВА 4
имеет нулевую меру во множестве «типичностей», и достоверность решения
прикладной задачи может быть оценена только экспериментально, часто в
сравнении со специально сконструированными тестовыми ситуациями, ко-
торые, в свою очередь, являются тестовыми лишь в предположении об адек-
ватности выбранной модели.
Значительным шагом вперед в понимании алгоритмов распознавания как
«точек» в некоторой алгебраической структуре со специфическими операци-
ями, отношениями, топологическими свойствами явились работы 60-х годов
отечественных математиков, приведшие, в частности, к созданию нового на-
правления в теории распознавания образов — алгебраической теории распоз-
навания. Разработанный в работах Ю.И. Журавлева [11] и его учеников фун-
даментальный алгебраический подход к решению задач распознавания обра-
зов представляет собой, прежде всего, метатеорию, позволяющую корректно
работать с некорректными (эвристическими) алгоритмами. Эвристический
алгоритм распознавания интерпретируется в этой метатеории как элемент
некоторой топологической алгебры.
К сожалению, алгебраическая поддержка конкретных эвристических алго-
ритмов оставляет желать лучшего. Отчасти это объясняется традициями ис-
пользования непрерывных моделей для решения дискретных задач. Это по-
нятно: многие задачи «непрерывной» математики и вычислительно проще
для решения, чем их дискретные аналоги, и используют более привычный
для практика математический аппарат.
Между тем именно в задачах, связанных с обработкой и распознаванием
цифровых (дискретных) изображений, применение детерминированного диск-
ретного математического аппарата является не только желательным, но и ре-
зультативным. Не задаваясь целью дать формальное определение понятию «изоб-
ражение», мы считаем, что его непременными атрибутами являются интерпре-
тируемость семантических связей и структурная избыточность. Первый из этих
атрибутов определяет разную степень информативности отдельных особеннос-
тей изображения для наблюдателя и интерпретируется, в большинстве случаев,
как некие геометрические характеристики или объекты-примитивы. Второй
можно интерпретировать как существование некоторой локальной доминанты
в окрестности каждой или большинства точек изображения (например, изоб-
ражение «ведет себя» подобно линейной функции).
В пользу этого прежде всего говорит анализ механизма зрения — способ-
ности живых организмов получать информацию от окружающей деятельнос-
ти за счет падающего на них света. Задача аппарата зрения — распознавание
внешних ситуаций для выбора целесообразного поведения. При рассматрива-
нии человеком некоторого объекта детали, привлекающие внимание, пооче-
редно проецируются на центральную зону сетчатки глаза, обладающую мак-
симальными информационными возможностями. На рис. 4.16 показана за-
пись движений глаза при свободном рассматривании в течение двух минут
портрета девушки [18, стр.96]. Эта запись является экспериментальным сви-
детельством в пользу того факта, что при решении задачи распознавания че-
4.6. Некоторые алгебраические методы в задачах распознавания изображений
277
ловек, прежде всего, руководствуется геометрическими особенностями изоб-
ражения как многомерного объекта.
Статистический подход к решению задач распознавания полностью игно-
рирует геометрические особенности изображения как многомерного сигнала.
Альтернативой этому является разработка методов анализа изображений, чув-
ствительных к уникальным геометрическим свойствам конкретного изобра-
жения. В этом случае используемый математический аппарат, поддерживаю-
щий такие методы, должен ставить в соответствие уникальным геометричес-
ким свойствам не менее уникальные свойства той алгебраической структуры,
которая используется как альтернатива полю действительных или комплекс-
ных чисел. Создание такого гипотетического математического аппарата пред-
ставляется в настоящее время перспективной задачей, а строгое обоснование
первых результатов в указанном направлении выходит далеко за рамки дан-
ной книги. В частности, в работах [24]—[26] в качестве альтернативных алгеб-
раических структур использовались целые, рациональные или алгебраичес-
кие числа, построение которых, в отличие от вещественных чисел, является
не топологическим, а чисто алгебраическим, и ко-
торые наследуют уникальные арифметические свой-
ства порождающих их алгебраических уравнений.
В качестве примеров, иллюстрирующих эф-
фективность намеченного подхода, в данном раз-
деле рассматриваются три связанные между со-
бой задачи.
1. Выделение локально-симметричных компо-
нентов (примитивов) из фрагментов изображений
при известной группе преобразований, относительно
которой объект-примитив инвариантен. Эта задача
может быть решена как в форме, позволяющей ви-
зуально выделить объект, так и позволяющей сфор-
мировать признаковое пространство и синтезиро-
вать алгоритм распознавания. В качестве альтерна-
тивной алгебраической структуры предлагается
многомерное пространство, ассоциированное с не-
которым полем алгебраических чисел.
2. Кластеризация объектов в признаковых про-
странствах, построенных при решении предыдущей
задачи, может быть существенно более сложной, чем
при традиционном подходе, а уравнение разделяю-
щей гиперповерхности — достаточно сложным. Аль-
тернативным решением в этом случае является за-
мена отношений «больше —меньше» для обычных
разделяющих поверхностей иными, но легко ана- Рис. 4.16.
лизируемыми, бинарными отношениями.
3. Выбор в качестве альтернативных структур числовых полей с «ярко выра-
женной индивидуальностью» элементов увеличивает теоретические ресурсы
278
ГЛАВА 4
распознающих алгоритмов, но делает их весьма чувствительными на практи-
ке к ошибкам представления входных данных (неустойчивыми). Необходи-
мые теоретические гарантии устойчивости полиномиальных решающих пра-
вил могут быть получены с привлечением известных фактов теории диофан-
товых приближений.
В разделах 4.6.2—4.6.4. данной главы рассматриваются некоторые подходы
к решению указанных выше задач.
4.6.2. Резонансный метод выделения геометрических примитивов
Реальное изображение есть, как правило, функция X(z,, t2) двух непре-
рывных аргументов. Переход к цифровому изображению (дискретизация)
ф: X (/j, ?2)ь->х:(п1, п2), (пр n2)eZ2,
включает в себя вычисление значений
«1 = (rt, ?2), п2 =n2(fp t2).
Природа функции ф известна специалисту-обработчику далеко не всегда,
и он работает с функцией x(np п2) (цифровым изображением) как двумер-
ным массивом данных — функцией, заданной на дискретной решетке (на-
пример, Z2). Визуализация этого дискретного массива представляет собой
уже кусочно-постоянную аппроксимацию исходного изображения Х(г,, г2),
узлы которой ассоциированы с рассматриваемой решеткой, выбираемой, во-
обще говоря, из соображений простоты записи и хранения информации и
никак не связанной с теми соотношениями инвариантности объекта на изоб-
ражении, выделение или распознавание которого предполагается в конкрет-
ной задаче. Мы покажем, что переход от «канонической» решетки Z2 к
другой, природа и свойства которой адекватны геометрическим свойствам
объекта, позволяет визуализировать распознаваемый объект или его как часть
некоторое бинарное изображение (бинарный примитив).
В основе рассматриваемого подхода лежит две связанные между собой идеи.
Первая идея. Пусть и2) — бинарное изображение:
X — const0, при пеДсХ2;
О, при п^Д,
где % д — характеристическая функция (индикатор) некоторого множества Д с Z 2.
Пусть известно достаточно много преобразований Тк, ( к = 1, 2, ..., К) относи-
тельно которых множество Д инвариантно. Тогда справедливо равенство
1 К
Мх(п) = —12х(ткп)= *(п)- (4-34)
К к=\
х(п) = ЛХд(п)
4.6. Некоторые алгебраические методы в задачах распознавания изображений
279
Пусть теперь изображение х(п) представимо в форме
х(п) = Х/гд (п) + v (п),
где функция v(n) интерпретируется как «шум». Тогда
Мх(п) — х(п) + ^(п) (4.35)
и, при достаточно общих предположениях о функции v(n) и преобразова-
ниях Тк, отношение сигнал/шум у изображения Л4х(п) станет больше, чем
у изображения х(п). Другими словами, усреднение (4.34) «подчеркивает»
инвариантный компонент, и «гасит» неинвариантный компонент (своеоб-
разный «резонанс»). Это соображение приводит к представлению изображе-
ния как суммы интересующего объекта и «всего остального». И основная
трудность состоит в отыскании таких преобразований Тк, относительно ко-
торых объект инвариантен, а «фон» преобразуется в некотором смысле «слу-
чайным образом».
Вторая идея. Свяжем с каждой точкой (и,, п2)е^2 комплексное число
г — «j +in2 бС. Пусть У],у2, ...» Yj — алгебраические иррационально-
сти. При фиксированном целом q рассмотрим множество точек
Yi+••• + «</ Ya); «и •••> ad
и поставим в соответствие точкам z = +in2 «достаточно близкие» точки
множества A(J . Иными словами, закодируем пары аргументов (п{, п9) точ-
ками множества Ад , то есть, в конечном счете, векторами (cg/q, ..., ad/q}
многомерного пространства. Элементы множества А^ — алгебраические
числа, для которых достаточно хорошо изучены «естественные» преобра-
зования, инварианты и связь с геометрическими свойствами. Именно из
этих «естественных» преобразований будем выбирать преобразования Тк,
действующие не на аргументы (и,, н2), а на их многомерные коды. Под-
робное обоснование рекомендаций по выбору конкретного выбора пара-
метров (у,, ..., у^; d, q) выходит за рамки книги (см., например, [24]).
Мы ограничиваемся в данном разделе лишь несколькими примерами.
Пример 4.1. На рисунке 4.17 представлено оригинальное изображение «Ва-
шингтон», из которого требуется выделить «пентагональный компонент» при
условии точечного и кусочно-постоянного зашумления (рис. 4.18а).
Пусть у = ехр{2711/5}; кодирование пар (пг и2) при подходящем q произ-
водится числами вида q~x [atf + a2y2 4-а3у3 + а4у4).
В качестве преобразований кодов рассматриваются линейные продолже-
ния отображений
Tjiy-^y, Т2:уь->у2, Т3:уь->у3, Г4:у.->у4.
280
ГЛАВА 4
Рис. 4.17. Исходное изображение «Вашингтон»
Результаты выделения пентагонального компонента представлены на
рис. 4.186— 4.18г.
Пример 4.2. Исходное изображение ордена Святой Анны (рис. 4.19а) под-
вергается зашумлению и нелинейным геометрическим искажениям
(рис. 4.196). Задача состоит в выделении компонентов с четырьмя осями сим-
метрии. Кодирование точек (пи л2) производится числами
q ’ (6j+62z+63a + 64za),
где a = у/?. . В качестве отображений Тк рассматриваются линейные продол-
жения отображений, порожденных <7 и т , где
т(сс) = а, т(/) = —/, o(z) = z, o(a) = z'a.
Действия группы отображений
{ id, т, о, о2, о3, то, то2, то3}
на числа ос, a + az , az , az —а сведены в таблицу 4.1 и демонстрируются
на рис. 4.20.
4.6. Некоторые алгебраические методы в задачах распознавания изображений
281
а
в
Рис. 4.18. Пример выделения геометрического примитива: а — фрагмент зашумленного изобра-
жения; б — пентагональный компонент: центр «скользящего окна» не совпадает с центром сим-
метрии; в — пентагональный компонент: центр «скользящего окна» совпадает с центром сим-
метрии; г — бинаризация выделенного пентагонального компонента (бинарный примитив)
На рис. 4.21 с—г представлены фрагменты изображения рис. 4.196, а на
рис. 4.22а—г — соответствующие выделенные примитивы.
Пример 4.3. Исходное изображение — «Футболист» (см. рис. 4.23). Задача
состоит в «обнаружении мяча», то есть выделении из фрагментов изображе-
282
ГЛАВА 4
Рис. 4.19. Исходное изображение ордена Святой Анны (а); искаженное и зашумленное изобра-
жение (6)
ния эллипсоидальных компонентов с заданным эксцентриситетом Е. В каче-
стве кодирующих чисел берутся при D = d(e) числа
q~x (а, ; а, b, qC/Z,
а в качестве преобразований Тк — преобразования, сохраняющие значение
квадратичной формы
Г(х, у) = х2+£)у2; х,
Результаты выделения эллиптических компонентов из различных фрагмен-
тов изображения (рис. 4.24) представлены на рис. 4.25, соответственно.
Таблица 4.1. Результат действия отображений Тк
№ Отображения Элементы id т О a2 a3 TO to2 to3
1 а а а ia -a -ia -ia -a ia
2 a+ai a+ia a-ia ia-a -a-ia -ia+a -ia-a -a+ia a+ia
3 ей ia -ia -a -ia a -a ia a
4 сй-а ia-a -ia-a -a-ia -ia+a -a-ia -a+ia ia+a ia-a
4.6. Некоторые алгебраические методы в задачах распознавания изображений
283
Рис. 4.20. Действие отображений Тк на элементы а, а + а/, а/, а/ - а
284
ГЛАВА 4
Рис. 4.21. Фрагменты искаженного и зашумленного изображения
Рис. 4.22. Выделенные бинарные примитивы
4.6. Некоторые алгебраические методы в задачах распознавания изображений
285
Отметим инвариантность предложенного метода относительно поворота
эллиптического объекта.
4.6.3. Линейная разделимость классов в пространствах
с р-адической метрикой
Решение задачи классификации точек в пространстве признаков предпо-
лагает построение разделяющей поверхности, причем решение о принад-
лежности точек тому или иному классу принимается в результате сравнения
значения разделяющей функции с некоторым эталонным значением. Как
правило, это сравнение связано с бинарными отношениями «больше — мень-
ше» на множестве действительных чисел. Ясно, что указанные бинарные
отношения могут быть заменены иными, но подчиняющимися естествен-
ными «пользовательским» требованием к вычислительной сложности алго-
ритмов разделения.
1. Существование вычислительно простой процедуры проверки, находит-
ся ли значение разделяющей функции в точке и эталонного элемента (числа)
в данном отношении.
2. Существование достаточно широкого класса функций, значение кото-
рых в точках признакового пространства легко вычисляются.
3. Согласованность выбора класса разделяющих функций. Бинарного от-
ношения и свойств той (числовой) структуры, элементы которой интерпрети-
руются как точки признакового про-
странства.
Практик имеет дело с признако-
выми пространствами, координаты
точек которых — рациональные чис-
ла. После масштабирования их можно
считать целыми числами. Для целых
чисел, в отличие от рациональных,
кроме обычного отношения порядка
существует и частичное отношение
порядка, связанное с делимостью. Это
отношение делимости может быть ин-
терпретировано и в метрической фор-
ме, в терминах удаленности одной це-
лочисленной точки от другой.
Введем несколько понятий, отно-
сящихся к такой метрической трак-
товке делимости.
Рис. 4.23. Исходное изображение «Футболист»
286
ГЛАВА 4
Пусть х, у 6Z, р — простое число. Следуя, например, [3], определим р-ади-
ческое расстояние (метрику) между х и у равенством
Dp(x, у) = р-^->\
где vp (а) — так называемый р-адический показатель целого числа а, пред-
ставимого в форме
а = pVp{a)B, н. о. д (В, р) = 1,
то есть максимальная степень простого числа р, на которое делится целое
число а. Два числа тем «р-адически ближе», чем на большую степень р делит-
ся их разность.
Сформулируем еще два утверждения, известных как китайская теорема об
остатках [3] в не самой общей, но достаточной для рассматриваемого случая,
форме.
Китайская теорема об остатках. Пусть Р\,рк — различные простые числа
Р — Р\’Р1 Рк- Пусть дана система сравнений л^гДтодр,), -х =
= rk (mod р*).Тогда существуют такие целые ос,, •••,осл, что
x = ^a7r7(modP).
j=i
4.6. Некоторые алгебраические методы в задачах распознавания изображений
287
В терминах метрик Dp китайская теорема об остатках приобретает форму
так называемой аппроксимационной теоремы ([3, глава 18]).
Метрическая форма китайской теоремы об остатках. Пусть г(, rk eZ,
р^...,рк — различные простые числа. Тогда существует такие xeZ , что
справедливы неравенства
Dpi(xi, п),<р *, i = l, 2, •••, к.
Определение4.1. Пусть Q = Qj UQ2, &|» ^2 — дваконечныхнепере-
секающихся множества; © = ©’U©2 п£)2=ф) — некоторое конечное
множество р-адических метрик. Будем говорить, что множества Q, и &2
(локально) линейно разделимы относительно семейства метрик ©, если суще-
ствует такая гиперплоскость
Г (z) = Ао + Е= 0, (z= (z„ -,z„)e Z”),
J=O
что для любой точки х G (i = 1, 2) существует такая метрика Dpe(D‘, что
Ор(г(х), о)<р-’, (4.36)
а для любой точки у е Q \ Q( и любой метрики Dp G выполняется нера-
венство
оДг(у), о)>1.
(4.37)
Основным результатом данного раздела является следующее утверждение.
Теорема 4.1. Любые два конечных непересекающихся множества
Q,, Q2 CZ" локально линейно разделимы относительно некоторого семей-
ства р-адических метрик 2).
Конечно, неравенства (4.36) и (4.37) можно переписать в терминах отно-
шения делимости (или сравнения по mod р), но мы предпочли метричес-
кую формулировку, чтобы сделать более явной аналогию с «обычным» пред-
ставлением о разделимости множеств (классов) Q, и Q2 : точки одного
класса «близки», в некотором смысле, к гиперплоскости L(z) = 0 , а друго-
го «далеки».
Основой доказательства теоремы 4.1 является следующее вспомогательное
утверждение.
Лемма 4.1. Пусть Q2 cZ" — два конечных непересекающихся подмно-
жества целочисленной решетки Z", Q = Q!UQ2, и Qj={x,} —
одноточечное множество. Тогда существует такое простое Р\, что классы
Q, и Q2 линейно разделимы относительно метрики Dp[.
288
ГЛАВА 4
Доказательство. Пусть
й —{x/.} = |(xl*,---,x*); хк gZ; к = l, -,7v|,
Q( x' eZ| .
Рассмотрим множество А целых чисел:
А = (М,---,х'Д j = к = 2, 3,---,/vl.
I \ J J I J J
Тогда множество т(л) простых делителей чисел множества Л конечно.
Далее, для каждого вектора а, множество различных зна-
чений функций
./=|
также конечно и, следовательно, имеет конечное число простых делителей.
Поэтому найдется такое достаточно большое простое Р\, что справедливо
соотношение
F(x1? xJ-z-0 (modp]). (4.38)
Выбирая целое а° таким, чтобы при фиксированном ранее векторе а и
найденном простом рх выполнялось сравнение
L\ (xi)= ао + = 0(mod рх),
/=1
получаем
£|(ха) = 0 (modp,) при к = 1; (4.39)
Lx (хк) 0 (mod рх) при к 1. (4.40)
Действительно, если (4.40) не выполняется, то в силу (4.39)
Л(х*)-Ц(х,) = Г(х4), (х,) = 0 (modpi),
что противоречит соотношению (4.38).
Доказательство теоремы 4.1. Пусть Q,, Q2cZ" — два произвольных
конечных непересекающихся множества. Применяя лемму 4.1 к каждой
точке хЛ множества (Л = 1, 2,-Л^) получим множество простых
4.6. Некоторые алгебраические методы в задачах распознавания изображений 289
чисел = {pi,• • • pNf} и множество гиперплоскостей, (х) = 0, таких, что
равенство
4° (хл) = «о + Е«Х = °(mod р‘)’
7=1
справедливо тогда и только тогда, когда k=t. Аналогично, применяя лем-
му 4.1 к каждой точке ут множества Q2 (™ — t А2), получаем мно-
жество простых чисел (Р2 = и множество гиперплоскостей,
(у) = о, таких, что равенство
42)(Ут)=«о + Е«>У7 = ° (mod<7.v)
7=1
справедливо тогда и только тогда, когда т = $.
Воспользуемся аппроксимационной теоремой и найдем такие целые
Aj{j = 0,---,п), что для всех простых ptePp выполняются нера-
венства
(4.41)
О,Дд;, «})<<'. (4.42)
Из неравенств (4.41), (4.42) и метода построения гиперплоскостей
1^ (х) = 0, (у) = 0 следует, что гиперплоскость
L*(z) = До + £д;г; = О
является искомой.
Действительно, для любой точки хЛ eQj найдется такое простое (а
именно р = рк), что выполняется сравнение
r(xJ = ° (mod?*).
В самом деле, неравенства (4.41) равносильны сравнениям
(ду- — я'-) = 0 (mod pt). Поэтому для t= к имеем, при некотором целом Л,
L*(х*) = Ло + ЕAjxkj = «о + Е«*** + Pkh-® (modР,)•
7=1 7=1
10 - 9044
290
ГЛАВА 4
С другой стороны, для любой точки у т е Q2, при любом pt , анало-
гично, имеем при некотором ht
Ь’(У„) = Ао + Т.А)У" = ^o+t,^y'j + P,h, =
j=i ;=!
= ai+iajyj‘ (m^p) = L\(yn,)^0 (modp,).
/=i
Теорема доказана.
Парадоксальное, на первый взгляд, утверждение теоремы 4.1 не следует
воспринимать как утверждение о «линеаризации» теории распознавания или
как метод, существенно упрощающий построение разделяющей функции.
Вычислительные трудности не исчезают, они просто становятся другими.
Действительно, коэффициенты разделяющей гиперплоскости L* (z) = 0 —
целые числа, которые могут оказаться нереалистично большими. Кроме того,
большими могут оказаться и простые числа pt, qx, причем их величина оп-
ределяется не только координатами точек классов Qj и Q2, но и тем, на-
сколько «удачно угаданы» координаты векторов (af, ..., а^ = ак в лемме 4.1.
Эти вычислительные трудности частично преодолеваются рекурсивным пост-
роением разделяющей гиперплоскости, коэффициенты которой последова-
тельно уточняются в процессе обучения [25].
Смысл утверждения теоремы 4.1 приобретает более отчетливый характер,
если воспользоваться некоторой аналогией между понятиями и объектами
«непрерывной» математики и теории чисел, замеченной математиками еще в
XIX веке. Выпишем аналогичные понятия.
Теория чисел
1. Натуральный ряд чисел.
2. Арифметическая прогрессия
с модулем р.
3. Периодическая функция натураль-
ного аргумента с целым периодом р.
и так далее (см., например, [14]).
Математический анализ
1. Отрезок [0, 1] вещественной оси.
2. Отрезок [а/p, (а + 1)/р].
3. Функция, кусочно-постоянная на
отрезках [а/p, (а + 1)/р].
Произвольную достаточно гладкую разделяющую функцию можно ин-
терпретировать как «локально линейную» функцию (аппроксимацию соб-
ственной касательной в точке). Параметрическое семейство таких каса-
тельных, в свою очередь, можно интерпретировать как одну линейную функ-
цию, зависящую от параметра (координат точки) и линейно разделяющую
те точки классов Q, и Q2, которые «достаточно близки» к фиксирован-
ной точке.
Теорема 4.1, в силу отмеченной выше аналогии, может интерпретировать-
ся как «модулярная версия» локально линейного разделения классов, а ко-
4.6. Некоторые алгебраические методы в задачах распознавания изображений
291
нечность множеств Qj и Q2 позволяет заменить термин «локально линей-
ное» на «кусочно-линейное».
В заключение отметим, что существует «глобальная» версия доказанной
теоремы, в которой вместо семейства р-адических метрик берется одна мет-
рика, связанная с кольцом так называемых полиадических чисел Прюфера
[14], [27], [29].
Несмотря на отмеченные выше вычислительные трудности, предложен-
ный метод построения разделяющий гиперплоскости вполне работоспособен
практически. Ниже приводятся экспериментальные результаты по разделе-
нию точек текстурного изображения на два класса.
4.6.4. Рациональные приближения иррациональных алгебраических чисел
и теоремы устойчивости полиномиальных решающих правил
Вопрос об устойчивости тех или иных решающих правил является одним
из основных в теории распознавания образов. Именно устойчивость опреде-
ляет, в конечном счете, достоверность решения практических задач методами
данной теории. Однако большинство методов и алгоритмов в теории распоз-
навания имеют ярко выраженный статистический характер. Именно, про-
странство признаков наделяется метрикой (метрикой Махаланобиса, напри-
мер), ассоциированной с некоторой вероятностной мерой, относительно ко-
торой проводятся все алгоритмические построения. Полученные результаты,
сформулированные, как правило, в вероятностных терминах, могут, конечно,
интерпретироваться и как метрические, но относительно специфической не-
евклидовой метрики. Исследование метрического «евклидового» аспекта про-
блемы устойчивости решающих правил представляется в настоящее время
лишь перспективной задачей. Между тем, математическая теория (теория
диофантовых приближений), в рамках которой может быть проведено такое
исследование, не только существует, но и имеет весьма почтенную историю.
Рис. 4.26. Пример разделения точек текстурного изображения
ю*
292
ГЛАВА 4
Поэтому основная цель данного раздела состоит в получении следствий из
известных теорем теории диофантовых приближений в форме, достаточной
для анализа «детерминированной» устойчивости решающих правил.
Мы рассматриваем следующую основную проблему.
Проблема. Пусть Хи Y — два конечных непересекающихся подмножества
пространства V (классы объектов); функция F (v) разделяет классы:
F (у) > О при v е X и F (v) < 0 при v е Y. (4.43)
Существуют ли такие подмножества X*, У* с R" (%*d X, У*э Y), что F (v)
разделяет и множества X* и Y*?
Мы рассматриваем количественный метрический аспект сформулирован-
ной проблемы: на сколько можно «пошевелить» множества Хи У (то есть
найти X* z> X, Y* z> У и метрические связи между этими множествами), чтобы
полиномиальные функции F (v) из некоторого конечного множества по-пре-
жнему разделяли множества X*, У*?
Другими словами, насколько устойчивы решающие правила, ассоцииро-
ванные с разделяющими функциями данного класса полиномов?
Пусть, как обычно, Q — поле рациональных, R — поле действительных
чисел; К — произвольное вещественное поле алгебраических чисел. Пусть Eq,
Er, Ек — открытые «-мерные единичные кубы в Q, R и К полях, соответ-
ственно. S (х, р) — шар радиуса р с центром в точке х,
EQ(q)= r€£Q:r-
а, а
1 п
q q
Определение 4.2. Пусть v —(v,,...,vn)€Rn ; F(v) — многочлен от п пере-
менных с рациональными коэффициентами. Полином F(v) степени d> 1 бу-
дем называть разделяющим полиномом для множеств X, У сЕ0(<у) ,
(X А У = 0), если для него справедливо соотношение (4.43).
Определение 4.3. Пусть
5= U =4Р) us{.₽) с Ев.
<хЕХ
Разделяющий полином F(v) для X, УС^(д) называется локально ус-
тойчивым на множестве Eq, если для любого натурального числа q существует
Р — р(?)>0 такое, что полином F(v) разделяет множества 5^ и
Определение 4.4. Точную верхнюю границу р* (q) чисел г, таких что при
фиксированном q полином F(v) разделяет и $(?) будем называть
радиусом устойчивости полинома F(v). Если р*(<?) = fiq1 (Р > 0 — абсолютная
константа), то число t называется индексом локальной устойчивости.
Отметим, что чем больше индекс устойчивости, тем «менее устойчиво»
полиномиальное решающее правило.
4.6. Некоторые алгебраические методы в задачах распознавания изображений
293
Определение 4.5. Разделяющий полином F(y) будем называть слабо локаль-
но устойчивым, если существование множеств 5^ и 5’^ имеет место для
всех достаточно больших q > qQ.
Аналогично определяются понятия индекса и радиуса слабой локальной
устойчивости.
Конечно, если множества X и У конечны, то (слабая) локальная устойчи-
вость полинома F(v), как всякой непрерывной функции, является тривиаль-
ным следствием хрестоматийных теорем математического анализа. Однако, в
общем случае непрерывной функции эти теоремы утверждают только суще-
ствование множеств 5^ и s(-p\ Основная цель дальнейшей работы — полу-
чение точных оценок радиуса и индекса локальной устойчивости, справедли-
вых для некоторых классов разделяющих многочленов.
Основанием для оптимизма является арифметическая природа полиноми-
альных функций с целыми коэффициентами, в частности, тот факт, что кор-
нями многочленов с целыми (или рациональными) коэффициентами от од-
ной переменной являются числа с уникальными свойствами, а именно, ирра-
циональные числа, плохо приближаемые рациональными.
Отметим два предполагаемых и легко обосновываемых «из общих сообра-
жений» свойства индекса (слабой) локальной устойчивости.
Индекс (слабой) локальной устойчивости не меньше единицы.
Действительно, если t < 1, то единичный куб Eq(q) при некотором q
покрывается шарами устойчивости, и все проблемы распознавания сводятся
к процессу обучения для конечных множеств X, У с £q . К счастью для
теории распознавания образов (и, к несчастью для приложений) это невоз-
можно.
При фиксированном q индекс (слабой) локальной устойчивости является не-
убывающей функцией от степени d разделяющего полинома.
Действительно, большему значению d соответствует большее число «сте-
пеней свободы» (коэффициентов) у многочлена F (у). Вследствие этого возра-
стает количество разделяющих многочленов, специфичных именно для дан-
ных конечных множеств X, У и, поэтому, не являющихся разделяющими для
х'зх, У*э К
Конечно, приведенные соображения не могут являться формальными ар-
гументами в пользу сформулированных свойств. Строгие доказательства с
точными количественными формулировками могут быть получены на основе
известных фактов теории приближения вещественных чисел рациональными
(теории диофантовых приближений).
Одной из основных задач этой теории является изучение функции
ц(х,о)= min х——
' ’ о<р<ч q
для различных вещественных хе [0,1], то есть изучение вопроса о наилучшем
приближении вещественных чисел рациональными числами с ограниченным
294
ГЛАВА 4
знаменателем. Отметим, что неравенство ц(х, q) < q~' является тривиальным:
любая точка отрезка [0,1] удалена на расстояние, меньшее, чем ql от точек
решетки действительной оси с шагом q~'. Получение более точных оценок
для различных классов действительных чисел является весьма сложной зада-
чей и предметом исследований специалистов в теории чисел. Для нас суще-
ственно, что иррациональные корни полиномов с рациональными коэффи-
циентами (то есть алгебраические числа) «плохо» приближаются рациональ-
ными числами. Формулировки и доказательства теорем Лиувилля, Рота и
Хинчина, Левека, используемые в данном разделе для получения следствий
об устойчивости полиномиальных решающих правил и относящиеся к «клас-
сике» теории приближений алгебраических иррациональностей рациональ-
ными числами, приведены, например, в монографиях [12], [21].
Первая из теорем утверждает, что алгебраические иррациональности не
могут «слишком хорошо» приближаться рациональными числами, а именно,
если х — иррациональный корень полинома степени d с рациональными ко-
эффициентами, не имеющего рациональных корней, то ц(х, q) > q'd. Осталь-
ные теоремы посвящены уточнению количественной формы этого тезиса.
Предположим для простоты, во-первых, что X, Y с Eq (q) и что, во-вторых,
размерность признакового пространства уже предварительно понижена за счет
исключения несущественных признаков.
Пусть F(v) — разделяющий полином для X, Y с Eq (<?). Пусть для неко-
торого
г = (П, гъ г„)е EQ{q)
определены полиномы
Fj-^ = F(ri, ..., х, гу+1..., г„).
Тогда корни этих полиномов есть алгебраические числа, «удаленность»
которых от рациональных чисел гарантируется упомянутыми выше теорема-
ми теории диофантовых приближений. Количественные формулировки этих
теорем позволяют довольно просто получить некоторые следствия в отноше-
нии устойчивости полиномиальных решающих правил.
Теорема 4.2. (Следствие из теоремы Лиувилля). Если разделяющий много-
член не обращается в нуль в точках множества Eq , то индекс локальной
устойчивости не меньше степени d разделяющего полинома.
Утверждение следующей теоремы кажется парадоксальным: степень поли-
нома не участвует (!) в формулировке теоремы.
Теорема 4.3. (Следствие из теоремы К. Рота). Если разделяющий много-
член не обращается в нуль в точках Eq , то индекс слабой локальной устой-
чивости при любом 5 > 0 не меньше (2 + 8).
Следующая теорема утверждает существование таких «частых» решеток в
Eq , что индекс слабой локальной устойчивости многочлена, разделяющего
подмножества Хи Yэтих решеток, может быть сколь угодно близок к 1.
Теорема 4.4. (Следствие из теоремы Хинчина). Пусть ф(<?) — любая поло-
жительная функция целочисленного аргумента «у, такая, что ф(<у) —> 0, q -+ оо.
4.6. Некоторые алгебраические методы в задачах распознавания изображений
295
Тогда существует такая последовательность \mq| [q < mq j , что для разделя-
ющего многочлена, не обращающегося в нуль в рациональных точках множе-
ства Eq , выполняется неравенство
P*(^)>(p(q)(wzJ
Неформальная интерпретация последней теоремы в терминах теории рас-
познавания: есть ли вообще практический смысл в увеличении объема обуча-
ющей выборки? Приводит ли процесс обучения к радикальному повышению
«детерминированной» устойчивости? Ответ: да, приводит. Однако, этот про-
цесс может оказаться нереалистично сложным.
Основная идея доказательств теорем, сформулированных выше, иллюст-
рируется для л = 2 на рис. 4.27. Если функция F(v) — полином, то график
функции E(v) = 0 не может быть «слишком кривым». Если, кроме того, hx и
h2 «достаточно велики» (то есть корни полиномов F(rXix) и Е(х, г2) «плохо»
приближаются рациональными г2 и rj, что гарантируется соответствующими
диофантовыми теоремами, то график функции F(v) = 0 не может быть распо-
ложен «слишком близко» к узлам решетки Eq(<?). Следовательно, при подхо-
дящем значении г, определяемом параметрами rh r2, hx, h2, существует такой
шар радиуса г с центром в точке (г(, г2), что во всех его внутренних точках
функция F(v) принимает значения того же знака, что и в точке (rh г2).
Допущение, принятое выше, о рациональности координат точек множеств
X и Y является естественным при формировании множеств X и Y в процессе
наблюдений. На практике часто эти множества
формируются как результаты некоторых вычис-
лительных процедур, не обязательно приводя-
щих к рациональным результатам. Например, при
использовании в качестве признаков компонен-
тов дискретных фурье-спектров многомерных
сигналов (изображений), координаты точек мно-
жеств X и Y являются алгебраическими иррацио-
нальностями. Так как при машинном представ-
лении алгебраических чисел используется их ра-
циональная аппроксимация, то естественной
Рис. 4.27. Иллюстрация к теоре-
мам 4.2—4.4
задачей является получение метрических резуль-
татов о достаточной точности такой аппрокси-
мации при априорно известной «разреженнос-
ти» точек обучающей выборки. Это приводит к необходимости использова-
ния диофантовых результатов о приближениях алгебраических чисел
алгебраическими меньшей степени. Среди многочисленных известных тео-
рем такого рода отметим результат В. Левека ([21], теорема 8А), являющийся
обобщением теоремы Рота. Его следствием (аналогом теоремы 4.3), служит
следующее утверждение.
Теорема 4.5. Пусть К — вещественное алгебраическое поле; X, Y с Ек.
Тогда существует такие абсолютные эффективно определяемые константы Н
296
ГЛАВА 4
Рис. 4.28. (1) — зона локальной устойчивости; (2)—(3) — зоны слабой локальной устойчивости;
(4) — terra incognita
и р, зависящие только от подрешетки в Ек, на которой могут лежать точки
множеств X, Y, что при любом 5 > 0 радиус слабой локальной устойчивости
разделяющего полинома не меньше, чем р* = рЯ-(2+5).
Приведенные выше теоремы позволяют сформировать определенное пред-
ставление о целесообразности применения детерминированных и/или статис-
тических методов в задачах распознавания и об их оптимальном соотношении.
Действительно (см. рис. 4.28), для зоны (1) локальной устойчивости досто-
верность результатов распознавания с использованием полиномиальных разде-
ляющих функций имеет детерминированный характер, гарантируется теоре-
мой Лиувилля и не требует привлечения каких-либо вероятностных методов.
Исключительное поле деятельности для статистических методов — зона
(4). В зонах (2) и (3) слабой локальной устойчивости статистические методы и
критерии качества алгоритмов распознавания являются паллиативом, позво-
ляющим уменьшить объем обучения за счет перехода к «недетерминирован-
ному», вероятностному представлению о достоверности результатов распоз-
нающих алгоритмов. Отметим также, что в зонах слабой локальной устойчи-
вости возможно применение комбинированных методов с использованием
вероятностной информации о распределении «плохо аппроксимируемых»
иррационал ьносте й.
В частности, в работе [28] исследовалось распределение значений функ-
ции ц(х, q) как случайной величины. Количественные результаты о мере («ве-
роятности») плохо аппроксимируемых чисел среди всех действительных чи-
сел генерируют количественные результаты об устойчивости полиномиаль-
ных решающих правил в вероятностной формулировке. Такое использование
вероятностной информации представляется абсолютно нетрадиционным. Дей-
ствительно, с необходимостью следует, что качество (то есть устойчивость)
решающих правил связана не с какими-то априорными предположениями о
Литература к части 1
297
статистических свойствах массивов обучающих выборок, а с объективными
арифметическими (диофантовыми) отличиями действительных чисел от ал-
гебраических иррациональностей. Разумеется, практическое использование
этого подхода сопряжено со значительными техническими и теоретическими
трудностями, но представляется достаточно перспективным средством для
повышения качества решения задач распознавания.
Литература к части I
1. Анисимов Б.В., Курганов В.Д., Злобин В.К. Распознавание и цифровая
обработка изображений (М.: Высшая школа, 1983)
2. Ахмед Н., Рао К. Р. Ортогональные преобразования при обработке цифро-
вых сигналов (М.: Связь, 1980)
3. Ван дер Варден. Алгебра (М.: Наука, 1976)
4. Виттих В.А., Сергеев В.В., Сойфер В.А. Обработка изображений в авто-
матизированных системах научных исследований (М.: Наука, 1982)
5. Горелик А.Л., Скрипкин В.А. Методы распознавания (М.: Высшая школа,
1984)
6. Гренандер У. Лекции по теории образов: Синтез образов 1 (М.: Мир, 1979)
7. Гренандер У. Лекции по теории образов: Анализ образов 2 (М.: Мир, 1981)
8. Гренандер У. Лекции по теории образов: Регулярные структуры 3 (М.: Мир,
1983)
9. Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов (М.:
Мир, 1988)
10. Дуда Р., Харт П. Распознавание образов и анализ сцен (М.: Мир, 1976)
11. Журавлев К).И. Избранные научные труды (М.: Магистр, 1998)
12. Касселе Дж. Введение в теорию диофантовых приближений (М.: ИЛ, 1961)
13. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов (М.: Связь,
1979)
14. Постников А.Г. Введение в аналитическую теорию чисел (М.: Наука, 1971)
15. Прэтт У.К. Цифровая обработка изображений (М.: Мир, 1982, 2 т.)
16. Рабинер Р., Гоулд Б. Теория и применение цифровой обработки сигналов
(М.: Мир, 1978)
17. Ту Дж., Гонсалес Р. Принципы распознавания образов (М.: Мир, 1978)
18. Физический энциклопедический словарь, 2 (М.: Советская энциклопе-
дия, 1962).
19. Фу К. Последовательные методы в распознавании образов и обучении машин
(М.: Наука, 1971)
20. Фукунага К. Введение в статистическую теорию распознавания образов
(М.: Наука, 1979)
21. Шмидт В. Диофантовы приближения (М.: Мир, 1983)
22. Ярославский Л.П. Введение в цифровую обработку изображений
(М.: Советское радио, 1979)
23. Ярославский Л.П. Цифровая обработка сигналов в оптике и голографии:
Введение в цифровую оптику (М.: Радио и связь, 1987)
298
ГЛАВА 4
24. Chernov V.M. Schriftenreihe der Oesterreichischen Computr Gesellschaft 130 169
(1999)
25. Chernov V.M. Proc, of the 10th Scandinavian Conference on Image Analysis
(SCIA’97) (Lappeenranta, Finland, 2, 1997) P. 803
26. Chernov V.M. Diophantine Theorems on Stability of Polinomial Decision Rules
Pattern. Recognition and Image Analysis 11(1) 16 (2001)
27. Hewitt E., Ross K. Abstract harmonic analysis (Berlin, Springer, 1963)
28. Kargaev P.P, Zhigljavsky A. Journal of Number Theory 65 130 (1996)
29. Pruefer H. Math. Ann. 94(3-4) 198 (1925)
ЧАСТЬ II
АЛГОРИТМЫ
И ИНФОРМАЦИОННЫЕ
ТЕХНОЛОГИИ
ОБРАБОТКИ
ИЗОБРАЖЕНИЙ
ГЛАВА 5
АЛГЕБРО-АРИФМЕТИЧЕСКИЕ МЕТОДЫ
СИНТЕЗА БЫСТРЫХ АЛГОРИТМОВ
ДИСКРЕТНЫХ ОРТОГОНАЛЬНЫХ
ПРЕОБРАЗОВАНИЙ
5.1. Предварительные сведения
5.1.1.0 проблеме синтеза быстрых алгоритмов дискретных ортогональных
преобразований
Одними из наиболее эффективных методов цифровой обработки сигналов
являются методы, связанные с использованием дискретных ортогональных
преобразований.
Определение 5.1. Пусть у(и)еС — периодическая с периодом N комп-
лексная последовательность, {hin — семейство /V-периодических комп-
лексных функций с условием ортогональности
{hm,hk)= ЕХ(Л)МИ)=5«* <51)
п=0
(ЗшА. — дельта-символ Кронекера, черта означает комплексное сопряжение).
Преобразование
f = (/(0),...,/(W -1)) (f(0) F(N -1))=F, (5.2)
определяемое соотношением
F(m)=S/(nK(n) (<" = 0. 1....Af-l), (5.3)
n=0
называется дискретным ортогональным преобразованием (ДОП) с базисом
302
ГЛАВА 5
Преобразование (5.3) линейно и может быть записано в матричной форме:
Fr=Hfr, (5.4)
где fт, F' — транспонированные к векторам (5.2) векторы-столбцы,
Ы°)
Kv-i(O)
UH.
(5.5)
Определение 5.2. Матрица Н, определенная равенством (5.5), называется
матрицей дискретного ортогонального преобразования (5.3).
Пример 5.1. Преобразование (5.3) с базисными функциями
1 L , тп
;=ехр{2га—
I /V .
(5.6)
называется дискретным преобразованием Фурье (ДПФ).
Пример 5.2. Преобразование (5.3) с базисными функциями
, / \ if 2птп . 2ппиГ
п„, и) = —cos----И sm----
К 7 ТАН /V N
(5.7)
называется дискретным преобразованием Хартли.
Пример 5.3. Преобразование (5.3) с базисными функциями
. . л тс(и + 1/2)т
/.„,(«) = A,„cos 1
(5.8)
где нормирующие коэффициенты Лт определены равенством
при т 0,
при т = 0,
(5.9)
называется дискретным косинусным преобразованием (ДКП).
Непосредственное матричное умножение в (5.4) или, что то же самое, вы-
числение массива F(m) в (5.3) требует ~/V2 арифметических операций. По-
этому в практических задачах предпочтение отдается таким ДОП, для кото-
рых арифметическая природа базисных функций позволяет синтезировать
алгоритмы с существенно более низкой вычислительной сложностью. Отли-
чительной особенностью преобразований в примерах 5.1-5.3 является воз-
можность синтеза таких высокоскоростных алгоритмов.
Мл)
5.1. Предварительные сведения
303
Определение 5.3. Число вещественных арифметических операций сложе-
ния и умножения, достаточных для реализации преобразования (5.3), будем
называть (вещественной) аддитивной и мультипликативной сложностью алго-
ритма вычисления ДОП и обозначать A (Л) и М (/V) соответственно.
Если для данного алгоритма вычисления ДОП при N —> оо справедливо
соотношение
A(W) + M(W) р
7V2
то алгоритм принято называть быстрым (БА ДОП).
В частности, в п.1.7.7 рассмотрен БА вычисления дискретного преобразо-
вания Фурье, для которого при N = 2к
A(/V), M(/v) = <?(Wlog2/v).
Историю быстрых алгоритмов обработки сигналов принято отсчитывать с
1965 г., когда Кули и Тьюки (33] опубликовали свой быстрый алгоритм вы-
числения дискретного преобразования Фурье (далее — БПФ), хотя ранее Гуд
(1960 г.) и Томас (1963 г.) опубликовали в практически незамеченных совре-
менниками работах (35, 42] свои быстрые алгоритмы дискретного преобразо-
вания Фурье, базирующиеся на несколько ином подходе.
За время, прошедшее с первых публикаций, дискретный спектральный
анализ стал одним из основных средств решения задач цифровой обработки
сигналов, распознавания образов, машинного зрения, компьютерной оптики
и т.д. Разработке эффективных (быстрых) алгоритмов вычисления спектров
различных дискретных преобразований посвящено большое количество пуб-
ликаций, как у нас в стране, так и за рубежом [1, 2, 3, 4, 6, 9, 10, 12, 14, 15, 16,
17, 19, 24, 32, 39, 43, 47]. Значительный вклад в развитие общей теории диск-
ретных преобразований и их быстрых алгоритмов внесли С.С. Агаян, Н.Н. Ай-
зенберг, В.А. Власенко, В.Г. Лабунец, А.М. Крот, А.М. Трахтман, Л.П. Яро-
славский, Р. Агарвал, Ш. Виноград, Г. Нуссбаумер, Ч. Рейдер и др. Высоко-
эффективные алгоритмы конкретных преобразований, адаптированные к
характеристикам применяемых вычислительных средств разработаны И.Е. Ка-
пориным, Е.Е. Тыртышниковым, А.М. Григоряном и другими исследователя-
ми (7, 8, 11, 34, 40, 45, 46].
До последнего времени наиболее известными общими подходами явля-
лись метод кронекеровской факторизации матриц ДОП [1, 6, 19, 24] и метод
полиномиальных преобразований [2, 12, 17, 47].
Первый из них опирается на известную теорему Гуда (см., например, [19]):
если матрица ДОП представима в виде кронекеровской степени некоторой
матрицы, то она представима и в виде обычной матричной степени некото-
рой «слабозаполненной» матрицы. К сожалению, отсутствие общих теорем о
кронекеровской факторизации матриц ограничивает возможности этого ме-
тода, по существу, классификацией алгоритмов, синтезированных независи-
мыми методами.
304
ГЛАВА 5
Метод полиномиальных преобразований (дискретного преобразования
Лапласа, z-преобразования) существенно опирается на наличие априорной
информации о факторизации некоторых полиномов, что уже является весьма
сложной вычислительной задачей, и, что еще более существенно, на исполь-
зование индивидуальных арифметических свойств коэффициентов этих по-
линомиальных сомножителей (например, метод Ш. Винограда).
В то же время анализ структур конкретных быстрых алгоритмов дискрет-
ных ортогональных преобразований позволяет утверждать, что их авторы
используют весьма ограниченный набор решений, базирующихся на действи-
тельно глубоких алгебраических идеях, в сочетании с эвристическими сооб-
ражениями, специфичными либо именно для данного ДОП, либо для конк-
ретно используемого вычислительного устройства. Структура БА представля-
ет собой, как правило, некоторую рекурсивную процедуру, последовательно
реализующую редукцию вычисления ДОП заданного объема к ДОП меньше-
го объема или более простых преобразуемых массивов. Типичными схемами
таких редукций являются:
- редукция Кули-Тьюки для N = рк (р — простое число);
- редукция Гуда-Томаса для N= PQ (Р, Q — взаимно простые числа);
- редукция Рейдера для N= р (р — простое число);
- методы «совмещенного» вычисления ДОП вещественных сигналов.
По мнению авторов, алгоритмы, использующие все вышеперечисленные
методы редукции могут быть интерпретированы единообразно:
- вложение поля, содержащего значения входного сигнала и базисных
функций преобразования в некоторую конечномерную алгебру (кодирование)-,
- вычисление некоторого вспомогательного преобразования со значения-
ми в этой алгебре;
- отображение полученного результата в поле, содержащее значения вы-
ходного сигнала (декодирование).
Следует отметить, что выбор алгебры для вычисления вспомогательного
преобразования определяет не только эффективность того или иного БА, но
и неявным образом задает структуру этого алгоритма.
Именно такая трехэтапная процедура принята в книге за основу достаточ-
но общей методики синтеза быстрых алгоритмов ДОП, примеры реализации
которой описаны в настоящей главе.
5.1.2. Конечномерные ассоциативные алгебры
Пусть А — конечномерное векторное пространство над полем 1F с базисом
{е0, ed_]} с обычными (покоординатными) правилами сложения и ум-
ножения на элемент поля 1F.
Определим бинарный закон € А умножения базисных эле-
ментов и распространим его на все множество векторов из пространства А
посредством равенства
5.1. Предварительные сведения
305
d-1
§n= Е (510)
k,j=O
где
£ ~ ^оео + + ^>d~ Iе d-1 ’
n = noeo+- + 11i/-ie(/_1.
Определение 5.4. Множество А с введенными операциями сложения, ум-
ножения на элемент из F, индуцированных операциями исходного векторно-
го пространства, и умножением, определенным равенством (5.10), называется
конечномерной (J-мерной) ассоциативной алгеброй над полем F (или, короче,
F-алгеброй).
Определение 5.5. Пусть А есть некоторая F-алгебра и 1€А — такой эле-
мент, что для всех х 6 А выполняются равенства
1х = х1- х.
Такой элемент 1 называется единицей алгебры А, а сама алгебра — алгеброй
с единицей.
Определение 5.6. Пусть А, В — две F-алгебры. Взаимно однозначное ото-
бражение ср: А —> В называется изоморфизмом алгебр, если для любых ^,-q е А
и A G F выполняются равенства:
(a) Qte+ij) = <pte)+<p(n);
(Ь) фЩ) = Аф(£);
(с) <р^п) = ф(§)-ф(п)-
Если А = В, то отображение ср называется автоморфизмом.
Приведем несколько примеров конечномерных ассоциативных алгебр, рас-
сматриваемых в настоящем разделе при синтезе БА ДОП.
Пример 5.4. Четырехмерная R-алгебра с базисом {1, i, j, к] и правилами
умножения базисных элементов
i2 = j2 = k2 = 1, ij = -ji = k
называется алгеброй кватернионов.
Пример 5.5. Двумерные R-алгебры с базисом {1, е} называются алгебра-
ми комплексных, дуальных или двойных чисел, если, соответственно, е~ =— 1,
е2 =1 или е2 =0.
Пример 5.6. Пусть G — конечномерная d-элементная группа с групповой
операцией (*) и нейтральным элементом g0 = 1 € G. Рассмотрим векторное
пространство над R с базисом {Xgp-.^gj-j} и определим умножение (5.10)
элементов этого пространства равенством
^i=Z 12
geG^<g,g;=g>
306
ГЛАВА 5
Введенная алгебра называется групповой алгеброй группы G.
Другие необходимые примеры алгебр рассматриваются в разделе по мере
их использования.
5.1.3. Основные схемы редукции
Декомпозиция Кули—Тьюки «по основанию 2». Пусть / (и) € С есть Апе-
риодическая последовательность, N = 2k, — ее дискретный спектр
Фурье имеет вид
N-1
F(ni)=^2f[n)wmtl, w = ехр{2ти/Л/}, 0<т< N — 1. (5.11)
n=0
Сумма в правой части соотношения (5.11) может быть представлена для
0 < т < % -1 в виде двух сумм длиной 7V/2:
А-i w_|
F(m)~ + w"'52/(2n + l)(w2) =
н=0 п=0
= Fo (m)+ wmF} (m).
(5-12)
Здесь
—-i —-i
FoW=ЕУ (2w)(w2)ww* FiM=Hf(2n+ ,)(и’2)mw
n=0 n~0
— спектры Фурье /V/2 -периодичных подпоследовательностей. Таким обра-
зом, ДПФ длиной /V сведено к двум преобразованиям Фурье длиной /V/2 и
к N/2 дополнительным умножениям на степени w для 0</п<%-1. Так
как и^2 =-1, то вычисление F (т) для N/2<m< N -1 выполняется без
дополнительных умножений:
F(zn* + ^2)-F0(/n*)-w"1*F1 (w*), 0<ю*<%-1. (5.13)
Мультипликативная A/(/v) и аддитивная A(n) сложность такого алго-
ритма равны, соответственно,
M(/V)<|/Vlog2/V-|/V, A(N)<^N\og2N-~N, (5.14)
Изложенный алгоритм принято называть быстрым преобразованием Фу-
рье (БПФ) по основанию 2 (см. также п. 1.7.7).
5.1. Предварительные сведения
307
Декомпозиция Кули-Тьюки «по основанию 4». Аналогичным образом стро-
ится алгоритм БПФ «по основанию 4» при /V =4*. Сумма для F (т) в (5.11)
разбивается на четыре части:
7~!
F(m} = У2/(4и)(и'4) + wmУ2 f (4п +1)(w4) 4-
п~0 л=0
А_1
+ w2mZf (4п + 2)Р )”” + »3” Е /(4и + 3)(w4 )"” =
(5.15)
л=0
= F0(/n) + wmF{ (/к)+ w2mF2 н'3т^з(/и)’
0</п<%-1.
Соотношение (5.15) редуцирует вычисление ДПФ (5.11) к вычислению
четырех ДПФ длиной 7V/4 и к 3 7V/4 дополнительным умножениям на степени w.
Так как при стандартном машинном представлении комплексных чисел ум-
ножения на степени мнимой единицы / являются тривиальными, значения
спектра при N/4 < т< N- 1 вычисляются без дополнительных умножений
следующим образом:
1
i
-1
—i
1
-1
1
-1
w^F^m*)
—1- (5-16)
Оценки вычислительной сложности такого алгоритма имеют вид
М (/V)<|wiog2/V-^/V, A(/V)<^/Vlog2A— ±~N. (5.17)
Декомпозиция Кули—Тьюки с расщеплением основания (сплит-радикс алго-
ритм). Пусть N = 2к, тогда преобразование (5.11) для 0 < т < — 1 может
быть записано в следующем виде [6]:
F(m)= +w"! J2/(4n+l)(w4j + и-3"'У^ /,(4n + 3)(w4^ .
л=0 п=0 л—0
308
ГЛАВА 5
Здесь ДПФ длиной N сведено к одному ДПФ длиной N/2, двум ДПФ дли-
ной N/4 и к 2N/4 дополнительным умножениям на степени w. Вычисление
X (ди) для N/4 <т< N - 1 выполняются без дополнительных умножений:
где
Fo ("О = 52 / (2n) (w2 ,
п=0 4 Z
F3 (т) = 52 f (4« + 3) (w4 Г".
н=0
Оценки вычислительной сложности для этого алгоритма равны:
M(tf)<tflog2W-3W , A(/V)<3/Vlog2/V — 3/V. (5.18)
Декомпозиция ДПФ Гуда—Томаса. Другим известным способом быстрого вы-
числения ДПФ является декомпозиция Гуда-Томаса [35,42], применяемая в тех
случаях, когда длина преобразования N = P Q , где Р и Q — взаимно просты.
Пусть а = ехр{2л//Р}, 0 = exp{2ni/Q} — первообразные комплексные кор-
ни из единицы степени Р и 0, соответственно. Представим индексы входной
и выходной последовательности в виде
п = Рпх + Qn2
т = Рат} + Qbm2,
где а и b определяются из условий
Ра = l(modQ)
Q b = 1 (mod Р).
(5.19)
(5.20)
После введения обозначений i(n1,n2) = x(Pn1 + 0и2), р(ди1,ди2) =
= F(Pam{ +Qbm2Y соотношение (5.11) примет вид
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
309
С-l р-1
р(т„т2)= Е Е 7(n„n2)w(P"'+e"!,(',”"+e'""2l =
Н| =0/12=0
С~1 Р“1 , ч 2
— У? У2 7(П1 n2)wP £",1"||+/ЭС(*И|"'2+««2"11)+<? Ь,,2т2
Л] =0 />2 =0
В силу (5.20) справедливо равенство
С-i р-i
F(mi,m2)= £ 12 7(П|,п2)и/,”|'">и'/’£?('”'1"'!""’,!’”'>и'е"!",> =
//]=0 /12=0
0-1 р-i
= Е Е7(п1.«2)₽"'"'«"2"'2. (5-21)
Л] =0 /12 = 0
где Р = ехр{2л1Р/Л/} = ехр{2ти/(2} = wp, a = exp{2niQ/N] = ехр{2ш/Р} = wQ .
Из (5.21) следует, что
F(m|
(5.22)
ИЛИ
р-1 0-1
F(Paml^-Qbm2)=^2 £ f(Pn\ + Cwi) Р"1"1'
Л2=0\л1=0
а"2"'2
(5-23)
Так как для описанного шага декомпозиции справедливо неравенство
M(n) = m(p)-Q + M(q)-P<QP2 + PQ2 = N{p + Q)<N\ (5.24)
то применение этого приема тем эффективнее, чем на большее число взаим-
но простых сомножителей разлагается число N.
5.2. Совмещенные алгоритмы дискретных ортогональных
преобразований
Совмещенные алгоритмы одномерного дискретного преобразования Фурье
вещественных 7V-периодических последовательностей,
F(m} = f(n)wmn, wCC , wN =1 ,
n=0
(5.25)
310
ГЛАВА 5
хорошо известны и подробно описаны [6, 13, 23]. В их основе лежит возмож-
ность получения дополнительных вычислительных преимуществ за счет из-
быточности представления вещественных чисел в комплексной арифметике.
Типичный пример: представляя (5.25) в форме
7-' У’1
F(m)= J2/(2n)(w2) +w"'S/(2«+1)(m'2)"" (5-26)
п=0 л=0
и вводя комплексную функцию
z(n) = /(2n) + Z/(2n + l), (5.27)
можно свести вычисление преобразования (5.25) к вычислению ДПФ z(m)
комплексной последовательности z(n) с периодом N/2 и некоторому (отно-
сительно небольшому) числу дополнительных вычислений, позволяющих найти
по известному спектру Z(m) спектры F0(m), F, (m) последовательностей
f(2n), /(2п + 1) и реконструировать полный спектр F(m). В самом деле,
такая возможность следует из равенств
Fo (m) = Z(m) + Z (-т),
Fl(m) = i(z(-m)-Z(m)),
F(m) = Fo(m) + w'nFl (m).
(5-28)
Выделение из Z(rn) частичных спектров F0(m), F^m) обеспечивается
наличием в алгебре комплексных чисел С двух автоморфизмов (тождествен-
ного и комплексного сопряжения), действующих на R тождественно, причем
переход к комплексно-сопряженному числу при стандартной машинной реа-
лизации не требует дополнительных арифметических действий.
В случае двумерного ДПФ с реализацией быстрого алгоритма в простей-
шей построчно-столбцовой форме
N—1
/=•("<.. "<2)= Е f(n„n2)w^+^ =
"|.«2=0
TV-1 /V-1
= Е Ef («и «г)»'"2"1, (5-29)
Л] =0 «2 =0
применение описанного выше алгоритма приема затруднительно из-за неве-
щественности внутренних сумм в правой части (5.29). Другими словами, поле
С имеет «слишком мало» автоморфизмов, позволяющих осуществить много-
кратное совмещение по каждому из аргументов с возможностью последующе-
го разделения спектров.
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
311
5.2.1. Двумерный БА ДПФ с совмещением в алгебре кватернионов
Естественным обобщением идеи комплексного совмещения является вло-
жение преобразуемого вещественного J-мерного массива /(n) в
другие, отличные от поля С, алгебры с достаточным числом тривиально реа-
лизуемых автоморфизмов.
В книге мы подробно анализируем только двумерные совмещенные алго-
ритмы, что объясняется широким использованием именно двумерного ДПФ
в задачах обработки и анализа изображений, в компьютерной оптике и т.п.
Напомним, что алгебра Н кватернионов определяется как четырехмерная
К-алгебра,
Н = {q = a + bi + cj + dk‘, a,fe,c,dGR}, (5.30)
с определяющими соотношениями для умножений базисных элементов:
i2 = j2 = к2 = -1, ij = -ji = k.
Поле комплексных чисел С канонически вкладывается в Н:
а + Ы—* а + Ы + О- J-1-О-Лг. (5-31)
Кроме того, справедливо соотношение
q = а + Ы + cj + dk = (а + bi) + (с + di) j. (5.32)
Умножение кватерниона q общего вида на комплексное число z = ct+pi в
кватернионной форме (5.31) требует шести вещественных умножений:
z9 = ((a-P)Z> + a(fl-Z>))+(a(a + P)-a(a-fc))i-l-
4-((a-p)d + a(c-d ))y + (c(a+p)-a(c-d ))k.
Отображения
, E; \q^>j~'qj ,
Ek :q>->k~'qk , E„ :q>~>q
являются автоморфизмами H над R., причем
Ео (q) = a+bi! + cj+ dk,
e^q) = a + bi — cj — dk,
£ j; (<?) = a — bi + cj — dk,
EA {q) = a~bi — cj-I-dk.
(5.33)
312
ГЛАВА 5
Система уравнений (5.33), рассматриваемая относительно a, b, с, d, разре-
шима при любых значениях левых частей и требует для решения только сло-
жений и умножений на степени двойки:
4а = Ео (q) + г. (?) + Е* (?),
4& = Ео (q) + £,- (q) - £ ; (?) - Е * (q),
4<7 = £0 (?) - Е/ (?) + Е; (?) - Е* (?),
4^ = Ео (q) — £;(?) — Е j (q)+zk (?)-
Пусть /(npn2) — вещественная Апериодическая по каждому аргументу
функция. Преобразуем выражение для двумерного ДПФ (5.29) к виду
F(m„ т2) = £ w‘m'+l’m'Fj<ml, т2), (5.35)
а, 6=0
где
JVj-l
F(//,(/ni,wi2)= $2 х(л, + а,л2+ b)(w2} *2'2. (5.36)
H|,zi2=O
Положим fah(n}, п2) = /(2П(+а, 2n2+b) и введем функцию qfn^ п2)
со значениями в алгебре Н:
/оо ("I ’n2) + Al (ni *п2 )* + /10 («1 ’ «2)/ + /11 (И),П2)к = ?(«1,п2). (5.37)
Определим «полукватернионный спектр» <2(т]э т2) равенством
/ \ А / э\»|.П| + т2п2
Q(mb т2)= 52 ?(ир «2)(w ) <5-38)
«р п2=0
Для реконструкции F(m{,m2) достаточно вычислить массив Q(mit т2) для
т2 =0, 1......../Vj — 1, а затем с помощью (5.34) найти x(n!,n2):
45(mp т2\ 0, О) = 0(тр /п2) + 0'(лир m2) + C?’(mp wi2) + (/(/nr m2),
4/5(mp т2, 0, l) = l2(nip /n2) + |2'(mp m2)-CJ*(wip т2) — Qk(m}, т2),
m2;l, 0) = б(тр т2) - Q' (n?j, m2) + Qj (пц, m2)-Qk(ml, т2),
IkS^m^ т2\ 1, 1) = С(/Ир m2) — Q'(nip /«2)~CJ(mi’ т2) + Qк (Ш1 ’ т2)»
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
313
<2'(дП1, m2) = ei(e(wil, т2)), w2) = £-m2)),
'n2) = £*(C(-Wp “"»2)),
и, наконец, выполнить 3(N} -1)2 умножений на степени константы w в соот-
ношении (5.35).
Таким образом, вычислительная сложность преобразований (5.35) и (5.38)
определяется, в основном, сложностью кватернионного аналога двумерного
БПФ. Различные реализации таких аналогов рассматривались в [18, 31].
5.2.2. БПФ с представлением данных в алгебре (2х2)-матриц
Идея двойного совмещения может быть реализована и в иной форме —
при рассмотрении вложения значений преобразуемой последовательности в
четырехмерную R-алгебру (2х2)-матриц М2 с базисом
Поле комплексных чисел С изоморфно вкладывается в алгебру (2х2)-мат-
риц М2:
a+bi
—b а
Рассмотрим преобразование
(5-39)
V(n1,n2) =
7оо(«1’«2) /о1("рИ2)1 w
/ю(«1’”2) /11("1,П2Я
— у
с = cos(2Tt/w), s = sin(2Tt/2V).
Умножение матрицы общего вида из M2(R) на матрицу W* может быть
реализовано с помощью шести вещественных умножений:
314
ГЛАВА 5
a P c s a(c + s) — (a+p)s a(c + s) + (p — ct)c
у 5Д-.У cj y(c + j)-(y + 5)s y(c + s) + (6 - y)c
Поэтому мультипликативная сложность вычисления (5.39) такая же, как и
(5.36).
Пусть
Ат=Т"'АТ, A°=S-1AS, AP = R AR
При реконструкции т2) для разделения частичных спектров вос-
пользуемся непосредственно проверяемыми матричными тождествами:
ао_( 5 “Y1 аР-( а
[р а]’ [-Р а]’ [-у 5J’
WT = W” = Wp = W*.
Отображения
A->AT, АнчАп, A^Ap
являются автоморфизмами М2. Справедливы также равенства
(R+E)(A + Ap) = 4aDn,
(R+E)(at-A°] = 4PD11,
(R+E)(at-A°)t = 4yDI],
(R + E)(A + Ap)T = 48Dn.
(5-40)
Пользуясь соотношениями (5.40), при известном матричном спектре (5.39),
нетрудно найти «частичные спектры»
Л/.-1
/ \ г / \( 2\ОТ|Л|+ "'2Л,2
2^ fab(ni’ ггг)[н’ )
Пр п2=0
из следующих соотношений:
4Лю(т1’ т2)~е(wi’ w2)+Tp(— mt, —/и2))^Т,
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
315
47^^ (zrzj, m2) = eT^'FT(—Шр —т2)~Т°(—
4Fi0(mj, m2) = e(wT(—m[t —m2) —Фо(——т2)]тЛг,
4F|l(m], /н2)= е(^(т1 ’ л«2) +'®rP(—wi» “"h))
где e = (l, 0), J=(l, i), Jr — транспонированный вектор-столбец; подпос-
ледовательности fah(ni, n2) определены в предыдущем разделе. Реконструк-
ция полного спектра F(m,,w2) осуществляется согласно (5.35).
5.2.3. Кватернионное двумерное ДПФ
Определение 5.7. Двумерным кватернионным спектром вещественного мас-
сива /(и|,и2) размером /Vx/Vдалее будем называть [20, 27] двумерный массив
кватернионов
АГ—1 /V—1
F(m},m2) = w\n'n'f(n\->n2)w22n2> 0</w(,/w2 <Л7 — 1, (5.41)
«(=0 «2=0
где Wj =ехр{2л//Л/}, w2 =ехр{2лу/Л/}.
Кватернионный спектр (5.41) связан с комплексным спектром Фурье,
2N-I
F(m1,m2) = £ /(”r«2)vvm,"'+m2"2’
z,l .n2~О
соотношением
F^m{,m2)=< F(mj,m2)> LI,
где матрицы L и I имеют вид
1 О
01 < (Л
L= , 1= .
0 1 и
-1 о,
(5.42)
(5.43)
316
ГЛАВА 5
Через < Г(ш1,/?22) > Для кватерниона
F(ли,,т2) = Хо ("*i ,m2) + Xi (Ш1 ’) i + Х2 (mi >т2) J + Хз (mi ,mi
обозначен вектор его компонентов
(Хо(™н™2)’ Xi(т„т2), X2(mi,/n2), Хз^Р^г))-
Переход от кватернионного спектра (5.41) к комплексному спектру (5.42)
осуществляется без дополнительных вещественных умножений и требует все-
го двух операций вещественного сложения на отсчет.
Далее приведены три способа декомпозиции кватернионного ДПФ (КДПФ),
являющиеся аналогами различных схем алгоритмов двумерного комплексно-
го БПФ.
Алгоритм КДПФ с декомпозицией по основанию 2. Пусть кватернионный
спектр вещественного (TVxTV)-сигнала задан соотношением (5.41). По анало-
гии с редукцией одномерного ДПФ каждое из множеств индексов nvn2 вход-
ного сигнала разбивается на подмножества четных и нечетных индексов, при
этом равенство (5.41) принимает вид
N-1
«[,«2=0
--1
_ am, ( 2\m'ni f ( \f 2V"2"2 bm2 _
~ 2^ Wl Ъ P j fab(n^n2)\W2) W2 ~
a,h—Q «[,«2=0
= 52 w“m' Fah(m},m2)w^2, (5.44)
a,b=0
где
fab(n\’n2)= /(2«i+«, 2n2 + b),
Fab(m^m2) = 52 (и'12)Р’1Л1ЛДп|,п2)(^)'П2"2,
0< m{,m2 < N/}— 1.
(5.45)
Вычисление спектра для остальных значений пар (тх, т2), лежащих вне
области (5.45), производится без дополнительных умножений и может быть
записано в матричной форме:
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
317
1 1 1 1 foo(m|.m2)
Ё(ш] +/V/2, т2) 1 -1 1 -1 w”'
F^m^ т2 + /V/2) 1 1 -1 -1 Л>|
F(m}+Nl2,m2 + Nl2) 1 -1 -1 1 и'|"'Л|(т1-т2)и’2!
(5.46)
Кроме того, умножения на множители w"1, w22 достаточно выполнять
только для фундаментальной области
{°- wi,,m2 </V/4} = n0.
Остальные значения спектра определяются с использованием автоморфиз-
мов поля кватернионов (5.33) без дополнительных умножений. Действитель-
но, пусть вычислены значения
w\m'^Uh(mi>m2)w2m2 Д™ (w|,m2)eQ0» и
тогда
Н'Г^' Fah(Ц1 *т2 ) = (- £ j (Wl""' Fab (™1 * т2) .
<m‘ Fab ^г)^2 = Ъ (<"' Fab (m,,m2)wb2m2)(-1)6,
^Г'^ДМрЦг)^2 =(-1)“£Ди;Г'Ль("г1>"12)и'2т2)(-1Л
Окончательное вычисление значений кватернионного спектра F(m],m2)
производится в следующем порядке. Находятся значения суммы в (5.44) для
(m1,wt2)€Q0. По формуле (5.46) вычисляются элементы спектра в областях,
отличающихся от Qo сдвигом на N/2 по каждой из координат. Наконец,
остальные области заполняются на основании следующих свойств КДПФ ве-
щественного сигнала:
F(^-w1,m2) = Ey(F(/n1,m2))J
(5-47)
F(N-m},N-/n2) = EA(F(m1,m2)).
Схема заполнения кватернионного спектра по формулам (5.44)-(5.47) при-
ведена на рис. 5.1.
318
ГЛАВА 5
(5.47)
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
319
Таким образом, для оценок вычислительной сложности КДПФ по основа-
нию 2 справедливы следующие рекуррентные соотношения:
M(NxN) = 4M
— x —
12 2
N2
16 ’
—2+9—
16 Г
A(NxN) = 4A
N2
/V /V „ ,c
— x — + 6------2 + 15
2 2)
16
N2
16
4.
16
(5.48)
Отсюда следуют оценки вычислительной сложности описанного алгорит-
ма КДПФ:
M(NxN)<QN2\og2N-3±N2, A(NxN)<^N2\og2N-^N2. (5.49)
х ' 16 16 х 7 16 16
Алгоритм КДПФ с декомпозицией по основанию 4. Рассмотрим алгоритм
КДПФ вещественного сигнала объемом NxN (W=4f) с декомпозицией по
основанию 4.
Пусть в (5.41) множество индексов nt,n2 разбивается на 16 подмножеств в
зависимости от остатков (mod 4), w2(mod 4). Тогда равенство (5.41) при-
нимает вид
(5 50)
«.6=0
где
"-1
- / \ ( л\т1п* г / \1 л\т2п1
F0»(ml,m2) = Ъ +) Лл(Я1.»2Д**2) •
П|,л2=0
Лб(и1’П2) = /(4и1+«’ 4n2+Z>),
0 < т1 ,т2 < — 1 •
(5.51)
Значения спектра для остальных пар (znj,zn2), лежащих вне области (5.51),
вычисляются без дополнительных умножений:
г- । 1^1 -ar am, г / \ 6/n5 -Ьр
F "1l+rT’"l2+PT I 1 Fah(ml>m2)W2 J ’
4 4 ' a,b=0
r,p = 0,l,2,3. (5.52)
Умножения на степени базисных элементов / и j тривиальны, они сводятся
к перестановкам компонентов кватернионов и/или смене знака компонентов.
320
ГЛАВА 5
Кроме того, при вещественном входном сигнале умножение на фазовые мно-
жители и’|Ит|, и>2 2 достаточно производить только в фундаментальной области
{0<л«|,ш2 < ^8} = Qr
Действительно, пусть для найдены значения
">2И'’>
и на основании равенства (5.50) вычислены значения кватернионного спектра
Тогда значения в областях, отличающихся от Qj ад-
дитивными сдвигами на N/4 , вычисляются по формуле (5.52), а остальные
находятся на основании симметрий кватернионного спектра вещественного
сигнала (5.47). Схема заполнения кватернионного спектра по формулам
(5.50)—(5.52) приведена на рис. 5.2.
Оценки вычислительной сложности такого алгоритма определяются из со-
отношений
M(NxN) = l6M
(N ЛИ
— х —
И 4)
N2 N2
+ 6—6 + 9—9
64 64
и равны:
A(NxN) = 16 А
(N /V)
— х —
(4 4
/V2 TV /V2
+ 6--6 + 15--9 + 64——4
64 64 64
М (N х N) < Щ N2 log э N - N 2,
' 128 64
^(wxw)<^№iog2w-^№.
(5.53)
Алгоритм КДПФ с расщеплением основания. Рассмотрим еще одну схему де-
композиции кватернионного спектра, в которой ДПФ объемом (TV х /V) сводит-
ся к ДПФ объемом (N/2xN/2) для элементов входного массива с четными
индексами и двенадцати ДПФ объемом (/V/4 x/V/4) для элементов входного
массива, имеющих хотя бы один нечетный индекс. Пусть
А = {(0,1),(0,3),(1,0),(1,1),(1,2),(1,3),(2,1),(2,3),(3,0),(3,1),(3,2),(3,3)},
тогда
#(/П1,/и2)= 52 (wi2) ‘'/(2л|,2п2)(^2) 22 +
И] ,Ит =0
+ 52 £ (^14) ” ' )12”2 w212- <5-54)
(a,b)€A «|,Н2=0
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
321
F(mt, mJ а,Ь = 0,1,2 3; 0<mpm2<N—1
(5.50)
(5.52)
Рис. 5.2. Порядок заполнения значений кватернионного спектра в алгоритме КДПФ по основа-
нию 4
11 — 9044
322
ГЛАВА 5
При этом, по-прежнему, умножения на множители и"'1, достаточно
выполнять для области Й,.
Рекуррентное соотношение для опенки мультипликативной сложности
описанного алгоритма в этом случае имеет вид
(/V /V] /V2 /V2
+ 12Л/ — х— +6——4 + 9——8,
(4 4 J 64 64
f/V /V]
— х —
U 2)
откуда следует оценка для М (TVxTV):
A/(7Vx/v) = |/V2log2/V + o(w2).
(5.55)
(5-56)
5.2.4. Совмещенные алгоритмы дискретного косинусного преобразования
Косинусное преобразование (см. пример 5.3) является одним из основных
дискретных преобразований, используемых в цифровой обработке изображе-
ний. Так, на нем основаны известные методы кодирования изображений (на-
пример, JPEG [44]); методы восстановления и фильтрации (например, метод
гибридного спектрально-реккурентного восстановления изображений [5]),
методы извлечения признаков [1]. Такое широкое применение дискретного
косинусного преобразования (ДКП) обусловлено целым рядом причин.
Во-первых, базисные функции ДКП хорошо аппроксимируют собствен-
ные функции преобразования Карунена—Лоэва для широкого класса стацио-
нарных случайных процессов, то есть позволяют описывать сигнал с доста-
точно малой среднеквадратичной погрешностью минимальным числом спект-
ральных компонентов:
£-Е^л
Л=1
—> min;
во-вторых, ДКП входит как составная часть в некоторые эффективные
алгоритмы дискретного преобразования Фурье (ДПФ) (например, алгоритм
Капорина-Уэнга [6]);
в-третьих, ДКП обладает рядом других полезных свойств, позволяющих, на-
пример, избежать краевых эффектов при блочном кодировании изображений.
Хорошо известен способ вычисления ДКП, основанный на его сведении к
ДПФ вещественной последовательности двойной длины [1], или, при исполь-
зовании совмещенных алгоритмов [23], к ДПФ комплексной последователь-
ности той же длины.
Описанный в [1] быстрый алгоритм сводит (ненормированное) ДКП
jV-1
7('Ф E/(«)cos
n=0
(п + 1/2) га
__
(5.57)
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
323
к вычислению ДПФ вещественной последовательности длиной 2N:
1 N—l N—1 '
f(m)=L =
2 n=0 л=0
1 2ЛМ
= <5 58>
2 л=о
где w — exp{27n/27V}, g (A) — вещественная 2/V-периодическая последователь-
ность, полученная четным продолжением f (п),
f(k) при 0<k<N-1
f(2N-k-l) при N<k<2N-\
Сложность такого алгоритма ДКП равна
Мдкп (*) = M„f№(2N)+3N, A4kI1('V) = ^(2/V) + 3W, (5.60)
где Мдпф(2М) , АдПФ(2/У) — оценки сложности ДПФ вещественной после-
довательности двойной длины.
Алгоритм одномерного ДКП четной длины. Пусть вещественная последова-
тельность g {к) длиной 2N получена четным продолжением исходной после-
довательности f (л) по формуле (5.59), и ДКП связано с ДПФ соотношением
(5.58).
Для вспомогательного ДПФ
2N-1
в(т) = Ё g(k)wkm, (5.61)
к=0
длиной 2N, проведем один шаг стандартной декомпозиции Кули—Тьюки (5.12):
N-1 Л/-1
G(m) = Е S (2k)w2km + w" Е g (2к +1) w2lm. (5.62)
Jt=O *=0
Из (5.59) следует, что последовательности четных g(2k) и нечетных g(2k + 1)
отсчетов связаны между собой соотношением
g(2t+l) = g(2W-(at+l)-l)=g(2^-*-l)) = g(2Z) при l = N-k-l.
N—l
Пусть g (т) = g (2^)w2te, тогда
*=0
U*
324
ГЛАВА 5
(2*+ 1)и'2‘“ = wmY,g{2l)w2(N4~'}"' =
к=0 1=0
= w-"'^g(2l)w-2,"‘ = w''‘g(m). (5.63)
1=0
Из (5.62) и (5.63) следует, что
G(m) = g(m) + wmg(m). (5.64)
Тогда равенство (5.58) с учетом (5.62)-(5.64) примет вид
/ W="Iwm/2 (s W+(т)}-
= 5 (пг))== Re("*)}, (5.65)
Преобразуемый
вещественный сигнал Дл)
н (5.59)
где g(m) — ДПФ вещественного сигнала длиной N, 0 < т < Л-1.
Из соотношения (5.65) следует, что при вы-
полнении комплексных умножений на wm^ до-
статочно вычислять только действительную часть
произведения, что потребует двух умножений и
одного сложения на отсчет:
Формирование
вспомогательного
сигнала g(k)
Выделение из
вспомогательного сигнала
отсчетов с четными
индексами g(2k)
Вычисление ДПФ длиной N
g(rn)=Y g(2A)wh"
w
u (5-65)
Получение косинусного
спектра
/m)=Re{w'n/2g(m)}
Re{(G-H'Z?)(p,-H’v)} = (Щ~ bv. (5.66)
Таким образом, ДКП сведено к ДПФ веществен-
ного сигнала той же длины, 2N дополнительным
умножениям и N сложениям. Обобщенная схема
изложенного алгоритма приведена на рис. 5.3.
Мультипликативная и аддитивная сложности
описанного алгоритма вычисления ДКП равны:
WflKn(A') = Mfln®(W) + 2W,
^дкп (^) = ^дпф (W)+N, (5.67)
где Л/ДПФ(Л), ^дпф(^) “ оценки сложности
ДПФ вещественной последовательности той же
длины N.
Рис. 5.3. Обобщенная схема алгоритма ДКП
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
325
Алгоритм двумерного ДКП четной длины. Пусть / (нрн2) — входной веще-
ственный сигнал объемом NxN, w = exp{2ni/2N} — корень степени 2/VH3 еди-
ницы; вспомогательный сигнал g(k{,k2) связан с /(п|,н2) соотношениями
?(Мг) =
f(kt,k2)
f(2N-k,-l,k2)
при 0 < к{ <N — 1;
при N < к{ < 27V — 1;
при 0 < к} < /V -1;
f [lN-kx-\,2N-k2-\] при N<k}<2N-\;
0<к2 </V-l;
0<к2 </V—1;
N<k2 <2N-\;
N<k2<2N-\.
(5.68)
Принцип построения такой вспомогательной функции показан на рис. 5.4.
На рис. 5.4л показан входной сигнал f (ni,n2), заданный в области
0<nj,n2<N- Вспомогательный сигнал g(k},k2) совпадаете /(n,,n2) в
области 0<£, ,к2 <N и симметричен относительно прямых к} = (/V + l)/2 и
к2 = (?V + l)/2 (рис. 5.46). На рис. 5.4в приведен пример переупорядочивания
индексов при формировании вспомогательного сигнала при 7V=4. Тогда для
двумерного ДКП справедливо соотношение, аналогичное (5.58), связывающее
ДКП с двумерным ДПФ (5.42) вещественной последовательности:
1 . .. 2W-1
= 52 *(Мг)
4 UbJk2=O
(5-69)
На основании (5.43), вместо двумерного ДПФ
2ЛМ
G(mi,w2)= 52 #(*1А)и/"‘ ,+л"2 2>
*1,*2=0
в равенстве (5.69) можно использовать КДПФ соответствующего размера:
2/v-i
С(т],ш2) = 52 w?'k'S^k^k^w^2, (5.70)
*,Jt2=0
где =exp{2jn/2/V}, w2 = exp{2лj/2/v}-Учет симметрий сигнала g(k^k2)
позволяет находить значения кватернионного спектра по следую-
щей схеме.
Пусть
N-1
i(mi,m2)= 52 wi2m,A,5(2^p2fe2)w2W2.
*|,*2=0
326
ГЛАВА 5
ftnb ъ)
а
б
Рис. 5.4. Построение вспомогательного сигнала по формуле (5.68): а — пример входного сигнала
/(прЛг); ~ вспомогательный сигнал g^ki,k2)', в — соответствие индексов исходного и вспо-
могательного сигнала при N = 4
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
327
После одного шага декомпозиции по основанию 2, соотношение (5.70) для
КД ПФ примет вид
N-1
G(mt,m2) = У? wxm'k'g(2kXy2k2}w2mik2 +
^,*2=0
a'-i
w^niki3{2kx+\,2k2)w2n2k2 +
kf »^2 ==0
/V-!
+ wl2w,A|g(2Jl1,2^2 + l)w2W2A2 w22 +
*|.*2=0
A'-l
+ <* E w12w,*,g(2^1+1.2Jl2+l)vv2w2A2vv2”2. (5.71)
A|,A2=O
Так как из соотношения (5.68) следует, что
^(2Л1+1,2Л2) = ^(2/|,2/2) при 7( =Л/—А, — 1, 12=к2,
g(2kx,2k2 +1) = g(2lx,2l2^ при lx=kx, l2 = N—k2—l,
g(2Л,+1,2к2 + 1) = ^(2/,,2/2) при Z, = ЛГ — — 1, /2 = /V —Л2 —1,
то вторая сумма в (5.71) преобразуется к виду
< £ +1.2Л2)и-^‘« =
Л|,/С2=О
= <’ Е w|2m,(N-'l"l)«(2Zl,2/2)w22'”A = <m' £ Mf2""'1 g{2l„2l2)w22'"^ =
/|(/2=0 /,./2=о
= Е,-
<' Е и-2га'''«(2/1;2/2)и/2”А
/1./2=0
= е,
Аналогично, третья и четвертая сумма могут быть представлены как
JV-1 с х
£ w12n-‘'s(2*1,2*2+l)w2^w^ =E,{g(m|,m2)w22|
Л|./С2=0
N-1 , г 1
^Г' wi2m,A| я(2*1 +1,2£2 +l)w2"'2 2 w22 = Е*
Л|,*2=0
Таким образом, кватернионные спектры G(mx,m2) и g(wl,m2) связаны
между собой соотношением
328
ГЛАВА 5
G(nz1,m2) = Ew{g(m1,m2)} + Ey{w|,"lg(ml,m2)} +
+Е; (W1(, m2 ) w22} + Ел {<' g (w1, m2) w22
где eo, Е/, Ey, e* — автоморфизмы алгебры кватернионов, реализация действий
которых сводится к смене знака части компонентов в кватернионном пред-
ставлении.
Учитывая, что g(/nl,m2) = G(ml,/n2)LI (см. (5.43)), равенство (5.69) мо-
жет быть переписано в следующей форме:
i(m1,m2) = ivv(ffi|+'"2)/2(£w{g(m1,m2)} + Ey.|w|m,^(m|,m2)} +
+ ei {^(w|,m2)w22}+ Ек {^Г1 g(m,,m2)w™2 })ы. (5.72)
Отметим, что оператор А = Ы коммутирует с оператором умножения на
степени w. Действительно, пусть А есть линейный оператор А: Н —> С, такой
что
A(l)=l; A(«)=f; A(j) = i; A(k) = -l, (5.73)
q = a+bi + cj + dk € H — произвольный кватернион, w, ~ a + pz € C j есть
/-кватернион, w2 = a + Ру e C2 естьу-кватернион. Вычисляя непосредствен-
но произведение кватернионов указанного вида, получаем
qw2 = (any—р£у — acS+Pd6) +
+(P«y -I- aby - Pc5 - ad5) z +
+(cuz5 - P&S+otcy - P dy) j +
4-(Pa5 + ah8+pcy4~ady)£. (5.74)
Тогда из соотношений (5.73), (5.74) следует, что
А (qw2) = [(оспу — Pby — occS+Pd5) - (Рпб + od>8 + Pcy + ady)]
+[(Pay + aby - pc?8 - adS)+(aa8 - РЬЗ + асу - Pdy)]z.
С другой стороны, произведение трех комплексных чисел
A(wj) = a+Pi, A(w2) = y+3z, A(q) = (a — d)+(b + c)z
также представляется в форме
А (и>|) A (g) А (w2) = [(оспу — pZ/у — асб -I- Pd3) — (PaS 4- a£8 -I- Pry + ady)]
+[(Р«У+aby — РсЗ — ocd3) + (апб — р/?5+асу ~ pdy)] i.
5.2. Совмещенные алгоритмы дискретных ортогональных преобразований
329
Значит справедливо соотношение
qw2) = A(wj)a(47)a(b>2).
Поэтому проектирование кватернионов в поле комплексных чисел посред-
ством оператора LI в (5.72) может быть выполнено после умножений на сте-
пени w и, следовательно, справедливо равенство
+ {<‘,/2ё (т1«т2 ) w22/2 } + Ек {^Г,/2£ (™1»т2 ) w22/2 })LI -
Из последнего равенства следует, что
7(w1,zn2) = Re|w1m,/2g(m1,m2)w^2/2J. (5.75)
Из (5.74) следует равенство
Re {wj qw2 } = ау а — fiyb — себе + (36 <7 .
Поэтому вычисление двумерного ДКП отличается от вычисления КДПФ
того же объема тремя операциями сложения и четырьмя операциями умноже-
ния на отсчет входного массива, необходимыми для выполнения дополни-
тельных умножений на степени м>ь w2, одновременно со взятием веществен-
ной части в (5.75) (мы, как обычно, предполагаем, что произведения ау, ру, а§
и (35 вычислены заранее, так как в рассматриваемом случае они представляют
собой константы — значения базисных функций). Следовательно, оценки слож-
ности описанного алгоритма ДКП имеют вид
«дкп(^х^) = ^кдпф(^х^+4№,
ABKn(NxN) = AK№S,(NxN)+3N2, (5.76)
где МКДПФ (W х 2V), АКДПФ (Nx/V) — оценки сложности используемого алго-
ритма КДПФ при вещественном входном сигнале.
На рис. 5.5 приведена обобщенная схема описанного алгоритма ДКП.
В таблице 5.1 даны оценки сложности разработанного алгоритма при ис-
пользовании алгоритмов КДПФ, описанных в п.5.2.3.
330
ГЛАВА 5
Рис. 5.5. Обобщенная схема двумерного ДКП при четном размере блока
Таблица 5.1. Оценки сложности двумерного ДКП (ДДКП)
Алгоритм КДПФ Оценки сложности КДПФ Оценки сложности ДДКП
по основанию 2 и КДПФ (N * N) < 21 № log; N - /'Wln.(A'>'W)<^N2logIN-22№ MflKn(A'xtf)<21№log2W+^N2 2'®n(A’xW)<S«2log2W+^A'2
по основанию 4 M.OT.(NxN)<112№log2N-^№ Лкдпф("хN) <^N2 log;N -2 WgKn(WxN)<112№log2W+^№ 1ZO 04 Wn (A2X N)<N2 log2 NN2 1ZO 04
5.3. Быстрые алгоритмы ДОП при специальном представлении
данных
5.3.1. Представление данных в круговых кодах
Декомпозиция Кули—Тьюки «по основаниюр». Пусть N = рг, преобразова-
ние входной последовательности/(л) определено соотношением (5.11). Тогда
N/
"" /Р
при т = 0, 1,
— 1 спектр F (т) может быть представлен в виде
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
331
F(tn + N/p) 1
F(m + 2N/P) = 1
1
Y
Y2
уР"1
1 Fo (m)'
Y'’4 w”F, (m)
y2(p_|) 2mr / \
I W Г2 (ш)
(5-77)
где Fj(m) (j = 0, 1,1) есть ДПФ длиной N/р,
7-1
Fj(m)= ^2f(pn+ j)(wpy\ * (5.78)
w = ехр{2тп/?/}, у — ехр{2ти/р} — первообразные корни из единицы степе-
ни N и р соответственно.
Равенства (5.77), (5.78) сводят вычисление ДПФ длиной N к вычислению р
раз ДПФ длиной N/р с последующей последовательной редукцией к вычис-
лению одноточечных преобразований. Спецификой случая N = рг, при
р?±2,4, является наличие в правой части (5.77) умножений на степени кон-
станты у, что увеличивает вычислительную сложность алгоритма по сравне-
нию с БПФ по основанию 2 и 4 [2, 17], где аналогичные умножения триви-
альны (умножения на ±1, +/).
В работе [29] предложено специальное представление данных (значений
преобразуемого сигнала f(n) и комплексных параметров) в так называемых
у-кодах, которое позволяет сделать эти умножения тривиальными.
Пусть у = схр {2л7/ /?} — первообразный комплексный корень степени р
из единицы. Тогда для комплексного числа с наряду с обычной алгебраичес-
кой формой представления c = « + Z?z возможна и форма
с = с[у-\-с2у2 + ... + c/?_1yp 1 “ a + bi, (5.79)
где вещественные q,...,с t связаны с вещественными а, 6 соотношениями
К 2пк
а= / , ск cos------,
jt=i Р
p-i
Ь = ^'к
к=]
. 2пк
sin---.
р
332
ГЛАВА 5
Упорядоченный набор из (р-1) чисел (ср...,ср__{), ассоциированный с
представлением с в форме (5.79), будем называть у-кодом числа z-
Арифметические действия над комплексными числами индуцируют пра-
вила действий над кодами. Сложение чисел в у-кодах производится покомпо-
нентно, умножение чисел ву-кодах сводится к нахождению циклической сверт-
ки у-кодов. Умножения на у,у2,...,ур-1 выполняются с помощью у-кодов
без вещественных умножений и сводятся лишь к смене знака, суммированию
и перестановке части компонентов кода [29].
Так как вычисление циклической свертки произвольной длины есть ти-
пичная (и непростая) задача цифровой обработки сигналов, то в настоящей
главе мы ограничиваемся рассмотрением случая р = 3, для которого переход
к у-кодам наиболее эффективен и нагляден.
5.3.2. Алгоритмы одномерного ДПФ при длине преобразования N-3k
Пусть р=3, N =Зк,
у = ехр(2тп/3) = ^(-1-нч/з), у = - /л/з),
тогда равенство (5.79) примет вид (см. рис. 5.6) с~ а + Ы = ху + уу , где
x = [b/4з^ — а, у = [—Ь/у[з} — а.
Арифметические операции над кодами определяются равенствами
(х,у) + (и,у) = (х + и,у+ v), (5.80)
(х,у)-(и,v) = ((y-x)(y-u)-xu, (y-x)(v-u)~ у v).
Поэтому сложность операций сложения и умножения в кодах совпадает со
сложностью сложения и умножения комплексных чисел, а именно, сложение
в кодах реализуется при помощи двух вещественных сложений, умножение в
кодах реализуется через три вещественных умножения и три вещественных
сложения (как обычно, считается, что сложения компонентов кода базисных
функций выполнены заранее).
Умножение на числа у и у, имеющие коды (1,0) и (0,1), соответственно,
определяется равенствами
(1,0) • (u, у) = (—V, и — v),
(0,1)-(м,у) = (у — и, —м),
и не содержит нетривиальных вещественных умножений.
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
333
Рис. 5.6. Представление комплексных чисел в у-кодах
Этот факт позволяет снизить вычислительную сложность алгоритма БПФ
именно благодаря простой реализации умножений на степени у, удельный
вклад которых в быстрый алгоритм ДПФ, реализуемый на основе декомпози-
ции (5.77) весьма высок.
При р — 3 соотношение (5.77) принимает вид
>(т)
F(m + W/3)
F(m+2JV/3)
1 1 1V F0(m)'
1 у у
.1 V
(5.81)
и нетрудно показать, что оценки вычислительной сложности такого алгорит-
ма для вещественного сигнала имеют вид [21, 29]
М (/V) < /VIg3 /V - /V, A(/V) < 37V lg3 /V + N/3. (5.82)
5.3.3. Алгоритмы дискретного косинусного преобразования длиной 7V= 3*
Следуя [21], представим ДКП нечетной длины N в виде
Л/-1
/Н= E/(«)cos
n—Q
(n + l/2)m
п
= Re
(5.83)
N
334
ГЛАВА 5
где w = exp{27ri/4/v} — первообразный корень степени 47Уиз единицы. Пусть
f (п) при к = 2п +1;
О при к = 2п\
тогда соотношение (5.83) примет вид
/(m) = Re
2/V-l
W
n=0
(5.84)
При нечетном W числа 4и /V взаимно просты, декомпозиция Гуда-Томаса
(см. п.5.1.3) по формулам (5.22), (5.23), при р = 4 и Q = N, выполняется без
дополнительных умножений.
Преобразование индексов (5.22), ограничения в (5.83) и (5.84) на диапазон
изменения индексов т и к, а также обращение в нуль функции g(k} при
четных к, выделяют в двумерных массивах размером 4x7V «допустимые» под-
множества К и М для пар (к{,к2} (аналог \п{,п2) в (5.22)-(5.24)) и (га,,т2)
(см. рис. 5.7, 5.8). Кроме того, при р = 4 корень а в (5.22) равен мнимой еди-
нице /. Тогда из (5.84) по аналогии с (5.24) получается, что
з /V-1
G(m„m2)=£ £
it2=o(*,=o
ik2m2
(5.85)
Так как «допустимое» подмножество индексов К сформировано так, что
#(^,£2) отлично от нуля только при (к},к2)е К, то и суммирование в (5.85)
выполняется только при то есть при к2 =1,3. Этот факт позво-
ляет привести выражение (5.85) к виду
/(m) = Re
N-l
>т2 £ ?(*,)₽*'”"
*1=о
(5.86)
где п₽и ММ в=ехрг2то/л,1
[,) Ь(л-4,.3) при (*„з)ек’р exPt27“/'vJ-
Таким образом, ДКП нечетной длины N сведено к вещественному преоб-
разованию Фурье той же длины. При N = 3Г и использовании ДПФ, описан-
ного в п.5.3.2, оценки вычислительной сложности такого алгоритма ДКП имеют
вид [211
М (/V) = Nlog37V-/V, A(/V) = 3/VIog37V--|/V.
(5.87)
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
335
Рис. 5.8. Допустимые области значений пар (ЛрЛ2) и (znt,/n2) при
336
ГЛАВА 5
5.3.4. Алгоритмы дискретных ортогональных преобразований, реализуемые
в кодах Гамильтона—Эйзенштейна
Использование представлений элементов R-алгебр, размерности больше
двух, приводит к синтезу БА многомерных ДОП с уменьшенной вычисли-
тельной сложностью.
Пусть кватернионы Yi и у2 - примитивные корни третьей степени из
единицы, лежащие в различных изоморфных копиях поля комплексных чи-
сел С, = R(i) и С2 ~R(j), каноническим образом вложенных в Н:
Yi =exp{2m/3}, у2 = ехр{271//3};
кватернионы У] и у2 ~ соответствующие образы в Н элементов, сопряжен-
ных в Cj и С2 элементам у( и у2:
Yi = ехр {-2тп/3}, у2 = ехр { 2тгj'/З}.
Кватернионы q = qQ + ^,/ + <727 + ^3^ с <?2 — будем называть
/-кватернионами. Аналогично определяются j- и А:-кватернионы.
Ряд свойств алгебры кватернионов сформулируем для удобства чтения в
форме лемм, доказательства которых сводятся к непосредственной проверке
тождеств для комплексных чисел.
Лемма 5.1. Для любого <убН существуют единственные а, 6, <?, <7eR
такие, что справедливо представление
^ = («Yi+^Yi)Y2 + (ni + ^Yi)y2-
(5.88)
Определение 5.8. Следуя [20], четверку вещественных чисел {a, b, с, d) в
представлении (5.88) для q назовем кодом Гамильтона—Эйзенштейна кватер-
ниона q и будем обозначать (q) .
В частности, кватернионы специального вида имеют следующие коды:
(Y,) = (-!, О, -1, 0), (7,) = (0. -1, 0, -1),
<Y2> = (-1. -•> о, 0), (г2)=(0.0, -1. -1).
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
337
Далее, если g = a€R , то (q} = (a, а, а, а).
Операции в теле кватернионов и автоморфизмы Н, как четырехмерной
R-алгебры, индуцируют преобразования ассоциированных кодов.
Лемма 5.2. Пусть = b, с, d), /еС2,
(5) = (а, р, а, Р), (t) = (о, и, т, т).
Тогда
(sq) = ((р - а)(а - Ь) + аа, (р - а)(а — b) + Р&),
(Р — а)(с — d) + ac, (Р~а)(с —d)+pd), (5.89)
/ ,\=[(т-ст)(о-с)+ста’ (t-a)(fr-rf)+<rt'.
(т-а)(а-“<?)+тс, (т —a)(b-d) + Td
В частности, справедливы равенства:
(Yi я}~ (~k a-b, —d, c — d}, q} = (b — a, —a, d — c, —c),
( Я Y2)~(“c’ —a~c-> b — d}, (q Y2)—(c —n, d—b, —a, —£>).
Таким образом, умножения (5.89) и (5.90) кватерниона q общего вида на 1~
или у-кватернионы требуют не более шести нетривиальных вещественных
умножений и шести вещественных сложений (если считать, что сложения
компонентов кодов /- иу-кватернионов выполнены заранее); умножения ква-
тернионов q общего вида на Yj , Yi » Y2 или Ъ требуют только двух веще-
ственных сложений. Непосредственное последовательное умножение кватер-
ниона общего вида на /- и у-кватернионы требует 12 вещественных умноже-
ний. Покажем, что одновременное выполнение такой пары умножений требует
в 1,5 раза меньшего числа вещественных умножений.
Лемма 5.3. Пусть q, s, t — кватернионы, определенные в лемме 5.2. Тогда
вычисление кода произведения sqt требует не более девяти нетривиальных
вещественных умножений и пятнадцати вещественных сложений.
Доказательство. В обозначениях леммы 5.2 последовательным применени-
ем (5.89) и (5.90) получаем равенство:
(sqt) = ((т — а) |(р — a)(d — с — b + а) — а(с — а)] — о(р — a)(fr — а) + ааа,
(x-a)[(P-a)(j -c-Z> + a)-p(d -fc)]-o(p-a)(fc-a) + (ypfc,
(т — а)[(р — a)(d — с — Ь + а) — а(с — а)] — т(р — a)(d — с) + тас,
(т-<т)[(р-а)(г/-c-Z? + a)-P(d-£>)]-т(р-а)(^ —c)+Tpd).
338
ГЛАВА 5
Также непосредственно легко убедиться, что автоморфизмы е, , и Ек
(см. (5.33) п.5.2.)) алгебры Н,
Ef: q^i~[qi , £ j : q j~lq j , Ek:q^k'qk,
индуцируют преобразования кодов, описываемые следующим предложением.
Лемма 5.4. Пусть (q) = (a, b, с, d], тогда
= d, a, b), (Ej(q)) = (b, a, d, с), (tk(qty = (d, с, b, а),
и, следовательно, переход от кватерниона q к его автоморфному образу реа-
лизуется в кодах тривиально.
Лемма 5.5. Пусть (q)~ (a, b, с, dty тогда для кода (q'} кватерниона
q'----(d — b — с) у, +(л — b — с)у15 полученного из кватерниона формальной за-
меной в представлении (5.88) элементов у2 и у2 элементами у, и у, с
последующим применением тождеств у, + у, = — 1, Yj У] =1, справедливо
следующее равенство:
(q'} = (a, b, с, d)L,
где L
1 о Г
-1 -1 -1
-1 -1 -1
О 1 О
Лемма 5.6. Пусть seC|, (s) = (a, (3, а, 0),
Тогда справедливо равенство
Re$-H’Im.s =(ос, 0, a, 0)V.
Леммы 5.5 и 5.6 обеспечивают возможность рассмотрения ДОП как «про-
екций» некоторых вспомогательных преобразований, базисные функции ко-
торых принимают значения не в изоморфных копиях алгебры С, а являются
кватернионами общего вида. Это позволяет более полно учесть симметрии
алгебры Н, ассоциированные с ее автоморфизмами.
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
339
Быстрый алгоритм двумерного ДПФ. Пусть /(nH н2)бК — преобразуе-
мый двумерный ( W х/V )-массив, Л/=3', F(ml, т2) — двумерный дискрет-
ный спектр Фурье:
N-1
т2)~ У? /(np n2)wn|/”l+"2 "'2, w = exp{27u//v}. (5.91)
и,, п2—О
Рассмотрим двумерный кватернионный спектр (5.41) (КДПФ):
W-1
F(w], т2) = У2 n2)w22fn2> (5 92)
л,, п2=0
Wj = exp{27u//v}, w2 --схр (2л у/Л''}, m2 =0, 1, ..., N — 1).
Константы w,, w2 будем считать заданными кодами Гамильтона—Эйзен-
штейна. Из лемм 5.5 и 5.6 следует следующее утверждение.
Лемма 5.7. Пусть матрицы L и V определены в леммах 5.5 и 5.6. Тогда
F(ni{, т2^ = w22))LV.
Таким образом, вычисление спектра F^m[t т2] только 2/V вещественными
умножениями отличается от вычисления кватернионного спектра (5.92). Пред-
ставление (5.88) кватернионов кодами позволяет учесть мультипликативную
тривиальность умножения на константы , у? в быстрых алгоритмах. Вы-
числение спектра яг2) с помощью кватернионнного спектра позволя-
ет в максимальной степени использовать симметрии, связанные с автомор-
физмами алгебры Н при выборе фундаментальной области индексов выход-
ного сигнала.
Действительно, представим (5.92) в форме
где Fab(m]t т2) = У2 ^|ЗЛ|",|/(Зн| + а, Зя2+ Z?)w2n2 "'2,
И|, «2=0
и оценим мультипликативную сложность вычисления кватернионного спектра.
Значения Fab (ли,, т2) достаточно вычислить для пар (wij, т2) = (я/f, т2j € Qo,
где Qo — фундаментальная область:
Qo —
* * 1 п *
Wil, т2 : US я?),
т
340
ГЛАВА 5
Значения F^^m^ т2} для пар (т}, т2) , лежащих в областях, получен-
ных из Qo аддитивными сдвигами на векторы
отличаются от соответствующих Fah\m^, т2) лишь множителями Yi, Ун
у2, у2 и не требуют для вычисления дополнительных вещественных умно-
жений. При вычислении Fahlml, т2\ достаточно ограничиться значениями
(пц, т2)€ Q, CQ0 :
Действительно, непосредственно проверяются тождества:
*1 \
/ * / \ * \ а-----MIi Л/ I *
_ 1 aflli г* I * * I /мь I__ I 3 r * * /жм
Y1£J^I Fab[m\,ml}W2 — m2\W2 '
(* ~ I \ . *\ , * ~ ( N ) hrr“m2
«шт г» / * *1 bm? \Л,Ь апц г * * 13 J /с
W, 'F^^, m2jw2 2jy2=wl —~m2 w2( (5.93)
/ ♦ _ / \ . ♦ \ «-----Ш|
/ ат, I * * \ btn\Л.Ь __ I 3 Гг1
Yl £k ^1 Fab (ml ’ m2 )W2 Д2 - ^1 Fab
. /V t
N * N fthr"‘z
— — nil, —- m2 w2
И так как умножения на у", у2 и выполнение отображений 8,-, 8у и е*
не требуют нетривиальных вещественных умножений, то для мультиплика-
тивной сложности Л/(7V) рассмотренного алгоритма вычисления спектра (5.91)
имеем окончательно
M(^x^) = C^2lg3^+o(/V2),
(5-94)
где С = 5/3 для вещественных и С = 10/3 для комплексных входных данных.
Быстрый алгоритм дискретного косинусного преобразования (БА ДКП). В ряде
работ [21, 36, 37] показано, что одномерное дискретное косинусное преобразова-
ние (ДКП) нечетной длины А может быть сведено к ДПФ вещественного сигна-
ла той же длины, полученного из исходного перестановкой отсчетов (см. п.5.2.).
Следуя [21], получаем аналогичное утверждение для двумерного дискрет-
ного косинусного преобразования.
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
341
Рассмотрим двумерное (ненормированное) ДКП в форме
\ к-'1 ( \ (и 4-1/2) ль (л4-1/2)т2
ДлП1,т2)= > . /(nbn2JcosJt--------------cosп-----------.
иь п2=0 м *’
Пусть
2N-1
б(п1|,Л12)= ехР
П. *2=0
2N
/ X • 12т2
g(t},t2)^TlJ-^
где
/(нР н2)’ ПРИ G —2л, 4-1, t2 = 2п2 4-1;
g (/|, t2) = О, в остальных случаях;
Г„ r2=0, 1, ..., 2/V —1.
Тогда
+e/g(w2i, лг2))+Е* тг))]> (5.95)
и основную трудность представляет вычисление G(mt, т2).
Пусть целые аир выбраны так, чтобы выполнялись соотношения
42ос = 4 (mod 4/v);
N2$ = N (mod 4JV).
Находя для каждого нечетного tx (0 < tx < 2/V; w = 1, 2) пару (г у1, tx2), как
решение сравнения
tx ~ 4г у] + /V tх2 (mod 4/V), (5.96)
и для каждого тх (0 <тх < N ) пару ( лиу1, тх2 ), как решение сравнения
тх = 4ату1 4- /Vp тх2 (mod4/v),
с условиями
О < fv,, mxl < N ; 0 < tx2, тх2 < 4,
(5-97)
(5.98)
получаем системы сравнений
?v=4 (mod /V); mx = mxl (mod IV);
tx=N tx2 (mod 4); mx=mx2 (mod 4).
342
ГЛАВА 5
Пусть Т — множество четверок чисел (hi* *12* *21* *22 )’ являющихся реше-
ниями сравнений (5.96) с условиями (5.98). Так как ts нечетно, то ts2 также
нечетные, поэтому множество Т представимо в виде объединения четырех
непересекающихся множеств: Т — Тх j U Т13 U Т3tU Т33, где
Т(0> ~ {(*11* *12’ *21* *22)^^ : *12 = а» *22 ~ .
Отметим ряд легко проверяемых свойств множеств Tilh:
а) преобразования
(п„3л21, l)M(w-tll,3,«2l,l), (5.99)
(»,„ 1,<21, 3)^(r„,l,W-«2l, 3), (5.100)
(tn, 3, r2„ 3)^(w-r„, 3, N-t2l, З) (5.101)
являются биекциями множеств Тзх , Т13 , Т33 , соответственно;
Ь) если card А — число элементов множества А, то
card Т} 3 = card Т3 j = ; card Т33 = ;
с) при (гц, tn\ r2i* *22) переменные гп и г21 принимают независимо
все значения 0, 1, TV —1 ровно по одному разу:
^(*11’ *12’ *21’ *22) ~&(4*ц 4“ W*12* 4f2( + ЛЬ22),
F(mn, т12, ш21, т22) = /(4а mn+N$ml2, 4am21 4-TVpm22).
Производя в (5.95) замены переменных (5.96) и (5.97), получаем после преоб-
разований (декомпозиция Гуда—Томаса) выражение
"*12 ’ m21, ^22)4-6/(^(юп, "Jt2* "hi* m22
+ej(c("1ll’ "*12*
"hl*
7ft] 2? ^21’ ^^2
где
w12, m2l, m22) =
= i'^»v1'"m"G(r11, r12, t2l, =
= S , E . a, r2l, b)w'2^jb^ =
a, b—1,3
= S ^(^ii* "*12* ™21* "*22)- (5.102)
a, 5=1,3
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
343
-г -3 - --1 -3 • --1 гг
Так как г =-i= i , j ~~j~ j , то, производя в выражении для ТиЬ
при а и/или b равных 3 замену переменных , г2] согласно (5.99)—(5.101),
получаем после несложных преобразований следующее равенство:
m2}= т]2, m2]t т?2) =
(5.103)
где
G(nx, 1, п2, 1), при (л„ I, п2, 1)еГ;
G(/V —И|, 3, п2, 1), при (N-nj, 3, п2, 1)еГ;
G(n]? 1, N — п2, 3), при (п1? 1, N — n2, 3)еТ;
G(jV — И|, 3, N — п2, 3), при (N-nit 3, N — n2, 3)еТ.
Равенство (5.103) доказано для любого нечетного N. В случае /V = 3Г вы-
числение (5.103) можно реализовать в кодах с помощью алгоритма предыду-
щего раздела, что приводит к следующей оценке:
M(N*N)=^N2\og3N + o[N2\
В этом случае, вычисление f(mx, т2) для т}, т2 одной четности не тре-
бует дополнительных умножений; при тх, т2 разной четности умножение
на константу / в кодах требует не более одного умножения на отсчет выходно-
го массива. В конкретных алгоритмах обработки сигналов эти умножения
могут быть объединены с нормированием косинусного спектра.
5.3.5. Алгоритмы дискретного косинусного преобразования коротких длин
Алгебраические принципы синтеза БА ДКП коротких длин. Рассматривае-
мый метод синтеза БА ДКП базируется на следующих алгебраических идеях.
1. Матрица ДКП имеет блочную структуру. Результат умножения такой
матрицы на входной вектор сводится к умножению векторов из подпространств
сигнального пространства на матрицы меньших размеров со специфически-
ми свойствами «симметрии».
2. Умножение этих подматриц на векторы соответствующих подпространств
эквивалентно умножениям элементов некоторых конечномерных алгебр.
3. В большинстве рассматриваемых случаев умножение элементов таких
алгебр эквивалентно умножению в полиномиальных кольцах (или циклической
свертке). Это позволяет воспользоваться известными быстрыми алгоритмами
циклических сверток с минимальным числом умножений.
344
ГЛАВА 5
В данном разделе рассматриваются следующие конечномерные алгебры.
1. Двумерная алгебра A] ' с базисом {1, ej и правилами умножения ба-
зисных элементов
е?=-1.
(Алгебра С комплексных чисел).
2. Двумерная алгебра А^ с базисом {1, et} и правилами умножения
базисных элементов
е?=1.
(Алгебра «двойных» чисел, изоморфная прямой сумме R ©R см. пример 5.5.).
3. Трехмерная алгебра А^ с базисом {1, еи е2} и правилами умножения
базисных элементов
с, = с*2, е2 = —С], eje2 =е2е, = — 1.
4. Четырехмерная алгебра Aj4^ с базисом {1, еь е2, е3} и правилами ум-
ножения базисных элементов
2 2 1 2
С । — е 1 ® 2 — 5 ® 3 — 2 5 ® | — С 2® 1 — 3 5
е2е3 —е3е2 =-е,, е1е3=е3е,=1.
5. Четырехмерная алгебра А^ с базисом {1, еи е2, е3} и правилами ум-
ножения базисных элементов
2 2 1 2
ei =е2, е2=1, е3=е2, е1е2 =е2е, =е3,
е2еЗ=еЗе2~еН е1е3 =СЗе1 “1 •
6. Четырехмерная алгебра А^ с базисом {1, ер е2, е3} и правилами ум-
ножения базисных элементов
е2=—1, е2=1, е3=-1, е,е2 =е2е, = -- е3,
е2е3 =е3е2 =-е15 е,е3 =е3е, = е2. (5.104)
Непосредственно проверяются следующие утверждения.
Лемма 5.8.
5.8а . Умножение элементов (осо 4-a^i), (P0 + Piei) бА}2' равносильно ум-
ножению полиномов
(a0+a1f)(P0+P1r) (mod(r2+l))
и требует, согласно [17], три умножения и три сложения.
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
345
5.86. Умножение элементов (а0 -t-o^e,), (р0 Ч-pje,) G А22- равносильно ум-
ножению полиномов
(ос0 +aj/)(p0 +pj/) (mod(z2-1))
и требует два умножения и четыре сложения [17].
5.8в. Умножение элементов (а0 ч-а^ Ч-а2е2), (Ро Ч-р1е1+Р2е2) е А^'
равносильно умножению полиномов
(а0 +a,z+ а2г)(роч-р^ + Рэ/2) (mod(r3 4-1))
и требует четыре умножения и четырнадцать сложений [17].
5.8г. Умножение элементов (сс0 -t-cqci Ч-а2е2 Ч-а3е3), (Ро Ч-р1е1 Ч-р2е2 Ч-Р3е3) €
GAp равносильно умножению полиномов
(осо 4-a,r-a2z2 -a3r3)(po ч-Р/-р2/2 -(З3/3) (modjz4 ч-ljj
и требует девять умножений и пятнадцать сложений [17].
д) Умножение элементов (ос0 Ч-а1е1 Ч-а2е2Ч-ос3е3), (р0 Ч-р,е] Ч-(32е2 Ч-(33е3)
равносильно умножению полиномов
(аоЧ-а1гч-сс2/2 + азг3)(Зо+3^+₽2г2 +Зз?3) (mod(z4-l))
и требует пять умножений и пятнадцать сложений [17].
Лемма 5.9. Алгебра А^ изоморфна прямой сумме СфС :
СфС = {(z!,z2): Zf =а, Ч-bjij, z2 ~a2-hb2i2, if = i2 = -l, «|,a2,b,,b2 GR
Доказательство. Элементы
E0=(l,l), E,=(i„-i2), E2=(-l,l), E3=(i„i2) 6 СфС
образуют базис алгебры СфС над R. Отображение ср, определенное для ба-
зисных элементов алгебр Ар и СфС как
<р:е,->(/,.-i2), cp:e2i-»(-l, 1), <p:e3~(ip i2), 1)
продолжается R-линейно до изоморфизма соответствующих четырехмерных
пространств и сохраняет равенства (5.104).
Линейный оператор L, определенный на пространстве алгебры СфС об-
разами базисных элементов
L(Eo)=A(Eo-E2), L(E,) = 1(E,+E3). L(E2)=1(Eo+E2),
l(e3)=A(e3-e,),
346
ГЛАВА 5
преобразует базис {Ео, Е], Е2, Е3} в «стандартный» базис {о0, ut, о2, о3}
алгебры СфС, рассматриваемой как четырехмерная К-алгебра:
Qq — L(E0) — (1 + 0 , 0 + 0-/2), O| = L(Ef) — (о + /|, 0 + 0/2),
o2 = t(E2) = (0 + 0-i1, 1 + 0-i2), CT3 = L(E3) = (O+O-ij, 0+i2).
Следствие. Умножение постоянного элемента а — сс0 + «,6, +сс2еэ + сс3е3
на вектор b = [30-Г^С]-r(32e2 | [33e3 алгебры требует 6 вещественных
умножений и 10 вещественных сложений.
Доказательство. Сложность рассматриваемого умножения складывается из
умножения двух пар комплексных чисел (элементов алгебры СфС в базисе
{а0, а,, о2, а3}) и сложности преобразования элементов при замене базиса
{Ео, Ег Е2, Е3} на базис {о0, о2, о3}. Для умножения двух пар комп-
лексных чисел достаточно 3+3 умножений и 3+3 сложений [17]. Для преобра-
зования элементов переменного вектора достаточно 4-х сложений.
Алгоритм дискретного косинусного преобразования длиной N = 8. Рассмот-
рим (ненормированное) ДКП (5.57) в матричной форме (5.4), где
F=(F(°).....f(7))> f = (/(0),...,/(7)).
После переупорядочивания компонентов входного и выходного векторов
G = (G(0),...,G(7)) = (F(l),F(5),F(7),F(3),F(2),F(6),F(4),F(0)),
g = («(0)...g(7)) = (/(o)./(2),/(4)./(6),f(7)./(5),/(3)./(L)),
матричное представление ДКП может быть записано в форме G' — Tgz, где
/ — знак транспонирования:
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
347
a =cos
b — cos
'Зп'
Д6,
c = cos
I = cos
'бпу
Д6,
(2л) (4л'
И—COS---- , V —cos --- .
(16 J (16
Формирование из компонентов вектора g вспомогательного массива,
z(0) = g(0)-g(4), z(l) = g(l)-g(5), z(2) = g(2)-g(6),
z(3) = g(3)-g(7),
z (4) = (g (0) + g (4)) - (g (2) + g (6)), z(5) = (g (1)+g (5)) - (g (3) + g (7)),
z (6) = [(s (°) + «(4))+G? (2) + «(6))| -
-|(^W + s(5))+(«(3) + g(7))|, (5.105)
z (7) = [(g (°) + g (4))+(g (2) + g (6))]+[(g (1) + g (5))+(g (3) + g (7))],
требует 14 операций вещественного сложения. После этого выполнение ко-
синусного преобразования сводится к следующим матричным вычислениям:
G(0)'
G(l)
G(2)
lG(3).
a
c
d
b
c —d
d —b
b a
—a c
(5.106)
G(4)] (u
-nfz(4)'
« Jlz(5)J’
(5.107)
б(б) = vz(6),
G(7) = z(7).
(5.108)
Вычисление матричного произведения (5.106) эквивалентно вычислению про-
изведения элементов s,pG Aj4^ и, в соответствии с леммой 5.8г, требует 9 опе-
раций вещественного умножения и 15 операций вещественного сложения:
sp = (c+ael 4-#е2 -|-£Ze3)(z(0) + z(l)e1 4-z(2)e2 4-z(3)e3).
348
ГЛАВА 5
Вычисление матричного произведения (5.107) эквивалентно вычисле-
нию произведения элементов q,reA(2^ и, в соответствии с леммой 5.8а
требует 3 операций вещественного умножения и 3 операций вещественно-
го сложения:
qr = (M-bZe1)(z(4) + z(5)e1).
Вычисление по формуле (5.108) требует одной операции вещественного
умножения.
Суммарная сложность алгоритма ДКП длиной N= 8 с учетом формирова-
ния вспомогательных переменных z0,...,z7 составляет 9 + 3+1 = 13 опера-
ций умножения и 14 + 15 + 3 = 32 операции сложения.
Структура рассмотренного алгоритма не зависит от конкретных значений
параметров a, b,..., v. Пусть v/ = Z/ = c, = l, и —и/l, а = а/с, d' = d/c,
b' = b/c. Тогда умножение в (5.108) становится тривиальным, в матричном
произведении (5.107) остается два умножения. Вычисление правой части со-
отношения (5.106) требует 8 операций умножения, а умножения на v, е, с
объединяются с нормализацией компонентов косинусного спектра (с умно-
жениями на Х,„ в (5.8)).
Таким образом, рассмотренный алгоритм ДКП длиной W=8 требует
2 + 8=10 операций умножения и 32 операции сложения, его схема приведена
на рис. 5.9.
Алгоритм ДКП длиной N= 9. После перестановки ряда строк и столбцов
матрица ДКП длиной 9 принимает вид
г а с d с -d а d а -с -d -c -a -a d -c c -a -d b -h —b b -b b 0" 0 0
е —и -v Т9 = v -е и и v -е -v -u e и —e v —evu h h -h -h —h —h -1 1 1
b -Ь -Ь b b -b 0 0 0
h h h h h h -1 -1 -1
1 1 1 k i i i 1 1
Матричные умножения
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
349
Рис.5.9. Направленный граф алгоритма ДКП длиной 8
эквивалентны умножению элементов алгебры :
(-tze2-cCj +J)(z(0)e( +z(l)e2 +z(2)) и (fe2-ge} -e)(z(6)e2-z(5)e, + z(7)),
соответственно, и требуют согласно лемме 5.8в 4 вещественных умножений и
14 вещественных сложений каждое.
Таким образом, ДКП длиной А =9 посредством умножения на матрицу
Т9 выполняется за 8 умножений и 44 сложения (то есть требует менее одного
умножения и около пяти сложений на отсчет). Схема рассмотренного алго-
ритма приведена на рис. 5.10.
Алгоритм дискретного косинусного преобразования длиной N— 10. После пе-
рестановки ряда строк и столбцов матрица ДКП длиной 10 принимает вид
f а b c d —d -c —b -a
b d —a -c c a -d -b -q q
с -а d —b b -d a —c q -q
d -с a -a b c -d q -q
1 и —u —I -I -it и I 0 0
Тм = и — 1 I —u —u I —l и 0 0
v —h -h v v -h —h v -i -i
h - v -v h h —v -v h i i
q ~cl Q Q -q -q q -q -q q
1 1 I 1 1 1 1 1 i i
V
350
ГЛАВА 5
Рис. 5.10. Направленный граф алгоритма ДКП длиной 9
Матричное умножение
эквивалентно вычислению произведения элементов алгебры
+ае2 — се3 +j)(z(o)e, + z(l)e2 + z(4)e3 - z(3)),
и требует, согласно лемме 5.8д, 5 вещественных умножений и 15 веществен-
ных сложений.
Вычисление матричного произведения
I и z(4)
и —ZJ z(5)
эквивалентно вычислению произведения элементов алгебры Aj2\
(Z + ие() (z (4) - z (5)et),
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
351
и, в соответствии с леммой 5.8а, требует три операции вещественного умно-
жения и три операции вещественного сложения.
Вычисление матричного произведения
v —h г(б)
Л -Jb(7),
эквивалентно вычислению произведения элементов алгебры
(v + Ae1)(z(6)-z(7)e1),
и, в соответствии с леммой 5.86, требует две операции вещественного умно-
жения и четыре операции вещественного сложения.
Таким образом, ДКП длиной 10 посредством умножения на матрицу
ТК) выполняется за 9 умножений и 43 сложения. Схема алгоритма приведена
на рис. 5.11.
Алгоритм дискретного косинусного преобразования длиной 12. После
перестановки ряда строк и столбцов матрица ДКП длиной 12 принимает
вид
a c c -a и d d -u -u -d -d и a c c -a d и -и d -c -a a -c —c -a a -c -d -u и -d b e -e b —e b —b —e -e -b —b e -b e e b
v I 1 V -v -I -I -v -I -v -v -I 1 V V I h —h —h h ~h h h -h
b ~e e b e b -b e —b -e -e b e -b -b -e e -b —b —e b -e e b
р-р р -р -р р -р р
я я я я я я я я
0 0 0 0
-1 -1 -1 -1
h —h —h h h -h -h h -h h h -h
111 111 11 1 1 11
352
ГЛАВА 5
A=(a' + d' + b'-c')/4-, B = {a, + d,-b'+c,'}lA\ C = (b'+ c'- a'+ d')/2;
D = (a'-d')/2; E = (b'+ c'+ a'-d')/2; F = (v' + /i')/2; G = (v'-h')/2.
Рис. 5.11. Направленный граф алгоритма ДКП длиной 10
Умножение матрицы ДКП длиной 12 на входной вектор эквивалентно:
а) умножению переменного элемента алгебры А^ на постоянный эле-
мент этой же алгебры;
б) умножению переменного элемента алгебры на постоянный эле-
мент этой же алгебры;
в) умножению переменного элемента алгебры А^ на постоянный эле-
мент этой же алгебры;
г) дополнительным умножениям констант на переменные и вспомогатель-
ным сложениям.
Согласно леммам 5.8, 5.9, ДКП длиной N= 12 посредством умножения на
матрицу Т12 выполняется за 13 умножений и 55 сложений. Схема алгоритма
приведена на рис. 5.12.
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
353
Л = (а'-а,-с'-и')/2- B = (a' + d' + c'-u,)l2\ С= (с' + и')/2;
D = (c'-u')/2; E = (a'-d' + c' + u')/2- F = (а'+ d' -с' + и’)/2.
Рис. 5.12. Направленный граф алгоритма ДКП длиной 12
12 — 9044
354
ГЛАВА 5
Алгоритм дискретного косинусного преобразования длиной N= 15. После пе-
рестановки ряда строк и столбцов матрица ДКП длиной 15 принимает вид
a d d У у -v v -а У v —v —a a -d -d у -V —у a v d —a У d -d -a -y -d v -y a -v b e -e b —b -e —e b —e -b —b e e b -b e c — c -c c c —c c —c 0 0 0 0
h р q -h s q p -s —s —q ~P s -h -p -q h -q —s ph s -p -h q -p -h q s h —q -s p I -r r -I -I r —r I -r I -I r r -I I -r и и -и -и -и -и и и -1 1 1 -1
b -e e b —b —e -e b e b -b e e —b —b -e e —b -b -e b —e e b 0 0 0 0 0 0
I -r r -/ I -r r -I —r I -I r -r I -I r -r I -I r I -r r -I -1 -1 1 1 -1 1
c -c c c —c —c c -c 0 0 0 0 -с с 0
и и и и и и и и -1 -1 -1 -1 и и -1
1 1 1 1 1 1 1 1 1 1 I 1 1 1 1
Умножение матрицы ДКП длиной 15 на входной вектор эквивалентно:
а) двум умножениям переменного элемента алгебры А^ на постоянный
элемент этой же алгебры;
б) умножению переменного элемента алгебры Ар на постоянный эле-
мент этой же алгебры;
в) умножению переменного элемента алгебры Ар на постоянный эле-
мент этой же алгебры;
г) дополнительным умножениям констант на переменные и вспомогатель-
ным сложениям.
ДКП длиной N= 15 посредством умножения на матрицу Т15 выполняется
за 24 умножения и 83 сложения. Схема алгоритма приведена на рис. 5.13.
В качестве основы для сравнительного анализа вычислительной сложнос-
ти синтезированных алгоритмов был использован алгоритм работы [26], син-
тезированный для ДКП произвольных длин, оценки сложности которого при
/V = 2* совпадают с оценками сложности лучших из известных алгоритмов
ДКП [38, 41].
В таблице 5.2 приведено количество операций необходимых для вычисле-
ния ДКП предложенным алгоритмом и известным способом. На рис. 5.14
5.3. Быстрые алгоритмы ДОП при специальном представлении данных
355
A = (h — 5 + р — q)/2\ B = (h — s — p + q)l2\ С = (р+ q — h —s)/2;
D = (h + s)/2; E = (h + s + p + q)/2; F = a1 + d' + /-v';
G = (df-vf)/2\ H=(d' + v')/2’ I=(l~r)/2\ J=(/ + r)/2.
Рис. 5.13. Направленный граф алгоритма ДКП длиной 15
12*
356
ГЛАВА 5
Таблица 5.2. Количество операций для вычисления ДКП
N Описанные алгоритмы Алгоритм работы [26]
* + * +
8 10 32 12 29
9 8 44 11 44
10 9 43 15 36
12 13 51 20 43
15 21 82 35 89
приводится зависимость удельной мультипликативной сложности алгоритмов
от длины преобразования.
На рис. 5.15 показана зависимость времени xN обработки изображения
блочным ДКП от размера квадратного блока N в виде относительной харак-
теристики Tyv/Tg, где т8 — это время обработки изображения блоками 8x8
(tn/t8= 1 ПРИ N= 8), размер изображения — 1024x1024 пиксела.
Таким образом, синтезированные алгоритмы ДКП гарантируют скорость
обработки изображения близкую к скорости обработки лучшим из известных
алгоритмов ДКП длиной А= 8. Время обработки практически не возрастает с
ростом N. В то же время, как будет показано в п.5.5, использование алгорит-
мов блочного кодирования на основе ДКП объемом (/V xN) для «неканони-
ческих» размеров блока (N* 8) позволяет в ряде случаев получить больший
коэффициент сжатия при той же среднеквадратичной ошибке восстановле-
ния изображения.
5.4. Унифицированный метрический подход к синтезу быстрых
алгоритмов многомерного ДПФ
Анализ соотношения (5.29), определяющего структуру простейшего (так
называемого, построчно-столбцового или каскадного) алгоритма двумерного
ДПФ, показывает, что, например, его мультипликативная сложность удовлет-
воряет равенству М (N х N) = 2NM (/V).
Рис. 5.14. Удельная мультипликативная слож- Рис. 5.15. Относительное время обработки изоб-
ность алгоритмов ражения 1024x1024 пиксела блочным ДКП
5.4. Унифицированный метрический подход к синтезу быстрых алгоритмов
357
Таким образом, при N = 2к верно соотношение
М(АхЛ-) = 2A(CA’log2A') = CA2log2A2.
Другими словами, сложность вычисления ДПФ двумерного массива объе-
мом (NxN) с помощью каскадного алгоритма равна сложности одномер-
ного ДПФ длиной А2. Но у двумерного (/V х А)-ДПФ число «степеней сво-
боды» (различных корней из единицы) равно N, а не А2, как у одномерно-
го. То есть каскадный алгоритм полностью игнорирует двумерную природу
обрабатываемого массива и, несмотря на простую структуру, очевидно, не
является наилучшим.
К настоящему времени разработано большое количество быстрых алгорит-
мов многомерных ДПФ, базирующихся на принципиально различных подхо-
дах: на факторизации матриц преобразований 11, 4, 9], на полиномиальных
преобразованиях [12], тензорной технике [23—27], преобразовании Радона [14,
15] и т.д. Несмотря на то, что арифметическая сложность таких алгоритмов
существенно ниже, чем у простейшего «построчно-столбцового» (каскадно-
го) алгоритма, относительно сложная структура делает эти алгоритмы весьма
неудобными для реализации и массового использования. Поэтому наиболее
широкое распространение у пользователей получили различные модифика-
ции двумерного БПФ Кули-Тьюки: «по основанию два», «по основанию че-
тыре», БПФ с векторным основанием (многомерное обобщение сплит-ра-
дикс БПФ) [8]. Арифметическая сложность таких алгоритмов несколько выше,
чем у БА, полученных методами работ [8, 14, 15]. Однако простая «однород-
ная» структура делает их привлекательными для практического использова-
ния и аппаратной реализации.
В данном разделе предлагается альтернативная интерпретация известной
схемы Кули—Тьюки редукции ДПФ. Если при ее классической интерпрета-
ции множество входных и выходных индексов разбиваются на подмножества,
определяющие конкретный выбор схемы редукции, то альтернативный ав-
торский подход связан с покрытиями области суммирования подмножествами
(возможно, пересекающимися) со специальными метрическими свойствами.
5.4.1. Альтернативная интерпретация редукции Кули—Тьюки
В одномерном случае классическая редукция БПФ Кули—Тьюки сводит
вычисления ДПФ длиной N = 2Г к двум ДПФ длиной N/2 и некоторому
числу дополнительных умножений на степени первообразного корня w степе-
ни N из единицы:
4"1
Е/(п)и'"т = E/(2n)n<2”'±lv'"E/(2n+l)lv2"m.
и=0 и=0 w=0
(5.109)
358
ГЛАВА 5
При этом область суммирования оказывается разбитой на два подмноже-
ства (четных и нечетных чисел). Введем в рассмотрение 2-адическую норму на
множестве Z целых чисел:
где v2(m) есть 2-адический показатель целого числа и,
u = 2v^v, (2, v) = l.
Тогда область суммирования в левой части соотношения (5.109) покрыва-
ется двумя множествами с 2-адическими диаметрами, равными 1/2: главной
подрешеткой четных чисел и множеством нечетных чисел — аддитивным сдвигом
главной подрешетки. Мультипликативная сложность БПФ определяется слож-
ностью умножений на коэффициенты при сумме в правой части (5.109), соот-
ветствующей сдвигу главной решетки.
Альтернативная интерпретация соотношения (5.109) связана с действием
проектирующего оператора А: п 2п (и eZ) .
Пусть D = 2Z — множество целых четных чисел, %D (и) — характеристи-
ческая функция множества D; положим
/V—1 /V—1 , ч
s=Z7(«)zd(«). ь‘(5)=е;/(а‘п),
я=0 я=0
тогда справедливы равенства 25 = £'(5), = f^2knj, и соотношение
(5.109) принимает форму
N—1 । /V—1 I Л/-1
=^E/(AH)wmA« ±4^Е/(Ан)^Аи, (5.110)
я=0 n=O я—О
определяющую схему редукции. В отличие от традиционной интерпретации,
вычисление ДПФ редуцируется не к вычислению более коротких сумм, а к
вычислению ДПФ той же длины, но для все более «простых» функций с все
более коротким периодом и, в конце концов, к вычислению ДПФ постоян-
ных функций.
Мультипликативная сложность БА определяется в этом случае сложнос-
тью умножений на коэффициенты при суммах, соответствующих сдвигу (сдви-
гам) главной подрешетки, то есть тем, насколько «большую часть» области
суммирования можно покрыть главной подрешеткой.
Рассмотрим некоторые примеры развития многомерной версии этой идеи.
5.4. Унифицированный метрический подход к синтезу быстрых алгоритмов
359
5.4.2. Алгоритмы двумерного ДПФ с покоординатным прореживанием
области суммирования
Целью настоящего раздела является явное описание алгоритма двумерного
ДПФ с достаточно простой структурой, имеющего меньшую сложность, чем
наилучший из известных БА (алгоритм с векторным основанием [20]), исполь-
зующий традиционную интерпретацию двумерной редукции типа Кули-Тью-
ки. Основным результатом здесь является следующее утверждение.
Теорема 5.1. Пусть /(и)бС ; n, meZ2:
п = («!, п2), m = (m,, т2), (n, т) = прщ + п2т2;
Qn ={n = (wI,n2):0<ny <АГ —1; 1<J<2}cZ2.
Пусть F(m) — двумерный дискретный спектр Фурье:
F(m) = /(n)w<m’n>, meQyy, W = 2*, (5.111)
we С — первообразный корень степени N из единицы.
Тогда существует алгоритм вычисления преобразования (5.111), для кото-
рого справедлива оценка мультипликативной сложности:
M(/V2)<-|w2log27V. (5.112)
Доказательству теоремы предпошлем ряд лемм.
Пусть комплексная N-периодическая по каждому скалярному аргументу
функция 5(и) определена на Z2,
D = |п = (2М],п2): 0<rij <N — 1; l<j<rf|cZ2,
функция Xd(h) — характеристическая функция множества D.
Лемма 5.10. Пусть А, В — линейные операторы из Z2 в Z2:
Ап —(2/12, nJ, Вп=-(п2, 2nJ,
(В = А* — оператор, сопряженный к А).
Положим
5= 22 l‘(s)= 22 4А'П)-
Тогда справедливы следующие равенства:
2S = L’(S), s(A2'n) = s(2'n), 5'[в2/п) = 5’(2гп).
360
ГЛАВА 5
Последовательное преобразование области суммирования при переходе от
S к L'(s) показано на рис. 5.16. Новая область суммирования выделена се-
рым фоном.
Положим далее Та 5(11) = ^(п + а). Следующее утверждение является ос-
новным в описании схемы редукции, учитывающей тривиальность умноже-
ний на (±z), и непосредственно следует из леммы 5.10.
Лемма 5.11. При А = 2Г и r = 0, 1, ... справедливо соотношение
L‘ (F(m)) = 2-1 L1 (f0 (B'm))+2~4 £ w^'B'm^4 (qo (в'т)), (5.113)
a€A
где
е„(т)= Е И'<т п>7;/(П)>
Д _ |а =(яр а2): а{ *0; aj =0, 1; 1 < j < 2} .
П2
(03}
(1,3)
2,3)
(3,3)
(1,2)
(3,2)
(0,1)
(1,1)
2,1)
(3,1)
(0,0)
(1,0)
2,0) (3,0)
«1
>»&•><>& S (2,0) (2,1) ;(2,2) (2,3)
/ Ч (0,0) (0,1) (0,2) (0,3)
(2,0) (2,1) (2,2) (2,3)
X.1 j’*'1'.™ (0,0) (0,1) (0,2) (0,3)
П2
(0,2) (2,2) J * (од); (2,2)
Л,л ОД. (2,0) ' ; V (0,0)’; (2,0)
(0,2) (2,2) (0,2) (2,2)
Vi-;-:. (0,0) (2,0) (0,0)1 (2,0)
в
п,
Рис. 5.16. Пошаговое преобразование области суммирования для L' (5)
а
5.4. Унифицированный метрический подход к синтезу быстрых алгоритмов
361
Лемма 5.12. Пусть а€Д, г = 2<7 + т, 0<т<2,
G^’T(m) = Nq=2~4N.
Тогда при фиксированном векторе а арифметическая сложность вычисле-
ния массива G^’T(m) для m€Qw равна сложности вычисления массива
G^,T(m) для ше^9’т,где О.ч,х — фундаментальная область:
{m:0<m, <Nq+2, 0<т2 <А^+1}
{m: 0<ти <Nq+i, и = 1, 2}
при t — 1;
при t = 0.
Доказательство. При т — 0 , например, функция G^’°(m) инвариантна от-
носительно преобразований сдвигов ш m + bNq для b е Z2 и, самое боль-
шее, меняет знак при преобразованиях
m m + 2 1 bNq = m i—> m + b7V^+1
Аналогично рассматривается случай т = 1.
Доказательство теоремы 5.1. Соотношение редукции (5.113) определяет по-
крытие решетки Z2 непересекающимися подрешетками (см. рис. 5.17) и, на-
пример, при / = 0, сводит вычисление спектра (5.111) к вычислению спектров
более простых функций: функции /(Ап), являющейся N/2-периодической по
аргументу п} и А-периодической по аргументу п2; jV/2-периодических функ-
ций (А2п) и некоторому числу дополнительных умножений на константы
(а,ш) ' ' *
w' ' для аеА.
При переходе от t к (г + 1) периодич-
ность преобразуемых функций попере-
менно по каждому из скалярных аргу-
ментов уменьшается в 2 раза. В конце
концов, 2г-кратное применение соотно-
шения (5.113) приводит к вычислению
ДПФ постоянных функций, для вычис-
ления которых не требуется умножений.
Поэтому равенство (5.112) следует из
(5.113) и леммы 5.12.
Рис. 5.17. Покрытие области суммирования непе-
ресекающимися множествами для алгоритма тео-
ремы 5.1 ( Т' — сдвиг решетки ArZ2 на вектор
а = (р q})
362
ГЛАВА 5
5.4.3. «Чесс-алгоритмы» двумерного ДПФ для N= 2Г
В данном разделе для N = 2Г описывается семейство алгоритмов двумер-
ного ДПФ усложняющейся структуры, мультипликативная сложность лучше-
го из которых меньше, чем у алгоритмов с векторным основанием [6]. В отли-
чие от алгоритмов п.5.4.2, схемы редукции порождаются несколько иными
покрытиями области суммирования. Характерная «шахматная» структура но-
вых областей суммирования в этих алгоритмах определила введенное для них
название «чесс-алгоритмов» (чесс-БПФ). Мы рассматриваем дополнительное,
хотя и необязательное, условие вещественности преобразуемой по-
следовательности, учет которого позволяет еще приблизительно в два раза
снизить мультипликативную сложность алгоритма.
Теорема 5.2. Пусть f (пх, п2) G R — преобразуемый двумерный (ft xW) -мас-
сив, N = 2Г. Тогда существуют алгоритмы вычисления двумерного ДПФ
(5.111), мультипликативная сложность М (/V2) которых имеет оценку
M(/V2)<A/V2log2N, (5.114)
где А = 1; 3/4; 3/5.
Доказательству теоремы предпошлем ряд лемм — аналогов лемм 5.10-5.12.
Пусть комплексная функция ^(/1], и2) определена на Z2 и Апериодич-
на по каждому аргументу; множество DcZ2 состоит из пар целых чисел
одной четности:
D = {(«], и2): пх = n2(mod 2)}. (5.115)
Лемма 5.13. Пусть
(5Ь)(м,, m2) = 5(u2-m1, w1+m2)Xd(m2-«1» и1+мг)>
SR' — t-я итерация оператора -R; пусть далее
N-1 /V—!
5= S п2>> L'(s)= Е м2)-
П|,и2=0 и1,и2=0
Тогда 2S-L’(S).
Доказательство. Достаточно показать, что для любой пары целых чисел
(и,, п2) с условиями
(п],и2)е£>, 0<H],n2</V —1
существуют ровно два решения системы сравнений:
и2— их=пх (mod /V)
и2+их=п2 (mod /V). (5.116)
5.4. Унифицированный метрический подход к синтезу быстрых алгоритмов
363
Так как (np w2)gD , то все решения системы (5.116) являются решения-
ми системы сравнений:
_(К1+Л2)
и, =-------
2
mod —
2
Пусть М] и и2 —вычетычисел v±=(n1±n2)/2 (modN/2), соответствен-
но. Тогда из четырех пар чисел,
(и, -ЬNa/2, и2 + М>/2), a, b~0, 1,
только две являются решениями системы (5.116) с условием (5.117) (см. рис. 5.18).
Преобразование области суммирования при переходе от 5 к £*(,$) изоб-
ражено на рис. 5.19; серым фоном выделены индексы, принадлежащие обла-
сти суммирования по главной подрешетке,
О<пр n2<JV-l. (5.117)
Отметим очевидные равенства:
(3?2^)(«!, u2) = s[2tul, 2lu2j xd^21Uj, 2'и2), 0, 1, .... (5.118)
Последовательное изменение областей суммирования в L' (5) изображе-
но на рис. 5.19а—5.19г.
Пусть далее Tilhs(n}, n2) = $(«] п2 +-£>). Следующая лемма является ос-
новной при описании предлагаемой схемы декомпозиции.
Лемма 5.14. При N~2r (г>3), г = 0, 1, ... и ст = 2, 3, 4, справедливы
равенства:
L2r(f(w|, аи2)) — (Foo(2;Ж], 2fwi2^+
+ — £ iv2'(‘™'+ta>’£a(^(2'mi, 2'm2)),
2° a, ьел„
L IZ |Wl2 W|l, Z I A71| r m2 j I j,
+ J_ £
2Q
364
ГЛАВА 5
где
N-1
Fah(m„m2) = Е и'"'",+"!"2Т0(,(/(П|,П2)),
Л|,л2=О
{0<п,Ь<1; b (mod 2)} , если ст = 2;
[0<а,Ь <3; a,b^O (mod 2)} , если ст = 3;
{0<л,£<1; a^b (mod 2)} , если ст = 4.
(5.119)
(5.120)
Таким образом, с помощью леммы 5.14 вычисление спектра Г(тпх, т2)
редуцируется к вычислению ДПФ того же размера, но для функций все более
простого вида и, в конце концов, к вычислению ДПФ константы.
Следующая лемма является аналогом леммы 5.12 для рассматриваемого
покрытия области суммирования.
Рис. 5.18. Главная подрешетка и новая система координат в алгоритме теоремы 5.2
5.4. Унифицированный метрический подход к синтезу быстрых алгоритмов
365
г
. < Л ' ' .г; ч.\
0,0 Л‘’* ' ,4 0,0
2,0 2,2 2,4 2,6 2,0 , ?}><< ? s;
4b S'.e- V 4,2 4,4 4,6 4,0 4,2
6,0 Ж 6,4 .6,6 6,0 6,2
Р,0 од 0,4 0,6 0,0 0,2
0 1 2 3 4 5
Рис. 5.19. Пошаговое преобразование области суммирования для чесс-БПФ теоремы 5.2
Лемма 5.15. Пусть N, = /v/2',
m2) = w2'^+b^L^Fab(2'mi, 2'm2)),
m2) = .v2'W";-"')+6(”'+"IV(Fat(2'(m2-m,), 2'(m,+ m2))).
Тогда при фиксированных a, a, b, t массив G^ (тх, т2) достаточно
найти для (тх, м2)ей^с; а массив Z^'(тх, т2) достаточно найти для
(amj, m2)e£llaZ ; где и ^g.z — фундаментальные области:
366
ГЛАВА 5
{р, m2i }-0<ml<Nl/2\ 0<m2<Nl/4}, если o = 2;
^o.G — {(wi,, т2) :0<ш1э т2 </V,/4}’ если а = 3;
{(m(, т2} :0<mj < Nj4\ 0<ж2<^/8}, если ст = 4;
{р, т2 jiOC/ri! <7V,/2; 0<m2<7V,/8}, если о = 2;
{(т„ т2 )-0<тх <JV,/4; 0<m2</V,/8}, если о = 3;
{(mi, /м2):0</И] < 7Vf/4; 0<т2 </У,/1б}, если 0 = 4.
Доказательство. Подробное доказательство проведем для ст —4. Осталь-
ные случаи рассматриваются аналогично.
Пусть т'р (сдвиг) и (зеркальное отражение) — преобразования фун-
даментальных областей:
j , \ | Nt aNt\
"h)-+ ^р (-1)"т2 +Ч7Г
7 = 1, 2, 3; а, ₽ = 0, 1, 2'-1; £, т] = 0, 1.
Пусть о = 4 . Тогда функции L4^Fab^2tmlt 2'm2)) инвариантны относи-
тельно преобразований т^р и т^р и Nt — периодичны. Кроме того, спра-
ведливо равенство
т2)] = {^аь‘(т^ тг)) = 2)
(* — знак комплексного сопряжения). Пусть
Q.k = , т2): 0 < тх, т2 < Nt} ,
тогда доказываемое утверждение для (тр т2) следует из соотношения
— U ('Сар(Р11 (^о,б))и'Гар (Qo,g)).
а, р \ \ v ' /
5.4. Унифицированный метрический подход к синтезу быстрых алгоритмов
367
Аналогично, функции
^4(^(2'("г2~И1|)’ 2'(т1+лпг)))
инвариантны относительно преобразований и и умножаются на ±1, ±i
при преобразованиях т„а. Доказываемое утверждение для т2) сле-
дует, например, из соотношения
1 f 3 7
S2tCU р° UtJo UT^fc.z) .
£=0 (а=0 \Р=0 ' j)
Доказательство теоремы 5.2. Из лемм 5.14 и 5.15, а также вида фундамен-
тальной областей Q'o с и Qjy z для о = 2, 3, 4 легко получаем рекуррент-
ные соотношения для мультипликативной сложности QN (г) вычисления
m2)):
Qn (t +1 ) + 20„(/ + 2) ЗА2 + 2/+2 ’ если о = 2;
Qn (t + 1 ) +4£?/y (/ + 3) 3N2 + 2t+2 ’ если o = 3; (5.121)
Qn (t +1 )+8Oy(r+4) ЗА2 + 2/+2 ’ если a = 4.
Как обычно, считаем, что умножения комплексных чисел реализованы по
схеме «три сложения, три умножения», а умножения на степени двойки не
учитываются. Так как
eN(0) = w(№), Q„(2r)=0,
то из (5.121) следуют неравенства основной теоремы:
м(а2) =
/V2log2/V, если о = 2;
^JV2log2/V, если o = 3;
3 Э -JV2log2/V, если o = 4.
Замечание. Как и в одномерном случае, покрытия, определяющие тот или
иной вариант чесс-редукции, допускают понятную метрическую (неархиме-
дову) интерпретацию. Отождествим пару индексов (и,, п2) входного сигнала
с целым гауссовым числом: (пр п2)^п{+ n2i .
368
ГЛАВА 5
Функция
Ч/1(я1 + a2i)=y[2 2( '+ 2) , 4/,(о)=О; at, a2€Q^,
является продолжением 2-адической нормы с Она алгебраическое расшире-
ние Q_(i) и индуцирует на множестве индексов (np п2) метрику, причем
неравенство T^Wj, и2)<1/2 равносильно соотношению nlf п2=0 (mod 2).
Именно относительно нормы 4х, неявно рассматриваются покрытия об-
ласти определения входных данных, определяющие схему редукции в извест-
ных алгоритмах.
Пусть теперь 4^(flj + a2i)= 2~v^a,+u^, 4/2(о) = О.
Тогда нетрудно проверить, что функция 4'2 индуцирует на Q_(i) метри-
ку, совпадающую на (Q^c метрикой, индуцированной 2-адической нормой.
Покрытия области определения входных данных в чесс-алгоритмах, опреде-
ляющие схему редукции, рассматриваются относительно Ч7 2.
Неравенство 4/2(л1, п2)< 1/2 равносильно соотношению и,, п2=0 (mod 2)
ит.д. Таким образом, сложность рассмотренных в разделе 5.4.3 алгоритмов
ДПФ при (5 = 2, 3, 4 определяется тем, «насколько экономно» покрыта по-
добласть 4Z2(лр п2)> 1/2 области суммирования 2-адическими Ч/2-шарами
с меньшими диаметрами.
Несмотря на то, что традиционные схемы редукции двумерного ДПФ не-
явно используют метрические свойства покрытий относительно метрики,
индуцированной нормой 4^, эти схемы могут быть также интерпретированы
в терминах метрических свойств относительно нормы 4' 2.
5.4.4. Алгоритмы двумерного ДПФ — алгоритмы с расщеплением основания
нецелого порядка
В настоящем разделе показывается, что известные БА двумерных ДПФ
(БПФ «по основаниям два и четыре», БПФ с векторным основанием) также
допускают описание в терминах соотношений редукции, аналогичных (5.113),
но реализуемым «с шагом два».
Пример 5.7. Двумерный БА ДПФ «по основанию два».
Традиционная интерпретация схемы редукции этого алгоритма имеет вид
1
F(w(, т2) = f(n\’ n2)wn'm'+m2n2 = 22 /(2«1, 2л2)(и/2] 1 ,+ 2 2 +
П|,п2=0 П|,л2—О
+ £ w"""+i™= Е /(2n, + «. 2n2+i)(W2)"'""+m!"!.
a,b—Q n|,n2=0
(а, /?)*(0,0)
5.4. Унифицированный метрический подход к синтезу быстрых алгоритмов
369
Это соотношение редукции равносильно соотношению
где
Д( = |а = (r/j, а2); aJt а2 — О, »
п = п2), т = ^т1,т2), (п, п0 = п{т{ + т2п2;
Bm = (wi2, 2az2j ).
Соответствующее покрытие области суммирования показано на рис. 5.20.
Закрашены элементы главной подрешетки A2Z2. Элементы подрешетки, сдви-
нутой на вектор а = (р, д) обозначены тД.
Пример 5.8. Двумерный БА ДПФ «по основанию четыре».
Интерпретация схемы редукции имеет вид
Г(т,,т2) = Z2 /(«р n^w"'”1'^2"2 = /(4nr 4и2)(и’4] 1 2 2 +
Л|,Л2=0 «^/12=0
——I
। V am, + hm2 f(A . A , i \( 4\nimi+ni2n2
+ > , w ' 2_> /(4И] + п, 4n2+ b)\w )
a,b=0 nt,n2— 0
(u,fc)*(0,0)
В обозначениях предыдущего примера это соотношение редукции равно-
сильно соотношению
где
Л2 ={а — (ар а2)‘, alt а2 =0, 1, 2, з}\{0} .
Соответствующее покрытие области суммирования показано на рис. 5.21.
Закрашены элементы главной подрешетки A4Z2. Элементы подрешетки,
сдвинутой на вектор а = (р, q) обозначены .
370
ГЛАВА 5
Рис. 5.20. Покрытие для двумерно-
го БПФ «по основанию 2»
Рис.5.21. Покрытие для двумерного БПФ
«по основанию 4»
Пример 5.9. БПФ с векторным основанием.
Соотношение редукции имеет вид
——1
F(mhm2) = Е /(«„ = £ /(2л„ 2л2)р)",”,+"!”Ч
П|,л2=0 Л|,л2=0
—-I
3 т 1
+ £ £ Г(4П1 + а,4И2+Ь)(^)Л,т'+"!"!.
u,h=O Л|,л2=0
a,h*0(mod 2)
В обозначениях предыдущих примеров это соотношение редукции равно-
сильно соотношению
F(m) = -UJ(Go(m))+± £ (ejm)),
4 10аел3
где
Л3 =|а = (а1, д2); л1» а2 = 0» 1» 2, 3}\{a = 2(flj, а2); а}, а2 =0, 1} .
Соответствующее покрытие области суммирования показано на рис. 5.22.
Закрашены элементы главной подрешетки A2Z2. Элементы подрешетки,
сдвинутой на вектор а = (р, q) обозначены тД.
5.4. Унифицированный метрический подход к синтезу быстрых алгоритмов
371
5.4.5. Алгоритмы двумерного ДПФ с «мультипокрытиями» области
суммирования
Анализ доказательств предыдущих теорем раздела и примеров 5.7—5.9, по-
казывает, что мультипликативная сложность алгоритмов с расщеплением ос-
нования нецелого порядка определяется количеством умножений на степени
w сумм, соответствующих покрытию области суммирования неглавными (сдви-
нутыми) подрешетками. Другими словами, чем большая часть области сум-
мирования покрывается главной (главными) подрешетками, тем меньшую
мультипликативную сложность имеет алгоритм.
Как известно [2], оценка мультипликативной сложности БА двумерного
ДПФ при N = 2Г имеет вид
A/(/V2)<CN2log2N + o(tV2). (5.122)
Наилучшим значением константы С в (5.122), а именно С = 9П, для БА
типа Кули-Тьюки обладает алгоритм с векторным основанием (Vector Radix
FFT [6]). Абсолютно лучшее, неулучшае-
мое, по мнению авторов [6], значение кон-
станты С = 1 у алгоритма Нуссбаумера
[17], синтезированного с применением
принципиально иной техники полиноми-
альных преобразований.
Ниже мы покажем, что, во-первых,
алгоритм двумерного ДПФ с мультипли-
кативной сложностью, равной сложности
алгоритма Нуссбаумера может быть син-
тезирован в рамках рассматриваемого под-
хода; во-вторых, может быть синтезиро-
ван алгоритм, для которого значение кон-
станты С равно 2/3.
Снижение сложности обеспечивается
применением рассматриваемой схемы де-
композиции с покрытием области сумми-
рования несколькими главными перекры-
Рис. 5.22. Покрытие для двумерного БПФ
с векторным основанием
вающимися подрешетками.
Теорема 5.3. Существует алгоритм вычисления преобразования (5.111) с
мультипликативной сложностью:
MpV2)<7V2log2 N.
(5.123)
372
ГЛАВА 5
Доказательство. Пусть А,, А2, В,, В2 — линейные операторы из Z2 в Z2:
А]П = (2к2, И]), Bjn = (n2, ); A2n = (n2, 2nJ, B2n = (2n2, nJ .
Тогда справедливо соотношение редукции
F(m) = 2-' L1, (Co(m))+ 2’1 (t'2 (c0 (m))- 2’1 L? (Oo (m)))+
+2-4][><a-,n>i.f(C(,(ni)), (5.124)
аел
где A = {a = (flp a2); alfa2=l, З}.
Соответствующее покрытие области суммирования изображено на рис. 5.23.
Цифрами 1 и 2 обозначены элементы подрешеток A,Z2 и A2Z2, соответ-
ственно; тД — элементы подрешеток A*Z2 = A2Z2, сдвинутых на вектор
Отметим, что А2 = А2 и Lj((2o(m)) = L2(C0(m)). Поэтому для мульти-
пликативной сложности V(J вычисления справедливо рекуррен-
тное соотношение
V(») = V(r + l) + (V(» + l)-V(r + 2))+4V(r+4) + 3-4—=
ЗЛ/2
= 2V(r + l)-V(r + 2) + 4V(r + 4) + ^-. (5.125)
Из соотношения (5.125) с помощью рассуждений, аналогичных соответ-
ствующей аргументации при доказательствах предыдущих теорем, следует ут-
верждение теоремы 5.4.
Теорема 5.4. Существует алгоритм вычисления преобразования (5.111) с
мультипликативной сложностью:
/ \ 7
A/(N2)<|/V2log2W.
(5.126)
Доказательство. Пусть А3, А4, В3, В4 — линейные операторы из Z2 в Z2:
A3n = (2n2, nJ, B3n = (n2, 2nJ; A4n = (n2, 4nJ, B4n = (4n2, nJ.
C — A 5 — оператор, отображающий решетку Z2 на чесс-решетку теоремы 5.2:
Сп = (и2 —пи П] + л2).
5.5. Некоторые приложения
373
Тогда справедливо соотношение редукции
F (ш) = 2~' L'2 (в0 (m))+(2-' Д (йо (т)) - 2"2 4 (е0 (т)))+
+(2-24(е0(т))-2-3(4-Д)(ес(т)))+
+2-‘£>Лт>4(ео(т)),
(5.127)
где Л = {а = (1, 2), (3, 2)} , из которого следует равенство (5.126).
Соответствующее покрытие области суммирования изображено на рис. 5.24.
5.5. Некоторые приложения
5.5.1. Задача вычисления ДПФ последовательности произвольной длины
Неблагоприятным следствием популярности БПФ-алгоритма Кули-Тью-
ки для W = 2Г является широкое распространение мнения о том, что приме-
нять дискретное преобразование Фурье практично лишь при такой длине
последовательности. В результате БПФ-алгоритмы стали диктовать парамет-
ры применяемых устройств вместо того, чтобы приложения диктовали выбор
подходящего алгоритма БПФ [2].
В задачах, не предполагающих жестких аппаратурных требований к длине
обрабатываемого сигнала, применение только традиционных алгоритмов БПФ
Рис. 5.24. Мультипокрытие для трех главных
подрешеток в теореме 5.4
Рис. 5.23. Мультипокрытие для двух главных
подрешеток в теореме 5.3
374
ГЛАВА 5
Кули—Тьюки приводит к необходимости увеличивать период обрабатываемых
сигналов ~ добавлять нулевые отсчеты до ближайшего «хорошего» целого чис-
ла вида /V* = 2Г. Такие числа расположены в натуральном ряду весьма редко,
что приводит к почти двукратному увеличению удельной вычислительной слож-
ности для «плохих» N, равных, например, 2'4-1 = /V (см. рис. 5.25 график 1).
Задача вычисления дискретного спектра последовательности произволь-
ной длины может быть решена на основе знания арифметических особенно-
стей базисных функций ДПФ, минимальной информации о последователь-
ности и информации о всевозможных алгоритмах БПФ. Цель раздела —
показать возможность синтеза «наилучших» алгоритмов, ориентированных
на вычисление ДПФ последовательностей (массивов) произвольного пе-
риода при наличии ограниченного количества базовых эффективных алго-
ритмов дискретного преобразования Фурье, реализованных для относи-
тельно небольшого числа длин преобразования. Такая задача решается в
несколько этапов.
На первом этапе специалист в области синтеза БА ДОП формирует на-
бор алгоритмов БПФ, ориентированных на различные типы входных дан-
ных (целые, вещественные, комплексные), длины входных последователь-
ностей (четные, нечетные, равные целой степени простого числа и т.п),
размерность входного сигнала и т.д. и описывает их свойства. Например,
алгоритм Кули—Тьюки наиболее эффективен для преобразования Фурье
комплексной последовательности, длина которой равна целой степени двой-
ки. При этом сформированный набор алгоритмов должен быть не слиш-
ком велик (для ускорения последующей работы по его анализу и формиро-
ванию наилучшего алгоритма) и, в то же время, содержать разнообразные
алгоритмы, учитывающие различные особенности параметров входного
сигнала. Особое значение на этом этапе имеет квалификация специалиста
в предметной области.
На втором этапе производится комплексный анализ вычислительной слож-
ности алгоритмов, исследуются возможности формирования на их основе
новых алгоритмов, например, алгоритмов промежуточных длин с использо-
ванием декомпозиции Гуда—Томаса или специализированных алгоритмов
для вещественного входного сигнала с использованием идеи совмещения
или уменьшения размера фундаментальной области. При подготовке систе-
мы к работе на конкретной ЭВМ исследуется также время выполнения от-
дельных алгоритмов на данном компьютере, для того чтобы впоследствии
система могла вырабатывать рекомендации по выбору конкретного алгорит-
ма в зависимости от пожеланий пользователя как по теоретической (ариф-
метической) или структурной сложности, так и по реальному времени рабо-
ты программы.
Предложенный специалистом набор алгоритмов и технологических при-
емов по их использованию, а также информация о теоретической сложности
и реальном быстродействии алгоритмов составляют первоначальное заполне-
ние базы знаний.
5.5. Некоторые приложения
375
Как уже отмечалось выше, типичными схемами редукции ДПФ являются
редукция Кули—Тьюки, редукция Гуда-Томаса, редукция Рейдера, методы
совмещенного вычисления ДОП.
Редукция Кули—Тьюки сводит, например, вычисление одномерного
ДПФ длиной N = рк к вычислению преобразований длиной /V] — pk~l и
неявно использует арифметические свойства представления значений пре-
образуемого сигнала, согласованные с конкретной машинной арифмети-
кой, а также топологические свойства множества индексов входных и
выходных данных [27].
Редукция Гуда—Томаса использует изоморфизм прямого произведения
циклических групп взаимно простых порядков и циклической группы поряд-
ка, равного произведению порядков прямых сомножителей.
Редукция Рейдера основана на известном факте цикличности мультипли-
кативной группы простого конечного поля и существенно использует алгеб-
раичность значений базисных функций ДОП.
Методы «совмещенного» вычисления ДОП используют избыточность пред-
ставления вещественного входного сигнала по отношению к представлению
значений базисных функций ДОП в базисе некоторого объемлющего поля
или алгебры. Их эффективность определяется наличием достаточно боль-
шого числа автоморфизмов этой объемлющей структуры, реализуемых три-
виально.
Таким образом, гипотетическая автоматизированная система «должна уметь»
анализировать для каждого значения N, ту арифметическую информацию,
которая в «рафинированном виде» проявляет себя при синтезе БПФ-алгорит-
мов для специальных длин Nk <N.
Автоматизированная система производит выбор оптимальной структуры БПФ-
алгоритма длиной N на основе информации о следующих БПФ-алгоритмах:
1) БПФ Кули—Тьюки с декомпозицией по основанию 2;
2) БПФ Кули-Тьюки с декомпозицией по основаниям 3 и 6;
3) редукция Гуда—Томаса, для формирования алгоритмов промежуточных
длин;
4) специальные алгоритмы ДПФ коротких длин.
Большинство алгоритмов представлены в интерпретации авторов данной
главы, например алгоритм преобразования Фурье по основанию 3 построен
на основании декомпозиции типа Кули—Тьюки, однако в нем использовано
специальное представление данных в у-кодах, что позволяет существенно сни-
зить арифметическую сложность преобразования по сравнению с известными
аналогами.
Для обработки конкретной последовательности системе предоставляется
информация о типе данных и длине последовательности, ее размерности;
пользователь выбирает способ оптимизации алгоритма — по теоретической
сложности или реальному быстродействию. Результатом работы системы яв-
ляется подготовленный набор аргументов для некоторого метаалгоритма ДПФ
[22, 29], по которым система формирует окончательный вид оптимального
376
ГЛАВА 5
алгоритма преобразования последовательности с заданными характеристика-
ми. После чего может быть непосредственно выполнено вычисление дискрет-
ного спектра заданной последовательности.
Система способна накапливать информацию, обучаться, поэтому для вы-
числения спектра другой последовательности с теми же характеристиками не
требуется повторения анализа. Система сразу готова к выполнению преобра-
зования.
Таким образом, информация, представленная в системе, обладает конст-
руктивными особенностями присущими базам знаний: внутренней интерпре-
тируемостью, структурированностью, связностью. Знания, накопленные в
системе, легко адаптируются к изменениям, например, к замене или допол-
нению алгоритмов в базовое множество.
На рис. 5.25 представлены графики удельной арифметической сложности
вычисления спектра комплексной одномерной последовательности произ-
вольной длины. Здесь N — реальный период; W* (7V) — удельная арифмети-
ческая сложность (число арифметических операций на один отсчет входно-
го сигнала) вычисления БПФ сигнала с увеличенным периодом /V* > N . На
графике 1 приведена сложность вычисления спектра традиционным спосо-
бом — на базе БПФ Кули-Тьюки по основанию 2. График 2 получен после
предоставления системе информации об алгоритмах БПФ по основаниям 3
и 6. Вычислительная сложность снижена в среднем на 5,2% (или в 1,1 раза).
После того как система была дополнена знаниями об использовании деком-
позиции Гуда-Томаса (график 3) выигрыш в среднем составил 27,6% (1,4
раза). Последний график 4 получен для случая, когда система в дополнении
к перечисленным получила знания о специальных алгоритмах преобразова-
ния Фурье коротких длин. При этом выигрыш возрастает до 37,2% или 1,6
раза в среднем. Отметим, что для ряда длин удельная сложность вычисления
спектра в случае 1 и 4 отличается более чем в два раза. Из графика явно
следует, что с ростом объема знаний, которыми обладает система, растет и
ее эффективность.
Рис. 5.25. Удельная сложность вычисления спектра комплексной одномерной последовательности
5.5. Некоторые приложения
377
Гистограммы распределения вычислительного выигрыша для случаев 2, 3,
4 по отношению к традиционному способу представлены на рис. 5.26 деталь-
но (а, б, в) и более крупными группами (г, д, е). Из них следует, что при
увеличении объема информации, которой обладает система, заметно возрас-
тает доля «больших» выигрышей. Если при использовании алгоритмов групп
1 и 2 практически весь выигрыш (91 случай из 100) не превышает 10%, то при
использовании всех знаний, доступных системе, удельная сложность вычис-
ления спектра может быть снижена в 2 и более раз в 37% случаев.
Построение аналогичной системы синтеза быстрых алгоритмов диск-
ретных ортогональных преобразований для двумерного случая позволяет
достигнуть еще более существенного снижения вычислительной сложнос-
ти. На рис. 5.27 приведены гистограммы распределения вычислительного
выигрыша, рассчитанные для тех же групп алгоритмов, использованных
для двумерного сигнала объемом NxN. Здесь максимальный выигрыш дос-
тигает 80%, причем в 52% случаев сложность может быть снижена более
чем в два раза.
Рис. 5.26. Гистограмма распределения вычислительного выигрыша в одномерном случае
Рис. 5.27. Гистограмма распределения вычислительного выигрыша в двумерном случае
378
ГЛАВА 5
5.5.2. Исследование алгоритмов ДКП в методе блочного кодирования
с преобразованием
В главе 6 подробно описан метод блочного кодирования изображений,
который в настоящее время получил чрезвычайно широкое распространение.
Он базируется на использовании обобщенного спектрального представления
сигнала. Эффективность метода обуславливается тем, что спектральные ком-
поненты изображения (трансформанты) могут быть статистически более не-
зависимы, чем сами отсчеты сигнала, и, следовательно, нести ту же информа-
цию при меньшем объеме передаваемых цифровых данных.
Выбор преобразования в этом методе обусловлен следующими требовани-
ями: преобразование должно быть обратимым, основная информация о сиг-
нале должна быть сосредоточена по возможности в меньшем числе трансфор-
мант для обеспечения эффекта сжатия, прямое и обратное преобразование
должны легко вычисляться. Идеальным по второму требованию является пре-
образование Хотеллинга (дискретная версия Карунена—Лоэва), у которого
наиболее быстро убывают дисперсии трансформант. Однако на практике оно
не используется, так как его базис жестко привязан к автоковариационной
функции сигнала, и его необходимо строить заново для каждого нового класса
сигналов. Кроме того, это преобразование не обладает быстрым алгоритмом.
Поэтому, как правило, используются известные алгоритмы спектральных пре-
образований, несколько проигрывающие в качестве, но выигрывающие в ско-
рости. Наиболее близким по своим характеристикам к преобразованию Кару-
нена—Лоэва для широкого класса изображений является дискретное косинус-
ное преобразование (5.8).
Схема метода представлена на рис. 5.28. Входное изображение разбивает-
ся на квадратные блоки размером Nx N отсчетов, в каждом блоке выполня-
ется двумерное ДКП. Затем производится отбор существенных трансфор-
мант и их квантование. Совокупность отобранных и квантованных транс-
формант для всех блоков составляет содержание сжатых данных. Принципы
отбора существенных трансформант и методы их кодирования подробно
описаны в главе 6.
Ниже описываются некоторые экспериментальные результаты по кодирова-
нию изображений с помощью ДКП блоками Nx Nпри различных значениях N.
Входное изображение подвергалось кодированию с заданными коэффици-
ентом сжатия Ке, размером блока N и типом преобразования Туре, затем
восстанавливалось, и по разности исходного и восстановленного изображе-
ний определялась среднеквадратичная ошибка (ошибка сжатия), внесенная в
данные сквозной процедурой кодирования/декодирования. Ниже для крат-
кости будем называть ее ошибкой сжатия (см. рис. 5.29).
На рис. 5.30, 5.31, 5.32 приведены тестовые изображения «Портрет», «Аэро-
фотосъемка», «Глазное дно» и результаты их сжатия/восстановления. Приве-
денные зависимости позволяют сделать вывод о том, что в принятом методе
5.5. Некоторые приложения
379
компрессии применение ДКП устойчиво дает хорошее качество сжатия. Рас-
ширение набора длин, для которых существуют эффективные алгоритмы ДКП,
позволяет выбрать размер блока, при котором ошибка сжатия при заданном
коэффициенте сжатия будет наименьшей. Использование блоков нестандарт-
ных размеров позволяет уменьшить ошибку сжатия в 1,3—1,5 раза.
Полученные результаты подтверждаются и визуальным качеством восстанов-
ленных изображений.
Рис. 5.29. Схема эксперимента по кодированию изоб-
ражений
Рис. 5.28. Схема метода кодирова-
ния с преобразованием
380
ГЛАВА 5
N — 21
г
Рис. 5.30. Результаты кодирования изображения «Портрет»: а — исходное изображение; б —
зависимость ошибки сжатия от размера блока; в — восстановленное изображения после кодиро-
вания при коэффициенте сжатия Кс = 6 и размере блока N— 9; г — восстановленное изображе-
ния после кодирования при коэффициенте сжатия Кс- 6 и размере блока N= 27
N = 9
в
5.5. Некоторые приложения
381
а
б
N= 9
в
N= 27
г
Рис. 5.31. Результаты кодирования изображения «Глазное дно»: а — исходное изображение; б —
зависимость ошибки сжатия от размера блока; в — восстановленное изображения после кодиро-
вания при коэффициенте сжатия Кс = 10 и размере блока 7V= 9; г — восстановленное изображе-
ния после кодирования при коэффициенте сжатия Кс= 10 и размере блока N- 27
382
ГЛАВА 5
а
б
N= 9
в
N=21
г
Рис. 5.32. Результаты кодирования изображения «Аэрофотосъемка»: а — исходное изображение;
б — зависимость ошибки сжатия от размера блока; в — восстановленное изображения после
кодирования при коэффициенте сжатия Кс=% и размере блока 7V=9; г — восстановленное
изображения после кодирования при коэффициенте сжатия Кс= 8 и размере блока N=T1
Литература к главе 5
383
Литература к главе 5
1. Ахмед Н., Рао К. Р. Ортогональные преобразования при обработке цифро-
вых сигналов (М.: Связь, 1980)
2. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов (М.: Мир,
1989)
3. Брейсуэлл Р. Преобразование Хартли (М: Мир, 1990)
4. Вариченко Л.В., Лабунец В.Г., Раков М.А. Абстрактные алгебраические
системы и цифровая обработка сигналов (Киев: Наукова думка, 1986)
5. Виттих В. А., Сергеев В. В., Сойфер В. А. Обработка изображений в авто-
матизированных системах научных исследований (М.: Наука, 1982)
6. Власенко В. А., Лаппа Ю. М., Ярославский Л. П. Методы синтеза быст-
рых алгоритмов свертки и спектрального анализа сигналов (М.: Наука, 1990)
7. Гречишников А.И. Радиотехника и электроника 27(10) 52 (1984)
8. Григорян А.М. Журнал выч. матем. и матем. физики 31(10) 1576 (1991)
9. Дагман Э.Е., Кухарев Г.А. Быстрые дискретные ортогональные преобразо-
вания (Новосибирск: Наука, 1983)
10. Залманзон Л.А. Преобразования Фурье, Уолша, Хаара и их применения в
управлении, связи и других областях (М.: Наука, 1989)
11. Капорин И. Е. Журнал вычислительной математики и математической
физики 20(4) 1054 (1980)
12. Крот А.М. Дискретные модели динамических систем на основе полиноми-
альной алгебры (Минск: Навука i тэхшка, 1990)
13. Крот А.М., Минервина Е.Б. РЭ 22(6) 1217 (1987)
14. Лабунец В.Г. Алгебраическая теория сигналов и систем (Свердловск: изд-
во УрГУ, 1989)
15. Лабунец В.Г. Алгебраическая теория сигналов и систем: Цифровая обработка
сигналов (Красноярск: Изд-во красноярского университета, 1984)
16. Маккелан Дж. X., Рейдер Ч.М. Применение теории чисел в цифровой обра-
ботке сигналов (М.: Радио и связь, 1983)
17. Нуссбаумер Г. Быстрое преобразование Фурье и алгоритмы вычисления свер-
ток (М.: Радио и связь, 1985)
18. Першина М. В., Чичева М. А. Компьютерная оптика, Часть 2 (14—15) 13
(1995)
19. Трахтман А.М., Трахтман В.А. Основы теории сигналов на конечных интер-
валах (М.: Советское радио, 1975)
20. Чернов В. М. Проблемы Передачи Информации 31(3) 38 (1995)
21. Чернов В. М. Автомат, и вычисл. техн. 3 62 (1994)
22. Чернов В.М. Доклады Академии наук 357(3) 317 (1997)
23. Ярославский Л. П. Введение в цифровую обработку изображений (М.: Со-
ветское радио, 1979)
24. Ярославский Л.П. Цифровая обработка сигналов в оптике и голографии:
введение в цифровую оптику (М.: Радио и связь, 1987)
384
ГЛАВА 5
25. Briggs W.L., Van Henson E. The DFT: An owner's manualfor the discrete Fourier
transform (SIAM, 1995)
26. Chan S.-С., Ho K.-L. IEEE Trans, on Circuits and Systems 39(3) 185 (1992)
27. Chernov V.M. Workshop on Digital Image Processing and Computer Graphics.
Proceedings SPIE 2363 134 (1994)
28. Chernov V.M. Pattern Recognition and Image Analysis 8(2) 506 (1998)
29. Chernov V.M. Pattern Recognition and Image Analysis 3(4) 455 (1993)
30. Chernov V.M. Pattern Recognition and Image Analysis 6(1) 73 (1996)
31. Chichyeva M.A., Pershina M.V. Image Processing and Communications, Institute
of Telecommunications Bydgoszcz, Poland 2(1) 13 (1996)
32. Cizek V. Discrete Fourier transforms and their applications (A. Hilger Publ., 1986)
33. Cooley J.W., Tukey J.W. Math. Comp. 19 297 (1965)
34. Duhamel L., Hollman H. Electron. Lett. 20(17) 14 (1984)
35. Good I. J. J. Royal Statist. Soc., Ser. B. 20 361 (1958)
36. Heideman M.T. IEEE Trans. Signal Process. 40(1) 54 (1992)
37. Hou H. S. IEEE Transactions on Acoustics, Speech and Signal Processing ASSP-
35(10) 1455 (1987)
38. Hou H.S., Tretter D.K. J. Visual Commun. and Image Represent. 3(1) 73 (1992)
39. Sipp F., Wade W.R., Simon P. Walsh series: An introduction to the dualic harmonic
analysis (A. Hilger Publ., 1990)
40. Sorensen H.V., Heideman M.T., Burrus C.S. IEEE Trans. ASSP-34(1) 152
(1986)
41. SuheiroN., Hatori M. IEEE Transactions on Acoustics, Speech and Signal
Processing ASSP-34(6) 642 (1986)
42. Thomas L.H. Using a computer to solve problems in physics, in applications and of
digital computer (Boston, Mass.: Ginn and Co., 1963)
43. Van Loan C. Computational frameworks for the fast Fourier transform (SIAM,
1992)
44. Wallace G.K. Communications of the ACM 34(4) 31 (1991)
45. WangZ. IEEE Trans. Acoust., Speech, Signal Processing ASSP-32 803 (1984)
46. Winograd S. Proc. Nat. Acad. Sci. USA 73 1005 (1976)
47. Winograd S. Arithmetic complexity of computations (SIAM, 1980)
ГЛАВА 6
КОМПРЕССИЯ ИЗОБРАЖЕНИЙ
6.1. Показатели качества методов компрессии
Как уже неоднократно отмечалось, цифровым изображениям соответству-
ют чрезвычайно большие объемы данных. Это ставит перед разработчиками
программно-аппаратных средств обработки изображений целый ряд серьез-
ных проблем. Требования быстрой передачи данных или их полной регистра-
ции вступают в противоречие с техническими характеристиками используе-
мой аппаратуры: недостаточной емкостью запоминающих устройств, ограни-
ченной пропускной способностью каналов передачи данных, недостаточным
быстродействием вычислительных машин и т.д. В подобных ситуациях боль-
шое значение приобретает особый вид обработки изображений — их кодиро-
вание с целью сокращения объема (компрессии) данных. Также будем ис-
пользовать термин «компрессия изображений», имея в виду цифровые изоб-
ражения, заданные в виде двумерного массива данных.
Технико-экономический эффект от использования компрессии данных
весьма многообразен, он обусловлен многими очевидными факторами. Так,
при передаче данных компрессия позволяет разгрузить канал и, следователь-
но, повысить достоверность полученной информации, сократить время и/или
снизить мощность и вес передающей аппаратуры. При регистрации изобра-
жений компрессия позволяет уменьшить необходимую емкость запоминаю-
щих устройств или улучшить использование существующих архивов данных,
благодаря чему сокращаются расходы на хранение и поиск информации в
архиве. При обработке данных на компьютере компрессия во многих случаях
дает возможность сократить время обработки, при этом появляется возмож-
ность использования компьютера меньшей вычислительной мощности и т.д.
Принципиальная возможность сокращения объема данных заключается в
том, что изображения (и их цифровые образы — матрицы пикселов) обладают
высокой степенью избыточности с точки зрения содержания информации.
Это связано, во-первых, с тем, что между близкими точками поля яркости
(соседними отсчетами матрицы) имеется сильная статистическая зависимость.
Из теории информации известно, что наличие зависимости между элементами
13 — 9044
386
ГЛАВА 6
сообщения приводит к уменьшению количества информации, переносимой
этим сообщением при том же его объеме (то есть объем сообщения использу-
ется неэффективно). Другая причина избыточности заключается в том, что
значения яркости распределены в диапазоне их возможного изменения суще-
ственно неравномерно.
Естественно, что внимание многих исследователей в течение уже длитель-
ного времени привлечено к задаче создания методов компрессии, примене-
ние которых позволило бы улучшить характеристики систем передачи, обра-
ботки и регистрации изображений. К настоящему времени разработано боль-
шое количество таких методов, однако работы в этой области интенсивно
продолжаются [8, 12, 14, 15, 16, 20]. Мы ограничимся изложением лишь не-
скольких классов методов компрессии, которые в той или иной степени явля-
лись предметом исследований авторов.
Прежде чем перейти к описанию этих методов, определим совокупность
показателей, которыми они будут характеризоваться.
6.1.1. Показатели эффективности
Рассмотрим сначала, как можно оценить эффективность метода компрес-
сии данных. Если говорить о цифровых изображениях, то показателем эф-
фективности обычно служит коэффициент сжатия (компрессии):
К=\
(6.1)
где 70, / — объемы данных соответственно до и после компрессии. Следует
отметить, что этот показатель является относительным, он характеризует эф-
фективность метода в сравнении с некоторым «эталонным» (исходным) спо-
собом цифрового представления данных. При этом эталонный способ может
быть выбран достаточно произвольно. Для изображений в качестве исходного
чаще всего используется представление в виде матрицы отсчетов с известным
форматом данных (например байт на отсчет).
Абсолютную эффективность метода можно охарактеризовать коэффици-
ентом эффективности:
(6.2)
где Zinjn — минимально достижимый объем данных (соответствующий случаю
полного устранения избыточности гипотетическим «оптимальным» методом).
Однако этот показатель используется редко из-за сложности определения /min
(эта величина определяется энтропией источника сообщений и легко вычисля-
ется лишь для некоторых простейших моделей источников) [10].
Приведенные показатели характеризуют эффективность кодирования дискрет-
ного изображения, то есть матрицы отсчетов. Если же говорить о физическом,
6.1. Показатели качества методов компрессии
387
непрерывном изображении (поле) /(х15х2), заданном в некоторой двумер-
ной области, например, при |х1|<Е1/2, |х2|<Е2/2, где 1Л, L2 — некоторые
положительные величины, то следует оценивать метод его компрессии с точ-
ки зрения эффективности дискретного представления этого непрерывного
поля. Такую оценку можно осуществить, используя еще показатель произво-
дительности источника
^1^2
(6.3)
При реализации процедуры компрессии данных естественно стремле-
ние обеспечить по возможности большее значение коэффициентов сжа-
тия (6.1) и эффективности (6.2) и, соответственно, меньшее значение по-
тока данных (6.3):
Ксж—>тах, А^ф—>тах, t/—> min.
Однако эта оптимизация ограничивается рядом объективных факторов и,
в частности, тем, что компрессия, как правило, вносит искажения в обраба-
тываемое изображение.
6.1.2. Показатели точности
Если произвести кодирование изображения с целью компрессии данных, а
затем его восстановление (декодирование), то в результате может получиться
изображение, отличающееся от исходного. Для характеристики величины этого
отличия чаще всего используют среднеквадратичный критерий и критерий
максимальной ошибки.
Ранее мы записывали приближенные выражения для полной среднеквад-
ратичной и максимальной погрешности цифрового представления непрерыв-
ного изображения (см. формулы (2.53) и (2.54)). Если считать отсутствующи-
ми посторонние искажения (шумы), то из них следует:
^КВ КВ КВ ^обр КВ ’
(6-4)
£ max х max "Е f max "Е обр max ‘
(6.5)
Первые две составляющие погрешности обусловлены дискретизацией
поля яркости по пространственным координатам и квантованием по уров-
ню. Третья составляющая это дополнительная погрешность, которая воз-
никает в процессе обработки (в данном случае компрессии и последующе-
го декодирования) цифрового изображения. Поскольку мы рассматриваем
13*
388
ГЛАВА 6
цифровую обработку, то компрессия применяется к матрице отсчетов изобра-
жения, то есть аналого-цифровое преобразование поля яркости уже осуще-
ствлено, составляющие погрешности ел, заранее известны и неизменны
(для заданных параметров модели изображения и способе интерполяции).
Метод компрессии изображения характеризуется третьей составляющей.
Поэтому почти всегда, когда говорят о показателе точности метода комп-
рессии, имеют в виду именно Еобр. Функцией этой погрешности является
и коэффициент сжатия: для любого разумного метода компрессии он рас-
тет с ростом еобр.
Зависимость Ксж (вобр) может быть построена для каждого изображения и
для каждого метода сжатия. Чем выше проходит график этой зависимости,
тем более эффективен метод (или тем «удобнее» изображение для компрес-
сии, то есть выше его избыточность).
На практике всегда оговаривается предельное допустимое значение по-
грешности обработки (некоторое е0), то есть требуется, чтобы
£ обр — 0 '
Этим условием и ограничивается рост эффективности процедуры комп-
рессии.
Зависимость от погрешности можно получить и для потока данных (6.3).
Эта функция будет убывающей. Это обусловлено тем, что поток данных
характеризует эффективность представления исходного непрерывного поля.
Соответственно, и ограничение налагается на общую погрешность (6.4)
или (6.5).
Отметим, что по способу управления показателями эффективности и точ-
ности и, соответственно, по режиму использования в системе обработки
изображений все методы компрессии разделяются на два больших класса.
В методах компрессии с фиксированной скоростью коэффициент сжатия явля-
ется наперед заданным (фиксированным). При этом для разных изображений
получается различная погрешность их восстановления по кодированным дан-
ным. Поэтому такие методы называются еще методами кодирования с неуп-
равляемой погрешностью. Их достоинство — простота использования в си-
стемах передачи данных, так как информационный поток на выходе блока
компрессии имеет постоянную скорость (если, конечно, постоянен входной
поток).
В другом классе — методах кодирования с переменной скоростью (или с
управляемой погрешностью) задается допустимая погрешность восстановле-
ния. При этом переменным оказывается коэффициент сжатия. Эти методы
более сложны в применении, т.к. в некоторых случаях требуют использова-
ния «буферного» запоминающего устройства на выходе устройства компрес-
сии для выравнивания скорости потока данных. Однако они потенциально
более эффективны в смысле устранения избыточности данных.
6.2. Статистическое кодирование
389
6.1.3. Системотехнические показатели
Для практического применения процедур компрессии данных важное зна-
чение имеют и их параметры, которые принято называть системотехнически-
ми. Их достаточно много, но главные — сложность (в смысле быстродей-
ствия) вычислительных процедур, реализующих методы компрессии и необ-
ходимые затраты памяти компьютера. Причем эти показатели следует относить
отдельно к процедурам компрессии (кодирования) и к процедурам восста-
новления (декодирования). Единицы измерения системотехнических показа-
телей зависят от конкретной реализации процедур обработки (например, слож-
ность может измеряться и числом операций на отсчет, и временем обработки
изображения).
Ниже мы перейдем к описанию конкретных методов компрессии изобра-
жений. Заметим предварительно, что задача компрессии хорошо исследована
и вне сферы обработки изображений. Большое число методов давно и успеш-
но используется при обработке «одномерных» сигналов, например, телемет-
рической информации [6, 9, 13, 18]. Для простоты изложения многие методы
мы будем вначале описывать в «одномерном» варианте, а только затем отме-
чать особенности их построения для изображений.
6.2. Статистическое кодирование
Начнем с «классических» методов, известных из теории информации. Они
служат для устранения статистической избыточности источника дискретных
сообщений, обусловленной неравномерностью сообщений и их взаимозави-
симостью. Напомним минимально необходимые сведения из теории инфор-
мации [10, 17].
Пусть имеет место простейшая ситуация, когда отсчеты сигнала (символы
сообщения) представляют собой независимые случайные величины и могут
принимать Q значений: /0,/Р .. ,/g-i с вероятностями р0,р}, *Pq-i со-
ответственно. Объем информации, приходящейся в среднем на каждое сооб-
е-|
щение (отсчет), есть энтропия источника сообщений: Н =-^Pi log 2Pi-
z~о
В то же время, чтобы закодировать сообщения в двоичной форме словами
одинаковой длины, как это обычно делается, длина кодового слова должна
быть, как минимум, равна b~ log2Q.
Эта величина (разрядность двоичного кодового слова) определяет макси-
мальное количество информации, которое потенциально может содержать
сообщение: Н inax = b — log 2 Q.
Если бы все вероятности сообщений были равны ( р{ = 1/Q, 0 < I < Q -1),
то Н — Н , то есть потенциальные возможности переноса информации были
390
ГЛАВА 6
бы полностью использованы, равномерный код был бы безызбыточен. Одна-
ко на практике вероятности различаются, поэтому Н </71тах. Коэффициент
эффективности (6.2) равномерного кода
1 max
Одним из важнейших результатов теории информации является доказа-
тельство возможности устранения избыточности сообщений путем их надле-
жащего кодирования. Основная идея указанного кодирования заключается в
переходе к кодовым словам различной длины: сообщениям с высокой вероят-
ностью назначаются более короткие кодовые слова, а сообщением с малой
вероятностью более длинные. В результате средняя длина кодового слова
<2-1
b = HPihi,
1=0
где bt — длина слова для сообщения xh уменьшается, приближаясь к И, и
К =
* ь
Такая обработка сообщений называется их эффективным кодированием [17].
Код, обеспечивающий нулевую избыточность — 1), называется оптималь-
ным статистическим кодом. Он позволяет уменьшить объем данных в
Н I
rz __ 11 max 1
ЛСЖ — д, ~ rz
/У лэф
раз по сравнению с кодированием словами одинаковой длины. На практике,
однако, построение оптимального статистического кода обычно оказывается
чрезвычайно сложным, поэтому используются квазиоптимальные коды с бо-
лее простой реализацией. Далее мы рассмотрим некоторые из них.
Предварительно заметим, что эффективное кодирование не сопровождает-
ся внесением погрешности в цифровые данные (дискретные сообщения), то
есть обеспечивается их точное воспроизведение, следовательно, Еобр =0.
Как следствие, получается кодирование с переменной скоростью.
Указанные результаты обобщаются и на случай статистически зависимых
сообщений. Здесь обычно осуществляется переход от кодирования отдель-
ных сообщений к кодированию их групп (блоков), то есть, как говорят,
«укрупненных» сообщений. Достаточно большие блоки можно считать прак-
тически независимыми, и для них задача кодирования сводится к рассмот-
ренной выше.
6.2. Статистическое кодирование
391
6.2.1. Код Шеннона—Фано
Код Шеннона—Фано — классическая иллюстрация описанного подхода к
эффективному кодированию. Рассмотрим его построение. Пусть опять (для
простоты изложения) сообщения независимы.
Все возможные сообщения упорядочиваются по убыванию их вероятнос-
тей. Затем их множество разбивается на две группы так, чтобы суммарные
вероятности сообщений в группах были по возможности одинаковы. Если
кодируемое сообщение относится к первой группе, то в качестве первого сим-
вола кода берется 0 (например), если ко второй группе — то 1. Затем каждая
из групп снова разбивается на две примерно равновероятные части, форми-
руется второй символ кодового слова и т.д. Разбиения продолжаются до тех
пор, пока в каждой группе не останется по одному единственному сообще-
нию. Поясним сказанное на примере.
Пример 6.1. Пусть имеется источник с алфавитом в 6 сообщений (см. пер-
вые два столбца таблицы 6.1). В остальных столбцах таблицы показан процесс
разбиения и результирующие кодовые слова.
Средняя длина кодового слова здесь равна
=2(0,3 + 0,25+ 0,2) + Зх0,15 + 4(0,05 + 0,05) = 2,35.
При равномерном кодировании пришлось бы взять b > 1g2 6 и целое, т.е.
Ь = 3 .
Таким образом, по сравнению с кодированием словами одинаковой длины
в данном примере код Шеннона—Фано обеспечил коэффициент сжатия
Ксж=Ь/Ья1,28.
Таблица 6.1. Пример построения кода Шеннона—Фано
Pl 1 -е разбиение 2-е разбиение 3-е разбиение 4-е разбиение Кодовое слово
вер-сть группы 1 l-й символ кода вер-сть группы 2-й символ кода вер-сть группы 3-й символ кода вер-сть группы 4-й символ кода
fo 0,3 0,55 0 0,3 0 - - - - 00
/1 0,25 0,25 1 - - - - 0 1
/2 0,2 0,45 1 0,2 0 - — - - 1 0
/з 0,15 0,25 1 0,15 0 - - 1 1 0
Л 0,05 0,10 1 0,05 0 1110
./5 0,05 0,05 1 1111
392
ГЛАВА 6
6.2.2. Код Хаффмена
Методика построения кода Хаффмена заключается в следующем. Сообще-
ния выписываются в порядке убывания вероятностей. Последние два сообще-
ния в списке объединяются в новое «вспомогательное» сообщение. Одному из
объединяемых сообщений приписывается символ 0, второму — 1. Оставшиеся
сообщения и только что полученное вспомогательное опять выписываются по
убыванию вероятностей и т.д. Процедура продолжается до тех пор, пока не
получится единственное вспомогательное сообщение с вероятностью 1. Кодо-
вое слово для каждого сообщения считывается в инверсном порядке, то есть,
начиная с последнего шага процедуры формирования кода к первому.
Пример 6.2. Возьмем тот же источник сообщений, что и выше, и построим
для него код Хаффмена. Процедура построения иллюстрируется таблицей 6.2,
где столбцы, содержащие исходные сообщения ft и вспомогательные сооб-
щения 5, помечены символом f.
Результирующие кодовые слова показаны в таблице 6.3.
В данном примере код Хаффмена по длинам слов (и, следовательно, по
эффективности) совпадает с кодом Шеннона—Фано, но, в принципе, здесь
могут быть и различия: код Хаффмена всегда равен или превышает по эффек-
тивности код Шеннона—Фано.
Достоинство подобных статистических кодов — сокращение объема дан-
ных до теоретически возможного предела без внесения искажений. Недостат-
ками являются, во-первых, сложность реализации, быстро возрастающая с
ростом числа сообщений и, во-вторых, необходимость знания распределения
вероятностей сообщений.
Коды Шеннона-Фано и Хаффмена используются преимущественно при
малом алфавите сообщений и играют вспомогательную роль. Обычно они
реализуются «внутри» других методов компрессии данных для дополнитель-
ного повышения их эффективности. Рассмотрим еще один метод статисти-
ческого кодирования.
6.2.3. Кодирование длин серий
Кодирование длин серий (КДС) довольно часто используется в задачах
компрессии данных (обычно как вспомогательная операция в более сложных
методах) [3, 14, 20, 26]. Его главное достоинство заключается в том, что, в
отличие от методов Шеннона—Фано и Хаффмена, оно не нуждается в форми-
ровании и хранении громоздких таблиц кодов. В то же время получаемые
результаты кодирования обычно мало отличаются от оптимальных.
Хотя метод КДС используется в различных ситуациях, по своей сути он
относится к кодированию двоичных последовательностей. Рассмотрением та-
кого типа данных мы и ограничимся.
6.2. Статистическое кодирование
393
Таблица 6.2. Пример построения кода Хаффмена
394
ГЛАВА 6
Таблица 6.3. Результирую-
щие кодовые слова кода
Хаффмена
/о 00
/1 01
fl 11
h 100
А 1010
fs 1011
Пусть имеется последовательность символов 0 и 1,
символы в последовательности статистически неза-
висимы, вероятность появления единицы равна р
(соответственно, вероятность нуля — (1 — /?)):
... О 1 0 1 00 1 1 00 00 1 1 00 ...
Энтропия таких сообщений
//= —plog2/? — (1 — p^log2 (1 — р).
Если р = 0,5, то такая последовательность безызбыточна: энтропия Н =1
и длина кодового слова на сообщение Ь = 1. Кодировать эту последователь-
ность не имеет смысла.
Далее будем рассматривать случай р<0,5 (вариант /? >0,5 приводит к
«симметричным» результатам). Здесь уже имеет место статистическая избы-
точность сообщений (Н <1, Ь = Г). Возникает вопрос, как ее уменьшить.
Кодирование каждого символа, например по Шеннону—Фано, здесь ниче-
го не дает (см. таблицу 6.4, представление данных остается без изменений).
Можно, конечно, перейти к кодированию блоков («укрупненных» симво-
лов). Например, если р = 0,1 и взять по два сообщения в блоке, то неравно-
мерный код Шеннона—Фано строится так, как показано в таблице 6.5
В этом случае избыточность уменьшится. Средняя длина кодового слова
здесь равна
- Зх(0,01+0,09) + 2х0,09 + 1x0,81 1,29 _ д
Однако до энтропии
Н = - - 0,01 log 2 0.01 - 0.99 log 2 0,99 « 0,47
еще далеко. Для того, чтобы и дальше приблизить b к Н, нужно увеличить
длину блоков, но при этом процедура кодирования (и соответственно де-
Таблица 6.4. Кодирование битового
потока по Шеннону—Фано
Сообщение Единственное разбиение
Вероятность Код
/о=’О' Р 0
/о=Т 1 -Р 1
Таблица 6.5. Использование «укрупненных»
символов для кодирования битового потока
Блок Вероятности Код
So=’l Г р2 = 0,01 0 0 0 0 0 0
$,= '0Г р(1 -р) = 0,09 1 0 0 1
р(1-р) = 0,09 1 - 0 1
S3=’00' (1 -р)2 = 0,81 1 - - 1
6.2. Статистическое кодирование
395
кодирования) становится громоздкой: длина таблицы кодов равна 2К", где
Кв — число двоичных сообщений в блоке. Следовательно, увеличивая блоки,
мы быстро подойдем к допустимому пределу сложности.
Иной подход реализуется в методе КДС. Здесь последовательность также
разбивается на блоки (укрупненные символы), но эти блоки имеют разную
длину. И наоборот, каждый блок кодируется двоичным словом фиксирован-
ной длины.
Пусть для кодирования блоков используются b-разрядные двоичные сло-
ва. Вместо самих двоичных сообщений рассматривается система из Q = 2h
укрупненных символов:
$0 = I,
S, =0 1,
S2 =00 1,
SQ^ =00 ...0 1,
SG„“ = 00 ...0 0.
Здесь каждый следующий блок содержит на один символ ‘0’ больше пре-
дыдущего. Предпоследний и последний блоки имеют одинаковую длину. Дан-
ная система блоков является полной, то есть разбиение произвольной после-
довательности на такие блоки всегда возможно. После выделения укрупнен-
ных символов из последовательности каждый из них кодируется своим
b -разрядным кодом. По сути, кодируется номер укрупненного символа или,
что одно и то же, число (длина серии) нулей в блоке. Отсюда вытекает и
название метода.
Реализация такого кодирования заключается в подсчете подряд идущих
нулей в последовательности двоичных сообщений, то есть оказывается пре-
дельно простой. Также проста и процедура декодирования. Причем очень
удобно, что КДС не зависит впрямую от статистики сообщений и имеет един-
ственный параметр — длину выходного кодового слова — b.
Для того, чтобы понять, как нужно выбирать Ь, оценим эффективность
метода. Коэффициент сжатия (6.1) для него равен
Ксж = —, (6.6)
ь
где К — средняя длина входного укрепленного сообщения.
Определим значение К . Вспомним, что длины блоков
•W1 > ^2’-"’ Sq-i ’ Q-1
равны соответственно 1, 2, 3, ..., (Q-2), (2 — 1) двоичным разрядам. А ве-
роятности их появления, в соответствии с принятой моделью источника —
р, (1-р)р. (1-р)2р,..., (1-р)°“2р. (1-р)е-‘.
396
ГЛАВА 6
Средняя длина входного укрупненного символа
ЯГ = 1-р+2-(1-р)р+3-(1- р)2 р+...+
+(е- 0(1- p)L 2 p+(q~ ОО- p)L 1 Р=
(6.7)
Учитывая, что Q~2h, и подставляя (6.7) в (6.6), получаем окончательно:
pb
(6.8)
Таким образом, коэффициент сжатия зависит от характеристики источни-
ка р и характеристики кода Ь. Зависимость (6.8) показана на рис. 6.1. На
Рис. 6.1. Зависимость коэффициента сжатия от
характеристики источника для КДС
этом рисунке сплошной линией
показана также функция 1/Н(р),
характеризующая максимально до-
стижимый коэффициент сжатия. Из
анализа этого рисунка можно сде-
лать следующие выводы:
1) при фиксированном b коэф-
фициент сжатия растет с уменьше-
нием р;
2) при надлежащем (оптималь-
ном) выборе разрядности выход-
ного кодового слова эффектив-
ность КДС лишь незначительно
отличается от эффективности оп-
тимального статистического коди-
рования;
3) каждое значение b является
оптимальным только для определен-
ного диапазона значений вероятно-
сти р . Это означает, что на практике необходимо производить оценку р по
реальным данным.
6.3. Оптимизация регулярного цифрового представления
изображений
Вернемся к рассмотрению цифрового представления непрерывного изоб-
ражения, при котором поле яркости описывается матрицей своих отсчетов,
6.3. Оптимизация регулярного цифрового представления изображений
397
взятых в узлах регулярной прямоугольной сетки с шагами дискретизации Л,
и Д2, а каждый отсчет кодируется b-разрядным двоичным кодом. В технике
связи такое регулярное цифровое представление непрерывной функции на-
зывается импульсно-кодовой модуляцией (ИКМ) [14, 20].
Даже не применяя специальные методы компрессии, можно попытаться
оптимизировать параметры ИКМ с точки зрения ее эффективности. Попро-
буем произвести минимизацию потока при заданном ограничении на погреш-
ность описания изображения.
Решение этой задачи важно в двух аспектах. Во-первых, оно позволяет
осуществить рациональный выбор параметров аналого-цифрового преобра-
зования видеосигналов в системе передачи изображений, использующей ИКМ.
Во-вторых, наиболее эффективное регулярное представление изображений
может служить хорошей базой для сравнения с ним более сложных способов
представления (и методов компрессии) данных.
Задача оптимизации регулярного цифрового представления ставится сле-
дующим образом. Целевой функцией является поток данных. Эта характери-
стика выражается через параметры дискретизации и квантования и должна
быть минимизирована:
U ——------>min. (6.9)
Д1Д2
Оптимизация осуществляется в пространстве переменных Ь, Дь Д2.
Ограничения выдвигаются со стороны общей погрешности цифрового пред-
ставления изображения, заданной соотношением (6.4) или (6.5). В данном
случае дополнительной обработки (и, соответственно, составляющей погреш-
ности Еобр в формулах (6.4) или (6.5) нет, поэтому общая погрешность скла-
дывается из погрешности квантования по уровню е^, зависящей от разряд-
ности кодовых слов Ь, и из погрешности дискретизации по пространствен-
ным координатам £Л, зависящей от шагов дискретизации Ди Д2. Если
рассматривать среднеквадратичную и максимальную ошибку, то ограничения
запишутся, соответственно, в форме неравенств:
E»=e/o(«’)+eJ„(A1. Д2)<е?к,
(6.10)
Е
’"max
£ f max (^) "E £ x max (Д I ’ Д 2 ) — 0 max ’
(6.П)
где еокв и max ~ средне квадратичная и максимальная погрешности.
Дополнительными ограничениями являются естественные требования по-
ложительности варьируемых переменных: Ь>0, Д] >0, Д2>0, а также
целочисленности Ь.
398
ГЛАВА 6
Для известной модели изображения и выбранного способа интерполяции
можно получить конкретное выражение для зависимостей £ f (/?) и £А. (др Д2);
эти вопросы рассмотрены в п.2.6. После этого поставленная задача оптимиза-
ции иногда легко решается даже аналитически.
Пример 6.3. Пусть непрерывное изображение описывается моделью стаци-
онарного поля с гауссовым распределением яркости и биэкспоненциальной
АКФ, изотропной в перпендикулярных направлениях:
Bf (*i > х2) = °/ ехр(-а(| х, | +1 х21)).
При квантовании по уровню шкала яркости выбирается по правилу «трех
сигм», квантованные уровни располагаются равномерно, шаги дискретиза-
ции по пространственным координатам выбраны равными, Д1 = Д9=Д, и
предполагается билинейная интерполяция отсчетов (эту совокупность исход-
ных данных будем также использовать и в последующих примерах).
Пусть задана допустимая среднеквадратичная погрешность цифрового пред-
ставления ЕОкв, и требуется определить оптимальные параметры ИКМ (Ь и
Д), минимизирующие поток данных.
Для рассматриваемой ситуации известно (см. п.2.6, формулу (2.23) и
табл. 2.1), что
£/ кв (^) — ^2/? ’ кв (A) = 01
(здесь применена приближенная формула для Ех кв, в предположении что
погрешность дискретизации мала). Выражение (6.10) для полной ошибки
цифрового представления изображения теперь конкретизируется:
(неравенство здесь брать не имеет смысла, т.к. минимум объема данных будет
достигаться при наибольшей погрешности, то есть именно при равенстве).
Таким образом, ограничение на варьируемые параметры имеет вид
2
3 2 Ео кв 1
-^- + -аД = -^- = ~, (6.12)
2“ 3 a2 d2
где d2 — соотношение сигнал/шум для цифрового представления изображения.
Нам требуется минимизировать поток данных (6.9):
U — b/Д2 —> min.
(6.13)
6.3. Оптимизация регулярного цифрового представления изображений
399
Для решения этой задачи найдем из (6.12) величину А и подставим ее в
(6.13). При этом, чтобы игнорировать физическую размерность координат
поля, перейдем к эквивалентным безразмерным характеристикам:
U 4Ь
* 3 1
а А-------
2R/2
+ min.
(6.14)
(6.15)
Таким образом, мы получили функцию (6.15), зависящую только от цело-
численного параметра b, ее минимум легко определяется перебором.
Конкретизируем исходные данные. Пусть d2=100. Тогда
3 3
аД = —0,01—5Т-
2 22Ь
U
4Ь
а2
0,01—
22\
9
Зависимость потока данных от разрядности кодовых слов представлена в
табл. 6.6, а также на рис. 6.2. В данном случае получается &opt = 6.
Соответственно
аДот = —0,01—2-
°1" 2[ 2 "
-0,01
2
3
4096
«0,014.
Рис. 6.2. Зависимость потока данных от раз-
рядности кодовых слов
Таблица 6.6. Зависимость
потока данных от разрядности
кодовых слов
ь С//а2
] - (Д<0)
2 - (А<0)
3 - (Д<0)
4 - (Д<0)
5 45 400
6 31 000
7 32 200
8 35 600
9 40 000
400
ГЛАВА 6
При этом обеспечивается
^-^31 ооо.
а
Повторим, что регулярное представление изображений в виде таблицы
пикселов на прямоугольной сетке выглядит естественным, ИКМ просто реа-
лизуется и потому чрезвычайно часто используется. Однако оно обладает од-
ним серьезным недостатком — является чрезвычайно избыточным. Действи-
тельно, для получения необходимых малых значений погрешности мы вы-
нуждены выбирать шаги дискретизации по координатам также достаточно
малыми. При этом между соседними отсчетами появляется сильная статисти-
ческая связь. Так, в рассмотренном выше примере коэффициент корреляции
между соседними отсчетами получается равным
р = е~аД-р‘ ^0,986.
Из теории информации известно, что наличие корреляции между элемен-
тами сообщения приводит к уменьшению количества информации, перено-
симого этим сообщением при том же его объеме. Иными словами объем со-
общения используется неэффективно, значения потока данных оказываются
сильно завышенными по сравнению с потенциально достижимым миниму-
мом. Далее мы попробуем приблизиться к этому минимуму, используя специ-
альные методы обработки данных.
6.4. Метод дифференциального кодирования
Рассмотрим группу методов компрессии данных, которые получили очень
широкое применение при обработке изображений. Методы этой группы но-
сят названия: дифференциальное (разностное) кодирование, кодирование с
предсказанием, дифференциальная импульсно-кодовая модуляция (ДИКМ)
и т.д. [8, 11, 14, 16, 20]. Они реализуют широко распространенный подход к
решению задачи компрессии. Вначале мы дадим общее описание метода, а
затем остановимся на важнейших деталях.
6.4.1. Общее описание метода
Суть метода дифференциального кодирования изложим применительно к
обработке одномерной последовательности отсчетов f(n), для изображения
такая последовательность может формироваться, например, в результате его
развертки по строкам.
6.4. Метод дифференциального кодирования
401
Идея метода заключается в том, что в порядке поступления отсчетов из
каждого отсчета f(n) вычитается некоторое опорное (предсказанное) значе-
ние f (и), то есть формируется разность
е(л) = /(«)-/(«). (6.16)
Поскольку обычно сигнал изменяется плавно (отсчеты являются сильно-
коррелированными), предсказывать значения отсчетов удается довольно точ-
но, то есть разностный сигнал е будет почти всегда близок к нулю (иметь
малую дисперсию). Благодаря этому при цифровом представлении е удается
обойтись меньшим числом разрядов, чем потребовалось бы для f (при той
же абсолютной погрешности квантования по уровню).
Итак, квантованию по уровню здесь подвергается не исходный сигнал,
а разностный. (Если обработке подвергаются уже оцифрованные отсчеты,
то соответствующая операция заключается в их загрублении (перекванто-
вании) с целью уменьшения числа двоичных знаков.) Квантованный раз-
ностный сигнал ё(п) поступает на выход системы (или процедуры) коди-
рования, см. рис. о.За:
При восстановлении (декодировании) отсчетов (на приемной стороне си-
стемы передачи данных) к получаемым значениям ё(и) прибавляется опор-
ный сигнал. При_этом формируются приближенные значения отсчетов пол-
ного сигнала — f(n), см. рис. 6.36.
Заметим, что в системе дифференциального кодирования должны исполь-
зоваться два идентичных устройства (алгоритма) формирования опорного
сигнала: на передающей и приемной стороне. При восстановлении в нашем
распоряжении имеется только восстановленный сигнал поэтому пред-
сказание должно осуществляться именно по нему. Соответственно, то же са-
мое приходится делать и при кодировании. Таким образом, приходим к об-
щей схеме дифференциального кодера и декодера, показанной на рис. 6.4.
Определим, с какой погрешностью здесь восстанавливаются отсчеты. Раз-
ностный сигнал описывается своими квантованными значениями с точнос-
тью до ошибки квантования по уровню:
Ё(н) = е(п)4-Еу(п). (6.17)
С такой же точностью получается и восстановленный сигнал:
7(Л) = Ё(и) + /(«) = Е(и) + Е у(п) + f(n) = f(n)+Е^ (и). (6.18)
Аналогичное соотношение имеет место и для случая простого квантования
сигнала по уровню. Однако здесь Еу — ошибка квантования не самого сиг-
нала /, а разностного — е. При фиксированной разрядности кодового сло-
ва ошибка квантования параметра по уровню тем меньше, чем меньше дис-
персия параметра (разумеется, в предположении, что всякий раз шкала пара-
метра согласуется с его дисперсией). Если < с , то при той же разрядности
402
ГЛАВА 6
Рис. 6.3. Пример дифференциального кодирования: а — кодирование, б — декодирование
Рис. 6.4. Схема дифференциального кодера (о) и декодера (б). УП — устройство предсказания,
КВ — квантователь
кодового слова дифференциальное кодирование обеспечивает более точное
восстановление отсчетов. При равных погрешностях восстановления диффе-
ренциальное кодирование позволяет обойтись меньшей разрядностью кодо-
вых слов, то есть обеспечивает получение эффекта сжатия данных.
Выигрыш от использования дифференциального кодирования тем больше,
чем меньше о“, то есть чем точнее осуществляется предсказание отсчетов.
При фиксированном алгоритме предсказания выигрыш тем больше, чем мень-
ше ошибка квантования разностного сигнала. Эти два фактора требуют спе-
циального рассмотрения, которое будет дано позже.
Основное достоинство дифференциального кодирования — это его про-
стота. Оно обеспечивает сравнительно высокую эффективность компрессии
и поэтому широко применяется на практике. Недостаток метода — низкая
помехоустойчивость при передаче закодированных данных из-за возможного
накопления ошибок на приемной стороне системы. В большинстве своих ва-
риантов эти методы относятся к методам кодирования с фиксированной ско-
ростью (и, следовательно, с неконтролируемой погрешностью). Качество вос-
становленных изображений для дифференциального кодера обычно оценива-
ется по критериям визуального восприятия или среднеквадратичной ошибки.
6.4.2. Выбор квантователя для разностного сигнала
Квантование разностного сигнала е по уровню имеет определенную спе-
цифику по сравнению с квантованием произвольного параметра, которое мы
рассматривали ранее.
6.4. Метод дифференциального кодирования
403
Первый фактор, определяющий эту специфику — малое число разрядов в
кодовом слове. Действительно, для того, чтобы обеспечить эффект сжатия в
системах, использующих ДИКМ, чаще всего длина кодовых слов Ь<3 (то
есть число квантованных уровней Q<8 — это довольно мало). Поэтому за-
дача назначения шкалы для сигнала в и оптимального расположения на ней
квантованных уровней становится довольно сложной. При решении этой за-
дачи приходится исходить из компромисса между двумя нежелательными яв-
лениями. С одной стороны, если взять широкую шкалу и «широко» располо-
жить на ней квантованные уровни, то получается большая ошибка квантова-
ния. С другой стороны, если попытаться уменьшить ошибку квантования путем
сужения шкалы, то это приведет к тому, что разностный сигнал в с большой
вероятностью будет выходить за ее границы («зашкаливать»), квантованный
разностный сигнал Ё будет ограничиваться по амплитуде по сравнению с
сигналом до квантования. Так как при этом утрачивается информация о
приращении сигнала (относительно предсказанного значения) большем, чем
ограниченное значение Ё, то резко возрастает погрешность восстановления
сигнала на его быстро меняющихся участках, и возникают так называемые
«перегрузки по наклону». Поиск компромиссного решения задачи выбора кван-
тователя приводит к использованию неравномерно расположенных кванто-
ванных уровней (нелинейных шкал).
Предложено довольно много таких шкал, построенных, исходя из различ-
ных критериев оценки качества передаваемых изображений. Еще в 1960 г.
Макс предложил строить нелинейную шкалу квантования, исходя из условия
минимизации среднеквадратичной ошибки квантования [14, 19, 33]. Эта шкала
применяется довольно часто, поэтому рассмотрим ее более детально.
Обозначим границы интервалов (шагов) квантования на шкале сигнала
как dQ,dx,...,dQ , а квантованные значения разностного сигнала — ео,е 1,..,е
(см. рис. 6.5).
Правило квантования сигнала задается выражением
Ё = Е/, если d{ <E<d[+l. (6.19)
Из (6.19) следует, что случайное значение ошибки квантования по уровню
равно Еу -Е —Ё = Е —Е/, если d{ <E<dl+}.
Если известна плотность распределения разностного сигнала ре(е), то
можно определить среднеквадратичную ошибку квантования:
£-1 di+}
= J (е-Е/)2А(£)^- (6.20)
/=0 d,
£/0=-°° dQ-\ dQ=°°
Рис. 6.5. Нелинейная шкала квантования
404
ГЛАВА 6
Для получения оптимальной шкалы нужно найти е, (0<г<(?-1) и dj
(1<J <<? — !)» минимизирующие ошибку (6.20). Возьмем частные производ-
ные по варьируемым параметрам и приравняем их нулю:
дг1 а с э г
f (е - Е<) л (E)rfe=2 Й£- Е<) (£)л=°-
di di
отсюда
(6.21)
отсюда
£j+£j-i
2
dJ =
(6.22)
Далее необходимо решить систему уравнений (6.21)—(6.22). В общем слу-
чае это решение заключается в применении итерационной процедуры, в ко-
торой параметры Ef, найденные из (6.21), подставляются в (6.22), затем dj,
найденные из (6.22), подставляются в (6.21), и так — многократно, до получе-
ния установившегося решения. Сама минимальная среднеквадратичная ошибка
(6.20) выражается с учетом (6.21) следующим образом:
£-1 dw
кв ^е J' Ре
/=0 di
(6.23)
Заметим, что общим недостатком всех нелинейных шкал является именно
то, что они нелинейны: номер квантованного уровня не пропорционален
физическому значению сигнала. Поэтому двоичный код, которым описыва-
ется разностный сигнал (Г, нельзя непосредственно использовать при даль-
нейшей обработке (например, при формировании предсказываемого значе-
ния сигнала — f ); необходимо вначале вернуться к «физической» шкале, то
есть при помощи хранимой в памяти таблицы соответствия осуществить
6.4. Метод дифференциального кодирования
405
переход от номера квантованного уровня I к его значению е, (которое, соб-
ственно, и передается в кодированной форме).
Остановимся на одном полезном факте, который понадобится нам при
дальнейшем анализе. При любом выборе шкалы погрешность квантования,
очевидно, уменьшается с увеличением разрядности и связана с размахом (то
есть дисперсией) квантуемого сигнала. Например, для параметра е с нор-
мальным распределением, шкалы, выбранной по правилу «трех сигм» и рав-
номерного квантования в соответствии с п.6.3 мы получаем
Для других шкал конкретный вид зависимости может быть другим, но в
целом ее характер сохраняется. Соответствие между дисперсией квантуемого
параметра и ошибкой квантования удобно записать в общем виде:
<624>
где Fq (b) — назовем характеристикой квантователя (величина, зависящая от
разрядности).
Функция FQ(b) экспоненциально убывает и стремится к нулю. При
Ь —0 FQ(b) = i, поскольку имеет место отсутствие передачи квантованного
параметра, и его значение должно быть принято равным математическому
ожиданию (ошибка ЕуКВ равна дисперсии о^). Подобную характеристику
можно ввести и для оценки погрешности квантования по другим критериям.
Еще одной особенностью процедуры квантования при дифференциальном
кодировании является то, что дисперсия разностного сигнала может значи-
тельно изменяться во времени в зависимости от коррелированности и, следо-
вательно, предсказуемости обрабатываемого сигнала (изображения практичес-
ки всегда являются неоднородными). Известны многочисленные варианты адап-
тивных шкал, меняющихся в зависимости от текущего поведения сигнала [11,
14, 20]. Однако и их рассмотрение выходит за рамки нашего анализа.
Выбор хорошего квантователя (то есть такого, который вносит прием-
лемо малые искажения) представляет собой сложную задачу. Поэтому в
заключение параграфа целесообразно указать вариант дифференциального
кодирования, при котором квантователя нет вообще. Это так называемое
обратимое дифференциальное кодирование, которое довольно часто исполь-
зуется в цифровых системах. В этом случае предполагается, что обрабатыва-
емый сигнал заранее равномерно квантован (то есть, представлен целыми
числами — условными значениями яркости). Формируемый разностный
сигнал полностью (без внесения погрешности квантования) передается по
каналу. Возникает вопрос, в чем здесь выигрыш, ведь количество разрядов
кода на выходе дифференциального кодера не уменьшается. В данном слу-
чае эффект сжатия обусловлен тем, что «узкое» распределение вероятностей
разностного сигнала позволяет применить методы статистического кодирования
406
ГЛАВА 6
а б
Рис. 6.6. Обратимое дифференциального кодирование: а — кодер, б — декодер
(например, код Хаффмена), что и обеспечивает необходимую компрессию
данных. Функциональная схема системы с обратимым дифференциальным
кодированием показана на рис. 6.6.
Поскольку в данном случае квантователя нет, то погрешность в разност-
ный сигнал не вносится, и в устройстве кодирования нет необходимости ис-
пользовать обратную связь.
Обратимое дифференциальное кодирование реализует сжатие данных с
контролируемой (нулевой) погрешностью, и, соответственно, с переменной
скоростью, что и определяет его достоинства и недостатки.
6.4.3. Алгоритмы предсказания отсчетов
Как уже отмечалось, при дифференциальном кодировании нужно стре-
миться как можно к более точному предсказанию отсчетов сигнала. Возмож-
ность этого предсказания обусловлена наличием статистической зависимости
отсчетов. Рассмотрим некоторые возможные подходы к синтезу алгоритмов
предсказания. Начнем с одномерного линейного случая.
Устройство линейного предсказания обычно строится как некоторая
ЛПП-система. Однако кодер системы ДИ КМ в целом является нелинейным
из-за наличия квантователя. Поэтому точный анализ его характеристик чрез-
вычайно сложен. При изучении дифференциального кодера обычно делается
ряд упрощающих допущений, которые, естественно, обуславливают прибли-
женность результата анализа (или оптимизации) системы, но, по крайней
мере, делают задачу разрешимой. В первую очередь, такое упрощение состоит
в замене квантователя источником независимого шума квантования, то есть в
переходе к эквивалентной схеме кодера, показанной на рис. 6.7.
На этом рисунке Нпр (?) — передаточная функция линейного предсказателя.
После очевидных преобразований схема, изображенная на рис. 6.7, может
быть представлена в виде рис. 6.8.
При анализе предсказателя нас в первую очередь интересует дисперсия
ст“ разностного сигнала е . Она, очевидно, складывается под влиянием двух
независимых случайных воздействий — полезного сигнала f (п) и шума кван-
тования еу(и):
е(н) = Еу(w) + ee (л). (6.25)
Преобразование /(и) в описывается эквивалентной ЛПП-систе-
мой, изображенной на рис. 6.9о.
6.4. Метод дифференциального кодирования
407
Рис. 6.7. Эквивалентная схема
кодера
Рис. 6.8. Преобразованная эк-
вивалентная схема кодера
Переходя к представлению последовательностей и систем с помощью
Z-преобразования, получаем:
£f(Z) = F(Z)----/_\-=F(Z)[1-/Jnp(z)]-
'-«пр z
(6.26)
Преобразование ev(h) в £е (л) описывается ЛПП-системой, изображен-
ной на рис. 6.96. Оно же в Z-области:
Мг)=Ыг)+/^
d -Hpp(z)
Zjll-Wnp(z)
или
а б
Рис. 6.9. Преобразование полезного сигнала (о) и шума квантования (б) в составляющие разност-
ного сигнала
408
ГЛАВА 6
Из (6.26) и (6.27) несложно получить энергетический спектр (точнее,
Z-преобразование АКФ) разностного сигнала:
ФеЫ = Ф/(г)[1-Н„р(г)][1- (6.28)
Отсюда можно перейти во временную область, определить дисперсию раз-
ностного сигнала как сумму двух дисперсий (сигналов Еу и Ее ) и далее оп-
тимизировать параметры передаточной функции /7пр (предсказателя) по кри-
терию минимизации этой суммарной дисперсии. Однако на деле все оказыва-
ется не так просто, поскольку дисперсия второй составляющей разностного
сигнала оказывается зависимой от всей дисперсии о2 (т.к. определяется про-
цедурой квантования сигнала е ).
Пример 6.4. Пусть имеет место предсказание по предыдущему отсчету пос-
л едовател ьности:
У(п) = а/(л-1), Hnp(z) = az~l. (6.29)
Определим параметр а в (6.29) исходя из условия минимизации ошибки
предсказания (тем самым продемонстрируем общий подход к синтезу линей-
ных процедур предсказания).
Фе(г) = Ф f аг)+Фе^ (z)fi2 =
= Фу (z)[l + a2(z)a2.
Переходя от Z-преобразования во временную область (от энергетических
спектров к АКФ), получаем
5E(^) = (14-a2)e/(A:)-6z5/ (Jt + 1)-а£у (к-1) + В£у (к)а2.
При к = 0 получаем выражение для дисперсии разностного сигнала:
o2=oj[l + fl2-2np] + a2EjKB. (6.30)
(В (6.30) АКФ входного сигнала дополнительно выражена через диспер-
сию о2 и коэффициент корреляции между соседними отсчетами — р.)
С другой стороны, известно что, ошибка е (п) возникает вследствие кван-
тования, то есть е2кв — где FQ(b} — характеристики квантователя
(см. общую формулу (6.24)). Так как все рассматриваемые последовательнос-
ти считаются стационарными, дисперсия разностного сигнала будет постоян-
ной, и ее можно выразить из соотношения
ст2 =а2 [1 + а2 -2ap] + a2FG(fe)a2,
6.4. Метод дифференциального кодирования
409
то есть
2 2 — 2fl Р
e=a'*-4W
Оптимальное значение параметра а получим, приравняв нулю производную:
do2 _(2a-2p)[l-a* 2Fe(fe)] + (l + a2-2aP)(2OFe(fe))
da -
Отсюда следует квадратное уравнение
a2pFc(fr)-fl[l + Fe(b)] + p =0,
решая которое определяем оптимум:
2pFe(fe)
(лишний корень отбрасывается из условия получения минимума, а не мак-
симума).
Конкретизируем результат. Пусть р -0,9, шкала — равномерна и выбрана
по правилу «трех сигм» (то есть fq (/>) = з/22Л), и b = 2. Тогда из полученных
соотношений находим:
2
«opt«0,86; -^-«0,222.
ст/
Рассмотренный подход неудобен тем, что уравнение для оптимального
параметра получается нелинейным (если параметров несколько, то есть алго-
ритм предсказания более сложен, задача может стать неразрешимой). На прак-
тике чаще всего делают еще одно допущение: при оптимизации коэффициен-
тов предсказателя полагают F6(b) = 0 (то есть Ь—>оо). В таком случае для
предсказателя по одному отсчету непосредственно из полученного выше квад-
ратного уравнения получаем, что -а + р = 0, и, следовательно, aopt =р.
Оказывается, такой выбор параметра практически не ухудшает точности
предсказания. Действительно, для наших числовых данных теперь получим:
«ор.=0.9; ^-«0.224,
410
ГЛАВА 6
что свидетельствует о том, что экстремум функции а2 (а) является достаточ-
но пологим.
Можно вообще взять а = 1 (так это часто и делается на практике из сооб-
ражений простоты), и даже в этом случае точность предсказания почти не
ухудшится. Так, для принятых числовых данных в этом варианте получим
2
--^0,246,
то есть всего лишь на 10% хуже, чем при оптимальном значении коэффи-
циента.
Следует отметить, что при вычислении дисперсии разностного сигнала (а
не при отыскании параметров предсказателя) квантование все же следует учи-
тывать (что и делалось выше), иначе погрешность в результатах может быть
уже заметной. Так, для наших числовых данных, если не учитывать квантова-
ние, для « — 1 получается, что
«2
->
14-а 2 — 2а р
l-a2Fe(Z>)
а=1 =1+1- 2- 0,9— 0,2;
^=0
это — заниженное значение, далекое от реальности. Впрочем, если значе-
ние Fq (/?) действительно мало (обычно при b > 3), то и этой погрешностью
можно пренебречь.
Далее мы будем рассматривать линейные процедуры предсказания общего
вида. При этом, учитывая сказанное, ограничимся приближенным методом
их расчета, полагая F0(h) = O, то есть, считая, что предсказание осуществля-
ется по точным (не квантованным) значениям отсчетов. Нужно найти пара-
метры физически реализуемой ЛПП-системы, минимизирующей дисперсию
ошибки предсказания, то есть обеспечивающей оптимальную (в среднеквад-
ратичном смысле) оценку сигнала на шаг вперед. Эта задача полностью впи-
сывается в известный класс задач синтеза линейных восстанавливающих фильт-
ров (см. п.3.4.1). Параметры оптимального (квазиоптимального) восстанавли-
вающего фильтра, как известно, определяются из системы (3.50), состоящей
из уравнения Винера-Хопфа и ограничения на импульсную характеристику,
а дисперсия ошибки восстановления определяется выражением (3.51) (с уче-
том замены в этих соотношениях Лвосст на йпр — импульсную характеристику
ЛПП-системы — предсказателя).
Особенности рассматриваемой ситуации заключаются в следующем.
Во-первых, в данном случае нет никаких искажений, то есть наблюдаемый
и полезный сигналы совпадают, и поэтому в указанных соотношениях
6.4. Метод дифференциального кодирования
411
Учитывая это, получаем те же соотношения в модифицированном виде
(заодно введем обозначение Bf(k) = GjRf(k) и вспомним, что у нас
ё2=а}):
k£D (6.31)
Лпр(и1) —О, m^D\
_2
-f=i-5X(*)R/(*)-
° f kED
(6.32)
Во-вторых, поскольку мы рассматриваем предсказание, область наблюде-
ния D может включать в себя только точки к >1.
Для предсказывающей КИХ-системы параметры определяются в результа-
те непосредственного решения уравнений Винера—Хопфа (6.31).
Пример 6.5. Определим параметры линейного предсказателя по двум от-
счетам: D : {1, 2}. В данном случае система (6.31) принимает вид
'np(l)+^(2)R/(*) = R/W. ПР” m = 1.
Лпр(1)хЯ/(1)+Лпр(2)х1 =^(2), при т = 2.
Ее решение:
J?z(l)[l-/?z(2)]
l-Rj(l)
A-(2)=_T^j(ir
Если сигнал имеет АКФ вида Rf = то
р(1-р2) о2-о2
/!-’W=4t^=p’ л''‘’(2) = 7ТР“=0’
то есть предсказание по двум отсчетам вырождается в предсказание по одно-
му. Можно показать, что для экспоненциальном АКФ предсказание по одно-
му отсчету уже является оптимальным. (Этот факт очень полезен в практи-
ческих задачах.) Для него (как следует из (6.32))
2
-1 = 1-Л1ф(1)Я/(1) = 1-р2.
аг
412
ГЛАВА 6
Предсказание при помощи БИХ-систем используется существенно реже,
поскольку здесь возникают сложности расчета и необходимо дополнительно
анализировать устойчивость предсказывающей системы.
Большой простор для творчества при синтезе алгоритмов предсказания
открывает переход к обработке изображений, при которой появляется воз-
можность построения «двумерных» предсказателей.
Если используются двумерные линейные предсказатели, то все очень
похоже на рассмотренный одномерный случай. Приведенные выше опре-
деляющие соотношения (6.31) и (6.32) записываются для двумерного сиг-
нала в виде
Е 1Хр(*ь n2-k2) = Rf(nx, п2), (щ, n2)ED,
(jtbJi2)eD (6.33)
л2) = 0, (и,, n2)&D-,
2
2г=1- Е EMMz)M*i.*2)- (6.34)
а/
Область наблюдения сигнала — D, очевидно, должна обеспечивать реа-
лизуемость системы при заданном виде развертки и не включать в себя точ-
ку (0,0).
Пример 6.6. Пусть имеет место простейший вариант двумерного линейного
предсказания — по двум точкам при построчной развертке изображения, а
именно предсказанное значение для отсчета, помеченного на рис. 6.10 круж-
ком, формируется как взвешенная сумма «прошлых» отсчетов (крестики).
На рис. 6.10 введены компактные обозначения для коэффициентов корре-
ляции между отсчетами (р,,р2,р3) и для двух ненулевых значений импульс-
ной характеристики предсказывающего КИХ-фильтра (aj,a2)- Построим си-
стему уравнений вида (6.33)
«l+^Рз = Р1»
а1Рз ^~а2 — Р2 •
Найденные из нее оптимальные коэффициенты имеют вид
_Р1~Р2Рз. _ _ Р2 "Р1Рз
“t — ; 2 ’ “2 — : 2 '
1-Рз 1-Рз
Пусть сигнал имеет АКФ, изотропную в перпендикулярных направлениях:
/?, («„ и2) = рМ+Ы
6.4. Метод дифференциального кодирования
413
и отсчеты, по которым ведется предсказание, расположены именно так, как
показано на рис. 6.10. Тогда р] = р, р2—р, р3=р2,
Относительная дисперсия разностного сигнала (6.34) имеет вид
£t = i_2p_^=lzPi,
о2 1 + р2 1 + р2
т.е. в (1 + р2) раз меньше, чем в одномерном случае.
В более общем случае можно использовать линейное предсказание по че-
тырем отсчетам (см. рис. 6.11) или большому их числу, то есть использовать
произвольную двумерную каузальную (или полукаузальную физически реа-
лизуемую) К.ИХ- или БИХ-систему. Однако, как показывают многочислен-
ные эксперименты, существенного выигрыша по сравнению с линейным пред-
сказанием по двум отсчетам это не дает.
Существуют адаптивные варианты линейных процедур предсказания, в
которых используется оценка локальных коэффициентов корреляции и соот-
ветствующая подстройка коэффициентов, однако они применяются редко ввиду
сложности.
Общий недостаток линейных предсказателей заключается в том, что они
всегда дают всплеск (выброс) ошибки предсказания (разностного сигнала)
при прохождении участков изображения со скачкообразным изменением яр-
кости. Это вызывает нежелательные перегрузки по наклону на наиболее ин-
формативных областях изображения — границах областей и контурных лини-
ях. От этого недостатка позволяют избавиться некоторые двумерные нели-
нейные алгоритмы предсказания.
Предсказатель Грехэма [16] обеспечивает точное предсказание отсчетов при
пересечении участков изображения с вертикальными и горизонтальными кон-
турами. Поясним принцип его действия (см. также рис. 6.12).
Рис. 6.10. Двумерное
линейное предсказа-
ние по двум отсчетам
Рис. 6.11. Двумерное линей-
ное предсказание по четырем
отсчетам
414
ГЛАВА 6
Для каждого отсчета /(И|,л2) вычисляются две величины:
д=|/(м], п2-1, «2-1)|,
# = n2)-/(nI-l, п2- 1)|.
В зависимости от значений этих величин производится переключение пред-
сказателя:
/(«1.
/(л,—1, п2), если А<В,
/(«1, л2-1), если А > В,
что обеспечивает предсказание всегда «вдоль» контура. Данный алгоритм,
обеспечивает «инвариантность» предсказания к контурам (скачкам яркости)
двух направлений — вертикального и горизонтального [5].
Предсказатель, инвариантный к контурам четырех направлений (см.
рис. 6.13) [5, 23]. Принцип здесь тот же, что и в предыдущем случае, но
процедура допускает переключение на четыре направления предсказания.
Направление выбирается из условия, что по нему сумма модулей отмечен-
ных на рисунке трех разностей отсчетов будет минимальной. Ввиду громозд-
кости формулы аналитическое представление здесь не приводится. Этот
предсказатель эффективен тогда, когда на изображении имеются протяжен-
ные линии (контуры) под углами 0°, 45°, 90°, 135е к строкам. Его очевидный
недостаток — сложность реализации.
Рис. 6.12. Преобразователь Грехема. Утолщенны-
ми линиями выделены анализируемые разности
отсчетов, стрелками — возможный выбор отсче-
тов в качестве предсказанного значения
Рис. 6.13. Предсказатель, инвариантный к
контурам четырех направлений (см. коммен-
тарии к рис. 6.12)
6.4. Метод дифференциального кодирования
415
6.4.4. Оптимизация дифференциального кодера изображений
При проектировании процедуры ДИ КМ возникает задача выбора ее пара-
метров. В общем случае решение этой задачи заключается в оптимизации
кодера по критерию минимума потока данных (см. формулу (6.13)). Именно
исходя из этого условия нужно выбрать:
1) шаги дискретизации непрерывного поля по пространственным коорди-
натам — Д,, Д2;
2) вид и параметры алгоритма предсказания;
3) вид шкалы квантования и разрядность кодовых слов — b.
Разработчик обычно располагает небольшим набором различных шкал и
предсказателей, поэтому по ним можно организовать прямой перебор. А
при каждом конкретном выборе типа шкалы и алгоритма предсказания за-
дача сводится к параметрической оптимизации, решаемой в пространстве
параметров предсказателя, а также величин Дн Д2 и Ь. Причем предсказа-
тель обычно рассматривается автономно и оптимизируется, например, по
методике, изложенной в предыдущем параграфе, его параметры определя-
ются моделью изображения и опять же шагами дискретизации Д(, Д2. Сле-
довательно, в конечном счете остаются только три свободные переменные —
д,, д2, ь.
Задача оптимизации решается с учетом ограничений со стороны общей
погрешности цифрового представления изображения. Эта погрешность, как
и в случае И КМ, складывается из погрешности квантования (теперь уже раз-
ностного) сигнала по уровню и из погрешности дискретизации по простран-
ственным координатам. В случае использования среднеквадратичного пока-
зателя качества ограничения записывается в виде, подобном (6.10). Погреш-
ность дискретизации зависит (при заданной модели изображения и выбранном
способе интерполяции) от шагов дискретизации Д,, Д2. Однако погреш-
ность квантования по уровню зависит теперь не только от разрядности дво-
ичных слов — b, но и от дисперсии квантуемого (разностного) сигнала, кото-
рая, в свою очередь, зависит снова от Aj, Д2 (то есть степени коррелирован-
ное™ и, следовательно, предсказуемости отсчетов). Поэтому неравенство (6.10)
в данном случае можно переписать в виде
Д|’ дг)+е?и(д1’ да)-«о»-
(6.35)
Кроме того, действуют ограничения: Д, >0, Д2>0, &>0; b — целое.
В случае нелинейного предсказания, а также сложной модели изображе-
ния, выходящей за рамки модели однородного поля, поставленная задача па-
раметрической оптимизации не имеет аналитического решения (или это ре-
шение оказывается чрезмерно громоздким). Поэтому чаще всего оптимиза-
ция дифференциального кодера производится путем его моделирование на
416
ГЛАВА 6
синтезированных или натурных тестовых изображениях, В простейших вари-
антах эту задачу можно решить аналитически.
Пример 6.7. Пусть непрерывное изображение описывается моделью стаци-
онарного поля с биэкспоненциальной АКФ вида
В/(л1, х2) = ф-*Н<
в дифференциальном кодере используется простейший алгоритм предсказа-
ния по предыдущему отсчету, f(n) = у(л-1), и равномерная шкала кванто-
вания, приведенная к интервалу «трех сигм» разностного сигнала (характери-
стика квантователя FQ (b) = 3/21Ь). Шаги дискретизации по пространствен-
ным координатам выберем равными: Д(—Д2 = Д, и будем предполагать
билинейную интерполяцию отсчетов при восстановлении непрерывного изоб-
ражения.
Пусть также задана допустимая среднеквадратичная погрешность цифро-
вого представления е0 кв. Требуется найти оптимальные параметры ДИКМ —
b и Д, минимизирующие поток данных.
Решение. Для рассматриваемой ситуации известно, что
2 2 2 л
^хкв ~
Ошибки квантования по уровню находим из уравнения
£/«.= а2сГе(Ь),
где для случая предсказания по одному отсчету (см. предыдущий параграф)
То есть при а = 1, для рассматриваемого простейшего предсказателя имеем
_2___2 2а Д
е~ 'i-W
Таким образом, ограничение (6.35) принимает вид
2 2 z> * \ 2/а\ 2 2(ХД$2(6) 2 т д 2
£кв =е)Кв(^Д) + ехкв(Д) = аГ-------О}аД-Еокв-
ли j ли х ' Л по ' f « О f v лв
1 - 3
6.4. Метод дифференциального кодирования
417
(Здесь использовано равенство, так как минимум достигается на границе.)
Таким образом,
2а A FQ(b) 2 . 1
l-FQ(b) 3 d2
где d2 — уже использовавшееся обозначение для отношения сигнал/шум по
мощности. Для случая равномерной шкалы
6аД 2 . 1
7~-----г + -аД~—.
(22fc-3) 3 d2
Выразим отсюда значение шага дискретизации (в нормированном, безраз-
мерном виде):
аД =----
2d2
1
_2_+1
2й -3 3
Очевидно, что при Ь>1 эта величина всегда положительна. Перейдя к
безразмерной характеристике потока данных, получим минимизируемое вы-
ражение в виде
U
а2
^ = 4d2b
___3
к22л—3 ' 3
1V
Конкретизируем исходные данные. Пусть d2=100. Значения {//а2 при
значениях b от 1 до 9 сведем в таблицу 6.7 и отобразим на графике (см.
рис. 6.14).
Таким образом, оптимальное значение длины кодового слова bopt = 3. Со-
ответственно аД % 0,013; при этом обеспечивается, что и/а2 % 17600, что
существенно меньше, чем в случае ИКМ (см. пример 6.3). Дифференциаль-
ное кодирование обеспечило получение эффекта сжатия данных.
Рассмотренная методика расчета и оптимизации дифференциального ко-
дера является приближенной. По ходу изложения мы делали много допуще-
ний, которые становятся все менее правомерными при уменьшении разряд-
ности Ь. Однако подобные расчеты обычно дают приемлемый для практики
результат.
14 — 9044
418
ГЛАВА 6
Таблица 6.7. Зависи-
мость потока данных
от длины кодового
слова
ь и а2
1 44400
2 25500
3 17600
4 19000
5 22600
6 26800
7 31100
8 35600
9 40000
U/a2
Рис. 6.14. Зависимость потока данных от длины кодового слова
6.4.5. Дифференциальное кодирование бинарных изображений
Дифференциальное кодирование часто применяется для компрессии дан-
ных при обработке бинарных изображений. При этом оно реализуется в до-
вольно специфическом виде. Кратко отметим основные особенности такого
применения.
Во-первых, предсказываемое значение двоичного отсчета здесь строится
как булева функция некоторой совокупности предыдущих отсчетов, и вместо
разностного сигнала формируется сигнал несовпадения предсказанного и
истинного значения отсчета, то есть их сумма по mod 2: 0 — предсказание
удалось, 1 — предсказание неверно.
Во-вторых, из схемы процедуры кодирования исключается квантователь,
то есть в данном случае используется обратимое дифференциальное кодиро-
вание (см. п.6.4.2). Эффект сжатия достигается здесь не сокращением числа
двоичных знаков на отсчет (ведь и так уже b = 1), а преобразованием последо-
вательности к виду, удобному для статистического кодирования. Если проце-
дура предсказания построена достаточно хорошо, то доля ошибочно предска-
занных отсчетов (то есть единиц в «разностном» сигнале) будет мала, и в
такой ситуации очень удобно использовать КДС, см. п.6.2.3.
Структура дифференциального кодера и декодера последовательности би-
нарных отсчетов показана на рис. 6.15.
Пример 6.8. Построим алгоритм двумерного булева предсказания, обеспе-
чивающий «инвариантность» к горизонтальным и вертикальным границам
объектов (контурам). Пусть предсказание строится на основе трех предыду-
щих отсчетов текущей и предыдущей строки (см. рис. 6.16). На этом рисунке
6.4. Метод дифференциального кодирования
419
Рис. 6.15. Дифференциальный кодер для бинарных изображений
и ниже для удобства введем краткие обозначения отсчетов: — уже
пройденные, /0 — предсказываемый.
Таблица 6.8 построена для булевой функции /0 Записанную
в таблице булеву функцию можно выразить и аналитически:
Продемонстрируем эффективность применения
такого предсказателя. Пусть имеется изображение —
«квадрат» (см. рис. 6.17а). После применения к нему
нашей процедуры предсказания получим изображе-
ние, показанное на рис. 6.17d. По оставшимся на
изображении трем точкам полностью восстанавли-
вается исходное изображение. В исходном изобра-
жении было 8x8 = 64 бит. Осталось 3 единицы. Если
использовать КДС при построчной развертке
Таблица 6.8. Булева
функция предсказания
по трем отсчетам
/> /2 /з /о
0 0 0 0
1 1
1 0 0
1 0
1 0 0 1
1 1
1 0 0
I 1
б — варианты, выбираемые при различных значениях пройденных отсчетов
14*
420
ГЛАВА 6
Рис. 6.17. Исходное бинарное изображение «квадрат» (а) и изображение ошибок его булева пред-
сказания по трем точкам (б)
изображения, и положить в нем b = 5, то получится всего 4 серии, то есть
4 х 5 = 20 бит. Возникающий при этом коэффициент сжатия Ксж = 64/20 = 3,2.
Дифференциальное кодирование бинарных изображений используется и
при обработке полутоновых изображений при их представлении и кодирова-
нии по битовым плоскостям.
6.5. Методы кодирования с преобразованием
6.5.1. Общая схема методов кодирования с преобразованием
Основная идея метода кодирования с преобразованием заключается в ис-
пользовании так называемых «обобщенных представлений» сигнала [13, 18].
Поясним, что это такое, на примере обработки одномерного сигнала.
Пусть имеется сигнал f(t) — непрерывная функция времени. Весь пери-
од, на котором этот сигнал рассматривается, (период наблюдения) разбивает-
ся на стыкующиеся интервалы представления — .. L^\ ... В резуль-
тате обработки сигнала на каждом из интервалов представления формируется
некоторый набор (вектор) параметров — обобщенных координат сигнала:
* 14°)’ 41)’•••’ Чл/(-1)р
где М. — число компонентов вектора на интервале см. рис. 6.18. Эти обоб-
щенные координаты, представленные в цифровой форме, используются везде
далее в системе вместо значений (отсчетов) самого сигнала. Они выбираются
так, что при необходимости из обобщенных координат можно восстановить (точно
или приближенно) исходный сигнал.
Очевидно, что представление регулярными отсчетами есть частный случай
обобщенного представления, для которого
£(<)=[;д, (>+!)&], м(=1. /$=/[;д].
6.5. Методы кодирования с преобразованием
421
F(1) F<2) F(0
Рис. 6.18. Обобщенное представление сигнала
В общем же случае координатами могут служить самые различные характе-
ристики сигнала на интервале представления.
Эффективность обобщенных представлений вытекает из того, что обоб-
щенные координаты могут быть менее коррелированными, чем отсчеты сиг-
нала (в ряде случаев — статистически независимыми). Следовательно, они
могут содержать ту же информацию при меньшем объеме данных. Обобщен-
ных координат может быть меньше, чем отсчетов на том же интервале.
Следует сказать, что есть два пути для получения обобщенных координат в
цифровой форме. Первый путь — их вычисление в аналоговой форме с даль-
нейшим преобразованием в цифровую. Общая структура устройства форми-
рования координат выглядит здесь так, как показано на рис. 6.19л.
Это так называемое обобщенное квантование сигнала (или квантование в
пространстве обобщенных координат). Обработка сигнала здесь ведется на
аналоговом уровне, что обеспечивает высокую скорость, но невысокую точ-
ность и малую гибкость процедуры обработки. Для цифровой вычислитель-
ной техники более естественна другая схема, показанная на рис. 196. Здесь
обработке подвергается сигнал, уже прошедший первичную дискретизацию
и квантование (то есть превращенный в последовательность цифровых от-
счетов). Блок вычисления координат в данном случае производит просто
некоторую перекодировку (преобразование) цифровых данных. Именно этот
вариант, называемый кодированием с преобразованием, и рассматривается
далее.
Итак, процедура кодирования с преобразованием заключается в следую-
щем. На этапе компрессии данных (кодирования):
422
ГЛАВА 6
Рис. 6.19. Вычисление обобщенных координат: а — обобщенное квантование, б — кодирование
с преобразованием
1) каждый блок отсчетов подвергается некоторому преобразованию, в ре-
зультате которого формируются обобщенные координаты сообщений;
2) осуществляется кодирование обобщенных координат с целью сокраще-
ния избыточности данных (достижения эффекта сжатия).
На этапе восстановления (декодирования):
1) декодируются обобщенные координаты;
2) вычисляется обратное преобразование, то есть по декодированным зна-
чениям обобщенных координат вычисляются сами отсчеты сигнала.
Достоинствами метода кодирования с преобразованием в общем случае
являются весьма высокая эффективность и высокая помехоустойчивость. В
отличие от дифференциального кодирования здесь сигнал обрабатывается
«блоками», то есть независимо на каждом интервале представления, поэтому
влияние помех на сжатые данные ограничивается размером блока, то есть
исключаются длинные «треки» ошибок при восстановлении.
Основной недостаток метода — его относительная сложность, как на этапе
компрессии, так и на этапе восстановления.
Отметим далее, что при кодировании обобщенных координат в данные
вносится погрешность, т.к. эта операция, как правило, связана с квантовани-
ем координат, отбрасыванием наименьших из них и т.п. В зависимости от
варианта метода эта погрешность может быть неконтролируемой (случай ко-
дирования с фиксированной скоростью) или контролируемой (случай коди-
рования с переменной скоростью, реализуемого некоторыми адаптивными
вариантами метода). Но в любом случае эта погрешность обычно количе-
ственно оценивается по среднеквадратичному критерию, поскольку для дру-
гих критериев возникают сложности при переводе погрешности из простран-
ства обобщенных координат в пространство отсчетов.
Очевидно, что при разработке процедуры кодирования с преобразованием
приходится решать две основные задачи:
1) выбор вида преобразования для получения обобщенных координат;
2) выбор метода обработки (кодирования) обобщенных координат.
Рассмотрим обе эти задачи более подробно.
6.5. Методы кодирования с преобразованием
423
6.5.2. Выбор преобразования
В принципе, обобщенными координатами сигнала могут служить любые
его характеристики на интервале представления. Но для рассматриваемой за-
дачи компрессии данных нужно, чтобы используемое преобразование отвеча-
ло нескольким требованиям.
1. Преобразование должно быть обратимым, то есть позволять переходить
от обобщенных координат обратно к отсчетам.
2. В результате преобразования основной объем информации о сигнале
должен быть сконцентрирован по возможности в меньшем числе обобщен-
ных координат (это обеспечит наибольший эффект сжатия).
3. Преобразование (прямое и обратное) должно достаточно просто вычис-
ляться.
Практически всегда в качестве обобщенных координат берутся коэффици-
енты разложения сигнала в ряд по какому-либо дискретному ортогональному
базису (иногда называемые трансформантами). Для одномерного сигнала /(м)
на интервале 0 < п < N — I такое разложение может быть записано в следую-
щей общей форме:
/V—I
F(m) = f(n)A(m, и) (6.36)
л=0
— прямое преобразование (вычисление трансформант);
лм
/(/и)= F(m)B(mt п) (6.37)
ли—О
— обратное преобразование, где матрицы А(т,п), в(т,п) — ядра прямого и
обратного преобразования. Если принять, что строки в(т,п) ортогональны:
дм ,
У2 В(т, п)В* (&, и) = ||#,и|| 5(т—Л), (6.38)
л=0
то можно получить, что
Если при этом все нормы равны:
Pm||2=||B|| = Const,
424
ГЛАВА 6
то будут ортогональны и столбцы матрицы в(т,п), то есть кроме (6.38) будет
справедливо и соотношение
/v—1 _
Х,В(т, п)В‘(т, *) = ||Вт|| 8(и-к).
т=0
И далее
N-1 1
5Хт- п)А‘(к, п) = —6(т-к),
»=о ||В||
N-l 1
£A(m, л)А*(т, *) = —8(л-Л).
"’=° И
Как видно, в данном случае первое требование (обратимость преобразова-
ния) является выполненным.
Ортогональным преобразованием, идеальным с точки зрения второго тре-
бования является так называемое преобразование Хотеллинга (дискретное
преобразование Карунена-Лоэва) [14, 20, 25]. Остановимся на нем подроб-
нее. Это преобразование строится из условия получения некоррелирован-
ных трансформант. Выведем основное соотношение для нахождения базис-
ных функций Хотеллинга. Пусть искомый базис — вещественный и ортого-
нальный:
А(т,п) = В(т,п) (||в|| = 1).
АКФ для трансформант (в предположении центрированности сигнала и
его трансформант), исходя из требования их некоррелированности, должна
иметь вид
TV-1 N-1
BF(m, к) = E{F(m)F(k)} = Е Ylf(n}A(m’ nY£f(l)A(k’
n=0
1=0
N-l N—l
= У2 У? n)A(k, l)Bf (w, /)= DF (m)S(zn— k) (6.39)
n=01=0
(при этом необязательно чтобы сигнал был стационарным).
Умножим обе части выражения на последнем шаге (6.39) на А(к, р) и про-
суммируем по к:
N-l N-} N—\ JV—I
£а(£, p)DF(m)&(m-k) = £ 12 ^А(к^ р)л(т, п)д(к, l)Bf(n, l),
к=О к=0 п=0 1=0
6.5. Методы кодирования с преобразованием
425
ИЛИ
N-l JV-1
DF (т)А(т, р)=Е £>(ли, ЛП
Л=О /=0
N-l 7V-1
w=0 1=0
р)л(к, 1)
к=0
Bf(n, 1) =
N-\
i)= п)вАп> р)'
п=0
Или окончательно
N-1
Df (т)А(т, р) — 52 А(т’ n)Bf (”’ р)- (6.40)
п=0
Видно, что строки A(zn,p) (и, соответственно, А (ли, л)) есть собственные
функции (векторы) ковариационной функции (матрицы) Bf , a DF (ли) — ее
собственные значения. Поэтому преобразование Хотеллинга называют еще
разложением по собственным векторам АКФ. Можно показать, что кроме
некоррелированности трансформант преобразование Хотеллинга обеспечи-
вает максимально быстрое убывание их дисперсии (собственных значений),
то есть обладает именно тем свойством, которое сформулировано выше во
втором требовании к преобразованию. Все другие базисы дают более медлен-
ное убывание, а значит, требуют для той же точности представления данных
использования (передачи) большего числа трансформант. Однако несмотря
на столь ценное качество преобразования Хотеллинга, на практике оно при-
меняется редко, так как, во-первых, его базис оказывается жестко привязан-
ным к АКФ сигнала (его пришлось бы все время пересчитывать, а уравнение
(6.40) чаще всего в явном виде не решается), и, во-вторых, для него в общем
случае не существует быстрого алгоритма вычисления, то есть оно совершен-
но не удовлетворяет третьему условию, сформулированному выше. Поэтому
преобразование Хотеллинга возникает обычно в теоретических рассмотрени-
ях как идеал, к которому нужно стремиться, а на практике применяются дру-
гие преобразования, для которых существуют быстрые алгоритмы.
Сравнительный анализ различных дискретных ортогональных базисов вы-
полнялся большим числом исследователей [1, 14, 20, 25]. Укажем некоторые
известные и наиболее важные факты, относящиеся к этому вопросу.
Найдено, что преобразование Хотеллинга хорошо аппроксимируется дис-
кретным преобразованием Фурье (в п.3.4.4 мы видели, что ДПФ тоже декор-
релирует сигнал, правда, не абсолютно, а асимптотически, при N —>оо). Не-
достатки ДПФ — его комплекснозначность, что затрудняет обработку транс-
формант. Разработаны и используются вещественные базисы: Фурье в форме
Хартли, косинусное, Уолша, семейство вейвлет-преобразований ит.д. [1, 24,
25, 31]. В настоящее время на первое место выдвинулось косинусное преоб-
разование, которое, как выяснилось, чрезвычайно близко подходит по свой-
ствам к преобразованию Хотеллинга для многих сигналов (например, экс-
поненциально коррелированных) [1]. Преобразование Уолша, Хаара и им
426
ГЛАВА 6
подобные применяются тогда, когда предъявляются жесткие требования к
сложности аппаратуры и скорости вычислений, однако для компрессии сиг-
налов они менее эффективны.
При обработке изображений все изложенное чаще всего используется в «дву-
мерной» модификации. Матрица отсчетов разбивается на блоки — двумерные
интервалы представления, и применяются двумерные преобразования.
Вопрос, который необходимо в этой связи затронуть, это выбор размеров
блоков. Известно, что декоррелирующие свойства преобразований усилива-
ются с увеличением размеров блока. В одномерном случае практически не-
коррелированные трансформанты получаются тогда, когда длина блока со-
ставляет хотя бы несколько интервалов корреляции сигнала. В двумерном
случае при кодировании изображений средней детальности чаще всего ис-
пользуют квадратные блоки 8x8, 16x16, 32x32. Дальнейшее увеличение
размеров блоков практически не повышает эффективность компрессии, а лишь
усложняет процедуру обработки как на кодирующей, так и на декодирующей
стороне.
6.5.3. Кодирование трансформант
Обработка результатов преобразования (трансформант) заключается в вы-
полнении двух основных операций:
1) отбора наиболее существенных трансформант;
2) их квантования, то есть представления определенным числом разрядов.
Обе эти операции приводят к уменьшению объема данных (то есть обеспе-
чивают эффект сжатия), и обе они вносят погрешность в обрабатываемый сиг-
нал. Иногда используется только одна из них: либо отбор, либо квантование.
Что касается квантования, его осуществление осложнено необходимостью
расчета шкал и разрядностей, который должен быть выполнен для каждой
трансформанты. Один из возможных вариантов определения разрядностей
для кодирования трансформант мы рассмотрим в следующем параграфе.
Реализация отбора проще, так как здесь имеется много простых эвристи-
ческих процедур, основанных на практическом опыте. Наиболее часто ис-
пользуется так называемый зональный отбор трансформант, при котором ос-
тавляются только те из них, которые попадают в зоны с наибольшими их
дисперсиями, а остальные полагаются равными нулю и не кодируются (не
передаются). Чем меньше трансформант мы оставим, тем выше будет эф-
фект сжатия, но тем больше и погрешность (разница между обобщенными
спектрами F( иг) и F (иг) и, соответственно, между исходным сигналом /(и)
и восстановленным /(и)).
В двумерном случае для блока N х N после преобразования получаем мат-
рицу трансформант того же размера. Процедура зонального отбора эквива-
лентна поэлементному умножению этой матрицы на бинарную маску, состо-
ящую из единиц и нулей.
Недостаток зонального отбора заключается в том, что маска выбирается
заранее, исходя из энергетических характеристик сигнала и базиса преобра-
6.5. Методы кодирования с преобразованием
427
зования, то есть метод является неадаптивным (не настраивается на текущие
особенности сигнала). Возможность адаптации заключается в применении для
отбора нескольких альтернативных масок, из которых для каждого блока вы-
бирается наиболее подходящая, при этом вместе с кодированными данными
должен регистрироваться и номер выбранной маски.
Еще одна возможность адаптации заключается в применении порогового
отбора трансформант. В этом случае обработке (квантованию и передаче)
подвергаются только те трансформанты, амплитуды которых в данном блоке
превысили некоторый порог. Причем, порог может быть фиксированным (тогда
его превысит случайное число трансформант, кодирование будет с перемен-
ной скоростью), а может изменяться от блока к блоку для того, чтобы выше
порога оказалось строго определенное число трансформант. Последний вари-
ант называется еще отбором максимальных трансформант.
Хотя пороговый отбор обеспечивает более правильный (с точки зрения
погрешности) выбор трансформант, общую эффективность метода компрес-
сии снижает необходимость регистрации служебной информации для указа-
ния положения («датирования») выбранных трансформант. Если трансфор-
мант немного, то можно непосредственно указать их адреса (номера) в блоке.
В общем случае, чтобы осуществить датирование, необходимо передавать дво-
ичную последовательность (в двумерном случае — двоичную матрицу) разме-
ром в блок, где выбранным трансформантом будут соответствовать, напри-
мер, единицы, а отброшенным — нули. Для сокращения объема данных при
передаче этой служебной информации можно использовать КДС.
Существует много других вариантов адаптивного отбора, однако здесь мы
не будем на них останавливаться. Квантованные трансформанты иногда до-
полнительно подвергаются статистическому кодированию. Следует отметить,
что все эти усовершенствования усугубляют главный недостаток метода коди-
рования с преобразованием — относительно высокую вычислительную слож-
ность. Сложная процедура кодирования с преобразованием может не подда-
ваться аналитическому расчету, в подобных ситуациях приходится исследо-
вать ее через моделирование. Один из немногих случаев, когда анализ и
оптимизация кодера с преобразованием может быть осуществлена аналити-
чески, рассматривается ниже.
6.5.4. Оптимизация процедуры кодирования с преобразованием
Рассмотрим задачу оптимального выбора параметров процедуры компрес-
сии данных, использующей кодирование с преобразованием. Для простоты
обозначений ограничимся случаем одномерных блоков. Примем следующий
простой алгоритм обработки сигнала.
Последовательность отсчетов /(п), полученная при построчной развертке
изображения, дискретизированного с шагами Ан Д2 по координатам, раз-
бивается на одинаковые интервалы представления — блоки по N отсчетов.
Пусть случайный сигнал стационарен, тогда все интервалы статистически
428
ГЛАВА 6
эквивалентны, и при анализе достаточно рассмотреть один из них при
0<n<W—1. На интервале представления сигнал подвергается ортогональ-
ному преобразованию, формируются его обобщенные координаты — транс-
форманты (6.36). Эти трансформанты представляются в цифровой форме, то
есть квантуются и кодируются двоичными словами. Каждой трансформанте
назначается своя шкала и своя длина кодового слова. Пусть Ьт — длина ко-
дового слова для трансформанты F(m). Для некоторых трансформант может
быть назначено Ьт ~ 0, это означает, что они не попали в зону отбора, и их
значения игнорируются (принимаются равными нулю).
Формируемый системой поток данных в рассматриваемом случае равен
/V-1
»i=0
М,Д2 '
(6-41)
В целях минимизации этой величины можно варьировать:
1) вид базисных функций /г)};
2) размер блока Д’ ;
3) шаги пространственной дискретизации Др Д2;
4) шкалы квантования и разрядности кодовых слов
Мы ограничимся рассмотрением «облегченного» варианта задачи оптими-
зации: будем считать, что вид шкалы квантования, базис преобразования и
размер блока заданы. Тогда она сводится к выбору оптимальных Д,, Д 2, [bm }.
Оптимизация кодера (минимизация величины (6.41)) осуществляется при
ограничении на погрешность восстановления сигнала. Как уже говорилось, для
методов кодирования с преобразованием обычно используется среднеквадра-
тичный критерий качества восстановления. Полная среднеквадратичная по-
грешность и ограничения на нее задаются формулой, подобной (6.10) и (6.35).
Погрешность пространственной дискретизации ел зависит от шагов дис-
кретизации Aj, Д2. Вторая составляющая погрешности — е, —определяет-
ся параметрами квантования трансформант. Дисперсии трансформант зави-
сят от степени коррелированности сигнала, то есть от Aj, Д2 (для одномер-
ных блоков существенна корреляция только по строке, поэтому будет
рассмотрена зависимость лишь от шага по горизонтали — Д2). Таким обра-
зом, ограничение на погрешность здесь может быть записано в виде
=Ех„(Д1, Д2)+е}„(д2, {bm})<elKt. (6.42)
Детально проанализируем второе слагаемое. В результате квантования транс-
форманты искажаются:
F [т] — X (m) + е(т},
где е(т) — ошибки квантования т-й трансформанты. Можно считать, что
в этом простом соотношении учтены и эффекты квантования, и эффекты
6.5. Методы кодирования с преобразованием
429
зонального отбора. Если трансформанта F(m) квантуется, то_е(т) — соответ-
ствующая ошибка квантования. Если она отбрасывается, то F(m) = 0, то есть:
е(т) = — F(m),
что эквивалентно кодированию трансформанты нуль-разрядным двоичным
словом.
Восстановленные отсчеты получаются обратным преобразованием иска-
женных трансформант:
/VI _ N-l 7V-1
/(«) = HF(m)B(m> п)= п) = «)•
m=0 m=0 m=0
Ошибки восстановления
_ W-l
е(п) = /(н)-/(n)= ^е(т)в(т, п).
т=0
Дисперсия ошибки восстановления, усредненная по интервалу представ-
ления,
1 N-1 , > 1 лм Л'-1 /v-i
®/K.=-EE{e2(,!)}=77S£ «) =
'* л=0 * л=0 1л1=0 А=0
1 N-l /V-1 , 4/V-l 1 N-l f ч _
= —£ SE{e(m)eW}SB(m’"И*’")=^£Me2W}llB™ll"’ (6ЛЗ)
N т—0 к=0 п=0 ™ т=0
где на последнем шаге учтена ортогональность базиса.
Будем считать, что шкала квантования каждой трансформанты согласова-
на с ее дисперсией, а характеристики всех квантователей одинаковы. Тогда
дисперсия ошибки квантования каждой трансформанты
fi{e2(m)} = a2 (m)Fe(Bm), (6.44)
где Of (?n) — дисперсия трансформанты Из (6.43) и (6.44) получаем
е?» lar(m)Fe(bm)- (6-45)
™ т=0
Далее необходимо определить дисперсии трансформант (считаем базис
вещественным):
2
/V-1
W-1
л=0
W-l N-1
= У1а(тп, п)А(т, 1}Вf(n— l).
п=0 1=0
(6.46)
430
ГЛАВА 6
Подставив (6.46) в выражение (6.45), окончательно получим
= (6.47)
где
1 /У-1ЛГ-1
^=—11^11 п)А(т, (6.48)
™ n=01=0
Поскольку базис и характеристики сигнала известны, значения весовой
функции Wm всегда могут быть вычислены (в простых случаях аналитически,
в более сложных — численно). Заметим, что весовой коэффициент Wm через
автоковариационную функцию В? зависит от шага дискретизации по стро-
кам Д2 (рассматривается случай одномерных блоков).
С учетом изложенного ограничение (6.42) принимает вид
7V-1
e„ = eJ„(A. A2)+Ec(bm)WM(A2)<eiL- <6-49»
т=0
Решать при таком ограничении задачу минимизации величины (6.41) весь-
ма сложно. Однако в нашем случае можно дать конкретные рекомендации.
По Д[, Д2 можно делать только перебор (почему, будет ясно из дальнейше-
го изложения). Диапазон перебора определяется, с одной стороны, есте-
ственными ограничениями: Aj >0, Д2>0, а с другой стороны, условием
Ej кв (Д।, Д2) < Eq кв (асимптотически, при Ьт —► оо, суммарная погрешность
состоит из погрешности пространственной дискретизации). Для фиксирован-
ных (Д], Д2) задача упрощается.
Действительно, из (6.41), (6.48) имеем:
/V-1
кв — — ^0 кв — кв — ^0 кв ’
т=0
W-]
X>m->rnin.
(6.50)
Для этой задачи существует простая процедура выбора (распределения)
разрядностей, суть которой заключается в следующем.
Вначале принимается, что все bm = 0(0<m<N — 1) — это ситуация, когда
передача информации отсутствует. Так как ^(0)= 1, то при этом
W-1
6/к. = £>„, = <?/
т=0
6.5. Методы кодирования с преобразованием
431
Естественно, это недопустимо большая величина. Для ее снижения далее в
цикле выполняются следующие действия:
1) делается попытка добавления одного разряда к каждому кодовому слову
и всякий раз определяется, на сколько уменьшается £ 2 кв. Если добавить раз-
ряд к кодовому слову с номером т , то это уменьшение составит
= Fq (ът)Wm - Fe (b„ +1>„ = [Fg (bm) - Fg (bm + ;
2) определяется кодовое слово, для которого указанное уменьшение мак-
симально (равно max {£„,}), и именно к нему прибавляется разряд;
ГН
3) величина е2 кв уменьшается на max {£,„}, и осуществляется возврат на п.1.
т
Процедура завершается, когда е2 кв станет меньше допустимой величины
Е(ГКВ (см.(6.50)). Возможна модификация этой процедуры при разработке
кодера с постоянной скоростью: процедура завершается, когда достигается
W-1
требуемый объем данных bw).
т=0
Поскольку на каждом шаге производится максимально возможное умень-
шение ошибки, необходимая точность будет достигнута за минимальное чис-
ло шагов. А так как на каждом шаге объем данных увеличивается на единицу,
то после завершения процедуры он будет минимально возможным.
Пример 6.9. Пусть непрерывное изображение описывается моделью ста-
ционарного поля с АКФ вида
Bf(x„ ^ = aXa(W+W)-
Шаги дискретизации выбраны равными: Д, =Д2 = Д, при восстановлении
предполагается использовать билинейную интерполяцию. Используется рав-
номерное квантование, согласованное со шкалой каждой трансформанты:
Fg(ft) = 3/22/’.
При кодировании с преобразованием используется простейший базис при
длине блока /V = 2:
При такой минимальной длине блока формулой (6.50) описываются поч-
ти все реально используемые базисы: конусный, Уолша, Хаара, Фурье и т.д.
432
ГЛАВА 6
Более длинные блоки, при которых между базисами появляются различия,
мы не можем взять из-за того, что пример станет слишком громоздким.
Пусть задана допустимая среднеквадратичная погрешность и требуется
найти: А, Ьо, , минимизирующие поток данных.
В этом случае целевая функция (см. (6.41))
Ограничение по погрешности (6.49) имеет вид
аД+[F0 (b0)W0 + FQ (6, )Ж, j < e* (6.52)
Определим весовые функции Wo и IV] для используемого базиса (см. (6.48)).
В данном случае
W2 = £b2(w,„)=1+1=1,
/2=0 Ч Ч Z
fi/(n-()= Bz(x„ x2)L=0 = а2 а2 pl-'l,
'х2=Д(и-/)
где при малых шагах дискретизации р~е”аЛ ~1-аД.
Поэтому из (6.48) получаем:
H^l+p]^
аД'
"Т
2
И/,=^[1-р]^2
То есть ограничение (6.52) приобретает вид
2 схД / \ аД / х 1
-аД+ 1-~
3 \ CL
Возможные значения аД удовлетворяют условию
0< аД<-1=.
2d1
6.5. Методы кодирования с преобразованием
433
Пусть б?2—100. Тогда 0<аД<0,015.
Организуем в этом диапазоне перебор по значению шага пространствен-
ной дискретизации. Для каждого конкретного (аД) определим разрядность
кодовых слов Ьо и bt.
Для различных значений аД с помощью описанной процедуры выбора
разрядностей подсчитаны параметры, приведенные в таблице 6.9.
Зависимость потока данных от шага дискретизации показана на рис. 6.20.
Эта зависимость получается не монотонной и не гладкой, именно поэтому
для поиска оптимального шага дискретизации и предлагался перебор.
В нашем конкретном численном примере:
<14^=0,0142, fe0opl=7, felopl=3, ^f- = 24800,
Таблица 6.9. Процедура выбора разрядностей
аД Ьо bi и/а2
0,0000 4-0,0061 5 0 «>4-67200
0,0061 4- 0,0079 6 0 80600 4-48100
0,0079 4-0,0089 6 1 56100 4-44200
0,0089 4-0,0122 6 2 50500 4- 26900
0,0122 4-0,0134 6 3 30200 4-25100
0,01344-0,0142 7 3 27800 4-24800
0,0142 4-0,0146 7 4 27300 4- 25800
0,0146 4-0,0148 8 4 28100 4-27400
Рис. 6.20. Зависимость потока данных от шага дискретизации
434
ГЛАВА 6
то есть получили некоторый эффект сжатия по сравнению с ИКМ (напом-
ним, там было 31000). При увеличении размера блока выигрыш, видимо, бу-
дет расти. Но одновременно будет усложняться и расчет кодера.
6.6. Метод адаптивных выборок
Рассмотрим еще одну группу методов компрессии, общий принцип дей-
ствия которых заключается в следующем [2, 6, 13, 18]. На этапе кодирования
из сигнала выделяется некоторый набор (подмножество) его отсчетов (значе-
ний). Эти значения берутся так, чтобы по ним можно было построить апп-
роксимирующую функцию, описывающую сигнал с требуемой точностью. При
декодировании вместо истинного сигнала строится именно эта аппроксими-
рующая функция.
Подобных методов существует довольно много. Самый простой из них —
регулярное прореживание отсчетов с последующей интерполяцией. Однако
наибольший интерес представляют методы, в которых отсчеты берутся не «всле-
пую», а адаптивно, в соответствии с текущим поведением сигнала. При этом
их можно взять ровно столько, сколько потребуется для восстановления с
заданной точностью. Центральное место среди таких методов занимают ме-
тоды адаптивных выборок.
6.6.1. Общая схема и примеры метода адаптивных выборок
Методы адаптивных выборок очень давно применяются при передаче те-
леметрической информации [2, 6, 13, 18]. Известны примеры их использова-
ния и при обработке (передаче) изображений [5, 14], но по своей сути они
рассчитаны на обработку одномерных последовательностей.
Действие метода адаптивных выборок заключается в следующем. Из пос-
ледовательности отсчетов выделяется некоторое число «существенных» от-
счетов, таких, что остальные отсчеты («избыточные») могут быть восстанов-
лены по существенным с необходимой точностью. При восстановлении су-
щественные отсчеты используются как узлы для интерполяции сигнала
какой-либо не очень сложной функцией, чаще всего кусочно-постоянной или
кусочно-линейной.
Из-за случайного характера сигнала существенные отсчеты случайным об-
разом и неравномерно располагаются на оси времени. Поэтому в состав ко-
дированных данных необходимо включать служебную информацию для ука-
зания положения (датирования) существенных отсчетов. Это является осо-
бенностью всех алгоритмов адаптивных выборок. Конкретные алгоритмы
адаптивных выборок весьма просты. Рассмотрим некоторые из них, считая,
что сигнал — последовательность f (и).
6.6. Метод адаптивных выборок
435
Предсказатель нулевого порядка (ПНП). Пусть в момент п = 0 зафиксиро-
ван очередной существенный отсчет fc ~ f (о).
Далее по мере возрастания дискретного времени (при п = 1,2,3,...) на каж-
дом шаге вычисляется ошибка представления текущего отсчета значением fr:
е(п) = f(n) — fe, и проверяется выполнение условия
(6.53)
где е0 тах — предельно допустимая максимальная ошибка, которая вносится
в сигнал в процессе обработки.
Пусть в момент п = п0 условие (6.53) нарушилось. Тогда фиксируется
новый существенный отсчет (принимается f(.= /(и0)), и процедура про-
должается. При восстановлении избыточных отсчетов на каждом интервале
между существенными используется экстраполяция (восстановление вперед)
постоянным значением f(;.
Иллюстрация к описанию алгоритма ПНП дана на рис. 6.21. На нем крес-
тиками помечены существенные отсчеты, кружками — восстановленные зна-
чения избыточных отсчетов.
Достоинство алгоритма ПНП — крайняя простота. Недостатком является
невысокая эффективность, особенно в условиях шумов, при которых наблю-
дается много «лишних» нарушений условия (6.53).
Интерполятор нулевого порядка (ИНП). Это немного более сложный, но
существенно более эффективный алгоритм. Опишем процесс обработки сиг-
нала для значений п > 0 .
Рис. 6.21. К описанию алгоритма ПНП
436
ГЛАВА 6
Начиная с первого отсчета рассматриваемого интервала (и = 0), по мере
возрастания и вычисляются максимальное и минимальное значения отсчетов
на интервале:
/щах (п) = шах {/(«')}
0<п'<п
/min («) = min {/(«)}•
(6.54)
Очередной существенный отсчет фиксируется в момент п = п0, когда впер-
вые нарушается неравенство
fmax (^) /min (^) — max • (6.55)
Значение существенного отсчета принимается равным
fc = |[/max («0 “ 0 + /min («0 ~ 0] ’ (6-56)
оно используется для восстановления избыточных отсчетов на интервале
О < л < л0 -1. С момента п = п0 процедура повторяется.
Алгоритм ИНП показан на рис. 6.22.
Восстановление сигнала здесь, как и в алгоритме ПНП, производится по-
стоянной величиной (полиномом нулевого порядка). Этот алгоритм эффек-
тивно применяется для обработки видеосигнала, так как обычно строки изоб-
ражения бывают близки к кусочно-постоянной функции (содержат области
близких значений, разделенные резкими границами, скачками яркости). Для
Рис. 6.22. К описанию алгоритма ИНП
6.6. Метод адаптивных выборок
437
плавно изменяющихся («гладких») сигналов целесообразно использовать бо-
лее сложную интерполирующую функцию. Рассмотрим один из соответству-
ющих алгоритмов.
Интерполятор первого порядка (ИПП). В нем используется линейная ин-
терполяция между существенными отсчетами. Существует несколько вариан-
тов ИПП, мы опишем один из наиболее эффективных — так называемый
«веерный» алгоритм.
Пусть в момент n = nG зафиксирован очередной существенный отсчет.
Рассмотрим, как выбирается следующий (см. рис. 6.23).
При п = 1 строятся два луча, ограничивающие множество всех лучей, ис-
ходящих из существенного отсчета и описывающих отсчет f (1) с погрешно-
стью, не большей ЕОтах-
При п = 2 из этих множеств лучей выбирается подмножество, которое
описывает с заданной точностью и отсчет f (2), и т.д. Поведение ограничива-
ющих лучей при этом, очевидно, таково: верхний может поворачиваться только
по часовой стрелке, нижний — только против часовой. Как только граничные
лучи «сомкнулись» (в момент и0), делается отступление на шаг и фиксирует-
ся существенный отсчет. Его значение берется лежащим на любом из допус-
тимых лучей.
Дадим формальное описание алгоритма. Вместо лучей можно исполь-
зовать тангенсы их наклонов. Поворот по часовой стрелке соответствует
уменьшению тангенса, против часовой стрелки — увеличению. В произ-
вольный момент п для верхнего граничного луча имеем тангенс (обозна-
чим его tg । (я))
tg. {п)= min --------t-----.
v 7 0<n'<n n
Рис. 6.23. К описанию алгоритма ИПП
438
ГЛАВА 6
Для нижнего граничного луча тангенс (обозначен tg2(n))
, / . /(«')“/<+£0т»
tg 2 (n) = min--.
0<п <п п
Очередной существенный отсчет фиксируется в момент п = п0, когда впер-
вые нарушается неравенство tg1 (и) > tg 2 (п).
Значение этого нового существенного отсчета принимается равным любо-
му из интервала
| /< + (tg 2 («О - О) Х («О - О • /< + (tg I («О - *)) Х ("О - 1) ]
(чаще всего среднему значению) и используется для восстановления избыточ-
ных отсчетов при 0 < п < п0 -1 путем линейной интерполяции.
Достоинство алгоритма ИНП — очень высокая эффективность при обра-
ботке плавно меняющихся сигналов. Правда, для реальных изображений это
достоинство проявляется редко, поскольку, как уже говорилось, функция рас-
пределения яркости обычно близка к кусочно-постоянной.
Остановимся на вопросе датирования существенных отсчетов. В основном
в литературе описывается два способа датирования [2, 5, 18].
В первом из них кодированные данные организуются в виде пар «отсчет-
дата», то есть создается последовательность кодовых слов длиной (bf
разрядов, в которых bf отводится на описание значения существенного от-
счета, а Ьх — на его датирование. Датирование здесь удобно производить,
указывая число пропущенных избыточных отсчетов между парой существен-
ных. Максимальное число, которое может быть указано в Ьх, двоичных раз-
рядов равно [1Ьх — , то есть ограничено. Поэтому для случаев, когда длина
серии избыточных отсчетов превышает это предельно допустимое значение, в
процедуре компрессии необходимо предусмотреть принудительную фикса-
цию существенного отсчета.
Достоинства такого способа датирования — в простоте реализации и в
удобстве обращения с кодированными данными, структура которых имеет
здесь регулярный характер. Этот способ можно использовать для алгоритмов
адаптивных выборок, работающих в реальном масштабе времени. Недостаток
способа — некоторое снижение эффективности сжатия за счет принудитель-
ной фиксации лишних существенных отсчетов.
Второй способ датирования существенных отсчетов заключается в следую-
щем. Каждому отсчету, обработанному алгоритмом компрессии данных, ста-
вится в соответствие двоичный символ: 1 — для существенного отсчета, 0 —
для избыточного. Эти двоичные символы образуют служебную датирующую
двоичную последовательность. Если единиц мало (существенных отсчетов на-
много меньше, чем избыточных), то с целью сокращения объема служебной
6.6. Метод адаптивных выборок
439
информации к датирующей последовательности можно применить КДС. Такое
датирование обеспечивает несколько больший эффект сжатия, чем предыду-
щее. Вместе с тем при формировании потока сжатых данных в реальном време-
ни такой поход менее удобен, «раздельная» регистрация существенных отсче-
тов и датирующей информации порождает некоторые проблемы, связанные с
усложнением структуры данных, их возможной де синхронизацией и т.д.
Говоря о методах адаптивных выборок в целом, можно отметить их несом-
ненные достоинства:
- простоту реализации,
- работоспособность при неизвестной или меняющейся статистике сигналов,
- гарантированные значения максимальной ошибки восстановления.
Эти методы реализуют компрессию данных с контролируемой (причем,
очень строго) погрешностью. Но отсюда вытекает и их основной недоста-
ток — нерегулярность выходного потока данных (переменный коэффициент
сжатия).
Применительно к изображениям можно отметить и еще один недостаток: в
методах адаптивных выборок полностью игнорируется двумерный характер
функции яркости, вся обработка ведется в рамках одномерного видеосигнала.
В то же время, несомненно, что учет «двумерности» данных мог бы повысить
эффект сжатия за счет использования статистических связей отсчетов функ-
ции яркости не только в строке, но и между строк.
6.6.2. Метод выделения областей и кодирования контуров
Известно несколько вариантов обобщения алгоритмов адаптивных выбо-
рок на двумерный случай. Одним из таких вариантов является метод выделе-
ния областей и кодирования контуров [5, 21, 22].
В общих чертах метод заключается в разделении (сегментации) всего изоб-
ражения на однородные области так, чтобы внутри каждой области отсчеты
поля с необходимой точностью описывались некоторой простой аппрокси-
мирующей функцией.
Кодированные данные здесь будут состоять из параметров аппроксимиру-
ющей функции для каждой области (то есть, если сохранять терминологию
«существенных» значений поля) и описания геометрических характеристик
(границ) областей («датирующей» информации). В принципе ту же операцию
над сигналом осуществляли и методы адаптивных выборок, только для них
изображение разворачивалось в одномерную последовательность отсчетов и,
как следствие, области получались одномерными.
Рассмотрим алгоритм построения (выделения областей), который является
обобщением на двумерный случай алгоритма ИНП (приведенные ниже фор-
мулы по своему смыслу являются обобщением на двумерный случай соотно-
шений (6.54)-(6.56)).
440
ГЛАВА 6
Пусть прямоугольная матрица отсчетов обрабатывается в порядке пост-
рочной развертки, то есть слева направо в строке и сверху вниз по строкам.
Пусть f(n{,n2) — некоторый отсчет, не принадлежащий первой строке и
первому столбцу матрицы («] ^1,и2 *1).
Обозначим через А и В области, к которым принадлежат уже пройден-
ные отсчеты, соседние с f(nifn2)\ f(n{— 1,и2) и y(nj,n2—1) соответствен-
но (рис. 6.24а).
Для каждого отсчета f(n},n2) нужно решить, отнести ли его к области А,
к области В, или же он не принадлежит ни А , ни В, а открывает собой свою
(новую) область. В соответствии с принципом работы ИНП, отсчет /(п},п2)
можно отнести к области А, если разность между максимальным и мини-
мальным значением яркости в этой области (включая и новый отсчет) не
будет превышать удвоенной допустимой погрешности восстановления, то есть
будет выполняться неравенство
max /(п[л2)- min f(n\tn2) < 2е0 max.
(п{ ,п2 )€ ди( л, ,л2) (nJ ,п2 )6 ди( л, ,п2)
Аналогично отсчет /(hi,«2) можно отнести к области В, если
max f(n{,n2)~ ; min /(n;,n'2)<2E0max.
(л{ ,п2 )GBU( л, ,л2) (nJ ,n2)6BU{n1 ,л2 )
Если оба неравенства нарушены, то f(n},n2) представляет собой новую
область, он отделяется от предыдущих отсчетов двумя элементами границы
(рис. 6.246).
Если выполняется только первое или только второе неравенство, то отсчет
присоединяется соответственно к А или В (при этом формируется верти-
кальный или горизонтальный элемент границы, см. рис. 6.24в и 6.24г).
Сложнее обстоит дело, если оба неравенства выполняются. Такая ситуация
возникает, например, когда предыдущие отсчеты /(и] -1,и2) и f(n^n2~^)
принадлежат одной и той же области (то есть А и В совпадают). В подобных
случаях нужно проанализировать, нельзя ли объединить А, В и отсчет
f(n}rn2) в одну область, то есть проверить выполнение неравенства
t max f(n[,n2)- min f(n\tn2) < 2e0
(nJ ,n2 )G4UBU(n, ,n2) (nJ,n2 )€ДиВи(П] ,n2)
Если оно выполняется, то происходит указанное объединение, при этом
между /(Hj,H2) и соседями элементов не появляется граница (см. рис. 6.246).
Если же неравенство нарушено, то отсчет как и прежде, присое-
диняется к А или к В, исходя из каких-либо дополнительных соображений.
Отметим очевидные особенности обработки отсчетов первой строки и пер-
вого (левого) столбца. Для первой строки не определена область А, а для
6.6. Метод адаптивных выборок
441
Рис. 6.24. К описанию алгоритма выделения областей на изображении
первого столбца — область В, поэтому проверки соответствующих неравенств
не производятся. Самый первый отсчет (в верхнем левом углу матрицы) все-
гда принимается за новую (первую) область.
Набор «существенных» значений (средних между максимумами и миниму-
мами яркости в областях) составляет первую часть кодированных данных.
Кроме того, в них должны содержаться сведения о форме и положении выде-
ленных областей (аналог — датирующая информация в методе адаптивных
выборок). Эти сведения удобнее всего давать через описание границ областей
(«контуров»).
В [5, 22] предложен способ такого описания, основанный на следующей
несложной статистической модели границ областей. Если представить отсче-
ты поля яркости в виде квадратных ячеек, то контурные линии (границы),
проходящие между отсчетами, составляются из горизонтальных и вертикаль-
ных элементов единичной длины (см. рис. 6.24 и далее рис. 6.25). Конфигура-
ция границы в каждой точке сопряжения контурных элементов определяется
наличием (или отсутствием) каждого из четырех стыкующихся контурных
элементов. Обозначим их через бинарные величины а1, а2, а3, а4.
442
ГЛАВА 6
Примем, что dj =
О —нет элемента
, 1
1 —есть элемент
< J<4.
В рамках принимаемой модели контуров считается, что их статистические
свойства, во-первых, не зависят от положения на плоскости изображения и,
во-вторых, полностью определяются четырехмерным распределением вероят-
ностей Р{ах,а2,а3,а^.
В соответствии с такой моделью контуры очень эффективно кодиру-
ются при помощи сочетания дифференциального метода (предсказания)
и КДС. В процессе строчной развертки для каждого отсчета изображения
по уже известным а{ , а2 предсказывается пара значений «3, а4. Если
Таблица 6.10. Булевы функции для
предсказателя контурных элементов
«1 а2 «3 «4
0 0 0 0
0 1 1 0
1 0 0 1
1 1 0 0
предсказание дало ошибку, то пара ис-
тинных значений а3, а4 считается «су-
щественной» и фиксируется вместе со
своей датирующей информацией — рас-
стоянием (по строке) до предыдущей
существенной пары.
Сами процедуры предсказания здесь
оказываются достаточно простыми. На-
пример, если известно, что границы в ос-
новном вертикальны и горизонтальны и
имеют мало разветвлений, то можно предсказывать контурные элементы так,
как показано на рис. 6.25.
Рис. 6.25. Вариант предсказателя контурных элементов
6.7. Другие методы компрессии изображений
443
Соответствующие булевы функции могут быть представлены в виде таб-
лицы (см. табл. 6.10) или записаны аналитически:
а3 — Л «2> «4 = а{ Л а2 ,
где — предсказываемые значения аь /—3,4, — отрицание п(, / = 1,2.
Можно использовать и адаптивную процедуру предсказания, которая стро-
ится по результатам оценки распределения Р(а1,а2,а3,д4) по самому изобра-
жению. Такая процедура обеспечит больший эффект сжатия, но обработка
изображения станет двухпроходной: первый переход — выделение областей и
сбор статистики для построения предсказателя, второй проход — собственно
кодирование контуров. Остановимся на деталях. Если известна статистика
контурных элементов, то можно найти апостериорное (условное) распределе-
ние вероятностей р(а1,а2/а3,а4).
Выбирать предсказываемые значения следует так, чтобы они обеспечили
максимум этой вероятности (соответственно, минимум вероятности ошибки
предсказания):
Р(л3,«4/«|,я2) — тахР(«3,а4/а|,а2) •
Умножив обе части этого выражения на безусловное двумерное распре-
деление Р[а1,а2), получим условие выбора предсказателя в более удобной
форме:
P{a3,a4la}ia2)= тахР(п1,п2,п3,п4).
К сожалению, метод выделения областей и кодирования контуров по-
чти не поддается теоретическому анализу и, соответственно, формальной
оптимизации; его можно исследовать только моделированием. Достоин-
ства метода:
- очень высокая эффективность,
- использование показателя максимальной ошибки,
- работа в условиях априорной неопределенности свойств изображения.
Недостаток — сложность (как самих процедур кодирования-декодирова-
ния, так и получаемой структуры кодированных данных).
6.7. Другие методы компрессии изображений
Опишем некоторые методы компрессии, которые либо не вошли ни в один
из рассмотренных классов, либо принадлежат сразу нескольким классам. Ко-
нечно, они представляют собой необозримое «все остальное», но среди них
имеются отдельные «яркие» методы, которые авторы считают необходимым
упомянуть.
444
ГЛАВА 6
6.7.1. Гибридные методы кодирования
Некоторые известные процедуры компрессии данных, используемые на
практике, представляют собой комбинации методов, отнесенных нами к раз-
ным классам. В сущности, в неявной форме мы уже вводили в рассмотрение
подобные «гибридные» методы, когда, например, говорили о сочетании диф-
ференциального кодирования с кодированием по Хаффмену или кодирова-
ние с преобразованием с КДС.
Теперь рассмотрим два других примера.
Методы преобразования и предсказания. Кодирование с преобразовани-
ем и дифференциальное кодирование основаны по сути на одном и том же
принципе: в них сначала производится разрушение корреляционных свя-
зей между элементами сообщения (декорреляция), а затем независимое
квантование (обработка) декоррелированных элементов. Эти методы раз-
личаются лишь в способах декорреляции. Каждый из них имеет опреде-
ленные преимущества и недостатки. Кодирование с преобразователем бо-
лее эффективно, но и более сложно, дифференциальные методы просты,
но менее эффективны.
Применительно к двумерным изображениям А. Хабиби в 1974 г. предложил
гибридный метод кодирования с использованием преобразования и предсказа-
ния, который по эффективности близок к методам кодирования с двумерным
преобразованием, но значительно проще в реализации [30]. Этот метод очень
похож на рассмотренный ранее однопроходный спектрально-рекуррентный ме-
тод восстановления изображений (см. п.3.4.8). Общая схема обработки данных
здесь такова. Пусть изображение /(«|,«2) представляет собой вертикальную
«ленту» прямоугольной сетки отсчетов, по Nотсчетов в строке (0< п < N — 1).
Для каждой строки выполняется одномерное преобразование (вычисляется «по-
луспектр»):
N-1
/*(«1.0= 12 f(nl,n2)A(l,n2), 0</</V-l.
н2=0
Преобразование декоррелирует сигнал, то есть полуспектр /*(п1,и2)
можно рассматривать как совокупность независимых случайных последо-
вательностей (и, — их аргумент, I — номер последовательности). Каждая
из этих последовательностей обрабатывается своим дифференциальным
кодером.
При восстановлении изображения обработка осуществляется в обратном
порядке: сначала по разностным сигналам «полуспектральных» компонентов
восстанавливаются сами компоненты (вернее их оценки — , а затем с
помощью обратного преобразования по строкам получаются оценки отсчетов
поля яркости,
_ /V-i _
/(«р«2)= 12/*(«i,wz,n2).
п2 =0
6.7. Другие методы компрессии изображений
445
Рис. 6.26. Схема устройства, реализующего метод компрессии изображений с преобразованием
и предсказанием
Структурная схема устройства компрессии/восстановления изображений при-
ведена на рис. 6.26. Изображенный в нем кодер канала служит для объедине-
ния данных от различных дифференциальных кодирующих блоков (декодер
играет обратную роль).
Если известны корреляционные свойства изображения и выбран базис
преобразования, то всегда можно вычислить АКФ «полуспектральных» ком-
понентов, рассматривая их как последовательности с аргументом и(. Следо-
вательно, можно обычным путем рассчитать параметры дифференциальных
кодеров (следует подчеркнуть, что по каждому столбцу параметры кодера бу-
дут индивидуальны).
Методы двумерного предсказания и адаптивных выборок. Эти методы соче-
тают в себе дифференциальное кодирование и методы адаптивных выборок.
Здесь снова делается попытка объединить положительные качества методов,
принадлежащих двум классам. Алгоритмы адаптивных выборок восстанавли-
вают в сигнал с качеством, оцениваемым по критерию максимальной ошибки
(и это достоинство), но игнорируют «двумерность» данных (недостаток). На-
оборот, дифференциальное кодирование позволяет на этапе предсказания
учесть двумерный характер изображений, но относится к методам с неконт-
ролируемой погрешностью. Рассматриваемые ниже гибридные методы и учи-
тывают двумерный характер изображений, и используют критерий максималь-
ной ошибки.
Принцип их работы в общих чертах заключается в следующем [4, 5].
Пусть отсчеты изображения f (nt,n2) обрабатываются в порядке построч-
ной развертки (по возрастанию nt и п2). Для каждого отсчета формируется
его предсказываемое значение /(щ,п2) по некоторой совокупности оценок
отсчетов, обработанных ранее. Как и в методах дифференциального кодиро-
вания вычисляется разностный сигнал
Е(П1,И2) = /(и1,П2)-7(«Р«2)’
446
ГЛАВА 6
но затем этот разностный сигнал подвергается обработке каким-либо алго-
ритмом адаптивных выборок (а не квантованию, как в ДИКМ).
При восстановлении отсчетов поля по сжатым данным, сначала восстанав-
ливаются оценки отсчетов разностного сигнала, которые отличаются от дей-
ствительных значений на величины, не превышающие допустимую макси-
мальную ошибку е0 (эта ошибка является параметром процедуры адап-
тивных выборок):
Ё(«1, п2 ) = В(П],п2) + («! ,п2 ), |еу («!, п2 )| < е01пах.
Далее эти оценки суммируются с результатами предсказания на «прием-
ной» стороне, при этом получаются оценки отсчетов изображения с той же
точностью:
/(Л1,/72) = Ё(Л1,Л2) + 7(Л1,«2) = /(Л1,Л2)+Е/ (Л1,«2),
Учет двумерного характера функции яркости в данном методе целесооб-
разно осуществлять при помощи нелинейных алгоритмов двумерного пред-
сказания, инвариантных к контурам (см. п.6.4.3). При использовании таких
предсказателей разностный сигнал (ошибка предсказания) не будет иметь
выбросы при пересечении в ходе развертки контурных линий (границ облас-
тей), то есть будет достаточно «гладкой», и поэтому алгоритм адаптивных
выборок будет работать эффективно. Из алгоритмов адаптивных выборок,
как показали исследования, здесь эффективнее всего работают простые ПНП
и ИНП.
Недостаток метода — низкая помехоустойчивость (как и для всех методов,
основанных на попиксельном предсказании в ходе развертки).
6.7.2. Стандарт компрессии изображений JPEG
В течение нескольких лет совместный комитет Международной Организа-
ции по Стандартизации (ISO) и группы экспертов по фотографии JPEG* раз-
работали международный стандарт JPEG компрессии черно-белых и цветных
полутоновых изображений [27, 28, 32]. Основной целью стандарта является
поддержка широкого многообразия программных приложений, которые об-
рабатывают полутоновые изображения и обмениваются ими. Каждое такое
приложение предъявляет различные требования к методу компрессии, поэто-
му стандарт JPEG включает в себя два базисных метода, каждый из которых
рассчитан на свои режимы работы. Метод, основанный на дискретном коси-
нусном преобразовании (ДКП), определен для компрессии изображений с
внесением допустимых искажений, и метод кодирования с предсказанием —
для компрессии без потерь.
1 Joint Photographic Experts Group.
6.7. Другие методы компрессии изображений
447
Ниже кратко описывается первый из указанных методов, который на прак-
тике применяется наиболее часто. Основными требованиями, которые были
приняты во внимание при его разработке, являются:
1) достижение наилучших, по мнению разработчиков, соотношений ко-
эффициента сжатия и точности восстановления изображения для широкого
диапазона уровней качества изображений, особенно для ситуаций, когда ви-
зуальное соответствие оригиналу характеризуется экспертами в пределах от
«очень хорошо» до «превосходно»;
2) параметризуемость кодера, то есть наличие управляющего параметра,
позволяющего пользователю выбрать желаемый компромисс между степенью
сжатия и качеством восстановленного изображения;
3) применимость к любому виду цифрового полутонового изображения,
то есть отсутствие ограничений на размерность, количество цветовых про-
странств, формат представления отсчетов и т.д., а также ограничений на со-
держимое сложность, цветовой диапазон или статистические характеристики
изображений;
4) возможность как программной реализации с приемлемой эффективно-
стью для широкого диапазона универсальных процессоров, так и аппаратной
реализации для приложений, требующих высокую эффективность.
Метод кодирования на основе ДКП, реализуемый в рамках стандарта JPEG,
является по существу наиболее полным и развитым методом компрессии,
достаточным для большинства приложений. На сегодня он обеспечил мини-
мально необходимую единую информационную инфраструктуру для представ-
ления разнообразных изображений и используется различными группами
пользователей, независимо от применяемого ими аппаратного и программно-
го обеспечения.
На рис. 6.27 и рис. 6.28 показаны ключевые шаги обработки, которые яв-
ляются основой метода кодирования с ДКП:
- дискретное косинусное преобразование блоков изображения размерами
8x8 отсчетов;
Исходное
изображение
Сжатые данные
изображения
Рис. 6.27. Схема кодера на основе ДКП
448
ГЛАВА 6
Сжатые данные
изображения
Восстановленное
изображение
Рис. 6.28. Схема декодера на основе ДКП
- квантование коэффициентов ДКП (трансформант) с использованием
таблиц, значения которых оптимизированы в соответствии с особенностями
визуального восприятия человека;
- статистическое кодирование квантованных трансформант.
На рисунках приведен частный случай компрессии однокомпонентного
(черно-белого) полутонового изображения. Процесс обработки можно рас-
сматривать как компрессию потока (последовательности) блоков такого изоб-
ражения. Компрессия цветного (многокомпонентного) изображения в целом
соответствует поочередной компрессии нескольких полутоновых изображе-
ний — цветовых компонентов.
На входе блока двумерного ДКП отсчеты исходного изображения сгруппи-
рованы в блоки размером 8x8.
Чтобы сохранить свободу новаций и настроек внутри реализаций ДКП, в
стандарте JPEG не фиксируется точно какой то один уникальный алгоритм
преобразования. Вместо этого определен тест на совместимость по точности,
которому должны удовлетворять все кодеры и декодеры, использующие ДКП.
Это должно отсечь грубые аппроксимации базисных функций преобразова-
ния, которые ухудшили бы качество восстановления сжатого изображения.
После прямого преобразования получаем 64 коэффициента двумерного
дискретного спектра входного сигнала. В декодере обратное ДКП по 64 коэф-
фициентам (которые при кодировании квантовались) восстанавливает фраг-
мент изображения. Основная информация о яркости блока в целом содер-
жится в коэффициенте с координатами (0,0), который называется DC-коэф-
фициентом. Оставшиеся 63 коэффициента обозначаются префиксом АС.
Так как обычно значения соседних отсчетов изображения меняются незна-
чительно, операция ДКП концентрирует основную информацию о сигнале в
трансформантах низких пространственных частот. Для блока 8x8 типичного
полутонового изображения большинство пространственных частот имеет нуле-
вые или почти нулевые коэффициенты и фактически не кодируются.
Следующий шаг — квантование всех 64 коэффициентов преобразования.
Трансформанты квантуются, чтобы уменьшить их величину и увеличить
6.7. Другие методы компрессии изображений
449
количество нулевых значений, то есть отбросить информацию, которая не
существенна для восстановления изображения с необходимым визуальным
качеством. Квантование — главный источник погрешностей в кодерах с ДКП.
Используется равномерное квантование, причем каждая трансформанта
матрицы 8x8 имеет свой шаг квантования в соответствии с таблицей. Таблица
шагов квантования выступает как параметр, определяющий желаемое соот-
ношение коэффициента сжатия и точности восстановления изображения.
В стандарте JPEG соответствующие таблицы квантования, оптимизирован-
ные для различных случаев по критерию наилучшего визуального восприя-
тия, приводятся в качестве информации, а не как требование.
После квантования DC-коэффициент обрабатывается отдельно от оставшихся
63 АС-коэффициентов. Операцию статистического кодирования для обоих ти-
пов коэффициентов удобно рассматривать в виде двухэтапной процедуры. На
первом шаге квантованные коэффициенты преобразуются в промежуточную
последовательность символов. На втором шаге данным символам назначаются
коды переменной длины в соответствии с алгоритмом Хаффмена.
Для кодирования DC-коэффициентов используется дифференциальный
метод кодирования, то есть на вход статкодера поступает разность квантован-
ного DC-коэффициента текущего блока и предыдущего.
Квантованные АС-коэффициенты переупорядочиваются в виде зигзагооб-
разной последовательности так, чтобы низкочастотные трансформанты (от-
личие от нуля которых наиболее вероятно) были сгруппированы перед высо-
кочастотными. Далее последовательность АС-коэффициентов преобразуется
с помощью алгоритма кодирования длин серий. То есть каждый отличный от
нуля АС-коэффициент зигзагообразной последовательности представляется в
виде пары символов, первый из которых определяет количество последова-
тельных нулевых трансформант перед ненулевой, а второй символ является
значением ненулевой трансформанты.
Итоговый шаг обработки — статистическое кодирование. Этот шаг дает
дополнительное сжатие без потери точности, кодируя отдельно разности кван-
тованных DC-коэффициентов и преобразованные АС-коэффициенты. Стан-
дарт JPEG определяет два метода статистического кодирования: кодирование
по Хаффмену и алгоритм арифметического кодирования. Метод арифмети-
ческого кодирования точно определяется стандартом JPEG. Для многих изоб-
ражений он обеспечивает лучшее сжатие (на 5—10%), но более высокая слож-
ность реализации этого алгоритма и наличие на него патента привели к тому,
что в Базовом алгоритме и большинстве реализаций стандарта используется
статкодер Хаффмена.
Дополнительным параметром при этом является таблица кодов переменной
длины (кодов Хаффмена). При компрессии используются предопределенные
таблицы кодов переменной длины, одна — для DC-разностей, и другая — для
промежуточной АС-последовательности. В некоторых случаях могут использо-
ваться таблицы, вычисленные специально для данного изображения с помо-
щью предварительного прохода, накапливающего статистику. Важно, чтобы
кодер и декодер использовали одинаковые соответствующие таблицы кодов
переменной длины.
15 - 9044
450
ГЛАВА 6
6.7.3. Метод иерархической сеточной интерполяции
Описанный в [7, 29] метод иерархической сеточной интерполяции основан
на многоуровневом представлении цифрового изображения. Его суть состоит в
следующем. В памяти ЭВМ хранится двумерный массив отсчетов изображе-
ния, прореженного в 2Л раз по каждой координате, и набор поправок, допол-
няющих его до массивов, имеющих коэффициенты прореживания 2R~l, 2R~2
и так далее, вплоть до полного изображения. На каждом иерархическом уровне
прореженный двумерный массив отсчетов используется для восстановления
(интерполяции) пропущенных отсчетов следующего, более детального уровня.
Формируемые при этом разности между исходными отсчетами и их интерпо-
лированными значениями квантуются так, чтобы гарантировалось их восста-
новление с заданной точностью. Для дополнительного уменьшения объема дан-
ных квантованные разности подвергаются статистическому кодированию.
Как показали теоретические и экспериментальные исследования, важней-
шими свойствами метода и конкретных алгоритмов иерархической сеточной
интерполяции, обусловившими их преимущества перед другими известными
алгоритмами компрессии изображений, являются:
- управление величиной ошибки восстановления отсчетов изображения
после компрессии;
- высокая эффективность, оцениваемая к координатах «коэффициент сжа-
тия - погрешность восстановления» изображения;
- малая вычислительная сложность;
- возможность мультиразрешения, то есть быстрого получения уменьшен-
ных (прореженных) копий входного изображения без его полного восстанов-
ления.
Дадим более детальное описание метода. В нем используется представление
исходного изображения F в виде объединения иерархических уровней Fr:
R
F=[jFr, Fr =
r=0
{fr(nl,n2)}X{fr+l («1»«2)}>
если
если
r = R,
0<r<K,
(6.57)
где fr(n},n2) — массив отсчетов изображения, взятых с шагом 2Г по каждой
координате. Представление (6.57) дает возможность обрабатывать уровни пос-
ледовательно, начиная со старшего, причем закодированные (и затем декоди-
рованные) отсчеты каждого более старшего уровня будут использоваться для
интерполяции отсчетов младшего (более детального) уровня.
Рассмотрим этап компрессии изображения. Самый старший иерархический
уровень Fr (максимально прореженное изображение) сохраняется в памяти
без обработки. На каждом из следующих уровней (Fr, 0<r<R) обработка
ведется следующим образом.
1. Производится интерполяция отсчетов уровня Fr+1 для того, чтобы по-
лучить более детальное представление изображения, то есть вычисляются ап-
проксимирующие («предсказанные») значения отсчетов fr(nl,n2). При этом,
6.7. Другие методы компрессии изображений
451
если г = то используются истинные значения отсчетов, а если нет, то
значения /г+1 (яр^г)» восстановленные после компрессии (см. ниже). Спо-
соб интерполяции не является специфичным для метода иерархической се-
точной интерполяции: в принципе, здесь может быть использована любая
известная интерполяция, отвечающая очевидным требованиям высокой точ-
ности и малой вычислительной сложности.
2. Вычисляется массив разностей истинных и предсказанных значений
отсчетов («постинтерполяционных остатков»):
еДирИ?) = ~ Л(л1’п2)- (6.58)
3. Выполняется квантование постинтерполяционных остатков (6.58). При
этом каждая разность ег заменяется на одно из ее квантованных значений
Ёг. Расположение квантованных значений в диапазоне возможного измене-
ния разностей, в общем, может быть произвольным при условии, что обеспе-
чивается требуемая (заданная) точность восстановления истинных значений
разностей.
4. По квантованным значениям постинтерполяционных остатков осуще-
ствляется восстановление иерархического уровня Fr:
7r("l’n2) = Er(npw2) + Л(П1’Л2)' (659)
Восстановленные отсчеты (6.59) нужны для использования в следующем
цикле обработки изображения, а именно, при получении аппроксимирующих
значений (интерполяции) отсчетов уровня Fr_{. Поэтому на этапе компрес-
сии данная операция выполняется для всех уровней кроме самого младшего
(для которого г = 0).
5. Осуществляется статистическое кодирование квантованных постинтер-
поляционных остатков. Поскольку распределение их вероятностей, как пра-
вило, является существенно неравномерным, в результате кодирования дос-
тигается значительный эффект сокращения объема данных, который и явля-
ется целью выполняемой обработки изображения. Для статистического
кодирования здесь могут быть использованы любые известные алгоритмы:
Хаффмена, КДС, а также их комбинации (см. п.6.2).
Обработанное (кодированное) изображение представляет собой набор дан-
ных, содержащий:
- массив отсчетов изображения, соответствующий старшему иерархичес-
кому уровню FR ;
- статистические коды квантованных постинтерполяционных остатков на
иерархических уровнях Fr, 0 < г < R ;
- необходимую вспомогательную информацию (заголовок, кодовые таб-
лицы, ключи режимов и т.п.).
На этапе восстановления изображения сначала берется максимально про-
реженное изображение (на иерархическом уровне FR), а затем последова-
тельно синтезируются изображения со все более высоким разрешением
15*
452
ГЛАВА 6
(соответствующие уровням Fr_i,Fr_2, —» Fo). При этом на каждом из этих
уровней обработка ведется следующим образом.
1. Как и на этапе сжатия, производится интерполяция отсчетов уровня
Fr+i, то есть вычисляются предсказанные значения отсчетов fr (n,,n2). Если
г = /? — !, то интерполяция ведется по истинным значениям отсчетов, а если
нет, то по восстановленным значениям — /г+1(и|,л2).
2. Осуществляется декодирование (восстановление из статистических ко-
дов) квантованных постинтерполяционных остатков ёг.
3. Осуществляется восстановление изображения на иерархическом уровне Fr:
Л(П|,П2) = + Л("1-«2)-
Дадим описание одного из возможных способов интерполяции отсчетов
уровня Fr+1 (то есть вычисления «предсказанных» значений отсчетов на уровне
Fr, г <R). Для этого рассмотрим ячейку из 3x3 отсчетов /г(п{,п2), показан-
ную на рис. 6.29. Она содержит отсчеты трех типов:
1) угловые отсчеты ячейки (на рисунке показаны темными). Они принад-
лежат уровню Fr+i и, следовательно, уже известны при интерполяции, то есть
являются опорными для предсказания остальных отсчетов ячейки;
2) отсчеты на краях (ребрах) ячейки, принадлежащие уровню Fr (показа-
ны косой штриховкой). При интерполяции должны быть сформированы их
предсказанные значения;
3) центральный отсчет ячейки (выделен сеткой). Он также принадлежит
уровню Fr и, следовательно, тоже требует предсказания.
Экспериментально установлено, что в большинстве практических случаев
хорошую точность дает следующий простой способ интерполяции изображе-
ния (так называемая схема «Прямой крест»). Сначала вычисляются аппрок-
симирующие значения отсчетов на краях ячейки как средние значения двух
ближайших угловых отсчетов. Затем центральный отсчет предсказывается как
среднее значение четырех отсчетов на ребрах. Последовательность указанных
вычислений иллюстрируется стрелками на рис. 6.29.
Следует заметить, что предложенная схема отличается от известного мето-
да билинейной интерполяции [19] тем, что перед вычислением центрального
отсчета имеется возможность скорректировать
(уточнить) значения отсчетов на ребрах, доба-
вив к ним значения соответствующих кванто-
ванных постинтерполяционных остатков.
Одной из важных отличительных особен-
ностей метода иерархической сеточной интер-
поляции является возможность гарантирован-
ной точности восстановления каждого отсче-
та изображения, оцениваемой по критерию
Рис. 6.29. Последовательность интерполяции изображения
6.7. Другие методы компрессии изображений
453
максимальной ошибки. Для реализации этой возможности можно использо-
вать следующую процедуру квантования постинтерполяционных остатков:
+ Б0 max
2^0 max + 1
(6.60)
где е0 — допустимая максимальная погрешность восстановления отсче-
тов, [..] — оператор выделения целой части вещественного числа. В формуле
(6.60) предполагается, что величины fr, fr и eOmax задаются целыми числа-
ми (причем е0 max — неотрицательное).
6.7.4. Экспериментальные исследования методов компрессии изображений
Как уже отмечалось выше, метод компрессии изображений JPEG является
в настоящее время наиболее распространенным среди множества известных
методов, широко применяется при хранении и передаче цифровых изображе-
ний, реализован практически во всех программных продуктах обработки и
анализа изображений. Тем не менее, как и любому из известных методов,
методу JPEG присущи определенные недостатки, препятствующие его при-
менению в областях, где предъявляются особо высокие требования по точно-
сти представления информации, скорости ее выдачи потребителю. В таких
областях более перспективным представляется применение разработанного
метода на основе иерархической сеточной интерполяции (ИСИ), обеспечива-
ющего не только требуемое качество, но и быстрый доступ к сжатым данным.
Именно для этих методов (ИСИ и JPEG), представляющих наибольший ин-
терес для многих практических приложений, проведен сравнительный ана-
лиз, результаты которого приводятся ниже.
В качестве тестовых выбраны изображения, показанные на рис. 6.30 и яв-
ляющиеся типичными представителями различных классов изображений.
Рис. 6.30. Исходные изображения: а — «Портрет», б — «Аэрофотосъемка»
454
ГЛАВА 6
Используя широко распространенную программу ADOBE PHOTOSHOP 4.0 и
разработанные программные средства, реализующие метод сжатия ИСИ, была
произведена оценка эффективности методов в координатах «степень сжатия —
точность восстановления». Путем варьирования параметра «качество» при
сжатии методом JPEG или максимальной ошибки восстановления при сжа-
тии методом ИСИ были получены сжатые изображения, и, соответственно,
восстановленные изображения. Для иллюстрации работы исследуемых мето-
дов на рис. 6.31—6.32 приведены погрешности восстановления изображений,
рассчитываемые как модули разностей исходных и декодированных изобра-
жений, для лучшей наглядности усиленные по яркости в 5 раз и представлен-
ные в виде негативов.
Для модулей разностей декодированных и исходных изображений постро-
ены гистограммы распределения яркостей (рис. 6.33), по критериям (2.4) и
(2.5) оценены максимальные ошибки етах восстановления и ошибки, соответ-
ствующие 95% и 99% квантилям соответствующих гистограмм (рис. 6.34), а
также рассчитаны среднеквадратичные отклонения (2.2) декодирован-
ных изображений от исходных (рис. 6.35).
Анализируя зависимости среднеквадратичных ошибок восстановления
легко видеть, что в приведенном примере метод ИСИ предпочтительнее
метода JPEG. Однако исследования, проведенные на значительном мно-
жестве различных изображений [7, 29], показали, что метод ИСИ выигры-
вает только при малых и средних коэффициентах сжатия (Х\ <10). Следу-
ет отметить, что среднеквадратичный критерий далеко не лучшим образом
отражает реальное качество восстановления изображения, поскольку дает
усредненное значение погрешностей и не учитывает локальные особенно-
сти поля яркости. Как отмечалось в п.2.1.3, в наиболее ответственных слу-
чаях при работе с уникальными видеоданными более корректным является
применение критерия максимальной ошибки. Результаты исследований
(рис. 6.34) продемонстрировали полное преимущество по этому критерию
алгоритма ИСИ при любых степенях сжатия. Оценка максимальной ошиб-
ки восстановления в ее вероятностно-зональной модификации (2.5) при
доверительных вероятностях 0,95 и 0,99 показала, что и по этим критериям
метод ИСИ более эффективен.
Приведенные гистограммы (рис. 6.33) наглядно демонстрируют принци-
пиальное отличие предлагаемого алгоритма ИСИ, гарантирующего заданную
максимальную ошибку, от алгоритмов с преобразованием, для которых впря-
мую не контролируются выходные показатели (степень сжатия и ошибка вос-
становления). Для разностных изображений (модулей разностей декодиро-
ванных и исходных изображений) для алгоритма ИСИ распределения ярко-
сти близки к равномерным, а для алгоритмов с преобразованием — подобны
экспоненциальным. Длинные «хвосты» распределений ошибок JPEG означа-
ют возможность сильных искажений и даже потерь на декодированном изоб-
жении мелких деталей размером до нескольких десятков отсчетов.
6.7. Другие методы компрессии изображений
455
Рис. 6.31. Погрешности восстановления изображений после компрессии методом JPEG: а —
«Портрет» (Кх ~ 5,5 ), б — «Аэрофотосъемка» ( Ks ~ 2,5 )
б
Рис. 6.32. Погрешности восстановления изображений после компрессии методом ИСИ: а —
«Портрет» ( КЛ. ~ 5,5 ), б — «Аэрофотосъемка» ( Кд. ~ 2,5)
Рис. 6.33. Гистограммы распределений ошибок для методов сжатия ИСИ, JPEG: а — «Портрет»
(Кх ~ 5,5), б — «Аэрофотосъемка» (Кх ~ 2,5)
456
ГЛАВА 6
а
Рис. 6.34. Зависимости максимальных ошибок от степени сжатия: а — «Портрет», б — «Аэрофо-
тосъемка»
Рис. 6.35. Зависимости среднеквадратичных ошибок от степени сжатия: а — «Портрет», б —
«Аэрофотосъемка»
Литература к главе 6
1. Ахмед Н.Д., Рао К.Р. Ортогональные преобразования при обработке цифро-
вых сигналов (М.: Связь, 1980)
2. Бабкин В.Ф., Крюков А.Б., Штарьков Ю.М., в кн.: Сжатие данных. Ап-
паратура для космических исследований (М.: Наука, 1972) С. 172
3. Блох Э.Л. Проблемы передачи информации 5 12 (1960)
4. Виттих В.А., Сергеев В.В. Известия вузов. Приборостроение 12 15 (1976)
5. Виттих В.А., Сергеев В.В., Сойфер В.А. Обработка изображений в авто-
матизированных системах научных исследований (М.: Наука, 1982)
6. Воздушно-космическая телеметрия / Под ред. К.Н. Трофимова (М.: Воен-
издат, 1968)
Литература к главе 6
457
7. Гашников М. В,, Глумов Н.И., Сергеев В.В. Известия Самарского научно-
го центра РАН 1 99 (1999)
8. Джайн А. К. Сжатие видеоинформации: Обзор. ТИИЭР3 71 (1981)
9. Евдокимов В.П., Покрас В.М. Методы обработки данных в научных кос-
мических экспериментах (М.: Наука, 1977)
10. Колесник В.Д., Полтырев Г.Ш. Курс теории информации (М.: Наука, 1982)
11. Коннор Д., Брей нард Р., Лимб Дж., в кн.: Обработка изображений при
помощи цифровых вычислительных машин (М.: Мир, 1973) С. 60
12. Кунт М., Икономонулос А., Кошер М. Методы кодирования изображений
второго поколения. ТИИЭР 4 59 (1985)
13. Мановцев А.П. Основы теории радиотелеметрии (М.: Энергия, 1973)
14. Методы передачи изображений. Сокращение избыточности / Прэтт У.К.,
Сакрисон Д.Д., Мусманн Х.Г.Д. и др. (М.: Радио и связь, 1983)
15. Мусман Х.Г., Пирш П., ГраллертХ.-Й. Достижения в области кодирова-
ния изображений. ТИИЭР 4 31 (1985)
16. НетравалиА., Лимб Дж. Кодирование изображений: Обзор. ТИИЭР 3 76
(1980)
17. Новик Д.А. Эффективное кодирование (М.-Л.: Энергия, 1965)
18. Ольховский Ю.Б., Новоселов О.Н., Мановцев А.П. Сжатие данных при
телеизмерениях (М.: Советское радио, 1971)
19. Прэтт У.К. Цифровая обработка изображений 1 (М.: Мир, 1982)
20. Прэтт У.К. Цифровая обработка изображений 2 (М.: Мир, 1982)
21. Сергеев В.В. Вопросы кибернетики Вып. 42. Кодирование и передача инфор-
мации в вычислительных сетях (11) 146 (М.: Научный совет по комплекс-
ной проблеме «Кибернетика» АН СССР, 1978)
22. Сергеев В.В., Сойфер В.А. Автоматика и вычислительная техника 3 76
(1978)
23. Сергеев В.В. Устройство формирования сигнала отсчета для дифференци-
ального кодера изображений / А. с. 906033 СССР, МКИ Н04п7/13. Бюлле-
тень изобретений 6 (1982)
24. СорокоЛ.М., СтрижТ.А. Спектральные преобразования на ЭВМ (Дубна:
ОИЯИ, 1972)
25. Уинтц П.А. Кодирование изображений посредством преобразований. Обра-
ботка изображений при помощи цифровых вычислительных машин (М.: Мир,
1973) С. 98
26. Штарьков Ю.М., Бабкин В.Ф., в кн.: Аппаратура для космических иссле-
дований. Кодирование, сжатие данных (М.: Наука, 1973) С. 3
27. Digital Compression and Coding of Continuous-tone Still Images, Part I,
Requirements and Guidelines. ISO/IEC JTCJ Draft International Standard
10918-1 (1991)
28. Digital Compression and Coding of Continuous-tone Still Images, Part 2, Compliance
Testing. ISO/IEC JTC1 Committee Draft 10918-2 (1991)
458 ГЛАВА 6
29. Glumov N., Gashnikov M., Sergeyev V. Proceedings of 15th International
Conference on Pattern Recognition — ICPR-2000 (Barselona, Spain) 3 232
(2000)
30. HabibiA., Robinson G.S. Computer, USA 5 22 (1974)
31. Mallat S.G. IEEE Trans, on Pattern Anal, and Mach. Intell. 11(7) 674 (1989)
32. Wallace G.K. The JPEG Still Picture Compression Standard. Communications of
the ACM (1991)
33. Max J. IRE Trans. Inform. Theory IT-6 7 (1960)
ГЛАВА 7
МЕТОД ПОЛЯ НАПРАВЛЕНИЙ
7.1. Изображения со структурной избыточностью
Известно, что многие изображения с информационной точки зрения явля-
ются избыточными. Особое место среди них занимают изображения со струк-
турной избыточностью, рассматриваемые в данной главе. Визуально такие
изображения воспринимаются как совокупность контурных линий, подчиня-
ющихся некоторому достаточно сложному порядку. Типичными представите-
лями изображений со структурной избыточностью являются интерферограм-
мы, дактилограммы и многие другие изображения естественного и искусст-
венного происхождения. Если рассмотреть пространственный спектр таких
изображений, он окажется расположенным в достаточно узкой полосе частот
в области некоторой характерной пространственной частоты, которую можно
назвать несущей частотой. Именно несущая частота воспринимается визуаль-
но как множество контурных линий и является основным фактором избыточ-
ности изображения. Процесс наложения информационной составляющей на
несущую, как правило, является весьма сложным и не всегда известен зара-
нее, что исключает применение простых методов выделения информации (де-
модуляции), применяемых в радиотехнике. Более того, при распознавании и
интерпретации изображений этого и не следует делать. Например, при интер-
претации интерферограмм широко применяется подход, основанный на вос-
становлении фазы предметной волны, по виду которой можно легко класси-
фицировать интерферометрируемый объект.
В данной главе последовательно развивается подход, основанный на вы-
числении поля направлений изображений со структурной избыточностью. До-
казывается, что именно поле направлений является наиболее удобным носи-
телем информации для решения задачи интерпретации и распознавании изоб-
ражений со структурной избыточностью. В качестве представителей данного
класса изображений будут рассматриваться изображения квазипериодических
структур. Примерами могут служить интерферограммы [1], дактилограммы
[2], кристаллограммы слезной жидкости [3], кристаллограммы кровяной плазмы
[4] и другие изображения (рис. 7.1).
460
ГЛАВА 7
Рис. 7.1. Различные квазипериодические структуры диагнос-
тических изображений: а — дактилограмма, б — кристалло-
грамма слезной жидкости, в — кристаллограмма плазмы кро-
ви, г — интерферограмма
Рис. 7.2. Описание поля
направлений
Квазипериодические структуры определяются наличием многоконтурной
упорядоченной текстуры с выраженной ориентацией. В каждой малой облас-
ти квазипериодической структуры функция яркости является периодической
вдоль определенного направления и визуально выражается в системе парал-
лельных полос. Основными параметрами таких изображений являются пре-
имущественное направление полос и их густота в каждой точке изображения.
Кроме того, на таких изображениях выделяются особые точки и линии (син-
гулярности), в которых нарушается периодическая структура. Для формиро-
вания геометрических характеристик такого класса изображений также пред-
лагается использовать подход, основанный на вычисле-
нии поля направлений. Как указывалось выше, поле
направлений является удобным носителем информации
для решения задачи интерпретации и распознавании
изображений с квазипериодической структурой.
Полем направлений будем называть поле углов пре-
имущественного направления полос в локальной окрес-
тности точки изображения. Угол направления полосы
,х2) в данной точке равен по определению углу ка-
сательной к линии уровня функции яркости (рис. 7.2).
Впервые идея метода поля направлений для интерпрета-
ции и анализа диагностических изображений была предложена в работе [5]
применительно к анализу дактилограмм. В работах [6, 7, 8] метод использо-
вался для диагностики кристаллограмм слезной жидкости [3]. Несколько позд-
нее в работе [9] были впервые представлены теоретические аспекты метода
поля направлений и определены некоторые подходы к построению алгорит-
7.2. Математическое описание поля направлений
461
мов его расчета (оптический метод и др.). В данной главе будет представлена
полная классификационная схема методов построения поля направлений,
проведено сравнительное исследование их точности и быстродействия и по-
казана интерпретация полей направлений в конкретных прикладных задачах
обработки изображений.
7.2. Математическое описание поля направлений
Согласно определению «Математической энциклопедии» [10] полем на-
правлений называется геометрическая интерпретация множества линейных
элементов, соответствующих обыкновенному дифференциальному уравнению,
которое в случае двух переменных имеет следующий вид:
^- = g(xi,x2). (7.1)
Линейным элементом называется набор чисел х,, х2, g (*i, х2), который мож-
но представить как совокупность точки (xj,x2)eGcR2 и соответствующего
ей направления с направляющими косинусами
1
Jl + g2(xj,x2)
a/1 + ^2(xi,x2)
которое отображается отрезком малой длины, проходящим через эту точку
параллельно вектору (l,g(x!,x2)).
В математике понятие поля направлений используется, в основном, для
качественной интерпретации поведения интегральных кривых и приближен-
ного графического решения дифференциальных уравнений. В монографии
К. Мардиа [11] приводится описание теории статистического анализа угло-
вых наблюдений. Однако эта теория не применима для анализа квазиперио-
дических структур, т.к. основана на традиционной векторной арифметике. В
подходе Мардиа к определению поля направлений важным является знак на-
правления, т.е. углы а и а+ 180° считаются различными. При обработке
изображений не имеет смысла понятие знака направлений линии и поэтому
данная теория не применима для операций усреднения, фильтрации, оценки
и др. В работе [9] понятие поля направлений адаптировано для использова-
ния в анализе изображений.
Рассмотрим произвольную функцию яркости изображения /(хих2), ко-
торую будем считать гладкой, т.е. имеющей непрерывные частные производ-
ные первого порядка. Рассмотрим множество кривых на плоскости
соответствующих линиям уровня функции яркости изображения:
/(х|,х2) = /„.
(7.2)
462
ГЛАВА 7
Легко видеть (рис. 7.2), что множество направлений касательных к линиям
(7.2) в соответствии с определением (7.1) образует поле направлений при
( , df(xl,x2)/dxl
df(xitx2)/dx2
Таким образом, классическое определение поля направлений приводит к
функции которая имеет физический смысл угла наклона касатель-
ной к линии уровня функции яркости изображения и задается следующим
уравнением:
tgv(xHx2
9/(Х|,Х2)/ЙХ1
^f(xj,x2)/9x2
О < ,х2) < л.
(7.3)
Очевидной является связь поля направлений с градиентом функции ярко-
сти: угол ,х2) задает направление, перпендикулярное вектору градиента
(df(xitx2)/dxlf df(xy,x2)/dx2). Характерным отличием поля направлений от
поля углов вектора градиента является область значений: [0,л) в отличие от
[0,2л), что сказывается на арифметических свойствах поля направлений, ко-
торые будут рассмотрены ниже.
7.3. Математическая модель изображений
со структурной избыточностью
Формула вычисления поля направлений (7.3) может быть непосредственно
применена к классу изображений со структурной избыточностью, функция
яркости которых должна обладать достаточной гладкостью для возможности
Рис. 7.3. Альтернативное опи-
сание поля направлений
ее дифференцирования. Таким классом изображе-
ний являются, в частности, интерферограммы, для
которых интуитивное понятие поля направлений
связывается с направлением интерференционных
полос и совпадает с определением (7.3). В произ-
вольной локальной области достаточно малых раз-
меров функция яркости таких изображений (рис. 7.3)
может быть описана гармонической функцией
/(X],X2) = AcOsjcD^j + W2%2 +<Po]+^> (7-4)
где <£>j =2tt/L|, со2 = 2ti/L2 — локальные простран-
ственные частоты, а ф0 — локальная начальная фаза.
Можно определить направление и пространственную частоту «интерферен-
ционных» полос в этой локальной области:
7.3. Математическая модель изображений со структурной избыточностью
463
tg V = — (Oj /со2,0 < V < Л,
/ 7 2*
(0 = ^(0] + С02 .
Рассматривая совокупность всех точек изображения, получаем альтерна-
тивное описание поля направлений \j/(x],x2) в виде уравнения
tgy(xj,x2
о>1 (^1,^2)
<02(хр*2)’
(7-5)
а также поле пространственных частот,
со(х1,х2) = ^со2(х1,л2) + (о2(л1,х2) ,
(7.6)
которое описывает плотность или густоту полос в малой окрестности задан-
ной точки (х,у) на изображении. Соотношение (7.5) задает альтернативный
к формуле (7.3) способ вычисления поля направлений для «гладких» изобра-
жений, содержащих квазипериодические структуры и удовлетворяющих ло-
кальной модели (7.4).
Модель «гладкого» изображения (7.4) может быть обобщена на случай про-
извольного изображения с квазипериодической структурой, в том числе на
изображения, содержащие перепады функции яркости (контуры) и на бинар-
ные (двухградационные) изображения. Так, например, изображение отпечат-
ка пальца, кристаллограммы слезной жидкости, кристаллограммы крови не
описывается гладкой функцией яркости, и к нему не может быть применено
классическое определение поля направлений (7.3). Однако такие изображе-
ния содержит локальные периодические структуры и могут быть описаны
следующей локальной моделью:
/(х!,х2) = Ae[W]X] +(02х2+<Ро] + Я’
(7-7)
где <?[-] ~ произвольная периодическая функция с периодом (для опреде-
ленности) 2л. В частности, контрастное изображение отпечатка пальца
может быть описано локальной моделью (7.7) с прямоугольной функцией
e[z] = signjcos(z)].
Таким образом, устранение структурной избыточности для рассматривае-
мого класса изображений приводит к описанию таких изображений парой
полей: полем направлений у(х1,х2) и полем пространственных частот
to(xi,x2). Построение поля пространственных частот описано в работе [12].
На рис. 7.4 приведен пример поля направлений v(xi,x2) и поля простран-
ственных частот (d(x],x2) для тестового изображения интерферограммы.
Поле направлений изображено градациями серого, причем нулевым значе-
ниям соответствует черный цвет, а значению л — белый цвет. Поле про-
странственных частот также представлено градациями серого в диапазоне от
минимального до максимального значения.
464
ГЛАВА 7
Рис. 7.4. Квазипериодическая структура интерферограммы и ее характеристики: а — исходная
функция яркости изображения, б — поле направлений, в — поле пространственной частоты
Для количественной оценки степени сокращения структурной избыточно-
сти при описании изображения полем направлений и полем пространствен-
ных частот были использованы два метода. Первый метод основан на измере-
нии эффективной ширины пространственного спектра. Для приведенного
примера тестового изображения интерферограммы сокращение эффективной
(на уровне 90%) ширины спектра составило 0,25 для поля направлений и для
поля пространственных частот. Второй метод основан на измерении сокра-
щения объема данных при кодировании без потери качества (архиватор pkzip).
Для приведенного примера объемы сжатых изображений поля направлений и
поля пространственных частот составили соответственно 0,19 и 0,24 от объе-
ма сжатого исходного изображения.
Таким образом, представление изображения, содержащего квазипериоди-
ческие структуры, в виде двух компонентов — поля направлений и поля про-
странственных частот — должно упростить обработку и анализ, а также повы-
сить качество распознавания. Это объясняется малой информационной на-
сыщенностью компонентных изображений и возможностью независимой их
обработки. На рис. 7.5 показано несколько видов простейших конфигураций
полей направлений (шаблонов).
Традиционные методы обработки изображений (линейная обработка ок-
ном, нелинейная фильтрация, и т.п.) не могут быть непосредственно приме-
нены к полям направлений. Это связано с особенностями арифметики на-
правлений, которая является периодической по значениям, причем период
равен л. В [9] показано, как можно решить некоторые проблемы арифметики
направлений, позволяющие применять традиционные методы обработки для
полей направлений. Для применения цифровых методов анализа полей на-
правлений для формирования геометрии пространства такого типа изображе-
ний в прикладных задачах необходимо модифицировать определение поля
направлений.
Для примера рассмотрим простейшую линейную операцию вычисления
среднего арифметического двух значений поля направлений: у, и \g2. Здра-
вый смысл подсказывает, что при Vi=0 и Vi—л/2 результатом должно
73. Математическая модель изображений со структурной избыточностью
465
f(x},x2) = AcosA(x2 -х2)
б
. х2
tgV = —-
д
f(xl,x2) = A cos£(X|2 + х2)
г
tg^ = - —
*2
3
f(r, (р) = A cos kip
в
* *1
tgV = —L
*2
е
Рис. 7.5. Стандартные конфигура-
ции полей направлений (а, б, в, г)
и соответствующие им интерфе-
рограммы (д, е, ж, з)
быть неопределенное значение с нулевым «весом» (ср. аргумент комплексно-
го числа, равного нулю). При у, = 0 и \у2 «л (\|/2 <тс) результат усредне-
ния должен быть равен нулю. Очевидно, правильный результат не может быть
получен ни в рамках обычной вещественной арифметики, ни в рамках век-
торной (или комплексной) арифметики. Проблема снимается при описании
направления комплексным числом вида
ф = wexp(i*2\j/),
(7-8)
466
ГЛАВА 7
где \|/ — вещественное значение направления в соответствии с введенными
выше определениями, aw— вес, некоторое вещественное число (0< w<l).
Для приведенных примеров, полагая w = l, получаем в первом случае:
V] =1, ф2= — 1, ф = 0, w = 0, ф — неопределенно; во втором случае:
ф, =1, ф2~1, ф = 1, = ф = 0.
На основе (7.8) можно записать определение комплексного поля направлений:
,х2) = w(xj ,х2 )exp(z2v(%] ,х2)). (7.9)
Весовая функция w(x1,x2) в (7.9) имеет смысл достоверности (выражен-
ности, надежности определения) поля направлений в данной точке. Очевид-
но, она должна иметь верхнее граничное значение, равное 1, на участках изоб-
ражения с отчетливо выраженным направлением периодической структуры.
Такими участками являются области с резкими перепадами яркости (конту-
ры). Минимального значения, равного нулю, весовая функция должна дости-
гать на участках с постоянной яркостью. Например, для изображения с глад-
кой функцией яркости [9] весовую функцию можно определить на основе
градиента функции яркости следующим образом:
и>(л„х2)= (^(^-^)/Эх,)2+(<У(х„хг)/Эх2)2 (7|0)
1 + +(df(*x,x2)ldx2)
При использовании модели изображения с квазипериодической функцией
яркости (7.4) весовую функцию w(x],x2) следует положить равной единице.
Использование определения (7.9) позволяет записать уравнение линейной
фильтрации комплексного поля направлений:
ф(хнх2) = JJ* й(«1,м2)ф(х1 — Uj,x2 — u2)du]du2, (7.11)
(ui,u2)GHZ
где й(м],м2) — вещественная функция, имеющая смысл импульсной характе-
ристики линейного фильтра, a W — область окна. В практических задачах
обработки изображений часто можно ограничиться сглаживанием поля на-
правлений по квадратному окну:
Xj — ИрХ2 — м2) duxdu2.
(7-12)
где L х L — размеры окна обработки.
Для дискретного поля направлений сглаживание по окну размером
(2М -М)х(2М +1) задается соотношением
7 А. Нелинейная фильтрация полей направлений
467
1 м м
V(ni.n2) = 7---77 Е Е Щщ-к,п2-1).
(2Л/+1) л=-м/=-м
Заметим, что, в отличие от традиционной фильтрации функции интенсив-
ности при фильтрации поля направлений по (7.11), не возникает проблемы
граничных значений, так как вне обрабатываемого фрагмента изображения
мы имеем возможность положить равной нулю весовую функцию w(jC],x2),
что соответствует неопределенным значениям поля направлений.
7.4. Нелинейная фильтрация полей направлений
Типичным представителем нелинейных алгоритмов обработки изображе-
ний является медианный фильтр [13]. Традиционное определение медианы
основано на построении ранжированного ряда вещественных чисел и опреде-
лении серединного значения в этом ряду:
|х1,х2,...,х2Л/+1}—>|xj,x2,...,x2JW+1 j-^xmed =хм. (7.13)
Очевидно, в силу периодичности значений направления и отсутствия от-
ношения порядка такое определение медианы для ряда значений направле-
ния невозможно. Однако можно доказать (см. также [13]), что определение
(7.13) эквивалентно следующему:
2Л/+1
= arg min Е |*л “ */1 • (7.14)
хк /=1
Определение (7.14) можно трактовать как уравнение нелинейного фильт-
ра, удовлетворяющего аддитивно-равномерному критерию оптимальности.
Соответствующий аддитивно-равномерный фильтр для дискретного комплек-
сного поля направлений, который в силу приведенных рассуждений является
аналогом медианного фильтра, имеет следующий вид:
у(и|,и2)= argmin Е |v(wi — — г,п2 —#)|. (7.15)
Можно записать более простой аналог фильтра (7.14), используя веще-
ственное поле направлений. Для этого следует определить «расстояние» меж-
ду двумя значениями направления и v2 не 110 хорде, как сделано в (7.15),
а по дуге:
r(Vi.V2) = min {krV2|’71 -|VrV2|}-
Получаем следующий аддитивно-равномерный фильтр для дискретного
вещественного поля направлений:
468
ГЛАВА 7
ф(и!,и2)= argmin 52 г(у(п} - к,п2~ r,n2~ q)). (7.16)
v(n1-i,H2-/),(i,z)ew' (r.g)ew
Заметим, что, в отличие от медианного фильтра, аддитивно-равномерный
фильтр в форме (7.15) или (7.16) не гарантирует однозначности выходного
значения, так как точки на (или внутри) единичной окружности не образуют
упорядоченного множества.
7.5. Цифровые методы построения поля направлений
Непосредственное использование численного дифференцирования по оп-
ределению (7.3) для цифрового построения поля направлений возможно лишь
для «гладких» изображений при условии полного отсутствия шумов наблюде-
ния. На практике необходимо использовать помехоустойчивые методы по-
строения поля направлений, основанные на аппроксимации и усреднении.
Используя различные модели представления поля направлений, выделим
пять обширных классов методов его построения: методы параметрической
аппроксимации, проекционно-дисперсионные и дифференциальные методы,
методы локальных градиентов и спектральные методы. На рис. 7.6 представ-
лена классификация методов построения полей направлений, разработанная
в ходе экспериментальных исследований. Целью данной классификации яв-
ляется выбор наилучших методов для конкретных приложений.
7.5.1. Методы параметрической аппроксимации
Класс методов параметрической аппроксимации основан на аналити-
ческом представлении функции яркости изображения в симметричном пря-
моугольном скользящем окне. Пусть f(xl,x2) — функция яркости изобра-
жения в точке (x1,x2)eG, где (/некоторая область изображения. Аппрок-
симация изображения /(^,х2) в симметричном прямоугольном окне
W = {(w,v): — L, <и < L,, — L2 <v <L2}, размером (2L{ +1)x(2L2 4-1) пред-
ставляет собой двумерный полином:
f(xi~u,x2-v)= 52 ai,j(xi^x2)u‘vJ’ (xltx2)eG, (u,v)eW, (7.17)
где D — { (i, j): 0 < i < S, 0 < j < S, 0 < i 4- j < $} множество показателей сте-
пеней.
Коэффициенты полинома (7.17) j(x},x2) являются функциями положе-
ния центра окна (xj,x2)-
Рассматриваемая локальная аппроксимация функции яркости позволяет
сгладить изображение для вычисления производных и получить некий гео-
метрический инвариант в виде поверхности первого или второго порядка. В
качестве аппроксимирующей функции используем следующие поверхности:
- плоскость: f(u,v) = au 4-fcv4-c;
7.5. Цифровые методы построения поля направлений
469
Рис. 7.6. Классификационная схема методов построения полей направлений
470
ГЛАВА 7
- квадратичную поверхность: f (и, v) = аи2 4- bv 2 + cuv 4- du 4- ev + f;
- цилиндрическую поверхность: f (u,v) = a(y + ku)2 + b(y +ku) + c.
Коэффициенты аппроксимирующих полиномов определим по методу наи-
меньших квадратов из условия минимума функционала J:
J= jj [/(*! ~иух2 — v) — dudv —> min .
(m.v)GW
В дискретном виде функционал имеет следующее выражение:
J= 52 52f/(nimin .
(uy)&V а'Ь'с-
Приравнивая к нулю частые производные функционала по полиномиаль-
ным коэффициентам, получаем систему линейных уравнений относительно
неизвестных коэффициентов:
- аппроксимация плоскостью:
aJ>2=Pio, Ь£>2=р01’ с521 = Ноо> (7-18)
где gw(*i,x2)~ локальные степенные моменты изображения в окне обра-
ботки,
£ upv4 f(xx-u,x2-v), (7.19)
(u,v)€W
быстрые алгоритмы рекурсивного вычисления моментов приведены в [14];
- аппроксимация квадратичной поверхностью:
+Ь^2 +
<£y+fc£«2v2 + /£v2=go2,
c£H2v2=nu, <fJ2«2=n10, e£v2=n0„
a£«2+fe£v2+/£l = goo;
- аппроксимация цилиндрической поверхностью:
а±У +6«*Z>2 V2 +ак4£и4 +сХУ+ск2Е“2 =
= Но2 4-&2Ц2о»
+M2J>2 =Moi Wio’
flJ2v2 +ak2 £м2 +с^1 = Цоо,
6a2Jt£>2v2 +2a2P£>4 +2лс*£М2 +Ь2к^и2 =
= 2apH 4-2^p20 4-Ьц10.
7.5. Цифровые методы построения поля направлений
471
Аппроксимация плоскостью. В системе координат, связанной с положением
скользящего окна W, зададим одномерный полином /(х,,х2), аппроксимиру-
ющий изображение /(x,,x2) в виде плоскости, f[xi,x2) = axl +bx2 + с,
коэффициенты которого имеют вид
_____бН ю_____ 01____
L(L+1)(2L + 1)’ Z,(t+1)(2L + 1)
Используя модель представления поля направлений (7.3) и систему (7.18),
получаем для его определения следующее выражение: tg\jjr(x1,x2) = ц10/ц01.
Квадратичная аппроксимация. Метод локальной квадратичной аппрокси-
мации основан на аппроксимации функции /(хх,х2) в пределах окна И7квад-
ратичной поверхностью:
/(х],х2) = oxj2 +bx2 +c*i*2 +^i +^г + /» (7.22)
За значение поля направления в точке (х1?х2)
принимается направление главной оси параболоида
(7.22) (рис. 7.7), когда центр окна W находится в
точке (Х|,х2). Численное решение данной задачи
приведено в [14], где предложен эффективный ал-
горитм вычисления коэффициентов с использова-
нием рекурсивного метода вычисления моментов
(7.19). Для определения направления главной оси
параболоида перейдем к каноническому виду урав-
нения поверхности [15]:
Рис. 7.7. Линии уровня квад-
ратичной поверхности
— 4"^x22 + f' •
Для этого используем следующие аффинные преобразования координат:
Х[ = х{ cos а—х2 sin ос + х10,
х2 =Х| sina4-x2cosa4-x20,
се — 2bd
*10 Г 2 ’
4аЬ — с
_ cd — 2ае
Л20 “ 2 '
4аЬ — с
(7.23)
Последние являются координатами вершины аппроксимирующего пара-
болоида, а угол а определяется из следующего уравнения: tg2oc = c/(a — b).
В результате решения данного уравнения получим два взаимно перпендику-
лярных направления а} и а2, соответствующие главным осям квадратичной
472
ГЛАВА 7
поверхности (7.22). Выбор направления большей полуоси осуществляется сле-
дующим образом:
cx = arg min [a',
{«i.ai}
где «7 = «cos2 ex+ /? sin 2 ex + с sin a cos а. Данное выражение получено при пе-
реходе к каноническому виду уравнения поверхности с помощью аффинного
преобразования координат (7.23). Вектор параметров аппроксимирующего
полинома найдем из системы (7.20):
__________45 И 2о_________________15^00_______
L(L + 1)(2L + 1)2(4L2 + 4£-з) (2£ + 1)2 (4Z,2+4£-3) ’
__________45Но2__________________оо_________
L(L + l)(2L + l)2(4L2+4L-3) (2L + 1)2 (4£2 + 4£-3)'
______ЗЦ pt______
t(L + l)(2L + l)2’
_ М оо (l4^2 +14L-3)-15(p 204-ц о2)
(2L + 1)2[4L2 + 4£ - з)
Цилиндрическая аппроксимация. Общая идея метода цилиндрической апп-
роксимации предложена в работе [16].
Рассмотрим построение системы нелинейных уравнений в явном виде.
В системе координат скользящего окна рассмотрим полином второго порядка
одной переменной, который повернут на плоскости изображения на некото-
рый угол , аппроксимирующий изображение /(х],х2) в виде цилиндра
= а(х2 +&ч) +^(-^2 +&К1)+с, где к — — tg\|/. За направление в цент-
ре окна (xj,x2) принимаем направление, вдоль которого повернут цилиндр, а
именно угол у. Параметры а, Ь, с, к аппроксимирующего полинома опреде-
лим из системы (7.21):
7.5. Цифровые методы построения поля направлений
473
5о(но2 +2Лр,ц +&2Р-2о) —Ноо(52
а =-1i
SQ (J4 +6Л$22 J4) — (^2 +
b______3(Цр1 ~Ь ^Цю)_
М(Л/+1)(2Л/+1)2(1 + Л2]’
Моо-«52(1 + ^2) (7'24)
с =----------
S0
6a2ks22 + 2a2k3s4 4-lacks2 +b2ks2 = 2ацп + 2акц20 +bp.l0,
r^C Srq= 22 XX*2> S0 =500=(2L + 1)2’
(.r,y)ew
L(L + 1)(2L + 1)2(3L2 + 3L-1)
5 4 ~ 540 = 504 — “
В отличие от аппроксимации плоскостью и квадратичной поверхностью
система (7.21) является нелинейной, что требует использования для ее реше-
ния соответствующих численных методов. Подставив выражения а, Ь, с в пос-
леднее уравнение системы (7.24) получим нелинейное уравнение относитель-
но параметра к, решение которого можно получить численными методами.
Метод комбинированной аппроксимации.
При проведении исследований рассмот-
ренных методов было замечено, что при
аппроксимации изображения плоскостью
возникает большая погрешность в точках
экстремума функции яркости, а при апп-
роксимации квадратичной поверхнос-
тью — в точках перегиба. Из рис. 7.8 вид-
но, что в точках экстремума функции (уча-
сток 1) погрешность можно уменьшить,
используя параболическую аппроксима-
цию, в точках перегиба (участок 2) — ап-
Рис. 7.8. Метод комбинированной апп-
роксимации
проксимацию прямой (для двумерного случая — плоскостью). Таким обра-
зом, воспользуемся методом комбинированной аппроксимации. Определим
две величины, характеризующие соответственно параметр крутизны и кри-
визны аппроксимируемой функции:
474
ГЛАВА 7
(7.25)
дх2
(7.26)
Величина (7.25) достигает высоких значений в точках перегиба, а величина
(7.26) — в точках экстремума. Согласно (7.22) данные характеристики будут
иметь следующие выражения:
|\7/ (%] ,х2 )| = d2+е2,
Д/(Л1,л2) = 4(о2+£2)(2£ + 1)2.
Использование конкретного способа аппроксимации определяется следу-
ющими условиями:
- аппроксимация плоскостью: |V/(x1,x2)| >Д/(х,,х2),
- аппроксимация параболическая: |V/(xpx2)| <Д/(х1,х2).
Экспериментальные исследования. Класс методов локальной параметричес-
кой аппроксимации обладает высокой устойчивостью к шумам, так как метод
наименьших квадратов имеет шумоподавляющее свойство. Недостатком же
является необходимость адаптивного выбора размеров окна обработки ^(раз-
мер окна должен быть меньше расстояния между соседними полосами). Про-
ведем исследование рассмотренных выше методов на тестовых изображениях
(см. рис. 7.9). Из-за специфики значений отсчетов поля направлений невоз-
можно использовать понятие среднеквадратичной ошибки в обычном смыс-
ле. В данном случае под среднеквадратичной ошибкой будем понимать следу-
ющую величину:
е2 =j^| JJ|v(x1,x2)-^(x1,x2)| dX'dx
2’
где D — область изображения, ф(хрх2) — истинное значение поля направле-
ния, ф(Х|,х2)— его оценка. Воспользуемся представлением поля направле-
ния в комплексной форме (7.9) с единичной весовой функцией:
е2 =
|°|
^'2у(^Л2)
(Х|,х2)ео
_e«2v(X!,x2)
= 4г ff sin2(v(x|,x2)-v(x|,x2)).
I 1(Л|,х2)€О
(7.27)
7.5. Цифровые методы построения поля направлений
475
Рис. 7.9. Иллюстрация работы методов параметрической апп-
роксимации: а — изображение интерферограммы; поле направ-
лений, полученное методом аппроксимации плоскостью (б);
методом параболической аппроксимации (в); комбинирован-
ным методом (г)
Значение среднеквадратичной погрешности находится в диапазоне от нуля
до четырех. При этом нулевое значение соответствует совпадению полей на-
правлений, а максимальное — расхождению на 90°. В качестве значения по-
грешности будем использовать угловую среднеквадратичную погрешность:
5° = arcsinVe2 /4 .
Исследование точности проводилось на серии тестовых изображений, от-
личающиеся наличием шума, равномерностью и неравномерностью простран-
ственной частоты и видом квазипериодической структуры (рис. 7.10). Рас-
сматривалась зависимость точности оценки от отношения шум/сигнал
h2 =oJ/Oy, где с2 — дисперсия функции яркости:
ст'
Полученная ошибка зависит от уровня шума, от пространственной часто-
ты (рад/пиксел) (или от периода анализируемой структуры J = (пик-
сел/период)) и от метода построения поля направлений. Для полноты экспе-
риментальных исследований данного класса методов проведем также тести-
рование переборного метода цилиндрической полиномиальной аппроксимации
[16]. Сравнивая между собой методы параболической аппроксимации и апп-
роксимации плоскостью (рис. 7.11 и 7.12), можно сделать вывод, что метод
аппроксимации плоскостью, обладая наименьшей вычислительной сложнос-
тью, обеспечивает наилучшую оценку поля направления. Это объясняется тем,
что на тестовом изображении площадь участков, соответствующих перегибу
функции яркости (рис. 7.8), больше, чем участков, соответствующих точкам
476
ГЛАВА 7
Рис. 7.10. Тестовые изображения
квазипериодических структур: а —
с постоянным полем направления;
б-г — различные виды полос; д —
с шумом 50%
экстремума. Можно заметить также существенное уменьшение погрешнос-
ти оценки поля направлений при использовании комбинированной аппрок-
симации.
7.5.2. Методы локальных градиентов
Рассматриваемый класс методов основан на том факте, что градиент функ-
ции в любой точке перпендикулярен касательной к линии уровня в этой точ-
ке (7.3). Методы локальных градиентов основаны на вычислении градиента
функции яркости при различных положениях локальной маски внутри ска-
нируемого по изображению симметричного прямоугольного внешнего окна
И" размером ^хЛ2 (локальный градиент): (У^’"2), где l<nx<L},
Рис. 7.11. Зависимость точности оценки поля направлений аппроксимационными методами от
интенсивности шума (маска 11x11, ш = 0,07 л)
7.5. Цифровые методы построения поля направлений
477
..... плоскость
—с— параболоид
----- комбинированный
-----переборный цилиндрический
Рис. 7.12. Зависимость погрешности оценки поля направления аппроксимационными методами
от пространственной частоты квазипериодической структуры (маска 9x9)
1 < и2 < Ь2 ~ координаты положения локальной маски в окне W. Использо-
вались два типа локальной маски (рис. 7.13).
За направление полос в точке сканирования принимаем угол у, вычислен-
ный на основе найденных локальных градиентов:
tg4>(-tp-'2) = -?x,/^2> °-v(*|.*2) <Л >
>Qx2 )
. 9х1 ' дх2 ,
Рассматриваемый класс методов нахождения поля
направления можно разбить на два подкласса, характе-
ризуемые различным способом использования локаль-
ных градиентов в общей схеме расчета поля направле-
ний: методы усреднения проекций градиента и методы
усреднения локальных углов направления.
Метод усреднения проекций градиентов основан на
использовании локальных градиентов (g”1’”2,
соответствующих положению (nlfn2) локальной маски,
в расчете градиента функции яркости в центре внешне-
го окна РИ:
Рис. 7.13, Иллюстрация
метода локальных гради-
ентов
п1=1л2=1
Метод усреднения локальных углов направлений использует локальные гра-
диенты (я”,,Л2, <7Л|,Л2) для расчета локальных углов:
\ •*! Х2 /
(7.28)
478
ГЛАВА 7
Тогда направление полосы в центре внешнего окна W можно вычислить,
усредняя поле локальных углов:
1 М l2
Ф = T-arg 22 22 exp(i2y„, „г )•
П|=1и2=1
(7.29)
Значение весовой функции поля направлений соответственно будет иметь
следующее выражение:
vv =
1
LXL
2 Л|=1п2=1
Фактически метод состоит из двух этапов: 1) определение градиента, либо
направления (на основе градиента) в каждой точке локальной маски (2x2,
крест); 2) сглаживание поля градиентов или поля направления в окне. Про-
цесс классификации методов градиентов можно продолжить, базируясь на
различных способах нахождения локальных градиентов: использование раз-
ностных схем и локальной аппроксимации гармоническими функциями. Об-
щая классификационная схема для класса методов локальных градиентов пред-
ставлена на рис. 7.14.
Градиентный метод с использованием разностных схем. В этом методе для
нахождения градиента используется его определение. При вычислении част-
ных производных применяется разностный метод со сканированием локаль-
ной маской двух видов: квадратная размером 2x2 и крестообразная. Эти мето-
ды, как и все градиентные, позволяют получить непрерывные значения угла
направлений, что обеспечивает повышение точности оценки по сравнению с
переборными алгоритмами. Быстродействие методов существенно зависит от
размера внешнего окна сканирования W. Недостатком метода является повы-
шенная чувствительность к шумам.
Рис. 7.14. Классификация методов локальных градиентов
КРЕСТОВИДНАЯ МАЖА
КВАДРАТНАЯ МАКА
7.5. Цифровые методы построения поля направлений
479
Локальная маска крестообразного типа. Локальные градиенты определяют-
ся по следующей разностной схеме (рис. 7.15):
л,л2 = гю ~г-ю _ f<xi +”i + 1»*2 +«2)~/<х1 +И1 -1,х2+л2)
Ях' 2 2
nt,n2 = Г01 ~Г0-1 = f(X\ + Ид, Х2 + И2 + 1) ~ /(Хд + /I, ,Х2 + /12 ~ 1)
2 2
0<xi<L1, 0<x2<L2, —W/2<nit n2<W/2.
Локальная квадратная маска размером 2x2. Разностная схема имеет вид
q™ =Кц W+fto W = ([/(Л| +И| +1Х2 +„2 +1)_
~f(xl +Лр*2 +и2 + 1)] + [/(*1 +И1+1,х2+л2)-
-/(х, + и,,х2 +и2)])/2,
q"'2'n2 + ----— = ([/(*! +л,,х2 +и2 +1)-/(х, 4-лрх2 +и2)] +
+[/(Xi 4-л, + 1,х2 +и2 + 1) —/(x, 4-л, + 1,х2 +и2)])/2.
Методы локальной синусоидальной аппроксимации. Методы описываемого
подкласса градиентных методов основаны на аппроксимации в пределах ло-
кального окна функции яркости синусоидальной функцией двух перемен-
ных: g (х,, х2) = A sin (содх, + со2х2 + <р).
Значения локальных проекций градиента в центре окна (при х, = х2 = 0)
имеют вид
=An'-"=iol"'-"2COs(<p"'-"j),
= Л"1."!о)2-.,л, со^ф'-.лг ).
Параметры А, со,, со2, (р можно определить методом наименьших квад-
ратов, который сводится к системе нелинейных уравнений, которую анали-
тически решить невозможно. Численные методы очень сложны в реализа-
ции, а в данном случае ненадежны в связи с неоднозначностью обратных
тригонометрических функций. Поэтому данная задача решается без исполь-
зования метода наименьших квадратов и формулируется таким образом,
что допускает аналитическое решение. Величина А является константой,
480
ГЛАВА 7
Рис. 7.15. Маска кре- Рис. 7.16. Локальная
стообразного типа квадратная маска
равной наибольшему значению функции яркости. Необходимо определить
параметры Шр cd2, (р.
Применим метод сведения переопределенной задачи к такой, где число
уравнений равно числу неизвестных. Для этого перейдем от используемого
нами вида локальной маски к маскам нескольких видов.
Маска первого типа ответствует наклону полосы в центре локального окна
на 45° и используется при определенной конфигурации значений функции
яркости (рис. 7.17), которую можно задать следующим условием:
[(*1 <*2)]v[(*i >^з)(^i >*2)]-
(7.30)
Выберем стандартную декартову систему координат, обеспечивающую наи-
меньшее значение фазы (что определяется неоднозначностью арксинуса при
выполнении условия (7.30)). Для данной задачи важен лишь знак частного
со2/<О]. Поэтому частоту (О) считаем всегда положительной, а со2 с данной
маской при выполнении условия (7.30) — отрицательной. Это всегда можно
сделать выбором начала отсчета и начальной фазы.
Таким образом, если условие (7.30) выполняется, то приходим к системе
следующего вида:
Asin (р = t ],
Asin(-co2 4-<р) = г 2,
Asin(co7 +<р) = г3,
решение которой имеет вид
• ^з
<p = arcsin—, О), = arcsin— — <р
А А
2
со9 = — (р — arcsin—.
А
Если первая маска не позволяет найти частоты (Oj и cd2 , т.е. условие (7.30)
не выполняется, воспользуемся маской второго типа (рис. 7.18), соответству-
ющей наклону полосы в центре локального окна на 135 градусов (усл. 7.30).
7.5. Цифровые методы построения поля направлений
481
Рис. 7.17. Маска первого типа
Рис. 7.18. Маска второго типа
В этом случае частоты СО] и со2
уравнений будет иметь следующий вид:
являются положительными и система
A sin (р = ,
Asin(—со2 +(р) = Г2,
Asin(—СО] +(р) = /3.
Решение системы имеет вид
• А •
(p = arcsin—, со, = (р—arcsin—
А А
(02 — (р —arcsin-^-.
Маска третьего типа соответствует наклону полосы в центре локального
окна на 90 градусов (рис. 7.19), что соответствует выполнению следующего
условия:
[(^2<^1) Л (*4 <'з)] V [(^2>^1) Л (^4>*з)]- (7.31)
В этом случае частоты cot > 0 и ш2 = 0; система уравнений будет иметь
следующий вид:
. . 11з
Asin<p = 2 ’
Asin (ci)/ + <p) = *2~fe4-.
Решение системы имеет вид
• + Z3 • *2 +*4
— arcsin---co, = arcsin —---- —(p
2A 2A
co2=0.
Маска четвертого типа соответствует горизонтальному расположению по-
лос (рис. 7.20), что соответствует выполнению следующего условия:
[(ri <*з) А (г2 <*4)] V [(?| >г3) A (t2 >*4)]-
(7.32)
16 — 9044
482
ГЛАВА 7
Рис. 7.19. Маска третьего типа
Рис. 7.20. Маска четвертого типа
Здесь также частоты со2 > 0
ющий вид:
и (Oj =0, и система уравнений имеет следу-
. . ^1^2
Asm(p= 1
A sin (—to2 + <р) = ,
соответственно, решение системы имеет вид
. ^1+^2 • *з+*4
(р = arcsin —---, = ф - arcsin —---
2А 2 2А
to) =0.
Во внешней маске Wукладывается (Lx — 1)х(£2 —1) локальных масок раз-
мером 2x2. Таким образом для определения частоты функции яркости, соот-
ветствующей центру глобального окна используются усредненные по окну
значения модулей локальных частот (о2Л|’”2:
(7.33)
При этом частотному компоненту со2 присваивается тот знак, который
преобладает во множестве локальных частот.
На рисунках 7.21, 7.22, 7.23, 7.24 приведено исследование точности оценки
поля направления градиентными методами в зависимости от интенсивности
шума и пространственной частоты квазипериодической структуры. Из этих
рисунков видно, что наибольшую точность оценки при малой интенсивности
шума обеспечивает метод локальных градиентов при использовании разно-
стных схем с усреднением углов, но наибольшую устойчивость при увеличе-
нии шума обеспечивают метод локальных градиентов при использовании раз-
ностных схем с усреднением проекций градиентов.
7.5. Цифровые методы построения поля направлений
483
Рис. 7.21. Зависимость погрешности оценки поля направления от интенсивности шума (маска
7x7) для класса градиентных методов, использующих стандартные разностные схемы
ба,°
синусоид, аппроксим. (проекции)
синусоид, аппроксим. (углы)
разност. схемы (крест-проекции)
разност. схемы (крест-углы)
разност. схемы (2х2-проекции)
разност. схемы (2х2-углы)
Рис. 7.22. Зависимость погрешности оценки поля направления от интенсивности шума (маска
7x7) для различных градиентных методов
Синусоидальный метод является устойчивым к шуму при увеличении про-
странственной частоты структуры. Методы, основанные на разностных схе-
мах, оказались неустойчивыми в случае использования усреднения по проек-
циям для больших размеров внешнего окна И< При использовании усредне-
ния по углам методы, основанные на разностных схемах, обладают большей
устойчивостью при увеличении пространственной частоты.
Таким образом, можно сделать общий вывод: методы, основанные на раз-
ностных схемах, использующие усреднение проекций обеспечивают более
высокую помехоустойчивость при достаточно большой интенсивности шума,
однако методы, использующие усреднение углов, обладают тем преимуще-
ством, что являются более точными при высоких пространственных частотах
квазипериодической структуры. Если сравнивать класс методов параметри-
ческой аппроксимации с классом градиентных методов, то можно заметить,
что точность оценки методами указанных классов близка, но заметна раз-
ность в скорости отдельных методов: синусоидальный метод позволяет рекур-
сивные вычисления по формуле (7.33), но объем вычислений на каждом шаге
рекурсии достаточно велик.
16*
484
ГЛАВА 7
Рис. 7.23. Зависимость погрешности построения полей направлений синусоидальным методом
от частоты интерферограммы: а — усреднение углов, б — усреднение проекций
Рис. 7.24. Зависимость погрешности построения полей направлений градиентными методами
(разностные схемы): а — крест-проекции, б — крест-углы, в — 2х2-проекции, г — 2х2-углы от
частоты интерферограммы
г
7.5. Цифровые методы построения поля направлений
485
7.5.3. Дифференциальные методы
Дифференциальных методы основаны на том факте, что производная функ-
ции яркости по направлению, совпадающему с направлением полосы, имеет
наименьшее (по модулю) значение среди производных по направлению в те-
кущей точке: фг — arg min |/^|.
При использовании дифференциального метода с маской
3x3 по отсчетам внутри окна вычисляем производные вдоль
направлений [5], определяемых углами 0, 45, 90, 135 градусов.
При этом используются симметричные разностные схемы:
*11 *12 *13
*11 *21 *23
*31 *31 *зз
Рис. 7.25. Эле-
менты маски 3x3
2Л
Оценки производной для различных направлений в дифференциальном
методе с маской 3x3 (рис. 7.25) имеют следующие выражения:
у' _ х13 *11+*23 *21+*33 *31
6
*12 ~*21 +О>5(*13 ~х31) + *23 ~*32
3>/2
» _ Х31 Xj ] + Х32 *]2 +*33 *13
/90 “ г
*23 ~~*12+0>5(*зз — *ц) + *з2 *21
Зл/2
Основным преимуществом дифференциальных методов является макси-
мально возможное быстродействие среди всех представленных классов мето-
дов построения поля направления. Конкретные данные по быстродействию
будут представлены ниже.
При использовании маски размеров 5x5 вычисляются производные по вось-
ми направлениям, определяемым углами: 0, 26,6 = arctg (1/2), 45, 63 = arctg (2),
90, 116, 135, 153 градуса. Оценки производных для различных направлений
имеют следующий вид:
*15 ~*11 + *25 ~ *21 +*35 ~~*31 +*45 ~ *41 +*55 ~*51
/ _ *15 — *32 + *25 *41 + *35 *51
26" 6^5
, _ 1,5(х13 -х31) + х14 -л4| +0,75(Х|5 -л51) + х25 + 1,5(х„ -х53)
И ~ ' 15^2
486
ГЛАВА 7
Л/ _ *13 *51
>з ~------------
*14 *52 + *15 *53
6л/5
1,5(*31 - *5з)+*21 -*54+0,75(лн -л55) + х12 -*45 + 1,5(х13 -х35)
15^2
/ _ *ц *35 +*21 *45 +*31 *55
JI53 ~
6^5
Весовую функцию определим с помощью следующего соотношения:
Существенным недостатком всех дифференциальных методов является
сильная чувствительность к шумам, что дает более низкое качество оценки по
сравнению с другими методами. На рис. 7.26 показана зависимость погреш-
ности построения поля направлений от интенсивности шума для различных
интерферограмм.
Рис. 7.26. Зависимость погрешности построения полей направлений дифференциальными ме-
тодами от интенсивности шума для двух типов квазипериодических структур
7.5. Цифровые методы построения поля направлений
487
Основным ограничением методов является принципиальная невозможность
уменьшения максимальной ошибки оценки до значений меньших чем 90/л,
где п — количество производных по направлению (л = 4 для маски 3x3, л = 8
для маски 5x5).
7.5.4. Проекционно-дисперсионные методы
Проекционно-дисперсионный метод [5, 9] построения поля направлений
основан на применении преобразовании Радона [17] для вычисления «томог-
рафических» проекций функции яркости изображения f (х,,л2) внутри сколь-
зящего окна вдоль направления, перпендикулярного направлению, задавае-
мому углом у (рис. 7.27):
I
L/2 ________ \ ________________________
J I \]l2 + у2 cos \g + arctg— ,\]l2 + у2 sin v + arctg—
-L/2 l> 1
Jy, (7.34)
I
где полагается, что центр окна размером LxL находится в точке (0,0).
Рассматривая функцию (7.34) при фиксированном значении параметра V
и значениях аргумента /б[—L/2, Z/2], можно измерить разброс ее значений
относительно среднего («дисперсию»):
488
ГЛАВА 7
L/2
DM= j [«(/.v)-r(y)] di,
-Цг
1 Ч-
Л(у) = -J K(Z,v)d/. (7.35)
1 -L/2
За оценку значения поля направлений принимается значение угла \|/, при
котором функция О (у) имеет максимум:
V = argmax£>(\|f).
v
Весовую функцию комплексного поля направления определим из следую-
щего соотношения:
max £>(у) - min D(\|/)
W = .
maxD(\|/)
v
Непосредственное использование преобразование Радона (7.34) для диск-
ретного случая вызывает трудности, связанные с невозможностью вращения
окна обработки.
Практическая реализация дисперсионного метода построения поля направ-
лений сводится к вычислению функции для частного случая четырех
(вертикального, горизонтального и двух диагональных) направлений на диск-
ретном множестве отсчетов функции яркости /(х, у) внутри окна.
Произведем сканирование изображения f (х, у) квадратной МхМ маской
и для каждого из ее положений сформируем четыре последовательности сред-
них значений для отсчетов, расположенных вдоль линий, параллельных од-
ному из четырех направлений — 0°, 45°, 90°, 135°:
R(k,45°] = -^f(.k-j+lj), k = l, 2.................. 2М-1;
k ' k 7=1
я(*,90°) = -1-Х/(Л*). *=1. 2...............
' ' M J=1
я(*. а’) = -1£жд *=1. 2„... M; (7.36)
V ' M >=1
K|i,135o) = -22/(M-t+j-l,A k=l, 2, ..., 2M- 1.
V ' kj=i
7.5. Цифровые методы построения поля направлений
489
В результате получаем дискретный аналог (7.35):
DW=Е£(*.'и)[я(*.'1') - «М]2.
*
к
(7.37)
5(*.у)=
—, к = 1, 2,...,М, \|/ = 0° или \|/ = 90°;
М
к = \, 2,..., 2М-1, \|/~ 45" или у = 135°.
Основным недостатком такой реализации проекционно-дисперсионно-
го метода является квантованность результирующих значений поля направ-
лений (0°, 45°, 90°, 135°/ Можно увеличить число градаций значения поля
направления до восьми, обобщив соот-
ношения (7.37, 7.36) за счет рассмотрения
четырех дополнительных направлений
(26° = arctg(l/2), 63° =arctg(2), 116°, 153°).
Однако такой метод увеличивает трудоем-
кость и громоздкость алгоритмов. Ниже
представлен подход к увеличению точнос-
ти за счет интерполяции.
Дисперсионный метод с интерполяцией.
Допустим, что функция (7.35) имеет вид си-
нусоиды: — Acos(2(\|/ — ф)) + В. Зная
значения данной функции Do, Ь45, Р90, D
Рис. 7.28. Иллюстрация дисперсионного
метода с интерполяцией
135 в точках \|/ = 0°, 45°, 90°, 135°,
можно оценить неизвестные значения параметров А, ф, В (рис. 7.28):
Acos2\jf + В = Dq,
A cos
71
j-2V
+ В = £>45,
.•Ц) 4- £>45 + Dqq + Dl35 — В,
откуда получаем
7^45 &
Do-B'
На отрезке [0°, 180°] данное уравнение имеет два решения, соответствую-
щих минимальному и максимальному значению функции £>(v). Для данного
490
ГЛАВА 7
метода весовую функцию поля направления определим следующим образом:
w = 2A/(A + B).
Исследование точности проекционно-дисперсионных методов (рис. 7.29—
7.31) показало, что интерполяционный метод в 2—12 раз увеличивает точность
оценки поля направления по сравнению с четырехградационным перебор-
ным методом (рис. 7.28). Интерполяционный метод проигрывает переборно-
му только для больших значений пространственной частоты и большой ин-
тенсивности шума.
Рис. 7.29. Зависимость погрешности построения полей направлений проекционно-дисперсион-
ными методами от интенсивности шума для двух типов квазипериодических структур
----- перебор 3x3 —о— перебор 9x9
—м— перебор 13x13 ...о-.. Интерпол. 3x3
-----Интерпол. 9x9 .... Интерпол. 13x13
Рис. 7.30. Зависимость погрешности построения полей направлений проекционно-дисперсион-
ными методами от интенсивности шума для различных масок
7.5. Цифровые методы построения поля направлений
491
б
Рис. 7.31. Зависимость погрешности оценки поля направлений проекционными методами от
пространственной частоты квазипериодической структуры: а — переборный метод; б — интер-
поляционный метод
7.5.5. Спектральные методы
Спектральный метод расчета поля направлений [9] основан на модели изоб-
ражения с локально-периодической функцией яркости (7.4). В соответствии с
этой моделью производится спектральный анализ функции яркости изобра-
жения в пределах скользящего квадратного окна задава-
емого областью
где — координаты центра окна, LxL— размеры окна. Рассмотрим
коэффициенты ряда Фурье функции яркости в пределах окна:
492
ГЛАВА 7
27ti
)ехр-------(mjjCj +m2x2) dxxdx.
2»
L
C(mpm2)= Jj /(x,.x2
»фМ)
и определим координаты максимального по модулю коэффициента (см.
рис. 7.32):
argmax |c(zn1,zn2)|-
(ffl|,m2)*(0,0)
В соответствии с моделью (7.4) индексы определяют превалирую-
щие в данном фрагменте изображения пространственные частоты co^x^xj),
<о2 (х{\ л:£) с точностью до знака и позволяют оценить значения поля направ-
лений и поля пространственных частот в точке (х^х®):
(7.38)
В отличие от метода локальной квадратичной аппроксимации здесь разме-
ры окна ограничены снизу: при каждом положении окна на плоскости изоб-
ражения оно должно пересекаться несколькими «интерференционными» по-
лосами. Чем больше полос попадает внутрь окна и чем меньше искривлен-
ность полос внутри окна, тем более точными будут оценки (7.38).
Рис. 7.32. Иллюстрация спектрального метода
7.5. Цифровые методы построения поля направлений
493
Практическая реализация спектрального метода расчета поля направлений
основана на использовании рекурсивных алгоритмов быстрого преобразова-
ния Фурье [БПФ]. Но, несмотря на это, данный метод чрез-
вычайно трудоемок с вычислительной точки зрения. Далее
рассмотрим метод основной локальной частоты, основан-
ный на непосредственном «геометрическом» способе оцен-
ки пространственных частот.
Метод основной локальной частоты. Этот метод также как
и представленный выше спектральный метод, основан на
поиске главной гармоники. Отличие заключается в проце-
Рис. 7.33. Иллюст-
рация метода ос-
новной локальной
частоты
дуре поиска.
Компоненты пространственной частоты для малой обла-
сти изображения квазипериодической структуры равны
CDj = 2л/dlf со2 = 2n/d2, где dlt d2 — периоды функции яркости f(x},x2) в
вертикальной и горизонтальной развертке, и задача сводится к определению
периода сечений функции яркости по горизонтали и вертикали.
На рис. 7.33 отмечены по вертикали и горизонтали периоды функции яр-
кости, равные удвоенному расстоянию между соседними экстремумами (ми-
нимумами и максимумами). В силу наличия шумов на рассматриваемых се-
чениях функции яркости присутствуют побочные минимумы и максимумы.
Поэтому необходима процедура их отсечения. Отбросим минимумы, лежащие
выше порогового значения Птт и максимумы — ниже порогового значения
Птах (на рис. 7.34 они соответственно обозначены — о и *). В результате на
Рис. 7.34. Удаление ложных экстремумов
ярких участках группируются максимумы, не разделенные минимумами,
на темных — соответственно минимумы (рис. 7.35).
Поскольку экстремумы разных типов должны чередоваться, то воспользу-
емся процедурой прореживания. При этом оставим один первый максимум
(минимум), остальные до ближайшего ми-
нимума (максимума) отсечем (рис. 7.36).
Для определения пространственной часто-
ты просканируем исходное изображение.
Размер маски должен составлять прибли-
зительно два-три периода функции ярко-
сти. При увеличении размера маски нару-
шается условие однородности квазипери-
одической структуры, при уменьшении —
возрастает влияние краевых эффектов.
Для каждой текущей точки, соответ-
ствующей центру окна, определим зна-
чения пространственных частот Wj, со2. В
соответствии с размером маски
сформируем периодически обновляемый буфер из строк (столбцов) изоб-
ражения.
- Выберем в маске первую, среднюю и последнюю строки (столбцы).
494
ГЛАВА 7
Рис. 7.35. Удаление группы экстремумов
- В каждой строке (столбце) определим количество и номера минимумов
и максимумов (отсчетов с наименьшими и наибольшими значениями функ-
ции яркости).
- Определим среднее расстояние между пиками (максимумами) в строке
(причем расстояние равно нулю, если пиков в строке (столбце) нет, и размеру
маски, если пик один), и определим соответствующее значение частоты.
- Результирующую частоту определим как среднее значение найденных
частот по выбранным строкам (столбцам) сканируемой маски.
Оценка значения поля направления принимается равной отношению най-
денных компонентов пространственной частоты СО], со2-
В отличие от спектрального или градиентных методов, представленных
выше, в данном случае возникает неоднозначность, связанная с невозможно-
стью определения знаков компонентов пространственной частоты. В данном
случае мы не сможем отличить направления а и (180 — а) градусов. Для опре-
деления знака частоты предлагается анализировать сдвиг экстремумов функ-
ции яркости в соседних линиях развертки изображениях.
На рис. 7.37 приведено исследование точности оценки поля направления
методом основной локальной частоты в зависимости от пространственной
частоты квазипериодической структуры для различных размеров окна ска-
нирования, а также приведена точность оценки поля направления при раз-
личной интенсивности шума для двух сечений данного графика, соответ-
ствующих низкой и высокой частоте квазипериодической структуры. При
увеличении пространственной частоты повышается точность оценки поля
направления (также как и предыдущего спектрального метода). При нали-
чии шумов погрешность достаточно высока, но не сильно увеличивается
при увеличении интенсивности шума (это объясняется природой наклады-
ваемого шума (высокочастотной) и тем, что спектральные методы хорошо
работают на высокочастотных квазипериодических структурах (размер окна
обработки ограничен снизу и должен содержать как минимум несколько
«интерференционных» полос).
7.5. Цифровые методы построения поля направлений
495
Пространственная частота со, рад/пикссл
Пиксел/период d
..... маска 5x5 —-— маска 7x7
..... маска 9x9 -----маска 11x11
—о— маска 13x13
в
Рис. 7.37. Зависимость погрешности построения полей направлений методом «основной ло-
кальной частоты»: а, б — от интенсивности шума для различных масок и различных частот (а —
со = 0,3л, б — о = 0,08л ); в — от пространственной частоты
7.5.6. Экспериментальные исследования методов построения поля
направлений
На рис. 7.38 приведено исследование точности оценки поля направления
различными методами в зависимости от пространственной частоты, а так же
от периода анализируемой квазипериодической структуры при обработке ок-
ном 9x9 (в случае дифференциальных методов окном 5x5) и в зависимости от
интенсивности шума для высокочастотной — рис. 7.38в и низкочастотной
рис. 7.386 интерферограмм, соответствующих сечениям графика рисунка 7.38а.
496
ГЛАВА 7
.....дифференциальные ------проекционные
—о— градиентные (2x2)-------аппроксимационные
спектральные
Рис. 7.38. Зависимость погрешности оценки поля направления разными методами (маска 9x9): а —
от пространственной частоты; б, в — от интенсивности шума (б — при ш = 0,07л рад/пиксел, изоб-
ражение 256x256, в — при о) = 0,3л, размер 128x128 пикселов)
7.5. Цифровые методы построения поля направлений
497
Анализ данных графиков позволяет сделать следующие выводы.
- Максимальную теоретическую точность (при отсутствии шумов) обеспе-
чивают градиентные и аппроксимационные методы построения полей направ-
лений.
- При отношении шум/сигнал 0,2% и выше преимуществом по точности
оценки поля направления (в диапазоне низких частот) обладают проекционно-
дисперсионные методы. Для высокочастотных квазипериодических структур
преимущество данных методов начинает проявляться при отношении шум/
сигнал 0,5% и выше. При этом в случае наличия большого шума методы явля-
ются достаточно помехоустойчивыми, и ошибка оценки практически не за-
висит от уровня шума.
- Для высокочастотных квазипериодических структур наилучшую точность
оценки поля направления обеспечивают спектральные методы. Влияние шума
начинает сказываться на работу спектральных методов (в диапазоне высоких
частот квазипериодических структур) при отношении шум/сигнал 5%.
- Для дифференциальных методов наблюдается резкое возрастание ошиб-
ки оценки поля направления при пространственных частотах квазипериоди-
ческой структуры выше 0,3л рад/пиксел. Для данных методов можно также
отметить сильную зависимость от шумов.
- Аппроксимационные методы обеспечивают хорошую точность оценки
поля направления, если окно обработки захватывает не более одной полосы
квазипериодической структуры.
- Наибольшим быстродействием обладают аппроксимационные методы,
метод основной локальной частоты и дифференциальные методы.
Рис. 7.39. Диаграмма затрат времени на обработку квазипериодической структуры размером
256x256 различными методами построения полей направлений для различных масок: 1 — дис-
персионный переборный метод, 2 — дисперсионный интерполяционный; 3 — дифференциаль-
ный; 4 — градиентный метод на основе синусоидальной аппроксимации с усреднением углов;
5 — градиентный метод на основе синусоидальной аппроксимации с усреднением проекций;
6 — градиентный метод на основе разностных схем с усреднением проекций с локальной мас-
кой 2x2; 7 — градиентный метод на основе разностных схем с усреднением углов с локальной
маской 2x2; 8 — градиентный метод на основе разностных схем с усреднением проекций с
локальной маской крест; 9 — градиентный метод на основе разностных схем с усреднением
углов с локальной маской крест; 10 — метод цилиндрической аппроксимации; 11 — метод аппрок-
симации плоскостью; 12 — метод аппроксимации квадратичной поверхностью; 13 — метод ком-
бинированной аппроксимации; 14 — спектральный метод (основной локальной частоты)
498
ГЛАВА 7
7.6. Обработка и интерпретация дактилоскопических
изображений
Дактилоскопические изображения используются в криминалистике для
идентификации личности, а также в последнее время широко применяются в
системах доступа. Представленная ниже методика кодирования изображений
отпечатков пальцев [2, 5] основана на обнаружении глобальных и локальных
особенностей и расчете их геометрических характеристик (расстояния и углы
между особыми точками). Глобальные особенности характеризуют тип узора
и включают в себя такие характерные конфигурации расположения папил-
лярных линий как «петля», «дельта», «спираль», центры петель.
Локальные особенности определяют мелкие нерегулярности папиллярного
узора и включают в себя точки разрыва, ветвления и слияния линий папил-
лярного узора, а также их комбинации: глазки, фрагменты линий, крючки и
мостики. Количество их намного больше, чем количество глобальных осо-
бенностей, поэтому они позволяют значительно точнее идентифицировать
отпечаток пальца.
Ниже показывается, как метод поля направлений может быть применен
для обнаружения и определения координат глобальных особенностей, для
оценки их геометрических характеристик и для процедур поиска локальных
признаков дактилограмм. Для вычисления поля направлений в данном случае
возможно использование спектрального (п.7.5.5) или проекционно-диспер-
сионных методов (п.7.5.4), так как методы параметрической аппроксимации
(п.7.5.1) не могут быть применены из-за высокой пространственной частоты
квазипериодической структуры, сравнимой с частотой дискретизации дакти-
лографического изображения. В данных исследованиях был использован про-
екционно-дисперсионный метод, дающий четыре градации направления, а
также градиентный метод с использованием синусоидальной аппроксимации
(п.7.5.2). На рис. 7.40 приведены исходное изображение и результаты расчета
поля направлений.
Непосредственное использование поля направлений (рис. 7.406) для об-
наружения глобальных особенностей невозможно из-за большого количе-
ства шумов. Для подавления шумов был использован сглаживающий линей-
ный фильтр (7.11). Многократное применение сглаживающего фильтра по-
зволяет восстановить «глобальное» поле направлений линий папиллярного
узора (рис. 7.416). При этом, естественно, теряется информация о локаль-
ных неоднородностях, что в нашем случае следует считать оправданным.
Заметим еще одну особенность линейного сглаживания поля направлений:
многократное применение линейного фильтра не приводит к вырождению
поля направлений в константу, как это имеет место при линейной фильтра-
ции функции яркости. Это утверждение справедливо при наличии на исход-
ном изображении замкнутых или радиально расходящихся линий, что всегда
выполняется для дактилоскопических изображений.
В целях сравнительного анализа был исследован также и аддитивно-рав-
номерный фильтр (7.15) и (7.16) применительно к тому же исходному полю
направлений (см. рис. 7.406). Результаты представлены на рис. 7.42.
7.6. Обработка и интерпретация дактилоскопических изображений
499
Рис. 7.40. Построение поля направлений для дактилоскопического изображения: а — функция
яркости исходного изображения; б — четырехградационное поле направлений, рассчитанное
проекционно-дисперсионным методом
Рис. 7.41. Результаты фильтрации поля направлений: а — линейное сглаживание (окно 7x7,
1 проход); б — линейное сглаживание (окно 7x7, 10 проходов)
а б -в
Рис. 7.42. Результаты применения аддитивно-равномерного фильтра к полю направления, пред-
ставленному на рис. 7.40ft а — без весовой функции, окном 5x5, количество итераций 228 (ста-
ционарная точка); б — с весовой функцией, окном 5x5, количество итераций 155 (стационарная
точка); в — без весовой функции, окном 7x7, количество итераций 176
500
ГЛАВА 7
В результате проведенных исследований было показано наличие стацио-
нарной точки аддитивно-равномерного фильтра, которая достигалась после
нескольких сотен итераций при размере окна обработки 5x5. Это свойство
также показывает родство аддитивно-равномерного фильтра с медианным
фильтром [13].
7.6.1. Геометрические характеристики глобальных особенностей
дактилограмм
Поиск глобальных особенностей основан на использовании четырехграда-
ционного поля направления. Для приведения непрерывных значений поля
направлений к четырем градациям воспользуемся номерами секторов (0, 1, 2, 3),
определяемыми следующим диапазоном углов: 0 — (0°-22° и 158°—180°), 1 —
(23°—67°), 2 — (68°— 112°), 3 — (113°—157°). Центры приведенных диапазонов
соответствуют углам 0°, 45°, 90°, 135°. Окрестность каждой точки изображения
отпечатка пальца характеризуется определенным порядком смены значений
поля направлений. Для глобальных особенностей этот порядок отличается от
порядка произвольной точки отпечатка. Так, например, особенность «дельта»
определяется следующей конфигурацией: 1—2—3—0. В табл. 7.1 приведено со-
ответствие различных конфигураций поля направлений и основных типов
особых точек, а соответствие исходного изображения и поля направления
вблизи особой точки показано на рисунке 7.43.
Определение глобальных особых точек осуществляется обработкой поля
направлений скользящим окном и поиском указанных конфигураций на его
границе. Размер окна должен быть достаточно большим, так как при фильт-
Таблица 7.1. Соответствие конфигураций поля направлений и типов особых точек
Конфигурация Тип особой точки
1-O-3-2-1-0-3-2 0-3-2-1-0-3-2—1 3-2-1-0-3-2-1-0 2-1-O-3-2-1-O-3 центр спирали
0-1-2-3 1-2-3-O 2-3-0-1 3-0-1-2 дельта
1-0-3-2 O-3-2-1 3-2-1-O 2-1-0-3 петля
2-1-0-1 продолжение двойной левой петли
3-2-3-O продолжение двойной правой петли
1-0-3-0 шатер
7.6. Обработка и интерпретация дактилоскопических изображений
501
рации поля направлений происходит сглаживание его значений. Сглажива-
ние особенно сильно заметно в областях больших перепадов значений поля
(стыковки различных направлений папиллярных линий), соответствующих
как раз окрестностям глобальных особых точек. С другой стороны большой
размер маски не дает точного местоположения найденной особой точки.
Уточнение ее расположения осуществляется следующим способом. Умень-
шим размер маски на единицу. Проанализируем четыре возможных положе-
ния малой маски: если хотя бы в одном из них требуемая конфигурация
сохраняется, то малую маску рассматриваем как исходную и процесс повто-
ряем. Иначе за местоположение особой точки принимаем координаты цент-
ра исходной маски.
Спираль
Дельта
Рис. 7.43. Интерпретация дактилограмм
502
ГЛАВА 7
Среди особых точек, найденных описанным выше способом, существует
множество ложных — из-за недостоверности определяемых значений поля
направлений на краях изображений. Кроме того, в силу специфики поля на-
Рис. 7.44. Поиск особых точек дактилограмм
правлений конфигурация особой точ-
ки типа «центр спирали» из-за раз-
мытости фильтрованного поля не до-
стигается, и в районе «центра»
появляется группа конфигураций
ложных особых точек типа «петля», а
при наличии конфигурации «петли»
ниже нее обязательно имеется мно-
жество конфигураций ложных «шат-
ров» (рис. 7.44). Для отделения истин-
ных глобальных особенностей точек
и определения их геометрических ха-
рактеристик производится анализ
списка всех найденных особых точек
по следующему алгоритму.
- Отсечение краевых точек по двум
порогам, пропорциональным разме-
ру изображения поля (коэффициент
определен из экспериментальных исследований). Меньший порог соответ-
ствует отсечению всех найденных точек, второй — всех кроме «дельт». Такой
подход обосновывается строением рисунка отпечатка пальца.
- Удаление ложных «шатров». Если выше «шатра» имеется какая-либо осо-
бая точка, то этот «шатер» является ложным.
- Объединение группы близко расположенных «петель» в особую точку
типа «центр» с координатой, равной центру тяжести группы.
- Определение геометрических характеристик «спиралей» (правое или ле-
вое закручивание, угол наклона большой оси симметрии) и «дельт» (углы,
определяющие ориентацию дельты).
- Классификация «петель» (простая, двойная, правая, левая), определение
угла наклона оси «петли».
7.6.2. Оценка геометрических характеристик глобальных особенностей
В качестве геометрических признаков особенностей типа «дельта» исполь-
зуются четыре угла наклона линий раздела областей с различными значениями
поля направления. Наклон большой оси симметрии «спирали» выражается че-
рез углы наклона двух секторов поля направлений, соответствующих горизон-
тальным папиллярным линиям. Для определения правого и левого закручивания
и его степени используется следующие три величины (признака).
7.6. Обработка и интерпретация дактилоскопических изображений
503
1. Признак К, характеризует степень отклонения оси спирали от вертикаль-
ного положения:
а-90°
к, —------,
90°
где а — угол наклона большой оси симметрии спирали.
При вертикальном расположении оси закручивание отсутствует и спираль
вырождается в серию концентрических эллипсов.
2. Признак К2 характеризует ширину вертикального пучка линий по разным
сторонам спирали:
К2 = --1 ~Si—,
max(5z,5r)
где длины сечений областей поля направлений со значениями 90°,
расположенных слева и справа от центра спирали. Сечение производится на
некотором расстоянии ниже центра по всей ширине изображения поля на-
правлений. Признак использует тот факт, что количество вертикальных ли-
ний меньше с той стороны спирали, куда направлен процесс закручивания.
3. Признак характеризует несимметричность расположения дельт отно-
сительно центра спирали:
К3 = ,
max( dhdr)
где dlydr — расстояние от центра спирали до соответственно левой и правой
дельт. Признак использует тот факт, что ближайшая «дельта» расположена со
стороны закручивания.
Каждый из описанных выше признаков характеризуется положительным
значением К, при правом закручивании. Для достоверности определения при-
знака закручивания используется следующая величина:
n=1(n,+n2+n3).
Направление закручивания определяется знаком К, а степень — ее моду-
лем. Анализ петель (простая, двойная, правая, левая), определение угла на-
клона оси петли основан на следующих утверждениях:
- если имеются точки типа «продолжение двойной петли» то петля явля-
ется двойной и признается правой или левой в соответствии с типом точек
продолжения петли;
- если петля является простой, то она признается правой или левой в за-
висимости от расположения дельты, а угол наклона простой петли выражает-
ся через один из углов, определяющих ориентацию дельты;
- угол наклона двойной петли при условии, что точек продолжения бо-
лее одной (рис. 7.45), выражается средним арифметическим двух углов: угла,
определенного по дельте, и угла наклона касательной к линии расположения
504
ГЛАВА 7
Рис. 7.45. Геометрические характеристики глобальных особенностей
точек продолжения; если точка продолжения одна, то угол наклона определя-
ется так же, как для простой петли.
7.6.3. Обнаружение мелких нерегулярностей отпечатка пальца
Кроме описанных выше особенностей, характеризующих отпечаток в це-
лом, существуют особенности другого типа. Это места разветвления, слия-
ния, обрыва линий, составляющих папиллярный узор. Метод обнаружения
точек нарушений основан на том, что вблизи искомой точки нарушается не-
прерывность (в случае обрыва) или однозначность касательной (в случае раз-
ветвления) папиллярной линии. Для поиска особенностей необходим бинар-
ный препарат папиллярного узора, который получается при помощи выделе-
ния хребтов и логической фильтрации (скелетизации и протяжки) (рис. 7.46).
Рис. 7.46. Предварительная обработка папиллярного узора при поиске локальных особенностей:
а — исходное изображение; б — выделение хребтов; в — скелетизация и протяжка бинарного
препарата
7.6. Обработка и интерпретация дактилоскопических изображений
505
Точки папиллярных линий лежат в центре светлых полос исходного изоб-
ражения (хребтов). Выделение центров полос можно рассматривать как зада-
чу выделения хребтов на двумерной поверхности, определяемой функцией
яркости изображения. Рассмотренный в [18] метод выделения полос, исполь-
зуемый для решения поставленной задачи, дает изображение папиллярных
линий, имеющее два недостатка: толщина линий более одного пиксела и на-
личие разрывов. Утоньшение папиллярных линий достигается с помощью
скелетизации бинарного изображения. Устранение ложных разрывов произ-
водится процедурой протяжки, основанной на построении четырех логичес-
ких фильтров, каждый из которых соответствует значению четырехградаци-
онного поля направления. Производится анализ всевозможных комбинаций
яркости внутри маски.
Поиск мелких нерегулярностей осуществляется сканированием скелетизи-
рованного бинарного изображения квадратной маской. Анализируя только
границы маски, фиксируется количество пересекающих ее папиллярных ли-
ний. Несовпадение количества входящих и выходящих линий означает нали-
чие точки нарушения. Стороны маски, пересечения которых соответствуют
входящим и выходящим линиям, определяются по значениям поля направле-
ний. Линии подсчитываются по количеству перепадов яркости точек грани-
цы. Результатом описанного процесса являются два изображения, одно из
которых характеризует местоположение точек нарушений, а другое является
изображением их плотности, определяющейся количеством нарушений внут-
ри маски большего размера с центром в текущей точке. Изображение отпе-
чатка пальца имеет высокое качество не по всей своей площади, что является
следствием неидеальных условий получения оттиска. В областях низкого ка-
чества папиллярные линии выделяются недостоверно, поэтому их нарушения
рассматривать нецелесообразно. В дальнейшем классификации подвергаются
точки нарушения, находящиеся в области высокого качества. Данная область
определяется с помощью описанного ниже критерия качества.
Оценка областей высокого качества папиллярного узора. Определим три кри-
терия качества. Первым критерием является плотность нарушений папилляр-
ного узора. При этом было установлено, что чем больше плотность наруше-
ний, тем ниже качество изображения. На качественных участках изображе-
ния отпечатка пальца разброс угла нефильтрованного поля направлений мал.
Благодаря этому коэффициент доверия (весовая функция) отсчетов фильтро-
ванного поля направлений достаточно велик в отличие от разрушенных участ-
ков. Поэтому вторым критерием качества можно взять значение весовой фун-
кции отсчета поля направлений. Отметим, что вес мал не только на участках
низкого качества, но и в окрестности глобальных особых точек из-за большо-
го изменения значения угла. Но это не влияет на результат, так как окрестно-
сти глобальных особых точек эквивалентны разрушенным участкам в смысле
достоверности папиллярного узора. При построении рассмотренных выше
критериев исходное изображение отпечатка пальца используем косвенно.
Для повышения качества выделения достоверных участков был использован
дополнительный критерий, получаемый непосредственно по исходному
506
ГЛАВА 7
изображению. Качественные участки изображения отпечатка пальца имеют
структуру чередующихся полос, что приводит к большему разбросу значений
яркости, чем на участках низкого качества, которые более однородны по яр-
кости. Таким образом, если строить локальные гистограммы по участкам изоб-
ражения, то количество пиков локальной гистограммы на разрушенных участ-
ках будет меньше, чем на качественных. Количество пиков локальной гистог-
раммы принято за третий критерий качества. На рис. 7.47 представлены этапы
формирования критериев качества и отсева ложных локальных особенностей
дактилограммы.
е
Рис. 7.47. Этапы формирования критериев качества и отсева
ложных локальных особенностей дактилограммы: а — дакти-
лограмма; б — точки нарушения папиллярного узора; в — плот-
ность нарушений узора; г — количество пиков локальной гис-
тограммы; д — весовая функция поля направлений; е — еди-
ный критерий качества; ж — истинные точки нарушения
7.6. Обработка и интерпретация дактилоскопических изображений
507
Для составления единого критерия качества воспользуемся методикой объе-
динения свидетельств, разработанной в экспертной системе MYCIN [19].
Согласно указанной выше методике каждому элементарному высказыванию
и правилу ставится в соответствие число (вес), называемое фактором уверен-
ности CF, определяемое следующими мерами:
МВ[Н,Е] — мера возросшей веры в гипотезу Н на основе свидетельства Е;
MD[H,E] — мера возросшего неверия в гипотезу Н на основе свидетель-
ства Е.
Указанные меры определяются через вероятности соответствующих выс-
казываний:
Р(Н) = 1
МВ[Н,Е] = так[Р(Н / Е),Р(Н)] — Р(Н)
1, Р(Н) = \
MD[H,E]= Р(Н)-тп[Р(Н / Е),Р(Н)]
Р(Н)
Р(Н)^\,
CF[H,E] = МВ[Н, Е] - MD[H, Е].
Необходимость введения, наряду с мерой подтверждения, независимой от
нее меры опровержения аргументируется ссылкой на мнение ряда филосо-
фов, занимающихся разработкой теории подтверждения. В соответствие с те-
орией субъективных вероятностей, авторы системы MYCIN полагают, что в
каждый момент времени вера субъекта в гипотезу Н выражается вероятнос-
тью Р(Н). При этом человек оперирует высказываниями вида: «Если про-
изошло событие Е, прирост моей веры в гипотезу Н характеризуется числом
х». Такой интерпретацией высказываний мотивируется принятие в качестве
основных мер возросшей веры и неверия. В системе MYCIN функции, реали-
зующие объединение двух свидетельств, постулируются, так как в общем слу-
чае меры МВ[Н,ЕХ &Е2] и MD[H,EX &Е2] нельзя выразить через величины
МВ\Н,ЕХ], MD[H,Ei\, МВ[Н,Е2], MD[H,E2]. По мнению авторов схемы
вполне удовлетворительной является аппроксимация истинных значений МВ
и MD по формулам:
(0, MD[H,E,&E2] = 1,
МВ[Н,Е,&Е2] = 1 2
1 2 [МВ[Н,ЕХ] + МВ[Н,Е2]-МВ[Н,ЕХ]-МВ[Н,Е2], MD[H,ЕХ&Е2\^\,
0, МВ[Н,Е} &Е2] = 1,
A/D[E,E,&E9]= 1 2
1 2 [Л/О[/7,Е1] + Л/В[Е,Е2]-Л/Р[Е,Е1]МО[/7,Е2], МВ[Н,Ех&Е2]*1.
Пусть Н — гипотеза о том, что текущая точка принадлежит области высоко-
го качества изображения. Исходя из экспериментальных данных, априорную
508
ГЛАВА 7
вероятность гипотезы Р(Н) принимаем равной 2/3. Пусть 7, — значения ярко-
сти в текущей точке изображения количества пиков на гистограмме, /9,/3 —
значения весов поля направлений и плотности нарушения папиллярного узора
соответственно. Тогда согласно построенным критериям качества изображе-
ния: Р(Я/Е1) = 71/255, Р(Н/Е2) = /2/255, Р(Я/Е3) = 1-73/255. Объедине-
ние трех свидетельств произведем в два этапа. Первым этапом объединяем два
свидетельства, вторым — результат и третье свидетельство. При этом общий
результат не зависит от порядка объединения.
Классификация локальных нарушений папиллярного узора. Классификации
будем подвергать только те точки, которые лежат на выделенных качествен-
ных областях изображения, где единый критерий качества превышает неко-
торый порог, установленный с помощью экспериментальных исследований.
Анализируем четыре типа точек: левое разветвление и обрыв, правое разветв-
ление и обрыв. Характерные конфигурации приведены для различных на-
правлений линий на рис. 7.48. Для большей досто-
верности распознавания анализу подвергаем допол-
нительно восемь граничащих точек, местоположение
которых зависит от значения поля направления дак-
тилограммы в особой точке. Полученную совокуп-
ность граничащих точек разобьем на две группы: с
местоположением до классифицируемой точки по
направлению линии и с положением после нее.
Последовательно выдвигаются четыре гипотезы
о типе точки и в каждой группе подсчитывается число
конфигураций, не противоречащих гипотезе. В ка-
честве типа точки нарушения выбирается тип, для
которого соответствующая гипотеза имеет наиболь-
шее число подтверждающих конфигураций. Если таких конфигураций мень-
ше двух, то это означает отсутствие нарушения папиллярной линии.
В результате процедуры распознавания особых точек можно сформировать
список, содержащий следующую информацию о локальных особых точках
(рис. 7.49): тип особой точки, декартовы координаты, угол, определяющий
направление линии в данной точке.
Для сличения следа и изображения отпечатка пальца на дактилокарте не-
обходимо, чтобы полученные характеристики особых точек были инвариант-
ны к различным геометрическим искажениям (изменение масштаба, поворот
изображения). Это достигается переходом к полярной системе координат, где
полюс находится в центре спирали, шатра или петли (предполагается, что
отпечаток имеет особую точку одного из этих трех типов). Полярная ось рас-
полагается вдоль главной оси отпечатка (оси «лапки», используемой в систе-
ме идентификации «фрагмент» (см. рис. 7.45). Преобразованный список то-
чек нарушений папиллярного узора содержит полярные координаты точки
нарушения (полярный угол отсчитывается против часовой стрелки и записы-
вается в градусах от 0° до 360°), тип точки нарушения, угол, определяющий
7.7. Обработка и интерпретация кристаллограмм слезной жидкости
509
Рис. 7.49. Классификация локальных особенностей папиллярного рисунка
направление линии в 4 градациях. Погрешность обнаружения локальных на-
рушений описанным выше методом составила 7—8% относительно априор-
ной информации данной дактилокарты.
7.7. Обработка и интерпретация кристаллограмм слезной
жидкости
В последние годы применение компьютерных методов обработки медико-
диагностических изображений стало одним из важнейших инструментов на-
учных исследований и повышения эффективности ранней диагностики глаз-
ных заболеваний.
Здесь рассматривается диагностика патологических изменений в органах
зрения [6, 20, 8, 7] на основе анализа кристаллограмм слезной жидкости
(рис. 7.50).
Слезная жидкость является индикатором нарушения обменных процессов
при различной патологии органа зрения. С биохимической точки зрения сле-
за представляет собой многокомпонентную химическую систему. Биохими-
ческие исследования позволяют оценить только некоторые ее показатели [21,
22]. Известные лабораторные тесты требуют значительного количества иссле-
дуемой жидкости, дорогостоящего лабораторного оборудования и реактивов.
В настоящее время невозможно провести одновременное тестирование слезы
на наличие всех составляющих ее компонентов. Поэтому сейчас представля-
ют интерес для клиницистов диагностические методики, позволяющие оце-
нить структурные нарушения исследуемой биологической жидкости доступ-
ными способами. В основу данных исследований был взят кристаллографи-
ческий метод, дающий представление о фундаментальной картине структуры
веществ. Он рекомендован в широкую медицинскую практику как дополни-
тельный тест для дифференцированной диагностики воспалительных, опухо-
левых и дистрофических заболеваний органа зрения.
510
ГЛАВА 7
Рис. 7.50. Кристаллизация слезной жидкости в присутствии
хлорной меди: а — изображение всего кристалла; б — увели-
ченные фрагменты
Основные принципы кристаллографического метода были разработаны
Т.Е. Ловицем в 1804 году. В офтальмологии он стал широко применяться в
последнее десятилетие.
Существует несколько способов получения кристаллограмм. В одном из
них в слезную жидкость до высушивания вводится кристаллообразующая
жидкость (см. рис. 7.50). Метод кристаллизации слезы в присутствии хлорной
меди был разработан О.Б. Ченцовой с соавторами в 1988 г. [3, 23]. Метод
считается значительно более чувствительным, чем другие, в которых биоло-
гическая жидкость высушивается и после чего проводится микроскопия сухо-
го остатка (рис. 7.51). Основу метода [3, 23] составляет кристаллографическое
Рис. 7.51. Чисто высушенная слеза: а — норма; б — патология
7.7. Обработка и интерпретация кристаллограмм слезной жидкости
511
исследование слезы с использованием классификационных диагностических
признаков анализируемой структуры.
Автоматизированный анализ является более объективным и дает возмож-
ность получать не только качественную, но и количественную оценки струк-
турных нарушений кристаллограмм [24, 25]. Ниже приводятся методы авто-
матизированного анализа кристаллограмм, исследование их диагностической
ценности, методы формализации медико-диагностических признаков и фор-
мирования количественных вероятностных оценок патологии на основе сис-
темы геометрических признаков кристаллограмм. Результатом работы диа-
гностики является интегральная оценка вероятности патологии исследуемой
кристаллограммы, объединяющая все критерии классификации.
7.7.1. Медико-диагностические признаки кристаллограмм
С помощью методики [26] на основе анализа изображений кристаллограмм,
априори разделенных врачом-офтальмологом на нормальные и имеющие па-
тологии (рис. 7.52), были выделены глобальные диагностические признаки
классификации кристаллограмм, базирующиеся на оценках геометрических
параметров исследуемой квазипериодической структуры и используемые для
экспертной оценки патологии глаза.
Согласно данной методике при отсутствии глазных заболеваний различно-
го рода кристалл слезы является прозрачным, содержит длинные, тонкие,
преимущественно одного направления лучи, которые имеют четкие границы
и исходят из единого центра, имеющегося на изображении или из невидимо-
го, воображаемого центра. При патологии лучи отличаются неровными кон-
турами, кристаллы непрозрачны (высокая плотность кристаллов), наблюдает-
ся много поломок, наростов, большой разброс направлений линий кристал-
лов, на изображении имеется множество центров, из которых исходят лучи.
Отличительной особенностью патологии является также большая густота лу-
чей кристаллов на отдельных участках.
На основе экспертных оценок выделены несколько формальных призна-
ков, позволяющих произвести классификацию кристаллограмм:
- однонаправленность лучей кристалла;
- относительная площадь участков с качественными лучами кристалла;
- густота лучей;
- прозрачность кристалла.
7.7.2. Оценка геометрических параметров кристаллограмм
Большинство из рассматриваемых характеристик кристаллограмм базиру-
ются на понятии поля направлений.
Критерий однонаправленности лучей кристалла слезы. Кристаллограммы слез-
ной жидкости при отсутствии патологических изменений в органах зрения
512
ГЛАВА 7
Кристаллограммы в норме
Кристаллограммы с патологией
Рис. 7.52. Характерные изображения кристаллограмм слезной жидкости в норме и при патоло-
гических изменениях органа зрения
характеризуются явно выраженной однонаправленностью лучей кристалла,
то есть имеют небольшой разброс направлений лучей (рис. 7.53).
Введем критерий однонаправленности лучей кристалла слезы следующим
образом: чем меньше значение показателя критерия однонаправленности К]у
тем меньше разброс направлений лучей. Показатель критерия вычисляется на
основе анализа фильтрованного поля направлений изображения кристаллов.
Для обнаружения скачков поля направлений (контуров) целесообразно ис-
7.7. Обработка и интерпретация кристаллограмм слезной жидкости
513
Исходное изображение
Фильтрированное поле
направлений
Контурный препарат поля
направлений
Кристаллограмма слезы в норме
Исходное изображение
Фильтрированное поле
направлений
Контурный препарат поля
направлений
Кристаллограмма слезы при патологии
Рис. 7.53. Иллюстрация критерия однонаправленности
пользовать квадрат модуля градиента комплексного поля направлений (7.9)
(см. п.7.2):
Т(*1»*г) =
ду(х!,х2)2
дх2
2
При единичной весовой функции получаем
c?sin 2\|/(jc1 , jc2 )
дх2
dcos2\|/(xi, х2 )V
дх2
(7.39)
За показатель критерия однонаправленности кристаллограммы можно при-
нять среднее по изображению значение величины у(х1}х2) (7.39):
Kl ^x^x2^dxidx2-
17 _ 9044
514
ГЛАВА 7
Контурная характеристика поля направлений показана на рис. 7.53.
Критерий относительной площади участков с четкими линиями. На рис. 7.52
можно заметить неоднородность изображения кристаллограмм слезной жид-
кости: существуют участки с нечеткими размытыми линиями, иногда имеют-
ся крупные однородные пятна. При патологических изменениях наблюдается
увеличение относительной площади данных участков. Весовая функция комп-
лексного поля направлений (7.9) принимает большие значения в областях
изображения, где линии выражены отчетливо (рис. 7.54) (см. п.7.1). Поэтому
введем критерий оценки областей с качественными линиями по относитель-
ной площади участков с наибольшим значением весовой функции поля на-
правления кристаллограммы. Из экспериментальных исследований установ-
лено пороговое значение веса, разделяющее области с явно выраженной чет-
костью линий от «плохих» участков. Алгоритм расчета заключается в пороговой
обработке изображения «весов» (см. рис. 7.54). Количественным показателем
критерия является коэффициент четких линий:
k2=sp/s,
где 5 — площадь всего изображения, Sp — суммарная площадь участков, на
которых значение весовой функции не меньше порогового значения.
Критерий густоты лучей кристалла. В ходе экспериментальных исследова-
ний в офтальмологии на натурных изображениях при значительном увели-
чении плотности лучей кристалла было отмечено повышение вероятности
заболевания. На основании этого был сформулирован признак плотности
линий на изображении кристалла. Его количественный показатель можно
определить, исходя из частотных свойств функции яркости изображения. В
качестве критерия классификации примем среднее значение густоты лучей
кристалла. Усреднение должно проводиться по областям изображения с боль-
шим значением весовой функции поля направлений, на которых значение
пространственной частоты является достоверным. Коэффициент густоты
определим как среднее значение квадрата пространственной частоты функ-
ции яркости кристаллограммы, найденной методом «основной локальной
частоты» (см. п.7.5.5):
*з=А»2.
где со2 =со2 +св|, ю1, — искомые пространственные частоты, D — область
четких линий.
Критерий прозрачности кристаллограммы. Вероятность наличия у человека
заболевания глазного дна увеличивается с уменьшением прозрачности крис-
таллограммы слезы. Введем критерий прозрачности кристалла. Прозрачность
кристаллограммы будем определять, используя вероятностное распределение
функции яркости. «Прозрачная» кристаллограмма характеризуется положи-
7.7. Обработка и интерпретация кристаллограмм слезной жидкости
515
Исходное изображение
«Вес» поля направлений
«Вес» поля направлений
после пороговой обработки
Кристаллограмма слезы в норме
Исходное изображение
«Вес» поля направлений
Кристаллограмма слезы при патологии
Рис. 7.54, Иллюстрация критерия относительной площади участков с четкими линиями
«Вес» поля направлений
после пороговой обработки
тельным смещением среднего значения яркости f относительно срединного
значенияf> fc, где fc = (/max + /min)/2. Для «непрозрачной» кристаллограм-
мы f <fc (рис. 7.55). Количественным выражением данного критерия явля-
ется коэффициент
K4=(f~fc)/f.
Гистограмма функции яркости определяется по областям четких линий.
Для уменьшения влияния шумов минимальная и максимальная яркость
вычисляются через квантили распределения:
/max > /max) = Ро > /min P(f <f^n) = P0^,
где pQ ^0,024-0,1.
Кристаллограммы характеризуются неравномерной яркостью. С другой
стороны, изображения различных кристаллов обладают неодинаковой ярко-
стью фона из-за невозможности обеспечения одинакового равномерного ос-
вещения слезной жидкости при фотосъемке и вводе изображения. Поэтому
необходимо проводить выравнивание яркости, при котором сохранится конт-
раст между лучами кристалла и фоном в их окрестности. Оценка параметров
производится по изображениям с выровненной яркостью.
17»
516
ГЛАВА 7
а
Рис. 7.55. Распределение яркости для прозрачного (а) и непрозрачного (б) кристаллов
7.7.3. Классификация кристаллограмм на основе объединения
диагностических признаков
Решение о наличии патологии зависит от уровня нормы образца по каждо-
му отдельно взятому параметру кристаллограммы: R = G(P}, Р2, Р3, Р4), где
Pi = Р(К,) — уровень (вероятность) нормы по /-му диагностическому при-
знаку, Ki — величина признака, R — уровень нормы по четырем признакам.
Оценка уровня нормы отдельного образца при классификации, проводимой
только по /-му признаку, строится следующим образом:
1, Kt>K^
к — кп
i i К П К < К Н
К “—К"' ‘
(7.40)
О, Ki<K-t
где К" — порог патологии, К" — порог нормы. Для конкретного признака
классификации пороги К", К" выбираются на основе априорной информа-
ции, известной по каждому признаку. В качестве оценки уровня нормы об-
разца при классификации, проводимой по четырем признакам, будем исполь-
зовать следующую линейную функцию:
r} =p1eJ+P2e2+P3e3+P404, (7.41)
где 6Z — весовые коэффициенты, =1. Экспериментальные исследова-
ния, проводимые по указанной методике, показывают, что рассмотренные
выше признаки имеют различную значимость при диагностике кристалло-
граммы. Некоторые кристаллограммы априорно отнесены врачами к пато-
логическим из-за явно выраженного патологического характера только по
одному критерию классификации, достаточно важного для диагностики, не-
смотря на высокие значения уровней нормы по другим признакам. Поэтому
введем понятия весового коэффициента оценок уровней нормы по /-му при-
знаку, учитывающему важность (значимость) данного признака и использу-
ем его при объединении критериев классификации. Вес признака можно
7.7. Обработка и интерпретация кристаллограмм слезной жидкости
517
задать величиной дискриминантной (разделяющей) способности данного при-
знака. Дискриминантную способность определим как обратную величину к
минимальному риску для порогового классификатора. Порог определяется
по выборочным данным на основе априорной информации врача. Можно
показать, что в этом случае весовые коэффициенты определяются следую-
щим образом:
©,=«,/£>*. (7.42)
i=k
где и, — количество правильно классифированных кристаллограмм по /-му
признаку.
Рассмотрим другой подход к оценке уровня нормы по всем выбранным
признакам (7.39) на основе оптимального объединения. Он использует ап-
риорную информацию врача р7 о наличие патологии на изображениях
обучающей выборки (у — номер изображения). Тогда параметры линейной
функции
/?2 = ©о + Р{ со, + Р2со2 + Р3со3 + Р4со4 (7.43)
определим из условия минимума среднеквадратичной ошибки аппроксима-
ции функции априорной оценки:
N
I = 52(соо + со,Р,' + со2Р' + со3Р' + со4Р4 - р7 )2 — min,
«=|
где р7 — априорная оценка врача (1 — норма, 0 — патология), N — объем
выборки.
Для интерпретации уровня нормы образца в качестве вероятности нормы
проведем нормализацию к диапазону [0;1 ] следующим образом:
р _ Р,со, + Р2со2 + Р3со3 + Р4со4
со, +со2+со3+со4
7.7.4. Экспериментальное исследование методов анализа кристаллограмм
Для нахождения параметров системы диагностики (границ нормы и патоло-
гии в (7.40), весовых коэффициентов функций (7.40, 7.42)) проводились иссле-
дования по обучающей выборке, состоящей из 20 натурных изображений (10 —
норма, 10 — патология). Результаты выборочной классификации показаны в
табл. 7.2. Здесь тип соответствует априорной оценке офтальмолога для изобра-
жения (Н — норма, П — патология); Р, — Р4 — оценки уровней нормы по
соответствующим признакам классификации; Р,, Р2 — результирующие оцен-
ки уровней нормы, полученные разными способами объединения критериев
518
ГЛАВА 7
Таблица 7.2. Результаты классификации по обучающей выборке
Изображение Поле направлений Тип Pl Pa Ps c. z?2 c2
SfcJl » * ' "W * H 0,634 0,4 0,964 1 0,72 + 0,73( +
k JRBW к я П 0,466 0,4 0,896 0,294 0,47 + 0,585 +
ggg пр 1 H 0,846 1 0,816 1 0,924 + 0,86 +
f- $'> H 1 1 0,44 0,294 0,72 + 0,782 +
’^•ЯКЯийЛ* w » A П 0 0 1 0 0,15 + 0,3 IS +
н 1 H 0,863 1 0,476 0,824 0,83 + 0,751
L П 0,614 0,525 0,456 1 0,67 - 0,57f +
7.8. Обработка и интерпретация кристаллограмм плазмы крови
519
классификации (R2 — ПРИ оптимальном); Сн С2 — соответствие результата
классификации априорной оценке при пороговом значении введенного уров-
ня нормы, отделяющем норму образца от патологии, полученном из условия
минимума ошибочной классификации: Р° =0,60. При объединении крите-
риев первым способом (7.40) ошибочная классификация составляла 10% (в
двух случаях априорной патологии наблюдалась норма). При оптимальном
объединении ошибок не наблюдается.
Для исследования качества диагностики были проведены испытания на
проверочной выборке, состоящей из 105 изображений (34 — нормы, 71 —
патология). Используя найденные параметры системы оптимального объе-
динения и оптимальное пороговое значение (Р° =0,5845), только на двух
образцах, имеющих априорную норму на выходе системы, получена патоло-
гия и на восьми образцах с априорной патологией — норма. Можно сделать
предположение, что одной из причин ошибочной классификации может
являться тот факт, что качество ввода изображения проверочной выборки в
ходе эксперимента было выше, чем обучающей, что привело к неоднород-
ности объединенной выборки. В ходе экспериментальных исследований в
сотрудничестве с офтальмологами была найдена вторая причина ошибочной
классификации кристаллограмм с априорной патологией. Часть признаков,
немаловажных для диагностики глазных заболеваний, оказалась за преде-
лом анализа. Они не были обнаружены и формализованы вследствие отсут-
ствия их в обучающей выборке, а также вследствие частичной потери их в
процессе ввода изображений (не достаточно высокое разрешение ввода, на-
личие шумов). Этими признаками являются локальные характеристики лу-
чей кристалла: отсутствие центра кристаллизации (рис. 7.56я), кристаллиза-
ция на посторонних включениях (рис. 7.566); мелкие дефекты: множествен-
ные включения — природные шумы кристалла (признак воспаления и
опухоли) (рис. 7.56в,г), обильные наросты на лучах кристалла (рис. 7.566),
неровные контуры луча (утолщения на концах, выемки на протяжения луча
(рис. 7.56е)).
Глобальная диагностика кристаллограмм, построенная с использованием
метода поля направлений, позволила выделить из множества кристаллограмм
группы нормы и патологии, определить количественное выражение глобаль-
ных признаков классификации кристаллограммы и определить уровень нор-
мы по каждому признаку классификации.
Для повышения достоверности классификации кристаллограмм слезной
жидкости необходимо провести изучение и формализацию локальных диа-
гностических признаков кристаллов, что составляет предмет дальнейших ис-
следований. Более детальная обработка на основе дополнительной серии при-
знаков позволит в дальнейшем перейти к дифференциальной диагностике, то
есть выявлять отдельные группы заболеваний: опухоли, дистрофические и
воспалительные заболевания.
520
ГЛАВА 7
а
б
в
Рис. 7.56. Примеры кристаллограмм с локальными признаками патологии
7.8. Обработка и интерпретация кристаллограмм плазмы крови
Впервые исследования в области анализа кристаллографических текстур
биологических субстратов были представлены Jiri Hozman в 1995 году. Объек-
том его исследований были кристаллограммы кровяной плазмы (рис. 7.57а).
В работах [4] им описаны методы автоматизированной компьютерной оцен-
ки характеристик кристаллограмм плазмы. Главный подход, предложенный
им к описанию данной кристаллографической структуры, — это количествен-
ная оценка ее текстуры. Для этого использовались спектральные методы.
В спектральном подходе было использовано преобразование Фурье и некото-
рые спектральные признаки текстуры: форма частотного спектра — располо-
жение, размер, ориентация главных пиков, энтропия нормализованного спектра
в областях частот и др. Спектр мощности и фазовый спектр определялись в
локальной области однородной текстуры. По выделенным локальным облас-
тям вычислялись среднее и дисперсия каждого текстурного признака. Был
также использован морфологический подход вместе с последующим анали-
зом форм. Морфологический подход анализа кристаллограмм основан на ис-
пользовании двумерного преобразования Фурье (Хартли), проведении мор-
фологии полутонового и бинарного изображения спектра и анализа получен-
ной в результате данной обработки формы (признак компактности). Указанные
7.8. Обработка и интерпретация кристаллограмм плазмы крови
521
Норма
Патология
Рис. 7.57. Этапы обработки кристаллограмм кровяной плазмы по представленной в п.7.7 мето-
дике: а — исходные изображения, соответствующие норме и патологии; б — поля направлений;
в — сглаженные поля направлений
522
ГЛАВА 7
Норма
Патология
а
б
Рис. 7.58. Этапы обработки кристаллограмм кровяной плазмы по представленной в п.7.7 мето-
дике: а — весовые функции полей направлений; б — пороговая обработка полей весов; в —
контурные препараты полей направлений
7.9. Обсуждение результатов
523
подходы чрезвычайно трудоемки с вычислительной точки зрения. Предлага-
ется использовать геометрический подход к анализу данной структуры, бази-
рующийся на методе поля направлений (рис. 7.57, 7.58). На представленных
на рис. 1.51а изображениях кристаллограмм кровяной плазмы можно заме-
тить сходство диагностических признаков (нормы и патологии) данных структур
с кристаллограммами слезной жидкости. Используем разработанную методику
анализа кристаллограмм слезной жидкости (п.7.7) для нового класса объектов.
На рис. 7.58, иллюстрирующем этапы обработки кристаллограммы плазмы
крови, можно зафиксировать заметную разницу результирующих изображе-
ний анализа структур с нормой и патологией. Особенно эта разница заметна
на препарате поля направлений (рис. 7.576), где в случае нормы ясно про-
слеживается направление лучей центрального кристалла. Препарат с пато-
логией характеризуется наличием более мелких кристаллов с искривленны-
ми лучами, что эквивалентно наличию множества центров кристаллизации
и беспорядочной структуре поля направления. То же самое можно сказать
про контурный препарат поля направлений (рис. 7.58в) и весовую функцию
(рис. 7.58я). Существенную часть кристаллограммы без патологии составляют
однонаправленные четкие лучи центрального кристалла (рис. 7.586). Они ха-
рактеризуются наибольшим значением весовой функции.
Для представленных на рис. 1.51а кристаллограмм плазмы крови с нормой
и патологией были определены абсолютные значения следующих параметров
квазипериодической структуры (табл. 7.3.), определенных в п.7.7.2: коэффи-
Таблица 7.3. Значения параметров для кристаллограммы плазмы крови (рис. 7.57с)
Признак Норма Патология
Коэффициент однонаправленности лучей 658 307
Коэффициент площади четких линий 0,4 0,19
Коэффициент густоты 45,6 72,8
Прозрачность кристалла -0,06 0,02
Признак компактности 1,871229 1,102622
циент однонаправленности лучей кристалла, коэффициент площади четких
линий, коэффициент густоты лучей и прозрачности кристалла. Для сравне-
ния приведены значения признака компактности для данного изображения,
представленного Jiri Hozman в статье [4], полученного на основе анализа формы
структуры бинарного изображения спектра кристаллограммы.
Сравнивая два различных подхода (геометрический и спектральный) для
анализа кристаллограммы плазмы крови, можно сделать вывод, что отличие
заключается лишь в использовании различных вспомогательных объектов
обработки: либо это изображение поля направления, либо изображение спектра
структуры (морфологический подход [4]). Поле направлений является пред-
почтительнее, т.к. позволяет сохранять пространственную структуру анализи-
руемого объекта и его локальные свойства и позволяет использовать простые
и быстрые алгоритмы его расчета.
524
ГЛАВА 7
7.9. Обсуждение результатов
Метод поля направлений является эффективным методом анализа изоб-
ражений, характеризуемых наличием квазипериодических структур. Приме-
нение метода поля направлений позволяет сократить структурную избыточ-
ность изображений за счет перехода от функции яркости к функции, опи-
сывающей локальную ориентацию квазипериодической структуры — полю
направлений. Признаки изображения, рассчитанные по полю направлений,
существенно отличаются от традиционно используемых признаков, таких
как моментные функции, геометрические параметры, спектральные при-
знаки и т.п. Использование признаков поля направлений позволяет эффек-
тивно решать задачи обработки интерферограмм, кристаллограмм и дакти-
лограмм. Предложенные численные методы оценивания поля направлений
имеют различные характеристики эффективности (точности и быстродей-
ствия). Все методы разбиты на пять классов в зависимости от используемой
модели представления поля направлений и подхода к его вычислению: ме-
тоды параметрической аппроксимации, методы локальных градиентов, диф-
ференциальные методы, проекционно-дисперсионные методы, спектраль-
ные методы. Для оценки точности методов в качестве критерия использова-
лась приведенная угловая среднеквадратичная погрешность, рассчитанная с
использованием комплексного поля направлений. Для каждого типа изоб-
ражений выявлен наиболее эффективный класс методов. Например, для
диагностики дактилограмм и кристаллограмм эффективными методами по-
строения полей направлений являются спектральные и проекционно-дис-
персионные методы.
Рассмотрен ряд прикладных задач обработки изображений с использова-
нием метода поля направлений. В задаче обработки дактилограмм использо-
вание поля направлений позволяет эффективно выделять глобальные особен-
ности отпечатков пальцев — тип узора (характерные конфигурации располо-
жения папиллярных линий: «петля», «дельта», «спираль», центры петель). Также
метод может быть применен для определения координат глобальных особен-
ностей, для оценки их геометрических характеристик и для процедур поиска
локальных признаков дактилограмм (мелких нерегулярностей папиллярного
узора, включающих в себя точки разрыва, ветвления и слияния линий папил-
лярного узора, а также их комбинации: глазки, фрагменты линий, крючки и
мостики). Глобальная диагностика кристаллограмм, построенная с использо-
ванием метода поля направлений, позволила выделить из множества кристал-
лограмм группы нормы и патологии, определить количественное выражение
глобальных признаков классификации кристаллограммы (однонаправленность
лучей кристалла, относительная площадь участков с качественными лучами
кристалла, густота лучей, прозрачность кристалла) и определить уровень нор-
мы по каждому признаку классификации.
Литература к главе 7
525
Литература к главе 7
1. Храмов А. Г. Методы восстановления интерферограмм на ЭВМ. Оптичес-
кая запись и обработка информации, (Куйбышев: КуАИ, 1988)
2. Руководство по системе «Фрагмент» (УВД Куйбышевского горисполко-
ма, 1976)
3. Ченцова О.Б., Прокофьева Г.Л. Кристаллографический метод обследования
при некоторых заболеваниях глаз (М.: 1988)
4. HozmanJ., Kubinec R., TrnkaJ., Varenka J. Biomedical Image Processing
Applications. Biomedical Engineering & Biotechnology, (Praha: Publishing House
of the Czech Technical University, 1995)
5. Ильясова Н.Ю., Устинов A.B., Храмов А.Г. Научное приборостроение
3 (Санкт-Петербург, 1993) С. 89
6. Ильясова Н.Ю., Устинов А.В. Тезисы доклада на 2-ой международной кон-
ференции «Распознавание-95» (Курск, 1995) С. 248
7. Дворянова Т.П., Ильясова Н.Ю., Устинов А.В., Храмов А.Г. Компьютер-
ная оптика 16 90 (1996)
8. Dvoryanova Т.Р., Ilyasova N. Yu., Ustinov A.V., Khramov A.G., in Proceedings
of 13th biennal international conference Biosignal-96, (Brno, Check Republic,
1996) P. 29
9. Soifer V.A., Kotlyar V.V., KhoninaS.N., and Khramov A.G. Pattern
Recognition and Image Analysis. 6(4) 710 (1996)
10. Математическая энциклопедия. T. 3 / Под ред. И.М. Виноградова (М.:
Советская энциклопедия, 1982)
11. Мардиа К. Статистический анализ угловых наблюдений (М.: Наука, 1978)
12. Устинов А. В. Компьютерная оптика 19 (1999)
13. Yustonson B.L, in Fast Algorithms in Digital Image Processing (M: Radio i Svyaz,
1984) P. 156
14. Glumov N.I., Krainukov N.I., Sergeyev V.V., Khramov A.G. Pattern Recognition
and Image Analysis 4 424 (1991)
15. Бронштейн И.Н., Семендяев К.А. Справочник no математике (1956)
16. Сергеев В.В., Фролова Л.Г. Автометрия 1 22 (1996)
17. Хермен Г. Восстановление изображений по проекциям: Основы реконструк-
тивной томографии (М.: Мир, 1983)
18. Крайнюков Н.И., Сойфер В.А., Храмов А.Г. Автометрия 1115 (1991)
19. Хачатрян А.Р. Техническая кибернетика 2 (1988)
20. Дворянова Т.П., Ильясова Н.Ю., Овчинников К.В., Устинов А.В., Хо-
нина С.Н. Материалы международной конференции офтальмологов, посвя-
щенной 75-летию профессора А.М. Водовозова, труды Волгоградской меди-
цинской академии наук 50(1) 172 (1995)
21. Чеснокова Н.Б. МРЖЗ (1986)
22. Харченко С., Корнеева Г., Ветров А. Известия АН СССР. Серия биологи-
ческая 3 (1988)
526 ГЛАВА 7
23. Модифицированная методика изучения кристаллограмм слезы. Тезисы док- ладов 6съезда офтальмологов России (М.: 1994)
24. KhoninaS.N., Kotlyar V.V., Soifer V.A., DvoryanovaT.P. Proceedings SPIE 2363 249 (1994)
25. Soifer V.A., Khonina S.N., Ilyasova N. Yu., and Kotlyar V.V. Structural methods in pattern recognition using optical Karhunen-Loeve expansion. Proceedings of SSPR (1994)
26. Дворянова Т.П. Кристаллографическое исследование слезной жидкости при воспалительных заболеваниях глаза. Диссертация на соискание степени канд. мед. наук. (Волгоград, 1999)
ГЛАВА 8
ПАРАЛЛЕЛЬНО-РЕКУРСИВНЫЕ МЕТОДЫ
ЛОКАЛЬНОЙ ОБРАБОТКИ ИЗОБРАЖЕНИЙ
8.1. Цифровые параллельно-рекурсивные фильтры
с конечной импульсной характеристикой
8.1.1. Обработка изображений в скользящем окне
В основе многих процедур обработки и анализа цифровых сигналов лежит
операция линейной обработки «скользящим окном». Как известно, ее смысл
состоит в том, что некоторая ограниченная двумерная область — «окно обра-
ботки» последовательно (например, в порядке построчной развертки) зани-
мает все возможные положения в плоскости изображения, и для каждого по-
ложения окна по значениям лежащих в нем входных отсчетов вычисляется
значение одного отсчета выходного изображения.
Пространственно-инвариантная (не зависящая от координат) обработка
такого вида описывается общим соотношением
£(п],п2) = б[{/(«1 (8.1)
где /(«1, я2)> ~ двумерные последовательности отсчетов входного и
выходного изображения соответственно; G — оператор преобразования, D —
конечное множество отсчетов, заданное относительно начала координат и
определяющее форму и размеры окна обработки (рис. 8.1).
Наибольший интерес представляет преобразование дискретизированного
сигнала Л ПП-системой с конечной импульсной характеристикой — КИХ-фильт-
ром [16, 25]. Как известно, значения сигнала на выходе КИХ-фильтра явля-
ются результатом цифровой свертки входного сигнала с импульсной характе-
ристикой фильтра и могут быть найдены взвешенным суммированием вход-
ных отсчетов в пределах окна обработки. Однако такое вычисление свертки
(«прямая» реализация КИХ-фильтра) имеет практический смысл лишь для
малых размеров окна, то есть для короткой импульсной характеристики, по-
скольку объем вычислений здесь пропорционален числу ненулевых отсчетов
последней. Для больших окон (в задачах фильтрации и восстановления
528
ГЛАВА 8
о о о о о о
о
о
о
о о о о о
D —
о о о о о
о о о ]о о
о о о о о о
о о о о о о
о О О о о о
о о о о О о
о о X о о о
о о о о о о
о о о о о о
о о о о о о
,«2 )
Рис. 8.1. Схема обработки изображения в скользящем окне
сигналов, корреляционного обнаружения объектов, синтеза изображений рель-
ефа по радиоголограммам и т.д.) прямое вычисление свертки оказывается чрез-
мерно трудоемким. Известные многочисленные алгоритмы быстрой свертки
для КИХ-фильтров общего вида также далеко не всегда решают проблему
сложности обработки данных даже при использовании алгоритмов, описанных
в главе 5. В этой ситуации представляется перспективным применение алго-
ритмов, воплощающих идею параллельной рекурсивной реализации КИХ-фильт-
ров [30, 31, 36, 37] позволяющей резко снизить вычислительные затраты при
обработке изображений.
При рекурсивном формировании результата обработки при каждом по-
ложении окна используются не только отсчеты входного изображения (из
множества Z)), но и вычисленные до данного шага отсчеты обработанного
изображения. Известные рекурсивные алгоритмы реализуют вычисление ло-
кальных спектров изображения, статистических характеристик (средней яр-
кости, дисперсии, гистограммы и т.д.), фильтрацию (линейную и нелиней-
ную) с целью подавления шумов, устранения частотных искажений, выделе-
ния контуров и т.д. [18, 20, 24, 35, 37, 40]. Линейные рекурсивные фильтры в
общем случае являются фильтрами с бесконечной импульсной характеристи-
кой (БИХ-фильтрами). Широкое использование двумерных БИХ-фильтров
затрудняется необходимостью решения проблемы их устойчивости [16, 28].
Однако существует класс заведомо устойчивых КИХ-фильтров, также допус-
кающих рекурсивную реализацию [30, 31].
Наиболее простую структуру имеют рекурсивные КИХ-фильтры с импульс-
ной характеристикой, разделимой по координатам. Применение такого фильт-
ра может быть сведено к обработке изображения одномерными рекурсивны-
ми КИХ-фильтрами (путем организации рекурсивной обработки каждого
столбца изображения по отдельности и построчной рекурсивной обработки
результатов фильтрации в столбцах). Вычислительная сложность рекурсив-
ных КИХ-фильтров не зависит от размеров окна обработки D (которое зада-
ет область ненулевых отсчетов импульсной характеристики фильтра), а оп-
ределяется только сложностью рекурсий.
8.1. Цифровые параллельно-рекурсивные фильтры
529
К сожалению, для области D произвольной формы нельзя организовать
разделимую рекурсивную фильтрацию. Однако на практике обычно ограни-
чиваются прямоугольными областями:
D: -М; <тх<М^\ -М2<т2<М2, (8.2)
где Л/j",М]+ ,М2 ,М2 — параметры, задающие границы окна по координа-
там (М]“ + > О, М2 + М2 > 0). Во многих алгоритмах обработки изоб-
ражений удобно использовать прямоугольное окно, симметричное относи-
тельно центрального элемента:
D: — Л/j <т1 <М,, — М2<т2< М2
(8-3)
8.1.2. Принципы построения параллельно-рекурсивных КИХ-фильтров
Рассмотрим сначала более простой и наглядный случай обработки одно-
мерных сигналов. Преобразование КИХ-фильтром бесконечной последова-
тельности отсчетов входного сигнала f (л) в выходную последовательность g (л),
как известно, описывается соотношением «конечной свертки»:
м +
g(«) = 52 Л(т)/(и-т), (8.4)
т——М ~
где h (w) — импульсная характеристика фильтра, равная нулю вне интервала
j—М~, М + ] длиной N — М~ + М + +1, величины М~, М + задают размер
окна обработки и его положение относительно формируемого выходного от-
счета. Параллельно-рекурсивный КИХ-фильтр представляется в виде К па-
раллельных звеньев, и, следовательно,
К-1
h(m) = ^2akhk (/и), (8.5)
к—0
К-1
у(п) = ^акук(п), (8.6)
к=0
М +
Ук(")= 52 hk(m)f(n~m), (8.7)
т=—М~
где ак — коэффициенты, hk (т) — линейно независимые базисные функ-
ции (конечные ядра) разложения h (т) в ряд (8.5), то есть импульсные харак-
теристики параллельных КИХ-звеньев, ук (л) — сигналы на выходах звеньев
(0<к < К — 1). Причем к каждому звену предъявляется требование эффек-
тивной рекурсивной реализации, то есть описания достаточно простым
530
ГЛАВА 8
разностным уравнением. Последнее означает, что передаточная функция
(^-преобразование импульсной характеристики) звена
«.(?) = Ё hk(rn)z-m
т=—<х
(8.8)
должна записываться в дробно-рациональной форме, как отношение полино-
мов от комплексной переменной z, состоящих из небольшого числа слагае-
мых [25, 29].
Исходя из сказанного, определим общий вид импульсных характеристик
рекурсивно реализуемых КИХ-звеньев. Интервал, ограничивающий ненуле-
вые отсчеты конечной импульсной характеристики, можно задать через «пря-
моугольный импульс»:
П (тп) = и [т — у) — и (тэт — 5),
(8.9)
где
м(т) =
1 при т > 0
0 при т < 0
— функция единичного скачка, у, S — целые константы, определяющие по-
ложение импульса на оси аргумента (у < 5). Последовательность (8.9) имеет
^-преобразование, которое может быть представлено в дробно-рациональной
форме:
ОС с 7 -у _ 7 5
Яп(г) = Е П(т)г~” = z~T+z~Y++—+z~8~'= f. (8.10)
т=—оо 1 Z
Известны трансформации произвольной последовательности, не увели-
чивающие ее длину и сохраняющие дробно-рациональность z-преобразова-
ния: умножение на коэффициент, целую положительную степень аргумента
и экспоненту [25, 29]. Применяя их к функции (8.9), получаем, что последо-
вательность
П(т) = Sm°p-mn(m),
(8.11)
при целом неотрицательном а и произвольных S, р, также будет иметь конечную
длину и дробно-рациональное ^-преобразование. Учтем далее, что каждая базис-
ная функция hk (т) может быть составлена из нескольких последовательностей
вида (8.11), и введя необходимую индексацию постоянных, получим, что
Lk-1
Мш) = 5/*)],
/=0
(8-12)
где Lk, а1к, у1к, 8ik — целочисленные (Lk >1, alk >0, —М <y/Jt <6ZJt <
<M+), a Slk, filk — произвольные вещественные или комплексные кон-
8.1. Цифровые параллельно-рекурсивные фильтры
531
станты. Подстановка выражения (8.12) в (8.8) с учетом (8.9), (8.10) и свойств
^-преобразования [25,29] дает
1=0
d d d
z— z— ...z~~
dz dz dz
а1к ' раз
(8.13)
Формулы (8.12), (8.13) могут использоваться для конструирования различ-
ных базисов разложения (8.5) и получения передаточных функций рекурсив-
ных звеньев. Так, при надлежащих значениях параметров из (8.12) следует
базис комплексных дискретных экспоненциальных функций, базис Фурье в
вещественной форме, косинусный базис и т.д. Выбор конкретных параметров
в (8.12), (8.13) следует производить из соображений простоты получающихся
КИХ-звеньев (очевидно, в частности, что Lk и а[к должны быть невелики) и
достаточности малого числа слагаемых в разложении (8.5) для качественного
решения определенной задачи обработки сигналов. Некоторые базисы для пред-
ставления импульсных характеристик параллельно-рекурсивных КИХ-фильт-
ров будут детально рассмотрены ниже.
Представленные выше результаты легко обобщаются на двумерный слу-
чай. Для двумерного сигнала (изображения), заданного отсчетами f(nltn2)
на бесконечном квадратном растре, результат обработки КИХ-фильтром вы-
ражается через двумерную свертку:
^(и],л2)= 52 (ni ~т{,п2~~т2\ (8.14)
(mj,/n2)
где /1(м|,м2) — импульсная характеристика двумерного фильтра, D — ко-
нечная область ее ненулевых значений. Как и в одномерном случае, для быст-
рого параллельно-рекурсивного вычисления свертки (8.14) необходимо, что-
бы импульсная характеристика фильтра имела представление в виде суммы
К-1
h[mxjn2} — '^akhk (т{,т2},
к-О
(8.15)
при небольших К, а базисные функции этого разложения соответствовали
импульсным характеристикам рекурсивных КИХ-звеньев. При выполнении
(8.15) выходной сигнал фильтра будет формироваться из сигналов с выходов
параллельных звеньев:
(8.16)
К-1
*==0
532
ГЛАВА 8
где
Ук^Ъ^ 12 Т\(т\’т2}/(п\~т\>п2~т2)- (8.17)
(mi ,т2) €D
Поскольку для области D произвольной формы нельзя предложить удоб-
ную общую формулу для двумерных рекурсивных базисных импульсных ха-
рактеристик hk (т},т2), то обычно рассматриваются прямоугольные области
вида (8.2) и разделимые звенья [6, 16, 36, 37р.
hk (wi. ™2) = hfi (wij)h® (m2). (8.18)
При этом для каждого сомножителя в (8.18) можно воспользоваться «од-
номерной» общей формулой (8.12). Реализация разделимого звена заключает-
ся в последовательной (каскадной) обработке двумерного сигнала сначала по
одной, а затем по другой координате:
^(м],л2)= 12
М 2
12 h^4m2)f(ni ~т[,п2 -т2)
т2~-М2
(8.19)
Значения у*(п,,п2) можно интерпретировать как линейные локальные
признаки изображения, которые используются при решении различных задач
обработки изображений. Поскольку вычисление этих признаков можно про-
изводить путем последовательной обработки по каждой из координат, то це-
лесообразно рассматривать построение базисов и алгоритмы обработки в од-
номерном варианте, а затем обобщать результаты на двумерный случай.
8.1.3. Рекурсивно реализуемые базисные функции
Задача конструирования базиса для разложения (8.5) импульсной харак-
теристики КИХ-фильтра решается эвристически с учетом удобства программ-
ной или аппаратной реализации фильтра, эффективного «покрытия» рас-
сматриваемого множества процедур обработки сигналов ит.д. Это решение
удобно разбить на два этапа. На первом определяется класс базисных функ-
ций, строится алгоритм и оценивается сложность их рекурсивного вычисле-
ния. На втором этапе из множества функций данного класса выбираются К
базисных функций, обеспечивающих требуемое качество и простоту обра-
ботки. Здесь мы остановимся на первом этапе решения задачи. Второй, тре-
бующий привлечения показателей эффективности обработки сигналов, бу-
дет рассмотрен ниже.
Опишем несколько видов одномерных рекурсивно реализуемых базисных
функций с указанием их соответствия общей модели (8.12) и выводом разно-
стных уравнений.
8.1. Цифровые параллельно-рекурсивные фильтры
533
Прямоугольный базис. Семейство прямоугольных ядер [36,37] состоит из
функций
Л* (т) = м(т-у*)-м(т-8*)
(8.20)
и соответствует случаю, когда в (8.12)
= Ро* = 1» аок Чок~Ук’ — М + .
Передаточная функция (8.10) записывается в виде
Из (8.21) следует простое разностное уравнение, описывающее процесс
рекурсивного вычисления свертки (8.7):
У к (п) = Ук (л+ )“/("" 5Д
(8.22)
Здесь и везде ниже при записи разностных уравнений не оговариваются
начальные условия, то есть все преобразуемые последовательности считаются
неограниченными по аргументу и принимающими нулевые значения в «ми-
нус бесконечности».
Для получения очередного значения последовательности ук (л) по форму-
ле (8.22) нужно выполнить всего две арифметические операции: сложение и
вычитание. Крайняя простота формирования локальных линейных призна-
ков, сводящегося здесь к рекурсивному суммированию отсчетов изображения
в скользящих прямоугольных окнах, является несомненным, но, возможно,
единственным достоинством ядер этого семейства.
Косинусный базис. В работах [6,18] при анализе сигналов на скользящем
интервале было предложено использовать семейство ядер косинусного бази-
са. В [31] показано, что для наиболее быстрого рекурсивного вычисления
свертки (8.7) такие ядра следует брать в нетрадиционной «разнормирован-
ной» форме:
М™) =
+ ^—и(т — М+ — 1^, (8.23)
где jk — целочисленный индекс ядра (0 <Д < TV- 1, jp j при р* q). Функ-
ции (8.23) получаются из общей формулы (8.12) при Lk = 2, аок = аи =0,
534
ГЛАВА 8
exp
л^Н-2Л/
2N
exp
к(1 + 2М“)л
—/—-------
2/V
$0к
2 cos
л .
2N Jk
$1к
п 71 •
2cos-----/л
2/V
Рол = ехР
. л .
I—Jk
N к
а . л I
Pi*=exp'i—Л ,
Чок=Ък=~М , bf)k=S[k=M + +1.
Подставив эти параметры в (8.13), находим выражение для передаточной
функции формирующего цифрового фильтра:
ZM~-(-lYk z~M^
]-2cos ^-jk z 1 +Z 2
(8.24)
N
Как видно из выражения (8.23), значение индекса jk = 0 порождает прямо-
угольное ядро, для которого свертка (8.7) рекурсивно вычисляется с помощью
простейшего алгоритма вида (8.22). Ненулевые значения индекса требуют по-
строения рекурсивного вычислительного процесса, исходя непосредственно из
передаточной функции (8.24). Легко показать, что получение любых ук (п) здесь
может быть описано следующей системой разностных уравнений:
71(л)=/(л+м)-/(я-м+-1)>
/2 (») = f(n + -М*-1),
/4(л) = /2 (л)-/2(л-1),
№ W = № («-O + Zi (л), при Д=0,
У к (л) = 2 cos jk j (п -1) - ук (п - 2) + /3 (п), при jk Ф 0 и кратных 2,
У к (л) = 2 cos Ijk j ук (п -1) - ук (л - 2) + /4 (л), при Jk не кратных 2,
(8.25)
8.1. Цифровые параллельно-рекурсивные фильтры
535
При использовании системы (8.25) для вычисления К значений одномер-
ных сверток (8.7) с косинусными ядрами (в том числе и с ядром при jk = 0),
число операций сложения и умножения равно соответственно (2К + 3) и
(К- 1). Иными словами, при /Г>>1 на одном шаге вычислительные затраты
в среднем составляют примерно по два сложения и одному умножению на
каждую свертку.
Базис комплексных дискретных экспонент. Базис комплексных дискретных
экспоненциальных функций (ДЭФ), рассматриваемый на TV-точечном окне,
состоит из N ортогональных функций одинаковой протяженности, которые
мы запишем в обобщенном (по сравнению с [1, 24, 36, 37]) виде:
hk(m) = exp i
т~ М +-
(8.26)
где jk — индекс функции (целочисленная «частота»), 0< jk <N — l, jk^ j
при p^q, (pk — ее фаза, вещественная постоянная. Выражение (8.26) соот-
ветствует общей формуле (8.12) при
Lk =1, S0Jt =exp(i(pj, аок =0, P0jt = ехр ~i—jk
У ok — — Л/ + +1.
После подстановки этих параметров в (8.13) получаем передаточную функ-
цию звена фильтра:
M
z — z_______
.2л .
211
Hk(z) = expi -jkM~+(pk
1 —exp Z~’
N
Положим
2л .
Тогда выражение (8.27) максимально упрощается:
„М" -м+-\
Z — Z
~ (.2л . 1 -j
l-exph~A z
(8.27)
(8.28)
536
ГЛАВА 8
и функции базиса ДЭФ приобретают вид
hk(m) = exp
т + М
(8.29)
Звену с передаточной функцией (8.28), осуществляющему преобразование
(8.7), соответствует разностное уравнение:
1 /
Ук (я) = ехР|'дГА Л (л-1) + /(л + Л/
)-/(«
-м+
-1
(8.30)
Заметим, что в уравнении (8.30) имеется комплексный множитель, из-за
которого и последовательность ук (и) оказывается комплекснозначной (ис-
ключение составляет только случай jk =0, когда базисная функция (8.29)
является прямоугольной, и формула (8.30) совпадает с (8.22)). При использо-
вании в разложении импульсной характеристики произвольного набора из К
базисных функций полный сигнал на выходе фильтра также будет принимать
комплексные значения. Отсюда можно заключить, что применение базиса
ДЭФ в параллельно-рекурсивных КИХ-фильтрах является естественным при
обработке именно комплексных сигналов.
Для сигналов, принимающих вещественные значения, следует рассматри-
вать только вещественную часть импульсной характеристики фильтра с бази-
сом ДЭФ. Однако можно показать, что такая модификация процедуры обра-
ботки, по существу, означает переход к базису Фурье в вещественной форме,
для которого достижима более простая реализация рекурсии.
Вещественный базис Фурье. Вещественный базис Фурье формируется из
взятых отдельно вещественных и мнимых частей функций базиса ДЭФ (8.26),
то есть включает в себя базисные функции двух видов:
/£os(w) = cos +
cpfc lulm + Af ) — —
(8.31)
^in(w) — sin^^ A'W 4-<p£'j +Af ^ — u[m - M+ -1J, (8.32)
где, как и раньше, jk, j[' — целочисленные индексы, не повторяющиеся для
функций каждого вида, jp jg , jp * j', при р q, (рк, <р^ — фазы, при-
нимающие равные значения для каждой пары функций (8.31) и (8.32) с оди-
наковыми индексами; <рА = ср^/, при jk = Jk>.
8.1. Цифровые параллельно-рекурсивные фильтры
537
Пусть для функции (8.32) с индексом д# = N/2 выполняется условие
(8.33)
для любых целых г. Тогда базис является ортогональным и полным на /V-точеч-
ном окне, если он включает в себя функции (8.31) и (8.32) со всеми значени-
ями индексов из интервалов
N
2’
N
2
Выражения (8.31) и (8.32) можно получить из общей формулы (8.12), если
в ней положить
~ Lk>—2, аол а1л ол'“а1л' О»
$0к'
=0,5ехр(/ф*), = 0,5ехр(-дрД
X]
Л
2J
t / /
= 0,5ехр i ф*/ — — , Slk> — 0,5ехр —/1фЛ
2)
Рол = ехР
,2л . 1 „ (.2л . 1
R -2Л •'
Рол'=ехР
R (-271 '
Р1л'“ехР t-jfh’
Тол *“ Т1Л ~ Тол' — У\кг “ М , 30А. — 8и — Ь()к> — 81Л/ — М +1.
Подставив эти параметры в формулу (8.13) и приведя в ней дробно рацио-
нальные слагаемые к общему знаменателю, получим выражения для переда-
точных функций КИХ-звеньев двух типов:
cos
2л ,
-cos 57
_____
+<Рл
(-Л/--1) +ф,
1 -2cos — jk z 1 + z 2
UV Ч
(8.34)
538
ГЛАВА 8
sin - — j'k'M 4- ip'., - sin - ~/к>(м
N k k ) N k\
2n
N
1- 2cos 2л ' z l + Z 2
(8.35)
Если взять конкретные значения фаз (удовлетворяющие условию (8.33))
Ф* =~Jk (M -0,5), ф'г =~j'k>(M -0,5),
то передаточные функции (8.34) и (8.35) упрощаются:
2л J|z z
cos — ik
(TV
(8.36)
2л .
. n . —1—2
l-2cos —jk z + z
N
. 2л
sin —jk>
t JV k
М~ —Л/ + —1
z -Z
2л ./
1 —2cos — jk> z + z
(TV
(8.37)
Отбросив в формулах (8.36), (8.37) постоянные для каждой функции коэф-
фициенты, приходим к еще более простым выражениям:
М~ _ г-/И + -1 -1
1 - 2cos '2л . 1 г-1 + z-2
(8.38)
М -М+-1
Z —Z
1 — 2cos '2л ' Л \ z~'+z~2
(8.39)
которые будем считать окончательными.
Выполнив те же упрощающие действия над последовательностями (8.31),
(8.32), можно убедиться, что ^-преобразованиям (8.38) и (8.39) соответствуют
модифицированные функции вещественного базиса Фурье:
8.1. Цифровые параллельно-рекурсивные фильтры
539
h^Cm)
(8.40)
sin
2п ./ _ 1 ]
— i,i т + М + —
JV Ч 2)
. | 7С ./
sin —J.i
{N к
и\т + М )— и(т~ М+— 1
(8-41)
Эти функции с точностью до коэффициентов совпадают с вещественными
и мнимыми частями комплексных базисных функций сдвинутого дискретно-
го преобразования Фурье (СДПФ) с параметрами сдвига (0,5; 0) [37] для сиг-
нала на интервале аргументов Л/+].
Из выражений (8.38), (8.39) видно, что передаточные функции звеньев имеют
общие независимые от индексов множители. Это позволяет построить эконо-
мичные с вычислительной точки зрения каскадные рекурсивные процедуры
получения отсчетов на выходах звеньев. Если не учитывать возможные совпа-
дения индексов базисных функций (8.40) и (8.41), то рекурсивный вычисли-
тельный процесс можно описать следующей системой разностных уравнений:
У к («) =
yr(n) = 2cos
nl’-V+JiW ПРИ
f 2it
2cos — jk Ук(п-1)-ук(п-2) + /2(П) при
177
Л2л
t N
— /г У к' (л-0-У к-("“ 2)+/з(») ЧРИ
jk=o>
Л . N (8-42)
0< Уг<—.
* 2
При построении этой системы учтено, что среди рассматриваемых базис-
ных функций, как и в базисе ДЭФ, имеется одна прямоугольная (функция
(8.40) с индексом jk =0), и для соответствующего ей КИХ-звена реализова-
на упрощенная схема рекурсивных вычислений.
Если базисные функции (8.40) и (8.41) входят в разложение (8.5) только
парами, при одинаковых значениях индексов (jk = за исключением «пря-
моугольника» (8.40) при jk = 0, для которого пары нет, то фильтр оказывается
540
ГЛАВА 8
более простым. Действительно, в данном случае вместо системы уравнений
(8.42) можно построить другую, обеспечивающую меньшие вычислительные
затраты:
fi (n) = f(n + M')-f(n-M + -1),
fP (") = J к) ("-!)- (« - 2) + fi W>
Ук (n-lj + f (n)
Ук' (n) + f^ (л-1)
при Л =0.
при о<Л«
при J к' “ J к
jV
2 ’
(8.43)
8.1.4. Секционирование импульсной характеристики КИХ-фильтров
Параллельно-рекурсивные фильтры позволяют резко снизить вычислитель-
ную сложность обработки сигналов по сравнению с прямой сверткой: объем
вычислений в них пропорционален не размерам окна обработки, а всего лишь
небольшому числу используемых параллельных звеньев. Но существует еще
одна, дополнительная возможность уменьшения сложности фильтров за счет
выбора в разложении (8.5) базисных функций специального вида.
Пусть базисные функции разложения (8.5) одномерной импульсной харак-
теристики КИХ-фильтра отличаются друг от друга только сдвигом, то есть
имеют вид
hk(m) = hx (m-yk)t (8.44)
где h* (m) — последовательность конечной длины, задающая базис разложе-
ния; ук — целая константа — параметр сдвига к-й базисной функции относи-
тельно А4 (ли). В свою очередь КИХ-фильтр с импульсной характеристикой
hs (m) представим в виде L параллельных рекурсивно реализуемых звеньев:
hs (т) = hi Н > (8.45)
z=o
где {А/}/=0 — коэффициенты разложения импульсной характеристики hs (т).
Подставим (8.44), (8.45) в (8.7) и далее в (8.6):
К-1 L—\ К-\ L\
8(n)-=^ak^biyi(n~yk)=^ (8.46)
к=0 1=0 к=0 1=0
8.2. Параллельно-рекурсивные КИХ-фильтры
541
где
м,+
yi(n)= zC т), (8.47)
т——М[
— целые константы, определяющие границы области ненулевых
значений функций Л/(т), ск1 — коэффициенты. Из полученных соотноше-
ний видно, что в рассматриваемом случае обработка данных может быть орга-
низована в два шага. Сначала, в соответствии с (8.47), производится рекур-
сивное вычисление сверток входного сигнала с импульсными характеристи-
ками Затем по (8.46) выполняется взвешенное суммирование только
некоторых точек (отсчетов) промежуточных последовательностей, получен-
ных на первом шаге.
В частном случае описанную процедуру можно интерпретировать как сек-
ционирование заданной импульсной характеристики h (т). Разобьем ее об-
ласть ненулевых отсчетов [— М~, М + ^ на К непересекающихся равных ин-
тервалов длиной 7V' = N/К. На каждом из интервалов h (т) представим в виде
линейной комбинации базисных функций:
L-1
i—о
Очевидно, свертка входного сигнала/(п) с секционированной импульсной
характеристикой h (т) может быть определена по формулам (8.46), (8.47).
Благодаря использованию базисных функций со сдвигом вида (8.44), для
разложения импульсной характеристики может быть значительно уменьшена
сложность рекурсивного вычисления сверток (8.47). Поэтому предлагаемый
метод секционирования во многих случаях позволяет дополнительно снизить
вычислительную сложность обработки сигнала.
8.2. Параллельно-рекурсивные КИХ-фильтры
с полиномиальными импульсными характеристиками
8.2.1. Полиномиальные базисы и обобщенные моменты
Во многих прикладных задачах анализа изображений возникает необходи-
мость обработки изображения КИХ-фильтром с импульсной характеристи-
кой, описываемой степенным полиномом:
К L
Ь{т^т2)=^И^к1т\т2^ (8.48)
*=0 /о
при (nZ|,m2)€£>, где К, L — степени полинома по каждой из перемен-
ных; {ац}*До ~ ег0 коэффициенты. Представление (8.48) является весьма
542
ГЛАВА 8
универсальным и может быть использовано при сглаживании изображений,
формировании признаков двумерных объектов в скользящем окне, цифровом
моделировании линейных искажений оптических сигналов ит.д. [7, 9, 14, 49].
Особое значение степенные полиномы имеют для вычисления так называе-
мых «моментных инвариантов» — признаков, обладающих инвариантностью
к преобразованиям изображения типа «поворот» и «масштабирование» [21,
38, 39, 48, 50].
Несложно показать, что, с одной стороны, степенной полином (8.48) все-
гда может быть преобразован к виду
К L
*=о/=о
(8.49)
где
к
Як № = 12^™
i=0
(8.50)
— любой «одномерный» полином к-го порядка с коэффициентами
{Pw}ju=o~ коэффициенты разложения импульсной харак-
теристики по двумерному факторизуемому полиномиальному базису, введен-
ному выражениями (8.49) и (8.50). С другой стороны, формула (8.48) может
считаться частным случаем формулы (8.49), в котором у базисных функций
(8.50) все коэффициенты кроме старших равны нулю. Таким образом, соот-
ношения (8.48) и (8.49) эквивалентны с точки зрения описания импульсной
характеристики КИХ-фильтра, однако, как будет показано ниже, выражение
(8.49) более удобно для построения быстродействующих алгоритмов обработ-
ки изображений.
Подставив (8.49) в (8.14), получаем выражение для сигнала на выходе
КИХ-фильтра, отличающееся от (8.16) двумерной индексацией линейных
признаков:
К L
g(nx,n2)^£ ЕРи Ц н (л, , п2). (8.51)
Jt=O/=O
Величины Hw(ni»n2)> называемые иногда «обобщенными моментами»,
определяются как свертки входного сигнала с полиномиальными факторизу-
емыми ядрами
Ц*/(л1««2)= 12 Ияк(т})Я1^2)/(п1-т\^п2~т2У (8-52)
8.2. Параллельно-рекурсивные КИХ-фильтры
543
Полагая, что окно обработки D имеет прямоугольную форму (8.2), получа-
ем для вычисления обобщенных моментов выражение, аналогичное (8.19):
Mt
m2— ~М 2
,т\=~М\
(8.53)
Как и в общем случае, описанном в п.8.1.2, вычисление обобщенных мо-
ментов можно производить путем последовательной обработки по каждой из
координат, что дает основание ограничиться построением и исследованием
одномерных полиномиальных базисов. Алгоритмы обработки сигналов фильт-
рами с полиномиальными импульсными характеристиками, разработанные в
одномерном варианте, легко обобщаются и на двумерный случай.
8.2.2. Параллельно-рекурсивные алгоритмы вычисления обобщенных
моментов
Вычисление обобщенных моментов для произвольного полиномиального бази-
са. Итак, для последовательно возрастающих значений аргумента п требуется
вычислять одномерные обобщенные моменты для полиномиальных базисных
функций (8.50):
м+
= 52 <Ик(т) Q<k<K. (8.54)
т—-М~
Очевидно, выражение (8.54) аналогично формуле (8.7), если в ней исполь-
зовать базисные функции
к .г \ / \1
hk (т)" Y^akim> м и” + A/'J- и (т - М+ -11. (8.55)
Поскольку формула (8.55) является частным случаем (8.12), то и здесь при-
менима общая методика построения разностных уравнений, описывающих
параллельное рекурсивное вычисление сверток (8.54), через передаточные
функции вида (8.13). Однако для полиномиального базиса разностные схемы,
сконструированные независимо для различных звеньев, оказываются весьма
громоздкими для реализации, хотя их вычислительная сложность (как и в
общем случае) не зависит от размеров окна обработки. Существует другая
возможность более быстрого вычисления моментов (8.54), а именно, отказав-
шись от полной независимости параллельных звеньев, можно построить «кас-
кадно-рекурсивные» процедуры [10-14, 43—47].
Для построения соответствующего алгоритма установим связь между момен-
тами на текущем и предыдущем шаге. Согласно (8.50), сдвинутая на шаг базис-
ная функция qk (т 4-1) остается степенным полиномом Л-го порядка и, следо-
вательно, единственным образом разлагается по базису полиномов {<7, (т)}* :
544
ГЛАВА 8
Qk (m +1) = ^aki £C/mJ = ^,bki qi (m),
(8.56)
(_o J=o i—0
где С- — биномиальные коэффициенты; {&*,•} *_0 — коэффициенты указан-
ного разложения.
В общем случае коэффициенты bkl определяется через aki следующим
образом:
ькк =1, bki = — - £ bkjaji
, i = k- 1Д-2, ...,0.
Из (8.54) и (8.56) выводится основная рекуррентная формула:
Мл(«) = £мч(п-1)+<1к(-м }f(n+M )-^(м++1)/(и-л/+- 1).
(8-57)
Из (8.57) видно, что вычисление любого момента щ (п) требует вычисле-
ния и всех моментов младших порядков. При этом сложность одного шага
формирования полного набора моментов при 0 < к < К оказывается доволь-
но высокой, она имеет примерно квадратичную зависимость от К: число опе-
раций сложения U+(k) и умножения составляет
( . ч (К + 4)
и+(к)=и.(к) = у-------->
(8.58)
Приведенный параллельно-рекурсивный алгоритм вычисления обобщен-
ных моментов в скользящем окне может применяться при локальном разло-
жении сигнала по любому известному полиномиальному базису: степенному,
базисам дискретных ортогональных полиномов и др. [41, 42]. Целесообразно,
однако, указать новый класс полиномиальных базисов, специально адаптиро-
ванных к рассматриваемой процедуре скользящего окна и позволяющих ра-
дикально снизить вычислительную сложность обработки сигналов (даже по
сравнению с оценками (8.58)), за счет обнуления большей части коэффици-
ентов в рекуррентной формуле (8.57).
Построение полиномиальных базисов с ускоренным вычислением обобщенных
моментов. В [12, 45, 46] было показано, что существуют полиномы (8.50), для
которых обеспечивается значительное снижение объема вычислений за счет
обнуления части коэффициентов в разностных уравнениях (8.57):
bki = 0 при 0 < i < к — 2.
(8.59)
8.2. Параллельно-рекурсивные КИХ-фильтры
545
Путем несложных преобразований выражение (8.56) приводится к виду
при к = 0,
Як (™+1) = Я\ W+—<7o(w) а00 при к = 1,
Qk W+ кк • ^akka(k-l)j , . _ 22 C/aki при к>2
а(к-!)(*— 1) J=° t=j+i
(8.60)
Подбирая коэффициенты таким образом, чтобы выполнялись равенства
Е С/«к-«(*-», = О. 0<j<*-1, t>l.
<=У+1
^кк _ ।
(8.61)
можно получить набор полиномиальных функций, для которых справедлива
следующая рекуррентная формула:
?oW~ 1 • (8.62)
Тогда схема расчета свертки (8.54) с учетом (8.59) записывается в следую-
щем виде:
цл(п) = цА.(м--1)4-цА:_1(м-1) + ^(-Л/ )f(n+M )-^(Л/+Н)/(и-Л/+-1),
.|io(«) = Ho(/I-1) + /(« + A/")-/(W“W+-l)» 1<к<К.
(8.63)
Сложность такой процедуры составляет:
U+(K) = 3K + 2, U*(K) = 2K+2, (8.64)
соответственно, сложений и умножений на отсчет сигнала. Сравнительный
анализ оценок (8.58) и (8.64) показывает, что для алгоритма (8.63) наблюдает-
ся радикальное снижение вычислительной сложности: вместо квадратичной
зависимости от порядка моментов К в (8.58) имеет место линейная зависи-
мость в (8.64).
18 — 9044
546
ГЛАВА 8
Полиномиальные базисы с минимальной вычислительной сложностью. Рас-
смотрим {цА. (и)} ^_0 как самостоятельные величины (признаки) и поста-
вим задачу разработки такого полиномиального базиса, для которого схема
рекурсивного пересчета (8.63) будет простейшей. Следует отметить, что при
расчете обобщенных моментов до АГ-ого порядка система (8.61) состоит из
К (К + 1)/2 уравнений с (АГ + 1)(ЛГ + 2)/2 неизвестными, то есть является
недоопределенной и имеет бесконечное множество решений. Таким образом
условия (8.61) задают семейство полиномиальных базисов с {К -Ь1)-степеня-
ми свободы, которыми можно воспользоваться для дополнительного сниже-
ния сложности алгоритма (8.63).
Используем одну степень свободы этого семейства полиномиальных функ-
ций для того, чтобы выполнялось условие
^0(п) = а00 =1’ (8.65)
а остальные К — для обнуления одного (для определенности последнего) ко-
эффициента во всех разностных уравнениях (8.63), кроме первого:
qk(M++V)~0, 1<к<К. (8.66)
При соблюдении обозначенных условий алгоритм вычисления обобщен-
ных моментов становится более простым:
р0(и) = р0(и -1) 4- f(n + М “) - f(n - М+ -1),
Нл(л) = Цл(л-1) + рл_1(д-1) + ^(-М")/(п+Л/"), 1 <к< К.
А его сложность определяется следующими выражениями:
U+(K)^2K+2, U*(K) = K, (8.67)
что, несомненно, лучше предшествующих оценок. Соответствующий базис,
задаваемый ограничениями (8.65), (8.66), был назван базисом с минимальной
вычислительной сложностью (МВС).
8.2.3. Алгоритмы формирования МВС и МВС-подобных базисов
Алгоритм построения базиса МВС с обнулением на краю окна обработки.
Обратимся к алгоритму параллельно рекурсивного расчета обобщенных мо-
ментов на основе базиса МВС. В приведенном выше описании алгоритма для
формирования базиса были указаны только соотношения в виде равенств (8.61)
и (8.65) и получаемый на их основе алгоритм рекурсивного расчета коэффи-
циентов. Иначе говоря, не был определен явный вид базиса МВС. Оказывает-
8.2. Параллельно-рекурсивные КИХ-фильтры
547
ся, это возможно сделать. Для этого перейдем от представления полиномов в
виде (8.50) к использованию формы записи с помощью корней. Для полино-
ма fc-го порядка будет справедливо следующее:
Jt-i .
qk = с*), ®<к<К, (8.68)
,=0
Г a-V' 1
где набор г. — корни полинома к-й степени, которые в общем случае
могут быть и комплексными. Вещественный множитель ак в нашем случае
будет отвечать за (К+1)-ю степень свободы, связанную с полиномом нулевой
степени. Пусть нам необходимо, чтобы все полиномы до К-й степени вклю-
чительно имели одним из корней некоторое число М, (М = —М~ или
М — М + +1), то есть
д*(м) = 0, \<к<К. (8.69)
Будем рассматривать полиномы «снизу-вверх», начиная с первой степени.
Для к = 1 представление (8.68) упрощается:
<7i H = «i (m-cj).
Из (8.69) следует, что Cq = М, и полином первого порядка имеет вид
q} = (m — Af). (8.70)
Из рекуррентного соотношение для полиномиального базиса (8.62) следу-
ет, что для полинома второго порядка выполняется равенство
q2 + W = 4i W,
или, посредством представления (8.68),
Учитывая условие (8.69) для полинома второго порядка, можно несколько
конкретизировать последнюю формулу:
Подставив т — М в последнее равенство, получим, что
1(м-(с? -1))-0 = 0,
18*
548
ГЛАВА 8
откуда С]2 = М 4-1, т.е. полином второй степени имеет вид
<72 {rn} = a2 (т — М}[т — (М +1)).
Аналогичные преобразования можно проделать для третьей, четвертой и
больших степеней. В результате делаем вывод, что полином к-й степени име-
ет вид
Як ('я) = «*П('”-(л/ +0)’
i=O
1<к<К.
При этом существует зависимость между вещественными множителями:
к-\ А-1
Як (^ + 1) - qk (т) = ак П (т +1 - (М 4- /)) - ак П [т - (М 4- /)) =
/=о /-0
<>к
(к-2 к-\
(/и - (Л/ 4- /)) - I"! (w - (Л/ 4- /))
j=-i /=0
= ((/и — М +1) - (т - М - к 4- 1))<зЛ PJ [т - (Л/ -Г /)) =
/=0
Л-2
=^П("Н^ + $ = Як-\ («)>
1=0
то есть все корни за исключением крайнего правого переходят к младшему
полиному, а множитель ак_х = как.
Используя оставшуюся степень свободы для выполнения условия а0 = 1,
запишем общий вид полиномиального базиса МВС:
4oW = l>
як (т)=т;П("1-(А/+0)’ **
(8.71)
где М ——М~ или М =М + +1 (см. рис. 8.2). Переход же от полученного
представления (8.71) к представлению (8.50), при необходимости, может быть
легко произведен на основании теоремы Виета [2], устанавливающей связь
между соответствующими коэффициентами. Необходимо отметить, что при
генерации рекурсивных полиномов с минимальной вычислительной сложно-
стью вовсе не обязательно генерировать все (ЛГ4- 1) полиномов по (8.71), а
затем переходить к представлению (8.50). Достаточно построить один стар-
8.2. Параллельно-рекурсивные КИХ-фильтры
549
Qk(m)
Рис. 8.2. Полиномиальный базис с минимальной вычислительной сложностью
ший полином в соответствии с приведенной формулой, привести его к виду
(8.50), а затем использовать процедуру построения рекурсивного полиноми-
ального базиса по полиному наивысшего порядка по следующей схеме:
к
a(k-l)j ~ Z2 ^iaki->
i=j+l
0<j<k-\,
\<к<К.
(8.72)
Отметим два важных свойства построенного набора полиномиальных фун-
кций, которые понадобятся в дальнейшем.
А. Целочисленность значений базиса МВС. Пусть М =—М~, тогда т>М.
Очевидно, что рк (т) = 0 при М <т<М 4-к. Тогда для интервала т>М + к
справедливо следующее:
т—М
{ } *7=0 v лГпЛ’ к'(т~м~к)'
0< к< К.
Очевидно, что значениями полиномиальных базисных функций являются
биномиальные коэффициенты, то есть целые числа:
Qk (т) = С
т+М —к
т+М ~
0<к<К.
550
ГЛАВА 8
Пусть теперь М = М + +1, тогда т<М <М + к , и для этого интервала
справедливо:
1=0
М —т—\~к
к
М —т—1
П i
М —т—\—к ’
То есть значения полиномов
в этом случае также являются целыми числами:
Я к w=
>М + -т
М+—т+к’
Б. Изменение области нулей в базисе МВС. Из выражения (8.71) очевидно,
что корни каждого из полиномов в базисе МВС расположены на действитель-
ной оси последовательно в отсчетах целочисленного аргумента. При этом, с
переходом от старшего полинома к младшему, эта «область нулей» сужается,
теряя один нуль с края области, как показано на рис. 8.3. Подобное можно
предположить, зная полином старшего порядка и рекурсивное выражение (8.62)
для полиномиальных функций.
МВС-подобные базисы с модифицированной схемой рекурсии. Имея пред-
ставление о том, как происходит изменение базисных функций, можно, не
используя рекурсивную схему пересчета коэффициентов (8.61), получить вы-
ражение для полинома старшего порядка в базисах с такой же вычислитель-
ной сложностью, как и базис МВС. А именно, необходимо расположить нули
полиномиальных функций последовательно в целочисленных отсчетах вбли-
зи границ окна обработки справа от них, как показано на рис. 8.4. При этом
Рис. 8.3. Изменение «области нулей» в базисе МВС
8.2. Параллельно-рекурсивные КИХ-фильтры
551
для полиномов старших степеней схема рекурсивного пересчета моментов
оказывается простейшей:
ц* (n) = JX* (л -1) + (п -1),
а для полиномов средних степеней — остается прежней:
gt(n) = g4(n-l) + H*-i(«-l)+9*(W++ D/(n- М+- 1).
Для полиномов младших степеней схема записывается в общем виде:
Mn) = ~ О +и*-|(й“ *) + ^(-Л/ )f(n+M )-qk(M+ + !)/(«-М*-1), к> О,
Ц0(л) = Но(л ~ 1) + /(« + м~) -1).
Можно показать, что сложность подобного рекурсивного алгоритма расче-
та моментов не зависит от соотношения в распределении корней полинома
между правым и левым краями окна обработки и определяется все той же
формулой (8.67).
Учитывая вышесказанное, а также требование нормировки для полинома
нулевого порядка в форме qQ (л) — 1, получаем следующее выражение для по-
линомов старшего порядка в наборах МВС-подобных полиномиальных бази-
сов + к2 — к):
1 *1-1/
z, Н П ~ [М ++ 1+ *2 ))-
»2=о'1 7
(8.73)
552
ГЛАВА 8
С
q к (">)=-
Все остальные базисные функции соответствующего набора могут быть
получены с использованием формулы пересчета (8.72).
Выражение для базиса МВС (8.71) оказывается частным случаем формулы
(8.73). Более того, как и для базиса МВС, для МВС-подобных базисов может
быть указано выражение (для полинома старшего порядка) с использованием
биномиальных коэффициентов. Можно показать, что справедливо следую-
щее представление:
/п-ЬМ ——т
т+М~ М+—т+К2
и целочисленность в общем случае не присутствует.
Таким образом, в рамках указанного обобщения может быть получено (К + 1)
различных наборов МВС-подобных полиномиальных базисов и схем рекурсив-
ного вычисления соответствующих обобщенных моментов. Вопрос целесооб-
разности использования того или иного набора для задач обнаружения и рас-
познавания может решаться либо на основе анализа информативности какого-
либо подмножества из набора, либо на основе анализа качества самого базиса.
8.2.4. Параллельно-рекурсивный алгоритм на основе полиномиальных
базисов четных степеней
В п.8.2.3. были введены семейства базисов, обеспечивающие вычисление
КИХ-свертки с минимальным количеством арифметических операций при
произвольном виде импульсной характеристики. Существует однако доста-
точно широкий круг задач, когда необходимо производить вычисление дву-
мерной свертки (8.14) с импульсными характеристиками специального вида.
Так например, в задачах фильтрации изображений и цифрового моделиро-
вания видеоинформационного тракта импульсные характеристики часто ока-
зываются четными функциями. В связи с этим представляется целесообраз-
ным построить семейство полиномиальных базисных функций, адаптиро-
ванных специально для описания четных импульсных характеристик, а также
разработать алгоритмы параллельно-рекурсивной фильтрации изображений
с использованием подобных базисов. Будем проводить рассуждения в тер-
минах одномерных сигналов, а затем обобщим результаты на двумерный
случай.
Семейство рекурсивных полиномиальных функций четных и нечетных степе-
ней. Как отмечается в [30, 36] расчет свертки вида (8.54) производится эф-
фективно в случае, если фильтр с конечной импульсной характеристикой
qk(m) описывается разностным уравнением, то есть реализуется рекурсив-
но. Таким образом, задача заключается в поиске полиномиальных функций
(8.50), позволяющих работать в рамках простых рекурсивных схем. При этом
8.2. Параллельно-рекурсивные КИХ-фильтры
553
границы поиска подобного полиномиального набора ограничены возмож-
ностью использования (К +1) степеней свободы, каждая из которых соот-
ветствует одному из коэффициентов в представлении полинома старшего
порядка.
Легко показать, что для произвольного полинома £-го порядка можно по-
добрать полином (А-1)-го порядка так, чтобы выполнялось условие
qk (т) = qк(т -1) + qk_} (т), (к > 0).
В свою очередь, для полинома (fc-l)-ro порядка можно подобрать поли-
ном (£-2)-го порядка, для которого справедливо равенство
^_i(/n) = qk-} (т - 1)4- qk2(m ~ 0, (к>2).
Тогда полиномы £-го порядка и (£-2)-го порядка связаны соотношением
qk(m)==2qk(m — V)—qk(m— 2)+qk_2(jn, (к>2). (8.74)
Набор базисных функций, отвечающих этому соотношению, может быть
использован в процедуре параллельно-рекурсивного расчета свертки (8.54).
Теперь определим общие ограничения, налагаемые на вид базиса и возни-
кающие при выполнении соотношения (8.74). Подставив выражение (8.50) в
последнее разностное уравнение, получим (к<К):
[* 12]
a(Jt-2)(2j) — 2 XL ak{2i)C{2i) ’
i—j+i
м
a -2? a C{2j+1}
a(k-2)(2j+l) ak (2i+l)u-(2i+f) ’
i=j+\
0 <./<[*/2]-1,
0<j<[(*-1)/2]-1,
(8-75)
где [...] — целая часть числа, С/ — биномиальные коэффициенты. Легко
показать, что семейству рекурсивных полиномиальных функций, заданных
выражением (8.74), присуще следующее свойство. Если известно, что одна
из базисных функций данного семейства является симметричной относи-
тельно нуля функцией, то и все базисные функции меньших степеней также
являются симметричными. Используем это свойство в дальнейшем, а набор
полиномиальных функций удовлетворяющих разностному уравнению (8.74)
и, соответственно, соотношению (8.75) с четными индексами к назовем се-
мейством полиномиальных функций четных степеней для рекурсивной об-
работки [13, 23, 47].
Параллельно-рекурсивный алгоритм вычисления одномерных обобщенных мо-
ментов четных степеней. Пусть для последовательности возрастающих значе-
ний целочисленного аргумента п требуется вычислить обобщенные моменты
554
ГЛАВА 8
четных степеней до Л'-го включительно. Подставляя в выражение для свертки
(8.54) рекуррентное соотношение (8.74), получаем (2<к<К, к, К — четные):
Но W = Но ~ i) + 4о + М) - /(ет - Л/ -1))
Нл (™) = 2ц* (т -1)+Нл-2 -1) - И* (т - 2) +qk (-M)f(tn + М) - (8.76)
-qk(M + -\)-qk (-M-1)/(/п + Л/ -V)-\-qk[M]f{m-M -2).
Вычислительная сложность предложенной процедуры равна (здесь и везде
далее умножение на «2» не учитывается)
Г7+(Л") = ЗАГ Ь2, t/.(A')= 2АЧ-1.
Используем факт сохранения симметрии в семействе полиномиальных
функций четных степеней для упрощения параллельно-рекурсивного алго-
ритма расчета обобщенных моментов. Пусть самая старшая полиномиальная
базисная функция является четной, тогда и весь базисный набор представля-
ет собой совокупность заданных на симметричном интервале функций, для
которых выполняется равенство (к — четное):
qk(m) = qk( т), тб[-Л/,М] , ®<к<К.
В этом случае схема (8.76) может быть преобразована к виду (к — четное)
Но = Но (т -1)+tfo (М)(/+ м) - м -1))>
Yi(/n) = /(w-Af-2) + /(m-hM), f(m-M-1)+/(/и + Л/-1),
ц*(/п) = 2ц*(/п-1)4-ц*_2(аи-1)-ц*(/п-2)-^(Л/ + 1)у2(?п)+^(Л/)у|(/и), к >2.
Вычислительная сложность алгоритма на одном шаге составляет
l/+(tf) = 2tf + 4, U^K) = K+\, К>0.
Заметим, что на обеспечение симметрии здесь были использованы К/2 сте-
пеней свободы, и одна степень свободы — на обеспечение равенства ат = 1.
Оставшиеся К/2 степеней свободы должны быть использованы для обнуления
значений части полиномиальных функций на границе интервала, не выходя
при этом за рамки четности базиса. Необходимого эффекта можно добиться
следующим образом. Перепишем разностное уравнение (8.74) в виде
q/c-ii^-^) = qk(m)-2qk(m-i) + qk(m-2)- (8-77)
Из (8.77) следует, что если корни полинома расположить на действитель-
ной оси последовательно в отсчетах целочисленного аргумента, то при пере-
ходе к полиному с меньшей степенью подобная «область нулей» сужается,
теряя два нуля по краям области. Следовательно, если «область нулей» вклю-
8.2. Параллельно-рекурсивные КИХ-фильтры
555
чает в себя интервал \М, М + 1], то
для (К/4) старших полиномов ко-
эффициенты цк (Л/) и qk(M+\)
будут нулевыми, а схема рекурсии
простейшей. Для (Л/4) младших по-
линомов схема рекурсии не изме-
нится, т.к. не будут равны нулю зна-
чения соответствующих коэффици-
ентов. В случае если количество
полиномиальных базисных функций
нечетно, возможно появление допол-
нительного рекурсивного звена для
полинома степени к = 2[Лг/4]+2 с ну-
левым значением одного из коэффи-
циентов qk(M} или qk (М +1) .
Учитывая симметричность всех ба-
зисных функций, это явление мож-
но показать на одной из двух схем
рис. 8.5.
Таким образом, задача сводится
к построению базиса по полиному
наивысшего порядка:
<7к(™) =
Л/+1+
К-2
4
Величина ХК =]/К1 — нормиру-
ющий множитель, обеспечивающий
выполнение равенства = 1. Мож-
но получить также выражение через
биномиальные коэффициенты:
Рис. 8.5. Изменение «области нулей» в четном по-
линомиальном базисе
гМ-Т-\ rm+T-KI2
qK(m)= ^r-wci2,m+r___ г = м + |+
С к
(8.78)
Представление младших полиномиальных базисных функций можно по-
лучить по формуле (8.75). На рис. 8.6 приведен типичный вид нормирован-
ных полиномиальных базисных функций четных степеней, получаемых при
использовании схемы формирования базиса (8.75) для заданного полинома
старшего порядка (8.78) при К — 12.
556
ГЛАВА 8
4к(т)
max q(m)
1
0,5
0
-0,5
М
-М
Рис. 8.6. Полиномиальные базисные функции четных степеней
Схема параллельно-рекурсивного расчета обобщенных моментов на осно-
ве полученного базиса имеет вид
ц0(ги) = ц0(ю -1) + Дт + Л/) - Дт - М -1),
Yi М = /('” + АС + /("* - Л/ -2), у2 (т) = Дт + М -1) + Дт - М -1),
= 2цк(т -1) - - 2) + Цк_2(т -1) + (тэт),
+ 1)у2(/я), если 2<к<2[К/4],
К *0 (mod 4), к = 2[К/4\ + 2,
где
М = Н, если
0, если
8.2. Параллельно-рекурсивные КИХ-фильтры
557
а сложность обработки определяется выражением
£7+(АГ) = 1,5^+4, U,(k) = K/2 (К>2),
и приблизительно в 1,33—2 раза ниже соответствующих затрат на алгоритм с
базисом МВС.
При использовании моментов для вычисления свертки сигнала с четной
конечной импульсной характеристикой, сложность алгоритма модифициру-
ется с учетом затрат на скалярное произведение и равна
1/+(/С) = 2/С-Ь4, U.(k)=K (ЛГ>2),
что приблизительно в 1,5—2 раза меньше, чем сложность алгоритма на основе
МВС базиса.
Параллельно-рекурсивный алгоритм вычисления двумерных обобщенных
моментов четных степеней. Зададим базисный набор, состоящий из разде-
лимых четных полиномиальных функций следующего вида: =
— <7* (wi (m2), здесь k, I — четные индексы, совместно задающие совокуп-
ность базисных функций и ограниченные некоторой парой (К, L). Подобное
представление позволяет, как отмечалось ранее, использовать построчно-стол-
бцовую схему обработки (8.53). В результате алгоритм параллельно-рекурсив-
ного вычисления двумерных четных обобщенных моментов примет следую-
щий вид (к — четное):
- формирование вектора одномерных моментов в процессе рекурсивной
обработки по строкам:
Ро('И|,'Н2) = Ш)('”| -1,т2) + /(/«! + Л/,,/п2)"/('”! ~м\
Yi W =/(™i +Mum2) + f(m\ -2,т2),
Тг("12) = f(m\ +ЛЛ -l,M2) + /(nii -Л/| -1,/п2),
.цА(/И1,т2) = 2цЛ(/П1 -1,т2)-^(лм1 -2,/п2) + ЦЛ_2(/п1 -1,т2) + ^ (ш2),
fltW)Yi(/n2)-^W +1)У2("12)» если 2 < Ас < 2[ЛГ/4],
где
если
если
tf*0(mod4), к = 2[К/4] + 2,
2 + 2[(/Г + 2)/4] < к < К ;
- вычисление матрицы двумерных моментов в процессе рекурсивной об-
работки по столбцам (0 < к < К):
558
ГЛАВА 8
Ило (^i, ) = цА0 (^1, т2 -1) + щ. (W1, т2 + М2) - р* (т}, т2 - М2 -1),
Vl (w,, tn2) = (лл/,, т2 + М2) + щ , т2 - М2 - 2),
Y?(Wi,M2) = gA(mI,w2 + 4/2-l) + g)t(/nl,w2-A/2-l),
где ^к1(тьт2) = <
= ,w2 -1)-цл/(т{,т2-2) + цк{1..2}(тьт2 -1) + {(mt,т2),
\qi{M2)^\(m^m2)~ql{M2 + 1)у£(т1}т2), 2 < I < 2[£/4],
^/(M2)\|/l-(W],/n2), если £*0(mod4), I ~ 2[£/4] + 2,
О, если 2 + 2[(£ + 2)/4]</<£.
Вычислительная сложность приведенной процедуры составляет
U+(K,L) = 0,25(А> 2)(3£ + 14)+1, U*(K,L) = 0,25(£Г + 2)(£ + 2)-1,
(К L > 2). (8.79)
В случае если моменты используются для расчета свертки с двумерным осе-
симметричным неразделимым КИХ-фильтром, то с учетом затрат на последу-
ющее вычисление скалярного произведения (8.51) получим:
£7+рГ,£) = (£Г + 2)(£ + 4), f/*(X',£) = 0,5(Ar + 2)(£ + 2)-l , (К, £>2),
вычислительная сложность приблизительно в 2—4 раза меньше, чем для бази-
са МВС. При вычислении свертки с разделимой импульсной характеристи-
кой (ИХ), оценки — следующие:
U+(K,L) = 2(K + L) + 8, U*(K)=K + L (К>2), (8.80)
а достигаемый выигрыш эквивалентен выигрышу одномерного фильтра.
8.2.5. Параллельно-рекурсивной алгоритм фильтрации сигналов
при нечетной полиномиальной импульсной характеристике
Полученные результаты для четного полиномиального базиса легко пере-
носятся на случай нечетных базисных функций.
Параллельно-рекурсивный алгоритм вычисления одномерных обобщенных
моментов нечетных степеней. Пусть для последовательности возрастающих
значений целочисленного аргумента п требуется вычислить обобщенные мо-
менты нечетных степеней до степени К включительно. Подставляя в выра-
жение для свертки (8.54) рекуррентное соотношение (8.77), получаем
(3<^<ЛГ; к,К — нечетные):
8.2. Параллельно-рекурсивные КИХ-фильтры
559
g, (т) = 2ц, (т -1) - ц, (т - 2) + (-M)f(m + М) -
-^(Л/ + 1)/(/л-М~ 1)/(//?+ M-l)+^j(M) f(m- А/-2),
Ц* (т) = 2ц* (т -1) + щ, 2 (т -1) - ц* (т - 2) + qk (-M)f(m + М) - (8.81)
-qk(M + l)f(m-M -1)- qk(-M- l)f(m+ M- 1)+ qk(M)f(m~ M- 2).
Вычислительная сложность подобной процедуры составляет
U+(K) = ЗК 4- 2, U*(K) = 2К+2.
Используем факт сохранения асимметрии в семействе полиномиальных
функций нечетных степеней для упрощения параллельно-рекурсивного алго-
ритма расчета обобщенных моментов. Пусть самая старшая полиномиальная
базисная функция является нечетной, тогда и весь базисный набор представ-
ляет собой совокупность заданных на симметричном интервале функций, для
которых выполняется равенство (к — нечетное)
qk (т) — — qk (—ли), т <= \-М, А/], 1 < к < К.
В подобной ситуации схема (8.81) может быть преобразована к виду
У1(т) = f(m -М-2)- f(m + М), у2(т) = f(m + М -V)~ f(m- Л/-1),
< щ (т) = 2ц, (/и — I) — ц, (т - 2)+у, (т) + ~~ Т2 И» (8-82)
И*(т) = 2ц.к(т-1) + |1Л-2(«-1)-Щ(т-2)+qk(М)у} (m)+qk(M + 1)у2 (т).
Вычислительные затраты подобного алгоритма на одном шаге составляют
U+(K)~2K + 3, U*(K)=K.
На обеспечение симметрии были использованы К/2 степеней свободы, и
одна степень свободы на обеспечение равенства д}(М) = \. Оставшиеся
К/2 степеней свободы должны быть использованы для обнуления значений
части полиномиальных функций на границе интервала, не выходя при этом
за рамки нечетности базиса. Необходимого эффекта можно добиться, распо-
лагая корни полинома старшего порядка тем же способом, что и для четного
полиномиального базиса, как показано на рис. 8.7.
Таким образом, как и в случае четных полиномиальных базисных функ-
ций, задача сводится к построению базиса по полиному наивысшего порядка,
который имеет вид
560
ГЛАВА 8
(К-1)# 0 (mod 4)
Рис. 8.7. Изменение «области нулей» в нечетном полиномиальном базисе
Величина =1/(К\м) — нормирующий множитель, обеспечивающий
выполнение равенства = Представление с использованием биноми-
альных коэффициентов с точностью до множителя т/М совпадает с соответ-
ствующей формулой для четных полиномиальных базисов (8.78). Аналогич-
но, значения базисной функции не являются целочисленными.
Выражения для младших базисных функций можно получить по формуле
(8.75). На рис. 8.8 приведен типичный вид нормированных полиномиальных
базисных функций нечетных степеней, получаемых при использовании схе-
мы формирования базиса (8.75) для заданного полинома старшего порядка
при К = 13.
Алгоритм параллельно-рекурсивного расчета обобщенных моментов на
основе полученного базиса имеет вид
У[(т) = Дт-М-2)-Дт+ М), у2(т) = Дт + М-V)- Дт- М- 1),
Hi (т) = 2pi (т -1) - щ (т - 2) + (т) + у2{т),
М
. ц* (т) = (т -1) - ц* (т - 2) + (т -1) + (т),
^WYi(^) + ^(M + 1)Y2("i)> если 3<fc<2[(tf-l)/4] + l,
где
^(^w) = Wjt(A/)Yi(w2), если (tf-l)*0 (mod 4), k = 2[(tf-l)/4] + 3,
.0, если 3 + 2[(/T + l)/4]<£<tf,
8.2. Параллельно-рекурсивные КИХ-фильтры
561
-М О М
Рис. 8.8. Полиномиальные базисные функции нечетных степеней
а сложность обработки равна
C/+(tf) = l,5tf + 3,5, U*(k]=(K-\)/2 (tf>3),
что приблизительно в 1,33—2 раза меньше соответствующих затрат на алго-
ритм с базисом МВС.
При использовании моментов для вычисления свертки сигнала с нечетной
конечной импульсной характеристикой, оценка сложности алгоритма моди-
фицируется с учетом затрат на скалярное произведение и равна
U+(tf) = 2K+3, ^(АГ) = К’ (К>3),
что в 1,5—2 раза лучше соответствующих оценок алгоритма с базисом МВС.
Параллельно-рекурсивный алгоритм вычисления двумерных обобщенных мо-
ментов нечетных степеней. Зададим базисный набор, состоящий из раздели-
мых нечетных полиномиальных функций следующего вида:
<7и(т1,тп2) = ^д.
562
ГЛАВА 8
здесь к, I — четные индексы, совместно задающие совокупность базисных
функций и ограниченные некоторой парой (К, L). Тогда алгоритм параллель-
но-рекурсивного вычисления двумерных нечетных обобщенных моментов
примет слдующий вид (к — нечетное):
- формирование вектора одномерных моментов в процессе рекурсивной
обработки по строкам:
p0(ml,/n2)=p0(m1-J,m2)+/(m1+Al1,m2)-/(rw1-Al1-l,m2)
Yi = -Alj -2,w2)~/(m1 +Mitm2),
< p.it(/n1,m2) = 2|>ijk(m] -I,m2)-p.zt(m]-2,m2)+pJt_2(m1-l,/«2)+^jt (m2),
где
^a (A1i)Yi (m2), если
О, если
если 3<£<2[(tf-l)/4]+l,
(K-l)*0(mod 4), Л = 2[(АГ-1)/4]+3,
3+2[(K+l)/4]<fc<K;
- вычисление матрицы двумерных моментов в процессе рекурсивной об-
работки по столбцам (1 < к < К ):
1,/n2-l)+^z(wJ,w2),
Нло(т1’т2)=Нло("г1>'”2”1) + И*(^1,АИ2+А^2)~НЛ"гь"12-А12-1),
x^Jt(ni|,m2)=pt(mI,m2-Al2-2)-pJt(mI,zn2 + Al2),
Wk (wl >т2) = Нк (т1.т2 + М2 -0-Цк (т1 ’ т2 -М 2 -1).
Ни К, т2) = 2ц w (т}, т2 (mt ,т2 - 2)+Цл(/_2) (т}
^/(^2)vL(mi.w2)-^(Al2+l)Y;(??i1,m2), 3<Z< 2[(L+l)/4],
<7z(A/2)Va(w1’w2)’ если (L-1)^0 (mod 4), / = 2[(L-l)/4]-f
0, если 3+2Г(л+1)/4“|</<£.
где ^к1(т},т2)--
Выражение для вычислительной сложности приведенной процедуры прак-
тически совпадает с соответствующим выражением для четного полиноми-
ального базиса (8.79)~(8.80).
8.2.6. Оценка качества полиномиальных базисов по различным критериям
Как уже отмечалось ранее, вопрос целесообразности использования того
или иного набора полиномиальных базисных функций для задач обработки
изображений может решаться либо на основе анализа информативности ка-
8.2. Параллельно-рекурсивные КИХ-фильтры
563
кого-либо подмножества из набора, либо на основе анализа качества самого
базиса.
Можно предложить три критерия для оценки качества базиса. Первый из
них связан со спецификой реализации вычислений на процессорах с фикси-
рованной разрядной сеткой. В такой ситуации нас интересует диапазон зна-
чений формируемых моментов, а значит и диапазон значений полиномиаль-
ных базисных функций. Диапазон моментов будем оценивать следующей ве-
личиной:
м+
diap = max |<7jt (w)|-
k m=-M~
Второй критерий для оценки качества набора базисных функций связан со
спецификой реализации вычислений на процессорах с плавающей точкой.
Тогда интерес представляет вопрос устойчивости вычисления или вопрос обус-
ловленности матрицы моментов. Из численных методов известно [2, 22], что,
чем лучше обусловлена матрица (взаимной корреляции базисных функций),
тем устойчивее получаемое решение (например, при решении системы ли-
нейных уравнений, обращении матрицы и т.д.). Число обусловленности для
матрицы В рассчитывается следующим образом:
condB = ||В||в-||,
где |...|— норма матрицы. Для квадратичной нормы число обусловленности
равно
condB— т-г35--
vW
1 I Imin
Здесь Xma¥,lm:n — максимальное и минимальное собственные значения
1ПаА 1111П
матрицы.
Третий критерий для оценки качества набора базисных функций связан с
различной степенью его «ортогональности» или «коррелированности». Чем
меньше уровень корреляции между базисными функциями, тем проще про-
изводить классификацию и тем лучше соответствующий набор. Принято оце-
нивать коэффициент сопряженности по норме Гильберта—Шмидта [7]:
norma В —
здесь by — элементы матрицы. Для ортогональной системы значение этой
величины равно нулю, максимальное значение этой величины равно единице.
564
ГЛАВА 8
Поскольку перебрать все возможные комбинации окон, степеней полино-
мов невозможно, приведем несколько примеров, по которым и определим
основные правила выбора наборов базисных функций. В качестве аргументов
на рис. 8.9 используется величина, задающая соотношение количества нулей
в правой и левой области, Л'1 — К2. Линии на графиках соответствуют следу-
ющим наборам базисных функций:
«-----» (сплошная линия) — МВС-подобные базисные функции;
«.....» (пунктирная линия) — четные полиномиальные базисные функции;
«-----» (штриховая линия) — нечетные полиномиальные базисные функции.
На основе полученных результатов можно сделать следующие выводы:
- общий вид зависимости введенных показателей для МВС-подобных ба-
зисов практически не зависит от размеров окна обработки;
- наилучшие значения показателей среди МВС-подобных базисов имеет
набор, порождающий полином которого имеет набор корней с приблизитель-
но равным распределением между правой и левой границей окна обработки;
- в целом матрица корреляций МВС-подобных базисных функций доста-
точно плохо обусловлена;
- среди всех базисов наименьшим диапазоном и наилучшей обусловлен-
ностью обладают нечетные полиномиальные базисы;
- базисные функции всех наборов сильно сопряжены.
/Гб
11
диапазон
обусловленность
сопряженность
100000 т
1000000 т
100000
10000
1000
100 7
ю —।—।—।—।—।—।
-6-4-2 0 2 4 6
1Е+07
1Е+06
100000-
10000
1,00Е+03 —।—।—।—।—।—।
-6-4-2 0 2 4 6
1000-1-—।—।—।—г
-6-4-2 0 2 4 6
Рис. 8.9. Исследование качества наборов полиномиальных базисов для рекурсивной обработки
8.3. Расчет и применение параллельно-рекурсивных КИХ-фильтров
565
8.3. Расчет и применение параллельно-рекурсивных
КИХ-фильтров в задачах обработки изображений
8.3.1. Общая схема расчета параллельно-рекурсивных КИХ-фильтров
При конструировании параллельно-рекурсивного КИХ-фильтра необхо-
димо решить три задачи:
- выбрать размеры окна обработки и класс базисных функций разложения
(8.5) или (8.15);
- из полного множества базисных функций выбранного класса выделить
фактически используемые в разложении К функций;
- рассчитать коэффициенты фильтра.
Первая задача может быть решена эвристически. Вторая и третья — ре-
шаются одновременно, в ходе переборной процедуры численных расчетов
[30, 32].
Выделенное подмножество из К базисных функций должно обеспечивать
как можно более высокую эффективность обработки сигналов. Для определе-
ния наилучшего подмножества в общем случае нужно перебрать все возмож-
ные сочетания по К базисным функциям в их полном множестве, вычислить
для каждого сочетания некоторый показатель качества R и найти вариант,
соответствующий максимальному значению показателя. Однако такой пере-
бор оказывается практически неосуществимым из-за чрезмерного объема не-
обходимых вычислений.
Наиболее просто было бы заранее ввести некоторое упорядочение базис-
ных функций (например, для базиса Фурье — по возрастанию «частотного
индекса») и использовать первые К функций из упорядоченного набора. Но,
во-первых, не всегда удается указать «естественный» порядок следования функ-
ций (для прямоугольного базиса, в двумерном случае и т.д.), и, во-вторых,
выбранное подмножество может оказаться весьма далеким от оптимального.
В [30, 32] для выбора базисных функций предлагается использовать субоп-
тимальный метод последовательного присоединения («селекции вперед»),
широко применяемый для выделения подмножества признаков в задачах рас-
познавания образов. Согласно ему, сначала выбирается единственная функ-
ция, обеспечивающая максимум показателя качества, затем к ней присоеди-
няется еще одна, максимизирующая показатель в паре с уже выбранной, и
так далее до получения набора из К функций. (Для базиса Фурье в варианте с
попарной реализацией звеньев процедура модифицируется: на каждом шаге
добавляется не по одной, а по группе функций, связанных одинаковыми зна-
чениями индексов.) Данный метод резко сокращает вычислительные затраты
по сравнению с полным перебором при незначительной потере оптимально-
сти формируемого подмножества базисных функций.
Как следует из сказанного выше, для каждого анализируемого подмноже-
ства базисных функций требуется рассчитывать показатель качества обработ-
ки сигналов, а для окончательного варианта подмножества — и коэффициен-
ты разложения импульсной характеристики фильтра в ряд (8.5) или (8.15).
566
ГЛАВА 8
Интересно, что для многих задач обработки сигналов схема этих расчетов
оказывается, по существу, идентичной [30, 32].
Вектор-столбец искомых коэффициентов А = {ал}л=0 задается матричным
соотношением вида
А = В'С, (8.83)
а показатель качества, максимизируемый в процессе выбора базисных функ-
ций, соотношением
/г = А7’С=-СгВ“,С, (8.84)
где В = {blk 20 ~ невырожденная симметрическая матрица, верхний ин-
декс —1 означает обращение матрицы, С — {q — вектор-столбец, верх-
ний индекс Т — транспонирование вектора. Специфика расчета фильтра для
каждой конкретной задачи заключается только в способе вычисления эле-
ментов матрицы В и вектора С.
Ниже выводятся соотношения, по которым рассчитываются указанные
элементы для некоторых наиболее важных прикладных задач. В целях ком-
пактности изложения детально рассматриваются случаи обработки одно-
мерных сигналов, а для двумерных даются основные расчетные формулы.
Все участвующие в преобразованиях последовательности считаются веще-
ственными.
8.3.2. Среднеквадратичная аппроксимация импульсной характеристики
Выведем соотношения, по которым рассчитываются указанные элементы
в задаче аппроксимации импульсной характеристики. Пусть требуется пост-
роить фильтр с импульсной характеристикой h (т),_которая аппроксимирует
некоторую заданную импульсную характеристику h (m). Для решения этой
задачи воспользуемся методом наименьших квадратов. Будем минимизиро-
вать величину:
е2 = У7 w(zn)|h (zn)—/i(zn)] ,
m=-oo
(8.85)
где w (tri) — некоторая неотрицательная весовая последовательность. Подста-
вим в формулу (8.85) выражение (8.5) для импульсной характеристики парал-
лельного фильтра:
е2= £ w(m)
m=—оо
T,akhk(™)
k=0
(8.86)
8.3. Расчет и применение параллельно-рекурсивных КИХ-фильтров
567
и приравняем нулю частные производные:
<Эе2
-----о, 0<1<К-1. (8.87)
dat
В результате получим систему линейных уравнений относительно коэф-
фициентов фильтра:
ВА-С, (8.88)
в которой элементы матрицы В и вектора С вычисляются по формулам
м+ м+ _
blk = 22 w^h^mjhb (т), ck = 52 w(m)h (m)hk (m). (8.89)
m——M ~ m=—M ~
Очевидно, решение данной системы определяется записанным выше соот-
ношением (8.83). Подставив найденные коэффициенты фильтра в (8.86), не-
сложно получить достигаемый минимум ошибки аппроксимации:
ОО _
Emin = Е R, (8.90)
оо
где R вычисляется по формуле (8.84). В разности (8.90) первый член не зави-
сит от параметров синтезируемого фильтра, поэтому уменьшение ошибки в
процессе подбора базисных функций обеспечивается максимизацией показа-
теля качества/?.
Для двумерного параллельно-рекурсивного КИХ-фильтра, описываемого
соотношениями (8.15)—(8.17), с импульсной характеристикой, аппроксими-
рующей двумерную функцию h (w],wi2), формулы (8.85), (8.89) и (8.90) мо-
дифицируются:
оо оо 2
е2= Е Е , т2 )[й [ml,tn2 )—, (8.91)
ГИ|=—оо ос
bik = 52 (т1,т2)Лл
ct = Е Е (/И],/и2)Л^ (mpm2)> (8.92)
ос ОС _
£min= 52 52 ^(rni,m2)h2(mbm2)-R, (8.93)
ос m2=—ос
где — двумерная неотрицательная весовая функция ошибки апп-
роксимации.
568
ГЛАВА 8
8.3.3. Среднеквадратичная аппроксимация частотной характеристики
Аппроксимация частотной характеристики ЛПП-системы является традицион-
ной задачей проектирования цифровых фильтров [25]. Частотная характеристи-
ка синтезируемого фильтра (спектр Фурье его импульсной характеристики)
/ \ 00
(8.94)
т——со
где о — безразмерный вещественный частотный аргумент, должна здесь при-
ближенно соответствовать некоторой требуемой частотной характеристике
Н\е‘®У Будем минимизировать погрешность аппроксимации, которую, при-
нимая во внимание периодичность спектров последовательностей [25, 29],
запишем в виде
। л 2
Е2= — J w(ei&] Jco, (8.95)
2л
где W — вещественная четная неотрицательная весовая функция. С уче-
том формул (8.5) и (8.94) представим выражение (8.95) в более конкретной
форме:
1 “ , . . . х-i , -
е2=—Jwe“> В е" -Х:«Л «“
Ml _
(8.96)
где Нк — частотные характеристики параллельных звеньев фильтра. И
далее через условие (8.87) перейдем к системе линейных уравнений вида (8.88)
и ее решению (8.83), в которых элементы матрицы В и вектора С определяют-
ся следующим образом:
~2л J W\elH‘\e
2л
(8.97)
Коэффициенты фильтра, найденные по формуле (8.83) с использованием
(8.97), обеспечивают минимум ошибки аппроксимации (8.96):
8.3. Расчет и применение параллельно-рекурсивных КИХ-фильтров
569
где R — подлежащий максимизации показатель качества фильтра, вычисляе-
мый по формуле (8.84). На практике может оказаться более удобным исполь-
зовать вместо спектральных функций, входящих в приведенные выше выра-
жения, соответствующие им последовательности. Опираясь на свойства пре-
образования Фурье [25, 29], несложно трансформировать соотношения (8.97)
и (8.98) к следующему виду:
м+ м +
btk= Е £ ftz(m)ht(n)w(m-n),
т=—М ” п——М ~
оо М+
ск = £ h(m)hk(n)w(m-n)t
т—-<х> п—М
(8.99)
оо оо _ _
Emm = £ £ h(m)h(n)w(m-n)~ R, (8.100)
т——оо п——оо
где
1 П
2nJ ' '
- последовательность, соответствующая спектральной весовой функции
п
-п
- импульсная характеристика идеального (аппроксимируемого) фильтра.
При переходе к двумерным сигналам полученные расчетные соотношения
претерпевают непринципиальные изменения. Выражение для погрешности
вместо (8.95) принимает вид
। К К
е2 =—f (8.101)
_п „п
где , е'“2) — вещественная неотрицательная весовая функция, облада-
ющая свойством центральной симметрии: e‘“2 I = W le ,C01 ,е~'“2 1,
570
ГЛАВА 8
Н (e'“‘, е'®2 j — аппроксимируемая частотная характеристика, Н (еи,>|, б'®2 j —
частотная характеристика рассчитываемого фильтра. Вместо соотношений (8.97)
следует использовать
. я л
Ь1к =—2 J f (8.102)
4тс _ _
—я —я
« Л 7Ь
ск =—-f f W^l,eia^H^a\ei<a2^Hk^~iWl,e~ia2jdG)ld(i)2, (8.103)
—я —л
где Нк (еи,>',^'“2 j —• частотная характеристика параллельных звеньев фильт-
ра, а вместо соотношений (8.99), (8.100) —
bik= Е ЕЕ EM™i’™2)M"i*«2M™]-"i,™2-«2),
(ш,, т2 )бО («I, л2 )ED
ОО 00 _ ___ _
Q = Е Е Е ЕЛ(™1’™2)МП1’П2М™1 “П1’™2 -«2)’ (8.104)
Л1] ——оо т2 ——ос (п|.п2)СО
ОС 00 оо оо _ _
emin= Е Е Е Е Л(т1,т2)Л(п1,п2)^(т1-П1,т2-Л2)-Л, (8.105)
М|~—ОО Ш2=—ОО Л] =—ОО Л2=—ОО
где w(n,,n2), h (и|,л2) — двумерные последовательности, соответствующие
спектральным функциям W(<?'“',е‘“2) и Н (е,а>1 , е'“2). Связь между всеми
последовательностями и их спектрами определяется двумерным преобразова-
нием Фурье [16, 26]. Например,
оо оо
lV^,<0,,ext°2 j— Е vvfnp^Jexpf-z^cOjn]+со2п2)],
ОС И2=—°C
j Л Я
м>(и|,и2) =—7 J* Уw(e‘w\e'“2)ехрр(Щ|И] d<o2.
4л _л _п
Заметим, что если минимизировать невзвешенную погрешность аппрокси-
мации, то нет необходимости рассчитывать фильтр с использованием частот-
ного подхода. В силу теоремы Парсеваля [16, 25], при отсутствующих (равных
единице) весовых функциях критерии (8.95) и (8.101) эквивалентны соответ-
ственно критериям (8.85) и (8.91). При этом задача расчета фильтра с требуе-
мой частотной характеристикой сводится к задаче аппроксимации импульс-
8.3. Расчет и применение параллельно-рекурсивных КИХ-фильтров
571
ной характеристики, решение которой в вычислительном плане проще. Од-
нако в общем виде весовых функций аппроксимация импульсной и частот-
ной характеристик приводит к разным фильтрам. В этой связи рассмотрим
отдельно частные случаи выбора спектральных весовых функций, имеющие
важное практическое значение.
8.3.4. Моделирование ЛПП-системы
Пусть требуется рассчитать фильтр, преобразующий входной сигнал /(л)
так же, как некоторая «идеальная» ЛПП-система с известными характеристи-
ками. Обозначим как g^(n) сигнал на выходе рассчитываемого фильтра и как
g^\n) сигнал на выходе идеальной системы. Далее рассмотрим два случая.
В первом случае предпсуюжим, что /(л) — детерминированная последова-
тельность со спектром Будем минимизировать квадрат отклонения
одного выходного сигнала от другого:
£
2= £ IA")- ЛмГ.
(8.106)
В соответствии с теоремой Парсеваля и другими свойствами преобразова-
ния Фурье
где — спектры выходных сигналов, — частотная
характеристика идеальной системы, Н — частотная характеристика рас-
считываемого фильтра. Сравнение последнего выражения с критерием (8.95)
показывает, что данная задача заключается в аппроксимации частотной ха-
рактеристики с весовой функцией
iv(e/w) = |r(eto)|2, (8.107)
при этом значения ошибок (8.95) и (8.106) совпадают. Спектральной весовой
функции (8.107) соответствует последовательность
оо
w(n) = 22 /Н/("»+л), (8.108)
т=—оо
она нужна при расчете фильтра с использованием соотношений (8.99) и (8.100).
Рассмотрим второй случай. Пусть /(л) — стационарная случайная после-
довательность с нулевым средним и энергетическим спектром Ф f (i. При
572
ГЛАВА 8
расчете фильтра потребуем минимизации дисперсии разности выходных
сигналов:
2
£2 =Е
8^ («)~ (”)
(8.109)
Известно [25], что эта дисперсия может быть вычислена через энергети-
ческий спектр разности, который, в свою очередь, выражается через энерге-
тический спектр входной последовательности и частотные характеристики
идеальной системы и рассчитываемого фильтра:
1 т* 2
Е2=^/ф/И1й(е'“)-яИ|J<o-
-л
Сопоставив это соотношение с критерием (8.95), видим, что мы снова при-
шли к задаче аппроксимации частотной характеристики при весовой функции
= (8.110)
а ошибки (8.95) и (8.109) опять совпадают. Для того, чтобы воспользоваться
при расчетах формулами (8.99), (8.100), выполним над весовой функцией (8.110)
обратное преобразование Фурье и получим, что
w(n) = Bz(n) (8.111)
— автоковариационная функция входного сигнала.
Для двумерных сигналов и систем аналоги формул (8.106)—(8.111) имеют
соответственно следующий вид:
Mj——00 оо
(8.112)
(8.113)
оо 00
^(^,«2)= 22 52 + n1,m2 + n2). (8.114)
mt—— 00 т2=—оо
(8.116)
8.3. Расчет и применение параллельно-рекурсивных КИХ-фильтров
573
w(n]^nl) = f (8.117)
где g(«j,п2) и g(«j, п2) — двумерные входные сигналы идеальной ЛПП-
системы и рассчитываемого фильтра, и г(е'Ш1 ,е'“2)—двумерная
входная детерминированная последовательность и ее спектр, В^(п},п2] и
Фу (е'Ю| ,е1™2 J — АКФ и энергетический спектр входного стационарного слу-
чайного сигнала. Минимальные значения ошибок (8.112), (8.115) равны зна-
чению критерия (8.101).
8.3.5. Преобразование стационарных случайных процессов
Во многих практических ситуациях требуется применение линейного фильт-
ра, преобразующего некоторый входной стационарный случайный процесс в
выходной процесс с заданным энергетическим спектром. Задача расчета та-
кого фильтра при его параллельной структуре является частным случаем рас-
смотренных выше задач. Известно [25], что энергетические спектры входного
сигнала фильтра — Ф/ и выходного сигнала — Ф^ связаны между
собой соотношением
ф«И=ф/(е'“)1йИГ’
где н{е,<й^ — частотная характеристика фильтра. Поэтому при заданных
энергетических спектрах сигналов на входе и выходе требуемая частотная ха-
рактеристика фильтра записывается в виде
(8.118)
(предполагаем, что энергетический спектр входного сигнала строго положи-
телен на всех частотах). Как следует из уже полученных результатов, в данном
случае расчет параллельного фильтра по условию минимума критерия (8.109)
сводится к аппроксимации частотной характеристики (8.118) с весовой функ-
цией (8.110). Общие расчетные соотношения (8.97) и (8.99) при этом конкре-
тизируются и записываются соответственно в следующем виде:
1 я
Ь,к = Ф/ (е’*>)</<0’
-п
-я
(8.119)
574
ГЛАВА 8
И
м+ м+
ь1к= Е Е hi(m)hk{n)Bf(tn-n),
т= —М " п—-М ~
М+ _
ск = h (m)hk (ли), (8.120)
т=—М "
где В f (m) — АКФ входного процесса, h(m) — последовательность, вычисля-
емая через обратное преобразование Фурье:
-л
При расчете коэффициентов параллельного фильтра по формуле (8.83) с
использованием (8.119) или (8.120) обеспечивается минимальное значение
ошибки (8.109), равное
^=Dg-R, (8.121)
где — дисперсия выходного случайного процесса.
Рассмотрим еще более конкретную задачу синтеза случайного процесса с
энергетическим спектром Фк из дискретного белого шума — последо-
вательности независимых случайных величин с единичной дисперсией. В дан-
ном случае фДе'“) = 1, и выражения (8.119) и (8.120) упрощаются:
1 к
(>«= —
-л
ct (<Tto)Ao, (8.122)
-л
М+ М+ _
bik= Е hi(m)hk(rn), ск= Е h(m)hk(m), (8.123)
т——М~ т——М~
где h (т) = f Лш.
—л
Сопоставление формул (8.123) и (8.89) показывает, что теперь задача све-
лась к_невзвешенной квадратичной аппроксимации импульсной характерис-
тики h(m).
8.3. Расчет и применение параллельно-рекурсивных КИХ-фильтров
575
В двумерном случае аналоги формул (8.119), (8.120), (8.122) и (8.123) име-
ют, соответственно, следующий вид:
. л л
b,t=-L.f f Фу , е'"2 )н, (е|Ш|, е“°2)яЛ («-'“, е‘‘“2
—л —л
. л л ----------------------------------
ct=-~2j е^фДе'"1, е’“‘!)d(O1dW2, (8.124)
ь1к= Е 12 12 12hi("h* Mi}hk(nx, n2)Bf(mi-ni, т2-п2),
(/И!, т2) GD («!, п2) fzD
Ск = 12 12h{mX4 m2)hk(n^ пг\ (8.125)
(rip тг) ED
где
h{mx, m2)=—vJ* j Дфj, e/fi>2jФ, е'Шг jexp^cOjWj4-co2Rt2)]j©|J©2;
471 —Я -n
и для случая Ф Де •/Ш|, е /с°2 j = 1:
1 л л ----------------------
ct=~~J /ЛфДе*”1. е'“2)нДе*‘ш', e^jdco^ojj, (8.126)
*“ТС ’’-ТС
b/k= Е 12hi(m\* m2)hk(nlt n2),
(»i|, m2) ED
ck= 12 12Цт}, m2)hk(nlt n2),
(mp m2) ED
(8.127)
X ---------------
JДфК^е‘“’, e'“2jexp^cOjm,+<o2WI2)]^oi)i^co2
-Л
Для минимального значения ошибки формирования выходного процесса
остается в силе выражение (8.121).
8.3.6. Восстановление сигналов
Рассмотрим линейную модель наблюдения случайного сигнала на фоне
помехи:
576
ГЛАВА 8
оо _
f(n) = 52 h(m)f0(n- т)+ v(n), (8.128)
m™—сю
где h(m) — импульсная характеристика «искажающей» ЛПП-системы, /0(п)
и v (л) — соответственно, полезный сигнал и помеха, некоррелированные между
собой стационарные случайные последовательности с нулевыми средними и
автоковариационными функциями (АКФ) В/0(т) и Bv(m). Потребуем, что-
бы рассчитываемый цифровой фильтр обеспечивал наилучшее в среднеквад-
ратичном смысле восстановление полезного сигнала или, иными словами,
чтобы для сигнала g (п) на выходе фильтра дисперсия
е2 = е|[/0(п)-£(и)]~}
(8.129)
принимала минимальное значение (здесь и далее Е{...} — оператор матема-
тического ожидания). С учетом формул (8.6) и (8.7) конкретизируем выраже-
ние (8.129):
£2 = Е
К-l м +
fo(n)~lL<h 52
к=0 т——М
hk(m) f(n~ т)
(8.130)
Далее через условие (8.87) перейдем к системе уравнений (8.88) и к формуле
(8.83) для расчета коэффициентов фильтра, в которых в данном случае
м+ м'
ь1к = 52 52 hl М (я) Вf (т-п),
т=—М~ п——М~
М +
Q ~ 52 hk(m)Bfof(-m),
т——М ~
(8.131)
где В^ (т) — АКФ наблюдаемого входного сигнала, и Вд (т) — взаимная кова-
риационная функция полезного и наблюдаемого сигналов. Эти функции выража-
ются через введенные выше характеристики модели наблюдения (8.128) [25]:
оо оо _ _
В/(т) = 52 52 h(r)h(r+ p)Bfo(m- р)+ Bv(m),
p=—cor——oo
52 h(p)Bfo(m-p).
p=—OC
Подставив найденные коэффициенты фильтра в формулу (8.130), после
ряда преобразований получаем значение минимальной дисперсии ошибки
восстановления:
8.3. Расчет и применение параллельно-рекурсивных КИХ-фильтров
577
е^=ОЛ-Я. (8.132)
где D — дисперсия полезного сигнала.
Для двумерных сигналов соотношения (8.128), (8.129) и (8.131) модифици-
руются. Модель наблюдения записывается в виде
/(л,,и2) = (8.133)
ГИ] ——ОО ЛИт ——ос
минимизируемая ошибка восстановления имеет вид
£2 = Е |[/0 (п1,п2 )-.?(«], я2)]2}- (8.134)
Элементы матрицы В и вектора С в формулах (8.83), (8.84) и (8.88):
bik= 22 22 22 22Л/("гот2)Лл(«1’«2)^/(mi-п^т2-п2\
(nt,n2)£D
22 22ЛДт1^2)^,/()/(-теп""12). (8.135)
(wp/njJCO
где
^ £ £ £ 22 h[rx,r2}h{rx +px,r2^ p2)Bfi\mx-px,m2-p2)+Bv[mx,m2),
p| ——ОС P2 ——ОС Г| =—ос r2 =“0C
B/()/(mi,m2)= £ £ h{px,p2)Btn{mx~p^m2-p2\
Pj—OCp2--OC
Все участвующие в данных выражениях двумерные последовательности
имеют тот же смысл, что и в одномерном случае. Выражение (8.132) для ми-
нимального значения ошибки остается без изменений.
8.3.7. Обнаружение объектов
Пусть сигнал на входе фильтра состоит либо из аддитивной смеси «объек-
та» Т(п) известной формы и «фона» — случайной последовательности v(n):
/(n)=T(n) + v(n), (8.136)
19 — 9044
578
ГЛАВА 8
либо только из фона:
f(n) = v(n). (8.137)
Задача состоит в том, чтобы отличить одну ситуацию от другой. Будем судить
о наличии объекта по уровню сигнала g (я) на выходе фильтра, то есть счи-
тать, что наблюдаемый входной сигнал соответствует модели (8.136), если
«(л)>Д, (8.138)
где Д — некоторое пороговое значение, или модели (8.137) в противном слу-
чае. Решение, принятое по правилу (8.138), означает обнаружение объекта,
при этом значение аргумента п позволяет указать положение (произвести ло-
кализацию) объекта на временной оси [37].
Данную задачу можно интерпретировать как задачу классификации вход-
ного сигнала, решаемую для каждого значения п. Примем в качестве класси-
фикационных признаков сигналы (8.7) на выходах параллельных звеньев ф^луг-
ра. Совокупность этих сигналов образует вектор признаков Y — {.У;. («)}*_
Будем считать, что фон v(n) стационарен, распределен по нормальному
закону, имеет нулевое среднее и АКФ Bv(m). Несложно получить, что для
модели сигнала (8.136) математическое ожидание вектора Y имеет вид
с = £{Y} = {с4‘;‘
м+
Е hk(m)T(-m)
т=-М
(8.139)
а для модели (8.137) оно равно нулю. Ковариационная матрица вектора в
обоих случаях одинакова:
B = £{(Y-C)(Y-C)T} ={ЫЦ =
м' м'
Е Е ht (т) hk (л) Bv (т - п)
т—-М^ п—-М~
(8.140)
Поскольку процедура формирования признаков линейна, вектор Y в каж-
дом классе сигналов, как и фон, распределен нормально. Известно [33, 34],
что в такой ситуации оптимальным является линейный классификатор, кото-
рый принимает решение о наличии объекта при
CrB-,Y >-5-СгВ-1С - d,
2
(8.141)
где d — параметр, зависящий от выбранного критерия обнаружения и апри-
орной вероятности появления объекта в наблюдаемом сигнале. Сопоставле-
8.3. Расчет и применение параллельно-рекурсивных КИХ-фильтров
579
ние неравенств (8.138) и (8.141), с учетом формулы (8.6), позволяет одновре-
менно найти вектор коэффициентов фильтра (он снова определяется соотно-
шением (8.83)) и пороговое значение выходного сигнала:
Д = --С7В 'С-</ = -/? J , (8.142)
2 2
где величина R опять выражается формулой (8.84) и в данном случае пред-
ставляет собой расстояние Махаланобиса между классами сигналов [33]. Па-
раметр R является показателем качества классификатора: чем больше его зна-
чение, тем меньше вероятность ошибок обнаружения объекта.
В задаче обнаружения двумерного объекта для наблюдаемого сигнала, вме-
сто моделей (8.136) и (8.137) используются, соответственно, модели
f(nl,n2) — T[nltn2) + v(nl,n2), (8.143)
f(nI,n2) = v(n1,«2), (8.144)
и решение о наличии объекта выносится, если сигнал на выходе двумерного
фильтра превышает пороговый уровень:
g(ni,n2)>A. (8.145)
Формулы (8.83), (8.84) и (8.142) для расчета и анализа фильтра сохраняют-
ся, но модифицируются выражения для элементов матрицы (8.140) и вектора
(8.139):
b^ — Е ЕЕ ^hl(mt,m2)hk(nl,n2)Bl,(m]-п]}т2 -п2), (8.146)
(mt,m2)€D (nt,n2)GD
ck= Е ЕЛл (m1,wt2)7’("Ihw2)-
(пц,т2)€О
Двумерные последовательности, которые присутствуют в соотношениях
(8.143)—(8.146), имеют тот же смысл, что и одномерные, введенные выше.
8.3.8. Анализ эффективности параллельно-рекурсивных КИХ-фильтров
в задачах обработки изображений
Анализ эффективности параллельно-рекурсивных КИХ-фильтров проведем
на простых примерах решения задач обнаружения объектов на изображении
и аппроксимации заданной ИХ. Ограничимся рассмотрением фильтров на
основе полиномиальных базисов, поскольку именно они обеспечивают наи-
более ярко выраженное преимущество над традиционными способами реше-
ния поставленных задач.
В задаче обнаружения в качестве объекта примем изображение «креста»
(рис. 8.10с) (размером 9x9 элементов) единичной яркости на нулевом фоне,
19*
580
ГЛАВА 8
подвергнутое линейному искажению путем двукратного усреднения квадрат-
ным окном 3x3 элемента и зашумлению аддитивным белым шумом с диспер-
сией Dv а.
Качество фильтра при обнаружении объектов характеризуется зависимостью
произведения RDV (здесь R — расстояние Махаланобиса между классами объек-
та и фона) от приведенной вычислительной сложности обработки (рис. 8.106):
U=U+ + т]£Л,
где Т| — коэффициент относительной сложности операции умножения (при
построении зависимостей примем типичное значение Т| =3).
Для сравнения результаты работы параллельно-рекурсивных алгоритмов
приведены вместе с традиционными, а именно на рис. 8.106 даны следующие
обозначения алгоритмов:
1 — обычный КИХ-фильтр в форме прямой свертки [15, 26, 27];
2 — быстрая свертка по схеме Кули—Тьюки с основанием «2» и процеду-
рой оптимального секционирования входного сигнала [15, 26];
3 — параллельно-рекурсивный фильтр на основе полиномиального бази-
са с минимальной вычислительной сложностью (см. п.8.2.3);
4 — параллельно-рекурсивный фильтр на основе четного полиномиаль-
ного базиса, предложенный в п.8.2.4.
Из рис. 8.106 видно, что наибольшим расстоянием Махаланобиса и, сле-
довательно, качеством обладает фильтр на основе четного полиномиального
базиса при любой сложности обработки.
При построении зависимостей качества фильтра от сложности для алго-
ритмов прямой и быстрой свертки варьировались размеры окна обработки, а
для параллельно-рекурсивных фильтров выбирались различные подмноже-
ства двумерных базисных функций из множества с индексами
0<к<К, 0<1<К.
Рис. 8.10. Анализ эффективности применения рекурсивных полиномиальных базисов в задаче
обнаружения объекта
8.4. Применение методологии распознавания образов
581
В задаче аппроксимации импульсной характеристики (ИХ) с помощью по-
линомиальных функций рассмотрим двумерную «гауссоиду», то есть раздели-
мую по координатам функцию вида
h (raj,ra2) = exp(—0,О1(га2 +
заданную на симметричном окне | raj <15, | га2| <15 и изображенную на
рис. 8.1 \а.
В силу разделимости искомой ИХ, ее аппроксимация сводится к аппрок-
симации каждой из одномерных составляющих функции:
h (га) = ехр(—0,01га2).
На рис. 8.1 И также показаны зависимости квадрата погрешности аппрок-
симации от вычислительной сложности для фильтров, реализованных выше-
означенными четырьмя способами.
Представленные результаты показывают, что разработанные параллельно-ре-
курсивные фильтры значительно увеличивают скорость обработки изображений —
в 10—100 раз по сравнению с известными алгоритмами прямой и быстрой свер-
тки. В случае осесимметричных импульсных характеристик, часто используемых
во многих прикладных задачах, при применении четных полиномиальных бази-
сов вычислительная сложность дополнительно снижается в 1,5—2 раза.
8.4. Применение методологии распознавания образов в задачах
цифровой обработки изображений
Необходимым свойством алгоритмов автоматической обработки изобра-
жений, рассчитанных на универсальное применение, является их адаптив-
ность, то есть способность само подстройки к меняющимся свойствам обра-
батываемых данных. Для задачи фильтрации и восстановления общая идея
Рис. 8.11. Анализ эффективности применения рекурсивных полиномиальных базисов в задаче
аппроксимации импульсной характеристики
582
ГЛАВА 8
адаптации может быть сформулирована следующим образом. Задается (фик-
сируется) некоторый параметрический класс алгоритмов обработки (напри-
мер, линейные цифровые фильтры с множеством возможных импульсных
характеристик). Объект обработки (изображение или его фрагмент) сначала
подвергается анализу с целью оценки его характеристик: статистических, струк-
турных и т.п. Затем по полученным значениям характеристик объекта рассчи-
тываются параметры алгоритма (в приведенном примере — конкретная им-
пульсная характеристика фильтра). И только после этого производится соб-
ственно обработка — фильтрация изображения. Заметим, что принципиальным
здесь является априорное выделение класса обрабатывающих алгоритмов,
именно для него описанная внутренняя структуризация адаптивной обработ-
ки может быть конкретизирована до уровня практической реализации. Если
же говорить о «сквозном» преобразовании объекта обработки в результат и
ставить задачу оптимизации такого преобразования в некотором (пусть дос-
таточно широком) классе объектов, то, с одной стороны, найденное опти-
мальное преобразование, безусловно, будет максимально адаптивным в рам-
ках рассматриваемого класса объектов, но, с другой стороны, само понятие
адаптации потеряет смысл, так как оно перестанет поддерживаться описан-
ной выше специфической структурой адаптивного алгоритма.
Традиционный путь решения задач обработки и анализа изображений вклю-
чает в себя подбор или полуэвристический синтез большого числа обрабатыва-
ющих процедур, что объективно обусловлено разнообразием и сложностью
математических моделей формирования оптических сигналов, плохой форма-
лизацией решаемых задач, критериев качества обработки и т.д. По этой причи-
не для современных компьютерных систем анализа видеоинформации харак-
терна весьма разветвленная и, как следствие, неудобная структура прикладного
программного и аппаратного обеспечения, в рамках которой представлена
широкая номенклатура алгоритмов обработки изображений, а сами алгорит-
мы, реализующие лишь отдельные шаги сквозных информационных техноло-
гий решения прикладных задач, обладают низкой вычислительной эффектив-
ностью и/или не обеспечивают требуемое качество обработки.
В то же время практически всегда можно неформально указать желаемый
результат обработки, например, предъявив согласованную пару изображений,
интерпретируемых как «входное» и «выходное». Поскольку сам механизм пре-
образования данных при этом остается неизвестным, мы имеем здесь типич-
ную для распознавания образов ситуацию необходимости «принятия реше-
ния по прецеденту» [4, 17]. Это позволяет применить к обработке изображе-
ний универсальную методологию распознавания, то есть свести синтез
обрабатывающего алгоритма к построению решающего правила, а саму зада-
чу обработки — к «узнаванию» результата во входных данных.
Возможность подобного подхода упоминается или лежит в контексте мно-
гих работ по распознаванию зрительных образов [4, 17, 19]. Однако ее прора-
ботка до уровня практической реализации впервые осуществляется в рамках
данного исследования.
8.4. Применение методологии распознавания образов
583
8 .4.1. Общее описание преобразования данных
Приложение методологии распознавания образов к обработке изображе-
ний можно проиллюстрировать несложными схемами, представленными на
рис. 8.12. На входе процедуры обработки мы имеем изображение F, являюще-
еся результатом искажений «идеального» изображения Fo, недоступного для
наблюдения (рис. 8.12а). Предполагается, что существует некоторое гипоте-
тическое «эталонное» преобразование идеального изображения к требуемому
выходному — (70. Это преобразование может быть как сколь угодно сложным
и плохо формализованным (сегментация изображения, устранение мешаю-
щих деталей, фона и т.п.), так и очень простым (пороговая обработка, выде-
ление контуров) и даже тождественным (восстановление изображения, иска-
женного в канале). В любом случае нам требуется получить результат G, дос-
таточно близкий к (70, имея доступ только к наблюдаемому изображению F.
Если рассматривать достаточно большое количество согласованных пар
(F, Gq) как обучающую выборку, то можно, в принципе, построить процедуру
обучения классификатора, ставящего в соответствие вектору признаков, вы-
числяемых по входному изображению F, выходное изображение G. Набор
признаков и вид классификатора при необходимости могут корректироваться
по результатам оценки качества обработки (то есть расхождения G и (70), что
отражено соответствующими обратными связями на схеме рис. 8.12а.
Процедуры формирования признаков и классификации, настроенные в
итоге обучения на неформально заданное преобразование данных, далее ис-
пользуются при обработке других изображений того же класса (см. рис. 8.126).
Разумеется, в общем случае практическому воплощению представленных
схем препятствуют чрезвычайно высокая размерность вектора признаков, с
должной полнотой описывающего входные видеоданные, и астрономическое
Рис. 8.12. Схема процедуры обучения классификатора (а), схема обработки изображения с при-
менением классификатора (б)
584
ГЛАВА 8
число классов для выходного изображения. В такой ситуации требуемая обу-
чающая выборка становится совершенно нереальной по объему, а процедура
обработки, даже если ее и удастся построить, будет неприемлемо сложной с
вычислительной точки зрения. Однако указанные препятствия в значитель-
ной степени снимаются, если ограничиться рассмотрением пространственно-
инвариантной обработки изображения в режиме «скользящего окна».
В рамках предлагаемого подхода для каждого положения окна формирует-
ся /^-мерный вектор признаков, который используется в процедуре класси-
фикации каждого выходного отсчета. Поскольку рассматриваются только ло-
кальные признаки изображения, вычисляемые по окну сравнительно неболь-
шого размера, то их число ограничено. Решение принимается индивидуально
для каждого отсчета выходного изображения и, следовательно, число классов
мало (равно числу уровней квантования выходного отсчета). И напротив, объем
обучающей выборки достаточно велик, он равен числу положений скользя-
щего окна на изображении, по которому производится обучение, то есть са-
мих отсчетов изображения. При необходимости выборку еще большего (тео-
ретически, неограниченного) объема можно получить с помощью компью-
терного моделирования тестовых изображений, их «эталонных» преобразований
и искажений в системе видеоизмерений.
Первая и основная задача, которую нужно решить для реализации предла-
гаемого подхода, состоит в разработке методов и алгоритмов формирования
локальных признаков изображений в скользящем окне. Простейшими при-
знаками могут служить сами значения отсчетов изображения в окне обработ-
ки. Однако их использование не всегда целесообразно, поскольку, во-первых,
даже для небольшого окна их оказывается слишком много и, во-вторых, та-
кие признаки сильно коррелированы между собой и, как следствие, малоин-
формативны.
Существенно более полезными являются локальные «обобщенные момен-
ты» — линейные признаки, вычисляемые с помощью быстрых параллельно-
рекурсивных алгоритмов, рассмотренных в п.8.1, 8.2, и обладающих доста-
точно высокой информативностью.
8 .4.2. Классификация отсчетов изображения
Задачи синтеза и обучения алгоритмов классификации отсчетов выходного
изображения по заданному вектору локальных признаков, вычисляемых в
скользящем окне, лежат в русле традиционной проблематики теории распоз-
навания образов и, в принципе, могут иметь достаточно стандартные реше-
ния [4, 17, 19, 34]. Тем не менее, предлагаемый подход к обработке видеоин-
формации требует выполнения классификации в весьма специфичных усло-
виях. Поскольку в его рамках делается попытка построения унифицированного
средства обработки изображений, при синтезе классификатора не удается
использовать важные упрощающие предположения о линейной разделимости
8.4. Применение методологии распознавания образов
585
классов, гауссовых распределениях признаков и т.п.; можно рассчитывать
лишь на компактность классов в пространстве признаков. В такой ситуации
наиболее естественным было бы применение классификатора Байеса, реа-
лизованного в табличной («гистограммной») форме, или какой-либо доста-
точно хорошей его аппроксимации [34]. Однако тот факт, что в данном слу-
чае классифицируется каждый отсчет выходного изображения, налагает не-
типично жесткие ограничения на сложность вычислительных процедур и ведет
к необходимости разработки ускоренных алгоритмов классификации.
Следует отметить, что номер класса здесь одновременно является значени-
ем выходного отсчета, что автоматически определяет понятие расстояния между
классами и порождает специфичный вид функции потерь. При этом оказыва-
ется целесообразным аппроксимировать не дискриминантные функции для
каждого класса, как это обычно делается в классификаторах, а непосредственно
функцию решений.
Вопрос построения алгоритма классификации отсчетов, наилучшим обра-
зом приспособленного к данной ситуации и отвечающего сформулирован-
ным требованиям, остается пока открытым. В качестве одного из вариантов
решения данной задачи можно предложить процедуру классификации Байе-
са, реализованную в иерархической (древовидной) форме при кусочно-ли-
нейной аппроксимации функции решений.
В процессе обучения область определения функции решения, представля-
ющая собой Химерный гиперкуб, последовательно разбивается по осям и
рождает в памяти компьютера древовидную структуру (см. «двумерную»
люстрацию на рис. 8.13). В
каждой из областей, полу-
ченных в результате раз-
биения, осуществляется
линейная аппроксимация
функции решений обыч-
ным методом наименьших
квадратов. Области с ма-
лой ошибкой аппрокси-
мации принимаются за
терминальные вершины
дерева. Те области, в ко-
торых ошибка велика,
подвергаются дальнейше-
му разбиению. Процедура
обучения завершается
либо при достижении за-
данной точности аппрок-
симации, либо при исчер-
пании ресурсов памяти компьютера, отведенной на хранение древовидной
структуры вместе с параметрами аппроксимирующих гиперплоскостей в тер-
минальных вершинах дерева.
ПО-
ИЛ-
Рис. 8.13. Пример построения иерархического классификатора
586
ГЛАВА 8
Как показывают эксперименты, описанные ниже, такой классификатор
при небольшой размерности признакового пространства достаточно быстро
обучается и далее демонстрирует хорошие результаты распознавания при
весьма незначительных вычислительных затратах. Точность предлагаемой
кусочно-линейной аппроксимации функции решений при заданных ресур-
сах памяти вычислительного комплекса, очевидно, будет тем выше, чем мень-
ше размерность вектора признаков. Описанные выше рекурсивные проце-
дуры вычисления обобщенных моментов для различных семейств ядер, для
разных размеров окна обработки и т.д. способны породить чрезвычайно боль-
шое количество линейных признаков, среди которых многие будут мало ин-
формативными (в контексте конкретной решаемой задачи) или даже линей-
но связанными с другими. Избыточное число признаков ведет к усложне-
нию процесса обучения классификатора, поскольку требует обучающей
выборки увеличенного объема, к росту вычислительной сложности (и вре-
мени) обработки изображений. Поэтому при реализации описанного подхо-
да к обработке изображений весьма полезно из заранее выбранного «полно-
го» набора признаков выделить их подмножество, фактически используемое
при классификации отсчетов.
Выделяемое подмножество из К признаков должно обеспечивать как можно
более высокую эффективность обработки сигналов. Для определения наилуч-
шего подмножества в общем случае нужно перебрать все возможные сочетания
по К признаков в их полном множестве, оценить для каждого сочетания неко-
торый показатель качества обработки (для фильтрации и восстановления изоб-
ражений — остаточную погрешность представления обработанных данных) и
найти вариант, соответствующий экстремальному значению показателя (ми-
нимальной погрешности). Однако такой перебор оказывается практически
неосуществимым из-за чрезмерного числа анализируемых вариантов и, как
следствия, объема необходимых вычислений.
В [8, 31] для выбора наилучших ядер при вычислении обобщенных момен-
тов предложено использовать субоптимальный метод последовательного при-
соединения, довольно широко применяемый в приложениях теории распоз-
навания образов. Согласно ему, сначала выбирается единственный обобщен-
ный момент (признак), обеспечивающий экстремальное значение показателя
качества, затем к нему присоединяется еще один, дающий наилучшее каче-
ство обработки в паре с уже выбранным признаком, и т.д. до получения набо-
ра из К признаков. Как показывает практика, данный метод резко сокращает
вычислительные затраты по сравнению с полным перебором при несуще-
ственной потере оптимальности формируемого подмножества признаков.
В некоторых случаях удается ввести некоторое «естественное» упорядочение
признаков. Например, обобщенные моменты, соответствующие семейству ко-
синусных ядер, можно рассматривать в порядке возрастания частотного индек-
са, а соответствующие полиномиальным ядрам — в порядке увеличения степе-
ни полинома. Тогда можно использовать первые К функций упорядоченного
набора, то есть вообще исключить перебор и, следовательно, дополнительно
упростить синтез процедуры обработки.
8.4. Применение методологии распознавания образов
587
Результаты экспериментальных исследований алгоритмов восстановления
изображений, основанных на применении методологии распознавания обра-
зов, приведены ниже.
8 .4.3. Вычислительные эксперименты по исследованию эффективности
алгоритмов локальной обработки изображений
Для оценки эффективности предложенного подхода к предварительной
обработке и адаптивному восстановлению изображений была выполнена се-
рия вычислительных экспериментов. При исследовании использовались пять
тестовых изображений. Первые три изображения — кусочно-постоянные «мо-
заичные» поля, полученные разбиением плоскости прямыми линиями четырех
направлений: вертикального, горизонтального и двух диагональных. Постоян-
ный шаг между параллельными прямыми выбирался так, чтобы обеспечить
типичные значения коэффициента корреляции между соседними отсчетами
цифрового изображения в строке: 0,8 — «Мелкая мозаика»; 0,9 — «Средняя
мозаика», 0,95 — «Крупная мозаика». Раскраска каждой области постоянных
значений осуществлялась независимыми случайными нормально распреде-
ленными значениями яркости. Подобные изображения очень просто синте-
зируются и в то же время удовлетворительно описывают пространственную
структуру многих типов подстилающих поверхностей, срезов кристалличес-
ких материалов ит.д. Четвертое изображение представляло собой «полуна-
турную» сцену, содержащую набор моделей технических объектов (самоле-
тов) на черном (нулевом) фоне. Пятое изображение — реальный оцифрован-
ный фотоплан участка территории с городской (промышленной) застройкой,
полученный при помощи высокоразрешающей аппаратуры дистанционного
зондирования.
Исследования проводились на примерах двух наиболее распространенных
задач обработки изображений: фильтрации зашумленного изображения и вос-
становления изображения при модели его наблюдения с динамическими (ли-
нейными) искажениями и шумом. В обоих случаях шум принимался «белым»
(некоррелированным) гауссовым однородным случайным полем, аддитивно
наложенным на основной сигнал. Динамические искажения для задачи вос-
становления описывались двумерной линейной системой с гауссовой импульс-
ной характеристикой
h(nitn,) =-----ехр
v 2яо2
и2 + и2
2g2
(8.147)
с достаточной степенью адекватности описывающей совокупное влияние на
оптический сигнал остаточных аберраций объектива и апертуры оптико-элект-
ронного видеодатчика [3, 5, 27].
588
ГЛАВА 8
В качестве прототипа (базы для сравнения) разработанных алгоритмов исполь-
зовался метод оптимальной линейной фильтрации (п.3.4.2), обеспечивающий
минимум среднеквадратичной ошибки линейной оценки изображения. Авто-
ковариационная функция полезного сигнала, необходимая для расчета вине-
ровского фильтра, оценивалась непосредственно по обрабатываемому тесто-
вому изображению (естественно, до его искажения).
В алгоритмах, реализующих предложенный подход к обработке через рас-
познавание, в качестве локальных линейных признаков изображения были
взяты обобщенные моменты с ядрами прямоугольного семейства, выбранны-
ми методом последовательного присоединения, и с полиномиальными (сте-
пенными) ядрами, упорядоченными по возрастанию степени полинома.
На рисунках 8.14—8.18 приведены тестовые изображения и результаты ис-
следования эффективности алгоритмов их фильтрации. Эти результаты пред-
ставлены в виде зависимостей коэффициента подавления шума от
соотношения сигнал/шум на входе (Dv/£>v).
Принята следующая нумерация рассмотренных методов (алгоритмов):
1 — оптимальный линейный восстанавливающий фильтр,
2 — распознавание на основе обобщенных моментов с прямоугольными
ядрами,
3 — распознавание на основе обобщенных моментов с полиномиальными
ядрами.
Здесь и везде ниже:
е2 — дисперсия погрешности фильтрации (восстановления), то есть раз-
ности идеального и обработанного изображений,
Dv — дисперсия аддитивного шума,
Z), — дисперсия полезного сигнала (неискаженного изображения).
Качественный эффект фильтрации иллюстрируют рис. 8.19—8.21, на кото-
рых для трех конкретных примеров приведены идеальные (неискаженные)
изображения, изображения с шумом, результаты фильтрации тремя разными
методами и поля остаточных погрешностей. Из иллюстраций видно, что пред-
ложенные методы фильтрации дают визуально лучшее качество обработки, не
обладают вредным «расфокусирующим» свойством, характерным для линей-
ного винеровского фильтра, существенно меньше искажают границы облас-
тей (контуры), практически полностью восстанавливают протяженные участ-
ки постоянной яркости (фон).
И, наконец, на рис. 8.22—8.24 для этих же трех изображений представлены
результаты исследования эффективности адаптивного восстановления. В этих
примерах для импульсной характеристики (8.147) было принято значение па-
раметра о =2, что соответствует удовлетворительному согласованию разреша-
ющей способности оптической системы с шагом пространственной дискре-
тизации двумерного сигнала. Соотношение сигнал/шум было постоянным и
соответствовало хорошим условиям видеоизмерений: Ds/Dv =50. Качествен-
ный эффект от применения новых методов здесь остается в целом таким же,
8.4. Применение методологии распознавания образов
589
Рис. 8.14. Фильтрация изображения «Мелкая мозаика»
e2/Dv
Рис. 8.15. Фильтрация изображения «Средняя мозаика»
e2/Dv
Рис. 8.16. Фильтрация изображения «Крупная мозаика»
590
ГЛАВА 8
как и в случае фильтрации: уменьшение расфокусировки, лучшее воспроиз-
ведение участков с контурами, повышение точности.
Из приведенных экспериментальных данных можно сделать общий вывод
о существенно более высокой эффективности предлагаемых методов по срав-
нению с оптимальным линейным восстанавливающим фильтром (в 1,1—3 раза
по дисперсии погрешности восстановления). Полученный выигрыш допол-
нительно может быть увеличен за счет оптимизации параметров обработки,
совершенствования классификатора отсчетов и процедур его обучения, отыс-
кания лучших семейств рекурсивно вычисляемых признаков в скользящем
окне ит.д.
Рис. 8.17.
Рис. 8.18. Ф '.льтрация изображения «Фотоплан;
8.4. Применение методологии распознавания образов
591
Метод 1
Метод 2
Метод 3
Идеальное изображение
Результаты восстановления
Рис. 8.19. Фильтрация изображения «Средняя мозаика»
592
ГЛАВА 8
Метод 1
Метод 2
Метод 3
Изображение с шумом (£>5/Рк=5)
Идеальное изображение
Остаточная погрешность
Результаты восстановления
Рис. 8.20. Фильтрация изображения «Самолетьг
8.4. Применение методологии распознавания образов
593
Метод 1
Метод 2
Метод 3
Изображение с шумом (Ds/Dv=5)
Остаточная погрешность
Рис. 8.21. Фильтрация изображения «Фотоплан,
594
ГЛАВА 8
Метод 1
е2 = 275
Метод 2
е2=184
Метод 3
е2=187
Идеальное изображение
Искаженное изображение (о = 2)
Результаты восстановления
Остаточная погрешность
Рис. 8.22. Восстановление изображения «Средняя мозаика»
8.4. Применение методологии распознавания образов
595
Метод 1
е2= 188
Метод 2
е2 = 157
Метод 3
е2 = 167
Идеальное изображение
Искаженное изображение (о — 2)
Результаты восстановления
Остаточная погрешность
Рис. 8.23. Восстановление изображения «Самолет»
596
ГЛАВА 8
Искаженное изображение (о = 2)
Метод 1
е2= 1876
Метод 2
£2 = 993
Метод 3
е2=1038
Идеальное изображение
Результаты восстановления
Рис. 8.24. Восстановление изображения «Фотоплан,
Остаточная погрешность
8.5. Заключение
597
8.5. Заключение
В этой главе рассмотрены методы локальной обработки изображений,
основанные на применении параллельно-рекурсивных фильтров с конеч-
ной импульсной характеристикой. При обработке изображений в режиме
«скользящего окна» оказывается возможным радикальное снижение вы-
числительной сложности обработки путем ее распараллеливания и рекур-
сивной реализации. Дано общее описание одно- и двумерных параллель-
но-рекурсивных КИХ-фильтров, обеспечивающее гибкость синтеза рекур-
сивно вычисляемых базисных функций. Сложность параллельно-рекурсивных
КИХ-фильтров определяется числом параллельных звеньев и не зависит от
размеров окна обработки, что обеспечивает рост их преимуществ при увели-
чении окна.
При построении параллельно-рекурсивных КИХ-фильтров возможно ис-
пользование известных базисов разложения импульсных характеристик, в част-
ности прямоугольного, косинусного базисов и базиса Фурье. Однако наи-
больший практический интерес представляют полиномиальные базисы, для
которых разработаны быстрые алгоритмы формирования моментных характе-
ристик, широко используемых при обнаружении и распознавании объектов
на изображении. Введено семейство полиномиальных базисных функций,
обеспечивающих минимальную вычислительную сложность обработки, а так-
же построены алгоритмы формирования полиномиальных базисов специаль-
ного вида (четных и нечетных), предназначенных для разложения осесиммет-
ричных импульсных характеристик.
Для многих задач моделирования и обработки сигналов расчет параллель-
но-рекурсивных КИХ-фильтров может производиться по единой схеме, спе-
цифика каждой задачи проявляется только в значениях параметров схемы.
Разработанная общая схема расчета конкретизирована для наиболее важных
прикладных задач — для аппроксимации импульсной и частотной характери-
стик, моделирования ЛПП-систем, преобразования и синтеза стационарных
процессов, восстановления сигналов, обнаружения объектов.
На основе локальных признаков, формируемых с помощью параллельно-
рекурсивных фильтров, строятся и нелинейные процедуры обработки изобра-
жений, основанные на методологии распознавания образов.
Таким образом, параллельно-рекурсивные алгоритмы фильтрации, обла-
дая низкой вычислительной сложностью, не зависящей от размеров окна об-
работки, позволяют радикально повысить скорость обработки изображений
(в 10—100 раз по сравнению с известными методами), могут быть использова-
ны в системах оперативного анализа видеоинформации, в том числе в реаль-
ном масштабе времени.
598
ГЛАВА 8
Литература к главе 8
1. Амин М.Г. ТИИЭР 11 112 (1987)
2. Амосов А.А., Дубинский Ю.А., Копленова Н.В. Вычислительные методы
для инженеров (М.: Высш, шк., 1994)
3. Бейтс Р., Мак-Доннелл М. Восстановление и реконструкция изображений
(М.: Мир, 1989)
4. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов (М.: Наука,
1974)
5. Василенко Г.И., Тараторин А.М. Восстановление изображений (М.: Радио
и связь, 1986)
6. Виткус Р.Ю., Ярославский Л.П. Адаптивные методы обработки изображе-
ний (М.: Наука, 1988) С. 6
7. Виттих В.А., Сергеев В.В., Сойфер В.А. Обработка изображений в авто-
матизированных системах научных исследований (М.: Наука, 1982)
8. Глумов Н.И., Коломиец Э.И., Сергеев В.В. Научное приборостроение 3(1)
72 (1993)
9. Глумов Н.И., Крайнюков Н.И., Сергеев В.В., Храмов А.Г. Компьютерная
оптика 13 47 (1993)
10. Глумов Н.И., Мясников В.В., Сергеев В.В. 3-я Всероссийская с участием
стран СНГ конференция «Распознавание образов и анализ изображений: но-
вые информационные технологии» (РОАИ-3-97) (г. Нижний Новгород,
Часть II, 1997) С. 8
11. Глумов Н.И., Мясников В.В., Сергеев В.В., в сб. Труды Пятого Меж-
дународного семинара «Распределенная обработка информации» (Ново-
сибирск, 10—12 октября, 1995) С. 272
12. Глумов Н.И., Мясников В.В., Сергеев В.В. Компьютерная оптика (14—15)
55 (1995)
13. Глумов Н.И., Мясников В.В., Сергеев В.В. Распознавание образов и ана-
лиз изображений: новые информационные технологии: 2-ая Всероссийская с
участием стран СНГ конференция (Ульяновск, Часть 2, 1995) С. 94
14. Глумов Н.И., Сергеев В.В. Тезисы докл. 6-й науч. конф. «Математические
методы распознавания образов» (Москва, 1993) С. 90
15. Голд Б., Рэйдер Ч. Цифровая обработка сигналов (М.: Сов. радио, 1973)
16. ДаджионД., Мерсеро Р. Цифровая обработка многомерных сигналов (М.:
Мир, 1988)
17. Журавлев Ю.И., Гуревич И.Б., в сб. Распознавание, классификация, про-
гноз. Математические методы и их применение. Вып. 2 (М.: Наука, 1989)
С. 5
18. Зеленков А.В. Автометрия 6 34 (1982)
19. Ковалевский В.А. Методы оптимальных решений в распознавании изобра-
жений (М.: Наука, 1976)
20. Краковский В.Я.. Чайковский В.Н. Автометрия 6 34 (1984)
Литература к главе 8
599
21. Майтра С. Моментные инварианты. ТИИЭР 4 297 (1979)
22. МудровА.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран,
Паскаль (Томск: МП «РАСКО», 1991)
23. Мясников В.В. Автометрия 1 80 (1996)
24. ОботнинА.Н., Страшинин Е.Э. Автометрия 1 30 (1975)
25. Оппенгейм А.В., Шафер Р.В. Цифровая обработка сигналов (М.: Мир, 1979)
26. Прэтт У.К. Цифровая обработка изображений 1 (М.: Мир, 1982)
27. Прэтт У.К. Цифровая обработка изображений 2 (М.: Мир, 1982)
28. Рабинер Л., Голд Б. Теория и применение цифровой обработки сигналов (М.:
Мир, 1978)
29. Сергеев В. В. Математические модели и методы в автоматизированных
системах научных исследований (Куйбышев: Куйбышевский авиационный
институт, 1986)
30. Сергеев В.В. Радиотехника 8 38 (1990)
31. Сергеев В.В. Компьютерная оптика (10—11) 186 (М.: МЦНТИ, 1992)
32. Сергеев В.В., Фролова Л.Г. Компьютерная оптика 12 72 (1992)
33. Ту Дж., Гонсалес Р. Принципы распознавания образов (М.: Мир, 1978)
34. Фуку нага К. Введение в статистическую теорию распознавания образов
(М.: Наука, 1979)
35. Ярославский Л.П. Введение в цифровую обработку изображений (М.: Со-
ветское радио, 1979)
36. Ярославский Л.П. Радиотехника 3 87 (1984)
37. Ярославский Л. П. Цифровая обработка сигналов в оптике и голографии:
Введение в цифровую оптику (М.: Радио и связь, 1987)
38. Abu-Mostafa Y., Psaltis D. IEEE Trans. Pattern Anal. Mach. Intell PAMI-7(1)
46 (1985)
39. Abu-Mostafa Y., Psaltis D. IEEE Trans. Pattern Anal. Mach. Intell PAMI-6(6)
698 (1984)
40. Chochia P.A. Computer Vision, Graphics, and Image Processing 44 211 (1988)
41. Glumov N.I., Kolomiyetz E.I., Sergeyev V.V. Optics & Laser Technology 27(4)
241 (1995)
42. Glumov N.L, Krainukov N.I., Sergeyev V.V., Khramov A.G. Pattern Recognition
and Image Analysis 4 424 (1991)
43. Glumov N.I., Myasnikov V.V., Sergeyev V.V. International Symposium «Optical
Information Science and Technology» — С) I SI"97 (Moscow, Russia, 27—30 August
1997)
44. Glumov N.I., Myasnikov V.V., Sergeyev V.V. Image Processing and Computer
Optics, 577E2363 40 (1994)
45. Glumov N.I., Myasnikov V.V., Sergeyev V.V. Proceedings of the Third IEEE
International Conference on Electronics, Circuits, and Systems ICECS’961 (Rodos,
Greece, 1996) P. 696
46. Glumov N.I., Myasnikov V.V., Sergeyev V.V. Pattern Recognition and Image
Analysis 4(4) 408 (1994)
600
ГЛАВА 8
47. Glumov N.I., Myasnikov V.V., Sergeyev V.V. Pattern Recognition and Image
Analysis 6(1) 122 (1996)
48. Hu M. IRE Trans. Information Theory IT-8 179 (1962)
49. Shen J., Shen D. Proceedings of 13th International Conference on Pattern
Recognition II (B) (Vienna, Austria, 1996) P. 241
50. Teh C.H. and Chin R.T. IEEE Trans. Pattern Anal, and Mach. Intell. 10(4) 496
(1988)
ГЛАВА 9
ОБНАРУЖЕНИЕ И РАСПОЗНАВАНИЕ ОБЪЕКТОВ
НА ИЗОБРАЖЕНИЯХ
Несмотря на высокий уровень развития современной компьютерной тех-
ники, до настоящего времени остается целый ряд практических задач, реше-
ние которых оказывается достаточно проблематичным. К числу подобных задач
относится задача распознавания образов. Обусловлено это во многом сложно-
стью формализации процесса восприятия видимых образов. Поэтому, несмот-
ря на очевидную легкость, с которой человек решает задачу распознавания
окружающих его предметов, все еще нет «универсального» математического
или технологического подхода, позволяющего конструктивно разрабатывать
методы, алгоритмы и автоматические устройства, эффективно осуществляю-
щие процесс распознавания. Однако для некоторых частных ситуаций, когда
математические модели оказываются подходящими для той или иной практи-
ческой задачи, удается получить приемлемые результаты.
Цель настоящей главы — познакомить читателя с рядом теоретических и
практических результатов в области статистического распознавания образов,
ориентированных на особенности и характер анализируемой информации —
изображения.
9.1. Задачи распознавания на изображениях
Весь спектр задач, которые приходится решать при распознавании на изоб-
ражениях, можно подразделить на две группы:
- распознавание или классификация изображений и
- поиск и распознавание объектов (специфических локальных областей)
на изображениях.
Это разделение связано с особенностями реализации процесса распозна-
вания. В первой группе задач распознавание или классификация производится
для всего изображения целиком. То есть, следуя принятой в главе 4 термино-
логии, все изображение целиком в процессе распознавания относят к одному
из нескольких классов. Таким образом решением задачи распознавания в этой
группе является реализация отображения: изображение — номер класса. Следуя
602
ГЛАВА 9
принятому в главе 4 разбиению процесса распознавания на два этапа, указан-
ное отображение реализуется в виде следующих двух отображений: отображе-
ния изображение-признаки и отображения признаки-класс. Это позволяет пред-
ставить процесс решения задачи классификации изображения в виде схемы,
приведенной на рис. 9.1, которая является традиционной и стандартной для
задач распознавания образов.
Примером задач первой группы являются задачи распознавания лиц по фо-
тографиям, распознавания дактилоскопических отпечатков, диагностики за-
болеваний по снимку того или иного человеческого органа и т.д.
В задачах второй группы процесс распознавания оказывается включенным
в более общую технологию обработки изображения, связанную с поиском
распознаваемых геометрических объектов на всей области наблюдения. Объек-
ты в данной ситуации представляют собой относительно небольшие локаль-
ные области, появление которых может произойти в любой точке изображе-
ния. Причем информация о том: имеются ли объекты на изображении, како-
во их количество, ориентация, размеры и т.д., чаще всего отсутствует.
Результатом решения задачи распознавания в этой ситуации является не
только класс найденного объекта, но также и его характеристики: положение,
возможно размер, цвет, ориентация объекта в плоскости изображения ит.д.
Примером задач второй группы являются задачи дешифрирования аэро-
космических снимков, автоматического чтения текстов, нахождения локаль-
ных патологий на медицинских снимках и многие другие. Неопределенность
в целом ряде характеристик объектов делает задачу их поиска и распознава-
ния на изображении в математическом и вычислительном плане более слож-
ной по сравнению с задачами первой группы. Это приводит к тому, что про-
цесс ее решения не укладываются в приведенную схему, а производится в
соответствие со схемой, в упрощенном виде представленной на рис. 9.2, то
есть включает в себя трудно формализуемую задачу выделения фрагментов
(«областей интереса»),
В соответствии с данной схемой анализу подвергается каждый фрагмент
на изображении. По текущему фрагменту, выделенному окном обработки,
производится формирование признаков и классификация. В зависимости от
результатов классификации происходит расчет дополнительных параметров
объекта.
Легко заметить, что схема решения задачи классификации изображения
входит как составной элемент в схему решения задачи поиска и распознава-
ния. Действительно, в более широком понимании задачи второй группы от-
носятся к группе задач высокого уровня — задачам анализа наблюдаемого
изображения или сцены. Под анализом сцены в данном случае понимается со-
признаки
изображение
номер
класса
Рис. 9.1. Схема решения задачи распознавания образов
9.2. Формирование признаков по изображению
603
параметров
Рис. 9.2. Схема поиска и распознавания объектов на изображении
ставление полного описания изображенных на снимке предметов с указани-
ем их местоположения и взаимного расположения. В то же время следует
заметить, что нередко наблюдается и противоположная ситуация, когда мето-
ды и технологии решения задач второй группы выступают в качестве состав-
ных элементов решения задач первой группы. Так, например, один из мето-
дов решения задачи распознавания людей по фотографиям их лиц заключает-
ся в нахождении на изображении ярко выраженных областей интереса: глаз,
носа, губ ит.д., и их последующего описания [81, 65].
Следует также отметить, что в рамках настоящей главы решается в основ-
ном вторая задача.
9.2. Формирование признаков по изображению
Формирование признаков — первый этап в любой системе распознавания
образов. И качество всей системы оказывается жестко зависимо от того, на-
сколько хорошо подобраны признаки для описания объекта — в данном слу-
чае изображения.
Задача формирования признаков достаточно сложна, потому что процесс
описания изображения, или построения набора признаков, до настоящего вре-
мени остается процедурой эвристической, во многом зависимой от опыта и
квалификации разработчика. В связи с этим при разработке каждой новой
системы распознавания чаще всего даже специалистам в распознавании об-
разов приходится решать ее заново, ориентируясь на специфику обрабатыва-
емых изображений и изображенных на них объектов.
В рамках данной главы представлены математические методы и алгорит-
мы, используемые для формирования описания изображений и эффективно
применяемые для решения целого ряда задач распознавания на изображени-
ях. Более подробно, в п.9.2.1 представлены основные требования, которые
обычно предъявляются к формируемым признакам изображения, а также
выделены методы и алгоритмы, используемые для удовлетворения этим тре-
бованиям. В п.9.2.2, описан ряд алгоритмов, используемых для «нормализации»
604
ГЛАВА 9
изображения. Процесс нормализации, как будет показано, позволяет привес-
ти само изображение и признаки к виду, более удобному для распознавания.
Обзор основных групп признаков изображений и математических основ их
формирования, включающий также и принципиальные для задачи распозна-
вания свойства признаков, был приведен в п.4.5. В настоящей главе, в п.9.2.4
представлен алгоритм формирования признаков (моментных инвариантов),
значения которых оказываются инвариантными (то есть неизменными) к наи-
более частым искажениям: изменению масштаба изображенного объекта и
его ориентации.
9.2.1. Основные требования к признакам, вычисляемым по изображениям
Основным требованием к используемой системе признаков анализируемо-
го изображения является требование эффективности процесса распознавания.
Это требование часто имеет ряд противоречивых аспектов, на которых мы
остановимся ниже.
Во-первых, оно предъявляет к признакам требования вычислительного ха-
рактера. Они заключаются в том, чтобы существовал алгоритм расчета при-
знаков, и этот алгоритм был вычислительно эффективен. Необходимость пер-
вого требования обусловлена тем, что разработка любой системой распозна-
вания происходит, как правило, в рамках некоторого лимита «ценового»
ресурса. Это ограничивает возможности использования ряда средств форми-
рования признаков. Например, подобное ограничение в области распознава-
ния изображений может отразиться на возможности использования видеоап-
паратуры, регистрирующей цветные изображения, либо обеспечивающей по-
вышенную разрешающую способность. Второе требование вытекает из
необходимости удовлетворения определенным временным ограничениям, на-
кладываемым на процесс распознавания в целом. Это требование достаточно
типично для систем распознавания в реальном времени, например, для бор-
товых систем дистанционного зондирования, систем оперативного контроля
и других.
Во-вторых, требование эффективности распознавания накладывает опреде-
ленные требования на значения признаков. А именно, для объектов различных
классов значения признаков должны отличаться сильнее, чем для объектов
одного класса. Это требование иногда интерпретируют как требование компак-
тности описания класса в пространстве признаков, когда образы объектов од-
ного класса в пространстве признаков образуют компактные области — клас-
теры или таксоны. Это не совсем корректно, так как на требование «различия»
или «близости» значений признаков следует смотреть с точки зрения использу-
емого при распознавании классификатора — решающего правила. В то же время
компактность образов, в случае ее достижимости, позволяет существенно уп-
ростить процедуру классификации и сделать ее более устойчивой.
В-третьих, требование эффективности распознавания приводит к необхо-
димости удовлетворения требования устойчивости или инвариантности обра-
9.2. Формирование признаков по изображению
605
за (описания) к ряду возможных искажений объекта. Действительно, класси-
фицируемые на изображении объекты в реальной жизни подвергаются цело-
му ряду изменений. Кроме того, процесс регистрации сцены привносит до-
полнительные искажения, связанные с неидеальностью приборов регистра-
ции, изменением освещенности, шумами и т.д. На практике это приводит к
изменению изображения объекта и, следовательно, изменению его образа в
пространстве признаков. Последнее в общем случае может повлиять на ре-
зультаты классификации и, следовательно, эффективность системы в целом.
Следует отметить, что, если характер требований эффективности призна-
ков, существования методов их расчета и наличия быстрых алгоритмов их
вычисления часто зависит от специфики решаемой задачи, то требование
инвариантности для целого ряда практических задач распознавания на изоб-
ражениях оказывается достаточно общим. В частности, оно подразумевает
все или некоторые из следующих требований:
- инвариантность к шумовым и динамическим искажениям;
- инвариантность к яркостным искажениям (изменению яркости и кон-
траста);
- инвариантность к изменению местоположения объекта;
- инвариантность к изменению масштаба объекта;
- инвариантность к изменению ориентации объекта (к повороту объекта в
плоскости изображения);
- инвариантность к произвольным аффинным преобразованиям;
- инвариантность к изменению ракурса съемки объекта (для трехмерных
объектов).
Инвариантность к указанным искажениям в общем случае достигается за
счет предварительного преобразования исходного изображения. В частно-
сти, первая группа искажений, связанная с шумовыми и динамическими
изменениями изображения, устраняется за счет использования методов и
алгоритмов восстановления. Подробно математические аспекты процесса вос-
становления и соответствующие алгоритмы описаны в пп.3.4—3.5.
Яркостные искажения, относящиеся ко второй группе, эффективно могут
быть устранены за счет приведения изображения к «нормализованному» виду.
Соответствующий математический аппарат и алгоритмы представлены в п.9.2.2,
В том же разделе приведены методы нормализации изображений объектов
для искажений, включающих в себя изменения положения, масштаба и ори-
ентации изображенного объекта (преобразования подобия).
9.2.2. Нормализация изображений при вычислении признаков
Под нормализацией в дальнейшем будем понимать такое преобразование
изображения, которое позволяет привести его к виду, удобному для распозна-
вания. Последнее подразумевает некий стандарт для нормализованного изоб-
ражения, в качестве которого могут выступать средняя яркость, разброс или
606
ГЛАВА 9
дисперсия яркости на изображении, ориентация изображенного объекта, его
размеры и т.д.
В соответствии с принятым в п.9.1 подразделением задач распознавания
на две группы наблюдается соответствующее разделение на группы для алго-
ритмов нормализации. Связано это с особенностями реализации вычислений
при нормализации изображения в целом — глобальная нормализация, либо его
фрагментов — локальная нормализация. В то же время математические основы
и методы нормализации оказываются одинаковыми. Они, в свою очередь,
подразделяются в соответствие с требованиями инвариантности к признакам,
которые представлены в п.9.2.1. А именно, основными являются следующие:
- яркостная нормализация,
- нормализация положения объекта,
- нормализация масштаба объекта,
- нормализация ориентации объекта.
Яркостная нормализации. Одним из важных этапов решения задачи обнару-
жения и распознавания объектов на цифровых изображениях является нор-
мализация яркостных искажений. Такие искажения в системах дистанцион-
ного формирования изображений возникают вследствие как природных, так
и технических факторов (условий наблюдения, освещенности, влияния ат-
мосферы, времени экспозиции ит.д.). В результате их действия яркостные
статистические характеристики фона и объектов на изображении могут суще-
ственно изменяться при сохранении неизменной формы объектов. Из пред-
положения, что основную информацию об объектах несут их геометрические
характеристики, следует необходимость яркостной нормализации, то есть
преобразования изображения к виду, независимому от случайного характера
яркостных искажений.
При отсутствии априорной информации об искажениях вид и параметры
нормализующего яркостного преобразования определяются непосредственно
по обрабатываемому изображению. Обычно вид преобразования задается, а
параметры вычисляются на основе яркостных статистических характеристик
(среднего, дисперсии, гистограммы) [23, 27, 41, 44], однако параметры могут
быть определены и с помощью других признаков изображения (например,
моментных инвариантов [21]).
Известные алгоритмы нормализации обеспечивают выравнивание («эква-
лизацию») гистограммы на изображении [26, 41, 44], приведение к заданным
значениям («стандартизацию») среднего и дисперсии [44]. Такие методы и
алгоритмы и их математические основы представлены в пп.3.1—3.2.
Следует отметить, что несмотря на большое количество работ по обработ-
ке изображений, в которых рассматривается нормализация яркостных иска-
жений [21, 23, 26, 27, 41, 44], данную проблему нельзя считать окончательно
решенной вследствие ряда причин.
Во-первых, алгоритмы яркостной нормализации оказываются существенно
различными по эффективности для различных классов изображений. Так,
9.2. Формирование признаков по изображению
607
для нормализации изображений крупномасштабных объектов оказывается
необходимым учитывать специфику математической модели такого изобра-
жения.
Во-вторых, анализ реальных изображений показывает, что на них всегда
присутствует шумовая составляющая яркости с характеристиками, часто раз-
личающимися на объекте и фоне. При этом в упомянутых работах не уделено
достаточного внимания влиянию шумов на яркостную нормализацию.
В-третьих, для обнаружения (распознавания) объектов на изображении
иногда более важной является «стандартизация» среднего значения не по все-
му изображению, а на объекте и фоне в отдельности.
В данном разделе рассматриваются вопросы построения и применения
нормализующего преобразования с учетом обозначенных вопросов.
Рассмотрим математическую модель изображения, в котором значитель-
ную часть поля яркости f (л,, п2) занимает пространственно-протяженный
объект. Тогда область изображения можно разбить на две, соответствующие
объекту D() и фону Dh: D = D()[J Db. Области D можно поставить в соответ-
ствие эталонное изображение, каждый элемент которого определяется в зави-
симости от его принадлежности области D() или Dh:
о, при (л11Яг)еол,
1, при (п1;и2)еО„.
Используя данное представление, получаем модель нормализуемого изоб-
ражения:
/(л1Л2) = (СДЯ|>Я2) + Л,)7(«1,'22) +
+ ?/,(rtl,n2)(1-7(n1,n2)) + ^ + v(nl,«2). (9.2)
Будем считать, что С,о(н1,л2), ~ центрированные однородные
случайные поля с заданными автоковариационными функциями, v(n},n2) —
шумовая составляющая наблюдаемого изображения, А и А(, --- параметры
яркостного преобразования изображения относительно эталона. Величина А()
является контрастом между объектом и фоном (разность между их средними
значениями), а величина А — средней яркостью фона.
Вначале определим основные требования к искомому нормализующему
преобразованию, которые естественным образом вытекают из самой поста-
новки задачи.
Преобразование $ устранения яркостных искажений изображения должно
обеспечивать:
- минимизацию некоторого критерия сходства нормализованного изобра-
жения в окне с эталонным:
||у(МЛ”1’ rt2)))-y(7(«p л2))||->тт, (nls n2)tD, (9.3)
о08
ГЛАВА 9
где у — вектор признаков, вычисляемых на области изображения D (в качестве
признаков можно использовать отсчеты изображения, тогда у(/(и|, и2)) =
= f(n^ я2)); ||у|| ~ норма вектора у в заданном пространстве функций
дискретного аргумента;
- инвариантность к линейному яркостному преобразованию изображения:
у(^(а/(«ь «2) + ^)) = у(^(/(”м «2)))’ (9.4)
где Л, В — параметры преобразования;
- для эталонного изображения (9.1) должно выполняться соотношение
у($(7("ь "2)))=y(7(”i, «2))-
При построении преобразования могут задаваться и дополнительные тре-
бования, например, условие несмещенности математических ожиданий при-
знаков на нормализованном изображении относительно признаков, опреде-
ляемых на эталонном изображении:
^{y(^(/("j- «2)))} = у(7("1, «2))- (9-5)
Построение нормализующего преобразования. Для построения нормали-
зующего преобразования рассмотрим некоторые свойства изображения,
удовлетворяющего (9.1) и (9.2). С учетом этих выражений нетрудно полу-
чить статистические характеристики изображения — среднее и дисперсию
Н/о} = A>(]-*) + o*(l-*) + o>, (9.6)
где щ — А, = A„ + А, gJ , — соответственно, средние значения
и дисперсии случайной составляющей на участках фона и объекта;
М KI+N
— доля площади изображения, занимаемая объектом; I D() I, |£)ft I — количе-
ство элементов в областях Do и Dh. Характеристики (9.6) соответствуют
также случаю, когда объект частично покрывается изображением. В зависи-
мости от расположения объекта на изображении происходит увеличение доли
площади к от нуля до максимального значения А, которое при заданных раз-
мерах изображения и формы объекта можно считать априорно известным.
Линейность яркостного искажения модели (9.2) дает основание для выбо-
ра нормализующего преобразования также из класса линейных поэлемент-
ных преобразований вида
g(n|t n2) = af(n}, w2)+b, (n„ n2)eO, (9.7)
где a, b — параметры преобразования.
9.2. Формирование признаков по изображению
609
Наиболее распространенным критерием сходства (9.3) изображений явля-
ется следующий критерий:
n2) + b-f(nly п2))2
—> min,
а, b
(9.8)
при минимизации которого определяются оптимальные параметры преобра-
зования (9.7):
(9.9)
Другой способ выбора параметров преобразования (9.7) заключается в при-
ведении среднего и дисперсии в окне к значениям, соответствующим эталон-
ному изображению. Нетрудно показать, что и в этом случае коэффициенты
преобразования (9.7) выражаются через характеристики А, А() яркостного
искажения и дисперсии случайных полей:
а ~
b = -[A + A()k]a + K, (9.10)
где К — доля площади объекта на изображении при его центральном располо-
жении (на эталонном изображении объекта).
При использовании параметров (9.9) и (9.10) преобразования (9.7) реали-
зуются два различных алгоритма нормализации, которые назовем соответ-
ственно:
- алгоритм МНК (с определением параметров по методу наименьших квад-
ратов) и
- алгоритм НСД (с нормализацией среднего и дисперсии).
Каждый из двух приведенных алгоритмов требует априорного знания (или
оценки) параметров искажения А, Ап, дисперсий случайных полей ^ь, и
величины к и, следовательно, является весьма трудоемким. Другими их недо-
статками являются невыполнение условия несмещенности (9.5) и зависимость
контраста (разности между средними яркости на объекте и фоне) на норма-
лизованном изображении от уровня шума: при увеличении дисперсий слу-
чайных составляющих на изображении контраст уменьшается. Кроме того,
для определения оптимальных параметров (9.9) должно быть известно точное
положение объекта на изображении.
20 — 9044
610
ГЛАВА 9
Тем не менее, алгоритм НСД широко используется для нормализации изоб-
ражений [44]. При этом параметры (9.10) вычисляются через оценки среднего
Ду и дисперсии в окне:
где = = — к] — среднее и дисперсия на эталонном изображении.
Более простой алгоритм нормализации можно построить, если пренебречь
случайной составляющей на изображении. Тогда параметры преобразования
(9.7) примут вид
1 А
а = —, Ь =------, (9.12)
в которых параметры искажения можно заменить оценками ру и |1„ средних
на фоне и объекте:
а=-----J--, Ь =------. (9.13)
Данные параметры при неограниченном росте отношения «сигнал/шум»
на изображении стремятся к оптимальным. Очевидно, что преобразование
(9.7) с параметрами (9.13) удовлетворяет требованиям, изложенным выше.
Особенности реализации алгоритма расчета параметров при локальной норма-
лизации изображения. Использование полученного преобразования возможно
как для глобальной, так и для локальной нормализации изображения. В пер-
вом случае формула (9.7) применяется с постоянными параметрами а и b для
всего изображения целиком. При локальной нормализации требование вы-
числительной эффективности вынуждает в ряде задач использовать дополни-
тельные элементы ускорения процессов расчета параметров преобразований
(9.9)—(9.13).
В частности, для практического применения преобразования (9.7) с па-
раметрами (9.13) применяется алгоритм (назовем его НЛК-алгоритмом нор-
мализации локального контраста), основанный на одновременном использо-
вании двух скользящих окон (см. п.8.1.1), в которых реализуется оценка сред-
них значений яркости на объекте и фоне. Одно из окон является основным,
и в нем реализуется обработка изображения (нормализация, обнаружение
объекта). Во втором (дополнительном) окне вычисляется только сумма зна-
чений элементов изображения. Форма этого окна выбирается таким обра-
зом, чтобы при центральном расположении объекта в окне, «разность» окон
(элементы изображения, принадлежащие только большему из двух окон)
соответствовала фону и использовалась для оценки среднего на фоне
Примером такой пары окон могут служить два прямоугольных окна с об-
9.2. Формирование признаков по изображению
611
щим центром, «разность» которых
является прямоугольной рамкой, как
показано на рис. 9.3.
Среднее значение яркости на «раз-
ности» окон определяется аналогич-
но (9.6):
Й/ (9.14>
вспомогательное
окно
г „ Рис. 9.3. Нормализация при обработке в сколь-
где к — доля площади, занимаемая к и
ЗЯЩСМ Uls-Hv
объектом на «разности» окон.
При обработке изображения «двойным» скользящим окном средние зна-
чения на основном окне D и на «разности» окон вычисляются через суммы
элементов в окнах:
И/
Е /(«н «г)
(n1>n2)eD_______
И
У /(«I. «г)- У, _/(«!. «1)
(п,,П2)ёГ>(П|,п2)ео
(9.15)
где D — область дополнительного окна; |П| , |Z)| — количества элементов в
окнах D, D.
С использованием оценок (9.15) строится нормализующее преобразование
вида (9.7), параметры которого определяются по формулам:
И/ Ц/ Ц/
(9-16)
Подставляя параметры (9.16) в (9.7) с учетом (9.6) и (9.14), получаем
«2
/(пи п2)-н* -(|1О ~)к
(9.17)
) =
(п],п2)ео
При центральном расположении объекта в окне, к =0, к = К, и нормали-
зующее преобразование (9.17) эквивалентно преобразованию (9.7) с парамет-
рами (9.13).
20*
612
ГЛАВА 9
Для повышения устойчивости работы алгоритма нормализации (9.17) на
участках фона, где разность оценок ц f и jiy близка к нулю, может быть
применена регуляризация Тихонова [2], в соответствии с которой вместо па-
раметров (9.16) используются параметры
а= * = (9.18)
(Н/-Й/) +Y2 +Y2
где у параметр регуляризации.
Следует отметить, что регуляризация необходима и при использовании
алгоритма НСД в случае наличия на изображении участков фона с малой
дисперсией яркости.
Рекурсивная реализация алгоритма расчета параметров локальной ярко-
стной нормализации. Определение оценок средних значений (9.15) локаль-
ного нормализующего преобразования (9.17) сводится к вычислению ло-
кальных сумм элементов изображения на основном и дополнительном ок-
нах, которое нетрудно организовать рекурсивным образом, если окна
являются прямоугольными.
Вычисление суммы в скользящем окне можно рассматривать как обработ-
ку изображения фильтром с конечной импульсной характеристикой вида
1 при (wij, wi2)e£>,
О при (w], m2)$D .
Для прямоугольного окна D
-N; <п,< W.+, -W2- < n2 < N+,
фильтр является факторизуемым и допускает параллельно-рекурсивную реа-
лизацию [41]:
5(ni, м2)~— 1, пг)+ f(ni + f(n]~ 1» лг)»
; _х / / <919>
n2) — s(n}, п2 -1)+ п2 + N2 Н , п2- 1^2 ~ 1)»
где 5 (и,, п2) — локальные суммы элементов изображения в столбцах окна.
Данные рекуррентные соотношения могут быть также реализованы, если
рассматривать локальные суммы как моменты нулевого порядка, при приме-
нении параллельно-рекурсивного алгоритма вычисления моментов изобра-
жения (см. п.8.2).
Основным достоинством алгоритма является независимость его вычисли-
тельной сложности от размеров окна (всего 4 арифметической операции для
каждого положения скользящего окна) при незначительном увеличении па-
мяти (для одномерного массива сумм элементов в столбцах).
h{mx, ^2) —
9.2. Формирование признаков по изображению
613
Приведенный алгоритм и оценка его сложности полностью распространя-
ются для второго прямоугольного окна (дополнительного):
D: -N7<nx <Nf, ~N2<n2<N^- (9.20)
Однако существуют возможности для упрощения реализации алгоритма. Так,
задавая окна равными по высоте (TVj- = /V(+, /V? =/V+)j получаем для допол-
нительного окна, что рекурсивное соотношение для столбцов в (9.19) остается
в силе, а вместо второго выражения необходимо использовать рекурсию:
n2) = s(nlt п2 — п2 ~\-N2^— п2 —N2 —1). (9.21)
В этом случае «разность окон», используемая для оценки среднего фона
(9.15) представляет собой пару вертикальных полос. Для вычисления суммы
на втором окне требуется только две операции сложения без дополнительно-
го увеличения памяти.
При реализации преобразования (9.7) с параметрами (9.11) кроме вычис-
ления среднего определяется дисперсия в окне. Для расчета дисперсии орга-
низуется рекурсивное вычисление сумм квадратов отсчетов изображения в
окне по формулам, аналогичным (9.19).
Особенности применения нормализующего преобразования в скользящем окне.
При обработке изображения для каждого положения скользящего окна вы-
числяются свои параметры нормализующего преобразования. Следовательно,
при скользящей нормализации невозможно сформировать единое нормали-
зованное изображение, а можно построить серию нормализованных (с раз-
личными параметрами а и Ь) фрагментов изображения, которые соответству-
ют всем возможным положениям скользящего окна на изображении.
Однако нормализация является, как правило, промежуточным этапом об-
работки изображения, после которого на нормализованном изображении фраг-
мента вычисляются признаки, используемые для обнаружения (распознава-
ния) объектов [11, 27]. Если процедура расчета признаков реализуется в виде
линейной системы с постоянными параметрами, можно вычислять признаки
у (например, моментные характеристики) непосредственно на исходном изоб-
ражении и далее преобразовывать их с помощью рассчитанных параметров
нормализации а и b для текущего положения окна:
у(#(”1> пг)) = «2))+уИ (ль n2)eD. (9.22)
Следует отметить, что предлагаемое преобразование (9.7) с параметрами
(9.16) обеспечивает нормализацию яркостных искажений только в случае
полного захвата объекта основным окном D. При частичном расположении
объекта в окне нормализация осуществляется неточно, поскольку на «раз-
ности» окон присутствует часть объекта. Тем не менее, для обнаружения
(распознавания) это обстоятельство не является существенным, поскольку в
пространстве признаков область, соответствующую объектам, определяют
614
ГЛАВА 9
только векторы признаков, вычисленные для положений окна, полностью
покрывающих объект [11].
Анализ эффективности алгоритмов яркостной нормализации в скользящем окне.
Для практического применения любого из рассматриваемых алгоритмов яр-
костной нормализации изображения необходимо проведение теоретического
анализа и экспериментальных исследований алгоритма с целью:
- оценки качества нормализации;
- определения оптимальных параметров нормализующего преобразования;
- определения допустимого диапазона параметров искажения, для кото-
рого алгоритм сохраняет работоспособность.
В общем случае оценить качество яркостной нормализации изображения
можно только по конечным результатам решения конкретной задачи обра-
ботки изображения (например, распознавания объектов в условиях неопреде-
ленности яркостных искажений). Однако такой подход требует чрезвычайно
трудоемкого моделирования всего многозвенного процесса решения приклад-
ной задачи. Поэтому целесообразно использовать некоторые частные крите-
рии, характеризующие качество решения отдельных этапов задачи и позволя-
ющие провести исследования алгоритмов с целью выработки рекомендаций
по их использованию. Здесь для оценки качества алгоритма нормализации
будем использовать критерии сходства нормализованного и эталонного изоб-
ражений или признаков, вычисляемых на этих изображениях:
- относительную величину квадрата отклонения нормализованного изоб-
ражения от эталонного:
г2
£2= —= Е
1^1
12 («/(«и
(лр л2)ео
"2) + £-/(и1, «г))2
(9.23)
1
где |£>| — число элементов изображения в окне;
- расстояние Махаланобиса [40] между векторами признаков, определяе-
мых на эталонном и нормализованном изображениях:
R = (Y(S)-y(/)f
где В — ковариационная матрица случайного вектора Y(g) (компоненты
вектора y(f) не являются случайными); y(f) — реализация вектора Y, со-
ответствующая эталонному изображению /(пр п2).
При исследовании алгоритмов будем рассматривать положение объекта в
центре изображения, поскольку, как отмечалось выше, основное значение
для распознавания объектов имеет качество нормализации именно в такой
ситуации.
Пусть заданное на области D и содержащее локальный объект изображе-
ние удовлетворяет следующей упрощенной математической модели:
/(rip n2) = A(tf[ni, z?2) + A + v(np n2), (9.24)
9.2. Формирование признаков по изображению
615
где
. [о при (лр n2)eDj,
f(n" П’Ь|1 при (л„ л2)еО„,
г(л], п2) — белый шум, то есть случайное поле с нулевым математичес-
ким ожиданием и автоковариационной функцией Bv(n{, п2\ т}, т2)~
= с; 5(п] — mi )б(п2 — m2), oj — дисперсия значений отсчетов изображения,
5(и) — единичный импульс.
Для яркостной нормализации изображения применим поэлементное ли-
нейное преобразование
#(п], n2)~af(ni, и2)+Ь, (ль n2)ED, (9.25)
где a, b — параметры преобразования, определяемые согласно одному из рас-
смотренных алгоритмов. Очевидно, что автоковариационная функция норма-
лизованного изображения имеет вид
Вк (и|, л2; /И], wi2) = a^ 8(и| —/П1)8(и2 —= («;, п2\ mt, w2),
причем, в соответствии с моделью (9.24), выполняется равенство
п2, mlt m2) = Bv (п1э п2\ т(, т2). (9.26)
Если признаками являются все элементы изображения в окне, то из (9.24)—
(9.26) выводится соотношение
(«I, nhjG©
v—\ / , . — / 1 E IdI
= E («(nb W2)-/(«H «2)) ~7““22
(«1, n2)eo a CTv
(9.27)
Для каждого из рассмотренных выше алгоритмов определения параметров
а, b преобразования (9.25) выведем оценки показателей качества, соответ-
ствующие упрощенной модели (9.24).
Алгоритм МНК. Определение параметров а, b путем минимизации (9.23)
сводится к решению системы линейных уравнений:
616
ГЛАВА 9
или с учетом (9.24)
fl(A2|D„| + A2|D| + 2AA„|D„| + OJ|D|) + fr(A„|D„| + A|£>|) = (A + A„)|D„|
«(A„|D„| + A|D|) + b|D| = |D„|A.
Из (9.27) находим:
а... А,|о»||Р/,| А„
A„2|d„||dJ+g?|d|2 2
о2
t-4, A|D„||Dt|+a?|D„||D| -А, л
А,2|ОМ1 + <*Ж л2 .
" + К(1-К)
где К = |Z)J/|£)| — доля окна, занимаемая объектом. При этих значениях а и
b значение "Ё2 достигает минимума и равно
=(|d„|-o(a„|d„|+a|do|)-*|d„|) ±=
9.2. Формирование признаков по изображению
617
где d = Ao/<3v — отношение «сигнал/шум» на искаженном изображении.
Расстояние Махаланобиса (9.27) в этом случае равно
Алгоритм НСД. Параметры а и b преобразования (9.10), обеспечивающие
нормализацию среднего и дисперсии в окне, для упрощенной модели изобра-
жения определяются следующим образом:
*(-*)
Ь — —А 4- А()К 4~ К.
(9.28)
Подставляя (9.28) в (9.23) и (9.27), получаем
и
°2 12 f2 (nit n2)+2ab 22 /(л1« «2) +
(л(, л2}€£> («/fn2)G£>
+ъ2 22 1-2а 12 zb. л2)7(«н «г)-
(пр (Л1»
-%> 12 /(«ь «2)+ 12 /2(п1> "2) =
(«(, n2)eD (прЛг)^
= а2 (а2К+А2+2А AoK+c2^+2ab(A()K + A)+b2 -
—2аК (А +А0)-2ЬК + К = 2 (/С - К2 )(1 - Аоа) =
= 2К(1-К) 1-
= 2/С(1-/С)
2^К - К2)(1 - А„а)|£>|
А2К(1-К) +oj
618
ГЛАВА 9
Алгоритм НЛК. При использовании алгоритма нормализации локального
контраста оцениваются параметры (9.12):
Путем подстановки этих величин и модели (9.24) в выражения (9.23) и
(9.27) определим показатели эффективности:
Я =
=14
Таким образом, получены формулы (9.29)-(9.31), используемые для оцен-
ки качества алгоритмов яркостной нормализации:
- алгоритм МНК:
(9.29)
- алгоритм НСД:
R = 2K(1-K) d2 +
1
к(1-4
(9.30)
9.2. Формирование признаков по изображению
619
- алгоритм НЛК:
Ё2=1/А К = |£>|.
(9.31)
Зависимости Ё2 и /?/|£)| от d (при К=0,5) и от К (при d = 5) для
рассмотренных алгоритмов показаны на рис. 9.4, на которых кривые соответ-
ствуют алгоритмам МН К, НСД, НЛК.
Анализируя теоретические оценки алгоритмов, можно сделать следующие
выводы'.
- алгоритм НЛК является наилучшим среди рассматриваемых по крите-
рию расстояния Махаланобиса в пространстве признаков, но худшим по кри-
2
терию минимума е ;
- при больших значениях сигнал/шум d >4 показатели качества (£2 и Я)
для различных алгоритмов нормализации достаточно близки между собой;
- показатели качества первых двух алгоритмов зависят от доли площади
объекта в окне и достигают экстремальных значений при К = 0,5.
Кроме этих выводов из общих соображений и ранее приведенных данных
можно дать следующие рекомендации по применению процедур яркостной
нормализации:
- наибольший практический интерес (с точки зрения вычислительной слож-
ности) представляют два алгоритма нормализации — НСД и НЛК; при больших
Рис. 9.4. Качество яркостной нормализации изображения с центральным расположением объек-
та («--» _ МНК, «-----» - НСД, «----- - НЛК)
620
ГЛАВА 9
d эффективность применения алгоритмов практически одинакова, поэтому
рекомендуется применять алгоритм НЛК, поскольку его вычислительная слож-
ность значительно меньше;
- размеры окон обработки должны обеспечивать необходимую устойчи-
вость статистических оценок и полностью покрывать объект.
Нормализация масштаба объекта. Для построения алгоритма воспользуемся
введенной ранее математической моделью наблюдения изображения (9.1), (9.2).
Изменение масштаба объекта приводит к тому, что доля относящихся к объекту
отсчетов будет увеличена или уменьшена пропорционально квадрату величи-
ны изменения линейных размеров. Пусть К — доля площади изображения,
занятая объектом на эталонном изображении, — А(, + А и цл = 4 — сред-
ние объекта и фона. При изменении масштаба средние изображения изменя-
ются в соответствии с изменением доли к отсчетов, относящихся к объекту:
Н/ = кР<> + откуда
В результате линейное изменение масштаба а = у]к/К .
При реализации данного алгоритма для локальной нормализации масшта-
ба, величина среднего с точностью до постоянного множителя может быть
эффективно вычислена с использованием параллельно-рекурсивного алгоритма
(9.19).
Заметим, что до использования алгоритма нормализации масштаба необ-
ходимо воспользоваться алгоритмом яркостной нормализации. В противном
случае средняя величина яркости, зависящая от яркости отсчетов изображе-
ния, не позволит получить корректное значение к и, следовательно, пра-
вильно определить изменение масштаба.
Нормализация положения объекта. При нормализации положения объекта
задачей является нахождение такого положения (xf, х‘2) нового начала ко-
ординат в плоскости изображения, при котором размещение этого объекта
окажется в определенном смысле стандартным (например, центральным).
Заметим, что данное преобразование изображения характерно лишь для гло-
бальной нормализации, поскольку при локальном подходе окно обработки
занимает все возможные положения на изображении, и обязательно найдется
такое, при котором объект будет иметь требуемое расположение в анализиру-
емом фрагменте.
Существует целый ряд подходов к нормализации положения объекта. Из
них наиболее типичным является подход к определению начала координат по
центру «тяжести» изображения [3].
Как известно [3], координаты центра тяжести (xf, x^j плоской фигуры S
определяются следующим образом:
9.2. Формирование признаков по изображению
621
jCjpfxj ,x2)dx}dx2
__£s___________________
ff p(xJtx2)dxidx2
D.s
ff x2p(xj,x2)dx1dK2
D.s_________________
ff p(x1,x2)dx1dx2
DS
(9.32)
здесь р(л1,х2) — функция плотности фигуры в точке (xltx2), Ds — область,
занимаемая фигурой. Интерпретируя значения функции яркости как значе-
ния «тяжести» в отсчетах наблюдаемого изображения, получаем следующие
выражения для вычисления положения нового начала координат в плоскости
дискретного изображения:
*1-1 *2-1
Е п2)
л с П|=Оя2=О
Л1 — /V,—I/V2—I
Е Е /(«I. «г)
П|=0 п2=0
/Vj-1 W2-l
Е Е «г)
» с П| =0 п2 =0
Х2 jV,-1jV2-1
Е Е /(«и и2)
П|—0 л2=0
Если функция яркости имеет всего две градации, т.е. наблюдаемое изобра-
жение бинарно, то приведенные выражения преобразуются к виду
где D] ={(*1, п2): /(пр п2)~^} ~ область отсчетов с ненулевыми значе-
ниями функции яркости. Полученные выражения отражают уже статис-
тический подход к нахождению нового начала координат — оно опреде-
ляется как средняя величина координат присутствующих на изображении
точек.
В дополнение к изложенному возможны также подходы к определению
начала координат, основанные на геометрической модели объекта (центр опи-
сывающего многогранника, окружности и т.п.), использующие степенные
моменты более высокого порядка [3, 6], и др.
Нормализация ориентации объекта. Изложенный ниже геометрический под-
ход к определению ориентации объекта предложен в монографии [3]. Он ос-
нован на использовании степенных моментов (см. п.4.5.4).
Выберем в качестве нормализованной ориентации такое положение цент-
рированного изображения, при котором момент второго порядка р,п = 0. Для
осесимметричного объекта данное условие соответствует ситуации, когда ось
симметрии объекта расположена вдоль оси абсцисс или ординат.
622
ГЛАВА 9
Пусть изображение некоторым образом повернуто относительно своего
нормализованного положения. Тогда соответствие между моментами второго
порядка запишется таким образом:
Ни (О) = |(Ц2О -Ho2)-sin 2ф + Ци cos ср ,
здесь Ц]](0) = 0 — момент нормализованного изображения, (р — угол пово-
рота изображения против часовой стрелки, относительно начального положе-
ния. Тогда
1 2ц<. я
ср = — arctg------Hr—, t =0,1,2.... (9.33)
2 Мог-М20 2
Данное выражение определяет ориентацию неоднозначно, а с точностью
до поворота на гл/2. Для однозначного ориентирования изображения (с не
более, чем двумя осями симметрии) можно воспользоваться значениями мо-
ментов ц02, ц01, ц30 следующим образом [3]: в выражении (9.33) коэффи-
циент t выбирается исходя из условий
О, при р20>Ц02> Мзо>°,
1, при И20<И02, Мзо>°.
2, при Н20 > М-о2, Мзо<°>
3, при М20 < Мо2, Мзо<°-
При наличии на объекте (изображении) более двух осей симметрии не-
обходимо использовать более сложные алгоритмы нормализации ориента-
ции [3].
В случае нормализации бинарного изображения, можно использовать ста-
тистический подход. В этом случае в качестве ориентации объекта выбирают
направление собственного вектора хх матрицы ковариации В координат от-
счетов ненулевой яркости. При этом собственный вектор должен соответ-
ствовать максимальному собственному числу Хтах матрицы ковариации, как
показано на рис. 9.5.
Пусть матрица ковариации имеет вид
возможные собственные значения X находятся из уравнения
(В-ЛЕ)хх=0,
(9.34)
9.2. Формирование признаков по изображению
623
Рис. 9.5. К определению ориентации по соб-
ственному вектору матрицы ковариации:
«—>» — собственный вектор, соответствующий
максимальному собственному числу, «-->» —
собственный вектор, соответствующий мини-
мальному собственному числу, «••••>» — оси
координат изображения
где Е — единичная матрица, х^ — собственный вектор, соответствующий
числу X. Из уравнения (9.34) получаем
^тах
а Ч- b +
Тогда собственный вектор, соответствующий ХПШЛ равен
с
b — а + — а)2 +4с2
_ —
что соответствует углу наклона <р такому, что
tg(p =
2с
b — a + yffb — a)2 +4с2
(9.35)
Для центрированного изображения b = |120 , а = ц02 , с = Цп,
<р = arctg
_______________2Цц________________
Р-20 — Р-02 + >/(Р-20 ~Р-02)
4 =
624
ГЛАВА 9
Перепишем полученное выражение в следующем виде:
tga =
Р-20 Р-02
(9.36)
2рц
Р- 20 ~РЛ2
Учитывая, что для произвольного угла а выполняется тригонометричес-
кое тождество
tga =
tg(2a)
1 + -Jl +[tg(2a)]
|a|
я
4
получаем окончательно
1
a =—arctg
^Pii
<P2O ~P02 ,
(9.37)
Легко заметить, что данное выражение для ориентации совпадает с глав-
ным значением угла (9.33). То есть результаты определения ориентации объекта
на изображении на основе геометрического и статистического подходов в
принципе совпадают. В то же время достоинство первого подхода состоит в
однозначности определения ориентации, в том числе при нескольких осях
симметрии изображенного объекта.
В заключение заметим, что необходимость нормализации зависит от того,
какие именно признаки используются при распознавании. Если используе-
мая система признаков инвариантна к некоторым преобразованиям (ярко-
стным, геометрическим), то необходимость предварительной нормализации
изображения отпадает. И наоборот, использование неинвариантных к иска-
жениям признаков приводит к необходимости применения к изображениям
нормализующих преобразований.
В п.4.5 выделены основные группы признаков, используемых при распоз-
навании на изображениях, а также указано, какие из них требуют нормализу-
ющих преобразований, а какие являются инвариантными.
9.2.3. Моментные инварианты как признаки изображения
Во многих задачах обработки цифровых изображений нашли широкое при-
менение моментные характеристики изображений и рассчитываемые на их
основе моментные инварианты [3, 6, 18, 19, 21, 45, 46, 52—57, 71, 73—75].
9.2. Формирование признаков по изображению
625
Основным достоинством моментных инвариантов является нечувствительность
к поворотам изображения, что делает эффективным их применение в каче-
стве признаков в задаче обнаружения и распознавания на изображении объек-
тов неизвестной ориентации. Более того, путем несложных преобразований
на базе моментных инвариантов формируются признаки, устойчивые к пре-
образованиям подобия. Наконец, при поиске и распознавании объектов на
изображении в рамках технологии «скользящего окна» применение момент-
ных инвариантов особенно уместно в связи с возможностью параллельно-
рекурсивного вычисления локальных моментных характеристик, алгоритм
которого рассмотрен в п.8.2.
В п.9.2.3.:
- произведена формализация общего алгоритма синтеза функционально
независимых моментных инвариантов произвольного порядка;
- приведен быстрый алгоритм расчета моментных инвариантов в режиме
скользящего окна (локальной нормализации) и приведены оценки вычисли-
тельной сложности;
- рассмотрен способ формирования на базе степенных моментов аффин-
ных инвариантов — признаков изображения, инвариантных к аффинным пре-
образованиям — по материалам работ [52, 53].
Моментные инварианты в обработке изображений. Рассмотрим сначала изоб-
ражение как функцию двух непрерывных аргументов /(jq, х2). Степенные
моменты порядка (к, I) определяются согласно формуле
= J J xfxl2 f(xt, x2)dxtdx2, к, I = 0, 1, ... . (9.38)
—оо—сю
Обычно в задачах распознавания используются центральные моменты, об-
ладающие инвариантностью к сдвигу изображения:
00 ОО к [
= J f (*! -xf) (х2 -*2) /(х1, x2}dxxdx2, к, 1 = 0, 1, ... , (9.39)
—оо —ОО
где А] = ц10/ц00, Х2 =ЦО|/роо — координаты «центра тяжести» изображе-
ния (9.37). Очевидно, что центральные моменты (9.39) выражаются через
моменты (9.38):
Р« = £ t, (-1)'+' с; C,J Г" , (9.40)
<=0 j=0
где С‘к , С{ — биномиальные коэффициенты. Для центрированного изобра-
жения (при Х]С = х2 =0) значения моментов (9.38) и (9.39) совпадают. Для
определенности в дальнейшем будем рассматривать именно эту ситуацию.
С помощью степенных моментов определяются характеристики, инвари-
антные к повороту изображения (моментные инварианты). Так, набор харак-
теристик, приведенный в [18, 21, 71], включает семь инвариантов:
626
ГЛАВА 9
Ф] —Ц.20 "ЬНо2 ,
Ф2=(Н2О-Но2)2+4Ни,
фз ^(Нзо ~ЗЦ|2) +(3р21 — Моз) >
ф4=(Мзо+М12)2+(Ш1+Моз)21 (9.41)
ф5 =(Мзо - 3М12 )(мзг> +И|2 )[(Изо +М|2)2 —3(иг, + Моз )2 ] +
+(3М2| -М<в)(м21 +Моз)[3(Мзо +Mi2)2 -(М21 +Моз)2]-
фб=(М20-Мо2)[(Мзо+М12)2-(М2|+Моз)2]+4М||(Мзо + М|2)(М2|+Моз).
ф? — (М21 ~Моз)(Мзо +М12)[(Мзо +Ми) — З(м2|+Моз) j +
+(мзо ~3М|2)(м2| +Моз)[з(Мзо+М12)2 — (М-21 + Моз)2]-
В данном наборе используются только моменты до порядка (к, I) при
&4-/<3. В работах [3, 45, 76] используется более узкий набор инвариантов,
входящих в указанное множество (9.41). Но при любом выборе набора возни-
кает два вопроса:
- о функциональной избыточности наборов, то есть о возможности выра-
зить один из инвариантов как функцию других [7, 54];
- о полноте набора, то есть о возможности с помощью моментов до задан-
ного порядка построения других функционально независимых инвариантов
[7, 54].
Метод построения моментных инвариантов произвольного порядка. Для отве-
та на поставленные выше вопросы кратко рассмотрим предложенный в [45,
46] метод построения моментных инвариантов с использованием комплекс-
ных моментов:
Мк[ — f J (xj + iх2)к (xj — ix2^1 /(xj, л2)^X1 dx2, к, 1 = 0,1,.... (9.42)
—00 —00
Комплексные моменты являются линейной комбинацией обычных моментов:
при i + j = k + l,
(9.43)
где «гу, bjj — некоторые целочисленные коэффициенты.
9.2. Формирование признаков по изображению
627
В полярных координатах комплексные моменты могут быть представлены
в виде
Mw = J*Jp*+/+1 /ел(рcos^, psindjdpdd, A, / — 0,1,... . (9.44)
о о
С другой стороны Mkl =|MA/|e'Vo, где |MW|, y0 — модуль и аргумент ком-
плексного числа. Путем несложных преобразований выражения (9.44) можно
показать, что при повороте изображения на угол Ad значение комплексного
момента примет вид
Mkl (Ad) = |Mw|ef ч'° е~* (9.45)
Из (9.45) следует [46], что при повороте изображения не меняются значе-
ния Ми(Дй) = Ми и Ми(ДО)МЛ (ДО)=|МИ|2.
Обобщая эти результаты, введем в рассмотрение произведение
мг, ,м?А ...м^ =|м;1, м?Л... +^> х
Хе~‘А4^1~/,)'’+(*2_/2)Г2+ • (9 46)
Оно является инвариантным к повороту, если выполняется условие
-1^=0. (9.47)
1=1
При этом условии в качестве инвариантов можно использовать модуль
произведения комплексных моментов |м^М^/2 ...M^z |, вещественную
Re^M^M^ ...М'^ ) и мнимую j часть произведения.
Можно показать, что набор моментных инвариантов (9.41) для центриро-
ванного изображения выражается через комплексные моменты следующим
образом:
Ф> =Мц , Ф2 —^20^02’ Фз — М21 М12> Ф4 —М30М03,
Ф5=Ке(м|1М03), Ф6=Ке(м^1М02), Ф7 =-1т(м^ Моз). (9.48)
Отметим, что данный набор является функционально избыточным, так как
инварианты Ф3, Ф4, Ф5, Ф7 связаны соотношением
ф52+ф2=ф’ф4.
628
ГЛАВА 9
Очевидно, что по заданному набору комплексных моментов можно по-
строить любое число инвариантов, так как любая функциональная комбина-
ция инвариантов также является инвариантом. Однако количество функцио-
нально независимых инвариантов ограничено и зависит от числа комплекс-
ных моментов, используемых при построении.
Алгоритм синтеза набора функционально независимых инвариантов на
основе множества Q комплексных моментов М^, М^, ..., / состоит
в следующем: 44
- из множества Q берутся моменты Мк1 при =lt, которые являются
инвариантами;
- задается базовый элемент (к0 =lG) множества Q и для остальных
моментов Мд..,, при к^1{ строятся инвариантные комбинации, удовлетво-
ряющие требованию (9.47):
Ф/ =МЦ'М^, при (к0 = /„>(*, = /,) (9.49)
Очевидно, что любое другое инвариантное произведение вида (9.46), при
условии (9.47), построенное из моментов множества Q, представляется через
инварианты (9.49).
Таким образом, число функционально независимых инвариантов, которое
можно построить из q комплексных моментов, составляет:
I q, если kt = /, при 1 < i < q,
<7 — 1, в противном случае.
Так, например, из треугольной матрицы комплексных моментов (9.42) при
1 <к+1 < К, включающей (К+1 )(Х+2)/2 элементов, можно сформировать
(неединственным образом) (К+1)(Ан-2)/2-1 независимых инвариантов вида
(9.46) при условии (9.47).
Для центрированного изображения комплексные моменты М0), М10 рав-
ны нулю, вследствие чего при построении инвариантов они не используются
(например, в (9.41) и (9.48)). Однако, как будет показано ниже, при обработке
цифровых изображений в режиме «скользящего окна» оказывается возмож-
ным и даже желательным использование моментов М01 и Mt0.
Особенности построения моментных инвариантов для обработки цифровых
изображений в режиме скользящего окна. Для обработки цифровых изображе-
ний используются дискретные аналоги моментных характеристик (9.38), (9.39),
(9.42), в которых операция интегрирования заменена на суммирование диск-
ретных значений произведений изображения на двумерную степенную функ-
цию. При этом моменты обычно вычисляются не по всему изображению, а
только по ограниченной области — окну обработки D:
Ни(яр w2)= 12 т^х^щ-т^ пг-тг). (9.50)
(тр/п2) GD
9.2. Формирование признаков по изображению
629
Вычисление моментных инвариантов в режиме скользящего окна и их ис-
пользование в качестве признаков для обнаружения и распознавания объек-
тов имеют следующие особенности, обусловленные спецификой этого режи-
ма [7]:
- исчезает необходимость центрирования моментов (путем вычисления по
дискретному аналогу формулы (9.39) или преобразованием моментов (9.50) в
центральные по формуле (9.40)), поскольку при обработке всегда найдется
положение окна, для которого геометрический центр окна будет близок к
центру тяжести объекта,
- возникают ситуации, когда окно захватывает только часть объекта, и эта
часть постепенно увеличивается при «наползании» окна на объект, при этом
центр тяжести изображения в окне смещается от края окна к его центру.
Для точной локализации (определения координат) объекта на изображе-
нии необходимо использовать признаки, характеризующие «захват» объекта
окном, например расстояние от центра тяжести изображения в окне до цент-
ра окна. Расстояние является инвариантным к повороту изображения и выра-
жается через моменты [3, 46]:
ф - л/МюМ01 = +Цр| (951)
М(х) Р-00
Вместо инварианта (9.51) в качестве признаков можно использовать инва-
рианты М10М01, Mqq по отдельности [3, 21, 46], а также другие инварианты,
построенные согласно (9.46), (9.47) с использованием комплексных моментов
Мю, М0| ( М2оМО1, М30М01 ит.д.).
Таким образом, набор признаков для распознавания объектов должен со-
стоять из инвариантов:
- построенных с использованием комплексных моментов младших поряд-
ков (к+1<\) и обеспечивающих локализацию объекта;
- построенных с помощью комплексных моментов старших порядков
(k+l>V) и обеспечивающих распознавание (различение) объекта.
Алгоритм расчета моментных инвариантов в скользящем окне. Алгоритм вы-
числения заданного набора моментных инвариантов для каждого положения
скользящего окна на изображении включает следующие этапы [7]:
- вычисление треугольной матрицы моментов (Л+/<Х') до заданно-
го порядка К;
- вычисление линейных комбинаций моментов, задающих вещественные
и мнимые части требуемых комплексных моментов;
- вычисление значений моментных инвариантов.
Рассмотрим указанные этапы и приведем выражения для вычислительной
сложности реализуемых алгоритмов.
При использовании окна обработки прямоугольной формы применим па-
раллельно-рекурсивный алгоритм расчета моментных характеристик (см. п.8.2)
с учетом того, что формируется не прямоугольная, а треугольная матрица
630
ГЛАВА 9
моментов [1к1 (0<к <К ,0<1 <К — к). Для вычисления треугольной матри-
цы моментов порядка К требуется операций сложения и операций
умножения на каждый отсчет обрабатываемого изображения [7], где
им (К + 1)(К + 3)(*+8), = К(К + 2)(К + 7) (9 52)
6 т 6
На этапе расчета линейных комбинаций моментов (9.43) число операций
зависит от набора комплексных моментов, необходимых при вычислении
инвариантов. Для пары комплексно сопряженных моментов достаточно оп-
ределения только двух комбинаций, поскольку
Re(Mj = Re(Mtt), Im(M„) = -Im(Mtt).
Следовательно, при использовании треугольной матрицы комплексных
моментов Мы (0<к<К,0<1<К—к) порядка К необходимо определить
только с элементов матрицы Mk[ (0<к<К,0<1< min (Л, К — к)):
К + 2 К + 3
~2 2~
где [...] — целая часть числа п. При этом количество арифметических опера-
ций сложения и умножения U™ составляет
1 К ffjkl
~+1
Jfc=2U2
На практике количество операций умножения может быть ниже приведенной
оценки за счет оптимизации вычислительного процесса (например, некоторые
коэффициенты в линейных комбинациях оказываются равными единице).
При вычислении моментных инвариантов согласно (9.46), (9.47) число
операций определяется количеством комплексных умножений, используемых
при построении набора инвариантов. В частном случае, при использовании
представленного выше алгоритма с выбором базового элемента (например,
М01) число операций для вычисления инвариантов составляет
# + 1 К + 2
2
2
+ /С-1, U*=2U*.
(9.54)
Вычислительная сложность отдельных этапов алгоритма вычисления мо-
ментных инвариантов, рассчитанные по формулам (9.52)—(9.54), а также сум-
марные количества операций {Uа и Vт) приведены в следующей табл. 9.1.
9.2. Формирование признаков по изображению
631
Таблица 9.1. Вычислительная сложность алгоритма расчета моментных инвариантов
К 0 1 2 3 4 5 6 7 8
Ua 4 12 25 44 70 104 147 200 264
0 4 12 25 44 70 104 147 200
им 0 0 2 6 15 29 52 84 130
им 17 т 0 0 5 13 27 47 77 117 172
иф 0 2 6 12 18 26 34 44 54
0 4 12 24 36 52 68 88 108
и0 4 14 33 62 103 159 233 328 448
ит 0 8 29 62 107 169 249 352 480
Таким образом, проведенный анализ показывает, что число выполняемых
операций на всех этапах расчета инвариантов не зависит от размеров окна
обработки, что делает рассмотренный алгоритм эффективным при больших
размерах окна обработки.
Аффинные инварианты. Аффинные моментные инварианты [52, 53, 55] — это
признаки изображения, построенные на основе степенных моментов и опи-
сывающие силуэт некоторого объекта. В соответствии со своим названи-
ем данные признаки являются инвариантными к аффинным преобразовани-
ям изображения:
«I — aQ 4-fljX] + а2х2,
и2 — +^1*1 +^2Л2-
Авторы [52, 53, 55] предложили рассматривать аффинное преобразование
как декомпозицию следующих шести элементарных трансформаций:
а) «1 — X] +р] £/ 2 — -^2 б) Mj = %, н2 =Х2+₽2 в) £ § 11 ’L ,3 3.
г) ST К м — II II х 8° д) М] + t2x2 — -^2 е) и} =Х] U2 =flXl + Х2
Трансформации (а) и (б) представляют преобразование изображения типа
сдвига, (в) — пропорциональное масштабирование. Преобразование (г) зада-
ет искажение масштаба вдоль одной из осей координат. Последние два пре-
образования характеризуют поворот и деформацию изображения, не описы-
ваемые преобразованием подобия.
632
ГЛАВА 9
Трансформации, связанные с изменением положения объекта, легко могут
быть устранены при использовании центрированных моментов (9.39) или,
что эквивалентно, введением нового начала координат. Поэтому далее пола-
гается, что вычисляемые моменты являются центрированными.
Рассмотрим, как последующие преобразования изменяют значения сте-
пенных (центрированных) моментов. Пропорциональное масштабирование
изображения
и, = ахр и2 = ах2 (9.55)
изменяет значение степенного момента следующим образом:
ОО 00
= J J u2)dutdu2 =
-00—00
00 оо
_a*+£+2 J J x1Ax2/(ax1, ax2)dx}dx2 =aA+£+2pw.
—00—00
Из полученного соотношения следует, что величина
*+£,,
Ноо) 2
(9.56)
является инвариантом относительно преобразования (9.55). В более общем
случае функционал
(9.57)
где г] — некоторые вещественные коэффициенты, является инвариантом к
этому виду преобразований, если выполняются равенства
ЙМ+МО)
= ~------------+с(|). (9.58)
Искажение масштаба вдоль оси х,, задаваемое преобразованием
и(=8х), и2= х2, (9.59)
приводит к подобным изменениям значений степенных моментов:
Ни =S/?+I Нн •
9.2. Формирование признаков по изображению
633
Подставив данное равенство в соотношение (9.57), получим выражение
для функционала Ф:
II
Ноо
Очевидно, для инвариантности к преобразованию (9.59) достаточно вы-
полнения соотношений
j=i
Учитывая выражение (9.58), получаем следующее условие, при выполне-
нии которого обеспечивается инвариантность к искажению масштаба вдоль
одной из осей координат:
Ф) Ф)
Vie/:
j=i 7=1
Преобразования (д) и (е) однотипны. Поэтому рассмотрим способ постро-
ения инвариантов к первому из них.
Из теории алгебраических инвариантов [55] известно, что условием инва-
риантности функционала Ф к преобразованию (д) является выполнение ра-
венства
(9.60)
к I Wkl
Подставляя выражение (9.57) для функционала Ф в уравнение (9.60), можно
найти выражение для коэффициентов гД/’Е/) при заданном конкретном мно-
жестве слагаемых /.
В заключение приведем шесть аффинных инвариантов, полученных в ра-
боте [52]:
h — 4~(Н2ОМО2 —
Ноо
1. / э о 2 2 \
— 6МзоИ21И12Иот +4ЦзоН12+4^03)121 -ЗИ21Ц12).
Ноо
634
ГЛАВА 9
'з
1
И 00
(р-2о(М-21М-ОЗ Р-12 )“ М-Ц (МзоР-03 ~ Р-21М-12 ) + М-02 (М-ЗоН
12 “Р-21
4 “ |]
Роо
Р2() Рад 6Ц20Р11Р12Р0З 6р20Ро2Р21Роз +9Р2ОРО2Р?2 +^РгоРГ|Р21РоЗ +
+6Р20Р11P02P30P03 “18Р2оР| 1Р02Р21Р12 “^РпРзоРоз “ 6Р20Р02Р30Р12 +
+ 9р20Р02Р21 +’2р?1РО2РзоР12 -6рПРо2РзоР21
^5 “ “б“(Р40Р04 “4Рз1Р]3 +3^22 )>
Роо
6 ~“9“(Р40Р04Р22 + 2|131р,22Ц13 — РдоРи “Po4P22)-
Роо
9.3. Обнаружение и локализация объектов на изображении
9.3.1. Постановка задачи и анализ современного состояния
Обнаружение и локализация объектов на изображении — один из основ-
ных этапов при решении задачи поиска и распознавания объектов на изобра-
жениях. Основными причинами этого являются следующие:
- любую задачу классификации для многих гипотез можно заменить не-
сколькими простыми задачами альтернативного распознавания - обнару-
жения;
- при классификации на изображении решающее правило работает в ус-
ловиях с пространственной протяженностью обрабатываемых данных, что
приводит к необходимости согласования критериев и/или алгоритмов обна-
ружения и локализации для качественного решения задачи [79];
- высокая вычислительная сложность «хорошего» алгоритма распознава-
ния и «хороших» признаков не позволяет практически использовать их при
поиске объекта по всему изображению, что приводит к необходимости при-
менения достаточно простых решающих правил предварительной обработки,
локализующей области возможного интереса, где может появиться соответ-
ствующий объект.
В настоящее время известно огромное число алгоритмов построения клас-
сификаторов для решения задачи обнаружения [13, 14, 17, 33, 38—40]. Каж-
дый из них имеет свои недостатки и свои преимущества. В настоящей работе
рассмотрена линейная модель. Это обусловлено следующими причинами:
- простотой применения (реализации) классификатора;
- возможностью приведения классификаторов с полиномиальной дискри-
минантной функцией к линейному виду путем повышения размерности про-
странства признаков;
9.3. Обнаружение и локализация объектов на изображении
635
- существованием для решающего правила явного выражения вычисли-
тельной сложности, которая, к тому же, является самой низкой среди всех
групп классификаторов (с тем же числом признаков);
- возможностью проведения аналитических расчетов.
Заметим, что при поиске объекта на изображении задача не исчерпывается
построением классификатора. Дополнительно к классификации возникает
необходимость локализации объекта — то есть определения координат его
местоположения. Это обусловлено следующими причинами:
- область, выделенная классификатором-обнаружителем и относящаяся к
одному объекту, как правило, является размытой и не дает конкретных коор-
динат объекта;
- возможно существование несвязных областей, относящихся к одному и
тому же объекту, что может привести к появлению ложного объекта;
- области, соответствующие различным объектам одного и того же класса
могут быть связными — это может привести к потери объекта;
- области, относящиеся к объектам разных классов, могут находиться
вблизи друг друга, что может привести к потере объекта или его неверной
классификации.
Локализация позволяет обойти обозначенные недостатки процесса обна-
ружения и распознавания. Однако для локализации должен быть выбран кри-
терий, по которому одно из возможных положений считается предпочтитель-
нее другого положения. Хотя количество работ в области обнаружения и рас-
познавания достаточно велико, вопросу локализации объекта на изображении
практически уделяется недостаточно внимания, хотя одно из основных свойств
изображения состоит в передаче человеку информации о взаимном располо-
жении объектов. Именно конкретные координаты играют для многих реаль-
ных задач ключевую роль. Так, например, все алгоритмы, использующие опи-
сание одной и той же реальной картины (сцены) в виде нескольких изобра-
жений, применяют так называемую процедуру согласования изображений.
Похожие процедуры используются и в задачах калибровки видеокамер, зада-
чах стереозрения, построения рельефа местности, привязки изображений к
реальным или существующим картам ит.д. [26, 44, 47, 85]. Все они, по суще-
ству, сводятся к вычислению корреляции изображения заданного объекта с
наблюдаемым изображением. Небольшие вариации в подходах и решениях
этой сложной задачи, предпринимаемые с целью увеличения качества обна-
ружения и локализации, связаны, как правило, с эвристическими соображе-
ниями. Это может быть и квантование сигнала, и специальное препарирова-
ние и т.д. Подобные пробные подходы к локализации объекта все чаще ис-
пользуются в связи с переходом от полутоновых к цветным изображениям —
локализацию предлагается проводить только по характерному цвету искомого
объекта [62, 68]. При этом подавляющее большинство алгоритмов определе-
ния местоположения не учитывает, что одновременно с локализацией проис-
ходит и обнаружение объекта.
Комплексный подход к рассмотрению задачи обнаружения и локализации
предложен в работах [43, 44]. Он определяет качество измерения координат
636
ГЛАВА 9
объектов ошибками двух видов. Ошибки первого рода возникают вследствие
неверных отождествлений искомых объектов с отдельными деталями на на-
блюдаемом изображении. Они дают большие отклонения результата измере-
ния координат от истинного значения, превышающие некоторые наперед за-
данные предельные размеры (или размеры объекта). Такие ошибки называют
аномальными. Аномальные ошибки характеризуются вероятностями ложного
обнаружения и пропуска объекта. Ошибки второго рода или нормальные ошибки
имеют величину меньше некоторого наперед заданного значения (или мень-
ше линейных размеров объекта). Можно считать, что нормальные ошибки
характеризуются своими среднеквадратичными значениями отклонения в
определении координат. Для построения локализатора с минимальным чис-
лом аномальных ошибок используется подход [41], принятый в обработке
изображений (использование частотной характеристики фильтра, гистограм-
мы и спектра изображения ит.д.). Однако этот подход невозможно приме-
нить для задачи локализации, где отсчеты входного изображения не исполь-
зуются в качестве признаков, и классификатор, в свою очередь, не является
линейным.
Все сказанное выше приводит к выводу об актуальности проблемы разра-
ботки и реализации критериев и алгоритмов локализации, согласованных с
показателями качества процесса обнаружения (нормальные ошибки, таким
образом, в данном случае не рассматриваются).
9.3.2. Критерии локализации объектов
Локализация, согласованная с критерием качества обнаружения и распозна-
вания. Качество процедуры обнаружения и распознавания может быть оха-
рактеризовано величиной (4.10) общего риска R. При этом оптимальный в
смысле минимума общего риска классификатор Байеса строится таким обра-
зом, чтобы при суждении о каждом конкретном векторе у выбирать тот
класс Clt (l ~ 0, £ —1), для которого значение условного среднего риска (4.8)
по этому классу,
кХуНЕлЖ/у)- /=ол-1.
1=0
минимально [13, 17, 33, 38, 40]. Здесь £>(£2/-/у) — апостериорная вероятность
отнесения данного конкретного вектора у к классу Для определеннос-
ти в дальнейшем будем интерпретировать класс £20 как класс, соответствую-
щий фоновой составляющей изображения.
Поскольку процедуру локализации объектов на изображении можно рас-
сматривать как частный случай процедуры обнаружения или распознавания,
то представляется целесообразным производить локализацию объекта по тому
же критерию, по которому производится и классификация, то есть по мини-
муму общего риска. Пусть и п2 — отсчеты в плоскости изображения.
9.3. Обнаружение и локализация объектов на изображении
637
Пусть область локализации (то есть область предполагаемого размещения
объекта у-го класса на изображении) обозначена Dj. Пусть у = у(п],п2) —
вектор признаков для фрагмента изображения с координатами п} и п2. Тог-
да критерий локализации выглядит следующим образом:
R: (у(м| ,п2 н— min R (у(п| — т},п2 — т21). (9.61)
' ' v " (т„тг^ ' х "
В силу реализационных ограничений области Dj, как правило, принима-
ются одинаковыми и равными некоторой наперед заданной области D, раз-
меры которой согласуют с размером искомого объекта. Тогда существует по-
тенциальная возможность упрощения процесса обнаружения и локализации,
если классификация также производится на основе анализа значения средне-
го риска. Используем тот факт, что выбор класса / для анализируемого фраг-
мента происходит по критерию (4.11), то есть
Л<(у(П1’п2))= ПЗ^КДу(п1-«2))- <9б2>
В этом случае общий критерий обнаружения (распознавания) и локализа-
ции запишется в следующем виде:
1П|,п2): К, ук ,п2 ]) = min R. (ylnj — т},п2 — т21). (9.63)
\ \ \ П i=Q,K-\ V \ 7 2
(ш1,ш2)^
Процесс обнаружения и локализации, основанный на приведенном крите-
рии реализуется следующим образом: область D (окно локализации) зани-
мает все возможные положения на плоскости изображения, и если при оче-
редном положении (п,,п2) координаты-аргументы оптимума критерия (9.63)
совпадают с текущими, а соответствующий номер класса отличен от нуля (не
фоновый класс), то текущее положение рассматривается как искомое поло-
жение объекта соответствующего класса.
Использование выражения (9.63) напрямую оказывается не всегда целесо-
образно, поскольку вычислять значения рисков Rj неудобно. Более того,
известные правила классификации Байеса [33, 40] существенно проще (9.62).
Возникает вопрос, нельзя ли упростить и правило локализации. Покажем,
что в общем случае сделать это невозможно.
Пусть сравниваются два значения риска для двух различных местоположений
предполагаемого объектау-го и /-го классов с координатами (п},п2) и (n},n2):
к-\
£'>2>(£Мр(у(«|.п2)/£1<) ______
кДу(«1.«2)) = —-------Г~7----Г)------’ j =
638
ГЛАВА 9
/Г-1
E^(^Jp(y("iA)/^J _____
Ъ(у(«I>«2)) = —----/ f=од,-1.
Здесь р(у/£2() — условная плотность вероятностей случайного векторного
признака Y в классе О.,, р(у) — безусловная плотность вероятностей случай-
ного вектораY. В случае, если = (й],п2), значения безусловной плот-
ности вероятности в этих двух формулах одинаково. Именно это обстоятель-
ство позволяет производить дальнейшие упрощения байесовского правила клас-
сификации при конкретном векторе признаков. Но при локализации координаты
различны, следовательно, различны векторы и, наконец, значения безусловной
плотности вероятности. Значит, в общем случае локализация по минимуму
риска должна производиться по самим значениям риска. Однако для задачи
обнаружения объектов можно получить существенные упрощения.
Локализация при обнаружении объекта. Пусть класс объектов — О,, класс
фона (шума) — О,0. Тогда значение риска для вектора у имеет вид
'W"”"2» р(п0)Р(у(п„П2)/п0)+/>(а,)Р(у(п„П2)/п1) 1 ’ h
Его можно переписать следующим образом:
^(у(«1*«2
/0 П Р(^о)р(у(п1>«2)/По)
1 | f(Ql)p(y(”l>”2)/Qj
/>(^о)р(у («h«2)/^o)
I = {0,1}.
Введем отношение правдоподобия:
А(п,,п2
р(у(”1.и2)/ло)
(9.64)
Тогда риск за принятие решения об отнесении текущего фрагмента к каж-
дому из классов будет равен
Р(П0) 2>
9.3. Обнаружение и локализация объектов на изображении
639
Зависимость рисков от Л, приведенная на рис. 9.6, построена с учетом
того, что за неверное решение штраф больше, чем за верное.
Классификация производится путем сравнения величины Л с порогом А:
X — г1° гоо . ^(^°)
Г01~Г11 ^(^1)
При Л > А принимается решение о наличие объекта и производится его
локализация. Очевидно, что значение риска R тем меньше, чем больше отно-
шение правдоподобия (9.64). Поэтому критерий локализации (9.61) может
быть приведен к виду
Л],л2): Л (у l/ij, п2)) = max _ Alyl«t — тх,п2 — /и2)/- (9.65)
Полученный результат тем более важен, поскольку выражение (9.64) ис-
пользуется для построения классификатора Байеса в виде (см. п.4.3)
П,
А значит, критерий обнаружения и локализации будет единым:
(м|,н2): A(y(n,,n2)) =
max
1,m2)eD£&A(y(n1 — т],п2 —т2
Л(у(л1 — т1,п2 — т2
здесь «&» — операция логической конъюнкции (логическое «и»).
Процесс обнаружения и локализации, основанный на приведенном крите-
рии реализуется следующим образом: область D занимает все возможные
положения на плоскости изображе-
ния, и если при очередном поло-
жении (п},п2) координаты-аргу-
менты оптимума критерия (9.66)
совпадают с текущими, то оно и
рассматривается как искомое по-
ложение объекта.
Рис. 9.6. Изменение риска в задаче обна-
ружения
640
ГЛАВА 9
Локализация объекта по максимуму правдоподобия. Пусть функция правдо-
подобия фонового класса такова, что для всех отличающихся от нуля значе-
ний функции правдоподобия класса объектов она приблизительно постоян-
на, то есть
р(у/^0)~ const для {у:р(у/П1)>Е}^(). (9.67)
Тогда критерий локализации (9.65) преобразуется к следующему виду:
P(y(wi.«2)/^i)=z ma? , р(у(«] ~т^пг-тг)1О.Х (9.68)
Ьп{,т2 ]EDl
Выражение (9.68) означает, что локализация производится по максимуму
правдоподобия класса объектов. Гипотезу (9.67) целесообразно использовать
в случае, если разброс значений векторов признаков в классах объектов и
фона существенно различается. С точки зрения статистических свойств век-
тора признаков это означает существенное различие в матрицах ковариации
векторов Y в каждом из классов (см. п.4):
где
b, = e{(y-e{y})(y-e{y})7<>,
или, в одномерном случае, это означает существенное различие в дисперсиях
случайных величин:
_2 _2
° О >>°| ,
где
о2 = е{(у-Е{у})2 /qz
Здесь Xmin (•) и Xmax — минимальное и максимальное собственные числа
соответствующих ковариационных матриц. Для одномерного случая выпол-
няется: Xmax — 2t,nin ~<т. Данный критерий целесообразно использовать так-
же в ситуации, если функция правдоподобия фонового класса неизвестна или
предполагается произвольной.
Локализация по максимуму функции правдоподобия имеет понятный
смысл: производится выбор того положения фрагмента, для которого пред-
положение о похожести на объект (его описание в признаковом простран-
стве) наиболее правдоподобно. Процесс локализации идентичен приведен-
ному ранее.
Локализация объекта по минимуму значения альтернативной функции правдо-
подобия. Пусть функция правдоподобия класса объектов такова, что для всех
9.3. Обнаружение и локализация объектов на изображении
641
отличающихся от нуля значений функции правдоподобия фонового класса
она приблизительно постоянна, т.е.
p(y/Q,) ~ const для {у : р(у/^о)>е}е_0• (9-69)
Тогда критерий локализации (9.65) преобразуется к следующему виду:
(л,,л2): р(у(«],«2)/^о)^, ~ р(у(«1 ~т^п2-т2)/£10),
JED
что означает, что локализация производится по минимальному значению функ-
ции правдоподобия фонового класса, то есть альтернативной к функции прав-
доподобия класса объектов. Аналогично предшествующему случаю, гипотезу
(9.69) целесообразно использовать в случае, если разброс значений векторов
признаков в классах объектов и фона существенно различается. С точки зре-
ния статистических свойств вектора признаков это означает существенное
различие в матрицах ковариации:
|^min (В 1 )| »l^-max (®0 )|
или, в одномерном случае, Qj >>g0.
Приведенный критерий целесообразно использовать также в ситуации, если
функция правдоподобия класса объектов неизвестна или предполагается про-
извольной. Такое часто происходит, когда производится поиск на изображе-
нии каких-либо локальных аномалий, характеристики которых, разумеется,
заранее неизвестны. При этом, как правило, большая часть изображения (фон)
заполнена некоторой однородной структурой (например, текстура) с совер-
шенно понятными для идентификации характеристиками. В такой ситуации
действительно целесообразно выбирать аномальные точки, т.е. те точки на
изображении, которые плохо согласуются с описанием фона. А поскольку
фон занимает основное пространство изображения, следовательно, вероятно-
сти появления аномальных фрагментов малы, то есть малы и значения функ-
ции правдоподобия класса фона.
Локализация по минимуму альтернативной функции правдоподобия имеет
понятный смысл: производится выбор того положения фрагмента, для кото-
рого предположение о похожести на «необъект» (описание в признаковом
пространстве) наименее правдоподобно (альтернативная функция правдопо-
добия имеет наименьшее значение). Процесс локализации по данному крите-
рию аналогичен изложенному ранее.
Предложенный здесь критерий локализации объектов достаточно интен-
сивно используется, но без постановки задачи именно таким образом. При-
мером могут служить работы [33, 77, 83] по распознаванию отпечатков пальцев.
21 — 9044
642
ГЛАВА 9
В качестве признаков для распознавания принимались те фрагменты изобра-
жения отпечатка, которые выглядели аномальными по сравнению с общей
структурой. А именно, предполагалось, что изображение при локальном рас-
смотрении состоит из параллельных и достаточно регулярных перепадов функ-
ции яркости, таких как на рис. 9.7а. Все, что значительно отличается от по-
добной модели принимается за аномальный фрагмент. Примеры аномалий
приведены на рис. 9.76—г. Именно величина отличия, с точки зрения теории
распознавания, может рассматриваться как значение признака, по которому
определяется значение функции правдоподобия. Очевидно, что для фонового
класса более правдоподобными оказываются более низкие значения призна-
ка (слабое отличие), а менее правдоподобными — более высокие, как изобра-
жено на рис. 9.8. В результате локализация производится по максимуму вели-
чины отличия. Пример обнаружения и локализации аномальных фрагментов
приведен на рис. 9.9. В качестве значения, характеризующего отличие фраг-
мента изображения от изображения регулярной структуры, была принята
ошибка аппроксимации фрагмента двумерной цилиндрической полиноми-
альной функцией.
В заключение отметим, что представленные здесь критерии могут быть
использованы безотносительно к тому, какой именно вид области исполь-
зует процедура локализации. Однако можно предположить, что если все же
а б в
Рис. 9.7. Схематичные изображения отдельных фрагментов дактилограмм: а — фрагмент изоб-
ражения с регулярной структурой; б — фрагмент изображения с искусственным нарушением
регулярной структуры; в — фрагмент изображения с естественным нарушением регулярной струк-
туры; г — фрагмент изображения с естественным нарушением регулярной структуры
Рис. 9.8. Функция правдоподобия фонового класса в задаче обнаружения и локализации осо-
бенностей на дактилограмме
9.3. Обнаружение и локализация объектов на изображении
643
Рис. 9.9. Процесс обнаружения и локализации аномальных фрагментов на дактилограмме: а —
исходная дактилограмма; б — изображение-аппроксимация; в — поле локальных ошибок апп-
роксимации; г — результаты обнаружения и локализации; д — функция правдоподобия (эмпи-
рическая) для класса регулярной структуры изображения (фоновый класс)
адаптироваться на вид конкретной области локализации, то результаты могут
быть лучше. Более того, не всегда построение классификатора связано с по-
строением функции правдоподобия. И тогда оказывается невозможным вос-
пользоваться данными критериями. Поэтому целесообразно произвести рассмот-
рение возможности построения совместного алгоритма обнаружения-локализа-
ции, который одновременно (а не последовательно, как это предполагалось
21*
644
ГЛАВА 9
ранее) выполнял бы и обнаружение, и локализацию по выбранному крите-
рию качества.
9.3.3. Совместное обнаружение и локализация объектов
Общее описание процедуры локализации. Вначале определим понятие «ло-
кализатора-обнаружителя» объектов. Очевидно, что он должен наследовать
свойства классификатора для обнаружения объектов, а следовательно со-
держать некоторую функцию (подобно дискриминантной функции) d(-),
задаваемую на пространстве признаков и имеющую некоторое заранее выб-
ранное пороговое значение, на основе которого определяется, нужно ли от-
носить данную точку на изображении к области локализации. Без ограниче-
ния общности можно считать порог равным нулю. В случае, если пороговое
значение не равно нулю, всегда можно сделать линейное преобразование
функции j(-) таким образом, чтобы пороговое значение обратилось в нуль.
С помощью функции </(•) для каждого положения (л,, п2) окна обработки
производится вычисление одного отсчета изображения дискриминантной функ-
ции T|(wi» пг}- Далее, в отличие от обычного классификатора, «локализатор-
обнаружитель» должен содержать некоторое правило, по которому среди
нескольких точек области локализации выбирается какая-либо одна. Для
этого целесообразно использовать известный в обработке изображений пи-
ковый фильтр [29]. Алгоритм его работы следующий:
min,
если Т]1П] ,п2)~ max rllni —Щ\,П'>—т-У
' 1 (т,,т2)ео V
если Л (л21 -> ^2 ) тах .Tl(wi ~ т.},п2— т2
(nij ,т2)сО
Величина D — заранее выбранная область локализации, min — некото-
рое постоянное значение, не превышающее ни одно из значений яркости
изображения #(ni’n2) ~ изображение, полученное в результате
пиковой фильтрации изображения T](nHw2)- Как правило, область локализа-
ции выбирается симметричной относительно нулевого отсчета, который и
принимается за выходной отсчет фильтра:
D = [-M, Д ]х[-М2,М2].
Здесь ^22Й, -Ь1), [1М2 +1) — размеры пикового фильтра по вертикали и
горизонтали, соответственно.
Принимая описанную модель локализатора-обнаружителя, схема процесса
обнаружения и локализации становится такой, как изображена на рис. 9.10.
Существенным отличием работы локализатора-обнаружителя от процесса ло-
9.3. Обнаружение и локализация объектов на изображении
645
Рис. 9.10. Схема процесса обнаружения и локализации
кализации, описанного в п.9.3.2, является то, что порядок следования лока-
лизации и классификации (процедур пиковой фильтрации и порогового от-
бора, соответственно) в данной ситуации не влияет на результат работы. Это
связано с тем, что одни и те же значения изображения используют-
ся и для локализации, и для порогового отбора. А значит, при реализации
алгоритма возможно построение процедуры, которая осуществляет локализа-
цию и обнаружение за один проход по изображению: выделенное процедурой
локализации экстремальное значение ,n2) просто сравнивается с неко-
торым порогом.
С целью упрощения дальнейшего изложения примем следующие соглаше-
ния. Считаем, что отсчеты в окне пикового фильтра упорядочены по мере
удаления от выбранного выходного отсчета фильтра, и их нумерация произ-
водится в диапазоне [0, N-1], где N = |£>| — число отсчетов в области лока-
лизации. Для определения аномальных ошибок процедуры совместного обна-
ружения и локализации (вероятностей ложной тревоги и пропуска объекта)
зададим событие Q, которое состоит в принятии процедурой решения о том,
что некоторый (случайный) фрагмент изображения содержит объект. В соот-
ветствии с выбранной схемой обнаружения и локализации это событие запи-
шется следующим образом:
e = {no(Y)>o}{no(Y)>ni(Y)}-{no(Y)>nW-i(Y)}-
Здесь первое из событий {т|0(Y) >о} отвечает за процедуру обнаружения,
а все остальные события — за пиковую фильтрацию. Тогда вероятности оши-
бок классификации для процедуры совместного обнаружения и локализации
запишутся в обычном виде:
p0 = P(Q/£lB), р, = />(ё/Я,). (9.70)
Критерием качества процесса «обнаружения-локализации» является кри-
терий минимума суммарной ошибки обнаружения в виде
= + —> min . (9-71)
4-)
где в качестве параметров оптимизации выступают параметры функции d(...).
646
ГЛАВА 9
При таком критерии формируемая процедура обнаружения и локализации
будет оптимальна только с точки зрения величины аномальных ошибок: объект
найден или не найден. Следовательно, возле конкретного местоположения
каждого из объектов однозначно должна быть задана некоторая область, для
которой принимается допущение, что для любой ее точки объект присутству-
ет. Вне такой области объект считается отсутствующим. Размеры области це-
лесообразно задавать, учитывая размер используемого при локализации пи-
кового фильтра. А именно, они должны быть такими, чтобы в пределах обла-
сти каждого конкретного объекта процедура совместного обнаружения и
локализации выделяла не более одного объекта. Такое возможно, только если
эта область имеет линейные размеры не больше половины соответствующих
линейных размеров пикового фильтра (области локализации), как показано
на рис. 9.11.
Один из приводимых ниже алгоритмов построения «локализатора-обнару-
жителя» основывается на моделях функции правдоподобия в признаковом
пространстве, а также на предположении линейности функции d (•) и на пред-
положении о фиксированном окне локализации. Процесс построения функ-
ции J(-) в такой ситуации возможен, если имеет место независимость значе-
ний отсчетов изображения дискриминантной функции в окне локализации.
Другой алгоритм не использует никаких априорных предположений, но тре-
бует для настройки «локализатора-обнаружителя» (то есть нахождения пара-
метров функции d () и размера окна пикового фильтра) исходные данные в
виде обучающей выборки. Этот алгоритм является итерационным.
Настройка процедуры обнаружения и локализации при независимых значениях
отсчетов изображения дискриминантной функции в пределах окна локализации.
Пусть плотность вероятности отсчетов изображения в окне пикового фильтра
задается следующим образом:
Нчо-П.....' = {0,1}. (9.72)
Тогда значение вероятностей классификации (9.70) равно
+оо По По
P(Q/&k)= f f-f р(По,’1|,. .,'П«-|/Н,)<'11«-|.•
0 —оо —оо
/ = {о,1}. (9.73)
Предположим независимость значений пикселов изображения дискрими-
нантной функции в окне пикового фильтра. Заметим, что такое предположе-
ние, как правило, не отражает реальную ситуацию. Поскольку значения изоб-
ражения функции в окне локализации рассчитываются по признакам сильно
перекрывающихся фрагментов изображения, то и зависимость значений, не-
сомненно, присутствует. Но предположение позволяет сделать существенные
9.3. Обнаружение и локализация объектов на изображении
647
Рис. 9.11. Обнаружение и локализация объекта: область расположения объекта на изображении
(1), область локализации (3), выходной отсчет пикового фильтра (2), плоскость изображения (4)
упрощения и, как будет показано, получить алгоритм настройки процедуры
совместного обнаружения и локализации. Этот же алгоритм можно использо-
вать и в ситуации, когда предположение не выполняется, понимая, однако,
что решение в этом случае не является оптимальным. Итак, пусть выполняет-
ся равенство
/V—I
Р^о.-П.....ЛлмДМ = П Pi )• I = {0. Q.
/=0
где Pi () — плотность вероятности /-го отсчета изображения в окне пикового
фильтра. В таком случае выражение (9.73) преобразуется:
+оо Л о Ло
P(Q/Q.[) = J* РоСЛо/^/)/* Pip(v/v-i/^/)^Л/v-i•• -^Л^Ло =
О -оо -оо
+°Р /V—1
= J Ро(ЛО/^/)П :(Ло/^/)^Ло> /={о,1}.
о /=1
Здесь p(t]0/<2z ) — функция распределения значений пикового фильтра в
классе .
В процессе обработки окно пикового фильтра последовательно занимает
все возможные положения в плоскости дискретных аргументов изображения.
Поэтому практически все пикселы изображения попадают в каждый из отсче-
тов окна пикового фильтра. А значит, разумно предположить, что законы
распределения значений отсчетов изображения дискриминантной функции,
попадающих в различные отсчеты окна пикового фильтра одинаковы, то есть
p,(T|/f2z) = p(T|/nz), ^(t]/Qz) = p(t]/Qz), i = О,ЛГ —1. Тогда [23]
p(e/n,)=7 z={o.i}.
648
ГЛАВА 9
а вероятности ошибок имеют вид
1-/>n(0/Qo) W-l , PN(0/Cl,)
Р0=------Р'=~7Г+—ЧН1- <974>
N N N
Для полученных значений вероятностей (9.74), критерий качества (9.71)
преобразуется (отбрасываем несущественные постоянные величины):
riPN(0/£l,)-roPN(OlQ0)^mn, (9.75)
4-)
а необходимое условие экстремума показателя качества будет иметь вид
Р'(О/П,)_го PN-'(O/Qo)
Р'(О/ао) Г, P"-,(O/QI)’
Производная вычисляется по неизвестным параметрам функции d(-), вид
которой оказывает влияние на функции распределения отсчетов изображе-
ния в окне пикового фильтра в каждом из классов.
Для окончательного построения алгоритма обнаружения-локализации не-
обходимо знание функции j(-) и параметров распределения вектора при-
знаков в признаковом пространстве. Аналитический результат можно полу-
чить, если предположить линейность функции d(-) и специальный вид ее
функции распределения в каждом из классов. В этом случае процесс по-
строения классификатора можно получить в виде алгоритма Петерсона—Мат-
сона [23, 82].
Случай линейной функции d (•) и функции распределения специального вида.
Пусть Pd (‘П/^/)|/_|0|| — функция распределения значений функции J(-) с
непрерывной плотностью вероятности И пусть при измене-
нии параметров функции d(-) изменения в законе распределения касаются
только параметров среднего и дисперсии (Ц/, G?) в каждом из классов:
g/2=WtB/W,
где W, WN — коэффициенты линейной формы и свободный член — неизвест-
ные параметры функции d(-), Mz, В/ — соответственно, математическое ожи-
дание и ковариационная матрица вектора признаков в каждом из классов:
M/=E{Y/Qj, Bz Z-O,L-1.
9.3. Обнаружение и локализация объектов на изображении
649
Тогда (см. п.9.3.4) поиск значений линейной функции можно представить
в следующем виде (алгоритм Петерсона—Матсона):
tOpW^M, +(l-t)a?WTM0
raj+(l-r)a?
Здесь параметр
критерия (9.75):
t € R. По этому параметру производится оптимизация
И1
\Pd
0rd
Но
—> min.
i
Заметим, что при достаточной разделимости классов и близких априорных
вероятностях значение параметра находится в диапазоне t с[0,1].
Настройка процедуры обнаружения и локализации при параметрическом зада-
нии дискриминантной функции. В ситуации, когда предположение о независи-
мости значений отсчетов изображения дискриминантной функции в окне
пикового фильтра не выполняется, для настройки локализатора-обнаружите-
ля можно предложить итерационную процедуру, которая в качестве априор-
ной информации использует выборочные данные в виде наборов векторов
признаков.
Решение о классе объекта в текущей точке изображения принимается в
ситуации, когда текущее значение d(-) оказывается больше, чем окружаю-
щие значения в области локализации, и выше порога, встроенного в качестве
параметра в выражение функции J(-). Тогда событие Q принятия решения
о том, что текущий фрагмент является искомым, представляется следующим
образом:
e = {rsd}, (9.76)
здесь d задает процесс расчета значений функции d (), Т — пороговый
отбор (значений функции J), S — процедура локализации (по значениям
функции d). Независимо от порядка следования процедур локализации и
порогового отбора и та, и другая работают со значениями функции d (•). По-
этому окончательное решение в действительности получается как совместное
решение процедур Т и S об отнесении текущего фрагмента к классу объек-
тов. Таким образом, событие (9.76) есть произведение двух событий — собы-
тия локализации значения функции г/Q и события превышения заданного
порога значением этой функции, т.е.
е={&/}{ти}.
650
ГЛАВА 9
Первое из событий происходит тогда, когда решение об отнесении теку-
щего фрагмента к классу объектов принимает процедура локализации. Второе
событие — когда подобное решение принимает процедура порогового отбора.
На процесс локализации-обнаружения, таким образом, можно смотреть как
на процедуру принятия коллегиального решения двумя простейшими класси-
фикаторами — пороговым и экстремальным. Однако полностью отождеств-
лять представление о локализаторе-обнаружителе как о двух независимых
классификаторах некорректно, поскольку величина порогового значения свя-
зана с видом функции J(-), которая и формирует новое признаковое про-
странство для вышеназванных простейших классификаторов.
Поскольку порядок следования событий несущественен, вероятности клас-
сификации, определяющие качество классификации, могут быть записаны
следующим образом:
Р(е/Й,) = />({&/} {та}/П,) = />({&/}/£>,)p({Sd}/{Td} П,). (9.77)
На основе (9.77) строится следующая итерационная процедура формиро-
вания локализатора-обнаружителя (для определенности а* — вектор пара-
метров функции j(-) на к-й итерации):
- задается некоторый начальный вид функции j(-), то есть задается собы-
тие |7W(a°)| путем решения, например, задачи обнаружения:
1 it > \ °
i(-i)44{ra(a°)}/£2'Pmi> а°=гй;
'“° u ' “ и и
- на очередной к-й итерации определяются оптимальные параметры и со-
ответствующее событие (а*как решение задачи:
£(-i)* пр ({SJ(a*-1)} /Q/ )P(Wa”)} I (a"~‘ )}Q')—min;
- найденный вектор а" рассматривается как направление на оптимум,
поэтому коррекция параметров осуществляется следующим образом:
- итерации заканчиваются, когда решение слабо меняется.
Для обеспечения сходимости итерационной процедуры используем извес-
тный из метода стохастической аппроксимации результат и зададим последо-
9.3. Обнаружение и локализация объектов на изображении
651
вательность величины коррекции таким образом, чтобы выполнялись
условия [40]:
оо оо
«* ~ £“*=°°. £“*<00.
к~0 п—0
Для иллюстрации работоспособности предложенного алгоритма рассмот-
рим две задачи обнаружения и локализации объектов на изображениях, при-
веденных на рис. 9.12а и рис. 9.126.
Функцию j(-) выберем линейной. В качестве признаков для первой зада-
чи используем нормализованные показатели выборочных среднего и средне-
квадратичного отклонения в окне обработки. Для второй задачи используем
единственный признак — локальное выборочное среднее.
На рис. 9.126—9.12г и рис. 9.12е—9.12з приведены результаты решения со-
ответствующих задач. Из иллюстрации к первой задаче, характеризуемой
высокой априорной вероятностью появления объекта на изображении, вид-
но, что суммарная ошибка обнаружения, пропорциональная в данном слу-
чае паре чисел (число пропущенных объектов, число ложно обнаруженных),
оказалась самой большой для ситуации, когда процедура обнаружения не
учитывала наличие последующей локализации (б) — (26, 0). Самый низкий
уровень ошибок оказался у процедуры совместного обнаружения и локали-
зации, настраиваемой в предположении независимости отсчетов в окне ло-
кализации (в) — (0, 2).
Из иллюстрации ко второй задаче, характеризуемой относительно низкой
априорной вероятностью появления объекта на изображении, видно, что без
учета локализации, при обнаружении, ни один из объектов не был на изобра-
жении обнаружен, и ошибка обнаружения в (е) составила (72, 0). Следует
заметить, что подобный результат типичен при обнаружении в ситуации с
низкими априорными вероятностями появления объектов. В отличие от клас-
сической схемы решения, при использовании совместных процедур обнару-
жения и локализации и соответствующих алгоритмов их настройки, ошибка
обнаружения оказалась достаточно низкой. Для представленных изображе-
ний (ж) и (з) она пропорциональна величинам (5,45) и (5, 21). Таким обра-
зом, очевидно преимущество процедур совместного обнаружения и локализа-
ции по сравнению с последовательным использованием алгоритма обнаруже-
ния объекта и его последующей локализацией.
9.3.4. Распознавание объектов двух классов
Модификация алгоритма Петерсона—Матсона. Алгоритм Петерсона—Мат-
сона [40, 82] был разработан для нахождения параметров линейной разделяю-
щей функции 6 (у), минимизирующей величину среднего риска в предполо-
жении, что значения этой функции имеют нормальный закон распределения
в каждом из классов. В данном разделе будет показано, что без каких-либо
652
ГЛАВА 9
а — исходное изображение
б — результат применения процедуры обнару-
жения с критерием (9.77) и последующей ло-
кализацией
в — результат локализации-обнаружения в
предположении независимости отсчетов в окне
локализации
г — результат локализации-обнаружения при
настройке процедуры с использованием ите-
рационного алгоритма
Рис. 9.12. Результаты обнаружения и локализации (задача 1)
изменений данный алгоритм может быть использован и без предположения о
нормальности закона распределения. Будет предложен алгоритм нахождения
параметров для случая, когда математические ожидания вектора признаков
для различных классов совпадают — для такой ситуации известный алгоритм
не позволяет получить решение. Далее будут сделаны некоторые замечания о
диапазоне параметра, используемого в алгоритме Петерсона—Матсона. И,
наконец, будет показано, что тот же самый алгоритм можно использовать и
при решении задачи Неймана—Пирсона. Для начала рассмотрим известный
алгоритм.
Линейная дискриминантная функция, минимизирующая величину общего рис-
ка (алгоритм Петерсона—Матсона). Пусть линейная дискриминантная функ-
ция d(y) = Wry имеет нормальный закон распределения в каждом из
классов. Для этого предположения есть две предпосылки:
- вектор признаков Y имеет нормальный закон распределения в каждом
из классов, тогда и линейная комбинация элементов вектора имеет нормаль-
ный закон распределения;
- вектор признаков Y не имеет нормального закона распределения, но
количество признаков достаточно большое. В силу центральной предельной
теоремы линейная комбинация элементов вектора имеет нормальный закон
распределения.
9.3. Обнаружение и локализация объектов на изображении
653
д — исходное изображение
е — результат применения процедуры об-
наружения с критерием (9.77) и последую-
щей локализацией
ж — результат локализации-обнаружения
в предположении независимости отсчетов
в окне локализации
з — результат локализации-обнаружения
при настройке процедуры с использовани-
ем итерационного алгоритма
Рис. 9.12. (продолжение) Результаты обнаружения и локализации (задача 2)
Поведение значений функции d(y) в каждом из классов полностью ха-
рактеризуется математическим ожиданием и дисперсией:
ц, =/?{<7(Y)/<2,} = WtM,+Wn,
о? = £{(d(Y) - И/ )2/п,} = WTB( W, I = {0,1}.
654
ГЛАВА 9
Здесь Mz, В/ — вектор математических ожиданий и ковариационная мат-
рица вектора признаков в классе Q,.
Пусть, далее, необходимо минимизировать величину среднего риска (по
параметрам дискриминантной функции):
*min ='bpte/^o) + rip(c/^i)"*min,
(9.78)
где событие Q = 1d(X)>0k Тогда этот критерий эквивалентен следующему:
Г]Ф
-г0Ф
ч
P-Q
—> min .
Здесь Ф(-) — функция Лапласа. Необходимым условием минимума, как
известно, является следующее:
Тогда, учитывая, что [40, 82]
а [ g,L м, wrB,n,
d f pj 1
dWN I CF/ J ’
Z = {0,1},
(9.79)
получаем систему уравнений:
Го
Р§
ехр Мо +
2ло0 2(Уо J,
Гр
2°оД
' 2 '
ехр —Ц- =-7==--
2Oq V27UO1
^WTB0
<*о
р?
ехР ’Й •
Р?
ехР “ГТ
2о?
Mi+b-w7») ,
(9.80)
Из этой системы очевидно следующее равенство:
M0+^WrB0 = M1+b-WrBl.
Go О?
(9-81)
9.3. Обнаружение и локализация объектов на изображении
655
Поскольку точного решения для выражения (9.81) получить невозможно,
Петерсон и Матсон предложили следующую итерационную процедуру. Век-
тор W определяется как функция некоторого числового параметра t:
W = a[?B0+(l-/)B1] '(Мо-М,),
(9.82)
где
-Но/<?о
a = Hi/°i-Во/°о-
(9.83)
Анализируя второе из равенств в (9.80), можно предположить, что опти-
мальное решение приведет к тому, что |Х0 и р.) будут иметь разные знаки,
т.е. ц0 <0, ц, >0. В этом случае величина а — всего лишь масштабный
множитель (всегда одного знака), и ее можно не учитывать, а диапазон t е [0,1].
Теперь значение WN находится по формуле
+(1 -z)o?WrM0
(9.84)
Существует обобщение изложенного подхода для произвольного вида функ-
ционала качества [40], которое, однако, приводит только к системе уравне-
ний и не дает окончательного решения. Одним из частных решений, полу-
ченных таким образом, является классификатор Фишера.
Обобщение процедуры Петерсона—Матсона на законы распределения специ-
ального вида. Требование нормальности распределений для получения проце-
дуры решения задачи построения классификатора является слишком жест-
ким. Для того, чтобы получить ту же самую итерационную процедуру, вполне
достаточно выполнения следующих требований:
- плотности вероятности должны быть дифференцируемыми функциями
по аргументу;
- изменение параметров функции J(-) должно приводить только к изме-
нению математического ожидания и дисперсии в функциях распределения
Тогда преобразуем критерий (9.78):
—» min .
Определим плотности вероятности:
, . . dP^(u/Q.i} , -
Р, «А = 'У ”, (={0.1}.
du
656
ГЛАВА 9
А система уравнений (9.80) примет следующий вид:
^0 f \ -Но м0 4-^WrB0 =—Р\ ( \ / м,- А
<*0 °0 _Цо =_1 °о J р, <*1 к °!
(9.85)
Откуда снова приходим к выражению (9.81) и итеративной процедуре Пе-
терсона-Матсона (9.82)—(9.84).
При этом нет необходимости адаптировать алгоритм Петерсона—Матсона
к какому-либо конкретному распределению — вполне достаточно лишь пред-
положения о выполнении указанных требований. Нахождение же оптималь-
ного значения параметра t, вообще говоря, можно производить и не зная
конкретный вид закона, то есть, проверяя оптимальность решения по выбо-
рочным данным при условии, что выборка репрезентативна.
Построение линейного классификатора при совпадающих средних вектора
признаков в классах. При построении классификатора возможна ситуация, когда
математические ожидания Мо и Mj вектора признаков оказываются одина-
ковыми, т.е.
М0=М,=М. (9.86)
Подобная ситуация может возникнуть, например, если набор признаков
не обладает достаточными дискриминантными свойствами. Совершенно оче-
видно, что итерационная процедура (9.82)—(9.84) не дает решения в такой
ситуации. Поэтому требуется так модифицировать алгоритм, чтобы получить
решение. Обратимся к выражению (9.81). Учитывая равенство (9.86), (9.81)
можно переписать следующим образом:
-^W7B0=-^WrB1>
здесь ц = ц0—Ц]. Перепишем последнее соотношение в виде
о2'В
ао
о-Лв.
of
w=o.
(9.87)
Решить такое уравнения, также как и
Поэтому введем переменную t:
(9.81), аналитически невозможно.
_ °о
L О?-о?'
О2 0?
9.3. Обнаружение и локализация объектов на изображении
657
Тогда, с точностью до ненулевого масштабного множителя, условие (9.87)
можно представить в виде
(rBI+(l-r)Bo)W = O.
(9.88)
Заметим, что диапазон изменения переменной t, в отличие от указанного в
[40, 82], не ограничен отрезком [0, 1], а определяется всей числовой прямой
t е R. Кроме того, для конкретного значения t вектор W может и не суще-
ствовать. Действительно, выражение (9.88) относительно вектора W есть
определение ортогонального векторного пространства к набору векторов-строк
матрицы
гВ, +(l-z)B0. (9.89)
Для существования такого ортогонального пространства необходимо (и
достаточно), чтобы среди строк матрицы (9.89) была хотя бы одна линейно
зависимая. В этом случае определитель матрицы оказывается нулевым. Если
же определитель ненулевой, значит, все строки независимы и ортогональное
пространство построить невозможно — оно оказывается пустым. Таким обра-
зом, бессмысленно решать уравнение (9.88) в ситуации, когда не выполняет-
ся условие
det(rBj 4-(1 — /)Во) = О.
(9.90)
Учитывая, что матрицы В] и Во невырожденные, последнее условие можно
преобразовать:
i_,
det В^оЧ---1 — О,
J
(9.91)
где I — единичная матрица. Значения величины i = (1 — t)/t лежат на всей
числовой оси, за исключением точки t =0 . Но при этом значении определи-
тель (9.90) ненулевой, так как матрица (9.89) оказывается равной ковариаци-
онной матрице Во. Поэтому можно представить (9.91) в виде
det(B,B01-4-/I) = 0,
(9.92)
Если при распознавании используется N признаков, то размер матрицы
В ,В"1 составляет N х N. Тогда, следуя определению определителя, (9.92) можно
переписать в виде уравнения jV-го порядка относительно величины i . А зна-
чит можно решать это уравнение относительно переменной i теми же метода-
ми, что и обычные уравнения такого рода [2, 22]. Максимальное количество
линейно независимых векторов-решений W исходного уравнения (9.88) не
превышает N, причем при одном значении переменной i (корне) их число
658
ГЛАВА 9
равно кратности корня. Сам же вектор W может легко быть найден путем
процесса ортогонализации Грама—Шмидта набора векторов: строк матрицы
(9.92) и некоторого произвольного вектора W.
Пусть теперь вектор W найден. Для получения окончательного ответа
необходимо определить значение свободного члена Ид,. Это можно сделать
на основе выражения (9.85). Покажем это на примере распределения Гаусса.
Учитываем, что выполняется равенство (9.85) в виде
2
Ц
2с?)
(9.93)
тогда
. 12 ГрО|
Ц = ±О0(\ —-----2~ln
Учитывая, что ц = WTM-f-Ww, получаем выражение для искомой величи-
ны:
WN =±о0о,
-WrM.
(9.94)
Задача неразрешима, если выражение под корнем отрицательно. Это про-
исходит, если выполняется одно из следующих соотношений:
о, >о0 и rQOjOiOQ, либо ог<о0 И Г0О| >Г]О0.
Графически эта ситуация выглядит так, как показано на рис. 9.13. То есть
штрафы за решения выбраны таким образом, что минимум риска достигается
только в ситуации, если все пространство классифицируется в какой-то один
класс. Такая ситуация невозможна, если штрафы одинаковы, и решение при-
нимается на основе анализа только плотностей вероятностей. Единственная
аномалия возникает, когда плотности вероятностей совпадают, но тогда аб-
солютно бессмысленно выбирать какое-либо конкретное решение, так как
У
все они дают одинаковую величи-
ну риска.
Рис. 9.13. Пример ситуации с отсутствием
решения
9.3. Обнаружение и локализация объектов на изображении
659
Двумерное пространство признаков (Л'= 2). Рассмотрим простую ситуацию,
когда пространство признаков двумерно. Тогда возможно получить оконча-
тельное аналитическое решение для классификатора. Итак, пусть матрицы
В1 и Во имеют следующий вид:
причем выполняются условия ab>c2 и de>q2. Тогда матрица (9.89) запи-
шется следующим образом:
ta + (l — t)d tc + (\~t)q
В~ . (9.95)
Zc + (1 — t)q tb + (1 — t)e]
Условие существования ортогонального пространства (9.90) преобразуется
к виду
(ta + (1 — t)d)[tb + (\ — Z)e)~ (zc + (l — t)q)2 = 0,
либо, в виде квадратного уравнения:
t2 ((а — d)(b — е) — (с — q}1 ) + z(ae + M-f-2g2 — 2cq — Idej 4-[de — q2 j =0.
Примем следующие обозначения:
A~[a — d)[b~ e) — (c — g)2, B = ae + bd + 2q2 — 2cq — 2de, C = de — q2.
Тогда решение будет иметь вид
_~В±у]в2-4АС
ti ? —
12 2А
Параметр определяется из равенства (9.85).
Наиболее простое решение получается в ситуации, когда дисперсии по
координатам одинаковы, то есть а — Ь и d—e. Тогда
/
а соответствующие векторы линейной дискриминантной функции, определя-
ющие ортогональное векторное пространство, имеют вид
(-1)
W| = , W| =
I j I’ lt2
На рис. 9.14 приведен пример двумерного случая.
660
ГЛАВА 9
Замечание о диапазоне переменной в итерационной процедуре алгоритма Пе-
терсона-Матсона. В работах [40, 82] диапазон величины t, определенной
выражением (9.83), принимается ограниченным: ге[О, 1]. Такое ограничение
следовало из выполнения в системе уравнений (9.85) второго равенства, кото-
рое предполагает ясную геометрическую трактовку, изображенную на рис. 9.15.
В такой ситуации ц0 <0<цр и значение t действительно принадлежит вы-
шеуказанному диапазону. Но это возможно только в ситуации достаточно
качественного разделения гиперплоскостью классов в пространстве призна-
ков. В действительности вполне возможна ситуация, изображенная на рисун-
ке рис. 9.16. Такое возможно, например, если одно из весовых значений в
целевой функции существенно больше другого, или если один из классов
существенно больше «размыт» в признаковом пространстве. А поскольку это
достаточно характерные ситуации, то необходимо, оставаясь в рамках линей-
ного классификатора, все же найти наилучшее решение. При этом заметим,
что возможно получения не одного, а нескольких классификаторов, среди
которых и надо отобрать наилучший.
Для указанного обобщения необходимо расширить область параметра t
на всю вещественную прямую: /6R. На рис. 9.17 приведен пример для
одной из ситуаций, когда оптимальное значение параметра t лежит вне
интервала [о, 1].
Рис. 9.14. Линейные разделяющие функции при равных средних вектора признаков
Рис. 9.15. Геометрическая интерпретация необходимого условия экстремума: ситуация высокой
разделимости классов
9.3. Обнаружение и локализация объектов на изображении
661
Рис. 9.16. Геометрическая интерпретация необходимого условия экстремума: ситуация низкой
разделимости классов
Линейный классификатор, оптимальный по критерию Неймана—Пирсона. Во
многих задачах вместо линейного критерия оптимизации используется кри-
терий Неймана—Пирсона (4.3.3):
р, —> min,
Ро = Ро-
(9.96)
Заметим, что в ситуации, когда множество значений вероятностей оши-
бок (po»Pi) имеет выпуклый характер, критерии Неймана—Пирсона и ми-
нимума риска эквивалентны при соответству-
ющем выборе параметров оптимизации, то
есть величин г,,г0 и р0 [40]. В альтерна-
тивной ситуации линейная задача оптими-
зации не позволяет получить все решения
на границе множества. В то же время крите-
рий Неймана—Пирсона позволяет это сде-
лать. Поэтому важно уметь решать задачу
Неймана—Пирсона для рассматриваемого ли-
нейного классификатора.
Итак, пусть решается задача (9.96) для ЛИ- Рис. 9.17. Множество локальных ре-
пейного классификатора со всеми описанны- шсний пин^й”°го классификатора:
ми выше предположениями на законы распре-
деления значений дискриминантной функции. Перепишем ее, используя ме-
тод множителей Лагранжа, в виде безусловной целевой функции:
Pi+a(A>o-Po)2“»min,
здесь а — множитель Лагранжа ( а >>0). Тогда необходимым условием ми-
нимума является следующее равенство:
р[ = 2а(ро
-Ро)
Ро-
662
ГЛАВА 9
Учитывая, что
Г
р,=р.
а|/
получаем следующее уравнение:
— 2а 1 pQ Pd
_/q
Оо/
/ v
_Но
Ро
а0,
Ро — 1 ?d
/
Подставляя в последнюю формулу выражение для производной по вектору
W и порогу WN, снова приходим к аналогичной (9.85) системе уравнений и,
далее, получаем такое же уравнение (9.81) относительно вектора W. Понят-
но, что результатом рассуждений снова окажется итерационная процедура
Петерсона—Матсона (9.82)—(9.84).
Тот факт, что, используя рассматриваемую процедуру, для любого значе-
ния вероятности ложной тревоги можно найти соответствующее ей наимень-
шее значение вероятности пропуска объекта, означает, что процедура Петер-
сона-Матсона позволяет получить всю границу множества значений вероят-
ностей ошибок. Следовательно, любую задачу оптимизации с критерием,
требующим совместного понижения значений вероятностей р0, р{ и линей-
ным классификатором, можно решить, используя алгоритм Петерсона—Мат-
сона — то есть простым перебором значений величины t. Этот факт очень
удобен при построении линейного классификатора на базе других критери-
ев — нет необходимости разрабатывать какую-то другую процедуру поиска
решающего правила.
9.4. Совместная классификация
Основной целью проектирования любой системы классификации является
построение такого решающего правила, которое обеспечивало бы максималь-
но возможное качество распознавания. Именно поэтому в последнее время
начали интенсивно развиваться математические методы и алгоритмы постро-
ения решающих правил с повышенной структурной сложностью — мульти-
классификаторов [49, 58, 66, 67, 69, 70, 72, 84, 87]’.
Идея мультиклассификатора достаточна проста — использовать результаты
распознавания сразу нескольких классификаторов для улучшения качествен-
ных показателей всей системы в целом. Подобная совместная классификация,
очевидно, в целом должна оказаться не хуже индивидуальных решений, кото-
рые принимаются каждым из используемых классификаторов, называемых в
ряде работ экспертами (experts) [80].
1 В настоящее время в рамках данного направления нет устоявшейся терминологии. В связи с
этим некоторые используемые далее термины не являются общепризнанными.
9.4. Совместная классификация
663
В то же время, ориентация на схему принятия решения со многими клас-
сификаторами породила целый ряд теоретических и практических проблем:
как наилучшим образом комбинировать классификаторы, как настраивать
параметры получаемого мультиклассификатора, можно ли улучшить качество
совместной классификации при коррекции параметров классификаторов-экс-
пертов и как это делать, какова граница качественных показателей при со-
вместной классификации и т.д. На многие из этих вопросов до сих пор нет
исчерпывающих и полных ответов. Это еще раз показывает, что теория и
методы совместной классификации — новое, развивающееся направление в
распознавании образов. Несмотря на это существует целый ряд теоретически
интересных и полезных с практической точки зрения результатов.
9.4.1. Стратегии совместной классификации
Поиски путей нахождения наилучшей схемы совместной классификации
привели к появлению целого ряда различных мультиклассификаторов. В то
же время стратегий совместной классификации, как показывает анализ этих
решающих функций, достаточно немного. Выделим их.
С точки зрения реализации процесса совместной классификации очевидно
разделение стратегий совместной классификации на последовательные и па-
раллельные.
В последовательной стратегии классификации векторы признаков подвер-
гаются последовательному анализу каждым из входящих в мультиклассифи-
катор экспертом. В случае, если данный эксперт достаточно «эрудирован»,
ответ о принадлежности к конкретному классу выносится немедленно. В про-
тивном случае анализ данных осуществляется следующим экспертом. Задачей
настройки последовательной схемы классификации является нахождение па-
раметров всех классификаторов и правила их взаимодействия. Схема после-
довательной стратегии классификации представлена на рис. 9.18. Число экс-
пертов в такой схеме принятия решения может быть различным: от двух клас-
сификаторов до неограниченного их количества.
Надо отметить, что появление и развитие последовательной стратегии клас-
сификации во многом было обусловлено существованием хорошо развитой
статистической теорией последовательного анализа гипотез [4, 5, 20, 30, 39].
Классической работой в области последовательного анализа считается ра-
бота Вальда (5]. Суть метода при проверке двух гипотез заключается в следу-
ющем. Все выборочные данные разбиваются, искусственным или естествен-
ным путем, на группы — наблюдения. Начиная с первого наблюдения произ-
водится расчет вектора признаков, а затем и отношения правдоподобия’.
664
ГЛАВА 9
Здесь ук — объединенный вектор признаков до А-го наблюдения. Значе-
ние отношения правдоподобия при очередном наблюдении используется для
вынесения одного из трех решений:
- если А(у*)<А, то принимается гипотеза £20,
- если А(у*)>В, то принимается гипотеза £2,,
- если А<А(у*)<В, то производится следующее наблюдение.
Пороговые значения А и В выбираются таким образом, чтобы обеспечить
требуемые значения ошибок классификации. Метод проверки двух гипотез,
называемый последовательным критерием отношения правдоподобия Вальда, яв-
ляется оптимальным в том смысле, что минимизирует одновременно средний
риск и среднюю длительность наблюдений [20]. Дальнейшее его развитие
привело к появлению методов последовательного анализа для многих гипо-
тез, методов усечения (остановки) последовательных процедур, различных
обобщений и дополнений [4, 30, 31, 32, 86]. В одной из последних отече-
ственных работ в области последовательной статистической оценки [32], вме-
сто отношения правдоподобия используется некоторая наперед заданная ста-
тистика, а пороги варьируются на каждом шаге.
Однако, несмотря на достаточно широкий круг работ в этой области, ис-
пользование методологии последовательного анализа для построения и опти-
мизации последовательной схемы совместной классификации в общем слу-
чае недостаточно эффективно. Это обусловлено несколькими причинами. Во-
первых, решение на каждом этапе анализа в последовательной схеме
классификации в общем случае принимается не на основании статистики, а
классификатором, параметры которого заранее могут быть неизвестными. Во-
вторых, эксперты различных уровней могут быть «компетентны» лишь на ог-
раниченном числе классов. Например, в двухэтапной процедуре распознава-
ния [24, 50] первый эксперт предназначен для решения задачи обнаружения,
а второй — задачи распознавания.
В последовательных же процедурах
классификации все элементы струк-
турно эквивалентны.
Выделенные основные недостат-
ки существующих решений в облас-
ти последовательной организации
классификации делают целесообраз-
ным разработку новых алгоритмов
параметрической и структурной
оптимизации последовательных
мультиклассификаторов. Этим обус-
ловлено появление большого числа
работ в этой области [30, 31, 32].
Рис. 9.18. Схема мультиклассификатора для
последовательной стратегии классификации
9.4. Совместная классификация
665
В параллельной стратегии классификации векторы признаков подвергаются
одновременному анализу несколькими классификаторами-экспертами. Каж-
дый их классификаторов выносит свое решение о принадлежности анализи-
руемых данных к тому или иному классу. В этом случае задачей настройки
параллельной схемы классификации является задача поиска функции «агре-
гирования» решений различных экспертов, а также поиск оптимальных пара-
метров классификации каждого эксперта в составе общей схемы. Структура
параллельного мультиклассификатора приведена на рис. 9.19.
Заметим, что при параллельной комбинации экспертов возможно различ-
ное представление информации об их решениях. Наиболее типичными фор-
мами представления решений являются:
- номер класса, к которому принадлежат классифицируемые данные по
мнению эксперта (минимальный объем информации);
- апостериорные вероятности принадлежности классифицируемых данных
к каждому классу (максимальный объем информации).
Появление параллельных стратегий классификации вначале было обуслов-
лено желанием разработчиков повысить качество систем распознавания. В
последнее время параллельная стратегия классификации бурным развитием
обязана в первую очередь возросшим потенциалом вычислительной техники,
в особенности компьютерам с параллельной архитектурой. Использование
многопроцессорных вычислительных комплексов для решения задачи рас-
познавания позволяет естественным образом разделить процедуру классифи-
кации на ряд параллельно выполняемых процессов, каждый из которых реа-
лизует процесс принятия решения некоторого конкретного эксперта. Подоб-
ная технология в настоящее время эффективно используется, например, в
нейронных сетях [66, 67, 84].
Заметим также, что поиск функции агрегирования в первое время проводил-
ся эвристическими методами, часто использовались аналогии с коллективными
Рис. 9.19. Схема мультиклассификатора для параллельной стратегии классификации
666
ГЛАВА 9
методами принятия решений, которые характерны для людей. Наиболее яр-
ким примером такой функции агрегирования является классификация по
правилу «максимального голосования». В соответствии с этим правилом ре-
шение о принадлежности к некоторому классу принималось, если за этот
класс «проголосовало» наибольшее число экспертов. Однако до недавнего
времени для большинства подобных схем классификации не были получены
теоретические обоснования эффективности. Поэтому их использование во
многом отражало детерминистический подход к построению мультикласси-
фикаторов.
Ниже представлены некоторые методы и алгоритмы для параллельной и
последовательной стратегий совместной классификации. В п.9.4.2, приведе-
ны алгоритмы настройки правила агрегирования параллельного мультиклас-
сификатора с минимальным объемом информации о решениях экспертов.
Рассмотрены особенности настройки и реализации мультиклассификатора в
частных случаях: при независимой работе экспертов, при малом числе клас-
сов. Даны выражения для оценки ошибок мультиклассификации.
Информацию о методе построения мультиклассификаторов, использую-
щих максимальную информацию о решениях экспертов, и математическое
обоснование соответствующих алгоритмов можно найти, например, в работе
[72]. Результаты этой работы направлены на теоретическое обоснование ряда
эвристических методов совместной классификации, широко используемых в
распознавании образов.
В п.9.4.3. приведен метод построения итерационных алгоритмов пара-
метрической оптимизации классификаторов-экспертов в составе двухэтап-
ной последовательной процедуры классификации. Рассмотрены особеннос-
ти реализации такой процедуры, алгоритмов ее настройки и эффективности
на примере решения задачи поиска и распознавания локальных объектов на
изображении.
9.4.2. Параллельная схема совместной классификации с минимальной
информацией о решениях экспертов
Как отмечалось в п.9.4.1, схемы параллельной классификации могут раз-
личаться способом представления информации о решениях экспертов. Рас-
смотрим ситуацию, когда информация от эксперта поступает в виде номера
класса. В этом случае не требуется никаких дополнительных предположений
о способе представления образа и виде решающей функции. Вначале дадим
формальную постановку задачи мультиклассификации, а затем рассмотрим
возможные методы ее решения.
Формальная постановка задачи мультиклассификации. Пусть все множество
объектов разделено на L классов , I = О, L — 1. Пусть для классификации
используется N классификаторов, каждый из которых выносит свое решение
9.4. Совместная классификация
667
Qn J п = 0, /V — 1 j относительно принадлежности конкретного объекта (о не-
которому классу. Для определенности будем считать, что л-й классифика-
тор относит анализируемый объект к /-му классу, если Qn~l. Таким об-
разом множество возможных решений каждого из классификаторов
{/: / ~ О, L —1|, и на решение Qn можно смотреть как на дискретную слу-
чайную величину с некоторым законом распределения. В этом случае на
вход мультиклассификатора (функции агрегирования) подается случайный
вектор Q~(C0, в качестве компонентов содержащий мнения эк-
спертов. Тогда решением задачи настройки мультиклассификатора является
нахождение функции или отображения, которое по заданному конкретному
вектору решений q = (<?0, ..., определяет, к какому именно классу Q.t
принадлежит соответствующий этому вектору объект со.
Очевидно, постановка задачи таким образом приводит нас к стандартной
процедуре классификации Байеса дискретного случайного вектора (см. п.4).
Процедура совместной классификации Байеса. Пусть на всем множестве воз-
можных векторов (возможных решений экспертов) q = (qG, для
каждого класса (/ — О, L~ 1) определена его функция правдоподобия
p(Q = Q/^/) • Тогда оптимальным решением задачи классификации, как из-
вестно, является правило максимума апостериорной вероятности (см. п.4.3)1:
объект относят к тому классу , для которого
P(n(/Q=q) = max p(ft -/Q=q). (9.97)
Здесь апостериорные вероятности P(fiy/Q=q) определяется по формуле
Байеса:
. . P(Q/.)p(Q = q/n,)
P(O;/Q = q)= V J>-±------У-Lb.
Sp(n()p(Q=q/ni)
i=0
На практике процедура построения мультиклассификатора Байеса сво-
дится к получению для каждого класса Q, (/=0, L —1) таблицы размером
Ln , которая задает распределение вероятностей случайного вектора Q,
P(Q = q/Qz). Таким образом, необходимо произвести оценку LN+1 вероят-
ностей P(Q = q/O|) () = 0, L — 1). При реализации процедуры распознава-
ния достаточно одной таблицы размером LN , которая содержит для каждо-
го возможного вектора q соответствующий номер класса, получаемый за-
ранее в соответствии с формулой (9.97). В табл. 9.2 приведены размеры такой
таблицы.
1 Здесь и далее в разделе матрица штрафов предполагается простейшей.
668
ГЛАВА 9
Таблица 9.2. Размер таблицы мультиклассификатора Байеса
число классов L
2 4 8 16 32 64 128 256
ЧИСЛО экспер тов/У 2 22 24 26 28 210 212 214 21б
4 24 28 212 2’6 220 224 228 232
8 28 2’6 г24 232 240 248 2» 2е4
16 216 232 г64 .4.
32 232 2W ...
Для реализации процедуры мультиклассификации Байеса в режиме реаль-
ного времени (например, при автоматическом чтении текста), занимаемый
соответствующей таблицей объем данных должен помещаться в оперативную
память компьютера, что означает практическую невозможность использова-
ния мультиклассификатора для тех параметров (W,L) таблицы, которые вы-
делены серым цветом.
Кроме того, при настройке такого мультиклассификатора возникают до-
полнительные ограничения, связанные с устойчивостью получаемых оце-
нок вероятностей соответствующих законов распределения. Действитель-
но, получение «хорошей» в статистическом смысле оценки одного значе-
ния вероятности требует десятков, а иногда сотен и тысяч экспериментов.
Так как число оцениваемых значений вероятностей составляет Lw+I, то
объем выборочных данных становится просто катастрофически большим.
Таким образом, объективно существуют причины, которые в ряде случаев
делают невозможным использование процедуры мульти классификации Байе-
са. Это привело к появлению различных алгоритмов, основанных на опреде-
ленных упрощениях. Одним из типичных упрощений является допущение
независимости решений классификаторов-экспертов и/или их признаков. Ниже
приведен подход построения мультиклассификатора для такой ситуации. Од-
нако надо заметить, что в ситуации небольшого числа классов и малого коли-
чества классификаторов оптимальной является приведенная выше процедура
Байеса.
Мультиклассификаторы при независимых экспертах. Предположим, что ре-
шения Qfn выносимые различными решающими правилами в мультикласси-
фикаторе, являются независимыми в каждом из классов. С вероятностной
точки зрения это предположение означает выполнение равенств:
N-J ______
P(Q = q/Q,) = П^(е„=«./П/), 1= 0,L- 1.
л=0
Тогда дискриминантная функция Байеса /-го класса
^(ч) =
= q/£2|), 1=0,L — 1
9.4. Совместная классификация
669
будет иметь вид
N-I _____
4/(ч) = Р(П/)П/’(е„ =l=O,L- 1.
Введем в рассмотрение функцию
G-W=
1, если q = s,
О, иначе.
Тогда значение вероятности P(Qn = qn/Q[) может быть представлено сле-
дующим образом:
р(с„=?„/«,)= Ер(с„=
.5=0
В этом случае выражение для дискриминантной функции мультикласси-
фикатора будет иметь вид
/V-l L-I
d, (q) = P(£l,) [I Е Р(Qn = V«i)Gr (<?„).
,;._0v-0
/= 0,L~ 1.
(9.98)
Применяя к полученному выражению логарифмическое преобразование, а
также учитывая, что для конкретного п функция Gx (qn) = 0 при всех 5 х qn,
получаем
N-1 L—I ______
d|(9) = lnP(n/) + EEGs.(9„)lnP(e„=i/n/), /=0,Л-1. (9.99)
п =0.1-0
Обозначим:
Zj ~Gx(qfl), где j = L-n + sy j = 0, L-N-l,
5 = 0, £-1, z-(z0, zLxN4). (9.100)
Введем z — (z0, ..., zLN^)T — бинарный вектор длиной L-N. Введем ко-
эффициенты
Wj =1пР(е„ =5/Q/), j = £h + 5, n = 0, N-l , 5 = 0, L-l. (9.101)
Тогда окончательным решением задачи является мультиклассификатор с
дискриминантной функцией вида
d,(y) = [w']7'z + lnP(n,).
здесь Wz — вектор-столбец, составленный из коэффициентов W-
(j = 0, L N — 1 ). Таким образом, оптимальный мультиклассификатор оказался
670
ГЛАВА 9
линейным относительно введенного бинарного вектора признаков (9.100) и
преобразованного признакового пространства.
Замечание 1. В качестве функции Gx (<у) может выступать, например, по-
лином (£-1)-го порядка:
<?.(«)=
1
П(‘-0
/=0
Ш-')-
/=0
(9.102)
Из выражений (9.99) и (9.102) видно, что в признаковом пространстве ре-
шений экспертов мультиклассификатор является полиномиальным, и степень
полинома, описывающего решающую функцию мультиклассификатора, рав-
на (£-1). То есть при построении совместного решения правила распознава-
ния для двух классов, мнения экспертов комбинируются в линейной форме,
для трех классов они учитываются в полиноме второй степени и т.д.
Замечание!. Представленный алгоритм построения мультиклассификато-
ра, при независимых решениях экспертов, естественным образом переносит-
ся на ситуацию распознавания векторов-признаков со значениями в конеч-
ном поле.
В дополнение к изложенному общему алгоритму мультиклассификации
рассмотрим один важный частный случай, когда решается задача альтер-
нативного распознавания (обнаружения) и мульт и классификатор, в соот-
ветствии с первым замечанием, комбинирует мнения экспертов в линей-
ной решающей функции. Данная задача известна как задача распознава-
ния бинарных векторов признаков, и ее решение дано, например, в
монографии [33]. В данном случае ее решение вытекает как частный слу-
чай (9.98) и (9.102).
Итак, пусть L = 2. Тогда функция Gs (g) определяется следующим образом:
М<7) = <7-
В результате дискриминантная функция (9.98) может быть переписана сле-
дующим образом:
d,(q) = = 1/П,))(!-«„)+ />(0„=1/П,)9„), /=0Д=Т
я=0
Окончательным решением задачи является мультиклассификатор с диск-
риминантной функцией вида
d,(q) = lln(P(n/))+Sto(l-P(Q„= 1/Н,))|+ ,
л=0 л--0 “ V5,2/))
который, как ожидалось, является линейным относительно решений экспертов.
9.4. Совместная классификация
671
Аналогичным образом можно получить выражение для мульти классифи-
катора в терминах отношения правдоподобия (см. п.4.2.):
Vj^l: A/7(g)>Xj7
где
P(Q„ =!/«>) ,
1-р(е„=1/П7)'
1-Р(С„ = 1ЛМ
Очевидно, отношение правдоподобия также является линейной функцией
решений экспертов.
Замечание 3. В отличие от общей ситуации построения мультиклассифика-
тора, количество требуемых для оценки параметров при независимых решени-
ях экспертов, в соответствии с выражением (9.101), составляет LxN для каж-
дого класса. В этом случае объем данных, используемых при классификации,
равен NxL2, что существенно меньше, чем приведенные в табл. 9.2 значения.
Это позволяет использовать представленную здесь процедуру совместной клас-
сификации для большого числа классов и классификаторов-экспертов.
Вычисление вероятностей ошибочной классификации при совместной класси-
фикации. Аналитическое выражение для вероятностей ошибок совместной клас-
сификации в общем случае не получено. Однако при небольшом количестве
экспертов значения этих вероятностей можно вычислить на ПЭВМ, исполь-
зуя дискретный аналог формулы (4.26):
Рц= Е P(Q = q/ft|), l^j,
qEDj
поскольку в признаковом пространстве находится всего LN элементов. Когда
число компонентов вектора решений экспертов велико, можно получить при-
ближенные выражения для вероятностей ошибочной классификации в случае
£ = 2, если предположить независимость решений экспертов. Результаты рас-
чета вероятностей известны для бинарного вектора признаков и даны, на-
пример, в [33]. В подобной ситуации в соответствии с центральной предель-
ной теоремой можно считать закон распределения случайной величины
Л у = A/y(Q) нормальным. Числовые характеристики закона распределения
случайной величины Л]0 имеют следующий вид:
' p(e„=i/g,) i-p(e„=i/n0)'
,i-p(e„=i/O|) p(e„=i/n0) ,
N-1
H/-£{A10(Q)/Qj= Е1п
л=0
672
ГЛАВА 9
/ — 0,1; с, —e{(A|0(Q) /о(
HJ pfe-i/n')
„=о| 11-Р(е„ = 1/£2,)
1-Р(б„ = 1/П0)>
P(C„=i/ft0) ,
2
p(e„=i/n,)(i-p(e„=i/fiz)).
Для вероятностей ошибочной классификации получаем следующие прибли-
женные выражения:
р0 = 1 - Ф ——— , р} = Ф ———
°0 °1 ;
Х = 1п
Рфо)
Р(П,)'
В ситуации, когда условия центральной предельной теоремы не выполня-
ются, а решения экспертов независимы, можно воспользоваться следующими
выражениями для верхних границ вероятностей ошибок, вытекающих из не-
равенства Чебышева:
р < °°
(мо-Х)
Pl <
(и.-*-)2
Исследование эффективности правил совместной классификации. Для оценки
эффективности использования совместного решающего правила был прове-
ден ряд экспериментальных исследований по классификации. Данные были
представлены в виде векторов смеси нормальных законов распределений,
как показано на рис. 9.20о. В качестве экспертов выступали линейные клас-
сификаторы, параметры которых оказывались локально оптимальными. Ре-
зультаты исследований представлены в табл. 9.3 и на рис. 9.206— в. Форми-
руемая разделяющая граница мультиклассификатора, базируясь на линей-
ных разделяющих границах экспертов, показанных на рис. 9.206, оказывается
кусочно-линейной (см. рис. 9.20в). Как следствие такой «адаптации» к типу
распределения данных, качество работы мультиклассификатора оказалось
Таблица 9.3. Эффективность совместной классификации с минимальной информацией
о решениях экспертов
Классификатор Ро Pi Риск
эксперт 1 0,785 0,085 0,435
эксперт 2 0,775 0,08 0,425
эксперт 3 0,23 0,12 0,175
Классификация оптимальным мультиклассификатором с независимыми решениями экспертов 0,23 0,055 0,143
9.4. Совместная классификация
673
лучше качества любого из экспертов и для вероятностей ошибок р0 и рх, и
для величины риска в целом (см. таблицу 9.3).
9.4.3. Двухэтапная последовательная процедура классификации
Структура двухэтапной последовательной
процедуры классификации. Примем модель
данных, в соответствии с которой большая
часть анализируемых (классифицированных)
данных относится к не интересующему нас
«фоновому» классу, а интересующие нас дан-
ные, интерпретируемые как «объекты», встре-
чаются достаточно редко. Подобная модель
характерна для многих приложений, в част-
ности для задач поиска и распознавания ло-
кальных объектов на изображении [1, 3, 9,
10, 11, 50].
Из принятой модели следует, что прямое
использование расширенного набора призна-
ков и качественного решающего правила для
большей части анализируемых данных неэф-
фективно и вычислительно избыточно, так как
их занимает не интересующая нас фоновая
составляющая. Поэтому представляется целе-
сообразным:
- до процесса распознавания провести
предварительный анализ данных с целью вы-
деления из них фрагментов, которые потен-
циально содержат интересующую информа-
цию — объекты. Объем «полезных» данных
по сравнению с первоначальным оказывает-
ся сравнительно небольшим;
- по выделенным данным производить по
возможности полный анализ с целью доста-
точно качественной классификации. Большая
вычислительная сложность производимого
анализа компенсируется малым числом ана-
лизируемых фрагментов.
Рис. 9.20. Векторы признаков и результаты классифи-
кации с минимальной информацией о решениях экс-
пертов: «...» — эксперт 1, «---»> — эксперт 2,
«----» — эксперт 3, «х» — объекты класса Г20, «о» —
объекты класса Q,
а — исходные данные
б — разделяющие границы экспертов
в — совместная классификация с неза-
висимыми решениями экспертов
22 — 9044
674
ГЛАВА 9
Тогда процесс распознавания данных может быть синтезирован в рамках
двухэтапной процедуры, представленной на рис. 9.21.
Для каждого фрагмента данных:
на первом этапе процедуры
- с использованием быстрого алгоритма производится формирование век-
тора признаков;
- на основе сформированного вектора принимается решение о принад-
лежности текущего фрагмента либо к классу объектов, либо к классу фона
(этап предварительного обнаружения).
Пусть текущий фрагмент классифицируется как «объект», тогда классифи-
катор второго этапа производит распознавание:
на втором этапе процедуры
- по выделенному фрагменту данных производится формирование при-
знаков, информативность которых должна быть достаточной для принятия
решения с необходимым качеством;
- производится классификация фрагмента с использованием достаточно
качественного классификатора второго этапа. При этом классификатор мо-
жет использовать информацию, полученную на первом этапе.
Легко заметить, что первый этап по своему содержанию близок к обычной
схеме обнаружения. Однако к нему предъявляются дополнительные требова-
ния низкой вычислительной сложности и малой вероятности пропуска объекта
при одновременно небольшом числе выделяемых фрагментов.
входной набор данных 72^
быстрое вычисление
признаков
• • • ¥
предварительное обнаружение
фрагменты данных
полная классификация
.......-.. j;.;.,,.,:...
формирование признаков ф
по фрагменту 2: . к
'".'О'. "И.1. ..I" .. " ... III I I. I... <
результаты классификации
Рис. 9.21. Схема двухэтапной последовательной процедуры классификации
9.4. Совместная классификация
675
Основное преимущество данной двухэтапной процедуры обнаружения и
распознавания состоит в возможности, с одной стороны, снижения вычисли-
тельной сложности (первый этап) и, с другой стороны, использования рас-
ширенного набора средств формирования признаков и классификации (вто-
рой этап).
Соглашения об обозначениях. Введем вначале обозначения для обычного
алгоритма распознавания, а затем, используя полученную терминологию, ис-
пользуем ее для описания двухэтапной последовательной процедуры класси-
фикации.
Пусть по фрагменту анализируемых данных у, являющемуся реализацией
случайного фрагмента у, с помощью однозначного (но не взаимнооднозначно-
го) преобразования ф формируется вектор признаков у = {уп}^ (в частно-
сти, вектор у может совпадать с самим фрагментом данных), который, в свою
очередь, рассматривается как реализация случайного вектора Y. Вектор при-
знаков, как показано на рис. 9.22, используется для классификации фрагмента
у в один из L классов {О., , представители которых и формируют исходный
набор данных. Следуя принятой выше терминологии, будем интерпретировать
класс По как класс фона, а оставшиеся (L —1) классов — как классы объек-
тов. Как известно, справедливы следующие соотношения [40]:
L-I ______
H=Un/’ nfnn; = 0, Л i,j=O,L-l.
/=о
Рис. 9.22. Схема процесса распознавания в признаковом пространстве
22*
676
ГЛАВА 9
В то же время, пространство £2, содержащее все возможные фрагменты
данных у, оказывается разбитым на множество областей 0/ (/ = 0, L — 1), оп-
ределяющих, по сути, работу классификатора. А именно, классификатор при-
нимает решение о принадлежности фрагмента у классу £2Z в том случае,
если /?(у) = у Е/9/, при этом 0/ = ф-Г(£>/) является прообразом области Dt
/V-мерно го метрического пространства признаков. Необходимость задания об-
ластей D[ и признакового пространства D обусловлена тем фактом, что
производить классификацию в исходном пространстве £2 затруднительно, так
как области Ql не являются компактными, а размерность самого простран-
ства часто оказывается достаточно высокой.
Преобразование ф позволяет, с одной стороны, снизить размерность
пространства признаков, а с другой стороны, добиться удобного для клас-
сификации вида областей ф(<2/). Заметим, что выполняются следующие
соотношения:
L-1 _____
Я'ПЯу=0, i*j, i,j=O,L-l,
1=0
и, соответственно, в силу однозначности преобразования ф,
L1 _____
£2=|j0{, 0/П©;=0, j, i,j=O,L-\.
1=0
В статистической теории распознавания описание классов производится
путем задания или определения функций правдоподобия в признаковом про-
странстве для каждого из классов [17, 33, 40]. Отойдем от подобного традици-
онного подхода. Будем производить все рассуждения в пространстве О, но
при этом рассматривать его как обычное признаковое пространство. В этом
случае для описания любого из классов достаточно знать соответствующую
область £2,, / = 0,L —1, а также единственную безусловную плотность вероят-
ности:
/(т)=£Ж)Р(у/я,),
1=0
где / = 0,£ —1 — функция правдоподобия /-го класса в признако-
вом пространстве фрагментов данных, P(£2Z), /=0,£—1 — некоторая чис-
ловая величина, задающая априорную вероятность появления объектов /-го
класса. Действительно, функция правдоподобия какого-либо класса легко
может быть получена следующим образом:
КЛ)=|/МЖ ,=ет.
u 1 |о,
9.4. Совместная классификация
677
А значение соответствующей априорной вероятности равно
P(n() = P(£2() l = f’(n/). f p(y/at)dy=
Й,
Г P(n,)p(Y/nz)dY= f p(y)dy = Ptfetll).
Тогда выражение для вероятностей классификации из класса в класс, зада-
ваемое в обычном признаковом пространстве как
P,7 = Jp(y/n>)rfy-
Д
в нашем случае преобразуется к виду
i, j = О, L — 1,
Р,у =/р(?/П7)б!Т = -^/р(П7)р(У/Пур7 = -1^ / p(y)dy=
0,- Ч“>)0,.ПП,.
р(уее,По;) _ p((Yee,)-(yeo,))
р(п7) р(тео,)
= р(уе©7ГёпД
i,y = O,L—1.
Здесь «» — произведение событий, а окончательное выражение для веро-
ятности задает обычную условную вероятность. Очевидное преимущество
предлагаемого описания состоит в том, что и классы, и классификатор опре-
деляются в исходном пространстве единообразно, используя области этого
пространства и , соответственно.
Введем теперь следующие обозначения событий:
а = {уе0/} = {ф(у) = уео,}.
wr/={ycn/}> z=o,L-i; (9.ЮЗ)
здесь Qt — событие, состоящее в принятии классификатором решения о
принадлежности случайного вектора признаков Y области Dl, то есть об
отнесении случайного фрагмента у к Z-му классу. Тогда выражение для ве-
роятностей классификации будет иметь вид
P,j = p('yee1./YeftJ)=/’(ei/wy), i,j=o,L-i.
678
ГЛАВА 9
Будем использовать введенные обозначения в рамках задачи распознава-
ния (второй этап). Для задачи обнаружения (первый этап) примем:
L = 2, Q = Qlt Q=Q0, €) = ©!, 0 —0О, D = D}, D = D0. (9.104)
Заметим, что в ситуации, когда для распознавания используется одно и то
же признаковое пространство, предлагаемое описание использовать нецелесо-
образно. Однако оно очень удобно, если имеется несколько признаковых про-
странств и несколько классификаторов. Действительно, пусть классификатор
первого этапа, подразделяющий пространство признаков на области «объек-
ты» — «фон» и решающий задачу обнаружения, связан с событием классифи-
кации Q и соответствующей областью 0, которые определены в формуле (9.104).
Событие Q, очевидно, в подобной ситуации интерпретируется как решение об
отнесении вектора признаков к классу объектов, a Q — к классу фона.
Для алгоритма классификации (распознавания), используемого на втором
этапе, в качестве событий и соответствующих областей примем и 0,,
определенные формулой (9.103). Событие Qo, таким образом, интерпретиру-
ется как решение классификатора второго этапа технологии об отнесении
вектора признаков к классу фона. Заметим, что в общем случае события Q и
Qo не являются несовместными (может выполняться неравенство P(QQ0)^0),
то есть заведомо допускается попадание «фоновых» фрагментов на второй
этап технологии.
В рамках вышеуказанных соглашений вероятности классификации при
обнаружении и распознавании в двухэтапной процедуре задаются следующим
образом:
PV = PtftQilWj}, i = l.L-l, j = O,L-1,
Poj=^(cM)+P(e<2o/W,). (9.105)
Здесь произведение событий QQi означает, что случайный фрагмент дан-
ных у классификатор первого этапа отнес к классу объектов, и одновремен-
но с этим классификатор второго этапа определил его к z-му классу. При
отнесении случайного фрагмента к классу фона возможно, с одной стороны,
сделать это на этапе предварительного обнаружения (событие О, с другой
стороны, отнести его к нулевому классу на втором этапе (событие Q£20). По-
скольку события QQ0 и Q несовместны, общая вероятность отнесения слу-
чайного фрагмента к классу «фон» может быть записана как сумма вероятно-
стей первого и второго случаев.
В дополнении к качественным показателям процесса распознавания вве-
дем в рассмотрение характеристику, характеризующую вычислительную слож-
ность процедуры. Заметим, что традиционно в обработке изображений [9, 10,
12, 28] оценка сложности алгоритмических и программных средств произво-
дится по формуле
(9.106)
9.4. Совместная классификация
679
где Ua, Um — количество, соответственно, сложений и умножений, ис-
пользуемых для обработки или классификации одного фрагмента изображе-
ния, то есть сложность на отсчет изображения; т] — коэффициент относи-
тельной сложности операции умножения по отношению к операции сложе-
ния, типичное значение которого для наиболее массовых компьютеров лежит
в диапазоне от 1 до 3.
В единицах (9.106) средняя вычислительная сложность одного акта обна-
ружения и распознавания составляет
U=U,+P(Q)U„, (9.107)
где t/j и t/jj, соответственно, сложность первого и второго этапов техно-
логии.
Разумный компромисс между качеством решения задачи и затраченными
вычислительными ресурсами достигается, если рассматривать величины слож-
ности и качества либо как составляющие некоторой целевой функции, которая
отражает приемлемость выбора каждой конкретной пары, либо как критерии
оптимальности и ограничения в задаче оптимизации технологии. Наиболее
часто встречающейся задачей параметрической оптимизации, используемой
при построении алгоритма распознавания, является задача улучшения его
качества при одновременном ограничении на сложность процесса принятия
решения [1, 3, 10, 11, 50]:
/?(а) —► min,
C/(a)<(/lim. (9.108)
Здесь t/|jm — верхняя граница сложности, а — вектор параметров алго-
ритма, по которому производится оптимизация.
Параметрическая оптимизация двухэтапной последовательной процедуры клас-
сификации. Пусть решается задача параметрической оптимизации двухэтап-
ной процедуры в виде (9.108) по вектору параметров
а=(а1«ап)>
где af и аи задают, соответственно, параметры первого и второго этапов.
Тогда, учитывая выражения (9.105), (9.107) и (9.108), задача оптимизации
формулируется следующим образом:
+ Е ('i -'by)^(’’,>)^(c(ai)ei(all)/W>)-» min
J=0 (аьаи)
680
ГЛАВА 9
Очевидно, что показатель сложности двухэтапной процедуры не содержит
зависимости от совместного вектора параметров а . В то же время показатель
качества функционально с ним связан, а, следовательно, не может выступать
в качестве критерия настройки ни одного из двух классификаторов-экспер-
тов. Получаем противоречие — мы не можем настроить процедуру без на-
стройки каждого из ее этапов, и не можем настроить ни один из этапов по
критерию качества процедуры в целом. Для того чтобы изменить эту ситуа-
цию, воспользуемся возможностью представления вероятностей классифика-
ции из класса в класс в виде альтернативных выражений:
P(QQi/Wj) = P{Q/Wj)p(Qi/QWj), -----------
\ \ i,j=O,L-]. (9.109)
f,(ce,/wy)=p(e,/wy)p(e/e,W;),
Пусть теперь в процессе оптимизации получено некоторое решение
(fix fix \
ai , ап j. Зафиксируем какой-либо один из этапов, например второй, и бу-
дем изменять параметры другого. Тогда получим:
р(е(а,)G,(айк)/Wj) = р(й(a?)/wj)/Qt(а“’) Wj), i,j =0,1-1.
To есть изменение вероятности классификации из класса в класс про-
порционально изменению вероятности p(<2(ai)/12i(апХ)^у), причем собы-
тие, стоящее как условие, является фиксированным в процессе изменения
параметров первого этапа. Аналогично, фиксированным оказывается и ко-
эффициент пропорциональности изменения />^(2l(anX)/w/J. Точно также, в
соответствии с первым выражением в (9.109), можно получить величину из-
менения искомой вероятности при фиксированном первом этапе.
Таким образом, используя представление классификатора как события,
можно, фиксируя то первое, то второе из них, находить вектор оптимальных
изменений и производить соответствующую коррекцию, что в целом должно
привести к решению задачи настройки последовательной процедуры класси-
фикации. Заметим, что подобный подход требует итерационного представле-
ния алгоритма оптимизации. При этом указанные возможности позволяют
построить итерационные алгоритмы различных типов. В настоящем разделе
рассматриваются два из них.
Итерационный алгоритм параметрической оптимизации на основе градиентно-
го метода. Для построения итерационного алгоритма оптимизации на основе
градиентного метода необходимым является наличие возможности вычисле-
ния действительного значения вектора изменения параметров. Для этого
требуется вычисление производных вида
Эф(а|)е,(ац)/и^)
да
9.4. Совместная классификация
681
Учитывая выражение (9.109), получаем следующий способ их вычисления
/ fix fix \
в некоторой точке (а! , ап I:
Зная теперь значения производных можно воспользоваться градиентным
или любым другим методом оптимизации первого порядка [2, 15, 22}.
Использовать тот же подход для получения матрицы вторых производных
не представляется возможным, поскольку невозможно записать выражение
для смешанных производных. Как следствие, метод Ньютона и другие методы
оптимизации второго порядка не могут быть использованы [2].
К сожалению, воспользоваться алгоритмом оптимизации на основе гради-
ентного метода достаточно сложно. Основной проблемой является то, что на
практике вид зависимости вероятностей классификации от вектора парамет-
ров алгоритма классификации не может быть представлен в аналитическом
виде, а значит и вычисление указанных производных невозможно. В тех ред-
ких случаях, когда получение градиента все же допускается, существуют до-
полнительные трудности применения градиентного алгоритма: учет ограни-
чений в задаче оптимизации, выбор шага при коррекции параметров, высо-
кая вычислительная сложность такого алгоритма применительно к задаче
оптимизации процедуры распознавания. Все это делает использование итера-
ционного алгоритма оптимизации на основе градиентного подхода малоэф-
фективным или невозможным в большинстве реальных задач. Поэтому необ-
ходима его модификация. Эта модификация, исходя из перечисленных недо-
статков градиентного алгоритма, должна касаться процесса модификации
параметров. А именно, если на очередной итерации происходит полная кор-
рекция вектора параметров каждого из этапов, то можно без каких бы то ни
было затруднений использовать известные алгоритмы оптимизации. Учет ог-
раничений по сложности в таком случае также не является проблематичным.
Таким образом, итерационный алгоритм параметрической оптимизации
двухэтапной последовательной процедуры классификации может быть пред-
ставлен следующим образом.
Итерационный алгоритм поэтапной параметрической оптимизации. Решает-
ся задача оптимизации алгоритма распознавания второго этапа (второго экс-
перта):
682
ГЛАВА 9
E'b; + Е (g7 - rO7)p(W'7)/>(e(a1)/W'7)p(e,(a„)/e(a1)lVJ.)- min. (9.110)
j=O i,j=O a"
Решается задача оптимизации алгоритма распознавания первого этапа (пер-
вого эксперта):
Епу + Е Ь - rOj)p{wi)p{Ql (an)/Wy)p(c(a1)/el(an)lV;)-‘ min.
J—О i,j—0 ai
(9.111)
Если точность решения задачи не удовлетворяет, то возвращаемся к реше-
нию задачи оптимизации второго этапа.
Для определенности будем считать, что алгоритм прекращает свою работу
в ситуации, если новые изменения величины риска R и сложности Р\0) не
превышают некоторых изначально заданных величин. В качестве начального
состояния в данном алгоритме выбирается такое состояние классификатора
первого этапа, когда Q = VV0, то есть на первой итерации в качестве условий
будут выступать только события W-.
Сделаем некоторые замечания относительно задач (9.110) и (9.111). При
решении задачи распознавания число сформированных классов не превы-
шает их количество в первоначальной задаче. В задаче же обнаружения
(9.111) число всех условных событий составляет L2, то есть квадратично
зависит от первоначального числа классов. Такое увеличение их числа мо-
жет привести к неэффективному решению задачи — известным является
факт повышения значения среднего риска при увеличении числа классов и
неизменном пространстве признаков [40]. Поэтому при решении каждой
конкретной задачи необходимо, учитывая конкретные значения штрафов
Гу, производить модификацию выражения (9.111) для снижения числа ус-
ловных событий. Это может быть эффективно сделано, если матрица штра-
фов является простейшей.
Итерационный алгоритм поэтапной параметрической оптимизации в случае
простейшей матрицы штрафов. Итерационные схемы алгоритма. Пусть матри-
ца штрафов является простейшей. В этом случае задачи оптимизации (9.110)
и (9.111) меняются. А именно, задача (9.110) будет иметь вид
А'—1
F(lV0)P(e(ai)/%)+X;/>(w'y)P(e(aI)/H5)p(ei(a„)/e(aI)W>)-min, (9.112)
Иц
Для задачи (9.111) показатель качества можно переписать следующим об-
разом:
9.4. Совместная классификация
683
*=£р(^)р(с/^)+£ £р(и'у)р(се,/и’у)=
7=1 j-О г=0,
L-I
/=1 ;=о
cw/Ua
= р a LM +Ёфи,А)= р Q LX-+ р eU%e>
7=1 7=0 V 7=1 I 7=0
/,1
Окончательно:
+ Р
L-\ _
< 7=0
->min,
»/
Р(С(а/))<£!!ш^
и и
(9.113)
Очевидно, что показатель качества этой задачи может быть представлен в
виде
p(e-v,)+p(cv0),
где
V, = u4- ^иЧё/. (9.114)
7=1 7=0
В то же время, используя другие преобразования, возможно получение и
других форм представления критерия (9.113). Некоторые из вариантов приве-
дены в табл. 9.4.
Аналогичным образом может быть изменено и выражение (9.112). Подоб-
ная неоднозначность представления задачи оптимизации в общем случае мо-
жет привести к множественности результатов ее решения. Однако если на
каждой итерации выносится оптимальное или решение Байеса, то результат
оптимизации не будет зависеть от выбора итерационной схемы. Покажем это
на примере второй и третьей схем. Для первой из них рассмотрим классифи-
катор Байеса. Как известно, его разделяющая граница определяется из нера-
венства [17, 33, 40]
L—1
рkolia р y/woUa
„ 1=1
1=1
LI ] ( /L-1
р U wtQ, py/u^a
u=i И / i=i
684
ГЛАВА 9
Таблица 9.4. Формы представления составляющих критериев качества
Итерационная схема Ио И
1 ^0 7=0
2 И'обо и’ид j=i
3 и^д /=0 L-I
4 UWjQj 7=0 L-] и^. 7=1
Граница не изменится, если к правой и левой частям неравенства добавить
L-]
одну и ту же величину Р |J W{Q{ р у/ U . Учитывая, что присутствую-
U=i
щее в этом выражении событие несовместно ни с одним из событий третьей
/-1
схемы, получаем:
Р
WoUe,
U i=i
и(иад
0=1
% lie,
/=1
и[иад
U=i
/71-1
/1-1
f Д—1
р и ад, и и ад, р у и ад, и и ад,
Д/=1 J и=1 JJ / u=i U=i
Из последнего неравенства следует, что
р 1>, р
/L-\
y/U^,
. / /=1
а это задает выражение разделяющей границы классификатора Байеса для
третьей итерационной схемы. Аналогичным образом можно показать эквива-
лентность, с точки зрения решающего правила Байеса, остальных итерацион-
ных схем. В то же время, при использовании классификатора, отличного от
байесова, результаты оптимизации будут зависеть от вида задачи, а следова-
тельно и от итерационной схемы. Значит, для нахождения наилучшего реше-
ния необходимо также исследовать результаты оптимизации для каждой из
схем и выбрать наилучшую.
Вернемся к вопросу размерности задач распознавания и обнаружения —
числу классов в каждой из них. Очевидно, что поскольку алгоритм обна-
9.4. Совместная классификация
685
ружения может быть сведен к виду (9.114), где Vo и V] выполняют роль
событий принадлежности к соответствующему классу, то и число классов в
задаче обнаружения снижено до двух. Число классов в алгоритме распозна-
вания (9.112), как и в (9.110), осталось идентичным числу классов в перво-
начальной задаче.
Результаты экспериментальных исследований. Для исследования предложен-
ного итерационного алгоритма оптимизации двухэтапной последовательной
процедуры классификации рассмотрим задачу поиска и распознавания ло-
кальных объектов на изображении.
Характер изображений в этой задаче и специфика процесса их анализа
позволяют говорить об удовлетворении принятой ранее модели данных. А
именно, для задачи поиска и распознавания локальных объектов на изобра-
жении характерно, что [1, 3, 9, 10, 11, 50]:
- подавляющую часть изображения занимает не интересующая нас «фоно-
вая» составляющая;
- интересующие нас на изображении локальные области — объекты —
малы по сравнению с размерами самого изображения;
- расположение объектов в плоскости изображения таково, что для каж-
дого из них можно указать такое положение некоторой выпуклой, заранее
заданной, области, что никакой другой объект в ней не будет присутствовать;
- количество содержащихся на изображении объектов мало по сравнению
с общим количеством отсчетов изображения.
В рамках данной модели одним из наиболее удобных способов анализа
данных является их локальная обработка [10, 11, 63]. В задачах обнаружения
и распознавания локальных объектов на изображении при каждом положе-
нии окна обработки анализируемый фрагмент рассматривается как отдельное
изображение, для которого и производится классификация.
Для экспериментальных исследований были выбраны изображения, со-
держащие объекты двух классов. Изображение, приведенное на рисунке
рис. 9.23а использовалось для обучения и оценки результатов классифика-
ции. В качестве признаков в работе были выбраны следующие:
- на первом этапе — два локальных средних с различными размерами окна
усреднения (15x15, 25x25), вычислительная сложность их расчета составляет
8 операций на отсчет (см. п.8.1.3);
- на втором этапе — пять моментных инвариантов (см. п.9.2.3), вычислен-
ных по градиенту выделенного фрагмента (25x25) изображения с использова-
нием алгоритма прямой свертки; вычислительная сложность расчета инвари-
антов составляет приблизительно 6300 операций на отсчет изображения.
В качестве классификаторов в работе были использованы:
- на первом этапе — линейный классификатор, рассчитываемый с исполь-
зованием процедуры Петерсона-Матсона; вычислительная сложность его
использования для классификации составляет 4 операции на отсчет (см. п.9.3.4);
- на втором этапе — квадратичный классификатор, вычисляемый в предпо-
ложении нормальности закона распределения вектора признаков на втором
686
ГЛАВА 9
6 — требуемая классификация
в — наилучший результат распознавания клас-
сификатора второго этапа (риск равен 0,05634)
и его состояние на первой итерации алгорит-
ма оптимизации
г — результаты работы двухэтапной проце-
дуры классификации на первой итерации
алгоритма оптимизации
д — результат работы классификатора второго
этапа на последней итерации алгоритма опти-
мизации
е — результаты работы двухэтапной процеду-
ры классификации на последней итерации ал-
горитма оптимизации
0,032 -г
0,03 X
0,028 - - \____________________________
g 0,026 --
0,024 --
0,022 --
0,02 4---1----1----1---1----1---1----1
1 2 3 4 5 6 7 8
номер итерации
ж — величина среднего риска при распозна-
вании
з— вычислительная сложность при распозна-
вании
Рис. 9.23. Экспериментальные результаты оптимизации двухэтапной последовательной проце-
дуры классификации
Литература к главе 9
687
этапе; вычислительная сложность его использования для классификации изоб-
ражения при двух классах объектов и одном классе фона составляет прибли-
зительно 200 операций на отсчет (см. п.4.4).
Таким образом, в проведенных исследованиях = 12, Un =6500.
Сравнение качества работы оптимизированной двухэтапной процедуры
производилось с наилучшим достижимым качеством классификатора второ-
го этапа. Ограничения на сложность процедуры не задавались. Процесс оп-
тимизации приведен на рис. 9.23в—з. Сравнение показателей работы при-
ведено на рис. 9.23^с—з. Сравнение позволяет утверждать о приблизительно
двукратном выигрыше в качестве распознавания при использовании двухэ-
тапной процедуры. При этом до 15% выигрыша достигалось за счет исполь-
зования итерационного алгоритма оптимизации. Заметим, что также умень-
шилась сложность процесса принятия решения: по сравнению со сложнос-
тью алгоритма классификации второго этапа значение вычислительной
сложности уменьшилось приблизительно в 10 раз (см. рис. 9.23з).
Литература к главе 9
1. АбчукВ.А., Суздаль В.Г. Поиск объектов (М.: Сов. радио, 1977)
2. Амосов А.А., Дубинский Ю.А., Копленова Н.В. Вычислительные методы
для инженеров (М.: Высш, шк., 1994)
3. Анисимов Б.В., Курганов В.Д., Злобин В.К. Распознавание и цифровая об-
работка изображений (М.: Высшая школа, 1983)
4. Башаринов А.Е., Флейшман Б.С. Методы статистического последователь-
ного анализа и их радиотехнические приложения (М.: Сов. радио, 1962)
5. Вальд А. Последовательный анализ (М.: Физматгиз, 1960)
6. Буреев В.А. и др. Зарубежная радиоэлектроника 4 52 (1980)
7. Глумов Н.И. Построение и применение моментных инвариантов для об-
работки изображений в скользящем окне. Деп. в ВИННИТИ, №1880-В94
(Самара: Самарский государственный аэрокосмический университет,
1994)
8. Глумов Н.И. Яркостная нормализация цифрового изображения в скользящем
окне. Деп. в ВИНИТИ, №1881-В94 (Самара: Самарский государственный
аэрокосмический университет, 1994)
9. Глумов Н.И., Егунов И.П., Коломиец Э.И., Мясников В.В., Сергеев В.В.,
в кн.: Распознавание образов и анализ изображений: новые информационные
технологии: 2-я Всероссийская с участием стран СНГ конференция (Улья-
новск, Часть 2, 1995) С. 91,
10. Глумов Н.И., Коломиец Э.И., Сергеев В.В. Научное приборостроение 1 72
(1993)
11. Глумов Н.И., Коломиец Э.И., Сергеев В.В. Тезисы докл. 6-й науч. конф.
«Математические методы распознавания образов» (Москва, 1993) С. 89
688
ГЛАВА 9
12. Глумов Н.И., Сергеев В.В. Тезисы докладов 6-й научной конф. «Матема-
тические методы распознавания образов» (Москва, 1993) С. 90
13. Горелик А.Л., Скрипкин В.А. Методы распознавания (М.: Высшая школа,
1984)
14. Горелик А.Л., Гуревич И.Б., Скрипкин В.А. Современное состояние про-
блемы распознавания (М.: Высшая школа, 1985)
15. Давыдов Э.Г. Исследование операций (М.: Высш, шк., 1990)
16. ДаджионД., Мерсеро Р. Цифровая обработка многомерных сигналов (М.:
Мир, 1988)
17. Дуда Р., Харт П. Распознавание образов и анализ сцен (М.: Мир, 1976)
18. Круглов В.Н., Лабунец В.Г. Быстрый алгоритм совмещения изображений,
инвариантный к повороту и масштабу. Деп. в ВИНИТИ, №5104-85 (Сверд-
ловск: Уральский политехнический институт, 1985)
19. Круглов В.Н., Лабунец В.Г. Распознавание образов при помощи модульных
инвариантов моментов. Деп. в ВИНИТИ, №5105-85 (Свердловск: Ураль-
ский политехнический институт, 1985)
20. Леман Э. Проверка статистических гипотез (М.: Наука, 1979)
21. Майтра С. ТИИЭР 4 297 (1979)
22. МудровА.Е. Численные методы для ПЭВМ на языках Бейсик, Фортран,
Паскаль (Томск: МП «РАСКО», 1991)
23. Мясников В.В. Сборник материалов 2-й международной конференции «Рас-
познавание 95» (Курск, 1995) С. 88
24. Мясников В. В. 3-я Всероссийская с участием стран СНГ конференция «Рас-
познавание образов и анализ изображений: Новые информационные техноло-
гии» (РОАИ-3-97) (Нижний Новгород, Часть I, 1997) С. 203
25. Прэтт У.К. Цифровая обработка изображений 1 (М.: Мир, 1982)
26. Прэтт У.К. Цифровая обработка изображений 2 (М.: Мир, 1982)
27. Путятин Е.П., Аверин С.И. Обработка изображений в робототехнике (М.:
Машиностроение, 1990)
28. Сергеев В.В. Радиотехника 8 38 (1990)
29. Сергеев В.В., ЧичеваМ.А. Компьютерная оптика 5 78 (1989)
30. Синдлер Ю.Б. Метод двухступенчатого статистического анализа и его
приложения в технике (М.: Наука, 1973)
31. Сосулин Ю.Г., Гаврилов К. Ю. 2-я Всероссийская с участием стран СНГ
конференция «Распознавание образов и анализ изображений: новые инфор-
мационные технологии» (Ульяновск, Часть 1, 1995) С. 23
32. Сосулин Ю.Г., Гаврилов К.Ю. 3-я Всероссийская с участием стран СНГ
конференция «Распознавание образов и анализ изображений: новые инфор-
мационные технологии» (Нижний Новгород, Часть 1, 1997) С. 84
33. Ту Дж., Гонсалес Р. Принципы распознавания образов (М.: Мир, 1978)
34. Федотов Н.Г. Методы стохастической геометрии в распознавании образов
(М.: Радио и связь, 1990)
35. Федотов Н.Г. Тезисы докладов III Конференции Распознавание образов и
анализ изображений: новые информационные технологии (РОАИ-3-97) (Ниж-
ний Новгород, 1997) С. 278
Литература к главе 9
689
36. Федотов Н.Г., Мельников М.М., ТужиловИ.В., Костюшин Р.А.,
Шульга Л.А. Труды IVКонференции Распознавание образов и анализ изоб-
ражений: новые информационные технологии (РОАИ-4-98) (Новосибирск,
1998) С. 187
37. Федотов Н.Г., Шульга Л.А. Труды VМеждународной Конференции Распоз-
навание образов и анализ изображений: новые информационные технологии
(РОАИ-5-2000) 1 (Самара, 2000) С. 156
38. Фор А. Восприятие и распознавание образов (М.: Машиностроение, 1989)
39. Фу К. Последовательные методы в распознавании образов и обучении ма-
шин (М.: Наука, 1971)
40. Фукунага К. Введение в статистическую теорию распознавания образов
(М.: Наука, 1979)
41. Ярославский Л.П. Введение в цифровую обработку изображений (М.: Со-
ветское радио, 1979)
42. Хелгасон С. Преобразование Радона (М.‘. Мир, 1983)
43. Ярославский Л.П. Радиотехника и электроника 5 17 (1972)
44. Ярославский Л.П. Цифровая обработка сигналов в оптике и голографии:
Введение в цифровую оптику (М.: Радио и связь, 1987)
45. Abu-Mostafa Y., Psaltis D. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-7(1)
46 (1985)
46. Abu-Mostafa Y., Psaltis D. IEEE Trans. Pattern Anal. Mach. Intell. PAMI-6(6)
698 (1984)
47. Aksak I., Feist Ch., KijkoV., Knoefel R., MatselloV., Oganovskij V.,
Schlesinger M., Schlesinger D., Stanke G. Proceedings of 7-th International
Conference on Computer Analysis of Images and Pattern (Kiel, Germany, Springer,
1997) P. 551
48. Dana H. Ballard, Christopher M. Brown. Computer vision (Prentice-hall, Inc.,
Englewood Cliffs, New Jersey, 1982)
49. Cao J., Ahmadi M., Shridhar M. Pattern Recognition 28(2) 153 (1995)
50. Casasent D. Proceedings of The ltfh Scandinavian Conference on Image Analysis
II (Lappeenranta, Finland, 1997) P. 597
51. Elms A.J. Proceedings 12h IAPR International Conference and Neural Networks,
Conference B: Pattern Recognition Methodology and Systems II (1994) P. 439
52. Flusser J. and Suk T. Pattern Recognition Letters 15 433 (1994)
53. Flusser J. and SukT. IEEE Transactions on Geoscience and Remote Sensing
32(2) 382 (1994)
54. Flusser J. Pattern Recognition 33(9) 1405 (2000)
55. Flusser J. and Suk T. Pattern recognition 26(1) 167 (1993)
56. Flusser J., SukT., Saic S. Pattern Recognition 28 1723 (1995)
57. Flusser J., SukT., Saic S. IEEE Trans. Image Proc. 5 533 (1996)
58. Franke J., Mandler E. Proceedings 11th IAPR International Conference on Pattern
Recognition, Conference B: Pattern Recognition Methodology and Systems II
(1992) P. 611
690
ГЛАВА 9
59. Freeman Н. Computer Surveys 6(1) 57 (1974)
60. Freeman H. IRE Trans. Elec. Comp. EC-10 260 (1961)
61. Freeman H. Proc. Natl. Elec. Conf. 18 312 (1961)
62. GeversT., Smeulders W. Proceedings of The ICfh Scandinavian Conference on
Image Analysis II (Lappeenranta, Finland, 1997) P. 861
63. Glumov N.I., Egunov I.P., Kolomiets E.I., Myasnikov V.V., Sergeyev V.V.
Pattern Recognition and Image Analysis 6(1) 120 (1996)
64. Glumov N.L, Krainukov N.I., Sergeyev V.V., Khramov A.G. Pattern Recognition
and Image Analysis 4 424 (1991)
65. Golovan A., Yoo M.H., Lee S.W. Proc, of the 15th Int. Conf. On Pattern
Recognition 1 (Barcelona, Spain, 2000) P. 1092
66. Hansen L.K., Salamon P. IEEE Transactions on Pattern Analyis and Machine
Intelligence 12(10) 993 (1990)
67. Hashem, B. Schmeiser. IEEE Transactions on Neural Networks 6(3) 792 (1995)
68. Healey G. Proceedings of The l(fh Scandinavian Conference on Image Analysis II
(Lappeenranta, Finland, 1997) P. 823
69. Ho J., Hull J., Srihari S.N. IEEE Transaction Pattern Analysis and Machine
Intelligence 16(1) 66 (1994)
70. Но T.K., Hull J.J., Srihari S.N. IEEE Transactions on Pattern Analysis and
Machine Intelligence 16(1) 66 (1994)
71. Hu M. IRE Trans. Information Theory IT-8 179(1962)
72. Kittier J., Hater M., Duin R. Proceedings of 13th International Conference on
Pattern recognition. Track B: Pattern Recognition and Signal Analysis II (Vienna,
Austria, 1996) P. 897
73. Lambert G., Noll J. Proceedings of 13th International Conference on Pattern
recognition. Track B: Pattern Recognition and Signal Analysis II (Vienna, Austria,
1996) P. 735
74. Li B. IEEE Trans, on Image Processing 4(4) 502 (1995)
75. Li B., Shen J. Pattern Recognition 27(6) 785 (1994)
76. Maghsoodi R., Rezaie B. Methods of Handling and Processing Imagery. SPIE
757 58 (1987)
77. Maio D., Maltoni D. IEEE Trans. Pattern Anal. Machine Intell. 19(1) 27 (1997)
78. Mattis F., Flusser J. IEEE Transactions on Pattern Analysis and Machine
Intelligence 15(10) 996 (1993)
79. Myasnikov V.V. Proceedings of the l(Ih Scandinavian Conference on Image Analysis
SC I A’961 (Lappeenranta, Finland, 1997) P. 405
80. Nair D., Aggarwal J.K. Proc. 13th Int. Confer. On Pattern Recognition 1 (Vienna,
Austria, 1996) P. 601
81. Nandy D., Ben-Arie J. Proc, of the 15th Int. Conf. On Pattern Recognition 1
(Barcelona, Spain, 2000) P. 1104
82. Peterson D.Y., Mattson R.T. IEEE Trans. Information Theory IT-12 (Chapter 4)
380 (1966)
Литература к главе 9
691
83. Prabhaker S., Jain А.К., Wang J., Pankanti S., Bolle R. Proc, of the 15th Int.
Conf. On Pattern Recognition 1 (Barcelona, Spain, 2000) P. 25
84. Rogova G. Neural Networks 7(5) 777 (1994)
85. Suri J., Haralick R., Sheehan F., Jamin V. Proceeding? of The l(Jh Scandinavian
Conference on Image Analysis I (Lappeenranta, Finland, 1997) P. 197
86. TungH., Lee J., Tsai I. Pattern Recognition 27(8) 1093 (1994)
87. Xu A., Krzyzak C., Suen Y. IEEE Trans. SMC 22(3) 418 (1992)
ГЛАВА 10
ПОСТРОЕНИЕ ОЦЕНОК ПО МАЛОМУ ЧИСЛУ
НАБЛЮДЕНИЙ В ЗАДАЧАХ ОБРАБОТКИ
ИЗОБРАЖЕНИЙ
ЮЛ. Примеры и формулировка задачи
При построении информационных технологий обработки и анализа изоб-
ражений характерной является ситуация, когда приходится сталкиваться с
проблемой обработки больших потоков данных, например, аэрокосмического
мониторинга Земли. Тем не менее, на отдельных этапах (в т.ч. геоинформа-
ционных технологий) часто, напротив, возникает проблема извлечения необ-
ходимой информации из малого числа наблюдений. Приведем несколько ти-
пичных примеров.
Пример ЮЛ. Идентификация неинвариантных к сдвигу (неизопланатичных)
систем формирования изображений, характеристики которых достаточно быстро
изменяются при переходе от одной точки изображения к другой. Если степень
неизопланатичности системы высока настолько, что оценка параметров «усред-
ненной» модели по всем отсчетам на изображении не обеспечивает требуемой
точности (моделирования, построения восстанавливающих фильтров и др.),
осуществляют оценку характеристик системы для совокупности малых фраг-
ментов изображений, используя для этой цели небольшое число измерений,
полученных на каждом фрагменте.
Пример 10.2. Распознавание образов при малом числе обучающих объектов.
Ограниченность числа изображений объектов, предъявляемых для обучения,
является скорее правилом, чем исключением. Иногда это связано с отсут-
ствием достаточного числа объектов, пригодных для обучения (например, при
быстро изменяющихся условиях функционирования системы), иногда — с
желанием экономии затрат и времени на обучение. Известно большое число
приложений (роботы и манипуляторы, адаптивные системы управления, сис-
темы технического зрения и др.), в которых оценка параметров разделяющих
поверхностей классификаторов должна осуществляться по малому числу на-
блюдений.
Пример. 10.3. Оценка разрешающей способности (PC) видеотракта. Эта за-
дача решается на этапе опытной эксплуатации системы с целью аттестации
10.1. Примеры и формулировка задачи
693
соответствия характеристик системы расчетным. Традиционный способ оценки
PC [10] заключается в том, что с помощью системы регистрируется известное
изображение (мира) в виде чередующихся темных и светлых полос, имеющих
различные размеры, частоту и ориентацию. Заключение о величине PC выра-
батывается по результатам установления изображения миры, на котором по-
лосы еще различимы.
Создание и поддержка полномасштабных мир на поверхности Земли для
оценки PC систем аэрокосмического мониторинга требует значительных ма-
териальных затрат. Поэтому часто оценку PC осуществляют по изображению
текущего сюжета без специальной миры. При визуальном анализе изображе-
ния экспертом вносится элемент субъективизма. Поэтому представляет инте-
рес разработка формализованных, утвержденных в качестве стандарта, авто-
матизированных методик оценки PC, свободных от особенностей восприятия
изображений отдельными экспертами. Проблема заключается в том, что раз-
меры фрагментов, пригодных для выработки количественных оценок PC по
изображениям текущих сюжетов (например, перепад яркости на границе осве-
щенной крыши здания и тени), как правило, оказываются небольшими, а их
число невелико.
Можно привести еще ряд примеров из других областей, например, анализ
сцен, оценка в медицинской диагностике и др., для которых проблема оцен-
ки по малому числу наблюдений актуальна. Ограничимся указанными, как
нам кажется, наиболее характерными примерами и приведем для них матема-
тические формулировки.
Для решения ряда задач обработки (например восстановления) изображе-
ний необходимо знание оператора системы. Этот оператор рассчитывают на
этапе проектирования с использованием физических и математических моде-
лей видеотракта. Вследствие неизбежных упрощений, связанных как с недо-
статочной изученностью явлений, так и с вычислительными аспектами опе-
ратор системы нуждается в уточнении. Для этого проводят испытания, за-
ключающиеся в «предъявлении» на вход системы известного изображения.
Затем по входному изображению и результатам его регистрации на выходе
системы строится оптимальная, в некотором смысле, модель. Эта задача из-
вестна как идентификация систем. Обычно она формулируется (в узком смысле
[30]) как задача оценки параметров модели системы формирования изобра-
жений из априори заданного класса. Наиболее широко используются описан-
ные в п.1.4 линейные модели типа (1.140) и/или (1.149) с постоянными по
пространственным координатам параметрами (ЛПП-системы). Вычислитель-
ные преимущества, связанные с применением таких моделей, очевидны. Если
в действительности искажения оказываются пространственно-зависимыми (не-
изопланатичными), то, как указывалось выше, линейные модели с постоян-
ными параметрами строят на малых фрагментах изображений.
Для формулировки задачи идентификации указанных линейных моделей
мы должны внести в уравнения (1.140), (1.149) некоторые важные дополне-
ния. Во-первых, нельзя оценить бесконечное число значений импульсной
694
ГЛАВА 10
характеристики, то есть число слагаемых в правой части (1.140) всегда огра-
ничено. Во-вторых, задача идентификации решается по результатам измере-
ний, которые всегда содержат погрешности. С учетом сказанного уравнения
перепишем, соответственно, в виде
#(п],п2)= 12 72hmi,m2f(n\ ~ml,n2-tn2) + ^g(nl,n2), (10.1)
g(n]tn2) = - £ -^,п2-т2) +
+ 52 52^1,m2/(«l-/nl>W2-W2) + ^(ni.n2). (10.2)
(ni,jn2) EQf
В (10.1), (10.2) используются те же обозначения, что и в (1.140), (1.149).
Дополнительно введены лишь обозначения для ошибок bg(n},n2) (измере-
ний, ограничений на порядок модели и др.), а фигурирующая в (10.2) ошибка
^(И],п2) определяется как
^(n],n2) = bg(n1,n2)~ £ 52%,/n2S^(«i-т^п2-т2). (10.3)
(mi.mz)
Модель, описываемую уравнением (10.1), в соответствии с принятой в пер-
вой части книги терминологией далее будем называть КИХ-фильтром, а мо-
дель, соответствующую уравнению (10.2) — БИХ-фильтром. Поскольку зада-
ча идентификации должна решаться по совокупности отсчетов f{n],n2) вход-
ного (неискаженного) и g(n}in2) выходного (искаженного) изображений, для
дальнейшего изложения удобно от уравнений (10.1), (10.2) перейти к их мат-
ричным представлениям.
Рассмотрим уравнение (10.2). Предположим, что общее число коэффициен-
тов {amitfn2{^/и„т2} этого уравнения равно М, а фрагмент на выходном изоб-
ражении содержит N различных отсчетов g(nitn2). Отсчеты, фигурирующие в
правой части (10.2) при одном из фиксированных положений (п},п2) выходно-
го отсчета, можно представить в виде элементов вектор-строки:
] = [•••» g(«i -т},п2-т2),..., f(n}
(mltm2)eQg{jQf, i = (10.4)
а соответствующий вектор искомых параметров будет иметь вид
c = [q,c2,...,cA/]7’ (10.5)
Заметим, что размерность вектора искомых параметров зависит от порядка
передаточной функции системы, то есть от размеров опорных областей как
на входном, так и на выходном изображении.
10.1. Примеры и формулировка задачи
695
Для N различных положений опорных областей из векторов-строк (10.4)
составим АхМ-матрицу X, аиз W отсчетов g(nj,/?2) на выходном изображе-
нии и 7V соответствующих им ошибок ^(П],и2) составим М<1-векторы у и
соответственно. Если вектор параметров с остается неизменным при любом
положении опорной области на фрагменте (для ЛПП-систем это всегда вы-
полняется), с использованием введенных обозначений можно записать следу-
ющее матричное равенство:
у = Хс + £. (10.6)
Задача заключается в том, чтобы по одной реализации (фрагменту изобра-
жения) построить оценку с вектора параметров с по доступным для непо-
средственного наблюдения АхЛ/-матрице X и /Vx 1-вектору у (N> М), при не-
известном ЛМ-векторе ошибок £,.
Аналогичное матричное равенство можно построить для модели (10.1)
КИХ-фильтра. Сопоставив приведенные выше обозначения с (10.1) нетрудно за-
метить, что вектор искомых параметров с в данном случае представляется в виде
с = [с1,с2,...,см]т= [...,г, (щ,m2) е Qf,
а каждая строка матрицы X состоит из отсчетов только входного изображения:
xi ...= -mhn2-m2),..], (mltm2)eQf, i = l,N -
Постановка задачи идентификации модели КИХ-фильтра формально со-
впадает с задачей идентификации БИХ-фильтра. Важные отличия состоят в
следующем. Компоненты TVxl-вектора ошибок в данном случае не зависят
от полезных сигналов (отсчетов поля яркости выходного изображения), как
это имеет место в (10.3) для БИХ-фильтра. Кроме того, размерность вектора
искомых параметров зависит лишь от размеров опорной области на входном
изображении. Это оказывается существенным для рассматриваемых в настоя-
щей главе методов. Подчеркнем, что с точки зрения задачи идентификации
порядок обхода точек на фрагменте (изображении) не играет роли. Это при-
водит лишь к перестановке строк в уравнении (10.6). В то же время примене-
ние оцененных моделей КИХ и БИХ-фильтров существенно различается.
Пример 10.4. Моделирование искажающей системы с использованием модели
КИХ-фильтра. Исходное тестовое изображение показано на рис. 10.1а (сюжет
на изображении выбирался из соображений иллюстрации возможности ис-
пользования для идентификации оптического канала естественных элемен-
тов: дорожных разметок, пешеходных переходов [32] и др.). Искаженное изоб-
ражение (рис. 10.16) получено из исходного моделированием расфокусиров-
ки. Использовалась модель расфокусировки с круговой (центральной)
симметрией. Параметры импульсной характеристики определялись в соответ-
ствии с выражением
h(i,j) = (у/2ка} ^хр^-г^До2),
696
ГЛАВА 10
Рис. 10.1. Тестовые изображения: а — исходное; б — расфокусированное
где г2 —i2 + j2, a /', j — координаты отсчетов в опорной области. Задавался
параметр расфокусировки с= 1,5. Указанное значение параметра о при допу-
стимой относительной погрешности (около 1%) соответствовует опорной об-
ласти 9x9. При этом число различных подлежащих оценке отсчетов импульс-
ной характеристики (размерность вектора с) составляет 15.
Пример 10.5. Моделирование искажений с использованием БИХ-фильтра.
Принималось, что опорные области на входном (неискаженном) и выход-
ном (зарегистрированном) изображениях — квадранты в квадрате 3x3, то
есть БИХ-фильтр имеет порядок (1,1). При этом соответствующее (10.2)
разностное уравнение, описывающее модель БИХ-фильтра, имеет вид
g (И1,И2) = «!Og(nl - 1»п2) + «01#*л2 - 0 + Яц£(п1 - 1>п2 - D +*оо/(«! ,П2) +
+ -l,n2) + feoi/(ni*n2 -D+WOh -1*п2 ~1)+5(л1»п2).
При реализации БИХ-фильтра возникают принципиальные трудности,
связанные с тем, что для вычисления выходных отсчетов g(n]tn2) использу-
ются отсчеты из той же опорной области. Поэтому для построения физичес-
ки реализуемых фильтров, как указывалось в п.1.4, необходимо согласовы-
вать направления «обхода» изображения и форму опорной области. Сказан-
ное относится как к моделированию искажений, так и к восстановлению
изображений.
На рис. 10.2 приведено исходное тестовое изображение. Параметры БИХ-
фильтра для различных вариантов передаточной функции искажающей систе-
мы приведены в таблице 10.1. Соответствующие этим вариантам искаженные
изображения, полученные методом итераций [4], показаны на рис. 10.3g—в.
Хотя во всех случаях использовались одинаковые опорные области (3x3), ха-
рактер искажений существенно различается. Эти изображения будут исполь-
зоваться нами для иллюстрации работы алгоритмов оценивания. Для просто-
ты ссылок указанные варианты искажений {а—в) далее будем называть «сла-
бым», «средним» и «сильным» соответственно.
Следует обратить внимание на тот факт, что в данном случае при решении
задачи идентификации независимо от интенсивности искажений не происходит
10.1. Примеры и формулировка задачи
697
Таблица 10.1. Параметры БИХ-фильтра
Рис. аю aoi ан boo bio boi bn
а 0,125 0,125 0,166 0,250 0,083 0,083 0,166
б 0,165 0,165 0,330 0,110 0,055 0,055 0,110
в 0,200 0,200 0,400 0,066 0,033 0,033 0,066
заметной потери точности, если оценивать лишь 7 коэффициентов. Это в два
с лишним раза меньше, чем в рассмотренном выше примере моделирования
искажений с помощью КИХ-фильтра притом, что интенсивность искажений
в примере 10.4 ниже. Ясно, что при решении задачи
идентификации сильных искажений (рис. Ю.Зв) в клас-
се КИХ-фильтров потребуется маска больших разме-
ров, а размерность соответствующей задачи иденти-
фикации существенно возрастет.
Несмотря на некоторые трудности реализации
БИХ-фильтров, с точки зрения вычислительной слож-
ности сквозной технологии оценки и восстановления,
их использование, как правило, предпочтительнее. Ис-
пользование модели БИХ-фильтра для решения за-
дачи идентификации (особенно при малых размерах
Обработка изображу
связана с решением
кик задач, в катары:
входные, и выкодны
ные являются изобр
ниями. Одним из пр
ров служат системы
редачи изображений
оазпабогчики стали
Рис. 10.2. Исходное изобра-
жение
используемых для этого фрагментов изображений) выгоднее, даже если на
этапе улучшения качества изображений, по каким-либо причинам, должен
использоваться КИХ-фильтр.
Матричное соотношение вида (10.6) можно построить при формулировке
различных задач оценки. Оно естественным образом «появляется» в задаче оце-
нивания параметров линейной или обобщенной разделяющей функции при
обучении распознаванию образов. Столбцы, фигурирующей в (10.6) матрицы X
в этом случае являются векторами (обобщенных) признаков, a NxA -вектор у
формируется по заданным допускам, определяющим область решений [6]. Эта
задача будет рассмотрена в п.10.14.
)6ра15шка изебраж
связана с решение»
Kitt задач, в «торы:
вктные, и выодднь
ные являются изобр
ниями. Одним из пр
ров служат системы
родами изображены
вазпабогчмям стала
а
мазание ривмлем»
Kiu V4U4H. жкшуры
и выхяымм
ные явджкнш жзыбр
ниями. Одним из пр
нмедуыт системы
книма «эибрашим
км талдс
ММ
ЬМЫМЬЫ, W*M*tbM*
в
Рис. 10.3. Варианты линейных искажений: а — слабое; б — среднее; в — сильное
698
ГЛАВА 10
10.2. Проблема оценки по малому числу наблюдений
Необходимость решения задач оценки по малому числу наблюдений по-
рождает ряд принципиальных проблем. Прежде, чем перейти к их обсуж-
дению, приведем стандартную постановку задачи. Обычно, когда нужно
построить оценку с вектора параметров с по /УхЛ/-матрице X и Nx\-векто-
ру у (N> М), связанным равенством (10.6), используют следующие пред-
положения [5].
1. Векторы и у = [у1,у2„..,ул,]7’ — случайные.
2. Матрица X детерминирована, то есть ее элементы не являются случай-
ными величинами.
3. Rank (X) = М.
4. Математическое ожидание вектора £ равно нулю, то есть A/{£J = O,
/ = 1, N или М{$} = ().
5. Для любых i j М ^1 = 0 , М |^2} = а2 для всех i = I, N. Дру-
гими словами, cov{^} = о2Ед,, где о2 — дисперсия отклонений, cov{ } —
WxTV-матрица ковариаций отклонений, а Ед, — единичная УУх?/-матрица.
Если эти предположения выполняются, то оценка метода наименьших квад-
ратов (МН К),
с = [х7'х]“'х7'у, (10.7)
является несмещенной и эффективной [5].
К сожалению, указанные предположения при малом числе наблюдений не
отвечают реальному содержанию задачи и оказываются, в лучшем случае, бес-
полезными. Действительно, даже если предположения 4 и 5 справедливы для
шумовой последовательности на всем изображении, оценки математического
ожидания и дисперсии на малых фрагментах этого изображения могут сильно
отличаться от декларированных в них свойств. При этом оценки искомых
параметров, построенные в рамках указанных предположений, также будут
получены с большими ошибками.
Предположение 3 также является традиционным, но его выполнение при
малых размерах фрагмента сомнительно. Дело в том, что при идентифика-
ции моделей искажающих систем по малым фрагментам изображений все-
гда сохраняется опасность попадания на неинформативный участок (фона),
даже если в целом для всего изображения это свойство имеет место. Стро-
го говоря, вместо предположения 3 в данном случае более реалистичным
является Rank (X) < М. Приведем простой пример, оправдывающий эту точку
зрения.
Пример 10.6. Пусть решается задача оценки параметров модели КИХ-фильт-
ра с опорной областью 3x3 на фрагменте 4x4, показанном на рис. 10.4о, кото-
рый содержит бинарное изображение темного квадрата. Для определенности
положим, что уровень яркости темного участка 10 единиц, а светлого — 50.
10.2. Проблема оценки по малому числу наблюдений
699
Рис. 10.4. Примеры расположения фрагментов
Предположим также, что искажения обладают свойством центральной симмет-
рии так, что описывающее их разностное уравнение можно представить в виде
2
А-0
где
/(0) = /(п|,И2),
/(')=[/(”| +1>0)+/(п,-1,0+/(0.л2 + 1) + /(0,„2-|))]/4>
/(2) = [/(«, + 1,л2 +1) + /(л, +1,Л2 -1 + /(л, -1,л2 +1) + /(п, — 1,л2 —1))]/4.
Матрицы Хо и Хб, сформированные путем последовательного сдвига опор-
ной области по строкам фрагмента 4x4 для двух положений фрагментов, по-
казанных на рис. 10.4g и б имеют следующий вид:
10 30 40 10 30 40
10 30 40 50 40 40
Хд =
10 30 40 50 40 40
10 30 40 50 50 40
Нетрудно заметить, что RankXo= 1, следовательно, матрица ^ХдХа| не
существует, а задача оценки параметров КИХ-фильтра указанного порядка
неразрешима. Ситуация коренным образом меняется после «сдвига» фраг-
мента на один отсчет вправо и вниз, так как показано на рис. 10.46. Легко
проверить, что RankX6=3. Ясно, что при решении задачи идентификации по
изображению, содержащему большое число (информативных) элементов, воз-
никновение таких ситуаций маловероятно.
Таким образом, при оценке по малому числу наблюдений, во-первых, все-
гда существует опасность попадания фрагмента на такой участок изображения,
700
ГЛАВА 10
где задача оценки оказывается плохо обусловленной или даже вырожденной,
во-вторых, условия предельных теорем теории вероятностей при малом числе
наблюдений не выполняются и, как следствие, невозможно обосновать апри-
орную вероятностную модель ошибок в исходных данных.
Свойство устойчивости статистических характеристик шумов на фрагмен-
тах изображений не проявляется и в случае, когда существует устойчивое рас-
пределение ошибок на множестве изображений данного класса. Поэтому мы
вынуждены отказаться от всех наиболее важных с теоретической точки зре-
ния предположений классической регрессии. С учетом сказанного сформули-
руем предположения, которые далее будут использоваться при решении зада-
чи оценки по малому числу наблюдений.
Предположение 1. Матрица X и вектор у фиксированы, то есть х(у,у(,
i — \yN , j = ], М известны в результате измерений на одной отдельно взятой
реализации.
Предположение 2. Rank(X) < М , то есть не гарантируется невырожденность
Х7Х.
Предположение 3. Статистические характеристики вектора у и матрицы X
на множестве реализаций считаются неизвестными.
Предположение 4. Относительно вектора ошибок ^ = [^] ,£2»—Л/v] извест-
но лишь то, что задано ограничение на его норму: ||£,|| < R .
Существенно также то, что мы отказываемся от наиболее важных с теоре-
тической точки зрения предположений классической регрессии: Rank (X) = М,
Л/ {£} =0 и cov{^} = o2E/v. Отказ от этих предположений является вынуж-
денным, а требование |||;||<Я более реалистичным. При сделанных предпо-
ложениях, вся неопределенность связана с произвольной ориентацией векто-
ра в TV-мерном пространстве. Необходимо отметить, что предположение 4
широко используется в теории возмущений [2] и в теории некорректных за-
дач [20], которые в основном связаны с алгебраическим подходом.
В дополнение к указанным может использоваться также предположение
об ограничениях параметров модели в виде неравенств. Эти ограничения за-
даются на основе априорной информации о допустимых диапазонах оценива-
емых характеристик. Аналогичные ограничения используются в традицион-
ной постановке задачи оценки параметров линейной регрессии [5] и в дан-
ном случае не являются принципиальными.
С учетом сказанного термин «оценка» мы будем употреблять, не связывая
его во всех случаях с прилагательным «статистическая». Наряду с ним, там,
где необходимо подчеркнуть нестатистический характер задачи, мы будем
вместо термина «оценка» использовать также термин «определение». Кроме
того, мы будем избегать употребления широко используемого в теории стати-
стических оценок термина «выборка», применяя вместо него термины «набор
данных» или «малое число наблюдений».
В связи с последним замечанием нуждается в уточнении само понятие «малое
число наблюдений». Важнейшим признаком, отличающим задачи оценки по
малому числу наблюдений от задач классической регрессии, является априорная
неопределенность информативных свойств полезных сигналов и статистических
10.2. Проблема оценки по малому числу наблюдений
701
характеристик шумов. Кстати заметим, что свойство статистической устойчиво-
сти может не проявляться и при достаточно большом числе наблюдений.
Попытки указать конкретное число наблюдений, которое может считаться
малым, бесплодны. Например, выборка 500 наблюдений может быть весьма
представительной при оценке одного параметра (сдвига), но это очень мало,
если решается задача оценки параметров разделяющей гиперплоскости в про-
странстве 400 признаков. Для того чтобы формально определить малое число
наблюдений, нам понадобятся некоторые дополнительные сведения о задаче
наименьших квадратов.
Введем в рассмотрение невязку
£ = у —Хс = у —у. (10.8)
Из (10.8) видно, что вектор у принадлежит пространству столбцов матри-
цы X: у е2?(х). Можно показать также [8], что вектор у декомпозируется на
два ортогональных компонента у = Хс+£ , £, ± Хс . Для более детального об-
суждения свойств МН К необходимо ввести в рассмотрение так называемое
сингулярное разложение.
Известно [8,31], что для /VxM-матрицы X ранга к<М существуют ортого-
нальные Л'хА-матрица Т и ЛхЛ-матрица F такие, что
TrXF = S, X = TSFr, (10.9)
где S — диагональная УУхЛУ-матрица, составленная из неотрицательных чи-
сел, среди которых ровно к строго положительны. Диагональные элементы sh
i = \tk, матрицы S называются сингулярными числами матрицы X. Из (10.9),
в частности, следует, что
ХГХ = FSTSFT = FAF7, (10.10)
Л О
XX7'=TSS7’Tr=T
Т7,
(10.11)
о о
где Л = diag(X] А,) — диагональная матрица. Числа X, являются квадра-
тами соответствующих сингулярных чисел sif i = 1, к, и называются характе-
ристическими числами или собственными значениями. Подчеркнем, что соб-
ственные значения матрицы ХГХ и ненулевые собственные значения матри-
цы XX7 совпадают.
Векторы-столбцы матриц F и Т являются соответствующими собственны-
ми векторами. Предположим, что Rank X = Л/, и пусть первые М столбцов
матрицы Т соответствуют ненулевым, tx-, i = \,M, а последние N-М столб-
цов — нулевым собственным значениям матрицы XX , tOji = М + 1,А , то
есть матрица Т представима в виде блочной:
т=[тх;т0].
(10.12)
702
ГЛАВА 10
Теперь подпространства, связанные с матрицей X, мы можем ввести сле-
дующим образом:
/?(Х) — span [t А1 м/ ]>
ЖХ ) — span[tOil,...,tOJV_wj.
Уже упоминавшееся выше 7?(Х) называют пространством столбцов (или
столбцовым пространством) матрицы X, a 2V(Xr) — нуль-пространством мат-
рицы Хг. Далее для краткости иногда мы будем их называть просто простран-
ством и нуль-пространством матрицы X соответственно.
Нуль-пространство Л/(ХГ) является ортогональным дополнением для Я(Х).
Поскольку в соответствии с (10.8) уея(х), а ^±Хс —у, ясно, что вектор
невязок принадлежит нуль-пространству £еЛДХг). На рис. 10.5 приведена
геометрическая интерпретация МНК для случая М =2, N—3.
Теперь мы готовы сформулировать еще одно требование к малым наборам
данных. В основу его положим следующий принцип: размерности подпро-
странств, которым принадлежат две указанные выше ортогональные состав-
ляющие векторов у и должны быть сопоставимы. Таким образом, число
наблюдений будем считать малым, если наряду с имеющей место априорной
неопределенностью вероятностных моделей полезных сигналов и шумов раз-
мерности пространств /?(х) и 2V(Xr) — одного порядка.
В заключение еще раз подчеркнем, что результат оценивания существен-
ным образом зависит от конкретной реализации (положения фрагмента на
изображении). Поэтому в контексте сформулированных выше предположе-
ний и введенных в настоящем разделе понятий мы сосредоточим внимание
на следующих двух вопросах:
1. Как велика может быть ожидаемая норма вектора ошибок оценки на дан-
ной конкретной реализации при заданной матрице X (предположение 1) и за-
данном ограничении на норму вектора ошибок измерений (предположение 2)?
2. Опираясь на какую дополнительную информацию и каким образом
следует строить процедуры оценки, обеспечивающие требуемую точность
оценки на каждой конкретной ре-
ализации, несмотря на отсутствие
априорной информации о распре-
делении ошибок измерений?
Для получения ответов на эти
вопросы нам необходимо выявить
структуру и основные закономер-
ности формирования ошибок оцен-
ки на конкретном наборе данных.
Рис. 10.5. Геометрическая интерпретация
МНК
10.3. Формы представления и ортогональные разложения ошибок
703
10.3. Формы представления и ортогональные разложения
ошибок
Для установления качества оценок на одной отдельно взятой реализации
большую пользу может принести непосредственный анализ соотношений для
ошибок измерений и ошибок оценки, а также их ортогональные разложения.
При использовании метода наименьших квадратов (10.7) искомые оценки
являются решением системы нормальных уравнений:
Ас = Ь. (10.13)
Здесь и далее используются обозначения А = ХГХ, b = Хгу, где X —
АхМ-матрица, а у — Ах1-вектор, фигурирующие в (10.6).
Предполагается, что соответствующая уравнению (10.6) точная модель иден-
тифицируемой системы,
у*=Х*с, (10.14)
существует, где X* и у* — незашумленные матрица и вектор. В действитель-
ности матрица X и вектор у фиксируются с ошибками. В первых трех строках
таблицы 10.2 приведены соотношения, иллюстрирующие структуру матрицы
X и векторов у и для моделей КИХ- и БИХ-фильтров.
Из геометрических представлений (рис. 10.5) ясно, что наиболее важными
представляются особенности формирования вектора ошибок оказывающе-
го непосредственное влияние на точность МНК-оценок. Заметим, что хотя
матрица X и вектор у формируются по зашумленным данным, они известны
до начала идентификации. Факт вхождения в X ошибок измерений напрямую
не влияет на точность оценивания. Это влияние опосредованное (через изме-
нение обусловленности задачи из-за ошибок измерений).
Действительно, поскольку в общем случае матрица X и вектор у содержат
ошибки 8Х и Sy, матрица А и вектор b также будут содержать возмущения,
которые обозначим SA и Sb, соответственно:
A = A*+SA, (10.15)
Таблица 10.2. Формирование измерений и ошибок
Матрицы и векторы КИХ-фильтр БИХ-фильтр
X X* X* + 8Х
У у’+8у у’ + 5у
5у 5у - ЗХс
зь ♦г X 8у Х’Г8у + 8Хгу* + 8Хг5у
ЗА 0 Х‘Г8Х + 8ХГХ‘ + 8ХГ8Х
704
ГЛАВА 10
b = b*+5b, (10.16)
где с учетом (10.14)
* Лс * ЛсТ Лс
А =Х X, b=Х у.
Выражения, показывающие структуру возмущений 5А и 8b, приведены в
последних двух строках таблицы 10.2.
Характеристики обусловленности матриц А и А могут существенно раз-
личаться. Например, если матрица А вырождена, соответствующая ей мат-
рица А —А + 5А может оказаться хорошо обусловленной. Поэтому далее в
случаях, когда в контексте конкретного исследования способ формирования
матрицы А имеет принципиальное значение, мы будем указывать тип модели
(КИХ-фильтр и/или БИХ-фильтр). При этом общие обозначения, при необ-
ходимости, могут быть заменены их конкретными выражениями из табли-
цы 10.2.
Теперь построим соотношения для ошибок МНК-оценок. Для этого в со-
ответствии с (10.14) запишем систему уравнений:
А*с = Ь*.
С учетом (10.15),(10.16) это равенство можно переписать в виде
Ас = Ь —£, (10.17)
где
^ = 5Ь-ЙАс. (10.18)
Сравнивая (10.17) и (10.13) можно записать выражение для ошибки оцен-
ки Дс = с — с:
Ac = A-1;. (10.19)
Можно показать, что векторы ошибок £ и связаны соотношением
; = (10.20)
Равенство (10.20) можно получить, произведя в (10.18) замену 5b, 5А их
выражениями из таблицы 10.2 или умножив обе части уравнения (10.6) слева
на Хт и затем осуществив подстановку £ = Ь —Ас из (10.17). Компоненты
вектора ошибок £ представляют собой скалярные произведения вектора £ и
соответствующих векторов матрицы X. В частности, если векторы-столбцы
матрицы X нормированы так, что ||xt-||2 = 1 для всех i = то имеет место
следующая геометрическая трактовка: компоненты вектора £ суть проекции
вектора ошибок на направления, задаваемые векторами независимых пере-
менных X/, i =
10.3. Формы представления и ортогональные разложения ошибок
705
С учетом (10.19) и (10.20) ошибку оценки Ас — с —с можно выразить также
посредством вектора
Ас = [хгх]-1 Хг£ = А-1ХГ£. (10.21)
В рамках статистических методов анализа точности, обе части равенства
(10.21) полагается подвергнуть операции математического ожидания, откуда
при выполнении предположений классической регрессии сразу следует не-
смещенность оценок. Мы не делаем этого, поскольку асимптотические свой-
ства оценок в настоящей главе не исследуются. .
Подчеркнем, что матричный коэффициент ХГХ| Хг =А-1ХГ в (10.7),
(10.21) при решении задачи оценки на конкретной реализации всегда извес-
тен. Это имеет место как в случае модели КИХ-фильтра, где X = X , так и в
случае модели БИХ-фильтра, для которой Х = Х*+5Х (см. таблицу 10.2).
Поэтому при анализе точности идентификации матрица А и вектор b счита-
ются заданными точно, а значение имеет лишь способ формирования оши-
бок и/или £).
Теперь, опираясь на выписанные выше соотношения (10.19), (10.21), вскро-
ем общие закономерности формирования ошибок оценки. Для этого вос-
пользуемся сингулярным разложением (10.9)~(10.11) задачи наименьших
квадратов [8]. Как и ранее здесь, пока, предполагаем, что RankX = М. Если
это так, то из последнего равенства в (10.9) с учетом блочной структуры
матрицы Т (10.12) и известных свойств, F-1 =Fr, [ft] =F, SrS = A2,
можно записать Ах Af-матрицу
TZ=XFA”1/2. (10.22)
Теперь умножим обе части (10.19) слева на F7, где F указанная выше орто-
гональная матрица: FrAFr= А. Тогда с учетом свойств FF7 = Е, F^A^F = А-1
можно получить, что
F7Ac = A“1Fr;. (10.23)
Равенство (10.23) допускает простую геометрическую трактовку: проекции
вектора ошибок оценки на базис, образованный собственными векторами
матрицы А, образуются из проекций вектора ошибок исходных данных (10.18)
на тот же базис с «коэффициентами усиления» обратно пропорциональными
соответствующим собственным значениям.
Аналогичное соотношение можно построить для вектора ошибок иденти-
фикации, представленного в виде соотношения (10.21). Для этого с учетом
связи между векторами ошибок £ и £ (10.20) перепишем (10.23) в виде
FrAc = Л ’ {F7 Х7'^ = А1/2 [л l/2F7X7'
23 — 9044
706
ГЛАВА 10
Подставляя в это равенство вместо матрицы A ^2FrXr равную ей, в со-
ответствии с (10.22), матрицу т£, получаем следующее представление:
FrAc = A“1/2T^. (10.24)
В данном случае имеет место весьма сходная геометрическая трактовка: про-
екции вектора ошибок идентификации на направления базиса, образованного
собственными векторами матрицы А = ХГХ, образуются из проекций векто-
ра ошибок Е, исходных данных на направления базиса, образованного соб-
ственными векторами, соответствующими ненулевым собственным значени-
ям матрицы В = ХХГ с «коэффициентами усиления» Х~’/2, i = 1,А/ .
Поскольку ненулевые собственные значения матрицы В = ХХГ совпада-
ют с собственными значениями матрицы А = ХТХ , в силу равенства Q = Хг£
(10.20), соотношение (10.23) легко может быть получено также из (10.24) под-
становкой Тх =XFA'"I'Z2 . Для теоретического анализа ошибок идентифика-
ции соотношение (10.24) представляет больший интерес, т.к. в нем использу-
ется исходный вектор ошибок фигурирующий в уравнении (10.6).
Соотношения (10.23), (10.24) представляются важными для понимания
общих закономерностей формирования ошибок идентификации. Однако для
сравнительного анализа точности более предпочтительными являются ска-
лярные характеристики векторов ошибок. Поэтому с использованием разло-
жений (10.23), (10.24) запишем выражения для квадрата евклидовой нормы
вектора ошибок оценивания.
Подвергнув операции транспонирования обе части равенства (10.23), пе-
репишем его в виде
AcrF —£rFA-1.
Далее умножив слева обе части последнего равенства на соответствующие
(левую и правую) части (10.23), с учетом свойств матрицы F получим, что
= ||Дс||* = ^FA-2F^= ||# cos2 ф,., (10.25)
1=1
л
где <р, =(§,f,-) — угол между вектором ошибок и направлением собственно-
го вектора fz, соответствующего /-му собственному значению Х(. матрицы ХГХ.
Аналогичное соотношение имеет место для случая представления ошибок
идентификации в виде (10.24). Для этого, транспонировав обе части (10.24),
запишем равенство
AcrF = ^rTzA-,/2.
Умножив обе части этого равенства на соответствующие части равенства
(10.24), аналогично предыдущему, получим, что
10.4. Оценки достижимой точности
707
п п Л/
АсгАс = ||Ас||| = ^тТкА-'Т^= cos2 V/, (10.26)
1=1
А
где \g( = w — угол между вектором и собственным вектором ,• (z-м столб-
цом матрицы Тх (10.22)).
Соотношения (10.25) и (10.26) имеют ясную геометрическую трактовку. Из
правых частей этих равенств видно, что норма вектора ошибок идентифика-
ции зависит не только от нормы вектора но также и от его ориентации
относительно подпространств матрицы X. Напомним, что в указанных соот-
ношениях Из В частности, в соответствии с (10.20),
Таким образом, связь двух форм представления ошибок также определяет-
ся числами X,, i = l,M , являющимися собственными значениями матрицы
Х7Х. Заметим, что каноническое представление (10.26) во многих случаях ока-
зывается более полезным, т.к. в нем фигурирует вектор ошибок которому
может быть поставлен в соответствие вектор невязок (10.8).
10.4. Оценки достижимой точности
Приведенные выше соотношения (10.25), (10.26) вскрывают закономерно-
сти формирования ошибок идентификации, однако они не пригодны для
оценки достижимой точности. Вычисление по этим формулам квадрата евк-
лидовой нормы вектора ошибок идентификации представляется проблема-
тичным, во-первых, из-за необходимости вычисления всех собственных зна-
чений матрицы А, во-вторых, значения косинусов никогда не известны, т.к.
не известна ориентация вектора ошибок относительно пространства матрицы X.
В настоящем разделе мы приведем некоторые результаты, использование ко-
торых для анализа точности идентификации, по крайней мере, не требует
решения полной проблемы собственных значений.
Обсуждая в разделе 10.2 содержательную постановку задачи оценки по ма-
лым фрагментам изображений, мы отказались от основных предположений
классической регрессии. Вместо этого мы ввели в рассмотрение предположе-
ние об ограниченности нормы вектора ошибок: ||£||<Я и констатировали,
что вся неопределенность связана с произвольной ориентацией этого вектора
в Л'-мерном пространстве.
Для построения количественных оценок точности идентификации во мно-
гих отношениях удобной является обладающая свойством инвариантности к
унитарным преобразованиям евклидова норма. При этом указанное ограни-
чение можно переписать в виде
И12<Л5. (10.27)
23*
708
ГЛАВА 10
Заметим, что в соответствии с выражениями для ошибок, приведенными в
таблице 10.2, неравенство (10.27) является следствием того, что при фиксиро-
ванной матрице X заданы также границы для согласованных евклидовых норм
возмущений 5у и 5Х.
Множество Е векторов, удовлетворяющих неравенству (10.27), принадле-
жит «шару»:
1;еЕ, S=^:(^)V2=h|2<«5=const|. (10.28)
Ориентация вектора ошибок £ относительно пространства столбцов мат-
рицы X случайна, и не делается никаких предположений относительно веро-
ятности различных направлений. Поэтому здесь и далее отсутствуют какие-
либо вероятностные оценки ошибок идентификации. Проблема обоснования
и учета априорных вероятностей направлений векторов из множества (10.28),
по-видимому, заслуживает отдельного серьезного исследования. В настоящей
главе эти проблемы не затрагиваются.
Из неравенства (10.27) в силу (10.20), устанавливающего связь между раз-
личными представлениями ошибок, следует также, что
1И2<^> (10.29)
где 7?^ — пока не известная, но фиксированная константа. Позже мы устано-
вим связь величин R^ и R^. Здесь, пока, заметим следующее. Искомый век-
тор параметров с удовлетворяет уравнению (10.17), то есть b — £ является «точ-
ной» правой частью. Поскольку вектор £ не известен, вместо (10.17) мы вы-
нуждены решать уравнение (10.13) Ас = Ь, относительно которого мы
утверждаем лишь то, что евклидова норма возмущений в правой части не
превышает величины R?. Ясно, что в ходе вычисления искомых оценок к
ним добавятся еще ошибки округления.
В теории возмущений известен подход к оценке влияния ошибок округле-
ния, так называемый обратный анализ ошибок [2]. В соответствии с этим
подходом влияние ошибок при вычислениях равносильно дополнительному
внесению ошибок в исходные данные. Обозначим эти дополнительные воз-
мущения матрицы А и вектора b соответственно ДА и ДЬ. Тогда соответствую-
щая (10.13) система, содержащая также и эквивалентные возмущения [2] мо-
жет быть представлена в виде
[а+да]-с, =[ь-;]+(5+дъ), (ю.зо)
где св — оценка, которая кроме ошибок Дс, определяемых равенствами (10.19),
(10.21), содержит также погрешности (округления), возникающие на этапе
вычисления оценок. Для наглядности в правой части (10.30) квадратными
скобками выделена правая часть точного (по отношению к искомому вектору с)
уравнения (10.17), а круглыми — суммарное возмущение правой части, свя-
занное с вычислениями и неточностью исходных данных.
10.4. Оценки достижимой точности
709
Для анализа общих ошибок Дсе = св — с, возникающих вследствие перво-
начальных ошибок исходных данных и эквивалентного возмущения при вы-
числениях, воспользуемся результатами теории возмущений. В частности, из-
вестна [2,21] следующая оценка для максимальной относительной погрешно-
сти Sc = |Асв||/||с|| в решениях:
8С< К(А\ (8й+5Д (10.31)
1-А(А)8/ ’
где /ЦАХАЛА]-1 — условное число или так называемое число обусловлен-
ности, а относительные погрешности исходных данных для наиболее общего
случая, когда оцениваются параметры модели БИХ-фильтра, в соответствии с
(10.30) определяются как
8Л =||ДА||/||А||, 8fc =|5+ДЬ|/|Ь-Ц=|5+Ab||/|b- + 8Ас|.
Поскольку в исходных предположениях (10.27), (10.29) используется евк-
лидова норма вектора, далее для числа обусловленности мы будем использо-
вать справедливое для согласованной с ней спектральной нормы веществен-
ной матрицы Грама соотношение
^(A) = Xmax(A)/lmi„(A), (10.32)
где Xmax(A), Xmin(A) — максимальное и минимальное собственные значения
матрицы А. Далее для сокращения записей мы будем обозначать их Xmax, Xmin
соответстве нно.
С учетом сказанного неравенство (10.31) можно записать в виде
8С< х (8>+8л). (10.33)
Подчеркнем, что при этом для характеристики фигурирующих в (10.33) от-
носительных возмущений также должны использоваться евклидовы нормы:
8е=||Дс.1МН2. =||ДА[|2/ЦА|(2, 8ь=||?+дь|2/|ь'+8Ас^. (10.34)
Если матрица А достаточно хорошо обусловлена, то при соответствующем
выборе разрядной сетки вычислителя Xmin >>А,тах5л, и условие (10.33) при-
нимает более простой вид:
8, <£=*-(8* +8Л) = К(А)(8Х + 86). (10.35)
^min
710
ГЛАВА 10
Часто оказывается (например, в случае идентификации модели КИХ-фильт-
ра), что относительной погрешностью 8^ можно пренебречь, по сравнению с
8Л, поскольку в последней содержатся также ошибки исходных данных (из-
мерений). Тогда справедлива более простая оценка:
X
8с<-^8ь = К(А)85, (10.36)
Amin
Наконец, если составляющей 8Ас в выражении (10.18) также можно пре-
небречь по сравнению с 8b (а тем более по сравнению с Ь), то существенно
упрощается и само выражение для относительных возмущений 8Л;
6t=||S + Ab||2/|bj2. (10.37)
В соответствии с неравенством треугольника наряду с (10.37) для 8Й мож-
но использовать также оценку сверху:
§ _ М2 , 11^^112 (10 38)
— и «и ' II «и > (Ю.Зб)
И Н
где, в соответствии с (10.18), (10.20), £ = ХГ^ = 8Ь-8Ас.
Построим теперь оценки для скалярной характеристики ДсгДс — ||Дс||2.
Будем полагать, что для нормы вектора ошибок исходных данных выполняет-
ся предположение (10.27): Будем также использовать допущение,
что норма (длина) вектора ошибок не зависит от ориентации этого вектора
относительно пространства столбцов матрицы X. Для решения задачи вос-
пользуемся каноническими разложениями (10.25), (10.26).
Разделим задачу на два этапа. Вначале решим более простую задачу: уста-
новим экстремальные (максимальную и минимальную) ошибки идентифика-
ции, которые могут возникать при фиксированной норме ||^||2 вектора оши-
бок, то есть при условии, что , а
(10.39)
Множество Ел — более узкое по сравнению с Е в (10.28). Оно представ-
ляет собой подмножество векторов ошибок, концы которых принадлежат сфере,
с радиусом 7^.
По предположению матрица X фиксирована и задана, а фигурирующие в
канонических разложениях (10.25), (10.26) собственные значения (ХГХ),
1 — 1,М не зависят от направления вектора Таким образом, задача сводится
к отысканию такой ориентации вектора ошибок относительно пространства
столбцов матрицы X, при которой квадрат нормы вектора ошибок идентифи-
кации будет достигать экстремальных значений (максимума или минимума).
= {(rtf’ =|Н2 = = const}
10.4. Оценки достижимой точности
711
Рассмотрим равенство (10.26) как функцию переменных V/ • При соответ-
ствующих предположениях непрерывности множества возможных реализа-
ций вектора шума £, на заданной сфере переменные у,-, i = \,М также непре-
рывны в интервале [0,2л]. Следовательно, квадрат евклидовой нормы вектора
ошибок идентификации, заданный в виде (10.26), является непрерывной функ-
цией М непрерывных аргументов V/ •
Для фиксированных матрицы X (Rank (X) = М) и собственных векторов,
образующих пространство /? (X), необходимые условия экстремума функции
(10.26) задаются следующей системой М уравнений:
—||Дс||2 = 2R^X4~1 cosy, siny, ”0.
(10.40)
Одно из возможных решений этой системы соответствует углам у,-, при
которых все косинусы обращаются в нуль. Это возможно в случае, когда век-
тор ошибок принадлежит нуль-пространству матрицы Хт: е У (X). Если это
не так, то (поскольку Rank(X) = Ми, следовательно, ^0) при у4 G [0,2л]
углы могут принимать одно из двух значений: у, = 0, ± л/2.
Таким образом, необходимые условия экстремума для величины ||Ас||2
выполняются либо при £ е N (X), либо на направлениях, задаваемых соб-
ственными векторами, образующими пространство R (X). Другими словами,
если £, е R (X), его направление должно совпадать с одним из (ортогональных
друг другу) векторов-столбцов М<Л/-матрицы Т^.
Теперь из геометрических соображений (рис. 10.5) легко установить макси-
мальное и минимальное значение квадрата нормы вектора ошибок идентифи-
кации. Ясно, что при £ е jV(X) имеет место равенство ||Ас||2 = 0. При е R (X)
зададим в качестве «подозрительного» на экстремум одно, например /-е, на-
правление (у, — 0) ортогонального базиса. Но тогда для всех j = 1,М, j i
yj = ±л/2, a cosy7 = 0. Следовательно, сумма в правой части функции (10.26)
будет содержать лишь одно слагаемое: ||Ас||2 = ||^||| соответствующее выб-
ранному (У-му) направлению, а экстремальные значения ||Ас||2 будут дости-
гаться на направлениях, соответствующих максимальному и минимальному
собственным значениям. Таким образом, имеет место
Утверждение 1. Пусть Rank (X) = М, а множество векторов ошибок £€ER:
SR ='^(^Ч)1/2 =Н2 = const}.
Тогда
(10.41)
712
ГЛАВА 10
если е R (X), и
М2 (10.42)
в остальных случаях.
Оценку (10.42) можно также получить из выражения для вектора ошибок
идентификации (10.21) используя неравенство треугольника [3]. Однако ут-
верждение 1 и использовавшиеся для его обоснования рассуждения дают бо-
лее полное представление о структуре и границах ошибок оценки. В частно-
сти, видно, что при построении МНК-оценок составляющая вектора ошибок,
принадлежащая нуль-пространству матрицы X, не влияет на точность оценок.
Проблема заключается в компенсации влияния проекции вектора ошибок на
R(X). В связи с этим, приведенная в (10.41) для случая £ е /?(Х), оценка
снизу квадрата евклидовой нормы вектора ошибок идентификации может быть
весьма полезной.
Аналогичные оценки могут быть построены также в случае, когда величи-
на квадрата нормы вектора ошибок идентификации представлена в виде со-
отношения (10.25). Действуя по той же, что и выше, схеме из (10.25) с учетом
ограничения (10.29) получаем неравенство
<10'43>
где в соответствии с (10.18) £ = Sb-SAc. В отличие от (10.41) здесь вместо
в качестве «коэффициента усиления» ошибок исходных данных фигури-
рует X“fn. Объяснение этому факту мы находим в соотношении (10.20), свя-
зывающем различные формы представления ошибок.
Установим связь величин R^ и R^. Применим к соотношению связи меж-
ду ошибками (10.20) стандартные преобразования:
Fr;=FrXr^=AV2[A“1/2FrXr]^ = A1/2Tx§, и £rF = §7Т{Л1/2.
Далее используя ту же, что и ранее, схему, по аналогии с (10.25), (10.26)
получаем, что
_ , м
Hl2=H2S>,COs2V,- (10-44)
1=1
Радиус «шара» для вектора Q должен быть равен минимальной из величин
полуосей эллипсоида (10.44) при максимальном значении Ц^Ц*. В соответ-
ствии с предположением (10.27) максимальное значение квадрата нормы век-
тора £ задается равенством ||£ |* = R^. Поскольку матрица X фиксирована,
числа i = \,М являются константами. С другой стороны, мы установили,
10.4. Оценки достижимой точности
713
что при экстремальных значениях величины ||АсЦ^ квадраты косинусов могут
принимать значения Оили 1. Обозначив R* минимально возможное значе-
ние суммы в правой части (10.44), при ||£||* — R^ получим, что
Отсюда, в частности, следует, что
=*!£а- (10-45)
Теперь вернемся к исходному предположению (10.27). Ясно, что ошибки
идентификации в общем случае, когда векторы и/или £ принадлежат шару,
не могут превышать ошибок, которые возникают в случае, когда они принад-
лежат соответствующим сферам. Поэтому с учетом (10.43), (10.45) справедли-
во следующее следствие (10.42).
Следствие утверждения 1.
Если
$GS, Е = |§:(^4)'/2 =И2 <Я? =constj,
ТО
||ас^<1;!пИ’<х;!пя52. (ю.4б)
Если
Z = ^:(^),/Z =М2 <яс =constj,
ТО
<10-47)
где Zmin — минимальное среди собственных значений Х( матрицы ХГХ, a R^
удовлетворяет равенству (10.45).
В заключение обсудим оценки, фигурирующие в утверждении 1 и его след-
ствии. Из (10.46) следует, что оценка сверху для квадрата нормы вектора
ошибок оценивания может быть улучшена, если осуществить преобразова-
ние данных, направленное на увеличение минимального собственного зна-
чения, при котором норма ||£||2 вектора ошибок в исходных данных, по
крайней мере, не увеличивается. Если все собственные значения одинаковы,
то есть = Х“|П = Х-1, оценки сверху и снизу (10.41) обязаны совпадать.
При этом число обусловленности К (А) равно единице, а || АсЦ^Х-'Н’.Это
равенство отражает известный факт: точность оценки повышается при возра-
стании отношения полезный сигнал/шум. В частности, если X • =1, z = 1,М,
714
ГЛАВА 10
то норма вектора ошибок идентификации равна норме вектора ошибок в ис-
ходных данных.
Оценки (10.46) и (10.47) получены в предположении, что переменные у, и
ср, могут принимать любые значения в интервале [0, 2л]. Это предположение
можно ослабить. В частности, можно допустить, что векторы £, и/или £ при-
надлежат некоторому конусу. Из геометрических соображений ясно, что ука-
занные неравенства при этом не нарушатся.
Соотношения (10.46) и (10.47) строились в расчете на наихудший случай,
когда направление вектора ошибок совпадает с направлением собственного
вектора, соответствующего минимальному ненулевому собственному значению
матрицы XXт. В действительности вероятность того, что в конкретном случае
реализуется неблагоприятное направление меньше единицы. Конечно, было
бы полезно использование априорных вероятностных характеристик, характе-
ризующих направление вектора Выявление таких характеристик, в особен-
ности для ситуаций, когда устойчивость самих распределений ошибок еще не
имеет места, является важной и, к сожалению, мало изученной проблемой.
В заключение подчеркнем, что в соответствии с (10.46), (10.47) решающее
значение при оценке ошибок идентификации имеют собственные значения
матрицы А. Поэтому в следующем разделе более глубоко исследуется связь
обусловленности и информативности данных со спектром этой матрицы.
В частности, с использованием приведенных неравенств будут построены про-
стые в вычислительном отношении оценки для характеристики информатив-
ности данных на фрагментах изображения.
10.5. Меры обусловленности и мультиколлинеарности
В п. 10.4 мы полагали RankX = M В то же время по предположению 2
(разд. 10.2) RankX<A/. Следовательно, для того, чтобы приведенные выше
оценки «работали» мы обязаны сначала применить к исходным данным про-
цедуры исключения линейно-зависимых или «почти» линейно-зависимых век-
торов (столбцов матрицы X). В настоящем разделе рассматриваются характе-
ристики, которые могут использоваться для входного контроля данных.
Точность оценок на каждой конкретной реализации существенным обра-
зом зависит от числа обусловленности матрицы А, которое при заданной со-
гласованной норме матрицы определяется формулой (10.32). Как следует из
соотношений (10.31), (10.35), (10.36), при большом значении числа обуслов-
ленности даже небольшие ошибки в исходных данных могут привести к боль-
шим ошибкам в решениях. Одной из основных причин плохой обусловленно-
сти матрицы А = Х7Х является «почти» линейная зависимость (мультикол-
линеарность) [5] векторов-столбцов матрицы X. Можно утверждать, что
следствием сильной мультиколлинеарности всегда является плохая обуслов-
ленность задачи. Обратное не всегда верно.
Векторы-столбцы матрицы X могут быть почти ортогональными, но силь-
но различаться параметрами масштаба, что неизбежно приведет к плохой
10.5. Меры обусловленности и мультиколлинеарности
715
обусловленности. Поэтому далее термин «обусловленность» употребляется для
общей характеристики чувствительности решений к ошибкам в исходных дан-
ных, а термин «мультиколлинеарность» используется в тех случаях, когда необ-
ходимо указать конкретную причину возникновения плохой обусловленности.
Как уже не раз подчеркивалось, в задаче оценки по малому числу наблюде-
ний характеристики обусловленности могут существенным образом изменяться
при переходе от одного фрагмента изображения к другому. Поэтому в данном
случае принципиально необходимым этапом является оценка обусловленнос-
ти и мультиколлинеарности на каждом полученном наборе данных. В насто-
ящем разделе наряду с широко известными мерами мультиколлинеарности
и/или обусловленности описываются меры, которые были специально разра-
ботаны [24] для оценки информативности данных по малому числу фиксиро-
ванных наблюдений.
В регрессионном анализе качество оценок обычно характеризуют диспер-
сией. Оценка МНК становится малоэффективной, т.е. дисперсия оценок су-
щественно возрастает, если имеет место мультиколлинеарность. Несмотря на
существование указанной зависимости, понятие мультиколлинеарности не
связано со статистическими характеристиками сигналов, а является мерой
сопряженности (но не корреляции) [5] независимых переменных в уравнении
(10.6). Поэтому использование этого понятия в контексте настоящей поста-
новки задачи является вполне уместным. Далее дадим сравнительную харак-
теристику мерам мультиколлинеарности [5], [24].
1. Определитель информационной матрицы (Грама) А= Х7Х имеет вид
м
det(A) = n^- (10.48)
<=i
Определитель может выступать в качестве меры мультиколлинеарности,
если матрица Грама определенным образом нормирована. Например, можно
вместо исходной матрицы А рассматривать матрицу А , полученную из нее по
правилу А=Л/ТгА (ясно, что для сравнения оценок по точности в этом
случае необходимо учитывать соответствующее изменение нормы вектора оши-
бок в исходных данных). При такой нормировке сумма собственных значе-
ний равна единице. Поэтому, если det(A) близок к нулю, то минимальное
собственное значение также близко к нулю и, следовательно, задача плохо
обусловлена. При отсутствии нормировки определитель может быть доста-
точно большим даже при близком к нулю минимальном собственном значе-
нии за счет большой величины максимального собственного значения.
2. Число обусловленности (10.32) — Л'(А) = A.max/Xmin. Соображения, по ко-
торым число обусловленности может выступать в качестве меры мультикол-
линеарности, те же, что и для определителя нормированной матрицы. Однако
в данном случае не требуется специальная нормировка матрицы А, т.к. число
обусловленности не чувствительно к параметру масштаба. Эта мера широко
используется в теории возмущений для анализа ошибок в решениях [2, 21]. В
работе [18] показана связь между числом обусловленности и определителем
716
ГЛАВА 10
матрицы. В частности, приводится следующая оценка сверху числа обуслов-
ленности
А?(а) <(тгм A^/det А.
3. Минимальное собственное значение ~~ Xmin (а) информационной матри-
цы А = ХГХ. Эта мера мультиколлинеарности является универсальной. Она
отражает как масштаб, зависящий от физической размерности независимых
переменных, так и мультиколлинеарность (сопряженность) соответствующих
им векторов. Это подтверждается приведенными выше оценками сверху для
нормы вектора ошибок идентификации (10.46), (10.47).
4. Показатель парной сопряженности, В регрессионном анализе часто ис-
пользуется матрица сопряженности:
1 Иг - Г\т
г21 1 ... г2т
'ml Гт2 - 1
(10.49)
где гу =(xfx7)/[(xfx1)1/2(xjxy)1/2] = cos(xJ,xy), a xf, ху — i-й иj-й векто-
ры-столбцы матрицы X. В качестве показателя мультиколлинеарности высту-
пает величина
г = шах г» ,
Г i J ।
(10.50)
i*7-
Важное достоинство этой меры — вычислительная простота. Однако по
сравнению с другими она является наиболее слабой. В [5] приводится пример
матрицы А = Х'Х, составленной с использованием трех компланарных, но по-
парно линейно независимых векторов. Матрица А при этом вырождена, но мера
(10.50) «не замечает» этого.
5. Показатель максимальной сопряженности. В качестве меры мультиколли-
неарности, свободной от указанного недостатка, рассматривают величину [5]
Я=тах|/?,.|, (10.51)
где A2 =xfXAr_I[xJ/_1XA/_|] Х^х,., xz — i-й вектор-столбец матрицы X,
а Хм. 7 — Nx(M-1)-матрица, полученная из исходной путем «вычеркивания»
этого (i-го) столбца. Геометрически — косинус угла между вектором-столб-
цом X; матрицы X и подпространством, натянутым на множество остальных
М-1 векторов этой матрицы.
Указанная мера, наряду с минимальным собственным значением и числом
обусловленности, является наиболее сильной. Если R* 1, гарантируется не-
вырожденность задачи. Недостатком этой меры является вычислительная
10.5. Меры обусловленности и мультиколлинеарности
717
сложность, связанная с необходимостью вычисления обратной матрицы. Но
даже если мы готовы пойти на эти затраты, то возникает «замкнутый круг»:
для того чтобы сделать заключение о характере обусловленности, необходимо
знать обратную матрицу, но если матрица А плохо обусловлена, то ее обраще-
ние становится серьезной проблемой.
6. Показатель минимальной сопряженности с нуль-пространством. Эта мера
мультиколлинеарности [24] позволяет в значительной мере избежать указан-
ных выше проблем и определяется как
Smin = min|5z|,
i
(10.52)
где S, > j~M,N , =(xJ-,tOy) — проекция вектора-столбца xf-
матрицы X на j-й собственный вектор, соответствующий нулевому собствен-
ному значению матрицы Х^Х^-р Здесь Хл/1 — Ах(М-1)-матрица, со-
ставленная из (А/-1) нормированных (||х(-|| — 1, i = l,Af) векторов-столбцов
матрицы X после исключения вектора х;. Геометрически 5, — косинус угла
между вектором х, и нуль-пространством матрицы Х^_н составленной из
Л/1 векторов-строк.
Для вычисления меры (10.52) необходимо вначале вычислить все i = M,N.
Можно показать [24], что для этого справедливы следующие соотношения:
5.=(’‘ГТ,м-1Т»л/-1’‘,)1/2/(х,Гх,)'/2, (10.53)
Здесь То м-i ~ матрица, размерности Ах(А-М+1), составленная из
N-M+1 собственных векторов, соответствующих нулевым собственным зна-
чениям матрицы . Подчеркнем, что в данном случае не требуется
обращать матрицу, вдобавок объем вычислений при малом числе наблюде-
ний, когда размерность нуль-пространства не превышает размерность про-
странства параметров, по сравнению с мерой (10.51) значительно меньше.
7. Показатель диагонального преобладания матрицы Грама. Соображения,
по которым показатель диагонального преобладания, определяемый как
Тг2А
ТгА2
(10.54)
может использоваться в качестве меры обусловленности и/или мультиколли-
неарности, связаны с известными свойствами матриц Грама [2,9]:
' м м
тг2а=£л( , тга2 = £а,2.
U=i ы
(10.55)
718
ГЛАВА 10
Ограничением на применение показателя (10.54) являются неравенства
М-1«Ь<М. (10.56)
Иногда [24] вместо показателя ф удобнее использовать приведенную к ин-
тервалу [0,Ц величину ф = ф-7И+1, характеризующую превышение диагональ-
ного преобладания ф над левой границей допустимых значений (10.56).
Точность вычисления показателя (10.54) не зависит от характера обуслов-
ленности и кратности собственных значений. Важным достоинством показа-
теля ф (или ф), по сравнению с большинством из указанных выше мер, явля-
ется вычислительная простота. Это имеет большое значение в системах обра-
ботки изображений. Общим недостатком показателя (10.54) является то, что в
силу ограничений (10.56) он «срабатывает» лишь на достаточно хорошо обус-
ловленных матрицах. Однако, если задача как раз и заключается в достиже-
нии хорошей обусловленности, то указанный недостаток следует считать до-
стоинством.
Из приведенного краткого обзора мер мультиколлинеарности видно, что
использование определителя и показателя парной сопряженности связано со
значительным риском. Их применение, по-видимому, возможно лишь при
наличии дополнительной априорной информации. Следующие три меры: число
обусловленности, минимальное собственное значение и показатель макси-
мальной сопряженности являются достаточно полными характеристиками
мультиколлинеарности, но две из них связаны с нахождением экстремальных
собственных значений, а третья требует вычисления обратной матрицы. Вы-
числение собственных значений и/или обратной матрицы в ситуациях, когда
задача плохо обусловлена, а среди собственных значений имеются кратные,
представляет серьезные трудности.
Поэтому наиболее привлекательными, с точки зрения построения проце-
дур контроля малых наборов данных в информационных технологиях обра-
ботки изображений, представляются две меры: показатель диагонального пре-
обладания (в силу вычислительной простоты) и показатель сопряженности с
нуль-пространством, который, также как и показатель (10.51), дает гаранти-
рованные оценки мультиколлинеарности, но при малом числе наблюдений
делает это сравнительно экономно. В силу сказанного далее рассмотрим бо-
лее детально связь этих двух мер с остальными, упоминавшимися выше.
10.6. Связь и сравнительная характеристика мер
обусловленности и мультиколлинеарности
Из приведенных в разделе 10.3 канонических представлений и оценок точ-
ности (10.25), (10.26) видно, что при сделанных относительно вектора оши-
бок исходных данных предположениях решающую роль в формировании
ошибок идентификации играют собственные значения информационной мат-
рицы А = ХГХ (Грама). Вместе с тем, решение полной проблемы собственных
значений является сложной вычислительной задачей. Поэтому в технологиях
10.6. Связь и сравнительная характеристика мер обусловленности и мультиколлинеарности 719
обработки изображений для контроля информативности данных желательно
использовать наиболее простую в вычислительном отношении меру обуслов-
ленности и мультиколлинеарности — показатель диагонального преоблада-
ния. Поэтому представляет интерес связь этого показателя с собственными
значениями.
Если показатель ф диагонального преобладания (10.54) удовлетворяет не-
равенствам (10.56): М — 1<ф<Л/, то имеют место следующие оценки сверху
и снизу для собственных значений:
1(A) < М ~1Тг А (1 + 7(М / ф - 1)(Л/ -1)), (10.57)
1(A) > АГ! Tr А (1 - / ф - 1)(М -1)). (10.58)
Доказательства этого утверждения можно найти в работах [23, 24]. Нагляд-
ное геометрическое объяснение неравенств (10.57), (10.58) — на рис. 10.6.
Для практических целей наибольший интерес, конечно, представляет оценка
снизу (10.58), т.к. она может использоваться для оценки верхней границы
возможной ошибки идентификации при заданном в (10.27), (10.29) ограниче-
нии на норму вектора ошибок исходных данных. Действительно, неравенство
(10.46) не нарушится, если вместо минимального собственного значения
Xmin = mmlf(A) подставить его оценку (10.58). При этом получаем следую-
щую легко вычисляемую оценку сверху для погрешности идентификации:
ЦАсЦз <М[тга(1-7(М/ф-1)(Л/-1))]
где — заданная в (10.27) максимально возможная норма вектора ошибок
Заметим, что если матрица А нормирована по правилу А=А/Тг А , то оцен-
ка максимальной погрешности идентификации зависит только от погрешно-
сти исходных данных и величины диагонального преобладания информаци-
онной матрицы. Если указанной нормировке подвергается набор данных, для
которого величина уже задана, то она также должна быть изменена соот-
ветствующим образом.
В работе [24] показано, что применение оценок (10.57), (10.58) во многих
отношениях является более предпочтительным по сравнению с использова-
нием аналогичных оценок, построенных на основе известных локализацион-
ных результатов Гершгорина и Брауэра [9].
С использованием неравенств (10.57), (10.58) может быть построена оцен-
ка сверху для спектрального числа обусловленности. В частности, подставляя
в (10.32) вместо lmax, Xmin оценки (10.57), (10.58), соответственно, получа-
ем следующую оценку сверху [24]:
к (А) = ^(А) k. = 1 + 7(Л£/ф-1)(ЛГ-1)
(10.59)
720
ГЛАВА 10
Рис. 10.6. Геометрическая интерпретация множества 02
Соображения, по которым мы обозначили эту оценку , будут понятны
из дальнейшего. Ясно, что для фигурирующего в этом неравенстве показателя
ф также должны выполняться ограничения (10.56): М — 1 < ф <М.
Существует более сильная при тех же ограничениях на показатель ф оценка
сверху для числа обусловленности:
К(А) = <к; = 1+У(Ф-^+2)~'(М-ф)
*mm(A) ' 1-7(ф-Л/+2)_1(Л/-ф)
(10.60)
Доказательство неравенства (10.60) можно найти в работах [24, 29], а гео-
метрическая интерпретация связи этой оценки с другими показана на рис. 10.6.
Для построения гарантированных оценок для относительных ошибок иден-
тификации, вычисляемых по соотношениям (10.33), (10.35), (10.36), должны
использоваться оценки сверху (10.59), (10.60). Поэтому проведем сравнитель-
ный анализ их эффективности.
На рис. 10.7 приведены зависимости оценок к*, к % от приведенной к диа-
пазону [0—1] величины диагонального преобладания ф=ф—Л/4-1. Получен-
ные подстановкой ф = ф+М—1 в соотношения (10.59) и (10.60) выражения
для оценок ку, по которым проводились расчеты, имеют вид
_1+7(1-ф)/(1+ф)
1-7(1-ф)/(1+ф)’
(10.61)
1 + ^(1-ф)(М- 1)(ф+ л/- I)-7
кв —
1-7(1“ Ф)(М- 1)-1(Ф+ М- I)1
(10.62)
10.6. Связь и сравнительная характеристика мер обусловленности и мультиколлинеарности 721
Из графиков видно, что оценка kf более сильная, чем , но преимуще-
ство незначительное и притом быстро убывает с ростом показателя ф. Более
того, хотя оценка к2 и зависит от порядка матрицы М, зависимость эта сла-
бая, так что она остается достаточно эффективной даже при М = 100. Поэто-
му выбор между этими оценками, по-видимому, должен определяться в пер-
вую очередь удобством вычислительной реализации.
Наглядное объяснение существа приведенных выше неравенств и ограниче-
ний дает геометрическая интерпретация для матрицы Грама размерности 3x3.
Предположим, что для такой матрицы с собственными значениями Aq, А2, А,3
строятся оценки по показателю диагонального преобладания (ф или ф). В соот-
ветствии со свойствами (10.55) матриц Грама введем в рассмотрение множество
матриц 02 =<A:TrА—Zj =const,
/ о х 1/2
(ТгА j =7 2= const
, одновременно удов-
летворяющих уравнениям
А| А2 А3 — / |, А^Н-А2-|-А3 — z2.
В трехмерном пространстве, образованном собственными значениями At,
А2, А3, первое уравнение описывает плоскость, отсекающую на осях величи-
ну Гр Второе уравнение описывает сферу с центром в начале координат и
радиусом t2. Подмножество 02, образованное пересечением плоскости и сфе-
ры, является окружностью. Очевидно, что для различных, но фиксированных
пар t2, можно построить различные окружности, каждой из которых будет
соответствовать фиксированная величина диагонального преобладания
(ф = tj/t2 или ф = ф- Af+l).
На рис. 10.6 показаны множества 02> соответствующие различным зна-
чениям ф (ф| > ф2>ф3). Для множества 02, соответствующего величине по-
казателя ф2 цифрами 1и 2 указаны точки, в которых достигаются оценки
(10.57), (10.58) для собственных значений, а в не-
посредственной близости от точки 1 показана так-
же точка /cf(A), в которой имеет место максималь-
но возможное для соответствующего множества мат-
риц число обусловленности.
Из рис. 10.6 видно, что построение гарантиро-
ванных оценок обусловленности по показателю ди-
агонального преобладания, при значениях ф в ди-
апазоне 1<ф<М—1, возможно только в случае,
когда априори задана граница снизу для минималь-
ного собственного значения. Использование такого
дополнительного условия неконструктивно, ПО- Рис. 10.7. Зависимости оценок
скольку наличие априорной информации о мини- к'• кг от показателя ф
мальном собственном значении вообще снимает проблему оценки обуслов-
ленности. Тем не менее, из приведенного примера ясно, что показатель ди-
агонального преобладания ф (или ф), наряду с минимальным собственным
24 — 9044
722
ГЛАВА 10
значением и числом обусловленности, является важной характеристикой мат-
рицы Грама.
Теперь покажем связь меры (10.52) с максимальной сопряженностью (10.51)
[5]. Для удобства их сопоставления величины Rif фигурирующие в (10.51),
представим в следующем виде:
(Хд,
где z( = [xJ/_1XAf_1] Xjf.jXp
Применяя к указанным соотношениям ортогональные преобразования,
можно убедиться, что показатель максимальной сопряженности (10.51) мож-
но также трактовать следующим образом:
R = тах|Я,|, Я, = а2;}1/2, j = 1.М-1, i = ЦЙ,
где ау ) — проекция вектора х- на j-й вектор базиса, образованного
собственными векторами, соответствующими ненулевым собственным зна-
чениям матрицы Хду^Х^.р Если вектор х(- принадлежит пространству столб-
цов матрицы Хм~1 (задача вырождена, а показатель R= 1), то он ортогона-
лен нуль-пространству этой матрицы (при этом Smin = 0). С уменьшением
величины R соответствующая ей величина Smin увеличивается. По существу,
показатели R и Sinin являются мерами одной и той же характеристики, но
вычисляются посредством разных подпространств.
Указанное обстоятельство является причиной вычислительных преимуществ
меры (10.52) при обработке малых наборов данных. Объем вычислительной
работы при использовании показателя Smin будет меньше в ситуации, когда
размерность нуль-пространства меньше, чем размерность пространства пара-
метров. В действительности эти преимущества проявляются и в случае, когда
общее число наблюдений превышает число оцениваемых параметров более
чем в два раза. Дополнительный выигрыш имеет место вследствие того, что
для определения матрицы То м_ь которая используется при вычислении Sb не
требуется решение полной проблемы собственных значений и (в отличие от
R) не нужно вычислять обратную матрицу.
Представляет также интерес использование меры
=(Е-?.2)1/2. E=E₽J. >=мл (ю.63)
— так называемого показателя суммарной сопряженности с нуль-пространством.
Здесь все обозначения те же, что и в (10.52).
Мера (10.63) является менее надежной, чем мера (10.52). Она может при-
нимать достаточно большие значения даже в том случае, когда 5min = 0, т.е.
задача вырождена. Тем не менее, вычисление показателя наряду с мерой
(10.52) целесообразно, т.к. он несет дополнительную информацию о структу-
ре пространства матрицы X. Это тем более оправдано, поскольку не требует
сколько-нибудь значительных дополнительных вычислительных затрат.
10.6. Связь и сравнительная характеристика мер обусловленности и мультиколлинеарности 723
Пример 10.7. На рис. 1CL8 приведены поля значений для показателей диа-
гонального преобладания ф > 0,1 (рис. 10.8я) и минимальной сопряженности
с нуль-пространством 5min > 0,5 (рис. 10.86) по полю тестового изображения,
моделирование которого описано примере 1.4. Для удобства визуального вос-
приятия значения ф и 5min, превышающие указанные пороги, заменены мак-
симальным значением в обычной [0—255] шкале яркостей (бинарные изобра-
жения удобно использовать в ходе идентификации для отбора информатив-
ных данных).
Пример 10.8. В качестве тестового использовался участок изображения типа
«текст», показанный на рисунке 10.8в. Для наглядной визуальной оценки свя-
зи показателя Smin с информативностью исходных данных он рассчитывался в
каждой точке исходного изображения. Результаты расчетов представлены в
виде изображения на рисунке 10.8г. Диапазон изменения показателя [0,1] также
приведен к интервалу [0,255]. Видно, что показатель 5min «безошибочно заме-
чает» строки и слова, т.е. наиболее информативные для идентификации уча-
стки изображения.
На рис. 10.9л и б показана связь показателей ф(А) и 5min со всеми, обсуж-
давшимися в предыдущем разделе, мерами мультиколлинеарности и обуслов-
ленности в двух крайних ситуациях, характеризующихся как «хорошо» (а) и
«плохо» (6) обусловленная задача. Схема напоминает модель направленного
графа. Идея этого представления заимствована из [5]. Так же как и там, сплош-
ная стрелка означает «из... обязательно следует...», а пунктирная — «из... как
правило, но не обязательно, следует...». Показанные на схемах связи вытекают
из анализа приведенных выше аналитических соотношений мер мультикол-
линеарности и обусловленности. В заключение напомним, что некоторые из
мер (Smin, шах/?) учитывают лишь сопряженность (мультиколлинеарность), а
другие (ф (А), /Г (A), A.min) «чувствуют» также и различия в масштабах векторов
независимых переменных, т.е. являются мерами обусловленности. Ниже при-
водятся результаты экспериментов, иллюстрирующие связь и сравнительную
эффективность мер мультиколлинеарности и обусловленности.
Пример 10.9. Решалась задача идентификации линейной модели систе-
мы формирования изображений с использованием тестовых изображений,
Обработка изобрази
связана с решением
ких задач, в кагоры:
входные, и выходны
ные являются изобр
ниями. Одним из пр
ров служат системы
редачи изображеню
оазоаботчики сталю
а б в г
Рис. 10.8. Поля мер обусловленности: а и б — для тестового изображения на рис. 10.1 (а — ф,
d — 5min); г — показатель Smin для изображения в
24*
724
ГЛАВА 10
б
Рис. 10.9. Схема связей показателей мультиколлинеарности и обусловленности: а — в случае
хорошо обусловленной задачи; б — в случае плохо обусловленной задачи
обладающих заведомо различной степенью обусловленности в достаточно ши-
роком диапазоне. В эксперименте осуществлялась оценка параметров импульс-
ной характеристики искажающей системы по изображениям № 1—5, которые
показаны на рис. 10.10. Наряду с проверкой устойчивости связей, показан-
ных на рис. 10.9 пунктирными стрелками, ставилась также задача дать срав-
нительную оценку эффективности мер.
Интуитивно ясно, что вызываемая мультиколлинеарностью обусловленность
задачи идентификации, решаемой по этим изображениям, должна ухудшаться
по мере увеличения номера изображения. Наиболее информативным, т.е. при-
водящим к хорошо обусловленной задаче, является тестовое изображение № 1.
Его генерация проводилась при помощи датчика псевдослучайных чисел, а
каждый отсчет этого изображения является реализацией случайной величины,
равномерно распределенной на интервале от Одо 255. Тесты № 2—5 формиро-
вались как фрагменты изображения из работы [25]. Выходные изображения
формировались путем моделирования расфокусировки, обладающей круго-
вой симметрией, с использованием разностного уравнения типа (10.1) [25]:
4
y("i.»2)=!>(*)•#).
к=0
10.6. Связь и сравнительная характеристика мер обусловленности и мультиколлинеарности 725
где
х(0)=х(лр п2),
x(l) = [x(«j + l,0) + x(^j-l,0)+x(0, л2+1)+х(0, л2-1)]/4,
х(2) = [х(Л] + 1, л2+1)+х(м1 + 1, л2—1) + х(я1-1, л2+1) + х(Л]-1, п2-1)]/4,
x(3) = lx(«j+ 2,0)+х(Л|-2,0) + х(0, л2 + 2)+х(0, л2-2)]/4,
х(4) = [х(л1 + 2, п2+ 1) + х(Л] +2, л2-1) + х(л1-2, п2 + 1) + х(л1-2, л2-1) +
+ х(п] + 1, п2 + 2) +х(/7| + 1, л2-2) + х(л1-1, п2 + 2) + х(л(-1, п2-2]/8.
Это уравнение соответствует опорной области 5x5 (без угловых отсчетов),
показанной на рис. 10.11. Значения импульсной характеристики искажающе-
го фильтра задавались равными: Л (0) = 0,102, Л(1) = 0,327, Л (2) = 0,245,
h (3) = h (4) = 0,163. Соответствующая этой опорной области матрица X для
каждого тестового изображения имела размерность 25x5, а матрица А = Х7Х —
5x5. Вектор оценок параметров искажающей системы Л = [/г(0),...,Л(4)| опре-
делялся с помощью метода наименьших квадратов.
В ходе эксперимента для показанных выше пяти тестовых изображений
№ 1—5 (рис. 10.10) рассчитывались следующие характеристики обусловленности
№ 1
№ 2
№ 3
Рис. 10.10. Тестовые изобра-
жения
№ 4
№ 5
726
ГЛАВА 10
и мультиколлинеарности: определитель нормированной матрицы — det (А),
спектральное число обусловленности — АГ(А) = A.max(A)/kmin (А), минималь-
ное собственное значение — A.min(A), показатель диагонального преоблада-
ния — ф(А), а также показатели максимальной сопряженности — шах/? и ми-
нимальной сопряженности с нуль-пространством —
Aniin. Результаты расчетов приведены в таблице 10.3.
Из таблицы 10.3 видно, что числовые значения
всех мер обусловленности указывают на ее ухудше-
ние с ростом номера изображения, в частности,
меры det (А/ТгА), Xmin, ф(А) и Amin, как и следовало
ожидать, уменьшаются, а для изображения № 5 зна-
чения Xmin и 5min оказались практически равными
нулю. Порождаемая этим тестовым изображением за-
дача идентификации характеризуется как плохо обус-
ловленная и по другим показателям (К(А)-+оо). Это
объясняется тем, что на нем присутствует в основном
фон. При хорошей обусловленности (изображение № 1) 5min->1, а показатель
диагонального преобладания ф(А) принимает значения существенно более
высокие, чем для изображения № 5.
Выбор одной из мер мультиколлинеарности и/или обусловленности в конк-
ретных информационных технологиях, конечно, должен осуществляться в за-
висимости от требуемой надежности вырабатываемых решений и вычислитель-
ных возможностей. Далее будут приведены конкретные примеры их использо-
вания. Здесь, пока, заметим, что применив к конкретному набору данных в
качестве меры обусловленности показатель диагонального преобладания ф(А),
мы можем всегда получить, по крайней мере, один из трех вариантов ответа:
1) задача плохо обусловлена и решение с требуемой точностью невозможно;
2) значение меры ф(А) на заданном фиксированном наборе данных не по-
зволяет сделать уверенное заключение о достижимой точности оценки,
т.к. 1 < ф(А) < М-1;
3) задача хорошо обусловлена (ф(А)>М-1) так, что существуют и могут
быть выработаны гарантированные оценки разрешимости задачи с требуемой
точностью при заданной точности исходных данных.
В первом случае решение, которое следует принять, очевидно. Во втором
случае возможность получения удовлетворительных оценок параметров
Таблица 10.3. Сравнение мер мультиколлинеарности и обусловленности
№ det (А/Tr А) *(А) ^min Ф(А) max/f с . иГП1Л
1 3,67х10‘5 16,72 12165,9 2,53024 0,58013 0,814522
2 6,42x10'6 37,85 2182,3 1,91591 0,87135 0,490654
3 7,96х10у 342,02 672,6 1,16107 0,98731 0,158775
4 5,07x1010 3011,98 35,2 1,21001 0,99883 0,057468
5 0,0 ОО 0,0 1,00000 1,00000 0,0
10.7. Построение проверочных неравенств для достижимой точности
727
вызывает сомнения и, следовательно, необходимо решить — готовы ли мы
пойти на увеличение вычислительных затрат, чтобы провести дополнитель-
ный анализ сформированного набора данных, например, по показателю 5min.
В третьем, последнем, случае представляют интерес точные количественные
оценки достижимой точности. Вопросам построения таких оценок посвящен
следующий раздел.
10.7. Построение проверочных неравенств для достижимой
точности
Если по сформированному набору данных задача оценки может быть ре-
шена с требуемой точностью, то такие данные называют информативными.
Термин «информативность» относится к числу наиболее часто употребляе-
мых в задачах оценки. Он, например, используется при исследовании при-
годности признаков в задачах обучения распознаванию образов. В задачах
идентификации систем формирования изображений этот термин, по суще-
ству, имеет тот же смысл, но его трактовка в данном случае нуждается в
уточнении.
В статистической теории оценок в качестве меры информативности широ-
ко используется фишеровская информация. В частности, известна нижняя
граница ковариаций оценок, определяемая как обратная информационная
матрица Фишера [28]. Поскольку мы определили точность решения задачи
как евклидову норму вектора ошибок оценки на одной конкретной реализа-
ции, указанная мера информативности здесь неприменима. Тем не менее, и в
данном случае удобно использовать понятие информативности как характе-
ристику потенциальных возможностей фиксированного набора данных, в част-
ности, достижимой точности оценивания параметров на заданном фиксиро-
ванном наборе данных.
На конкретной реализации нижняя граница для погрешности идентифи-
кации (аналогичная неравенству Крамера—Рао), как это видно из (10.46),
(10.47), отсутствует. Однако это не может служить основанием для оптимиз-
ма. Если дополнительная информация об ориентации вектора ошибок от-
сутствует, гарантированные оценки погрешности идентификации (10.46),
(10.47) имеют место лишь в случае, когда указанные неравенства превраща-
ются в равенства. Поэтому, говоря об информативности данных, как о свой-
стве, определяющем достижимую точность, мы будем иметь в виду лишь
величину верхних границ для ошибок идентификации в (10.46), (10.47). Ин-
формативность каждого конкретного набора данных в указанном смысле
определяется характеристиками обусловленности матрицы Грама. Поэтому
анализ обусловленности и/или мультиколлинеарности задачи должен являться
важной составной частью анализа информативности данных. В настоящем
разделе приводятся оценки для относительной погрешности идентифика-
ции моделей искажающих систем в классе КИХ-фильтров и БИХ-фильтров,
728
ГЛАВА 10
построенные с использованием оценки (10.60) и неравенств (10.31), (10.33),
(10.35) и (10.36).
Справедливость неравенств (10.33), (10.36) не нарушится, если вместо
числа обусловленности АГ(А) подставить его оценку сверху к* (10.61). При
этом получаем
8С < АГ(А)5Й =-У. _ _ 86, (10.64)
1-7а-Ф)/(1ч-Ф)
где, как и в (10.61), (10.62)
ф=ф-ЛГ4-1, ф G [0,1].
Обращает на себя внимание вычислительная простота этой оценки. Ана-
логичные оценки могут быть построены с использованием соотношений (10.31),
(10.35). Неравенство (10.64) указывает на существование, возможно более глу-
бокой, чем это может показаться на первый взгляд, связи погрешности оце-
нивания с диагональным преобладанием матрицы Грама. Поэтому представ-
ляет интерес построить неравенства, позволяющие осуществлять оценку воз-
можности решения задачи идентификации с требуемой точностью минуя
оценку числа обусловленности и/или минимального собственного значения,
т.е. непосредственно по величине показателя ф диагонального преобладания
матрицы А = ХГХ.
Для установления связи показателя ф и/или ф с погрешностью идентифи-
кации вначале построим соотношения, связывающие этот показатель с допу-
стимыми значениями минимального собственного значения и числа обуслов-
ленности. Для этого будем использовать наиболее сильные из полученных
выше оценок: (10.60) — для числа обусловленности и (10.58) — для собствен-
ных значений.
В частности, подставив в неравенство (10.58) вместо показателя ф правую
часть равенства ф = ф +М-1 и осуществив формальную замену Xmjn на А.доп
после несложных преобразований получаем следующее неравенство:
_ Хлоп (М - 1)(2Тг А - ХДОПМ)
Ф>_=1-------л---------(10.65)
ТгЧ-гТгАЛ.^+А.^М
гае Хдо„ = Я(/|Дс|, =(й?7ЦДс||^1/' ; это получаем на основе неравенств (10.46),
(Ю.47). 7
Для нормированной по правилу А = МА/ТгА матрицы как частный слу-
чай из неравенства (10.65) получаем более простое условие:
(10.66)
10.7. Построение проверочных неравенств для достижимой точности
729
Аналогичное неравенство можно также построить с использованием наи-
более сильной из полученных выше оценок для числа обусловленности. Для
этого произведем в (10.60) формальную замену к* на КДОП(А). После соответ-
ствующих преобразований получаем условие
2*доп(а)
~^о„(А) + 1’
(10.67)
где
^ДОп(А) „ О о ,
6а+6л+\
а , 5Л, 5Л определяются из соотношений (10.34) или (10.37), (10.38).
На рис. _10.12 показаны области допустимых значений для величины ф, гра-
ницы ф = ф(Хдоп) и ф = ф(£доп) которых построены по соотношениям (10.66)
и (10.67). При значениях показателя ф, принадлежащих области выше ука-
занных кривых погрешность идентификации не превышает допустимого зна-
чения. На рис. 10.12*7 показано несколько кривых для 47=2,3,4,5. При
фиксированном Хдоп ординаты кривых растут с ростом М. На основе этих
графиков или непосредственно по соотношениям (10.65), (10.66) может быть
определено допустимое значение приведенной величины диагонального пре-
обладания для каждого заданного Хдоп или /ГД0П(А).
Приведенные соотношения и графики являются еще одним доказатель-
ством тесной связи показателя диагонального преобладания с известными
мерами мульти коллинеарности и/или обусловленности. Однако нас интере-
суют зависимости, связывающие допустимые значения величин фиф непо-
средственно с допустимыми погрешностями идентификации.
Для этого исключим в (10.66) Хдоп заменив его значением, выраженным в
соответствии с (10.46) через |Ас||2 и В результате получаем следующую,
несложную в вычислительном отношении, оценку:
Рис. 10.12. Связь показателя ф с допустимыми мерами: а — Каоп; б — Хдоп
730
ГЛАВА 10
М-1
Ф_М5-1’
(10.68)
где 5 = ||Ас||4 /(2||Дс||2 r£ - .
Величина о может быть рассчитана заранее по априори заданной величине
#2 и допустимому значению нормы вектора ошибок идентификации. Величи-
на 5 может изменяться в пределах М-1 <8<1. Заметим, что если 6 = 1 (при
этом ф = 1), должно также выполняться требование ||Ас|| =||^||"- Это, как и
следовало ожидать, имеет место в случае, когда все собственные значения
одинаковы: lmax = A.min = Х; = 1, i = \,М , а К (А) = 1.
Аналогично предыдущему, подставляя в неравенство (10.67) фигурирую-
щее там же выражение для АГДОП(А), получаем, также простую в вычислитель-
ном отношении, оценку
2(8е8с+8с28д)
Ф“ 82+8^ +28е 8с8л +8282 ’
(10.69)
где 8^- = 8Й + 8л , а 8л, 8Л — указанные в (10.34) или (10.37), (10.38) относи-
тельные погрешности для матрицы А и вектора Ь. Напомним, что погрешно-
сти 5л возникают лишь в ходе вычислений, а 8д включает также и погреш-
ности исходных данных.
Если погрешности, связанные с округлениями в ходе вычислений, суще-
ственно меньше погрешностей в исходных данных, а задача достаточно хоро-
шо обусловлена, то можно считать 8л — 0, при этом = 6Л. Тогда из (10.69),
как частный случай, вытекает следующая оценка:
26А
8?+82
(10.70)
Необходимо иметь в виду, что в данном случае должно выполняться выте-
кающее из (10.39) неравенство 8С >8Й. С учетом этого из (10.70) следует, что
уменьшение величины приведенного показателя диагонального преоблада-
ния до значений близких к нулю (ф -+ 0) свидетельствует о значительном
увеличении погрешности 8(., т.к. при этом должно выполняться 6С>>8Й.
Интересно, что равенство бс = 8й возможно, только при ф=1. Напомним,
что все приведенные в этом разделе оценки могут использоваться лишь для
значений величины диагонального преобладания, удовлетворяющих неравен-
ствам М — 1 <ф<Л/ (ф>0).
Из неравенств (10.68)—(10.70) видно, что оценка возможности достижения
требуемой точности сводится к сравнению величины диагонального преобла-
дания ф = ф — М +1 матрицы Ас некоторой константой, определяемой допу-
стимой погрешностью оценки и заданными погрешностями исходных дан-
ных. Эта константа, определяемая как
10.7. Построение проверочных неравенств для достижимой точности
731
Г| _М -14- Е < ф = М -14-ф, 0 < £ < 1,
(10.71)
может быть вычислена заранее. Тогда задача текущего контроля информатив-
ности предъявленного набора данных сведется к проверке выполнения про-
стого неравенства:
п<Ф(а).
(10.72)
В таблице 10.4 приведена сводка построенных с использованием соотно-
шений (10.68)—(10.70) выражений, которые могут использоваться при опре-
делении величины порога т] в (10.72) для различных типов идентифицируе-
мых моделей.
Величины относительных погрешностей, фигурирующие в таблице 10.4,
определяются по соотношениям в (10.34) или (10.37), (10.38). Иногда сами
относительные погрешности не известны, но может быть задан допустимый
коэффициент Лотн, показывающий во сколько раз относительная погреш-
ность оценивания параметров может превышать погрешность исходных дан-
ных: 8С. = £отн8. Если вдобавок (как это часто имеет место для моделей типа
БИХ-фильтра) выполняется приближенное равенство 8Й=8Л=8, то вели-
чина 8j- = St + 8Л = 28. При этом можно построить более простые выраже-
ния для границ 11,-113. Сводка соответствующих этому случаю формул приве-
дена в таблице 10.5. Расположение пороговых значений по строкам таблицы
такое же, как и в таблице 10.4.
Если исходная матрица X и вектор у перед решением задачи оценки масш-
табированы по правилу X = Х-(ТгА)1/2, у = у *(Тг А)1^2, величина ||Ас||2 не
изменяется, а ||<|| =И2-ТгА. При этом величина kt для масштабированных
данных совпадает со значениями параметра к в аналогичном соотношении,
приведенном в последней строке таблицы 10.4.
В таблице 10.6 приведены результаты расчета порогового значения т]3, кото-
рое может использоваться для контроля информативности данных как КИХ-,
так и БИХ-фильтра при различных размерностях (Л/) задачи. Данные из
Таблица 10.4. Соотношения для вычисления пороговых значений
№ Выражение для вычисления порогового значения Тип фильтра Примечание
1 „ . 28Д п, =М -П—, ь 3 5й2+62 КИХ СП II _oj о ‘V О’ м " II ,05
2 Лг М —1-1 б2+8^ +26Г8,8Л+5,2&д БИХ 8f>5fc, -ьЗЛ
3 Лз к 2Тг2Л - (М -1)2 (к Тг А - МУ Л/—14- — у- к 2Тг2 А + (М -1) (к Тг А - М) КИХ, БИХ det(A) = Ц 1=1
732
ГЛАВА 10
Таблица 10.5. Соотношения для вычисления пороговых значений
№ п. Выражение для вычисления порогового значения Тип фильтра Примечание
1 Л1 м -1+ КИХ ^ОГЦ ~ 1
2 Л2 м , , 2*та(2+* 8) 4(1 + (1 + 52) БИХ ^отн — 1
3 Пз м ^-(М-Г^к.-М}2 к?+(М — 1)(£г — л/)2 КИХ, БИХ к, =А-ТгА = 1^4-‘ТгА> Н М-2
Таблица 10.6. Значения порога Пз Для различных ktn М
Л
К М — 2 Л/= 3 УИ = 4 М=5
1 1,0000 - - -
1,5 1,8000 - - -
2 2,0000 2,0000 - -
2,5 1,9230 2,7778 - -
3 1,8000 3,0000 3,0000 -
3,5 1,6897 2,8824 3,7692 -
4 1,6000 2,6667 4,0000 4,0000
4,5 1,5283 2,4545 3,8571 4,7647
5 1,4706 2,2727 3,5714 5,0000
5,5 1,4235 2,1228 3,2700 4,8400
6 1,3846 2,0000 3,0000 4,5000
таблицы могут непосредственно использоваться для выбора конкретных чис-
ловых значений порога в решающем правиле (10.72). Из таблицы видно, что
гарантирующие высокую точность оценки допустимые значения порогов долж-
ны принимать также высокие значения. Это не всегда достигается, особенно
на полутоновых изображениях. В ряде случаев этого удается добиться про-
стым масштабированием исходной матрицы А = ХТХ по правилу
A = DAD,
(10.73)
где D = diag(fZ1,fZ2»”->^w) — диагональная Л/хЛ/-матрица масштабных коэф-
фициентов dk = Jak>k , к — 1»^ •
10.7. Построение проверочных неравенств для достижимой точности
733
Заметим, что получаемая в результате такого масштабирования матрица,
является матрицей сопряженности (10.49):
a(d) = dad = r.
Пример 10.10. В таблице 10.7 еще раз для сравнения приведен фрагмент
таблицы 10.3 (один столбец с показателем ф(А)), а рядом помещен столбец со
значениями показателя ф(К), рассчитанного после масштабирования тех же
матриц в соответствии с (10.73). Из таблицы видно, что для матрицы, сфор-
мированной по тестовому изображению № 1 (см. пример 6.1), показатель ф(Я)
значительно выше показателя ф(А), в то же время на изображении № 2 на-
блюдается обратное.
Описанный в примере 10.10 эффект не является неожиданным. Ясно, что
если недиагональные элементы матрицы А пренебрежимо малы, по сравне-
нию с диагональными, матрица R становится единичной и для нее ф=1.
Если же после масштабирования показатель ф по-прежнему «не срабатыва-
ет», это свидетельствует о сильном влиянии мультиколлинеарности. Это вов-
се не означает, что задача оценивания не может быть решена с требуемой
точностью, а может означать, что на данной конкретной реализации следует
использовать другие более сильные оценки, например, основанные на вычис-
лении показателя сопряженности с нуль-пространством 5min. Объем вычисле-
ний при этом, конечно, неизмеримо больше. Но это неизбежная плата за
эффективность оценок. Утешением в данном случае является неоспоримый
факт меньшей, по сравнению с показателем максимальной сопряженности,
вычислительной сложности метода на малых наборах данных. Тем не менее,
использование показателя сопряженности с нуль-пространством может быть
оправдано лишь высокой стоимостью риска, связанного с возможными ошиб-
ками оценивания.
В заключение отметим, что применение процедур анализа обусловленности
в задачах обработки изображений может преследовать разные цели. Если предъяв-
ленный фрагмент изображения явля-
ется единственным, то результаты срав- „ , .... ’ J Таблица 10.7. Сравнение ф(А) и ф(К) нения допустимых пороговых значений
с фактическими значениями мер обус- ловленности и/или мультиколлинеар- ности являются лишь констатацией факта (хорошей или плохой) его ин- формативности. Иногда преследуется цель подыс- кать на изображении наиболее под- ходящие для решения задачи идеи- тификации фрагменты. Тогда анализ № ф(А) ф(И)
1 2,53024 4,26353
2 1,91591 1,88864
3 1,16107 1,15292
4 1,21001 1,21259
5 1,00000 1,00000
информативности должен заключаться в сравнении показателей диагонально-
го преобладания на различных фрагментах и отборе тех из них, для которых он
734
ГЛАВА 10
оказался выше по сравнению с другими или заданными порогами. Такая
задача рассматривалась, например, в работе [25].
10.8. Общие принципы и схема построения оценок по малому
числу наблюдений
После того как установлено, что сформированный набор данных инфор-
мативен, можно перейти к решению собственно задачи построения оценок.
В рамках статистической теории критерий качества оценки задается на ос-
нове априорной информации о распределении ошибок [30]. Если такая ин-
формация отсутствует, выдвигается какая-либо правдоподобная априорная
гипотеза относительно распределения ошибок, а построенная на ее основе
процедура подвергается статистическим испытаниям с целью уточнения ве-
роятностной модели. При решении задачи оценки по одному малому набору
данных такая возможность отсутствует. При этом возникают следующие прин-
ципиальные вопросы.
1. Какая априорная информация должна и может использоваться для по-
лучения оценок?
2. Если такая информация имеется, то какая схема построения оценок
наиболее приемлема с точки зрения эффективного использования этой ин-
формации?
Из выражения (10.7) для МНК-оценок видно, что источником погрешно-
стей в оценках параметров могут быть плохая обусловленность матрицы А и
наличие в исходных данных ошибок (измерений). Однако наличие обоих ука-
занных факторов не означает, что мы обречены на неудачу. Для того, чтобы
понять почему это может быть, вначале приведем один известный интерес-
ный результат [8].
Пусть с — МНК-оценка (10.7) векторного параметра с, удовлетворяющего
уравнению (10.6), а % = у —Хс — соответствующий этой оценке вектор невя-
зок (10.8). Тогда справедливы равенства
T^T^ToY (10.74)
где То — фигурирующая в (10.12) Nx(N-М)-матрица, составленная из нор-
мированных собственных векторов, соответствующих нулевым собственным
значениям матрицы ХХГ. Равенство (10.74) утверждает, что проекции вектора
ошибок и вектора невязок £ на собственные векторы, образующие нуль-
пространство матрицы Хт совпадают. Доказательства равенств (10.74) можно
найти в работе [8].
Еще раз обратимся к геометрической интерпретации МНК (рис. 10.5). Из
рисунка видно, что при сделанном предположении (10.27) об ограничении
нормы вектора ошибок свойства оценок параметров определяются лишь
его ориентацией вектора относительно пространства столбцов матрицы X.
10.8. Общие принципы и схема построения оценок по малому числу наблюдений
735
В частности, если он ортогонален этому пространству, ошибка оценки отсут-
ствует. Ясно, что получающийся при этом вектор невязок совпадет с векто-
ром ошибок, что следует также и из равенств (10.74).
Если же вектор т.е. является линейной комбинацией векторов
измерений, ошибка оценки может оказаться значительной, хотя вектор невя-
зок при этом равен нулю. При этом левые и правые части равенств (10.74)
одновременно обращаются в нуль. Из приведенных геометрических сообра-
жений, в частности, следует, что само по себе большое значение нормы век-
тора невязок еще не может служить достаточным основанием для предполо-
жения, как это иногда считают, о большой величине ошибки оценивания,
как, впрочем, не всегда обоснован также критерий минимума нормы вектора
невязок.
Теперь обсудим вопрос формирования эффективной схемы оценки. Из
рис. 10.5 видно, что улучшить точность оценок на конкретной реализации
можно либо изменив (уменьшив) длину вектора либо изменив его ориен-
тацию относительно пространства столбцов матрицы X. Это можно сделать
как корректировкой только вектора у, так и путем одновременной деформа-
ции матрицы X и вектора у. С точки зрения вычислительной простоты целе-
сообразно использовать для этого простейшие линейные преобразования ис-
ходных данных.
Будем рассматривать следующие два типа преобразований.
1. Непосредственная корректировка вектора выхода модели:
У = у-|, (10.75)
где 2, — так называемый корректирующий вектор.
2. Преобразование взвешивания:
y = Gy, X = GX, (10.76)
где G = diag(gj ,g2> — диагональная матрица. В п.10.10 мы покажем,
что при определенных требованиях должны также выполняться условия:
G2 = GrG>0, detG^O. Заметим, что при этом неизвестный вектор оши-
бок также преобразуется в
< = G^. (10.77)
Практическая реализация геометрически совершенно очевидного способа
повышения точности оценок путем преобразований (10.75), (10.76) наталки-
вается на все те же трудности: отсутствие априорной информации. Некото-
рую надежду хотя бы что-то узнать о векторе ошибок дают равенства (10.74).
Конечно, из факта равенства проекций векторов ошибок и невязок на
базис нуль-пространства не следует равенство их компонентов. Тем не ме-
нее, в /V-мерном пространстве исходных измерений можно указать множе-
ство близких к соответствующим векторам невязок векторов ошибок «почти»
принадлежащих нуль-пространству. Такая близость может также иметь место
736
ГЛАВА 10
для достаточно большого множества векторов ошибок, имеющих промежу-
точное положение (по отношению к пространству столбцов матрицы X и нуль-
пространству матрицы Хг), если какой-либо компонент вектора ошибок зна-
чительно превосходит по абсолютной величине остальные. Тогда, как видно
из (10.74), его влияние на формирование вектора проекций будет определяю-
щим и, следовательно, соответствующий компонент вектора невязок, скорее
всего, также будет выделяющимся.
Указанная близость компонентов носит случайный характер. Поэтому как
только мы потребуем, чтобы эта информация использовалась в ходе оценки,
нам понадобятся априорные вероятностные модели. Вероятностная природа
этих моделей, к сожалению, пока недостаточно изучена. Однако есть основа-
ния предполагать, что близость некоторых компонентов векторов ошибок и
невязок в основном определяется их сравнительной величиной. Поэтому в
ряде случаев они могут быть заданы в виде ограничений, аналогичных огра-
ничению на значение нормы вектора ошибок (10.27), (10.29).
Если в качестве источника дополнительной информации мы хотим ис-
пользовать вектор невязок (10.8), то схема оценки должна быть итерацион-
ной. На первом шаге этой схемы должна вычисляться МНК-оценка (10.7).
Затем с использованием дополнительной информации, содержащейся в не-
вязках, осуществляется преобразование типа (10.75) и/или (10.76) и вычисля-
ется новая (МНК) оценка:
с = [хгх]-1Ху. (10.78)
Вычисление оценок и преобразование могут повторяться несколько раз.
Правило остановки может заключаться в сравнении меры близости оценок на
соседних шагах с заданным порогом. Ошибка на каждом шаге зависит от
того, насколько удачно построено очередное преобразование данных.
В рамках указанной схемы оценки основными являются следующие во-
просы.
1. Всегда ли возможно достижение требуемой точности оценивания на
любом заданном наборе данных X, у с использованием указанных преобразо-
ваний данных?
2. Если требуемая точность достижима, то насколько возможно для по-
строения этих преобразований использовать текущие значения векторов не-
вязок £?
3. И, наконец, как должны строиться указанные преобразования?
Подчеркнем, что применение итерационной схемы оценки вовсе не ис-
ключает использования априорной статистической информации, если такая
имеется. Однако чаще всего при малом числе наблюдений такая информация
ненадежна. При построении указанных преобразований гораздо большую
пользу может принести непосредственный детальный анализ конкретного
фрагмента (например, формы и геометрических размеров регистрируемых
объектов, допустимых функций яркости на объектах и др.).
10.9. Построение оценок путем непосредственной корректировки вектора выхода модели 737
В связи с последним замечанием следует также развеять часто имеющее
место мнение, что обработка малых объемов данных требует меньшего объе-
ма вычислений. Если априорная информация бедная, то для достижения та-
кой же, как и на большой выборке точности может потребоваться гораздо
больше вычислений (переборов), прежде чем удастся подобрать подходящее
преобразование. Не заплативший за измерения, должен заплатить за вычис-
ления. К счастью, именно в силу малого числа наблюдений появляется воз-
можность непосредственного анализа каждого отсчета и их верификации с
учетом информации, получаемой от различных источников.
10.9. Построение оценок путем непосредственной корректировки
вектора выхода модели
Принципиальная возможность повышения точности оценок на каждой кон-
кретной реализации путем корректировки (10.75) не вызывает сомнений.
Интуитивно ясно, что если удастся «угадать» корректирующий вектор так,
чтобы выполнялось = £, то искомые параметры модели будут определены
точно. Заметим, что задача восстановления (устранения шумов) изображе-
ний, которая часто решается на этапе предварительной обработки изображе-
ний, по существу, и есть корректировка вектора выхода модели.
Можно показать, что в R (X) существует множество проекций корректиру-
ющих векторов для которых ||Дс||2 >||Ас||2 , где [|Дс||2 — норма вектора
ошибок оценки по скорректированным данным. Компоненты w(, этих векто-
ров, определяемых как w = ТГ|, удовлетворяют неравенству
м м
EX’Ч -2£ Хг'у. и,. <0. (10.79)
i—1 (=1 '
где v, — компоненты вектора (проекции) v =ТГ£, а Х(- — собственные зна-
чения матрицы Грама. Неравенство (10.79) неконструктивно в том смысле,
что оно указывает лишь на существование корректирующих векторов, обес-
печивающих повышение точности, но не дает способ их построения. Ока-
зывается, однако, что дополнительные возможности для корректировки
появляются в ходе оценки в рамках описанной выше схемы. Необходимая
дополнительная информация для этого содержится в невязках, вычисляемых
на промежуточных шагах оценки.
Пример 10.11. Приведем результаты, полученные в эксперименте [27]. Ис-
ходный набор исходных данных задавался в виде произвольной, случайным
образом формируемой матрицы X и вычисляемого при заданном с вектора у
модели вида (10.6) (7V= 15, Л/~5). Набор реализаций векторов ошибок
генерировался в виде смеси случайных чисел с произвольными законами рас-
пределения. Число реализаций векторов ошибок, на которых проводился экс-
перимент, равнялось 1000.
738
ГЛАВА 10
Таблица 10.8. Связь векторов ошибок
и невязок
№ комп. Среднее СКО к{ Относит, число сов- падений знаков
1 0,961 0,352 0,986
2 1,240 2,430 0,967
3 1,599 3,769 0,923
4 2,583 11,448 0,856
5 3,960 11,699 0,807
6 8,127 32,767 0,708
7 9,328 26,793 0,676
8 11,847 37,639 0,630
9 9,882 29,474 0,634
10 7,192 23,666 0,709
И 3,846 11,032 0,810
12 2,524 13,851 0,878
13 1,502 3,902 0,926
14 1,099 0,519 0,976
15 0,966 0,336 0,986
Для каждой реализации строилась МНК-
оценка (10.7) параметров модели, рассчи-
тывались невязки (10.8) и из компонентов
вектора невязок строился вариационный ряд
i1<^<...<u,<e,<ii+1<...<eI3. ис-
пользуя эти данные, рассчитывались набо-
ры коэффициентов связи для
которых затем вычислялись среднее и сред-
неквадратичное отклонение (СКО). Кро-
ме того, для одноименных компонентов
векторов ошибок и невязок вычислялось
относительное число совпадений знаков.
Количественные характеристики связи
между компонентами этих векторов при-
ведены в таблице 10.8. Из таблицы видно,
что максимальные по абсолютной величине
компоненты вектора невязок (первая и пос-
ледняя строки таблицы) имеют значения
близкие к соответствующим элементам век-
тора ошибок, а их знаки совпадают в подав-
ляющем большинстве случаев.
Приведенный пример подтверждает вы-
сказанное нами ранее предположение о близости выделяющихся компонентов
векторов ошибок и невязок и возможности использования этой информации
для итерационного уточнения оценок. Опираясь на этот пример, рассмотрим
возможность формирования корректирующего вектора по правилу
^=g£, (10.80)
где G = diag(gj ,g2,т.е. путем простого умножения компонентов век-
тора невязок на соответствующие коэффициент (вещественные числа).
Если вектор получается из вектора невязок £ путем умножения какого
его компонента на коэффициентgh то его можно представить в виде = Е g,
где Е — диагональная jVk/V-матрица, составленная из компонентов вектора
невязок (порядок следования двойных индексов такой же, как и для исходного
вектора невязок), a g — вектор коэффициентов «связи», компонентами которо-
го, наоборот, являются элементы диагональной матрицы G. Если среди компо-
нентов вектора невязок отсутствуют нулевые, то с использованием фигурирую-
щих в (10.79) проекций w из последнего равенства следует, что
g = E-,Tw.
Здесь компоненты вектора w должны удовлетворять (10.79).
Условия, при которых возможно построение диагональной матрицы для
преобразования вектора невязок в корректирующий вектор, вообще говоря,
10.9. Построение оценок путем непосредственной корректировки вектора выхода модели 739
очевидны. Тем не менее, последнее равенство полезно, тж. акцентирует вни-
мание на том, что если невязки близки к нулю, ничего скорректировать нельзя.
Рассмотрим теперь один из методов построения корректирующего векто-
ра. В методе эксплуатируется связь выделяющихся компонентов, а также мо-
жет использоваться информация из других источников. Задача заключается в
построении корректирующего вектора £ или вектора поправок А2, ——по
вектору невязок £ для каждого фиксированного набора данных. Из рис. 10.13
видно, что при использовании любого из указанных корректирующих векто-
ров (или Д£,) точность оценки будет одинаковой.
Предположим, что с использованием характеристик связи ошибок и невя-
зок или путем дополнительных более точных измерений нескольких отсчетов
удалось задать ровно М (любых) компонентов вектора достаточно близки-
ми к соответствующим компонентам вектора ошибок Из соображений удоб-
ства изложения эти М компонентов путем перестановки и перенумерации
строк сделаем первыми, а соответствующий им вектор, являющийся состав-
ной частью вектора обозначим
Введем в рассмотрение (У-Л/)х1 -вектор £,нМ, составленный из оставших-
ся компонентов вектора £, которые нам пока не известны. Корректирующий
Ух 1-вектор £ = ^tv-л/] представляет собой прямую сумму векторов и
. Задача заключается в определении недостающих компонентов, т.е. век-
тора по известным Л/компонентам вектора ^м.
Будем искать вектор из условия
Тог(М) = О.
Основанием для этого служат следующие соображения. В соответствии с
(10.74) ТО^ = ТОГ£. Следовательно, если компоненты вектора £, совпадают с
истинными значениями компонентов вектора ошибок: то корректи-
рующий вектор А^ = £ — £ = , удовлетворяющий этому равенству, бу-
дет ортогонален нуль-пространству. Свойство ортогональности вектора АЁ,
с нуль-пространством сохранит-
ся и в случае, когда это равен-
ство приблизительное: Та-
ким образом, реализация указан-
ного условия позволит оценить
составляющую вектора ошибок,
принадлежащую пространству
столбцов матрицы X.
Рис. 10.13. Геометрическая интерпретация
метода корректировки вектора выхода мо-
дели
740
ГЛАВА 10
С использованием ортогональной матрицы То, построенной для матрицы
X, которая уже подверглась перестановке и перенумерации строк так, что ее
первые М строк соответствуют М компонентам вектора а последние —
N-М компонентам вектора в соответствии с указанным выше услови-
ем сформируем следующую систему уравнений:
~ *0,М‘
(10.81)
Здесь — матрица составленная из последних N-М столбцов матри-
цы Tq . Вектор t0 A/ размерности (N-M)*\ формируется в соответствии с ра-
венством
*о,м =Т0<- ТодДду,
где Tq M — (7У-Л/)хЛ/-матрица, составленная из первых М столбцов той же
матрицы Тр .
Так как Rank То = (N-М), существует единственное решение системы
(10.81), а искомый вектор определяется как
%>N-M —
(10.82)
Заметим, что при задании компонентов вектора равными соответству-
ющим компонентам вектора невязок: =Км , ва( 10.82) будут получены ос-
тавшиеся компоненты вектора невязок: =^N_M. Это не удивительно,
т.к. задавая компоненты подоб-
Об работка изображу
связана с решение!/
кик задач, в которы:
входные, и выходны
ные являются изобр
ниями. Одним из пр
ров служат системы
редачи изображены
оазоабогчики стал»
а
• pm»*'»'**
мм i• впи/м:
4WM — J—IV» мв4р
«•мм Оввамм
б
Рис. 10.14. Тестовые изображения: а — исходное,
б— искаженное
ным образом, мы не вносим ни-
какого нового знания. Для того
чтобы улучшить результат оцен-
ки, мы должны в компоненты век-
тора «вложить» дополнитель-
ное знание. Это могут быть лю-
бые априорные сведения, в т.ч.
показанная в примере 9.1 связь
между реализациями £ и Ниже
приводится пример, в котором ис-
пользовался описанный метод.
Пример 10.12. Использовались
показанные на рисунках 10.14л и б тестовые изображения. Изображение
(рис. 10.146) получено путем моделирования искажений с использованием
БИХ-фильтра порядка (2,2), который описывается передаточной функци-
ей вида
^(z„z2) = B(zi»z2)/a(z1,z2),
10.9. Построение оценок путем непосредственной корректировки вектора выхода модели 741
где
^(zl»z2) = ^00 +*10*1 +k-10zl +^01Z2 ^~^0-lZ2
+^11Z]Z2 +£_]_]Z] Z2 + ^1-1Z]Z2 z2*
^(zi,z2) = l + eioZi +«-ioZi 1 +aoiz2 +flo-iz2 +
+«nZiZ2 +a_i-iZ^lZ2l +0i-iZJz^1 +a_nZilz2.
Переменная Zi соответствует горизонтальному направлению на изображе-
нии, a Z2 — вертикальному. Параметры передаточной функции задавались
так, чтобы обеспечивалась радиальная симметрия искажений:
= ^01 ~ *-10 = *0-1 ’ *11 ~ *1-1 = *11 ~ *-1-1 ’
«ю ~ floi = °-ю ~ яо-1» а11 = fll-l =аи= fl-i-i •
При выполнении указанных условий полиномы числителя и знаменателя
представляются в следующем компактном виде:
^(zi,z2) = h0[l+*i(zi H-zf1 + z2 + z2 + гГ'г21 + zjz21 +гГ'г2)|,
A(zi,z2) = l + fli[zi +zf’ + z2 +z^,)+<22(z1z2 Ч-гГ’гг1 4-ZjZ^1 + гГ’г2),
где bQ= 0,02834, bj=l,2, &2=0,27, ax= —1,2, д2=0,27.
В соответствии co схемой идентификации задача решалась итерационно.
Вначале строилась МНК-оценка. С ее использованием вычислялся вектор
невязок и задавался вектор . Затем с использованием полученного вектора
невязок в соответствии с (10.82) вычислялся корректирующий вектор осу-
ществлялась корректировка вектора у и вновь вычислялась МНК-оценка.
Оценивались 5 параметров фильтра (b0, bx, b2i ах, а2) на фрагменте,
содержащем 24 наблюдения. Ошибки формировались в виде векторов одина-
ковой длины с произвольной ориентацией относительно пространства матри-
цы X. Это достигалось соответствующей нормировкой векторов ошибок, име-
ющих случайное направление. Для одноименных компонентов векторов оши-
бок и невязок подсчитывались: число совпадений знаков; усредненные по
100 реализациям отношения одноименных компонентов и сумма квадратов
отклонений этих отношений от найденного среднего значения.
Полученные результаты приведены в таблице 10.9. Номера компонентов в
первом столбце таблицы упорядочены по убыванию их абсолютных значе-
ний. Из таблицы видно, что выделяющимся компонентам вектора ошибок
соответствуют выделяющиеся компоненты (с тем же знаком) вектора невя-
зок, а коэффициент связи между ними достаточно устойчив.
Для того, чтобы показать возможность увеличения точности идентифика-
ции по мере более точного задания небольшого числа (в данном случае 5)
742
ГЛАВА 10
Таблица 10.9. Связь реализаций ошибок и невязок для модели БИХ-фильтра
№ п./п. Относи- тельное число сов- падений знаков Отноше- ние мч Дисперсия отношений № п./п. Относи- тельное число сов- падений знаков Отноше- ние Ы/Н Дисперсия отношений
1 0,992 0,994 0,073 13 0,816 1,2514 1,436
2 0,975 0,987 0,177 14 0,841 1,3291 1,549
3 0,983 1,0480 0,210 15 0,750 1,3395 2,198
4 0,933 1,0167 0,288 16 0,791 1,5177 3,362
5 0,933 1,0689 0,414 17 0,699 1,4881 3,915
6 0,942 1,0962 0,483 18 0,675 1,9899 8,199
7 0,908 1,0250 0,516 19 0,741 2,0329 6,805
8 0,949 1,0065 0,561 20 0,649 2,3555 24,24
9 0,883 1,1810 0,811 21 0,733 3,0389 52,83
10 0,891 1,1005 0,776 22 0,592 3,9789 87,83
11 0,850 1,2369 1,162 23 0,467 5,4769 276,9
12 0,808 1,2023 1,519 24 0,433 12,956 64387
компонентов вектора , в этом эксперименте указанные компоненты зада-
вались с возрастающей точностью в соответствии с формулой
=1,4а£м+(1-1,4)а£м.
Уточнению подвергались 19 компонентов корректирующего вектора по за-
данным 5 компонентам. Для сравнения точности оценивания при различных
а использовалась скалярная характеристика ||Дс||2/||с||2, где ||Ас||2 и ||с||2 —
евклидовы нормы векторов ошибок оценивания и параметров модели соот-
ветственно. Результаты приведены в таблице 10.10.
Из таблицы 10.10 видно, что при задании компонентов вектора равны-
ми невязкам (а = 0) повышения точности, по сравнению с МНК, как и сле-
довало ожидать, не происходит. Однако по мере более точного задания этих
компонентов происходит увеличение точности и при = ^м (а = 0,71) ошиб-
ка составляет всего лишь около одного процента. Эта ошибка связана с неиз-
бежными погрешностями округления. Заметим, что погрешность МНК-оце-
нок при этом составляет почти 20%.
Пример 10.13. Этот пример является продолжением примера 10.11, в ко-
тором были приведены результаты исследования связи выделяющихся ком-
понентов векторов ошибок и невязок. Эксперимент проводился по той же
схеме. Для построения корректирующего вектора использовались М ком-
понентов вектора , соответствующих наибольшим по абсолютной вели-
чине невязкам. Они задавались с использованием коэффициентов связи,
приведенных в таблице 10.8. В качестве меры точности оценок на каждом
шаге использовалась евклидова норма отклонения оценки от точного значения
10.9. Построение оценок путем непосредственной корректировки вектора выхода модели 743
Таблица 10.10. Связь точности оценки с точностью задания вектора
Параметр Параметры модели БИХ-фильтра к
а Ьг Ьг «1 а2 н2
Параметры 0,028340 0,034008 0,007652 -1,200000 0,270000
МНК-оценки 0,022962 0,057481 0,006793 -1,029265 0,114629 0,189
а=0 0,023002 0,057663 0,006808 -1,026394 0,111991 0,191
а=0,14 0,024483 0,050960 0,008005 -1,067358 0,149081 0,147
о =0,28 0,026047 0,044293 0,009344 -1,105419 0,183520 0,104
а=0,42 0,027685 0,037637 0,010813 -1,141070 0,215756 0,065
cy~0,56 0,029445 0,031336 0,012390 -1,169678 0,241525 0,034
а=0,71 0,031265 0,025105 0,014061 -1,195811 0,265037 0,011
а=0,86 0,033172 0,019205 0,015788 -1,216209 0,283283 0,022
а=1 0,035153 0,013615 0,017550 -1,231559 0,296894 0,039
вектора параметров |Ас*| =||с —с*||, а так же вычислялись нормы отклоне-
ния от обычных МНК-оценок ||Дс^1|к|| = ||см||к — с*|| и нормы отклонения
оценок на соседних шагах ||Ас*|| = ||с* — с*-1||. Результаты оценки приведе-
ны в таблице 10Л (здесь к номер шага итерационной схемы).
Из таблицы 10.11 видно, что корректиров-
ка уже на втором шаге приводит к заметному
улучшению точности оценок и далее качество
оценок не изменяется. Этот и другие экспе-
рименты показывают, что для корректировки
в соответствии с описанным методом, как пра-
вило, достаточно одного шага. Тем не менее,
как видно из (10.82) объем вычислений дос-
таточно большой.
Таблица 10.11. Нормы разностей
оценок, при корректировке всех
компонентов
к KI |Дс* II 1 мнк|| м
1 0,6566
2 0,4465 0,2489 0,2489
3 0,4465 0,2489 0
Рассмотрим другой, не требующий большого числа вычислений, способ
корректировки. Корректирующий вектор на каждом шаге итерационной схе-
мы строится в виде £ = [о,...,оДл,О,...,о], где к: | = max |.
Другими словами, корректируется только один компонент вектора вы-
хода модели с номером, равным номеру наибольшей по абсолютной ве-
личине невязки. С учетом данных предварительных исследований вы-
бранный компонент может умножаться на соответствующий коэффици-
ент связи. Ниже приводится пример, иллюстрирующий работоспособность
указанной процедуры.
Пример 10.14. Процедура с корректировкой на каждом шаге итерацион-
ной схемы лишь одного выделяющегося компонента исследовалась на тех
же исходных данных, которые использовались для модели в примере 10.13, а
744
ГЛАВА 10
для оценки качества алгоритма вычислялись те же меры точности. Результаты
приведены в таблице 10.12.
Эксперимент повторялся на 500 реализациях исходных данных. При фор-
мировании вектора ошибок намеренно, но случайным образом, вводился
один выделяющийся (большой по абсолютной величине) компонент. После
Таблица 10.12. Точность оценок
к к *11 |Дсмнк|| м
1 0,6566
2 0,4494 0,2543 0,2543
3 0,3827 0,3562 0,1018
4 0,3606 0,3970 0,0407
5 0,3527 0,4133 0,0163
6 0,3497 0,4198 0,0065
7 0,3486 0,4224 0,0026
8 0,3481 0,4235 0,0010
9 0,3479 0,4239 0,0004
10 0,3478 0,4241 0,0001
каждого эпизода оценивания анализи-
ровался факт улучшения точности оце-
нок. В эксперименте зафиксировано
улучшение по сравнению с МНК-оцен-
кой в 406 случаях из 500, что свидетель-
ствует о достаточной высокой устойчи-
вости наблюдаемого эффекта.
Последний пример подтверждает воз-
можность повышения точности оценок
путем последовательной корректировки
одного выделяющегося компонента век-
тора выхода модели. Из таблицы 10.12 вид-
но, что имеет место заметный выигрыш в
точности по сравнению с начальной
МНК-оценкой, хотя для этого, по суще-
ству, не используется никакая априорная информация кроме знания о том, что
выделяющиеся компоненты векторов ошибок и невязок близки по величине.
10.10. Построение алгоритмов оценки по методу
взвешивания
В настоящем разделе мы рассмотрим построение итерационных алгорит-
мов оценки, в которых на промежуточных шагах осуществляется линейное
преобразование типа взвешивания (10.76). Напомним, что оно заключается
в том, что исходная матрица X и вектор у умножаются на диагональную
NxА-матрицу G. При рассмотрении вопросов построения этой матрицы мы
будем предполагать, что одним из описанных в п.10.5 способов установлено,
что Rank X = М. Поскольку возможность повышения точности этим спосо-
бом на любой конкретной реализации, вообще говоря, не очевидна, вначале
получим условия, при которых это возможно.
Предположим, что на некотором этапе идентификации получена МНК-оцен-
ка (10.7). Для квадрата евклидовой нормы ошибки идентификации, соответ-
ствующей этой оценке, (10.21) имеет место равенство
ИАсЦз = Ac7Ac = ^x[x7xjx7^.
Пусть также каким-то образом задана диагональная матрица
G =diag(g1 ,g2,...,gN I, и после линейного преобразования данных (10.7)
10.10. Построение алгоритмов оценки по методу взвешивания
745
y=Gy, X = GX построена новая оценка, для которой мера близости по
аналогии с предыдущей имеет вид
ЦДсЦ* = ДсгДс = £7х[х7х]х7’<.
(10.83)
Зададимся вопросом: всегда ли можно при произвольном, но фиксирован-
ном векторе ошибок £ подобрать диагональную матрицу G так, чтобы при
этом выполнялось неравенство
'ДСг^Де:*.
Нетрудно заметить, что неравенство (10.83) эквивалентно требованию не-
отрицательной определенности квадратичной формы:
х[хгх] 2x7’-g7’x[x7’x] 2XrG$>0.
(10.84)
Проанализируем, в каких случаях это возможно.
Вновь воспользуемся ортогональной WxЛ-матрицей Т = [Т\:Т0] (10.12).
Учитывая блочную структуру этой матрицы, а также свойства
Тхх[х7’х]"2х7'тх = Л“|,
ХгТо=0 (ТогХ-0), T?fGfVGTz =Л
где V ~х[хгх| Хг. Неравенство (10.84) можно переписать в виде
0
TorGrVGTx
TxGrVGT0
T0rGrVGT0
Тг£<0.
Здесь ^т=^[тк;т0]=[^тхлгт0|> а тЧ = [тхЧ,ТоЧ]Г
С учетом блочной структуры матрицы, фигурирующей в последнем нера-
венстве, квадратичную форму (10.84) можно представить в виде
5t[t0T07G7VGTjT/' +TATjG7VGT0T07' +T0T07'G7'VGT0T07']§<0. (10.85)
На основе (10.85) можно сделать следующие выводы. Если вектор оши-
бок £ принадлежит нуль-пространству матрицы ХГ(Т^£, —0), то никаким
выбором весовой матрицы нельзя улучшить точность оценок. Действитель-
но, матрица T0Tq GvGT0Tq неотрицательно-определенная (по построению),
746
ГЛАВА 10
и все ее собственные значения могут обращаться в нуль лишь при G — оЕл,,
где а любое число, а Ел-— единичная Л/х/У-матрица. При этом квадратичная
форма (10.85) принимает вид £zT0Tq х[хгх] XrToTQ^ = 0. Для всякой дру-
гой весовой матрицы G собственные значения указанной матрицы неотрица-
тельны и указанное неравенство (10.85) (для отличающегося от нулевого) век-
тора ошибок невозможно.
Этот вывод не является неожиданным. Действительно, в случае, когда
£ е N(XT), в соответствии с (10.24), ошибка идентификации равна нулю, а вся-
кое изменение ориентации вектора ошибок относительно пространства столб-
цов матрицы X может лишь ухудшить качество оценки. Если £, G R (X), то с
изменением весовой матрицы G также ничего сделать нельзя. Этот вывод оче-
виден, т.к. при Tg £ = 0 все слагаемые в левой части (10.85) обращаются в нуль.
Во всех остальных случаях (Т^^О, Т(^^0) в классе диагональных мат-
риц (включая вещественные и комплексные с чисто мнимыми элементами)
всегда можно подобрать, и притом не единственную, матрицу G, для которой
в (10.85) будет иметь место строгое неравенство. Для того чтобы убедиться в
этом, рассмотрим условие, при котором вектор ошибок идентификации по
преобразованным, в соответствии с равенствами (10.84), данным, равен нулю:
Xr| = XrG4=0.
Так как матрица G2 диагональная, в последнем равенстве ничего не изме-
нится, если мы представим его в виде
XrE-z = 0,
(10.86)
где д — диагональная матрица, составленная из компонентов вектора оши-
бок так, что цифры индексов матрицы совпадают с цифрами индексов соот-
ветствующих компонентов вектора S = diag(^I,^2,...,^/v), az - /Vxl-век-
тор-столбец, компоненты которого, наоборот, составлены из элементов диа-
гональной матрицы G = diag^ , притом так, что z(- = g?, i = \,N .
По предположению вектор и матрица X фиксированы, следовательно
последнее равенство (10.86) можно интерпретировать как недоопределенную
систему уравнений с заданной Mx/V-матрицей XrS и N неизвестными ком-
понентами вектора z. Для получения какого-то решения этой системы N-M
компонентов вектора z могут быть заданы. ___
С учетом того, что должно выполняться = gj, i = \,N, зададим их веще-
ственными и положительными. Если Rank X = М, то задаваемые компоненты
всегда могут быть подобраны так, что будет существовать решение системы
(10.86) относительно оставшихся М компонентов. При этом возможно, по
крайней мере, два варианта решения: 1) все М компонентов неотрицательны;
2) среди полученных М компонентов имеются (или даже все) отрицательные.
Первый вариант приводит к получению вещественной диагональной весо-
вой матрицы G = diag(g1,g2,—>#Jv) • Он возможен, если в N-мерном про-
странстве существует множество Z точек, z; е Z:
10.10. Построение алгоритмов оценки по методу взвешивания
747
Z = (z:h^z = 0, i=l,M, =M1,xy^,...,x^jV],
г it —1 (W-87)
z = [z1,z2,...,zjV] , Zj>0, 7 = l,2Vk
Ясно, что это требование может выполняться не всегда.
Во втором случае решение существует всегда. Однако среди элементов мат-
рицы G, в силу равенств zi — g2, i = 1,/V, мы должны допустить комплексные
числа, лежащие на мнимой оси (с нулевой вещественной частью). Следова-
тельно, если Хг^0, с использованием множества чисел, лежащих только
на мнимой и/или вещественной оси комплексной плоскости, всегда можно
построить, и притом не единственную, диагональную матрицу G такую, что
X^ = XrG4 = 0.
Заметим, что комплексность весовой матрицы G, вообще говоря, не
создает вычислительных проблем. Дело в том, что для формирования сис-
темы уравнений (10.13) фактически используется не исходная матрица
G =diag(g1,g2,...,g/v), a G2, элементы которой всегда вещественны и при-
нимают отрицательные значения лишь в случае, когда соответствующий
элемент исходной матрицы G оказывается на мнимой оси комплексной
плоскости. Однако получающаяся при этом матрица Хл, уже не является
матрицей Грама, и для нее нельзя построить оценки точности, приведен-
ные в п.10.7. Для того, чтобы это свойство не нарушалось, мы должны
потребовать выполнения условий G2 — GrG >0, detG ^0, о которых уже
упоминалось в (10.76).
Пример 10.15. Покажем образование множества (10.87) точек z€ Z для слу-
чая, когда размерности пространства параметров и пространства исходных на-
блюдений соответственно равны М = 2 и 3. В примере используются следу-
ющие исходные данные.
Матрица X и соответствующая ей матрица А = ХГХ имеют следующий вид:
0,691234
X = -0,70629
0,384033
1,072726
-0,302148 - 0,796138
1,067942 -0,251647
-0,251647 1,932058
Собственные значения матрицы А (ненулевые собственные значения мат-
рицы XX7), соответственно, равны =1, А2 = 2, а соответствующие им
ортогональные матрицы имеют вид
F =
0,965431 -0,260658
0,260658 0,965431
T = [TJ т0]=
0,767440
-0,402260
-0,499223
0,134762
0,862489
-0,487804
0,626798
0,307084
0,716117
748
ГЛАВА 10
Здесь и далее для матриц используются те же обозначения, что и в тексте.
Вектор ошибок формировался в виде взвешенной суммы векторов
§ = а§п+(1-а)§го,
принадлежащих пространству столбцов матрицы X:
=[0,637953 0,325431 -0,697933]
и нуль-пространству матрицы Хт:
=[0,626798 0,307084 0,716117]Т,
где а — некоторое положительное число (0<а< 1).
На рис. 10.15. показана область значений параметра а, для которой суще-
ствует вещественная диагональная весовая матрица G, обеспечивающая нуле-
вую ошибку идентификации. Множество векторов, для которых это, возмож-
но, образует внутренность конуса, граница которого соответствует предель-
ному значению параметра а = 0,5. Ясно, что каждому вектору, принадлежащему
внутренности конуса в верхней полусфере, соответствует вектор х противопо-
ложного направления в нижней полусфере.
Приведенная геометрическая интерпретация, еще раз наглядно иллюстри-
рует тот факт, что наиболее сложная ситуация при оценке по методу наи-
меньших квадратов возникает в слу-
чае, когда е /?(Х). При этом, если
мы хотим сохранить «хорошие»
свойства матрицы Грама, то ника-
ким выбором вещественной весо-
вой матрицы G нельзя повысить
точность оценок параметров. Воз-
можный путь повышения точности
идентификации в этом случае мо-
жет заключаться только в непосред-
ственной корректировке вектора у.
Рассмотрим теперь способы по-
строения весовой матрицы. При по-
Рис. 10.15. Разбиение пространства измерений строении ЭТИХ методов, ПО-Прежне-
му, будет полезен выявленный факт
близости выделяющихся компонентов векторов ошибок и невязок. Опираясь
на указанное свойство, мы будем непосредственно в функции невязок фор-
мулировать различные критерии и с их использованием строить локально оп-
тимальные (на шаге) процедуры преобразования.
В рамках этого подхода ищется матрица
G=diag(gl,g2,Q (G,<) -> min
G
10.10. Построение алгоритмов оценки по методу взвешивания
749
при заданных ограничениях. В таблице 10.13 приведено четыре варианта фор-
мулировки критериев и соответствующие им выражения для вычисления
весовых коэффициентов. Метод близок к оптимизационному подходу в за-
дачах идентификации. Однако, в отличие от него, экстремум ищется не в
пространстве искомых оценок, а в пространстве параметров весовой матри-
цы преобразования. Другими словами, идея заключается в построении оп-
тимальных преобразований отдельно для каждого шага процесса последова-
тельных МНК-оценок. Этот подход наиболее близок к методам построения
адаптивных систем, в которых критерий качества корректируется на проме-
жуточных этапах с учетом дополнительной информации, появляющейся в
процессе.
Нетрудно заметить, что при использовании для вычисления весовых коэф-
фициентов соотношений, приведенных в п.1 и 3 указанной таблицы, могут
возникнуть проблемы при =0 =0). Их можно преодолеть путем до-
бавления в знаменателях соответствующих выражений малых положительных
чисел. Для других критериев элементы весовой матрицы могут быть вычисле-
ны, даже если среди компонентов вектора невязок есть нулевые. Легко заме-
тить, что этого удалось добиться соответствующим изменением критерия. Далее
Таблица 10.13. Критерии и соотношения для определения весовых коэффициентов
№ п/п Вид критерия и ограничений Выражения для вычисления весовых коэффициентов
1 £rG2£—»min , G Е g,.• = N . gi > 0 • r=I S(=|f. * = где g0 = /v/^^*2. Л=1Л. / ,=1
2 (pro + тг Im* ..+ > 1Л_ 11 “ Oq “ bJ •A ’ 1 . t>o 4- IA V «1 * q + <r N л V 9 . ) E S;2 Ed (H+i j] I
gk = <7 4=1
F’ k=(q+X),N 3k
3 1—1 Е#-=Л'’ 8i>°- i-l 8 к — где g0 = £[ k = \,N, M"'-
4 iPTO Oq (pro + (РГО tr In* Л- ; *> "n — S' (prt> * T IA V g r—! Ot=. .pro a a 8« 8к = 89 q+<T $<l] •Нт» __ - -2—I "7^ 11
750
ГЛАВА 10
приводится пример использования полученных соотношений в задаче иден-
тификации модели системы формирования изображений.
Пример 10.16. Осуществлялась параметрическая идентификация линейной
модели КИХ-фильтра в соответствии с соотношениями (10.76), (10.78). Ис-
пользовались тестовые изображения из примера 10.4 и бинарные поля пока-
зателей ф и 5min из примера 10.7. Для идентификации отбирались фрагменты
изображений, для которых масштабированное значение показателя 5min пре-
вышало 0,5.
Выражения для расчета весовых коэффициентов зависели от номера ите-
рации. На первой итерации вычислялись оценки МНК с одинаковыми веса-
ми равными единице. Весовые коэффициенты на второй и третьей итерациях
вычислялись по следующим соотношениям:
«I =£о(*+|С|) .
Si =So(s2+V) •
Вычисленные весовые коэффициенты затем подвергались нормировке так,
чтобы выполнялось условие i=l,N.
Определялся параметр расфокусировки о по оценкам вектора параметров
импульсной характеристики. Для этого решалась задача аппроксимации с
Таблица 10.14. Сравнение точности
МНК-оценок и метода взвешивания
Метод идентификации |До|/о
Одношаговый МНК 32,33
Трехшаговая процедура с весами 0,034
помощью этого же алгоритма оцен-
ки. В таблице 10.14 приведены срав-
нительные данные, показывающие
точность оценки параметра расфоку-
сировки с при идентификации с ис-
пользованием описанного алгоритма
и обычного МНК. Большое преиму-
щество метода взвешивания в данном
случае объясняется тем, что в исходные данные наряду с нормальными поме-
хами, относительная интенсивность которых составляла около 3%, добавля-
лись (менее 5%) сильно выделяющиеся импульсные помехи.
Еще раз подчеркнем, что описанный в настоящем разделе подход близок к
схеме идентификация по настраиваемой модели [30]. Однако последователь-
ная МНК-оценка с перестраиваемой весовой матрицей, по сравнению с иден-
тификацией по настраиваемым моделям, имеет более широкие возможности.
Как показано в примере 10.16, здесь критерий качества может изменяться на
каждом шаге с учетом требований к повышению точности оценок на очеред-
ном шаге и дополнительной информации, содержащейся в искомых оценках
параметров и невязках.
10.11. Идентификация моделей восстанавливающих фильтров
751
10.11. Идентификация моделей восстанавливающих фильтров
Проблема восстановления изображений сводится к некорректной обрат-
ной задаче построения обратного оператора искажающей системы с регуля-
ризацией решений. При этом предполагается, что оператор №(•), действую-
щий на входную последовательность f(nltn2), задан. Часто оператор JV()
определяют путем предварительного решения задачи идентификации харак-
теристик искажающей системы по специально подобранным для этой цели
тестовым изображениям.
Если задачи идентификации и восстановления решаются изолированно,
то усилия, направленные на определение, по возможности, более точной мо-
дели искажающей системы на этапе идентификации, могут оказаться, в зна-
чительной степени, напрасными. Дело в том, что на этапе восстановления
изображений обычно все равно приходится в той или иной степени (в зави-
симости от свойств оператора) осуществлять регуляризацию решений, по су-
ществу, означающую намеренное искажение обратного оператора с целью
уменьшения чувствительности к ошибкам в исходных данных. Поэтому пред-
ставляется целесообразным задачи идентификации моделей искажающих си-
стем и восстановления изображений с самого начала рассматривать с учетом
их взаимосвязи.
Рассмотрим возможность использования КИХ-фильтра (10.1), которому
на фрагменте, содержащем N отсчетов, соответствует уравнение вида (10.6).
По аналогии с (10.1) модель инверсного тракта (если она существует) можно
представить в виде
f(nlfn2)= 22 hr(mlfm2)g(ni-mlfn2-т2)+у(п11п2). (10.88)
{/nt,/n2}67?
Для L опорных областей, каждая из которых включает S отсчетов выходно-
го (искаженного) изображения, по аналогии с (10.6) можно записать матрич-
ное соотношение
x = Yhr+i|/> (10.89)
где х, у — вектор £xl, Y — матрица £х5, a hr - вектор 5x1.
Восстанавливающий фильтр будем строить также в классе КИХ-фильтров:
f(n]yri2) = 22 ^г{т},т2^{щ— т1,п2—т2). (10.90)
{лп, ,т2}еЛ
В матричном виде
x = Yhr, (10.91)
где Y — фигурирующая в (10.89) матрица размерности LxS, h; — вектор
оценок коэффициентов описывающего инверсный фильтр разностного урав-
нения размерности — 5^1. Компоненты £х!-вектора х — суть оценки значений
752
ГЛАВА 10
поля яркости восстановленного изображения. Они содержат ошибки, связан-
ные с наличием ошибок Sg(n](n2) в исходных данных, ограничением поряд-
ка КИХ-фильтра и погрешностями оценки его параметров.
При определении вектора hr есть, по крайней мере, две возможности. Во-
первых, можно по вектору у и матрице X, фигурирующим в (10.6), найти
оценку с вектора с модели искажающей системы, а затем одним из известных
способов построить вектор hr восстанавливающего фильтра. Во-вторых, можно
(поменяв изображения местами) по х и Y сразу найти оценку hr — парамет-
ров инверсного фильтра (10.91), решив соответствующую задачу идентифика-
ции. В настоящем разделе описывается второй подход.
Задача идентификации инверсной модели видеотракта имеет некоторые
специфические, по сравнению с оценкой модели прямого тракта, особенно-
сти. Если оцениваются непосредственно параметры инверсного фильтра, то
МНК-оценка hr вектора параметров hr инверсного тракта, по аналогии с
(10.7), определяется как
hr = [y7 G 2y|’‘ Y7G 2х. (10.92)
В (10.92) матрица У, в отличие от фигурирующей в (10.7) матрицы X, со-
ставлена из искаженных и зашумленных отсчетов изображения. Поэтому
соответствующая (при G2 =Е) матрица [УГУ] может оказаться невырожден-
ной даже в ситуациях, когда исходное неискаженное и незашумленное изоб-
ражение не содержит никаких информативных элементов, т.е. отсутствуют
объекты на фоне с одинаковыми значениями двумерной функции яркости).
Результаты оценки параметров инверсного тракта на таких фрагментах изоб-
ражения могут ввести в заблуждение.
Вторая важная особенность заключается в следующем. Для задачи (10.7)
естественным является требование достижения наивысшей точности опреде-
ления h в смысле близости к h. В случае идентификации параметров восста-
навливающего фильтра требование определения точной инверсной модели не
всегда оправдано. Например, оценка (10.92) является наилучшей в смысле
среднеквадратичного критерия:
<2(hf) — minC(hr) = min ([х - Yhr ]Г [х - Yhr
Поскольку hr ищется в условиях присутствия в элементах матрицы Y
ошибок измерений, то эта оценка фактически оказывается регул яризован-
ной в среднеквадратичном смысле. Как показывают исследования [13], ре-
зультаты восстановления наилучшим в среднеквадратичном смысле инверс-
ным фильтром субъективно не всегда воспринимаются как лучшие. Поэто-
му представляет интерес построение процедур идентификации, позволяющих
достаточно просто реализовывать различную степень близости к истинным
значениям параметров модели, в т. ч. и по субъективным оценкам качества
восстановления.
10.11. Идентификация моделей восстанавливающих фильтров
753
Метод взвешивания данных открывает для этого широкие возможности.
В данном случае взвешиванию должны подвергаться матрица Y и вектор х:
Y = GY, x = Gx.
(10.93)
При этом можно изменять свойства восстанавливающих фильтров путем
непосредственного изменения матрицы преобразования G. Если вдобавок
параметризовать матрицу G, то изменением одного (или небольшого числа)
параметров можно добиваться различного регуляризующего эффекта. Это осо-
бенно удобно в случае, когда имеется возможность непосредственного визу-
ального контроля качества восстановления. Проиллюстрируем это на тесто-
вых изображениях.
Пример 10.17. Использовался метод построения диагональной матрицы G
преобразования взвешивания, основанный на использовании семейства кри-
териев вида
/V 1 IV
где sk, Л = 1,2,3 — параметр, обеспечивающий различную степень близости
оценок h, к истинным параметрам hr.
Это равносильно построению трех моделей по критерию
б(Ьг) = ([х-Yh,]T[x — Yhr]
в котором матрица преобразования G, определяющая в (10.93) преобразован-
ные данные Y и х, изменяется от итерации к итерации так, что при определе-
нии моделей на завершающих этапах критерий оказывается «менее регуляризу-
ющим», т.е. обеспечивающим получение более точной инверсной модели.
Исследовалась процедура, предусматривающая построение набора из трех
моделей инверсного тракта с помощью последовательности трех оценок с из-
меняющимися от шага к шагу значениями параметра st: = 2, s2 = 1, 0.
На рис. 10.16 приведены тестовые фрагменты, использовавшиеся для непо-
средственной идентификации восстанавливающего фильтра, а на рис. 10.17в —
результаты восстановления изображения, подвергшегося таким же искажени-
ям, как и тестовые фрагменты.
Для идентификации использовалась основанная на указанном выше кри-
терии трехшаговая процедура с весами
8,(*) = 8о|^|
где st(&)=0 при всех А: =1,3, и i<q,
25 — 9044
754
ГЛАВА 10
10.16. Тестовые фрагменты
а
б
в
Рис. 10.17. Результаты восстановления фильтрами, полученными путем их непосредственной
идентификации: а — исходное изображение; б — искаженное изображение; в — восстановлен-
ное изображение
а для остальных компонентов 5,(1) = 2, 5/(2) = 1, 5|-(з) = 0.
Параметр ^определялся из условия нормировки:
При моделировании искажений тестовых фрагментов и изображения «са-
молет» использовалась такая же, как и в примере 10.4, параметрическая мо-
дель искажений с о = 1,5. Соответствующая указанному значению параметра
расфокусировки опорная область имеет размеры 9x9. Изображение, восста-
новленное фильтром, полученным в результате решения задачи оценивания,
описанным выше способом, показано на рис. 10.17в. Заметим, что в данном
случае даже с учетом центральной симметрии искажений число оцениваемых
параметров равно 15.
Проблема большой размерности задачи идентификации при оценке мо-
делей КИХ-фильтров может быть преодолена применением итерационной
процедуры восстановления изображений с использованием набора инверс-
ных КИХ-фильтров невысокого порядка. Общая схема формирования сово-
купности моделей следующая. По исходным тестовым изображениям иден-
тифицируется модель инверсного тракта невысокого порядка. С помощью
10.11. Идентификация моделей восстанавливающих фильтров
755
полученной модели восстанавливающего фильтра осуществляется обработ-
ка искаженного тестового изображения. Затем исходное искаженное тесто-
вое изображение заменяется обработанным и вновь решается задача иден-
тификации. В результате определяется новый КИХ-фильтр невысокого по-
рядка и т.д. Процесс формирования множества моделей останавливается,
если очередной шаг не дает существенного улучшения качества восстанов-
ления тестового изображения.
Задача восстановления натурных изображений должна решаться путем их
последовательной обработки полученным набором инверсных фильтров в той
же последовательности, как они были оценены. Если опорная область — квад-
рат со стороной /V отсчетов, то каждые два соседних шага обработки фор-
мально соответствуют одному шагу обработки фильтром с опорной областью
2N-1. Действительно, подставляя выражение для каждого отсчета обработан-
ного тестового изображения (10.90) в аналогичное соотношение для следую-
щего шага обработки, получаем
Л/—1/2 TV—1/2 А
/<,+1,(п1,П2)= Е ^+'Чк„к2) Е h(rn(l„l2)y(nl-k,-l„n2-k2-l2)=
kX1k2=\-N/2 lx,l2^-N!2
N-\
= 12 hr'+l’m2)У(п\ -m]vn2-m2),
mi ,m2=l—N
где ml = 4-/1э m2=k2+l2,a
N—\/2
к‘;м(т1,т2)=Х, Z h^(k„k2)h^(l„l2).
kx,k2Jx,l2=l-N/2,
k{ +1х—тх,
Л2 + 12—/П2
Для реализации указанной итерационной схемы восстановления изобра-
жений, даже при сравнительно больших размерах размазывающих масок, мо-
жет применяться набор КИХ-фильтров фиксированного и притом невысоко-
го порядка.
Пример 10.18. Использовались тестовые изображения 128x128 с диапазо-
ном яркости 0—256, показанные на рис. 10.18 (а, би в). Линейные искажения
формировались трехкратным «проходом» КИХ-фильтром, обладающим ради-
альной симметрией с опорной областью 5x5 (без угловых отсчетов), показан-
ной на рис. 10.11.
Компоненты вектора, характеризующего импульсный отклик системы,
задавались следующими: Ло = 0,359118, 7^ = 0,39503, h2 = 0,19033, А3 = 0,04991,
h4 = 0,00560 (корни соответствующего разностного уравнения: -0,4; -0,3;
-0,2±i0,3). Аддитивный шум моделировался в виде псевдослучайной
25*
756
ГЛАВА 10
Рис. 10.18. Тестовые изображения: а — неискаженное; б — искаженное; в
искаженное и
зашумленное
последовательности с дисперсией о2 =36. По приведенным тестовым изобра-
жениям строился набор из трех инверсных восстанавливающих КИХ-фильт-
ров с такой же опорной областью.
Подлежавшее восстановлению изображение «часы» (размером 256x256)
приведено на рисунке 10.19о. Для его искажения и зашумления использова-
лась та же, что и для тестового изображения модель (различались лишь гене-
рирующие числа псевдослучайной последовательности шумов). В частности,
средний квадрат разности исходного и расфокусированного изображений
(о^ = 0) =464, а при добавлении шумов (о^ =36) =500.
На рисунке 10.196 приведено изображение, полученное путем последова-
тельного применения к показанному на рисунке 10.19д искаженному и за-
шумленному изображению набора из трех КИХ-фильтров, построенных по
методу наименьших квадратов, а на рисунке 10.19в — полученное с использо-
ванием такого же набора фильтров, оценивавшихся с использованием метода
взвешивания данных с изменяющимися от шага к шагу значениями парамет-
ра sk: = 2 , s2 =1, 53 —*0. Отчетливо наблюдается эффект подчеркивания
Рис. 10.19. Результаты восстановления изображения «часы» (а), фильтром оцененным по методу
МНК (б) и с использованием метода взвешивания (в)
10.11. Идентификация моделей восстанавливающих фильтров
757
шумов инверсным фильтром, хотя контуры и элементы восстановленного
изображения воспринимаются более четкими.
Описанных в примере 10.18 усложнений, связанных с быстрым ростом раз-
мерности задачи оценки модели КИХ-фильтра, можно избежать применени-
ем модели БИХ-фильтра. Ниже приводится пример, показывающий эффек-
тивность восстанавливающих фильтров этого класса, полученных путем иден-
тификации.
Пример 10.19. Структура инверсной модели БИХ-фильтра задавалась в виде
разностного уравнения того же, что и для модели прямого тракта в примере
10.5, порядка:
}{n^n2)=b^f(nx -\,n2)+b^f{n{,n2 -1,л2-1) +
+«оо^(Л!+ «1во#(Л1 -tn2)-\-aemg(n{,n2 + -l,n2 -1).
Использовались те же, что и в указанном примере 10.5, тестовые изобра-
жения. Точные значения параметров приведенной выше инверсной модели
для трех, указанных в примере 10.5, типов искажений (рис. 10.3л, б и в), полу-
ченные путем непосредственного вычисления коэффициентов обратной пе-
редаточной функции, приведены в первых трех строках таблицы 10.15. Те же
коэффициенты, полученные путем непосредственной идентификации инверс-
ной модели, приведены в последних трех строках таблицы.
Далее из таблицы 10.15 брались коэффициенты восстанавливающего БИХ-
фильтра, полученные путем непосредственной идентификации и осуществ-
лялось восстановление двух других изображений: «текст» и «город» (рис. 10.20),
искаженных с использованием тех же трех вариантов моделей, соответствую-
щих «слабому», «среднему» и «сильному» искажениям. Искаженные изобра-
жения в той же последовательности приведены на рис. 10.21.
На рис. 10.22 приведены изображения, полученные путем восстановления
наиболее сильно (по варианту в) искаженных изображений (результаты для
вариантов а и б, по крайней мере, не хуже). Для моделирования и восстановле-
ния искаженных изображений использовался итерационный метод [4] реализа-
ции БИХ-фильтров. Подчеркнем, что опорные области восстанавливающих
Таблица 10.15. Параметры и оценки параметров инверсной модели
Вариант Ь.“о Ь\\ **00 **ю **01 **н
а -0,332 -0,332 -0,664 4,000 -0,500 -0,500 -0,664
б -0,500 -0,500 -1,000 9,090 -1,500 -1,500 -3,000
в -0,500 -0,500 -1,000 15,15 -3,030 -3,030 -6,060
а -0,335 -0,333 -0,658 4,008 -0,502 -0,499 -0,673
б -0,510 -0,501 -1,012 9,114 -1,487 -1,484 -3,025
в -0,492 -0,485 -1,000 15,02 -2,995 -2,941 -6,080
758
ГЛАВА 10
В задачах обработки из
сообщениями являются
слу«-аиные параметры и
определение которых и
печной целью интерпре
жения. Это могут быть.1
ма, раз мер ы, о риента ц га
ное расположение дета
н и й, п а ра метр ы, оп редег
Рис. 10.20. Исходные изображения
6 эамымлх с&рв&ти *а
являются
Ой рШМЛЛен*’* моторшх и
«•мной мелою ’•«терлре
чепмя Это мемуг
woe лете
«ий, плра«етрыколредш
а
I на
^ОХн •*'►’** •• « и
ч«км**я»’*
Сч > .ям»мт in» ж
he' <к>4 щмйнно
мт*“м шмут
й*.
*«*s
> ~ V. 4V, VA. ~ -М)^. -«. ™ W
б
в
Рис. 10.21. Изображения, подвергшиеся линейным искажениям: а — слабое, б — среднее, в —
сильное
В задачах обработки из
сообщениями являются
случайные параметры и
определение которых и
печной целью интерпре
жения. Это могут быть.1
ма, раз мер ы, о риента ц га
кое расположение дета
к и й, п а ре метр ы, оп редег
а
Рис. 10.22. Результаты восста-
новления изображений: а —
«текст»; б — «город», оценен-
ный инверсным БИХ-фильтром
б
10.12. Идентификация кусочно-постоянных моделей
759
фильтров на входном и выходном изображениях для всех трех вариантов ли-
нейных искажений имели размеры 3x3. Ясно, что при моделировании
«сильных» линейных искажений (по варианту в) с помощью КИХ-фильтра
размеры опорной области должны быть значительно большими, а размер-
ность задачи оценки — существенно выше.
Таким образом, восстанавливающий фильтр может быть построен путем не-
посредственной идентификации инверсного тракта в виде моделей КИХ-фильт-
ра и БИХ-фильтра с использованием каких-либо характерных фрагментов на
изображении. При этом возможно достижение различного регуляризующего
эффекта путем непосредственного «управления» весовой матрицей. Качество
восстановления, в конечном итоге, будет зависеть от типа и характеристик
используемой модели, а также от того, насколько она в действительности
соответствует модели реальных искажений.
Конечно, такое качество восстановления как показано в примерах не все-
гда достижимо. Если оцененный БИХ-фильтр оказывается неустойчивым, мы
вынуждены, в интересах реализуемости, изменить его параметры, принеся в
жертву качество восстановления. Проблемы, связанные с обеспечением ус-
тойчивости БИХ-фильтров, являются важными и представляют самостоятель-
ный интерес.
Тем не менее, необходимо подчеркнуть, что несмотря на некоторые труд-
ности, связанные с реализацией БИХ-фильтров, вычислительная сложность
сквозной технологии оценки и восстановления, особенно при интенсивных
линейных искажениях, может быть меньшей, по сравнению с использовани-
ем КИХ-фильтров. Связано это с возможностью использования опорных об-
ластей небольших размеров при любых искажениях. Это представляется осо-
бенно выгодным при проведении идентификации моделей искажающих сис-
тем и восстанавливающих фильтров по малым фрагментам изображений.
10.12. Идентификация кусочно-постоянных моделей
в случае пространственно-зависимых искажений
В системах формирования изображений искажения часто оказываются
пространственно-зависимыми (неизопланатичными). Задача коррекции та-
ких искажений может быть решена применением линейных восстанавливаю-
щих фильтров с перестраиваемыми по пространственным координатам пара-
метрами. Если модель неизопланатичности может быть представлена в виде
зависящего от небольшого числа параметров семейства двумерных функций,
параметры восстанавливающего фильтра могут быть легко вычислены в каж-
дой точке обрабатываемого изображения. В настоящем разделе рассматрива-
ется информационная технология оценки параметров такой функции по тес-
товым изображениям.
При идентификации модели пространственно-зависимых искажений в виде
совокупности пространственно-инвариантных моделей на малых, насколько
760
ГЛАВА 10
это возможно, фрагментах изображения, возникает проблема отбора малых
фрагментов изображений, на которых измерения являются информативными,
т.е. таких на которых задача идентификации может быть решена с требуемой
точностью. Ниже показано, как эта проблема может быть решена с использо-
ванием описанных выше методов.
Наиболее характерным типом искажений, вносимых оптическими систе-
мами, является расфокусировка, связанная с аберрациями различных поряд-
ков. Предположим, что эти искажения на малом фрагменте изображения мо-
гут быть описаны уравнением КИХ-фильтра. Задачу идентификации этой
модели в случае пространственно-зависимых искажений можно представить
в виде следующей последовательности действий [15, 35].
1. Идентификация импульсной характеристики на малых фрагментах.
2. Оценка на каждом фрагменте параметра расфокусировки о.
3. Оценка параметров функции, описывающей изменения параметра рас-
фокусировки по полю изображения (модели неизопланатичности).
4. Оценка параметров восстанавливающих фильтров, соответствующих
полученным значениям параметра расфокусировки о.
Фрагменты для идентификации отбираются по заданному пороговому зна-
чению показателя 5min. Для каждого выбранного фрагмента задача идентифи-
кации параметров импульсной характеристики (этап 1) решается, как описа-
но выше в примере 10.16.
По полученным на каждом фрагменте оценкам значений импульсной ха-
рактеристики ЦЛрЛз), к1,к2—\,М , далее строится оценка д параметра с
модели из примера 10.4. Для этого решается задача определения
о,: e(dj = mi_n<2(a), (10.94)
где 5 — номер фрагмента, aS — область допустимых значений параметра
расфокусировки. В частности, для получения МНК-оценки ду параметра ол
минимизируется функция
<?(«*,) = Е Е /т- ехР —-h(k>’k2) (Ю.95)
kt=—N/2 k2=-N/2 \у12Я0х 2Gs
Далее (этап 3) по совокупности бл. строятся оценки параметров модели
неизопланатичности с = с(п}, п2). Для этого необходимо задать параметри-
ческое семейство двумерных функций, описывающих характер неизопла-
натичности. Для выбора этого класса функций можно осуществлять пред-
варительный визуальный просмотр полученного множества оценок ду. На-
пример, если расфокусировка увеличивается по мере удаления от центра
изображения, удобно изменение параметра о описать параметрическим се-
мейством функций вида
о(п|,п2) = XX + Руи2 +о0,
10.12. Идентификация кусочно-постоянных моделей
761
где п2 — текущие координаты точки, а 1Х, Ху, рх (3v, о0 — кон-
станты, зависящие от степени неизопланатичности.
Иногда можно ограничиться рассмотрением частного случая указанной
зависимости, когда неравномерность расфокусировки обладает радиальной
симметрией. Параметрическое семейство функций, описывающих такую мо-
дель неизопланатичности имеет вид
Q(n1,n2) = Xxn12 +Хул2 +о0>
(10.96)
где 'кх='ку — коэффициенты, характеризующие изменения искажений по
мере удаления от центра п} = п2 = 0.
Четвертый, заключительный этап технологии — определение параметров
восстанавливающих фильтров. С использованием оцененной на третьем этапе
модели неизопланатичности, в принципе, в любой точке изображения можно
строить соответствующий восстанавливающий фильтр. Однако при этом объем
вычислительной работы оказывается весьма значительным. Для сокращения
времени обработки изображений целесообразно заранее построить множество
фильтров, соответствующих различным значениям параметра о, в виде некото-
рой таблицы соответствия, а затем в ходе обработки выбирать «ближайший».
Для составления такой таблицы можно воспользоваться методом непо-
средственной идентификации характеристик инверсного тракта, описанным
в предыдущем п.10.11. Для этого необходимо осуществлять идентификацию
параметров восстанавливающего фильтра при различных искажениях, пола-
гая входным — искаженное, а выходным — неискаженное изображение. До-
стоинство такого подхода мы уже обсуждали в п.10.11.
Пример 10.20. Для получения таблицы соответствия параметра с и парамет-
ров инверсных фильтров (4-й этап) в качестве тестового использовалось изобра-
жение «текст», показанное на рисунке 10.8. Из этого
изображения было получено множество искаженных
в соответствии с моделью (пример 10.4) изображений
при различных значениях параметра с. Последователь-
ность параметров s задавалась в диапазоне 0,5—3,5 с
шагом 0,1. Полученные таким образом для каждого
фиксированного значения s искаженные изображения
использовались в качестве входных для идентифика-
ции параметров восстанавливающего фильтра.
Осуществлялось экспериментальная проверка эф-
фективности описанной выше четырехэтапной ин-
формационной технологии построения корректиру-
ющих фильтров неизопланатичных искажений. Для
этого использовалось изображение (рис. 10.23), по-
лученное из исходного (рис. 10.8) моделированием
мых искажений. Расфокусировка осуществлялась КИХ-фильтром, значения
импульсной характеристики которого определялись по формуле из примера
& реввгмее
ie О Димы mi W
me слеп
Рис. 10.23. Тестовое изобра-
жение
пространственно-зависи-
762
ГЛАВА 10
Таблица 10.16. Оценки параметров модели (10.96)
Параметры Оценки параметров Абсолютная погрешность Относительная погрешность
VI, 0,000231 0,00000306 0,01350
Оо 0,928000 0,00438000 0,00470
10.4, а параметр о в каждой точке изображения рассчитывался по соотноше-
нию (10.96) при =Ху =0,0002275, о0 =0,932.
Для указанных параметров модели неизопланатичности размер опорной
области должен увеличиваться от центра изображения к периферии. В каче-
стве критерия для выбора размеров маски использовалась величина отноше-
ния значения гауссиана на границе опорной области к его значению в цент-
ральной точке. Для величины отношения не более 0,01 минимальный размер
маски равен 5, а максимальный — 13. На рис. 10.23 видно, что при описанном
способе моделирования расфокусировка, как и следовало ожидать, возрастает
от центра изображения к периферии.
В результате реализации первых двух этапов описанной технологии на
фрагментах изображения, отобранных по показателю Smin, было получено
множество оценок параметра расфокусировки dv. Далее с использованием
полученного множества оценок на третьем этапе — оценивались параметры
функции, описывающей изменение параметра о по полю изображения (моде-
ли неизопланатичности). Результаты оценки, полученные в рассматриваемом
примере, приведены в таблице 10.16.
Осуществлялась обработка изображения текста, показанного на рис. 10.24а.
Это изображение получено с использованием той же модели искажений, но
на другом тексте. Восстановленное изображение приведено на рис. 10.25а. На
рис. 10.256 для сравнительной визуальной оценки приведено изображение этого
же текста, полученное обработкой «средним» фильтром, т.е. инверсным фильт-
ром, построенным по той же методике, но без учета пространственной неин-
вариантности искажений.
««м»
Рис. 10.24. Исходное изобра-
жение
которы» «и
юрчной цолыо mwfWfw
гздт, Это могут
иЙ ГвбЯЭЛСЖЯМ»» jmp
««НА. Это мо<ут Омгк.»
Рис. 10.25. Результаты восстановления: а — пространственно-
зависимым фильтром; б — «средним» фильтром
10.13. Оценка разрешающей способности видеотракта
763
В примере рассмотрена простейшая модель неизопланатичности, обладаю-
щая центральной симметрией. В действительности, изменение характеристик
искажений на изображении может иметь более сложный характер. Для оце-
нивания модели неизопланатичности в общем случае полезными могут быть
методы двумерной сплайн-аппроксимации.
10.13. Оценка разрешающей способности ввдеотракта
Задача оценки разрешающей способности (PC) описана в п.2.5, а также кратко
обсуждалась в примере 10.3. Она является одной из типичных, в которых тре-
буется решать задачу оценивания по малому числу наблюдений. Рассмотрим
информационную технологию оценки PC видеоинформационного тракта по
регистрируемым изображениям текущих сюжетов в значительной мере свобод-
ную от особенностей восприятия изображений отдельными экспертами.
Основой технологии является оценка частотной характеристики системы
на фрагментах изображений небольших размеров. Рассматриваемый здесь метод
оценки PC, по существу, является реализацией описанной в разделе 2.5 мето-
дики, допускающей ее автоматизацию. Общая схема решения задачи состоит
из двух этапов. На первом этапе строится процедура, копирующая действия
эксперта при ручном выделении участков на изображении и их ретуширова-
нии. При этом для автоматизированной «прорисовки» функции яркости в
виде ступеньки используется предположение о том, что граница перепада яр-
кости соответствует величине полусуммы уровней
яркостей на примыкающих («светлой» и «темной»)
ступеньках.
На втором этапе по исходному искаженному и
отретушированному фрагментам оценивается час-
тотная характеристика системы. Задача оценки ре-
шается по малому числу наблюдений на фрагмен-
тах с использованием описанных в настоящей гла-
ве методов. В качестве дополнительной используется
информация о том, что распределение яркости имеет
вид ступенчатой функции.
Схема фрагмента со ступенчатой функцией яр-
кости показана на рис. 10.26. Здесь темные и свет-
x(i,n)
x(i,l), i=l,m
• •••ООО о
• •••ООО о
• •••ООО о
•••ООО О"
• •••ООО о
• •••ООО о
Рис. 10.26. Фрагмент изображе-
ния тхп со ступенчатой функ-
цией яркости
лые точки соответствуют отсчетам с низким и высоким уровнем яркости. Для
отыскания таких фрагментов на изображении ищутся участки, имеющие рез-
кие перепады яркости в направлении, перпендикулярном средней линии фраг-
мента, притом такие, что изменения яркости в пределах каждого из двух со-
седних уровней незначительны.
Поиск осуществляется следующим образом. Вначале для каждой точки
изображения определяется перепад яркости к =1 — х2 I, где
764
ГЛАВА 10
о "I п)2
*1 -----Ь2Л»’Д
т-п i=xj=x
- т п
*2 =—-Ё Ё *(и),
т‘п
x(i, j) = j = \,n) — i, j-й отсчет яркости на фрагменте, a х,,х2 “
средние значения яркости, вычисленные в левой и правой половинах прямо-
угольного участка размером тхп (рис. 10.26). Далее на заданном (в процен-
тах к общему числу) множестве точек изображения, являющихся центрами
Алхл-фрагментов, определяется минимальное (кт) значение величины перепа-
да яркости и сравнивается с заданным допустимым значением (кг). Если кт > кп
то отобранное множество точек может использоваться для оценки разреше-
ния, а величина кт принимается в качестве порогового значения, определяю-
щего это множество фрагментов (претендентов).
Для каждого отобранного таким способом фрагмента (претендента) вы-
числяются СКО яркости в каждой зоне (темной и светлой):
•vi =
т п/2
— ЕЁ(*(м)~*1)2
V/2
2
т-п
*2
Е Е U0’J)-*2)2
1 п
<—1 ;-j_i
где л,, х2 — средние значения яркости в каждой из двух зон. Затем из
числа претендентов отбираются фрагменты, для которых полусумма СКО
5 — (л, +s2)/2 имеет допустимое значение. Могут использоваться одновре-
менно фрагменты с перепадом яркости «темный — светлый» и «светлый —
темный», либо только одного типа.
Заключительная операция первого этапа состоит в формировании тесто-
вых «неискаженных» фрагментов. Она заключается в компьютерном ретуши-
ровании отобранных фрагментов. Предполагается, что наименьшим искаже-
ниям подвергаются участки фрагментов, наиболее удаленные от линии пере-
пада яркостей. Поэтому процедура ретуширования сводится к замене значений
яркости в каждой из половинок выбранного фрагмента их средними значени-
ями, вычисленными по формулам:
1 т
—Е*(*>),
mi=l
где x(i,n), i = l,m — отсчеты, расположенные на линиях, параллельных
линии, разделяющей светлую и темную зону на уровне яркости 5, и наиболее
удаленных от нее (рис. 10.26).
10.13. Оценка разрешающей способности видеотракта
765
При воссоздании фрагментов «неискаженного» изображения могут исполь-
зоваться, вообще говоря, любые знакомые элементы регистрируемых сюже-
тов. Желательно использовать такие элементы, относительно которых имеется
априорная информация о геометрической форме и размерах. В любом случае
идея заключается в том, чтобы эту априорную информацию «обменять» на
информацию о частотной характеристике системы.
Частотную характеристику системы можно оценить в классе КИХ- или
БИХ-фильтров. Для оценки в данном случае можно использовать итерацион-
ную схему с промежуточными преобразованиями взвешивания и/или коррек-
тировки данных. Важно то, что матрица X в данном случае формируется по
отсчетам функции яркости известного (ступенчатого) вида. Эта дополнитель-
ная априорная информация может эффективно использоваться для построе-
ния преобразований взвешивания и корректировки данных.
Пример 10.21. В таблице 10.17 приведены результаты исследования связи
компонентов векторов ошибок и невязок, полученные по 500 реализациям.
Номера столбцов в таблице соответствуют номерам столбцов на фрагменте
(рис. 10.26). Из таблицы видно, что наиболее информативными для построе-
ния корректирующего вектора являются компоненты вектора невязок, соот-
ветствующие отсчетам, расположенным в 1, 4, 5 и 8-м столбцах фрагмента
(рис. 10.26).
Связь компонентов векторов ошибок и невязок всегда более тесная, если в
расчет принимать меньшее число выделяющихся компонентов вектора невя-
зок. Обладая априорной информацией о коэффициентах можно определить
заранее матрицу К = diag (к{, к2,..., к^), с использованием которой в ходе оце-
нивания строятся корректирующий вектор и/или матрица весов G. Ниже при-
водится пример оценки модели видеотракта в сквозной технологии оценки
разрешающей способности, в котором эффективно эксплуатируется допол-
нительная информация о выявленных связях.
Пример 10.22. Использовался простейший способ построения корректиру-
ющего вектора | по правилу.
где К = diag (£b к2,..., kN) — диагональная матрица коэффициентов связи,
фигурирующих в таблице 10.17.
Таблица 10.17. Связь компонентов векторов ошибок и невязок
Номера столбцов 1 2 3 4 5 6 7 8
Значения 1,262 1,200 1,285 0,779 0,810 1,070 1,200 1,259
СКО отношений |£(|/ 0,114 0,146 0,169 0,143 0,155 0,169 0,155 0,125
766
ГЛАВА 10
Рис. 10.27. Тестовые изображения: а — исходное; б — расфокусированное с выделенными фраг-
ментами
На рисунках 10.27а, б приведены изображения участка автодороги с раз-
меткой, использовавшиеся для оценки эффективности технологии. Исходное
изображение (рис. 10.27а) подвергалось расфокусировке путем преобразова-
ний в частотной области с использованием модели искажающей системы с
импульсным откликом гауссовой формы (см. пример 10.4) с параметром рас-
фокусировки о=1.
Выделенные на первом этапе технологии, в соответствии с описанной ме-
тодикой, тестовые фрагменты показаны на рис. 10.276 прямоугольниками.
Исследовалась возможность оценки фигурирующей в (2.18) частотной харак-
теристики на указанных фрагментах. В частности, проводилось срав-
нительное исследование точности аппроксимации гауссовой частотной ха-
рактеристики БИХ-фильтром первого порядка и фильтрами с конечной им-
пульсной характеристикой (КИХ-фильтрами) различных порядков.
Использовался БИХ-фильтр первого порядка с опорными областями 3x1:
g (л) = 52 a(k)g{n- к)+ £(и), к* 0.
/=-1 к=-\
Соответствующая этому разностному уравнению передаточная функция, опи-
сывающая симметричные искажения в направлении оси хь (рис. 2.4) имеет вид
tf(z) = B(z)/A(z),
где A(z) = l + al(z + z'1), fi(z) = 60+Z>|(г+ ?"'),
тотная характеристика вещественна:
а соответствующая ей час-
н = »0 + 2&,cos(Qr)
l + 2a|Cos(nT)
Результаты оценки приведены в таблице 10.18. Из таблицы видно, что при
слабых искажениях использование КИХ-фильтра третьего порядка (размер
маски=5х1) и БИХ-фильтра первого порядка обеспечивает сравнимую точность
10.13. Оценка разрешающей способности видеотракта
767
Таблица 10.18. Точность аппроксимации
G Тип фильтра Маска Атах СКО
1 КИХ 5 0,02398472 0,00038715
БИХ 3 0,02816998 0,00045672
1,2 КИХ 5 0,04219072 0,00082203
БИХ 3 0,04545734 0,00075587
1,5 КИХ 5 0,11187530 0,00206668
БИХ 3 0,09013103 0,00147081
2 КИХ 9 0,10613500 0,00142538
БИХ 3 0,08086268 0,00129539
аппроксимации как по критерию максимального (Атах), так и среднеквадра-
тичного отклонения (СКО) оцененной частотной характеристики от исход-
ной (гауссовой). При увеличении степени размытия (параметра а) точность
оценки параметров в классе КИХ-фильтров того же порядка убывает быстрее,
чем в классе БИХ-фильтров, а повышение порядка КИХ-фильтра не позволя-
ет достичь более высокой точности по сравнению с точностью оценок пара-
метров БИХ-фильтра первого порядка.
Приведенные результаты показывают возможность построения более точ-
ных (по сравнению с МНК) оценок параметров модели БИХ-фильтра по ма-
лому числу наблюдений на фрагментах изображений при отсутствии априор-
ной информации о распределении ошибок измерений. При этом, что весьма
важно для оценки PC, интенсивность искажений может иметь большую не-
определенность в весьма широком диапазоне.
Продолжение примера 10.22. На рис. 10.28 для сравнения приведены ис-
ходная гауссова частотная характеристика и вычисленная в примере 10.22 с
использованием оценок параметров модели БИХ-фильтра. Ошибка аппрок-
симации АЯ зависит от частоты. Максимальная и среднеквадратическая по-
грешности аппроксимации передаточной функцией БИХ-фильтра соответ-
ственно составили: Атах = 0,0325, Дск0 = 0,0005.
Необходимо иметь в виду, что ошибка АП определения зачетной частоты
разрешения зависит не
только от ошибок аппрок-
симации частотной ха-
рактеристики АН, но и
от параметра Св (2.19).
Характер зависимости
ошибки АП от частоты
П связан также с видом
Рис. 10.28. Аппроксимация га-
уссовой частотной характери-
стики передаточной функцией
БИХ-фильтра
___Гауссова частотная характеристика
768
ГЛАВА 10
Таблица 10.19. Параметры фрагментов
Параметры фрагментов Тип перехода
«темный- светлый» «светлый- темный»
Перепад 142,8 141,5
СКО 15,6 15,34
к 3,0 3,0
т 0,1 ед. дл. 0,1 ед. дл.
Рис. 10.29. Зависимость погрешности ДП от
параметра Q и погрешности Д/7
частотной характеристики системы. Для показанной на рис. 10.28 гауссовой час-
тотной характеристики ошибка ДО монотонно увеличивается с уменьшением па-
раметра Q. На рис. 10.29 представлено полученное в ходе экспериментов семей-
ство зависимостей ошибок ДО оценки зачетной пространственной частоты О от
параметра а = arctg (Q при различных значениях погрешности аппроксимации Д//.
Полученная путем аппроксимация моделью БИХ-фильтра оценка гауссо-
вой частотной характеристики использовалась затем для определения часто-
ты О и соответствующего ей показателя линейного разрешения по соотноше-
ниям (2.18), (2.19), (2.10) с использованием данных, приведенных в таблице
10.19. Параметры КнТ задавались, а амплитуда А и СКО о„ оценивались по
сформированным тестовым фрагментам.
В результате решения задачи получены следующие результаты: зачетная
круговая частота 16,43 рад/ед. длины, зачетная частота —• 5,23 1/ед. длины,
линейное разрешение — 0,19 ед. длины. Полученные результаты хорошо со-
гласуются с результатами моделирования при исходном интервале дискрети-
зации Т= 0,1 ед. длины.
10.14. Информационная технология совмещения изображений
по информативным фрагментам
Во многих алгоритмах и информационных технологиях (калибровка ви-
деокамер, стереозрение, построение рельефа местности, привязка к существу-
ющим картам и т.д.), использующих описание одного и того же сюжета, при-
меняют процедуры согласования (совмещения) изображений. При совмеще-
нии изображений с целью распознавания (например, идентификации личности
по отпечаткам пальцев и др.) параметры взаимных сдвигов и поворота совме-
щаемых изображений, как правило, сильно различаются. Более того, сюжет
совмещаемого изображения может являться лишь частью сюжета, хранящего-
ся в памяти в качестве образца.
Известно [13], что для совмещения плоских изображений, имеющих одина-
ковый масштаб, достаточно найти на этих изображениях по три соответственные
10.14. Информационная технология совмещения изображений
769
точки. В ситуации, когда одно изображение является частью другого, для по-
вышения надежности целесообразно вводить избыточность, т.е. число «подо-
зрительных» точек, претендующих на соответственные, брать больше трех. Если
априорная информация о величине относительных сдвигов и поворотов отсут-
ствует, то для нахождения соответственной точки каждому отсчету необходимо
сопоставлять его со всеми отсчетами совмещаемого изображения. Это требует
проведения большого объема вычислений. Для их сокращения на совмещае-
мых изображениях осуществляют [14] предварительное выделение сравнитель-
но небольшого числа наиболее информативных фрагментов (точек «претен-
дентов»), большинство из которых должны быть соответственными.
В настоящем разделе описывается технология, опирающаяся на следую-
щие три идеи, развивающие этот подход:
- для установления информативности и соответствия точек наряду с сами-
ми (в данном случае центральными) отсчетами используется совокупность
отсчетов, близких к концентрическим окружностям заданных радиусов, кото-
рые далее для краткости будем называть круговыми масками;
- в качестве характеристики информативности точек «претендентов» ис-
пользуется показатель диагонального преобладания информационной матри-
цы, составленной из отсчетов на заданных круговых масках (способ форми-
рования описывается ниже);
- для определения параметров сдвига и поворота решается задача оценки
линейной по параметрам модели линейных преобразований с ограничениями,
формируемой по координатам сравнительно небольшого числа, но существен-
но более трех, выявленных среди информативных соответственных точек.
При формировании круговой маски из отсчетов обычной прямоугольной
сетки неизбежно возникают зависящие от размера маски погрешности. При
этом возникают следующие вопросы.
1. Можно ли в принципе строить надежные процедуры отыскания соот-
ветственных точек с использованием круговых масок небольших размеров?
2. Если это возможно, то как выбирать параметры маски, чтобы, по воз-
можности, снизить вносимые погрешности?
Возникают также трудности на этапе оценки параметров сдвига и поворо-
та по малому числу наблюдений, связанные с отсутствием априорной инфор-
мации о статистических характеристиках ошибок оценивания координат со-
ответственных точек. Рассмотрим, основные этапы технологии, позволяю-
щей преодолеть указанные трудности.
Выделение информативных областей на совмещаемых изображениях. Анализ
информативности фрагментов в окрестности каждой точки с координатами
(п],п2) осуществляется с использованием показателя диагонального преоб-
ладания [5, 6]:
Tr2R(n,,n2) _ М2
TrR2(n1,«2)“M+£r{2’
(10.97)
/, j = 1..М, i j, М — 1<<J)[r(«],m2)]<M,
770
ГЛАВА 10
где
R(nhn2) = С(я1,п2)А(л|,п2)С(л|,п2), A(n|,n2) = Xr(n|,n2)X(nj,n2), (10.98)
— так называемая информационная матрица,
C(n1,n2)=diag(a-'/2,a;2'/2.а^м).
a X(n,,n2) — АхЛУ-матрица составленная из отсчетов поля яркости на фрагмен-
те в виде круговой маски с центром в точке (м],п2)- Применение такой маски
обеспечивает инвариантность информативных точек к углу поворота изображе-
ния. Элементы матрицы X формируются из отсчетов,
находящихся в узлах прямоугольной сетки, ближай-
, ших к точкам пересечения концентрических окруж-
ностей и радиальных лучей. Столбцы соответствуют
М-1 концентрическим окружностям и центральной
точке, строки — N радиальным лучам (рис. 10.30).
При указанном способе формирования матрицы
, X соответствующая ей матрица А = Х7Х (если не при-
нимать во внимание погрешности, связанные с пере-
ходом от прямоугольной сетки к круговой маске) не
зависит от углового положения фрагмента. При из-
„ .л ,л „ менении углового положения фрагмента происходит
Рис. 10.30. Пример кругового
фрагмента, вписанного в квад- Циклическая перестановка строк матрицы X, что при-
рат 7x7 водит лишь к изменению порядка суммирования про-
изведений соответствующих элементов. Вследствие
умножения слева и справа на матрицу С диагональное преобладание получаю-
щейся из А матрицы R не зависит также и от различий среднего уровня яркости
совмещаемых изображений. Поэтому выделяемые на совмещаемых изображени-
ях информативные точки, с близкими значениями показателя ф[r] , в большин-
стве случаев оказываются соответственными.
В действительности при переходе от прямоугольной сетки к круговой маске
неизбежно возникают погрешности. Интуитивно ясно, что величина этих по-
грешностей зависит от радиусов окружностей (круговых масок). Поэтому пред-
ставляет интерес выявление радиусов, при которых эти ошибки минимальны.
При переходе от прямоугольной системы координат к полярной целесооб-
разно брать отсчеты в узлах прямоугольной сетки, ближайшие к пересечени-
ям радиусов и концентрических окружностей. Для такой процедуры считыва-
ния установим радиусы концентрических окружностей, для которых ошибки
несовпадения координат отсчетов на изображении минимальны.
Выбор параметров круговой маски. На рис. 10.31 приведены подсчитанные
по соотношениям
/ N г ,
£<г)=(>)+и]
(10.99)
10.14. Информационная технология совмещения изображений
771
Рис. 10.31. Зависимость Е(г): а • для 24 сегментов; б — для 16 сегментов
зависимости ошибок Е(г) несовпадения координат от величины радиуса г для
двух вариантов задания радиальных лучей, при которых круговая маска раз-
бивается на 16 и 24 одинаковых секторов. Здесь Дх?(г) = [х;(г) —хДг)] ,
=[у.(г) —у,(г)| ; х.-.у;— прямоугольные координаты точек пересечения
лучей с концентрической окружностью радиуса г, а хг,у;— координаты бли-
жайших к ним точек прямоугольной сетки в той же системе координат.
В таблице 10.20 приведены радиусы и величины ошибок, соответствующие
точкам локальных минимумов, выделенных на рис. 10.31 (по 14 точек на каж-
дом) вертикальными пунктирными лини- ™ ~ к
” ' г j г Таблица 10.20. Ошибки несоответствия
ями. Графики и таблицы дают представ- ддЯ выделенных 14 радиусов
ление о наиболее предпочтительных ра-
диусах, однако, сам по себе переход к радиусу, которому на графике соответству- ет меньшее значение ошибки, не гаран- тирует уменьшения погрешности, т.к. в действительности такие переходы совер- шаются дискретно. Все возможные варианты круговых масок для радиусов в диапазоне от 0 до 20 в случае разбиения на 16 сегментов приведены в таблице 10.21 (нумерация лучей против часовой стрелки начиная с «горизонтального» направления в пер- вом квадранте). Наконец, ошибки несовпадения ко- ординат лишь опосредованно влияют на ошибки в определении соответственных точек. Непосредственной причиной 16 сегментов 24 сегмента
г Е(г) г Е(г)
1,050 0,4625 1,150 0,6778
3,030 0,1753 3,190 0,7177
4,230 0,4165 3,950 0,5152
5,290 0,3337 4,200 0,3865
7,260 0,4489 5,990 0,6776
8,710 0,4565 7,150 0,5485
9,920 0,1655 8,160 0,2317
10,97 0,2528 10,19 0,5485
12,95 0,0864 11,35 0,5263
14,00 0,3142 12,65 0,7124
15,20 0,3131 14,15 0,6344
15,97 0,3577 15,84 0,5039
17,10 0,3912 18,35 0,6082
18,23 0,2316 19,79 0,2053
772
ГЛАВА 10
Таблица 10.21. Круговые маски для 16 сегментов несоотвествия между точками со- вмещаемых изображений являют- ся различия функций яркости на сравниваемых фрагментах. Эти пааличия связаны не только
№ Ради- Координаты точек на луче №:
маски ус г 1 2 3 4
1 1,7 (2;0) (2;1) d;D (1;2)
2 2,2 (2;0) (2;1) (2;2) (1;2) с несоответствием координат точек, но и со спектральными характерис- тиками рассматриваемого класса
3 2,5 (3;0) (2;1) (2;2) (1;2)
4 2,8 (3;0) (3;1) (2;2) (КЗ)
5 3,5 (4;0) (3;1) (2;2) (1:3) изображений. В качестве меры этих
6 3,6 (4;0) (3;1) (3,3) (г.З) различий обычно используется ко-
7 4,1 (4;0) (4;2) (3;3) (2;4) эффициент корреляции.
8 4,5 (5.0) (4;2) (3;3) (2,4) На рис. 10.32 приведены резуль-
9 4,9 (5;0) (5;2) (3;3) (2;5) таты исследования зависимости ко- эффициента корреляции от радиу- са при различных углах поворота (22°, 45° и 67°) исходного изобра- жения. Сплошной жирной линией показан график изменения коэф-
10 5 (5,0) (5;2) (4;4) (2:5)
11 5,6 (6;0) (5;2) (4;4) (2;5)
12 6 (6;0) (6;2) (4;4) (2,6)
13 6,4 (6;0) (6;3) (5;5) (3;6)
14 6,7 (7;0) (6;3) (5;5) (3;6) фициентов корреляции, получен-
15 7,1 (7;0) (7;3) (5;5) (3;7) ный их усреднением. Коэффициен-
16 7,6 (8;0) (7;3) (5;5) (3;7) ты корреляции рассчитывались для
17 7,8 (8;0) (7;3) (6;6) (3;7) заведомо соответственных точек. Цифры по оси абсцисс указывают номера масок из таблицы 10.21. Из этих графиков видно, что исполь- зование масок с номерами 3, 5, 6, 9, 12 и 13 (в особенности с номе- ром 6) менее предпочтительно. Необходимо заметить, что ре-
18 8,2 (8;0) (8;3) (6;6) (3;8)
19 8,6 (9;0) (8;3) (6;6) (3,8)
20 9,2 (9;0) (9,3) (7,7) (4;8)
21 9,4 (9;0) (9;4) (7;7) (4,9)
22 9,6 (Ю;0) (9;4) (7;7) (4;9)
23 10,3 (10;0) (Ю;4) (7;7) (4;9)
24 10,4 (Ю;0) (Ю;4) (7;7) (4;10) зультаты получены для дактилоско-
пических изображений (рис. 10.33).
Свойства круговых масок могут отличаться от приведенных для классов изоб-
ражений, обладающих специфическими спектральными характеристиками
полей яркости. Поэтому исследования по описанной схеме, вообще говоря,
10.14. Информационная технология совмещения изображений
773
Рис. 10.33. Тестовые изоб-
ражения: а — исходное;
б — повернутое на 90°
Рис. 10.34. Поля инфор-
мативности: а — исходно-
го; б — повернутого на 90°
Определение соответственных точек. Для определения соответственных то-
чек можно использовать обычный корреляционный метод. Для уменьшения
числа сравнений информативные точки предварительно разделяются на
2—3 группы. Сравнение точек внутри каждой группы осуществляется по прин-
ципу: «каждая — с каждой». Эта информация является достаточно надежной,
т.к. показатель диагонального преобладания информационной матрицы яв-
ляется носителем локальных автокорреляционных свойств сигнала.
Для перебора всех возможных дискретных значений взаимного углового
положения в данном случае формируется матрица (X) для каждой точки (пре-
тендента) и совмещаемых изображений. Матрица X получается путем цикли-
ческой перестановки строк, соответствующих различным положениям круго-
вого фрагмента на сюжете совмещаемого изображения. Для проверки соот-
ветствия фрагментов вычисляется матрица
Rc=CAcC, (10.100)
где АС=ХГХ,
С = diag
Ясно, что при угловом положении соответственных фрагментов, приво-
дящем к одинаковой последовательности строк матриц X и X и при отсут-
ствии ошибок в измерениях матрица Rc совпадает с R, определяемой соот-
ношением (10.98). След матрицы Rc представляет собой сумму М коэффи-
циентов корреляции, вычисленных для М концентрических масок:
тм
ГЛАВА 10
TrRc
м
где A:f-= (xf--х/)/||х/|’||х<-|, z = 1,М . Если нормы векторов ||х( ||, i — \,М оди-
наковы, величина к совпадает с обычным коэффициентом корреляции. При
наличии шумов или неточном совпадении положений фрагментов будут иметь
место различия. Тем не менее, величина к, определяемая соотношением, яв-
ляется достаточно информативной характеристикой соответствия искомых
точек (фрагментов).
С использованием величин к, для каждой точки исходного изображения
подбирается точка из совмещаемого изображения с учетом взаимного углово-
го положения фрагментов соответствующих точкам. Соответственными счи-
таются лишь те точки, для которых оценки угловых положений фрагментов
(т.е. номера переставленных строк в матрице X) совпадают.
Оценка параметров сдвига и поворота. Для оценки параметров сдвига и по-
ворота используются уравнения аффинных преобразований [6]:
X* X сохф —sin <р а
у * = Т у , Т = sin9 СО8ф Р
1 1 0 0 1
(10.101)
где а, р — параметры, зависящие от конкретных значений сдвига х0, у0,
поворота ф, и типа афинного преобразования (последовательности сдви-
гов и поворотов). В частности, по L координатам информативных точек
|(xf-,y(): / = 1,bj исходного изображения и соответственных им точек
{(х*,Уу): z = 1,l} искаженного изображения, в соответствии с (10.186),
формируется уравнение вида
q = Sc + £,
(10.102)
где TVxl -вектор q, №<4-матрица S (7V=2£, JV>4) и
искомый 4x1-вектор с
задаются, соответственно, в виде
-У1 1 О
~Уь 1 О
X! О 1
Ч 0 1.
(10.103)
10.14. Информационная технология совмещения изображений
775
a TVxl-вектор £ составлен из ошибок, связанных с неправильным определе-
нием соответственных точек.
Далее по S и q решается задача оценки векторного параметра с при огра-
ничении
с\ + с2 — cos 2 <Р + sin 2 ср = 1. (10.104)
С использованием полученных оценок с, = cos<p, с2 =sin9, с3 =d, с4 = 0
формируется система двух уравнений, вид которых определяется типом (по-
следовательностью) аффинных преобразований, и вычисляются искомые па-
раметры сдвига _х0, у0.
Поскольку число используемых информативных точек невелико, для ре-
шения задачи оценки используется итерационная процедура с взвешиванием
данных на промежуточных шагах. Весовая матрица строится с учетом ограни-
чений-равенств (10.104). При построении корректирующего вектора £, фор-
мируются лишь несколько компонентов, соответствующих наиболее выделя-
ющимся невязкам.
Далее в малой окрестности точки с координатами, равными ближайшим
целым числам вновь осуществляется поиск соответственных точек к скоррек-
тированным компонентам (включая также точки с более низким порогом
информативности). Если находятся точки, обладающие более высокой корре-
ляцией, осуществляется замена соответствующих компонентов вектора g. В
противном случае соответствующие строки в уравнении (10.102) исключают-
ся из рассмотрения до тех пор, пока соблюдается условие N > 4k, где к > 0 —
заданное (целое) число.
Пример 10.23. Для экспериментальной проверки работоспособности опи-
санных процедур совмещения, использовались дактилоскопические изобра-
жения 256x256 пикселов. Исходное изображение приведено на рис. 10.33*7.
Изображение на рис. 10.336 получено из него поворотом на 90° относительно
точки (127, 127). Для этого использовалось следующее преобразование:
х* = ТЛТфТ_л = Тх, где
1 0 х0 costp -sincp 0 1 0 0 0 -1 254
ТЛ = о 1 >0 т = sincp coscp 0 .Т_Л = 0 1 0 , а Т = 1 0 0
0 0 1 0 0 1 “*o “Уо 1 0 0 1
(вычислена при (р=90°, х0-127, у0=127).
На рисунке 10.34 приведены полученные по этим изображениям так назы-
ваемые «поля информативности», рассчитанные по (10.97) для 100 наиболее
информативных точек. Для оценки на изображениях было отобрано 85 (из 100)
соответственных точек. Затем по этим точкам были вычислены оценки компо-
нентов вектора с = [cos (р, sin ср, а, 0]: cos<p = 0, sin<p = l, а = 254, 0 = 0. Ясно,
что с использованием этих оценок изображения совмещаются точно.
776
ГЛАВА 10
Если относительные повороты изображений отличаются от углов кратных
90°, возможна ошибка совмещения, вследствие неизбежных ошибок округления
оценок координат до целых. На рис. 10.35а и б приведены тестовые изображе-
ния (512x512 пикселов), имеющих относительный поворот 30°. Для поворота на
30° относительно точки (160,180) использовалась матрица преобразования
0,866
0,5
0
-0,5
0,866
0
111,436
-55,884
1
Поля информативности исходного и повернутого изображения (по 100 точек)
показаны на рис. 10.36а и б соответственно. Для оценки на изображениях было
отобрано 86 (из 100) соответственных точек. Оцененные по этим точкам компо-
ненты вектора с = [cos<p,sin<p,a,p] равны соответственно: cos ср = 0,866156 ,
sin<p= 0,50011, a = 111,397, Р =-55,9869.
Ошибка совмещения с изображением, полученным из «повернутого» об-
ратным аффинным преобразованием с использованием указанных оценок,
составила 1 пиксел. Ясно, что устранение этой ошибки на заключительном
этапе технологии с использованием обычной прямоугольной маски не потре-
бует значительных вычислительных затрат.
10.15. Оценка по малому числу наблюдений в задачах обучения
распознаванию образов
Обучение распознаванию образов часто осуществляется по малому числу
наблюдений. Это может быть связано с нестационарностью распределений
образов в признаковом пространстве, требующей частой перенастройки клас-
сификатора. При этом использование априорных параметрических семейств
распределений образов может ввести в заблуждение. В указанной ситуации
осуществляют уточнение оценок параметров классификатора при каждом вновь
поступающем наборе данных и после каждого такого шага обучения пере-
страивают классификатор.
Как указывалось в п.4.1, задача распознавания образов включает две зада-
чи: отбор и упорядочивание признаков и собственно классификацию, которая
Рис. 10.35. Тестовые изоб-
ражения: а — исходное;
б — повернутое на 30°
10.15. Оценка по малому числу наблюдений в задачах обучения распознаванию образов 777
Рис. 10.36. Поля инфор-
мативности изображений:
а — исходного; б — по-
вернутого на 30°
включает задачу оценки параметров разделяющей функции. При решении
обеих указанных задач по малому числу наблюдений оказывается полезным
применение рассмотренных выше методов, основанных на использовании
нуль-пространства транспонированной матрицы признаков. Преимущества
этого подхода в данном случае связаны с тем, что при малом числе наблюде-
ний размерность нуль-пространства сопоставима с размерностью простран-
ства признаков.
Рассмотрим применение метода в рамках традиционной постановки зада-
чи распознавания образов в классе линейных или обобщенных разделяющих
функций вида (4.4) (см. п.4.1). Задача оценки параметров классификатора для
двух классов в этом случае формулируется следующим образом. По совокупно-
сти Мх\-векторов наблюдений признаков у; (/ = l,^), полученных на /Vобъек-
тах, принадлежность которых к классам известна, найти оценку ЛМ-вектора
параметров а разделяющей функции вида (4.4)
J(y) = arx,
(10.105)
где а = [w0, w]r= [w0, wb... wj, a x =[1, y]r.
При выборе системы обобщенных признаков решающее значение имеют
сингулярные числа 7УхЛ/-матрицы X, строками которой являются векторы
xf, i = \,N. Столбцы матрицы X будем обозначать X •, j — \,M . Если векто-
ры Ху линейно-зависимы (или «почти» линейно-зависимы), при вычисле-
нии сингулярных чисел и/или соответствующих им собственных значений
матрицы ХГХ могут возникнуть серьезные трудности.
Можно избежать вычисления собственных значений, если воспользовать-
ся показателем максимальной сопряженности (10.51). Более эффективно в
вычислительном отношении при малом числе наблюдений использование
процедуры, основанной на вычислении показателей сопряженности с нуль-
пространством (10.52).
Пусть XL — Nx 1-матрица, составленная из L нормированных (||Ху-| = 1,
j = i,L) векторов-столбцов матрицы X (2<LxM). В качестве количественных
характеристик взаимной ориентации векторов обобщенных признаков будем
использовать величины (10.53)
=(xJ.T0>lT’;ix^l/7(x7xJ)'/2.
(10.106)
778
ГЛАВА 10
Для матрицы из М столбцов возможно Jм = ^С'М (i = 3,M — 1) различ-
ных вариантов подпространств. Обычно число используемых характеристик
значительно меньше. Их выбор определяется конкретными особенностями
задачи, например, взаимной независимостью групп признаков и др.
Формирование пространства обобщенных признаков может осуществлять-
ся либо путем наращивания числа признаков, либо путем их исключения. В
последнем случае число обобщенных признаков задается большим, насколь-
ко это возможно. Затем для каждого из них вычисляются показатели Sj. Век-
торы обобщенных признаков, для которых эти величины не удовлетворяют
заданным граничным значениям, исключаются из матрицы X.
После того как признаковое пространство сформировано, решается задача
оценки параметров классификатора. Ищется разделяющий вектор а, удовлет-
воряющий уравнению
Ха = Ь,
(10.107)
где b — вектор, формируемый по заданным допускам, определяющим область
решений.
Процедура оценки может быть построена по схеме вложенных итераций.
Внутренний цикл обеспечивает получение устойчивых к ошибкам предъявле-
ния обучающих объектов оценок а вектора параметров а. Внешний цикл
реализует настройку вектора Ь, обеспечивающего наилучшее, в смысле задан-
ного критерия, положение разделяющей гиперплоскости.
Для получения оценок а при малом числе обучающих объектов эффективно
применение рассмотренных выше процедур оценки по малому числу наблюде-
ний, основанных на методе взвешивания или корректировке вектора выхода
модели. Для настройки вектора допусков могут использоваться традиционные
критерии качества классификатора, рассматривавшиеся, например, в [6].
Пример 10.24. Рассмотрим применение показателя сопряженности для оцен-
ки информативности признаков. Проводился эксперимент по классификации
Рис.10.37. Поле
показателей Sj
цифр. Изображения цифр были преобразованы в бинарный растр
32x64. Растр был поделен на фрагменты 8x8, а в качестве при-
знаков использовалось количество черных пикселов в фрагменте.
Использовалось по 20 образцов каждой цифры.
На рис. 10.37 приведено поле показателя сопряженности
признаков (10.106) (фрагментов растра) для цифр «2» и «3»
(более темный цвет соответствует меньшему значению ^).
Для двух фрагментов все компоненты вектора Ху оказались
равными нулю (на рисунке соответствующие фрагменты от-
мечены крестиками). Эти признаки были исключены из даль-
нейшего рассмотрения. Таким образом, матрица X из урав-
нения (10.107) имела размерность 40x31.
В таблице 10.22 приведены минимальные и максималь-
ные значения Sj для матрицы X и X', полученной после ис-
ключения из X восьми столбцов с минимальными значениями (5ДОП = 0,05).
Оказалось, что заданным требованиям на величину показателя сопряженности
Литература к главе 10
779
удовлетворяют столбцы, соответствующие на рисунке фрагментам 13, 24, 34,
64, 74, 81, 82 и 83 (первая цифра — номер строки, вторая — номер столбца
фрагмента на рисунке). Как видно из таблицы, после исключения группы признаков их сопря- женность уменьшилась. Имеет место связь между количеством исклю- ченных по показателю сопряженности призна- ков и количеством неправильных классификаций. В данном примере все объекты классифицирова- Таблица 10.22. Предельные значения показателей 5",
X X'
•-’mm 0,026 0,092
^mu 0,210 0,510
лись правильно при исключении до 10 признаков, имеющих наименьшие зна-
чения показателя сопряженности. При исключении более 15 признаков число
ошибок классификации возрастало.
Рассматриваемый подход хорошо приспособлен к ситуации, когда класси-
фицируемые объекты изменяют свои свойства (признаки) в процессе функ-
ционирования. Параметры алгоритмов оценки в методе взвешивания и/или
корректировки вектора выхода могут быть определены путем анализа невязок
на предшествующем наборе данных с учетом вновь поступающих данных.
В данной процедуре легко учитывать также мнение квалифицированного экс-
перта, осуществляющего обучение системы. Это реализуется путем непосред-
ственного внесения изменений в вектор Ь, формируемый по допускам, опре-
деляющим область решений.
Литература к главе 10
1. Веллман Р. Введение в теорию матриц (М.: Наука, 1976)
2. Воеводин В.В. Вычислительные основы линейной алгебры (М.: Наука, 1977)
3. Гантмахер Ф.Р. Теория матриц (М.: Наука, 1967)
4. Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов (Пер.
с англ. М.: Мир, 1984)
5. Демиденко Е.З. Линейная и нелинейная регрессии (М.: Финансы и статис-
тика, 1981)
6. Дуда Р., Харт П. Распознавание образов и анализ сцен (Пер с англ. М.:
Мир, 1976)
7. Калман Р.Е. Успехи математических наук Т. 40, вып. 4 (244) 27 (1985)
8. Лоусон Ч., Хенсон Р. Численное решение задач метода наименьших квадра-
тов (Пер. с англ. — М.: Наука, Гл. ред. физ.-мат. лит., 1986)
9. Маркус М., Минк X. Обзор по теории матриц и матричных неравенств
(Пер. с англ. М.: Наука, 1972)
10. Мельканович А.Ф. Фотографические средства и их эксплуатация (М.: Изд-
во МО, 1984)
11. Мудров В.И., Кушко В.Л. Методы обработки измерений (М.: Сов. радио. 1976)
12. Поляк Б.Т., Цыпкин Я.З. В сб. Идентификация и оценка параметров сис-
тем. Тр. IV Симпоз. ИФАК (Тбилиси, Мецниереба, ч. I, 1976) С. 190
13. Прэтт У.К. Цифровая обработка изображений (М.: Мир, 1982)
780
ГЛАВА 10
14. Сергеев В.В., Фролова Л.Г. Автометрия 1 (1996)
15. Сергеев В.В., Фурсов В.А., Максимов М.В. Тр. III конф. «Распознавание
образов и анализ изображений: новые информационные технологии» (РОЛИ-
97) (Н. Новгород, 1—7 декабря, Тез докл., Ч. I, 1997) С. 252
16. Сергеев В.В., Фурсов В.А., Парфенов С.И. Тезисы докладов IV конферен-
ции «Распознавание образов и анализ изображений: новые информационные
технологии (Новосибирскк, Ч. I, 1998) С. 378
17. Сойфер В.А., Котляр В.В., Фурсов В.А. Тр. конф. Волжского регионального
центра РАРАН (Саров, 1998) С. 108
18. Солодовников В.В., Бирюков В.Ф., Тумаркин В.И. Принцип сложности в
теории управления (М.: Наука, 1977)
19. Теряев Е.Д., Шамриков Б.М. Цифровые системы и поэтапное адаптивное
управление (М.: Наука, 1999)
20. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач (М.:
Наука, 1974)
21. Уилкинсон Дж. X. Алгебраическая проблема собственных значений (Пер. с
англ. М.: Наука, 1970)
22. Фурсов В.А. Техн, кибернетика 6 130 (1991)
23. Фурсов 'В.К. Введение в идентификацию по малому числу наблюдений (Изд.
МАИ, 1991)
24. Фурсов В.А. Идентификация моделей систем формирования изображений
по малому числу наблюдений (Самара, СГАУ, 1998)
25. Фурсов В.А. Компьютерная оптика (Вып. 14—15, 78, 1995)
26. Фурсов В.А. Компьютерная оптика (Вып. 16, 103, 1996)
27. Фурсов В.А., ЧудилинА.Г. В сб. Искусственный интеллект (Симферо-
поль, 2, 2000) С. 212
28. Цыпкин Я.З. Основы информационной теории идентификации (М.: Наука,
1983).
29. Шамриков Б.М., Фурсов В.А. Техн, кибернетика 6 173 (1979)
30. Эйкхофф П. Основы идентификации систем управления (Пер. с англ. Под
ред. Райбмана Н.С. — М.: Мир, 1975)
31. Bjorck Ake. Least Squares Methods. (Elsevier Science Publishers B.V. North-
Holland, 1990)
32. Fursov V.A. Journal: Proc. SPIE 3087 34 (1997)
33. Fursov V.A. 5th International Workshop on Digital Image Processing and Computer
Graphics. «Image Processing and Computer Optics» (Samara, Russia, Aug, 22—
26, 1994) P. 2
34. Fursov V.A. Journal: Proc. SPIE 2363 62 (1995)
35. Sergeyev, Vladislav V., Fursov, Vladimir A., & Maksimov, M.V. Journal: Proc.
SPIE 3348 275 (1998)
36. Fursov V.A. Pattern recognition and image analysis 8(2) (1998)
Учебное издание
МЕТОДЫ КОМПЬЮТЕРНОЙ обработки изображении
Гашников Михаил Валерьевич
Глумов Николай Иванович
Ильясова Наталья Юрьевна
Мясников Владислав Валерьевич
Попов Сергей Борисович
Сергеев Владислав Викторович
Сойфер Виктор Александрович
Храмов Александр Григорьевич
Чернов Андрей Владимирович
Чернов Владимир Михайлович
Чичева Марина Александровна
Фурсов Владимир Алексеевич
Редактор М.Б. Козинцева
Оригинал-макет: О.А. Пелипенко
ЛР № 071930 от 06.07.99. Подписано в печать 11.06.03. Формат 70x100/16.
Бумага офсетная. Печать офсетная. Усл. печ. л. 63,52. Уч.-изд. л. 65.
Заказ № 9044
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов
в ППП «Типография «Наука».
121099 Москва, Шубинский пер., 6
Издательская фирма
«Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117864 Москва, Профсоюзная ул., 90
В издательстве «ФИЗМАТЛИТ» вышли из печати
(2000 2003 гг.)
Аракин В.Д. История английского языка: Учеб, пособие. — Изд. 2-е. — 2001. — 272 с.
Аракин В.Д. Сравнительная типология английского и русского языков: Учеб, пособие. —
Изд. 3-е. - 2000. - 256 с.
Афанасьева О.В.} Резвецоеа М.Д., Самохина Т.С. Сравнительная типология английского
и русского языков (практикум): Учеб, пособие. — Изд. 2-е, испр. — 2000. — 208 с.
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры: Учеб, для вузов. —
Изд. 8-е. - 2000. - 320 с.
Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической гео-
метрии и линейной алгебре / Под ред. Д.В. Беклемишева: Учеб, пособие. — Изд. 2-е,
перераб. — 2001. — 496 с.
Бендриков Г.А., Буховцев Б.Б. и др. Физика. Задачи для поступающих в вузы: Учеб,
пособие для подготов, отделений вузов. — Изд. 9-е. — 2000. — 400 с.
Бугров С.Я., Никольский С.М. Сборник задач по высшей математике. — 3-е изд. — 2001. —
304 с.
Бутиков Е.И., Кондратьев А. С. Физика. В 3-х кн.: Учеб, пособие.
Кн. 1. Механика. — 2000. — 352 с.
Кн. 2. Электродинамика и оптика. — 2000. — 336 с.
Кн. 3. Строение и свойства вещества. — 2000. — 336 с.
Бутузов В.Ф., Крутицкая Н.Д., Шишкин А.А. Линейная алгебра в вопросах и задачах
/ Под ред. В.Ф. Бутузова: Учеб, пособие. — Изд. 2-е, испр. — 2002. — 248 с.
Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А. А. Математический анализ
в вопросах и задачах / Под ред. В.Ф. Бутузова: Учеб, пособие. — Изд. 5-е, испр. —
2002. - 480 с.
Буховцев Б.Б., Кривченков В.Д. и др. Сборник задач по элементарной физике / Под
ред. В.Ф. Бутузова. — Изд. 6-е — 2000.
Владимиров В.С., Жаринов В.В. Уравнения математической физики: Учеб, для вузов. —
Изд. 2-е., стереотип. — 2003- — 560 с.
Волковыский Л.И., Лунц Г.Л., Араманович И.Г. Сборник задач по теории функций ком-
плексного переменного: Учеб, пособие для вузов. — Изд. 4-е, перераб. — 2002. — 312 с.
Гантмахер Ф.Р. Лекции по аналитической механике / Под ред. Е.С. Пятницкого: Учеб,
пособие для вузов. — Изд. 3-е. — 2001. — 264 с.
Гильденбург В.Б., Миллер М.А. Сборник задач по электродинамике. — Изд. 2-е, доп. —
2001. - 168 с.
Гольдштейн Б.В., Городцов В.А. Механика сплошных сред. Ч. 1. — 2000. — 256 с.
Елютин И.В., Кривченков В.Д. Квантовая механика (с задачами) / Под ред. Н.Н. Бого-
любова. — Изд. 2-е, перераб. — 2001. — 304 с.
Задачи по общей физике / Белонучкин В.Е., Заикин Д.А., Кингсеп А.С., Локшин Г.Р.,
Ципенюк Ю.М. — 2001. — 336 с.
Зайцев В.Ф., Полянин А.Д. Справочник по обыкновенным дифференциальным уравне-
ниям. — 2001. — 576 с.
Зимина О.В., Кириллов А.И., Сальникова Т.А. Решебник. Высшая математика — 2000. —
368 с.
Ильин В.А., Позняк Э.Г Основы математического анализа. В 2-х ч. — 2001. — 648 с.; 464 с.
Ильин В.А., Позняк Э.Г. Линейная алгебра: Учеб, для вузов. — Изд. 5-е — 2001. — 320 с.
Ильин В.А., Позняк Э.Г. Аналитическая геометрия: Учеб, для вузов. — Изд. 5-е. — 2001. —
240 с.
Кадомцев С. Б. Аналитическая геометрия и линейная алгебра. — 2001. — 160 с.
Карманов В.Г Математическое программирование: Учеб, пособие. — Изд. 5-е, стерео-
тип. — 2001. — 264 с.
Кингсеп А.С., Локшин ГР., Ольхов О.А. Основы физики. Курс общей физики. В 2 т. Т.
1. Механика, электричество и магнетизм, колебания и волны, волновая оптика / Под
ред. А.С. Кингсепа: Учебник. — 2001. — 560 с.
Кострикин А.И. Введение в алгебру. В 3-х кн.: Учеб, для вузов.
Кн. 1. Основы алгебры. — Изд. 2-е. — 2000. — 352 с.
Кн. 2. Линейная алгебра. — Изд. 2-е. — 2000. — 352 с.
Кн. 3. Основные структуры алгебр!я. — Изд. 2-е. — 2000. — 336 с.
Кудрявцев Л.Д. Краткий курс математического анализа. В 2-х тл Учеб, пособие. — Изд.
3-е, перераб. — 2002. — 400 с.; 424 с.
Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и те-
ории алгоритмов. — 4-е изд. — 2001. — 256 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. В 10 т.: Учеб, пособие для вузов. —
2001.
Лебедев В.И. Функциональный анализ и вычислительная математика.:
Учеб, пособие. — Изд. 4-е, перераб. и доп. — 2001. — 296 с.
Лурье М.В. Геометрия. Техника решения задач: Учеб, пособие. — 2001. — 240 с.
Медведев ГН. Абитуриенту о письменном экзамене по математике. Физический факультет
МГУ. 1997-2000 гг. - 2001. - 64 с.
Назаретов А.П., Пигарев Б.П., Садовничая И.В., Симонов А.А. Задачи и варианты их
решения на вступительных экзаменах в московских вузах (экономические специаль-
ности): Учеб, пособие. — Изд. 2-е, перераб. и доп. — 2001. — 458 с.
Никольский С.Н. Курс математического анализа: Учеб, для вузов — Изд. 5-е. — 2000. —
640 с.
Пинский А.А. Задачи по физике / Под ред. Ю.И. Дика. — 2000. — 336 с.
Полянин А.Д. Справочник по линейным уравнениям математической физики. — 2001. —
576 с.
Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Конкурсные задачи по математике: Спра-
вочное пособие. — 2001. — 400 с.
Пугачев В. С. Теория вероятностей и математическая статистика: Учебник для вузов. —
Изд. 2-е, испр. и доп. - 2002. — 496 с.
Рябенький В. С. Введение в вычислительную математику. — Изд. 2-е. - 2000. — 296 с.
Сборник задач по алгебре / Под ред. А.И. Кострикина: Учеб, для вузов. — Изд. 3-е, испр.
и доп. — 2001. — 464 с.
Сборник задач по уравнениям математической физики / Владимиров В. С., Вашарин А. А.,
Каримова Х.Х., Михайлов В.П., Сидоров Ю.И., Шабунин М.И. — Изд. 4-е, стерео-
тип. — 2003. — 288 с.
Сигал И.Х., Иванова А.П. Введение в прикладное дискретное программирование. Учеб,
пособие. — 2002. — 240 с.
Треногий В.А. Функциональный анализ: Учеб, пособие. — Изд. 3-е, испр. — 2002. — 488 с.
Треногий В.А., Писаревский Б.М., Соболева, Т.С. Задачи и упражнения по функциональ-
ному анализу: Учеб, пособие. — Изд. 2-е, испр. и доп. — 2002. — 240 с.
Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной
математики. Геометрия. Стереометрия. — 2000. — 248 с.
Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной
математики. Геометрия. Планиметрия. — 2000. — 248 с.
Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной
математики. Арифметика и алгебра. — 2000. — 320 с.
Элементарный учебник физики / Под ред. Г.С. Ландсберга. В 3-х кн.: Учеб, пособие. —
2000. - 512 с.; 400 с.; 400 с.
Яворский Б.М., Пинский А. А. Основы физики / Под ред. Ю.И. Дика.
В 2-х кн. - 2000. - 624 с.; 576 с.
Яворский Б.М., Селезнев Ю.А. Физика: Справочное пособие для поступающих в вузы. —-
Изд. 5-е, перераб. — 2000. — 592 с.
По вопросам приобретения книг обращаться:
Издательская фирма
«Физико-математическая литература»
117864 Москва, Профсоюзная ул., 90
тел./факс (095) 334-7421, e-mail: fizmat@maik.ru