ОБЩАЯ ЧАСТЬ
ГЛАВА I.
Введение.
§ 1. Астрономия, ее задачи и методы. Астрономия изучает движение^ строе/ше, взаимную связь и процессы развития небесных тел Ч Науку астрономию справедливо считают древнейшей из наук. Уже за 5 — 6 тысяч лет до нашего времени кочевники Африки и Азии при своих передвижениях в пустынях ориентировались по звездному небу. Конечно, их познания еще не представляли собой науки, но они положили ей начало путем накопления фактов и установления простейших закономерностей. С течением времени, общее развитие экономики и всех наук вообще оказало воздействие и на развитие астрономии. Уже во П в. до н. э. древнегреческий астроном Гиппарх определил положения на небе свыше тысячи звезд и изучил видимое движение Солнца и Луны, тем самым положив начало астрономии как науке и увеличив возможности ее практического применения, необходимого для развития торговли и мореплавания. Сначала занятия астрономией, главным образом, имели целью вести счет времени, а также дать возможность мореплавателям точнее ориентироваться в море. С течением времени общее культурное развитие народов все больше и больше побуждало ученых не только разрабатывать практическое применение знаний, но и стремиться познать мир, исследовать закономерности и причины явлений. При этом очень большое значение имел переход от видимых движений небесных светил к их действительным движениям. Этот переход, сделанный на основе предыдущих многовековых наблюдений величайшим астрономом К о-перником, положил границу между древней астрономией, изучавшей лишь видимые движения, и новой астрономией, знающей действительные движения небесных тел.
Развитие астрономической теории открыло широкие возможности как для практического применения астрономии, так и для понимания закономерностей и причин изменений, происходящих во вселенной. Общее развитие науки и техники давало норые возможности для исследований и ставило в то же время и новые задачи. Науки, особенно сильно влиявшие на развитие астрономии, были математика и физика. Физика в соединении с техникой дала возможность астрономии применить для изучения неба зрительные трубы, спектральный анализ, фотографию и фотометрию и в то же время поставила перед астрономией задачу исследования процессов развития материи во вселенной. В настоящее время связь астрономии с физикой стала так глубока, что появилась особая
1 Слово „астрономия* — греческого происхождения и имеет два корпя: „астрой* — светило и „номос* — закон.
1*	5
ветвь астрономии — астрофизика. Астрофизика, пользуясь теориями физики и химии, пользуясь инструментами, построение которых было бы невозможно без физики, в то же время дает все новый й новый материал для более глубокого познания форм существования материи и
Рис. 1. Вид южной половины небосвода 23 сентября в 10 часов вечера (в средних широтах СССР).
применяет теорию для углубленного исследования развития небесных тел. Ряд наиболее важных исследований строения материи, произведенных учеными новейшего времени, связан с результатами астрономиче-* ских наблюдений, и, наоборот, исследования развития небесных тел неизменно проводились на основе знания физических законов. Математика дает астрономии методы, необходимые, для обработки произведенных наблюдений и для развития астрономической теории.
Коренное отличие астрономии от физики представляет самый метод получения материала. Физика—наука опытная, астрономия — наблюдательная. Физика, стремясь исследовать закономерности и причины явлений, проводит в любое время опыты в наиболее подходящих для исследования условиях. Астрономия вынуждена следить за ходом явлений, так как не имеет возможности ни повторить, ни изменить движений небесных тел. Поэтому астрономы наблюдают явления тщательно, со всеми подробностями их описывают, точно отмечая при этом время, и только после накопления таких наблюдений имеют возможность сделать выводы. Астрономические наблюдения иногда оказываются необходимыми для физики. Например, современная физика не может поставить опыта для изучения материи при 11 000°; астрономы же могут наблюдать светила этой температуры и приходить здесь на помощь физикам, но уже Путем наблюдений, а не опытов.
§ 2.	Очерк вселенной. После захода Солнца ночь наступает не сразу, небосвод темнеет постепенно, и с такой же постепенностью появляются на небе звезды; сначала их немного, но позже число звезд становится больше, и при этом звезды, появившиеся раньше» оказы-4
ваются ярче, чем появившиеся позже. При наступлении полной ночи небо усеяно звездами различной яркости, а среди звезд проходит слабо светящаяся полоса, которую называют Млечным Путем. Среди групп звезд— созвездий — можно наблюдать Луну и яркие, похожие на звезды све-
Рис. 2. Вид южной половины небосвода 23 сентября в И часов вечера (в средних широтах СССР),
тила — планеты. Планеты по их виду можно отличить от звезд, так как они дишь слабо мерцают.
Вид неба непрерывно меняется. Взаимное расположение звезд при наблюдениях невооруженным глазом остается неизменным, но все они перемещаются по небосводу (рис. 1 и 2). Их перемещение можно заметить невооруженным глазом за 15—20 минут, ас астрономическими трубами — в доли секунды. Луна и планеты изменяют свое место среди звезд, но неодинаково быстро; легче всего заметить движение Луны (рис. 3). Это явление можно пронаблюдать невооруженным глазом в течение получаса. Перемещение планет менее заметно — нужно следить за ними по меньщей мере несколько дней, чтобы уста
новить, что планеты изменили свое положение относительно какой-нибудь из звезд.
Не следует, однако, думать, что звезды представляют собой образец покоя и неподвижности. Долголетние наблюдения с большими астрономическими трубами показывают, что и звезды перемещаются на небе одни относительно других, но нужно наблюдать много лет, чтобы
5
Рис. 3. Область неба, на которой отмечены видимые перемещения среди звезд: Луны—за 3 часа и планеты Сатурн—за 3 месяца (отре-зок около звезды |&).
специальными инструментами обнаружить эти перемещения (рис. 4). Таким образом, небо со всеми своими светилами является образцом вечной изменчивости.
В сущности говоря, всякое движение, которое мы наблюдаем на небе, — относительно, так как все светила находятся в движении. Знание расстояний до небесных тел показывает, что наши непосредственные впечатления часто дают нам представление, обратное тому, что есть на самом деле. При наблюдениях передвижений Луны по звездному небу оно нам представляется наиболее быстрым
Рис. 4. Видимые перемещения звезд созвездия Дельфина за 10 тысяч лет. Кружок изображает видимые размеры Луны на небе, величины и направления стрелок — перемещения звезд.
потому, что Луна — ближайшее к нам светило; в действительности же как планеты, так и звезды, по отношению к которым мы наблюдаем движение Луны, имеют линейные скорости, несравненно ббльшие, чем Луна.
Вообще наблюдая движение светил, мы должны всегда помнить, что с какого-нибудь другого, отдаленного от Земли небесного тела и самое звездное небо и движения небесных светил представляются в ином виде.
Мы говорили пока лишь о перемещениях самих светил, т. е. об изменениях механического характера./Астрономические наблюдения показывают, что и на поверхностях и внутри светил происходят изменения не только механические. Как пример можно привести ближайшую к нам звезду— наше Солнце, на поверхности которого наблюдаются появление и исчезновение темных пятен, глубокие физико-химические процессы, электромагнитные изменения, выделение тепла и света и связанные с этим быстрые движения громадных масс раскаленных газов. Хотя мы и не можем наблюдать поверхностей отдаленных звезд, но, изучая излучаемый ими свет, мы приходим к выводу, что и на их поверхностях происходят подобные же изменения, иногда даже еще более грандиозные. Самое свечение небесных тел представляет собой процесс особого рода, связанный с физико-химическими изменениями на поверхности и внутри светила. Таким образом, во вселенной всюду и вечно происходит движение в самом общем смысле этого слова. Астрономическая наука может в ряде случаев описать не толькд перемещения небесных тел в пространстве, но и внутренние процессы, происходящие в них. Законы, по которым происходят эти движения, известны уже настолько, что наука в состоянии рассчитать происходящие изменения как вперед, 6
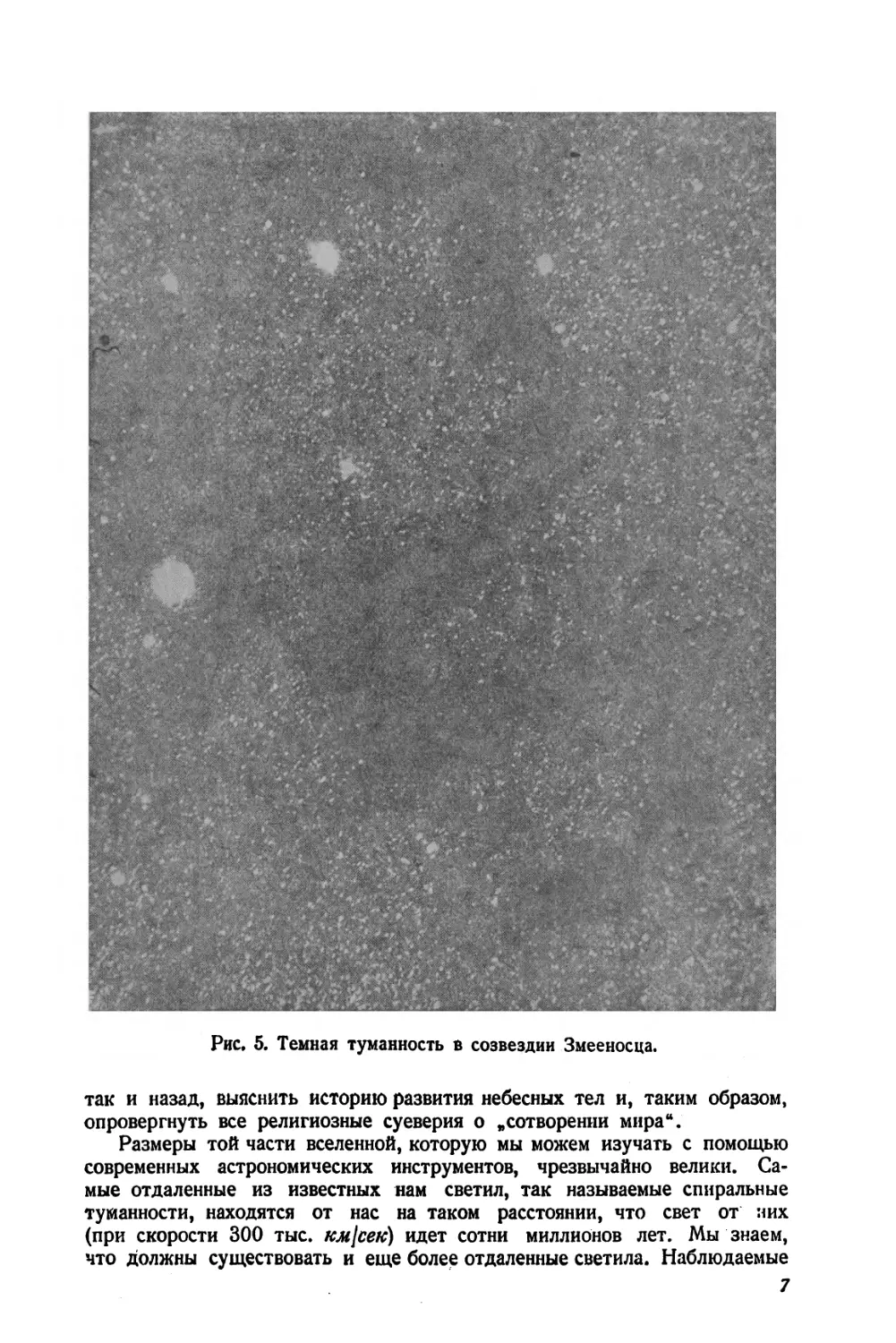
Рис, 5. Темная туманность в созвездии Змееносца.
так и назад, выяснить историю развития небесных тел и, таким образом, опровергнуть все религиозные суеверия о „сотворении мира44.
Размеры той части вселенной, которую мы можем изучать с помощью современных астрономических инструментов, чрезвычайно велики. Самые отдаленные из известных нам светил, так называемые спиральные туманности, находятся от нас на таком расстоянии, что свет от них (при скорости 300 тыс. км/сек) идет сотни миллионов лет. Мы знаем, что должны существовать и еще более отдаленные светила. Наблюдаемые
7
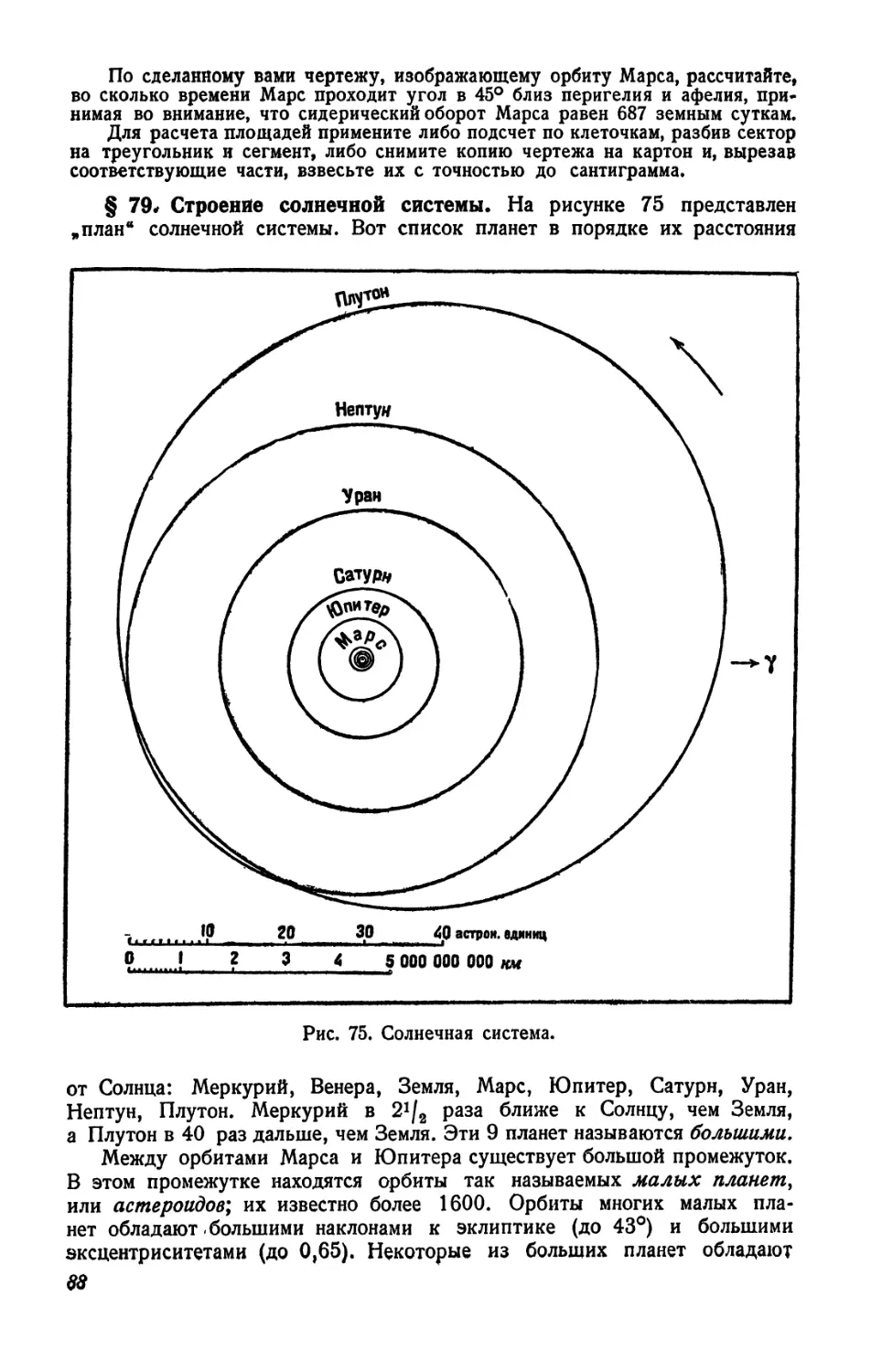
Рис. 6. Орбиты четырех планет, ближайших к Солнцу.
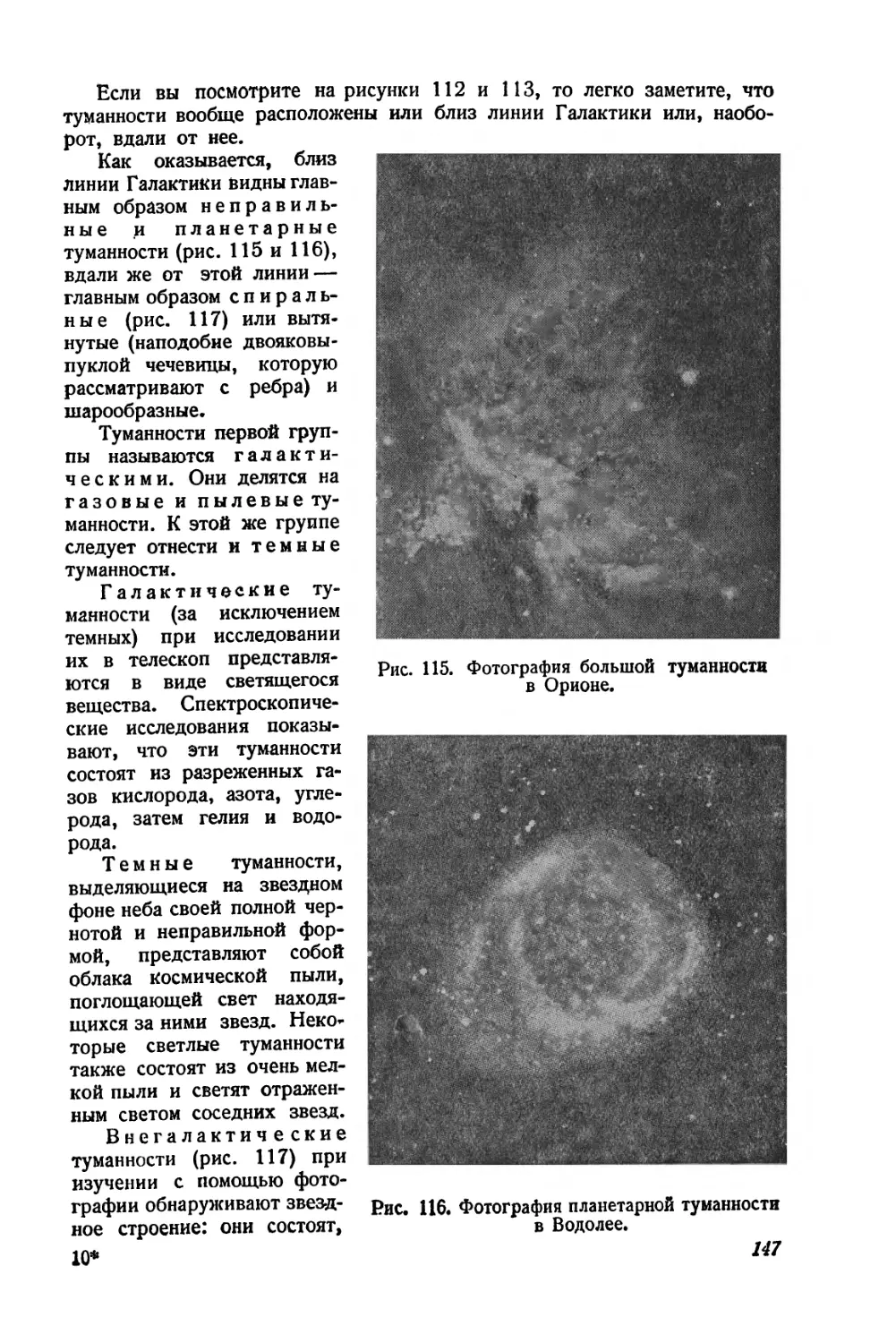
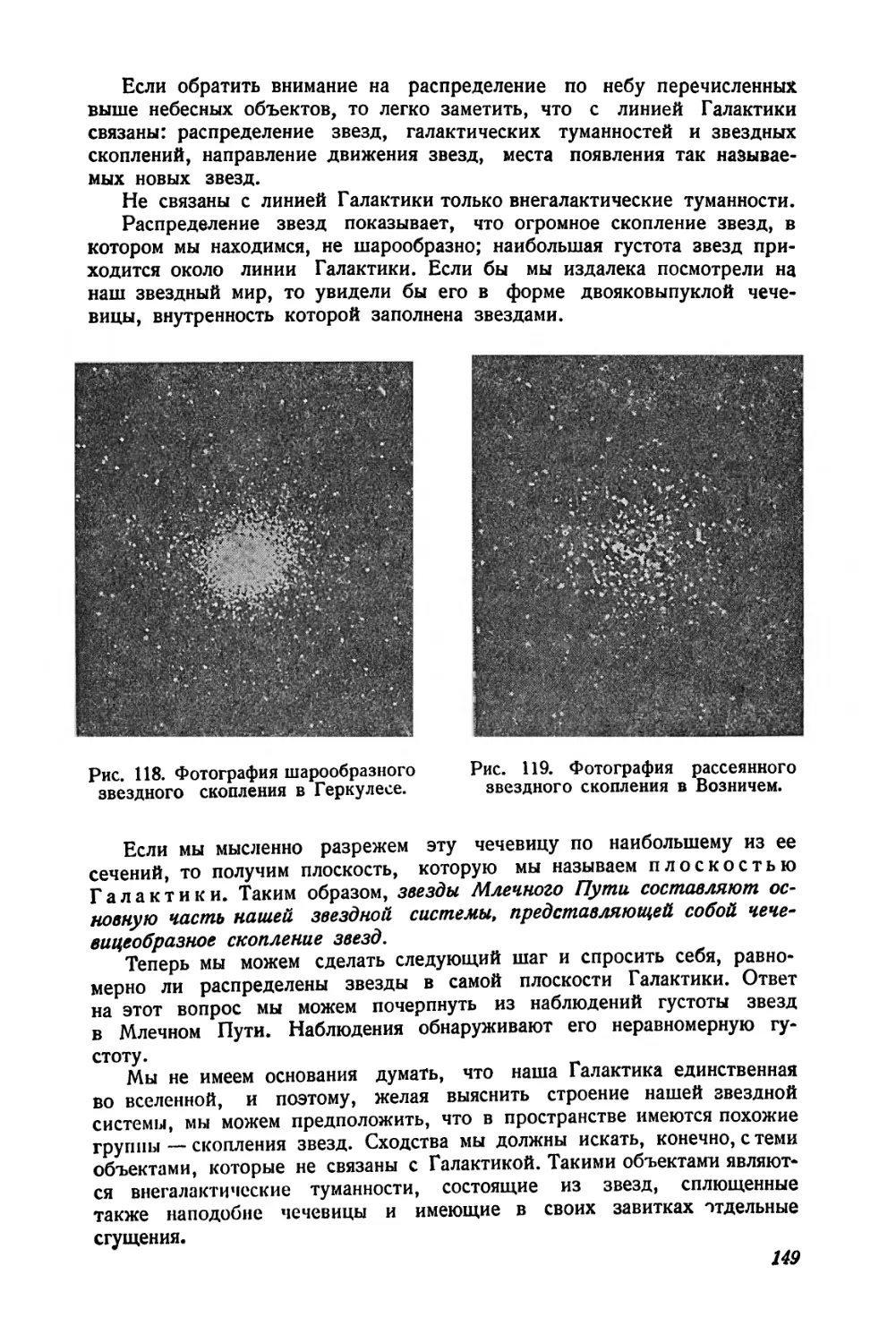
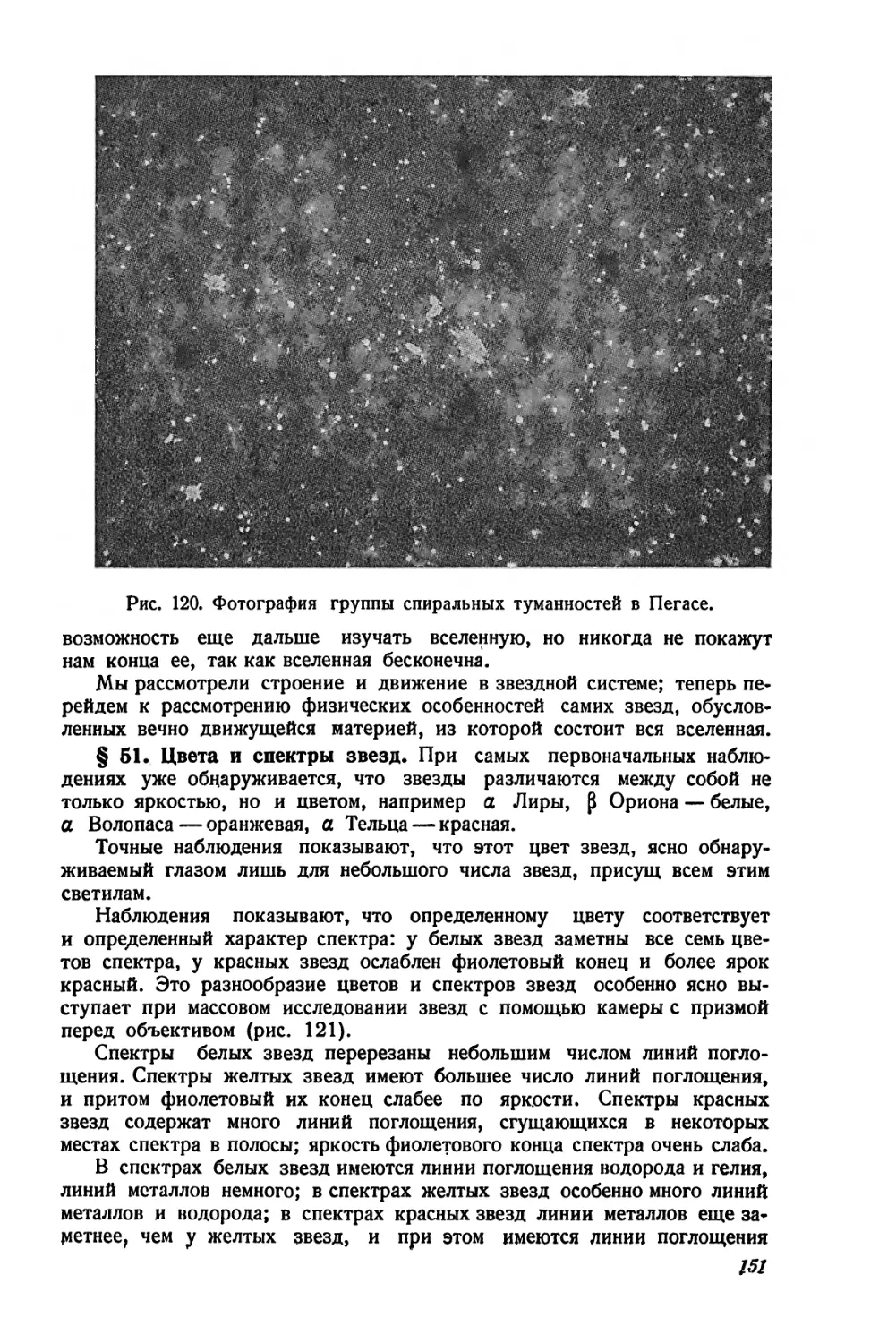
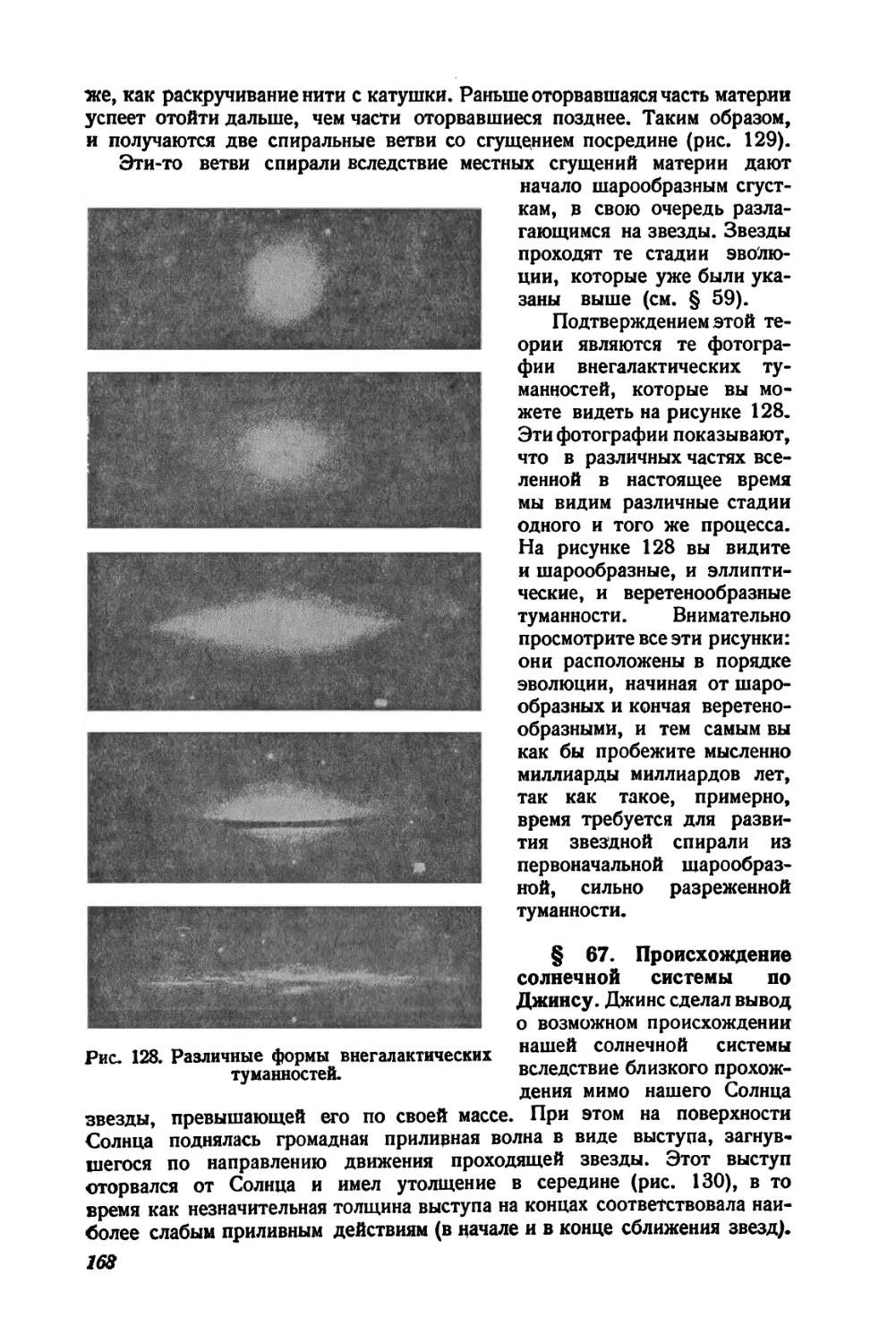
нами небесные тела состоят из материи, находящейся в самых разнообразных формах, начиная от темных, несветящихся, облакообразных „туманностей * (рис. 5) и кончая материей, сгустившейся в газовые шары громадных размеров, — звезды, излучающие свет и тепло при температурах их поверхности от 3000° до 30 000°. Наше Солнце — лишь одна из звезд и притом сравнительно небольшая и не особенно горячая (температура поверхности Солнца около 6000°). Звезды находятся в различных стадиях своего развития, они возникают из холодных газовых еще более громадных шаров, сжимаются и разогреваются до наивысшей температуры, а затем постепенно гаснут. Эти процессы развития звезд происходят очень медленно — в течение биллионов лет. В различных местах вселенной звезды рассеяны не беспорядочно — они расположены так, что образуют спиралеобразные иля шарообразные скопления. Такие звездные скопления вследствие большой отдаленности представляются рам маленькими светящимися объектами, различимыми лишь с помощью больших телескопов. Наше Солнце — одна из звезд подобного скопления, которое мы видим на небе, как светлую полосу Млечного Пути. В мощные телескопы возможно обнаружить, что полоса Млечного Пути состоит из громадного числа звезд, невооруженным же глазом мы видим лишь клочковатое, облакообразное строение. Млечного’ Пути. Есть основание предполагать, что звездное скопление — Млечный Путь — в действительности имеет спиралевидное строение, подобное' наблюдаемым на небе спиральным туманностям, причем все звезды, входящие в него, движутся вокруг общего центра. Наша Земля является,
спутникомодной из звезд — Солнца, вокруг которого обращаются светящие отраженным солнечным светом темные шары — планеты (рис. 6). Земля — одна из сравнительно небольших планет, обращающаяся вокруг Солнца на расстоянии около 150 млн. км. Самая дальняя из планет, известных в настоящее ’время — Плутон — обращается вокруг Солнца на расстоянии, в 40 раз большем, чем Земля. Около большинства планет обращаются меньшие тела, получившие название „спутников планет*. Луна—спутник Земли, обращающийся вокруг нее на расстоянии 380 тысяч километров; это самое близкое к наМ небесное тело.
Кроме туманностей, звезд и планет, в небесном пространстве движутся скопления небольших телец. Когда эти скопления приближаются к Солнцу, из них начинают выделяться газы, которые под действием давления лучей Солнца, отбрасываются в противоположную от Солнца сторону. С Земли мы наблюдаем это как' появление на небе сначала светлого пятна, а потом удлиненного „хвостатого светила*. Такие светила полу- . чили название „комет*. Кометы движутся около Солнца по очень вытянутым траекториям. Траектории многих комет изучены настолько, что астрономы предвычисляют появление этих светил.
8
Из этого краткого очерка видно, что наука уже многое изучила во вселенной. Происходящее с каждым годом расширение и углубление научных исследований дает нам уверенность, что явления, непонятные нам в настоящее время, будут нами разгаданы и поняты после более глубокого их изучения. Следует помнить, что та звездная вселенная, которую мы теперь изучаем, соответствует лишь одной из стадий ее эволюции.
Систематическое изучение отдельных небесных объектов и прежде всего переход от видимых их движений к действительным дают нам возможность глубже и подробнее разобраться в изменениях, происходящих во вселенной.
§ 3.	О наблюдениях. При изучении начал астрономйи в школе необходимо, согласно указаниям учителя, производить наблюдения для того, чтобы лучше понять выводы науки и способы ее исследования. В этом учебнике одновременно с описанием явлений будурданы(в особых отделах) указания к выполнению наблюдений с простыми, иногда даже самодельными, инструментами.
Некоторые наблюдения надо проводить в течение месяца или года, затрачивая на каждое из них немного времени. В отделах, где описываются наблюдения, указывается, сколько времени и как чдсто надо проводить каждое из них.
Наблюдение надо тщательно и аккуратно записывать с указанием всякий раз даты (год, месяц, число) и времени (час, минута, а по возможности и секунда). Для записи всех наблюдений за год следует завести особую тетрадку, надписав на ее заглавной странице свою фамилию и место наблюдения (название места наблюдения и, если это известно, географическое положение, его).
§ 4.	Небосвод и созвездия. На открытом месте, где бы ни велось наблюдение, небо, как ясное, так и облачное, представляется нам похожим на внутреннюю поверхность полушара, простирающуюся над головой и спускающуюся к краям наблюдаемого земного ландшафта. Земная поверхность нам представляется кругом, в середине которого мы находимся и края которого, как кажется на первый взгляд, сходятся сf небом. Линия, по которой (как нам представляется) небо сходится с землей, называется линией видимого горизонта.
В течение дня мы наблюдаем движение по небосводу Солнца, которое восходит в каком-нибудь месте линии горизонта, поднимается все выше, затем начинает опускаться и заходит. После захода Солнца голубой небосвод темнеет, и на нем ^появляются звезды.
Взаимное расположение звезд .на небе не меняется заметно в течение очёнь долгого времени, и поэтому еще с древних времен стали выделять на небе группы особенно ярких звезд и называть их созвездиями. Каждой группе звезд — созвездию — придавали наименование сказочных героев, зверей, а в некоторых случаях эти названия соответствовали тем житейским хозяйственным работам Или религиозным обрядам, с временем которых совпадала видимость на небе данного созвездия. Так получились созвездия со странными для нашего времени названиями Большой Медведицы, Ориона, Цефея, Весов и т. д.
Одно время христианские церковники пытались переименовать созвездия и поместить на небе вместо зверей и легендарных героев христианских святых, но эта попытка потерпела полную неудачу.
В настоящее время астрономия изучила расположение на небе очень многих звезд, даже тех, которые невидимы невооруженным глазом. Древнее название созвездий потеряло прежний смысл, и поэтому теперь созвездием называют определенный район неба, в пределах которог 9
9
Рис. 7. Созвездие Большой Медведицы; яркости звезд: Обозначения звезд 1 234567 SQXQWabcdef Звездные величины Р/а 2 2*/2 3 3*/3 4 41/2 5 5*/2 6 6*/2 7 7х/2 8 8*/а 9 9*/3 Границы созвездия, отмеченные черной сплошной линией, проведены согласно постановлению Международного астрономического союза.- Пунктиром обозначены прежние границы созвездия. Прямоугольником около звезды 3 отмечена область, более подробная карта которой дана рядом.
заключается группа звезд'большей частью с каким-нибудь характерным взаимный расположением.
На рисунке 7 изображено созвездие Большой Медведицы так, как его рисуют на современных звездных картах — точных рисунках неба с определенными условными обозначениями яркости звезд и границ созвездий. Условность обозначения яркости звезд заключается в том, что они изображаются (обычно на белом фоне) черными маленькими кружками, размеры которых тем больше, чем больше Яркость звезды. Границы созвездий изображаются сплошной или пунктирной линией.
§ 5.	Яркости звезд. Для обозначения яркостей звезд установлена особая единица, получившая название „звездной величины*. Эта единица обозначает не размеры звезд, а определенную степень их яркости. При этом принято считать, что если яркость одной звезды составляет 0,4 яркости другой, то первая звезда на 1 звездную величину слабее, чем вторая. Таким образом, получается распределение звезд по яркости. Самые яркие звезды обозначаются как . звезды 1-й величины, яркость звезды 2-й величины составляет 0,4 яркости звезды 1-й величины, яркость звезды 3-й величины составляет 0,4 яркости звезды 2-й вели-, чины и т. д. Подробный разбор этого способа обозначений мы рассмотрим в астрофизической части учебника. Теперь же заметим, что самые слабые звезды, видимые невооруженным глазом, 5-й или 6-й величины (в зависимости от зоркости), t. е. почти в 100 раз слабее звезд 1-й величины (см. § 42 второ^части книги, а также наблюдение 4).
§ 6.	Число наблюдаемых звезд. Если вести наблюдения с биноклем или с астрономической трубой, то можно заметить еще более слабые звезды в тех местах, где они невооруженным глазом невидимы (рис. 7). Уже обыкновенный призматический бинокль дает возможность 19	,	‘
видеть звезды до 8-Й звездной величины, в сравнительно небольшую трубу видны звезды до 10—11-й звездной величины, а в современные гигантские телескопы можно усмотреть звезды до 18-й звездной величины.
Невооруженным глазом на всем небе (на обоих его полушариях) можно насчитать около 6—7 тыс. звезд, в бинокль — около 45 тыс., в астрономических списках зарегистрировано около 1 миллиона звезд, яркости и положения которых на небе измерены.
В следующих двух строках приведены числа звезд первых шести величин на всем небе:
Звездные величины............. 1	2	3	4	5	6
Число звезд.................. 20	46 134 458 1476 4840
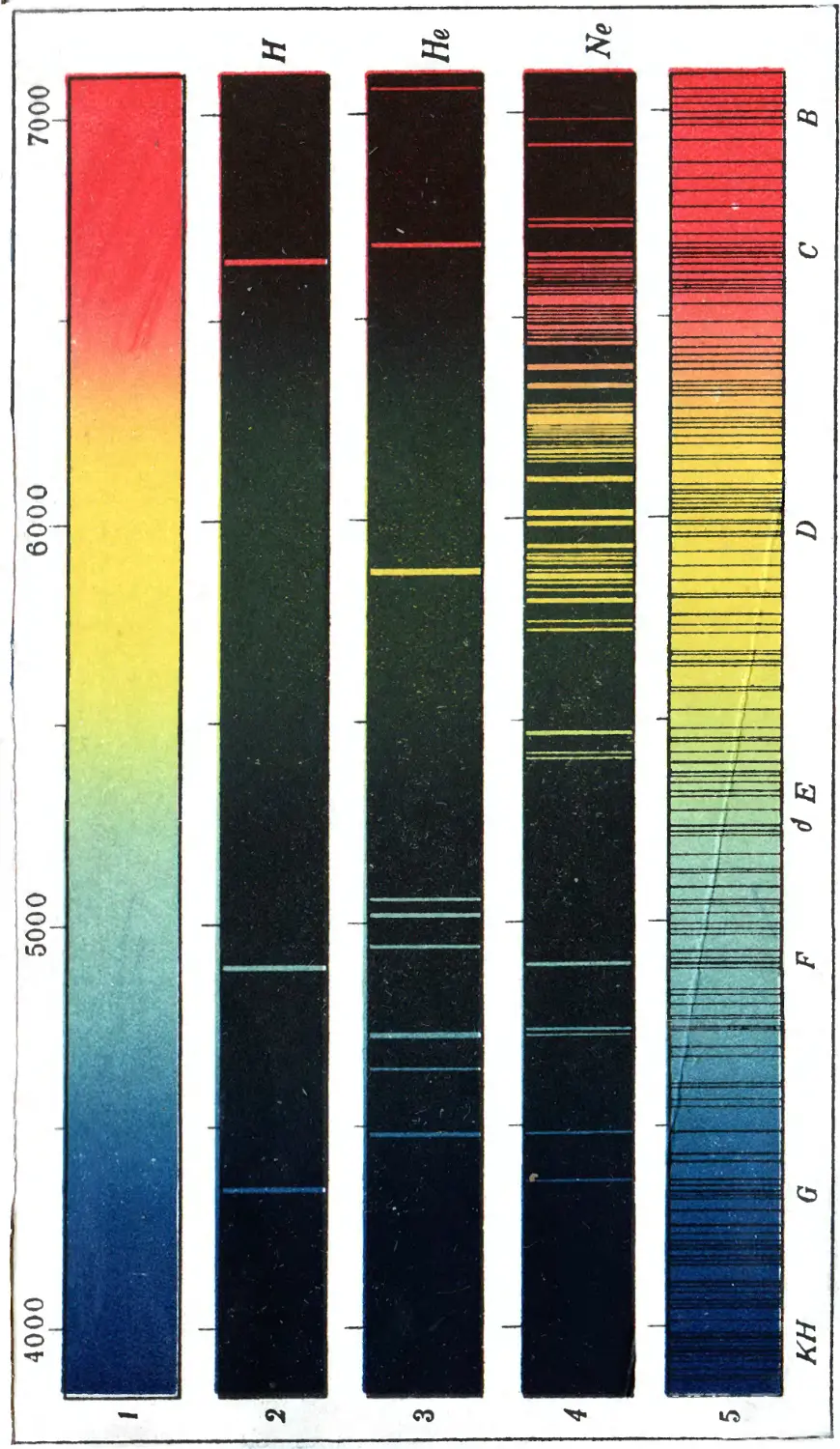
§ 7.	Цвета звезд. Звезды отличаются между собой не только яркостью, но и цветом, малозаметным с первого взгляда, но точно измеренным для многих звезд с помощью специальных приборов и методов. У некоторых звезд этот цвет'очень заметен. Цвета звезд бывают: красный, оранжевый, желтый, белый и голубовато-белый.
§ 8.	Обозначения звезд. Для обозначения звезд уже давно приняли способ именования их буквами греческого алфавита с добавлением названия созвездия, например а (альфа) Большой Медведицы^ Когда в XVII в. составлялись первые подробные карты неба, не было еще точных фотометров, предназначенных для измерения яркостей небесных светил. Тогда яркости звезд оценивали на-глаз, а звезды обозначали буквами греческого алфавита в порядке их яркости. Наиболее яркие звезды получили и особые названия.
Таким образом, самое буквенное обозначение показывает приближенно последовательность яркости звезд в пределах данного созвездия, но лишь приближенно, так как современные точные измерения яркости дают иногда несколько иной порядок.
В настоящее время это обозначение буквами сохранено по международному соглашению для ярких звезд, вообще же принято обозначать звезду номером того «каталога* звезд, в котором отмечены ее положение на небе и ее яркость.
§ 9.	Суточное вращение звездного неба. Точное изображение звездного неба может быть сделано на шаре (небесном глобусе, см. § 14).
Но шаровая поверхность не принадлежит к числу поверхностей, развертывающихся на плоскости, поэтому для изображения звездного неба на плоскости приходится применять искусственные способы (картографические проекции), как и в географии.
Один из таких способов применен при составлении рисунка 1,чгде изображена южная половина небосвода с главнейшими созвездиями; Э^от рисунок изображает йид звездного неба осенью в 10 часов вечера, а рисунок 2 —на 1 час позже (в 11 часов вечера). Сопоставив оба эти рисунка, а также свои наблюдения (набл. 1, 2, 3), вы можете сделать следующий вывод: в южной половине небосвода все созвездия передвигаются с течением времени слева направо (с востока на запад), поднимаясь в восточной части и опускаясь в западной, подобно .тому, как движется по небу днем Солнце. Подобная* же картина наблюдается в северной половине небосвода, где легко проследить, что созвездия обращаются вокруг одной его точки. Это обращение удобнее всего заметить по
11
Большой Медведице, если есть возможность пронаблюдать се положение на небе в начале и в середине ночи (рис. 8). Общее движение звездного неба, при котором взаимное расположение созвездий не меняется, может быть названо вращением вокруг некоторой точки. На рисунке- 9 изобра-
Рис. 8. Положение созвездий Большой и Малой Медведиц в начале и в середине ночи осенью.
жена фотография северной части небосвода, снятая при неподвижном аппарате. Изображения звезд на этом рисунке получились в виде дуг различной толщины. Из того, что все дуги стягивают равные углы и принадлежат концентрическим окружно-(г •	стям, вытекает, что здесь имеет место
‘	обращение звезд вокруг одной точ-
&;	 ки. Эту точку на фотографии вы.
уможете найти обыкновенным геомет-рическим построением (центр круга
••? по его ДУге)* Ее называют полюсом J мира.
Й <	м: i Северный полюс мира находится в
J ! созвездии Малой Медведицы, вблизи
	звезды, обозначаемой на звездных кар-
тах греческой буквой а. Поэтому а Малой Медведицы называют еще и Полярной звездой (рис. 10).
Точку горизонта, которая прихо-
/	дится под Полярной звездой, услов-
лено называть северной точкой го-
Рис. 9.	ризойта и обозначать буквой N
(„норд“ —север).
Все небо вращаемся как одно целое; светила поднимаются-—восходят— в одной сторонеб горизонта и заходят в другой; то же происходит и с Солнцем днем. Отсюда мы можем заключить, что звездное небо представляется нам подобным громадному шару, в центре которого мы находимся и одна половина которого для нас видима,, другая же скрыта 12
от наших глаз под горизонтом. Этот шар вращается вокруг некото* рой воображаемой оси с востока на запад, и поэтому мы наблюдаем восход и заход светил и их движение над горизонтом.
Чтобы получить наглядное представление о том, что мы наблюдаем, возьмите шарообразную колбу, наполните ее наполовину водой и, хорошо закупорив отверстие, переверните, а на внешней поверхности колбы нанесите точки, изображающие звезды (рис. И). Если 1вы будете вращать колбу вокруг оси, проходящей по сере- ’ дине горлышка, то, представив себе, что вы находитесь внутри колбы, получите модель вращения небесного свода (в этой модели плоскость воды изображает плоскость горизонта). Нечто в этом же роде можете получить, если, наметив мелом на внутренней поверхности раскрытого зонтика звезды, станете вращать его вокруг ручки, как оси, а сами будете находиться под зонтиком и наблюдать движения отмеченных на зонтике точек.
Обратимся снова к нашей модели — колбе, представив себе, что она увеличилась в размерах -и превратилась в огромный шар — небосвод, имеющий ту же воображаемую ось вращения, вокруг которой мы вращали колбу, и что мы сами находимся внутри него в точке С (рис. 12).
Ось вращения этого шара условились называть осью мира, а точки ее пересечения с небесным шаром, — полюсами мира. Ось мира наклонена к горизонту, и поэтому светила поднимаются выше всего в южной стороне небосвода.
Так как взаимное расположение созвездий не зависит от положения их над го-
n
,.n



z
p

Рис. 11.
С С
*М51
^*0
*мз? Y
12
Рис. 10, Созвездия Большой и Малой Медведиц.
На рисунке показано, что Полярная звезда находится на воображаемой линии, соединяющей аир Большой Медведицы/
ризонтом, то ознакомление с созвездиями легко провести независимо от их положения над горизонтом. 6На» рисунке 13 изображена на плоско* сти половина звездного неба в виде круга, в центре которого находится
Полярная звезда. На этом круге изображены очертания главнейших созвездий и линиями со стрелкой показано, как по созвездиям Большой и Малой Медведиц можно отыскать другие созвездия (набл. 5).
Сопоставив дневное движение Солнца и ночное движение светил по отношению к горизонту, можно притти к выводу, что они совершенно одинаковы по характеру. Солнце есть одно из светил на небе и его дневное движение объясняется общим вращением звездного неба. Невидимость звезд днем объясняется лишь освещением земной атмосферы Солнцем, превышающим яркость звезд. Наблюдение Появления звезд в сумерки подтверждает это; подтверждение того же самого дают наблюдения в астрономические трубы, при помощи которых мы можем
видеть звезды и днем.
При подъеме на большие высоты на стратостатах дневное небо представляется темносиним, и на нем бывают видны звезды.
§ 10. Угловые измерения. Не имея непосредственного представления о расстояниях до светил, мы невольно относим их все на одинаковое расстояние от нашего глаза; поэтому все светила представляются нам на внутренней поверхности шара, в центре которого находится наш глаз. Радиус этого шара может быть какой угодно (см. § 14).
На поверхности шара через любые две точки мы
можем провести дугу окружности и выразить ее длину в градусах и их частях. Проведя мысленно из глаза наблюдателя две прямые (радиусы), проходящие через две точки на поверхности шара, мы можем измерить центральный угол, соответствующий дуге между этими точками
на шаре.
На небе мы можем вести измерения только в угловой мере. Если мы смотрим последовательно на одну, а потом на другую звезду, то между направлениями на эти звезды получается некоторый угол, называемый угловым расстоянием. Угловое расстояние измеряют в угловой же мере, построив прибор, дающий возможность измерять угол между двумя направлениями.
Простейший вид такого прибора — транспортир. Держа около глаза центр транспортира, повернем его так, чтобы его плоскость проходила через две точки, угловое расстояние между которыми мы измеряем. Заметив деления, по направлению которых мы видим эти точки, и вычислив разность между отсчетами, получим интересующее нас угловое расстояние. Угловое расстояние мы можем мерить между двумя любыми точками: между двумя звездами на небе, межд$у двумя удаленными предметами, между краями какого-нибудь светила или предмета. Если светило на небе представляется нам кружком, то угловое расстояние между двумя противоположными концами его диаметра называют 14
пальцами вытянутой правой
Рис. 14.
17
угловым диаметром светила; например видимый угловой диаметр Солнца */Л Луны — тоже 1I2q.
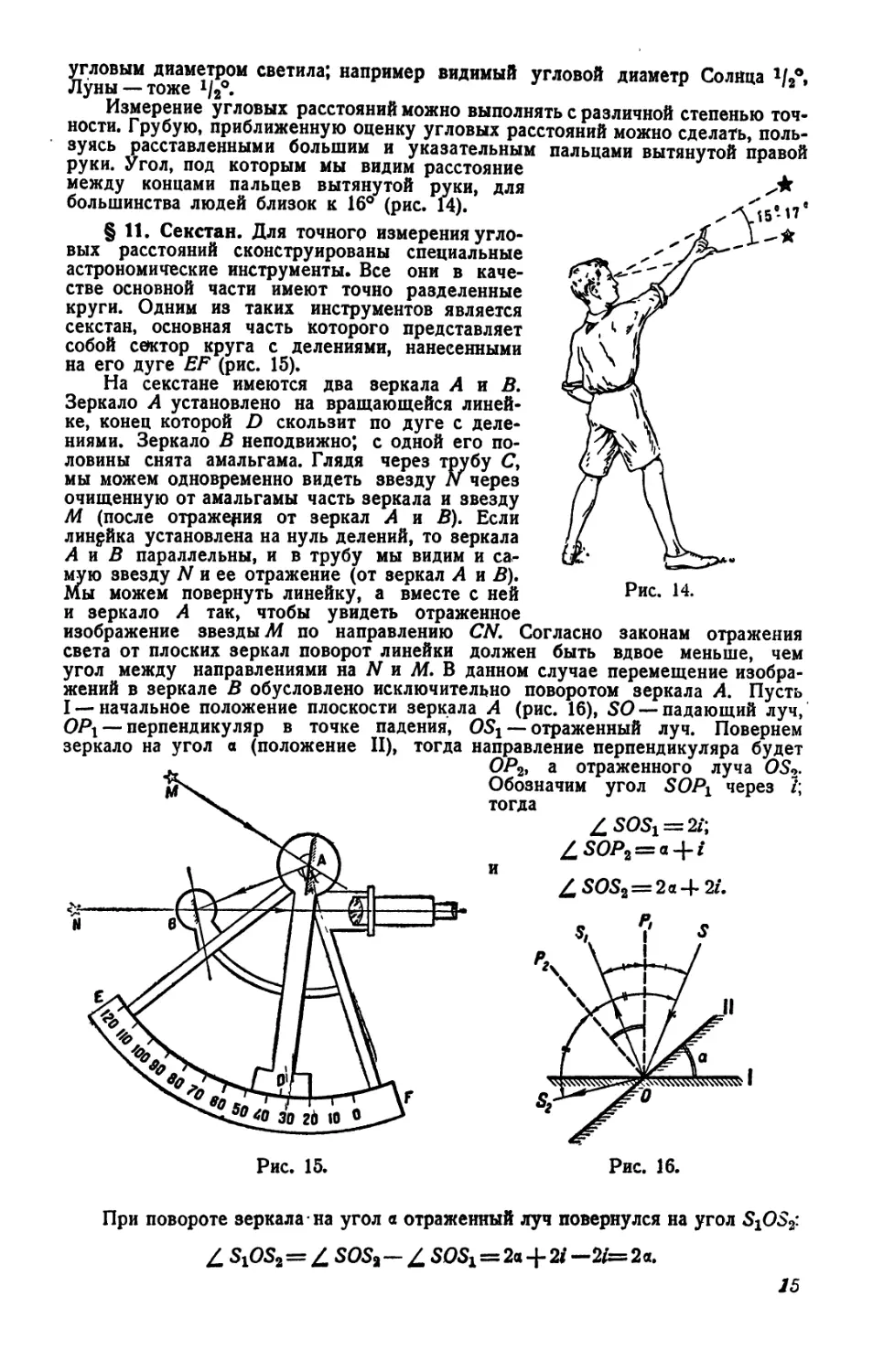
Измерение угловых расстояний можно выполнять с различной степенью точности. Грубую, приближенную оценку угловых расстояний можно сделать, пользуясь расставленными большим и указательным руки. Угол, под которым мы видим расстояние между концами пальцев вытянутой руки, для большинства людей близок к 16° (рис. 14).
§ 11. Секстан. Для точного измерения угловых расстояний сконструированы специальные астрономические инструменты. Все они в качестве основной части имеют точно разделенные круги. Одним из таких инструментов является секстан, основная часть которого представляет собой сектор круга с делениями, нанесенными на его дуге EF (рис. 15).
На секстане имеются два зеркала А и В. Зеркало А установлено на вращающейся линейке, конец которой D скользит по дуге с делениями. Зеркало В неподвижно; с одной его половины снята амальгама. Глядя через трубу С, мы можем одновременно видеть звезду N через очищенную от амальгамы часть зеркала и звезду М (после отражения от зеркал А и В). Если линейка установлена на нуль делений, то зеркала А и В параллельны, и в трубу мы видим и самую звезду N и ее отражение (от зеркал А и В). Мы можем повернуть линейку, а вместе с ней и зеркало А так, чтобы увидеть отраженное изображение звезды М по направлению CN. Согласно законам отражения света от плоских зеркал поворот линейки должен быть вдвое меньше, чем угол между направлениями на N и М. В данном случае перемещение изображений в зеркале В обусловлено исключительно поворотом зеркала А. Пусть I — начальное положение плоскости зеркала А (рис. 16), SO — падающий луч, ОРг — перпендикуляр в точке падения, OSr — отраженный луч. Повернем зеркало на угол а (положение II), тогда направление перпендикуляра будет ОР2, а отраженного луча OS2-Обозначим угол SOPi через Z; тогда
£SOP2 = * + i
Z$OS2 = 2a-4-2Z.
N
Рис. 16.
Рис. 15.
При повороте зеркала на угол а отраженный луч повернулся на угол
Z SxOSa = Z — Z	= 2a + 2i —2Z= 2 a,
15
Таким образом, при повороте зеркала на какой-нибудь угол отраженный луч поворачивается на угол, вдвое больший. Это именно и происходит в секстане. Поэтому деления по дуге EF отмечены числами, вдвое ббльшими, чем соответствующие центральные углы.
Секстан был изобретен в начале XVIII в., почти одновременно, Ньютоном и двумя его современниками, независимо друг от друга. Изобретение это произошло не случайно, — оно было вызвано требованиями мореплавания.
§ 12; Небесный меридиан. При наблюдении суточного движения светил легко заметить, что в одной половине небосвода все светила поднимаются над горизонтом, в другой же половине — опускаются. Получается естественное разделение всего небосвода на две половины — восточную и западную. Воображаемая линия, делящая таким образом весь небосвод, имеет большое значение для всех расчетов, связанных с суточным движением небесных светил.
Тот момент, когда Солнце бывает на этой линии, называют моментом полудня. Эту воображаемую линию называют небесным меридианом (полдень на латинском языке — меридиес).
Точку, лежащую над наблюдателем (по вертикали), называют точкой зенита. Положение небесного меридиана определяется геометрически. Плоскость, проходящую через глаз наблюдателя, полюс мира и зенит называют плоскостью меридиана. На рисунке 17 плоскость CSZPN есть плоскость меридиана, a Z— зенит места наблюдения. Пересечение плоскости меридиана с небосврдом является раздельной линией между восточной и западной половинами небосвода. Линия пересечения плоскости меридиана с небосводом называется небесным меридианом.
Эта линия проходит (рис. 17) через точки 5, Z, Р и N.
Всякое светило в момент прохождения через небесный меридиан находится или на наибольшей угловой высоте над горизонтом, или на наименьшей.
Плоскость меридиана мы можем мысленно продолжить и ниже плоскости горизонта (также и линию небесного меридиана).
Когда Солнце в момент полудня поднимается выше всего, то оно „проходит меридиан", и в этот момент тень от вертикально стоящего предмета падает по направлению СП. Поэтому линия CN, продолженная по направлению на точку 5, получила название полуденной линии. Полуденная линия есть пересечение тальной плоскостью.
Так как ту сторону горизонта, где шую .высоту1, называют южной, то точки горизонта: юга (S), севера (N), но. определить, если знать направление полуденной линии. Момент, когда светило, проходя через меридиан, находится на наибольшей высоте, принято называть моментом верхней кульминации светила, и, наоборот, моментом нижней кульминации называется момент наименьшей высоты светила.
И верхняя, и нижняя кульминации могут происходить только на
плоскости меридиана с горизон*
Солнце поднимается на наиболь-очевидно, что четыре главные востока (Е) и запада (W), мож-
1 В северном полушарии Земли.
16
линии небесного меридиана. Верхние кульминации бывают к югу от полюса мира, нижние — к северу от него. Кульминации происходят и под плоскостью горизонта, например полночь мы имеем право называть моментом нижней кульминации Солнца.
§ 13.	Определение положения меридиана. Знание положения плоскости меридиана является весьма важным для всех наблюдений и вычислений. Оно вполне определяется, если известно направление полуденной линии, т. е. направление SN (рис. 17). В практической астрономии изучается много способов определения положения плоскости меридиана и полуденной линии.
Здесь мы остановимся на более простых и приближенных способах.
Имея точные часы, можно определить положение меридиана по Солнцу, наблюдая его на небе в полдень1. Если в этот момент мы мысленно^ проведем плоскость через Солнце, зенит и глаз наблюдателя, то это и будет плоскость меридиана. Без часов можно определить направление полуденной линии путем наблюдения тени на горизонтальной плоскости от вертикально стоящего
Рис. 18.
Рис. 19.
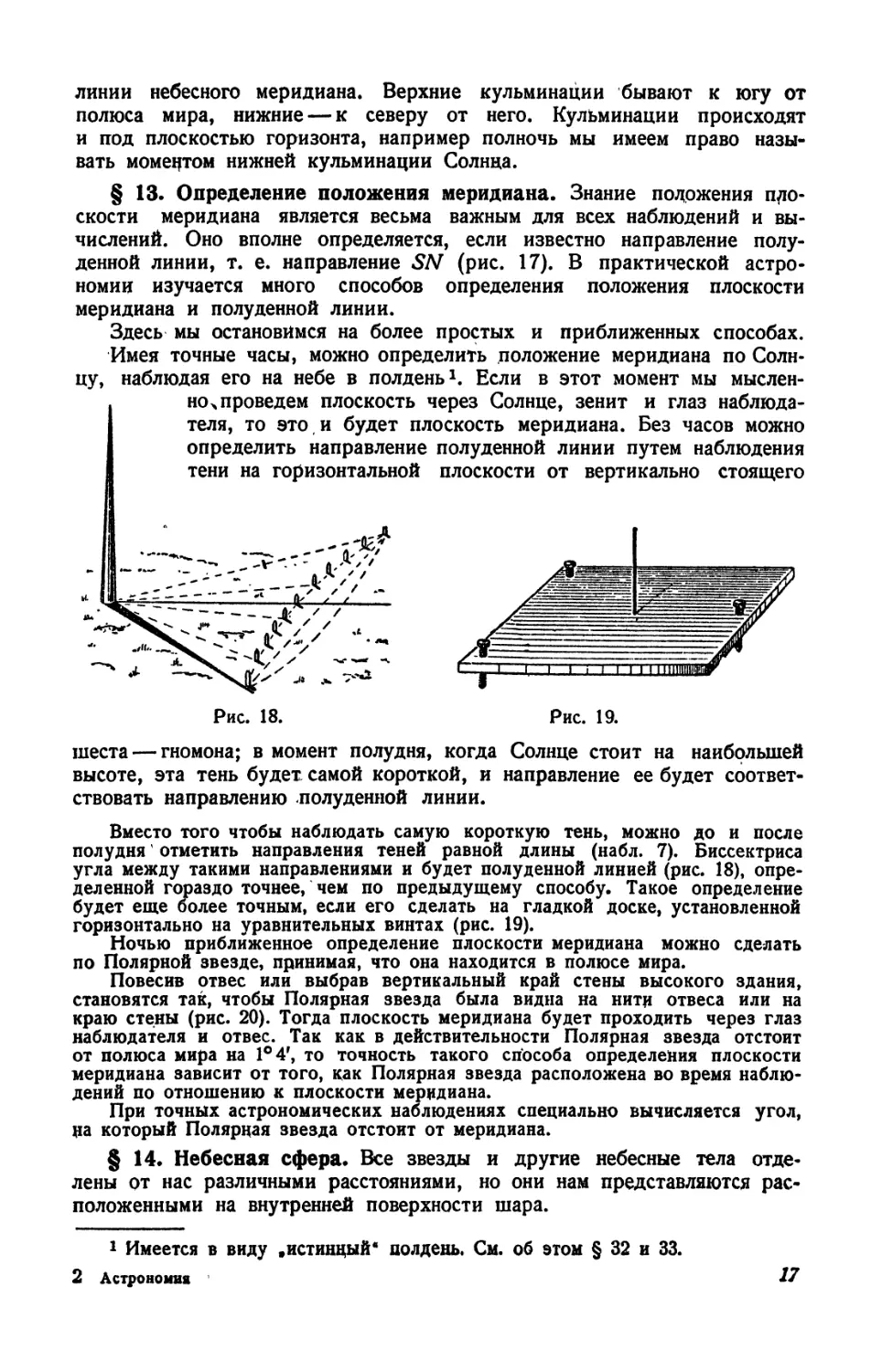
шеста — гномона; в момент полудня, когда Солнце стоит на наибольшей высоте, эта тень будет самой короткой, и направление ее будет соответствовать направлению полуденной линии.
Вместо того чтобы наблюдать самую короткую тень, можно до и после полудня отметить направления теней равной длины (набл. 7). Биссектриса угла между такими направлениями и будет полуденной линией (рис. 18), определенной гораздо точнее, чем по предыдущему способу. Такое определение будет еще более точным, если его сделать на гладкой доске, установленной горизонтально на уравнительных винтах (рис. 19).
Ночью приближенное определение плоскости меридиана можно сделать по Полярной звезде, принимая, что она находится в полюсе мира.
Повесив отвес или выбрав вертикальный край стены высокого здания, становятся так, чтобы Полярная звезда была видна на нити отвеса или на краю стены (рис. 20). Тогда плоскость меридиана будет проходить через глаз наблюдателя и отвес. Так как в действительности Полярная звезда отстоит от полюса мира на 1°4Г, то точность такого способа определения плоскости меридиана зависит от того, как Полярная звезда расположена во время наблюдений по отношению к плоскости меридиана.
При точных астрономических наблюдениях специально вычисляется угол, на который Полярная звезда отстоит от меридиана.
§ 14.	Небесная сфера. Все звезды и другие небесные тела отделены от нас различными расстояниями, но они нам представляются расположенными на внутренней поверхности шара. 1 2
1 Имеется в виду •истинный* полдень. См. об этом § 32 и 33.
2 Астрономия	17
Например, на рисунке 21 звезды $ и S' мы можем представить себе находящимися как на поверхности А, так и на поверхности В, — их угловое расстояние от этого не изменится.
Когда мы разбирали способы измерений на небе, мы уже говорили, что, не воспринимая непосредственно расстояния до небесных светил, мы представляем их находящимися на внутренней поверхности шара (по-гречески — сферы) какого угодно радиуса. Поэтому в астрономии для удобства расчетов пользуются этим представлением и, называя поверхность этого шара (на самом деле несуществующего) небесной сферой, придают ему мысленно такое же вращение, какое наблюдается у звездного неба.
Итак, небесная сфера — шар произвольного радиуса, в центре которого мы можем поместить глаз наблюдателя. Этот центр может быть мысленно перенесен в любую точку при условии сохранения соответствия всех направлений, по которым мы наблюдаем светила.
Рассматривая небесный свод, мы помещаем себя в центре небесной сферы. В нашей модели (см. рис. 11) мы не находимся в ее центре, но самую модель можем поставить так, чтобы все направления соответствовали наблюдаемым.
Наконец, мы можем изобразить небесную сферу на чертеже и по этому чертежу делать расчет различных небесных явлений.
Суточное вращение небесного свода мы должны представлять себе как вращение небесной сферы вокруг оси, проходящей через центр сферы
и пересекающей ее в точках, которые мы будем называть полюсами мира.
Горизонтальная плоскость, как известно, есть плоскость, перпендикулярная к отвесной линии; эта плоскость совпадает с направлением поверхности налитой в сосуд жидкости.
Математическим горизонтом мы будем называть линию пересечения небесной сферы горизонтальной плоскостью, проходящей через центр этой сферы.
Эту горизонтальную плоскость мы должны изображать на чертеже так же расположенной по отношению к оси мира, как это имеет место в действительности.
Если из центра небесной сферы мы восставим перпендикуляр к горизонтальной плоскости, то его направление называется зенитным направлением, а точка его пересечения с видимой половиной сферы называется зенитом, а с невидимой — надиром.
Моделью небесной сферы может служить любой шар с отмеченными на нем звездами. Такой шар с нанесенными на нем, кроме звезд, некоторыми линиями, укрепленный на оси вращения, получил название небесного глобуса, 49
На небесном глобусе фигуры созвездий изображены зеркально. Планетарий — это тоже большой небесный глобус, но на его поверхность смотрят изнутри; поэтому фигуры созвездий в планетарии не зеркальны.
Небесные глобусы ценны тем, что дают возможность делать различного рода расчеты с помощью соответствующей установки оси глобуса по отношению к горизонтальному кольцу, изображающему плоскость горизонта.
§ 15.	Горизонтальные координаты. Для многих задач, как теоретических, так и практических, нужно бывает точно отметить положение светил по отношению к горизонту.
На рисунке 22 изображена половина небесной сферы. NESW есть плоскость горизонта, наблюдатель находится в точке С, и над ним возвышается половина небесной сферы. М обозначает наблюдаемое светило.^
Плоскость меридиана SZN, полуденная линия SCN, зенит Z. Представьте себе, что наблюдатель сначала смотрит по направлению 5 (плоскости меридиана), а затем смотрит на светило М. Для этого ему необходимо: 1) повернуться на угол SCm
(вокруг вертикальной оси) до тех пор, пока он не станет лицом по направлению к СМ; 2) повернуть голову вверх на угол тСМ до тех пор, пока он не увидит светила.
Указанные два угла вполне определяют местонахождение светила на небесной сфере, причем угол поворота от плоскости меридиана считается от точки юга (5) по часовой стрелке, если смотреть с зенита. Два угла, определяющие положение светила, получили название „горизонтальных координат*. Угол между плоскостью меридиана и вертикальной плоскостью, в которой видно светило (угол SCm), называют азимутом (на рис. 22 он больше 270°). Угол от горизонтальной плоскости до наблюдаемого светила (измеряемый в вертикальной плоскости) называют высотой (угол тСМ).
Таким образом, вместо обозначения стран горизонта S, W, N, Е, можно сказать, что это те точки, для которых высоты равны нулю, а азимуты 90°, 180°, 270°.
Высота точки зенита 90°. азимут 315°, а высота 45°.
5
N
Рис. 22.
равны 0°,
На рисун-
ке 22 координаты точки
В практической астрономии предпочитают вместо высоты угол ZC/W, который называют зенитным расстоянием. Очевидно, что / ZCM Аг / ЛЮи==90°. и поэтому, зная высоту, можно вычислить зенитное расстояние, и наоборот. Высота может быть положительной и отрицательной, а зенитное расстояние может заключаться в пределах от 0° до 180°.
Для обозначения горизонтальных координат приняты знаки: азимут обозначается А, высота Л, зенитное расстояние z; h = 90° — z. Применяя 2*
М:
определять
эти знаки, мы выведенное выше соотношение высоты и зенитного расстояния можем написать так: г==90° — h. В Москве, например, положение полюса мира мы можем указать такими координатами: А = 180°, й = 55°45'20" или Л =180°, z=34° 14'40".
Вследствие вращения небесной сферы горизонтальные координаты непрерывно меняются, и, чтобы указать положение светила на небе с помощью горизонтальных координат, следует указать одновременно и момент времени, к которому относятся эти координаты.
§ 16.	Универсальный инструмент. Для измерения горизонтальных координат применяют специальный инструмент, называемый универсальным инструментом. Универсальный инструмент (рис. 23) представляет собой соединение двух вращающихся, разделенных на градусные деления, кругов, плоскости которых взаимно перпендикулярны. Горизонтальный
Рис. 23. Универсальный инструмент.
круг установлен на трех уравнительных винтах, вращением которых он может быть приведен в строго горизонтальное положение (с помощью уровня). В центре этого круга расположена вращающаяся вертикальная ось, на которой укреплены две стойки одинакового размера с вырезами в верхней части. В вырезах леЖит горизойтальная ось, к которой неподвижно прикреплен вертикальный круг с градусными делениями. На горизонтальной оси вращается зрительная труба с крестом нитей в поле зрения.
Для определения с помощью универсального инструмента зенитного расстояния и азимута какого-либо светила зрительную трубу наводят на это светило и делают отсчеты на вертикальном и горизонтальном кругах инструмента.
На вертикальном круге универсального инструмента нулевой отсчет
может и не соответствовать направлению трубы в зенит. Поэтому специальным наблюдением определяют то деление круга, которое соответствует наведенной на зенит трубе. (Для этого дважды наводят трубу на один и тот же отдаленный неподвижный предмет: один раз так, что круг приходится справа от наблюдателя, другой раз так, что он приходится влево. Полуразность отсче* тов круга даст „место зенита на круге*, и после этого любой отсчет' круга можно перевести в зенитное расстояние.)
Для получения же из отсчета, сделанного на горизонтальном круге, азимута светила, нужно после отсчета направить зрительную трубу на земной предмет или на небесное светило с известным азимутом и снова сделать отсчет на горизонтальном круге инструмента. Тогда по разности двух отсчетов горизонтального круга можно вычислить искомый азимут
20
небесного светила. Для увеличении точности отсчетов они обычно производятся с, помощью нониусов.
§ 17.	Небесный экватор и горизонтальная плоскость. На рисунке 24 изображены: небесная сфера, горизонт ESWN, ось мира СР, полуденная линия SCN и плоскость меридиана SAPN. Проведем через центр небесной сферы плоскость перпендикулярно к оси мира и будем называть эту плоскость плоскостью экватора, а линию пересечения ее с небесной сферой — небесным экватором. Экватор делит сферу на две половины — северную и южную.
Прямая EW перпендикулярна и к СР и к направлению CZ; следовательно, она перпендикулярна и к SN.
Экватор пересекается с линией горизонта в точках востока и запада, и во всяком месте на Земле видима лишь половина небесного экватора.	2
В разных'местах на Земле высота по-
люса .различна. Эту высоту мы будем в	/Ч
дальнейшем обозначать буквой <р.	\
Найдем теперь правило вычисления	\
угла между плоскостями горизонта и эква-
тора, который обозначим й0. Это правило	______-чДГ
мы можем найти таким рассуждением:
-SA 4- 90° 4- ? = - PN = 180°,	\	----""у
\ / 4 "-------------л
откуда получаем	X /	/
Ло = -SA = 90° — <р.
Значит, вычисление угла Ло между пло-	Рис. 24.
скостью экватора и плоскостью горизонта очень просто: искомый угол равен дополнению до 90° высоты полюса.
В Москве, например, ср = 55°45'20'г, следовательно, самая высокая точка экватора А находится над горизонтом на высоте 34°14г40*.
§ 18.	Экваториальные координаты. При ознакомлении с горизонтальными координатами мы видели, что для них основными плоскостями служат плоскости горизонта и1 небесного Меридиана. Вследствие видимого вращения небесной сферы все светила описывают круги, параллельные экватору, и поэтому, чтобы указать положение светила на звездном небе, нужно иметь три данных: h — высота, А — азимут и t—время. Так как небесная сфера вращается как одно целое и на ней есть основная линия — экватор, то, чтобы определить взаимное положение Светил на небесной сфере, можно применить координаты, подобные по своей основе горизонтальным. В этом случае основной плоскостью является плоскость экватора небесной сферы; время же нужно указывать лишь для светил, передвигающихся по самой сфере (например, Солнце, Луна, планеты).
Если мы (рис. 25) через звезду М и ось мира проведем плоскость, то она разрежет небесную Сферу по большому кругу. Этот круг на сфере, проходящий через звезду, мы будем называть кругом склонения светила. Угол от экватора до светила, измеряемый дугой (тМ) по кругу склонения, называют склонением светила. Склонение мы будем считать положительным (-{-) в сторону северного полюса мира и отрицательным (—) в сторону южного полюса мира.
21
Легко понять, что через каждую точку на нёбесной сфере можно провести круг склонения и для каждого заданного склонения можно наметить на сфере бесчисленное множество точек. Чтобы избегнуть неопределенности в указании положения светила на небесной сфере,
определяют положение самого круга склонения, на котором находится светило. Это положение определяется двугранным углом ^СРт между плоскостями круга склонения светила М и начального круга склонения уР.
Угол, считаемый в плоскости экватора между начальным кругом склонения и кругом, проходящим через звезду, условились называть прямым восхождением и считать его в направлении, противоположи
ном вращению небесной сферы.
На нашем чертеже ут есть прямое восхождение, тМ — склонение светила. Начальная точка
Отсюда
счёта на экваторе обозначается греческой буквой у, на ребе в этом месте нет никакой яркой звезды, самая точка находится в созвездии Рыб.
Причину выбора именно такой точки мы разберем дальше.
Прямое восхождение и склонение выражаются в угловой мере (градусах, минутах и секундах). Прямое восхождение принято обозначать буквой а, склонение — буквой 81. Прямое восхождение в астрономической практике принято выражать в мерах времени (часах, минутах и секундах времени), принимая время полного оборота небесной сферы (т. е. .поворота начального круга склонения) на 36Q0 за 24 часа, получается простой перевод:
360° соответствуют 24 часам
15°	„	1	часу
15'	»	1	минуте
15*	.	1	секунде.
Любое прямое восхождение, таким образом, можно перевести из градусной меры в меру времени.
Для всех звезд, видимых невооруженным глазом, и для многих звезд, видимых в зрительные трубы, определены экваториальные координаты. Списки звезд с указанием их яркости и экваториальных координат называются звездными каталогами.
Для наглядного представления двух систем координат воспользуйтесь моделью небесной сферы из колбы (см. рис. И), нанесите на ее поверхности чернилами или тушью экватор и сетку кругов склонений и параллельных кругов. Из проволоки сделайте подобную же сетку и покройте колбу ею, как колпаком. Придерживая проволочную сетку рукой, вращайте колбу, и вы сможете проследить, как взаимно располагаются сетки экваториальных и горизонтальных координат.
§ 19.	Звездные карты. Подобно географической карте с ее сеткой меридианов и параллелей можно построить по данным звездных каталогов звездную карту. На такой карте невозможно с полной точностью
1 а—-греческая буква .альфа*; В—.греческая буква .дельта*.
22
изобразить расположение звезд на небесной сфере, так как поверхность шара невозможно без разрывов наложить на плоскость. Однако имеется много способов перенесения на плоскость поверхности небесной сферы путем проектирования поверхности шара или непосредственно на плоскость или на цилиндрическую или коническую поверхности, которые возможно развернуть на плоскости. Каждый из этих способов связан с некоторыми неточностями, но чем меньше поверхность сферы таким образом проектируется, тем менее заметны эти неточности.
На рисунке 26 показан один из таких способов, называемый стереографической проекцией. В этой проекции сфера проектируется на плоскость, касательную к поверхности шара. Из точки, диаметрально противоположной, проводятся лучи через каждую из проектируемых точек сферы до пересечения с плоскостью. Посмотрев на рисунок 26, можно понять, что параллели получатся в виде кругов, если плоскость каса-
тельна к полюсу, но расстояния между	рис 26.
этими кругами не равны и увеличиваются от полюса к экватору. На карте звездного неба, полученной с помощью такой проекции, экваториальные созвездия изобразятся в бблыпем масштабе, чем околополярные. Несмотря на некоторые недостатки этой проекции, ею часто пользуются при вычерчивании общей карты неба.
В звездных атласах на одном листе изображают ре все небо, а отдельные его части. По большей части в таких атласах дают отдельно изображение околополярной области неба, остальные же части звездного неба Дают в виде прямоугольных полос.
На звездных картах и атласах около линий, изображающих параллели и круги склонений, ставят числа, соответствующие значениям склонений и прямых восхождений. Границы созвездий отмечаются по направлениям параллелей или кругов склонений. Для звезд различной яркости, звездных скоплений и туманностей имеется система условных обозначений, указанных при карте.
Наиболее правильное изображение небесной сферы дает небесный глобус, на ко-I экваториальные координаты.
При изучении созвездий с помощью общей звездной карты ее следует расположить над собой так, чтобы полюс мира на карте был виден по тому же направлению, по которому мы его видим на небе (см. рис. 27). После этого надо повернуть карту вокруг ее центра так, чтобы изображение какого-нибудь известного созвездия было так же расположено, как и на небе в момент наблюдения. Благодаря такому расположению карты легко будет находить все другие созвездия. Когда создастся навык в пользовании картой и часть
созвездий будет известна, можно класть ее на стол и мысленно переносить изображение созвездий на небо так, как выше было указано. На рисунке 27 показано, как при начальном знакомстве с созвездиями карту удобно прикрепить в ее центре булавкой к палке, врытой в землю и направленной вдоль оси мира.
§ 20	Эклиптика. Известно, что летом Солнце в полдень стоит высоко, зимою же низко: летом день длиннее ночи, зимою — наоборот.
Так как в полдень Солнце бывает в верхней кульминации, то, измерив в это время его высоту, можно, вычислив по формуле (стр. 21) высоту экватора в меридиане, найти склонение Солнца.
Пусть, например, в каком-нибудь месте высота Солнца в полдень была 48°', а высота полюса ср = 651/2°, тогда угол Л0 = 241/1,0. Вычитая 241/2° из 48°, получаем 231/2°. Следовательно, склонение Солнца 231/2°.
Рис. 28. Южная половина небосвода 22 декабря около 10 часов вечера (в средних широтах СССР).
Делая ежедневно такие наблюдения, можно для каждого дня года рассчитать склонение Солнца. Тогда окажется, что за год Солнце бывает то выше, то ниже небесного экватора.
Наблюдения в любом месте на поверхности Земли дают таблицу склонений Солнца (месяцы отмечены римскими цифрами):
1/1 — 23°2' 1/II —17°9' 1/Ш — 7°40/
l/IV4-4°28' 1/V —15°1' 1/VI —22°2'
1/VII 4-23°8' 1/VIII —18°5' 1/IX — 8°22'
1/X — 3°6' 1/XI —14°22' 1/XII — 21°47'.
Построив по данным этой таблицы график, легко заметить, что только два раза в году (21 мартами 23 сентября) Солнце бывает на экваторе.
Ночью Солнце, будучи под горизонтом, проходит северную часть меридиана в полночь. В это время звезды видны, и мы можем, наблюдая небо в полночь, подменить, какие звезды находятся в кульминации.
Различи^ вида северной половины небосвода легко проследить по околополярным созвездиям: осенью в нижней кульминации в полночь бывает Большая Медведица, зимою — Дракон, весною — Кассиопея, летом — Жираф и Возничий.
24
Изменение вида южной половицы ночного небосвода изображено на рисунках 1, 28, 29, 30. Сопоставление данных всех наблюдений приводит нас к следующим выводам:
Рис. 29. Южная половина небосвода 21 марта около 10 часов вечера (в средних широтах СССР).
1. В течение года Солнце непрерывно меняет свое положение по отношению к экватору: полгода оно бывает выше экватора, полгала — ниже экватора. Склонение его меняется ot-J-231/^0 до — 23J/2O.
Рис. 30. Южная половина небосвода 21 июня около 10 часов вечера (в средних широтах СССР).
2. Одновременно Солнце передвигается среди звезд справа налево: его прямое восхождение меняется — оно всегда бывает на 12 часов больше, чем прямое восхождение звезд, верхняя кульминация которых бывает
25
з полночь. Следовательно, Солнце вообще передвигается по самой небес* ной сфере, но не параллельно небесному экватору, а то выше, то ниже его и два раза в год пересекает его.
Каждый год все явления периодически повторяются; инрми словами, черев год Солнце приходит в прежнее положение.
Рис, 31.
На карте экваториальной полосы неба (рис. 31) мы можем отметить положения Солнца, полученные по следующим данным: склонение Солн-
ца— по полуденным наблюдениям его высоты, прямое восхождение Солнца — по прямым восхождениям звезд, находящихся в цолночь в
Рис. 32.
нижней кульминации.
Построив по этим данным путь видимого движения Солнца на карте среди звезд, мы видим, что он дважды пересекает экватор и отходит от экватора не более как на 231/2°.
Линию видимого пути Солнца на небесной сфере называют эклиптикой.
Эклиптика — большой круг небесной сферы» плоскость его наклонена к экватору на угол в 232f2O (рис. 32).
На эклиптике есть 4 замечательные точки,
координаты которых таковы:
Прямое восхождение	Склонение	Название	Условное обозначение и время
0 часов	0°	Точка весеннего равноденствия	V 21 марта
6	4-231/2о	Точка летнего солнцестояния	© 22 июня
12 »	0°	Точка осеннего равноденствия	23 сентября
18	— 2342°	Точка зимнего солнцестояния	% 22 декабря
Когда склонение Солнца 0°, оно находится на экваторе, плоскость горизонта делит экватор пополам, и поэтому день равен ночи. При склонении в -р^З1^0 в северном йолушарии Земли бывают наиболее длинные, а при склонении в —23!/2° наиболее короткие дни (см. § 24).
Солнце совершает по эклиптике! один оборот в течение года. Год делят на 12 месяцев, и соответственно этому еще в древности на эклиптике выбрали 12 созвездий. Эти созвездия носят названия различных животных, и поэтому их назвали зодиакальными (животное по-гречески — зоон), а самую область неба, где расположена эклиптика, — поясом 26
зодиака. Зодиакальные созвездия следующие: Рыбы, Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Козерог, Водолей.
§ 21. Звездные сутки, звездное время и часовой угол. Из того, что было сказано при описании экваториальных координат, следует, что склонения светил отсчитываются по кругу склонений от небесного экватора. За начало счета прямых восхождений выбирается точка, через которую Солнце из южного полушария (8 < 0) переходит в северное (5 > 0). Таким образом, точка весеннего равноденствия есть начало счета прямых восхождений (см. § 18).
Мы знаем, что небесная сфера имеет видимое вращение с востока на запад. При помощи часов и трубы, установленной в плоскости меридиана, мы можем установить время одного полного оборота небесной сферы, — стоит только выбрать какую-нибудь звезду на небе и дважды пронаблюдать ее в верхней кульминации (набл. 14).
Время одного полного оборота небес-ной сферы называют звездными, сутками.	'х'ч
Звездные сутки равны промежутку вре- / мени между двумя последовательными [ верхними кульминациями точка весеннего /	s' V
равноденствия. Звездные сутки принято де- I лить на 24 части — звездных часа, каждый I	I
час—на 60 звёздных минут, каждую мину-	\	/
ту—на 60 звездных секунд.	\	/
Представьте себе, что сделаны часы	/
с делением циферблата на 24 часа и что их часовая стрелка делает полный оборот	$
за одни звездные сутки. Такие часы по-	рИСв З2а,
стоянно применяют при наблюдениях в астрономических обсерваториях и называют звездными часами.
Звездные часы можно установить так, что они будут показывать 0 ч. 0 м. 0 с. в тот момент, когда в верхней кульминации находится точка весеннего равноденствия, положение которой среди звезд определяется из наблюдений Солнца и звезд. Время, которое показывают звездные часы, будем называть звездным временем.
Легко понять, что звездное время всегда равно прямому восхождению звезд» находящихся в верхней кульминации. Представим себе, что мы отметили момент верхней кульминации точки весеннего равноденствия и поставили стрелки наших звездных часов на 0 ч. 0 м. 0 с. Если после этого прошло 2 часа, то небесная сфера повернулась на 2/24 своего оборота, т. е. в верхней кульминации находятся звезды с прямым восхождением, равным 2 часам, и звездное время совпадает с прямым восхождением звезд, находящихся в верхней кульминации. Это рассуждение справедливо для любого момента, соответствующего другому повороту небесной сферы.
Зная прямое восхождение какого-нибудь светила и звездное время й данный момент, легко рассчитать, какой угол (считая по экватору) образует круг склонения этого светила с меридианом. Угол между плоскостью меридиана и плоскостью круга склонения данного светила называют часовым углом светила и отсчитывают от юга к западу.
На рисунке 32а изображен небесный экватор, если на него смотреть с северного полюса мира. Из этого чертежа видно, что часовой угол
27
точки у, т. е. звездное время, состоит из прямого восхождения светила и его часового угла, т. е.
и t=S — а.
В этой формуле S означает звездное время. При вычислении по этой формуле знак Ц- при / означает, что светило находится к западу от меридиана.
Пример, а светила равно 17 ч. 35 м., звездное время равно 20 ч. 45 м. Тогда часовой угол светила равен: 20 ч. 45 м.—17 ч. 35 м. = 3 ч. 10 м.
Следовательно, светило находится к западу от меридиана, т. е. оно прошло через меридиан 3 ч. 10 м. назад.
Вычисление часового угла светила бывает нужно при расчетах с небесным глобусом и при наведении трубы на светило. Установив по часовому углу какой-либо звезды небесный глобус, можно рассчитать вид всего звездного неба.
Как было сказано выше, началом счета прямых восхождений принята точка весеннего равноденствия. В день весеннего равноденствия, в пол-
2	день, Солнце бывает в верхней кульмина-
—J	ции, и в это время звездные часы пока-
\ ]	зывают 0 ч. Ом. Ос. На следующий день
\	/ \$э Солнце передвинется от точки весеннего
/	\ I // >< \ равноденствия, и когда Солнце будет в
I	1	верхней кульминации, звездные часы уже
st—------—-------------\N не будут показывать 0 ч. 0 м. 0 с.; они
с	будут показывать столько, каково запоз-
Рис*’	дание верхней кульминации Солнца по от-
ношению точки весеннего равноденствия. Показания звездных часов будут всегда в момент полудня равны прямому восхождению Солнца. Отсюда легко понять, что звездные сутки-короче промежутка между двумя последовательными верхними кульминациями Солнца и начало звездных суток (верхняя кульминация точки у) приходится на разное время солнечных суток.
Правило о равенстве звездного времени прямому восхождению, звезд, находящихся в верхней кульминации, дает возможность по наблюдениям звезд в верхней кульминации поверять звездные часы и, наоборот, по верно идущим звездным часам знать, какие звезды находятся в верхней кульминации.
§ 22.	Высота светила в момент кульминации. В тот момент, когда светило проходит южную или северную часть небесного меридиана, можно, измерив его высоту, вычислить его склонение, и наоборот.
На рисунке 33 изображена плоскость меридиана SPN; СР — ось мира, СЛ — пересечение плоскости экватора с плоскостью меридиана, ^ACS1 — склонение светила проходящего через южную часть меридиана, —высота полюса мира над горизонтом места.
Имеем: / АС8Л = 3;
^WCP=2/4CZ==(p, Z.SCA = <№ — ^ ^SxCZ=z.
Рассматривая £ACZ, можем записать:
£ACZ = £ACSV±£SXCZ или ф =
28
откуда получаем
*=Ф—8;
так как z=90° —А, то
90°—А = <р —8, или А = 90°— ф-{~&.
Эти две формулы, А = 90°— и 2=ф— Ь, связывают каждая по три величины. Поэтому, зная две из этих величин, можно при помощи простых арифметических действий вычислить третью.
Так, например, в случае, если мы при помощи универсального инструмента измерим h (или z) и знаем ф, мы можем вычислить д наблюдавшегося светила.
Если бы звезда проходила меридиан между полюсом и зенитом (в точке 52) или ниже полюса (в точке S8—нижняя кульминация), то соотношения между величинами z, ф и 8 получились бы иные, чем для случая кульминации звезды в южной части меридиана (в точке S,).
Для звезды, кульминирующей в точке 52, имеем:
£ZCS2 = ,/ACS2 — £ACZ\ z = 8 —ф,
и для звезды, кульминирующей в точке 53:
ZZCSz -=£ZCP+£pcs^ т. е.
z = 90° —ф-|-90о— 5, или z==180° — ср — 5.
Во всех трех приведенных нами формулах 8 входит со своим знаком.
Эти формулы показывают, что в момент кульминации светила перечисление горизонтальных координат в экваториальные и обратно выполняется путем простых арифметических вычислений.
В дальнейшем изложении будет доказано, что высота полюса равна географической широте места наблюдения. Поэтому видимость светил зависит не только от их склонения, но и от широты места наблюдения.
§ 23.	Видимость светил в зависимости от их склонений. Часть Светил для какого-либо места земной поверхности никогда не бывает видима, так как в момент прохождения через небесный меридиан в верхней кульминации высота их или отрицательна (т. е. z > 90°), или равна нулю. Мы можем по формуле
А = 90° —
вычислить склонение тех светил, которые не поднимаются над горизонтом места, высота полюса которого равна ф.
Полагая А = 0 в формуле А = 90°—ф-|-8, находим:
0 = 90° —ф-|-8 и 8 = ф —90°= —(90°—ф).
Таким образом, все светила со склонением, большим по абсолютной величине, чем ф — 90°, не поднимаются над горизонтом.
Часть светил, окружающих полюс, никогда не заходит за горизонт. Склонения этих светил мы можем рассчитать, принимая во внимание, что их высота всегда больше нуля в момент прохождения ими меридиана в нижней кульминации.
В момент нижней кульминации
А = 8 — 90°-J-ф, при А=0; 8 = 90° — ф.
29
Рис. 34. Экваториальная установка.
А — объектив; В — окуляр; CD — ось склонений; РЕ — полярная ось; R — часовой механизм; KL — часовой круг; НМ — круг склонений: Р — кремальера для передвижения окуляра; Т — искатель; S — уравнительный винт; U — ключ для микрометрического движения.
Формулы эти выведены для северного полушария Земли. Для южного полушария формулы получаются такие же, но с обратным знаком при 90< Таким образом, в каждом месте на Земле может быть наблюдаема не вся небесная сфера: одна ее часть (со склонением, меньшим, чем ср — 90°) никогда не бывает видима, другая часть (со склонением, ббльшим, чем 90° — ср) остается постоянно видимой; вся остальная часть благодаря вращению небесной сферы может быть наблюдаема, но не одновременно. Легко понять, что область невидимых светил окружает один полюс до параллели, соответствующей склонению ср — 90°; область незаходящих светил окружает другой полюс до параллели 90°—ср, и, наконец, область восходящих и заходящих светил есть полоса между указанными параллелями, в середине которой проходит экватор.
Для Москвы, например, ср = 55°45'; постоянно видимы все светила со склонением, ббльшим, чем 90° — 55°45' = = —}— 34°15'; никогда невидимы светила со склонением, меньшим, чем 55°45' — 90° = — _ 34°15'.
§ 24.	Равноденствие и солнцестояние. Длительность дня. Мы уже знаем, что эклиптика наклонена к экватору на угол в 231/2°; склонение Солнца при его движении по эклиптике постоянно меняется. Когда склонение Солнца равно 0°, то его центр находится на экваторе, и дневная дуга по небу равна ночной, т. е. продолжительности дня и ночи почти одинаковы Это бывает около 21 марта и 23 сентября, по-этому-то эти моменты получили название моментов весеннего и осеннего равноденствий, так же называются и те точки эклиптики, где в это время находится Солнце.
При отрицательных склонениях дневная дуга короче ночной, при- положительных — наоборот. В течение приблизительно полу
года, от 23 сентября до 21 марта, дни короче ночей, в остальное время — наоборот.
Наиболее длинные и наиболее короткие дни бывают при склонениях Солнца, равных -j-231/2O и ~ 231/2°- Этя моменты названы солнцестояниями: летним и зимним, так же называют и соответствующие точки эклиптики (точки летнего и зимнего солнцестояний).
В южном полушарии наиболее длинные дни бывают при склонении Солнца, равном — 231/2°, а наиболее короткие — при склонении —231/2°.
§ 25.	Экваториальная установка трубы. Для длительных наблюдений светил астрономические трубы, установленные подобно зрительной трубе
1 За полсуток склонение Солнца изменяется.
30
универсального инструмента, неудобны: приходится для непрерывного наблюдения не только поворачивать трубу слева направо, но и изменять ее наклон.
Для такого рода наблюдений устраивают установку трубы на двух перпендикулярных осях, одна из которых направлена по оси мира и называется «полярной* осью. При таких трубах имеется особый «часовой механизм", вращающий трубу так, что она, будучи в начале наблюдения наведена на какое-либо светило, остается все время направленной на него. При осях установки, так же как и в универсальном инструменте, делаются разделенные круги, дающие возможность по экваториальным координатам светила навести на него трубу.
Только что описанная установка называется экваториальной (рис. 34), и применяется при научных наблюдениях в астрономических обсерваториях. Даже и без часового механизма и разделенных кругов такая установка заметно облегчает наблюдения (см. приложение X — описание астрономической трубы).
При наблюдениях трубой с экваториальной установкой сначала устанавливают трубу по данному склонению-светила, а потом, вычислив часовой угол светила, поворачивают трубу на соответствующий угол вокруг полярной оси установки.
§ 26.	Меридианный инструмент. Для определения склонения светила универсальный инструмент должен быть установлен в плоскости меридиана. Чем точнее будут деления его кругрв, тем с большей точностью будет определено склонение светила.
Инструмент, предназначенный как для определения склонений светила, так и для их прямых восхождений, называют меридианным кругом (рис. 35). Труба меридианного круга вращается около горизонтальной оси, опирающейся на два каменных столба; она при любом наклоне расположена в плоско-
сти меридиана. Скрепленный с	Рис. 35. Меридианный круг,
нею круг, разделенный на градусы и их доли, при вращении трубы двигается вместе с ней. Таким образом, пользуясь нониусами при столбе, можно точно отсчитать наклон трубы, а следовательно, и высоту светила. Для уточнения наблюдений отсчет делений производят, глядя в микроскоп. При наблюдениях с меридианном кругом необходимо учитывать влияние преломления света в атмосфере (см. § 28).
Для точного наведения на звезду в поле зрения меридиапнрй трубы натянуты нити. Момент наблюдения при помощи электрической сигнализации записывается с точностью до сотых долей секунды времени.
Меридйанный инструмент, таким образом, может служить для определения как склонения, так и прямого восхождения светил, — нужно только при нем 31
поставить выверенные звездные часы и точно отмечать момент кульминации светила. В астрономических обсерваториях точные звездные часы (рис. 36) помещают в подвалах с постоянной температурой и, применяя принцип электромагнитного телеграфа, на особой ленте отмечают удары секунд часов и моменты прохождения звезд через меридиан. Таким способом можно определить прямое восхождение с точностью до 0,01 секунды.
§ 27. Пассажный инструмент. Имея список звезд с точно определенными координатами, можно, наоборот, проверить ход звездных часов
Рис. 36. Астрономические часы.
Два малых циферблата показывают часы и минуты, большой — секунды. Часы заключены в стеклянный колпак, в котором поддерживается постоянное давление*
по наблюдениям звезд с известным прямым восхождением. Инструментом для таких определений может служить меридианный круг, но в астрономических обсерваториях для поверки часов устанавливают особые «пассажные инструменты*.
При наблюдениях с пассажным инструментом, так же как и с другими астрономическими инструментами, кроме неподвижных часов, пользуются еще и переносными точными часами —хронометрами. Астрономические часы и хронометры четко отбивают секунды времени, и поэтому с их помощью можно вести счет времени на-слух. В хронометрах, как и в карманных часах, двигателем механизма является раскручивающаяся пружина. В конструкции механизма имеются специальные детали, делающие ход его более точным. Хронометры хранятся в особых ящиках . на подвесах, обеспечивающих постоянство горизонтального положения циферблата.
Пассажный инструмент подобен меридианному кругу, но для него нет необходимости делать точные круги для отсчета склонений. Круги при пассажном инструменте служат лишь для быстрой установки трубы по координатам звезды, согласно формуле г==ср —S.
Для установки таких меридианных и пассажных инструментов в обсерваториях устраивают
32
специальные неотапливаемые й хорошо вентилируемые помещения. Это необходимо для точности наблюдений, так как токи теплого воздуха не дают возможности получить спокойные изображения светил*
§ 28. Рефракция и ее учет в астрономии. Преломление света в земной атмосфере должно быть учтено как при обработке наблюдений, так и при расчете горизонтальных координат светил. Луч света, входя в земную атмосферу извне, преломляясь, меняет свое направление. Если бы земная атмосфера была вполне однородна, то луч, преломившись на верхней границе атмосферы, шел бы внутри нее прямолинейно. На самом деле показатель преломления атмосферы тем больше, чем ближе к поверхности Земли тот слой воздуха, через который проходит свет (рис. 37). В сущности показатель пре-
ломления изменяется непрерывно от верхних слоев до нижних, и поэтому луч света, проходя атмосферу, непрерывно изгибается, и светило (S) наблюдателю с поверхности Земли представляется выше (S^, чем это есть в действительности. Это явление называется атмосферной рефракцией. Исследования целого ряда физиков и астрономов дали возможность выработать формулу для вычисления рефракции в зависимости от давле-	$
ния и Температуры воздуха.
Исследование показывает, что рефракция тем больше, чем меньше высота светила. В зените рефракции нет. В горизонтальном направлении рефракция равна 34г, на высоте 10° — равна 5, на высоте 40° —• равна Г.
Таким образом, рефракция поднимает видимое место светила над горизонтом в частности, мы видим иногда светила над горизонтом в то время, когда они еще находятся ниже его. При восходе и заходе Солнца и Луны рефракция больше поднимает нижний край светила, чем верх-
ний, и поэтому Солнце и Луна представ-	рис> 37.
ляются нам близ горизонта сплюснутыми.
Полученную из наблюдений высоту светила, пользуясь точной формулой, исправляют на величину рефракции. Если, например, получена из наблюдений высота светила 10°, то на самом деле она равна 9*55'. У^ет рефракции представляет один из примеров учета факторов, влияющих на точность наблюдений. Такой учет с максимальной заботливостью выполняется астрономами и дает результат высокой точности.
§ 29. Сумерки. Земная атмосфера удлиняет продолжительность светлой части суток. Вследствие преломления и отражения в земной атмосфере сотнеч-ных лучей освещение небосвода продолжается и тогда, когда Солнце нахо-дится под горизонтом. В промежуток времени от момента захода Солнца и до момента, когда оно бывает на б1/^0 под горизонтом, еще настолько светло, что можно в домах не пользоваться искусственным ссвещением, и лишь постепенно на небе становятся видимы наиболее яркие звезды. Этот промежуток времени называют гражданскими сумерками. Только после того как Солнце зайдет на 18° под горизонт, становятся видимы слабые звезды и светлая полоска Млечного Пути.
Этот момент считается концом астрономических сумерек. Длительность сумерек зависит от места (широты) наблюдения и времени года. Чем место наблюдения ближе к экватору, тем сумерки короче, так как там Солнце быстрее заходит, его параллель составляет больший угол с горизонтом. На самом экваторе гражданские сумерки длятся 26 минут, на полюсах Земли —до 16 суток (при шестимесячной ночи), В СССР их продолжительность изменяется от 30 минут (в дни равноденствий) до 1 и даже 2 часов (летом). В северных частях СССР сумерки длятся всю ночь (белые ночи).
Расчет длительности сумерек бывает нужен во многих областях народного хозяйства (например, освещение улиц, сигнальные огни на транспорте, оборона страны).
3 Астрономия	33
§ 30. Измерение времени. Для измерения времени, как и для всякого измерения, необходима однородная постоянная единица меры.
Уже издавна было замечено, что вращение небесной сферы по отношению к плоскости меридиана совершается с неизменной правильностью. Современная наука установила, что промежуток времени между двумя последовательными кульминациями точки весеннего равноденствия постоянен и вращение небесной сферы строго равномерно (см. § 21).
Уже издавна люди начали распределять время своей работы, руководствуясь дневным движением Солнца, и считали серединой дня полдень — момент верхней кульминации центра Солнца. Этот момент мы будем
называть истинным полуднем.
Промежуток времени между двумя последовательными верхними кульминациями Солнца мы будем называть истинными солнечными
сутками.
Солнечные сутки длиннее звездных. Солнце перемещается по эклиптике
и поэтому запаздывает каждый день в кульминации по отношению к той звезде, вместе с которой оно было в кульминации в какой-нибудь полдень. Практически оказывается удобнее и
точнее поверять часы по наблюдениям звезд. Поэтому в обычной жизни пользуются часами, соответствующими дневному движению Солнца, поверяют же часы по звездам. Чтобы иметь возможность так измерять время, необходимо установить точную связь между видимым вращением звездного неба и
видимым движением Солнца.
§ 31. Среднее и истинное время; Вращение небесной сферы совершается равномерно, и если бы Солнце было неподвижно на небесной
сфере, то часовой механизм, которым мы пользуемся в обычной жизни, можно было бы очень просто, без всяких пересчётов, проверять по Солнцу. На самом деле Солнце перемещается по эклиптике.
Если мы, имея звездные часы, поверяемые по астрономическим наблюдениям; будем наблюдать ежедневно момент полудня, то заметим, что промежутки между двумя последовательными полуднями в разное время года неодинаковы. Согласно правилу об определении момента кульминации мы можем сказать, что прямые восхождения Солнца изменяются неравномерно.
Причина этого состоит в том, что Солнце:
1) перемещается по эклиптике, а не по экватору;
2) движется по эклиптике неравномерно.
Если бы даже Солнце передвигалось по эклиптике равномерно, то все-таки промежутки между полуднями не были бы равны. На рисунке 38 изображены два места небесной сферы с экватором и эклиптикой. Правая часть рисунка соответствует весеннему времени, левая — летнему времени.
Если мы на эклиптике отложим равные, отрезки, соответствующие пути, который Солнце проходит по эклиптике в течение суток,—у Л, АВ> ВС,.MN, NP, PQ, и через точки А,В, С, ..., Л4, N, Р, Q, проведем круги склонений, то соответствующие отрезки (проекции отрезков уЛ, АВ, ВС и т. д.) по экватору ya, ab, Ьс, ..., тп, пр, pq будут не равны и на правой части чертежа крроче, чем на левой. Отсюда следует, что промежутки между полуднями летом длиннее, чем весной.
34
Солнце по эклиптике движется неравномерно — зимою быстрее, чем летом; это вносит1 дополнительные неравенства в длительность промежутков между полуднями.
Чтобы избежать необходимости ежедневно подгонять часовой механизм к наблюдаемому истинному Солнцу, условились вести счет времени по так называемому „среднему Солнцу*. Среднее Солнце есть воображаемая точка, которая движется по экватору и притом равномерно.
Точное знание движения истинного Солнца по эклиптике дает возможность вычислить разницу между верхними кульминациями среднего и истинного Солнца для любого дня. Часовые механизмы идут по среднему Солнцу, поверяют же их или по звездам или по истинному Солнцу, внося в вычисления указанную выше разность
Момент верхней кульминации среднего Солнца будем называть средним полуднем^ промежуток времени между двумя последовательными одноименными кульминациями среднего Солнца будем называть средними солнечными сутками.
Таким образом, на небесной сфере мы представляем себе два Солнца: истинное и среднее.
Истинное Солнце	Среднее Солнце
1)	Движется по эклиптике.	1) Движется по экватору.
2)	Движется по эклиптике	2) Движется по экватору равнонеравномерно.	мерно.
3)	Оба Солнца четыре раза в году имеют равные прямые восхождения.
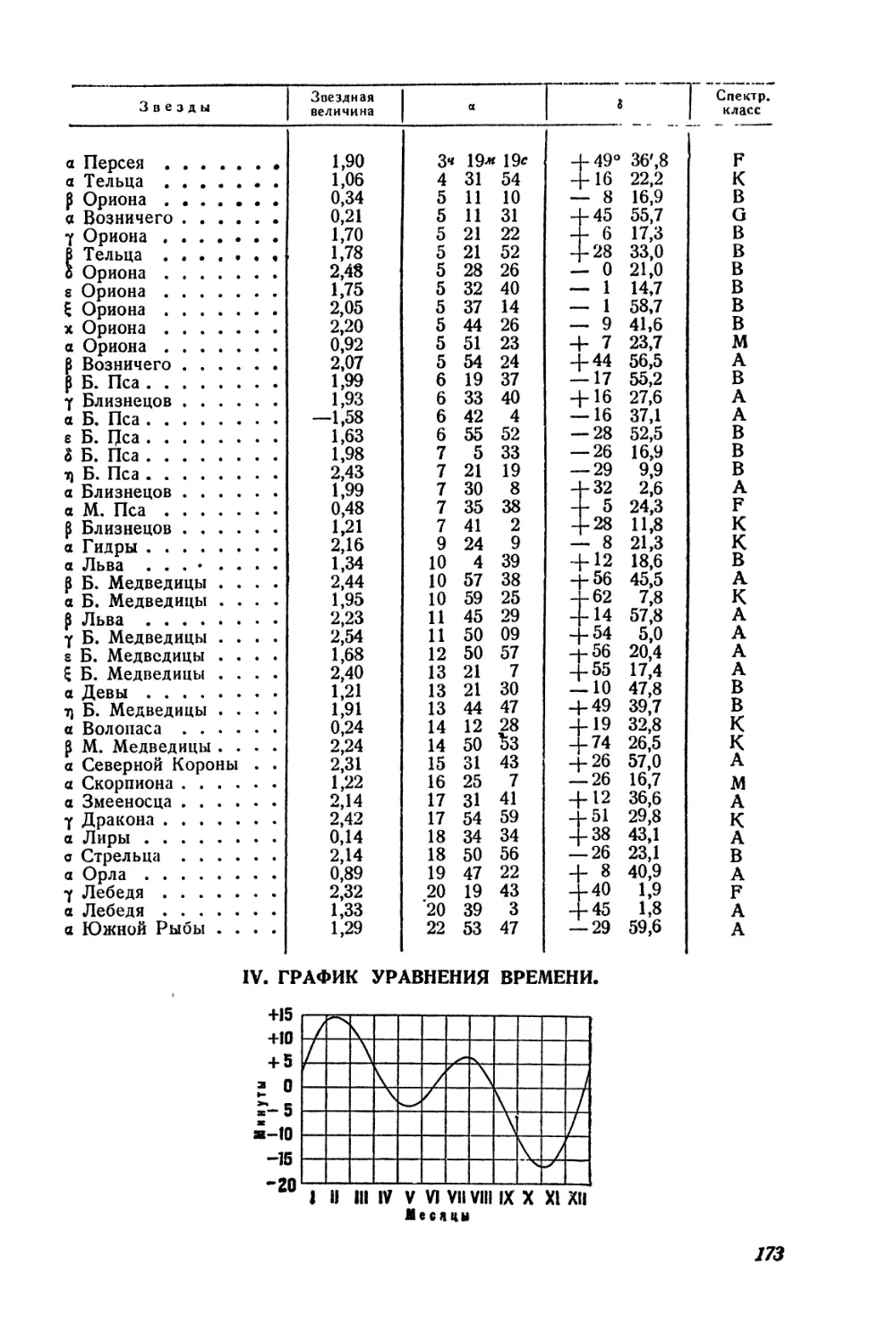
§ 32. Уравнение времени. Истинное Солнце то отстает от среднего, то опережает его, поэтому среднее время бывает или впереди или позади истинного. Движение истинного Солнца изучено настолько точно, что для всякого момента можно» рассчитать вперед разницу среднего и истинного времени. Эта разница получила название уравнения времени. Если мы обозначим /ф —момент по истинному солнечному времени, /и —момент по среднему солнечному времени, т] — уравнение времени, то
/и~^о4-г(;
Т) может быть и положительным и отрицательным.
Уравнение времени дается в астрономических календарях на каждую полночь. Оно по абсолютной величине не превышает 17 минут и четыре раза в году бывает равно нулю. Изменения уравнения времени в пределах четырехлетия невелики; поэтому для подсчетов, не ^требующих точности, можно пользоваться графиком, даваемым в конце настоящей книги.
Зная уравнение времени, можно проверить часы по солнечным часам или по гномону (см. § 33)..
Пример. 15 мая в момент истинного полудня часы показывают 12 ч. 1 м. Верно ли показывают часы среднее время?
На 15 мая уравнение времени: —4 минуты.
В момент истинного полудня часы должны показывать;
12 часов — 0 ч. 4 м. —11 ч. 56 м.
Значит, часы показывают неверно на
12 ч. 1 м.—-11 ч. 56 м. xss-j—5 минут.
Часы ушли вперед на 5 минут против правильного среднего времени, 3*	Л
§ 33.	Поверка местного времени по Солнцу. Для определения истинного полудня или истинного времени можно устроить различные приборы, дающие тень от какого-либо стержня при освещениц его Солнцем. Такие приборы называют солнечными часами. Наиболее простые солнечные часы можно устроить так.
Установить стержень по направлению оси мира (т. е. направив его на Полярную звезду) на циферблате, разделенном на 24 части и перпендикулярном к направлению стержня. Плоскость циферблата, очевидно, будет совпадать с плоскостью небесного экватора, и тень от стержня в солнечный день будет равномерно перемещаться по циферблату, соответственно углу отклонения Солнца от плоскости меридиана.
Можно устроить часы и с горизонтальным циферблатом (рис. 39), но в таких часах часовые деления циферблата Не будут равными, так как Солнце при своем суточном движении равномерно перемещается па-
раллельно экватору, но неравномерно по отношению к горизонту.
Для расчета делений приходите^ применять правила тригонометрии. С помощью графика, помещенного в приложении IX, можно получить углы, которые надо отложить от направления полуденной линии для 1, 2, 3 и т. д. часов до и после полудня. Эти углы получаются различными для разных широт, и поэтому график дан для широт 40°, 45°, 50°, 55°, 60°.
§ 34.	Звездное и среднее время. И звездные и средние сутки одинаково подразделяют на часы, минуты и секунды. Продолжительность этих делений суток для
Рис. 39. Солнечные часы. звездных и средних единиц времени’ неодинакова. Так как среднее Соднце мы представляем себе равномерно движущимся по экватору, то его кульминация ежедневно отстает от кульминации той звезды, которая в какой-нибудь
полдень кульминировала, вместе с ним.
Среднее Солнце делает полный оборот по экватору за год. В году бывает 3651/4 суто& Следовательно, ежесуточно вреднее Солнце отстает от выбранной звезды на 360° _______________________________24 часа
W/7” 3651/< •
Это число, приближенно вычисленное, равно 4 минутам. Следовательно, ежедневно верхняя кульминация Солнца запаздывает на 4 минуты по отношению к той звезде, которую мы можем представить себе в точке весеннего равноденствия.
Звездные сутки короче средних солнечных на 4 минуты (приближенно). Точный расчет показывает, что зврздные сутки имеют продолжительность 23 ч. 56 м. 4,1 с. среднего солнечного времени. Когда не тр^ буется при вычислениях большой точности, можно считать разницу средних и звездных суток в 4 минуты и переводить среднее время в звездное и обратно, пользуясь этим числом.
Пусть в какой-нибудь день средние и звездное верно идущие часы одновременно показывают 0 я, Q м, 0 с.; это значит, что Солнце как 36
раз находится в точке весеннего равноденствия. На следующий день средние часы будут показывать 0 ч. О м. О с., звездные часы будут показывать 0 ч. 4 м. Мы можем составить таблицу, указывающую на сколько уходят звездные часы от средних за разные промежутки времени.
За | сутки звездные часы уходят вперед на 4 минуты .	1 месяц	ж	.	„	„	,	2	часа
.	3 месяца	„	„	»	.	„	6	часов
„	12 месяцев	»	.	»	»	.	24	часа
Точка весеннего равноденствия бывает в полдень в верхней кульминации около 21 марта каждого года (вследствие чередования простых и високосных годов этот день бывает 21 или 22 марта). Будем считать, что 21 марта каждого года бывает совпадение среднего и звездного времени. Пользуясь упомянутой выше Таблицей, мы можем рассчитать, что 21 апреля в полдень звездные часы будут показывать 2 часа, 21 мая — 4 часа и т. д.
Если мы можем рассчитать звездное время в полдень любого дня, то отсюда можно перейти и к расчету Звездного времени для любого момента.
Пусть мы хотим рассчитать, сколько будут показывать звездные часы в 10 часов вечера 18 февраля. Вычисления будем делать так: 21 марта в полдень звездные часы показывают 0 часов (или 24 часа)е 21 февраля они показывают в полдень 22 часа, а 18 февраля на 4 минуты ХЗ меньше, т. е. 21 ч. 48 м. В 10 часов вечера показания звездных часов будут 21 ч. 48 м. -J-10 часов = 31 ч. 48 м.; откидывая отсюда полные звездные сутки, т. е. 24 часа, получаем, что 18 февраля 10 часов среднего времени соответствуют 7 ч. 48 м. звездного времени. Такой расчет лишь приблизительный.
При точных расчетах применяют точное значение звездных суток, причем учитывают уход вперед звездных часов после момента полуночи не только за сутки, но и за их доли, и пользуются при этом даннымй астрономического календаря, в котором на каждый день указывается звездное время в средний полдень.
Все данные, нужные для точных вычислений, у нас в СССР можно найти в „Астрономическом календаре* Горьковского астрономо-геодезического общества (б. Нижегородского кружка любителей физики и астрономии).
Перевод звездного времени в среднее следует делать таким же способом, учитывая разницу Между звездным и средним временем. Пусть, например, нам нужно перевести 8 ч. 45 м. звездного времени в среднее для вечера 18 февраля.
В полдень 18 февраля звездные часы, как нами было рассчитано выше, показывают 21 ч. 48 м., т. е. они впереди средних на
21 ч. 48 м. —12 часов = 9 ч. 48 м.
Следовательно, в 8 ч. 45 м. средние часы должны показывать:
8 ч. 45 м. —— 9 ч. 48 м. = —1 ч. 03 м. =22 ч. 57 м.
§ 35.	Расчет вида звездного неба. Умение перевести среднее время в звездное очень полезно для расчета вида звездного неба, потому что звездное время равно прямому восхождению звезд, находящихся в верхней кульминации. Произведем, например, расчет вида звездного неба 26 апреля в 11 часон вечера,
26 апреля звездное время в полдень: 2 часа + 4 минутыХ 5 = 2 ч. 20 и. 26	„	„	9 в 11 ч. веч: 2 ч. 20 м. +11 часов = 13 ч. 20 м.
Следовательно, в И часов вечера 26 апреля в верхней кульминации нахо* дятся звезды с прямым восхождением 13 ч. 20 м. Возьмем звездную карту или: звездный атлас и посмотрим, в каких созвездиях есть звезды, имеющие прямое восхождение, близкое к 13 ч. 20 м. Почти такое прямое восхождение имеет середина созвездия Девы, то^ же прямое вдсхбжденйе имеют средние части созвездий Волос Вереники, Гончих Псов и звезда 6 Большой Медведицы. Следовательно, эти созвездия будут видны в южной стороне неба; к западу будут созвездия, звезды которых имеют меньшее' прямое восхождение (Лев, Рак, Близнецы), к востоку — звезды которых имеют ббльшее прямое восхождение (Волопас, Геркулес), на севере’ будут видны созвездия со звездами, имеющими прямое восхождение: 13 ч. 20 м.+ 12 часов = 25 ч. 20 м.= = 1 ч. 20 м., т. е. Кассиопея и Андромеда.
По обыкновенной карте звездного неба расчеты видимости легко выполнить для звезд в кульминации, но гораздо труднее подсчитать, какие созвездия в данный момент восходят и заходят. Такой подсчет можно сделать с помощью небесного глобуса, но ввиду его громоздкости брать его для наблюдения с собой неудобно.
Для быстрых расчетов вида неба обычно применяют „подвижную звездную карту*. Такая карта представляет собой круглую карту неба, на которую накладывается вторЪй круг с круглым же прорезом. В прорез видны только те области небесной сферы, которые'можно наблюдать на определенной широте (см. § 23) поверхности Земли. Делений по краям дают возможность, совместив месяц и число по краю одного круга с чесом суток на другом, получить сразу вид звездного неба ц расположение созвездий по отношению к горизонту (см. приложение XIV);
НАБЛЮДЕНИЯ.
1.	В начале вечера выйдите на открытое место и наблюдайте появление звезд при наступлении ночи в восточной части неба* Заметив» какую-нибудь, появившуюся на темнеющем небе звезду, запишите момент наблюдения и в записной тетради изобразите звезду точкой. Продолжайте наблюдения р, заметив появление других звезд в той же области неба, отмечайте положение каждой из них на том же листе и при этом нумеруйте звезды в порядке их появления, записывая для каждого номера время наблюдения. Когда окончательно, стемнеет, обведите точки на рисунке кружочками тем большего размера, чей1 ярче звезды. Сопоставьте нумерацию звезд ,с наглядным изображением их яркости на вашем рисунке. Вы убедитесь, что видимость звезд зависит от их яркости и от освещенности неба, откуда можно сделать , вывод, что звезды невидимы днем только вследствие светлого фона неба.
2.	Закончив наблюдение первое, изобразите несколько созвездий в южной и северной половинах небосвода на двух полукругах х, отметив на них час и минуту наблюдения. В тот же вечер через 2 часа после первого Наблюдения сделайте еще два таких же рисунка тех же созвездий.
Изменилось ли взаимное расположение звезд в созвездиях? Изменилось ли положение созвездий по отношению к горизонту? На каких рисунках /северной или южной части неба) это изменение заметнее?
3.	Чтобы убедиться, что звездное небо с течением времени передвигается по отношению к горизонту, выберите в четырех сторонах неба какие-нибудь вертикальные предметы (например, мачты, телеграфные столбы и т. п.) или, еще лучше, повесьте на высоких столбах шнуры с грузами на конце. Расположите стул так, чтобы, сидя на нем, видеть какую-нибудь звезду слева от вертикального предмета, понаблюдайте за ней, оставаясь неподвижным. Сделайте такие наблюдения по четырем, направлениям. Как меняется положение звезд?
Это наблюдение можно заменить еще более наглядным, если установить неподвижно бинокль или зрительную трубу (например, прикрепив их к неподвижному предмету), наведенными на какое-нибудь светило на небе. Достаточно нескольких минут, чтобы заметить передвижение этого светила.
1 Как на рисунках 1 и я,

4	По карте созвездия Большой Медведицы (рис 7) проследите, до какой звездной величины вы видите звезды невооруженным глазом, в бинокль и в астрономическую трубу
5.	Сделайте на прозрачной кальке копию рисунка 13 и перенесите его в свою тетрадь для наблюдений В первый же ясный вечер ознакомьтесь по этому чертежу со всеми главными созвездиями, видимыми в это время на небе, и зарисуйте их расположение на двух полукругах
6	Измерьте с доступной для вас точностью угловые расстояния между яркими звездами Большой Медведицы и по этйм данным начертите карту этого созвездия
7	Выберите близ школы ровное, с горизонтальной поверхностью место, не закрытое строениями, и на этом месте установите гномон, проверив его вертикальность Гномон нужно прыть в землю на 1/2 ле, сначала разрыхлив ее, после этого (в рыхлой земле гномон можно отклонять в стороны) устанавливайте его по отвесу и одновременно утрамбовывайте землю около гномона Когда гномон будет окончательно установлен вертикально, нужно у его основания положить несколько камней, чтобы он стоял крепко
Начиная с восхода Солнца, отмечайте конец тени гномона, втыкая в землю колышки Делайте это через каждые 20—30 минут и закончите эту работу около 3 часов дня
Когда наблюдения закончены, то около гномона будет целый ряд колышков (§ 13), которые отмечают и длину и направление тени По этим отметкам можно определить, как передвигалась тень от Солнца и как передвигалось само Солнце над линией горизонта
Чтобы отметить полуденную линию, надо выбрать из всех длин тени гномона самую короткую, но так как сделать это точно очень трудно, следует воспользоваться уже сделанными отметками конца тени и отмечать тени равной длины.
Легко понять, что самая короткая тень должна находиться как раз посредине между тенями равной длины, так как тени бывают равной длины за одинаковое время до и после полудня.
Поэтому, подыскав по поставленным колышкам отметки теней равной длины, расстояние между соответствующими колышками разделите пополам, и вы найдете на поверхности земли ту точку, которая должна находиться на полуденной линии (рис 18) Так как может случиться, чТо не отмечено в точности равных теней до и после полудня, то лучше применять более простой и точный способ, описанный ниже
Для этого надо начертить на земле линию движения конца тени гномона и притом так, чтобы она как можно лучше подходила к сделанным колышкам и отметкам
Сделав петлю на бечевки и надев эту петлю на гномон у его основания, прочертите часть окружности так, чтобы захватить линию концов тени Отметьте точки пересечения этой линии с окружностью, воткнув два колышка в этих местах. Между этими двумя колышками натяните бечевку и отметьте ее середину третьим колышком Зацепив петлей бечевки за основание гномона, натяните ее так, чтобы она проходила через этот колышек Вдоль протянутой бечевки положите и забейте в землю ряд камешков или битого кирпича.
Отмеченная линия и есть полуденная линия1.
Если никак нельзя отыскать подходящего ровного и горизонтального места для этой работы, можно сделать доску на трех винтах с гномоном посредине (§ 13)
Для определения полуденной линии доску надо установить горизонтально, все отметки делать на ней карандашом и, когда линия полудня будет на ней отмечена, воткнуть булавки по^ концам линии; глядя по направлению булавок, установить на земле два кола и забить их накрепко в землю. Полуденную линию можно наметить и на полу комнаты Для этого закрывают окно доской с небольшим круглым отверстием и отмечают на полу движение солнечного кружка
8	Подвесив на открытом месте отвес, встаньте по отношению к нему так, чтобы его нить проходила через Полярную звезду Отметьте место, на котором стоите, и точку над Грузом отвеса По этим отметкам нанесите на земле линию, имеющую направление С—Ю
1 Для увеличения точности следует определение полуденной линии сделать несколько раз и взять среднее из полученных ее направлений*
39
9	Пользуясь сделанными уже работами (или Полярной звездой), найеТьтё Мысленно по небу небесный меридиан и по звездной карте определите, какие созвездия находятся в верхней и нижней кульминациях.
10.	Пользуясь простейшими угломерами, определите высоты и азимуты нескольких ярких звезд, выбрав их в разных местах неба.
11	Наметьте мысленно линию экватора и созвездия, находящиеся на экваторе. После этого, справившись по звездной карте, мысленно проведите эклиптику и заметьте зодиакальные созвездия
12.	Пользуясь высотомером-эклиметром, определяйте высоту Солнца каждый ясный день около полудня (от Ш/2 часов утра до 12у2 часов дня). Измеренные высоты отмечайте на графике, на котором по одной оси отмечены числа года, а по другой — градусы
13.	Выпишите из астрономического календаря координаты планет на тот день, когда собираетесь наблюдать. Наметив положение планет по звездной карте, отыщите их на небе.
14	Пронаблюдайте внимательно заход Солнца или Луны в возможно более открытом месте Зарисуйте фигуры диска этих светил, начиная с того момента, когда нижний край светила касается горизонта.
15.	Начните наблюдение передвижения планеты среди звезд. Сделайте карту е изображением кругов склонений и параллелей, надпишите соответствующие числа а и 8 при них и после каждого наблюдения отсчитывайте по этой карте координаты планеты. Наблюдения продолжайте в продолжении всего времени видимости планеты.
16.	Наблюдения передвижения Луны среди звезд делайте, пользуясь звездной картой и отсчитывая координаты Луны Вычислите среднюю часовую скорость движения Луны по небу в угловой мере. Если около Луны (слева) заметите звездочку, то попытайтесь наблюдать „покрытия звезды Луною"
17.	Измерьте высоту нескольких ярких звезд (не менее трех) в момент верхней кульминации Измерьте высоту Полярной звезды Взяв из справочника склонения всех этих звезд, вычислите по ним высоту полюса, выведите среднее арифметическое из наблюдений звезд и сравните с измерением высоты Полярной звезды.
18	Установив по линии меридиана отвес и столб с пластинкой, имеющей отверстие (4 мм в диаметре), наблюдайте несколько вечеров подряд прохождение одной и той же звезды через меридиан При этом отмечайте время по возможно более точным часам, которые проверяйте ежедневно*по радио или на телеграфе
19.	По моменту кульминации какой-нибудь яркой звезды найдите поправку ваших часов.
Задачи и вопросы.
1.	Сколько звезд 5-й величины имеют такую же яркость, как одна звезда 1-й величины?
2	При наблюдении звезды замечают, что она поднимается выше и выше. В восточную или в западную сторону небосвода смотрит наблюдатель?
3	Путешественник, смотря в правое окно вагона (по движению поезда), сначала видел Полярную звезду по направлению движения поезда, а через некоторое время из того же окна заметил, что Полярная звезда видна прямо из окна. В какую сторону поезд изменил направление своего движения?
4.	Красноармеец идет под утро в разведку по направлению Полярной звезды. После восхода Солнца он возвращается обратно Как он должен итти, руководясь Солнцем, если ему надо итти обратно 1 час времени?
5.	На земном полюсе Полярная звезда видна в зените Как там расположен небесный экватор?
6	На земном экваторе небесный экватор проходит через точку зенита. Видна ли там Полярная звезда и если видна, то в каком месте небесного свода?
7.	Меняются или не меняются с течением времени горизонтальные координаты светил?
8.	В каких частях небосвода зенитные расстояния светила непрерывно увеличиваются и в каких уменьшаются?
9.	Азимут светила 45°, высота 60°. В какой стороне неба надо искать это светило?
10.	Когда высота Солнца равна 0°?
11.	Когда азимут Солнца равен 0°?
40
12	Высота полюса под горизонтом 65*/»° Какой угол образует с горизон-ылыюй плоскостью плоскость экватора?
13	Высота звезды, находящейся на небесном экваторе, в момент ее верхней кульминации равна 30°. Какова высота -полюса?
14	Определить широту места, в котором зенитное расстояние звезды, имеющей склонение 60°20', в момент верхней кульминации оказалось равным 7°35' к северу от зенита.
15	Насколько градусов от полюса мира отстоит звезда со склонением в 0°? л 30°? в 50°?
16	. Каково склонение звезды, отстоящей от полюса на 40°?
17	. Склонение светила + 30°, прямое восхождение 7 часов. В каком созвездии оно находится? •
18	В астрономическом календаре даны экваториальные координаты планеты Марс на 1939 г.
	а	а
1 июля	20 ч 32 м.	— 24° 5'
16 в	20 . 21 .	— 25*40'
1 августа	20 .	3 ,	— 27° 3'
16	19 » 50 „	— 27*22'
1 сентября	19 я 49 .	— 26*39'
16	20 . 2 .	— 25*15'
1 октября	20 . 24 „	— 23*15'
16 в	20 , 52 »	— 20*43'
1 ноября	21 » 27 „	— 17*26'
16	,	22 , 2 .	— 13*52'
1 декабря	22 „ 38 в	— 9*56'
16	.	23 , 14 „	— 5*45'
1 января 1940 г.	23 „ 53 в	— 1°3'
23 июля 1939 г произойдет противостояние Марса; его видимый диаметр будет 24", а расстояние от Земли 58 млн /см.
Нарисуйте на звездной карте путь Марса среди звезд
19	. Пользуясь звездной картой с нанесенной на ней эклиптикой, укажите (приблизительно) точку, в которой Солнце находится сегодня, будет находиться через месяц.
20	. Как располагается эклиптика по отношению к горизонту на Северном полюсе?
21	. Каков азимут Солнца в момент его восхода на земном экваторе (высота полюса 0°) 22 марта? 22 июня? 22 сентября? 22 декабря?
22	В какое время года (месяц, число) в полночь эклиптика выше всего поднимается над горизонтом?
23	. Высота полюса 56°. Солнце в полдень имело высоту 34°, а через несколько дней посте этого 341/2° В какое время года были сделаны наблюдения и каково было склонение Солнца?
24	. Какова высота полюса в том месте Земли, где высота Солнца в полдень 22 июля оавна 69°38'? Какова высота Солнца в том же месте в полдень 22 декабря?
25	Определите (по формуле) наибольшую полуденную высоту, на которую может подняться Солнце в вашем городе, наименьшую высоту, полуденную высоту сегодня
26	Звезда а Лебедя имеет склонение 4~ 45°2'. На каком зенитном расстоянии она будет в момент верхней кульминации в месте, где высота полюса 40°14' (Ереван)?
27	Какова высота полюса в том месте на Земле, где 22 июня Солнце в полночь наполовину заходит за горизонт (предположите, что рефракции нет)?
28	. Какова высота пойюса (шйрота) в том месте, где 22 июня момент окончания вечерних астрономических сумерек совпадает с началом утренних астрономических сумерек?
29	Высота полюса 441/2°- Отметьте на карте созвездия, постоянно видимые над горизонтом.
30	. Звезда а Возничего в момент нижней кульминации видна на горизонте. Какова высота Полярной звезды?
ЗЬ Сколько показывают звездные часы в момент кульминации а Орла?
4/
32 Какие звезды проходят меридиан 3 октября в 10 ч 30 м вечера* Какие созвездия уже прошли меридиан и видны на юго-западе и какие видны на юго-востоке?
33	. Звезда 3 Малой Медведицы наблюдалась в нижней кульминации, причем звездные часы в это время показывали 5 ч. 59 м 33 с Какова поправка часов?
34	Астроном пронаблюдал прохождение светила через меридиан (верхняя кульминация) в 7 ч< 35 м 15,4 с звездного времени и определил зенитное расстояние светила в 44° 15' Поправка часов, определенная в этот вечер, была равна +0 м. 33,4 с. Каковы координаты светила, если высота полюса 56°20'*
35	В устье Беломорско-Балтийского канала (Сорокская Губа) наблюдаемая высота полюса 64°33' На какой высоте бывает там Солнце в полдень 22 декабря*
36	. Каково прямое восхождение Солнца 7 ноября, если в этот день уравнение времени равно —16 минутам?
37	20 ноября созвездие Большой Медведицы видно в плоскости меридиана В северной стороне неба Вычислите среднее местное время.
38	. На какой высоте видно Солнце на Южном полюсе 22 декабря?
39	15 июля солнечные часы показывают 4 часа дня Сколько должны показывать часы по местному времени и сколько по звездному?
ГЛАВА II.
Форма Земли и ее вращение»
§ 36. Развитие взглядов на форму Земли. В древние времена, когда люди не имели ни необходимости, ни возможности перемещаться на значительные расстояния от места своего жилья, они считали Землю плоской Небо по их представлениям было чем-то вроде перевернутой чаши, по которой двигались Солнце и звезды. Но уже недалекие перемещения от места жилья вынуждали людей искать какие-нибудь признаки, по которым можно было бы выбирать нужные для перемещения направления Одним из таких признаков И притом самым надежным оказались звезды, не менявшие на небе своего положения вследствие близости к полюсу мира
Таким образом, с самого начала жизни человечества познание Земли соединилось с изучением неба, а хозяйственные потребности, развитие торговых сношений заставляли совершать все более отдаленные путешествия и подробнее изучать небо
Особенно важно было изучение неба для первобытных кочевников В результате путешествий знакомство с поверхностью Земли становилось все более обширным, карты земной поверхности делались все ббльшими по количеству изображенных на них земель и морей, но все же долгое время Землю продолжали считать плоской
Первый толчок к изменению взглядов на форму Земли был дан той практикой наблюдений неба, к которой первобытные люди вынуждены были обращаться для отыскания нужных им направлений Они заметили, что при перемещениях на дальние расстояния Меняется и вид неба, одни звезды перестают быть видимы, другие, наоборот, появляются над горизонтом Это то явление, которое мы можем пронаблюдать, переехав из северных частей СССР в южные или обратно.
На рисунке 40 изображены созвездия, видимые в одно и то(.же время в Москве (правая часть рисунка) и в Крыму Небольшое сравнительно перемещение из Москвы в Крым дает изменение вида неба, вполне заметное Сравните части этого рисунка; вы видите, что в Москве Полярная звезда стоит выше, чем в Крыму, но зато в южной части небосвода 42
созвездие Скорпиона в Москве видно не все, в Крыму же оно стоит высоко над горизонтом. Таким образом, перемещению по Земле с севера на юг всегда соответствует как бы поворот небесной сферы, при котором ее северные части опускаются, а южные поднимаются. К этим соображениям можно добавить еще й то, что всюду, во всех местах Земли горизонт представляется кругообразным.
Можно думать, что именно подобные наблюдения побудили ассиро-вавилонян изменить первоначальное представление о Земле и небе.
По представлениям ассиро-вавилонян Земля была полушарообразная гора, над которой про-
стирается твердый небо- рИс. 40. Положение созвездий в южной и север-свод, а все это „здание* ной сторонах небосвода в Крыму (налево) покоится на „мировом	и в Москве (направо).
океане". В этом пред-
ставлении (рис. 41) сказалось и знакомство с отдаленными странами (мировой океан, полушарообразная гора), и в то же время большая наивность (так как „мировой океан" где-нибудь тоже должен
Рис. 41. Земля и небо по представлению вавилонян»
был находиться), и слепая вера в сверхъестественное, поддерживаемая жрецами.
Дальнейшее развитие торговых сношений, путешествия финикиян, греков, походы до самой Индии Александра Македонского — все это не только давало новые сведения о поверхности Земли, но и ставило под сомнение представления о Плоской или полушарообразной Земле. Наблюдения лунных затмений, во время которых на лунном диске виден
43
неизменно круглый край земной тени, доказывали, что Земля имеет фор* му шара.
Живший в IV в. до н. э. величайший греческий ученый Аристотель развил и обосновал учение о шарообразности Земли. Аристотель считал, что все „тяжелые* тела стремятся приблизиться к центру мира и, собираясь вокруг этого центра, образуют земной шар» Взгляды Аристотеля, воспринятые как его современниками, так и последующими поколениями греческих ученых, легли в основу Древнегреческого учений о строении мира (см. § 37) и привели к первым попыткам определить размеры земного шара (Эратосфен).
О высоте, на которой в то время стояло изучение поверхности Земли, можно отчасти судить по современным Аристотелю географическим картам. На рисунке 42 вы видите, что греческий ученый Г е к а т е й
Рис. 42. Карта Земли Гекатея (V в. до н. э.).
Очертания материков и морей, изображенные на карте, в общем напоминают действительные.
в V в. до н. э. дал в общем правильную карту известной в то время части поверхности Земли.
Но после того как христианская религия сделалась господствующей в Римской империи и началось гонение „языческой* науки, учение о шарообразности Земли стало рассматриваться как противоречащее *свя* щенному писанию*, и ему на смену пришли примитивные взгляды на Землю как на плоское тело, прикрытое твердым колпаком — небесным сводом. Реакционные взгляды церкви быстро сказались и на общих практических знаниях. Если во времена Гекатея карта Земли достаточно близко подходила к истинной, то в средние века географические карты (рис. 43) стали почти фантастическими. На рисунке 43 поверхность Земли изображена так, что северные части находятся слева, а южные— справа. Если, принимая во внимание это расположение, вы сравните рисунки 42 и 43, то легко убедитесь в несовершенстве второго рисунка.
44
Знакомых очертаний Евразийского материка вы не найдете, но зато в угоду церкви изображены «священные* земли, Иерусалим и воображаемый рай. Даже в конце XV в., когда Колумб собирался совершить свое знаменитое путешествие через Атлантический океан, ему пришлось подвергнуться издевательствам и насмешкам со стороны «отцов* христианской церкви, отрицавших возможность приплыть в Индию западным
Ряс. 43. Карта Земли средних веков —эпохи господства христианской церкви.
На карта аавар — слева, ttr— е;травз- Карта совершенно неверна по расположению и очертанию морей и материков.
морским путем. Кругосветное путешествие Магеллана дало доказательства того, что Земля изолирована в пространстве, не имеет никаких мнимых подпор и, невидимому, шарообразна.
§ 37. Вращение Земли. Как мы видели, церковь своим сопротивлением греческому учению о шарообразности Земли сумела временно приостановить прогресс знаний о Земле. В учении о вращении Земли и обращении ее около Солнца сопротивление церкви было еще более жестоким.
В древности первые наблюдатели неба думали, что небо действительно вращается вокруг Земли. Если путешествия смогли опровергнуть теорию плоской Земли, то теорию ее неподвижности опровергли наблюдения
45
движения небесных светил, которые для путешественников были указателями направлений и служили для счета времени. Однако не только эти наблюдения ставили под сомнение теорию неподвижности Земли и вращающегося вокруг нее неба: общий подъем наук, сопротивление гнету библейского толкования мира, стремление объяснить явления природы
не чудесами, а естественными причинами создали впоследствии почву для нйвой теорий о вращении самой Земли и ее обращении вокруг Солнца.
В древней Греции получила общее признание геоцентрическая система мира („ге*— по-гречески Земля), согласно которой'шарообразная Земля неподвижно расположена в центре мира, а вокруг нее обращаются все небесные тела — Солнце, планеты, звезды. Эта система мира часто называется Птолемеевой системой мира — по имени греческого ученого Птолемея, 'подробно изложившего ее в своем сочинении, известном под арабским названием „Альмагест* (что значит „Великое построение*).
Птолемей, живший во II в., был
Рис. 44. Николай Коперник (7473—1543).
qjhylwa из выдающихся астрономов древности и в своих сочинениях собрал все достижения астрономии своего времени. Его теория об обращении светил вокруг Земли была геометрически довольно удачно рассчитана и могла служить практическим целям предвычисления положения Солнца и планет. Однако бблыпая точность наблюдений и ббльшие требования к точности расчетов впоследствии уже не удовлетворялись теорией Птолемея (см. § 62).
Христианская церковь приняла теорию Птолемея довольно поздно, по существу только в XIII в., а до тех пор ее приверженцы, как мы видели, отказывались даже от учения о шарообразности Земли. Невежественные монахи средневековья представляли Землю и небо в виде
плоского круга, покрытого стеклянным колпаком со звездами, за которым находилась „божественная небесная машина*. Однако передовые ученые отнюдь не были сторонниками такого мировоззрения, и многие из них, хотя и недостаточно определенно, высказывали мнение не только о шарообразности, но и о вращений. Земли.
Завершителем и выразителем этих идей был Николай Коперник (рис. 44), который после долгих лет исследований и наблюдений в книге „Об обращениях небесных шаров* развил и обосновал учение о. движении Земли (подробнее о значении учения Коперника и о его последователях см. § 69).
§ 38. Доказательства шарообразности Земли. Существуют несколько доказательств кривизны поверхности Земли, ее изолированности в пространстве и ее шарообразности.
Поверхность Земли имеет кривизну, так как:
1.	При наблюдении корабля, приближающегося к наблюдателю, стоящему на берегу, сначала появляются мачты корабля, а пот'ом уже самый корпус.
45
2.	При поднятии на высоту кругозор расширяется, и тот же корабль (рис. 45) становится видим с более далекого расстояния.
3.	После захода Солнца вершины гор или даже высоких строений остаются некоторое время освещенными, так как Солнце, зашедшее за выпуклость Земли для наблюдателя в точке А (рис. 45), еще не зашло для наблюдателей в точках В и С.
4.	При перемещении наблюдателя по поверхности Земли изменяется высота полюса мира.
Земля изолирована в пространстве, так как:
5.	Кругосветные путешествия ясно показывают возможность, двигаясь все время в одном и том же направлении, притти к месту выезда.
Земля шарообразна, так как:
6.	При перемещении по поверхности Земли наблюдатель всюду видит себя в середине круга, а это может быть только при условии, что он находится на шарообразной поверхности.
7.	Во время затмений тень Земли, падающая на Луну, всегда имеет вид круга, а ведь только шарообразное тело при любом положении может дать круглую тень.
Мы пока что называем Землю шарообразной; в дальнейшем мы рас* смотрим вопрос, насколько близко форма Земли соответствует геометри* ческому шару. Геодезические измерения точнее доказывают кривизну земной поверхности, но в то же время убеждают нас в том, что Земля не является в точности шарообразной.
§ 39.	Доказательства вращения Земли. Для доказательства вращения Земли .невозможно привести такие же простые наблюдения, как для доказательства ее шарообразности. Непосредственные ощущения такого доказательства нам не дают, но это еще не означает, что Земля неподвижна. Действительно, сидя в вагоне поезда и глядя через окно на вагон рядом стоящего поезда, мы, замечая передвижение, часто не можем определить, какой именно из поездов сдвинулся.
Непосредственных доказательств существования вращения Земли во времена Коперника еще не было, так,как не были еще известны законы механики, с помощью которых впоследствии были даны эти доказательства.
Все доказательства вращения Земли, в сущности, имеют в основе закон инерций и независимости движений. Одно из доказательств, получаемых путем опыта, основано на инерции качающегося маятника, выражающейся в том, что плоскость качания маятника, как бы мы ни поворачивали штатив, на котором он привешен, сохраняет свое направление в пространстве.
47
Представим себе длинный и тяжелый маятник, подвешенный к предмету, стоящему на поверхности Земли. Предположим, что мы дали возможность маятнику качаться в направлении меридиана. Через определенное время Земля повернется на некоторый угол, маятник же будет качаться по прежнему направлению, и нам, находящимся на Земле и движущимся вместе с нею, будет представляться, что маятник отклонен от прежней плоскости своего качания и качается уже не в плоскости меридиана, а по линии, составляющей с меридианом некоторый угол.
Такой опыт был сделан
в 1851 г. в Париже физиком Фуко, который использовал для этой цели высокое здание парижского Пантеона (рис. 46). При этом блестяще подтвердилось учение о вращении Земли — маятник отклонялся от первоначального направления в каждую минуту именно настолько, насколько было это предусмотрено по вычислениям. Легко понять, что если такой опыт производить на полюсе Земли, то отклонение маятника за 1 час должно быть 15°. На всякой иной широте отклонение тем меньше, чем ближе место опыта к земному экватору. На экваторе отклонение не имеет места совсем.
Опыт Фуко повторяли много раз в различных местах Земли. В СССР опыт Фуко публично демонстрируется в Антирелигиозном музее в Ленинграде (в помещении бывшего Исаакиев-
Рис. 45. Опыт Фуко в парижском Пантеоне в 1851 г.
ского собора), причем и размеры и продолжительность качаний маятника гораздо больше, чем в предыдущих опытах.
Все опыты с маятником Фуко давали и дают один и тот же результат плоскость качаний маятника отклоняется так, как это должно быть при вращении Земли.
Другое доказательство вращения Земли получается при падении тел с большой высоты. Представим себе высокую башню, вращающуюся вместе с Землей (рис. 47); ее основание и вершина имеют неодинаковую линейную скорость вращения. Скорость на вершине башни больше, у подножия — меньше. Представим себе теперь, что тяжелый предмет, находившийся на вершине башни, потерял опору и начинает падать к ее подножию. Падая, этот предмет будет сохранять то движение, которое он имел на вершине. За один и тот же промежуток, времени 48
вершина и подножие башни проходят неодинаковые пути, вершина — больший, чем подножие. Поэтому предмет, падая с вершины башни, будет все время отклоняться от вертикального направления и, коснувшись поверхности Земли, окажется смещенным к востоку. Это «отклонение падающих тел к востоку* тем больше, чем с ббльшей высоты падает предмет. Его величина может быть вычислена теоретически.
Опыт с падением тел нельзя проделывать на открытом воздухе, так как при малости отклонения случайные воздушные течения или ветер
могут совершенно исказить все явление.
Обычно такие опыты производились в глубоких шахтах, причем неизменно оказывалось, что отклонение очень близко соответствует тео-
ретически вычисленному.
При первых опытах такого рода (1804 г.), сделанных внутри вертикальной шахты глубиной 85 м, отклонение оказалось 11,4 мм, а теоретически вычисленное должно быть 10,5 мм. Разница была очень мала (0,9 мм}> что вполне объяснимо случайными токами воздуха
внутри шахты.
Таким образом, два описанных опыта с несомненностью доказывают существование вращения Земли.
§ 40.	Видимы^ и математический горизонт. В предыдущей главе мы рассмотрели целый ряд явлений, видимых с поверхности Земли, а также некоторые геометрические схемы этих явлений и движений. Теперь, исходя из теории шарообразности Земли, мы все эти представления можем пересмотреть и разъяснить. Представим себе наблюдателя, вернее сказать, глаз наблюдателя, находя
щийся на поверхности гладкой, без выступов и впадин, шарообразной Земли. Этого наблюдателя мы можем изображать как точку на поверх-
ности шара.
Плоскость, проходящую через точку земной поверхности и перпендикулярную к отвесному направлению, мы уже условились называть горизонтальной. Горизонтальная плоскость может быть или касательной к земной поверхности или находиться выше поверхности Земли. Линию пересечения небесной сферы горизонтальной плоскостью мы будем называть математическим горизонтом места наблюдения. На самом деле глаз наблюдателя всегда выше земной поверхности. Поэтому линия пересечения горизонтальной плоскости с небесной сферой всегда несколько выше, чем видимая граница земной поверхности. Эту пограничную Линию мы будем называть видимым горизонтом (см. § 4). Математический горизонт всегда делит небесную сферу пополам, видимый горизонт оставляет видимой тем большую часть небесной сферы, чем выше расположен наблюдатель (рис. 45). Только стоя на берегу большого водоема или с большой высоты (дирижабль, самолет), мы можем наблюдать видимый горизонт как ровную линию. Понижением горизонта мы будем называть угол между горизонтальной линией и лучом зрения на край видимого горизонта. Этот угол тем больше, чем больше высота наблюдателя. Измерив этот угол и зная высоту подъема, можно вычислить размеры земнбго шара. Практически такой способ не применяется вследствие
4 Астрономия
49
того, что угол понижения горизонта, даже при больших высотах, Не* велик и точное измерение его ненадежно- (вследствие рефракции).
§ 41.	Географические координаты. Названия географических координат —. долготы и широты — очень древнего происхождения; в древности поверхность Земли была лучше изучена по направлению с запада на восток, чем с юга на север. Поэтому первые карты Земли, обладавшие формой прямоугольника, имели бблыпую сторону по направлению 3 — В, что и дало основание это направление назвать долготой.
Чтобы определить положение какого-нибудь места на земном шаре, проведем плоскость через земную ось и данное место; эта плоскость разрежет земной шар по окружности.
Дуга большого круга, проходящая через полюсы Земли и заданное место, называется меридианом этого места. Меридианов на поверхности земного шара можно провести сколько угодно. Поэтому, указав широту в градусах, надо еще указать угол, который составляет плоскость данного меридиана с плоскостью какого-нибудь другого меридиана, от которого условлено вести счет.
Угол между плоскостью меридиана данного места и плоскостью начального £ меридиана называют долготой.
Долгота считается в сторону вращения Земли и выражается как в угловой мере (т. е. в градусах, минутах и секундах), так и в единицах времени (часы, минуты, секунды).
Можно сказать, что долгота есть дуга,
Рис- 48.	считаемая по земному экватору qt началь-
ного меридиана до данного. За начальный принимают меридиан, проходящий через астрономическую обсерваторию в Грйниче (Англия).
Угол FCK (рис. 48) между плоскостью экватора и направлением из центра земного шара на данную точку земной поверхности называют широтой места; можно сказать иначе: широтой называется дуга между экватором и данной точкой. Так как от экватора можно отмерить широту и в сторону севера и в сторону юга, то условились северные широты обозначать знаком-}-, а южные знаком—. Круги на земном шаре, соединяющие места с равной широтой, называют параллелями.
§ 42. Земной шар и небесная сфера. Мы ознакомились в главе I с целым рядом понятий, относящихся к видимом явлениям, происходящим на небосводе, и представляем себе плоскость горизонта, меридиана и полуденную линию так, как мы их мысленно проводим, находясь на поверхности Земли. Мы уже перешли частично от видимого к действительному, когда рассматривали Землю как вращающийся шар и плоскость горизонта как касательную плоскость к земной поверхности. Заключим этот переход путем дальнейшего сопоставления видимого и действительного.
Мы можем считать, что наблюдатель С на поверхности Земли (рис. 49) видит все светила на звездном небе по тому же направлению, что и воображаемый наблюдатель, смотрящий на небо из центра Земли,
Происходит это потому* что размеры Земли ничтожно малы по сравнению с расстояниями до звезд. Продолжение земной оси вращения имеет направление на какую-то точку небосвода, и наблюдатель в С видит эту точку по тому же направлению. Представим себе часть небесной сферы с центром в -точке С. Линия СР — ось мира, она параллельна земной оси вращения, CZ есть направление в зенит —оно представляет собой продолжение земного радиуса, проведенного из центра в точку С. Плоскость NPZS преходит через ось мира и отвесную линию; для наблюдателя в точке С—это плоскость । небесного меридиана, но эта же самая плоскость есть плоскость географического меридиана в точке С; направление полуденной линии SN есть направление географического меридиана в точке С. Плоскость небесного экватора ЕА W параллельна плоскости земного экватора, направление EW есть касательная к параллели точки С. Земля вращается по направлению WE (^) (если смотреть с Северного полюса) и увлекает наблюдателя С
.вместе с построенной им небесной сферой; наблюдателю же представляется, что небесная сфера вращается по направлению EW (“^.) и через меридиан проходят последовательно круги склонений РА, РВ, PD.
Если наблюдатель перемещается по поверхности Земли, то вместе с ним перемещается небесная сфера; при этом изменяется как высота полюса мира, так и положение небесного экватора.
§ 43.	Широта места и высота полюса. Мы уже говорили, что высота полюСа* над горизонтом меняется в зависимости от местоположения .наблюдателя на Земле. Легко доказать, что высота полюса над горизонтом равна широте этого места. На рисунке 50 изображено сечение земного шара и небесной сферы плоскостью, проходящей через ось вращения Земли и точку наблюдения С. В точке С наблюдатель по направлению Р видит полюс, по направлению Z — зенит места. Плоскость ZCP—плоскость небесного меридиана наблюдателя. Угол PCD — высота полюса над горизонтом. Угол CTF —г широта места. Легко видеть, что == ^/СТТ7 как Углы со взаимно перпендикулярными сторонами. Отсюда вытекает очень важный вывод: широта места равна угловой высоте полюса над горизонтом.
формулу высоты звезды для момента ее верх-полюса, то теперь
Так как мы уже йа!веЛй
ней кульминации h = 90° — ср-Ц-S, где ср— высота можем применить ее как для расчета высот светил, зная широту, так 4*	51
и, наоборот, для вычисления широты, когда нам известны высота и склонение светила в момент его верхней кульминации.
Пользуясь только что сделанным выводом, мы можем представить себе как вид звездного неба, так и ряд явлений, связанных с вращением небесной сферы.
Начнем разбор с Северного полюса Земли. Находясь на нем, наблюдатель будет видеть полюс мира в зените, небесный экватор будет совпадать с горизонтом, светила не будут восходить и заходить, а лишь обращаться параллельно горизонту. Любое направление в плоскости горизонта будет лежать в плоскости какого-либо меридиана, а полуденной линии не будет, так же как и стран горизонта. В местах с какой-нибудь северной широтой явления происходят так, как мы уже разбирали во всех рассуждениях главы I. На земном экваторе ось мира лежит в плоскости горизонта, небесный экватор проходит через зенит места и суточное движение светил происходит перпендикулярно к горизонту (рис. 50а).
В южном полушарии Земли все происходит так же, как в северном, но светила движутся для наблюдателя справа налево.
а	б	в
Рис. 50а. Суточные цути светил относительно горизонта для наблюдателя, находящегося: а — на Северном полюсе Земли, б — в средних широтах, в — на экваторе.
Так как Солнце, двигаясь по эклиптике, может иметь склонение от 4“23* 1/2° до — 231/2°, то на полюсах оно может быть одновременно1 видно лишь в дни равноденствий, но во всякое другое время оно видимо или на одном или на другом полюсе. На полюсах шесть месяцев длится ночь и шесть месяцев — день, восход и заход Солнца обусловлены его движением по эклиптике и продолжаются 83 часа.
На Северном полюсе восход Солнца начинается несколько раньше весеннего равноденствия1. До дня летнего солнцестояния Солнце, непрерывно обращаясь по небосводу, поднимается до высоты в ЗЗ1/^ и затем также начинает снижаться к горизонту. Заходит оно несколько позже осеннего равноденствия. От полюса до полярного круга (широта 66х/2°) в течение года бывают два периода: светлый и темный, когда Солнце или не восходит или не заходит. Эти периоды тем короче, чем. ближе место к широте 66*/2°: на самом полярном круге (широта бб1/^) вдень летнего солнцестояния Солнце не заходит, лишь касаясь в полночь
1 Этот, более ранний, восход обусловлен двумя обстоятельствами:
1) Солнце имеет видимый диаметр около */2° и поэтому верхний Край его должен появиться над горизонтом еще тогда, когда склонение Солнца (отрицательное) равно */4°; 2) рефракция, как бы поднимающая светила, дает возможность видеть верхний край Солнца еще тогда, когда этот край более чем на !/2° ниже математического горизонта.
52
горизонта. А в день зимнего солнцестояний оно там не должно было бы восходить, но вследствие рефракции и видимого диаметра оно короткое время бывает видно над горизонтом.
От этой широты и до широты 231/2° Солнце восходит и заходит, но никогда не бывает в зените места наблюдения. На широте -|~ 231 Солнце бывает в зените один раз в году — в день летнего солнцестояния.
На экваторе день всегда равен ночи. Солнце бывает в зените два раза в году, в дни равноденствий.
§ 44.	Вращение Земли и счет времени. Мы уже ознакомились с основой счета времени: истинными, средними и звездными сутками. Теперь, рассматривая шарообразную, вращающуюся Землю, мы можем разъяснить и расширить вопрос об определении времени и поверке часов.
Поставьте яркую лампу и на некотором расстоянии от нее земной глобус с воткнутой в него булавкой, изображающей гномон. Вращая глобус, вы воспроизведете для любого места его поверхности смену дня и ночи и передвижение тени от гномона. Легко уяснить себе с помощью этой модели, что в полдень тень от гномона идет вдоль земного меридиана, что в один и тот же момент на разных меридианах будет разное время: в западных частях — утро (до полудня), в восточных частях — вечер. Если бы Земля не двигалась вокруг Солнца, то промежуток между полуднями в одном и том же месте был бы равен звездным суткам. На самом деле вследствие движения Земли по ее орбите всякий следующий полдень наступает спустя некоторый промежуток времени после того, как место нахождения наблюдателя на Земле обернется к той же звезде, которая в предыдущий день одновременно с Солнцем была в верхней кульминации (рис. 51).
Таким образом, после того как Земля сделает пол
ный оборот вокруг своей оси, ей еще надо повернуться на угол SjBS, чтобы для места наблюдения Солнце находилось в верхней кульминации.
Если бы Земля обращалась около Солнца по круговому пути и ось ее вращения была перпендикулярна к плоскости движения, то разность между солнечными сутками и звездными была бы всегда одинакова и равна 3 м. 56 с., т. е. как раз тому времени, которое нужно Земле, чтобы повернуться на угол S\BS.
На самом же деле Земля обращается около Солнца по эллипсу и летом движется несколько медленнее, чем зимою. Мы с Земли наблюдаем это как неравномерность движения Солнца пр эклиптике и для упрощения дела измерения времени вводим понятия истинного и среднего Солнца.
§ 45.	Местное время и .долгота» С помощью простой модели, описанной в предыдущем параграфе, легко себе уяснить, что на каждом из земных меридианов в один и тот же физический момент Солнце видно под разными углами к плоскости небесного меридиана данного места. Если мы выберем какой-нибудь меридиан с долготой £, на котором в данный момент полдень, то в другом месте на Земле с другой долготой наблюдают Солнце, отстоящим от небесного меридиана на некоторый часовой угол.
Таким образом, в этих двух местах в один и тот же физический момент Солнце находится не в одном и том же положении по отношению
53
к плоскости меридиана, и каждое из этих мест должно считать свое „местное* время, равное часовому уму Солнца. Разница „местных* времен равна разности часовых углов Солнца, или, что то же, промежутку времени между прохождениями его через меридианы мест с долготами L и Lv Так как небесный меридиан есть пересечение плоскости земного меридиана небесной сферой, то разность часовых углов должна быть равна углу между плоскостями меридианов L и £р т. е. £ — £Р
Всякое место на Земле имеет свое „местное* время, и разность долгот,равна разности времени двух мест. Поэтому долготы земных* пунктов принято выражать не только в градусной мере, но и во времени, исходя из расчета 360° = 24 часам.
§ 46.	Международный поясной счет времени. Местное время было бы вполне удобно для счета, если бы люди жили изолированной не имели способов быстрого передвижения. Современная жизнь человечества, установившего технику быстрых переездов и еще более быстрой связи (телеграф), требует большого единообразия в счете времени. Действиу тельно, представьте себе путешественника, переезжающего из Москвы во Владивосток. Такой путешественник должен оыл бы непрерывно следить за своими часами, и непрерывно переводить их стрелки вперед, чтобы они показывали местное время тех бесчисленных меридианов, которые он проезжает. Это, конечно, крайне неудобно. Чтобы устранить такое неудобство, принят почтц по всему земному шару поясной счет времени. Представим себе земной шар разделенным на 24 равные полосы, ограниченные меридианами, отстоящими на 15° друг от друга. Средние меридианы всех этих полос будут отличаться между собой по своему местному времени ровно на 1 час. Такие полосы назвали поясами. Все места внутри пояса считают время не свое, местное, а по времени среднего меридиана своего пояса. Таким образом, это условное поясное время может отличаться от местного не более как на полчаса.
Наш путешественник, едущий из Москвы во Владивосток, должен переводить стрелки своих часов ровно на 1 час всякий раз, как он переезжает пограничный меридиан. Пояса называют по номерам, показывающим, насколько их время впереди времени нулевого гриничского пояса. Западная Европа занимает 2 пояса (нулевой, и 1-й), СССР занимает 10 поясов (от 2-го до 12-го) (см. приложение VI — карту часовых поясов).
Счет времени по часовым поясам разработан и принят на международной конференции, к постановлениям которой присоединилось большинство стран. Правители царской России не желали присоединяться к этому интернациональному соглашению, и в России до 1918 г. счет времени велся по долготам некоторых городов: было время московское, петербургское, киевское и т. д. Только советская власть декретом от 8 февраля 1919 г. установила в РСФСР поясной счет времени.
Практически оказывается неудобно устанавливать границы поясов точно по меридианам, так как при этом разделяются области, экойомит чески связанные. Поэтому граница поясов проводится в общем по меридиану, но следует по извилинам областных границ или пограничных рек., При составлении расписания движения по всей транспортной сети СССР счет времени по поясам вносит затруднения в расчет графиков. Поэтому для транспортной сети применяется общий счет времени по главному московскому узлу.
54
Это „транспортное* время называют железнодорожным. Кроме того, в целях экономии электроэнергии в настоящее время особым распоряжением правительства СССР часы переведены на 1 час вперед так, что всякий пояс в СССР живет, в сущности, по времени следующего восточного пояса. Время с учетом этого перевода на 1 час вперед называют „декретным* временем.
Границы поясов для РСФСР, подробно перечисленные в декрете Совета народных комиссаров от 8 февраля 1919 г., затем были распространены на СССР. В Западной Европе нет государств, столь обширных по долготе, потому границами поясов служат границы самих государств.
Развитие международных отношений и средств сообщения вызвало необходимость установить „линию изменения даты* на земном шаре. Представим себе путешественника, выехавшего в кругосветное путешествие и едущего все время на восток. Переезжая из одного пояса в другой, он будет 24 раза переводить свои часы на 1 час вперед, и если бы на, его часах (как это иногда бывает) была стрелка, указывающая дни, то за время такого кругосветного путешествия эта стрелка передвинулась бы на одно деление больше, чем на часах в том месте, откуда он выехал. Происходит это потому, что для такого путешественника сутки должны быть как бы короче, так как он движется в ту же сторону, куда вращается Земля, и, объехав Землю, сделает один лишний оборот вокруг оси Земли. С путешественником, едущим на запад, произойдет обратное. Если каждый из путешественников имеет при себе отрывной календарь, то едущий на восток оторвет на 1 листок больше, едущий на запад — на 1 листок меньше, чем живущие в одном и том же месте. В каждом месте на Земле сутки начинают считать с полуночи, а каждое место имеет свое „местное* время, поэтому начало суток в разных местах различно. Ввиду этого и установлена „линия изменения даты* — линия, идущая приблизительно по 180° долготы. К востоку от этой линии число месяца всегда меньше на 1, чем к западу. Поэтому капитан корабля, пересекая границу дат с запада на восток, два раза подряд считает одно и тоже число и тем устраняет указанную выше ошибку в счете времени. При пересечений границы дат с востока на запад один день из счета выбрасывается.
§ 47.	Перевод времени. Так как мы живем по поясному времени, то для расчета моментов астрономических явлений в поясном времени следует вводить в расчеты и долготу места. Схема перехода такова:
1) наблюдение Солнца-> истинное время-> среднее местное время * поясное время;
2) наблюдение звезды-*звездное время-* среднее местное время-* поясное время.
Для удобства перехода от местного среднего времени к поясному мы можем для любого места на Земле ввести „поправку на пояс*. Поправка на пояс равна разности поясного и местного времени и показывает, сколько надо прибавить к местному времени, чтобы, получить поясное (с учетом алгебраического знака). Например, Москва лежит во 2-м (часовом) поясе, а ее долгота от Гринича 2 ч. 30 м. 17 с.
Поправка на пояс (для Москвы): 2 ч. 0 м. 0 с. — 2 ч. 30 м. 17 с == ^ — 30 м. 17 с.
Пример 1. Сколько должны показывать часы, идущие по поясному времени, 20 сентября в Москве в момент истинного полудня? По таблице или 55
по календа рю находим, что уравнение- времени равно — 5 мин. Следовательно, местное время равно 11 ч. 5о м. О с.
Учитываем поправку на пояс: 11 ч. 55 м. О с. — 30 м. 17 с. = И ч. 24 м. 43 с., столько должны показывать правильно идущие поясные часы. Если часы показывают, например, 11 ч. 23 м. 10 с., то их поправка будет: 4-1 М..-33 с. Если мы обозначим Т{—поясное время, tQ — истинное время, ч — уравнение времени, О — поправку на пояс, то
Отсюда легко видеть, что, зная 3 величины этой формулы, мы можем вычислить четвертую, т. е., например, по поясному времени найти сначала местное, а потом истинное.
Пример 2. Сколько должны, показывать часы, идущие по поясному времени в момент верхней кульминации звезды Сириус 9 ноября в Москве?
Прямое восхождение Сириуса 6 ч. 42 м*> следовательно, в момент кульминации звездные часы должны показывать 6 ч. 42 м. Перевод звездного времени В среднее местное время:
вреднее местное время Звездное время 21 ноября	12 часов	16 часов
9 .	12 .	15 ч. 12 м.
Следовательно, 9 ноября звездные часы впереди средних на 3 ч. 12 м. 6 ч. 42 м. — 3 ч. 12 м. =»3 ч. 30 м. (среднего местного времени).
Беря поправку на пояс в Москве, имеем:
3 ч. 30 м. —30 м. 17 с. = 2 ч. 59 м. 43 с.
В момент кульминации Сириуса поясные часы должны показывать 2 ч. 59 м. 43 с.
§ 48.	Служба времени. В астрономических обсерваториях часы поверяются по наблюдениям звезд, причем учитываются самые малые неправильности хода часов.
Главные часы обсерватории идут по местному звездному времени, но, кроме этих часов, в обсерваториях Имеются часы, идущие по поясному времени, поверяемые по звездным часам.
Все государственные часы (на телеграфе, на почте, на железных дорогах, во многих правительственных учреждениях, на площадях и улицах больших городов) в сущности идут по часам астрономической обсерватории, так как основное время „хранится* на этих часах. Таким образом, астрономические обсерватории несут „службу точного времени*, заключающуюся в хранении и передаче точного времени. Хранение точного времени выполняется с помощью меридианных наблюдений звезд, поверки часов и записи их хода.
Передача времени выполняется, главным образом, путем широкого применения достижений современной техники, в частности электротехники. Простейший из этих способов — передача времени по телефону и телеграфу — применяется для передачи точного времени государственным учреждениям (почте, телеграфу, наркоматам, городским советам). В больших городах часы в учреждениях нередко электрифицированы — это собственно не часы, а указатели времени, соединенные проводом с настоящими точными часами, находящимися в правительственном здании и поверяемыми по часам обсерваторий» Благодаря электрической связи такие циферблаты показывают то же время, что и основные часы. Наиболее широкий способ передачи времени — радиовещание. Передача времени по радио устроена так: астрономическая обсерватория соединена прямым проводом с радиостанцией, провод подходит к часам и может быть 56
йключен, Кош происходит передача. Сначала включают микрофон, по которому дежурный астроном говорит о предстоящей передаче и о точном моменте ее. В надлежащий момент провод переключается на часы, и
в пространство передается удар маятника часов в виде короткого гудка. Эта передача времени выполняется с точностью до 0,1 секунды.
Передача точного времени по радио организована широко во всех государствах, и каждая обсерватория не только подает сама время, но и сравнивает свои часы с часами других обсерваторий (для контроля).
Служба точного времени неминуемо влечет интернационализацию
всей организации этого дела, так как и В практических и в теоретиче-
ских задачах этой работы заинтересованы и мореплавание, и авиация, и разведки полезных ископаемых. Поэтому организовано Международное
бюро службы времени, которое заботится о планомерности и увязке
работы всех государств в этом деле.
Наш Союз, раскинувшийся на 10 часовых поясов, особенно нуждается в организации службы времени по радио, и вскоре же после Великой Октябрьской социалистической революции у нас была организована передача времени по радио из Главной астрономической обсерватории (в Пулкове); в настоящее время такая передача ведется многими обсерваториями.
Рис. 52. Солнечное кольцо.
§ 49.	Способы поверки часов. Простейшие способы поверки часов по Солнцу уже были изложены (§ 33). Если не требуется большой точности, ими можно пользоваться. Солнечные часы в местностях с малой облачностью могут в течение дня заменять обыкновенные часы с часовым механизмом, давая при тщательной установке достаточную точность для обыденной жизни.
Очень удобен и сравнительно точен прибор, особенно полезный в экспедициях при отсутствии универсальных инструментов, конструкции проф. С. П. Глазенапа.	t
Для определения моментгк истинного полудня проф. С. П. Глазенап сконструировал „солнечное кольцо* (рис. 52). Кольцо свободно висит на штифте, имея одну точку опоры. Под действием собственной тяжести кольцо висит всегда в одном положении относительно отвесной линии, независимо от передвижения подставки. В верхней части .кольца просверлено отверстие диаметром в 1 мм, а на противоположной, внутренней стороне кольца наклеена бумага с
миллиметровыми делениями, занумерованными в определенном порядке.
До и после полудня наблюдают светлый кружочек от отверстия на одном и том же номере деления, поворачивая при этом весь приборчик так, чтобы плоскость кольца была направлена на Солнце. При этом записывается по часам момент, когда светлый кружочек делится пополам каким-нибудь штрихом. Эти записи моментов, соответствующие одинаковым высотам Солнца до и после полудня, складывают, и делением получившейся суммы пополам находят момент истинного полудня. Прибавив с соответствующим знаком уравнение времени, получают момент среднего полудня и таким образом узнают, верны ли часы. Так как до и после полудня, можно сделать несколько таких наблюдений, то, взяв среднее арифметическое из них, можно получить поправку часов более точно.
Вследствие движения Солнца по эклиптике вычисленный таким образом момент истинного полудня не будет соответствовать моменту прохождения Солнца через меридиан. Поэтому при наблюдениях солнечным кольцом ло особым
57
таблицам вычисляется поправка полудня (она, впрочем, невелика и для средних широт не превышает 30 секунд).
Таким образом, пользуясь солнечным кольцом дажеи без учета собственного движения Солнца, возможно поверить часы с точностью до г/2 минуты; если же при вычислении принять во внимание поправку на движение Солнца, то поверка часов может быть сделана с точностью до 1 секунды.
№ штриха 18,5 19 20 21	Пример наблюдения и вычисления 1 октября 1926 г. До полудня	После полудня	Полус 9 ч.	1	м.42	с.	14	ч.	38	м.	48	с.	11	ч.	50 9 „	4	„	44	„	14	„	35	„	49	„	11	„	50 9 „	11	„	47	„	14	„	28	„	45	„	11	„	50 9 „	18	„	28	„	14	„	21	„	58	„	11	„	50				умма м. 15 с. . 161/г. . 16	, . 13	.
	Среднее	11	ч.	50	м. 15 с.
Следовательно, по часам истинный полдень наступил в 11 ч. 50 м. 15 с. Так как уравнение времени 1 октября 1926 г. равно—10 м. 8. с., то по средним часам истинный полдень должен быть в 12 час. — 10 м. 8 с. =11 ч. 49 м. 52 с., т. е. часы впереди на 23 секунды.
При поверке часов по небесным светилам далеко не Всегда переводят стрелки на циферблате часов. Если поправка невелика, то замечают разницу и называют ее „поправкой часов“.
Поправка часов показывает, сколько надо придать (со знаком -\*или —) к показаниям часов, чтобы получить верное время. В нашем примере поправка часов: минус 23 секунды (— 23 секунды).
§ 50.	Измерение диаметра земного шара. В §36 указывалось, что первое определение размеров Земли было сделано еще Эратосфеном. С течением времени такие определения были повторяемы с большей точностью и выросли в целую отрасль астрономической науки—геодезию, науку, изучающую размеры и форму Земли, а кроме того, постоянно применяемую и для построения географических карт.
В способе, которым Эратосфен определил размеры земного шара, применяется формула высот (см. § 22). Пусть из двух точек на Земле, находящихся на одном меридиане, с широтами лр и <рх одновременно наблюдают одно и то же светило в момент его кульминации; склонение светила — Для широты ср высота светила А, для широты cpt высота светила Ах;
А =90° —<р
Aj=90° — <Pi + &.
Если мы вычтем второе равенство из первого, то получим: h—*! = <?! — <₽;
это значит, что разность высот Солнца равна разности широт.
Следовательно, по наблюдениям одного и того же светила мы можем выразить в градусах дугу по меридиану между местами наблюдения. Если эту дугу измерить в линейных мерах, то можно по ее длине вычислить всю окружность, а затем и радиус ее, т. е. радиус земного шара.
Вычисление можно производить по известной формуле, дающей длину дуги I окружности радиуса
где а — угол, стягиваемый дугой U 58
В нашем случае а = гр, — <р = Л— Лр и нашу формулу мы можем переписать так:
/==21Г₽^А;
А
Рис. 53.
того, узнал высоту
и А1 (оис. 53). Изме-
решая это уравнение относительно 7?, получаем;
г» - 180/
1с(Л —/h)*
Так именно и поступил в древности (III в. до н. э.) Эратосфен. Он определил расстояние между двумя городами в Африке по времени перехода каравана из одного места в другое, а кроме Солнца в этих городах и отсюда впервые вычислил размер земного шара.
§ 51.	Триангуляция. Чем длиннее дуга, измеренная по поверхности Земли, тем точнее определение радиуса Земли. Однако измерение длинных дуг на поверхности Земли представляет трудности вследствие разнообразия земной поверхности. Поэтому для измерения длины дуги в настоящее время применяют способ триангуляции, изобретенный голландцем Снеллиусом в начале XVII в. Триангуляция (от латинского слова „триангулум* — треугольник) состоит в построении на земной поверхности ряда треугольников и в вычислении их сторон по одной стороне и углам (которые легче измерить, чем стороны).
Пусть надо измерить расстояние между точками А
ряется в линейных мерах сначала длина отрезка АВ, один конец которого находится в точке А, другой же может быть расположен где угодно. Этот отрезок АВ получил название базиса (основания) измерения.
После этого выбирается несколько точек С, D, Е и F, расположенных около линии АА'.
С помощью угломерных инструментов измеряются углы в каждом из треугольников, которые получаются, если соединить прямыми линиями точки А, В, С, D, Ей F.
Зная в треугольнике АВС сторону АВ и углы СВА и САВ, определяют стороны АС и ВС. Так как в треугольнике BCD углы тоже измерены, а сторона ВС определена, то вычисляют стороны BD и DC и т. д. Таким образом, все отрезки АВ, ВС, АС и т. д. известны, а также известны углы между ними. По этим данным можно в любом масштабе построить всю сеть треугольников и, наложив масштаб, измерить длину. При расчетах построение заменяется вычислением с помощью тригонометрических формул. При этих вычислениях учитывают шарообразность Земли.
Так как направление базиса можно выбрать любое, то обычно его располагают в наиболее удобной местности, и измерение его длины производит с особой тщательностью,
Одной из наиболее крупных работ по измерению Земли было измерение парижского меридиана, выполненное французскими академиками с 1792 по 1798 г, с целью установления единицы длины — метра. Измерение велось методом триангуляции и захватило дугу от Дюнкерка (наиболее северной точки Франции на берегу Ламанша) через Париж, Перпиньян (нц берегу Средиземного моря) до Барселоны (в Испании).
Рисунок 54 представляет часть этого большого измерения, причем толстая линия около Мелэна изображает непосредственно измеренный в туазах1 базис.
§ 52.	Форма Земля. При вычислении результата триангуляционных измерений получается длина одного градуса по меридиану, и если триангуляционные работы ведутся в разных широтах, то возможно сопоставить между собой эти длины* При сопоставлении оказывается, что измерения, произведенные близ полюса» дают для одного градуса дуги меридиана ббльшие значения, чем измерения близ экватора. Если бы Земля была совершенно шарообразна, то таких результатов не должно было бы получаться: во всех широтах длина одного Градуса должна была бы быть неизменной.
Следовательно, сечение Земли, проходящее через ось ее вращения, дает не окружность, а какую-то иную кривую линию. Кривая линия характеризуется радиусом кривизны.
Радиусом кривизны в какой-либо точке кривой линии мы будем называть предел радиуса окружности, проходящей через три точки дуги кривой при слияинии их в одну.
Очевидно, что чем больше кривизна дуги, тем короче радиус соот-
Рис. 54. Французская триангуляция (1792—1798). ветствующей окружности,
и наоборот.
Так как из измерения Земли длина одного градуса меридиана получается большей в близполюсных областях, то, следовательно, на экваторе кривизна Земли наибольшая, а на полюсе кривизна Земли наименьшая.
Таким образом, в сечении по оси Земля имеет вид замкнутой кривой с ббльшей кривизной в экваториальной области (рис. 55). Наиболее подходящей замкнутой кривой линией, дающей такое же соотношение кривизны, является эллипс. Земля, оказывается, не шарообразна, а имеет форму тела, получающегося от вращения эллипса вокруг малой оси. Такое тело называется эллипсоидом вращения. Эллипсоид вращения похож на шар, как бы сдавленный, сжатый по концам одного и того же диаметра; поэтому принято говорить, что Земля сжата у полюсов.
^Туаз—-старая французская мера длины, которая равна 1,949 м<
66
Размеры всякого эллипсоида определяются размерами большой и ма* лой полуосей того эллипса, от вращения которого получен эллипсоид. Для характеристики сжатая эллипсоида пользуются отношением раз* ности большой и малой его полуосей к большой полуоси.
Обозначая сждтие буквой а, а длину большой и малой полуосей эллипса а и Ь, получаем:
а—b
Для земного эллипсоида а=6378,388 км-,
1
§ 53.	Сжатие Земли и его причины. Сжатие Земли объясняется вращением ее вокруг оси: центробежная сила вращения, отбрасывая экваториальные части Земли, способствовала образованию эллипсоидальной
формы ее. Подобное же явление сжатия наблюдается и у других планет;
особенно оно заметно у Юпитера и Сатурна.
Чтобы получить наглядное представление о сжатии вследствие вращения, установите на центробежной машине гибкий пружинный обруч и Приведите обруч во вращение: на ваших глазах обруч будет сжиматься тем больше, чем больше будет скорость вращения.
Вопрос об истинной форме Земли был предметом большого научного спора в начале XVIII в. Исаак Ньютон теоретически вывел, что Земля должна иметь форму сплюснутого по оси вращения эллипсоида. ЖакКассини считал, наоборот, что Земля должна быть вытя-
нута по оси вращения, причем в своих взглядах он основывался на измерениях, сделанных в 1718 г. французскими учеными. Так как сами измерения, в смысле своей точности, возбуждали сомнение, решено было организовать новые. Эти измерения были выполнены двумя экспедициями Французской академии наук. Одна экспедиция измеряла дугу меридиана около полярного круга (в Лапландии), другая около экватора (в Перу).
Обе экспедиции работали в конце 30-х годов XVIII в., и к середине этого же столетия, когда были закончены вычисления и сопоставлены результаты, спор был окончательно решен в сторону подтверждения теоретических расчетов Ньютона. Последующие измерения, производившиеся более точными методами,
подтвердили то же самое.
Существование сжатия Земли еще раз дает подтверждение учению о вращении Земли.
Современные методы исследования Земли дают возможность еще точнее определить форму Земли и ее отклонения от эллипсоида.
§ 54.	Построение Географических карт. Земной шар еще не вееь исследован, на географических картах есть еще „белые пятна", обозначающие мало или совершенно не исследованные места. Наш Союз в наследие от царской России получил особенно много таких „белых мест" Между тем для нужд социалистического строительства нам нужно использовать не только известные нам области, но и неизвестные, а для этого прежде всего следует составить для них географические карты, чтобы промышленноисследовательские экспедиции могли уверенно совершать свои разведки.
Для этой цели необходимо определить из наблюдений географические координаты этих пунктов на Земле. Определение географических Координат также необходимо в мореплавании, авиации, деле обороны страны.
Астрономия дает методы таких определений и помогает им передачей точного времени.
Широта места определяется помощью наблюдений высот звезд в кульминации универсальным инструментом. Для этого служит формула: h =90°—<р —J—S, преобразованная к виду: ср =90°+ 8 — h. Определяется высота звезды, склонение которой точно известно, и отсюда вычисляется широта. Точность определения широты зависит от точности инструмента и от точности, с которой известно склонение звезды. В астрономических обсерваториях меридианными кругами специально определяют склонение ряда ярких звезд, удобных для наблюдений, универсальным инструментом. Таким образом, далекая, на первый взгляд, от практики теория меридианных наблюдений на самом деле имеет громадное значение для определения широты.
Долгота места определяется путем сравнения местного времени с временем какой-нибудь обсерватории.
Наблюдатель каким-нибудь из способов (для этого существует несколько осдбо разработанных приемов) определяет момент кульминации светила с известным прямым восхождением.
Момент кульминации определяется по имеющимся у наблюдателя часам — хронометру. Эти часы путем приема сигналов времени сравниваются с часами какой-нибудь обсерватории.
Наблюдатель переводит прямое восхождение звезды (т. е. звездное время) в местное время, находит поправку своих часов, а затем вычисляет долготу путем вычитания времени передачи сигнала из показаний своих часов.
Пример. Наблюдатель, пронаблюдав кульминацию звезды и перечислив звездное время в местное, получил 11 ч. 2 м. 5 с., а его часы показывали 11ч. 15 м. 40 с. Значит, поправка его часов—13 м. 35 с.
При приеме сигналов времени московский сигнал (подаваемый в б часов вечера времени III пояса) был слышен в 9 ч. 22 м. 0 с. вечера.
Находим местное время момента приема сигнала:
9 ч. 22 м. 0 с. —13 м. 35 с. = 9 ч. 8 м. 25 с.
Отсюда разница долгот места наблюдения и Москвы равна:
9 ч. 8 м. 25 с. — 6 ч. 0 м. 0 с. == 3 ч. 8 м. 25 с.
В этот же вечер наблюдатель определил h (высоту) звезды 8 Змееносца; Склонение 8 Змееносца— 3°30',9. Высота (из наблюдений) оказалась 47°23',7. Следовательно, широта места наблюдения:
т = 90° — 47°23',7 + (— 3°30',9) = 90° — 47°23',7 — 3°30',9 = 39°5',4.
Подобным же способом мореплаватели определяют свое положение в море, а авиаторы — над поверхностью Земли.
В морской и авиационной практике вместо универсального инструмента применяют специально изготовляемые для этой цели секстаны.
В СССР для' целей уточнения географической карты такого рода работы планируются Главным управлением государственной съемки и картографии, а на заводах точной механики изготовляются необходимые для этой цели инструменты.
Съемки для уточнения карты СССР делаются при помощи метода триангуляции, В разных местах СССР можно видеть «геодезические 62
сигналы*, сделанные из бревен пирамиды; эти пирамиды ставятся в местах триангуляций, и географические координаты их определяются из астрономических наблюдений.
В настоящее время советскими геодезистами проведены новые триангуляционные работы в несравненно бблыпем количестве* и лучшего качества, чем это было в царской России. Эти работы уточняют карту СССР и дают некоторые новые выводы для теории о форме Земли. Кроме того, советскими геодезистами поднят ряд вопросов о международной геодезической работе и нашими же геодезистами начаты работы по соединению советской триангуляции с американской.
Работы советских геодезистов и астрономов имеют большое значение для задачи освоения Арктики, поставленной и успешно выполняемой советским правительством. Перелеты через Северный полюс героями-летчиками и дрейф героев-папанинцев совершались успешно отчасти и потому, что астрономическая и геодезическая части этих экспедиций были тщательно разработаны учеными, вооружившими славных исследователей и заранее подготовленными таблицами и соответствующими приборами. С другой стороны, сделанные наблюдения дают новый богатый материал для науки.
Точные определения долгот и широт важны и в другом отношении — они могут послужить материалом для исследования постоянства земной поверхности. Изменения в широте или долготе могут показать, что данное место поверхности Земли сдвигается.
В настоящее время на Международном астрономическом конгрессе запроектирована большая работа по сравнению долгот обсерваторий путем передачи времени по радио. Эта работа может выяснить, действительно ли происходит медленное передвижение материков, как это предполагает теория Вегенера.
Задачи и вопросы.
1.	Выберите ровное место на земле, установите на нем два шеста и тщательно измерьте расстояние между ними. Простым угломерным прибором 1 измерьте углы между отмеченным отрезком и поставленным на некотором расстоянии третьим шестом. По формулам тригонометрии вычислите две другие стороны треугольника.
2.	Для вычисления размеров земного шара Эратосфен использовал следующие данные.
В день летнего солнцестояния в Сиене (в верхнем Египте) Солнце стойт в зените (высота 90°), в тот же день в Александрии высота Солнца 82°48'. Оба наблюдения дают высоту Солнца в полдень. Расстояние между Сиеной и Александрией 5000 стадий.
Принимая стадию равной 185 м, вычислите радиус земного шара и подсчитайте в процентах ошибку первого определения размеров Земли.
3.	При триангуляциях, произведенных французскими академиками для вывода длины метра, получены следующие данные:
Место
Дюнкерк
Пантеон (Париж)
Эво
Каркассона
Наблюденная широта
51° 2' 8",50 48° 50' 49",37 46° 10' 42",54 430 12' 54",30
Расстояние в туазах
124 944,8
152 293,1
168 846,7
1 Модель угломерного прибора можно сделать из фанеры и металлических частей „Конструктора* по тому же принципу, по которому устроен универсальный инструмент. Он может состоять из двух взаимно перпендикулярных кругов с градусными делениями.
63
По этим данным вычислите в туазах среднюю длину одного градуса.
4.	В результате Лапландской и Перуанской градусных экспедиций в 1736 г. Получено для длины одного градуса:
в Перу	362000 футов
• Лапландии	367000 9
Вычислите радиус кривизны Земли для широты Перу и Лапландии.
5.	Сколько километров надо проехать по направлению меридиана от вашего города, чтобы переместиться на 1° южнее?
6.	Размеры земного эллипсоида по данным Кларка (1880 г.):
а =±6378,249 км>
по данным Хайфорда (1909 г.):
а = 6378,388 км, « = ян^я-.
Какова разница полярных полуосей земного эллипсоида по этим определениям?
7.	Экваториальный диаметр планеты Юпитер 140 000 км9 сжатие */16. Чему равен полярный диаметр Юпитера?
8.	Полдень на Чукотском полуострове наступает на 10 ч. 54 м. раньше, чем. в самом западном городе СССР. Сколько градусов по долготе занимает СССР?
9	В каком месте земного шара экватор проходит через зенит места?
10» Работа героической экспедиции папанинцев продолжалась с 21 мая1937 г. до 19 февраля 1938 г. Самолеты перелетели через Северный полюс и место, где началась работа папанинцев, находилось на широте 89°41', а самое южное на широТе 70°54'. Вычислите зенитное расстояние Солнца в верхней и нижней кульминациях при начале дрейфа и в день окончания экспедиции. (Справка: склонение Солнца 21 мая 1937 г. + 20°3\ склонение Солнца 19 февраля 1938 г. —11°35г.) На основе этих расчетов сделайте вывод об условиях освещения в начале и в конце дрейфа.
11.	На каких широтах северного и южного полушарий Земли 20 марта, 20 июня, 20 сентября и 20 декабря высота Солнца в полдень бывает одновременно равна 60°?
12.	Экскурсия школьников выехала из Москвы, по дороге велись наблюдения высоты Полярной звезды и сравнение своих часов, поставленных по московским, с городскими часами тех мест, где они проезжали. Здесь приведены данные наблюдений.
Время наблюдения	Способ передвижения	Высота Поляр* ной звезды	Сравнение часов
Конец 1-го дня пути	Жел. дор.	52*	Разницы йет
.2	,	.	» »	44Ч«*	» •
.4	,	.	Пароход	441/8°	•	0
.6	,	,	Жел. дор.	48е	• •
.7	.	.	Пароход	52®	• •
.9	.	.	Жел. дор.	5U/S«	Часы отстали на 1 час от городских
Определите по этим данным направление пути экскурсии,
13.	В Москве полдень, а в Казани в то же время часы показывают 12 ч. 46 м.
Какова долгота Казани от Гринича, если известно, что долгота Москвы от Гринича 2 ч. 30 м.?
64
14.	Выразить во времени долготу места, которое по карте обозначено имеющим долготу от Гринича 36°30‘.
15.	В прежнее время считали нулевым меридианом меридиан острова Ферро, и на некоторых картах долготы отмечаются от Ферро. Ферро лежит к западу от Гринича на 17°40'. Какова долгота места от Гринича, которое на карте лежит от Ферро на 50° к востоку? Выразить эту долготу во времени.
16.	Который час во Владивостоке, когда в Москве 6 часов утра?
17.	Экспедиция О. Ю. Шмидта высадилась на лед с затонувшего .Челюскина* 13 февраля 1934 г.
15 февраля Кренкель подал радиограмму: .Второй день челюскинцы живут на льду. Ночью прояснело. По звездам определили свое местонахождение: 67°17" северной широты, 172°51' западной долготы...*
Сколько ^должны были показывать часы в лагере (по местному времени), когда Кренкель принимал московские сигналы времени, подаваемые в 12 часов дня (по времени III пояса)? Каково было зенитное расстояние полюса мира?
ГЛАВА III.
Развитие представлений о солнечной системе.
Среди бесчисленного множества небесных светил лишь небольшая часть их находится сравнительно близко к Земле, образуя так называемую солнечную систему. В состав членов солнечной системы входят Солнце, Луна, планеты с их спутниками и кометы. Благодаря сравнительной близости этих светил к Земле человек изучил их видимые и истинные движения, а также расстояния и истинные размеры гораздо раньше, чем ему удалось разгадать строение и движе*
Ш\
§ 55. Параллактическое смещение. Зная точные IhwSk \ размеры и форму Земли, можно по наблюдениям по-	\
ложений светил на звездном небе вычислить расстояния Ж ✓' С до них и их размеры в линейных мерах. В основе таких	IvjX
определений лежит измерение параллактического сме-щения светил.
Параллактическим смещением пользуются при зем- \\\\ 'до лемерных работах, при измерении расстояния до недоступного предмета. Пусть, например, надо определить Рис. 56. расстояние до предмета Д, находящегося по другую сторону реки (рис. 56). В этом случае поступают так. Выбирают две точки В и С, из которых виден предмет А. Длину линии ВС, называемой базисом, измеряют при помощи рулетки. В точках В и С по очереди устанавливают какой-нибудь угломерный инструмент, при помощи которого измеряют углы между направлениями, по которым из этих точек видны точка А и второй конец базиса. Таким образом, в получившемся треугольнике ВАС оказываются измеренными сторона ВС и два прилегающих к ней угла. Отсюда по правилам тригонометрии можно вычислить расстояние АВ или расстояние АС.
Эти расстояния определяются тем точнее, чем больше угол при точке А, т. е. чем больше сумма углов. В и С отличается от 180°. Другими словами, базис ВС н£до брать тем больше, чем дальше находится предмет А.
Передвигаясь вдоль базиса от точки В к точке С, мы заметим, что направления на точку А меняются в зависимости от того, откуда мы 5 Астрономия
на нее смотрим; точка А как бы смещается. Это смещение, равное углу ACD, и называется параллактическим смещением.
Нетрудно сообразить, что вследствие параллельности линий ВА и CD угол ACD равен углу ВАС, т. е. параллактическое смещение точки А равно углу, под которым из этой точки виден базис ВС.
Из сказанного выше понятно, что параллактическое смещение предмета с его удалением от наблюдателя уменьшается и превращается в нуль для бесконечно удаленных предметов.
В этом можно убедиться при помощи следующего опыта. Проведите на черной доске мелом ряд вертикальных линий через 5 см. Поставьте перед доской на расстоянии 1 м шарик на стойке (рис. 57), расположив его так, чтрбы, глядя на него с расстояния в 3—4 м, видеть его посреди начерченных на доске линий.
Не двигая головой, закрывайте попеременно то правый, то левый глаз,— вы заметите, что шарик будет виден то в одном, то в другом месте ряда линий. Чтобы проследить, как изменяется смещение при приближении наблюда-
Рис. 57.	теля, подойдите вдвое ближе к шарику
и повторите этот опыт, — вы заметите, что смещение стало больше, и можете оценить на-глаз, во сколько раз оно увеличилось.
Если вы все время будете смотреть только одним глазом и, не приближаясь и не удаляясь от шарика, станете сами передвигаться вправо и влево, то заметите, что бблыпему вашему перемещению соответствует и бблыпее параллактическое смещение. Параллактическое смещение, таким образом, оказывается тем больше, чем ближе шарик и чем больше смещение наблюдателя.
§ 56. Горизонтальный экваториальный параллакс. Солнце, Луна и планеты должны обнаруживать параллактическое смещение, если их наблюдать с разных мест земного шара. Положения этих светил мы относим к небесной сфере, центр которой перемещается вместе с наблюдателем,—точки небесной сферы не обнаруживают параллактического смещения. Предположим, например (рис. 58), что Луна L одновременно наблюдается с двух точек
земной поверхности Ли В. Тогда наблю-	Рис. 58.
датель, находящийся в Л, увидит Луну
на небесной сфере в точке £2 (на зенитном расстоянии Z2), а наблюдатель из В увидит Луну в точке Lx (на зенитном расстоянии ZJ. Угол ALB> соответствующий дуге £х£2, на которую Луна как бы переместилась по небесной сфере, и называется, как мы знаем, параллактическим смещением. Зная еще расстояние между пунктами наблюдения, т. е. длину хорды АВУ можно в треугольнике ALB вычислить все его углы и стороны, а зная их, можно вычислить и расстояние между Луной и Землей. То же самое расстояние (конечно, с меньшей точностью) можно
66
было бы определить геометрически, построив треугольник ALB по известной стороне АВ и по двум прилегающим к ней углам. Вся трудность определения расстояния до небесных светил заключается в практическом измерении углов Zx и Z2, необходимых для определения параллактического угла (т. е. угла ALB} с требуемой степенью точности. Вычисление же расстояний по известному параллаксу производится настолько просто и быстро, что эта задача считается уже решенной, если параллактическое смещение, соответствующее определенному базису, измерено.
Можно поэтому, вместо того чтобы сравнивать расстояния светил от Земли, сравнивать их параллактические смещения, относящиеся, конечно, к одному истому же базису, взятому на поверхности Земли.
Наиболее удобным базисом для определения параллактических смещений членов солнечной системы является экваториальный радиус Земли, длина которого нам известна. На рисунке 59 точка С—центр Земли, S — какая-нибудь планета, Солнце или Луна. Когда в точке А земного экватора светило видно как раз на	I ~
горизонте, наблюдатель из точки В	1
(также лежащей на экваторе) видит это светило прямо в зените по на-правлению BS, и в этом же самом	Рис. 59.
направлении увидел бы светило наблюдатель из С. Поэтому угол ASB равен параллактическому смещению, соответствующему базису С4, который есть экваториальный радиус Земли. Вследствие этого параллактическое смещение, измеряемое углом AS С» называется горизонтальным экваториальным параллаксом, и, когда говорят Или пишут о параллаксе каких-либо членов солнечной системы, обычно имеют в виду именно этот горизонтальный экваториальный параллакс.
Очевидно, что если бы наблюдатель находился на светиле S, то он видел бы экваториальный радиус Земли под тем же самым углом ASC. Поэтому рассматриваемый нами параллакс можно определить двояко:
1. Г	оризонтальный экваториальный параллакс есть кажущееся сме* щение светила по отношению к двум экваториальным наблюдателям, из которых один видит светило в горизонте» а другой — в зените.
2. Г	оризонтальный экваториальный параллакс светила есть угол, под которым с этого светила виден радиус Земли (проведенный в ту точку экватора, для которой данное светило находится на горизонте).
Зная размеры Земли, мы можем, измерив параллаксы Солнца, Луны и планет, вычислить расстояния до них.
§ 57.	Расстояние и параллакс. Расстояние от светила S до центра Земли С вычисляется так (см. рис. 59). В треугольнике SAC угол А прямой, CA — R (/?— экваториальный радиус Земли в километрах). Тогда
sin ASC’
Практически наблюдать так, как это показано на рисунке 59, неудобно, и поэтому измерения производятся из двух точек Земли, расположенных более удобно для организации наблюдений (рис. 58). Затем при помощи 5*	67
специальных формул вычисляется угол AS С, а по нему по приведенной выше формуле и расстояния SC.
§ 58.	Определение линейных диаметров светил. Непосредственные наблюдения дают нам только угловые диаметры светил, например, диаметр Солнца 32', Юпитера — около 50" (в противостоянии) и т. д. Действительные линейные диаметры светил можно определить, если, кроме их угловых диаметров, известны еще и расстояния этих светил от Земли. Пусть на рисунке 60 точка О есть центр Земли, Ох — центр светила, имеющего линейный радиус R и находящегося от Земли на расстоянии OOV Угол ВОЬХ представляет видимый угловой радиус этой планеты. В таком случае из чертежа прямо видно, что
R — OO-l sin р.
§ 59.	Видимое движение Луны среди звезд. Наблюдения движения тел солнечной системы легче всего произвести, начав с наблюдений над движением Луны.
Наблюдая внимательно за положением Луны на небе в различные дни, легко убедиться, что она не только восходит и заходит, подобно Солнцу и звездам, но еще и перемещается сре-в ди звезд в направлении с запада на во-(	А——г-*-***-—сток (см* § НРИ своем Движении от-
I q~ Т -------------гД } носительно звезд Луна меняет фазы, т. е.
k J	изменяет свой вид. Находясь на небес-
ной сфере вблизи Солнца, она имеет вид узкого серпа, а находясь в про-”ис* 6 ’	тивоположной от него стороне, выгля-
дит как полный круг (полнолуние).
За каждые сутки Луна смещается влево (к востоку) приблизительно на 13°, и вследствие этого каждые сутки ее верхняя кульминация запаздывает приблизительно на 50 минут. Луна перемещается среди звезд так быстро, что за двое с четвертью суток переходит из одного зодиакального созвездия в другое.
Наблюдая за Луной в течение одного вечера, можно без труда подметить ее движение, так как уже за час Луна смещается к востоку на 13°: 24 = 32', т. е. приблизительно на величину своего видимого диаметра. Такие наблюдения удобнее производить, когда Луна еще не слишком ярка, так что вблизи нее видны слабые звездочки. При этом случается, что Луна загораживает от нас по временам те звездочки, которые лежат на ее пути2. Иногда можно наблюдать, как Луна загораживает от нас Солнце и планеты. Из всего этого можно вывести заключение, что Луна является наиболее близким к нам и к тому же непрозрачным небесным телом.
При этом легко запомнить, что она движется среди тех же зодиакальных созвездий, что и Солнце. Если точно проследить ее путь среди звезд и нанести его на звездную карту, то обнаружится, что Луна возвращается к тем же звездам, около которых она была 27,32 суток назад, описав полный круг по звездному небу. Видимый путь Луны
1 Моменты этих так называемых покрытий звезд Луной ежегодно даются в жАстрономическом календаре*.
68
не совпадает с эклиптикой, а дважды с ней пересекается, причем Луна никогда не отходит от эклиптйки больше, чем на б1//5. Период в 27,32 суток называется звездным (сидерическим) месяцем и равняется продолжительности истинного обращения Луны вокруг Земли.
§ 60.	Видимые движения планет. Среди ярких звезд, видимых на небе, люди уже с давних времен стали выделять пять „блуждающих светил" (по-гречески планет). Эти планеты ведут себя не так, как остальные. Они постоянно меняют свои места среди остальных так называемых „неподвижных" звезд.
В прежнее время истинное строение вселенной не было известно. До изобретения телескопа о физической природе планет не могли даже догадываться, и потому планеты отличали от звезд только по их видимым движениям. В то время было известно только пять наиболее ярких планет, видимых невооруженным глазом: Меркурий, Венера, М-арс, Юпитер и Сатурн. После изобретения телескопа в течение трех столетий были открыты еще другие планеты: Уран, Нептун, Плутон и более тысячи маленьких планеток — астероидов.
Отличить пять главных планет от ярких звезд на небе можно по их движениям и по тому признаку, что планеты мерцают меньше, чем звезды. После Венеры Юпитер является самой яркой из планет и светит спокойным желтоватым светом. Он ярче самых блестящих из „неподвижных" звезд. Найти на небе Сатурн немного труднее, так как он менее ярок. Марса легко распознать по его красному цвету и быстрому перемещению среди звезд. Его движение можно заметить уже после нескольких дней наблюдения.
Названия планет пришли к нам из глубокой древности. Они связаны с римской мифологией, например, имя Марса у римлян носил бог войны, и планета была названа этим именем благодаря своему кровавому цвету.
Присмотревшись в течение нескольких месяцев к движению планет (лучше всего Марса), можно заметить, что их движение значительно сложнее, чем движение Луны. В общем, планеты Марс, Юпитер и Сатурн значительно медленнее, чем Луна, движутся среди звезд с запада на восток (как говорят, прямым движением). По временам, однако, это движение прекращается (наступает так называемое „стояние* планеты), затем снова возобновляется, но уже в противоположном направлении, происходит попятное движение планеты среди звезд (с востока на запад), продолжающееся до новой остановки и возобновления прямого движения. Так как при этих движениях склонение планеты несколько меняется, то в конце-концов получается, что планета выписывает на звездном небе как бы петлю. Рисунки 61 и 62 изображают части карты звездного Неба, на которых вычерчены видимые пути Марса и Юпитера среди звезд в 1939 г. Из рисунков видно, что путь планеты не совпадает с эклиптикой. Однако все главные планеты передвигаются в области двенадцати зодиакальных созвездий. Размеры петель в градусах, описываемые разными планетами, различны; например, у Марса (рис. 61) эта петля составляет 11°, в то время как у Юпитера она составляет всего 8°.
Различие в быстроте движения планет и в величине их петель уже издавна наводило на мысль, что в этом в бблыпей или меньшей степени сказывается действие перспективы. Планета с более быстрым видимым движением и большей петлей (например Марс) должна быть к нам ближе, 69
чем более медленная планета, описывающая меньшие петли (например Юпитер). Совершенно так же нам кажется, когда мы наблюдаем толпу людей, что более близкие к нам люди перемещаются быстрее, а более далекие медленнее.
Перемещаясь по небу, планеты Марс, Юпитер и Сатурн временами оказываются вблизи Солнца, которое, как уже говорилось, тоже перемещается по небу. Теряясь в лучах Солнца, они не могут быть наблю-
даемы. Моменты, когда планета и Солнце видны с Земли по одному направлению, называются соединениями планеты с Солнцем. Иногда планеты наблюдаются на небе как раз в стороне, противоположной Солнцу (и проходят верхнюю кульминацию в полночь). Это положение планеты называется противостоянием, или оппозицией.
§ 61.	Видимые движения Меркурия и Венеры. Эти планеты движутся в общем так же, как и остальные, т. е. описывают петли, причем
их движения наиболее быстры. Однако характерной особенностью Меркурия и Венеры является их постоянная видимая близость к Солнцу. Они никогда не удаляются от него на большое угловое расстояние и. потому могут наблюдаться только на заре, или в начале вечера, или незадолго до восхода Солнца по утрам* Венера отходит от Солнца не дальше, чем на 47°, а Меркурий не дальше, чем на 28°. Наибольшие удаления этих планет от Солнца называются элонгациями. Во время 70
таи называемой восточной элонгации Меркурий и Венера могут быть видимы лучше всего вечером после захода Солнца. Постепенно они идут попятным движением навстречу Солнцу и скрываются в его лучах. Через некоторое время они больше всего удаляются от Солнца к западу — происходит западная элонгация. В это время планеты восходят раньше Солнца и могут наблюдаться перед утренней зарей. Меркурий довольно ярок, но всегда настолько близок к Солнцу, что его увидеть (особенно в северных широтах) очень трудно. Венера отходит от Солнца дальше, чем Меркурий, кроме того, она является самой яркой из всех планет, так что наблюдать ее можно очень часто. Иногда её можно видеть даже днем, при полном блеске Солнца, если только знать приблизительно ее положение на небе в это время. Некоторые несведущие люди называют Венеру то утренней, то вечерней звездой (смотря по тому, когда она видна) и думают, что это два различных светила.
§ 62.	Взгляды на устройство Странные движения планет пытались пие времена. Это было нужно для того, чтобы можно было предсказывать наперед, где в любой момент времени будет находиться данная планета. До Коперника Землю считали неподвижной и небо представляли себе в виде хрустального шара (сферы), окружающего эту неподвижную Землю. В средние века думали даже, что Земля плоская и что небо прикрывает ее наподобие стеклянного колпака. По учению средневековых монахов, звезды являлись светильниками, которые по вечерам зз
представление о вселенной вытекало неизбежно из того, что в то время наука всецело находилась во власти духовенства, под влиянием религиозных суеверий.
Во II в. знаменитый греческий ученый Птолемей, являясь выразителем взглядов древнегреческой науки на мироздание, объяснял движения планет следующим образом. Он считал, что Солнце, Луна и все планеты движутся вокруг неподвижной Земли. Для объяснения петлеобразного движения планет он предположил, что каждая из планет движется по маленькому кругу, называемому эпициклом^ в то время как центр этого эпицикла равномерно движется по кругу (названному деферентом) около Земли. Плоскости деферента и эпицикла Птолемей предположил немного не совпадающими. Эта „птолемеева система мира* изображена на рисунке 63 (направления движений планет и центров эпициклов обозначены на этом рисунке стрелками). Если бы, например, Марс находился в точке А эпицикла, с Земли должно было бы казаться, что он имеет попятное движение. Пройдя по эпициклу до точки В, Марс стал бы двигаться прямым движением. Так как в то же время центр эпицикла двигался бы по деференту прямым движением, получилось бы, что Марс описал на небе петлю. Обратите внимание на значки,
71
солнечной системы в древности, как-нибудь разгадать еще в древ-
Рис. 63.
ангелами.
стоящие вместо названий планет (эти условные обозначения планет употребляются и в настоящее время) к
Развитие астрономических наблюдений показало, однако, неудовлет? ворительность птолемеевой системы мира. Последователям Птолемея для согласования теории с наблюдениями пришлось допустить, что по эпициклам движутся не самые планеты, а центры воображаемых кругов еще меньшего размера — вторичных эпициклов, по которым уже движутся сами планеты. Таким образом, теорию Птолемея приходилось усложнять все больше и больше, нагромождая друг на друга новые эпициклы. Вследствие этого вычислять наперед движения планет сделалось не толькб неудобно, но и вообще самое объяснение планетных движений, исходящее из теории Птолемея, стало маловероятным.
§ 63	Теория Коперника. Великий ученый Николай Коперник, родившийся в 1473 г. в польском городке Торне, пришел к заключению, что все видимые движения небесных светил можно объяснить гораздо, проще и естественнее, если допустить что Земля вращается вокруг своей оси и вместе с тем движется (обращается) вокруг Солнца.
Подобные догадки высказывались и раньше, но они не подтверждались научными доказательствами. Эпоха XV—XVI вв., вызвавшая к жизни начатки революционной человеческой мысли, не могла не отразиться и в науке, и Коперник явился одним из мощных выразителей уже назревавших революционных научных идей. Он собрал все доступные в его время доказательства того, что Земля действительно вращается вокруг оси и вокруг Солнца. Он показал также, что другие планеты подобно Земле обращаются вокруг Солнца по определенным путям (орбитам), находясь от него на разных расстояниях. Меркурий и Венера должны двигаться ближе к Солнцу, чем Земля, и быстрее. Орбиты остальных планет расположены за орбитой Земли, дальше от Солнца, и время их полного обращения по орбитам тем больше, чем дальше они от Солнца. Только Луна, по теории Коперника, действительно обращается вокруг Земли и вместе с ней движется вокруг Солнца.
Согласно объяснению Коперника, восход и заход светил вызываются тем, что Земля вращается вокруг оси. Сложные петлеобразные движения планет вызываются* тем, что мы наблюдаем их движения по орбитам вокруг Солнца с движущейся Земли и вместе с ней или перегоняем их или отстаем от них. Поэтому нам и кажется, что планеты движутся то в одну сторону, то в другую. Коперник не имел в своем распоряжении тех доказательств движения Земли, которыми мы располагаем в настоящее время, но все же его доводы были достаточно убедительны (см. § 70 и 71).
§ 64.	Объяснение видимых движений планет. По теории Коперника, видимые прямые и попятные движения планет объясняются очень просто. Рассмотрим рисунок 64, изображающий часть солнечной систему. Точка., отмеченная буквой 5, обозначает положение Солнца. Первый окружающий ее круг изображает орбиту Земли. Второй круг изображает орбиту какой-нибудь внешней планеты (например Марса), т. е. планеты, расположенной дальше от Солнца, чем Земля. Часть самого внешнего круга
1 На рисунке 63 значки слева направо обозначают последовательно Луну, Меркурий, Венеру, Солнце, Марс, Юпитер и Сатурн.
72
изображает часть поверхности небесной сферы, которую в данном случае мы будем рассматривать как сферу, центр которой совпадает с точкой S, т. е. с Солнцем. Глядя с Земли на Марс, мы видим его в какой-либо точке небесной сферы, среди звезд, расположенных по тому же направлению. Пусть, например, в некоторый момент времени Марс находится в точке Pt своей орбиты, а Земля — в точке 7\ своей орбиты. В таком случае с Земли Марс будет виден на небесной сфере в точке Bv Известно (§ 76), что чем ближе планета находится к Солнцу, тем быстрее она движется. Поэтому, когда через некоторое время Земля перейдет по своей орбите в точку Т2, Марс, двигаясь медленнее, передвинется по своей орбите на меньшее расстояние и придет в точку Р2. В это время он будет виден с Земли в точке В2 небесной сферы. С Земли будет казаться, что за протекший промежуток времени Марс двигался по небесной сфере из точки в точку В2, т. е. двигался прямым двц*
жением. Еще через некоторое время Земля дойдет до точки Т8, а Марс —До точки Р3 и будет виден с Земли по направлению В3. Очевидно, что в течение этого времени с Земли казалось, что Марс, остановившись при своем „прямом движении*, сменил его на „попятное*, двигаясь от точки В2 к точке В8 как бы „назад*. По прошествии еще некоторого времени Земля и Марс займут положения 7\ и Р4. Марс на этот раз передвинулся из В8 в точку В4 прямым движением. Таким образом, Марс на нашем рисунке сменил первоначальное прямое движение на обратное, а затем обратное снова на прямое. Так как плоскость орбиты не совпадает с плоскостью эклиптики, а наклонена к ней под небольшим углом, то в результате получилось, что Марс описал на небесной сфере нечто вроде петли (рис. 64а). Точно так же, как в разобранном примере, объясняются петлеобразные движения и других внешних планет» т. е. тех, орбиты которых расположены от Солнца дальше, чем орбита Земли. К таким внешним планетам принадлежат Марс, Юпитер, Сатурн и открытые после Коперника еще более далекие планеты — Уран, Нептун и Плутон. Подобным же образом объясняется видимое движение внутренних планет — Меркурия и Венеры.
73
Упражнение. Начертите орбиту Земли и Венеры, а также небесную сферу и проследите, каким образом движется Венера по небесной сфере, если ее наблюдать с Земли. Учтите при этом, что радиус орбиты Венеры составляет 0,7 радиуса земной орбиты и что за одно и то же время Венера описывает по своей орбите дугу, в Р/2 раза большую, чем Земля (если эти дуги выражать в градусах).
§ 65.	Планетные конфигурации. Внешние планеты, двигаясь по своим орбитам, могут занимать относительно Земли различные положения, называемые конфигурациями. Некоторые определенные взаимные расположения Земли, Солнца и планет носят специальные названия. На рисунке 65 изображены орбиты внутренней планеты (например Венеры), Земли и внешней планеты (например Марса). Допустим, что Земля находится в точке Е. Тогда Марс может занимать по отношению к ней различные
положения, конечно, в разные моменты времени. Из этих положений наи-
более интересны положения Марса в точках Р2, Р4, Рг и Р3. Положение Р2 называется противостоянием, и оно наиболее благоприятно для на-
блюдения планеты, так как в это время Марс виден на небе в точке, прямо противоположной Солнцу. В это время он бывает в верхней кульминации в полночь и видим в течение всей ночи. Вместе с тем в это время Марс ближе всего подходит к Земле, и его видимый угловой диаметр в телескоп кажется наибольшим. А это значит, что на его поверхности в это время можно увидеть больше всего подробностей. Когда внешняя планета находится в точке Р4 (верхнее соединение), то она расположена относительно Земли прямо за Солнцем, кульминирует
вместе с ним и, следовательно, теряется днем в его лучах, так что совсем не может наблюдаться. Если внешняя планета находится в точках Рг или Р8 (эти положения называются квадратурами), угол между направлениями с Земли на Солнце и на планету составляет 90°.
В этих положениях планета дальше от Земли, чем в противостоянии, и- может наблюдаться только или в первую или только во вторую по-
ловину ночи, в зависимости от того, какая квадратура — восточная или западная (Р8 — западная квадратура).
Внутренняя планета (например Венера) может находиться или прямо перед Солнцем, в нижнем соединении с ним в точке Р2, или в верхнем соединении с Солнцем, прямо за ним (в точке Р4). В первом положении планета ближе всего к Земле, во втором положении — дальше всего, но в обоих случаях планету нельзя наблюдать, так как она теряется в ярких солнечных лучах. Внутренние планеты можно наблюдать только вблизи восточной или западной элонгации — точка Р[ или Р8 — в первом случае рано вечером, во втором — перед восходом Солнца. Угол P^ES определяет наибольшее из возможных видимых удалений (элонгаций) планеты от Солнца. Для Венеры этот угол не превосходит 47°, для Меркурия 28° (см. § 61).
§ 66.	Фазы Меркурия и Венеры. Благодаря особенностям своего положения и движения относительно Земли, а также тому, что они светят 74
исключительно отраженным солнечным светом, Меркурий и Венера меняют фазы, подобно Луне. Другими словами, они бывают или совсем невидимы, или видны в виде серпа, полукруга и, наконец, в виде полного светящегося кружка. Эти изменения фаз внутренних планет понятны из рисунка 66. Когда планета находится между Землей и Солнцем, к нам повернута ее темная, не освещенная Солнцем сторона. Когда планета находится за Солнцем, к Земле обращена освещенная часть ее поверхности. Однако в это время планета близка к Солнцу и, теряясь в его лучах, практически невидима. В промежуточных положениях Меркурий и Венера имеют вид серпа или части круга, и .гмена фаз этих
планет доказывает, что они являются непрозрачными шарами^ не излучающими собственного света, так как только такой шар, будучи освещен со стороны, может иметь вид, подобный изображенным на рисунке 66. Фазы Венеры можно видеть даже в сильный бинокль или в небольшую подзорную трубу. Внешние планеты также имеют небольшие изменения фаз, но в телескоп их легко можно заметить только у Марса.
Обыкновенно Меркурий и Венера в нижнем соединении проходят то выше, То ниже Солнца, но иногда они проходят прямо перед ним и
проектируются на солнечную поверхность в виде маленьких черных кружков. Эти явления называются прохождениями Венеры и Меркурия по диску Солнца. Прохождения Венеры по диску Солнца бывают редко; они были в 1639, 1761, 1769, 1874 и
1882 гг. и будут в 2004 и 2012 гг. С Меркурием это происходит чаще: в 1907, 1914, 1924, 1927, 1937, 1940 (12/XI), 1953, 1960, 1970, 1973, 1986 и 1999 гг.
§ 67.	Сидерические и синодические периоды обращений планет. Продолжительность полного оборота планеты вокруг Солнца называется сидерическим (т. е. звездным) периодом обращения планеты. Промежуток времени» протекающий между двумя одинаковыми конфигурациями планеты, называется синодическим периодом обращения. Что сидерический и синодический периоды обращения не равны, легко понять из того, что, двигаясь вокруг Солнца с различными скоростями, Земля и планета по истечении сидерического периода обращения планеты уже не будут иметь такого же расположения относительно друг друга и относительно Солнца, какое они имели раньше.
Для Меркурия, Венеры и Марса сидерический период меньше синодического, для остальных планет — наоборот.
Из наблюдений известно, что сидерический период (время истинного обращения планет около Солнца) тем больше» чем дальше планета находится от Солнца (см. приложение VIII).
Благодаря последнему обстоятельству в единицу времени радиус-вектор Земли (линия, соединяющая ее с Солнцем) поворачивается на ббль-ший угол, чем радиус-вектор внешней планеты. Рассмотрим, например, движение Юпитера, начав с момента его противостояния. Через сколько дней наступит следующее противостояние, если сидерический период Юпитера (S дней) известен?

и *	360° о	360°
Юпитер проходит по своей орбите за сутки -73-, а Земля -~-о	1
(Т—сидерический период Земли, равный году, т. е. 3651/4 суткам). Земля движется быстрее, и потому за каждые сутки будет опережать 360°	360° w	„
Юпитер на ----------я- • Увеличиваясь ежедневно, эта дуга через Р су-
л	О
ток (через время синодического периода) достигнет 360°, т. е. Юпитер х	360° \ n QCAO
снова будет в противостоянии. Следовательно -у-------^-J.p = 360,
откуда находим:
1 ±_ 1 Р = Г S*
Эта формула называется уравнением синодического движения. Пользуясь ею и зная кроме Т какую-либо другую из входящих в нее величин, можно вычислить третью величину. Для внутренней цдацеты, движущейся быстрее Земли, эта формула будет иметь вид:
1 1 1 Р= S 7’
в чем можно убедиться, пользуясь рассуждением, подобным предыдущему.
§ 68. Астрология. С древних времен существовала ложная наука — астрология, считавшая, что по расположению небесных светил можно предсказать судьбу человека и даже целого народа. Вера во влияние светил на судьбу человека и на его деятельность, вера в возможность предсказать эту судьбу и в согласии с этими предсказаниями предпринять те или другие действия—эта вера возникла почти так же давно, как и сама астрономия. Особым вниманием пользовалась астрология у правящих классов. Цари, князья и различные богачи часто нанимали специальных лиц — астрологов, на обязанности которых лежало составлять гороскопы для их семейств, т. е. таблички, в которых в туманной и противоречивой форме предсказывались события, интересовавшие их хозяев. Для возможности делать .предсказания* была необходима теория, позволявшая вычислять наперед положения планет на небе. Такой теорией являлась теория Птолемея. Но для усовершенствования теории необходимы наблюдения неба.
Таким образом, ложная в своей основе астрология, предъявляя практические требования, способствовала развитию астрономических наблюдений и математической теории движения планет, подготовив, таким образом, почву и для появления теории Коперника и для дальнейшей ее разработки. Теория Коперника сильно подорвала веру в чудесное и вместе с тем веру в астрологию. Последующие научные открытия окончательно доказали нелепость и ложность астрологии.
§ 69. Революционное учение Коперника и борьба церкви с ко-перниканством. Идеи Коперника были новы и необычны. Они не вязались с многовековыми представлениями о строении вселенной и о роли Земли в мироздании. Они противоречили всем установившимся взглядам и понятиям. Мало того, они противоречили тому, что говорилось в библии о „тверди небесной* и о том как „Иисус Навин остановил Солцце*. Представление о человеке как о божьем творении, цели существования вселенной и о Земле как об арене сошествия бога на Землю — все это решительно не позволяло церковникам признать теорию Коперника и позволить ей распространяться.
Это предвидел и сам Коперник; и именно поэтому он долго не решался напечатать свою книгу. Только к концу жизни Коперника друзьям удалось уговорить его опубликовать свое замечательное открытие, плод 76
поручено редактировать книгу,
Рис. 67. Джордано Бруно $548—1600).
многолетней работы. Опасаясь обвинения в безбожии и преследований со стороны церкви, Коперник был принужден посвятить свою книгу римскому папе. Монахом, которому было было написано предисловие, извращавшее мысли Коперника. В предисловии говорилось, что излагаемая Коперником система мира не существует в действительности, а придумана лишь в качестве одного из возможных способов вычислять положения Солнца и планет на небе. Сам Коперник был убежден, однако, в том, что таково действительное строение солнечной системы.
Антирелигиозное* значение книги Коперника (напечатанной к концу его жизни) во всей его полноте было понято католическим духовенством не сразу. Это случилось уже позднее, и тогда ненависть церкви к свободной науке обрушилась уже на последователей Коперника—Джордано Бруно и Галилея.
Учение Коперника неминуемо вы
звало целый поток новых мыслей, свободных от гнета религии. Становилось ясно, что различие между небом и Землей совсем не такое, как учили библия и монахи. Становилось понятным, что за пределами Земли находится огромная или даже бесконечная вселенная, в которой, может быть, существуют другие миры, населенные живыми разумными существами. Такие взгляды вскоре после смерти Коперника стал излагать философ Джордано Бруно.
Бруно, будучи противником церкви и книжного, мертвого учения средневековья, боролся, главным образом, за философскую сторону учения Коперника — единство представления вселенной, отрицая деление ее на Землю и небо. Конечно, его мысли шли в разрез с учением церкви и подрывали ее авторитет, уничтожая вместе с тем невежество народных масс, в котором их старались держать для своей выгоды правящие классы. Поэтому Джордано Бруно был схвачен католической инквизицией и заточен в тюрьму на 8 лет, после чего (в 1600 г.) его сожгли на костре как злостного еретика.
Галилей, знаменитый ученый той же эпохи, сделал много открытий в области физики и механики и борьбу за коперниканскую систему вел, главным образом, путем собирания фактов, доказывающих ее правильность. Он первый применил зрительную трубу для наблюдения небесных тел и сделал с ее помощью ряд открытий, подтверждавших теорию Коперника и широкие обобщения Бруно (фазы Венеры, спутники Юпитера, строе* ние Млечного Пути и т. д.). В своей книге „Разговоры о двух системах мира* он не только заявил себя сторонником взглядов Коперника, но и высмеял господствовавшее в те времена учение о неподвижной Земле. Церковь после этой книги подвергла Галилея суду инквизиции и, пользуясь его старостью и слабостью, заставила его отречься от своей „ереси* и до конца жизни продержала его в ссылке.
77
Книга Коперника была сожжена и внесена в список книг, которые верующие католики не должны были читать. Из этого списка запрещенных книг труд Коперника был изъят только в 1835 г.
Все основные догматы христианской церкви подрывались учением Коперника, и неудивительно, что в дальнейшем, хотя учение Коперника уже было принято наукой, церковь с тупым упорством долго старалась поддерживать старое учение о неподвижности Земли.
Значение работы Коперника было громадно не только для астрономии, но и для всего естествознания. Энгельс так говорит об этом: „Революционным актом, которым естествознание заявило о своей независимости, было издание бессмертного труда, творения, в котором Коперник бросил — хотя и скромно и, так сказать, лишь на ложе смерти — перчатку церковному авторитету в естественных делах*.
§ 70. Аберрация. Во времена Коперника не были известны два из
основных доказательств движения Земли вокруг Солнца: явление годичной аберрации света и годичный параллакс.
В настоящем параграфе мы познакомимся с первым из этих явлений— с годичной аберрацией света, открытой в 1721 г. Брадлеем.
Если бы Земля была неподвижна, то все звезды постоянно были бы видны на одних и тех же местах небесной сферы. В случае движения
Рис. 69.
Земли этого не должно быть, так как сочетание скорости движения Земли со скоростью, распространения света, идущего к нам от звезд, вызовет кажущееся смещение последних. Этого не было бы лишь в том случае, если бы свет распространялся мгновенно; между тем, мы знаем, что он распространяется с конечной скоростью 300 тыс. км(сек.
Для уяснения явления аберрации рассмотрим такой пример. Если вы находитесь во время дождя в вагоне трамвая или поезда, стоящего 78
неподвижно, то дождевые капли вам кажутся падающими отвесно (при отсутствии ветра). Если же в это время вагон движется, то вам будет
казаться, что дождевые капли падают наклонно, навстречу вашему движению (рис. 69), и наклонность их падения будет тем больше, чем больше скорость вагона по сравнению со скоростью падения капель. Опи-
санное явление происходит вследствие известного из физики сложения скоростей в относительном движении. За время вашего перемещения из а в Ь дождевые капли проходят расстояние с'а и на вас упадет не капля с\ бывшая над вашей головой, когда вы находились в а, но
капля, занимавшая при начале движения место с. В результате вам
покажется, что капли дождя падают не вертикально (как в действительности), а в косом направлении cb навстречу движению. Подобное же
явление происходит в небесном пространстве; только надо заменить на
этом рисунке вагон Землей, движущейся вокруг Солнца, а струи, дождя — лучами света, идущими от звезды. От звезды 5 (рис. 70) свет идет к наблюдателю по направлению 54 со скоростью с. Расстояние ОА
(длину телескопа) свет проходит за время /, т. е. ОА — ct. Но за то же время глаз наблюдателя и конец телескопа А переместятся вместе с Землей в точку В, двигаясь со скоростью движения Земли вокруг Солнца V. Чтобы луч света 54 попал в глаз наблюдателя, необходимо наклонить телескоп по направлению движения, в положение АО. Если телескоп будет наклонен на угол а, то на это же угловое расстояние звезда покажется сместившейся со своего нормального положения. Так как при движении вокруг Солн-
ца направление скорости движения Земли все время изменяется и в течение года меняется на 360°, то звезда, находящаяся в полюсе эклип-
тики, опишет в течение года окружность около своего истинного положения (в каждый момент смещаясь в сторону движения Земли).
Звезды, находящиеся на небесной сфере между эклиптикой и. полюсом последней, описывают в течение года под влиянием аберрации не окружности, а эллипсы. Звезды, лежащие на самой эклиптике, описывают в течение года отрезок — прямую линию. Длина этого отрезка, как и большие оси эллипсов (в предыдущем случае), одинаковы и равны диаметру аберрационного круга, описываемого звездой, находящейся в полюсе эклиптики.
Явление годичной аберрации света, невозможное в случае неподвижности Земли, является физическим доказательством ее обращения вокруг Солнца. Наблюдения показывают, что величина наибольшего аберрационного смещения любой звезды составляет 20*,5 и называется постоянной аберрации.
Определив из наблюдений эту величину, зная из опыта скорость света и причину происхождения аберрации, можно определить скорость движения Земли вокруг Солнца. Допустим для простоты, что угол при точке В прямой. Тогда из чертежа ясно, что
sina=54:04 = ^:c^ = v:300 ООО.
79
Подставляя в эту формулу 20",5 вместо а, получаем tr = 30 км/сек, т. е. что Земля движется по своей орбите вокруг Солнца со скоростью 30 км)сек. Скорость движения Земли по орбите может быть определена и многими другими способами.
§ 71. Годичный параллакс. Еще Коперник указал, что звезды должны обнаружить параллактическое смещение, вызываемое орбитальным движением Земли около Солнца. Действительно, наблюдая какую-нибудь звезду В из точки Е (рис. 71), а потом из точки Ev куда Земля вместе с наблюдателем переносится через полгода, мы увидим ее не по одному и тому же направлению. Нам покажется, что звезда сместилась на небесной сфере на угловое расстояние, измеряемое углом ЕВЕг в направлении, противоположном смещению наблюдателя. Годичным параллаксом звезды называется половина угла ЕВЕХ, соответствующая базису ES=a, т. е. большой полуоси земной орбиты. Как и для случая земных предметов (см. § 63), параллакс ............	звезд должен быть тем больше, чем они
I !	к нам ближе (на рис. видно, что па-
> I Dj	раллакс звезд D и С, более далеких, чем
\ /	/ ft' •	— меньше). Вследствие непрерывного
\\	//	\ движения Земли по орбите нам должно
V // ft \ казаться, что звезды в течение года опи-Л / //	\	сывают на небесной сфере маленькие эллип-
Д/by	\	сы, так как видимое смещение их пред-
\ ставляет собой отражение годичного дви^ fcgj/	: жения Земли вокруг Сблнца (рис. 71). Сле-
* з Е\	дует запомнить следующее определение:
рис# 71 е	годичным параллаксом звезды называет-
ся угол (наибольший), под которым с нее виден радиус земной орбиты. Открытие годичных параллаксов звезд дало еще одно подтверждение правильности теории Коперника. Если бы Земля была неподвижна, то никакого годичного параллакса не существовало бы. Вместе с тем измерения звездных параллаксов позволяют определить расстояние до звезд и изучить расположение их в пространстве.
Чтобы разобраться в том, как происходит параллактическое смещение звезд вследствие движения Земли по орбите, проделайте следующий опыт. Подвесьте к потолку на бечевке шарик, причем бечевку нужно пропустить через крюк так, чтобы шарик можно было под* тягивать к потолку на разные расстояния (если к потолку подвешена электрическая лампа, то можно воспользоваться ею, особенно когда она висит на так называемом „блочном подвесе*). Если вы станете кругообразно ходить по полу (рис. 72), глядя на шарик (или на' лампу), то заметите, что он виден в разных местах потолка и описывает по потолку круг. Чем ближе к вам шарик, тем заметнее это кругообразное движение. Обходя по кругу в стороне от шарика, вы заметите, что видимое движение его из кругообразного обратится в эллиптическое. В этом опыте передвигающийся наблюдатель изображает перемещающуюся до своей орбите Землю, шарик — звезду, а потолок — небесную сферу.
§ 72. Параллаксы звезд. Долгое время не удавалось измерить годичных параллаксов звезд, и можно было заключать только о том, что 80
звезды находятся от Земли гораздо дальше, чем Солнце и планеты. Только в 1838 г., когда техника постройки точных измерительных инструментов, употребляемых в астрономии, развилась в достаточной степени, это удалось немецкому астроному Бесселю. Бессель измерил параллакс слабой звезды 61 в созвездии Лебедя. Ее параллакс равен всего лишь 0",30, поэтому неудивительно, что с прежними инструментами грубой конструкции такую маленькую угловую величину не удавалось измерить. В старину не могли себе представить, чтобы звезды могли быть так далеки, а их параллаксы так малы. Поэтому отсутствие у звезд заметного годичного параллакса служило одним из возражений против теории
Рис. 72.
Коперника и в частности привело датского астронома Тихо Браге к созданию собственной теории строения солнечной системы.
Наибольший параллакс имеет самая близкая к нам звезда, так называемая Proxima, или „ближайшая* Центавра. Параллакс этой слабой звезды (10г/2 величины), невидимой невооруженным глазом, равен 0",760. Следующее за ней место занимает очень яркая звезда а Центавра с параллаксом 0",756. Параллаксы остальных звезд значительно меньше и лишь в немногих случаях превосходят 0",1.
Горизонтальные экваториальные параллаксы (см. § 55) каждой звезды меньше этих годичных во столько же раз, во сколько диаметр земной орбиты больше диаметра Земли (т. е. приблизительно в 25 тыс. раз). Понятно поэтому, что горизонтальные экваториальные параллаксы звезд невозможно измерить.
6 Астрономия	81
Если величину годичного параллакса звезды обозначить р, расстояние до звезды г может быть определено по формуле:
r=t^aCTp- ед’
Вместо этой формулы можно пользоваться следующей, в которой р jhmv&w быть выражено в секундах дуги1:
206265	206265-149500000
г = —-— астр. ед. =------------------км.
Р	Р
.Ближайшая* Центавра отстоит от нас, таким образом, приблизительно на 273 тыс. астр, ед., т. е. около 40000000 млн. км* а другие звезды находятся еще гораздо дальше.
§ 78. Движение Земли вокруг Солнца. Земля, как и все планеты, обращается около Солнца по орбите, очень близкой к круговой. При
этом Земля вращается вокруг своей оса, сохраняющей в пространстве постоянное направление. На рисунке 73 изображены 4 положения Земли на ее орбите.
Для северного полушария Земли положение II соответствует началу лета, III — началу осени, IV — началу зимы, I — началу весны. Если сопоставить эти положения с чертежом эклиптики, то легко понять, что в то время как Земля бывает в положении I, Солнце с нее видно на экваторе и, так как экватор делится горизонтом пополам, в это время день равен ночи, и потому эта точка называется точкой весеннего равноденствия. По тем же причинам точка III называется точкой осеннего равноденствия. Точки II и IV называют точками солнцестояний (летнего и зимнего).
Наблюдения показывают, что видимое движение Солнца по эклиптике совершается неравномерно. Можно вычислить среднюю суточную скорость движения Солнца, если разделить 360° на продолжительность полного обращения Земли вокруг Солнца.
1 206 265—число секунд в дуге, равной по длине радиусу (т. е. число секунд в радиане).
82
За время полного обращения Земли вокруг Солнца, называемое го* дому на Земле 3651/4 раз происходит смена дня и ночи. Следовательно, среднее суточное движение Солнца по эклиптике равно 360°:365,25 = 59\
Однако около времени летнего солнцестояния (для северного полушария) среднее суточное движение 57', а около времени зимнего солнцестояния 1°,1. Исследования причин этого явления показывают, что оно происходит вследствие того, что путь Земли вокруг Солнца не круговой, а эллиптический, и зимою Солнце несколько ближе к Земле, вследствие чего скорость движения Земли по ее орбите зимой больше, чем летом (см. §78 — второй закон Кеплера).
Изменение расстояния Земли от Солнца оказывает сравнительно небольшое влияние на количество тепла и света, получаемого от Солнца Землей, так как эти изменения составляют всего лишь 3,3°/0 среднего расстояния Земли от Солнца.
В соответствии с видимым перемещением Солнца по небесной сфере, являющимся отражением обращения Земли вокруг Солнца (причем угол падения его лучей на земную поверхность периодически изменяется), происходит смена времен года. Кроме того, различие в наклоне земной поверхности к направлению солнечных лучей создает на Земле различные климатические пояса. Таких поясов, как известно из географии,, различают пять; два полярных, два умеренных и один экваториальный. Границы этих поясов совпадают с параллелями, проведенными на определенной широте.
Линии раздела климатических поясов называют: 1) полярными кругами, проходящими на широтах Ч^бб1/^ между полярными и умеренными поясами; 2) тропиками, проходящими на широтах Ч^З1/^ между умеренными поясами и экваториальным.
Применив формулу высоты светила в момент кульминации й = 90°— — ср-|-J и подставив в нее крайние значения склонений Солнца-J-231/^0 и — 23г|2°, а также J = 0°, можно вывести, что на линиях тропиков Солнце один раз в году проходит через зенит (<р=±231/2°), а на полярных кругах один день в году не восходит (cp = 661/2°) и один день не заходит.
Таким образом, в местах между тропиками Солнце может проходить зенит. В местах между тропиками и полярными кругами оно никогда зенита не проходит. В местах между полярным кругом и соответствующим полюсом оно на некоторое время бывает невидимо в течение нескольких. Суток и тем дольше, чем ближе местность к полюсу. На полюсе невидимость Солнца продолжается полгода. Тропики северный и южный носят названия тропика Рака и тропика Козерога.
Все эти явления смены сезонов обусловлены в сущности наклоне* нием земной оси к эклиптике и движением Земли вокруг Солнца.
Неравномерность движения Земли создает неравное деление года на сезоны, четыре сезона не равны между собой, что можно заключить из следующей таблички точных средних моментов начал сезонов:
Весеннее равноденствие	21 марта, т.	е.	начало весны
Летнее солнцестояние	22 июня	„	.	лета
Осеннее равноденствие	23 сентября	„	в	осени
Зимнее солнцестояние	22 декабря	„	„	зимы
Нетрудно рассчитать, что в северном полушарии Земли летнему сезону соответствует 186 суток, а зимнему — только 179.
6*	S3
§ 74.	Основа календаря. Основой для счета времени является движение небесных тел, наблюдаемое с Земли. Для счета времени сначала пользовались только суточным движением Солнца над горизонтом, тем более, что смена дня и ночи соответствует трудовому укладу жизни человечества.
Для измерения более длительных промежутков времени, чем 1 сутки, естественно воспользоваться видимыми движениями двух наиболее ярких светил — Солнца и Луны.
Синодический месяц (т. е. время полной смены фаз Луны) имеет продолжительность 29,5305881 средних суток, а год (время полного оборота Земли вокруг Солнца) содержит 365 средних суток 5 ч. 48 м 46,1 с., или 365,24219879 средних солнечных суток.
Ни одно из этих чисел, взятых с полной точностью, не содержится целое или дробное число раз в другом, а потому невозможно выбрать единицы времени, соизмеримой одновременно с продолжительностью средних суток, синодического месяца и года.
Способ считать время так, чтобы, принимая во внимание движение небесных тел, в то же время не создавать сложных числовых расчетов, получил название календарного счета времени. У разных народов в разные времена были различные календари, основанные либо на движении Луны, либо на годичном движении Солнца. Были и такие, где исчисление времени основывалось и на движении Луны и на движении Солнца. Они были сложны.
Наш современный календарь является усовершенствованием старинного календаря, в котором основой счета было годичное движение Солнца. В нем было неверно то, что продолжительность года принималась равной 365 суткам, т. е. была (почти) на 1L суток меньше, чем следует, п	365 1	*	.
Легко рассчитать, что через -у: -j лет должна была накопиться ошибка в полгода, т. е. если, например, начало первого года приходилось на день весеннего равноденствия, то через 730 лет оно стало бы приходиться на осеннее равноденствие.
§ 75.	Старый и новый календарные стили. Чтобы исправить этот недостаток календаря, при римском правителе Юлии Цезаре астроном Созиген предложил изменить календарь таким образом: три года считать по 365 суток, а каждый четвертый год считать в 366 суток, и лишние сутки прибавлять в феврале, считая в нем не 28, а 29 суток.
Тот год, в котором присчитывался лишний день, назвали високосным и установили считать високосными те года, число которых делится без остатка на 4. Этот календарь принято называть юлианским, так как он был узаконен Юлием Цезарем.
Однако и этот календарь не соответствует истинной продолжительности года, потому что в нем предположено, будто бы в году 365,25 суток. Юлианский год длиннее действительного на: 365,25 суток — — 365,24219879 суток = 0,00780121 суток.
Эта разница в 0,0078 суток (за 1 год) через 128 лет накапливается, в целые сутки. К 1582 г, она составляла уже 10 суток (относительно 325 г., когда юлианский календарь был принят христианской церковью).
К 1576 г. астрономами был предложен новый способ счета времени, состоящий в том, что три раза за 400 лет пропускаются високосные 84
года, и, таким образом, накопляющаяся за 400 лет ошибка в 3 суток уничтожается. Распоряжением римского папы Григория XIII этот календарь в 1582 г. был введен среди католических народов, а ошибка в 10 дней была сразу уничтожена тем, что следующий после 4 октября день сосчитали не 5, а 15 октября. При этом было условлено из общего счета високосных годов исключать, т. е. считать простыми, те года целых столетий, число сотен которых не делится на 4.
Таким образом, после перехода к новому календарю, года 1700, 1900, 2100 и т. д. являются простыми, между тем как по старому (юлианскому) календарю эти года — високосные. К настоящему времени разница между старым и новым календарем („старым* и „новым* стилями) составляет уже 13 суток (до 1900 г. она была 12 суток).
В 2100 г. старый календарь отстанет от нового на 14 суток.
Самый новый (григорианский) стиль не свободен от ошибок, но ошибка нового стиля накапливается через 3000 лет на 1 день. Эта ошибка так невелика, что нет никакой необходимости изменять еще и новый стиль.
§ 76.	Узаконенный в СССР счет времени. Необходимость правильного и общего счета времени вытекает из все более оживляющихся международных деловых отношений, при которых крайне неудобйо было бы каждому народу вести счет времени по-своему. В настоящее время все культурные народы ведут счет времени по новому (григорианскому) стилю.
В нашей стране, в дореволюционное время, царское правительство упорно держалось старого юлианского стиля, главным образом, уступая требованию церковных властей (синода), хотя в научных работах уже применялся новый стиль и неоднократно ученые поднимали вопрос о необходимости перехода к григорианскому счету времени.
Вскоре после Великой Октябрьской социалистической революции Совет народных комиссаров РСФСР несколькими последовательными декретами установил в нашей стране международную систему в календарном счете времени и в счете часов по поясам. Декрет о введении нового стиля был опубликован в 1917 г., но самое введение нового стиля было приурочено к 1 февраля (старого стиля) 1918 г. Так как к 1918 г. старый стиль отстал от нового на 13 суток, то, чтобы исправить эту ошибку, вместо 1 февраля стали считать 14 февраля и, продолжая, таким образом, счет дальше, сразу перешли к новому стилю.
Совет народных комиссаров СССР в 1925 г. в законе о мерах подтвердил и распространил все правила счета времени на весь Союз, причем установил деление суток на 24 часа (от полуночи до полуночи). Последнее пока еще не вполне привилось в жизни, отчасти вследствие привычки называть время с обозначением дня и ночи, отчасти же потому, что часы изготовляются с двенадцатичасовым циферблатом. Двадцатичетырехчасовой счет времени применяется на транспорте, на почте и на телеграфе.
§ 77.	Эра# Началом счета годов можно принять любой день и от него считать время вперед и назад, придавая для краткости знак плюс или минус к числу, обозначающему протекшее время. Разные государства в разное время за начальный принимали год какого-либо события в своей жизни. Римляне, например, считали время от основания своего главного города Рима. Нередко началом счета служило какое-либо
85
мифическое событие, которое считалось происшедшим за определенное число лет от более близкого по времени и действительного события. Начало счета времени принято называть эрой,
В настоящее время многие государства считают эрой рождение Христа и от него ведут счет, но эта эра совершенно условна, так как исторические исследования доказывают, что Христа не было.
В восточных странах счет лет долго велся по императорам, и лишь много лет спустя один римский монах 248 год от начала правления Диоклетиана (римского императора) принял за 532 год от рождества христова, и это его предложение вошло в обычай у всех бывших тогда христианских народов. Таким образом, совершенно произвольно была установлена новая эра (обозначаемая „н. э.“). В течение полутора тысячелетий бблыпая часть культурного человечества пользуется этой эрой отчасти в силу религиозных предрассудков, отчасти потому, что удобно иметь всем народам общий счет времени и общую начальную эру.
§ 78» Законы Кеплера. Практика составления таблиц планетных движений согласно теории Коперника вскоре показала недостаточную точность теории. Вычисленные положения планет недостаточно точно согласовались с наблюдениями. Немецкий астроном Иоганн Кеплер устано-вил три закона, дополняющие теорию Коперника и названные в его честь законами Кеплера. Эти законы Кеплер установил, изучая многолетние ряды наблюдений Марса, произведенные Тихо Браге. Первый закон Кеплера определяет форму планетных орбит и положение последних относительно Солнца.
Он формулируется следующими словами: орбита каждой планеты есть эллипс» в одном из фокусов которого находится Солнце.
Эллипс является плоской кривой, напоминающей более или менее вытянутый круг (рис. 74). Коперник допускал для планет возможность только круговых движений. Кеплер определяет орбиты планет как эллипс (геометрическое место точек, сумма расстояний которых от двух точек, называемых фокусами, постоянна и равна большой оси эллипса). На рисунке 74 AD является большой осью, ОА — большой и ОВ — малой полуосями. Точки S п К являются фокусами. Для любой точки эллипса (например, для точки М) сумма ее расстояний от точек К и 5 (т. е.
равна AD. Большая полуось обозначается буквой а, малая полуось — буквой Ь. Если рисунок 74 изображает планетную орбиту, то мы должны себе представить, что Солнце находится в одном из ее фокусов, например в точке & Ближайшая к Солнцу точка планетной орбиты называется перигелием» а самая далекая — афелием (на рис. 74 точки А и D), Эксцентриситетом эллипса (е) называется отношение расстояния между фокусами эллипса к его большой оси.
Первый закон Кеплера был большим шагом вперед в том отнощении, что он совершенно устранил эпициклы, которые Копернику частично пришлось сохранить в своей теории для объяснения второстепенных неравномерностей в движении планет.
86
С D
Рис. 74.
Чтобы вычертить эллипс, надо воткнуть на некотором расстоянии друг от друга две булавки — это будут два фокуса. Затем к булавкам надо привязать концы нитки, длина которой равнялась бы желаемой длине большой оси будущего эллипса. Вставив карандаш так, чтобы его конец все время натягивал нитку, вычерчивают эллипс. Он получится тем более вытянутым, чем дальше друг от друга будут расставлены булавки.
Второй закон Кеплера определяет скорость движения планеты в разных точках ее орбиты. Он формулируется так: радиус-вектор планеты описывает в равные времена равные площади. Это означает, что вблизи Солнца планета движется быстрее, чем вдали от него, и притом следующим образом. Пусть, например, за 100 дней планета описала по своей орбите дугу АН (рис. 74). Ее радиус-вектор за эти ТОО дней перешел из, положения 5Л в положение 5/7, т. е. описал площадь SAH.
По второму закону Кеплера в других участках орбиты планета за 100 дней опишет меньшие дуги CD или ЕР, но так, что площади SCD или ESF будут равны площади HSA.
Третий закон Кеплера связывает расстояния планет от Солнца с временами их сидерических обращений. Если большие полуоси двух планет (т. е. средние расстояния их от Солнца) обозначить ах и а2, а их сидерические периоды обращения обозначить Т\ и Т2, то третий закон Кеплера выразится следующей формулой:
7*2	_3
71 а1
Т*2	Z.3 *
Т2 а2
или словами: отношение квадратов сидерических периодов обращения планет равно отношению кубов больших полуосей их орбит.
Благодаря этому закону, зная из наблюдений сидерические периоды обращения планет и зная среднее расстояние одной из них до Солнца, можно легко определить расстояния всех других планет. Среднее расстояние Земли от Солнца называется астрономической единицей. Если мы примем среднее расстояние Земли от Солнца за единицу и время 3/-----------------------------------------------------
обращения станем выражать в годах, то формула а = у Г2 даст нам большую полуось орбиты любой планеты, имеющей сидерический период Т лет, причем а будет выражено в астрономических единицах.
Законы Кеплера имеют большое значение в астрономии, так как они позволяют вычислить, в какой точке своей орбиты будет находиться данная планета в интересующий нас момент времени. Зная это, легко вычислить и ее видимое положение среди звезд на небесной сфере для любого момента вперед или назад. Список таких вычисленных положений планет называется эфемеридой.
Пользуясь законами Кеплера, моэрно решить и обратную (более трудную) задачу: из наблюденных положений (новооткрытой) планеты на небесной сфере можно определить размеры, форму и положение ее орбиты.
Законы Кеплера приложимы не только к планетам, но и к кометам, к спутникам планет, к двойным, звездам и т. п. Кроме того, ими пользуются в физике при изучении строения мельчайших частиц вещества (атомов).
Упражнение. Для пданетыМарс а = 1,524 астр, ед., е = 0,14. Вычертите его орбиту, приняв за единицу масштаба (астр» ед.) 20 см.
87
По сделанному вами чертежу, изображающему орбиту Марса, рассчитайте, во сколько времени Марс проходит угол в 45° близ перигелия и афелия, принимая во внимание, что сидерический оборот Марса равен 687 земным суткам.
Для расчета площадей примените либо подсчет по клеточкам, разбив сектор на треугольник н сегмент, либо снимите копию чертежа на картон и, вырезав соответствующие части, взвесьте их с точностью до сантиграмма.
§ 79< Строение солнечной системы. На рисунке 75 представлен „план* солнечной системы. Вот список планет в порядке их расстояния
от Солнца: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон. Меркурий в 2*/2 раза ближе к Солнцу, чем Земля, а Плутон в 40 раз дальше, чем Земля. Эти 9 планет называются большими.
Между орбитами Марса и Юпитера существует большой промежуток. В этом промежутке находятся орбиты так называемых малых планет^ или астероидов} их известно более 1600. Орбиты многих малых планет обладают большими наклонами к эклиптике (до 43°) и большими эксцентриситетами (до 0,65). Некоторые из больших планет обладают 88
спутниками — небольшими планетами, обращающимися вокруг них и вместе с ними обращающимися вокруг Солнца. У Земли 1 спутник — Луна, у Марса 2 спутника, у Юпитера 11, у Сатурна 9, у Урана 4 и у Нептуна 1. Как уже указывалось, спутники обращаются вокруг планет по законам Кеплера, только для них роль центрального тела в этих законах играет не Солнце, а планета, вокруг которой каждый из них обращается.
Кроме планет, в состав солнечной системы входят некоторые, так называемые периодические кометы, обращающиеся вокруг Солнца по очень вытянутым эллипсам.
§ 80.	Параллаксы Солнца и Луны. Пользуясь третьим законом Кеплера и зная из наблюдений сидерические периоды обращения планет, можно легко вычислить их относительные расстояния от Солнца. Чтобы эти расстояния выразить в километрах, достаточно знать в километрах расстояние одной какой-нибудь планеты от Солнца. Обычно мы все расстояния измеряем в единицах расстояния Земли от Солнца (в астрономических единицах), и поэтому задача сводится к тому, чтобы определить, сколько километров заключено в этой астрономической единице. Для этой цели необходимо измерить параллакс Солнца.
Измерения приводят к следующим значениям параллакса и расстоя* ния между Землей и Солнцем: параллакс Солнца 710=8",80; среднее расстояние от Земли до Солнца 149500000 км. Последнее расстояние представляет в то же время большую полуось земной орбиты.
Подобные же наблюдения для Луны дают: параллакс Луны	54'2", 7;
среднее расстояние Луны от Земли 384 400 км.
При определении параллакса планет мы не можем взять базис больше экваториального радиуса Земли. Поэтому при заданной величине базиса параллакс может быть точнее всего измерен для самых близких к Земле планет. Вследствие этого расстояние от Земли до Солнца обычно определяют не непосредственно, а сначала измеряют параллакс какой-либо из тех планет, которые ближе всего подходят к Земле, а затем находят параллакс Солнца путем вычислений. В этом отношении наиболее благоприятны для наблюдений Марс и малые планеты (в частности так называемый Эрот).
§ 81.	Размеры планет и Солнца. После того как удалось, пользуясь параллаксом, определить размеры всех планет, Солнца и Луны, оказалось, что Солнце — самое большое из светил солнечной системы; Юпитер, Сатурн, Уран и Нептун — наибольшие по размерам планеты; близкие к Солнцу планеты (от Меркурия до Марса включительно) — значительно меньше; наибольшая из них — Земля, затем — Венера. (Сравнительные размеры Солнца и планет изображены на рисунке 76.) Каждая из планет значительно больше, чем ее спутники. Малые планеты имеют совсем ничтожные размеры. Наибольшая из них Церера имеет в диаметре всего 770 км и ее поверхность немногим больше Великобритании и меньше Кавказа* Большинство малых планет по размерам похожи на большие скалы, и некоторые из них можно было бы погрузить в Черное море, не повысив при этом заметно его уровня.
§ 82.	Лунные фазы и пепельный свет. Познакомившись с основными чертами строения солнечной системы, можно теперь подробнее 89
изучить движение нашего ближайшего небесного соседа — Луны. Луна обращается вокруг Земли и вместе с Землей обращается вокруг Солнца, поэтому Луну называют спутником Земли. Изменения вида Луны — сме~ на ее фаз — происходит от того, что при своем движении вокруг Земли она занимает различные положения относительно Солнца. подобно планетам, является шарообразным непрозрачным телом, и мы видим только те ее части, которые освещены Солнцем; когда Луна находится между Землей и Солнцем, к нам повернута ее теневая, не освещенная Солнцем половина, и мы Луну не видим (новолуние). Когда Луна находится как раз против Солнца, т. е. Земля находится между
Солнцем и Луной, мы ви-
Рис. 76. Сравнительные размеры Солнца и планет.
дим всю ее освещенную половину (полнолуние). В промежуточных положениях Луны мы видим ее освещенную половину сбоку, отчего Луна имеет вид неполного круга или серпа. Рисунок 77 поясняет связь лунных фаз с положением Луны на ее орбите. На этом рисунке солнечные лучи падают сверху, в плоскости чертежа.
Понятно, что верхняя кульминация Луны происходит при новолунии в полдень, при полнолунии — в полночь, при первой четверти— около 6 часов вечера и при последней четверти — около 6 часов утра.
Если бы мы находились на Луне, то для нас Земля также занимала бы различные положения относительно
Солнца, и ее освещенную половину мы также видели бы под разными углами.
Поэтому Земля при наблюдении с Луны должна также менять фазы и с тем же периодом в 29*/2 суток, с той только разницей, что когда на Земле наблюдается полнолуние, на Луне должно наблюдаться „новозе-
мелие", и наоборот. Вы это легко можете понять, исходя из того же рисунка 77. Надо только теперь себе представить, что наблюдатель движется вместе с Луной и с нее смотрит на Землю.
Диаметр Земли больше диаметра Луны, и потому в „полноземелие* Луна освещается Землей значительно сильнее, чем в полнолуние Земля освещается Луной1. Этим объясняется явление „пепельного света" — умеренно яркое голубовато-зеленоватое свечение неосвещенной Солнцем
1Это происходит также и от того, что земная поверхность отражает солнечные лучи лучше, чем лунная.
90
10
части лунного диска незадолго до и вскоре после новолуния, когда яркая часть Луны видна в виде узкого серпа. В это время Земля освещает лунную поверхность лучами, отраженными ею от Солнца.
§ 83.	Месяц. Сидерический месяц, т. е. период обращения Луны вокруг Земли, составляет 271/8 суток (см. § 59). Промежуток вре-мени между двумя последовательными одинаковыми фазами Луны называется синодическим месяцем и равняется 29*/2 суткам. Сидерический и синодический месяцы аналогичны сидерическому и синодическому периодам обращения планет. Луна совершает полный оборот по звездному небу в течение сидерического месяца, а полнолуния наступают тогда, когда Луна находится в поло
жении, противоположном Солнцу.
Продолжительность синодического месяца (29,53 суток), известную из наблюдений, можно вычислить, зная из наблюдений продолжительность сидерического месяца (27,32 суток). Действительно, от новолуния до новолуния, т. е. от соединения Луны с Солнцем до следующего соединения, протекает Р суток; Луна движется со скоростью 360	~
градусов в сутки, а Солнце —
360 со скоростью градусов в сутки (365,24 — продолжительность года в сутках). По истечении синодического месяца (Р суток) Луна опере-„	/ 360	360 \ D
жает Солнце на
градусов. При этом Луна успеет, обежав небо, „догнать сзади*, отставшее от нее Солнце. Следовательно,
/ 360	360 \
к 27^2 “365^4 ?Р-360’
Рис. 77. Фазы Луны.
откуда получаем о— 27,32-365,24 опсо 365,24—27,32 “ 29,53 СуТ0К'
Обратите внимание на сходство формул этого параграфа с формулами § 67.
§ 84.	Затмения. Если бы плоскость лунной орбиты совпадала с плоскостью эклиптики, то ежемесячно происходили бы затмения (рис. 78).
Каждое новолуние Луна оказывалась бы рак раз на прямой линии между Землей и Солнцем и загораживала бы от нас последнее своим непрозрачным телом. Вследствие этого всякий раз наблюдалось бы явление, которое мы называем затмением Солнца. Совершенно так же каждое полнолуние Луна попадала бы в тень, отбрасываемую Землей в сторону, противоположную Солнцу, вследствие чего происходило бы лунное затмение. Но из-за наклонения лунной орбиты к эклиптике Луна в но-, волуние и в полнолуние большей частью проходит выше или ниже эклиптики, и затмений не происходит. Затмения могут произойти только тогда, когда новолуние или полнолуние случаются вблизи двух узлов лунной
91
орбиты, т. е. вблизи точек пересечения лунной орбиты с плоскостью эклиптики. Иными словами, Солнце и Луна должны одновременно находиться вблизи узлов лунной орбиты.
Так как этих узлов два, а Солнце делает полный круг по эклиптике в течение года, то ежегодно бывают два периода (разделенных промежутком в полгода), когда могут происходить затмения. Более точные подсчеты показывают, что ежегодно должно происходить не менее двух и не более пяти солнечных затмений и не более трех лунных, причем последних может и не быть вовсе.
§ 85.	Лунные затмения. Земля, будучи непрозрачным телом шарообразной формы, отбрасывает тень в форме конуса в сторону, противоположную Солнцу. Если полнолуние происходит достаточно близко от
Рис. 78. Затмения Луны и Солнца.
узла лунной орбиты, то Луна частично, или полностью погружается в земную тень, так что происходит лунное затмение.
Диаметр тени Земли на том расстоянии, на котором в эту тень погружается Луна, больше диаметра самой Луны. В этом месте ширина тени еще настолько велика (равна 22/3 диаметра Луны), что Луна может погрузиться в нее целиком, и иногда полное лунное затмение длится в течение 1 ч. 40 м. Во время затмений Луна не исчезает совершенно, а продолжает светиться, хотя и очень слабо. При этом она обычно имеет красноватогбурьгй оттенок. Причина этого заключается в том, что солнечные лучи, преломляясь, в атмосфере, окружающей Землю, попадают внутрь конуса земной тени. Однако из всех цветов радуги, составляющих белый солнечный свет, атмосфера сильно поглощает голубые лучи, а пропускает внутрь этого конуса тени преимущественно красные, 92
которые она поглощает слабее. Сильное поглощение атмосферой голубых лучей обнаруживается также при восходе и заходе Солнца. При косом ходе лучей через атмосферу утром и вечером солнечный свет пронизывает бблыпую толщу воздуха, чем среди дня, и фиолетовые лучи поглощаются сильнее. Поэтому при восходе и заходе Солнце кажется красным. Лунное затмение бывает видимо одновременно со всех мест земного шара, обращенных во время затмения к Луне.
Земля отбрасывает не только тень, но и полутень (рис. 78). Поэтому еще до начала вступления Луны в конус тени она погружается в полутень, но при этом ее яркость ослабевает незначительно.
§ 86.	Солнечные затмения. Луна меньше Земли, и поэтому поперечник отбрасываемого ею теневого конуса меньше поперечника Земли. Тень Луны не может одновременно покрывать не только всю Землю, но даже значительную ее часть. Полное затмение Солнца наблюдается только внутри того сравнительно небольшого пятна, которое лунная тень образует на поверхности Земли. Это теневое пятно, имеющее форму
Рис. 79. Последовательные
стадии кольцеобразного затмения.
круга, никогда не превосходит 250 “ 300 км в диаметре. Вне этого пятна, в области, куда падает лунная полутень, наблюдается частное затмение, т. е. закрывается Луной только часть солнечного диска. В остальных частях Земли, вне тени и полутени, затмения Солнца нет. Благодаря тому, что Земля вращается вокруг своей оси, а Луна движется вокруг Земли по своей орбите, тень Луны перемещается по поверхности Земли, и последовательно (в разные моменты) солнечное затмение наблюдается в различных местностях той полосы, которую перемещение лунной тени создает на поверхности Земли. Эта полоса (шириной не свыше 250 — 300 км) называется полосой полного затмения. В сторону от нее наблюдается лишь частное затмение, и тем меньшее (с тем меньшей фазой), чем дальше находится местность от полосы полного затмения.
Вследствие эллиптичности кай лунной, так и земной орбит видимый (угловой) диаметр Луны бывает то больше, то равен, то меньше солнечного. В первом случае полное затмение Солнца длится определенное время (не свыше 7 м. 40 с.)
Во втором случае полное затмение может длиться только одно мгновение. В последнем случае Луна не покрывает Солнца целиком, его края остаются видны вокруг темного круга Луны, — происходит кольцеобразное затмение (рис. 79),
93
§ 87.	Полные солнечные затмения. Картина солнечного затмения протекает так. Сперва на правом (западном) краю Солнца появляется маленькая черная выемка. Постепенно она растет, и Солнце все больше и больше закрывается Луной. До наступления полного затмения солнечный свет ослабевает не очень сильно. С наступлением полного затмения картина сразу меняется: становится темно, и на небе делаются видимыми более яркие звезды. В это время животные испытывают сильное беспокойство, вылетают ночные бабочки (если затмение случилось летом). Вокруг Солнца появляются яркие огненные выступы (протуберанцы), в виде небольших розоватых язычков, вытягивающихся от Солнца, а кругом затмившегося Солнца вспыхивает солнечная корона, представляющая собой крайние части солнечной атмосферы. После окончания полного затмения из-за правого края Луны появляется узкий солнечный серпик, и сразу исчезает корона, протуберанцы и звезды. Этот серпик растет, и постепенно Луна сходит с солнечного диска.
Хотя, вообще говоря, солнечные затмения происходят чаще лунных, но в одном и том же месте Земли солнечные затмения, в особенности полные, происходят гораздо реже лунных. Полные солнечные затмения наблюдаются в определенном месте Земли примерно один раз в 300 лет. В пределах СССР полные солнечные затмения наблюдались в 1914 г., 1936 г., и ближайшее следующее произойдет в 1941 г. Во время полных затмений удается наблюдать такие явления, какие в другое время невозможно увидать. Поэтому для наблюдения полных затмений в, полосу полного затмения снаряжаются специальные экспедиции.
Полное солнечное затмение 1936 г. было видимо на всем протяжении СССР (см. рис. 80). Это давало возможность поставить не только обычные наблюдения солнечной короны, но и решить целый ряд специальных астрономических и физических вопросов. Академия наук СССР организовала целый ряд советских экспедиций в полосе полного затмения и многие экспедиции получили ценные результаты. Кроме советских экспедиций, в полосе полного затмения работали научные экспедиции из США, Франции и других стран.
Раньше, когда еще не умели предсказывать момента наступления затмений и не знали причины их, затмений очень боялись, считая их за дурное предзнаменование. Церковники в этих случаях никогда не упускали случая воспользоваться народным невежеством и суеверием. Они пользовались затмениями для целей своей наживы (проповедуя конец мира) и для пропаганды религии. Малокультурные народы и сейчас боятся затмений и думают, что при затмениях демон съедает Солнце.
§ 88.	Орбита Луны. Орбита Луны является мало вытянутым эллипсом, в фокусе которого находится Земля. Точка этой орбиты» ближайшая к Земле» называется перигеем» а наиболее далекая точка — апогеем1. Когда Луна в перигее, ее диаметр кажется больше (33'30"), когда она в апогее — диаметр кажется меньше (29'21"). Плоскость лун* ной орбиты наклонена к плоскости орбиты Земли на б1/^, и поэтому Луна в течение месяца только дважды бывает на самой эклиптике* когда она ее пересекает, в так называемых восходящем и нисходящем узлах своей орбиты.
1 Перигей — значит .ближайший к Земле", апогей — „дальнейший от Земли".
94
Орбита Луны, не меняя своего наклонения к эклиптике, вращается в пространстве. При этом узлы лунной орбиты скользят по эклиптике навстречу движению самой Луны. В 18 лет 7 месяцев узлы делают полный оборот цо эклиптике и занимают прежнее положение. Это влияет на эпоху видимости затмений, которая ежегодно наступает поэтому на 20 дней, раньше.
Время, протекающее между двумя прохождениями Луны через один и тот же узел, называется драконическим месяцем. Последний, конечно, короче звездного месяца и равен 27,21 суток. По истечении 242 драконических месяцев Луна оказывается в прежнем положении относительно Солнца, и
Рис. 80. Карта солнечного затмения 1936 г.
На чертеже продольными линиями соединены точки, в которых фаза затмения одинакова (изофазы). Поперечными линиями соединены точки, в которых затмение происходило в одно и то Же время (указано мировое время). Средняя заштрихованная полоса обозначает места, где затмение было полное.
если когда-либо случилось затмение, то оно должно будет повториться и через 242 драконических месяца, что составляет 18 лет 11 суток. Этим и объясняется существование периода, называемого саросом (см. § 89).
§ 89.	Предвычисление затмений. Время наступления затмений ученые вычисляют заранее с точностью до десятой доли секунды, зная теорию движения Земли и Луны.
При этом обычно составляется карта (рис. 80), на которой вычерчивается путь луной тени по Земле и проводятся линии — изохроны (линии одинаковых моментов начала, середины и конца затмения) и изофазы (линии одинаковых фаз). Фазой затмения называется отношение отрезка диаметра Солнца, наиболее закрытого Луной, ко всему диаметру.
Можно вычислить моменты затмений как будущих, так и прошедших для любого места Земли, а так как в одном и том же месте Земли
95
солнечные затмения бывают редко, это позволило установить даты многих событий, происходивших в древности, если в описании событий упоминаются наблюдения затмений.
Ученые некоторых древних народов могли, хотя и грубо, предсказывать затмения. Наблюдая чередование затмений, они подметили цикл, называемый саросом. По истечении 18 лет и 11 суток затмения повторяются, но наблюдаются в другой местности.
§ 90.	Вращение Луны и либрация. Физические условия на Луне в значительной степени обусловливаются особенностями ее вращения вокруг своей оси. Период вращения Луны около своей оси в точности равняется периоду ее обращения вокруг Земли, т. е. 27,32 суток. Благодаря этому Луна всегда повернута к Земле одним и тем же полушарием, и мы всегда наблюдаем одну и ту же ее сторону.
Чтобы понять лучше, как происходит вращение Луны вокруг оси, проделайте следующий опыт. Пусть один из ваших товарищей станет посреди комнаты, изображая Солнце, а другой станет напротив него, изображая Землю. Третий ваш товарищ должен обходить вокруг „Земли", изображая Луну и ее движение. При этом обходе он должен все время поворачиваться к „Земле" (своему второму товарищу) лицом. Второму товарищу будет поэтому видно всегда только лицо тоге, кто его обходит (т. е. с Земли будет всегда видимо одно и то же полушарие Луны). Легко заметить при этом, что в течение одного обхода (обращения) третий ваш товарищ („Луна") один раз повернется вокруг своей оси и первый товарищ („Солнце") увидит за время одного обращения голову второго товарища и спереди и сзади. Последнее означает, что Солнце в течение одного обращения Луны освещает по очереди обе ее половины — и видимую для нас, и невидимую.
Таким образом, на Луне день длится половину лунного месяца, т. е. почти 15 земных суток, и столько же там длится ночь.
Хотя Луна повернута к Земле всегда одной и той же стороной, мы изучили не половину всей ее поверхности, а несколько больше. Это произошло от того, что Луна, двигаясь вокруг Земли, как бы покачивается немного вокруг своей оси,—эти явления, отчасти действительные, отчасти кажущиеся, происходят по различным причинам и называются либрацией. Главная из этих причин заключается в том, что вращение Луны вокруг своей оси совершается равномерно, в то время как ее движение вокруг Земли (по эллиптической орбите) не вполне равномерно. Благодаря этой, либрации мы можем по временам видеть небольшую часть другого полушария Луны. Таким образом, мы изучили в общей сложности 0,6 всей ее поверхности.
НАБЛЮДЕНИЯ.
1.	Следите за фазами Луны, зарисовывая ее вид и положение относительно Горизонта (высоту и азимут). Не забывайте при этом записывать год, день и час наблюдения. Если при этих наблюдениях вы заметите слева, совсем близко (не далее 30')» какую-нибудь звездочку, то, подождав некоторое время, сможете пронаблюдать, как она скроется за луной и появится из-за нее не позднее, чем через час. Выбрав время, когда около Луны видно несколько ярких звезд, зарисуйте среди них положение Луны и повторите зарисовку часа через два. Сравнивая рисунки между собой, вы убедитесь, что Луна перемещается среди звезд с запада на восток.
2.	Узнав по астрономическому календарю время вечерней элонгации Венеры, проследите, начав наблюдения до элонгации, как она постепенно удаляется от Солнца, достигает наибольшего удаления и затем снова начинает к нему 95
приближаться. Проследите, как меняется при атом видимая яркость Венеры, а если есть возможность воспользоваться астрономической трубой, то проследите за изменением фаз этой планеты и зарисуйте их.
3.	Узнав по астрономическому календарю моменты покрытия звезд Луною, пронаблюдайте их, отметив время исчезновения звезды за лунным краем и время ее появления из-за противоположного края. Обратите внимание на то, сразу ли исчезает звезда или же ее яркость постепенно ослабевает по мере приближения звезды к краю Луны.
Задачи и вопросы.
1.	Во время „покрытия звезды Луною" звезда была скрыта Луною в течение 20 минут. Было ли покрытие центральным? (Диаметр Луны принять равным 1/2°.)
2.	Может ли быть Меркурий видим по вечерам на востоке?
3.	Почему не может произойти прохождения Марса по диску Солнца?
4.	Может ли Марс ежегодно подходить к Земле на наименьшее расстояние, т. е. ежегодно быть в противостоянии?
5.	Какой вид имели бы видимые движения планет, если бы плоскости их орбит совпадали с эклиптикой?
6.	Зная, что от одного противостояния Юпитера до следующего проходит 399 дней, вычислите период обращения Юпитера около Солнца.
7.	Какую форму должна 'иметь орбита планеты, чтобы ее движение по орбите было строго равномерным?
8.	Пользуясь результатом решения задачи б, вычислите большую полуось орбиты. Юпитера, принимая расстояние от Земли до Солнца за единицу.
9.	Диаметр Луны составляет 0,27 диаметра Земли. Пренебрегая расстоянием от Земли до Луны, определите горизонтальный параллакс Солнца для наблюдателя, находящегося на Луне.
10.	Чему должен быть равен угловой диаметр Земли, если ее наблюдать с Меркурия во время противостояния? (Нужные данные взять из приложе-
11.	Когда расстояние от Земли до Марса составляло 55 млн. км, его угловой диаметр был равен 25",I. Чему равен линейный радиус Марса?
12.	Человеческий глаз видит две точки раздельно друг от друга, если угловое расстояние между ними не меньше 4'. Можно ли при этих условиях со звезды а Центавра обнаружить движение Земли около Солнца невооруженным глазом?
13.	Сколько времени луч света идет от Солнца до Земли?
14.	Сколько времени курьерский поезд, идущий без остановок со скоростью 80 км1час, должен был бы итти от Земли до орбиты Плутона?
15.	Как объяснить происхождение выражения „первая четверть Луны*?
16.	В какие месяцы Луна в полнолуние кульминирует на наибольшей высоте над горизонтом?
17.	Может ли быть кольцеобразное затмение Луны?
18.	Может ли произойти кольцеобразное затмение Солнца, когда Луна во время затмения находится в перигее? в апогее?
19.	Пользуясь картой солнечного затмения на рисунке 80, рассчитайте фазу затмения и момент его середины (в Москве, в Тбилиси, в Иркутске).
ГЛАВА IV.
Всемирное тяготение.
§ 91.	Закон всемирного тяготения. После обострения классовой борьбы, происходившей в XVI в., сопутствуемой ломкой общественных форм и ломкой идеологической, новый развивающийся класс торговой и промышленной буржуазии стал обращать большое внимание на развитие точных наук. Усилившееся к этому времени влияние буржуазии на государственный аппарат сказалось, между прочим, и в покровительстве 7 Астрономия	97
Рис. 81. Исаак Ньютон (1643—1727).
государством тем наукам, которые способствовали развитию механики, мореплавания, геодезии и давали в руки буржуазии экономическое и идеологическое оружие для борьбы с другими классами. Развитие мореплавания требовало развития и астрономических наблюдений и теорий, которые позволяли бы предвычислять с нужной точностью положения светил на небе. В связи с этим в 1675 г. была основана вблизи Лондона широко известная теперь Гриничская обсерватория, а за ней и другие астрономические обсерватории.
К той же эпохе ремесла, носившие прежде кустарный характер, стали вытесняться промышленными предприятиями с разделением трудовых процессов, с изобретением новых машин, с развитием индустрии. Эта область требовала глубокой разработки законов механики, без которой построение и развитие машин было невозможно.
Новая эпоха выдвинула ряд ученых, пошедших далее в этом направлении. Галилей установил некоторые из основных явлений в механике, изучил падение тел на землю, а Гюйгенс разработал понятие о центростремительном ускорении и теорию движений маятника. Кеплер вывел свои законы из наблюдений, но не имел ясного представления о причинах открытого им движения планет.
В XVII в. у некоторых ученых стал возникать взгляд, что причиной криво* линейного движения планет является притяжение их Солнцем, Ньютон, исходя из законов Кеплера, математически разработал этот вопрос и показал, как сила этого взаимодействия, этого притяжения изменяется с изменением расстояния планет от Солнца. Разрабо
тав математически ряд понятий и законов механики, он убедился в том, что притяжение Земли простирается до Луны. Он доказал, что на том расстоянии, на котором Луна находится от Земли, ускорение силы тяжести таково же, каково центростремительное ускорение Луны при ее движении вокруг Земли. Отсюда он сделал заключение, что как падение тел на землю, так и обращение Луны вокруг Земли вызваны одной и той же причиной — взаимным притяжением, тяготением, существующим между ними.
Далее Ньютон доказал, что обращение спутников вокруг своих планет происходит по тому же закону всемирного тяготения. Ведь законы Кеплера вытекают как следствие из закона тяготения и применимы не только к планетам, движущимся около Солнца по эллипсам, но и вообще ко всем телам, движущимся по закону тяготения. Последующая проверка показала полную справедливость закона Ньютона и за пределами солнечной системы — в звездной вселенной.
Открытие Ньютоном законов динамики и закона тяготения явилось могучим толчком к дальнейшему развитию техники и естествознания, в особенности к развитию измерительной и теоретической астрономии. Эти открытия являются одними из величайших в истории всего человечества. 98
Обратимся теперь к рассмотрению закона тяготения.
Английский ученый Исаак Ньютон (1643—1727) установил, что всякие две материальные частицы взаимно притягиваются с силой (F), пропорциональной произведению их масс (mt и т^) и обратно пропорциональной квадрату расстояния между ними (г).
Математически этот закон выражается формулой:
где k — коэфициент пропорциональности. Если мы хотим вычислить F в динах, то массы надо выражать в граммах, а расстояние — в сантиметрах. Величина Л, называемая постоянной тяготения, численно равна силе (в динах), с которой притягиваются друг к другу два шарика с массами по одному грамму, помещенные на расстоянии 1 см друг от друга По современным определениям k ==6,68-1О"8, илиуу^^дины.
Величина притяжения двух металлических шаров друг к другу впервые была на опыте измерена физиком Кэвендишем (в 1798 г.), что дало ему возможность определить величину постоянной тяготения k. Кроме упомянутых открытий, Ньютону принадлежит огромное количество чрезвычайно ценных научных трудов по механике, математике, физике и астрономии. Он положил основы высшей математики (анализа бесконечно малых величин). Главные его открытия изложены в книге „Philosophia Naturalis Principia Mathematical^ („Математические начала натуральной философии"). Духовенство очень боялось, чтобы открытия Ньютона не способствовали развитию материалистического мировоззрения, и приложило много стараний к тому, чтобы эта книга не возбуждала неугодных церкви заключений. Несмотря на эти старания, открытия Ньютона явились одной из основ материалистического взгляда на природу.
§ 92.	Распределение тяжести на поверхности Земли. Ученые, пользуясь современными методами, основанными, главным образом, на наблюдениях качания маятников, определяют ускорение силы тяжести с точностью до 0,001 CMfcetfi, Из наблюдений выяснилось, что это ускорение в разных местах земной поверхности разлйчно. Чем ближе к экватору, тем ускорение тяжести меньше. Вот величина ускорения на разных широтах.
Географическая	Ускорение силы
широта	тяжести
0° (экватор)	978,030	см/сек2
45°	980,616
90° (полюс)	983,216
Это различие объясняется двумя причинами. Во-первых, Земля не шар, а эллипсоид. Она сплюснута у полюсов, и полюсы находятся б^яиже к центру Земли, чем ее экваториальные части. По закону тяготения предметы на полюсах сильнее притягиваются к центру Земли. Во-вторых, благодаря суточному вращению Земли на все предметы, находящиеся на поверхности Земли, действует центробежное ускорение, стремящееся оторвать эти предметы от земной поверхности. Центробежное ускорение равно нулю на полюсах и имеет наибольшую величину на экваторе, где оно сильнее всего противодействует земному цритяжению, уменьшая ускорение силы тяжести.
Действие двух приведенных причин можно выразить в виде формул, при помощи которых нетрудно вычислить, каково должно быть в данной местности ускорение силы тяжести. Наблюдения показывают, что в некоторых местах Земли существуют большие аномалии силы тяжести, т. е. наблюденное ускорение силы тяжести сильно отличается от теоретического. Иногда сила тяжести бывает больше, чем дает теория, иногда — меньше. Это объясняется тем, что
Чела шарообразной формы и однородной структуры притягиваются так, как если бы вся их масса была сосредоточена в их центре.
7*	Я9
строение Земли не вполне однородно. В ее коре, на небольшой глубине под поверхностью, залегают и очень тяжелые, и очень легкие горные породы: их масса в сравнении с массой всей Земли ничтожна, но зато они находятся гораздо ближе к поверхности, чем центр Земли, в котором можно считать сосредоточенной всю ее массу. Поэтому они оказывают заметное действие на колебание находящегося над ними маятника. Например, более тяжелые массы вызовут в местности, рассположенной над ними, увеличенную относительно нормы силу тяжести. Таким образом, изучение аномалий силы тяжести позволяет исследовать не только форму Земли, нои строение ее коры.
Часто аномалии силы тяжести вызываются залеганием под землей железных РУД, угля или нефти, и их изучение является средством находить полезные ископаемые. В Советском Союзе за последние годы такие способы нахождения полезных ископаемых очень развились, наука здесь идет непосредственно на службу социалистическому строительству. Для всех этих работ необходимо крайне точно определять период колебания маятников, для чего в свою очередь необходимо иметь часы, поправка которых была бы всегда точно известна на основании астрономических наблюдений.
§ 93.	Определение массы Земли. Массу Земли М можно вычислить после того, как определена величина постоянной тяготения А, вставив в формулу § 91 известные уже нам из измерений значения /? (радиуса Земли) и g (взяв его среднее значение 980,6 см/сек2):
К	0,0 ’lU—®
Разделив эту величину на объем Земли, получим среднюю плотность Земли, равную 5,5 г/см3. В действительности внутренние части Земли имеют гораздо бблыиую плотность, а поверхностные слои вдвое меньшую. Масса Земли может быть определена и другими способами.
§ 94.	Движение Луны. К открытию закона всемирного тяготения Ньютона, как мы видели, привело (см. § 91) рассмотрение движения Луны вокруг Земли. Луна обращается вокруг ЗеМли, потому что последняя притягивает /	4^
Lo\
Рис. 82.
ее так же, как она притягивает к себе предметы, нахо-дящиеся у земной поверхности. Если бы Луна была неподвижна, то она упала бы на Землю. Этого не происходит от того, что Луна движется с определенной скоростью в направлении, касательном к лунной орбите, т. е. в направлении, перпендикулярном к направлению ускорения силы тяжести. Из физики известно, что всякое тело, движущееся по кругу, должно испытывать центростремительное ускорение. В движении Луны таким центростремительным ускорением является ускорение силы тяжести. Каждую секунду Луна падает к Земле с такой же скоростью, с какой на Землю находящийся от последней на том же расстоянии, на
падал бы камень,
каком находится Луна. Если бы в тот момент, когда Луна находилась в точке L (рис. 82), притяжение Земли перестало на нее действовать, она прошла бы по инерции за одну секунду расстояние ££х—по прямой линии. Благодаря притяжению Земли Луна за ту же секунду упала к ней на расстояние LxLq. Складывая эти два движения, мы убедимся, что в действительности Луна за секунду прошла путь не LLV не £х£0, а дугу ££0. Так как земное притяжение действует на Луну непрерывно, то путь Луны все время искривляется.
100
§ 95.	Вывод закона тяготения из законов Кеплера. Ньютон вывел свой закон тяготения, исходя из законов Кеплера. Такой вывод в упрощенной форме (не строго и не полно) можно получить, приняв орбиты планет за круги. Рассмотрим две планеты, движущиеся вокруг Солнца по круговым орбитам с радиусами гх и г2 и с периодами 7\ и Г2. Испытываемые ими центростремительные ускорения Д и Добудут относиться одно к другому так.
j\___4Л1	__rx Tl
Л—:’zf ~	*
По третьему закону Кеплера
21=^
Л
Подставляя это значение в предыдущую формулу, получаем:
т1
1	f* 9^
rl r2	r2
Ji ~ Л ri	Г1 ’
т. e. центростремительные ускорения, испытываемые планетами, обратно пропорциональны квадратам их расстояния от Солнца. Так как силы относятся, как сообщаемые ими ускорения, то наш вывод означает, что силы притяжения, испытываемые планетами, обратно пропорциональны квадратам их расстояний от Солнца. При одном и том же ускорении сила пропорциональна массе, испытывающей это ускорение. Поэтому, обозначив массы наших планет т1 и т2, а испытываемые ими силы притяжения к Солнцу Д и Д’ получаем:
/1 _т1 J1 __т1Г2 ft та Ja тгг%
Эта формула и выражает закон тяготения. Она показывает, что сила, с которой планета притягивается Солнцем» пропорциональна ее массе и обратно пропорциональна квадрату ее расстояния от Солнца, Из первого и второго законов Кеплера можно вывести, что сила, заставляющая планеты совершать движение по эллиптическим орбитам, направлена к Солнцу.
§ 96. Ускорение движений планет относительно Солнца. Солнце своим притяжением вызывает ускорение в движении планеты, но и планета в свою очередь притягивает Солнце и сообщает ему некоторое ускорение, направленное к планете. Массы планет очень малы сравнительно с массой Солнца, но все же они притягивают к себе Солнце и сообщают ему небольшое ускорение. Поэтому в действительности не планета движется вокруг неподвижного Солнца, а и планета и Солнце движутся вокруг их общего центра тяжести с одним и тем же периодом. При этом планета описывает вокруг центра тяжести солнечной системы большой эллипс, а Солнце — очень маленький эллипс. То же самое можно сказать о движении планет и их спутников. Особенно сильно это сказывается для Земли и Луны, так как масса последней, хотя и значительно меньше массы Земли, но сравнима с ней.
В большинстве случаев представляет интерес движение планет не относительно центра тяжести солнечной системы, а относительно Солнца. Величину этого действительного ускорения планет относительно Солнца можно рассчитать так. Пусть масса Солнца будет М, а масса планеты т и среднее расстояние между ними будет а. Тогда на основании закона тяготения ускорение планеты к Солнцу j выразится так:
х) Центростремительное ускорение при круговом движении равно (как показал еще Гюйгенс) квадрату скорости, деленному на радиус, т. е. и2:г; нот/ — г=2лг:Г, следовательно, центростремительное ускорение равно 4я2г:Г2 (Г— период).
101
4it2
xL ^—(Af + zn) П
Подобно этому, ускорение Солнца под действием притяжения планеты будет: . _ F ~ьт
Ускорение относительного движения планеты относительно Солнца G выразится суммой ускорений J и /0:
I ; ЬМ'Ьт-ЬМ+т G=J+J0 = bTi + k-2 = k—.
Эта поправка позволяет вывести более точно третий закон Кеплера, что в свою очередь дает возможность определять массы двойных звезд и планет, имеющих спутников.
§ 97. Точное выражение третьего закона Кеплера. Ускорение планеты относительно Солнца О, выведенное в предшествующем параграфе, равняется центростремительному ускорению, которое может быть выражено формулой 4я2я
-р-. Мы можем поэтому написать:
4я2л М + т
• -РЛ =~*	л > ИЛИ
к!2 а2
Подобным же образом для другой планеты с массой ть периодом обращения 7\ и средним расстоянием ах получится выражение:
^.в’=(М+да1)7?.
Деля эти два равенства почленно одно на другое, получаем:
дЗ	pa
+/»!) Tl'
Это равенство представляет третий закон Кеплера в более точной форме: кубы средних расстояний планет от Солнца относятся, как квадраты их сидерических периодов обращения, умноженные на сумму масс соответствующей планеты и Солнца.
Выведенный самим Кеплером третий закон, с которым мы познакомились раньше, лишь приближенный. Он получается, если пренебречь массами планет сравнительно с массой Солнца. Другими словами, он получается, если в предыдущей формуле массы т и тх считать равными нулю. Именно благодаря тому, что массы планет гораздо меньше массы Солнца, Кеплеру и удалось вывести свой третий закон в его приближенной форме.
§ 98.	Возмущения. Законы Кеплера справедливы в точности только для того случая, когда по закону тяготения взаимодействуют лишь два тела.
В солнечной системе Солнце и все планеты взаимодействуют друг с другом, и потому, хотя взаимное притяжение планет сравнительно с притяжением Солнца очень мало (так как массы планет гораздо меньше массы Солнца), все тела солнечной системы движутся не точно по законам Кеплера. Эти отклонения в движении от законов Кеплера называются возмущениями. Возмущения можно учесть и вычислить точную эфемериду движения небесного тела, т. е. составить таблицу, в которой заранее указаны видимые небесные координаты данного светила в определенные моменты времени.
Величина притяжения зависит не только от массы, но и от расстояния между телами. Поэтому чем ближе какое-нибудь небесное тело подходит к массивной планете, тем больше сказывается притяжение последней. На небольшом расстоянии притяжение планеты даже небольшой массы может быть больше притяжения Солнцем и может вызвать очень большие возмущения. Наибольшие возмущения вызывает Юпитер, 102
масса которого — наибольшая из масс остальных планет. Он производит огромные возмущения в движении тех малых планет и комет, которые близко к нему подходят. Если движения небесных тел не надо знать с большой точностью, их эфемериду можно вычислять, не учитывая влияния возмущений.
Математическая теория возмущений позволяет также определять массы планет по производимым ими возмущениям, предсказывать наступление океанских приливов и отливов для целей мореплавания и дает возможность точно вычислять наперед положения всех светил солнечной системы, что в свою очередь очень важно для различных практических потребностей (например для нужд мореплавания).
§ 99.	Вычисление масс небесных тел. Закон всемирного тяготе-ния позволяет вычислять массы небесных тел. Для планет, имеющих спутников, это вычисление производится так. Пусть одна планета, имеющая спутника, обладает массой М, а другая планета (также имеющая спутника) имеет массу Afv Расстояния спутников от своих планет и периоды их обращений обозначим соответственно через а, ах и т. д. Тогда ускорения, сообщаемые этими планетами своим спутникам, соответственно будут:
• 1М • гЛ
, =	" У1 = &^2-
а2	аг
С другой стороны, как мы уже знаем, эти ускорения являются центростремительными, выражаемыми формулой v2.a> т. е. для двух планет соответственно равны 4я2а	4ic2ai
---- и —
Г2	Г2
Беря отношение этих двух пар выражений и приравнивая их друг другу, получаем:
Ш kMi 4 л2 a 4^aL	М дЗ rj
~a*'	'~т1 ’ т‘е‘ of* К*
Это позволяет определить отношение масс М и двух планет. Если за первую планету принять Землю, то массы остальных планет, имеющих спутников, можно выразить в массах Земли. Аналогичной формулой можно пользоваться для вычисления массы Солнца.
Определить массы планет, не имеющих спутников, труднее. Это можно сделать, изучая возмущения, производимые их массами в движениях других планет. Среди тел солнечной системы после Солнца наибольшими массами обладают Юпитера а затем Сатурн. Масса Солнца приблизительно в 750 раз больше массы всех планет, вместе взятых (см. приложение VIII).
Задача. Вычислите массу Солнца, приняв массу Земли за единицу, взяв расстояние Земли от Солнца а=1, период Обращения Земли вокруг Солнца Г=1, расстояние Луны от Земли а1 = 1/890, период обращения Луны вокруг Земли Т1 = 1|134. При этом Луну надо рассматривать как спутника Земли, а Землю — как спутника Солнца.
§ 100.	Устойчивость планетной системы. Под влиянием возмущений планетные орбиты все время изменяются. Доказано, что большие
103
полуоси планетных орбит не могут достигнуть нуля или бесконечности, т. е. планеты (в том числе Земля) не могут упасть на Солнце или уйти от него. Однако это доказано для большого, но не для бесконечно большого промежутка времени, т. е. не исключена возможность того, что через какие-нибудь миллиарды миллиардов лет какая-нибудь из планет упадет на Солнце.
Таким образом, и в солнечной системе происходят непрерывные изменения, она не является застывшим миром с раз навсегда определенным строением и движениями.
§ 101.	Открытия Нептуна и Плутона. В 1781 г. английским астрономом Гершелем была открыта планета Уран, невидимая невооруженным глазом. Постепенно стало выясняться, что движение Урана всё сильнее и сильнее уклоняется от вычисленной эфемериды, которая учитывала возмущения, производимые известными планетами. Это могло быть объяснено предположением, что движение Урана возмущается какой-то неизвестной планетой, находящейся от Солнца дальше, чем Уран. Французский ученый Леверье и английский ученый Адамс, независимо друг от друга, с помощью очень сложных вычислений определили место, где на небесной сфере должна быть видна неизвестная планета. Пользуясь указанием Леверье, берлинский астроном Галле нашел на небе эту планету (1846 г.). Она была названа Нептуном. Поразительное предсказание существования Нептуна на основании теории всемирного тяготения служит одним из лучших доказательств правильности этой теории и является торжеством человеческой мысли.
После открытия Нептуна в движении Урана остались неправильности, необъяснимые возмущениями известных планет. Американский астроном Ловелл вычислил, что отклонения в движении Урана могуть быть объяснены возмущениями, вносимыми существованием еще более далекой, занептунной планеты, орбиту которой он вычислил. Долгое время эту планету не удавалось найти, и только через 14 лет после смерти Ловелла (в 1930 г.) эта планета была найдена и названа Плутоном.
§ 102.	Зависимость вида орбиты от начальной скорости. Подробные вычисления показывают, что форма орбиты зависит от скорости движения тела относительно притягивающего его центра. Камень, брошенный рукой, имеет малую скорость и падает на Землю. Если его бросить горизонтально, со скоростью 7,9 км/сек, то он станет двигаться вокруг Земли по круговой орбите в качестве ее спутника. При большей скорости он будет двигаться вокруг Земли по эллиптической орбите, с тем ббльшим эксцентриситетом, чем больше была его скорость. При скорости в 11 км/сек камень полетит по разомкнутой кривой — параболе — и навсегда удалится от Земли. При еще большей скорости камень улетит от Земли по кривой, называемой гиперболой. Ньютон доказал, что второй закон Кеплера справедлив для светил, движущихся по любой из этих орбит, а не только для планет, движущихся по эллипсам.
Точно так же небесные тела (например некоторые из комет), вступая из межзвездного пространства в пределы солнечной системы, движутся вокруг Солнца по разным орбитам, в зависимости от того, с какой скоростью они пришли. Эти выводы явились обобщением законов Кеплера для всех тел, движущихся по закону тяготения, и заслуга этого обобщения также принадлежит Ньютону.
§ 103.	Межпланетные путешествия. С давних пор человек задавался мыслью, нельзя ли с Земли полететь на дру! не планеты. Очевидно, что для этого надо преодолеть притяжение Земли, т. е. надо вылететь с Земли со скоростью не меньше 11 км/сек. В настоящее время теоретически вопрос о межпланетных сообщениях разработан: придумана особая летательная 104
машина — ракета, которая может вылететь с Земли с необходимой начальной скоростью. Первая научная работа по этому вопросу была опубликована в 1903 г. русским ученым К. Э. Циолковским (умер в 1935 г.).
Такая ракета основана на том же принципе, на котором основано употребление обыкновенных ракет, применяемых, например, в войсках для сигнализации. Снаряд выбрасывает из себя с большой силой газы и по закону равенства действия и противодействия движется благодаря этому вперед с огромной скоростью. В последнее время уже производились удачные опыты с моделями такого аппарата. Для того чтобы совершить межпланетный полет, остается преодолеть некоторые, еще довольно значительные технические затруднения и придумать способы, обеспечивающие безопасность людей, которые будут находиться в аппарате, во время полета.
§ 104.	Приливы и отливы. На рисунке 83 изображены две фотографии одного и того же места морского берега в Мурманске. Заметно, что на второй фотографии вода как будто отошла от берега и стоит на более низком уровне. Одна фотография сделана через 6 часод после другой. Подобные же явления наблюдаются на всех океанских берегах:
а	б
Рис. 83. Прилив (а) и отлив (б) в Кольском заливе.
через каждые 6 часов1 вода то прибывает (приливает), то отливает, так что каждые сутки бывают два прилива и два отлива. Приливы и отливы имеют большое значение в мореплавании, а также в будущей экономике приморских стран. В прилив океанские пароходы могут входить в устья мелких рек, в отлив — обнажаются подводные камни и многие места становятся опасными для плавания. Огромная масса воды, приходящая в движение при приливах и отливах, обладает колоссальной энергией. Во Франции (в Бретани) сделана попытка использовать эту энергию при помощи особых плотин, и даже эта пробная маленькая гидроэлектростанция дает 7500 кет энергии. В будущем использование этой природной энергии принесет громадные результаты. Каждые сутки отливы и приливы наступают примерно на 50 минут позднее. Эта величина совпадает с ежесуточным запаздыванием кульминаций Луны и наводит на мысль, что причиной приливов и отливов является притяжение Луны.
1 Более точно — через 6 ч. 12 м.
105
§ 105.	Объяснение приливов. Явление приливов объясняется притяжением Луны. Для простоты мы можем представить себе Землю как твердый шар, окруженный водяной оболочкой океанов. На рисунке 84 изображен земной Шар (если на него смотреть с полюса) и окружающая его водная оболочка. Луна на рисунке изображена маленьким кругом L. Точки В, Т и А находятся на разных расстояниях от Луны и поэтому притягиваются ею неодинаково — точка А сильнее всего, точка В — слабее всего. Поэтому слой воды вблизи точки А оттягивается от Земли, а вблизи В твердый земной шар оттягивается от своей водной оболочки. В результате около точек А и В получаются два водяных выступа — две приливные волны. Одновременно с этим в точках С и D уровень воды становится меньше, она спадает, и там наблюдается отлив. Так как Земля вращается вокруг своей оси, а следовательно, и по отношению к Луне, то в течение суток приливная волна последовательно поднимается в разных местностях Земли. Пусть сперва данная местность находится
С	в точке £>, где наблюдается от-
•	лив. Через 6 часов вследствие
д	вращения Земли эта местность
............. (Ц 4 займет положение Л, где Луна оттягивает воду, и там наступит прилив. Еще через 6 часов эта местность попадет в положение. 84......ние С, вследствие чего снова
наступит отлив. А еще через
6 часов (в положении В) будет наблюдаться второй прилив (через полсуток после первого прилива) и т. д.
Благодаря тому что Луна обращается вокруг Земли в ту же сторону, в какую последняя вращается вокруг оси, приливы и отливы следуют друг за другом не точно через 6 часов, а через 6 ч. 12 м. Расположение материков на Земле и трение воды о земную поверхность создают различные неправильности в чередовании приливов, достигающие иногда нескольких часов.
Солнце точно так же вызывает приливы и отливы, но примерно вдвое меньшие по величине, чем Луна. Складываясь, солнечные и лунные приливы вызывают изменения во времени наступления приливов и в их высоте. Как легко понять, наибольшие приливы наступают в моменты новолуний и полнолуний и в некоторых местностях достигают 21 м в высоту. Построены специальные машины, которые позволяют предсказывать величину и время наступления приливов, что для океанских портов очень важно. В закрытых морях, как, например, в Азовском и Каспийском, приливы очень невелики.
Помимо практического значения изучение приливов позволяет понять эволюцию (развитие) небесных тел, так как явления приливов существуют не только на Земле, но и на других небесных телах и оказывают на них большое влияние.
§ 106. Роль приливов в эволюции Земли и Луны. По отношению к развитию Земли и Луны создана гипотеза, достаточно хорошо разъясняющая весь процесс этого развития, исходя из приливного взаимодействия.
В очень отдаленные времена Земля и Луна вместе составляли одну общую полужидкую вращающуюся массу шарообразной формы. Враще-106
ние было очень быстрым — около 5 часов. Так как все тело было полу жидким, то притяжение Солнца создавало на его поверхности приливы.
Эти приливы повторялись каждые 2—21/9 часа и заставляли колебаться всю массу, вследствие чего произошел разрыв ее — от нее отделилась меньшая часть. Перед моментом разрыва все тело уже имело форму груши (рис. 85), но вращалось как одно целое.
После разрыва обе части, ббльшая — Земля и меньшая — Луна, уже не составляли одного целого: Земля вращалась попрежнему, Луна же, оторвавшись от Земли, обращалась вокруг нее медленнее. Но Луна не только обращалась вокруг Земли, оба тела своим притяжением создавали приливы на своих поверхностях. Выступы этих приливов были направлены по линии центров Земли и Луны. Таким образом, угловая скорость приливной волны на поверхности Земли оказывалась меньше, чем ее
собственная угловая скорость вращения, — в результате вращение Земли стало замедляться, но и на Луне создавались приливы под действием притяжения Земли, и у нее происходило замедление вращения. Оба за-
медления вращения действовали неодинаково, — прилив как тормоз больше действовал на Луну, потому что Земля,
как более массивная, вызывала на Луне более высокий прилив, чем Луна на Земле. Кроме того, Луна отдалялась от Земли и медленнее обращалась вокруг нее.
Все эти изменения происходили в согласии с законом о сохранении количества движения и третьим законом Кеплера; замедление вращения Земли и Луны вокруг оси влечет за собой увеличение их расстояния, а увеличение расстояния — замедление обращения Луны. При этом наиболее быстро развивается процесс замедления вращения Луны вокруг оси.
Этот процесс закончился тогда, когда Луна навсегда повернулась к Земле одной стороной (как это имеет место теперь). После этого все приливное действие влияло уже только на Землю, ко
торая продолжает замедляться в своем вращении. Настанет время, когда угловая скорость вращения Земли сравняется с угловой скоростью обра-
щения Луны вокруг Земли, которая тоже уменьшается, но более медленно,
т. е. Земля и Луна станут повернутыми одна к другой всегда одной и
той же стороной.
107
§ 107. Явление прецессии. Еще во П в. до н. э. греческий астроном Г и п п а р х обнаружил, что точка весеннего равноденствия, т. е. пересечение экватора с эклиптикой, непрерывно перемещается навстречу движению Солнца
по эклиптике. По точным современным определениям, основанным на совокуп-
ности наблюдений, произведенных до настоящего времени, это смещение точки весеннего равноденствия по эклиптике составляет 50",2 в год. Явление это называется прецессией, или предварением равноденствий, так как Солнце ежегодно вступает в точ-
ку весеннего равноденствия раньше, чем в том случае, если бы эта точка оставалась неподвижна и не двигалась навстречу Солнцу. Перемещение точки весеннего равноденствия (а также, конечно, и точки осеннего равноденствия) происходит оттого, что небесный экватор, не меняя своего наклона к эклиптике, поворачивается. Вследствие этого ось мира непрерывно меняет свое направление в пространстве. Ось мира параллельна оси вращения Земли, так что смещение оси мира означает, что земная ось, не меняя своего наклона к эклиптике, меняет свое направление в пространстве (рис. 86).
Оказывается, что земная ось описывает в про-
Рис. 87. Перемещение полюса мира вследствие странстве конус вокруг
прецессии.	полюса эклиптики с перио-
дом в 26 тыс, лет (рис. 86 и 87).
Следствием прецессии оказываются следующие явления: 1) Солнце ежегодно приходит в точку весеннего равноденствия раньше, чем это было бы при отсутствии прецессии; 2) полюс мира перемещается на небесной сфере по кругу, в центре которого находится полюс эклиптики (рис. 87). Таким образом, а Малой Медведицы не всегда была и не всегда будет полярной звездой. Через 14 тыс. лет земная ось будет направлена в сторону созвездия Лиры, и звезда а Лиры будет считаться полярной. Теперешняя полярная звезда — а Малой Медведицы — отстоит от полюса на l1^0, а во времена Гиппарха, две тысячи
лет назад, она отстояла от полюса мира на 12°,3.
Координаты звезд, т. е. прямые восхождения и склонения, вследствие прецессии непрерывно меняются. Поэтому и в списке звезд или на звездной карте всегда должно быть указано, к какому году относится координатная сетка, или значения координат звезд а и 3. Существуют специальные таблицы, позволяющие учесть влияние прецессии на координаты звезд. Вследствие из-
менения координат звезд с течением времени некоторые новые созвездия становятся незаходящими, а другие созвездия уже никогда не появляются над горизонтом.
§ 108. Причины предварения равноденствий. Чтобы понять причины перемещения земной оси в пространстве! сделаем следующий опыт: возьмем волчок и заставим его быстро вращаться на столе. Цели в это время толкнуть 108
волчок сбоку, to его ось, не изменяя своего наклона к плоскости стола, станет медленно поворачиваться в пространстве, описывая конус. Земля является таким же волчком. Сила, стремящаяся повернуть земную ось, подобно толчку, сообщаемому рукой волчку, создается благодаря притяжению Солнцем и Луною экваториального выступа Земли. Если бы Земля была шаром, этого явления не происходило бы. Земля сплюснута у полюсов, и потому на экваторе ее получается как бы выступ (рис. 88). Притяжение Луны, находящейся вблизи плоскости эклиптики, действует на этот экваториальный выступ по направлению ЕМ, т. е. под углом к плоскости земного экватора. Поэтому получается, что притяжение Луны стремится повернуть ось Земли и поставить ее перпендикулярно к плоскости эклиптики. Вследствие вращения Земли вокруг оси последняя по закону инерции стремится сохранить направление оси вращения. Законы механики показывают, что в результате сложения этих двух вращательных движений ось Земли, как и ось волчка, будет описывать в пространстве конус. Такое же действие, как Луна, оказывает и Солнце, почему описанное явление называется лунно-солнечной прецессией.
Задачи и вопросы.
1. Представьте себе, что притяжение Солнца внезапно исчезло. Как бы тогда стали двигаться планеты?
2. Вычислите центростремительное ускорение, испытываемое Луной, и ускорение силы тяжести на расстоянии Луны и сравните их. Для последнего расчета надо учесть, что Луна отстоит от Земли на 60 земных радиусов, так что на этом расстоянии ускорение силы тяжести в 602 раз меньше, чем на поверхности Земли. Центростремительное ускорение вычислите по формуле:
; р — расстояние Земли от Луны — надо выразить в сантиметрах, а
Т—сидерический месяц — надо выразить в секундах.
3.	Во сколько раз сила тяжести на поверхности Луны меньше, чем на поверхности Земли, если масса Луны в 81 раз, а радиус в 3,7 раза меньше массы и радиуса Земли?
4.	Вычислите массу Нептуна относительно массы Земли, зная, что его спутник отстоит от центра планеты на 354 000 км и период его обращения равен 5 с. 21 ч. Вычисление произвести, сопоставляя движение спутника Нептуна с движением Луны вокруг Земли.
5.	Где между Землей и Луной на линии, их соединяющей, находится точка, в которой притяжение со стороны обоих этих небесных тел одинаково?
6.	Во сколько лет полюс мира вследствие прецессии опишет на небесной сфере дугу в 10°?
ЧАСТЬ АСТРОФИЗИЧЕСКАЯ
ГЛАВА I,
Методы астрофизических исследований.
§ 1.	Астрофизика. Переходя к изучению физической природы небесных светил, необходимо познакомиться с теми методами, которыми пользуется современная астрофизика — наука о физическом строении и развитии небесных тел. Эта область астрономии является самой молодой; она возникла во второй половине прошлого столетия, с тех пор как была изобретена фотография и был открыт спектральный анализ. До этой эпохи о физической природе небесных тел и о совершающихся на них явлениях было известно очень мало. Развитие астрофизики тесно связано с успехами опытной и теоретической физики, с развитием математики и техники изготовления точных оптических приборов. Область астрофизики развивается исключительно быстрыми темпами, и каждый год приносит новые поразительные открытия. Астрофизик изучает материю, находящуюся в таких условиях, которые искусственно в физических лабораториях в большинстве случаев еще не могут быть созданы. На поверхности и в недрах Солнца, звезд и туманностей вещество находится нередко в таких формах и в таком движении, которые еще не наблюдались на Земле. В бесконечном мировом пространстве мы встречаем разнообразнейшие условия температур, плотностей и давлений. Поэтому изучение материи в таких условиях позволяет глубже проникнуть в ее свойства и использовать эти свойства для различных практических применений. Развитие астрофизики идет рука об руку с развитием физики и других смежных наук, так что открытия в одной из этих наук способствуют достижениям другой науки и стимулируют ее дальнейшее развитие.
§ 2.	Астрономические обсерватории. Астрономическими обсерваториями называются учреждения, предназначенные специально для наблюдения и изучения небесных светил. В таких обсерваториях, устраиваемых по преимуществу в местностях с большим количеством ясных ночей и с прозрачным воздухом, устанавливаются различные инструменты: рефракторы, рефлекторы, фотографические камеры, меридианные круги и другие приборы, с которыми мы отчасти познакомились выше. Помимо изучения светил эти обсерватории несут регулярную службу времени, содействуют государству в составлении географических карт, в разведке полезных ископаемых методами гравиметрии и т. п.
Самая большая астрономическая обсерватория Советского Союза находится в Пулкове (вблизи Ленинграда). При Советской власти в нашем Союзе организовано несколько астрономических институтов — научных учреждений, подобно обсерваториям ведущих изучение вселенной и удовлетворяющих хозяйственным и культурным запросам страны. Работа каждой обсерватории протекает по заранее составленному плану.
110
§ 3.	Астрофотография. Применение фотографии (Изобретенной в 1839 г. Дагерром) к астрономии оказалось исключительно плодотворным. Достоинства, которыми обладает фотографическая пластинка по сравнению с человеческим глазом, следующие:
1. Ф	отографическая пластинка накапливает световое действие так, что чем дольше ее подвергать действию света (чем больше делать экспозицию, выдержку), тем яснее получается на ней изображение светящегося предмета. Благодаря этому на фотографической пластинке при долгой экспозиции получаются даже такие слабые звезды, которые не видны глазом ни в какой телескоп.
Звезды на фотографиях получаются в виде кружков тем большего размера, чем они ярче. Действительно, сколько бы времени мы ни смотрели, наш глаз, в противоположность фотопластинке, не увидит звезд более слабых, чем те, которые он может увидеть в течение первых минут наблюдения. Кроме того, форма и строение многих небесных светил, как, например, туманностей, фотографически воспроизводятся гораздо точнее, чем при помощи рисунка, сделанного при непосредственном наблюдении глазом.
2. В	то время как глаз одновременно может сосредоточить внимание только на одной точке,«а фотографии одновременно получается большая область неба.
3. Ф	отография неба является документом, который можно хранить, рассматривать и изучать в течение неопределенно долгого периода времени. Особенно большая коллекция астрономических фотографий собрана в Гарвардской обсерватории в Америке. Там хранится свыше 300 тыс. фотографий, снятых на этой обсерватории за последние 45 лет. Эти фотографии постоянно изучаются и дают возможность установить историю жизни различных звезд.
§ 4.	Астрофотометрия. Наряду с фотографией большое значение для изучения природы небесных тел имеет астрофотометрия — отрасль астрономии, занимающаяся измерением яркостей светил. Для этой цели служат специальные приборы — астрофотометры. В большинстве из них яркость звезд сравнивается с яркостью какой-нибудь искусственной светящейся точки, получаемой, например, при помощи электрической лампочки. Яркости звезд можно измерять также по величине или по черноте тех изображений, которые они дали на фотографической пластинке. Особенно большую точность (до тысячных долей звездной величины) дают измерения при помощи так называемого фотоэлектрического фотометра. Благодаря особому устройству свет от звезды, попадая в этот фотометр, вызывает в нем появление электрического тока. Измеряя силу этого тока, можно определять яркость различных звезд очень точно.
§ 5.	Спектроскопия. Как известно из физики, луч белого света, пропущенный через стеклянную призму, разлагается в цветную полоску, состоящую из всех цветов радуги и называемую спектром. Прибор, основной частью которого является призма и который позволяет изучать спектры светящихся тел, называется спектроскопом. Спектр, состоящий из полоски, в которой цвета: красный, желтый, зеленый, синий и фиолетовый непрерывно переходят из одного в другой, называется непрерывным спектром. Такой спектр дают твердые и жидкие раскаленные тела (например нить электрической лампочки), а также раскаленные газы, находящиеся под большим давлением. При малом давлении газы и пары металлов дают спектр, состоящий из ярких цветных линий на темном фоне. Каждый химический элемент дает в спектре всегда одни и те же (одного и того же цвета, т. е. одной и той же длины волны) характерные для него линии. Это дает возможность определять химический состав светящихся тел по их спектрам', стоит только, изучив положение линий видимых в спектрах светил, сравнить их с линиями в таблице спектров известных химических элементов. Например, натрий дает в своем спектре яркую линию строго определенного желтого оттенка (определенной длины волны). В спектрах других элементов тоже есть желтые линии, но они при более тщательном исследовании имеют, как оказывается, несколько другой оттенок (немного другую длину волны), чем желтая линия натрия. Обнаружив в. спектре каких-либо паров желтую линию этого определенного оттенка, мы можем утверждать, что в его состав входят пары натрия.
Если перед раскаленным телом, испускающим непрерывный спектр, поместить слой более холодных паров натрия, то будет наблюдаться следующее явление. Спектр окажется уже не непрерывным: в желтом цвете, именно там, где раньше наблюдалась яркая желтая линия натрия, появится темная, черная линия. То же наблюдается, если взять вместо паров натрия пары других элементов —
Ш
яркие линии их спектра превращаются в темные, перерезывающие непрерывный спектр. Это явление можно выразить так: газы и пары поглощают как раз те лучи спектра, которые они сами способны испускать. По положению темных линий в спектре также можно определить химический состав светящегося тела. Описанным способом,называемым спектральным анализом, можно определить химический состав как земных, так и небесных тел. Вместо глаза в спектроскопе можно поместить фотографическую пластинку, на которой отпечатывается спектр. Такие приборы называются спектрографами.
§ 6.	Определение лучевых скоростей светил. Лучевой скоростью светил называется скорость, с которой они приближаются к нам или удаляются от нас, т- е. их скорость по направлению луча зрения. В том случае, если тело движется хотя бы с огромной скоростью перпендикулярно к лучу зрения, оно не приближается к нам и не удаляется от нас, и его лучевая скорость равна нулю. Лучевую скорость светил можно измерить, изучая их спектр. По закону, называемому законом Допплера-Физо, спектральные линии движущегося предмета смещаются со своего нормального положения тем больше, чем больше лучевая скорость тела. При приближении к нам источника света спектральные линии смещаются к фиолетовому концу спектра, при удалении они смещаются к красному концу спектра.
Измеряя величину смещения спектральных линий относительно их нормального положения, можно вычислить скорость приближения или удаления светила, пользуясь формулой
Х'~Х = Х~, с
в которой v есть скорость звезды, с — скорость света, X — нормальная длина волны линии и Хг — наблюдаемая длина волны той же линии в спектре светила.
§ 7.	Определение температур небесных светил. Температуры небесных светил можно определять различными способами. Вот два из них:
1. Можно при помощи особых чувствительных приборов непосредственно измерить количество тепла, получаемого нами от данного светила.
2. Температуры тел, светящих собственным светом, можно определить по их спектру. У едва раскаленных тел самой яркой является красная часть спектра. Чем выше температура тела, тем ближе к фиолетовому концу находится самая яркая- часть в его непрерывном спектре. Измеряя положение (длину волны) самого яркого места в спектре светила, можно вычислить его температуру. Таким же образом иногда определяют температуру руд, расплавленных в доменных печах.
ГЛАВА IL
Солнце.
§ 8.	Общие данные о Солнце. Солнце — центральное светило планетной системы. Оно гораздо больше и массивнее всех планет, вместе взятых. Его масса в 332 тыс. раз больше массы Земли, а диаметр в 109 раз больше земного, так что внутри него могли бы свободно поместиться не только все планеты, но даже орбита Луны, отстоящей от Земли на 30 земных диаметров. Все планеты, в том числе Земля, освещаются светом Солнца и согреваются его теплом. Люди с давних пор сознавали, какое огромное значение имеет Солнце для жизни на 112
Земле, и обожествляли его. Во многих странах жрецы заставляли народ строить храмы в честь Солнца и приносить ему жертвы. Даты многих религиозных праздников и обычаев связаны с астрономическими явлениями, касающимися Солнца (днями равноденствий, солнцестояний и пр.).
В наше время наука еще лучше разобралась в значении Солнца для жизни на Земле, но в ее задачу входит не обожествление Солнца, а изыскание способов наилучшего использования солнечной энергии. Изучая Солнце, ближайшую к нам звезду, наука позволяет исследовать строение и движение вещества, изучить влияние изменений на Солнце на жизнь Земли, научиться предсказывать эти изменения и вместе с тем установить, как развиваются небесные тела, как они произошли и каково их будущее.
§ 9.	Жизнь Солнца и жизнь Земли. Свет и тепло, получаемые от Солнца, поддерживают жизнь на поверхности нашей планеты — Земли. Испарение воды, дождь, выпадение снега, течение рек, бури, грозы, засухи и все другие явления, обусловливающие климат и погоду на Земле, зависят от нагревания Земли Солнцем и должны изменяться в зависимости от изменений, происходящих на Солнце. Дальше мы увидим, как удалось установить взаимоотношение между некоторыми изменениями, происходящими на Солнце и на Земле.
Человечество широко пользуется не только прямой солнечной энергией в виде тепла и света, но и другими формами, в которые она переходит: энергией воды, ветра (посредством водяных турбин на гидроэлектростанциях, ветряков и т. п.). Каменный уголь — окаменевшие остатки растений, существовавших благодаря солнечному теплу, — это тоже запасы солнечной энергии, как бы скрытые в Земле. Огромная часть солнечной энергии, падающей на Землю, остается, однако, неиспользованной. В настоящее время разработаны проекты устройства так называемых солнечных машин — аппаратов, собирающих непосредственно солнечную энергию и превращающих ее в другие виды — в энергию паровых и электрических двигателей. Этим солнечным машинам предстоит большая будущность в народном хозяйстве нашего Союза, особенно в южных его районах, где бывает много ясных, солнечных дней.
§ 10.	Общий вид Солнца в телескоп. Если посмотреть через темное стекло на Солнце в телескоп, то мы увидим его в виде большого круглого диска, слегка ослабевающего по яркости у краев (рис. 89).
Почти ежедневно на Солнце можно видеть темные пятна различных размеров, а вблизи краев Солнца можно заметить маленькие яркие блестки, называемые факелами. Если присмотреться, то можно заметить и то, что поверхность Солнца не равномерно светлая, а как бы рябая, как будто она состоит из тесно расположенных мелких зерен. Описанное явление называется грануляцией, а светящиеся зерна — гранулами, вся же видимая в телескоп поверхность Солнца называется фотосферой ( по-гречески „фотос* означает „свет*). Солнечные пятна были открыты еще в 1611 г. Фабрицием, а затем Галилеем, тотчас после изобретения телескопа. Духовенство, узнав об открытии на Солнце пятен, отнеслось к этому открытию очень враждебно, так как оно противоречило учению о совершенстве и неизменяемости небесных тел.
§ 11.	Вращение Солнца. Если наблюдать Солнце и находящиеся на нем пятна изо дня в день, то легко можно заметить, что они по-степеннно перемещаются по диску Солнца от восточного края диска 8 Асгрэчомнц	НЗ
Рис. 89. Фотография Солнца.
к западному (если смотреть с Земли). Это происходит от того, что Солнце вращается вокруг своей оси с периодом в 26 суток. Для земного наблюдателя вращение Солнца кажется происходящим в течение 27 суток, потому что, пока Солнце один раз повернется вокруг своей оси, Земля пройдет по своей .орбите вокруг Солнца некоторую дугу в том же направлении, и Солнце должно будет повернуться еще на некоторый угол, чтобы прежнее пятно снова оказалось как раз против Земли. Экватор Солнца наклонен к плоскости эклиптики на угол в 7°.
Наблюдения над видимым движением пятен и других образований на диске Солнца показывают, что различные части его вращаются с разными скоростями. Быстрее всего вращаются экваториальные части, делая один оборот в течение 25 дней. Чем ближе к полюсам Солнца, тем медленнее происходит вращение, и на расстоянии 10 градусов от солнечных полюсов один оборот длится 34 суток. Следовательно, Солнце вращается не как твердое тело, а как жидкое или газообразное, и это находится в полном соответствии с малой плотностью Солнца (1,4) и с его высокой температурой.
114
§ 12.	Солнечные пятна и их изменения. Размеры солнечных пятен весьма разнообразны. Иногда эти пятна так велики, что видны невооруженным глазом (через темное стекло). Большинство пятен по своему диаметру больше диаметра Земли. Часто пятна располагаются целыми группами. Видимая форма пятен бывает весьма разнообразна (рис. 90) и зависит не только от их истинной формы, но и от их положения на диске Солнца. Приближаясь вследствие вращения Солнца к краю его видимого диска, пятна вытягиваются рследствие перспективы, так как в это время мы на них смотрим не прямо, а сбоку. Почти каждое пятно, кажущееся при наблюдениях черным, бывает окружено более светлой, серой каемкой, так называемой полутенью.
С давних пор чернота пятен наводила на мысль, что они являются наиболее холодными участками солнечной поверхности. И действительно, позднейшие наблюдения показали, что температура газов в солнечных пятнах значительно ниже температуры остальной поверхности, — она не достигает 5000°. Таким образом, газы внутри пятен тоже раскалены и кажутся темными только благодаря контрасту с более горячими и яркими частями поверхности (поверхностная яркость пятен в 500 раз больше яркости Луны в полнолуние).
Солнечные газы находятся в постоянном движении, и это движение проявляется и в пятнах, причем происходящие изменения пятен колос-
Рис. 90. Изменения солнечных пятен за одни сутки.
Черный кружок вверху дает понятие о размерах Земли в том же масштабе. 8*	Ш
сальны и по характеру и по масштабу. Обычно пятна появляются в виде маленьких черных точек (так называемых пор), постепенно увеличиваются, окружаются другими пятнами, дробятся на части, сливаются друг с другом, меняют свою форму и даже передвигаются по самой солнечной поверхности. Редкая группа пятен существует в течение 3—4 оборотов Солнца. Обычно они распадаются и исчезают, а на смену им появляются новые группы. В противоположность пятнам, факелы являются наиболее горячими участками поверхности. Гранулы следует рассматривать как облака раскаленных газов, плавающих в атмосфере Солнца. И факелы и гранулы также возникают, исчезают и непрерывно перемещаются над солнечной поверхностью.
§ 13* Периодичность солнечных пятен. Многолетние наблюдения над солнечными пятнами, подсчет их числа и площади показали существование периодичности солнечных пятен. После года, когда число и площадь пятен были наибольшими (год максимума солнечной деятельности), их количество и размеры уменьшаются все сильнее и сильнее и лет через 6 достигают минимума (год минимума солнечной деятельности). Затем снова начинается увеличение числа пятен, достигающее нового максимума, в среднем через 11 лет после первого (см. рис. 95). В начале каждого периода (цикла) солнечных пятен последние появляются далеко от солнечного экватора (но никогда не бывают в полярных областях) и постепенно спускаются к нему, где и исчезают. Благодаря существованию периодичности можно наперед предсказать, в каком году солнечных пятен будет больше всего или, наоборот, мало. Последний максимум пятен наблюдался в 1928 г., а следующий нужно ожидать около 1939 г. Периодичность солнечных пятен была открыта в 1851 г. любителем астрономии аптекарем Швабе.
§ 14.	Спектр и химический состав Солнца. Спектр Солнца состоит из непрерывного спектра, перерезанного темными, так называемыми фраунгоферовыми линиями (см. таблицу в конце книги). Это указывает, что раскаленная поверхность Солнца — фотосфера — окружена слоем менее горячих газов, вызывающих своим поглощением появление в спектре темных линий. Эти более холодные слои Солнца можно назвать его атмосферой. Благодаря поглощению света в толще этой атмосферы, если на нее смотреть в косом направлении, края Солнца кажутся темнее его центра. По измерениям положений фраунгоферо-вых линий удалось установить, каким химическим элементам они принадлежат, т. е. удалось установить химический состав паров и газов, составляющих солнечную атмосферу. Главные из этих элементов следующие: водород, натрий, кальций и железо. Каков состав внутренних частей Солнца, нам пока точно неизвестно.
Кроме фраунгоферовых линий, принадлежащих самому солнечному спектру, в нем наблюдаются еще некоторые так называемые теллурические (земные) темные линии, вызванные поглощением солнечного света в земной атмосфере. Главные из этих линий принадлежат кислороду, озону и водяному пару земной атмосферы.
§ 15.	Свет и теплота Солнца. Земля получает от Солнца огромное количество тепла и света. Так как Солнце находится очень далеко от Земли и излучает энергию во все стороны, то на Землю падает только ничтожная часть этой энергии. Можно поэтому себе представить, как 116
велика должна быть его температура, как много тепла и света оно посылает. Один квадратный сантиметр поверхности, выставленный на Солнце перпендикулярно к его лучам, получает за каждую минуту около одной малой калории тепла. Если учесть, что солнечное тепло предварительно поглощается земной атмосферой, то оказывается, что поверхность в 1 см2, перпендикулярная к солнечным лучам и помещенная на границе земной атмосферы, получает в минуту 1,93 малых калорий.—эта величина называется солнечной постоянной.
Зная величину солнечной постоянной, можно рассчитать температуру Солнца. То же можно сделать, пользуясь способами, описанными в § 7, а также и другими. Один из таких способов, примененный в Москве проф. Цераским, очень интересен. Проф. Цераский собирал при помощи
Облакообразные.
Языки пламени.
Смерчи.	Древовидные.
Рис. 91. Различные формы протуберанцев.
вогнутого зеркала солнечные лучи в одну точку. В этой точке, как показывают расчеты, температура должна быть не выше температуры Солнца. Оказалось, что все вещества, известные на Земле, будучи помещены в эту точку, моментально плавились. Совокупность результатов показывает, что температура Солнца составляет 6000°, считая от абсолютного нуля, и, следовательно, все вещества на Солнце должны находиться в раскаленном, газообразном состоянии.
Средняя плотность Солнца равна 1А» т. е. почти в Р/2 раза больше плотности воды. Это показывает, что в недрах Солнца газы, его составляющие, чрезвычайно сильно сжаты.
Общее количество энергии, испускаемой Солнцем, чрезвычайно велико, и составить о нем некоторое представление можно на основании следующего расчета. Если бы Солнце замерзло кругом на глубину 14 м.
117
излучаемого им тепла было бы достаточно, чтобы растопить всю эту кору в течение одной минуты.
§ 16.	Обращающий слой и хромосфера. Непосредственно к фотосфере прилегает тонкий слой более холодных газов, которые, поглощая свет, испускаемый фотосферой, вызывают появление темных фраунгофе-ровых линий на фоне яркого непрерывного спектра Солнца.
Рис, 91а. Изменения протуберанца*
Фотографии сделаны через промежутки в 10 минут. Белые кружки дают понятие о размерах Земли в масштабе рисунка.
Этот слой называется обращающим слоем. Он является нижним слоем солнечной атмосферы. Над обращающим слоем находится более обширный, вечно волнующийся слой — хромосфера, состоящая преимущественно из водорода и кальция. Плотность наружных слоев Солнца, в частности хромосферы, очень невелика и меньше плотности воздуха у земной поверхности. Обращающий слой и хромосфера раньше могли наблюдаться только во время полных солнечных затмений, когда непрозрачный диск Луны закрывает видимый диск Солнца — фотосферу. Тогда в момент полного затмения становятся (как бы в разрезе) видимы обращающий слой и хромосфера в виде розоватого кольца, окружающего солнечный диск. В этот момент спектр обращающего слоя наблюдается непосредственно в виде ярких линий на темном фоне, причем эти линии видны как раз в тех местах спектра, где в обычном солнечном спектре 118
находятся темные линии, т. е. линии обычного спектра Солнца как бы обращаются в яркие. Поэтому обращающий слой и получил свое название. Над поверхностью хромосферы тут и там высовываются огромные огненные языки, фонтаны раскаленных газов, выбрасываемых вверх с поверхности Солнца. Эти светящиеся выступы над солнечной поверхностью называются протуберанцами. Они поднимаются над поверхностью Солнца на громадную высоту, достигающую сотен тысяч километров (в десятки раз больше диаметра Земли), и бывают весьма разнообразной формы (рис. 91). Они испытывают непрерывные, быстрые и сильные изменения (рис. 91а). Протуберанцы состоят преимущественно из водорода и кальция, причем водородные протуберанцы претерпевают наиболее бурные изменения.
Рис. 92. Фотография солнечной короны.
Сделана во время полного солнечного затмения 19 июня 1936 г. в Куйбышевке (Дальневосточный край) экспедицией Государственного астрономического института им. П. К. Штернберга.
§ 17.	Солнечная корона. В моменты полных солнечных затмений вокруг Солнца на большом пространстве от него, над слоем хромосферы, наблюдается нежное жемчужное, серебристое сияние, вроде., ореола. Оно называется солнечной короной, которая в своих внутренних частях (внутренняя корона) вблизи солнечного края наиболее ярка. Более слабые лучи внешней короны простираются от него на градус и больше (рис. 92). Солнечная корона является внешней разреженной частью солнечной атмосферы» она состоит частично из газов, частично из мельчайших твердых частиц пыли. Вид солнечной короны меняется: в годы максимума солнечных пятен она имеет одну форму, в годы минимума—другую (рис. 92а).
119
§ 18.	Зодиакальный свет. Под этим названием известно слабое сияние в форме конуса, поднимающееся из-под горизонта перед наступлением рассвета или после окончания вечерних сумерек. Основание этого конуса ярче и находится на горизонте в стороне, ближайшей к Солнцу. Это показывает, что данное явление связано с Солнцем. Зодиа-
Рис. 92а. Изменения формы солнечной короны.
Левая часть рисунка — корона при минимуме пятен, правая — при максимуме пятен, средний рисунок — корона в промежуточную эпоху.
кальный свет, хорошо видимый в южных странах, вытягивается всегда
вдоль эклиптики по зодиакальным созвездиям, от чего и получил свое название. Повидимому, зодиакальный свет представляет наиболее внешние и разреженные, вытянутые вдоль эклиптики части солнечной атмосферы, которая ближе к Солнцу переходит в солнечную корону. Зодиакальный свет состоит, вероятно, из частиц пыли, сосредоточенных
преимущественно в плоскости эклиптики на огромном протяжении вокруг Солнца и освещаемых Солнцем, в то время как корона состоит из смеси пылинок и газовых молекул. Солнечная атмосфера в обычном смысле этого слова непосредственно прилегает к поверхности Солнца и состоит уже
исключительно из газов.
Рис. 93. Строение солнечной атмосферы.
§ 19.	Строение Солнца. Подводя итоги сказанному выше, мы можем представить себе строение Солнца следующим образом. Видимая поверхность Солнца — фотосфера — состоит из раскаленных паров и газов, нагретых до 6000°. В этой фотосфере появляются охлажденные места — воронкообразные углубления, своего
рода вихри солнечных газов, — это солнечные пятна. По мере приближения к центру Солнца давление, плотность и температура газов возрастают,
причем в самом центре последняя достигает, повидимому, нескольких десятков миллионов градусов. Солнечный шар, ограниченный фотосферой, окружен гигантской атмосферой — несколькими слоями газов меньшей плотности. Толщина этих слоев, их состав и расстояние от фотосферы
видны из следующей таблицы (см.
Обращающий слой 300 км Хромосфера до 20 000 км Протуберанцы до 250000 км Солнечная корона 2 000 000 км Зодиакальный свет>150000000 км
также рисунок 93):
Железо и другие элементы Водород, гелий, кальций, магний и др. Водород, гелий, кальций
Мелкая пыль н газы
Мелкая пыль
120
§ 20.	Наблюдение протуберанцев и короны вне затмений. В Обычное время протуберанцы и корона не видимы от того, что их мешает видеть яркий фон неба вблизи Солнца, создаваемый рассеянием его света молекулами воздуха. Если перед наступлением полного солнечного затмения навести на край Солнца касательно к его диску щель спектроскопа, то в момент полного затмения вместо обычного спектра с фраунгоферо-выми линиями мы увидим внезапное появление ярких линий на темном фоне. Таким образом, можно убедиться, что хромосфера излучает свет, дающий спектр, состоящий из ярких линий. Эти линии соответствуют тем газам, которые находятся в составе хромосферы. Если вне солнечного затмения щель спектроскопа поставить касательно к солнечному диску, то свет дневного неба, разлагаясь в непрерывный спектр, будет очень слаб. Между тем свет хромосферы, разлагаясь в спектр, сосредоточится в отдельных узких линиях, благодаря чему каждая из этих линий будет достаточно ярка. Если щель спектроскопа сделать настолько широкой, чтобы в нее поместилось все изображение какого-нибудь протуберанца, мы увидим яркие изображения этого протуберанца в тех же самых местах, где при узкой щели наблюдались узкие яркие линии. Действительно, в этом случае протуберанец сам как бы является щелью. Яркие изображения протуберанца будут видны в тех самых местах спектра, где находятся спектральные линии веществ, входящих в его состав. Применяя этот способ (изобретенный в 1868 г.), протуберанцы можно наблюдать ежедневно, а в последнее время их научились и фотографировать (рис. 91а и 93).
В 1931 г. была сделана удачная попытка изучать солнечную корону в любое время при помощи особых приемов (на высокогорных обсерваториях с крайне прозрачным воздухом).
Рис. 94. Спектрогелиограмма и соответствующая ей фотография Солнца.
§ 21.	Спектрогелиограф. И теория и практика показывают, что фраунго-феровы линии кажутся черными только вследствие контраста с прилегающим к ним ярким непрерывным спектром. В действительности в „темных* линиях солнечного спектра свет все-таки излучается, причем этот свет излучается только теми частями солнечной поверхности, в которых содержатся газы, в спектре которых имеется данная линия. Получим при помощи спектроскопа
121
спектр Солнца, а за спектром поставим ширму со щелью, приходящейся как раз на место какой-нибудь „темной*, например водородной линии спектра. Тогда за ширму будет проходить свет только через эту вторую щель, и притом свет, идущий только от нашей водородной линии. Поставив за ширмой фотографическую пластинку, мы получим на ней отпечаток, указывающий, каким образом водород располагается по тому узкому участку солнечной поверхности, который вырезается из солнечного диска первой щелью (щелью самого спектроскопа). Перемещая первую щель вдоль солнечного диска, оставляя вторую щель Неподвижной относительно спектра и двигая фотопластинку с той же скоростью, с какой движется первая щель, мы получим ряд прилегающих друг к другу фотографий узких участков поверхности Солнца. В конце концов, продвинув первую щель от одного края Солнца до другого, мы получим полную фотографию Солнца, показывающую, как над его поверхностью распределяется водород. Такой прибор называется спектрогелиографом, а получаемые при помощи него фотографии — спектрогелиограммами.
§ 22.	Спектрогелиограммы Солнца. С помощью спектрогелиограмм изучаются преимущественно распределение и движение в атмосфере Солнца водорода и паров кальция. Одна из таких спектрогелиограмм, полученная в лучах водорода, воспроизведена на рисунке 94. На „кальциевых* снимках видны темные продолговатые полоски, называемые волокнами, — это протуберанцы, проектирующиеся на солнечный диск. Как и протуберанцы, они испытывают сильные и быстрые изменения. На „водородных* спектрогелиограммах видно, как вокруг пятен массы водорода охвачены мощным вихревым движением.
§ 23.	Цикл солнечной деятельности и его связь с земными явлениями. Специальные Наблюдения показывают, что в солнечных пятнах существуют мощные магнитные поля. Эта магнитность солнечных пятен обнаруживает изменения с периодом в 22 года, т. е. вдвое большим периода солнечных пятен. Одиннадцатилетний период колебаний обнаруживают и другие явления на Солнце: число факелов, протуберанцев
Рис. 95. Связь между числом солнечных пятен и магнитными явлениями на Земле.
и т. п. В годы максимума пятен солнечная постоянная становится несколько больше, чем в годы минимума. Таким образом, вся солнечная деятельность в целом изменяется с периодом в 11 лет (вернее, с периодом в 22 года, если учитывать период изменения магнитного поля солнечных пятен).
Изучение явлений, протекающих в земной атмосфере, показывает у многих из них существование такой же периодичности в 11 лет. К ним т
относятся магнитные бури (колебания стрелки компаса), полярные сияния, грозы и др. (рис. 95). Число гроз и полярных сияний с наступлением максимума солнечной деятельности возрастает. Несомненно, характер деятельности Солнца должен влиять на климат Земли.
В нашем Союзе земледелие составляет видную отрасль народного хозяйства, и для проведения планового земледелия в крупных масштабах важно было бы иметь возможность предвидеть наступление жарких, засушливых или дождливых периодов, холодных зим и т. п. Иметь такую возможность было бы очень ценно и для ряда других областей хозяйственной жизни (в транспорте, строительстве и т. п.). Ученые Советского Союза — астрономы и метеорологи — совместно взялись за разрешение вопроса, — как солнечная деятельность влияет на погоду и как можно научиться заранее предвидеть наступление солнечных и связанных с ними земных явлений.
Мы видим в области изучения Солнца такое же единение теории и практики, как и в большинстве других областей астрономии. Мы видим снова, что Земля не является изолированным небесным телом и что движения ее атмосферы связаны взаимодействием с явлениями, протекающими на других небесных телах, главным образом с явлениями в атмосфере Солнца»
НАБЛЮДЕНИЯ.
Наблюдения Солнца удобно вести, проектируя его изображение с помощью трубы на белый экран или рассматривая его в трубу сквозь очень темное стекло. Изучите вид Солнца, найдите на нем пятна и сосчитайте их число. Обратите внимание, нет ли на Солнце факелов и заметна ли его грануляция, одинаково ли ярок весь его диск или он темнее к краям. Выбрав группу солнечных пятен, проследите ее видимое положение на диске в течение нескольких дней, чтобы убедиться в том, что Солнце вращается.
Выбрав характерную группу солнечных пятен, проследите за ней в течение 10—12 дней, аккуратно зарисовывая ее вид, — расположение пятен, их форму и относительные размеры. Сравнив потом свои рисунки, рассмотрите, какие изменения происходили с этой группой.
Задачи.
1.	Рассчитайте мощность, получаемую 1 м2 земной поверхности от Солнца.
2.	Последний максимум пятен был в 1938 г. Когда можно ожидать следующие два максимума?
3.	Высчитайте скорость движения протуберанцев, измерив на рисунке 91а положение протуберанца в разные моменты.
ГЛАВА III.
Луна и планеты»
§ 24.	Строение лунной поверхности. Поверхность Луны, спутника Земли, ее движение и физические условия на ней изучены лучше, чем у какого-либо другого небесного тела, благодаря тому, что она является наиболее близким к нам небесным телом. Это позволяет очень подробно изучать и особенности ее поверхности. Многие подробности лунной поверхности видны даже в сильный бинокль.
Уже простым глазом на диске Луны видны темные пятна, которые в XVII в. были названы морями. Это название сохранилось и до настоящего времени, хотя уже давно установлено, что на Луне воды нет
123
Рис. 96. Фотография участка лунной поверхности.
(Море Дождей; цирки Архимед, Аристилл, Автолик и Платон.)
(см. § 25). В телескоп бросается в глаза, что вся поверхность Луны крайне неровна — вся она как бы изрыта „оспинами* или гигантскими воронками всевозможных размеров. Эти ямы, эти воронки имеют круглую форму. На краях лунного диска они кажутся вытянутыми, но это есть следствие перспективы — мы смотрим на них не прямо сверху, а сбоку (см. карту Луны в конце книги). Наблюдая их в телескоп, легко распознать, что они представляют собой кольцеобразные горы (рис. 96). Бла-
годаря некоторому сходству их с кратерами земных вулканов им было дано название кратеров. Кратеры особенно большого размера называются цирками и достигают 250 км в диаметре. Дно кратеров и цирков довольно ровное, но горный вал, окружающий эти равнины в виде кольца, имеет очень сложное строение. Высота этих горных валов достигает нескольких километров. В действительности лунные кратеры очень мало похожи на обычные кратеры земных вулканов. Соотношения высоты горы и размера самого кратерного углубления у тех и у других совершенно различны (рис. 97). Горы, лежащие на лунном диске у границы
света и тени, называемой терминато-	0 10 20 км
рОМ, ОТбраСЫВаЮТ ДЛИННЫе Тени, ПО КО-	Тихо'
торым можно определить высоту гор.
Терминатор представляет границу дня и ночи, и в областях, лежащих вблизи него, на Луне наблюдается либо вое-	'
ход, либо заход Солнца. В полнолуние	L? ? М ?
земные наблюдатели смотрят на Луну	Везувий
с той же стороны, с которой на нее рис 97 профили лунного цирка светит Солнце, поэтому им не видны	и земного вулкана,
тени, отбрасываемые лунными горами, что лишает их возможности разобрать рельеф лунной поверхности.
В некоторых местах на поверхности Луны видны громадные горные
цепи, сходные с земными, и длинные трещины, пронизывающие ее кору. Если бы на Луне существовали разумные существа, возводящие искусственные сооружения вроде наших городов, мы бы это увидели, так как современные телескопы позволяют видеть на Луне образования размером в несколько сот метров.
При наблюдениях Луны в полнолуние бросаются в глаза светлые лучи, радиально расходящиеся от некоторых лунных цирков. Наиболее длинные лучи выходят из цирка Тихо (в южном полушарии Луны).
§ 25.	Физические условия на Луне. Физические условия на Луне очень своеобразны и резко отличны от земных. Сила тяжести на Лу-не в шесть раз меньше, чем на Земле, и потому человек мог бы, например, подпрыгнуть там в шесть раз выше, чем у нас. Это же обстоятельство послужило причиной того, что частицы воздуха и водяного пара отлетели от ее поверхности—Луна не могла их удержать около себя. Поэтому Луна лишена атмосферы, и в ее „морях" нет ни капли воды — это безводные, каменистые низменности.
Отсутствие на Луне атмосферы доказывается несколькими явлениями. Одно из них заключается в том, что при покрытиях звезд Луною они не гаснут постепенно, приближаясь к лунному краю, а скрываются за ним сразу. Если бы на Луне была атмосфера, звезды в этих случаях
125
постепенно гасли бы, приближаясь к ее краю, вследствие поглощения света лунным воздухом. Отсутствие у Луны атмосферы вызывает следующие явления: тени лунных гор черные и резкие; нет на Луне ни зари, ни сумерек; небо кажется совершенно черным, и на нем можно одновременно видеть Солнце, Землю и звезды (голубой цвет нашего неба, сумерки, зори и тому подобные явления вызываются рассеянием света частицами воздуха). На Луне никогда не бывает дождя, и мы никогда не видим над ее поверхностью облаков, или тумана.
Отсутствие атмосферы, смягчающей колебания температуры, и большая продолжительность дня и ночи вызывают на Луне резкие смены жары и холода. В течение 354-часового лунного дня почва накаляется до120°, а затем в течение 354-часовой ночи охлаждается до —160°. Нет никакого основания предполагать, чтобы условия на невидимой для нас половине Луны были отличны от условий на видимой для нас половине ее. При таких условиях органическая жизнь на Луне, повидимому, невозможна.
Удивительные формы многочисленных лунных гор, подобных которым на Земле мы почти не встречаем, несомненно, обязаны своим происхождением физическим условиям на Луне. Существуют два предположения. Эти горы могли возникнуть (подобно воронкам от взрыва снарядов) при падении на Луну больших камней (метеоритов), носящихся в межпланетном пространстве. Падая на Землю, такие камни не могли образовать больших воронок, так как их удары должны были смягчаться сопротивлением атмосферы. Если же иногда такие воронки и образовывались, то большинство из них не сохранилось благодаря разрушительному действию воды и ветра.
По другому предположению лунные цирки образовались благодаря усиленной вулканической деятельности в давно прошедшие времена. При некоторых условиях эта деятельность может проявляться не в форме извержений из кратеров конусообразных вулканов, а в форме излияний лавы через широкие отверстия, образующие лавовые озера. Согласно этой гипотезе лунные цирки следует рассматривать как озера застывшей лавы.
Каков вид противоположной части лунной поверхности мы совершенно не знаем, но имеем все основания полагать, что его характер тот же, что и у видимого нам полушария Луны»
§ 26.	Две группы больших планет. Планеты можно разделить на две весьма различные группы.
К первой принадлежат планеты типа Земли — Меркурий, Венера, Земля и Марс. Размеры их сравнительно невелики, они близки к Солнцу, плотность их велика и поверхность их твердая. Физические условия на некоторых из этих планет допускают существование органической жизни. Вероятно, эти планеты давно уже охладились, сжимаясь, и уже давно покрылись твердой корой.
Вторая группа планет — далекие от Солнца громадные небесные тела малой плотности, вероятно еще не отвердевшие и находящиеся в жидком или полужидком состоянии. Все они окружены гигантскими плотными атмосферами, совершенно скрывающими от нас поверхность этих планет. Эти планеты быстро вращаются около своей оси и потому сильно сплющились. К этим большим и массивным планетам принадлежат Юпитер, Сатурн, Уран и Нептун.
126
§ 27.	Меркурий и Венера. При наблюдениях в телескоп и Мерку-рай и Венера обнаруживают фазы, что придает им сходство с Луной, только на их поверхности не видно почти никаких подробностей.
Об этих планетах, вследствие их неблагоприятного положения для наблюдений, известно немного. Обе планеты, особенно Меркурий, близки к Солнцу и потому получают солнечного света и тепла гораздо больше, чем Земля. Ни у Меркурия, ни у Венеры нет спутников; Мер-курий, повидимому, лишен атмосферы, а время обращения его вокруг оси равняется времени его обращения вокруг Солнца. Таким образом, одна его половина постоянно обращена к Солнцу и чрезвычайно накалена, другая же находится во мраке вечной ночи и очень холодна.
Венера окутана густой облачной атмосферой, которая скрывает от нас ее поверхность. Поэтому нам неизвестно точно время ее вращения около оси. Может быть оно равно 6 или 20 с лишком суткам.
§ 28.	Земля и ее атмосфера. Земля обладает почти такими же размерами, как и Венера, и имеет спутника — Луну. Последняя сравнительно со своей планетой так велика, что Землю правильнее было бы назвать двойной планетой. Для Меркурия и Венеры Земля самая яркая из планет, видимых в ночное время. Для остальных планет Земля оказывается то утренней, то вечерней звездой, меняющей свои фазы, — она имеет в общем такой же вид, какой для нас имеет Венера. Наблюдателям, смотрящим на Землю в телескоп с других планет, должны быть видны океаны, сверкающие снега и льды, окружающие ее полюсы. Благодаря этому присутствие атмосферы, играющей огромную роль в жизни на Земле, сразу же могло бы быть обнаружено при наблюдении Земли из мирового пространства. Около половины поверхности Земли скрыто облаками, плавающими в ее атмосфере. Однако даже с ближайшей звезды Земля (так же как и все другие планеты) не была бы видима хотя бы в величайший из телескопов, подобных сооруженным на Земле, потому что звезды слишком от нее далеки.
§ 29.	Марс. После Венеры из больших планет Марс является ближайшим к нам небесным соседом, наблюдаемым, однако, в значительно более удобных условиях. Иногда он приближается к нам на расстояние всего в 55 млн. км. Такие сближения, называемые великими противостояниями, повторяются каждые 15 лет.
Марс вращается вокруг своей оси в течение 24 ч. 37 м. 23 с., так что его сутки всего на 37 м. 23 с. отличаются от земных. Ось планеты наклонена к плоскости его орбиты на 25° 10', так что на Марсе регулярно происходит смена времен года, и в этом отношении он очень похож на Землю.
Первое, что бросается в глаза при телескопических наблюдениях Марса, — это красноватый цвет большей части его поверхности. Именно благодаря этому обстоятельству для невооруженного глаза Марс представляется в виде светила красного цвета. Меньшую часть поверхности планеты занимают темные пятна, названные морями, в то время как красноватые области носят название суши. Как и в случае Луны, названия морей и материков на Марсе являются условными. Всего лучше на поверхности Марса бывают видны яркие белые пятна, расположенные на полюсах планеты. Они называются полярными шапками и, повидимому, состоят из снега, напоминая скопления льда и снега
127
у полюсов Земли. Подобно земным полярным шапкам они испытывают сезонные изменения в своих размерах (так как ось вращения Марса наклонена к плоскости его орбиты). Когда, например, на южном полушарии Марса зима, южная полярная шапка очень велика. С наступлением весны она тает — дробится и уменьшается в размерах (рис. 98). Вместе с тем вокруг полярной шапки образуется и распространяется темное окаймление.
Марс по диаметру вдвое меньше Земли. Он в Р/2 раза дальше от Солнца» чем Земля, и потому получает значительно меньше тепла и света. Марс окружен атмосферой гораздо более разреженной» чем земная» содержащей небольшое количество кислорода и водяного* пара, столь необходимых для существования органической жизни. Водяного пара в атмосфере Марса так мало (не более 5°/0 того, что наблюдается в атмосфере у поверхности Земли), что там никогда не бывает облаков, но изредка наблюдаются туманы. Содержание кислорода в единице объема атмосферы Марса по сравнению с земной атмосферой не превышает 15°/0. Вследствие разреженной и безоблачной атмосферы поверхность Марса, так же как и лунная, всегда доступна для наблюдений.
Неопытный глаз на диске Марса почти ничего не видит. Опытные же наблюдатели, работающие с большими телескопами, смогли постепенно изучить всю его поверхность и даже составили подробные карты Марса (рис. 99 и 100). Между прочим, оказалось, что окраска темных пятен, их густота и цвет также испытывают изменения, связанные с переменой марсианских времен года.
Во многих местах маленькие темные пятнышки на Марсе при наблюдении в небольшие телескопы сливаются для глаз в тонкие, нежные темные линии, которые были названы каналами.
Эти каналы не являются, однако, искусственными сооружениями жителей Марса, так как часть их является обманом зрения, а часть представляет в действительности не линии, а ряды неправильных мелких пягнышек.
Рис. 98. Изменения поляр- в самых теплых местностях Марса темной шапки Марса.
F	пература не превышает тепла, а в хо-
лодных доходит до —100°.
Есть ли на Марсе органическая жизнь мы не знаем, но вполне можем допустить ее существование, так как физические условия на этой планете похожи на земные, хотя они несравненно более суровы.
Предполагают, что красноватые места поверхности Марса являются песчаными пустынями, а „моря"—низменностями, в которых скопляется в небольших количествах влага, необходимая для развития раститель-128
Рис. 99. Вид Марса в большой телескоп (по рисунку Антониади).
ности. Возможно, что сезонные изменения в темных пятнах вызваны явлениями, подобными появлению и опаданию листвы на деревьях в наших земных условиях. Больших гор на Марсе нет, и вся его поверхность довольно ровная. Повидимому, Марс является стареющей планетой, развитие которой зашло уже далеко. Мы можем себе представить физическое состояние Марса промежуточным между состоянием Луны и состоянием Земли. Различные данные позволяют предполагать, что с течением времени поверхность Земли тоже станет ровной и лишенной воды.
Марс имеет двух спутников—Деймоса и Фобоса (в переводе с греческого на русский —* Страх и Ужас). Эти луны Марса крайне малы и сравнительно слабо освещают его ночи. Фобос, диаметр которого не больше 20—30 км, находится от
поверхности Марса в 36 раз ближе, чем Луна от Земли, и обращается вокруг своей планеты в течение 7 ч. 30 м., т. е. скорее, чем сам Марс вращается вокруг своей оси. Поэтому он восходит на западе и заходит на востоке.
Рис. 100. Карта поверхности Марса.
9
Асгрономкя
129
Рис. 101. Вид Юпитера в телескоп.
§ 30.	Юпитер — самая большая из планет солнечной системы: в 1312 раз больше Земли по объему и в 317 раз больше ее по своей массе. Уже в небольшую астрономическую трубу видны темные полосы облаков, вытянутые вдоль экватора планеты (рис. 101). Заметив какое-нибудь из пятен в этих полосах, находящихся в обширной и плотной атмосфере планеты, уже через час можно убедиться в том, что Юпитер быстро вращается вокруг своей оси. Вследствие быстрого вращения Юпитер сжался
у полюсов, его сжатие составляет 1|1в и хорошо заметно в телескоп. Юпитер вращается не как твердое тело — как и у Солнца его экваториальные области вращаются быстрее (9 ч. 50 м.), чем полярные (9 ч. 59 м.).
У Юпитера одиннадцать спутников, из которых четыре самых больших видны даже в шестикратный бинокль, а в телескоп легко следить за их обращениями около планеты.
§ 31.	Сатурн. Сатурн несколько меньше Юпитера и очень похож на него по своему строению. Он точно так же окружен густым облачным покровом, сквозь который поверхность планеты видеть нельзя. Облака на Сатурне, как и на Юпитере, вытягиваются полосами вдоль экватора, но рассмотреть эти полосы очень трудно. Замечательна малая средняя плотность Сатурна, которая составляет всего лишь 0,7 плотности воды. Вследствие быстрого вращения вокруг своей оси (101/а часов) Сатурн сплюснулся у полюсов еще сильнее, чем Юпитер.
Замечательно широкое плоское кольцо, опоясывающее планету в плоскости ее экватора (рис. 102). В кольце можно заметить темные промежутки или щели. Доказано, что кольцо Сатурна не сплошное, а состоит из бесчисленного множества небольших частиц, которые подобно спутникам обращаются около планеты по законам Кеплера. Этих частиц так много и они так близки друг к другу, что на том расстоянии, с которого мы на них смотрим, они сливаются в сплошное светящееся кольцо. В зависимости от наклона оси вращения Сатурна относительно Земли, который периодически изменяется, меняется вид кольца. Когда мы на него смотрим с ребра, то оно, будучи крайне тонким, не видно. Иногда же кольцо Сатурна бывает повернуто к нам так, что мы его видим, как говорят, в наибольшем раскрытии.
Вокруг Сатурна обращается девять спутников^ из которых один (Титан) бывает видим в небольшие телескопы.
130
Рис. 102. Вид Сатурна в телескоп.
§ 32.	Уран» Нептун и Плутон. Уран и Нептун являются довольно большими планетами, похожими на Юпитер. Они также окружены плотными атмосферами, в которых облака вытягиваются полосами, параллельными экватору нланет. Они также сильно сжаты и вращаются вокруг оси очень быстро — Уран в течение 10,7 часа, Нептун в течение 16 часов. Наблюдать их даже в сильные телескопы очень трудно, так как они очень далеки и от Солнца и от Земли. Уран обладает четырьмя спутниками, а Нептун — одним.
Все большие планеты — от Юпитера до Нептуна,—повидимому, еще не затвердели, и органическая жизнь на них едва ли возможна. Быть
может, эти планеты еще йе вполне
остыли и состоят из расплавленной жидкости.
Плутон, открытый в 1930 г., повидимому, меньше Земли и даже в самые сильные телескопы виден с трудом в виде слабой звездочки без заметного диска.
§ 33.	Астероиды. Малые планеты, или астероиды, обращающиеся вокруг Солнца между орбитами Марса и Юпитера, очень многочисленны. Каждый год их открывается несколько десятков, а всего их известно
Рис. 103. Орбиты малых планет Амура и 1932 НА.
уже более 1600. Диаметр самой боль-
шой из них — Цереры—составляет всего 770 км, а диаметры боль-
шинства из них измеряются несколькими километрами.
9*
131
Орбиты малых планет крайне разнообразны. У некоторых из них наклон к эклиптике и вытянутость орбиты очень велики. Особенно замечательны в этом отношении малые планеты Эрот и Амур, орбиты которых, благодаря большой вытянутости, пересекают орбиту Марса. Иногда эти планеты подходят к Земле значительно ближе, чем Марс (рис. 103), и тем дают возможность точнее определить величину солнечного параллакса.
За последнее время обнаружены астероиды, орбиты которых пересекают орбиты Земли и Венеры, как, например, планета, обозначенная 1932 НА. Одна из них (Гермес) может приближаться к Земле почти так же близко, как Луна,
ГЛАВА IV.
Кометы и метеоры.
§ 34. Вид комет и его изменения. Кометами называются время от времени появляющиеся на небе светила своеобразного и изменчивого вида1: когда комета далека от Солнца, она имеет вид слабого туманного пятнышка с расплывчатыми очертаниями; приближаясь к Солнцу, комета
Рис. 104. Слабая (телескопическая) комета.
становится более яркой, постепенно выбрасывая светящийся хвост, всегда направленный в сторону, противоположную Солнцу.
Солнце отталкивает частицы, находящиеся в кометном хвосте. Причина этого отталкивания будет объяснена в § 36. Размеры кометных хвостов бывают громадны; они часто охватывают на небе по нескольку десятков градусов, а в пространстве тянутся на десятки и даже сотни миллионов километров. На фотографиях комет (рис. 104 и 105) звезды выходят в виде черточек оттого,
что кометы передвигаются среди звезд, а фотографическая камера во время фотографирования перемещается за кометой. В голове кометы, в самой яркой ее части, наблюдается обычно некоторое уплотнение — ядро кометы. Каждый год открывается по нескольку комет, но большинство из них видно только в те
лескоп.
§ 35. Орбиты комет. Яркие кометы, имеющие длинные хвосты, появляются неожиданно. Их орбиты имеют большое сходство с параболами (рис. 106). Огибая Солнце, эти кометы снова уходят в межзвездное пространство и, по крайней мере, некоторые из них, вероятно, никогда больше не возвращаются в пределы солнечной системы.
Часть комет, большинство которых не видно для невооруженного глаза, движется по не особенно вытянутым эллипсам и периодически приближается к Солнцу. Такие кометы называются периодическими.
1 Комета в переводе с греческого означает «косматая звезда*. 132
Большие полуоси кометных орбит очень разнообразны, а эксцентриситеты значительно больше эксцентриситетов планетных орбит.
Самый короткий период обращения (3,3 года) имеет комета Энке: ее приближение к Солнцу наблюдалось 32 раза. Широко известна также яркая комета Галлея, имеющая период обращения, равный 75 годам. Последний раз она приближалась к Солнцу и наблюдалась в 1910 г.
§ 36. Физическая природа комет. Спектроскопические наблюдения комет показывают, что кометы состоят из крайне разреженных газов — окиси углерода (угарного газа СО) и циана. Свечение этих
газов вызывается действием ультрафиолетовых солнечных лучей. Возможно, что в хвостах некоторых комет присутствуют мельчайшие частицы пыли, светящие отраженным солнечным светом. Особенно подробно природа комет изучалась русскими учеными. Несколько комет было открыто советскими астрономами. Хвосты комет бывают иногда прямыми, иногда несколько изогнутыми. Как доказал русский астроном Бредихин, хвост кометы тем прямее, чем больше отталкивательная сила Солнца, действующая на частицы, по сравнению с силой солнечного притяжения.
Известно, что лучи света производят давление на освещенные ими тела. Величина этого давления, обнаруженного на опыте русским физиком Лебедевым и теоретически предсказанного английским физиком Максвеллом, зависит от величины освещаемых тел. На крупные частички пыли это давление заметно не действует, а на мелкие оно действует заметно и может в несколько раз превышать силу тяготения. Таким образом, давление солнечных лучей на газовые частички, выделяющиеся из кометного ядра по мере его приближения к Солнцу и нагревания, заставляет их удаляться от него с большой скоростью и образовывать кометный хвост. Возможно, что в образовании кометных хвостов играет роль и электрическое отталкивание, так как газовые частички в кометах заряжены электричеством. Некото
рые кометы обладают несколькими хвостами, и это показывает, что в их состав входят частицы с разным зарядом и различных размеров.
Твердая часть кометного ядра, вероятно, ничтожна по размерам и состоит, повидимому, из скопища камней или глыб, разделенных друг от друга промежутками. Масса комет ничтожно мала и не превышает масс небольших астероидов.
Рис. 105. Комета Морхауза.
133
§ 37. Метеоры. Метеоры, или падающие звезды, лучше всего наблюдаются в безлунные ночи, особенно осенью в поздние часы. Пролетая по небу, они производят впечатление, как будто упала звезда. В некоторые ночи, например 10 и И августа, таких падающих звезд наблюдается очень много, по нескольку десятков в 1 час. Если видимые пути метеоров по небу мысленно продолжить назад, то оказывается, что некоторые из них пересекаются почти в одной точке. Эта точка называется радиантом (рис. 107). Радиант есть перспективное явление, когда рой метеоров (поток) движется в атмосфере по одному направлению.
В действительности метеоры не имеют ничего общего со звездами. Это явление вызывается крошечными камешками, несущимися с большой скоростью в межпланетном пространстве и при встрече с Землей проникающими в ее атмосферу. Влетая в атмосферу со скоростью от 10 до 200 км в секунду, они от взаимодействия /	с молекулами воздуха накаляются и затем
ъсЗ/	распыляются, не достигая поверхности Зем-
ли, на высотах порядка 80—150 км* В спек-тре метеоров наблюдаются раскаленные ________________________________паРы тех веи*еств, из которых состоит метеорная частица (железо, кремний, каль-ций и др.). Температура их около 2—3 ________________X- тыс. градусов. Иногда после полета ме-J теоров ненадолго остается туманная по* лоска — это метеорный след.
§ 38. Распад комет и метеоры. Есть
\	основания предполагать, что метеорные
\	частички являются продуктом распада
комет. Замечено, что периодические коме-
\	ты по мере своих последовательных возвра-
Рис. 106. Различные формы щений к Солнцу становятся менее яркими.
орбит.	Некоторые из них обнаружили дробле-
ние, т. е. наблюдалось, как комета постепенно распадалась на несколько частей. Наиболее замечательна была в этом отношении комета Биэлы. После ее распадения на две части в 1846 г. комету еще видели при ее следующем возвращении к Солнцу в 1852 г., но с тех пор комета исчезла. В ноябре 1872 г., когда Земля пересекла орбиту этой кометы, внезапно наблюдался целый дождь падающих звезд, наблюдавшийся ежегодно в ноябре и в дальнейшем, но только уже не столь обильный. Когда по положению радианта ноябрьских метеоров был вычислен путь метеоров в пространстве, оказалось, что они движутся сплошным роем или потоком по такой же орбите, по какой двигалась раньше комета Биэлы. Повидимому, комета Биэлы окончательно распалась на части, превратившись в маленькие камешки, наблюдаемые при встрече с Землей в виде метеоров. Такое же сходство обнаруживается между орбитами некоторых комет и орбитами некоторых потоков метеорных частиц. Рой метеорных частиц постепенно растягивается по орбите, а сама орбита вследствие возмущений планетами иногда отклоняется от орбиты Земли, и потому некоторые богатые метеорные потоки с течением времени ослабевают или прекращаются, так как Земля уже перестает встречаться с этими метеорными частицами.
134
Рис. 107. Радиант метеоров.
§ 39. Болиды и метеориты. Гораздо реже наблюдаются очень крупные метеоры, или огненные шары, называемые болидами. Они происходят от проникновения в земную атмосферу метеорных тел значительного размера, появляющихся также из межпланетного пространства. Благодаря большим размерам они распыляются не так скоро, как маленькие метеоры, пролетают больший путь и погасают гораздо ниже, на высоте 30—60 км. Еще более крупные метеорные тела, опускаясь еще ниже в более плотные слои атмосферы, теряют от сопротивления воздуха свою огромную скорость (в среднем на высоте 20—25 км) и падают на землю в виде твердых и почти остывших каменных (реже железных) масс. Рассекая воздух с большой скоростью, летящее метеорное тело в атмосфере вызывает звуковую волну, воспринимаемую ухом как громовой удар с раскатами. Эти звуки становятся слышными в том случае, когда высота полета не превосходит 50—55 км. Упавшие на землю метеорные тела называются метеоритами. Их собирают и хранят в музеях.
По своему составу метеориты бывают двух типов — каменные и железные. Размеры метеоритов очень разнообразны. Самый большой из них, найденный в 1931 г. в Южной Африке, весит 70 т. Иногда наблюдаются целые дожди из падающих камней — это происходит от дробления метеорита в атмосфере. Ныне известно около 1000 падений метеоритов.
Метеориты являются, может быть, самыми крупными осколками распавшихся комет или осколками каких-либо других небесных тел. В них найдены все те же химические элементы, какие известны на Земле, но иногда в других комбинациях.
135
В нашей стране упавший метеорит является собственностью государства и подлежит сдаче его в научное учреждение.
В 1908 г. в сибирской тайге около реки Подкаменной Тунгузки упал гигантский метеорит, произведший своим падением большие разрушения в лесу. Экспедиции Академии наук СССР исследуют место падения, чтобы выкопать этот метеорит, который, повидимому, является крупнейшим в мире.
§ 40. Возможно ли столкновение Земли с кометой? Церковники часто пугают народ, предсказывая конец мира при солнечном затмении или угрожая столкновением Земли с кометой. Вычисления показывают, что такое столкновение чрезвычайно мало вероятно. Случайное столкновение может произойти один раз в 80 млн. лет.
Что же, однако, произойдет в результате такого столкновения? Если комета „заденет* своим хвостом Землю, то разреженные газы кометного хвоста даже не смогут проникнуть в плотные слои земной атмосферы. Мы даже не заметим, что Земля находится в хвосте кометы. Такие случаи уже бывали и не влекли за собой никаких особенных последствий. Если случится еще менее вероятное столкновение Земли с самим ядром кометы, то скорее всего будет наблюдаться только обильный дождь метеоров и, может быть, произойдет выпадение большого количества метеоритов, не угрожающее, во всяком случае, нанести сколько-нибудь заметный ущерб жизни на Земле.
Таким образом, комет не следует бояться-—это „безобидные*, хотя и большие по размерам, небесные светила.
Появление комет не имеет, конечно, никакого отношения к земным событиям: войнам и т. п., как это думали раньше. Современная наука не только разрушает все предрассудки, связанные с появлением комет, но уже после нескольких дней наблюдения появившейся кометы позволяет наперед вычислить весь ее. дальнейший путь в пределах солнечной системы.
НАБЛЮДЕНИЯ.
1.	Располагая телескопом или сильным биноклем, изучите поверхность Луны; Проследите, как меняется длина теней лунных гор по мере удаления от терминатора к краю Луны. Выберите какую-нибудь характерную небольшую местность на Луне и зарисуйте ее вид. Повторите зарисовку этой местности на следующий день и сравните рисунки, заметив, как меняется рисунок вида местности в зависимости от ее освещения Солнцем. Заметьте, как от одного дня к другому перемещается граница тени по лунной поверхности. В полнолуние обратите внимание на светлые лучи, выходящие из цирка Тихо в южном полушарии Луны.
2.	Пользуясь телескопом, изучите вид тех планет, которые по своему положению доступны для наблюдений: Венера, Марс, Юпитер и Сатурн. Зарисуйте вид Венеры. Найдите около Юпитера его главных спутников. Зарисуйте полосы на диске Юпитера и убедитесь в его быстром вращении вокруг оси, заметив перемещение какого-нибудь пятна по его диску в течение часа. Обратите внимание на сжатие Юпитера. Зарисуйте расположение спутников Юпитера и, повторив наблюдение и рисунок, часа через два посмотрите, заметно ли за это время передвинулись спутники.
3.	Пронаблюдайте в течение нескольких часов какой-нибудь метеорный поток в ту ночь, когда по данным постоянной части „Астрономического календаря* число принадлежащих к нему метеоров ожидается особенно большим. Сосчитайте число метеоров в час и нанесите их путь на копию, снятую со звездной карты. Определите, из какого созвездия вылетают эти метеоры — где их радиант. Попробуйте оценить яркость метеоров в звездных величинах и длину их пути в градусах; наблюдения занесите в журнал.
Задачи.
1.	Сколько бы весил (на пружинных весах) человек, попавший на Луну?
2.	Могут ли наблюдаться на Луне восход и заход Земли?
3.	Если скорость движения ракеты для межпланетных путешествий будет 11 км1сек> сколько времени понадобится, чтобы долететь до Луны? до Марса? 136
4.	Рассчитайте, во сколько раз угловой диаметр Венеры, видимый с Земли во время нижнего соединения, больше, чем во время верхнего соединения.
о. Сколько марсианских суток длится марсианский год?
6.	Считая, что человеческий глаз еще может различить детали, видимые под углом 4', вычислите в километрах размер наименьших деталей, видимых на Марсе в телескоп с увеличением в 600 раз (во время противостояния Марса).
7.	Во сколько раз Меркурий и Плутон получают больше или меньше тепла и света от Солнца, нежели Земля?
8.	Каков угловой диаметр Солнца, видимый с Нептуна?
9.	У орбиты кометы Энке большая полуось составляет 2,22 астрономической единицы и эксцентриситет 0,847. Начертите орбиту этой кометы и определите по чертежу ее расстояние от Солнца в перигелии и в афелии.
10.	Как можно доказать, что в действительности звезды с неба не падают?
11.	Как спектр кометы может дать ответ на вопрос, есть ли в ее составе твердые пылинки?
12.	Какая разница между метеором, болидом и метеоритом?
ГЛАВА V.
Звездная вселенная.
§ 41.	Методы изучения звезд. Изучение звездной вселенной совре-менная астрономия выполняет теми же методами, как и изучение Солнца и планет, но в применении этих методов к звездам есть некоторые особенности. Многочисленность звезд вынуждает применять эти методы так, чтобы получать сразу данные для значительного числа объектов. Незначительность видимой яркости звезд заставляет делать инструменты для их изучения с большими объективами или зеркалами, которые, захватывая широкий пучок света, идущий от звезд, дают возможность рассмотреть или сфотографировать даже очень слабые по яркости звезды (рис. 108). При изучении туманностей применяют светосильные объективы, дающие яркое изображение поверхностей фотографируемых светил.
При изучении звездной вселенной широко применяется фотография, благодаря которой на пластинке получаются изображения большого числа звезд. Измеряя негативы, можно определить взаимное положение звезд, относительную яркость и если перед объективом поставлена призма, то и спектр.
При рассматривании звезд в трубу можно сравнивать яркости звезд, но при этом нередко получается другое отношение яркостей, чем при изучении звездных фотографий. Это происходит оттого, что глаз чело* века наиболее чувствителен к желто-зеленой части спектра, фотографи» ческая же пластинка — к сине-фиолетовой.
Если при наблюдении глазом две звезды представляются одинаково яркими, но одна из них белая, а другая красноватая, то на фотографии изображение красноватой звезды получится меньшим кружочком, чем белой, и, исследуя негатив, мы придем к выводу, что эти звезды неодинаково ярки. Соотношение яркостей, получаемое по фотографиям звезд, рассчитанное в звездных величинах, оказывается не таким, как для глаза, и называется фотографическим, в отличие от визуального, воспринимаемого глазом.
Для исследования фотографий звезд в астрономических обсерваториях имеются специальные приборы, дающие возможность измерять с большой точностью взаимное положение звезд, их яркость и спектр.
Звездное небо, уже знакомое вам по наблюдениям невооруженным глазом и с небольшими инструментами, оказывается значительно более разнообразным и по качеству и по числу наблюдаемых объектов при
137
Рис. 108. Величайший в мире телескоп с зеркалом диаметром в 2^ м (100 дюймов) на горе Вильсона в США.
наблюдении и фотографировании современными гигантскими инструментами. Светила, наблюдаемые в обсерваториях, по внешнему виду подразделяются на такие группы: звезды, неправильные туманности (клочкообразные), планетарные туманности, скопления звезд неправильные и шарообразные, туманности вытянутой, шарообразной и спиральной формы, Млечный Путь.
Изучение спектров этих светил показывает, что все они имеют химический состав, подобный той материи, которую мы изучаем в лабораториях на Земле. Известно, что материя находится в постоянном движении и смене форм, и мы имеем полное основание предполагать, что все разнообразие светил вселенной есть результат этого вечного движения, что мы одновременно видим материю в разных стадиях ее развития. Научные исследования доказывают правильность этих предположений, 138
В древности, когда только еще началось знакомство со звездным небом, наиболее доступным было изучение положения светил на небе, и лишь развитие оптики дало возможность исследовать физическое строение светил и углубить знания о туманностях, звездных скоплениях и Млечном Пути.
Исследования звездной вселенной начаты сравнительно недавно. Начало этим исследованиям было положено Вильямом Гершелем в конце XVIII в. Гершель с самого начала своих работ наметил новый для его времени путь исследования вселенной. Считаясь с громадным числом звезд на небе, он понял невозможность подробного исследования распределения всех звезд и вместо этого предпочел путь массового изучения отдельных участков неба с последующим сравнением между собой результатов статистических подсчетов. Современная астрономия дала блестящее подтверждение правильности избранного Гершелем пути и, пользуясь математикой, расширила и углубила егб способы. Так, пользуясь даже самыми простыми способами подсчетов, Гершель еще в конце XVIII в. наметил в основных чертах верную кар-тину
Современная астрономия эту карти-ну не только расширила, уточнила и распространила на громадные расстоя-ния, но и изучила физическое строе- Рис> 109. Сравнительная яркость ние звезд.	звезд четырех смежных звездных
§ 42.	Число и яркости звезд. Чис-	величин.
ло звезд, наблюдаемых и фотографируемых в современные телескопы, значительно превышает то, которое мы видим невооруженным глазом. Вспомним, что при первом же знакомстве с небом мы разбирали способ обозначения их яркости с помощью звездных величин.
Звездная величина есть ступень яркости, соответствующая ее изменению в 2,512 раза (число, логарифм которого равен 0,400).
Таким образом, обозначая звездную величину звезды, имеющей яркость буквой mv а яркость и звездную величину звезды, избранной стандартом, /0 и /и0, получаем формулу:
Если принять /0 за единицу и прологарифмировать формулу, то получим другую, более удобную для вычислений:
1g Л °,4 Ио—^i)-
Если в листе картона прорезать четыре кружка следующих диаметров: 2, 3, 5 и 8 мм, закрыть с обратной стороны листком полупрозрачной бумаги и смотреть на них, осветив Их сзади и отойдя от них так далеко, чтобы они представлялись светлыми точками, то они будут неодинаковой яркости. При таком подборе диаметров разница в яркости между каждыми двумя последовательными кружками будет близко соответствовать одной звездной величине. На рисунке 109 изображены 4 таких кружка, смежные площади которых относятся между собой, как число 2,5 относится к 1.
Так как соотношения яркости могут быть очень разнообразны, то звездные величины считают не только в целых единицах, но и в долях 139
единицы. Например, если отношение яркостей двух звезд равно 10, то разница в их звездных величинах будет 2,5. Если светило ярче, чем звезда нулевой величины, то его яркость выражается отрицательной звездной величиной. Например, яркость Сириуса равна минус 1,6 звездной величины (—1,6 звездной величины). Для быст-
Рис. ПО. Вильям Гершель (1738—1822).
рого перечисления разности звездных величин в отношения яркостей и обратно удобнее всего вычислить таблицу и по ней построить график.
Наблюдения в астрономические трубы дают возможность измерять яркости слабых звезд. Определение яркости выполнено для очень многих звезд. Наиболее обширный в настоящее время каталог Гарвардской обсерватории (в Америке) включает точно измеренные яркости всех звезд до 71/т величины и многих более слабых.
В § 6 приведены числа звезд первых шести величин. Они дают число звезд от самых ярких до 1,5 звездной величины (1-й звездной величины), потом от 1,5 звездной величины до 2,5 звездной величины и т. д.
Общее число звезд до 20-й звездной величины получено статистическими методами. Для этого сосчитывалось число звезд различной яркости на небольших участках в разных местах неба, а отсюда выводилось среднее число звезд на 1 квадратный градус.
После этого было вычислено общее число звезд на всем небе.
Однако, не подсчитывая всех звезд той или иной звездной величины, возможно сделать это на многих небольших участках неба и отсюда вывести среднее число звезд определенной яркости на 1 квадратный градус небесной сферы, а затем получить приблизительно общее число звезд этой яркости для всего неба.
По таким наблюдениям получена следующая таблица:
Построив график зависимости числа звезд от яркости или вычислив отношение последующего числа к предыдущему, можно убедиться, что нарастание числа звезд с увеличением звездной величины идет все медленнее и медленнее. Отсюда можно естественно сделать заключение, что число звезд ограничено. Однако современные исследования показывают, что эта кажущаяся ограниченность
Звездная величина	Полное число звезд на небе	Звездная величина	Полное число звезд на небе
До 5-й	2134	До 13-й	5 700 000
9 6-й	6974	, 14-й	13800 000
, 7<й	14 300	, 15-й	32 000 000
, 8-й	41 300	, 16-й	70800000
, 9-й	117 000	, 17-й	148 700 000
, 10-й	324 000	, 18-й	296 000000
, 11-й	868 000	, 19-й	560 000000
, 12-й	2 260000 1	. 20-й	1000 000000
происходит от поглощения света очень разреженной материей, находящейся повсюду между звездами и потому ослабляющей свет, идущий
от наиболее далеких из них.
140
§ 43.	Параллаксы звезд» Звезды находятся от нас на различных расстояниях. Определение расстояний до звезд основано на измерении их параллаксов. Измерение параллаксов производится при помощи угломерных инструментов или путем фотографирования с последующим измерением полученных негативов.
Вычисление расстояния, как мы видели в первой части этой книги, ведется таким же способом, как и по измерениям экваториального параллакса, только основанием (базисом) треугольника является радиус земной орбиты.
Параллаксы звезд весьма малы, они не превышают нескольких десятых долей секунды; отсюда легко высчитать, что расстояния до звезд очень велики, и их неудобно выражать не только в километрах, но и в „астрономических единицах*. В качестве примера можно указать на одну из ближайших звезд, расстояние до которой составляет около 273 тыс. астрономических единиц.
Для выражения звездных расстояний в настоящее время приняты два способа. Первый способ, установившийся уже давно, состоит в том, что единицей считают расстояние, проходимое светом за 1 год. Так как скорость света равна 300 тыс. км) сек, то в этих единицах даже звездные расстояния выражаются небольшими числами. Эта единица полу* чила название светового года.
Второй способ, введенный сравнительно недавно, состоит в том, что за единицу считают расстояние, соответствующее годичному параллаксу в 1 секунду. Меньшему параллаксу, т. е. большему расстоянию соответствует и большее число таких единиц. Эта новая единица получила название парсек (сокращение слов „параллакс в секунду*).
Соотношение между единицами длины в астрономии
Единицы длины	Километр	Астрономическая единица	Световой год	Парсек
Километр		1	—	—	—
Астрономическая единица • •	149,5 «10е	1	——	—
Световой год 		9,56.1012	6,3.10*	1	0,307
Парсек		3,1-1018	206 265	3,26	1
В настоящее время определены параллаксы свыше 6000 звезд. Из этого числа 123 находятся от нас на расстоянии, меньшем, чем 10 парсеков.
Некоторые звезды с известным параллаксом.
„Ближайшая" Центавра.................0",760 rfc 0",006
а Центавра...........................0 ,756 zt 0 ,003
а Большого Пса	(Сириус)............ 0 ,379 * 0 ,004
т Кита...........,.....................0,315*0,009
а Малого Пса (Процион)...............0 ,310 * 0 ,006
а Орла (Альтаир).....................0 ,204 * 0 ,004
а Лиры (Вега)........................0 ,124*0 ,010
а Возничего (Капелла)................0 ,063 *0 ,002
а Орион (Бетельгейзе)................0 ,012*0 ,004
1 В этой таблице для краткости числа, состоящие из единицы с нулями, изображаются соответствующей степенью 10, например: 10= 101, 100= 102. 1000000= 106.
141
В этой таблице число со знаком + показывает возможные ошибки определений. Из таблицы видно, с какой высокой точностью делаются современные определения малых углов, а следовательно, и расстояний.
Кроме уже описанного способа определения звездных растояний по величине годичных параллаксов современная астрономия разработала и применяет также и другие способы, с которыми мы познакомимся в § 44.
§ 44.	Видимая и абсолютная яркости звезд. Так как звезды находятся от нас на различных расстояниях, то наблюдаемые соотношения их яркости не соответствуют действительным. Но если известны расстояния до некоторых звезд, то уже есть возможность рассчитать истинное отношение яркостей этих звезд, принимая во внимание закон ослабления яркости пропорционально квадрату расстояния.
Представьте себе, что все звезды, находящиеся от нас на разных расстояниях, передвинулись и все оказались на одинаковом расстоянии; сравнив при этих новых условиях звездные величины всех этих звезд, мы сможем определить соотношения их действительных яркостей.
Таким образом, для звезд, расстояния до которых удалось определить, можно сравнить их истинную яркость, вычислив ее для одного и того же расстояния, как это обычно делается, например, для расстояния в 2 062 650 большего, чем расстояние Солнца от Земли (10 парсеков).
Для всех звезд, параллаксы которых известны, можно, пользуясь формулой	у Г2
7Г=^°’
вычислить их яркость, приведя их к одному расстоянию. В этой формуле I есть видимая яркость звезды, /0 — яркость, которую она имела бы, если бы находилась от нас на расстоянии 10 парсеков, г — расстояние до звезды и г0=1О парсекам. Вычисленную абсолютную яркость /0 можно перевести в звездные величины. Звездная величина, которую имела бы данная звезда, если бы она находилась на расстоянии в 10 парсеков, называется абсолютной звездной величиной.
Когда для многих звезд были определены тригонометрические параллаксы и вычислены по ним абсолютные яркости, то астрономам удалось установить зависимость между видом спектральных линий и абсолютной звездной величиной.
Знание этой зависимости в настоящее время позволяет по наблюдению звездных спектров вычислять абсолютную величину звезд.
Сопоставляя видимую и абсолютную яркости, астрономы вычисляют и расстояния звезд, пользуясь для этого приведенной выше формулой.
Таким образом, по абсолютным и по наблюдаемым звездным величинам можно вычислить расстояние до любой далекой звезды, лишь бы она была доступна спектральному исследованию.
§ 45.	Млечный Путь. Светлая полоса, проходящая по всему небу и называемая Млечным Путем, при рассматривании в сильный телескоп или фотографировании, оказывается состоящей из миллиардов слабых по яркости звезд, неодинаково густо рассеянных в различных его частях (рис. 111). Если рассматривать Млечный Путь невооруженным глазом, то он представляется клочковатым, с местными сгущениями и как бы отдельными завитками и облаками. Наблюдения как южной, так и северной половин неба показывают, что Млечный Путь тянется 142
Рис. 111. Фотография участка Млечного Пути.
непрерывной полосой через всю поверхность небесной сферы. На рисунках 112 и ИЗ изображены северная и южная половины неба и отмечен Млечный Путь, а также места нахождения звездных скоплений и туманностей.
Рассматривая эти рисунки, вы видите, что Млечный Путь делит все небо на две приблизительно равные части. Рисунки изображают всю небесную сферу, разделенную по линии небесного экватора; но небесную сферу можно разрезать на равные части и многими другими способами. Наиболее удобно для рассмотрения строения звездного мира провести эту линию по середине полосы Млечного Пути.
Таким образом, получается своеобразный экватор небесной сферы — его называют линией Галактики (Галактика — звездная система, образуемая звездами Млечного Пути).
Линия Галактики имеет большое значение для изучения расположения различных небесных объектов и исследования движений звезд.
143
Рис. 112. Млечный Путь в южном полушарии.
Точками отмечены туманности, крестиками — звездные скопления.
§ 46.	Видимое распределение звезд. Мы уже говорили, что В. Гершель положил начало массовому исследованию вселенной путем подсчета числа звезд, видимых на разных участках неба. Эти подсчеты показали неравномерное распределение звезд и их большую густоту в областях
Среднее число звезд на 1 квадратном градусе.
Звезде ая величина	Угловое расстояние от линии Галактики		
	0° |	I 30°	1 80°
До 5-й	0,045	0,022	0,013
. 9-й	2,8	1,3	0,75
. 15-й	910	270	92
. 21-й	74 000	8700	1800
неба, близких к Млечному Пути. Подсчеты Гершеля были повторены с лучшими наблюдательными средствами современными нам учеными и показали подробности строения Млечного Пути.
Подсчет числа звезд на одинаковых площадках неба вдали от Млечного Пути и вблизи ясно показывает, что, чем слабее звезды, тем они более сгущены близ линии Галактики. Это видно из таблицы слева.
244
Рис. 113. Млечный Путь в северном полушарии.
Точками отмечены туманности, крестиками — звездные скопления.
§ 47.	Движения звезд. Долгое время звезды считались неподвижными, а их взаимное расположение — неизменным; однако современные точные определения положения звезд показывают, что очень многие из них обнаруживают движения, незаметные для глаза, но измеримые точными инструментами. Собственным движением называется угловое перемещение звезды по небесной сфере за один год. Накапливаясь в течение веков, эти движения могут стать заметными и ощутительно изменить вид неба (рис. 114).
Собственные движения, выраженные в дуговой мере, показывают лишь кажущееся движение по небесной сфере, но не дают знания истинного движения небесных объектов. Если такой объект достаточно ярок, то, исследуя его спектр, можно определить его передвижение по отношению к наблюдателю и выразить величину перемещения в километрах. Эта скорость движения звезды имеет то же направление, что и луч зрения, направленный на звезду. Такую скорость называют лучевой. Если для какой-нибудь звезды известны и лучевая скорость, и 10 Астрономия	145
собственное движение по небу, выраженное в угловой мере, и, наконец,
ее расстояние, то возможно рассчитать скорость и направление движения
звезды в пространстве.
Собственные движения звезд очень малы: наиболее быстрая „летящая звезда Барнарда* перемещается по небу на угловое расстояние, равное видимому диаметру Луны, лишь за 180 лет. Все другие звезды передвигаются еще медленнее. За последнее время собственные движения звезд благодаря точности наблюдений удалось обнаружить у многих звезд. Это и неудивительно: во вселенной все тела находятся в движении, мы же
замечаем только те движения, которые доступны нашим инструментам.
Рис. 114. Движение звезд в созвездии Большой Медведицы.
Верхняя часть рисунка — вид созвездия 50 тыс. дет назад, середина —в настоящее время, нижняя часть рисунка — через 50 тыс. лет.
Большое число изученных движений звезд дало возможность разобраться в характере этих движений.
Исследование собственного движения звезд показало, что, хотя отдельные звезды движутся по самым разнообразным направлениям, в общем в одной половине неба звезды как бы расходятся во все стороны от одной точки на небесной сфере, находящейся на границе созвездия Лиры и Геркулеса, и, наоборот, сходятся к прямо противоположной точке. Отсюда астрономы пришли к выводу, что сама наша солнечная система движется в пространстве по направлению к созвездию Лиры. Скорость движения нашей солнечной системы равна 20 гсм^ек.
Чтобы уяснить себе идею способа определения направления движения солнечной системы, представьте себе, что вы идете по
лесу: тогда деревья в том направлении, куда вы идете, будут все время как бы отодвигаться одно от другого, в противоположном же направлении будет наблюдаться об
ратное явление.
Помимо этого общего движения звезд — отраженного движения нашей солнечной системы — у некоторых групп звезд обнаружены еще и другие преимущественные движения, направленные к каким-нибудь определенным точкам на небе. Наличие этих движений показывает, что целые группы звезд, отделенные друг от друга громадными расстояниями, представляют собой системы звезд, имеющие общее движение. Замечательно, что направления общих движений по большей части параллельны линии Галактики.
§ 48.	Туманности. Туманности, которые представляются глазу, вооруженному небольшим телескопом, светлыми маленькими пятнами на темном фоне неба, при рассматривании в более мощные телескопы или при их фотографировании оказываются весьма разнообразного вида.
140
Если вы посмотрите на рисунки 112 и ИЗ, то легко заметите, что туманности вообще расположены или близ линии Галактики или, наобо-
рот, вдали от нее.
Как оказывается, близ линии Галактики видны главным образом неправильные и планетарные туманности (рис. 115 и 116), вдали же от этой линии — главным образом спиральные (рис. 117) или вытянутые (наподобие двояковыпуклой чечевицы, которую рассматривают с ребра) и шарообразные.
Туманности первой группы называются галактическими. Они делятся на газовые и пылевые туманности. К этой же группе следует отнести и темные туманности.
Галактические туманности (за исключением темных) при исследовании их в телескоп представляются в виде светящегося вещества. Спектроскопические исследования показывают, что эти туманности состоят из разреженных газов кислорода, азота, углерода, затем гелия и водорода.
Темные туманности, выделяющиеся на звездном фоне неба своей полной чернотой и неправильной формой, представляют собой облака космической пыли, поглощающей свет находящихся за ними звезд. Некоторые светлые туманности также состоят из очень мелкой пыли и светят отраженным светом соседних звезд.
Внегалактические туманности (рис. 117) при изучении с помощью фотографии обнаруживают звездное строение: они состоят, 10*
Рис. 115. Фотография большой туманности в Орионе.
Рис. 116. Фотография планетарной туманности в Водолее.
147
подобно Млечному Пути, из отдельных звезд, причем спектроскопическое исследование показывает у них звездные спектры. Видимая форма туманности спиральная, или веретенообразная, зависит от того, как расположена по отношению к нам данная туманность.
Две группы туманностей различаются и по своим расстояниям от нас. Галактические туманности находятся сравнительно недалеко: на расстояниях в сотни или тысячи световых лет, между тем как внегалактические — на расстояниях в миллионы световых лет.
Новейшие исследования туманностей наиболее сильными телескопами показывают, что внегалактические туманности рассеяны по всей вселенной. Отсутствие их близ линии Галактики объясняется тем, что в этом направлении разреженная межзвездная материя производит значительное поглощение света и скрывает от нас эти туманности.
§ 49. Звездные скопления. Звездные скопления при фотографировании большими телескопами ясно обнаруживают звездное строение и увеличение числа звезд к середине (рис. 118); такие скопления называют шарообразными. Другой тип звездных скоплений— это рассеянные или неправильные (например Плеяды) и другие (рис. 119).
Звездные скопления разбро-
_	„	саны по небу неравномерно;
Р“С- "’•XT&.3S0’ t,““' большинство их находится близ Млечного Пути.
Звездные скопления как шарообразные, так и рассеянные видны в областях неба, близких к линии Галактики, причем больше всего их оказывается в областях созвездий Стрельца и Скорпиона. Расстояния до шарообразных звездных скоплений очень велики, они выражаются в десятках тысяч световых лет. Расстояния до рассеянных звездных скоплений значительно меньше.
Туманности и звездные скопления перечислены в „Новом генеральном каталоге* (составленном Дрейером), номерами которого они обозначаются; ийогда звездные скопления обозначают номерами каталога, составленного астрономом Мессье. В первом случае перед номером пишется символ NGC, ар втором — фамилия Мессье. Например звездное скопление в Геркулесе обозначают или Мессье 13. (сокращенно М 13), или NGC 6205.
§ 50.	Строение вселенной. Имея данные о расстояниях и видимом распределении звезд, туманностей и звездных скоплений, мы можем составить себе представление о строении нашей звездной вселенной.
118
Если обратить внимание на распределение по небу перечисленных выше небесных объектов, то легко заметить, что с линией Галактики связаны: распределение звезд, галактических туманностей и звездных скоплений, направление движения звезд, места появления так называемых новых звезд.
Не связаны с линией Галактики только внегалактические туманности.
Распределение звезд показывает, что огромное скопление звезд, в котором мы находимся, не шарообразно; наибольшая густота звезд приходится около линии Галактики. Если бы мы издалека посмотрели на наш звездный мир, то увидели бы его в форме двояковыпуклой чечевицы, внутренность которой заполнена звездами.
Рис. 118. Фотография шарообразного звездного скопления в Геркулесе.
Рис. 119. Фотография рассеянного звездного скопления в Возничем.
Если мы мысленно разрежем эту чечевицу по наибольшему из ее сечений, то получим плоскость, которую мы называем плоскостью Галактики. Таким образом, звезды Млечного Пути составляют основную часть нашей звездной системы, представляющей собой чечевицеобразное скопление звезд.
Теперь мы можем сделать следующий шаг и спросить себя, равномерно ли распределены звезды в самой плоскости Галактики. Ответ на этот вопрос мы можем почерпнуть из наблюдений густоты звезд в Млечном Пути. Наблюдения обнаруживают его неравномерную густоту.
Мы не имеем основания думать, что наша Галактика единственная во вселенной, и поэтому, желая выяснить строение нашей звездной системы, мы можем предположить, что в пространстве имеются похожие группы — скопления звезд. Сходства мы должны искать, конечно, с теми объектами, которые не связаны с Галактикой. Такими объектами являются внегалактические туманности, состоящие из звезд, сплющенные также наподобие чечевицы и имеющие в своих завитках отдельные сгущения.
149
Поэтому мы приходим к выводу, что наш Млечный Путь как звездная система, вероятно, не что иное, как спиральная туманность, внутри которой находится наша солнечная система и которую мы поэтому видим изнутри.
На рисунке 117 изображена спиральная туманность, на которую, как надо думать, похожа наша Галактика. Если вы проведете прямые линии по разным направлениям из ее средней части, то увидите, что по одним направлениям эти линии пересекут сравнительно негустые ее части, а по другим, наоборот, — очень густые и широкие. Диаметр Галактики около 30 000 парсеков. Наша солнечная система находится в средней части Галактики, но не в ее центре.
Звездные скопления находятся на границах Галактики, рассеянные же скопления находятся внутри Галактики, так же как и галактические туманности.
Если мы представим себе, что все небесные тела в ближайших к нам частях звездной вселенной обращены в равномерно плотную материю и она распределена по всему этому пространству, то средняя плотность ее будет невелика — менее чем 0,00005 mz на 1 км3.
Изучение собственных движений звезд показывает, что направление этих движений в среднем параллельно плоскости Млечного Пути.
Современные исследования звездных движений приводят к выводу, что звезды Галактики составляют вращающуюся систему.
Поэтому Галактику мы в настоящее время представляем себе находящейся в общем вращении. Каждая звезда, в том числе и наша солнечная система, участвует в этом общем вращении, происходящем в плоскости Галактики. Период обращения солнечной системы составляет 250 млн. лет, а его расстояние от центра вращения — центра Галактики (расположенного по направлению к созвездию Стрельца) — 10 000 парсеков.
Подобное же вращение подмечено и у некоторых спиральных туманностей.
Применение разнообразных способов дало возможность определить расстояние до различных небесных тел. В приводимой ниже таблице даны эти расстояния.
Наиболее близкая звезда . . . Галактические туманности . . Рассеянные скопления . . . . Шарообразные скопления . . . Внегалактические туманности .
Расстояния в парсеках 1,3 100—10000 40— 4000 5000— 60 000 250000 и больше
Диаметры в парсеках
0,01 — 10
5
25 10000—30 000
Ход этих чисел, а также наличие на небе внегалактических туманностей показывают, что наша Галактика, при всей громадности ее размеров, — лишь одна из многих звездных систем, рассеянных на громадных расстояниях друг от друга в бесконечном пространстве вселенной. За последнее время с помощью сильнейших телескопов и фотографий обнаружены в пространстве целые группы внегалактических туманностей очень малого углового диаметра (рис. 120). Это показывает, что они удалены от нас на громадные расстояния. Улучшение техники построения инструментов и усовершенствование способов наблюдения дают нам 150
Рис. 120. Фотография группы спиральных туманностей в Пегасе, возможность еще дальше изучать вселенную, но никогда не покажут нам конца ее, так как вселенная бесконечна.
Мы рассмотрели строение и движение в звездной системе; теперь перейдем к рассмотрению физических особенностей самих звезд, обусловленных вечно движущейся материей, из которой состоит вся вселенная.
§ 51.	Цвета и спектры звезд. При самых первоначальных наблюдениях уже обнаруживается, что звезды различаются между собой не только яркостью, но и цветом, например а Лиры, Ориона — белые, а Волопаса—оранжевая, а Тельца — красная.
Точные наблюдения показывают, что этот цвет звезд, ясно обнаруживаемый глазом лишь для небольшого числа звезд, присущ всем этим светилам.
Наблюдения показывают, что определенному цвету соответствует и определенный характер спектра: у белых звезд заметны все семь цветов спектра, у красных звезд ослаблен фиолетовый конец и более ярок красный. Это разнообразие цветов и спектров звезд особенно ясно выступает при массовом исследовании звезд с помощью камеры с призмой перед объективом (рис. 121).
Спектры белых звезд перерезаны небольшим числом линий поглощения. Спектры желтых звезд имеют большее число линий поглощения, и притом фиолетовый их конец слабее по яркости. Спектры красных звезд содержат много линий поглощения, сгущающихся в некоторых местах спектра в полосы; яркость фиолетового конца спектра очень слаба.
В спектрах белых звезд имеются линии поглощения водорода и гелия, линий металлов немного; в спектрах желтых звезд особенно много линий металлов и водорода; в спектрах красных звезд линии металлов еще заметнее, чем у желтых звезд, и при этом имеются линии поглощения 151
титана и его соединений. По положению линий поглощения можно определить состав атмосфер звезд.
Как и в случае Солнца, линии, видимые в спектре звезды, зависят не только от ее химического состава, но и от ее температуры.
Здесь перечислены только основные типы спектров, между ними есть, конечно, переходные типы. Все спектры звезд распределены на 8 классов, которые по международному соглашению обозначаются большими буквами латинского алфавита (рис. 122):
Белые Желтые Красные
О, В, A F, G, К М, N
Особенности цвета и спектра наводят на мысль, что звезды не вечно остаются одинаковыми, и, наблюдая их, мы видим различные стадии единого процесса развития звезд, подобно тому как, видя толпу людей
Рис. 121. Негатив фотографии звездных спектров, полученной с помощью объективной призмы (буквами отмечены типичные спектры).
всех возрастов — от младенцев до стариков, — мы имеем перед глазами стадии человеческого возраста.
§ 52.	Температуры звезд. Для звезд, как и для Солнца, по исследованию спектра можно определить температуру поверхности, измеряя положение в спектре наиболее яркой его части.
Как и следовало ожидать, белые звезды оказались наиболее горячими, с температурами от 10 000° до 25 000°, а красные — наиболее холодными, с температурой около 3000°; температура желтых звезд оказывается промежуточной— около 6000°.
Чтобы пополнить весь материал, имеющий значение для познания физических процессов в звездах, нам нужно еще изучить некоторые особые виды звезд.
Это даст нам возможность построить общую картину эволюции
звезд, уже намечающуюся по данным о их спектре и температуре.
§ 53.	Двойные звезды. Визу а л ь н о-д войными звез
дами принято называть такие две звезды» которые кажутся настолько близко расположенными одна к другой» что они не могут быть видимы раздельно иначе» как при помощи астрономической трубы. Когда при наблюдениях таких звезд стали производить точное измерение их взаимного положения, то обнаружилось, что иногда одна из звезд, составляющих двойную звезду, обращается вокруг другой, при-152
В A F G КМ
Рис. 122. Классы звездных спектров.
чем период обращения составляет годы, а иногда и столетия. Отсюда ясно, что некоторые двойные звезды в действительности расположены близко на небе и представляют собой систему двух солнц, причем меньшее обращается около большего по закону тяготения Ньютона (рис. 123). Такие двойные звезды называют физическими парами, в отличие от оптических, ничем между собой не связанных и находящихся на разных расстояниях от Земли. Двойные звезды при наблюдениях
153
одна по массе на 24% больше
Рис. 123. Орбита двойной звезды (Т Девы).
нередко представляются резко различающимися по цвету, но по большей части это явление оптического обмана (цветового контраста).
Звезды, составляющие физические пары, совершают свои движения по закону тяготения. Поэтому по движению двойных звезд возможно сделать расчеты формы и расположения их орбит, а если известен параллакс, то и размера орбит. Кроме того, применение закона Ньютона дает возможность вычислить отношение их масс и сравнить их с массой Солнца.
Массы двойных звезд находятся в самых различных соотношениях. Есть двойные звезды, массы которых почти равны между собой. Ближайшая к нам звезда а Центавра состоит из трех звезд: одна из них несколько массивнее Солнца (на 14%), другая несколько менее массивна (97% массы Солнца), третья же очень мала по яркости сравнительно с первыми двумя. Ее масса пока неизвестна. Но имеются и другие соотношения: так, например, звезда а Малого Пса состоит из двух, причем лица, масса же другой составляет всего 39% массы Солнца. Время обращения этих звезд очень различно: есть звезды с обращением в несколько десятков лет и есть такие, которые заканчивают один оборот в сотни лет.
Кроме визуально-двойных звезд существуют еще так называемые спектрально-двойные звез-д ы, т. е. такие, которые, обращаясь друг около друга, даже в сильные телескопы сливаются вместе, не разделяясь на две отдельные звезды.
Благодаря тому, что каждая из этих очень близких друг к другу звезд имеет собственный спектр, мы наблюдаем сложный спектр, состоящий из этих двух наложенных друг на друга спектров. Однако при своем орбитальном движении друг около друга одна из звезд временно приближается к Земле, а другая в это же время удаляется от Земли. Вследствие этого, согласно правилу Доп
плера, темные линии в спектрах этих звезд смещаются, но в противоположные стороны. Когда обе звезды движутся по своим орбитам перпендикулярно к тому направлению, по которому мы на них смотрим, они обе ни приближаются к нам ни удаляются от нас, и каждые две темные линии, принадлежащие наложенным друг на друга спектрам двух звезд, сливаются в одну линию. Понятно, что период раздвоения линий в спектре таких спектрально-двойных звезд равен периоду их обращения друг около друга.
§ 54. Переменные звезды. Переменными звездами названы такие, у которых замечены колебания яркости. Наблюдения изменения яркости переменных звезд чаще всего производятся путем сравнения их с соседними звездами, обладающими постоянной яркостью. Из таких наблюдений получается материал в виде таблицы, в которой отмечены время наблюдения и яркость переменной звезды. Построение графика по такой таблице показывает, что у многих переменных звезд в изменениях яркости имеется закономерность^ проявляющаяся в том, 154
что через определенные промежутки времени» называемые периодом» изменения яркости повторяются» и кривая этих изменений по общему виду остается такой же, как и в предыдущий период. Изучение кривых яркости и периодов показало, что все переменные можно разделить на несколько групп по признакам периода или вида кривой. Основные группы названы по тем звездам, которые являются наиболее типичными
их представителями.
§ 55. Затменные звезды. Переменные типа Ал го л я названы так по звезде 0 Персея (Алголь), которая меняет cboIo яркость в течение небольшого промежутка времени, оставаясь более долгое время неизменной по яркости.
Звезды типа [5 Лиры названы по звезде Лиры, которая все время плавно меняет свою яркость, причем имеет два минимума яркости: один сильнее, другой слабее (рис. 124). Сравнение кривых обоих типов показывает в них нечто общее: в том и в другом случаях звезда гаснет не надолго, и кри-
вая изменения яркости совершенно оди- рИСф ^24. Кривая изменения ярко-накова до и после минимума. Подобную сти переменной звезды ₽ Лиры же кривую яркости можно получить (площади кружков пропорциональ-во время солнечного затмения, опре- ны ЯРКОСТИ звезды).
деляя общую яркость Солнца. Есте-
ственно предположить подобное же явление и в случае переменных типа Алголя и $ Лиры, тем более, что эти звезды оказывается в то
Рис. 125. Схема, поясняющая изменение блеска звезды типа Алголя.
(Положения В2 и В4 соответствуют началу и концу затмения, В3 — его середине, В6 соответствует середине затмения звезды В звездою Д.)
же время спектрально-двойными, причем период обращения их друг около друга равен периоду изменения яркости.
В силу этого звезды типов Алголя и р Лиры называют затменными звездами. Из наблюдений и построенной по ним кривой яркости можно вычислить отношение размеров и взаимное положение главной звезды и затмевающего ее спутника (рис. 125). Различие кривых объясняется тем, что в звездах типа р Лиры спутник и главная звезда вытянуты по направлению линии, соединяющей их центры или даже, может быть, представляют собой как бы слившуюся двойную звезду. Таких звезд на небе известно более 800, причем большинство из них принадлежит к типу Алголя. Изменения яркости этих переменных невелики (от одной до двух звездных величин), а периоды по преиму-
ществу короткие (от долей суток до 5 суток); немногие звезды имеют периоды больше 5 суток.
155
§ 56.	Цефеиды и долгопериодические переменные звезды. Переменные типа цефеид названы по звезде S Цефея, кривая яркости которой имеет своеобразный вид с быстрым подъемом и медленным падением яркости (рис. 126). Периоды этих звезд очень разнообразны, а изменения яркости достигают двух звездных величин. Для этих звезд подмечена очень существенная особенность, заключающаяся в том, что периоды их находятся в зависимости от абсолютной яркости, так что, зная период звезды, можно вычислить и абсолютную яркость ее, а зна
чит и расстояние, на котором она находится.
Это имеет большое значение для определения расстояний до тех звездных систем, в которых есть цефеиды. Если, например, в отдаленной туманности обнаруживают цефеиды, то, определив их периоды, вычисляют и их абсолютные яркости. Сопоставив эту абсолютную яркость с наблюдаемой видимой яркостью, вычисляют расстояние до туманности. Расстояния до туманностей и звездных скоплений определены именно таким способом.
Рис. 126. Кривая изменения яркости цефеиды.
знания их природы, и дальнейшие наблюдения в этой обла-помочь углубить и пополнить теорию эволюции звезд.
указанных типов переменных звезд существуют и такие, закономерность изменений не найдена или же эти звезды
Долгопериодические переменные звезды изменяются по яркости очень сильно — на 4—5 звездных величин, и периоды изменений их доходят до двух лет, а по большей части бывают порядка 300 суток. Как периоды таких звезд, так и кривые яркости бывают не вполне постоянны.
Наиболее замечательная звезда этой группы— это о Кита, названная еще в древности „ Удивительной “. Изменения ее яркости так велики, что она то бывает видна невооруженным глазом (2-й звездной величины), то становится невидимой даже в небольшие трубы (10-й звездной величины). Почти все звезды этой группы красноватые.
Объяснения изменения яркости этих групп
звезд носят более предположительный характер, чем в случае затменных звезд. Предполагается, что изменения в яркости цефеид могут быть обусловлены периодическим расширением и сжатием звезды. Изменение яркости долгопериодических звезд может иметь аналогичное объяснение. Наблюдение переменности звезд дает, таким образом, новые материалы для сти могут Кроме у которых представляют как бы переходный вид от одной группы к другой. Общее число открытых переменных звезд к началу 1938 г. было уже около 6500, но с каждым годом открываются все новые переменные. Можно думать, что переменность яркости связана с эволюцией звезд, что за время своего существования всякая звезда проходит стадию переменности.
§ 57.	Новые звезды. Иногда на небе неожиданно вспыхивают звезды, которые поэтому называют новыми. Новые звезды ярче 2-й звездной величины в максимуме яркости появляются не часто, в среднем около трех за одно столетие, и при этом преимущественно в областях неба, близких к Млечному Пути. Благодаря фотографии открытия новых звезд за 156
последней время стали более часты. При своем появлении новые звезды бывают иногда очень ярки, но скоро яркость их уменьшается с периодическими колебаниями, и, наконец, звезда становится очень слабой по яркости — она ослабевает на 11 звездных величин в среднем. До появления новой звезды по каталогам звезд или по фотографиям иногда обнаруживали существование слабой звездочки на том месте, где появилась новая звезда. Поэтому ясно, что новая звезда — это своеобразная переменная, яркость которой сразу увеличивается, звезда „загорается", а потом, постепенно уменьшаясь, возвращается к прежней яркости.
Исследования последнего времени показывают, что, повидимому, в таких звездах в процессе их эволюции происходит скачок, обусловленный нарастанием противоречивых процессов: строение такой звезды делается неустойчивым. Взрываясь, она выделяет огромное количество световой энергии, после чего ее строение совершенно меняется, и температура становится гораздо выше.
§ 58.	Связь между абсолютными звездными величинами и спектрами. При сравнении абсолютных звездных величин с типом спектра звезд обнаружилось очень интересное и важное обстоятельство: красные звезды оказались или очень яркими или очень слабыми, желтые звезды— менее отличающимися по абсолютной яркости и, наконец, белые звезды— с наименьшими различиями в яркости. Кроме того, по подсчетам на звездном небе красных звезд в общем оказывается больше, чем белых, но многие из них очень слабы по своей видимой яркости.
В окружающем нас мире мы наблюдаем непрерывные изменения, мы знаем, что на поверхности Земли все меняется стечением времени, что материя меняет свои формы. Невероятно было бы предполагать, что изменения форм материи не вызывают в свою очередь и изменений в состоянии звезд.
Так как разница в цвете соответствует разнице температур, то можно думать, что мы наблюдаем звезды в различных стадиях их существования, которые отмечаются переходом от более высокой температуры к более низкой с одновременным изменением цвета.
Понижение температуры в газообразных телах может происходить или при расширении таких тел (работа расширения происходит за счет теплоты тела) или вследствие отдачи тепла в окружающее пространство, если газ не сжимается. При сжатии газовый шар будет разогреваться.
§ 59.	Эволюция звезд. Эти соображения и послужили для объяснения странного на первый взгляд факта, что низкие температуры свойственны и очень ярким и очень слабым звездам. Если мы представим себе, что звезды образуются путем сгущения, вещества в мировом пространстве, то в то время как эта материя, собравшись в громадный шар, станет сжиматься, температура сначала будет еще невысока, газовый шар будет светиться красноватым светом, и так как он очень велик, то общая яркость его тоже будет велика. В дальнейшем газовый шар продолжает сжиматься, и его поверхность разогревается, цвет становится желтым, но Яркость не меняется, так как уменьшение размеров возмещается увеличением яркости каждой единицы поверхности. Эти последовательные изменения доводят звезду до белого свечения и высокой температуры.
Такое состояние оказывается для звезды критическим. В дальнейшем приток тепла из недр звезда пррцс^рдит б&&ее ^ддедно и не возме-157
щает охлаждения звезды вследствие излучения ею тепла в мировое пространство (по всей вероятности, помимо сжатия в недрах звезд существуют еще другие источники энергии, но какое физическое явление лежит в основе их, пока еще неизвестно).
Белый газовый шар, усиленно излучая тепло в окружающее пространство, станет охлаждаться, переходить от белого цвета через желтый к красному и, наконец перестанет светиться — станет невидим для отдаленных наблюдателей. Красная громадная звезда к концу своего существования обратится в небольшую красную звезду, а потом — в темное тело.
За многие миллиарды лет вследствие действия причин, обусловленных самим существованием и свойствами материи, происходят непрерывные изменения звезды. Эти изменения совершаются не все время в сторону увеличения яркости и температуры звезды. То самое сжатие, которое сначала вызывает повышение температуры, доводит звезду до такого состояния, что начинается обратный процесс, приводящий звезду опять к охлаждению и отсутствию свечения. Таким образом, разогревание звездного шара уже в самом себе содержит причину и обратного процесса, начинающегося после достижения наивысшей для данной звезды температуры.
§ 60.	Звезды-гиганты и звезды-карлики. Так как для довольно большого числа звезд уже известны абсолютные яркости, то можно высчитать, во сколько раз ббльшая красная звезда должна превышать, по размерам меньшую. Такого рода вычисления показали, что яркие красные звезды имеют диаметры, в сотни раз ббльшие, чем слабые по яркости красные звезды. Поэтому абсолютно яркие красные звезды стали называть звездами-гигантами, а маленькие красные — звездами-карликами. Например, по сравнению с нашим Солнцем звезда а Ориона больше его по диаметру в 300 раз.
В следующей ниже таблице приведены размеры звезд-гигантов и звезд-карликов, полученные по вычислениям:
Название	Яркость сравнительно с Солнцем	Диаметр сравнительно с Солнцем	Спектральный класс
Р Центавра		3100	11	В
а Лиры		50	2,4	А
а Возничего		150	12	G
Солнце			1	1	G
а Волопаса		100	30	К
а Тельца		90	60	К
а Ориона		1200	290	М
а Скорпиона .			3400	480	М
Крюгер 60 ... • ...	0,003	%	М
Звезда Барнарда ....	0,0004	2/б	М
Эта таблица показывает, что наше Солнце по своим размерам и яркости отнюдь не принадлежит к звездам-гигантам и относится к звездам-карликам. Во всяком случае оно уже перешло через наибольшую свою яркость, постепенно сжимаясь и угасая, дошло до звезд класса G (желтых) и имеет сравнительно небольшой диаметр. Так как общая теория эволюции звезд применима и к Солнцу, мы можем сказать, что в будущем оно станет красным карликом.
Теория звезд-гигантов и карликов получила подтверждение, когда оказалось возможным измерить видимые диаметры некоторых звезд, а после 158
этого, зная их расстояния, вычислить и истинные. Такие измерения применены еще к немногим звездам, так как они возможны лишь с наибольшим из существующих телескопов и требуют помимо сильной трубы еще и особого очень сложного прибора — интерферометра.
Измерения, сделанные с наибольшим в мире телескопом (обсерватории на горе Вильсона в Калифорнии) в соединении с интерферометром, показали, что яркие красные звезды действительно громадных размеров. Вот таблица, дающая результаты измерений углового диаметра d некоторых звезд, а также их параллаксы р и вычисленные отсюда линейные диаметры £>, причем за единицу принят диаметр Солнца.
d	р	D
а Ориона........... О",047	0",017	300
а Скорпиона ....	0,040	0,0095	450
а Тельца........... 0 ,020	0,057	38
а Волопаса.........	0 ,020	0 ,080	27
Из таблицы видно, что определенные из наблюдений размеры звезд-гигантов достаточно хорошо согласуются с теоретическими расчетами.
Для тех двойных звезд, расстояние до которых удалось определить, возможно и определение их массы. Оказывается, что массы звезд в общем, за некоторыми исключениями, содержатся в пределах от 1/J0 до 10 масс Солнца. Сопоставим эти числа с данными о диаметрах звезд и примем во внимание, что объемы звезд относятся, как кубы их диаметров. Тогда оказывается, что при небольшом сравнительно разнообразии масс крайние величины объемов колеблются приблизительно от 0,001 до 108 (если объем Солнца принять за единицу). Это показывает, что плотности звезд очень сильно различаются: красные гиганты имеют ничтожно малые плотности (меньше плотности воздуха), а красные карлики, наоборот, обладают большей плотностью, чем Солнце.
Известно несколько удивительных звезд — белых карликов, выделившихся, быть может, по особым причинам из обычного эволюционного ряда. У этих звезд температура высока (около 8000°), а плотность исключительно велика: например,^ спутника Сириуса плотность вещества 34 000 г)см3 (его вещество состоит из атомов с оторванными электронами).
Продолжительность переходов звезд от одного типа к другому очень велика и измеряется биллионами лет.
§ 61.	Итоги изучения строения вселенной. Выше уже было указано, что установлено наличие целых групп внегалактических туманностей — галактик, еле заметных даже на фотографиях, полученных сильнейшими современными инструментами.
Это указывает на то, что вселенная простирается бесконечно далеко, и основная форма развития ее частей есть спиральная звездная система.
Вспомним путь, который прошло человечество к этому познанию: сначала — представление о плоской Земле и шарообразного неба над ней, будто бы приводимого в движение волею таинственного и чудесного божества; следующая стадия познания — отказ от этой теории и представление о Солнце как о центре системы планет; далее — представление о группе звезд, среди которой Солнце лишь одна из рядовых и неярких звезд; наконец — современное представление о системах галактик, к одной из которых принадлежит и наш Млечный Путь. Так развивалось наше представление о вселенной вширь, но в то же время оно развивалось и вглубь. Наука в настоящее время не только установила, что всюду
159
во вселенной звезды и целые системы галактик состоят из той же материи, из которой состоит наша Земля, но, что самое важное,—эта материя всюду проявляет одинаковые свойства. Всюду мы замечаем наличие закона вечности материи, но изучение небесных светил показывает, что возможные формы бытия материи более разнообразны, чем те, которые мы имеем возможность изучить, пользуясь только земными условиями наших лабораторий.
Этот путь, пройденный человечеством, подтверждает нам возможность еще более широкого и глубокого изучения и понимания всех форм бытия материи и, таким образом, опровергает как агностицизм (утверждение ограниченности человеческого познания), так и вытекающую из него веру в божество. Мир бесконечен как во времени, так и в пространстве, но и так же бесконечны возможности познания его человеком.
НАБЛЮДЕНИЯ.
1.	При наблюдениях яркости звезды ее часто оценивают так называемым способом Пиккеринга. Способ этот заключается в том, что исследуемую звезду сравнивают с одной более яркой и с другой более слабой звездой. Звезды, с которыми ведут сравнение, называют „звездами сравнения". При оценке разность яркостей звезд сравнёния мысленно делят на десятые доли и оценивают, сколько таких десятых долей заключается между исследуемой звездой и звездами сравнения. Наблюдение записывают, например, так: аЗх7Ь. Это значит, что звезда яркости х на 0,3 слабее звезды а и на 0,7 ярче звезды Ь. (Не следует забывать, что здесь говорится о десятых долях разности звездных величин звезд а и Ь.) По этому наблюдению вычисляют яркость изучаемой звезды х:
x = a + 0,3(& — а), или х — Ь — 0,7 (Ь — а).
Если, например, по звездному каталогу а = 4,7 и & = 5,3 звездной величины, а запись наблюдения: я4х6£, то х = 4,7 + 0,4 (5,3 — 4,7) = 4,7 4-0,4-0,6 = 4,7 + + 0,24 = 4,9 звездной величины (с округлением до десятых долей). После небольшой практики легко освоиться с этим способом наблюдений.
Определите таким образом яркость двух, трех звезд какого-либо созвездия, взяв яркость соседних звезд сравнения из звездного каталога. Вы убедитесь, что первый же опыт оценки уже даст близкие к точным измерениям результаты.
2.	Изберите какой-нибудь большой участок Млечного Пути и зарисуйте его очертания на бумаге негативным изображением (белое — черным). Продолжая присматриваться к отдельным частям наблюдаемого участка, отметьте самой слабой штриховкой наименее яркие части, потом — более яркие и т. д., пока не получите полный рисунок с распределением на нем яркостей.
3.	Применяя наиболее подходящий по силе из имеющихся у вас инструментов, ознакомьтесь (разыскав их с помощью карты) с туманностями Андромеды, Ориона и звездными скоплениями в Геркулесе и Возничем. Сделайте рисунки того, что удалось пронаблюдать.
4.	Применяя обозначения: б (белый), ж (желтый), о (оранжевый), к (красный) и промежуточные, например жо (желто-оранжевый) или ож (оранжевожелтый), оцените цвета звезд а Лиры, а Орла, а Волопаса, а Возничего, а Ориона, р Ориона, а Лебедя, а Тельца.
5.	Пронаблюдайте способом Пиккеринга звезды 8 Цефея и р Лиры в течение нескольких дней подряд. При этом особенно аккуратно записывайте время наблюдения. Постройте график изменения яркости этих звезд.
Яркости звезд сравнения:
Для 3 Цефея		Для р Лиры	
v Цефея	4,46 зв. в.	у Лиры	3,30 зв. в.
в »	4,23 » »		4,46 „ „
	4,40 . .		4,46 , „
7 Ящерицы	3,85 „ „	X	4,34 „ „
i Цефея	3,68 , ,	о Геркулеса	3,83 „ „
С ,	3,62 , .	£ ,	3,82 . .
160
6.	В наибольший из имеющихся у вас инструментов посмотрите на двойные звезды: С Большой Медведицы (11' 48"), е Лиры (3' 27"), а Ориона (2' 15"), р Лебедя (34"), у Андромеды (10"). Отметьте, какие из них инструмент „разделяет* (в скобках при каждой звезде отмечено расстояние между звездами).
7.	Наведите фотографическую камеру на какие-нибудь созвездия с яркими звездами, откройте объектив на 1 минуту, на полученном негативе оцените по величине изображений порядок яркости звезд и сравните с тем, что наблюдается глазом.
Задачи.
1.	Звездная величина нашего Солнца равна —26. Вычислите, какую оно имело бы ридимую звездную величину, находясь на расстоянии ближайшей к нам звезды а Центавра.
2.	Во сколько раз уменьшается в минимуме яркость переменной звезды, если в максимуме она бывает 9,5 звездной величины, а в минимуме 12,5 звездной величины?
3.	В 1933 г. один из минимумов Алголя приходился на 3 декабря в 17,1 часа. Исходя из продолжительности периода Алголя (2,8673 суток), вычислите ближайший минимум в текущем году и месяце.
4.	Максимум звезды ч Лебедя был в 1929 г. 1 июня, период ее 412,9 суток. Когда должен быть максимум в 1938 г.?
5.	Изменится ли вид кривой яркости Алголя и как, если спутник (имея те же размеры) не совсем темный, а сам светится в несколько раз слабее, чем главная звезда?
6.	„Летящая* звезда в Змееносце, наиболее быстрая из известных, имеет собственное движение 10",3 в год. Через сколько времени она переместится на величину, еле заметную глазом (Г)?
7.	Видимая яркость звезды а Центавра равна 0,33 звездной величины, а ее абсолютная звездная величина 4,7. Каково расстояние этой звезды в парсеках?
8.	Расстояние до туманности Андромеды считается 850 000 световых лет. Зная что угловой размер туманности около 2° (по длине), вычислите ее истинные размеры и сравните их с размерами нашей звездной системы.
9.	Звездное скопление в Геркулесе отдалено от нас на 10,3 тыс. парсеков, его угловой диаметр 12* и общая яркость 5,9 звездной величины. Вычислите действительный диаметр скопления и его абсолютную звездную величину.
10.	Во сколько раз (по объему) а Скорпиона больше нашего Солнца (см. § 60)?
11.	Чтобы наглядно представить себе размеры звезд, сделайте сначала чертеж, изображающий планетную систему, а потом на этом же чертеже, приняв за центр положение Солнца, изобразите и размеры перечисленных в таблице (§ 60) четырех звезд, сохраняя все время одинаковый масштаб.
ГЛАВА VI.
Эволюция вселенной и происхождение солнечной системы.
§ 62.	Легенды о ,,сотворении мира". Знакомство со строением нашей Галактики, расположением в пространстве систем галактик, эволюцией звезд показывает нам, что в мире совершаются постоянные, вечные движения материи и преобразования форм ее бытия.
В древности люди имели смутное представление о том, что вселенная не всегда была такой, какой мы ее наблюдаем в настоящее время, и пытались создать теорию ее происхождения. Однако отсутствие точных знаний о закономерностях явлений природы, с одной стороны, и стремление касты ученых жрецов искать причину не в естественном, а, наоборот, в чудесном и таинственном — с другой, способствовали созданию идеи о сотворении мира богом. Введение божества как необходимого создателя всего существующего было не случайным. Господство И Астрономия
правящих классов могло быть обосновано в глазах трудящихся масс отчасти именно при помощи идеи божества, вручившего будто бы эту власть жрецам и воинам.
Древнейшие легенды о „сотворении мира* поражают своей наивностью. Так, например, халдеи предполагали, что бог Мардук разрубил тело богини Тиамат, олицетворявшей хаос, и из одной половины сделал небо, а из другой Землю. Подобные же фантастические сказания о сотворении мира существовали и у других народов древности.
Халдейское сказание о сотворении мира было повторено с небольшими изменениями древними евреями в так называемой Библии. Они, так же как и халдеи, предполагали чудесное сотворение мира из первичного хаоса волею божества, которое они называли Елоимом. По еврейскому сказанию Елоим1 в течение шести дней последовательно сотворил небо и Землю, отделил на Земле сушу от воды, сотворил на Земле растения, животных и человека. Основное предположение о творении, а также и противоречия в самом сказании остались такими же, как и у халдеев. Это сказание является в сущности видоизменением халдейского учения о сотворении мира и, так же как и халдейское учение, обусловлено незнанием устройства вселенной.
Как уже говорилось, это сказание было записано в Библию, которую жрецы-священники объявили „священной*, написанной со слов самого бога. Христианство, возникшее в среде еврейского народа, признало Библию, а вместе с тем и это учение священным, и, таким образом, слегка измененное сказание невежественных халдеев дошло и до нашего времени в тех книгах, которые как священные хранятся в церквах и содержание которых, вопреки всем данным науки, христианская церковь лицемерно продолжает защищать.
В настоящее время, когда наука точно изучила движения небесных тел и нашла их причину, когда мы знаем строение отдельных частиц вещества — атомов, мы, конечно, не можем удовлетвориться такой сказкой о происхождении мира. К тому же само по себе библейское сказание совершенно противоречит нашим знаниям природы.
Мы, например, знаем, что изменения, происходящие с неживой и живой материей, протекают в течение сотен и тысяч лет, а этим сказанием думают уверить нас, что весь мир мог создаться в 6 дней. Да и библейский счет „творения* надо признать невозможным, так как день и ночь являются следствием вращения Земли вокруг оси. Какие же „дни* могли быть тогда, когда еще и Земли как небесного тела не было?
Самое выражение Библии: „бог отделил свет от тьмы* не имеет никакого смысла, так как свет мы получаем от Солнца, и разделение на дни и ночи могло быть только после образования Солнца и планет, между тем как по Библии это разделение предшествует „созданию* Солнца и планет.
1 Слово „Елоим* значит „боги* и употребляется в I главе Библии; в других главах бог называется „Иегова*. Такое противоречие даже в названии „творца* отражает разные стадии развития религии: многобожие (Елоим) и единобожие (Иегова). В библейских сказках различны и способы творения: в I главе Библии Елоим создают мир и человека словом: „да будет*, а во II главе Иегова якобы вылепил человека из глины, вдохнул в него жизнь и так устал, что на седьмой день ему пришлось отдыхать. Разногласие между этими сказками объясняется тем, что они складывались у народов, живших в разных местностях и ведших различный образ жизни.
162
Из этих примеров видно, что библейское сказание противоречит пауке. Его ложность совершенно очевидна, точно так же как и основное предположение о „создании" мира богом из „ничего". Закостенелая мысль церковников сохранила это сказание как „священное", но современная наука не может с ним считаться.
Наука в лице мыслящих людей разных эпох шла и идет иными путями; она не признает ничего чудесного, сверхъестественного, она ищет естественных причин для всех явлений, признает лишь движущуюся материю и старается найти те закономерности, по которым происходят изменения материи. Наука, конечно, не может сразу разрешить всех возникающих вопросов, но весь ход научной мысли за много столетий ясно показывает, как с каждым годом, шаг за шагом наука всё глубже и глубже проникает в причины, в сущность явлений.
Вместо теории о „сотворении вселенной" наука, отбрасывая „творца" как ненужную основу, выдвигает теорию развития небесных тел из вечно движущейся материи.
Сторонники такого взгляда на происхождение вселенной были уже в древности, но они еще не имели того теоретического и технического аппарата, которыми владеет современная наука, и поэтому их теории, будучи верны в своей основе, не давали удовлетворительного объяснения всех возможных деталей развития вселенной и их последствий.
Уже в V в. до н. э. греческий ученый Демокрит утверждал, что всё вещество состоит из отдельных частичек — атомов. Перемещения и различные соединения атомов создают все тела нашей вселенной, а всё, что совершается в ней, подчинено неизменным законам природы. Демокрит не считал Солнце только светящимся диском, — он утверждал, что оно огромно и что Млечный Путь состоит из подобных Солнцу звезд. Демокрит прекрасно понимал, что вселенная не может быть создана кем-либо: она существует вечно и вследствие действия законов природы медленно, но непрерывно изменяется.
Во времена Демокрита изучение природы далеко еще не находилось на той высоте, как теперь: не столько исследовали природу, сколько рассуждали о том, что может и чего не может быть. Демокрит в сущности не знал почти никаких известных теперь законов природы, но, наблюдая обычные явления, пришел к выводу, что материя вечна и ее изменения совершаются независимо от каких-либо таинственных богов.
Жрецы и народ, находившийся под влиянием жрецов, не соглашались с таким здравым взглядом на мир и смотрели на Демокрита как на безбожника и отступника от привычной им веры.
Древние римляне мало интересовались наукой и без споров приняли древнегреческие сказания о мире, подобные легендам халдеев и евреев. Но мысли Демокрита не пропали: римский поэт Лукреций Кар в своих поэмах описывает образование мира очень близко к тому, как это было дано в учении Демокрита.
Вот перевод отрывка поэмы Лукреция Кара „О природе вещей":
„Но, как раньше сказал я тебе, ничего не родится Из ничего и обратно не может в ничто обратиться. Ныне не стрелами яркими дня и не Солнца лучами Надо рассеивать ужасы и помрачение духа, Но изучением и толкованием законов природы... Первоначальное правило ставит природа такое: Из ничего — волей богов — ничего не творится."
11*
163
§ 63.	Противодействие христианской церкви созданию научных космогонических гипотез. Эпоха христианства не приняла этих мыслей, а, наоборот, целиком внесла наивные древние легенды халдеев и евреев в официальное религиозное учение.
В мрачную эпоху средневековья христианская церковь жестоко расправлялась с учеными, решавшимися смотреть на мир не глазами церковников. Джордано Бруно и Галилей подверглись ожесточенному преследованию церкви.
Наступившая эпоха „возрождения наук и искусств", когда лучшие люди отошли от религиозного толкования мира и снова стали изучать природу независимо от „священных" книг, дала человечеству начало улучшения знаний строения вселенной и ее законов.
В XVIII в., когда буржуазия в своем стремлении занять первенствующее место боролась с церковью и феодализмом, группа ученых, названных энциклопедистами по их главному коллективному труду—„Энциклопедии", впервые научно поставила целый ряд вопросов, касающихся происхождения мира и жизни Земли. Бюффон, принадлежавший к этой группе, в своей „Естественной истории" уже пытался объяснить происхождение солнечной системы. Эпоха Французской революции, предтечами которой были энциклопедисты, произвела такой сдвиг в мировоззрении, что в XVIII в. немецкий философ Кант (1755 г.) и французский математик Лаплас (1796 г.) выдвинули теорию развития солнечной системы из туманности. Лаплас выпустил книгу „Изложение системы мира". В конце этой книги Лаплас дал первую научную космогоническую гипотезу, т. е. научное предположение о том, как могла произойти из вечной материи и развиться наша планетная система при действии закона Ньютона о взаимном тяготении частиц материи.
П. А. Кропоткин рассказывает в одной из своих книг: „Наполеон I сделал Лапласу замечание, что в его „Изложении системы мира" нигде не упоминается имя бога, и Лаплас ему ответил: „Я не нуждался в этой гипотезе (предположении)". Этот ответ Лапласа показывает, что истинно научное отношение к изучению мира не имеет ничего общего с религией и отрицает какую бы то ни было мысль о чудесном происхожении мира, но в то же Ьремя он характерен для буржуазного мыслителя, не решающегося итти на прямое отрицание бога.
Так на протяжении веков шла борьба двух групп: церковников, поддерживающих в интересах капиталистического строя бессмысленную и невежественную гипотезу о сотворении мира, и естествоиспытателей-материалистов, неустанно искавших причин явлений природы и шаг за шагом проникавших всё далее в закономерности ее. Теоретическим оружием пролетариата в его борьбе с буржуазией и ее орудием угнетения трудящихся — религией — является философия пролетариата — диалектический материализм. Борьба за мировоззрение продолжается и до сих пор. Современные церковники отнюдь не так невежественны, чтобы целиком поддерживать библейскую легенду, они понимают всю ее нескладность и невозможность ее защиты. Церковь теперь идет по иным путям: она пытается утверждать, что библейское сказание о сотворении мира в общем не противоречит науке, если понимать ее не буквально. Однако уже давно были доказаны явные нелепости этого сказания как в деталях, так и в основном положении, поэтому ухищрения церковников несостоятельны и недоказательны. В настоящее время церковь стремится 164
подорвать авторитет научного мировоззрения, указывая, что научные теории развития вселенной — только „гипотезы*, „предположения* и что полного знания развития вселенной наука не имеет. Но и это утверждение в своей основе имеет ложное положение о непознаваемости мира и о существовании его мистического творца.
Научная гипотеза есть необходимая форма, необходимая ступень беспредельно развивающегося познания.
„Формой развития естествознания, поскольку оно мыслит является гипотеза... Дальнейший опытный материал приводит к очищению этих гипотез, устраняет одни из них, исправляет другие, пока, наконец, не будет установлен в чистом виде закон*1.
Так говорит Энгельс о значении гипотез в науке. Такое значение имеют и космогонические гипотезы, со всё большей точностью и ясностью вскрывающие нам процесс происхождения вселенной.
О том же говорит В. И. Ленин: „Познание человека не есть прямая линия, а кривая линия, бесконечно приближающаяся к ряду кругов, к спирали. Любой отрывок, обломок, кусочек этой кривой линии может быть превращен (односторонне превращен) в самостоятельную, целую, прямую линию, которая (если за деревьями не видеть леса) ведет тогда в болото, в поповщину (где ее закрепляет классовый интерес господствующих классов)*1 2.
Таким образом, в противовес материалистическому мировоззрению, говорящему о познаваемости мира, церковники л своих возражениях против космогонических гипотез в скрытом виде проводят свое собственное положение об ограниченности познания.
Весь ход развития космогонических гипотез, начиная от Лапласа, показывает, как каждая новая гипотеза становится совершеннее и глубже.
Процесс развития небесных тел проходит очень медленно, и мы его «епосредственно наблюдать не можем, но зато, собирая наблюдения туманностей и распределяя их по их форме и строению на группы, мы можем проследить по этим формам, как могло итти их развитие, и, пользуясь известными нам законами природы, разъяснить последовательность и неизбежность этих стадий и переходов.
§ 64.	Гипотеза Лапласа. В своей гипотезе Лаплас осторожно подходит к решению вопроса, применяя лишь бесспорные механические законы и не пытаясь давать объяснения тому, что по состоянию науки еще было недостаточно известно.
Лаплас предполагает, что планетная система образовалась из громадной, состоящей из раскаленных газов, вращающейся туманности. Эта туманность имела шаровидную форму, но вследствие ее вращения центробежная сила вызвала ее сплющивание и вместе с тем непрерывное выделение в плоскости экватора частиц этой туманности. Получался широкий тонкий пояс, окружающий шаровидное уплотнение, находящееся в его центре. Одновременно шло последовательное разделение пояса на ряд концентрических колец, продолжавших обращаться вокруг центрального сгущения (рис. 127).
При этом скорость вращения центральной части все увеличивалась (в силу закона сохранения количества движения), и поэтому централь-
1 „Диалектика природы*, Партиздат, 1933, стр. 6.
2 Сочинения, 3-е изд., т. XIII, 1935, стр. 304.
12 Астрономия	165
Рис. 127. Происхождение солнечной системы по гипотезе Лапласа.
ная часть туманности, сгустившаяся в Солнце, вращалась быстрее, чем оставшиеся кольца. Плотность материи колец, как это показывает Лаплас, не могла быть равномерной, и поэтому материя постепенно собиралась в большие скопления и всё более уплотнялась.
Эти скопления и стали началом планет.
С каждым таким шарообразным сгущением могло произойти то же самое, что и с начальной туманностью, так как внешние молекулы имели большую линейную скорость и своим движением могли привести образовавшийся шар во вращение. Таким путем возникли спутники, и только в одном случае, около Сатурна, часть кольца сохранилась.
Помимо чисто механических процессов происходили и физические: планеты, бывшие горячими при своем возникновении, затем, когда уплотнение закончилось, стали отдавать тепло в мировое пространство. Шары планет с большей массой имели бблыпий запас теплоты, и поэтому их охлаждение шло медленно; наиболее медленно шло охлаждение центрального громадного шара — Солнца. Небольшие планеты охладились значительно быстрее и, наконец, покрылись с поверхности твердой корой». Конечно, весь этот процесс продолжался не шесть суток, а миллиарды лет»
Гипотеза Лапласа не только развивает старую гипотезу Демокрита о создании мйра благодаря действию естественных сил, — эта гипотеза объясняет, как всё это могло произойти, и приводит к выводам, па большей части согласным с тем, что мы наблюдаем в планетной системе» Действительно, планеты обращаются вокруг Солнца в одну сторону — в ту же, что и само Солнце, и их Орбиты очень близко лежат около одной плоскости.
Но известны факты, не соответствующие гипотезе Лапласа, например обратное вращение некоторых спутников. Поэтому в настоящее время: гипотезу Лапласа считают не охватывающей всех фактов» 166
В гипотезе Лапласа мы уже видим применение законов механики, и в том числе закона всемирного тяготения и известных в то время законов физики, главным образом в области теплового обмена.
Недостатки гипотезы Лапласа вызвали попытки исправить ее путем уточнения расчетов и введения в рассуждения дополнительных соображений. Однако все эти попытки не приводили к положительным результатам, так как основы теории не учитывали всех явлений, могущих иметь место при развитии солнечной системы.
§ 65.	Накопление наблюдательных данных. Когда в конце XIX и в начале XX вв. были исследованы явления приливов, то попытка применить теорию приливного взаимодействия к вопросам образования небесных светил сразу же значительно продвинула вопрос вперед.
При изучении солнечной системы мы ознакомились с гипотезой Д. Дарвина образования системы Земля — Луна. Эта гипотеза является лишь частной, но имеет очень большое значение потому, что она наметила новый этап в развитии гипотез о происхождении солнечной системы, этап, характеризуемый учетом приливного взаимодействия. После гипотезы Д. Дарвина целый ряд ученых ("Мультон, Си и др.) в своих теоретических выводах не пропускает этого фактора.
Наиболее широко и глубоко все факторы и особенно приливное взаимодействие учтены в гипотезе Д. Джинса, основанной на современных данных о внегалактических туманностях.
Наблюдения туманностей поставили вопрос не только о развитии планетной системы, но и целых звездных систем — галактик. Поэтому усилия астрономов направились к тому, чтобы дать гипотезу, наиболее общую.
Исследования внегалактических туманностей показывают, что эти туманности бывают шарообразные, эллиптические и спиральные. При этом оказывается, что на фотографиях туманностей, имеющих веретенообразный вид (а по существу линзообразных, но рассматриваемых сбоку), почти всегда можно заметить темную полосу, как бы разрезающую туманность симметрично (рис. 128).
Кроме того, было обнаружено и другое обстоятельство: около одной спиральной туманности нередко можно заметить другую такую же.
Отсюда возникла мысль, что развитие системы звезд или планет может происходить вследствие взаимодействия двух газообразных масс, вызывающих приливы и отделения части вещества туманности. Современный английский ученый Д. Джинс всесторонне разработал эту теорию.
§ 66.	Эволюция больших туманностей. Если в пространстве находится шаровая вращающаяся газообразная туманность, то вследствие близости других небесных тел она испытывает их притягивающее влияние. Вследствие сжатия скорость вращения туманности увеличивается, и она всё больше и больше сплющивается. Но одновременно с этим вращение туманности создает по ее краям выделение материи, неравномерное по всему ее краю, так как ближайшее небесное тело, возбуждая приливное действие, дает толчок к выделению ее сначала в двух противоположных местах экватора сплющенного эллипсоида. Таким образом, вместо кольца получаются два выступа, из которых извергается материя. Если бы туманность не вращалась, то с двух противоположных краев ее получились бы два выступа, отходящие своими вершинами от нее все дальше и дальше. Вследствие вращения туманности отрывание продолжается так
167
же, как раскручивание нити с катушки. Раньше оторвавшаяся часть материи успеет отойти дальше, чем части оторвавшиеся позднее. Таким образом, и получаются две спиральные ветви со сгущением посредине (рис. 129).
Эти-то ветви спирали вследствие местных сгущений материи дают начало шарообразным сгуст-

Рис. 128. Различные формы внегалактических туманностей.
кам, в свою очередь разлагающимся на звезды. Звезды проходят те стадии эволюции, которые уже были указаны выше (см. § 59).
Подтверждением этой теории являются те фотографии внегалактических туманностей, которые вы можете видеть на рисунке 128. Эти фотографии показывают, что в различных частях вселенной в настоящее время мы видим различные стадии одного и того же процесса. На рисунке 128 вы видите и шарообразные, и эллиптические, и веретенообразные туманности. Внимательно просмотрите все эти рисунки: они расположены в порядке эволюции, начиная от шарообразных и кончая веретенообразными, и тем самым вы как бы пробежите мысленно миллиарды миллиардов лет, так как такое, примерно, время требуется для развития звездной спирали из первоначальной шарообразной, сильно разреженной туманности.
§ 67. Происхождение солнечной системы по Джинсу. Джинс сделал вывод о возможном происхождении нашей солнечной системы вследствие близкого прохождения мимо нашего Солнца
звезды, превышающей его по своей массе. При этом на поверхности Солнца поднялась громадная прилирная волна в виде выступа, загнувшегося по направлению движения проходящей звезды. Этот выступ оторвался от Солнца и имел утолщение в середине (рис. 130), в то время как незначительная толщина выступа на концах соответствовала наиболее слабым приливным действиям (в начале и в конце сближения звезд).
168
Рис. 129. Фотография спиральной туманности в Большой Медведице.
Оторвавшийся выступ впоследствии распался на части, и из средней части его получились наибольшие планеты, меньшие же планеты получились из более тонких частей.
Каждая космогоническая гипотеза представляет собой движение науки вперед в познании возможных причин образования небесных тел. Каждая гипотеза в связи с общим прогрессом науки обнаруживает противоречия и проверяется на новых теориях и фактах. Эта проверка дает возможность сделать следующий шаг к лучшему познанию причин к более совершенной гипотезе.
Изложенная гипотеза Джинса в настоящее время подвергается проверке, некоторые ее положения поставлены под сомнение и уже намеча-169
Рис. 130. Происхождение планет по гипотезе Джинса.
ются черты новой космогонической гипотезы, которая полнее разъяснит происхождение солнечной системы и устранит недостатки гипотезы Джинса.
§ 68. Возраст небесных тел. Гипотезы Дарвина и Джинса уже достаточно хорошо разъясняют возможные причины возникновения галактик, солнечной системы и двойных звезд, но эти гипотезы не учитывают еще всех физических условий развития миров, так как такой учет пока еще невозможен. Время, в течение которого происходят эти процессы, громадно, но все-таки может быть приблизительно подсчитано.
Основой таких подсчетов для Земли являются не столько астрономические данные, сколько физико-химические: в этом случае можно исходить от процесса распада урана на свинец и гелий, при котором за 100 млн. лет получается 13°/0 свинца от начального веса урана.
Исследования свинца, находящегося совместно с ураном в горных породах, показывают, что возраст земной коры заключается между 1 и 2 миллиардами лет. Но Земля моложе, чем вся солнечная система.
Различные соображения о процессах, происходящих в материи, составляющей звезды, а также результаты изучения орбит двойных звезд показывают, что возраст звезд может быть от 5 до 10 биллионрв лет.
§ 69. Заключение. В начале этой главы была рассказана краткая история двух различных по существу учений о строении и развитии мира: религиозного, упорно хранящего наивные представления первобытных народов о чудесном сотворении мира богами, и научного, отбросившего всё фантастическое, не основанное на опыте и наблюдениях, и рассматривающего лишь вечную материю, взаимодействие частиц ее и происходя
дящие отсюда ее видоизменения. Научное учение, отбрасывая ненужную и вредную гипотезу бога, не закрывает глаз на то, что в настоящее время не все еще законы природы выяснены до конца; поэтому в той общей картине мира, с которой мы имели возможность ознакомиться, наука считает необходимым продолжать разработку некоторых деталей, еще недостаточно выясненных до сих пор. Таким образом, картина мира исправляется и видоизменяется в деталях, но в своем основном положении— учении о вечной материи и ее превращениях — научное мировоззрение остается и останется таким же, как и теперь. Весь ход мыслей от Демокрита и до нашего времени подтверждает это мировоззрение, а факты, получаемые из астрономических наблюдений, дают для него всё новый и всё более прочный материал.
Религия и буржуазная идеология, исходя от принципа непознаваемости мира, подчиненности человека мистическому существу (как бы его ни называли церковники и „мыслители “ разных толков), утверждают тем самым слабость человека, его бессилие перед природой, невозможность перестройки ее для себя.
Материалистическая диалектика, выводя из истории развития науки познаваемость мира и признавая единую объективную реальность — вечно движущуюся и изменяющуюся материю, отрицает всё мистическое, чудесное, и тем самым утверждает силу и способность человечества перестроить мир.
Слова В. И. Ленина, что материалистическая диалектика есть учение оптимизма, подтверждаются всем развитием науки, всем ходом техники, всем строительством социализма в СССР и дают уверенность ученым в их работе по исследованию вселенной.
Задачи а вопросы.
1.	Лукреций Кар, описывая, согласно Демокриту, образование вселенной, говорит: «Частицы от времен бесконечны повсюду носилися, частью движимы собственной тяжестью, частью гонимы «толчками". Что в этом описании соответствует современному нам научному представлению о материи и происхождении вселенной и что неверно?
2.	Кант в своем сочинении ,Общая естественная история и теория неба", излагая образование планетной системы из хаоса, говорит, что «частицы могут продолжать свободное круговое движение". Удовлетворяет ли эта часть теории Канта тому, что наблюдается в действительности в планетной системе?
3.	В том же сочинении Кант говорит, что «возникновение и образование миров началось впервые у центра вселенной". Ошибочно ли это выражение? Почему?
4.	В нашей планетной системе обращения и вращения планет и их спутников называются прямыми, когда они совершаются (еслй смотреть с северного .конца оси мира) против часовой стрелки. В планетной системе оказываются:
Вращение Обращение спутников планеты прямое обратное
Земля 		Прямое	1 спутник	—
Марс		»	2 спутника	——
Юпитер			7 спутников	2 спутника1
Сатурн 		м	8	1 спутник
Уран ......	Обратное	—	4 спутника
Нептун		Прямое	—	1 спутник
Имеют ли значение эти факты (и какое) для теории Лапласа?
5. Один из спутников Марса обращается вокруг него скорее, чем вращается он сам. Соответствует ли это гипотезе Лапласа?
1 Движение двух спутников Юпитера, открытых в 1938 г., еще не исследовано,
171
ПРИЛОЖЕНИЯ.
I.	ГРЕЧЕСКИЙ АЛФАВИТ.
А а — альфа В р— бэта Г 7 — гамма А 8 — дельта Е е — эпсилон Z С — дзета Н т) — эта 000—тэта
I i — йота К х — каппа A X — ламбда М р— ми N v — ни S Е — кси О о — омикрон Пл — пи
Р р —ра 2 а — сигма Т т — тау Г □ — ипсилон Фу — фи X х —ХИ Ф <0 — пси 2 а) — омега
II.	НАИБОЛЕЕ УПОТРЕБИТЕЛЬНЫЕ НАЗВАНИЯ ЯРКИХ ЗВЕЗД.
Алгол ь — р Персея Альдебаран — а Тельца Альтаир — а Орла Антарес — а Скорпиона Арктур — а Волопаса Бетельгейзе — а Ориона Вега — а Лиры Капелла — а Возничего Кастор — а Близнецов
Мицар— $ Б. Медведицы Поллукс — р Близнецов Полярная — а М. Медведицы Процион — а М. Пса Регул — а Льва Ригель — р Ориона Сириус — а Б. Пса Спика — а Девы Фомальгаут — а Южной Рыбы
III.	КАТАЛОГ ЯРКИХ ЗВЕЗД (до 2,5 ЗВЕЗДНОЙ ВЕЛИЧИНЫ и 30° ЮЖНОГО СКЛОНЕНИЯ).
В каталоге даны яркость звезд, прямое восхождение а, склонение 8, обозначение спектра, которое в то же время служит указанием цвета: белые звезды — О, В, А, желтые — F, G, К> красные — М.
Звезды	Звездная				Спектр.
	величина	а		о	класс
а Андромеды		2,15	о* 4* 46с		|-280 42',2	А
р Кассиопеи 		2,42	0 5 26		-58 45,8	F
а Кассиопеи		2,1—2,61	0 36 31		-56	9,2	К
р Кита		2,24	0 40 5		-18 22,2	К
у Кассиопеи		2,25	0 52 28		к 60 20,3	В
р Андромеды		2,37	1	5 48		-35 15,0	м
а М. Медведицы ....	2,12	1 36 54		-88 55,7	F
у Андромеды		2,28	1 59 36		-41 59,7	К
а Овна		2,23	2 3 13		-23 7,9	К
о Кита		2,0—10,11	2 15 48		- 3 17,7	М
р Персея		2,2— 3,51	3 3 36	4-40 41,2		В
1 Переменная звезда.
172
	Звездная				Спектр.
Звезды	величина	а		О	1 класс
а Персея			1,90	3** 19* 19*	н	1-49° 36',8	F
а Тельца 		1,06	4 31 54	н	Р16 22,2	К
р Ориона	  •	0,34	5 И 10		- 8 16,9	В
а Возничего 		0,21	5 11 31		- 45 55,7	G
7 Ориона		1,70	5 21 22		- 6 17,3	В
В Тельца	1,78	5 21 52		-28 33,0	В
о Ориона		2,48	5 28 26		- 0 21,0	В
s Ориона 		1,75	5 32 40		- 1 14,7	В
£ Ориона		2,05	5 37 14		- 1 58,7	В
х Ориона 		2,20	5 44 26		- 9 41,6	В
а Ориона		0,92	5 51 23	4- 7 23,7		м
Р Возничего 		2,07	5 54 24	н	1-44 56,5	А
р Б. Пса		1,99	6 19 37		-17 55,2	В
у Близнецов 		1,93	6 33 40	4-16 27,6		А
а Б. Пса		—1,58	6 42	4		-16 37,1	А
s Б. Цса		1,63	6 55 52		-28 52,5	В
3 Б. Пса		1,98	7 5 33		-26 16,9	В
*4 Б. Пса .		2,43	7 21 19		-29 9,9	В
а Близнецов		1,99	7 30	8		- 32 2,6	А
а М. Пса		0,48	7 35 38		- 5 24,3	F
р Близнецов 		1,21	7 41	2		-28 11,8	К
а Гидры		2,16	9 24	9		- 8 21,3	К
	1,34	10 4 39		И12 18,6	В
р Б. Медведицы ....	2,44	10 57 38		-56 45,5	А
а Б. Медведицы ....	1,95	10 59 25		-62 7,8	К
f Льва		2,23	11 45 29		-14 57,8	А
7 Б. Медведицы ....	2,54	11 50 09		-54 5,0	А
s Б. Медведицы ....	1,68	12 50 57		- 56 20,4	А
5 Б. Медведицы ....	2,40	13 21	7		-55 17,4	А
а Девы		1,21	13 21 30		-10 47,8	В
7) Б. Медведицы ....	1,91	13 44 47	4-49 39,7		В
а Волопаса 		0,24	14 12 28		-19 32,8	К
£ М. Медведицы ....	2,24	14 50 ЬЗ		-74 26,5	К
а Северной Короны . .	2,31	15 31 43		— 26 57,0	А
а Скорпиона		1,22	16 25	7		-26 16,7	М
а Змееносца		2,14	17 31 41		-12 36,6	А
7 Дракона		2,42	17 54 59		- 51 29,8	К
а Лиры		0,14	18 34 34		-38 43,1	А
а Стрельца 		2,14	18 50 56		-26 23,1	В
а Орла		0,89	19 47 22		- 8 40,9	А
7 Лебедя 		2,32	20 19 43		-40	1,9	F
а Лебедя 		1,33	20 39 3		-45 1,8	А
а Южной Рыбы ....	1,29	22 53 47		-29 59,6	А
173
V. ШИРОТЫ и ДОЛГОТЫ ГОРОДОВ СССР (от Гринича) (жирным шрифтом напечатаны названия столиц союзных республик).
Широта Долгота	Широта Долгота
Алма-Ата ♦ ♦ . 43° 16' 4-5* 7-и,8	Новосибирск > .55° 1' + 5*31^,6
Архангельск. . . 64	34	4-2	42,1	Новочеркасск . . 47	25	4-	2	40,4
Астрахань ... 46	21	4-3	12,1	Одесса , .... 46	29	4-	2	3,0
Ашхабад . ... 37	45	4” 3	53,6	Омск ..............54	59	4“	4	53,5
Баку............. 40	21	-4-3	19,4	Орел.............. 52	58	4-	2	24,3
Белосток . . . . 53	07	4-2	16,0	Орджоникидзе. . 43	02	4-	2	58,7
Благовещенск . . 50	15	4-8	30,1	Пенза . . . , . 53	11	+	3	0,1
Витебск . . , .55	10	4-2	0,8	Петрозаводск . . 61	47	4-	2	17,6
Владивосток ... 43	07	4-8	47,5	Петропавловск на
Владимир , . . . 55 12 4-2 41,6	Камчатке . , . 53	0 4-10 34,9
Вологда .	а ...	58	13	4-2 39,5	Полтава...... 49	35	4- 2	18,3
Воронеж	....	51	39	4-2 36,8	Псков........ 57	49	+ 1	53,3
Горький........ 56	20	4-2	56,0	Ростов на Дону .47	13	4-	2	38,9
Днепропетровск .	48	28	4-2 20,3	Рязань . .	*	•	.	54	38	4- 2	39,0
Енисейск	....	58	27	Ц- 6 8,8	Самарканд	♦	.	.	39	39	4- 4	27,9
Ереван......... 40	14	4-2	58,0	Саратов......... 51	32	4-	3	4,3
Житомир .... 50	15	4-1	54,7	Свердловск	...	56	49	4~	4	2,4
Иваново	.	.	.	.	57	0	4-2 43,9	Севастополь.	.	.	44	37	4- 2	14,1
Иркутск	.	.	.	.	52	16	4-6 57,1	Семипалатинск	.50	24	4- 5	20,4
Казань......... 55	48	4-3 16,5	Симферополь	,	.	44	57	4- 2	16,4
Калинин........ 56	52	4-2 23,6	Смоленск . <	>	.	54	46	4-2	18,2
Калуга......... 54	31	4-2	25,0	Ставрополь	...	43	03	4-	2	48,0
Каменец-Подольск48	40	4-1	46,3	Сталинабад...	38	33	4“ 4	35
Киев ...... 50	27	4-2	2,0	Сталинград	...	48	42	4- 2	58,1
Киров............ 58	36	4-3	18,7	Тамбов....... 52	44	4- 2	45,8
Кишинев .... 47	02	4-1	55,3	Ташкент	....	41	20	4“ 4	37,2
Кострома .... 57	46	4-2	43,7	Тбилиси	....	41	42	4- 2	59,3
Краснодар .... 45	03	4“ 2	35,9	Тобольск	....	58	12	4- 4	33,1
Красноярск ... 56	01	4-6	II»4	Томск............. 56	30	4-5	39,8
Куйбышев. . . .53	II	4-3	20,4	Тула......... 54	12	4- 2	30,5
Курск............ 51	44	4-2	24,8	Ульяновск	....	54	19	4- 3	13,6
Кутаиси........ 42	15	4-2	50,8	Уральск .....	51	42	4- 3	25,4
Ленинград .... 59	57	4-2	1,0	Уфа.......... 54	43	4- 3	43,8
Львов............ 49	49	4-1	36,1	Фрунзе....... 42	53	4- 4	58,5
Минск.......... 53	54	4-1	50,3	Хабаровск....	48	28	4- 9	0.2
Могилев .... 53	54	4“ 2	1,3	Харьков...... 50	00	4- 2	24,9
Молотов .... 58	01	4~3	45,1	Херсон....... 46	38	4- 2	10,5
Москва......... 55	45	4-2	30,3	Чернигов	....	51	29	4“ 2	5,2
Мурманск .... 68	59	4- 2	12,2	Чита..........52	01	4-7	34,0
Николаевск на	Чкалов.......... 51	45	4- 3	40,4
Амуре ... .53	08	4-9	22,9	Якутск....... 62	02	4- 8	39,0
Новгород .... 58	31	4“ 2	5,1	Ярославль	....	57	38	4“ 2	39,о
VI. ШИРОТЫ И ДОЛГОТЫ АСТРОНОМИЧЕСКИХ ОБСЕРВАТОРИЙ (от Гринича).
	Широта	Долгота	
1. Берлип-Бабельсберг4- 52°24'24",2		4- 0*52*25<\5	
2. Вашингтон	4" 38 55 12 ,3			— 5 8 18 ,3
3. Гора Вильсона	4“ 34 12 59 ,5			- 7 52 14 ,3
4. Гринич	4- 51 28 38 ,2			0 0	0
5. Мадрид	-40 24 30 ,1		-0 14 45 ,0
6. Москва	-55 45 20 ,2		1-2 30 17
7. Нанкин	-32 4 2		-7 55 18
8. Париж	-48 5011		-0 9 20
9. Прага	-50 4 36,0		-0 57 35
10. Пулково	- 59 46 18 ,5		-2 1 18,6
11. Рим	-41 53 33 ,2		-0 49 56 ,3
12. Токио	-35 40 21		-9 18 10 ,1
174
VII. КАРТА ЧАСОВЫХ ПОЯСОВ.
VIII. ТАБЛИЦА СОЛНЕЧНОЙ СИСТЕМЫ.
	Сидерический период обращения в гддах	Синодический период обращения в сутках	Среднее расстояние от Солнца		Эксцентриситет	Наклонение	Масса (Земля =1)	Плотность	Экваториальный диаметр		Сжатие	Время вращения вокруг оси	Наклон экватора к плоскости орбиты	Число спутников 1
			в астр. ед.	в млн. км					Земля = 1	в км				
Меркурий $		0,241	116	0,387	58	0,206	7°	0,04	3,8	0,39	5000	?	88 суток	0°	—
Венера $ 		0,615	584	0,728	108	0,007	3	0,81	4,9	0,97	12 400	?	6 суток?	?	—
Земля 5 		1,000	—•	1,000	150	0,017	0	1,00	5,5	1,00	12742	V297	23* 56* 4*	23°27'	1
Марс С?		1,881	780	1,524	228	0,093	2	0,11	4,0	0,53	6770	V192	24* 37*23*	25°ю'	2
Юпитер 21		11,86	399	5,203	778	0,048	1	316,9	1,3	10,95	139560	Х/13	9* 50*	3° 6'	11
Сатурн tl		29,46	378	9,539	1426	0,056	2	94,9	0,7	9,02	115110	VlO	10* 14*	26°45'	9
Уран	.		84,01	370	19,19	2868	0,047	1	14,66	1,3	4,00	51 000	Vu	10,7*	98°	4
Нептун Ф		164,7	368	30,07	4494	0,099	2	17,16	1,6	3,92	50000	V40	15,8*	29°	1
Плутон F2,		248,9	367	39,58	5915	0,247	17	0,5 ?	?	0,4?	5 000	?	?	?	—
Солнце 0 		1		—	—	—	—-	331 950	1,4	109,1	1 390600		25 суток	7°15’ (к эклиптике)	—•
Часы до или после полудня
При построении горизонтальных солнечных часов стержень, по тени которого отсчитывается истинное солнечное время, должен быть направлен по оси мира, т. е. расположен в плоскости меридиана под углом к горизонтальной плоскости, равным широте места. Углы откладываются от полуденной линии и имеют общую вершину в точке укрепления стержня на горизонтальной плоскости. Для каждого часа до и после полудня эти углы вычисляются по тригонометрической формуле. Формула такова:
tgx ® sin
где т — угол, ? — широта, f© — истинное солнечное время, выраженное в градусах.
График дает возможность найти эти углы без»вычислений для широт от 40 до 70°. Задавшись данными щиротой и часом, находим место пересечешя соответствующих вертикальной и часовой линий и производим отсчет по левой шкале чертежа. Например, для широты 57° и для 3 часов искомый угол равен 40°.
IX. ГРАФИК ДЛЯ ПОСТРОЕНИЙ ГОРИЗОНТАЛЬНЫХ СОЛНЕЧНЫХ ЧАСОВ.
X. АСТРОНОМИЧЕСКИЕ ТРУБЫ И ОБРАЩЕНИЕ С НИМИ.
В астрономических трубах основные линзы — объектив и окуляр. Объектив дает изображение, а в окуляр, как в лупу, это изображение рассматривается. Так как заменой окуляров можно получить и изменение увеличения трубы, то при трубах обычно бывает несколько окуляров, которые можно по желанию вставлять в выдвигающийся окулярный конец трубы. Все астрономические трубы во время наблюдения устанавливаются на подставки (штативы) с шарнирами, позволяющими передвинуть трубу по любому направлению. Иногда при таких штативах бывают микрометрические движения, осуществляющиеся посредством особых винтов или ручек.
И объектив и окуляры должны храниться в чистоте: объектив вне времени наблюдений обязательно должен быть закрыт крышкой, а окуляры — лежать в ящике с гнездами для них.
В астрономической трубе поле зрения тем меньше, чем больше увеличение: поэтому трудно бывает сразу навести трубу на светило. Для облегчения наведения трубы очень часто к ней прикрепляется небольшая труба-искатель. В поле зрения искателя натянуты две ниточки, а сам искатель с помощью уравнительных винтов может быть слегка передвинут на трубе. Правильное положение искателя такое, при котором на перекрестке нитей видно то же самое, что видно в центре поля зрения трубы.
Предварительная установка окуляров. Чтобы ночью во время наблюдений сразу устанавливать окуляры на резкие изображения предметов, следует днем перепробовать окуляры и сделать на трубе отметки глубины вдвига каждого окуляра.
Общая окулярная трубка вдвигается или рукой или помощью особого винта (кремальеры). Днем надо нацелиться трубой на какой-нибудь отдаленный, хорошо освещенный предмет и ввинтить в окулярную трубку самый слабый окуляр (назовем его № 1, он будет наиболее длинным), установить его так, чтобы наблюдаемый предмет был совершенно ясно и четко виден, острым перочинным ножом отметить черту, по которую выдвинута трубка, и около черты начертить № L Так же поступить (не сдвигая трубы во время смены окуляров) со следующим окуляром, поставив метку № 2, и т. д.
Установка искателя. Навести трубу на отдаленный предмет, ввинтить самый слабый окуляр, передвинуть трубку так, чтобы резко выделяющаяся часть наблюдаемого предмета была в центре поля зрения. Не сдвигая трубы, посмотреть в искатель и, если предмет не на пересечении нитей, то, действуя упорными винтиками, соответственно переместить искатель. Еще раз проверить точность установки. Последовательно произвести то же самое со всеми окулярами до окуляра с наибольшим увеличением.
Наблюдения ночью. Начиная наблюдать, вдвинуть окуляр до соответствующей ему метки. Если при трубе есть искатель, то, пользуясь им, навести трубу на светило. Если искателя при трубе нет, то наведение надо делать с наименьшим увеличением, нацеливаясь трубой, как целится стрелок из ружья по мушке (тут нужна некоторая сноровка, и поэтому лучше приобрести эту сноровку днем).
Если светила все же не видно, подвигать слегка трубу вправо-влево, вверх-вниз, пока светило не будет поймано в поле зрения. Тогда, установив изображение его в центре поля зрения, быстро сменить слабый окуляр на более сильный, следя за тем, чтобы в это время труба не сдвинулась.
Качество изображений и выбор окуляра. Не всегда воздух бывает вполне прозрачным и спокойным, и поэтому наибольшее увеличение не всегда применимо, так как при нем изображения не только не становятся лучше, но делаются совершенно мутными и дрожащими. Не надо гнаться обязательно за наибольшим увеличением, а выбирать, последовательно сменяя окуляры, то* при котором атмосферные недостатки не сказываются на отчетливости изображений.
Движение светила по полю зрения. Вследствие суточного вращения небесной сферы наблюдаемое светило быстро (тем быстрее, чем больше увеличение) перемещается по полю зрения справа налево (астрономическая труба переворачивает изображения). Следует приучиться по возможности плавно, без толчков, передвигать трубу за светилом непрерывно или же давать светилу пройти по середине поля зрения, следя за ним глазом и, когда оно дойдет до противоположного края, слегка передвинуть трубу и привести тем светило к правому краю» 178
XL КРАТКАЯ ХРОНОЛОГИЧЕСКАЯ ТАБЛИЦА ПО ИСТОРИИ АСТРОНОМИИ.
Дата
Первые записи астрономических наблюдений у египтян, вавилонян и китайцев........................................ 3000	лет до н. э.
Несомненные записи астрономических наблюдений . . . 800 „ „ , „
Первое (в Греции) предсказание солнечного затмения (Ф а-лесМилетский)........................................... 585	г. „ 9 9
При помощи 19-летнего цикла упорядочен календарь {греком Метоном)................................................ 440	г. „ „ г
Разработана теория планетных движений на концентрических сферах (Евдокс)......................................IV	в.	„	„	„
Изложение взглядов на вселенную в книге „О небе* Аристотелем .................................................IV	в.	„	Я9
Определение размеров земного шара из измерений (Эратосфен) ...................................................III	в.	„	9	9
Первые идеи о гелиоцентрической системе. Попытки определения расстояния до Солнца (Аристарх) ... •...........III в. „ „ 9
Разработка теории эпициклов..........................III	в. „ „ „
Определение элементов движения Солнца и Луны и главного неравенства лунной орбиты. Обработка прежних наблюдений и открытие явления прецессии. Первый звездный каталог (Гиппарх — величайший астроном древности)........... II в. „ , 9
„Альмагест* — книга с изложением геоцентрической системы мира. Первый из дошедших до нашего времени звездный каталог (Клавдий Птолемей)............................... II	в. н. э.
Перевод на арабский язык сочинений Аристотеля и Птолемея ..................................................VIII	и IX вв.
Градусное измерение Дуги между Тигром и Евфратом (А л ь-
Мамун).................................................. 827 г.
Астрономические (гакамитские) таблицы. Астрономические наблюдения в специально построенном здании...............X	и XI вв.
Астрономические (альфонсинские) таблицы. Открытое выражение сомнения в правильности птолемеевой системы . . .	1252 г.
Повторение наблюдений звезд Птолемея в специально построенной (в Самарканде) обсерватории Улуг-бек (татарский хан) .............................................. 1394 — 1449 гг.
Научное обоснование гелиоцентрической системы мира (НиколайКоперник)......................................... 1543	г.
Наблюдения над движением Марса, точнейшие из полученных до изобретении телескопа (ТихоБраге) ................ Конец	XVI в.
Сожжение Джордан о Бруно.............................. 1600	г.
Первый звездный атлас с обозначением ярких звезд буквами греческого алфавита (Байер).......................... 1603	г.
Применение изобретенной зрительной трубы к астрономическим наблюдениям, открытие солнечных пятен, лунных гор, фаз Венеры, спутников Юпитера и т. д. (Галилей, Шей-н е р, Ф а о р и ц и й)................................... 1610	г. и след.
Открытие законов движения планет Кеплером........... Около 1620 г.
Суд над Галилеем...................................... 1633	г.
Изучение силы тяжести, установление простейших законов кинематики и динамики (Галилей, Гюйгенс).................. XVII	в.
Изобретение часов с маятником (Гюйгенс)............... 1656	г.
Изобретение триангуляции и применение зрительных труб к градусным измерениям (Снеллиус, Пикар).................. XVII	в.
Определение скорости распространения света (Ремер). .	1675 г.
Установление закона тяготения. Возникновение теоретической астрономии (Ньютон)..........................•	. . .	1682 г.
Первое определение солнечного параллакса (Жан Кассини) 1671 г.
Основание Гриничской обсерватории в Англии и составление первого большого звездного каталога (Флемстид). .	1676 и 1725 гг.
Первый звездный каталог южного полушария. Открытие периодических комет и собственного движения звезд (Эдмунд
Галлей)................................ 1678,	1705 и 1718 гг.
179
1781 г.
1787 г.
1796 г.
1797 г.
1799 г.
1801 г.
—1817 гг.
1838 г.
1839 г.
1844 г.
1846 г.
1851 г.
1859 г.
1859 г.
1860 г.
Открытие аберрации света и развитие методики точных наблюдений (Брадлей) *............................,.................... 1728г.
Составление точных звездных каталогов (Брадлей, Лакайль, Л а л а н д)......................	.. . ............... 1758	г. и след.
Космогоническая гипотеза Канта............................ 1755	г.
Изобретение ахроматического объектива (Д о л л о н д)..... 1758	г.
Определение плотности Земли (Маскелайн, Кавендиш) 1774 —1798 гг. Возникновение небесной механики (Эйлер, Клер о, Лагранж, д’Аламбер, Лаплас)............*...........Конец	XVIII — начало XIX в.
Изготовление гиган7ских рефлекторов. Открытие орбитального движения двойных звезд, движения Солнца. Изучение строения звездной вселенной (В. Г е р ш е л ь)...................Конец	XVIII в.
Открытие Урана (В. Г е р ш е л ь).......................
Усовершенствованный хронометр (Гаррисон).............. . .
Научно обоснованная космогоническая гипотеза (Лаплас) . . .
Развитие методов определения кометных орбит (О л ь б е р с) . . • Начало специального производства точных измерительных приборов (Р е п с о л ь д)...........................................
Открытие первой малой планеты Цереры (П и а ц ц и). • • .
Усовершенствование ахроматических объективов и первое изме рение длин волн линий солнечного спектра (Фраунгофер). 1806 Измерение первого годичного параллакса звезды (Бессель). Основание Пулковской обсерватории ..........................
.Астрономия невидимого*—открытие существования спутников у Сириуса и Проциона (Бессель)................................
Открытие Нептуна и составление таблиц движения планет (Л е -веррье).....................................................
Открытие периодичности солнечных пятен (Швабе) ...... Составление каталога и атласа всех звезд северного неба до 10-й величины и начало изучения переменных звезд (Аргеландер). . .
Начало применения спектрального анализа (Кирхгоф). . • • Начало спектроскопии звезд (Секки, Хёггинс).............
Разработка способа наблюдать солнечные протуберанцы вне затмений (Ж а н с е и и Л о к а й е р)................ . т . . . .
Разработка теории строения комет (Бредихин) . ..........
Подробное изучение поверхности Марса и связи падающих звезд с кометами (Скиапарелли)....................................
Развитие теории приливов и гипотез в образовании Луны (Дж. Дарвин) ... ., ........... ............................ 1879—1881 гг.
Первые идеи о звездной эволюции (ЛокайериЛэн). • • Около
Начало составления каталогов точной яркости и спектров звезд, установление современной классификации спектров (Гарвардская обсерватория) ...........................................Около
Фундаментальный каталог звезд (Босс) и начало работы по составлению фотографической карты неба........................
Применение принципа Допплера в астрофизике (Д у н е р) . . . Изобретение спектрогелиографа (X э л, Д е л а н д р).  .
Начало развития звездной статистики................Около
Открытие зависимости между периодом цефеид и абсолютной яркостью их (Л и в и т т)...................................
Обнаружение существования звезд карликов и гигантов (X е р ц-шнрунг и Ресседл)...........................................
Гипотеза об эволюции звезд (Ресселл)....................
Нахождение метода определения параллаксов звезд по их спектрам (АдамсиКольшюттер)...........................................
Исследование системы звездных скоплений (Ш а п л и).....
Первое измерение диаметра звезды, интерферометром (Пиз). • . Применение теории ионизации к объяснению звездных спектров (Саха)......................................................
Открытие вращения Галактики (Оорт). . ..................
Открытие существования звездных сйстем, подобных Галактике.
Открытие планеты Плутон (Л о в е л л и Т ом б о) . .....
Открытие космического поглощения (Трюмплер).............
1868 г.
1877 г.
1877 г.
1880 г.
1884 г.
1887 г.
1887 г.
1892 г.
1900 г.
1908 г.
1913 г.
1913 г.
1914 г.
1918 г.
1920 г.
1921 г.
1924 г.
1924 г.
1930 г.
1930 г.
180
XII. ОБЩАЯ КАРТА ЛУНЫ.
Ниже приводятся названия главных лунных кратеров и цирков, обозначенных на карте Луны цифрами по квадрантам лунного диска.
Карта Луны дана для наблюдений в астрономическую трубу, перевертывающую изображения. Для наблюдений с биноклем карту надо рассматривать в перевернутом виде (север — кверху, юг — книзу). Чтобы удобнее было в этом случае прочитывать номера, лучше снять копию с карты и на этой копии поставить надписи и номера в перевернутом виде.
3 — Штёффлер
4 — Мавролик
б Фризиус
7 — Цагут
8 — Али аценз
10 — Катарина
11 — Кирилл
72 — Теофил
19 — Фабриций
20 Фраунгофер
21 — Фурнерии
25 — Петавий
30 — Лангрен
112 — Бланка» 114 — Клавий 115 — Магинус
115 — Лонгомонтан
117 — Тихо
118 — Вальтер
119 — Питат
123 — Тебит
Юг
125— Арзахель 127 — Альфонс 128 — Птолемей
134 — Шиллер 135 — Фосилид 137 — Шикард 144 — Гассенди 148 — Гримальди
Север
35 — Аристотель 35 — Евдокс
40 — Ари стилл 41 — Автолик 42 — Посидоний 53— Агриппа 61 — Атлас
66 — Геми нус 69 — Клеомед 77 — Тарунций
79 — Платон
83	— Архимед
84	— Тимохарис
85	— Ламберг
86	— Эйлер
88 — Эратосфен
90 — Коперник
102 — Аристарх
108 — Кеплер
181
ХШ. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА.
Пособия для наблюдений.
1.	Астрономический календарь-ежегодник. Переменная часть, Изд. Горьковского астрономо-геодезического о-ва и Горьковского изд-ва (на данный год).
2.	Русский астрономический календарь. Постоянная часть, Изд. 4-е, перераб., Изд. Нижегородского кружка любителей физики и астрономии, 1930.
3.	Проф. С. П. Г л а з е н а л, Друзьям и любителям астрономии, Изд. 3-е, дополн. и перераб под ред. проф Б А. Воронцова-Вельяминова, ОНТИ, М. — Л. 1936.
4.	М. Е. Н а б о к о в, Астрономия с биноклем, Изд. 2-е, Учпедгиз, М. 1937.
М ^^1935° А0/ АСГР°Н0МИЯ НЯ основе наблюдений» Перевод с франц. С. А. Шорыгина, ОНТИ,
6.	А. А. Ч и к и н, Астрономическая труба из очковых стекол, С добавлением П. В. Албычева. ГТТИ, М. 1932.	’
7.	П.П. Паренаго и Б. В. Кукаркин, Переменные звезды и способы их наблюдения. ОНТИ, М.—Л. 1938.
8.	Проф. А. А. Михайлов, Звездный атлас, Четыре карты звездного неба до 40° южного склонения, содержащие все звезды до 5'/2 величины, Изд. 2-е Московского о-ва любителей астрономии, М. 1920.
Пособия по вопросам определения времени.
9.	В. А. Р о с с о в с к а я, Время и его измерение, Гос. изд-во «Стандартизация и рационализация», Л. — М. 1933.
10.	Проф. И. Ф. П о л а к, Время и календарь, Изд. 2-е, ГТТИ, М. — Л. 1934.
О солнечной системе.
11.	Проф. В. М. Шульгин, Энергия Солнца, Изд. 2-е, дополн., Учпедгиз, М. 1937.
12.	Ч. Аббот, Солнце, Перевод Н. Я. Бугославской, ОНТИ, М. — Л. 1936.
13.	К. Л. Б а е в и В. А. Шишаков, Луна, Изд-во Академии наук СССР, М. —Л. (печатается).
14.	Проф. Б. А. Воронцов-Вельяминов, Как открывают планеты, ГАИЗ, 1937.
15.	Проф. К. Л. Баев, Обитаемы ли планеты, ГАИЗ, М. 1936.
16.	С. А. Ш о р ы г и и, Планеты, Изд-во Академии наук СССР, М. (печатается).
17.	Проф. И. Ф. П о л а к, Планета Марс и вопрос о жизни на ней, Изд. 3-е, ГОНТИ М.—Л, 1939.
18.	Проф. С. К. Всехсвятский, Что такое кометы. Изд-во Академии наук СССР, М — Л. 1938.
19.	Й. С. Астапович и В. В. Федынский, Метеоры, Изд-во Академии наук СССР, М. Л. (печатается)
20.	К. Л. Б а е в, Всемирное тяготение, ОНТИ, М. — Л. 1936
21.	Я- И. Перельман, Межпланетные путешествия, Изд. 10-е, ОНТИ, М. — Л. 1936.
22.	Я. И. Перельман, Занимательная астрономия, Изд. 3-е, под ред. проф. Б. А. Воронцова-Вельяминова, ГОНТИ, М. — Л. 1938.
О звездной вселенной и космогонии.
23.	Проф. К. Ф. Огородников, Как наблюдали небо прежде и как его наблюдают теперь, Изд-во Академии наук СССР, М. — Л. 1938.
24.	Проф. Б. А. Воронцов-Вельяминов, Строение вселенной, ОНТИ, М. — Л. 1936.
25.	Проф. И. Ф. П о л а к, Происхождение вселенной, Изд. 4-е, ОНТИ, М. — Л. 1934.
26.	Дж. Г. Д ж и н с, Движение миров, Переработка под редакцией Э. Кольмана, Детиздат. М. - Л. 1937.
По истории астрономии.
27.	Г. А. Г у р е в, Коперниковская ересь в прошлом и настоящем, Из истории взаимоотношений науки и религии, Изд. 3-е, перераб., ГАИЗ, М. 1938.
28.	Проф. Р. В. К у н и ц к и й, История развития взглядов на строение солнечной системы, ГАИЗ, М.1933.
29.	К. Л. Б а е в, Коперник, Журнально-газетное объединение, М. 1935.
30.	Б. А. Воронцов-Вельяминов. Лаплас, Журнально-газегное объединение, М. 1937.
Пособия для преподавателей.
31.	П. И. Потов, К. Л. Баев, Б. А. Воронцов-Вельяминов, Р. В. Куницкий, Астрономия, Учебник для высших педагогических учебных заведений, Учпедгиз, М. —- Л. 1940.
32.	Проф. М. Е. Н а б о к о в, Методика преподавания астрономии, Учпедгиз, М.—*Л. (печатается).
33.	Проф. Б. А. Воронцов-Вельяминов, Сборник задач и упражнений по астрономии. Учпедгиз, М. —Л. 1939.
34.	Доц. А. М. Смирнов. Пособия по астрономии, Учпедгиз, М. — Л. 1936.
35.	Проф. И. Ф. Полак, Курс общей астрономии, Изд. 5-е, пересмотр, и дополн., ГИТТЛ, М.—Л, 1939,
ОГЛАВЛЕНИЕ.
ЧАСТЬ ОБЩАЯ.
Глава I. Введение.
Стр,
§ 1.	Астрономия, ее задачи и методы .	3
§ 2.	Очерк вселенной . . . .»....... 4
§ 3.	О наблюдениях • • •	9
§ 4.	Небосвод и созвездия............—
§ 5.	Яркости звезд.................. 10
§ 6.	Число наблюдаемых звезд........—
§ 7.	Цвета звезд..................•	11
§ 8.	Обозначения звезд ......... —
§ 9.	Суточное вращение звездного неба —
§ 10.	Угловые измерения.............. 14
§ 11.	Секстан........................ 15
§ 12.	Небесный меридиан ........ 16
§ 13.	Определение положения меридиана 17
§ 14.	Небесная сфера.................. —
§ 15.	Горизонтальные координаты .... 19
§ 16.	Универсальный инструмент .... 20
§ 17.	Небесный экватор и горизонтальная плоскость....................... 21
§ 18.	Экваториальные координаты. ... —
§ 19.	Звездные карты................ 22
§ 20.	Эклиптика..................... 24
§ 21.	Звездные сутки, звездное время и часовой угол........................ 27
Стр.
§ 22.	Высота светила в момент кульминации .............................. 28
§ 23.	Видимость светил в зависимости от их склонений........................ 29
§ 24.	Равноденствие и солнцестояние. Длительность дня.................... 30
§ 25.	Экваториальная установка	трубы .	—
§ 26.	Меридианный инструмент.....31
§ 27.	Пассажный инструмент...... 32
§ 28.	Рефракция и ее учет в астрономии.	33
§ 29.	Сумерки.................... —
§ 30.	Измерение времени..........34
§ 31.	Среднее и истинное время... —
§ 32.	Уравнение времени......... 35
§ 33.	Поверка местного времени	по
Солнцу...................... 36
§ 34.	Звездное и среднее время....... —
§ 35.	Расчет вида звездного неба	. •	« •	37
Наблюдения.........................  38
Задачи и вопросы...............• . . 40
Глава II. Форма Земли и ее вращение.
§ 36.	Развитие взглядов на форму Земли 42
§ 37.	Вращение Земли.................45
§ 33.	Доказательства шарообразности Земли.................•.............. 46
§ 39.	Доказательства вращения Земли . 47
§ 40.	Видимый и математический горизонт ................................ 49
§ 41.	Географические координаты . • . . 50
§ 42.	Земной шар и небесная сфера ...
§ 43.	Широта места и высота полюса. . 52
§ 44.	Вращение Земли и счет времени . 53
$ 45. Местное время и долгота.......--
§ 46.	Международный поясной счет времени ............................ 54
§ 47.	Перевод времени............. 55
§ 48.	Служба времени..............56
§ 49.	Способы поверки часов.......57
§ 50.	Измерение диаметра земного шара 58
§ 51.	Триангуляция............... 59
§ 52.	Форма Земли................ 60
§ 53.	Сжатие Земли и его причины ... 61
§ 54.	Построение географических карт . —
Задачи и вопросы..................63
Глава III. Развитие представлений о солнечной системе*
§ 55. Параллактическое смещение .... 65
$ 56	. Горизонтальный экваториальный параллакс........................... 66
§ 57.	Расстояние и параллакс	67
§ 53.	Определение линейных диаметров светил.............................. 68
§ 59.	Видимое движение Луны среди звезд —
§ 60.	Видимые движения планет. . . • . 69
§ 61.	Видимые движения Меркурия и Венеры ............................... 70
§ 62.	Взгляды на устройство солнечной системы в древности..................71
§ 63.	Теория Коперника.............. 72
§ 64.	Объяснение видимых движений планет ...............................   —
§ 65.	Планетные конфигурации........74
§ 66.	Фазы Меркурия и Вейеры........—
§ 67.	Сидерические и синодические периоды обращений планет..............75
§ 68.	Астрология...................  76
§ 69.	Революционное учение Коперника и борьба церкви с коперникан-ством •.................*	...........—.
§ 70.	Аберрация.................... 78
§ 71.	Годичный параллакс............80
§ 72.	Параллаксы звезд............. ...
§ 73.	Движение Земли вокруг Солнца. . 82 $ 74. Основа календаря............. 84
§ 75.	Старый и новый календарные стили —
§ 76.	Узаконенный в СССР счет времени 85 § 77. Эра..........................
§ 78.	Законы Кеплера..............  86
§ 79.	Строение солнечной системы . • . 88
§ 80.	Параллаксы Солнца и Луны .... 89 § 81. Размеры планет и Солнца...... —
§ 82.	Лунные фазы и пепельный свег . .	—
§ 83.	Месяц.......................  91
§ 84.	Затмения..................... ...
§ 85.	Лунные затмения...............90
§ 86.	Солнечные затмения............93
§ 87.	Полные солнечные затмения .... 94
§ 88.	Орбита Луны................... —
§ 89.	Предвычисление затмении......95
§ 90.	Вращение Луны и либрация .... 96 Наблюдения.........................  —
Задачи и вопросы..................•	97
Стр.
§ 91. Закон всемирного тяготения. ... 97
§ 92» Распределение тяжести на поверхности Земли . •.....................  99
Глава IV. Всемирное тяготение.
Стр.
§ 93.	Определение массы Земли.......100
§ 94.	Движение Луны.................. —
§ 95.	Вывод закона тяготения из законов Кеплера.............................101
§ 96.	Ускорение движений планет относительно Солнца . . . •.............. —
§ 97.	Точное выражение третьего закона Кеплера ............................102
§ 98.	Возмущения..................... —
§ 99.	Вычисление масс небесных тел. . . 103
§ 100.	Усюйчивость планетной системы. 103
§ 101.	Открытия Нептуна и Плугона . . 104
§ 102.	Зависимость вида орбип от на-
§ 103.	Межпланетные путешествия .... —
§ 104.	Приливы и от швы...........105
§ 105.	Объяснение приливов........106
§ 106.	Роль приливов в эволюции Земли и Луны.......................- . . —
§ 107.	Явление пр мессии...........ЮЗ
§ 108.	Причины предварения равноденствий ............................ —
Задачи и вопросы...................109
ЧАСТЬ АСТРОФИЗИЧЕСКАЯ.
Глава /. Методы астрофизических исследований.
ПО
111
§ 1.	Астрофизика..................
§ 2.	Астрономические обсерватории . .
§ 3.	Астрофотография..............
§ 4.	Астрофотометрия..............
§ 5.	Спектроскопия................
Глава II.
§ 8.	Общие данные о Солнце........112
§ 9.	Жизнь Солнца и жизнь Земли . . • 113
§ 10.	Общий вид Солнца в телескоп ... —
§ 11.	Вращение Солнца............... —
§ 12.	Солнечные пятна и их изменения . 115
§ 13.	Периодичность солнечных пятен . . 116
§ 14.	Спектр и химический состав Солнца ................................. —
§ 15.	Свет и теплота Солнца......... —
§ 16.	Обращающий слой	и	хромосфера . 118
§ 17.	Солнечная корона.............119
§ 6.	Определение лучевых скоростей светил..........................112
§ 7.	Определение температур небесных тел.............................. —
Солнце.
§ 18.	Зодиакальный свет . ,......120
§ 19.	Строение Солнца............. —
§ 20.	Наблюдение протуберанцев и короны вне затмений...............121
§ 21.	Спектрогелиограф............ —
§ 22.	Спектрогелиограммы Солнца .... 122
§ 23.	Цикл солнечной деятельности и его связь с земными явлениями ....	—
Наблюдения ............... 123
Задачи............................ —
Глава III. Луна и планеты.
§ 24.	Строение лунной поверхности . . . 123
§ 25.	Физические условия на Луне . . . 125
§ 26.	Две группы больших планет .... 126
4 27. Меркурий и Венера ... • . . . . 127
§ 28.	Земля и ее атмосфера.......... —
§ 29.	Марс........................127
§ 30.	Юпитер......................130
§ 31.	Сатурн....................... —
4 32.	Уран, Нептун п Плутон.......131
§ 33.	Астероиды.................... —
Глава IV. Кометы и метеоры.
$ 34. Вид комет и их	изменения......132
§ 35. Орбиты комет.................. —
4 36. Физическая природа комет......133
4 37. Метеоры .....................134
4 38. Распад комет и	метеоры...... —
§ 39. Болиды и метеориты.............135
§ 40. Возможно ли столкновение Земли с кометой?.......................136
Наблюдения ...............
Задачи..................
Глава V. Звездная вселенная.
§ 41.	Методы изучения звезд..........137
§ 42.	Число и яркости звезд..........139
§ 43.	Параллаксы звезд..............141
§ 44.	Видимая и абсолютная яркости
звезд...........................142
§ 45.	Млечный Путь................... —
§ 46.	Видимое распределение звезд ... 144
§ 47.	Движения звезд.................145
§ 48.	Туманности....................146
4 49.	Звездные скопления............148
§ 50.	Строение вселенной............. —
4 51.	Цвета и спектры звезд.........151
4 52.	Температуры звезд.............152
§ 53.	Двойные звезды................. —
§ 54.	Переменные звезды.............154
§ 55.	Затменные звезды...............155
§ 56.	Цефеиды и долгопериодические переменные звезды......................156
§ 57.	Новые звезды................... —
§ 58.	Связь между абсолюшыми звездными величинами и спек i рами . . 157
§ 59.	Эволюция те зд.......... —
4 60 Звезды-пи анты и зпс зш-картикп . 158
§61. Итоги изучения с троения вселенной 159
Наблюдения ............. . . 160
Задачи.......................161
Глава VI. Эволюция вселенной и происхождение солнечной системы.
§ 62.	Легенды о „сотворении мира" ... 161
§ 63.	Противодействие христианской церкви созданию научных космогонических гипотез.....................164
§ 64.	Гипотеза Лапласа...............165
§ 65.	Накопление наблюдательных данных .................................167
§ 66. Эволюция больших туманностей . . —
§ 67.	Происхождение солнечной системы по Джинсу........................168
§ 68.	Возраст небесных тел.......170
§ 69.	Заключение................. —
Задачи и вопросы.................171
Приложения ......... . . ... . 172