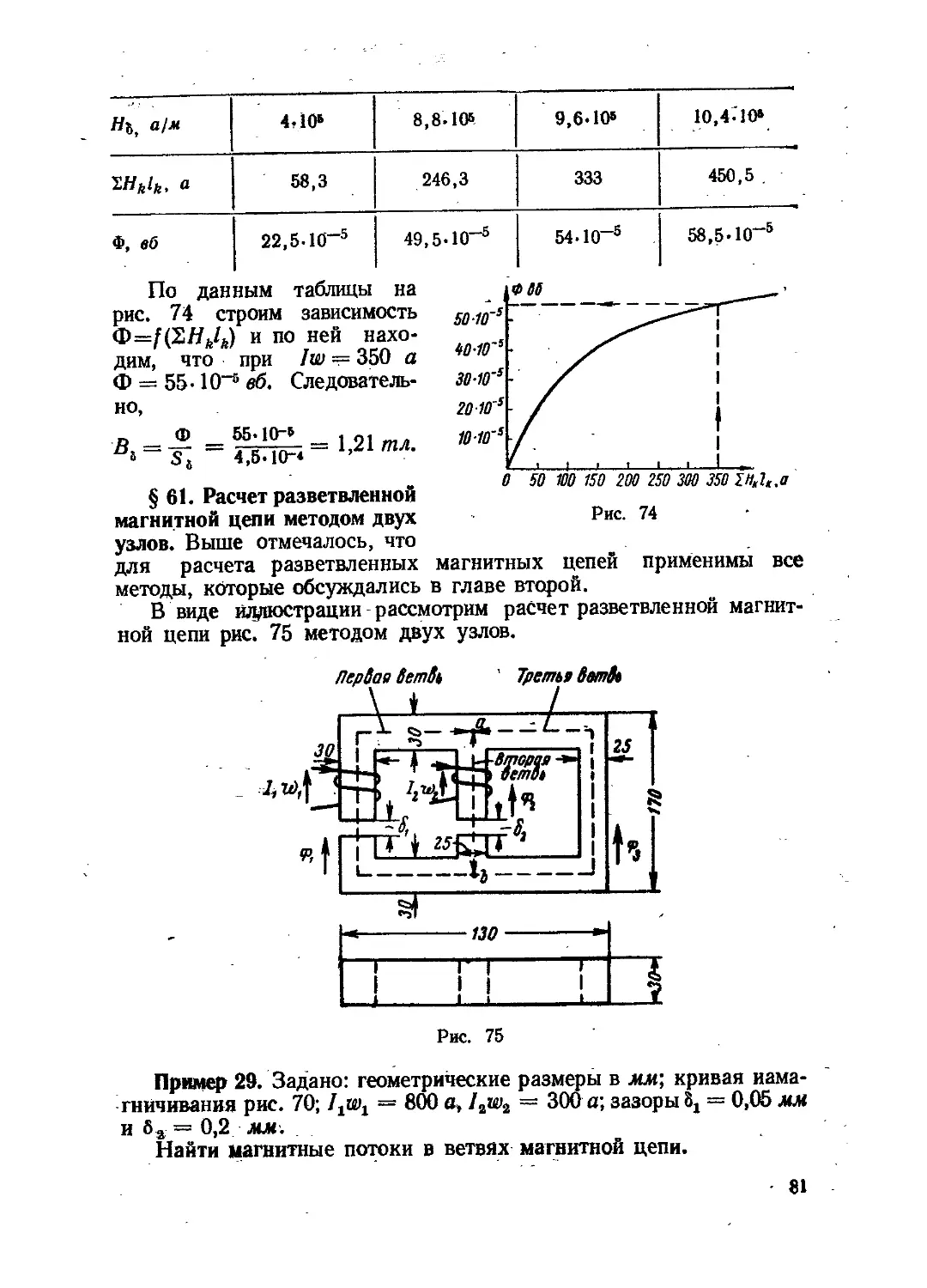
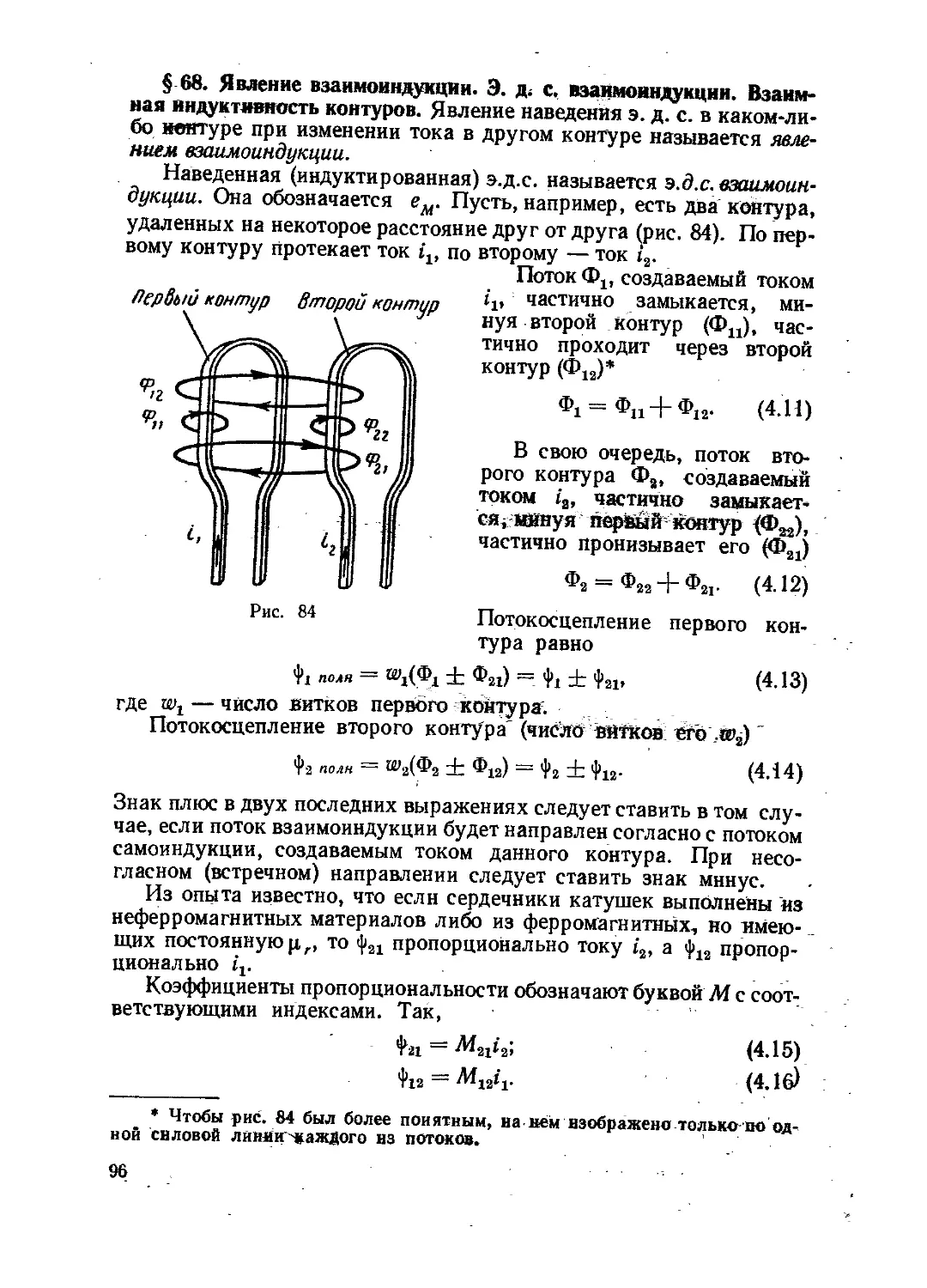
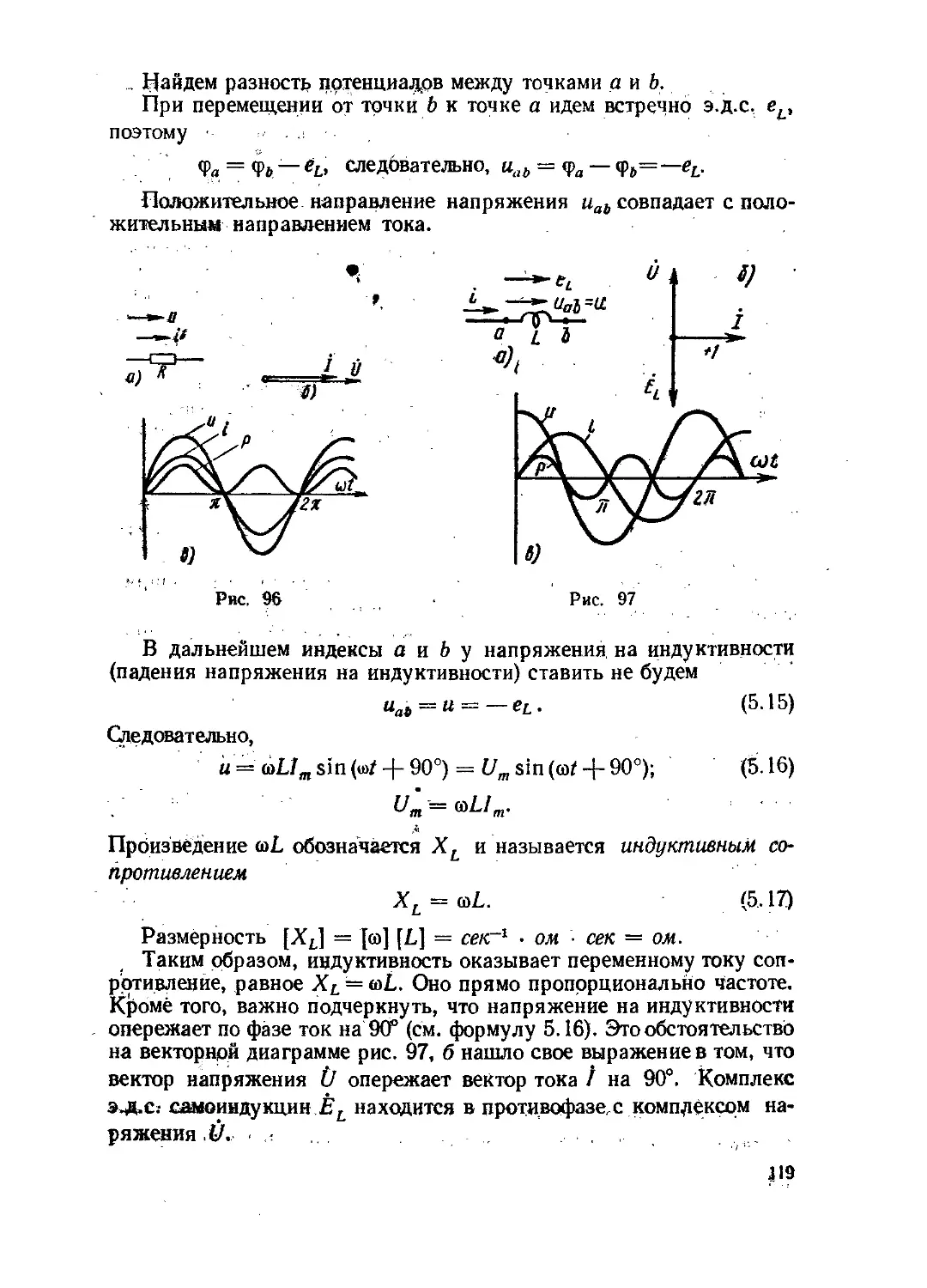
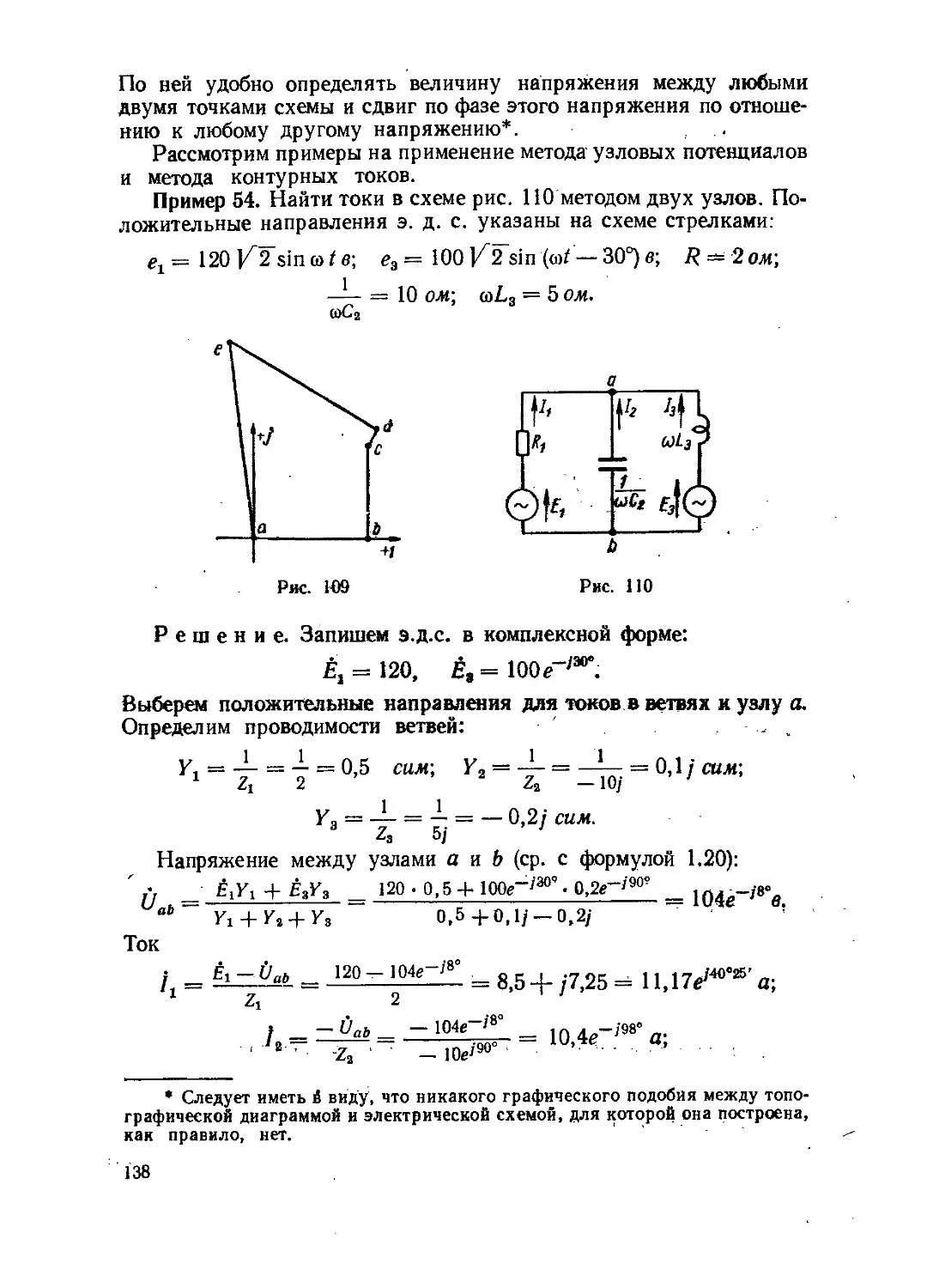
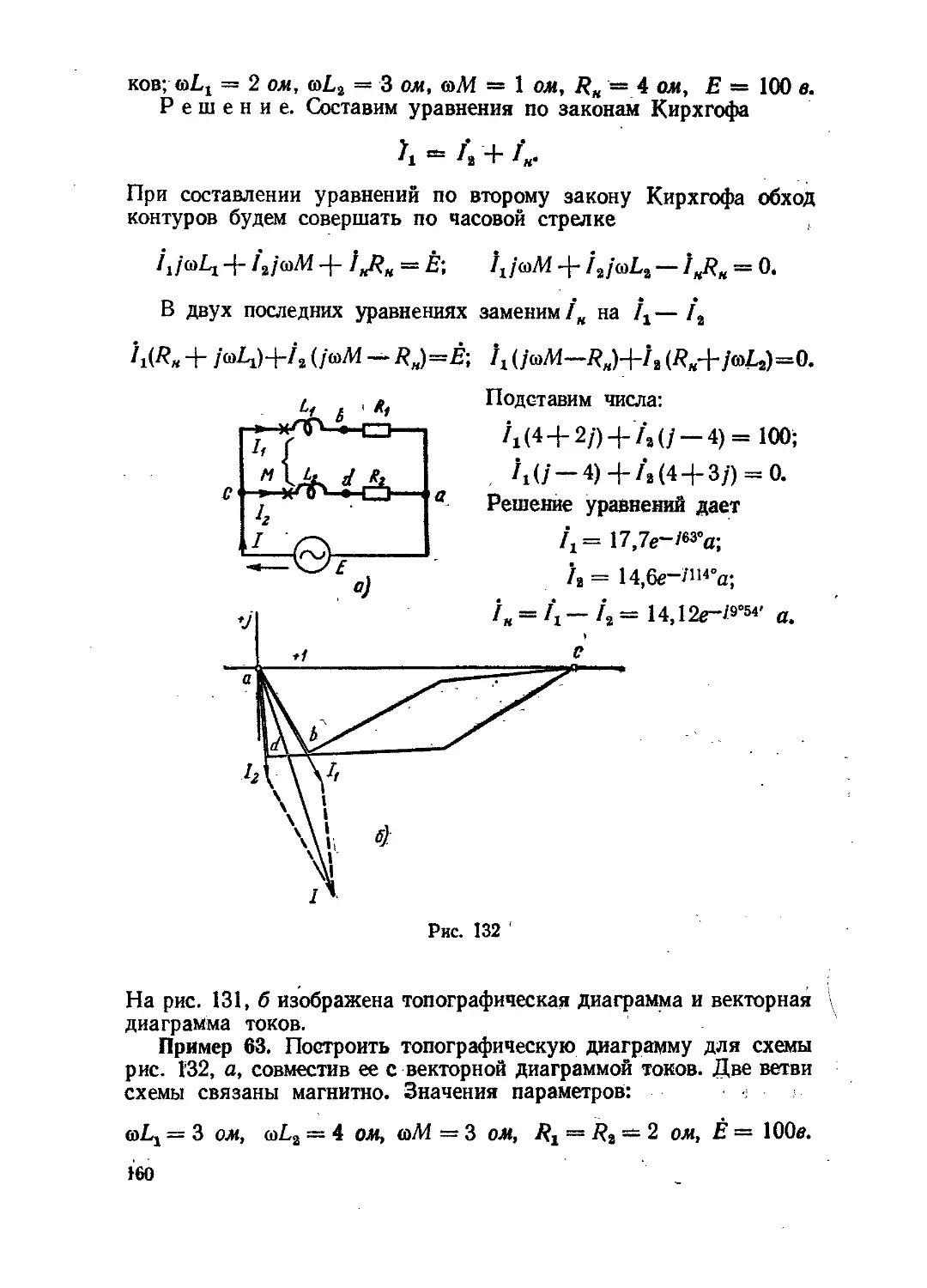
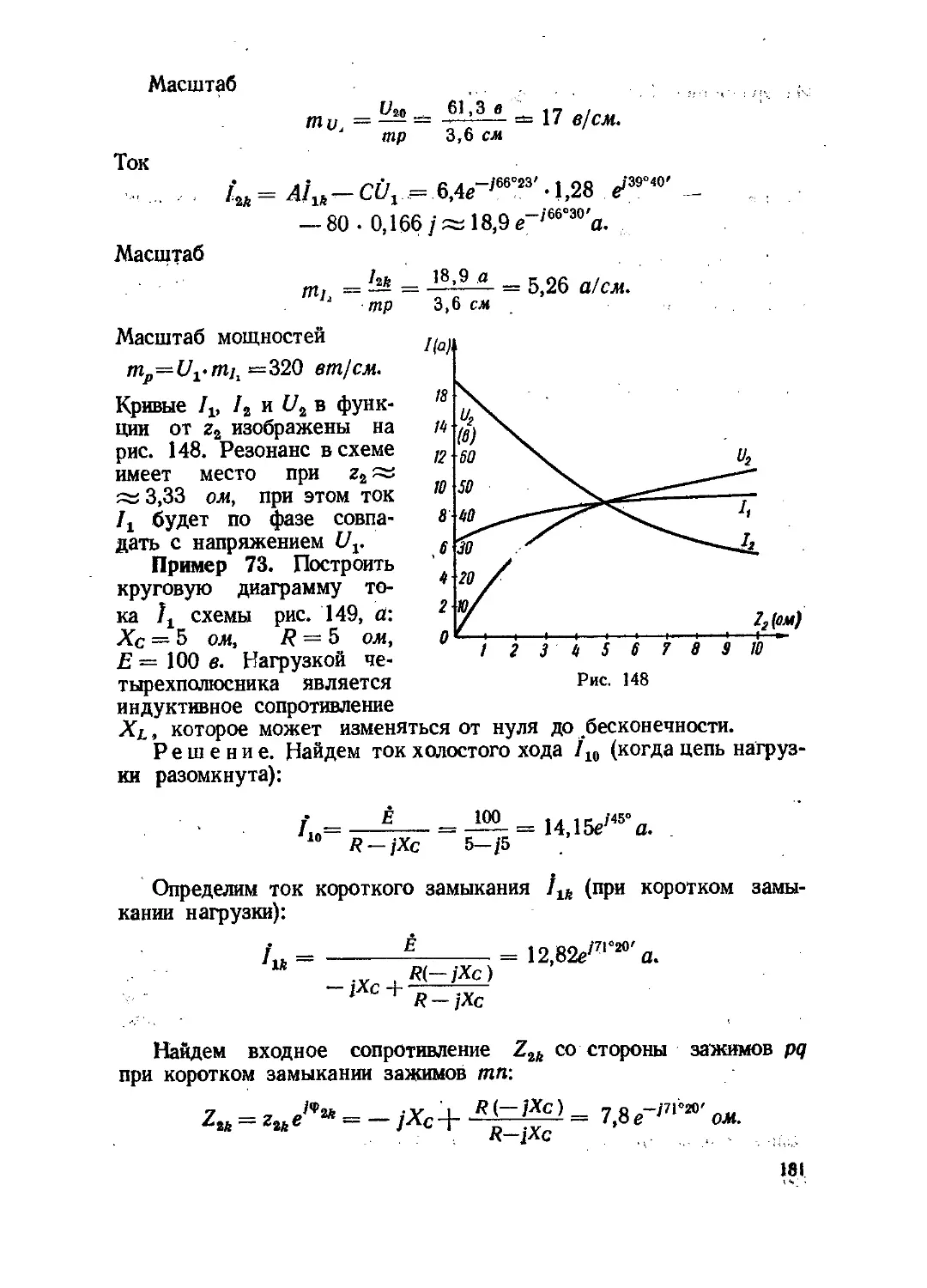
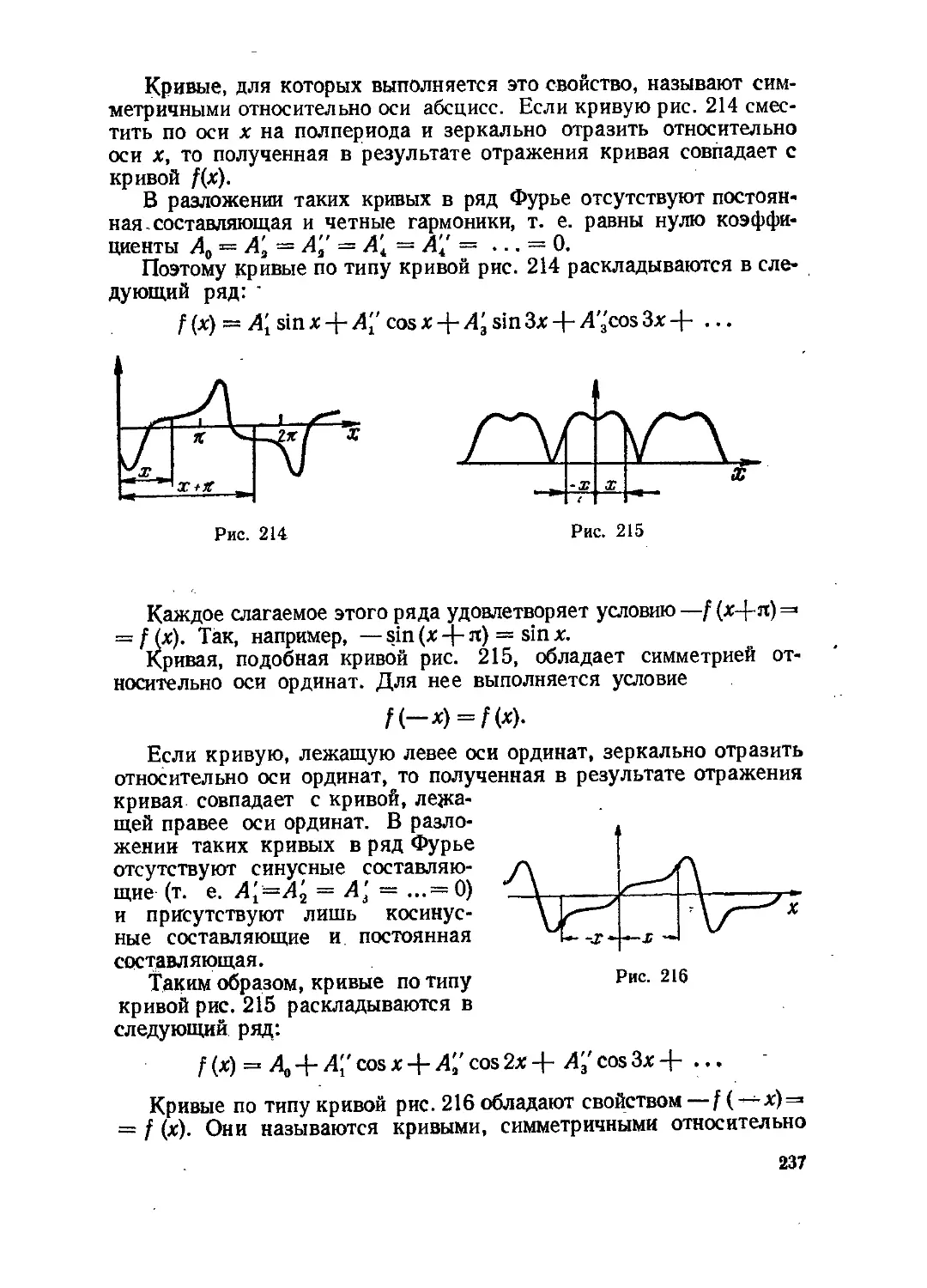
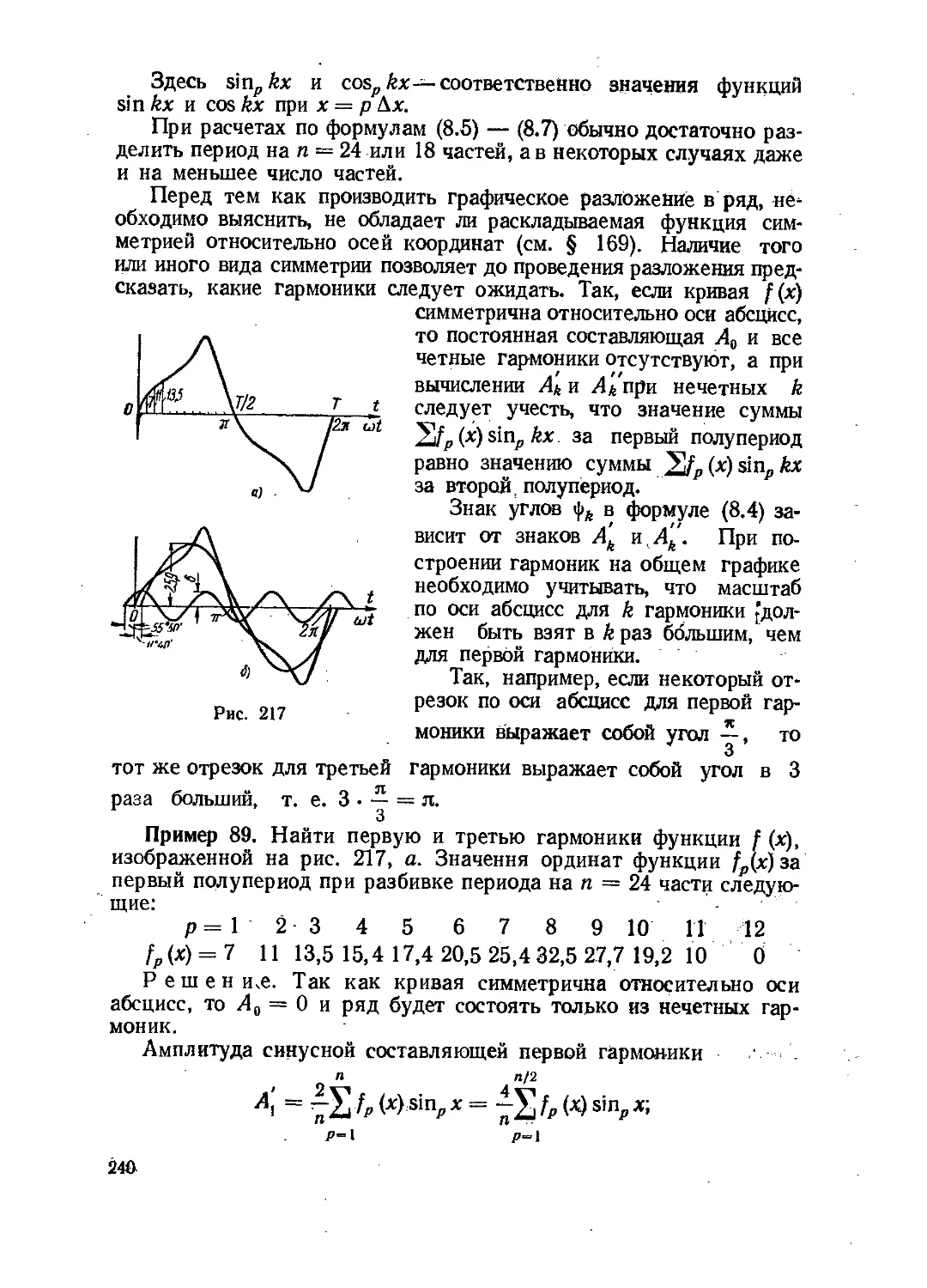
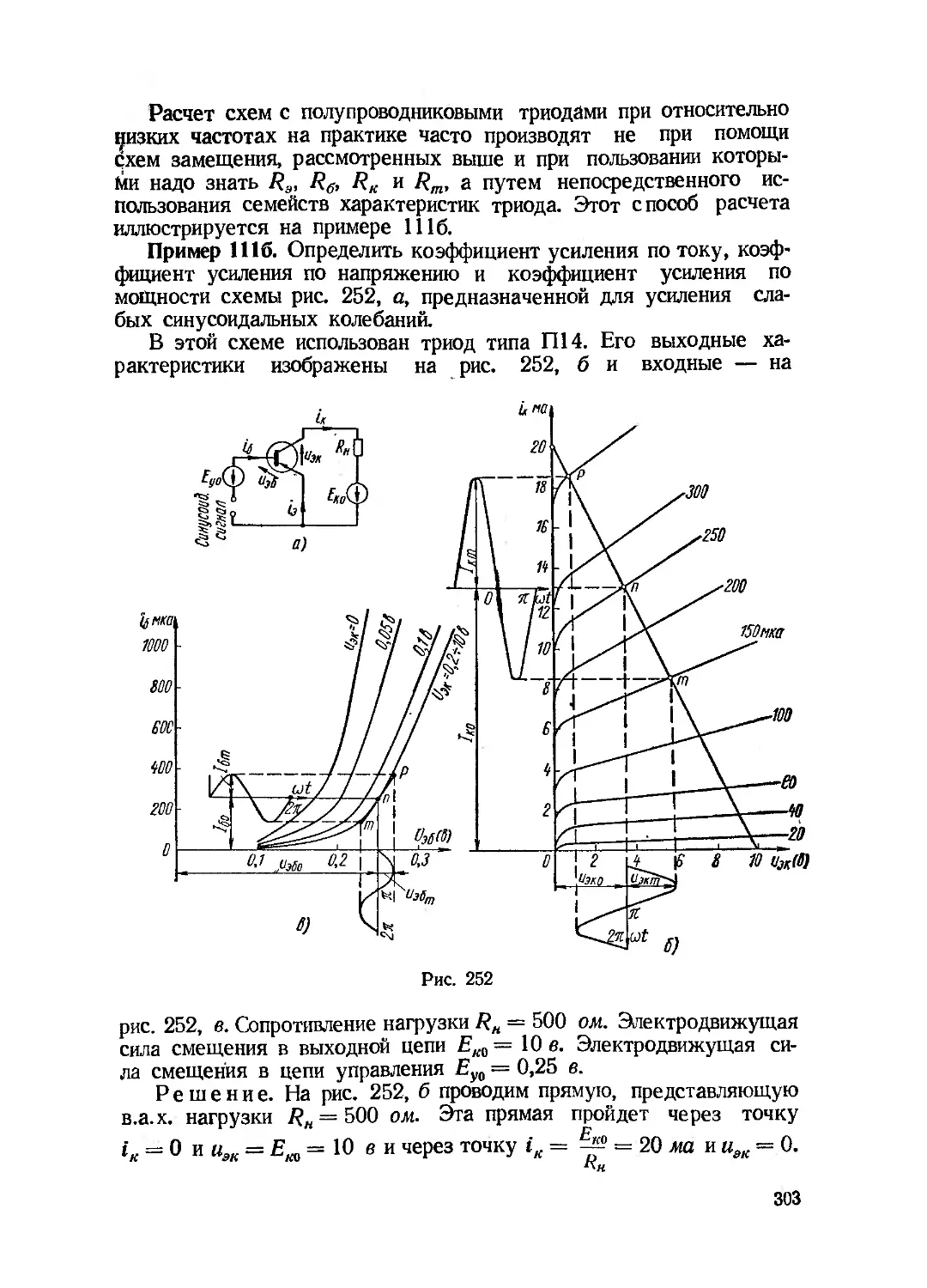
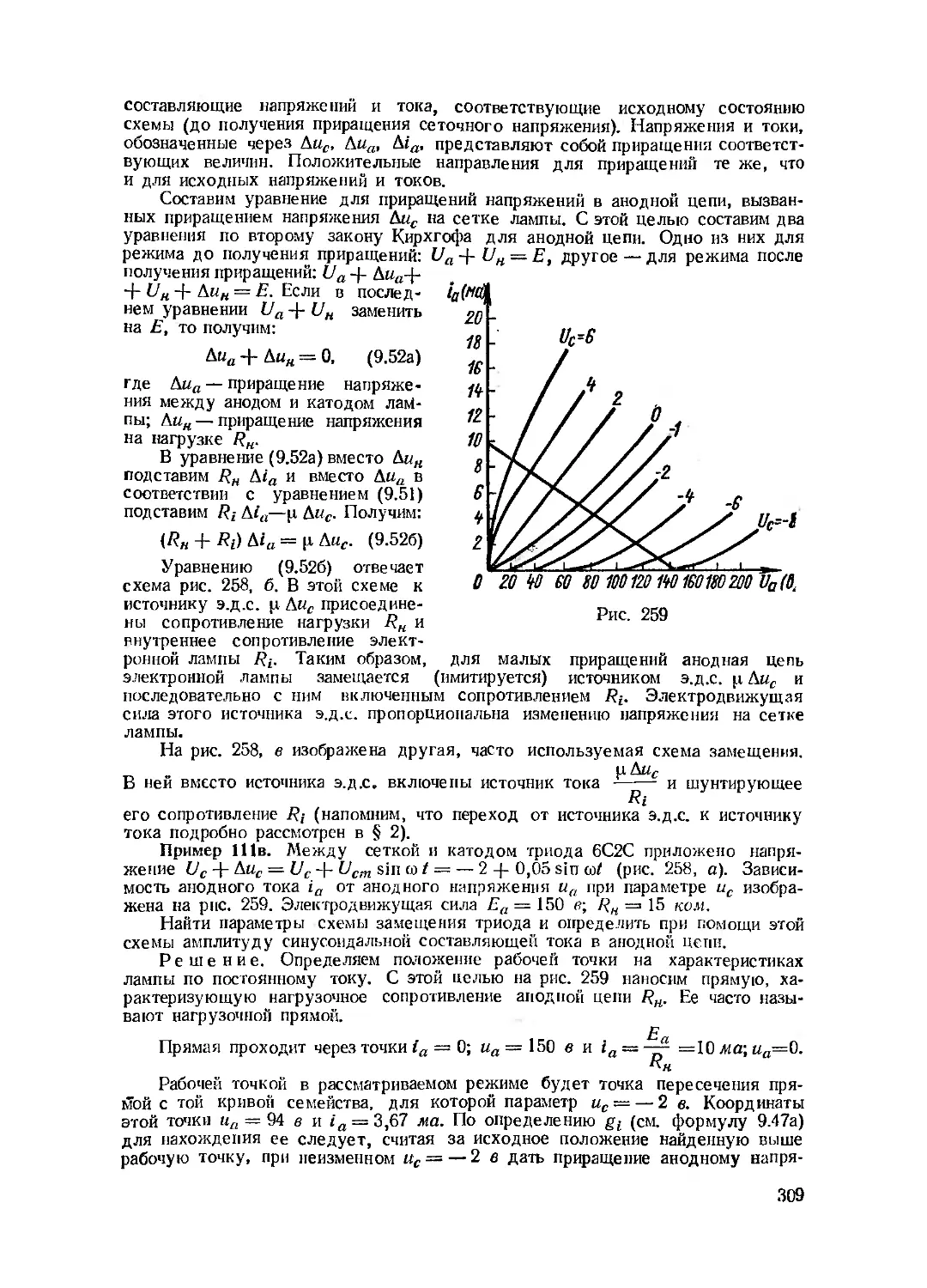
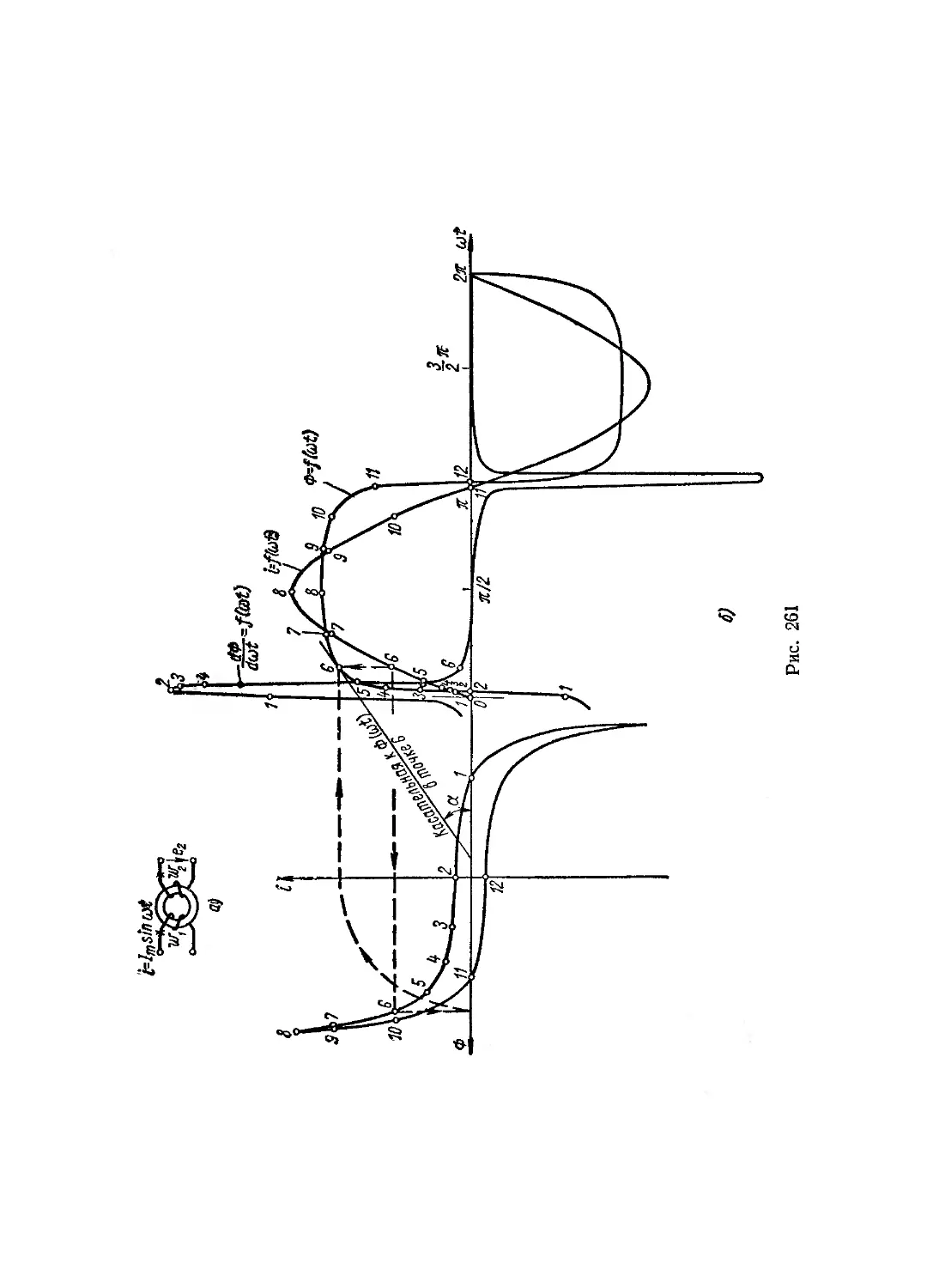
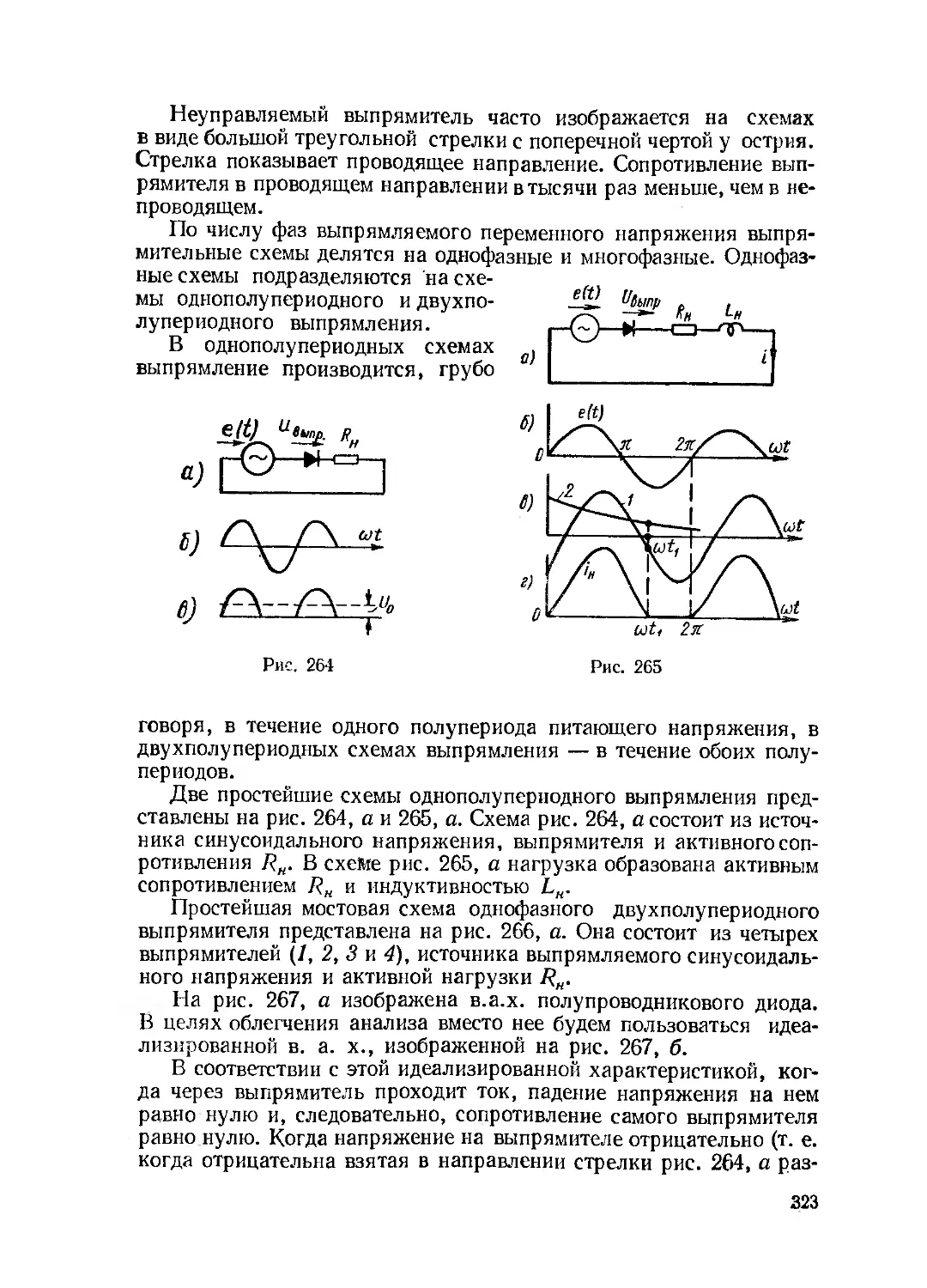
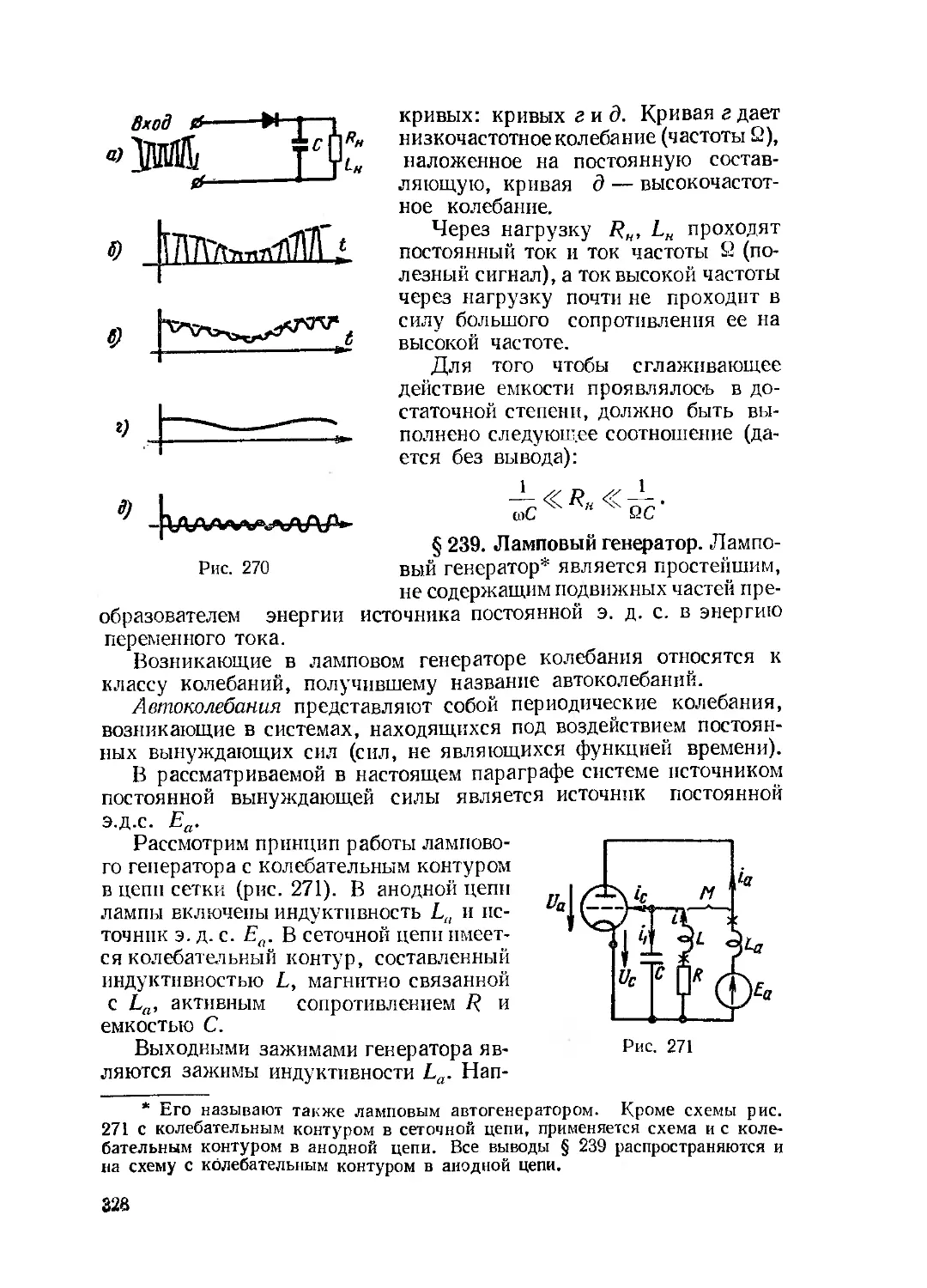
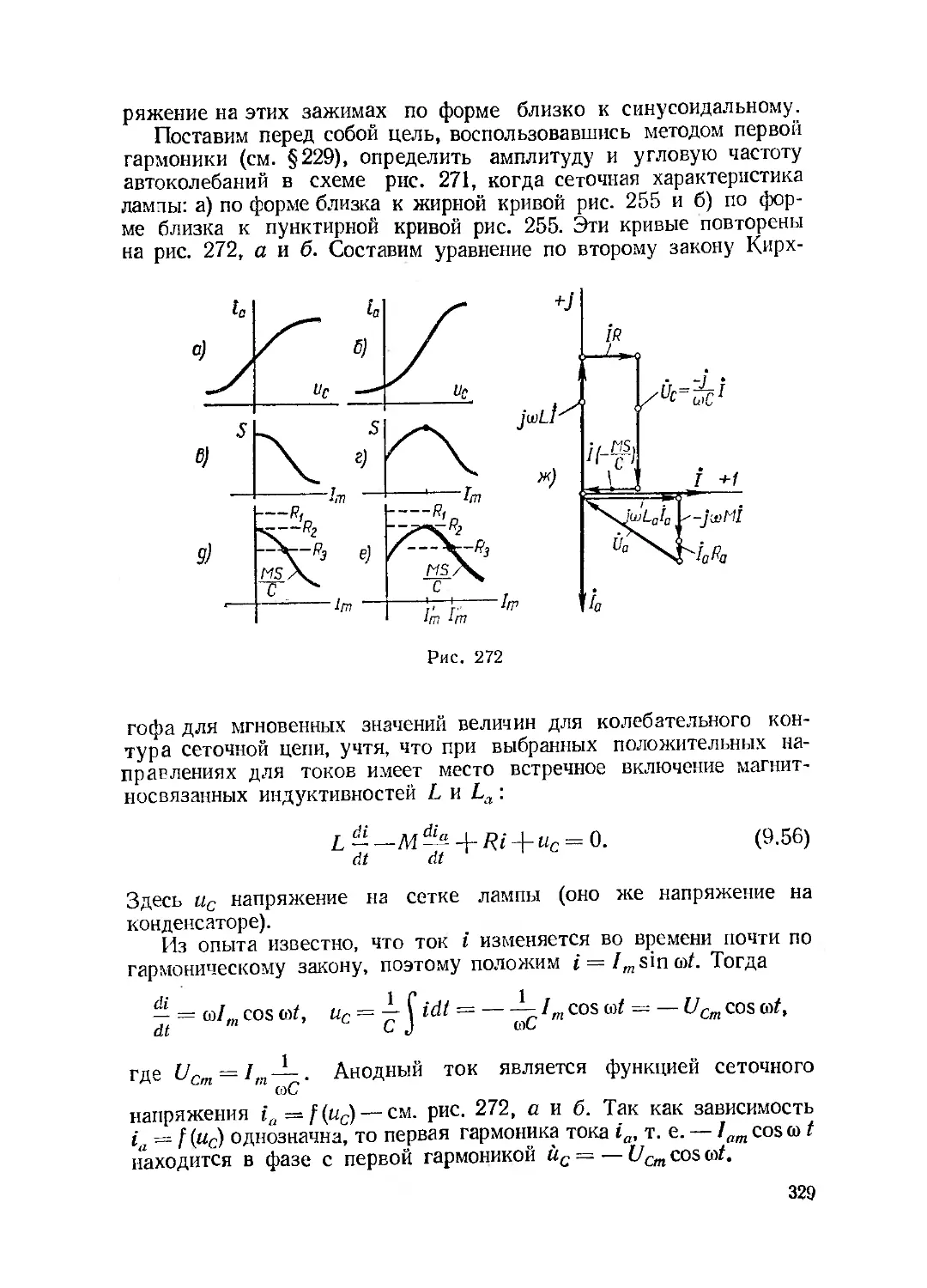
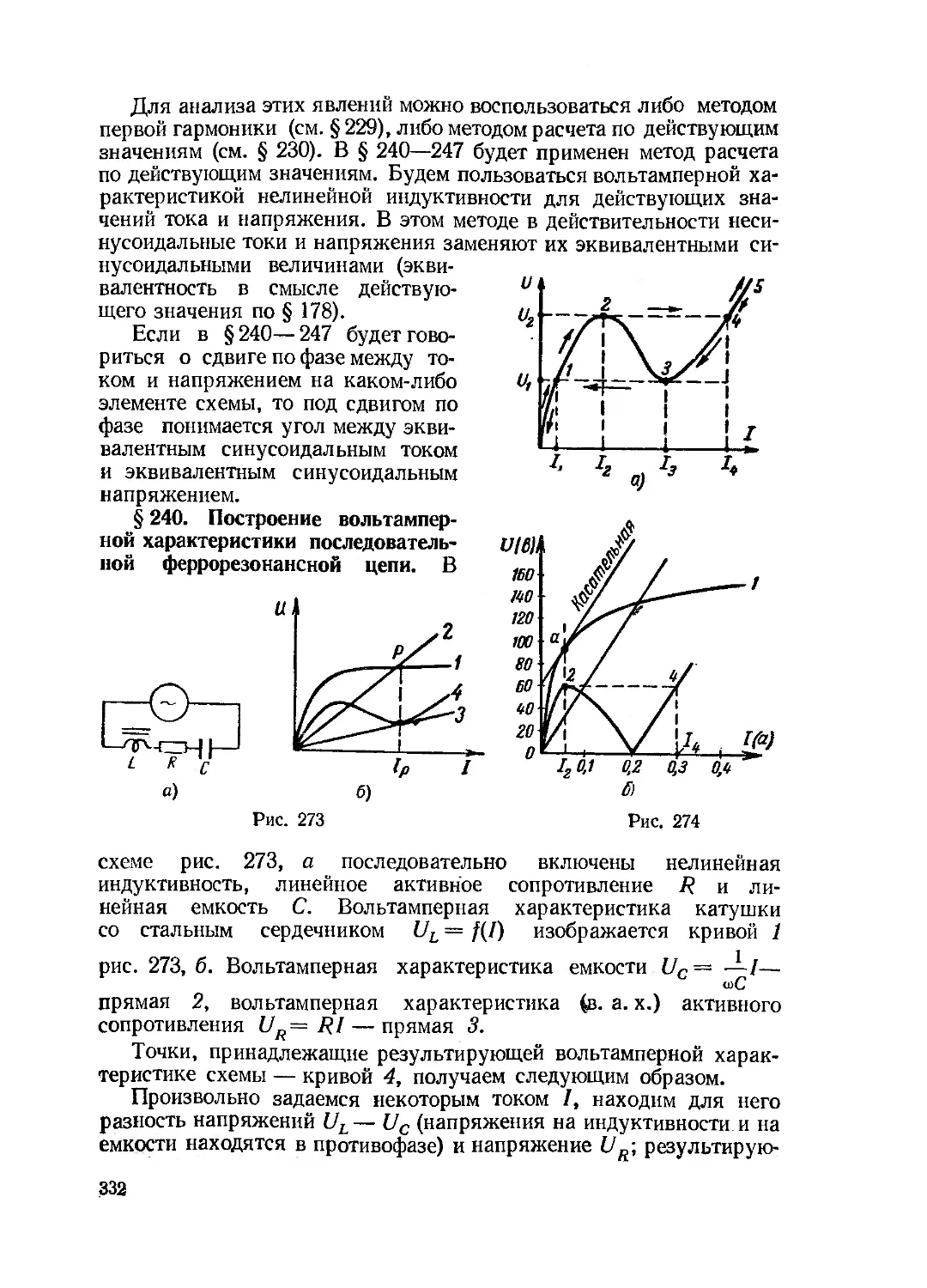
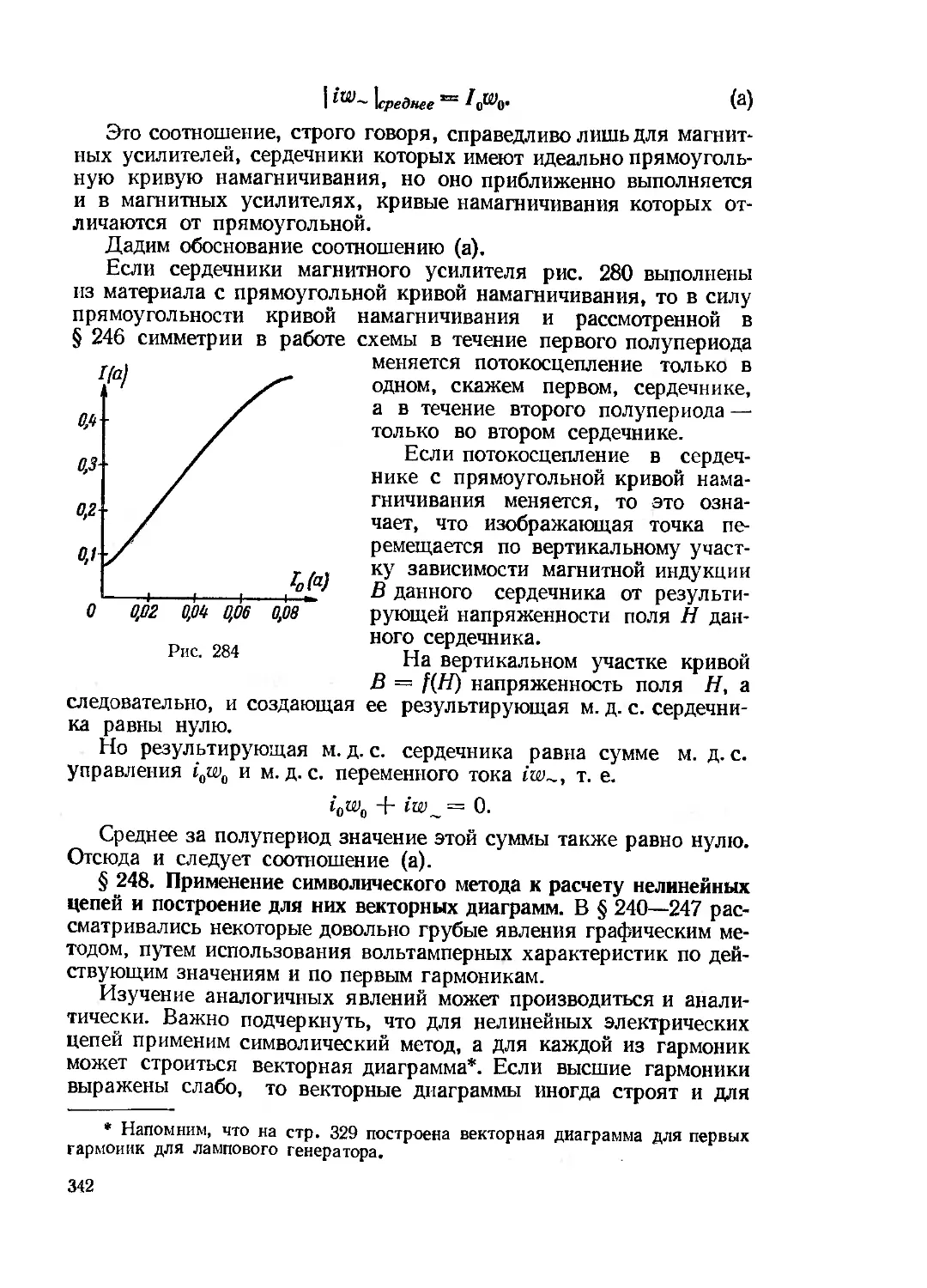
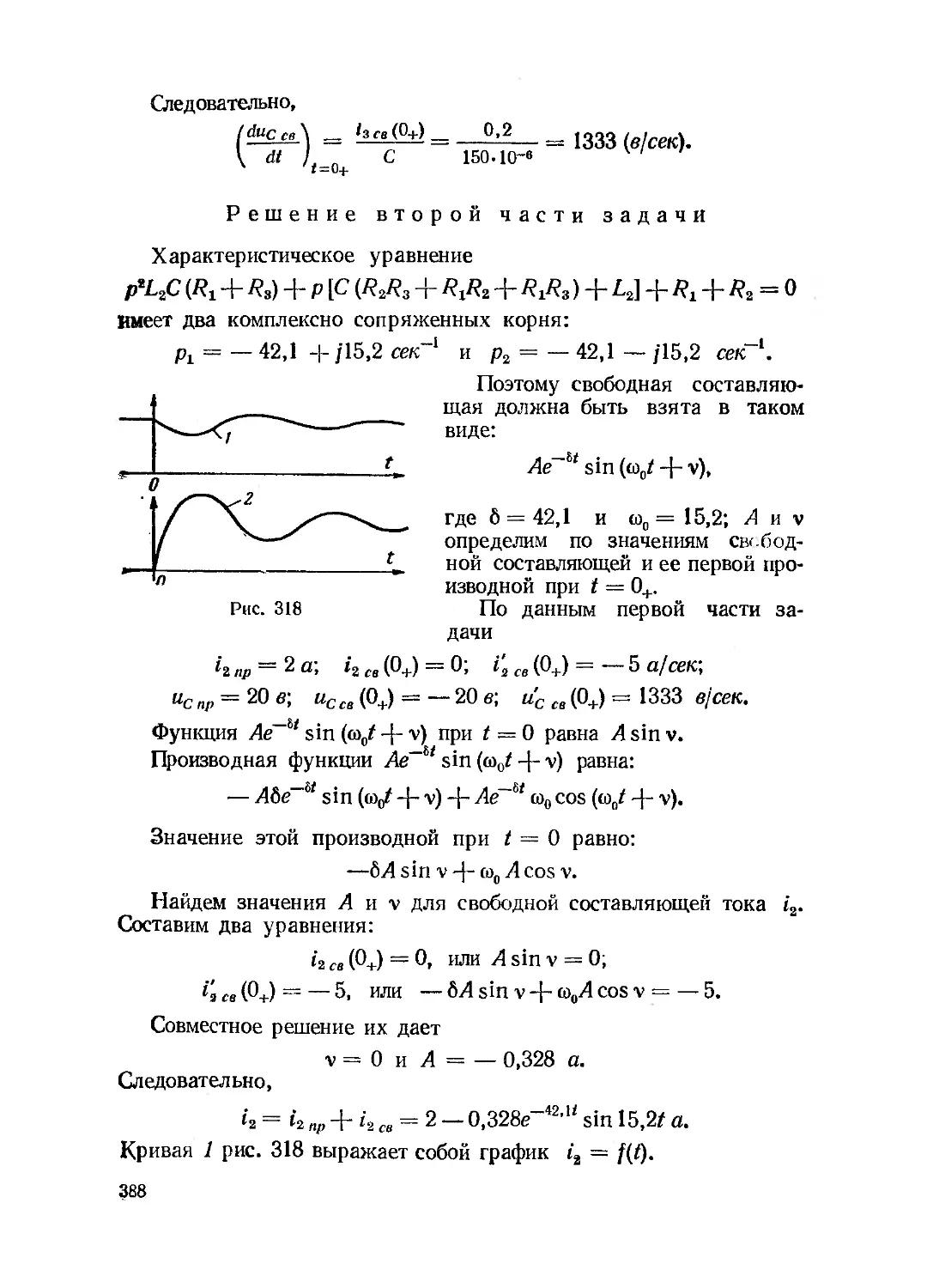
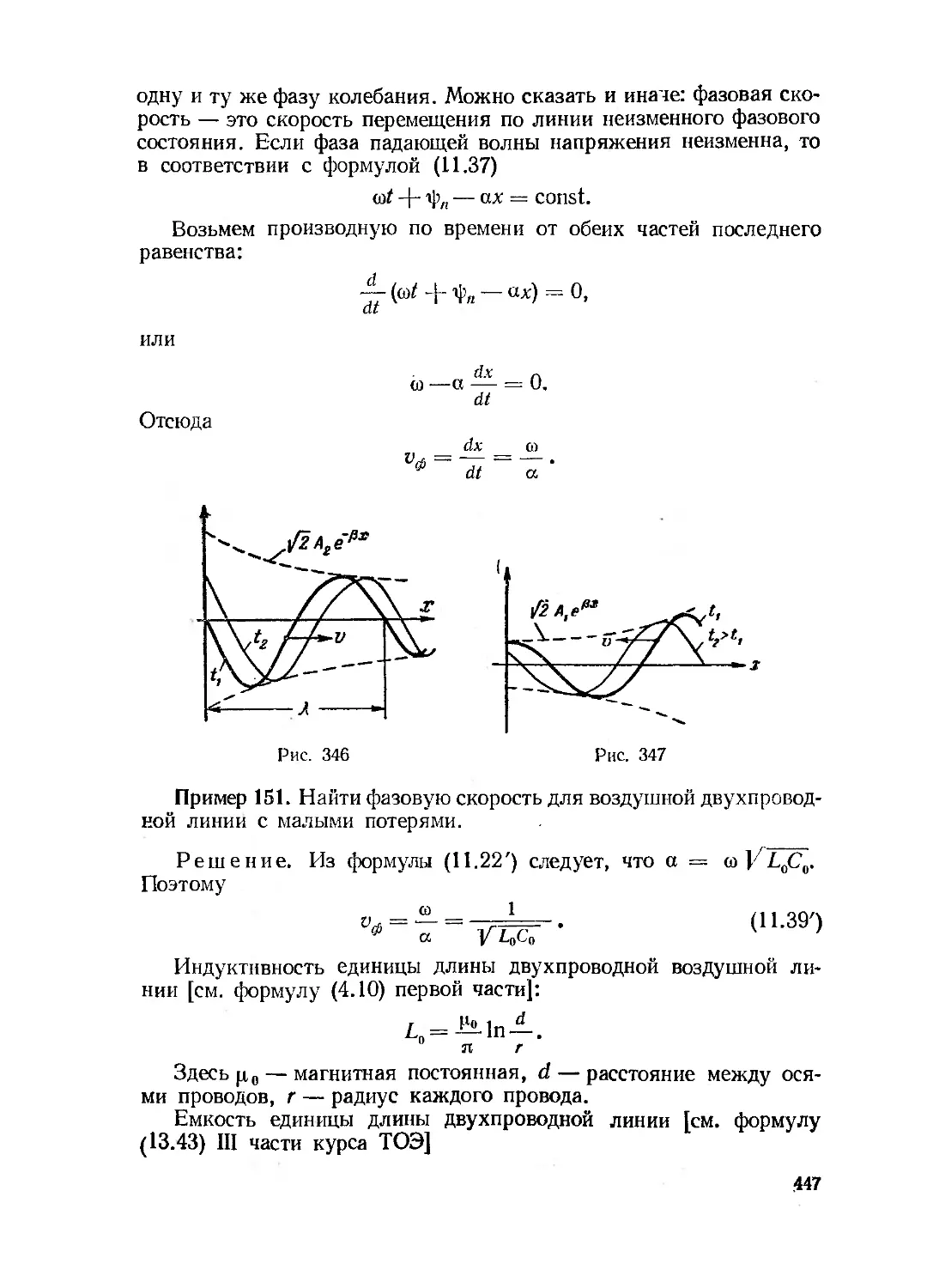
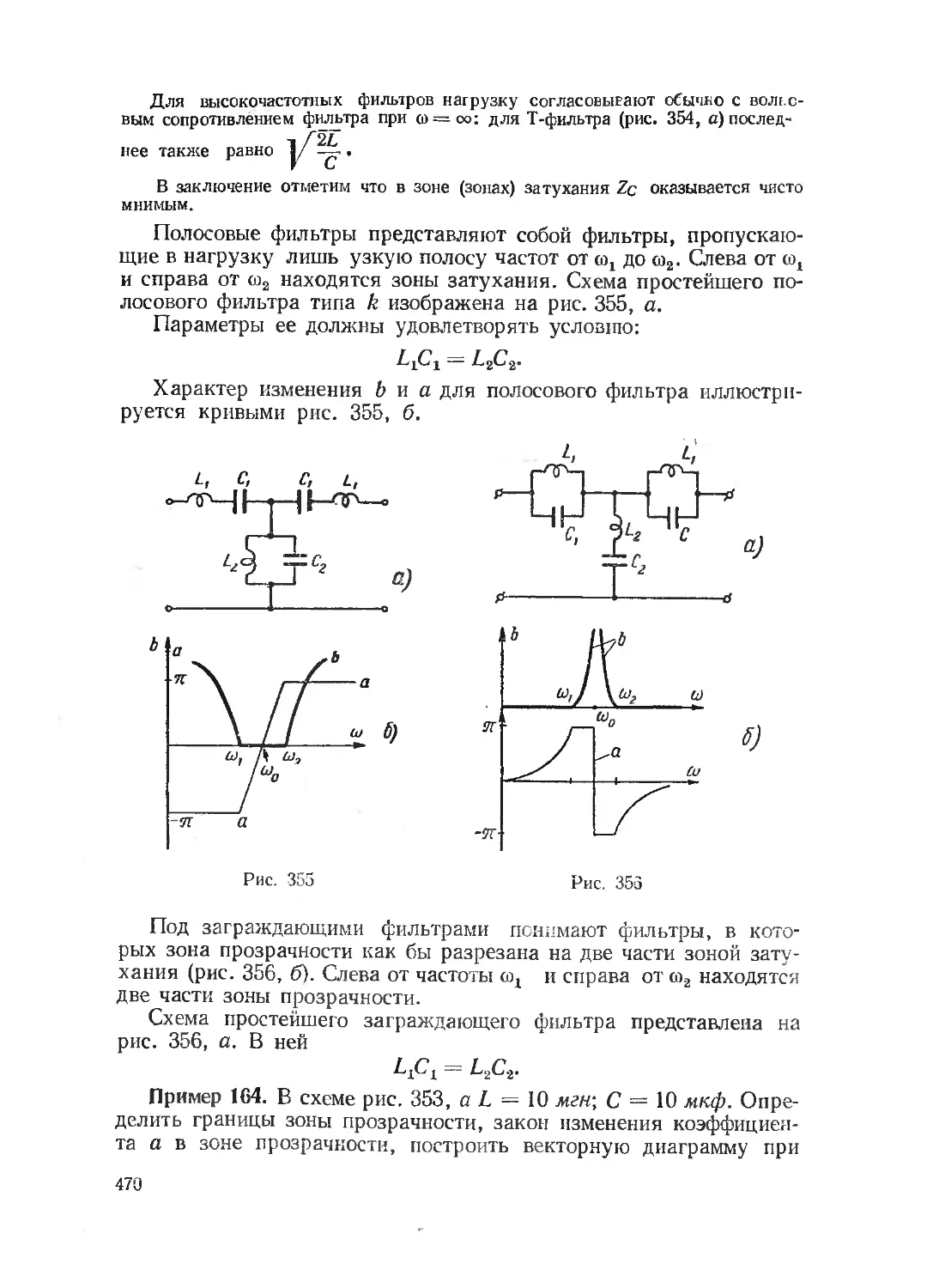
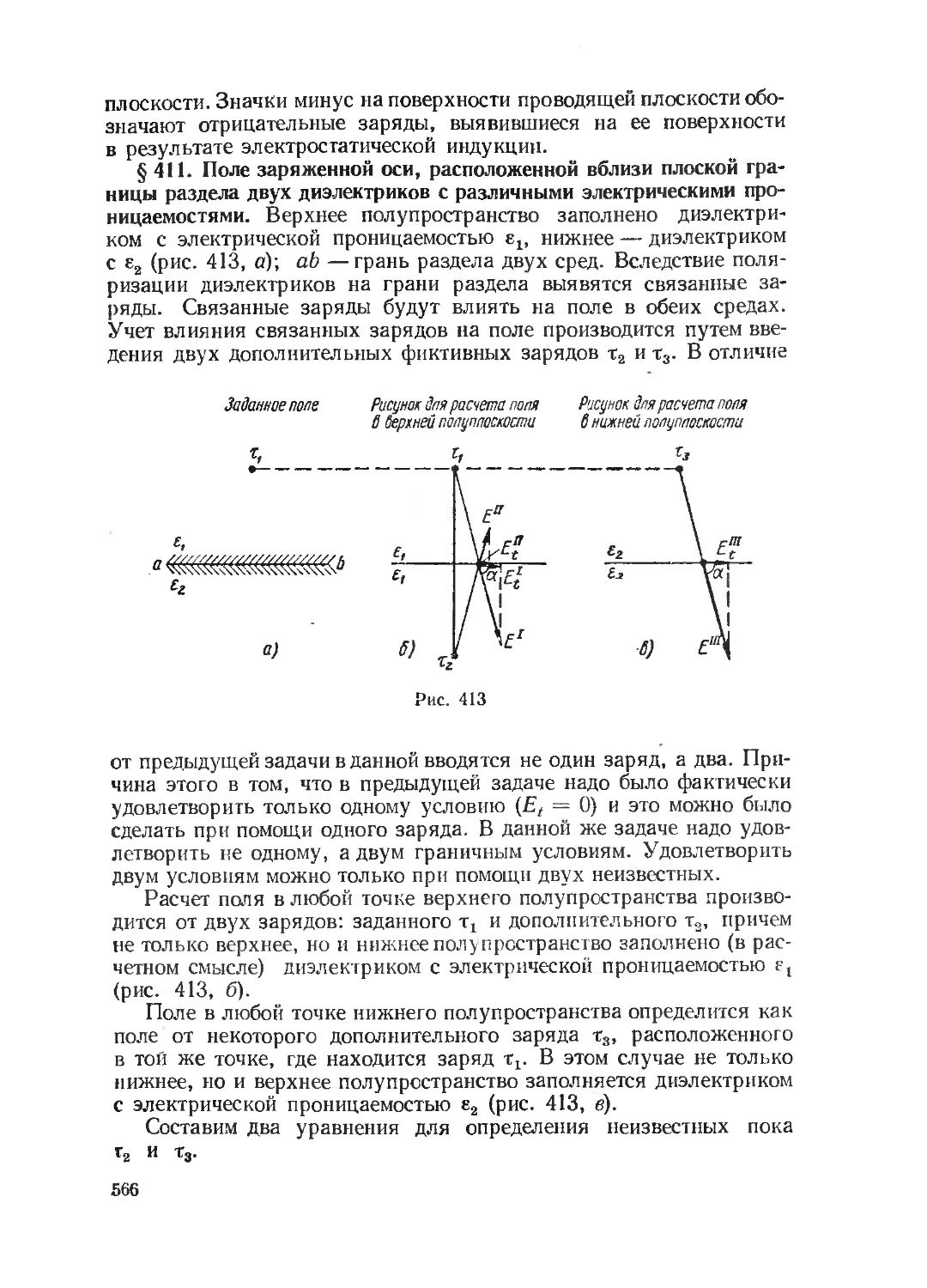
Текст
Л. А. БЕССОНОВ
ТЕОРЕТИЧЕСКИЕ
ОСНОВЫ
ЭЛЕКТРОТЕХНИКИ
В ТРЕХ ЧАСТЯХ
Издание четвертое
Допущено
Министерство и высшего и среднего
специального образования СССР
в качестве учебника
для внерге/ических и ? тектротсхнических
вузов и факу 1ьтетов
ИЗДАТЕЛЬСТВО «ВЫСШАЯ ШКОЛА!
Москва — 1964
ПРЕДИСЛОВИЕ
Теоретические основы электротехники (ТОЭ) являются одной
из основных дисциплин многих высших технических учебных заве-
дений. На ней базируются профилирующие дисциплины этих вузов.
Курс ТОЭ изучается студентами в течение трех семестров. В
соответствии с этим 'предлагаемый вниманию читателя учебник
по курсу ТОЭ издается в трех частях.
Первая и вторая части курса посвящены теории электрических
цепей, третья часть — теории электромагнитного поля.
Содержание учебника соответствует программе по ТОЭ (ин-
декс УМУ-Т-3/23 ), утвержденной в 1962 г. Министерством высше-
го и среднего специального образования СССР для высших учеб-
ных заведений по всем специальностям, в учебных планах кото-
рых имеется этот курс.
С целью облегчения усвоения курса ТОЭ в книгу включено бо-
лее 220 численных примеров с решениями. Примеры подобраны
так, что образуют полный цикл упражнений по всем трем частям
курса.
Наличие большого количества примеров по всем разделам кур-
са особенно существенно для тех, кто собирается изучать ТОЭ са-
мостоятельно и в первую очередь для студентов заочных и вечерних
учебных заведений.
Основной материал курса набран обычным шрифтом (корпу-
сом). Материал, набранный петитом, является относительно вто-
ростепенным и может быть опущен. Однако с ним все же рекомен-
дуется ознакомиться, для того чтобы подготовиться по ТОЭ лучше,
чем минимально необходимо.
Естественно, что по указанию кафедры ТОЭ того или иного
вуза часть материала книги, набранного петитом, может счи-
таться обязательной для студентов какой-либо специальности и,
наоборот, часть материала книги, набранного корпусом, необя-
зательной.
Десять параграфов третьей части курса, набранных кор-
пусом, помечены звездочками. Пометка звездочкой у номера
параграфа означает, что студент должен уяснить основные положе-
3
ния данного параграфа, понять идею вывода, уметь пользоваться
выведенными в параграфе формулами, но подробного зияния всех
выкладок, выполненных в этом параграфе, от него не требуется.
Изложение материала ведется в Международной системе единиц
СИ.
По сравнению с предыдущим изданием полнее рассмот-
рен вопрос о синтезе электрических цепей и добавлены разделы
о применении матриц в электротехнике, о электромеханических
аналогиях, о методе сеток, о моделировании полей по методу
электрических сеток, об уравнениях активных четырехполюсников,
понятие о графах и ряд других.
При подготовке рукописи к печати учтены замечания, содержа-
щиеся в официальной рецензии на книгу кафедры ТОЭ Новочеркас-
ского политехнического института («Известия высших учебных за-
ведений», серия Электромеханика, № 12, 1962) — заведующий ка-
федрой проф. В. М. Алехин, учтены также замечания товарищей
по кафедре и в особенности доц. В. П. Олексевича и пожелания,
высказанные проф. Ю. Г. Толстовым.
Автор выражает благодарность всем лицам, своими критическими
замечаниями способствовавшим улучшению книги. Весьма ценная
помощь при корректуре книги мне была оказана В. П. Каменской
и С. Э. Расовской, за что им очень благодарен.
Автор
ЧАСТЬ 1
Глава первая
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПОСТОЯННОГО ТОКА
§ 1. Определение линейных и нелинейных электрических цепей.
Совокупность соединенных друг с другом источников электри-
ческой энергии и нагрузок, по которым может протекать электри-
ческий ток, называют электрической цепью.
В данной главе будут рассматриваться электрические цепи пос-
тоянного тока. Постоянным током называют ток, неизменный во
времени. Постоянный ток представляет собой направленное упоря-
доченное движение частиц, несущих на себе электрические заряды.
Как известно из курса физики, носителями зарядов в металлах
являются свободные электроны, а в жидкостях — ионы. Упорядо-
ченное движение носителей зарядов в проводниках вызывается элект-
рическим полем, созданным в них источниками электрической энер-
гии. Источники электрической энергии представляют собой такие
источники, которые преобразуют химическую, механическую и
другие виды энергии в электрическую. Источник электрической
энергии характеризуется величиной н направлением электродви-
жущей силы (э. д. с.) и величиной внутреннего сопротивления.
Условимся обозначать постоянный ток буквой /, э. д. с. источ-
ника — буквой Е и сопротивление — буквой R. В Международ-
ной системе единиц (в системе СИ*) ток измеряется в амперах (а),
э. д. с. — в вольтах (в) и сопротивление — в омах (ом).
Изображение электрической цепи на рисунке с помощью услов-
ных знаков принято называть электрической схемой (рис. 1, а).
Условным знаком сопротивления R на электрической схеме яв-
ляется вытянутый прямоугольник. Условным знаком источника
электрической энергии является кружок с изображенной внутри
него стрелкой. Стрелка указывает положительное направление
э. д. с. (более подробно об источниках энергии см. в § 2).
* От первых букв слов The International System of Units. Введена как
предпочтительная система с 1 января 1963 г. (ГОСТ 9867—61).
7
За положительное направление э. д. с. источника энергии
принимается направление возрастания потенциала внутри этого
источника.
Приемник энергии и провода, соединяющие приемник с источ-
ником энергии, называют «внешней» частью электрической цепи, или
короче, внешней цепью. Во внешней цепи ток течет от плюса источ-
ника энергии к минусу, а внутри источника — от минуса к плюсу.
Зависимость тока, протекающего по сопротивлению, от напряже-
ния на этом сопротивлении принято называть вольтамперной харак-
теристикой. Вольтамперные характеристики изображают графи-
чески. В этом случае по оси абсцисс на графике в некотором мас-
штабе обычно откладывается напряжение, а по оси ординат — ток.
Рис. 1
Различают два принципиально отличных типа вольтамперных
характеристик. В первой из них вольтамперная характеристика
представляет собой прямую линию (рис. 1, б), во втором — неко-
торую кривую линию (рис. 1, в).
Сопротивления, вольтамперные характеристики которых явля-
ются прямыми линиями, называют линейными сопротивлениями,
а электрические цепи с входящими в них только линейными сопро-
тивлениями принято называть линейными электрическими цепями.
Сопротивления, вольтамперные характеристики которых не яв-
ляются прямыми линиями (т. е. нелинейны), называют нелинейными
сопротивлениями, а электрические цепи с нелинейными сопротивле-
ниями называют нелинейными электрическими цепями.
§ 2. Источник э. д. с. и источник тока. При расчете и анализе
электрических цепей источник электрической энергии заменяют рас-
четным эквивалентом. В качестве последнего может быть взят:
1. Либо источник э. д. с. и последовательно с ним включенное
сопротивление равное внутреннему сопротивлению реального
источника энергии (рис. 2, а).
2. Либо источник тока с параллельно включенным С ним сопро-
тивлением Лв, равным внутреннему сопротивлению реального источ-
ника энергии (рис. 2, б).
Под источником э. д. с. условимся понимать такой идеализиро-
ванный источник питания, э. д. с. которого постоянна, не зависит
от величины протекающего через него тока и равна э. д. с. реаль-
8
ного источника энергии. Внутреннее сопротивление этого идеали-
зированного источника питания равно нулю.
Источник э. д. с. на схемах изображают в виде кружка со стрел-
кой и написанной рядом буквы Е. Стрелка указывает положитель-
ное направление э. д. с. (направление возрастания потенциала внут-
ри источника).
Под источником тока понимают такой идеализированный источ-
ник питания, который дает ток Ik, не зависящий от величины на-
грузки R цепи и равный частному от деления э. д. с. реального источ-
ника на внутреннее сопротивление Re его .
Для того чтобы источник тока мог давать ток /й, не зависящий
от величины сопротивления нагрузки, внутреннее сопротивление
его и его э. д. с. теоретически должны стремиться к бесконечности.
Рис. 2
По определению источник тока дает ток /^, не зависящий от величины соп-
ротивления нагрузки /?. Другими словами, сопротивление /? в схеме рис.
2,6 может быть взято равным нулю (короткое замыкание) или равным бес-
конечности (холостой ход), а ток I ь должен остаться неизменным. Рассмот-
рим, при каких условиях это возможно. С этой целью через Ram обозначим
внутреннее сопротивление источника тока, а через Еит его э. д. с. и запишем
два уравнения, описывающие работу схемы рис. 2, б для упомянутых двух
крайних режимов работы.
При R = О
Ik Rum Ецт. (а)
При R = <х>
(R \
1 4* п ) = Еит- (б)
Кит>
R
Уравнения (а) и (б) совместны только в том случае, если —— -> оо.
. Re
Другими словами, сопротивление источника тока Rum теоретически стремится
к бесконечности (/?в — величина конечная). Но если Rum стремится к беско-,
иечиости, а /& величина конечная, то и Е„т = Ram теоретически тоже стре-
митси к бесконечности (отношение двух бесконечно больших величии Еит и
Rum Равио конечной величине —току Z&).
Как уже говорилось, и источник э. д. с., и источник тока представляют
собой расчетные идеализированные источники. Физически осуществить их,
строго говоря, невозможно, поскольку внутреннее сопротивление реальных
источников не может быть равно нулю и при конечном токе не может быть рав-
но бесконечности..
9
Однако, если внутреннее сопротивление Re реального источника пита-
ния мало по сравнению с сопротивлением R внешней цепи (например, при всех
возможных режимах работы сопротивление нагрузки R на несколько поряд-
ков оказывается больше, чем /?в), то источник питания будет работать в ре-
жиме, близком к режиму, характерному дли источника э. д. с. Аналогично,
если внутреннее сопротивление реального источника питания во всех воз-
можных режимах работы схемы будет много больше сопротивлении внешней
цепи R (например, на несколько порядков), то источник питания будет ра-
ботать в режиме, довольно близком к режиму, характерному для источника
тока (в том случае, когда сопротивление R меняется в относительно неболь-
ших пределах, нет необходимости требовать, чтобы Rttm и Еит стремились
к бесконечности).
Следует отметить, что схема рис. 2, б эквивалентна схеме рис. 1, а толь-
ко в отношении энергии, выделяющейся в сопротивлении нагрузки R, и не
эквивалентна' ей в отношении энергии, выделяющейся во внутреннем сопро-
тивлении источника тока.
На схеме источник тбка изображают в виде кружка со стрелкой,
рядом с. которым написана буква I с тем илй иным индексом (напри-
мер, k). Стрелка показывает положительное направление тбка Ik.
Ток в нагрузке (в сопротивлении 7?).будет одинаков в обеих эк-
вивалентных схемах (в схеме рис. 2, а и в схеме рис. 2, 6} и.равен
ТО^У --
: ' • J =
R + Re
в схеме рис. 1, а.
Для. схемы рис. 2,. а это.настолько очевидно, что не требует по-
яснений.
Убедимся в этом для схемы рис. 2, б. Ток Ik источника тока в этой
схеме распределяется обратно пропорционально, сопротивлениям
двух параллельных ветвей с сопротивлениями и /?в. Ток / в на-
грузке R равен
- ] — / — &
~ k R+Re Re R +Re R+Re'
Таким образом, совершенно безразлично, каким из рассмотрен-
ных расчетных эквивалентов пользоваться. В дальнейшем, как пра-
вило, будем пользоваться «эквивалентом номер один», т. е, будем
заменять реальный источник электрической энергии источником
э. д. с. и последовательно с ним включенным сопротивлением 7?в.
В заключение отметим, что свойства источника э. д. с. и источ-
ника тока можно довольно наглядно характеризовать графиками,
изображенными на рис. 3, а и б. На этих графиках даны зависимос-
ти тока /, протекающего через идеализированный источник энергии,
в функции от напряжений U на его зажимах (на рис. 3, а изобра-
жена зависимость I = f (U) для источника э. д. с. и на рис. 3, б —
для источника тока).
Пример 1а. В /схеме рис,! 2;б источник тока дает ток 7*^=50а.
Шунтирующее его сопротивленце = 2 ом. Найти величину э.д.с.
эквивалентного источника э.д.с. в сх&ме рис. 2, а.
10
Решение. Э. д. с. Ё = IkRa= 100в.
Таким образом, параметры эквивалентной схемы рис. 2, а та-
ковы: Е = 100 в и Rs = 2 ом.
§ 3. Разветвленные и неразветвлеиные электрические цепи. Элек-
трические цепи подразделяются на неразветвлеиные н разветвлен-
ные. Схема рис. 1, а представляет собой простейшую неразветвлен-
иую цепь, в которой во всех ее элементах течет один и тот же ток.
Простейшая разветвленная цепь изображена на рис. 4, а; в ней
имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь
можно определить как участок цепи, образованный последователь-
но соединенными элементами и заключенный между двумя узлами.
В свою очередь узел есть точка цепи, в которой сходится не менее
трех ветвей. Если в месте пересечения двух линий на электрической
схеме поставлена.«жирная» точка (рис. 4, б), то
в этой точке есть электрическое соединение двух _____
линий, в противном случае (рис. 4, в) линии пе- —
ресекаются без электрического соединения. . —»-i-------1—. .
§ 4. Напряжение на участке цепи. Под напря- я я Ь
жением на некотором участке электрической це- р
пи понимают разность потенциалов, между край- ис’
ними точками этого участка.
На рис. 5 изображен участок цепи, на котором есть сопротивле-
ние R и нет э. Д. с. Крайние точки этого участка обозначены буква-
ми а и Ь. Пусть ток / течет от точки а к точке Ь.
На участке цепи без э. д. с. ток течет от более высокого потенциа-
ла к более низкому. Следовательно, потенциал точки а (фа) выше по-
тенциала Точки b (фй) на величину, равную произведению тока 1
на сопротивление R:
Ф. = Ф»-ЫЯ
В соответствии с определением напряжение между точками а и &
uat> = % — Ф»-
Следовательно, Uab = IR. Другими словами, напряжение на
И
сопротивлении равно произведению тока, протекающего по сопро-
тивлению, на величину этого сопротивления.
В электротехнике разность потенциалов на концах сопротивле-
ния принято называть либо «напряжением на сопротивлении» (так
принято, например, в Л. 2*), либо «падением напряжения» (так при-
нято в Л. 1 а и б).
В дальнейшем разность потенциалов на концах сопротивления,
т. е. произведение /У?, будем именовать падением напряжения. По-
ложительное направление падения напряже-
—ния совпадает с положительным направлени-
г-—ем тока, протекающего по данному сопротив-
а в с лению.
Рассмотрим теперь вопрос о напряжении
на участке цепи, содержащем не только со-
противление, но и э. д. с.
На рис. 6, а и б показаны участки некото-
с рых цепей, по которым протекает ток I. Най-
7 дем разность потенциалов (напряжение) меж-
ду точками а и с для этих участков.
По определению
Uac^4a~ фс- (1-1)
Выразим потенциал точки а через потенциал точки с. При пере-
мещении от точки с к точке Ь (рис. 6, а) идем встречно э. д. с. Е, по-
этому потенциал точки b оказывается ниже (меньше), чем потенциал
точки с на величину э. д. с. Е, т, е.
<Рй = <рс —£•
Для рис. 6, б при перемещении от точки с к точке b идем соглас-
но э.д.с. Е и потому потенциал точки b оказывается выше (больше),
чем потенциал точки с, на величину э.д.с. Е, т. е.
Фг. = <Р« + Е-
Ранее говорилось, что на участке цепи без э. д. с. ток течет от
более высокого потенциала к более низкому. Поэтому в обеих схе-
мах рис. 6 потенциал точки а выше, чем потенциал точки b на вели-
чину падения напряжения в сопротивлении 7?:
Таким образом, для рис. 6, а имеем <ра == <рс — Е -{- //?, или
^ас==Фа —Фс = —(1-2а)
и для рис. 6, 6 — <ра = фс -{- Е 4~ //?, или
t/oc = <pe-<pc = //? + £. (1.26)
* Букиа Л с цифрой справа обозначает ссылку на литературу, перечень
которой приводится в конце книги.
12
Положительное направление напряжения указывают на схемах
стрелкой. Стрелка должна быть направлена от первой буквы ин-
декса ко второй. Так, положительное направление напряжения Uac
изобразится стрелкой, направленной от а к с.
Из самого определения напряжения следует также, что Uca —
= Фс — фа. Поэтому Uca = — Uac. Другими словами, изменение
чередования (последовательности) индексов равносильно измене-
нию знака этого напряжения. Из изложенного ясно, что напряже-
ние может быть и положительной, и отрицательной величиной.
§ 5а. Закон Ома для участка цепи, не содержащего э. д. с. За-
кон Ома устанавливает связь между током и напряжением на не-
котором участке цепи. Так, применительно к участку цепи, изобра-
женному на рис. 5, запишем
или
J __ ab __ фа ф& . (13)
R R ’
§ 56. Закон Ома для участка цепи, содержащего э. д. с.
Закон Ома для участка цепи, содержащего э.д.с., позволяет
найти ток этого участка по известной разности потенциалов
(фа — Фс) на концах участка цепи и имеющейся на этом участке
э.д.с. Е. Так, из уравнения (1.2а) для схемы рис. 6, а имеем
у Фа — фС + g = Цдс + Е
R R
Аналогично из уравнения (1. 26) для схемы рис. 6, б следует,
что
у -- Фо Фс Е _ Еде Е
R R '
В общем случае
г _ Едс i Е _ (ф I фс) ± Е (14)
R R ’ У '
Уравнение (1.4) математически выражает собой закон Ома для
участка цепи, содержащего э. д. с.; знак плюс перед Е соответствует
рис. 6, а, знак минус — рис. 6, б.
В частном случае при Е = 0 уравнение (1.4) переходит в урав-
нение (1.3).
Пример 16. К зажимам а и с схемы рис. 7 подключен вольтметр,
имеющий очень большое, теоретически бесконечно большое сопро-
тивление (следовательно, его подключение или отключение не пов-
лияет на режим работы цепи).
Если ток 1 = 10 а течет от а к с, то показание вольтметра Uac =
=» — 18 в.
Если ток / = 10 а течет от с к а, то показание вольтметра Uac —
= —20 в.
13
Определить величину сопротивления /? и э. д. с. Е.
Решение. В первом режиме £7а/ = — 18 = — £-{-//? =
= —£+10/?.
Во втором режиме UaclJ = —20 = — £ — //? = — £ —10/?.
Совместное решение дает: £ = 19 в и /? = 0,1 ом.
§ 6. Законы Кирхгофа. Все электрические цепи подчиняются
первому и второму законам Кирхгофа.
Первый закон Кирхгофа может быть сформулирован двояко.
Первая формулировка: алгебраическая сумма токов, подтекающих
к любому узлу схемы, равна нулю. Вторая формулировка: сумма
подтекающих к любому узлу токов, равна сумме утекающих от узла
токов.
Так, применительно к рис. 8, если подтекающие к узлу токи счи-
тать положительными, а утекающие — отрицательными, то, со-
гласно первой формулировке
Л /а /3 /4 = 0»
согласно второй
Физически первый закон Кирхгофа означает, что двйжение за-
рядов в цепи происходит так, что ни в одном из узлов они не скап-
ливаются.
Второй закон Кирхгофа также может быть сформулирован двоя-
ко.
Первая формулировка: алгебраическая сумма падений напряже-
ний в любом замкнутом контуре равняется алгебраической сумме
э. д. с. вдоль того же контура. Записывается он следующим образом:
В каждую из сумм соответствующие слагаемые входят со зна-
ком плюс, если они совпадают с направлением обхода контура, и ср
знаком минус, если они не совпадают с ним. ,
Вторая формулировка: алгебраическая сумма напряжений (не
падений напряжений!) вдоль любого замкнутого контура равна ну-
лю
•Так,- для периферийного контура схемы рис. 9,
uae-]-uet-\-ued-\-uda = o.
14
§ 7. Составление уравнений для расчета токов в схемах при по-
мощи законов Кирхгофа. Законы Кирхгофа используются для
нахождения токов в ветвях схемы. Так как в каждой ветви схемы
течет свой ток, то число неизвестных токов равняется числу ветвей
схемы. Перед тем как составлять уравнения, необходимо:
а) произвольно выбрать положительные направления токов в
ветвях и обозначить их на схеме;
б) выбрать положительные направления обхода контуров для
составления уравнений по второму закону Кирхгофа.
Для единообразия рекомендуется положительные направления
обхода контуров выбирать одинаковыми для всех контуров, напри-
мер все по часовой стрелке.
Обозначим число ветвей схемы через в а е
и число узлов через у. Для того чтобы
получить линейно независимые уравнения, (Т)£> ’ ПЛг 1/
по первому закону Кирхгофа составляется дд
число уравнений, равное числу узлов без Гр» (лХ* Т
единицы, т. е. у — 1. По второму закону L____|
Кирхгофа составляется число уравнений, в
равное числу ветвей, за вычетом числа Рис э
уравнений, составленных по первому за-
кону Кирхгофа, т. е.
а—(у—1).
При составлении уравнений по второму закону Кирхгофа необ-
ходимо следить за тем, чтобы были охвачены все ветви схемы. В
большинстве случаев стремятся при составлении линейно независи-
мых уравнений по второму закону Кирхгофа составлять их так,
чтобы в каждый новый контур, для которого составляется уравне-
ние, входила хотя бы одна новая ветвь, не вошедшая в предыдущие
контуры, Для которых уже составлены уравнения по второму зако-
ну Кирхгофа. Такие контуры условимся называть независимыми.
Следует иметь в виду, что требование, чтобы в каждый новый
контур входила хотя бы одна Новая ветвь, является в некоторых
случаях излишне жестким требованием (достаточным, но не необ-
ходимым условием) и для ряда сложных многоконтурных схем не
может быть выполнено.
В таких случаях часть уравнений по второму закону Кирхго-
фа приходится составлять для контуров, все ветви которых уже во-
шли в предыдущие контуры.
Пример 2. Найти токи в ветвях схемы рис. 9, в которой
Ег = 80 в, Eg = 64 в, = 6 ом, = 4 ом, /?з = 3 ом, — I ом.
Решение. Произвольно выбирем положительные направле-
ния токов в ветвях (рис. 9). В схеме два узла. Следовательно, по пер-
вому закону Кирхгофа можно составить только одно уравнение
= (а)
15
Нетрудно убедиться в том, что для второго узла уравнение будет
аналогичное. По второму закону Кирхгофа надо составить в — (у —
— 1) = 3 — (2 — 1) = 2 уравнения. Положительные направления
обхода контуров выбираем по часовой стрелке.
Для 'контура KjE^E^
/2/?2 = /?£-{-£2- (б)
Знак плюс перед взят потому, что направление тока /х сов-
падает с направлением обхода контура. Знак минус перед /2/?2
— потому, что направление /2 встречно обходу контура.
Для контура EtRtRsRi
+ (^з + — —• ^2- (в)
Совместное решение уравнений (а), (б), (в) дает 1г = 14 а, /2 =
= — 15 а, 1а = — 1а. Поскольку положительные направления то-
ков выбираются произвольно, то в результате расчета какой-либо
один или несколько токов могут оказаться отрицательными. Так,
в рассмотренном примере отрицательными оказались токи /2 и /3.
Отрицательные знаки у токов следует понимать так: направле-
ния токов /2 и /3 не совпадает с направлениями, принятыми для
них на рис. 9 за положительные, т. е. в действительности токи /2
и /3 текут в обратном направлении.
§ 8. О заземлении одной точки схемы. При заземлении одной лю-
бой точки схемы токораспределение в схеме не меняется, так как
никаких новых ветвей, по которым могли бы протекать токи, при
этом не образуется. Иначе будет, если заземлить две или большее
число точек схемы, имеющих различные потенциалы. В этом слу-
чае через землю (любую проводящую среду) образуются дополни-
тельные ветви, сама схема становится отличной от исходной, и то-
кораспределение в ней меняется.
§ 9. Потенциальная диаграмма. Под потенциальной диаграммой
понимают график распределения потенциала вдоль какого-либо
участка цепи или замкнутого контура. По оси абсцисс на нем от-
кладывают сопротивления вдоль контура, начиная с какой-либо
произвольной точки, по оси ординат — потенциалы. Каждой точке
участка цепи или замкнутого контура соответствует своя точка на
потенциальной диаграмме.
Рассмотрим последовательность построения потенциальной диаг-
раммы по данным примера 2.
Пример 3. Построить потенциальную диаграмму для контура
abcea (рис. 9).
Решение. Подсчитываем суммарное сопротивление контура.
Оно равно: 4 -|- 3 + 1 = 8 ом. Выбираем масштаб пр оси абсцисс
(ось х) и масштаб по оси ординат (ось у).
Произвольно примем потенциал одной из точек, например точ-
16
ки а, равным нулю. Эту точку на диаграмме рис. 10 поместим в на-
чало координат.
Потенциал точки Ь равен ф* = фа + /2 • 4 = <ра — 60 = — 60 в.
Координаты ее: х = 4, у = —60.
Потенциал точки с: <рс = фй-|-Е2 = 4 в. Координаты точки с: х=4,
У = 4.
Точка е: = <рс + /3 = 4 — 1.1=3 (в). Координаты точки ё:
х = 5, у = 3.
Тангенс угла наклона прямой ab к оси абсцисс пропорциона-
лен току /2, а тангенс угла а2 наклона прямой се — току /3.
§ 10. Энергетический баланс в электрических цепях. При проте-
кании токов по сопротивлениям
На основании закона сохране-
ния энергии количество тепла,
выделяющееся в единицу време-
ни в сопротивлениях схемы,
должно равняться энергии, до-
ставляемой за то же время ис-
точником питания.
Если через источник э. д. с.
Е течет ток / так, что направле-
ние тока совпадает с направле-
нием э. д. с., то источник
э. д. с. доставляет в цепь в еди-
ницу времени энергию (или Рис. 10
мощность *), равную Е1 (про-
изведение EI входит с положительным знаком в уравнение
энергетического баланса). Если же ток / направлен встречно э. д. с.
Е, то источник э. д. с. не поставляет энергию, а потребляет ее (на-
пример, заряжается аккумулятор), и произведение Е1 входит в урав-
нение энергетического баланса с отрицательным знаком. Уравне-
ние энергетического баланса при питании только от источников
э. д. с. записывается следующим образом:
2/2/? = 2н/.
Если схема питается не только от источников э. д. с., но и от ис-
точников токд, т. е. к отдельным узлам схемы подтекают и утекают
токи от источников тока, то при составлении энергетического ба-
ланса необходимо еще учесть энергию, доставляемую источниками
тока. Допустим, что к узлу а схемы подтекает ток 1к от источника то-
ка, а от узла b этот ток утекает. Доставляемая источником тока мощ-
ность равна Uab lk. Напряжение Uab и токи в ветвях схемы должны
быть подсчитаны с учетом тока, подтекающего от источника то-
ка. Последнее проще всего сделать по методу узловых потен-
циалов (§ 20). Общий внд уравнения энергетического баланса
* Мощность равна энергии, расходуемой в единицу времени.
17
запишется так:
2/г/? = 2£/+21/аЛ-
Для практических расчетов электрических цепей разработан
ряд методов, более экономных в смысле затраты времени и труда,
чем метод расчета цепей по законам Кирхгофа. Рассмотрим эти ме-
тоды.
§ 11. Метод пропорциональных величин. В чистом виде метод
применим для расчета цепей, состоящих только из последовательных
и параллельных соединений сопротивлений и наличии в схеме од-
ного источника. Но этот метод может комбинироваться и с другими
приемами (преобразование треугольника в звезду, метод наложения
и т. п.)„ которые будут рассмотрены в дальнейшем, что расширяет
его расчетные возможности. Согласно методу пропорциональных
величин, в самой удаленной от источника э. д. с. ветви схемы (ис-
ходной ветви) произвольно задаемся некоторым током, например
током в 1 а. Далее продвигаемся от конца схемы к началу и находим
токи в ветвях и напряжения иа различных участках схемы. В резуль-
тате расчета получаем значения напряжения в начале схемы и то-
ков в ветвях, если бы в исходной ветви протекал ток в 1 а.
Так как найденное значение напряжения в начале схемы в об-
щем случае не будет равняться э. д. с. источника, то следует во всех
ветвях изменить токи, умножив их на коэффициент, равный отно-
шению э. д. с. источника к найденному значению напряжения в на-
чале схемы.
Пример 4. Найти токи в ветвях схемы рис. 11 методом пропор-
циональных величин. Сопротивления даны на схеме в омах.
Решение. Задаемся тском в сопротивлении 4 ом, равным 1 а,
и подсчитываем токи в остальных ветвях. Эти токи обведены на ри-
сунке кружками. Напряжение между точками т и п при этом ока-
зывается равным Г-4 4-3-3 4-4-3 = 25 (в). Так как э. д. с. рав-
на 100 в, то все токи надо умножить на коэффициент k = ~ = 4.
§ 12. Метод контурных токов. В методе контурных токов прини-
мается, что в каждом независимом контуре* схемы течет свой кон-
турный ток. Уравнения составляются относительно контурных то-
ке». После нахождения их определяют токи ветвей через контурные
токн.
Таким образом, метод контурных токов можно определить как
метод расчета, в котором за неизвестные (за искомые) принимаются
контурные токи. Число неизвестных в этом методе равно числу
уравнений, которые надо было бы составить для схемы па второ-
му закону Кирхгофа.
Вывод основных расчетных уравнений проведем применительно
к схеме рис. 12. В ней два независимых коктура. Положим, что в
девая контуре по часовой стрелке течет контурный ток /и и в пра-
* Для сложных схем надо учесть еще два последних абзаца $ 7.
И
вом (также по часовой стрелке) контурный ток /22. Для каждого
из контуров составим уравнения по второму’закону Кирхгофа. При
этом учтем, что по смежной ветви (ветви с сопротивлением те-
чет сверху вниз ток (/и — /22). Направления обхода контуров при-
мем также по часовой стрелке.
Для первого контура
/и (*i + Яа) + ((и ~ /22) = Е, + Е„
или
/ц (/?!+*2+я6) 44-W22 == 4-£s.
Для второго контура
U1V I4~ ^22 (^?s4- ^4) — ------ Е5--f4,
(—£5) 1144 22 (R3 4- ^4 4- R&) — — Et — Е-„.
Рис. 11 Рис. 12
В первом уравнении множителем при токе 11г является сумма
сопротивлений первого контура, которую обозначим через
множителем при токе /22 в первом уравнении является сопротивле-
ние смежной ветви, взятое со знаком минус, обозначим его через Т?12.
v Перепишем эти уравнения следующим образом:
/ 1Л14- — Ец I Н 4'1
/nR214- ^22^22= Ei2 j
Здесь
R11~ ^?14*^?г4"^?з, ^Xi — ^i 4‘^5>
Я22 = Ri+Rt + Ri,’ е22 = — е4 — Е;„
Rn = Rn =
В первом из уравнений (1.4') множителем при контурном токе
первого контура /п является полное или собственное сопротивле-
ние этого контура /?и, а множителем при токе /22 — сопротивле-
ние,смежной между первым и вторым контурами ветви, взятое со
знаком минус’.
•В общем случае можно сказать, что сопротивление смежной, ветви
мёжДу k я т контурами входит в уравнение со знаком минус, если нап-
раваеиия хентурныхтОков lhk и 1тт вдоль этой ветви встречиы/ в се зйашмг
плюс, если направления токов согласны.
(1.4")
Еп есть контурная э. д. с. первого контура, она равна алгебра-
ической сумме э. д. с. этого контура. В нее со знаком плюс входят
те э. д. с.,направления которых совпадают с направлением обхода
контура.
R22 есть полное или собственное сопротивление второго контура.
Т?21 — сопротивление смежной ветви между первым и вторым
контурами, взятое со знаком минус.
Е22 — контурная э. д. с. второго контура.
Если бы в схеме было больше двух контуров, например три, то
система уравнений выглядела бы следующим образом:
7 11^11 ~~ 132^12 4“ I33R13 ~ ^11
1 11^21 122R22 133^23 ~ ^22
1ц7?31 7 22^32 4“ 733R33 ~ ^33
Рекомендуется для единообразия в знаках сопротивлений с разны-
ми индексами все контурные токи направлять в одну и ту же сто-
рону, например все по часовой стрелке.
Если в результате решения системы уравнений какой-либо кон-
турный ток окажется отрицательным, то это будет означать, что
в действительности направление контурного тока обратно приня-
тому за положительное.
В ветвях, не являющихся смежными между соседними контурами
(например, в ветви с сопротивлениями 7?а схемы рис. 12), най-
денный контурный ток будет являться истинным током. В смеж-
ных ветвях надо через контурные токи найти истинные. Например,
в ветви с сопротивлением Rs протекающий сверху вниз ток равен
разности 112 — /22.
Если в электрической цепи будет иметься п независимых конту-
ров, то количество уравнений будет равно п.
Общее решение системы п уравнений относительно тока Ikk
Ikk = Eu^L+£22^4-E3. 4
Кк 11 Д I йй Д I О<
Здесь Д есть определитель системы
7?11 ^12 7?,
T?21 R22
R31 ^32
(1.5)
'13 ••• Rm
*23 ••• ^2п
R33 • • • ^Зп
(1-6)
Rnl %п2 ^пЗ • • • Впп
Д4т есть алгебраическое дополнение, полученное из опреде-
лителя Л путем вычеркивания k столбца и т строки и умноже-
ния полученного определителя на (— l)ft+/n.
Если провести из левого верхнего угла определителя диаго-
наль в правый нижний угол его (она называется главной диаго-
налью) и учесть, что А?12 = /?2i и вообще Rkn = 7?^, то можно
20
убедиться в том, что определитель делится на две половины,
являющиеся-зеркальным изображением одна другой. Это свойст-
во определителя называют симметрией относительно главной диа-
гонали. В силу симметрии определителя относительно главной диа-
гонали
^ktn ^mk'
Пример 5. Найти токи в схеме рис. 13 при помощи метода кон-
турных токов. Численные значения сопротивлений и э. д. с. ука-
заны на рисунке.
Решение. Выбираем направления всех контурных токов 7Ш
722 и /33 по часовой стрелке.
Определяем:
Ru = 54-54-4= 14 (ои);
/?22 = 54-104-2= 17 (ом),
/?зз = 24-24- 1 = 5(ож);
= /?21 = 5 (ОМ),
/?13 — Rsi = 0, /?23 = ^?32 = 2 ОМ',
Еи = — 10 в, Е22 = Ю в,
Е^ ~ 8 в.
Записываем систему уравнений:
147и-5/22
5/u4“ 17722 2733— 10;
2722 4- 5733 ---- 8.
14 —5 0
Определитель системы
—5 17 —2 = 1009.
0—2 5
7 22
—10 —5 0
10 17 —2
— 8—2 5
Д
14 —10 0
—5 10 —2
0—8 5
Д
14 —5 —10
—5 17 10
_ о—2 —8
'зз - д
—640
= —0.635(a).
-^- = 0,225 (а).
1009 '
—1524
1009
= —1.52(a).
21
Ток в ветви cm lem = Ki — ZM =—0,635 — 0,225 = —0,86 (а).
Ток в ветви ат 1ат = /и — /м = 0,225 + 1,52 = 1,745 (в).
Формула (1.5) метода контурных токов в ряде последующих па-
раграфов используется в качестве исходной формулы для рассмот-
рения некоторых важных вопросов теории линейных электрических
цепей, таких как: определение входных и взаимных проводимостей
ветвей, принцип взаимности, метод наложения и линейные соот-
ношения в электрических цепях.
§ 13. Принцип наложения и метод наложения. Будем интересо-
ваться током в k ветви сложной схемы. При составлении уравнений
по методу контурных токов распорядимся выбором контуров так,
что k ветвь будет входить только в один k контур. Эго всегда воз-
можно сделать.
Тогда ток в k ветви будет равен контурному току по урав-
нению (1.5). Каждое слагаемое правой части (1.5) представляет
собой ток, вызванный в k ветви соответствующей контурной э.д.с.
Например, Еи есть составляющая тока k ветви от контурной
э.д.с. Еи. Каждую из контурных э.д.с. можно выразить через э.д.с.
ветвей Ev E2f Е3, ..., Ek, ..., Е„, сгруппировать коэффици-
енты при этих э.д.с. и получить выражение следующего вида:
h ~ E2gki-\- Egg^-^- ... + Ekgkk-\- ... -\-Engk„. (1.7)
Если контуры выбраны таким образом, что какая-либо из э.д.с.,
например Ет, -входит только в один т контур и в другие контуры
не входит, то gkm = ^5-.
Уравнение (1.7) выражает собой принцип наложения. Принцип
наложения формулируется следующим образом: ток в k ветви ра-
вен алгебраической сумме токов, вызываемых каждой из э. д. с.
схемы в отдельности. Этот принцип справедлив для всех линейных
электрических цепей, т. е. таких цепей, вольтамперные характе-
ристики сопротивлений которых представляют собой прямые ли-
нии.
Принцип наложения используется в методе расчета, получив-
шем название метода наложения,-
При расчете цепей по методу наложения поступают следующим
образом: поочередно рассчитывают токи от каждой из э. д. с., мыс-
ленно удаляя остальные из схемы, но оставляя в схеме внутренние
соНротивлення источников, и затем находят токи в ветвях путем ал-
гебраического сложения частичных токов. Заметим, что метбдом'на-
ложения нельзя пользоваться для подсчета выделяемых в сопротив-
лениях мощностей, как суммы мощностей от частичных токов, по-
скольку мощность является квадратичной функцией тока (Р =
= /?/«).
Так, если через некоторое сопротивление R будут протекать
согласно направленные частичные токи /t и /8, то выделяемая в нем
»
мощность равна Р — R (7Х + 72)2 и она не равна сумме мощностей
от частичных токов
Л¥=/?7? + /?/2.
Пример 6. Найти токи в .схеме рис. 9 при помощи метода наложе-
ния.
Решение. Представляем схему рнс. 9 в виде двух схем: схе-
мы рис. 14, а и б. Значения сопротивлений и э. д. с. указаны в чис-
лах на схемах. В схеме рис. 14, а оставлена э, д. с. Ех — 80 в, э. д. с.
Ей удалена; в схеме рис. 14, брставлена Е$ и удалена Ev
Найдем токи для схемы рис. 14, а
• Л=-----~- = W); 7;=/; = 5а.
В схеме рис. 14, б
/’2 =--^—— = 10 (а); 7' == 10.-4— =4(а); 7’3 = 10-4=6 (а).
0*4 , о -f- 4 .
Для нахождения результирующих токов алгебраически сумми-
руем частичные токи, приняв за положительные направления для
токов в ветвях направления, указанные на рис. 9:
Л = Л+Л = Ю + 4= 14(a); -72 = 7;+7’s = 10 + 5 = 15 (а);
—73 = 73 —73 = 6 —5 = 1 (а).
§14. Входные и взаимные проводимости ветвей. Входное сопро-
тивление. На рис. 15, а изображена так называемая «скелетная схема»
пассивной цепи. На ней показаны только ветви и узлы. В каждой
ветви имеется сопротивление. Выделим в схеме две ветви. Одну
из них назовем ветвью т, другуй — ветвью k. Прместйм в ветвь
гп э.д.с. Ет (Других э.д.с. в схеме нет). Выберем контуры в схе-
ме так, что k ветвь входит только в k дрнтур, а ветвь /я толь-
ко в т контур, Тогда э.д.с. Ет вызовет ток в вфвйк + ,,
??
и ток в ветви т
I k ^mSim
I т ^тётт
(1.8)
Коэффициенты g имеют размерность проводимостей. Коэффи-
циент g с одинаковыми индексами (gmm) называют входной прово-
димостью ветви (ветви т). Он численно равен току в ветви т от
действия э.д.с. Ет, равной 1 в (единичной, э.д.с.): 1т = 1-Ятт-
Коэффициенты g с разными индексами называют взаимными
проводимостями. Так, gkm есть взаимная проводимость k и т вет-
вей. Величина gkm численно равна току в k ветви от действия еди-
ничной э.д.с. в т ветви*.
Рис. 15
Входные и взаимные проводимости ветвей используются при
выводе общих свойств линейных электрических цепей (§ 15 и 17)
и при расчете цепей по методу наложения — формула (1.7).
Собственные и взаимные проводимости могут быть определены
расчетным и опытным путями.
Рассмотрим, как найти их расчетным путем. С этой целью надо
составить для схемы уравнения по методу контурных токов, следя
за тем, чтобы ветви, взаимные и входные проводимости которых пред-
ставляют интерес, входили каждая только в свой контур и в другие
контуры не входили. Далее находится определитель системы А и по
нему необходимые алгебраические дополнения
(1-9)
gkm = ^-‘ (1-Ю)
д
* Входные и взаимные проводимости ветвей можно определить и несколь-
ко иначе.
Входная проводимость какой-то т ветви— это коэффициент пропорцио-
нальности между током этой ветви и э. д. с. той же ветви (при отсутствии э. д. с.
в других ветвнх схемы).
Взаимная проводимость ветвей k и т есть коэффициент пропорциональ-
ности между током k ветви и э. д. с. т ветви при отсутствии э. д. с. в других
ветвях схемы.
24
При опытном определении gmm и gkm поступают следующим
образом: в т ветвь схемы включают э.д.с. Ет и в k ветвь ампер-
метр (или миллиамперметр). Деление тока k ветви на э.д.с. Ет и
дает gkm. Для нахождения входной проводимости ветви т (gmm)
надо измерить ток в т ветви от э.д.с., включенной в т ветвь.
Частное от деления тока т ветви на э.д.с. т ветви и дает gmm.
Выделим т ветвь, обозначив всю остальную часть схемы (не со-
держащую э. д. с.) некоторым прямоугольником (рнс. 16). Вся схе-
ма, обозначенная прямоугольником, по отношению к зажимам ab
обладает некоторым сопротивлением. Его называют входным со-
противлением. Так как в рассматриваемом
примере речь идет о входном сопротивлении
для т ветви, то обозначим его Rex т.
= (1-П)
‘т gmm
Таким образом, входное сопротивление т
ветви есть величина, обратная входной про-
водимости т ветви. Его не следует смеши-
вать с полным сопротивлением т контура в
методе контурных токов, оно не имеет с ним ничего общего.
Пример 7. Определить входную проводимость gu и взаимную про-
водимость g12 в схеме рис. 13.
Решение. Контуры на схеме рис. 13 выбраны так, что ветвь 1
(ветвь cbm) с э.д.с. ^ входит только в первый контур, а ветвь 2
(ветвь са) с э.д.с. £2—в0 второй, поэтому можно воспользоваться
определителем системы А и алгебраическими дополнениями Лц и Д12,
составленными по данным примера 5 к схеме рис. 13:
I 5 2 | (—1)1+2
= Д12 = I 0 5 I _
®12 Д 1009
I 17 —2 I
; Д1Л..| -2 5|<-1)1+1
Д 1009
— = 0,025 (ф-1)*;
1009 ‘ '
— = 0,081 (ом-1).
1009 ' '
§ 15. Теорема взаимности. Теорема формулируется следующим
образом:
В любой, сколь угодно сложной линейной цепи ток в k ветви,
вызванный э.д.с. Ет, находящейся в т ветви
I k ~
будет равен току 1т в т ветви, вызванному э.д.с. Еь (численно
равной э.д.с. Ет), находящейся в k ветви
1 т Ekgmk'
* Единица проводимости ом 1 в системе СИ называется сименс (сим).
25
Для доказательства теоремы взаимности обратимся к рис. 15, а.
Как и при выводах в предыдущем параграфе, выделим две веган
схемы: ветвь k и ветвь т. Включим в ветвь т э. д. с. Ет, в
ветвь k амперметр* для измерения тока Ik. Пусть ветви k й т
каждая входят, соответственно, только в k и т контуры. Тогда
по методу контурных токов Ik = Ет . Затем поменяем места-
Д
ми э. д. с. и амперметр, т. е. э. д. с. переместим из ветви т в
ветвь k и назовем ее теперь Ek, а амперметр — из ветви k в
ветвь т. В этом случае ток Im — Ek-^^~ •
Рис. 17
Так как Ek = Ет, а ДшА = \т в силу симметрии определителя
системы Д относительно главной диагонали (см. § 12), то ток Ik в
схеме рис. 15, б равняется току 1т в схеме рис. 15, в.
При практическом использовании теоремы взаимности важно
иметь в виду взаимное соответствие в направлениях токов и э. д. с.
в схемах рис. 15, бив.
Так, если э.д.с. Ek, находящаяся в k ветви схемы рис. 15, в,
будет направлена согласно с контурным током Ik в схеме рис. 15, б,
то положительное направление тока 1т в схеме рис. 15, в будет
совпадать с направлением э. д. с. Ет в схеме рис. 15, б.
Пример 8. В схеме рис. 17 переключатели Pv Р2, Р3 и Р4 мо-
гут находиться либо в первом, либо во втором положениях. Если
они находятся в первом положении (1), то в схеме включена толь-
ко одна э. д. с. Ел. Под действием Ei протекают токи: Гл = t, 5 dr
12 = 3 a, I3 = 1 а.
Найти ток /4, если все переключатели будут находиться в по-
ложении 2, полагая, что Е, = 20 в, Еъ — 40 в, Е3 = 50 в, Е4 10 в.
Решение. Для нахождения тока /4 воспользуемся принципом
наложения и принципом взаимности. Если бы в схеме была включена
лишь одна э. д. с. Ег и равнялась бы она 10 в, а остальные э. д. с. (Е2 и
* Амперметр включаем для наглядности. Сопротивление амперметра по-
лагаем равным нулю. .,";
26
Еа} отсутствовали, то в ветви 4* по принципу взаимности протекал
бы сверху вниз ток 1,5 а. Так как э. д. с. в действительности рав-
20
на 20 в вместо 10 в, то от нее в ветви 4 протекает ток 1,5 • — = 3 (а).
Аналогично определим токи в ветвн 4 от действия э. д. с. Ег и затем
от э. д. с. Е3 и произведем алгебраическое сложение частичных то-
ков (учтем их направление)
, , с 20 . о 40 , 50 , ,
/, = 1.5--кЗ-------1. — = 10 (а).
4 ’ 10 1 10 10 ' '
§ 16. Теорема компенсации. В любой электрической цепи без
изменения токораспределения в ней сопротивление может быть за-
менено э. д. с., численно равной падению напряжение в заменяемом
сопротивлении и направленной встречно току в этом сопротивлении.
Для доказательства теоремы компенсации выделим из схемы од-
ну ветвь с сопротивлением R, по которой течет ток /, а всю осталь-
Если в выделенную ветвь включить две равных и противополож-
но направленных э. д. с. Е, численно равных падению напряже-
ния в сопротивлении R от тока I (Е — IR; рис. 18, б), то ток / в
цепи от этого не изменится. Убедимся в том, что разность потенциа-
лов между точками а и с в схеме рис. 18, б при этом будет равна нулю.
Действительно,
Фс = Фа — + Е = Фа — IR + 1R = фо.
Но если <рс =<ра, то точки а и с можно объединить в одну точку или,
другими словами, закоротить участок ас и получить схему 18, в.
В ней вместо сопротивления R включена э. д. с. Е:
Пример 9. Убедиться в тождественности схем рис. 19, а и б.
Решение. В схеме рис. 19, а ток 7 ==—&—. Для схе-
Ri + Я*
мы рис. 19, б
Е Е
. _ _ 1 + 7?» _ Ei
Ri Ri Ri + Rg’
* Номер ветвей соответствует индексу в. д. с.
27
Таким образом, замена сопротивления R2 на э. д. с. Е2 в схеме
рис. 19, как это и следует из теоремы компенсации, не вызвала из-
менения тока в схеме.
§ 17. Линейные соотношения в электрических цепях. Если в ли-
нейной электрической цепи изменяется э. д. с. или сопротивление в
какой-либо одной ветви, то две любые величины (токи и напряже-
ния) двух любых ветвей связаны друг с другом линейными зависимос-
тями вида у — а + Ьх.
Роль х играет ток или напряжение одной ветви, роль у выпол-
няет ток или напряжение другой ветви.
Доказательство. Согласно методу контурных токов, об-
щее выражение для тока в k ветви записывается в виде (1.7). Если
в схеме изменяется только одна э. д. с., например э. д. с. Ет, то все
Кг
Рис. 19
слагаемые в (1.7), кроме слагаемого Emgkm, постоянны и могут быть
для сокращения записи заменены некоторым слагаемым Ak. Сле-
довательно,
- Ik — Ak-\-Em8km’ (1-12)
Аналогично для какой-то р ветви
7р = Ар + Еот^. (1.13)
Выразим Ет из (1.13)
gpm
и подставим в (1.12). Получим
Ik = ak+bkIp. (1.14)
Здесь
а =Л4 —Л_^ и bk=&*-
Р gpm gpm
Из (1.14) следует, что при изменении э. д. с. Ет токи Ik и 1р связаны
линейной зависимостью. Из теоремы компенсации известно, что
любое сопротивление может быть заменено э. д. с.
Следовательно, изменение сопротивления в т ветви эквивалент-
но изменению э. д. с. Ет. Таким образом, линейноесоотношение меж-
ду двумя любыми токами (1.14) имеет место не только при измене-
нии э. д. с. Ет, но и при изменении сопротивления какой-то т ветви.
28
Если обе части (1.12) умножить на сопротивление k ветви Rk
и проделать аналогичные выкладки, то можно, убедиться в том, что
напряжение на k ветви линейно связано с томом в р ветви.
Коэффициенты ak и bk в (1.14) и в других подобных выражениях
могут быть определены либо расчетным, либо опытным путями.
При опытном определении коэффициентов.достаточно определить
значения двух токов (или, соответственно, напряжений) при двух
различных режимах работы схемы и затем решить систему из двух
уравнений с двумя неизвестными. Пусть, например, в первом опыте
Ik = Iki и = lpv а во втором опыте Ik = /А2 и 1р = 1р2, тогда
Если в схеме одновременно изменяются э. д, с. или сопротивления
в каких-либо двух ветвях, то любые три величины в этой схеме (то-
ки, напряжения) связаны друг с другом линейным соотношением
вида у — а + bx + cz.
Доказательство этого соотношения проводится аналогично при-
веденному выше.
Пример 10. На рис. 20 изображена схема, в которой выделено
три ветви. В ветви 1 включен амперметр Alt в ветви 2 — амперметр
А2. Третья ветвь имеет рубильник Р и сопротивление Ря. Если
рубильник Р разомкнут, то Л1 показывает 1 а, а А2 показывает 5 а.
При замкнутом рубильнике Р Аг показывает 2 а, а А2 — 4 а. При
замкнутом рубильнике Р сопротивление /?3 изменили так, что пока-
зание амперметра А2 стало 4,5 а. Каково показание амперметра Аг
в этом режиме?
Решение. Выразим /, через /2
/,= а+6/2.
Составим два уравнения для определения а и Ь:
1 = а + 56;
2==а + 46,
отсюда а = 6 и 6 — —1.
При /2 — 4,5 а
/, = 6 —4,5-1 = 1,5(а).
29
§ 18. Замена нескольких параллельных ветвей, содержащих ис-
точники э. д. с., одной эквивалентной. Существенное облегчение
при расчете сложных схем дает замена нескольких параллельно
включенных ветвей, содержащих источники э. д. с. и сопротивления,
на одну эквивалентную ветвь.
Участок цепи рис. 21, б будет эквивалентен участку цепи, изо-
браженному на рис. 21, а, если при любых значениях тока 7, под-
текающего из всей остальной, не показанной на рисунке части схе-
мы, напряжение на зажимах аи b (Uab) в обеих схемах будет одина-
ковым. Для того чтобы выяснить, чему должно равняться и
составим уравнения для обеих схем.
Для схемы рис. 21, а
НО
/2 = (Д2 Uab) Sit 7 г.
7n = (£„-(/of)g„. - (1.15)
Следовательно,
л п л
Л= S= S E^-yab IX (ив)
4=1 4 = 1 . v 4=1
Здесь через п обозначено число параллельных ветвей. Для схемы
рис. 21, б справедливо следующее тождество
l = Egg3-Uabg3, (1.17)
где =
Равенство токов I в схемах рис. 21, а и б должно иметь место
при любых значениях Uab, а это возможно только в том случае,
когда коэффициент при Uab в (1.16) равен коэффициенту при f/aZ>B
(1.17). Следовательно,
п
IX
Но если слагаемые с Uab в (1.16) и (1.17) равны, й токи 7 по
условию! эквивалентности двух схем также равны» то
п
E3g3,
- *=>
эе
отсюда
= —. (1.19)
Формула (1.18) дает возможность найти проводимость ga и по
ией R3 в схеме рис. 21, б. Из формулы (1.18) видно, что проводимость
ga не зависит от того, есть в ветвях схемы рис. 21, а э. д. с. или нет.
При подсчетах по формуле (1.19) следует иметь в виду следую-
щее: если в какой-либо ветви схемы э. д. с. будет отсутствовать,
то соответствующее слагаемое в числителе (1.19) выпадает, но про-
водимость этой ветви в знаменателе формулы (1.19) не выпадает;
если какая-либо э. д. с. в исходной схеме имеет направление, обрат-
ное изображенному на рис. 21, а, то соответствующее слагаемое
войдет в числитель формулы (1.19) со знаком минус.
Рис. 21
Ветви схемы рис. 21, а и ветвь 21,6 эквивалентны только в смыс-
ле поведения их по отношению ко всей остальной части схемы, не
показанной иа рис. 21, но они не эквивалентны в отношении мощ-
ности, выделяющейся в иих. Качественно поясним это. В ветвях
схемы рис. 21, а токи могут протекать даже при 1 = 0, тогда как
в ветви аЬ рис. 21, б при 1 = 0 ток и потребление энергии отсутст-
вуют.
Пример 11. Заменить параллельные ветви рис. 22 одной экви-
валентной. Дано: Е' = 10 в, E*t — 30 в, Еа = 40 в, Е3 = 60 в и
= 2 ом, = 4 ом, /?а = 1 ои, /?4 = 5 ом.
Решение. Находим
gt = 0,5 сим\ gt = 0,25 сим\ g9 = 1 сиМ", gt = 0,2 сим.
= 0,513 (ом).
4
P — — (10 — 30)-0,5-40-0,25 + 60-1 _ 9n r , 4
a v <т 1,95 ’
Таким образом, параметры эквивалентной ветви рис. 21, б таковы:
Ra = 0,513 ом и Еа — 20,5 в.
§ 19. Метод двух узлов. Очень часто встречаются схемы, содер-
жащие всего два узла. В качестве примера на рис. 23 изображена од-
Рис. 23
на из таких схем. Наиболее рациональ-
ным методом расчета токов в них являет-
ся метод, получивший название метода
двух узлов.
Под методом двух узлов понимают ме-
тод расчета электрических цепей, в кото-
ром за искомое принимается напряжение
между двумя узлами схемы.
Расчетные формулы этого метода не-
посредственно следуют из формул (1.15)
и (1.16); они также могут быть весьма
просто получены из рассматриваемого в следующем параграфе
более общего метода — метода узловых потенциалов.
В отличие от схемы рис. 21, а ток 1 к узлам а и b схемы рис. 23
не подтекает. Поэтому, если в формуле (1.16) принять / = 0, то
из нее может быть найдено напряжение Uab между двумя узлами
иаЬ
^Ekgk
(1.20)
После того, как напряжение Uab будет найдено, определяется ток
в любой (п) ветви по формуле (1.15).
Пример 12. Найти токи в схеме рис. 23 и сделать проверку
баланса мощности, если Ек = 120 в, Е3 — 50 в; Rx = 2 ом, R2 =
= 4 ом, 2?з = 1 ом и Т?4 = 10 ом.
120-0,5 — 50-1
, _£2
а —
Р,, 1ZU-U.O — OU-1 10 г а
е ш е н и е. U„b —---------:---------=-------= 5,4 в;
аа 0,5 + 0,25+14-0,1 1,85
/. = = 1?° ~ 5/1 = 57,3 (а);
2
= 0-5.4 = _ | 35
/?2 4
I = = - 50 ^J?,4 = _ 55 4 (а)
3 /?з 1
. = Ei-Uah = 0-М_ = _ 054
* Я* 10 7
32
В схеме потребляется мощность
= 57,32.24-1,346s. 4 4-
4-55,4’- 14-0,54®-10 = 9647 (e/n).
Источники э.д.с. доставляют мощность Е1114- Е3/э = КО. 57,3 4“
4-50-55,4 = 9647 (ет).
§ 20. Метод узловых потенциалов. Ток в любой ветви схемы мо-
жет быть найден по закону Ома для участка цепи, содержащего
э. д. с. Для того чтобы можно было применить закон Ома, надо знать
потенциалы узлов схемы. Метод расчета электрических цепей, в ко-
тором за неизвестные принимаются потенциалы узлов схемы, на-
зывают методом узловых потенциалов.
Допустим, что в схеме п узлов. Так как любая (одна) точка схе-
мы может быть заземлена без изменения токораспределения в схе-
Рис. 24
ме, то мы вправе один из узлов схемы мысленно заземлить, т. е. при-
нять потенциал его равным нулю. При этом число неизвестных
уменьшается с п до (п — 1).
Число неизвестных в методе узловых потенциалов равно числу
уравнений, которые надо составить для схемы по первому закону
Кирхгофа. Метод узловых потенциалов, как и метод контурных то-
ков является одним из основных расчетных приемов. В тех случа-
ях, когда число узлов без единицы меньше числа независимых кон-
туров^'в схеме, данный метод является более экономным, чем метод
контурных токов. '
Обратимся к схеме рис. 24. Схема имеет довольно большое ко-
личество ветвей (11 ветвей) и сравнительно небольшое число узлов
(4 узла). Если один из узлов схемы, например узел 4, мысленно за-
землить, т. е. принять <р4= 0, то необходимо будет определить по-
тенциалы только трех узлов <рх, <ра, <р3. Для единообразия в обозна-
ченияху с ловимся, что токи будут иметь два индекса. Первый ин-
декс утока будет соответствовать номеру узла, от которого ток уте-
кает, второй индекс отвечает номеру узла, к которому ток подте-
2 Л. А. Бессонов
33
кает. Проводимости ветвей также будем снабжать двумяиндексами.
В соответствии с обозначениями токов на рис. 24составим .урав-
нение по первому закону Кирхгофа для первого узла , \
о,
или
l£4i — fa — ф«Л£« — — Ф1Л 84i +
+ [0 — 6Р1 — Фг)] £1'2' — [£'12 — (фа — Фi) ]g'a +
4~ (Ф1 Фа>)] 8 12 + [£31 ~ (Ф1 Фа)] gi» = О*
Перепишем последнее уравнение следующим образом:
: ’ ф/*11 4~ (Р2^12-Ь Фз^13 = ^11- (1.21)
Здесь
Оц = g'4t + 813 + g"i2 + g4l 4* g’l2 + g'vi'’ '
^12 — [g 12 4"812 ”4~ ^12)’ G13 = 813’
Л1= £41814 + £318314"“ £21821 ~~ £“1'4^41 £i$zv
Обсудим структуру уравнения (Г.21). Множителем при <pt в нем
является коэффициент Gu, равный сумме проводимостей'всех* вет-
вей, сходящихся в первом узле. G12 равняется сумме проводимостей
всех ветвей, соединйющих узел 1с узлом 2, взятой со знаком минус.
Аналогично 613 есть сумма проводимостей всех ветвей, соеди-
няющих узел / с узлом 3, взятая со знаком минус. Ток /и называ-
ют узловым током первого узла. Это расчетная величина, равная
алгебраической сумме токов, полученных от деления э. д. с. вет-
вей, подходящих к узлу 1, на сопротивления данных ветвей. В эту
сумму со знаком плюс входят токи тех ветвей, э. Д. с. которых нап-
равлены к узлу 1. Необходимо заметить, что записанные выше про-
водимости с двумя индексами не имеют ничего общего с входными
и взаимными проводимостями ветвей, которые рассматривались
в § 14.
Подобные же. уравнения могут быть записаны и для остальных
узлов схемы. Если схема имеет п узлов, то ей соответствует система
из (п — 1) уравнений вида
Фх^и + <₽2Gi2 4- • • • +ф„_1б1, „_| = Iи>
Ф1^21 4" ф2С22 4- • • . 4- Фп-1^2, п-1 — 122»
(1.22)
узле k",
k и т.
Ф1Ся-1,14~ф2^п—1,2 4~ • • • 4-ф«-А-1. п—1 ^п—1, п—1
Здесь Gkk— сумма проводимостей ветвей, сходящихся в
GAm —сумма проводимостей ветвей, соединяющих узлы
взятая со знаком минус; Ikk есть узловой ток k узла. Если к k
узлу подтекает ток от источника тока, то он должен быть включен
в ток Ikk со знаком плюс, если утекает, то со знаком минус.
Если между какими-либо двумя узлами нет ветви, то соответ-
34
ствующая проводимость равна нулю. После решения системы (1,22)
относительно потенциалов определяют токи в ветвях по закону
Ома для участка цепи, содержащего э. д. с.
Пример 13. Найти токи в ветвях схемы рис. 24 н сделать проверку
по второму закону Кирхгофа.
Дано: £', — 10 в, Е’14 — 6 в, Е'12 = 20 в, Е“2{ = 30 в, £31=14в,
£24= 10в, £43 = 8в, £"3 = 12в, £'2= 7в; /?'( = 1ом, /?"4=2ол,
R'l2— 10 ом, /?"2 = Ю ом, R'^ = 5 ом, RM = 2 ом, R2i = 4 ом,
R3i= 2 ом, R''23 = 4 ом, ₽2з = 2 ом-
Источник тока, включенный между узлами 3 и 2, дает ток 1 кзг =
= 1,5 а.
Решены е..Записываем систему уравнений
Ф1®11 4- ф2®12 4- Фз®13 ~ 7ц>
Ф1®21 4“ Фа®22 4- Фэ®23 ~ ^22, .'
Ф1®ЭД 4* Фа®за 4“ Фз®зз = 733.
Подсчитываем проводимости
С 1 , 1 t 1 ! 1 ,1 ,1 •
: “*+4+4+4+т+т=2’4<“*
~ = 1 I 1 I 1 , 1 |1 . 1 _
#12 #12 #12 #24 #23 #23.
= 0,2 4- 0,1 4- 0,1 4- 0,25 4- 0,25 + 0,5 = 1,4 (сим);
®33 = 4г 4- 4- 4* = 0,5 4- 0,5 4- 0,25 4- 0,5 = 1,75 (сим);
^23 ^23 ^31
®12 *= ®21 = — (0,2 4- 0,1 4- 0,1) = — 0,4 (сим);
®3i = ®1з = — 0,5 сим;
®аз ®за — — (0,25 4-0,5) — — 0,75 (сил).
При подсчете G22, G33 и учтено, что проводимость ветви с источ-
ником тока равна нулю (сопротивление источника тока равно бес-
конечности).
Узловые токи
, ' #41 #14
Ц #41
аа
#81___ #12
#31 # 12
#23 #12
#23 #12
#21
#;2 =
#я
10 _ J6 14 _ 20 , 30=
1 2 2 10 ' ю"
-^ + /Иа = -1.5 (а);
^2| ^24
#м
#32
#32
/33 = —3,5 + 3 —74-4— 1,5 = — 5(a).
2*
35
Система уравнений
2,4ф!^—0,4ф2— 0,5ф3 = 15;
—0,4фх 4" 1.4фг — 0,75фз = — 1,5;
—0,5ф1 — 0,75ф2 + 1,75ф3 = — 5.
Определитель системы
2,4 —0,4 —0,5
= 3,62.
—0,5 —0,75
Фа —
2,4 15 —0,5
—0,4 —1,5 —0,75
->0,5 —5 1,75
Д
^ = 0,06 (в),
М07 (в).
Заключительный этап расчета состоит в подсчете токов по зако-
ну Ома. Разумеется, перед определением токов в ветвях схемы сле-
дует эти токи обозначить и выбрать для них положительные направ-
ления.
Напомним, что в соответствии с принятыми в настоящем параг-
рафе обозначениями первый индекс у тока дает номер узла, от ко-
торого ток утекает, а второй индекс — номер узла, к которому ток
подтекает: ‘ 1'
^4 —(<Р1 —ф4) _ Ю —(6 —0) _
' «41 “ 1 “ W’
== = — 1,185 (а);
я12 5 5
= = 7-(0,06+2,1) =. М4 = _
«И 2 2
j ««-(Фз-Ф4). = 8-(-1,107-0) _4 55 и т д
Сделаем проверку решения по второму закону Кирхгофа для пери-
ферийного контура.
Алгебраическая сумма падений напряжений равна
4-1 — (— 1,185)).5 — 2,92.2 — 4,55-2» —5 (в).
Алгебраическая сумма э. д. с. равна
10 —7—8=. —5(e).
36
Покажем, что основная формула (1.20) метода двух узлов получает-
ся как частный случай из формулы (1,22). Действительно, если один
узел схемы рис. 23, например узел ft, заземлить, то остается найти
только один потенциал <ра = Uai. Для получения формулы (1.20)
в (1.22) следует положить:
Фх = Фе ~ Uatr> Фа — Фз = Ф* = • • • 1=3 0; /22 = — /д;
G21 = Gu; Z33 =/44 = ... = 0.
§ 21. Преобразование звезды в треугольник и преобразование тре-
угольника в звезду. Условимся соединение трех сопротивлений, име-
ющее вид трехлучевой звезды (рис. 25), называть соединением «звез-
да», а соединение трех сопротивлений так, что они образуют собой
стороны треугольника (рис. 26), называть соединением «треуголь-
ник». В узлах 1, 2, 3 (потенциалы их <р1( <р2 и <р3) и треугольник и
звезда соединяются с остальной частью схемы, не показанной на
рисунках.
Обозначим токи, подтекающие к узлам 1, 2, 3, через 11г /2 и 1Я.
Рис. 26
Очень часто при расчете электрических цепей оказывается полез-
ным преобразовать треугольник в звезду или совершить преобразо-
ваний звёзды в треугольник. Практически чаще встречается потреб-
ность в преобразовании треугольника в звезду, чем в обратней* пре-
образовании. Если преобразование выполнить таким образом, что
при одинаковых значениях потенциалов одноименных точек тре-
угольника и звезды подтекающие к этим точкам токи будут одина-
ковы, те вся внешняя схема «не заметит» произведенной замены.
Выведем формулы преобразований. С этой целью выразим токи /v
Z^ и /3 в звезде и в треугольнике через разности потенциалов.точа*
и соответствующие проводимости. ,т ,
Для звезды. .
/1 + /2 + /8 = 0. (1.23)
но
Zj = (ф1 Фе) = (фа Фо) ёгг 1 (1.24)
7» -(фз —Фо) &- Г
37
Подставим (1.24) в (1.23) и найдем фв
Ф1Д1 + ФгЙз + Фз£з— Фв(£1 + £г + й») = &
Отсюда
<р0 = Ф1£к±Ф*£1±Ф»^. (1.25)
Si + St + s»
Далее, введем <р0 в выражение для тока /х
Л = (Ф1—Фо) Si = в* (g2-+g3) ~ • (1.26)
Si + gt 4- g»
Обратимся к соединению треугольником. В соответствии с обо-
значениями на рис. 26
' Л Ла Л1 ~ (ф« Фа) 512 ' (Фз Ф1) 5аз =
* “ Ф1(51а + 51з) — Фз51Л — ф2512- (1-27)
Так как ток /х в-схеме рис. 25 должен равняться току Л в схеме
рис. 26 при любых значениях потенциалов фх, ф2, ф3, то коэффи-
циент при <р2 в правой части (Г.27) должен равняться коэффициен-
ту при ф2 в правой части (1.26), а коэффициент при ф3 в правой час-
ти (1.27) должен равняться коэффициенту при <р3 в правой час-
ти (1.26).
Следовательно,
(1.28)
gl + gi + gt
gi3- -• (1-29)
Si + g% + gl
Аналогично
£зз = - <L3°)
’ Si + St + gt
Формулы (1.28) — (1.30) дают возможность найти проводимости
сторон треугольника через проводимости лучей звезды. Они имеют
очень легко запоминающуюся структуру: индексы у проводимостей
в числителе правой части соответствуют индексам у проводимости
в левой части, а в знаменателе стоит сумма проводимостей лучей
звезды.
Из уравнений (1.28) — (1.30) выразим сопротивления лучей
звезды
#х==—; #2 = — и /?3== —
Si gt g»
через сопротивления сторон треугольника
#12 ~ '> #23 ~ ~ 1 #13 ~ ~ •
git gtt gl3
36
С этой целью запишем дроби, обратные (1.28) — (1.30)
1 1 . 1 Л1Ла 4~ Л2Л3 4~ ЛзЛ,
п Лх Ла Лэ Л1Л2Л3 _______ т ?, о,.
1г = “Т7Г“----------------ZT-----------V ( }
Лх Иг RiRz
Здесь
m = /?1/?2 + /?2/?s + ??3/?1; (1.32)
^аз = ^-; (1.33)
> (1.34)
*<8
В (1.32} подставим (1.31), (1.33) и (1.34), получим
т „а / 1 । 1 । 1 \ ms Ли 4-Лаз 4* Ли
т = т!--------)- -----1- 1 — т —_ _ •
Следовательно,
т RnRmRn
ш = —,————,
Ли 4* Лаз “t Лзх
Подставим т в (1,33) и найдем
Jf __ ЛйЛп '
Ли 4" Лаз 4" Лз1
Аналогично
— ЛазЛи .
Ли 4- Лаз 4" Ли
• __ ЛхзЛаз . -
Лха 4- Лаз 4* Ли
(1.35)
(1.36)
(1.37)
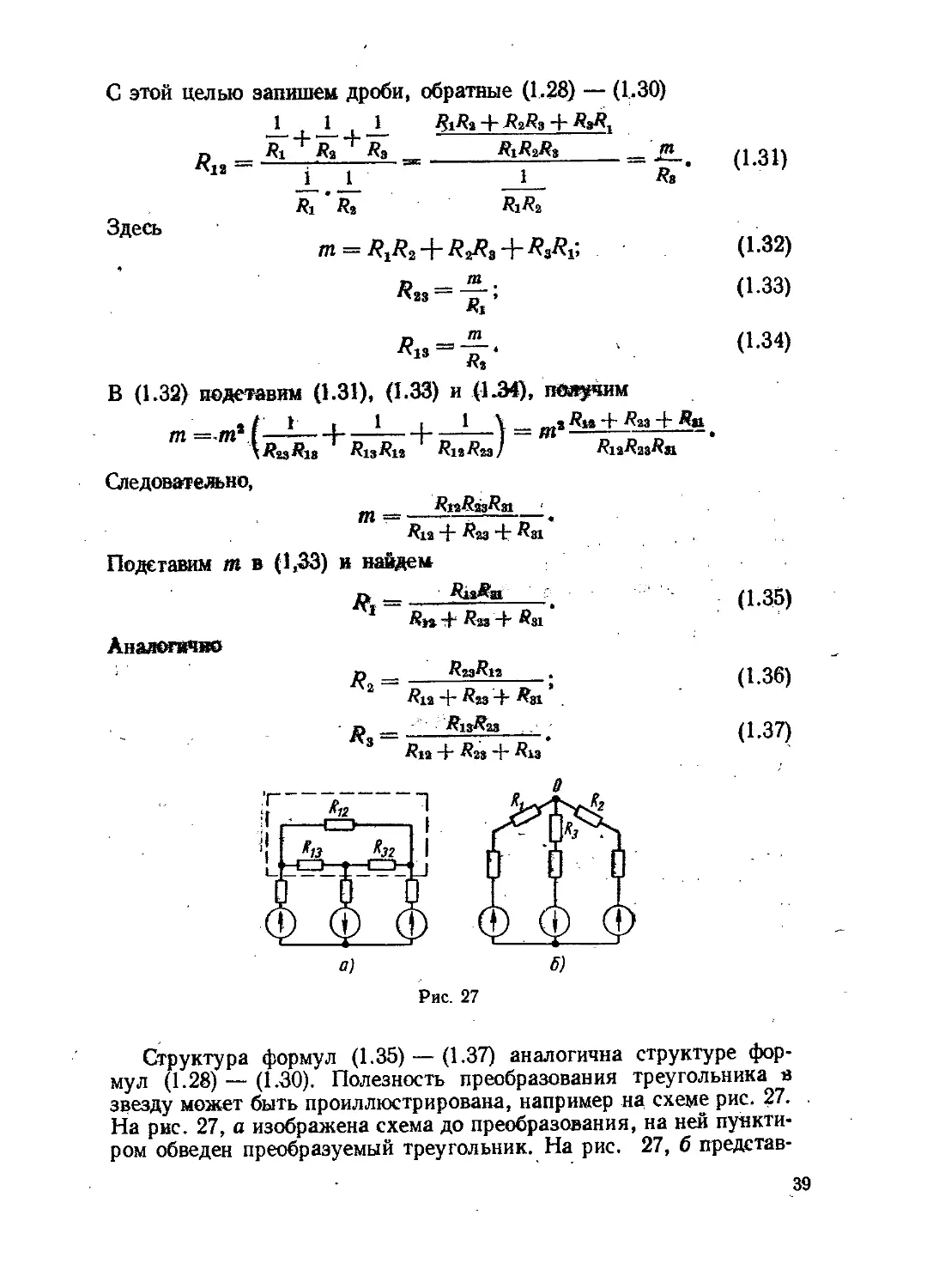
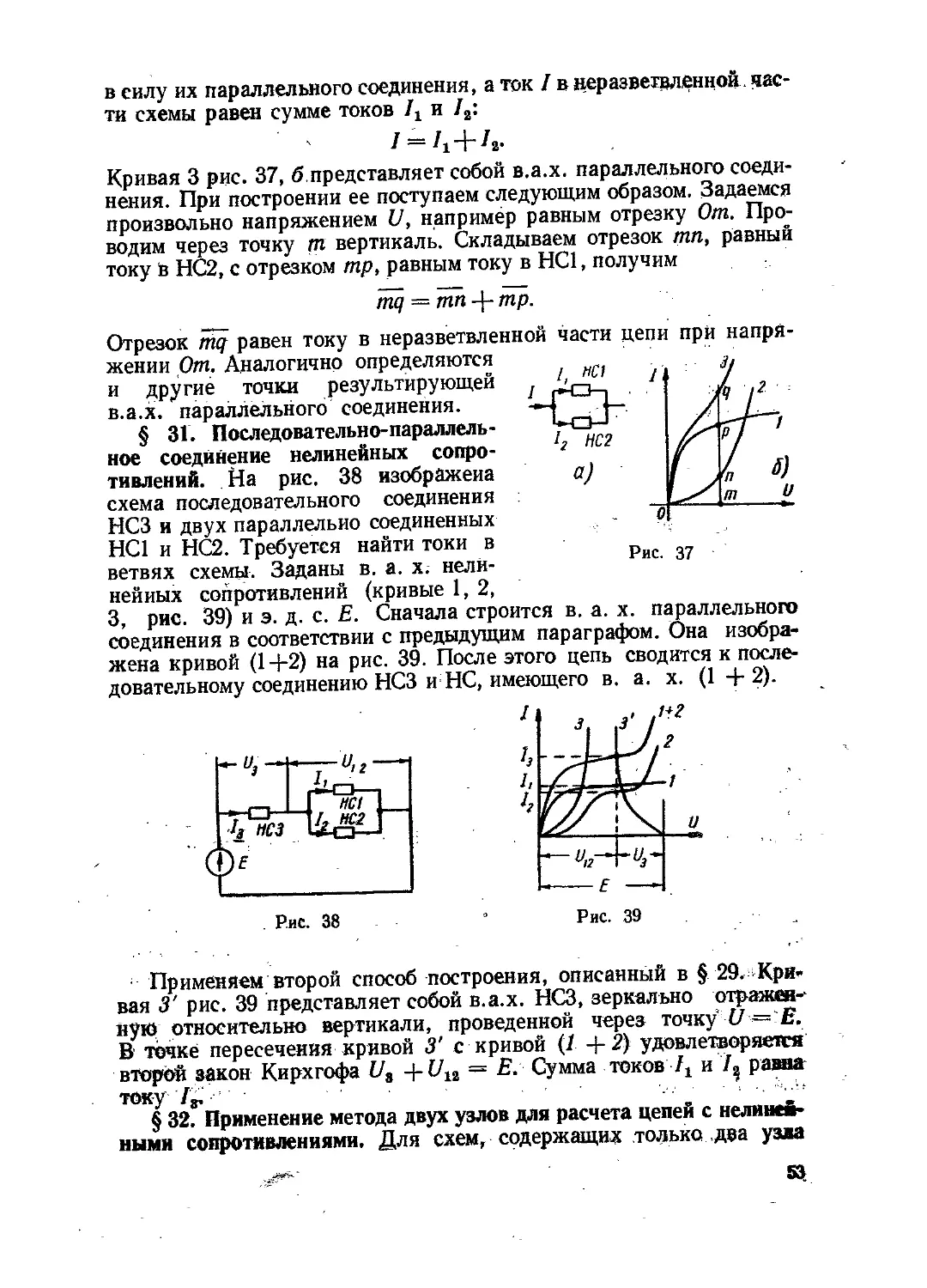
Рис. 27
Структура формул (1.35) — (1.37) аналогична структуре фор-
мул (1.28) — (1.30). Полезность преобразования треугольника в
звезду может быть проиллюстрирована, например на схеме рис. 27.
На рис. 27, а изображена схема до преобразования, на ней пункти-
ром обведен преобразуемый треугольник. На рис. 27, б представ-
39
лена та же схема, ио после преобразования. Расчет токов в ней зна-
чительно проще (например, -методом двух узлов), чем расчет токов
в схеме рис. 27, а. В полезности преобразования звезды в треуголь-
ник можно убедиться на примере схемы рис. 28. На рис. 28, а изоб-
ражена схема до преобразования. Пунктиром обведена преобразуе-
мая в треугольник звезда. На рис. 28, б представлена схема после
преобразования. Схема свелась к последовательному и параллель-
ному соединению сопротивлений.
Пример 14. Найти значения сопротивлений Ri, R3, R3 в схеме
712, Я13, /?32 В схеме рис. 27, а
равны, соответственно, 2,3,5 ом.
Решение. По формуле
(1.35)
рис. 2/, о, если сопротивления
по формуле (1.36)
₽2 = ^=1 (ом)
и по формуле (1.37)
1,5 (ом).
§ 22. Активный и пассивный двухполюсники. Познакомимся с
понятием двухполюсника, которым довольно широко пользуются
в Теории электрических цепей.
В любой электрической схеме всегда можно мысленно выделить
какую-то одну ветвь, а всю остальную часть схемы, вне зависимости
от ее структуры и сложности, условно изобразить некоторым пря-
моугольником (рис. 29, а). К такому приему мы прибегали и рань-
ше (§ 16) без специальных объяснений. По отношению к выделенной
ветви вся схема, обозначенная прямоугольником, представляет со-
бой так называемый двухполюсник.
.. Таким образом, двухполюсник. — это обобщенное название схе-
мы, которая своими двумя выходными зажимами (полюсами) при-
-соединяется к выделенной ветви.
40
Если в двухполюснике есть э.- д. с. или (и) источник тока;, то та-
кой двухполюсник называют активным. В этом случае на прямо-
угольнике ставится буква Л (первая буква слова активный, см.
рис. 29, а, б и в). ' “ '
Если в двухполюснике нётэ. д. с. и источника тока, то его назы-
вают пассивным? В этом случае на прямоугольнике либо ие ставит-
ся никакой буквы, либо ставится буква П (первая буква слова пас-
сивный, см. рис. 29, г).
§ 23. Замена активного двухполюсника эквивалентным генерато-
ром. Метод холостого хода и короткого замыкания. По отношению
к выделенной ветви двухполюсник в расчетном отношении можно
заменить эквивалентным генератором, э. д. с. которого равна нап-
ряжению холостого хода на зажимах выделенной ветви, а внутрен-
нее сопротивление равно входному сопротивлению двухполюсника.
Это полсйкение используется в методе-расчета электрических
цепей, который имеет несколько названий, а именно: Метод холос-
того хода и короткого замыкания, метод эквивалентной генератора,
метод активного двухполюсника.
Пусть задана некоторая, сколь угодно сложная схема, и требует-
ся найти ток в одной ее ветви. Мысленно заключим всю схему, со-
держащую э.д.с. и сопротивления, в прямоугольник, выделив из
нее одну ветвь ab, ток I в которой требуется найти (рис. 29, а).
Буква А на прямоугольнике свидетельствует о том, что в нем есть
э.д.с.'(активный двухполюсник).
Естественно, что ток 1 не изменится, если в ветвь ab включить
две равные й противоположно направленные э.хд. с, иЕа(рнс.
29, б). На основании принципа наложения ток можно представить
в виде суммы двух токов Г и 1"
Под током /' будем понимать ток, вызванный э.д.с. и всеми
э.д.с. активного двухполюсника, заключенными в прямоугольник,
а ток /" вызывается только одной э.д.с. Е2. В соответствии с этим
для нахождения токов Г и 1" используем схемы рис. 29, виг. Бук-
ва П на прямоугольнике схемы рис. 29, г свидетельствует о том,
что двухполюсник в этой схеме пассивный, т. е. в нем отсутствуют
все э.д.с., но оставлены внутренние сопротивления источников.
Э.д.с. Et направлена встречно напряжению Uab. По закону Ома
для участка цепи, содержащего э.д.с.,
I' —
R .
Выберем Ех так, чтобы ток Г был равен нулю. Отсутствие тока в вет-
ви эквивалентно ее размыканию (холостому ходу).Ндаряжение
н'а заййймах об при холостом ходе (хф аетви обозначим Uat,xx.
Следовательно, если выбрать Е± равной Uat)XX, то /' ==О. Так
’41
как 1=Г-{-1", а 7' = О, то 7=7". Ноток I" в соответствии со
схемой рис. 20, в определяется так;
7"=ч- & -й
И + Иах Я + Ивх w
Здесь Rex— входное сопротивление двухполюсника по отношению
к зажимам ab\ R — сопротивление ветви ab.
Уравнению (а) отвечает эквивалентная схема рис. 30. В этой
схеме вместо двухполюсника изображены источник э.д.с. Ua6xx = Е2
и сопротивление
Совокупность э.д.с. E2 — Uabxx и сопротивления 7?^ можно
рассматривать как некоторый эквивалентный генератор (ЦЙХ явля-
ется его внутренним сопротивлением, a Ueixx
RSx его э.д.с.).
1 Таким образом, по отношению к выделеи-
ffn ной ветви (ветви ab рис. 29, а) всю остальную
' т часть схемы можно заменить эквивалентным
--------* генератором с названными выше значениями па-
Рис. 30 раметров. .
Метод расчета тока в выделенной ветвн, ос-
нованный на представлении активного двухпо-
люсника эквивалентным генератором, принято называть методом
эквивалентного генератора, методом активного двухполюсника или
методом холостого хода и короткого замыкания.
В дальнейшем мы чаще всего будем пользоваться последним наз-
ванием.
Последовательность расчета тока этим методом рекомендуется
следующая:
а) найти напряжение на зажимах разомкнутой ветви оЬ;
б) определить входное сопротивление 7?вЛ всей схемы по отноше-
нию к зажимам ab при закороченных источниках э.д.с;*;
в) подсчитать ток по формуле
7 = (1.38)
* + /?«
Если сопротивление ветви ab сделать равным нулю (7? = 0), то
для нее будет иметь место режим короткого замыкания, а протека-
ющий по ней ток будет являться током короткого замыкания (7КЗ).
Из (1.38) при 7? = 0 получим
; (1.39)
"вх
* Если среди источников питания схемы есть источники тока, то при
определении входного сопротивления всей схемы по отношению к зажимам
ab ветви с источниками тока следует считать разомкнутыми. Это станет по-
нятным, если вспомнить, что внутреннее сопротивление источников тока рав-
но бесконечности ( § 2).
42
или
= (1-40)
‘КЗ
Из формулы (1.40) следует простой метод опытного определения
входного сопротивления. Для этого необходимо измерить напряже-
ние холостого хода на зажимах разомкнутой ветви (Uab хх) и ток ко-
роткого замыкания (Z^) при коротком замыкании ветви и найти
R„x как частное <эт деления Uat> хх на 1К3.
Название метода — метод холостого хода и короткого замыка-
ния — объясняется тем, что при решении этим методом для нахож-
дения Uab хх используется холостой ход ветви ab, а для определения
входного сопротивления двухполюсника может использоваться опыт
короткого замыкания ветви ab.
Рис. 3f,
Пример 15. Определить ток в диагонали ай мостовой схемы рис.
31, а, полагая = 1 ом, = 4 ом, R3 = 2 ом; = 2 ок;
= 10 в.
Решение. Размыкаем ветвь ab (см. рис. 31, б).и находим нап-
ряжение холостого хода
। г г> т п — I ЯхЯг Я1Я1
т. = Ф. + /л -1Л - Ф.+-
2 _ । р I Яг Ях \
Ф» + ^1^Я2 + Я4 Я1 + Яз/
или
Uab хх ~~ Фа, Ф» 4-/? R J- R ) =
\Яг + Я* Т лз/
= 10(—-----------—А = 4,67 (в).
(,44-1 1.+ 2 / '
Подсчитываем входное сопротивление всей схемы по отношению
к зажимам ab при закороченном источнике э.д.с. (рис. 31, в). Точки
с и d схемы оказываются соединенными накоротко. Поэтому
4- = 1,47 (оя).
Ri + Яз Яг + Я* 14-2 4 + 1 ’
43
Определим ток в ветви по формуле (1.38)
Ugbxx 4.67
Ri + R,x 2+1,47
= 1,346 (а),
§ 24. Передача энергии от активного двухполюсника нагрузке.
Если нагрузка R подключена к активному двухполюснику
(рис. 29, а), то через нее пойдет ток / = - , и в ней бу-
дет выделяться мощность
р _ у in U2ab хХ
(R + R'x?
Выясним, каково должно быть соотношение между сопротивле-
нием нагрузки R и входным сопротивлением двухполюсника Rex,
чтобы в сопротивлении нагрузки выделялась максимальная мощ-
ность; чему будет она равна и каков при этом будет к.п.д. передачи.
С этой целью найдем первую производную Р по R и приравняем ее
нулю:
ЛР (Я + ад8 - 2/?(7? + ад = о -4
dR (R + RexY
Отсюда
--=/?„. (1.42)
Нетрудно найти вторую производную и убедиться в том, что
она отрицательна I< 0 L поэтому соотношение (1.42) соответ-
ствует максимуму функции Р =±= f (Р).
Подставим (1.42) в (1.41) и найдем максимальную мощность, ко-
торая может быть выделена в нагрузке R
(1-43)
**\9Х
Полезная мощность, выделяющаяся в нагрузке, определяется
уравнением (1.41). Полная мощность, выделяемая эквивалентным
генератором, равна
р —U I УЧь XX
г полн ^аЪхх* п id*
К&х "Г К
Коэффициент полезного действия
Рполн R + Rex
Если R = то т] = 0,5. : -
Если мощность Р значительна,то работать с таким низким к.п,д.,
как 0,5, совершенно недопустимо. Но если мощность Р мала, на-
пример составляет всего несколько милливатт (такого порядка мощ-
44
ности отдаются различными датчиками устройств автоматики),
то с низким к. п. д. можно и не считаться, поскольку в этом режиме
датчик отдает нагрузке максимально возможную мощность. Выбор
величины сопротивления нагрузки 7?, равного входному сопротивле-
ний Rex активного двухполюсника, называют согласованием нагрузки.
Пример 16. Найти, При каком значении сопротивления R6 схемы
рис. 31, а в нем будет выделяться максимальная мощность и чему
она будет равна.
Р е ш е н и е. Из условия (1.42) находим
P5 = Pe.r = М7 ом
к
Рис. 32
и
U!abxx „ 3.71 (в/п).
р
1 макс »п л 1 л?
4RSX 44,47
§ 25. Передача энергии по линии передачи.
Схема линии передачи электрической энер-
гии изображена на рис. 32. На ней — напряжение генерато-
ра в начале линии, t/a — напряжение на нагрузке Р — сопро-
тивление проводов линии, Р2 — сопротивление нагрузки в конце
линии.
При передаче больших мощностей (например, нескольких де-
сятков мегаватт) в реальных линиях передач к. п. д. составляет
практически 0,94—0,97, а С/а лишь
на несколько процентов мень-
ше l/j.
Если по линии передачи с со-
противлением R нагрузке должна
быть передана мощность Ра, то
коэффициент полезного действия
передачи будет тем выше, чем
больше напряжение Ut в начале
линии. В этом можно убедиться
путем следующих рассуждений:
снижение Ut вызовет снижение
С/а, а уменьшение U2 при неизмен-
ном Ра приведет к уменьшению
/ U2 \
Ра1 Р2 = —). Снижение Ра при
\ Рз I
R = const приведет к уменьшению к.п.д. т] = .
R + А2
Характер изменения мощности в начале линии Рх, мощности
в нагрузке Ра, коэффициента полезного действия и напряжения
на нагрузке Ut в функции от тока по линии при неизменном напря-
жении на входе линии и неизменном сопротивлении проводов
линии Р йллюстрируется кривыми рис. 33. По оси абсцисс на этом
рисунке отложен ток/, по оси ординат — Plt Pa, С/а,т].
45
Максимальное значение тока 1маке — имеет место при ко-
г\
ротком замыкании нагрузки. Кривые построены по уравнениям:
^ = 6//;
Pz = UlI — PP\
Ч = А_=1_^;
Pl Ul
и^и.—т.
Глава вторая
НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПОСТОЯННОГО ТОКА
§ 26. Основные определения. Как уже говорилось в § 1, под не-
линейными электрическими цепями принято понимать электриче-
ские цепи, содержащие нелинейные элементы. Нелинейные элементы
подразделяются на нелинейные сопротивления, нелинейные индук-
тивности и нелинейные емкости.
Нелинейные сопротивления (НС)*, в отличие от линейных, обла-
дают нелинейными вольтамперными характеристиками. Напомним,
что вольтамперная характеристика (в.а.х.)—это зависимость тока,
протекающего через нелинейное сопротивление, от напряжения
на нем. Нелинейные сопротивления могут быть подразделены на две
большие группы: группу неуправляемых НС и группу управляе-
мых НС. В управляемых НС, в отличие от неуправляемых, кроме ос-
новной цепи, как правило, есть еще по крайней мере одна вспомо-
гательная или управляющая цепь, воздействуя на ток или напряже-
ние которой можно деформировать в. а. х. основной цепи. В неуправ-
ляемых НС в.а.х. изображается одной кривой, а в управляемых —
семейством кривых.
В группу неуправляемых НС входят: лампы накаливания, элект-
рическая дуга, бареттер, газотрон, стабиловольт, тиритовые и ви-
литовые сопротивления, полупроводниковые выпрямители (диоды)
и некоторые другие НС.
В группу управляемых НС входят трех- (и более) электродные
лампы и полупроводниковые трех- (и более) электродные выпря-
мители (триоды).
§ 27. Вольтамперные характеристики нелинейных сопротивлений.
На рис. 34 изображено одиннадцать типов наиболее часто встречаю-
щихся вольтамперных характеристик неуправляемых НС.
* В даинов главе приняты следующие сокращения в записи: НС — не-
линейное сопротивление, в. а. х. — вольтамперная характеристика (подоб-
но тому, как э. д. с. = электродвижущая сила).
47
В.а.х. типа рис. 34, а имеют, например, лампы накаливания с
металлической нитью. Чем больше протекаюнщй через 41Й^"ток,
тем нить сильнее нагревается и тем больше становится ее сопроти-
вление.
Если условиться величину, откладываемую по оси абсцисс,
обозначить через х, а величину, откладываемую по оси ординат, че-
рез f (х), то характеристика типа «а» подчиняется условию
f(x) = — f( — х).
Нелинейные сопротивления, для которых выполняется это усло-
вие, называют нелинейными сопротивлениями с симметричной вольт-
амперной характеристикой.
Рис. 34
В.а.х. типа рис. 34, б обладают тиритовые и вилизрвые сопро-
тивления, некоторые типы термисторов (гермосо11рбЙ1йе®йЛУ« Лам-
пы с угольнбй нитью накаливания.
Основу тирита и вилита составляют мелкоизмельчениый графит
и карборунд. После соответствующей технологической обработки
эта масса прессуется в виде дисков и запекается. Вилитовые и тири-
товые HG используются в нелинейных мостовых схемах автоматики,
применяемых, например, в качестве индикаторов отклонения нап-
ряжения генераторов от номинала. Они широко используются в за-
щитных устройствах при передаче энергии высоким напряжением.
Для представителей данной группы характерно, что с увеличением
протекающего тока сопротивление их уменьшается. В^а.х. их сим-
метрична.
В.а.х. типа рис. 34, в обладает, например, устройство, называе-
мое бареттером. Бареттер выполняется обычно в виде спирали из
стальной проволоки, помещенной в стеклянный сосуд, заполненный
водородом при давлении порядка 80 мм рт. ап-. В определенном
диапазоне изменения тока в. а. х. бареттера расположена почти
горизонтально. Бареттер используется для стабилизации тока на-
кала электронных ламп при изменении напряжения питания. В- а. х,
типа рис. 34, в также симметрична.
48
В.а.х. типа рис. 34, г в отличие от предыдущих, несимметрична.
Ею обладают полу проводниковые выпрямители (меднозакисные,.се-
леновые, кремниевые, германиевые), очень широко применяемые
для преобразования переменного тока в постоянный. Они способ-
ны пропускать ток практически только в одном, проводящем, нап-
равлении. Широко применяются они также в различных датчиках
и преобразователях устройств автоматики. В.а.х. типа рис. 34, д
имеет электрическая дуга с разнородными электродами, газотрон
и некоторые типы термисторов. Если напряжение повышать, начи-
ная с нуля, то сначала ток растет, но остается весьма малым; после
достижения напряжения Ur (напряжения зажигания) происходит
резкое увеличение тока в цепи и снижение напряжения на электри-
ческой дуге или газотроне. Для верхнего участка в.а.х. прираще-
нию тока соответствует убыль напряжения на нелинейном сопротив-
лении.
Участок в.а.х. по типу верхнего участка кривой рис. 34, д на-
зывают падающим участком вольтамперной характеристики *.
Электрическая дуга широко применяется при сварке металлов,
в электротермии (в дуговых электропечах), а также в качестве мощ-
ного источника электрического освещения, например в прожекто-
рах.
Газотрон представляет собой лампу с двумя электродами, за-
полненную благородным газом или парами ртути.'
В. а. х. по типу рис. 34, е имеет, двухэлектродная выпрямитель-
ная лампа — кенотрон. По нити накала лампы пропускается ток.
Этот ток разогревает катод (один из двух электродов лампы) до вы-
сокой температуры, в результате чего с поверхности катода начи-
нается термоэлектронная эмиссия. Под действием электрического
поля поток электронов направляется ко второму—холодному элект-
роду — аноду. В начальной части в. а. х. (рис. 34, е) зависимость
тока от напряжения подчиняется закону трех вторых: i = au3/2.
В.а.х. кенотрона несимметрична, это объясняется тем, что поток
электронов направляется с катода на анод только в том случае,
если анод положителен по отношению к катоду.
В.а.х. по типу рис. 34, ж обладают лампы с тлеющим разрядом.
К числу их относятся стабиловольты и неоновые лампы. При тлею-
щем разряде благородный газ, которым заполнена лампа (неон, аргон
и др.), светится. В.а.х. потипу рис. 34, ж обладает той особенностью,
что в определенном диапазоне значений токов напряжение на лампе
остается практически неизменным.
Некоторые типы точечных германиевых и кремниевых выпрями-
телей имеют в. а. х. по типу рис. 34, з.
* Падающий участок в. а. х. представляет-собой такой ее участок, йа
котором положительному приращению тока через НС соответствует отрица-'
тельное приращение напряжения на НС. . ’
49
Электрическая дуга между электродами, выполненными из од-
ного и того же материала и находящимися в одинаковых условиях,
имеет в.а.х. по типу рис. 34, и.
В.а.х. трехслойного германиевого (кремниевого) диода — три-
нистора — изображена на рис. 34, к.
В.а.х. туннельного диода — на рис. 34, л (о принципах работы
тринйстора и туннельного диода см., например Л. 18).
В качестве управляемых нелинейных сопротивлений широко при-
меняются полупроводниковые триоды и трехэлектродные электрон-
ные лампы.
О полупроводниковых'триодах, их характеристиках и об их при-
менении сказано в девятой главе курса ТОЭ.
Вольтамперные характеристики трехэлектродной лампы рассмот-
рены в §41.
§ 28. Общая характеристика методов расчета нелинейных элект-
рических церей постоянного тока. В первой части курса ТОЭ рас-
сматривается , методика расчета простейших нелинейных электри-
ческих цепей; образованных последовательно, параллельно н пос-
ледовательно-параллельно соединенными НС и источниками э. д. с.
Кроме тбго, рассматривается методика расчета сколь угодно слож-
ных цепей, в состав которых входит только одно НС (или цепи, сво-
дящиеся к таким).
Вопросы расчета более сложных Схем выходят за рамки курса.
При необходимости можно ознакомиться с несколькими различными
приемами расчета более сложных схем по литературе Л, 1а (стр.
166), а также в журнале «Электричестве», № 12, 1955.
’ Обратим внимание на то, что с линейной частью любой сложной
разветвленной цепи, содержащей нелинейные сопротивления, мож-
но проделывать любые преобразования, рассмотренные в первой гла-
ве. Разумеется, такого рода преобразования целесообразно делать
только в том случае, если они позволяют облегчить расчет всей слож-
ной схемы.
Применение одного из таких преобразований — перехода от
треугольника сопротивлений к звезде — для облегчения нахожде-
ния входного сопротивления линейной части схемы дано в § 34.
Из рассмотренных в главе первой методов расчета в данной гла-
ве к нелинейным цепям применены следующие методы:
метод двух узлов;
замена нескольких параллельно включенных ветвей одной эк-
вивалентной; .
метод Холостого хода и короткого замыкания.
Перед проведением расчета нелинейных цепей должны быть из-
вестны вольтамперные характеристики входящих в схему нелиней-
ных сопротивлений. Расчет нелинейных цепей постоянного тока про-
изводится, как правило, графическим путем.
§ 29. Электрические цепи с последовательным соединением нели-
нейных сопротивлений. На рис. 35, а изображена схема последователь-
50
ного соединения НС с заданной в.а.х. и линейного сопротивления R. В
схему включен источник э.д.с. Е. Требуется найти ток в цепи.
В.а.х. НС обозначена на рисунках как i = f (UHC), в. а. х. линейного
сопротивления есть прямая линия. В. а. х. всей цепи, т. е. зависи-
мость тока в цепи от суммы падений напряжений на НС и J?, обо-
значена через i = Расчет основывается на законах
Кирхгофа. Обсудим два способа расчета. Первый способ иллюстри-
руется рис. 35, б, второй—рис. 35, в.
В первом способе строится результирующая в.а.х. всей пассив-
ной части схемы, исходя из того, что при последовательном соедине-
Рис. 35
нии через НС и R течет одинаковый ток. Для построения результи-
рующей в.а.х. задаемся произвольным током, проводим через него
горизонталь и складываем напряжение на НС (отрезок тп на рис.
35, б) с напряжением на R (отрезок /пр).
тп 4- тр = mq*.
Точка q принадлежит результирукадей в.а.х. всей схемы. Анало-
гично строятся и другие точки результирующей в.а.х. Определение
тока в цепи при заданной э.д.с. Е производится графически по ре-
зультирующейв.а.х. (рис. 35, б). С этой целью следует заданную
величину э.д.с? Е отложить по оси абсцисс и через полученную точ-
ку на оси абсцисс провести вертикаль до пересечения с результиру-
ющей в.а.х. в точке q. Ордината точки q равна искомому току.
При расчете цепи по второму способу нет необходимости стро-
ить результирующую в.а.х. всей пассивной части схемы. В этом спо-
собе из точки i = О, U = Е в точку
. / = -Ё, t/ = 0
R
* Черта, поставленная над отрезком, означает, что речь идет о длине
Этого отрезка.
51
следуе! провести йрямую - '
так, как показано на рис. 35, в. Тангенс угла а наклона её к
вертикали с учетом масштабов по осям численно равен /?. Точка
пересечения прямой с в.а.х. НС и дает решение. Действительно,
для этой точки ток через НС и через /? одинаков, а сумма паде-
ний напряжений £7НС -f - UR ** Е. При изменении э.д.с. со значения
Е до Et надо прямую / = f (UR) переместить параллельно себе
так, чтобы она исходила из точки / = О, U = Ех (пунктирная пря-
мая на рис. 35, в).
Аналогично рассчитывают цепи при последовательном соедине-
нии двух и большего числа НС. В этом случае сначала находится
в.а.х. двух НС, затем трех и т. д.
В)
Обсудим применение второго способа для расчета цепи рис. 36, а
с двумя различными НС. В.а.х. НС1 и НС2 изображены на рис. 36, б.
Так как НС2 имеет нелинейную в.а.х., то вместо прямой I=f (U^),
как это было на рис. 35, в, теперь надо нанести нелинейную за-
висимость 7 = /(^НС2)- Начало ее (рис. 36, в) расположено в точке
/ = 0, Ut = Е. Отсчет положительных значений f/HC2* производит-
ся влево от этой точки. Так как положительные значения <7НС2на
рис. 36, б откладываются вправо от начала координат, а на рйс.
36, в-—влево, то кривая / = /(^НС2) рис. 36, в представляет собой
зеркальное изображение кривой 2 рис. .36, б относительно верти-
кальной оси, проведенной через точку Ut=E.
§ 30. В.а.х. параллельного соединения нелинейных сопротивлений.
Схема параллельного соединения двух НС изображена на рис. 37, а.
В.а.х. НС изображены на рис. 37, б. При построении результирую-
щей в.а.х. исходим из того, что напряжения на НСГ и на НС2 равны
• На рис. 36, в вместо £/НС2 обозначено lft.
52
в силу их параллельного соединения, а ток I в неразвегвленной час-
ти схемы равен сумме токов и /2:
Кривая 3 рис. 37, ^представляет собой в.а.х. параллельного соеди-
нения. При построении ее поступаем следующим образом. Задаемся
произвольно напряжением U, например равным отрезку От. Про-
водим через точку т вертикаль. Складываем отрезок тп, равный
току В НС2, с отрезком тр, равным току в НС1, получим
mq = тп -f- тр.
Отрезок mq равен току в неразветвленной части цепи при напря-
жении От. Аналогично определяются
и другие точки результирующей ;
в.а.х. параллельного соединения.
§ 31. Последовательно-параллель-
ное соединение нелинейных сопро-
тивлений. На рис. 38 изображена
схема последовательного соединения
НСЗ и двух параллельно соединенных
НС1 и НС2. Требуетея найти токи в
ветвях схемы. Заданы в. а. х. нели-
нейных сопротивлений (кривые 1,2,
3, рис. 39) и э. д. с. Е. Сначала строится в. а. х. параллельного
соединения в соответствии с предыдущим параграфом. Она изобра-
жена кривой (1 +2) на рис. 39. После этого цепь сводится к после-
довательному соединению НСЗ и НС, имеющего в. а. х. (1 +2).
Применяем второй способ построения, описанный в § 29. Кри-
вая 3' рис. 39 представляет собой в.а.х. НСЗ, зеркально отражен-
ную относительно вертикали, проведенной через точку U — Е.
В точке пересечения кривой 3' с кривой (/ + 2) удовлетворяется
второй закон Кирхгофа Us -{-(/12 = Е. Сумма токов 7Х и /2 равна
току- /8. • '
§ 32. Применение метода двух узлов для расчета цепей с нелиней-
ными сопротивлениями. Для схем, содержащих только два узжа
53
или приводящимся к ним, широко применяется метод двух узлов.
Рассмотрим его на примере схемы рйс.40. В схеме три НС й три э.д.с.
Пусть в.а.х. НС изображаются кривыми рис. 41, а, б ив. Для оп-
ределенности положим, что Е± > £2 > Е3. Выберем положитель-
ные направления для токов. Пусть, например, все токи направлены
к узлу а. Тогда по первому закону Кирхгофа
Л+Л+Л = о. (2.1)
Каждый, из токов является нелинейной функцией падения напря-
жения на «своем» нелинейном сопротивлении. Так, /х является функ-
цией Ult /2 — функцией Ug и 13 — функцией (/3.
Поставим перед собой задачу выразить все токи в функции не от
различных переменных (Ult U2, Us), а в функции одного перемен-
ного — напряжения Uab между двумя узлами. Это сделать возмож-
но, так как
U^E.-U^ (2.2)
(^2 == Е2 U (2-3)
U3 —Eg — Uab. (2.4)
Ъ -и;
Рис. 40 Рис. 41
Таким образом, возникает задача о перестройке кривой
4 = f (С\) в кривую Д = f(Uab)’ кривой Ig = f (Ug) в кривую
Ig = f(Uab) и т- Д- Перестроим кривую Л=/(Ц) (рис. 41, а)
в кривую 4 = / (Uab) (Ряс- 42). Соответствующие друг другу
точки обозначены одинаковыми цифрами...
Для точки 5 /j = 0 и ^=0; при этом Uab = Et (см. формулу
2.2). Другими словами, начало кривой Д — f (Uab) сдвинуто в точку
Uab =
Росту (при > 0) соответствует убыль Uab. Для точки 2
при значении U = Ег Uab = 0. Росту | | (при < 0) отвечает
рост Uab, причем Uab > Ег
На основании предыдущих рассуждений и построений рис. 42
рекомендуется проводить перестройку следующим образом:
1. Сместить кривую Д = f (Ц) параллельно самой себе так, что-
бы начало ее находилось в точке Uab = Ev Кривая, полученная в
результате переноса, представлена пунктиром на рис. 42.
54.
2. Провести через точку Uab == вертикаль и зеркально отра-
зить пунктирную кривую относительно вертикали.
Аналогичным образом производится перестройка кривых и для
других ветвей схемы. Нанесем кривые 1Л = f (Uab), /а = / (Uab) и
4 = /(#«*) на одном рисунке' (на рис. 43 они обозначены цифрами
1, 2, 8) и построим кривую Zx-|- /2-(-/3 = f(Uab) (на рис. 43 она
обозначена цифрой 4), просуммировав ординаты кривых 1, 2, 3.
Точка т пересечения кривой 4 с осью абсцисс дает значение Uab,
при котором удовлетворяется уравнение (2.1). Восставим в этой
точке перпендикуляр к оси абсцисс. Ординаты точек пересечения
§ 33. Замена нескольких параллельных ветвей, содержащих НС
и э. д. с. , одной эквивалентной ветвью. Обсудим постановку задачи.
Пусть есть совокупность нескольких параллельных ветвей, содер-
жащих НС и э.д.с. (рис. 44). Параллельные ветви входят в состав
сложной схемы, не показанной на рис. 44. Спрашивается, какова
должна быть э.д.с. и в.а.х. эквивалентного нелинейного сопротив-
ления НСЭ участий схемы рис. 45, чтобы он был эквивалентен па-
раллельным ветвям рис. 44? Для того чтобы одна ветвь рис. 45 была
эквивалентна ветвям рис. 44, необходимо, чтобы ток / в неразвет-
вленной части цепи рис. 44 при любых значениях напряжения Uab
равнялся току / в ветви рис. 45.
Воспользуемся построениями на рис. 43 предыдущего параграфа.
Кривая 4 рис. 43 есть не что иное, как зависимость
/1 + 4 + /з = М^).
Другими словами, кривая 4 есть не что иное, как результирую-
щая в.а.х. трех параллельных ветвей. Такую же в.а.х. должна иметь
ветвь рис. 45. Если ток I в схеме рис. 45 будет равен нулю, то Uab=
= Еа. Следовательно, Е3 на рис. 43 определяется значением напря-
жения Uab, при котором кривая 4 будет пересекать ось абсцисс.
Для определения в.а.х. нелинейного сопротивления НСЭ необхо-
55
димо кривую 4 рис. 43 зеркально отобразить относительно вертика-
ли, проведенной через точку т. .
В.а.х. НСЭ изображена на рис. 46. Важно подчеркнуть, что вклю-
чение э.д.с. в параллельные ветви привело к тому, что в.а.х, НСЭ
стала несимметричной, несмотря на то, что в.а.х. нелинейных соп-
ротивлений 1, 2, 3 в схеме рис. 40 были взяты симметричными.
Таким образом, изменяя э.д.с. в ветвях параллельной группы,
можно изменять результирующую в.а.х. ее ц как бы искусственно
создавать НС с самыми причудливыми в.а.х.
Рис. 44
Рис. 46
§ 34. Применение метода холостого хода и короткого замыкания
к расчету цепей с нелинейными сопротивлениями. Если в сложной
электрической цепи есть одна ветвь с НС, то определение тока в ней
может производиться С этой целью выделим ветвь
с йИВвеййым сопротивлением,
а всю остальную линейную схе-
а) б)
му представим в виде активно-
го двухполюсника (рис. 47,а).
Как известно из предыдуще-
го (§ 22), схему линейного актив-
ного двухполюсника по отно-
шению к зажимам а и b выде-
Рис. 47 ленной ветви можно предста-
вить в виде последовательного
соединения источника э.д.с. с э.д.с., равной напряжению'на зажи-
мах ab при размыкании ветви (Uabxx), сопротивления, равного
входному сопротивлению Rex линейного двухполюсника, и сопро-
тивления ветви ab (рис. 47, б).
’ Определение тока в схеме рис. 47, б не представляет труда и мо-
жет проводиться в соответствии с § 29.
' Пример 17. Определить ток в ветви ab схемы рис. 48, а по ме-
тоду хх и кз, при /^ = /?# == 2 ом, = 8 ом, Я* = 4 ом, &4=6 ом.
В.а.х. НС изображена на рис. 49, а; Е —58,4 в.
Решени’е. Размыкаем ветвь ab и определяем напряжение хо-
лостого хода
Uabxx —• 8,35 в.
Для подсчета входного сопротивления линейной части схемы
относительно зажимов ab необходимо преобразовать треугольник
сопротивлений /?2, /?0 (или /?4, /?0> /?3, рис. 48,6) в эквивалент-
ную звезду (рис, 48, в) по формулам (1.35—1.37):
RiRo
+ Ro
#5 =
-- = 1,333 (ом); /?в = 0,33 ом
2+8+2 ' ’
Ri — 1,333 ом, Rgx = /?5
= 4,05 ом.
№ + Rs) (Ry + Rt)
Ro + Rs + Ry + Ri
a)
' Рис. 48
Для определения тока в ветви ab схемы рис. 48, а на рис. 49, а
из точки т(С7ЖЛ.=8,35в) проводим луч тп, тангенс угла наклона у
которого к вертикали (с учетом масштабов по осям абсцисс и ор-
динат) равен Rex. Точка п пересечения луча тп с в.а.х. нелиней;
кого сопротивления определяет рабочий режим схемы
у ; / = 0,22 а.
§ 35. Статическое н дифференциальное сопротивления. Свойства
нелинейного сопротивления могут быть охарактеризованы либо
его в. а. х., либо зависимостями его статического и дифференциаль-
ного сопротивлений от тока (или напряжения).
Статическое, сопротивление Rcm равно отношению напряжения
на НС к протекающему по нему току
7^ = ^-. (2.5)
Статическое сопротивление численно равно тангенсу угла о, на рис.
49, а (между осью ординат и прямой, идущей в точку Ь). :
При переходе от одной точки в.а.х. к соседней статическое соп-
ротивление изменяется. Оно характеризует поведение НС в режи-
ме неизменного тока. +
Под дифференциальным сопротивленцем R() принято понимать
отношение малого (теоретически бесконечно малого) приращения
57 .
напряжения dU на НС к соответствующему приращению тока di
(2.6)
al
Дифференциальное сопротивление (раньше называлось динами-
ческим) численно равно тангенсу угла 0 (рис. 49, а) наклона каса-
тельной к в. а. х. в рабочей точке и характеризует поведение НС при
достаточно малых отклонениях от предшествующего состояния. Дру-
гими словами, приращение напряжения на нелинейном сопротивле-
нии связано с прирсищнием тока, проходящим через него, соотно-
шением dU = Radl.
Если в.а.х. НС имеет падающий участок, т. е. такой участок,
на котором увеличению напряжения на величину Д1/ соответствует
убыль тока на величину Д/, что имеет место, например, для элект-
рической дуги (см. ее в.а.х. на рнс. 34, д'), то дифференциальное соп-
ротивление на этом участке оказывается отрицательным.
Из двух сопротивлений (Rem и Rd) наибольшее применение на-
ходит Rd. Оно используется, например, при замене НС эквивалент-
ным линейным сопротивлением и э.д.с., а также при исследовании
вопроса об устойчивости режимов работы нелинейных цепей (см.
вторую часть курса).
Пример 18. Построить кривые зависимости Rcm и Rd в функции
от тока / для нелинейного сопротивления, в.а.х. которого изобра-
жена на рис. 49, а.
Кривые построены на рис. 49, б. г
§ 36. Замена нелинейного сопротивления эквивалентным линей-
ным сопротивлением и э. д. с. Если заранее известно, что НС будет
работать лишь на определенном участке своей в. а. х. и этот участок
может быть с известной степенью приближения заменен прямой ли-
нией, то в таких случаях НС в расчетном отношении может быть
заменено эквивалентным линейным сопротивлением и источником
э. д. с.
58 ч
Пусть рабочая точка будет перемещаться лишь по участку ab
рис. 49, а (см. также рис. 50).
Для этого участка
и = Ua +1 tg₽ = Ue +1 Rd. (2.7)
Уравнению (2.7) удовлетворяет участок цепи рис. 51. На нем
Е — Uo и линейное сопротивление R = Rd.
Привлекательная сторона замены НС на линейное сопротивление
и э.д.с. заключаёт/я в том, что после такой замены вся схема ста-
новится линейной и ее работа может быть исследована методами,
разработанными для линейных цепей. Конечно, при этом прихо-
дится особенно внимательно следйть за тем, чтобы рабочая точка не
выходила за пределы линейного участка в.а.х.
Пример 19. Выразить аналитически участок в.а.х. рис. 49, а
в интервале между точками я и с.
- Из рис. 49, я находим t/0 — — 45 в и Rd = tg р = 220 ом. Сле-
довательно, U яЬ — 45 + 220 /.
*
’ * * J
Нелинейные сопротивления могут придать й В' ряде случаев при-
дают электрическим цепям свойства, принципиально недостижимые
в линейных цепях. К числу таких свойств относятся: стабилизация
тока, стабилизация напряжения, усиление постоянного тока, ло-
гарифмическое и степенное преобразование функций и т. п. Эти свой-
ства будут рассмотрены ниже.
. Рис. 50
Рис. 51
Рис. 52
§ 37. Применение нелинейных сопротивлений для получения произведения
-" хДЧР1 Функций. Пусть есть два постоянных'напряжения и U2. Каждое из них
выражает какую-то физическую величину. Требуется получить напряжение,
. пропорциональное произведению двух физических величин, выражаемых на-
пряжениями и U2. Простейшее преобразующее устройство рис. 52 основано,
на Применении нелинейных сопротивлений с квадратичной в. а. х. вида I =
= kU* и магнитного усилителя. Квадратичной в. а. х. обладают, например,
меднозакисные полупроводниковые выпрямители. Магнитный усилитель
(МУ; теорию его См. во второй части курса) имеет две одинаковых управляю-
щих обмотки Wyi и (на рисунке ие показаны). Сопротивления их иесьма
59
малы по сравнению с сопротивлениями НО и НС2. Поэтому можно с большой
степенью приближения считать, что напряжение на входе первойцепи, рав-
ное Ui + Us, приложено к НС1, а напряжение на входе второй цепи U2
приложено к НС2. Характеристики НС1 и НС2 одинаковы. Напряже-
ние на выходе МУ пропорционально результирующей м. Д. с. управлений
(м. д. с. — магнитодвижущая сила). Последняя равна разности м. д. с. пер-
вой и второй обмоток управления:
м. Д. с.реа = /, о)у1 — /2 wyt == (4 — 4) tt>y.
Но »
4 =r k (Ut + Utf = k (U2 -f- 2{/x Ut + U%)
И
4 = k (Ut — t/a)2=A (U2 — 2(4 Ut + C/|)
или - . •
M. Д. Z.pea = 4toy U1Ui.
Следовательно, напряжение на выходе магнитного усилителя действительно
пропорционально произведению Ух и t/2.
Рис. 53
§ 38. Логарифмические преобразователи на нелинейных сопротив-
лениях. Если нелинейное сопротивление с в.а.х. по .типу в.ал.
рис. 34, г, например селеновый выпрямитель, зашуйтирОВать линей-
ным сопротивлением R (рис. 53) и от внешнего источника подвести
к схеме ток /, то ответвляющийся в сопротивление 7? ток I# будет
нелинейно зависеть от тока /. При малых токах статическое сопро-
тивление НС много больше сопротивления 7?, поэтому через НС
ток почти не пойдет.
При больших токах статическое сопротивление НС становится
малым, много меньше сопротивления 7?, и большая часть тока I
идет по НС.
, Зависимость тока IR от тока / показана на рис. 54. Подбором ви-
да в.а.х. НС и величины шунтирующего сопротивления 7? можно
добиться того, что зависимость = f(7) будет близка к логарифми-
ческой, т. е. иметь такой вид:
IR = a\gI.
Таким образом, выходная величина преобразователя (7^) пропор-
циональна логарифму входной величины (/).
. Преобразователи такого рода широко используются в качестве
составных элементов различных счетно-решающих устройств'.
60
§ 39. Стабилизатор тока. Под стабилизатором тока понимают
устройство, которое способно поддерживать в нагрузке неизменный
ток при изменении 'сопротивления нагрузки и при изменении нап-
ряжения на входе всей схемы.
Стабилизация постоянного тока может производиться при по-
мощи различных схем. Наиболее распространенной и в то же вре-
мя простейшей схемой стабилизатора тока является схема рис. 55.
В ней последовательно с нагрузкой включено НС типа барет-
тера Б. На рис. 56 в качестве примера приведена в. а.х. бареттера
типа 0.3Б17-35. Первая цифра дает ток в амперах, который барет-
тер способен поддерживать постоянным, цифры 17-35 дают область
изменения напряжения на бареттере в вольтах на участке барет-
тирования (поддержания постоянства тока).
Пример 20. Бареттер типа 0,ЗБ 17-35 используется для стаби-
лизации тока накала электронной лампы. Номинальный ток начала
0,3 а и напряжение 6 в. Требуется найти, в каких пределах можно
изменять напряжение U на входе схемы, чтобы ток нити накала лам-
пы оставался практически неизменным и равным 0,3 а.
Р е ш е н И е. Находим сопротивление нити накала лампы
= ± = 20(ом).
Проводим через точки аи b (рис. 56), ограничивающие участок барет-
тирования, две прямые под углом a (tg а = 20 ом) к вертикали. Из
рис. 56 находим, что напряжение U можно изменять в интервале от
23 до 41. в.
Пример 21. В схему предыдущей задачи введено последователь-
ное сопротивление /?г Полагая напряжение на входе схемы неиз-
менном и равным 41 в, найти, до какого максимального значения
в схеме будет иметь место стабилизация тока.
Решение. Если = 0 и U — 41 в, то рабочий режим ха-
рактеризуется положением точки b (рис. 56). С увеличением сопро-
тивления. /?г рабочая точка на в. а.х. перемещается по направлению
’ 61
к точке а. В граничном режиме в точке а tga2 = 80 ом.
Следовательно, = 80 — 20 = 60 (ом).
§ 40. Стабилизатор напряжения. Под стабилизатором напряже-
ния понимают устройство, напряжение на выходе которого Uh под-
держивается постоянным или почти постоянным при изменении со-
противления нагрузки RH или величины напряжения на входе
устройства.
Простейший стабилизатор напряжения осуществлен по схеме
рис. 57. В качестве нелинейного сопротивления используется ста-
биловольт; Re — балластное сопротивление. На рис. 58 изображе-
на в.а.х. стабиловольта 150С5-30.
Анализ работы стабилизатора
включает в себя определение
пределов допустимых изменений
Ul при RH = const, а также ис-
Рис. 57
следование работы стабилизатора при одновременном изменении
и RH-
Для оценки качества работы &ТШЬшзатора иногда пользуются
понятием коэффициента стабилизации. Под йгйлюнййют отноше-
ние относительного приращения напряжения на входе стабилизатора
IWi \
I —i к относительному приращению напряжения на выходе стаби-
\ Ui )
лизатора I —- I. Рассмотрим два численных примера.
\ н I
Пример 22. В схеме рис. 57 RH = 5 ком, R6 = 2 ком. Характе-
ристика стабиловольта соответствует рис. 58. Определить границы
допустимого изменения Ult чтобы стабилизатор давал на выходе
стабилизированное напряжение 150 в.
Решение. Воспользуемся методом хх и кз. Разомкнем ветвь
стабиловольта и найдем напряжение хх:
Uabxx = Ur — = 0,713(7,
abxx 1 1
Определим входное сопротивление-линейной части схемы (рис. 57)
по отношению к зажимам ab
R =^е = i427 ож.
Rh+R6
62.
На рис. 58 проводам две прямые (сплошные линии) через точки
т н п в.а.х. стабиловольта так, чтобы тангенс угла, образованного
ими с вертикалью, численно равнялся Rex — 1427 ом.
Отрезки, отсекаемые этими прямыми на оси абсцисс, равны
Uxx. Из рисунка находим 0,713t/ljHUM — 157 в. Следовательно,
UiMUH ™ 220 в. Аналогично, 0,713£/1лш/а, = 192 в или ^<,^=269 в.
Следовательно, напряжение может изменяться от 220 до 269 в.
Пример 23. Для схемы рнс. 57 при R6=2 ком, характеристике
стабиловольта по рис. 58 и {/х = 250 в определить, в каких преде-
лах можно изменять сопротивление нагрузки RH, чтобы стабили- х
затор мог выполнять свои функции по стабилизации выходного
напряжения.
Решение. Воспользуемся методом хх и кз. _
Определим
Uxx = Ur—^-=250----------.
х . + Нб + 2000
Находим
Rt == fg а = —= -?002g« ...
* ; Нн + Иб 2000 RH •!
Задача сводится к определению значений RH, при которых прямые,
характеризующие собой Rex, будут проходить через точки т и п
характеристики стабиловольта. В данном примере не известны ни
тангенсы углов, а, ци исходные точки на оси абсцисс, из которых
должны быть проведены прямые, поэтому решаем задачу путем
пробных построений. С этой целью задаемся значениями под-
считываем соответствующие им Uxx и Rex.
ком 3 4 5 6 7 8
Uxx> в 150 167 178 187 194 200
Rex» 1200 1330 1425 1500 1555 1600
По данным таблицы проводим несколько лучей.
Графически находим, что прямые (см. пунктирные прямые на
рис. 58) пройдут через точки тип, соответственно при RM —
= 3,3 ком и RHMaKC = 8 ком.
§ 41. Усилитель постоянного напряжения. Под усилителем по-
стоянного напряжения понимают устройство, величина приращения
напряжения на выходе которого больше величины приращения нап-
ряжения на входе. Усилители постоянного напряжения часто вы-
полняют на управляемых нелинейных сопротивлениях — трехэлект-
63
родных лампах или полупроводниковых триодах. На рде. 59 изоб-
ражены анодные (по существу, вольтамперные) характеристики трех-
электродной лймпы типа 6С2С. Под ними понимают зависимость
анодного тока лампы 1а от анодного напряжения Ua при сеточном
напряжении Uc в качестве параметра.
Схема усилителя постоянного напряжения изображена на рис.
60. Входное (усиливаемое) напряжение подается на сетку лампы.
На выходе усилителя (зажимы
а и Ь) включена нагрузка RH.
Сетка триода расположена
ближе к катоду, чем анод. Влия-
ние поля сетки на поток элект-
ронов с катода на анод значи-
тельно больше влияния поля
анода. Поэтому сравнительно
незначительные изменения нап-
ряжения на сетке приводят к
резкому изменению анодного то-
ка и напряжения на выходе уси-
лителя. Для анодной цепи Е =
=Ua -J- IaRH. Зависимость нап-
ряжения выхода (JaRH=E— Ua)
от напряжения входа (6Д) строится при помощи семейства кривых
рис. 59.
Пример 24. Построить зависимость Ueblx=f (Uc) для схемы рис. 60,
если RH = 12 ком и Е = 240 в. Триод 6С2С.
Решение. Из точки 1а = 0 Ua=E под углом а к вертикали
(tg а — 12000 ом) проводим прямую. Точки пересечения ее. с анодны-
ми характеристиками дают соответствующие друг другу значения
1а и Uc. Зависимость UeblX = f (Uc) отличается от зависимости
Ia = f{Ve) (рис. 61) только масштабом (UH — IaRH, RH = const).
Глава третья
МАГНИТНЫЕ ЦЕПИ
* § 42. Разделение всех веществ на две группы — ферромагнитные
и неферромагнитные. Из курса физики известно, что все вещества
в отношении их магнитных свойств делятся на три группы: диамаг-
нитные, парамагнитные и ферромагнитные. У диамагнитных веществ
относительная магнитная проницаемость рг немного меныпе еди-
ницы, например у висмута она равна 0,99983. У парамагнитных ве-
ществ относительная магнитная проницаемость немного больше
единицы, например платины равна 1,00036. У ферромагнитных
веществ (железо, никель, кобальт и их сплавы, ферриты и др.)
много больше единицы (например, доходит до 104, а у некоторых ма-
териалов даже до 10е).
Электрики делят все вещества не на диа-, пара- и ферромагнит-
ные, как это принято в физике, а на ферромагнитные и неферромаг-
нитные. У ферромагнитных веществ много больше единицы, у
всех неферромагнитных практически равно единице.
§ 43. Основные величины, характеризующие магнитное поле.
Напомним, что основными величинами, характеризующими магнит-
ное поле, являются: магнитная индукция В и намагниченность J*.
Магнитная индукция — это векторная величина, определяемая
по силовому воздействию магнитного поля на ток. Намагничен-
ность есть магнитный момент единицы объема вещества.
Кроме этих двух величин, магнитное поле характеризуется еще
одной величиной — напряженностью магнитного поля Н. Три вели-
чины В, J, Н связаны друг с другом следующей зависимостью:
В = РО(Я + Д ' (3.1)
В международной системе единиц СИ индукция измеряется в тес-
лахДгпл):
1 тл = 1 в-сек/м2 = 1 вб/л2.
Индукция также измеряется в кратных ей единицах аб/сж® шш
!"Стрелка над буквой свидетельствует о том, что речь вдето векторе
в пространстве. ,
3 Л. А. Бессонов fjg
в единицах системы СГСМ гауссах (1 гс = 10~8 вб/смг). Намагничен-
ность J и напряженность поля Н в системе СИ измеряют в а/м, а
в системе СГСМ — в эрстедах (э).
На практике часто измеряют индукцию В в единицах системы
СГСМ (гс), а напряженность поля Н в а! см (см. также, сноску на
стр. 75).
Намагниченность J есть вектор, направление которого совпа-
дает с направлением Н в данной точке,
7 = хЯ. (3.2)
Коэффициент х для ферромагнитных веществ сам является функцией
Н. Подставим (3.2) в (3.1) и, обозначив 1 +* = р,г, получим
В = Hog,//. (3.3)
где р,0 — постоянная, характеризующая магнитные свойства ваку-
ума. В системе СИ р0 = 4л • 10-7 гн!м= 1,256 • 10-8 гн/м.
В системе СГСМ р0= 1.
Безразмерный коэффициент р,г называют относительной магнит-
ной проницаемостью. Для ферромагнитных веществ р,, есть функ-
ция Н.
Магнитный поток Ф есть поток вектора магнитной индукции
через площадь S
Ф = J BdS, (3.4)
з
где dS —элемент поверхности S. В системе СИ поток измеряется
в в . сек или веберах. В-системе СГСМ поток измеряют вхгаксвел-
лах (мкс) или кратных единицах киломаксвеллах (клкс)
1 мкс — 10~8 вб\ 1 кмкс = 108 мкс.
Расчеты магнитных цепей проводят обычно путем использова-
ния двух величин — магнитной индукции В и напряженности по-
ля Н.
Что касается третьей величины — намагниченности J, то ее в
расчетах, как правило, не используют (но при необходимости зна-
чение J, отвечающее соответствующим друг другу значениям В нН;
всегда может быть найдено из формулы (3.1).
§ 44. Элементы теории ферромагнетизма. Как известно из курса
физики, ферромагнитные тела состоят из областей самопроизволь-
ного (спонтанного) намагничивания. Ширина этих областей очень
мала и составляет, примерно, 1СГ2 мм. Ширина границ между со-
седними областями около КГ-8 мм. Каждая область определенным
образом намагничена, и магнитное состояние ее характеризуется
вектором намагниченности. Направление вектора намагниченности
зависит от внутренних упругих напряжений и от кристаллической
структуры ферромагнитного тела.
66
. Векторы намагниченности отдельных областей направлены в раз-
личные стороны, поэтому во внешнем по отношению к ферромагнит-
ной среде пространстве намагниченность ферромагнитного тела,
если тело не помещено во внешнее магнитное поле, нн в чем не про-
является. Если же ферромагнитное тело поместить во внешнее маг-
нитное поле, то под действием этого поля векторы намагниченности
отдельных областей будут поворачиваться по внешнему полю. В
результате этого, индукция результирующего магнитного поля ока-
зывается во много раз (сотни и даже сотни тысяч раз) больше, чем
магнитная индукция воздействующего на ферромагнетик внешне-
го поля.
Атом любого элемента схематически можно представить в виде положи-
тельно заряженного ядра и движущихся вокруг него электронов. Электроны
вращаются не только вокруг ядра, но и вокруг собственной оси.
Решающую роль в создании магнитных свойств ферромагнитных мате-
риалов играет магнитный момент электрона при вращении его вокруг своей
оси — так называемый спин электрона.
В атомах ферромагнитных материалов имеются не полностью заполнен-
ные электронные оболочки с нескомпенсированными спинами. Так, например,
в атоме железа на третьей, считая от ядра, электронной оболочке (вместе с
двумя подоболочками) вместо 18 электронов находятся всего 14. Причем су-
щественно, что на одной из подоболочек этой электронной оболочки 5 элект-
ронов имеют одно направление спина, а 1 электрон имеет противоположное
направление спина.
Благодаря тому, что в атоме железа имеются 4 нескомпенсированных
спина, атом в целом обладает магнитным моментом.
Как уже говорилось выше, в ферромагнитных материалах имеются об-
ласти самопроизвольного намагничивания. Каждая из этих областей образо-
вана совокупностью атомов, магнитные моменты которых параллельны (не
антипараллельны). Рассмотрим причины, вызывающие появление таких об-
ластей.
В силу наличия незаполненных электронных оболочек с нескомпенси-
рованными спинами часть электронов одного атома располагается настоль-
ко близко к ядру другого атома, что между соседними атомами как бы имеет
место обмен электронами.
Благодаря этому между соседними атомами действуют не только магнит-
ные силы, вызванные взаимодействием спинов, но имеются силы, обусловлен-
ные наличием обменных электронов. Этн силы называют обменными силами.
С обменными силами связана энергия, которую называют обменной энергией
или обменным интегралом. Обменный интеграл может быть положительным
и отрицательным. Ферромагнитные свойства проявляются в том случае, ког-
да обменный интеграл положителен и имеет некоторое определенное зна-
чение.
Обменные силы стремятся установить соседние атомы таким образом,
чтобы магнитные моменты их были параллельны. В свою очередь магнитные
силы взаимодействия между соседними снинами стремятся установить сосед-
ние атомы так, чтобы магнитные моменты их были антипараллельны.
Обменные силы убывают с расстоянием быстрее, чем магнитные силы
взаимодействия между соседними спинами. Поэтому, начиная с некоторого рас-
стояния, магнитные силы взаимодействия между соседними спинамй~нЗЧи»~—
нают превышать обменные силы. Этим и объясняется, что спонгинтго намаг-
ничениые области имеют малые размеры. • •
Кроме того, в энергетическом отношении наиболее выгодным оказывает-
ся такое состояние, при котором ферромагнитное тело оказывается подразде-
ленным на небольшие области, намагниченные антипараллельно. Такое сос-_
3*
67
тойние ^энергетическом отношении наиболее выгодно потому, что вся систе-
ма в целом обладает минимумом энергии.
При повышении температуры железа до 760°С (до точки Кюри) скорости
движения электронов становятся настолько большими, что происходит раз-
рушение спонтанных областей.
§ 45. Основные характеристики ферромагнитных материалов.
Свойства ферромагнитных материалов принято характеризовать
зависимостью магнитной индукции В от напряженности магнитно-
го поля Н. Различают два основных типа этих зависимостей: кривые
намагничивания и гистерезисные петли.
яСпинка”превельнпо
цикла или кривая >
размагничивания
Предельный
цикл
Основная
кривая
намагничивания
Симметричные
гистерезисные
петли
Рис.
Под кривыми намагничивания будем понимать однозначную за-
висимость между В и Н. Кривые намагничивания подразделяют на
начальную, основную и безгистерезисную. Что понимается под ни-
ми, будет пояснено несколько позже.
Из курса физики известно, что ферромагнитным материалам при-
суще явление гистерезиса. Под ним понимают явление отставания
в изменении магнитной индукции от изменения напряженности маг-
нитного поля Н. Гистерезис обусловлен, грубо говоря, внутреннем
треннем областей самопроизвольного намагничивания. Он находит
свое выражение в том, что при периодическом изменении напряжен-
ности поля зависимость между В и Н приобретает петлевой харак-
тер.
Различают несколько типов гистерезисных петель — симметрич-
ную гистерезисную петлю, предельную петлю (цикл) и несимметрич-
ную гистерезисную петлю или частный цикл.
На рис. 62 изображено семейство симметричных гистерезисных
петель. Для каждой симметричной петли максимальное положитель-
ное значение “В равно максимальному отрицательному значению В
й, соответственно, равно |—.
Геометрическое место'вершин симметричных гистерезисных пе-
68 '
коэрцитивной силой и
Несимметричные
гистерезисные кВ
петли или
частные циклы
Рис. 63
Основная
Начальная
безгистерезисная
Н
тель принято называть основной кривой намагничивания. При очень
больших И вблизи ± Нмпкс восходящая и нисходящая части гис-
терезисной петли практически сливаются.
Предельной гистерезисной петлей или предельным циклом назы-
вают симметричную гистерезисную петлю, снятую при очень боль-
ших Нмакс. Значения индукции при Н = 0 называют остаточной
индукцией и обозначают Вг. Значение напряженности поля при В = О
называется задерживающей или
чается Нс. Участок предельно-
го цикла ВГНС (рис. 62) принято
называть кривой размагничива-
ния или «спинкой» гистерезис-
ной петли.
Этот участок используется
при расчетах магнитных цепей
с постоянными магнитами.
Если изменять Н периодиче-
ски, но так, что значение
не будет равно значению |— Нт1(^
то зависимость между В и Н
будет иметь петлевой характер, но центр петли не будет совпадать с
началом координат (рис. 63). Такие гистерезисные петли приня-
то называть частными петлями гистерезиса или частными цик-
лами.
Если предварительно размагниченный ферромагнитный мате-
риал (В = О, Н = О) намагничивать, монотонно увеличивая Н, то
зависимость между В и Н, имеющая место при этом процессе, назы-
вается начальной кривой Намагничивания.
Начальная и основная кривые намагничивания настолько близ-
ко расположены друг к другу, что для многих практических целей
» их можно считать совпадающими (рис. 63).
Безгистерезисной кривой намагничивания называют зависимость
между В и Н, которая имеет место в том случае, когда при намагни-
чивании ферромагнитного материала его периодически постукивают
или воздействуют на него затухающим по амплитуде синусоидаль-
ным полем. При этом гистерезис, т. е. явление отставания изменений
В от изменений Н, имеющий место вследствие внутреннего тре-
ния областей самопроизвольной намагниченности, как бы сни-
мается.
Безгистерезисная кривая намагничивания весьма резко отли-
чается от основной кривой (рис. 63).
В различных справочниках, а также в Государственном стан-
дарте ГОСТ 802-58 в качестве однозначной зависимости между В я Н
дается Основная кривая намагничивания.
§ 46. Магнитномягкие и магнитиотвердые материалы. Все фер-
ромагнитные материалы могут быть подразделены на две большие
группы: магнитномягкие и магнитиотвердые.
69
Магнитномягкие материалы обладают круто поднимающейся
основной кривой намагничивания и относительно малыми площадя-
ми гистерезисных петель.
Они применяются во всех устройствах, которые работают или
могут работать при периодически изменяющемся магнитном пото-
ке (трансформаторах, электрических двигателях и генераторах, ин-
дуктивных катушках и т. п.).
В группу магнитномягких материалов входят электротехничес-
кие стали, железо-никелевые сплавы типа пермаллоя и др.
Магнитнотвердые материалы обладают полого поднимающейся
основной кривой намагничивания и большой площадью гистерезис-
ной петли.
В группу магнитнотвердых материалов входят углеродистые
стали, вольфрамовые сплавы, сплавы магнико, платино-кобаль-
товые сплавы и др. Из магнитнотвердых материалов выполняют
постоянные магниты.
На рис. 64 качественно сопоставлены гистерезисные петли для
магнитномягкого материала типа пермаллоя (кривая 1) и для маг-
нитнотвердого материала (кривая 2).
§ 47. Материалы с прямоугольной петлей гистерезиса. Некоторые
магнитномягкие материалы, например перминвар, сплавы типа
Н60П, Н65П и другие обладают петлей гистерезиса по форме близ-
кой к прямоугольной (рис. 65). Такие материалы получили распро-
странение в счетно-решающих устройствах и в устройствах авто-
матики.
§ 48. Магнитодиэлектрики и ферриты. В радиотехнике, где при-
меняются колебания высокой частоты, сердечники катушек индук-
тивности изготовляют из магнитодиэлектриков или из ферритов.
Магнитодиэлектрики — материалы, полученные путем смеше-
ния мелкоизмельченного порошка магнетита, железа или пермал-
лоя с диэлектриком. Эта смесь формуется и запекается. Каждую
ферромагнитную крупинку обволакивает пленка из диэлектрика.
70
Благодаря наличию таких пленок сердечники из магнитодиэлектри-
ков не насыщаются; их находится в интервале от нескольких еди-
ниц до нескольких десятков.
Ферриты изготовляют из окислов меди или цинка и окислов же-
леза или никеля. Смесь формуется и обжигается. В результате по-
лучается твердый раствор, например Zn-Fe2O8. По своим электри-
ческим свойствам ферриты представляют собой полупроводники.
Объемное сопротивление их порядка 1 — 107 ом-м, тогда как для
железа р ~ 1(Гв ом-м.
Магнитные свойства ферритов могут быть получены самые раз-
личные. В отличие от магнитодиэлектриков ферритй могут насы-
щаться. Коэрцитивная сила ферритов составляет примерно 10 а/м.
Маркируют их двумя буквами и цифрой. Например, феррит типа
НЦ-1000 есть никель-цинковый феррит, у которого на начальном
участке кривой намагничивания равно 1000.
§ 49. Закон полного тока. Магнитное поле создается электричес-
кими токами. Количественная связь между линейным интегралом от
вектора напряженности магнитного поля Н вдоль любого произ-
вольного контура и алгебраической суммой токов 2/, охваченных
этим контуром, определяется законом полного тока
Закон полного тока есть опытный закон. Он может быть экспери-
ментально проверен путем измерения <$)Hdl при помощи специаль-
ного устройства, известного из курса физики, называемого магнит-
ным поясом.
§ 50. Магнитодвижущая сила. Магнитодвижущей силой (м. д. с.)
катушки (или обмотки) с током называют произведение числа витков
катушки w на протекающий по ней ток /.
М.д.с. Iw вызывает магнитный поток в магнитной цепи подобно
тому, как э.д.с. вызывает электрический ток в электрической цепи.
Как и э.д.с., м.д.с. есть величина направленная. Положительное нап-
равление ее обозначают на схеме стрелкой.
Положительное направление м.д.с. совпадает с движением ост-
рия правоходового винта, если его вращать по направлению тока
в обмотке.
Для определения положительного направления м.д.с. часто поль-
зуются следующим мнемоническим правилом: если мысленно охва-
тить правой рукой сердечник, расположив ее пальцы по току в обмот-
ке, а затем отогнуть большой палец, то последний укажет направле-
ние м.д.с.
На рис. 66 дано несколько эскизов с различным направлением
намотки катушек на сердечник и различным направлением м.д.с.
§51. Магнитная цепь. Магнитной цепью называется совокупность
м. д. с., ферромагнитных тел или каких-либо иных тел или сред, по
которым замыкается магнитный поток.
71
§ 52. Разновидности магнитных цепей. Магнитные цепи могут
быть подразделены на неразветвлеиные и разветвленные. Примером
неразветвленной цепи может служить цепь рис. 67. Разветвленные
цепи делятся на симметричные и несимметричные. Магнитная цепь
рис. 68 будет симметричной: в ней поток <f\ будет равняться пото-
ку Ф2, если обе части ее , расположенные слева и справа от верти-
кальной пунктирной линии, будут одинаковы в геометрическом от-
ношении, изготовлены из одного и того же материала и если =
- Рис. 67
Рис. 66
Достаточно сделать =/= /2а>2 или изменить направление то-
ка в одной из обмоток, или сделать воздушный зазор в одном из край-
них стержней магнитопровода, чтобы магнитная цепь рис. 68 стала
несимметричной. В несимметричной цепи рис. 68 поток Фх Ф2.
Рис. 68
Рис. 69
§ 53. С какой целью в магнитную цепь электрических машин,
электрических аппаратов и других устройств вводя/ ферромагнит-
ные материалы? Электрические машины, трансформаторы и другие
аппараты конструируют так, чтобы поток в них был по возможности
наибольшим. Убедимся в том, что если в магнитную цепь входит
ферромагнитный материал, то поток в магнитной цепи при одной и
той же м. д. с. и прочих равных условиях оказывается во много раз
больше, чем в случае отсутствия ферромагнитного материала в той
же цепи. С этой целью рассмотрим численный пример.
* Левую ветвь назовем первой и все относящиеся к ней величины снаб-
дим индексом 1 (ток 1Х, число витков обмотки ид).
Правую ветвь назовем второй и все относящиеся к ней величины снаб-
дим индексом 2 (/2, w$.
72
Пример 25. Возьмем два одинаковых в геометрическом отноше-
нии кольцевых сердечника (тора) рис. 69. Пусть радиус средней
магнитной линии их — 10 см и поперечное сечение 5 = 2 см9.
Один сердечник неферромагнитный, например деревянный, а дру-
гой —>• ферромагнитный (кривая намагничивания рис. 70). Намо-
таем на каждый кольцевой сердечник обмотку с числом витков
w = 200 и пропустим по ним одинаковый ток I, скажем в один ам-
пер. Найдем потоки в теле торов.
По закону полного тока напряженность поля И — оди-
накова в обоих торах и не зависит от материала сердечника
Н = -LJ00- = 318 (а]м).
2л . 0,1 '
Н(а/н)
Рис. 70
Поток в неферромагннтном сердечнике
Ф^ = BS = йвИгЯ5 = 1,256-1(Г«.318-2-10“* = 8-ИГ8' (вб).
По кривой намагничивания (рис. 70) находим, что для Н — 318 а/м
В 1,02 тл. Поток в ферромагнитном торе
Ффм = BS = 1,02 • 10““ • 2 = 20,4 • 10-5 (вб).
20 4 • 103
Таким образом, поток в ферромагнитном торе в ——---------=
” . в
= 2550 раз оказался больше, чем поток в неферромагнитном торе.
Кроме усиления магнитного потока, введение ферромагнитных
материалов в магнитную цепь преследует также и другую
цель, а именно: сосредоточения магнитного поля в определенной
области пространства и придания ему определенной конфигура-
ции.
§ 54. Падение магнитного напряжения. Падением магнитного на-
пряжения между точками а и b магнитной цепи называют линей-
73
ный интеграл от напряженности магнитного поля между этими
точками
ь
UMab=^HdL
а
(3.6а)
Если на этом участке Н
—>
с элементом пути dl, то
из-под знака интеграла.
постоянно и совпадает по направлению
Н dl — Hdl cos 0° и Н можно вынести
Тогда
ъ
ab ~ Н J* =
а
(3.66)
где 1аЬ — длина пути между точками а и Ь. Магнитное напряже-
ние измеряется в амперах.
В том случае, когда участок магнитной цени между точками а
и b может быть подразделен на «-отдельных частей так, что для каж-
дой части Н = Hk постоянно, то
п
UMab = ^Hhlk. (3.7)
k=l
§ 55. Веберамперные характеристики. Под веберамперной (или
максвелламперпой) характеристикой будем понимать, зависимость
потока Ф по какому-либо участку магнитной цепи от паденйй маг-
нитного напряжения на этом участке
6
Рис. 71
Они играют такую же важную роль при расчетах и исследова-
нии магнитных цепей, какую играют вольтамперные характеристики
нелинейных сопротивлений при расчетах
и исследовании электрических цепей с
нелинейными сопротивлениями (глава вто-
рая).
Веберамперные характеристики при
расчетах магнитных цепей в готовом виде
не задаются. Перед расчетом их надо по-
строить при помощи кривых намагничива-
ния ферромагнитных материалов, входящих в магнитную цепь.
§ 56. Построение веберамперных характеристик. На рис. 71
изображен участок магнитной цепи, по которому идет поток Ф.
Пусть участки 1г и /2 сечением S выполнены из ферромагнитного
материала, кривая В = f (Н) для которого задана, например кри-
вой рис. 70. На участке длиной б магнитный поток идет по воздуху.
74
Требуется построить в.а.х. * * участка цепи между точками а и Ь.
При построении допустим: 1) что магнитный поток вдоль всего
участка от а до b постоянен (отсутствует рассеяние) и 2) что сечение
магнитного потока в воздушном зазоре такое же, что и на участках
/j и /2 (отсутствует боковой распор силовых линий в зазоре).
В действительности оба эти допущения справедливы лишь в из-
вестной мере.
Построение в.а.х. производим следующим образом. Задаемся
рядом значений индукции В, например для электротехнических
сталей значениями 0; 0,5; 0,8; 1,0; 1,1; 1,2; 1,3; 1,4; 1,5 тл идля
каждого значения В находим напряженности поля на всех участках
(/1( /,ив).
На участках из ферромагнитного материала (участки и /2,
рис. 71) напряженности = /72 (так как^ Вг =Вг) находим
по кривой намагничивания.
Для неферромагнитных участков (участок б)
Я , = ----- = о,8 . 10«Втл = 80S **.
м У-Огн/м 1,256 .10-е гм/л тя гс
Таким образом, для определения Н (в а/м) в воздухе надо по-
множить индукцию, выраженную в тл, на коэффициент 0,8.10е.
Для каждого значения В определим поток Ф = BS и найдем
магнитное напряжение
По результатам подсчетов строим кривую Ф = f (UM).
Пример 26. Построить в.а.х. для участка цепи рис. 71 для трех
значений б: 0, 0,005 и 0,05 см, ^=10 см, /2 = 5 см-, S = 5 см2.
Решение. Определим падение магнитного напряжения меж-
ду точками ab участка магнитной цепи рис. 71 при б = 0,005 см
и В = 0,5 тл.
Из кривой рис. 70 находим, что индукции В = 0,5 тл соответ-
ствует напряженность поля Н = 40 а/м.
Таким образом, при В — 0,5 тл, Нх =. Я2 = 40 а/м.
По формуле Uт аЬ = //1/1 /72/2 + Н& 6 подсчитываем
Umab = 40-0,1 + 40.0,05 + 0,8.0,5- 10е. 5 . 10~5 = 26 а.
Значения УмаЬ при иных зазорах и индукциях находим анало-
гичным образом.
Подсчеты сводим в таблицу.
* В третьей главе (в отличие от.второй главы) под в.а.х. понимается
веберамперная характеристика.
• ** Обратим внимание на то, что в большинстве книг, изданных, пример-
но, до 1960 г. и посвященных различным магнитным устройствам, магнитную
индукцию измеряют в гауссах (не в веберах иа м2), а напряженность поля из-
меряют в а)см. Такое сочетание единиц различных систем можно' встретить
и в ГОСТ 802—58 на магнитные материалы.
75
В, ftiA' 0,5 ' 0,8 1,0 1,1 1,2 1,8 м
Ф, вб 25-10-5 40-10-5 50-10-5 55. Ю-5 60.10*"5 65-Ю-5 70.ГО-4 ..
U\=Hi, а/м 40 • 130 300 440 700 1080 1800
Hl , д/ж 4-10» 6,4.10» 8-10» 8,8.10» 9,6-10» 10,4-10» 11,2-10»
Uj) аЬ ри 8=0, а 6 19,5 45 64 105 162 270
«м аЬ ри 8= =0,005сж, а 26 51,5 85 108 153 214 326
Ujh ab ири 8 = =0,05сж, а 206 339,5 445 504 585 682' 830
По данным таблицы на рис. 72 построены в.а.х. при трех зна-
чениях б. Из построений видно, что если участок, для которого стро-
100 2003001)00500 600
Рис. 72
потоков в любом узле магнитной
он следующим образом:
ится в.а.х., не имеет «воздушно-
го» включения, то в.а.х. круто
поднимается вверх. При нали-
чии воздушнб^о включения
в.а.х. спрямляется й идет бо-
лее полого.
§ 57. Законы Кирхгофа для
магнитных цепей. При расчетах
магнитных цепей, как и при ра-
счетах электрических цепей,
используются первый и второй
законы Кирхгофа.
Первый закон Кирхгофа: ал-
гебраическая сумма магнитных
цепи равна нулю. Записывается
£Ф = О. (3.8)
Второй закон Кирхгофа: алгебраическая сумма падений магнит-
ного напряжения вдоль любого замкнутого контура равна ал-
гебраической сумме м.д.с. вдоль того же контура
(3.9)
76
Второй закон Кирхгофа для магнитных цепей по сути дела есть
иная форма записи закона полного тока.
Перед тем как для магнитной цепи записать уравнения по зако-
нам Кирхгофа, следует произвольно выбрать положительные нап-
равления потоков в ветвях магнитной цепи и положительные нап-
равления обхода контуров.
Если направление магнитного потока на некотором участке сов-
падает с направлением обхода, то падение магнитного напряжения
этого участка входит в сумму У UM со знаком плюс; если будет
встречно ему, то со знаком минус.
Аналогично, если м.д.с. совпадает с направлением обхода, она
входит в У Iw со знаком плюс, в противном случае — со знаком
минус.
В качестве примера составим уравнения по законам Кирхгофа
для разветвленной магнитной цепи, изображенной на рис. 75 (см.
стр. 81). Магнитная цепь имеет три ветви и две м.д. с.
Левую ветвь назовем первой и все относящиеся к ней величины
снабдим индексом 1 (поток Фп напряженность поля Hlt длина пу-
ти в стали /х, длина пути в воздушном зазоре м.д.с.
Среднюю ветвь назовем второй и все относящиеся к ней величи-
ны снабдим индексом 2 (поток Ф2, напряженность поля Н2, длина
пути в стали 1г, длина воздушного зазора 62, м.д.с. I2wt).
Все величины, относящиеся к правой ветви, снабдим индексом
3 (поток Ф8, длина пути на вертикальном участке Z8, суммарная дли-
на пути на двух горизонтальных участках
Произвольно выбираем направление потоков в ветвях.
Положим, что все потоки (Фх, Ф2, Ф3) направлены вверх (к уз-
лу а). Число уравнений, которое следует составить по законам Кирх-
гофа, равно числу ветвей цепи (в рассматриваемом случае надо сос-
тавить три уравнения — в цепи три ветви).
По первому закону Кирхгофа необходимо составить столько урав-
нений, сколько в цепи узлов без единицы (см. § 7).
В цепи рис. 75 два узла, следовательно, по первому закону Кирх-
гофа надо составить одно уравнение:
Ф1 + Фа + Ф3 = 0* (а)
По второму закону Кирхгофа надо составить число уравнений,
равное числу ветвей за вычетом числа уравнений, составленных по
первому закону Кирхгофа. В рассматриваемом примере по второму
закону Кирхгофа следует составить 3 — 1=2 уравнения.
Первое из этих уравнений составим для контура, образованного
первой и второй вётвями, а второе — для контура, образованного
первой и трётьей ветвями (для периферийного контура).
Перед составлением уравнений по второму закону Кирхгофа
надо выбрать положительное направление обхода контуров. Будем
обходить контуры по часовой стрелке,.
77
Уравнение для контура, образованного первой и второй ветвя-
ми:
Я, - ^2 - - № (О
Здесь Яг1 и Hi2 — напряженности поля соответственно в воз-
душных зазорах и б2.
Слагаемые Я1/1 и вошли в уравнение со знаком плюс, так
как на первом участке поток Фг направлен согласно с обходом
контура.
Слагаемые Н212 и Я82й2 вошли в левую часть уравнения со зна-
ком минус, так как поток Ф2 встречен направлению обхода кон-
тура.
В правую часть уравнения м.д.с. I1w1 вошла со знаком плюс,
так как она направлена согласно с обходом контура. М.д.с. /2а>2
вошла в правую часть уравнения со знаком минус, так как она
направлена встречно обходу контура.
Составим уравнение для периферийного контура, образованного
первой и третьей ветвями:
Я1/1 + /7г]б1-/7'/'-/73/3=/1№1. (в)
На совместном решении трех уравнений (а, б, в) с тремя неиз-
вестными (Фх, Ф2, Ф3) останавливаться не будем, так как в § 61
дается решение рассматриваемой задачи более совершенным мето-
дом, чем метод, основанный на непосредственном использовании за-
конов Кирхгофа, а именно методом двух узлов.
§ 58. Распространение на магнитные цепи всех методов, приме-
няемых для расчета электрических цепей с нелинейными сопротив-
лениями. Во второй главе подробно обсуждались различные прие-
мы расчета электрических цепей с НС. Все эти методы полностью
применимы и к расчету магнитных цепей, так как и магнитные и
электрические цепи подчиняются одним и тем же законам — за-
конам Кирхгофа.
Аналогом тока в электрической цепи является поток в магнит-
ной цепи. Аналогом э.д.с. — м.д.с. Аналогом вольтамперной ха-
рактеристики нелинейного сопротивления — веберамперная харак-
теристика участка магнитной цепи.
§ 59. Определение м. д. с. неразветвленной магнитной цепи по
заданному потоку. Задано: конфигурация и геометрические размеры
магнитной цепи, кривая (или кривые) намагничивания ферромаг-
нитного материала и магнитный поток или индукция в каком-либо
сечении.
Требуется найти м.д.с., ток или число витков намагничивающей
обмотки.
Расчет проводим в следующей последовательности:
1. Разбиваем магнитную цепь на участки постоянного сечения
и определяем длины 1к (в м) и площади поперечного сечения Sk
78
(вл2) участков. Длины участков берем по средней силовой линии.
2. Исходя из постоянства потока вдоль всей цепи, по заданному
потоку и сечениям находим магнитные индукции на каждом
участке
3. По кривой намагничивания определяем напряженности поля
Нь для ферромагнитных участков магнитной цепи.
Напряженность поля в воздушном
зазоре находим по формуле
/7а/я = 0,8-10^. (3.10)
4. Подсчитываем сумму падений маг-
нитного напряжения вдоль всей магнит-
ной цепи 2 и на основании зако-
на полного тока приравниваем эту сум-
му полному току Iw;
^Hklk = Iw.
Основным допущением расчета явля-
ется то, что магнитный поток вдоль всей
магнитной цепи полагается неизменным.
В действительности небольшая часть по-
тока всегда замыкается, минуя основной
путь. Например, для магнитной цепи рис. 67 поток, выйдя из лево-
го сердечника, в основном направляется по пути macbn, но неболь-
шая часть потока идет по воздуху по пути mqn. Поток, который замы-
кается, мииуя основной путь, называют потоком рассеяния.
Пример 27. Геометрические размеры магнитной цепи даны на рис.
73 в мм. Кривая намагничивания изображена на рис. 70. Найти,
какой ток должен протекать по обмотке с числом витков w = 500,
чтобы магнитная индукция в воздушном зазоре равнялась 1 тл.
Решение. Магнитную цепь разбиваем на три участка:
/j = + 4 == 30 см; Sx = 4,5 см2; = 13,5 см; S2 = 6 см2.
Воздушный зазор:
6 = 0,01 см; Ss = = 4,5 см2.
Индукция
Bt = Z?s == 1 тл.
Индукцию на участке /2 найдем, поделив поток Ф = Z?8S8 на
сечение S2 второго участка
д _ ф _ В8 1 • 4>5 п 7С
— sa ~ Ss ~ 6 ~ тл’
79
Напряженности поля на участках и Z, находим по кривой
намагничжания (рис. 70) по известным значениям В1нВ^
— 300 а/м, Н2— 115 а/м.
Напряженность поля в воздушном зазоре
Hi = 0,8.10".Вг = 0,8.10е. 1 = 8.10® (а/м).
Подсчитываем падение магнитного напряжения вдоль всей маг-
нитной цепи
= 300.0,34-115.0,135 4- 8.105.10"4= 185,6 (а).
Ток в обмотке
j = Wklk = 18М = 0 71 <
w 500 '
§ 60. Определение потока в неразветвлениой магнитной цепи по
заданной м. д. с. Заданы геометричёские размеры магнитной цепи,
кривая намагничивания и полный ток. Требуется найти поток или
индукцию.
Для решения задачи необходимо построить зависимость потока
в функции от Hklk и на ней найти рабочую точку.
Пример 28. Найти магнитную индукцию в воздушном зазоре
магнитной цепи предыдущей задачи, если Iw = 350 а.
Решение. Задаёмся значениями В,в зазоре равными 0,5; 1,1;
1,2; и 1,3 тл и для каждого из них подсчитываем подобно
тому, как в предыдущей задаче определялась J] Hklk при
56= 1 тл. Подсчеты сводим в таблицу:
Bt, тл 0,5 1,1 1,2 1,3
Bi, тл 0,5 1,1 1,2 1,3
В2, тл 0,375 0,825 0,9 0,975 •
а/м .50 . .460 .. 700 • J020
Н2, а/м 25 150 200 300
во
9
а/м 4-10® 8,8-10» 9,6.10» 10,440»
XHklk, а 58,3 246,3 333 450,5 .
Ф, вб 22,5.1С-5 49.5.10-5 54-10-5 58,5-10-5
По данным таблицы на
рис. 74 строим зависимость
Ф=/(2Яа/а) и по ней нахо-
дим, что при Iw == 350 а
Ф = 55. 10-6 вб. Следователь-
но,
д __Ф _ 55-10-» тл
S5 ~ 4,5-1О"< “ 1,21 тЛ‘
§ 61. Расчет разветвленной
магнитной цепи методом двух
узлов. Выше отмечалось, что
для расчета разветвленных
Рис. 74
магнитных цепей применимы все
методы, которые обсуждались в главе второй.
В виде иллюстрации рассмотрим расчет разветвленной магнит-
ной цепи рис. 75 методом двух узлов.
Рис. 75
Пример 29. Задано: геометрические размеры в мм; кривая нама-
гничивания рис. 70; /1г^1 = 800 в, /2а>2 = 300 о; зазоры — 0,05 мм
и 6а = 0,2.-Mr.
Найти магнитные потоки в ветвях магнитной цепи.
«1
Решение. Как и в схеме рис. 40, узловые точки обозначим
буквами а и Ь. Выберем положительные направления потоков Фх,
Ф2, к узлу а- Построим зависимость потока Фх от падения маг-
нитного напряжения первой ветви (кривая 1 рис. 76). Для ее постро-
ения задаемся произвольно рядом численных значений Фр для каж-
дого значения его находим индукцию и по кривой намагничива-
ния напряженность Нх на пути в стали по первой ветви.
Магнитное напряжение на первом участке равно UM1 = Нх/х +
+ 0,8-106 В161; здесь = 0,24 м есть длина пути в стали по пер-
вой ветви.
Таким образом, для каждого значения потока Фх подсчитываем
100 200300 ООО 500 500100 800 UM(a)
Рис. 76
UM1 и по точкам строим зависимость Фх = f (UMJ) — кривая 1
рис. 76.
Аналогично строим зависимость Ф2 = f —кривая 2; UMi —
== Яа/а-|-0,8.10в.В2д2; /2=0,138 м— длина пути в стали по второй
ветви. Кривая <3 есть зависимость Ф3=/:(^з)' — Н'Л + Н’31”3:
здесь 13 ^0,1 м и /3"^=0,14 м. Им соответствуют участки треть-
ей ветви, имеющие сечения 9 и 7,5 см2.
Магнитная цепь рйс. 75 формально аналогична нелинейной элек-
трической цепи рис. 40.
Аналогом токов /х и /2 электрической цепи рис. 40 являются
магнитные потоки Фх и Ф2 магнитной цепи рис. 75.
Аналогом э.д.с. Et является м.д.с. Аналогом зависимости
тока в первой ветви от падения напряжения на сопротивлении пер-
вой ветки является зависимость магнитного потока Фх в
первой ветви магнитной цепи от падения магнитного напряжения UM
вдоль первой ветви [Ф1 = /Г(^Л1)1 и т.д.
Воспользуемся этой аналогией для определения потоков Фь Ф2,
Ф8. С этой целью выполним графические построения, полностью ана-
логичные графическим построениям, выполненным на рис. 43.
Вспомним, что кривые рис. 43 представляют собой зависимости
токов в ветвях схемы в функции не от падений напряжений (Ult
№2
U2, U3,) вдоль этих ветвей, а в функции от напряжения Uab между
двумя узлами (а и Ь) схемы рис. 40.
В соответствие с этим введем в расчет магнитное напряжение —
разность магнитных потенциалов—между узлами а и Ь:
U’ле eeb Флеа ФлеЬ'
Выразим магнитный потенциал точки а (?ма) через магнитный по-
тенциал точки b (<?мЬ), идя от точки b к точке а сначала по первой
ветви, затем по второй и, наконец, по третьей. Для первой ветви
Фле а — Фле Ъ ~ (#Л + #8181) + hWf
Здесь Я1/1 -|- = UM1 представляет собой падение магнитного
напряжения по первой ветви. Знак минус перед скобкой поставлен
в соответствии с тем, что при перемещении согласно с направле-
нием потока магнитный потенциал (как и электрический при пере-
мещении по току) снижается (если бы двигались против потока, то
магнитный потенциал возрастал и надо было бы поставить плюс).
Плюс перед поставлен потому, что при перемещении от точки
b к точке а идем согласно с м.д.с. Таким образом для первой
ветви имеем
имаь = Фяа — Фмь*= — им1 + 1^ + (а)
Аналогично для второй ветви (перемещаясь от b к а по пото-
ку Фг и согласно см.д.с. I2w2) получим
Уле2 ~ ле ab ~Ь hW2- (б)
Для третьей ветви (в ней м.д.с. отсутствует)
УлеЗ =• —- ab- (в)
Графическое решение задачи приведено па рис. 77. На нем
кривая 1 есть = f(UMab); кривая 2 Ф2 = f(UMaby, кривая 3 Ф8 =
S3
= Д{/л ab). Построение их производилось так же, как и построение
соответствующих кривых рис. 43. Начало кривой 1 смещено в точ-
ку ^маь = Kwi — 800 а. Начало кривой 2 в точке UMab — 12юг —
= 300 а. Кривая 123 представляет собой кривую Ф, -f- Фа -f- Ф8 ==
— f(UM ab). Она пересекает ось абсцисс в точке т. Проведем через
точку т вертикаль и найдем потоки в ветвях:
Фх = 126,2 -10-5 вб; Ф2 = — 25 -10—5 вб;
Ф3 = — 101,2-10-5 вб.
То обстоятельство, что в результате расчета потоки Фа и Ф3 ока-
зались отрицательными, означает, что в действительности эти потоки
направлены противоположно положительным направлениям для них,
показанным стрелками на рис. 75.
Рассмотрим, какие изменения произошли бы в построениях на рис. 77,
если бы какая-либо из м. д. с. изменила направление на противоположное (на-
пример, в результате изменения тока в этой обмотке}. Пусть, например, изме-
нилось на противоположное направление м. д. с. /Зю2. В уравнение (б) м. д. с.
/2ш2 войдет теперь с отрицательным знаком. Это найдет свое отражение при
построениях в том, что кривая 2 на рис. 77 переместится влево параллельно
самой себе так, что она пересечет ось абсцисс не в точке UMab=300 а, а в точ-
ке имав= — 300 а (см. пунктирную кривую 2' на рис. 77). Кривые 1 и 3
останутся без изменений, но суммарная кривая Ф2 + Ф2 -j- Ф3 = f(UMab),
разумеется, станет иной.
§ 62. Как получить постоянный магнит? Возьмем замкнутый то-
роид (тороидальный сердечник) из магнитнотвердого материала. Сде-
Рнс. 78
лаем в нём два очень тонких
радиальных пропила на расстоя-
нии 8 друг от друга (рис. 78, а).
Выпиленный кусок тороида оста-
вим пока на месте. Затем намо-
таем на тороид обмотку и про-
пустим по ней ток достаточной
величины, чтобы намагнитить то-
роид до насыщения. После это-
го ток выключим и обмотку
смотаем. Тороид окажется на-
магниченным. Намагниченность
тороида есть следствие того, что магнитные моменты областей са-
мопроизвольного намагничивания сохранили свою ориентацию, вы-
званную предшествующим воздействием внешнего поля.
Магнитный поток в теле тороида определяется суммой магнит-
ных моментов всего тороида.
Вынем выпиленный кусок из тела тороида (рис. 78, б).
Объем намагниченного вещества уменьшится на объем вынутой
части, что приведет к уменьшению магнитного потоке теле то-
роида.
34
В воздушном зазоре тороида при отсутствии на тороиде обмот-
ки с током проходит магнитный поток— устройство представляет
собой постоянный магнит.
§ 63. Расчет магнитной цепи постоянного магнита. Величина маг-
нитной индукции в зазоре магнита (В8) зависит от соотношения меж-
ду длиной воздушного зазора В и длиной ферромагнитной части магни-
та 1е (рис. 78,6). Обозначим: Нъ—напряженность поля в воздушном
зазоре; Вс — магнитная индукция в те-
ле магнита; Нс — напряженность маг-
нитного поля в теле магнита.
Найдем две неизвестных величины
Ве и Нс, полагая известными кривую
размагничивания ферромагнитного ма-
териала, величину зазора 8 и длину
1С. Одна связь между ними (нелиней-
ная) дается кривой размагничивания
(рис. 79)*. Другая связь (линейная)
следует из закона полного тока.
Действительно, если воспользовать-
ся законом полного тока, то можно записать
+ = (3.11)
В правой части уравнения (3.11) стоит нуль. Это объясняется
тем, что на постоянном магните нет обмотки с током. Но
Если зазор достаточно мал, то можно в первом приближении
принять, что рассеяние потока отсутствует и BCSC — BsSs
Здесь Sc — площадь поперечного сечения магнита, Ss — пло-
щадь поперечного сечения воздушного зазора.
и
/Л = 0,8.10е. В. = 08.10е- —В_.
8 8 Ss с
Подставим Нь в уравнение (3.11). Получим
Н с (a/jKj = NBa (тл), (3. 12)
где
W = 0,8.10*. —(3.13)
1с *8
* По оси абсцисс на рис. 79 влево от точки О И = Не отрицательна.
85
Коэффициент N, зависящий от геометрических размеров, называется
размагничивающим фактором*.
Для определения Нс и Вс следует на рис. 79 нанести прямую
по уравнению (3.12). В точке пересечения прямой с кривой размаг-
ничивания удовлетворяются обе связи между Вс и Нс, которым
должно быть подчинено решение.
Пример 30. Найдем Вс, В&, Нс и Н6, если постоянный магнит
(рис. 78, б) имеет 7? = 5 см, 8 = 1 см. Кривая размагничивания изо-
бражена на рис. 79.
Решение. Если пренебречь боковым распором магнитных си-
ловых линий в зазоре, то S8 = Sc. При этом размагничивающий
фактор М = 0,8. —— = 263.102. На рис. 79 проводам прямую
Оа по уравнению Нс — —263.102 Вс.
Точка а пересечения ее с кривой размагничивания даетВе= 0,3 тл.
Такая же индукция будет в воздушном зазоре. Напряженность
поля в теле магнита Нс — —SQQQa/м. Напряженность поля в воз-
духе Д8 = 0,8.10е.0,3 = 24.10* (а/м).
§ 64. Прямая возврата и* коэффициент возврата. Частично за-
полним зазор 8 на длине (см. рис. 78,6) куском магиитномягкого
материала. Под действием поля постоянного магнита внесенный
кусок намагнитится, и поток в теле магнита возрастет.
В силу наличия гистерезиса магнитное состояние постоянного
магнита будет изменяться не по участку ab (рис. 79) кривой раз-
магничивания, а по нижней ветви ас частного цикла.
Для упрощения расчетов принято заменять частный цикл пря-
мой данией, соединяющей его вершины. Эту прямую данию назы-
вают прямой возврата. -
Тангенс угла наклона прямой возврата к оси абсцисс называют ко-
эффициентом возврата. Численные значения его для различных
магнитнотвердых материалов даются в руководствах по постоян-
ным магнитам.
Обозначим длину оставшегося воздушного зазора через 8Х (см.
рис. 78, б)
8i = 5-^
и на основании закона полного тока запишем
НС1С + Н.. 81 + 7лиЯ^ = О.
Напряженность поля в мягком магнитном материале Нмс мно-
* Название коэффициента W подчеркивает, что при помощи его можио
определить то размагничивание (уменьшение магнитного потока в теле маг-
нита), которое происходит при введении воздушного зазора в магнитную
цепь постоянного магнита.
86
го меньше, чем напряженность поля в магнитнотвердом материале
и в воздушном зазоре при одном и том же значении магнитной
индукции, поэтому слагаемым H^l^ пренебрегаем по сравнению
с остальными. При этом
Нс (а/м) = -0,8-10*^- ^-Вс(тя). (3.12Э
‘с
Магнитное состояние постоянного магнита определяется пересече-
нием прямой возврата с прямой по уравнению (3.12z).
Пример 31. Воздушный зазор магнита примера 30 уменьшен
вдвое. Найти индукцию в нем.
Решение. Находим N = 131,5-102. Прямая О А рис. 79 пересе-
кается с прямой возврата в точке d. Поэтому Вс = 0,4тя. Такая же
индукция будет и в воздушном зазоре, так как S5 = Sc.
Таким образом, уменьшение зазора со значения 8 до 8Х приве-
ло к увеличению магнитной индукции в нем с 0,3 до 0,4тл.
Если же зазор получить не путем сокращения зазора со зна-
чения 8 до 8V как это было в предыдущем примере, а путем вы-
емки из тела намагниченного тороида куска длиной 8Х, то магнит-
ное состояние магнита определится пересечением луча ОА с кри-
вой размагничивания ЬаНс в точке е. В этом случае Вс = В6 =«
= 0,48тл, т. е. йозрастет по сравнению с магнитной индукцией при-
мера 31 на 0 ’48 100 = 20%.
0,4
Из этого примера наглядно видно, что магнитный поток в по-
стоянном магните зависит не только от величины воздушного за-
зора, но и от предыстории установления этого зазора.
§ 65. Магнитное сопротивление и магнитная проводимость
участка магнитной цепи. Закон Ома для магнитной цепи- По опре-
делению падение магнитного напряжения UM — Hl, но
Н = В = —5—.
Здесь Ф — поток, aS — поперечное сечение участка. Следователь-
но,
им = Ф-----1-~- = Ф^. (3.14)
Уравнение (3.14) называют законом Ома для магнитной цепи;
Это уравнение устанавливает связь между магнитным напряже-
нием UM и потоком Ф; RM называется магнитным сопротивлени-
ем участка магнитной цепи. Обратная величина магнитному со-
87
противлению называется магнитной проводимостью
Q _ 1 _
(3.16)
I
Rm
Из предыдущего известно, что веберамперная характеристика
участка магнитной цепи в общем случае нелинейна. Следовательно,
RM и @м являются функциями магнитного потока. Это обстоятель-
ство приводит к тому, что пользуются понятиями и GM практи-
чески лишь в таких случаях, когда магнитная цепь в целом или
участок ее, для которых определяются RM и GM, не насыщены.
Чаще всего это имеет место, когда в магнитной цепи имеется до-
статочно большой воздушный зазор, спрямляющий веберамперную
характеристику магнитной цепи в целом или участка ее.
Пример 32. Найти RM воздушного промежутка постоянного маг-
нита и по нему магнитный поток, если 8 = 0,5 ом, площадь попе-
речного сечения воздушного зазора S = 1,5 с-и®. Магнитное напря-
жение на воздушном зазоре 1920 а.
Решение.
Ф = Ча ----------*920----в 7230.10~8|
R* 0,265-10е
Глава четвертая
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
И МЕХАНИЧЕСКИЕ СИЛЫ В МАГНИТНОМ ПОЛЕ
§ 66. Явление электромагнитной индукции. Явление электро-
магнитной индукции представляет собой одно из важнейших явле- *
ний, наблюдаемых в магнитном поле. Оно было обнаружено в 1831 г.
английским физиком Майклом Фарадеем. Суть явления состоит в
том, что при всяком изменении магнитного потока, пронизывающе-
го какой-либо контур, вне зависимости от того, чем вызвано изме-
нение потока, в контуре наводится электродвижущая сила е.
Опыт показывает, что наведенная или индуктированная э.д.с. е
прямо пропорциональна скорости изменения потокосцепления конту-
ра <|>
Потокосцепление контура ф равно алгебраической сумме потоков
пронизывающих отдельные витки обмотки
Ф = Ф1+Ф2 + Ф3 + . . . 4-Ф„- (4.2)
Если все витки обмотки w пронизываются одним и тем же потоком
Ф, то
ф = щф. (4.3)
Так как число витков w есть величина безразмерная, то измеря-
ется потокосцепление в тех же единицах, что и поток. Важно сде-
лать два замечания к формуле (4.1).
Первое замечание: ф есть полное или результирующее потоко-
сцепление контура или обмотки; оно создается не только внешним
по отношению к данному контуру потоком, но и собственным пото-
ком, пронизывающим контур при протеканий по нему электриче-
ского тока.
Второе замечание относится к знаку минус. Знак минус в фор-
муле (4.1) объясняется тем, что положительное направление для
наведенной э.д.с. и положительное направление линий магнитной
89
индукции, пронизывающих контур при возрастании потока, принято
связывать правилом правоходового винта.
Если закручивать правоходовой винт так, что его острие будет
двигаться по направлению магнитных силовых линий при возрастании
потока, то положительное направление для наведенной э.д.с. будет
совпадать с направлением вращения головки этого винта.
Знак минус в правой части формулы (4.1) поставлен с целью
приведения в соответствие действительного направления для э.д.с.
при оговоренных выше условиях с направлением, принятым для
нее за положительное.
Рис. 80, а поясняет сказанное.
Свои эксперименты Фарадей проводил с замкнутыми проводни-
ковыми контурами. Наведение э.д.с. он трактовал как следствие
пересечения проводами контура магнитных силовых линий.
В 1873 г. английский физик Джеймс Кларк Максвелл обобщил
и развил идеи Фарадея. Он показал, что явление электромагнит-
ной индукции наблюдается не только в замкнутых проводниковых
контурах, но и в замкнутых не проводниковых контурах. Обобще-
ния Максвелла рассматриваются в дальнейшем в третьей части
курса.
Пример 33. Вывести формулу для определения э.д.с. в об-
мотке с числом витков wt намотанной на прямоугольной рамке
площадью S. РаМка вращается с угловой скоростью ш в одно-
родном магнитном поле с индукцией В = Вйе~а* (рис. 80, б).
Подсчитать численное значение э.д.с. в при ш/ — В№= 1тл;
а = 10 сек-1; S = 4 см2-, <» = 31,4 сек-1; w = 100.
Решение. Потокосцепление обмотки
ф = доф = wBS cos а = wBbSe cos wt.
Здесь угол а — ю/ представляет собой угол, образованный плоско-
стью рамки и горизонтальной плоскостью
90
е = —~ = — B£w(— ae~at cos <at — <we-a< sinW) =
= B£we~ai (a cos <ot -f- «sin <ot).
Подсчитаем численное значение e при w/ — ~:
t = a/= 0,5; <? = 1-4-IO"4-1OO<?~0-5.31,4 = 0,761 (e).
2-31,4 i v ’
Определение э.д.с., наведенной в проводнике длиной dl, пере-
секающем магнитные силовые линии неизменного во времени маг-
нитного поля, часто производится по формуле
de—B {dl v ]. - (4.4) -
>
Здесь de — э.д.с. в участке проводника длиной dr, о — скорость
перемещения проводника относительно магнитного поля.
В формуле (4.4) индукция В скалярно умножается на вектор-
—> —>
ное произведение dl и о.
Если в результате расчета по формуле (4.4) э.д.с. окажется по-
ложительной, то это означает, что э.д.с. de направлена согласно с
положительным направлением элемента проводника dl.
Формула (4.4) в одинаковой мере пригодна для определения э.д.с.
при движении проводника в неравномерном и в равномерном маг-
нитном полях, лишь бы магнитное поле было неизменно во вре-
мени.
При движении проводника длиной I в равномерном поле э.д.с.
удобнее определять по формуле
е = В1ип. (4.5)
Здесь В—индукция равномерного поля, / — длина активной части
проводника (пересекающей магнитные силовые линии) и vn— со-
ставляющая скорости движения проводника, нормальная (перпендику-
лярная) магнитному полю.
Направление наведенной э.д.с. при пользовании формулой (4.5)
определяют по правилу правой руки, известному из курса физики:
если расположить правую руку таким образом, что магнитная 'ин-
дукция входит в ладонь, а отогнутый большой палец направить по
нормальной составляющей скорости проводника, то возникающая в
проводнике э.д.с. совпадает с направлением четырех остальных вы-,
тянутых пальцев правой руки.
*
♦ *
Можно показать, что из формулы (4.5) может быть получена формула (4.1)
С этой целью обратимся к рис. 81 и проделаем некоторые выкладки. 1
91
На рис. 81 изображено неравномерное магнитное поле, направленное пер-
пендикулярно чертежу. В этом поле Может перемещаться проводник длиной I,
являющийся составной частью некоторого контура. Нормальная к полю состав-
ляющая скорости проводника
dx
где х — координата в направлении vn. В отрезке проводника длиной dl
наведется э. д. с., которую определим по формуле (4.5); имеете I подстав-
ляем dl: de = Bvn dl. Э. д. с. в проводнике
длиной I
• • •/•
1
L
. I
• /*
Рис. 81
Vn
Bdxdl
di
элементарная площадка
dS, пронизываемая магнитным потоком, a I BdS ==
о
<= d® есть 1фиращение потока в рассматриваемом контуре.
Таким образом, численное значение э.д. е. равно . Так какположнтель-
di
ное направление для наведенной э. д. с. и положительное направление индук-
ционных линий при возрастании потока связаны правилом правоходового
винта, то следует учесть еще знак минус. Окончательно (при w = 1)
d®
di ’
е
»
Поясним явление возникновения Э. д. с. на концах движущегося в маг-
нитном поле проводника путем использования понятйя-о силах Лоренца.
Из курса физики известно, что на движущиеся и магнитном поле заряды
действуют механические силы, пропорциональные величине зарядов и состав-
ляющей скорости, перпендикулярной силовым линиям магнитного поли. Эти
силы принято называть силами Лоренца по имени голландского физика Ген-
рика Лореица (1853=4928), Сида, действующая иа электрический заряд q,
двигающийся со скоростью v в магнитном поле индукции В, равна q [о В].
Если какой-либо проводник будет перемещаться в магнитном поле так,
что ои будет иметь составляющую скорости, перпендикулярную силовым ли-
ниям магнитного' поля, то на положительные и отрицательные заряды, вхо-
дящие и состаи атомов и молекул этого проводника, будут действовать силы
Лоренца. ,
Силы, действующие на носителей отрицательных зарядов, будут дейст-
вовать в одну сторону, а на носителей положительных зарядов — в противо-
положную сторону.
Если движущийся в магнитном поле проводник металлический, то в силу
большой способности к перемещению в ием носителей отрицательных заря-
дов (свободных электронов) иа одном конце проводника образуется избыток
отрицательных зарядов, а иа другом его конце ~ недостаток отрицательных
зарядов (т. е. избыток положительных зарядов).
Другими словами, благодаря тому, что иа носители зарядов в металли-
ческом проводнике воздействуют силы Лореица, в этом проводнике произой-
дет разделение зарядов. На одном конце проводника в избытке появятся поло-
жительные заряды, иа другом •— отрицательные. .
92
Но явление разделения зарядов а движущемся в магнитном поле провод-
нике представляет собой не что иное, как явление возникновения в нём индук-
тированной э. д. с.
§ 67. Явление самоиндукции и э. д. с. самоиндукции. Индуктив-
ность. Явление наведения э.д.с. в каком-либо контуре при изменении
тока, протекающего по этому же контуру, называется самоиндук-
цией. Наведенная (индуктированная) э.д.с. называется э.д.с. са-
моиндукции. Э.д.с. самоиндукции обозначается Для определе-
ния ее надо продифференцировать потокосцепление контура ф, вы-
званное собственным током i.
Из опыта известно, что для контуров (катушек) с неферромаг-
нитным сердечником или для катушек с сердечником из магнитоди-
электриков, у которых р.г почти постоянна и не зависит от напря-
женности магнитного поля, потокосцепление ф пропорционально то-
ку i, т.е.
ф = Li. (4.6)
Коэффициент пропорциональности L между ф и i называется
собственной индуктивностью контура или, проще, индуктивностью.
Индуктивность как элемент схемы замещения реальной цепи дает
возможность учитывать в расчетном смысле явление самоиндукции
И явление накопления энергии в магнитном поле катушки.
Индуктивность L зависит от геометрических размеров контура
(катушки) и от числа витков w, но не зависит от величины тока,
протекающего по катушке; измеряется L в в-сек/а= ом-сек = ген-
ри (гн):
и
~ = —(Li)=L —
dt dt di
eL = -LdA
L di
(4.7)
Таким образом, э.д.с. самоиндукции в катушке пропорциональ-
на скорости изменения тока в этой катушке; э.д.с. самоиндукции
равна нулю, если ток не изменяется.
Положительное направление э.д.с. совпадает с положительным
направлением тока.
Знак минус в формуле (4.7) свидетельствует о том, что мгно-
венное значение э.д.с. отрицательно, если приращение тока поло-
/ di^ п
жительно если —> О
\ dt
Для катушек с ферромагнитным сердечником потокосцепление ф являет-
ся нелинейной функцией тока ф (/), и э. д. с. самоиндукции по правилам диф-
ференцирования сложной функции равна
eL
dip di
И ~dt
г *-
~Ld dt
(4.8)
93
4ф
Производная — называется собственной дифференциальной индуктивностью
di
или проще, дифференциальной индуктивностью и обозначается Lq.
Динамическая индуктивность является функцией тока. Для подсчета как
4ф
функции времени по формуле (4.8) следует построить крввую Lq = — =
di
di
— f (i), а значения — определять путем либо аналитического, либо графнчес-
dt
кого дифференцирования зависимости i = f (t) по времени.
di </ф
Значение е определяется произведением — на — , соответствующих
ь dt di
взятому моменту времени t.
Рис. 82
Полный поток
Пример 34. Определить индуктивность катуш-
ки, равномерно намотанной на тороид прямоуголь-
ного сечения (рис. 82). Внутренний радиус тороида
/?! = 4 см, наружный — /?2 = 6 см. Высота торои-
да Л = 2 см. Число витков w = 1000. р.г = 80
(тороид из магнитодиэлектрика).
Решение. Напряженность поля в тороиде
по закону полного тока
Н-^-.
2.R
Поток через полоску hdR, заштрихованную на
рис. 82,
^trIwh
2я/?
ЛФ = BhdR =
dR.
Rz HI?
_ С С * I4>p.r/wh Т?2
ф= рф = -^- j Т=-^— 1П-.
Л,
Потокосцепление
ф = шф.
Индуктивность
ф Ш2р0ргЛ , Кг
L = T = ~ 2*
Следовательно,
(4.9)
10002 • 1,256 • 10-• • 80 • 2 • 10—2 , 6
L = ------------------------------------1пт = 0,131 (гн).
Пример 35. По катушке примера 34 течет ток i = /OTsin<irf.
Определить э. д. с. самоиндукции в катушке при /и = 0,1.ан
ш = 103 сек~\
94
Решение. е£ = —L^- = _ ш£/ cosW;
at
eL= — 103 • 0,131 • 0,1 cos <ot = — 13,1 cos We.
Пример 36. Определить индуктивность двухпроводной линии
передачи длиной I = 10 км при расстоянии d
между проводами 2 м. Диаметр проводов
12 мм.
Решение. Двухпроводная линия (рис. 83)
представляет собой как бы один большой
виток с током i=I.
Напряженность поля в пространстве меж-
ду проводами в произвольной точке на линии,
соединяющей оси проводов, создается обоими
проводами и равна сумме напряженностей,
каждая из которых находится по закону пол-
ного тока:
I___. / Рис. 83
2хх • 2я (</ — х) ’
где d — r^x^r. Поток через элементарную площадку dS = Idx
равен
с!Ф —BdS = Bldx =
2к \ х
Полный поток*
Подставляя численные значения:
1,256 • 10-е . 200
L —-----------------------In “TV = 0,0232 (г«).
Я U,0
* Потокосцеплением в теле самих проводов при решении задачи прене-
брежен о.
95
§68. Явление взаимоиндукции. Э. д. с. взаимоиндукции. Взаим-
ная индуктивность контуров. Явление наведения э. д. с. в каком-ли-
бо контуре при изменении тока в другом контуре называется явле-
нием взаимоиндукции.
Наведенная (индуктированная) э.д.с. называется э.д.с. взаимоин-
дукции. Она обозначается ем. Пусть, например, есть два контура,
удаленных на некоторое расстояние друг от друга (рис. 84). По пер-
вому контуру протекает ток it, по второму — ток /2.
Поток Фр создаваемый током
iv частично замыкается, ми-
нуя второй Контур (Фи), час-
тично проходит через второй
контур (Ф12)*
Ф1==Фп + Ф12. (4.Н)
В свою очередь, поток вто-
рого контура Ф2, создаваемый
током ia, частично замыкает-
ся, минуя первый контур <ФИ),
частично пронизывает его (Ф21)
®2 = ®22 + ®2l- (4.12)
Потокосцепление первого кон-
тура равно
Ф1 поля = ®1(®1 ± Ф21) = Ф1 ± Ф21» (4.13)
где — число витков первого контура.
Потокосцепление второго контура' (число витков его ,®2)'
Ф2 поля = ®2(®2 ± Ф12) = ф2 ± Ф12- (4.14)
Знак плюс в двух последних выражениях следует ставить в том слу-
чае, если поток взаимоиндукции будет направлен согласно с потоком
самоиндукции, создаваемым током данного контура. При несо-
гласном (встречном) направлении следует ставить знак минус.
Из опыта известно, что если сердечники катушек выполнены из
неферромагнитных материалов либо из ферромагнитных, но имею-
щих постоянную цг, то ф21 пропорционально току i2, а ф12 пропор-
ционально iv
Коэффициенты пропорциональности обозначают буквой М с соот-
ветствующими индексами. Так,
Ф21 = Л121»2; (4.15)
Ф12 = Л41211. <4.16>
* Чтобы рис. 84 был более понятным, нанем изображено тольконо од-
ной силовой линии -каждого из потоков.
96
и лМй- численно фамцс друг другу: (дойаза*
тевЙеЙо/в § 72): \ > :
; -ДМ = Мп == М. : v - ‘, - >, (4J7)
Коэффициент М называется взаимной индуктивностью контуров
(или катушек). Он имеет ту же размерность, что и собственная ин-
дуктивность L.
Полная э.д.с., индуктируемая в первом контуре,
.....
'• '' —(4.18)
at at
Аналогично для второго контура
е2Пол« = — 7-2 ~ -+ М ~ = ец -|- 02м- (4.19)
dt dt
Э. д. с. взаимоиндукции
= (4.20)
аг
ewi = ^Md±. (4.21)
<//
В двух последних выражениях знак минус следует ставить при со-
гласном направлении потоков самоиндукции и взаимоиндукции, а
плюс — при встречном. При таком обозначении коэффициент М
всегда будет величиной положительной.
Как элемент схемы замещения реальной цепи М позволяет в
расчетном смысле учесть явление взаимоиндукции.
; Влитературе встречается и другой способ записи э. д. С. самоиндукций.
Пишут так;
'и—<4-20)
'«—"Th
и принимают, что коэффициент М может быть либо положительным (при со-
гласном направлении потоков самоиндукции и взаимоиндукции), либо отри-
цательным (при встречном направлении потоков).
4*21
Взаимная индуктивность М определяется как отношение — или
412 '
—• Ни от ф21, ни от г2 (и, соответственно, от ф12 и i\) порознь она
не зависит, если сердечники катушек неферромагнитны или если сер-
дечники ;выполнены из ферромагнитного материала с постоянной |лг.
Взаимная индуктивность М зависит только от взаимного располо-
.женин катушек, числа витке® их, геометрических размеров катушек
и от постоянной для данного сердечника
4 Л. А. Бессонов $7
Прй любой форме й любоы распбложеййи Матй’йТйоейяэёййык кй-
тушек определение взаимной индуктивности "М между1’ йимй :Ч5ёз
затруднений можеТ быть проведено' опЫтййм Путей На’ ПфёкённЬй'
токе (§ 115). Расчетное же определение М при сложном характере
распределения магнитного поля в силу трудностей математического
характера удается произвести лишь для катушек простейших геомет-
рических фОрМ. ' :!, >
Если магнитносвязанные катушки имеют ферромагнитные сердеч-
ники с непостоянной рг, например намотаны на одном сердечнике,
рг которого является функцией результирующей напряженности
магнитного поля, то в этом случае М будет непостоянной .вели-
чиной. i; , ,
Вводить понятие взаимной индуктивности для таких катушек
нецелесообразно. , .
Пример 37. На тороид примера 34, кроме первой обмотки с чис-
лом витков = 1000, намотана вторая а>2 = 500. Определить
взаимную индуктивность между обмотками.
Ре Шен й е. Если принять, что весь поток, созданный'первой об-
моткой, Д> =__________^!_(см. пример 34) пронизывает и вторую об-
2ft
могку (потоком рассеяния пренебрегаем), то *= ш8Ф и
. . R»
М = £!• = ------(4.22)
4 2я
Подставим числовые значения
м _ ,оов55м.
§ 69. Энергия магнитного поля уединенной катушки. Включим
к источнику э. д. с. Е индуктивную катушку с сопротивлением R
и индуктивностью L. Пусть в момент времени t = 0 в ней i = 0 и
ф = 0. Той в цепи по закону Ома будет равен
£ + eL & ,
1 ~ R ~ R
или
Е = . (4.23)
Умножим обе части равенства на i dt. Получим
Eidt — »2/? dt 4- i dty. (4.24)
Левая часть (4.24) представляет собой энергию/отдаваемую источ-
ником э. д. с. за время d/. Слагаемое J2/? (//—энергия, выделяющаяся
98
в рнда;,тецлоты за вр|едр .((/ в сопротивлении 1?. Слагаемое <4$ есть
энрргця, идущая на создание магнитного поля уединенной непо-
движной редеформирующейся катушки; обозначим ее dty
'Л',' .; 1 <4.25)
Полная энергия, запасенная в магнитном поде катушки при изме-
нении ф от О до -фт,
.... _ пп
ДЛ катушек с неферромагнитным сердечником ф = Li и </ф=
= L di. Поэтому
W^Lpdi = ~ (4.26)
Здесь / — некоторое установившееся значение тока в цепи.
<§ Ж Плотность энергии магнитного поля. Пусть на тороидальный
сердечник, у которого отношение внутреннего радиуса к внешнему
близко к единице*, равномерно намотано w витков; I—длина
средней линии сердечника. На основании закона полного тока Hi =
Hi ~
= IW или t == —.
В свою очередь t/ф = uiS dB и
Н ♦ в •. в
</ф= — f H dB = V f H dB.
M J w J J
о о 0 n ;
Поделим обе части равенства на объем тороида V
в
^^-f=jHdB. (4.27)
. ° / 'Л..'
Таким образом, плотность энергии магнитного поля равна '
в
J И dB.
е
Если цг сердечника тороида постоянна, то
м. В = popr Н и dB = pe р, dH.
Следовательно,
н
и/ \ н dH = = .
, , м * r J 2 2
! - - о
(4.28)
^ Благодари мому можно, с известным приближением считать, что яа-
ррдфенв|9сть,др^д й а теле тороида во всех точкам одна и та же.,
4* 99
8 кЙвдоЙ^Щйнйцё объейа", зан!гй5го пблёй, соД^йййёй' зМё^гия
‘Ши(и'й«й4б'поля, равная- - ’ ' ; •« -- v i f >, tf
Для ферромагнитного сердечника pr 5^ const, и поэтому гдля
подсчета энергии единицы объема формула (4.28) не годится. Для
подсчета энергии единицы объема ферромагнитного сердечника слё-
дует исходить из формулы (4.27)
wM = lHdB.
о
Произведение Н dB изображено на [
ной площадкой. Весь интеграл пред-
ставляет собой площадь, ограничен-
ную кривой В — /(Я), осью ординат
и прямой В = const.
§ 71. Потери на гистерезис за один
цикл перемагничивания. При перио-
дическом намагничивании ферромаг-
нитного материала в нем совершают-
ся необратимые процессы, на кото-
рые расходуется энергия от намаг-
;. 85 дважды заштрихован-
В
Н
j!
Рис. 86
Рис. 85
ничивающего источника. Потери в сердечнике состоят из потерь на
гистерезис и из потерь на вихревые токи. В настоящем парагра-
фе обсудим вопрос о потерях на гистерезис. Потери на Вихре-
вые токи будут обсуждены во второй части курса. Физически поте-
ри на гистерезис обусловлены главным образом потерями от мик-
роскопических вихревых токов при скачкообразных поворотах век-
торов намагниченности отдельных намагниченных областей (скач-
ки Баркгаузена, известные из курса физики).
Площадь гистерезисной петли представляет собой энергию, выде-
ляющуюся в единице объема ферромагнитного вещества за один цикл
перемагничивания.
100
Д^с-пви^^до, пл^адь гидт^резиа^й лпетли, равнд -
Чтобы убедиться в этом, представим площадь гистерезисной петли
рис. 86 в виде суммы четырех площадей
$)Н dB = Sj + S2 + S3 + S4.
*: Площадь Sj соответствует движению от точки 1 до точки 2; так
как на этом участке Н > 0 и dB > О, то произведение
Н dB > 0 и Sx > 0.
Площадь S2 соответствует движению от точки 2 до 3; так как
в этом интервале Н > 0 и dB < 0, то S2 < 0.
Площадь S3 — движение от 3 до 4; S3 > 0, так как Н < 0 и
dB<0..............
” Площадь S4—движение от 4 до Г, S4 < 0, так как Н <0 и
dB> 0. -
Вели ферромагнитный сердечник подвергается периодическому
намагничиванию (например, в цепях переменного тока), то для умень-
шений потерь на гистерезис в нем он должен быть выполнен из маг-
нитномягкого материала (§ 46).
§ 72. Магнитная энергия дву^ магиитносвязаниых контуров. Пусть
есть два неподвижных магнитносвязанных контура, не изменяющих
свои размеры и находящихся в неферромагнитной среде. Индуктив-
ность Первого контора Lx, второго L2, взаимная индуктивность
между контурами М. Подсчитаем магнитную энергию двух конту-
ров для, двух режимов, отличающихся друг от друга только после-
довательностью установления токов ц и i2 в контурах. Последова-
тельность установления токов в первом режиме выберем следующую:
сначала включим первый контур к источнику э. д. с. при разомкну-
том втором контуре, затем включим второй контур к источнику
э. д. с. н будем поддерживать ток в первом постоянным.
Во втором режиме последовательность установления токов вы-
берем следующую: включим сначала к источнику э.д.с. второй кон-
тур при разомкнутом первом, а затем включим первый, поддержи-
вая постоянным ток второго контура.
, Подсчитаем магнитную энергию контуров в первом режиме.
., При росте тока в первом контуре от 0 до и разомкнутом вто-
ром контуре запасенная первым контуром магнитная энергия равна
* Кружок на знаке интеграла свидетельствует о том, что Jf/dfi подсчи-
тывается за полный цикл изменения В. • г
101
Цри росте тока i2 от 0 до ia и при = const энергия запасает-
ся не только вторым, но и первым контуром. Энергия, запасаемая
вторым контуром, J i2d\|)2. Но хр2 = L2i2 Af 12i, (положим, что име-
ет место согласное включение). Так как
ix = const,
то
^Ф2 == 7,2</f2
и
У = Л2 у (2Л2 = 2 • !
О О
Рост токаТ2 вызывает изменение потокосцепления первого контура
vpj. Оно становится равным + M2li2. Поэтому энергия,
обусловленная потоком взаимоиндукции, будет равна
Суммарная магнитная энергия двух магнитносвязанных контуров
при установлении токов в них по первому режиму
Рассуждая совершенно аналогично, для второго режима установ-
ления получим
Так как режимы отличаются друг от друга только последова-
тельностью установления токов, то естественно, что магнитная энер-
гия в этих двух режимах будет одинакова. Отсюда следует, во-пер-
вых, что
М21 = М12 = М . (4.29)
и, во-вторых, что
± (4.30)
Плюс перед слагаемым Mi^ соответствует согласному включению
контуров, минус — встречному.
Пример 38. По обмотке тороида примера 37 течёт ток 0,5 а и
пр обмотке с»2 ток 0,4 а. Определить магнитную энергию при со-
гласном и при встречном направлении потоков обмоток. . .
Решение. По формуле (4.9) определим индуктивность вто-
рой обмотки
La = 0,0327 гн.
102
: В Соответствии е (4.30) при согласном направлении Потоков
, F, = + b£L + мгц = -0,131~ °’.-- +
ж 2 । 2 112. 2
^0,0327.0,f _|_0 0655 . о,5.0,4 = 0,032 {дж).
При встречном направлении потоков
WM = 4- — Mid* = 0,00585 дж.
м 2'2 1 s
§ 73. Принцип взаимности взаимной индукции. Проделаем два
опыта. В первом из них изменяющийся во времени ток ix(/) пропус-
тим по первой катушке (контуру) и измерим (подсчитаем) э. д. с.
взаимоиндукции, возникающую во второй
катушке (контуре), магнитносвязанной
первой. Эта э. д. с. будет равна
Во втором опыте тот же ток (той
амплитуды и изменяющийся по тому
закону во времени, что и в первом ой;
назовем его ta(Z), пропустим по второй
тушке и измерим (или подсчитаем) э.д.с.
взаимоиндукции, возникающую в первой ка-
тушке. Эта з.д.с. будет равна
о —_____М —
егм м
, До условию постановки опыта h(0 = *а(Л» поэтому = е2л) •
Другими словами, э. д. с. взаимоиндукции в описанных выше двух
опытах будут одинаковы. Это положение принято называть принци-
пом взаимности взаимной индукции.
Так как = М, то при расчетном и опытном опреде-
лении М всегда следует выбирать наиболее простой и удобный путь
из двух возможных.
Пусть, например, через равномерно нанесенную на тороид обмотку wt
проходит произвольно расположенный внутри тороида провод (рис. 87). Этот
провод является частью одновиткового контура, полностью не показанного
на рисунке. Требуется найти аналитическое выражение для Л/ между. Торои-
дом и одиовитковым контуром. Это можно сделать двумн путями.
Первый Путь: мысленно пропустим по первому контуру (обмотке to, то-
роида) ток 4, найдем потокосцепление второго (одновиткового) контура 4м
с, потоком первого и определим 4
4
гоз
Второ* путь: мысленно пропустим по второму (одиовитковому) контуру
с числом витков ®j = 1 ток it, найдем потокосцепление первого контура (фьО
с потоком второго н определим
44 = -^- •
i»
В расчетном отношении эти два пути ие эквивалентны. Первый путь мно-
го проще второго. Объясняется это тем, что поток, создаваемый первым кои-
туром, весь замыкается внутри тороида и полностью сцепляется с одновитко-
вым контуром, “и потокосцепление ipi, можно легко найти, тогда как найти
поток, создаваемый одновнтковым контуром и сцепляющийся со вторым кон-
туром, если ировод расположен внутри тороида произвольно, весьма затруд-
нительно.
Поток тороида
R* ., -
GИоIV®!л f
Ф1“ to J R “ 2л 1П Rt
я,
Поток осцеп ле вне
фа! = = 1 •
и
44 = (431)
G to . R,
Пример 39. Через тороид примера 34 пропущен одиночный про-
вод. Найти М между одиночным проводом и обмоткой w.
Решение. По формуле 4.31 (ср. ее с формулой 4.22) при
= 1 найдем
1,256. 10*® • 80. 1000.2 - 10-2.0,41
2л
Пример 40. По одиночному проводу примера 39 проходит ток
ia = 100(1—е~2/) а. Определить э.д.с., наводимую в обмотке а^.
Решен ие. ем, =—М — —— 1,31 • 10-3 • 100 • 2е-а/==
лн dt
‘ =—0,262е-“ в.
§ 74. Коэффициент связи. Под коэффициентом связи k двух
магтштносвязанных контуров с индуктивностями £ди Lg и взаимной
индуктивностью М понимают отношение Л4* к у LxLa
V ^Lt
Можно показать, что k не может быть больше единицы. Для ло-
го чтобы убедиться в этом, составим выражение для и если вы-
яснится, что k* = -^-<С1, то й 1. Воспользуемся обозначе-
ниями § 68 и запишем
= 1,31 (мгн).
* Заметим, кстати, яте 44 может быть-больше Li (или Lj), ио не мржет
быть больше и Li и Lt. -
104
£2 = *1 1 ** 3_
£i£s и*1(Ф12 4~ Фх1) tt>a (Фгх j~ Фаг)
‘1 ii
ФцФм < р
(Ф12 4- Ф11ХФ21 + Фаг)
С будет равно 1 только в случае, если весь поток, создаваемый пер-
вом контуром, будет сцепляться со вторым.
§ 75. "Магнитная энергия системы контуров с токами. Запишем
общее выражение для магнитной энергии системы магнитносвя-
занных контуров. С этой целью обратимся к уравнению (4.30) и пе-
репишем его следующим образом:
____ £х^? I Mijit, । £2/а ।______________ (£xG ~4~ t
м~ 2 2 ' 2 2 2 '
2
I (£z*2 zfc _ fx'l'i j M's _ 1 ут .
2 Ы
Аналогичное выражение будет иметь место, если магнитносвязаны
не два, а п контуров:
п
= 7 2 (4. 33)
Й-I
где фй представляет собой полное потокосцепление k контура.
§ 76. Механические усилия в магнитном поле. В § 66 говорилось
о явлении электромагнитной индукции как одном из важнейших
свойств магнитного поля. Назовем это свойство первым свойством.
Вторым важнейшим свойством магнитного поля является ме-
ханическое взаимодействие его с электрическим током. Оно было
обнаружено еще в 20-х годах прошлого столетия (опыты Эрстеда
и Ампера). Эксперимент показывает, что магнитное поле индукции
В (рис. 88) взаимодействует с элементом тока Idl с силой
F = I[dlB]. (4.34)
Этасила перпендикулярна dl и В. Если угол между din В равен
нулк>, то векторное произведение | dl В | равно нулю, и магнитное
поле не оказывает механического воздействия на элемент тока Idl.
Сила максимальна, если В и dl взаимно перпендикулярны;
Механическое воздействие поля на ток физически объясняется
стремлением силовых линий, искаженных внесением провода, вы-
прямиться.
105
На рис. 89 изображено три эскиза. На первом — силовые линии
равномерного магнитного поля до внесения в него провода с током.
На втором —‘ силовые линии уединенного провода с током. На треть-
ем— силовые линии результирующего поля. Слева от провода си-
ловые линии собственного поля провода направлены встрёчно сило-
вым линиям внешнего равномерного поля, а справа — согласно с
ним. Поэтому результирующее поле слева от провода разрежено,
а справа сгущено. Силовые линии, стремясь выпрямиться, произ-
водят давление на провод справа надевр.
Рис. 88
Внешнее
однородное
поле
Собственное
поле провода
Рис. 89
Резцшпирцлцее
попе
При взаимно перпендикулярном расположении магнитного поля
и провода с током направление действия силы часто определяют по
мнемоническому правилу, получившему название правила левой
руки: если расположить левую руку таким образом, что силовые
линии будут входить в ладонь, вы-
I,у , тянутые пальцы направить по току,
У то отогнутый большой палец покажет
/ направление действующей силы.
/ f .fdL Взаимодействие поля с током име-
ет место вне зависимости от того,
4 а / вследствие каких причин возникло
, у/, ~ магнитное поле: возникло ли оно в
в результате протекания макротоков в
ри M электрических контурах, или оно
ис‘ есть следствие протекания микротоков
в ферромагнитных материала^, или
потока электронов в вакуумном приборе и т. п. Оно наблюдается
как в постоянном, так и в изменяющемся во времени поле.
Механические силы, возникающие в магнитном поле, часто на-
зывают электродинамическими силами, как бы подчеркивая самим
названием то обстоятельство, что под действием этих сил в системе
может возникнуть и часто действительно возникает перемещение
тел, т. е. динамический процесс.
Пример 41. На рис. 90 изображены два параллельных провода,
расстояние между которыми а — 10 см. По первому проводу течет
ток = 1000 а, по второму — /г = 500 а. Направления- токов
106
показаны стрелками. Определить силу взаимодействия между про-
водами иа длине Г м. > : >
Решение; Воспользуемся формулой (4.34). Учтем, что угол
между элементом длины провода dl и индукцией В равен 90°.
Поэ+бйу модуль векторного произведения [d/S] равен
dl В sin 90° = dl В. /
Магнитная индукция S,! создаваемая первым проводом в точках,
где расположен второй провод, по закону полного тока равна
В = Сила
2яв F = I„dtВ =* ;
2 2ла
1000 • 500 • 1,256 • 10-« • 1 . . .
------ —1 («).
2л. 0,1
Под действием силы провода стремятся сблизиться.
В заключение обратим внимание на следующее положение. Принято гово-
рить, что магнитное поле оказывает механическое воздействие на проводник с
током, помещенный в это поле. Это выражение требует некоторых уточнений.
Дело в том, что магнитное поле механически воздействует на упорядочен-
но движущиеся в проводнике заряды (силы Лоренца —см. § 66), а уже этн
заряды, сталкиваясь при своем упорядоченном движении с другими частица-
ми вещества проводника, передают силу самому проводнику.
§77. Выражение, механической силы в виде производной от энергии маг-
нитного ноля по координате. Возьмем систему из л контуров стоками. Пусть
одйя из контуров под действием механической силы F на него со стороны ос-
тальных контуровперемещаетсятак, что координата х его изменяется на ве-
личия/ dx. Требуется выяснить, какая связь существует между силой F и из-
менением энергии магнитного поля системы dWм-
Для какого-то k контура системы запишем уравнение (ср. с уравнением
(4.35)
dt
где ф* есть полное, потокосцепление k контура. Оно зависит не только от
тока В k контуре, но н от токов других контуров, магнитносвязаниых с k
контуром. Умножим (4.35) на ikdt-.
Запишем аналогичные уравнения для остальных контуров и просумми-
руем их;
п п п
^ек1к<И = J i2kRkdt+ £ ikd*t. (4. 36)
*=l A=f
п
Слагаемое £ 1к dty представляет собой ту часть энергии, которую получают
k=l
все цепи от источников э, д. с. за вычетом тепловых потерь.
При перемещении какого-то одного контура иа расстояние dx изменяет-
ся магнитная Энергия системы на величину d и совершается механичес-
кая работа Fdx, rgiF составляющая силы, действующая по направлению х.
^гИззаканасохраненияэнергии следует, что энергия,, доставляемая .источ-
никами э. д. с. за время dt, должна равняться энергищвыделяющейсяэа то
жевремя в виде теплоты в сопротивлениях контура, плюс энергня/пошед-
шая. на покрытие механической работы Fdx, плюс приращение энергннмагг
нитного поля dWM: , ,
п я • - , •- ..
S«4M'=S ik^di + Fdx + dWM. \ (4.37)
4 = 1 4=1 : , г’.'
Из сопоставления (4.36) н (4.37) следует, что
Л
У ‘4 ditk = F dx + d WM, (4.38)
4=1
Уравнение (4.38) означает, что механическая работа и приращение Виер-
rt
гни магнитного поля совершаются за счет той части энергии У сЦнсточ-
4=1-
ников, которую последние отдают в цепи за вычетом тепловых потерь. Из
(4.38) получаем
'. л ....
У'4^4 — dWM
Ъ — |
F= —----------------- (4.39)
dx
Уравнение (4.39) является достаточно общим. Из него вытекают, два важных
частных случая. В первом из них пусть перемещение происходит таким обра-
зом, что ' потокосцепления контуров остаются неизменными. При этом
dipt = 0; Fdx = — dWM и
Знак минус означает, что механическая работа совершается за счет убы-
ли энергии магнитного поля.
Во втором частном случае пусть перемещение происходит так, что токи
в контурах остаютси неизменными (»£ = const). Это может быть, 'иапримёр,
тогда, когда перемещение происходит настолько быстро, что токи не успевают
нзменитьси.
Из предыдущего (см. формулу 4.33) следует, что
= У ^4 ^4- . - < : .
Следовательно,
d^ ySz*dfr . (4.41)
Подставим (4.41) в (4.39)
г- Л л п
У lk ^4 ~ — У ‘4 ^4 “ S ^4
4 = 1 2 4=1 2 4 = 1 : " <fWM
" 1 -1—1” .' т-- s= I .. " j 1 - as — »
dx dx dx •
(4.42)
108
" 'Во ЬтОрбмчастйом случае выражение дай Механической сияы-втлйЧает-
ся от (4?40)'лй1йъ'ЗйакЬм1-s ’
‘,л;ИриЧ^ = const ДдстайДяемая вдели от источников э.- д. с» эйертк» за вй*
чё*бм "гёКлОВыХ ;П<йДр1>:*делйтСйгна две-равные пасти. Одна часть ’Идет пгчфк»
ращение энергии магнитного поля dWM, другая—иа механическую работу Fdx?
Уравнения (4.40) и (4.42) часто используются для нахождения механической
силы. Для того чтобы найти силу F, радо либо составить аналитическое вы-
ражение для магнитной энергий системы и продифференцировать его по из-
меняющейся координате, либо опытным путем снять зависимость магнитной
энергии от изменяющейся координаты и затем графически продифференци-
ровать ее. ’ . .- !
§ 78. Сила тяги электромагнита. Пусть якорь электромагнита иа неко-
торое расстояние х удален от ярма (рис. 91). И якорь, и ирмо выполнены из
мйгийтномягкого материала и иеиасыщеиы. Обо-
значим площадь поперечного сечения двух воз-
душных зазоров через S. Подсчитаем энергию
магнитного’ пОля, запасенную в воздушном зазо-
ре, пренебрегав выпучиванием силовых линий.
Магнитная энергия в воздушном зазоре будет
ВН
равна произведению
объем воздушного
нитным полем:
плотности энергии на
зазора (вз) Sx, занятый маг-
ВН
Как уже отмечалось, и якорь, и ярмо вы-
полнены из магнитиомягкого материала и нена-
сыщены. Поэтому напряженность поля в них в
сотии и даже тысячи раз меньше, чем напряжен-
ность поля в воздушном зазоре при одной и той
же магнитной индукции. Следовательно, магнит-
ная энергия в якоре н ярме, если воздушный зазор не очень мал, составляет
лишь небольшую часть от магнитной энергии, запасенной в воздушном за-
зоре
4* ^яя и ярма w
Для определения силы воспользуемся формулой (4.40), т. е. подсчитаем силу
при условии неизменности магнитного потока:
г \dWM\* ВН В* „
F = —— =—- S =-------S.
| dx I 2 2pe
Подставим р0 = 1,256 • 10“• гн/м и возьмем В в тл. Получим
F(h) = 0,398 - 10»-B?m4) SW. (4.43)
Физически якорь и ярмо испытывают механическую силу (стремятся сбли-
зиться) вследствие того, что они представляют собой как бы огромное коли-
* Силу вычисляем по модулю. Получаемый по формуле (4.40) знак ми-
нус свидетельствует о том, что сила получена за счет убыли энергии магнит-
ного поля.
Если вычислить силу по формуле (4.42), исходя из неизменности тока,
то можно убедиться в том, что она будет обратно пропорциональна квадрату
расстояния х.
199
;<$<лдо,1давр(жогаческн! мадых коятуровс ^окдми, ,
Механическая сила возникает вследствие взаимодействия микротоков в
якоре с микротоками в ярме.
Лример 42. Сопротивление R обмотки электромагнита (ш = 900), рнс. 91
равно 13,8 см. ,,
Пренебрегая потоком рассеяния и выпучиванием магнитных линий в зазоре,
определить величину э. д. с. Е источника питания, при которой якорь Элект-
ромагнита будет притягиваться; к ярму с силой F = 100 кГ = 981 л; 3=2-20=
= 40 (си2); 4 = 55сл; х = 0,2 см; 1Я = 15 см. Якорь и ярмо выполнены из
магнитномягкого материала, кривая намагничивания которого дана на рис. 70.
Решение. По формуле (4.43) находим
В = п [-------------------= -1/----------——-------------- = 0,785 (тл).
у 0,398 . 10е • S у 0,398• 10" • 40 • 1О-* ’ ' '
, По закону полного тока У, UM = Jw:
^UM= 0,8.10«.ВЯ1Л.2х+(11+11!)Яс = 0,8.0,785.10«.4.10-з-{-0,7.120 = 2589 (в).
Ток
1 = = 2589 _ 2 €73
w 900
Э. д. с.
E = /R = 40e.
§ 79. Закон электромагнитной инерции. Правило Ленца. В 1883 г.
русский акад*. Э. X. Ленц установил закон электромагнитной инер-
ции, получивший название закона или правила Ленца. Формули-
руется он следующим образом: при всяком изменении магнитного
потока, сцепляющегося с каким-либо проводящим контуром, в по-
следнем возникают силы электрического и механического характера,
стремящиеся сохранить постоянство магнитного потока.
«Силу электрического характера» следует понимать в том смыс-
ле, что при всяком изменении магнитного потока, сцепленного с зам-
кнутым проводящим контуром, в этом контуре возникает индукти-
рованная э.д.с., которая стремится вызвать в контуре ток, препят-
ствующий изменению потокосцепления контура.
Механическая сила, воздействующая на контур, будет препят-
ствовать изменению линейных размеров контура или повороту кон-
тура.
Рассмотрим эти силы на примере.
Пример 43. Перпендикулярно равномерному и неизменному во
времени магнитному полю (рис. 81) индукции В = 1,5 тл распо-
ложен прямой провод длиной / = 0,5 м. Гибкими проводниками он
соединен с нагрузкой RH. Полное сопротивление замкнутого кон-
тура R пусть будет 20 ом. Если провод будет неподвижен, то в нем
ПО
не наведется э.д.с. и на него не будет Действовать МёхйИич^кйя
сила. . Г
Если же провод начнет двигаться, например влево, со скоростью
= 10 м/сек, так что контур будет оставаться замкнутым, то в нем
наведется Э.д.с. (см. формулу (4.5))
е ^Blv„ = 1,5 • 0,5 • 10 = 7,5 (в);
и по проводу, пойдет ток
I = 0,375 а.
R
При движении провода влево поток в контуре от внешнего маг-
нитного поля возрастает. Индуктированный ток (направлен по ча-
совой стрелке) будет вызывать магнитное поле, направленное встреч-
но внешнему полю, и будет препятствовать росту потока контура.
На провод действует механическая сила. Эта сила направлена
противоположно скорости ип и также стремится сохранить постоян-
ство магнйтного потока;.
Глава пятая
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО
СИНУСОИДАЛЬНОГО тока
§80. Синусоидальный ток и основные характеризующие его вели-
чины. Синусоидальный ток представляет собой ток, изменяющийся
во времени по синусоидальному закону
i = Im sin + ф) = /т sin (at + if). (5.1)
График его дан на рис. 92. Максимальное значение функции назы-
вается амплитудой. Амплитуда тока обозначается /т; Т—период
колебания, т. е. время, за которое совершается одно полное коле-
бание.
Частота
f = Y . (5-2)
равна числу колебаний за одну секунду. Измеряется f в \/сек илн
герцах (гц).
Величина
л <• 2зт
со = 2л/ = у
называется угловой частотой и измеряется в рад/сек или в \/сек.
Аргумент синуса, т. е. величина (at + ф) называется фазой.
Фаза характеризует состояние колебания (т. е. численное значение
величины) в данный момент времени t.
Значение фазы при t = 0, т. е. угол ф, называется начальной
фазой.
Любая синусоидально изменяющаяся функция вполне опреде-
ляется тремя величинами: амплитудой, угловой частотой и началь-
ной фазой:
Наибольшее практическое распространение в СССР и в Запад-
ной Европе получили установки синусоидального тока частоты 50 ец,
»2
которая принята за стандартную*. В QUA стандартной является час-
тота 60 гц. Вообще же диапазон частот практически применяемых
синусоидальных токов очень широк. Он начинается с долей герца,
например в геологоразведке, до многих миллиардов герц в радио-
технике.
Синусоидальные токи и э.д.с. сравнительно низких частот (приб-
лизительно до нескольких килогерц) получают обычно при помощи
вращающихся машин — синхронных генераторов, которые изучают-
ся в курсе электрических машин. Синусоидальные токи и э.д.с.
высоких частот получают при помощи ламповых генераторов, под-
робно изучаемых в курсе радиотехники и менее подробно во второй
части курса ТОЭ. Принцип получения синусоидальной э.дс.
путем вращения витка с постоянной, угловой скоростью в равно-
мерном магнитном поле рассматривался в примере 33 (при а = 0).
Генератор синусоидальной э.д.с.
на электрических схемах обозна-
чают в виде кружка со знаком
синусоиды ~ и изображенной ря-
дом стрелкой. Стрелка дает на-
правление, принятое для э.д.с. за
положительное.
§ 81. Среднее и действующее зна-
чения синусоидально изменяющей-
ся величины. Под средним значе- Рис. 92
нием синусоидально изменяющейся
величины понимают среднее значение ее за полпериода. Так, сред-
нее значение тока
Т/2
j/msin<o/d/ = -bm, (5.4)
: У °
2
т. е. среднее значение синусоидального тока составляет —= 0,638
Л
от амплитудного. Аналогично
£ — £ Е • U —— U
^ср ‘-‘mi иср ит‘
Л Л
Очень широко применяется понятие действующего значения си-
нусоидально изменяющейся величины (его называют также эффек-
тивным или среднеквадратичным). Действующее значение тока
' ° ° (5.5)
- • -* В электроэнергетике. „
ИЗ
Следовательно, действующее значение синусоидального тока равно
<У,:707 от амплитуды. Аналогично . >
£ = —= Ж
У2 /2
Можно сопоставить тепловое действие синусоидального тока с
тепловым действием постоянного тока 1„ост, текущего то же время
по тому же сопротивлению.
Количество теплоты, выделенное за один период синусоидальным
током, равно
г
J т 2
0
Выделенная за то же время постоянным током теплота равна
RI2nocmT. Приравняем их:
т = RFnocmT И®1 ^пост =' / = ;
2 у"2 .
Отсюда слёХует, что действующее значение синусоидального тока
I численно; равно значению такого постоянного тока, который за
время, равное периоду синусоидального тока, выделяет такое же
количество теплоты, что и синусоидальный ток.
Большинство измерительных приборов показывает действующее
значение измеряемой величины*.
§ 82. Коэффициент амплитуды и коэффициент формы. Познакомимся
с понятиями коэффициента амплитуды (ka) и коэффициента формы (кф).
Коэффициент амплитуды представляет собой отношение амплитуды периоди-
чески изменяющейся функции к ее действующему значению. Так, для
синусоидального тока
(5.6)
Под коэффициентом формы понимают отношение действующего значении пе-
риодически измениющейся функции к ее среднему за полпериода значению.
Для синусоидального тока
fteS=^'==li7=^r=al’ll**‘
Я ,т
(5.7)
* Действующее значение измеряют приборы электромагнитной, элект-
родинамической к тепловой систем. Принцип действия измерительных при-
боров различных систем изучается в курсе электрических измерений.
** Для несииусондальных периодических токов ка #=]Л2 и 1,11.
Отличие ка от У~2 и кф от 1,11 позволяет судить отом, насколько иесинусо-
идальиый ток отличается от синусоидального.
114
; § 83.Изображение синусоидально изменяющихся величин векто-
рами на комплексной плоскости. Комплексная амплитуда. Комплекс
действующего значения. Рассмотрим вопрос об изображении си-
нусоидально меняющихся функций векторами на комплексной плос-
кости. На рис. 93 изображена комплексная плоскость. На ней могут
быть изображены комплексные числа. Комплексное число имеет
действительную и мнимую пасти. По оси абсцисс комплексной плос-
кости будем откладывать действительную часть комплексного чис-
ла, по оси ординат — мнимую часть. Условимся на оси действитель-
ных значений ставить значок +1, а на оси мнимых значений зна-
чок 4- j (/ = V — 1).
Из курса математики известна формула Эйлера
= cos а 4- / sin а. (5.8)
Комплексное число ^“ изображается на комплексной плоскости
вектором, численно равным единице и составляющим угол а с осью
вещественных значении (осью 4- 1). Угол а
отсчитывается против часовой стрелки от
оси 4-1. Модуль функции е1а равен единице.
Действительно,
j/cos2«4-sin2a = 1.
Проекций функции eja на ось 4-1 рав-
на cos а, а проекция на ось 4- / равна sin а.
Возьмем теперь'Вместо функции е>а функцию
Imeia. Очевидно, что
/m^«^4cosa4-/7msina. Л
На комплексной плоскости эта функция, так же, как и” функция
eia, изобразится под углом а к оси 4" 1. но величина вейтбра бу-
дет в 1т раз больше.
Угол а в формуле (5.8) может быть любым. Положим, что
а т. е. положим, что угол а изменяется прямо: про-
порционально времени. Тогда
1т = cos 4- ц,) 4- j/m sin (at + ф). (5.9)
Слагаемое /„cos (at 4~ ф) представляет собой действительную часть
(Re) выражения /„е;<т<++):
/„cos (at 4~ Ф) = Re/„e/(“<’w>,
а фуйкция 7„sin(w/-|_’‘l5) есть коэффициент при мнимой части
(Im) выражения т- е.
' ' " е‘ 1 i = /ЯШ(М+‘Ф) := Im/„e/M+4), \ ;-(5.10)
Д+5
под которым вектор 1т
'Такилс ;образб»7 можно ’утверждать," что .сийугощймъ1к>“иам^’?
няющийся ток i (ср. формулы 5.1 и 5.10) может быть йрёдетай*'*
лен как ImZme^(m/+<,') или, что. то же самое, как проекция враща-
ющегося вектора 7„е/ на ось 4- / (см. рис. 94).
Для единообразия принято на комплексной плоскости изобра-
жать векторы синусоидально изменяющихся во времени величин
для момента времени <ot = 0. Для этого момента времени вектор
будет равен -г'
" .7 * (5.П)1
где 1т есть комплексная величина, модуль ее равен 1т, а угол,
, проведен к оси -j-1 на комплексной
плоскости, равен начальной фазе ф. "
Величину 1т называют комплексной амп^
литудой тока i. Комплексная амплитуда
изображает ток i на комплексной плос-
кости для момента времени <at =0. . Wc-1
смотрим Два численных примера На пере-
ход от мгновенного значения тока к ком-
плексной амплитуде и от комплексной ам-
плитуды к мгновенному значению.
Пример 44. Ток i = 8 sin (соТ-|-20°) а.
Записать выражение комплексной ампли-
туды этого тока.
В данном случае 1т = 8а, ф = 20°. Следовательно, 1т = 8 е^°’.
Пример 45. Комплексная амплитуда тока 1т = 25 е~^°а. За-
писать выражение мгновенного значения этого тока. , , ’
.РеЩение. Для перехода от комплексной амплитуды к мгно-
венному значению надо умножить tm на efmt и взять коэффи-
циент при мнимой части от полученного произведения (см. форму-
лу 5.10)
i = Im 25е-/30° elmi = Im 25e'w-30°’ = 25 sin (<ot — 30°).
Под комплексом действующего значения тока или, проще, под
комплексом тока (комплексным током) 1 понимают частное от ле-
чения комплексной амплитуды на 1^2:
/ - -Izl = /"L. = 1еМ.
/2 V2
Пример 46. Записать выражение комплекса действующего зна-
леиия тока для примера 44.
М»^ = 5,67Л -
§ 84. Сложение й вычитание синусоидальных функций времен»
при помощи комплексной плоскости. Положим, что необходимо сло^
U6
(5.12)
жить два TOKa.4it в ij одной и той же частоты. Сумма их дает неко-
торый ток/той же частоты
i = /14_|2‘,
•.•<i = 4*sin(«rf + l’i); G = /amsin(®/4-i|)a); '
J, ’? i =7„sin («>/-f-ф).
Требуется найти амплитуду Im и начальную фазу ф тока i.
С этой целью ток ix изобразим на комплексной плоскости (рис. 95)
вектором 11т .== IlmeJ\ а ток t3 вектором /2т = /а„Л Геоме-
трическая сумма векторов 11т и /2ж даст комплексную амплиту-
ду суммарного тока /„ = 7Амплитуда тока lm буррт оп-
ределяться длиной суммарного вектора, а начальная фаза ф уг-
лём, составленным этим вектором и осью -|- 1,
Для определения разности двух токов (или э.д.с., напряжений)
надо на комплексной плоскости п)роизвести не сложение, а; вычи-
тание соответствующих векторов.
Обратим внимание на то, что если бы векторы 11т, и Гт, изображенные
на рис. 95, мы стали вращать иокруг начала координат с угловой скоростью
<о, то взаимное расположение векторов по отношению друг к другу осталось
бы без изменений.
§ 85. Векторная диаграмма. Векторная диаграмма представляет
собой совокупность векторов на комплексной плоскости, изобража-
ющих собой синусоидально изменяющиеся функции одной и той же
частоты, построенных с соблюдением правильной ориентации отно-
сительно друг друга по фазе.
Рис. 95 представляет собой пример векторной диаграммы.
§ 86. Мгновенная мощность. Протекание синусоидальных токов
по участкам электрической цепи сопровождается потреблением энер-
гии от источников. Скорость поступления энер-
гии характеризуется мощностью. Условимся
под мгновенным значением мощности или, ко-
роче, мгновенной мощностью понимать произве-
дение мгновенного значения напряжения и на
участке цепи на мгновенное значение тока I,
протекающего по этому участку
р = ui, (5.13)
где р есть функция времени..
Перёд тем как приступить к изучению ос-,
нов расчета сложных цепей синусоидального
тока, обсудим соотношения между токами и
напряжениями в простейших цепях, векторные
диаграммы для, них и кривые мгновенных значен
ЛИЧИН' /
Рис. 95
различных ве-
Составными элементами цепей синусоидального тока являются
активное сопротивление R, индуктивность L и емкость С; 1 ‘
Термин «сопротивление» для цепей синусоидального тока, в от-
личие от цепей постоянного тока, оказывается недостаточно полным,
поскольку сопротивление переменному току оказывают не только
те элементы цепи, в которых выделяется только энергия в виде теп-
лоты (их условимся называть активными сопротивлениями), но и
те элементы цепи, в которых энергия в виде теплоты не выделяется,
но периодически запасается энергия в электрическом или магнит-
ном полях. Такие элементы цепи условимся называть реактивными,
а сопротивления, оказываемые ими переменному току, реактивными
сопротивлениями. Реактивным сопротивлением обладают индуктив-
ности и емкости (подробнее см. § 88 и 89).
§ 87. Синусоидальный ток в активном сопротивлении. На рис. 96
представлено три эскиза. На первом из них (рис. 96, а) изображено
активное сопротивление R, по которому течет ток i=/ffl sinco/.
По закону Ома напряжение •
и — iR = Rlm sin a>t '
или ’ :
u= (/msin©/, (5.14)
где Um = RIm.
Комплекс тока I и совпадающий с ним по фазе комплекс напря-
жения U изображены на векторной диаграмме рис. 96, б.
На рис. 96, в даиы кривые мгновенных значений тока i, напря-
жения и й мгновенной мощности р
р = Umlm sin wt&in&t = (1—cos2®Z).
, Мгновенная мощность имеет постоянную составляющую —
и составляющую cos 2ш/, изменяющуюся с частотой 2<о. По-
требляемая от источника питания за время dt энергия равна pdt.
§ 88. Индуктивность в цепи синусоидального тока. Практически
любая обмотка (катушка) обладает некоторой индуктивностью L
и активным сопротивлением R. На схеме катушка может быть пред-
ставлена в виде последовательного соединения индуктивности L и
активного сопротивления R.
Выделим из схемы одну индуктивность L (без активного со-
противления) — рис. 97, а. Если через L течет ток i = Im sin &t,
то в катушке наводится э. д. с. самоиндукции eL .
6l — — = C0S s*n (®^ — 90е)"
Положительное направление э.д.с. eL на рис. 97, а обозначено
стрелкой, совпадающей с положительным направлением токай
118
... Зайдем разность потенциалов между точками а и Ь.
При перемещении от точки Ь к точке а идем встречно э.д.с, е£,
поэтому ' .
Фа = ф» — eL> следовательно, иаЬ = Фа — ф»=— eL.
Положительное направление напряжения иаЬ совпадает с поло-
жительным направлением тока.
В дальнейшем индексы а и b у напряжения на индуктивности
(падения напряжения на индуктивности) ставить не будем
uat = u = —eL. (5.15)
Следовательно,
и = (oL/msin(«>/-|-900) = sin (со/90°); (5.16)
Произведение ©L обозначается XL и называется индуктивным со-
противлением
XL = aL. (5.17)
Размерность [XL] = Jco] [L] = сект1 • ом • сек = ом.
Таким образом, индуктивность оказывает переменному току соп-
ротивление, равное XL = ю£. Оно прямо пропорционально частоте.
Кроме того, важно подчеркнуть, что напряжение на индуктивности
опережает по фазе ток на 90° (см. формулу 5.16). Это обстоятельство
на векторной диаграмме рис. 97, б нашло свое выражение в том, что
вектор напряжения I) опережает вектор тока / на 90°. Комплекс
Э.Д.С: самоиндукции Ёь находится в противофазе, с комплексом на-
ряжения .(/.
JI9
Трафики мгновенных значений t, и, р изображены нй'рис. 97, в.’
Мгновенная мощность
р = ui = Um cos и/ lm sino>/ = ЧтЬи sjn 2o>t
Она проходит через нулевое значение, когда через нуль проходит
либр, и, либо i. За первую четверть периода, когда и й i положитель-
ны, р также положительна. Площадь, ограниченная кривой р
и осью абсцисс за это время, представляет собой энергию, которая
Рис. 98
взята от источника питания и
пошла на создание анергии
магнитного поля в индук-
тивности.
Во вторую четверть перио-
да, когда ток в цепи умень-
шается от максимума До ну-
ля, энергия магнитного по-
ля отдается обратно источ-
нику питания, при этом
мгновенная мощность отри-
цательна. За третью четверть
периода от источника снова
забирается энергия, за чет-
вертую отдается и т. д., т. е.
энергия периодически то за-
бирается индуктивностью от
источника, то отдается ему
обратно.
§ 89. Конденсатор в цепи
синусоидального тока. Если
приложенное к конденсатору
напряжение во времени не
меняется, то заряд q — Си на
одной его обкладке и заряд
— q= — Си на другой (С—ем-
кость конденсатора)* неизме-
нен и через конденсатор не проходит тока (i = — = о\» Иначебу-
\ dt /
дет обстоять дело, если напряжение на конденсаторе меняется во
времени, например по синусоидальному закону (рис. 98, а)
u = i/msin(o/. (5.18)
В этом случае по синусоидальному закону будет меняться заряд
q конденсатора: q = Си = CUm sin ш/, и конденсатор будет перио-
* Емкость как элемент схемы замещения реальной цепи дает возможность
учитывать в расчетном смысле явление зарядки конденсатора и накопление им
энергии (о емкости см. также § 407 в III части курса).
120
днч^скц^терезаряжаться. Периодическая перезарядка конденсатора
вызовет протекание через него зарядного тока < j
! = Й = — (CUmsintot) =
.dt dt т ’
= 4>CUm cos tot = toCUm sin (at -j- 90°). (5.18')
Положительное направление тока черед конденсатор на схеме
рис. 98, а совпадает с положительным направлением напряжения.
Из сопоставления (5.18) и (5.18') видно, что ток черед конденсатор
по фазе опережает напряжение на конденсаторе на 90°. Поэтому на
векторной диаграмме рис. 98, б вектор тока / опережает вектор нап-
ряжения {/„да 90°. Амплитуда тока 1т равна амплитуде напряжения
Um, поделенной на емкостное сопротивление Хс
*с = Л. (5.19)
©С
Действительно,
/ —мСП t)m _ит
' t ~Хс-
toC
Емкостное сопротивление обратно пропорционально частоте
и измеряется в омах. Графики мгновенных значений и, I, р изобра-
жены на рис. 98, в. Мгновенная мощность
р — ui = Ч-Ш-Ш sin 2иЛ
2
За первую четверть периода конденсатор потребляет энергию от ис-
точника питания. Эта энергия идет на создание электрического по-
ля в конденсаторе. Во вторую четверть периода напряжение на кон-
денсаторе уменьшается от максимума до нуля, и запасенная в элект-
рическом поле энергия отдается источнику (мгновенная мощность
отрицательна). За третью четверть периода энергия снова запасает-
ся, за четвертую отдается и т. д.
Если проинтегрировать по времени обе части равенства
1 = С~,
dt
то получим
и » 1 J idt. (5.20)
Равенство (5.20) позволяет определить напряжение на конденсаторе
черед ток по .конденсатору.
' При изложении вопроса о прохождении синусоидального тока через кон-
денсатор предполагалось, что диэлектрик, разделяющий пластины конден-
сатора, является идеальным диэлектриком, в котором нет потерь энергии.
Одиако при приложении синусоидального напряжения к пластинам конден-
сатора, разделённым твердым или жидким диэлектриками, в последних веег-
121
да имеются иеиоторые потери энергии. Эти потерн относительно малы и ими
часто, можно пренебречь. Если требуется учесть их в расчете, то . конденсатор
заменяют расчетной схемой замещении, изображенной на рис. 98, г. В этой
схеме параллельно емкоств С присоединено активное сопротивление R, по-
тери энергии в котором имитируют потери'энергии в реальном диэлектрике.
Ток / через конденсатор равен геометрической сумме Двух токов: тока 4
через емкость, на 90° опережающего напряжение t/ на конденсаторе (рис. 98, д'),
н Относительно малого по величине тока 4 через активное сопротивле-
ние R, совпадающего по фазе с напряжением 0.
Таким образом, ток через конденсатор е иеидеальным диэлектриком опе-
режает напряжение на угол, немного менывий 90°. Угол 8, который составляет
ток I с током 4, принято называть углом потерь. Он зависит от сорта диэлек-
трика и от частоты и составляет в лучшем случае несколько севунд, в худ-
шем — несколько градусов. Величина tg8 дается в таблицах (см. стр. 717),
характеризующих свойства различных твердых и жидких диэлектриков.
§ 90. Умножение вектора на j и на — J.
. *J . Пусть есть некоторый вектор Л = Ле/<Ра (рис.
у4 99). Убедимся в том, что умножение его на
х. ‘ / j дает вектор, по модулю равный А, йо по-
- х/ _ вернутый в сторону опережения (против: ча-
х. + / совой стрелки) по отношению к исходному
. . вектору А на 90°. Умножение А на (— j)
~JA поворачивает вектор А на 90° в сторону от-
Рис. 99 ставания (по часовой стрелке) также без из-
менения его модуля.
Чтобы убедиться в этом, представим вектор J и вектор — / в
показательной форме:
/ = 1.е^=^;
Тогда
= Ае;Фае?90° = Ле/(Фа+9°в); (5.21)
— Aj = Ае^ае~’^° = Ае’{^~^. (5.22)
Из (5.21) следует, что вектор /А, по модулю равный А, со-
ставляет с осью -j-1 комплексной плоскости угол фй-(-90о, т. е.
повернут против часовой стрелки на 90° по отношению к век-
тору А.
Аналогично из (5.22) вытекает, что умножение вектора А*
на (— /) дает вектор, по модулю равный А, но повернутый по
отношению к нему на 90° по часовой, стрелке.
§ 91. Основы символического метода расчета цепей синусдовдль-
ного тока. Исключительно широкое распространение на практике
Получил метод расчета цепей синусоидального тока, который при-
нято называть символическим или комплексным методом.
Сущность символического метода расчета состоит в том, что для
режима синусоидального тока можно перейти от уравнений, состав-
ленных для мгновенных ’значений и являющихся по сути дела диф-
ференциальными уравнениями (см. уравнение 5.23), к алгебраичес-
ким уравнениям, составленным относительно комплексов тока и
э.д.с. Этот переход основан на том, что в любом уравнении, со-
ставленном по законам Кирхгофа для установившегося про-
цесса, мгновенное значение тока i заменяют комплексной
амплитудой тока 1т, мгновенное значение напряжения на актив-
ном сопротивлении /?, равное /?/, заменяют комплексом /?/от, по фа-
зе совпадающим с током /и, мгновенное значение напряжения на
индуктивности и, — L— заменяют комплексом опережаю-
ь at
щим ток на 90°. Мгновенное значение напряжения на емкости
u„= — С idl заменяют комплексом /' ( , отстающим от тока
с С J....... \ <оС /
на 90°. Мгновенное значение э.д.с. е заменяют комплексом Ёт.
Справедливость замены = £ — на следует из § 88
dt . 4
и § 90.
Действительно, в § 88 было показано, что амплитуда напря-
жения иа индуктивности равна произведению амплитуды тока
на Хд = <в£; Присутствие множителя / говорит о том, что вектор
напряжения на индуктивности опережает вектор тока на 90®.
Аналогично из § 89 следует, что амплитуда напряжения на
емкости равна амплитуде тока, умноженной на = — . Отста-
вание напряжения на емкости от протекающего по ней тока
на 90° привело к появлению множите-
ля — /. /
Например, для схемы рис. 100 уравне- _г—xZnrUI
ние для мгновенных значений запишется Д d-j* £ ’V
так: X
«я4-«д + “с=в
или
//? 4- L С idf = е. (5.23)
Рис. 100
Запишем его в комплексной форме
/т/? 4- + =
Вынесем /т за скобку
(5.24)
Следовательно, для схемы рис. 100 .
Ёт
Im j
•• --
Последнее уравнение позволяет найти комплексную амплитуду
тока ]'т через комплексную амплитуду э.д.с. Ет и сопротивле-
ния цепи /?, аЬ и —.
ч>С
Метод , называется символическим потому, что ток. и, каждое
напряжение заменяются своими комплексными изображениями
или символами.
Так, есть изображение или символ падения напряжения
iR, je>Lim есть изображение или символ падения напряжения на
индуктивности uL = L — \------- 1т есть изображение падения
ь dt <оС
напряжения на конденсаторе ± idt.
Переход от уравнения (5.23) к уравнению (5.24) может быть проведен и
другим путем, более строгим, ио и более громоздким. Рассмотрим этот путь.
В (5.23) вместо тока i подставим его эквивалент Im lm elmt и вместо е Irn£„e,mt
Получим . .
R 4- £ 3; Im 4- ~ f Im /те,0>* di = Im Ё e'mt.
er C J
Операция дифференцирования по времени функции imeiat и операция
взятия мнимой части (Im) от этой функции взаимно переместимы, т. е. совер-
шенно безразлично, в какой последовательности совершать эти операции: взять
ли сначала миимую часть от функции lm а затем продифференцировать
полученное выражение по времени или сначала продифференцировать функцию
lm etwt по времени, а затем взять мнимую часть от продифференцированной
функции — результат будет одинаков.
Аналогичное заключение справедливо и по отношению к интегралу по
времени от функции lme,,at. Поэтому можем записать
I -J Im lm = L Im у lm е iat= Im / »L1 (5.25)
at - at
± f Im/m e,0>* dl =-7 Im f s . (5,26)
Постоянную интегрирования при взятии интеграла опустили, так как прн
установившемся синусоидальном токе и отсутствии постоянной составляющей
в э.д.с. е напряжение иа конденсаторе не содержит постоянной составляю-
щей.
Перепишем уравнение (5.23) с учетом (5.25) и (5.26):
Im R 1т 4. Jm /®£/да e/<u' 4- Im Im № = Im Ёт ei<at; (5.27)
124
lmlR + ^L + -^}lfnef(Bi==Yrn&fn^t. (5.28)
\ № )
Если бы э. д. с. е и ток i в цепи рис. 100 изменились не по синусоидально-
му закону, а по косинусоидальному:
• \ е =т=.Дп COS , ..
и
< = /<nCos(<o/4-|f),
вйейо Уравнения (5.28) аналогичным путем было бы Получено уравнение
(5.29). • у. г
. , !?е(л+^+ (5.29)
Умножим обе части уравнения (5.28) иа / и, сложив с (5.29), получим
Re ( R + /ш£ + —) 1т е1ш*+ i Im ( R + frL + ) 1т е1а>‘ =
\ J(dG / \ /0>G /
= ReEOTe/'°<-f-/ImEme/<B<
ИЛИ
(я + /ш L + -тМ 4 еМ = Ёт e,at. (5.30)
\ /ши /
Физически уравнение (5.30) описывает два независимых и одновременно
происходящих в цепи рис. 100 процесса, а именно: протекание синусоидаль-
ного тока /от sin (ш / + ф;) под действием э. д. с. Еи sin (<о / + фе) н протека-
ние косинусоидального тока lm cos (tot ф,) под воздействием э. д. 6.
Ет cos (<ot + фе). Амплитуды токов 1т и фазовые углы фе и ф, в этих двух
режимах одинаковы. Процессы происходят независимо друг от друга, так как
цепь рис. 100 линейна и параметры /?, L, С не зависят от токов.
Поэтому наложение на исследуемый режим, режим протекания синусо-
идального тока Im sin (ш/ 4- ф;) под действием э. д. с. Ет sin (cot фД второго
режима не влияет на амплитуду и фазу тока первого режима. В уравнении
(5.39) сократим множитель e,a>i, не равный нулю, учтем, что
й Получим
1 _ /__L_=_±.
/шС / /шС ш С
( R + 4 = Ет
\ Ши /
(5.31)
Уравнение (5.31) совпадает с уравнением (5.24).
§ 92. Комплексное сопротивление. Закон Ома для цепи синусо-
идального тока. Вернемся к уравнению (5.24). Множитель /? Ц- jaiL —
— -L представляет собой комплекс, имеет размерность сопротив-
шС
125
ления, обозначается через 1 (зет большое) и называется комплекс-
ным сопротивлением , \
Z=ze/4, = /?+/o)L —-i- (5.32)
(йС '
Как и всякий комплекс, Z может быть представлен в показательной
форме. Модуль комплексного сопротивления принято обозначать
через z (зет малое). Несмотря на то, что Z является комплексом, точ-
ку над ним не ставят: точку принято ставить только над такими ком-
плексными величинами, которые изображают собой синусоидаль-
ные функции времени. ’
Уравнение_(5.24) запишется так; = Ёт, Поделим обе час-
ти его на К2 и перейдем от комплексных амплитуд /т и Ёт к
комплексам действующих значений I и Ё
/ = f. (5.33)
Уравнение (5.33) представляет собой закон Ома для. цепи сину-
соидального тока. '.. , '
В общем случае Z имеет некоторую действительную часть /? и
некоторую мнимую часть ]Х
Z = R + jX, (5.34)
где R — активное сопротивление, X — реактивное сопротивление.
ДлЯ схемы рис. 100 X = <oL------—.
§ 93. Комплексная проводимость. Под комплексной проводимостью
Y понимают величину, обратную комплексному сопротивлению Z
Y=± = g~jb = ye^9- -- <5.35)
Измеряется комплексная проводимость в ом~1 или сименсах. Дейст-
вительная часть ее обозначается через g, мнимая—через Ь. Так как
Z R+jX R2 + X2 R2 + X2 ‘ IF + X2 6 J
TO
g=-*—, b=-*—,
IV+X2 R2 + X2
(5.36)
Если X положительно, то и b положительно, при отрицательном
X b также отрицательно.
При использовании комплексной проводимости закон Ома (см.
5.33) запишется так: . . > >,
/ = (7У
или
l=ug-jUb = ia+\L
(5.33')
126
Здесь 1а называют активной составляющей тока, /г -^ реактивней
составляющей тока; U — напряжение на участке цепи, сопротивле-
ние которого равно Z.
§ 94. Треугольник сопротивлений и треугольник проводимостей.
Из (5.34) следует, что модуль комплексного сопротивления
' г=:у^+х\ (5.37У
Следовательно, z можно представить как гипотенузу прямоуголь-
ного треугольника (рис. 101) —треугольника сопротивлений, —
один катет которого равен /?, другой X:
. tgq> = £. . (5.38)
А
Аналогичным образом, модуль комплексной проводимости в соот-
ветствии с (5.36) у = К g2 + b2. Следовательно, у есть гипотенуза
прямоугольного треугольника (рис. 102),
катетами которого являются активная g
и реактивная б проводимости:
tg<p = -. (5.30)
g
Треугольник сопротивлений дает
графическую интерпретацию связи меж-
ду модулем полного сопротивления г и
активным и реактивным сопротивления-
ми цепи. Аналогично, треугольник проводимости — графическая
интерпретация связи между модулем полной проводимости у и ее
активной и реактивной составляющими.
§ 95. Применение логарифмической линейки для перехода от ал-
гебраической формы записи комплекса к показательной и для обрат-
ного перехода. При расчете цепей переменного тока все время при-
ходится иметь дело с комплексными числами. Действительно, сопро-
тивление участка цепи или цепи в целом — это комплекс, проводи-
мость — комплекс, ток, напряжение, э. д. с. —комплексы. Для со-
вершения такой простой операции, как нахождение тока по закону
Ома, надо комплекс э. д. с. разделить на комплекс сопротивления.
Из курса математики известно, что комплексное число может
быть представлено в трех формах записи: алгебраической а + jb,
показательной celv и тригонометрической с coscp -f- jc sinq>.
Сложение двух и большего числа комплексов удобнее всего про-
изводить, пользуясь алгебраической формой записи. При этом по-
рознь складываются их действительные и мнимые части:
(а1 ~Ь /М + (аз + /^з) + (аз — /М — (а1 + а1 + аз) +
+ / (^1 + — Ь-Л-
127
уДобиеевсепонрОиз-
водить, пользуясь показательной формой записи. Пусть,- например,
наДо'поделить комплекс на. комплекс са/ф*. В результате деле-
Нйя будет получен комплекс cad<t*
с е/^=‘ - •/ ', г'-
Модуль результирующего комплекса (с8) равен частному —»
а аргумент <р8 = <pi — <ра, При умножении двух комплексов ctei9i
и csei4>’ результирующий комплекс
ciel4,‘ — c1el's’‘ сйе1ч>а = с1сае/(*'+ч>’).
При расчетах электрических цепей часто возникает потребность
в переходе от алгебраической формы записи комплекса к показатель-
ной или в совершении обратного перехода.
Наиболее удобный путь Для этого — применение логарифмиче-
ской линейки.
Пусть задано комплексное число a + jb. Из предыдущего (§ 92
и 94) ясно, что а и Ь есть катеты прямоугольного треугольника,
а гипотенуза его с = у/о2 4- Ьа. Частное от деления меньшего ка-
тета на больший катет дает тангенс меньшего острого угла прямо-
угольного треугольника, а деление меньшего катета на синус мень-
шего угла дает гипотенузу треугольника или модуль комплекса.
Эти соображения положены в основу определения модуля и ар-
гумента комплекса по его алгебраической форме a +/6 при помоши
логарифмической линейки.
С этой целью движок линейки повертываем обратной стороной,
так что на лицевой части линейки будет та сторона движка, на кото-
рой написаны «сннус» и «тангенс».
Последовательность операций нахождения аргумента и модуля
следующая:
1. Значение меньшего по абсолютной величине катета отклады-
ваем на основной нижней шкале линейки и против него ставим рис-
ку визира.
2. Значение большего катета откладываем также по основной
шкале и против него ставим конец движка. Этим произведено Деле-
ние меньшего катета на больший.
3. По шкале тангенсов против риски визира отсчитываем вели-
чину наименьшего угла прямоугольного треугольника.
4. Не сдвигая визира, перемещаем движок так, чтобы против
риски визира пришелся' только что найденный угол на шкале «си-
нус». Последняя операция есть деление меньшего катета на си*
нус меньшего угла.
128
5. Модуль комплекса (гипотенуза прямоугольного треугольни-
ка) отсчитывается против конца шкалы движка по основной ниж-
ней шкале линейки.
Переход от показательной формы к алгебраической совершается
в обратной последовательности. Для того чтобы не совершить ошиб-
ки при записи показательной формы комплекса, рекомендуется сна-
чала качественно изобразить заданный своей алгебраической фор-
мой комплекс на комплексной плоскости. Это построение позволит
правильно выразить угол между осью + 1 н вектором через угол,
найденный по линейке. Углы против часовой стрелки от оси + 1 счи-
таются положительными, по ча-
совой стрелке — отрицательны-
ми.
Пример 47. Перевести в по-
казательную форму следующие
комплексы: а) 3 + 2/; б) 2 + 3/;
в) 4 — 5/; г)— 6 — 2/; д)—9,2+
+ 0,4/; е) 10 — /0,8.
Решение, а) Ставим ви-
зир против цифры 2 на нижней
шкале линейки и конец движка
против цифры 3. По шкале тан-
генса находим угол 33°40'. Пе-
редвигаем движок так, чтобы
против риски визира на шкале
синусов пришелся угол 33°40'.
Отсчет по нижней шкале против
конца шкалы движка дает мо-
дуль 3,6. Вектор 3 + 2/ качест-
венно изображен на рис. 103, а.
осью + 1 н
вектором равен
Из рисунка видно, что угол между
33°40'. Поэтому 3 + 2/ = 3,6 е/33°40'.
б) По линейке находим угол 33°40' и модуль 3,6. Диаграмма на
рис. 103, б. Угол между осью + 1 н вектором равен 90° — 33°40' =
= 56°20'. Следовательно, 2 + 3/ = 3,6е/56 20 .
в) Линейка дает угол 38°40' и модуль 6,4. Из диаграммы рис. 103, в
видно, что вектор находится в четвертом квадранте. Угол между
осью +1 н вектором- равен—5Г20'. Таким образом.
4-5/ = 6,4а-'5’020'.
г) По линейке определим угол 18°35' н модуль 6,32. Из диаграм-
мы рис. 103, г видно, что угол между осью + 1 и вектором может
быть выражен двояко: либо как — (180° — 18°35') — — 16Г25',
либо как + (180° + 18°35') = 198°35'. Поэтому
— 6 — 2/ = 6,32е~Л61025' = 6,32?198035', •
5 Л. А. Беесоноа
д) Линейка дает угол 26°35' и модуль 0,448. Вектор находится во
втором квадранте (рис. 103, д). Следовательно, — 0,2 + / 0,4 =
= 0,448е/116^'.
е) Этот случай принципиально отличается от рассмотренных вы-
ше тем, что составляющие комплекса (катеты прямоугольного тре-
угольника) по абсолютной величине различаются более, чем на поря-
док. При этом гипотенуза прямоугольного треугольника практичес-
ки равна большему катету, а угол определяется по средней шкале
движка. Линейка дает угол 4°40', угол находится в четвертом квад-
ранте (рис. 103, е). Поэтому 10—/0,8?^ 10е~/4 4° .
§ 96. Законы Кирхгофа в символической форме записи. По пер-
вому закону Кирхгофа алгебраическая сумма мгновенных значений
токов, сходящихся в любом узле схемы, равна нулю, т. е.
Е/ = 0. (5.40')
Заменим в этой сумме каждый ток его комплексным изображением
/, получим
S/ = 0. . (5.40)
Уравнение (5.40) представляет собой первое уравнение Кирхгофа
в символической форме записи.
Обсудим, далее, символическую форму записи второго закона
Кирхгофа.
Для любого замкнутого контура сколь угодно сложной электри-
ческой цепи синусоидального тока может быть оставлено уравнение
по второму закону Кирхгофа для мгновенных значений токов, напря*
жений и э.д.с. :
Пусть замкнутый контур содержит п ветвей и каждая (А) ветвь
вобщем случае включает в себя э.д.с. ек, активное сопротивление
индуктивность Lk и емкость Ckt по которым протекает ток ik. Тогда
по второму закону Кирхгофа ,
п п
Но каждое слагаемое левой части уравнения, в соответствии с § 92,
можно заменить на а каждое слагаемое правой части на Ек. i
Поэтому уравнение (5.4Г) переходит в следующее: |
Л л
. = S4. (5-41) I
k = \ . ]
Уравнение (5.41) представляет собой второй закон Кирхгофа в сим-
волической форме записи. 1
§97. Применение к расчету цепей синусоидального тока всех мето-
дов, обсуждавшихся в главе «Электрические цепи постоянного тока».
130
Для анализа и расчета электрических цепей постоянного тока раз-
работан ряд методов и приемов, облегчающих решение по сравне-
нию с решением системы уравнений, составленных путем непосред-
ственного использования законов Кирхгофа. Из главы первой из-
вестно, что к числу таких методов относятся, например, метод кон-
турных токов, метод узловых потенциалов, метод хх и кз и т,. д.
Из главы первой известно также, что окончательные расчетные
формулы этих методов получены в результате выводов, в основе ко-
торых были первый и второй законы Кирхгофа.
Поскольку первый и второй законы Кирхгофа справедливы и для
цепей синусоидального тока, то можно было бы записать уравнения
для мгновенных значений величин цепей синусоидального тока,
перейти от них к уравнениям в комплексах и затем повторить вывод
всех формул главы первой и для цепей синусоидального тока.
Разумеется, проделывать выводы заново нет необходимости.
В том случае, когда отдельные ветви электрической цепи сину-
соидального тока не будут связаны между собой магнитно, все рас-
четные формулы главы первой будут пригодны и к расчету цепей
синусоидального тока, если в них вместо постоянного тока / под-
ставить комплекс тока /, вместо проводимости g— комплексную про-
водимость Y, вместо сопротивления А?—комплексное сопротивление
Zu вместо постоянной э.д.с. Е—комплексную э.д.с. Ё.
Если же отдельные ветви электрической цепи синусоидального
тока связаны друг с другом магнитно — это будет иметь место при
наличии взаимоиндукции, — то падение напряжения на каком-ли-
бо участке цепи будет зависеть не только от тока данной ветви, но
и от токов тех ветвей, с которыми данная ветвь связана магнитно.
Это обстоятельство приводит к тому, что расчет электрических цепей
синусоидального тока при наличии в них магнитносвязанных вет-
вей приобретает ряд особенностей, которые не будут учтены, если
в формулах главы первой непосредственно заменять Е на Е, R на Z
и g на Y. Особенности расчета магиитиосвязанных цепей будут обсу-
ждаться в § 113.
§ 98. О применении векторных диаграмм при расчетах электри-
ческих цепей синусоидального тока. Токи и напряжения на различ-
ных участках электрической цепи синусоидального тока, как пра-
вило, по фазе не совпадают. Наглядное представление о фазовом рас-
положении различных векторов дает векторная диаграмма токов
и напряжений. Аналитические расчеты электрических цепей сину-
соидального тока рекомендуется сопровождать построением вектор-
ных диаграмм. Они дают возможность качественно контролировать
аналитические расчеты.
качественный контроль заключается в сравнении направлений
различных векторов на комплексной плоскости, которые получают-
ся из аналитического расчета, с направлением этих векторов, ис-
ходя из физических соображений. -
5*
‘131
Например, на векторной диаграмме напряжение UL на индуктив-
ности L должно опережать протекающий через нее ток на 90°, а на-
пряжение на емкости Uc должно отставать от протекающего через
нее тока на 90°.
Если аналитический расчет будет давать результаты, не совпа-
дающие с такими очевидными положениями, то, следовательно, в
него вкралась ошибка, которая должна быть найдена и устранена.
Кроме того, векторная диаграмма часто используется также и как
Рис. 104
средство расчета, например в мето-
де пропорциональных величин.
Рассмотрим несколько примеров.
Пример 48. В схеме рис. 104, а
задана э.д.с. е = 141 sin at (в) и па-
раметры схемы: 7?х= 3 ом; /?а=2 ом;
L = 0,00955 гн. Угловая частота
и=314 сек~1. Определить ток и напря-
жения на элементах цепи.
Решение. Запишем уравне-
ние для мгновенных значений:
at
Перейдем от него к уравнению в
комплексах '
+ j®Ll = Ё
или
1Z = E, где Z = + #а + jaL = 3-f-2-f-/314.0,00955 =
= 5-]-3/= 5,82?31°.
Комплекс действующего значения э.д.с.
i’-yy = "«(«)
Находим
Напряжение на сопротивлении Rt
URt = Ua6 = = 51,6е-'3,°л.
Напряжение на сопротивлении 7?а
URi = = /7?а = З4,4е-'31°в.
Напряжение на индуктивности
UL = Uca = jaLi = 3/ • 17,2е-/3|° = 51,6е/59°в.
132
Векторная диаграмма изображена на рис. 104, б. Вектор Ё направ-
лен по оси + 1. Ток отстает от него на 31°.
Пример 49. Решить задачу примера 48 методом пропорциональ-
ных величин.
Решение. Зададимся током в цепи в 1 а и направим его на
векторной диаграмме рис. 104, в по оси 4-1 (/ — 1). Напряжение
на активном сопротивлении Rr будет совпадать по фазе с током и чис-
ленно равно 1 3 = 3 (в). Напряжение на Т?2 также будет совпадать
с током и равно 2 в. Напряжение на индуктивности равно Зе и опе-
режает ток на 90°. Из прямоугольного треугольника следует, что
при токе в цепи в 1 а на входе должна быть э.д.с.
/б2 + З2 = 5,82 (в).
Так как на входе действует э.д.с. в
100 ,
Раза больше, то
все токи и напряжения должны быть умножены на коэффициент
17,2. На векторной диаграмме рис. 104, в все векторы повернуты на
ЗГ против часовой стрелки по сравнению с соответствующими век-
торами на векторной диаграмме рис. 104, б. Ясно, что взаимное рас-
положение векторов на диаграмме при этом не изменилось.
Пример 50. В цепи рис. 105, а включены последовательно актив-
ное сопротивление н емкость: R=4 ом‘, угловая частота со—105 сек-1.
Определить величину емкости С, если при э.д.с. Е = 10 мв ток
в цепи был 2 ма.
Решение. Комплексное сопротивление цепи
Z = R------j—-
аС
Модуль его
По закону Ома
/ = -.
г
Отсюда
„ Е 10.10-3
z = — = —-----— — 5 (ом).
I 2.10-» ’
Следовательно,
Хс = — = Vz* — R* = V 52 —42 = 3
соС
с = -— = —1— = 3,33 (мкф).
®ХС 10». 3 '
Векторная диаграмма изображена на рис. 405, б.
133
Пример 51. На участке ab разветвленной цепи рис. 106, а парал-
лельно включены индуктивное сопротивление XL — &L и активное
сопротивление R, численно равное Хд. Показание амперметра Ла
равно 5 а. Определить показание амперметра Л3, полагая сопротив-
ления амперметров настолько малыми, что их можно не учитывать.
Решение. На рис. 106,6 качественно построим векторную
диаграмму. Напряжение Uab совпадает по фазе с током /а, Ток /г
отстает от тока 7а на 90° и равен ему по величине. Ток в нераз-
ветвленной части схемы 13 — /2. Модуль тока 13 равен
5И2 — 7,05 (а). Амперметр А3 покажет 7,05 а.
Пример 52 а. Построить векторную диаграмму токов и напря-
жений для схемы рис. 107, а, если ток /j = 1 а; = 10ом\
u>L.= Юолс; — = 14,1 о.и; aL3— 20 ом и R3 = 2,5 ом.
а>С
Решение. Обозначим токи и выберем положительные направ-
ления для них в соответствии с рис. 107, а. Выберем масштаб для
токов trij — 0,5 а/см и масштаб для напряжений 4 в/см. Ток
/| направим по оси -{-I (рис. 107,6). Падение напряжения О R
чиеленно равно 10 в и по фазе совпадает с током /х. Падение на-
пряжения в индуктивном сопротивлении cdAx также равно 10 в, НО
опережает ток /х на 90°. Геометрическая сумма по мо-
дулю равна 10 И2 = 14,1 (в). Емкостный ток /а опережает это
напряжение на 90°.
Модуль тока
, 14,1
1, = —— = 1 (а).
2 14,1 '
Ток в неразветвленной части цепи равен геометрической сумме
токов 73= /х+4. Модуль его равен 0,8 а (найдено графически).
Падение напряжения на сопротивлении R3 равно 2 в я совпадает
134
по фазе с током. Падение напряжения на индуктивности L9
опережает ток /3 на 90° и численно равно 0,8.20 = 16(e). Напря-
жение на входе схемы равно э.д.с. и составляет—18,3 в.
Пример 526. Решим теперь задачу, обратную рассмотренной
в п^мере 52 а.
Пусть в схеме рис. 107, а опытным путем были найдены значе-
ния токов Ilt и /8 (в ветви схемы включили амперметры и запи-
сали их показания): Il=la, 1а, /3^а0,8а и опытным путем
Рис. 107
бьиш определены три напряжения, а именно: напряжение на входе
схемы, равное э. д. с. Е — 18,3 в, напряжение на емкости Uc = 14,1 в
(оно же напряжение на первой ветви) и напряжение U8 на третьей
ветви (на /?3 и L3) U9 — 16 в. Напряжения были определены путем
подключения вольтметра поочередно к зажимам а и е, а и с, е и с.
Требуется по опытным данным (по значениям трех токов и
трех напряжений) .достроить векторную диаграмму.
Решение. На рис. 107,в отложим вектор равный 14,1 в.
Для сопоставления с рис. 107,6 расположим его на диаграмме так
же, как он расположен на рис. 107,6.
Изобразим на диаграмме ток /2. Он на 90° опережает напря.
жение йс и по модулю равен 1а. После этого можно построить на
диаграмме токи и /3, воспользовавшись тем, что три тока (/г, /3 и
/^ образуют замкнутый треугольник (см. рис. 107, 6).
133
Для построения треугольника по трем сторонам (т. е. фактически
для определения третьей вершины его) из конца тока /2 (из одной
вершины треугольника) проводим дугу радиусом, равным току Iv
а из начала тока /а (т. е. из второй вершины треугольника) прово-
дим дугу радиусом, равным току 13.
Точка пересечения этих дуг дает искомую третью вершину тре-
угольника, т. е. точку, в которой оканчиваются векторы токов /Зи
После того, как на диаграмме определено положение тока /3,
можно изобразить на ней векторы напряжения U3 и э. д. с. Е.
Напряжения Uc, U3 и э.д. с. Е также образуют замкнутый тре-
угольник. Для построения его поступаем, как и при построении
треугольника токов.
Из конца вектора Uc проводим дугу радиусом, равным U3, а из
начала вектора ис — дугу радиусом, равным Е. Дуги пересекаются
в двух точках: в точках е и f.
Так как напряжение (J3 представляет собой падение напряже-
ния от тока 13 на последовательно соединенных R3 и L3, то оно
по фазе должно опережать ток /3, а не отставать от него,
Поэтому из двух точек (е и [) выбираем точку е (если бы выбрали
точку f, то в этом случае напряжение 03— см. пунктир на
рис. 107, в — отставало бы от тока /3, а не опережало его).
В заключение отметим, что в треугольнике токов дуги тоже
пересекаются в двух точках, но вторая (лишняя) точка на рис. 107, в
не показана.
§99. Изображение разности потенциалов на комплексной плоскос-
ти. Потенциалы цепи переменного тока являются комплексными
числами. На комплексной плоскости комп-
лексное число можно изображать либо точ-
кой, координаты которой равны действи-
тельной и мнимой частям комплексного по-
тенциала, либо вектором, направленным от
начала координат к данной точке плоскости.
В качестве примера на рис,. 108 пред-
ставлены два вектора, изображающие со-
бой комплексные потенциалы
фа = —2 + 5/ и Ф» = 4 + /.
По определению, разность потенциалов £/в»=фв—ф» = —6 +
+ 4j; Uab изобразится вектором, направленным от b к а. Первый
индекс у напряжения (в нашем примере индекс а) указывает, к ка-
кой точке следует направить стрелку вектора напряжения. Естест-
венно, что
А,= -0at.
136
§100. Топографическая диаграмма. Каждая точка электрической
схемы, в которой соединяются друг с другом сопротивления, имеет
свое значение комплексного потенциала.
Совокупность точек комплексной плоскости, изображающих со-
бой комплексные потенциалы одноименных точек электрической
схемы, называется топографической диаграммой.
Термин «топографическая» объясняется тем, что диаграмма напо-
минает топографическую карту местности. На топографической
карте каждой точке местности отвечает определенная точка. Рас-
стояние между двумя точками на местности может быть определено
путем измерения расстояния между одноименными точками на
карте.
Аналогичные измерения могут быть проведены и на топографи-
ческой диаграмме. Напряжение между любыми двумя точками элек-
трической схемы, например между точками а и Ь, по величине и на-
правлению определяется вектором, проведенным на топографичес-
кой диаграмме от точки b к точке а.
При построении топографической диаграммы, как и при построе-
нии потенциальной диаграммы (см. § 9), потенциал любой одной точ-
ки схемы может быть принят равным нулю. На диаграмме эта точ-
ка помещается в начало координат. Тогда положение остальных
точек схемы на диаграмме будет, вполне определенным. Оно будет
определяться параметрами цепи, э.д.с. и токами ветвей. Рассмот-
рим пример иа построение топографической диаграммы.
Пример 53. По данным примера 52а построить топографическую
диаграмму для схемы рис. 107, а.
Решение. Обозначим буквами а, Ь, с,... точки схемы
рис. 107, а, которые хотим отобразить на топографической диаграмме.
Примем потенциал точки а равным нулю:
Ф« = 0.
Выразим потенциал точки Ь через потенциал точки а:
<Р«+10-
Плюс перед слагаемым I1Rl объясняется тем, что при переходе от
точки а к точке b перемещаемся против тока Точка Ь на диаграм-
ме будет иметь координату по оси абсцисс + 10. Аналогично
Фс = Ф» + ijnLi =• Ю + /Ю;
Фй = фс + Л^3;
Фе = Ф« + 4/®^8.
Совокупность точек a, b, с, d, е на комплексной плоскости рис. 109
и представляет топографическую диаграмму для схемы рис. 107, а.
- 137
По ней удобно определять величину напряжения между любыми
двумя точками схемы и сдвиг по фазе этого напряжения по отноше-
нию к любому другому напряжению*. .
Рассмотрим примеры на применение метода узловых потенциалов
и метода контурных токов.
Пример 54. Найти токи в схеме рис. ПО методом двух узлов. По-
ложительные направления э. д. с. указаны на схеме стрелками:
ег = 120 К2 sin и/ в; е3 — 100 К2 sin (со/— 30°) в; /? = 2олс;
—— = 10 ом; a>La = 5 ом.
соС2
Рис. 1-09
Рис. ПО
Решение. Запишем э.д.с. в комплексной форме:
4 = 120, Ея= МОГ'3"*.
Выберем положительные направления для токов в ветвях к узлу а.
Определим проводимости ветвей: - , . в
Y. = — = — = 0,5 сим; У2 = — = —= 0,1/сим;
1 Zj 2 Z2 —10/ '
Ya = — = — = —0,2/ сим.
Z3 5/ '
Напряжение между узлами а и b (ср. с формулой 1.20):
'(j = i2o.o,5 + iooe-/3°Q-o,2e-/90° = 104е-/8«в
аЬ Yi + Yi+Уз 0,5+0,1/-0,2/ ’
Ток
/t e = 120-104е-'8 = g 5 .7 25 j 1j17^40«25- а.
Z. 2
* Следует иметь й виду, что никакого графического подобия между топо-
графической диаграммой и электрической схемой, для которой она построена,
как правило, нет.
138
i _ — = 1ООе~/зо1> — 104е~/8° _
3 Z3 Ь}
100 (cos 30° — / sin 30°) — 104 (cos 8° — / sin 8°) _ — 16,2 — 35,5/
5/ 5/
Рис. 111
Пример 55. Найти токи в схе-
ме рис. 111, а методом контур-
ных токов и построить топогра-
фическую диаграмму: Ёг = 100 в
Ёъ = 100е/9О° в;
= 2 ом;
с аС
R = аЬ — 5 ом.
Решение. Выберем направ-
ления контурных токов /и и /аа
по часовой стрелке. Запишем в
общем виде уравнения для контур-
ных токов (ср. с уравнениями 1.4'):
Л1^21 4~ ^22^22 = ^22.
Здесь Zlt есть собственное сопро-
тивление первого контура
= = 5-2/;
(0G
Zaa — собственное сопротивление второго контура;
^22 ~ R 4" /®^-= 5 —5/.
Zia = Zai — сопротивление смежной ветви между первым и вто-
рым контурами, взятое с обратным знаком
Zia = — R = — 5;
Ёа равна алгебраической сумме э.д.с. первого контура
£^=^=100;
£аа равна алгебраической сумме э.д.с. второго контура
£аа = — = — 100/.
Следовательно,
139
/и(5-2/)-5/22 = 100;
-5/и4->гг(54-/5) = -100/.
системы
(5-2/) -5
-5 (54-5/) ’ '
/ = —•
11 д’
(5 — 2/) 100
— 5 —100/
Д,=
Определитель
= 104-15/= ISe'’56”20';
Д2 —
г ___ ^2.
1м ” д’
= 300 — 500/ = 582е~/59°;
= 500;
100 —5
- 100/ (5 4-5/)
/ At 500 97 о -/56°20'
/н=7 = ^7»- = 27.^ «;
; Да _ 582е~/59° ч _/115°20' „
/аг = Т = 32,3
Ток в сопротивлении R (направлен от точки b к точке т)
1и - = а.
Топографическая диаграмма изображена на рис. 111, б.
§ 101. Активная, реактивная и полная мощности. Под активной
мощностью Р понимают среднее значение мгновенной мощности р за
период Т
т т
P = ^pdt = ^uidt. ' (5.42)
о о
Если ток i — Im sin at, напряжение на участке цепи и =
= Z7msin (at 4-ф), то
т
Р = J lmUm sin и/sin (at -j- <p) dt = eos <р = UI cos ф. (5.43)
о
Активная мощность физически представляет собой энергию,
которая выделяется в единицу времени* в виде теплоты на участке
цепи в сопротивлении R. Действительно, произведение U совф =
= //?; следовательно,
Р = PR. (5.44)
Активная мощность измеряется в ваттах (вт.)
Предполагается, что в 1 сек укладывается целое число периодов Т.
140
Под реактивной мощностью Q понимают произведение напряже-
ния U на участке цепи, на ток / по этому участку и на синус угла <р
между напряжением U и током /
Q = LVsin<p. (5.45)
Реактивную мощность принято измерять в «вольтамперах реак-
тивных»— сокращенно, вар. Если sin<p > 0, то и Q > 0, если
sin ф < 0, то Q < б.
Рассмотрим, что физически представляет собой реактивная мощ-
ность. С этой целью возьмем участок цепи, на котором последователь-
но соединены /?, L и С. Пусть по нему протекает ток i = Im sin со/.
Запишем выражение для мгновенного значения суммы энергий маг-
нитного и электрического полей цепи:
sin2 со/ +
С/2 „ 7/2
+ 2(^)2 cos2 со/= (1 — cos2co/)4-
72
+ w5(1+“s2“')-
Из полученного выражения видно, что WM3 имеет постоянную
составляющую Wяа, неизменную во времени, и переменную сос-
тавляющую изменяющуюся с двойной угловой частотой:
W — W —wM3;
ж= — + —~ И wM3 =--------------------cos 2co/.
мэ* 2 2cd«C i \ 2 2o2C /
На создание постоянной составляющей была затрачена
энергия в процессе становления данного периодического режима.
В дальнейшем при периодическом процессе энергия №мэ остается
неизменной и, следовательно, от источника питания не требуется
доставки энергии на ее создание.
Среднее значение энергии wM3, поступающей от источника за
Т ~ т
интервал времени от------до -|-----, равно
f w^dt=n{LI2~'^ =
= — ЦХ. — Xr) = — UI 5Шф= — Q.
ж» ь с жо жо
(5.46)
141
Таким образом, реактивная мощность Q пропорциональна сред-
нему за четверть периода значению энергии, которая отдается ис-
точником питания на создание переменной составляющей электри-
ческого и магнитного поля индуктивности и емкости.
За один период переменного тока энергия WMg£^ дважды отдает-
ся генератором в цепь и дважды он получает ее обратно.
Другими словами, реактивная мощность характеризует собой
ту энергию, которой обмениваются генератор и приемник.
Полная (кажущаяся) мощность
S = UI. (5.47)
Она измеряется в вольт-амперах, сокращенно ва. Между Р, Q и S
существует соотношение
Р2 + Q2 = S2. (5.48)
Можно графически представить эту связь в виде прямоугольного
треугольника (рис. 112), треугольника мощности, один катет ко-
торого равен Р, другой катет равен Q и гипоте-
.. нуза S.
Ъ/у На щитке любого источника электрической
р энергии переменного тока (генератора, транс-
I форматора и т. д.) указывается величина S. Она
? характеризует ту мощность, которую этот ис-
Ряс. 112 точиик может отдавать потребителю, если пос-
ледний будет работать при cos ф = 1 (т. е. будет
представлять чисто активное сопротивление).
§ 102. Выражение мощности в комплексной форме записи. Пусть
задан некоторый комплекс
А = Ае^л = A cos фл jA sin <рд.‘
Под комплексом А, сопряженным с комплексом А, будем пони-
мать комплекс
А — Ae~j4lA == A cos <рл — jA sin <рл.
Рассмотрим простой прием определения активной и реактивной
мощностей через комплекс напряжения и сопряженный комплекс
тока. Напряжение на некотором участке цепи обозначим через
U = Uei<iu, ток по этому участку / = . Угол между напря-
жением и током <р = <рц — фр Умножим комплекс напряжения на
сопряженный комплекс тока I — le jWi и обозначим полученный
комплекс через S
S = t/Z=Z/Ze><<V4’P = Ulei'f = UI cos ф + jUI sin ф = P -|- /Q. (5.49)
Значок— (тильда) над S, означает, что речь идет о комплексе (а не
142
(5.50)
о сопряженном ; комплексе) полной мощности, составленном при
участии сопряженного комплекса тока I.
Таким образом, активная мощность Р есть действительная часть
(Re), а реактивная мощность Q есть мнимая часть (Im) пройзве-
, *
дения и!
Р = Ке£77;
Q = ImUI.
Пример 56. Определить активную, реактивную и полную
мощности по данным примера 48.
Решение. Напряжение на входе всей схемы равно э.д.с.:
й = Ё = 100 в.
Ток в цепи 7 = 17,2е"^31°а.
Сопряженный комплекс тока / — 17,2^31°.
S = (H= 100-17,2^31° = 1720cos31° + / 1720 sin 31°= 1475+/886,
ReZ7/= 1475, Im67 = 886.
Следовательно, активная модность Р = 1475 вт, реактивная
Q = 886 вор и полная S = 1720 ва. '
§ 103, Измерение мощности ваттметром. Измерение мощности
производится обычно при помощи ваттметра электродинамической
системы. Последний представляет собой прибор, в котором в маг-
нитном поле неподвижной катушки может вращаться подвижная
катушка, жестко скрепленная со стрелкой — указателем.
Неподвижная катушка выполнена из достаточно толстого прово-
да, имеет очень малое сопротивление и называется в дальнейшем
последовательной обмоткой. Она включается в цепь последователь-
но, подобно амперметру. Подвижная катушка выполнена из очень
гонкого провода, имеет’практически чисто активное сопротивление и
называется в дальнейшем параллельной обмоткой. Она включается
'• параллельно участку цепи, подобно вольтметру.
На электрической схеме ваттметр изображается в виде кружка
с буквой W, из которого выходят четыре конца (рис. 113). Одна па-
ра концов на рисунке (обычно горизонтальные концы) принадлежит
последовательной обмотке, другая пара концов — на рисунке это
обычно вертикально расположенные концы — параллельной. На
концах одноименных зажимов обмоток принято ставить звездочки.
Вращающий момент ваттметра, а следовательно, и показание
его пропорциональны скалярному произведению напряжения Uab
на параллельной обмотке на ток /, протекающий по последователь-
ной обмотке.
143
Напряжение на параллельной обмотке берется равным разности
потенциалов между концом ее, имеющим звездочку (точка а на рис.
113) и вторым концом ее, не имеющим звездочки (точка Ь).
Ток / входит в конец последовательной обмотки, имеющий звез-
дочку.
При записи скалярного произведения, выражающего собой пока-
зание ваттметра, над векторами напряжения и тока ставим черточ-
ки. Так, показание ваттметра (рис. 113^ определяется скалярным
произведением Uab I = UabI cos Как правило, ваттметр
включают в схему так, что измеряемое им скалярное произведение
напряжения на ток оказывается активной модностью.
Рис. 113
Рис. 114
Однако в специальных случаях включения скалярное произве-
дение напряжения на ток может дать и не активную модность, а
реактивную (подробнее об этом см. в § 144).
Цена деления ваттметра определяется как-частное от деления про-
изведения номинального напряжения на номинальный ток — они
указываются на лицевой стороне прибора — на число делений
шкалы.
Пример 57. Номинальное напряжение ваттметра 120 в. Номиналь-
ный ток 5 а. Шкала имеет 150 делений. Определить цену деления
ваттметра.
§ 104. Двухполюсник в цепи синусоидального тока. На схеме
рис. 114 изображен пассивный двухполюсник, включенный к источ-
нику э. д. с. Входное сопротивление двухполюсника <
В общем случае
ZeX^ReX+jXeX = ze^
Если ХвХ > 0, то входное сопротивление имеет индуктивный ха-
рактер, при XsX <0 — емкостный и при Хвх =. 0 чисто активный.
1.4+
Входная проводимость Увх представляет собой величину, обратную
входному сопротивлению
У = —.
л 6Х 7 *
^вх
Входное сопротивление может быть определено либо расчетным
путем, если известна схема внутренних соединений двухполюсника
и значения сопротивлений, либо опытным путем.
При опытном определении входного сопротивления двухполюс-
ника собирают схему рис. 115, а. В ней амперметр измеряет ток /,
вольтметр напряжение Uab = U на входе двухполюсника. Ваттметр
равно активной мощности Р = UI coscp. Модуль входного сопро-
тивления г—у-. Деление Р на произведение/J// дает косинус
Р
угла между напряжением и током cos ф = —.
По косинусу угла находится sin ф и затем определяются
Rex = z cos ф и Хйх — z sin ф.
Так как косинус есть функция четная, т. е. cos (—ф) = cos ф, то
обсуждавшиеся выше измерения для определения входного соп-
ротивления должны быть дополнены еще одним опытом, который поз-
волил бы путем сопоставления показаний амперметра в двух опытах
определить знак угла ф.
Для определения знака угла ф параллельно исследуемому двух-
полюснику путем замыкания ключа К. подключают небольшую ем-
кость С (рис. 115, а).
Если показания амперметра при замыкании ключа Д' станут
меньше, чем они были при разомкнутом ключе, то угол ф положи-
телен, и входное сопротивление Z = ze/4> имеет индуктивный харак-
тер (этому случаю отвечает векторная диаграмма рис. 115, б).
Если показания амперметра при замыкании ключа станут боль-
ше, то ф отрицательно, и входное сопротивление имеет емкостный
характер (векторная диаграмма рис. 115, а).
145
На диаграмме рис. 115, бив обозначено: /—ток через двухполюс-
ник, 1С — ток через емкость, который на 90’ опережает напряже-
ние U на входе двухполюсника. Пунктиром изображен ток через
амперметр при замкнутом ключе. Сопоставление пунктиром изоб-
раженного тока с током I и дает возможность сделать приведенное
выше заключение.
Пример 58. Измерения по схеме рис. 115, а дали: U — 120 в;
/ = 5 а; Р = 400 вт.
Замыкание ключа К. приводило к уменьшению показаний ватт-
метра. Определить входное сопротивление двухполюсника.
Решение. Модуль входного сопротивления
г = — = 24 ом\ cos и = — = = 0,666; sin ф = 0,745;
I UI 120-5 > > т > >
Rex = 2 cos ф = 24-0,666 = 16 (ол);
Хвх = гэшф = 24-0,745 = 17,9 (ом).
Комплекс входного сопротивления
Zex = (16+/17,9) ом.
§ 105. Резонансный режим работы двухполюсника. Пусть двух-
полюсник содержит одну или несколько индуктивностей и одну или
несколько емкостей. Под резонансным режимом (или режимами) ра-
боты такого двухполюсника понимают режим (или режимы), при
котором входное сопротивление двух-
Дк подюсника является чисто актив-
ным*.
г £ С | По отношению к внешней цепи
* L~l—^~Т~И— двухполюсник в резонансном режиме
а) ведет себя как активное сопротивле-
+J ние, поэтому ток и напряжение на
входе двухполюсника совпадают по
/ X J фазе.
— Г >----Реактивная мощность двухполю-
\ / *1 сника при этом равна нулю.
\ / Различают две основные разновид-
f) ности резонансных режимов — резо-
• нанс токов и резонанс напряжений.
Ркс’ 6 § 106. Резонанс тбков. Явле-
ние резонанса в схеме рис. 116, а,
образованной двумя параллельными ветвями с разнохарактерными
реактивными сопротивлениями, называют резонансом токов. Пусть
* Отсюда следует, что для определения условий наступления резонанса
надо приравнять нулю мнимую часть комплекса входного сопротивления
двухполюсника.
Такой способ определения условий наступления резонанса справедлив,
если не пренебрегать активными сопротивлениями индуктивных катушек.
146
первая ветвь имеет активное сопротивление Rx и индуктивное <о£,
а вторая ветвь — активное R, и емкостное —.
<оС
Ток /х первой ветви отстает от напряжения U — Uab (см. рис.
116, б) и может быть записан так:
/>^ = (7^-/^).
Ток /а второй ветви опережает напряжение
А = &¥ч, — U (ёч ~
Ток в неразветвленной части цепи
i — 4+h — й (ё\+ёч) — (^i + ь^.
По определению резонансного режима, ток / должен совпадать
по фазе с напряжением U. Это будет при условии, что сумма реак-
тивных проводимостей ветвей равна нулю:
bt -J- ь2 — о.
В соответствии с (5.36), 1
V e£ „ . <оС = п И VO t' «?+«»»£* 2 р» к _А_ * w’C3
Следовательно, условие наступления режима резонанса токов в схе-
ме рис. 116, а запишется так:
а>£
/??+«2£2
1
аС
агъ2
(5.51)
На рис. 116, б изображена векторная диаграмма для резонансно-
го режима. Из (5.51) следует, что при = 0 резонанс наступит
при условии
ю£
/?1+<й2£2
= (оС.
(5.51Э
В еще более частном случае, когда R2 = 0 и 4С coL, резонанс нас-
тупит при
<o2LC « 1. (5.51")
Резонанса можно достичь путем изменения co, L, С или путал из-
менения и /?2. Ток в неразветвленной части схемы по величине
может быть меньше, чем токи в ветвях схемы. При R2 = О и
Rx ~ 0 ток / может оказаться ничтожно малым по сравнению с то-
ками /х и /2. ........... ‘
И7
В идеализированном, практически не выполнимом режиме рабо-
ты, когда = /?2 = 0, ток в неразветвленной части схемы равен ну-
лю, и входное сопротивление схемы оказывается равным бесконеч-
ности.
Обратим внимание еще на следующее. В формулу (5.51) входит
пять величин (L, С, R2, со). Если определять из нее L или С, то'
может оказаться, что
Рис. 117
для искомой величины будут получены два
действительных значения. Получение двух
действительных значений для L и С сви-
детельствует о том, что при неизменных
четырех параметрах изменением пятого
параметра можно получить два резонанс-
ных режима (пояснения к возникновению
двух резонансных режимов при изменении
одного параметра и неизменных остальных
дается в примере 70 на стр. 176).
Если для искомой величины, например
для ю, будет получено мнимое значение,
то это свидетельствует о том, что при за-
данном сочетании четырех параметров из-
менением пятого нельзя достичь резо-
нанса.
Пример 59. В схеме рис. 116, а /?1=30 ом;
<dL = 40 ом; /?2 = 0; со = 103 сек-1. При ка-
кой емкости в схеме будет резонанс то-
ков?
Решение. По формуле (5.51)
Хе = -L- = e 62,5 (ом);
40 ' '
шС <x>L
С — 1 _____________
®*С 103-62,5
= 16 (мкф).
§ 107. Компенсация сдвига фаз. Входное сопротивление боль-
шинства потребителей электрической энергии имеет индуктивный
характер. Для того чтобы уменьшить потребляемый нми ток за счет
снижения его реактивной составляющей и тем снизить потери энер-
гии в генераторе и подводящих проводах, параллельно приемнику
энергии включают батарею конденсаторов.
Процесс уменьшения угла сдвига фаз между напряжением на
приемнике и током, потребляемым от генератора, называют компен-
сацией сдвига фаз.
§ 108. Резонанс напряжений. Резонанс в схеме последовательного
соединения 7?, L, С (рис. 117, а) называют резонансом напряжений.
При резонансе ток в цепи должен совпадать по фазе с э.д.с. Е.
Ток будет совпадать по фазе с э.д.с. Е, если входное сопротивление
схемы
148
будет чисто активным. Условие наступления резонанса в схеме
<552>
При этом I — Напряжение на индуктивности будет равно нап-
ряжению на емкости
U, — Ur = wLI = — U.
L С R
Отношение
' 9 - = о
R R
называют добротностью резонансного контура. Добротность пока-
зывает, во сколько раз напряжение на индуктивности (или на ем-
кости) превышает напряжение на входе схемы в резонансном
режиме.
Практически Q может доходить до 200 и даже больше. Век-
торная диаграмма для режима резонанса изображена на рис. 117, б.
§109. Исследование работы схемы рис. 117, а при изменении час-
тоты и при изменении индуктивности. Пусть в схеме рис. 117, а па-
раметры R, L, С и величина э.д.с. Е постоянны, но меняется частота
со. Обсудим характер изменения тока / и напряжений на индуктив-
ности UL и на емкости Uc в функции от со.
Ток в цепи
(5.53)
При изменении со меняется реактивное сопротивление цепи
со/. ——:
шС
и ток / -> 0;
Г Е
и ток / = —;
R
ток / -»0.
при СО* —> 0 X —> — ос
при со = —Д=г- X = 0
Н V LC
при СО —> ос X —> оо И
Чем меньше активное сопротивление резонансного контура при неиз-
менных остальных параметрах схемы, т. е. чем больше доброт-
ность контура Q, тем более острой (пикообразной) становится
* Стрелка -> заменяет слово «стремящийся» или, соответственно,' «стре-
мится».
149
форма кривой I — f (со). Напряжение на индуктивности U L = wLI.
При со — О UL — о> при со —* со UL Е (рис. 118, а). Не приве-
денный здесь подробный анализ показывает, что при Q > —7=
у 2
кривая UL (и кривая Uc) проходят через максимум, при Q<-^
V 2
кривая UL монотонно стремится к Е.
Напряжение на емкости Uc = / — при со -> О стремится к Е,
ПрИ со -*
женйя на индуктивности UL и максимум напряжения на емкости
Uc имеют место при частотах, не равных резонансной частоте
&р = • Максимум UL имеет место при частоте, большей чем
евр, а максимум Uc — при частоте, меньшей сор.
Если в схеме 117, а менять не частоту, а индуктивность L, то
зависимости /, UL в функции от XL = coL (со = const) изобразятся
кривыми рис. 118, б*.
Пример 60. В схеме рнс. 117, a R = 10 олс; L = 1 гн; С — \мкф.
Определить резонансную частоту, добротность Q, а также нап-
ряжение на емкости, если иа вход схемы будет подано напряжение
. 10 мв при резонансной частоте.
Решение. Резонансная частота ыр — со
со = -4= = — Ю3 (сек-1).
V LC К1О-“
Добротность
Q = — = = 100.
__________ 7? 10
Так как Uc— — I, а —- = const, то кривая Uc = f (coi) качёствен-
<яС »С '
но имеет такой же вид, что и кривая I = f (<bL).
150
Ток в цепи
г Е 0,01 1 / ч
/ = — = —-— = 1 (ма).
R 10
Напряжение на емкости
[7C = Q£= 100-0,01 = 1 (в).
§110. Частотная характеристика двухполюсника. Входное со-
противление двухполюсника и входная проводимость его есть функ-
ции частоты. Зависимости действительной и мнимой частей .вход-
ного сопротивления или входной проводимости двухполюсника от
частоты называют частотными характеристиками двухполюсника.
Частотные характеристики получили широкое распространение
в радиотехнике и связи. Они либо рассчитываются, если известна
схема внутренних соединений двухполюсника и значения активных
сопротивлений, индуктивностей и емкостей в ней, либо снимаются
опытным путем.
При снятии частотных характеристик опытным путем на вход
схемы подается напряжение, частота которого может меняться в ши-
роких пределах, и по результатам измерений подсчитывается дейст-
вительная и мнимая части входного сопротивления.
В схему двухполюсника могут входить последовательно и парал-
лельно соединенные индуктивности, емкости и активные сопротив-
ления. Наибольший интерес представляют частотные характеристи-
ки двухполюсников, составленных только из индуктивностей и ем-
костей. Если частота источника питания двухполюсника высока,
то индуктивные сопротивления катушек индуктивности оказываются
много больше собственных активных сопротивлений катушек, и для
упрощения построения частотных характеристик последними часто
пренебрегают. В такой идеализированной упрощенной схеме будут
только индуктивности иь емкости, и построение частотных характе-
ристик схемы резко упрощается.
В качестве примера рассмотрим построение частотных характеристик
двухполюсников, изображенных на рис. 119, а и а. Двухполюсник рис. 119, а
образован последовательно соединенными индуктивностью Lr и емкостью
Ci. Двухполюсник рис. 119, г — параллельным' соединением £2 и С2. При
построении частотных характеристик будем полагать, что в реактивных сопро-
тивлениях всех элементов, из которых составлены двухполюсники, отсутст-
вуют потери энергии. Входное сопротивление и входная проводимость для
двухполюсников рис. 119, а равны соответственно
1 \ у , 1
-----I > л = <oLi — ——— ;
<oCj / (nCi
, d = _L =---------.
-17 ‘ \ Х , 1
I <aL,-----— I coLj-----—
1 \ 1 <oCj / coC,
.Прямая 1 рис. 119, б изображает зависимость = /(<о). Кривая 2 — зависи-
мость ——- = / (со). Кривая 3 — зависимость X = f (со).
со С, ’
Г = -/б
. 151
. Значение ш = шо, при котором кривая 3 (рис. 119, б) пересекает ось абс-
Иисс, дает значение угловой частоты, при которой в двухполюснике рнс. 119, а
наступает резонанс напряжений.
При со < ©о входное сопротивление имеет емкостный характер (X отрица-
тельно), при со > шо входное сопротивление имеет индуктивный характер
(X положительно).
Так как реактивная проводимость для схемы рис. 119, а b =——
то кри-
вая b = f (со), изображенная на рис. 119, в, взаимнообратна кривой 3 рис. 119, б.
При со < соо входная проводимость имеет емкостный характер, при со > со0 —
индуктивный. В точке со = Шо кривая b = f (со) претерпевает разрыв от — оо до
4-оо. Для двухполюсника рис. 119, г входное сопротивление и входная прово-
димость соответственно равны:
/со£2 ( — —тг)
2 = jX =--------= . х (oL^ .
\ CO ct / 1 1
co C2 co C2
J cola
- 1
,, „ . 1—w2£2C2 , ®C2
у = -;& = -?--------------; &=—-----------
co La
Зависимости X =*f (co) и b ~ f (co) для схемы рис. 119, г изображены соответ-
ственно на рис. 119, д и е. При со =со'о реактивная проводимость b становится
равной нулю, а реактивное сопротивление претерпевает разрыв от 4- «до
— оо. При со = <о'о в двухполюснике рис. 119, г имеет место резонанс токов.
На основании изложенного можно сказать, что по виду характеристики
X — f (®) или характеристики b = f можно судить о том, какого типа ре-
зонансные режимы и в каком количестве будут возникать в исследуемой схе-
ме при изменении частоты от 0 до до.
152
Точки, в которых кривая (X = f (ш) пересекает ось абсцисс (или соответ-
ственно кривая b = f (ш) претерпевает разрыв от — <х> до + оо), дают зна-
чения угловой частоты, при которых в исследуемой схеме возникают режимы
резонанса напряжений.
Точки, в которых кривая X = f (ш) претерпевает разрыв от + оо до
— оо (или кривая b = f (ш) пересекает ось абсцисс), соответствуют режимам
резонанса токов.
В качестве иллюстрации сформулированного правила исследования пос-
троим частотные характеристики X = f (ш) и Ь = f (ш) для схемы рис. 119, ж
и по ним определим, какие резонансные режимы и в каком количестве воз-
можны в схеме при изменении частоты от 0 до оо.
Для двухполюсника рис. 119, ж реактивное сопротивление равно сумме
реактивных сопротивлений двухполюсников рис. 119, а и г. В соответствии
с этим ординаты кривой X = f (ш) для схемы рис. 119, ж получаем путем сум-
мирования ординат кривых X (со) рис. 119, б и д (см. рис. 119, з).
Зависимость Ь = f (ш) для схемы рис. 119, ж изображена на рис. 119, и.
Из рис. 119, а и и видно, что в схеме рис. 119, ж при увеличении частоты от О
до оо будет происходить следующее: при ш ==<0! возникает резонанс напря-
жений, при ш =<о2 — резонанс токов, затем при ш =<0з вновь возникает ре-
жим резонанса напряжений. При последующем увеличении частоты резонан-
сов в схеме не будет. Обратим внимание на то, что режимы резонанса токов и
резонанса напряжений чередуются.
§ 111. Передача энергии от активного двухполюсника нагрузке.
К зажимам ab активного двухполюсника рис. 120 подключена наг-
рузка Z„~RH + jXH. Требуется выяснить, при соблюдении каких
условий в нагрузке будет выделяться максимальная активная
мощность.
По методу хх и кз (§ 23) ток в нагрузке
г __ Ugb хх
%вХ + %н
Здесь ZM — Rax + jXax есть входное сопро-
тивление двухполюсника по отношению к за-
жимам ab. Поэтому Рис. 120
i ______U ab хх_____
Rsx +Rh-H (Хвх+Хн)‘
По условию, Rax и Хах заданы и менять их нельзя. Менять мож-
но лишь RH и Хн. Выберем Хн так, чтобы ток в цепи был максималь-
ным, это имеет место при Хах + Хн = 0. При этом двухполюсник
работает в резонансном режиме: ток через нагрузку будет по фазе
совпадать с напряжением Uab хх
j U ab хх
Rex + Rh
Как и в цепи постоянного тока (§ 24), если взять RH = Rex, то
выделяющаяся в нагрузке мощность будет максимальна и равна
г/2
г>___ uab хх
. 4Rex ’
Таким образом, Для того чтобы выделить в нагрузке, прйсоединя-
. 153
емок к активному двухполюснику с входным сопротивлением Rex +
+ ]Хвх, максимально возможную мощность, необходимо сопротив-
ления нагрузки выбрать следующим образом: Хн = — Хвх и RH =
Rex'
§ 112. Падение и потеря напряжения в линии передачи энергии.
Генератор соединен с приемником энергии линией передачи. Линия
передачи обладает активным RA и индуктивным X, = и>Ьл сопротив-
лениями.
Построим векторную диаграмму для цепи, состоящей из генера-
тора, линии передачи и приемника. Для определенности положим,
Рис. 121
что нагрузка приемника имеет индуктив-
ный характер. Вектор напряжения в кон-
це линии (на приемнике) направим по оси
+ 1 (рис. 121), ток 1 отстает от него в
силу индуктивного характера нагрузки.
Падение напряжения в активном сопро-
тивлении линии 1Ra совпадает по фазе с
током, падение напряжения в индуктив-
ном сопротивлении линии 1}ХЛ опережает ток на 90°.
Познакомимся с двумя терминами, встречающимися в литера-
туре: падением напряжения в линии передачи и потерей напряже-
ния в линии передачи.
Под падением напряжения в линии передачи понимают модуль
геометрической разности векторов напряжения в начале ((7Х) и кон-
це ((7g) линки; оно равно
Потеря напряжения равна разности модулей напряжения в на-
чале и конце линии, т. е. равна | | — | U21.
Потеря напряжения в линии передачи показывает, на сколько
вольт напряжение в конце линии меньше, чем напряжение в начале
линии.
Как правило, падение напряжения больше потери напряжения.
§ 113. Расчет электрических цепей при наличии в них магнитио-
связанных катушек. В состав электрических цепей могут входить
катушки, магнитносвязанные с другими катушками. Поток одной
из них пронизывает другие и наводит в них э. д. с. взаимоиндукции,
которые должны быть учтены в расчете. При составлении уравне-
ний для магнитносвязанных цепей необходимо знать, согласно или
встречно направлены потоки самоиндукции и взаимоиндукции.
Правильное заключение об этом может быть сделано, если извест-
но направление намотки катушек на сердечнике и выбрано положи-
тельное направление токов в них.
На рис. 122, а катушки включены согласно, на рис. 122, б —
встречно. Изображение на электрических схемах сердечников ка-
тушек загромождает чертеж, и поэтому обычно избегают изобра-
154
жать сердечники на схемах, ограничиваясь тем, что одноименные
зажимы (скажем, начала катушек) помечают одинаковыми знач-
ками, например звездочками.
Схема рис. 122, в полностью эквивалентна схеме рис. 122, а,
а схема рис. 122, г эквивалентна схеме рис. 122, б.
Если на электрической схеме токи двух магнитносвязанных ка-
тушек одинаковым образом ориентированы относительно одноимен-
но (звездочками) обозначенных зажимов катушек, например оба
направлены к звездочкам или оба направлены от звездочек, то име-
ет место согласное включение, в противном случае — встречное.
Для расчетов магнитносвязанных цепей применяется символи-
ческий метод расчета. На примере схемы рис. 123 обсудим вопрос о
составлении уравнений для расчета магнитносвязанных цепей.
Произвольно выберем положительные направления токов в вет-
вях (см. рис. 123). Направления обхода контуров выберем по часо-
вой стрелке. Сначала составим уравнения для мгновенных значений:
Ч = 4 + Ч-
Для левого контура (ветви 1 и 2)
+ С + + + f ta d/ + f8/?a=et.
Ц J . ^2 J
Перед слагаемым M поставлен тот же знак, что и перед L^1,
так как ток и ток is входят в одноименные зажимы магнитносвя-
занных катушек, т. е. имеет место согласное включение. Сумма
слагаемых
dt 1 dt
представляет собой падение напряжения в первой катушке.
Все слагаемые левой части последнего уравнения взяты со зна-
ком плюс, так как на всех участках первого контура положительные
155
направления токов совпадают с направлением обхода контура. Со-
ставим уравнение для второго контура (ветви 2 и 3). Направление
тока i2 встречно направлению обхода контура, поэтому сумма па-
дений напряжений во второй ветви войдет в уравнение со знаком
минус
*
-A f t-2d/_t-a/?a + L8^ + M^4-t-8/?8=-e8.
С 2 J dt dt
Перейдем к комплексной форме записи
/1 = / я + / 3.
. Л(Я1----Кг------------------------ = Ev
\ (оС| / \ (oCj j
iyjuiM. — —i—) 4~ /3 (K3 + /®^8)= — K3.
На решении трех уравнений с тремя неизвестными останавливаться
не будем.
§ 114. Последовательное соединение двух магнитносвязанных ка-
тушек. На рис. 124 изображена схема последовательного согласно-
го включения двух катушек и на рис. 125 — последовательного
встречного включения тех же катушек. При согласном включении
dt dt dt dt
В комплексной форме записи
/ [/?! + /?2 + /® (£ + ^-2 + 2Л1)] = Ё;
17 = Р
* ^согл >
%согл = 4" R2 + (^i + ^2 ~Ь 2Л4). (5.54)
Векторная диаграмма для согласного включения изображена на
рис. 126. На ней U1 — Напряжение на первой катушке, {7а — на
второй.
При встречном включении
iR^L,-------М — + Ь3 — — М — -]-1К3 = е.
1 dt dt 1 2 dt dt 1 2
156
Отсюда
IZa.„„ = Ё.
встр
Здесь
zecmp = /?! + /?2 + /® (L, + L, - 2Л4). (5.55)
Векторная диаграмма для встречного включения и при Lr > М и
La > М изображена на рис. 127.
§ 115. Определение М опытным путем. Обсудим два практически
важных способа опытного определения взаимоиндукции М. двух маг-
нитносвязанных катушек.
Первый способ. Проделаем два опыта. В первом из них
включим катушки последовательно и согласно. Измерим ток и нап-
Рис. 126
Рис. 127
ряжение на входе и активную мощность цепи. В другом — те же
катушки включим последовательно и встречно и также измерим I,
U, Р. По результатам измерений найдем
Хсогд = и>(Ё1 + Ь2 + 2М)
И
Xecmp = a)(L1 + L2-2M).
Разность
Х.п,, — Х..тп = 4юЛ1,
сисл остр *
следовательно,
М = Хеогл-Хи^ (515б)
4(0
Второй способ. Включим первую катушку к источнику
• синусоидальной э.д.с. через амперметр (рис. 128), а к зажимам
второй катушки подключим вольтметр с большим внутренним соп-
ротивлением. Измерим ток /j и напряжение U%.
Мгновенное значение напряжения
и2 = М —,
2 dt>
157
Действующее значение его
1/2 = о)М/х.
Следовательно,-
М = (5.57)
<о/1
Пример 61. В схеме рис. 128 вольтметр показал 100 в, ампер-
метр 10 а\ <о = 314 сект1. Определить М.
Решение. По формуле (5.57)
М = .. 100 = 0,0319 (гн).
314-10
§ 116. Трансформатор. Вносимое сопротивление. Трансформа-
тор представляет собой статическое * устройство, служащее для
преобразования переменного во времени напряжения по величине.
Передача энергии из одной цепи в другую в трансформаторе про-
исходит путем использования явления взаимоиндукции.
Трансформатор имеет две обмотки-, находящиеся на общем сер-
дечнике. Магнитную проницаемость сердечника будем полагать по-
стоянной. Параметры первичной обмотки и Lx; вторичной — и
Рнс. 129
Рнс. 130
La. Взаимоиндукция между обмотками М. (рис. 129). Сопротивле-
ние нагрузки, подключенной к зажимам вторичной обмотки, рав-
но ZH.
Выберем положительные направления токов /х и /2. Обозначим
напряжение на нагрузке UH. Запишем уравнение в комплексах.
Для первичной цепи
-{-/j/coAl = Lj. (5.58)
Для вторичной цепи
- + /2/tt>L2 -j- i1j<nM -j- UH — 0. (5.59)
На рис. 130 качественно построим векторную диаграмму, по-
лагая для определенности, что нагрузка ZH = zHeI9ft имеет инду-
* Т. е. не имеющее подвижных частей.
•158
ктивный характер. Ток /2 направим по оси -ф-1. Напряжение на
нагрузке UK опережает ток /2 на Угол Ф«- Падение напряжения
/2Л?2 совпадает по фазе с током /а. Вектор /2/«L2 опережает
ток /а на 90°.
В соответствии с уравнением (5.59) вектор /1/«M проводим так,
чтобы геометрическая сумма падений напряжений во вторичной
цепи равнялась нулю.
Ток 7t отстает от вектора /jwAf на 90°. Вектор совпада-
ет с током /, по фазе, а вектор опережает Ц на 90°.
Вектор /а/аМ опережает/а на 90°. В соответствии с уравнени-
ем (5.58) геометрическая сумма /1/?1 -ф- дает Д.
В (5.59) подставим
йн = = h (RH + iXH)
и решим уравнения (5.58) и (5.59) относительно
Ё
(/?i 4* RSH) -f- j (Xi —
Здесь
ReH
<агМ*
mV4-(»MW2
вн (%4-««)24-(“^4-Хк)2
ReH и Хан называют вносимыми из вторичного контура в первич-
ный активным и реактивным сопротивлениями.
Вносимые сопротивления представляют собой такие сопротивле-
ния^ которые следовало бы «внести» в первичную цепь (включить
последовательно с Rx и XJ, чтобы учесть влияние нагрузки вто-
ричной цени трансформатора на ток в первичной цепи его.
Пример 62. Определить токи в схеме рис. 131, а и построить то-
пографическую диаграмму, совместив ее с. векторной диаграммой то-
159
ков; <й£х = 2 ом, aL2 = 3 ом, аМ = 1 ом, RH = 4 ом, Е — 100 в.
Решение. Составим уравнения по законам Кирхгофа
При составлении уравнений по второму закону Кирхгофа обход
контуров будем совершать по часовой стрелке
/’i/wLj + 7a/«M + /= Ё; lyjaM 4- 72)^2 — iHRH — 0»
В двух последних уравнениях заменим /ж на
+ —/?и)=£; ЛС/соМ—/?и)4-/а(/?я4-/®Д2)=0.
Подставим числа:
Л (4 +2/)+7, (/-4) =100;
Л(/-4) +4(4 + 3/) = 0.
Решение уравнений дает
/1= 17,7е-/вз»а;
7а= 14,6е-пм»а;
7И = 4 — /а = 14,12е~^9°54' а.
Л
Рис. 132 '
На рис. 131, б изображена топографическая диаграмма и векторная \
диаграмма токов.
Пример 63. Построить топографическую диаграмму для схемы
рис. 132, а, совместив ее с векторной диаграммой токов. Две ветви
схемы связаны магнитно. Значения параметров:
®LX= 3 ом, аЬ2 — 4 ом, шЛ1 — 3 ом, = 7?а = 2 ом, Ё — ЮОв.
160
Решение. Обозначим токи в ветвях через/, и /2 и ток в
неразветвленной части схемы через 1. Составим уравнение по второму
закону Кирхгофа для согласного включения катушек:
^1(^1+ /®^1) + /а/юМ = Ё;
IjaM -f - /2 (/?2 4- /ш£2) = Ё.
Совместное решение их дает
а; /2 = 14,27с’'86030'а.
Топографическая диаграмма, совмещенная с векторной диаграм-
мой токов, изображена на рис. 132, б.
§ 117. Теорема о балансе активных и реактивных мощностей. В
любой линейной электрической цепи сумма активных мощностей
источников э. д. с. равна сумме активных мощностей приемников,
а сумма реактивных мощностей источникрв э. д. с. равна сумме реак-
тивных мощностей приемников энергии.
При этом под реактивной мощностью приемников энергии пони-
жается сумма произведений квадратов токов ветвей, умноженных
на реактивные сопротивления ветвей, подсчитанных без учета яв-
ления взаимоиндукции*, плюс алгебраическая сумма мощностей,
переносимых магнитными потоками из одних ветвей в другие вслед-
ствие -явления взаимоиндукции.
Доказательство. Пусть Схема содержит f узлов, b ветвей и все
ветви или часть их связаны друг с другом магнитно. По первому закону Кирх-
гофа сумма токов в любом узле равна нулю. Например, для k узла, в кото-
ром сходится п ветвей,
р
IX = 0.
Или
п
?itp 0*
₽=1
Умножим каждое слагаемое этой суммы на потенциал k узла <pfc:
я
Фа /ftp =
₽=1
Просуммируем аналогичные выражения для всех [ узлов схемы
~ t п
Xj Фа = О'
. а=1 р-i
* Имеется ,в виду, что подсчитываются без учета взаимоиндукции только
реактивные сопротивления ветвей, токи же подсчитываются с учетом явле-
ния взаимоиндукции.
6 Л. А. Бессонов
161
В двойную сумму любой ток схемы, например ток 7^, входит дважды й
притом с разными знаками. Действительно, при k — т и р = q соответствующее
• *
слагаемое двойной суммы равно а при k — q и р =т слагаемое
равно Так как
* • * S
Луги= ^mqt . <
то эти слагаемые можно объединить, и получим 7ОТ« (фт — ф?)-
Пусть какая-то ветвь схемы, например ветвь kq, магнитно связана с ветвью
Рис. 133
sr так, что сопротивление взаимоиндукции
между ними XMkq (см. рис. 133).
ST
В соответствии с рис. 133
Ф? ФА = ^kq hq %kq hr iX-jukq-
sr
В свою очередь для ветви sr
Фг ?s Esr lsr Zsr — Iftq jXjtkq'
sT'
Если принять, что ,?!-
hq=3lkqe kl> isr = lsr e V
н учесть, что
Ikq ~hqe и hr = hr e ‘
то сумма двух слагаемых
# # /{ф ~ф i **~ф )
Ikq hr !*м b 'i'lkq hr jX. k ~ hq hr l^JUkq Iе ** + e *9 I ="
sr sr sr
= / Ikq hr cos (Vkq fsr)-
sr _ „
Таким образом, попарное рассмотрение слагаемых двойной суммы позволя-
ет переписать ее в таком виде:
hp — Zt hp ^kp~i~ /*2 7kq hr Хм/iq cos (фА? ф$г)- (5.60)
» sr
Слагаемые типа Ekplkp представляют собой произведение э. д. с., находя-
щейся в ветви kp (k и р — текущие индексы узлов схемы), на сопряженный
комплекс тока этой же ветви; 7|р — квадрат модуля тока ветви kp;
%kp — Rkp + / XkP-
В сумму/-2^/й9/5ГХЛ^со8(ф^ —ф„) по одному разу входят попар-
sr
ные произведения токов магнитносвязанных друг с другом ветвей, умножен-
ные на соответствующие сопротивления взаимоиндукции и на косинусы углов
между токами этих ветвей.
Например, если в некоторой схеме магнитно связаны три ветви (ветви
12, 13 и 23), то сумма
1’2 hq hr X»kq cos (ф«ед Ф«г)
sr
162
запишется так:
/ • 2 {Ла Лз Xj<12COS (<Р12 — <Р1з) 4- /12 /23 ^Ck12cos (<Р12—ф2з) + /2з/13 COS(<p23—<Р1з)|
13 23
Левая и правая части формулы (5.60) представляют собой комплексы. Ра-'
венство действительных частей комплексов дает формулу (5.61), а равенство
мнимых — формулу (5.62):
Re Ё&р 1&р= /ftpR*p> (5- 61)
I111 ^kp ^kp — У kp Xkp + 2 Ifcq Isr ^-Mpq COS (<f hq ф^г)- (5. 62)
sr
В этой формуле ^Mk4 принято положительным при согласном направлении
ST
потоков взаимоиндукции н самоиндукции ветвей hq и Sr и отрицательным при
встречном их направлении.
Формулы (5.61) и (5.62) представляют собой математическую запись сфор-
мулированной выше теоремы.
Пример 64. По данным примера 62 в числах убедиться в справед-
ливости’ теоремы о балансе мощности применительно к схеме рис.
131, а.
Решение. Активная мощность, доставляемая источником
э.д.с., равна
ReE/ = Re 100 . 17,Те'63" = 1770 cos 63 е = 800 (ет).
Активная мощность, потребляемая приемниками, равна
12HRH = 14.122 - 4 = 800 (em).
Следовательно, равенство активных мощностей выполнено.
Реактивная мощность источника э.д.с.
Im£7 = 1770 sin 63° = 1582 (вар).
Реактивная мощность приемников энергии с учетом согласного вклю-
чения катушек равна
4- 1'2<лЬ2 4-2/1/2(йМ cos (ф/: — ф;2) =
= 17,72. 24- 14,62 - 34- 2. 17,7. 14,6 cos (63° — 114°) = 1582 (вар).
Таким образом, баланс реактивных мощностей также удовлетво-
ряется.
Глава шестая
ТЕОРИЯ ЧЕТЫРЕХПОЛЮСНИКА И КРУГОВЫЕ
ДИАГРАММЫ
Рис. 134
§ 118. Четырехполюсник и его основные уравнения. Четырехпо-
люсником принято называть электрическую схему, имеющую два
входных зажима и Два выходных зажима. В качестве примера могут
быть названы трансформатор, линия передачи энергии, мостовая
схема и т. п.
Принято четырехполюсник изображать в виде прямоугольника
с выходящими из него концами (полюсами) тп и pq (рис. 134).
Если электрическая схема, которую изображает собой четырех-
полюсник, содержит э.д.с., то в прямоугольнике
ставится буква А (первая буква слова «актив-
ный»).
Если буква А отсутствует, то это свидетельст-
вует о том, что четырехполюсник пассивный, т. е.
не содержит э.д.с. В дальнейшем рассматривается
теория пассивного четырехполюсника.
Входной ток обозначают 7Х, входное напряже-
ние (7Х; ток и напряжение на выходе — через /2 и 02.
Четырехполюсник является передаточным звеном между источ-
ником питания и нагрузкой. Зажимы тп являются входными; к ним,
как правило, присоединяется источник питания. Зажимы pq «—
выходные; к ним, как правило, присоединяется нагрузка*.
При работе четырехполюсника в качестве связующего звена меж-
ду источником и нагрузкой предполагается, что могут изменяться
нагрузка четырехполюсника и напряжение на входе, но схема внут-
ренних соединений четырехполюсника и значения сопротивлений
в ней остаются неизменными.
Для любого пассивного (не содержащего э.д.с.) линейного че-
тырехполюсника напряжение и ток на входе и 1\ связаны с на-
пряжением и током на выходе Ь2 и /2 двумя уравнениями, которые
принято называть основными уравнениями четырехполюсника;' '*
164
+ (6.1)
/х = CU2 4- Dl\. (6.2)
В этих уравнениях комплексные коэффициенты А, В, С, D за-
висят от схемы внутренних соединений четырехполюсника, от зна-
чений сопротивлений схемы и от частоты. Для каждого четырехпо-
люсника они могут быть определены расчетным или опытным путя-
ми.
Коэффициенты связаны соотношением
AD — ВС = 1. (6.3)
Выведем уравнения (6.1 и 6.2). С этой целью к зажимам тп вклю-
чим источник э. д. с. Ёг = Umn = Uv а к зажимам pq — нагрузку Z2
(рис. 135, а).
Напряжение на нагрузке й2 = /2 = См. Согласно теореме
компенсации (§ 16) заменим нагрузку Z2 на э.д.с. Ё2, направленную
встречно току /2 и численно равную й2 (рис. 135,6). Запишем
выражения для токов и /2 через £г и £2 и входные и взаимные
проводимости ветвей (см. § 13).
Если токи /х и /2 рассматривать как контурные токи, то э.д.с.
контуров, совпадающие с направлением контурных токов, войдут
в уравнения, подобные уравнению (1.7), со
знаком плюс, а э.д.с., не совпадающие с
направлением соответствующих контур-
ных токов, войдут в уравнения со знаком
минус.
Э.д.с. Ёг направлена согласно с /х, по-
этому она войдет в уравнения (6.4 и 6.5) со
знаком плюс, Ёа направлена встречно Л>
поэтому она войдет в уравнения (6.4 и 6.5)
со знаком минус:
А = (6.4)
I2 = E1Y12-E2Y22. (6.5)
Из (6.5) найдем
Подставим (6.6) в (6.4), получим
• _ а УиУи-У?2 • У»
‘1~ --V----
г 12 г м
(6.7)
Обозначим
165
Заменим в (6.6) и (6.7) на Ut, £2 на (72, воспользуемся обозна-
чениями (6.8) н получим основные уравнения четырехполюсника
(6.1 и 6.2)
Ul А(72 + В/8; /\ = сй2 4- Df2.
Проверим справедливость уравнения (6.3)
I,
р.——
9
Рис. 136
YuY* rnr22-y»
AD-BC= —--------------------«= 1.
^12 Yj2
Таким образом, уравнение (6.3) дей-
ствительно выполняется. Далее обсудим,
какая связь будет существовать меж-
ду 7j и /а и^а, если источникэ.д.с.
Ё1 присоединить к зажимам pq, а наг-
рузку к зажимам тп (рис. 136).
Как и в предыдущем выводе, заменим Za на э.д.с. Ег, направ-
ленную встречно току /2, и запишем выражения для токов 1\ и /8 :
току it, и запишем выражения для токов и /8 :
i^-EtY^E.Y^ (6.9)
4 ^-EtY^+E'Yvt, (6.10)
Из (6.9) найдем
4 = ^+4^. (6.Ц)
*12 *12
‘Подставим (6.11) в (6.10)
Заменим Ёг на 0^, Ёг на й2, воспользуемся (6.8) и перепишем
(6.11) и (6.12) следующим образом:
U^DUt + Blt, (6.13)
4 = Cl)t + Ait. (6.14)
Уравнения (6.1) и (6.2) описывают работу четырехполюсника при
питании со стороны зажимов тп н присоединении нагрузки к зажи-
мам pq, тогда как уравнения (6.13) и (6.14) описывают работу того
же четырехполюсника при питании его со стороны зажимов pq и при-
соединении нагрузки к зажимам тп.
166
Четырехполюсник называют симметричным, если при переме-
не местами источника питания и нагрузки токи в источнике питания
и в нагрузке не изменяются. В симметричном четырехполюснике
А = D.
Заметим, что системы уравнений (6.1 — 6.2; А-форма)и (6.4— 6.5; У-форма)
не являются единственно возможными формами записи уравнений четырехполюс-
ников, Так, разрешив систему (6.1—6.2) относительно l/t и 1/2, получим фор-
му уравнений, которая называется Z-формой:
171 — Zll/l -|- Zlt l\; = Z2iZi -|- Z22 /2.
Разрешив (6.1 — 6.2) относительно U1 и /2> получим Я-форму уравнений четы-
рехполюсника:
(71 = Яп 4 + я1£ и* h = я21 h + Нт й2.
Существуют и другие формы записи уравнений четырехполюсника.
§ 119. Определение коэффициентов четырехполюсника. Как уже
отмечалось в предыдущем параграфе, поведение четырехполюсни-
ка в различных режимах его работа описывается формулами (6.1,
6.2, 6.13 и 6.14). В эти формулы входят комплексные коэффици-
енты А, В, С, D. Определение их может производиться по форму-
лам (6.8), если схема внутренних соединений четырехполюсника и
параметры ее известны, либо путем использования входных сопро-
тивлений четырехполюсника, полученных опытным или расчетным
путями.
Определение комплексов входных сопротивлений производится
опытным путем при помощи ваттметра, амперметра и вольтметра по
схеме, повторяющей схему рис. 115, а с тем отличием, что вместо
двухполюсника к источнику питания зажимами тп или pq (смотря
по тому, какое входное сопротивление определяется) подключается
испытуемый четырехполюсник.
Проведем опыты по определению входного сопротивления четы-
рехполюсника в трех различных режимах его работы.
1. Определим комплекс входного сопротивления со стороны за-
жимов тп при разомкнутой ветви pq (холостой ход ветви pq, ин-
декс ноль)
7 — 2 р'4’"'
•^10 —
2. Определим комплекс входного сопротивления со стороны за-
жимов тп при коротком замыкании ветви pq (к. з., ставим индекс
k)
Zlk = zlhe^.
3. Найдем комплекс входного сопротивления со стороны зажимов
pg при коротком замыкании зажимов mn
7 _ у pi’fzk
В результате обработки данных трех опытов будут получены ком-
плексные сопротивления Zlo, Ztk, Zik, Выразим их через коэффи-
167
циенты А, В, С, D. С этой целью из уравнений (6.1) ж (6.2)найдем»
ZM и Zlfe через А, В, С, D, а из (6.13) и (6.14) выразим Zak через
В и А.
В первом опыте, при определении Zlo, ветвь pq была разомк-,,
нута, поэтому/2 = 0. Следовательно, из (6.1) и (6.2) получаем
ila = си*.
Отсюда входное сопротивление 7 ,
7 _ ^1» А
Ч» — —.
Ло G
Во втором опыте, когда определялось Zlft, ветвь pq была корот-
козамкнута, поэтому t/2 = 0, и из (6.1) и (6.2) находим:
^ift = ^4*1 = D 4*
В третьем опыте при питании со стороны зажимов pq и коротком
замыкании на зажимах тп из формул (6.13) и (6.14) при
Ua = 0 следует, что
7 — в — JL
2к Ahk А '
Таким образом, для определения четырех неизвестных коэф-
фициентов А, В, С, D располагаем четырьмя уравнениями:
AD — ВС = I;
Составим разность
1 _ z!fe = 1 _ Вс = JL
. Zjo AD AD
ИЛИ
Zip — Zlk 1_
Zip AD
Поделим (6.17) на (6.16)
zik A
(6.3)
(6.15)
(6-16)
(6.17)
(6.18)
(6119)
168
Помножим (6.18) на (6.10)
(Ао—^ife) zik _ _i_
2ift A*
Отсюда
A .= 1Л___z>° .
' 2з*(210—Zift)
(6.20)
Формула (6.20) позволяет определить А через Zu, Zik и Zik.
После нахождения А определяется коэффициент С из (6.15), В из
(6.17) и D из (6.16).
Коэффициенты А и D безразмерны, коэффициент В имеет раз-
мерность ом, коэффициент С—сим.
Пример 65. Опытным путем было найдено, что Z,o =
= 7,815е-/м°12' ом, Zik = 12,5е'66°23’ ом и Z2k = З.ЗЗе'27’33' ом.
Определить коэффициенты А, В, С, D четырехполюсника.
Решение. Находим
210—2^ = 5 —6/ —5—12/ = —18/ = 18е”/90° .
По формуле (6.20) подсчитаем А:
А =
7,815е_'50°12' • 12,5е/66°23'
З.ЗЗб'27°33' • 186-7’°°
г А _________ 1,28е/39°40 n /до»
С~ 2И “ 7,8156-/50°12' ~°’166е CUM'<
в = AZik== 1,28е'’39°40'. 3,ЗЗе/27°33’ « 4,26е'67° ом-,
п_ в _ 4,2бе'67°
Zlk~ 12,5ei^&' ~°’34>
1,28е/39°40';
Пример 66. К зажимам pq (рис. 134) четырехполюсника примера
65 присоединена нагрузка Za = (6 4 /6) ом. К зажимам тп присо-
единяется источник э.д.с. Найти йг и Д, если /а = 1а.
Решение. По формуле (6.1)
йк = л(7а + в/2 = л/2га 4- в/а = /а (AZB 4- в);
(?!= 1.(1,28439Ч0\бГ1е'450+ 4,26е/67О) = 14,85е/79^ о.
По формуле (6.2)
[\ = сйа 4- О7а = /а (CZa 4-О)=
= 1.(0,166е'90° • 6 И'2е/45’ 4- 0.34) = 1,165е/123° а.
Пример 67. К зажимам тп четырехполюсника примера 65 при-
соединена нагрузка Za = (6 4- /6) ом. К зажимам pq включается
источник э.д.с. При каком значении напряжения источника э.д.с.
ток /а в нагрузке будет 1а?
169
Решение. По формуле (6.13)
=• /2 (DZ2 + В) = 0,34 (6 + /6) + 4,26е'67” = б.ЭЗе'58'’20' в.
§ 120. Схемы замещения пассивного четырехполюсника. Функ-
ции пассивного четырехполюсника как передаточного звена между
источником питания и нагрузкой могут выполнять простейшие элект-
рические схемы, схемы замещения: трехлучевая звезда (Т-схема)
рис. 137 или эквивалентный ей треугольник (П-схема) рис. 138 *.
Три сопротивления Т- или П-схем должны быть рассчитаны ис-
ходя из того, чтобы схема замещения обладала такими же коэффи-
Рис. 137
Рис. 138
циентами А, В, С, D, какими обладает заменяемый ею четырехпо-
люсник.
Задача эта однозначна, так как схема замещения содержит три
параметра, и четырехполюсник характеризуется тоже тремя пара-
метрами (одна связь между А, В, С, D задана уравнением
AD — ВС=1).
Выразим напряжение (X и ток в начале Т-схемы (рис. 137)
через напряжение Ua и ток /2 в конце схемы:
/,_/,+ «L^_0,^+/t(I+^)i_ (6.21)
и, = и2 + /2z2 + 1& = йг (i+AUzt4-Z2+ (6.22)
Сопоставим (6.22) c (6.1) и (6.21) c (6.2). Из сопоставления найдем
Л=1 + ^; в-А+>2 + ^; с = A; d = 14-A;
^3 ^3 ^3 ^3
Следовательно,
Z3 = 3 С ’ (6.23)
Z1==AU; 1 с ’ (6.24)
7 D—1 2 с • (6.25)
* Другими словами, любой линейный четырехполюсник при фиксирован-
ной частоте может быть заменен эквивалентной Т- или П- схемой.
170
Формулы (6.23—6.25) дают возможность найти сопротивления
Zs, Zt и Z2 схемы рис. 137 по коэффициентам четырехполюсника
А, С, D. Аналогичные выкладки для П-схемы рис. 138 дают:
д == 14-А • в == z с = А±А±£« £> = j _ьА.
*’ ZBZ. ' z6
Следовательно,
Z4 = В; (6.26)
(6-27)
= <6-28>
Если четырехполюсник симметричный, то А — D, ив Т-схеме
замещения Zt = Z2, а в ГТ-схеме Z5 = Ze.
Пример 68. Найти параметры Т-схемы для четырехполюсника
примера 65.
Решение. По формулам (6.23) — (6.25)
Z1 « —/90° -7 D — 1
з = — ~ бе ' ом\ Z., —------=
3 С -С
— )’34 ~7jL- ~ 4е/90° ом, Zt = 5 ом.
' ОДббе/90 1
Исследование работы электрических цепей часто проводят гра-
фическими методами путем построения круговых и линейных диа-
грамм. Перед тем как приступить к изучению круговых диаграмм,
обсудим вопрос о построении дуги окружности по хорде н вписан-
ному углу.
§ 121. Построение дуги окружности по хорде и вписанному углу.
Из геометрии известно, что вписанным углом называется угол, вер-
шина которого находится на окружности, а стороны являются хор-
дами.
Вписанный угол измеряется половиной дуги, на которую он опи-
рается. Так, Z.ABC — ф (рис. 139) измеряется ^ADC, a Z.ADC
измеряется — АВС. Сумма двух углов Z АВС + Z. ADC = л.
Угол EDC является дополнительным до л к Z.ADC, и поэтому
Z.EDC = ф.
Какое бы положение ни занимала точка D в интервале от А до С,
угол между продолжением хорды AD (т. е. линией DE) и хордой
DC остается неизменным и равным ф.
Угол между продолжением хорды АС и касательной к окруж-
ности в точке С также равняется углу ф.
Центр окружности О находится на пересечении перпендикуля-
ра к середине хорды и перпендикуляра к касательной (рис. 140).
171
Из изложенного следует, что если, задана хорда ивписанный
угол ф, то для нахождения центра окружности (см. рис. 140) необ-
ходимо:
1. Восставить перпендикуляр к середине хорды.
2. Под углом ф к продолжению хорды провести прямую, которая
будет являться касательной к окружности.
3. Восставить перпендикуляр к касательной. Пересечение пер-
пендикуляра к хорде и перпендикуляра к касательной даст центр
окружности.
§ 122, Уравнение дуги окружности в векторной форме записи.
Построения, аналогичные построениям рис. 139, могут быть выпол-
нены и на комплексной плоскости. В этом случае все хорда, напри-
мер СА, DA, CD, будут являться векторами.
На комплексной плоскости рис. 141 совместим хорду С А — F
с осью-|-1. Если угол ф положителен, то от продолжения хорды
он должен быть отложен против часовой стрелки, при ф<0угол
откладывается по часовой стрелке.
Обозначим DA = G и CD = И. Тогда
~G + H = 'F, (6.29)
Вектор Н опережает вектор G на угол ф. Пусть модуль век-
тора Н будет в k раз больше модуля вектора G. Тогда
H^kGe’t (6.30)
Если А = 0, то 77 -= 0 a G = F .
При k — оо Н = F и G = 0.
• Подставим (6.30) в (6.29). Получим
G (l+ke^^F,
или
X _ 7
\ + ^'
(6.31)
172
Уравнение (6.31) называют уравнением дуги окружности в вектор-
ндйформе записи . >
При изменении коэффициента k от 0 до <» меняются оба векто-
ра G и Н, но так, что угол ф между ними остается неизменным, а сум-
ма векторов равна вектору F. Конец вектора G скользит по дуге ок-
ружности, хордой которой является вектор F. Поэтому можно ска-
зать, что дуга окружности является геометрическим местом кон-
цов вектора G.
Важно обратить внимание на то, что рабочей частью окружности
или рабочей дугой является та часть окружности, которая по от-
ношению к хорде F лежит по обратную сторону от касательной (ра-
бочая дуга на рис. 141 вычерчена сплошной линией, не рабочая —
пунктиром).
§ 123. Круговые диаграммы. Из предыдущего (§ 83) известно,
что Синусоидально изменяющиеся функции времени (токи, напря-
жения) могут быть изображены векторами на комплексной плоскос-
ти. Если процесс в электрической цепи будет описываться уравне-
нием:, по форме тождественным с уравнением (6.31), то геометричес-
ким местом концов вектора тока или напряжения, выполняющего
в уравнений, электрической цепи ту же роль, какую играет вектор G
в уравнении (6.31), будет являться окружность.
Под круговой диаграммой тока или напряжения понимают ду-
гу окружности, являющуюся геометрическим местом концов векто-
ра тока или, соответственно, напряжения при изменении по модулю
какого-либо сопротивления электрической цепи н сохранений не-
изменными остальных сопротивлений, частоты и э.д.с. источников
энергйи.
При помощи круговых диаграмм производится графический ана-
лиз работы электрических цепей.
, Ввопросы теории круговых диаграмм большой вклад был сде-
лан основателем Московской электротехнической школы чл.-корр.
АН СССР К. А. Кругом.
§ 124. Круговая диаграмма тока для последовательного соеди-
нения двух сопротивлений. Пусть к источнику э.д.с. включены
последовательно Zt —г^91 и Z — ze141 (рис. 142). Сопротивление
Zx неизменно, a Z может меняться лишь по модулю, так что угол
<р остается постоянным. Ток в цепи
А
/ = =------А"------• (6-32')
2 . j_|_ е/(ч>—<₽i)
Здесь
173
представляет собой ток в цепи при коротком замыкании сопротив-
ления Z.
Обозначим <р — Фх = 'Ф- Тогда
/ =------L-. (6.32)
l+_Le'*
Z1
Уравнение (6.32) тождественно с (6.31).
Роль вектора F играет комплекс роль коэффициента k—- ;
роль G — вектор I. При изменении г вектор / будет скользить
по дуге окружности, хордой которой является Ik.
Круговая диаграмма построе-
на на рис. 143. На нёй вектор
э.д.с. направлен по оси-р- 1. Ток
i = &
отстает на угол фг от э.д.с. Ё. Для определенности построим диа-
грамму при ф<0. Выберем масштаб токов: нусть отрезок ас
в масштабе /п, выражает собой модуль тока !k. Отрезок da изо-
бражает собой ток I, отрезок cd в соответствии с уравнением "
(6.32) изображает произведение / —. Отложим на направлении
Z1
Ik отрезок ае, в произвольном масштабе тг выражающий модуль
постоянного сопротивления
^^ае-тг.
Из точки е под углом минусф к линии ас проводим прямую ef,
которая является, как будет показано ниже, линией модуля пере-
менного сопротивления г при отсчете от точки е. На ней в масштабе
тг нанесем деления для измерения z.
Из подобия треугольников adc и aef следует
ad ае с de г. г. г
— - - —; ef — ае — = —---— =____
de ef' ad т2 .1 тг'
174
Или
z — ef тг.
Следовательно, отрезок ef в масштабе тг измеряет модуль перемен-
ного сопротивления г.
Проекция 1 на направление Ё — отрезок ag—в масштабе тр =
— Ет{ измеряет активную мощность
Р = ag • тр = ag . Е • tnl — ag.E, — = El cos<p.
_ l ag
tn, = —; — = cos ф.
‘ ad ad
Проекция I на направление, перпендикулярное Ё,— отрезок ah —
в масштабе тр измеряет реактивную мощность
Q — ah •— ah • Е • — = Е! sin<p.
F ad
§ 125. Круговая диаграмма напряжения для дзух последовательно
соединенных сопротивлений. Умножим обе части уравнения (6.32)
на Zx = z1e'4'1. Учтем, что I Zt—Uz . Получим
... ' (J, =--------------- (6.33)
1+Ае/«₽-Ф,)
Уравнение (6.33) свидетельствует о том, что геометрическим
местом конце» вектора Uz^ является дуга окружности, хорда кото-
рой Ё.
§ 126. Круговая диаграмма для активного двухполюсника. Ток
1Н в цепи нагрузки ZH = гяе/ф« активного двухполюсника рис. 120
равен
t-'afr хл-
f = -J^xx = -----------. (6.34)
Z»x 4" J_|_ ,Z|t g! ^H ®вх^
гвх
Здесь Zex = z„x е!<Рах есть комплекс входного сопротивления двух-
полюсника по отношению к зажимам ab выделенной ветви.
Из уравнения (6.34) следует, что при изменении модуля сопро-
тивления нагрузки гн ток /н скользит по дуге окружности.
Рассмотрим два простейших примера на круговые диаграммы.
Пример 69. Параметры схемы рис. 142 таковы: Ё = 120 в;
Z1 — Pt = 24 ом; сопротивление Z чисто емкостное и модуль его
изменяется от 0 до со. Построить круговую диаграмму тока и
круговую диаграмму напряжения на сопротивлении Zt.
* 120
Решение. Ток Ik = — = 5 (а). Выберем масштаб для токов
24
= 1,31 ajсм и масштаб для напряжений та = 26 в/см.
175
,.i -Найдем угол ф = <р —<Pj = — 90° —fO* = .•—•90S. <
На рис. 144 построены круговая диаграмма тока на токе 1к,
как на диаметре, и круговая диаграмма напряжения на э. д. с. Е,
как на диаметре. Масштаб для сопротивлений тг = 10 ом/см. Для
любого значения сопротивления г по диаграмме находим ток и
напряжение U2l. Так, при z = 9,5 ом I = 4,65 a, U21= 111,5 в.
Пример 70. Построить геометрическое место концов тока 1
неразветвленной части схемы рис. 145 и графически исследовать
возможность возникновения резонансных режимов, при следующих
Рис. 144
Рис. 145
данных: Ё — 30 в\ ом’ Хс — 8 ом’’ = 3 ом<
может
изменяться от 0 до
Решение. Ток
оо.
/2 в схеме остается неизменным:
. b
Л
: 30
2~6 —/8
= Зе/53о,0'а.
2 Гчометрическое место
концов Вектора Ц и
1 резон, ч
*нин
Рис. -146
. \геометрическое место
концов Вектора /
В 7 8 9 10 ом
' Пиния
Он на 53°10' опережает э.д.с. Ё
(рис. 146). Ток /j при изменении
XL меняется так, что конец его
скользит по дуге окружности, диа-
метром которой является ток
Ilk = — = 10 fl, tn j = 2,65 al см.
Ri ,
-Ток в неразветвленной части
схемы / = Iv
Геометрическим местом его яв-
ляется также дуга окружности
а12Ь. В режимах, соответствую-
щих точкам 1 и 2,ток совпадает
по фазе с э.д.с. Ё. Следовательйо,
в этих режимах в схеме имеет мес-
то резонанс токов.
176
Выберем масштаб сопротивлений тг == 2 ом)см. Графически
найдем л£ для точек 1 и 2,
Для точки 2 ом, для точки 1 Хья?Ю,6 ом. При
этом ток / равен: / — 11,1 а и / = 2,4 а.
§ 127. Круговая диаграмма четырехполюсника. Пус1ъ напряжение
c/j на входе четырехполюсника рис. 135, а неизменно по вели-
чине, фазе и частоте, а нагрузка Z2 — z2el^ на выходе четырех-
полюсника изменяется только по модулю, так что характеризую-
щий ее угол <р2 остается постоянным.
В этом случае для тока /2, напряжения и2 и тока ^существуют
круговые диаграммы. Покажем, что для тока /2 существует
круговая диаграмма. С этой целью всю схему четырехполюсника
рис. 135, а, за исключением нагрузки Z2, заменим активным двух-
полюсником, и по методу хх и кз найдем ток /2 в ветви pq
Под Upqxx донимается напряжение между точками р и q при
размыкании ветви pq, а под Zexpq — Z2k — z2kei<fyt—входное соп-
ротивление по отношению к зажимам pq при короткозамкнутых
зажимах тп. Поделим и числитель и знаменатель правой части
(6.35х) на ZMpg — Zik и учтем, что .
V РЧ хх f
--------
где l2k— ток короткого замыкания ветви pq.
j _ __________________________________Ъь _______
. , га /(Фа—Ч>24> (6.35)
.с , *+• *
Z2*
Из уравнения (6.35) следует, что вектор тока /2 скользит по
дуге окружности, хордой которой является I2k.
Обсудим далее вопрос о круговой диаграмме тока Zj на входе
четырехполюсника.
Из предыдущего (см. например, формулу 1.14) известно, что
в линейной цепи любые два тока при изменении сопротивления в
любой ветви схемы связаны соотношением вида
= а-\-Ып.
Следовательно, ток //может быть линейно выражен через j'a:
1\ = а + Ь12. (6.36)
Найдем коэффициенты а и Ь. Если ветвь pq будет разомкнута,
то /2 == 0, а
177
Из уравнения (6.36) найдем
а = /10. . . <6;37)
Если ветвь pq будет короткозамкнута, то /2 == i2t и = /и.
Поэтому
4s = Ло +
Отсюда
Ь = -1к~ 1«, (6.38)
^2ft
Подставим (6.37), (6.38) и (6.35) в (6.36); получим
/ _ / ।_________________________________Aft~ hf>
1 . 10 1+’ (6,39)
*2*
Уравнение (6.39) свидетельствует о том, что геометрическим
местом концов вектора Ц также является дуга окружности.
Выше был рассмотрен вопрос о настроена круговой диаграм-
мы для тока. Аналогичным образом производится построение кру-
говой диаграммы для напряжения. Так, если в какой-то схеме
изменяется по модулю сопротивление Z2 — г2е,ф’ водной, скажем,-
второй ветви, то для напряжения на некотором участке ab этой
схемы можно записать выражение, аналогичное (6.39):
Uai = Uak хЯ
Ugb кз Оab хх
1+Л. е/(ф’-ф2*)
*2ft
Здесь Оаьхх напряжение на зажимах ab при z2 = оо, Uabk3 на-
пряжение на зажимах аЬ при z2 = 0.
Величина Z2k = z2k ei<f2k — входное сопротивление всей схемы по
отношению к зажимам, к которым присоединяется сопротивле-
ние Z2.
Последовательность построения круговой диаграммы проиллю-
стрируем численным примером.
Пример 71. Построить круговую диаграмму тока Л четырех;
полюсника примера 65, если U1 — 80 в и <р2 — —32°27'.
Решение. 1. По данным примера 65 выпишем значения
входных сопротивлений: Zte == 7,815е_у'50’12';
Zu= 12,5е'б6°23’; Z2k = 3,33е'27°33'.
2. Найдем
4 = г* = ю'2ет'; 4“^ =6,4
Z10 Zlft
- 178
3. В масштабе tn<j = 20 в/см на рис. 147 изобразим вектор
4. В масштабе тц — 4 а/см на рис. 147 нанесем токи /10
и ilk; /10 опережает на 50° 12', а отстает от на 66°23'<
5. Проводим хорду /1й — /10 и по хорде и углу
ф = ф2 — <р2А = — 32°27' — 27°33' - — 60°
находим центр окружности.
6. Выберем масштаб для со-
противлений тг = 2 ом/ см и в
этом масштабе вдоль хорды
от точки т отложим отрезок
mq, выражающий собой модуж>
сопротивления z2ft = 3,33 ом;
mq-mz — г2к; mq — 1,66 см.
7. Под углом минус -ф, т. е.
4-60°, проводим линию qr, ли-
нию модуля переменного соп-
ротивления z2, и на ней в мас-
штабе mt наносим деления для
отсчета сопротивления zv
Дуга тпр представляет со-
бой геометрическое место концов
тока при изменении Zj. Для
определения величины и фазы
тока при заданном z2 необходимо на линии переменного сопро-
тивления, линии qr, отложить отрезок, например отрезок qs,
в масштабе тг равный сопротивлению z2, и соединить точку s
с точкой т. Пересечение прямой ms с дугой тпр дает точку п.
Вектор пО в масштабе гл/, дает ток /г Угол между и век-
тором /х есть угол <р. Например, при za = 6 ом /х = 9,1 а и ф=16°.
§ 128. Определение /2, (J2, Pt и Qx по круговой диаграмме
четырехполюсника. Круговая диаграмма четырехполюсника рис.
147 служит не только для определения тока при любом z2. По
ней можно определить также модуль тока /2, модуль напряжения
на нагрузке £/2, активную и реактивную мощности для лю-
бого сопротивления z2. Каждая из перечисленных величин на диа-
грамме измеряется своим отрезком. Так, ток /2 измеряется отрез-
ком тп; U2 — отрезком пр; Рг — отрезком OT;Ql — отрезком О/*.
Убедимся в этом.
Из основных уравнений четырехполюсника (6.1) и (6.2) опре-
делим U2 и 72:
U2 — DU1 — BI,; (6.40)
i2 = Al1 — CU1. (6.41)
* Обведен скобкой на рис. 147.
159
Из уравнения (6.40) следует, что
иг = В F-7i 1 = в(/1А—/j.
\ D /
Разность — /х на круговой диаграмме изображается отрезком
рп. Таким образом, отрезок рп пропорционален U2.
При холостом ходе, когда /2 = 0, а = /10, точка п сливается
с точкой т, при этом хорда тр дает значение Uw. Масштаб ти2,
в котором отрезок пр выражает напряжение U2, равен
_____ ^20 ‘
ти, = —•
тр
Из уравнения (6.41) найдем
— \ с /
Разность /,— ^ изображается отрезком тп. Если учесть, что
для данного четырехполюсника А есть Постоянная величина,
то можно сказать, что отрезок тп пропорционален току /а.
При коротком замыкании зажимов pq, когда /а = f2k, a l\ — Ilk,
точка п совпадает с , точкой р, и хорда тр будет выражать
ток I2k. Отсюда масштаб для тока /а
т _
тг——. , ,
2 тр
Отрезок ОТ представляет собой проекцию вектора тока 4
на направление напряжения в масштабе тр1 — он дает
активную мощность Рг == Z/^ cos <р. Проекция вектора тока
на направление, перпендикулярное — отрезок о/, — в том же
масштабе измеряет реактивную мощность фл = ZZ/jsinq).
Для каждого значения za по круговой диаграмме можно най-
ти Ilt Za, U2, Plt Qj и построить трафики этих величин в функции
от za, т. е. произвести весьма полное графическое исследование
работы четырехполюсника.
Пример 72. По круговой диаграмме четырехполюсника примера
71 и данным примера 65 построить графики Ilt /а, U2 в функции
от za. Выяснить, при каком значении za будет резонансный режим.
Решение. Подсчитаем напряжение U2 при холостом ходе:
U2Q = В (Ilk — /10) = 4,26 eie7'(G,4e-l66m'— 10,2 е/50°12' )== •
- 61,Зе-/39’ в.
Длина хорды тр на рис. 147 равна 3,6 см.
180
Масштаб
Ток
Масштаб
61,3 в i
тц, — — — — =»= 17 в см.
тр 3,6 см
= A*- C(JX = 6,4е-/66°23' - 1,28
— 80 • 0,166 /^18,9 е-766°30'а.
/2Й 18,9 а
mh---------
тр
= 5,26 а!см,
3,6 см
Масштаб мощностей
mp=U1. тц —320 вт/см.
Кривые Iv, 12 и U2 в функ-
ции от г2 изображены на
рис. 148. Резонанс в схеме
имеет место при г2 ~
3,33 ом, при этом ток
/2 будет по фазе совпа-
дать с напряжением Ur
Пример 73. Построить
круговую диаграмму то-
ка \ схемы рис. 149, «:
Хс = 5 ом, R — 5 ом,
Е — 100 в. Нагрузкой че-
тырехполюсника является
индуктивное сопротивление
Х^, которое может изменяться от нуля до бесконечности.
Решение. Найдем ток холостого хода /10 (когда цепь нагруз-
ки разомкнута):
10 R~jXc 5-/5
Определим ток короткого замыкания /1А (при коротком замы-
кании нагрузки):
к = -------*-------= 12,82е'7™' а.
1 R-jXc
Найдем входное сопротивление Z2k со стороны зажимов pq
при коротком замыкании зажимов тп:
Z№ = zik= - /Хс+ = 7,8e-'7,O2°' ом.
к—1Хс
181
Следовательно, <p2ft =— 71°20'.
Угол ip = ф2 — ф2А = 90 — (—71?20') = 161°20'.
Круговая диаграмма тока построена на рис. 149, б.
Хордой окружности является разность Ilk— 110. Угол if, поло-
жителен, поэтому для определения положения касательной он от-
ложен от продолжения хорды против часовой стрелки.
Диаграмма носит несколько необычный характер: рабочая часть
дуги занимает почти целую окружность.
Рис. 149
I)
Для определения положения конца вектора тока из конца
вектора /10 через точку на линии XL, соответствующую заданной
величине XL, проводится прямая до пересечения с рабочей частью
дуги окружности. При XL = 5 ом ток опережает э.д.с. £ на 90°.
Рис. 150
§ 129. Линейные диаграммы. Под линейными диаграммами по-
нимают диаграммы, в которых геометрическим местом концов век-
тора тока или напряжения является прямая линия.
182
По сути дела линейная диаграмма представляет собой частный
случай круговой диаграммы, поскольку прямая есть дуга окруж-
ности с бесконечно большим радиусом.
Пример 74. Построить геометрическое место концов вектора
тока / в схеме рис. 150, а при изменении Лс. Напряжение Uab~
— const, и Xl неизменны.
Решение. На рис. 150, б изображаем вектор Uab. Ток Д от-
стает от него на угол
. Xl
Ф = arc tg—.
Ki
Ток /2 опережает Uab на ЭО"5. Геометрическим местом концов об-
щего тока 1 — 4- /2 будет прямая линия pq. Она и является ли-
нейной диаграммой тока I.
Ц т____________р It т__________________р
Рис. 151
§ 130. Уравнения активного четырехполюсника. Положим, что в первой
ветви (ветви тп) активного четырехполюсника рис. 151, а есть источник э. д. с.
Ег, во второй ветви (pq) — нагрузка ZH, а в остальных ветвях (3—р), находя-
щихся внутри четырехполюсника, имеются или могут быть э. д. с. Ёь (индекс
k может пробегать значения от 3 до р). Тогда, заменив по теореме компенса-
ции сопротивление Za на э. д. с. Ё2 (рис. 151, б), запишем выражения для токов
Ан А:
р
h = £1 У и - £г Ум + S Yik’ (6- 42>
fe = 3
р
12 ЁгУ21 — Ё2 У22 + У Уik- 1®- 43)
6 = 3
Осуществим короткое замыкание одновременно на зажимах тп и pq. При этом
р
по первой ветви будет протекать ток Абб = УУб Y 1й,а по второй 1гьь =>
ьэ
Р : .
s y^k'
k = 3
183
р
В (6.42) вместо £ЁьУ1Ь подстаним а в (6.43) вместо
4=3
р
Ё& Ка*. Кроме того, заменим на Ut и £а на Уа. Получим:
4=3
K-iibk^OiYu-U^, (6.42')
7а — 7а*д[ = 1/1К21 — {72У22. (6.43')
Уравнения (6.42') н (6.43') отличаются от уравнений (6.4) и (6.5) только
тем, что в левых частях нх находятся соответственно /х — и 72 — ltkk
вместо lt и /а. Отсюда следует, что все уравнения, получающиеся из (6.4) —
(6.5) в результате их преобразований, будут справедливы и для активного
четырехполюсника, только в ннх Д надо заменить на 7t — 7^, а /8 на
1г — lank-
Так, A-форме уравнений для пассивного четырехполюсника
(j\ = A Ut -|- В
h^cut + Di„
соответствует A-форма уравнений для активного четырехполюсника
йг = A Us -|- В (Д — 7ajj), /j — = С Ut + D (/а — Afefe).
Коэффициенты А, В, С, D активного четырехполюсника удовлетворяют усло-
вию AD — ВС => 1 н определяются так же, как и для пассивного.
Глава седьмая
ТРЕХФАЗНЫЕ ЦЕПИ,
ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ
И МЕТОД СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ
§ 181. Трехфазная система э. д. с. Под трёхфазной симметричной
системой э. д. с. понимают совокупность трех синусоидальных э. д. с.
одинаковой частоты и амплитуды, сдвинутых по фазе на 120Q. Гра-
фик мгновенных значений их изображен на рис. 152, Векторная
диаграмма на рис. 153.
Трехфазную систему э.д.с. получают при помощи трехфазного
генератора. Принцип работы его иллюстрируется рис. 154. В равно-
мерном магнитйом поле с постоянной угловой скоростью со вращают-
ся три одинаковых жестко скрепленных друг с другом катушки.
Плоскости катушек смещены в пространстве на 120°. В каждой
из катушек наводится синусоидальная э.д.с. одинаковой амплиту-
ды, но по фазе они сдвинуты на 120°.
Аналогичным путем может быть получена двух, четырех и более
фазная система э.д.с. Наибольшее практическое распространение
получила трехфазная система.
Чтобы отличить три э.д.с. трехфазного генератора друг от
друга, их обозначают соответствующим образом. Если одну из
э.д.с. обозначить Ёд, то отстающую от нее на 120° э.д.с. приня-
то называть Ёв, а опережающую на 120°—Ёс.
185
Последовательность прохождения э.д.с. через одинаковые зна-
чения (например, через нулевое значение) называют последователь-
ностью фаз.
§ 132. Трехфазная цепь. Расширение понятия фазы. Совокупность
трехфазной системы э. д. С., трехфазной нагрузки или нагрузок и
соединительных проводов называют трехфазной цепью.
Токи, протекающие по отдельным участкам трехфазных цепей,
сдвинуты друг относительно друга по фазе. Под фазой трехфаз-
ной цепи понимают участок трехфазной цепи, по которому протекает
один и тот же (одинаковый) ток*.
§ 133. Основные схемы соединения трехфазных цепей, определе-
ние линейных и фазных величин. Обмотки генератора должны быть
соединены с нагрузкой. Самым неэкономичным способом является
соединение каждой обмоткн генератора с нагрузкой двумя прово-
дами. В этом случае в системе было бы шесть соединительных про-
водов. Для экономии числа соединительных проводов обмотки трех-
фазного генератора соединяют в звезду или в треугольник. Трех-
фазную нагрузку также соединяют в звезду или в треугольник. При
этом число соединительных проводов от генератора к нагрузке умень-
шается с шести до трех или до четырех.
На электрической схеме трехфазный генератор принято изобра-,
жать в виде трех обмоток, расположенных под угле»* 120^ друг к
другу. При соединении его в звезду объединяются в одну точку
одноименные зажимы (например, концы) трех обмоток. Ее принято
называть нулевой точкой генератора и обозначать буквой О (рис. 155).
Начала обмоток генератора принято обозначать буквами А, В, С.
Буква А ставится у начала первой фазы, В— у начала второй и С —
у начала третьей.
При соединении обмоток генератора треугольником (рис. 156)
конец первой обмотки генератора соединяется с началом второй, ко-
нец второй с началом третьей, конец третьей с началом Первой.
Геометрическая сумма э.д.с. в замкнутом треугольнике равна нулю.
Поэтому, если к зажимам Л, В, С не присоединена нагрузка, то по
обмоткам генератора не будет протекать ток.
Пять простейших способов соединения трехфазного генератора
с трехфазной нагрузкой изображено на рис. 157—160.
Точку, в которой объединены трн конца трехфазной нагрузки
при соединении ее звездой, называют нулевой точкой нагрузки и
обозначают О'. Нулевым проводом называют провод, соединяющий
нулевую точку генератора с нулевой точкой нагрузки. Ток нулево-
го провода назовем /0. Положительное направление для него возь-
мем от точки О' к точке О.
* Под фазой будем также продолжать понимать аргумент синусоидаль-
но изменяющейся величины.
Таким образом, в зависимости от рассматриваемого вопроса фаза —
это либо участок трехфазной цепи, либо аргумент синусоидально изменяю-
щейся величины. '
186
Провода, соединяющие точки А, В, С генератора с нагрузкой,
называют линейными - проводами.
Схема рис. 157 называется звезда — звезда с нулевым проводом;
схема рис. 158 звезда — звезда без нулевого провода; схема рис.
159, а звезда — треугольник; рис. 159, б — треугольник — тре-
угольник; рис. 160 — треугольник — звезда.
Текущие по линейным проводам токи называют линейными то-
ками, их обозначают 7д,/в, /с. Условимся за положительное
направление для них принимать направление от генератора к нагруз-
ке. Модули линейных токов часто обозначают через /Л, не указы-
вая никакого дополнительного индекса. Такое обозначение особен-
но часто применяется тогда, когда все линейные токи по модулю
одинаковы.
Напряжение между линейными проводами называют линейным
напряжением. Как и любое напряжение, его снабжают двумя ин-
дексами. Например UAB есть линейное напряжение между точками
А и В. Модуль линейного напряжения обозначают ил.
Рис. 157
Рис. 158
Познакомимся с понятиями фазовых напряжений и фазовых токов.
Каждая из трех обмоток генератора называется фазой генератора.
Каждая из трех нагрузок называется фазой нагрузки. Протекаю-
щие по ним токи называют фазовыми токами генератора I $ или,
соответственно, нагрузки, а напряжения на них — фазовыми или
фазными напряжениями (U#).
§ 134. Соотношения между линейными и фазовыми напряжениями
и токами. При соединении генератора в звезду (рис. 157, 158,159, а)
линейное напряжение по модулю в И З раз больше фазового напря-
W
жения генератора {ифгеш;^. Это следует из того, что Пл есть основание
равнобедренного треугольника с острыми углами nd Ж (рис. 161)
'Л := IV2COS30” - (7.1)
Линейный ток 1Л при соединении генератора в звезду равняется
фазовому току генератора
Рис. 159
При соединении генератора в треугольник линейное напряжение
равняется фазовому напряжению генератора. Это следует из рис. 156
При соединении нагрузки в звезду (см. рис. 157, 158, 160) соответ-
ствующий линейный ток равен соответствующему фазовому току
нагрузки
При соединении нагрузки треугольником токи в сторонах тре-
угольника также снабжают двумя индексами (см. рис. 159, а и б).
Положительные направления токов выбираем по часовой стрелке.
Индексы у токов соответствуют выбранным для них положитель-
ным направлениям. Первый индекс у тока отвечает точке, от кото-
рой ток утекает, второй — точке, к которой ток подтекает.
188
При соединении нагрузки в треугольник (см; рис. 159, а и б) ли-
шённые токи не равны фазовым и определяются через них по пер-
вому закону Кирхгофа
А = ~ 7СЛ» В = 1вс ~~ IАВ* k = IСА ~ ВС'
§ 135. Преимущества трехфазных систем. Все элементы трехфаз-
ной системы: генератор, трансформатор, трехфазный асинхронный
двигатель, трехфазная линия передачи, в своей основе были разра-
ботаны русским инженером М. О. Доливо-Добровольским в 1891 г.
Широкое распространение трехфазных систем объясняется глав-
ным образом тремя основными причинами:
а) передача энергии на дальние расстояния трехфазным током
в экономическом отношении более выгодна, чем передача энергии
переменным током с иным числом фаз;
б) элементы трехфазной системы — трехфазный асинхронный
двигатель и трехфазный трансформатор — весьма просты в произ-
водстве, экономичны и надежны в работе;
в) трехфазная система обладает при определенных условиях свой-
ством неизменности величины мгновенной мощности системы за пе-
риод синусоидального тока. Это свойство справедливо в том случае,
если нагрузка во всех трёх фазах трехфазного генератора будет оди-
накова.
§ 136. Расчет трехфазных цепей. Трехфазные цепи представляют
собой разновидность цепей синусоидального тока, и потому расчет
и исследование их производится теми же методами и приемами,
которые обсуждались в главах пятой и шестой.
Для цепей трёхфазного тока также применим символический
метод расчета, могут строиться векторные, топографические и кру-
говые диаграммы.
Аналитический расчет трехфазных цепей рекомендуется сопро-
вождать построением векторных или топографических диаграмм.
Векторные диаграммы облегчают нахождение углов между токами
и напряжениями, предохраняют от возможных ошибок аналити-
ческого расчета и делают все соотношения более наглядными.
Рассмотрим некоторые простейшие трехфазные цепи.
§ 137. Звезда—звезда с нулевым проводом. Если нулевой провод
в схеме рис. 157 обладает весьма малым сопротивлением, то потенциал
точки О' практически равен потенциалу точки О; точки О' и О
фактически представляют собой одну точку. При этом в схеме
образуются три обособленных контура. Токи в них:
f _ &а . ; __Ёв . _______Ёс
А~ гЛ'
По первому закону Кирхгофа ток в нулевом проводе равен геомет-
рической сумме фазных токов
4-4 +/в + /с- <7-3>
189
Если Z4 = ZB = ZC (такая нагрузка называется равномерной),
то ток /0 равен нулю, и нулевой провод может быть изъят из схе-
мы без изменения режима ее работы.
При неравномерней нагрузке фаз ток /0 в общем случае не ра-
вен нулю.
При наличии в нулевом проводе некоторого сопротивления Zo
расчет схемы производится по методу двух узлов (см. § 140)..
Пример 75. В схеме рис. 162, а э. д. с. каждой фазы трехфазного
генератора равна 127 в. Сопротивления фаз нагрузки равны по ве-
личине (6,35 ом), но имеют различный характер:
2Л—/?, ZB — Zc----------
Определить ток в нулевом проводе.
Решение. На рис. 162,6 построим векторную диаграмму. Токи
всех фаз по модулю равны —— — 20 (а). Ток 1А 'по фазе совпа-
6,35 <
дает с ЁА. Ток 1В на 90° отстает от Ёв. Ток 1Сопережает Ёс на
90°. Сумма /л +/в4-/'с дает ток/0. По модулю он равен 14,6 а.
Пример 76. Какой величины должно быть взято сопротивление /?
в фазе А схемы рис. 162, а, чтобы ток в нулевом проводе стал
равным нулю?
Р е ше ние. Геометрическая сумма токов 1в-\-1спо модулю
равна 2-20.cos30° = 20/з"(а). ’
Ток в нулевом проводе станет равным нулю, если ток jA, на-
правленный противоположно сумме 1в-\- 1С, по модулю станет рав-
ным 20 К 3 а. Прн этом сопротивление фазы А
Я = —= 3,66 (ом).
20 3 20)Л 3
Пример 77. Определить ток в нулевом проводе схемы рис. 162, а,
если в фазе А будет включено активное сопротивление 3,66 ом,
а индуктивность и емкость фаз В и С поменять местами
190
gjL = — = 6,35 ом.
шС
Решение. Векторная диаграмма изображена на рис. 163.
Из нее следует, что
/0 = 34,6 + 34,6 = 69,2 (а).
§ 138. Соединение нагрузки треугольником. Выберем
направление токов в фазах треугольника в соответствии
с рис. 159, а. Ток /лв вызывается напряжением лв. Величина и
фаза его" по отношению к напряжению UАВ определяются сопро-
тивлением нагрузки ZAB. Ток /вс вызван напряжением UBC, Величи-
на и фаза его по отношению к определяются сопротивлением
ZBC. Ток 1СА вызван напряжением UCA и определяется комплек-
сом ZCA. Линейные токи определяются через фазовые токи по пер-
вому закону Кирхгофа
1А = I АВ— 1сА'
1в = ^ВС IABt
IcA—^вс-
(7.4)
При равномерной нагрузке фаз линейные токи по модулю в Из
раз больше фазовых токов. При неравномерной нагрузке линейные
токи могут быть и больше и меньше фазовых токов.
Пример 78. В схеме рис. 164, a ZAB = — 19/; ZBC = 19/; ZCA —
= 19 ом. Э.д.с. каждой фазы генератора 220 в. Определить все
токи и построить векторную диаграмму.
Решение. Решение будем сопровождать векторной диаграм-
мой (рис. 164, б). Напряжения на фазах нагрузки в | 3 раз больше
фазовых э.д.с. генератора и равны 220 К 3 = 380 (в). Ток /АВ опе-
Г$1
режаёт напряжение Г7Лв на 90° и по величине расён — = 20 (а).
Ток 1ВС отстает от Свс на 90° и также равен 20 а. Ток- /сл , по
модулю равен .20 а и совпадает по фазе с напряжением 0сл. Ли-
нейные токи 1А, 1В, 1С найдем графически путем использования
соотношений (7.4). По модулю /л = /с^ 10 а; /в = 20а.
§ 139. ^Оператор а трехфазной системы. Условимся комплексное
число е>120°, по модулю равное единице, обозначать через а и на-
зывать оператором трехфазной системы.
щ Тогда
g/240^ (еУ120 )2 == fl2.
. . , Три вектора: 1, а и а2 образуют симмет-
14-------—1 ричную трехфазную систему (рис. 165).
14-а4-а2 = 0. (7.5)
рнс igg Умножение какого-либо вектора на а по-
ворачивает его без изменения модуля на угол
120° против часовой стрелки. Умножение
вектора на о2 поворачивает его на угол 240° против часовой стрелки
или, что то же самое, поворачивает его по часовой стрелке на 120й.
При помощи оператора а можно выразить э.д.с. Еви э.д.с. Ёс,
симметричной трехфазной системы э.д.с. через э.д.с. ЁА.
О
Ёв = а2£л;
Ёс = аЁА.
§ 140. Соединение звезда — звезда без нулевого провода. Схема
рис. 158 представляет собой схему с двумя узлами (точки О и
Наиболее целесообразным приемом расчета токов в ней является
метод двух узлов (§ 19). Напряжение между двумя узлами равно
U ЁаУа + ЁвУв + Ёс¥с _ EA(YA + ^YB + aYc) (7
° Уа+Ув+Ус Уа+.Ув+Ус.
Если нагрузка равномерна (Ул = YB = Ус), то (см. соотноше-
ние 7.5)
fi ____ ЁаУл (1 + я + о2) л
3Y.a
и напряжение на каждой фазе нагрузки равно соответствующей
э.д.с.:
АО' = U ВО' = йСО'
Иначе будет обстоять дело, если нагрузка неравномерна., В этом
случае (J0,0^Q и
192
Uaq' Ёа Uq'O’ &во' Ёв ^о'О’ й CQ! Eq U о'о’
Токи в фазах нагрузки
; U АО' f U во'. г Uсо'
1А — 1В = —--> 1С — --•
ZA ZB ZC
Численные подсчеты см. в примере 80.
Если в двух фазах нагрузка одинакова, например ZB — Zc ¥= ZA,
то формула (7.7) после преобразований получает следующий уп-
рощенный* вид:
Цуо = “ГЗ#- <7-8)
о о л ZB-\-
§ 141. Трехфазные цепи при наличии взаимоиндукции. Расчет трех-
фазных цепей, содержащих магнитносвязанные катушки, произво-
Рис. 166 Рис. 167
дится так же, как и расчет магнитносвязанных цепей однофазного
синусоидального тока.
Пример 79. Определить показание амперметра и показание вольт-
метра в схеме рис. 166. Построить топографическую диаграмму,
совместив ее с векторной диаграммой токов. Дано: Еф = 127 в;
шЬ — — = 4 ом', и>М — 2 ом.
<пС
Решение. Выберем положительные направления токов в соответ-
ствии с рис. 166. По первому закону Кирхгофа 1А 4~ /в + 7*с = 0.
Примем э.д.с. Еа направленной по оси -}* 1. Составим уравнение но
второму закону Кирхгофа для контура ОАО'ВО
iА]шЕ 4- iBj^M — (/в]^Ё / л/'ыМ) = йАВ.
После подстановки числовых значений
или
2/ (/л- /в) = 220е7‘80°
1’л— ^В —
22Ое>зо»
2ело»
= 110е->даоа.
7 Лг А. БессОнвв-
193
Для контура ОСО’ВО
I (——'j—UвР°Ь-}~ IА]'шМ) — l)CB
G \ шС I
“Н - 4//с - 2jlA - 4jiB = 220/.
Совместное решение трех уравнений дает
1А = ПО, 1В = 1 We0°, [с = 110 V3e~i^a.
Топографическая диаграмма, совмещенная с векторной диаграм-
мой токов, изображена на рис. 167. Амперметр показывает ПО а,
вольтметр ~ 640 в;
;<Ро' = Фо +еа
§ 142. Активная, реактивная и полная мощности трехфазной
системы. Под активной мощностью трехфазной системы понимают
сумму активных мощностей фаз плюс активная мощность, выделя-
емая в сопротивлении, включенном в нулевой провод
Р=^а+Рв+Рс + Р<г (7.9)
Реактивная мощность — сумма реактивных мощностей фаз плюс
реактивная мощность сопротивления, включенного в нулевой про-
вод
Q = Q4+Qb + Qc+Qo- (7.10)
Полная мощность
S = (7.11)
Если нагрузка равномерная, то
Р. = (?о = О
Ра = рв = Рс = иф1ф cos <p^; QA = QB = Qc = иф1ф sin ф^.
Здесь под <рф понимается угол между напряжением 1Уф на фазе
нагрузки и током 1ф фазы нагрузки. При равномерной нагрузке фаз
Р = 3^/в6созфв6;
Q = ЗЦ^зшф^;
5 = ШфГф.
(7.12)
* При равномерной нагрузке вне зависимости от Способа ее соединения
в звезду или в треугольник
Ыф1ф = Уз ~У~ъиф!ф = К зил1л.
Здесь ил — линейное напряжение на нагрузке, 1Д — линейный ток на-
грузки.
Поэтому вместо формул (7.12) часто пользуются следующими:
Р = УЗ ид1д cos <р;
Q = У£УЛзшф;
з = уз ия1д.
194
§ 143. Измерение активной мощности в трехфазной системе. Для
измерения активной мощности трехфазной системы в общем случае
(неравномерная нагрузка и наличие нулевого провода) необходимо
три ваттметра включить по схеме рис. 168.
Активная мощность системы равна сумме показаний трех ватт-
метров. Если нулевой провод отсутствует, то измерение мощ-
ности производится двумя ваттметрами по схеме рис. 169.
Сумма показаний двух ваттметров в схеме рис. 169 дает активную
мощность всей системы вне зависимости от того, в звезду или в тре-
угольник соединена нагрузка
(треугольник нагрузки всегда
Рис. 168
Рис. 169
Показание первого ваттметра равно скалярному произведению
напряжения U Ас на ток IА, т. е. UACIA, показание второго UBC[B.
Сумма показаний двух ваттметров
ас/aвс/в =_/У ао — [/со) Iа([/во~jJ(Xl)lв=_ _
— U АО^А-}- Uво 1в— ^СО^аЛ-^в) = U АО 1а ^Г^ВО^В -VUcoIc.
Последнее выражение есть не что иное как сумма активных мощ-
ностей всех трех фаз.
При равномерной нагрузке фаз достаточно измерить мощность
одной из ^фаз и результат утроить.
Если в схеме рис. 169 нагрузка будет равномерная, то по показаниям
двух ваттметров (Pi и Р2) может быть определен тангенс угла фи нагрузки.
Обсудим как это можно сделать.
На рис. 170 изображена векторная диаграмма для равномерной индуктив-
ной нагрузки. Угол между напряжением UAc и током 1А равен (<р—30й),
а угол между напряжением UBc и током 1В равен (<р + 30°). Поэтому пока-
зание первого ваттметра
Р1 ₽= У АС ТА = ид1л СОЗ (ф — 30°)
и показание второго
Ра = йвС Тв = ил1лсоь(Ч+ 30°).
Если ф > 60°, то ф + 30° > 90° и Р2 <.0. Стрелка второго ваттметра
. при ф > 60° будет ударяться об упор слева. В этом случае для замера вели-
7*
195
(7.13)
чины Р2 следует поменять местами концы параллельной обмотки и измерен-
ную мощность взять со знаком минус.
Составим разность и сумму показаний ваттметров:
Pi — Pi = 1Л sin q>;
Pi + Pi = КЗ ид 1Л cos ф.
Отсюда после деления первой строчки на вторую, получим
Ч Т 2
§ 144. Измерение реактивной мощности при равномерной нагруз-
ке фаз. Убедимся в том, что показание ваттметра в схеме рис. .171
при равномерной нагрузке фаз пропор-
ционально реактивной мощности всей си-
стемы. Ваттметр измеряет величину
ВС I А~ U ВС IA C0S №ВС Л i д)-
Угол между U&. и /А .равен 90° — ф (см.
рис. 170). Поэтому показание^ ваттметра
равно
Пример 80.
Найти
Уъиф1ф sintp.
Следовательно, реактивная мощность си-
стемы (см. формулу 7.12) равна показа-
нию ваттметра, умноженному на К3.
показания ваттметров в схеме рис. 172
и сумму показаний их сравнить С активной мощностью системы,
подсчитанной как 2 I2R', R — “ = 7^ ом.
шС
Решение. Для сокращения записи обозна-
Ус=~4- = /<оС - /у.
"/шС
196
По методу двух узлов
Z7 _ р Уд+°2Гв+аГС _ а 1 — ]аг+]а _
u°'°~ А ya+yb+yc -Са i-7 + j
= ЁА(1 — /3) = —0,73-220 = — 160 (в).
Напряжение на фазе А нагрузки йА0, = ЁА— Uo,o = 220 —
— (— 160) = 380 (в). Ток фазы А 1А=^ — 5 (а). Он совпадает
по фазе с UA0, (см. векторную диаграмму на рис. 173). Напря-
жение на фазе В нагрузки йво,=Ёв—f70,0 = 50 — / 191. Мо-
дуль напряжения (JBQ, равен 197 в. Модуль напряжения Uco,
197
также равен 197 в. Токи 1В = 1с— = 2,6 (а). Угол между то-
ком 1А и напряжением l)AC равен — 30°. Угол между током /в
и напряжением равен 76°. Показание первого ваттметра^
Р,= Л1А) = 380-5-cos30° = 1650 (вт).
Показание второго ваттметра
р2 = UBCIB cos (1)^ *1В) = 380-5. cos 76° = 253 (вт).
Суммарная мощность
Рх + Р2 = 1903 вт.
Правильность этой цифры подтверждается подсчетом мощности
в системе по формуле
2 ГЁ.
Так как активное сопротивление есть только в фазе А, то
% PR = РАр = 52-76 = 1900 (вт).
197
Результат совпадает с суммой показаний ваттметров с точностью
подсчетов на логарифмической линейке.
Пример 81. Определить показания ваттметров в схеме рис. 172 прн
обрыве линейного провода С в точке tn, находящейся у начала фазы
С приемника.
Решение. При обрыве провода в точке т схема из трехфазной
переходит в однофазную. К линейному напряжению Uдв включены
последовательно соединенные /? и L
j______/ ___ Оле — 380е^3|>3 _ о 54е-/ха®
/д- iB — R+jaL— 76-Н76 ’
Векторная диаграмма изображена на рис. 174 . Показание пер-
вого ваттметра
Pt=UAC Та ~ 380-3,54cos 15° = 1295 (ет).
Показание второго ваттметра
/>a=I/BC7s = 380.3,54 cos 105° = —345 (ет).
Pl-{-Pi = 950 ет.
Проверка:
РАРА =3,542-7бда950 (ет).
Пример 82. Известны показания ваттметров в схеме 169 при рав-
номерной индуктивной нагрузке фаз: Pt= 766 ет и Ра= — 174 ет.
Определить угол <р нагрузки, а также реактивную и полную
мощность системы.
Р ешен йе. По формуле (7.13)
tg<р = Уз = 2,65; ф«69°20';
~ = tg<p; Q = Ptg<p = (766— 174).2,65 = 1600 (еар)\
S = Vp*-\-Q*= 1716 еа.
§ 145. Круговые и линейные диаграммы в трехфазных цепях.
Если меняется модуль сопротивления одной из фаз трехфазной це-
пи, то геометрическим местом концов вектора напряжения или тока
любой из фаз цепи будет являться окружность или прямая линия.
В качестве примера обсудим вопрос о круговой диаграмме на-
пряжений в схеме рис. 175, а, если ZB= Zc= г = const и изменяет-
ся только модуль сопротивления фазы A ZA.
С этой целью воспользуемся методом холостого хода и короткого
замыкания. При холостом ходе фазы А к линейному напряжению
Uвс присоединены последовательно два сопротивления Zs = Zc =
= г фаз В и С. Падения напряжения на них будут одинаковы и равны
половине напряжения Use- Следовательно, нулевая точка прием-
ника — точка О', на схеме находящаяся между'этими сопротивле-
198
ниями, при холостом ходе фазы А окажется посредине отрезка ВС
(там, где на рис. 175, б поставлена буква т).
Напряжение холостого хода между точками А и О' схемы
рис. 175, a (иА0,хх) равно разности потенциалов точек А и О' (по-
следняя, как уже говорилось, при холостом ходе находится в точке tn).
Из векторной диаграммы рис. 175, б видно, что это напряжение
в полтора раза больше фазной э.д.с. ЁА
фазе.
и совпадает с ней по
б)
Эквивалентная схема для определения тока в сопротивлении
ZA по методу хх и кз изображена на рис. 176. Из нее следует
/ 1’ЬЕа
‘a- Zex + ZA
(7-14)
здесь Zex представляет собой входное ' сопротивление схемы
рис. 175, а по отношению к зажимам АО'. Из схемы рис. 177 найдем
Напряжение
L) = / 7. =
' иО'т 1
Рис. 176
Ь5.ЁЛ
гА
При ZA =0 U0,m = 1,5ЯЛ, и точка О' совпадает с точкой А рис. 175, б.
При ZA — оо, U0,m = 0 и точка О' совпадает с точкой т рис. 175, б.
199
Эти два граничных положения точкй О' на круговой диаграмме
рис. 175, б (при 2Л = 0 и при ZA — оо) не зависят от характера со-
противления в фазе А.
Что касается положений точки О' (геометрического места этой
точки) при значениях ZA, находящихся в интервале от 0 до оо,
то они зависят не только от модуля сопротивления ZA, но и от ха-
рактера этого сопротивления (т. е. угла <рл)
Если сопротивление ZA чисто активное и равно /?, то фл==0,
Фл —= 0 и
ft _ 1>5£д
Геометрическим местом концов вектора й0>т в этом случае
будет являться прямая Ат рис. 175, б. При /? = г U0'm = •
Если сопротивление ZA чисто .емкостное, то <рл==—90°, <рл—<рвх=
=—90°, и геометрическим местом концов вектора Ь0,т будет являть-
ся полуокружность трА. При
* = г Л = = 0,67 £ле>«3 0 25'.
<вС О’т 1 — 2/ л
Положение точки О' в этом режиме (при — = г) показано на
<оС
рис. 175, б. Если сопротивление 2Л будет чисто индуктивным
(2Л = ja>L), то фл—Фе»—90°, и геометрическим местом концов век-
тора й0,т будет являться полуокружность mqA.
Таким образом, при изменении сопротивления в фазе А схе-
мы рис. 175, а нулевая точка приемника перемещается по полу-
окружности трА рис. 175, б, если ZA имеет емкостный характер;
по прямой тОА, если ZA есть активное сопротивление, и по по-
луокружности тцА, если ZA есть чисто индуктивное сопротивление.
Напряжение между нулевой точкой приемника (точкой О')
и нулевой точкой генератора (точкой О), т. е. f/o'o на рис. 175, б
определится вектором, проведенным из точки О в перемещаю-
щуюся точку О'.
§ 146. Указатель последовательности чередования фаз. Опреде-
ление порядка или последовательности чередования фаз в трехфаз-
ной симметричной системе э.д.с. или напряжений производится при
помощи устройства, называемого указателем последовательности
чередования фаз. Он состоит из двух одинаковых ламп накаливания
и емкости С (рис. 178). Емкость С берется такой величины, что ем-
1
костное сопротивление — равно сопротивлению г каждой лампы.
<»С
200
Если три конца фазоуказателя подключить к трем концам сим-
метричной трехфазной системы э.д.с., то потенциал нулевой точки
схемы рис. 178 будет определяться положением точки О' на вектор-
ной диаграмме рис. 175, б.
Из диаграммы рис. 175, б видно, что напряжение на лампах
накаливания будет различно. На лампе, включенной в фазу В, оно
определяется вектором йво,\ на лампе, включенной в фазу С,
вектором Uсо,. Так как UB0, > Uco„ то лампа в фазе В будет
гореть более ярко, чем лампа в фазе С. Следовательно, если фа-
зу трехфазной системы э.д.с., к которой подключен конец от
емкости, принять за фазу А, то фаза, к которой окажется
Рис. 178
Рис. 179
подключенной ярко горящая лампа, есть фаза В, а фаза с туск-
ло горящей лампой — фаза С.
Одним из важнейших свойств многофазных и, в частности, трех-
фазных токов является способность их создавать круговое вращаю-
щееся магнитное поле.
§ 147. Определение кругового вращающегося магнитного поля.
Круговое вращающееся магнитное поле представляет собой маг-
нитное поле, вектор результирующей магнитной индукции которо-
го по величине неизменен и вращается с постоянной угловой ско-
ростью о.
§ 148. Магнитное поле катушки с синусоидальным током. Прежде
всего убедимся в том, что магнитное поле одной катушки, по кото-
рой протекает синусоидальный ток, представляет собой пульсирую-
щее*, не вращающееся магнитное поле. С этой целью обратимся к
рис. 179. На рис. 179 изображена катушка. По ней проходит сину-
соидальный ток i = Im sin о/. Магнитное поле характеризуется
вектором магнитной индукции В. Направление В определяется на-
правлением намотки катушки и направлением тока в ней в данный мо-
мент времени. Пусть буква Н обозначает начало и К — конец ка-
тушки на рис. 179. Если ток входит в зажим Н и выходит нз зажи-
ма К. (это направление тока будем считать положительным; ему соот-
* Под пульсирующим полем понимают поле, вектор магнитной индук-
ции которого изменяется (пульсирует) вдоль оси создающей его катушки с то-
ком.
201
ветствует интервал времени от 0 до w)-, то вектор магнитной индук-
ции направлен вверх. В следующий полупериод, когда ток отрица-
телен, вектор В направлен вниз. Таким образом, геометрическим
местом концов вектора В является ось катушки.
§ 149. Получение кругового вращающегося магнитного поля. Рас-
положим три одинаковые катушки так, что оси их смещены на 120’
по отношению друг к другу (рис. 180). Присоединим катушки к сим-
метричной трехфазной системе э. д. с. Пусть токи входят в начала
катушек и изменяются следующим образом:
= Im sin
t2 = Im sin (<of — 120°); is = lm sin (at + 120°).
Графики их изображены на рис. 181. Каждый из токов будет созда-
вать пульсирующее поле, направленное вдоль оси своей катушки.
Рис. 180
Рис. 181
Положительное направление оси первой катушки обозначим -f-1,
второй +2, третьей +3. Индукцию первой.катушки обозначим
Ви второй — В2, третьей — В3.
На рис. 182 изобразим мгновенные значения Bt, Bit Ва и ре-
зультирующую индукцию для моментов времени at = 0, -2., я,
— я. На первом эскизе
. я
втором при at = — и
рис. 1 о/ даны построения для at = и, на
т. д.
Рис. 182
202
С увеличением времени вектор результирующей магнитной ин-
дукции, оставаясь по величине равным 1,5Вт, вращается с угло-
вой скоростью ш по направлению от начала первой катушки с то-
ком /т sin со/ к началу второй катушки с током lm sin (at — 120°).
Можно сказать, что вектор результирующей магнитной индукции
вращается в сторону катушки с отстающим током.
Если ток lm sin (<о/—120°) пропустить по третьей, а ток
/msin (W-j-120°) по второй катушке, то направление вращения
поля изменится на обратное.
В § 53 отмечалось, что если магнитная цепь полностью или час-
тично выполнена из ферромагнитного материала, то при том же
токе магнитный поток в ней резко возрастает по сравнению с маг-
нитным потоком в отсутствии ферромагнитного материала.
Для того чтобы усилить вращающееся магнитное поле, внутрь
катушек (рис. 180) помещают полый или сплошной ферромагнитный
цилиндр, а стороны катушек заключают в пазы
внешнего ферромагнитного цилиндра (рис. 183).
Вращающееся магнитное поле используется
в электрических двигателях.
§ 150. Принцип работы асинхронного двига-
теля. Наиболее распространенным в промыш-
ленности типом двигателя переменного тока
является трехфазный асинхронный двигатель.
В нем имеется неподвижная часть — статор, в
пазах которого помещены три катушки, создаю-
щие круговое вращающееся магнитное поле,
часть — ротор, в пазах которого находятся три замкнутых на себя
или на внешнее сопротивление катушки (рис. 183).
Чтобы не затемнить рис. 183, катушки на нем даны в разрезе,
торцовые части катушек не показаны, а каждая из них занимает
лишь небольшую часть окружности статора (или ротора).
В действительности каждая из катушек (прямые и обратные про-
вода ее) занимает 7з окружности расточки статора (или окружности
ротора).
Вал ротора двигателя соединен с валом рабочей машины.
Допустим, что вначале ротор неподвижен. При этом вращающее-
ся магнитное поле, созданное обмотками статора, пересекает провода
катушек неподвижного ротора с угловой скоростью ш и наводит в
них э.д.с. Э.д.с. вызовут токи в катушках ротора. По закону Лен-
ца эти токи стремятся своим магнитным полем ослабить вызвавшее
их магнитное поле.
- Механическое взаимодействие токов ротора с вращающимся маг-
нитным полем приведет к тому, что ротор начнет вращаться в ту
же сторону, в какую вращается магнитное поле (в этом можно убе-
диться, применив правило левой руки).
В установившемся режиме скорость вращения ротора арот со-
ставляет (0,98-7-0,95) со. Двигатель называется асинхронным пбто-
203
му, что ротор его вращается не синхронно (асинхронно) с вращаю-
щимся полем; ырот принципиально не может равняться угловой ско-
рости вращающегося поля. Это станет понятным, если учесть, что
при <ирот— о» вращающееся поле не пересекало бы провода обмоток
ротора, в них отсутствовал бы ток, и ротор не испытывал бы вра-
щающего момента.
В курсе ТОЭ мы ограничиваемся качественным рассмотрением
основных положений, характеризующих принцип работы асинхрон-
ного двигателя. Более обстоятельно все эти вопросы изучаются в
курсе электрических машин.
Рис. 184
СерВечник
Рис. 185
§ 151. Эллиптическое вращающееся магнитное поле*. Кроме кругового
вращающегося магнитного поля на практике приходится иметь дело также и
с эллиптическим вращающимся магнитным полем. Под ним понимают магнит-
ное поле, вектор результирующей магнитной индукции которого скользит
по эллипсу и вращается с периодически изменяющейся угловой скоростью.
Круговое вращающееся магнитное поле переходит в эллиптическое
в результате нарушения нормального режима работы, например при обрыве
в одной' из катушек или если протекающие по катушкам (см. рис. 180) токи
будут ие равны по амплитуде или сдвинуты Не иа^ 120° по отношению друг к
другу. Оно образуется также, если в одной катушке будут перепутаны нача-
ло и конец. - • - -
Пример 83. Построить геометрическое место концов вектора результирую-
щей магнитной индукции схемы рис. 180, если в результате аварии прекра-
тилось протекание тока в первой катушке, а токи во второй и третьей катуш-
ках остались прежними.
Решение. Вращающееся поле будет создаваться только второй и третьей
катушками. Составим таблицу значений В2 и В3 в долях от Вт для at = 0
л л
4 ’ 2
Для построения вектора результирующей индукции для фиксированного
момен’Га времени надо на оси второй катушки отложить В3, а на осн третьей
катушки отложить В3 и затем их геометрически сложить. Если Вг > О, то
она откладывается по положительному направлению оси 4- 2, при Вг < 0
она откладывается в обратном направлении.
В результате построений получен эллипс рис. 184. Большая полуось его
* Дальнейший материал главы седьмой, начиная с § 151, для студентов
РТФ не обязателен.
204
0 В | в | сч 3 —л 4 Я 4* | СИ Я 3 7 —л 4
Sa =sin(m/—120°) вт Гз~ —0,97 —0,5 0,259 Уз 2 0,97 0,5- -0,259
2
В, — =sin(m/-|-120°) Вт /з~ 2 0,259 —0,5 —0,97 Уз —0,259 0,5 0,97
2
Рис. 186
При расчетах трехфазных цепей, содержащих вращающиеся
машины и трансформаторы, применяется расчетный прием, который
получил название метода симметричных,
составляющих. Перед тем как приступить
к изучению основ этого метода, оказывает-
ся необходимым рассмотреть вопрос о за-
висимости входного сопротивления трех-
фазного трансформатора и асинхронного
двигателя от сдвига фаз между фазными
э.д.с. питающей его системы.
§ 152. Зависимость входного сопротив-
ления трехфазного трехстержневого транс-
форматора от сдвига фаз между фазными э. д. с. питающей его
системы. На рис. 185 схематически изображен широко применяе-
мый на практике трехфазный трехстержневой трансформатор.
Магнитная система его состоит из трех стержней или сердеч-
ников, которые соединены при помощи ярм.
На первом сердечнике расположены первичная и вторичная об-
мотки первой фазы, на втором — второй фазы, на третьем — треть-
ей. Соединим первйчные обмотки в звезду.
Рассмотрим два различных режима работы трансформатора.
В первом режиме входные зажимы трансформатора подключены
к симметричной трехфазной системе э.д.с. рис. 186, а.
Во втором режиме входные зажимы присоединены к системе
э.д.с. рис. 186, б, в которой все э.д.с. имеют одинаковую амплитуду
и совпадают по фазе.
Для того чтобы различие в двух режимах работы трансформато-
ра стало более ясным, обсудим сначала особенности работы двух сход-
* нах электрических схем рис. 187 и 188.
В схеме рис. 187 э.д.с. образуют симметричную систему, такую
Же, что и на рис. 186, а, т; е.
_ Ёв = а2ЁА и Ёс = аЁА,
а проводимости ветвей
205
ya = yb = yc = y.
В схеме рис. 188 по-прежнему
ya = yb = yc=y,
но система э.д.с. другая (рис. 186, б), а именно:
£л= £в= £с.
В схеме рис. 187
fl _ + « + «2) _ П
о'о ~ ЗУ
Токи в фазах
/л= (£л-^О'о)Ул=ад
iB—EBY', ic = EcY.
О' О'
Рис. 187 ' Рис. 188
В схеме рис. 188 (сначала без учета пунктирного добавления)
°6'0 = + = £л. /л= (£л_ {/о,о) у = 0;
/в=/с = 0.
Физически все токи в этом случае равны нулю потому, что по
любому контуру алгебраическая сумма э.д.с. равна нулю.
Режим работы схемы рис. 188 существенно изменится, если
между нулевыми точками О' и О включить сопротивление Z0,Q — '
= — (пунктир на схеме рис. 188). В этом случае
YO’O
и - 3£ЛУ
ЗУ + Уо,о ’
ток в нулевом проводе
/ _ п у _ З^лТУр'о **
и 0'0 0'0 Зу + уо,о •
Токи в фазах
/л = iB = /с = (£л - (J0,q} у = = 1/0,0,
or -f-1 о О d
.206
т.е. ток в нулевом проводе будет в три раза больше фазных
токов.
Вернемся к обсуждению двух режимов работы трехфазного транс-
форматора. Режим работы схемы 187 аналогичен первому, а ре-
жим работы схемы рис. 188 с пунктирным добавлением аналогичен
второму режиму работы трансформатора.
В схеме рис. 188 с пунктирным добавлением токи ветвей замы-
каются по сопротивлению Zo'o- Во втором режиме работы трансфор-
матора магнитные потоки стержней, не имея возможности (подоб-
но токам в схеме рис. 188 без пунктирного добавления) замыкаться
по соседним стержням, могут замыкаться и действительно замыкают-
ся по воздуху (силовые линии изображены пунктиром на рис. 185).
Таким образом, в первом режиме работы трехстержневого трехфаз-
ного трансформатора магнитные потоки проходят по сердечникам
и ярмам, а во втором режиме магнитные
потоки, выйдя из сердечников, вынужде- £
ны замыкаться по воздуху. При одном и том "
же значении токов в обмотках в этих двух
режимах магнитные потоки будут резко
различны. Во втором режиме потоки будут
много меньше, чем в первом режиме, еле-
довательно, индуктивность обмоток и вход-
ное сопротивление на фазу во втором ре-
жиме (назовем его Zo) будет меньше, чем в ис’
первом режиме Zv
Допустим далее, что к входным зажимам трехстержневого транс-
форматора приложено одновременно две системы э.д.с.: система
э.д.с. рис. 186, а и система э.д.с. рис. 186, б. Первую из них будем
называть системой прямой последовательности фаз (в ней э.д.с. фа-
зы В отстает от э.д.с. фазы Л), вторую систему будем называть сис-
темой нулевой последовательности фаз.
Примем, что трансформатор работает на линейном участке его
веберамперной характеристики и потому применим принцип нало-
жения. Для расчета токов в обмотках трансформатора надо порознь
найти токи от системы э.д.с. прямой последовательности, исполь-
зовав для этой цели сопротивление Zlt и токи от нулевой последо-
вательности по сопротивлению Zo, а затем геометрически сложить
токи прямой и обратной последовательностей в каждой фазе,
Кроме систем э.д.с. прямой и нулевой последовательностей, су-
ществует еще система э.д.с. обратной последовательности (рис. 189).
В ней э.д.с. фазы В опережает э.д.с. фазы А. Входное сопротивле- *
ние на фазу трехстержневого трансформатора для обратной после-
довательности Za равно входному сопротивлению трансформатора
для прямой последовательности Zt.
Еще большее различие во входных сопротивлениях для различ-
ных последовательностей имеется в трехфазном асинхронном дви-
гателе.
207
§ 153. Входные сопротивления на фазу трехфазного асинхронно-
го двигателя для прямой, обратной и нулевой последовательностей
фаз. Если к входным зажимам трехфазного асинхронного двигате-
ля рис. 183 одиовремеиио подвести систему напряжений прямой,
нулевой и обратной последовательностей фаз, то входное сопротив-
ление иа фазу двигателя, для прямой последовательности не бу-
дет равно входному сопротивлению на фазу для обратной последо-
вательности Z2, и оба они будут отличны от входного сопротивления
для нулевой последовательности Ze. Разберемся, чем это объясня-
- ется.
Под действием напряжения прямой последовательности в дви-
гателе создается круговое вращающееся магнитное поле. Оно,увле-
кает за собой ротор двигателя. Ротор вращается с угловой частотой
<орот. Система напряжений обратной последовательности также соз-
дает круговое вращающееся поле, но направление вращения его
обратно направлению вращения поля прямой последовательности.
Система напряжений нулевой последовательности вращающегося
магнитного поля не создает. Вокруг статорных обмоток ею созда-
ются пульсирующие потоки, замыкающиеся по воздушному зазору
между статором и ротором, подобно тому, как в трехстержневом
трехфазиом трансформаторе рис. 185 потоки от нулевой последо-
вательности, выходя из сердечников, замыкались по воздуху.
Входное сопротивление на фазу двигателя для данной последо-
вательности зависит не только от активного и реактивного сопротив-
лений фазы статорной обмотки, но и от активного и реактивного соп-
ротивлений фазы роторной обмотки для данной последовательности*.
Индуктивное сопротивление фазы ротора прямо пропорционально
частоте. Прямая последовательность создает в роторе токи частоты
(о> — wpom) в пределах от 0,02 до 0,05 о>, тогда как токи ротора от об-
ратно вращающегося поля имеют частоту о> (1,98-~1,95) ш.
.Так как частоты токов в роторе, создаваемые прямой и обратной
последовательностями, различны, то различны и входные сопротив-
ления на фазу для прямой Zx и обратной Z2 последовательностей.
* Подобно тому как в трансформаторе входное сопротивление определя-
ется яе только собственным сопротивлением первичной обмотки, ио и сопро-
тивлением, вносимым вторичной обмоткой (см. § 116).
208
Магнитные потоки' нулевой последовательности замыкаются,?,
минуя ротор, тогда как потоки прямой и обратной последователь-^
ностей проходят через ротор. При одном и том же токе прямой и ну-
левой последовательностей потоки прямой и нулевой последова-
тельностей будут различны. Поэтому для асинхронного двигателя
4 ^2*
§ 154. Разложение несимметричной системы на системы нулевой
прямой и обратной последовательностей фаз. Любая несимметрич-
ная система трех токов, напряжений, потоков одинаковой частоты —•
обозначим их для общности Л, В, С — может быть однозначно
представлена в виде трех систем, систем нулевой, прямой и обрат-
ной последовательностей фаз.
Система прямой последовательности (рис. 190) состоит из век-
торов Лх, Blt Ср причем
^ = агЛр | (7 J5)
Сх = aAr J
Система обратной последовательности (рис. 191, а) состоит- из
Аг, В2, С2'.
Вг^аА^ 1
С2 = ааЛ2. I
Система нулевой последовательности Ло, Во, Со (рис. 191, б)
(7.17)
векторы сим-
(7.18)
Ао — Вл — Се.
Выразим заданные три вектора А, В, С через
: метричных систем следующим образом:
А — Ло -j- А4~ А2;
в = вв4- вх4-в2;
с = со4~ Cj-f- с2.
Перепишем (7.18) с учетом (7.15) и (7.16):
Л = Ло4- Лх4- Л2;
В = Лп 4~ ааЛх 4~ аА2;
_ С = Ло 4- aAi4-a2Aa.
(7.19)
(7.20)
(7.21)
Из системы уравнений (7.19 — 7.21) найдем Ло, Лх и Л2 че-
рез заданные векторы А, В, С. Для нахождения Ло сложим
уравнения (7.19 — 7.21) и учтем, что 1 4~ a -J- а2 — 0. Получим
А=4М + В+С). (7.22)
209
Для нахождения Д, надо геометрически сложить три заданных
вектора и взять одну треть от суммы.
Для определения к уравнению (7.19) прибавим уравнение
(7.20), умноженное на а, и уравнение (7.21), умноженное на а2:
Лх = - (Л 4- аВ + агС). (7.23)
3
Следовательно, одна треть суммы, состоящей из вектора А, плюс
вектор В, повернутый против часовой стрелки на 120°, плюс
вектор С, повернутый по часовой стрелке на 120°, дает вектор Лг
Для определения Л2 к уравнению (7.19) Прибавим уравнение
(7.20), предварительно умноженное на а2, и уравнение (7.21),
умноженное на а. Получим
Л = - (Л 4- а2В 4- аС). (7,24)
3
*/
Рис. 192
Пример 84. Задана система трех напряжений (рис. 192, а):
С?А — 220 в, UB = 220/ и Uc = — 220/.
Найти симметричные составляющие этой системы.
Решение. По формуле (7.22)
(70 = 1 (йА 4- 0в 4- 0с) ~ - (220 4- 220/ — 220/) = 73,4 в.
3 3
Графические построения для определения (70 = UA0 даны на
рис. 192, б.
По формуле (7.23)
~ Wa 4- айв^аЮс) = 2В[1 4- / (а - а2)) = - 53,4 в,
О Ч
а — а2 — / ИЗ.
ЭТО
Графические построения для определения UAl даны на рис, 192, в.
По формуле (7.24) — построения см. на рис. 192, г— имеем
= ^[1+/(а2-а)]=2оо в.
о
§ 155. Основы метода симметричных составляющих*. Если в сос-
тав трехфазных цепей входят трехфазные трехстержневые трансфор-
маторы и (или) вращающиеся электрические машины, например
асинхронные двигатели и генераторы, или те и другие вместе, то
расчет аварийных режимов, например коротких замыканий одной
или двух фаз на землю, короткого замыкания двухд^аз без соедине-
ния с землей, обрыва одной фазы и других режимов, при которых
на двигателях и трансформаторах возникают несимметричные сис-
темы напряжений, производится по методу симметричных состав-
ляющих. Рассмотрим основы этого метода.
На основании принципа наложения, применимого к линейным
цепям, заданный несимметричный режим работы схемы в методе
симметричных составляющих представляется как результат наложе-
ния трех симметричных режимов.
В первом симметричном режиме все токи, э.д.с. и напряжения
содержат только составляющие прямой последовательности фаз,
а вращающиеся машины и трехфазные трансформаторы пред-
ставлены на схемах их сопротивлениями для прямой последователь-
ности Zr
Во втором симметричном режиме все токи, э.д.с. и напряжения
содержат составляющие только обратной последовательности, а ма-
шины и трансформаторы представлены их сопротивлениями обрат-
ной последовательности Za. В третьем симметричном режиме все токи
э.д.с. и напряжения содержат только составляющие нулевой после-
довательности, а машины и трансформаторы представлены соот-
ветствующими сопротивлениями нулевой последовательности Zo.
Для того чтобы от несимметричной исходной схемы прийти к трем
симметричным схемам, поступают следующим образом: в том месте
схемы, где создается несимметрия, в схему вводится система трех
несимметричных напряжений UA, UB, Uc**. Далее система трек
несимметричных напряжений в соответствии с § 154 раскладывает-
ся на три симметричные системы, основные векторы которых 0Q, Ut
и 172 подлежат определению.
Точно так же система трех несимметричных токов 1А, !в, 1С
раскладывается на три симметричные системы токов, основные век-
торы которых /в, /х, /2 подлежат определению.
* Изучение данного параграфа обязательно для студентов энергетичес-
кого и электромеханияеского факультетов.
•• Система этих трех напряжений (или э. д. с.) на основании теоремы
компенсации заменяет собой три неодинаковых сопротивления, образовавших-
ся в месте аварии и приведших к несимметрии во всей схеме.
21Г
В методе симметричных составляющих неизвестными являются
Шесть величин: три напряжения — Uo, U1 и {7а и три тока /0, /х
и /2, через которые могут быть выражены любые напряжения и
токи в цепи.
Для определения шести неизвестных составляются шесть урав-
нений. По одному уравнению составляются для каждой из трех сим-
метричных схем, остальные три уравнения составляются для того
участка схемы, где создается несимметрия. Вид трех последних
уравнений зависит от характера несимметрии в схеме.
Обсудим применение метода на примере схемы рис. 193. Эта схе-
ма состоит из трехфазного генератора с заземленной нулевой точ-
кой, дающего симметричную систему э.д.с., линии, трехфазного
асинхронного двигателя, соединенного в звезду, и трехфазного трех-
Рис. 193
стержневого трансформатора с заземленной нулевой точкой. На
участке линии между двигателем и трансформатором произошло
однофазное короткое замыкание на землю.
Сопротивления обмоток генератора для прямой, обратной и нуле-
вой последовательностей обозначим, соответственно, через ZUt
^ог-
Аналогично сопротивления на фазу для трехфазного двигателя
Zia, Z2d и Zod; для трансформатора — Z1T, Z2r и Z0T. Сопротивление
на фазу трехфазной линии передачи для прямой, обратной и нуле-
вой последовательностей фаз обозначим соответственно Zu, Z24
и Z04. Сопротивление линии для прямой последовательности Zu
равно сопротивлению линии для обратной последовательности Z?ji,
но не равно сопротивлению линии для нулевой последовательности
фаз Z04 за счет различия в значениях индуктивности на фазу трех-
фаЗной линии для систем прямой и нулевой последовательностей фаз.
Различие в значениях индуктивности на фазу для прямой и нуле-
вой последовательностей фаз объясняется двумя причинами.
Во-первых, тем, что индуктивность линии передачи для прямой
и для обратной последовательностей определяется только лишь гео-
метрическими размерами петель, образованных линейными прово-
дами, тогда как индуктивность линии для нулевой последователь-
ности определяется не только геометрическими размерами петель,
212
образованных линейными проводами, но и геометрическими раз-
мерами петель, образованных линейными проводами и нулевым
проводом.
Во-вторых, тем, что э.д.с., наводимые в проводах линии для пря-
мой и для обратной последовательностей, представляют собой геомет-
рическую, сумму э.д.с. от сдвинутых по фазе на 120° токов в линей-
ных проводах, тогда как э.д.с., наводимые в проводах линии для ну-
левой последовательности, созданы совпадающими по фазе токами
нулевой последовательности.
Более подробно вопрос об
линии для систем прямой и
нулевой последовательностей
фаз изложен в приложе-
нии В в Л. 5.
В рассматриваемом при-
мере будем учитывать сопро-
тивление на фазу участка
линии между двигателем и
местом короткого замыкания.
Остальные участки линии
имеют малую протяженность,
и сопротивление их учиты-
вать не будем. Сопротивление
между нулевой точкой генератора и
а сопротивление между нулевой точкой
лей — ZSt.
Обозначим напряжения между линейными проводами и землей
в том месте, где произошла авария, через UA, йв и йс (см.
рис. 194, а), а токи через 1А, 1В и 1С. Несимметричную систему
напряжений l)A, UB, Uc представим тремя симметричными систе-
мами:
индуктивности
к/. b. 1м.
А о Ь
на фазу трехфазной
Л
(/,♦□ ед вг/Зп
0
Рис. 194
землей обозначим
трансформатора и
73г,
зем-
В соответствии с этим напряжение VA между линейным про-
водом А и землей заменим тремя напряжениями: Uo, и1 и
(рис. 194, б); 0в заменим на напряжения £70, и aUv Анало-
гично заменим и напряжение Uc. Далее три несимметричных тока
IА, 1в, представляем тремя симметричными системами токов
Др ^1’ ^2'
Л^Л+4+4'* Дв=
ic~ 1 а*
213
Следовательно, ток 1А на схеме рис. 194, б (и на схеме рис. 193)
можно заменить суммой трех токов /0 -|~ А + 12‘, ток I в—суммой
трех токов /0+ а/а; ток 1С— суммой /0 4-а/14-а8А.
Следующий этап расчета состоит в переходе от заданной несим-
метричной системы (схемы) к трем симметричным расчетным систе-
мам (схемам): к схеме прямой последовательности, к схеме обрат-
ной последовательности и к схеме нулевой последовательности.
Схема прямой последовательности состоит из генератора, трех
сопротивлений Z12, соединенных в звезду, трех симметричных
напряжений Uv a20lt аС\, трех симметричных токов
allt трех Соединенных в звезду сопротивлений Zjt , трех соеди-
ненных в звезду сопротивлений
Zig и трех сопротивлений ли-
нии Zlt.
Так как эта схема симметрич-
на, то расчет ее может прово-
диться на одну фазу. Схема пря-
мой последовательности на одну
*)
Рис. 195
фазу (на фазу А) изображена на ряс. 195, а. Упростим ее, не
затрагивая неизвестное пока напряжение С этой целью . сна-
чала заменим ветвь с ЁА и ветвь с Zld одной эквивалентной
с э.д.с. Ё'3 и проводимостью Уз!:
Р' ___ ЕАУ±г , у, ______ у . у е у ______ 1 , у _____ 1
Yu + Yld' 31 Z12 ’ Г*> Z^‘
Далее полученную ветвь с последовательно соединенным с ней
сопротивлением Z1A и ветвь с сопротивлением Z1T заменим одной
эквивалентной с параметрами Ё3 и Z31 (рис. 195, б)
6 . <7 Z17(Z^+ZU).
3 ~ +У1Т ’ ~ z1T + z'3l + ’
7' __ 1 . у ______ 1 . у _ 1
V' ’ 1 эл, 7' । 7, > * 1т 7 •
Г 91 1 Z31 + Z1T
Для схемы рис. 195, б
214
E9=iMUv (7.25)
Аналогичным путем составляем однофазную схему рис. 196 для
обратной последовательности (также для фазы А). Так как генера-
тор дает симметричную систему э.д.с. прямой последовательности,
то в схеме рис. 196 источник э.д.с. обратной последовательности от-
сутствует.
В этой схеме взято напряжение обратной последовательности
(j2 и ток обратной последовательности /2 вместо и1 и Zx, взятых
в схеме прямой последовательности. После замены двигателя и
трансформатора их сопротивлениями обратной последовательности
Zid и Z2t и преобразований, подобных тем, которым была подвер-
гнута схема прямой последовательности, найдем
у __ ^2т( + ^2л) .
э2~ z2t + z;2 + z24’
Е2 = Г2г + Уад; У2г = -^-;
1 э2
JAjisi схемы рис. 196
/2Z,2 + &2 = 0. (7.26)
Составим схему для нулевой последовательности. В ней также
будет отсутствовать источник э.д.с. нулевой последовательности,
но будет введено напряжение нулевой последовательности Uo и ток
нулевой последовательности /0. При составлении ее надо учесть,
что через сопротивления Z3! и Z3t в исходной схеме рис. 193 текут
токи нулевой последовательности в три раза большие, чем по со-
ответствующим участкам линии (см. § 152), поэтому в однофаз-
ную схему рис. 197, а введены сопротивления З23г и 3ZSr. Нуле-
вая точка асинхронного двигателя не соединена с землей, поэто-
му через него не текут токи нулевой последовательности, и в схе-
ме рис. 197, а сопротивление Zor) отсутствует. От схемы рис. 197, а
перейдем к схеме рис. 197, б. В ней
Рис. 197
_ ____ (3Z32 + ^Ог + Ze4)(Z()T + 3Z3j.)
30 “ 3Z„ + 2», -I- Z04 + Zor + 3Z3/ * ...
215
Для Схемы рис. 197, б .
/Х + (7о = О. (7.27)
К трем уравнениям (7.25)—(7.27) добавим еще три уравнения, харак-
теризующие несимметричную нагрузку (участок, на котором
произошло кз на землю, см. рис. 193). Из схемы рис. 193 видно, что
= 0; 7в = 0; /с —0.
Каждая из этих величин может быть выражена через симметрич-
ные составляющие:
^А=^о+^1 + ^=0; (7.28)
/в= /в -J- aiI1 о1г — 0; (7.29)
7С= Л + аЛ + ^/^О. (7.30)
Совместное решение уравнений (7.25)—(7.30) дает возможность
найти напряжения £70, и (72 и токи /0, 1г и /2. По ним мо-
; гут быть определены токи и напряжения на любом участке схемы.
Например, ток короткого замыкания на землю
Л=/о+Л + Л-
В примере на метод симметричных составляющих, разобранном
да стр. 212—216, несимметричный режим работы схемы рис. 193
был вызван коротким замыканием линейного провода фазы А на
землю. Рассмотрим теперь последовательность расчета при возник-
новении другого вида аварии, а именно, при обрыве одного из ли-
нейных проводов.
На рис. 198, а изображена схема, повторяющая схему рис. 193
с тем только отличием от нее, что вместо короткого замыкания ли-
нейного провода А на землю в том же месте, где ранее было корот-
кое замыкание, произошел разрыв линейного провода А без соеди-
216
нения с землей. Трехфазный генератор по-прежнему дает, симмет-
ричную систему э.д.с.
Как и в рассмотренном выше примере, не будем учитывать соп-
ротивления на фазу проводов линии от места аварии до трансформа-
тора, полагая, что расстояние от трансформатора до места аварии
; мало. В соответствии с основными положениями метода симметрич-
: ных составляющих, в место разрыва провода вводим систему трех
несимметричных напряжений UA, XJB и йс (см. рис. 198, б), кото-
рые на основании теоремы компенсации заменяют собой три не-
одинаковых сопротивления, образовавшихся в месте аварии и при-
ведших к несимметрии во всей схеме.
Рис. 199
Подобно тому как это было показано на рис. 194, б, три не-
симметричных напряжения UA, UB и Uc заменяем тремя симме-
тричными системами напряжений:
Аналогично три несимметричных тока 1А, 1В, 1С заменяем
тремя симметричными системами токов:
1а= 4 + Л + Л,
Л?— 4 + % +
217
После этого от заданной несимметричной схемы рис. 198 переходим
к трем симметричным схемам: к схемам рис. 199, а, 200, а и 201, а.
Схема рис. 199, а составлена для прямой последовательности
применительно к фазе А, схема рис. 200, а —для обратной после-
довательности и схема рис. 201, а—для нулевой последователь-
ности. Эти схемы преобразуем подобно тому, как это ранее было сде-
лано в отношении схем рис. 195—197, не затрагивая преобразова-
нием неизвестные пока напряжения Ult U2 и Uo. Получаем три рас-
четные схемы для прямой, обратной и нулевой последовательное-
тей, изображенные соответственно на рис. 199, б, 200, б и 201, б.
Для этих схем составим уравнения по законам Кирхгофа
+ (7.31)
0 = (72 + /2Z32- (7.32)
0={7о + /Ло- (7.33)
Уравнения (7.31—7.33) внешне полностью совпадают с уравнения-
ми (7.25—7.27), однако Zal, Z.2 и Z№ в схемах рис. 199, б—201, б
отличны от значений 2Э1, Zai н ZM в схемах рис. 195, б—197, б.
Далее составляем три уравнения для места аварии:
Л= 4+Л+Л^ 0, (7.34)
UB = 0 + аЮ1 + ай2 = 0, (7.35)
*7с = # о + = °- (7.36)
Уравнение (7.34) состазлено на основании того, что при нали-
чии разрыва в линейном проводе А ток IА — 0.
Уравнения (7.35) и (7.36) выражают равенство, нулю напряже-
ний ив и Uc, введенных в схему рис. 198, б в месте аварии.
Совместное решение уравнений (7.31—7.36) дает возможность
найти Ux, U2, Uo, ilt i2, iQ, а по ним любой ток и любое напря-
жение в схеме. '
Аналогичным образом производится расчет н при других видах
аварий в трехфазных системах.
ПРИЛОЖЕНИЯ К I ЧАСТИ курса тоэ
Приложение А
ЭЛЕКТРОСТАТИЧЕСКИЕ ЦЕПИ
5 15 6. Определение электростатической цепи. Цепи, образованные источ-
никами постоянной э.д.с. и идеальными конденсаторами, принято называть
электростатическими цепями.
Идеальные конденсаторы представляют собой конденсаторы, сопротив-
ление между обкладками которых в установившемся режиме на постоянном
токе равно бесконечности.
Для электростатических цепей характерно, что в установившемся режи-
ме работы, когда заряды на обкладках (пластинах) конденсаторов ие меняют-
ся во времени, токи через конденсаторы не протекают (токи через идеальные
конденсаторы протекали, когда последние заряжались, т. е. когда они накап-
ливали заряды).
В качестве примера электростатической цепи на рис. 202 изображена схе-
ма с двумя источниками э. д. с. EY и Е2, тремя конденсаторами С1г Сг, Ся,
и одним сопротивлением.
Через сопротивление R схемы рис. 202 в установившемся режиме ток не
протекает, падение напряжения на нем равно нулю и потому на распределе-
ние напряжений в схеме это сопротивление никакого влияния не оказывает.
§ 157. Что понимают под расчетом электростатической цепи? Под рас-
четом электростатической цепи понимают определение напряжений и зарядоз
на конденсаторах, входящих в состав цепи. Важную роль при расчетах имеет
положение, вытекающее из первого закона Кирхгофа и заключающееся в том,
что алгебраическая сумма зарядов на пластинах конденсаторов, присоединен-
ных к любому узлу схемы, всегда равна либо нулю, либо сосредоточенному
на них начальному заряду.
Начальным зарядом (обозначим его qH) будем называть заряд, сосредо-
точенный на этих пластинах к началу процесса, приведшего к установивше-
муся режиму.
Перед началом расчета величина и знак qH должны быть определены по
данным предшествовавшего режима или известны из каких-либо иных сооб-
ражений.
§ 158. Алгебраическая сумма зарядов иа пластинах конденсаторов, при-
соединенных к любому узлу схемы, равна либо нулю, либо начальному заряду,
сосредоточенному на них к началу процесса. Для доказательства этого общего
положения обратимся к рис. 202. Заряды иа обкладках конденсатора Ct
обозначим через qlt иа обкладках конденсатора С2 через qit на обклад-
218!
ках конденсатора С3 через qs. Хотя в установившемся состоянии (когда за-
ряды во времени не меняются) токи во всех ветвях. схемы (их назовем ilt 1г
и i3) и равны нулю, но в процессе зарядки (или разрядки) конденсаторов,
т. е. в процессе становления установившегося режима (когда qlt q2 и q3
менялись во времени) токи в ветвях схемы не были равны нулю.
Как известно из предыдущего (§ 89), ток через конденсатор равен скорос-
ти изменения заряда на нем. Поэтому
. . dqt . dqs
dt ’ dt ’ is= dt *
По первому закону Кирхгофа, алгебраическая сумма токов, сходящихся
в любом узле любой схемы, равна нулю. Для узла а (рис. 202) ймеем
Производная от алгебраической суммы (Л — 9» — =2j <?) будет рав-
на нулю только в том случае, если эта сумма будет равнавекрторой-Ьостоян-
ной величине, которую назовем qH. ~ " ''
Следовательно, в самом общем случае
= Чн- (АЛ)
Наиболее часто встречаются случаи, когда qK = 0. При этом
S<7==°- (А.2)
§ 159. Распределение напряжений между двумя последовательно соеди-
ненными идеальными конденсаторами. Если два предварительно незаряженных
идеальных коидеисатора Ct и С2 присоединены к источнику С напряжением
V (рис. 203) и в схеме имеет место установившийся режим, то отношение нап-
ряжений иа конденсаторах (t/x и l/s) обратно пропорционально отношению
емкостей конденсаторов
Это соотношение является следстввем того, что через оба конденсатора
при заряде прошел одинаковый ааряд q — CxUi — C2U2.
Пример 85. К источнику напряжения с э. д. с. £ — 120 в последователь-
но включены два конденсатора (рис. 203): Ci = \5мкф, Са == 45 мкф. Най-
ти Ut и U2. х
220
с
Решение. Так как их 4- U2 = Е и U2 = Ul —— , то
Са
/ С. \
!+-—- =£•
\ '-'2 /
120
Следовательно, I/, =------j— = 90 в, U2 = 30 в.
1+т
Заряд q = Cit7i = 15 • IO-* • 90 — 1,35 • 10-3 (к).
§ 160. Методика расчета разветвленных электростатических цепей. Все
методы расчета электрических цепей постоянного тока, рассмотренные в гла-
ве первой, основывались на первом и втором законах Кирхгофа и законе Ома.
Напомним эти законы:
Первый закон Кирхгофа:
^/ = 0 (А.4)
Второй закон Кирхгофа:
(А-5>
Закон Ома
l = Ug. (А.6)
Для электростатических цепей имеют место аналогичные уравнения.
Действительно, вместо уравнения (А.4) при начальных зарядах, равных ну-
лю, имеет место уравнение (А.2). Вместо уравнения (А.6) справедливо урав-
нение
q = UC. (А.6')
Уравнение (А.5) является общим для электрических и для электростати-
ческих цепей.
Таким образом, между электрическими и электростатическими цепями
имеет место формальная аналогия: та роль, которую играет ток / в уравне-
ниях электрических цепей, в уравнениях электростатических цепей выполня-
ет заряд q; роль, которую играет проводимость g в уравнениях электрических
цепей, в электростатических цепях выполняет емкость С.
Эта формальная аналогия дает возможность использовать все методы рас-
чета электрических цепей постоянного тока для расчета электростатических
цепей, надо лишь в формулах для расчета цепей постоянного тока (выведен-
ных вглаве первой) токи заменить на заряды, а проводимости g на емкости С.
Практически наиболее приспособленными к расчету электростатических
цепей оказываются метод узловых потенциалов н вытекающий из него метод
двух узлов.
Дело в том, что в расчетные формулы этих методов в явном виде входят
проводимости (см. формулы 1.20 н 1.22), поэтому замена проводимостей, на
емкости производится весьма просто.
Если начальные заряды qH на отдельных конденсаторах не равны нулю,
то учет влияния этих зарядов на распределение напряжений в схеме произво-
дится путем добавления нх (с соответствующим знаком) в правые части урав-
нений метода узловых потенциалов (формула (1.22)) подобно тому как в этом
методе учитываются токи, подтекающие к отдельным узлам~схемы от источ-
ников токов (см. стр. 34). Расчет электрической цепи начинался с выбора по-
ложительных направлений токов в ветвях. Расчет электростатических це-
пей начинают с того, что произвольно выбирают положительные направления
для напряжений на конденсаторах. Причем положительное направление нап-
ряжения на конденсаторе связано с распределением зарядов на его обкладках
в соответствии с рис. 204,
221
Пример 86. Методом двух узлов найти напряжения на конденсаторах и
заряды на обкладках их в схеме ряс. 205. Начальный заряд qH = 0. Значении
э. д. с. в вольтах и емкостей в микрофарадах даны на ряс. 205.
Решение. Выберем положительные направления напряжений на кон-
денсаторах к узлу а и воспользуемся формулой (1.20), заменив в ней прово-
димости g на емкости С
„ —£2С2 100 - 60 — 80.40
°Ь~- C1 + G + C3 = 60 + 40 + 20 -23>3<в)-
Таким образом, напряжение на конденсаторе С3
= — Uаь = — 23,3 в.
Напряжение на конденсаторе С2равно
U± = — Uab = 100 — 23,3 = 76,7 (в).
Напряжение на конденсаторе С2 равно
Иг = — Ег — Uab = — 80 — 23,3 = — 103,3 (в).
Рис. 205
Рис. 204
Найдем заряды на обкладках конденсаторов, присоединенных к узлу а.
Так как U± > 0, то в соответствии с рис. 204 на обкладке конденсатора Cj,
обращенной к точке а, будет отрицательней заряд, равный
— = — ULCL = — 76,7 • 60 • 10-« = — 4,6 . 10-з
Напряжения U2 и U3 меньше нуля, поэтому на обкладках конденсаторов С2
и С3, обращенных к точке а (с учетом рис. 204), заряды будут положительные
</2 = — t/2C2= 103,3 • 40 • 10-» — 4,13. 10~3 (к).
q3 = — tl3C3 = 23,3 • 20 • 10-« = 0,463 . 10-3 (х).
Алгебраическая сумма зарядов на обкладках, присоединенных к узлу
а по условию задачи должна быть равна нулю. Проверим это:
— <Zi + <?2 + <1з = 10-з (—4,6 + 4,13 + 0,466) « 0.
Пример 87. Условия те же, что и в примере 86, но пластинам конденса-
торов, соединенным в точке а схемы рнс. 205, перед сборкой схемы сообщили
начальный заряд <?„ = 3,2- 10-«х. Найти напряжения на конденсаторах.
Решение. Воспользуемся методом узловых потенциалов. Мысленно
заземлим узел Ь. Неизвестным будет потенциал узла а, т. е. <ра. Если бы произ-
водился расчет электрической цепи аналогичной конфигурации, то расчетное
уравнение по методу узловых потенциалов записалось бы следующим обра-
зом:
Фе Е>аа = аг
где Gaa— сумма проводимостей всех ветвей, сходящихся в узел а, 1а — узло-
вой ток, равный алгебраической сумме токов, полученных как произведение
э. д. с. ветвей на проводимости данных ветвей, плюс ток, подтекающий к дан-
ному узлу от источника тока. В соответствии с изложенным в § 160 заменяем
сумму проводимостей Gaa суммой емкостей (Сг + С2 + С2), а узловой ток 1а
заменяем узловым зарядом ЕхСг — Е2С2 + qK-, qH в последнем выражении
играет ту же роль, что и ток, подтекающий к узлу а от источника тока в ана-
логичной электрической цепи. .
222
Получаем следующее уравнение:
Фа (Cj + С2 4* Сз) = — Е3С3 + <?«•
Подставим числа: 120 • 10“• фа = 60 • 10~«, отсюда
Фа = 50 в.
Напряжение на первом конденсаторе
£/, = £1 — фа = 100 — 50 = 50 (в).
Напряжение на втором конденсаторе
С/2 = — Е2 — фв == — 80 — 50 = — 130 (в).
Напряжение на третьем конденсаторе
U3 = — фа = — 50 в.
Пример 88. На рнс. 206, а показано соединение в звезду трех емкостей
С,, С2 и С3. Значения емкостей в микрофарадах записаны на рисунке. Тре-
буется наитн величины емкостей С12,
ка емкостей рнс. 206, б, полагая,
что начальные заряды на емкостях
равняются нулю.
Решение. Ввиду аналогии
между электрическими и электроста-
тическими цепями (§ 160) восполь-
зуемся формулами (1.28) — (1.30),
заменив в ннх проводимости на ем-
кости: •
Q__________£1^2 _
Ci + С2 С3
10 • 20
= = 3,33 (мкф);
Сгз н С,j эквивалентного треугольни-
С13 = 5 мкф\ С23 — 10 мкф.
§ 161. Расчет цепей с неидеальными конденсаторами. Под нендеальными
конденсаторами понимают конденсаторы, проводимость между обкладками
которых не равна нулю (или, другими словами, сопротивление между обклад-
ками которых не равно бесконечности).
Если к нендеальному конденсатору приложить постоянное напряжение,
то через него будет протекать ток утечки.
Нендеальный конденсатор в расчетном отношении можно представить
схемой замещения на рнс. 207. На этой схеме параллельно включены идеаль-
ный конденсатор (который накапливает заряды на обкладках) и активное соп-
ротивление по которому протекает ток утечки конденсатора вследствие
несовершенства диэлектрических свойств среды, разделяющей его. пластины.
Ток утечкн обычно мал, так как сопротивление составляет несколько
десятков или сотен мегом. Однако токн утечкн, несмотря на их малость, иг-
рают принципиальную роль н приводят к тому, что напряжения в цепях с
нендеальными конденсаторами и источниками постоянных э. д. с. в устано-
вившемся режиме распределяются уже не в зависимости от величин емкостей
конденсаторов (что имело место в цепях с идеальными конденсаторами), а в
зависимости от сопротивления утечек конденсаторов (т. е. распределяются
так же, как н в «обычных» цепях постоянного тока).
В качестве простейшего примера рассмотрим схему рнс. 208. Эта схема
в отличие от схемы рнс. 203 содержит два неидёальных конденсатора, сопро-
тивления утечек которых равны Kyi и Ку2.
223
В установившемся режиме работы через последовательно соединенные
•' Е
сопротивления R, Ryl н Ry2 течет ток утечкн, равный Ly — ---------------.
R 4* Ryi + Ryz
От этого тока на сопротивлении Ryi будет падение напряжения
и на сопротивлении £у2 падение напряжения U2 = lyRyz- У '
Напряжение на емкости Ci будет равно Ut, а на емкости С2 равно U2.
Таким образом, в цепях постоянного тока с нендеальными конденсаторами на-
пряжения на емкостях не зависят от величин емкостен, а зависят от сопротив-
лений утечек конденсаторов.
Все рассмотренное в приложении А относилось к установившимся режи-
мам работы. Как происходит переход от одного установившегося режима ра-
боты к другому, по каким законам в функции времени меняются при этом то-
ки и напряжения — все этн вопросы изучаются во II части курса ТОЭ.
С, С.
Приложение Б
ДУАЛЬНЫЕ ЦЕПИ
§ 162. Определение дуальных электрических цепей. Две электрические
цепи называют дуальными, если законизменения донтурных токов в одной иэ
инх подобен закону изменения узловых потенциалов и другой. .
В качестве простейшего примера на рис. 209 изображены две дуальные
цепи. '
Схема рнс. 209, а составлена источником э. д. с. £ н последовательно с
ннм включенными активным, индуктивным н емкостным сопротивлениями
(R, L, С). Схема рнс. 209, б образована'источником тока /э н тремя параллель-
ными ветвями.
Первая ветвь содержит активную проводимость ga, вторая — емкость Сэ,
третья — индуктивность L3.
224
Для того чтобы показать, какого рода соответствие имеет место в дуаль-
ных цепях, составим для схемы рис. 209, а уравнение по- методу контурных
токов, а для схемы рнс. 209, б уравнение по методу узловых потенциалов.
Для схемы рис. 209, а
I + + = £ (Б.1)
\ 1®с /
Для схемы рис. 209, б обозначим потенциал точки а через фЛ и составим
уравнение по методу узловых потенциалов*:
1
jaLa
Если параметры схемы рис. 209, б (т. е. ga, La и Ca) согласовать в пара-
метрами схемы рис. 209, а (т. е. с R, L и С) таким образом, что
~Ь /®Са I (Б .2)
ёэ “ Са с
Элементы
исходной схемы
Эхйидалентные элементы
дуальной схемы
Рис. 210
где k есть некоторое произвольное число, имеющее размерность ом*, то
1 R 1 jcoL 1 / 1 . \
8а ТУ "+ = ь + У + ь ~ ь \ йтГ i<£>L / ‘
С учетом последней строки уравнение (Б.2) перепишем следующим
образом:
' Сопоставим уравнения (Б.4) и (Б.1). Из сопоставления следует, что если
ток 1а источника тока в схеме рнс. 209, б будет изменяться с той же угловой
частотой , что и э. д. с. Е в схеме рис, 209, а, а параметры обеих схем согла-
сованы в соответствии с уравнением (Б.З), то закон изменения во времени
потенциала фа в схеме рис. 209, б будет совпадать с законом изменения во
времени тока 1 в схеме рис. 209, а.
Если свойства какой-либо из схем изучены, то онй полностью могут быть
перенесены на дуальную ей схему.
* Потенциал второго узла схемы рнс. 209, б принят равным нулю.
8 Л. А. Бессонов
225
§ 163. Взаимно дуальные элементы схем. Каждому элементу исходной
схемы (схемы с источниками э. д. с. Ей параметрами R, Е, С) Отвечает свой
элемент экнивалеитиой дуальной схемы (схемы с источниками тока 1а и пара-
метрами ga, Са, La).
Так, источнику э. д. с. Е исходной схемы отвечает в дуальной схеме
источник тока 1а (рис 210); активному сопротивлению R исходной схемы— про-
водимость индуктивности L — емкость Са, емкости С — индуктинность La.
§ 164. Как образовать дуальную схему из исходной? Каждому независи-
мому контуру исходной схемы (а также области, являющейся внешней по
отношению к схеме) соответствует свой узел дуальной схемы.
Если в какой-либо ветви исходной схемы, являющейся смежной между
двумя контурами, имеется п последовательно включерных элементов, то этой
ветви соответствует п параллельных ветвей, соединяющих узлы дуальной
схемы, отвечающие этим контурам. Каждому элементу исходной схемы (Ё,
R, Ly С) в дуальной схеме соответствует свой эквивалент (Z3, g3, Са, La).
Для преобразования исходной, схемы в дуальную поступают следующим
образом.
Внутри каждого независимого контура (и вр внешней области) ставят по
точке н именуют ее. Эти точки будут являться узламк эквивалентной дуаль-
ной схемы.
В схеме рис. 211, а три независимых контура, поэтому внутри них ставим
точки 1, .2, 3, (точка / соответствует первому контуру, точка 2 — второму и
т. д.).
Во внешней по отношению к схеме области ставим точку 4. Между полу-
ченными четырьмя узлами проводим пунктирные линии — ветвн дуальной
схемы. Эти линнн проводим через элементы исходной схемы (через R, L, С, Ё)
и в дуальной схеме рнс. 211, б включаем в них соответствующие эквиваленты.
Так, узел 1 рис. 211, а соединен с узлом 4 одной пунктирной линией, так
как в ветвн, являющейся Смежной между первым и внешним контуром, вклю-
чено лишь одно сопротивление (активное сопротивление R^. На схеме рнс.
211, б между узлом 1 и узлом 4 включена активная проводимость §э1.
Узел 1 и узел 2 на рис. 211, а соединены двумя пунктирными линиями
(одна из них проходит через источник э. д. с. Ё5, другая через индуктивность
Aj, поскольку в ветви, являющейся смежной между 1 н 2 контурами, после-
довательно соединены два элемента схемы (Ё5 и L6). Узел 1 и узел 2 на схеме
рис. 211, б соединены двумя ветвями. В одну из них включен источник тока
As, в Другую — емкость Сэ5 (элементы, дуальные Ё5 н А5).
226
,Положительные направления токов источников тока должны быть сог-
ласованы с положительными направлениями э. д. .с. источников э. д. с.
Если при.обходе k контура по часовой стрелке какая-то э. д. с. этого кон-
тура будет совпадать с направлением обхода контура, то ток эквивалентного
ей источника тока должен быть направлен к k узлу.
Приложение В
МАТРИЦЫ В ЭЛЕКТРОТЕХНИКЕ
§ 165. Основные свойства матриц. Матрица — это совокупность величин,
расположенных в виде прямоугольной таблицы. Чтобы отличать матрицу по
внешнему виду от определителя, ее обрамляют квадратными скобками [ ]
или двойными вертикальными чертами || || . Каждый элемент матрицы часто
снабжают двумя индексами. Первый соответствует номеру строки, вто-
рой — номеру столбца.
Матрица называется квадратной, если число строк в ней равно числу
столбцов. Пример квадратной матрицы
°11 °12 °13
^21 ^22 ^23
°31 °32 °33 •
аП °12 ^13
[Д] = О 21 О 22 023
о31 а32 а33
Диагональной называется матрица вида Гап О 1.
(О O32J
Матрица, у которой элементы, расположенные по главной диагонали, равны
1, а все остальные — нули, называется единичной. Пример
Г1 0 01
О 1 О
О 0 1
Неопределенной называется матрица, в которой сумма элементов любой стро-
ки и любого столбца равна нулю.
Две матрицы равны, если равны соответствующие элементы этих матриц.
Например, матрица [4] = д12] равна матрице [В] = j^11 ^iaj, если ап ==>
— Ьц, 012 = ^12, а21 “= 1*21, ^22 = ^22*
У равных матриц равны определители. Так, для рассмотренного выше при-
мера Оц а22 — o2i 012 = Ьи Ь22 — Ь1г Ь21, но из равенства определителей
двух матриц еще не следует равенства самих матриц.
При сложении (вычитании) матриц следует сложить (вычесть) соответ-
ствующие элементы этих матриц.
Например,
[Д1 4- (Cl = F0*1 °1а1 I [с*х с*а1 = Гаы ~Ьсп + cial
[021 a22j 1^21 C22J 1а21 4~ С21 °22 4* С22_|.
Умножение двух матриц (число столбцов первой должно быть равно числу
строк второй) производится по правилу « строка первой матрицы умножается
на k столбец второй»,
Для иллюстрации этого правила умножим две матрицы, элементами ко-
торых являются числа
21Г5 61Г1 -54-2.7 1-64-2-81
4][7 8J “ [з • 5-I-4 - 7 3.6 4-4.8].
227
8*
Руководствуясь приведенным правилом, нетрудно убедиться в том, что [Л|
[В| [В] |4], т. е. результирующая матрица зависит от последовательности
расположения матриц сомножителей.
По отношению к матрице [4] можно составить обратную матрицу [4]-1.
Для этого необходимо: а) каждый элемент исходной матрицы {4] заменить его
алгебраическим дополнением; б) транспонировать полученную Матрицу, т. е.
строки сделать столбцами; в) разделить транспонированную матрицу на оп-
ределитель исходной матрицы [4].
Рассмотрим пример. Пусть [4] = J®*1 требуется найти [4]-1. Заме-
нив элементы матрицы [4] на алгебраические дополнения, получим матрицу
д”] • После транспонирования будем иметь £______________
Следовательно, Г а22 —а1г1
[Д]-1 _ L—Дат aii]
а11а22—a12a21
Произведение [4] [4]_ 1 = [ 1 ] = 1.
Для решения уравнения [4] [В] = [С] относительно матрицы [В] сле-
дует обе части этого уравнения умножить на [4]“1:[4j—1 • [4] [В]=[4]_1-[С]
. и учесть, что [4]_*• [4] = 1, Получим [В] = [4]—*• [С],
где Hj-Rf1].
Для второго = U3,
1-2 — 7 + А,
§ 166. Применение матриц в электротехнике. Матрицы применяются!
а) для сокращенной записи систем уравнений;
б) для некоторого упорядочения решения систем уравнений;
в) при исследовании топологических свойств электрических цепей (см.,,
например, Л. 10) в теории графов и при синтезе цепей.
Сокращение записи при помощи матриц проиллюстрируем на следующем
примере. Положим, что для некоторой цепи записана система уравнений по
методу контурных токов
2цА + Z12/2 -|- Z13A = Ё1(
^>iA + Z22/2 -f- Z23I3 = Ё2, (а)
Z3111 + Z32/2 4- Z33/3 = £3.
Zj-, Z12 z13
Z21 Z22 Z23 ;
^31 Z32 Z33
то систему (а) можно заменить одним матричным уравнением
lZ|[/] = [£].
228
Некоторое упорядочение решения
систем уравнений при помощи матриц
проиллюстрируем на примере состав-
ного четырехполюсника. Найдем мат-
рицы [41J и]4а]двух последовательно
соединенных четырехполюсников 1 и2
рис. 212 и матрицу [4] эквивалентного
им четырехполюсника.
Для первого
4=za.
Следовательно,
ИЛИ
где
’ 1 О'
Л1.
В правой части уравнения (в) заменим
на его эквивалент из (г).
4/1
h
Получим
== И11 Иг]
. Матрица двух последовательно
соединенных четырехполюсников
И] — И1] Иг] — Q ।
Zj 4- Z%
Z2
1
Следовательно,
Z. +Z2 . . . 1 .
4/1 7 47з 4* Zj/з и /1 = — 47g 4" 1 • 1з.
^2 ^2
Приложение Г.
ИССЛЕДОВАНИЕ ПРОЦЕССОВ
в неэлЕктрических системах на электрических
МОДЕЛЯХ- АНАЛОГАХ
Исследование процессов в неэлектрнческих системах (механических, акус-
тических, тепловых, гидравлических н др.) илн в частично неэлектрическия
(например в электромеханических) зачастую производят на электрическик
моделях-аналогах.
229
Стремление использовать дЛя! этой' целй электрические модели объясня-
ется тем, что: 1) электрические параметры можно легко Изменять в широких
пределах; 2) токи и напряжения можно измерять с большой точностью;
3) токи и напряжения относительно просто записать на осциллографе. Для
определенности в качестве неэлектрнческой будем рассматривать механи-
ческие системы.
Механические системы подразделяются на системы поступательного, вра-
щательного, поступательно-вращательного движения. В каждой из этих сис-
тем могут быть активные н пассивные элементы. Активными являются источ-
ники силы f н нсточннкн скорости v для систем поступательного движения н
источники вращающего момента М н угловой скорости <» для систем вра-
щательного движения.
Пассивными элементами являются элементы упругости, трения н массы.
Как н при рассмотрении электрических цепей, этн элементы часто идеализи-
руют, например считают, что идеальная пружина обладает только упругостью
н не обладает массой.
Для заданной механической системы сначала составляется схема заме-
щения, а затем, используя аналогию между механическими н электрически-
ми величинами, о которой будет идти речь ниже, образуют электрическую
схему-аналог, которую н подвергают исследованию (экспериментальному нли
теоретическому).
Перед составлением схемы замещения механической системы необходимо:
1. Выбрать систему отсчета для снл и скоростей (нлн соответственно для
вращающих моментов н угловых скоростей).
2. Соединить между собой узлы, имеющие одинаковую скорость нлн оди-
наковую величину смещения.
3. Соединить неподвижные узлы в одни узел.
4. На схеме замещения между соответствующими узлами изобразить ак-
тивные н пассивные элементы, имеющиеся в изучаемой системе.
Рассмотрим простейший пример.
Механическая система рнс. 213, а образована телом массой т, опираю-
щимся на пружину упругости S (S = — , где е — податливость). На тело
е
действует внешняя сила f(f), являющаяся функцией времени t, При движе-
нии тела в вертикальном направлении возникает вязкое треине о среду. Сила
вязкого трення пропорциональна скорости v перемещения тела. В схеме все-
го два узла. Подвижный а н неподвижный Ь.
Выберем положительное направление для отсчета величины перемещения
тела х, считая за исходное положение тела прн отсутствии силы f(f). Поло-
жительное направление для скорости v выберем вниз, как это показано на
ряс. 213, а. Схема замещения изображена на рнс. 213, б. В ней четыре ветвн.
Рнс. 213
В первой включен источник силы f(t), во второй — масса т, в третьей — иде-
альная пружина упругости S, в четвертой — сопротивление трення гтр.
23(1
Для схемы замещения составим уравнение по .первому закону мехавики.
Согласно этому закону сумма всех внешних сил, действующих в некотором
узле, должна быть равна сумме снл реакций в этом же узле. В узле « действу-
ют трн, силы реакцни.’(
, dv „
fm~m-------реакция системы, обусловленная силой тревня,
dt
f^—^vdt— реакция системы, обусловленная деформацией пружины,
е J
fmp — rmpv —реакция системы, обусловленная трением.
По первому закону механики
frn + fs + fmp—fff)
или
dv 1 (*
т — + rmpv + — I v dt = f (/).
u» € J
Между отдельными элементами механической системы н элементами соот-
ветствующей ей электрической модели (системы) может быть аналогия двух
типов в соответствии с тем, что для каждой электрической цепи может быть
составлена дуальная ей цепь.
В первом типе аналогий сопоставимыми величинами являются:
сила f — напряжение и,
скорость v — ток I,
масса т — индуктивность L,
податливость пружины е — емкость С,
сопротивление трения гтр — электрическое сопротивление R.
Во втором типе аналогий сопоставимыми величинами являются:
сила f — ток I,
скорость v — напряжение и,
масса т — емкость С,
податливость е — индуктивность L,
сопротивление трения гтр — электрическая проводимость G.
На рис. 213, в изображена электрическая схема по второму типу анало-
гий, соответствующая схеме замещения механической системы рис. 213, б.
Для схемы рис. 213, в
гС + *£ + < (О
или
du 1 С
С — + — 1 и dt -)- Qu = i (t).
dt L J
Здесь и — напряжение между узлами а и Ь.
Закон изменения напряжения и во времени в схеме рис. 213, в соответ-
ствует закону изменения скорости v в системе рис. 213, а, если параметры
электрической схемы соответствующим образом подобраны.
ЧАСТЬ II
Глава восьмая
ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ТОКИ
В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
§ 167. Определение периодических несинусоидальных токов и на-
пряжений. Периодическими несинусоидальными токами и напряже-
ниями будем называть токи и напряжения, изменяющиеся во вре-
мени по периодическому несинусоидальному закону.
Они возникают в четырех принципиально различных режимах
работы электрических цепей. В первом из них источник э.д.с. или
источник тока дает несииусоидальную э.д.с. или соответственно не-
синусоидальный ток, а все элементы цепи — активные сопротив-
ления, индуктивности и емкости — линейны, т. е. от величины тока
не зависят.
Во втором режиме работы источник э.д.с. или источник тока дает
синусоидальную э.д.с. или синусоидальный ток, но один или не-
сколько элементов цепи нелинейны.
В третьем режиме работы источник э.д.с. или источник тока дает
несинусоидальную э.д.с. или несинусоидальный ток, а в состав элект-
рической цепи входят одно или несколько нелинейных сопротив-
лений.
В четвертом режиме работы источник э.д.с. дает постоянную или
синусоидальную э.д.с., а один или несколько элементов цепи пери-
одически изменяются во времени.
В данной главе рассматриваются методика расчета и особенности
работы линейных электрических цепей при воздействии на них не-
синусоидальных э.д.с. и токов — первый из перечисленных выше
режимов работы. Второй и частично третий режимы работы обсуж-
даются в главе девятой. Четвертый режим работы рассмотрен в при-
ложении А.
§ 168. Изображение несииусоидальных токов и напряжений ря-
дами Фурье. Из курса математики известно, что любая периоди-
ческая функция f(x) с периодом 2л, удовлетворяющая условиям
Дирихле*, может быть разложена в ряд Фурье.
* Все периодические функции, с которыми имеют дело электрики, ус-
лоииям Дирихле удовлетворяют. Поэтому производить проверку на ныполне-
, ние условий Дирихле не требуется.
235
’ Переменная величина х связана со временем t соотношением
х = at — 2л —,
т
где Т — период функции во времени.
Таким образом, период функции по х равен 2л, а по времени пе-
риод той же функции равен Т.
Ряд Фурье записывается так:
/ (х) = Д) -j- A't sin х+Л' sin 2х -f- Л'3 sin Зх 4- Л' siri 4х 4- ... 4“
4- л;' cos х4-Л'' cos 2х 4- Л''cos Зх 4~ Л'' cos 4х 4- •.. (8.1)
Здесь Ло — постоянная составляющая, А[— амплитуда синусной
(изменяющейся по закону синуса) составляющей первой гармоники,
А’ — амплитуда косинусной составляющей первой гармоники, А'а-^~
амплитуда синусной составляющей второй гармоники и т. д.
2гг
A=-^-fH*)dx; (8,2)
zn j
о
2it
Л' = -i- J f (x) sin x dx; A" = J f (x) cos x dx;
о 0
2л 2«
A'k = —- J f (x) sin kx dx; A'k = J f (x) cos kxdx.
о о
Так как
(8.3)
A'k sin kx 4- Л" cos kx = Ak sin (kx 4- фй),
где Ak = )Л(Л*)24-(Л”)2 и tgt* = ^-, то ряд Фурье (8.1) может
Ak
быть записан в другой форме:
/(*)== Л^Л^шСх4-фх)4-Л2sin(2x4-ф2)4- “
= А+S 4sin (kx+М (8-4)
где Ак — амплитуда k гармоники ряда Фурье.
Гармоники, для которых k — число нечетное, называ1от нечет-
ными гармониками; гармоники, для которых k — число четное, —
четными гармониками.
§ 169. Некоторые свойства периодических кривых, обладающих
симметрией. На рис. 214—216 изображены три кривые, обладаю-
щие некоторыми специфическими свойствами.
Кривая рис. 214 удовлетворяет условию
— f(x + ^) = f(x).
236
Кривые, для которых выполняется это свойство, называют сим-
метричными относительно оси абсцисс. Если кривую рис. 214 смес-
тить по оси х на полпериода и зеркально отразить относительно
оси х, то полученная в результате отражения кривая совпадает с
кривой f(x).
В разложении таких кривых в ряд Фурье отсутствуют постоян-
ная, составляющая и четные гармоники, т. е. равны нулю коэффи-
циенты А9 = Л' = Л'' = А< — A'i = ... — 0.
Поэтому кривые по типу кривой рис. 214 раскладываются в сле-
дующий ряд: ’
f (х) — А[ sin х -f- A'/ cos х -f- Л' sin Зх Л'3'соз Зх ...
Каждое слагаемое этого ряда удовлетворяет условию —f (х-|-л) =»
= fix'). Так, например, —sin(хл) = sinх.
Кривая, подобная кривой рис. 215, обладает симметрией от-
носительно оси ординат. Для нее выполняется условие
/(— x) = f(x).
Если кривую, лежащую левее оси ординат, зеркально отразить
относительно оси ординат, то полученная в результате отражения
кривая совпадает с кривой, лежа-
щей правее оси ординат. В разло-
жении таких кривых в ряд Фурье
отсутствуют синусные составляю-
щие (т. е. Л1=Л2 = Л' = ...= 0)
и присутствуют лишь косинус-
ные составляющие и постоянная
составляющая.
Таким образом, кривые по Типу
кривой рис. 215 раскладываются в
следующий ряд:
f(x) = Ло+ Л''совх + А'* са&2х-\- Лз'совЗх-|- ...
Кривые по типу кривой рис. 216 обладают свойством —f ( — х)=>
= / (х). Они называются кривыми, симметричными относительно
237
♦ f'\ AXsT 2л. ан- -»iaftc /<*>t /(иЛ)=^(зйк1!1т1Л+^1пЗаИпЗ<о1-1-^-51п5а51п5ш^...)
/ 2л 'Ч / Ut f(ut)=^(sina}t--j-sin Jut+^-sin5ut-^Sin7at+...)
fa 5Г 2л. f(ajt)= ^^(sinut +jsln3ut+ j- sin 5wt-t у sin 7vt+...)
| bit
~| fat Л Г?7Г f(il)t)=^a^in^cosut+jsin~^cos3ut+jsin^-ais5b)t+...)
4>£ -чатг —
Л fftc \ 1 / ' ut f^)t)^^(j+^-cosut+^cos2ut-^cos4ut+^cos6(i)t-..)
,/\ Л Zz\ Mt f(ut)=‘^t-(j+pjeos2ut-j^-cos4ut+-^-cos6a)t-...J
Z\°t"/i\ / » < x% У f^t^^^^^+j^cosSui-jjcosBwt+^coseutt.^
°. F >Ч'/ЛуАу^~уУ/Av^r / yz V? У 'y/'y/'</^ >г >c^_'xS<'- 4>/-n 3am 2 cos But 2cos 12 ut , 2cos18ut ) 5 7 'У 11-13 ' 17-19 ~ -J .
начала координат. Разложение их в ряд Фурье имеет такой вид:
f (х) = A’t sin х-j- A' sin 2х4- A's sin Зх-f- ...
§ 170. О разложении в ряд Фурье кривых геометрически правиль-
ной формы и кривых геометрически неправильной формы. Встреча-
ющиеся в электротехнике периодические кривые могут быть раз-
биты на две группы. Первая группа включает в себя периодические
кривые геометрически правильной формы, например трапецеидаль-
ной, треугольной, прямоугольной и т. п. Разложение их в ряд Фурье
дается в таблице (см. стр. 238). В ней вместо х написано at.
Вторая группа кривых включает в себя кривые произвольной
(геометрически неправильной) формы. Чаще всего периодические
кривые второй группы задаются в виде графика. Разложение их
в ряд Фурье производится графически (графоаналитически).
§ 171. Определение гармоник ряда Фурье графическим (графоана-
литическим) путем. Графический метод определения гармоник ря-
да Фурье основан на замене определенного интеграла суммой ко-
нечного числа слагаемых. С этой целью период функции f(x), рав-
ный 2л, разбивают на п равных частей Дх
Л 2л
Дх = —
п
и заменяют интегралы суммами.
По определению постоянная составляющая
2гс 0==П П
л.=-И
О Р=1 р=1
или
п
= (8>5)
р-i
где р — текущий индекс; он пробегает значения от 1 до n; fp (х)—
значение функции f (х) при значении х = р \х.
Амплитуда синусной составляющей k гармоники ряда
2-гс п
А' = i J f (х) sin kxdxx 2 . £ fP (х) sinP kx>
о Р=1
или
п
А’к = -у fp (х) sinp kx. (8.6)
Pel
Амплитуда косинусной составляющей k гармоники
п
Ак ~ S fp w cosp kx’ 7)
23»
Здесь sinp£x и cosp йх—соответственно значения функций
sin kx и cos kx при х = р \х.
При расчетах по формулам (8.5) — (8.7) обычно достаточно раз-
делить период на п = 24 или 18 частей, а в некоторых случаях даже
и на меньшее число частей.
Перед тем как производить графическое разложение в ряд, не-
обходимо выяснить, не обладает ли раскладываемая функция сим-
метрией относительно осей координат (см. § 169). Наличие того
или иного вида симметрии позволяет до проведения разложения пред-
сказать, какие гармоники следует ожидать. Так, если кривая f(x)
симметрична относительно оси абсцисс,
то постоянная составляющая Ло и все
четные гармоники отсутствуют, а при
вычислении Л* и Л^при нечетных k
следует учесть, что значение суммы
2/p(x)sinp£x за первый полупериод
равно значению суммы ^fp (х) sinp kx
за второй, полупёриод.
Знак углов в формуле (8.4) за-
висит от знаков Ak и ЛА. При по-
строении гармоник на общем графике
необходимо учитывать, что масштаб
по оси абсцисс для k гармоники ’дол-
жен быть взят в k раз большим, чем
для первой гармоники.
Так, например, если некоторый от-
резок по оси абсцисс для первой гар-
моники выражает собой угол у, то
гармоники выражает собой угол в 3
раза больший, т. е. 3 • = л.
Пример 89. Найти первую и третью гармоники функции f (х),
изображенной на рис. 217, а. Значения ординат функции /р(х)за
первый полупериод при разбивке периода на п = 24 части следую-
щие:
р = 1 2 3 4 5 6 7 8 9 10 11 12
/р(х) = 7 11 13,5 15,4 17,4 20,5 25,4 32,5 27,7 19,2 10 О
Решение. Так как кривая симметрична относительно оси
абсцисс, то Ло = 0 и ряд будет состоять только из нечетных гар-
моник.
Амплитуда синусной составляющей первой гармоники
тот же отрезок для третьей
п п/2
л' = ^£fp (х) sinp х = 42 fp (х) sinp Х-,
ll fl
p=l p-i
240.
л' = ^ I7sin 150 +11 sin 30° +13,5 sin 450+15’4 sin 60° +
+ 17,4 sin 75° + 20,5 sin 90° + 25,4 sin 105° + 32,5 sin 120° +
+ 27,7 sin 1359+ 19,2 sin 150° 4-10 sin 165°) = 25,3.
Амплитуда косинусной составляющей первой гармоники
л/2
+'' = fP х;
p=i
А” = (7 cos 15° + 11 cos 30° + 13,5 cos 45° + 15,4 cos 60° +
+ 17;4 cos 75° + 20,5 cos 90° + 25,4 cos 105° + 32,5 cos 120° +
+ 27,7 cos 135°+ 19,2 cos 150°+ 10 cos 165°) =—5,23.
Амплитуда синусной составляющей третьей гармоники
12
А'3 = M*)sin,3x =
p=i '
= - (7 sin 45° + 11 sin 90° + 13,5 sin 135° + 15,4 sin 180° +
. + 17,4 sin 225° +20,5 sin.270° +25,4 sin 315° +
+32,5 sin 360°+ 27,7 sin 45°+19,2 sin 90°+ 10 sin 135°) = 3,47.
Амплитуда косинусной составляющей третьей гармоники
12
4' = -~S fp(x)cosp3x^
p-i
= - (7 cos 45° + 11 cos 90° + 13,5 cos 135° + 15,4 cos 180° +
+ 17,4 cos 225° + 20,5 cos 270° + 25,4 cos 315° +
+ 32,5 cos 360° + 27,7 cos 45° + 19,2 cos 90° + 10 cos 135°) = 5,1.
Амплитуда первой гармоники ряда А± — V(А')а + (А")а = 25,9.
Тангенс угла -ф1( на который начало первой гармоники смещено
по отношению к началу кривой /(х),
tg= ^- = ~5— = — 0,206; ik =— 11°40'.
. 25,3 1
Амплитуда третьей гармоники /13 = 1+ (Л3 )2 + (Л3 )2 = 6;
tgib = -+= 1,47; if, = 55°50'.
si <-
241
Следовательно, если ограничиться третьей гармоникой, то '
— 25,9 sin (<о/— 11°40') 4- 6 sin (&»/ + 55°50').
На рис. 217, б изображены первая и третья гармоники получен-
ного ряда, а также результирующая (суммарная) кривая. Ее мож-
но сопоставить с кривой рис. 217, а.
В заключение рассмотрения вопроса о разложении кривой f(x) в’ ряд
Фурье следует сказать, что несколько более точные результаты будут полу-
чены, если под/j, (х), sinpAx, cospkx в формулах (8.5)—(8.7) понимать значения
перечисленных функций не в конце, а в середине р интервала, т. е. не при
х = рДх, а при х = (р — 0,5)Дх.
§ 172. Расчет токов и напряжений при несинусоидальных э. д. с.
Перед проведением расчета э. д. с. должна быть представлена ря-
дом Фурье.
Согласно принципу наложения мгновенное значение тока любой .
ветви схемы равно сумме мгновенных значений токов отдельных
гармоник. Аналогично, мгновенное значение напряжения на любом
участке схемы равно сумме мгновенных значений напряжений
отдельных гармоник на этом участке. Расчет производится для
каждой из гармоник в отдельности при помощи приемов, известных
из первой части курса.
Сначала производится расчет токов и напряжений от действия
постоянной составляющей э.д.с. После этого производится расчет
токов и напряжений от действия первой гармоники э.д.с., затем
от второй гармоники э.д.с., от третьей и т. д.
При расчете токов и напряжений от постоянной составляющей
э.д.с. необходимо иметь в виду, что падение напряжения на индук-
тивности L от постоянного тока равно нулю, а также следует иметь
в виду, что постоянный ток через емкость С не проходит.
При расчете необходимо учитывать, что индуктивное сопротив-
ление растет прямо пропорционально частоте, поэтому индуктив-
ное сопротивление для k гармоники XLk в k раз больше, чем индук-
тивное сопротивление для первой гармоники XLi:
XLk = k<pL = kXLl,\
(i)L. J
Емкостное сопротивление уменьшается с ростом частоты, поэто-
му емкостное сопротивление для k гармоники XCk в k раз меньше,
чем емкостное сопротивление ХС1 для первой гармоники:
Ack — k<»C “ k ’ lQ
Для каждой из гармоник может быть построена своя векторная
диаграмма. Однако следует иметь в виду, что откладывать на вектор-
242
ной диаграмме токи, и падения напряжения различных .частот и,
тем более, векторно складывать токи различных частот и векторно
складывать падения напряжения различных частот недопустимо,
поскольку угловые скорости вращения векторов различных частот
неодинаковы.
Активные сопротивления, если частоты не очень велики, пола-
гают от частоты независящими*.
Пример 90. Электродвижущая сила в схеме рис. 218, а изменя-
ется по закону
е (0 = Elm sin (at -f- фх) -f- ESm sin (3®/ + Фз); Elm = 25,9 в,
E3m = 6 в; ф1 —— 11 °40', ф3 = 55°50'; /? = 10 ом;
4 = 9 ом; aL = 6 ом.
d)C
Рис. 218
Требуется записать выражения для мгновенных значений токов
в ветвях и тока в неразветвленной части схемы.
Решение. Обозначим токи в соответствии с рис. 218, а. Пер-
вая гармоника тока i{ равна:
^2- sin (at -j- фх) = 2,59 sin (at — 11 °40').
R
Третья гармоника тока
^2-sin (3 <о/ + Фз) = 0,6 sin (3®/Ц-55°50').
Полный ток первой ветви
i, = 2,59 sin (at — 11 °40') + 0,6 sin (3at + 55°50').
Первая гармоника тока in равна:
^2- sin (at + + 90°) = 2,87 sin (at -j- 78°20').
и>С
* Строго говоря, величина активного сопротивления зависит от частоты
вследствие явления поверхностного эффекта. Явление поверхностного эффек-
та (см. третью часть курса ТОЭ) здесь не учитывается.
243
Третья гармоника тока in равна:
^2- sin (За/ +1|)3 + 90°) = 2sin (3®* + 145’50').
ЗшС
Полный ток второй ветви
tn = 2,87 sin (a>t + 78’20') + 2 sin (3<at + 145’50').
Первая гармоника тока z’ni равна:
^-sin(<1)/ + i|)1 —90°) = 4,32 sin (®Z — 101’40').
coL
Третья гармоника тока im
sin (3®/ 4- 1|>з — 90’) = 0,33 sin (3®/ — 34’ 10').
Полный ток третьей ветви
Ли = 4,32 sin («/ — 101’40') 4-0,33 sin (3®/ —34’10').
Ток в неразветвленной части схемы
i — i\ 4- *н4" *нь
Первая гармоника тока i равна сумме первых гармоник токов
ветвей*. Аналогично, третья гармоника тока i равна сумме третьих
гармоник токов ветвей. Окончательно получим:
i = 3 sin (®/ — 40°) + 1,8 sin (3®^ + 125°) а.
Пример 91. Определить мгновенные значения токов и напря-
жений в схеме рис. 218, б: е (f) — 100 + 8Q sin (а/ + 30°) +
4" 60 sin (3m / + 20’) + 50 sin (5m + 45°) e; R = 3 ом; ®L = 3 ом;
— = 27 ом.
<йС
Решение. Определяем комплекс сопротивления участка Ьс
схемы для первой, третьей и пятой гармоник:
z _ g/ (-J7/) = 3 38 z = _9/(-—9/) =
ьл _ 27/4-3/ 1 М 9j — 9j
15/ — 5,4/
Полное сопротивление цепи для первой гармоники
= R 4-Zbcl = 34- 3,38/ = 4.5?48’30' ом.
* Каждую гармонику выражают комплексным числом. Суммирование
одноименных гармоник производится путем сложения комплексных чисел
или путем сложения векторов на комплексной плоскости, т. е. так же, как
это делалось в I части курса ТОЭ.
244
Полное сопротивление цепи для третьей гармоники
Z3 = об.
Полное сопротивление для пятой гармоники
Z6 = 3-8,5/ = 9^-/70030' ом.
Сопротивление цепи для постоянной составляющей тока равно
3 ом (на участке Ьс постоянный ток течет через индуктивность L,
активное сопротивление которой полагаем равным нулю).
Находим составляющие тока в неразветвленной части схемы.
Постоянная составляющая тока = 33,3 а. Комплекс тока
первой гармоники равен:
.89е.—__= 17 8 е-/18°30' а
45е/48°30' 1,’ое “•
На третьей гармонике имеет место резонанс токов. Поэтому в
токе I третьей гармоники нет, но в токах и 12 третья гармоника
присутствует. Комплекс пятой гармоники тока I равен:
5Qg/45° ggg J115°30'
9е—/7о°зо' ~~ 0,006 а.
Определяем падения напряжения на участке Ьс от каждой из
гармоник. Падение напряжения на участке Ьс от постоянной состав-
ляющей равно нулю.
Комплексная амплитуда от первой гармоники тока (индекс 1)
= 17,8е—/18030 . 3,38/ = 6О,2е/71<>30'.
Аналогично
Мгновенное значение напряжения иЬс\
иЬс = 60,2 sin (at + 71 °30') 60 sin (Зш/ 20°)
4-47,1 sin (5<в/ + 25°30') в.
Находим комплексные амплитуды токов первой, третьей и пя-
той гармоник через емкость:
первая гармоника
60,2е/71°3(!' _ g 23^161030'-
- третья гармоника
— 9/
245
пятая гармоника
Мгновенное значение тока через емкость
= 2,23 sin (ю/ + 161 °30') + 6,67 sin (Зсо/ 4-1Юй) +
4-8,72 sin (5W+115°30') а.
Определяем составляющие тока через индуктивность:
постоянная составляющая равна 33,3 а;
первая гармоника
6O,2e,7l°зo,__20 ig—/18’30'.
третья гармоника
пятая гармоника
i2 = 33,3 + 20,1 sin (<о/ — 18°30') + 6,67 sin (Зю/ — 70°) +
4-3,13sin(5<^ —64’30').
Ток неразветвленной части схемы
i = 33,3 + 17,8 sin (at — 18°30') -f- 5,55 sin (5at -f- 115°30') a.
§ 173. Резонансные явления при иесинусоидальных токах. Как
известно из первой части курса ТОЭ, резонансным режимом работы
электрической цепи, содержащей одну или несколько индуктив-
ностей н одну или несколько емкостей, называют такой режим ра-
боты ее, при котором ток на входе этой цепи совпадает по фазе с дей-
ствующей на входе э. д. с.
Если воздействующая э.д.с. несинусоидальна, то в электричес-
кой цепи могут возникать резонансные режимы (резонансы токов
или резонансы напряжений) не только на первой гармонике, но и
на высших гармониках.
Условимся под резонансом на k гармонике понимать такой ре-
жим работы, при котором ток k гармоники на входе цепи по фазе
совпадает с k гармоникой, действующей на входе э.д.с. (но при
этом токи остальных гармоник не совпадают по фазе с вызвавшими
их э.д.с.).
Если учитывать активные сопротивления индуктивных катушек,
то условие возникновения резонанса для какой-либо гармоники за-
ключается в том, что реактивная составляющая входного сопротив-
ления для этой гармоники должна быть равна нулю.
246
Исследование резонансных явлений при несинусоидальных то-
ках часто производят, полагая активные сопротивления индуктив-
ных катушек равными нулю.
В последнем случае входное сопротивление при резонансе токов
равно бесконечности, а входное сопротивление при резонансе напря-
жений равно нулю.
Обратим внимание на то, что при возникновении резонансного
и близкого к нему режима-на какой-либо высшей гармонике токи
и (или) напряжения этой гармоники могут оказаться большими, чем
токи и напряжения первой гармоники на тех же участках цепи,
несмотря на то, что амплитуда соответствующей высшей гармоники
э.д.с. на входе схемы может быть в не-
сколько раз меньше амплитуды первой
гармоники э.д.с.
Пример 92. В схеме рис. 219 задана ин-
дуктивность £2. Полагая активное сопро-
тивление индуктивной катушки равным ну-
лю, найти, при каких значениях емкостей
С± и С2 входное сопротивление схемы для
первой гармоники равняется нулю, а для
девятой гармоники равно бесконечности.
Решение. Запишем выражение входного сопротивления схе-
мы для первой гармоники и приравняем его нулю:
Приравняем бесконечности входное сопротивление для девятой
гармоники:
Ze = -^--
9 ЭшС!
Совместное решерие дает:
с < \ jtoCg /
-------------------- = ОО .
§174. Действующее значение несинусоидального тока и действую-
щее значение несинусоидального напряжения. По определению
(см. § 81) квадрат действующего значения тока I выражается через
мгновенное значение тока i следующим образом:
т
I2 = - f i2dt.
т.)
О - .
.247
Если ток
1 = zo + sin (<»/ + фх) + /2ffisin (2<о/-Ma) -Ь .
то
»2 = zo+£ ZLsin2 и™*+w +
4=1
+S /₽'Л'иsin (pat+%)sin №+%)•
P=0
9=0 p+q
. Ho
T
J sin2 (kat 4- qk)dt =
0
T
f sin (pat 4- фр) sin (qat 4~ %) dt = 0-
*o )
P + 9
(8.10)
Поэтому
I2 i2
2tn [ 3m
2'2
ИЛИ
/= V zo4-—+ —+•••
у °“ 2 2
Так как амплитуда k гармоники тока Ikm в раз больше
действующего значения k гармоники Ik, то
^4m _ Ikm. tkm _ ^2
2 /2 V2 k
И
z = /zo2 + zi2+z2a + z32+--- (8.1 1')
Следовательно, действующее значение несинусоидального тока
равно квадратному корню из суммы квадратов постоянной состав-
ляющей тока и действующих значений отдельных гармоник. Отсдви-.
гов фа? 'Фа действующее значение не зависит.
Аналогичным образом действующее значение I/ несинусоидаль-
ного напряжения равно корню квадратному из суммы квадратов
постоянной составляющей и действующих значений отдельных гар-
моник: -
{/= /(/24-(/2 4-(/2 4 (/2 + ... / (8.11)
248
Пример 93. По данным примера 91 определить действующее зна-
чение тока I в неразветвленной части схемы и действующее значе-
ние э.д.с. е.
Решение
I = |/зз,32+-^^- + Ц^ = 35,6 (а);
Е = У 100»+^ + ? + = 127,1 (в).
§ 17S. Среднее по модулю значение несинусоидальной функции. Под сред-
ним по модулю значением функции понимается среднее_значенне, определя-
емое следующим образом:
2 к
fl/(o>OI<W. (8.12)
2Л J
0
В отличие от действующего значения оно зависит от углов ф^.
Пример 94. Если за начало счета времени принять момент прохождения
через нуль первой гармоники тока н учесть, что начало k гармоники тока
смещено по отношению к началу первой гармоники на угол (ф^ — k^)
(см. § 171), то для кривых не содержащих постоянной составляющей,
и четных гармоник, после интегрирования получим;
2 Г V1 1 1
JCP =— AmC0Sa + 2jT /Л»»СО8(Ф4 — £ф! — ka) , (8.13)
по модулю Л I к J
*=3,5,7, ...
где минус а — угол, при котором /(ш/) принимает нулевое значение (предпо-
лагается, что за полпернода она не меняет знака).
§ 176. На какие величины реагируют амперметры и вольтметры
различных систем при несинусоидальных токах? Несннусоидальные
токи и напряжения могут измеряться приборами различных систем.
Изучение принципа действия приборов производится в курсе элект-
рических измерений. Поэтому здесь упомянем лишь, на какие
величины реагируют вольтметры и амперметры различных си-
стем.
Приборы электромагнитной, электродинамической и тепловой
систем реагируют на действующее значение, магнитоэлектриче-
ские приборы с выпрямителем — на среднее по модулю значение
величины, магнитоэлектрические без выпрямителя — на постоян-
249
ную составляющую, амплитудные электронные вольтметры — на
максимальное значение функции*.
§ 177. Активная и полная мощности несинусоидального то-
ка. Под активной мощностью Р несинусоидального тока понимают
среднее значение мгновенной мощности за период первой гармони-
ки:
т
Р = — С ui dt.
Т J
о
Если представить напряжение и и ток i рядами Фурье:
и = Ц> + Ulm sin Н + ф() + U2m sin (2со^ + ф2) -J-
-j-(73m S1П (3<й/-j-ф3)••• ;
I = ^o + /imSin((d^4-i|)1 — (p1) + /2OTsin(2(BZ + i|)3 — (p2)4-
+ ^3mS’n (3®^ + Фз— фз) + ••• > .
подставить эти ряды под знак интеграла и проинтегрировать, учтя
соотношения (8.10), то получим:
р = t/o/o + t/i/icosTi + t/2/2Cos<p2 + t/3/3cos(p3+ .., (8.14)
Таким образом, активная мощность несинусоидального тока рав-
на сумме активных мощностей отдельных гармоник.
Полная мощность S равна произведению действующего зна-
чения несинусоидального напряжения на действующее значение
несинусоидального тока:
S = UI, (8.15)
где
I/ - + + ;
/ = ]/^ /ц -f- 4- 4" • • •
* Напомним, что на лицевой стороне прибора всегда имеется условный
злачок, свидетельствующий о том, какой системы данный прибор.. На рис.
Рис. 220
220 приведены эти условные значки: а — магнитоэлектрическая система; б
электромагнитная система; в — электродинамическая система; г —тепловая
система; д — магнитоэлектрическая система с выпрямителем.
250
Пример95. Найти Р и S, если
и = 25,9 sin (ю/ — 11°40') 4- 6 sin (Зсо/ 4- 53°50') в;
: i = 3 sin(w/—4(П-Ь0,9 J/”2 sin (3®/4- 125°) а.
Решение. UY= = 18,3 (в); U3— = 4,26 (в);
/х = 2,13 а; /3 = 0,9а;
<рх = — 11° 40' — (— 40°) = 28° 20'; <р3 = — 71° 10';
Р = 18,3 • 2,13 cos 28° 20'4-4,26.0,9 cos (—71° 10') = 35,5 (вт)-,
U V = К 18,324-4,26г = 18,55 (в);
/ = V 2,1324-0,92 = 2,31 (а); S = UI= 18,55 - 2,31 = 42,8 (ва).
§ 178. Замена несинусоидальных токов и напряжений эквивалент-
ными синусоидальными. При изучении некоторых простейших
свойств нелинейных электрических цепей (об этом будет идти речь
в главе девятой) несинусоидальные токи и напряжения заменяют
эквивалентными синусоидальными. Замена производится таким
образом, что действующее значение синусоидального тока принимает-
ся равным действующему значению заменяемого несинусоидального
тока, а действующее значение синусоидального напряжения берет-
ся равным действующему значению несинусоидального напряже-
ния.
Угол сдвига фаз фэ между эквивалентными синусоидами напря-
жения н тока берегся таким, чтобы активная мощность эквивалент-
ного синусоидального тока была равна активной мощности неси-
нусоидального тока:
c°sq>3 = -^-. (8.16)
Пример 96. Заменить несинусоидальные ток и напряжение при-
мера 95 эквивалентными синусоидальными и найти угол сдвига фаз
Ф3 между ними.
Решение. Действующее значение синусоидального напря-
жения U = 18,55 в.
Действующее значение синусоидального тока / = 2,31 а;
cos <рэ =---------= 0,828, а>э = 34°.
э 18,55-2,31 3
§ 179. Особенности работы трехфазных систем, вызываемые
гармониками, кратными 3. Электродвижущие силы каждой фазы
трехфазного трансформатора или трехфазного генератора часто
оказываются несинусоидальными. Каждая из э.д.с. (ел, ев, ес)
повторяет по форме остальные со сдвигом на одну треть периода
251
Так
а э.д.с.
э.д.с. в
и может быть разложена на гармоники. Постоянная Состав-
ляющая обычно отсутствует.
Пусть k гармоника э.д.с. фазы А равна *
= (^ + ФА). .
как э.д.с. фазы В отстает от э.д.с. фазы Л на — ,
т
фазы С опережает э.д.с. фазы А на —, то k гармоники
фазе В и фазе С равны соответственно:
Чв = Ekm sin^ffl (t — -у) 4- =
= Ekm sin (kat—120% Ц-
ekc~ Ekms>in |£‘йР+4-')+11’Л =
| \ о J I
- Ekm sin (kat 4- 120% 4- фй);
ka —= k — — = k—= 120%.
3 T 3 3
Если k принимает значения 1,4, 7,10, то k гармоника э.д.с. фазы
В отстает на 12Q° от k гармоники э.д.с. фазы А. Следовательно, 1,
4, 7, 10 гармоники образуют систему прямой последовательности
фаз (что понимают под прямой последовательностью фаз, см. § 154).
Если k = 2, 5, 8, 11, то k гармоника э.д.с. фазы В опережает k
гармонику фазы А на 120°. Следовательно, вторая, пятая, восьмая
и т. д. гармоники образуют системы обратной последовательности.
Гармоники, кратные 3 {k = 3, 6, 9, ...), образуют систему нуле-
вой последовательности, т. е. третьи гармоники во всех трех фазах
совпадают по фазе (3-120° = 360°):
еЗА = езв = езс = E3m sin (3at 4- ф3);
шестые гармоники также совпадают по фазе и т. д.
То обстоятельство, что третьи гармоники во всех трех фазах сов-,
падают по фазе, полезно проиллюстрировать графически.
На рис. 221 э.д.с. еА, ев, ес представляют собой три фазные э.д.с.
трех фазного генератора. Они имеют прямоугольную форму и сдви-
нуты по отношению друг к другу на одну треть периода основной
частоты.
На том же рисунке показаны первая и третья гармоники каж-
дой э.д.с. Из рисунка видно, что третьи гармоники действительно
находятся в фазе. ...
Обсудим особенности работы трехфазных систем, вызываемые-
гармониками, кратными 3.
252
1. При соединении обмоток трехфазного генератора или трех-
фазного трансформатора в. треугольник (рис. 222, а) по ним будут
протекать токи гармоник, кратных 3, даже при отсутствии внешней
нагрузки.
Алгебраическая сумма третьих гармоник э.д.с. в треугольнике
равна З£3*. Обозначим сопротивление обмотки каждой фазы для
третьей гармоники через Z3, тогда ток третьей гармоники в треуголь-
нике равен:
где Ев — действующее значение шестой гармоники фазной э.д.с.,
Ze — сопротивление фазы по шестой гармонике.
Действующее значение тока, протекающего по замкнутому тре-
угольнику в схеме рис. 222, а, равно:
I — V П + ^6 + ^9 + • • •
2. Если соединить обмотки трехфазного генератора или трех-
фазного трансформатора в открытый треугольник (рис. 222, б), то
при наличии в фазных э.д.с. гармоник, кратных 3, на зажимах т
и п будет напряжение, равное сумме э.д.с. гармоник, кратных 3:
Umn = 3E3m sin (За/ 4- ф3) ЗЕ6т sin (6а/ 4- фв) 4- ...
Показание вольтметра в Схеме рис. 222, б равно:
з/£32 4-£62 4- ...
* Однако алгебраическая сумма первых гармоник э. д. с. и всех гар-
моник э. д. с., не кратных 3, равна нулю, поэтому от перечисленных гарйёник
при отсутствии нагрузки по замкнутому треугольнику ток протекать иебудет.
253:
3. В линейном напряжении вне зависимости от того, звездой или
треугольником соединены обмотки генератора или трансформато-
ра, кратные 3 гармоники отсутствуют.
Третье свойство докажем для случая холостого хода генератора
или трансформатора, т. е. когда внешняя нагрузка отсутствует.
Однако это свойство справедливо и при наличии нагрузки.
Рассмотрим сначала схему соединения треугольником (рис. 222, а).
Обозначим (р/д — потенциал точки А и фВз — потенциал точки В
по третьей гармонике, получим
Флз= Тв.ч— Ё3 з^з-
Но Ё3= /3Z3, следовательно, фЛз — фвз.
Рис. 223
Рнс. 224
При соединении в звезду (рис. 223) линейное напряженье третьей
гармоники равно разности соответствующих фазовых напряжений.
Так как третьи гармоники в фазовых напряжениях совпадают по
фазе, то при составлении этой разности они вычитаются.
В фазовом напряжении могут присутствовать все гармоники (пос-
тоянная составляющая обычно отсутствует). Поэтому действующее
значение фазового напряжения
•••
В линейном напряжении схемы рис. 223 отсутствуют гармоники,
кратные 3, поэтому
= |/ з Knf
О ношение — <2 У" 3 , если есть гармоники, кратные 3.
Оф
4. При соединении генератора и равномерной нагрузки в звез-
ду и отсутствии нулевого провода токи третьих и других гармоник
нулевой последовательности не могут протекать по линейным про-
водам (подробно это обсуждалось в § 152). Поэтому между нулевыми
точками приемника О' и генератора О (рис. 224 при Zo = оо) будет
действовать напряжение
ио’о ~ sin (Зю/ 4- ф3) Ц- Ейт sin (бы/ -|- ф6) -(- ...
254
Действующее значение его
/"р2
Г/ =. Л/ 3m । 6m .
V ~2~ + ^~ +
5. Если в схеме звезда — звезда при равномерной нагрузке фаз
сопротивление нагрузки для третьей гармоники обозначить Z„3,
а сопротивление нулевого провода для третьей гармоники обо-
значить Zo3 (рис. 224), то по нулевому проводу будет протекать ток
третьей гармоники, равный:
f __
03 ~ 7 , ZK3«
Z°a + T‘
По каждому из линейных проводов будет протекать ток третьей
гармоники
Аналогично находятся токи и от других гармоник, кратных 3.
Пример 97. Дано мгновенное значение напряжения фазы А трех-
фазного генератора:
иА = 127 sin (со/ + 10°) 4- 30 sin (Зсо/ ф- 20°) ф-
4-20 sin (11 at 4- 15°) в.
Требуется записать мгновенное значение линейного напряжения
иАВ при соединении генератора звездой.
Решение. В линейном напряжении третья гармоника отсут-
ствует.
Первые гармоники фаз Л и В по фазе сдвинуты на 120°.
Поэтому линейное напряжение йАВ первой гармоники в V 3 раз
больше фазного напряжения первой гармоники UA и на 30°
будет опережать его по фазе.
Одиннадцатая гармоника (обратная последовательность фаз)
линейного напряжения будет отставать по фазе от одиннадцатой
гармоники напряжения фазы А на 30° и будет в V 3 раз больше ее:
иАВ = 127 V"3 sin (со/ 4- 40°) 4- 20 /У sin (11 at — 15°) в.
Пример 98. Э.д.с. фазы Л в схеме рис. 225 равна: еА = 170sinco/4~
4-80cos3co/4~34cos9cd/ в; /? = 9олг, coL = 2 ом.
Определить показания всех приборов. Приборы электродинами-
ческой системы.
Решение. Действующие значения э.д.с.:
El = = 121 (в); Е3 = 56,5 в; Е9 = 24,2 в.
г 2
255
По линейным проводам течет первая гармоника тока
/х = . Л = 13,2 (а).
1 ]ЛЯ2+(ыЙ2 9,2
Показание вольтметра Уг равно
]^ + E23+E2s = 136 в.
Показание вольтметра У2 равно:
/^ = 13,2.9 = 118,5 (в).
Показание вольтметра V3 равно:
У~3 . 118,5 = 205 (в).
Показание вольтметра V4 равно:
/jCoL = 26,4 в.
Показание вольтметра V6 равно:
]/£з4-£д = 62,3 в.
Пример 99. Э. д. с. каждой фазы генератора (рнс. 226) изменяет-
ся по трапецеидальному закону: ат = 220 в; а = 10°.
Нагрузка равномерная; R = 6 ом, a>L— 0,5 ом, = 12 ом.
(£>С
Записать мгновенное значение тока по нулевому проводу, пре-
небрегая гармониками тока выше седьмой.
Решение. При помощи таблицы (см. стр. 238) записываем
разложение трапецеидальной э.д.с.:
еА = (sin a sin cot -f~ — sin За sin Зю/ 4“
ал \ 9
-4- — sin 5а sin 5ю/ —— sin 7аsin 7ю/ ),
' 25 1 49 J
256
или
sin 10° sin at sin 30° sin Зсо/ Ц-
•л
4 • 220
еЛ = ~~
Л
18
-I—— sin 50° sin 5co/ -4—5- sin 70° sin Tat'i.
25 1 49 /
Следовательно,
eA = 274 sin at -f- 89,3 sin Зсо/ -f- 49,5 sin 5co/ -f- 30,9 sin 7at.
По нулевому проводу будет протекать только третья гармоника
тока:
/оз =----^г-: £з= 5# = 63’3
7 . Лнз у 2
z03+ 3
Z03 = l,5/; Z„s = 6-4/;-^ = 2-/l,33;
О
Мгновенное значение тока /сз = 44,8 sin (Зсо/ — 4'40') а.
§ 180. Биения. Колебательный процесс, получающийся в резуль-
тате сложения двух синусоидальных колебаний с равными ампли-
тудами А и близкими, но не равными частотами сох и со2, дает коле-
бание, которое называется биением.
Пусть
f (/) = A sin со/ + Л sin со2/.
Воспользуемся известным тригонометрическим преобразованием:
- о л а — В . а + ₽
sin а + sin р = 2 cos---L sin —— .
1 2 2
Следовательно, /(/) можно представить следующим образом:
/(/) = 2Л cos Й/ sin со/,
где
Й = и и =
2 2
(Q «со).
График результирующего колебания изображен на рис. 227.
Амплитуда колебания изменяется по закону 2Л cos Й/. Огибаю-
щая колебаний нанесена пунктиром.
Возникновение биений при сложении двух синусоидальных колебаний
с равными амплитудами и близкими (но не равными) частотами используется
на практике в различных целях, в частности как средство, позволяющее уста-
новить, что складываемые колебания имеют неодинаковые частоты.
9 Л. А. Бессонов
257
§ 181. Модулированные колебания. В телефонии и радиотехнике
очень широко применяются модулированные колебания. Модули-
рованным колебанием f(t) = A sin (со/ ф- ф) называется колебание,
в котором амплитуда А, частота со, фаза ф, или и те и другие вместе
изменяются во времени.
Колебание, в котором изменяется только амплитуда А, а угло-
вая частота со и фаза ф неизменны, называют колебанием, модули-
рованным по амплитуде.
Колебание с изменяющейся угловой частотой со, но неизменны-
ми амплитудой А и фазой ф называют колебанием, модулированным
по частоте.
Рис. 227
Рис. 228
Колебание, в котором изменяется только фаза ф, а амплитуда
А и угловая частота со неизменны, называют колебанием, модули-
рованным по фазе.
Простейшим амплитудно-модулированным колебанием являет-
ся колебание, в котором амплитуда модулирована по закону сину-
са:
/(/) = Ао (1 ф- т sin Qf) sin (со/ ф- ф),
где S2 со; т называют глубиной модуляции, как правило т < 1.
График колебания изображен на рис. 228; на нем огибающая
дана пунктиром.
Если воспользоваться известным из тригонометрии тождест-
вом sin a sin Р = у cos (а — р) — у cos (а ф- Р), то колебание
Ло(1 ф-msin Q/) sin (а>/ф-ф) можно представить в виде суммы
трех колебаний:
/ (/) = Д sin (со/ ф~ ф) ф- 'у-0 cos [(со -Й)/ф-ф] —
_£^оС08[(соф-Й)/ф-ф].
Частоту со называют несущей, а частоты (со — Q) и (со ф- Q) —
боковыми частотами,
258
Пример 100. Разложить функцию f(t) — 20 (1 + 0,6 sin 103/)Х
X sin 106/ на составляющие.
Решение, co — Q = 99 . 103; co4-Q = 101 . 103; ^ = 6.
1 2
Следовательно,
f(0 = 20sinl05/ + 6cos(99.1030 — 6 cos (101 . 103Л)
§ 182. Расчет линейных цепей, находящихся под воздействием
модулированных колебаний. Расчет токов и напряжений в линей-
ных электрических цепях при воздействии на них модулированных
колебаний производится путем разложения модулированных коле-
баний на составляющие, расчета токов и напряжений от каждой
составляющей в отдельности и затем суммирования соответствую-
щих токов и напряжений на основании принципа наложения.
9*
Глава девятая
НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПЕРЕМЕННОГО ТОКА
§ 183. Определение нелинейных электрических цепей перемен-
ного тока. Нелинейными электрическими цепями переменного тока
называют электрические цепи переменного тока, в состав которых
входят одно или несколько нелинейных сопротивлений.
§ 184. Подразделение нелинейных сопротивлений на три основные
группы. Как известно из первой части курса, прохождению перемен-
ного тока оказывают сопротивление не только активные сопротив-
ления, но и индуктивности и емкости. В соответствии с этим нели-
нейные сопротивления для переменного тока могут быть разделены
на три обширные группы: на группу нелинейных активных сопро-
тивлений, группу нелинейных индуктивных сопротивлений и груп-
пу нелинейных емкостных сопротивлений. Каждая из этих групп
может быть подразделена на две подгруппы: управляемые и неуправ-
ляемые.
Управляемые нелинейные сопротивления обычно представляют
собой такие сопротивления, которые имеют один или несколько уп-
равляющих электродов (зажимов) или управляющих обмоток, вклю-
чаемых в управляющую цепь или цепи, воздействуя па ток или нап-
ряжение которых можно управлять величиной сопротивления в глав-
ной цепи. При отсутствии специальных управляющих электродов
или обмоток управляющий ток или напряжение могут воздейст-
вовать на нелинейное сопротивление через электроды или обмотки
главной цепи
§ 185. Общая характеристика нелинейных активных сопротив-
лений. Наиболее широкое распространение в качестве управляемых
нелинейных активных сопротивлений получили трех-(и более) элект-
родные лампы и полупроводниковые триоды. Свойства, принцип
работы, характеристики и применения их будут рассмотрены в
§ 210—225.
Неуправляемыми нелинейными активными сопротивлениями
являются электрическая дуга, меднозакисные и селеновые выпря-
мители, тиритовые и вилитовые сопротивления, термисторы, барет-
260
теры, лампы накаливания и др. Основные свойства и вольтамлер-
ные характеристики их обсуждались в главе второй.
Кроме классификации нелинейных активных сопротивлений по
принципу управляемости, они могут быть классифицированы по
степени влияния температуры нагрева сопротивления, обусловлен-
ной протекающим по сопротивлению током, на форму вольтамперной
характеристики его.
Так как тепловые процессы (процессы нагрева и остывания) яв-
ляются процессами инерционными, то сопротивления, нелинейность
вольтамперных характеристик которых всецело обусловлена изме-
нением температуры в результате нагрева протекающим через соп-
ротивления током, принято называть инерционными сопротивле-
ниями.
Сопротивления, нелинейность вольтамперных характеристик
которых обусловлена иными (не тепловыми) процессами, принята
называть безынерционными*.
Наиболее типичными представителями группы инерционных
сопротивлений являются электрические лампы накаливания, тер-
мисторы и бареттеры. Наиболее типичными представителями груп-
пы безынерционных сопротивлений являются электронные лампы
и полупроводниковые диоды и триоды.
Если постоянная времени нагрева инерционного сопротивления много
больше периода переменного тока, то величина сопротивления за период пе-
ременного тока практически не меняется и определяется не мгновенным, а
действующим значением переменного тока. Если к нелинейному инерцион-
ному сопротивлению подвести синусоидальное напряжение (при условии что
постоянная времени нагрева сопротивления значительно больше периода
синусоидального напряжения), то ток через него будет практически синусо-
идальным.
Можно сказать, что инерционные нелинейные сопротивления занимают
промежуточное положение между линейными и нелинейными сопротивления-
ми. К нелинейным они тяготеют вследствие того, что сопротивление их явля-
ется функцией действующего значения тока, к линейным они тяготеют потому,
что в установившемся режиме работы сопротивление их для различных мо-
ментов времени внутри периода воздействующей на схему э. Д. с. остается
практически неизменным.
§ 186. Общая характеристика нелинейных индуктивных сопротив-
лений. Под нелинейными индуктивными сопротивлениями или,
проще, под нелинейными индуктивностями понимают катушки ин-
дуктивности, намотанные на замкнутых сердечниках из ферромаг-
нитного материала, для которых зависимость магнитного потока
в сердечнике от протекающего по катушке тока нелинейна. Индук-
тивное сопротивление таких катушек, оказываемое прохождению
переменного тока, непостоянно; оно зависит от величины перемен-
ного тока.
Катушка со стальным сердечником в литературе называется еще
иногда дросселем со стальным сердечником.
Более правильно было бы называть их почти безынерционными.
261
Нелинейные индуктивности подразделяются на управляемые и
неуправляемые, но деление на безынерционные и инерционные на
них не распространяется, так как нелинейность их обусловлена
свойствами ферромагнитного материала, а не тепловым эффектом.
На электрических схемах нелинейная индуктивность изобра-
жается либо в виде замкнутого сердечника с нанесенной на нем об-
моткой (рис. 229, а), либо в виде индуктивности с нанесенными око-
ло нее двумя чертами (рис. 229, 6).
Сердечники нелинейных индуктивностей при относительно низ-
ких частотах делают обычно двух типов: пакетные и спиральные.
Пакетные сердечники представляют собой сердечники, образо-
ванные тонкими пластинами ферромагнитного материала кольцевой
или П-, или Ш-образной формы.
Спиральные сердечники представляют собой сердечники, туго
навитые из тонкой ферромагнитной ленты. По форме они напомина-
ют туго навитую часовую пружину.
Рис. 229
Пластины пакетного сердечника и отдельные витки спирального
сердечника изолируют друг от друга эмалевым лаком, жидким стек-
лом или каким-либо иным изолирующим составом и запекают. Изо-
ляция необходима для уменьшения потерь энергии в сердечнике от
вихревых токов (см. § 187).
При высоких частотах резко возрастают потери в листовых сер-
дечниках, и потому при высоких частотах сердечники выполняют
обычно из феррита (о свойствах феррита см. § 48 первой части кур-
са).
§ 187. Потери в сердечниках нелинейных индуктивностей от вих-
ревых токов. Если по катушке со стальным сердечником проходит
переменный ток, то в сердечнике возникает переменный магнитный
поток. Под действием переменного магнитного потока в листах сер-
дечника возникают вихревые токи. На рис. 230 изображен один лист
сердечника. Пусть магнитный поток, увеличиваясь, направлен вверх
(вдоль листа). В листе в плоскости его, перпендикулярной магнит-
ному потоку, по закону электромагнитной индукции наводится
э. д. с. Эта э. д. с. вызывает в нем ток, который называют вихревым
током. Контур, по которому замыкается вихревой ток, изображен
пунктиром на рис. 230. Вихревые токи по закону Ленца стремятся
создать поток, встречный по отношению к вызвавшему их потоку.
262
Потери энергии в листе на вихревые токи пропорциональны квад-
рату наведенной в контурах листа э.д.с. и обратно пропорциональ-
ны сопротивлению контуров. Электродвижущие силы, наводимые
в контурах, по которым замыкаются вихревые токи, при заданной
ширине листа пропорциональны толщине листа А, амплитудному
значению индукции и частоте. В свою очередь сопротивление кон-
тура пропорционально периметру контура и удельному сопротив-
лению. При b А периметр контура почти не зависит от толщины
листа. Поэтому потери энергии на вихревые токи пропорциональ-
ны квадрату амплитудного значения индукции, квадрату частоты
и квадрату толщины листа.
Уменьшение потерь в листовом сердечнике на вихревые токи
достигается двумя путями: 1) изготовлением сердечника из тонких
изолированных друг от друга листов (о чем говорилось в § 186) и
2) добавлением в ферромагнитный материал примесей, увеличиваю-
щих его удельное сопротивление.
При частоте 50 гц толщина листов составляет обычно 0,35—
0,5 мм; при высоких частотах она доходит до 0,005 мм.
Кроме потерь от вихревых токов, в сердечнике есть еще потери,
обусловленные гистерезисом.
§ 188. Потери на гистерезис. Из § 46 первой части курса извест-
но.что ферромагнитному материалу присуще явление гистерезиса.
Площадь гистерезисной петли в координатах В, Н (В — индукпия,
Н — напряженность поля) характеризует собой энергию, выделяю-
щуюся в единице объема ферромагнитного материала за один пери-
Рис. 231
Рис. 232
од переменного тока (за одно перемагничивание). Потери в сердеч-
нике, обусловленные гистерезисом, пропорциональны объему сердеч-
ника, первой степени частоты и площади гистерезисной петли. От
толщины листов потери на гистерезис не зависят*.
§ 189. Схема замещения нелинейной индуктивности. В расчетном
отношении нелинейную индуктивность рис. 229, а можно предста-
вить в виде схемы рис. 231, а. В ней параллельное идеализирован-
* Явления поверхностного эффекта (см. третью часть курса) не учиты-
ваем.
263
ной (без потерь) нелинейной индуктивностью включено сопротив-
ление Rie, потери в котором имитируют потери энергии в сердечни-
ке на гистерезис и вихревые токи, а последовательно включено ак-
тивное сопротивление самой обмотки /?об; U — напряжение на не-
линейной индуктивности.
Как уже отмечалось, потери энергии на гистерезис и вихревые
токи Рге зависят от качества ферромагнитного материала и толщины
листов сердечника.
Если сердечник выполнен из низкокачественного магнитного
материала, то потери в нем достаточно велики, а сопротивление /?г8
г U
достаточно мало и ток 1гв = —- может оказаться соизмеримым
Вгв
с током / , протекающим по идеализированной (без потерь) не-
линейной индуктивности, и ветвь с сопротивлением Rie надо учитывать
в расчете.
Если же сердечник изготовлен из тонких листов высококачест-
венного мягкого магнитного материала, то потери в сердечнике
472
малы, а сопротивление R28 = — очень велико, и потому ветвь
Де
с сопротивлением Rig можно не учитывать.
Часто идут еще на одно упрощение, а именно полагают, что актив-
ное сопротивление обмотки Ro6, настолько мало, что с падением нап-
ряжения в нем можно не считаться. Аналогичное упрощение часто
делалось и при расчете линейных индуктивностей. В этом случае
сопротивление катушки со стальным сердечником оказывается чи-
сто индуктивным (соответствующая схема замещения представлена
на рис. 231, б).
Переход от схемы замещения рис. 231, а к схеме замещения рис.
231, .б вызван стремлением облегчить расчеты цепей, учтя основной
полезный нелинейный эффект — релинейность между индукцией
В и напряженностью Н и пренебрегая побочным вредным эффектом—
потерями, обусловленными гистерезисом и вихревыми токами в сер-
дечнике.
При периодическом процессе нелинейность между В и Н учи-
тывают, ведя расчет по кривой, абсциссы которой равны полусум-
ме абсцисс восходящей и нисходящей ветвей предельной гистере-
зисной петли (рис. 232).
§ 190. Общая характеристика нелинейных конденсаторов. В обыч-
ных конденсаторах обкладки разделены веществами, диэлектричес-
кая проницаемость которых не является функцией напряженности
электрического поля. Для них зависимость мгновенного значения
заряда на одной обкладке от мгновенного значения напряжения меж-
ду обкладками (кулонвольтная характеристика) представляет собой
прямую линию (рис. 233), а емкость их не зависит от напряжения и.
Для нелинейных конденсаторов зависимость q от и нелинейна (см.
рис. 235).
264
Нелинейные конденсаторы называют еще варикондами.
Пространство между обкладками нелинейного конденсатора за-
полнено сегнетодиэлектриком. Сегнетодиэлектриками называют ве-
щества, диэлектрическая проницаемость которых является функцией
величины напряженности электрического поля. Собирательное наз-
вание— сегнетодиэлектрики — им присвоено потому, что впервые
это свойство было обнаружено у кристаллов сегнетовой соли.
На электрических схемах вариконды изображают в виде конден-
саторов, в пространстве между обкладками которых делается косая
штриховка (рис. 234, а).
Сегнетодиэлектрики подобно ферромагнитным веществам обла-
дают гистерезисом. Электрическим гистерезисом называют явление
отставания изменения электрического смещения D от изменения наи-
Рис. 235
Рис. 234
ряженности поля Е. Подобно тому как это имеет место в ферромаг-
нитных веществах, площадь гистерезисной петли в координатах
D, Е характеризует собой потери на электрический гистерезис в
единице объема сегнетодиэлектрика за один период изменения Е.
Кроме потерь на гистерезис, в варикондах есть еще потери, обус-
ловленные тем, что проводимость сегнетодиэлектрика не равна ну-
лю, а также рядом других причин.
На схеме замещения (рис. 234, б) вариконд можно представить
в виде параллельного соединения идеализированного (без потерь)
вариконда и ветви с активным сопротивлением Ягп, потери в кото-
ром имитируют в расчетном отношении активные потери в вари-
конд е.
Наличие потерь в варикондах является вредным побочным эф-
фектом. Чем выше качество сегнетодиэлектрика, тем уже петля
гистерезиса и меньше потери в нем. Для облегчения исследования
свойств электрических цепей, содержащих вариконды, гистерези-
сом и потерями обычно пренебрегают и зависимость q—f(u) прини-
мают в виде пунктирной кривой рис. 235. Абсциссы ее равны полу-
сумме абсцисс восходящей и нисходящей ветвей предельной гис-
терезисной петли. Лишь при исследовании схем, в основе действия
которых лежит явление гистерезиса, например при анализе работы
некоторых запоминающих и счетных устройств, гистерезис необ-
ходимо учитывать.
265
§ 191. Нелинейные сопротивления как генераторы высших гар-
моник тока и напряжения. Если нелинейное сопротивление присоеди-
нить к генератору синусоидального напряжения, то протекающий
через сопротивление ток будет иметь несинусоидальную форму, и
потому нелинейное сопротивление будет являться генератором выс-
ших гармоник тока. Для того чтобы убедиться в этом, рассмотрим
рис. 236. На нем кривая 1 — вольтамперная характеристика соп-
ротивления, кривая 2 — синусоидальное напряжение на нем, кри-
вая 3 — ток i через сопротивление.
Для построения кривой i = /(со/) последовательно придаем со/
значения, например равные 0, и т. д.; для каждого
из них находим напряжение и, переносим соответствующее значе-
ние и на кривую и = f(i) и из нее опре-
деляем значение тока i для взятого мо-
мента времени. Найденное значение то-
ка i откладываем на той ординате, ко-
торой соответствует выбранный момент
времени.
Эти операции показаны на рис. 236 стрелками. Так, по точкам
строится кривая 3. Она имеет пикообразную форму и может быть
разложена на гармоники.
Аналогично, если через нелинейное сопротивление пропустить
синусоидальный ток, то напряжение на нем будет иметь несинусои-
дальную форму. Соответствующие построения приведены на
рис. 237. Следовательно, нелинейное сопротивление будет являться
генератором высших гармоник напряжения.
Амплитуды первой и высших гармоник токов нелинейно зави-
сят от амплитуд первой и высших гармоник напряжений на нелиней-
ных сопротивлениях.
Все это затрудняет анализ и расчет нелинейных цепей и в то же
время позволяет осуществить с их помощью ряд важных в практи-
ческом отношении преобразований, принципиально невыполнимых
при помощи линейных электрических цепей.
§ 192. Основные преобразования, осуществляемые при помощи
нелинейных электрических цепей. На рис. 238, а схематически изоб-
266
ражен четырехполюсник, в состав которого входят одно или несколь-
ко нелинейных сопротивлений. Будем называть такой четырехполюс-
ник нелинейным (ИЧ).
На рис. 238, б представлен нелинейный шестиполюсник (НШ).
В отличие от четырехполюсника он имеет еще два зажима («полюса»),
к которым присоединяется источник управляющего напряжения
или тока.
При помощи нелинейных четырехполюсников и шестиполюсни-
ков можно осуществить ряд очень важных преобразований, а имен-
но:
1. Преобразовать переменный ток в постоянный. Устройства,
позволяющие осуществить это преобразование, называются выпря-
мителями (см. § 236).
Цепь управления
Рис. 238
2. Преобразовать постоянный ток в переменный. Это преобразо-
вание производится при помощи устройств, которые называются ав-
тогенераторами (см. § 239) и инверторами.
3. Осуществить умножение частоты, т. е. получить па выходе че-
тырехполюсника напряжение, частота которого в несколько раз
больше частоты входного напряжения. Четырехполюсники, при
помощи которых производится умножение частоты, называются
умножителями частоты; устройство, удваивающее частоту, называет-
ся удвоителем частоты; устройство, утраивающее частоту, — утро-
ителем и т. д. Принцип работы простейшего утроителя частоты рас-
смотрен в § 233.
4. Осуществить процесс деления частоты, т. е. выполнить опе-
рацию, обратную умножению частоты.
Четырехполюсники, позволяющие осуществить деление частоты,
называются делителями частоты. Теория работы их здесь не рас-
сматривается; с ней можно ознакомиться по Л. 18.
5. Стабилизировать напряжение или ток, т. е. получить на вы-
ходе четырехполюсника напряжение или ток, почти не изменяющий-
ся по величине при значительном изменении величины входного нап-
ряжения. Такие четырехполюсники называются стабилизаторами
напряжения (или тока). Устройства, позволяющие осуществить ста-
билизацию напряжения в цепях постоянного тока, были рассмот-
267
рены. в главе второй. Стабилизация напряжения переменного тока
рассмотрена в § 245.
6. Осуществить триггерный эффект. Под ним понимают эффект
резкого (скачкообразного) изменения выходной величины при не-
значительном изменении входной величины. Триггерный эффект
обсуждается в § 241 и 244.
7. Как уже говорилось в § 181, модуляция есть процесс, при ко-
тором амплитуда (фаза или частота) высокочастотного колебания,
поступающего на вход четырехполюсника, преобразуется таким
образом, что характер изменения ее повторяет характер изменения
управляющего низкочастотного сигнала.
В результате получается высокочастотное колебание, в характере
изменения амплитуды (фазы или частоты) которого запечатлен ха-
рактер изменения низкочастотного управляющего сигнала.
Устройства, позволяющие осуществить модуляцию, называются
модуляторами. Принцип работы одного из модуляторов обсуждает-
ся в § 237.
8. Осуществить демодуляцию. Под демодуляцией понимают про-
цесс выделения из высокочастотного модулированного колебания
запечатленного в нем низкочастотного управляющего сигнала.
Устройства, позволяющие осуществить демодуляцию, называ-
ются демодуляторами или детекторами.
Простейшее детекторное устройство рассмотрено в § 238.
9. Преобразовать желаемым образом форму входного напряже-
ния. Так, например, при подаче на вход нелинейного четырехполюс-
ника напряжения синусоидальной формы на выходе его можно по-
лучить напряжение прямоугольной или пикообразной формы.
Некоторые устройства, применяемые для такого рода преобра-
зований, получили свое название в соответствии с формой выходного
напряжения или тока. Так, пик-трансформатор есть устройство,
которое позволяет при подаче на вход его синусоидального напря-
жения или синусоидального тока на выходе получить короткие им-
пульсы (пики) тока или напряжения. Принцип работы одного из
пик-трансформаторов рассмотрен в § 234.
10. Осуществить усиление напряжения (или тока).
Под усилением напряжения будем понимать процесс получения
на выходе нелинейного устройства напряжения значительно боль-
шей величины, чем управляющее напряжение на входе его. Управ-
ляющее напряжение может быть напряжением постоянного и пе-
ременного тока.
Обычные трансформаторы также позволяют усиливать напря-
жение, однако в усилителях напряжения на нелинейных сопротив-
лениях энергия, потребляемая управляющей цепью, может быть
в сотни, тысячи и даже сотни тысяч раз меньше энергии на выходе
усилителя, тогда как в обычных трансформаторах эти энергии, гру-
бо говоря, равны.
268
Кроме того, усилители напряжения, использующие нелинейные
сопротивления, позволяют осуществить усиление не только пере-
менного, но и постоянного напряжения и притом с плавным изме-
нением коэффициента усиления. Простейший усилитель напряже-
ния постоянного тока был рассмотрен в § 41.
11. Осуществить усиление мощности.
Усилением мощности называется процесс выделения на выходе
устройства (в нагрузке) мощности, значительно большей мощности,
поступающей в управляющую цепь.
Устройство, позволяющее получить эффект усиления мощности,
называют усилителем мощности. Простейший усилитель мощности
рассмотрен в § 246.
Эффект усиления мощности требует дополнительных пояснений. Энергия,
поступающая на вход усилителя мощности (на вход четырехполюсника рис.
238, а), доставляется находящимся вне четырехполюсника источником сиг-
нала и расходуется на управление режимом работы нелинейного сопротив-
ления, входящего в состав четырехполюсника.
Выделяющаяся в нагрузке энергия доставляется совсем от иного источ-
ника — от источника энергии, либо находящегося внутри рассматриваемого
четырехполюсника, либо включаемого на выходе четырехполюсника последо-
вательно с нагрузкой.
Когда говорят об эффекте усиления мощности, то имеют в виду, что при-
ращение мощности, выделяющейся в нагрузке, оказывается больше прира-
щения мощности, потребовавшейся для изменения режима работы нелиней-
ного сопротивления.
12. Осуществить степенное и логарифмическое преобразование
входного напряжения и тока.
Эти виды нелинейных преобразований обсуждались в главе вто-
рой (см. § 37 и 38).
Кроме перечисленных, прн помощи нелинейных электрических
цепей могут быть осуществлены и другие нелинейные преобразова-
ния. К нх числу относится, например, плавное преобразование час-
тоты прн помощи нелинейных четырехполюсников и шестиполюсни-
ков, не содержащих подвижных частей. Рассмотрение этого преоб-
разования выходит за рамкн курса (с ним можно ознакомиться по
Л. 19).
Нелинейные устройства находят широкое применение для осу-
ществления электрическим путем операции умножения двух, трех
и большего числа функций (см. § 37 первой части курса), а также
в электрических счетных и запоминающих устройствах (часть маг-
нитных устройств такого рода рассмотрена в Л. 18) в качестве не-
линейных фильтров и т. п. Нет сомнений в том, что по мере разви-
тия техники и изучения свойств нелинейных цепей последние будут
находить применение для выполнения и других функций.
Многие из перечисленных в данном параграфе типов преобразований (пре-
образование постоянного тока в переменный и обратное преобразование, мо-
дуляция и демодуляция, усиление тока, напряжения, мощности), хотя и осу-
ществляются при помощи нелинейных устройств — ив этом смысле они яв-
ляются нелинейными преобразованиями, — но при определенных условиях
269
в относительно небольшом диапазоне изменений входной величины осущест*
вляющие эти преобразования преобразователи могут обладать почти линей*
ной зависимостью амплитуды (действующего или среднего значения) выход*
иой величины от амплитуды (действующего или среднего значения) иходной
величины.
Вне этого диапазона зависимость выходной величину от входной являет*
ся в той или иной степени (часто в очень значительной) нелинейной.
Для многих других типов преобразователей (например, для логарифми»
ческих и степенных преобразователей) зависимость выходной величины eft
входной принципиально не может быть линейной, так как это противоречило
бы самому назначению и самому принципу работы преобразователей этого
типа.
Если же зависимость выходной величины от входной может быть линей*
ной или близкой к линейной, то в большинстве случаев стремятся выбрать ре-
жим работы преобразователя таким образом, чтобы работа его проходила
именно на линейном участке.
Так поступают, в частности, при использовании электронных, полупро-
водниковых и магнитных усилителей тока, напряжения, мощности.
§ 193. Некоторые физические явления, наблюдаемые только в не-
линейных цепях. В электрических цепях переменного тока, содержа-
щих нелинейные индуктивности и линейные емкости или нелиней-
ные емкости и линейные индуктивности, а также нелинейные
индуктивности и нелинейные емкости, при определенных усло-
виях (далеко не всегда!) могут возникать физические явления, ко-
торые не могут возникать в линейных цепях*. Таких явлений весь-
ма много. Мы ограничимся кратким рассмотрением только неко-
торых наиболее важных из них.
К числу таких явлений относятся:
1. Явление возникновения интенсивных колебаний в цепи на выс-
шей гармонике при отсутствии этой гармоники во входном напря-
жении.
В линейных цепях возникновение интенсивных колебаний на
высшей гармонике может быть только при наличии этой гармоники
во входном напряжении, и они не могут наступить, если во входном
напряжении нет данной гармоники.
2. Явление, возникновения субгармонических колебаний.
Под субгармоникой понимают гармонику, частота которой в це-
лое число раз меньше частоты источника э.д.с.
Субгармонические колебания представляют собой колебания
какой-либо из субгармоник. Чаще всего наблюдаются на частотах
—, —, — и т. д. (<о — частота источника э.д.с.).
v Z О
3. Явление возникновения колебаний в цепи на гармонике
* Имеются в виду «обычные» линейные цепи, параметры которых не яв-
ляются функцией времени.
О линейных цепях е непостоянными во времени параметрами см. в при-
ложении А.
270
с частотой ™ и, где т и п — целые числа (по-прежнему со-ча-
И
стота источника э.д.с.).
4. Явление зависимости характера установившегося режима
в нелинейной цепи переменного тока от предшествовавшего этому
режиму состояния схемы и начальной фазы источника э.д.с., от
которого питается схема.
Это явление может наблюдаться в нелинейных электрических
цепях в зоне существования триггерного эффекта, о котором было
упомянуто в предыдущем параграфе. Суть явления состоит в том,
что при подключении нелинейной резонансной цепи к источнику
э.д.с. в ней может возникнуть один из двух возможных режимов.
Какой из двух режимов возникнет, зависит от начальной фазы ге-
нератора и состояния цепи, предшествовавшего включению (см.
§ 241).
5. Явление возникновения автомодуляции.
Автомодуляция представляет собой процесс периодического или
почти периодического изменения амплитуд токов и напряжений в
нелинейных электрических цепях без воздействия на них внешне-
го модулирующего фактора, т. е. без воздействия на них низкочастот-
ного сигнала.
Перечисленные выше физические явления имеют место в резо-
нансных цепях только в определенной для каждой схемы области
значений параметров.
Области значений параметров, как правило, оказываются та-
кими, что практически эти явления наблюдаются сравнительно
редко.
Если к этому же учесть, что исследование условий возникнове-
ния этих явлений часто связано с весьма громоздкими математи-
ческими выкладками, то станет ясно, что в курсе с достаточной пол-
нотой отразить эти явления трудно. Читателей, интересующихся
ими, отсылаем к специальной литературе (Л. 18 и 19).
§ 194. Разделение нелинейных сопротивлений по степени симмет-
рии характеристик относительно осей координат. Кроме деления не-
линейных сопротивлений на активные, индуктивные и емкостные,
управляемые и неуправляемые (а активных — еще на безынерцион-
ные и инерционные), нелинейные сопротивления могут быть клас-
сифицированы еще по одному признаку — по степени симметрии
характеристик для мгновенных значений относительно осей коор-
динат.
Пусть х и у будут величины, характеризующие режим работы
нелинейного сопротивления. Условимся через х обозначать вели-
чину, откладываемую по оси ординат декартовой системы, а через
у — величину, откладываемую по оси абсцисс.
Характеристики, для которых выполняется условие — у{— х) =
= у(х), принято называть симметричными характеристиками; ха-
271
рактеристики, не удовлетворяющие этому условию, — несиммет-
ричными.
Симметричные характеристики имеют нелинейные индуктивнос-
ти и нелинейные емкости, а из активных сопротивлений — тирито-
вые и вилитовые сопротивления, электрическая дуга с однородны-
ми электродами и некоторые другие типы сопротивлений.
Однако основные типы нелинейных активных сопротивлений —
электронная лампа и полупроводниковый триод — обладают несим-
метричными характеристиками.
На протяжении ближайших 13 параграфов (исключение состав-
ляет § 201) рассматриваются основные положения, характеризую-
щие особенности работы нелинейных сопротивлений с симметрич-
ными характеристиками.
Основные положения, характеризующие особенности работы не-
линейных сопротивлений с несимметричными характеристиками —
электронной лампы и полупроводникового триода, излагаются в
§ 210—225.
§ 195. Аппроксимация характеристик нелинейных сопротивлений.
Для проведения математического анализа нелинейных цепей пере-
менного тока и изучения общих свойств их оказывается полезным
выразить аналитически зависимость между мгновенными значения-
ми и и i для нелинейного активного сопротивления, зависимость
между В и Н для нелинейной индуктивности, зависимость q и и для
нелинейной емкости. Приближенное аналитическое описание харак-
теристик нелинейных сопротивлений принято называть аппрокси-
мацией характеристик.
§ 196. Аппроксимация симметричных характеристик для мгновен-
ных значений гиперболическим синусом. При исследовании свойств
электрических цепей явлением гистерезиса, как правило, можно
пренебречь. Лишь при исследовании схем, в основе действия кото-
рых лежит это явление (например, при исследовании работы запо-
минающих магнитных устройств с прямоугольной петлей гистере-
зиса), гистерезис необходимо учитывать.
На рис. 239, а изображена типичная симметричная характери-
стика
У = f(*).
В нелинейной индуктивности роль х играет мгновенное значе-
ние индукции В\ роль у выполняет мгновенное значение напряжен-
ности поля И.
Для нелинейной емкости роль у выполняет напряжение и, роль
х — заряд q.
Для нелинейных активных сопротивлений (например, тирито-
вых и вилитовых сопротивлений) роль х выполняет напряжение,
роль у — ток.
Существует большое количество различных аналитических вы-
ражений, в той или иной мере пригодных для аналитического опи-
272
сания характеристик нелинейных сопротивлений (Л. 18 и 20). При
выборе наиболее подходящего аналитического выражения для функ-
ции y=f(x), исходят не только из того, что кривая, описываемая ана-
литическим выражением, должна достаточно близко всеми своими
точками расположиться к опытным путем полученной кривой в пред-
полагаемом диапазоне перемещений рабочей точки на ней, но учи-
тывают и те возможности, которые выбранное аналитическое выра-
жение дает при анализе свойств электрических цепей. В дальней-
шем для аналитического описания характеристик симметричных
сопротивлений по типу рис. 239, а будем пользоваться гиперболи-
ческим синусом
у = a sh р х. (9.1)
В этом выражении а и Р — числовые коэффициенты; а измеряет-
ся в тех же единицах, что и у, Р измеряется в единицах, обратных
единицам измерения х, так что произведение р% есть величина без-
размерная. Для определения двух неизвестных коэффициентов а
и Р следует на полученной опытным путем зависимости у = f(x) в
предполагаемом рабочем диапазоне произвольно выбрать две наибо-
лее характерные точки, через которые должна пройти аналитичес-
кая кривая, подставить координаты этих точек в уравнение (9.1)
и затем решить систему из двух уравнений с двумя неизвестными.
Пусть координаты этих точек будут: уи хг и у2, х2 (рис. 239, а).
Тогда
ух = a sh Pxt;
у2 = а sh рх2.
Поделим их:
t/i sh₽x/ ( ’
Трансцендентное уравнение (9.2) служит для определения коэф-
фициента р. После этого определяется коэффициент а:
273
Пример 101. Кривая намагничивания трансформаторной стали
Э41 (толщина листов 0,5 мм) изображена на рис. 239, б. Найти ко-
эффициенты а и ₽.
Решение. Выбираем две точки на кривой» 200 а/м,
В. = 1Д тл\ Н2 = 2400 а/м; В2 = 1,532 тл.
sh (1,532 6)
имеем: —= 12,
sh (1,1 ₽)
подсчеты:
По уравнению (9.2)
вольными значениями ₽
проводим
Задаемся
произ-
р 6
РВ2 9,2
рв. 6,6
sh р В2 13,5
sh pBt
5,22 4,57 3,92 8,26
8 7 6 5
5,74 5,03 4,32 3,59
9,58 7,25 6,24 4,1
и
___. Sh В ^9 £ /О\
По результатам подсчетов строим кривую = /дР) и из
sh р
кривой находим р = 5,75 \/тл. Далее, определяем а = =«
SH р Jog
= ТУёг ~ "169?) = О’7* Пунктирная кривая рис. 239, б построе-
на по уравнению
Н = 0,71 sh (5,75 В).
§ 197. Понятие о функциях Бесселя. При анализе нелинейных цепей
широко пользуются функциями Бесселя*. Перед тем как записать общее вы-
ражение для них, вспомним, что тригонометрические, показательные и гипер-
болические функции выражаются степенными рядами.
Известно, что
X3 X5 X7 Sinx = x-- + --- + ... (9.4)
X2 X4 Xе cosx=l-- + --- + ... (9.5)
X2 X3 X4 ^=14- + ^|+3i + Zi + - (9.6)
X2 X3 X4 (9.7)
X3 X5 X7 Sh*==x + 3l+5!+7l+-- (9.8)
X2 X4 Xе chx=l+- + - + - + ... (9.9)
* Функции Бесселя являются решением известного уравнения Бесселя
dx* х dx \ х2
ля не используется. ,
j у = 0. Однако в данной главе само уравнение Бессе-
274
В этих формулах аргумент х может быть действительным, чисто мнимым
или комплексным числом. Значения записанных выше функций для конкрет-
ных значений х можно определить при помощи выписанных выше рядов, что
в качестве примера будет сделано ниже . Однако практически их следует оп-
ределять, разумеется, при помощи графиков или таблиц.
Л
Пример 102. Известно, что sin— = sin 30° = 0,5. Проверить этот резуль-
6
тат при помощи формулы (9.4).
л
Решение. В формулу (9.4) подставляем — вместо х и ограничиваемся
6
тремя членами ряда:
л _ л 1
6 “7 3 • 2
sin
( пу । 1 (—\6
\ б" / + 5 • 4-3-2 \ 6 )
= 0,5228 — 0,02385 4-0,0032 » 0,5.
Функции Бесселя также выражаются степенными рядами и для них так-
же составлены таблицы. Функция Бесселя от аргумента х обозначается Jp(x)
Индекс р дает порядок функции Бесселя. Общее выражение для Jp (х) в виде
степенного ряда такое:
(х\р / х \р+2 //2^\₽+б
2 / \ 2 / \ 2 / \ 2 /
JpW = 0! р! “ 1! (Р4-1)! + 2! (р 4-2)! ~ 3! (р 4-3)! + ’ * * (9Л°
Для дальнейшего наибольший интерес представляют функции Бесселя от
чисто мнимого аргумента. Для получения их в общее выражение (9.10)
вместо х следует подставить jx, где / = V — 1 . Бесселева функция нулевого
порядка
(9.П)
Пример 103. При помощи формулы (9.11) найти /0(/4).
22 2« 2’ 2е 2“>
Решение. Je (j4) = 1 + -+ - + - 4- + ... = 1+4 +
64 256 102£
36г576 1 14 400
Бесселева функция первого порядка от чисто мнимого аргумента jx равна
х I х Г I — \6 I х V
.2 . \ 2 / ,\2/ Д 2 J
Л (/*) = 1 -yj- + i 1|2j + I 2| з| +1 з|4[ +•••
(9-12)
Бесселева функция второго порядка от чисто мнимого аргумента jx равна
Аналогично записываются ряды для функций Бесселя и более высоких
порядков.
При помощи этих рядов для функций Бесселя составлены приведенные
ниже таблицы функций Бесселя и по ним построены кривые рис. 240.
275
Обратим внимание на то, что в таблице дана не функция Jj (jx), а функция
— / Л (/*)•
Точно так же вместо функции J3(jx) в таблице дана зависимость
j Ja (jx) = f(x). Сделано это потому, что функции (jx), J3 (jx), Jb (jx) без
дополнительного множителя j не встречаются.
Так как функция J2 (jx) = f(x) отрицательна, то в таблице дана зависи-
мость — J2 (jx) = f(x). При х = 0 не равна нулю только функция Бесселя
нулевого порядка (Jo(0) = 1).
Из таблиц и графиков рис. 240 видно, что с ростом х значения функций
увеличиваются. Чем выше порядок функций Бесселя, тем меньше ее значе-
ние при одном и том же х.
Значения бесселевых функций мнимого аргумента
X Л(М) —/Л(М) -Л(м) 1Л>(М)
6,0 1,00 0,00 0,00 0,00 0,00
0,2 1,01 0,10 0,005 0,17.10-3 0,42.10-5
0,4 1,04 0,20 0,02 0,13-Ю-2 0,67. IO-'1
0,6 1,09 0,32 0,046 0,46-10~2 0,34.10-3
0,8 1,16 0,43 0,08 0,01 0.Ц.10-2
1,0 1,26 0,56 0,14 0,02 0,27-10—2
1,2 1,39 0,72 0,20 0,04 0,58-10~2
1,4 1,55 0,88 0,29 0,06 0,011
1,6 1,75 1,08 0,39 0,10 0,019
1,8 1,99 1,32 0,53 0,15 0,032
2,0 2,28 1,59 0,69 0,21 0,051
2,2 2,63 1,91 0,89 0,30 0,077
2,4 3,05 2,30 1,13 0,41 0,114
2,6 3,55 2,76 1,43 0,55 0,165
2,8 4,16 3,30 1,80 0,73 0,234
3,0 4,88 3,95 2,24 0,96 0,325
3,2 5,75 4,73 2,79 1,25 0,446
3,4 6,78 5,67 3,45 1,61 0,605
3,6 8,03 6,79 4,25 2,07 0,810
3,8 9,51 8,14 5,23 2,63 1,076
4,0 11,30 9,76 6,42 3,34 1,416
4,2 13,44 11,70 7,87 4,21 1,851
4,4 16,01 14,04 9,63 5,29 2,405
4,6 19,09 16,86 11,76 6,63 3,106
4,8 22,79 20,25 14,35 8,29 3,992
5,0 27,23 24,34 17,50 10,33 5,108
5,2 32,58 29,25 21,33 12,84 6,510
5,4 39,01 35,18 25,97 15,94 8,268
5,6 46,73 42,32 31,62 19,74 10,468
5,8 56,03 50,94 38,47 24,41 13,21
6,0 67,23 61,34 46,78 30,15 16,63
7 168,6 156 124 85,17 51,0
8 427,56 399,87 327,6 236,07 150,5
9 1093,59 1030,91 864,50 646,69 433,3
10 2815,7 2671 2281 1758 1226
11 7288 6948,9 6025 4758 3430
12 18 948 18142 15 924 12 834 9507
276
§ 198. Разложение гиперболического синуса и гиперболического косинуса
от периодического аргумента в ряды Фурье, коэффициентами которых являют-
ся функции Бесселя. Если аргумент х изменяется по периодическому закону,
например по закону синуса х = хт sin со/, где хт — амплитуда колебания,
то по периодическому закону будут изменяться и функции sh (xmsincof) и
ch(xmsinco/). Так как периодические функции могут быть представлены ряда-
ми Фурье, то в ряд Фурье могут быть разложены функции sh (xmsinco/) и
ch (xmsin со/). С этой целью в (9.8) и (9.9) надо вместо х подставить xmsinco/,
учесть известные из тригонометрии формулы
1 — cos 2a
sin2 a
2
1 3
sin3 a —-------sin За J------sin a,
4 4
sin4 a = — (3 — 4 cos 2a + cos 4a) и т. д.,
8
сгруппировать все слагаемые с sin со/, сгруп-
пировать все слагаемые с sin Зсо/, а также от-
дельно выделить постоянную составляющую.
В результате группировки окажется, что ко-
эффициентами при тригонометрических функ-
циях будут ряды, которыми изображаются
функции Бесселя различных порядков от чи-
сто мнимого аргумента jxm. Окончательно получим:
sh (xm sin cd/) = 2 [— /Jj (jxm)] sin at — 2jJ3 (jxm) sin Зсо/ —
— 2JJ5 (jxm) sin 5<o/ — ...
(9-14)
ch (xm sin co/) = Jo (jxm) -j- 2J2 (/*m) cos 2co/ + 2J4 (jxm) cos 4co/ + .., (9.15)
Формулы (9.14) и (9.15) в дальнейшем часто будут использоваться. Ряд
для sh (xmsinco/) состоит только из нечетных гармоник и не имеет постоянной
составляющей. Ряд для ch (хт sin со/) имеет постоянную составляющую и чет-
ные гармоники.
Пример 104. Разложить в ряд Фурье sh (4 sin со/) и ch (4sinco/),
Решение. Значения функций Бесселя берем из таблицы:
- /Л (/4) = 9,76; jJ3(j4) = 3,34;
— ЁМ/4) = 0,505; Уо(/4) =11,3; J2 (/4) = — 6,42.
В соответствии с формулами (9.14) и (9.15) имеем:
sh (4sinco/) = 2- 9,76 sin со/ — 2 • 3,34 sin Зсо/ + 2- 0,505 sin 5со/ — ...
ch (4 sin co/) = 11,3 — 2- 6,42 cos 2 co/ + 2- 1,416 cos 4co/ — ....
§ 199. Разложение гиперболического синуса от постоянной и синусоидаль-
но меняющейся составляющих в ряд Фурье. Из предыдущего (см. § 196) извест-
но, что мгновенное значение функции у связано с мгновенным значением х
формулой (9.1):
у = a sh Px.
В этой формуле аргументом гиперболического синуса является не х, как
было в § 197, а произведение §х. В соответствии с этим для получения разло-
жения sh фхт sin со/) и ch (P*m sin со/) в формулах (9.14) и (9.15) следует за-
менить х на рхт.
Если х = х0 + хт sin со/, где х0— постоянная составляющая и хт—ам-
плитуда синусоидальной составляющей, то
у = a sh (Рх0 -|- P*m sin со/) = a sh Рх0 ch (§xm sin co/) -j-
-|- a ch px0 sh (P*m sin co/).
277
Следовательно,
у = a sh рл'о |Jo (/К) + 2Л (/P*m) cos 2coZ + 2J4 (jfixm) cos 4<oZ -Ф- ...] +
4- a ch px0 {2 1— j (/0Am)] sin a>t — 2jJ3 (ff>xm) sin 3 <oZ — ... }. (9.16)
Из формулы (9.16) следует, что постоянная составляющая функции у (на-
зовем ее у0) равна:
i/о = a sh PVo GPx,„). (9.17)
Первая гармоника функции у (обозначим ее у4)
tji = 2a clipA'ol — jJiGPx,,,)] sincoZ. (9.18)
Вторая гармоника
Уч = 2a sh p*0 1Л (/P*m)l cos 2co Z. (9.19)
Третья гармоника функции
Уз = 2a ch Px0 [— jJ3 GP*m)l sin 3coZ (9.20)
и T. д.
Пример 105. Разложить в ряд Фурье функцию А = sh (2 -|-4 sin coZ).
Решение. По таблицам находим: sh 2 = 3,63*, ch 2 = 3,76. Зна-
чения функций Бесселя также берем из таблицы.
В соответствии с формулой (9.16) имеем:
— = sh (2 + 4 sincoZ) = 3,63 (11,3 — 12,844 cos 2coZ + 2,832 cos 4<oZ — ...) +
+ 3,76 (19,52sincoZ — 6,674 sin 3coZ + 1,01 sin 5coZ— ...).
Таким образом, постоянная составляющая — = 3,63- 11,3 = 41 1.
a
Амплитуда первой гармоники = 3,76 • 19,52 = 73,4.
a
Амплитуда второй гармоники ^^- = 3,63- 12,844 = 46,7.
а
§ 200. Некоторые общие свойства симметричных нелинейных сопротив-
лений. Если нелинейное сопротивление с симметричной характеристикой
работает в условиях, когда одна из определяющих его состояние величин, а
именно величина х, изменяется во времени по закону х = х0+ хт sincoZ, то
в отношении другой определяющей его состояние величины — величины у —
можно сделать следующие выводы:
1. Величина постоянной составляющей функции у (т. е. у0) зависит не
только от величины хп, но и от величины х,,,. Это свойство следует нз формулы
(9.17):
Уо = a shp.v0J0 G'Pxrn)-
2. В кривой у ~ f (coZ) появляются четные гармоники. Четные гармоники
исчезают при ха = 0. Фаза четных гармоник зависит от знака постоянной сос-
тавляющей (от знака х„).
3. Путем изменения величины х0 или у0 можно изменять амплитуды пер-
вой и высших гармоник функции y(coZ).
Первое из этих свойств поясним графически. Пусть нелинейное сопротив-
ление работает прн отсутствии синусоидальной составляющей (хт= 0). Тог-
да изображением этого процесса на характеристике нелинейного сопротив-
ления будет точка а (рнс. 241, а). Для нее
* Таблицы sh х и ch х см. на стр. 428.
278
У ~ Уп, ₽х= ₽х' = Ar sh —.
о а
Этот результат следует из формулы (9.17), если учесть, что Jo (0) = !.
Напомним, что размерность коэффициента р обратна размерности х, а
коэффициент а имеет ту же размерность, что и у; поэтому произведение рх
у
и частное — являются безразмерными величинами.
Если теперь нелинейное сопротивление будет работать при хт А 0, то
для того, чтобы постоянную составляющую функции у, т. е. 1/0, сохранить
прежней, постоянная составляющая х0 должна
быть снижена или снизится сама со значения х'о
до значения х".
Величина flx'o определяется из формулы
Уо
а
Р4 = Лг sh- (2.2!)
'о(/Рл';к)
где х" определяется ординатой точки Ь, располо-
женной ниже точки а (рис. 241, б).
Первое и третье из этих свойств широко ис-
пользуются в теории управляемых нелинейных
сопротивлений. Второе свойство используется в
теории умножителей частоты.
Пример 106. Нелинейное сопротивление с ха-
рактеристикой у = a sh рх сначала работало при
— = 41,1 и при отсутствии переменной состав-
ляющей (Рхт = 0). Затем режим работы его из-
Уп
менялся: постоянная составляющая _ осталась
а
прежней, но появилась переменная составляю-
щая, амплитуда которой Рхт = 4. Найти постоян-
ные составляющие рх0 в этих двух режимах.
Решение. В первом режиме
Pxg = Аг sh 41,1 = 4,41.
Во втором режиме
41 1
Рхл = Ar sh -----— — Ar sh 3,63 = 2.
Jo <j4)
Таким образом, при переходе от первого режима ко второму постоянная
составляющая рх0 изменилась с 4,41 до 2, т. е. более чем в 2 раза.
§ 201. Некоторые общие свойства нелинейных сопротивлений с несиммет-
ричными характеристиками. Нелинейным сопротивлениям с несимметрич-
ными характеристиками также присущи перечисленные в § 200 общие свой-
ства. Однако в отношении второго свойства между несимметричными и сим-
метричными сопротивлениями имеет место существенное различие: четные
1 армоники функции у появляются у несимметричного сопротивления и при
х(| = 0.
Следует, конечно, иметь в виду, что сами формулы, дающие количествен-
ную связь между отдельными величинами в нелинейных сопротивлениях с
симметричными н несимметричными характеристиками, разумеется, различ-
ны, поскольку характеристики несимметричных нелинейных сопротивлений
не описываются формулой у — х sh рх.
279
§ 202. Типы характеристик нелинейных сопротивлений. При ана-
лизе и расчете электрических цепей с нелинейными сопротивления-
ми в зависимости от характера рассматриваемого вопроса исполь-
зуется несколько различных типов характеристик одного и того же
нелинейного сопротивления, а именно:
характеристики, связывающие мгновенные значения определя-
ющих величин;
вольтамперные характеристики, связывающие амплитуды или
действующие значения первых гармоник тока и напряжения;
вольтамперные характеристики, связывающие действующие зна-
чения тока и напряжения.
§ 203. Характеристики для мгновенных значений. Основным ти-
пом характеристик являются характеристики, связывающие мгновен-
ные значения основных определяющих величин, например тока и
напряжения на нелинейном активном сопротивлении, мгновенные
значения индукции и напряженности в сердечнике нелинейной ин-
дуктивности, мгновенные значения заряда и напряжения для не-
линейной емкости.
Такие характеристики будем называть характеристиками для
мгновенных значений. Иногда перед этим названием добавляют
слова: вольтамперные, веберамперные или кулонвольтные.
§ 204. Вольтамперные характеристики по первым гармоникам.
Под вольтамперными характеристиками по первым гармоникам по-
нимают графическую или аналитическую связь между амплитудой
или действующим значением первой гармоники тока и амплитудой
или действующим значением первой гармоники напряжения на не-
линейном сопротивлении.
Этот тип характеристик подразделяется на две подгруппы. В
первой подгруппе принимается, что напряжение (поток или заряд) на
нелинейном сопротивлении изменяется по синусоидальному за-
кону.
Во второй подгруппе характеристик принимается, что по сину-
соидальному закону во времени меняется ток через нелинейное ак-
тивное сопротивление (или напряженность в сердечнике нелиней-
ной индуктивности, или напряжение на нелинейной емкости).
Если воздействующие на нелинейное сопротивление синусоидаль-
ное напряжение или синусоидальный ток не содержат постоянной
составляющей, то вольтамперная характеристика для первых гар-
моник для данного нелинейного сопротивления изображается какой-
то одной кривой. Если же воздействующее напряжение или ток со-
держат постоянную составляющую, то вольтамперные, веберампер-
ные или кулонвольтные характеристики изображаются семействами
кривых, на которых постоянная составляющая тока, напряжения,
потока или заряда является параметром.
Этот тип характеристик получают расчетным или графическим
путем из соответствующих характеристик для мгновенных значе-
ний, либо снимают экспериментально.
280
При графическом построении задаются различными значениями
амплитуды воздействующего на нелинейное сопротивление напря-
жения (или тока, индукции, заряда), по точкам строят кривую тока
(напряженности, напряжения) в функции времени и путем разло-
жения ее в ряд Фурье находят соответствующие амплитуды первой
гармоники тока (напряженности, напряжения).
Пример графического построения кривой тока в функции вре-
мени для управляемой нелинейной индуктивности см. в § 207 на
рнс. 245.
Аналитический (расчетный) путь состоит в том, что построение
точек обсуждаемой характеристики производится путем исполь-
зования формул (9.17) и (9.18) или любых иных, подобных им.
Рис. 242
В § 206 рассмотрено применение формул (9.17) и (9.18) для полу-
чения единых характеристик по первым гармоникам для управляе-
мых симметричных нелинейных сопротивлений.
Для нелинейной индуктивности вольтамперные характеристики
по первым гармоникам можно получить опытным путем при помо-
щи схемы рис. 242, а.
В этой схеме ИТ1 — источник синусоидальной э.д.с., ИТ2 —
источник постоянной э.д.с.
Зажимы ab — это зажимы управляемой цепи нелинейного соп-
ротивления, зажимы cd — зажимы управляющей цепи нелинейного
сопротивления.
Измерительный прибор Vt реагирует на первую гармонику на-
пряжения, а измерительный прибор Аг—на первую гармонику тока.
На рис. 242, б качественно изображены вольтамперные харак-
теристики управляемой нелинейной индуктивности по первым гар-
моникам. Параметром на них является ток управления /0.
281
Вольтамперные характеристики по первым гармоникам для
управляемой нелинейной емкости изображены на рис. 242, в. Пара-
метром на них является управляющее постоянное напряже-
ние Uo.
Снятие характеристик рис. 242, б производится следующим обра-
зом. Устанавливают некоторое произвольное значение тока /0 в це-
пи управления, затем плавно повышают напряжение U\ и для каж-
дого его значения записывают величину тока
Затем то же проделывают при новом значении /0 и т. д. Резуль-
таты измерений наносят на график, и соответствующие точки соеди-
няют плавной кривой.
Вольтамперные характеристики для первых гармоник исполь-
зуются в методе расчета установившихся режимов в нелинейных
цепях, который получил название расчета по первой гармонике
(см. § 22S).
При расчете применяют вольтамперные характеристики той под-
группы, которая по условиям работы данного нелинейного сопро-
тивления более подходит, чем другая.
§ 205. Вольтамперные характеристики для действующих значений.
Под вольтамперными характеристиками для действующих значе-
ний понимают зависимость между действующим значением синусо-
идального (или несинусоидального) напряжения на нелинейном
сопротивлении и действующим значением тока, протекающего че-
рез нелинейное сопротивление. Если напряжение или ток содержат
постоянную составляющую, то вольтамперные характеристики для
действующих значений изображаются семейством кривых, на кото-
рых постоянная составляющая тока, потока, напряжения или за-
ряда является параметром.
Эти характеристики получают графическим или аналитическим
путем из характеристик для мгновенных значений или снимают опыт-
ным путем при помощи схемы рис. 242, а, но приборы Vj и Л1 в этом
случае должны измерять действующие значения.
Следует иметь в виду, что вольтамперные характеристики для
действующих значений зависят от формы напряжения на нелиней-
ном сопротивлении и (или) от формы протекающего через него тока,
поэтому необходимо указывать, при каких условиях они полу-
чены.
При качественном и грубом количественном анализах, в кото-
рых используются вольтамперные характеристики для действую-
щих значений, полагают, что характеристики, снятые при одной
форме напряжения на нелинейном сопротивлении, близки к харак-
теристикам, снятым при другой форме напряжения. В действитель-
ности же количественное различие в характеристиках может ока-
заться значительным. Вольтамперные характеристики для дейст-
вующих значений используются в методе расчета, получившем наз-
вание расчета по вольтамперным характеристикам для действую-
щих значений (см. § 230).
2₽2
§ 206. Получение аналитическим путем обобщенных характеристик уп-
равляемых нелинейных сопротивлений по первым гармоникам. Как уже гово-
рилось выше, нелинейные индуктивности нелинейные емкости и большая груп-
па нелинейных активных сопротивлений имеют характеристики для мгновенных
значений, которые могут быть приближенно описаны формулой у = a sh 0х.
Для каждого вида нелинейного сопротивления под х и у следует понимать
свои величины. Для нелинейной индуктивности: х — магнитная индукция, у —
напряженность магнитного поля. Для нелинейной емкости: х — заряд, у — на-
пряжение. Для нелинейного активного сопротивления: х — напряжение (или
ток), у — ток (или напряжение).
Таким образом, х и у — обобщенные обозначения определяющих работу
нелинейного сопротивления величин.
243
Для всех перечисленных видов сопротивлений можно построить единые
характеристики по первым гармоникам.
С этой целью положим х = хв хт sin a>t.
Тогда в соответствии с формулой (9.18) амплитуда первой гармоники
функции у (назовем ее t/tm) равна:
Ут = 2achp%0[ — /Л(/Рхт)]. (9.22)
Формула (9.22) устанавливает связь между амплитудой у1т первой гармо-
ники у, амплитудой хт первой гармоники х и постоянной составляющей х0.
На рис. 243, я изображены характеристики управляемого нелинейного
сопротивления pxm = f j при параметре fk0 = 0, 1, 2, 3, 4, 5, по-
строенные по формуле (9.22).
Кривыми рис. 243, а можно пользоваться при известном значении пара MOT-
РО
ра р%0. Если известно не рх0, а постоянная составляющая —, то семейство
кривых рх,п = f ( j при параметре может быть построено следующим
образом: из формулы (9.17) находим
Уо
sh рх0 = ----~----
Jo (ffiXm)
283
и вместо ch Р%0 в формулу (9.22) подставляем
Получаем:
1 -|- sh2p%0 —•
* Е» I2
а
Кривые (рис. 243, 6) построены по формуле (9.23). Они представляют со»
бой характеристики управляемого нелинейного сопротивления при значениях
(9.23)
параметра—= 0, 50, 100, 150 и 200. Обратим внимание на то, что ₽-*т.
— есть безразмерные величины. Если масштабы по осям уменьшить в]Л2 раз,
то кривые рис. 243, б будут представлять собой характеристики по действу-
ющим значениям первых гармоник.
Характеристика неуправляемого нелинейного сопротивления изображается
одной кривой рис. 243, б, для которой — = 0.
Рис. 244
§ 207. Простейшая управляемая нелинейная индуктивность.
Простейшая управляемая нелинейная индуктивность изображена
на рис. 244. Она состоит из катушек w1 и
ю2, намотанных на замкнутый ферромаг-
нитный сердечник. Пусть площадь попе-
речного сечения сердечника будет 5(л!2),
а длина средней магнитной линии Цм).
Обмотка w1 включена в цепь перемен-
ного тока, и по ней протекает переменный
ток I, содержащий первую и высшие гармо-
ники.
Обмотка управления w0 — ее называют
также обмоткой подмагничивания — при-
соединена к источнику постоянной Э.Д.С.
Ео через дополнительную индуктивность
Lo и регулируемое активное сопротивление. По обмотке проте-
кает постоянный ток
' __ ^2
Ro
где — активное сопротивление цепи подмагничивания.
Хотя переменный магнитный поток и наводит в обмотке wB пе-
ременную э.д.с., но переменного тока по обмотке we практически не
284
протекает, так как дополнительная индуктивность Lo взята такой,
что она образует для переменного тока достаточно большое индуктив-
ное сопротивление.
Пусть приложенное к обмотке напряжение равно Um cos at.
Это напряжение равно э.д.с. самоиндукции, взятой с обратным зна-
ком (активное сопротивление обмотки считаем весьма малым):
и = — е. = w. — = cos at.
L 1 dt m
Отсюда магнитный поток
Ф = — sin at -j- Фо = Ф sin at + Ф/,
Ф . HjH.
т »
(OWi
(9.24)
где Фт — амплитуда переменной составляющей магнитного потока,
Фй — постоянная составляющая магнитного потока.
Управляемая нелинейная индуктивность позволяет путем из-
менения величины постоянного тока 10 в обмотке управлять ве-
личиной переменного тока I.
Принцип управления режимом работы нелинейной индуктив-
ности и характер изменения во времени отдельных величин пояс-
ним при помощи рис. 245, а и б. На этих рисунках кривые Ф = f(Hl)
представляют собой зависимости потока Ф в сердечнике в функции
от произведения напряженности магнитного поля И на длину сред-
ней магнитной линии I сердечника.
285
Построения на рис. 245, а соответствуют случаю, когда /0 — О,
а на рис. 245, б — когда /0 Ф 0. На обоих рисунках переменная
составляющая потока Ф,л sin <в/ одинакова. Для рис. 245, а постоян-
ная составляющая потока равна нулю, а для рис. 245,6 Фо=у=О.
На кривой Ф = /:(о>/), на кривой Ф = /(Д/) и на кривой iwt — f(at)
наиболее характерные соответствующие друг другу точки обозна-
чены одинаковыми буквами.
Построения производим в следующей последовательности:
1. Сначала откладываем значение постоянной составляющей
потока Фо и строим кривую Фт sin <в/ = f (со/) (для рис. 245, а
Фо = 0).
2. Затем произвольно задаемся различными моментами времени,
Тдг
например равными at = 0; —; л; — л; 2л, и для каждого значе-
ния со/ при помощи кривой Ф —/(///) находим соответствующие
значения HI и строим кривую iwA Д- = f (at) (для рис. 245, а
Jew0 = 0). Ось времени для этой кривой направлена вертикально
вниз и проходит через точки а, с, е в нижней части рисунка.
Обратим внимание на то, что ток i не содержит постоянной состав-
ляющей, так как в цепи обмотки нет источника постоянной э.д.с.
и выпрямителей.
Прямая А — А рис. 245, б является нулевой линией для кривой
iwt = f(at). Ток i колеблется около этой прямой так, что среднее
значение его за период от <в/ = 0 до at — 2л равно нулю.
Другими словами, проводим прямую А — А так, чтобы площадь
Sj была равна площади S2.
Расстояние, на которое удалена прямая А — А от оси ординат,
равно /одао.
Полезно сопоставить выводы § 200, сделанные в общей форме, с теми вы-
водами, которые применительно к нелинейной индуктивности могут быть сде-
ланы путем рассмотрения рис. 245, а и б. Сопоставимыми величинами явля-
ются: х — Ф; у — (iwx + /„Wo); х0 — Фо; хт — Фт; у0 — /ow„; у = /(ео/) —
— (iwt + /оЩс) = f (at).
В § 200 говорилось, что путем изменения величины уе можно изменять
амплитуды первой и высших гармоник функции у = f(at). Этот вывод под-
тверждается построениями рис. 245, о и б — амплитуды первой и высших гар-
моник функции iwj = f(at) зависят от величины /о®0. Чем больше /owo,
тем больше амплитуда первой гармоники тока I.
В § 200 отмечалось, что у0 зависит не только от х0, но и от хт. В свою оче-
редь из построений рис. 245, а и б следует, что величина /ошо зависит не толь-
ко от Фо, но и от Фт.
В § 200 говорилось, что при наличии постоянной составляющей в соста-
ве функции х в кривой у = f(at) появляются четные гармоники. Из рис. 245, б
следует, что при наличии постоянной составляющей Фо в составе магнитного
потока Ф в кривой iwj = f (at) появляются четные гармоники — кривая
iwt = f(at) несимметрична относительно прямой А — А.
Выведем зависимости, позволяющие подсчитать амплитуду пере-
менной составляющей магнитной индукции Вт через амплитуду при-
286
воженного напряжения Um, угловую частоту <в, площадь попереч-
ного сечения сердечника S и число витков wL.
Выведем также формулы, позволяющие подсчитать постоянную
составляющую напряженности поля Но через постоянный ток /0,
амплитуду первой гармоники напряженности поля Н1т через амп-
литуду первой гармоники 11т переменного тока и т. д.
Имеем:
Фт = BmS-, (9.25)
Фй = B0S, (9.26)
где Во — постоянная составляющая магнитной индукции.
Из формул (9.24) и (9.25) следует, что
В =-^-- (9.27)
Если магнитную индукцию измерять в гауссах, S — в сж2, заменить Um
на 1/^2, где U — действующее значение напряжения на обмотке то
V2 U • 108 V • 10е
Вт = —---------=----------. (9.27 )
т ZnfWiS 4,44/w.S
Формула (9.27) дает возможность найти амплитуду переменной
составляющей магнитной индукции по амплитуде синусоидального
напряжения U, частоте f, числу витков wt и сечению S.
По закону полного тока произведение напряженности поля Н
на длину средней магнитной линии / должно равняться алгебраи-
ческой сумме м. д. с. Следовательно,
iwr -ф- Iowo — Hl. (9.28)
Уравнение (9.28) распадается на ряд уравнений: на уравнение
для постоянных составляющих, на уравнение для первой гармоники,
второй гармоники и т. д.
Равенство постоянных составляющих левой и правой частей урав-
нения (9.28) дает:
Ш = Н„1, (9.29)
где Но — постоянная составляющая напряженности поля.
Переменный ток I содержит первую, вторую и другие высшие
гармоники, но постоянной составляющей не содержит, так как в
цепи обмотки нет источника постоянной э.д.с. и выпрямителей.
Амплитуда первой гармоники левой части уравнения (9.28) рав-
на амплитуде первой гармоники правой части уравнения. Следо-
вательно,
= (9.30)
где /1т — амплитуда первой гармоники тока I, — амплитуда
первой гармоники напряженности поля.
Аналогично
= (9-31)
287
Из (9.29) —(9.31) следует, что
Lf __
, 0 1 '
Н —
lm~ I '
JJ __ hmwl
J12m —
ИТ. Д.
(9.32)
(9.33)
(9.34)
Формула (9.32) дает возможность определить постоянную состав-
ляющую напряженности поля Но через постоянную составляющую
тока /0. Формула (9.33) позволяет найти Н1т через 11т и т. д.
§ 208. Вольтамперные характеристики управляемой нелинейной
индуктивности по первым гармоникам. Под вольтамперными ха-
рактеристиками управляемой нелинейной индуктивности по пер-
вым гармоникам будем понимать зависимость действующего зна-
чения первой гармоники переменного напряжения Ux на обмот-
ке w1 нелинейной индуктивности от действующего значения первой
гармоники переменного тока 11 прн постоянном токе /е, взятом в ка-
честве параметра.
Как уже говорилось в § 203, вольтамперные характеристики не-
линейной индуктивности можно получить либо опытным путем при
помощи схемы рис. 242, а, либо расчетным путем.
Рассмотрим расчетный путь, основанный на использовании обоб-
щенных характеристик, о которых шла речь в § 206.
Примем, что зависимость между мгновенным значением напряженности
магнитного поля Н и мгновенным значением магнитной индукции В выражает-
ся гиперболическим синусом:
И = a sh РВ. (9.35)
В формуле (9.35) Н играет ту же роль, какую играет у в формуле (9.1),
а В — ту же, что и х.
На основании аналогии между формулой (9.35) и формулой (9.1) ясно,
что характеристики управляемой нелинейной индуктивности по первым гар-
моникам будут полностью совпадать с характеристиками рис. 243, б, только
надо Вхт заменить на РВ,,,, —— заменить на —— и параметр — на —.
2а 2а а а
Из формулы (9.27) следует, что
PV2 £7
=3 ,
<DW1S (0ПУ1О
или
.. п ©Wi S
и = ₽ mруТ (9-36)
С другой стороны, из (9.33) имеем
/1т = Г2/1^-^£
288
Следовательно,
1 2a tt>!
На основании формулы (9.32)
, Ho al
lo —
a w0
(9.37)
(9.38)
Таким образом, для перехода от семейства кривых в безразмерных едини-
цах
/70
при параметре — к семейству кривых Ц = / (/х) прн параметре /0 надо масштаб
wttijS а/ (Л2
по оси ординат изменить в ——7= раз, масштаб по оси абсцисс — в ---------
р ]/ 2
al
раз и значения параметра — в — раз.
Пример 107. Управляемая нелинейная индуктивность рис. 244 имеет
следующие данные: S = 2,2 см2; 1 = 25см; wt = 250; ш0 = 1775.
Аналитическое выражение кривой намагничивания
И = 0,71 sh(5,75 В).
Воспользовавшись кривыми
о г I У1т \
Уо
при параметре (рис. 243, б) построить для нее семейство в. а. х. по
первым гармоникам I/, = f (/г) при параметре /0.
Решение. Подсчитываем коэффициент для перехода от &хт к напря-
жению U:
awtS 314.250 • 2,2 - 10"*
---— = ——------------: =,214
Р1/2 5,75]/’2-’ ‘
Таким образом, при переходе от $хт к напряжению V масштаб по оси
ординат на рис. 243, б должен быть увеличен в 2,13 раза. Определяем коэф-
77
фициент для перехода от к действующему значению первой гармоники
тока:
а/]Л2 0,71 . 0,25 У? _3
250
Следовательно, масштаб по оси абсцисс должен быть изменен в 10~3 раз.
/7о
Коэффициент для перехода от — к току /0 равен
al 0,71-0,25
w0 1775
10 Л. А. Бессонов
289
Семейство в. а. х. изображено на рис. 246.
В литературе, посвященной электрическим цепям с нелинейными индук-
тивностями, используется термин индуктивное сопротивление нелинейной ин-
дуктивности по первой гармонике.
Под индуктивным сопротивлением по первой гармонике понимают отно-
шение действующего значения первой гармоники напряжения (Д на зажимах
обмотки нелинейной индуктивности, включенной в цепь переменного тока,
к действующему значению первой гармоники тока /х, протекающего через
эту обмотку:
Х1”7?
где Xt является функцией величины напряжения Ui и величины тока подмаг-
ничивания /в.
О том, как меняется Хъ в функции от Ц при /й = const, и о том, как
меняется в функции от /0 при Ul = const, можно сделать заключение, вос-
пользовавшись кривыми рис. 246.
Так, если принять Ui — 8,52 в, то
при /0 = 0, Ii = 0,01 а и, следо-
вательно,
8,52
----- 852 (ом).
Xl-o,oi
При /0 => 0,01 а
8,52
Xi => = 10> (ож).
0,084 ' '
При /0 = 0,015 а
8,52
Х,= —-— =66,5 (ом).
1 0,128 ' '
Таким образом, путем изменения
можно управлять величиной сопро-
величины тока подмагничивания 10
тивления Хг.
Это положение будет учтено в § 246 при рассмотрении принципа работы
магнитного усилителя.
Пример 108. Обмотка управляемой индуктивности примера 107 под-
ключена к синусоидальному напряжению U = 12,2 в (f — 50 гц). Обмотка
управления ю0 подключена к источнику постоянной э. д. с. Ео = 1 в. Актив-
ное сопротивление цепи подмагничивания Ro = 50 ом. Определить ампли-
туду переменной составляющей Вт и постоянную составляющую Во магнит-
ной индукции.
Решение. По формуле (9.27)
12,2-УТ
Вт =•---------~ * -------= 1 тл- $Вт = 5,75.
т 2л • 50 • 250 • 2,2.10-*
Постоянная составляющая тока
/в = & = Го = °’о2(а)-
Постоянная составляющая напряженности поля
//„=^=141,5^.
290
Параметр
По формуле (9.21)
200
РВО = Аг sh =1,86;
Jo(l 5,75)
„ РВО 1,86 „
Во= = ~ = 0,324 (тл).
Р 5,75
§ 209. Вольтамперные характеристики управляемой нелинейной емкости
по первым гармоникам. Кулонвольтная характеристика нелинейной емкости
с достаточной степенью точности может быть выражена гиперболическим си-
нусом:
и = a sh pg. (9.39)
Пусть заряд
<7 = Qo + Qm sin at.
Здесь Qo — постоянная составляющая заряда, Qm — амплитуда первой гармо-
ники заряда.
При этом напряжение на емкости будет иметь постоянную составляющую
Un, а также первую и высшие гармоники. Формулы (9.17) — (9.20) можно
распространить на нелинейную емкость, если заменить у0 на Uo, у1т на Uim,
хт на Q„, и Хо на Qo. В соответствии с этим постоянная составляющая напря-
жения на емкости
t70 = ashpQ0JG(/PQm). (9.40)
Первая гармоника напряжения на емкости равна 2achpQc |—jJi(iPQm)l since/.
Т dq г
1ок через емкость равен—. Следовательно, первая гармоника тока через
at
емкость запишется так:
d
— (Qm sin со/) = со Qm cos со /.
dt
Ее амплитуда равна:
а
wQm = Р Qm а >
Р
а действующие значения — в '[Л2 раз меньше:
/1 = ₽Qm-p7T- (9-41)
Под вольтамперными характеристиками управляемой нелинейной емкости
по первым гармоникам будем понимать зависимость действующего значения
первой гармоники тока через емкость от действующего значения первой
гармоники напряжения Ur при параметре Ua.
На основании записанного выше соответствия между С'о и уй, у1т и Ulm
и т. д. можно сказать, что семейство кривых
ив
при параметре — полностью повторяет семейство кривых
a
₽Xm=^(“&r)
при параметре —, изображенное на рис. 243, б.
а
10*
291
к семейству вольт-
Для перехода от семейства кривых PQm = /|
\ 2а
амперных характеристик управляемой нелинейной емкости по первым гармо-
никам надо учесть формулу (9.41), учесть, что действующее значение первой
гармоники напряжения на емкости
U, = —— а
1 2а
V2,
и что
Uo
и„ = ~
а
а.
семейства кривых р Qm
Другими словами, для перехода от
при параметре— к семейству кривых /1 = /(171) при параметре Uo надо
а
масштаб по оси ординат изменить в
параметр — в а раз. Подобно тому
СО
——7= раз, по оси абсцисс — в а ]/ 2 раз и
РУ 2
как для нелинейной индуктивности вводится
понятие индуктивного сопротивления
по первой гармонике (см. § 208), для
нелинейной ----------’
емкостном
гармонике*
емкости вводят понятие об
сопротивлении по первой
X
Здесь lJt — действующее значение первой
гармоники напряжения на нелинейной
емкости, Д — действующее значение пер-
вой гармоники тока через нелинейную
емкость, Xj является функцией величи-
ны Ut и величины Uo.
109. На рис. 247 изображена кулонвольтная характеристика вари-
ВК1-3. Найти значения коэффициентов а и р в выражении
Пример
коида типа
и = a sh р q.
Решение. Выберем две точки на характеристике
= 120 в; ?! = 3,7 10-в/с; ц2 = 320 в; qt = 8 • 10~3 к.
Составим уравнение для определения коэффициента Р:
42 = 2 67 = sh(8- 10~6Р)
ur ’ sh(3,7 • 10~ер)
Отсюда
Р = 0,17-10е 1/к; а=-----—-----=^-=>175,5(0).
' ' sh(8 • 10~ср) 1,82
Пример ПО. Заряд q вариконда предыдущего примера изменяется по
закону 9 = <2о + <2m sin <2о => 3 • 10-e к; Qm = 4 • 10~e к; <o = 3140 сект1.
Записать выражение для мгновенного значения напряжения иа конденса-
торе и иайти ток через конденсатор.
Решение. Находим:
PQo=>3 -0,17 = 0,49; рQm = 4.0,17 = 0,68;
shp<20 = 0,51; chpQ0 = 1,12;
292
Uo = a sh PQoJo (/PQm) = 175,5 - 0,51 - 1,12= 100 (e);
и == Uo + Ulm since/ + U2m cos2coZ Usm sin Зсо/ + ...
Ulm = 2a ch PQo [— /Д (/PQm)] = 2 . 175,5 . 1,12.0,368 = 144 (e);
U2m = 2a sh PQ0 |J2 (/ p Qm)| = — 2-175,5.0,51.0,065 = — 11,6 (e);
U3m = 2a ch PQo [— jj3 (/PQm)] = 2 . 175,5 1,12 . 0,008 = 3,14 (e).
Амплитуда тока
Im = coQm = 3140 • 4 . 10-’ = 0.012(a).
Пример 111а. Через нелинейный конденсатор с характеристикой
и = 175,5 sh (0,17 • 10е</) протекает ток, первая гармоника которого
(со = 3140 cetr1) имеет амплитуду 11т == 18,45 ма. Постоянная составляющая
напряжения на конденсаторе й/0 == 106,2 в. Амплитуда первой гармоники
напряжения 111т = 217,5. Найти постоянную составляющую заряда Qu и
амплитуду первой гармоники Qm.
Решение. Определяем:
11т 0,01845
Qm = = —-------= 5,88 • 10-е (К).
со °
3140
Составим уравнение для определения PQ0:
______________________________sh PQo^o (/PQm)
Him 2 ch PQo [ (/PQm)]
Отсюда
_ 2^o 1-Mi (/PQm)] 106,2.0,56 _
P tWo(/₽Qm) ’217,5.1,26
PQo = 0,463; Qo = 2,72 • 10“’ к.
0,432;
§ 210. Основные сведения об устройстве полупроводниковых трио-
дов. В настоящее время подавляющее большинство полупроводни-
ковых триодов (транзисторов) выполняют из элемента германия,
подвергнутого специальной обработке.
Область полупроводникового триода, образованная германием,
в который добавлены примеси, легко отдающие электроны (фосфор,
сурьма, мышьяк), называют «-областью (« — первая буква слова
negativ). Название обусловлено тем, что проводимость «-области
создается в основном носителями отрицательных зарядов. Добав-
ление к германию ничтожного количества примесей, имеющих на
внешней орбите на один электрон меньше, чем германий (бора, алю-
миния, галия или индия), приводит к тому, что в германии образует-
ся избыток носителей положительных зарядов.
Область триода с избытком носителей положительных зарядов
называют p-областью (р — первая буква слова positiv). Проводи-
мость p-области обусловлена в основном носителями положитель-
ных зарядов*.
Полупроводниковый триод типа р — « — р представляет собой
кристалл германия (р-германий), в середине которого при изготов-
* Носителями положительных зарядов в полупроводниках являются дыр-
ки. Дырками называют незаполненные валентные связи атомов. Дырки спо-
собны перемещаться по кристаллической решетке так, как будто они являют-
ся положительными зарядами.
293
лении его сделана весьма тонкая «-прослойка (толщиной 0,02 —
0,025 мм) (рис. 248, а). В другом, в настоящее время пока менее рас-
пространенном и не рассматриваемом здесь типе триода — триоде
типа п — р — п — средняя область — область р, а крайние —
«-области. Знаками « + » в p-области условно обозначены носите-
ли положительных зарядов, знаками «—» в «-области — носители
отрицательных зарядов. Переходный слой между р- и «-областями
(таких слоев в триоде два) обладает односторонней проводимостью.
Ток через этот слой может течь практически только в случае, если
потенциал p-области будет выше потенциала «-области.
Триод имеет три вывода. Первый вывод сделан от первой р-об-
ласти и называется коллектором (К), второй вывод сделан от вто-
рой p-области и называется эмиттером (3), третий вывод сделан от
«-области и называется базой (Б). На электрических схемах триод
изображают в виде кружка, внутри которого вычерчена утолщен-
ная линия (см. рис. 248, б). От этой линии отходят три вывода. С
одной стороны есть один вывод (от базы), с другой — два вывода.
Из этих двух выводов один имеет стрелку — это вывод от эмиттера,
другой не имеет стрелки — вывод от коллектора.
§ 211. Три основных способа включения триодов в схему. Разли-
чают три основных способа включения триодов в схему. Эти спосо-
бы отличаются друг от друга тем, какой из электродов триода явля-
ется общим для управляющей и управляемой цепей. На рис. 249, а
изображена схема с общей базой, на рис. 249, б — схема с общим
эмиттером и на рис. 249, в — с общим коллектором.
Во всех схемах Ен— источник э.д.с. в цепи нагрузки; Еу — источ-
ник э.д.с. в цепи управления. Для всех схем, использующих трио-
ды типа р — « — р, полярность источников э.д.с. должна быть та-
кой, что коллектор должен иметь отрицательный потенциал по от-
ношению к базе, а эмиттер — положительный потенциал по отно-
шению к базе.
§ 212. Принцип работы полупроводникового триода в качестве
управляемого сопротивления. Основные положения, характеризую-
щие принцип работы триода, рассмотрим применительно к схеме
с общей базой (рис. 249, а).
$94
В переходном слое между эмиттером и базой и в переходном слое
между базой и коллектором имеются объемные заряды*. В р-облас-
ти объемные заряды отрицательны, а в «-области объемные заря-
ды положительны.
Объемные заряды в каждом переходном слое создают электри-
ческое поле, вектор напряженности которого направлен от п-обла-
сти к p-области. Другими словами, это поле препятствует движению
носителей положительных зарядов из p-области в «-область и дви-
жению носителей отрицательных зарядов из n-области в р-область.
Разность потенциалов на переходном слое между р- и «-обла-
стями называют потенциальным барьером.
Величины разностей потенциалов на переходных слоях зависят
от величины и полярности каждой из э.д.с.. включенных в схему.
Рис. 249
Так, включение э.д.с. Еу в схеме рис. 249, «приводит к уменьше-
нию разности потенциалов на переходном слое между эмиттером и
базой по сравнению с величиной разности потенциалов на этом слое,
когда э.д.с. Еу не была включена. В свою очередь включение э.д.с.
Ен приводит к увеличению разности потенциалов между базой и
коллектором по сравнению с величиной разности потенциалов на
этом слое, когда Ен не была включена.
Объясняется это тем, что результирующая напряженность поля
на переходном слое коллектор — база при наличии э.д.с. Ен рав-
на сумме напряженностей от объемных зарядов и от э.д.с. Ен, тогда
как на переходном слое эмиттер — база результирующая напряжен-
ность поля при наличии э.д.с. Еу равна разности напряженностей
от объемных зарядов и от э.д.с. Еу.
Кривая 1 рис. 248, в качественно иллюстрирует зависимость
изменения потенциала ф вдоль триода при отсутствии э. д. с. Ен
и Еу. Кривая 2 того же рисунка — при наличии э. д. с. Ен и Еу.
При сниженном потенциальном барьере между эмиттером и базой из
области эмиттера в область базы, соединенной с отрицательным по-
На рис. 248, а они не показаны.
295
люсом э.д.с. Еу, движутся дырки (носители положительных заря-
дов)*.
Хотя в «-области при этом и происходит частичная рекомби-
нация положительных и отрицательных зарядов, однако благодаря
малой толщине «-слоя большая часть носителей положительных за-
рядов успевает продрейфовать к переходному слою между базой
и коллектором. В переходном слое между базой и коллектором но-
сители положительных зарядов оказываются под воздействием силь-
ного электрического поля, образованного источником э.д.с. Ен (обыч-
но Ен > Еу). Под действием этого поля носители положительных
зарядов втягиваются в область коллектора и движутся к электроду
коллектора. Таким образом, большая часть носителей положитель-
ных зарядов, вышедших из эмиттера и прошедших в «-область, уст-
ремляется к коллектору (потенциал коллектора отрицателен по от-
ношению к потенциалу базы и к потенциалу эмиттера).
В результате к электроду базы подходит лишь незначительное
количество носителей положительных зарядов из числа тех, кото-
рые вышли из области эмиттера и прошли в область базы.
При принятых на рис. 249, о положительных направлениях для
токов ток эмиттера (is) равен сумме тока коллектора (ij и тока ба-
зы (Q:
h = Ё + h.
Отношение тока коллектора к току эмиттера принято обозна-
чать через а:
а = \
^3
В плоскостных триодах (см. § 213) а равно 0,95—0,98 и зависит
ст режима работы триода. В точечных триодах а может быть и боль-
ше единицы. Полупроводниковый триод является управляемым
активным сопротивлением. В нем величиной коллекторного тока и
величиной падения напряжения между электродами коллекторной
цепи можно управлять путем изменения величины э.д.с. Еу.
Следует иметь в виду, что при изменении полярности э.д.с. Ен
в схеме рис. 249, а триод теряет свойство управляемости и на участ-
ке между базой и коллектором работает как обычный неуправляе-
мый диод. Этот режим является ненормальным режимом работы
триода.
§ 213. Плоскостные и точечные полупроводниковые триоды. Трио-
ды делятся на плоскостные и точечные. У плоскостных трио-
дов р- и «-области переходят одна в другую через относительно боль-
шую площадь. У точечных триодов переход p-области в «-область
происходит в месте точечного контакта этих областей. Другими сло-
вами, площадь перехода одной области в другую у точечных трио-
дов очень мала.
* Небольшое количество отрицательных зарядов движутся при этом от
базы к эмиттеру, но ток, создаваемый ими, относительно мал.
296
Плоскостные триоды применяют при низких и средних частотах
и относительно больших токах, точечные триоды — при более вы-
соких частотах и малых токах*.
§ 214. Вольтамперные характеристики триодов. Свойства каждо-
го триода вполне определяются двумя семействами его вольтампер-
ных характеристик. Первое семейство — зависимость тока вы-
ходной цепи от напряжения между электродами триода, включен-
ными в выходную цепь, при каком-либо из остальных токов трио-
да, взятом в качестве параметра. В качестве параметра может быть
взята и какая-либо другая величина, например напряжение между
электродами триода, включенными в цепь управления. Это семей-
ство описывает свойства триода по отношению к выходной цепи.
Второе семейство — зависимость тока входной цепи— цепи управ-
ления — от напряжения между электродами триода, включенны-
ми во входную цепь, при напряжении между электродами трио-
да, включенными в выходную цепь (или при токе выходной цепи),
взятом в качестве параметра. Это семейство характеристик описы-
вает свойства триода по отношению к цепи управления.
На рнс. 250, а качественно изображено семейство выходных ха-
рактеристик iK — f(.u3K) при параметре ia для схемы с общим эмит-
тером (рис. 249, б). Правее вертикальной пунктирной прямой А —
А кривые начинают круто подниматься; там может произойти про-
бой триода. Поэтому правее прямой А — А работать нельзя.
Расположенная в третьем квадранте кривая ОВ иллюстрирует
потерю управляемости триода при изменении полярности э.д.с. в
выходной цепи.
* В настоящее время и при высоких частотах больше применяют плос-
костные триоды вместо точечных.
297
При протекании тока по триоду он нагревается выделяющимся
в нем теплом. Каждый триод в зависимости от его размеров и усло-
вий охлаждения может отдавать в окружающее пространство опре-
деленное количество теплоты. Допустимое количество выделяюще-
гося в триоде тепла характеризуется так называемой мощностью
рассеяния = иэк1к (дается в каталогах). На рис. 250, а пункти-
ром нанесена гипербола iK = — = f (иэк). Для того чтобы триод
иэк
не перегревался в условиях длительного режима, рабочая точка
должна находиться внутри заштрихованной области на рис. 250, а
(кратковременно можно работать и в области, находящейся выше
пунктирной кривой). На рис. 250, б качественно изображено семей-
ство входных характеристик триода i6 — при параметре изк
в схеме с общим эмиттером (рис. 249, б).
Важно обратить внимание на то, что любой ток триода (напри-
мер, 1К или Q является функцией не одного, а двух переменных.
Так, ток iK является функцией иак и гэ. Ток 1б есть функция иэб
и «ак> Это положение будет учтено в § 218.
Полупроводниковый триод может быть использован в качестве
усилителя тока, усилителя напряжения и усилителя мощности.
§ 215. Полупроводниковый триод в качестве усилителя тока.
Триод может служить усилителем тока тогда, когда приращение
(А) тока управляемой цепи (той, где включена э.д.с. Ен) оказы-
вается во много раз больше приращения тока управляющей цепи
(той, где включена э.д.с. Еу). Из трех схем рис. 249 в качестве уси-
лителя тока могут быть использованы две: схема с общим эмит-
тером (рис. 249, б) и схема с общим коллектором (рис. 249, в). В
обеих схемах током управления является ток базы i6. Током управ-
ляемой цепи в схеме с общим эмиттером является ток коллектора
iK, а в схеме с общим коллектором — ток эмиттера 1Э.
Так как iK = aia (см. § 212) и в то же время
G = iK + ^б>
то
1б = Ь — = — а) 1Э.
Как уже говорилось в § 212, коэффициент а зависит от режима
работы триода, т. е. от величины токов триода, и несколько изме-
няется при переходе от одного режима работы триода к другому.
Однако при нахождении связи между малыми приращениями
токов можно в первом приближении принять a=const, и тогда
AiK = aAia
и
Ei6 = (!—«) Aia.
Коэффициент усиления по току kt равен отношению прираще-
ния тока выхода к приращению тока входа. Коэффициент уси-
298
ления по току для схемы с общим эмиттером, где выходным то-
ком является iK, а входным — i6, равен:
k- = = а
' Мд 1 — а
Коэффициент усиления по току для схемы с общим коллекто-
ром, где выходной ток Д, а входной 1б, равен:
k, = = ——
Мд 1 — а
Коэффициент а для плоскостных триодов примерно равен
0,95 — 0,98, поэтому kt 19 — 50.
§ 216. Полупроводниковый триод в качестве усилителя напряже-
ния. При работе триода в качестве усилителя напряжения важно,
чтобы приращение напряжения на нагрузке &ивых, включенной в
выходную цепь, было больше приращения напряжения на входе
управляющей цепи Ьивх.
Коэффициент усиления по напряжению равен ka = -~вых-. При
^вХ
использовании триода в качестве усилителя напряжения его вклю-
чают либо по схеме с общей базой (см. рис. 249, а), либо по схеме
с общим эмиттером (рис. 249, б).
Качественно покажем, что коэффициент усиления по напряже-
нию для обеих схем может достигать значений порядка нескольких
сотен. С этой целью обратим внимание на два положения: на соот-
ношение между входным и выходным сопротивлениями триода и на
соотношение между сопротивлением нагрузки и выходным сопро-
тивлением триода.
1. Соотношение между входным и выход-
ным сопротивлениями триода. Входное сопро-
тивление триода Rer равно отношению приращения напряжения
на входных зажимах триода к приращению входного тока.
Выходное сопротивление триода Квых равно отношению прира-
щения напряжения на выходных зажимах триода к приращению
выходного тока.
В схеме с общей базой
р : р ____ ^иэб.
*^вх ^ехэб >
р _ р _ ^иэк
^вЫХ f'-eux эк . . •
Для схемы с общей базой Кеых оказывается примерно на 2 поряд-
ка больше, чем Ке..
В схеме с общим эмиттером
7?вл = /?г...,=
и
Мд
р = В _____________ &иэк
*^6ЫХ вых эк
299
Для схемы с общим эмиттером /?еыА. обычно в несколько раз
больше
2. Соотношение между сопротивлением на-
грузки и выходным сопротивлением триода.
При работе триода в качестве усилителя напряжения (и в ка-
честве усилителя мощности) в обеих схемах сопротивления на-
грузки -RH берут обычно того же порядка, что и выходное сопро-
тивление триода со стороны зажимов эмиттер — коллектор, т. е-
R-вЫХ эк-
Составим выражения для определения ku в схеме с общей
базой:
Д. _ ^ВЫХ___
^ивх ^aRex эб
ио = а, а - R"~ ^вых зк, следовательно, ku = а —— эк. Если
Rex эб Rex эб Rex эб
учесть, что а близко к 1, то для схемы с общей базой
Reux эк и СС)Ставляет величину порядка нескольких сотен.
Rex эб
Составим выражение для ku в схеме с общим эмиттером.
Входным током в схеме с общим эмиттером является ток
базы, а выходным — ток коллектора. Поэтому
& АНдЫХ AIkRh Rвых эк
^tlex ^if)Rex эб 1 а Rex эб
Если учесть, что ——— = 19 4-49, а отношение -еых эк в схеме
1 а Rex эб
с общим эмиттером составляет величину порядка нескольких
единиц, то для схемы с общим эмиттером ku составляет величину
от нескольких десятков до нескольких сотен.
§ 217. Применение полупроводникового триода в качестве усили-
теля мощности. Усиление по мощности достигается во всех схемах
включения рис. 249. Коэффициент усиления по мощности kp равен
отношению приращения мощности в нагрузке к приращению мощ-
ности на входе триода:
Для схемы рис. 249, а
(МкУ^н Reux эк
(^afRex эб Rex эб
Таким образом, коэффициент усиления по мощности для схемы
рис. 249, а в первом грубом приближении примерно равен коэффи-
циенту усиления по напряжению для этой схемы. Наибольшее уси-
ление по мощности достигается в схеме с общим эмиттером. Для
нее kp может достигать значений 104 и более.
300
§ 218. Связь между приращениями входных и выходных величин полу-
проводникового триода. Напряжение на входных зажимах триода (назовем его
для общности иг) и напряжение на выходных зажимах (и2) являются функция-
ми входного (ix) и выходного (i2) токов триода, т. е.
«1 = Ui (.И, О), (9.42а)
иг = U2 (ilt i2). (9.426)
Запись «1 = U± (i’i, свидетельствует, что ut есть функция двух пе-
ременных (ь и г2). Условимся исходные значения токов и напряжений обо-
значать большими буквами U, I, а приращения — через Д( и Ди. Пусть токи
получили малые приращения Д1\ и Д(2 и стали равными (Zj + Дг’1) и (Z2 +
+ Д(2). При этом напряжения также получили приращения и стали равными
(Ui + Дих) и (t/2 + Ди2). Следовательно,
t/i + ДМ1 = [(/L + Дч); (Z2 + Д«2)], (9.43а)
U2 + Ди2 = U2 [(Zi + ДМ; (Z2 + ДМ). (9.436)
Найдем связь между приращениями напряжений Ди2 и Ди2 и приращени-
ями токов Д?! и Д12. С этой целью разложим правые части равенств (9.43а) и
(9.436) в ряд Тейлора для функции от двух переменных по степеням прира-
щений Дг, и Д»2 и воспользуемся тем, что в силу малости приращений можно
пренебречь слагаемыми, содержащими Д^ и Д12 в степенях выше первой. По-
лучим
Ui ДИ1 = Ui (Zj, Z2) -|- Д/j I — I -j- Д»2
V dii I h, h
ldU2 \
t/2 -J- Ди2 = U-2 (fi, I2) -J- Д«1 I -— j -J- Af2 . . ,
\ d‘1 I, \ di2 //„ /a
fdUt\
Здесь ------ означает частную производную 1/х по току ii, в которую
\ dii /Ц; /2
подставлены значения li и Z2, определяющие собой исходные значения токов
/ dUi\
(до получения приращений);-------1 —частная производная Ui по »2, в ко-
\ ot2 / /„ /а
торую подставлены значения Z] и Z2.
Для-сокращения записи введем обозначения:
dUi \
di2 ) it. i3 ’
dUt\ I dUi\
— = Ru, —1
dll //,. h \ Ol2 / I„ I,
Обратим внимание па то, что
не равно
W -Р
I ->• I ~~ Атг-
\ dtz //,; Ц
Значения /?ц, Z?12, Z?21 и /?22 могут быть найдены графическим путем
из характеристик полупроводникового триода, поэтому в дальнейшем будем
полагать их известными. Если из уравнения (9.43а) вычесть уравнение (9.42а),
а из уравнения (9.436) — уравнение (9.426) и затем частные производные за-
менить соответственно на Z?u, /?12, Rzi, Rzz, то получим
Ди( = Rn Дч + Ri2 (9.44а)
Ди2 = R2i Д<1 Rn Д42. (9.446)
301
Формулы (9.44) связывают малые приращения токов Ai'i и Д12 с малыми
приращениями напряжений ДИ1 и Ди2. Из формул (9.44) следует, что по от-
ношению к малым приращениям триод, являющийся управляемым нелиней-
ным сопротивлением, можно заменить эквивалентной линейной схемой за-
мещения.
§ 219. Схема замещения полупроводникового триода для малых прираще-
ний. В специальной литературе по полупроводниковым триодам в схемы за-
мещения триодов для малых приращений вводят не сопротивления 1?ц, /?12,
/?21, ^22> 0 которых шла речь выше, а некоторые расчетные сопротивления—
сопротивление базы Rg, сопротивление коллектора R3, сопротивление эмит-
тера R3 и некоторый расчетный источник э. д. с., величина э. д. с. которого
равна произведению тока управляющей цепи на расчетное сопротивление Rm.
Значения Rg, RK, R3 и Rm определяются через /?п, R12, R2l и R22.
Рассмотрим схему замещения триода, когда общим электродом является
база. На рис. 251, а изображена схема с общей базой. Входным током в ней
является ток 4, равный току эмиттера = i3, выходным током — i2, рав-
ный взятому с обратным знаком току коллектора i2 ~ — 1К (положительное
направление для тока i2 принято противоположным положительному направ-
Рис. 251
лению тока iK на рис. 249, а). Схема рис. 251, б заменяет схему рис. 251, а
для малых приращений. По второму закону Кирхгофа составим уравнения
для двух контуров схемы рис. 251, б:
Дых = (R3 + Rg) Д/x + Rg Д12; (9.45а)
Ды2 — Rm &i3 = Rg fill (RK Rg) Дl2\ (9,456)
ДИ1 ” llmn = фт фл» 6dl2 = llpq — фр ф^,
где фт — потенциал точки и; фп — потенциал точки п и т. д.
Сопоставление уравнений (9.45) с уравнениями (9.44) дает
К9 4- Kg = Яи» Kg — ^?121
Кт 4* Кб — К2б Кк “Ь Кб = К22.
Последние уравнения дают возможность найти сопротивления Rg, R3, RK
и R^ по известным сопротивлениям /?и, R21, Rl2, R22. Источник э.д.с.
Кт = Дц) введен в схему замещения рис. 251, б для того, чтобы
учесть в расчете усилительное действие триода: величина э.д.с. этого источ-
ника пропорциональна входному току.
Таким образом, для расчета малых приращений входных и выходных то-
ков в нелинейной схеме рис. 251, а, для определения коэффициентов усиле-
ния и входных сопротивлений в этой схеме для малых приращений следует
произвести расчет линейной схемы рис. 251, б, подключив к входным зажимам
ее тп источник малой (обычно синусоидальной) э. д. с., а к выходным зажи-
мам pq нагрузку RH.
302
Расчет схем с полупроводниковыми триодами при относительно
цизких частотах на практике часто производят не при помощи
схем замещения, рассмотренных выше и при пользовании которы-
ми надо знать R6, RK и Rm, а путем непосредственного ис-
пользования семейств характеристик триода. Этот способ расчета
иллюстрируется на примере 1116.
Пример 1116. Определить коэффициент усиления потоку, коэф-
фициент усиления по напряжению и коэффициент усиления по
мощности схемы рис. 252, а, предназначенной для усиления сла-
бых синусоидальных колебаний.
В этой схеме использован триод типа П14. Его выходные ха-
рактеристики изображены на рис. 252, б и входные — на
Рис. 252
рис. 252, в. Сопротивление нагрузки RH = 500 ом. Электродвижущая
сила смещения в выходной цепи Ек0 = 10 в. Электродвижущая си-
ла смещения в цепи управления Еуо = 0,25 в.
Решение. На рис. 252, б проводим прямую, представляющую
в.а.х. нагрузки #„ = 500 ом. Эта прямая пройдет через точку
1К = 0 и изк = Ем = 10 ей через точку iK = = 20 ма и иэк = 0.
303
Семейство входных характеристик триода П14, как это видно
из рис. 252, в, обладает той особенностью, что в интервале значений
иэк — 0,2—10 в зависимость тока базы i6 от напряжения между эмит-
тером и базой изображается одной и той же кривой (практически
не зависит от величины иак). Найдем значение тока i6 — 1бл при
отсутствии синусоидального сигнала на входе, т. е. в режиме, когда
на вход цепи управления действует только постоянная э.д.с. Еуо=
— 0,25 в (цепь управления замкнута через источник сигнала).
Из рис. 252, в следует, что при иаб = 0,25 в ток i6 = 1бо =
= 250 мка (точка и). Далее найдем ток iK = 1т и напряжение иэк =
— в этом режиме.
На семействе кривых рис. 252, б режим работы при Еу = Еу0
определяется точкой п, полученной в результате пересечения
в.а.х. нагрузки с той кривой семейства iK = f(uaK), для которой
параметром является i6 = 250 мка.
В точке п iK~IK0— 13,1 ма и иэк = UaKQ = 3,5 в. Линеаризи-
руем входную характеристику в рабочей точке. С этой целью про-
ведем в окрестности точки п (рис. 252, в) прямую так, чтобы она
на возможно большем участке совпала с касательной к кривой
*5 = f (иэб) в точке п. Крайними точками проведенной прямой бу-
дем считать точки р и т. В точке р i6 = 350 мка и идб = 0,27 в.
В точке т 1б= 150 мка и нЭ(?=0,23 в. Этим точкам соответству-
ют одноименные точки р и т на рис. 252, б.
В точке р (рис. 252, б) iK = 18,6 ма, в точке tn iK = 8,6 ма.
Таким образом, при подаче на вход схемы синусоидального нап-
ряжения с амплитудой Ug6m — 0,02 в в цепи управления появится
синусоидальная составляющая тока, имеющая амплитуду 1бт =
= 1ут = 100 мка, а в выходной цепи, кроме постоянного тока
/к0, появится синусоидальный ток с амплитудой Iкт — 5,0 ма*. При
этом на выходных зажимах триода будет действовать синусоидаль-
ная составляющая напряжения, имеющая амплитуду UaKm — 2,45 в.
Найдем искомые коэффициенты усиления.
Коэффициент усиления по току
k. = Em 5,0 =50.
^Ex Iym Ю0 XIKQ
Коэффициент усиления по напряжению
д, __ &ивых_RHEm _ 500*5,0* 10~3 _ j gg
&иех эбт 0,02
Коэффициент усиления по мощности
ь — ^вых R-нЕкт 500 (5,0* 10~3)2 СОСА
р ЛРвх и9бт1ут 0,02.100. 10-»
* Берем первую гармонику переменной составляющей коллекторного
тока.
304
Входное сопротивление триода между зажимами эмиттер —
база для синусоидальной составляющей равно:
КвХ!* = ^ = = 200 ом.
1ут 100 мка
Выходное сопротивление между зажимами эмиттер — коллек-
тор для синусоидальной составляющей равно:
= = 1^ = 490 ом.
* кт 5,0 ма
В тепловом отношении триод работает в ненапряженных усло-
виях, так как мощность, выделяемая в самом триоде в режиме, соот-
ветствующем точке п (рис. 252, б), равна:
^эко^ко = 3.5 в - 13,1 ма = 45,8 мет,
что значительно меньше допустимой для данного триода мощности
рассеяния 150 мет.
§ 220. Основные сведения о трехэлектродной лампе. Электрон-
ная лампа имеет три электрода: катод, анод и сетку. Эти электроды
находятся в вакуумированном стеклянном или металлическом бал-
лоне. Катод, подогреваемый нитью накала от вспомогательной ба-
тареи (обычно не показываемой на схемах), испускает электроны
вследствие явления термоэлектронной эмиссии. Поток электронов
направляется ко второму (холодному) электроду — аноду — толь-
ко в том случае, если потенциал анода выше потенциала катода.
Если же потенциал анода сделать ниже потенциала катода, то по-
тока электронов от катода к аноду не будет (в этом случае анод бу-
дет не притягивать электроны, а отталкивать их). В результате
этого электронная лампа обладает несимметричной вольтамперной
характеристикой.
Третий электрод — сетка — расположен ближе к катоду, чем
анод. Поэтому электрическое поле, создаваемое между сеткой и ка-
тодом, даже при малых напряжениях между сеткой и катодом ока-
зывает сильное влияние на поток электронов с катода на анод.
Сетка является управляющим электродом. Путем изменения потен-
циала сетки можно управлять величиной диодного тока лампы.
Как и полупроводниковый триод, электронная лампа может быть
включена в схему тремя основными способами: с общим катодом,
с общей сеткой и с общим анодом (в зависимости от того, какой из
электродов будет являться общим для анодной и сеточной цепей).
На рис. 253 изображена схема с общим катодом. Она является
наиболее часто употребляемой схемой. Как и полупроводниковый
триод, электронная лампа может служить в качестве усилителя
тока, усилителя напряжения и усилителя мощности. Возможность
выполнения лампой всех этих функций основывается на том, что
изменение разности потенциалов между сеткой и катодом оказыва-
ет более сильное влияние на поток электронов с катода на анод,
11 Л, А, Бессонов
305
чем изменение (на ту же величину) разности потенциалов между
анодбм и катодом.
§ 221. Вольтамперные характеристики трехэлектродной лампы
для мгновенных значений. Цепь, образованную анодом и катодо»м
электронной лампы, источникохм э.д.с. Еа и нагрузкой RH, будем
называть анодной цепью.
Цепь, образованную сеткой и катодом электронной лампы и ис-
точником э.д.с. Ес, будем называть сеточной цепью.
Напряжение между анодом и катодом будем обозначать иа и
называть анодным напряжением. Напряжение между сеткой и ка-
тодом будем обозначать ис и называть сеточным напряжением.
Рис. 254
Ток в анодной цепи ia нелинейно зависит от. анодного и сеточ-
ного напряжений. Ток в сеточной цепи ic также нелинейно зависит
от иа и ис.
Под анодными характеристиками трехэлектродной лампы пони-
мают зависимость анодного тока ia от анодного напряжения иа
при сеточном напряжении ис, взятом в качестве параметра.
В виде примера на рис. 254 изображено семейство анодных ха-
рактеристик лампы. Если семейство анодных характеристик рас-
сечь прямыми иа = const, то можно получить семейство кривых
ta= /(wc) при параметре иа. Такие кривые называются сеточными
(анодно-сеточными) характеристиками трехэлектродной лампы.
Кривые этого семейства изображены на рис. 255. Для них харак-
терно, что ток 1а не равен нулю при ис = 0, а также то, что имеется
область насыщения, в которой ток 1а почти не увеличивается с рос-
том ис.
Семейство зависимостей сеточного тока ic от сеточного напряже-
ния ис при различных значениях анодного напряжения иа при поло-
жительных значениях ис изображено на рис. 256.
306
В общем случае при работе лампы одновременно меняются иа и
ис и изображающая точка на семействах анодных и сеточных ха-
рактеристик перемещается с одних кривых на другие. В частном
случае работы, когда иа остается неизменным или почти неизмен-
ным, ia= f(uc) изображается одной кривой семейства кривых
рис. 255.
Если электронная лампа работает при отрицательных или срав-
нительно малых положительных напряжениях на сетке, то сеточ-
ный ток имеет малую величину и его в расчете, как правило, не
учитывают.
Следует отметить своеобразие сеточной характеристики по сравнению с
обычными вольтамперными характеристиками. Дело в том, что сеточная ха-
рактеристика дает связь не между током через нелинейное сопротивление и
напряжением на нем, что характерно для «обычных» в. а. х., а между мгновен-
ным значением тока через нелинейное сопротивление и мгновенным значением
управляющего напряжения на этом сопротивлении.
§ 222. Аналитическое выражение сеточной характеристики элект-
ронной лампы. Сеточная характеристика при иа = const может быть
приближенно представлена отрезками прямых (рис. 257). Часть
сеточных характеристик, например характеристика, выделенная
жирной линией на рис. 255, может быть описана полиномом треть-
ей степени:
ia = + аис — (9-46)
Здесь ia0 есть значение тока ia при ис — 0; а и b — числовые
коэффициенты; а измеряется в а • в-1; b измеряется в а • в-3.
Для определения коэффициентов а и b следует выбрать на
характеристике две точки с координатами ial, ис1 и ie2, ис2 и ре-
шить систему двух уравнений с двумя неизвестными:
*й2 = »во + ам«2 —би-
характеристика по типу пунктирной кривой на рис. 255 может
быть приближенно описана полиномом второй степени:
Д = До + Рис +
где р и q — числовые коэффициенты.
Существуют аналитические выражения и для анодных харак-
теристик.
§ 223. Связь между малыми приращениями входных и выходных величин
электронной лампы. Как уже говорилось в предыдущем параграфе, анодный
ток ia является функцией не только анодного, но и сеточного напряжения;
ia = 1а (иа, ис). Если по отношению к некоторому исходному состоянию
(Ua, Uс) сеточное напряжение получит небольшое приращение Дис, то оно вы-
зовет приращение анодного напряжения Диа и приращение анодного тока ДД.
Если проделать выкладки, аналогичные выкладкам § 218, то получим
ldla\ ldla\
Д*в = ЧГ +Д“с ДТП
\dua!ua,Uc \SucJua.Ue.
11* 807
[dl„\
Частную производную I - 1 , в которую подставлены значения
Va и Uc, соответствующие исходному состоянию, принято обозначать через
gi и называть внутренней проводимостью электронной лампы (проводимость
между анодом и катодом):
\ диа / ип, ис.
(9.47а)
Величину Rit обратную gi, называют внутренним сопротивлением лампы
(сопротивление между анодом и катодом):
Rt = — • (9.476)
Si
Частную производную I — 'j , подсчитанную при исходных значе-
\ дис j Ua, Uс
ииях 1)а и Uc, называют крутизной характеристики лампы и обозначают бук-
вой S:
(9.48)
имеет размерность проводимости; gi и S зависят от вида характеристик лам-
пы и величин исходных напряжений Ua и Uc. Отношение S к gi называют
коэффициентом усиления лампы и обозначают буквой р:
(Ola \
Ц = А = W/t/д, и с. (9.49)
Si ("'а\
\диа) иа. Uс
Коэффициент усиления показывает, во сколько раз приращение напряже-
ния между сеткой и катодом Дис оказывается более эффективным, чем при-
ращение напряжения между анодом и катодом Диа в отношении получения
одинакового приращения анодного тока Д/д. С учетом сказанного выше фор-
мула для Д/а запишется следующим образом:
Ма = Дид gi -j- Дис S, (9.50)
или
Дид = Rt Ма — И (9.51)
§ 224. Схема замещения электронной лампы для малых приращений. На
схеме рис. 258, а большими буквами UH, Va< Uc> la обозначены постоянные
.308
1а(ИЧ
20
10
10
К
12
10
8
0
Ч
2
w' еГТо 100120 шшжгоо ua(i
Рис. 259
для малых приращений анодная цепь
1митируется) источником э.д.с. и Ли,, и
составляющие напряжений и тока, соответствующие исходному состоянию
схемы (до получения приращения сеточного напряжения). Напряжения и токи,
обозначенные через Лыс, Диа, Д«й, представляют собой приращения соответст-
вующих величин. Положительные направления для приращений те же, что
и для исходных напряжений и токов.
Составим уравнение для приращений напряжений в анодной цепи, вызван-
ных приращением напряжения Дцс на сетке лампы. С этой целью составим два
уравнения по второму закону Кирхгофа для анодной цепи. Одно из них для
режима до получения приращений: Ua -f- UH — Е, другое — для режима после
получения приращений: Ua -f- Ди«+
+ Uн + ДнЛ = Е. Если в послед-
нем уравнении Ua -ф- UH заменить
на Е, то получим:
Днй + Дия = 0, (9.52а)
где Дий — приращение напряже-
ния между анодом и катодом лам-
пы; Дик — приращение напряжения
на нагрузке RH.
В уравнение (9.52а) вместо Дц„
подставим RH №а и вместо Дп„ в
соответствии с уравнением (9.51)
подставим Ri Ыа—р Дцс. Получим:
(/?„ + Ri) Ма = р. Дис. (9.526)
Уравнению (9.526) отвечает
схема рис. 258, б. В этой схеме к
источнику э.д.с. р Днс присоедине-
ны сопротивление нагрузки RH и
внутреннее сопротивление элект-
ронной лампы R-l. Таким образом,
электронной лампы замещается
последовательно с ним включенным сопротивлением R^ Электродвижущая
сила этого источника э.д.с. пропорциональна изменению напряжения на сетке
лампы.
На рис. 258, в изображена другая, часто используемая схема замещения.
Ц
В ней вместо источника э.д.с. включены источник тока ---- и шунтирующее
Ri
его сопротивление (напомним, что переход от источника э.д.с. к источнику
тока подробно рассмотрен в § 2).
Пример 111в. Между сеткой и катодом триода 6С2С приложено напря-
жение Ис + Оыис = Uc 4- Uст sin со t = — 2-[-0,05 sin со/ (рис. 258, а). Зависи-
мость анодного тока ia от анодного напряжения иа при параметре ис изобра-
жена на рнс. 259. Электродвижущая сила Еа = 150 fi; RH = 15 ком.
Найти параметры схемы замещения триода и определить при помощи этой
схемы амплитуду синусоидальной составляющей тока в анодной цени.
Решение. Определяем положение рабочей точки на характеристиках
лампы по постоянному току. С этой целью на рис. 259 наносим прямую, ха-
рактеризующую нагрузочное сопротивление анодной цепи RH. Ее часто назы-
вают нагрузочной прямой.
£
Прямая проходит через точки ia = 0; нй=150 в и = =10 ма\ иа=0.
R»
Рабочей точкой в рассматриваемом режиме будет точка пересечения пря-
мой с той кривой семейства, для которой параметр ис — — 2 в. Координаты
этой точки иа = 94 в и /й = 3,67 ма. По определению gt (см. формулу 9.47а)
для нахождения ее следует, считая за исходное положение найденную выше
рабочую точку, при неизменном ис = — 2 в дать приращение анодному напря-
309
жению Дый, найти соответствующее ему приращение анодного тока Д/я и по-
делить Д/й на Дин:
dla Л.1а 5ма 1
g, = — « = —— = 10~4 сим; = = 104 ом;
81 диа Киа 50 в 4 Si
gi пропорционально тангенсу угла наклона касательной в рабочей точке к кри-
вой Ia = f(.ua)> Для которой ис = — 2 в. Для определения крутизны характе-
ристики S при иа — 94 в <= const даем приращение сеточному напряжению
Дпс =— 1 — (—2) = 1 в и из рисунка находим соответствующее ему прира-
щение Д/д = 5,37 — 3,67 =а 1,7 (ма). Следовательно,
— = 1,7 • IO-3 а/в.
Ьис
Коэффициент усиления
ц = — = 17.
gi
Амплитуда синусоидальной
уравнению (9.526):
составляющей тока в анодной цепи, согласно
»У'^'ст
lm~ RH + Ri
= 3,39 - IO-5 а.
Анодный ток равен 1а -|- Д/й = 3,67 -|- 0,339 sin at ма.
§ 225. Построение зависимости вход — выход для электроииой лампы при
больших сигналах. Напряжение между сеткой и катодом ис является входным
напряжением, а напряжение на нагрузке RH (схема рис. 258, а) — выходным.
Напряжение на нагрузке равно произведению тока ia на сопротивление RH.
Если амплитуда переменной составляющей напряжения ис будет достаточно
большой (например, соизмерима или больше постоянной составляющей напря-
жения Uc), то линейные схемы замещения рис. 258, бив применять уже нельзя.
Определение зависимости тока 1а от времени t при подаче на сетку лампы
напряжения любой формы и любой амплитуды может производиться путем
графических построений. Существо последних состоит в следующем:
1. Придавая времени t различные значения, находим отвечающие им мгно-
венные значения ис.
2. Для каждой пары соответствующих друг другу значений t и ис анод-
ный ток ia определится ординатой точки пересечения нагрузочной прямой и
той кривой семейства ia = f (иа), для которой данное значение ис является
параметром.
3. Далее, строится кривая зависимости ia— f (/). Разложение ее в ряд
Фурье дает возможность найти постоянную составляющую, а также амплиту-
ду первой и высших гармоник ряда Фурье. Повторив построения при иной
амплитуде или иной форме напряжения ис, найдем новые значения постоян-
ной составляющей и амплитуд первой и высших гармоник тока ia. В резуль-
тате ряда таких построений будут получены данные, на основании которых
можно построить любые представляющие интерес зависимости между вход-
ными и выходными величинами. Разумеется, в принципе аналогичные по-
строения могут быть проделаны и для полупроводникового триода.
§ 226. Общая характеристика методов анализа и расчета нелиней-
ных электрических цепей переменного тока. Анализ нелинейных
явлений и получение числовых соотношений в нелинейных цепях
переменного тока оказываются делом гораздо более сложным и бо-
лее трудоемким, чем анализ и расчет линейных электрических цепей.
Как правило, нелинейные электрические цепи в своем составе
содержат либо нелинейные индуктивности, либо нелинейные ем-
840
кости, либо безынерционные в тепловом отношении нелинейные
активные сопротивления.
Токи и напряжения в таких цепях в той или иной степени неси-
нусоидальны.
Токи и напряжения в большей степени синусоидальны в цепях,
содержащих только инерционные в тепловом отношении нелиней-
ные активные сопротивления.
Все методы анализа нелинейных цепей могут быть подразделе-
ны на две большие группы: аналитическую и графическую. Аналити-
ческие методы в отличие от графических дают возможность прово-
дить анализ в общем виде, а не только для частных значений па-
раметров.
Недостатком аналитических методов является то, что прихо-
дится выражать аналитически характеристики нелинейных сопро-
тивлений, что всегда связано с некоторой погрешностью. При рас-
чете сколько-нибудь сложных нелинейных электрических цепей
переменного тока приходится мириться с тем, что расчет может быть
произведен лишь с известной степенью приближения.
Наиболее широкое распространение получили следующие ме-
тоды анализа и расчета нелинейных цепей переменного тока:
1. Графический метод, использующий характеристики нелиней-
ных сопротивлений для мгновенных значений.
2. Аналитический метод, использующий характеристики нели-
нейных сопротивлений для мгновенных значений при их кусочно-
линейной аппроксимации.
3. Аналитический или графический метод, использующий вольт-
амперные характеристики по первым гармоникам.
4. Аналитический или графический метод, использующий вольт-
амперные характеристики по действующим значениям несинусои-
дальных величин.
5. Аналитический метод расчета по первой и одной или несколь-
ким высшим или низшим гармоникам.
6. Расчет при помощи линейных схем замещения.
7. Применение математических счетных машин.
Из перечисленных семи методов* обязательными для изучения
являются первый, второй, третий и четвертый.
В дальнейшем будет кратко охарактеризован каждый из семи
методов. В зависимости от характера цепи, формы в.а.х. нелиней-
ного сопротивления, а также от того, какое нелинейное явление в
цепи исследуется, целесообразно применить тот или иной метод
из перечисленных.
Естественно, что чем сложнее характер нелинейного явления,
тем более сложным и громоздким оказывается метод анализа его.
* Седьмой метод не является самостоятельным методом. Он используется
совместно с любым из предыдущих шести методов.
311
И, наоборот, анализ грубых нелинейных явлений производится бо-
лее простыми средствами.
§ 227. Графический метод, использующий характеристики не-
линейных сопротивлений для мгновенных значений. Этот метод при-
меним, как правило, к цепям, в которых по тем или иным сообра-
жениям известен закон изменения во времени какой-либо одной
определяющей работу нелинейного сопротивления величины, на-
пример тока, напряжения, заряда. Метод иллюстрируется на при-
мере анализа работы пик-трансформатора (см. § 234) и утроителя
частоты (§ 233).
Последовательность расчета этим методом такова:
1. Сначала, исходя их тех или иных физических предпосылок,
положенных в основу анализа, находят закон изменения во времени
одной из определяющих работу нелинейного сопротивления величин.
Так, в § 233 (см. стр.316), полагая активное сопротивление пер-
вичных обмоток w1 и w2 равным нулю, принимают, что по синусои-
дальному закону изменяется сумма потокосцеплений этих обмоток.
В § 234 (стр. 318) принято, что по синусоидальному закону во
времени изменяется ток намагничивающей обмотки пик-трансфор-
матора.
2. Затем путем использования характеристики (или характерис-
тик) нелинейного сопротивления для мгновенных значений графи-
ческими построениями находят закон изменения во времени вто-
рой величины, определяющей работу нелинейного сопротивления.
В § 233 такой величиной является ток, в § 234 — магнитный по-
ток.
3. После этого по результатам п. 2 путем вспомогательных гра-
фических построений и простейших расчетов находят выходную
величину и искомое соотношение между параметрами схемы.
, Достоинствами метода являются простота и наглядность, а так-
же легкость учета гистерезисных явлений.
§ 228. Расчет нелинейных цепей путем применения кусочно-ли-
нейной аппроксимации характеристики нелинейного сопротивления
для мгновенных значений. Основным содержанием метода является
сведение задачи о нахождении периодического решения нелиней-
ных уравнений к нахождению периодического решения системы ли-
нейных уравнений.
Основные этапы метода:
1. Замена вольтамперной (веберамперной, кулонвольтной) ха-
рактеристики нелинейного сопротивления для мгновенных значе-
ний отрезками прямых линий.
2. Подстановка в нелинейные дифференциальные уравнения
уравнений прямых п. 1. Этим нелинейные дифференциальные
уравнения будут сведены к линейным.
Каждому нелинейному уравнению будет соответствовать столь-
ко линейных уравнений, сколько отрезков прямых заменяет харак-
теристику нелинейного сопротивления.
312
3. Решение системы линейных дифференциальных уравнений.
Каждому линейному участку характеристики нелинейного сопро-
тивления будет соответствовать свое решение со своими постоян-
ными интегрирования.
4. Определение постоянных интегрирования, исходя из согла-
сования решения на одном линейном участке с решением на другом
линейном участке.
Наиболее эффективен метод тогда, когда характеристика нели-
нейного сопротивления с известной степенью приближения может
быть заменена отрезками прямых, расположенных таким образом,
что когда одна величина, определяющая режим работы нелинейного
сопротивления, например ток, меняется, то другая, например пото-
косцепление, неизменна.
Еще более эффективен метод тогда, когда отрезки прямых, заме-
няющие собой в.а.х. нелинейного сопротивления, могут быть взя-
ты совпадающими с осями координат.
Пример решения задачи для этого случая см. § 235.
§ 229. Аналитический (или графический) метод расчета по пер-
вым гармоникам токов и напряжений. В этом методе по сложному
закону изменяющиеся токи и напряжения на нелинейном сопротив-
лении заменяются их первыми гармониками. В расчете используют-
ся вольтамперные характеристики по первым гармоникам в анали-
тической форме или в виде графической зависимости.
Основные этапы расчета в аналитическом варианте:
1. Сначала выражают аналитически в.а.х. нелинейного сопро-
тивления для мгновенных значений.
2. Путем подстановки в нее первой гармоники напряжения или
тока получают формулу, которая дает нелинейную связь между амп-
литудой первой гармоники тока через нелинейное сопротивление и
амплитудой первой гармоники напряжения на нем [в качестве при-
мера такой связи можно назвать формулу (9.22)].
3. В уравнение, составленное для исследуемой цепи по
второму закону Кирхгофа, подставляют вместо мгновенных
значений тока и напряжения на нелинейном сопротивлении
мгновенные значения их первых гармоник, а высшими гармоника-
ми пренебрегают.
4. После этого уравнение разбивается на два уравнения. Одно
из них выражает собой равенство коэффициентов при синусных сла-
гаемых левой и правой частей уравнения, другое — равенство ко-
эффициентов при косинусных слагаемых обеих частей уравнения.
5. Далее, производится совместное решение этих двух уравне-
ний.
Основные черты расчета методом первой гармоники в графичес-
ком варианте:
1. В качестве зависимости между амплитудой первой гармоники
напряжения на нелинейном сопротивлении и амплитудой первой
гармоники тока через него берется нелинейная зависимость в виде
313
графика. Эта зависимость может быть получена любым способом,
в том числе и опытным путем.
2. Произвольно задаются амплитудой 11т первой гармоники тока
через нелинейное сопротивление, из графика находят соответствую-
щую ей амплитуду первой гармоники напряжения на нелинейном
сопротивлении и затем путем построения векторной диаграммы по
первой гармонике для всей схемы определяют амплитуду Ulm пер-
вой гармоники напряжения на входе схемы. Построение векторной
диаграммы принципиально производится так же, как и для обыч-
ных линейных цепей синусоидального тока, а именно: если не учи-
тывать потери в сердечнике, то первая гармоника напряжения на
нелинейной индуктивности опережает первую гармонику протекаю-
щего через нее тока на 90°; первая гармоника напряжения на нели-
нейной емкости отстает от протекающего через нее тока на 90°; пер-
вые гармоники напряжения и тока на нелинейном активном соп-
ротивлении по фазе совпадают.
3. Путем построения нескольких векторных диаграмм для раз-
личных значений 11т находят соответствующие им Ulm и строят
вольтамперную характеристику всей схемы Ulm =
Метод позволяет исследовать такие нелинейные явления, как
преобразование постоянного тока в переменный и обратное преоб-
разование, явление резонанса на основной гармонике, триггерный
эффект на первой гармонике, некоторые типы автомодуляционных
процессов, но он не позволяет исследовать более сложные явления,
как, например, резонанс на высших и низших гармониках, резонанс
на дробных гармониках и другие сложные вопросы.
Если пользоваться аналитическим вариантом этого метода, то
решение можно получить в общем виде, что весьма существенно, так
как становится возможным исследовать решение при изменении
любого из параметров цепи.
Этот метод будет применен ниже для анализа работы автогене-
ратора (см. § 239) и для анализа цепи с нелинейной емкостью (см.
пример 118).
§ 230. Анализ нелинейных цепей переменного тока путем исполь-
зования вольтамперных характеристик для действующих значений.
В этом методе графический расчет проводится путем исполь-
зования вольтамперных характеристик нелинейных сопротивлений
для действующих значений, полученных расчетным или опытным
путем.
В этом методе принимается, что в действительности несинусои-
дально изменяющиеся токи и напряжения могут быть заменены их
эквивалентными синусоидальными величинами (эквивалентность
в смысле действующего значения).
Все этапы расчета рассматриваемым методом полностью совпа-
дают с перечисленными в предыдущем параграфе этапами графичес-
кого расчета по методу первой гармоники.
Отличие между методами состоит только в том, что в данном ме-
314
тоде используется в.а.х. не для первых гармоник, а для действу-
ющих значений.
Метод применяется в дальнейшем для исследования простейших
явлений в феррорезонансных цепях (см. § 240—245).
Если исследуются нерезонансные электрические цепи или резо-
нансные, но для которых по тем или иным соображениям заранее
известно, что в изучаемых режимах работы в них не могут возни-
кать резонансные явления на высших и низших гармониках, то
амплитуда первой гармоники тока, как правило, оказывается боль-
ше амплитуд высших гармоник тока. При этом действующее значе-
ние тока в цепи обычно сравнительно мало отличается от действую-
щего значения первой гармоники тока.
Чтобы убедиться в этом, рассмотрим следующий пример: пусть
ток в цепи содержит первую и третью гармоники и действующее
значение третьей гармоники тока составляет 40% действующего
значейия первой гармоники (73 = 0,4/J. Действующее значение
несинусоидального тока будет равно:
//f+/33 = 1,075/i,
т. е. всего на 7,5% больше действующего значения первой гармо-
ники 7Г
Метод позволяет изучать некоторые свойства нерезонансных
электрических цепей, как, например, эффект усиления мощности
(§ 247). Для исследования свойств резонансных нелинейных цепей
метод пригоден в ограниченной степени. Так, им можно приближен-
но исследовать простейший триггерный эффект (см. § 241), но нель-
зя исследовать более «тонкие» вопросы, как, например, резонанс-
ные явления на высших гармониках.
§ 231. Аналитический метод расчета по первой и одной или нескольким
высшим или низшим гармоникам. Решение этим методом складывается из
следующих этапов: составляется система дифференциальных уравнений цепи,
характеристики нелинейных сопротивлений выражаются аналитически, и эти
аналитические выражения подставляются в дифференциальные уравнения
цепи.
Решение для искомой величины изображается в виде ряда, состоящего из
первой и одной или нескольких высших или низших гармоник, например в виде
х = xlm sin wi + xsm sin (3 и/ + ^3). Предполагаемое решение подставляется в
уравнения системы.
В результате этой подстановки оказывается возможным разбить уравне-
ния системы на несколько трансцендентных алгебраических уравнений, со-
ставленных относительно амплитуды первой гармоники, амплитуд высших
(или соответственно низших) гармоник и их фаз.
Число трансцендентных уравнений в общем случае оказывается в 2 раза
больше числа учитываемых гармоник, поскольку для каждой из гармоник
уравнение разбивается на два — на уравнения для синусной и косинусной
составляющих.
Далее совместно решается система трансцендентных уравнений. Труд-
ность решения состоит в том, что каждое из трансцендентных уравнений со-
держит все неизвестные. Поэтому при решении часто пользуются методом по-
следовательных приближений.
315
Решение этим методом оказывается, как правило, довольно громоздким.
Однако метод позволяет исследовать такие сложные явления в нелинейных
цепях, как резонанс на высших гармониках, резонанс на низших и дробных
гармониках и т. п. Более подробное рассмотрение метода выходит за рамки
курса, и потому интересующихся им отсылаем к специальной литературе (на-
пример, к Л. 18).
Рассматриваемый метод в литературе называют также методом гармо-
нического баланса. Частным случаем его является метод первой гармоники
(§ 229).
§ 232. Расчет при помощи линейных схем замещения. Этот метод приме-
ним к расчету нелинейных электрических цепей, на которые воздействуют
постоянные и синусоидально изменяющиеся э. д. с., если переменные состав-
ляющие токов и напряжений относительно малы, например во много раз
меньше соответственно постоянных составляющих токов и напряжений.
Последовательность расчета такова;
1. Сначала определяется положение рабочей точки на характеристике
нелинейного сопротивления по постоянному току. В окрестности этой точки
будет перемещаться изображающая точка под воздействием малой перемен-
ной э. д. с.
2. Затем в рабочей точке по постоянному току проводится касательная к
характеристике нелинейного сопротивления и производится замена участка
характеристики нелинейного сопротивления отрезком касательной.
3. Далее составляется линейная схема замещения для расчета перемен-
ной составляющей. Вид схемы зависит от характера нелинейного сопротив-
ления, а параметры ее — от величины тангенса угла, составленного касатель-
ной к характеристике и одной из осей координат.
Схема замещения полупроводникового триода для малой переменной со-
ставляющей дана на рис. 251, б, для трехэлектродной лампы — на рис. 258, б
или 258, в. Примеры на данный метод см. на стр. 302 и 309.
§ 232а. Расчет путем применения математических счетных машин. Ма-
тематические счетные машины применяются для табулирования решений сис-
тем трансцендентных уравнений и систем алгебраических уравнении высоких
степеней, для табулирования решений, выраженных в виде медленно сходя-
щихся рядов, для интегрирования линейных дифференциальных уравнений
(главным образом высоких порядков), к которым сводятся нелинейные диф-
ференциальные уравнения при кусочно-линейной аппроксимации характе-
ристики нелинейного сопротивления, а также в некоторых других случаях.
Рассмотрим несколько примеров.
В первых двух примерах (см. § 233 и 234) анализ проводится
графически, путем использования характеристик Ф =/(t) для нели-
нейной индуктивности.
В первом из этих примеров характеристика берется без учета
гистерезиса, во втором — с учетом гистерезиса (т. е. в виде петле-
вой зависимости).
§ 233. Простейший утроитель частоты. Утроитель частоты пред-
ставляет собой устройство, напряжение на выходе которого имеет
частоту в 3 раза большую, чем напряжение на входе. Схема простей-
шего утроителя изображена на рис. 260, а. Она состоит из двух транс-
форматоров (/ и 2). Поток первого трансформатора назовем Фх,
второго—Ф2. В сердечнике первого трансформатора имеется воз-
душный зазор. Благодаря этому веберамперная характеристика его
Ф = f(i) представляет собой прямую (прямая Фх на рис. 260, б)*.
* В правом верхнем углу рис. 260, б.
316
Сердечник второго трансформатора не имеет воздушного зазора.
Веберамперная характеристика его изображается кривой Ф2 рис.
260, б. На сердечник первого трансформатора нанесены обмотки wt
и ws, на сердечник второго — w2 и w.v Обмотки и w2 соединены
согласно, а обмотки w3 и —встреч-
но друг другу.
Пусть приложенное к первичной
цепи напряжение и — Umcosat.
По закону электромагнитной ин-
дукции и= ~ + йу2Ф2).
at
Отсюда следует, что
— Фх -]- Ф2= — Sin at.
w2
Положим w1 = w.2 = tv, тогда
Фх -ф- Ф2 = — sin att
aw
Рпс. 260
т. е. сумма потоков первого и второ-
го трансформаторов изменяется во
времени по синусоидальному закону.
Построим кривую i = f(at). С этой
целью, просуммировав ординаты кри-
выхФх иФ2, построим сначала кривую
Ф1 + (1)2=Н0.
а затем нанесем на рисунок синусо-
иду Фх + Ф-2 — Z (ш0> амплитуда ко-
торой равна —.
C0U)
Задаемся произвольным значением
суммарного потока (точка а), проектируем эту точку на кривую
Ф4 -|-Ф2 = f(i), находим соответствующий ток I и затем откладыва-
ем этот ток на вертикали, проведенной через точку а на рис. 260, б.
Получаем точку Ь, принадлежащую кривой i = /(со/).
Так как первый трансформатор не насыщен и зависимость Ф( =
= /(/) есть прямая линия, то кривая Фх(со/) имеет такую же заост-
ренную форму, как и форма тока i — f(at).
Ординаты кривой Ф2(со/) равны разности ординат кривой Фхф-
-J- Ф2 = / (со/) и кривой Фх(со/).
Кривая Ф2(со/) имеет «уплощенную» форму.
Кривые Фх (со/) и Ф2 (со/) могут быть разложены на гармоники.
Первая и третья гармоники потоков изображены на рисунке. В по-
токах будут и более высокие гармоники, но они относительно ма-
317
лы. Из рисунка видно, что первая гармоника потока Фх (она обо-
значена Ф'5 и первая гармоника потока Ф2 (Ф0 находятся в фа-
зе, тогда как третья гармоника потока Ф1(Ф") находится в про-
тивофазе с третьей гармоникой потока Ф2 (Ф'").
В каждой из вторичных обмоток (ш3 и о>4) наводятся первая и
третья гармоники э. д. с. В силу встречного включения обмоток
w3 и wi первые гармоники э. д. с. в них будут вычитаться, а
третьи гармоники — складываться. В результате, если подобрать
число витков wt так, чтобы первые гармоники э. д. с. в обмотках
w8 и wt были равны по величине, а это будет при условии Ф4ьу3==
= Ф2№4, то на выходе утроителя будет э. д. с. только лишь
утроенной частоты.
Для нормальной работы утроителя необходимо, чтобы суммар-
ная э. д. с. утроенной частоты в обмотках и w2 первичной це-
пи равнялась нулю, т. е. чтобы и^Ф"' — ш2Ф'" = 0. Нетрудно убе-
диться в том, что это условие выполняется, так как ьух == и>2, а
Ф[" = ф"' (сумма потоков <1>4 -ф- Ф2 синусоидальна).
Пример 112. В результате графических построений было найде-
но, что в утроителе по рис. 260, а Ф'т = Ф'т — 0,0027 в.сек, а
Ф"^= Ф"'т = 0,0006 в-сек. Определить число витков обмотки w4 и
напряжение на выходе утроителя при холостом ходе, полагая, что
iWj = w2 — w3 = w = 100, f = 50 гц.
Решение. Находим число витков: ш. — шаФ1т- = 100.
Фцт.
Мгновенное значение напряжения на выходе
“еых = Ф1т Sin 3wZ — Ф2т S'" 3(00.
Действующее значение его
Uebix = Зю = 100 • 3 • 314 • 2'0’0006 = 80 (в).
У‘2 V2
§ 234. Пик-трансформатор. Пик-трансформатор представляет
собой устройство, на выходе которого получают э. д. с. пикообраз-
ной формы.
Электродвижущая сила пикообразной формы требуется, напри-
мер, для управления моментом зажигания ртутных выпрямителей.
Рассмотрим принцип работы простейшего пик-трансформатора
(рис. 261, а).
На замкнутый тороидальный сердечник из материала с почти
прямоугольной кривой намагничивания наматываются две обмот-
ки (о»! и w2). По обмотке пропускают синусоидальный ток от ис-
точника тока. На зажимах обмотки w2 наводится э.д.с. пикообраз-
318
Рис. 261
ной формы. Принцип получения ее иллюстрируется рис. 261, 6.
В левой части рис. 261, б изображена петля гистерезиса Ф =
= f(i). С целью удобства дальнейших построений оси Ф и i повер-
нуты по сравнению с обычным начертанием их на 90° против часо-
вой стрелки. В правой части рисунка построены три кривые: кривая
заданного синусоидального тока i = f(at) по обмотке кривая
магнитного потока в сердечнике Ф = /(га/) и кривая = /(oiZ),
dwt
ординаты которой пропорциональны искомой э.д.с. е2 на зажимах
обмотки w2:
аф аФ dent
е2 — — w., — = — w, ---------------------
dt dent dt
= — aw2
dcot
Соответствующие друг другу точки кривых обозначены одина-
ковыми цифрами.
Последовательность построения такова.
Сначала строим кривую i = /(со/). Амплитуда тока соответству-
ет ординате точки 8 на кривой Ф = /(/). Затем при помощи кривой
i = /(со/) и кривой Ф = /(/) строим кривую Ф = /(со/). В качестве
примера на рисунке стрелками показана последовательность нахож-
дения точки 6 кривой Ф = /(со/).
После этого путем графического дифференцирования строим
кривую — = / (со/). Ординаты ее пропорциональны тангенсам уг-
dint
ла наклона касательных к кривой Ф = / (со/) с осью абсцисс. Так,
z. d®
для точки 6 — пропорционально тангенсу угла а.
dent
т С?Ф
На участках, где Ф увеличивается в функции времени, — по-
с.’со/
ложительно. Чем больше крутизна кривой Ф = / (со/), тем больше
. Кривая = f (ш/) имеет пикообразиую форму. Такую же
(.'(о/ dent
форму имеет и э. д. с. е2.
§ 235. О расчете электрических цепей, содержащих индуктивные
катушки, сердечники которых имеют почти прямоугольную кривую
намагничивания. Некоторые высококачественные магнитномягкие
материалы, например Н60П, Н65П и др., обладают тем свойством,
что кривая намагничивания их близка по форме к прямоугольной:
на участке О — а (рис. 262, а) кривая почти совпадает с осью орди-
нат, а на участке а — b она расположена почти параллельно оси
абсцисс.
На рис. 262, а пунктиром показана предельная петля гистере-
зиса. Коэрцитивная сила Нс для таких материалов очень мала и со-
ставляет всего 1—10 а/м.
Расчет электрических цепей переменного тока, содержащих ин-
дуктивные катушки, сердечники которых выполнены из упомяну-
тых выше магнитных материалов, обычно производят при помощи
метода кусочно-линейной аппроксимации (см. § 228). Для облегче-
320
ния расчета кривую намагничивания заменяют идеально прямо-
угольной (рис. 262, б). Участки 4—1 и 2—3 параллельны оси
абсцисс, а участок 1—2 совпадает с осью ординат.
Если изображающая точка будет перемещаться по участку 1—2,
то изменяется только индукция в сердечнике, а напряженность
поля в сердечнике будет равна нулю.
При движении изображающей точки по участкам 4—1 и 2—3
меняется только величина напряженности поля Н, а индукция в
сердечнике будет оставаться неизменной.
Рис. 262
Схема рис. 262, в состоит из источника синусоидальной э.д.с.
е = Ет sin и/, нелинейной индуктивности с заданной зависимостью
потокосцепления ф от тока i и активного сопротивления R. Требует-
ся вывести формулы для определения ф и I и построить графики из-
менения ф и i во времени в установившемся режиме.
Так как потокосцепление ф равно произведению индукции в сер-
дечнике В на площадь поперечного сечения сердечникаS и на число
витков обмотки w, т. е. ф = BSw, а по закону полного тока ток I
пропорционален напряженности магнитного поля в сердечнике,
то зависимость потокосцепления ф от тока i (рис. 262, г) качествен-
но такая же, как и зависимость В = f(H) (рис. 262, б). Имеем:
+ = Ет sin at. (а)
В интервале времени от bit = 0 до cot = (btl — назовем этот ин-
тервал первым интервалом — ток i = 0, все напряжение приходит-
ся на нелинейную индуктивность, = Ет sin ы/ и потокосцепле-
ние ф изменяется от — фт до 4~ ф,„ (изображающая точка на рис.
262, б перемещается от 1 к 2).
321
В этом интервале dip = Ет sin at dt, следовательно,
р
ip =------- cos at 4- С. (б)
а
Здесь С — постоянная интегрирования.
На втором интервале времени от at = att до at — л потоко-
сцепление ip остается постоянным и равным ipm, — = 0 и из
dt
уравнения (а) имеем:
£
Ri = Ет sin at, или i = sin at. (в)
Таким образом, на втором интервале времени ток I изме-
няется по закону синуса, а потокосцепление ib постоянно
Рис. 263
и равно ipm. При этом изобра-
жающая точка на рис. 262, б
перемещается по участку 2—3.
Найдем постоянную интег-
рирования С и величину со^. Для
определения С запишем уравне-
ние (б) при at = 0. При at = 0
ip = — ipm, поэтому
— 1[?,л = — — Д- С. Отсюда
ы
C = -ip,„+^.
ы
Для определения вос-
пользуемся также уравнением (б),
учтя, что при at = at± ip = ipm.
£
Получим: =------cosort.—
to
Отсюда cos at. = 1 — , или at, = arc cos (1 — .
1 F 1 \ F 1
m V tod/
Характер изменения тока i, потокосцепления ip и —, когда 1,
dt Ет
показан на рис. 263.
Если амплитуда э. д. с. Ет будет меньше, чем onpm, то вто-
рого интервала времени не возникает; другими словами, ток i бу-
дет равен нулю в течение всего периода.
§ 236. Выпрямление переменного напряжения. Под выпрямле-
нием переменного напряжения понимают процесс преобразования
переменного напряжения в постоянное или пульсирующее. Выпрям-
ление производится при помощи полупроводниковых, ламповых или
других типов выпрямителей.
322
Неуправляемый выпрямитель часто изображается на схемах
в виде большой треугольной стрелки с поперечной чертой у острия.
Стрелка показывает проводящее направление. Сопротивление вып-
рямителя в проводящем направлении в тысячи раз меньше, чем в не-
проводящем.
По числу фаз выпрямляемого переменного напряжения выпря-
мительные схемы делятся на однофазные и многофазные. Однофаз-
ные схемы подразделяются на схе-
мы однополупериодного и двухпо-
луперподного выпрямления.
В однополупериодных схемах
выпрямление производится, грубо
Рис. 265
Рис. 264
говоря, в течение одного полупериода питающего напряжения, в
двухполупериодных схемах выпрямления — в течение обоих полу-
периодов.
Две простейшие схемы однополупериодного выпрямления пред-
ставлены на рис. 264, а и 265, а. Схема рис. 264, а состоит из источ-
ника синусоидального напряжения, выпрямителя и активного соп-
ротивления RH. В схеме рис. 265, а нагрузка образована активным
сопротивлением RH и индуктивностью LH.
Простейшая мостовая схема однофазного двухполупериодного
выпрямителя представлена на рис. 266, а. Она состоит из четырех
выпрямителей (/, 2, 3 и 4), источника выпрямляемого синусоидаль-
ного напряжения и активной нагрузки RH.
На рис. 267, а изображена в.а.х. полупроводникового диода.
В целях облегчения анализа вместо нее будем пользоваться идеа-
лизированной в. а. х., изображенной на рис. 267, б.
В соответствии с этой идеализированной характеристикой, ког-
да через выпрямитель проходит ток, падение напряжения на нем
равно нулю и, следовательно, сопротивление самого выпрямителя
равно нулю. Когда напряжение на выпрямителе отрицательно (т. е.
когда отрицательна взятая в направлении стрелки рис. 264, а раз-
323
ность потенциалов на самом выпрямителе), выпрямитель не прово-
дит тока (i = 0) и сопротивление его равно бесконечности.
Рассмотрим сначала работу схемы рис. 264, а. Кривая рис. 264, б
изображает собой э. д. с. источника питания схемы, кривая рис. 264,
в — напряжение на нагрузке RH. В первый полупериод, когда э.д.с.
источника положительна и действует согласно с положительным
направлением напряжения на выпрямителе, выпрямитель пропус-
кает ток, и напряжение на нагрузке в точности равно э.д.с. источ-
ника. Во второй полупериод, когда э. д. с. источника питания отри-
цательна, выпрямитель не пропускает тока и напряжение на наг-
рузке равно нулю (в этот полу-
Рис. 266 Рис. 267
Таким образом, напряжение на нагрузке в схеме рис. 264, а
имеет форму полусинусоид. Через UB обозначено среднее значение
напряжения на нагрузке.
Пример 113. Если в схеме однополупериодного выпрямления нагрузка
будет активно-индуктивной (см. рис. 265, о), то режим работы схемы су-
щественно изменится по сравнению с режимом работы при чисто активной
нагрузке.
Уравнение, составленное по второму закону Кирхгофа для схемы
рис. 265, а, запишется так:
“в + in RH + LH — = Ет sin ыб (а)
at
Это уравнение является нелинейным, так как напряжение на выпрямителе
нв = и8ыпр нелинейно зависит от тока iH = i.
Проведем решение уравнения (а) методом кусочно-линейной аппрокси-
мации характеристики нелинейного сопротивления (см. § 228). С этой целью
заменяем в. а. х. диода отрезками прямых в соответствии с рис. 267, б.
Уравнение (а) записано в общем виде и годится как для проводящей, так
и для непроводящей частей периода.
В проводящую часть периода, когда ток iH =/= 0 и движение изображающей
точки происходит по вертикальному участку в. а. х. рис. 267, б, напряжение
иа диоде ив = 0. При этом уравнение (а) приобретает такой вид:
iHRH + LH^ = Ет sin at. (а')
at
324
В непроводящую часть периода, когда через RH и LH пе протекает ток, па-
дения напряжения на сопротивлении RH и индуктивности LH равны нулю и
изображающая точка движется по горизонтальному участку в. а. х.
рис. 267, б. При этом уравнение (а) переходит в следующее
ие = Ет sin со/. (а")
Таким образом, вместо одного нелинейного уравнения (а) мы получили
два линейных уравнения (а') и (а").
Решение уравнения (а') запишется следующим образом*
Е L
iH = —— sin (со/ — ср) 4- Ле н (б)
z
Первое слагаемое правой части последней формулы представляет собой
принужденный ток, а второе — свободный ток:
л / 9 а
г = V ф = аГС tg ~R^ •
Выпрямитель открывается (проводит ток), начиная с со/ = 0. Составим
уравнение для определения постоянной интегрирования А. С этой целью за-
пишем уравнение (б) при / = 0:
„ Ет .
0 = — — sm ср -|- А.
z
Нуль в левой части последней строки объясняется тем, что при ш/ = 0
£
/„ = 0. Следовательно, А => —2 sin ср. Подставим в формулу (б) значение А
z
и запишем окончательное выражение для тока в проводящую часть периода:
tH = ~— sin (cot — <p) + "— sin cpe
z z
В непроводящую часть периода iH = 0.
На рис. 265, б изображена э.д.с. источника питания схемы Ет sin со/.
£
На рис. 265, в кривая 1 — принужденный ток —” sin (со/ — ср), кри-
z
вая 2— свободный ток. С увеличением времени / свободный ток затухает по
экспоненциальному закону.
Кривая рис. 265, г изображает ток iH. Ординаты этой кривой равны сум-
ме ординат кривой 1 и 2 рис. 265, в.
В момент времени co/j, когда ток iH становится равным нулю, выпрями-
тель переходит от состояния проводимости в состояние непроводимости.
В интервале времени оты/х до 2к выпрямитель закрыт и ток в нагрузке
равен нулю.
В следующий период процесс повторяется.
Рассмотрим теперь работу мостовой схемы рис. 266, а.
В этой схеме источник синусоидальной э.д.с. е(/), выпрямители
1, 2, 3, 4 и нагрузка RH образуют мостовую схему.
Источник э.д.с. включен в одну диагональ этой схемы, а нагруз-
ка RH — в другую.
* Несколько следующих абзацев рекомендуется читать после ознаком-
ления с классическим методом расчета переходных процессов в главе десятой.
325
Выпрямители работают попарно.
В первый полупериод, когда э. д. с. e(t) действует согласно с по-
ложительным направлением напряжения на выпрямителях 1 и 3*,
эти выпрямители проводят ток, а выпрямители 2 и 4 тока не прово-
дят. Во второй полу пер иод, когдаэ. д. с. е(/) изменит знак и дейст-
вует согласно с положительным направлением напряжения на вып-
рямителях 2 и 4, ток проводят выпрямители 2 и 4, а выпрямители
1 и 3 тока не проводят. Направление протекания тока через нагруз-
ку показано на рис. 266, а стрелкой. Ток через нагрузку протекает
все время в одном и том же направлении. Форма напряжения на
нагрузке иллюстрируется кривой рис. 266.
§ 237. Амплитудная модуляция. На схеме рис. 268 пунктиром об-
веден нелинейный активный четырехполюсник. Он состоит из трех-
электродной лампы, анодной батареи Еа и параллельно включен-
ных индуктивности L и емкости С, настроенных в резонанс на час-
тоту со. Если к входным зажимам четырехполюсника (зажимы а и Ь)
подвести сумму двух синусоидальных напряжений
ис = sin at 4- U2 sin £2/ (co £2), (9.53)
то на выходных зажимах (зажимах cd) будет действовать амплитуд-
но-модулированное напряжение.
Рассмотрим работу схемы при условии, что падение напряжения
на зажимах cd мало по сравнению с величиной э. д. с. Еа. При этом
условии анодный ток 1а будет зависеть только от сеточного напря-
жения ис.
Соответствующим подбором величины э. д. с. Еа добьемся того,
что сеточная характеристика лампы ia — f(uc) при малых значениях
напряжения на сетке будет представлена в виде полинома второй
степени (рис. 269)1
ia = + аис + (9.54)
Рис. 268
Уравнение (9.54) описывает кривую, подобную пунктирной кри-
вой рис. 255.
♦ Для того чтобы убедиться в этом, следует обойти по часовой стрелке
контур е (01RH Зе (f).
326
Подставим (9.53) в (9.54). Получим:
ie — I'm + а (^i sin и/ + U2 sin Q/) -f-
Г7/э r/s 1
4- b (1 — cos 2со/) + -g5 (1 — cos 2Q/) -f- 2t71t72 sin Qt sin at I,
или
= l‘«o + ± (Ut + И) + aU1 (1 + tn sin Qt) sin at —
— cos 2co£ — cos 2QZ -ф- aU2 sin Qt\ (9.55)
2W2
tn = ---.
a
Следовательно, протекающий в анодной цепи ток содержит пос-
тоянную составляющую te0+~ {U\ -f-t/j), модулированную по ам-
плитуде первую гармонику аиг(1 -|-msinQZ) sin и/, гармонику
частоты 2со и гармоники частот 2Q и Q.
На зажимах резонансного контура, настроенного на частоту
со, будет действовать практически только амплитудно-модулирован-
ное напряжение, поскольку для постоянной составляющей, а так-
же для частот 2со, 2 и 22 сопротивление резонансного контура, а
следовательно, и падение напряжения на нем во много раз меньше,
чем для частоты со и близких к ней.
Появление амплитудно-модулированного напряжения на вы-
ходе четырехполюсника вызвано квадратичным членом в аналити-
ческом выражении сеточной характеристики лампы.
§ 238. Детектирование. Выделение низкочастотного сигнала, за-
печатленного в модулированном колебании, называют детекти-
рованием. Принципиальная схема детектора, позволяющего осу-
ществить детектированием амплитудно-модулированного колеба-
ния, изображена на рис. 270. Она состоит из выпрямителя и емкости
С, шунтирующей нагрузку RH, LH. В качестве нагрузки могут быть
телефон, репродуктор, реле и подобные им устройства.
Выпрямитель срезает отрицательные полуволны модулирован-
ного напряжения. Если бы емкость отсутствовала, то характер
изменения напряжения на выходе выпрямителя после среза отри-
цательных полуволн изобразился бы кривой рис. 270, б. В дей-
ствительности на выходе выпрямителя есть емкость. В промежу-
тки проводимости конденсатор заряжается, а в промежутки не-
проводимости — разряжается на нагрузку RH, LH.
В силу этого напряжение на выходе оказывается «сглажен-
ным» (см кривую в рис. 270). Напряжение, изображаемое кривой
рис. 270, в, качественно можно представить в виде суммы двух
.327
кривых: кривых гид. Кривая г дает
низкочастотное колебание (частоты 2),
наложенное на постоянную состав-
ляющую, кривая д — высокочастот-
ное колебание.
Через нагрузку RH, LH проходят
постоянный ток и ток частоты 2 (по-
лезный сигнал), а ток высокой частоты
через нагрузку почти не проходит в
силу большого сопротивления ее на
высокой частоте.
Для того чтобы сглаживающее
действие емкости проявлялось в до-
статочной степени, должно быть вы-
полнено следующее соотношение (да-
ется без вывода):
Л I
v К.л л «л д лг ыС QC
§ 239. Ламповый генератор. Лампо-
Рис. 270 вый генератор* является простейшим,
не содержащим подвижных частей пре-
образователем энергии источника постоянной э. д. с. в энергию
переменного тока.
Возникающие в ламповом генераторе колебания относятся к
классу колебаний, получившему название автоколебаний.
Автоколебания представляют собой периодические колебания,
возникающие в системах, находящихся под воздействием постоян-
ных вынуждающих сил (сил, не являющихся функцией времени).
В рассматриваемой в настоящем параграфе системе источником
постоянной вынуждающей силы является источник постоянной
э.д.с. Еа.
Рассмотрим принцип работы лампово-
го генератора с колебательным контуром
в цепи сетки (рис. 271). В анодной цепи
лампы включены индуктивность Lu и ис-
точник э. д. с. Еа. В сеточной цепи имеет-
ся колебательный контур, составленный
индуктивностью L, магнитно связанной
с La, активным сопротивлением R и
емкостью С.
Рис. 271
Выходными зажимами генератора яв-
ляются зажимы индуктивности La. Нап-
* Его называют также ламповым автогенератором. Кроме схемы рис.
271 с колебательным контуром в сеточной цепи, применяется схема и с коле-
бательным контуром в анодной цепи. Все выводы § 239 распространяются и
на схему с колебательным контуром в анодной цепи.
328
ряжение на этих зажимах по форме близко к синусоидальному.
Поставим перед собой цель, воспользовавшись методом первой
гармоники (см. §229), определить амплитуду и угловую частоту
автоколебаний в схеме рис. 271, когда сеточная характеристика
ламлы: а) по форме близка к жирной кривой рис. 255 и б) по фор-
ме близка к пунктирной кривой рис. 255. Эти кривые повторены
на рис. 272, а и б. Составим уравнение по второму закону Кирх-
гофа для мгновенных значений величин для колебательного кон-
тура сеточной цепи, учтя, что при выбранных положительных на-
правлениях для токов имеет место встречное включение магнит-
носвязанных индуктивностей L и La:
+ + =
dt dt
(9.56)
Здесь tic напряжение на сетке лампы (оно же напряжение на
конденсаторе).
Из опыта известно, что ток i изменяется во времени почти по
гармоническому закону, поэтому положим i — Imsina>t. Тогда
di t .
— -- Ci)/„, COS (£>t,
dt m
idt =--------5- Im cos co/ = — UCm cos co/,
coC
где ^cm = hn— • Анодный ток является функцией сеточного
<>c
напряжения ia — f(uc) — см. рис. 272, а и б. Так как зависимость
ia = f (uc) однозначна, то первая гармоника тока ia, т. е. — lam cos со t
находится в фазе с первой гармоникой йс = — UCm cos со/.
329
В уравнении (9.56) участвует производная Она может быть
найдена следующим образом: — = . Но
dt due dt
dig .—, __ I am COS cot /atil
duc~A.uc —uCm cos at UCm
где S — крутизна лампы по первой гармонике. Она находится гра-
фическим или аналитическим путем по характеристике ia = f («с)»
придавая 1т различные значения. Каждому значению 1т соответ-
ствует некоторое (7Оп, а стало быть, и некоторые 1ат и S.B свою
очередь
= £ (- UCm COS 0)0 = Sin О)/ (UCm
at at С \ <оС /
На рис. 272, виг изображены зависимости S = соответ-
ствующие рис. 272, а и б. Для рис. 272, в с ростом 1т умень-
шается S вследствие насыщения (из рис, 272, а видно, что при
больших ис анодный ток почти не увеличивается при росте ис).
Зависимость S = изображенная на рис. 272, г имеет другой
характер: сначала S возрастает вследствие перехода на более кру-
той участок кривой ia — f(uc) рис. 272, б, а затем уменьшается
вследствие насыщения. Подставим найденные значения —, ис и
dt
тока i в уравнение (9,56). Получим:
(coL--—7mcos at -j- (Д—/msinco7 = 0. (9.58)
\ ыС} \ С /
Сумма двух функций, одна из которых изменяется во времени
по закону синуса, а другая по закону косинуса, равна нулю для
любого момента времени. Это может быть либо в случае, когда
1т = 0 (т. е. когда колебания отсутствуют), либо при 1т + 0, когда
выполняются два условия:
o)L = —
соС
(9.59)
(9.60)
Из (9.59) следует, что угловая частота автоколебаний
® = (9.61)
]/LC
Исследуем условия возбуждения колебаний, используя (9.60).
С этой целью построим зависимость левой и правой частей (9.60) в
функции от 1т — см. рис. 272, д и е (рис. 272, д соответствует
рис. 272, в, а рис. 272, е — рис. 272, г), полагая, что изменяется
R, а М. и С неизменны. Сопротивление 7? не является функцией
330
амплитуды тока 1т, поэтому левая часть (9.60) представляет со-
бой прямую, параллельную оси абсцисс. Чем меньше R, тем ниже
расположится прямая. Левая часть — кривая, подобная кривой
рис. 272, в или кривой рис. 272, г.
При 7?> прямая не пересекается с кривой, поэтому коле-
бания будут отсутствовать. Колебания возбудятся при
Рис. 272, д иллюстрирует так называемое мягкое возбуждение
колебаний, когда при уменьшении R амплитуда тока 1т плавно
увеличивается, начиная с нулевого значения. Рнс. 272, е иллюстри-
рует так называемое жесткое возбуждение колебаний, когда при
плавном уменьшении R амплитуда 1т скачком увеличивается с
нуля до некоторого относительно большого значения, например
при R = R2 до Гт, а при R = R3 до Я,.
Аналогичным образом могут быть рассмотрены условия возбужде-
ния колебаний, если оставить неизменными R и М и изменять С,
или если R и С неизменны, а меняется М. Правая ветвь кривой
рис. 272, е соответствует устойчивым колебаниям (она вычерчена
утолщенной линией), левая — неустойчивым колебаниям (левая ветвь
кривой является нерабочей ветвью). Для токов и напряжений
сеточной и анодной цепей (для их первых гармоник) могут быть
построены векторные диаграммы для действующих значений пер-
вых гармоник (см. рис. 272, ж). Уравнению (9.58) соответствует
уравнение в комплексах:
/<оТ7---^7-|-7/?—7—=0. (9.G2)
шС С
Для анодной цепи для мгновенных значений изменяющихся во
времени величин (постоянная составляющая тока напряжения
иа и постоянная э. д. с. Еа не учитываются) справедливо уравнение:
L - -М - + laR + иа = 0.
" dt dt 1 а а 1 а
Ему соответствует уравнение в комплексах
j^Laia-ie>Mi + iaRa + Ua = 0. . (9.63)
Здесь Ra — активное сопротивление индуктивности La, Ua — ком-
плекс первой гармоники анодного напряжения.
Энергия на покрытие потерь в сеточной цепи доставляется из
анодной цепи вследствие наличия магнитной связи между ними.
Воздействие выходной цепи (в данном случае анодной) на
входную цепь (в рассматриваемом случае на сеточную) называют
обратной связью. Обратная связь является необходимым условием
существования автоколебаний.
*
* *
Рассмотрим теперь группу довольно грубых явлений, которые
имеют место в цепях, содержащих нелинейную индуктивность и ли-
нейную емкость. Такие цепи принято называть феррорезонансными.
331
Для анализа этих явлений можно воспользоваться либо методом
первой гармоники (см. § 229), либо методом расчета по действующим
значениям (см. § 230). В § 240—247 будет применен метод расчета
по действующим значениям. Будем пользоваться вольтамперной ха-
рактеристикой нелинейной индуктивности для действующих зна-
чений тока и напряжения. В этом методе в действительности неси-
нусоидальные токи и напряжения заменяют их эквивалентными си-
нусоидальными величинами (экви-
валентность в смысле действую-
щего значения по § 178).
Если в § 240— 247 будет гово-
риться о сдвиге по фазе между то-
ком и напряжением на каком-либо
элементе схемы, то под сдвигом по
фазе понимается угол между экви-
валентным синусоидальным током
и эквивалентным синусоидальным
напряжением.
§ 240. Построение вольтампер-
ной характеристики последователь-
ной феррорезонансной цепи. В
Рис. 274
Рис. 273
схеме рис. 273, а последовательно включены нелинейная
индуктивность, линейное активное сопротивление 7? и ли-
нейная емкость С. Вольтамперная характеристика катушки
со стальным сердечником UL = /(/) изображается кривой 1
рис. 273, б. Вольтамперная характеристика емкости Uc— —I—
прямая 2, вольтамперная характеристика (в. а. х.) активного
сопротивления UR= RI — прямая 3.
Точки, принадлежащие результирующей вольтамперной харак-
теристике схемы — кривой 4, получаем следующим образом.
Произвольно задаемся некоторым током I, находим для него
разность напряжений UL— Uc (напряжения на индуктивности и на
емкости находятся в противофазе) и напряжение U результирую-
332
щее напряжение U равно гипотенузе треугольника, построенного
на катетах Up и UL — Uc .
При сравнительно малом активном сопротивлении R на резуль-
тирующей в. а. х. цепи имеется падающий участок, а сама в.а.х. име-
ет N-образную форму. С увеличением R падающий участок на в.а.х.
исчезает.
§ 241. Триггерный эффект в последовательной феррорезонансной
цепи. На рис. 274, «отдельно представлена кривая 4 рис. 273, б. Бу-
дем, начиная с нуля, плавно увеличивать напряжение источника
э.д.с. в схеме рис. 273, а. При этом изображающая точка на рис. 274, а
будет перемещаться от точки 0 через точку 1 к точке 2. Если нап-
ряжение и дальше повышать, то изображающая точка скачком пе-
реместится из точки 2 в точку 4, а затем движение будет происхо-
дить по участку 4—5.
При уменьшении напряжения изображающая точка будет пере-
мещаться от точки 5 через 4 к точке 3, затем произойдет скачок в
точку 1, далее движение будет происходить от точки 1 к точке 0.
Таким образом, при плавном подъеме напряжения и достижении им
значения U2 в цепи происходит скачкообразное увеличение тока со
значения 12 до значения /4. При этом резко изменяется угол сдвига
фаз между током в цепи и общим напряжением: в точке 2 ток от-
стает от напряжения (UL > Uc), в точке 4 ток опережает напряже-
ние (Uc > UL). При плавном уменьшении напряжения источника
э. д. с. и достижении им значения Ux ток в цепи скачком уменьшает-
ся со значения 13 до значения Ц.
Явление резкого изменения тока в цепи при незначительном из-
менении напряжения на входе будем называть триггерным эффектом
в последовательной феррорезонансной цепи.
Если схему рис.273, а включить к напряжению U, величина кото-
рого находится в интервале между Ur и U2, то в схеме установит-
ся один из двух возможных режимов. Первый режим соответствует
нахождению рабочей точки на участке между точками 1 и 2, вто-
рой — на участке между точками 3 и 4.
На каком из двух участков окажется рабочая точка, это зави-
сит от характера переходного процесса в цепи при подключении ее
к источнику э. д. с.
§ 242. Феррорезонанс напряжений. Феррорезонансом напряже-
ний называют режим работы цепи рис. 273, а при котором первая гар-
моника тока в цепи совпадает по фазе с напряжением U источника
э. д. с. На рис. 273, б, где построены вольтамперные характеристики
для действующих значений, феррорезонанс напряжений приблизи-
тельно соответствует точке р.
Феррорезонанса напряжения можно достичь путем изменения
напряжения или частоты источника питания схемы, путем измене-
ния емкости и параметров катушки со стальным сердечником.
Пример 114. Кривая / рис. 274, б представляет собой в.а.х.
нелинейной индуктивности. Пренебрегая активным сопротивлением,
333
найти, какой величины емкость следует включить последователь-
но с нелинейной индуктивностью (схема рис. 273, а), чтобы триггер-
ный эффект происходил при 60 в. Найти, во сколько раз ток после
скачка /4 будет больше тока до скачка /2; со — 314 сект1.
Решение. Из точки U = 60 в, I = 0 проводим касательную
к в. а. х. нелинейной индуктивности. Касание произойдет в точке
а. Вольтамперная характеристика емкости (прямая) должна быть
проведена из начала координат параллельно касательной. Тан-
генс угла наклона ее к оси абсцисс численно равен — .
Из рис. 274, б находим:
— — 690 ом', С = ——-------= 4,52 (мкф)'
шС 314.690
Ток при скачке изменяется с /2 = 0,06 а до /4 — 0,29 а;
= 4,83.
h
§ 243. Вольтамперная характеристика параллельного соединения
емкости и катушки со стальным сердечником. Феррорезонанс токов.
Кривая 3 рис. 275 представляет собой результирующую вольтам-
перную характеристику для схемы рис. 276. Ток I в неразветвлен-
ной части схемы равен алгебраической сумме токов IL и /с. Абсцис-
Рис. 276
сы кривой 3 равны разности соответствующих абсцисс кривых 2
и 1.
До точки р ток /с по модулю больше тока /£. В точке р
кривые 1 и 2 пересекаются. Выше точки рток/л по модулю боль-
ше /с. Под феррорезонансом токов в схеме рис. 276 понимают
режим работы ее, при котором реактивная составляющая первой
гармоники тока /д равна току /с. В этом режиме (точка о на
рис. 277) ток в неразветвленной части цепи не равен нулю, он
содержит активную составляющую и высшие гармоники тока 1Ь.
334
§ 244. Триггерный эффект в параллельной феррорезонансной цепи.
На рис. 277 изображена результирующая вольтамперная характе-
ристика схемы рис. 276.
Если в качестве источника питания схемы взять источник тока
и (начиная с нуля) плавно увеличивать ток / в цепи, то при дости-
жении им значения /2 напряжение на входе цепи скачком возрас-
тает со значения Ua до значения Ub.
При плавном уменьшении тока и достижения им значения /г
напряжение скачком уменьшается со значения Uc до значения Ud.
Пример 115. В. а. х. нелинейной индуктивности в схеме рис. 276
изображается кривой 1 на рис. 278. Пренебрегая активным сопро-
тивлением и высшими гармоника-
ми, определить величину емкости
С, которую надо включить в схе-
ме рис. 276, чтобы триггерный эф-
фект имел место при токе 12 =0,15 ст,
со — 314 сек-1.
Решение. Из начала коор-
динат произвольно проводим не-
сколько лучей (a, b,c,d). На в. а. х.
нелинейной индуктивности находим
точки, касательные в которых к ней
параллельны проведенным лучам.
Так, касательная к в. а. х. ин-
дуктивности в точке а параллель-
на лучу а, касательная в точке
b параллельна лучу b и т. д.
Проводим кривую 2. Она прове-
дена через точки, подобные точ-
Рис. 278
ке а рис. 277 для различных значений емкости.
Пересечение вертикали /2 = 0,15 а с кривой 2 дает значение
напряжения U2.
Вольтамперная характеристика искомой емкости должна быть
проведена через точку k. Точка k находится на горизонтали, про-
веденной через точку т. Отрезок
nk — пт-\- пс'*.
Точке k соответствует ток Ik = 0,235 а:
J- = = ALL = 478 (ом\, С = 6,68 мкф.
о>С /А 0,235
§ 245. Простейший феррорезонансный стабилизатор напряже-
ния. Принцип стабилизации величины напряжения переменного то-
ка собственно тот же, что и стабилизации напряжения постоянного
* Точка с’ находится на пересечении прямой nk с в. а. х. нелинейной ин-
дуктивности.
335
тока (§ 40), а именно: выходное напряжение снимается с такого участ-
ка цепи, на котором оно по величине остается почти постоянным при
изменении величины входного напряжения.
Для стабилизации напряжения переменного тока широко при-
меняются различные феррорезонапсные схемы. Простейшая из них
представлена на рис. 279, а. Она состоит из параллельного ферро-
резонансного контура и последовательно с ним включенной линей-
ной индуктивности.
На рис. 279, б кривая 1—в. а. х. нелинейной индуктивности;
прямая 2—в. а. х. емкости; кривая 3—в. а. х. параллельного ферро-
резонансного контура; прямая
4 — в. а. х. линейной индуктив-
ности L; кривая 5—результирую-
щая в. а. х всей схемы: ординаты
ее равны сумме ординат кривой 3
и кривой 4.
Намотаем на сердечник линей-
ной индуктивности дополнитёль-
Рис. 279
Рис. 280
ную обмотку w,. и присоединим ее к основной схеме, как показано
пунктиром на рис. 279, а.
Напряжение на выходе стабилизатора равно напряжению на за-
жимах ей минус э. д. с., наводимая в обмотке wK. Последняя линей-
но зависит от тока / (прямая 6 рис. 279, б). Напряжение на выходе
стабилизатора изобразится кривой 7. Ординаты ее равны разности
соответствующих ординат кривой 5 и прямой 6. Зависимость напря-
жения на выходе стабилизатора U№lx от напряжения на входе Uex
при холостом ходе стабилизатора дана на рис. 279, в. Для построе-
ния ее следует придавать току произвольные значения и для каж-
дого его значения по кривым 7 и 5 найти соответствующие величи-
ны иоых и Uex.
336
Стабилизация имеет место только при Uet > 7/1. Поэтому
в область Uex < кривая на рис. 279, в не продолжена.
§ 246. Магнитный усилитель и дроссель насыщения. Устройст-
ва, составленные из нескольких управляемых нелинейных индук-
тивностей и служащие в качестве регулируемых индуктивных соп-
ротивлений, называют магнитными усилителями или дросселями
насыщения.
На схеме рис. 280 к источнику э. д. с. напряжением Uc и часто-
той / последовательно подключены магнитный усилитель и нагруз-
ка RH.
Магнитный усилитель обведен пунктиром на схеме рис. 280.
Он составлен из двух одинаковых управляемых нелинейных ин-
дуктивностей.
Обмотки переменного тока их (отсоединены согласно, а обмот-
ки постоянного тока (w0) — встречно.
Магнитный поток в первом сердечнике назовем Фп во втором Ф2.
Положительные направления потоков показаны стрелками на рис. 280.
Вследствие симметрии обеих половин магнитного усилителя
относительно^ вертикальной прямой А—А (рис. 280) и симметрии
кривой Uc = относительно оси времени о/ в характере из-
менения потоков Фх и Ф2 в функции времени также должна быть
симметрия.
Симметрия состоит в том, что кривая Ф2 =• /(со/) может быть
получена из кривой Фх = /(со/) путем смещения последней на пол-
периода и зеркального отражения относительно оси времени. Дру-
гими словами, имеет место соотношение
Ф2(со/) = —Ф^со/ — л).
Из рис. 280 следует, что потокосцепление обмоток равно
а>_(Ф2+Ф2), а потокосцепление обмоток w0 равно —Ф2).
Если мгновенное значение тока в цепи переменного тока обо-
значить через i, а мгновенное значение тока в цепи управления —•
i0, то по второму закону Кирхгофа можно записать уравнение (а)
для цепи переменного тока и уравнение (б) для цепи управления:
Д- у (Фх + Ф2) = VTUC cos со t-, (а)
at
1^ + ^(Ф1-Ф2) = Ев. (б)
at
Ток i0 в общем случае содержит постоянную составляющую
10 = ~ И переменную i0_ составляющую: iB = /0-Н0~. Форма кри-
Ко ~
вой потока Фх — f (со/) и симметричной ей в указанном выше смысле
кривой Ф2 = f (ю/) зависит от многих факторов: от формы кривой
намагничивания В = f (//), от величины сопротивления 7?0 и от ве-
личины сопротивления /?„, от величины э. д. с. Ео и амплитуды на-
пряжения синусоидальной э. д. с. Но какова бы ни была форма по-
12 Л. А. Бессонов
337
токов, в силу соотношения Ф2(<о?) = —Ф1(о/ — л) сумма потоков
Ф1 + Ф2 может состоять только из нечетных гармоник, а разность
потоков Фх— Ф2 — только из постоянной составляющей и четных
гармоник.
В качестве примера на рис. 281, а показаны зависимости пото-
ков Фх, Ф2, разности Фх —Ф2 и суммы Фх +Ф2 потоков в функ-
ции времени для частного случая работы схемы рис. 280, когда
сопротивление нагрузки ^0 и сопротивление цепи управления
/?0 весьма мало.
На рнс. 281, б показаны зависимости от времени тех же величин,
что и на рис. 281, а, но для другого режима работы, а именно когда
Ro очень велико (/?„ теоретически стремится к бесконечности), а
RH по-прежнему очень мало.
Рис. 281
Сопоставим кривые рис. 281, а с соответствующими кривыми
рис. 281, б. Для обоих рисунков выполняется условие Ф2(со/) =
= —Фх(<в/ — тс). В обоих случаях постоянная составляющая
потока Фх равна и противоположна по знаку постоянной составляю-
щей потока Ф2, в обоих случаях сумма потоков Фх + Ф2 дает си-
нусоиду частоты источника питания, а разность потоков состоит
из постоянной составляющей и четных гармоник. Различие в зна-
ке у постоянных составляющих потоков Фх и Ф2 объясняется тем,
что постоянная составляющая м. д. с. первого сердечника направ-
лена согласно с Фх, а постоянная составляющая м. д. с. второго
сердечника направлена встречно Ф2.
Анализ схемы рнс. 280 может проводиться различными метода-
ми. Чаще всего анализ проводится двумя методами: методом первой
гармоники и методом кусочно-линейной аппроксимации кривой
намагничивания.
Метод первой гармоники находит применение в том случае,
когда сердечники магнитного усилителя выполнены из ферромаг-
нитного материала, например из электротехнических сталей Э4А
338
и ХВП, кривые намагничивания которых имеют плавный харак-
тер, без резкого изгиба.
Если же сердечники магнитного усилителя выполнены из ма-
териала, кривая намагничивания которого приближается к идеаль-
но прямоугольной (см. рис. 262, б), например из материалов 65НП
или 50НП, то анализ схемы рис. 280 целесообразно проводить
методом кусочно-линейной аппроксимации (основы этого метода
см. в § 228, а пример на него — в § 235).
В дальнейшем анализ схем рис. 280 будем проводить методом
первой гармоники, как это и принято в учебной литературе по
ТСЭ.
Из предыдущего известно, что при анализе цепей с управляе-
мыми нелинейными индуктивностями используется семейство вольт-
амперных характеристик по первым гармоникам.
Вольтамперные характеристики по первым гармоникам (см.
§ 204) представляют собой зависимости действующего значения
первой гармоники напряжения на нелинейной индуктивности от
действующего значения первой гармоники тока через нее при токе
управления 10, взятом в качестве параметра.
Из предыдущих рассуждений и построений рис. 281, а и б
ясно, что в любом режиме работы магнитного усилителя постоян-
ная составляющая потока Фх численно равна постоянной состав-
ляющей потока Ф2, а амплитуда первой гармоники потока Фх рав-
на амплитуде первой гармоники потока Ф2. Кроме того, в любом
режиме работы схемы рис. 280 постоянная составляющая м. д. с.
первого сердечника равна постоянной составляющей м. д. с. второ-
го сердечника и каждая из них равна Iowo.
Магнитный усилитель состоит из двух последовательно соеди-
ненных нелинейных индуктивностей.
Вольтамперные характеристики обеих индуктивностей одина-
ковы и имеют качественно такую же форму, как и кривые рис.
243, б. Поэтому семейство вольтамперных характеристик магнит-
ного усилителя подобно семейству кривых рис. 243, б.
' § 247. Применение магнитного усилителя для усиления мощности.
Для объяснения принципа работы схемы рис. 280 обратимся к рис.
282.
На рис. 282 изображена схема, эквивалентная схеме рис. 280
в отношении первой гармоники. Напряжение Uc источника пита-
ния и сопротивление RH в ней те же, что и в схеме рис. 280, а маг-
нитный усилитель замещен его индуктивным сопротивлением Хг
по первой гармонике. Сопротивление Хг является функцией вели-
чины тока подмагничивания /0 и напряжения на обмотках маг-
нитного усилителя и определяется принципиально так же, как
индуктивное сопротивление по первой гармонике для одной не-
линейной индуктивности (см. § 208).
Для схемы рис. 282 действующее значение первой гармоники
переменного тока равно:
12*
339
1 = -~е -
VW + R?
Активная мощность, выделяющаяся в сопротивлении RH,
равна:
Рк = /2/?„.
Если ток подмагничивания /0 магнитного усилителя будет мал,
то сопротивление окажется относительно большим, а ток 1
и мощность Рн будут относительно малыми. При увеличении тока
подмагничивания /0 Хо уменьшится, а ток / и мощность Рн воз-
растут.
Таким образом, путем изменения величины тока подмагничи-
вания можно управлять величиной переменного тока и величиной
активной мощности, выделяющейся в сопротивлении /?в.
Рис. 282
Рис. 283
Если сопротивление цепи подмагничивания RB сделать доста-
точно малым, то активная мощность I^Ro, выделяющаяся в цепи
подмагничивания и затрачиваемая на управление режимом работы
магнитного усилителя, будет значительно меньше той мощности
I2RH, которая выделится в нагрузке RH в цепи переменного тока.
При этом магнитный усилитель будет работать в качестве усилите-
ля мощности.
Способность магнитного усилителя служить в качестве усили-
теля мощности характеризуется величиной коэффициента усиления
по мощности kyM. Под ним понимают отношение приращения мощ-
ности в нагрузке RH к мощности, затраченной в цепи управления:
^ = ^4^. (9.64)
где 1ХХ — ток / в нагрузке при /0 — 0, RB — сопротивление цепи
управления.
340
Для получения количественных соотношений в схеме рис. 28G
воспользуемся семейством вольтамперных характеристик, изобра-
женных на рис. 283.
Под UMy будем понимать действующее значение первой гармо-
ники падения напряжения на магнитном усилителе.
Напряжение на индуктивности (на магнитном усилителе) и на-
пряжение на активном сопротивлении сдвинуты по фазе на 90° по
отношению друг к другу. Сумма квадратов падения напряжения
на магнитном усилителе и нагрузке равна квадрату напряжения
сети. Следовательно,
^жу + (ад=^Л
Поделим обе части равенства на t/c2; обозначим 1макс — тогда
Ян
V 4- = 1. (9.65)
\ Uc / \1макс]
Уравнение (9.65) представляет собой уравнение эллипса. Одна
полуось его равна напряжению сети Uc, другая — току 1микс-
Дуга эллипса изображена на рис. 283. Точки пересечения ее с се-
мейством вольтамперных характеристик магнитного усилителя
дают соответствующие друг другу значения 1 и /0.
Пример 116. Построить кривую / = f (/0) для магнитного уси-
лителя, семейство в. а. х. которого изображено на рис. 283: Uc —
= 60 в; RH = 120 ом. ,
Решение. Определяем полуоси эллипса. Одна полуось
Uc — 60 в, другая
1макс = — = 0,5 (а).
ММлС «О/Л ' *
Эллипс построен на рис. 283. По точкам пересечения его с се-
мейством в. а. х. строим кривую I = Д/о). Она изображена на рис.
284.
Пример 117. Сопротивление цепи обмотки управления магнит-
ного усилителя примера 116 равно А?о = 100 ом. Определить коэф-
фициент усиления по мощности при I = 0,462 а.
Решение. По формуле (9.64) находим:
, 120(0,4622 —0,0752) „с с
==—=3 ’ '
В заключение обсудим важное соотношение, которое имеет ме-
сто в магнитных усилителях.
Среднее за полупериод значение м. д. с., создаваемой перемен-
ным током i, равно постоянной составляющей м. д. с., создаваемой
током управления, т. е.
341
| вреднее “
(a)
Это соотношение, строго говоря, справедливо лишь для магнит-
ных усилителей, сердечники которых имеют идеально прямоуголь-
ную кривую намагничивания, но оно приближенно выполняется
и в магнитных усилителях, кривые намагничивания которых от-
личаются от прямоугольной.
Дадим обоснование соотношению (а).
Если сердечники магнитного усилителя рис. 280 выполнены
из материала с прямоугольной кривой намагничивания, то в силу
прямоугольности кривой намагничивания и рассмотренной в
§ 246 симметрии в работе схемы в течение первого полупериода
следовательно, и создающая
меняется потокосцепление только в
одном, скажем первом, сердечнике,
а в течение второго полупериода —
только во втором сердечнике.
Если потокосцепление в сердеч-
нике с прямоугольной кривой нама-
гничивания меняется, то это озна-
чает, что изображающая точка пе-
ремещается по вертикальному участ-
ку зависимости магнитной индукции
В данного сердечника от результи-
рующей напряженности поля Н дан-
ного сердечника.
На вертикальном участке кривой
В — f(H) напряженность поля Н, а
ее результирующая м. д. с. сердечни-
ка равны нулю.
Но результирующая м. д. с. сердечника равна сумме м. д. с.
управления iowo и м.д.с. переменного тока iw~, т. е.
iou)o + iw~ = 0.
Среднее за полупериод значение этой суммы также равно нулю.
Отсюда и следует соотношение (а).
§ 248. Применение символического метода к расчету нелинейных
цепей и построение для них векторных диаграмм. В § 240—247 рас-
сматривались некоторые довольно грубые явления графическим ме-
тодом, путем использования вольтамперных характеристик по дей-
ствующим значениям и по первым гармоникам.
Изучение аналогичных явлений может производиться и анали-
тически. Важно подчеркнуть, что для нелинейных электрических
цепей применим символический метод, а для каждой из гармоник
может строиться векторная диаграмма*. Если высшие гармоники
выражены слабо, то векторные диаграммы иногда строят и для
* Напомним, что на стр. 329 построена векторная диаграмма для первых
гармоник для лампового генератора.
342
действующих значений величин. Аналитический расчет по пер-
вой гармонике иллюстрируется примером 118.
Применение символического метода и построение векторной диа-
граммы для действующих значений см. в § 249 и 250.
Пример 118. В схеме рис. 285, а Еа = 106,2 в, R = 2 ком.
При каком значении индуктивности L и э. д. с. £\ в цепи будет резонанс
по первой гармонике, если в цепь включен нелинейный конденсатор с такой
же характеристикой, как и в примере 109? Угловая частота <о = 3140 сек-1 и
ток в цепи 11т = 18,45 ма.
Решение. Явление резонанса по первой гармонике состоит в том, что
первая гармоника напряжения на емкости равна первой гармонике напря-
жения на индуктивности; при этом первая гармоника тока в цепи по фазе
совпадает с э. д. с. Ех.
Рис. 285
Используем данные примера 111а. Из них находим, что амплитуда пер-
вой гармоники напряжения на емкости равна:
ипт=з 217,5 в.
Следовательно,
= Ucim =217,5 в,
отсюда
217,5
L =---------------= 3,76 (гн).
0,01845 • 3140 v
Электродвижущая сила
0,01845
£\ = !t R = - -- . 2000 = 26,2 (в).
V *
Так как постоянный ток в цепи не протекает, то постоянная составля-
ющая напряжения на конденсаторе Uq0 равна э. д. с. Ей.
Векторная диаграмма для режима резонанса по первой гармонике в схе-
ме рис. 285, а изображена на рис. 285, б. Так как потери в емкости не учиты-
вались, то напряжение на емкости точно на 90° отстает по фазе от тока.
При рассмотрении характеристик управляемой нелинейной ин-
дуктивности в § 207, при обсуждении основных свойств феррорезо-
нансных схем в § 240—244, при изучении магнитного усилителя
в § 246 и стабилизатора напряжения в § 245 нелинейная индуктив-
343
ность рассматривалась идеализированно, а именно: не учитывались
потери в ее сердечнике, не учитывалось наличие потока рассеяния
и падение напряжения в активном сопротивлении самой обмотки.
Делалось это для того, чтобы основные свойства перечисленных
схем и устройств не «затемнялись» упомянутыми выше факторами.
Теперь настала очередь изучить вопрос о векторной диаграмме
нелинейной индуктивности с учетом этих факторов.
§ 249. Векторная диаграмма нелинейной индуктивности. Нели-
нейная индуктивность изображена на рис. 286, а. Активное сопро-
тивление самой обмотки w назовем 7?.
Протекающий по обмотке ток создает в сердечнике магнитный
поток. Большая часть этого потока — поток Фт—замыкается по
сердечнику, а меньшая часть — поток Ф4 — по воздуху. Поток Фт
называют основным потоком, а поток Ф4— потоком рассеяния.
Обычно поток Ф4 составляет всего несколько процентов от по-
тока Фт. Однако могут быть и такие режимы работы, в которых
а)
поток Ф^ оказывается соизмеримым с потоком Фт. Такие режимы
имеют место, если сердечник работает при большом насыщении
или когда в сердечнике имеется относительно большой воздушный
зазор 8.
При построении векторной диаграммы заменим в действитель-
ности несинусоидальный ток и несинусоидальный поток эквива-
лентными синусоидальными величинами.
Отношение потокосцепления рассеяния ьуФ4 к току I при-
нято называть индуктивностью рассеяния и обозначать Lsl
Ls = ^ = ^. (9.66)
Индуктивное сопротивление Xs = wLs называют индуктивным
сопротивлением рассеяния.
Схема замещения нелинейной индуктивности изображена на
рис. 286, б. Она отличается от схемы рис. 231, а тем, что в ней
добавлено сопротивление Xs. В неразветвленной части схемы вклю-
чены активное сопротивление R обмотки w и индуктивное сопротив-
ление рассеяния Xs.
344
На участке cb есть две ветви. Правую ветвь образует идеализи-
рованная нелинейная индуктивность, по которой проходит намаг-
ничивающий ток 1р. Левую ветвь образует активное сопротивление,
потери в котором равны потерям Рс на гистерезис и на”вихревые
токи в сердечнике нелинейной индуктивности. По левой ветви те-
чет ток
Рс
Ucb
(9.67)
На рис. 286, в изображена векторная диаграмма нелинейной
индуктивности в соответствии со схемой рис. 286, б. Эта векторная
диаграмма строится так же, как и для обычных линейных схем.
Начнем ее построение с построения потока Фт.
Оба потока (Фт и Ф4) пронизывают обмотку w рис. 286, а
и наводят в ней э. д. с. самоиндукции.
Напряжение Ucb на зажимах идеализированной нелинейной
индуктивности равно по величине и противоположно по знаку
э. д. с. самоиндукции, возникающей в обмотке w схемы рис. 286, а
под действием основного потока Фт:
Ucb=jaJW-^r.
V 2
Деление Фт на 1^2 объясняется переходом от амплитудного
значения потока к действующему. Напряжение tjcb на 90° опере-
жает поток Фт.
Ток 1р — это ток через идеализированную индуктивность (т. е.
через индуктивность, в сердечнике которой нет потерь энергиии);
он на 90° отстает от напряжения Vcb и по фазе совпадает с по-
током Фт. Ток 1С совпадает по фазе с напряжением Ucb. О том,
как определять токи 1р и 1С, сказано в следующем параграфе.
По первому закону Кирхгофа 7 = 1р -ф- 1С.
Напряжение Uab на входе схемы равно геометрической сумме
напряжения Ucb, падения напряжения /7? в активном сопротивле-
нии и падения напряжения jIXs в индуктивном сопротивлении
рассеяния.
Обратим внимание на то, что величина тока 1р и величина то-
ка 1С не пропорциональны величине напряжения Ucb, а следователь-
но, и величине напряжения Uab на входе схемы.
Другими словами, если напряжение Uab увеличить, скажем, в
1,3 раза, то токи 1р и 1С увеличатся не в 1,3 раза, а больше, чем в
1,3 раза.
345
При построении векторной диаграммы мы исходили из того, что величина
напряжения Ucb известна. По напряжению мы определили токи / и 1С и
затем нашли напряжение Uab на входных зажимах индуктивной катушки.
Однако обычно бывает известно напряжение Uob, а напряжение Ucb не-
известно. Поэтому прн построении векторной диаграммы при заданном Uab сна-
чала следует разобраться, может ли напряжение Ucb в исследуемом режиме
работы схемы значительно отличаться от напряжения Uab.
Если падения напряжения в сопротивлениях R и Xs составляют малую
величину по сравнению с Uab, например всего 3—8% от Vub, то можно в пер-
вом приближении считать, что U(b fc Uab. Если же падения напряжения в со-
противлениях 7? и Xs соизмеримы с напряжением Ucb, то тогда для определе-
ния напряжения 1)сЬ приходится проделывать вспомогательную работу, а именно:
построить векторные диаграммы для нескольких значений Ucb, например рав-
ных 1; 0,9; 0,8; 0,7 от Uub, для каждого из этих значений Ucb найти свое Dob,
по результатам построить вспомогательную кривую l/eb — f (Uab), из нее найти
Ucb при заданном Uab н затем уже строить искомую векторную диаграмму.
§ 250. Определение величины намагничивающего тока и величины
тока потерь. Ток /0 и его составляющие /и и 1С находят либо опыт-
ным путем, либо аналитическим.
Рассмотрим вопрос об аналитическом определении их. Если
через I обозначить длину (л) средней магнитной линии на пути
в стали (рис. 287), через 6 длину «воздушного» зазора (лг) в маг-
нитной цепи, через В мгновенное значение магнитной индукции
в тл, через Н мгновенное значение напряженности поля в сердеч-
нике в а/м, то мгновенное значение намагничивающего тока iv. в а
на основании закона полного тока равно (см. стр. 75);
Н/+0.8Й6 • 10»
. (9.68)
На векторной диаграмме откладывается действующее значение
намагничивающего тока /()..
Для определения действующего значения намагничивающего тока надо
(ф„,\
Вт —---- , Н заменить на
a sh (pBm sin и/), разложить гиперболический синус от периодического аргу-
мента в ряд по функциям Бесселя (см. формулу 9.14) и воспользоваться фор-
мулой (8.11'), при помощи которой определяется действующее значение тока
через амплитуды отдельных гармоник. В результате получим
/„=& х
W1
Л 0,8 106]2г————————’ ~ -
X У [-/А 9Ж,) + —~—J + [jJ3 (if>Bm)]2 +[- jj5 (j$Bm)]2 +....
(9.69)
Если воздушный зазор 6 = 0, то формула (9.69) упрощается:
/р = У [- /Л (/PBm)J2 + [/Л (/ps„,)]2 + [- /Л (/₽йт)12 + ... (9.70)
В свою очередь ток /с, обусловленный потерями в стальном
сердечнике, определяется как частное от деления потерь в сердеч-
нике от вихревых токов и гистерезиса на величину э.д.с., наведен-
346
ную рабочим потоком Фт в обмотке w, и равную напряжению
исЬ-
= (9.71)
и сЬ
Ueb = ?^ = 4,44fW1<Zm,
где Рс — полные потери в стали от вихревых токов и гистерезиса:
Рс = трс;
здесь т — масса сердечника в кг; рс — потери в 1 кг сердечника.
На рис. 288 изображена кривая, вы-
/„ к>1
ражающая собой зависимость !_- - =
}<2а1
= / (Psm), построенная по формуле
(9.70). При помощи этой зависимости по
PBm находится
Ip. wt
VTal
, а затем опреде-
ляется а и I известны).
Величина потерь в 1 кг электро-
технической стали прн индукциях 1,0 и
1,5 тл и частоте 50 гц нормирована государственным стандартом ГОСТ 802-58.
Обозначим: р( 0 — потерн в 1 кг стали при Вт = 1 тл и f = 50 гц;
pj 5 —потери в 1 кг стали при Вт = 1,5 тл и f = 50 гц.
Значения Р] 0 и р) 5 приведены в следующей таблице:
Марка стали Толщина листа, мм р, 0 вт1кг pi 5 вт-кг
Э41 0,5 1,6 3,6
Э42 0,5 1,4 3,2
Э43 0,5 1,25 2,9
Э41 0,35 1,35 3,2
Э42 0,35 1,2 2,8
Э43 0,35 1,05 2,5
Потери прн других индукциях и частотах, мало отличающихся от 50 гц,
определяются следующей эмпирической формулой;
347
/ f \1,3
Рс = ₽1,ов" вт1кг>
Pl,5
n - 5,691g —— .
Pl.o
(9-71)
§ 251. Основные соотношения для трансформатора со стальным
сердечником. В § 116 рассматривались соотношения, характеризую-
щие работу трансформатора, для которого зависимость между на-
пряженностью поля и потоком в сердечнике была линейной, а поте-
ри в сердечнике отсутствовали.
Для улучшения магнитной связи между первичной (ьух) и вто-
ричной (ет2) обмотками трансформатора сердечник его выполняется
из ферромагнитного материала*.
В данном параграфе рассматриваются соотношения, характери-
зующие работу трансформатора с учетом того, что зависимость
между напряженностью поля и потоком в ферромагнитном (сталь-
Рис. 289
ном) сердечнике нелинейна, а также с учетом того, что в сердечнике
есть потери, обусловленные гистерезисом и вихревыми токами.
Для уменьшения тока холостого хода стремятся сердечник тран-
сформатора изготовить таким образом, чтобы он имел возможно
меньший воздушный зазор, расположенный перпендикулярно маг-
нитному потоку, либо совсем не имел его.
В силу нелинейной зависимости между потоком и напряженно-
стью поля в сердечнике по обмоткам трансформатора протекают
несинусоидальные токи**.
Анализ работы трансформатора будем проводить, заменив в дей-
ствительности несинусоидальные токи и потоки их эквивалентны-
ми в смысле действующего значения величинами. Комплекс дейст-
вующего значения тока первичной обмотки /г, комплекс действующе-
го значения тока вторичной обмотки — /2; Фт — амплитуда основ-
ного магнитного потока, проходящего по сердечнику трансфор-
* На рис. 289 и 290 для большей наглядности обмотки Wj и w2 показа-
ны находящимися на разных стержнях. Практически их располагают обыч-
но на одном и том же стержне.
** Несинусоидальность проявляется главным образом в режимах работы,
близ! их к холостому ходу.
348
матора, пронизывающего обе обмотки wx и ьу2 и наводящего
в них э.д.с.
Вследствие наличия рассеяния небольшой по сравнению с Фт
поток Ф1? — поток рассеяния первичной обмотки — замыкается по
воздуху, образуя потокосцепление только с обмоткой ьух. Другой,
также небольшой по сравнению с Фт поток — поток рассеяния
.вторичной обмотки Ф25 — замыкается по воздуху, сцепляясь толь-
ко с обмоткой ЬУ2.
Полагают, что потокосцепление потока Ф1Л с обмоткой w1 про-
порционально току /х:
= ^Фи — Л* (9.72)
Коэффициент пропорциональности Lls между потокосцеплением
фХл и током 7Х называют индуктивностью рассеяния первичной
обмотки; Lls зависит от числа витков и конструкции обмотки.
Принимают также, что потокосцепление ф25 потока Ф24 с об-
моткой ьу2 пропорционально току вторичной цепи /2:
К = ^2Ф26. = Lj2. (9.73)
Коэффициент пропорциональности между потокосцепле-
нием” ty2i, обусловленным потоком рассеяния Ф25, и током /2 на-
зывают индуктивностью рассеяния вторичной обмотки; L^. зави-
сит от числа витков и конструкции вторичной обмотки.
Индуктивное сопротивление первичной обмотки, обусловлен-
ное потоком рассеяния Ф15, обозначают Х14.:
XXi = <bLu. (9.74)
Аналогично, индуктивное сопротивление вторичной обмотки,
обусловленное потоком рассеяния Ф24 , обозначают
= G)L2i. (9.75)
Пусть 7?х — активное сопротивление первичной цепи, Д2 —
активное сопротивление вторичной обмотки, Z„ — сопротивление
нагрузки.
На рис. 290 изображена схема того же трансформатора, что и
на рис. 289, но на ней активные сопротивления и индуктивные со-
противления, обусловленные потоками рассеяния, представлены
отдельно выделенными сопротивлениями: 7?х, X л, /?2, Xs2. Запи-
шем уравнение по второму закону Кирхгофа для обеих цепей.
Для первичной цепи
+ /Vx Д- /<^х = (7Х. (9.76)
349
Для вторичной цепи
/2Яа + + /®«>2 +ин = 0. (9.77)
V 2
ф„
Здесь /(ОКУ!—— напряжение, численно равное э. д. с., на води-
17” 2
мой в обмотке wt основным рабочим потоком Фт. Деление Фт на
1^2 объясняется переходом от амплитудного значения к действу-
Ф
ющему. Аналогично, — напряжение, численно равное
]Л2
э. д. с., наводимой в обмотке wz основным рабочим потоком Фт.
Обозначим ток Д при холостом ходе трансформатора через /0-
Магнитодвижущая сила трансформатора при холостом ходе равна
М. д. с. трансформатора при наличии тока /а равна Ц-
-ф- i2w2. Трансформаторы конструируют обычно таким образом,
что падения напряжения и 1гХ31 много меньше, чем паде-
ние напряжения ыщ, Фп\ Если это учесть, то для правильно
V 2
сконструированных трансформаторов уравнение (9.76) запишется
так:
jaWy U,. (9.76')
V 2
Последнее уравнение справедливо как при холостом ходе, так
и при нагрузке. Другими словами, при переходе от холостого хода
к режиму работы при нагрузке поток Фт практически остается
неизменным по величине.
Но если в этих двух режимах Фт одно и то же, то должны быть
равны и создающие его м. д. с. в этих двух режимах, т. е.
/1и)1 + /2щ2 = />1. (9,78')
Отсюда, поделив обе части равенства на wlt получим:
Л=4+М (9.78)
где
Таким образом, ток первичной цепи l\ может быть представ-
лен как геометрическая сумма двух токов: тока холостого хода
10 и тока Г2. Ток /2 принято называть приведенным (к числу вит-
350
ков первичной обмотки) вторичным током. Он численно равен то-
ку /2, измененному в — раз.
Кроме того, в правильно сконструированных трансформаторах
падения напряжения /2/?2 и/2Х.2 малы по сравнению с ши» 2 -Ф2з»
Г 2
поэтому из уравнения (9.77) следует, что приближенно
/юа, (9.79)
V 2
Если почленно поделить (9.76') на (9.79) и перейти к модулям,
то получим:
L'-(9.80)
1/„ w2
т. е. отношение напряжения на входе трансформатора к напряже-
нию на выходе трансформатора (на нагрузке) приблизительно рав-
но отношению числа витков первичной обмотки к числу витков
вторичной обмотки.
В правильно сконструированных трансформаторах при нагруз-
ке, близкой к номинальной, ток /0 составляет всего 1—10% тока
/х; поэтому уравнение (9.78) можно приближенно представить так:
7X©X^—/2Щ2.
Между модулями токов /х и /2 при нагрузке, близкой к но-
минальной, имеет место следующее приближенное соотношение:
(9.81)
Другими словами, ток /х почти пропорционален току /2.
Эта пропорциональность немного нарушается за счет тока хо-
лостого хода
В активных сопротивлениях вторичной цепи выделяется энер-
гия. Эта энергия переносится магнитным потоком из первичной
цепи во вторичную и восполняется источником питания схемы.
§ 252. Векторная диаграмма трансформатора со стальным сердеч-
ником. На рис. 291, а изображена векторная диаграмма при индук-
тивной нагрузке
!Хн-
Построение диаграммы начнем с тока /2, расположив его про-
извольно. Под углом <рк = arc tg — к нему расположим вектор на-
Ян
пряжения на нагрузке йн. Прибавим к йн векторы i2R<* и I2jXs2.
На рис. 291, а вектор 12R2 должен быть параллелен вектору 7а,
351
Сумма падений напряжения во вторичной цепи равна нулю. Это
дает возможность построить вектор коо>2 Далее строим век-
V 2
тор Фт|он на 90° отстает от вектора /сои>2-^£|.
V V2/
В сердечнике трансформатора, как и в сердечнике нелинейной
индуктивности, есть потери, обусловленные гистерезисом и вихре-
выми токами. Благодаря этому ток холостого хода 70 состоит из
геометрической суммы намагничивающего тока /„ и тока потерь 1С
(рис. 291, б):
4 = Л 4-4-
Рис. 291
Ток /р. совпадает по фазе с потоком Фт, а ток 1С опережает
поток Фт на 90°.
Токи /ц и 1С определяют так же, как для нелинейной индуктив-
ности.
Ток холостого хода /„ опережает поток Фт на некоторый
угол у.
В соответствии с уравнением (9.78) ток Ц равен геометричес-
кой сумме тока L и тока /' =— /2—. Геометрическая сумма па-
дений напряжений/х/Х41и/cooij—дает напряжение на
]Л2
входе первичной цепи Uv
С целью удобочитаемости рис. 291, а на нем не выдержаны
имеющие место в действительности соотношения между модулями
напряжений, а также между модулями токов.
352
Пример 119, Повышающий трансформатор имеет сердечник из трансфор-
маторной стали Э41 (толщина листов 0,5 мм). Кривая намагничивания
Н = 0,71 sh (5,75 В). Сердечник выполнен из пластин, имеющих форму колец
и не имеющих воздушного зазора: = 250; ау2 = 1750; S = 2,2 см2; I = 25 см.
Пренебрегая Rt и Ха, определить ток холостого хода /0 при Ui ==> 15 в и
f = 50 гц.
U
Решение. Вт = ------------ = 1,22 тл.
4,44/ teijS
Произведение f>Bm = 5,75 • 1,22 = 7,02. По кривой рис. 288 при fBm=7,02
находим:
Но
а<У"2 = 0,71 -0,25 У 2~
250
Следовательно, = 185 • IO'*3 = 0,185 (а). Масса сердечника т =
= 7,8 г/см2 • 2,2 см2 -25 см = 0,428 кг. Из таблицы находим: = 1,6 вт/кг,
Р\ 5 = 3,6 вт /кг-.
3,6
« = 5,691g — « 1,13.
1,6
Удельные потери в стали при Вт = 1,22 тл-.
рс = 1,6 - 1.221,13 • 1 = 2,1 (вт/кг).
Потери в сердечнике массой 0,428 кг.
Рс = 0,428 • 2,1 = 0,9 (вт).
Рс 0,9
Ток, обусловленный потерями в стали 1С = — = 0.06(a). Ток хо-
лостого хода /о практически равен току 1^.
Пример 120. Ко вторичной обмотке трансформатора предыдущего приме-
ра включена нагрузка индуктивного характера ZH = 300 + j 300 ом. Пре-
небрегая активными сопротивлениями и индуктивностями рассеяния обмо-
ток, найти ток 7t.
Решение. Направим потом Фт по оси действительных значений (рис.
и>2 1750
291, а). Напряжение на нагрузке 17а = 1/х — = 15 • —— = 105(e). Комплекс
юх 250
напряжения {/2 = 105 е~s0° в:
U2 105е_/ 90° . l4RO
12 = — =--------77Г- = 0,248 е~’ 135 = 0,176 — j 0,176 а.
ZH 423 е' 45 '
Приведенный ток
/' = —Д— = 1,23 + / 1,23 а.
3 wt
Ток
/1=4 + Г = 0,185 + / 0,06 + 1,23 + / 1,23 = 1,92 е< 42<,2°' а.
Глава десятая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ
В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
§ 253. Введение. До сих пор мы ограничивались расчетом и изу-
чением свойств электрических цепей постоянного, синусоидального
и периодического несинусоидального токов. Как происходит уста-
новление режима в цепи при включении и отключении источников
э. д. с., по каким законам происходит переход от одного режима к
другому при изменении параметров цепи, при отключении и под-
ключении ветвей, при коротких замыканиях и подобных им процес-
сах, — все эти вопросы до сих пор были вне нашего внимания.
В данной главе будут изучаться переходные процессы. Под пе-
реходными процессами будем понимать процессы перехода от одного
режима работы электрической цепи (обычно периодического) к дру-
гому (обычно также периодическому), чем-либо отличающемуся от
предыдущего, например: величиной амплитуды, фазы, формой или
частотой действующей в схеме э. д. с., значениями параметров схе-
мы, а также конфигурацией цепи.
Периодическими режимами обычно являются режим синусои-
дального тока, режим постоянного тока, а также такой режим, как
режим отсутствия тока в ветвях цепи.
Переходные процессы вызываются коммутацией в цепи. Комму-
тацией называют процесс замыкания или размыкания рубильни-
ков или выключателей.
Операцию, которую производят над рубильником, на рисунках
поясняют стрелкой. Так, операция включения рубильника на схе-
мах показывается, как правило, в соответствии с рис. 292, а, а опе-
рация размыкания рубильника — в соответствии с рис. 292, б.
Переходные процессы обычно являются быстропротекающими
процессами; длительность их составляет часто десятые, сотые, а
иногда даже миллионные доли секунды; сравнительно редко про-
исходят переходные процессы, длительность которых составляет
секунды и десятки секунд. Тем не менее изучение переходных про-
цессов весьма важно, так как оно позволяет выявить возможные
354
превышения напряжения на отдельных участках цепи, которые
могут оказаться опасными для изоляции установки, позволяет
выяснить возможные увеличения амплитуд токов, которые могут
в десятки раз превышать амплитуду тока установившегося перио-
дического процесса.
Изучение переходных процессов позволяет решать и такие во-
просы, как вопрос о том, как деформируются по форме и амплитуде
сигналы при прохождении их через усилители, фильтры и другие
радиотехнические устройства.
§ 254. Задача о переходном процессе в любой линейной электри-
ческой цепи с сосредоточенными параметрами сводится к решению
линейного дифференциального уравнения с постоянными коэффи-
циентами*. Запишем уравнения по второму закону Кирхгофа для
Рис. 292
Рис. 293
схемы рис. 293 при замкнутом рубильнике. Сумма падений напря-
жения на индуктивности L и сопротивлении равна э. д. с. Е:
ul + Ri = Е,
или
L-^-Ri = E. (10.1)
dt
Как известно из математики, уравнение, содержащее неизвест-
ную функцию (в нашем случае t) и ее производные (в нашем слу-
чае L — j , называется дифференциальным уравнением.
Таким образом, задача об определении тока как функции вре-
мени по сути дела есть задача о решении дифференциального урав-
нения.
Из курса математики известно, что решение дифференциального
уравнения есть не что иное, как отыскание функции, удовлетворяю-
щей дифференциальному уравнению. Подстановка этой функции и
ее производных превращает дифференциальное уравнение в тож-
дество.
Решение линейных дифференциальных уравнений будет прово-
диться в данной главе тремя методами: классическим, оператор-
ным и методом, использующим интеграл Дюамеля.
* Имеются в виду цепи с неизменными во времени параметрами R, L,
С, М.
355
Перед тем как изучать эти методы, необходимо рассмотреть
общие свойства линейных цепей при переходных процессах, а
также общие законы, которым подчиняются переходные процессы
в линейных электрических цепях.
Перечисленным вопросам посвящены § 255—278.
Рассматриваемые в § 255—278 вопросы имеют отношение ко
всем перечисленным выше методам расчета переходных процессов,
однако часть этих параграфов (§ 255, 261, 263, 264 и 265) следует
рассматривать также как введение к классическому методу расчета
переходных процессов.
§ 255. Принужденные и свободные составляющие токов и напря-
жений. Из курса математики известно также, что общий интеграл
линейного дифференциального уравнения равен сумме частного
решения неоднородного уравнения плюс полное решение однород-
ного уравнения.
Частное решение уравнения (10.1) равно— (£—постоянная э. д. с.)..
R
Однородное уравнение получается из исходного, если в нем
взять правую часть равной нулю. В нашем случае
Z.S + W=O.
Решением однородного уравнения является показательная функ-
ция вида Aept.
Для всех переходных процессов условились, что момент t = 0
соответствует моменту коммутации.
Лир есть некоторые постоянные числа, независящие от време-
ни. Без вывода дадим значения их для рассматриваемого примера:
Л = -* ир = -*.
R L
Следовательно, решение уравнения (10.1) запишется так:
я.
Е Е -l*
i = —----е
R R
о Е
в нем слагаемое — есть частное решение неоднородного урав-
Е ~~
нения (10.1), а слагаемое — — е —общее решение однородно-
го уравнения (10.2). Подстановка (10.3) в (10.1) дает тождество:
--------
dt\R R
R\ L
(Ю.2)
(10.3)
е~"‘
R I
Л'
Ее L — E.
356
Следовательно, (10.3) действительно является решением урав-
нения (10.1).
Частное решение неоднородного дифференциального уравнения
будем называть принужденной составляющей тока (или, соответ-
ственно, напряжения), а полное решение однородного уравнения —
свободной составляющей.
Так, применительно к рассмотренному выше примеру принуж-
денная составляющая тока равна — , а свободная составляющая
Е
Е ~~г
----е « Для того чтобы различать, о каком токе (полном,
А
принужденном или свободном) идет речь, условились принужден-
ную составляющую снабжать индексом пр, свободную — индек-
сом св- полная величина без индекса. Так,
i = ‘пр +‘св-
Кроме индексов пр и св, токи и напряжения могут иметь и допол-
нительные индексы, соответствующие номеру ветвей на схеме.
Принужденная составляющая тока или напряжения физиче-
ски представляет собой составляющую, изменяющуюся с той же
частотой, что и действующая в схеме принуждающая э.д.с. Так,
если в схеме действует принуждающая синусоидальная э.д.с. ча-
стоты со, то принужденная составляющая любого тока и любого
напряжения в схеме представляет собой соответственно синусои-
дальный ток или синусоидальное напряжение частоты со.
Определяются принужденные составляющие в цепи синусои-
дального тока при помощи символического метода (см. главу пя-
тую). Если в схеме действует источник постоянной э.д.с (как,
например, в схеме рис. 293), то принужденный ток есть постоян-
ный ток и находится он при помощи тех методов, которые были
изучены в главе первой.
Следует иметь в виду, что постоянный ток через емкость не
проходит, поэтому принужденная составляющая тока через ем-
кость в цепях с источниками постоянной э.д.с. равна нулю. Кроме
того, напомним очевидное положение — падение напряжения на
индуктивности от неизменного во времени тока равно нулю.
Во всех линейных электрических цепях свободные составляю-
щие токов и напряжений затухают во времени по показательному
закону ept. Так, в рассмотренном выше примере
С увеличением времени t множитель е L * быстро уменьшает-
ся. Название «свободная» составляющая объясняется тем, что эта со-
357
ставляющая есть решение уравнения, «свободного» от вынуждаю-
щей силы (однородного уравнения без правой части).
Из трех токов (полного, принужденного и свободного) и трех
напряжений (полного, принужденного и свободного) основное
значение имеют полный ток и полное напряжение.
Полный ток является тем током, который в действительности
протекает по той или иной ветви цепи при переходном процессе.
Его можно измерить и записать на осциллограмме. Аналогично, пол-
ное напряжение — это то напряжение, которое в действительности
имеется между некоторыми точками электрической цепи при пере-
ходном процессе. Его также можно измерить и записать на осцилло-
грамме.
Что касается принужденных и свободных составляющих токов
и напряжений во время переходного процесса, то эти составляющие
играют вспомогательную роль; они являются теми расчетными
компонентами, сумма которых дает действительные величины.
При любых переходных и установившихся процессах соблю-
даются два основных положения: ток через индуктивность и напря-
жение на емкости не могут изменяться скачком. Рассмотрим эти
положения.
§ 256. Ток через индуктивность и напряжение на емкости не мо-
жет изменяться скачком*. Доказательство того, что ток через индук-
тивность не может изменяться скачком, проведем на примере схемы
рис. 293. По второму закону Кирхгофа
dt 1
Ток I и э.д.с. Е могут принимать только конечные (не бесконеч-
но большие) значения.
Допустим, что ток I может измениться скачком. Скачок тока
означает, что за бесконечно малый интервал времени А/, стремя-
щийся к нулю, ток изменится на конечную величину Ай При этом
= со. Если вместо L — в уравнение (10.1) подставить оо, толе-
вая часть уравнения не будет равна правой части и не будет вы-
полнен второй закон Кирхгофа.
Следовательно, допущение о возможности скачка тока через
индуктивность противоречит второму закону Кирхгофа.
Невозможность скачка тока через L следует также и из энерге-
тических соображений. Действительно, если допустить, что ток
через L может измениться скачком, то скачком изменится и запас
энергии в магнитном поле индуктивной катушки (Ди»Л[). Конеч-
ное приращение энергии магнитного поля &wM можно представить
в виде произведения мощности источника энергии Р на время Д(,
за которое произошло приращение энергии. Отсюда
Они могут изменяться только плавно, без скачков.
358
Р = lim = оо.
Af-»O А/
Но ни один из источников энергии не может отдавать в цепь
бесконечно большую мощность.
Ток через L не может измениться скачком, но напряжение на
индуктивности, равное L— скачком измениться может. Это не
dt
противоречит второму закону Кирхгофа и энергетическим соотно-
шениям.
Доказательство того положения, что напряжение на емкости
не может изменяться скачком, проводится аналогично доказатель-
ству первого положения.
Рис. 294
Обратимся к простейшей цепи с емкостью (рис. 294, а). Соста-
вим для нее уравнение по второму закону Кирхгофа:
Ri + ис = Е.
В нем Е — э.д.с. источника, конечная величина, ис — напря-
жение на емкости.
Так как
то
RC^~-\-uc = E. (10.4)
dt
Если допустить, что напряжение ис может измениться скачком, то
= °° И левая часть уравнения (10.4) не будет равна
правой части. Отсюда следует, что допущение о возможности скач-
кообразного изменения напряжения на емкости противоречит вто-
рому закону Кирхгофа.
Можно показать, что допущение о возможности скачка «с про-
тиворечит и энергетическим соотношениям*.
* Это доказательство проводится аналогично тому, как проводилось до-
казательство невозможности скачка тока, исходя из энергетических соотно-
шений.
359
Однако ток через емкость, равный С^~- может изменяться
at
скачком; это не противоречит второму закону Кирхгофа и энерге-
тическим соотношениям.
Из перечисленных выше двух основных положений следуют два
закона коммутации.
§ 257. Первый закон коммутации. Ток через любую индуктивность
непосредственно до коммутации — назовем его iz, (0_) — равен току
через ту же индуктивность непосредственно после коммутации —
назовем его о. (0+) , т. е.
/г(0_) = /д(0+). (10.5)
Время t = 0_ есть время непосредственно до коммутации, t = 0+
есть время непосредственно после коммутации (рис. 294, б). Равен-
ство (10.5) и выражает собой первый закон коммутации.
§ 258. Второй закон коммутации. Обозначим напряжение на ем-
кости непосредственно до коммутации через ис (0_) и через ис (0+)—
напряжение на ней непосредственно после коммутации.
В соответствии с невозможностью скачка напряжения на ем-
кости
ис (0_) = ис (б+). (10.6)
Равенство (10.6) выражает собой второй закон коммутации.
Перед тем как приступить к изучению методов расчета переход-
ных процессов, необходимо условиться о некоторых дополнитель-
ных определениях.
§ 259. Что понимают под начальными значениями величин? Под
начальными значениями (в литературе их называют еще начальны-
ми условиями) понимают значения токов и напряжений в схеме при
t = 0.
Как уже говорилось, токи через индуктивности и напряжения
на емкостях непосредственно после коммутации всегда равны их
значениям непосредственно до коммутации. Что касается осталь-
ных величин: напряжений на индуктивностях, напряжений на
активных сопротивлениях, токов через емкости, токов через актив-
ные сопротивления, то все эти величины могут изменяться скач-
ком, и потому их значения непосредственно после коммутации ча-
ще всего оказываются не равными их значениям до коммутации.
Поэтому следует различать докоммутационные и послекоммута-
ционные начальные значения.
§ 260. Докоммутационные и послекоммутационные начальные зна-
чения. Докоммутационными начальными значениями условимся на-
зывать значения токов и напряжений непосредственно до коммута-
ции (при t — 0_ ). Послекоммутационные начальные значения —
значения токов и напряжений непосредственно после коммутации
(при t = 0+).
360
Ч Л С
-с/Ъ-СЭ'Т'-
а R, 4
'4
/?г
С
d
Рис. 295
§ 261. Независимые и зависимые (послекоммутационные) на-
чальные значения. Для любой схемы после происшедшей в ней ком-
мутации можно записать уравнения по законам Кирхгофа. Из этих
уравнений можно определить значения токов во всех ветвях и на-
пряжений на любых участках схемы в послекоммутационном режи-
ме (при t = 0+).
G этой целью значения токов в ветвях, содержащих индуктивно-
сти и значения напряжений на конденсаторах, берутся равными
тем значениям, которые они имели в режиме до коммутации при
t — 0_, а остальные токи и напряжения после коммутации нахо-
дятся из уравнений Кирхгофа, поскольку часть слагаемых в них
известна. Значения токов через индуктивности и напряжения на
емкостях, известные из докоммутаци-
онного режима, условимся называть
независимыми начальными значениями.
Значения остальных токов и напря-
жений при t = 0+ в послекоммутацион-
ной схеме, определяемые по независи-
мым начальным значениям из законов
Кирхгофа, будем называть зависимыми
начальными значениями.
§ 262. Нулевые и ненулевые начальные условия. Если к началу
переходного процесса непосредственно перед коммутацией все
токи и все напряжения на пассивных элементах схемы равны нулю,
то говорят, что в схеме имеют место нулевые начальные условия.
Если же к началу переходного процесса токи и напряжения в схе-
ме не равны нулю, то говорят, что в схеме имеют место ненулевые
начальные условия.
При нулевых начальных условиях токи в индуктивностях и на-
пряжения на емкостях начнут изменяться с нулевых значений,
при ненулевых условиях — с тех значений, которые они имели не-
посредственно до коммутации.
§ 263. Составление уравнений для свободных токов и напряжений.
Для послекоммутационной схемы составляются уравнения по за-
конам Кирхгофа для полных токов и напряжений так же, как это
делалось и раньше. Л именно: сначала обозначаем токи в ветвях
и произвольно выбираем для них положительные направления. За-
тем составляем уравнения по первому и второму законам Кирхгофа.
Так, для схемы рис. 295 после выбора положительных направлений
для токов запишем:
4 1*2 4 '— 0;
at
4^2 — J i3dt = 0.
361
В этих уравнениях i\, i2 и i3 — полные токи. Каждый из них
состоит из свободного и принужденного токов. Для того чтобы
от этой системы уравнений перейти к уравнениям для свободных
токов, «освободим» систему от вынуждающих э. д. с. (в нашем слу-
чае от э. д. с. Е) и вместо запишем i1CB, вместо i2 — i2<0 и т- Д-
Получим:
ев С св ?3 св О,
+ (Ю7)
С св R?. 77 f 13 св =
Cf J
Заметим, что для любого контура любой электрической цепи
сумма падений напряжений от свободных составляющих токов
равна нулю.
§ 264. Алгебраизация системы уравнений для свободных токов.
В § 255 говорилось о том, что свободный ток представляет собой ре-
шение однородного дифференциального уравнения (уравнения без
правой части).
Как известно из курса математики, решение однородного диф-
ференциального уравнения записывается в виде показательных
функций Aept. Таким образом, каждый свободный ток может быть
представлен в виде:
iee = Aept-
Постоянная интегрирования А для каждого свободного тока —
своя (или свои), а показатели затухания р одинаковы для всех
свободных токов. Физически показатели затухания одинаковы
для всех свободных токов потому, что вся цепь охвачена единым
(общим) переходным процессом.
Составим производную от свободного тока:
^- = £(Л^) = м^ = р4в.
Следовательно, производная от свободного тока может быть
заменена произведением piCB, а свободное напряжение на индук-
тивности L на LpiCB. Найдем интеграл от свободного тока:
J J Р Р
Постоянную интегрирования взяли здесь равной нулю, так
как свободные составляющие не содержат от времени не завися-
щих слагаемых.
Следовательно, интеграл от свободного тока можно заменить
на а свободное напряжение на конденсаторе J ice di па ~«
362
В систему дифференциальных уравнений для свободных токов
вместо L подставим LpiCl3 и вместо — С i в dt -» — . Получим:
dt С J Ср
Ч св Ч св hce ~ О»
(^1Р “Ь Ч св 4“ Ч св^г ~ 0» (10 8)
»-гсЛ-^ = о.
Ср
Система уравнений (10.8) представляет собой систему алгебра-
ических уравнений относительно ilce, i2ce, i3ce и, в отличие от
исходной системы, не содержит производных и интегралов.
Переход от системы линейных дифференциальных уравнений
к системе алгебраических уравнений называют алгебраизацией
системы дифференциальных уравнений для свободных токов. Мож-
но сказать, что система (10.8) есть результат алгебраизации систе-
мы дифференциальных уравнений (10.7).
§ 265. Составление характеристического уравнения системы. Чис-
ло алгебраических уравнений равно числу неизвестных свободных
токов. Положим, что р нам известно (в действительности оно пока
не найдено и будет определено в дальнейшем), и решим систему
(10.8) относительно ilce, i2ce и iSce. Получим:
; _ М . : _ А? . ; ______ А?
св д > ‘2 св д’ 13 св д'
Здесь А есть определитель системы. В рассмотренном примере
1 —1 — 1
А = ^1Р + R1 ^2 0
о я2 ц Ср
Дг получается из определителя системы А путем замены пер-
вого столбца правой частью уравнений (10.8):
А1== 0 —1 —1 0 Я2 0 о r2 — — 2 Ср 1
А2 получается из А путем замены второго столбца правой частью
системы (10.8).
Так как в правой части системы (10.8) стоят нули, то в каж-
дом из определителей А1Г Аа и Д3 один из столбцов будет состоять
из нулей.
363
Известно, что если в определителе один из столбцов составлен
из нулей, то этот определитель равен нулю. Следовательно, Дг =
= О, Д2 = О, Д3 = 0.
Из физических соображений ясно, что каждый из свободных то-
ков не может быть равен нулю, ибо в этом случае не будут выполне-
ны законы коммутации.
Однако из предыдущего следует, что
• _ £ • _ £ • — £
hre-д. 12Св-д, ‘зев-д-
Свободные токи могут быть не равны нулю только в том случае,
если определитель системы Д будет равен нулю:
Д = 0. (10.9)
При этом каждый из токов будет представлять собой неопреде-
ленность:
• _ 4г — £ • _ 4а — £
Чев— д — 0 > Чев — д - о ’ • • ’
раскрыв которую можно получить действительное значение каждого
свободного тока.
Раскрытием неопределенностей здесь заниматься не будем, а
воспользуемся тем существенным для дальнейшего выводом, что
определитель Д алгебраизированной системы уравнений должен
равняться нулю.
Уравнение Д = 0 называют характеристическим уравнением.
Единственным неизвестным в нем является р. В рассматриваемом
примере после раскрытия уравнения Д = 0 получим:
+ Ъ (L1P + = о,
Ср Ср
или
4~ р (R1R2C Li) 4~ 4~ __q
рС
Если дробь равна нулю, то равен нулю числитель ее. Следователь-
но,
р2Я2ЕхС + ptR&C + Lx) + + R2 = 0 (10.10)
Корни квадратного уравнения:
_ _ (R1R2C Li) jz V (R1R2C 4- £t)2 — 4 (7?х Rz) RzLjC . jq j j.
112 2R2L+C • ( f
В самом начале § 264 говорилось о том, что решение для
свободного тока берется в виде АеР*. Если характеристическое
уравнение будет иметь не один корень, а несколько, например, п,
то каждый свободный ток должен быть взят в виде
364
S Ake’k‘ .
fe=i
Пример 121. Найти корни характеристического уравнения схемы
рис. 295 при трех значениях С: 1) С = 1 мкф; 2) С — 10 мкф;
3) С = 100 мкф. К, = Я2 = ЮО ом; = 1 гм.
Решение. При С = 1 мкф
R&C + L^ 100 • 100 . 10-e+ 1 = 1,01;
4 (/?! + /?2) = 4 • 200 . 100 . 10-е = 0,08;
2R2L1C = 2 • 100 . IO"8 = 2 . 10-4;
„ — 1,014-V1.012 —0,08 осп _.
Р1.2 =-------^гпо^— • Pi =—250 сек ;
р2 ~ — 9850 сек-1.
При С = 10 мкф
R&C + £х = 1,1; 4 (Rx + R2) R2L£ = 0,8;
2/?2£1С == 2 - 10“3;
pt = — 230 сек-1; р2 = — 870 сект1.
При С = 100 мкф
R1R2C-]-L1 = 2; 4(R1 + R2)R2L1C = 8;
2R2L1C = 2 . IO-2;
px = — 100 4- 100/; p2 = — 100 — 100/.
§ 266. Составление характеристического уравнения путем исполь-
зования выражения для входного сопротивления цепи на перемен-
ном токе. Характеристическое уравнение для определения р часто
составляют более простым путем по сравнению с путем, обсуждав-
шимся в предыдущем параграфе. С этой целью составляют выраже-
ние входного сопротивления для любой ветви цепи на переменном
токе [обозначим его Z(jco)], заменяют в нем /со на р [получают Z(p)]
и приравнивают Z(p) нулю.
Уравнение Z(p) = 0 всегда будет совпадать с характеристиче-
ским. Убедимся в этом на примерах.
Пример 122. Для схемы рис. 295 входное сопротивление относи-
тельно зажимов ab для переменного тока равно:
Zab U®) ~ ----~~ •
365
Заменим в нем > на р, вместо Zob (ja>) запишем Zab (р) и при-
равняем его нулю:
^2-—
Zab (Р) = Рк + R, +----= 0.
*2+ —
Ср
Отсюда
P2LiCR2 -Р р (Д -Р P1P2Q -Р Pi -Р Рг _ g
1 -р R2Cp
или
p2LxCR2 + р (^ + R&C) + R, + R2 = 0. (10.1 О')
Уравнение (10.10') полностью совпадает с уравнением (10.10),
составленным иным путем.
Уравнение (10.10') было составлено путем использования выра-
жения для входного сопротивления первой ветви схемы рис. 295
относительно зажимов ab. В точности такое же уравнение будет
получено, если записать выражение для входного сопротивления
любой другой ветви.
Пример 123. Убедиться в том, что уравнение (10.10) может быть получе-
но путем составления входного сопротивления для третьей ветви рис. 295 за-
меной в нем ja> на р и приравнивания Z(p) нулю.
Решение. Входное сопротивление для третьей ветви
7 .. . 1 . Ri (Ri -р /’м Д)
(/to) =э ~ -р
j b>C Ра 4- Pl -р /toLi
Заменим в нем /со на р и приравниваем Z (р) нулю:
7 . - 1 , ^(Pl + pLl)
%cd (Р) — г + D . D . - — 0.
рС Pa + Pi + рД
Отсюда
р2 Lj СРа -р р (Lj -р Р1 Рг С) -р Pi ~р Р2 => 0.
(10.10")
Уравнение (10.10") совпадает с (10.10).
§ 267. Подразделение независимых начальных значений на ос-
новные и неосновные . Для сложных схем со многими накопителя-
ми энергии может оказаться, что число независимых начальных зна-
чений (начальных условий) окажется большим, чем порядок харак-
теристического уравнения, и, следовательно, больше числа постоян-
ных интегрирования.
В этом случае при определении постоянных интегрирования бу-
дут использованы не все независимые начальные условия, а часть
из них.
366
Условимся называть основными независимыми начальными усло-
виями те токи в индуктивностях и напряжения на емкостях, ко-
торые могут быть заданы независимо от других. Остальные неза-
висимые начальные условия назовем неосновными.
В качестве иллюстрации этого подразделения обратимся к схеме рис.
296. Она содержит три индуктивности и одну емкость.
В схеме всего четыре независимых начальных значения (начальных ус-
ловия):
1) tl (0+) = 0; 2) i2 (0+) = 0; 3) 13 (0+) = 0; 4) ис (0+) = 0.
Из них три являются основными и одно — неосновным. При выборе ос-
новных допустим известный произвол. Так, если за основные взять первое,
второе и четвертое условия, то неосновным
будет »3(0-|-) = 0. Это условие автоматиче-
ски вытекает из первого закона Кирхго-
фа вне зависимости от того, есть индук-
тивность в третьей ветви или нет ее.
Если за основные взять первое, третье
и четвертое условия, то неосновным будет
второе.
Пример 124. Убедиться в том, что для
схемы рис. 296 характеристическое урав-
нение будет иметь не четвертый, а третий
Рис. 296
порядок.
Решение. Составляем выражение для входного сопротивления
/ 1 \
I pL3 + ~ I pL3
Z (р) = /?! + pLt + -А--------’ — - 0.
pZ-2 + pl-3 +
рС3
Отсюда
(Rl + pl-l) [1 + Р2 ^-2 (1-2 + Ез)1 + pl-3 (1 + ^2 l-г Р2) — 0-
Следовательно, характеристическое уравнение имеет третий порядок.
§ 268. Чем определяется степень характеристического уравнения?
Взглянув на схему, переходный процесс в которой исследуется,
необходимо уметь быстро ответить на вопрос о том, какова будет
степень характеристического уравнения цепи. Умение быстро ориен-
тироваться в этом вопросе дает возможность оценить трудоемкость
предстоящих выкладок и способствует выявлению ошибки, если
последняя возникает при составлении характеристического урав-
нения.
Степень характеристического уравнения равна числу основ-
ных независимых начальных условий в послекоммутационной
схеме после максимального ее упрощения и не зависит от вида
э. д. с. в схеме.
Упомянутое выше упрощение состоит в том, что последовательно
и параллельно соединенные индуктивности должны быть замене-
367
ны одной эквивалентной и емкости, включенные последовательно и
параллельно, тоже должны быть заменены эквивалентной*.
Так, применительно к схеме рис. 297 последовательно вклю-
ченные Li и Li следует заменить на -{- £/' + 27И, если
между ними есть магнитная связь (если нет магнитной связи, то
М. = 0), а емкости С3', С3" и С4 — на емкость
С3' С3"
С3' -|- С3"
+
Начальное значение напряжения на емкости Съ равно начально-
му значению напряжения на С4.
В результате упрощений схема рис. 297 приводится к схеме
рис. 298. В последней две индуктивности и одна емкость, все три
независимых начальных значения — основные. Следовательно, по-
рядок характеристического уравнения будет третий.
Рис. 298
Две параллельно соединенные индуктивности и Л2 (без
активных сопротивлений), между которыми есть взаимная индук-
тивность М, с начальными значениями токов г\(0) и z2(0), могут
быть заменены одной эквивалентной
L = Д£2 - ЛР
Z-i + L2 Ц- 2М
Минус в знаменателе соответствует согласному, плюс встречному
включению. Начальное значение тока через равно i\(0) i2(0).
В заключение обратим внимание на то, что порядок характе-
ристического уравнения не зависит от того, имеется ли магнитная
связь между индуктивностями схемы или она отсутствует.
§ 269. О корнях характеристического уравнения. Число корней
характеристического уравнения равно степени этого уравнения.
Так, если характеристическое уравнение представляет собой урав-
нение первой степени, то оно имеет один корень, если второй сте-
пени — два корня, если третьей степени — три корня и т. д. Урав-
* Имеется в виду, что других сопротивлений, например активных, в вет-
вях с емкостями нет, что начальные напряжения на последовательно соеди-
ненных емкостях относятся обратно пропорционально этим емкостям, а так-
же что начальные токи через последовательно соединенные индуктивности
одинаковы.
368
некие первой степени имеет всегда действительный (не мнимый и
не комплексный) корень.
Уравнение второй степени может иметь:
а) два действительных неравных отрицательных корня;
б) два действительных равных отрицательных корня;
в) два комплексно сопряженных корня с отрицательной дейст-
вительной частью.
Уравнение третьей степени может иметь:
а) три действительных неравных отрицательных корня;
б) три действительных отрицательных корня, из которых два
равны друг другу;
в) три действительных равных отрицательных корня;
г) один действительный отрицательный корень и два сопряжен-
ных с отрицательной действительной частью.
§ 270. Все действительные корни характеристических уравнений
всегда отрицательны, а комплексные корни всегда имеют отрицатель-
ные действительные части. Свободный процесс происходит в цепи, ос-
вобожденной от источников э. д. с. Он описывается слагаемыми вида
Aept. В цепи, освобожденной от источников э. д. с., свободные токи не
могут протекать сколько угодно длительно, так как в цепи отсутст-
вуют источники энергии, которые были бы способны в течение сколь
угодно длительного времени покрывать тепловые потери от свобод-
ных токов. Другими словами, свободные токи непременно долж-
ны затухать.
Но если слагаемые ept должны затухать (спадать) во времени,
то действительная часть р должна быть отрицательной.
В таблице приведены значения экспоненциальной функции
e~at — f (at).
at 0 0,1 0,2 о,з 0,4 0,5 0,6 0,7
е 1 0,905 0,819 0,741 0,67 0,606 0,549 0,5
at 0,8 0,9 1 1,5 2 3 4 5
e-at 0,45 0,406 0,368 0,223 0,135 0,05 0,018 0,0067
Обсудим характер изменения свободных составляющих для
простейших переходных процессов в цепях с характеристическим
уравнением первого и второго порядков.
Если число корней характеристического уравнения будет боль-
ше двух, то свободный процесс может быть представлен как про-
цесс, составленный из нескольких простейших процессов.
13 Л. А. Бессонов
369
§ 271. Характер свободного процесса, когда характеристическое
уравнение имеет один корень. В этом случае свободный ток выра-
жается так:
ice = Ае~“‘,
(10.11)
где р = — а зависит только от параметров цепи, А — от парамет-
ров цепи, э. д. с. и момента включения. Характер изменения ice при
А > 0 иллюстрируется рис. 299.
За интервал времени t — т = — функция Ае ~а1 уменьшится в
е = 2,71 раза. Действительно, при / = -г = —
at = ат -- а — = 1; e~at — е~ах = е~1 — — = —-—.
а е 2,71
Величину т— — = — принято называть постоянной времени
а |р|
цепи*-, т зависит от вида схемы и параметров ее. Так, для цепи
рис. 293 т = —, для цепи рис. 294, a r=RC,
R R С
для цепи рис. 309 т= ——— и т. д.
/?i + Rt
§ 272. Характер свободного процесса при
двух действительных неравных корнях ха-
рактеристического уравнения. Пусть рг = — а
и р2 = — Ь. Для определенности положим
b > а-.
1св = А1е-“'+А2е~1’'. (10.12)
Характер изменения свободного тока при
различных по величине и знаку постоянных
интегрирования Аг и А2 качественно иллю-
Рис. 300
Рис. 299
стрируется «жирными» кривыми рис. 300, а, б, в, г. На всех
* Название «постоянная времени» отражает постоянство величины под-
__________________________________________________£
касательной к экспоненте; подкасательная к экспоненте е т численно рав-
на т.
370
рисунках кривая 1 представляет функцию Axe~at, кривая 2—функ-
цию A2e~bt. Результирующая («жирная») кривая получена путем
суммирования ординат кривых 1 и 2.
Для рис. 300, а А± > 0 и Л2 > 0-
Для рис. 300, б Аг > 0, А2 < о, | А2
Для рис. 300, в Аг > 0, А2 < О, IА2
Для рис. 300, г А± > О, А2 < 0, | Л2 = Л*.
4-
Л,.
§ 273. Характер свободного процесса при двух равных корнях.
Из курса математики известно, что если среди корней харак-
теристического уравнения есть два равных корня рг = р2 = — а,
то соответствующие слагаемые решения должны быть взяты в та-
ком виде:
АгеР( 4- A2tep( = (Лг + A2t) e~at. (10.13)
На рис. 301 построено пять кривых. Они иллюстрируют воз-
можный характер изменения функции (Лх ф- A2f)e~at при различ-
ных знаках постоянных интегрирования Лг и Л2, а также когда
одна из постоянных равна нулю.
Рис. 301 Рис. 302
Кривая 1 — при At > 0 и Л2 > 0.
Кривая 2 — при Аг < 0 и Л2 > 0.
Кривая 3 — при Л± > 0 и Л2 < 0.
Кривая 4 — при Лх = 0 и Л2 > 0.
Кривая 5 — при Л, > 0 и Л2 = 0.
§ 274. Характер свободного процесса при двух комплексно со-
пряженных корнях. Комплексные корни всегда встречаются попар-
но сопряженными. Так, если один корень pt = — 6 /и0, то
другой будет равен р2 = — 6 —- /соо. Из курса математики извест-
но, что соответствующее им слагаемое решения, например дол-
жно быть взято в таком виде:
ice — А ё~и sin (о»(/ 4- v). (10.14)
Формула (10.14) описывает затухающее синусоидальное колеба-
ние (рис. 302). Оно имеет угловую частоту <ос и начальную фазу v.
Огибающая колебания определяется кривой Ле-£\ Чем больше 6,
3*
371
тем быстрее затухает колебательный процесс; А и v определяют-
ся значениями параметров схемы, начальными условиями и величи-
ной э. д. с. источника; <о0 и 6 зависит только от параметров' цепи пос-
ле коммутации; <о0 называют угловой частотой свободных колеба-
ний; 6 — коэффициент затухания.
§ 275. Некоторые особенности переходных процессов. Как извест-
но из предыдущего, полное значение любой величины (тока, напря-
жения, заряда) равно сумме принужденной и свободной составляю-
щих. Если среди корней характеристического уравнения есть ком-
плексно сопряженные корни 2 = — 6 + /соо и значение угло-
вой частоты свободных колебаний <о0 почти равно угловой частоте
со источника синусоидальной э.д.с. (источника питания), а коэф-
фициент затухания 8 мал (цепь с малыми потерями), то сложение
принужденной и свободной составляющих дает колебание, для
которого характерно биение амплитуды по рис. 303.
Рис. 304
Колебание по рис. 303 отличается от биений, рассмотренных
в § 180, тем, что здесь у одной из составляющих колебания ампли-
туда медленно уменьшается.
Если угловая частота свободных колебаний ю0 точно равна
угловой частоте источника синусоидальной э. д. с., то результи-
рующее колебание часто имеет форму, изображенную на рис. 304.
Рис, 305
Рис. 306
Простейшим примером колебаний такого типа является колеба-
ние, возникающее на конденсаторе в схеме рис. 306 в результате
сложения принужденного колебания UCmcosat и свободного коле-
бания —UCme~i( cos at:
ис = и Cm (1 — e~sz) cos at.
Амплитуда результирующего колебания нарастает по экспо-
ненциальному закону.
372
При наличии емкости (или емкостей) в схеме могут возникать
большие начальные броски токов, в несколько раз превышающие
амплитуды тока установившегося режима. Так, в схеме рис. 305
при нулевых начальных условиях в первый момент после замыка-
ния рубильника напряжение на емкостях равно нулю и ток в не-
разветвленной части цепи равен -Um sin . Если ф = 90°, то
в первый момент после замыкания рубильника ток равен —.
При размыкании рубильников в индуктивных цепях возникают
опасные увеличения напряжения на отдельных участках цепи.
Этот вопрос рассмотрен в § 277.
Пример 125. Осциллографирование показало, что при подключении схе-
мы рис. 306 к синусоидальному напряжению, имеющему угловую частоту
и = 10 100 рад/сек, переходный процесс сопровождался биениями амплиту-
ды в соответствии с рис. 303.
Период биения равнялся 0,1255 сек. За одно биение амплитуда колеба-
ния уменьшилась в е раз. Найти значения L и R схемы, если известно, что
С ~ 1 мкф.
Решение. По-прежнему через и0 будем обозначать угловую частоту
собственных колебаний. Тогда в соответствии с § 180 частота биений:
и — йо 2л 2л
Ш(5 = = - = — = 50 рад/сек*.
Следовательно,
йо = (о — 2а>б = 104 рад/сек.
По условию амплитуда результирующего колебания за время Т = 0,1255 сек
уменьшилась в е раз. Поэтому е~~ы = е~1, нли
б = —=7,97 сек-’.
0,1255
Для схемы рис. 306 из решения характеристического уравнения следу-
ет, что
где
Отсюда
VALC — (RCf
2LC
б = ^.
2Z,
1 2
— = 6К 4- б2 и 108 и £
LC °
1
— — о2,
LC
С.108 = 0’01гН;
R = б • 2L = 7,97.0,02 = 0,159 (ом).
1
* Формула для (£>б была выведена в § 180 в предположении, что амплиту-
ды А, и А2 двух складываемых колебаний постоянны (не меняются во вре-
мени). Здесь мы полагаем, что эта формула приближенно справедлива и в том
случае, когда амплитуда одного из колебаний, например Дъ весьма медлен-
/ dAL Д
но изменяется во времени < «Д I.
373
§ 276. О переходных процессах, сопровождающихся электричес-
кой дугой. Если переходный процесс вызывается размыканием ру-
бильника в электрической цепи, содержащей индуктивности, то
между расходящимися ножами рубильника при определенных усло-
виях может возникнуть электрическая дуга. Если электрическая
дуга возникает, то расчет переходного процесса становится делом
весьма трудным и не может проводиться методами, изучаемыми в
данной главе. Объясняется это тем, что сопротивление электричес-
кой дуги является нелинейной функцией протекающего через нее
тока. В этом случае, если известна вольтамперная характеристика
дуги, для расчета переходных процессов могут применяться мето-
ды, излагаемые в приложении В.
Рис. 308
Пример 126. Выяснить, можно ли ожидать возникновения электричес-
кой дуги (искры) при размыкании рубильника в схеме рис. 307.
Решение. До размыкания рубильника в цепи был установившийся
режим
Допустим, что при достаточно медленном размыкании рубильника дуга
ие возникает. При этом ток мгновенно спадает до нуля, a i (0+) должен бу-
дет равняться (0+). Но этого быть не может, ибо каждый из токов (i и i2)
по первому закону коммутации не может измениться скачком.
Следовательно, между достаточно медленно расходящимися ножами ру-
бильника в схеме рис. 307 при определенных условиях можно ожидать возни-
кновения электрической дуги (искры).
§ 277. Об опасных перенапряжениях, вызываемых размыканием
ветвей в цепях, содержащих индуктивности. При размыкании ру-
бильников в электрических цепях, содержащих значительные индук-
тивности, на отдельных участках электрических цепей могут воз-
никать напряжения, во много раз превышающие установившиеся.
Напряжения, превышающие установившиеся, будем называть пере-
напряжениями. Они могут оказаться настолько значительными, что
вызовут пробой изоляции и выведут из строя измерительную аппа-
ратуру.
Пример 127. Рассмотрим числовой пример.
К зажимам индуктивной катушки R = 100 ом, L = 10 гн подключен
вольтметр (рис. 308). Сопротивление вольтметра Rv — 3000 ол; Е — 100 в
374
Найти, чему будет равно напряжение на зажимах вольтметра при t = О,
если допустить, что размыкание рубильника произойдет мгновенно и дуги
не возникнет.
Е
Решение. До размыкания рубильника через L протекает ток i = —
-t la. В индуктивности была запасена магнитная энергия
£/2
". Если допус-
тить, что размыкание рубильника произошло мгновенно и дуги не возникло, и
учесть, что ток через индуктивность должен оставаться равным 1 а, то по
замкнутому контуру, составленному вольтметром и катушкой, за счет запа-
са энергии магнитного поля индуктивности в первое мгновение будет проте-
кать ток в 1 а. При этом на вольтметре будет пик напряжения порядка 3000 в.
Протекание большого импульса тока через вольтметр может вызвать перего-
рание катушки прибора и выход его из строя.
При размыкании рубильника с конечной скоростью между расходящи-
мися контактами рубильника схемы рис. 308 возникнет электрическая дуга.
Это приведет к тому, что увеличение напряжения на вольтметре будет мень-
ше, чем в рассмотренном выше идеализированном случае, когда рубильник
размыкался мгновенно без дуги*.
Чтобы не «сжечь» вольтметр в цепи рис. 308, сначала надо отключить
вольтметр, а затем разомкнуть рубильник.
Перенапряжения проявляются тем сильнее, чем больше индуктивности
L в цепях. Особенно опасны они в цепях постоянного тока, содержащих ин-
дуктивности порядка единиц и десятков генри. В таких цепях при отключе-
ниях соблюдают специальные меры предосторожности (отключение рубиль-
ника после введения дополнительных активных сопротивлений в цепь).
На этом закончим общее рассмотрение характера изменения
свободных токов и напряжений и некоторых общих особенностей
переходных процессов и перейдем к изучению методов анализа и
расчета переходных процессов.
Начнем это изучение с общей характеристики различных мето-
дов.
§ 278. Общая характеристика методов анализа переходных про-
цессов в линейных электрических цепях. Расчет переходных процес-
сов в любой линейной электрической цепи состоит из следующих
основных операций:
1. Выбор положительных направлений токов в ветвях цепи.
2. Определение значений токов и напряжений непосредственно
до коммутации.
3. Составление характеристического уравнения и определение
корней его**
* При более детальном рассмотрении процесса необходимо было бы
еще учесть влияние междувитковых емкостей и емкостей па землю (см. § 316).
При неучете дуги, распределенных емкостей и величины индуктивности L
приведенный выше расчет является весьма грубым и неточным и носит ил-
люстративный характер.
** Если в практической деятельности встретится потребность в опреде-
лении корней характеристических уравнений высоких степеней (например,
4 — 6-ой степени), то, как их определять, сказано в книге: Е. П. Попов.
Динамика систем автоматического регулирования, Гостехиздат, 1954, § 39.
375
4. Получение выражений для искомых токов и напряжений
как функции времени.
Широко распространенными методами расчета переходных про-
цессов являются;
1) метод, получивший в литературе название классического;
2) операторный метод;
3) метод расчета путем применения интеграла Дюамеля.
Для всех этих методов перечисленные выше четыре операции
или этапа расчета являютсячобязательными.
Для всех методов первые три операции (они были кратко рас-
смотрены выше) совершаются одинаково, и их нужно рассматри-
вать как общую для всех методов часть расчета.
Различие между методами имеет место на четвертом, наиболее
трудоемком, этапе расчета.
Из перечисленных выше трех методов наиболее широко при-
меняются классический и операторный, менее широко использует-
ся метод расчета путем применения интеграла Дюамеля. В даль-
нейшем, после того как мы достаточно ознакомимся с этими метода-
ми, будут даны сравнительная оценка и рекомендуемая область
применения каждого из них (см. § 307).
В радиотехнике, кроме трех перечисленных выше методов, применяют еще
метод анализа переходных процессов, основывающийся на интеграле Фурье.
Краткое изложение вопроса об интеграле Фурье см. в приложении Б.
§ 279. Определение классического метода расчета переходных про-
цессов. Классическим методом расчета переходных процессов назы-
вают метод расчета, в котором решение дифференциального уравне-
ния берется в виде суммы принужденного и свободного решений и
в котором определение постоянных интегрирования, входящих в
выражение для свободного тока (или напряжения), производится
путем совместного решения системы линейных алгебраических урав-
нений по известным значениям корней характеристического урав-
нения и известным значениям свободной составляющей тока и ее
производных, взятых при t = 0+.
§ 280. Определение постоянных интегрирования в классическом
методе. Как известно из предыдущего, любой свободный ток или
любое свободное напряжение могут быть представлены в виде сум-
мы экспоненциальных слагаемых. Число членов суммы равно чис-
лу корней характеристического уравнения.
Так, при двух действительных неравных корнях
при трех действительных неравных корнях
ice = А^( 4- Л2ем + А3еРз(-
Для любой схемы при помощи уравнений Кирхгофа и законов
коммутации можно найти: 1) числовое значение искомого свобод-
376
кого тока при t = 0+, обозначим его 1св (0+) и 2) числовое значение
первой, а если требуется, то и высших производных от свободного
тока, взятых при t — 0+. Числовое значение первой производной от
свободного тока при t — 0+ обозначим через Св(Р+). Числовое зна-
чение второй производной от свободного тока при t = 0+ обозначим
через 4(°+) и т. д.
Рассмотрим методику определения постоянных интегрирования
4. Л. .. •. полагая известными ice(0+), ice(0+), /«в(0+) и значения
корней plt рй, ...
Если характеристическое уравнение цепи представляет собой
уравнение первого порядка, то ice = Aept. Постоянная интегриро-
вания А определяется по значению свободного тока tfe(0+):
Я = 4в(0+). (10.15)
Если характеристическое уравнение имеет второй порядок и
корни его действительны и неравны, то
^« = 4^ + 4^. (10.16)
Продифференцируем это уравнение по времени:
i'ce = + Рг^ерЛ. (10.16')
Запишем уравнения (10.16) и (10.16') при / = 0 (учтем, что
при t — 0 е₽,< = ePlt = 1); получим:
/св(0+) = 4+4; (10.17)
ice (0+) = рг4 + р2Л2. (10.17')
В этой системе уравнений известными являются zcs(0+), «св(0+),
рг и р2; неизвестные Лг и Л2.
Совместное решение (10.17) и (10.17') дает:
Л __ >СО (0+) - Pilce (0+) .
A1 ~ Pi-P2 ”
(10.17")
Л2 — ice (0+) Av
Если корни характеристического уравнения являются ком-
плексно сопряженными, то свободный ток берется в таком виде:
ice = Ae~lt sin (<о0/ 4- v). (Ю.18)
Угловая частота <в0 и показатель затухания 6 известны из реше-
ния характеристического уравнения.
Определение двух неизвестных Л и v производится и в этом
случае по значениям ice(0+) и 4в(0+).
Продифференцируем по времени уравнение (10.18); получим:
ice — — A&e~if sin (cooZ -р v) -р Ашйе~ч cos^t -j- v). (10.18')
377
Запишем уравнение (10.18') при t = 0+:
ice (0+) = — Л8 sin v 4- Лсо0 cos v.
Таким образом, для определения двух неизвестных А и v имеем
два следующих уравнения:
ice (0+) = A sin v;
ice (0+) = — Л 6 s i n v 4~ cos v.
(10.19)
Для цепи, имеющей характеристическое уравнение третьего
порядка, свободный ток
ice = А^е?'1 + A2ePst A^pJ.
(10.20)
Найдем первую, а затем вторую производную от левой и пра-
вой частей уравнения (10.20):
ice — PiA^* 4~ p2A2fAJ 4~ PsA^'*',
ice = p] A^lt 4- P2 A^ 4- Рз Ae₽sZ.
Запишем (10.20), (10.21) и (10.22) при t = 0+:
iCB (0+) — A + a2 4- A;
ice (0+) — PiAt 4- p2A2 4~ P3A3',
ice (0+) = /\ A 4" P2 A2 4~ P3 A3.
(10.21)
(10.22)
(10.23)
Система уравнений (10.23) представляет собой систему трех
линейных алгебраических уравнений с тремя неизвестными: Alt
А2 и As. Все остальные входящие в нее величины [р^ р2, р3,
(° , ). С«(0+), С(0+)] известны.
Обратим внимание на то, что в сложных разветвленных цепях при нали-
чии в них многих накопителей энергии и некоторых частных соотношениях
между параметрами начальные значения одного или нескольких свободных
токов или напряжений могут оказаться равными нулю. При этом число сво-
бодных составляющих в том или ином токе пли напряжении окажется мень-
ше числа корней характеристического уравнения и не равно числу свобод-
ных составляющих в других токах. Такое явление может иметь место, на-
пример, если одна из угловых частот<о0 свободных колебаний окажется в точ-
ности равна собственной угловой частоте последовательного или параллель-
ного резонансного контура, имеющегося в схеме. В этом случае на этой час-
тоте для свободной составляющей последовательный резонансный контур
будет практически закорачивать участок цепи, к зажимам которого он при-
соединен, а параллельный — как бы разрывать цепь для нее.
Теперь рассмотрим несколько числовых примеров на расчет
переходных процессов классическим методом в цепях первого и
второго порядков с источниками постоянной и синусоидальной
э. д. с. с нулевыми и ненулевыми начальными условиями.
Пример 128. В схеме рис. 309 до замыкания рубильника были
нулевые начальные условия: Е = 210 в; R, = 1000 ом, /?»=2000 ом\
С = 50 мкф.
378
Требуется! 1) найти начальные значения полных, принужден-
ных и свободных составляющих всех токов и напряжения на ем-
кости; 2) определить закон изменения во времени токов во всех
ветвях и напряжения на емкости.
Решение первой части задачи
Выбираем положительные направления для токов в ветвях
в соответствии с рис. 309. Положительные направления для напря-
жений примем, как это обычно и делает-
ся, совпадающими с токами.
До замыкания рубильника напря-
жение на конденсаторе равно нулю:
пс(0_) = 0.
По второму закону коммутации оно
остается равным нулю и непосредствен-
но после коммутации при t = 0+. Со-
ставим уравнения по законам Кирхгофа:
«Л + «с =
«С =
i’i = i2 is.
Перепишем их для t = 0+:
^Л(0+)4-ис(0+) = £;
UC (0+) ~ l2 (0-4-)
4(0+)=4(0+)4-»3(0+),
Так как
ис(0+) = 0,
то
»\(0+) = / = = 0,21 (а) и i2 (0+) = 0;
/\1 AUvU
i3 (0+) = ii (0+) — i2 (0+) = 0,21 а.
Независимое начальное значение в схеме одно:
ис(0+) = 0.
Все остальные начальные значения зависимые.
Найдем принужденные значения токов.
В схеме действует источник постоянной э. д. с. Для постоянного
тока емкость представляет собой разрыв цепи.
Поэтому
1'зпр = 0
и
379
Е 210 л лт / ч
= 12Пл =-----=-----— 0,07 (а).
Принужденное напряжение на конденсаторе равно принужден-
ному напряжению на сопротивлении Т?2:
ис = 140 в.
ПР 2ПР Я1 + /?2
Найдем свободные составляющие токов. С этой целью каждый
ток при t = 0+ представим в виде суммы принужденного и свобод-
ного:
h(0+)=/w(0+) + ^e(0+);
отсюда
(0+) = ч (0+) - (0+) = 0,21 - 0,07 = 0,14 (о);
кв (0+) = (0+) - кр (0+) = 0 - 0,07 = -0,07 (а)»
кв (0+) == h (0+) - кР (0+) = 0,21 - 0 = 0,21 (а);
«&в (0+) = «с (0+) - иСпр (0+) = 0 - 140 = - 140 (в).
Решение второй части задачи
Характеристическое уравнение (о составлении его см. стр. 365):
/ад2с+яг4-я2 = о
имеет один корень:
р = = -30 шТ1.
RiRzC
Так как характеристическое уравнение имеет только один
корень, то свободную составляющую каждой искомой величины
возьмем в виде АеР‘ (у постоянных А будем ставить те же индек-
сы, что и у искомых токов):
4 = кр + кв = = 0,07 + 0,14е-30/ а-
i2 = iinp 4- кв = 4- А^ = 0,07 - 0,07е-30/ а;
h = кР + кв = 0 + = 0,21е~30/ а;
«с = Чспр кисее = +Л^ = 140 - 140е-3^ в.
-Г ^2
Графики токов и напряжения ис в функции времени изображе-
ны качественно на рис. 310.
Постоянная интегрирования Аг равна значению свободной со-
ставляющей тока ilce при t = 0+, т. е.
+ = +в(0+) = 0,14 а.
380
Постоянная интегрирования
•^2 ~ Чсв(®+) — —0,07 а;
Л = *'зсв (0+) ~ 0,21 а; Ал — иСсв (0+) = — 140 в.
Выше было записано решение в числовом виде. Запишем теперь
решение в буквенном виде:
E
Л1=г1(0+)-»1яр(0+) = 4
Al
712 — 4 (0+) i^np (®+) = 0-
A=/3(o+)-«3np(o+) = -^-o=
Al
At = uc (0+) - uCnp (0+) = 0 E
R1 + «2 ’
Е
«1 + /?2 ’
Е
Ri ’
Ri + Rt $2'
В общем виде искомые величины запишутся так:
Я1 + М Ri }
А1 4- А2
‘з=~^; ис — Е(I — ept).
Al Al -f- A2
Пример 129. В схеме рис. 311 до замыкания рубильника был ус-
тановившийся режим: 7?! = = 7?3 = 50 ом\ С = 100 мкф\
Е = 150 в.
Рис, 311
Рис. 310
Требуется: 1) найти полные, принужденные и свободные со-
ставляющие токов и напряжения на конденсаторе, а также началь-
ное значение производной от свободного напряжения на конден-
саторе; 2) определить токи ilt i2, i3 и напряжение ис в функции
времени.
381
Решение первой части задачи
До коммутации г2 (0_) = 0 и
4 (ОJ = 4 (0_) = —= 1 (а).
ах -г Ах -г /\3 150
Напряжение на конденсаторе равнялось напряжению на со-
противлении /?3:
«с (0-) = »з (0_) Я3 = 1 • 50 = 50 (в).
Найдем принужденные значения после коммутации:
£ 150 - _ .
г1лр — 'з,ф — Ri + Кз — 100 — > (G)>
иСпр (ОД = i3np (ОД А>3 = 1,5 • 50 = 75 (в).
По второму закону Кирхгофа составим уравнение для контура,
образованного первой и второй ветвями для t — 0+:
G (°+) + «с (ОД = Е, но ис (ОД = ис (ОД.
Поэтому
/х(0Д = = J50 - 50 =
И +/ Rt 50 7
Из уравнения
ис (ОД “ *3 (ОД Яз
найдем:
<3(0+) = ^=1а.
Аз
По первому закону Кирхгофа
1'1 (ОД = С (ОД + С (ОД.
Следовательно,
(ОД = (ОД - i3 (ОД = 2-1 = 1 (а).
Свободные составляющие найдем как разности между полными и
принужденными величинами:
«с се(0+) = ис (ОД — ис пр (ОД = 50 — 75 = — 25 (в);
4 се (ОД = h (ОД - пр (ОД = 2 - 1,5 = 0,5 (а);
«2 се (ОД = к (ОД - г2 пр (ОД = 1-0 = 1 (а);
г’з св (°+) = i3 (ОД — is пр (ОД = 1 — 1,5 = — 0,5 (а).
Так как свободный ток через емкость
due ре
св____________________________dt
то
св ice
dt ~ с '
382
В рассматриваемом примере
/ dUCce \ _ ^2са (0+)
\ dt / /=о+ С
1
100-10-8
= 101 (ejсек).
Решение второй части задачи
Характеристическое уравнение для послекоммутационной схе-
мы имеет один корень:
р = — А±А = — 400 сек'.
RiRfi
Рис. 312
Каждый ток равен сумме принуж-
денной составляющей и свободной со-
ставляющей Aept, где А равно значе-
нию свободной составляющей при
t= 0+:
г1= 1,54-0,5е-4е0'а;
i2 = e~iWta\
is= 1,5 —О,5е-400/а;
uc=75 — 25e“«we.
Графики изображены на рис. 312.
Пример 130. В схеме рис. 313 до
коммутации был установившийся ре-
Рис. 313
жим: = 40 ом, R2 — R-< — 160 ом\ L = 2 ен; Е— 120 в.
Требуется: 1) найти свободные составляющие токов и свобод-
ную составляющую напряжения на индуктивности при t = 0+;
2) найти токи 1х, i211 ul в функции времени.
Решение первой части задачи
В установившемся режиме до коммутации (от постоянного тока
на индуктивности нет падения напряжения) токи определяются
следующим образом:
G (0_) - (0_) 4- i3 (0-) = 2i2 (0_) =-А— = 1 а.
п , А2АЗ
383
Следовательно, i2 (0_) = 0,5 а.
Принужденные токи после коммутации
Е ПС
11пр — 12пр — ~п , р ' 0’° а‘
*\1 Т ^2
По первому закону коммутации j2 (0_) = г2 (0+) = 0,5 а.
Найдем (0+) = ilce (0+):
^2св (0+) = Ч (0+) iznp (0+) — 0,5 0,6 = — 0,1 (а).
Для определения свободного напряжения на индуктивности при
I = 0+ составим уравнение по второму закону Кирхгофа для после-
коммутационной схемы:
Отсюда
t2ce(0+)(^ + /?2) + u£fe(0+) = 0.
«£св (°+) = 20 <?•
Решение второй части задачи
Характеристическое уравнение pL -ф- /?2) = 0 имеет один
корень р = — 100 сек"1.
Значения принужденных и свобод-
ных составляющих возьмем из первой
части задачи. Имеем:
^=^ = 0,6 —0,1е~1О%
и uL = 20е~100/в.
Кривые 1\, i2 и uL изображены качест-
венно на рис. 314.
Пример 131. В схеме рис. 315 до
замыкания рубильника был установив-
шийся режим: =R2— 2 ом\ aL—З ом',
е (t) = 127 sin (a>t — 50°) в.
Требуется: 1) найти ife(0+); 2) определить закон изменения
тока в цепи после коммутации.
384
Решение первой части задачи
Находим комплексную амплитуду тока в цепи до коммутации!
7/п=-124 + Г -25,4е~/86О50,а.
Мгновенное значение тока до коммутации
i = 25,4 sin (at — 86° 50').
В момент коммутации (при со/ = 0)
i (0_) — 25,4 sin (— 86° 50') — — 25,35 а.
Принужденный ток после коммутации
. _ 127е~/о0° _ „ /106°20’
*т 2 + 3/ “
Мгновенное значение принужденного тока
1пр = 35,2 sin (со/ — 106° 20');
inp (°+) = 35,2 sin (— 106° 20') = — 33,8 а.
По первому закону коммутации
i (0_) = i (0+) = — 25,35 а.
Но
i (°+) = inP (°+) + ice (°+)«
Следовательно,
ice (0+) = i (0+) - inp (0+) = - 25,35 + 33,8 = 8,45 (а).
Решение второй части задачи
Характеристическое уравнение pL — 0 имеет корень
/?2 _ /?2
L со/.
2-314
3
210 (сек-1).
со
По данным первой части задачи ток в цепи до коммутации
(кривая 1 рис. 316 до со/ = 0) равен:
i = 25,4 sin (со/ — 86° 50') а.
Принужденный ток после коммутации
inp = 35,2 sin (со/—106° 20') а (кривая 2, рис. 316);
»св(0+) = 8,54О.
Следовательно,
i = inp -j- ice = 35,2 sin (со/ — 106° 20') + 8,54e~21()' a.
Кривая 3 рис. 316 — свободный ток, кривая 4 — полный ток
после коммутации (ординаты кривой 4 при со/ 0 равны сумме
ординат кривых 2 и 3).
385
Пример 132. В схеме рис. 317 замыкается рубильник в третьей
ветви. До этого был установившийся режим; e(t) = Е = 120 в.
Требуется:
1) найти
«2с«(о+); J «Сс.(о+) и ;
\ dt 1 /=о. \ dt /t=0.
+ +
2) определить г2(/) и uc(f).
Решение первой части задачи
До замыкания рубильника
; (0 ) = i9(0 ) =---= - - — = 2 (а).
2V-/ R1 + Rs 50+ 10
Найдем принужденные токи и напряжение на конденсаторе
после коммутации:
Ч пр *2 пр
Постоянный ток через конденсатор не течет, поэтому
hnp = 0.
От постоянного тока на индуктивности нет падения напряжения,
следовательно,
и1Лпр ~ 0.
Принужденное напряжение на конденсаторе равно падению
напряжения на сопротивлении от тока i2lip:
иСпр = 2.10 = 20 (а).
По первому закону коммутации
г2(0_) = 4(0+) = 2а.
Но
la (0+) — i2 пр (0+) + i2 св (0+),
386
откуда
h св (0+) = »‘2 (0+) - »2 пр (0+) =2-2=0
Ч(0+) = 4(0+) + г3(0+),
или
h(0+) = 24-/3(0+).
Составим уравнение по второму закону Кирхгофа для замкну-
того контура, образованного первой и третьей ветвями:
Так как
то
G (0+) Ъ + is (0+) 7?3 4- ис (0+) = Е.
и g (04 = 24-/3(04,
»з(0+) =
Ri +
120 — 2-50
50 + 50
= 0,2 (а).
Найдем i3fe(0+):
ia св (0+) = i3 (0+) - i3 пр (0+) = 0,2 - 0 = 0,2 (а).
Для определения uLce(0+) составим уравнение для свободных
составляющих по контуру, образованному первой и второй вет-
*1 св (0+) R1 4“ С Св (0+) ^2 + UL св (®+) = 0,
«Lce(0+) = - = -0,2-50 4-0 = - 10 (6).
Но
Следовательно,
(= = -jo = _ 5 ^feeKV
v 4 Л=о+ 2
Свободное напряжение на конденсаторе при t = 0+ найдем по
второму закону коммутации:
wc(0_) =«с (0+);
wc (0+) = ис ,1р (0+) 4- ис св (0+);
0 = 20 4- ис (в (0+),
отсюда
«с.в(0+) = -20 в.
Определим скорость изменения свободного напряжения на кон-
денсаторе при t = 0+.
С этой целью воспользуемся тем, что
- __due св
dt *
387
Следовательно,
/ d»C св \ _ св (0+) _
V dt I п С
4 Ч = 0+
- - ’ = 1333 (в/сек).
150.10-е ' '
Решение второй части задачи
Характеристическое уравнение
ргЬ2С (Ях + Яз) + р [С (ад 4- ад + ад) + Л2] + 7?г + Т?2 = 0
Имеет два комплексно сопряженных корня:
р± — — 42,1 + /15,2 сек"1 и р2 — — 42,1 — /15,2 сек~1.
Поэтому свободная составляю-
щая должна быть взята в таком
виде:
Ae~u sin (соо/ + v),
где 6 = 42,1 и соо = 15,2; А и v
определим по значениям свобод-
ной составляющей и ее первой про-
изводной при t — 0+,
По данным первой части за-
дачи
пр = 2 a; i2 св (0+) = 0; Г, св (0+) = — 5 а/сек-,
«с пр = 20 в; иСсв (0+) = — 20 в; ас св (0+) = 1333 в/сек.
Функция Ae~il sin (ы(/ -ф- v) ПРИ 7 = 0 равна A sin v.
Производная функции Ae~tl sin (aot -ф- v) равна:
— Лбе-М sin (<0(/ v) 4~ Ae~&i ю0 cos (соо7 4~ v)-
Значение этой производной при t = 0 равно:
—6Л sin v 4~ <о0 cos v.
Найдем значения Лит для свободной составляющей тока i2.
Составим два уравнения:
t2 св (0+) = 0, или Л sin v = 0;
г’я св (0+) — — 5, или — 6Л sin v ю0Л cos v = — 5.
Совместное решение их дает
v = 0 и Л = — 0,328 а.
Следовательно,
*2 = »2 Пр + *2 св = 2 — 0,328е-42,1/ sin 15,2/ а.
Кривая 1 рис. 318 выражает собой график i2 — f(t).
388
Найдем А и v для свободной составляющей напряжения ис:
ис св (0+) = — 20. или A sin v — — 20;
(0+) = 1333, или —6 Л sin v-j-cOjHcosv = 1333.
Отсюда
А — 37,9 и v = —31°52'.
Таким образом,
«с = «с пр + «сев = 20 + 37,9е~42,1' sin (15,2t — 31°52>.
Кривая 2 рис. 318 изображает ис = f(f).
Пример 133. В схеме рис. 317
е(/) = 127 sin (314/+ 40°) в.
Параметры схемы те же, что и в примере 132. До включения
рубильника в схеме был установившийся режим:
«с(°-) по-
требуется:
1) найти
<2св(0+); ; исМ и ;
\ at ) \ dt I
t=o+ t=o+
2) определить i2(/) и uc(/).
Решение первой части задачи
До коммутации
/ _ j — 127g)'1° — о 2О2е—,44°30' а'
•lm — 12т — 60 + /628 u.zuze а>
ix = i2 = 0,202 sin (со/ — 44°30');
(0_) = i2 (0_) = 0,202 sin (— 44°30') = — 0,1415 a.
Определим принужденные токи и напряжения на конденсаторе
после коммутации.
Входное сопротивление цепи
Ъ
(R? + /w72) ( Яз— ।
+ /<°72 + Rg — ~
<оь
= 104,ве-7950';
/ _ _ 127^/40_____ । 213е,'49°50' а
Ilm~ ZeX 104,8е-р°Б°' а-
Мгновенное значение принужденного тока после коммута-
ции
389
i\ = 1,213 sin (at 49°50');
imp (°+) = 1.213 sin 49° 50' = 0,923 a.
Комплекс сопротивления параллельно соединенных второй и
третьей ветвей
= 56,Зе-'18 0 35’.
^23 —
(Rz + /(«A) I Rs — г )
Ra + Мг + Rs — Лг
<вС
Комплекс напряжения на параллельном участке
(723„, = Л/Лз = 1,21 Зе/49°50' . 56,Зе“;18035' = 68,2е/31°15' в;
j 0_2зт 68'2е?31 ‘.L — о 1085е~/58045' I
3 2m Z2 10 +/628 U,1UOOe »
/ = = 68.2eJ2LL. = 1 253е /54°20'.
т Z3 50-/21,3
Мгновенные значения принужденных токов t2 и is после ком-
мутации:
12 = 0,1085 sin (at — 58°45');
is = 1,253 sin (at + 54°20');
i2 nP (0+) = 0,1085 sin (— 58°45') = — 0,0928 a;
is nP (0+) = 1.253 sin 54° 20' =1,016 a.
Принужденное напряжение на конденсаторе
(j -I (--------Ц = 1,253e/54°20'. 21, 3e~‘ 90° = 26,7e~/®o«>'.
Cm '3m^
Мгновенное значение принужденного напряжения на емкости
после коммутации
ис пр — 26,7 sin (at — 35°40');
«с пр (°+) = 26,7 sin (— 35°40') = — 15,57 в.
Найдем г2с.в(0+). По первому закону коммутации
is (0_) = «2 (0J = - 0,1415 = i2 пр (0+) + i2ce (0+);
»2Пр(0+) = -0,0928 а-
i2 св (0+) = — 0,1415 + 0,0928 = — 0,0487 а.
Свободное напряжение на конденсаторе ис св (0+) найдем по вто-
рому закону коммутации:
«с (0_) = ис Пр (0+) + ис св (0+);
иСсМ = «с(0_)-«Сяр(0+) = 0-(- 15,57) = 15,57 (в).
390
Для определения is св (0+) составим уравнение по контуру, обра-
зованному первой и третьей ветвями:
Ч св (0)) R1 4" Ч св (ОД R3 4" св (ОД = 0*
Заменим в нем i’ife(0+) через
[—0,0487 Д-13св (ОД]
и учтем, что
«с«(0+) = 15,57 в.
Найдем:
iSce (ОД = —5’?7-±-2’— = — 0,1314 (а);
йев (ОД = /2 св (ОД + Чсв (ОД = - о,18 а.
Для определения
составим уравнение для контура, образованного первой и второй
ветвями:
Ч св (ОД Ri +Ч св (ОД Rz + uL св (ОД — 0,
откуда
(ОД = 9,487 в-
( d‘2 св \ _ Ul св ^Д — 9’48? _ 4 74 M/cei
\ dt )t=o+ L 2 > V z '
/duc св __ Ч св (0+) __ 0.1314 _____gyg ,
\ dt ]t=o+ C 150.10-e V
Решение второй части задачи
По данным, полученным при решении первой части,
i2 пр = °>1085 sin (го/ — 58°45/), i2 св (0+) = — 0,0487 п;
Ч св (°+) = V4 а/сек-,
иСпР ~ 25,7 sin (го/ — 35°40z), ticce (0+) = 15,57 в,
ис се (0+) = — 876 в/сек.
Корни характеристического уравнения те же, что и в предыду-
щем примере. Для определения Дит для /2 се составим два урав-
нения:
A sin v = — 0,0487;
— М sin v Д- ю0 A cos т = 4,74,
А = 0,184 а и v = — 15°20'.
откуда
391
Следовательно,
i2 = i2 ,ip + i2 св = О, 1085 sin (orf — 58°45') -f-
+ 0,184e~421U sin (15,2/ — 15°20') a.
Для определения постоянных А и v для иСсв составим два
уравнения:
A sin v = 15,57;
— М sin v 4- &>0Л cos v = — 876.
Совместное решение дает:
А = 21,3 и v = 136°50',
ис — ис пр ~\~^ссв== 26,7 sin W — 35°40') Д-
Д-21,Зе—42,1Z sin(15,2/Ч- 136°5(У) в.
*
* *
Перейдем теперь к изучению основ второго метода расчета пе-
реходных процессов в линейных электрических цепях — оператор-
ного метода.
Предварительно вспомним некоторые уже известные положения.
§ 281. Логарифм как изображение числа. Еще из средней школы
известно, что для выполнения умножения, деления, возведения в
степень и извлечения корня из многозначных чисел целесообразно
пользоваться логарифмами.
Действительно, операция умножения сводится к сложению
логарифмов, операция деления — к вычитанию логарифмов и
т. д.
Таким образом, облегчение в расчете получается в силу того,
что сравнительно сложная операция сводится к более простой.
Каждому числу соответствует свой логарифм, поэтому логарифм
можно рассматривать как изображение числа.
Так, 0,30103 есть изображение (логарифм) числа 2 при основа-
нии 10.
§ 282. Комплексы тока и напряжения есть изображения синусо-
идальных функций. Второй раз с понятием изображения мы столк-
нулись при изучении символического метода расчета цепей синусо-
идального тока. Согласно символическому методу комплексная ам-
плитуда есть изображение синусоидальной функции. Так, 1т есть
изображение синусоидального тока /„sin (at +ф). Между изобра-
жением числа в виде логарифма и изображением синусоидальной
функции времени в виде комплексного числа есть существенная
разница.
В первом случае речь идет об изображении числа (не функции),
во втором — об изображении функции времени.
Подобно тому как введение логарифмов упростило проведение
операций над числами, введение комплексных изображений сину-
392
соидальных функций времени позволило упростить операции над
функциями времени — свести операции по расчету цепей сину-
соидального тока к операциям, изученным в главе первой «Линей-
ные электрические цепи постоянного тока».
§ 283. Введение к операторному методу. Операторный метод, к изу-
чению которого мы приступаем, также основан на использовании
понятия об изображении функций времени. В операторном методе
каждой функции времени соответствует функция новой переменной,
обозначаемой буквой р, и, обратно, функции переменной р отве-
чает определенная функция времени.
Переход от функции времени к функции р совершается при
помощи преобразования Карсона — Хевисайда.
Таким образом, операторный метод расчета переходных процес-
сов представляет собой метод расчета, основанный на преобразо-
вании Карсона — Хевисайда.
Забегая вперед, отметим, что операторный метод позволяет
свести операцию дифференцирования к операции умножения, а
операцию интегрирования — к делению. Это облегчает интегри-
рование дифференциальных уравнений.
§ 284. Преобразование Карсоиа — Хевисайда. Условимся под
р понимать комплексное число:
р — а 4- jb, (10.24)
где а — действительная часть, b — мнимая часть этого комплекс-
ного числа.
В дальнейшем в соответствии с установившейся практикой ко-
эффициент b с учетом знака условимся называть не коэффициен-
том при мнимой части комплекса (чем он в действительности явля-
ется), а «мнимой частью». Функцию времени (ток, напряжение,
э.д.с., заряд) будем обозначать f(t) и называть оригиналом. Ей
соответствует функция F(p), называемая изображением, опреде-
ляемая следующим образом:
F(p) = р f f(t)e~ptdt. (10.25)
о
Соответствие между функцией Р(р) и функцией /(/) записывают
так:
^(Р^НО.
Знак == называют знаком соответствия.
Верхний предел интеграла (10.25) равен бесконечности. Интег-
ралы с бесконечным верхним пределом называют несобственными.
Если в результате интегрирования и подстановки пределов будет
получено конечное число (не бесконечность), то говорят, что интег-
рал сходится.
В курсе математики доказывается, что интеграл (10.25), в сос-
тав которого входит функция e~pt — e~at e~ibtt сходится только в
393
— J d (e-pl) = — Ae-pt
Следовательно, изображением постоянной является
стоянная:
А = А.
Наряду с преобразованием Карсона — Хевисайда (10.25) в
F(p) = р j Ae~pl dt = Ар
о
том случае, когда модуль функции f(t) если и увеличивается с
ростом t, то все же медленнее, чем модуль функции ept, равный е°1.
Практически все функции f(f), с которыми имеют дело электри-
ки, этому условию удовлетворяют.
Найдем изображения некоторых простейших функций.
§ 285. Изображение постоянной есть сама постоянная. Требует*
ся найти изображение функции f(t) = А, где Л есть постоянная
величина.
С этой целью в (10.25) вместо /(/) подставим А и проведем ин*
тегрирование:
|° = А
о
сама по-
(10.27)
научной и
учебной литературе широко пользуются преобразованием Лапласа. Оно
отличается отсутствием множителя р перед интегралом в (10.25), т. е. при
преобразовании по Лапласу принимают
F (р) = J f (t) e~pt dt.
b
По Карсону — Хевисайду изображение и оригинал имеют одинаковую
размерность, а изображение постоянной А равно самой постоянной.
По Лапласу размерность оригинала не равна размерности изображения,
а изображение постоянной А равно —.
Р
Следует сказать, что основная заслуга в разработке интегрального пре-
образования функции f(t) в функцию р принадлежит Лапласу. Карсон и
Хевисайд добавили к преобразованию Лапласа лишь нормирующий множи-
тель р, благодаря введению которого оригинал и изображение стали иметь
одинаковую размерность.
§ 286. Изображение показательной функции е’7. Вместо f(t) в
(10.25) подставим ё^;
F (р) = р j1 eal e~pl dl = р § e~f(p~a) dt =
b о
= p (— j J e-t(p~-'j d[— t(p — a)] =
о
----e~t(p~u.)
р — a
—Р— (0 — 1) = —Р—
р — а р — a
3S4
Таким образом,
е°*= —. (10.28)
р —а
При выводе формулы (10.28) (при подстановке пределов) было
учтено, что действительная часть оператора р больше, чем а, т. е.
а > а. Только при этом условии интеграл сходится.
Из формулы (10.28) вытекает ряд важных следствий.
Положив в ней а = /со, получим:
еМ = _Р_. (10.29)
Р - /">
Формула (10.29) дает возможность найти изображение комп-
лекса синусоидального тока:
[mei(*t+*) =
С этой целью обе части (10.29) умножим на постоянное число
1т. Получим:
imeimt = im-^. (10.30)
Р —/ш
Аналогично, изображение комплекса синусоидального напряже-
ния:
ите>ы^ит-^. (10.31)
Р —/ш
Функция e~at имеет своим изображением —-—, т. е.
Р + “
(10.32)
Р + “
§ 287, Изображение первой производной. Известно, что функ-
ции f(t) соответствует изображение F (р). Требуется найти изобра-
жение первой производной зная, что значение функции f (t)
dt
при t = 0 равно f (0).
Подвергнем функцию -^-^преобразованию Карсона—Хевисайда:
р С e-pt dt = e~pt d [f (/)].
J dt J
о о
Интегрирование произведем по частям; обозначим
e~pt = и и d [f (01 = dv, ^udv =uv — J vdu.
395
Следовательно,
р J е~Р‘ d [f (01 = pe~pt / (0 | - P f f(t)d ИП
о о 0
Ho
pe~p‘f(t) | = P[O-f(O)]=-pf(O),
0
a
- P J f (0 d (e~pt) = p.p J f(t) e~ptdt = pF (p).
о о
Таким образом,
P №?-e-P‘dt==pF(p)-pf(P),
J
0
или
^=pF(p)-pH0). (10.33)
dt
§ 288. Изображение напряжения на индуктивности. Изображе-
ние тока i равно / (р). Запишем изображение напряжения на ин-
дуктивности
, di
tir — L ~~ •
L di
По формуле (10.33)
^ = p/(p)-pi(0).
dt
Здесь i (0) есть значение тока i при t = 0*.
Следовательно,
L-==LpI (р) — Lpi (0). (10.34)
dt
Если i (0) = 0, то
L^=Lp/(p). (10.34')
dt
§ 289. Изображение второй производной. Без вывода дадим формулу
rf2 • 2 р / \ 2 f /о\ „Г^01 11Л
-г-р2Р(р) — P2f (0) — Р —— • (1U.36)
dr L dt Jz=o
Следовательно, изображением второй производной тока i будет следующее
выражение:
* Для сокращения записи вместо i (0_) пишем i (0); i (0) может быть и
положительной и отрицательной величиной: i (0) положительно, когда нап-
равление тока i (0) совпадает с произвольно выбранным положительным нап-
равлением послекоммутационного тока в индуктивности L.
396
—^p4(p)-p4(Q)-pl'(p).
§ 290. Изображение интеграла. Требуется найти изображение
функции J f (0 dt, зная, что изображение функции f (t) равно F (р).
о
t
С этой целью подвергнем функцию J f (0 dt преобразованию Кар-
о
сона — Хевисайда:
ОО t ОО t
Р f [f f (0 Л] e~pt dt = - J [ J f (0 dt\ d
о о о 0
Примем
' t
J f (0 dt = tr, d (e~pt) = du
о
и возьмем интеграл по частям:
Первое слагаемое правой части при подстановке и верхнего
и нижнего пределов дает нуль. При подстановке верхнего предела
нуль получается за счет ранее наложенного ограничения на функ-
цию f(t) (см. § 284), а именно, что функция f(0 если и растет с уве-
личением t, то все же медленнее, чем растет функция е°*, где а —
действительная часть р. При подстановке нижнего предела нуль
t
получается за счет того, что обращается в нуль J f (0 dt. Следова-
ло
тельно, если f(t)^F(p), то
t
^f(t)dt^=^. (10.36)
§ 291. Изображение напряжения на конденсаторе. Напряжение
на конденсаторе ис часто записывают в таком виде: ис = С i dt.
397
В такой форме записи не указаны пределы интегрирования по вре-
мени. Более полной формой записи будет являться следующая:
t
ис — ис (0) Ч- — f i dt.
С J
о
В последнем выражении учтено, что к моменту времени t на-
пряжение на конденсаторе определяется не только током, проте-
кавшим через конденсатор в интервале времени от 0 до t, но и
тем напряжением ис (0), которое на нем было при t — 0. В со-
t
ответствии с формулой (10.36) изображение — {idt равно
С J
о
а изображение постоянной пс(0) есть сама постоянная*. Поэтому
изображение напряжения на конденсаторе запишется следующим
образом:
«С==^ + «С(0). (Ю.37)
ср
/(g)
Ср
В таблице даны простейшие операторные соотношения; часть
их была выведена выше, другая дается без вывода.
1. —-— =
р — а
2. —5—
р + «
3. —-— == eimt.
p — ju ‘
4. — = l-rt
р + а
5. - = te~at.
(р + «)2 '
Р2
6.
7.
i г - : (1 —Ч
(р + а)-
1
8.
=-[1— «-»'(!+<
(Р-! «) а2* V Н
___1__.t 1 . e~at
р (Р а) ' а а2 а2
* Для сокращения записи вместо ис (0_) пишем ис (0); ис (0) может
быть и положительной и отрицательной величиной. В формуле (10.37) пс(0)
берется положительной величиной, если направление напряжения tic (0)
совпадает с произвольно выбранным положительным направлением послеком-
мутационного тока через конденсатор.
398
r)2 1
9. ---------P---------= _L_ iae~at — be~bt).
(p + a)(p + b) a — b ’
1 o. -------P--------= _1_ le~bi — e~at).
(P + «) (P + b) a — b
Л 1 ,____1 te~bt e~at \
(p + a) (p + b) ’ ab b — a\ b a J
12. - = Z.
P
§ 292. Закон Ома в операторной форме. Внутренние э. д. с. На
рис. 319 изображена часть сложной разветвленной электрической
цепи. Между узлами а и b этой
цепи включена ветвь, содержа-
щая R, L, С и источник э.д.с.
e(t). Ток по ветви обозначим че-
рез i.
В схеме замыкается рубиль-
ник К, что приводит к переход-
ному процессу. Непосредствен-
но до коммутации ток i = i (0_)
и напряжение на конденсаторе
Выразим потенциал точки а через потенциал точки b в после-
коммутационном режиме:
<Ра = <ъ + «с + «ь + «я—е(0;
иаЬ = — % = UR + UL + UC — е (0*
Вместо uL запишем L —, вместо ис запишем
dt
t
О
Тогда
t
uab ^iR-\-L-+ Uc$) + ~\idt-e(t). (10.38)
dt C J
о
Применим преобразование Карсона — Хевисайда к уравнению
(10.38). Преобразование Карсона — Хевисайда является линейным
преобразованием, поэтому изображение суммы равно сумме изоб-
ражений.
Каждое слагаемое уравнения (10.38) заменим операторным
изображением:
вместо i7? запишем А7 (р);
399
вместо uab запишем Uab(py,
LTt^LpI ~ Lpi (°); Uc (0) “c (0);
t
1C idt^nEL e(t)=:E(p).
C J Cp
0
Получим:
U«b (P) = I (P) ( R + PL + - Lpi (0) + uc (0) - E (p). (10.39)
Смысл проведенного преобразования состоит в том, что вместо
дифференциального уравнения (10.38) мы получили алгебраиче-
ское уравнение (10.39), связывающее изображение тока 7(р) с изоб-
ражением э.д.с. £(р) и изображением напряжения Uab(p). Из
уравнения (10.39) следует, что
/ (п) = Uab (р) + Lpi (0) ~ ис (0) + Е (р) (Ю 40)
Z(p) ’ 7
Здесь
Z(p) = /?+p£+A;
Ср
Z(p) представляет собой операторное сопротивление участка цепи
между точками а и Ь.
Структура его аналогична структуре комплекса сопротивления
того же участка цепи переменному току, если ja заменить на р
(ср. с § 266).
Уравнение (10.40) может быть названо законом Ома в опера-
торной форме для участка цепи, содержащего э.д.с. Оно записано
при ненулевых начальных условиях.
Слагаемое Lpt (0) представляет собой внутреннюю э.д.с., обу-
словленную запасом энергии в магнитном поле индуктивности L
вследствие протекания через нее тока i (0) непосредственно до ком-
мутации.
Слагаемое ис(0) представляет собой внутреннюю э. д. с., обу-
словленную запасом энергии в электрическом поле конденсатора
вследствие наличия напряжения на нем ис(0) непосредственно до
коммутации.
В частном случае, когда на участке ab отсутствует э. д. с.
е (I) и когда к моменту коммутации I (0) = 0 и ис (0) = 0, уравне-
ние (10.40) приобретает более простой вид:
7 (р) =
Z(p)
(10.41)
400
Уравнение (10.41) представляет собой математическую запись
закона Ома в операторной форме для участка цепи, не содержа-
щего э. д. с., и при нулевых начальных условиях.
§ 293. Первый закон Кирхгофа в операторной форме. По
первому закону Кирхгофа алгебраическая сумма мгновенных зна-
чений токов, сходящихся в любом узле схемы, равна нулю. Так,
для узла а схемы рис. 319
4 — i — z2 = 0. (10.42)
Применим преобразование Карсона — Хевисайда к уравне-
нию (10.42) и воспользуемся тем, что изображение суммы равно
сумме изображений.
Имеем
ЛСД — Лр) — /2(Р) = °-
В общем случае
S/(P) = 0. (10-43)
Уравнение (10.43) выражает собой
первый закон Кирхгофа в оператор-
ной форме.
§ 294. Второй закон Кирхгофа в опе-
раторной форме. Для любого замкнутого
Рис. 320
контура любой электрической цепи можно составить уравнение по
второму закону Кирхгофа для мгновенных значений величин.
Как известно, с этой целью предварительно необходимо вы-
брать положительные направления для токов в ветвях и положи-
тельное направление обхода контура.
Запишем уравнение по второму закону Кирхгофа для контура
рис. 320.
Контур обходим по часовой стрелке.
Учтем, что индуктивности L± и L.2 связаны магнитно. При вы-
бранных положительных направлениях для токов i± и z2 между
и L, имеет место согласное включение.
Падение напряжения на Lt состоит из двух слагаемых L^-l-
-\-М~. Падение напряжения на Ьг равно Ls —. При со-
ей dt dt
ставлении уравнения учтем, что начальное напряжение на конден-
саторе равно zzc. (0). Пусть оно действует согласно с током i3. На-
чальное значение тока z\ равно z\(0), а начальное значение тока
z2 равно г2 (0). Имеем:
Li м + ис (0) +1 f i3 dt - z2/?2 -
dt dt C J
о
- L2 £ - M J- = ex (0 - e3 (t). (10.44)
dt dt
14 «И. А. Бессонов
401
Каждое из слагаемых (10.44) заменим операторным изображе-
нием;
Li ~ LtPl 1 (Р) — (0);
С11
м = Mpl2 (р) — Mpi2 (0);
«2^2 И RJz (РУ
£•2 V L2P/2 ~ L2^£ '2 (°>:
at
M^MpI^-Mpi^O)-
dt
<М=Е№
ей (0 = Е3 (р).
(10.45)
Подставив (10.45) в (10.44), объединим слагаемые с (р), /2 (р),
/3(р), перенесем в правую часть ис(0), /.рот^О) и другие внутрен-
ние э. д. с. и получим:
li (р) А (Р) + Л (р) Z2 (р) + /, (р) Zs (р) =
= E’i(P) —£’з(Р) + £’в„(Р)- (10.46)
Здесь
Zi (Р) = Р (Lr - М); Z2 (р) = р (М - LJ - /?3; Z3 (р) = ±;
Ср
Еен (Р) = Р [(^1 — М) 4 (0) + (М — L,) 12 (0)1 — ис (0).
В более общем виде уравнение (10.46) можно переписать так:
24(р)/Ир) = 2^(р).
(10.47)
Уравнение (10.47) представляет собой математическую запись
второго закона Кирхгофа в операторной форме. В состав £,, (р)
в общем случае входят и внутренние э. д. с.
§ 295. При составлении уравнений для изображений применимы
все методы, рассматривавшиеся в разделе синусоидального тока.
Из уравнений, составленных по законам Кирхгофа для мгновенных
значений, вытекают соответствующие уравнения, составленные по
законам Кирхгофа для изображений.
Уравнения для изображений совершенно аналогичны по форме
уравнениям, составленным для той же цепи символическим методом
для комплексов токов и напряжений.
Но если каждому уравнению для комплексов отвечает соответ-
ствующее уравнение для изображений, то все основанные на за-
конах Кирхгофа приемы и методы составления уравнений (метод
40?
эквивалентного генератора, метод контурных токов, метод узло-
вых потенциалов, метод наложения и т. и.) могут быть применены
и при составлении уравнений для изображений.
При составлении уравнений! для изображений учет ненулевых
начальных условий производится путем введения «внутренних»
э.д.с., обусловленных начальными токами через индуктивности
и начальными напряжениями на емкостях.
§ 296. Последовательность расчета в операторном методе. Расчет
состоит из следующих двух основных этапов:
1. Составление изображения искомой функции времени.
2. Переход от изображения к функции времени.
На нескольких примерах покажем, как производится первый
этап. Второй этап будет рассмотрен
в § 298.
Пример 134. В схеме рис. 321 при
нулевых начальных условиях вклю-
чается рубильник. Составить опера-
торные изображения токов и ia,
пользуясь методом контурных токов.
Решение. Направления кон-
турных токов in и iM показаны на
схеме. Имеем
НЛ + Ь Ду + Я2 (in - t22) = е (ty,
dt
J i2-2 dt -|- /?2 (г'22 *11) = 0-
Переходим к изображениям:
Л, (р) (Р^ + - '22 (Р) ^2 = Е (р);
- /и (Р) R-2 + /гг (Р) (+ -Д == 0.
\ Ср}
Совместное решение двух уравнений с двумя неизвестными
дает;
{ { } _ £(р)(1 + ^Ср) . 11W р2Е,ЕС 4- р {RtR2C 4- £j) 4- Rt 4- R2 ’ I E (p)R-2Cp . 22 p2/?.£1C + p (RiR.C 4- Lt) 4- Rt 4- R2 (10.48) (10.49)
Изображение контурного тока /п(р) равно изображению
тока /Др). Изображение /22(р) равно изображению /3(р).
В (10.48) и (10.49) Е(р) есть изображение э.д.с. е(/). Если
е (/) = Е, то Е (р) тоже равно Е\ если
е (/) = Ет sin (и/ -|- ф),
14*
403
то
£(р) = 4
II т. д.
Пример 135. Составить изображения токов ir и i3 схемы рис.
321, пользуясь законами Ома и Кирхгофа.
Решение. Так как в схеме нулевые начальные условия и
нет магнитно связанных индуктивных катушек, то составить урав-
нения можно даже проще, чем по методу контурных токов.
Изображение тока
Л(р) =
Е(Р) .
Zex (Р)
Zev(p) есть входное сопротивление схемы в операторной форме
по отношению к зажимам ab. Оно определится так же, как опре-
деляется входное сопротивление для переменного тока, только
надо /со заменить на р.
Для переменного тока
z„-«,+K+—
Rz + гд
/соС
Входное операторное сопротивление
„ ,ч n . т . Ср Р2£1С/?2 + р(£1 + /?1/?2С) + /?1 + /?2
гвЛР)=^р1^----------•
R*+ Ср
Следовательно,
[ (р) = = —------£(р)(1 + ^Ср)------ (10.48')
Z(p) p^CRz + р (Д + RiR2C) + Rt + R2 '
уравнение (10.48') совпадает с уравнением (10.48).
Найдем изображение /а(р). С этой целью выразим /3(р) через
/Др) и операторные сопротивления второй и третьей ветвей. Вос-
пользуемся аналогией с переменным током. Для переменного тока
/ = t
‘з — 'i . •
+ 7ГД
/сов
Следовательно,
/з(р) = Л(р) ——•
404
Если в последнее выражение подставить /Др) из уравнения
(10.48), то будет получено уравнение (10.49).
Таким образом, совершенно безразлично, каким способом со-
ставлять изображения токов: результат будет одинаков.
Пример 136. Для схемы рис. 321 составить изображение напря-
жения на зажимах се, считая начальные условия нулевыми (как и
в примере 135).
Решение. Изображение напряжения на зажимах се
равно произведению изображения тока /3(р) на операторное со-
противление конденсатора:
(Р) = Л (Р) — =-----------£(p)Pi-----------. (10.50)
Ср p"R:L1C + p(R1R.C + L1)+R,+R2
§ 297. Изображение функции времени может быть представле-
но в виде отношения двух полиномов по степеням р. Так,
М (р)
для тока /и(р) в примере 134, если принять Е(р) = Е,
N (р) = Е (IR^Cp)',
М (р) = pR.Rfi + р (RR.fi + + Rt -Ь R.2.
Если в том же примере принять, что
е (/) = Ет sin (со/ -ф- ф),
то
Е (р) = Ёт и N (р) = Ёт р (1 + /?2Ср);
р —/со
м (р) = (Р - /®) [pRJL.fi + р (RR.fi J-LJfiRfi /?2].
Обозначим наивысшую степень оператора р в полиноме Л’(р)
через п, а наивысшую степень р в полиноме Л1(р) — через т.
Во всех физически осуществимых электрических цепях при
воздействии любых практически встречающихся э.д.с. всегда
п <_ т. Лишь для физически неосуществимых электрических цепей
п может оказаться больше т, по такие задачи не представляют
интереса.
Пример физически неосуществимой электрической цепи, для
которой степень п будет больше степени т, дан на рис. 322. Если
считать, что активное сопротивление цепи равно нулю, что физи-
чески неосуществимо, то
/ (р) = JL =
Д_ 1
Ср
В этом случае п = 1 и т ~ 0.
§ 298. О перехода от изображения к функции времени. В § 296 ука-
зывалось, что вторым этапом расчета переходных процессов ври
405
помощи операторного метода является переход от изображения к
функции времени. Эта операция может осуществляться различны-
ми путями. Первый путь состоит в применении формул соответствия
между функциями оператора р и функциями времени.
Часть формул соответствия приведена в таблице на стр. 398.
Вообще же в научной литературе есть специальные исследования,
содержащие обширные таблицы формул соответствия (1518 формул),
охватывающих все возможные практические задачи. Формулами
соответствия (стр. 398) рекомендуется пользоваться в том случае,
если среди корней уравнения Л4(р) = 0 есть несколько одинако-
вых корней (кратные корни) или (и) корень, равный нулю (р = 0).
Второй путь состоит в применении так называемой формулы
разложения (см. § 301). Формула разложения в § 301 выведена,
исходя из предположения, что уравнение М (р) = 0 не имеет крат-
кие. 322
Рис. 323
ных корней и корня р — 0 (при наличии кратных корней формула
разложения записывается иначе — см. например, |Л. 2]).
Для подавляющего большинства задач эти ограничения не
имеют существенного значения.
Формулой разложения широко пользуются на практике, и ее
принято рассматривать как основную формулу для перехода от
изображения к функции времени.
Рассмотрим два примера на применение формул соответствия,
а затем — после рассмотрения вопроса о разложении сложной
дроби на более простые — перейдем к выводу формулы разложе-
ния.
Пример 137. В схеме рис. 323, а напряжение источника изме-
няется по закону и (t) = 2500/ в (рис. 323, б), R — 400 ом,
С = 200 мкф. Найти закон изменения напряжения на конденсато-
ре и значение ис при t = 0,1 сек.
Решение. Z (р) = R -]—- = RCp- + ,
Ср Ср
Изображение напряжения 2500/ равно ^5? (см. соотношение
р
12 в таблице на стр. 399). Следовательно,
j /р\ __ U (р)________________ 2500 Ср .
Z (р) р (RCp + 1) ’
406
Uc(p) = I(p)± = сг
Ср Г\С
2500 1
/ 1
'V+rc
Из таблицы (стр. 398) находим, что
----!---==1 — 1(1 — e~at).
Р (Р + а).' а а2
В рассматриваемом примере
а = — = — = 12,5 сек-1;
RC 0,08
— = 31300; к. = 31 300
RC с
При t = 0,1 сек
ис = 31 300 (0,008 — 0,00645.0,714) = 106,5 (е).
Пример 138. В схеме рис. 324
u(t) = 100е“й/ в,
где а = 0,5 сек-1; /? — 2 ом\ L — 4 гн.
Найти i = f (t) и uL = f(t), а также зна-
чения i и uL при t = 1 сек.
Решение. Из таблицы (стр. 398) следу-
ет, что функция e~at имеет своим изображе-
нием —-—. Следовательно,
р + а
(10.51)
t
12,5
- = — = 0,00645;
а2 155
- 0,00645 (1 — е-12 -!
Рис. 324
t/(p) = _122р_;
Р + а
Z(p) = R + pL-,
100
Р
2(р) (р + a) (pL + /?) L (p + a)(p + b)’
^ = 25 а/сек.
р
Так как b — — = 0,5 — а, то
/(р) = 122—
L (р+а?
Из таблицы (стр. 398) находим
(Р + а)2 ’
i (t) = 25 te~at-
Напряжение на индуктивности
uL = L = 100 е-°>ы (1—0,50.
Поэтому
407
При t = 1 сек,
i = 25 • 1 • е~0-5 = 15,15 a- uL = 100 е~0-5 (1 —0,5) = 30,3 в.
§ 299. О разложении сложной дроби на более простые. Из
курса математики известно, что дробь вида
N (х) __ О-п^П ~Ь Дп—1 1 Т • 4~ Я Iх <Z()
М (*) bm хт + bm_! Xй-1 + . .. + btx + b0
при условии, что п т и полином
М (х) = bm х™ + bm_t xm~' +... + b±x 4- bn = 0
не имеет нулевого корня и кратных корней, может быть представ-
лена в виде некоторого постоянного числа Л(| и суммы более про-
стых дробей:
= —+ А —+... + Л,—. (Ю-52)
М (*) X — хг X — Х2 X —х,л
или
N (х) — Д I V д х
М (х) 0 1г х — хъ
k~\
Здесь xk — корни уравнения М (х) = 0.
Постоянные Л(|, Alt А2, ..., Ат можно найти двояко. Первый
путь — метод неопределенных коэффициентов — элементарнее, но
требует проведения более громоздких вычислений, второй — внеш-
не сложнее, но по существу удобнее, проще, а главное «упорядочен-
нее».
Познакомимся с этими приемами определения коэффициентов.
Первый путь состоит в том, что в уравнении (10.52) приводим
правую часть к общему знаменателю и затем путем сопоставления
коэффициентов при одинаковых степенях х составляем систему
уравнений для определения коэффициентов Ао, Аи А2,...
Пример 139. Разложить дробь -----------на сумму более простых дро-
х2 — 5х 4- 6
бей.
Решение. В рассматриваемом примере N (х) = 1 и М (х) — х2 — 5х -|-6.
Находим корни уравнения Л1 (х) = 0:
М (х) = х2 — 5х -j- 6 = 0.
Отсюда
Следовательно, ху => 2 и х3 = 3. Поэтому
1 хх
Tg Ё J- At I + Az ~ •
х‘ ~ 5х + 6 х — 2 х — 3
408
Приводим правую часть к общему знаменателю;
1 _ Ai(x2 —5x4-6)4-Ai(x2 —Зх)Ц~ АДх2 —2х)
х2 — 5х + 6 х2 — 5х + 6
Сопоставление коэффициентов при х2 в числителе левой и правой частей
дает:
О == Др 4" Д14" Да-
Сопоставление коэффициентов при х:
О = — 5Д0 — 3At — 2Да.
Сопоставление свободных членов дает:
1 = 6Д0.
Совместное решение приводит к следующему результату;
1 1 1
Д°- 6 ; Дт--2 ; 3 •
Таким образом:
1 1 1 х । 1 X
х2 — 5х 6 6 2 х — 2 3 х — 3
Теперь рассмотрим второй способ определения коэффициентов
До, Дх, А2, ... G целью определения коэффициента Ао положим
х = 0, что можно сделать, ибо М(х) не имеет корня х — 0 и поэто-
му ни левая, ни правая часть (10.52) при этом не обращаются в бес-
конечность. Обозначим значение N(x) при х = 0 через 7V(0) и зна-
чение Л4(х) при х = 0 через М(0). Получим:
М (0) 0 0—Х1 1 1 т 0-хт
Отсюда
д (10.53)
0 М (0)
Для определения коэффициента Аг помножим обе части урав-
нения (10.52) на (х — хг). Получим:
k -т
^(х-хх) = До(х-х1)+Д1х+(х-х1)2Ак-^—. (10.54)
Л1(х) " х—хк
Л-2
Рассмотрим выражение (10.54) при х, стремящемся к xv Пра-
вая часть дает Д^, левая часть будет представлять собой неопре-
деленность, так как множитель (х — xj, при х -» хг дает нуль и
знаменатель М(х) при значении х = хг тоже дает нуль [хх есть
корень уравнения М(х) = 0].
Раскроем неопределенность по правилу Допиталя. С этой целью
производную от числителя поделим на производную от знаменате-
ля и найдем предел дроби:
409
.. (x—X!)N(x) _ ]jm (x) + (x — xt)N' (x) __ N (Xi)
Lx, M(x) x^xt M'(x)
Здесь M'(x) есть производная от M(x) по х; M'ixJ — значе-
ние М'(х) при х = xr; N(X]) — значение N(x} при х = хг.
Следовательно, из (10.54) при х -> хх получаем следующее
уравнение:
им — А х
М'(Х1) r 1
откуда
Аналогично
N(xJ
xtM' (xi)
(10.55)
Вообще
N (ха)
х£ЛГ (х2)
(10.56)
Таким образом,
U (xfc)
xkM' (*«)
(10.57)
4 =
4 =
или
N (х) Д' (0) . N (xt) х , N (х2) х ।
М (х) М (0) Xi М' (х,) х—xj х2 М' (х2) х—х2
+-+ ) 7Z7- <,0-58)
U(x) = ЛГ(О) , N(xk) х
Л1 (х) М (0) xk М' (xk) х — хй’
А = 1
(10.58')
Пример 140. Найти коэффициенты разложения дроби---------,
Xs— 5х -f- 6
пользуясь вторым способом.
Решение. Корни уравнения М(х) = 0 известны из приме-
ра 139. Они равны хг = 2 и х2 — 3.
А(0) = 1; Л4(0) = 6.
По формуле (10.53)
А - 1
0 М (0) 6 ‘
М'(х) = 2х — 5; М'(х1) = 2. 2 —5 = — 1; ^(x1)= 1.
По формуле (10.57)
А - - NM - _______!_ = _I-
1 xxM'to) 2(-1) 2*
А = N(Xi) = 1 = 1
2 х2 М' (х2) 3-1 3 ’
410
что совпадает с результатами, полученными первым способом.
Пример 141. Разложить дробь
N (х) __х2 — 6х -J- 5
М (х) ~~ х2 — х — 2
на сумму более простых дробей.
Решение. Находим корни уравнения М(х) = 0:
х2 — х — 2 = 0; х13 = -^ ± + 2; xt = 2; ха = — 1.
W(0) = 5; 7И(0) = —2; Лв=—
д/(хх) = 4 — 12-|-5 = — 3; М'(х) = 2х — 1; M'(xt) = 3;
А - - ~3 - 1 •
1 xtM'(xj 2-3 2*
IV (х3) = 1 4-6 + 5 = 12; М' (х3) = - 3;
А = = 4
2 х2М'(х2) (-1Х-3)
Следовательно,
х2 — 6х + 5 _____________ 5 х , 4х
х2 — х — 2 2 2(х—2) х + 1
§ 300. Формула разложения. Переход от изображения к
функции времени часто производится при помощи формулы:
т
Л/(р)^Л/(О) , у N(pk) t . (10.59)
М(р) М (0) ркМ' (рк)е
Л-1
ее и принято называть формулой разложения.
Левая часть формулы является функцией р, правая часть соот-
ветствующая ей функция времени t.
§ 301. Вывод формулы разложения. Пусть изображение какой-
либо функции времени, например тока, представлено в виде дроби:
/(Р)=
w М (р)
Для получения тока как функции времени i (/) представим
сначала в виде суммы более простых дробей — разложим .
М (р) М(р)
С этой целью в формуле (10.58') заменим х на р:
I = /VM = Л'(0) I V N<Pfe) р
М(р) м PkM'(pk) р — Pk"
k = 1
(10.60)
Перейдем от изображения к оригиналу. Оригиналом левой час-
ти является i (/). Оригинал правой части равен сумме оригиналов
ее слагаемых.
411
N(0) N(pk)
Учтем, что слагаемое —— и множители-----------—— у слагаемых
м (0) pkM' (pfe)
суммы правой части (10.60) есть постоянные числа (не функции р!)
и что изображение постоянной есть сама постоянная. Затем учтем,
что функциями р в правой части являются только множители
—-—; им соответствуют функции времени вида ер k [см. форму-
лу (10.28)]. Поэтому
*(0 =
(°) I V N(Pk) vkl
М(0)^ pkM'(pk) •
ft=l
(10.61)
Переход от изображения (функции р) к оригиналу (функции f)
при помощи формулы разложения (10.61) основан на том, что изо-
бражение было представлено в виде постоянного числа и СУМ*
N (р,.) р
мы более простых дробен вида -----------— , а оригиналы этих
РкМ' (pk) p — pk
дробей являются показательные функции - N - ер
n PkM'(Pk)
„ А'(О) й „
Слагаемое представляет собой составляющую искомого
тока или соответственно напряжения, обусловленную постоян-
т N (0) „
ными э. д. с. Если постоянных э. д. с. в схеме нет, то —— = 0.
М (0)
Число слагаемых - равно числу корней уравнения
М (р) = 0. Коэффициенты —можно сопоставить с постоян-
PkM (pk)
ными интегрирования дифференциального уравнения (или уравне-
ний) цепи в классическом методе расчета.
Важно сделать следующие замечания к формуле (10.61):
1. Формула разложения применима при любых начальных ус-
ловиях и при любых практически встречающихся формах напряже-
ния, воздействующего на схему.
2. Если начальные условия не нулевые, то это находит свое
выражение в том, что в состав N(p) войдут «внутренние» э.д.с.
3. Если уравнение М(р) = 0 имеет комплексно сопряженные
корни, то слагаемые, соответствующие им в формуле (10.61), ока-
зываются также комплексно сопряженными и в сумме дают дейст-
вительное слагаемое.
4. Если воздействующая на схему э. д. с. синусоидальна
[Е„. sin (at ф)] и изображение э. д. с. взять в виде ,
р — ja
где комплексная амплитуда Ет — Ете>’\ то при пользовании
формулой разложения от правой части ее для перехода от комплек-
412
са к мгновенному значению надо взять коэффициент при / (взять
мнимую часть)*.
В соответствии с этим «внутренние»э. д. с., которые появляются
в правой части формулы разложения при ненулевых начальных
условиях в цепях с синусоидальной э. д. с., должны быть умножены
на коэффициент j.
Умножать внутренние э.д.с. на / необходимо потому, что толь-
ко в этом случае наличие внутренних э.д.с. будет учтено при взя-
тии мнимой части от правой части формулы разложения. В цепях
с постоянной э. д. с. внутренние э. д. с. умножать на / не нужно.
5. Если воздействующее на схему напряжение синусоидаль-
но, то принужденная составляющая решения входит в число слага-
емых и определяется корнем р = /со. Вычисле-
ние принужденной составляющей в виде члена этой суммы, соот-
ветствующего корню р = /со, для сложных схем, оказывается, как
правило, делом несколько более громоздким, чем непосредствен-
ное вычисление ее при помощи символического метода. Поэтому
для сложных схем переменного тока принужденную составляю-
щую рекомендуется вычислять символическим методом, а не как
составляющую суммы формулы (10.61), соответствующую корню
Р =
Разумеется, при помощи формулы, подобной формуле (10.61),
можно определять не только токи и напряжения, но и любые дру-
гие функции времени (заряд конденсатора, скорость перемещения
какого-либо тела механической системы и т. п.).
Рассмотрим два примера на применение формулы разложения.
Пример 142. Определить ток ix (i) в схеме рис. 311 при помощи
формулы разложения и сравнить с результатом решения класси-
ческим методом (см. пример 129 на стр. 381): Е — 150 в; R{ =
= R't = R3 = 50 ом\ С = 100 мкф.
Решение. Составим уравнения для изображений токов по
законам Кирхгофа**. Учтем, что в схеме ненулевые начальные ус-
ловия:
Л (Р) + «о (0) + ^ = £; Ц (р) + /3 (р) R3 = Е-
ср
— — (р) = 0,
где пс(0) = 50 в представляет собой «внутреннюю» э. д. с., обуслгз-
ленную запасом энергии в электрическом поле конденсатора к на-
чалу переходного процесса.
* Мнимая, а не действительная часть от формулы разложения берется
потому, что заданная э. д. с. Ет sin (<ut + ф) есть мнимая часть комплекса
Ёте< "1 (см. стр. 115).
** Уравнения составляем для послекоммутационной схемы.
413
Из системы трех уравнений найдем 7/р):
/ (р\ = 1£-Цс(0)1£зСр + £ = N(p)
11 7 RiRsCp + Ri + R3 М (р) ’
Уравнение М (р) = 0 имеет корень р = —fa ф = — 400 сек-';
RiR^C
N(Q) = Е= 150;
M(0) = Z?1 + /?3= 100;
М' (pr) = R&C = 50 50 . 100 • 10-е = 0>25;
yV(pj = (150 — 50). 50 • 100 . (—400). 10~6+ 150 = — 50;
i (0 = — ф- <-59)g~*c0< = 1,5 + 0,бе-400' а,
1X 1 100 1 (—400). 0,25 1
что совпадает с результатом примера 129.
Пример 143. Найти i(t) в схеме рис. 315 путем применения фор-
мулы разложения и сравнить результат с результатом решения той
же задачи классическим методом (см. пример 131 на стр. 384).
Решение. Изображение синусоидальной э. д. с. 127 sin
(314/ — 50°) равно:
Е(р) =
р —/со
где Ёт — 121е~>50° в.
В схеме ненулевые начальные условия:
/(р)(/?2 + р£) = £(р) + ^(0).
Так как действующая в схеме э. д. с. синусоидальна и изобра-
жение ее взято в виде Ёт—-— (где Ёт— комплексная амплиту-
р — /а
да) и в дальнейшем в связи с этим от правой части формулы раз-
ложения надо будет взять коэффициент при мнимой части (см. п. 4
§ 301), то умножим «внутреннюю» э. д. с. Lpi (0) на /.
После небольших преобразований находим I (ру.
I (р) = £mP + /'M(0) (Р —/<о) _ N (р).
7 (p-j^^ + pL) М(рУ
N(p)= Ётр ф- jLpi (0) (р —/со); М (р) = (р — /со) (/?2 ф- рЕ).
Уравнение М (р) = 0 имеет два корня:
Pi — ja сек.-1 и р2 = — — — 210 сек-1; N (0) — 0,
поэтому первое слагаемое в формуле (10.61) выпадает.
М' (р) = /?2 + pL ф- L (р — /со);
М' (Р1) = 2 + 3/ = 3,61 ?56°20'; М' (р2) = - 3,61 е756’20';
414
i (t) — Im
127е/<ю<-50°) . 127 e-/50°-}- j 3,61e/56°20' -25,35 g-21 of
3,6k'56°20' + -3,61 el S6’20'
= 35,2 sin (co< — 106°20')+ 13sin40°20'e~2I0'a;
13sin40°20' =8,54.
Результат совпадает с результатом примера 131.
§ 302. Переходная проводимость. В главе «Линейные электричес-
кие цепи» (§ 14) говорилось о том, что ток i в любой ветви схемы мо-
жет быть представлен в виде произведения напряжения U на входе
схемы на собственную или взаимную проводимость g:
г = Ug.
При переходных процессах это соотношение также имеет силу.
Если на вход какой-либо цепи в момент t = 0 включается по-
стоянное напряжение U (или э. д. с. Е), то ток 1(f) в любой ветви
этой схемы будет равен произведению постоянного напряжения U
на проводимость g(Z):
i(O = t/g(O- (10.62)
При переходном процессе проводимость является функцией
времени. Это находит свое отражение в том, что в скобках указы-
вается время /; g(t) называется переходной проводимостью. Она
измеряется в тех же единицах (сим), что и «обычная» проводимость.
Если в формуле (10.62) принять V равным 1 в, то при этом i(t) =
= g(t). Другими словами, переходная проводимость какой-
либо ветви схемы численно равна току 1(f) в этой ветви при под-
ключении цепи к постоянному напряжению в 1 в; g(f) будем снаб-
жать двумя индексами. Индексы указывают, о какой именно пе-
реходной проводимости идет речь. Если индексы одинаковы, то
речь идет о собственной переходной проводимости ветви, номер
которой соответствует цифре, указанной в индексе. Если индексы
разные, то речь идет о проводимости между теми ветвями, номера
которых указаны в индексе.
Так, например, если источник постоянного напряжения U
при нулевых начальных условиях включается в первую ветвь, то
ток первой ветви i^t) = Ugu(t), а ток третьей ветви i3 (t) =
= Ugsl(t).
Переходную проводимость можно определить либо расчетным,
либо опытным путем. При расчетном определении gkk(t) класси-
ческим или операторным методами находят ток k ветви при вклю-
чении источника постоянного напряжения в k ветвь. При опреде-
лении gi:m(t) находят ток k ветви при включении постоянного
напряжения U в т ветвь. Далее, в полученных формулах пола-
гают U равным 1 в. При опытном определении переходной про-
водимости ток i (t) соответствующей ветви находится путем осцил-
лографирования.
415
В § 15-было доказано, что Это свойство вытекает из симметрии
определителя системы относительно главной диагонали.
Аналогичным путем можно доказать, что операторное изображение про-
водимости gkm (р) равно операторному изображению gmk (р) . Но если рав-
ны изображения двух переходных проводимостей, то равны и сами переход-
ные проводимости, т. е.
gkm (О —g mk (О-
(а)
Равенство (а) свидетельствует о том, что на переходные процессы распро-
страняется теорема взаимности-.
Для переходных процессов теорема взаимности формулируется следую-
щим образом (см. «скелетные» схемы рис. 325).
В любой линейной электрической цепи ток переходного процесса k ветви
ik (/), вызываемый включением э.д.с. ет (t) в т ветвь (рис. 325, а), равен току
переходного процесса «„,(/) в т ветви, вызываемому включением э.д.с. е/г(0
в k ветвь (рис. 325, б) при условии, что ек (/) = ет (f).
§ 303. Понятие о переходной функции по напряжению. При под-
ключении линейной электрической цепи с нулевыми начальными
условиями к постоянному напряжению U между какими-то двумя
точками а и b схемы возникает напряжение uab(t), являющееся
функцией времени и пропорциональное воздействующему напря-
жению U. Напряжение иаЬ (/) может быть представлено в виде
произведения
(10.62')
.%(/) называют переходной функцией по напряжению.
Это безразмерная величина, численно равная напряжению
между точками а и b схемы, если на вход схемы подать постоянное
напряжение в 1 в\ k(f), так же как и g(t), можно определить либо
расчетным, либо опытным путем.
Пример 144. Определить переходную проводимость схемы рис.
293 (схему см. на стр. 355).
Решение. При замыкании рубильника i(f) ( 1—е L )•
416
По определению переходная проводимость равна току в цепи при
1 -Л
Е = 1 в. Следовательно, g(f) = — (1 — eL ).
Пример 145. Найти собственную переходную проводимость пер-
вой ветви взаимную переходную проводимость между
третьей и первой ветвями £зх(/) и переходную функцию для напря-
жения на конденсаторе kUc(t) для схемы рис. 309 (схему см. на
с гр. 379). Параметры схемы: /?х = 1000 ом, = 2000 ом;
С — 50 мкф. Источник э. д. с. £ = 210 в включаем в первую
ветвь.
Решение. По определению
l'i ~ (О’ *'з = Eg31 (/); ис = Ekn(. (/).
При помощи классического метода получаем (см. стр. 381):
Ё = —-------1- £-----------ept; i3 = — ер‘;
Я1 + Я2 1 £i(£i + ^2) /?1
„ р = _А+^.
/?г 4- /?з
Полагая в этих формулах £ = 1 в, находим:
к.-W t
g (0 = __!_ +----------Ъ---е r,r.c
11 ' £х4-£3 /?i(£i + £2)
R,+R, .
g31«) = ±e ;
«г
Rl+Rl . .
\-е R^c ).
£„(/)=
/?1 +
Подстановка числовых значений дает:
£ii(0 = 0,00033 + 0,00067 e~30t сим; g31(t) = 0,001 e-30Z сим;
^с(0 = |(1-е-300.
Пример 146. Определить взаимную проводимость между первой
и третьей ветвями схемы рис. 295 (схему см. на стр. 361) при
включении э.д.с. в первую ветвь и следующих значениях парамет-
ров: /?х = /?2 = 100 ом; L1 = 1 гн; С — 100 мкф.
Решение. Изображение тока третьей ветви равно:
13(р)= = ^.
pW + p(W + tx) + ^i + /?2 М(р)
Корни уравнения М(р) = 0 таковы (см. пример 121 на стр.
365):
рх = — 100 + /100; р2 = —100 — /100.
417
Полагаем Е = 1 в и в соответствии с формулой разложения
находим;
i (t) =------------------------ер,<ф-
при £=1 в ZpiRzLjC 4- (РХР^С Lj)
_1__________Ы
ЪрЛгЦС 4~ (R1R2C 4~ Pi)
После подстановки значений параметров, значений корней р±
е) Х ____________________________ e-jx
и р2 и использований формулы ------—— — sinx получим:
g31(/) = 4(0 = 0,01 a"190-sin 100/.
при Е = I в
Таким образом, взаимная переходная проводимость между
схемы рис. 295 при записанных выше
значениях параметров представляет
собой затухающую синусоиду.
Пример 147. В схеме рис. 326
«(0=170sin (314/+300) в; ом,
R., = 5 ом, R:t = 15 ом; Lx = 30 мгн,
L.2 = 50 мгн; М = 25 мгн.
Найти ф(/) при помощи формулы
разложения.
Решение. Составим уравне-
ния по методу контурных токов:
К (Р) + Я2 + Р (М + + 2Л4)] -
- /2 (р) [Я2 + Р + М)] = и (р);
- h (р) [Я2 + Р (7-2 + М)1 + /2 (Р) (R2 + R3 + pL2) - 0.
Совместное решение дает:
(р —/w)Zi(p)
___________0тР (20 4- 0,05р)_________ N (р)
“ (Р — /и) (0,000875р2 4- 2,6р 4- 275) М (р)"
Корни уравнения Л4(р)= 0 таковы:
рх = 314 j; р2 =—2S60; р3 = — 114 сск~‘.
N (0) = 0.
М' (р) = 0,000f75;;2 ф- 2,6р + 275 (р— /о>) (0,00175р ф- 2,6),
Pi/И' (рх) = /(оЛГ(/(о) = 314/835е-й’54' ,
р,Л-Г (р;) = — 2860 . М' (— 2860) =
= — 2860.2870е-/173 )1’ (—2,4),
р3ЛГ (р3) = — 11434' (— 114) = — 114.800е-/П1°«
Лфр,) = 314/25,4 • 170е-'(30 +38'0'),
N (Рг) = _ 2860 . (— 123) • 170е,30°,
418
N(p3) = — 114. 14,3- 170t-/30°,
i(t]= Im f N _JY_(£bL (Jp-^ I 'v ePi,t
I Pi-W'lPi) p2 M' (p2) p3 M' (p3)
= Im {5,17еН®/-8-50') 3,03^/20344' . e-28ecz
H-3,04ei'«° . e-inq = 5,17 sin («/ —8c50') —
—1,16 e-2860/_]_ 1,97
Познакомимся теперь с третьим методом расчета переходных
процессов в линейных электрических цепях — с расчетом при
помощи интеграла Дюамеля.
§304. Интеграл Дюамеля. При пользовании интегралом Дюамеля
условимся переменную, по которой
обозначать через т, а под t по-
прежнему будем понимать тот мо-
мент времени, в который требует-
ся найти ток в цепи. Пусть в цепь
с нулевыми начальными условия-
ми в момент времени t — 0 под-
ключается напряжение и (?) (рис.
327). Для того чтобы найти ток
в цепи в момент времени t, заме-
ним плавную кривую ступенчатой
и просуммируем токи от началь-
ного напряжения zz(O) и от всех
ступенек напряжения, вступающих
производится интегрирование,
в действие с запозданием во
времени.
Напряжение п(0) в момент времени t вызовет в цепи ток
u(0)g(/), где g(f) — переходная проводимость.
В момент времени т+Ат (рис. 327) возникает скачок напряже-
ния
Ат = н' (т) Ат.
Для того чтобы найти составляющую тока в момент времени t,
вызываемую этим скачком напряжения Azz, надо величину zzz(t)At
умножить на значение переходной проводимости с учетом времени
действия скачка до момента времени t.
Из рнс. 327 видно, что это время равно t—т—Ат. Следова-
тельно, приращение тока равно:
н' (т) g (t — т — Ат) Ат.
Полный ток в момент времени t получим, если просуммируем
все частичные токи от отдельных скачков и прибавим их к току
u(0)g(0=
419
i (t) = и (0) g (t) + 2 «'(t) g (t — t — At) At.
Число членов суммы равно числу ступенек напряжения. Оче-
видно, что ступенчатая кривая тем лучше будет заменять плавную
кривую, чем больше будет число ступенек. С этой целью заменим
конечный интервал времени Ат на бесконечно малый dx и перей-
дем от суммы к интегралу:
i(0 = «(0)g(0+ ^u'(x)g(t — x)dx.
о
(10.63)
Формула (10.63) называется интегралом Дюамеля.
Интеграл Дюамеля может быть записан и в ином виде. На дру-
гих формах записи не останавливаемся, так как существенных пре-
имуществ перед (10.63) они не имеют.
При помощи интеграла Дюамеля можно найти не только ток,
но и любую другую величину, например напряжение. В этом слу-
чае в формулу вместо переходной проводимости g(t) будет входить
переходная функция по напряжению k(f).
§305. Последовательность расчета при помощи интеграла Дюаме-
ля. Расчет состоит из четырех этапов.
Первый этап — определение переходной проводимости g(f) для
исследуемой цепи.
Второй этап — определение g(t — г). С этой целью в формуле
для g{t) надо t заменить на (t — т).
Третий этап —определение н'(т). Для этого находим производ-
ную от заданного напряжения u(f) по времени /ив полученном
выражении заменяем t на т.
Четвертый этап — подстановка найденных в этапах 1, 2, 3 функ-
ций в формулу (10.63), интегрирование по переменной т и подста-
новка пределов.
Пример 148. Найти = f (/) и u2 = f(f) при включении рубиль-
ника в схеме рис. 328, а. Напряжение источника э.д.с.
420
u(f) = 100(1 —e~ai) в, a — 0,25 сек-1;
R = 0,5 ом-, L± = 1 гн; M — 0,5 гн.
Решение. Переходная проводимость цепи, состоящей из
последовательно включенных R и L, равна:
Л
где
Л
Первое слагаемое в формуле (10.63) выпадает, так как «(0) = 0.
Находим и'(т):
и' (0 = - 100 (1 — e~ai) = 100 ас-"';
(U
и' (х) = 100ае~а\
t
h (0 = J и' (т) Ё — т) dr =
о
= J е~^[ 1 — е-^е-^ ] dr.
О
При интегрировании учитываем, что e~bt от т не зависит:
(/) = 200 (1 + е~0-51 — 2е~о.®) а.
Напряжение на зажимах вторичной обмотки
щ (/) = м = 50 (е-о.25« _ е-о,5<) в<
dt
§ 306. Применение интеграла Дюамеля при сложной форме напря-
жения. Пусть напряжение и (т) изменяется во времени по сложному
закону, например в соответствии с рис. 328, б. Начальное напря-
жение равно w(0). В интервале от т = 0 до т = t1 напряжение
плавно растет, и закон его изменения в этом интервале времени
пусть будет u^f). В момент т = t1 оно меняется скачком от иа до
иь, затем снова плавно меняется, но уже по другому закону п2(т)
во времени, чем в первом интервале. При т == /2 напряжение скач-
ком уменьшается со значения ис до нуля.
Требуется найти ток в каждом из трех интервалов времени.
Под первым интервалом будем понимать интервал времени от т = О
до т = /j (не включая скачка напряжения от иа до н£). Второй
интервал — от до /2, включая скачок от иа до иь, но не вклю-
чая скачок от ис до нуля. Третий интервал — при т > /2, вклю-
чая скачок от ис до нуля.
421
Интегрирование по-прежнему проводим по т, понимая под t
фиксированный момент времени, в который требуется найти ток.
Ток в любой момент времени t определится действием всех
напряжений, вступивших в действие до момента t.
На первом интервале
г (/) = и (0) g (/) -J- j* и/ (т) g (t — т) с/т.
о
На втором интервале
i (/) = и (0) g (Г) 4- | м/ (т) g (/ — т) dx 4- (ub — иа) g (/ — .4) 4-
о
+ J «2' W g (/ — Т) dx.
tt
Слагаемое (мй— ua)g (t — /г) обусловлено скачком напряжения
от иа до щ в момент времени tv
На третьем интервале
i (/) = и (0) g (/) 4- J и/ (т) g (/ — т) с/т 4- (иь — иа) g(t —
О
И2' (т) g (t — г) с/т 4- (0 — и(.) g (t
Пример 149. В электрической цепи рис. 328, а в момент времени t—Q
замыкается рубильник, и напряжение и (С) изменяется в соответствии с рис. 328,6;
и (0) = 50 в.'
На первом интервале времени от 1 = 0 до t = tL =- 4 сек zz1(/) = 150—
— 100 e~at, где а = 0,25 сект1.
На втором интервале времени от t = tL => 4 сек до t = /3 = 6 сек
и% (О = 50 -j- 100 е~с с = 0,4 с<,к-1.
Параметры схемы рис. 328, а таковы: — 0,5 о,и; Lr = 1 гн (вторичная
цепь разомкнута).
Haiir.i закон изменения тока g во времени для обоих интервалов времени,
а также значения тока iL при / = 2 сек и при 1 = 5 сек.
Реше п и е. g (t) = -у- (1 — e~bt); b = -у- = 0,5 сект1,
R
На первом интервале
u'i (T) == 100 a e~a';
422
4 (f) = « (0) g (0 + f “i (t) g (i — т) A == —p- (1 — e b‘) +
J A
-az [1 — e~~b !/~T)] A = 100 (1 —e~°’5'H
+ 200 (1+ e—P,5Z—2e—°
При t = 2 сек it = 100 (1 — e 1) + 200 (l-j-e 1 — 2e °-5) = 94,9 a.
На втором интервале времени (включая скачок tit,— иа = 36,9 в)
Л (/) = и (0) g (/) + щ (т) g (t—Т) dr +
+ — иа) g — h) + j* W g № "*)
u2 (T) = — 100 ce CTect';
-0.5 Л_2е-0,25Л) +
it (/) = 100 (1 — e~°’5 ') + 200 (1 + e
При t = 5 сек
it = 100 (1 - e~2'5) + 200 (1 + e~2 — 2g-1) +
+ 0,25 e-*’6 +e~0'4'4 e-0’5) e1’6 =91,79 + 80 + 29— 14,67 = 186,12 (a).
§ 307. Сравнение различных методов расчета переходных процес-
сов. И классический и операторный методы расчета могут приме-
няться для решения задач практически любой сложности. Каким
из них пользоваться, зависит от навыка и привычки.
Однако бесспорно, что классический метод более физически
прозрачен, чем операторный, в котором решение дифференциаль-
ных уравнений весьма сильно «механизировано». Интеграл Дюаме-
ля рекомендуется применять в тех случаях, когда напряжение
изменяется по сложному закону во времени, например при нали-
чии скачков напряжения (см. § 306), или когда переходная прово-
димость g(t) и (или) воздействующее на схему напряжение заданы
графически (в последнем случае интеграл Дюамеля берется путем
численного интегрирования).
423
*
* «
Рассмотрим некоторые дополнительные вопросы. На практике
часто встречается потребность электрическим путем получить про-
изводную и интеграл от тока или напряжения.
§ 308. Простейшее электрическое дифференцирующее устройство.
На рис. 329 представлен четырехполюсник, который при определен-
ных условиях может служить в качестве простейшего дифференци-
рующего устройства. Он состоит из последовательно соединенных
активного сопротивления 7? и индуктивности L.
По второму закону Кирхгофа
L^ + Z?z = uev(O.
at
Если параметры цепи выбрать таким образом, что L — будет
dt
много меньше Ri, то приближенно
Ri^uex(f) и
Рис. 330
Рис. 329
При этом напряжение на выходе четырехполюсника
________ т di __. duex (t)
выЛ’ dt~ R dt
будет пропорционально производной от напряжения на входе.
§ 309. Простейшее электрическое интегрирующее устройство.
На рис. 330 представлен четырехполюсник, напряжение иа
выходе которого при определенных условиях пропорционально
интегралу от входного напряжения. Он состоит из последовательно
соединенных R и С. По второму закону Кирхгофа
iR + ис = ивх (7).
Выберем параметры схемы (7? и С) таким образом, что падение
напряжения ис будет много меньше iR\ тогда приближенно
iR^ueAty, i =
i\
424
Напряжение на выходе
ивых (0 «с г. {i dt С ивх (f) dt,
ь J kl j
t. e., действительно, напряжение на выходе пропорционально
интегралу от напряжения на входе.
Напряжение с выхода дифференцирующего и интегрирующего
устройств подается для наблюдения или записи на катодный или
электромагнитный осциллограф
(предполагается, что последний
обладает достаточно большим
входным сопротивлением).
§ 310. Применение метода эк-
вивалентного генератора для ра-
счета переходных процессов. Для
расчета переходных процессов с
успехом применяется метод эк-
вивалентного генератора. Рас-
смотрим его на примере трех-
фазной цепи рис. 331, а. В ней
ев = Ет sin (at — 120° 4- <р);
ес = Ет sin (at 4-120° + <р).
Внутреннее сопротивление ис-
точника трехфазной э.д.с. по-
ложим равным нулю.
В фазах В и С включены
и С, в фазе А — R и L. Тре-
буется составить операторное
изображение тока фазы А при
замыкании рубильника.
Согласно методу эквивалент-
Рис. 331
ного генератора надо оператор-
ное изображение напряжения разомкнутой ветви Оло'хх(р) поделить
на сумму операторного сопротивления включаемой ветви 7л(р)
и входного операторного сопротивления всей схемы по отношению
к точкам А и О'; обозначим его Zex(p):
Т , ч ОА0,хх(Р)
1а(р) ZA(p) + Zex(p)
При разомкнутом рубильнике мгновенное значение напряжения
(см. стр. 199)
ыло'^ = y£-sin(®z + <p);
425
его изображение
АО'хх(Р) ~ . 5
2 р — до
ZA(P) = R-\-pU zei(p) =1 [/?-[- _L_у
2 \ Cp J
Следовательно,
/ (г)\ ___________ЗЁтСр2__________
A {р _ ;(О)(2Р2£С + 3pRC 4- 1) ’
Для перехода к функции времени следует применить формулу
разложения.
По существу поступаем в точности так же, как и в § 22 первой части кур-
са при обосновании применения метода эквивалентного генератора к расчету
цепей постоянного тока.
Всю схему за исключением ветви, в которой производится замыкание ру-
бильника, представляем активным двухполюсником. Зажимы подключаемой
ветви обозначим через А и О'.
Вводим в эту цепь две равные и противоположно направленные э.д.с
ei (0 и (0- Величина каждой э.д.с. равна напряжению на зажимах ветви при
холостом ходе ее — обозначим его через «ло'.гл-(0-
Далее, замыкаем рубильник и для нахождения тока в любой ветви схемы
пользуемся принципом наложения. Ток в любой ветви схемы — обозначим
его через z (/) — представляем в виде суммы двух токов: i (/) = i'(t) + i" (О-
Тох i'(t) вызван всеми э.д.с. активного двухполюсника и э.д.с. е± (/),
направленной встречно Щдо'хгСО-
>. Ток i"(t) вызван только одной э.д.с. е2 (/), направленной так же, как и
^АО'хх (О’
Поскольку э.д.с. eL(i) направлена встречно напряжению иАо'хх(0> то ток
«'(/) в подключенной ветви как был, так и останется равным нулю, а в осталь-
ных ветвях схемы токи останутся теми же, какими они были до замыкания
рубильника. Что касается тока i" (/), то он находится ст действия в.д.с.
ez(0 = Мао' хх(О> когда во всей схеме имеют место нулевые начальные
условия.
В заключение необходимо отметить, что если производится размыкание
какой-либо ветви некеторой схемы и при этом не нарушаются законы комму-
тации, то токй в остальных ветвях схемы после размыкания упомянутой вет-
ви могут быть найдены путем наложения двух режимов:
первый режим — это докоммутационный режим;
второй режим — режим, возникающий в соответствующих ветвях пас-
сивной схемы при нулевых начальных условиях от включения в размыкаемую
ветвь источника тока.
Источник тока дает ток, равный и противоположно направленный току
в размыкаемой ветви.
В качестве иллюстрации методики расчета переходных процессов путем
введения источника тока найдем для схемы рис. 313 примера 130 (стр. 383)
ток z’2 при размыкании рубильника в третьей ветвн. После размыкания рубиль-
ника z2 = z' + :
12=0,5а— ток докоммутационного режима,
.11
t2 — ток от источника тока /3 = 0,5 а (в данном случае постоянного)
в схеме рис. 331, б.
I! с 11
Изображение тока z2 равно
426
Ri
Z2 (P)=Z3 „ , n , . .
-г Ri + pL
Следовательно,
ill =
2
0,1 (1— е-1°0/)д;
1 — е
Ri + Rs
*з = 0,5 0,1 (1 —е~100z), что совпадает с результатом примера 130.
§ 311. Переходные процессы при воздействии импульсов напря-
жения. Ток в любой сколь угодно сложной схеме при воздействии на
нее импульса напряжения, изображенного на рис. 332,можно найти,
например, следующими тремя способами:
1. Применением интеграла Дюа-
меля.
2. При t ток определяется
так же, как от действия посто-
янного напряжения U.
Рис. 333
Рис. 332
При t > tr действующее на систему напряжение равно нулю.
Следовательно, система освобождается от вынуждающих э.д.с. и
по ней будут протекать свободные токи, начальные значения кото-
рых соответствуют полным токам в цепи при t =
3. Импульс представляют в виде двух постоянных напряжений.
Положительное напряжение U действует, начиная с 1-0; отри-
цательное напряжение U действует, начиная с 1- 1г При t < tv
токи в цепи определяются одним напряжением U.
При t > tL токи определяются обоими напряжениями с учетом
сдвига второго напряжения иа время tr.
Третий способ проиллюстрируем еще одним примером. Поло-
жим, что требуется найти ток в цепи при подключении ее к на-
пряжению, имеющему форму равнобедренного треугольника и
изображенному на рис. 333, а. Задача решается в три приема.
Сначала определяем ток в интервале времени от I = 0 до t tL
от действия напряжения иг = kt (рис. 333,6). Затем для интерва-
ла времени /2 5- t tx находим ток в цепи от действия двух на-
пряжении (рис. 333,6 и в): от продолжающего действовать напря-
427
жения Uy — kt и от вступающего в дей-
ствие при t = ty дополнительного напря-
жения и2 — — 2kt.
Для интервала времени t > t2 ток оп-
ределяется действием трех напряжений:
продолжающих действовать напряжений
Uy и и2 и вновь вступающего в действие
при t=t2 напряжения u3 = kt (при t~^ t2
сумма напряжений иг, и2 и us — рис.
333, г—даст нуль).
Из трех перечисленных выше способов
обычно наиболее экономным оказывается
первый.
§ 312. Некоторые схемы, обладающие спе-
циальными свойствами. Если в схемах рис. 334
взять Ry — R%= = R, составить операторные сопротивления, то ока-
жется, что оно будет равно R. Это означает, что при оговоренном выше со-
отношении параметров ток в неразветвленной части обеих цепей во време-
ни будет изменяться по тому же закону, по которому будет изменяться нап-
ряжение на входе.
Таблица значений показательной и гиперболической функций
X 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,2
6х 1 1,10 1,22 1,35 1,49 1,65 1,82 2,01 2,22 2,46 2,72 3,32
sh х 0,00 0,10 0,20 0,30 0,41 0,52 0,64 0,76 0,89 1,03 1,17 1,51
ch х 1,00 1,005 1,02 1,04 1,08 1,13 1,18 1,25 1,34 1,43 1,45 1,81
X 1,4 1,6 1,8 2,0 2,5 3,0 3,5 4,0 4,5 5 5,5 6
gX 4,05 4,95 6,05 7,39 12,18 20,09 33,11 54,6 90 148 244,7 400
sh х 1,90 2,38 2,94 3,63 6,05 10,01 16,54 27,29 45,00 74,20 122,3 200
ch х 2,15 2,58 3,10 3,76 6,13 10,07 16,57 27,30 45,01 74,21 122,3 200
§ 313. Понятие о передаточных функциях и о частотных характеристиках
звеньев и систем. В ряде отраслей техники и в особенности в теории автома-
тического регулирования об устойчивости
и о характере переходного процесса судят
по виду частотной характеристики систе-
мы. Принято расчленять систему на отдель-
ные элементы или звенья.
Каждое звено можно схематически
а)
представить либо в виде некоторого четы- Рис. 335
рехполюсника рис. 335, а, либо в одноли-
нейном начертании, как это показано
на рис. 335, б. Входными хех и выходными хвых величинами могут быть
как электрические величины, например ток, напряжение, заряд, так и не-
электрпческие величины, например координата или скорость перемещения
какого-либо тела механической системы.
На рис. 335, a Uex—входное напряжение, Чеых — выходное напряже-
ние.
428
Если звеньев в системе несколько, то входные и выходные величины бу-
дем снабжать числовыми индексами. Какова бы ни была схема внутренних
соединений каждого звена, всегда можно выразить операторное изображение
выходной величины хвых(р) через операторное изображение входной вели-
чины хвк(р)-.
Хвых(р) ' Хвх(р)К(р).
Коэффициент пропорциональности К(р) между хвых(р) и xev(p) приня-
то называть передаточной функцией звена:
К(р) = -вЫХ-\-. (Ю.64)
*вх (Р)
Передаточная функция зависит от схемы внутренних соединений звена и яв-
ляется функцией оператора р.
В качестве примера составим выражение для передаточной функции
четырехполюсника рис. 336, а. Операторное изображение напряжения на вы-
ходе ивык(р) запишется следующим образом через операторное изображение
напряжения на входе Uex (р):
,, , . Uex (Р) г,
Uвых (р) 1
я + тг
Ср
Отсюда
. .__ Ц^ых (р)____Р
= UBX(p) ~ р+а'
где
С понятием передаточной функции звена тесно связано понятие о частот-
ной характеристике звена.
Выражение для частотной характеристики получают из выражения для
передаточной функции путем замены оператора р на /со, где со — угловая час-
тота:
. v ХвЫХ (М) Л /1П KCi
К (/и) = —тгг; (10.65)
хвх (/<•>)
К (|<й) представляет собой комплексное число и может быть записано в алгеб-
раической и в показательной формах:
К(|«в) = С + /К = Ле/ф,
_____ V
Д ==рЛС2+1/2 , q> = arc tg — .
429
стотной характеристикой звена
к,(р)~
__J *2 —
Рис. 337
Зависимость U = /(со) называют действительной (вещественной) ча-
яли соответственно системы. Зависимость
V — /(со) — мнимая частотная характери-
стика. Зависимость А = /(со) — амплитуд-
ная частотная характеристика иф=/(<о) —
фазовая частотная характеристика. За-
висимость А = /(1g со) называют лога-
рифмической частотной характеристикой.
Характеристика Ae,<s> = {(<£>), построенная
в полярных координатах, называется амплитудно-фазовой частотной харак-
теристикой.
В качестве примера построим в координатах U, jV зависимость Д’ (/со) и в
координатах £/,<о зависимость £/==/ (со) для четырехполюсника рис. 336, а.
р
С этой целью в выражении К (р) —------- заменим р на /со и получим
р + «
к _ /со = /<о (а—/со) со2 . аа>
а -ф /со а2-фсо2 а2-фсо2 ^а2-фсо2'
Таким образом, для рассматриваемого примера
со2 ,, ссо
-------и V = ------------.
ла-фсо2 а2-фсо2
Придавая^ различные значения, например — = 0; 0,5; 1; 2; 10; ...; оо, мож-
а
но подсчитать значения U и V и построить на комплексной плоскости зависи-
мость К(/со) = /(со) в декартовой системе координат на рнс. 336, б. На рис.
336, в построена вещественная частотная характеристика U = /(со) для че-
тырехполюсника рис. 336, а.
Частотные характеристики отдельных звеньев и всей системы в целом мож-
но определять либо расчетным путем, если известны схемы внутренних соеди-
нений звеньев и значения параметров, либо получать опытным путем. При
опытном определении частотных характеристик поступают следующим обра-
зом.
На вход звена (или соответственно системы в целом) подают синусоидаль-
ное напряжение неизменной амплитуды и, изменяя частоту от 0 до максималь-
но возможной (теоретически до бесконечности), определяют амплитуду и фа-
зу выходной величины. Отношение амплитуды выходной величины к ампли-
туде входной величины дает значение А, а сдвиг по фазе выходной величины
по отношению ко входной — значение <р.
Вернемся теперь к вопросу о передаточных функциях. Положим, что сис-
тема образована несколькими последовательно включенными звеньями, на-
пример тремя (рис. 337). Обозначим: Ki(p) — передаточная функция пер-
вого звена, К2(р) — второго звена; К3(р) — третьего. Тогда операторные
изображения выходных величин звеньев можно выразить через операторные
изображения входных величин звеньев следующим образом:
Хг (р) = Xi (р) Ki (р),
Х3 (р) = х2 (р) Кг (Р).
Хл (Р) = х3 (р) К3 (Р).
Для того чтобы выразить выходную величину всей системы (р) через
входную величину лу (р), перемножим записанные выше три строчки. Получим
Хг (р) *з (Р) х4 (р) = х2 (р) Ki (р) х2 (р) Кг (р) х3 (р) К3 (р).
430
Отсюда
х4(р)=х1(р)К(р),
где
К(р) = К1(р)К2(р)Кз(Р). (10.66)
Таким образом, для получения передаточной функции нескольких по-
следовательно включенных звеньев следует перемножить передаточные функ-
ции этих звеньев.
§ 314. Основные сведения о синтезе электрических цепей. Синтезом элект-
рических цепей называют определение структуры электрических цепей и зна-
чений параметров входящих в них элементов по заданным частотным или
временным свойствам цепей.
В руководствах по синтезу цепей рассматриваются вопросы о синтезе
двухполюсников и о синтезе четырехполюсников.
При решении задачи о синтезе двухполюсников задается либо зависи-
мость его входного сопротивления от частоты, либо зависимость тора на вхо-
де двухполюсника в функции от времени при подаче на вход двухполюсника
прямоугольного импульса напряжения.
При синтезе четырехполюсника задается обычно либо зависимость его
передаточной функции от частоты, либо зависимость от частоты его коэффи-
циента затухания или коэффициента фазы, либо задается временная харак-
теристика четырехполюсника при подаче на вход его прямоугольного импуль-
са напряжения.
Каким бы образом ни были заданы характеристики двухполюсника или
четырехполюсника, они должны удовлетворять условию физической реали-
зуемости.
Все задачи на синтез цепей являются, как правило, задачами, допускаю-
щими неоднозначные решения.
Другими словами, заданным условиям можно удовлетворить при помо-
щи нескольких схем с сосредоточенными параметрами. Преимущество от-
дается схеме с наименьшим числом элементов и с наименьшим значением
параметров.
В технике автоматического регулирования и в технике связи синтез цепей
находит применение при проектировании корректирующих звеньев — уст-
ройств, улучшающих частотные характеристики всей системы в целом.
§ 315. Синтез двухполюсников, основанный на последовательном выде-
лении из функции входного сопротивления простейших составляющих. Зада-
ча ставится следующим образом. Известно выражение входного сопротивле-
ния некоторого двухполюсника Z(p) = удовлетворяющее условиям фи-
В(Р)
зической реализуемости. Требуется образовать схему и найти значения вхо-
дящих в нее элементов методом последовательного выделения из функции вход-
ного сопротивления простейших составляющих. Рассмотрим один из возмож-
ных путей решения задачи.
1. Сначала выделим из состава Z(p) составляющую, пропорциональную
первой степени р. Она будет иметь место, если степень А (р) на единицу выше
степени В (р). Выделенная составляющая имеет вид агр, где а±— некоторая
индуктивность, с которой начинается схема двухполюсника (рис. 338).
А (Р)
2. Выясняем, нет ли у Z (р) = ~ полюса при р = 0 (полюсами пазы-
’ \Р'
ваются корни уравнения В (р) = 0). Если Z (р) имеет полюс при р => 0, то из
а0
Z(p) следует выделить слагаемое вида — . Коэффициент ай представляет со-
бой интегральный вычет функции Z (р) при р = 0, т. е.
431
а0 = Res Z (p)= [ ’7^7“')
₽->0 \ b (p) ]p-()
ao
Величина В' (p) — производная от В (р) по р. Слагаемому — в двухполюснике
соответствует последовательно включенная емкость Со =
Рис. 338
3. Выясняем нет ли у Z(p) полюсов, лежащих на мнимой осн р112=+/со/,.
Если такие полюсы имеются, а они могут быть только простые, не кратные,
то каждой паре таких полюсов в разложении Z (р) соответствуют слагаемые
вида
2akP
р +
Коэффициент ак находится путем вычисления интегрального вычета функции
Z (р) при р = /со. Другими словами,
n/; = ResZ(p)= ——— .
(P/Jp-jm
2а/г р
Слагаемому —------г в искомой схеме соответствует последовательно вклю-
Р +ий
ченный контур, образованный индуктивностью L), и параллельно ей присоеди-
ненной емкостью С^. Действительно, операторное сопротивление параллельно
соединенных и Cf, равно
1 1
PLk PLk Р -Г
___________________________ , _______
1 _ =_ , •
pLk+~— P2LkCk+l P2+—-
P'-k Lk
20/, p 1 n 2 1
Сопоставление последнего выражения с —-------- дает — = 2о/г; и = -——.
р2+со/г2 Cfi к L;.Ck
4. Операции, проделанные в п. 1—3, позволяют выделить из Z(p) состав-
т
ляющне «1 р + — + у1 —2о^р— — число пар корней, лежащих на мнимой
Р Р2 + С0/г2
Л= 1
т
(По V1 2а», р
at Р + — + 7, —~—г
Р Р + со
fe = l k
уже не содержит
полюсов на мнимой оси. Функцию Z± (р), выражающую собой операторное
432
сопротивление некоторого двухполюсника, не содержащего полюсов на
мнимой осн, условились называть функцией минимального реактивного сопро-
тивления.
5. Дальнейшее формирование двухполюсника состоит в реализации функ-
ции минимального реактивного сопротивления Zj (р).
При осуществлении этой операции могут встретиться следующие случаи:
a) Zt (р) действительное и положительное число. В схеме двухполюсника
сио реализуется последовательным активным сопротивлением рис. 339, а.
б) Zj (р) представляет собой дробь вида —причем (р) не содержит
постоянного, не зависящего от р слагаемого. Другими словами, (р) таково,
что р = 0 представляет собой нуль Z, (р).
Р
В этом случае Z± (р) может быть разложено на сумму дрооей вида ---,
Р + «А
т. е.
7 ГгЛ V а,гР
Р
Каждой дроби вида •-----• в схеме двухполюсника соответствует после-
P+mk
довательно включенный контур, образованный параллельно соединенными
индуктивностью Ln и активным сопротивлением Rn — см. рис. 339, б.
В этом можно убедиться, образовав операторное сопротивление параллельно
соединенных Ln и Rn,
Р Rn ’ akp
---и сопоставив его с--------. Сопо-
Р+^ P+tnk
Lfl
которое равно
Rn
И tnk = —.
в схеме, реализующей Zj (р), появляется последова-
ставление дает ak=Rn
Если тк => 0, то
тельно включенное активное сопротивление, равное а/..
в) Z, (р) = таково, что /j (р) содержит постоянное, не зависящее
В1(Р)
от р слагаемое. В этом случае Zt (р) может быть представлено следующим
образом:
2г(р)
I Л ' со-
Р +dk
bk
Каждой дроби вида -------— в схеме Z,(p) соответствуют параллельное соеди-
Р + 4
пение емкости Ck и сопротивления R/: (рис. 339, в). Действительно, оператор-
Q
ное сопротивление параллельно соединенных Ск и Rk равно --------.
P+^cZ
„ bk 1 1
Сопоставление последнего выражения с ------- дает: Р>,= — и dh=---
Р + 4 Ck RkCk
6. В заключение необходимо отметить, что если функция минимального
Л, (Р)
реактивного сопротивления Zj (р) = такова, что Ах (р) имеет нули, т, е
"i (Р)
15 Л. А. Бессонов
433
корни уравнения Лх (р) = 0 на мнимой оси при p = ±jak и при р = со, то
21 (р) формируют путем составления обратной дроби:
zi(.p) Л(р)
разлагая ее в тон же последовательности, которая была дана выше в п. 1—4.
Разумеется, при этом следует иметь в виду, что разложение
1 о,
5'1 (Р) -= , • «1 Р + '
А (Р) Р
Y,(P)
Рис. 339
физически осуществляется уже не в виде последовательно соединенных со-
Оо 2акр
противлении ах р, —, —---------г и А (Р), как это имело место для Z(p), а в
Р Р +
а„ 2акр
виде параллельного соединения ветвей с проводимостями а1 р, — ,----------—— и
Р Р'1 Ч-«;
У2 (р).
Л(р) р!-|-р2-)-2р
Пример 150. Требуется реализовать функцию Z (р) = —----------------------
В(р) рЗ_,_р2_|.р_|..1
Решен и е. Действуем в соответствии с изложенным выше мето-
дом.
1. Так как степень А(р) равна степени В(р), то aL = 0. Другими
словами, в составе двухполюсника нет последовательно включенной индук-
тивности.
2. Z (р) не имеет полюса при р = 0. Поэтому в состав искомого двухпо-
люсника не входит последовательно соединенной емкости.
3. Z (р) имеет два полюса, лежащих на мнимой оси. Действительно,
В (р) = (р2 + 1) (Р + !)• Следовательно, р( 2 = ± /. Находим вычет Z (р) при
р = + / (ему же будет равен вычет при р = — /, так как они оба действи-
тельны):
ai = Res Z (р) = ЛЮ = = + = 1
рЧ В'(р) Зр2 + 2р+1 — 3 +2/4-1 2’
p=i p=-i
434
Определяем величины параллельно соединенных £t и Ср
Ci = ^- = —Цг = 1, Л = —Ц- = — = 1.
2«i о . — Cj со 1-1
2 1
2nt р р
4. Из Z (р) вычитаем —--j = —-- и находим функцию минимального
р2 + р2+ 1
реактивного сопротивления Z, (р):
Z ip\ _ Р3 + Р2 + 2Р _ Р _ Р
1 Р3+Р2+Р+1 Р2 + 1 р + 1’
5. Так как структура Zi (р) подходит под описанную в п. 5 6, то Zt (р)
осуществляется в виде параллельного соединения £2 = 1 и /?2= 1.
Схема искомого двухполюсника изображена на рис. 340.
§ 315 а. Понятие о графах. Формула Мэзона. Графом называют совокуп-
ность узлов и соединяющих их ветвей. Имеются два типа графов: ненаправ-
ленные и направленные. Узлы и ветви ненаправленного графа соответствуют
узлам и ветвям исследуемой электрической цепи. Каждая ветвь его характе-
ризуется величиной проводимости. Ненаправленный граф это как бы геомет-
рический образ или скелетная схема исследуемой электрической цепи.
В направленных графах—они называются также графами сигнала или
диаграммами прохождения сигнала — узлами являются обычно токи и (или)
напряжения, а каждая ветвь характеризуется величиной передачи (отноше-
нием выходной величины ветви ко входной величине этой ветви). На ветвях
направленных графов ставят стрелки, указывающие направление передачи.
Основной формулой в теории графов является формула Мэзона. Рассмотрим
ее применительно к ненаправленным графам:
/ £с,дг
Втп А
Здесь: 1 — ток, протекающий по некоторой выбранной ветви графа, по отно-
шению к которой определяется входная или взаимная проводимость, Втп —
напряжение источника э. д. с. или ток источника тока, присоединяемого
к узлам т и п; Сг — произведение проводимостей ветвей пути между узлами
тип, проходящего по выбранной ветви. Сг берется со знаком плюс, если
при прохождении по этому пути выбранная ветвь обходится согласно с услов-
но выбранным положительным направлением вдоль этой ветви. ДЛ— опреде-
литель схемы, полученной из исходной путем закорачивания всех ветвей пу-
ти Сг. Число членов суммы равно числу возможных путей между узлами т
и п, графа (в число этих путей не входит путь от т к п через источник
питания схемы). Д — определитель всей схемы.
Для облегчения подсчета Д и Дг разработано несколько способов (разло-
жение по узлам, разложение по ветви), которые за недостатком места здесь
не рассматриваются (см. например Л. 9).
15:
Глава одиннадцатая
УСТАНОВИВШИЕСЯ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ И
МАГНИТНЫХ ЦЕПЯХ, СОДЕРЖАЩИХ ЛИНИИ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ.
ОСНОВЫ ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ
§ 316. Введение и основные определения. В данной главе будут
рассмотрены основы теории установившихся процессов в электри-
ческих и магнитных цепях, содержащих линии с распределенными
параметрами.
Электрическими линиями с распределенными параметрами бу-
дем называть такие линии, в которых ток и напряжение непре-
рывно изменяются при переходе от одной точки (сечения) линии
к другой, соседней точке.
Под магнитными линиями с распределенными параметрами по-
нимают такие линии, магнитный поток и магнитное напряжение
вдоль которых непрерывно меняются при переходе от одной точки
линии к соседней.
Эффект непрерывного изменения тока (или потока) и эффект
непрерывного изменения электрического (магнитного) напряже-
ния вдоль линии имеют место вследствие того, что линии обладают
распределенными продольными и поперечными сопротивления-
ми (рис. 341).
На схеме рис. 341 изображен участок линии с распределенными
параметрами. Через dx обозначен бесконечно малый элемент дли-
ны линии.
Сопротивления Zn Z2, ••• будем называть продольными со-
противлениями; в них включены сопротивления и прямого и об-
ратного проводов. Сопротивления Z4, Z5, Ze,... будем называть
поперечными сопротивлениями.
Благодаря утечке тока через сопротивление Z4 ток ia не равен
току iv Аналогично ток i3 не равен току i2 и т. д. Напряжение
между точками а и b не равно напряжению между точками с и d
и т. д.
В электрических линиях с распределенными параметрами про-
дольные сопротивления образованы активными сопротивлениями
436
проводов линии и индуктивностями двух противостоящих друг дру-
гу участков линии длиной dx. Поперечные сопротивления состав-
лены сопротивлениями утечки, появляющейся вследствие несовер-
шенства изоляции между проводами линии, и емкостями, образо-
ванными противостоящими друг другу элементами (участками)
линии. В магнитных линиях с распределенными параметрами про-
дольные сопротивления образованы магнитными сопротивлениями
самих магнитных стержней, образующих магнитную линию, а
поперечные сопротивления обусловлены утечкой магнитного по-
тока по воздуху между противостоящими друг другу участками
линии.
Линия с распределенными параметрами называется однородной,
если равны друг другу все продольные сопротивления участков
линии одинаковой длины и если
равны друг другу все поперечные
сопротивления участков линии
одинаковой длины. Так, участок
линии рис. 341 будет однородным,
если Z1 — Z„ = Z3 = ... и Zi —
= = Z6.
Линию с распределенными па-
раметрами будем называть неодно-
родной, если продольные сопро-
тивления в ней различны или ес-
ли поперечные сопротивления нео-
динаковы.
Кроме того, линии с распреде-
ленными параметрами могут быть
и—dr—«+•—йг »!« di
Рис. 341
подразделены на две большие группы: нелинейные и линейные.
В нелинейных линиях с распределенными параметрами продоль-
ные и (или) поперечные сопротивления являются функциями про-
текающих по ним токов, в линейных — продольные и поперечные
сопротивления не являются функциями протекающих через них
токов.
В качестве примера нелинейной электрической линии с распре-
деленными параметрами может быть названа электрическая линия
передачи высокого напряжения при наличии между проводами
линии тихого электрического разряда — явление короны на про-
водах. В этом случае емкость между противостоящими друг дру-
гу участками линии является функцией напряжения между этими
участками линии.
В качестве примера нелинейной магнитной линии с распреде-
ленными параметрами может быть названа линия, образованная
параллельно расположенными магнитными сердечниками, которые
в процессе работы линии могут насыщаться. Когда говорят о линии
с распределенными параметрами, то обычно этот термин мысленно
связывают с мощными линиями передачи электрической энергии
437
на большие расстояния, с телефонными и телеграфными воздушны-
ми и кабельными линиями, с рельсовыми линиями автоблокировки
на железнодорожном транспорте, с антеннами в радиотехнике и
другими родственными линиями и установками.
В то же время с линиями с распределенными параметрами при-
ходится сталкиваться и тогда, когда «линии» в буквальном смысле
этого слова, казалось бы, вовсе пет. Так, обычная индуктивная
катушка представляет собой, строго говоря, линию с распределен-
ными параметрами. Действительно, между каждыми двумя сосед-
ними витками катушки, как и между каждыми двумя теламп, есть
емкость (рнс. 342). Кроме того, между каждым витком и корпусом
прибора (землей) также есть емкость.
Если по катушке будет протекать переменный ток, то через
межвптковые емкости и емкости на землю потечет ток. При одном
и том же напряжении между соседними
витками ток через емкости будет тем
(ПЦТ’ПТ'Цд большим, чем выше частота переменно-
________________________L I- го тока. При низкой частоте (десятки,
сотни, тысячи герц) ток через емкости
будет несоизмеримо мал по сравнению
„___________с токами через витки катушки и нали-
чпе емкостей можно не учитывать в
расчете, что и делалось до сих пор*.
Если же частота тока будет весьма велика, например будет
достигать миллионов и даже миллиардов герц, то токи через емко-
сти могут во много раз превышать токи через витки катушки.
В этом случае вся катушка в целом будет оказывать прохождению
переменного тока емкостное, а не индуктивное сопротивление —
количество перешло в новое качество. При промежуточных часто-
тах порядка сотен килогерц индуктивная катушка, если не приня-
то специальных мер, представляет собой типичную линию с рас-
пределенными параметрами. Если индуктивная катушка намотана
на стальной сердечник, который способен насыщаться, и частота
тока достаточно велика, то все устройство в целом представляет
собой сложную совокупность из электрической и магнитной нели-
нейных цепей с распределенными параметрами.
В курсе ТОЭ изучаются только основы однородных линейных
цепей с распределенными параметрами. Вся теория излагается
применительно к электрическим линиям с распределенными пара-
метрами на переменном токе. Теория однородных линейных элек-
трических цепей с распределенными параметрами на постоянном
токе непосредственно следует из теории цепей переменного тока,
если принять угловую частоту равной нулю.
* В дальнейшем (см. § 341—345) при рассмотрении теории электричес-
ких фильтров, работающих при относительно низких частотах, наличие рас-
пределенных емкостей в самих индуктивных катушках также не учитывается.
438
Теория однородных линейных магнитных линий на постоянном
токе в значительной мере аналогична теории однородных линейных
электрических линий с распределенными параметрами, только
вместо тока в уравнения должен быть подставлен магнитный по-
ток, вместо электрического напряжения — магнитное напряжение,
вместо продольного активного сопротивления — продольное маг-
нитное сопротивление, вместо поперечной электрической проводи-
мости — поперечная магнитная проводимость.
§ 317. Составление дифференциальных уравнений для однород-
ной линии с распределенными параметрами. Пусть /?,, — продольное
активное сопротивление единицы длины линии, Lo—индуктив-
ность единицы длины линии, Св — емкость единицы длины линии
и Go — поперечная проводимость единицы длины линии. Подчерк-
нем, что поперечная проводимость
Go не является обратной величи-
ной по отношению к продольному
сопротивлению 7?(|.
Разобьем линию на участки
длиной dx (рис. 343); х — это рас-
стояние, отсчитываемое от начала
линии. На длине dx активное со-
противление равно Rodx, индук-
тивность Lodx, проводимость утеч-
ки Gndx и емкость Codx. Обозначим
ток в начале рассматриваемого
участка линии через i, а напря-
жение между проводами линии в
начале участка и. И ток, и напряжение являются в общем случае
функциями расстояния вдоль линии х и времени t. Поэтому в
дальнейшем в уравнениях будут участвовать частные производные
от и и от i по времени t и по расстоянию х.
Если для некоторого момента времени t ток в начале рассмат-
риваемого участка равен I, то в силу наличия утечки тока через
поперечный элемент ток в конце участка для того же
момента времени будет равен i dx; есть скорость
изменения тока в направлении х. Скорость, умноженная на рас-
стояние dx, дает приращение тока на пути dx.
Аналогично, если напряжение в начале участка и, то в конце
участка для того же момента времени напряжение равно
и -j- — dx. Составим уравнение по второму закону Кирхгофа
дх
для замкнутого контура, образованного участком линии длиной
dx, обойдя его по часовой стрелке:
— и -ф- 7?0 dx i -ф- Lo dx -ф- и -ф- dx = 0.
439
После упрощения и деления уравнения на dx получим:
= (11.1)
dx dt
По первому закону Кирхгофа
i = di 4- i 4- — dx. (11.2)
дх
Ток di (см. рис. 343) равен сумме токов, проходящих через
проводимость GBdx и через емкость CBdx:
di= (и-{- — dx\ GBdx-[-— CBdx(u-{- —dx\.
\ дх / dt \ дх )
Пренебрегаем слагаемыми второго порядка малости, тогда
di = uGBdx-\-CBdx —. (П-3)
dt
Подставим (11.3) в (11.2), упростим и поделим уравнение на dx:
— = G0tz4-C0 —. (11.4)
дх 0 1 .° dt ' ’
Уравнения (11.1) и (11.4) являются основными дифференциаль-
ными уравнениями для линии с распределенными параметрами.
§ 318. Решение уравнений линии с распределенными параметрами
при установившемся синусоидальном процессе. Пусть напряжение
и ток в линии изменяются по синусоидальному закону во времени.
Воспользуемся символическим методом.
Изображение тока i = /msin (со/ +ф/) равно Здесь
V2
Изображение напряжения и — Um sin 4~ф„) равно Ue,mt, где
r‘j_
V2
Комплексы U а I являются функциями расстояния х, но не
являются функциями времени. Множитель е‘ш* есть функция вре-
мени t, но не зависит от х.
Представление изображения тока и изображения напряжения
в виде произведения двух множителей, из которых один является
функцией только х, а другой — функцией только t, дает возмож-
ность перейти от уравнений в частных производных [уравнений
(11.1) и (11.4)] к уравнениям в простых производных. Действи-
тельно,
ди 1ш1 dU
-- —- р • . •
дх dx 9
т di г ; d fat . j :
L4i‘-LJ'die - !
440
di _ i,,.t dl ф А^ »
Со~ = i^fie^1 . (11.6)
Подставим (11.5) и (11.6) в (11.1) и в (11.4) и ченных уравнениях множитель е,ю<. Получим: сократим в полу-
= Z /; ах 0 (11.7)
т- = dx ° ’ (П-8)
где Zo = Уо = Go+ /<оСо. (U.9) (11.10)
Решим систему уравнений (11.7) и (11.8) С этой целью продифференцируем (11.7) по х: относительно U.
_ d2U _ ? dl dx* — Zo dx ' (11.11)
В (11.11) вместоподставим правую часть Получим: = Z0Yfi. dx2 0 0 уравнения (11.8). (11.12)
Уравнение (11.12) представляет собой линейное дифференци-
альное уравнение второго порядка. Решение его:
(7 = А^ + А^. (11.13)
Комплексные числа Лг и А2 есть постоянные интегрирования,
которые в дальнейшем определим через напряжение и ток в начале
линии или через напряжение и ток в конце линии.
Коэффициент
(11.14)
принято называть постоянной распространения-, у — комплекс-
ное число, и потому его можно представить в таком виде:
Y = ₽ + /a, (11.15)
где р называется коэффициентом затухания. Забегая несколько
вперед, скажем, что он характеризует собой затухание падающей
волны на единицу длины линии (на 1 км), а — коэффициент фазы-,
он характеризует изменение фазы падающей волны на единицу
длины линии (на 1 км):
[у] = [Pl = [а] = 1/гсж.
441
Ток I найдем из уравнений (11.7):
1 dU Аге~^х-А^х
V
(11.16)
Величину — = -р—г- = 1/^, имеющую размерность сопро-
Y V Ъл* о “ Yв
тивления, обозначают Zc и называют волновым сопротивлением:
zc = V¥ = У , о l i7)
G Г Го Г Go + /coCo с ’
где zc — модуль, а <рс — аргумент волнового сопротивления Zc.
Следовательно,
/ = ф-е-тх— ~еу\ (11.16')
zc zc '
§ 319. Постоянная распространения и волновое сопротивление. Как уже
говорилось выше, постоянная распространения
Y = Р + fa — V"(fa> 4* /соЛ>) (Go + faC0) . (11.18)
Для линии постоянного тока со => 0, и потому
У = • (11-19)
Для линии переменного тока без потерь (До = 0 и Go = 0)
у = /соУЦс;. (11.20)
Составим выражения для приближенного определения f и а в линии с ма-
^0 <?0
лыми потерями, когда---- < 1 и —— 1. С этой целью перепишем (11.18)
сое-о соСо
следующим образом:
\ COLq / \ (ОСц J
и разложим биномы в ряды, ограничившись двумя членами каждого ряда.
Получим
+ /“ (11-21)
Z. г JLq Z Т Со
Следовательно,
₽=V Vr +§У£-° ’ (,L22)
£. Г L.Q £. Т Cq
а = соУ£оСо . (11.22')
Рассмотрим теперь выражение для волнового сопротивления. Для постоян-
ного тока (и = 0) нз (11.17) следует, что
Zc = 1/ ^9 .
го
(11.23)
442
Для линии переменного тока без потерь (/?0 = Go = 0)
ZC= ]/£<!. (11.23)
F Со
Для линии переменного тока с малыми потерями, когда —— <1 и
соСр
2С«1/с» [1 +/ (- (п-24)
’ Со L \ zojCq 2ojCq j _|
§ 320. Формулы для определения комплексов напряжения и тока
в любой точке линии через комплексы напряжения и тока в начале
линии. Как и раньше, через х будем обозначать расстояние от на-
чала линии до текущей точки на ней.
Пусть в начале линии при х = 0 напряжение равно Ult а ток /г
Составим уравнения для определения постоянных Лх и Л2 через
и /г Из (11-13) и (11.16) следует (при х = 0):
<4 = 4+4; (Н-25)
44=4-4 (Н-26)
Для определения из уравнения (11.25) вычтем уравне-
ние (11.26):
4 = , (11.27)
где Л,— модуль, ф0— аргумент комплекса Л,;
4= (?1+2?14 = л/*'1 , (11.28)
где Л2 — модуль, — аргумент* комплекса Л2.
Подставим (11.27) и (11.28) в (11.13):
Л_^-/12Сртх , 4 + AZc^ f, е^+е-^ /7 е'х-е"1х
и ~ 2 е ”1 2 С ~2 11Лс 2 ~ '
Введем гиперболические функции. Известно, что
рХ _L р—Х рХ _ р—Х
ch х = —±---- и sh х =---------.
2 2
Поэтому
Л* I e~tx
— = chYX (11.29)
и
ft*— е~'х
2-— = shyx. (11.30)
* Индексы о и п — начальные буквы слов отраженная впадающая (вол-
ны) — см. § 323.
443
Следовательно,
U = C\ch ух — itZc sh ух. (11.31)
Аналогичные преобразования, примененные к (11.16), дают:
/=/1chyx— ~shyx. (11.32)
Формулы (11.31) и (11.32) дают возможность найти комплексы
напряжения и тока в точке линии, расположенной на расстоянии х
от начала линии.
Следует иметь в виду, что аргументом гиперболических функ-
ций в этих формулах является комплексное число
ух — рХ /«X.
§ 321. Графическая интерпретация гиперболического синуса и
гиперболического косинуса от комплексного аргумента. Гипербо-
лические функции от комплексного аргумента сами являются ком-
плексами и могут быть изображены векторами на комплексной плос-
кости.
Заменим ух в уравнениях (11.29) и (11.30) на рх + /ах:
ch ух = 1 (е?х е,ах + е~?х еЧах)-,
sh ух = е1™ - е~?х е~,ах).
По таблицам показательных функций найдем значения ех и
на комплексной плоскости (рис. 344) отложим вектор
и вектор е~9хё~‘ах.
Первый из них по модулю равен е9х и по отношению к оси дей-
ствительных значений повернут на угол ах против часовой стрелки.
Второй по модулю е~9х и повернут по отношению к оси действи-
тельных значений на угол ах по часовой стрелке.
Гиперболический косинус равен полусумме этих векторов, а
гиперболический синус — полуразности их.
444
§ 322. Формулы для определения напряжения и тока в любой точ-
ке линии через комплексы напряжения и тока в конце линии. Обоз-
начим расстояние от текущей точки на линии до конца линии че-
рез у и длину всей линии (рис. 345) через /:
у = 1-х. (11.33)
Пусть будут известны напряжение и ток в конце линии
и /а. Подставим в (11.13) и (11.16') х = I, U = U2, 1 = /2, и со-
ставим два уравнения для определения постоянных интегрирования
А1 и Л2:
^2 ~ А6
1^С=А^1-А^1.
Отсюда
л;^2~/2^е~т' = л/ч
Л2 = йл±кгсе11= А^п .
(11.34)
Если подставить (11.34) в (11.13) и (11.16'), заменить I — х на
у и перейти к гиперболическим функциям, то получим:
yy4-72Zcshyz/; (11.35)
/=-g-shYy+/2chYy. (11.36)
Формулы (11.35) и (11.36) дают возможность, зная и /2,
найти комплексы напряжения и тока в точке, находящейся на
расстоянии у от конца линии.
§ 323. Падающие и отраженные волны в линии. Подставим
в формулу (11.13) Л1е/ ’'° вместо Л1( А2е'*п вместо Л2 [см. (11.34)]
и заменим Y на Р —/а. Получим:
С/ = А/х еМо+ах} + Л2е~?х ~ах\ (11.37')
Аналогичную операцию проделаем с формулой (11.16), причем
в дополнение к сказанному заменим Zc на г(е''Гс [см. форму-
лу (11.17)],
/ = __ А е/(1'о+а*-ч’с) _|_ А е~?хеМп , (и 3g/)
zc zc
Для перехода от комплексов напряжения и тока к функциям
времени умножим правые части формул (11.37') и (11.38') Ha[/2e-zW
и от произведений возьмем мнимую часть:
и = Лх ф 2 е15* sin (tot + ф0 + ах) Л2 К2 е-*”* sin (ы/ -ф- — ах);
(11.37)
443
i— — — V 2 epx sin (<at -j- ф0 -J- ax — <pf) -|-
zc
К2 si n (<£>t 4” 'Фл — ax — q>f). (11.38)
2C
Условимся падающей электромагнитной волной называть про-
цесс перемещения электромагнитного состояния (электромагнит-
ной волны) по направлению от источника энергии к приемнику,
т. е. в нашем случае в направлении увеличения координаты х.
Электромагнитное состояние определяется совокупностью элек-
трического и магнитного полей. Падающая волна, распростра-
няясь От источника энергии к приемнику, несет энергию, заклю-
ченную в ее электрическом и магнитном полях. Отраженной элек-
тромагнитной волной будем называть процесс перемещения элек-
тромагнитного состояния (электромагнитной волны) по направле-
нию от приемника энергии к источнику энергии, т. е. в нашем
случае в сторону уменьшения координаты х.
Падающая электромагнитная волна составлена падающей вол-
ной напряжения [второе слагаемое формулы (11.37)] и падающей
волной тока [второе слагаемое формулы (11.38)]. Отраженная
электромагнитная волна образована отраженной волной напряже-
ния [первое слагаемое формулы (11.37)] и отраженной волной
тока [первое слагаемое формулы (11.38)].
Знак минус у отраженной волны тока математически выражает
то обстоятельство,' что поток энергии, который несет с собой отра-
женная электромагнитная волна, движется в обратном направле-
нии по сравнению с потоком энергии, который несет с собой падаю-
щая волна.
Каждая из составляющих падающей волны (волна напряже-
ния или волна тока) представляет собой синусоидальное колеба-
ние, амплитуда которого уменьшается по мере роста х (множи-
тель ё~$х), а аргумент является функцией времени и координаты х.
Каждая из составляющих отраженной электромагнитной вол-
ны затухает по мере продвижения волны от конца линии к началу
(множитель е₽х). Физически эффект уменьшения амплитуд падаю-
щей и отраженной волн по мере продвижения их по линии объяс-
няется наличием потерь в линии.
На рис. 346 изображены графики распределения падающей
волны напряжения вдоль линии (в функции х) для двух смежных
моментов времени: при tr — утолщенная кривая и при t2 > tY —
тонкая кривая. Падающая волна распространяется слева направо.
При построении принято = 0.
На рис. 347 представлены графики распределения отраженной
волны напряжения для двух смежных моментов времени: и
t2 > tr Отраженная волна распространяется справа налево.
§ 324. Фазовая скорость. Фазовой скоростью иф называют ско-
рость, с которой надо перемещаться вдоль линии, чтобы наблюдать
446
одну и ту же фазу колебания. Можно сказать и иначе: фазовая ско-
рость — это скорость перемещения по линии неизменного фазового
состояния. Если фаза падающей волны напряжения неизменна, то
в соответствии с формулой (11.37)
ю/ 4~ Фл — ах — const.
Возьмем производную по времени от обеих частей последнего
равенства:
И + Фи — ах) = °>
или
dx г.
ю —а — = 0.
dt
Отсюда
Пример 151. Найти фазовую скорость для воздушной двухпровод-
ной линии с малыми потерями.
Решение. Из формулы (11.22') следует, что а = й/Ц?,.
Поэтому
_ о __ 1
Индуктивность единицы длины двухпроводной воздушной ли-
нии [см. формулу (4.10) первой части]:
£ = -ЕМп —.
п г
Здесь р,о — магнитная постоянная, d — расстояние между ося-
ми проводов, г — радиус каждого провода.
Емкость единицы длины двухпроводной линии [см. формулу
(13.43) III части курса ТОЭ]
(11.39')
447
ле0
1Л
где е0 — электрическая постоянная;
«ф = - 1 — = __= 1 ^300 000 км/сек.
VLoco V Ново т / 1,256. io-в ,8>86. ЦК* ф/м
§ 325. Длина волны. Под длиной волны А, понимают расстоя-
ние, на которое распространится волна за один период Т — —:
l = vT = y. (11.40)
Пример 152. Найти длину электромагнитной волны при/ =
= 50 гц и при f — 50 • 10s гц.
Решение. При f = 50 гц
, 300 000 км/сек
А, =---------'-- = 6000 КМ.
50 \/сек
При f = 50- 10е гц
А, = 6 м.
§ 326. Линия без искажений. Линия без искажений представляет
собой линию, в которой волны всех частот распространяются с оди-
наковой фазовой скоростью и все затухают в равной степени.
При движении электромагнитной волны по линии без искаже-
ний волна напряжения и волна тока уменьшаются по амплитуде,
но формы волн напряжения в конце линии и начале линии будут
подобны; точно так же будут подобны формы волн тока в начале
и конце линии.
Неискажающие линии находят применение в телефонии. При
телефонном разговоре по таким линиям не искажается тембр голо-
са (другими словами, не искажается спектральный состав голоса).
Для того чтобы линия была неискажающей, необходимо, чтобы
коэффициент затухания Р и фазовая скорость сф не зависели от час-
тоты; Р и Сф не будут зависеть от частоты, если между параметрами
линии имеет место следующее соотношение?
2?» = А. (11.41)
Л> Со
Для сокращения записи обозначим:
Ro _ Ср _
Ср Ср
По определению
?=₽ + /«= К/рУр.
448
Но
(11.42)
(11.43)
z<> = + /ю£0 = £0 (£ 4~ /со);
Y. ~ Go 4- /шС0 = Со (k 4- /®)
и
у = (£4-/<о)/£А.
Следовательно,
Р = £/£Л = /адГ
о = со У' L0C0
и
_________________________ со __ I
Уф — “o' ~ У *
Из формул (11.42) и (11.43) следует, что коэффициент затухания
Р и фазовая скорость уф в линии без искажений действительно
ie зависят от частоты.
В линии без искажений волновое сопротивление
является действительным числом и также не зависит от частоты.
Для того чтобы убедиться в том, что форма волны напряжения в конце
линии и2 будет полностью подобна форме волны напряжения в начале линия
«!, возьмем напряжение на входе линии в виде суммы двух синусоидальных
колебаний, одно из которых имеет частоту со, а другое 2со, и составим выраже-
ние для н2. Пусть
“г = Uim sin (со/ + фО 4- U2m sin (2<о/ + ф2).
Так как для линии без искажения коэффициент затухания Р не зависит от
частоты [см. формулу (11.42)], то амплитуды обоих колебаний на расстоянии I
уменьшаются в одинаковой степени и становятся равными и U2me~^1.
Для линии без искажения коэффициент фазы а прямо пропорционален
частоте, поэтому для частоты 2со коэффициент а в 2 раза больше, чем для час-
тоты со.
Следовательно, мгновенное значение напряжения в конце линии запишет-
ся следующим образом:
u2 = Ulme pz sin (со/+ Фт— а/) + U2me ₽z sin (2со/ + ф2 — 2аЛ) =
= Uime~pzsin I со (/ —----) + Фс + U2me ₽z sin
I \ co / J
Вынесем e~®1 за скобку и обозначим время /--------через т. Получим:
w2 = sin (сот + Ф1) + U2m sin (2сот + ф2)Ь
Если сопоставить последнее выражение с выражением для ult то можно
сделать вывод, что напряжение в конце линии имеет ту же форму, что и напря-
жение в начале линии. Однако оно уменьшено по амплитуде за счет затуха-
449
ния и смещено во времени на — = — {сек). Это время есть время движения
СО Сф
волны по линии длиной /.
§ 327. Согласованная нагрузка. Линия с распределенными па-
раметрами, как правило, служит в качестве промежуточного звена
между источником энергии и нагрузкой.
Обозначим сопротивление нагрузки через Z2 \Z2 = —). Если
Z2 не равно волновому сопротивлению линии Zc, то падающая
волна частично пройдет в нагрузку, частично отразится от нее
(возникает отраженная волна). Часто берут Z2 = Zc. Такая на-
грузка называется согласованной; при ней отраженная волна от-
сутствует.
В последнем можно убедиться при помощи формулы (11.34).
Действительно, отраженная волна будет отсутствовать, так как
Аг будет равно нулю:
Л = j (<>2 - Л/с) e~yl = ± (02-й2)е-'<1 = 0.
§ 328. Определение напряжения и тока. при согласованной
нагрузке. Для того чтобы получить формулы для определения на-
пряжения и тока в любой точке, удаленной от конца линии на рас-
стояние у, в формулы (11.35) и (11.36) вместо Zc подставим Z2,
заменим ^4 на U2 и на /2. Получим:
Z2
0 = U2 (ch у у 4- sh у у) = U2elv-,
1 = /2 (ch уу 4- sh уу) = /2 е™.
В начале линии при у = I
U2e11 = U2el4>u2 ер‘ е’”1 1
/1 = Цё'1 = I2ei<fhepieial, J
(11.44)
(11.45)
(11.46)
где U2 — модуль, а фц —аргумент комплекса й2; 12 — модуль,
a <jpz —аргумент комплекса /2.
§ 329. Коэффициент полезного действия передачи при согласо-
ваннрй нагрузке. Коэффициент полезного действия передачи равен
отношению активной мощности в конце линии Р2 к активной мощ-
ности Рг в начале линии:
Р2 = U212 cos (фу — <р/з) = 2 cos <рс;
фс — аргумент волнового сопротивления Zc.
При согласованной нагрузке угол между 1)г и также равен
Фс, поэтому в соответствии с формулами (11.46)
Pi = t/^iCOStp^ = U2I2e2^1 cos<pc.
450
Следовательно,
n = %. = е~™. (Н.47)
§ 330. Непер — единица измерения затухания. Произведение
р/ характеризует собой затухание падающей волны на длине ли-
нии/. Из формулы (11.47), логарифмируя ее, найдем, что при согла-
сованной нагрузке
₽/=41п£-. (11.48)
Z Гд
Произведение р/ является, строго говоря, безразмерной вели-
чиной, но в технике связи условились измерять его в неперах.
Линия обладает затуханием в 1 неп,
если
т. е. если
При этом
17а /а
где е есть основание натуральных логарифмов*.
§ 331. Входное сопротивление нагруженной линии. На рис. 348
изображена схема, составленная источником напряжения Ult
линией с распределенными параметрами длиной I и нагрузкой Z2.
Входное сопротивление Zex равно отношению й1 к /г В формулах
(11.35) и (11.36) вместо у подставим I и заменим U2 на /2Z2. Полу-
чим:
7 __ I2Z2 ch yl + i2Zc sh yl
. z2 . ’
Ii -sh yl +12 ch у I
или
Z^^.^hyz + Zcshy/, (1I49)
----sh yl +ch yl
7C
Если нагрузка согласована (т. е. Z2 = Zc), то из (11.49) следу-
ет, что входное сопротивление равно волновому:
_ Zc (ch yl + sh yl) _ 7
ex sh yl -j- ch yl C
* Затухание измеряется также в белах (б) или в децибелах (дб): 1 неп =>
= 8,686 дб.
. 451
§ 332. Уравнение для определения напряжения и тока в линии
без потерь. Строго говоря, линий без потерь не существует. Однако
гзжно- создать линию с очень малыми потерями (с очень малыми
/?„ и G*) и распространить на нее теорию линий без потерь.
Из предыдущего [см. формулу (11.22)] известно, что если
/?0 = Go = О,
то
у = ₽ + /а= jaVLfi'o,
т. е. коэффициент затухания ₽ — 0, а коэффициент фазы
При этом волновое сопротивление Zc является чисто актив-
ным [см. формулу (11.23')] и равно 1/ ~.
Для определения напряжения U и тока 7 в любой точке линии
обратимся к формулам (11.35) и (11.36). Повторим их:
0 = 02 ch уу+ f2Zc sh уу; (11.35)
7 = sh уу+ i2 ch уу. (11.36)
Учтем, что
УУ = (Р + /«) У = (0 + /“) У = jay.
Гпперболический косинус от мнимого аргумента jx равен кру-
говому косинусу от аргумента х:
. . е^х 4-е~^х 1 . ... . . . .
ch ]Х =--------= — (COS X 4" ] Sin X 4" COS X — / sin x) = COS X.
Следовательно,
ch yy — ch jay = cos ay.
Гиперболический синус от аргумента jx равен синусу кругово-
му от аргумента х, умноженному на
eJX . g-JX {
sh jx —--------= — (cosx-j- j sinx—cosx-]-/sinx) = /sinx.
Следовательно,
sh yy — sh jay = j sin ay.
Поэтому для линии без потерь формулы (11.35) и (11.36) пере-
пишем следующим образом:
О —й2 cos ay -j- jizZc sin ay, (11.35')
7= / ^-sin ay4~ 72cosaj/. (11.36')
* По сравнению c coL0 и wCo соответственно.
452
§ 333. Входное сопротивление линии без потерь при холостом хо-
де ее. При холостом ходе /2 = 0. Поэтому
V __U 2 cos ay __ — jZc __ V Со
7 j^sinay ~ ^аУ
Zc
(11.50)
Исследуем характер изменения Zexxx при изменении расстоя-
ния у от конца линии до текущей точки на ней.
В интервале значений ау от 0 до — tgay изменяется от 0
до оо, поэтому Zexxx имеет емкостный характер (множитель— /)
и по модулю изменяется от оо до 0. В интервале значений ау
от у до л tg ау отрицателен и изменяется от — °о до 0, поэтому
Zexxv изменяется по модулю от 0 до оо и имеет индуктивный
характер (множитель ф- /) и т. д. Таким образом, изменяя длину
отрезка линии без потерь, можно имитировать любой величины
емкостное и индуктивное сопротивления. Практически это свой-
ство используется при высокой частоте в различных радиотехни-
ческих установках.
§ 334. Входное сопротивление линии без потерь при коротком за-
мыкании на конце линии. При коротком замыкании на конце линия
U2 = 0 и из формул (11.35) и (11.36) следует, что входное сопротив-
ление
кз = jZc tgay = tg ay, (11.51)
где ______
a = co V L0C0.
Будем менять длину отрезка линии у и исследуем характер
изменения входного сопротивления.
В интервале значений ау от 0 до
tgay положителен и
изменяется от 0 до оо; следовательно, в этом интервале вход-
ное сопротивление имеет индуктивный характер и по модулю
изменяется от 0 до
В интервале ау от до л входное сопротивление имеет
емкостный характер и изменяется по модулю от — °о до 0
^в точке ay = ~ tg ау скачком изменяется от 4" 00 ДО — °° j.
Таким образом, изменяя длину отрезка линии, короткозамкнутой
на конце, также можно создавать различные по величине индуктив-
ные и емкостные сопротивления.
453
В линиях без потерь при холостом ходе, при коротком замыка-
нии, а также при чисто реактивных нагрузках образуются так на-
зываемые стоячие электромагнитные волны.
§ 335. Определение стоячих электромагнитных волн. Стоячая
электромагнитная волна представляет собой электромагнитную вол
ну, полученную в результате наложения движущихся навстречу
падающей и отраженной электромагнитных волн одинаковой интен-
сивности.
Стоячая электромагнитная волна образована стоячей волной
напряжения и стоячей волной тока. Математически стоячая волна
напряжения и стоячая волна тока описываются произведением
двух периодических (в нашем случае — тригонометрических)
функций. Одна из них — функция координаты текущей точки на
линий (в нашем случае ш/), другая — функция времени (at). Всегда
стоячая волна напряжения и стоячая волна тока сдвинуты по от
ношению друг к другу в пространстве и во времени.
Сдвиг во времени между стоячей волной напряжения и стоячей
волной тока равен 90°. Сдвиг в пространстве между стоячей волной
напряжения и стоячей волной тока равен четверти длины волны
[см. формулы (11.52') и (11.53'), (11.54') и (11.55')].
Точки линии, где периодическая функция координаты прохо-
дит через нуль, называются узлами, а точки линии, в которых пе-
риодическая функция координаты принимает максимальные зна-
чения, — пучностями.
При возникновении стоячих воли электромагнитная энергия
от начала линии к концу линии не передается. Однако на каждом
отрезке линии, равном четверти длины волны, запасена некоторая
электромагнитная энергия.
Эта энергия периодически переходит из одного вида (из энергии
электрического поля) в другой вид (в энергию магнитного поля).
В те моменты времени, когда ток вдоль всей линии оказывается
равным нулю, а напряжение достигает максимального значения,
вся энергия перешла в энергию электрического поля.
В те моменты времени, когда напряжение вдоль всей линии
равно нулю, а ток достигает максимального значения, вся энергия
перешла в энергию магнитного поля.
§ 336. Стоячие волны в линии без потерь при холостом ходе ли-
нии. Из формул (11.35') и (11.36') следует, что при холостом ходе
U = (72 cosay; (11.52)
I = iy^s'nay' (1L53)
Для перехода к функциям времени умножим правые части двух
последних формул на V2 е<<1Л и от полученных произведений возь-
мем мнимые части:
454
и — V 2f/2cosaysin at;
i = sin ay sin (at -f- 90°).
(11.52')
(11.53')
Угол 90° в аргументе у синуса в формуле (11.53') соответствует
множителю / в формуле (11.53).
В точках ay = kit, где k — 0, 1, 2,..., будут узлы' тока и пуч-
ности напряжения.
График стоячих волн напряжения и тока для трех смежных
зт 3
моментов времени atx — 0, <о/2 = — и at3 — — л показан на рис.
349; на верхнем графике — напряжение, на нижнем—ток. Утол-
щенными линиями показана волна при ait = 0, тонкими линия-
ми — при со/2 = — , пунктирны-
ми — при at3 = -|- л для напряже-
ния и при ats = л для тока.
§ 337. Стоячие волны в линии
без потерь при коротком замыка-
нии на конце линии. Из формул
(11.35') и (11.36') следует, что при
коротком замыкании на конце ли-
нии (U2 = 0)
= //2 1Л—sin ау; (11.54)
г Со
/=/2 cosay. (11.55)
Для перехода к мгновенным значениям умножим правые части
двух последних формул на ]^2 е'ш* п от произведений возьмем мни-
мые части:
и = /2 /2 1Л£о. sin ay sin (at ф 90°); (11.54')
г Св
i = И 2 /2 cos ay sin at. (11.55')
В правой части формулы (11.54') — в формуле для напряже-
ния — есть множитель sin ay sin (at ф 90°). Такой же множитель
есть в формуле (11.53') для тока i.
Следовательно, картина стоячей волны напряжения при корот-
ком замыкании на конце линии качественно повторяет картину
стоячей волны тока при холостом ходе линии.
Аналогично, картина стоячей волны тока в короткозамкнутой
линии качественно повторяет картину стоячей волны напряжения
при холостом ходе линии.
л 55
§ 338. Аналогия между уравнениями линии с распределенными
параметрами и уравнениями четырехполюсника. Напряжение и ток
на входе линии с распределенными параметрами (Ult /х) связаны с
напряжением и током в конце линии с распределенными парамет-
рами (й2, /а) следующими уравнениями [они получены из (11.35)
и (11.36), в которые вместо у подставлена длина всей линии /]:
= U2 ch у/ l2Zc sh
/\ = ^shyZ4- Л ch у/.
Сопоставим их с известными из первой части курса ТОЭ уравне-
ниями четырехполюсника:
(71=Z(/24-BZ2;
4 = ей,4- Di2.
Из сопоставления следует, что уравнения по форме полностью
аналогичны, и если принять, что
A = D = chyZ; (11.56)
B = ZcshyZ; (11.57)
C = ±l£, (11.58)
zc
то зависимость между Ц и й2 и /2 и зависимость между и Z/a
и /2 в линиях с распределенными параметрами будут в точности
Рис. 351
такими же, как и в четырехполюснике. Другими словами, при
соблюдении условий (11.56) — (11.58) четырехполюсник будет эк-
вивалентен линии с распределенными параметрами в отношении
связи между входными и выходными токами и напряжениями.
§ 339. Замена четырехполюсника эквивалентной ему линией с
распределенными параметрами и обратная замена. При перемене
местами источника и нагрузки в схеме рис. 348 токи в источнике и
нагрузке не изменятся. Таким же свойством обладает симметричный
четырехполюсник. Поэтому однородная линия с распределенными
параметрами может быть заменена симметричным четырехполюсни-
ком и, обратно, симметричный четырехполюсник можно заменить
участком однородной линии с распределенными параметрами. При
456
замене будем исходить из уравнений (11.56) — (11.58) и зависи-
мостей, при помощи которых параметры симметричного четырех-
полюсника связаны с коэффициентами А, В, С.
Из первой части курса известны (см. § 120) две схемы замеще-
ния четырехполюсника: Т схема (рис. 350) н П схема (рис. 351).
Для симметричной Т схемы
Zj=~- (11.59)
И 1 с
= (11.60)
или Л = О=1-[-^; (11.61) 6 = 27,4-1; (11.62) С = -. (11.63)
Для симметричной П схемы
или Z4 = B. (11.64) Z5=-^-, (11.65) А — 1 ^=i + g; (П-66) B = Z4; (11.67) С = f + 4- (11-68)
Рассмотрим сначала последовательность операций при замене
Т и П схем замещения четырехполюсника эквивалентной ему ли-
нией с распределенными параметрами*.
Пусть известны параметры Z, и Z3 в Т схеме (или Z4 и Z5 в П
схеме). Требуется найти Zc и yl для эквивалентной линии.
Последовательность решения.
По формулам (11.61) — (11.63) [или соответственно (11.66) —
(11.68)] находим коэффициенты А, В, С.
Для определения волнового сопротивления Zc поделим (11.57)
на (11.58) и найдем:
(11.69)
* Речь идет о замене при фиксированной частоте.
457
Для определения yl поступим следующим образом: составим
выражение для th yl, использовав (11.56), (11.57) и (11.6$):
th у/, использовав (11.56), (11.57) и (11.6$):
В
sh -tl
th yl = =
• ch yl
/ B
c =Vbc
A ~ A
(11.70)
Но
Умножим и
е11. Получим:
,, , е11 — е
th yl =-----------
е7'4-е-7*
числитель, и знаменатель последней формулы на
e2'!1__1
th yl = ±----------*
+ 1
Отсюда
(Н.71)
e e — i _ th V "
Правую часть формулы (11.71) переведем в показательную
форму. Пусть она будет равна Мег\ Тогда
е™ = М
2al — V.
и
Следовательно,
1 V
₽/ = In М и al == —.
Рассмотрим теперь последовательность операций для замены
линии с распределенными параметрами эквивалентным ей четы-
рехполюсником.
Известны yl и Zc.
Требуется найти сопротивления Zx и Z3 в Т схеме (или Z4 и Zs
в П схеме). С этой целью по формулам (11.56) — (11.58) находим
значения коэффициентов А, В, С, а затем по формулам (11.59) и
(11.60) определяем Zx и Z3 для Т схемы [или по формулам (11.64)
и (11.65) сопротивления Z4 и Zs для П схемы].
Остановимся на вопросе о том, любой ли симметричный четырехполюсник
можно заменить участком линии с распределенными параметрами н любую
ли линию с распределенными параметрами можно заменить четырехполюс-
ником.
Очевидно, что такая замена может быть осуществлена, если полученные
в результате расчета параметры таковы, что заменяющее устройство физи-
чески можно выполнить. Как правило, замена участка линии с распределен-
ными параметрами четырехполюсником всегда возможна. Что касается обрат-
458
ной замены, то она возможна не всегда. Невозможна она в тех случаях, когда
в результате расчета волновое сопротивление окажется чисто мнимым чис-
лом: в реальных линиях этого не бывает.
§ 340. Цепная схема. На практике приходится встречаться со
схемой, представляющей собой последовательное включение несколь-
ких одинаковых симметричных четырехполюсников (рис. 352).
Такую схему принято называть цепной схемой. Исследование
распределения тока и напряжения вдоль цепной схемы удобно про-
водить, используя теорию линий с распределенными параметрами.
Действительно, в предыдущем параграфе говорилось о замене од-
ного четырехполюсника отрез-
ком линии длиной /, имеющей
коэффициент распространения у
и волновое сопротивление Zc.
Если число четырехполюсников
равно п, то длина отрезка ли-
нии с распределенными пара- рис 352
метрами будет в п раз больше,
т. е. равна nl.
Обозначим напряжение и ток на выходе п четырехполюсника
через Un + i и 1п + Г, тогда напряжение и ток на входе первого
четырех полюсника:
Ц = б/„+1 chyn/ + zn+[ZcShYH/;
Л = UjZ±~ Sh y,li U Ch Y nl'
(11.72)
(11.73)
Напряжение и ток на входе k от начала четырехполюсника (k - п):
Uk = f7„+1ch (n - k + 1) yl + in+izc sh (n - k + 1) yl', (11.74)
/A=^±ish(n-^+l)y/ + 7„+1ch(n-^+ l)y/. (11.75)
Рассмотрим несколько числовых примеров на материал, изло-
женный в § 316—339.
Пример 153. Для некоторой линии длиной 5 км на частоте
1000 гц были проведены опыты по определению ее входного сопро-
тивления при холостом ходе и коротком замыкании на конце ли-
нии. Оказалось, что Zexxx = 535е~/64 ом и Zex кз = 467,5е~'10 ом.
Требуется найти волновое сопротивление Zc и коэффициент рас-
пространения -у этой линии на частоте 1000 гц.
Решение. Из формулы (11.49) следует, что при холо-
стом ходе, когда Z2 = со,
Z -
вххх thyZ
459
При коротком замыкании, когда Z2 — О,
%вх кз ~ ?С th ТЛ
отсюда ________________
zc = VZexxxZex кз = /535е-'«4' 467,5е^ = 500с-/37° ом;
th yl = -\[ = -1 / 4б7,5е-/|0° = 0,935еу27.
Г Zex хх у 535е
По формуле (11.71)
g2T! __ 1 4- th yZ
1 — th yl
Следовательно,
g2₽Z ^2al __ 1 H-0,935ef27 | |e/8IcI0' _ g\,414 JI.414 .
1— 0,935e/27°
2pZ = 1,414; p = = 0,1414;
2а/= 1,414; a = 0,1414;
у = P-f-/a = 0,2e/45°
Пример 154. Определить Z?o, Lo, Go, и C? для линии предыду-
щего примера, полагая известными Zc= 500е-1 7° ом и у=0,2е/45° 1/км>
Решение. В соответствии с формулами (11.17) и (11.18) про-
изведение
yZc = Ro jwL0.
Следовательно,
яо4- /<oLo = 0,2е'45°. 500c“j37° = 100еу8 = 99 + /13,9.
Или
Ro = 99 ом/ км
и
£0 = = 0,00222 гн/км;
° 2л. 1000 1
— = +iaCo'
Zc
Таким образом,
Go + /®С0 = -0,2еН5 = 0,0557 . IO”3 4- /0,396 . 10~3.
500е-'37°
Пример 155. Линия предыдущего примера подключена к постоян-
ному напряжению (со = 0). Определить величину напряжения
и величину тока в начале линии, если на конце линии включена
нагрузка 400 ом и ток в нагрузке 0,5 а.
4€0
Решение. По формуле (11.23) находим волновое сопро-
тивление линии Zc для постоянного тока:
Zc = -1 = -1/------------== 1330 (ом).
У Go у 0,0557.10-3
Постоянная распространения [см. формулу (11.19)]
у = /ад = /99 • 0,0557.10-3 = 0,0743 (1/км).
По формулам (11.35) и (11.36) при у=~-1
Ut U2 ch yl + I2ZC sh у/; /, = Z2 ch yl -f- sh yl.
zc
По условию
/2 = 0,5 a; U2 = Z2/?2 = 0,5 • 400 = 200 (e);
yl = 0/ = 0,0745 • 5 = 0,371; ch у I = ch 0,371 = 1,07*;
sh yl = sh 0,371 =0,379.
Следовательно,
= 200.1,07 -]-0,5 • 1330.0,379 = 466 (e);
/. = 0,5 • 1,07 4- — . 0,379 = 0,694 (a).
1 1 1330
Пример 156. Линия примера 153 короткозамкнута на конце и
присоединена к источнику синусоидального напряжения 1000 гц.
Определить напряжение и ток в начале линии, если ток в конце
линии/а = 1 а.
Решение. При коротком замыкании
Ul = l2Zc sh yl и /г= /2 ch yl.
По данным примера 153
у = 04- /а = 0,1414 4- /0,1414 (Чкм)\ I = 5 or,
yl = 0,707 4- /0,707, Zc = 500е~'37° ом\
= е0,707 е'0’707 = 2,02 (cos 40с20' 4- / sin 40°20') = 1,54 4- /1,305;
= е-°-707 е“/0,707=0,495 (cos 40°20'—/ sin 40°20')=0,377— /0,32;
ch yl = 0,5 (ет/ 4-е-1') = 0,96 4- /0,4925 = 1,О7е'27°20';
sh yl = 0,5 (е11 — е—т/) = 0,582 4- /0,812 ^/4°20'.
Следовательно,
t/x= i2Zc sh у/ = 1 • 500е-/37° е'54°20' = 500/7°20' в,
/,= Z2chyZ= l,07e/27°20’a.
• Таблицы функций sh х, ch х и ех см. иа стр. 428.
461
Пример 157. Линия примера 153 замкнута на активное сопро-
тивление Z2 — 400 ом. Определить U1 и /1Э если по нагрузке про-
текает ток /2 = 0,5 a; f = 1000 гц.
Решение. = U2 ch у/ + I2ZC sh у/ = 200 . 1,07е/27°20' +
+ 0,5 • 500е-/37°е,54°20, = 463Л;
/\ = /2 ch у/ + ^- sh у/ = 0,5-1,07е'27°20' +
_|---22° ej54C20' = 0,8е/5з»з8'
1 500е~/37
Пример 158. По данным примера 157 определить комплекс
действующего значения падающей волны в начале линии (Л2).
Решение. В соответствии с формулой (11.28)
Л, = = -‘+2,,Ze;
Л, = + е.
2
Пример 159. Записать выражение для мгновенного значения па-
дающей волны напряжения в начале и конце линии по данным пре-
дыдущего примера.
Решение. Мгновенное значение падающей волны напряже-
ния в начале линии при х = 0 равно:
УТ - 431 sin(co/+ 19с30').
Мгновенное значение падающей волны напряжения в конце
линии при х — I в общем виде запишется так:
V'2A2e~l sin (со/ + — al);
е-3' = е_0,7С7 = 0,495. а[ = 0.707 = 40с30,;
/2Л2е -3' = V2 . 431 • 0,495 = 301 в;
tyn — al — 19°30' —40°30'=—21°.
Следовательно, мгновенное значение падающей волны напря-
жения в конце линии таково: 301 sin (со/ — 21°) в.
Пример 160. Определить величину затухания в неперах для ли-
нии примера 153, если на конце ее включена согласованная на-
грузка.
Решение. Затухание в неперах равно величине р/. Так как
произведение р/ равно 0,1414 • 5 = 0,707, то затухание линии равно
0,707 неп.
Пример 161. Какой величины дополнительную индуктивность
Lodon ,1аД° включить на каждом километре телефонное! линии с
462
параметрами: = 3 ом/км\ Lo = 2 • 10-3 гн/км:, Go — 10“6
Со= 6 . 10-9 ф/км, чтобы линия стала неискажающей?
Решение. Для того чтобы линия была неискажающей, ее
параметры должны удовлетворять уравнению (11.41). Следователь-
но,
ООП + = 3-^-1-0-- = 18 . 10-3 (гн/км)
о0 10 6
И
Lod07 = 18 — 2 = 16 (мгн/км).
Пример 162. Определить наименьшую длину короткозамкнутой
на конце двухпроводной воздушной линии, чтобы при частоте 108 гц
входное сопротивление ее равнялось 800/ ом.
Расстояние между осями проводов d — 20 см, радиус каждого
провода г = 2 мм.
Решение. В соответствии с формулой (11.51)
Z.x к, = / 1 f — tg аУ-
f со
Для двухпроводной линии
(1 d
1П —
г
п
По условию
800/ = /553 tg ау.
Отсюда
tgKy = §22 = 1,445; ау = 55°20' = 0,963 рад-,
553
V Роеп = —~— сек/см;
° з • IO1»
а = <о /ДД = «Ура = = 2,092 . 10~3 (УСД.
Искомая длина линии
у —-----!------= 46,1 (ел).
* 2,092 .10-» 7
463
Пример 163. В Т схеме рис. 350 Z, = 100 ом, Z3 = — 500 / см.
Определить волновое сопротивление четырехполюсника и ве-
личину у/ эквивалентной ему линии с распределенными парамет-
рами.
Решение. В соответствии с формулами (11.61) — (11.63)
А = 1 4-| = 1 + = 1 +0,2/ = 1,02е/1118' ;
ZSg -DUUy
В = 2ZX + = 200 + = 200 + 20/ ^2OOe/s°40';
z3 —500j
—J— = 0,002e/S°.
— 500/
C = —
z3
По формуле (11.69)
2OOe,S40'
0,002e/9°°
= 316e“>i2°w ом.
По формуле (11.70)
, V~BC /гоое^40’ • 0,002ej9° n .oe . .„ Qcn
th у/ = -L— =--------1--------------= 0,498 + /0,369.
По формуле (11.71)
e2V = e2?i 1 + tb yZ _ 1,498 4-/0,369 _ 2 475e/50°i0'.
1 — th yZ 0,502-/0,369
₽/ = ~In 2,475 = 0,454; al = 25c5' ^0,437 pad;
у/ = 0,454 + /0,437.
*
* *
Перейдем теперь к изучению основ теории электрических фильт-
ров.
§ 341. Определение электрических фильтров. Под электрически-
ми фильтрами понимают четырехполюсники, включаемые между
источником питания и приемником (нагрузкой), назначение которых
состоит в том, чтобы беспрепятственно — без затухания — пропус-
кать к приемнику токи одних частот и задерживать или, лучше ска-
зать, пропускать, но с большим затуханием, токи других частот.
§ 342. Введение к теории фильтров. Диапазон частот, пропуска-
емых фильтром без затухания, называют зоной прозрачности. Диа-
пазон частот, пропускаемых с затуханием, — зоной затухания.
Электрические фильтры собирают из индуктивных катушек и
емкостей. Фильтры используются главным образом в радиотехни-
ке и телефонии. В том и другом случаях применяются токи доволь-
но высоких частот.
При высоких частотах индуктивные сопротивления coL катушек
индуктивностей во много раз больше их активных сопротивлений.
464
Поэтому в излагаемой ниже упрощенной теории фильтров будем
полагать активные сопротивления катушек индуктивности равны-
ми нулю. Другими словами, будем полагать, что фильтры со-
ставляются только из реактивных элементов.
Фильтры обычно собирают по симметричной Т или П схеме
(см. рис. 350 и 351). Из предыдущего известно, что линия с распре-
деленными параметрами также может быть замещена симметрич-
ной Т или П схемой. Таким образом, схема фильтра та же, что и
схема замещения линии с распределенными параметрами. Поэто-
му при изучении фильтров можно будет воспользоваться понятием
о коэффициенте затухания и коэффициенте фазы, первоначально
введенными применительно к линиям с распределенными парамет-
рами.
Условимся сопротивление Zt в схеме рис. 350 и сопротивление
Z, в схеме рис. 351 называть продольными сопротивлениями,
а сопротивление Z3 в схеме рис. 350 и сопротивление Z5 в схеме
рис. 351 — поперечными сопротивлениями.
Фильтры, в которых произведение продольного сопротивления
на соответствующее поперечное сопротивление представляет собой
некоторое постоянное для данного фильтра число (число Л), не
зависящее от частоты, принято называть фильтрами типа k.
Фильтры, в которых это произведение зависит от частоты, на-
зывают фильтр аг и типа т*. В фильтрах типа k сопротивление
присоединяемой к выходу фильтра нагрузки равняется волновому
сопротивлению фильтра (согласованная нагрузка). В фильтрах
типа т нагрузка мсжет быть несогласованной (в них волновое со-
противление меньше зависит от частоты, чем в фильтрах типа k).
В курс ЗОЭ входит рассмотрение основ теории простейших
фильтров — фильтров типа k. Основы теории фильтров типа т
излагаются в специальных руководствах по технике связи и радио-
технике.
Качество фильтра тем выше, чем более резко выражены его
фильтрующие свойства.
Фильтрующие свойства четырехполюсников физически основа-
ны на возникновении в них резонансных режимов — резонансов
токов или резонансов напряжений.
§ 343. Основы теории фильтров. Из предыдущего известно, что
если нагрузка Z2 согласована с волновым сопротивлением Zc
четырехполюсника (или эквивалентной ему линии с распределен-
ными параметрами), то напряжение U2 и ток в нагрузке /2 связа-
ны с напряжением (7Х и током 1г на входе четырехполюсника (или
эквивалентной ему линии с распределенными параметрами) сле-
дующими соотношениями:
* Фильтры типа т обладают лучшими фильтрующими способностями,
но теория их немного сложнее теории фильтров типа k.
16 Л. А. Бессонов
465
t>2 = й^1-
Обозначим
yl = р/ -j- jal = & -f- ja.
Тогда
U2 - С^е-» e ~ia- j2 = iie~b e~ia.
Множитель e~b характеризует, во сколько раз модуль напряже-
ния (тока) на выходе фильтра меньше модуля напряжения (тока)
на входе фильтра.
Если 6 = 0, то е~ь= е° = 1 и фильтр пропускает колебания без
затухания. Таким образом, в зоне прозрачности b = 0.
В зоне затухания b >0. Множитель е~'а, по модулю равный 1,
свидетельствует о том, что напряжение U2 и ток /2 на угол а от-
стают соответственно от и /х. Подход к вопросу о фильтрующих
свойствах четырехполюсника основан на сравнении выражения
для коэффициента А четырехполюсника с равным ему [см. форму-
лу (11.56)] выражением гиперболического косинуса от аргумента
b + ja:
А = ch (b + ja).
Гиперболический косинус от суммы двух аргументов (с учетом
того, что ch ja = cos а и sh/a=/sina) может быть представлен
следующим образом:
ch (b + ja) = ch b cos а ф- / sh b sin a.
Для любого фильтра, собранного по симметричной Т схеме
[см. формулу (11.61)],
Для фильтра, собранного по П схеме [см. формулу (11.66)],
А = 1-]-^.
4,
Из каких бы реактивных сопротивлений ни был собран
Z Z
фильтр, отношение — в Т схеме и отношение — в П схеме
Z3 ^5
всегда будет действительным (не мнимым и не комплексным) чис-
лом — отношение двух мнимых чисел всегда есть число дей-
ствительное.
Следовательно, всегда будет действительным и коэффициент А.
Но если А действительно, то действительным должно быть и вы-
ражение равного ему ch (b -ф ja):
ch (6 + ja) = ch b cos a + j sh b sin a — A.
466
Выражение ch (b -j- ja) будет действительным числом, если
sh b sin a = 0. (11.76)
При этом
ch b cos a = A. (11.77)
Уравнения (11.76) и (11.77) используются для определения гра-
ниц зоны прозрачности и характера изменения угла а в зоне про-
зрачности, а также для определения характера изменения коэф-
4ициента затухания b в зоне (зонах) затухания.
Уравнение (11.76) в зоне прозрачности (Ь — 0) удовлетворяется,
так как sh b = sh 0 = 0. В силу того, что ch 0 = 1, уравнение
(11.77) для зоны прозрачности переходит в следующее:
cosa = /l. (11.78)
Круговой косинус (cos а) может изменяться в пределах от +1
до —1. Поэтому крайние значения коэффициента А [являющегося
функцией частоты — А (ю)] в зоне прозрачности равны +1.
Зона прозрачности в общем случае лежит в диапазоне частот
от сох до <в2. Значения Wj и м2 для низкочастотных и высокочастот-
ных фильтров (подробнее см. § 344) определяются путем решения
уравнений
Л(со)=+1. (11.79)
Для полосовых и заграждающих фильтров (см. § 344) сох и а>2
определяются как корни уравнения Д(со) = —1. Для них уравне-
ние А (со) = 1 дает возможность определить так называемую резо-
нансную частоту соо, находящуюся в интервале между <ог и ®2.
Характер изменения угла а в функции от® для зоны прозрач-
ности определяется в соответствии с уравнением (11.78) следую-
щим образом:
а = arc cos А (со). (11,78')
Далее обсудим, как определить b и а для зоны затухания. В зо-
не затухания b > 0. Уравнение (11.76) удовлетворяется при уело-
НИИ sin а = 0, (11.80)
т. е. при а — 0 (11.80')
и (или) при а = + л. . (11.80")
Из уравнения (11.77) при а == 0 следует, что
ch b = А (со), (11.8Г)
а при а — + л ch Л = — А (со). (11.81")
Уравнения (11.81') и (11.81") позволяют по значениям А как
функции со найти ch b в зоне затухания, а по ch & найти b и, таким
16* 467
образом, построить кривую b = Ди). Из уравнений (11.80) и
(11.80") следует, что в зоне затухания напряжение 02 на выходе
фильтра находится либо в фазе (при а — 0), либо в противофазе
(при а = ± л) с напряжением 01 на входе фильтра.
В заключение необходимо отметить два важных положения.
Первое: с изменением частоты со меняются коэффициенты В и С
четырехполюсника, поэтому изменяется и волновое сопротивле-
ние Zc = -
с V с
Для того чтобы фильтр работал на согласованную нагрузку
(только в этом случае справедлива изложенная выше теория фильт-
ров), при изменении частоты надо менять и величину сопротивле-
ния нагрузки*.
Второе: в зоне прозрачности волновое сопротивление фильтра
всегда активное, а в зоне затухания оно чисто реактивное (индук-
тивное или емкостное).
§ 314. Подразделение фильтроз на низкочастотные, высокочас-
тотные, полосовые и заграждающие. Низкочастотными фильтрами
называют фильтры, пропускающие в нагрузку лишь низкие часто-
ты, начиная с о>х = 0 до со2. Зона затухания их находится в интер-
вале от со2 ДО оо .
Схемы двух низкочастотных фильтров приведены на рис. 353, а
и б. Характер изменения коэффициента затухания b и коэффициен-
та фазы а качественно иллюстрируется кривыми рис. 353, в.
Под высокочастотными понимают фильтры, пропускающие в
нагрузку лишь высокие частоты, начиная с частоты <пг до оо. Зона
затухания у них находится в интервале значений частоты от 0
ДО сог
Схемы двух высокочастотных фильтров приведены на рис. 354, а
и б. Характер изменения b и а для них иллюстрируется кривыми
рис. 354, в.
Рассмотрим вопрос об изменении величины волнового сопротивления
фильтра Zc в зоне прозрачности для низкочастотного Т-фильтра (см. рис.
353, а) и для высокочастотного Т-фильтра (см. рис. 354, а).
* Если нагрузка фильтра не чисто активная или не согласована с вол-
новым сопротивлением фильтра, или если требуется учесть влияние активного
сопротивления индуктивных катушек на работу фильтра (что особенно су-
щественно для низких частот), то для построения зависимости = f(cn) и
"г
зависимости угла сдвига фаз между и U2 в функции от частоты можно вос-
пользоваться, например, методом пропорциональных величии, известным из
первой части курса ТОЭ.
С этой целью следует задаться несколькими значениями угловой часто-
ты и для каждого ее значения аналитическим или графическим путем иайти
комплекс напряжения на входе фильтра, положив ток на выходе фильтра
равным, например, 1 а.
468
С этой целью в формулу Zc = подставим для В и С их значения
в соответствии с формулами (11.59) — (11.63) и проанализируем полученные
выражения.
Для низкочастотного Т-фильтра (см. рис. 353, a) Zc = - co2L2. При
co = coi = O Zc — . С увеличением частоты Zc уменьшается, ио сна-
чала мало отличается от значения 1/ _. При достижении значения со=со2=
Zc становится равным нулю.
Б)
Для высокочастотного Т-фильтра (рис. 354, a) Zc—
Ха-
С со2С2
1
рактер изменения Zc в этом случае иной, а именно: при со == од =
Zc = 0, затем с увеличением со Zc увеличивается и при со-> оо Zc становится
равным .
Аналогичным образом можно проанализировать зависимость Zc от со для
П-фильтра.
Если фильтр предназначен для работы прн частотах, находящихся внутри
зоны прозрачности данного фильтра и относительно далеко удаленных от зна-
чения со, при котором Zc = 0, то сопротивление нагрузки Z„ на выходе низ-
кочастотных фильтров принято брать равным волновому сопротивлению филь-
"2L
С '
тра при со = со2 = 0; для Т-фильтра (см. рис. 353, а) оно равно
469
Для высокочастотных фильтров нагрузку согласовывают обычно с вол: с-
вым сопротивлением фильтра при го = оо: для Т-фильтра (рис. 354, а) послед-
1 /24
нее также равно I/ —.
В заключение отметим что в зоне (зонах) затухания Zc оказывается чисто
мнимым.
Полосовые фильтры представляют собой фильтры, пропускаю-
щие в нагрузку лишь узкую полосу частот от со1 до со2. Слева от гог
и справа от ю2 находятся зоны затухания. Схема простейшего по-
лосового фильтра типа k изображена на рнс. 355, а.
Параметры ее должны удовлетворять условию:
= L2C2.
Характер изменения b и а для полосового фильтра иллюстри-
руется кривыми рис. 355, б.
Под заграждающими фильтрами понимают фильтры, в кото-
рых зона прозрачности как бы разрезана на две части зоной зату-
хания (рис. 356, б). Слева от частоты (Oj и справа от со.2 находятся
две части зоны прозрачности.
Схема простейшего заграждающего фильтра представлена на
рнс. 356, а. В ней
LiCi = L2C2.
Пример 164. В схеме рис. 353, a L = 10 мгн\ С = 10 мкф. Опре-
делить границы зоны прозрачности, закон изменения коэффициен-
та а в зоне прозрачности, построить векторную диаграмму при
470
to — 2000 рад/сек и /2 = 0,2 а и определить закон изменения коэф-
фициента Ь в зоне затухания.
Решение. Для Т-схемы
А = I —- = 1 -j- /toL/coC =1 — a2LC.
Z3
Приняв А = 1, найдем:
©j = 0.
Приняв А = — 1, найдем:
— 1 = 1— a>2LC ,
отсюда
<оа = -у/ = 4470 рад/сек.
В зоне прозрачности а = arc cos А — arc cos (1 — <о2£С).
При частоте <о = 2000 рад/сек., находящейся в зоне прозрачности,
Zc — — <oaZ? — 40 ом. При нагрузке фильтра на волновое со-
противление напряжение на выходе U2— l2Zc — 0,2 • 40 = 8 (в).
Напряжение на входе t/1 также равно 8 в и опережает t/2 на
угол а = arc cos 0,6 53° (см. рис. 357).
Для определения закона изменения Ь в зоне затухания, в кото-
рой для данного фильтра А отрицательно, используем уравнение
ch b =—А — a>2LC — 1.
Найдем Ь, например, при <о = 2<о2 = 8940 рад/сек-.
ch b = (8940)2 • 10"2 • 10~3 * 5 = 8; b = 2,77 неп.
Без вывода дадим формулы для определения параметров поло-
сового фильтра рис. 355, а по заданным частотам f1 и f2 и задан-
ной величине сопротивления нагрузки фильтра Zc при частоте
_ “>0 .
2л _
1) резонансная частота /с= КД/г!
ft — fi .
2afifiZC ’
3)
4)
5)
л2с (f2 — fd ’
ZC(fi-fi)t
^fifi
471
Пример 165. Определить параметры полосового фильтра рис.
355, а, исходя из того, что он должен пропускать полосу частот
от /у=750 до /2=850 гц и что сопротивление нагрузки, равное вол-
новому сопротивлению фильтра Zc при резонансной частоте, со-
ставляет 800 ом.
Решение. 1) резонансная частота =-• = V750 • 850 =
= 798 (ач);
2) С.=-------850 - 750--= 0,0312 (цкф);
1 2л • 750.850 • 800 '
3) L. =-------—-------= 1,273 (гн)-,
2л (850 — 750) ' '
4) С2 =------------ = 3,94 (мкф);
л • 800 • 100
с. т 800- 100 п ni / ч
5) £2 =------------ = 0,01 (ан).
§ 345. Качественное определение типа фильтра. В заключение
укажем, как по схеме фильтра без проведения подробного матема-
тического анализа можно судить о том, к какому из перечисленных
выше типов может быть отнесен тот или иной фильтр. Заключение
основывается на характере продольного сопротивления фильтра*.
Если продольное сопротивление состоит только из индуктив-
ностей, то фильтр относится к категории низкочастотных.
Если продольное сопротивление чисто емкостное, то фильтр
высокочастотного типа.
Если продольное сопротивление состоит из последовательно
соединенных L и С, то фильтр полосового типа. Если продольное
сопротивление состоит из параллельно соединенных L и С, то фильтр
заграждающего типа.
* Характер продольного сопротивления фильтра, как правило, прямо
противоположен характеру поперечного сопротивления. В этом можно убе-
диться путем рассмотрения схем рис. 353, а, 354, а и 355, а. Действительно,
если продольное сопротивление индуктивное, то поперечное емкостное. Если
продольное составлено последовательно соединенными L и С, то поперечное
образовано параллельно соединенными L и С и т. д.
Глава двенадцатая
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ,
СОДЕРЖАЩИХ ЛИНИИ С РАСПРЕДЕЛЕННЫМИ
ПАРАМЕТРАМИ
§ 346. Введение. В главе десятой рассматривались переходные
процессы в линейных электрических цепях, содержащих сосредо-
точенные параметры.
Между тем для электроэнергетики, телефонии, телеграфии,
счетно-решающей техники и радиотехники существенное значение
имеют также и переходные процессы в электрических цепях, содер-
жащих линии с распределенными параметрами.
В тех участках цепей, которые могут быть представлены как
участки с сосредоточенными параметрами, расчет переходных про-
цессов производится рассмотренными в главе десятой методами.
В данной главе будут обсуждаться особенности переходных про-
цессов в самих линиях с распределенными параметрами, вопросы
согласования и увязки их с переходными процессами в участках
цепей с сосредоточенными параметрами.
Как уже говорилось в § 317, основными уравнениями для ли-
ний с распределенными параметрами являются уравнения (11.1)
и (11.4). Они справедливы и для установившихся и для переходных
процессов.
В силу того что интегрирование двух совместных дифферен-
циальных уравнений в частных производных [уравнений (11.1) и
(11.4)1 Б общем виде представляет собой довольно сложную в мате-
матическом отношении задачу, в курсе ТОЭ переходные процессы
изучаются в несколько упрощенной постановке, а именно: изу-
чаются переходные процессы в однородных линиях без потерь,
т. е. при Ло = 0 и Go = 0.
Такая постановка вопроса и практически вполне оправдана,
поскольку реальные линии с распределенными параметрами, как
правило, обладают относительно малыми потерями.
Изучение переходных процессов при Ro = 0 и Go= 0 дает воз-
можность качественно исследовать основные черты процессов. В ко-
личественном отношении неучет Ro и Go для начальных стадий пе-
473
реходного процесса существенного влияния обычно не оказывает,
однако для последующих стадий учет А?о и Gc представляется жела-
тельным. В энергетических, телефонных и телеграфных устройст-
вах, содержащих линии с распределенными параметрами, переход-
ные процессы возникают при подключении линий к источнику
э. д.с., при отключении от источника э. д. с., при подключении и
отключении нагрузки, а также при атмосферных (грозовых) раз-
рядах.
В радиотехнических устройствах и устройствах, используемых
в счетно-решающей технике, также происходят переходные процес-
сы по типу рассматриваемых в данной главе. Они имеют место, на-
пример, в линиях задержки и формирующих линиях.
§ 347. Исходные уравнения и решение их. Из уравнений (11.1) и
(11.4) при Ro — 0 и Ge= 0 следует, что
(12.1)
CU о/
di ___р ди
о "7?
дх ct
(12-2)
Ток и напряжение являются функциями двух переменных: рас'
стояния л- от начала линии и времени t. Продифференцируем (12.1)
по х, (12.2) по /:
д2и __ d2i
д^~ ° dxdt’
(12.3)
d2i _ d2u
dxdt ~ °dt2'
правую часть (12.3) вместо ------
дх dt
v2
В соответствии с (12.4) в
подставим —Со — и обозначим £0С0 =
дх2 v2 dt2
(12.4)
(12.5)
Из предыдущего [см. § 324, формулу (11.39)] известно, что
v — есть скорость распространения электромагнитной вол-
ны по линии. Если уравнение (12.2) продифференцировать по х, а
(12.1) по / ив продифференцированное уравнение (12.2) подставить
правую часть продифференцированного уравнения (12.1), то полу-
чим уравнение:
дЧ _ \_дЧ
дх2 v2 dt2
(12.6)
Уравнения (12.5) и (12.6) являются уравнениями второго поряд-
ка в частных производных. Из курса математики известно, что такого
вида уравнения называются волновыми уравнениями.
474
Решением уравнения (12.5) является сумма любых функций
h и f2, причем аргументом функции является •—), а ар-
гументом функции f2 является + —
« = (12-7)
\ V / \ v /
Для сокращения записи в дальнейшем часто будем обозначать:
,12'8>
«. = ?.(<+ 7)' <|2-9>
Следовательно,
h = + (12.10)
Вид функций ft и Д определяется граничными условиями в на-
чале и конце линии.
Функции ft и /2 в общем случае должны позволять дважды диф-
ференцировать их по х и по t.
Подстановка функций L I t— —) и/2н + —| в (12.5) дает
\ v) \ v /
тождество.
Решение уравнения (12.6):
।- = <pi (t—<р2 (t 4—у (12.11)
\ Г / \ V
Обозначим для сокращения записи:
»П = Ф1(* —~У
\ v!
I , t х \
го = ФаМ 4"~ b
Тогда
1 = 1п4“'о-
(12.12)
(12.13)
(12.14)
§ 348. Падающие и отраженные волны на линиях. В
соответствии с уравнениями (12.7) и (12.11) напряжение и
ток в линии могут быть представлены в виде двух функ-
/ х \ / X \
ций. Функции / j t---I и cpr \t---представляют собой пада-
\ v / \ v)
ющие волны. Функции /» It -ф- — ) и ф, (t -ф- —) — отраженные всл-
" \ VI \ v !
ны. Падающие волны перемещаются со скоростью v по направ-
лению от источника энергии к приемнику, т. е. в сторону увели-
чения координаты х.
Отраженные волны перемещаются по линии от приемника
энергии к источнику, т. е. в сторону уменьшения координаты х.
475
Обсудим, как следует понимать то обстоятельство, что
аргументом функции f1 является t— — (аналогичные выводы мо-
гут быть сделаны и по отношению к другим функциям).
Пусть в некоторой точке линии х = хх при t = значение
функции ) равно Fv Это значение функция будет
принимать во всех точках линии, где х > xlt с запозданием во
времени, равным -——, обусловленным конечной скоростью пере-
мещения волны по линии.
Так, в точке х = х2 значение функции Д будет равно Fx при
V
Действительно,
Таким образом, каков бы ни был закон изменения напряжения
падающей волны Д в начале линии, по такому же закону, но с за-
позданием во времени будет изменяться напряжение падающей вол-
ны в любой точке линии.
§ 349. Связь между функциями Д, /2 и функциями <₽!, ф2. Найдем
связь между функцией Д и функцией а также между f2 и<р2.
С этой целью в (12.1) и (12.2) подставим (12.7) и (12.11) и для
сокращения записи обозначим:
Тогда уравнение (12.1) дает:
Л — 7 f'a = + 4<Рз-
В свою очередь из (12.2) следует, что
—= ^одч-сод,
(12.15)
(12.16)
476
Перепишем (12.15) и (12.16):
f'i — +ф2); (12.15')
Но fi+f* = ^(Ф1— <рг). vL — — ifLo 7 • (12.16')
0 , г-. г ~ “ ZC> L0C0 ’ с® __ V LqCo ifLo 7 vC0 Co V Co “ °
где Zc есть волновое сопротивление однородной линии без потерь
[см. формулу (11.23')]. Таким образом,
f'i—f — Zc (Ф1 + фг); fi + f'2 — Zc (q\ — <Рг)- (12.15") (12.16")
Следовательно, <₽; = «-; 1 Zc’ (12.17)
Ф2 = — • Zc (12.18)
Если производные двух функций (например, <р' и /\) равны
при любых значениях х и t, то это значит, что сами функции
(Ф1 и /\) равны с точностью до постоянной. Поэтому
О2-19)
\ V } Zc \ V ]
и
ф2Ь + А\=_±/2Р + А\ (12.20)
\ Г ) Zc \ V I
Постоянные интегрирования опустили, так как будем полагать,
что в токах и напряжениях падающей и отраженной волн отсутству-
ют постоянные составлющие, не зависящие от х и от t. Два последних
уравнения можно переписать с учетом (12.8 и 12.9) и (12.12 и 12.13):
= (12.19')
Zc
lo = -u^-t (12.20')
Zc
индексы n и о — начальные буквы слов падающая и отраженная
(волны).
Из (12.19) следует, что ток падающей волны для любого момента
времени и для любой точки на линии равен частному от деления
напряжения падающей волны для того же момента времени и для
той же точки линии на волновое сопротивление Zc.
Из (12.20) вытекает, что ток отраженной волны для любого мо-
мента времени и для любой точки линии равен взятому с обратным
477
знаком частному от деления напряжения падающей волны в той же
точке линии и для того же момента времени на волновое сопротив-
ление.
Знак минус в (12.20) имеет тот же смысл, что и знак минус в (11.38).
§ 350. Электромагнитные процессы при движении прямоуголь-
ной волны по линии. Пусть источник постоянного напряжения и,
имеющий внутреннее сопротивление, равное нулю, подключается
к незаряженной однородной линии с распределенными параметра-
ми, у которой Ro = G„ = 0 (рис. 358).
По линии будет перемещаться падающая электромагнитная вол-
на. Начальный участок волны, первым продвигающийся по ли-
нии, принято называть фронтом волны.
В данном случае волна имеет прямоуголь-
ный фронт.
Двигаясь по линии, волна создает меж-
ду проводами линии электрическое и маг-
нитное поля.
Приращение магнитного потока на
фронте волны за время dt, равное произ-
ведению тока i на индуктивность участка
линии длиной dx (т. е. на £„ dx);
(/ф = i£0 dx.
Приращение магнитного потока на фронте волны вызывает
э. д. с.
= —i
c = = ==_/£oU=_t-_^ =
dt _ ° Уйс0
=— iZc=—ип—-—и.
Таким образом, на фронте волны возникает э. д. с. самоиндук-
ции, численно равная напряжению генератора.
На фронте волны происходит зарядка проводов линии: один про-
вод, например верхний, присоединенный к плюсу источника э. д. с.,
приобретает положительный заряд, другой (нижний) — отрица-
тельный заряд (такой же величины).
На фронте волны возникает ток смещения i — — . Здесь dq
dt
есть приращение заряда на одном из проводов линии за время dt;
dq = Сви dx = Со uvdt
и
iCM = — = Couv — —.
см dt 0 Zc
Следовательно, проходящий по диэлектрику на фронте волны ток
смещения в точности равен току падающей волны, проходящему
по проводам линии.
478
Электромагнитная волна, продвигаясь по линии, каждой еди-
нице последней сообщает энергию электрического поля Qfn и энер.
w; 2
гию магнитного поля----.
2
Можно показать, что эти количества энергий равны друг дру-
гу. Действительно,
ип = 1"л ~ 01 ~\f •
F Cq
Следовательно,
Colln _ CoinLg __ Ьр<я
~2~- 2C0 2
Когда падающая волна достигнет конца линии, к которому в об-
щем случае присоединена некоторая нагрузка или другая линия
Рис. 360
(с другим волновым сопротивлением), то часть падающей волны
пройдет в нагрузку (или соответственно во вторую линию), а часть
отразится — возникнет отраженная волна.
Для выяснения вопроса о том, какова будет форма волны, про-
ходящей в нагрузку, какова будет форма отраженной волны и как
они будут деформироваться во времени, применяют расчетную схе-
му, которую принято называть схемой замещения для исследова-
ния волновых процессов в линии с распределенными параметрами.
§ 351. Схема замещения для исследования волновых процессов
в линиях с распределенными параметрами. Для обоснования мето-
дики составления схемы замещения обратимся к рис. 359. На нем
изображена линия с распределенными параметрами, на конце ко-
торой включена некоторая нагрузка. Начиная с того момента, когда
падающая волна дойдет до конца линии, по нагрузке пойдет ток iH
и на ней будет напряжение и*.
В соответствии с формулами (12.10) и (12.14) напряжение и ток
в любой точке линии можно представить в виде суммы падающих
* Для этого времени и изображены на рис. 359 эпюры волн напряжения
и тока на линии.
479
и отраженных волн. Это положение справедливо и в отношении
напряжения и тока в конце линии. Следовательно,
«я + «о = и«. (12.21)
4, + ^ = ^ (12.22)
Заменим i„ на ~, a i0 на . Получим:
zc '-с
Ч/l Н-
ип и0 ~ iHZc.
Или
2un = uH + iHZc. (12.23)
Таким образом, напряжение на конце линии икиток в нагрузке
1Н вне зависимости от характера нагрузки связаны с напряжением
падающей волны ип уравнением (12.23).
Последнему удовлетворяет схема с сосредоточенными парамет-
рами, изображенная на рис. 360. В ней к источнику э. д. с. напря-
жением 2ип подключаются последовательно соединенные Zc и на-
грузка.
Расчет переходного процесса в схеме рис. 360 — в схеме с со-
средоточенными параметрами — производится любым из методов,
рассмотренных в главе десятой.
Расчет переходного процесса в схеме рис. 360 дает возможность
найти iH = f (/) и ин = f(f). После того, как эти зависимости будут
найдены, может быть определен характер изменения во времени
напряжения и тока отраженной волны: ио = f(f) и io =f(t). Действи-
тельно, из уравнений (12.21) и (12.20') следует, что
u0(t)
= (12.2Г)
Рассмотрим несколько примеров, иллюстрирующих примене-
ние схемы замещения.
§ 352. Подключение разомкнутой на конце линии к источнику пос-
тоянного напряжения (рис. 361, а). В линии без потерь, так же как
и в колебательном контуре без потерь, возникают незатухающие ко-
лебания. Период колебаний состоит из четырех частей или стадий
одинаковой продолжительности —, где I — длина линии, v — ско-
V
рость распространения волны. Для рассмотрения этих стадий необ-
ходимо будет использовать две различные схемы замещения. Пер-
вая схема (рис. 362) соответствует разомкнутому концу линии (Z„=
= оо), когда к нему подойдет падающая от начала линии волна.
480
Вторая схема (рис. 363) соответствует подходу отраженной волны
к началу линии, где включен генератор постоянного напряжения,
внутреннее сопротивление которого полагаем равным нулю (ZH = 0)
Рассмотрим каждую из стадий процесса в отдельности.
Первая стадия. От генератора к концу линии распространяет-
ся волна напряжения ип1 = и и волна тока inl = — = i.
,, zc
Первая стадия иллюстрируется рис. 361, а.
Вторая стадия заключается в том, что от конца линии к нача-
лу ее движется отраженная волна ио1 и iol. Для определения ы01 и
служит схема рис. 362. Она составлена
в соответствии с общим методом, изло-
женным в § 351. В ней к напряжению
2ип1 = 2и подключаются волновое соп-
ротивление линии Zc и сопротивление
нагрузки ZH— оо (линия на конце ра-
зомкнута!).
Из схемы рис. 362 следует, что на-
пряжение на нагрузке равно удвоенно-
Рис. 362
ZUorZU
Рис. 363
му значению напряжения падающей волны. Действительно, при
оо
и7 = 2«я1 —— = 2 и. = 2и.
,л zH + zc л
В соответствии с формулой (12.21') отраженная волна напря-
жения
и01 = ин ип1 — 2ип1 ип1 — ип1 — и.
Отраженная волна тока [см. (12.20')]
1О1 — 1п1
Z-C
481
Таким образом, в течение второй стадии процесса от конца ли-
нии к началу продвигается отраженная волна ио1 = и, iol — — i.
Результирующее состояние на линии определяется наложением пер-
вой падающей волны (ип1, inl) и первой отраженной волны (ио1, i01).
На рис. 361, б дана эпюра распределения напряжения и тока по
линии для некоторого момента времени во второй стадии*.
Третья стадия процесса состоит в том, что волна ио1, iol, дой-
дя до начала линий, отразится от него как от короткозамкнутого
конца линии (внутреннее сопротивление генератора принято рав-
ным нулю) и вызовет распространение по линии в направлении от
генератора к концу линии второй падающей волны (ип2, in2), яв-
ляющейся по существу отраженной волной по отношению к вол-
не ио1, i01.
Для определения характера отражения волн от начала линии
используем схему рис. 363. В ней ZK = 0, напряжение 2ио1 = 2и.
Так как Z„ = 0, то и напряжение на нагрузке Z„ равно нулю. Но
напряжение на нагрузке в соответствии с (12.2 Г) равно сумме па-
дающей волны (в данном случае и01 = ц) и напряжения отражен-
ной от начала линии волны, распространяющейся от генератора к
концу линии и потому названной выше второй падающей волной.
Следовательно,
о = и + «л2-
Отсюда
«П2 = —«. t„2=v = — t’-
Результирующее состояние на линии в третью стадию процесса
изображается рис. 361, в. Оно получено в результате наложения
трех волн: первой падающей волны ип1, inl, первой отраженной от
конца волны и01, iol и второй падающей волны игЛ, 1гЛ.
Четвертая стадия процесса заключается в том, что на три преды-
дущие волны накладывается четвертая волна, представляющая со-
бой отражение от разомкнутого конца линии второй падающей вол-
ны.
Отражение второй падающей волны от конца линии произойдет
в соответствии со схемой замещения рис. 362, с тем только отличи-
ем, что вместо 2ипХ = 2и в схеме будет напряжение
2цп2 = — 2ц.
Вторая отраженная волна будет иметь цо2 = — и, io2 = i. Ре-
зультирующее состояние на линии в четвертой стадии (см. рис. 361, г)
есть результат наложения четырех волн:
* В этой стадии для участков линии, на которые прошли отраженные
волны, результирующее напряжение равно 2и, а результирующий ток равен
нулю.
482
uni+uoi4-uni+uo2 = и+и—и—и~ 0;
1Л1 + »о1 + z«2 + 'о2 = i — i — i + i — о.
Таким образом, к концу' четвертой стадии напряжение вдоль
всей линии и ток вдоль всей линии равны нулю — линия приобре-
тает такое же состояние, какое на ней было к началу первой стадии.
Затем процесс повторяется до бесконечности, так как Ro и Go были
приняты равными нулю. В действительности благодаря наличию
сопротивления Rb и утечки Go колебательный процесс постепенно
затухает и вдоль линии устанавливается режим, соответствующий
установившемуся процессу в линии при постоянном напряжении.
В рассмотренном выше примере линия на конце была разомк-
нута, поэтому отраженные волны имели такую же прямоугольную
форму, как и падающие.
Отраженные волны будут иметь форму, в общем случае не похо-
жую на форму падЯющей волны, если в состав нагрузки на конце
линии входят емкости и (или) индуктивности, а также в том случае,
Рис. 364
Рис. 365
если в месте перехода с одной линии на другую есть сосредоточен-
ные индуктивности и (или) емкости.
§ 353. Переходный процесс при подключении источника постоян-
ного напряжения к двум последовательно соединенным линиям при
наличии емкости в месте стыка линий. Пусть первая линия имеет
длину и волновое сопротивление ZC1, вторая линия — длину /2
и ZC2 =# ZC1. Напряжение источника э.д.с. равно и (рис. 364). В
месте стыка линий есть сосредоточенная емкость С.
Требуется определить форму волны, проникающей во вторую
линию, характер изменения тока через сосредоточенную емкость,
а также результирующее распределение напряжения и тока вдоль
первой линии при движении по ней отраженной от стыка линий вол-
ны.
Переходный процесс начинается тем, что от генератора по пер-
вой линии распространяется падающая волна с прямоугольным
фронтом ип1 — и и ток tnl =---.
ZC1
Для определения характера изменения токов и напряжений, ког-
да падающая волна дойдет до стыка линий, обратимся к схеме за-
мещения с сосредоточенными параметрами (рис. 365).
В этой схеме нагрузка образована двумя параллельными вет-
вями — емкостью С и волновым сопротивлением второй линии ZC2.
483
Две параллельные ветви появились в схеме замещения потому
что в исходной схеме рис. 364 падающая волна, дойдя до места сты-
ка линий, встречает два пути для своего дальнейшего распростра-
нения: первый путь — через емкость С, второй путь — по второй
линии с волновым сопротивлением ZC2.
Переходный процесс в схеме, аналогичной схеме рис. 365, был
рассмотрен в примере 128. Из него следует (при замене Е на
2и, 7?! на ZC1 и /?2 на ZC2), что
г2--Ц^(1-^); (12-24)
ZC1 "Г ZC2
i8 = — ePf- (12.25)
?С1
; =-----2tz / j I ^C2_ . ,12 26)
Z-Cl + ^C2 \ •Zci /
UC = - ePt^ (12-27>
ZCl + ZC2
p = —Zci + Zc2. (12.28)
ZC1 Zc-2C
Характер изменения i2, i3, и uc в функции от времени изоб-
ражен на рис. 366. В первый момент после подхода волны к месту
стыка линий напряжение падает до нуля, так как незаряженная
емкость в первый момент представляет собой как бы короткое за-
мыкание.
Начальное значение тока через емкость равно Затем емкость
заряжается, напряжение на ней растет, а ток через нее уменьшается.
Ток /2 в схеме замещения представляет собой ток электромагнитной
волны, распространяющейся по второй линии; напряжение волны,
распространяющейся по второй линии, равно f^Z^.
Для получения отраженной волны напряжения, распространяю-
щейся по первой линии по направлению от стыка линий к генерато-
ру, надо из ординат кривой рис. 366, г вычесть напряжение падаю-
щей волны и и затем перенести полученную кривую на линию, зная
скорость отраженной волны.
На рис. 367, аи б изображены соответственно отраженная вол-
на напряжения и отраженная волна тока.
Эпюра распределения напряжения и тока вдоль первой и второй
линий для момента времени, когда отраженная от стыка волна до-
шла до середины первой линии, представлена соответственно на рис.
368, а и б.
Перепад тока ef в кривой рис. 368, б равен току через емкость
для данного момента времени. По второй линии волна продвину-
лась на расстояние, вдвое большее, чем прошла отраженная волна
по первой линии. Это объясняется тем, что первая линия кабельная*
484
а вторая — воздушная. Скорость продвижения волны по воздуш-
ной линии 300 000 км/сек, а по кабельной — около 150 000 км/сек*.
Пример 166. В схеме рис. 364 ZCl = 50 ом, ZC2 = 400 ом;
12— 100 км; С ==5,62 мкф; 1Х — 60 км; и = 10 кв. Первая линия — ка-
бельная, вторая—воздушная. Построить эпюру распределения если
напряжения и тока вдоль линий для момента времени, когда распрост-
раняющаяся по второй линии волна дойдет до конца второй линии.
Решение. По формуле (12.28)
50 400 /лпп / — 1 \
—!------— —4000 (сек ').
Ток падающей волны по первой линии
и
1п ~
ZC1
р = —
50 • 400 . 5,62-IO-6
— = 200
50
(«)•
о)
Рис. 367.
Рис. 366
138,7
32,7
5) 400
Падсющш ।
по первой
пинии
Ьопна
Сумма 9Падающая
пада-
ют, и
атра*
бопн
по бторой
линии
Ьопна
Рис. 368
По формуле (12.24)
»2 = 44,5 (1 — е"403»') а.
График i2 = f (t) изображен на рис. 366, а.
По формуле (12.25)
«з = 400 е-4(10Э/ а.
График i3 = f (/) представлен на рис. 366, б.
* Формула для скорости v движения волны по линии приведена на стр.
474, а входящие в нее Lo и Со определены на стр. 447—448.
485
По формуле (12.26)
г\ = 44,5(1 4-8е-дао<) а.
График тока изображен на рис. 366, в.
По формуле (12.27)
«с = «zc2 = 17 750 (1 в.
Кривая ис изображена на рис. 366, г.
По условию падающая по второй (воздушной) линии волна
должна дойти до конца второй линии. Расстояние Z2, равное 100 клг,
, /2 100 1 .
она пройдет за время Z = — =--------=------(сек).
r v 300 000 3000
За это время отраженная от стыка волна пройдет по первой (ка-
бельной) линии расстояние в 2 раза меньшее.
Графики распределения и и i вдоль линии изображены на рис.
368.
Перепад ef на рис. 368, б равен току Z3 при t — сек;
Z3 = 400 е 3 = 106 а.
Отрезок fg равен току Z2 при t = сек;
i2 = 44,5 (1 — е"”3) = 32,7 а.
Отрезок тп на рис. 368, а равен напряжению ис при
ис = 13 050 в.
Пример 167. Воздушная линия длиной 100 км с волновым соп-
ротивлением 500 ом имеет на конце нагрузку, состоящую из парал-
лельно соединенных активного сопротивления RH — R = 700 ом
и индуктивности L = 0,1 гн (рис. 369). Линия включается к нап-
ряжению и = 30 кв. Построить эпюры распределения напряжения
и тока вдоль линии для момента времени, когда отраженная от кон-
ца линии волна дойдет до середины линии.
Решение. Сначала определим ток падающей волны:
. и 30 • 103 r-п , ,
1п = — =---------= 60 (а).
п Zc 500
Затем составим схему замещения (рис. 370). Из нее следует, что
Zc-|-—
R + Pi-
486
Отсюда
700 - 500 omn / -n
— ----------- — 2910 (сек *);
1200 - 0,1
ept^ = 120(1 —0,583е'29Ш) zz;
ia = 7- (1 — ept) = 120 (1 — e-291»9 a;
p =_______
(R + ZC)L
R + zc
2u ..
Zc
UL = инагр = L~T = 2u~-~ ePt = 35 • 103е-28Ш в.
dt R -|- Zc
Рис. 369
Рис. 370
Кривые инагр = f(f) и tj = f(t) изображены на рис. 371.
Эпюры распределения напряжения и тока для заданного момен-
та времени изображены на рис. 372, а и б.
В рассмотренных выше примерах электрическая цепь, содержа-
Рис. 372
щая линию с распределенными параметрами, подключалась к ис-
точнику постоянного напряжения.
Между тем часто встречаются цепи, в которых э.д.с. источника
изменяется по синусоидальному закону во времени. Если длина
линии с распределенными параметрами и частота синусоидальной
, I, I \
э.д.с. таковы, что время пробега волны по линии И = — | много
\ v 1
487
меньше периода переменного тока Т, например составляет вели-
чину порядка (—4- — ^ Т, то при исследовании первых стадий
\30 50 J
переходного процесса в первом грубом приближении можно при-
нять, что линия подключается к источнику постоянного напряже-
ния, э.д.с. которого равна амплитуде синусоидальной э.д.с. (рас-
чет на наиболее тяжелый случай).
Если же время пробега волны по линии составляет большую, чем
часть периода, то при расчетах необходимо учитывать
изменение э.д.с. источника при перемещении падающей волны по
линии.
ПРИЛОЖЕНИЯ КО II ЧАСТИ КУРСА ТОЭ
Приложение А
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
С ПЕРЕМЕННЫМИ ВО ВРЕМЕНИ ПАРАМЕТРАМИ
§ 354. Введение. Электрические цепи с переменными во времени парамет-
рами представляют собой такие электрические цепи, в состав которых входят
активные сопротивления, индуктивности, емкости и взаимные индуктивности,
изменяющиеся во времени (достаточно, чтобы в состав цепи входило хотя бы
одно изменяющееся во времени сопротивление, и она будет принадлежать к
рассматриваемому классу цепей).
Угольный микрофон — простейшее изменяющееся активное сопротив-
ление (рис. 373, а). Сопротивление его является функцией звукового давле-
ния, оказываемого мембраной на порошок графита. Индуктивная катушка с
Рис. 373
незамкнутым ферромагнитным сердечником, который выдвигается из катуш-
ки и вдвигается в нее (рис. 373, б),— пример переменной во времени индук-
тивности.
Конденсатор, пластины которого раздвигаются и сдвигаются, не сопри-
касаясь (рис. 373, в),— пример емкости, изменяющейся во времени.
Две индуктивные катушки и £2 (рис. 373, г), взаимное расположение
которых меняется во времени (например, если одна из них вращается вокруг
оси, перпендикулярной рисунку), — пример взаимоиндукции, меняющейся
во времени.
Изменение параметров цепи во времени обычно происходит под действием
внешней механической силы. Чем вызывается эта сила — этот вопрос мы де-
489
тализировать не будем. Параметр цепи может изменяться во времени перио-
дически и непериодически. Рис. 374 иллюстрирует несколько различных
периодических законов изменения параметра.
§ 355. Некоторые общие свойства электрических цепей с переменными па-
раметрами. Несмотря на то, что цепи с переменными во времени параметрами
являются линейными цепями (т. е. описываются линейными дифференциаль-
ными уравнениями), они обладают свойствами, сближающими их с нелиней-
ными цепями.
Переменные во времени сопротивления подобно нелинейным сопротив-
лениям являются генераторами высших гармоник тока. В силу этого в це-
пях с переменными параметрами протекают токи не только тех частот, ко-
торые имеют источник э. д. с. и переменная составляющая сопротивления,
но и токи множества других частот.
Благодаря этому в цепях с переменными параметрами при наличии в сос-
таве их индуктивностей и емкостей могут возникать резонансные явления на
высших и низших гармониках при отсут-
ствии гармоник данной кратности у ис-
LTO4HHKa э. д. с.
Обратим внимание на то, что ам-
t плитуды отдельных гармоник тока в це-
пях с переменными параметрами линейно зависят от значений амплитуд ос-
тальных гармоник (в нелинейных цепях аналогичная зависимость нелиней-
на).
Наряду с этим цепи с переменными во времени параметрами обладают
линейным свойством, принципиально отличающим их от нелинейных цепей.
Дело в том, что в цепях с переменными во времени параметрами амплиту-
ды гармоник тока и напряжения пропорциональны амплитуде э. д. с. источ-
ника. Другими словами, если э. д. с. источника увеличить вдвое, то и амплиту-
ды токов и напряжений увеличатся вдвое. В цепях с нелинейными сопротив-
лениями, где имеет место насыщение, такой пропорциональности, как извест-
но, нет.
Выше говорилось, что переменное сопротивление является генератором
высших гармоник тока. Убедимся в этом иа простейшем примере. На рис.
375 изображена схема, состоящая из источника постоянной э. д. с. Е и актив-
ного сопротивления, изменяющегося во времени в соответствии с кривой рис.
374, б:
= — Л sin со/). (АЛ)
k<l
л Е Е 1
По закону Ома ток в цепи равен i = —— = —---------------. Известно,
“(О “о 1—fesincoZ
1
что функция ——— при |х| < 1 может быть разложена в степенной ряд:
1-^=1 + х + х2 + *3+ ... +*”. (А.2)
490
Роль, которую играет х в формуле (А.2), в формуле (А.1) выполняет ftsinw/.
Поэтому при k < 1
I
= 1 + k sin со/ + й2 sin2 at + й3 sin3 at -f- .. • (A.3)
~Ro
Воспользуемся известными из тригонометрии формулами:
1—cos 2а 1 1
sin2 а =-------------; sin3 а =i — — sm За 4- — sin а;
2 4 г 4
3 1 1
sin* а = — — — cos 2а +~ cos 4а
и объединим слагаемые правой части ряда (А.З) с аргументами одинаковой
кратности. Получим:
i I й2 Зй« \ / й3 \
"Т_=,(1 + Т + “я''1--- +*+ • ••jsinco/ —
с \ Z о /\4 /
«о
/ й2 й1 \ / й3 \
— I —- — + — + . •. I cos 2at— I — + ... 1 sin Зсо/ + •..
Таким образом, несмотря на то, что в цепи рис. 375 включена постоянная
э. д. с., а переменная составляющая сопротивления изменяется по закону
синуса с частотой со, ток имеет и высшие гармоники (частоты 2а, Зсо). Постоян-
ная составляющая и амплитуды гармоник тока нелинейно зависят от коэффи-
циента й, но линейно зависят от э. д. с. Е.
Обратим внимание также на то, что при й О постоянная составляющая
р
тока в цепи рис. 375 не равна — Другими словами, в схеме наблюдается сво-
Ro
еобразный выпрямительный эффект.
Если в схеме рис. 375 сопротивление /?(/) изменять по более сложному за-
кону во времени, например по закону
/?011 — йх sin со/ — й2 sin (2со/+ <?)]; < 0,5; й2 < 0,5,
то, проделав аналогичные выкладки, можно было бы убедиться в том, что
постоянная составляющая, а также амплитуды всех гармоник тока зависели
бы от й1( k2 и ср.
Энергия, выделяющаяся в виде теплоты в цепи с переменными во вре-
мени параметрами, доставляется не только источниками э. д. с. (или тока),
имеющимися в цепи, но и теми внешними источниками (например, механичес-
кими двигателями), которые совершают работу при изменении параметра
(или параметров) цепи.
Какую долю энергии доставляет источник э. д. с., какую дает внешний
источник, совершающий работу при изменении параметра, — эти вопросы
для каждой цепи с переменными параметрами следует рассматривать приме-
нительно к конкретным условиям, и более подробно мы их касаться здесь не
будем. Отметим только, что доля энергии, доставляемая внешним источником,
может составлять в пределе нуль и в другом крайнем случае 100%.
Отметим, что незатухающие электрические колебания, возникающие
в электрических цепях вследствие периодического изменения во времени ин-
дуктивности или емкости цепн прн отсутствии источников электрической энер-
гии, называют параметрическими (гетеропараметрическими). Они поддер-
живаются за счет работы механической силы при изменении параметра (ин-
491
дуктивности или емкости) цепи. Частота этих колебаний в 2 раза меньше час-
тоты изменений параметра.
§ 356. Методика расчета электрических цепей с переменными параметрами
в установившемся режиме. Если переменный параметр изменяется во времени
периодически, претерпевая резкие скачкообразные изменения (см. рис. 374, а),
то расчет цепей целесообразно проводить при помощи классического метода
расчета переходных процессов. В этом случае постоянные интегрирования оп-
ределяют, исходя из законов коммутации и периодичности процесса. Метод
иллюстрируется ниже на примере 168.
Если же переменный параметр изменяется так, что его можно предста-
вить в виде постоянной составляющей и одной или нескольких синусоидаль-
ных составляющих, то расчет производят путем применения метода гармони-
ческого баланса.
Метод гармонического баланса применительно к нелинейным цепям был
рассмотрен в § 231. Основные черты его остаются и здесь теми же. Последо-
вательность расчета следующая: искомый ток (или какая-либо другая вели-
чина) изображается в виде ряда Фурье, например в виде:
/о + in sin at + /12 cos at /21 sin 2co< -|- /22 cos 2at + ...
Затем этот ток подставляют в дифференциальное уравнение цепи и вы-
деляют из него уравнение, выражающее собой равенство постоянных состав-
ляющих левой и правой части его, уравнение, выражающее собой равенство
синусных составляющих левой и правой частей, и т. д. Каждое нз этих урав-
нений будет в общем случае содержать несколько неизвестных (70, 7Ц, 112,
1ц, /гг)> но будет являться линейным уравнением относительно /0, /ц, /i2,
/22 (в этом отличие от нелинейных цепей). Далее решается система линей-
ных уравнений относительно /0, /и, /12, /21, /22. Метод гармонического ба-
ланса может применяться к расчету цепей, содержащих несколько перемен-
ных во времени параметров (например, изменяющееся во времени активное
сопротивление и изменяющуюся во времени индуктивность), а э. д. с. может
изменяться по любому периодическому закону. Метод иллюстрируется ниже
на простейшем примере 169.
Пример 168. В схеме рис. 376, а э. д. с. Е и индуктивность L постоянны,
а сопротивление 7? меняется в соответствии с рис. 376, 6. Определить закон
изменения тока в цепи в установившемся режиме.
Решение. Так как сопротивление изменяется периодически, то и ток
будет изменяться периодически. Обозначим значение тока в момент t = 0 че-
рез /2. В этот момент сопротивление цепи скачком возрастает со значения /?2
до /?!, и ток в цепи начинает уменьшаться. В момент t = т ток принимает
значение Ilt и в этот момент сопротивление скачком уменьшается со значения
7?! до значения /?2. Последнее приводит к тому, что ток начинает увеличивать-
ся.
492
В интервале времени от t = 0 до t = т ток можно представить в виде
£ j
суммы принужденного тока — и свободного тока Cie₽1 . Причем pi есть
Ri
корень характеристического уравнения цепи pL Ri = 0', Pi = — С»—п°*
стояиная интегрирования.
Во втором интервале времени i = — + С2е₽а^—тр2 = —Задача сво-
R2
дится к определению двух постоянных: Ci и С2.
При t = 0 i = /2; следовательно,
4 = +
При t — т i = /1, поэтому
4 = 4 + с‘с₽,т- (а-5>
Ki
Начальное значение тока для второго интер-
вала времени (/t) можно найти и иначе, а именно:
/1 => •—- + С2. (А.6)
А2
К концу второго интервала времени, когда t = 2т, i = /2, поэтому
12^4-+С^' (А’7)
R-2
Приравнивая правые части уравнений (А.4) и (А.7), получаем:
А+С1==А + С^.
I\l М2
Аналогично, из уравнений (А.5) и (А.6) следует, что
F F
-+с2 = - + с1е^.
М2 Ml
Совместное решение двух последних уравнений дает:
C2^-a + Ciep‘\ (А.9)
Е Е
Здесь а = — - —.
На первом интервале времени i = — Cieplt, на втором i — х)-
£1 ^2
Кривую i = f (t) см. на рис. 376, с.
Пример 169. В схеме рис. 377 э.д.с. е =з Е Ц- Em sin (со/ + 4); L = Ao (1 +•
+ k sin со/); активное сопротивление R не является функцией времени. Опре-
делить постоянную составляющую, а также первую и вторую гармоники
тока (k < 1).
493
Решение. В дифференциальное уравнение
d
Ri + ~ (Li) — Е ф- Ет sin (at ф- ф) (А. 10)
подставляем ток
* = /» + /и sin со/ ф- /к cos at ф- l21 sin 2со/ ф- /22 cos 2<о/. (А.11)
Выделив постоянную составляющую, получим уравнение (А.12):
RI0 = E. (А. 12)
Равенство коэффициентов при sin со/ в обеих частях уравнения (А. 10)
после подстановки в него (А. 11) и деления на R дает:
, . La , Ет
/и — с/is — ~ hi = D cos ф. (А.13)
z К
Равенство коэффициентов при cos о/ (и деления на R) дает
я/ц ф- /12 — /22 = — akh ф- — sin ф. (А.14)
z
Равенство коэффициентов при sin 2со/:
akin ф- /21 — 2п/22 = 0. (А.15)
Равенство коэффициентов при cos 2со/:
ай/12 ф- 2а/21 ф- /22 = 0, (А. 16)
<oLn
<АЛ7)
г\
Из уравнения (А.12) следует, что в схеме рис. 377 постоянная составля-
ющая тока 10 не зависит от переменной составляющей индуктивности и от пе-
ременной составляющей э.д.с. Однако постоянная составляющая потокосцеп-
й/.0/ц
ления, равная £0/0 ф- -—-—, зависит от амплитуды переменной составляющей
индуктивности (kL0) и от амплитуды первой гармоники переменного тока.
Это свойство в известном смысле напоминает первое из свойств нелиней-
ных симметричных сопротивлений, описанное в § 200.
Уравнения (А.13) —• (А.16) представляют собой систему четырех линей-
ных уравнений относительно четырех неизвестных токов /ц, Il2, /21, /22.
На решении четырех уравнений (два из них с правой частью, равной нулю)
останавливаться не будем. Дадим окончательный результат:
2akEm cos ф 4а j 4Ет sin ф 4Ет cos ф
/?(1 ф-4а2 —а2й2) ~ й /о + .Зй/? + ZakR
Zak ай2 1
•------------4- а — — 4- —
1 ф- 4а2—a2k 4 а
2akEm
—-— cos ф — Zakin
____R
1 ф- 4а2 — а2А2
(А.18)
Далее находятся /г2 из (А.15) и /12 из (А. 13). Из формул (А.18) следу-
ет, что амплитуда первой гармоники тока зависит не только от Ет, а и А, но
и от постоянной составляющей тока в цепи. Другими словами, изменяя ве-
личину постоянной э. д. с. Е в схеме рис. 377, можно управлять величиной
переменного тока.
494
Приложение Б
ИНТЕГРАЛ ФУРЬЕ
§ 357. Введение. В радиотехнике, технике связи, акустике, оптике, гид-
родинамике и других отраслях техники для выявления частотных и энерге-
тических свойств непериодических импульсов и результатов нх воздействия
на избирательные (резонансные) системы применяется интеграл Фурье. В тео-
рии автоматического регулирования интеграл Фурье используется в качестве
основы для вывода приближенных формул, позволяющих определить харак-
тер изменения искомой величины по снятой опытным путем частотной харак-
теристике входного сопротивления цепи (см., например, Л. 11). Все перечис-
ленные выше вопросы выходят за рамки курса ТОЭ, тем не менее иметь пред-
ставление об интеграле Фурье и связанных с ним вопросах (о спектре функции,
о связи спектра функции с изображением по Лапласу) полезно, так как это
подготавливает к чтению специальной литературы по упомянутым отраслям
техники.
§ 358. Ряд Фурье в комплексной форме записи. Как известно из предыду-
щего (см. § 168), в ряд Фурье может быть разложена любая периодическая
функция f(t), удовлетворяющая условиям Дирихле.
2зт
Обозначим период функции через Т и основную частоту через со0 = —
Ряд Фурье может быть записан двояко.
Первая форма записи:
f(/) = А; ЛА sin (kaot ф/г). (Б.la)
k~i
Вторая форма записи:
оо
f(f) — Ло + V (Л^ sin kaot + A"k cos kaat), (Б. If)
k^i
где Ло — постоянная составляющая ряда, Лд. — амплитуда k гармоники ряда,
фй — начальная фаза k гармоники;
Afk = Ak cos A"k = Ak sin ifo,
т
о
Ло = у I’ (Б.2)
Lz
2
JT
2
2 f
A’k \ fit) sink dt, (Б.З)
__
2
L
2
Ank — — f(t) cos ku>Qt dt, (Б.4)
V
495
Из курса математики известно, что
_ g-А
sin х =--------
2/
Следовательно,
sin (k<s>ut + фА) = -4[e/(W+<pft ) _ e-i(^ot+<pk) ],
(Б.5)
Подставим правую часть формулы (Б.5) в формулу (Б.1а). Получим:
/(/) = А, + X Л [ey(W+'4'fe) — +**> ].
*=1
Условимся, что
4 = Ake^k ;
A_k = - Ake->^ .
Тогда ряд (Б.5а) можно записать так;
Л = со
/(7) = До + -^7 J Akeik^.
2/ "
* = -оз
(Б.Са)
(Б.6)
(Б.7)
(Б.8)
Формула (Б.8) представляет собой комплексную форму записи ряда
Фурье. Текущий индекс k может принимать все целочисленные значения от
— со до + оо, но не может равняться нулю, так как постоянная составляю-
щая ряда выделена в виде отдельного слагаемого.
Пример 170. Представить функцию f (/)=>2 + 3 sin (ы0/ + 30°)+2 sin (2а>0/—
— 45е) в комплексной форме записи.
Решение. Ло = 2; 4 = Зе730°'» А_г= — Зе-уз0°; Л2 = 2е-у46°; Л_2 =
= f (I) = 2 + — [зеК<во/+30°> зе-/(и./+30°)^2е)(2<М—45°)
2/
__2g—/(2ш0<—45е)
Составим выражение для комплексной амплитуды Л*. По определению
|см. формулу (Б.6)]
4 = Ле/4'* = Лйсо5фЛ+/ЛА81пфА = Л^ +/Х (Б.9)
Величина /Ik определяется формулой (Б.З) и Ak — формулой (Б.4).
Подставим правые части формул (Б.З) и (Б.4) в формулу (Б.9):
Г
2
А =* 'y J (sin k cos
Т
2
Т
2
2/ Г ,
— ДО (cos ka>ot— I sin ta>oO dt.
_z
2
Или
т
2
• 2/ Г
Zft== T) f^e~ “ dt‘ (БЛ0)
Y
2
Подставим правую часть формулы (Б. 10) в формулу (Б.8). Будем иметь:
т
k = ~\~ оо 2
/(П = А> + ~ dt. (Б.11)
k —— ОО '/
2
§ 359. Спектр функции и интеграл Фурье. Ряд Фурье — это тригомет-
рический ряд, представляющий собой изображение периодической функции
суммой синусоид, амплитуды которых конечны, а аргументы кратны основ-
ной частоте <Во
Под интегралом Фурье понимают тригометрический ряд, представляющий
непериодическую функцию суммой бесконечно большого числа синусоид,
амплитуды которых бесконечно малы, а аргументы соседних синусоид отли-
чаются на бесконечно малую величину.
Формула для интеграла Фурье получается из формулы для ряда Фурье
[из форму/ы (Б.11)] предельным переходом при устремлении периода Т к бес-
конечности.
На функцию f (/) при представлении ее интегралом Фурье накладывают
+ ~
ограничение, а именно: полагают, что J f (f) dt есть величина конечная (не
— ОО
бесконечно большая). Это — серьезное ограничение. Ряд функций этому ус-
ловию не удовлетворяет*.
Так как по определению [см. формулу (Б.2)]
г
2
/l0 = y-J /(О Л.
_т
2
+ “
а при Т -> оо f f(t)df есть величина конечная, то Ло= 0. Преобразу-
* Наиболее важным для практики представителем функций f ((), для ко-
00
торых интеграл J / (0 dt расходится, является функция f (/) = Л, где А —
постоянное число. Для того чтобы столь важную для практики функцию, как
все же представить интегралом Фурье, пользуются следующим
приемом. Находят интеграл Фурье для функции / (/) = Ае~где р > 0 и
+ ~
/(() = 0 при t < 0. Для этой функции J f(t)dt сходится, поэтому она мо-
жет быть представлена интегралом Фурье. Далее в полученном выражении
устремляют р к нулю.
17 Л. А. Бессонов 497
г
2
ем величину J
т
е jkwj стоящую под знаком суммы в
формуле
co будем
разность
(Б. 11). С этой целью произведение kaa заменим на со, и под
понимать изменяющуюся (текущую) частоту. В ряде Фурье
. 2л 1 Дсо
двух смежных частот Дсо = соо = — . Следовательно, — —-----.
Т Т 2л
При Т оо Дсо заменим дифференциалом dco. В результате получим:
т
2 +«.
\ f(t)e-iwi dt.
2л J
Обозначим
г
2
J f(t)e~iai dt.
G(co)
(Б. 12)
Формула (Б. 12) дает возможность преобразовать функцию времени f (t)
в функцию частоты G (со); G (со) называют спектром функции / (/). Это ком-
плексная величина, зависящая от вида функции f (t). В соответствии с фор-
мулой (Б.12) в формуле (Б.11) заменим f/(Oe—dt на — G (со) das и
Т j 2л
учтем, что при изменении k от — оо до + оо со=> Асоо также изменяется от
— °° до + оо. Следовательно,
= оо
/ (О = ~ У с (“)
2л “
О) = — оо
Заменим сумму интегралом. Получаем:
+ °°
HO = V f G^e^da.
2л J
(Б. 13)
Формула (Б. 13) представляет собой запись интеграла Фурье. Она вы-
ражает непериодическую функцию f (t) в виде бесконечно большого числа си-
нусоидальных колебаний с бесконечно близкими частотами н бесконечно ма-
лыми амплитудами G (a) da [ G (ы) конечно, но произведение G(co) da беско-
нечно мало, так как бесконечно мала величина dco|.
Преобразования (Б.12) и (Б.13) являются взаимно обратными преобра-
зованиями.
Отметим, что представление функции f(t) в комплексной форме в виде
интеграла Фурье привело к необходимости формально ввести отрицательную
угловую частоту.
§ 360. Связь спектра функции с изображением по Лапласу. Сопоставим
формулу (Б.12) с формулой (Б. 14) преобразования-по Лапласу:
1Цр)=>] f (t) e~~pt dt (Б.14)
о
при условии, ЧТО /(/) = 0 при t < 0.
498
Если учесть, что /(/) = О при t < 0, и заменить р на ]а>, то формула (Б. 14)
переходит в формулу (Б. 12). Следовательно, формулы для спектра функции
С(со) могут быть получены из соответствующих формул для изображений по
Лапласу, если в последних р заменить на /со.
Пример 171. Пользуясь таблицей (см. стр. 398), найти спектр G (<о) функ-
ции /(/) = ё~at, полагая, что f (/) = 0 при t < 0.
Решение. Б таблице (см. стр. 398) дано изображение функций по Кар-
сону (не по Лапласу). Для получения изображения функции /(/) по Лапласу
следует поделить изображение этой функции по Карсону на р. Изображение
____________ л р 1
функции е по Карсону таково: -—- . Изображение по Лапласу: .
аф-р аф-р
Заменим р на /сои получим спектр G (со) = -; G(co) есть комплексная величи-
а+/со
на, равная Ge Модуль ее G равен —-===.; аргумент <рг = агс tg — .
j/ а2 + со2 и а
§ 361. Последовательность определения тока в цепи при помощи интегра-
ла Фурье. Расчет при помощи интеграла Фурье физически означает, что для
нахождения реакции системы на любое воздействие следует это воздействие
представить в виде бесконечно большого числа гармонических воздействий,
символическим методом найти реакцию системы на каждое из воздействий и
затем просуммировать реакции от всех воздействий.
Пусть на цепь с нулевыми начальными условиями, параметры которой
известны, воздействует э. д. с. e(t). Требуется найти ток i(t) при помощи ин-
теграла Фурье. Задача решается в четыре этапа. Первый этап — при помоши
таблиц изображения по Лапласу находим спектр Е(ю) заданной э. д. с. е(/).
Второй этап — определяем входное сопротивление Z(co) как функцию час-
тоты. По сути дела Z(co) представляет собой входное сопротивление цепи для
переменного тока. Третий этап — на основании закона Ома находим спектр
гока:
Л«) == Г = £(ы) У (и).
Z((0)
Четвертый этап — по спектру тока 7(<о) находим ток как функцию време-
ни. Переход от /(<о) к i(t) принципиально может быть осуществлен при по-
мощи формулы (Б.13). Однако практически определение 1(f) по /(со) произво-
дится часто при помощи той же таблицы соответствия между изображением по
Лапласу и функцией времени, которая использовалась в первом этапе рас-
чета при нахождении спектра э. д. с. Е(со).
Все изложенные выше этапы расчета по сути дела полностью повторяют
все этапы расчета, которые приходится проделывать при пользовании опе-
раторным методом.
В заключение необходимо отметить, что расчет при помощи интеграла
Фурье зачастую значительно упрощается для резонансных систем с малыми по-
терями (с большой добротностью).
В этом случае можно учитывать не всю характеристику ¥(со), а только
основную ее часть вблизи резонансной частоты сов. В пределах учитываемой
части характеристики У(<о) можно считать, что £(<») равна ее значению при
резонансной частоте Е(Юр).
Благодаря этому при воздействии на резонансный контур некоторым им-
пульсом контур будет выбирать частоты, соответствующие собственной ре-
зонансной частоте, и колебания в контуре будут иметь форму свободных ко-
лебаний.
17*
499
Приложение В
ПЕРЕХОДНЫЕ ПРОЦЕССЫ
В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
§ 362. Введение и общая характеристика методов анализа и расчета пе-
реходных процессов в нелинейных электрических цепях. При изучении главы
девятой можно было убедиться в том, что сама природа явлений в нелиней-
ных цепях гораздо сложнее и многообразнее, чем в линейных. Поэтому впол-
не естественно, что анализ и расчет переходных процессов в нелинейных элект-
рических цепях оказываются зачастую делом в значительной степени более
сложным, чем в линейных.
Известно несколько различных приемов и методов расчета переходных
процессов в нелинейных цепях. В дайной главе будут обсуждаться только
те их них, которые представляют наибольший интерес.
Рассматриваемые ниже методы анализа и расчета переходных процессов
в нелинейных цепях могут быть классифицированы следующим образом:
1) по виду основных операций, которые необходимо выполнять для интег-
рирования нелинейных дифференциальных уравнений, — на графические
(графоаналитические) и аналитические;
2) по характеру величины, для которой производится расчет, — на рас-
чет для мгновенных значений токов и напряжений и на расчет для мгновен-
ных значений огибающих токов и напряжений.
Условимся под графическими (графоаналитическими) методами расчета
понимать такие методы, в которых основными операциями при определении
зависимости от времени искомых токов и напряжений являются графические
построения, зачастую сопровождаемые и некоторыми вспомогательными чис-
ленными подсчетами.
Важно подчеркнуть, что в графических (графоаналитических) методах
расчета характеристики нелинейных сопротивлений обычно не требуется вы-
ражать аналитически.
В данной главе рассмотрены следующие графические методы:
1. Метод, основанный на графическом подсчете определенного интеграла
(§ 363).
2. Метод Волынкина (§ 366).
Аналитическими методами будем называть такие методы расчета, в ко-
торых основной операцией при определении зависимостей искомых токов и
напряжений от времени является точное или приближенное аналитическое
интегрирование дифференциальных уравнений цепи, в которые подставляют-
ся аналитические выражения характеристик нелинейных сопротивлений.
Ниже рассматриваются следующие аналитические методы:
1. Метод интегрируемой нелинейной аппроксимации (§ 364).
2. Метод кусочно-линейной аппроксимации (§ 365).
3. Метод медленно меняющихся амплитуд (§ 368).
Графические методы имеют следующие преимущества перед аналитичес-
кими:
1. В них не требуется, как правило, выражать характеристики нелиней-
ных сопротивлений аналитически, и поэтому они свободны от погрешностей,
связанных с аналитическим представлением характеристик нелинейных соп-
ротивлений.
2. Они довольно просто позволяют учесть гистерезис и другие сложные
нелинейные зависимости.
В свою очередь аналитические методы имеют перед графическими свои
преимущества. Из них основным является то, что они дают возможность по-
лучить решение в общем виде, а ие для какого-то одного конкретного сочета-
ния параметров. Получить решение в общем виде часто очень желательно,
500
так как анализ его позволяет выяснить все особенности процесса при изме-
нении всех параметров.
Как уже упоминалось выше, все методы расчета могут быть подразделе-
ны также на две подгруппы: на расчет по мгновенным значениям токов и нап-
ряжений и на расчет по мгновенным значениям огибающих токов и напряже-
ний.
Расчет по огибающим очень важен, так как он дает возможность, не вда-
ваясь в мелкие детали процесса внутри каждого периода действующей в схе-
ме периодической э. д. с. или внутри каждого периода автоколебаний в авто-
колебательной системе, судить о макроструктуре процесса.
Разумеется, расчет по огибающим возможен не только для нелинейных
цепей; он представляет существенный интерес и для линейных цепей.
Естественно, что точность расчета по огибающим уступает точности рас-
чета по мгновенным значениям. Однако относительная быстрота проведения
расчета по огибающим и возможность судить о макроструктуре процесса час-
то оказываются решающими факторами.
Рис. 378
Вообще же наиболее целесообразно там, где это необходимо, дополнять
расчет по огибающим расчетом по мгновенным значениям. Метод расчета по
огибающим представлен методом медленно меняющихся амплитуд (см. § 368).
Все же остальные методы относятся к подгруппе расчета по мгновенным зна-
чениям.
Довольно часто электрические цепи содержат несколько нелинейных
сопротивлений. Переходные процессы в таких цепях могут рассчитываться
путем применения метода Волынкина (см. § 366).
Теория переходных процессов в электрических цепях с управляемыми
нелинейными индуктивными, емкостными и активными сопротивлениями вы-
ходит за рамки курса. Интересующиеся этим вопросом могут ознакомиться
с ним, например по (Л. 18).
§ 363. Метод расчета переходных процессов в нелинейных цепях, основан-
ный на графическом подсчете определенного интеграла. Метод применим к
электрическим цепям, приводящим к дифференциальным уравнениям пер-
вого порядка, допускающим разделение переменных. Последняя оговорка
очень существенна. Она свидетельствует о том, что метод применим к цепям
постоянного тока и, как правило, не применим к цепям переменного тока.
Основные этапы и последовательность расчета проиллюстрируем на кон-
кретном примере.
Пример 172. Нелинейный конденсатор через сопротивление R подклю-
чается к источнику напряжения U (рис. 378). Кулонвольтная характеристика
конденсатора задана графически (рис. 379). Полагая, что в схеме нулевые
начальные условия, построить кривые изменения заряда q, напряжения иа
емкости ис и тока i в функции времени.
501
Решение. Составим дифференциальное уравнение
dq “с (?) + R— = и. dt
Разделим переменные dq dt-R ч (B.i) и — udq)
или dt = RF(q) dq.
Функция .. (B.3) U — «c(?)
(рис. 380) строится прн помощи кулонвольтной характеристики. С этой целью
задаемся произвольными значениями q, по кулонвольтной характеристике
находим соответствующее ему ис и по формуле (В.2) подсчитываем F(q).
При q — 0 ис = 0 и F(q) = — ; при ис = U F(q) =оо. Левую часть урав-
нения (В.1) интегрируем по t от 0 до текущего значения t. а правую— по q
от q => 0 до текущего значения q. Получаем:
t = R
F{q)dq.
(В.З)
Подынтегральное выражение F(q) dq представляет собой заштрихован-
ную площадку на рнс. 380.
Согласно уравнению (В.З) для определения времени t, соответствующего
какому-то конкретному значению q, надо подсчитать площадь, выраженную
Рис. 382
определенным
интегралом
dq,
и умножить ее на сопротивление R.
Кривая 1 рис. 381 качественно представляет собой зависимость q от t.
При помощи кривой q = f(t) и кулонвольтной характеристики нелинейной
емкости строится зависимость ис = f(t) — кривая 2 рис. 381.
Величина тока в цепи для произвольного момента времени определяется
при помощи формулы
{/ — ис
—R *
Кривая 3 рис. 381 качественно представляет собой i = f(t).
502
§ 364. Расчет переходных процессов в нелинейных цепях методом интег-
рируемой нелинейной аппроксимации. Метод основан на аппроксимации ха-
рактеристики нелинейного сопротивления такой нелинейной функцией, ко-
торая, во-первых, достаточно точно отображает характеристику нелинейного
сопротивления на предполагаемом интервале перемещения изображающей
точки по ней и, во-вторых, 1— и это главное — дает возможность точно про-
интегрировать уравнение в известных функциях.
Ценность метода заключается в том, что в результате интегрирования по-
лучается зависимость исследуемой величины от времени и от всех параметров
схемы.
Метод применим к дифференциальным уравнениям первого порядка, а
также к уравнениям, сводящимся к уравнениям первого порядка путем за-
мены переменных.
Пример 173. Определить закон нарастания во времени тока i при вклю-
чении рубильника в схеме рис. 382. Принять, что зависимость тока i от по-
токосцепления ф нелинейной индуктивности может быть выражена формулой
i = Аф4. В схеме нулевые начальные условия.
Решение. Дифференциальное уравнение цепи
перепишем следующим образом:
Вынесем из знаменателя множитель 7? и заменим i на Аф4:
dt —— ' •
7? ly — Аф4
U
Здесь 1у => ——.
А
Обозначим /у = а2 и заменим на Ф?» на —4/— '
1 у k
1
____L_ =_L(________L_ , ,,. J.....V
a2 — Ф1 2а \ а — Ф1 а + Ф? / ’
. Получим
(В.4)
503
При помощи формулы (В.4) можно определить значение времени, кото-
рое необходимо, чтобы отношение — достигло заданной величины.
'у
§ 365. Метод расчета переходных процессов в нелинейных электрических
цепях, основанный на замене характеристики нелинейного сопротивления
отрезками прямых линий (метод кусочно-лииейной аппроксимации). Замена
характеристики нелинейного сопротивления отрезками прямых линий дает
возможность перейти от нелинейного дифференциального уравнения к несколь-
ким линейным уравнениям, отличающимся друг от друга лишь значениями
коэффициентов.
Каждое из линейных уравнений справедливо для того интервала време-
ни, в течение которого рабочая точка перемещается по данному линеаризиро-
ванному участку. Метод применим к цепям, содержащим источники постоян-
ной и (или) синусоидальной э. д. с., к цепям пер-
вого и более высоких порядков.
Для сложных нелинейных цепей с источни-
ком (нсточннкамн) синусоидальной э. д. с. основ-
ная трудность расчета данным методом заключа-
ется в определении постоянных интегрирования
и времени работы на каждом линейном участке,
исходя из законов коммутации. В сложных це-
пях неизвестные определяются обычно из транс-
цендентных уравнений. Для решения трансцен-
дентных уравнений часто применяют математи-
ческие счетные машины.
Впервые идея метода была высказана рус-
ским физиком Н. Д. Папалексн в 1912 г.
Рассмотрим основные этапы расчета на прос-
тейшем примере.
Пример 174. Конденсатор заряжается через
нелинейное сопротивление от источника постоян-
ного напряжения U (рнс. 383, а). Определить
закон изменения тока в цепи при зарядке.
Решение. Вольтамперную характеристику
нелинейного сопротивления заменим двумя отрез-
ками прямых линий (рис. 383, б). Пусть на участке от i — 0 до i = й
инс = >
где и[[с — напряжение на нелинейном сопротивлении.
На участке i > ii
иНС ~
Размерность коэффициентов и k2 равна размерности сопротивления.
В уравнение цепи
ис + инс ~ U
вместо «с подставим J I dt и для первого участка заменим инс на Uo +
+ М, а для второго — на k2i.
При зарядке конденсатора ток будет постепенно уменьшаться от макси-
мального значения до нуля. Поэтому изображающая точка будет перемещать-
ся сначала по первому участку, а затем по второму. Для первого участка
Y + + W =
Для второго участка
504
idt + k2i = U.
Решение для первого участка
I
i = ^пр + ice = 0 + -
Постоянную интегрирования найдем из начального
ис = 0, поэтому
Uo + kiii (0+) = U;
условия: при t = О
Следовательно, при работе на первом участке
I_ u — Uq
ki
Пусть при / = /х ток t станет равным /±. Подставим в (В.5) it
и вместо t и решим полученное уравнение относительно tt
U — Uo
ti = kiC In ——-— .
(В.5)
вместо i
(В-6)
Дальнейшая работа происходит по второму участку; на нем
«-<)
I =□ Л2е k‘c ,
причем Л2 = <1.
Практически важной является задача о переходном процессе при подклю-
чении ненагруженного трансформатора (с разомкнутой вторичной обмоткой)
Рис. 384
или нелинейной индуктивности к источнику синусоидальной э. д. с.
Ет sin (<о/+ ф) (рис. 384, а). Рассмотрим эту задачу качественно.
Если активное сопротивление первичной обмотки трансформатора Ri мало.
Е
а амплитуда установившегося значения потокосцепления фот =----- соответ-
со
ствует окрестности точки а (рис. 384, б), то при включении рубильника в мо-
мент, когда э.д.с. Ет sin (со/ -ф ф) проходит через нулевое значение, в цепи
возникают очень большие кратковременные броски тока. Последние могут
превышать амплитуду тока холостого хода трансформатора в 20—50 и даже
более раз.
505
Физически они возникают вследствие того, что к концу первого полупе-
/2к \
риода ( — I после включения потокосцепление достигает величины, очень
\2<о /
близкой к 2фт.
Из кривой рис. 384, б, видно, что если фа 2i|>m, то в цепи будет очень боль-
шой ток, во много раз превышающий ток при ф=фт.
Хотя толчкн и очень кратковременны, но все же в системах с мощными
трансформаторами они нежелательны, так как требуют принятия специаль-
ных мер для устранения вредных последствий от них.
§ 366. Основы расчета переходных процессов в нелинейных цепях путем
замены определенного интеграла приближенной суммой. В 1916 г. Волынки-
ным был разработан графоаналитический метод расчета переходных процес-
сов в нелинейных цепях, основанный на замене определенного интеграла
приближенной суммой по формуле трапеций.
чда да)
Рис. 386
Из курса математики известно, что если интервал интегрирования (Ь — а}
ъ
в определенном интеграле J/W dx разбить на п равных частей и через у0, у1г
а
Уг, Уп обозначить значения функции f (х) соответственно при х0 = а, х± =
b — а
= а + Л, х2 — а + 2h и т.д., где h =-----, то
п
ь
С Ь — а
J f(x) dx яг — (у0 + 2У1 4* 2у% + • < • + 2{/л_! уп). (В.7)
а
Рассмотрим метод на примере цепи рис. 385. Цепь состоит из нелинейной
индуктивности и сопротивлений и /?а. Зависимость ф от I для нелинейной
506
индуктивности задана кривой рис. 386. Пусть э. д. с. е± (/) имеет форму, изоб-
раженную на рис. 387.
Обозначим токи в ветвях в
по законам Кирхгофа:
соответствии с рнс. 385. Составим уравнение
1
Rz
dip . dty
hRi+^r^-e^t).
dt dt
Отсюда
dtp
dt
Rt
, Rr
Rt ei
(В.8)
Rt
Для сокращения записи
обозначим:
n_
1+lr
e(0 =-----n—«1K).
1 + ^T
Тогда уравнение цепи запишется так:
dtp
dr
(В.9)
Разобьем время t на равные промежутки т (t = пт); тогда вместо
b — а
—----будем
2п
иметь:
nr — 0 r
2
2п
Последовательно проинтегрируем (В.9) от t = 0 до I =
t = 0 до t = 2т и т. д. и воспользуемся формулой трапеций.
Получим для первого интервала:
затем от
dt = J e(t) dt,
0 0
но по формуле (В. 7) имеем:
2
о
Следовательно,
(В.10)
2
e(t) dt,
о
где фо есть остаточное потокосцепление. В дальнейшем примем его равным
нулю.
507
Для t = 2т
но по формуле (В.7)
2т 2т
ifc + Я Ji di = Je(i)di,
О о
Поэтому для t = 2т
2т
J i di = — (2ix 4* is) -
о
При t = nx
2т
i?T . f
'h + ~ = j
о
/?т!х.
(В.11)
2
nt
(В.12)
k=n — 1
о
Уравнение (В. 12) позволяет последовательно находить ilt i2, i3 и т.д.
В левой части его стоят неизвестный ток i„ и соответствующее ему потоко-
t
12
Рис.
388
3. Значение
сцепление фп> а величина У th в правой части
известна по результатам подсчета за предыдущие
интервалы времени.
Последовательность расчета следующая:
П1
1. По заданной e(t) строим кривую j e(t)dt
i>
(рис. 388).
2. На том же рисунке (см. рис. 386), где
изображена кривая ф=>^(1), проводим прямую
OS пол углом а к оси абсцисс, тангенс которого
равен — .
по уравнению (В.10). С этой целью из рис.
ii находим
J e(t)dt. Пусть оно будет равно отрезку 11'. Переносим
о
отрезок на рис. 386 и перемещаем его параллельно оси ординат до тех
пока один конец его не окажется на кривой ф(«) — точка В, а другой—на
прямой OS — точка D.
Rx
При этом отрезок ВС равен фх, отрезок CD равен —ix.
Ток fx равен отрезку ОС.
4. Значение тока i2 находится аналогично, только в соответствии с урав-
2т
пением (В.11) из J e(Z) dt, равного отрезку 22', надо предварительно вы-
о
честь Rxilt а затем уже перемещать полученный отрезок параллельно оси
ординат.
Зт
5. Для определения i3 нз J e(t) dt надо вычесть Rx (ix + i2) и т.д.
о
берем значение
388
этот
пор,
508
Если е(0 — функция периодическая с периодом Г, то рекомендуется брать
Если е(0 — функция непериодическая, то величину т выбирают после
предварительных пробных подсчетов.
Рассмотрим числовой пример.
Пример 175. В схеме рис. 385 Rj = R-2 = 2ом. Зависимость ф = /(/) изоб-
ражается кривой рис. 386.
В интервале от t = 0 до t = 0,1 сек e(f) = 400 t, далее е(<) = 0. Пост-
роить кривую i = f(f), полагая начальные условия нулевыми и остаточное
потокосцепление ф0 = 0.
Решение. Принимаем интервал времени х = 0,025 сек. Результаты
подсчетов сводим в таблицу:
По данным таблицы на рис. 388 построен график
J =
а на рис. 389 построен график
1 = М-
§ 367. Расчет переходных процессов в схемах с несколькими нелинейными
сопротивлениями. Метод Волынкина может применяться и к цепям с несколь-
кими нелинейными сопротивлениями, а также к цепям, приводящим к урав-
нениям второго, третьего и более высоких порядков.
В качестве примера рассмотрим вопрос о переходном процессе в простей-
шей цепи с двумя нелинейностями.
509
В схеме рис. 390 к источнику э. д. с. e(f) подключаются последовательно
соединенные нелинейная индуктивность (зависимость ip от i задана) и нели-
нейное активное сопротивление с заданной вольтамперной характеристикой
nl( = f(i). Проинтегрируем уравнение цепи
с/ф
(0 = «(0
по t от 0 до t = пт.
Учтем, что
т
J и (0 dt =• |2«л 01) + 2к^ (*а) + • • • + 2«^ 0п-1) + иц (*«)!•
о
Получим формулу, аналогичную (В. 12):
пт
(В. 13)
Последовательность расчета по формуле (В. 13) такая же, как и по фор-
муле (В. 12). Отличие состоит лишь в том, что вместо прямой —-— (прямой
т
OS рис. 386) надо навести на рис. 386 кривую — uR («).
§ 368. Метод медленно меняющихся амплитуд. В электротехнике, радио-
технике и других отраслях техники исключительно широко применяется ме-
тод расчета переходных процессов, получивший название метода медленно
меняющихся амплитуд.
Этот метод был предложен в 1921 г. голландским физиком Ван-дер-Полем.
Рассмотрим основы этого метода на примере нелинейной цепи второго
порядка, находящейся под воздействием периодической возмущающей силы.
Пусть уравнение этой цепи записывается следующим образом:
d^x dx
—+/(*)—+cog* = Л sincot (B.14)
Про исследуемую цепь известно, что под действием периодической силы
с частотой со в ней устанавливается вынужденное колебание с частотой со, а
высшие гармоники выражены слабо.
Примем, что искомая функция x(t) может быть представлена так:
х = a sin a>t + b cosco/; (В.15)
а и b есть медленно меняющиеся во времени амплитуды искомого колебания.
510
Медленность изменения а и Ь во времени определяется тем, что производ-
ные от них по времени являются величинами первого порядка малости по
сравнению с произведениями (оа и соб, т. е.
da db
И — < cob. (В.16)
at dt
„ dx
Если это учесть, то вместо того, чтобы взять — равным
dt
dx da db
— =>aacosat— ba sin at 4-sin at — cosat —, (B.17)
dt dt dt
можно в первом приближении принять
dx
— ss аш cos at — ba sin at. (В. 18)
dt
Аналогично вместо того, чтобы вторую производную брать в таком виде
сРх da db dPa
— = — ага sin at — a*b cos at 4- co cos at — — co sin at — + TJ sin 4~
dt* dt dt at*
d*b da db
+ — cos co< + cocosco< —--co sincoZ — ,
dt* dt dt
пренебрежем в ней слагаемыми второго порядка малости и оставим слагае-
мые первого порядка малости. Получим:
сРх [ db\ / da\
—- « — I ага -(- 2со — I sin at + I — a*b + 2co — I cos at. (B. 19)
dt2 \ dt] \ dt]
Обратим внимание на то, что слагаемые первого порядка малости остав-
d?x
лены в выражении для — и слагаемыми первого порядка малости пренебре-
dt*
dx
жено в выражении для —.
dt
Объясняется это тем, что исследуемая цепь обладает малыми потерями,
поэтому амплитуда второго слагаемого левой части уравнения (В.14) отно-
сительно мала по сравнению с амплитудами первого и третьего слагаемых ле-
вой части уравнения (В. 14).
Далее, в функцию f(x) вместо х подставим (В.15) и разложим Дх) в ряд
Фурье. Затем умножим ряд Фурье, которым выразилось f(x), на — (на пра-
вую часть формулы В. 18). Получим:
dx
f(x) — = (a, b) -|- fj (a, fe) sin ы/ + F3 (a, 6) cos co/ + F3 (a, 6) sin 2co/ +
dt
Ft (a, b) cos 2coZ + ... (B.20)
Так как расчет ведется по первой гармонике, то постоянной составляю-
щей F0(a, b) и высшими гармониками ряда Фурье [т. е. F3 (a, b), F4(a, fe)] в
дальнейшем пренебрежем.
d*x
В уравнение (В.14) подставим вместо —правую часть (В.19), вместо
dx
f(x) — подставим
dt
Fi (a, b) sin at -f- F2 (a, b) cos at
511
и вместо со®х подставим
<о® (a sin at + b cos at).
Тогда уравнение (В.14) разобьется на два уравнения. Одно из них —
уравнение (В.21) — будет выражать собой равенство коэффициентов при
sin<a< в левой и правой частях уравнения (В. 14), другое—уравнение (В.22)—
равенство коэффициентов при cos at в левой и правой частях уравнения
(В.14):
db .
— 2со - + F1 (а, Ь) + а (со® — со2) = Л; (В.21)
2а — + F2 (a, b) + b (со® — со2) = 0.
at
(В.22)
Система уравнений (В.21) и (В.22) представляет собой два совместных
дифференциальных уравнения, составленных относительно мгновенных зна-
чений медленно меняющихся амплитуд а и Ь.
В общем случае решение системы (В.21) — (В.22) может производиться
методами численного интегрирования или при помощи метода Волынкина.
В частном случае, когда внешняя периодическая сила равна нулю (Л = 0)
и функция F\ (а, Ь) = 0, система сводится к одному дифференциальному урав-
нению первого порядка:
da
di
Fj(a)
2а
= 0).
(В.23)
Выше были рассмотрены основные этапы перехода от дифференциаль-
ного уравнения для мгновенных значений [уравнение (В. 14)] к дифференциаль-
ным уравнениям для медленно меняющихся амплитуд. Метод применим и к
другим, более сложным уравнениям.
В заключение необходимо отметить, что если максимальное значение сла-
dx
гаемого f(x) — в уравнении (В.14) (и подобных ему), выражающее собой па-
dt
дение напряжения в активном сопротивлении контура (или контуров), соиз-
меримо с максимальными значениями остальных слагаемых уравнения (В.14),
dx
то в выражении —
dt
должны быть сохранены слагаемые первого порядка, ма-
лости, которыми выше было пренебрежено. Огибающая колебаний определяется
уравнением f(t) = У"а2(0 + &2(0-
Пример 176. Определить закон нарастания амплитуд колебаний напря-
жения на сетке лампового генератора § 239.
Решение. Уравнение лампового генератора было выведено ра-
нее [см. уравнение (9.56)] . Ниже оно повторено:
.~d?uc „„duc
LC—г + ЯС—- +ис — М
d? dt с
dig
dt
0.
В свою очередь анодный ток ia выразится через сеточное напряжение ut
следующим образом:
33 ^аО + а'ис Ьис
|ср. с уравнением (9.46), см. пунктирную кривую рис. 255[.
Производная от анодного тока по времени
dig . 9 dllg
; (6
512
Подставим ее в уравнение (9.55). Получим:
LC~ + (RC ~ а'М + 3WMw‘ }^dt+Uc “°’
Поделим последнее уравнение на LC =——, где сов — угловая частота ав-
cog
токолебаний [см. формулу (9.61)], и обозначим
t Ala' —RC
1 “ LC ’
ь _ 3bM
ki~ Ma' ~RC'
(В.24)
(В.25)
Тогда
Примем
сРн, . . о dur ,,
------ — (1 — k2u2) --- + о? ис = 0.
dt2 dt ос
in: du<
х = ис у k2;
1 dx
Получим
Л yk2dt’
d?ue 1 <Рх
”^Г= ут2^2'
d2x dx ,
-----k± (1 — x2) ---[- co x = 0.
dt2 1V ' dt~ 0
Множитель — ^i(l — x2) и представляет собой функцию Дх) уравне-
ния (В.14).
Так как на систему не действует внешняя периодическая сила и частота
автоколебаний равна соо, а
(В.26)
Тогда
не со, то примем, что
х = a sin ы0/.
dx
— X ясоо cos со0/,
dt
da 2
2coo — cos a>ut — coo a sin coj/.
dt
(В-27)
(Рх
dt2
Подставим (В.27) и (В.28) в (В.26). Учтем, что
sin2 coof cos соо/ = — (cos — cos Зсо0/).
4
(В.28)
Получим
2coo cos co0Z —— aco’ sin coo( -|- aco’ sin coo/ — /^awo cos co0(-f-
dt
/г1<Ооа — cos 3 о
4
Так как расчет ведется по медленно меняющейся первой гармонике, то
слагаемое с cos Зсоо< не учитываем. Получаем
da
2 — = akt (1 — 0,25 а2).
dt
(В.29)
513
Введем новую переменную:
у = 0,25 а2.
Вместо (В.29) будем иметь:
dy
= (В.30)
Уравнение (В.30) представляет собой уравнение с разделяющимися пе-
ременными;
= f ——------;
kA = — In Co + In —-— .
I—У
Здесь через — In Co обозначена постоянная интегрирования
_±_=СеМ. Ц==-С^. =_J_________________
1 — У ° ' 1 + Сов*1' 1+Cie ***
Ci = ; а = 2 Уу~ = , =- — •
L° V l+Cje-*''
2
* = asin<B(/= ......... sin foct
V i+cie-fc^
Амплитуда напряжения на конденсаторе изменяется во времени следую-
щим образом;
1/с=-^ = - -2- - (В.31)
V k2 V у зьм
Постоянная интегрирования Ct определяется по начальному значению
амплитуды напряжения Uc. Так, если при t = 0
Uc = С с (0_),
то
4 а'М -- RC
1 “ 1^с (0_) ЗШ ~ L
Мгновенное значение напряжения на конденсаторе
2 Г ~--------------
“С = Сс sin со0/ = — — / п М — ЯС sino0t
V 14-Cje-*^ I ЗЬМ
(В.32)
Приложение Г
ОСНОВЫ ТЕОРИИ УСТОЙЧИВОСТИ РЕЖИМОВ РАБОТЫ
НЕЛИНЕЙНЫХ ЦЕПЕЙ
§ 369. Введение. Устойчивость « в малом» и устойчивость «в большом» .
Устойчивость по Ляпунову. Режим работы той или иной электрической цепи,
содержащей нелинейные сопротивления, мо>кет быть либо устойчивым, либо
неустойчивым. Как правило, режим работы подавляющего большинства элект-
514
рических цепей оказывается устойчивым и в относительно редких случаях —
неустойчивым.
Различают устойчивость «в малом» и устойчивость «в большом». Под ус-
тойчивым «в малом» режимом работы будем понимать такой, при котором дос-
таточно малое отклонение режима работы от исходного (установившегося) —
в независимости от того, какими причинами оно вызвано — с течением вре-
мени уменьшается и система возвращается к исходному состоянию.
При неустойчивом «в малом» режиме работы достаточно малое отклоне-
ние с течением времени увеличивается и система не возвращается в исходное
состояние.
Устойчивым «в большом» режимом работы будем называть такой режим
работы, при котором система, получив достаточно большое начальное откло-
нение, возвращается к исходному состоянию после прекращения действия
возмущения.
Если при достаточно большом отклонении от исходного состояния по
прекращению действия возмущения система не возвращается к исходному
состоянию, то ее называют системой, неустойчивой «в большом».
Различие между устойчивостью «в малом» и устойчивостью «в большом»
наглядно можно проиллюстрировать при помощи рис. 391, а. На этом рисун-
ке изображен желоб с помещенным в нем шариком. Если шарик толкнуть так,
что он придет в положение 2, а затем предоставить его самому себе, то под
действием силы тяжести шарик возвратится в исходное положение 1 (положе-
ние равновесия). Если же шарик толкнуть с большей силой, то он пройдет
через положение 5 и выскочит из желоба. Таким образом, система рис. 391, а
устойчива «в малом» и неустойчива «в большом».
В литературе можно встретить также термин устойчивость по Ляпунову.
Системой, устойчивой по Ляпунову, называют систему, для которой можно
указать область допустимых отклонений (область б(е) на рис. 391, б] от со-
стояния равновесия (точки О), что ни одно из движений, начинающихся внут-
ри области б, никогда не достигнет границ некоторой заданной области е.
Величина области t зависит от величины области е.
В нелинейных электрических цепях в общем случае возможны следую-
щие режимы (типы движения): 1) состояние равновесия; 2) периодическое дви-
жение при отсутствии в системе источников периодической э. д. с. или тока—
автоколебания; 3) периодическое движение с частотой источника периоди-
ческой э. д. с. (или тока) — вынужденные колебания; 4) резонансные явле-
ния на высших, низших и дробных гармониках; 5) квазипериодические (как
бы периодические) процессы по типу автомодуляции, а также ряд других,
более сложных типов движений. Каждый из этих режимов (типов движений)
может быть исследован на устойчивость.
Основы теории устойчивости были заложены крупнейшим русским ма-
тематиком А. М. Ляпуновым, в 1892 г. выпустившим книгу «Общая задача
об устойчивости движения».
515
В подавляющем большинстве практических задач производится исследо-
вание устойчивости «в малом». Этот вопрос и рассматривается в следующих
параграфах. Исследование устойчивости «в большом» производится путем
анализа хода интегральных кривых на фазовой плоскости или путем исполь-
зования «второй методы Ляпунова» (Л. 14) и здесь не рассматривается. Не рас-
сматривается здесь также методика исследования устойчивости по Ляпунову,
§ 370. Общие основы исследования устойчивости «в малом». Рассмотрим
общие основы исследования устойчивости «в малом». Они применимы ко всем
или, лучше сказать, почти ко всем известным в настоящее время типам дви-
жения, Разумеется, в каждом конкретном случае могут быть некоторые осо-
бенности в применении общих принципов. Об этих особенностях будет гово-
риться в следующих параграфах.
Для исследования устойчивости исследуемой величине х (или величи-
нам) дают малое приращение Дх, развертывают уравнения, описывающие про-
цесс, в ряд по степеням малого приращивания Дх и ввиду малости Дх отбра-
сывают все члены ряда, содержащие Дх в степенях выше первой.
В полученном уравнении (уравнениях) выделяют слагаемые, содержа-
щие Дх и производные от Дх по времени, и образуют из них дифференциаль-
ное уравнение (уравнения) относительно Дх. Уравнение относительно Дх
алгебраизируют, получают характеристическое уравнение и определяют его
корни.
Если хотя бы один корень характеристического уравнения (при дейст-
вительных корнях) будет положительным или будет положительной действи-
тельная часть комплексно сопряженных корней, то это явится свидетельством
того, что возникшее приращение Дх будет не убывать, а возрастать во вре-
мени.
Другими словами, исследуемое движение будет неустойчивым.
Если же все действительные корни характеристического уравнения будут
отрицательными, а все комплексно сопряженные корни имеют отрицательную
действительную часть, то исследуемое движение будет устойчивым.
При наличии нулевого корня и (или) чисто мнимых корней для исследо-
вания вопроса об устойчивости движения недостаточно учитывать только пер-
вые степени приращения исследуемой величины Дх. В этом случае следует
учитывать также и вторую степень приращения Дх. Характеристическое урав-
нение, составленное относительно приращения Дх, для системы второго по-
рядка имеет вид:
Д0Р2 а^р -|- д2 = 0.
Для системы третьего порядка
ДоР3 + Д1Р2 + a-ip + д3 = 0.
Для суждения о характере корней характеристического уравнения раз-
работано несколько математических критериев. Воспользуемся для этой це-
ли критерием Гурвица.
Критерий (теорема) Гурвица состоит в следующем: для того чтобы дей-
ствительные части корней характеристического уравнения
аоРп + Я1Р"-1 + Д2ря-2 + . .. + fl^-iP"-1 + д„ = 0
были отрицательными, необходимо и достаточно, чтобы все диагональные ми-
норы (Д1, Д2, ... , Д„_!) определителя Гурвица (Д„) были больше нуля.
Определитель Гурвица
Д
дх д3 д5 ... 0
До Д.2 «4 • . . 0
0 Дх Д3 »
. . . . дл-а а„ .
516
Следовательно, условия отрицательности действительных частей корней
характеристического уравнения выразятся следующим образом:
IGj 6Z3 I
= аха2 — а0а3 > 0;
ао I
д3 ==
аз аъ
Qq С12 П4
0 аг а3
> 0 и т. д.
Сам определитель Гурвица составляется так:
1. По главной диагонали определителя в порядке возрастания индексов
выписывают коэффициенты от at до ап.
2. В ту часть каждого столбца, которая расположена выше главной диа-
гонали, вписывают коэффициенты в порядке возрастания индексов.
3. В ту часть каждого столбца, которая расположена ниже главной диа-
гонали, вписывают коэффициенты в порядке уменьшения индексов (до с0
включительно).
Следствием теоремы Гурвица является лемма:
Все коэффициенты характеристического уравнения (а0, at, а2, .... сл)
устойчивой системы положительны.
Из изложенного выше вытекает, что для системы с характеристическим
уравнением второго порядка положительные вещественные корни (или ком-
плексно сопряженные с положительной действительной частью) будут
в том случае, если какой-либо из коэффициентов уравнения (а0, аг, а2) ока-
жется отрицательным. Для системы с характеристическим уравнением треть-
его порядка положительные вещественные корни (или комплексно сопряжен-
ные с положительной действительной частью) будут в том случае: 1) если ка-
кой-либо из коэффициентов (а0, а2, а3) окажется отрицательным или 2) если
^1^2 — «0^3 < О-
Аналогичные заключения могут быть сделаны и для систем с характе-
ристическими уравнениями более высоких порядков.
Коэффициенты а0, ait а2, а3, .... могут оказаться отрицательными в
следующих основных случаях:
1. Когда в состав исследуемой на устойчивость системы входят нелиней-
ные активные сопротивления, обладающие падающим участком характерис-
тики, и когда точка равновесия оказывается на падающем участке характе-
ристики.
2. В схемах с чрезмерно большим воздействием выходной цепи на вход-
ную цепь — в схемах с чрезмерно большой положительной обратной связью.
В этом случае поступление энергии из выходной цепи во входную превышает
потребление энергии во входной цепи и приращение Дх возрастает.
3. В схемах с управляемыми нелинейными индуктивностями и управля-
емыми нелинейными емкостями при наличии неявно (а в некоторых случаях
и явно) действующих обратных связей. В таких схемах обратные связи при
определенных условиях приводят к появлению на характеристиках нелиней-
ных индуктивностей или нелинейных емкостей падающих участков. Режим
работы системы может оказаться неустойчивым, если изображающая точка
скажется на падающем участке управляемой нелинейной индуктивности или
управляемой нелинейной емкости.
4. В схемах, содержащих нелинейные сопротивления с большой тепловой
инерционностью.
§ 371. Исследование устойчивости положения равновесия н системах с
постоянной вынуждающей силой. Обратим внимание на две особенности при
исследовании устойчивости положения равновесия в системах с постоянной
вынуждающей силой:
1. Характеристики всех нелинейных сопротивлений обычно заменяют от-
резками прямых линий, совпадающими с касательными к характеристикам не-
линейных сопротивлений в точке равновесия.
517
2. Если точка равновесия в системе с нелинейным активным сопротивле-
нием," имеющим S- или //-образную в. а. х., окажется на падающем участке
в. а. х., то при исследовании устойчивости положения равновесия следует учи-
тывать'малые «паразитные» параметры нелинейного сопротивления. Послед-
ние не играют сколько-нибудь существенной роли в установившемся (стацио-
нарном) процессе, но при переходном процессе, в особенности при быстро про-
текающих процессах, роль их становится значительной.
Опыт показывает, что нелинейное сопротивление с S-образной в. а. х.
(рис. 392, а) в схеме замещения для исследования устойчивости должно быть
представлено в виде последовательного соединения дифференциального сопро-
тивления Rtf с весьма малой «паразитной» индуктивностью Ln нелинейного со-
противления (рис. 393, г). НС с Л^-образной в. а. х. (рис. 392, б) в схеме заме-
щения должно быть представлено в виде параллельного соединения диффе-
ренциального сопротивления R() с весьма малой паразитной емкостью Сп нели-
нейного сопротивления*.
В § 373 дан пример на исследование устойчивости положения равновесия
в релаксационной автоколебательной системе с НС, имеющим S-образную
в. а. х.
В § 374 дан пример на исследование устойчивости положения равновесия
в автоколебательной системе с явно выраженной обратной связью.
§ 372. Исследование устойчивости автоколебаний и вынужденных коле-
баний по первой гармонике. В качестве исходных уравнений при исследовании
устойчивости автоколебаний и вынужденных колебаний обычно служат урав-
нения, получаемые по методу медленно меняющихся амплитуд (см. § 368).
Если через а и 6 обозначить медленно меняющиеся амплитуды синусной
и косинусной составляющих исследуемого колебания, то из исходных урав-
нений системы можно получить два уравнения для медленно меняющихся
амплитуд:
da
-r = A(a.by, (Г.1)
at
db
- = В(а,Ь). (Г.2)
Здесь А и В являются функциями амплитуд а и 6, а также функциями
всех параметров схемы, угловой частоты колебаний и и амплитуды вынужда-
ющей силы. Обозначим значения а и Ь в установившемся режиме (когда ам-
плитуды не изменяются во времени) через а0 и Ьо. Для определения а0 и Ьо
* Учитывая тот «паразитный» параметр, роль которого при возможном
триггерном эффекте в НС становится особенно значительной.
618
в уравнениях (Г.1) и (Г.2) следует положить — = 0и — = 0и решить сис-
dt dt
тему уравнений
А (а0, Ьо) = О, (Г.3)
В(ао,Ьо)=0. (Г.4)
Пусть в результате возмущения амплитуды колебания получили малые
приращения Да и ДЬ и стали равными:
а = а0 + ка и Ь = Ьо -|-
Подставим эти значения а и Ь в уравнения (Г.1) и (Г.2), развернем
Л(а0 + Да, Ьо + ДЬ) и В(а04-Да, Ьо + ДЬ) в ряд Тейлора по малым прира-
щениям Да и ДЬ и в силу малости приращений ограничимся слагаемыми ря-
да с первыми степенями Да и ДЬ. Получим:
Л (а0 -[- Да, Ьо ДЬ) = А (Й0, Ьо) ДаЛ^ -|- (Г.о)
В (а0 Да, Ьо -}- ДЬ) = В (а0, Ь<>) -}- ДаЛ2 4- ЛЬВ%. (Г.6)
Здесь для сокращения записи обозначено:
= дА (а’ b> I
да (Г.7)
д _ дА <а’ I ,
1 db L’
_[дВ(а,_Ь)_1
2~| да |/ (Г.8)
519
Индекс «/свидетельствует о том, что в частные производные должны быть
подставлены значения а и b установившегося режима, т. е. а0 и Ьо.
Коэффициенты Alt Bt, Аг, В2 являются функциями а0 и Ьо, но ие яв-
ляются функциями приращений Да и Дб. Подставим правые части уравнений
(Г.5) и (Г.6) в уравнения (Г. 1) и (Г.2), учтем уравнения (Г.З) и (Г.4), а также
то, что
d(a0 + Aa) d(Aa) d(60-f-Aft) d(bb)
dt dt dt dt
Получим два уравнения:
d(Aa) n ,
—— = At Ла + B^b. (Г.9)
dt
Алгебраизируем их: d(A&) — Л2Л0 4“ ^2^^» at (Г. 10)
р Ла = Д Да + Bj ЛЬ; (Г.9')
р ЛЬ — А2 Ла + В2 ЛЬ. (Г. 10')
Составим характеристическое уравнение
Здесь рг + тр + q = 0. (Г.11)
/п = — (Л( -|- В2); (Г.12)
(Г. 13)
В соответствии с критерием Гурвица для затухания Да и ЛЬ необходи-
мо, чтобы
В автоколебательных системах периодические вынуждающие силы, как
правило, отсутствуют, поэтому обычно можно взять b = 0, т. е. взять коле-
бание в виде a(f) sincoZ (см., например, автоколебания лампового генератора,
пример 176). В этом случае вместо двух уравнений (Г. 1) и (Г. 2) будет одно
da
уравнение — = А (а). Точно так же вместо двух уравнений (Г. 9) и (Г. 10)
dt
будет одно уравнение (Г. 15):
где d(Aa) dt (Г. 15) dA (а) I а- 2 • <гл6> da 1 а==а0
Для устойчивости автоколебаний в этом случае необходимо выполнение
условия At < 0.
Пример на исследование устойчивости автоколебаний по формуле (Г. 15)
см. в § 374.
Вопрос о том, как проводится исследование устойчивости вынужденных
колебаний на высших гармониках и субгармониках, а также о том, как про-
изводится исследование устойчивости процессов автомодуляции, рассмотрен,
например, в (Л. 18).
Рассмотрим теперь два примера на исследование устойчивости режимов
работы.
520
Первый пример — исследование устойчивости режима равновесия в ге-
нераторе релаксационных колебаний. Второй пример — исследование устой-
чивости периодического движения в ламповом генераторе синусоидальных
колебаний.
§ 373. Релаксационные колебания. Исследование устойчивости положения
равновесия в генераторе релаксационных колебаний. Релаксационные колеба-
ния представляют собой автоколебания, при определенных условиях возни-
кающие в нелинейных электрических цепях с одним накопителем энергии,
например в цепи с одной емкостью (без индуктивности) или в цепи с одной
индуктивностью (без емкости).
На рис. 393, а изображена принципиальная схема генератора релакса-
ционных колебаний. Она состоит из источника постоянной э. д. с. Е, линей-
ного сопротивления 7?, емкости С и параллельно соединенного с ней нелиней-
ного сопротивления НС, имеющего в. а. х. S-образной формы.
В качестве НС с такой в. а. х. могут быть взяты неоновая лампа или ти-
ратрон. На рис. 393, б дана схема генератора с неоновой лампой.
Кривая 1 рис. 393, в представляет собой в. а. х. неоновой лампы, прямая
2 того же рисунка — в. а. х. линейного сопротивления R.
Если бы не было релаксационных колебаний, то режим работы опреде-
лился бы точкой т пересечения кривой 1 и прямой 2.
Для этой точки сумма падений напряжений на НС и на сопротивлении
R равна в соответствии со вторым законом Кирхгофа э. д. с. Е.
Точку т будем называть точкой равновесия. Она определяет собой ре-
жим работы схемы при протекании по сопротивлению R и по неоновой лампе
постоянного тока.
Убедимся в том, что режим работы, определяемый точкой т, является
неустойчивым режимом: достаточно ничтожно малого отклонения от положе-
ния равновесия, чтобы изображающая точка «ушла» из точки т и не возвра-
тилась в нее. В схеме начнутся релаксационные колебания.
Для того чтобы убедиться в неустойчивости состояния равновесия, со-
ставим линейную схему замещения релаксационного генератора.
Так как НС имеет S-образную в. а. х., то в схеме для исследования устой-
чивости оно имитировано (в соответствии с § 371) дифференциальным сопро-
тивлением Rd и последовательно с ним включенной ничтожно малой «паразит-
ной* индуктивностью Ln.
Дифференциальное сопротивление 7?э в точке т пропорционально тан-
генсу угла а на рис. 393, е и является отрицательной величиной.
Источник э. д. с. в схеме замещения (рис. 393, г) отсутствует, так как ис-
следуется поведение схемы в режиме приращений по отношению к режиму,
определяемому точкой т.
Найдем входное сопротивление схемы в операторной форме:
7, (Rd + pLn)
Ср
Z(p)=R + ----------------.
7 + Rd + P^n
Cp
Характеристическое уравнение
p2 + 2bp + <o2 = 0,
где
, Ln + RRdC Rd ,
b —------------~ ---- и ы1 =---------,
2RLnC 2Ln RLnC
имеет корни
pM, 2 = — b ± Vb2 — <o2.
Так как
Rd < 0, то н b < 0.
521
Если соотношение между параметрами таково, что Ь2 > со2, то оба корня
будут вещественными и положительными.
Если Ь2 < со2, то корни комплексно сопряжены и имеют положительную
сещественную часть.
Таким образом, вне зависимости от соотношения между Ь2 и ш2 состояние
равновесия, определяемое точкой т, неустойчиво. Рассмотрим теперь после-
довательность смены состояний прн релаксационных колебаниях.
Пусть в схеме рис. 393, б прн нулевых начальных условиях замыкается
ключ К. Конденсатор С начнет заряжаться, и напряжение на нем будет рас-
ти (рис. 394, а). Так как конденсатор и неоновая лампа НЛ включены парал-
лельно, то в любом режиме работы напряжения на них одинаковы.
Как только напряжение на конденсаторе возрастет до величины, равной
напряжению зажигания и3 неоновой лампы, последняя зажигается и ток в ней
скачком возрастет с нуля до величины i4 (рнс. 394, б).
Конденсатор быстро разрядится через НЛ, внутреннее сопротивление
которой мало по сравнению с
сопротивлением R. При этом изображающая
точка на в. а. х. НЛ переместится нз
точки 4 в точку 1. В точке 1 напряжение
на НЛ равно напряжению гашения ее
иг, поэтому неоновая лампа гаснет, и
ток в ней становится
(точка 2).
Далее, конденсатор
ется до напряжения и3,
па снова зажигается и
ряется.
Траектория движения изображаю-
щей точки на рис. 394, б образует зам-
кнутую петлю 1234.
Важно подчеркнуть, что если ус-
ловия возбуждения колебаний в схеме
выполнены, то размах колебаний на-
пряжения на емкости не зависит от ве-
личины нагрузки R н величины э. д. с.
Е и определяется напряжениями зажи-
гания и3 и гашения иг НЛ. Период ко-
лебаний равен сумме времени зарядки
конденсатора н времени разрядки кон-
денсатора. Он зависит от величины э. д. с.
внутреннего сопротивления НЛ. Обратная
равным нулю
вновь эаряжа-
неоновая лам-
процесс повто-
и
£, емкости С, сопротивления R
связь в схеме находит свое выражение в том, что конденсатор управляет ре-
жимом работы неоновой лампы.
§ 374. Исследование устойчивости синусоидальных колебаний в ламповом
генераторе. В качестве второго примера на применение общей теории, изло-
женной в § 372, рассмотрим вопрос об исследовании устойчивости синусои-
дальных колебаний в ламповом генераторе (см. рис. 271). С этой целью вос-
----- • ----- (В.24).
(Г. 16) производная от амплитуды колебаний
пользуемся формулами (В.29) и
В соответствии с уравнением
da
A^dt
= 0,5 0^(1 —0,25 а2).
В установившемся режиме работы амплитуду колебаний обозначим
п da
через Яо- Для определения я0 приравняем — нулю и решим уравнение
1 — 0,25яо = 0. Отсюда я0 = 2.
В соответствии с § 372 для исследования устойчивости периодического
движения asintoZ в автоколебательной системе, на которую не действует
522
внешняя периодическая сила частоты со, достаточно найти знак производной
dA (a) dA (а)
—~— при а — а0. Если при этом - будет отрицательна, то процесс устой-
чив. В нашем случае
(а) .
V— ------= 0,5 ^(1-0,75^) = -^
4Ша=-а0=2
Ранее [см. (В. 32)] было выяснено, что a’ M>RC и что Лг>0, так как толь-
ко в этом случае амплитуда колебания представляет собой вещественную ве-
личину.
„ dA(a) „ л
Следовательно,------- < 0. Процесс устойчив.
da а=а0
Приложение Д
ФАЗОВАЯ ПЛОСКОСТЬ
§ 375. Определение фазовой плоскости н краткая характеристика областей
ее применения для исследований процессов в нелинейных цепях. Качествен-
ное исследование различных процессов в электрических цепях, описываемых
дифференциальными уравнениями первого и, в особенности, второго порядка,
производится в ряде случаев при помощи фазовой плоскости.
Фазовой плоскостью называют плоскость, по осн абсцисс которой откла-
дывается исследуемая величина (назовем ее х), а по оси ординат — пронзвод-
dx
ная от исследуемой величины — (последнюю принято обозначать через у),
dt
В каждой конкретной задаче подх понимают либо ток, либо напряжение,
либо заряд, либо индукцию. Любому сочетанию значений х и у исследуемой
цепи соответствует вполне определенная точка фазовой плоскости.
Для качественного исследования процессов в электрических цепях, опи-
сываемых уравнениями третьего порядка, применяют трехмерное фазовое про-
странство. На одной оси декартовой системы этого пространства откладыва-
dx d2x
ют значение функции х, на другой — —, на третьей — —.
dt aR
Качественное исследование представляет собой выявление общих свойств
исследуемой цепи без интегрирования нелинейного дифференциального урав-
нения. Под общими свойствами понимают обычно выяснение зависимости ха-
рактера переходного процесса от начальных условий, выяснение возможнос-
ти возникновения в схеме автоколебаний, резонансных явлений, автомоду-
ляцни, а также исследование устойчивости перечисленных режимов н режи-
мов равновесия.
Все эти вопросы в ряде случаев могут быть решены и иными путями, без
привлечения фазовой плоскости. Применение последней делает исследование
более наглядным и оправдано в тех случаях, когда объем работы соизмерим
или меньше объема работы при решении тех же задач иными методами.
Обычно фазовая плоскость применяется для исследования процессов
в электрических цепях, содержащих источники постоянной э. д. с. н не со-
держащих источников периодической э. д. с.
Однако фазовая плоскость может быть использована н для исследования
процессов в цепях, содержащих источники синусоидальной (и постоянной)
э. д. с., если предварительно перейти от уравнений, составленных для мгно-
венных значений, к уравнениям для медленно меняющихся составляющих
523
§ 376. Интегральные кривые, фазовая траектория и предельный цикл. За-
висимость у = f(x), получаемая из решения дифференциального уравнения
системы, определяет собой семейство кривых на фазовой плоскости, соответ-
ствующих различным значениям постоянных интегрирования. Кривые у —
= f(x), соответствующие различным начальным условиям, называются ин-
тегральными кривыми.
Начальное положение изображающей точки на фазовой плоскости опре
dx
деляется значениями х и — = у при t — 0.
dt
Интегральная кривая, проходящая через точку фазовой плоскости с за-
данными начальными условиями, называется фазовой траекторией.
Внд фазовой траектории зависит от конфигурации схемы, от характера
нелинейности и от соотношения между параметрами.
Если процесс в цепи является периодическим, то через интервалы вре-
мени, равные периоду процесса, соответствующие друг другу значения х и
dx
— = у повторяются, и фазовая траектория в этом случае является замкну-
dt
той кривой.
Рис 395
Замкнутая фазовая траектория называется предельным циклом. Если же
процесс является непериодическим, то фазовая траектория представляет со-
бой незамкнутую кривую.
Фазовую траекторию можно наблюдать на экране электронно-лучевого
осциллографа. С этой целью на одну пару отклоняющих пластин его подают
исследуемую величину х, а на другую пару — производную от х.
§ 377. Изображение простейших процессов на фазовой плоскости. Рас-
смотрим несколько простейших примеров на описание процессов в линейных
цепях (о релннейных цепях будет говориться позже).
Требуется изобразить на фазовой плоскости переходный процесс в схеме
рис. 395, а, вызываемый при нулевых начальных условиях замыканием ру-
бильника. Обозначим: i — ток в цепи, ис — напряжение на конденсаторе.
В уравнение цепи
Ri + ис = Е
due
вместо I подставим С — ; получим:
dt
Положим
RC ~77 -\-ис=>Е.
at
due dx
Uc = x; lt^dry-
524
Тогда
Е — х
Последнее уравнение описывает прямую ab рис. 395, б. Эта прямая и яв-
ляется фазовой траекторией рассматриваемого процесса. Точка b является
точкой равновесия.
В качестве второго примера рассмотрим
изображение
колебания
синусоидального
i = lm sin со/ (рис. 396, а).
Обозначим I — х; тогда
dx
у = — ^ы1т cosco/,
at
т. е
х — Im sin со/;
у = (л1т cos со/.
Поделим первое уравнение на 1т, второе
на а>1т, затем возведем в квадрат полученные
уравнения и сложим их. Будем иметь урав-
нение эллипса:
/ х \2 I у \ 2
( 7~ ) + ( i I = 1-
\Лп/ ' /
Следовательно, изображением синусои-
дального процесса (фазовой траекторией) на
фазовой плоскости будет эллипс (рис. 396, б).
На рис. 396, в изображено несколько эл-
липсов, соответствующих синусоидальным ко-
л.баниям с различными начальными усло-
виями.
Направление движения изображающей
точки показано стрелкой. В верхней полупло-
скости у = — < 0; следовательно, в верхней
полуплоскости изображающая точка движется Рис’ 396
в сторону увеличения координаты х. В нижней
dx
полуплоскости у = — < 0, поэтому в нижней полуплоскости изображающая
точка движется в сторону уменьшения координаты х. В целом можно сказать,
что перемещение изображающей точки на фазовой плоскости происходит
всегда в направлении движения часовой стрелки.
Важно обратить внимание на то, что хотя х и у и ивляются функциями
времени, но на фазовой плоскости время в явном виде никак не отображено.
Изображением затухающего синусоидального процесса является сверты-
вающаяся спираль.
Изображением нарастающего синусоидального колебания является рас-
кручивающаяся спираль.
ЧАСТЬ III
ВВЕДЕНИЕ
Третья часть курса «Теоретические основы электротехники» по-
священа электромагнитному полю.
Теория электромагнитного поля представляет собой учение о
электрических и магнитных явлениях, о теоретических положе-
ниях и законах, которым подчиняются эти явления, и о вытекаю-
щих из них методах расчета.
Изложение основных свойств и методов расчета полей произво-
дится в порядке перехода от более простых типов полей к более слож-
ным. В соответствии с этим вначале рассматриваются неизменные
во времени поля — электростатическое поле, электрическое поле
постоянного тока в проводящей среде, магнитное поле постоянно-
го тока — и лишь после этого рассматривается переменное элек-
тромагнитное поле. Изучение всех этих видов полей расширяет фи-
зические представления о поле, известные из курса физики, способ-
ствует более глубокому пониманию процессов, происходящих в
электротехнических установках, а также важно с прикладной точ-
ки зрения, поскольку оно дает возможность решать многие задачи,
имеющие существенное значение не только для теории электричес-
ких цепей, но и для решения задач, которые выходят за рамки тео-
рии цепей и имеют самостоятельное значение, как, например, зада-
чи об излучении и канализации энергии высокой частоты.
Ознакомление с материалом, излагаемым в разделе «Электроста-
тическое поле» позволяет понять, например, в каких условиях рабо-
тает электрическая изоляция в той или иной электрической установ-
ке, какое влияние на электрическую прочность оказывают электри-
ческие свойства диэлектрика, изменение этих свойств от точки к точ-
ке, посторонние включения и т. п. Изучение раздела «Электростати-
ческое поле» дает также возможность определять такие интеграль-
ные величины, как собственные и частичные емкости — понятия,
широко используемые в теории электрических цепей.
Изучение раздела «Электрическое поле постоянного тока в про-
водящей среде» дает возможность решать, например, следующие
практические задачи: находить распределение потенциалов и плот-
ностей токов в заземляющих установках, токи утечки в устройствах
с несовершенной изоляцией, распределение тока в морской воде в
18 Л. А. Бессонов
529
установках для траления, определять такие интегральные величи-
ны, как проводимость и сопротивление между электродами сложной
конфигурации и т. п.
Ознакомление с материалом, излагаемым в разделе «Магнитное
поле постоянного тока», также подготавливает к решению многих
задач, имеющих существенное практическое значение.
В качестве примеров таких задач могут быть названы следую-
щие: расчет магнитных экранов, расчет устройств для магнитной
записи звука, расчет установок для магнитной дефектоскопии, оп-
ределение сил взаимодействия, возникающих в электрических ап-
паратах при токах короткого замыкания, нахождение индуктив-
ностей и магнитных сопротивлений и т. п.
Наиболее обширным разделом третьей части курса ТОЭ является
раздел «Переменное электромагнитное поле». В этом разделе рас-
сматриваются вопросы излучения электромагнитной энергии, рас-
пространения электромагнитных волн в идеальном диэлектрике,
в проводящей и полупроводящей средах.
Изучение всего комплекса вопросов этого раздела также под-
готавливает к решению многих практических задач, как, например,
задач, связанных с высокочастотным нагревом и закалкой, канали-
зацией энергии высокой частоты, задач на определение активного
и реактивного сопротивлений проводников на переменном токе и т. п.
Глава тринадцатая
ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ
§ 378. Определение электростатического поля. Электромагнит-
ное поле является особым видом материи, оно является носителем
энергии и обладает характерными для него электрическими и маг-
нитными свойствами.
Электростатическое поле представляет собой^частный вид элек-
тромагнитного поля. Оно создается совокупностью электрических
зарядов, неподвижных в пространстве по отношению к наблюдате-
лю и неизменных во времени*.
В дальнейшем, как правило, будем иметь дело с полем, созда-
ваемым в однородной и изотропной среде, т. е. в такой среде, элек-
трические свойства которой одинаковы для всех точек поля и не за-
висят от направления. В противоположном случае будут делаться
соответствующие оговорки.
Электростатическому полю присуща способность воздействовать
на помещенный в него электрический заряд с механической силой,
прямо пропорциональной величине этого заряда.
В основу определения электростатического поля было положе-
но механическое его проявление. Оно было обнаружено много лет
назад и нашло свое выражение в известном из курса физики законе
Кулона (1785).
* Из курса физики известно, что любое вещество состоит из элементарных
заряженных частиц, окруженных электромагнитным полем. Таким образом,
в любом веществе всегда имеется микроскопическая неоднородность в прост-
ранстве.
Кроме того, элементарные заряженные частицы, входящие в состав ато-
мов и молекул, находятся в беспрерывном хаотическом движении. Следова-
тельно, кроме микроскопической неоднородности в пространстве всегда имеет-
ся неодинаковость расположения микроскопических зарядов в смежные мо-
менты времени.
В теории поля осредняют микроскопические неоднородности вещества
в пространстве и во времени, т. е. рассматривают процессы в макроскопичес-
ком смысле.
В заряженном теле (если общий заряд его неизменен во времени) эле-
ментарные заряды движутся хаотически. Поэтому даже в непосредственной
близости от поверхности этого тела создаваемое элементарными зарядами маг-
нитное поле практически отсутствует.
Это и дает возможность рассматривать в электростатическом поле лишь
одну «сторону» электромагнитного поля, а именно, электрическую «сторону».
18*
531
§ 379. Закон Кулона. Два точечных заряда <?, и ?2 в вакууме
взаимодействуют друг с другом с силой F, прямо пропорциональной
произведению зарядов и q2 и обратно пропорциональной квадра-
ту расстояния R между ними. Эта сила направлена по линии, со-
единяющей точечные заряды. Если заряды имеют одинаковые зна-
ки, то они стремятся оттолкнуться друг от друга; заряды про-
тивоположных знаков стремятся сблизиться:
(13.1)
где R„ — единичный вектор, направленный по линии, соединяющей
заряды (см. рис. 397)*.
Если пользоваться системой единиц СИ и кратными долями
единиц этой системы, то расстояние R обычно измеряют в
метрах (jh), заряды в кулонах (к), е0 = 8,86 10~12 ф/м, тогда
сила будет получена в ньютонах.
____Хотя в формулировке закона Кулона и
упоминаются «точечные» заряды, но это
не значит, что взаимодействующие друг
Рис. 397 с другом заряды расположены на те-
лах, имеющих бесконечно малые раз-
меры. Когда говорят о точечных зарядах, то имеют в виду следую-
щее: линейные размеры тел, на которых расположены взаимодей-
ствующие заряды, много меньше расстояния между телами.
§ 380. Основные величины, характеризующие электростатическое
поле: потенциал и напряженность. Всякое поле характеризуется
некоторыми основными величинами. В электростатическом поле
основными величинами, характеризующими его электрическое поле,
являются напряженность Е и потенциал <р.
Напряженность электрического поля есть величина векторная,
определяемая в каждой точке и величиной и направлением, потен-
циал является величиной скалярной. Значение потенциала опреде-
ляется в каждой точке поля некоторым числом.
Электростатическое поле определено, если известен закон
изменения Е или ф во всех точках этого поля.
Если в электростатическое поле поместить настолько малый (не-
подвижный) положительный заряд, что он своим присутствием не
вызовет сколько-нибудь заметного перераспределения зарядов на
телах, создающих поле, то отношение силы, действующей на заряд,
к величине заряда q и определяет напряженность поля в данной точке
Е = —.
9
* Напомним, что стрелка над буквой свидетельствует о том, что речь
идет о векторе в пространстве.
532
Напряженность численно равна силе, действующей на заряд, по
величине, равный единице.
В том случае, когда поле создается несколькими зарядами (qt,
q2, q3,...), напряженность поля равна геометрической сумме нап-
ряженностей от каждого из зарядов в отдельности:
Е = £1 + £2 + Ез + ...
из точки I в
Другими словами, при расчете электрического поля применим метод
наложения.
Рассмотрим вопрос о работе, совершаемой силами поля при пе-
ремещении заряда, и о связанных с работой понятиях потенциала и
разности потенциалов.
Поместим в электростатическое поле некоторый заряд q. На за-
ряд будет действовать сила qE. Пусть заряд q из точки 1 перемес-
тился в точку 2 по пути 132 (рис 398). Так как направление силы
qE, воздействующей на заряд в каждой точке пути, может не сов-
падать с элементом пути dl, то работа на перемещение заряда на пу-
ти dl определится скалярным произведением силы на элемент пути
qEdl. Работа, затраченная на перенос заряда q
2 по пути 132 определится как сумма эле-
ментарных работ qEd.1. Эта сумма может
быть записана в виде линейного интеграла
2
q J Е dl.
1
Заряд q может быть любым. Положим его
равным единице (единичный заряд). Под раз-
ностью потенциалов <рг—<р2 принято пони-
мать работу, затрачиваемую силами поля при
переносе единичного заряда из начальной
точки 1 в конечную точку 2:
2
^-^^Edl. (13.2)
1
Формула (13.2) позволяет определить разность
1 и 2 как линейный интеграл от напряженности поля.
Если бы потенциал конечной точки пути (точки 2) был равен
нулю, то тогда потенциал точки / определился бы так (при <р2 — 0):
m
Рис. 398
потенциалов точек
2
1
—> —>
Е dl,
533
т. е. потенциал произвольной точки поля 1 может быть определен
как работа, совершаемая силами поля по переносу единичного поло-
жительного заряда из данной точки поля в точку поля, потенциал
которой равен нулю.
За точку, имеющую нулевой потенциал, может быть принята
любая точка поля. Если такая точка выбрана, то потенциалы всех
точек поля определяются совершенно однозначно.
Часто принимают, что точка с нулевым потенциалом находится
в бесконечности. Поэтому, в особенности в курсах физики, распро-
странено определение потенциала как работы, совершаемой силами
поля при переносе единичного заряда из данной точки поля в бес-
конечность
оо
q>j = J Е dl.
1
Часто считают, что точка с нулевым потенциалом находится на
поверхности земли (земля в условиях электростатики есть прово-
дящее тело, поэтому безразлично, где именно — на поверхности зем-
ли или в толще ее — находится эта точка).
§ 381. Потенциал определяется с точностью до постоянной вели-
чины. Из предыдущего следует, что потенциал любой точки поля за-
висит от того, какой точке поля придан нулевой потенциал. Други-
ми словами, потенциал определяется с точностью до постоянной ве-
личины. Однако существенного значения это обстоятельство не име-
ет. Дело в том, что практическое значение имеет не потенциал ка-
кой-либо точки поля, а разность потенциалов и производная от по-
тенциала по координатам.
При составлении разности потенциалоз произвольная постоян-
ная, с точностью до которой определяется потенциал, вычтется, и в
разность потенциалов она не войдет. На величине производной от
потенциала по координатам произвольная постоянная, с точностью
до которой определяется потенциал, также не скажется, поскольку
производная от постоянной величины равна нулю.
§ 382. Электростатическое поле — поле потенциальное. Соста-
вим выражение для разности потенциалов в поле точечного заряда.
С этой целью положим, что в точке т рис. 398 находится положи-
тельный точечный заряд qY, создающий поле, а из точки 1 в точку 2
через промежуточную точку 3 перемещается единичный положи-
тельный заряд q = 1.
Обозначим: — расстояние от точки т до исходной точки 1,
— расстояние от точки т до конечной точки 2, R — расстояние
от точки т до произвольной точки 3 на пути 132. Направление на-
пряженности поля Е и направление элемента пути dl в промежуточ-
ной точке 3 показано на рис. 398. Скалярное произведение Е dl =
534
— Е dR, где dR есть проекция элемента пути dl на направление ра-
диуса, соединяющего точку т с точкой 3.
F
В соответствии с определением, напряженность поля Е = — •
По закону Кулона
F = —R..
4ле0/?а
q — 1, то модуль напряженности поля в поле
равен
Е = —.
4ш0/?2
Подставим в формулу (13.2) вместо Е dl величину
Получим
Так как 17?о| = 1 и
точечного заряда qx
—— dR.
4ле0/?2
Ф1~ <р2
91
4этеп
2
С dR 91 / _1_
I R2 4ле„ \ /?,
Ч)(ВД
2
2
Таким образом, разность потенциалов между исходной и ко-
нечной точками пути {точками 1 и 2) зависит только от положения
этих точек и не зависит от пути, по которому происходило пере-
мещение из исходной точки в конечную точку. Другими словами,
если перемещение из точки 1 в точку 2 будет происходить по како-
му-то другому пути, например по пути 142, то разность потенциа-
лов д>! — <р2, полученная в этом случае, будет в точности равна раз-
ности потенциалов <р, — <р2 при перемещении из точки 1 в точку 2
по пути 132.
Если поле создано совокупностью точечных зарядов, то проде-
ланный выше вывод справедлив для поля, созданного каждым из то-
чечных зарядов в отдельности. А так как для электрического поля
в однородном и изотропном диэлектрике справедлив принцип нало-
жения, то вывод о независимости величины разности потенциалов
— Фа от пути, по которому происходило перемещение из точки
1 в точку 2, справедлив и для электрического поля, созданного сово-
купностью точечных зарядов.
Если пройти по замкнутому пути 13241 (рис. 398), то исходная
точка пути {!) и конечная точка пути (/) совпадут, и тогда и левая
и правая части формулы (13.2) будут равны нулю
<Pj — <рх = 0 = (f) Е dl. (13.3)
Кружок на знаке интеграла свидетельствует о том, что интеграл
берется по замкнутому контуру.
Соотношение (13.3) означает, что в электростатическом поле
линейный интеграл от напряженности электрического поля, взятый
вдоль любого замкнутого пути, равен нулю.
535
Физически это объясняется тем, что при движении вдоль замк-
нутого пути совершена определенная работа силами поля и такая
же работа совершена внешними силами против сил поля.
Если условиться работу, совершенную силами поля, считать
положительной, а работу, совершенную против сил поля, отрица-
тельной, то сумма «положительных» и «отрицательных» работ рав-
на нулю.
, Выражение (13.3) можно трактовать и так: циркуляция вектора
Е вдоль любого замкнутого контура равна нулю. Это соотношение
выражает собой основное свойство электростатического поля. Поля,
для которых выполняются подобного рода соотношения, называют-
ся потенциальными. Потенциальными являются не только электро-
статические поля, но и все гравитационные поля (поля сил тяготе-
ния между материальными телами), установившиеся температур-
ные поля около нагретых тел и т. д.
§ 383. Силовые и эквипотенциальные линии. Электростатическое
поле можно наглядно характеризовать совокупностью силовых и
эквипотенциальных линий. Силовая линия — это мысленно про-
веденная в поле линия, начинающаяся на положительно заряжен-
ном теле и оканчивающаяся на отрицательно заряженном теле. Про-
водится она таким образом, что касательная к ней в любой точке ее
дает направление напряженности поля Е в этой точке. Вдоль сило-
вой линии передвигался бы весьма малый положительный заряд,
если бы он имел возможность свободно перемещаться в поле и если
бы он не обладал инерцией. Таким образом, силовые линии имеют
«начало» (на положительно заряженном теле) и имеют «конец» (на
отрицательно заряженном теле). Так как положительный и отрица-
тельный заряды, создающие поле, не могут быть в одной и той же
точке, то силовые линии электростатического поля не могут быть
замкнутыми сами на себя линиями.
В электростатическом поле могут быть проведены эквипотен-
циальные (равнопотенциальные) поверхности. Под эквипотенциаль-
ной поверхностью понимают совокупность точек поля, имеющих
один и тот же потенциал. Если мысленно рассечь электростатичес-
кое поле какой-либо секущей плоскостью, то в полученном сече-
нии будут видны следы пересечения плоскости с эквипотенциаль-
ными поверхностями. Их называют эквипотенциальными линиями
(или эквипотенциалями). Из самого определения эквипотенциаль-
ной поверхности следует, что перемещение по ней не вызовет изме-
нения потенциала. Точно так- же и перемещение вдоль эквипо-
тенциальной линии не связано с изменением потенциала.
Эквипотенциальные и силовые линии в любой точке поля пере-
секаются под прямым углом. На рис. 399, а для примера изображе-
ны два заряженных тела и проведено несколько силовых и эквипо-
тенциальных линий.
В противоположность силовым линиям эквипотенциальные ли-
536
нии электростатического поля являются замкнутыми сами на себя
линиями. Как уже говорилось, напряженность электрического поля
Е и потенциал <р связаны друг с другом связью интегрального вида
(13.2). Кроме нее между Е и <р существует и связь дифференциаль-
ного вида. Она рассмотрена в следующем параграфе.
§ 384. Выражение напряженности в виде градиента от потен-
циала. Как уже говорилось, электростатическое поле является
полем потенциальным. Между двумя близко расположенными
точками поля имеется в общем случае некоторая разность потен-
циалов.
Если эту разность поделить на кратчайшее расстояние между
взятыми точками, то полученная величина будет характеризовать
СипоВыетмш
Рис. 399
5)
скорость изменения потенциала в направлении кратчайшего рас-
стояния между точками. Эта скорость будет зависеть от направления,
вдоль которого взяты точки. В курсе математики пользуются по-
нятием градиента скалярной функции. Под градиентом скалярной
функции понимают скорость изменения скалярной функции, взятую
в направлении ее наибольшего возрастания. В этом определении гра-
диента существенны два положения. Первое то, что направление, в
котором берутся две близлежащие точки, должно быть таким, что
скорость изменения потенциала максимальна. Второе то, что нап-
равление это таково, что скалярная функция в этом направлении
возрастает (не убывает). На рис. 399, б изображены отрезки двух
весьма близко расположенных эквипотенциалей. Одна из них имеет
потенциал другая — <р2. Пусть <рх > <р2. Тогда, в соответствии
с приведенным определением градиента потенциала, последний изоб-
разится на рис. 399, б вектором, перпендикулярным к эквипотен-
циальным линиям и направленным от <р2 к <рг (в сторону увеличе-
ния потенциала).
537
Напряженность электрического поля направлена от более высо-
кого потенциала (фх) к более низкому (ф2). Если расстояние по пер-
пендикуляру (по нормали) между эквипотенциальными поверхно-
стями обозначить dn и через dn обозначить вектор, совпадающий
с направлением Е,
dn — пп dn
(здесь н°—единичный вектор по направлению dn), то тогда можно
на основании соотношения (13.2) записать выражение:
2
Ф1 — Ч’г — J Ё dl Edn = — dq?,
1
де через dtp = <р2 — <рг обозначено приращение потенциала при
переходе от точки 1 к точке 2.
Так как векторы Е и dn совпадают по направлению, то ска-
лярное произведение Е dn равно произведению модуля Е на модуль
dn (Edn = Е dn).
Таким образом, Edn = — dtp. Отсюда модуль напряженности
поля Е = — -^2. Вектор напряженности поля Ё = Еп°. Следова-
dn
тельно,
£ = —-^2-и". (13.4)
dn
В свою очередь из определения градиента следует, что
gradq>= ( — 7) = -=^2. ( — «"). (13.5)
dn dn
Сопоставляя (13.4) и (13.5), замечаем, что
Е = — grad ф. (13.6)
Соотношение (13.6) может быть истолковано следующим образом:
напряженность в какой-либо точке поля равна скорости измене-
ния потенциала в этой точке поля, взятой с обратным знаком. Знак
минус имеет вполне определенный смысл: направление Е и направ-
ление grad ф противоположны (см. рис. 399, б).
Нормаль dn в общем случае может быть расположена таким об-
разом, что не совпадет с направлением какой-либо координатной
оси. И потому градиент потенциала в общем случае может быть
представлен в виде суммы трех проекций по координатным осям.
Например, в декартовой системе координат
grad ф = 7-^2. + f + , (13.7)
dx dy dz
538
где i —— представляет собой скорость изменения <р в направлении
dx
оси х, — есть числовое значение (модуль) скорости (скорость—
—> —> —>
величина векторная), i, /, k — единичные орты, соответственно,
по осям х, у, z декартовой системы.
В свою очередь, вектор напряженности Е = iEx-\- jEy-\-kEz.
Таким образом,
7£x + /Ey+X = - (7-^+7^-4-7-g-).
Л \ dx dy dz ]
Два вектора равны друг другу только тогда, когда равны друг дру-
гу соответствующие проекции их.
Следовательно,
р ____ д<р . р _________ d(f . р _________ д<р
dx у ду dz
(13.8)
Соотношения (13.8) следует понимать так: проекция напряжен-
ности поля на ось х равна проекции скорости изменения потенциа-
ла вдоль оси х, взятой с обратным знаком, и т. д.
Для сокращения записи различных операций над скалярными
и векторными величинами употребляется дифференциальный опе-
ратор Гамильтона (оператор набла).
§ 385. Дифференциальный оператор Гамильтона (оператор набла).
Под оператором набла понимают сумму частных производных по
трем координатным осям, умноженных на соответствующие единич-
ные векторы (орты). В декартовой системе координат он запи-
шется так:
д
I —
дх
ду dz
Формально его можно рассматривать как вектор. Оператор наб-
ла может быть применен к скалярным и векторным функциям. Та
функция, действие над которой хотят произвести (дифференцирова-
ние ее по координатам или, другими словами, «пространственное»
дифференцирование), пишется справа от оператора набла. Если же
справа от него не указана эта функция, то сам по себе оператор наб-
ла не употребляется. Здесь можно провести аналогию с хорошо из-
вестными понятиями каких-либо других функций. Так, например,
если написано sin а, то совершенно ясно, что речь идет о синусе
угла а, т. е. о совершении определенной операции (нахождении си-
нуса) угла а. Если же было бы написано sin и после значка sin у и л
отсутствовал, то такая запись была бы лишена смысла.
Применим оператор v к потенциалу <р. С этой целью запишем
539
Если сравнить последнее выражение с (13.7), то можно заметить,
что правые части у них одинаковы. Следовательно, равны и левые.
Поэтому
grad ф = уф.
Другими словами, запись эквивалентна записи gradcp, а «при-
писывание» слева к какой-либо скалярной функции (в нашем слу-
чае к ф) оператора означает взятие градиента от этой скалярной
функции.
§ 386. Выражение градиента потенциала в цилиндрической и сфе-
рической системах координат. В цилиндрической системе (обозна-
чения см. на рис. 400, а):
Рис. 401
Рис. 400
В сферической системе (обозначения см. на рис. 400, б):
ёгабф = /?0-^4-Т°— L_ (13.10)
dR R dfJ Rsinfi да
§ 387. Поток вектора через элемент поверхности и поток век-
тора через поверхность. Пусть в векторном поле (например, в
поле вектора напряженности электрического поля Е) есть некото-
рый элемент поверхности, площадь его с одной стороны численно
равна ds. Выберем положительное направление нормали (перпен-
дикуляра) к элементу поверхности; Вектор ds в некотором масш-
табе на рис. 401 равен площади элемента поверхности, а его нап-
равление совпадает с положительным направлением нормали. Будем
считать, что площадь элемента достаточно мала, чтобы в пределах
этого элемента вектор Е можно было считать одним и тем же во
всех точках.
Если бы Е было перпендикулярно ds, то вектор Е не пронизы-
вал бы элемент поверхности; если Е будет направлено по ds, то
через данный элемент поверхности будет максимальный поток век-
540
тора Е. В общем случае поток вектора Е через элемент поверх-
ности ds определится скалярным произведением Е ds.
Произведение Е ds является величиной скалярной. Следователь-
но, поток вектора через элемент поверхности есть величина ска-
лярная. Поток вектора может оказаться положительным или отри-
цательным. Если скалярное произведение Е ds окажется положи-
тельным, то это будет означать, что поток вектора направлен в сто-
рону ds. Отрицательное значение потока вектора означает, что он
направлен в обратную сторону.
Если поверхность, через которую ищется поток вектора, велика,
то тогда уже нельзя считать, что во всех точках ее Е одна и та же.
В этом случае поверхность подразделяется на отдельные элементы
малых размеров, и полный поток вектора через поверхность будет
равняться алгебраической сумме потоков через все элементы
поверхности. Сумма потоков может быть записана в виде интеграла
J Е ds.
S
Значок s под знаком интеграла означает, что суммирование про-
изводится по элементам поверхности.
Если поверхность, через которую ищется поток вектора, замк-
нутая, то это обстоятельство находит свое выражение в том, что на
знаке интеграла ставится кружок:
Е ds.
§ 388. Свободные и связанные заряды. Поляризация вещества.
Свободными зарядами называют заряды, которые под воздействием
сил поля могут свободно перемещаться в веществе, их перемещение
не ограничивается внутримолекулярными силами.
Под связанными зарядами принято понимать электрические за-
ряды, входящие в состав вещества и удерживаемые в определенных
положениях внутримолекулярными силами. Такие заряды «связа-
ны» с данным веществом, неотделимы от него. Сумма положитель-
ных связанных зарядов равна сумме отрицательных связанных за-
рядов.
Если какое-либо диэлектрическое тело поместить в электриче-
ское поле, то оно поляризуется.
Под поляризацией понимают упорядоченное изменение располо-
жения связанных зарядов в теле, вызванное электрическим полем.
Это изменение расположения проявляется в том, что отрицательные
связанные заряды в теле переместятся в направлении более высо-
кого потенциала, а положительные связанные заряды переместят-
511
ся в сторону более низкого потенциала. Заряды сместятся настоль-
ко, что силы воздействия электрического поля на связанные заряды
уравновесятся внутримолекулярными силами. В результате поля-
ризации на поверхности вещества как бы обнажаются связанные
заряды.
§ 389. Вектор поляризации. Электрическим моментом двух рав-
ных по величине и противоположных по знаку зарядов, находящих-
ся друг от друга на расстоянии / (диполя), называют произведение
ql. Это векторная величина, направленная от заряда — q к заряду
+ q (рис. 402, с).
В поляризованном веществе молекулы в электрическом отноше-
нии представляют собой диполи. Под действием внешнего электри-
ческого поля диполи стремятся ориентироваться в пространстве
таким образом, чтобы электрический мсмент их был направлен па-
раллельно вектору напряженности электрического поля. Практи-
ческий интерес представляет электрический момент не одной моле-
кулы, не одной пары зарядов, а суммы диполей, находящихся в
единице объема вещества. Электрический момент суммы диполей, на-
ходящихся в единице объема вещества, называют вектором поля-
ризации и обозначают буквой Р
~Р=Л^-. (13.11)
Для большинства диэлектриков Р пропорционален напряжен-
ности электрического поля Е. Коэффициент пропорциональности
между ними обозначают обычно через k и называют электрической
восприимчивостью
~P = kE. (13.12)
542
Все диэлектрики в отношении происходящих в них процессов
при поляризации могут быть разбиты на 2 группы.
В первую группу входят диэлектрики, молекулы которых при
отсутствии внешнего электрического поля электрически нейтраль-
ны, т. е. в них центры действия положительных и отрицательных
зарядов совпадают. К числу таких диэлектриков относятся водород,
азот, парафин, слюда и др.
Поляризация в диэлектриках первой группы состоит в том, что
под действием внешнего электрического поля центр действия поло-
жительного заряда молекулы сместится по внешнему полю, а центр
Iя группа
Е--0 E/D
2 я группа
Е=0 Е*0
Рис. 403
действия отрицательных зарядов сместится против поля. В резуль-
тате молекула становится диполем.
Это смещение зарядов молекулы пропорционально величине
напряженности внешнего поля. Смещению противодействуют внут-
римолекулярные силы.
Во вторую группу диэлектриков входят диэлектрики, молеку-
лы которых при отсутствии внешнего электрического поля пред-
ставляют собой диполи. Другими словами, центры действия поло-
жительных и отрицательных зарядов этих молекул при отсутствии
внешнего электрического поля не совпадают (полярные молекулы).
В качестве диэлектрика с полярными молекулами может бьнь
назван, например, хлористый водород.
Благодаря тепловому движению диполи располагаются хаотич-
но, так что при отсутствии внешнего электрического поля их элект-
рические поля взаимно нейтрализуются.
Поляризация в диэлектриках второй группы состоит в том, что
полярные молекулы стремятся повернуться таким образом, чтобы
их электрический момент был направлен по внешнему электричес-
кому полю.
Поляризация диэлектриков первой группы иллюстрируется рис.
403, а и б и поляризация диэлектриков второй группы рис. 403, виг.
Рис. 403, айв соответствуют случаю, когда внешнее поле от-
сутствует. Рис. 403, биг при наличии внешнего поля.
543
§ 390. Вектор электрической индукции D. Кроме двух вектор
ных величин Е и Р, имеющих рассмотренный выше физический
смысл, в электротехнические расчеты вводят еще вектор D.
Вектор D называется вектором электрической индукции или
вектором электрического смещения. Он следующим образом вы-
ражается через векторы Е и Р:
D=^ + P.
Так как
Р = £Е = е0Е—, (13.13)
ч
то 3 = евЕ(1 + —'j = %егЕ= ^Е, (13.14)
е = е0 е/, er = 1 -j- — • (13.15)
Со
Коэффициент в, называют относительной электрической про-
ницаемостью*. Он показывает, во сколько раз электрическая про-
ницаемость вещества (в) больше, чем электрическая постоянная (е0),
характеризующая электрические свойства вакуума; ег величина без-
размерная.
В Международной системе единиц «СИ» [D] = [Р] = к/м2. Од-
ной из важнейших теорем электростатики является теорема Гаусса.
§ 391. Теорема Гаусса в интегральной форме. Поток вектора элект-
рического смещения через любую замкнутую поверхность, окружа-
ющую некоторый объем, равен алгебраической сумме свободных за-
рядов, находящихся внутри этой поверхности:
(13.16)
S
Так как D—eoer Е, то теорема Гаусса для однородной и изо-
тропной среды может быть записана и в такой форме
&Eds = - Чс^- , (13.17)
J Ео Ег
т. е. поток вектора напряженности электрического поля сквозь
любую замкнутую поверхность равен сумме свободных зарядов,
находящихся внутри этой поверхности, поделенной на произве-
дение е0Е,,.
Обе формы записи находят себе применение. Существенно под-
черкнуть, что поток вектора зависит лишь от суммы зарядов и не
* ъг называют также диэлектрической проницаемостью.
544
/и*,
зависит от расположения зарядов внутри замкнутой поверхнос^аю-
Существует еще одна форма записи теоремы Гаусса, отли^1^
щаяся от (13.17).
-* УЮ
Дело в том, что поток вектора Е через любую замкну1 ),
поверхность создается не только суммой свободных зарядов (2 Я^^по-
но и суммой связанных зарядов (2 Ясвяз)> находящихся внутри
верхности. ЗОЗЬ
Из курса физики известно, что поток вектора поляризации скР' ком
любую замкнутую поверхность равен взятой с обратным знаР^ури
алгебраической сумме связанных зарядов, находящихся вну9'
этой поверхности
V, с (а)
/ । Ясвяз ' (j) T’tfS.
рлот-
Напомним вывод формулы (а). С этой целью сначала покажем, что Пп'<1ект-
ность поверхностных связанных зарядов на грани поляризованного диэ/1
рика и вакуума равна модулю вектора поляризации. д ди-
На рис. 402, б изображено расположение диполей в поляризоваиномм,рзаи-
электрике длиной L, сечением s. На торцах диэлектрика образуются свЯ^е L'
ные заряды. Поверхностную плотность их обозначим через о. На длин^^руга.
положительные и отрицательные заряды взаимно компенсируют друг дрР как
Поэтому поляризованный диэлектрик рис. 402, б можно рассматривать ’
диполь длины L с сосредоточенными на концах зарядами os. х^'гРи"
Электрический момент всего диэлектрика длиной L равен osL. Элек*
ческий момент единицы объема диэлектрика равен
„ osL osL
Р= — = — = о.
V sL
лиого
Таким образом, плотность связанных зарядов на торцах поляризованную,
диэлектрика равна модулю вектора поляризации Р (вектор Р перпеидик’Чюжи-
рен торцам). Обратимся к рис. 402, в. На нем изображен свободный пол<|С1а.
тельный заряд, вызвавший поляризацию окружающего его диэлектрик^иные
Окружим заряд сферой и подсчитаем нескомпенсированные связа^^аря-
ааряды, попавшие внутрь сферы. Нескомпенсированными связанными з^'
дами оказываются заряды диполей, пересекаемых поверхностью s.
Так как поверхностная плотность их равна о, то
2<7«>яз= — § cds = —j Pds.
..иных
Знак минус появился вследствие того, что знак нескомпенсировагта)2, в),
связанных зарядов противоположен знаку свободного заряда (см. рис. 40.
----------- .Л3.17)
* Забегая вперед, отметим, что теорема Гаусса (формула 13.16 или 15%х ус-
примеиима не только к электростатическому полю, но при определенный
ловиях и к переменному электромагнитному полю. ^овии,
К переменному электромагнитному полю она применима при усло®,:я иа-
что расстояние от заряда, создающего поле, до точки, в которой ищется"долны
пряженность, должно быть много меньше длины электромагнитной вб'с'
(подробнее см. § 481). поле
Распространил теорему Гаусса иа переменное электромагнитное , Одному
Д. Максвелл. В честь последнего теорему Гаусса в применении к переменил Л. 1)
электромагнитному полю в литературе называют иногда (см. например,
постулатом Максвелла.
545
Поэтому формулу (13.16) можно переписать следующим образом
фо ds = ф ( е0Е-|-Р jds = еоф Е ds ф- фр ds = £ясвоб.
Следовательно,
®О ф У Чсвоб фр ds \ t Qceog ф" У Ясвяз
или
(f) Е d7= -<?C80g+--^^3. (13.17')
J *0
Формулы (13.17) и (13.17') отличаются своими правыми частями.
Теорема Гаусса в интегральной форме с большой эффективностью
и простотой может быть использована для нахождения напряжен-
ности или электрического смещения в какой-либо точке поля, если
через эту точку может быть проведена замкнутая поверхность та-
ким образом, что все эти точки этой поверхности будут в одинако-
вых (симметричных) условиях по отношению к заряду, находяще-
муся внутри замкнутой поверхности.
Такой поверхностью является обычно сфера (если заряд точеч-
ный) или боковая поверхность цилиндра (если заряд «линейный»).
При этом в силу симметричного расположения всех точек поверх-
ности относительно заряда численное значение напряженности поля
в различных точках этой поверхности будет одинаковым.
§ 392. Применение теоремы Гаусса для определения напряжен-
ности и потенциала в поле точечного заряда. В качестве примера ис-
пользования теоремы Гаусса найдем напряженность поля, создава-
емую точечным зарядом в точке, удаленной на расстоянии R от
центра заряда. С этой целью проводим через заданную точку сфе-
рическую поверхность радиуса R, полагая, что заряд находится в
центре сферы, и применяем к этой сфере теорему Гаусса (рис. 403, д).
Элемент поверхности сферы ds перпендикулярен к поверхнос-
ти сферы* и направлен в сторону внешней (по отношению к объему
внутри поверхности) нормали.
В данном примере в каждой точке сферы Е и ds совпадают по
направлению. Угол между ними равен нулю. Если учесть, что чис-
ленное значение Е во всех точках сферы одно и то же, то Е
может быть вынесено из под интеграла:
Eds = E
ds = Е 4л/?2 =
4
Wr
* Имеется в виду вектор, изображающий собой элемент поверхности
сферы.
546
Следовательно, напряженность, создаваемая точечным зарядом
q на расстоянии 7? от него, определится следующим образом
Е=------?___(13.18)
В силу сферической симметрии напряженность поля имеет только
одну R-ю составляющую в сферической системе координат. Следо-
вательно,
E = Er = . dR dR
Отсюда <p = -{EdR = -—q- hC. (13.19)
Таким образом, потенциал в поле точечного заряда обратно пропор-
ционален первой степени расстояния R от точечного заряда до точ-
ки, в которой определяется потенциал; С представляет собой пос-
тоянную интегрирования, с точностью до которой определяется по-
тенциал. Напомним, что аналогичные выражения для Е и«р были
получены в § 382 путем использования закона Кулона.
§ 393. Теорема Гаусса в дифференциальной форме. Теорема Гаус-
са была записана в интегральной форме. Интегральная форма дава-
ла связь между потоком вектора Е через поверхность s, ограничи-
вающую некоторый объем, и алгебраической суммой зарядов, нахо-
дящихся внутри этого объема. Интегральная форма не дает ответа
на вопрос, как связан исток линий D в данной точке поля с плот-
ностью свободных зарядов в той же точке поля. Ответ на этот вопрос
дает дифференциальная форма теоремы Гаусса. Чтобы прийти к ней,
поделим обе части уравнения (13.16) на одну и ту же скалярную ве-
личину — на объем V, находящийся внутри замкнутой поверх-
ности s:
$ D ds _ ^Чсеоб
V ~ V *
Последнее выражение остается справедливым для объема V лю-
бой величины. Устремим объем к нулю:
$ D ds .. ^Ясвоб
В m ------= 11 m------•
v-»o V у-»о V
При стремлении объема к нулю D ds также стремится к ну-
лю, но отношение двух бесконечно малых величин ф D ds и V есть
547
величина конечная*. Предел отношения потока векторной величины
D сквозь замкнутую поверхность, ограничивающую некоторый объем
к объему V называют дивергенцией вектора D (div D). Часто вмес-
то термина дивергенция употребляют ему эквивалентный термин
расхождение или исток вектора D.
В правой части последнего выражения находится объемная
плотность свободного заряда, ее обозначают рсвоЛ
Таким образом, теорема Гаусса в дифференциальной форме
записывается следующим образом:
div D — рееоб, (13.20)
div^<0
Рис. 404
т. е. исток линий D в данной точке поля определяется величиной
плотности свободных зарядов в этой точке. Если объемная плотность
зарядов в данной точке положительна (рсеоб > 0), то из бесконечно
малого объема, окружающего данную точку поля, линии вектора
D исходят (исток положителен, рис. 404, а). Если в данной точке
поля pfeO5<0, то в бесконечно малый объем, внутри которого
находится данная точка, линии вектора D входят. И, наконец, если
в какой-либо точке поля рсвоб = 0, то в данной точке поля нет ни
истока, ни стока линий D, т. е. в данной точке линии вектора D
не начинаются и не заканчиваются.
* В третьей части курса ТОЭ неоднократно приходится пользоваться
величинами, которые определяются при стремлении рассматриваемого объ-
ема или площади к нулю.
Необходимо заметить, что стремление к нулю не следует понимать дос-
ловно: речь идет лишь о таком уменьшении линейных размеров объема или
площадки, при котором еще не сказывается дискретность материи.
148
Если среда однородна и изотропна, то ее е = const, и потому
вместо (13.20) можно записать следующее выражение
dive£ = Pceod.
Вынесем е за знак дивергенции
е divE = рсв0(5,
следовательно,
div£ = P^. (13.21)
е
Это есть вторая форма записи теоремы Гаусса в дифференциаль-
ном виде. Она справедлива только для однородной и изотропной
среды. Для неоднородной среды е является функцией координат,
и потому е не может быть вынесена за знак дивергенции.
Уравнение (13.17') в дифференциальной форме запишется так:
divE = PCTog + Pc«”3 . (13.21')
во
Следовательно, истоком вектора Е, в отличие от истока векто-
• У
ра D, являются не только свободные, но и связанные заряды.
В различных системах координат div Е раскрывается различно.
§ 394*. Вывод выражения для div Е в декартовой системе ко-
ординат. Выделим в пространстве весьма малый параллелепипед с
ребрами dx, dy, dz. Расположим ребра параллелепипеда параллель-
но осям декартовой системы (рис. 404, б). Для нахождения истока
вектора Е из данного объема составим разность потоков, вытека-
ющих из объема и втекающих в него, и поделим разность потоков
на величину объема параллелепипеда, равную dx dy dz.
Левую грань площадью dx dz пронизывает только одна соста-
вляющая вектора Е, а именно составляющая / Еу, остальные соста-
вляющие (i Ех и k Ег) скользят по грани. Поток вектора Е, вхо-
дящий в эту грань, равен Eydxdz.
Так как Е есть функция координат, то и ее составляющие так-
же есть функции координат. Правая грань площадью dx dz отстоит
от левой грани на расстоянии dy. Проекция вектора Е на ось у для
нее равна Еу -|- dy.
* Что означает звездочка у номера данного и некоторых других параг-
рафов III части курса, пояснено в предисловии на стр. 3.
549
Здесь есть скорость изменения Е в направлении оси у;
ду
<77 dy есть приращение «игрековой» составляющей напряженности
ду
поля на пути dy.
Поток, выходящий из правой грани площадью dxdz, равен
Ev аХ(}г
ду I
дЕ
Исток через грани площадью dxdz равен —^-dxdydz.
ду
Таким же путем получим разность потоков через грани dydz
дЕх , , .
—-dxdydz.
дх
Разность потоков через грани dxdy (верхнюю и нижнюю стенки
объема): ^-dxdy dz.
Для нахождения divE сложим разности потоков через все
грани и поделим на объем параллелепипеда dxdydz, получим
divE = ^-4-^ + ^. (13.22)
дх ду дг
§ 395. Использование оператора набла для записи операции
взятия дивергенции. Ранее было показано, что умножение опера-
тора V на скалярную функцию равносильно взятию градиента от
этой скалярной функции. Покажем, что скалярное умножение
оператора V на векторную функцию, например на функцию Е,
означает взятие дивергенции от этой векторной функции.
Произведение VE может быть записано так:
X Ё = { 71 + 7 f + 7 | \ (7Ех + 7 Еу + k Егу =
\ дх ду дг / 7
= (13.23)
дх ду dz
Правые части (13.22) и (13.23) равны друг другу, следователь-
но, должны быть равны и левые части их. Поэтому
VE = divE,
* Почленно умножаем слагаемые первой скобки на слагаемые второй
скобки. Учитываем, что скалярное произведение одноименных ортов равно
единице, а скалярное произведение разноименных ортов равно нулю:
И = / / = kk — 1
ij = ik = jk = 1 • 1 •
1 . cosO°= 1,
cos 90° = 0,
550
т. е. действительно, умножение оператора v на вектор Е означает
взятие дивергенции от этого вектора.
• * >
§ 396. Выражение div Е в цилиндрической и сферической системах коор-
—>
динат. Без вывода запишем выражение div £ в цилиндрической системе коор-
динат:
-» 1 д 1 дЕа дЕг
div Е = - - (гЕг) + - + —2
г дг г да dz
(1324)
и в сферической системе координат-
div~E = — — [R2E J
R2 dR \ я/
1 d
R sin в d6
sin 0 Efl +--------——
° / R sin 6
0Еа
да
(13.25)
§ 397. Уравнение Пуассона и уравнение Лапласа. Уравнения
Пуассона и Лапласа являются основными уравнениями электроста-
тики. Они вытекают из теоремы Гаусса в дифференциальной форме.
Действительно, известно, что Е — — grad <р. В то же время соглас-
но теореме Гаусса
div£ = Рг?°Д. (13.21)
в
Подставим в (13.21) Е из (13.6). Получим
div Е = div (— grad <р) = —
Вынесем минус за знак дивергенции
div grad <р — —
Вместо того, чтобы писать gradcp, запишем его эквивалент у?Ф-
Вместо div напишем у. Тогда
V(V(f) = -Pf (13.26')
или
— (13.26)
Уравнение (13.26) называется уравнением Пуассона. Частный
вид уравнения Пуассона, когда pfeo(? = 0, называется уравнением
Лапласа. Уравнение Лапласа запишется так:
V2T = 0. (13.27)
Оператор у?2 — div grad называют оператором Лапласа или лапла-
сианом и иногда обозначают еще символом Д. Поэтому можно встре-
тить иногда и такую форму записи уравнения Пуассона:
Д<р = _ Рсвоб'
е
551
Раскроем у2ф в Декартовой системе координат. С этой целью
произведение двух множителей v и V<p запишем в развернутом
виде
v(v )== (Т£+7 *+
’ \ дх ду дг/ \ дх ду дг ]
Произведем почленное умножение и получим
V<P ck2"' ду2' дг2'
Таким образом, уравнение Пуассона в декартовой системе коор-
динат запишется следующим образом:
^2Ф । дЛФ । ^2Ф _Рсвоб / ] з 28)
дх2 ду'2 дг2 е
Уравнение Лапласа в декартовой системе координат
^_1_?Ф_1_^ = 0. (13.29)
дх2 ду2 дг2
*
* *
Приведем без вывода выражения у2<р в цилиндрической системе
координат
гДр = -И/гЁ1 (13.30)
v т г дг\ дг ]' г2 да2 ' дг2’
в сферической системе координат
= — ~ ------—-(sin 0^4---------(13.31)
v) R2 dR\ dR j R2 sin 6 0Э \ 09 I R2 sin2 0 da2
*
* *
Уравнение Пуассона дает связь между частными производными вто-
рого порядка от <р в любой точке поля и объемной плотностью сво-
бодных зарядов в этой точке поля. В то же время потенциалф в ка-
кой-либо точке поля зависит, разумеется, от всех зарядов, создаю-
щих поле, а не только от величины свободного заряда, находяще-
гося в данной точке.
Уравнение Лапласа (1780) первоначально было применено для
описания потенциальных полей небесной механики и впоследствии
было использовано для описания электрических полей. Уравнение
Пуассона применяется к исследованию потенциальных полей (элек-
трических и магнитных) с 1820 г.
Рассмотрим вопрос о том, как в общем виде может быть записано
решение уравнения Пуассона.
552
Пусть в объеме V есть объемные (р), поверхностные (о) и линей-
ные (т) заряды. Эти заряды представим в виде совокупностей точеч-
ных зарядов pdV, о ds, rd!; dV—элемент объема, ds —элемент за-
ряженной поверхности, dl — элемент длины заряженной оси. Со-
ставляющая потенциала dtp в некоторой точке пространства, уда-
ленной от р dV на расстояние R, в соответствии с формулой (13.19)
равна
pdV
4 ле/?
Составляющие потенциала от поверхностного и линейного за-
рядов, рассматривая их как точечные, определим аналогичным
образом:
с ds т dl
и -•
4ле/?--------------------------------4ле7?
Полное значение <р определим как сумму (интеграл) составля-
ющих потенциала от всех зарядов в поле:
Ф = _L_ С _1_ _LC2^_. (13.31')
4ле J R 4ле J 7? 4ле J R
V s /
В формуле (13.3Г) р, о и т есть функции радиуса /?. Практичес-
ки формулой (13.3Г) пользуются редко, так как распределение о
по поверхности, т по длине и р по объему сложным образом зави-
сит от конфигурации электродов и, как правило, перед проведением
расчета неизвестно; иначе говоря, интегрирование произвести затруд-
нительно, так как обычно неизвестно, как р, о и т зависят от ра-
диуса ₽.
§ 398. Граничные условия. Под граничными условиями понимают
условия, которым подчиняется поле на границах раздела сред с
различными электрическими свойствами.
При изучении раздела «переходные процессы» исключительно
большое значение имел вопрос о начальных условиях и о законах
коммутации. Начальные условия и законы коммутации позволяли
определить постоянные интегрирования при решении задач класси-
ческим методом. В классическом методе они использовались в яв-
ном виде, в операторном методе — в скрытом. Без использования
их нельзя решить ни одной задачи на переходные процессы.
Можно провести параллель между ролью граничных условий в
электрическом (или в любом другом) поле и ролью начальных ус-
ловий и законов коммутации при переходных процессах.
При интегрировании уравнения Лапласа (или Пуассона) в
решение войдут постоянные интегрирования. Их и определяют, ис-
ходя из граничных условий. Прежде чем перейти к подробному об-
суждению граничных условий, рассмотрим вопрос о поле внутри
проводящего тела в условиях электростатики.
§ 399. О поле внутри проводящего тела в условиях электростати-
ки. Пусть какое-либо проводящее тело находится в электростати-
553
ческом поле. Тело может быть заряжено, т. е. ему извне дан неко-
торый заряд, может быть и не заряжено. Рассмотрим эти два слу-
чая отдельно.
Если тело не заряжено, то естественно, что суммарный заряд
тела равен нулю. Так как тело помещено в поле, то вследствие яв-
ления электростатической индукции в нем произойдет разделение
зарядов. В результате этого разделения на поверхности тела, обра-
щенной в сторону более высокого потенциала (см. рис. 405), высту-
пят отрицательные заряды и на противоположной стороне — поло-
жительные заряды. Хотя сумма зарядов тела и будет равна нулю,
но заряды, выступившие на поверхности тела, окажут существен-
ное влияние на поле вне проводящего тела и на
» поле внутри проводящего тела. В области вне
f \ тела, в особенности вблизи от него, поле может
\_____ существенно исказиться по сравнению с тем по-
лем, которое было бы, если проводящее тело в
поле отсУтствовало-
Все точки проводящего тела в условиях
у электростатики имеют один и тот же потенциал.
1» В этом можно убедиться, исходя из противного.
Если допустить, что в условиях электростатики
между двумя точками проводящего тела может
Рис. 405 быть разность потенциалов, то тогда под дейст-
вием этой разности потенциалов электроны в те-
ле начали бы перемещаться. Упорядоченное движение зарядов в
теле противоречило бы самому определению электростатического по-
ля, как поля, созданного неподвижными зарядами (в макроскопи-
ческом смысле слова).
Так как все точки проводящего тела имеют один и тот же потен-
циал, то между двумя любыми бесконечно близко расположенны-
ми друг к другу точками приращение потенциала равно нулю, следо-
вательно, и Е = —— и® тоже равно нулю. Физически напряженность
дп
роля внутри проводящего тела равна нулю (в макроскопическом
смысле слова) потому, что напряженность от внешнего поля компен-
сируется равной ей по величине и противоположной по знаку нап-
ряженностью от зарядов, расположившихся на поверхности тела.
Если тело будет заряжено, то все принесенные извне на тело за-
ряды и заряды, разделившиеся в теле вследствие явления электро-
статической индукции, также расположатся на поверхности тела
таким образом, что потенциал всех точек будет один и тот же, а
напряженность внутри тела будет равна нулю.
§ 400. Условия на границе раздела проводящего тела и диэлект-
рика. На границе проводящее тело — диэлектрик всегда выполня-
ются два условия: 1) отсутствует тангенциальная (касательная к
поверхности) составляющая напряженности поля:
554
(13.32)
и 2) вектор электрического смещения D в любой точке диэлектрика,
непосредственно примыкающей к поверхности проводящего тела,
численно равен плотности заряда о на поверхности проводящего
тела в этой точке, т. е.
(13.33)
D = о.
Рассмотрим первое условие. Все точки поверхности проводящего
тела имеют один и тот же потенциал. Следовательно, между двумя
любыми весьма близко расположенными друг к другу точками по-
верхности приращение потенциала dtp = 0, но dtp — Etdl,
следовательно, Efdl = 0.
Так как элемент пути dl между течками на поверхности не ра-
вен нулю, то равно нулю Et.
Для доказательства второго условия мысленно выделим беско-
нечно малый параллелепипед (рис. 406). Верхняя грань его парал-
лельна поверхности проводящего те-
ла и расположена в диэлектрике. К __
Нижняя грань находится в прово- | ds
дящем теле. Высоту параллелепипе- Диэпектрик f
да возьмем весьма малой (сплющим
его). Применим к параллелепипеду ’’п^оВящее
теорему Гаусса. В силу малости ли- тело.бнемЕ^О
нейных размеров можно принять,
что плотность заряда о на поверхно- ис’
сти ds проводящего тела, попавшей
внутрь параллелепипеда, одна и та же. Полный заряд внутри
рассматриваемого объема равен о ds.
Поток вектора D через верхнюю грань объема равен Dds = D ds.
Потока вектора D через боковые грани объема в силу малости
последнего и в силу того, что вектор D скользит по ним, нет. Че-
рез «дно» объема поток также отсутствует, так как внутри про-
водящего тела Е = 0 и 0 = 0 (е проводящего тела есть величина
конечная). Таким образом, поток вектора D из объема равен D ds = о ds
или D — о.
§ 401. Условия на грани раздела двух диэлектриков с различными
электрическими проницаемостями. На грани раздела двух диэлект-
риков выполняются два следующих условия:
1. Равны тангенциальные составляющие напряженности поля
(13.34)
2. Равны нормальные составляющие электрической индукции
(13.35)
555
Индекс 1 относится к первому диэлектрику, индекс 2 — ко вто-
рому.
Первое условие вытекает из того, что в потенциальном поле
(р?// = 0 по любому замкнутому контуру. Второе условие пред-
ставляет собой следствие теоремы Гаусса. Покажем справедливость
первого условия. С этой целью выделим плоский замкнутый контур
mnpqm (рис. 407) и составим вдоль него циркуляцию вектора нап-
ряженности электрического поля. Верхняя сторона контура распо-
ложена в диэлектрике с электрической проницаемостью е2, ниж-
няя — в диэлектрике с ег Длину стороны тп, равную длине сто-
Рис. 407
роны pq, обозначим dl. Контур возьмем так, что размеры пр и qm
бесконечно малы по сравнению с dl. Поэтому составляющими ин-
теграла <§> Е dl вдоль вертикальных сторон в силу их малости
пренебрежем.
Составляющая § Е dl на пути тп равна E2dl2— E2(dl, по пути
pq E1dl1= — Eltdl.
Знак минус появился как следствие того, что элемент длины
на пути pq и касательная составляющая вектора Ег направлены
в противоположные стороны (cos 180° — — 1).
Таким образом, Е dl = E2tdl — Eltdl = 0 или Еи — £2/.
Убедимся в справедливости второго условия.
С этой целью на грани раздела двух сред выделим очень малых
размеров параллелепипед (рис. 408). Внутри выделенного объема
есть связанные заряды и нет свободных (случай наличия свобод-
ных зарядов на грани раздела рассмотрим отдельно), поэтому
(|)D ds = 0.
Поток вектора D через верхнюю грань площадью ds равен
Z)2 ds2 — Din ds. Поток через нижнюю грань Djdsj^ cos 180° =
= — Dlnds;
|dsx) = |ds2 ] = ds.
556
Следовательно,
ф D ds = — Dln ds -j~ D2tl ds = О или
Dln ~
При наличии на грани раздела двух сред свободных зарядов с
плотностью о (это встречается весьма редко)
D ds= D2n ds — ds — о ds,
т. e. при этом
D2„-Dln = o. (13.36)
Другими словами, при наличии на грани раздела двух сред сво-
бодных зарядов нормальная составляющая вектора D скачком из-
меняется на величину плотности свободных зарядов на грани раз-
дела.
Потенциал есть работа (см. стр. 534). На границе раздела
двух сред потенциал не претерпевает скачков.
§ 402. Теорема единственности решения. Электростатическое по-
ле описывается уравнением Лапласа (или Пуассона). Последнее
является уравнением в частных производных. Уравнения в частных
производных в отличие от обыкновенных дифференциальных урав-
нений допускают в общем случае множество линейно независи-
мых друг от друга решений. Естественно, что в любой кон-
кретной практической задаче есть одна единственная картина поля,
т. е. одно единственное решение. Из множества линейно независи-
мых решений, допускаемых уравнением Лапласа — Пуассона, вы-
бор одного единственного, удовлетворяющего конкретной задаче,
производится при помощи граничных условий*.
Если есть некоторая функция, удовлетворяющая уравнению
Лапласа — Пуассона и граничным условиям в данном поле, то
эта функция и представляет собой то едш ственное решение, кото-
рое ищется. В этом состоит смысл важного положения, которое при-
нято называть теоремой единственности решения**.
§ 403. Общая характеристика задач электростатики и методов
их решения. В зависимости от того, что задано и что определяется,
задачи электростатики могут быть разделены на следующие три
типа задач.
Задача первого типа: по заданному закону распределения по-
тенциала в пространстве ср (х, у, г) найти распределение свободных
зарядов, вызвавших поле. Такого рода задачи могут быть решены
при помощи уравнения Пуассона. Это наиболее простой тип
задач; —в данной точке поля, согласно уравнению Пуассона, * * § **
* Каким образом путем использования граничных условий производит-
ся отбор нужных и отсев «лишних» решений уравнения Лапласа, показано в
§ 417 и § 418.
** Доказательство ее см., например в (Л. 4).
557
равняется сумме частных производных второго порядка от <р, в
которую подставляются координаты данной точки поля.
Одна из задач первого типа рассмотрена в примере 189*.
Задача второго типа: задан закон распределения свободных
зарядов в пространству в функции координат ревоб(х, у, z). Найти
закон изменения потенциала в пространстве <рсвоб(х, у, г). Эта
задача является обратной к первой и значительно сложнее ее.
Принципиально задача состоит в решении уравнения Пуассона
относительно <р, т. е. в решении дифференциального уравнения
второго порядка в частных производных.
В примерах 184—187 рассмотрено несколько задач второго типа.
Задачи первого и второго типов практически встречаются редко.
В подавляющем большинстве приходится иметь дело с задачами
третьего типа.
Задача третьего типа: известны потенциалы (или полные заря-
ды) и геометрия тел, создающих поле. Требуется найти закон из-
менения Е или <р во всех точках поля.
Несколько задач третьего типа рассмотрено в § 416—419 и в при-
мерах 177, 182, 183.
Если среда, в которой создано поле, является неоднородной, то
она подразделяется на однородные области и решение уравнения
Лапласа производится для каждой области в отдельности. Основ-
ная трудность задачи состоит в том, что хотя полные заряды тел и
известны, но с какой плотностью на отдельных участках заряжен-
ного тела распределены заряды неизвестно. Решения уравнения
Лапласа для отдельных областей должны быть согласованы друг
с другом: на границе раздела двух сред с различными е должны вы-
полняться граничные условия. На грани раздела проводящего тела
и диэлектрика также должны выполняться свои граничные условия.
Задачи, отнесенные к группе задач третьего типа, могут быть
решены аналитическим или графическим путями, либо путем элект-
ромоделирования.
В данном параграфе дадим этим методам (путям решения) лишь
краткую характеристику с тем, чтобы читатель составил некоторое
предварительное впечатление о тех методах, с которыми ему при-
дется иметь дело. Более обстоятельное изложение этих методов бу-
дет дано в дальнейшем на конкретных примерах.
В самых простейших случаях задачи на аналитический расчет
полей решаются путем использования теоремы Гаусса в интеграль-
* Близкой к задачам первого типа является задача,в которой известно
выражение для потенциала <р как функции координат и требуется найти рас-
пределение поверхностных или линейных зарядов, создающих поле, когда
объемные заряды в поле отсутствуют. Если заряды расположены на поверх-
ностях проводящих тел, то в соответствии с формулой (13.33) плотность заря-
да о — е,ЕП, где Е„= — —. Индекс л обозначает направление, нормальное
к поверхности тела.
558
ной форме (§ 391). В более сложных случаях аналитическое реше-
ние задач третьей группы производится путем решения уравне-
ния Лапласа.
Аналитические методы решения задач третьей группы могут
быть подразделены на две подгруппы. В первой из них производит-
ся интегрирование уравнения Лапласа без использования вспомо-
гательных (искусственных) приемов. Во второй подгруппе задача
решается путем использования искусственного приема — метода
зеркальных изображений. По методу зеркальных изображений ре-
шение производится путем введения вспомогательного заряда или
зарядов, которые в расчетном отношении заменяют связанные за-
ряды, выявившиеся на границах тел или сред в результате
их поляризации или в результате электростатической индук-
ции (§ 409—412).
В тех случаях, когда1 потенциал <р является функцией только од-
ной координаты выбранной системы координат, уравнение Лапласа
из уравнения в частных производных переходит в обыкновенное
дифференциальное уравнение второго порядка, которое интегри-
руется без затруднений (примеры 182—184).
Если же потенциал <р является функцией двух или трех коор-
динат то для того, чтобы проинтегрировать уравнение Лапласа,
в этом случае путем применения метода Фурье — Бернулли следует
перейти от уравнения в частных производных к равносильной ему
совокупности двух или, соответственно, трех обыкновенных диф-
ференциальных уравнений (§ 416).
Графический метод анализа и расчета задач третьей группы
представляет собой метод, в котором по определенным правилам
производится построение семейств силовых и эквипотенциальных
линий путем использования некоторых заранее известных свойств
исследуемого поля. Эти правила практически одни и те же для всех
неизменных во времени полей, т. е. для электростатического поля,
электрического поля постоянного тока в проводящей среде (глава
четырнадцатая) и для магнитного поля постоянного тока (глава
пятнадцатая). В силу того, что графический метод решения наибо-
лее часто применяется для анализа магнитных полей, он рассмат-
ривается не в данной главе, а в главе магнитное поле постоянного
тока (§ 456).
Анализ и расчет электростатических полей методом моделирова-
ния основывается на использовании аналогии между электростати-
ческим полем и электрическим полем постоянного тока в проводя-
щей среде.
Метод моделирования основан на том, что каждой задаче элект-
ростатики может быть сопоставлена сходная задача на электрическое
поле постоянного тока в проводящей среде, в которой совокупность
силовых и эквипотенциальных линий практически такая же, что и
в электростатической задаче.
Это обстоятельство дает возможность перенести результаты эк-
559
спериментального исследования поля в проводящей среде на родст-
венную электростатическую задачу. Подробно об этом говорится
в главе четырнадцатой (§ 429—431). Следует заметить, что при рас-
четах полей широко применяется метод наложения.
В заключение отметим, что в задачах электростатики расчет
может производиться либо с целью определения «точечной» ха-
рактеристики поля (напряженности или потенциала в заданной точ-
ке), либо с целью определения интегральной характеристики дан-
него поля, например емкости или
разности потенциалов.
Перейдем к рассмотрению неко-
торых простейших электростати-
ческих задач.
§ 404. Поле заряженной оси.
Под заряженной осью понимают
весьма тонкий теоретически бес-
конечно длинный металлический
проводник (тонкая проволока). За-
Рис. 409
ряд на единицу длины ее принято
обозначать через т. Электрическая проницаемость среды, окружаю-
щей ось, равна е. Для нахождения напряженности поля в некоторой
точке, удаленной на расстоянии г от оси (рис. 409), проведем через
эту точку цилиндрическую поверхность так, что ось цилиндрической
поверхности совпадет с заряженной осью. *
Применим теорему Гаусса. Теорема Гаусса применима к замкну-
той поверхности. В нашем случае последняя образована боковой
поверхностью цилиндра и двумя его донышками. Поток вектора
Е имеется только через боковую поверхность цилиндра. Через до-
нышки поток вектора Е отсутствует, так как элемент поверхности
ds каждого донышка перпендикулярен Е.
Элементы ds боковой поверхности и напряженность электри-
ческого поля Е в любой точке цилиндрической поверхности по
направлению совпадают, поэтому
Е • 2лг 1 = — или Е = --------.
е 2леГ
(13.37)
Напряженность в поле заряженной оси изменяется обратно про-
порционально расстоянию г точки от оси.
Потенциал
<р = — f Edr — — Г —— dr --— In г -4- С =
J J 2лег 2ле
= i'"y+c- <13-38»
Потенциал изменяется по логарифмическому закону.
560
§ 405. Поле двух параллельных заряженных осей. Пусть одна ось
имеет заряд 4- т на единицу длины, другая — заряд — т. Возь-
мем в поле некоторую произвольную точку М (рис. 410). Резуль-
тирующая напряженность поля в ней Ем равна геометрической сум-
ме напряженностей от обоих зарядов. Расстояние точки М до поло-
жительно заряженной оси обозначим через а, до отрицательно заря-
женной оси — через Ь. Потенциал есть функция скалярная. По-
тенциал точки М
= + —1п- + С= -^1п- + С.
2ле а 2ле Ъ 2ле
(13.39)
а
Уравнением эквипотенцнали в поле двух заряженных осей будет
являться выражение — = const.
а
Эквипотенциаль будет представлять собой совокупность точек,
отношение расстояний которых до двух заданных точек есть вели-
чина постоянная.
В геометрии известна теоре-
ма Аполлония. Согласно теореме f" Р
Аполлония геометрическим мес- ”
том точек, отношение расстояний /
которых до двух заданных точек / //Vx
есть величина постоянная, является / /яЧ
окружность. Поэтому эквипотен- £<<----£-—Z—1——.С^—
циаль в поле двух заряженных осей V г
есть окружность. Рассмотрим, как \ J
можно построить ее. Соединим точ- У
ку М с осями. Проведем биссект- ---------
рисы внутреннего (аМЬ) и внешне- рис 4щ
го (рМа) углов. Точки 1 и 2 пере-
сечения биссектрис с линией, про-
веденной через заряженные оси, и точка М будут являться тремя
точками искомой окружности.
Для нахождения положения центра окружности (точки О) раз-
делим пополам расстояние между точками 1 и 2.
§ 406. Поле двухпроводной линии. Расстояние между осями двух
проводов линии (рис. 411) обозначим через d, радиус каждого про-
вода— через г. Если левому проводу будет сообщен, например,
заряд т на единицу длины, а правому заряд — т, то в пространстве
между проводами возникнет электрическое поле. Заряды проводов
распределятся по поверхности с неодинаковой плотностью.
Поверхность каждого провода в отдельности будет являться эк-
випотенциалью. Внутри проводов Е = 0. Задача о поле двухпро-
водной линии сводится к только что рассмотренной задаче о поле
двух заряженных осей. Расположим две заряженных оси так, чтобы
поверхности проводов являлись эквипотенциальными.
19 Л. А. Бессонов
561
Точки Oj и О2 означают геометрические оси проводов. Заряжен-
ные оси пусть будут расположены в точках т и п. Из условия сим-
метрии они на одинаковое расстояние х удалены от геометрических
осей.
Запишем условие равенства потенциалов точек / и 2 левого про-
гу b , d — г — х
вода. Отношение — для точки 1 есть не что иное, как-------;
а г — х
b п d + г — х
отношение — для точки 2 равно —!.
а г -|- х
Из равенства
d — г — х_d -|- г — х
г — х r-р х
получим
Х==|±/(|-)2-'-2- <13-40)
В последнем выражении знак минус перед радикалом соответ-
ствует положению точки п, знак плюс — точке т.
d
Рис. 411
Вместо подсчетов по формуле (13.40) положение заряженных осей
(часто их называют электрическими осями проводов) находят путем
следующих графических построений.
Проводят общую касательную к проводам (прямая pq), делят
расстояние между точками касания пополам (точка s) и проводят
окружность радиуса ps. Точки пересечения (т и п) окружности с ли-
нией OjO2 дают положения электрических осей, т. е. таких осей,
на которых надо было бы мысленно сосредоточить заряды проводов,
чтобы поверхности проводов являлись эквипотенциалями. Так как
поле от двух заряженных осей вне проводов удовлетворяет уравне-
нию Лапласа и в то же время удовлетворяются граничные условия
(поверхность каждого провода является эквипотенциалью, на ней
Et = 0), то на основании теоремы единственности полученное реше-
ние является истинным.
562
Нетрудно убедиться в том, что если d г, то х становится много
меньше г. При этом электрические и геометрические оси практически
совпадают.
§ 407. Емкость. Если два каких-либо проводника разделены ди-
электриком и несут на себе равные по величине и противоположные
по знаку заряды Q, то в пространстве между ними создается элект-
рическое поле. Пусть разность потенциалов между телами равна U.
Под емкостью С между двумя телами, на которых имеются рав-
ные и противоположные по знаку заряды, принято принимать абсо-
лютную величину отношения заряда на одном из тел к напряжению
между телами U
С = ^. (13.41)
Из определения емкости следует единица ее размерности 1-=
вольт
= 1 фарада (ф). Это очень крупная единица, и потому на практике
пользуются более мелкими кратными ей единицами: микрофарадой
(мкф) и пикофарадой (пф):
1 мкф = 10-е ф,
1 пф = КГ12 ф.
Устройства, предназначенные для получения определенной вели-
чины емкости, называюткснденсаторами. Однако не следует думать,
что емкостью обладают только специально для ее получения соз-
данные устройства. Емкостью обладают всякие два проводящих тела,
разделенных диэлектриком*.
Так как напряжение между двумя телами в электростатическом
поле может быть линейно выражено через заряд Q (исключение сос-
тавляют только устройства, в которых используются сегнетодиэлек-
трики — вещества, у которых е является функцией Е), то отноше-
Q
ние — оказывается независящим ни от величины и, ни от вели-
U
чины U.
Емкость зависит только от конфигурации тел, их размеров, от
расстояния между телами, от электрических свойств диэлектрика
(величины е). В качестве примера рассмотрим определение емкости
двухпроводной линии.
§ 408. Емкость двухпроводной линии. Выразим напряжение меж-
ду двумя проводами через заряд т на единицу длины. Точка 1 (рис.
411) принадлежит поверхности левого провода, точка <3 — поверх-
ности правого провода. Разность потенциалов между ними
* В литературе также можно встретить термин — емкость уединенного
тела. Под ней понимают отношение заряда на этом теле к его потенциалу,
полагая, что второе тело удалено в бесконечность и что потенциал его равен
нулю.
19*
563
r. т , d — г — x т , г -
U1, = ок —= — In-------------------------— In---------
13 v3 2ле Г—Х 2lte d —
При d^r х<?г, поэтому
f/13 = -L • 2- ln- = -In-. (13.42)
2ju r ns r
Следовательно, емкость единицы длины линии при условии d г
определится следующим образом
С = — = (13.43)
1/13 1п-
Она действительно зависит только от геометрических размеров
и от свойств среды и не зависит от величины заряда г и от величины
напряжения L/1?. Если расстояние между двумя проводами увели-
чивать, то емкость будет уменьшаться.
§ 409. Метод зеркальных изображений. Для расчета электроста-
тических полей, в особенности ограниченных какой-либо прово-
дящей поверхностью правильной формы или в которых есть геомет-
рически правильной формы граница между двумя диэлектриками,
широко применяется расчетный прием, который называют методом
зеркальных изображений.
Это искусственный прием расчета. В нем кроме заданных заря-
дов вводят еще дополнительные заряды, величины и местоположе-
ние которых выбирают так, чтобы удовлетворить граничным усло-
виям в поле. Если граница между двумя средами плоская, то допол-
нительные («фиктивные») заряды помещают территориально там,
где находятся зеркальные (в геометрическом смысле) отображения
заданных зарядов. Метод зеркальных изображений широко приме-
няется не только для расчета электростатических полей. Он приме-
няется также для расчета электрических полей в проводящей среде
и магнитных полей. Обоснованием метода, обоснованием правиль-
ности даваемого им решения, является теорема единственности.
Рассмотрим два примера на метод зеркальных изображений.
§ 410. Поле заряженной оси, расположенной вблизи проводящей
плоскости. Заряженная ось (т — заряд на единицу длины) распо-
ложена параллельно поверхности проводящей среды (рис. 412, а).
Проводящей средой может быть какая-либо металлическая стенка
или, например, земля. Требуется определить характер поля в верх-
ней полуплоскости (диэлектрике).
Вследствие явления электростатической индукции на поверх-
ности проводящего тела выступают заряды. Плотность их меняется
с изменением координаты х. Поле в диэлектрике создается не толь-
ко заряженной осью, но и зарядами, выступившими на поверхности
проводящего тела вследствие электростатической индукции. Не-
смотря на то, что распределение плотности зарядов на поверхности
564
неизвестно, данная задача сравнительно легко может быть решена
по методу зеркальных изображений.
Поместим в точке т фиктивный заряд обратного знака ( — т) по
отношению к заданному заряду т. Расстояние h от точки т до плос-
кости раздела сред такое же, что и расстояние от действительного
заряда до плоскости раздела. В этом смысле осуществлено зеркаль-
ное изображение. В данной задаче фиктивный заряд численно ра-
вен заданному, но имеет обратный знак. Так будет не всегда, т. е.
не во всех задачах искусственно введенный заряд будет численно
равен заданному и иметь противоположный знак.
Убедимся, что напряженность поля от двух зарядов (т и — т)
в любой точке границы раздела имеет только нормальную к граница
Рис. 412
составляющую и не имеет тангенциальной составляющей. Действи-
тельно, тангенциальные составляющие от обоих зарядов имеют про-
тивоположные направления и в сумме дают нуль в любой точке
поверхности.
Можно убедиться в том, что потенциал от каждой из осей, опре-
деляемый формулой (13.38), удовлетворяет уравнению Лапласа (фор-
муле 13.30). Для того чтобы проверить это, следует подставить пра-
вую часть формулы (13.38) в формулу (13.30) и убедиться в том, что
\72ф будет равно нулю
1£ГгЛ(Д_1п1У1 = о.
г дг ( дг \ 2ле г ] J
Так как потенциал от каждой из осей удовлетворяет уравнению
Лапласа и в то же время удовлетворено граничное условие, то на ос-
новании теоремы единственности полученное решение есть истин-
ное.
Картина поля заряженной оси, расположенной параллельно
проводящей плоскости, изображена на рис. 412, б. Силовые линии
перпендикулярны поверхности провода и поверхности проводящей
565
плоскости. Значки минус на поверхности проводящей плоскости обо-
значают отрицательные заряды, выявившиеся на ее поверхности
в результате электростатической индукции.
§ 411. Поле заряженной оси, расположенной вблизи плоской гра-
ницы раздела двух диэлектриков с различными электрическими про-
ницаемостями. Верхнее полупространство заполнено диэлектри-
ком с электрической проницаемостью е1( нижнее — диэлектриком
с е2 (рис. 413, о); ab —грань раздела двух сред. Вследствие поля-
ризации диэлектриков на грани раздела выявятся связанные за-
ряды. Связанные заряды будут влиять на поле в обеих средах.
Учет влияния связанных зарядов на поле производится путем вве-
дения двух дополнительных фиктивных зарядов т2 и т3. В отличие
Рис. 413
от предыдущей задачи в данной вводятся не один заряд, а два. При-
чина этого в том, что в предыдущей задаче надо было фактически
удовлетворить только одному условию (£z = 0) и это можно было
сделать при помощи одного заряда. В данной же задаче надо удов-
летворить не одному, а двум граничным условиям. Удовлетворить
двум условиям можно только при помощи двух неизвестных.
Расчет поля в любой точке верхнего полупространства произво-
дится от двух зарядов: заданного тт и дополнительного т2, причем
не только верхнее, но и нижнее полу пространство заполнено (в рас-
четном смысле) диэлектриком с электрической проницаемостью е,
(рис. 413, б).
Поле в любой точке нижнего полупространства определится как
поле от некоторого дополнительного заряда т3, расположенного
в той же точке, где находится заряд Тр В этом случае не только
нижнее, но и верхнее полупространство заполняется диэлектриком
с электрической проницаемостью е2 (рис. 413, в).
Составим два уравнения для определения неизвестных пока
т2 И т3.
566
Из условия равенства тангенциальных составляющих напряжен-
ности поля на границе раздела следует, что
или
~~ fri + т2]cos а — —— тч cos а.
2nejr 1 2яг2г '
Отсюда
Т1 + Т2 = Т3—• (13.44)
Из условия равенства нормальных составляющих вектора D на гра-
ни раздела, приняв за положительное направление для нормали
направление вниз, имеем
£>' — D11 = Г»'11.
п п п
Запишем последнюю строку в развернутом виде:
— (т, — т9) sin а = — т„ sin а.
2ят 1 27 2яг 3
Следовательно,
тг — т2 = т3. (13.45)
Совместное решение (13.44) и (13.45) дает
^=—^1 (13.46)
Е1 + е2
И
т3=-^-тг. (13.47)
Знак т2 совпадает со знаком заряда т,, если е, > е2. Знак т3
всегда тот же, что и знак tv
Если поле будет создаваться не заряженной осью, а точечным
зарядом, то вся методика сохраняется, и формулы (13.46) и (13.47)
годятся и для точечных зарядов. Но под т теперь следует понимать
величину точечного заряда.
§ 412. Электростатическое поле системы заряженных тел, рас-
положенных вблизи проводящей плоскости. В качестве системы за-
ряженных тел рассмотрим многопроводную линию из п весьма длин-
ных проводов с зарядом т/; на единицу длины (индекс у заряда соот-
ветствует номеру провода), протянутых параллельно поверхности
земли*. Высота подвеса и радиус каждого провода известны. Извест-
ны также электрическая проницаемость е среды, окружающей про-
вода.
* В более общем случае параллельно поверхности любой проводящей
среды.
567
Возьмем в диэлектрике некоторую произвольную точку М (рис.
414) и найдем потенциал ее. Потенциал точки М будет равен сумме
потенциалов, создаваемых каждым проводом и его зеркальным изоб-
ражением. Составляющая потенциала точки М от провода 1 и его
зеркального изображения
в соответствии с формулой (13.39) запи-
шется следующим образом (посто-
янную, с точностью до которой оп-
ределяется потенциал, опускаем):
4^1 = T^-ln^,
2ле а1м
где Ь1м есть расстояние точки М
до зеркального изображения пер-
вого провода, а1м есть расстояние
точки М до первого провода.
Будем полагать, что высоты под-
веса проводов над землей много
больше радиусов проводов. При
этом электрические оси практиче-
ски совпадут с геометрическими.
Составляющая потенциала точ-
ки М от второго провода и его
зеркального изображения
Фиг=Тг Л In—
Таким
образом,
Фл< = Фл<1 + Фл<2 + <Р„а + ••• =т1-1-1п^4-
2яе а1м
4-Т ’ ln^ + т ’ 1п^+ ...
Потенциальные коэффициенты. Первая группа формул
§ 413. Потенциальные коэффициенты. Первая группа формул
Максвелла. Точка М может быть помещена на поверхность первого
провода. При этом <рм = Ф1; bMl = 2/ip а1м = гр Ьм2 =Ь12 — расстоя-
ние первого провода до зеркального изображ-ения второго провода,
ам2 — а12 — расстояние первого провода до второго провода и т. д.1
Ф1 — In —+ т2-^-In —ts-^-ln —-ф- ...
Г £ ^12 2jTE ^13
Коэффициенты при зарядах тг, т2 и др. зависят только
от геометрических размеров тел, взаимного их расположения и от
свойств среды. Они не зависят ни от величины, ни от знака зарядов
и потенциалов.
Для сокращения записи последнюю строчку и другие аналогич-
ные ей запишем следующим образом:
568
Ф1 = *1аП + Т2«12 + Тза13 + > • •
Фг = + т2а22 4- т3а234- ...
<Рз = Т1аз1 + Тгаз2 + тзазз + ...
(13.48)
Здесь
«Атн =
— Jn^,
2ле akm
akk —
1 i 2Л*
--In—.
2ле rk
(13.48')
Коэффициент . Так как bmk=-bkm и amk = акт,
akm
то aftm = итк. Систему уравнений (13.48) принято называть первой
группой формул Максвелла (ее не следует смешивать с первым
уравнением Максвелла, о котором идет речь в § 460).
Коэффициенты а называют потенциальными коэффициентами.
Размерность их равна размерности единицы длины, поделенной
на фараду.
Так как у всех коэффициентов а под знаком логарифма стоит
дробь, числитель которой всегда больше знаменателя, то все коэф-
фициенты а положительны.
Коэффициентам а может быть дано следующее толкование: пусть
заряды всех проводов, кроме первого, равны нулю
т2 = т3 = г4 = ... =0, а тг= 1.
Тогда ф! = au, т. е. au численно равно потенциалу первого про-
вода, если на первом проводе находится единичный заряд, а заряды
на остальных проводах отсутствуют. Аналогично а21 численно рав-
но потенциалу второго провода в тех же условиях. Система (13.48)
позволяет подсчитать потенциалы заряженных тел по известным об-
щим зарядам тел.
Может встретиться и обратная задача: по известным потенциа-
лам тел найти общие заряды тел.
§ 414. Емкостные коэффициенты. Вторая группа формул Максвел-
ла. Решим систему (13.48) относительно зарядов, полагая потенциа-
лы ф и коэффициенты а известными:
Т4 — Р11Ф1 4~ Р12Ф2 4“ Р1зФз 4“ • • •
т2 = Р21Ф14- Р22Ф2 4- РгзФз 4- • • •
тз = Рз1Ф14- Р32Ф2 + РззФз 4- • • •
(13.49)
Коэффициенты Здесь через Д обозначен определитель сис-
569
темы (13.48)
А =
а11 И12 а13 • • •
И21 а22 °23 • • •
(Х3| a32 a33 • • •
Алгебраическое дополнение Aftn получается из определителя системы
А путем вычеркивания k строки и п столбца и умножения таким
путем полученного определителя на (—
Система (13.49) является второй группой формул Максвелла.
Коэффициенты Р называют емкостными коэффициентами. Размер-
ность их обратна размерности коэффициента а. Так как определи-
тель системы А симметричен относительно главной диагонали, то
Aftn = А,Л, и потому = pnft. Все р с одинаковыми индексами по-
ложительны, все р с разными индексами отрицательны.
о)
Рис. 415
Убедимся, например, в том, что Ри положительно, а Р21, Р31
отрицательны. С этой целью проделаем такой опыт: все провода,
кроме первого, соединим тонкими (чтобы не искажать поля) про-
водниками с землей. Потенциал земли примем равным нулю. При
этом из (13.49) следует, что
*1 = Р11<Р1>
Т2 = Рг1Ф1>
Т3 = Рз1Ф1‘ .
(13.49)
Придадим первому проводу положительный по отношению кземле
потенциал, соединив его с землей, например через батарею (рис.
415, а). Заряд первого провода положителен и потенциал первого про-
вода положителен (tpr > 0; > 0). Отрицательный заряд растечет-
ся по земле и по всем телам, с ней электрически соединенными. Все
провода, кроме первого, поскольку они электрически соединены
с землей, приобретут отрицательные заряды
ф2 = 0 т2 0,
Фз = 0 Т3 < °.
570
Из системы (13.49') следует, что ₽и = — > 0, а ₽21 = — < 0 и
<₽1 <Р1
Ч>1
Коэффициенты и PW; могут быть определены и опытным
путем. Рассмотрим как определить коэффициенты Рп и Р22.
Если после зарядки провода 1 (ключ /< на рис. 415, а включен)
до известного потенциала <рх ключ Д' разомкнуть, убрать батарею,
включить гальванометры Gx и G2 (рис. 415, б) и затем замкнуть
ключ Д’, то система разрядится; измерит заряд G2 измер it
заряд т2. Далее находим ₽и = — и Р21 — —.
<Pi <Р1
§ 415. * Частичные емкости. Третья группа формул Максвелла.
Систему (13.49) принято записывать еще и в иной форме, а именно
так, чтобы в каждой строчке справа были не потенциалы, а разнос-
ти потенциалов между данным телом и всеми остальными, в том
числе и землей.
В соответствии с (13.49) заряд k тела равен
^k Рд&Ф/г ""Н 1 Р^тФ/тГ
m— 1
m^k
Слагаемое
Pft/пФт Pfem (ф/п Фб Н” Ф&) ^km^ km ”1“ Р&тФк*
Поэтому
т=п т=п т=п т^п
ФаР/У? 4~ Фл । Pfcm I km ~ Ф/г > $km X РапЗ km'
т-^\ m-l т-1 т=|
m+k m*k m=kk
Обозначим
т=п
Ckk = Pftl + ₽*2 +••+₽*•*+•• • + Р/гл — (13.50)
т-1
с.т =—в. . (13.51)
km v^km ' '
Тогда
т=п
rk= <pftGw4-GftlCA.14-t/fr2Cft2+ ... = ф*Сл*+GftmCAm. (13.52)
m=l
m^k
Если придать k значения 1, 2, 3 ..., то получим
Ti = 4’1^11 + ^12^12 + ^13^13+ •••
Т2 — _Н ^2+21 + ^23^23 + • • •
(13.53)
571
Система (13.53) является третьей группой формул Максвелла.
Коэффициенты Ckk называют собственными частичными емкостями,
коэффициенты Скт — взаимные частичные емкости. Часто слова
«собственная» и «взаимная» опускают.
Так как
то И
С =С
^Ч:т mk*
Размерность частичных емкостей та же, что и размерность емкост-
ных коэффициентов р. Все частичные емкости положительны. Так
как С7ОТ=—a то, очевидно, что Cftm>0. Для
того чтобы убедиться в том, что Ckk положительно, проведем
следующий опыт: соединим тонкими металлическими проводниками
все провода с k проводом. Все Ukm = 0, и из (13.52) следует, что
т* =
Если k проводу сообщить положительный по отношению к зем-
ле потенциал (потенциал земли принят равным нулю), соединив
его с плюсом батареи, минус которой соединен с землей, то tk и
Фл будут положительными и отношение их
«Р*
Ckk оказывается положительной, несмотря на то, что в состав ее
(см. формулу 13.50) может входить большое число отрицательных
т~п
коэффициентов Р/гт (коэффициент Р/;/г больше, чем У, (3ftm). Соглас-
/п=1
т+Л
но (13.53) полный заряд k тела равен сумме зарядов. Заряд qkCkk
обусловлен разностью потенциалов между k телом и землей; UkmCkm
есть заряд, обусловленный разностью потенциалов между k и т
телами. Поэтому частичной емкости Ckm между k и т телами мож-
но дать следующее толкование: Скт есть отношение составляющей
заряда k тела, обусловленной разностью потенциалов Ukm между k
и т телами, к величине этой разности потенциалов.
Для более наглядной иллюстрации системы (13.53) можно пред-
ставить. что в системе трех проводов (рис. 416, а) первый провод
как бы соединен с обкладками трех конденсаторов СД, С12 и С13.
Заряды на обкладках этих конденсаторов, обращенных к проводу 1,
соответственно равны 4>iCu; 6\2С12; Д13С13. Заряды на других об-
кладках записаны на рис. 416, а.
Три группы формул Максвелла справедливы для системы заря-
женных тел любой формы, однако если тела имеют произвольную
форму, то потенциальные коэффициенты уже ле могут определяться
по формулам (13.48'), справедливым только для системы линейных
параллельных достаточно длинных проводов.
572
Определение емкостных коэффициентов и частичных емкостей
в этом случае производится опытным путем.
Частичные емкости используются при расчетах не только элек-
тростатических полей, они находят применение при расчетах быст-
ропротекающих процессов в электрических цепях, а также при рас-
четах таких процессов в электрических цепях, в основу которых по-
ложено использование частичных емкостей, например при емкост-
ном отборе мощности от высоковольтной линии электропередачи.
Частичные емкости между электродами электронных ламп, между
электродами полупроводниковых триодов учитывают при расчетах
быстропротекающих процессов.
§ 416*. Шар в равномерном поле. Если в равномерное поле*, нап-
ряженность которого равна Ео (см. рис. 416, б), внести металличес-
Рис. 416
кий или диэлектрический шар (е шара отлично от е окружающей сре-
ды), то электрическое поле, в особенности вблизи от шара, исказит-
ся, перестанет быть равномерным. Характер искажения поля зави-
сит от размеров шара, от его е и от величины заряда на шаре.
Если шар металлический, то силовые линии должны подходить
к его поверхности поД прямым углом. Если металлический шар не
заряжен, то на нем вследствие явления электростатической индук-
ции произойдет разделение зарядов. Силовые линии будут закан-
чиваться или начинаться на них.
Металлический шар может быть и заряжен, т. е. нести на себе
избыточный заряд, который также расположится на поверхности.
Если шар из диэлектрика, то под влиянием внешнего по отноше-
нию к нему поля шар поляризуется. Заряды, выявившиеся на шаре
вследствие поляризации, исказят прежде (до внесения шара) равно-
мерное поле. Силовые линии будут подходить к поверхности шара
так, что будут выполняться два граничных условия. (§ 401).
* Направлено сверху вниз (вдоль оси — г).
573
Эта задача является одной из наиболее типичных «классических»
задач. Если шар металлический, то внутри шара Е = 0 и ф = const.
Вне зависимости от того, металлический шар или диэлектрический,
во внешней по отношению к шару области нет свободных зарядов,
и потому поле в наружной по отношению к шару области описывает-
ся уравнением Лапласа.
Если шар из диэлектрика и свободный заряд на нем равен нулю,
то поле внутри шара описывается также уравнением Лапласа. Та-
ким образом, для решения той и другой задачи необходимо проин-
тегрировать уравнение Лапласа V2«p — 0. Любая конкретная задача
на интегрирование уравнения Лапласа в качестве первого этапа
предполагает правильный выбор системы координат. Система коор-
динат должна быть выбрана таким образом, чтобы граничные поверх-
ности в поле описывались наиболее удобным образом. В нашей за-
даче граничная поверхность — сфера. Сфера наиболее удобно опи-
сывается в сферической системе координат. Поэтому будем поль-
зоваться сферической системой координат.
Вторым этапом решения является выяснение вопроса о том, не
обладает ли изучаемое поле тем или иным видом симметрии. Усло-
вия симметрии поля часто в значительной мере облегчают решение
задачи. В рассматриваемой задаче поле не зависит от координаты а.
Чтобы убедиться в этом, поступим следующим образом. Мысленно
рассечем поле плоскостью, перпендикулярной оси Z декартовой сис-
темы, и проведем в этой плоскости окружность так, чтобы центр ее
лежал на оси Z. Все точки этой окружности имеют одно и то же зна-
чение радиуса R, соединяющего точку на этой окружности с началом
координат, и, кроме того, угол 0 в меридианной плоскости между
радиусом 7? и осью Z один и тот же.
Все точки окружности находятся в поле в одинаковых условиях.
Поэтому потенциал их один и тот же. Но значение угла а, характе-
ризующего положение точек этой окружности, различно. Если для
совокупности точек, обладающих 7? = const и 0 — const и различ-
ными значениями угла а, ф одно и то же, то это означает, что в дан-
ном поле ф не зависит от угла а. Поэтому поле будет описываться
уравнением (см. уравнение 13.31):
(т?2 -----’----- (sin 0^ = 0 (13.54)
R2 dR \ dR I R2 sin 6 50 \ 50 /
, 1 52<р „ ,,
(составляющая----------выпала, так как ф не зависит от а). Урав-
7?2sin2 0 5а2
нение (13.54) представляет собой уравнение в частных производных.
Для интегрирования уравнений в частных производных применяет-
ся метод Фурье — Бернулли. Согласно методу Фурье — Бернулли
решение для искомой функции (в нашем случае для ф) полагается
в виде произведения двух пока неизвестных функций М и 7V, одна
из которых (/И) зависит только от 7?, другая (Д') только от 0:
574
Ф = М (R) N (9) = MN. (13.55)
Вид функций М и 7V подлежит определению. Принятие решения в
виде произведения двух функций (13.55) позволяет разбить урав-
нение в частных производных (13.54) на два обыкновенных диффе-
ренциальных уравнения, из которых одно составлено будет относи-
тельно М, другое относительно Л/.
Подставим (13.55) в (13.54)
= д/ —. = м—
dR dR' дО д<) *
Поэтому
----± ( sin 9 —) = 0. (13.56)
R2dR\ dR j ' R2 sin 0 di \ d9J
D2
Умножим (13.56) на —
' ’ MN
t---1—±(sino =o. (13.57)
M dR \ OR ) 1 Wsin 0 аи di)
Особенностью уравнения (13.57) является то, что первое слагае-
мое в нем представляет собой функцию только R, а второе слагаемое
функцию только 9. Сумма двух функций, из которых одна зависит
только от R, а другая только от 0, равна нулю для бесчисленного
множества пар значений R и 9 [уравнение (13.57) годится для всех
точек поля]. Это может быть либо тогда, когда каждая из этих функ-
ций равна нулю
0 и—--------— f sin 6 —) = 0, (13.57')
MdR\ dR ) N sin 0 di \ 30 /
либо когда
1 d /dM \
--— = P
M dR \ dR
(13.57")
_____O_
N sin 0 30
Здесь p есть некоторое число, пока неизвестное.
Таким образом, задача свелась к интегрированию уравнений
(13.57') и (13.57"). Общее решение для фбудет равносогласно (13.55)
произведению решений уравнений (13.57') плюс произведение ре-
шений для М и Д' по уравнению (13.57"). Найдем решение уравне-
ний (13.57'). Так как в (13.57') М зависит только от R, а Д' только
от 9, то от частных производных можно перейти к простым:
1 d / n2 dM \ _g
М dR\ dR /
1 d I . r. dN \ n
---------Sin 9 — 1=0.
N sin 0 d& \ dO /
575
Интеграл первого из них
Найдем интеграл
М = -1 + д,.
второго уравнения
«in fl dN __ д . AN _ Л3
sin о — = /к, — =---------
dO dO sin 0
(13.58)
или
N = Aintg |- + A.
(13.59)
Покажем, что Л3 непременно должно равняться нулю, так как
только в этом случае в решении отсутствует слагаемое
A, In tg —.
2
Потенциал есть функция непрерывная и на конечном отрезке
он не может измениться на бесконечно большую величину. Из фи-
зических соображений ясно, что потенциал точек оси Z
вблизи шара не может быть равен бесконечности. Между тем,
если бы А3 =/= 0, то в выражении для потенциала присутство-
Л 1 L О
вало бы слагаемое А3 In tg — , которое равно — со для всех точек,
у которых 6 = 0 (tg 6 = 0; In tg 9 = — со).
0—0 при 0-0
Таким образом, частное решение для<р, вытекающее из (13.57'),
таково
<р = |’4-с2 (С^лл; с2 = а2а4). (13.60)
К
Найдем решение уравнений (13.57')
или
1 d / n! dM'
1 К —
MdR\ dR,
dM , d2M
dR dR2
= рМ.
CRn
2R
Применим подстановку Эйлера: М =
— = nCRn~!; — = п (п — 1) CR‘-2.
dR dR2
Подставим производные в уравнение
SRiiCR*-14- R2(n — 1) nCRn~2 = pCRn
или
n2 -ф- n — p = 0,
Решение квадратного уравнения
«1.2 =
2 ± рЧ' + Р-
(13.61)
576
Значение p определим при интегрировании второго уравнения
(13.57")
d . n dN
— Sin 9—
dO \ d6
1 d / • п dN\
N sin 0 dO \ d6 J
Решением его является выражение N = В cos 9. Убедимся в этом
путем подстановки и одновременно найдем значение р:
— ——В sin 9; sin 9— = — В sin2 9,
de de
1 d [ . dN\ —2Bsinficos6 o
---------Sin 9 — I = ---------------- = — 2 = — p.
N sin 0 db \ dO j В cos 0 sin в
Следовательно,
р = 2.
После нахождения числа р подставим его в (13 61) и найдем
Пу = 1 и — — 2.
Таким образом, совместное решение уравнений (13.57") дает сле-
дующее выражение для
Полное решение
(13.62)
В (13.62) присутствуют четыре неизвестных постоянных Clt С2,
С3 и С4. Значения постоянных зависят от того, какой шар (проводя-
щий или диэлектрический) внесен в поле*.
§ 417. Проводящий шар в равномерном поле. Для определения че-
тырех постоянных придется привлечь не только условие на поверх-
ности шара, но и условия на весьма большом удалении от шара,
теоретически на бесконечно большом удалении от шара или, как
принято говорить, «условия на бесконечности».
Совокупность весьма удаленных от шара точек в условном смыс-
ле рассматривается при этом как «бесконечность». Если шар будет
не заряжен, то все точки плоскости XOY, проходящей через центр
шара, имеют один и тот же потенциал. Обозначим его <р0.
При удалении от шара на большое расстояние Z = R cos 9, по
сравнению с которым радиус шара а весьма мал, возмущающее дей-
ствие шара на поле либо вовсе не проявится (если суммарный заряд
шара будет равен нулю), либо проявится как возмущение от точеч-
* Задачи теории поля, в которых приходится решать уравнения в частных
производных и из большого числа решений выбирать такие, которые удов-
летворяют граничным условиям, в математических работах принято назы-
вать краевыми задачами.
577
ного заряда (если шар будет иметь на себе суммарный свободный
заряд Q). И потенциал <р «на бесконечности» определится так:
Ф = + Фо + w cos9- (13.63)
Первое слагаемое правой части дает составляющую потенциала от
заряда шара Q, слагаемое E0R cos О учитывает прирост потенциала
от напряженности равномерного поля Ео на пути Z= 7? cos 9.
Так как решение (13.62) годится и для точек поля весьма далеко
(«бесконечно» далеко), удаленных от шара, то можно сопоставить
выражения (13.62) и (13.63). Они должны давать один и тот же ре-
зультат. Это будет только в том случае, когда соответствующие сла-
гаемые в обоих выражениях равны друг другу. Из сопоставления
следует, что
^2 ~ ф(р = ~г~ • С3 = Ей.
4ле
Сопоставление «на бесконечности» не дает возможности найти ве-
личину С4, так как в (13.63) нет слагаемого, изменяющегося обрат-
но пропорционально второй степени R. Для нахождения С, восполь-
зуемся тем, что в условиях электростатики все точки поверхности
шара имеют один и тот же потенциал, это условие равносильно тому,
что тангенциальная составляющая напряженности поля на поверх-
ности шара равна нулю. При R — а
Ф = const = -5- 4- I Еоа-\- cos 9Д- Фо.
4леа \ а2 ]
Очевидно, что правая часть будет постоянной при изменении
0 только при условии, что ( Еоа ) = 0. Отсюда
\ а2 /
С^-Е„а».
Таким образом, для всех точек диэлектрика
Ф = 7% + фо + Ео (Я —~Jc°s9.
\ R2/
(13.64)
Так как потенциал зависит только от R и 0, то напряженность
электрического поля имеет только две составляющих (см. стр. 540):
E6 = -
d<p
RdQ
ER = _*L = _2_
dR 4mR2
sin 9.
(13.64')
Если Q = 0, то на поверхности шара (при R = а)
Er = — 3E0cos9.
578
При 0 - О £л = — 3£с; при 0 = 18СГ ER = 3£0, т. е. в этих
точках напряженность поля стала в три раза больше напряженнос-
ти равномерного поля £0, в которое был внесен шар. На «экваторе»
при ( 6 = 90°) напряженность, напротив, стала равной нулю.
Таким образом, капелька воды, попав в бак трансформатора
с масляным заполнением, вызовет значительное местное увеличение
напряженности поля.
§ 418 *. Диэлектрический шар в равномерном поле. Если в равно-
мерное поле помещен незаряженный диэлектрический шар, то как
внутри шара, так и вне шара нет свободных зарядов и потому
поле описывается уравнением Лапласа. И общее решение (13.62)
годится и для данной задачи. Величинам, служащим для описания
поля внутри шара, «припишем» индекс i, а величины, при помощи
которых записывается потенциал во внешней по отношению к шару
области, снабдим индексом е. Таким образом, для «внутренней»
области
Ф/ = Cli + С2/ -j- ( C3tR + cosO.
А \ А /
Для «внешней» области
Ф« = + С2.+ ( C3eR + cos 0.
R \ R2 /
Н до найти 8 постоянных интегрирования.
Потенциал «на бесконечности» в этом случае
Ф = Фо + cos '*•
Сопоставляем последнее выражение с (13.66):
= Фо И С3е = Ео.
(13.65)
(13.66)
В § 392 было рассмотрено поле точечного заряда. Там было пока-
зано, что потенциал в поле точечного заряда изменяется обратно
Q
пропорционально R. Поэтому составляющая — есть не что иное,
как составляющая потенциала от суммарного заряда шара, рас-
сматриваемого как точечный заряд. Так как суммарный заряд ша-
ра равен нулю, то в выражении для <ре эта составляющая должна
выпасть. Другими словами,
С1е = 0.
Следовательно,
Ф£ = Фо+ (£<7?+§eVos0.
(13.66')
В последнем выражении осталась неизвестна лишь одна постоян-
ная Cte. Рассмотрим выражение потенциала <р; для внутренней
области. Оно должно давать конечное значение для всех точек
.579
внутри шара. Это может быть только тогда, когда Си — О
и С4/ = 0 (если бы Си ф 0, то слагаемое — в центре шара при
R
R — 0 давало бы бесконечно большое значение). Постоянная С2;,
с точностью до которой определяется потенциал в рассматривае-
мом поле, равна аналогичной постоянной С2е = <р0 для внешней
области.
Таким образом, для внутренней области
Ф( = Фо 4~ C3IR cose. (13.65')
Две оставшиеся неизвестными постоянные Cie и Csl найдем из
граничных условий.
Из равенства потенциалов <р( и <ре при R — а (это условие, как
нетрудно убедиться, эквивалентно условию Еи = E2t) следует, что
6^ = ^ + %
а2
Из равенства нормальных составляющих вектора D на границе
следует, что
_ Е /^Р<\ = —е
1 \ дЦ)к=а е \ dR J R=a
т. е.
Совместное решение двух последних уравнений дает
Потенциал внутренней области
Ф, = Ф0 + ^-^-со89 =Фо + Д0-^-г, (13.67)
2ее J- е, 2ее + ег
z = R cos 9.
Потенциал внешней области
Фг = Фо + £<1 (А? + cos 9.
е ° ° \ 1 R22ee + 4)
Напряженность поля внутри шара
g ___ __.
dz 2ее-|- ej
(13.68)
(13.69)
Е направлена вдоль оси г и не зависит от координат точки. Это оз-
начает, что поле внутри шара однородное.
На рис. 417 изображены линии вектора D и эквипотенциальные
линии («картина поля») для трех случаев:
580
а) когда в равномерное (до внесения шара) поле помещен неза-
ряженный проводящий шар;
б) когда в равномерное (до внесения шара) поле помещен диэлек-
трический шар, е; которого больше ге окружающей среды;
в) когда ez диэлектрического шара меньше окружающей среды.
Как известно из предыдущего (см. § 393 ), линии вектора D на-
чинаются на свободных зарядах. Эти линии прерываются на поверх-
ности металлического шара (рис. 417, а) и проходят, не прерываясь,
через диэлектрический шар (рис. 417, б и в).
Если на рис. 417, бив вместо линий вектора D изобразить ли-
нии вектора напряженности поля Е, то линии Е претерпевали бы
разрыв на поверхности шаров.
Рис. 417
Картина поля
при '
§ 419 *. Диэлектрический цилиндр в равномерном поле. Анало-
гичным образом выводятся формулы, позволяющие определить
потенциал и напряженность равномерного поля, возмущенного
внесением в него диэлектрического цилиндра (ось цилиндра пер-
пендикулярна Ес). ,
Пусть напряженность Ео равномерного (до внесения цилиндра)
поля направлена параллельно оси х декартовой системы (рис. 418, в).
Поместим в это поле диэлектрический цилиндр так, что ось ци-
линдра совпадет с осью г.
Путем решения уравнения Лапласа в цилиндрической системе
координат получим следующие формулы для определения потенциа-
ла внутри цилиндра (<pz) и вне цилиндра (<ре):
<р, =-----Ейг cos а =--------Еох, (13.70)
е»+Ее zi~F ее
Ю = Е f 4~~Eg- — — г Vos а. (13.71)
\ ei_l_ec г /
Напряженность равномерного поля внутри цилиндра направле-
на по оси х и равна
Е. = — Ео. (13.72)
4л
581
В заключение параграфа отметим, что если в равномерное поле
напряженностью Ео внести проводящий цилиндр, расположив его
так, что его продольная ось будет перпендикулярна £0, то потенциал
в области вне цилиндра
р / а2 \
= Ео I----r COS а.
§ 420. Понятие о плоскопараллельном, плоскомеридианном и рав-
номерном полях. В литературе можно встретить термины плоскопа-
раллельное поле, плоскомеридианное поле и равномерное поле*.
Под плоскопараллельным полем понимают поле, картина которого
(т. е. совокупность силовых и эквипотенциальных линий) повторяет-
ся во всех плоскостях, перпендикулярных какой-либо одной оси
декартовой системы координат.
Другими словами, в плоскопараллельном поле картина поля не
зависит от какой-то одной координаты декартовой системы.
В качестве примера плоскопараллельного поля может быть наз-
вано поле двухпроводной линии (двух заряженных проводов). Если
ось z декартовой системы направить вдоль оси одного из проводов,
то потенциал <р не будет зависеть от координаты z.
* Обратим внимание на то, что физики и математики в термин поле часто
вкладывают свое («профессиональное») содержание. Когда говорят о поле
в физическом смысле (электромагнитном, гравитационном, тепловом, поле
ядерных сил),то под ним понимают вид материи. Когда о поле говорится в ма-
тематическом смысле, то имеется в виду поле величины, которой оно описы-
вается. С чисто математической точки зрения поля могут быть векторные
и скалярные, вихревые и безвихревые, плоскопараллельные, плоскомеридиан
ные и др.
582
Под плоскомеридианным полем понимают поле, картина которо-
го повторяется во всех меридианных плоскостях, т. е. в плоскоме-
ридианном поле картина поля не зависит от координаты а цилиндри-
ческой или сферической системы координат. В литературе встре-
чается еще определение плоскомеридианного поля в иной форму-
лировке — как поля, образованного телами вращения с общей осью.
В качестве примера плоскомеридианного поля может быть наз-
вано поле, образованное внесением металлического шара в равно-
мерное до внесения шара поле (рис. 417) или поле диполя, о котором
идет речь в примере 192. В обоих этих случаях потенциал зависит
только от радиуса 7? и угла 0 сферической системы координат, но
не зависит от угла а.
Частным случаем плоскомеридианного поля является поле, в
котором потенциал зависит только от какой-либо одной координа-
ты сферической или цилиндрической систем координат.
В равномерном поле напряженность одинакова во всех точках
поля, т. е. величина ее не зависит от координат точки.
Равномерное поле образуется, например, между обкладками
плоского конденсатора, если в.пространстве между обкладками от-
сутствуют свободные заряды и если пренебречь искажающим влия-
нием краев конденсатора.
Следует иметь в виду, что весьма большое количество встречаю-
щихся на практике полей не обладает ни одним из перечисленных
выше видов симметрии, и потому не может быть отнесено ни к плос-
копараллельному, ни к плоскомеридианному, ни к равномерному
полям.
§ 421. Объемная плотность энергии электрического поля и выражение ме-
ханической силы в виде производной от энергии электрического поля по из-
меняющейся координате. Положим, что в некоторый момент времени напря-
жение на конденсаторе равно и. При увеличении напряжения на конденса-
торе на величину du заряд на одной из пластин конденсатора увеличится на
величину dQ, а на другой пластине на величину — dQ:
dQ = С du.
Здесь С — емкость конденсатора.
Для переноса заряда dQ источник энергии должен затратить работу, рав-
ную udQ = Cudu. Эта работа затрачивается на создание электрического по-
ля в конденсаторе.
Энергия, доставленная источником при заряде конденсатора от напря-
жения и = 0 до напряжения и = U и перешедшая в энергию электрического
поля конденсатора, равна
и
с си*
№э = С 1 и du = ——
о
Q2
2С'
Рассмотрим вопрос об объемной плотности энергии электрического поля.
С этой целью возьмем плоский конденсатор и положим, что расстояние меж-
ду пластинами его равно х, а площадь каждой пластины с одной стороны рав-
на S. Электрическая проницаемость среды между пластинами равна в. На-
'583
пряжение между пластинами U. Пренебрежем искажающим влиянием краев
конденсатора на поле между пластинами. При этом условии поле можно счи-
тать равномерным. Напряженность электрического поля Е по модулю равна
Е=Л.
CU2 eSU2
---- = ----— на
2 2х
объем
Q
Вектор электрической индукции по модулю равен D = еЕ — —Емкость
О
eS
плоского конденсатора С =------ . Для нахождения объемной плотности энер-
х
гни электрического поля разделим энергию =
V = Sx, «занятый полем». Получим
e.SU2 гЕ2 ЕР
Vr= 2Sx2 = 2 ~ 2
Таким образом, объемная плотность энергии электрического поля
еЕ2
-у . Если поле неравномерно, то напряженность будет изменяться при
ходе от одной точки поля к соседней, но объемная плотность энергии поля
еЕ2
будет по-прежнему равна —, так как в пределах бесконечно малого объема
поле можно считать равномерным.
Выделим в поле элементарный объем dV. Энергии в объеме dV равна
е.Е2
— dV.
2
Энергия, заключенная в объеме V любых размеров, равна
равна
пере-
V
В § 77 первой части курса ТОЭ рассматривался вопрос о выражении
механической силы, действующей на контур с током в магнитном поле, в ви-
де производной от энергии магнитного поля по изменяющейся координате.
В электрическом поле между заряженными телами также действуют ме-
ханические силы и их также можно выразить в виде производной от энергии
поля по изменяющейся координате. С целью рассмотрения этого вопроса об-
ратимся к рис. 418, а. На нем изображен плоский конденсатор, который при-
соединен к источнику напряжения U. В соответствии с предыдущим расстоя-
ние между пластинами назовем х, а площадь пластины S. На каждую пласти-
ну конденсатора действует сила Е. Под действием этих сил пластины кон-
денсатора стремятся сблизиться. Сила, действующая на нижнюю пластину,
направлена вверх, на верхнюю пластину — вниз.
Положим, что под действием силы Е нижняя пластина весьма медленно,
теоретически бесконечно медленно, переместилась вверх на расстояние dx
и приняла положение, показанное пунктиром на рис. 418, а.
Составим уравнения для баланса энергии при таком перемещении плас-
тины. На основании закона сохранения энергии, доставленная источником
питания энергия dWtl должна равняться сумме трех слагаемых:
1) работе силы Е на расстоянии dx : Fdx = Fdx.
2) изменению энергии электрического поля конденсатора dW3,
3) тепловым потерям от тока i, который протекает по проводам сопро-
тивлением R в течение времени от 0 до оо;
584
dWu = Fdx + dW3 + f Ri2 dt.
о
Так как по условию проведения эксперимента пластина конденсатора
перемещается вверх теоретически бесконечно медленно, то изменение заря-
дов на пластинах также происходит весьма медленно, а следовательно, и про-
ходящий через конденсатор ток смещения бесконечно мал.
оо
Другими словами, тепловыми потерями J Ri2 dt в силу их малости в
о
уравнении энергетического баланса можно пренебречь и тогда
dWu = Fdx + dW3.
Отсюда сила
d(Wu-W3)
F =---------— .
dx
Таким образом, силу F можно выразить в виде производной от разности
энергий (№„ — №3) по изменяющейся координате х.
В общем случае при перемещении пластины могут изменяться и напря-
жение между пластинами U и заряд Q.
Рассмотрим теперь два характерных частных случая перемещения плас-
тины конденсатора.
В первом из них конденсатор отсоединен от источника напряжения и пе-
ремещение пластины происходит при неизменных зарядах на пластинах.
Во втором случае перемещение пластины происходит при неизменном
напряжении между пластинами (конденсатор присоединен к источнику не-
изменного напряжения U).
П ервый случай. Так как конденсатор отсоединен от источника
энергии, то последний энергии не доставляет и потому dWu = 0, При этом
F — —-----_
dx
Таким образом, в этом случае сила, действующая на пластину, равна взя-
той с обратным знаком производной от энергии электрического поля конден-
сатора по изменяющейся координате. Знак минус свидетельствует о том, что
в рассматриваемом случае работа силы производится за счет убыли энергии
в электрическом поле конденсатора.
Если учесть, что энергия электрического поля конденсатора
то сила F по модулю равна
dW3 Q2 tE2S
IEI =—- = =.
1 1 dx 2eS 2
Второй случай. Энергия, доставляемая источником питания при
U = const, равна
dWu =~UdQ = U2 dC.
Здесь dC — приращение емкости, вызванное уменьшением расстояния
между пластинами на величину dx.
Изменение энергии электрического поля конденсатора
585
Разность
dWu — d\V3 = U2dC— — dC = -у- = dW3.
Поэтому во втором случае
dx 2 dx
Таким образом, и во втором случае сила равна производной от энергии
электрического поля по изменяющейся координате.
Емкость
потому
dC_ eS
dx х2'
1
| F | == — eS
2
Сила, действующая на пластину конденсатора во втором случае, в точ-
ности равна силе, действующей на пластину конденсатора в первом случае.
F
На единицу поверхности конденсатора действует сила -— . Эта сила рав-
О
еЕ2
на —.
2
e£2
Обратим внимание на то, что величина -^-выражает собой не только плот-
ность энергии электрического поля, но и численно равна силе, действующей
на единицу поверхности пластины конденсатора.
Действующие на пластины конденсатора силы можно рассматривать как
результат проявления сил продольного сжатия (вдоль силовых трубок) и сил
бокового распора (поперек силовых трубок). Силы продольного сжатия стре-
мятся укоротить силовую трубку, а силы бокового распора — расширить ее.
На единицу боковой поверхности силовой трубки действует сила; численно
tE2
равная —. Эти силы проявляются не только в виде сил, действующих на
пластины конденсатора. Они проявляются также на границе раздела двт х
диэлектриков. На границе раздела двух диэлектриков действует сила, направ-
ленная в сторону диэлектрика с меньшей электрической проницаемостью.
Примеры
Пример 177. Два провода диаметром 10 мм расположены парал-
лельно (рис. 418, б). Расстояние между осями проводов 20 мм. За-
ряд каждого провода на метр длины 10-8 к. Левый провод несет по-
ложительный заряд, правый — отрицательный. Найти наибольшую
и наименьшую плотности заряда на поверхности провода.
Решение. Находим положение электрических осей: х =
= 1,35 мм. Плотность заряда на поверхности металла о = D =
— гЕ. Следовательно, о будет больше там, где Е наибольшая.
586
Если учесть, что напряженность поля, создаваемая положитель-
ным зарядом, направлена от этого заряда, а напряженность поля,
создаваемая отрицательным зарядом, направлена к заряду, то ста-
нет ясно, что наибольшая напряженность поля будет в точке А,
наименьшая — в точке В. Напряженность поля в точке А
£___ Q_______I_________Q___
А 2ml(r—х) 2ml (D — г—х)'
а в точке В
Е _ Q f 1_______________1 \
В 2ml V + * D-\-r—x]
Напряженность поля в точке А равна сумме напряженностей от
обоих зарядов, а в точке В равна разности напряженностей.
Следовательно,
п с Ю-« I 1 । 1 \
л л А 2л-1 \0,005 — 0,00135 0,02—0,005—0,00135 ;
= 0,544 (мкк/м?),
п с 10-8 [ 1 1 \
“ 2л-1 \0,005+0,00135 0,02+0,005—0,00135 }
— 0,186 (мкк/'м2).
Таким образом, плотность заряда в точке А в 2,92 раза больше,
чем плотность заряда в точке В.
*
* *
По условию предыдущей задачи найти градиент потенциала в
точке М (расположенной посредине между проводами на линии,
соединяющей центры их).
Так какЕ = —gradcp, то модуль gradcp равен модулю Е, а на-
правление grad ср противоположно направлению Е. В точке М
Ем= _о_7—1_+—!_\ ==
2ml D ' D 2л • 8,86 - 10“12 • 1 • 0,00865
I----х — —х I
\2 2 /
= 41 600 в/м.
Направление Е и grad <р дано на рис. 418, б.
Пример 178. Определить частичные емкости на один метр длины
двухпроводной линии. Геометрические размеры (в метрах) см. на
рис. 419, а. Радиусы проводов 6 мм.
Решение. В соответствии с формулой (13.48)
а12^2>
— <^21^1 0-22^2'
587
Отсюда
<рх а12
_ q>2 «22 _ „ ®!2 1 ( «12 \
Ti—
или
Ti = Ф1Р11Ч- ФгРи-
Здесь
₽1 Р12 = -^; А= 011 012
Д Д а21 «22
Таким образом,
Т1 — Р11Ф1 Ч- Р12 (Фг Ф1 “Г Ф1) — ^i (Ри Ч- Р12)
Рис. 419
Д
2лг г 2л • 8,86 - 10“12
а22 “ ~ 1П
2ле
1 1 ^12
а12 = а21 = — 1п -1- =
2ле а12
«11 «12
«12 «22
Следовательно, для двухпроводной линии
Си = РиЧ-Р12 = ^^-, с12 = -₽12 = ^.
Аналогичным путем найдем С22 = Р2г Ч~ Р12= .
По формуле (13.48') найдем
а,, =------In — =-----------------In----• = 12,4 • 1010 (м ф),
q ое in—t2 g
= 12,9 - 1010 м!ф,
1-------1п — = 2,9 • 1010 (л*/ф),
2л 8,86 • 10-Х2 1410 '
| = 1020 (12,4 • 12,9 — 2,92) = 151,6 • 1020 (л12/^2),
Си==«2 2-«12 =0>659 . 10-н ф/м>
С22= -ч-”1?- = 0,626 . IO’11 ф/м,
Д
Д =
588
С12=^ = 0,191 • 10-и ф/м.
Пример 179. Провод 1 примера 178 соединен с землей через ис-
точник э.д.с. Е = 127 в. Провод 2 соединен с землей металлическим
проводником, так что его потенциал равен нулю (рис. 419, б).
Определить заряды на проводах 1 и 2 на один погонный метр.
Решение. Из формулы (13.49) при <р2 = 0 следует, что
Т1 Ф1Р11 И Т2 — Ф1Р121
р = 2®? = -12'9- 1010 = 0,852.10(ф/м),
Д 151,6 •10®°
₽12 = — С12 = — 0,191 -10 "и ф/м.
Заряд первого провода
т1== 127.0,852.10-"=- 1,08-10~9 (к/м).
Заряд второго провода
т2 = —0,191 • IO"11- 127 = —0,242. 10"9 (к/м).
Пример 180. Заряд тх на единицу длины провода 1 рис. 419, а
равен 2 10-9 к/м. Заряд т2 на единицу длины провода 2 ра-
вен—10~9 к/м.
Определить потенциал точки М, полагая потенциал земли рав-
ным нулю.
Г, Т! ,
Решение. «р„ = —— In ----
м 2ле а1М * Е
b-^in =
2ле а2м
2 • 10-9 |п У~72+12 10-9 |п
2л • 8,86 • 10~lz 2п • 8,86 . Ю-i2 2
(в).
Пример 181. Определить плотность наведенного заряда на по-
верхности земли в точке N (рис. 419, а), полагая, что заряды на про-
водах такие же, что и в примере 180.
Решение. В соответствии с формулой (13.33) плотность за-
ряда на поверхности проводника равна напряженности в этой точ-
ке, умноженной на е.
Напряженность поля в точке N (рис. 419, в) равна геометрической
сумме напряженностей от четырех зарядов: от заряда (обозна-
чим ее Ег), от заряда *т2 (Е2) и от зеркальных изображений этих
зарядов (Е1 и Е2')
Е = + Я +
Напряженности Ег и Е} направлены по одной прямой (по вертика-
ли) и складываются. Для нахождения проекций Е2 и Е'2 на верти-
каль умножаем Е2 и Е'2 на cos а
589
Т2
. 8--------------
0 = 2- Т1-е— 2---------12 • е—--------=0,1375- 10~8к/л«2.
2neftx 2ле + а2 + с2
а = 1; й2 = 4.
Пример 182. Две металлические пластинки (теоретически беско-
нечной протяженности) находятся в воздухе (рис. 420), образуя,
не соприкасаясь, двугранный угол а2. Потенциал первой пластины
<рх, второй <р„. Вывести формулы для определениями Е в любой точ-
ке поля внутри двугранного угла, а также формулу для определе-
ния плотности заряда на пластинках. Дать численный ответ при
<рх = 0, <р2 = ЮО в, а2 = 30е.
Решение. “
можно описать в
Поскольку граничные поверхности проще всего
цилиндрической системе координат, то решение
будем проводить именно в этой системе.
В пространстве между пластинками отсут-
ствуют свободные заряды, поэтому поле под-
чиняется уравнению Лапласа (уравнение
13.30).
Потенциал <р зависит только от угла а и
из условий симметрии не зависит от коорди-
наты z и радиуса г цилиндрической системы
координат. Поэтому
= 0.
da2
Решение последнего уравнения
2-
По условию при
се = 0 ф — — 0, а при а = а2
Ч> = <р2 = 100 в.
Следовательно,
с2 = О, С\ = —
2 1 л/6
Напряженность поля имеет только
щую
600
л
600
ср = —а.
л
одну альфовую составляю-
Плотность
р ____ _______С
Л и(Х Г
600 ,
----в/м.
ш
Например,
заряда
о = £> = е0£' = е0Еа
6О0ео
Л/
при
г-2 см о = D = — 8,48 • 10 ~8 к/м-.
Пример 183. Две металлические конусообразные воронки нахо-
дятся в воздухе, обращены остриями друг к другу и не соприка-
саются (рис. 421). Угол = 30°, 02 = 135°, потенциал первой
воронки <рх = 0, потенциал второй воронки <р2 = 1000 в.
и
590
Вывести формулу для определения <р и Е в пространстве между
воронками и найти по ним Е и д> в точке М с координатами R ~ 2 см
и 9 = 120°.
Решение. Воспользуемся сферической системой координат,
поскольку поверхности воронок проще всего описываются именно
в этой системе координат. В пространстве между воронками отсут-
ствует объемный заряд, поэтому поле описывается уравнением Лап-
ласа (формула 13.31).
В силу симметрии ф зависит только от угла 9 и не зависит от
радиуса R и угла а — двух остальных координат сферической сис-
темы. Таким образом,
sin 9 = 0, откуда sin 9 =Ct
de j J de 11
<p = Cjln tg y + C2.
Найдем постоянные интегрирования C± и C2. При 9 = 30° ф = 0,
при 9 = 135° <р = 1000 в. Следовательно,
0 = Сх In tg 15° + С2,
1000 = Q In tg 67° 30' + С3.
Отсюда
= 461 в, С2 = 608 в.
Потенциал точки М
Фм = 461 In tg 60° + 608 = 856,5 (в).
Напряженность поля имеет только в составляющую
£е =----------------------=----------——.
/?d6 /? sin О
Напряженность в точке М
E/j д1 -----------= — 26,6 (кв/м).
0,02 sin 120°
Пример 184. В вакууме на расстоянии 2 см друг от друга распо-
ложены два плоских электрода (рис. 422). Правый электрод зазем-
591
лен, а левый соединен с плюсом батареи, э.д.с. которой 200 в; от-
рицательный зажим батареи заземлен.
В пространстве между электродами распределен объемный заряд
с плотностью
Р = — аеох,
где а = 30 кв/см3.
Требуется найти закон изменения потенциала в пространстве
между электродами.
Решение. Полагаем, что размеры электродов много больше
расстояния между электродами. Направляем ось х, как показано
на рис. 422.
Потенциал зависит только от %; от у и от z он в данной задаче не
зависит. Следовательно,
Определяем постоянные интегрирования из граничных условий:
при х = 0 <р = 200 = С2,
прих=2 <р = 0= 200 + 2C,+ ~-'8' 103; С^ —20100 в/см.
6
Следовательно,
ф = 30 • _ 20 100% + 200 = 5000х3 — 20100% + 200 в.
Пример 185. В цилиндрическом конденсаторе с воздушной изо-
ляцией вокруг внутреннего электрода радиусом г0 располагается
заряд короны с объемной плотностью р к/см3. Наружный радиус ко-
роны(рис. 423). Радиус наружного электрода г2. Потенциал внут-
реннего электрода %, потенциал наружного электрода нуль.
Вывести формулу для определения <р в пространстве, занятом
объемными зарядами (назовем его областью I), и в пространстве,
не занятом свободными зарядами (область II).
Решение. В первой области
1 d
7 dr
Р
Ео
Двукратное интегрирование по г дает
592
<P, =-f-24-C1lnr + C2.
че0
Во второй области
ritPn \ =0>
г dr \ dr )
Откуда
Фп = С31пг4-С4.
Составим четыре уравнения для определения четырех постоян-
ных интегрирования (Cr, С2, С3, CJ.
При г — г0 <Р] = <р0. Поэтому
Фо Ч-С^п^ + С,. (а)
4е0
При г = гг Ф, = Ф1Г Следовательно,
„.2
-^ + С11пг1 + С2 = С31пг1 + С4. (б)
4е<>
При г — г2 фп = 0, тогда
0 = С31пг2 + С4. (в)
При г = гг равны нормальные составляющие вектора электри-
ческого смещения О:
или
2
С8 = С1-р-. (Г)
ZEq
Совместное решение уравнений (а), (б), (в), (г) (опущено) дает
Далее определяются Cs из уравнения (г), С4 из уравнения (в) и Са
из уравнения (а).
Пример 186. Над поверхностью земли расположилось грозовое
облако, заряженное положительным электричеством. Пространст-
во между облаком и землей можно рассматривать как огромных раз-
меров плоский конденсатор. Напряженность поля Е в нем направ-
лена от облака к земле.
Найти потенциал точки А, расположенной на расстоянии 8 м
от поверхности земли в двух случаях: 1) когда над поверхностью
20 Л. А. Бессонов
593
земли не протянут заземленный трос (рис. 424) и 2) когда над по-
верхностью земли над точкой А на высоте 10 м от земли протянут
заземленный стальной трос диаметром 10 мм (рис. 425).
Решение. В случае отсутствия троса
<Рд = EhA, где йл=8 м.
При наличии троса потенциал в точке А создается не только рав-
номерным полем «плоского конденсатора», но и зарядом на тро-
се qmp:
Фд =EhA-\-qmpalv
А
Облако
'Трос
Аа—8м
Земля
Рис. 424
Земля
Рис. 425
Здесь через а12 обозначен потенциальный коэффициент
1 . b12 1 . 10 + 8
а.„ = — In — = — In —!—
2ле а12 2ле 2
Составим уравнение для определения заряда троса:
Следовательно,
и
Фтрося Ehmp -|- qmp ап 0.
_ ____Ehmp
q"’~
й = в( Лл-Л.,Й).
\ а11/
Изменение потенциала в точке А, отнесенное к значению потенциа-
ла в точке А до появления троса:
Д«Рд_ Фд~Фд = £{hA (hA = 10.0,251
фГ фд EhA 8
594
. 1«
in —
«п =______2 _ 2.08 _ п nr«
an In 4000 8,3 ’ ° '
Пример 187. В равномерное поле с напряженностью £'о=103кв/л{
внесен незаряженный металлический шар радиусом а = 1 см.
Найти Er и Ef в точке А. Координаты точки A: R = 2 см и
О = 30°.
Решение. В соответствии с формулами § 417 имеем:
Ец = — - — Eocos0 (1 + —) =
dR \ R3/
— 1,082 . 106 (в/м)-
-^- = E0sinO (1 ——\ ==
Rdf) ° \ R3 )
4 — -'j = 0,4375 106 (в/м).
Резул ьтиру ющая
напряженность поля по модулю равна
Е = Уе^е^ = 1,168 . 106 в/м.
Пример 188. В воздухе создано равномерное электрическое поле
напряженностью Ео — 103 кв/м. В этом поле поместили диэлектри-
ческий цилиндр (е; = 4), так что ось цилиндра перпендикулярна
полю. Найти напряженность поля Et внутри цилиндра.
Решение. Воспользуемся формулой (13.72)
Et = Ео = 103 = 4 . 102 (кв/м).
Пример 189. В некоторой области пространства имеется поле,
потенциал которого зависит только от координаты х декартовой сис-
темы
<р = бх3 — 60х2.
Найти закон изменения плотности свободных зарядов в этом поле.
Решение. Уравнение Пуассона, описывающее поле, за-
пишется так:
_______ ______Рсвоб
dx2____е
Дважды дифференцируем <р по х
= 15х2 — 120х; = ЗОх — 120.
dx dx2
Следовательно, ревоб— (—30х-{-120) е.
Пример 190. Вывести формулу для определения напряженности и потен-
циала поля, создаваемого заряженной осью длины / (рнс. 426). Заряд на еди-
ницу длины оси равен т^
20*
595
Решение. Определим E и q> в произвольной точке К. Расположим оси
декартовой системы координат в соответствии с рис. 426. Выделим отрезок
оси длиной dx, на нем будет заряд т dx. В силу малости dx будем считать этот
заряд точечным и по теореме Гаусса найдем создаваемую им напряженность
поля в точке К:
idx
dE — --------.
4 ле/?2
Проекция dE на ось к
Jr. Jr. о rcos0dx
— dEx = dE cos 0 —---------.
4 ле/?2
Рис. 427
Проекция dE на ось у
dEy — dE sin 0
Заменим
т sin 0 dx
AmR2
h
R =-----x=/zctg0, dx =
sin 0
hd0
sin2 0 ’
E
т f* т
= :—Г I COS 0 d0= -—- (sin pa — Sin Pt);
4 лей J 4лей
p2
Ev = ------ I
Л Aneh j
3,
------ (cos 02 — cos 0J;
4 лей
2 2
£ = ’ £л 4-Ey
Составляющая потенциала в точке К от точечного заряда т dx равна
Р-2 ₽2
С
— I —7= Arsh(ctg0) ,
J Sill 0
3. ₽.
/ — а а \
т dx — т d0
dtp --- ----- -------------;
4ле/? 4 ле sin 0
<p = ------
4 ле
Ar sh---
h
596
Пример 191. Вследствие неравномерного нагрева диэлектрическая про-
ницаемость изоляции коаксиального кабеля (рис. 427) изменяется в функции
, т
радиуса г следующим образом: е = —. Вывести формулы для определения
напряженности электрического поля Е и смещения D. Радиус жилы кабеля
гг, внутренний радиус оболочки г2. Напряжение между жилой и оболочкой
U. Объемный заряд отсутствует.
Решение. Воспользуемся теоремой Гаусса (формула 13.20) в дифферен-
циальной форме (применять уравнение Лапласа в данном случае нельзя, по-
скольку оно выведено при условии, что е = const; см. § 393). В формуле
(13.24) заменим Е на D, учтем, что D имеет только одну г составляющую и
в силу симметрии не зависит от координат г и а. Будем иметь
div П = —4 (rDr) = 0.
г dr
Отсюда следует, что
rl)r = rD = С; D = —,
г
где С — постоянная интегрирования.
Таким образом, D изменяется обратно пропорционально радиусу. Напря-
женность поля
D Cr С
Е — — = — = — ,
е тг т
т. е. напряженность поля является величиной постоянной. Определим пос-
тоянную интегрирования С. С этой целью воспользуемся тем, что
С С С С (г2 — гл
J J in tn
Г1 r,
c mU
f 2 1
Графики изменения E, D и <p см. на рис. 427*.
Пример 192. Вывести формулы для расчета поля диполя.
Решение. Диполь изображен па рис. 428. Расстояние между центра-
ми зарядов обозначим через I. При решении воспользуемся сферической сис-
темой координат. Обозначим расстояние от произвольной точки а до заряда
4- q через Rr, до заряда — q через /?2 и до середины диполя через R. Угол
между вертикалью и радиусом R равен 6. Потенциал точки а определим как
потенциал в поле двух точечных зарядов:
* Обратим внимание на то, что если бы электрическая проницаемость е изо-
ляции коаксиального кабеля примера 191 была постоянной величиной (не явля-
лась бы функцией г), то тогда имели бы место следующие зависимости:
С71п —
U г
Е = -------; D — е,Е, <р = ----------•
rln — 1п —
И ri
т. е. в этом случае напряженность поля будет не постоянна, а изменяется об-
ратно пропорционально радиусу г, а потенциал ер изменялся бы не линейно в
функции г, а по логарифмическому закону.
597
<7 Rz — Ri
4ле
Если R~2> I, то RtR2 ~ R2, a R2 — Rt и I cos 0, поэтому
qlcos 0
4 ле/?2 ’
По формулам § 386 найдем
(13.73)
Рис. 428
Рис. 429
£=Ге^ + ^=-^'--Г1 + зс052о . (13.76)
Таким образом, в поле диполя при I потенциал <р изменяется обратно
пропорционально второй, а напряженность обратно пропорционально
третьей степени расстояния R рассматриваемой точки до диполя; <р и Е
являются функциями угла и.
Картина поля диполя изображена на рис. 429. Напряженность поля в
некоторой произвольной точке а равна геометрической сумме напряженностей
и Е2 от зарядов + q и — q. Если воспользоваться сферической системой
координат, то напряженность поля в той же точке а можно представить в ви-
де суммы напряженностей ЕЛ и Ее ; Ед направлена вдоль радиуса R, а Ед
имеет 0 направление.
Пример 193. Вывести формулы для определения величины на-
пряженности поля и емкости двухслойного плоского конденсатора
рис. 430, а также построить графики изменения модуля вектора на-
пряженности электрического поля, модуля вектора электрической
индукции D и потенциала <р в функции расстояния х.
598
Толщина первого слоя диэлектрика dlt второго слоя d2. Элект-
рическая проницаемость первого слоя elf второго слоя еа. При-
нять = 2ег и d2 = l,5dr
Решение. Всем величинам, относящимся к первому слою,
придадим индекс 1, а ко второму слою — индекс 2. Положим, что
разность потенциалов между обкладками конденсатора равна U.
Искажающее влияние краев конденсатора
не будем. При этом условии в каждом
слое поле будет равномерным. В силу то-
го, что нормальная составляющая вектора
D непрерывна, имеем Din — D2n.
Но Dln == е1Е1, D2n = е2Еа. Следова-
тельно,
00
Таким образом, отношение напряженно-
стей обратно пропорционально отношению
электрических проницаемостей.
Уравнение (а) связывает две пока не-
известные величины Ег и Е2. Второе
уравнение относительно Ег и Е2 составим,
исходя из того, что
на поле учитывать
или С, Сг
E.d.-\-E2d„= U. (б)
J 1 Рис. 430
Совместное решение (а) и (б) дает
U
di + — d2
е2
Графики зависимостей D, Е и ф от расстояния х изображены на
рис. 430.
Для нормальной работы конденсатора необходимо, чтобы на-
пряженность электрического поля ни в первом, ни во втором слоях
конденсатора не достигла значения напряженности, при котором
происходит пробой данного диэлектрика.
Напряженность равномерного поля, при которой происходит
пробой данного диэлектрика, принято называть пробивной напря-
женностью. Пробивная напряженность диэлектриков, в особен-
ности газообразных, сильно зависит от температуры и давления.
Пробивная напряженность воздуха равна 30 кв/см при нормальном
атмосферном давлении и температуре 18СС.
599
При выводе формулы для емкости двухслойного плоского кон-
денсатора на грань раздела двух диэлектриков мысленно поместим
бесконечно тонкий металлический листок. Эта операция вполне до-
пустима, так как поверхность раздела диэлектриков как была эк-
випотенциальной поверхностью до помещения листка, так и оста-
нется эквипотенциальной поверхностью после помещения на нее
листка, причем значение потенциала ее при этом не изменится.
После проведения такой операции емкость двухслойного конден-
сатора можно подсчитать как емкость двух последовательно вклю-
ченных конденсаторов С\ и С2; С2 — емкость первого слоя конден-
сатора, С2 — емкость второго слоя конденсатора:
dl #2
где S — площадь одной пластины конденсатора с одной стороны.
Емкость двух последовательно включенных конденсаторов равна:
-р <1% di
е2 е1
Глава четырнадцатая
ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
ПОСТОЯННОГО ТОКА В ПРОВОДЯЩЕЙ СРЕДЕ
§ 422. Плотность тока и ток. Если под воздействием внешних
источников в проводящей среде (металлических проводниках, земле,
жидкостях и т. д.) создано электрическое поле, то в ней будет про-
текать электрический ток. Электрический ток представляет собой
упорядоченное движение заряженных частиц под действием элект-
рического поля.
Носителями зарядов в металлах являются свободные электроны,
носителями зарядов в жидкостях являются ионы.
Упорядоченное движение свободных электронов в металле и ио-
нов в жидкости под действием электрического поля принято назы-
вать током проводимости.
При своем упорядоченном движении носители зарядов испыты-
вают многочисленные столкновения с другими частицами вещества,
которые находятся в тепловом движении. Эти столкновения затруд-
няют упорядоченное движение носителей зарядов и являются при-
чиной сопротивления, оказываемого проводящей средой прохож-
дению тока.
Свойство среды, характеризующее ее способность проводить ток,
называют удельной проводимостью и обозначают у. Удельная про-
водимость зависит от физических свойств проводящего материала
и от температуры; у имеет размерность оиг^м~1 = сим/м.
Электрическое поле в проводящей среде подчиняется опреде-
ленным законам и ближайшей задачей в данной главе является
рассмотрение этих законов.
Основной величиной в электрическом поле проводящей среды
является плотность тока 6. Это векторная величина, направленная
по напряженности поля. Она численно равна отношению тока At,
протекающего через элемент поверхности as (перпендикулярный
к направлению напряженности поля в данной точке), к величине
As этой поверхности.
601
Если поверхность имеет конечные размеры, то направление век-
тора плотности тока во всех элементах, на которые может быть раз-
бита эта поверхность, и направление элементов поверхности может
быть различно, и ток определится так:
Таким образом, ток есть поток вектора плотности тока.
В отличие от плотности тока ток является величиной скалярной.
При протекании постоянных токов по проводящим телам как
внутри проводящих тел, так и вне их существуют постоянные (неиз-
менные во времени) магнитные поля. Так как эти поля неизменны
во времени, то в поле не возникает явления электромагнитной ин-
Рис. 431
дукции. Другими словами, магнитное поле, созданное постоянным
током, не оказывает влияния на электрическое поле постоянного
тока. Благодаря этому оказывается возможным раздельно рассма-
тривать электрическое и магнитное поля постоянного тока.
Электрическое поле постоянного тока рассматривается в данной
главе, а магнитное поле — в главе пятнадцатой.
§ 423. Закон Ома в дифференциальной форме. Второй закон Кирх-
гофа в дифференциальной форме. Выделим в проводящей среде не-
большой параллелепипед объемом дК Длина ребра параллеле-
пипеда Д/, площадь поперечного сечения As. Расположим этот
объем так, что напряженность поля в нем направлена параллель-
но ребру (рис. 431, а). В силу малости объема можно считать, что
напряженность электрического поля Е одна и та же во всем эле-
ментарном объеме:
Д? = Д/п°,
Д$ = Д5П°,
G02
где n° — единичный вектор по направлению Д/, Да и Е.
Ток I = J 6 ds = б Дь\
Напряжение на элементе объема U = Е Ы = RI.
Сопротивление элемента объема
/? = — .
уДз
Подставив в выражение RI = EM эквиваленты R и 1, получим:
-^-'dAs’n° = ЕД/п°.
у is
Отсюда
К=уЕ. (14.1)
Соотношение (14.1) называют законом Ома в дифференциальной фор^
ме. Оно устанавливает связь между плотностью тока в данной точ-
ке проводящей среды и напряженностью поля в этой же точке.
Уравнение (14.1) справедливо для областей вне источников э. д. с.
В областях, занятых источниками э. д. с., кроме «кулонова» (элект-
ростатического) поля существует еще так называемое стороннее
электрическое поле, обеспечивающее непрерывное движение заря-
дов в электрической цепи.
Под сторонним электрическим полем понимают электрическое
поле не электростатической природы (например, обусловленное
химическими, электрохимическими, тепловыми, термоэлектриче-
скими, механическими или электромагнитными процессами).
Напряженность стороннего поля обозначается Естор. В областях,
занятых источниками э. д. с., полное значение напряженности поля
равно геометрической сумме напряженности «кулонова» и сторон-
него полей Е-[-Естор.
На рис. 431, б схематически изображена электрическая цепь постоян-
ного тока. Она состоит из источника питания и нагрузки.
Источник сторонней э.д.с. создает внутри источника питания стороннюю
напряженность поля Егтор_
Линейный интеграл от сторонней напряженности поля внутри источника
называется э. д. с. источника (Ед-
з
У ECmopdl—Ei-
I
Под действием стороннего поля в источнике непрерывно происходит разде-
ление электрических зарядов. Положительные заряды перемещаются к плю-
су источника, а отрицательные — к минусу.
603
Эти заряды в области внутри и вне источника создают электрическое по-
ле, напряженность которого, как и напряженность электростатического (ку-
лонова) поля направлена от положительных зарядов к отрицательным.
При протекании постоянного тока по цепи одни электрические заряды
непрерывно сменяются другими, такими же, что и в предыдущие моменты вре-
мени. Таким образом, картина поля в макроскопическом смысле повторяется
в смежные моменты времени. Поле носит как бы статический характер. Это
обстоятельство послужило основанием для того, чтобы поле, созданное в про-
водящей среде разделившимися зарядами, называть кулоновым полем, а его
напряженность Е называть напряженностью кулонова поля.
Внутри источника кулоново поле направлено навстречу стороннему полю.
Полное значение напряженности поля внутри источника равно Е + Естор. Вне
источника кулоново поле направлено от положительного электрода к отрица-
тельному. Под действием этого поля и происходит упорядоченное движение
зарядов в области вне источника. Прн протекании тока по цепи | Efmop| >| Е |.
При разомкнутой цепи |Efmop | = | Е .
В соответствии с этим закон Ома в дифференциальной форме для
областей, занятых источниками э. д. с., запишется следующим об-
разом
6 = у(£+Ятор). (14.1')
Уравнение (14.1') в литературе называют обобщенным законом
Ома в дифференциальной форме.
Если от обеих частей уравнения (14. Г) взять интеграл по замк-
нутому контуру, включающему в себя источник э.д.с., то из урав-
нения (14.1') будет получен второй закон Кирхгофа.
Последнее обстоятельство послужило основанием для того, что-
бы уравнение (14.1') называть также вторым законом Кирхгофа в
дифференциальной форме.
На рис. 431, е изображен замкнутый контур, по которому течет ток 1. На
участке 123 имеется источник сторонней э. д. с. Ер На участке 341 нет ис-
точников сторонней э.д.с. Обозначим через Щ сопротивление участка 123 и
через /<? сопротивление участка 341. Примем, что площадь поперечного сече-
ния всех участков замкнутого контура достаточно мала для того, чтобы мож-
но было считать, что направление плотности тока и направление напряжен-
ности поля в некоторой точке совпадает с направлением элемента пути dl в той
же точке.
<Н
Умножим обе части (14.1') на — и составим циркуляцию вдоль замкну-
Y
того контура 12341 рис. 431, в:
Интеграл от суммы равен сумме интегралов. Поэтому
(Е + Ё*стор) dl = ф ~Edl + ф Ecmopdl.
ф E di = 0 в силу потенциального характера «кулонова» поля.
604
В свою очередь
(Ю Ecmopdl ~ ) Естар dl -J- f Естор dl •
/23 341
но J Ecinofldl равен сторонней э. д. с. Elt a J Ecmopdl = 0, так как на участ-
123 341
ке 341 нет сторонней э. д. с.
„ Г ^dl
Для подсчета величины (V)----- умножим и поделим подынтегральное вы-
J V
ражение на площадь поперечного сечения S, от плотности тока б перейдем к
, dl
току / и заменим — на сопротивление участка пути dR.
VS
Получим
б dl S Idl , ,
---- — = — —IdR,
у S yS
=/ (j) dR=> I J dR+ I ^dR=>IR{ + IR.
123 341
Таким образом,
l(Rl + R) = E1.
(a)
Следовательно, из уравнения (14.1') образовано уравнение (а), представ-
ляющее собой уравнение, составленное по второму закону Кирхгофа.
§ 424. Первый закон Кирхгофа в дифференциальной форме. Если
в проводящей среде выделить некоторый объем, по которому про-
текает постоянный, не изменяющийся во времени ток, то можно ска-
зать, что ток, который войдет в объем, должен равняться току, вы-
шедшему из объема, иначе в этом объеме происходило бы накопле-
ние электрических зарядов, что опыт не подтверждает. Сумма вхо-
дящего в объем и выходящего из объема токов запишется так
dds = 0.
(14.2)
Если поделить и левую и правую части (14.2) на одно и то же
число (на объем, о котором шла речь выше), то равенство остане гея
справедливым
-----= 0.
V
Очевидно, что последнее соотношение будет справедливо и в том
случае, если объем, находящийся внутри замкнутой поверхности,
будет стремиться к нулю:
ф Ms’ _
Игл ---- = div 6 = 0.
v^o V
605
Таким образом, для постоянного, неизменного во времени поля
в проводящей среде
divl = 0. (14.3)
Это соотношение называют первым законом Кирхгофа в дифферен-
циальной форме. Оно означает, что в установившемся режиме в лю-
бой точке поля нет ни истока, ни стока линий fi.
§ 425. Уравнение непрерывности. Соотношение (14.3) годится только для
установившихся полей, неизменных во времени. Для неустановившихся полей,
когда электрические поля изменяются во времени, div 6 =/= 0. В этом случае
выходящий из какого-либо объема ток определяется скоростью изменения
заряда q, находящегося внутри объема:
С dq
(T)6ds= —— . (14.4)
J dt
Знак минус в последнем выражении объясняется тем, что если ток выходит
из объема, то это может быть только за счет убыли заряда в объеме.
Поделим обе части уравнения (14.4) на объем V, находящийся внутри
замкнутой поверхности з, и найдем предел отношения при V, стремящемся
к нулю:
dp * *
div б = — — . (14.5)
dt
Через р обозначена объемная плотность заряда в данной точке поля.
§ 426. Дифференциальная форма закона Джоуля — Ленца. В
разделе постоянного тока первой части курса отмечалось, что если
по какому-либо проводнику сопротивлением R протекает постоян-
ный ток I, то в единицу времени (в сек) в нем выделяется энергия,
равная PR. Определим энергию, выделяющуюся в единицу време-
ни в единице объема проводящей среды. С этой целью воспользуем-
ся рис. 431, а
— = = — = уЕ2. (14.6)
V \ yis ) у 1 ' 7
Таким образом, в единице объема проводящей среды выделяет-
ся в единицу времени энергия, численно равная уЕ2.
§ 427. Электрическое поле в проводящей среде подчиняется урав-
нению Лапласа. Так же, как и в электростатическом поле, напря-
женность электрического поля в проводящей среде Е = —grad<p.
В неизменном во времени поле
div 6 = divyE =0. (14.7)
* Об уравнении непрерывности, как об уравнении, выражающем собой
непрерывность полного тока (тока проводимости и тока электрического сме-
щения), говорится в § 460.
606
Если у среды не изменяется от точки к точке, т. е. если
среда однородна и изотропна, то у как постоянную величину
можно вынести за знак дивергенции и, следовательно, вместо
div уЕ = 0 можно написать у div Е = 0 или
divE = 0. (14.8)
Другими словами,
div (— gradtp) — О
или
Vq> = 0. (14.9)
Таким образом, поле в однородной проводящей среде подчиняет-
ся уравнению Лапласа. Уравнение Лапласа описывает потенциаль-
ные поля. Следовательно, поле постоянного тока в проводящей сре-
де является полем потенциальным. В нем, в областях, не заня-
тых источниками, ф Edl = 0.
§ 428. Переход тока из среды с одной проводимостью уу в среду
с другой проводимостью у2. Граничные условия. Выясним, какие
граничные условия выполняются при переходе тока из среды с од-
ной проводимостью в среду с другой проводимостью.
На рис. 432 линия ОО есть грань (граница) раздела сред.
Возьмем на грани плоский замкнутый контур 1234.
Составим циркуляцию вдоль этого контура.
Стороны 12 и 34 его весьма малы по сравнению со сторонами 23
и 41 (длину последних обозначим dl).
Так как (§)Edl вдоль любого замкнутого контура равен нулю,
то он равен нулю и для контура 1234.
В силу малости отрезков 12 и 34 пренебрежем составляющими
интеграла вдоль этих путей и тогда
Eltdl — E2tdl = 0 или Еи = Е21. (14.10)
Это соотношение совпадает с соотношением (13.34).
607
На грани раздела равны нормальные составляющие плотностей
токов. Докажем это.
На грани раздела выделим сплющенный параллелепипед (см.
рис. 433). Поток вектора б, втекающий в объем через нижнюю грань,
равен — поток вектора б, вытекающий из объема через верх-
нюю грань, 62иАХ. Так как ф; fids — 0, то
-б1пД5Н-62„Д5 = О,
и
61п = 62п. (14.11)
Таким образом, при переходе тока из среды с одной проводимо-
стью в среду с другой проводимостью непрерывна тангенциальная
составляющая вектора Е (Еи = Е2/, но Е1п =£ Е2п) и непрерывна
нормальная составляющая плотности тока fii;j=fi2;i (но i>lt =У= б2/).
Отсюда следует, что полные значения вектора Е и вектора fi
в общем случае меняются скачком на грани раздела.
Найдем связь между углом падения и углом преломления ₽2:
= tg₽2 = -^ = ^
с1л °2п °2л
или
(14.1'2)
tg ₽2 Y2
Если ток переходит из среды с большой проводимостью (напри-
мер, из металла) в среду с малой проводимостью (например, в землю),
то тангенс угла преломления tg§2 = tgр. '—будетменьшетанген-
Vi
са угла падения и, следовательно, угол Р2 будет меньше угла
Если у2 весьма мало, то угол ₽2—>0.
§ 429. Аналогия между полем в проводящей среде и электроста-
тическим полем. По своей природе поле электростатическое и поле
постоянного тока в проводящей среде различны. Электростатичес-
кое поле создается электрическими зарядами, неизменными во вре-
мени и неподвижными в пространстве, тогда как электрическое по-
ле в проводящей среде есть поле, в котором электрические заряды
имеют упорядоченное движение под действием внешнего источни-
ка. Тем не менее между двумя полями может быть проведена оп-
ределенная формальная аналогия. Действительно, электростатичес-
кое поле в областях, не занятых зарядами, удовлетворяет уравне-
нию Лапласа. Электрическое поле постоянного тока в проводящей
среде вне сторонних источников также ему удовлетворяет. В обоих
полях имеют дело с вектором напряженности поля Е. С вектором
электрического смещения D = еЕ может быть сопоставлен вектор
плотности тока 6 ,= уЕ.
С08
Dds мо-
С потоком вектора D (обозначим его буквой ф) ф =
жет быть сопоставлен поток вектора плотности электрического тока
/ = f bds .
можно сказать, что со-
Граничные условия на поверхности раздела двух диэлектриков:
~ и Dln — D2n.
Граничные условия на поверхности раздела двух сред с различ-
ной проводимостью:
E1Z = E2t и 61я = 62п.
Но если два поля удовлетворяют одному и тому же уравнению =
= 0 и в них выполняются тождественные граничные условия для
сходных величин, то при одинаковой форме граничных поверхнос-
тен на основании теоремы единственности ------- ------ — —
вокупность силовых и эквипотенциаль-
ных линий в этих двух полях (т. е.
«картина поля») будет одинаковой.
Эта формальная аналогия на прак-
тике широко используется. Так, на-
пример, если какое-либо электростати-
ческое поле уже изучено, то все сведе-
ния о поле могут быть перенесены и на
геометрически подобное поле в проводя-
щей среде.
Справедливо, разумеется, и обратное
заключение.
§ 430. Экспериментальное исследова-
ние полей при помощи электролитиче-
ской ванны. Если форма граничных
поверхностей (электродов) сложна, то
аналитический расчет поля часто ока-
зывается делом весьма трудным. И в
этом случае прибегают к эксперимен-
тальному исследованию полей. Обычно исследуют поля в электро-
литической ванне. Допустим, что требуется построить картину
плоскопараллельного электростатического поля. Непосредствен-
нее определение потенциалов электростатического поля путем поме-
щения в отдельные точки поля зондов не удается, так как зонды да-
же при малой мощности, потребляемой индикаторами, своим при-
сутствием все же искажают поле.
Поэтому прибегают к моделированию. С этой целью в ванну
с электролитом (например, с подкисленной водой), помещают элек-
троды (рис. 434). Форма и взаимное расположение их должны быть
в точности такими же, что и в изучаемом электростатическом поле.
Для того чтобы стенки ванны по возможности меньше искажали
исследуемое поле, линейные размеры ванны должны в несколько
609
раз превышать соответствующие линейные размеры исследуемого
поля.
Электроды соединяют с источником э.д.с. низкой частоты (обыч-
но 50 гц). Использовать в качестве источника питания э.д.с. пос-
тоянного тока нельзя, так как при постоянном токе будет происхо-
дить электролиз подкисленной воды и пузырьки газа, осаждаясь
на электродах, будут искажать исследуемое поле. По электролиту
проходит переменный ток.
При помощи вспомогательного реостата, зонда (щупа) и инди-
катора нуля можно снять семейство эквипотенциальных линий в
поле. С этой целью устанавливают движок реостата в каком-либо
фиксированном положении и, перемещая зонд (щуп) так, чтобы
индикатор показывал нуль, находят совокупность точек, потен-
циал которых равен потенциалу движка реостата. Далее переме-
щают движок реостата в новое положение и определяют коорди-
наты точек второй эквипотенциал и и т. д. Затем по семейству экви-
потенциален строится сетка силовых линий. При построении пос-
ледней руководствуются тем, что силовые линии в любой точке поля
должны быть перпендикулярны эквипотенциалям, в том числе и
поверхностям электродов.
В электростатическом поле силовые линии перпендикулярны
поверхностям электродов. В поле проводящей среды силовые ли-
нии, строго говоря, немного не перпендикулярны поверхностям
электродов. Но если проводимость электродов будет во много раз
больше проводимости электролита, то (см. формулу 14.12) с боль-
шой степенью точности можно считать, что силовые линии будут
подходить к поверхностям электродов практически под прямым
углом*.
§ 431. Соотношение между проводимостью и емкостью. Если ка-
кие-либо электроды поместить в проводящую среду и присоединить
к источнику э.д.с., то по проводящей среде пойдет ток. Если напря-
жение между электродами 1 и 2 равно Ul2 и по среде проходит ток
7, то проводимость среды
G = - .
1/12 2
Так как ток 7 = J 6 ds = у Je ds и Ul2 — JEdl.
i
то
V J ErfF
G = ------ (14.13)
J'e dF
____________ i
* В приложении Б на стр. 718 рассматриваются основы моделирования
полей при помощи метода электрических сеток.
610
В свою очередь, в электростатическом поле с электродами такой же
конфигурации емкость между двумя частями электродов, на кото-
рых располагаются одинаковые по величине и противоположные
по знаку заряды Q, создающие поток ф вектора электрической
индукции D
ф - - Q = J D ds ,
определится так:
1
Если поделить (14.14) на (14.13), то после сокращений получим
4 = — ’ <14Л5)
6 у
т. е. емкость С между двумя телами, разделенными диэлектриком
с электрической проницаемостью е, так относится к проводимости G
между теми же телами, если поместить их в среду с электрической
проводимостью у, как е относится к у.
Соотношение (14.15) позволяет по известному выражению емкос-
ти между какими-либо двумя телами получить выражение для про-
водимости или совершить обратную операцию.
Так, например, емкость двухпроводной линии
С___ ml
In —
(14.16)
Здесь I — длина проводов, d — расстояние между осями проводов
иг — радиус провода.
Для того чтобы получить выражение для проводимости между
двумя параллельными проводами (цилиндрами), погруженными в
среду с проводимостью у, надо в соответствии с (14.15) заменить в
(14.16) е на у. Получим
G = J^L. (14.17)
In А
Другой пример. Емкость коаксиального кабеля (рис. 435, а)
С ______________________________ 2ml
In А.
'1
Проводимость между двумя соосными цилиндрами длиной /,
которые разделены средой с проводимостью у (рис. 435, б)
6И
G =
In 21
Аналогия может быть распространена и на более сложные по-
ля. Например, если в равномерное поле, созданное в среде с про-
водимостью у,,, поместить шар с проводимостью у;, то в соответст-
вии с (13.67) потенциал внутри шара определится следующим об-
разом:
4'i= + - г-
2уе + У/
§ 432. Общая характеристика задач на расчет электрического по-
ля в проводящей среде и методов их решения. Так же, как и задачи
Рис. 435
электростатики, задачи на расчет электрического поля в проводя-
щей среде могут быть классифицированы по характеру величины,
которая определяется в результате расчета, на задачи, в которых
определяются точечные характеристики (плотность тока, потен-
циал), и на задачи, в которых находятся интегральные характерис-
тики поля, например сопротивление между электродами.
В зависимости от того, что задано и что определяется, все за-
дачи на расчет электрического поля в проводящей среде можно
разделять на два основных типа.
В первом из них задана форма и расположение электродов, гео-
метрия поля, свойства среды и интенсивность источников, создаю-
щих поле. Требуется найти либо точечные, либо интегральные ха-
рактеристики поля.
Второй тип задач является обратным по отношению к первому.
Одной из задач второго типа может быть, например, следующая:
при заданной точечной характеристике поля, заданной форме и рас-
положении электродов и свойствах среды, найти интенсивность
источников, создающих это поле.
612
Задачи на расчет электрического поля в проводящем среде могут
быть решены:
1. Путем непосредственного интегрирования уравнений, опи-
сывающих поле (см. примеры 195 и 198).
2. Путем использования аналитических решений для других
статических невихревых полей (см. примеры 194 и 200).
3. Экспериментальным (§ 430) или графическим путями.
Графический метод построения картины поля применительно
к плоскопараллельному магнитному полю рассматривается
в § 456.
Изложенная в этом параграфе методика полностью пригодна и
для построения картины плоскопараллельного электрического поля
в проводящей среде.
*
* *
В заключение необходимо остановиться на вопросе о том, как
производится расчет электрического поля в диэлектрике, окружаю-
щем проводники с токами.
Принято считать, что картина электрического поля в диэлектри-
ке, окружающем проводники стоками, тождественна картине элект-
рического поля в условиях электростатики.
Строго говоря, это верно лишь приближенно, поскольку в ус-
ловиях электростатики тангенциальная составляющая напряжен-
ности электрического поля на поверхности
проводящего тела равна нулю, тогда как
при протекании постоянного тока по про- s&’Et
воднику тангенциальная составляющая на- )
пряженности электрического поля на по- /
верхности проводника, хотя и очень мала I Jj
по сравнению с нормальной составляющей (s'
напряженности в той же точке, но все же
не равна нулю. На численном примере убе-
димся в том, что тангенциальная состав- Рис. 436
ляющая напряженности поля Et во мно-
го раз меньше нормальной составляющей напряженности поля £„.
Положим, что разность потенциалов U между двумя параллель-
ными токонесущими медными шинами (рис. 436) равна 100 в, рас-
стояние b между шинами 2 см и плотность тока 6= 2,5 • 106 а/м2.
Тогда
Et = — = 4,46- IO"2 в/м,
Еп=-=5- 103 в/м,
-^Д-^1,12 . 10s.
Et
С13
Примеры
Пример 194. Определить ток утечки коаксиального кабеля на
1 км длины. Пространство между жилой и оболочкой заполнено не-
идеальным диэлектриком, который обладает проводимостью
у = 10~8 ОМ-1’М~1.
Радиус жилы rlt радиус оболочки r2 — ert, где е — основа-
ние натуральных логарифмов. Напряжение между жилой и обо-
лочкой 10 кв.
Решение. Ток утечки I ~ UG. Проводимость
п 2л у/ 2л • 10-8 • ю3 с OQ 1П_Б , .
G —----— =-----------—- = 6,28 • 10 6 (сим).
In 1
П
Ток утечки через несовершенную изоляцию:
1 = 104 • 0,628 • 10-4 = 0,628 (а/км).
2
Заземлитель
/ 1 2
Пример 195. Рассмотрим простейшую задачу на расчет поля зазем-
лителя. Подвод тока к земле производится при помощи погруженных в
землю заземлений. Ток стекает
через заземлитель в землю и
растекается по толще земли
с тем, чтобы собраться у дру-
гого электрода заземлителя.
Земля выполняет роль обрат-
ного провода.
Если погрузить в землю
металлическую полусферу, че-
рез которую в землю стекает
ток / (рис. 437), и принять,
что второй электрод, к кото-
рому ток будет подтекать, находится очень далеко, то плот-
ность тока в землю на поверхности полусферы
будет равна б = - Z (поверхность сферы 4л/?2,
полусферы 2л/?2). Напряженность поля
Е - 6 - 1
у 2лу/?а ’
Напряжение между двумя точками на поверхности
ки 1 и 2):
Ur2 = ( EdR=~
I 2лу
Полусфера
радиуса К
Рис. 437
£ / / /
радиуса 7?
поверхность
земли (точ-
Ri
Г dR
J R ‘!
/
2лу Rl ) 2пу
Ri Ri /
1 1
1 1
614
На рис. 437 изображена кривая изменения потенциала на поверх-
ности земли.
В качестве примера найдем напряжение между точками 1 и 2,
расположенными на расстоянии, примерно равном шагу человека
(А’( = 22 м, /?2 = 23 м). Через заземлитель стекает ток / = 1000 а
(ток короткого замыкания), проводимость земли у — 10-2 ом^-м"1!
t/12 = — /—----------) = —(J-------------31,9 (в).
12 2яу \ /?! /?2 / 2л • 10-2 \ 22 23 / '
Пример 196. В морскую воду у = 0,1 олС1-^-1 вертикально
опущены две металлические трубы наружным диаметром 50 см
и длиной 3 м.
Найти проводимость G между трубами. Оси труб удалены на
расстояние d — 25 м.
Решение. G — —У1 = п ' -°" — = -—= 0,205 (сим).
In — In 25 4,605
г 0,25
Пример 197. Вывести формулу для определения проводимости G
между плоскостями и S2 проводящего тела, имеющего форму кли-
на (рис. 438).
Решение. Проводимость заштрихованного пояска высотой
га, толщиной dr и шириной b равна
аг
где у — удельная проводимость:
С = Vfc 1п
air а Г]
Пример 198. Пространство между двумя коаксиальными цилин-
дрическими металлическими трубками длиной / и радиусами г,
и г2 заполнено двумя различными проводящими средами (рис. 439).
618
Среда 1 имеет проводимость среда // — проводимость у2. Най-
ти проводимость G между трубками.
Решение. Для вывода формулы положим, что между труб-
ками имеется разность потенциалов U. Пусть под действием напря-
жения U через первую среду течет ток а через вторую — ток /2.
Линии плотности тока б направлены радиально.
Обозначим через S площадь, равную половине цилиндрической
поверхности текущего радиуса г
S = Лг1 (rt < г < г2),
где бх — плотность тока в первой среде, ба — во второй:
Л = 6XS = yj^nr/, £х = —у— ; /2 = 62S = yJEjirl, Е2= ;
Лг/у! Л/-/у2
и = [ E,dr = f E,dr, и = In ZL
J I “ ЛУ1/ rl пуг1 rl
J = j I / = Uni (Yl + Y-.) . g = n/ (Yl + Ya)
Пример 199. Воспользоваться результатами примера 198 и на-
писать формулу для вычисления емкости коаксиального цилинд-
рического конденсатора, обкладки которого имеют радиусы гх и г2.
Пространство между обкладками заполнено двумя различными диэ-
лектриками в соответствии с рис. 439 (ех вместо у1 и е2 вместо у3).
Решение. На основании аналогии, о которой шла речь в
§431, имеем
с _ л / (е, + е-,)
In
'1
Пример 200. В пластинке из алюминия (уг=3,57-107 ши-1 -ж-1)
создано равномерное электрическое поле напряженностью £„ =
= 0,1 в/м. Определить плотность тока в медном включении [у;=
= 5,6 • 10’олг* • м~‘, имеющем цилиндрическую форму и распо-
ложенном перпендикулярно полю.
Решение. Воспользуемся формулой (13.72) и аналогией, рас-
смотренной в § 431:
£ = £ = Ю-1 - 2 --57 = 0,78 . 10-* (в/м);
Ye+Yi 3,57 + 5,6 7
6. = ylEl = 5,6 . 10’ . 0,78 . 10"1 = 436 . 10*(а/м2).
Глава пятнадцатая
МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА
§ 433. Введение. В главе «Магнитные цепи» первой части ТОЭ
рассматривались методы расчета магнитных цепей и основные по-
нятия, характеризующие магнитное поле. Там отмечалось, что маг-
нитное поле характеризуется индукцией В, намагниченностью J
и напряженностью магнитного поля Н
Эти три величины связаны соотношением
в = Ио(^+7)=р(|рД (15.1)
где р.о — есть магнитная постоянная. В системе СИ
р0 = 4л • 10-’ гн/м = 1,256 - 10-с гн/м.
Одним из основных проявлений магнитного поля является воз-
действие его на проводник с током, помещенный в это поле.
Опыт показывает, что сила F, с которой магнитное поле действу-
ет на элемент проводника длиной dl с током /, определяется сле-
дующим образом
F = I[cUB\. (15.2)
Эта сила направлена перпендикулярно индукции в данной точ-
ке поля и перпендикулярна элементу тока Idl (рис. 440). Из вы-
ражения (15.2) следует, что индукция может быть определена как
сила, действующая на проводник длиной dl, равной единице, если
по нему протекает ток /, равный единице.
В Международной системе единиц «СИ» единицей измерения
индукции является тесла (1 тл = 1 в сек/лг).
Единицей измерения индукции в системе СГСМ является гаусс.
Если индукция В и элемент dl параллельны, то элемент тока не
испытывает механического воздействия со стороны магнитного по-
ля Механическое воздействие магнитного поля на элемент тока
максимально, когда В и dl взаимно перпендикулярны.
617
§ 434. Определение магнитного поля. Электромагнитное поле
представляет собой совокупность взаимно связанных друг с другом
электрического и магнитного полей. Таким образом магнитное
поле есть одна из сторон электромагнитного поля. В данной главе
рассматривается магнитное поле постоянного тока, для которого
характерно, что на помещенный в поле проводник с током дейст-
вует сила, прямо пропорциональная величине тока.
Поскольку эта сила зависит от ориентации элемента тока в
пространстве, то полное представление о поле в данной точке мо-
жет быть составлено только в том случае, если будут известны
силы при трех взаимно перпендикулярных положениях элемента
тока (векторная величина определяется тремя проекциями).
§ 435. Связь магнитного поля с током. Магнитное поле создается
током. Если где-либо протекает электрический ток, то он неизбеж-
но создает магнитное поле. Справедливо
и обратное заключение: если в какой-ли-
бо точке или точках есть магнитное поле, то
оно вызвано некоторым током. Этот ток
может протекать не обязательно в непо-
средственной близости от точек простран-
ства, в которых создано магнитное поле.
Магнитное поле создается в равной ме-
ре током проводимости и током электри-
ческого смещения. Ограничимся здесь толь-
ко упоминанием о токе электрического
смещения, как о токе, вызванном изменением напряженности элект-
рического поля во времени (подробнее см. стр. 651—653). В дан-
ном же разделе , как уже говорилось, рассматривается магнитное
поле постоянного тока, когда ток смещения отсутствует.
§ 436. Основной закон магнитного поля — закон полного тока.
Количественная связь между циркуляцией вектора Н по замкну-
тому контуру и током внутри контура определяется законом пол-
ного тока
dT= I. (15.3)
Формулируется он так: линейный интеграл от напряженности маг-
нитного поля вдоль любого замкнутого контура равен полному то-
ку, пронизывающему замкнутый контур.
Под полным током понимают весь ток (ток проводимости и ток
смещения), пронизывающий контур интегрирования.
Математическая запись закона полного тока в виде уравнения
(15.3) получила название интегральной формы закона полного тока.
Смысл термина «интегральная форма» состоит в том, что уравнение
(15.3) дает связь интегрального вида, т. е. связь между интегралом
от Н по некоторому замкнутому контуру и током, а не связь между
напряженностью поля в какой-то точке поля и плотностью тока в
618
той же точке поля (последняя связь называется диффереп*
циальной).
Интегральная форма закона полного тока применяется, когда
может быть использована симметрия в поле. Так, например, нап-
ряженность поля в некоторой точке А в поле уединенного прямого
провода с током / (рис. 441) по закону полного тока определится
следующим образом: проведем через точку А окружность радиуса
R в плоскости, перпендикулярной оси провода, так что центр ее на-
ходится на оси провода. В силу симметрии напряженность поля во
всех точках окружности численно одна и та же. Направление нап-
ряженности совпадает с касательной к окружности. Поэтому
§Hd7 = §HdlcosO° = И §dl = Н • 2л/? = /, Н=
С увеличением радиуса R напряженность магнитного поля убывает
по гиперболическому закону.
Если какое-либо поле имеет сложный характер и не удается сос-
тавить замкнутый контур, все точки которого находились бы в сим-
метричных условиях, то хотя интегральная форма записи закона
полного тока справедлива и для такого контура, но использовать
ее для нахождения напряженности в любой точке поля не удается
(И нельзя вынести из под знака интеграла).
§ 437. Дифференциальная форма закона полного тока. Соотно-
шение (15.3) годится для контура любых размеров, в том числе и
для весьма малого контура.
Выделим в какой-либо среде небольшой контур («жирно» об-
веден на рис. 442) и составим вдоль него циркуляцию вектора Н.
Циркуляция напряженности поля вдоль этого контура равна току, п[ о-
низывающему «жирно» обведенную площадку.
Если площадка мала, то можно полагать, что плотность тока
6 в пределах этой площадки одинакова, и тогда ток, пронизываю-
щий площадку, будет равен
619
At — ё As — ёп As.
Здесь ё„ есть проекция вектора плотности тока ё на нормаль к
площадке, т. е. на направление As:
(|л dT= 6„As.
За положительное направление нормали к площадке принимают
направление движения острия правоходового винта, головка кото-
рого вращается в направлении, принятом за положительное при
обходе контура при составлении циркуляции.
Поделим обе части равенства на As и устремим As к нулю. Это
будет соответствовать стягиванию «жирно» обведенной на рис. 442
площадки к нулю. Предел полученного отношения равен
(£ я аТ
lim —-----= ё„.
As—>0 As
В левой части равенства стоит величина, которую в курсе ма-
тематики называют проекцией ротора Н на направление нормали
к площадке As. Проекция ротора на направление нормали обоз-
начается так:
rot;i Н.
Следовательно,
rot„tf = 6„.
Если площадку As ориентировать в пространстве так, что на-
правление нормали к ней совпадет с направлением вектора плот-
ности тока ё в данной точке поля, то тогда вместо того, что-
бы писать равенство проекций двух векторов (rotn Н и ё„), можно
записать равенство самих векторов, т. е.
rot Н = 7. (15.4)
Последнее выражение и представляет собой закон полного тока
в дифференциальной форме. В дальнейшем он часто используется
для расчета магнитных полей.
Ротор может быть определен как функция, характеризующая
поле в рассматриваемой точке в отношении способности к образова-
нию вихрей.
Уравнение (15.4) записано в общей форме, безотносительно к
системе координат, и в каждой конкретной системе координат оно
раскрывается по-своему.
§ 438*. Раскрытие выражения rot Н — ё в декартовой системе
координат. Равенство двух векторов rot Н и ё означает, что
620
равны проекции их на ось х, равны проекции на ось у и проекции
<сн *
на ось z. Проекция rot// на ось z равна roL,// = —------, проек-
fts2 -> 0 Дзг
ция вектора 6 на ось z есть и т. д.
На рис. 443 в декартовой системе координат изображен малый
прямоугольный контур mnpq. Обойдем этот контур против часовой
стрелки и составим циркуляцию вектора //. При составлении цир-
куляции необходимо учесть изменение вектора Н от точки к точ-
ке. Обозначим проекции Н на оси х и у в точке т, соответствен-
но, через Нх и Ну. В точке п про-
екция на ось х изменится по срав-
нению с проекцией в точке т и ста-
нет равной Нх dx; проекция на
дх
дНи
ось у. // -4--—dx.
v ч дх
В точке q\
дН ,
/7 -4-——dy и //„ -\-~~dy.
х 1 ду ' у ' ду J
Рис 443
В точке р.
дН дН дН„ дН„
// -4--^-dy-[--5—dx и Н..Д- ~~dy dx.
х 1 ду J 1 дх У ' ду ' дх
При составлении циркуляции на участках тп и pq надо при-
нять во внимание лишь «иксовые» составляющие Н («игрековые»
составляющие перпендикулярны элементу пути).
Составляющая &Hdl на пути тп найдется как произведение
среднего значения «иксовой» составляющей напряженности на этом
пути на длину пути dx, т. е.
dx = (Н 4- — ^^dx\dx.
\ 2 дх )
На участке пр
I дН \ I дН„ дН \
I Н + —dx ) -р I Н 4- -У- dx 4- —d.dy 1
\ ' дх ) \ ч дх ду /
dy.
621
На
участке pq:
(— dx) =
дН v . . 1 дН. ,
—- dq-]------—*dx
ду ' ' 2 дх
{—dx).
На участке qm
2 ду
dy}(—dy)-
Если просуммировать все составляющие циркуляции вдоль
контура mtipq, то получим
(дН дН \
\ дх ду~ / dxdy-
В соответствии с определением проекции ротора на ось z по-
делим циркуляцию на площадку dsz = dx dy, после чего проекция
ротора на направление оси z запишется следующим образом:
-» дН„ дН
rot_ // = = Л .
г дх ду г
Аналогично
Таким образом,
rot Н = i (д~ -
\ ду
дг
rot>// =
Т0{уН>
ду дг
дНх дН?
дг дх
дНх дНг
= й
(15.6)
дх ду ) ' '
дг дх
§ 439. Выражение ротора в виде векторного произведения [V И].
Формально rot// можно представить в виде векторного произве-
дения оператора пространственного дифференцирования V па
вектор Н, т. е. rot 77 = [V //].
В этом нетрудно убедиться путем непосредственного умно-
жения v на Н\
и
ГМ д . -» д . д \ -* \1
[О &+ / ГУ+k Гг) V )] =
= _дН± \ ; 1дН± _дНД . (дН^_дНХ
\ ду дг ) ' ‘ \ дг дх )' \ дх ду )'
§ 440. Раскрытие rot// в виде определителя в декартовой сис-
теме. Ротор любого вектора, используемого в теории электромаг-
622
нитного поля, может быть представлен в виде определителя треть-
его порядка.
Так, rot И в декартовой системе запишется в виде такого
определителя
-» i -> / k
rot Н = £ д_ д_
дх ду дг
"х И У
(15.6)
Непосредственное раскрытие определителя показывает, что
получается выражение (15.5).
§ 441*. Выражение проекций ротора в цилиндрической системе
координат. Без вывода приведем выражение проекций ротора Н в
цилиндрической системе координат
. -й 1 дНа
rot,// =-----,------,
' г да дг ’
rot 7/ = ^-^
° дг
дг
(15.7)
rot
z г I дг
Mr
да
§ 442 *. Выражение проекций ротора в сферической системе коор-
динат. В сферической системе координат:
rot „ Н = —!— Г — (sin GZ/„) — 1,
л R sin е L <36 да ]
rote = R sin 0 да R"dR
15.8)
§ 443. Принцип непрерывности магнитного потока. Магнитный
поток есть поток вектора магнитной индукции через некоторую по-
верхность
Индекс s под знаком интеграла свидетельствует о том, что речь
идет об интеграле, взятом по поверхности s. Если поверхность зам-
кнута сама на себя (например, поверхность шара), то поток, про-
низывающий замкнутую поверхность, запишется так:
Ф = £ В ds.
623
Опыт показывает, что вошедший внутрь любого объема магнитный
поток равен магнитному потоку, вышедшему из того же объема.
Следовательно, сумма вошедшего в объем и вышедшего из объема
потоков равна нулю:
= 0. (15.9)
Последнее выражение представляет собой математическую запись
принципа непрерывности магнитного потока.
§ 444. Дифференциальная форма принципа непрерывности маг-
нитного потока. Поделим обе части (15.9) на объем V, находящийся
внутри замкнутой поверхности s, и найдем предел отношения, ког-
да объем V стремится к нулю:
lim —-----
г->о V
= 0 или divB = 0.
(15.10)
Соотношение (15.10) можно трактовать как дифференциальную
форму принципа непрерывности магнитного потока. Оно годится
для любой точки магнитного поля. Следовательно, в любой точке
магнитного поля нет ни истока, ни стока линий вектора магнитной
индукции. Линии вектора В нигде не прерываются, они представ-
ляют собой замкнутые сами на себя линии (окружность — пример
замкнутой на себя линии).
§ 445. В областях, «занятых постоянным током» , магнитное
поле есть поле вихревое, в областях, не «занятых током» , его мож-
но рассматривать как поле потенциальное. Вихревыми принято на-
зывать поля, ротор которых отличен от нуля. Так как для магнит-
ного поля постоянного тока
rot Н = Г,
—>
то во всех точках пространства, где 6 =/= 0, там поле вектора
Н является полем вихревым.
В областях пространства, где 6=0, там rot Н = 0 и магнит-
ное поле можно рассматривать как поле потенциальное.
§ 446. Скалярный потенциал магнитного поля. Для совокупно-
сти точек, где 6=0, там rot Н = 0 и магнитное поле можно рас-
сматривать как поле потенциальное, т. е. как поле, каждая точка
которого имеет скалярный магнитный потенциал <рт. Следовательно,
для таких областей можно принять
//=—gradcfm. (15.11)
Так как div В = div рЯ = 0, то при р = const div /7 = 0.
624
В последнее выражение подставим — grad <pm вместо Н, получим
div grad <pm = 0.
Таким образом, скалярный потенциал магнитного поля <рот, о кото-
ром может идти речь только для областей, не занятых током, под-
чиняется уравнению Лапласа
V2<Pm = 0. (15.12)
Разность скалярных магнитных потенциалов между точками /
и 2 называют падением магнитного напряжения между точка-
ми 1 и 2 (см. стр. 74):
2
j«12=(Pjki Тлг = J//d/ .
1
Падение магнитного напряжения между точками 1 и 2 по ка-
кому-то одному пути (например, по пути 132, рис. 444, а) в точнос-
ти равно падению магнитного напряжения между теми же точка-
ми по какому-то другому пути (например, по пути 142) в том слу-
чае, когда эти пути образуют замкнутый контур, ток внутри кото-
рого равен нулю.
Если же замкнутый контур, образованный двумя путями, ох-
ватывает некоторый ток, то падение магнитного напряжения по
первому пути не равно падению магнитного напряжения по второ-
му пути — они будут различаться на величину тока, охваченного кон-
туром. Последнее следует из закона полного тока. Так, примени-
тельно к рис. 444, а II dl =/= J Н dl (ибо из закона полного то-
752 132
ка следует, что J Н dl Ч~ J 7/ dl = —I, или J 7/ dl ——1~\- J H dl ).
132 251 132 152
Следует различать понятия падения магнитного напряжения
и магнитное напряжение. Первое определяется только линейным
интегралом от Н на dl по выбранному пути. Второе — не толь-
ко этим интегралом но и м.д.с., имеющейся на пути (см. стр. 83).
21 Л. А. Бессонов
625
Здесь имеется полная аналогия с понятиями падение напряже-
ния и напряжение для электрической цепи.
§ 447. Граничные условия. Подобно тому как в электростатичес-
ком поле и в поле проводящей среды выполнялись определенные
граничные условия, в магнитном поле также имеют место свои гра-
ничные условия. Их два:
Hlt = H2t, (15.13)
В1п = В2п. (15.14)
Условие (15.13) означает, что на грани раздела двух однород-
ных и изотропных сред, различных в магнитном отношении (раз-
личные р), равны тангенциальные составляющие векторов напря-
женности магнитного поля.
Условие (15.14) свидетельствует о равенстве нормальных сос-
тавляющих векторов магнитных индукций на грани раздела.
Условие (15.13) выводится путем составления линейного интеграла
§HdT по плоскому контуру mnpq (рис. 444, б) подобно тому,
как в разделе электростатического поля (стр. 556) составлялся ин-
теграл $Edl = 0. Стороны пр и qm ничтожно малы по сравнению со
сторонами тп и pq. Длину стороны тп и равную ей по величине
длину стороны pq обозначим через dl. Тогда
Н± sin 04 dl — Н2 sin а2 dl = 0,
но Н1 sin аг = Hlt, Н2 sin а2 = Н21, следовательно, Н1( = H2t.
Необходимо заметить, что условие (15.13) не выполняется, если
на поверхности раздела двух сред протекает так называемый «по-
верхностный ток». Под ним понимают ток, протекающий по бес-
конечно тонкому плоскому проводнику, помещенному на грань
раздела.
В этом случае <§)Н dl будет равняться не нулю, а поверхност-
ному току cdl, который попал внутрь замкнутого контура:
/Д sin аг dl — Н2 sin а2 dl = о dl,
и в силу этого, Hlt— Н21 = о.
Другими словами, при наличии поверхностного тока с плот-
ностью о тангенциальная составляющая напряженности поля тер-
пит разрыв. Как правило, однако, поверхностный ток отсутствует,
и равенство (15.13) имеет силу.
Равенство нормальных составляющих векторов магнитной ин-
дукции следует из принципа непрерывности магнитного потока
(р/ ds = 0.
Для того чтобы убедиться в справедливости (15.14), выделим
на грани раздела небольшой плоский параллелепипед и подсчитаем
626
потоки вектора В через нижнюю грань (рис. 445) —Bln As и че
рез верхнюю грань B2nAs.
Сумма потоков равна нулю:
—Bln AsB2n As = 0.
Следовательно,
Bin — в.2п.
Из (15.13) и (15.14) вытекает соотношение
= (15.15
tg «2 Р-2
Оно дает связь между углом падения ах и углом преломления
а2 (см. рис. 444, б). Если магнитные силовые линии выходят из
среды с большой магнитной проницае-
мостью, например pt= 104ро, в среду с
малой магнитной проницаемостью, на-
пример в воздух р2 = р0, то
^£3=104 и tga2 = 10-4tgar
tg И2
Следовательно, угол a2 много мень-
ше угла аг.
Пример 201. Найти угол а2, под ко-
торым силовые линии выходят в среду
с магнитной проницаемостью р,2, если
угол аг = 89е; щ = 104 ц,„ р2 = р0.
Решение, tgax = tg89° = 57,29.
tg a2 = tg aj = 10~4 tg ax = 0,005729; a2 = 20'.
Pi
§ 448. Векторный потенциал магнитного поля. Для расчета маг-
нитных полей широко используется векторный потенциал или век-
тор-потенциал магнитного поля. Его обозначают через А. Это ис-
кусственно введенная векторная величина, плавно изменяющаяся
от точки к точке, и такая, что ротор ее равен магнитной индукции:
В = rot А (15 16)
Основанием доя представления индукции в виде ротора от век-
тора-потенциала служит то, что дивергенция любого ротора тож-
дественно равна нулю.
Известно, что в магнитном поле div В = 0. Подстановка в
это равенство rot А вместо В дает выражение, тождественно рав-
нее нулю:
21*
627
div rot A = 0*.
Если вектор-потенциал как функция координат будет известен,
то индукция в любой точке поля определится путем взятия ротора
от вектора-потенциала в соответствии с (15.16). В отличие от ска-
лярного магнитного потенциала <рт, пользоваться которым можно
только для областей, «не занятых током» ( см. § 446), векторным
потенциалом можно пользоваться как для областей, «не занятых
током», так и для областей, «занятых током».
В электротехнических расчетах векторный потенциал приме-
няется для достижения двух целей.
Первая цель — определение магнитной индукции при помощи
уравнения (15.16).
Вторая цель — определение магнитного потока, пронизываю-
щего какой-либо контур (см. § 450).
Векторный потенциал в произвольной точке поля связан с плот-
ностью тока в этой же точке уравнением Пуассона.
§ 449. Уравнение Пуассона для вектора-потенциала. Умножим
обе части (15.4) на магнитную проницаемость среды р,:
pi rot Н = цб.
Условимся, что будем иметь дело со средами, которые могут
быть подразделены на отдельные области, так что магнитные про-
ницаемости pi в каждой отдельной области постоянны. Если ц пос-
тоянно, то его можно подвести под знак ротора
rot ц/7= rot В = рб*. (15.17)
В (15. 17) вместо В подставим rot Л, будем иметь
rotrot>l=p6. (15.18)
Операция взятия ротора от ротора есть по сути дела операция
раскрытия двойного векторного произведения и выполняется так**:
rot rot А = [V [V Л]] = grad div А — V2 А = р б (15.19)
* Равенство нулю div rot А можно пояснить при помощи оператора V.
С этой целью вместо rot А запишем |УД]. Тогда div rot А = V|V Л]. Век-
торное произведение [VД] перпендикулярно и к V и к Д. Скалярное произ-
ведение V на [УД], т. е. у [УД], равно нулю потому, что равен нулю коси-
нус угла между У п [УД].
** Из курса математики известно, что двойное векторное произведение
раскрывается следующим образом
[« ( b с)] = Ь( а с) — с (а Ь).
В нашем случае роль векторов а и Ь играет оператор V. а роль вектора с
играет вектор-потенциал Д. Таким образом [у [у Д|] — у (уД) — ~Д(уу; =
= grad бД’Д — у2Д.
628
До сих пор к вектору-потенциалу никаких дополнительных тре-
бований не предъявлялось, если не считать того, что это должна
быть функция, имеющая пространственные производные. Так как
А есть расчетная функция, то мы вправе подчинить ее в магнитном
поле постоянного тока требованию
сПуЛ=О. (15.20)
Это требование означает, что линии вектора А есть замкнутые
сами на себя линии. С учетом (15.20) уравнение (15.19) приобретает
следующий вид
?2Л=—цГ. (15.21)
Уравнение (15.21) есть не что иное, как уравнение Пуассона.
В отличие от уравнения (13.26) оно составлено относительно век-
торной величины, тогда как уравнение (13.26) составлено относи-
тельно скалярной величины <р. Вместо А в (15.21) подставим
iAx -ф- jA kAz и плотность тока б заменим на «Д.+
У21’4+ ^Аг = — Р'6х—Н/Ч— А •
Последнее уравнение разбивается на три уравнения, составлен-
ные относительно скалярных величин Ах, Ау, Аг :
VM v = — цбЛ,
?2Л2 =— рбг.
Общее решение их по аналогии с решением уравнения (13.26) за-
пишется так:
№
V
л = Г f (15.226)
v 4л J R ' '
Г
(15-22В)
V
—> —>
Если (15.22а) умножить на i, (15.226) на / и (15.22в) на k
и сложить, то получим
Х+Х +Х = £ С Х+Х+ь,>1У
* 1 ' У 1 г 4л J R
V
629
(15.24)
может
(15.25)
(15.26)
прони-
цирку-
ИЛИ Х== С (15.23)
4 л. J
V
Уравнение (15.23) есть общее решение уравнения (15.21) Вектор-
потенциал в любой точке поля Может быть определен путем вычис-
ления объемного интеграла (15.23). Объемный интеграл должен
быть взят по всем областям, занятым током.
§ 450. Выражение магнитного потока через циркуляцию вектора-
потенциала. Магнитный поток, пронизывающий какую-либо поверх-
ность s, равен р _» -»
Ф = j В ds .
S
Так как В = rot А, то Ф = j rot A ds .
s
На основании теоремы Стокса поверхностный интеграл
быть преобразован в линейный:
J rot A ds A dl.
s
Таким образом, „ , >
Ф = ф A dl.
Другими словами, для определения магнитного потока,
зывающего некоторую площадь s, необходимо подсчитать
ляцию вектора потенциала по замкнутому контуру, на который опи-
рается поверхность s.
Определение потока по (15.26) часто имеет преимущества по
сравнению с определением потока через магнитную индукцию по
(15.24). Дело в том, что соотношением (15.24) можно пользоваться
только в том случае, когда известно значение В в любой точке по-
верхности s, тогда как для вычисления потока при помощи соот-
ношения (15.26) достаточно знать значение А на контуре и не тре-
буется знание А в точках внутри контура.
Переход от [ rot A ds к интегралу ([’ A dl может быть пояснен
S
следующим образом.
Разобьем площадь s на элементарные площадки (см. рис. 446).
Заменим интеграл суммой и под интегралом вместо rot А подставим
г д’ J7 ’ . .
в соответствии с определением ротора m —— (предел опущен), тогда
J rot A ds* У ф
S
Таким образом, для вычисления J rot A ds необходимо найти
5
630
составляющие циркуляции вектора А по контурам всех элементар-
ных площадок и затем сложить их. Так как при составлении цир-
куляции обход участков, являющихся смежными между какими-ли-
бо двумя соседними площадками, совершается дважды и притом
в противоположных направлениях, то составляющие циркуляции на
всех смежных участках взаимно уничтожаются и остается цирку-
ляция только по периферийному контуру mnpq
по контуру
mnpq
§ 451. Векторный потенциал элемента тока. Определим величину
и направление составляющей векторного потенциала А, создавае-
мую током I, протекающим по элементу линейного проводника дли-
ной dl. Пусть расстояние от элемента тока до произвольной точки
пространства будет обозначено через R (рис. 447). В соответствии
с общим выражением
d А = i, но 1 dV =1 ds dl = id/;
4л. R
ds площадь поперечного сечения проводника. Следовательно,
= . (15.27)
4л R
Составляющая векторного потенциала от элемента тока имеет
такое же направление в пространстве, как и ток в элементе провод-
ника*.
§ 452. Взаимное соответствие электростатического поля и маг-
нитного поля постоянного тока. Между картиной электростатичес-
* Заметим, что единицей измерения для А является е • сек/м.
631
кого поля и картиной магнитного поля постоянного тока в областях,
не занятых током, может быть соответствие двух типов.
Первый тип соответствия — когда одинаково распределение
линейных зарядов в электростатическом поле и линейных токов в маг-
нитном поле. В этом случае картина магнитного поля (сетка поля)
подобна картине соответствующего электростатического. Отличие
состоит лишь в том, что силовым линиям электростатического поля
отвечают эквипотенциальные линии магнитного поля, а эквипотен-
циалям электростатического поля соответствуют силовые линии
магнитного.
В качестве примера на рис. 448 слева изображена картина по-
ля, образованного уединенным линейным зарядом + т, а справа
Электрическое попе Магнитное поле
заряженной оси линейного тока
Силойые пинии СилоНые линии
Рис. 448
на том же рисунке картина поля уединенного проводника с током
/ (для области вне проводника).
Второй тип соответствия, когда одинакова форма граничных
эквипотенциальных поверхностей в электростатическом поле и в
магнитном поле постоянного тока. В этом случае картина поля
оказывается совершенно одинаковой.
Соответствие второго типа проиллюстрируем при помощи
рис. 450. На нем изображена картина магнитного поля в воздушном
промежутке между полюсом и якорем машины постоянного тока
(обмотки не показаны). Если допустить, что полюс и якорь этой
машины используются в качестве электродов некоторого конден-
сатора, то картина электрического поля в воздушном промежутке
между электродами соответствовала бы картине магнитного поля —
в обоих случаях силовые линии выходили бы из полюса и входили
в якорь.
§ 453. Типы задач на расчеты магнитных солей. Различных типов
задач на расчет магнитных полей очень много. Рассмотрим вкратце
только некоторые из них в качестве иллюстрации.
Очень часто приходится определять индуктпвнос1ь какого-лп-
632
бо контура или взаимоиндуктивность двух контуров. Это первый
тип задач. Вторым типом задач являются задачи на определение
сил, действующих в магнитном поле на движущийся электрон, на
неподвижный проводник с током, на ферромагнитные массы в маг-
нитном поле*. Определение этих сил часто очень важно. Так, на-
пример, при работе электрических аппаратов при коротких замы-
каниях в цепи по ним могут протекать настолько большие токи,
что силы взаимодействия токов с полем, если не принято необхо-
димых мер, могут разрушить аппарат.
Третьим типом задач являются задачи на расчет магнитных эк-
ранов. Магнитными экранами называются устройства, предназна-
ченные для ослабления магнитного поля в заданной области про-
странства по сравнению с магнитным полем вне экрана. К магнит-
ной экранировке прибегают, например, для защиты чувствитель-
ных приборов от влияния посторонних магнитных полей, в част-
ности от влияния магнитного поля земли.
Четвертым типом задач является задача о распределении токов
в некотором объеме так, чтобы получить заданное магнитное поле.
Так, например, в морском деле большое значение имеет дегаусси-
ровка кораблей: корабль, обладая большой ферромагнитной мас-
сой, возмущает магнитное поле земли не только в непосред-
ственной близости от него, но и на достаточно большом удале-
нии. Соответствующие индикаторы на возмущение магнитного по-
ля земли могут привести в действие находящиеся поблизости са-
модвижущиеся мины и в результате корабль может оказаться подор-
ванным. Чтобы этого не случилось, на кораблях устанавливают спе-
циальные намагничивающие обмотки, которые располагают та-
ким образом, чтобы скомпенсировать возмущение магнитного поля
земли вблизи корабля. Много различных задач на расчет магнит-
ных полей возникает при магнитной записи звука, а также при
магнитной дефектоскопии. Магнитная дефектоскопия позволяет по
картине магнитного поля судить о наличии раковин, трещин и других
дефектов в изделиях из ферромагнитных материалов. Особенно ши-
рокое распространение магнитная дефектоскопия получила на же-
лезнодорожном транспорте при контроле целостности рельсов же-
лезнодорожного пути.
§ 454. Общая характеристика методов расчета и исследования маг-
нитных полей постоянного тока. Все известные методы расчета и
исследования магнитных полей могут быть подразделены на три
группы: аналитическую, графическою и экспериментальную.
Аналитическая группа объединяет в себе все чисто аналитичес-
кого порядка приемы: интегрирование уравнения Пуассона (для
областей, запятых током), интегрирование уравнения Лапласа
(для областей, не занятых током), применение метода зеркальных
изображений и др.
* См. § 77—78.
633
В силу трудностей математического характера аналитические
методы позволяют решать только весьма небольшой круг задач.
В тех случаях, когда расчет поля аналитическими методами вызы-
вает затруднения, прибегают к графическому методу построения
картины поля или к исследованию магнитного поля на модели. Гра-
фические методы построения картины поля применимы к двухмер-
ным безвихревым полям. Существует несколько различных приемов.
Один из них подробно рассматривается ниже. Описания других
приемов читатель найдет в книге В. А. Говоркова «Электрические
и магнитные поля» (Л.26).
§ 455. Опытное исследование картины магнитного поля. Опыт-
ное исследование картины магнитного поля производится несколь-
кими методами. Первый метод основан на явлении электромагнит-
ной индукции и состоит в следующем: плоская очень малых разме-
ров рамка с намотанной на ней обмоткой помещается в исследуемую
область поля и соединяется с баллистическим гальванометром. При
коммутации тока в обмотках аппарата или машины, поле в воздушном
зазоре которого исследуется, или при быстром удалении рамки в
область, где магнитное поле заведомо слабое (в последнем случае
ток в обмотках не переключается), измеряется количество электри-
чества, протекшее по баллистическому гальванометру, и по нему
судят о среднем значении индукции в рамке. Затем рамку поме-
щают в другую точку поля и снова определяют индукцию и т. д.
Этот метод дает возможность исследовать магнитные поля практи-
чески любой конфигурации в пространстве вне ферромагнетиков.
Второй экспериментальный метод исследования безвихревого
поля — метод моделирования полями тока в проводящей среде. Он
основан на аналогии между полем в проводящей среде и магнитным
безвихревым полем. Этот метод был разработан Л. Р. Нейманом и
состоит в следующем: для снятия картины плоскопараллельного
поля в воздушном зазоре какого-либо аппарата или машины из
листа металла (например, из стального листа) изготовляют уве-
личенную модель исследуемого участка поля. Так, на рис. 449 изоб-
ражена модель для исследования поля рассеяния между полюсами
машины постоянного тока. Так как м.д.с. распределена вдоль по-
люса, то подвод тока к краю полюса производится от нескольких
припаянных к листу проводов. Токи в них могут регулироваться
и этим может задаваться закон распределения м.д.с. по высоте
полюса. Отвод тока от линии тп, являющейся эквипотенциальной,
производится при помощи массивной проводящей колодки (подроб-
нее см. Л. 39).
Щуп и индикатор служат для построения эквипотенциалей в
поле проводящей среды.
Качественное исследование магнитного поля часто производят
при помощи стальных опилок. Опилки насыпают на плоский лист
из неферромагнитного материала, помещают в магнитное поле и
слегка по листу постукивают. Опилки расположатся вдоль сило-
634
вых линий. По густоте силовых линий можно качественно судить
об интенсивности магнитного поля.
Вместо опилок часто используют мельчайшие порошки окислов
железа, находящихся во взвешенном состоянии в какой-либо жид-
кости, например керосине.
Последний способ особенно широко применяется при магнитной
дефектоскопии изделий из ферромагнитных материалов.
§ 456. Графическое построение картины поля и определение по
ней магнитного сопротивления. Рассмотрим методику графическо-
го построения картины плоскопараллельного магнитного поля на
конкретном примере.
На рис. 450 изображены полюс и якорь машины постоянного то-
ка. Размер, перпендикулярный рисунку, принят достаточно боль-
шим — только при этом условии поле можно считать плоскопарал-
лельным.
Так как магнитная проницаемость стали много больше магнит-
ной проницаемости воздуха, то магнитные силовые линии перпен-
дикулярны поверхности полюса и якоря. Следовательно, поверх-
ности полюса и якоря являются эквипотенциальными поверхностя-
ми. Построение семейства силовых и эквипотенциальных линий про-
изводят «на глаз», руководствуясь следующим: силовые линии дол-
жны быть перпендикулярны поверхностям полюса и якоря и дол-
жны быть так расположены по отношению друг к другу, чтобы пос-
ле проведения эквипотенциалей образовались криволинейные квад-
раты, для которых отношение средней ширины квадрата (назовем
ее Ь) к средней длине квадрата (а) было приблизительно одинаково
для всех квадратов. При первом построении это возможно не удаст-
ся сделать достаточно хорошо, но после нескольких попыток, в осо-
бенности при наличии некоторого навыка и с учетом симметрии в
поле (если она имеется), удается построить сетку поля так, что
fet б2 Ьз _
G± Gz G$
635
При этом потоки во всех силовых трубках будут одинаковы. Это
облегчает подсчет магнитного сопротивления.
Пусть число криволинейных квадратов в силовой трубке равно
п, а число трубок т (для рис. 450 п = 2 ат - 11).
Магнитное напряжение между полюсом и якорем
= dl~ + Н2а2 + Н.ла3 + ... = 2
*=L
В свою очередь поток в одной силовой трубке
ДФ = — lb2\iH2 — ,
где I — размер в направлении, перпендикулярном чертежу, р —
магнитная проницаемость воздуха (равна р0).
Следователю ю,
,, ДФ ,, ДФ
, //, =
Zb1(x 2
Магнитное напряжение
,, __ДФ / в]
~ I Т
---- и т. д.
1Ь^
По построению все слагаемые —, — и т.
61 ь2
слагаемых равно п. Поэтому
г, ДФ а
ит = — п-
т ц! Ь
Отсюда
Дф =
па
Поскольку для всех квадратов — const,
а
лись проведенными так, что потоки ДФ во
д. одинаковы. Число
то построения оказа-
всех силовых трубках
одинаковы.
Полный поток с якоря на полюс равен
Ф = m ДФ = t/mpZ -
а п
где т — число силовых трубок.
Магнитное сопротивление
D ____
*\tn — --- — “ •
Ф \ilbm
Магнитная проводимость
____________________________ \ilbm
(15.28)
(15.29)
Графический метод построения картины поля применяется не
только для расчета магнитных полей, он широко используется и
для других невихревых полей, а именно для расчета электростати-
ческого поля и для расчета поля постоянного тока в проводящей
636
среде. Так, электрическая проводимость G между двумя телами оп-
ределяется по формуле (15.30), которая получается из форму-
лы (15.29), если р, заменить на. у
G = ^-. (15.30)
ап
Емкость между двумя телами в плоскопараллельном поле
c=slbm^ (15.31)
ап
§ 457*. Магнитное экранирование. Положим, что в равномерном
магнитном поле напряженностью /70 надо заэкранировать некото-
рую область пространства, например цилиндрическую, так, чтобы
напряженность поля в ней была во много раз меньше, чем напря-
женность внешнего поля.
Цилиндрический экран внутренним радиусом а, наружным b
имеет относительную магнитную проницаемость р2г (рис. 451, а).
Внутреннюю область обозначим /, область тела экрана II, об-
ласть снаружи экрана III.
В областях I и III относительная магнитная проницаемость
равна единице. Так как во всех трех областях нет тока, то магнит-
ное поле в них описывается уравнением Лапласа v2<pm = 0. Экран
будем полагать достаточно протяженным вдоль осп z (ось z
перпендикулярна чертежу); ср,„ зависит только от координат г и а
цилиндрической системы. Раскроем уравнение V2q,n = 0 в цилин-
дрической системе
Ч"‘ г дг\ dr J г2 да1
0.
637
Решение его методом Фурье — Бернулли (см. раздел Электр®,
статики) дает:
для первой области «р^ = [сгг -|- — j cos а,
для второй области <р” = (csr -|—cos а,
для третьей области ср”1 = (сьг -J- —'j cos а.
Постоянная интегрирования, с точностью до которой опреде-
ляется потенциал, принята здесь равной нулю.
Для определения шести постоянных (С\, С2, С3, С4, Сь и Св)
составим 6 уравнений:
1. Сопоставим <р”! с выражением <рт «на бесконечности»
<рт = HBr cos а. Из сопоставления находим, что СБ = Нв,
2. В первой области при г = 0 <рт должен оставаться конечным,
это может быть только в том случае, если в выражении <р^ будет
Q
отсутствовать слагаемое —. Оно будет отсутствовать при С2 — 0.
Г
3. Равенство <р^ и «р” при г = а дает уравнение
С.а = С,а + -4.
‘ а
Нетрудно убедиться в том, что условие непрерывности потенциа-
ла эквивалентно условию равенства тангенциальных составляющих
напряженности поля на грани раздела при г = а. Действительно*,
На =— г да
Следовательно, Нх =—С. sin а а г=а
и Д11 = —sina/C,4-^\ г=а \ «2/
Таким образом, с. = с.+&
Последнее уравнение совпадает с полученным ранее.
4. Равенство <рт на грани между второй и третьей (при г = Ь)
областями приводит к уравнению
сБь+^в = с3ь+^.
* Напомним, что И = —grad ут. Формулы, позволяющие определить На
и Нг через q>m, следуют из соотношения (13.9) на стр. 540.
638
5. Равенство нормальных составляющих индукции
В = и-^2'”-
г дг
на грани между первой и второй областями (при г = а)
Сх= (сз
\ а2 /
6. Равенство нормальных составляющих индукции при г = b
дает уравнение
Сб ~ = (Сз — ь?) И2г-
Совместное решение всех уравнений приводит к выражению по-
тенциала в первой области
I и 2qb2
<р = Н.——г cos а
о д
или, переходя к декартовой системе координат (ось х направлена
вверх, х = г cos а)
= (15.32)
Здесь 9 = A = fe2-|3W,
(1 + |1‘2л) Р2г Ц2л+1
(15.33)
4 Ь2
,2 ‘
(15.34)
нее
Напряженность поля в первой области (по модулю)
,,1 "Ч'т г, 24ft2
И =------= //,.---.
дх ° А
Отношение напряженности поля внутри экрана к напряженности
внешнего поля Нй".
— 2?fe2
Н„ А Ц2г Ь2 — а‘
Формула (15.34) приближенна ^принято ₽ = 1 и q —
можно заключить, что чем больше р2г и чем толще стенка экрана,
тем сильнее экранирующее действие его.
На рис. 451, б качественно показана картина линий магнитной
индукции при наличии экрана. Из рисунка видно, что силовые ли-
нии магнитного поля в своем подавляющем большинстве стремят-
ся пройти по стенкам экрана и лишь небольшая часть их заходит
в экранируемую область.
Пример 202. p2r = 104; а — 5 см, b = 5,5 см.
Наити отношение -----.
Н1 4
= 0,0023,
Но 104 5,58 — 5а
639
т. е. напряженность поля внутри экрана составляет всего 0,23%
от напряженности Нь.
§ 458. Применение метода зеркальных изображений. Для рас-
чета магнитных полей, создаваемых линейными токами, протекаю-
щими вблизи стальных масс, широко применяется метод зеркаль-
ных изображений. Допустим, что в воздухе или в какой-либо другой
среде с магнитной проницаемостью pj параллельно плоскости раз-
дела сред проходит провод с током /х (рис. 452, а).
Вторая среда пусть имеет магнитную проницаемость р2. Тре-
буется найти напряженность поля в любой точке первой и второй
сред. С этой целью вводят в расчет фиктивные или расчетные токи
^(заданный ток)
Л* а
а)
Доя определения поля в
Верхней полуплоскости
Ц (заданный ток)
ток)
Рис. 452
Для определения поля В
нижней полуплоскости
(расчетный ток)
Дг
6)
/2 и 1Я. Провод с током /а помещают зеркально по отношению к
проводу с током /*, а провод с током /3 помещают там, где располо-
жен провод с током lv
Двумя пока неизвестными токами /2 и 73 распорядимся таким
образом, чтобы удовлетворить двум граничным условиям на грани
раздела сред.
Поле в верхней полуплоскости (там, где расположен ток
(рис. 452, б) определится от двух токов: от заданного /1; и от фик-
тивного /2, причем и верхнее и нижнее полупространства при
этом заполняет среда с магнитной проницаемостью Поле в лю-
бой точке нижней полуплоскости определится током /3, а верхнее
и нижнее пространства имеют ц = ц2 (рис. 452, в). Составим урав-
нения для определения токов /2 и /3. Если взять произвольную
точку а на грани раздела сред, то ее можно считать принадлежащей
как первой, так и второй средам. Если считать ее принадлежащей
первой среде, то тангенциальная составляющая напряженности
поля в ней изобразится левой частью уравнения (15.35'), а танген-
циальная составляющая напряженности поля в ней, если считать
ее принадлежащей второй среде, изобразится правой частью (15.35')
640
Ii >ь \ h
—4------------cos a —. —— cos a.
2л/? 2л/? I
(15.35')
Отсюда получается первая связь между токами
Л—/3.
Для получения второй связи составим уравнение, выражающее
собой равенство нормальных составляющих магнитной индукции
в произвольной точке а на грани раздела:
т. е.
Рис. 453
Совместное решение дает
Иг — Pi j
Р-1 + Р-2
2Ц1 ,
|Ч + Ц2
Пример 203. Найти напряженности поля в точках т и п (рис.
453, а). Геометрические размеры в сантиметрах даны на рисунке.
Относительные магнитные проницаемости plr=p1 = 1, р2л=М2 = 999,
= 10 а. '
Решение. По формулам § 458 находим
/2 = Ь = 9,98 а,
|Ч + Ц2
/3 = I = о,О2 а.
Pi +
Для определения напряженности поля в точке tn, расположен-
ной в той же полуплоскости (среде), что и ток Ilt служит рис. 453, б
641
По заколу полного тока
1 2Л/?!
10
= 79,5(а/лг), А/, ==-А_
2л. 0,02 ' " 2л/?2
9,98 nr А г / х
---------------- — 35.4 (а л).
2л.4,48.10~2
Графическим путем находим Нт — 101 а/м.
Напряженность поля в точке п (рис. 453, в)
Нэ = Нп = -±-
п 2л/?3
0,02
2л • 4,48 • 10~2
= 0,0715 (а/л<).
На рис. 454, а качественно изображена картина линий магнит-
ной индукции В для случая, когда провод с током проходит в воз-
духе параллельно поверхности стальной плиты. На рис. 454, б —
картина линий В для слу-
чая, когда провод с током
проходит через узкий канал
в стальной плите параллель-
но поверхности плиты.
Воздух
7777/77/
Сталь
а)
Рис. 454
Рис. 455
Пример 204. По весьма длинному биметаллическому проводу
(рис. 455) протекает постоянный ток /. Радиус внутренней жилы г1(
наружного слоя г2. Проводимость внутренней жилы ух, наружного
слоя у2.
Определить закон изменения векторного потенциала А и маг-
нитной индукции внутри провода [во внутренней (/)] и наружной
(//) областях и вне провода (область Ill).
Решение. Определим плотности тока в первой области (60
и во второй области (62).
642
Так как Ev = E2t, то — = —. С другой стороны,
Vl
+ ^2 (ЛГ5 --ЛГ1) = Е
Следовательно,
=---------------------- И г>г = бхА
nrj-|-^?(nr|—W?) У’
V1
При раскрытии выражения в цилиндрической системе коорди-
нат учтем, что в данной задаче А имеет только одну составля-
ющую А = z° Az = г°Д направленную по оси провода (по оси г),
и эта составляющая зависит только от г:
— pijfij для первой области,
— — (г — \ = —р262 Для второй области,
г dr \ dr ] q ДЛя третьер1 области.
Двукратное интегрирование по г дает
Л„ = -^ + С31пг + С4,
= Съ In г Св.
Слагаемое С\1пг должно отсутствовать, так как А не может
принимать бесконечно больших значений при г — 0, отсюда сле-
дует, что CL = 0.
Вектор-потенциал определяется с точностью до постоянной, при-
мем эту постоянную равной нулю, С2 = 0. При этом на оси про-
вода А — 0. Из граничных условий составим уравнения для опре-
деления оставшихся четырех постоянных:
1. При г ~r± At = Аи, следовательно,
|чМ =_ И2М__|_Сз1пГ1_|_с4.
4 4
2. При г — г2 Ап — Апр т. е.
_ Ся In r2 + С4 = С5 In r2 + Q.
4
I dA. 1 dAu
3. При г — г. = H2t или--------------------——, т. е.
F 11/2/ & df
Ь\Г 1 62г । Од
2 2 p2'i
4. При г — г2 должны быть равны тангенциальные составляю-
щие напряженности поля
643
^2*2 С3 Cg
2 ц2г2 Цз<2
Имеем;
С3 = ^(6г-д.г),
/-> ^2 Pg — f 1) 4~ t>lr 1
с5 2 Рз>
Г» __ Н1®1Г1 I Р-2^2^1 /-> ] . (> 1*2^2^ I
с4 — — -| -------U 3 1П Гр с0 —-----------(-
4 4 4
~Ь С3 1П Г2 ~Ь ^4 ^5 Г2.
На рис. 455 одна кривая дает характер изменения — А = f (г);
другая кривая — характер изменения B = f(r) при — = — и рх =
?2 3,5
= Нг = Из.
Пример 205. Воспользоваться выражением Ф = A dl и данны-
ми примера 204 и найти магнитный поток, пронизывающий биметал-
лический провод примера 204 на длине I — 1 м.
Рис. 456
Решение. По формуле (15.26) Ф= (j A dl Разобьем путь ин-
тегрирования на четыре участка.
Первый участок от точки 1 до точки 2 (см. рис. 436, а).
Второй участок — от точки 2 до точки 3.
Третий — от 3 до 4 и четвертый от точки 4 до точки I.
В соответствии с этим
2 3 4 1
<f ~А di = J A dl + J Л dl f A dl -ф- f A dl.
I 4 J 4
2
J A dl равен нулю, так как значение А при г == 0 равно пу-
1
641
лю. На втором и четвертом участках J A dl также равен нулю,
так как угол между А и dl равен ± 90°, a cos 90° = 0.
J A dl не равен нулю только на третьем участке. На третьем
участке
А =нМ+Сз1п/.2+С4>
г-г, 4
а угол между А и dl равен 180° (cos 180° = — 1). Поэтому
4
Ф = f A dT=— А- 1.
3 г=г2 г = г2
Пример 206. Воспользоваться построениями рис. 450 и опреде-
лить магнитную проводимость воздушного зазора между полюсом и
якорем машины постоянного тока на единицу длины якоря (1 м).
Решение. В соответствии с рис. 450 п — 2 и tn = 11;
— = 0,9. По формуле (15.29)
а
Gm = 1,256 ' 10-6 ' 1.'0’9' 11 = 6,23 • 10-" (гн).
m 2 ’ \ /
Пример 207. Определить емкость и индуктивность на 1 м длины
кабельной двухпроводной линии с цилиндрической проводящей
броней. Картина поля в сечении кабельной линии дана на рис. 456, б
(ег = 2,5).
Решение. Изображенная на рис. 456, б картина поля спра-
ведлива и для электрического и для магнитного поля. Причем в со-
гласии с § 452 силовым линиям электрического поля соответствуют
эквипотенциали магнитного.
Число силовых трубок электрического поля т = 10,5 • 2 = 21.
Число ячеек в трубке п = 10 (пять от провода до брони, пять от
брони до провода). Отношение — ^1. Число силовых трубок маг-
нитного поля tn = 10, число ячеек в трубке п = 21. По формуле
(15.31) найдем емкость на 1 м длины кабеля (/ = 1 м):
С = 2,5.8,86.10-». ЬЬ21 в 46 . 10-12
10
По определению, индуктивность L равна отношению потоко-
сцепления к создающему его току L = у. В данной задаче име-
ется всего один виток (прямой и обратный провода). Поэтому
потокосцепление ф равно потоку Ф между проводами (индуктив-
ностью, обусловленной потокосцеплениями в теле проводов, в
силу их малости пренебрегаем).
645
По закону полного тока ток / может быть заменен на у Н dl
по замкнутому контуру, окружающему провод. В свою очередь
(fttdT представляет собой падение магнитного напряжения Um по
этому контуру. Следовательно,
Г ________ Ф ф
ь = —- ~ —-------— (j
I dl ит
Таким образом, индуктивность L в данном примере равна маг-
нитной проводимости Gm. Для определения последней воспользуем-
ся формулой (15.29)*
г , 1,256 10-е. 1 . ] . ю 7
G,n = L =---------------------= 6-10 (гн).
Пример 208. Найти разность скалярных магнитных потенциалов
(магнитное напряжение) между точками А и В, расположенными
в магнитном поле линейного тока I = 10а (рис. 457).
в
Решение. UmAB = J Н dl = Н dl \ Н (1Г,
А по пути АтС по пути СпВ
/ 2л/?д /
2л/?д 4 4 *
7/ dl = Н
по пути АтС
J Н dl =0, так как на этом участке угол между Н и dl ра-
по пути СпВ
вен 90°. Следовательно,
UmAB = \ = 2,5 а.
Пример 209. В воздухе создано равномерное магнитное поле на-
пряженностью Н„ — 240 а/м. В это поле поместили ферромагнит-
ный шарик, относительная магнитная проницаемость которого
р( = 20. Найти индукцию в шарике.
Решение. Воспользуемся аналогией между электростати-
ческим и невихревым магнитным полями. В формуле (13.69) заменим
£0 на Но и е на р.
Получим
И. = Н„ —3|tf
2ре + р.
240 . Ai_L = 32,7 а[м.
2+20
Индукция в шарике
Bt = 20.32,7 . 1,256 . 10-6 = 8,21 . 10~4 тл.
* При вычислении L по формуле для Gm число ячеек в силовой трубке
должно быть взято по замкнутому контуру.
646
Пример 210. Вдоль трубы с внутренним радиусом и наружным
радиусом г2 (рис. 458) протекает постоянный ток /. Вывести фор-
мулы для определения напряженности поля Н для внутренней
полости трубы, для тела трубы и снаружи трубы.
Решение. Напряженность поля в любой из указанных об-
ластей найдем по закону полного тока.
Если провести окружность радиуса г < гг с центром на оси
трубы, то эта окружность не охватит тока. Поэтому при г < гг
Н = 0. Другими словами, во внутренней полости трубы магнитное
поле отсутствует. Плотность тока в трубе
л (г| — г’)
Рис. 457 Рис. 458 Рис. 459
Окружность радиуса < г < г2 охватывает ток дл (г2 — г2).
Поэтому в этом интервале изменений г
я /(г2-г?)
2nr(r| — rl)
Снаружи трубы при г^> г2 напряженность поля убывает по гипербо-
лическому закону
2лг
График Н = f (г) изображен на рис. 458.
*
* *
-Из курса физики известен закон Био—Савара—Лапласа.
Согласно этому закону при отсутствии ферромагнитных сред отре-
зок линейного провода dl, по которому течет ток /, создает магнит-
ную индукцию dB в точке, удаленной на расстояние /? от элемента
тока, определяемую следующим образом:
_ trfZ /?о]
4л~ Я2
—>
Здесь /?0 — единичный вектор, проведенный от dl к точке, в ко-
торой определяется магнитная индукция (рис. 459). Результирую-
щая индукция в этой точке
(15.36)
647
В = I W яЛ . (15.37)
4л J Я1 2 '
l
В формуле (15.37) интегрирование производится по всей длине зам-
кнутого контура с током.
Если в формуле (15.36) ток I как постоянную величину ввести
в векторное произведение и заменить Idl на SdV, где dV — элемент
объема проводника с плотностью тока 6, то
н
= Но /?f|W
4л В2
(15.38)
(15.39)
В формуле (15.39) интегрирование производится по объему, «заня-
тому током».
Формула (15.38) в литературе встречается под названием за-
кона Ампера.
Практически формулы (15.37) — (15.39) применяются в тех слу-
чаях, когда интегралы могут быть взяты без больших затруднений.
Два простейших примера на применение
формулы (15.37) приводятся на стр. 649.
В заключение обратим внимание на
два положения.
в известной мере сходна
Рис. 460
1. Структура формул (15.36) и (15.38)
со структурой формулы для напряженности электрического поля
в поле точечного заряда, полученной в § 382 из закона Кулона.
2. Полезно сопоставить закон полного тока с законом Био —
Савара — Лапласа. Оба эти закона позволяют определять магнит-
ную индукцию, создаваемую током. Однако закон полного тока
применим только к замкнутым контурам с токами, тогда как закон
Био — Савара — Лапласа применим не только к замкнутым кон-
турам с токами, но в к отрезкам проводников стоками (кэлементам
648
тока). В этом смысле закон Био — Савара — Лапласа является
более универсальным.
Пример 211. При помощи формулы (15.37) определить магнитную
индукцию в точке т, создаваемую отрезком линейного провода с
током / (рис. 460). Точка т удалена от провода на расстояние Ь.
Решение. Угол между dl и Р обозначим а. Из геометричес-
ких соображений имеем
R =—-—, I = — b ctg а.
sin а
Следовательно, dl — ---------.
sin2 а
| [dZ/?0] | = dl • 1 • sin а,
dB = sin a da.
4nb
a2
В = — f sin a da = — - (cos a, — cos a2).
4nb J 4nb ' 1 27
a.
Вектор В направлен к читателю.
Если провод будет бесконечно длинный, то at = 0, а2 = 180°,
cos a. — cos a, = 2 и В = , что совпадает с результатом, полу-
2л6
чаемым по закону полного тока.
Пример 212. Вывести формулу для определения напряженности
магнитного поля на оси кругового витка с током 1 (рис. 461). Ра-
диус витка принять равным а.
Решение. Выделим элемент тока Idl. Напряженность поля
dH', создаваемая этим элементом в точке b на оси витка, находящейся
на расстоянии г от плоскости витка, равна
/1*0,1 .
4л (а2 + г2) ’
напряженность dH' перпендикулярна dl и /?„. От диаметрально
противоположного элемента тока I dl в той же точке b будет
напряженность dH". По модулю dH' и dH" одинаковы.
При геометрическом суммировании dH' и dH" будет получен
вектор, направленный по оси витка:
dl = a da,
2п 2г
уу__Г la sin [3 da __ la а Г da________
J 4л (a2 -L- z2) 4л (a2 + z2) (ач 22)'/a J 2 (a2 + z2)*/a
и
0
Глава шестнадцатая
ОСНОВНЫЕ УРАВНЕНИЯ
ПЕРЕМЕННОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
§ 459. Определение переменного электромагнитного поля. Под
переменным электромагнитным полем понимают совокупность из-
меняющихся во времени и взаимно связанных друг с другом элект-
рического и магнитного полей.
Переменное электромагнитное поле является одним из видов ма-
терии. Оно обладает энергией, массой и количеством движения и
может превращаться в другие виды материи. Любые возмущения
поля в диэлектрике с огромной скоростью, равной примерно
ЗЮ8 м/сек, передаются на большие расстояния.
При исследовании процессов в переменном электромагнитном
поле пользуются уравнениями, которые принято называть уравне-
ниями Максвелла.
Систему уравнений Максвелла образуют четыре уравнения:
1. Уравнение, выражающее связь между ротором напряженности
магнитного поля и плотностью тока в той же точке поля. Это урав-
нение называется первым уравнением Максвелла.
2. Уравнение, которое дает связь между ротором напряженности
электрического поля и скоростью изменения магнитного поля в той
же точке поля. Это уравнение называется вторым уравнением Мак-
свелла.
3. Уравнение div В = 0, выражающее принцип непрерывности
магнитного потока.
4. Уравнение div Е = ?се°б , выражающее связь между истоком
е
напряженности электрического поля и плотностью свободных заря-
дов в той же точке поля.
При исследовании энергетических соотношений в электромаг-
нитном поле применяют также теорему Умова — Пойнтинга, кото-
рая рассматривается в дальнейшем в § 463.
§ 460. Первое уравнение Максвелла. Первое уравнение Максвел-
ла записывается следующим образом:
650
rot Н = б + e —-
dt
(16.1)
В правой части его есть две плотности тока: плотность тока про-
водимости 6 и плотность тока электрического смещения е —. Ток
dt
электрического смещения возникает в любом диэлектрике, в том
числе и в вакууме, при изменении напряженности электрического
поля во времени. Ток смещения порождает магнитное поле так же,
как и ток проводимости. Хотя природа тока проводимости и природа
тока смещения не одна и та же, но оба вида тока обладают одним и
тем же свойством — вызывать магнитное поле.
Физический смысл первого уравнения Максвелла состоит в том,
что всякое изменение электрического поля во времени
(Л F\
— 1 вызывает в той же точке поля вихрь поля магнитного
dt I
(rot Я).
Введение в основные уравнения переменного электромагнитного
поля тока смещения является заслугой Джеймса Максвелла. В
1873 г. Максвеллом была издана книга «Трактат об электричестве
и магнетизме». В этой книге и был введен в электротехнические рас-
четы ток смещения.
С током смещения в предыдущих разделах (в особенности в раз-
деле «Переходные процессы» второй части курса ТОЭ) приходилось
встречаться неоднократно.
Так, известно, что при зарядке какого-либо конденсатора через
него протекает ток. Этот ток протекает через диэлектрик и являет-
ся не чем иным, как током смещения.
Таким образом, если в диэлектрике изменяется электрическое
поле во времени, то по диэлектрику протекает ток. Если, напри-
мер, взять незаряженный плоский воздушный конденсатор и под-
ключить его к источнику э. д. с. напряжением U через сопро-
тивление R, то напряжение на обкладках конденсатора будет
( t \
1 —е RC / . Так как напряженность
электрического поля в плоском конденсаторе
Е = ,
d
где d — расстояние между обкладками, то
d
1-е RC
651
Емкость плоского конденсатора С = —.
d
Ток смещения, про-
текающий через один квадратный сантиметр сечения диэлектрика,
взятый перпендикулярно силовым линиям, будет равен
нс \ U кс
’ — с С- - — —• -------- с. •
dt d RC Rs
Ток смещения через поверхность s равен
JL е «с
R
т. е. он в точности равен току проводимости, протекающему по про-
водникам, соединяющим конденсатор с источником э. д. с.
Важно обратить внимание на то, что линии тока являются зам-
кнутыми линиями.
В заключение рассмотрения вопроса о первом уравнении Макс-
велла заметим, что по сути дела первое уравнение Максвелла есть
не что иное, как закон полного тока в дифференциальной форме.
Убедимся в том, что из закона полного тока следует уравнение (16.1).
С этой целью возьмем произвольный контур и составим для него уравнение по
закону полного тока. Полный ток, пронизывающий площадку, ограниченную
контуром, равен сумме тока проводимости и тока смещения. Поэтому
T + ds.
S
На основании теоремы Стокса Н d / — J rot Hds. Следовательно,
s
Jrot Eds’ = J .
S £
Последнее равенство должно выполняться при любых площадках s. Это
может быть только в том случае, когда равны подынтегральные функции левой
и правой частей последней строчки, т. е.
rot Н = 6 + е •
dt
Выше говорилось о том, что линии тока являются замкнутыми линиями.
Можно математически сформулировать принцип замкнутости линий полно-
го тока. С этой целью от обеих частей уравнения (16.1) возьмем диверген-
цию. Из предыдущего известно, что дивергенция от ротора тождественно рав-
на нулю (см. § 448). Поэтому
div rot Н — div 16 4-е — 1 = 0.
\ dt )
Отсюда
/-^ дЕ \
div I 6 + е — | = 0.
\ dt 1
652
Таким образом, в любой точке поля нет ни истока, ни стока линий полного
тока.
/-» З/Л
Уравнение div о + е — = 0 представляет собой в иной форме запи-
\ dt /
санное уравнение непрерывности (14.5), рассмотренное в § 425. Действительно,
(-+ дЕ\ д —
из уравнения div I о + е -— ) = 0 имеем div 6 — — — divD . Но div D =
\ dt I dt
= Pceotf Поэтому div 6 = — - P™°- .
dt
§ 461. Второе уравнение Максвелла. Второе уравнение Максвел-
ла записывается следующим образом
rotE =-------— . (16.2)
dt
Физический смысл его состоит в том, что всякое изменение маг-
( д1Г\ „ , л
нитного поля во времени I I в какой-либо точке поля возбуж-
дает вихрь или ротор электрического поля в той же точке поля,
т. е. вызывает вихревое электрическое поле.
Второе уравнение Максвелла есть не что иное, как дифференци-
альная форма закона электромагнитной индукции.
Для того чтобы убедиться в этом, проведем следующие рассуждения.
Мысленно возьмем некоторый замкнутый контур, расположенный в перемен-
ном электромагнитном поле. Падение напряжения в нем равно ф Edl, это па-
дение напряжения должно равняться э. д. с., нитным потоком, пронизывающим контур; е = Е *dt. дФ Ноэ д. с. ₽ = -— • Таким образом, С — -> <ЗФ В свою очередь, ф = У В ds и е = — J S S Следовательно, 1 S причем площадь s опирается на контур 1. На основании теоремы Стокса Е dl = С - Г cffi I rot Е ds = — I J J dt s s наведенной переменным маг- дВ + —- ds, dt J rot Eds, поэтому ds .
653
Последнее равенство должно выполняться при любых площадках в, это
может быть только в том случае, когда равны подынтегральные функции
обоих интегралов. Следовательно,
rotf
дВ
dt'
Знак минус в правой части второго уравнения Максвелла (как и в формуле
6Ф
е =— —) объясняется правилом правоходового винта. Если завинчивать пра-
воходовой винт так, что положительное направление вектора магнитной ин-
—
дукции В в некоторой точке пространства при возрастании индукции в этой
точке совпадет с направлением движения острия винта, то положительное нап-
равление для вектора напряженности электрического поля Е при составлении
циркуляции вектора Е вдоль бесконечно малого контура, окружающего эту
точку и лежащего в плоскости, перпендикулярной вектору В, совпадет с нап-
равлением вращения головки винта.
Знак минус в правой части (16.2) поставлен для того, чтобы привести в
—$
соответствие действительное направление для Е при оговоренных выше уело-
—
виях с направлением, принятым для Е за положительное.
Как в первом, так и во втором уравнениях Максвелла участвуют
частные (не полные) производные во времени. Объясняется это тем,
что уравнения Максвелла записаны для таких тел и контуров, кото-
рые неподвижны по отношению к выбранной системе координат.
Следует обратить внимание на то, что в переменном электромаг-
нитном поле, кроме силовых линий электрического поля, «начина-
ющихся» и «оканчивающихся» на электрических зарядах (как в
электростатическом поле), могут быть и замкнутые на себя сило-
вые линии электрического поля, охватывающие замкнутые на себя
силовые линии магнитного поля (см., например, рис. 484).
§ 462. Уравнение Максвелла в комплексной форме записи. Урав-
нения (16.1) и (16.2) записаны для мгновенных значений. Если Н
и £ во времени изменяются синусоидально, то можно воспользо-
ваться символическим методом и записать уравнения (16.1) и (16.2)
в иной форме. Пусть
Л/ = Нт sin (ю/ + фн) и Е = Ет sin (щ/ -ф- ф£).
Можно записать Н = \тНте‘ш* (Im — «мнимая часть») или, условно,
п —> пте , где комплексная амплитуда
Н = Н е*н-
• jоз/
В свою очередь Е —> Ете (—> значок соответствия).
Так как напряженности Е и Н, кроме того, что они меняются
во времени по синусоидальному закону, являются функциями
векторными, т. е. определенным образом ориентированными в
654
пространстве векторами, то будем ставить над ними стрелку и
точку
Ет И Нт.
Стрелка означает, что речь идет о векторе в пространстве,
точка — о том, что проекции этого вектора на любую из коорди-
натных осей во времени изменяются синусоидально. Тогда б
можно заменить на усе ,
дЕ . E-t [ д у? l«>t . \
е— на /ыеЕе \~^Ете = 1ыЕте I *
rot Н — rot [Н ешг ] = е °4 rot Н
jut
(е как постоянная величина, не зависящая от координат, может
быть вынесена за знак ротора). При этом первое уравнение
Максвелла запишется так:
e^rolH = (уЕ /есоЕ) е ‘.
После сокращения на e'mt получим
rot// = yE-j- jcoeE. (16.3)
Аналогичным образом второе уравнение Максвелла в комплек-
сной форме запишется так:
rotE=-—(16.4)
§ 463 *. Теорема Умова — Пойнтинга для мгновенных значений.
Кроме уравнений Максвелла, большое значение в теории электро-
магнитного поля имеет теорема Умова — Пойнтинга. Она дает воз-
можность выяснить энергетические соотношения в поле.
Теорема Умова — Пойнтинга имеет две формы записи. Первая
форма записи—для мгновенных значений, вторая — в комплекс-
ной форме — для синусоидально изменяющихся величин.
Из § 421 известно, что энергия электрического поля в единице
е£2 * цЯ2
объема равна —. Энергия магнитного поля в единице объема—.
Энергия в объеме dV равна
+ ^.]dK
\ 2 2 /
Для того чтобы образовать выражение, в которое вошла бы пол-
ная энергия в объеме dV, умножим (16.1) на EdV, а (16.2) на
Н dV. Получим
655
E rot Н dV = ( уЕЕ-\- eE~^ dV = (yE2 + -- (16.5)
H rot E dV = (— u/7 —\ dV = (— - \dV. (16.6)
\ dt ) \ dt 2 J
Из (16.5) вычтем (16.6):
(E rot H — H rot E) dV = |yE2 + ~ (I67)
Так как div[EE] = Hrot E — E rot//, то* левая часть (16.7) есть
— div[EE]dl/.-
Следовательно,
- div [ЕЕ] dV = [уЕ2 + 1 j dV.
_ •—>
Обозначим для сокращения записи векторное произведение Е
на Е через S, т. е. примем, что S = [ЕН ]; S — это вектор, кото-
рый принято называть вектором Пойнтинга; размерность его равна
произведению размерности Е на размерность Н:
[S] = [E][E]=^ = ва/м.2.
Таким образом, вектор Пойнтинга имеет размерность мощности
(или энергии в единицу времени), отнесенной к единице поверхно-
сти, и направление его (рис. 462) совпадает с направлением дви-
жения острия правоходового винта, если головку последнего вращать
по кратчайшему направлению от Е к Н. Итак:
- div S dV = [уЕ2 + ^)) dV. - (16.8)
Распространим (16.8) на некоторый объем конечных размеров.
С этой целью проинтегрируем (16.8) по объему V:
— fdivSdP = J у£МУ + ^ П^ + ^ldP. (16.8х)
V V v L
* Напомним вывод этого соотношения. Введем индексы а и Ь, указываю-
щие, по какой переменной (а или Ь) производится дифференцирование, и уч-
тем, что можем в циклическом порядке менять множители. Будем иметь
div [Л й) = vjZfii = Vo рГв| + == В Л] + 7[B Vt] =
= В [уа Д] — A [v6 В| = В rot А — Hrot В.
Замена А на Е и В на Ни дает соотношение
div [ЕН] = /Trot Е — Е rot Н.
656
Подобно тому, как поверхностный интеграл по теореме Стокса пре-
образовывается в линейный, с чем имели дело в предыдущей главе
(§ 450):
J rot A ds = A dl ,
S
объемный интеграл в свою очередь может быть преобразован в по-
верхностный. Это преобразование производится при помощи теоре-
мы Остроградского — Гаусса
J div = §~Sd~s.
Качественно поясним это преобразование. Разобьем объем V (рис. 463) на
2 S A s /
отдельные объемы ДУ, заменим divS на-------— I строго говоря, надо было бы
ДУ \
§ SAs*\ -»
взять lim —) где As есть элемент поверхности объема AV, а знак S
ЛГ-»О AV /
обозначает суммирование по всем поверхностям объема AV. Тогда
j div'SdV = У, У A V
v
Первый знак суммы означает суммирование по поверхностям малого объема,
а второй знак суммы — суммирование по отдельным объемам.
Сумма 2 2 S As может быть разбита на две суммы: на сумму выраже-
ний S As по всем поверхностям, отделяющим один объем от соседнего (по
«внутренним» поверхностям), и на сумму S As по всем «периферийным» по-
верхностям. Первая сумма равна нулю, так как для двух смежных объемов
внешние нормали к общей поверхности направлены встречно. Рис. 464 пояс-
няет это; тп есть общая грань двух объемов. Для верхнего объема нормаль
к грани направлена вниз ( As,), для нижнего объема нормаль к поверхности
направлена вверх (As2 ), вектор S, будучи умножен на (Asj-J-Asz), даст
нуль. Сумма S As по всем периферийным поверхностям и представляет собой
$ ~S ds .
22 Л А. Бессонов
657
Таким образом, теорема Умова — Пойнтинга для мгновенных
значений записывается следующим образом:
Левая часть (16.9) представляет собой поток вектора Пойнтинга
(направленный внутрь объема) сквозь любую замкнутую поверх-
ность s, ограничивающую некоторый объем V*. В соответствии
с уравнением Джоуля — Ленца в дифференциальной форме
уЕ2 есть энергия, выделяющаяся в виде теплоты в единице объема
в единицу времени.
Поэтому j yEidV есть энергия, выделяющаяся в виде теплоты
в единицу времени в объеме V;
д UE2 . и№\
—------г -— есть скорость изменения запаса электромагнит-
dt\2 2 I
ной энергии в единице объема.
Но скорость изменения электромагнитной энергии есть мощ-
ность. Следовательно, поток вектора Пойнтинга сквозь любую зам-
кнутую поверхность, ограничивающую объем V, равен мощности,
выделяющейся в объеме V в виде теплоты, и мощности, идущей на
приращение энергии электромагнитного поля.
Теорему Умова — Пойнтинга можно трактовать как уравне-
ние энергетического баланса; левая часть (16.9) есть мощность или
энергия в единицу времени, доставляемая в виде потока вектора
Пойнтинга внутрь некоторого объема; правая часть (16.9) есть энер-
гия, расходуемая в единицу времени внутри объема.
Николай Алексеевич Умов (1846—1915) долгое время являл-
ся профессором Московского университета. В 1874 г. защитил док-
торскую диссертацию «О движении энергии в упругих средах», где
развил вопрос о потоке энергии в упругих средах и о плотности по-
тока энергии. Применительно к электромагнитному полю понятие
о потоке энергии было развито английским физиком Пойнтингом
в 1885 г.
Соотношение (16.9) было получено в предположении, что среда
внутри объема V однородна и изотропна, а также в предположении,
что отсутствует отраженная волна и внутри объема V нет источни-
ков электродвижущей силы.
* Поясним смысл знака минус в левой части формулы (16.9). Элемент по-
верхности ds в любой точке ее направлен в сторону внешней по отношению
к рассматриваемому объему нормали. Вектор Пойнтинга S направлен внутрь
этого объема. Поскольку угол между S и ds больше 90°, то скалярное произ-
ведение Sds < 0, а —Sds > 0. Таким образом, в силу наличия знака минус
левая часть формулы (16.9) является величиной положительной.
658
Если поле не изменяется во времени, то
и
А = 0
dt \ 2 ~ 2 /
— (f Sds = J yE2dV.
Электромагнитная энергия от места ее генерирования передает-
ся к месту потребления по диэлектрику (провода же выполняют
двоякую роль: они являются каналами, по которым проходит ток, и
являются организаторами структуры поля в диэлектрике).
Покажем справедливость этого утверждения на простейшем
примере. Пусть энергия постоянного тока передается по коаксиаль-
ному кабелю (рис. 465). Радиус
жилы гг , внутренний радиус
оболочки г2. Примем проводимость
материала жилы и оболочки
настолько большой (теоретически бесконечно большой), что напря-
женности поля Е = — в жиле и оболочке стремятся к нулю. Про-
V
странство между жилой и оболочкой заполнено диэлектриком.
Убедимся, что энергия, передаваемая приемнику в единицу
времени, равная UI, действительно канализируется по диэлектрику.
С этой целью подсчитаем поток вектора Пойнтинга через попе-
речное сечение диэлектрика, в рассматриваемом примере представ-
ляющее собой кольцо внутренним радиусом и наружным г2. Нап-
ряженность магнитного поля в диэлектрике по закону полного тока
Напряженность электрического поля в диэлектрике на постоянном
токе определяется так же, как и в условиях электростатики:
е
2лег/ га
г In —
22*
659
Здесь Q — полный заряд жилы на длине I, U —напряжение
между жилой и оболочкой. Следовательно, в некоторой точке ди-
электрика, расположенной на расстоянии г от оси (гх <; г <; г2),
S = ЕН = ———.
2№ In —
(Е и Н — взаимно перпендикулярны; см. рис. 465). Поток вектора
Пойнтинга через кольцо с радиусами гг и г2:
Таким образом, вся поступающая к приемнику энергия действитель-
но передается по диэлектрику. По жиле и оболочке энергия к прием-
нику не передается. Более того, если учесть, что у конечна и что
напряженность электрического поля в жиле и оболочке направлена
по току и не равна нулю, то нетрудно убедиться в том, что имеется
поток вектора Пойнтинга через боковую поверхность провода внутрь
провода, т. е. провода сами потребляют из диэлектрика энергию на
покрытие тепловых потерь.
Пример 213. Определить тангенс угла, составляемого напря-
женностью электрического поля с нормалью к поверхности жилы
в точке, принадлежащей поверхности жилы коаксиального кабеля
(рис. 465), а также подсчитать величину потока вектора Пойнтинга
через боковую поверхность жилы на длине в 1 м и сопоставить ве-
личину потока вектора Пойнтинга с потерями энергии в жиле на
длине в 1 м. Радиус медной жилы гх = 0,3 см. Внутренний радиус
оболочки r2 = 1 см. Протекающий по кабелю постоянный ток / =
= 50 а. Напряжение U между жилой и оболочкой 10 кв.
Решение. Нормальная составляющая напряженности
электрического поля на поверхности жилы
Еп = =------—------= 2,77 105 (в/м).
г. In — 0,003 • In —
г, 0,3
Тангенциальная составляющая напряженности электрического
поля Et на поверхности жилы по закону Ома равна
/
ЯГ1У
_________50_________
л • 0,0032 • 5,8 • 107
= 3,05 • IO’2 (в/м).
Вектор напряженности электрического поля Е составляет с нор-
малью к поверхности жилы угол а (рис. 466), тангенс которого
tga = —= 1,1 • ЮЛ
660
Напряженность магнитного поля на поверхности жилы по за^о
ну полного тока
Н = ~ = —-— = 2650 (а/м).
2лГ1 2л • 0,003
Для определения величины потока вектора Пойнтинга внутрь
жилы на длине в 1 м следует умножить составляющую вектора
Пойнтинга EtH, проникающую внутрь жилы, на величину боковой
поверхности жилы на длине в 1 м
EtH 2лГ1. 1 = 3,05 - 10“2 - 2650 • 2л 0,003 • 1 = 1,523 (вт).
Эта величина в точности равна потерям энергии в жиле кабеля
на длине в 1 м: Z2/? = /2-— = 502 - —------?-----= 1,523 (ет).
yS 5,8-107л-0,0032
Рис. 466
Рис. 467
Пример 214. На рнс. 467 изображено поперечное сечение сердечника транс-
форматора. Сердечник окружен витком. К разомкнутым концам а и b это-
го витка присоединены два одинаковых электродинамических вольтметра V,
и У2. Как расположены провода от вольтметров к точкам а и Ь, показано на
рис. 467. Отдельные точки витка и проводов обозначены буквами.
Поток Ф по сердечнику трансформатора направлен вдоль сердечника
трансформатора (перпендикулярно рисунку) и изменяется во времени следую-
щим образом:
Ф = 0,001 cos 500 t еб.
Определить показания вольтметров, полагая, что вне сердечника магнит-
ный поток отсутствует и что сопротивление Rv каждого вольтметра много
больше сопротивления самого витка Re , т. е. что
^«L
Решение. Обозначим через — ток по вольтметру Vt, i2 — ток
по вольтметру V2, i — ток по витку. Положительные направления для токоз
показаны стрелками на рис. 467.
По первому закону Кирхгофа
‘1 + 4 = «- (а)
Составим два уравнения по второму закону Кирхгофа. Одно из них для
контура, образованного вольтметром Vj и витком, т. е. для контура acck'bVta.
При записи уравнений учтем, что контур охватывает сердечник и потому кон-
тур пронизывается потоком Ф
66)
hRy + iRe + , = 0.
at
(6)
Другое уравнение запишем для контура, образованного вольтметром V2 и
витком (контур agV2fbedca). Этот контур не охватывает сердечник и потому
магнитный поток его не пронизывает
iiRy + IRe = 0.
Из уравнения (в) найдем i«==— i2 и подставим в (а). Получим /j =
R R
- ii I ~ + 1 ). в силу того, что —— » 1, — j2 —L .
\ Re / Re Re
Подставим j = jj + j2, где i2 — — h рв~, в уравнение (б). Будем иметь
(в)
/о Г, , Z/kVl D
J ]«h/?v=-dz ,
(1Ф
— — — 0,5 sin 500 t.
dt
Показание вольтметра I7! равно действующему значению величины lt Rv ,
0,5
т. е. равно 'у— — 0,355 (s).
Показание вольтметра V2 равно действующему значению величины
i2 Ry ~ 0.
Рассмотренный пример может служить наглядной иллюстрацией того по-
ложения, что при измерениях в переменном электромагнитном поле показание
вольтметра зависит от того, как расположены провода от вольтметра до
объекта измерения.
§ 464 *. Теорема Умова — Пойнтинга в комплексной форме записи.
Перед тем как приступить к вопросу о записи теоремы Умова —
Пойнтинга в комплексной форме, рассмотрим вопрос о полной
мощности в цепи переменного тока. Полная мощность
S = UI =Р-]~ jQ.
Пусть цепь переменного тока содержит последовательно со-
единенные активное сопротивление /?, индуктивность L и емкость С.
Тогда реактивная мощность
Q = РХ= /2 fcoL — — 'j = со f/2£ — /2 (—Г cl = 2w — а/.).
\ <оС/ L \«С/ J Л э
Здесь
Uc — напряжение на конденсаторе.
Таким образом, реактивная мощность Q равна разности между
магнитной wM и электрической шя энергиями цепи, умноженной на
2со. Подобно тому как в цепи переменного тока для вычисления
662
~ $S dt = — J div S'dV = J
полной мощности S надо умножить комплекс напряжения U на
*
сопряженный комплекс тока I, вводится в употребление комплекс-
ный вектор Пойнтинга S. Он равен
~ * у
S^[EH].
Вместо — S ds теперь будет
(£ rot 77 — Н rot £) dV.
V V
В соответствии с (16.3) и (16.4)
rot И — уЕ 4- /сое£
и
—> —>
rot £ —— ](оцН,
* _*
Следовательно, rot Н = уЕ — ja>eE и
£ rot Н — //rot £ = уЕЕ — jasJE £ /ыр//77 = у£2-|-
+ 2/ш^-£А2\
1 ' [ 2 2 J
Поэтому
— §Sd? = J уЕа dV + /2(о J <W. (16.10)
V v
Первое слагаемое правой части представляет собой активную мощ-
ность, второе — реактивную мощность. Таким образом, теорема
Умова —Пойнтинга может быть записана еще следующим образом
- j)SdT = P-[-]'Q.
В таком виде она часто используется для определения активного
и внутреннего реактивного сопротивления проводников на пе-
ременном токе (подробнее см. § 472).
§ 465. Некоторые дополнительные замечания. В заключение главы шестнад-
цатой необходимо сделать четыре замечания.
Первое замечание. В уравнения Максвелла входят параметры
(е, у, р), характеризующие усредненные в пространственном и временном
смысле свойства вещества. При низких частотах эти параметры представляют
собой действительные (иекомплексные) числа — такими мы и будем их счи-
тать в курсе ТОЭ.
При высоких частотах в диэлектриках существенную роль начинают иг-
рать диэлектрическая визкость, релаксационные и другие процессы. В фер-
ромагнитных веществах резко сказываются явлении гистерезиса, магнитной
вязкости и ряд других. В силу этих причин е, у и р, оказываются функциями
частоты и комплексами.
663
Зависимость параметров вещества от частоты впервые была обнаружена
русским ученым В. К- Аркадьевым в 1908—1911 гг. Физическое объяснение
этим явлениям было дано им в 1913 г. в работе «Теория электромагнитного
поля в ферромагнитном металле».
Второе замечание. В§ 460 рассматривалось первое уравнение
Максвелла (уравнение 16.1). В.правой части этого уравнения записаны две
плотности тока — плотность тока проводимости б и плотность тока электри-
веского смещения е—. Но, кроме тока проводимости и тока электрическо-
dt
го смещения, существует и третий вид тока — ток переноса. Ток переноса —
это собирательное название.
Под током переноса понимают ток, природа которого отлична от приро-
ды тока проводимости и от природы тока смещения. Наиболее типичным пред-
ставителем тока переноса является ток, возникающий в электронной лампе
вследствие явления термоэлектронной эмиссии.
Плотность тока переноса равна объемной плотности переносимых зарядов
—>
р, умноженной на скорость их переноса о. Если ток переноса создается дви-
жением со скоростью о+ положительно заряженных частиц с объемной плот-
ностью р+ и движущихся со скоростью о- отрицательно заряженных частиц
с объемной плотностью р_, то плотность тока переноса равна р+ о+ + р_о_-
Ток переноса так же, как и остальные виды токов, создает магнитное поле.
С учетом тока переноса первое уравнение Максвелла запищется следую-
щим образом:
-> - дЕ
rot И = б + е — + ро.
dt
Для тех задач, которые рассматриваются в третьей части курса ТОЭ, ток пе-
реноса отсутствует, поэтому первое уравнение Максвелла и берется в форме
(16.1).
Третье замечание. При чрезвычайно высоких частотах, когда
длина электромагнитной волны становится соизмеримой с линейными раз-
мерами, характеризующими молекулярную структуру самого вещества, ве-
щество уже нельзя рассматривать как континуум. В этом случае уравнения
Максвелла должны быть заменены уравнениями, учитывающими молекуляр-
ную структуру вещества.
Четвертое замечание. В §459 упоминалось о том, что элект-
ромагнитное поле обладает не только энергией, но и массой и количеством дви-
жения. Масса электромагнитного поля в-единице объема определяется как
частное от деления энергии поля, заключенной в единице объема, на квадрат
скорости распространения электромагнитной волны в пустоте
еД2 р Д2
2 + 2
М = ------г-----'
V2
Количество движения электромагнитного поля G, отнесенное к единице
объема, равно произведению массы поля в единице объема на скорость элект-
ромагнитной волны в пустоте
G = Mv.
Когда говорят о распространении электромагнитного поля, то имеют в
виду, что одновременно с движением потока электромагнитной энергии про-
исходит движение потока массы поля и потока количества движения поля.
664
Масса электромагнитного поля, заключенная в единице объема, несоиз-
меримо мала по сравнению с массой (плотностью) всех известных иам_'веществ.
Даже при максимально достижимых в настоящее время значениях напряжен-
ностей электрического и магнитного поля масса электромагнитного поля в
единице объема оказывается равной всего 10-20 — 10-15е/сл3.
Тем не менее наличие массы у электромагнитного поля имеет прин-
ципиальное значение: в самом факте наличия массы поля находит свое отра-
жение известная инерционность процессов в электромагнитном поле.
Хотя наличие массы и количества движения у электромагнитного поля
и имеет принципиальное значение, но в курсе ТОЭ эти понятия не используют-
ся — основное внимание в курсе уделяется энергетическим соотношениям.
Глава семнадцатая
ПЕРЕМЕННОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
В ОДНОРОДНОЙ И ИЗОТРОПНОЙ ПРОВОДЯЩЕЙ СРЕДЕ
§ 466. Уравнения Максвелла для проводящей среды. Пусть про-
водящая среда имеет проводимость у, магнитную проницаемость
р и в ней распространяется электромагнитная волна. Распростра-
нение электромагнитной волны в проводящей среде имеет ряд особен-
ностей. Эти особенности и являются предметом изучения в данной
главе.
Обратимся к первому и второму уравнениям Максвелла, запи-
санным в комплексной форме для синусоидально изменяющихся во
времени Е и Н
rot Н = уЕ -|- /соеЕ'
и
rot Е =—
В проводящей среде даже при весьма высоких частотах произведе-
ние сое много меньше проводимости у. Поэтому с большой степенью
точности слагаемым jcoeE в первом уравнении Максвелла можно
пренебречь.
В настоящее время наука не располагает точными данными о численном
значении относительной электрической проницаемости ег для металлов. Име-
ются лишь сведения, что порядок ег для металлов такой же, что и для боль-
шинства диэлектриков (т. е. от нескольких единиц до нескольких десятков).
В качестве примера возьмем ег для меди равной 10 и найдем, во сколько раз
ток проводимости в ней будет больше тока смещения при(0 = 103 и при (о =
= 10® рад/сек. При (о = 103
1 5,6.10’
— =--------------л; =6,33-104
ше 103-10-8,86-10-12
При ы = 108
JL =. б,зз- ю»,
<ле
т. е. в рассмотренном выше численном примере даже приш = 108 ток прово-
димости оказался больше тока смещения в 6,33 • 10° раз.
666
Таким образом, первое и второе уравнения Максвелла для про-
водящей среды приобретают вид
rot Н = уЕ (17.1)
и
rot Е =— /сор,//.
(17.2)
Эти два уравнения представляют собой уравнения с двумя
неизвестными Еп Н, Проведем совместное решение их. С этой це-
лью возьмем ротор от уравнения (17.1)
rot rot Н = grad div Н — V2H = у rot Е.
Учтем, что div Н = 0 и поэтому grad div Н — 0. Вместо rot Е в
соответствии с (17.2) подставим— /сор//. Получим
V2// = /соур//. (17.3)
Уравнение (17.3) представляет собой дифференциальное урав-
нение относительно Н. В самом общем случае, когда Н зависит
от всех трех или даже только от двух
координат, решение (17.3) представляет
собой не простую задачу. Поэтому ограни-
чимся рассмотрением решения уравнения
(17.3) для частного случая — для плоской
электромагнитной волны.
§ 467. Плоская электромагнитная вол-
на. Под плоской электромагнитной волной
условимся понимать такую волну, для ко-
торой характерно, что во всех точках плос-
кости (например, плоскости хоу), перпен-
дикулярной направлению распространения
волны (оси z), напряженность электри-
ческого поля Е в данный момент времени
Рис. 468
одинакова (по величине и направлению) и лежит в плоскости хоу,
точно так же и напряженность магнитного поля во всех точках
плоскости хоу одинакова и лежит в плоскости хоу. Рис. 468 служит
графической иллюстрацией к приведенному определению плоской
электромагнитной волны. На этом рисунке изображены для одного
и того же момента времени векторы Е и Н в двух параллельных
плоскостях, перпендикулярных оси z декартовой системы коорди-
нат. Во всех точках первой плоскости напряженность электричес-
667
кого (магнитного) поля одинакова по величине и по направлению.
Во всех точках второй плоскости напряженность электрического
(магнитного) поля также одинакова по величине и по направлению,
но она не равна напряженности поля в первой плоскости.
В силу самого определения плоской волны
дН п дН п дЕ п дЕ г.
дх ду дх ду
В плоской волне Е и Н являются функциями только одной ко-
ординаты, в нашем случае функцией только г.
Повернем координатные оси таким образом, чтобы ось у совпа-
ла с напряженностью магнитного поля Н. При этом
Здесь / единичный орт оси у декартовой системы координат
Подставим Н — )Н в уравнение (17.3) и раскроем V2.
(— 4- = jawjH. (17.4)
\дх2 1 ду2 ' dz2)'
Учтем, что
д2/) л о2Н п
-я-=- = 0 и 2 = 0.
дх2 ду2
Поэтому будем иметь
— = jayyH. (17.5)
В последнем уравнении вместо частной производной написана прос-
тая производная. Переход от частной производной к простой для
плоской волны вполне естественен, так как Н является функцией
только одной переменной г.
Уравнение (17.5) представляет собой линейное дифференциаль-
ное уравнение второго порядка. Его решение запишется следующим
образом
И = С1е^4-С2е-рг; (17.6)
С\ и С2 есть постоянные интегрирования; это комплексы, они оп-
ределяются из граничных условий и для каждой конкретной зада-
чи свои.
В свою очередь коэффициент
р = К/соуц. (17.7)
Если у берется в единицах олт1 лг1, р в гн/м, то р измеряется в
1/х.
668
1ак как
еще и так
У j = У = е/45° _ 1 +/
то р можно представить
P = k(\ + j), (17.8)
где
k = -i/^. (17.9)
У 2
Напряженность электрического поля найдется при помощи урав-
нений (17.1) и (17.6). Из (17.1) следует, что
Е = —rot/7.
V
Найдем rot Н. В соответствии с уравнением (15.6) в самом общем
виде
i / k
д д д
дх ду dz ’
ИНН
X у г
В рассматриваемой задаче
дН л дН п
-5— = О и -д— = О,
дх ду
поэтому выражение rot Н в значительной мере упрощается:
rot 7/ — i j k 0 0- dz fl dH \ ~ Ц dz Г (17.10)
OHO
Следовательно, Е -* ( 1 i — ~ \ у dH \ dz )' (17.10')
Производная dH dz = p [C^p* — С2е-рг]. (17.H)
Выражение (17.10') показывает, что напряженность электрического
поля в плоской волне при выбранном расположении осей координат
направлена вдоль оси х, об этом свидетельствует присутствие еди-
ничного орта оси х (орта i). Таким образом, в плоской электро-
магнитной волне между Е и Н есть пространственный сдвиг
в 90° {Е направлено по оси х, а /7 по оси у).
669
Частное от деления р на у принято называть волновым сопро-
тивлением и обозначать Zc:
Zc=^ = е,45°. (17.12)
Y ' Y
Волновое сопротивление измеряется в омах. Оно зависит от
свойств среды (от у и р) и от угловой частоты со. В соответствии
с (17.10') и (17.11) проекция Е на ось х равна
Ё Ёпад Ч- Eompt
где
Проекция И на ось у в соответствии с (17.6)
Н = Нпай Ч" Hompt
где
finad- С2е~рг и Йотр = С\еР\
Составляющие падающей волны Епад и Йпад дают вектор Пойнтинга
S пад (рте. 469, а). Он направлен вдоль положительного направ-
ления оси г. Следовательно, движение энергии с падающей вол-
ной происходит вдоль положительного направления оси г.
Составляющие отраженной волны Ё^ и Йотр дают вектор
Пойнтинга Somp (см. рис. 469, 6). Последний направлен вдоль
отрицательного направления оси г. Это означает, что отраженная
волна несет с собой энергию, и направление движения энергии про-
исходит вдоль отрицательного направления оси г.
Волновое сопротивление Zc можно трактовать как отношение
^.пад *. Так как волновое сопротивление является числом комплек-
Нпад
* Отношение Еотр к — Ёотр также равно Zc-
670
сным (см. 17.12), то сдвиг во времени между Ёпад и Нпад для од-
ной и той же точки поля равен 45°.
§ 468. Распространение плоской электромагнитной волны в од-
нородном проводящем полупространстве. Рассмотрим вопрос о рас-
пространении плоской электромагнитной волны в однородной про-
водящей среде, простирающейся теоретически в бесконечность (рис.
470).
Электромагнитная волна проникает из диэлектрика в проводя-
щую среду и распространяется в последней. Так как среда прости-
рается теоретически в бесконечность и падающая волна в толще
проводящей среды не встречает границы, которая «возмутила» бы
z
Рис. 471
ее распространение, то отраженной волны в данном случае пе воз-
никает.
При наличии только одной падающей волны
Н = C.2e~pz и Ё = ZcC.2e~pz.
Постоянную интегрирования С2 найдем из граничных условий.
Если обозначить напряженность магнитного поля на поверхности
проводящей среды через На — На е1* , то при z = 0
Сг = На.
Поэтому с учетом (17.8)
Н = Нae~hz e~ikz. (17.13)
В свою очередь
Ё = На e~kz -i/^ e~ikz (17.14)
Можно записать выражения для мгновенных значений Н и Е.
С этой целью надо правые части (17.13) и (17.14) умножить на
е'ш* и взять мнимые части от получившихся произведений.
671
Получим
Н — Hae~kz sin (со/ — kz 4- %) (17.15)
и
E = Ha y^e-fesin(co/ — £z4-ipQ4-45°). (17.16)
Проанализируем полученные выражения. Амплитуда Н равна
л Hae~kz. Амплитуда Е равна На e~kz- По мере увеличения z
множитель e~kz уменьшается по показательному закону. Следо-
вательно, по мере проникновения электромагнитной волны в прово-
дящую среду амплитуды Е и И уменьшаются по показательному
закону. На рис. 471 изображены огибающие амплитуд Н, построен-
ные по уравнению Нae~kz. Мгновенное значение Н и Е определяет-
ся аргументом синуса. Аргумент синуса в выражении (17.15), на-
пример, зависит от z и от со/. Если принять со/ = const и поинте-
ресоваться графиком мгновенных значений Н в функции от г, то
будет получена кривая 1 рис. 471 при со/-]-фа = О и кривая 2 при
со/ ~ 90°’
Для того чтобы охарактеризовать, насколько быстро уменьшает-
ся амплитуда падающей волны по мере проникновения волны в про-
водящую среду, вводят понятие глубины проникновения.
§ 469. Глубина проникновения и длина волны. Под глубиной
проникновения Д понимают расстояние вдоль направления распро-
странения волны (вдоль оси г), на котором амплитуда падающей
волны Е (или Н) уменьшается в е = 2,7183 раз. Уравнением для
определения глубины проникновения является выражение
-*д
е = е .
Отсюда следует, что АА = 1 или
Д = Х. (17.17)
Глубина проникновения зависит от свойств проводящей среды
(у и |i) и от частоты со. Так, если электромагнитная волна имеет
частоту f = 5000 гц и проникает в проводящую среду, у которой
у = 107олс-1 • лг1 и = 103, то*
k= = Л/^--5000 10Л-.1,256 • ю-6.-10! = 14 100 (1/лс).
У 2 У 2 ’
Глубина проникновения Л = — ?»7 • 10~Б м, т. е. на ничтожном
расстоянии в 0,007 см амплитуды Н и Е снизились в 2,7183 раза.
Полагаем, что не зависит от величины Н.
672
Под длиной волны X в проводящей среде понимают расстояние
вдоль направления распространения волны (вдоль оси z), на кото-
ром фаза колебания изменится на 2л. Длина волны определится из
уравнения kk = 2л , отсюда
% = -. (17.18)
k
Для рассмотренного выше численного примера
% = ^0,000445 (Л1).
14100
Иногда пользуются понятием фазовой скорости распространения
электромагнитной волны в проводящей среде. Под фазовой ско-
ростью понимают скорость, с которой надо было бы перемещать-
ся вдоль оси г, чтобы колебание имело бы одну и ту же фазу. Фаза
колебания определяется выражением
(со/ — /ez + %).
Производная от постоянной величины
^(ю/ —Л2 + Фо) = 0.
Или
.dz г, dz
»-‘S = 0; « =’*••
^. = ”- (17.19)
к
Для рассмотренного численного при-
мера
®фаз
2 л • 5000
14100
2,25 (м/сек).
§ 470. Магнитный поверхностный эффект. В качестве второго
примера распространения плоских электромагнитных волн в про-
водящей среде рассмотрим поле в стальном листе при прохождении
вдоль листа переменного магнитного потока Фт. Лист (рис. 472)
имеет толщину 2а, высоту h (h 2а) и весьма большую протяжен-
ность в направлении, перпендикулярном рисунку. Средняя плот-
ность магнитного потока по сечению листа
Задача состоит в определении законов изменения Н и Ё по сече-
нию листа. В силу симметрии напряженность магнитного поля на
левой поверхности листа и на правой поверхности листа одинаковы.
673
Обозначим ее через На и будем полагать известной (в даль-
нейшем выразим ее через Вср).
Так как толщина листа 2а много меньше высоты листа h, то
искажающим влиянием краев листа на поле можно в первом при-
ближении пренебречь и считать, что в лист с двух сторон проника-
ет плоская электромагнитная волна.
Расположим оси координат декартовой системы в соответствии
с рис. 472. Примем, как и прежде, Н — }Н. Общее решение для
Н таково
H = Cxepz -\-С^~рг.
Из граничных условий найдем постоянные интегрирования. При
z——а, т. е. для точек, находящихся на левой стороне листа:
На = Сге~ра + С^Ра\ (17.20)
при z—-\-a
Ha = C1^’a-]-CSie-pa. (17.21)
Совместное решение (17.20) и (17.21) относительно и С2 дает
С = С "° -
1 а ера + е-ра 2с\\ра
Следовательно, в произвольной точке
• II • ch 02
2chpa сп ра
Напряженность электрического поля
\ у dz ] \ у a ch ра ]
Здесь
= (17.23)
•у ch ра
Приг=4~аЕ направлена вверх (вдоль оси — х). При z =—а Е
направлена вниз (вдоль оси х, рис 472). Вектор Пойнтинга направ-
лен к средней плоскости листа (внутрь листа).
Как известно из второй части курса ТОЭ, ток, возникающий
при прохождении по листу переменного магнитного потока, приня-
то называть вихревым током.
Вектор плотности вихревого тока б = уЕ в любой точке листа
коллинеарен с вектором Е в этой же точке.
674
(17.24)
(17.25)
(17.25) мо-
о
Магнитная индукция В в произвольной точке
ch ра
Среднее значение магнитной индукции в листе
|i/fash ра рЙа th ра
ар ch ра ар
Если считать В,„ известной и равной то из
жет быть найдена напряженность поля На на поверхности листа
уу _ арВср (17.26)
° р th ра ’
Заметим, что аргумент ра = ka + jka является комплексом
и th ра есть гиперболический тангенс от комплексного аргумента:
он также является комплексом
л. .и-/!. । • г. \ sh 2ka 4- j sin 2ka
th pa = th (ka 4- ika) =-----—----------
ch 2ka + cos 2ka
Отношение среднего значения магнитной индукции по сечению
листа Вср к напряженности поля на поверхности листа На называ-
ют комплексной магнитной проницаемостью и обозначают р
- и th ра ~ .
Н = “ (и = РоНг)-
(17.27)
ар
Она зависит от рг, частоты ю и от толщины листа. При больших
значениях аргумента 2ka sh 2 ka ch 2 ka, и значения этих функ-
ций намного больше 1. Поэтому при больших значениях 2ka
th pazz------~1.
сЬ2Ла
И комплексная магнитная проницаемость рг оказывается равной
Hr
Рг = —•
ра
Так, например, при толщине листа 2а = 0,015 см, р, = 20 000,
у = 1,8 • 10е омг1. мг1 и f = 50 000 гц\
= 84 200; р = 84 200 V2 е/45°; ka = 6,31; 2ka = 12,62;
.. _ sh 12,62 ,
th pa 1.
ch 12,62
Следовательно,
ра
20000_____________ 2250е—?4Бв(
84 200 /2 е,45<>. 0,000075
675
Напряженность поля в средней плоскости листа (при z = 0)
равна Л7г=0 = . Отношение напряженности поля на краю лис-
та (при г — а) к напряженности поля в средней плоскости листа
равно
= ch ра. (17.28)
Wz=0
В левой и правой частях (17.28) стоят комплексы. Модуль ch ра
показывает, во сколько раз модуль На больше модуля fiz=0.
Найдем модуль ch pa. С этой целью запишем два сопряженных
комплекса
ch (ka 4- jka) = ch ka cos ka -f- j sh ka sin ka
и
ch (ka — jka) — ch ka cos ka — j sh ka sin ka.
Произведение сопряженных комплексов дает квадрат модуля.
Следовательно,
| ch ра [2 = ch (ka -ф- jka) ch (ka — jka) = — [ch 2 ka + cos 2 ka]* *.
Таким образом,
I ch pa I = |/ch2feg+cos2fea. (17.29)
Рассмотрим численный пример. Пусть p.r = 100; f = 500 гц
у = 107 ом~1 • м~1. При этом k = 1410 l/м.
Найдем отношение напряженности поля в средней плоскости
к напряженности поля на поверхности листа при толщине листа
2а = 1 мм; 2 мм; 4 мм,
2/га=1,41 2,82 5,64,
—— = 0,91 0,52 0,1.
| ch ра |
Таким образом, напряженность поля в средней плоскости листа
может быть много меньше напряженности поля на краю листа.
Явление неравномерного распределения поля по сечению прово-
дящего тела, вызванное затуханием электромагнитной волны, назы-
вается поверхностным эффектом. Если вдоль листа направлен маг-
нитный поток, то поверхностный эффект часто называют магнит-
ным, если вдоль плоской шины направлен переменный ток, то име-
ющий место при этом поверхностный эффект часто называют элект-
рическим поверхностным эффектом.
. .. . X у , X— у
* В силу того, что ch х + ch у = 2ch --------ch------
2 2
676
Природа их одна и та же. И дополнительное прилагательное
(магнитный или электрический) свидетельствует лишь о том, что
направлено вдоль листа (шины), поток или ток.
На рис. 473 построены две кривые. Первая из них дает характер
изменения модуля напряженности магнитного поля в функции от
z. В средней плоскости листа Н до нуля не снижается, так как
ch 0=^0. Кривая Н (г) строится по уравнению (17.22). Вторая кривая
на рис. 473 дает характер изменения модуля напряженности электри-
ческого поля в функции от z. Эта кривая строится по (17.23);
sh pz = 0 и потому кривая проходит через нуль при z = 0. Кривая
z-0
плотности вихревых токов 6 = уЁ качественно повторяет кривую
Е от z (разница только в масштабе).
§ 471. Прохождение переменного тока по плоской шине (электри-
ческий поверхностный эффект). Рассмотрим задачу, родственную
предыдущей. Пусть,вдоль шины направлен не переменный магнит-
ный поток, а переменный ток.
Положительное направление тока и расположение осей декар-
товой системы координат даны на рис. 474.
По закону полного тока найдем напряженность магнитного поля
на поверхности шины. Так как в данной задаче, как и в предыду-
щей, h 2а, то при подсчете Н dl можно в первом приближе-
нии пренебречь составляющей интеграла вдоль горизонтальных сто-
рон шириной 2а.
Тогда, обозначив напряженность поля на поверхности шины
через На, получим
На 2h = I.
677
Отсюда
z
2ft’
При составлении уравнений для определения постоянных ин-
тегрирования учтем, что слева от шины напряженность ориенти-
рована вдоль положительного направления оси у, а справа — в от-
рицательном направлении оси у.
Общее решение для плоской волны
й = с1еРг-\-с^~рг.
Постоянные интегрирования: при z = — а
На = C1e~Pa-j-C2ePa,
при г — а
-На^СхеРа-\-С2е-Ра.
Совместное решение двух последних уравнений дает
С, =— С2=—
2sh ра
Подставим иС2 в общее решение. Будем иметь
['-/ __// shpz __£ sh pz
sh pa 2h sh pa
Напряженность электрического поля Ё направлена вдоль оси х и
равна по предыдущему
л, 1 dH
Е —----------
у dz
или
Ё — р chpz
у 2h sh ра
Плотность тока в любой точке пластины
2ft sh ра
Минимальное значение плотности тока будет в средней плоскости
шины при 2 = 0. Оно равно
я 1 1
г=0 P2hshpa'
График изменения модуля Н в функции от г представлен на
рис. 475. На том же рисунке изображена вторая кривая, она дает
зависимость модуля плотности тока от г. Если сравнить кривые
рис. 475 с кривыми рнс. 473, то можно убедиться в том, что
678
графики изменения Е и Н при электрическом поверхностном эф-
фекте и при магнитном поверхностном эффекте как бы поменялись
местами.
Чем толще шина, чем больше у, р, и ы, тем сильнее проявля-
ется поверхностный эффект, т. е. тем более неравномерным
становится распределение плотности тока по сечению шины. И ес-
ли частота со очень велика, то может оказаться, что ток будет про-
текать только по тонкому поверхностному слою шины.
При тонких шинах и относительно небольших частотах поверх-
ностный эффект проявляется в малой степени.
Рассмотрим численный пример. Медная ши-
на высотой h — 2см и толщиной 2а = 0,1 см
имеет:
у = 5,6 • Ю7 ом-1 • .м-1; == 1.
По ней протекает переменный ток / = 10 а,
угловая частота = 105 рад]сек.
Требуется выяснить, во сколько раз плот-
ность тока на краю шины будет больше плот-
ности тока, соответствующей равномерному рас-
пределению (когда поверхностный эффект от-
сутствует).
Определяем
1870 \/м,
ka = 1870 - 0,0005 = 0 935
2ka= 1,87.
Плотность тока на поверхности шины
г „ > 1
о = р--------,
2h th ра
„ __ sh2fea-|- f sin2fea _3,167 /0,956 _ j gg ^/16°»'
ch 2ka -f- cos 2£a 3,32 — 0,292 ’
Следовательно,
A = 1870 /2 в'45'-------------------------= 60,6 • 104 . в'28035' а/м2.
2-0,02 -1,09 • e716 25'
Плотность тока при равномерном распределении
/ _ 10
h-2a 0,02 - 0,001
= 50.104 а/м2.
Таким образом, в рассматриваемом примере плотность тока по-
(60 6
—— ^1,2) больше, чем
50
плотность тока при равномерном распределении.
679
§ 472. Применение теоремы Умова — Пойнтинга для определения
активного и внутреннего индуктивного сопротивления проводни-
ков па переменном токе. Определение активного и внутреннего ин-
дуктивного сопротивления проводников на переменном токе часто
производят при помощи теоремы Умова — Пойнтинга в комплекс-
ной форме. С этой целью подсчитывают поток вектора Пойнтинга
через боковую поверхность проводника надлине в один метр и делят
его на квадрат тока, протекающего по проводнику, получают комп-
лекс сопротивления проводника на единицу длины (на один метр).
Действител ьно,
— $ [ен] ds = Р + /<2 = I2R + = !"Z
и
— (£ Г ЕН 1 ds
В качестве примера определим активное и внутреннее индуктив-
ное сопротивление прямоугольной шины длиной в один метр.
Энергия в шину проникает с двух сторон. Поверхность шины с двух
сторон на длине в 1 м равна 2/i-1.
£ 1
Z = R 4- jX = w у th ра ___________р-----
' 1 Р Р у th ра
или
„ 1870 ]f2e'45° nc . ,C1C in_4 ,
Z —-----------------------— 9,5 • 10 4 -4- t 5,16 • 10 4 om/m.
5,6 • 10’ 0,04 . l,O9e,lb°20'
Стедовательно, активное сопротивление провода на 1 м длины
шины равно 9,5. 10 ~4 ом и внутреннее индуктивное сопротивле-
ние 5,16 • 10 “4 ом.
Для сравнения заметим, что омическое сопротивление единицы
длины плоской шины, т. е. сопротивление постоянному току, рав-
но 8,92. 10"4 ом. Таким образом, в силу поверхностного эффек-
та активное сопротивление увеличилось с 8,92 10-4 до 9,5 • 10-4 ом,
т. е. на 6%.
В рассматриваемом численном примере в силу того, что шина
довольно тонкая и частота сравнительно невысока, активное сопро-
тивление шины лишь очень на немного превышает омическое соп-
ротивление. В других случаях это превышение может быть много
больше.
§473. Эффект близости. До сих пор рассматривалось прохождение
переменного тока по уединенному проводнику. Если поблизости от
проводника, поле в котором исследуется, есть другой проводник с
током, то, естественно, что второй проводник влияет на картину
поля в первом проводнике. В результате этого влияния активное
680
сопротивление одного провода, как правило, увеличивается по срав-
нению с активным сопротивлением уединенного провода. Влияние
близлежащих проводников с током на комплекс сопротивления ис-
следуемого проводника называют эффектом близости. Рассмотрим
эффект близости на примере двух плоских шин, близко расположен-
ных одна к другой (рис. 476). Одна шина является прямым прово-
дом, другая обратным.
- Если расстояние между шинами 2Ь такого же порядка, что и
толщина шин (2а) и много меньше высоты h, то можно показать,
что с известной степенью приближения напряженность магнитного
поля в пространстве между шинами в два раза больше напряжен-
ности магнитного поля от одной шины в непосредственной близости
от шины. А снаружи шин напряженность магнитного поля равна
нулю.
Для того чтобы убедиться в этом, воспользуемся принципом
наложения.
Сплошные стрелки на рис. 476 представляют напряженность поля
от левой шины, пунктирные — от правой. В пространстве между
шинами напряженности складываются, снаружи вычитаются. В ре-
зультате оказывается, что напряженность поля в пространстве меж-
ду шинами /7 = 2. — = —, а снаружи шин напряженность магнит-
2ft ft
ного поля равна нулю. Найдем постоянные интегрирования в вы-
ражении Н — Схерг-j-C2e ~рг.
При г = — а 0 = Схе~ра -j- С2ера.
При z = а — — = С^11" -ф С2е ~ра.
Отсюда
А __ - 1 ера „ А . _ f е~ра
-а ~~~ Н О —“* •
1 ft-2sh2pa ft 2sh2pa
681
Следовательно,
H = _ (gpo+рг _ е -Ра -рл *ЪР<а+3.
h-2&2pa ' h sh2pa
и напряженность электрического поля
Ё = Р ' chP(« + ?)
у h sh2pa
Если придавать г значения от — а до а, то по написанным вы-
ше формулам могут быть построены кривые изменения модулей Е
и /7 в функции от z. Такие кривые качественно изображены на рис.
477. Для правой шины кривые построены на основании симметрии
воля. Если не учитывать искажающего действия торцов, то элект-
ромагнитная волна в каждую из шин проникает только через по-
верхности их, обращенные друг к другу. Через наружные поверх-
ности электромагнитная волна не проникает, так как там Н = 0.
Комплекс сопротивления одной шины на единицу длины
7 __ EHh • 1 _ р
^енутр одной шины ~ р •
Рассмотрим численный пример. Пусть ток в 10 а течет по двум та-
ким же шинам, с которыми имели дело в предыдущем параграфе
(й = 2 см, 2а = 0,1 см). Одна из шин является прямым проводом,
другая обратным. Подсчитаем комплекс сопротивления одной ши-
ны на единицу длины с учетом эффекта близости и сравним его с
сопротивлением одной уединенной шины (когда эффекта близости
нет):
1870 . V~2 -е/45<
22,5- КГ4.^46’30'
th2p«= sh3’74.+.ls»^ = 1,04 е-/,03°',
ch 3,74 + cos 214°
Следовательно,
Z =_________Е
eNi"np yh th 2pa 5,6 • 107.0,02 . 1,04 . e-'1”30'
R = 15,7 . 10~4 om/m-, X„Hymp = 16,34 • IO'4 ом/м.
- Таким образом, влияние второй шины на поле в первой ши-
не привело к тому, что активное сопротивление одной шины воз-
росло с 9,5 • 10 “4 до 15,7 • 10 ~4 ом]м.
Для определения комплекса полного сопротивления едини-
цы длины петли, образованной двумя шинами, кроме собствен-
ного сопротивления самих шин, надо учесть еще индуктивное
сопротивление, обусловленное магнитным потоком, проходящим
в пространстве между шинами.
Последнее равно:
X _ _ .. <+<Л • 2Ь • 1 _ ро<о2Ь
^•внешн ш1-внешн 10 , , д •
1
682
Комплекс полного сопротивления единицы длины петли
^ПОЛН ~ 2 ReHymp +i&X'llvmp+x BHemtii*
В качестве примера найдем комплекс полного сопротивле-
ния на 1 м длины линии, составленной двумя шинами преды-
дущей задачи, если 2Ь = 0,4 см:
хвнешн = -л256 , 10~6;2106,0,004 = 2,51 . 10-* (рм1м\
ZnoJlH = 3,14 . ’10-3+ j 28,4 • 10-3 ом/м.
В заключение отметим, что в приложении В рассмотрен вопрос
о поверхностном эффекте в цилиндрическом проводе.
Глава восемнадцатая
РАСПРОСТРАНЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
В ОДНОРОДНОМ И ИЗОТРОПНОМ ДИЭЛЕКТРИКЕ
И В ПОЛУПРОВОДЯЩЕЙ СРЕДЕ
§ 474. Распространение электромагнитных волн в однородном и
изотропном диэлектрике. Проводимость у идеального диэлектрика
равна нулю. Поэтому в первом уравнении Максвелла (16.1) пер-
вое слагаемое правой части (6 = уЕ) выпадает, и уравнения Мак-
свелла для диэлектрика получают следующий вид:
rot Н = /<оеЕ, (18.1) rot £ = — /сор/7. (18.2) div В =0 и divE = е
Так как мы будем рассматривать диэлектрики однородные и
изотропные, то р = const и условие div р77 = 0 равносильно ус-
ловию div 77 = 0.
Проведем совместное решение уравнений (18.1) и (18.2). С этой
целью возьмем ротор от уравнения (18.1). Получим
rot rot Н = grad div И — V2 Н = /сое rot Е.
Так как div Н = 0, то и grad div Н = 0. В свою очередь rot Е
на основании второго уравнения Максвелла равен — /сор И. По-
этому — V2 Н = /сое (— /сор и)
или \"11 = — ®2ерН. (18.3')
684
Произведение ер, измеряется в сек11м2'.
Iе] [14 =----------= сек2 м2,
в • м. а • м.
т. е. ер имеет размерность, обратную размерности квадрата
скорости, и потому можно принять ер = — . После введения
t>2
такого обозначения уравнение (18,3') получает следующий вид:
"* / со\2 —»
V2/7 = — (-) И. (18-3)
Будем рассматривать распространение плоской электромагнит-
ной волны. Для плоской волны, распространяющейся в направ-
лении оси г, в соответствии с предыдущим, можно принять, что
напряженность магнитного поля направлена вдоль оси у, т. е.
принять, что
Я = 7^- (18.4)
Так как для плоской волны И зависит только от координаты z
и не зависит от координат х и у, то уравнение
\дх2 ду2 дга/ \vj
переходит в следующее:
Уравнению (18.5) соответствует характеристическое уравнение
„ /СО \2 .(0 . (О
р2 = — — , корни которого Pi = 1 — и р2 = — / —. Общее ре-
\ v / v v
шение уравнения (18.5)
J — г — /— г
H = Cte v'+ С.,е ° ; (18.6)
С1 и С2 есть комплексные коэффициенты, зависящие от граничных
условий. Как и всякое комплексное число, их можно представить
в показательной форме:
С, = и С2 = С2е/Ф" .
. — i — г
Слагаемое С2е v есть падающая волна, продвигающаяся в поло-
• 1 v 2
жительном направлении оси г. Слагаемое Сге есть отражен-
ная волна, распространяющаяся в отрицательном направлении оси г.
Напряженность электрического поля Е найдется по уравнению
(18.1)
£ = — rot 77.
/сое
685
Как следует из предыдущего (см. формулу 17.10), для плоской
волны
f dH \
rot п = i I-----I.
\ dz )
Поэтому
Е = Т[— [ (- j-\ (f?/7* — С2е~' “2) IV
Ijae L V f / JJ
Величину 1 — — 1/h. обозначают через Zc и называют
ес е Г е
волновым сопротивлением диэлектрика:
Волновое сопротивление является чисто действительным числом,
измеряется оно в омах:
Zc ~ 1/Ё = 1/S = = 377 1/£ ом.
G г е г еоег г 8,86 • 10 12ф/м • ег У
Оно не зависит от угловой частоты колебаний <о. Для вакуума
е, = 1 и р, — 1, поэтому Zc = 377 ом. Следовательно,
Е = 7е, (18.7)
где
Ё = ZcC2e~'’ * — ZcCre **.
Присутствие единичного орта оси х (орта 0 в уравнении (18.7)
свидетельствует о том, что вектор напряженности электрического
поля направлен по оси х.
Таким образом, в плоской электромагнитной волне, распро-
страняющейся в диэлектрике, как и для проводящей среды,
Е и Н взаимно перпендикулярны — Н направлено по оси у,
Е по оси х.
Запишем выражения для мгновенных значений Н и Е падаю-
щей волны.
Для получения мгновенного значения падающей волны Н надо
— / — z
комплекс Н == С2е’^п е ° умножить на eiwt и от произведения
взять мнимую часть. Получим
Н = Сг sin фп — ~zj’ (18.8)
аналогично
Е — C2Zcsin — ~ZY (18-9)
6«6
По мере продвижения падающей волны вдоль оси г амплитуда
Е и амплитуда И остаются неизменными, другими словами, за-
тухания волны не происходит. И это совершенно естественно,
так как в диэлектрике нет токов проводимости и нет выделения
энергии в виде теплоты.
На рис. 478 изображены пространственные кривые, представ-
ляющие собой графики мгновенных значений Н и Е. Эти графи-
ки построены по уравнениям (18.8) и (18.9) для момента времени
<в* + ф„ = 0.
Для более позднего момента времени, например для <о£-|-фл=9О°
аналогичные кривые изображены на рис. 479.
Как видно из рис. 478 и 479, вектор Е при своем изменении
остается направленным в плоской волне вдоль оси х, а вектор
Н — вдоль оси у, сдвига по фазе между Н и Е нет.
^Огибающая H(zt
Огибающая Е (Z)
Огибающая Е(г)
Рис. 478
Огибающая O(z)
Рис. 479
Проверим правильность построения графика Е = f(z) на рис. 478.
Кривые на рис. 478 построены при at -ф- % = 0, поэтому уравне-
нием кривой E — f(z) на рис. 478 будет являться выражение
(в соответствии с 18.9):
'при mt 4 = О
= C2Zcsin ( — — z).
При 2=0 Е = 0. В интервале от — z = 0 до — г = л Е отрица-
тельно. При — г = л£ = 0ит. д.
Вектор Пойнтинга падающей волны направлен вдоль оси г.
Модуль S изменяется по закону
—C2Zc sin2 (at — — z -ф-
Так как
687
то
s==C^c 1_СОЦ2(0/— ~?+2ф„)
т. е. вектор Пойнтинга изменяется во времени с двойной угловой
частотой и имеет постоянную составляющую .
Фазовая скорость электромагнитной волны в диэлектрике
= (18.10)
Если волна распространяется в вакууме, то е = е0 и р, = р,0 и
тогда фазовая скорость равна скорости света v = 300 000 км/сек-.
______________1____________
V 1,256- 10~с 8,86- 10~12
300 000 (км/сек).
Таким образом, фазовая скорость электромагнитной волны
в диэлектрике очень велика и она несоизмеримо больше фазовой
скорости плоской электромагнитной волны в проводящей среде.
Длина волны X есть то расстояние вдоль оси z, на котором фа-
за колебания изменится на 2л. Она найдется из соотношения
-Х = 2л.
V
Отсюда
(18.11)
Из (18.11) видно, что длина волны в диэлектрике обратно
пропорциональна частоте f. Так, при / = 103 гц:
__ 300 000 км/сек ^qq
106 \/сек
Рассмотрим численный пример.
Пример 215. В плоскости z = 0 напряженность электрического
поля плоской волны изменяется по закону Е=Ет sin (at + ф„),
где Ет = 0,2 в/м, а = 10s сект1 и = 30°; диэлектрик — воздух.
Записать выражения для мгновенного значения напряженности
магнитного поля и вектора Пойнтинга в плоскости z = 0,5 км.
п и Ет . / , . . <о X Ет 2 • КУ*1
Решение. Н = —— sin ( at -4---------г I; — = —------_
2С \ 1 v / 2С 377
= 5,315 • КН (а/м)\ г = = 1.665 радиана ~ 95°20'.
Следовательно,
Н = 5,315 • 10-«sin (106£ — 65°20') а/м.
688
Мгновенное значение вектора Пойнтинга при z = 0,5 км
3==£^Г1 —cos(2o)/-|-2t|)„ — =
2 L \ v J
= 5,31 . 10-6[1 —cos(2 . 106Z— 130o40z)] вт/м2.
§ 475. Плоские волны в однородной и изотропной полу проводя щей среде.
Кратко рассмотрим вопрос о распространении плоской электромагнитной вол-
ны в однородных и изотропных полупроводящих средах (морской воде, почве,
ионосфере, ферритах). При достаточно высоких частотах токи проводимости
и токи смещения в полупроводящих средах оказываются соизмеримыми.
Уравнения rot И = (l+/wf) Е и rot Е => — JwjcH после введения обозначе-
ний = е — /_Х = е — /е', где с' = -1, для плоской волны приводятся к сле-
<0 со
дующему
<РЙ
di2
Последнему соответствует характеристическое уравнение д2 => — ш8е1р. Решение
его
Н = С1£ р‘г + С^.
Здесь Ci и С2 — постоянные интегрирования, зависящие от граничных условий
<0 (О
₽! = ₽ + /'- И ₽2 =—₽—/-------
V1 V
Коэффициент затухания
е'
зависит от отношения —,
£
Фазовая скорость
V 2
е'
также зависит от величины —.
£
Напряженность электрического поля
£ = HZC,
где волновое сопротивление
23 Л. А. Бессонов
689
Глава девятнадцатая
ЗАПАЗДЫВАЮЩИЕ ПОТЕНЦИАЛЫ
ПЕРЕМЕННОГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
И ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ЭНЕРГИИ
§ 476. Вывод уравнений для А и <р в переменном электромагнит-
ном поле и решение их. Переменное электромагнитное поле создает-
ся токами и зарядами, зависящими не только от координат, ’но и
от времени. Рассмотрим, каким уравнениям подчиняется век-
торный потенциал А и скалярный потенциал <р в переменном элек-
тромагнитном поле. С этой целью выпишем систему уравнений
Максвелла:
rot Н=‘б4-е--1
1 dt
дН дВ
rot Е = — ц-----—--------
dt dt
div В = О
div£ =
е
(19.1)
(19.2)
(19.3)
(19.4)
Дополним ее уравнением непрерывности
div's = —
dt
(19.5)
и выражением магнитной индукции через векторный потенциал
В = rot А.
(19.6)
* В дальнейшем индекс «своб» писать не будем.
690
Для того чтобы составить уравнение относительно векторного
потенциала, необходимо проделать ряд выкладок. Помножим (19.1)
на р, получим
rot В = рб -}- ре
В последнем уравнении изменим ре на —:
rotB=p6 + l-§-. (19.7)
v2 dt
В (19.7) вместо 13 подставим rot Л
rot rot Л = рб .
г ' г» at
Или
grad div Л — VM = рб -J- (19.8)
-* —
Затем в (19.2) вместо — подставим — rot Л = rot (операция
взятия ротора и операция дифференцирования во времени есть
операции, не зависящие друг от друга, и потому взаимно пере-
местимые). Тогда (19.2) приобретает следующий вид:
rot£ = — rot-M (19.9)
(—>
от £ и от----I , то са-
й< /
ми функции равны с точностью до градиента от некоторой скаляр-
ной функции. Последнее потому, что ротор от градиента скаляр-
ной функции тождественно равен нулю
(rot grad <р ss 0).
Таким образом,
£ =—~ —gradcp. (19.10)
В (19.10) в качестве градиента скалярной функции взят grad <р.
Объясняется это тем, что уравнение (19.10) должно быть спра-
ведливо и для статического поля. А так как в статическом поле
= 0, то выражение, которое получается из (19.10) для ста-
тического поля, должно совпадать с известным из электростатики
выражением
£ — —gradtp.
fJ91
23*
В соответствии с (19.10) можно сказать, что в переменном электро-
магнитном поле напряженность электрического поля имеет две
составляющие. Одна из них обусловлена переменным
магнитным полем, другая ( — grad ср) обусловлена неподвижными
зарядами*. Чтобы убедиться в этом, достаточно взять циркуля-
цию от вектора Е по любому замкнутому контуру
(§)Edl = — ^§Adl —(j)grad<p dl.
Циркуляция от градиента <p тождественно равна нулю, а ф A dl
в соответствии с уравнением (15.26) есть магнитный поток Ф,
пронизывающий выбранный контур. Таким образом,
В уравнении (19.8) участвует производная —. Найдем ее из (19.10)
dt
д Е d2 А , dm
— =-----------grad —
dt dt2 dt
и подставим в (19.8):
grad div Л —V2 Л = uT — - — — grad -
v2 dt2 v2 dt
Последнее уравнение можно переписать следующим образом:
grad(div2 + l^)-vM 4-1 (19.11)
\ v* dt ) v2 dt*
Вектор-потенциал есть искусственно введенная функция, ро-
тор которой равен В. При рассмотрении вопроса о векторе-поген-
циале А в разделе магнитного поля отмечалось, что на вектор-
потенциал может быть наложено определенное условие, а именно —
в постоянном магнитном поле div А = 0, т. е. линии вектора А
есть замкнутые сами на себя линии.
В переменном электромагнитном поле таким требованием к
вектору-потенциалу является требование
div7 = —1^. (19.12)
_________ v2 dt
* Цервую из них можно назвать вихревой составляющей, вторую —
потенциальной (или «кулоновой»).
692
Нетрудно убедиться в том, что для неизменного во времени
поля условие (19.12) вырождается в условие div А = 0. В дальней-
шем. будет показано, что условие (19.12) является не чем иным,
как в иной форме записанным уравнением непрерывности (19.5).
Вместе с тем уравнение (19.12) свидетельствует о том, что в
переменном электромагнитном поле между векторным потенциа-
лом А и скалярным потенциалом ф существует определенная связь
и что функция А и <р являются зависящими друг от друга функ-
циями.
С учетом (19.12) уравнение (19.11) приобретает вид*
vm —<19ЛЗ>
Если А не является функцией/, то — ® и уравнение (19.13)
переходит в обсуждавшееся в разделе магнитного поля уравнение
Пуассона.
Уравнение (19.13) является неоднородным векторным волно-
вым уравнением. Его часто записывают в иной форме
□2Л= — jiK. (19.13')
1 д2
Оператор D2=V2----г — называют четырехмерным Лапласиа-
ном (за «четвертое измерение» принимается время /). Выясним,
какому уравнению в переменном электромагнитном поле подчиня-
ется потенциал <р. С этой целью в уравнение (19.4) вместо напря-
женности Е подставим ее эквивалент по (19.10)
div |-— — grad <р ) = —
\ dt / е
или
— — div А — div grad <р = —.
dt е
Но
V2 dt
и, следовательно,
dt dt2
Уравнение (19.13) принято называть уравнением Даламбера,
693
в свою очередь div grad q> = у2<р. Поэтому уравнение (19.4)
приобретает следующий вид:
v2 dt2 е
(19.14)
Таким образом, в переменном электромагнитном поле скалярный
потенциал <р удовлетворяет неоднородному волновому уравнению
(19.14). Если поле статическое и потенциал не является функцией
времени, то ~ = 0 и уравнение (19.14) переходит в уравнение
Пуассона у2ф — — — > обсуждавшееся в разделе электростатики.
Для того чтобы убедиться в том, что уравнение (19.12) совпа-
дает с уравнением непрерывности (19.5), проделаем следующие
выкладки.
Применим оператор С2 к обеим частям уравнения (19.12)
□ 2div Л = — С2 ——.
v2 dt
Внесем оператор D2 под знак дивергенции и под знак производ-
ной ло времени. Получим
div О2 Л =— --n2<p. (19.15)
v2 dt
В соответствии с (19.13') в (19.15) вместо О2Л подставим — рб,
а вместо D2<p подставим — —. Будем иметь:
— div у. б = — — —.
v2 dt е
Вынесем р из-под знака дивергенции, а в из-под
ной по времени, поменяем знаки и поделим обе
на р:
знака
части
(19.15')
производ-
равенства
(19.16)
иное, как
div б =-----— —.
v2ep dt
Так как —— = 1, то уравнение (19.16) есть не что
ь,2ер
уравнение непрерывности (19.5). Таким образом, можно считать
доказанным, что уравнение div Л =—сводится к уравнению
непрерывности div б = — —.
Обсудим вопрос о решении уравнения (19.14). К составлению
решения уравнения (19.14) подойдем следующим образом: запишем
решение уравнения для двух частных случаев: для случая, когда
694
= 0, но — =# 0, и затем когда — = 0, но О. И после
dt2 е е й/2
этого на основании физических соображений запишем решение
уравнения (19.14) в общем виде, так что оно будет переходить в
известные решения для частных случаев.
Если = 0, то уравнение (19.14) переходит в уравнение
Пуассона, общее решение которого известно из раздела электро-
статики (см. § 397):
1 f pdV
Ф = — \ --—.
4 ле J R
v
Составляющая потенциала ф от элементарного заряда pdV равна
1 pdV
4ле R
При р = 0 уравнение (19.14) приобретает вид
VST = --<P. (19.17)
V2 б/2 ' '
В частном случае для плоской волны ф зависит только от
пространственной координаты z:
(19.17')
йг2 v2 dt2
Решением (19.17') является выражение
Причем функции и /2 могут быть любыми, лишь бы они позво-
ляли производить над собой двукратное дифференцирование по I
и по z. Вид функций определяется граничными условиями.
Убедимся в том, что функция Л I t — — ) удовлетворяет уравнению (19.17’).
\ v /
Действительно,
696
В свою очередь
02<р д2<р
Подставим — и —— в уравнение (19.17'). Получим
т.е. имеет место тождество вне зависимости от вида функции Следователь-
(z \
I----) удовлетворяет уравнению
v 1
(19.17'), если она может быть дважды дифференцируема по z и по t. Точно
7 , 2 \
таким же путем не составит труда убедиться в том, что и функция М------I
\ v )
удовлетворяет уравнению (19.17').
Напомним, что с волновым уравнением (19.17') мы уже имели дело при
рассмотрении вопроса о переходных процессах в линиях с распределенными па-
раметрами в главе двенадцатой.
fi\t — —j представляет собой падающую волну, распространяю-
щуюся в направлении оси -j-z*, функция f2 есть отраженная
волна, двигающаяся в направлении оси —z. Покажем, что в
сферической системе координат уравнению (19.17) удовлетворяет
функция — * * v ; R — есть координата сферической системы,
v — скорость распространения волны. Действительно, в сфери-
ческой системе координат
♦ Чтобы определить, в каком направлении перемещается волна
/1(/ — —), надо выяснить, как должно изменяться г с увеличением времени t,
v I
7 z \
чтобы аргумент функции Lit—— оставался постоянным, например рав-
\ v J
г
ным нулю. Если принять t — — = 0, то z = vt, т. е. с ростом t увеличивает-
V
ся г. Это означает, что волна распространяется вдоль положительного направ-
ления оси 2.
696
1±(^аФ\+_!_а fsine^\ + __L_^.
Y R*dR\ dR) R* sin 0 39 \ 08 / 1 R2 sin2 0 0a2
Так как в силу сферической симметрии <р является функцией толь-
ко R, то — = 0 и — = 0. Поэтому
00 0a
V2cp =
1 д_ / £>2dq>\
R2dR\ dR/’
Если в V2<p подставить
то окажется, что
V2q> = — f
Т Rv2 '
Таким образом, функция
02ф 1
также равно —
dt2 Rv2
удовлетворяет уравнению
(19.17) в сферической системе координат.
Для неизменного во времени поля (см. § 397) <р= -у—-
4 ле 7?
и в то же время решение для <р в пространстве, не занятом заря-
дами, такое:
Сопоставляя эти два выражения, находим
Таким образом, составляющая потенциала от заряда р(/) dV, изме-
няющегося во времени, равна
4ле7?
Выражение р (t---) следует понимать так: объемный заряд р
\ V
(R \
t----1. Результирующее значение
потенциала получим, если просуммируем составляющие потенциа-
ла от зарядов, распределенных в объеме V
697
1
<р = —
4 ле
(19.19)
R
Обсудим решение уравнения (19.13). В общем случае уравнение
(19.13) может быть разбито на три уравнения для трех проекций
вектора-потенциала*. Каждое из уравнений в проекциях будет
составлено относительно скалярной величины (проекция вектора
есть величина скалярная). Общее решение для каждой из проекций
проводится точно так же, как проводилось выше решение для
скалярной величины <р с тем отличием, что вместо объемного заря-
да будет участвовать соответствующая проекция плотности тока и
1
р вместо —.
е
После умножения решений на соответствующие орты и сложе-
ния окажется, что составляющая вектора потенциала от элемента
тока
тока
S dV в некоторой точке пространства, удаленной от элемента
на расстоянии R, будет равна
dV
(19.20)
dA
4л/?
получения результирующего значения А надо геометрически
Для
просуммировать составляющие от всех элементов тока
„ /—— Vv
v /
(19.21)
А = ,
4л J R
v
§ 477. Запаздывающие потенциалы переменного электромагнит-
ного поля. Обсудим, в чем состоит физический смысл выражений
(19.18) и (19.20). Электромагнитная волна распространяется со
скоростью V. Расстояние R она пройдет за время —. Поэтому зна-
V
чение составляющей потенциала <р в переменном электромагнит-
ном поле в некоторой точке, удаленной от заряда на расстояние R
в момент времени t, определяется значением заряда в момент вре-
Точно так же следует понимать и выражение
dA =----->---.
4л/?
В силу конечной скорости распространения электромагнитной
* Подобно тому, как это сделано на стр. 629 —630.
698
волны значение вектора-потенциала от элемента тока б dV в точ-
ке, удаленной от элемента тока на расстояние 7?, изменяется с
запаздыванием во времени на величину —.
V
Благодаря наличию запаздывания потенциалы переменного
электромагнитного поля называют «запаздывающими потенциала-
ми».
Так как скорость распространения электромагнитной волны
в диэлектрике очень велика (v = 300 000 км/сек}, то запаздывание
проявляется заметно только при значительных R, при малых R
запаздывание настолько незначительно, что им практически мож-
но пренебречь.
Наиболее часто понятием запаздывающих потенциалов пользу-
ются в радиотехнике при изучении вопросов, связанных с излу-
чением электромагнитной энергии.
§ 478. Комплексная форма записи запаздывающего векторного
потенциала. В главе «Магнитное поле постоянного тока» (см. урав-
нение 15.27) отмечалось, что составляющая векторного потенциала
от элемента линейного тока i dl равна dA = — .
г 4л R
В переменном электромагнитном поле с учетом явления
запаздывания
Ток I может изменяться во времени по любому закону. Наиболее
интересен с практической точки зрения синусоидальный закон
изменения тока во времени. Пусть
i — lm sin (at ф).
Ток можно представить в показательной форме Im e'mt, где
/т = 1те>* (строго говоря, надо было бы писать символ мнимой
части, цо его часто опускают).
Ток i — — j = 7msin £<» (t-------'j -|~ф^ или
в показательной
форме ime ' v '.
Следовательно, комплексное
элемента тока d!Imsin —
значение вектор-потенциала от
4- ф] запишется так:
. . /“u 1—»
- p. I v!dl
Л 4л R
(19.22)
699
Аналогичным образом, если электрические заряды, создаю-
щие поле, меняются во времени по синусоидальному закону, то
составляющая комплексного потенциала q> от объемного заряда
Р„,бИ v> dV
равна
• = _L Р^е 1 v’dV (19.23)
* 4ле 7?
Пример 216. Найти закон изменения векторного потенциала от
тока '100sin(105/-J-30°)a, протекающего по элементу проводника
длиной dl = 30 см, в точке, удаленной от элемента тока на рас-
стояние 7? = 100
Решение
КМ.
p/m sin
dA =-------
dl
4nR
10-® • 0,3- 100 sin Г 10®(t---
[ \ 300 000 /
4л • 100 • 103
= 3. 10-11sin(105/ —80е) е-сек/м
(33,3 радианам 110°; —110е 4-30° =—80°).
1,256 •
Рис. 480
§ 479. Излучение электромагнитной
энергии. Рассмотрим вопрос об излучении
электромагнитной энергии элементом то-
ка. Пусть по отрезку проводника длиной
dl протекает ток Im sin со/ (рис. 480). В даль-
нейшем будем пользоваться цилиндриче-
ской и отчасти сферической системами ко-
ординат. Ось z цилиндрической системы
направим вдоль проводника. Положи-
тельное направление тока по проводни-
ку пусть совпадает с положительным на-
правлением оси 2.
Найдем значение вектора-потенциала
в произвольной точке, удаленной от эле-
мента тока на расстояние R. В соответствии с (19.22)
dA =
± Ime ' v,dl
4л R
(19.22)
или, если исключить множитель
. . -/-« -а
Л - Ime v dl
4л R
700
Направление dA* совпадает с направлением вектора dl (вдоль
оси z).
Найдем магнитную индукцию в произвольной точке поля
В = rot Л.
Раскроем ротор в цилиндрической системе координат:
В = гоЙ = 7° + а° (_ I'M
\ гда дг ] \ дг dr )
। ^/д(гАа)__ дЛд
дг гда)'
Так как А имеет единственную составляющую Az и она зависит
только от R и в силу симметрии поля не зависит от а, то
В = а°(— • (19.24)
Последнее выражение означает, что магнитная индукция имеет
«альфовое» направление.
Для нахождения комплекса магнитной индукции надо вычис-
дА
лить------Аг зависит в явном виде от R, а не от г. Поэтому
дг
дЛг dAz dR
___± У'У (1 о огл
dr ~ dR дг • (1У./&)
Для любой точки пространства справедливо, очевидно, соотно-
шение, вытекающее из теоремы Пифагора:
z2 + г2 = R2.
Продифференцируем (19.26) по г, получим
2г = 2/?—.
дг
(19.26)
Следовательно,
dR
дг
(19.27)
состоит из произведения двух функций R:
функции е '~-v и функции — . Поэтому
R
d dA,dR р /mdl . л
в — — ----й--si п о
dR дг 4л
ИЛИ
Составляющая А2
—
_с
— = sin 9.
R
. R
, — /СО —
______L е v
R2
a sin 0
° “ 4S
е~ Iю Г
R2
'“4
(19.28)
—jJ^-e 'ю v
J vR
r vR
* В дальнейшем для сокращения записи вместо dA будем писать А.
701
Выражение (19.28) можно переписать и в ином виде, перейдя к
мгновенным значениям:
I- ( 1
Sin! Of———I . n\ I
—• <19-28')
Последнее выражение позволяет сделать вывод, что в любой
точке пространства магнитная индукция от элемента переменного
тока имеет две составляющие, одна из них убывает обратно про-
порционально квадрату радиуса и изменяется по закону синуса
во времени, другая убывает обратно пропорционально первой сте-
пени радиуса и изменяется по закону косинуса во времени.
Найдем закон изменения напряженности электрического поля.
В соответствии с первым уравнением Максвелла:
£ = ,4^1//. (19.29)
. -А>
Так как Н = —, то
И
Г.
ЛтД/sinO е ° . jcoe ° (19.30)
П L 4Й 7? Г vR~ J J ’
Далее целесообразно перейти к сферической системе координат-
Проекции rot Н в сферической системе таковы:
rot„Н = -р 1 „ f J- (sin 6 Н ) — ^-1
Л R sin 0 [ 30 ' да J
4» 1 дЙр 1 д
rot. Н = т. (RH ),
6 R sin 0 да RdR' ’
. Д 1Г д дН., 1
Г0 ° Н = —|^(/?/70) — J
Так как Не ~ 0, Йк = 0, то
го|«« = «41Я<81"ойЛ 0931)
1 д
rote # = -R- (^о)>
(19.32)
rota Н = 0.
Найдем проекцию rot Н на направление 7?:^
( .. к . R
— ]<м— — /ео —
е v ( /юе v
R2 "1 vR
702
или,, после сокращения на sin 0,
_ /m r _ •<„ R
. 'n— imdl cos ее * * * * v lmdl cose joe v /19 33)
гоГд/7 — 2л/?3. ‘ v '
В свою очередь, проекция rot Н на направление 0 такова
_ ju> R _ ,ш R \
/т dl sin бе v । lm dl sin 0 /<oe ° j _
4л/?
, X
. - /Ш —
lm dl sin 0e ° I lm dl sin 0 j<o
4л/?3 4л/?2о
— l„> —
)m dl sin 0<oze °
4л Rv2
4ло
-/<Л
е
(19.34)
Для того чтобы получить проекции Е на направления R и 0, надо
соответствующие проекции rot Н поделить на /сое (см. уравнение
19.29). Будем иметь:
£ sin в । 7md/sin0e “о ।
jQ» —— 1 C V 1 '
6 4л/?3®е
. R
. — /со —
। ]Imdl sin Qae °
4л/?ч2е
4ne/?2t)
(19.35)
и
-i»*
g _____— ]lm dl cos 0e v
Л 2л/?3<08
lmdl cos 0 e ' °
2nR2ve
(19.36)
Таким образом, напряженность электрического поля имеет две
составляющие: одна из них направлена по 0, другая по /?; 0-ая
составляющая содержит три слагаемых (см. уравнение 19.35), из-
меняющихся обратно пропорционально, соответственно, третьей,
второй и первой степени расстояния R\ ER состоит из двух слага-
емых, изменяющихся обратно пропорционально R3 и R2. Частное
v v vT X
а> 2л/ 2л 2л
Отношение модуля первого слагаемого (в 19.33) к модулю
X
второго равно ----- .
Если R , то первым слагаемым можно пренебречь
2л
X
по сравнению со вторым; если R<^ —, то, наоборот, второе
2л
слагаемое много меньше первого.
703
Аналогичные соотношения имеют место между модулями
слагаемых в (19.34).
Принято все поле делить на ближнюю зону, среднюю и
дальнюю. Для ближней зоны А . для дальней зоны
2л
. В средней зоне соизмеримо с —. В соответствии с
этим в ближней зоне
7/ — а° lm dl е v
4*Да
_ . R
. _ — )7mdZ sin Ое ' v
Е'Ь 4л7?3юе
(19.37)
. R
. — /“> —
• _ —j/m dl cosfle________"
Er 4л/?3юе
Для дальней зоны
___a°/7mdZsinfl
~~ 2/?1
£е =
'т dl sin fl
-/«А
е v
2RK
Запишем мгновенные значения Н и Е в дальней зоне:
(19.38)
2RK \ v
dl sin fl
2R).
COS
(19.39)
Таким образом, в «дальней» зоне, т. е. в зоне, для которой
X
, напряженность магнитного поля имеет только одну «аль-
фовую» составляющую, а напряженность электрического поля
имеет только одну «тэтовую» составляющую (см. уравнение 19.38).
Если провести сферу радиуса /?, то во всех точках этой сферы Н
имеет одну и ту же фазу колебания в какой-то конкретный момент
времени (фаза колебания определяется аргументом косинуса). Ам-
плитуда Н для точек сферы R = const различна, она зависит от
угла 0; на «полюсах» при 0 = 0 и при 0 = 180е амплитуда колеба-
ния для любого момента времени равна нулю, так как
sin 0 — sin 180° = 0,
704
амплитуда колебания максимальна на «экваторе» сферы при G =
= 90°. По фазе Н и Е совпадают (см. уравнение 19.39). Модуль Е
в Е. = Zc раз больше модуля Н, т. е.
Е = HZC.
Полярную диаграмму зависимости модуля Е или Н в дальней
зоне от угла 0 принято называть диаграммой направленности. В рас-
сматриваемом случае она будет представлять две соприкасающихся
окружности (рис. 481, а).
Составим выражение вектора Пойнтинга в дальней зоне:
5=[£Д]= SR.
Векторное произведение двух векторов, один из которых имеет
«тэтовое» направление, а другой «альфовое», дает вектор, напра-
вленный по радиусу (см. рис. 481, б).
Так как Н и Е в дальней зоне по фазе совпадают, то с измене-
нием направления Я на противоположное (Н изменяется во вре-
мени по косинусоиде) одновременно меняется на противоположное
и направление вектора Е. Но вектор S своего направления не ме-
няет, он все время направлен вдоль радиуса.
Найдем величину модуля вектора Пойнтинга. G этой целью ум-
ножим модуль Е на модуль Я
Zc sin2 6 cos2 <o
S =--------------------------
47?2Х»
(19.40)
705
Среднее значение модуля вектора’ Пойнтинга за период Т равно
_Zc(dOV^sinae
з^период № ‘
Т
[ 1 Г о / , (fl/Л ,, 1 \
(— I cos2 I (at--------) dt — — |.
\ T J \ v J 2 1
о
Подсчитаем поток вектора Пойнтинга через сферическую поверхность
радиуса /?. Элемент ds сферической поверхности радиуса R направ-
лен по радиусу. Вектор Пойнтинга S также направлен по радиусу.
Угол между ними равен нулю (рис. 482). Элемент сферической по-
верхности можно рассматривать как криволинейный квадрат, пло-
щадь его (рис. 482):
ds = R d$R sin 0 da — R2 sin 0 d9 da.
к -1 -1
Jsin39d9 =— f sin2 0 ci cos 0 = C (cos29 — l)dcosG —
oil
_4
3 ’
2it
J da = 2л.
о
Далее заменим P на 2/2 (/ — действующее значение тока). В ре-
зультате окажется, что поток векто-
ра Пойнтинга через сферическую по-
верхность радиуса R, представляю-
щий собой мощность Ps, излученную
элементом тока, не зависит от радиуса
R и будет равен
$Sds = Ps = RsP, (19.41)
где
„ _ 2 nZc(dl)2
s 3 X2
(19.42)
Rs называют сопротивлением излуче-
ния. Чем больше Rs, тем больше из-
лученная мощность при том же то-
ке I. Сопротивление излучения прямо пропорционально квадрату
длины излучателя и, что особенно важно, обратно пропорцио-
нально квадрату длины волны X.
Так как длина волны А = у» то излученная мощность прямо
пропорциональна квадрату частоты. Если частота мала, например
всего 50 гц, то излучения практически нет. При радиочастоте излу-
706
чение значительно. Например, при частоте 50 • 10е гц излучение
больше, чем при частоте 50 гц в 1012 раз.
Пример 217. По отрезку линейного провода длиной Д/ = 3 см
протекает переменный ток I — 0,2 а. Частота тока f = 10s гц.
Найти сопротивление излучения и мощность излучения.
Решение. Длина волны к = 30 см. По формуле (19.42)
п 2 377 • з2 _ о , .
= — л. —— 7,8 (ом).
3 30“
По формуле (19.41)
Ps = Rsp = 7,8 • 0,22 = 0,312 (вт).
§ 480. Понятие о излучающем диполе. При выводе формул § 479
в качестве излучателя электромагнитной энергии был взят неболь-
Рис. 483
шой отрезок провода, по которому протекал синусоидальный ток.
Но в точности такие же формулы были бы получены, если вместо
элемента тока был взят излучающий диполь. Под излучающим ди-
полем понимают отрезок линейного провода с сосредоточенными
на концах его емкостями в виде шаров (рис. 483, а).
Полагают, что длина диполя / много меньше длины волны А и что
сечение провода ничтожно мало. При этих условиях распределенную
емкость самого проводника можно в первом приближении не при-
нимать во внимание и учитывать только емкости шаров.
На рис. 483, б показана схема, в которой генератор синусоидаль-
ного напряжения высокой частоты через коаксиальный кабель при-
соединен к двум вертикально расположенным проводничкам — изоб-
ражены «жирными» линиями на рис. 483, б, — соединенным в свою
очередь с двумя шарами (шариками), из которых составлен диполь.
Под воздействием напряжения генератора шарики диполя перио-
дически перезаряжаются.
Положим, что заряд верхнего шарика q изменяется по закону
— cos со/, а заряд нижнего шарика — q по закону Qm cos со/. Тогда
по вертикальным проводничкам, подходящим к шарикам, при перио-
дической перезарядке шариков будет протекать ток проводимости
707
i = — — aQn sin at.
at
Этот ток замыкается через диэлектрик в виде тока смещения, как
это показано пунктирными линиями на рис. 483, б.
Важно обратить внимание на то, что по двум вертикальным про-
водникам длиной у каждый при периодической перезарядке ша-
риков протекает ток проводимости i. Другими словами, два верти-
кальных проводничка длиной-^-(или с током i, которыми со-
единены шарики диполя, представляют собой элемент тока И (или
idl), о котором шла речь в § 479.
То обстоятельство, что посредине элемента тока на рис. 483, б
есть разрыв, а в элементе тока рис. 480 разрыва нет, не имеет су-
щественного значения, так как этот разрыв может быть взят весьма
малым по сравнению с длиной I (dl).
Таким образом, все выводы § 479, сделанные применительно к
излучателю в виде элемента тока i dl, применимы и к излучателю
в виде диполя, т. е. к излучателю, составленному двумя периоди-
чески перезаряжающимися шариками, соединенными тонким про-
водничком.
§ 481. Дополнительный анализ поля излучения. Как уже говори-
лось в § 479, в ближней зоне излучателя основную роль играют сос-
тавляющие напряженности электрического поля Eg и ER, обрат-
но пропорциональные третьей степени расстояния рассматриваемой
точки до излучателя.
Эти составляющие на 90° отстают по фазе от протекающего по
проводнику тока или, другими словами, по фазе совпадают с заря-
дом одного из шаров излучающего диполя.
Из предыдущего [см. формулы (13.74)—(13.75)] известно, что на-
пряженность электрического поля, созданного диполем, заряды
которого неизменны во времени, также обратно пропорциональна
третьей степени расстояния рассматриваемой точки до центра ди-
поля.
Следовательно, для определения мгновенного значения напря-
женности электрического поля излучающего диполя в ближней зо-
не практически можно пользоваться формулами, вытекающими
из закона Кулона. В свою очередь напряженность магнитного поля
в ближней зоне излучателя [см. формулу (19.37)] обратно пропорцио-
нальна квадрату расстояния рассматриваемой точки до элемента
тока и по фазе совпадает с током.
Из закона Био — Савара — Лапласа [см. формулу (15.36)] сле-
дует, что напряженность магнитного поля, создаваемого элементом
постоянного тока, также обратно пропорциональна квадрату рас-
стояния рассматриваемой точки до элемента тока.
708
На основании этого сопоставления можно сделать вывод, что
в ближней зоне (при R < X) для определения мгновенного значе-
ния напряженности магнитного поля практически можно пользо-
ваться формулой Био — Савара — Лапласа. Применимость фор-
мул, описывающих статические поля, для подсчета мгновенных зна-
чений Е и Н переменных полей в ближней зоне (при R < X) объяс-
няется тем, что в ближней зоне можно пренебречь запаздыванием.
Границы ближней зоны зависят от частоты. Так, например, при
f = 50 гц X = 6-106 м. При / = 1010 гц X = 3 см. Следовательно,
при частоте в 50 гц законами Кулона и Био — Савара —Лапласа
можно пользоваться практически при любом расстоянии точки до
элемента тока или диполя. Совершенно иная картина будет при час-
тоте 1010 гц. В этом случае границы ближней зоны удалены от излу-
чателя всего на доли сантиметра, и практически все пространство
вокруг излучателя следует рассматривать как дальнюю зону. В даль-
ней! зоне «кулонова» составляющая напряженности электрического
поля ничтожно мала по сравнению с волновой составляющей Е,
а «био — саварова» составляющая напряженности магнитного
поля ничтожно мала по сравнению с волновой составляющей И.
В ближней зоне поток вектора Пойнтинга имеет две составляю-
щие. Первая составляющая изменяется во времени по закону
sin 2и/ или cos2<o/. Вторая составляющая изменяется во времени
по закону sin2(o/ или coszcot
При подсчете потока вектора Пойнтинга через сферическую по-
верхность радиуса R в ближней зоне за период переменного тока
окажется, что поток от первой составляющей будет равен нулю,
поскольку среднее за период значение функции sin 2<о/ или cos2io/
равно нулю. Поток вектора Пойнтинга от второй составляющей бу-
дет отличен от нуля. Физически это означает, что в ближней зоне
происходит два качественно отличных в энергетическом отношении
процесса. Первый процесс—это процесс периодического обмена
энергией между источником энергии, к которому присоединен излу-
чатель, и ближней зоной.
Энергия то забирается от источника и накапливается в электро-
магнитном поле ближней зоной, то отдается обратно источнику. Этот
процесс характерен для «кулонова» и «био — саварова» полей
ближней зоны.
Второй процесс — это процесс излучения энергии. Он характе-
ризует волновой процесс в ближней зоне.
Излученная энергия составляет относительно небольшую вели-
чину по сравнению с энергией, периодически накапливаемой в элект-
ромагнитном поле ближней зоны и затем отдаваемой источнику пи-
тания.
От излучателя распространяются в пространство электромагнит-
ные волны. Эти волны для фиксированного момента времени схема-
тически можно представить рис. 484, а. На нем линии Е образуют
замкнутые фигуры, лежащие в меридиональных плоскостях. Линии
709
Е охвачены линиями Н. Последние представляют собой окружности
с центром на оси элемента тока.
Чтобы не загромождать рисунок 484, а, на нем изображено всего
две линии Е и две линии Н.
Характер электрического поля в меридиональной плоскости для
волновой зоны излучателя для различных моментов времени пока-
зан на рис. 484, б. На этом рисунке изображена также кривая из-
менения заряда излучающего диполя в функции времени. Чем боль-
ше по абсолютной величине становятся заряды диполя, тем боль-
шее количество линий Е начинается или, соответственно, оканчива-
ется на них.
Рис, 484
По мере распространения электромагнитной волны в окружа-
ющее пространство форма линий Е непрерывно меняется. Когда
заряды диполя по абсолютной величине начинают уменьшаться, то
начинает уменьшаться и число исходящих из них линий Е. При
этом образуются замкнутые на себя линии Е. Пакет замкнутых
на себя линий Е сцеплен с пронизывающими их линиями И (рис.
484, а). В следующий полупериод, когда заряды шаров меняют зна-
ки на противоположные, образуется аналогичный пакет замкнутых
на себя линий Е, отличающийся от предыдущего лишь направле-
нием вихря Е.
§ 482. О расчете поля реальных излучателей. Практически в ка-
честве излучателей используются антенны. Простейшая антенна
представляет собой отрезок провода длиной I, расположенный вер-
тикально по отношению к поверхности земли (рис. 485, а). Генера-
тор высокой частоты включается между антенной и землей. За счет
наличия распределенных емкостей антенны и проходящих через
ПО
них токов смещения ток по высоте антенны меняется по амплиту-
де и фазе (см. эпюру изменения амплитуд на рис. 485, а). Антенна
обладает высокой способностью к излучению вследствие того, что
создаваемые ею электрическое поле и магнитное поле распределе-
ны в одной и той же области пространства, окружающем антенну
(рис. 485, а).
Влияние земли на поле учитывают, вводя в расчет зеркальное
изображение антенны (полагая, что земля является идеальным про-
водником). При этом длина антенны оказывается равной 21, а эпю-
ра тока дополняется второй половиной (рис. 485, б). Для расчета
поля, создаваемого антенной, ее заменяют совокупностью малых
отрезков длины dl, на каждом из которых ток принимают неизмен-
ным по амплитуде и фазе. Тогда напряженность поля в произволь-
ной точке пространства может быть найдена как геометрическая
сумма напряженностей, создаваемых всеми малыми отрезками ан-
тенны.
Для увеличения емкости антенны, а следовательно, и проходя-
щего по ней тока при том же напряжении генератора, антенну час-
то дополняют горизонтальным участком (рис. 485, в).
§ 483. Переход плоской электромагнитной волны из одной среды
в другую. Рассмотрим условия перехода плоской синусоидально
изменяющейся электромагнитной волны из первой среды с волновым
сопротивлением ZC1 во вторую среду с волновым сопротивлением
ZC2. Примем, что волна падает перпендикулярно грани раздела сред
(рис. 486). Волна частично пройдет во вторую среду, частично от-
разится.
Условимся, что индекс 1 соответствует первой среде, индекс 2 —
второй. Индекс п свидетельствует о падающей волне, индекс о —
об отражающей. В первой среде будет падающая и отраженная
волны, во второй — только падающая (поэтому индекс п у нее не
будем ставить). Падающую во второй среде волну называют также
преломленной.
Для удобства чтения рис. 486 вектора, характеризующие пада-
ющую и отраженную волну в первой среде, смещены по вертикали
711.
и несколько отодвинуты от грани раздела сред. На грани раздела
сред должны быть равны тангенциальные составляющие напряжен-
ности электрического поля и должны быть равны тангенциальные
составляющие напряженности магнитного поля, т. е.
^1П Ё10 ~ ^2>
^ + ^0 = ^2-
(19.43)
(19 44)
Уравнения (19.43) и (19.44) полностью тождественны уравнениям,
которыми связаны напряжения и токи падающей, отраженной и
преломленной волн при переходе волны с одной линии с распреде-
ленными параметрами на другую линию (см. § 351 второй части).
Комплекс напряженности электрического поля Ё1п равен ком-
плексу напряженности магнитного поля Н1п, умноженному на Zcv
^ln ~
Для отраженной волны в соответствии
с изменением направления движения
энергии на противоположное
^0 ~ ^10 ^Cl-
Для преломленной волны
Ё2— Н2 ZC2.
Из уравнений (19.43) ^и (19.44) с учетом
предыдущих строчек получим
= (19.45)
ZC2 + ZC1
//10= (19-47)
Проанализируем полученные результаты. Значения £10, Н10 и
Ё2, Н2 зависят от соотношения между волновыми сопротивления-
ми обеих сред. Наибольший практический интерес представляет
случай, когда волна падает из воздуха на поверхность металла.
В этом случае первой средой является воздух, а второй средой —
металл. Так как волновое сопротивление проводящей среды за-
висит не только от ее проводимости и магнитной проницаемости,
но и от частоты (см. формулу 17.12), то для определенности по-
ложим, что проводящей средой является медь, а частота /= 10® гц.
Сопоставим значения волновых сопротивлений для диэлектрика и
для металла (см. формулы для Zc на стр. 670 и 686). Для воз-
712
духа ZCl — 377 ом. Для меди (у = 5,6 • 107 ом~* • лг1) пр",
f = Ю8 гц, ZC2 = 0,00357 е/45 ом. Если подставить эти значения
ZC1 и ZC2 в (19.45), то получим
^10~ ^1п‘> ^10 ~ ^1п<
т. е. от поверхности металла электромагнитная волна почти пол-
ностью отражается с переменой знака у напряженности электри-
ческого поля. Та часть волны, которая все же проникает в металл,
быстро в нем затухнет. Если бы проводящая среда имела у, стремя-
щееся к бесконечности, то тогда она являлась бы идеальным зерка-
лом для электромагнитной волны.
Явление отражения электромагнитных волн от проводящих сред
лежит в основе радиолокации.
§ 484. Экранирование в переменном электромагнитном поле. Яв-
ление затухания электромагнитной волны в поверхностном слое
металла используется для экранировки в переменном электромаг-
нитном поле.
Электромагнитные экраны представляют собой полые цилиндри-
ческие, сферические или прямоугольные оболочки, внутрь которых
помещается экранируемое устройство (например, катушка индук-
тивности, измерительный прибор и т. п.).
Экран выполняет две функции. Во-первых, он защищает устрой-
ство, заключенное в экран, от влияния внешнего по отношению к
экрану электромагнитного поля. Во-вторых, он защищает внешнее
по отношению к экрану пространство от электромагнитного поля,
создаваемого устройством, заключенным в экран.
Поскольку на расстоянии, равном длине волны в металле, элект-
ромагнитная волна почти полностью затухает, то для хорошей эк-
ранировки толщина стенки экрана должна быть примерно равна
длине волны в металле. Практически приходится учитывать и дру-
гие факторы (механическую прочность экрана, его стоимость и т. д.).
§ 485. Сопоставление принципов экранирования в электростати-
ческом, в магнитном и электромагнитном полях. Электростатическое
экранирование основано на компенсации внешнего поля полем за-
рядов, выявившихся на стенках экрана вследствие электростати-
ческой индукции (§ 399). Толщина стенок экрана при электроста-
тическом экранировании в отличие от экранирования в магнитном
и электромагнитном полях может быть сколь угодно малой. Экра-
нирование в магнитном поле постоянного тока (§ 457) основано,
грубо говоря, на том, что силовые линии магнитного поля преиму-
щественно проходят по участкам с меньшим магнитным сопротив-
лением (по стенкам экрана).
Экранирование в переменном электромагнитном поле основано
на том, что электромагнитная волна, проникающая в стенки экрана,
быстро затухает, расходуя энергию на покрытие потерь, обусловлен-
ных вихревыми токами в стенках экрана.
713
§ 486. Высокочастотный нагрев металлических деталей и несо-
вершенных диэлектриков. Поверхностная закалка стальных изделий.
Нагрев металлических деталей перед ковкой и штамповкой, суш-
ку древесины, наплавку и реставрацию инструментов часто произ-
водят путем помещения этих предметов (деталей) в электромагнит-
ное поле сравнительно невысокой частоты (1—20 кгц). Стальные
изделия (например, валы, шестеренки) часто подвергают поверх-
ностной закалке, помещая их в электромагнитное поле более вы-
сокой частоты (порядка 10—500 кгц).
Как известно из предыдущего (§ 468), электромагнитная волна,
проникая в толщу металла, быстро затухает. Поэтому теплота вы-
деляется практически лишь в относительно тонком поверхностном
слое стального изделия.
Под действием теплоты, выделившейся в поверхностном слое,
последний быстро разогревается до температуры, необходимой для
поверхностной закалки. Область еще более высоких частот
(1—ЗОМе^) используется для высокочастотного нагрева пластмасс
перед штамповкой, для термической обработки пищевых продуктов,
вулканизации резины и для других целей.
§ 487. Понятие о волноводах. Канализация энергии очень высо-
кой частоты по обычным двухпроводным линиям передачи оказы-
вается практически невозможной ввиду того, что: 1) провода линии
играют роль антенн и, вместо того чтобы передавать энергию потре-
бителю, излучают ее в пространство и 2) активное сопротивление
проводов линии при сверхвысоких частотах в силу резко выражен-
ного поверхностного эффекта оказывается настолько большим, что
весьма значительная часть энергии затрачивается на нагрев прово-
дов.
Применение коаксиального кабеля (коаксиальной линии) рис. 465
для канализации энергии весьма высокой частоты также не-
выгодно. Хотя в этом случае энергия в окружающее пространство
и не излучается (так как оболочка кабеля одновременно является
и экраном), однако в кабеле великн потери энергии в жиле и в ди-
7Г4
электрических шайбах, при помощи которых жила крепится внут-
ри кабеля.
При частотах больше 10* гц энергию передают по волноводам.
Волновод представляет собой полую трубу прямоугольного или
круглого сечения.
На рис. 487, а изображен прямоугольный волновод. Размеры
а и Ь находятся в определенном соотношении с длиной волны*.
Так, например, при длине волны Л = 10 см. берут b = 3,54 см и
а — 7,2 см.
Энергия внутрь волновода доставляется при помощи неболь-
шого стерженька, помещенного в волноводе, и коаксиального ка-
беля, соединенного с генератором высокой частоты (рис. 487, а),
или при помощи петли с током, также помещаемой в волноводе,
и коаксиального кабеля, соединенного с генератором высокой час-
тоты (рис. 487, б).
Отвод энергии с другого конца волновода производится также
при помощи стерженька или петли.
Энергия передается вдоль волновода, отражаясь от его стенок
(рис. 487, в). Стенки волновода являются как бы направляющими
для потока энергии. Небольшая часть энергии проникает в стенки
волновода и выделяется в них в виде теплоты. Для уменьшения по-
терь энергии в стенках волновода внутреннюю поверхность труб по-
лируют и покрывают слоем хорошо проводящего металла, напри-
мер серебра. Элементы теории волноводов рассмотрены в приложе-
нии Г.
*
* *
Основоположником теории переменного электромагнитного по-
ля является английский физик проф. Джеймс Кларк Максвелл
(1831—1879). Из его «Трактата об электричестве и магнетизме» (1873)
вытекал вывод о существовании электромагнитных волн, распро-
страняющихся со скоростью света.
Теория Максвелла была экспериментально подтверждена рабо-
тами немецкого физика проф. Генриха Рудольфа Герца
(1857 —1894) и русского физика проф. Петра Николаевича Ле-
бедева (1866—1912).
Генрих Герц в 1887—1888 гг. экспериментально доказал сущест-
вование электромагнитных волн и исследовал их свойства (отраже-
ние от зеркал, преломление в призмах). Он подтвердил выводы Макс-
велла о том, что скорость электромагнитных волн равна скорости
света. Профессор Московского университета Петр Николаевич
Лебедев в 1895 г. измерил давление света, теоретически вычислен-
ное Максвеллом. Своими опытами он доказал справедливость элект-
ромагнитной теории света.
• Размеры а и b см. на рис. 490, а на стр. 726.
713
Дальнейшее развитие теории излучения электромагнитной энер-
гии и использование свойства элемента тока излучать электромаг-
нитную энергию для создания радиосвязи было сделано проф. Алек-
сандром Степановичем Поповым (1856—1906). А. С. Попов являлся
первым выборным директором Петербургского электротехническо-
го института.
7 мая 1895 г. на заседании Русского Физико-химического общест-
ва им был прочитан доклад о проведенных им успешных опытах по
приему и передаче радиосигналов. Поэтому день 7 мая 1895 г. отме-
чается как день изобретения радио.
ПРИЛОЖЕНИЯ К Ш ЧАСТИ КУРСА ТОЭ
Приложение А
СВОЙСТВА НЕКОТОРЫХ ПРОВОДНИКОВЫХ
МАТЕРИАЛОВ И ДИЭЛЕКТРИКОВ
Значения электрической проводимости у в сим/м при 20° С для
различных проводниковых материалов
Алюминий (3,47 4-3,8) >10’ Ста ль (0,73 4- 0,97) • 10’
Бронза (1,92 4-4,76)-10’ Латунь (1,26-j-3,23). 10’ Серебро (6,174-6,25) • 10’ Чугун (24-2,5). 10»
Медь (5,5 4-5,72). 10’ Константан (1,9 4* 2,22) • 10»
Никель (1,26 4- 1,32)-10’ Нихром (0,735 4- 0,48) • 10»
Основные свойства некоторых диэлектриков
В таблице даны значения относительной электрической проницаемости ег
при частоте 100 г<(, тангенса угла потерь tg д при частоте 1000 гц и пробивной
напряженности (кв • афф!см) в равномерном поле при частоте 50 гц.
Материал В Г tg8 Епроб
Бакелит 4,9 0,03 240
Бумага 3,7 0,009 160
КкарЧ 3,8 0,001 80
Плексиглас 3,4 0,06 400
Полихлорвинил 3,2 0,01 320
Полистирол 2,55 0,0005 240
Слюда 5,4 0,002 100—1000
Трансформаторное масло 2,24 0,001 120
Фарфор 7 ’— 57
717
Приложение Б
ПОНЯТИЕ О РАСЧЕТЕ ПОЛЕЙ ПО МЕТОДУ СЕТОК И О МОДЕ-
ЛИРОВАНИИ ПОЛЕЙ ПО МЕТОДУ ЭЛЕКТРИЧЕСКИХ СЕТОК
За последние годы широкое распространение получили: а) метод числен-
ного расчета электрических и магнитных полей по методу сеток, б) модели-
рование электрических и различных неэлектрических полей по методу элект-
рических сеток.
Несмотря на близость названий, содержание методов существенно различ-
но.
§ 488. Расчет полей по методу сеток. Метод сеток представляет собой чис -
ленный метод интегрирования дифференциальных уравнений в частных про-
изводных путем сведения их к уравнениям в конечных разностях.
Рис. 488
На рис. 488, а изображен участок двухмерного поля. На нем показаны
оси х и у декартовой системы и квадратная сетка со стороной Ь. Точки (узлы)
сетки обозначены цифрами 0, 1, 2, 3, 4;ф0 — потенциал точки 0, ф! — потен-
циал точки 1 и т. д. Выведем приближенное соотношение между потенциалами
Фо. Ф1» Фз» Фз. Фл» вытекающее из уравнения Пуассона. Среднее значение пер-
дф
вой производной —
дх
иа участке 1 —> 0 приближенно равно
Дф
Дх
1-0
У1~ ?о
Ь '
718
На участке 0—2i
д? \ ?о — ?а
/0—2
d^f
Вторая производная —- в точке 0 приближенно равна разности средних зиаче-
дх2
dv
ний первых производных —— на участках 1 — 0 и 0 — 2, отнесенных к расстоя-
дх
нию Ъ между серединами отрезков 1 — 0 и 0 — 2, т. е.
(Д?\ _ / Ду\ <н~ то _?о — ?а
~ t _ &х/1-о \д*/о-2 Ь ь + Уз — 2?1>
дх2 Дх8 Ъ Ь Ь2
Аналогично,
д8? ~ ?з + ?4~2?0
ду*~ Ь2
Запишем уравнение Пуассона для двухмерного электростатического поля
д;? , д8<р _ _ Рсаоб
дх2 ' ду2 в ’
Рсвоб ““ свободный заряд в точке 0.
д2^ d^f
Подставим в уравнение Пуассона приближенные выражения для — и —.
Получим
Рсвоб Ь2
е
+ ?8 + ?3 + ?4 — 4tf0
(а)
Если поле описывается уравнением Лапласа, то рсвоб = 0 и
У1 + Уз + Уз + У4 — 4<f0 = 0. (б)
Уравнения (а) и (б) дают связь между потенциалами квадратной сетки. Они
являются основными в методе сеток. Чем меньше шаг сетки Ь, тем меньше
погрешность от замены уравнений Пуассона или Лапласа соответственно иа
уравнения (а) или (б). При расчете по методу сеток применяются не только
квадратные, но и иные виды сеток, например полярные. Для них будут свои
формулы в конечных разностях, в общем случае отличные от формул (а) и (б).
Допустим, что двухмерное поле, подчиняющееся уравнению Лапласа,
ограничено некоторыми поверхностями, и известны потенциалы этих поверх-
ностей (задача Дирихле), либо известны значения производной от потенциала
по нормали к каждой граничной поверхности во всех их точках (задача Ней-
мана). Возможны и комбинированные типы задач, когда для одной части
граничных поверхностей известны значения потенциалов, а для другой —
значении нормальной производной от потенциала.
Требуется найти значения потенциалов прямоугольной сеткн этого поля.
Последовательность расчета для задачи Дирихле проиллюстрируем на при-
мере расчета поля, образованного двумя параллельными прямыми углами
рис. 488, б. В месте поворота расстояние между параллельными сторонами уг-
ла изменяется. Потенциал верхней границы положим равным 75 единицам,
нижней — нулю. Будем полагать, что объемные заряды отсутствуют.
1. Тонкими сплошными линиями нанесем квадратную сетку. Обозначим
узлы получившихся квадратов буквами а, б, в, г, д,... (расположены в круж-
ках).
2. Следующий этап расчета состоит в произвольном выборе потенциалов
узлов а, б, в,... Объем дальнейшей вычислительной работы в значительной ме-
719
ре зависит от того, насколько близко к действительному выбрано первоначаль-
ное распределение потенциала. Поэтому всеми возможными средствами сле-
дует стремиться к возможно более правдоподобному первоначальному распре-
делению потенциала.
В рассматриваемом примере для этой цели нанесем на рисунок пример-
ный ход силовых и эквипотенциальных линий и, руководствуясь этими ли-
ниями, записываем начальные значения потенциалов узлов (цифры слева н
вверху у каждого узла).
3. Для каждого узла находим величину остатка в формуле (б). Так, оста-
ток для точки б равен 53 + 50 + 75 + 25 — 4- 50 = 3. Записываем вели-
чину остатка в правом верхнем углу у каждого узла* *.
4. Так как в каждом узле остаток должен быть равен нулю, то дальней-
ший и наиболее трудоемкий этап расчета состоит в таком изменении потенциа-
лов узлов, чтобы остатки во всех узлах не превышали некоторой заданной ве-
личины (скажем 1 или 2).
С этой целью в одной из точек с наибольшим значением остатка изменяем
потенциал приблизительно на 1/4 от остатка (в нашем случае в точке б умень-
шаем потенциал на 1) и затем пересчитываем остатки во всех остальных узлах.
Вновь полученные остатки записываем в левом нижнем углу у каждого узла
(на рисунке они выписаны не для всех узлов). Такая операция выполняется
несколько раз до тех пор, пока все остатки не станут равны или меньше за-
данной величины. Процесс является сходищимся. При расчетах используют
счетные машины.
Метод применим для магнитных и электрических полей, для линейных
и нелинейных сред, для неизменных и для изменяющихся во времени полей.
Более подробные сведения о методе сеток даны, например, в (Л. 26).
§ 489. Моделирование полей по методу электрических сеток. Моделирова-
ние полей при помощи электрических сеток представляет собой метод экспе-
риментального исследования полей путем измерения потенциалов узлов элект-
рической сетки, которой заменяется сплошная среда. Положим, что требует-
ся выяснить распределение потенциалов в некоторой проводящей области
(сплошной среде), причем потенциалы границ области заданы. Кроме того,
известна проводимость среды у и плотность тока б(х, у, г) как функция коор-
динат.
Моделируемую область подразделим на отдельные элементарные объемы,
например на кубы. Каждый элементарный объем заменим электрической схе-
мой замещения в соответствии с рис. 488, в.
Пусть ребро куба имеет длину 2а. Центр куба обозначим ( 'буквой О, а
точки, лежащие в серединах его граней, назовем цифрами 1, 2, 3, 4, 5, 6.
Шаг сетки в направлении осей к, у, г обозначим Дх, At/, Дг
(Дх = Д{/ = Дг = а).
Проводимость между любой из точек 1—би центральной точкой О равна
аа
g=t ~ = ta.
а
К узлу О от источника тока подтекает ток /0 = Й(х, у, г) а3. По первому за-
кону Кирхгофа сумма токов, подтекающих к узлу О, должна быть равна ну-
лю, т. е.
(<Рг — Фо)Я + (Фг — Фо) 8 + (4>з — Фо) g + (Ф4 — фо)£ + (Фе — Фо)£ +
+ (Фе — Фо)& + 4 — 0. (в)
Потенциал точки О
Фо = Ф (*> У> 2)-
* В правом верхнем углу У точки б на рис. 488, б должна быть
цифра + 3 вместо + 5.
720
Потенциал точки 1
Дх <?ф (Дх)2 д2 ф
фх= ф (х + Дх, j/, г) яе ф (х, у, г)— — +~^-^ +
(Дх)3 й3 ф (Дх)4 й4 ф
+ 3! 4! ахГ+ ”
Потенциал точки 2
&Х Йф
ф2=ф(х— Дх, у, г) » ф(х1{/,г) — — - — 4-
(Дх)2 д2ф (Дх)3 й:,ф
+ 2! дх2 ~ 31 дх2 + ‘ ‘ '
Следовательно,
д2ф д2ф
(<Р1 — фо) g + (<Р-2 — <Ро) g = (Л*)2 = •
Проделав аналогичные выкладки с остальными слагаемыми уравнения (в),
подставив в него выражение для /0 и сократив на а3, получим уравнение
Пуассона
й2ф й2ф , й2ф 6 (х, р, г)
йх2 + йр2 + дг2 у
Таким образом, распределение потенциалов в электрической сетке с точностью
а2
до частных производных четвертого порядка от ф, умноженных на
77- УД06'
летворяет тому же уравнению, что и распределение потенциала в сплошной
среде.
Распределение потенциалов в узлах О элементарных объемов измеряет-
ся компенсационным способом.
Приложение В
ПОВЕРХНОСТНЫЙ ЭФФЕКТ В ЦИЛИНДРИЧЕСКОМ
ПРОВОДЕ
По цилиндрическому проводу радиуса а протекает синусоидальный ток I
частоты со. Требуется вывести формулы для определения плотности тока б
и напряженности Н в любой точке сечения провода, а также формулы для под-
счета активного и внутреннего индуктивного сопротивления провода. При ре-
шении будем полагать, что обратный провод настолько далеко удален от пря-
мого провода, что влияние обратного провода на поле в прямом проводе можно
не учитывать.
Решение проведем в цилиндрической системе координат (рис. 489). Плот-
ность тока 6 направлена по оси г. поэтому 6 = г» б. Воспользуемся урав-
нением (17.1) и уравнением (17.2), предварительно умножив последнее на у.
Получим
rot Н — 6 , (П.1)
rot 6 = — .
(П 2)
24 Л. А. Бессонов
721
Или
rot rot б = — /<о у р. б,
т. е.
(grad div б — v2 б) z® = (— / <о у р.) 5 z® .
В установившемся режиме div 5=0. Поэтому
V2 6 — /соур 5.
Раскроем ^2б в цилиндрической системе координат
учтем, что б от а и от z не зависит. Получим
(см. формулу 13.30) и
Или
Обозначим
Тогда
d2 б 1 d5
dr1 r dr
<72 = — /WYP-
d26
dr2 +
d5
dr
+ <?26
или
d2 6
d (<7r)2 qrd (qr) +
(Г1.3)
(П.4)
1 / d 5 rfa в \
— 5
I
= 0
Уравнение (П.4) является частным случаем более общего уравнения (П.5),
которое называется уравнением Бесселя:
d2y 1 dp
dx2 х dx
(П.5)
. Уравнение (П.5) переходит в уравнение (П.4) при п = 0 (роль у играет
6, роль х играет qr).
Как известно из курса математики, решение уравнения (П.4) запишется
следующим образом
5 = Л/о(90 + BN0(qr). (П.6)
Здесь Л и В’ постоянные интегрирования; /0(</г) — функция Бесселя
нулевого порядка первого рода, Nolqr) — функция Бесселя нулевого поряд-
ка второго рода.
Функция N0(qr) обладает той особенностью, что при qr = 0 (т. е. на оси
провода при ' = 0) функция А'о(О) обращается в бесконечность. Но из физи-
ческих соображений ясно, что плотность тока должна быть всюду конечна,
в том числе и на осп провода. Поэтому слагаемое BN0(qr) в решении отбра-
сываем (принимаем В = 0). Следовательно,
b—AJ0(qr). (П..-)
D соответствии с уравнением (П.2) и формулами (П.З) и (15.7)
! ->
Н = ~т rot б = а°
Я
1 db
q2 dr
= 7 Н ,
722
1 d Г , 1 A d [Л (у)] dqr
AJ0(qr) = —
А А
== — ~2,cil—Ji (<7r)l = - Ji (qr),
. А
Н = — Ji(qr),
q
(П.8)
2па
А =
(П9)
(П. 10)
(П.! I)
(П.!2)
где J^qr) есть функция Бесселя первого рода первого порядка.
Определим постоянную интегрирования А. С этой целью по закону пол-
ного тока найдем Н на поверхности провода (при г — а) и приравняем ее зна-
чению Н, которое получается из формулы (П.8)
1 А
= — Л (<?о),
q
ql
2naJt(qa)
Подставим найденное значение А в формулы (П.7) и (П.8). Получим
• = д / /0 (дг)
2naJl(qa)
Л i-fi(qr)
п = --------------.
2naJ,(qa)
При помощи формул (П.10) и (П.11) можно определить комплекс плотности
тока 6 и комплекс напряженности поля Н в любой точке сечения провода.
Радиус г может принимать значения от 0 до а. Для точки на оси провода
г = 0. Для точек на поверхности г = а. Так как Jo(0) = 1 (см. ниже табли-
цу), то плотность тока на оси провода So
t.-
2naJl(qa)
Сопоставим (П.12) с (П.10). Сопоставление дает
б = 60Т0(9г), (П.13)
т. е. плотность тока в произвольной точке равна плотности тока на оси прово-
да, умноженной на функцию Бесселя нулевого порядка от аргумента qr
Из формулы (П, 13) следует, что плотность тока на поверхности провода
6 = 60J0(?o). (П.13')
г=а
Из предыдущего известно, что произведение qr есть комплексное число
<?г = г соур —/. (П.14)
Бесселевы функции J0(qr) и А (дг) от комплексного аргумента qr тоже явля-
ются комплексами и могут быть представлены в показательной форме:
Jo (qr) = Ьв е' ₽°, (П.15)
Ji (qr) = bt e*' ₽>, (П.16)
где b0 есть модуль, a po — аргумент функции Jo (qr); bx есть модуль, a p! —
аргумент функции J, (qr); bB,blt Po.Pi(Po и pi в градусах) определяются го
24*
723
значению г У оур. при помощи приведенной ниже таблицы. При составлении
этой таблицы наличие множителя У—j в составе аргумента qr уже учтено.
Таблица модулей и аргументов функций J0(qr) и Ti(qr)
гУ у р. Ьо ₽о Ь, Р,
0 1 0 0 —45,00
1 1,015 14,22 0,501 —37,84
2 1,229 52,28 1,041 —16,73
3 1,95 96,52 1,Ь0 + 15,71
4 3.439 138,19 3,173 53,90
5 6,231 178.93 5,812 •93,55
6 11,501 219,62 10,850 133,45
7 21,548 260,29 20,50 173,51
8 40.82 300,92 39,07 213,69
9 77,96 341,52 74,97 253,95
10 149,8 382.10 144,586 294,27
Для определения активного R и внутреннего индуктивного X сопротивления
единицы длины провода следует применить теорему Умова—Пойнтинга в комп-
лексной форме записи, т. е. проделать выкладки, подобные тем, которые для
плоской шины приведены в § 472.
В результате получим
7? = t2rnL±ocos(po_pi_45o)j (П.17)
2лауЬ1
X = sin (0О - 0, - 45°), (П. 18)
Пример 218. По стальному проводу (у=107 ом~'-м~\ p,r = 103) диаметром
6,04 лич течет синусоидальный ток I = 100 а частоты 50 гц. Определить плот-
ность тока на поверхности и на оси провода.
Решение. У соур. — У 2л 50 1,256 • 10_,i • 103 • 107 = 1985,
q = 1985 = 1985 е~> 45°,
о 0,00302 - 1985 = 6.
По таблице находим
J0«?o)=J0 (6Г~/) = И^е/219-6’; Ьо=1!,5;
р0 = 219,5°; J, (qa)=J, (б]Л-/) = Ю,85е' ,33’45°.
6, = 10,85; 0j = 133.45°.
По формуле (П.12) найдем плотность на оси провода
б =,----ql-----=________1985 е ,45 -100------- == 9б.5е 104 е-/178-30' а/ж2
гла^а) 2л • 0,00302-10,85 • eJ,33,4°
Плотность тока на поверхности провода (формула П.13')
6 = Vo (qo)=96,5-10«- е-/,78°30' . 11,5е/2,9,6° = 111. Ю3 - е/4,л° о/л2.
г = а
Таким образом, модуль плотности тока на поверхности провода в 11,5раза
больше модуля плотности тока на оси провода. По фазе 6 на 219,6° опережает 60.
724
Пример 219. Определить активное и внутреннее индуктивное сопротив-
ления 1 ж провода примера 218.
Решение. 7? и X найдем по формулам (П.17) и (П.18)
У"<оур Ьв 1985.11,5
= 1,11 • 10-2 ,
2лоу&! 2 • 0,00302 • 107 • 10,85
Ро — Pi — 45° - 219,6° — 133,45° — 45° а 41,1°,
/?= 1,11 10-2cos41,l°=0,835 • 1СГ2 ом,
X = 1,11 • 10~2 sin 41,1° = 0,731 • 10-2 ом.
Для сравнения отметим, что сопротивление 1 м провода примера 218 на пос-
8,35
тоянном токе равно 3,5- 10-3 ом, т. е. а —— ~ 2,39 раза меньше, чем на
3,5
переменном токе.
Пример 220. При какой частоте активное сопротивление алюминиевого
провода |у = 32- 10е ом-1- ж-1] диаметром 10 мм будет в три раза больше,
чем на постоянном токе?
Решение. Сопротивление провода (длиной в 1 ж) на постоянном токе
Rnocm =* —“—• Активное сопротивление провода (длиной в 1 ж) на перемен-
ло2у
ном токе определяется формулой (П. 17). Следовательно,
У соур Ьоа
2 bi
cos(P0-P1-45°)=3.
(П.19)
Уравнение (П.19) является трансцендентным относительно со. В нем b0, blt Pt
и Усоур являются функциями со. Для решения уравнения задаемся различ-
ными значениями со и строим график зависимости левой части уравнения (П.19)
от со. Из графика находим со я: 8800 гц.
Приложение Г
ОСНОВЫ ТЕОРИИ ВОЛНОВОДОВ
Процесс распространения электромагнитных волн в полости прямоуголь-
ного волновода будем рассматривать, полагая, что стенки волновода выполне-
ны из сверхпроводящего материала (у = оо ). При этом условии напряжен-
ность электрического поля на стенках волновода будет равна нулю (плот-
ность тока на стенках волновода S = у£ есть величина конечная, поэтому
при у = оо Е ->0).
Полость волновода заполнена диэлектриком, электрическая проницае-
мость которого е и магнитная проницаемость р. Оси координат расположим
в соответствии с рис. 490, а. Размер полости волновода в направлении оси х
назовем ,а н размер в направлении оси i/ обозначим Ь. Длина волновода в на-
правлении оси z не ограничена. Электромагнитное поле в волноводе описыва-
ется уравнением (18.3'):
V2// + иРщН =0
или аналогичным ему уравнением
V2 Е -f- <о2ер£ =0.
725
Распространяющиеся в волноводе электромагнитные волны являются вол-
нами, бегущими вдоль оси волновода (вдоль оси г) и стоячими в двух осталь-
ных направлениях. Стоячие волны в направлениях х и у образуются вслед-
ствие многократных отражений волн от стенок волновода.
Тот факт, что волны являются бегущими вдоль оси г, в формально мате-
матическом отношении находит свое выражение в том, что каждая из состав-
ляющих волн подобно бегущим волнам в линии с распределенными иарамет-
рами при записи ее имеет мно-
житель e~kp г, где kp —коэф-
фициент распространения.
Волны, распространяю-
щиеся в волноводах, разде-
ляются на два типа волн. Эти
два типа волн принято назы-
вать Д-волнами и Е-волнами.
Структура /7-волны тако-
ва, что составляющую вдоль оси
волновода имеет только нап-
ряженность магнитного поля,
а напряженность электричес-
кого поля расположена в пло-
скостях, перпендикулярных
оси волновода. Другими сло-
вами, для Д-волны
/7 = / Нх + / Ну-\- кНг-,
Ё’ =1Ёх (П.20)
Для Е-волны имеет место
обратная картина.
Составляющую вдоль оси
волновода имеет только напря-
женность электрического по-
ля, а векторы напряженности
магнитного поля расположены
в плоскостях, перпендикуляр-
ных оси волновода, т. е. для
Е-волны
Е = i Ех j Ёу Д- k Ёг и
Д — i Нх-\- j Ну.
Какой из этих типов волн возникает, это зависит от условий возбуждения
волновода Если возбуждение производится при помощи штырька по рис.
487, о, то в волноводе возникнут Е-волпы.
При возбуждении с помощью петли с током, расположенной вблизи уз-
кой стенки волновода в соответствии с рис. 487, б, в последнем возникают
Д-волны.
Приводимые ниже выкладки проделаны для Д-волны, но онн почти в точ-
ности такие были бы и для Е-волны. Еслиподставить (П. 20)в уравнение^ 8.3'),
то последнее разобьется на три уравнения для проекций. Для проекции на
ось z будем иметь следующее уравнение:
/ д2 д2 д'2 \ •
-2 “Ь Л *2 I НZ “ О"
\ дх2 ду2 дг2) (
(П.21)
726
Воспользуемся методом разделения переменных Фурье — Бернулли, идея
которого была рассмотрена в § 416. С этой целью положим
Нг = ХУ е~кр г , (П.22)
где X — есть функция только х, У — есть функция только у. Множитель e~kpz
выражает собой то обстоятельство, что вдоль оси г движется бегущая волна.
Подставим (П.22) в (П.21):
Уе-ftpz НА _|_ Xe-kpz — 4-Л’ХУе-*₽г ьРгрХУ e~k pz =0. (П.2Г)
дх3 ду2 р
Обозначим
kp -|- и2ец = k2
]Ь 'у
и поделим (П.21') на ХУе р . Будем иметь
1 а2х _1_^у
Г ду2
(П.23)
(П.24)
X /?х2
1 d2Y
-------, из которых одна является
У ду2
1 ff2X
Сумма двух функций — —— и
X дх2
только х, а другая функцией только у, может равняться постоянному числу—k2
только в том случае, если каждая из этих функций есть постоянное число.
Перейдем от частных производных к простым и положим
1 d2X
X dx2
1 d2Y
= -р2.
функцией
(П.24а)
(П.246)
--------= — а2.
У dy2
Здесь р и q есть некоторые постоянные числа. Решением уравнений (П.24а
и б) являются функции
X = Ct sin (рх + <р),
У = C2 sin (од-|-ф).
Здесь С2, <р и ф есть постоянные интегрирования, которые найдем из гра-
ничных условий. Таким образом, в соответствии с (П.22)
/72 = Нт sin (рх + <р) sin (од + ф) e~kP z
Здесь комплексная амплитуда Нт=С\ Сг. (П.25)
Для определения значений р, q, <р, ф обратимся к первому и второму урав-
нениям Максвелла, записанным через проекции напряженностей на оси коор-
динат:
дНг ду дНу дг (П.26) дЁг ду дЁу дг — j(pyHx, (П.29)
дНх дН2 (П.27) дЁх дЁг — /ыр7?у , (П.30)
дг дх —1 у, дг дх
дНу дНх = №Ёг, (П.28) дЁх —/юиД- . (П.31)
В силу того, что для /7-волны Ег =0, и поскольку волны
являются
727
dEv . дЁг
бегущими вдоль оси г, то —-< = — kpEv, а —i = — k„ Ех, и из уравне-
дг г дг
ния (П.29) и (П.30) следует, что
= | (П.32)
kpEx — /cofi//v. J
Как уже говорилось выше, на внутренних поверхностях стенок волновода
напряженность электрического поля равна нулю. Следовательно, Ёх — 0 при
у = 0 и у = Ъ, а = 0 при х = 0 и х — а. Если это учесть, то из уравне-
ний (П.32) имеем
Поскольку
дНу
дг '
Ну = Ну =0 и Нх = Hv=0.
f/-0 у=Ь х=0 х=а
дН *
- kpHу , —— = — kp Нх, а Ну равно нулю при у — 0
и у — b и Нх = 0 при х — 0 и х = а, то из (П.26) и (П.27) находим
—- •== 0; ' дУ Д- 0 ( ^нД —? =0; \ дУ Д-Ь (П.ЗЗ)
1 дНД (^нД
\ дх Л=о ~ °’ (П.34)
Уравнения (П.ЗЗ) — (П.34) служат для определения значений р, q, ср, тр.
Подставив (П.25) в (П.ЗЗ), найдем тр = и q = .
. _ , л тл
Из(П.34) определим <р = — и р=----, где тип целые числа; т—равно
2 а
числу полуволн электромагнитной волны, которое разместится по ширине волно-
вода. Число п показывает, сколько полуволн разместится по высоте волновода
Таким образом,
Hz = Нт cos
тлх плу г
-----cos-----е р .
а b
(П.35)
Найдем теперь Нх, Ну и Ёх, Ёу. Для определения Ёх поступим следующим
dWy . kpEx
образом; в уравнении (П.26)----- заменим на — k„Hv = — kp ~-------. Тогда
дг н у н /сор
Отсюда
/?2
Аналогично
дНг
Ь1 Г
кр сх
/®р
дНг /рсо пл
ду k2 Ь
kpE,
/сор.
— /сое Ех.
нт cos
а
тлх . плу -к „г
----sin----е р
b
k2 = k2p -j- со2 ер.
kn пл • тлх плу -к„г
~~ ~ Wmcos--------sin—— е Р
k2 b а b
(П.36)
(П.37)
Яу =
728
Ь W дНг . «И тп . . тпх ппу _ь z .п „й.
(П.ЗЯ
/сор. r k2 а а Ь
Проанализируем полученные результаты. Коэффициент kp играет роль
постоянной распространения электромагнитной волны вдоль оси г.
Если kp будет действительным числом, то волна при своем продвижении
по волноводу будет затухать. Затухание будет отсутствовать, если kp будет
мнимым числом.
Для того чтобы связать kp с геометрическими размерами волновода а и Ь
/ тп\2 / п л\2
и числами тип. подставим (П.35) в (П.21). Получим k2 = I ---] -j- I — I .
\ a ) \ b )
„ 2 / mn \2 / nn \2 ,9
Ho k2 — kp -f-co ер. Поэтому I---1 = kp + co2 ep; kp=0 при
л Г I m \2 I n \2
co = co0 = i?= -I/ — + —) ; (П.40)
V ер V \ a j \ b ]
kp является МНИМЫМ ЧИСЛОМ при СО > СОо.
Таким образом, по волноводу с заданными размерами а и b могут распро-
страняться электромагнитные волны, если частота волны больше со0. Разме-
ры а и b волноводов стандартизованы.
Числа тип могут принимать любые значения, но не могут одновременно
равняться нулю, так как тогда все составляющие Е и все составляющие И
были бы равны нулю.
Наибольшее практическое значение имеет основная волна, для которой
т — 1 и п — 0 Для этой волны по ширине волновода укладывается одна
полуволна, а по высоте волновода интенсивность поля не изменяется.
Для того чтобы оценить порядок величины соо для основной волны, возь-
мем размер а/р 7,2 см и по формуле (П.40) найдем
со0 я; 13,1 • 109 рад! сек.
Таким образом, по волноводу может передаваться энергия лишь весьма вы-
сокой частоты.
Картина поля для основной /7-волны для некоторого момента времени
изображена на рис. 490, б.
ЛИТЕРАТУРА ПО КУРСУ ТОЭ И СМЕЖНЫМ ВОПРОСАМ
а) Учебники и учебные пособия по всему курсу
1. Л. Р. Нейман, П. Л. Калантаров. Теоретические основы
электротехники. Госэнергоиздат, а) часть первая, 1959, б) часть вторая, 1959,
в) часть третья, 1959.
2. Г. В. Зевеке, П. А. Нонкин, А В. Не ту ши л, С. В. Стра-
хов. Основы теории цепей. Госэнергоиздат, 1963.
3. А. В. Н е т у ш и л, КМ. Поливанов. Основы электротехни-
ки, ч. 111 Госэнергоиздат, 1955.
4. Основы электротехники под ред. К А. К р У г а. Госэнергоиздат, 1952.
5. Л. А. Бессонов. Теоретические основы электротехники. «Высшая
школа», 1961.
6. А. Е. Каплянский, А. П. Лысенко, Л. С. Полотовский.
Теоретические основы электротехники Госэнергоиздат, 1961.
7. М. А. П е р е к а л и н. Электрические цепи. Госэнергоиздат, 1950.
б) Руководства по линейным электрическим цепям
8. Н. Г. Максимович. Линейные электрические цЛш и их преоб-
разования. Госэнергоиздат, 1961.
9. С. Мэзон, Г. Циммерман. Электронные цепи, сигналы и сис-
темы. ИЛ, 1963.
10. М. Ф. Гарднер, Д. А. Б э р н с. Переходные процессы в линей-
ных системах. Физматгиз, 1961.
11. А. А. X а р к е в и ч. Спектры и анализ. Гостехиздат, 1962.
12. К. А. Круг. Переходные и установившиеся процессы в линейных
электрических цепях. Госэнергоиздат, 1948.
13. Л. А. Бессонов. Линейные электрические цепи, издание ВЗЭИ,
1963.
в) Руководства по нелинейным цепям и системам
14. А. А. А н д р о н о в, А. А. В и т т, С. Э. X а й к и и. Теория коле-
баний, Физматгиз, 1959.
15. Е. П. П о п о в, И. П. П а л ь т о в. Приближенные методы иссле-
дования нелинейных автоматических систем. Физматгиз, 1960.
16. А. А. В о р о н о в. Элементы теории автоматического регулирования.
Воен из дат, 1954 .
17. К- Ф- Т е о д о р ч и к. Автоколебательные системы. Гостехиздат,
1952.
18. Л. А. Б е с с о н о в. Нелинейные электрические цепи. «Высшая
школа» 1964.
730
19. Л. А. Б есс о и о в. Автоколебания в нелинейных электрических
цепях со сталью. Госэпергоиздат, 1958.
20. Я. С. И ц х о к и. Нелинейная радиотехника. Советское радио, 1955,
21. Полупроводниковые приборы и их применение, под редакцией Ш и.
Госэнергоиздат, 1957.
22. В. К а и н и н г х э м. Введение в теорию нелинейных систем. Гос-
энергоиздат, 1962.
23. Г. Е. Пухов. Комплексное исчисление и его применение. Изд.
АН УССР, 1961.
г) Руководства по теории электромагнитного поля
24. И. Е. Т а м м. Основы теории электричества. Гостехиздат, 1956.
25. Г. А. Гринберг. Избранные вопросы математической теории
электрических и магнитных явлений. Изд. АН СССР, 1948.
26. В. А. Г о в о р к о в. Электрические и магнитные поля. Госэнергоиздат,
1960.
27. В. В. Н и к о л ь с к и й. Теория электромагнитного поля. «Высшая
школа», 1963.
28. И. М. Т е т е л ь б а у м. Электрическое моделирование. Физматгиз,
1959.
29. О. Б. Брон. Электромагнитное поле как вид материн. Госэнерго-
издат, 1962.
30. Л. Д. Г о л ь д ш т е й н, Н. В. 3 е р н о в. Электромагнитные поля
и волны. Советское радио, 1956.
д) Задачники
31. И. А. 3 а й ц е в, А. Г. Л у р ь е. Задачник по теоретическим осно-
вам электротехники. Госэнергоиздат, 1960.
32. О. Е. Г о л ь д и н. Задачник по курсу теоретических основ электро-
техники. Госэнергоиздат, 1960.
33. Задачник по теоретическим основам электротехники, под редакцией
К.'А. Круга, В. Ю. Ломоносова, М. А. Перекалина, К- М.
П бливанова. Госэнергоиздат, 1948.
34. В. А. Г о в о р к о в, С. Д. Купал я н. Теория электромагнит-
ного поля в упражнениях и задачах. «Высшая школа», 1963.
35. Задачник по теоретическим основам электротехники (теория цепей),
под редакцией К- М. Поливанова. Госэнергоиздат, 1962.
36. Л. А. Б е с с о н о в, И. Г. Д е м и д о в а, Л. Ф. К о т о в а, Н. Н.
Линниченко, Л. М. Середницкий. Задачник по теоретичес-
ким основам электротехники. Изд. ВЗЭИ, 1963.
37. М. Р. Ш е б е с. Сборник упражнений и задач по теоретическим ос-
новам электротехники. «Высшая школа», 1962.
38. В. Н. Б а ш а р и н а, Е. И. Б о г д а н о в, М. С. Гл азен ап,
В. Г. Григорьев, С. И. Куренев и др. Сборник задач по расчету
электрических цепей переменного тока. Изд. ЛЭТИ. Л. 1958.
е) Руководства к лабораториям
39. Л. Р. Н е й м а н, К. С. Д е м и р ч я н. Руководство к лаборатории
электромагнитного поля. «Высшая школа», 1961.
40. П. Л. Калантаров. Руководство к лаборатории переменных
токов. Госэнергоиздат, 1949.
41. О. И. Д о л г и х, М. Е. 3 а р у д и, Л. Ф. Котова. Руководство
к лабораторным работам по первой части курса ТОЭ. Изд. ВЗЭИ, 1964.
42. А. С. Б л и н к о в а, Л. Ф. К о т о в а, В. П. О л е к с е в и ч, В. В.
О ч а н. Руководство к лабораторным работам по второй части курса ТОЭ. Изд.
ВЗЭИ, 1962.
731
ж) Контрольные задания и методические руководства
43. Л. А. Бессонов, В. П. Олексевнч, И. Г. Демидова,
Н. Н. Линниченко. Контрольные задания и методические указания
по курсу ТОЭ. «Высшая школа», 1964.
44. А. Е. К а п л я н с к и й. Методика преподавания теоретических ос-
нов электротехники. Госэнергонздат, 1959.
СОДЕРЖАНИЕ
Предисловие
Часть I
Глава первая. Линейные электрические цепи
постоянного тока
§ 1. Определение линейных и нелинейных электрических цепей . . 7
§ 2. Источник э. д. с. п источник тока..................... 8
§ 3. Разветвленные и неразветвлениые электрические цепи .... ц
§ 4. Напряжение на участке цепи............................. . ] 1
§ 5а . Закон Ома для участка цепи, не содержащего э. д. с. 13
§ 56. Закон Ома для участка цепи, содержащего э. д. с..... 13
§ 6. Законы Кирхгофа .......................................... 14
§ 7. Составление уравнений для расчета токов в схемах при помощи
законов Кирхгофа ............................................... 15
§ 8. О заземлении одной точки схемы ............................. 15
§ 9. Потенциальная диаграмма .................................. 16
§ 10. Энергетический баланс в электрических цепях ................ 17
§ 11. Метод пропорциональных величин ............................. 18
§ 12. Метод контурных токов ...................................... 18
§ 13. Принцип наложения и метод наложения ........ 22
§ 14. Входные и взаимные проводимости ветвей. Входное сопротивление 23
§ 15. Теорема взаимности ......................................... 25
§ 16. Теорема компенсации......................................... 27
§ 17. Линейные соотношения в электрических цепях ..... 28
§ 18. Замена нескольких параллельных ветвей, содержащих источ-
ники э. д. с., одной эквивалентной ............................. 30
§ 19. Метод двух узлов ..................................г . . . 32
§ 20. Метод узловых потенциалов ................................ 33
§ 21. Преобразование звезды в треугольник и преобразование треуголь-
ника в звезду................................................... 37
733
§ 22. Активный и пассивный двухполюсники ........................ 40
§ 23. Замена активного двухполюсника эквивалентным генератором
Метод холостого хода и короткого замыкания ................ 41
§ 24. Передача энергии от активного двухполюсника нагрузке ... 44
§ 25. Передача энергии по линии передачи......................... 45
Глава вторая. Нелинейные электрические цепи
постоянного тока
§ 26. Основные определения ...................................... 47
§ 27. Вольтамперные характеристики нелинейных сопротивлений 47
§ 28. Общая характеристика методов расчета нелинейных электричес-
ких цепей постоянного тока..................................... 50
§ 29. Электрические цепи с последовательным соединением нелинейных
сопротивлений .................................................. 50
§ 30. В. а. х. параллельного соединения нелинейных сопротивлении 52
§ 31. Последовательно-параллельное соединение нелинейных со-
противлений .................................................. 53
§ 32. Применение метода двух узлов для расчета цепей с нелинейными
сопротивлениями ................................................ 53
§ 33. Замена нескольких параллельных ветвей, содержащих НС и
э. д. с., одной эквивалентной ветвью ...................... 55
§ 34. Применение метода холостого хода и короткого замыкания к рас-
чету цепей с нелинейными сопротивлениями .............. . 56
§ 35. Статическое и дифференциальное сопротивления .............. 57
§ 36. Замена нелинейного сопротивления эквивалентным линейг ым
сопротивлением и э. д. с........................................ 58
§ 37. Применение нелинейных сопротивлений для получения произве-
дения двух функций ............................................ 59
§ 38. Логарифмические преобразователи на нелинейных сопротивле-
ниях ........................................................... 60
§ 39. Стабилизатор тока ......................................... 61
§ 40. Стабилизатор напряжения ................................... 62
§ 41. Усилитель постоянного напряжения .......................... 63
Глава третья. Магнитные цепи
§ 42. Разделение всех веществ на две группы — ферромагнитные и
неферромагнитные ............................................... 65
§ 43. Основные величины, характеризующие магнитное поле .... 65
§ 44. Элементы теории ферромагнетизма ........................... 66
§ 45. Основные характеристики ферромагнитных материалов ... 68
§ 46. Магнитномягкне и магнитнотвердые материалы ................ 69
§ 47. Материалы с прямоугольной петлей гистерезиса .............. 70
§ 48. Магнитодиэлектрики и ферриты .............................. 70
§ 49. Закон полного тока ........................................ 71
§ 50. Магнитодвижущая сила ...................................... 71
§ 51. Магнитная цепь ............................................ 71
734
§ 52. Разновидности магнитных цепей 72
рических аппаратов н других устройств вводят ферромагнитные
материалы? ? • -..............„......................... , 72
§ 54. Падение магнитного напряжения . . .................. 73
§ 55. Веберамперные характеристики .............................. 74
§ 56. Построение веберамперных характеристик (в. а. х) .......... 74
§ 57. Законы Кирхгофа для магнитных цепей ....................... 76
§ 58. Распространение на магнитные цепи всех методов, применяемых
для расчета электрических цепей с нелинейными сопротивлениями 78
§ 59. Определение м. д. с. неразветвленной магнитной цепи по задан-
ному потоку ............................................... 78
§ 60. Определение потока в неразветвленной магнитной цепи по задан-
ной м. д. с...................................................... 80
§ 61. Расчет разветвленной магнитной цепи методом двух узлов ... 81
§ 62. Как получить постоянный магнит? ........................... 84
§ 63. Расчет магнитной цепи постоянного магнита ................. 85
§ 64. Прямая возврата н коэффициент возврата .................... 86
§ 65. Магнитное сопротивление н магнитная проводимость участка маг-
нитной цепи. Закон Ома для магнитной цепи.................. 87
Глава четвертая. Электромагнитная индукция
и механические силы в магнитном поле
§ 66. Явление электромагнитной индукции ........................ 89
§ 67. Явление самоиндукции и э. д. с. самоиндукции. Индуктивность 93
§ 68. Явление взаимоиндукции. Э. д. с. взаимоиндукции. Взаимная
индуктивность контуров .......................................... 96
§ 69. Энергия магнитного поля уединенной катушки................. 98
§ 70. Плотность энергии магнитного поля ......................... 99
§ 71. Потери на гистерезис за одни' цикл перемагничивания . . . 100
§ 72. Магнитная энергия двух магннтносвязанных контуров ... 101
§ 73. Принцип взаимности взаимной индукции ..................... 103
§ 74. Коэффициент связи ........................................ 104
§ 75. Магнитная энергия системы контуров с токами............... 105
§ 76. Механические усилия в магнитном поле ..................... 105
§ 77. Выражение механической силы в виде производной от энергии
магнитного поля по координате .................................. 107
§ 78. Сила тяги электромагнита ................................. 109
§ 79. Закон электромагнитной инерции. Правило Ленца ............. ПО
Глава пятая. Электрические цепи однофазного
синусоидального тока
§ 80. Синусоидальный ток н основные характеризующие его величины 112
§ 81. Среднее и действующее значение синусоидально изменяющейся
величины ............................................... . . ИЗ
§ 82. Коэффициент амплитуды и коэффициент формы ............... 114
735
§ 83. Изображение синусоидально изменяющихся величин векторами
на комплексной плоскости. Комплексная амплитуда. Комплекс
действующего значения. ......................................... 115
§ 84. Сложение и вычитание синусоидальных функций времени прн
помощи комплексной плоскости.................................... 116
§ 85. Векторная диаграмма ............................................... 117
§ 86. Мгновенная мощность ............................................... 117
§ 87. Синусоидальный ток в активном сопротивлении. 118
§ 88. Индуктивность в цепи синусоидального тока . 118
§ 89. Конденсатор в цепи синусоидального тока. 120
§ 90. Умножение вектора на j и на — / 122
§ 91. Основы символического метода расчета цепей синусоидального
тока ........................................................... 122
§ 92. Комплексное сопротивление. Закон Ома для цепи синусоидаль-
ного тока ................................ 125
§ 93. Комплексная проводимость..................... 126
§ 94. Треугольник сопротивлений и треугольник проводимостей . 127
§ 95. Применение логарифмической лннейкн для перехода от алгебра-
ической формы записи комплекса к показательной и для обрат-
ного перехода ............................................................................... 127
§ 96. Законы Кирхгофа в символической форме записи.......................................... 130
§ 97. Применение к расчету цепей синусоидального тока всех методов,
обсуждавшихся в главе «Электрические цепи постоянного тока» 130
§ 98. О применении векторных диаграмм при расчетах электрических
цепей синусоидального тока...................................... 131
§ 99. Изображение разности потенциалов на комплексной плоскости 136
§ 100. Топографическая диаграмма ............................................................ 137
§ 101. Активная, реактивная и полная мощности •.......................................... 140
§ 102. Выражение мощности в комплексной форме записи......................................... 142
§ 103. Измерение мощности ваттметром ........................................................ 143
§ 104. Двухполюсник в цепи синусоидального тока ............................................ 144
§ 105. Резонансный режим работы двухполюсника ............................................ 146
§ 106. Резонанс токов ....................................................................... 146
§ 107. Компенсация сдвига фаз ............................................................... 148
§ 108. Резонанс напряжений .................................................................. 148
§ 109. Исследование работы схемы рис. 117, а, при изменении частоты
и при изменении индуктивности .................................. 149
§ НО. Частотная характеристика двухполюсника ............................................... 151
§ 111. Передача энергии от активного двухполюсника нагрузке . . 153
§ 112. Падение и потеря напряжения в линнн передачи энергии . . 154
§ 113. Расчет электрических цепей при наличии в них магнитносвязан-
ных катушек .................................................... 154
§ 114. Последовательное соединение двух магнитносвязанных катушек 155
§ 115. Определение М опытным путем .......................................................... 157
§ 116. Трансформатор. Вносимое сопротивление ................................................ 158
§ 117. Теорема о балансе активных и реактивных мощностей .... 161
736
Глава шестая. Теория четырехполюсника и круговые
диаграммы
§ 118. Четырехполюсник н его основные уравнения ................ 154
§ J19. Определение коэффициентов четырехполюсника .............. 167
§ 120. Схемы замещения пассивного четырехполюсника ............. 170
§ 121. Построение дуги окружности по хорде н вписанному углу . 171
§ 122. Уравнение дуги окружности в векторной форме записи .... 172
§ 123. Круговые диаграммы ...................................... 173
§ 124. Круговая диаграмма тока для последовательного соединения
двух сопротивлений ............................................ 173
§ 125. Круговая диаграмма напряжения для двух последовательно
соединенных сопротивлений ..................................... 175
§ 126. Круговая диаграмма для активного двухполюсника .... 175
§ 127. Круговая диаграмма четырехполюсника ..................... 177
§ 128. Определение /2, U2, Plt и Q, по круговой диаграмме четырех-
полюсника ..................................................... 179
§ 129. Линейные диаграммы ...................................... 182
§ 130. Уравнения активного четырехполюсника .................... 183
Глава седьмая. Трехфазные цепи, вращающееся магнит-
ное поле и метод симметричных составляющих
§ 131. Трехфазная система э. д. с............................... 185
§ 132. Трехфазная цепь. Расширение понятия фазы................. 186
§ 133. Основные схемы соединения трехфазных цепей, определение
линейных и фазных величин ..................................... 186
§ 134. Соотношения между линейными и фазовыми напряжениями и
токами ........................................................ 187
§ 135. Преимущества трехфазных систем .......................... 189
§ 136. Расчет трехфазных цепей ................................. 189
§ 137. Звезда — звезда с нулевым проводом ...................... 189
§ 138. Соединение нагрузки треугольником ....................... 191
§ 139. Оператор а трехфазной системы ........................... 192
§ 140. Соединение звезда — звезда без нулевого провода.......... 192
§ 141. Трехфазные цепи при наличии взаимоиндукции............... 193
§ 142. Активная, реактивная и полная мощности трехфазной сис-
темы .......................................................... 194
§ 143. Измерение активной мощности в трехфазной системе ........ 195
§ 144. Измерение реактивной мощности при равномерной нагрузке
фаз ........................................................... 196
§ 145. Круговые и линейные диаграммы в трехфазных цепях .... 198
§ 146. Указатель последовательности чередования фаз ............ 200
§ 147. Определение кругового вращающегося магнитного поля . . . 201
§ 148. Магнитное поле катушкн с синусоидальным током............ 201
§ 149. Получение кругового вращающегося магнитного поля .... 202
§ 150. Принцип работы асинхронного двигателя ................... 203
§ 151. Эллиптическое вращающееся магнитное поле ................ 204
737
§ 152. Зависимость входного сопротивления трехфазного трехстерж-
невого трансформатора от сдвига фаз между фазными э. д. с.
питающей его системы ......................................... 205
§ 153. Входные сопротивления на фазу трехфазиого асинхронного дви-
гателя для прямой, обратной и нулевой последовательностей фаз 208
§ 154. Разложение несимметричной системы на системы нулевой, пря-
мой и обратной последовательностей фаз ....................... 209
§ 155. Основы метода симметричных составляющих ............... 211
Приложения к I части курса ТОЭ ................ 219
Приложение А. Электростатические цепи....................; . . 219
§ 156. Определение электростатической цепи ................... 219
§ 157. Что понимают под расчетом электростатической цепи...... 219
§ 158. Алгебраическая сумма зарядов на пластинах конденсаторов,
присоединенных к любому узлу схемы, равна либо нулю, либо
начальному заряду, сосредоточенному на них к началу процесса 219
§ 159. Распределение напряжений между двумя последовательно сое-
диненными идеальными конденсаторами .......................... 220
§ 160. Методика расчета разветвленных электростатических цепей . 221
§ 161. Расчет цепей с неидеальными конденсаторами ............ 223
Приложение Б. Дуальные цепи................................... 224
§ 162. Определение дуальных электрических цепей............... 224
§ 163. Взаимно дуальные элементы схем ........................ 226
§ 164. Как образовать дуальную схему из исходной? ............ 226
Приложение В. Матрицы в электротехнике........................ 227
§ 165. Основные свойства матриц .......................... . . 227
§ 166. Применение матриц в электротехнике .................... 228
Приложение Г. Исследование процессов в неэлектрических сис-
темах на электрических моделях — аналогах ............. 229
ЧАСТЬ II
Глава восьмая. Периодические несинусоидальные токи в
линейных электрических цепях
§ 167. Определение периодических несннусондальных токов и напря-
жений ........................................................ 235
§ 168. Изображение несинусоидальных токов и напряжений рядами
Фурье ........................................................ 235
§ 169. Некоторые свойства периодических кривых, обладающих сим-
метрией ...................................................... 236
§ 170. О разложении в ряд Фурье кривых геометрически правильной
формы и кривых геометрически неправильной формы .... 239
§ 171. Определение гармоник ряда Фурье графическим (графоанали-
тическим) путем ......................................... ... 239
§ 172. Расчет токов и напряжений при несинусоидальных э. д с. 242
§ 173 Резонансные явления при несинусоидальных токах......... 246
738
§ 174. Действующее значение несинусоидального тока и действующее
значение несинусондального напряжения ........................... 247
§ 175. Среднее по модулю значение несинусоидальной функции . . . 249
§ 176. На какие величины реагируют амперметры и вольтметры раз-
личных систем при несинусоидальных токах? ....................... 249
§ 177. Активная и полная мощности несннусоидального тока .... 250
§ 178. Замена несинусоидальных токов и напряжений эквивалентны-
ми синусоидальными .............................................. 251
§ 179. Особенности работы трехфазных систем, вызываемые гармони-
ками, кратными 3 251
§ 180. Биения ................................................... 257
§ 181. Модулированные колебания ................................ 258
§ 182. Расчет линейных цепей, находящихся под воздействием моду-
лированных колебаний ............................................ 259
Глава девятая. Нелинейные электрические цепи
переменного тока
§ 183. Определение нелинейных электрических цепей переменного тока 260
§ 184. Подразделение нелинейных сопротивлений на три основные
группы .......................................................... 260
§ 185. Общая характеристика нелинейных активных сопротивлений 260
§ 186. Общая характеристика нелинейных индуктивных сопротивлений 261
§ 187. Потери в сердечниках нелинейных индуктивностей от вихревых
токов ........................................................... 262
§ 188. Потери на гистерезис ..................................... 263
§ 189. Схема замещения нелинейной индуктивности.................. 263
§ 190. Общая характеристика нелинейных конденсаторов ............ 264
§ 191. Нелинейные сопротивления как генераторы высших гармоник
тока и напряжения ............................................... 265
§ 192. Основные преобразования, осуществляемые при помощи нели-
нейных электрических цепей .................................... 236
§ 193. Некоторые физические явления, наблюдаемые только в нелиней-
ных цепях ....................................................... 270
§ 194. Разделение нелинейных сопротивлений по степени симметрии
характеристик относительно осей координат........................ 271
§ 195. Аппроксимация характеристик нелинейных сопротивлений . 272
§ 196. Аппроксимация симметричных характеристик для мгновенных
значений гиперболическим синусом ................................ 272
§ 197. Понятие о функциях Бесселя ............................... 274
§ 198. Разложение гиперболического синуса и гиперболического коси-
нуса от периодического аргумента в ряды Фурье, коэффициен-
тами которых являются функции Бесселя ........................... 277
§ 199. Разложение гиперболического синуса от постоянной и синусо-
идально меняющейся составляющих в ряд Фурье ..................... 277
§ 200. Некоторые общие свойства симметричных нелинейных сопротив-
лений .................................-......................... 278
739
§ 201. Некоторые общие свойства нелинейных сопротивлений с несим-
метричными характеристиками .................................... 279
§ 202. Типы характеристик нелинейных сопротивлений ............. 280
§ 203. Характеристики для мгновенных значений ................. 280
§ 204. Вольтамперные характеристики по первым гармоникам . . 280
§ 205. Вольтамперные характеристики для действующих значений 282
§ 206. Получение аналитическим путем обобщенных характеристик
управляемых нелинейных сопротивлений по первым гармоникам 282
§ 207. Простейшая управляемая нелинейная индуктивность .... 284
§ 208. Вольтамперные характеристики управляемой нелинейной ин-
дуктивности по первым гармоникам ............................... 288
§ 209. Вольтамперные характеристики управляемой нелинейной емкос-
ти по первым гармоникам ........................................ 291
§210. Основные сведения об устройстве полупроводниковых триодов . 293
§211. Трн основных способа включения триодов в схему........... 294
§ 212. Принцип работы полупроводникового триода в качестве управ-
ляемого сопротивления ....................................... . 294
§ 213. Плоскостные и точечные полупроводниковые триоды.......... 293
§ 214. Вольтамперные характеристики триодов..................... 297
§ 215. Полупроводниковый триод в качестве усилителя тока . . . 298
§ 216. Полупроводниковый триод в качестве усилителя напряжения 299
§217. Применение полупроводникового триода в качестве усилителя
мощности ....................................................... 300
§ 218. Связь между приращениями входных и выходных величин полу-
проводникового триода..................................... 301
§ 219. Схема замещения полупроводникового триода для малых при-
ращений ....................................................... 302
§ 220. Основные сведения о трехэлектродной лампе ............... 305
§ 221. Вольтамперные характеристики трехэлектродной лампы для
мгновенных значений ..................................... 306
§ 222. Аналитическое выражение сеточной характеристики электрон-
ной лампы ...................................................... 307
§ 223. Связь между малыми приращениями входных и выходных ве-
личин электронной лампы ........................................ 307
§ 224. Схема замещения электронной лампы для малых приращений 308
§ 225. Построение зависимости вход — выход для электронной лампы
прн больших сигналах ........................................... 310
§ 226. Общая характеристика методов анализа и расчета нелинейных
электрических цепей переменного тока ........................... 310
§ 227. Графический метод, использующий характеристики нелиней-
ных сопротивлений для мгновенных значений ...................... 312
§ 228. Расчет нелинейных цепей путем применения кусочно-линей-
ной аппроксимации характеристики нелинейного сопротивле-
ния для мгновенных значений .................................... 312
§ 229. Аналитический (нлн графический) метод расчета по первым гар-
моникам токов и напряжений ..................................... 313
740
§ 230. Анализ нелинейных цепей переменного тока путем использования
вольтамперных характеристик для действующих значений . 311
§ 231. Аналитический метод расчета по первой и одной или нескольким
высшим или низшим гармоникам .................................. 315
§ 232. Расчет при помощи линейных схем замещения ............... 316
§ 232 а. Расчет путем применения математических счетных машин 316
§ 233. Простейший утроитель частоты ............................ 316
§ 234. Пик-трансформатор ....................................... 318
§ 235. О расчете электрических цепей, содержащих индуктивные ка-
тушки, сердечники которых имеют почти прямоугольную кри-
вую намагничивания ............................................ 320
§ 236. Выпрямление переменного напряжения ...................... 322
§ 237. Амплитудная модуляция .................................. 326
§ 238. Детектирование .......................................... 327
§ 239. Ламповый генератор ...................................... 328
§ 240. Построение вольтамперной характеристики последовательной
феррорезонансной цепи ......................................... 332
§ 241. Триггерный эффект в последовательной феррорезонансной цепи 333
§ 242. Феррорезонанс напряжений ................................ 333
§ 243. Вольтамперная характеристика параллельного соединения
емкости и катушки со стальным сердечником. Феррорезонанс
токов ......................................................... 334
§ 244. Триггерный эффект в параллельной феррорезонансной цепи . 335
§ 245. Простейший феррорезонансный стабилизатор напряжения . 335
§ 246. Магнитный усилитель и дроссель насыщения ................ 337
§ 247. Применение магнитного усилителя для усиления мощности 339
§ 248. Применение символического метода к расчету нелинейных це-
пей и построение для них векторных диаграмм.................... 342
§ 249. Векторная диаграмма нелинейной индуктивности............. 344
§ 250. Определение величины намагничивающего тока и величины то-
ка потерь ..................................................... 346
§ 251. Основные соотношения для трансформатора со стальным сер-
дечником ...................................................... 348
§ 252. Векторная диаграмма трансформатора со стальным сердечником 351
Глава десятая. Переходные процессы в линейных
электрических цепях
§ 253. Введение ................................................ 354
§ 254. Задача о переходном процессе в любой линейной электрической
цепи с сосредоточенными параметрами сводится к решению ли-
нейного дифференциального уравнения с постоянными коэффи-
циентами ...................................................... 355
§ 255. Принужденные и свободные составляющие токов и напряжений 356
§ 256. Ток через индуктивность и напряжение на емкости не может
изменяться скачком ........................................ . . 358
§ 257. Первый закон коммутации ................................. 360
741
§ 258. Второй закон коммутации ........................................... 350
§ 259. Что понимают под начальными значениями величии?.................... 360
§ 260. Докоммутационные и послекоммутационные начальные зна-
чения ............................................. 360
§ 261. Независимые и зависимые (послекоммутационные) начальные
значения .......................................... 361
§ 262. Нулевые и ненулевые начальные условия ............................. 361
§ 263. Составление уравнений для свободных токов и напряжений . 361
§ 264. Алгебраизация системы уравнений для свободных токов . . . 362
§ 265. Составление характеристического уравнения системы. . . . 363
§ 266. Составление характеристического уравнения путем использо-
вания выражения для входного сопротивления цепи на перемен-
ном- токе ..................................................... 365
§ 267. Подразделение независимых начальных значений на основные
и неосновные ..................................... 366
§ 268. Чем определяется степень характеристического уравнения? . 367
§ 269. О корнях характеристического уравнения .......................... 368
§ 270. Все действительные корни характеристических уравнений всег-
да отрицательны, а комплексные корни всегда имеют отрица-
тельные действительные части ................................... 369
§ 271. Характер свободного процесса, когда характеристическое урав-
нение имеет один корень ........................................ 369
§ 272. Характер свободного процесса при двух действительных нерав-
ных корнях характеристического уравнения ....................... 370
§ 273. Характер свободного процесса при двух равных корнях . . . 371
§ 274. Характер свободного процесса при двух комплексно сопряжен-
ных корнях ..................................................... 371
§ 275. Некоторые особенности переходных процессов ........................ 372
§ 276. О переходных процессах, сопровождающихся электрической
дугой .......................................................... 374
§ 277. Об опасных перенапряжениях, вызываемых размыканием вет-
вей в цепях, содержащих индуктивности .......................... 374
§ 278. Общая характеристика методов анализа переходных процессов
в линейных электрических цепях.................................. 375
§ 279. Определение классического метода расчета переходных процес-
сов ............................................................ 376
§ 280. Определение постоянных интегрирования в классическом мето-
де ............................................................, 376
§ 281. Логарифм как изображение числа .................................... 392
§ 282. Комплексы тока и напряжения есть изображения синусоидаль-
ных функций .................................................... 392
§ 283. Введение к операторному методу .................................... 393
§ 284. Преобразование Карсона— Хевисайда ............................... 393
§ 285. Изображение постоянной есть сама постоянная ....................... 394
§ 286. Изображение показательной функции eat............................. 394
§ 287. Изображение первой производной ............................... 395
742
§ 288. Изображение напряжения на индуктивности ................. 396
§ 289. Изображение второй производной .......................... 393
§ 290. Изображение интеграла ................................... 397
§ 291. Изображение напряжения на конденсаторе .................. 397
§ 292. Закон Ома в операторной форме. Внутренние э. д. с.........399
§ 293. Первый закон Кирхгофа в операторной форме ............... 401
§ 294. Второй закон Кирхгофа в операторной форме ............... 401
§ 295. При составлении уравнений для изображений применимы все
методы, рассматривавшиеся в разделе синусоидального тока . 402
§ 296. Последовательность расчета в операторном методе ......... 403
§ 297. Изображение функции времени может быть представлено в
виде отношения двух полиномов по степеням р .... 405
Л1(р)
§ 298. О переходе от изображения к функции времени ............. 405
§ 299. О разложении сложной дроби на более простые ............. 408
§ 300. Формула разложения ...................................... 411
§ 301. Вывод формулы разложения ................................ 411
§ 302. Переходная проводимость.................................. 415
§ 303. Понятие о переходной функции по напряжению................416
§ 304. Интеграл Дюамеля ........................................ 419
§ 305. Последовательность расчета при помощи интеграла Дюамеля . 420
§ 306. Применение интеграла Дюамеля при сложной форме напряже-
ния ............................................................ 421
§ 307. Сравнение различных методов расчета переходных процессов 423
§ 308. Простейшее электрическое дифференцирующее устройство . 424
§ 309. Простейшее электрическое интегрирующее устройство . . . 424
§ 310. Применение метода эквивалентного генератора для расчета
переходных процессов .................................... 425
§311. Переходные процессы при воздействии импульсов напряжения 427
§ 312. Некоторые схемы, обладающие специальными свойствами . . 423
§ 313. Понятие о передаточных функциях и о частотных характерис-
тиках звеньев и систем .................................. 428
§ 314. Основные сведении о синтезе электрических цепей ....... 431
§ 315. Синтез двухполюсников, основанный на последовательном вы-
делении из функции входного сопротивления простейших сос-
тавляющих ...................................................... 431
§ 315 а. Понятие о графах. Формула Мэзона...................... 435
Глава одиннадцатая. Установившиеся процессы в
электрических и магнитных цепях, содержащих линии с распределен-
ными параметрами. Основы теории электрических фильтров
§ 316. Введение и основные определения ......................... 436
§ 317. Составление дифференциальных уравнений для однородной
линии с распределенными параметрами ............................ 439
§ 318. Решение уравнений линии с распределенными параметрами при
установившемся синусоидальном процессе ......................... 440
743
§ 319. Постоянная распространения и волновое сопротивление . . . 442
§ 320. Формулы для определения комплексов напряжения и тока в
любой точке линии через комплексы напряжения и тока в нача-
ле линии ....................................................... 443
§ 321. Графическая интерпретация гиперболического синуса и гипер-
болического косинуса от комплексного аргумента ................. 444
§ 322. Формулы для определения напряжения и тока в любой точке
линии через комплексы напряжения и тока в конце линии . . 445
§ 323. Падающие и отраженные волны в линии ..................... 445
§ 324. Фазовая скорость ........................................ 446
§ 325. Длина волны ............................................. 448
§ 326. Линия без искажений ..................................... 448
§ 327. Согласованная нагрузка................................. 450
§ 328. Определение напряжения и тока при согласованной нагрузке 450
§ 329. Коэффициент полезного действия передачи при согласованной
нагрузке ....................................................... 450
§ 330. Непер — единица измерения затухания ..................... 451
§ 331. Входное сопротивление нагруженной линии ................. 451
§ 332. Уравнение для определения напряжения и тока в линии без
потерь ......................................................... 452
§ 333. Входное сопротивление линии без потерь при холостом ходе ее 453
§ 334. Входное сопротивление линии без потерь при коротком замы-
кании на конце линии ........................................... 453
§ 335. Определение стоячих электромагнитных волн ............... 454
5 336. Стоячие волны в линии без потерь при холостом ходе линии . 454
§ 337. Стоячие волны в линии без потерь при коротком замыкании на
конце линии .................................................... 455
§ 338. Аналогия между уравнениями линии с распределенными пара-
метрами и уравнениями четырехполюсника ......................... 456
§ 339. Замена четырехполюсника эквивалентной ему линией с распре-
деленными параметрами и обратная замена ........................ 456
§ 340. Цепная схема ............................................ 459
§ 341. Определение электрических фильтров ...................... 464
§ 342. Введение к теории фильтров .............................. 464
§ 343. Основы теории фильтров .................................. 465
§ 344. Подразделение фильтров на низкочастотные, высокочастотные,
полосовые и заграждающие ....................................... 468
§ 345. Качественное определение типа фильтра ................... 472
Глава двенадцатая. Переходные процессы в электрических
цепях, содержащих линии с распределенными параметрами
§ 346. Введение ................................................ 472
§ 347. Исходные уравнения и решение их.......................... 474
§ 348. Падающие и отраженные волны на линиях.................... 475
§ 349. Связь между функциями fi, f-г и функциями <pi, <р2 ...... 475
§ 350. Электромагнитные процессы при движении прямоугольной вол-
ны по линии .................................................... 478
744
§ 351. Схема замещении для исследования волновых процессов в ли-
ниях с распределенными параметрами ............................ 479
§ 352. Подключение разомкнутой на конце линии к источнику постоян-
ного напряжения (рис. 361, а) ................................. 480
§ 353. Переходный процесс при подключении источника постоянного
напряжения к двум последовательно соединенным линиям при
наличии емкости в месте стыка линий............................ 483
Приложения ко II части курса ТОЭ ............................. 489
Приложение А. Электрические цепи с переменными во времени
параметрами.............................................. 489
§ 354. Введение .............................................. 489
§ 355. Некоторые общие свойства электрических цепей с переменными
параметрами ................................... 490
§ 356. Методика расчета электрических цепей с переменными парамет-
рами в установившемся режиме............................ 492
Приложение Б. Интеграл Фурье ........................... 495
§ 357. Введение .............................................. 495
§ 358. Ряд Фурье в комплексной форме записи .................. 495
§ 359. Спектр функции н интеграл Фурье ....................... 497
§ 360. Связь спектра функции с изображением по Лапласу........ 498
§ 361. Последовательность определения тока в цепи при помощи ин-
теграла Фурье ................................................. 499
Приложение В. Переходные процессы в нелинейных электричес-
ких цепях...................................................... 500
§ 362 Введение и общая характеристика методов анализа и расчета
переходных процессов в нелинейных электрических цепях 500
§ 363. Метод расчета переходных процессов в нелинейных цепях, ос-
нованный на графическом подсчете определенного интеграла 501
§ 364. Расчет переходных процессов в нелинейных цепях методом ин-
тегрируемой нелинейной аппроксимации........................... 503
§ 365. Метод расчета переходных процессов в нелинейных электри-
ческих цепях, основанный на замене характеристики нелиней-
ного сопротивления отрезками прямых линий (метод кусочно-
линейной аппроксимации)........................................ 504
§ 366. Основы расчета переходных процессов в нелинейных цепях пу-
тем замены определенного интеграла приближенной суммой . 506
§ 367. Расчет переходных процессов в схемах с несколькими нелиней-
ными сопротивлениями .......................................... 509
§ 368. Метод медленно меняющихся амплитуд..................... 510
Приложение Г. Основы теории устойчивости режимов работы не-
линейных цепей.............................................. . 514
§ 369. Введение. Устойчивость «в малом» и устойчивость «в большом».
Устойчивость по Ляпунову ...................................... 514
§ 370. Общие основы исследовании устойчивости «в малом» .... 516
§ 371. Исследование устойчивости положения равновесия в системах
с постоянной вынуждающей силой ................................. °*
745
§ 372. Исследование устойчивости автоколебаний и вынужденных ко-
лебаний по первой гармонике ................................... 51В
§ 373. Релаксационные колебания. Исследование устойчивости поло-
жения равновесия в генераторе релаксационных колебаний . ^21
§ 374. Исследование устойчивости синусоидальных колебаний в лам-
повом генераторе ............................................. 522
Приложение Д. Фазовая плоскость................................ 523
§ 375. Определение фазовой плоскости и краткая характеристика об-
ластей ее применения для исследований процессов в нелиней-
ных цепях ..................................................... 523
§ 376. Интегральные кривые, фазовая траектория н предельный цикл 524
§ 377. Изображение простейших процессов на фазовой плоскости . . 524
ЧАСТЬ III
Введение ...................................................... 529
Глава тринадцатая. Электростатическое поле 531
§ 378. Определение электростатического поля ................... 531
§ 379. Закон Кулона ........................................... 532
§ 380. Основные величины, характеризующие электростатическое поле:
потенциал и напряженность ........................... 532
§ 381. Потенциал определяется с точностью до постоянной величины 534
§ 382. Электростатическое поле — поле потенциальное ........... 534
§ 383. Силовые и эквипотенциальные линии....................... 536
§ 384. Выражение напряженности в виде градиента от потенциала . 537
§ 385. Дифференциальный оператор Гамильтона (оператор набла) . 539
§ 386. Выражение градиента потенциала в цилиндрической и сферичес-
кой системах координат . . .................................... 540
§ 387. Поток вектора через элемент поверхности и поток вектора через
поверхность ................................................... 540
§ 388. Свободные и связанные заряды. Поляризация вещества . . . 541
§ 389. Вектор поляризации ..................................... 542
§ 390. Вектор электрической индукции D ........................ 544
§ 391. Теорема Гаусса в интегральной форме .................... 541
§ 392. Применение теоремы Гаусса для определения напряженности
и потенциала в поле точечного заряда........................... 546
§ 393. Теорема Гаусса в дифференциальной форме ................ 547
§ 394. Вывод выражения для div Е в декартовой системе координат . 549
§ 395. Использование оператора набла для записи операции взятия
дивергенции ................................................... 550
§ 396. Выражение div Е в цилиндрической и сферической системах
координат ..................................................... 551
§ 397. Уравнение Пуассона и уравнение Лапласа.................. 551
§ 398. Граничные условия....................................... 553
745
§ 399. О поле внутри проводящего тела в условиях электростатики . 553
§ 400. Условия на границе раздела проводящего тела и диэлектрика . 554
§ 401. Условия на грани раздела двух диэлектриков с различными
электрическими проницаемостями................................ 555
§ 402. Теорема единственности решения ...................... 557
§ 403. Общая характеристика задач электростатики и методов их ре-
шения ............................................ 557
§ 404. Поле заряженной оси.................................. 560
§ 405. Поле двух параллельных заряженных осей .............. . 561
§ 406. Поле двухпроводной линии ... .... 561
§ 407. Емкость .......................................... 563
§ 408. Емкость двухпроводной линии................................ 563
§ 409. Метод зеркальных изображений .............................. 564
§ 410. Поле заряженной оси, расположенной вблизи проводящей плос-
кости .................................................. . . . 564
§ 411. Поле заряженной оси, расположенной вблизи плоской границы
раздела двух диэлектриков с различными электрическими про-
ницаемостями ................................................. 566
§ 412. Электростатическое поле системы заряженных тел, расположен-
ных вблизи проводящей плоскости .............................. 567
§ 413. Потенциальные коэффициенты Первая группа формул Макс-
велла .......................................................
§ 414. Емкостные коэффициенты. Вторая группа формул Максвелла . 669
§ 415. Частичные емкости. Третья группа формул Максвелла .... 571
§ 416. Шар в равномерном поле .................................... 573
§ 417. Проводящий шар в равномерном поле................... 577
§ 418. Диэлектрический шар в равномерном поле .................... 579
§ 419. Диэлектрический цилиндр в равиомериом поле.......... 581
§ 420. Понятие о плоскопараллельном, плоскомеридианном и равномер-
ном полях ................................................... 682
§ 421. Объемная плотность энергии электрического поля и выражение
механической силы в виде производной от энергии электричес-
кого поля по изменяющейся координате ......................... 583
Примеры .......................................................... 586
Глава четырнадцатая. Электрическое поле постоянного
тока в проводящей среде
§ 422. Плотность тока и ток ...................................... 601
§ 423. Закон Ома в дифференциальной форме. Второй закон Кирхгофа
в дифференциальной форме ..................................... 602
§ 424. Первый закон Кирхгофа в дифференциальной форме ............ 605
§ 425. Уравнение непрерывности ................................... 606
§ 426. Дифференциальная форма закона Джоуля — Ленца............... 606
§ 427. Электрическое поле в проводящей среде подчиняется уравнению
Лапласа ...................................................... 606
§ 428. Переход тока из среды с одной проводимостью yi в среду с дру-
гой проводимостью у«. Граничные условия....................... 607
747
§ 429. Аналогия между полем в проводящей среде и электростатичес-
ким полем ...................................................... 608
§ 430. Экспериментальное исследование полей при помощи электро-
литической ванны ............................................... 609
§ 431. Соотношение между проводимостью и емкостью................ 610
§ 432. Общая характеристика задач на расчет электрического поля
в проводящей среде и методов их решения.................... 612
Примеры .......................................................... 614
Глава пятнадцатая. Магнитное поле постоянного тока
§ 433. Введение .................................................. 617
§ 434 Определение магнитного поля ............................... 618
§ 435. Связь магнитного поля с током............................. 618
§ 436. Основной закон магнитного поля — закон полного тока . . . 618
§ 437. Дифференциальная форма закона полного тока ................ 619
§ 438. Раскрытие выражения rot Н- 6 в декартовой системе координат 620
§ 439. Выражение ротора в виде векторного произведения [VH] . . 622
§ 440. Раскрытие rot Н в виде определителя в декартовой системе . 622
§441. Выражение проекций ротора в цилиндрической системе коор-
динат .......................................................... 623
§ 442. Выражение проекций ротора в сферической системе координат 623
§ 443. Принцип непрерывности магнитного потока ................... 623
§ 444. Дифференциальная форма принципа непрерывности магнитно-
го потока 624
§ 445. В областях, «занятых постоянным током», магнитное поле есть
поле вихревое, в областях, не «занятых током», его можно рас-
сматривать как поле потенциальное............................... 624
§ 446. Скалярный потенциал магнитного поля ...................... 624
§ 447. Граничные условия ............................ 626
§ 448. Векторный потенциал магнитного поля ...................... 627
§ 449. Уравнение Пуассона для вектора-потенциала................. 628
§ 450. Выражение магнитного потока через циркуляцию вектора-потен-
циала .......................................................... 630
§ 451. Векторный потенциал элемента тока ....................... 631
§ 452. Взаимное соответствие электростатического поля и магнитного
поля постоянного тока ................................. 631
§ 453. Типы задач на расчеты магнитных полей ..................... 632
§ 454. Общая характеристика методов расчета и исследования магнит-
ных полей постоянного тока ..................................... 633
§ 455. Опытное исследование картины магнитного поля .............. 634
§ 456. Графическое построение картины поля и определение по ней
магнитного сопротивления .................................... . 635
§ 457. Магнитное экранирование ................................... 637
§ 458. Применение метода зеркальных изображений .................. 640
748
Глава шестнадцатая. Основные уравнения переменного
электромагнитного поля
§ 459. Определение переменного электромагнитного поля........ 650
§ 460. Первое уравнение Максвелла .............................. 650
§ 461. Второе уравнение Максвелла .............................. 653
§ 462. Уравнение Максвелла в комплексной форме записи....... 654
§ 463. Теорема Умова—Пойнтинга для мгновенных значений . . . 355
§ 464. Теорема Умова—Пойнтинга в комплексной форме записи . . 662
§ 465. Некоторые дополнительные замечания ..................... 663
Глава семнадцатая. Переменное электромагнитное поле
в однородной и изотропной проводящей среде
§ 466. Уравнения Максвелла для проводящей среды................. 666
§ 467. Плоская электромагнитная волна .......................... 667
§ 468. Распространение плоской электромагнитной волны в однород-
ном проводящем полупространстве ................................ 671
§ 469. Глубина проникновения и длина волны...................... 672
§ 470. Магнитный поверхностный эффект........................... 673
§ 471. Прохождение переменного тока по плоской шине (электрический
поверхностный эффект) .......................................... 677
§ 472. Применение теоремы Умова — Пойнтинга для определения ак-
тивного и внутреннего индуктивного сопротивления проводни-
ков на переменном токе .................................... ... 680
§ 473. Эффект близости ......................................... 680
Глава восемнадцатая. Распространение электромагнитных
волн в однородном и изотропном диэлектрике
и в полупроводящей среде
§ 474. Распространение электромагнитных волн в однородном н изот-
ропном диэлектрике ............................................. 684
§ 475. Плоские волны в однородной н изотропной полу проводя щей
среде .......................................................... 689
Глава девятнадцатая. Запаздывающие потенциалы
переменного электромагнитного поля и излучение электромагнитной
энергии
§ 476. Вывод уравнений для А и <р в переменном электромагнитном
поле и решение их .............................................. 690
§ 477. Запаздывающие потенциалы переменного электромагнитного
поля .................................................... 698
§ 478. Комплексная форма записи запаздывающего векторного потен-
циала .......................................................... 699
§ 479. Излучение электромагнитной энергии ............. 700
§ 480. Понятие о излучающем диполе ............................. 707
749
§ 481 Дополнительный анализ поля излучения .................... 70S
§ 482. О расчете поля реальных излучателей............. . . 710
§ 483. Переход плоской электромагнитной волны из одной среды в
другую ................................................ . . . 711
§ 484. Экранирование в переменном электромагнитном поле .... 713
§ 485. Сопоставление принципов экранирования в электростатическом,
в магнитном и электромагнитном полих ......................... 713
§ 486. Высокочастотный нагрев металлических деталей и несовершен-
ных диэлектриков. Поверхностная закалка стальных изделий 714
§ 487. Понятие о волноводах ................................... 714
Приложения к III части курса ТОЭ .............................. 717
Приложение А. Свойства некоторых проводниковых материалов
и диэлектриков ............................................... 717
Приложение Б. Понятие о расчете полей по методу сеток и о мо-
делировании полей по методу электрических сеток............... 718
§ 488. Расчет полей по методу сеток ........................... 718
§ 489. Моделирование полей по методу электрических сеток .... 720
Приложение В. Поверхностный эффект в цилиндрическом проводе 721
Приложение Г. Основы теории волноводов ........................ 725
Литература по курсу ТОЭ и смежным вопросам .................... 730
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стра- ница Строка или рисунок Напечатано Следует читать По чьей вине
59 144 179 228 542 707 Л. А. Рис. 51 9 сверху Рис. 147 19 сверху Рис. 402, б сверху Рис. 483, а снизу Бессонов «Т( L Uab = uab I cos (иа1>М) f 0 где Для второго йг=иъ, L Q еретические основы э. / Ц,67= = /cos(H;i// 7 ) 7^-0 Этот текст должен быть на стр. 229 после формулы (в) L' —q пектротехнпкн», издан Типографии Издатель- ства Типографии Издатель- ства Типографии Типографии ие четвертое
Лев Алексеевич Бессонов
Теоретические
основы электротехники
Редактор И. А. Иванов
Художественный редактор И. Ф, Муликова
Технический редактор Р. К. Воронина
Корректор В. А. Орлова
Сдано в набор 14. VIII—63 г. Подписано к печати 25/Ш—64 г. Бумага
60X90'1,,,. 47 печ. л. 41,47 уч.-изд. л. Тираж 150,000 Т—04139
Тип. заказ 423 Изд. № ФМФ/174. Цена в переплете № 5—1 р. 34 к.,
в переплете №7 — I р. 44 к.
Издательство «Высшая школа» Москва, К-62, Подсосенский пер., 20
Саратовский полиграфический комбинат Росглан.полиграфпрома Государ-
ственного комитета Совета Министров РСфСР по печати,
г. Саратов, ул. Чернышевского, 59.