Автор: Глейзер Г.Д.
Теги: высшее образование университеты академическое обучение педагогика школы (теория образования, учебы и воспитания) математика история методология учебное пособие дидактика
ISBN: 5-204-00249-9
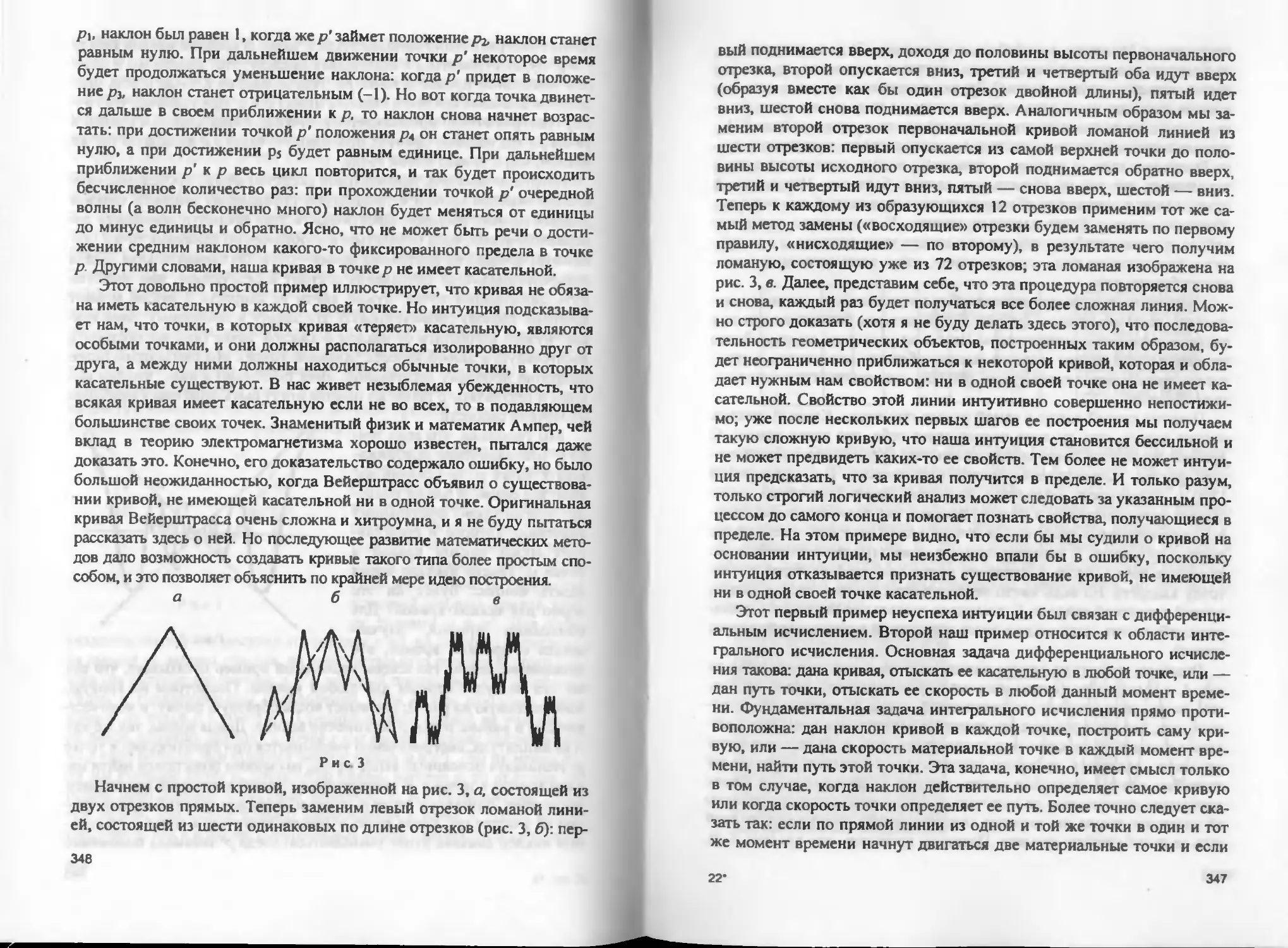
Год: 2001
МАТЕМАТИКА
Хрестоматия
по истории, методологии, дидактике
УНИВЕРСИТЕТ
РОССИЙСКОЙ АКАДЕМИИ ОБРАЗОВАНИЯ
МАТЕМАТИКА
Хрестоматия
по истории, методологии, дидактике
Составитель
профессор Г. Д. ГЛЕЙЗЕР
Допущено
Министерством оброзовония Российской Федерации
в качестве учебного пособия для студентов
высших учебных заведений гуманитарного профиля
Москва
Издательство У РАО
2001
УДК 378 147
ББК 74.202
Г 53
Рекомендовано
редакционно-издательским
советом У РАО
Рецензенты.
ГЛ Луканкин, чл.-корр. РАО, д-р пед. наук, проф.;
НX. Розов, д-р физ.-мат. наук, проф.
Математика: Хрестоматия по истории, методоло-
Г 53 гии, дидактике / Сост. Г.Д. Глейзер. — М.: Изд-во УРАО,
2001. —384 с.
ISBN 5-204-00249-9
Хрестоматия содержит статьи и фрагменты из книг выдаю-
щихся ученых о сущности и значении математики, ее истории, ме-
тодологии. дидактике В иих раскрывается роль математики в со-
временном мире как средства решения прикладных задач, эффек-
тивного стимулятора интеллектуального развития личности, вос-
питания математической культуры и стиля мышления, формиро-
вания интереса к изучению математики.
Книга предназначена студентам в качестве дополнительного
учебно-методического пособия по общеобразовательному курсу
математики. Содержащиеся в сборнике вопросы и упражнения
могут быть использованы для организации семинарских звнятий, в
самостоятельной работе студентов.
Хрестоматия может быть интересна учителям и всем любите-
лям математики.
УДК 378 147
ББК 74 202
ISBN 5-204-00249-9
С ГД. Глейзер, сост., 2001
Содержание
Предисловие ................................................ 5
Математика и история ее развития
М. Клайн. Зарождение математики и ее роль в познании ....... 8
Н. Виленкин. Основные этапы развития математики............ 21
Г.Фройденталь. Аксиоматическая абстракция Математика понятий и
математика алгоритмов......................................... 37
Р Курант, Г Роббинс. Что такое математика?................. 48
Д. Гильберт. Математические проблемы и их источники........ 50
Н. Бурбакн. Архитектура математики......................... 57
Вопросы и упражнения для индивидуального осмысления и коллектив-
ного обсуждения............................................... 70
Элементы математики
Г. Фройденталь. Логика .................................... 73
А. Колмогоров. О языке математических знаков 97
Т. Даннинг. Символы ........................................ 102
Р. Курант, Г. Роббинс. Алгебра множеств. Математический анализ
бесконечного................................................. 112
М. Kau, С. Улам. Мера..................................... 129
А Пуанкаре. Пространство и геометрия ....................... 134
А. Норден. Открытие Лобачевского и его место в истории новой гео-
метрии....................................................... 147
Вопросы и упражнения для индивидуального осмысления и коллектив-
ного обсуждения ............................................. 160
Математика в современном мире
Р Курант. Математике в современном мире .................. 163
М. Клайн. Математика и поведение природы ................. 178
Б. Гнеденко. Математика — язык науки Математические модели. 196
А. Колмогоров. Автоматы и жизнь............................„ 211
А. Пуанкаре. Опыт н геометрия ............................ 227
Вопросы и упражнения для индивидуального осмысления и коллектив-
ного обсуждения.............................................. 236
Математика и воспитание ума
А. Колмогоров. О математических способностях ............. 239
А. Хинчин. О воспитательном эффекте уроков математики .... 243
3
У. Сойер. О красоте и силе Какими качествами должен обладать ма-
тематик......................................................... 263
Д. Пойя. Умственная работа. Дисциплина ума................... 280
Вопросы и упражнения для индивидуального осмысления н коллектив-
ного обсуждения................................................. 300
Математика и психология
Ж. Пиаже. Структуры математические и оперативные структуры мыш-
ления .......................................................... 302
Г. Биркгофф. Психология математики........................... 322
Г. Хаи. Кризис интуиции...................................... 340
А. Пуанкаре. Математическое творчество....................... 357
Ж. Адамар. Различные типы математических умов................ 367
Вопросы и упражнения для индивидуального осмысления н коллектив-
ного обсуждения................................................. 374
Комментарии составителя...................................... 377
Источники ................................................... 382
Дополнительная литература.................................... 382
Предисловие
Настоящая хрестоматия предлагается в качестве учебно-методи-
ческого пособия по общеобразовательному курсу «Математика», пре-
дусмотренному в высших учебных заведениях.
Общее математическое развитие является одним из необходимых
условий и важнейшим фактором эффективного развития мышления
человека. В связи с этим общеобразовательный курс математики сей-
час изучается не только в общеобразовательных школах, но и во всех
высших учебных заведениях. Особую и пока не до конца разрешен-
ную проблему представляют собой содержание и методы математиче-
ского образования гуманитариев.
Мы исходим из предположения, что цели обучения математике
представимы в виде органического синтеза общекультурных, научных
(собственно математических) и прикладных целей. Общекультурные
цели обучения математике, конечно же, в первую очередь предпола-
гают всестороннее развитие мышления студентов. Не только мышле-
ния вербально-логического, но и в не меньшей степени наглядно-
действенного (или практического), а также наглядно-образного. В ак-
тивном развитии последних двух видов мышления и должна прояв-
ляться специфика ознакомления студентов, например, с развитием
идей и методов геометрии, изучающей свойства различных про-
странств, в том числе пространств, которые на небольших околозем-
ных участках не слишком сильно отклоняются от геометрии реального
физического пространства и вполне обеспечивают обслуживание на-
шего земного существования и земной инженерно-технической дея-
тельности. Отсюда становится ясным, что обучение математике долж-
но быть направлено на развитие у студентов интуиции, образного
(пространственного) и логического мышления, формирование у них
конструктивно-геометрических умений и навыков. Следовательно,
планируемые цели обучения математике будут достигнуты, если курс
математики не замкнут на узких чисто научных целях, а сконструиро-
ван таким образом, чтобы он в органической взаимосвязи эффективно
развивал у студентов такие свойства интеллекта, как математическую
5
интуицию, пространственное мышление, логическое мышление, тех-
ническое мышление, владение символическим языком математики.
Итак, математическое образование важно с различных точек зрения:
логической — изучение математики является источником и средст-
вом активного интеллектуального развития человека, его умственных
способностей;
познавательной — с помощью математики познается окружающий
мир, его пространственные и количественные отношения;
прикладной — математика является той базой, которая обеспечива-
ет готовность человека как к овладению смежными дисциплинами, так
и многими профессиями, делает для него доступным непрерывное об-
разование и самообразование;
исторической — на примерах из истории развития математики про-
слеживается развитие не только ее самой, но и человеческой культуры
в целом;
философской — математика помогает осмыслить мир, в котором
мы живем, сформировать у человека развивающиеся научные пред-
ставления о реальном физическом пространстве.
На достижение этих целей ориентирована программа общеобразо-
вательного курса «Математика», составленная для студентов УРАО
(авторы Г.Д. Глейзер, Н.Х. Розов).
Программой по математике предусмотрено изучение следующих тем:
Особенности математического мышления;
Множества;
Развитие понятия числа,
Функции. Основные понятия математического анализа и примеры
их применения;
Пространства. Методы изучения пространств;
Комбинаторика. Вероятность. Примеры решения задач математи-
ческой статистики;
Фундаментальные математические концепции. История, методоло-
гия и философия математики.
Как видно из названий тем, пособие позволит студентам глубже
осмыслить сущность многих проблем, изучаемых в этом курсе, озна-
комиться с высказываниями выдающихся ученых о сущности матема-
тики, ее истории, методологии и философии, роли в современном мире
как мощного средства решения прикладных задач, универсального
языка науки, эффективного стимулятора интеллектуального развития
личности и средства активного воспитания культуры и математиче-
ского стиля мышления.
Ознакомление студентов с текстами пособия, обдумывание ответов
на предлагаемые вопросы и упражнения будет способствовать форми-
6
рованию у них общего видения мировоззренческого характера, широ-
ких представлений о роли и месте математики в современной цивили-
зации и мировой культуре.
Книга носит чисто хрестоматийный характер — в ней собраны
только оригинальные статьи, отрывки, фрагменты из книг выдающих-
ся математиков. Мною даются к этим материалам лишь небольшие
комментарии, относящиеся в основном к источникам, из которых они
взяты, и предлагаются более 100 вопросов и упражнений для индиви-
дуального обдумывания и коллективного обсуждения, сгруппирован-
ных по пяти разделам в соответствии со структурой книги. В предла-
гаемых статьях и отрывках опущены комментарии редакторов и тек-
стовые ссылки авторов на литературные источники При желании с
ними можно познакомиться, обратившись к источникам, список кото-
рых приведен в конце пособия.
Подбор источников и эпиграфов, помещенных в пособии, а также его
композиция носит сугубо субъективный характер и отражает лишь лич-
ный опыт преподавания математики составителем в Университете Рос-
сийской академии образования в 1999/2000 учебном году.
Мною выборочно использовались материалы пособия для органи-
зации семинарских занятий.
Пособие не может заменить рекомендованной программой литера-
туры. Оно служит лишь дополнительным источником знаний, облег-
чающим студентам доступ к классическим произведениям. Надеюсь,
что хрестоматия будет способствовать пробуждению у студентов ин-
тереса к рассматриваемым проблемам и желания обратиться к перво-
источникам.
В заключение хочу выразить глубокую благодарность рецензентам
пособия профессорам Г.Л. Луканкину и Н.Х. Розову, рекомендациями
которых я воспользовался при отборе текстов и включении их в хре-
стоматию.
Москва, август 2000 г.
Г.Д. Глейзер
МАТЕМАТИКА И ИСТОРИЯ ЕЕ РАЗВИТИЯ
Со времен греков говорить «математика» зна-
чит говорить «доказательство».
Н. Бурбаки
М Т&айн
ЗАРОЖДЕНИЕ МАТЕМАТИКИ И ЕЕ РОЛЬ В ПОЗНАНИИ1*
Учение о природе будет содержать науку в соб-
ственном смысле лишь в той мере в какой может
быть применена в ней математика
Кант
Боги открыли людям не все В поиск пустившись,
люди сами открыли немало.
Ксенофан
Платье нередко многое говорит о человеке.
Шекспир
Хотя информация, которую мы получаем от наших органов чувств,
рассматривается, анализируется, подвергается экспериментальной
проверке и хотя мы располагаем ныне такими мощными вспомога-
тельными средствами, как телескоп, микроскоп и различного рода
приборы, позволяющие производить всевозможные наблюдения, а
также точнейшими измерительными устройствами, полученное с их
помощью знание ограниченно и может считаться достоверным лишь в
определенных пределах. Нам гораздо больше известно, чем раньше, о
числе планет, о существовании у некоторых из них спутников, о тем-
ных пятнах на Солнце, о применении компаса в навигации. Но достиг-
нутый прогресс знания составляет лишь крохотную толику того поис-
тине неисчерпаемого множества разнообразных и важных явлений,
которые нам необходимо и желательно знать.
Решающий, гигантский по своим масштабам и непреходящий по
своему значению шаг к расширению и приумножению нашего знания
Здесь и далее таким образом пронумерованы комментарии составителя к
публикуемым текстам
8
внешнего мира был сделан, когда для изучения его стали применять
математику Математика не только уточнила и расширила наше знание
явлений, доступных органам чувств человека, но и позволила открыть
весьма важные явления, не воспринимаемые нами, но оттого не менее
реальные по их воздействию, чем прикосновение к раскаленной плите.
То, что в нашей повседневной жизни незримо присутствуют такие фи;
зические «духи», не вызывает сомнений. О том, как они были откры-
ты, и пойдет наш рассказ.
Для нас, получивших современное образование, природа и «зем-
ные» приложения математики хорошо известны и воспринимаются как
нечто само собой разумеющееся Еще цивилизации, которые мы счи-
таем творцами западно-европейской математики, а именно цивилиза-
ции Древнего Египта и Вавилона, около 3000 лет до н.э. создали набор
полезных, но не связанных между собой правил и формул для решения
практических задач, с которыми люди сталкивались в повседневной
жизни. Вавилоняне и египтяне не сознавали, что математика способна
распространить их знание природы за пределы доступного чувствен-
ному опыту. Созданную ими математику можно сравнить с алхимией,
предшествовавшей химии.
Математика как логический вывод и средство познания природы —
творение древних греков, которым они начали всерьез заниматься
примерно за шесть веков до новой эры. Не сохранилось никаких доку-
ментов VI—V вв. до и.э., способных рассказать нам, что заставило
древних греков прийти к новому пониманию математики и ее роли.
Вместо этого мы располагаем лишь более или менее правдоподобны-
ми догадками историков, один из которых, в частности, утверждает,
что греки обнаружили противоречия в результатах, полученных древ-
ними вавилонянами при определении площади круга, и вознамерились
выяснить, какой из результатов верен Аналогичные расхождения об-
наружились и по другим вопросам. В качестве еще одного объяснения
историки ссылаются на философские интересы греков, ио это только
догадки, которые скорее поднимают вопросы, чем дают объяснения.
Кое-кто считает, что дедуктивная математика ведет свою родословную
от аристотелевской логики, возникшей в пылу дискуссий на общест-
венно-политические темы. Однако древнегреческая математика заро-
дилась до Аристотеля.
По-видимому, нам остается лишь констатировать, что у греков на-
чиная с VI в. до н.э. сложилось определенное миропонимание, сущ-
ность которого сводилась к следующему. Природа устроена рацио-
нально, а все явления протекают по точному и неизменному плану, ко-
торый в конечном счете является математическим. Человеческий ра-
зум всесилен, и если эту могучую силу приложить к изучению приро-
9
ды, то лежащий в основе мироздания математический план удастся
раскрыть и познать.
Как бы то ни было, именно греки были первыми, кому достало дер-
зости и гения дать рациональное объяснение явлений природы. Не-
уемная тяга греков к познанию была окрашена волнующими пережи-
ваниями поиска и исследования. Занимаясь изысканиями, греки нано-
сили новые области знания на «карты» (примером такой «карты» мо-
жет служить геометрия Евклида), чтобы те, кто идет следом, могли
скорее достичь границ неведомого и принять участие в освоении но-
вых областей.
На несколько более прочной исторической основе мы стоим, когда
ссылаемся на то, что Фалес (около 640—546 до н э.) из греческого города
Милета в Малой Азии доказал несколько теорем евклидовой геометрии.
Никаких документов того времени не сохранилось, и утверждение, что
Фалес Милетский доказал теоремы логическими средствами, довольно
спорно. Не подлежит, однако, сомнению, что и он, и его современники в
Малой Азии размышляли о плане, заложенном в основы мироздания.
Более достоверно известно, что разработанная пифагорейцами (мисти-
ческо-религиозным орденом, существовавшим в VI в. до н.э.) программа
выявления рационального плана, лежащего в основе природы, преду-
сматривала использование математики Пифагорейцев поражало, что
физически столь разнообразные объекты обнаруживают тождествен-
ные математические свойства. Например, Луна и резиновый мяч име-
ют одинаковую форму и много других общих свойств, присущих всем
шарам. Разве не очевидно, что математические соотношения, кроющиеся
за внешним разнообразием, и должны быть сущностью явлений?
Если говорить более конкретно, то пифагорейцы усматривали сущ-
ность вещей и явлений в числе и числовых соотношениях Число для
них было первым принципом в описании природы, и оно же считалось
материей и формой мира. По преданию, пифагорейцы полагали, что
«все вещи суть числа». Их вера в число станет более понятной, если
учесть, что пифагорейцы представляли числа наглядно в виде мно-
жеств точек (возможно, символизировавших для них частицы) и рас-
полагали точки в виде фигур, которые могли представлять реальные
объекты Например, множества
. . и ...
назывались соответственно треугольными и квадратными числами и
вполне могли представлять треугольные и квадратные объекты. Не под-
лежит сомнению и то, чю, когда пифагорейцы развили и усовершенст-
вовали свое учение, они начали понимать числа как абстрактные поня-
тия, а физические объекты как их конкретные реализации.
Ю
Пифагорейцам принадлежит идея сведения музыкальных интерва-
лов к простым соотношениям между числами; они пришли к этой
мысли, совершив два открытия. Первое — что высота звука, издавае-
мого колеблющейся струной, зависит от ее длины, и второе — что
гармонические созвучия издают струны, длины которых относятся
между собой, как некоторые целые числа. Например, гармоническое
созвучие возникает, если заставить колебаться две одинаково натяну-
тые струны, одна из которых вдвое длиннее другой. Музыкальный ин-
тервал между издаваемыми такими струнами тонами ныне называется
октавой. Другое гармоническое созвучие создают две струны, длины
которых относятся, как три к двум: в этом случае тон, издаваемый бо-
лее короткой струной, на квинту выше тона более длинной. Длины
любых двух струн, рождающих гармоническое созвучие, действитель-
но относятся между собой, как целые числа.
Движения планет пифагорейцы также сводили к числовым соотно-
шениям. По их представлениям, тела, перемещаясь в пространстве,
производят звуки, причем быстро движущееся тело издает более высо-
кий звук, чем движущееся медленно. Возможно, такого рода идеи бы-
ли навеяны свистящим звуком, который возникает при раскручивании
веревки с тяжелым предметом на конце. Согласно пифагорейской ас-
трономии, чем больше расстояние от планеты до Земли, тем быстрее
планета движется. Следовательно, звуки, издаваемые планетами, из-
меняются в зависимости от их удаленности от Земли, и все звуки под-
чиняются определенной гармонии. Как и всякая гармония, такая «му-
зыка сфер» может быть сведена к чисто числовым соотношениям. Но
тогда и движения планет можно свести к числовым соотношениям.
Другие характерные особенности природы пифагорейцы также
сводили к числу. Особенно высоко они ценили числа 1,2, 3, 4, обра-
зующие четверицу. или тетрактис По преданию, клятва пифагорей-
цев гласила- «Клянусь именем Тетрактис, ниспосланной нашим ду-
шам. В ней источник и корни вечно цветущей природы». Природа, по
мнению пифагорейцев, состояла из «четверок» — четырех геометри-
ческих элементов (точки, линии, поверхности и тела) и четырех мате-
риальных элементов (земли, воздуха, огня и воды), — игравших важ-
ную роль в философии Платона.
Четыре числа, входившие в тетрактис, в сумме давали десять, поэто-
му число «десять» пифагорейцы провозгласили идеальным числом и
усматривали в нем символ всего мира. Но так как число «десять» иде-
ально, в небесах должны быть десять тел. Чтобы получить нужное чис-
ло небесных тел, пифагорейцы придумали Центральный огонь, вокруг
которого обращаются Земля, Солнце, Луна и пять известных тогда пла-
нет, а также Антиземлю, лежащую по другую сторону от Центрального
I
11
огня. Ни Центральный огонь, ни Антиземля невидимы, так как мы оби-
таем на той части Земли, которая обращена в противоположную от них
сторону. Так пифагорейцы построили астрономическую теорию, осно-
ванную на числовых соотношениях.
Приведенные примеры позволят нам понять высказывание, припи-
сываемое знаменитому пифагорейцу Филолаю, жившему в V в. до н.э.:
«Если бы ни число и его природа, ничто существовавшее нельзя было
бы постичь ни само по себе, ни в его отношении к другим вещам .
Мощь числа проявляется, как нетрудно заметить, не только в деяни-
ях демонов и богов, но и во всех поступках и помыслах людей, во всех
ремеслах и музыке».
Натурфилософию пифагорейцев трудно назвать состоятельной. Не
удалось им продвинуться сколько-нибудь далеко ни в одной из облас-
тей естествознания. Их теории с полным основанием можно назвать
поверхностными. Тем не менее то ли благоприятное стечение обстоя-
тельств, то ли гениальное прозрение позволили пифагорейцам создать
два учения, первостепенное значение которых обнаружилось лишь
позднее. Первое — что природа устроена на математических принци-
пах и второе — что числовые соотношения суть основа, единая сущ-
ность и инструмент познания порядка в природе.
Атомисты Левкипп (ок. 440 до н.э.) и Демокрит (ок. 460—ок. 370
до н.э.) также отводили математике немаловажную роль. Они считали,
что вся материя состоит из атомов, различающихся положением, раз-
мерами и формой. Эти свойства атомов физически реальны. Все ос-
тальные свойства, такие, как вкус, теплота и цвет, присущи не самим
атомам, а обусловлены воздействием атомов иа воспринимающего
субъекта. Такое чувственное знание ненадежно, так как меняется от
одного воспринимающего субъекта к другому. Подобно пифагорей-
цам, атомисты утверждали, что реальность, лежащая в основе посто-
янно меняющихся свойств реального мира, может быть выражена на
языке математики. Все происходящее в этом мире строго предопреде-
лено математическими законами.
Первым из греков, кому мы обязаны наиболее существенным про-
движением в математическом исследовании природы, был Платон
(427—347 до н.э.). Он не только воспринял некоторые учения пифаго-
рейцев, но и был выдающимся философом, чьи идеи во многом опре-
деляли развитие мысли в Греции достопамятного IV в. до н.э. Платой
основал в Афинах Академию, ставшую центром притяжения мыслите-
лей его времени и просуществовавшую девять веков. Свои взгляды
Платон особенно отчетливо и ясно изложил в диалоге «Филеб». В ввод-
ной главе «Историческая ретроспектива» мы упоминали о том, что ре-
альный мир, согласно Платону, построен на математических принци-
12
пах. То, что воспринимают наши органы чувств, ие более чем несо-
вершенное представление реального мира. Реальность и рациональ-
ность физического мира может быть постигнута только с помощью
математики, ибо «Бог вечно геометризует». Платон пошел дальше, чем
пифагорейцы: он стремился не только познать природу, но и выйти за
ее пределы, чтобы постичь идеальный мир, построенный на математи-
ческих принципах, который, по мысли Платона, и есть подлинная ре-
альность. Чувственное, преходящее и несовершенное подлежало заме-
не на абстрактное, вечное и совершенное. Платон полагал, что не-
сколько тонких наблюдений внешнего мира позволят составить пред-
ставление об основных идеях, которые затем могут быть развиты ра-
зумом. Необходимость в дальнейших наблюдениях отпадала. После
того как исходные наблюдения произведены, природа должна бьпъ
полностью заменена математикой. Платон подверг критике пифаго-
рейцев за то, что они, исследовав числа, в которых запечатлена гармо-
ния музыкальных созвучий, так и не дошли до изучения естественной
гармонии самих чисел. Для Платона математика была ие только по-
средником между идеями и данными чувственного опыта: математи-
ческий порядок он считал точным отражением самой сути реальности.
Платон заложил также основы дедуктивно-аксиоматического метода,
который мы кратко обсудим. В этом методе Платон видел идеальный
способ систематизации уже накопленного знания и получения нового.
Наиболее выдающиеся из последователей Платона разделяли его
мысль, что математика занимается изучением внешнего мира и позволя-
ет получать о нем истинное знание. Хотя Аристотель и его сторонники
занимали несколько иную позицию, чем платоники, тем не менее по во-
просу об отношении математики к реальному миру школа Аристотеля
также отстаивала версию о математическом плане, лежащем в основе
всего мироздания. Аристотель утверждал, что математические абстрак-
ции почерпнуты из материального мира, однако в его сочинениях нигде
не говорится, что математика вносит поправки в чувственное знание,
расширяя его. Аристотель считал, что в основе движения небесных тел
лежат некие математические принципы, но для него математические за-
коны были не более чем описанием событий. Самым важным для Ари-
стотеля была конечная причина, или цель, событий, т.е. он исходил из
телеологической концепции.
Когда Александр Македонский (356—323 до н.э.) вознамерился по-
корить мир, он перенес центр греческой Ойкумены из Афин в один из
городов Египта, который он с присущей ему «скромностью» переиме-
новал в Александрию. Именно там, в Александрии, Евклид (около 300
до и.э.) написал первый достопамятный документ математического
знания — свои классические «Начала». В этой работе впервые было
13
применено доказательство. Помимо «Начал» Евклиду принадлежат
также сочинения по механике, оптике и музыке, в которых основная
роль отведена математике. Математика выступала как идеальная вер-
сия того, что составляло содержание известного нам реального мира.
Некоторые из теорем Евклида несли в себе новое знание геометриче-
ских фигур и свойств целых чисел. Но поскольку оригинальные ману-
скрипты Евклида до нас не дошли, мы не знаем, было ли это новое
знание его целью и в какой мере он заботился о надежности знания,
добытого чувственным опытом. Одно можно сказать с уверенностью:
Евклид проложил путь другим творцам и создателям математики
Греки «Александрийского периода» (около 300 до н.э.—600 н.э.)
необычайно расширили математику. Упомянем лишь обширный труд
Аполлония (ок. 262—ок 190 до н.э.) «Конические сечения», серию
первоклассных работ Архимеда (ок. 287—212 до н.э.) по многим об-
ластям математики и механики, труды по тригонометрии Гиппарха,
Менелая и Птолемея (ок. 90—160) и в конце периода «Арифметику»
Диофанта. Во всех этих сочинениях так же, как в «Началах» Евклида,
излагались идеальные версии объектов, отношений и явлений реально-
го мира. Все они внесли свою лепту в расширение нашего знания
Греческая цивилизация погибла под натиском римских и мусульман-
ских завоевателей. С ее падением Европа вступила в период Средневеко-
вья, продолжавшийся целое тысячелетие — с 500 по 1500 г. Главенст-
вующую роль в средневековой культуре играла церковь, рассматриыи-
шая жизнь на Земле как подготовку к загробной жизни на небесах. Иссле-
дование природы любыми средствами, как математическими, так и нема-
тематическими, считалось предосудительным занятием. Тем не менее от-
дельные мыслители и даже целые группы (Роберт Гроссетест, Роджер Бэ-
кон, Джон Пекхэм, мертонианцы из Оксфорда, к числу которых принад-
лежали Уильям Оккама, Томас Брадвар, Абеляр из Бата, Тьерри из Шар-
тра и Уильям из Конка) предпринимали попытки продолжить математи-
ческие и физические исследования. В частности они видели в математике
не противоречащее истине описание физических явлений, и некоторые из
них, главным образом Абеляр и Тьерри, настаивали на эксперименталь-
ном изучении природы. Все эти мыслители считали, что реальный физи-
ческий мир в основе своей рационален и математическое рассуждение
способно дать знание о нем. Не следует забывать и о вкладе, который в
период Средневековья внесли в математику индийцы и арабы и который
постепенно вошел в общий свод математического знания.
Началом современного периода, о котором в основном и пойдет речь в
нашей книге, принято считать конец XV—начало XVI вв. Что касается
XVI в., то его часто называют эпохой Ренессанса — возрождения греческой
14
мысли. Для нас сейчас несущественно, каким образом греческие мануск-
рипты попали в Италию, ставшую центром Возрождения.
Европейцы не сразу откликнулись на новые веяния. На протяжении
этого периода, который нередко называют гуманистическим, европей-
ские мыслители ие столько следовали высоким целям древних греков,
сколько изучали труды греческих авторов, но примерно к 1500 г. евро-
пейские умы, воспринявшие направленность античной мысли — при-
ложение разума к исследованию природы и поиск математического
плана, лежащего в основе мироздания, — принялись действовать. Од-
нако они столкнулись с серьезной проблемой, поскольку цели, кото-
рые ставили перед собой греки, находились в противоречии с культур-
ной традицией, сложившейся в Европе того периода. В то время как
греки не сомневались, что природа устроена на математических прин-
ципах и неизменно и неуклонно следует некоему идеальному плану,
мыслители конца Средневековья приписывали весь план и все дейст-
вие христианскому Богу. Именно Бог был для них творцом и создате-
лем плана мироздания, и все явления природы неукоснительно следо-
вали предначертаниям этого высшего существа. Весь мир — творение
Бога и беспрекословно подчиняется его воле. Математики и естествоис-
пытатели эпохи Возрождения, будучи правоверными христианами, раз-
деляли эту доктрину. Но католическое вероучение отнюдь не включало
в себя греческое учение о математическом плане, лежащем в основе
природы. Каким же образом можно согласовать тогда попытку понять
созданное Богом мироздание с поиском математических законов при-
роды? Пришлось добавить (к уже существовавшим учениям) новый
тезис — о том, что христианский Бог сотворил мир на математической
основе. Католическое вероучение, постулирующее первостепенное зна-
чение попыток понять волю Господа и его творения, приняло форму по-
иска математического плана, заложенного Богом в основу мироздания.
Как мы вскоре убедимся, узнав некоторые подробности, работа математи-
ков на протяжении XVI—XVIII вв. была по существу религиозным иска-
нием. В поисках математических законов природы они священнодейст-
вовали, раскрывая славу и величие творения божьего.
Математическое знание, истина о плане, положенном Богом в осно-
ву мироздания, при таком подходе обретали столь же боговдохновенный
характер, как и любая строка Священного писания. Разумеется, смертным
не дано постичь божественную мудрость плана с той полнотой и ясно-
стью, с какой она ведома самому Господу Богу, но люди могли смиренно
и с подобающей скромностью по крайней мере пытаться приблизиться к
божественному разуму и понять, как устроен мир.
Можно пойти дальше и утверждать, что математики XVI—XVIII вв
были уверены в Существовании математических законов, лежащих в
основе всех явлений природы, и настойчиво стремились найти их, ибо
15
исходили из априорного убеждения, что Бог и эти законы включил в
общую схему мироздания. Каждое открытие закона природы провоз-
глашалось как еще одно свидетельство мудрости Бога, а не проница-
тельности исследователя. Убеждения и взгляды математиков и естест-
воиспытателей распространились по всей Европе эпохи Возрождения.
Незадолго до того обнаруженные работы греческих авторов противо-
стояли глубоко религиозному христианскому миру, и духовные лиде-
ры Возрождения, рожденные в одном мире, но тяготевшие к другому,
слили учения обоих миров воедино.
Наряду с этим новым интеллектуальным увлечением стало приоб-
ретать все более широкую поддержку направление, основанное на
идее «назад к природе». Многие естествоиспытатели отвергли нескон-
чаемое умствование на основе догматических принципов, туманных
по смыслу и оторванных от опыта, и обратились к самой природе как
источнику подлинного знания. К началу XVII в. в Европе сложились
предпосылки того, что нередко называют «научной революцией».
Многие события способствовали или ускорили ее наступление: гео-
графические экспедиции открыли новые земли и народы; изобретение
телескопа и микроскопа позволило обнаружить новые явления; компас
облегчил навигацию в условиях открытого моря; гелиоцентрическая
теория Коперника заставила по-новому взглянуть иа нашу планетную
систему. Реформация пошатнула догмы католицизма. Математика
вскоре снова стала играть главную роль — ключа к природе.
Бегло обозревая исторический фон, на котором происходило разви-
тие европейской математики, мы стремились главным образом пока-
зать, что математика и применение ее к исследованию природы (ос-
новная тема последующих глав нашей книги) не возникли неожидан-
но, как гром среди ясного неба. Свое внимание мы сосредоточим не на
элементарной математике, дающей средства для корректировки и рас-
ширения нашего знания о явлениях, в основном доступных нашим ор-
ганам чувств, а на успехах, достигнутых математикой в открытии и
описании явлений, либо не доступных непосредственному воспри-
ятию, либо вообще не воспринимаемых нами. При этом нам не пона-
добится постигать тонкости математических методов, но важно будет
понять, каким образом математика позволяет описывать физические
явления и получать знание о них.
Каковы существенные особенности математического метода? Пер-
вая отличительная особенность — введение основных понятий. Неко-
торые из таких понятий, например точка, линия и целое число, подска-
заны непосредственно материальным, или физическим, миром. Поми-
мо элементарных понятий в математике немаловажную роль играют
понятия, созданные человеческим разумом. Примерами таких понятий
16
могут служить понятия отрицательного числа, буквенные обозначения
классов чисел, комплексные числа, функции, всевозможные кривые,
бесконечные ряды, понятия математического анализа, дифференци-
альные уравнения, матрицы и группы, многомерные пространства.
Некоторые из перечисленных нами понятий полностью лишены
интуитивной основы. Другие, например понятие производной (мгно-
венной скорости изменения), имеют под собой некую интуитивную
основу в физических явлениях. Но хотя производная и связана с физи-
ческим понятием скорости, ее в гораздо большей степени можно рас-
сматривать как конструкцию, созданную разумом, причем на качест-
венно совершенно ином уровне, нежели, скажем, понятие математиче-
ского треугольника.
На протяжении всей истории математики новые понятия поначалу
вызывали весьма настороженное отношение. Даже понятие отрица-
тельного числа сначала было отвергнуто серьезными математиками.
Тем ие менее каждое новое понятие, хотя и неохотно, принималось
после того, как становилась очевидной его полезность в приложениях.
Вторая существенная особенность математики — ее абстрактность.
Платон в диалоге «Государство» так сказал о геометрах:
«Но ведь когда они вдобавок пользуются чертежами и делают отсюда выводы,
их мысль обращена не на чертеж, а на те фигуры, подобием которых он служит
Выводы свои они делают только для четырехугольника самого по себе и его диа-
гонали, а не для той диагонали, которую оии начертили. Так н во всем остальном
То же самое относится и к пронзведениям ваяния и живописи: от них может па-
дать тень, н возможны их отражения в воде, но сами они служат лишь образным
выражением того, что можно видеть ие иначе, как мысленным взором».
Если математика должна быть могучей, то в одном абстрактном
понятии она должна охватывать существенные особенности всех фи-
зических проявлений этого понятия. Например, математическая пря-
мая должна включать в себя все наиболее значительные особенности
туго натянутых веревок, краев линеек, границ полей и траекторий све-
товых лучей.
В том, что математические понятия представляют собой абстрак-
ции, нетрудно убедиться на примере наиболее элементарного понятия —
числа Непонимание абстрактного характера этого понятия может при-
водить к недоразумениям. Поясним эту мысль на простом примере.
Человек заходит в обувной магазин и покупает три пары обуви по
20 долл, за пару. Продавец говорит, что три пары обуви по 20 долл, за
пару стоят 60 долл., и ожидает, что покупатель уплатит ему эту сумму.
Покупатель же возражает, утверждая, что три пары по 20 долл, за пару —
это 60 пар обуви, и настаивает, чтобы продавец приготовил 60 пар
обуви. Прав ли покупатель? Прав, как прав и продавец. Если чщу^гцр
обуви, умноженное на доллары, может давать доллара, га ночс-тлдбЬ
/ Z ^*миняя твхм-
3 Зак 72 I '“'ЧП*.
У Л ^^КОВА В.*-
тому же произведению не давать пары обуви? Ответ, разумеется, со-
стоит в том, что мы не умножаем туфли на доллары. Мы абстрагируем
числа 3 и 20 из физической ситуации, умножаем одно число на другое,
получаем число 60 и интерпретируем результат в соответствии с фи-
зической ситуацией.
Еще одна отличительная особенность математики — идеализация.
Математик идеализирует, намеренно отвлекаясь от толщины меловой
линии при рассмотрении прямых или принимая Землю при решении
некоторых задач за идеальную сферу. Сама по себе идеализация не яв-
ляется серьезным отступлением от реальности, но при любой попытке
приложить ее к реальности возникает вопрос, достаточно ли близок
исследуемый объект (например, реальная частица или траектория) к
его идеальному образу.
Наиболее поразительной особенностью математики является ис-
пользуемый ею метод рассуждения. Основу его составляет набор ак-
сиом и применение к этим аксиомам дедуктивного доказательства
(вывода). Слово «аксиома» происходит от греческого «мыслить подо-
бающим образом». Само понятие аксиомы — истины, столь самооче-
видной, что она ни у кого не вызывает сомнения, — введено греками.
Платоновское учение об анамнезисе утверждало, что люди обладают
априорным знанием истин, почерпнутым их душами в объективном
мире истин, и что аксиомы геометрии представляют собой воспомина-
ния о некогда известных истинах. Аристотель во «Второй аналитике»
упоминает об «общих [положениях], называемых нами аксиомами, из
которых, как первичного, ведется доказательство», истинность кото-
рых мы постигаем своей безошибочной интуицией. Если бы в доказа-
тельстве использовались какие-то факты, не известные нам как исти-
ны, то потребовалось бы дополнительное доказательство, которое ус-
танавливало бы эти факты, и этот процесс пришлось бы повторять
бесконечно. Аристотель также указывал на то, что некоторые понятия
должны оставаться неопределяемыми, ибо в противном случае доказа-
тельство не имело бы начала. В наше время такие понятия, как точка и
прямая, остаются неопределяемыми. Их значение и свойства зависят
от аксиом, предписывающих свойства «точек» и «прямых».
Подобно тому как многие используемые в математике понятия изо-
бретены человеческим разумом, аксиомы об этих понятиях изобрете-
ны с таким расчетом, чтобы понятия раскрывали те или иные стороны
реальности. Например, аксиомы для отрицательных и комплексных
чисел с необходимостью должны отличаться от аксиом для положи-
тельных чисел или последние должны по крайней мере допускать
обобщения, охватывающие отрицательные и комплексные числа. Ра-
зумеется, аксиоматизация более новых понятий требует более тонкого
подхода, поэтому правильные аксиоматические обоснования некото-
18
рых областей математики удалось создать лишь через много лет после
возникновения этих областей.
Помимо математических аксиом значительную часть лепты, вно-
симой математикой в наш физический мир, должно составлять и фи-
зическое знание. Оно может принимать форму физических аксиом
(например, законов движения Ньютона), обобщений эксперименталь-
ных наблюдений или чистой интуиции. Эти физические допущения
формулируются на языке математики, что позволяет применять к ним
математические аксиомы и теоремы.
Но сколь ни фундаментальны понятия и аксиомы, именно дедук-
тивные выводы из аксиом дают нам возможность получать полностью
новое знание, вносящее надлежащие поправки в наши чувственные
восприятия. Из многих типов рассуждений (индуктивных, по анало-
гии, дедуктивных и т.д.) только дедуктивное рассуждение гарантирует
правильность заключения. Например, придя к заключению «Все ябло-
ки красные» на том основании, что тысяча просмотренных нами яблок
были красными, мы пользуемся индуктивным рассуждением, поэтому
наше заключение ненадежно. Заведомо ненадежно и заключение
«Джон не мог не закончить этот колледж», которое мы делаем на том
основании, что брат-близнец Джона, унаследовавший от родителей та-
кие же способности, как и сам Джон, закончил этот колледж. В этом
случае мы рассуждаем по аналогии, и наше рассуждение также нена-
дежно. В отличие от этого дедуктивное рассуждение, хотя оно может
принимать разнообразные формы, гарантирует правильность заключе-
ний. Тот, кто считает, что все люди смертны, не может не согласиться
с тем, что Сократ смертен. Лежащее в основе этого рассуждения логи-
ческое правило является разновидностью того, что Аристотель назы-
вал силлогистическим рассуждением, или силлогизмом. К числу дру-
гих законов дедуктивного рассуждения Аристотель относил закон
противоречия (любое утверждение не может быть одновременно ис-
тинным и ложным) и закон исключенного третьего (любое утвержде-
ние должно быть либо истинным, либо ложным).
И сам Аристотель, и мир в целом не сомневались в том, что сфор-
мулированные Аристотелем принципы дедуктивного рассуждения, ес-
ли их применить к любым посылкам, приводят к заключениям столь
же надежным, как и посылки. Следовательно, если посылки были ис-
тинными, то заключения также будут истинными. Заметим попутно,
что принципы дедуктивного рассуждения Аристотель абстрагировал
из рассуждений, которыми уже пользовались математики. Дедуктив-
ная логика — дитя математики.
Необходимо по достоинству оценить, сколь радикальным было не-
укоснительное следование принципам дедуктивного доказательства.
Мы можем проверить сколько угодно чисел и убедиться, что каждое
з-
19
из них представимо в виде суммы двух простых чисел. Одиако мы не
можем утверждать, что наш результат есть математическая теорема,
поскольку он не был получен путем дедуктивного доказательства.
Приведем еще один аналогичный пример. Предположим, что какой-то
ученый измерил суммы углов 100 различных треугольников, отличав-
шихся по расположению, размерам и форме. В пределах точности из-
мерений все суммы оказались равными 180°. Ученый, разумеется, сде-
лал бы вывод, что сумма углов любого треугольника равна 180°. Но
такое заключение верно только в пределах точности измерений. Кроме
того, оставался бы открытым вопрос о том, не дадут ли существенно
иной результат измерения, производимые над треугольником какой-
нибудь еще не испробованной формы. Индуктивное заключение наше-
го естествоиспытателя математически неприемлемо. В отличие от него
математик начинает с фактов или аксиом, которые представляются на-
дежными. Кто может усомниться в том, что если к равным величинам
прибавить равные величины, то суммы окажутся равными9 С помо-
щью таких неоспоримых аксиом можно, рассуждая дедуктивно, дока-
зать, что сумма углов любого треугольника равна 180°.
В описанном нами дедуктивном процессе для обоснования рассужде-
ния используется логика При этом, по существу, мы до сих пор применя-
ем так называемую аристотелеву логику. Естественно спросить, почему
заключения, полученные с помощью такой логики, должны иметь какое-
то отношение к природе. Почему теоремы, доказанные человеческим ра-
зумом в тиши кабинетов, должны быть применимы к реальному миру,
как, впрочем, и аксиомы, которые во многих случаях являются не более
чем измышлениями того же человеческого разума?
Необходимо отметить еще одну важную характерную черту матеье-
тики: использование специальных обозначений. Хотя страница, испещ-
ренная математическими символами, способна отпугнуть непосвященно-
го, нельзя не признать, что без специальных обозначений математики по-
грязли бы в неразберихе слов. Все мы используем те или иные символы,
когда прибегаем к множеству общепризнанных сокращений Например,
мы часто пишем N.Y., вместо New York (Нью-Йорк), и, хотя смысл таких
аббревиатур нужно знать заранее, не подлежит сомнению, что краткость
символики способствует постижению сути дела, в то время как словесное
выражение перегружает разум.
Резюмируя, суть тех средств, которыми математики добывают фак-
ты о внешнем мире, можно сформулировать следующим образом: ма-
тематика строит модели целых классов реальных явлений. Понятия,
обычно идеализированные (независимо от того, почерпнуты они из на-
блюдений природы или являются плодами человеческого разума), аксио-
мы, которые также могут быть подсказаны физическими фактами или
придуманы людьми, процессы идеализации, обобщения и абстракции, а
20
также интуиция — все идет в ход при построении моделей. Доказательст-
во цементирует элементы модели воедино. Наиболее известная модель —
евклидова геометрия, но мы познакомимся со многими более изощрен-
ными и простыми моделями, рассказывающими нам гораздо больше о
менее очевидных явлениях, чем это делает евклидова геометрия
Наша цель состоит в том, чтобы показать, как прочно входит мате-
матика в современный мир не только как метод, позволяющий ком-
пенсировать несовершенство наших органов чувств, но и в гораздо
большей степени как метод расширения того знания, которое человек
способен обрести об окружающем мире. Как сказал Гамлет, «и в небе
и в земле сокрыто больше, чем снится вашей мудрости, Горацио». Нам
необходимо выйти за пределы знания, добытого чувственным опытом.
Суть математики в отличие от чувственного восприятия состоит в том,
что, опираясь на человеческий разум и способность человека к рас-
суждениям, она порождает знание о реальном мире, которое среднему
человеку, даже если он воспитан на рациональной западной культуре,
кажется полученным исключительно путем чувственного восприятия.
Важность математики для исследования реального мира под-
черкивал Алфред Норт Уайтхед в своей книге «Наука и современный
мир»: Ничто не производит столь сильного впечатления, как то об-
стоятельство, что математика, чем выше она возносится в горные
области все более абстрактной мысли, неизменно возвращается на
землю, обретая все большее значение для анализа конкретного фак-
та... Парадокс, окончательно установленный ныне, состоит в том
что именно предельные абстракции являются тем истинным оружи-
ем, которое правит нашим осмыслением конкретного факта
И как заметил однажды Давид Гильберт, один из самых выдаю-
щихся математиков XX в., физика в наше время слишком важна, что-
бы оставлять ее физикам.
(Виленкин
ОСНОВНЫЕ ЭТАПЫ РАЗВИТИЯ МАТЕМАТИКИ2
1. Введение. В школьном курсе математики сейчас мирно ужива-
ются разделы математической науки, возникшие на протяжении ее
многотысячелетней истории. Например, арифметика была (по крайней
мере в своей практической части) создана более 5 тыс. лет назад еги-
петскими и вавилонскими писцами и жрецами; геометрия в значитель-
ной части восходит к трудам древнегреческих ученых, развивавших
эту науку в VII—III вв. до н.э.; начала алгебры можно усмотреть еще в
трудах вавилонских математиков, а ее дальнейшее развитие связано с
21
именами арабских ученых IX—XIII вв. н.э. и европейских алгебраи-
стов XVI—XVII вв; формулы дифференцирования и интегрирования
были выведены в конце XVII в. Ньютоном и Лейбницем, а понятия
теории множества в основном сформулированы в работах Г. Кантора,
относящихся к концу XIX в.
Чтобы разобраться в этом конгломерате идей и понятий, необходи-
мо знать основные этапы развития математики, понимать, как матема-
тика постепенно расширяла свой предмет в процессе исторического
развития. Историю математики условно разбивают на четыре основ-
ных периода, причем начало каждого периода ознаменовалось вы-
дающимися научными достижениями, определявшими переход мате-
матики в новое качественное состояние.
2. Зарождение математики. Период зарождения математики на-
чался с древнейших времен и закончился в VII—V вв. до н.э. Это был
период накопления фактического материала, тесно связанного с по-
требностями хозяйственной жизни — развитием ремесла, земледелия,
обмена и торговли, исчислением податей, обеспечением войска продо-
вольствием и оружием, измерением площадей земельных участков и
объемов сосудов и т.д. Накопленные эмпирические знания подверга-
лись систематизации, что привело к выделению особого вида понятий
и методов решения задач, явившихся зачатками будущей математиче-
ской науки.
Уже в этот период формируются три основные понятия, изучение
свойств и взаимосвязей которых легло в основу дальнейшего развития
математики: число, величина и геометрическая фигура. Пересчет эле-
ментов конечных множеств (убитых на охоте зверей, сделанных горш-
ков, изготовленных стрел и т.д.), а также упорядочивание этих элемен-
тов привели к возникновению понятия натурального числа, как коли-
чественного, так и порядкового. Сравнение масс различных предметов,
объемов сосудов, расстояний и т.д. привели к понятию величины. При
этом первоначально величины различного вида рассматривались раз-
дельно, так что точнее было бы сказать не о величине, а о величинах
(например, меры массы не были связаны с мерами объема). Наконец,
изучение формы изделий, зданий, земельных участков и т.д. привели к
понятию геометрической фигуры — части геометрического простран-
ства (само слово «геометрия» означает землемерие).
Уже в глубокой древности были введены арифметические действия
над натуральными числами, отражавшие операции над конечными
множествами. Далее была установлена связь между натуральными
числами и величинами — в некоторых случаях измерение данной ве-
личины определенной единицей давало ответ в виде натурального
числа. В случаях, когда результат измерения не выражался натураль-
22
ным числом, либо переходили к более мелкой единице измерения, ли-
бо выражали результат измерения дробью. Во всех практических зада-
чах для выражения результатов измерения величин было достаточно
дробей. С помощью наблюдений и простейших рассуждений люди
пришли к формулам для вычисления геометрических величин — длин,
площадей и объемов различных фигур. Тем самым был перекинут
мост между арифметикой и геометрией. Более того, можно сказать,
что в этот период геометрия и арифметика не разделялись, геометри-
ческие задачи ставились как особого вида задачи на вычисление.
В дошедших до нас древнеегипетских папирусах и древневавилон-
ских клинописных табличках уже содержатся правила выполнения
арифметических действий, вычисления геометрических величин, ме-
тоды решения типовых арифметических задач (некоторые из которых
и сейчас встречаются в школьных задачниках), таблицы квадратов, ку-
бов, обратных величин и т.д. Не только понятия натурального числа и
измерения величины свободно использовались в то время, но и были
созданы некоторые общие методы решения арифметических задач, ко-
торые можно назвать «праалгеброй»,— вместо привычного сейчас ис-
пользования букв давались образцы решения задач.
Все это свидетельствует о довольно высоком уровне абстрактного
мышления тогдашних математиков, которые выделили три централь-
ных понятия: «фигура», «величина» и «число», нашли некоторые клас-
сы геометрических фигур (квадрат, прямоугольник, треугольник, пря-
моугольный параллелепипед, шар и т.д ), отметили типичные связи ве-
личин в материальном мире, зафиксировав их в виде типовых задач.
Решение практических задач потребовало умения обозначать нату-
ральные числа и дроби, воплощать понятие числа в определенных сим-
волах. Были разработаны различные системы счисления, тесно связан-
ные со счетом на пальцах (десятичная, двадцатеричная), а также двена-
дцатеричная и шестидесятеричная системы счисления, которые были
очень удобны, так как давали возможность делить «круглые» числа без
остатка на 3 (происхождение этих систем счисления не установлено до
конца историками науки).
Вавилонские ученые умели решать уравнения первой и второй сте-
пеней (а в некоторых случаях — и более высоких степеней), решать
задачи на прогрессии и т.д.
Однако, несмотря на накопление известного теоретического мате-
риала, математика того времени еще не была дедуктивной наукой —
наряду с результатами, полученными путем тех или иных выводов, она
содержала много эмпирических результатов, часть которых была даже
ложной. Например, в некоторых древнеегипетских папирусах утвер-
23
ждается, что площадь произвольного четырехугольника равна произ-
ведению полусумм длин противоположных сторон.
Задачи в древнеегипетских папирусах классифицировались не по
методам решения, а по содержанию (задачи на припек, на вместимости
сосудов и т.д.). Вместо доказательств писалось: «Делай, как делается»,
т.е. основой было не логическое рассуждение, а ссылка на авторитет
предшественников. Основной задачей обучаемого было не понимание
правил, а их запоминание.
3. Математика постоянных величин Второй период развития ма-
тематики известен в литературе как период математики постоянных
величин (или элементарной математики). Он начался в VII в. до н.э. и
закончился в XVII в. н.э. Основным достижением математической
мысли, характеризующим начало этого периода, было возникновение
и развитие понятия о доказательстве. Греческие математики созна-
тельно стремились расположить математические доказательства в та-
кие цепочки, чтобы переход от одного звена к следующему не остав-
лял никакого места сомнениям и заставлял всех с ним согласиться.
К сожалению, до нашего времени не дошли тексты, по которым
можно было бы судить о возникновении этого «дедуктивного метода».
Традиция называет первым из философов, применившим в математике
доказательства, греческого ученого Фалеса из Милета (города в Малой
Азии), жившего в VII—VI вв. до н.э. По дошедшим до нас сведениям,
Фалес доказал некоторые простейшие геометрические утверждения:
равенство углов при основании равнобедренного треугольника, равен-
ство вертикальных углов, один из признаков равенства треугольников,
равенство частей, на которые диаметр разбивает круг, и т.д.
Созданный Фалесом метод логического доказательства математи-
ческих утверждений был развит и усовершенствован учеными пифаго-
рейской школы в период между концом VI в. и серединой V в. до н.э.,
которые доказали, в частности, утверждение, называемое теперь тео-
ремой Пифагора (формулировка этого утверждения была известна еще
вавилонянам).
Пифагорейцы предприняли первую попытку свести геометрию и
алгебру того времени к арифметике. Они считали, что «все есть чис-
ло», понимая под словом «число» лишь натуральные числа. В частно-
сти, они были долгое время убеждены, что длины любых отрезков со-
измеримы друг с другом, а потому для измерения любых величин дос-
таточно рациональных чисел.
Поворотным пунктом было открытие пифагорейцами того, что диаго-
наль квадрата несоизмерима с его стороной. Это открытие, сделанное на
основе теоремы Пифагора, показало несостоятельность попытки свести
всю геометрию к натуральным числам. Анализ полученного доказатель-
24
ства привел к исследованию начальных вопросов теории чисел (четности
и нечетности простых чисел, разложения чисел на простые множители,
свойств взаимно простых чисел и т.д.).
После работ Пифагора стало ясно, что не все величины выражают-
ся рациональными числами. Поскольку понятие иррационального чис-
ла не могло быть создано в ту эпоху, греческие математики предпри-
няли иную попытку — обосновать всю математику на основе геомет-
рических понятий. Они стали развивать геометрическую алгебру, ис-
толковывая, например, сложение величин, как сложение отрезков, а
умножение — как построение прямоугольника с заданными сторона-
ми. При этом говорили о равенстве отрезков, а не о равенстве их длин,
поскольку длина отрезка выражается числом, а числа были изгнаны из
древнегреческой математики. Следы такого подхода к алгебре сохра-
нились в современных терминах квадрат числа, куб числа, геометри-
ческое среднее, геометрическая прогрессия и т.д.
Древнегреческие математики продвинулись очень далеко. Они про-
вели, например, классификацию квадратичных иррациональностей,
открыли все виды правильных многогранников, вывели формулы для
объемов многих тел, исследовали разнообразные кривые линии (эл-
липс, гиперболу, параболу, спирали). Выдающуюся роль в формиро-
вании математики как теоретической науки сыграла знаменитая книга
Евклида «Начала», представлявшая синтез и систематизацию основ-
ных результатов древнегреческой математической мысли и длительное
время служившая источником знаний и образцом строгого математи-
ческого изложения.
Книга Евклида является первой из дошедших до нашего времени
попыток аксиоматического изложения математической дисциплины.
Хотя во времена Евклида не вставал еще вопрос об описании логиче-
ских средств, применяемых для извлечения содержательных следствий
из аксиом, в системе Евклида была уже четко проведена основная идея
получения всего основного содержания геометрической теории чисто
дедуктивным путем из небольшого числа утверждений — аксиом, ис-
тинность которых представлялась наглядно очевидной.
В XIX в. было показано, что список аксиом Евклида неполон и
многие теоремы он доказывал, привлекая утверждения, не вошедшие в
этот список. Не было у Евклида и аксиом порядка. Признаки же равен-
ства треугольников доказывались на основе понятия наложения фигур,
т.е., по сути дела, на основе идеи движения, относящейся скорее к ме-
ханике, чем к математике.
В течение двух тысячелетий основное внимание критиков и ком-
ментаторов Евклида было направлено на аксиому о параллельных, по-
скольку предполагалось, что ее можно доказать на основе остальных
2 Зак 72
25
аксиом. Лишь открытие в начале XIX в. неевклидовой геометрии пока-
зало безнадежность попыток такого доказательства.
На формулировку аксиом Евклида сильное влияние оказали длив-
шиеся долгое время споры между сторонниками и противниками ато-
мизма. Атомисты (Демокрит, Левкипп) утверждали, что материя со-
стоит из неделимых атомов, причем существует предел делимости
пространства (т.е. что и пространство состоит из неделимых далее час-
тиц). Их противники полагали, что пространство безгранично делимо
и потому недопустимо считать, что линии состоят из точек, поскольку
точки не имеют ни частей, ни размеров, а линии имеют определенную
длину.
Хотя атомисты достигли больших успехов в геометрии (например,
Демокрит вывел формулу объема пирамиды), их попытки дать логиче-
ское обоснование геометрии не увенчались успехом. Дело в том, что
из атомистических воззрений вытекала соизмеримость любых двух от-
резков, а это противоречило известной уже в то время теореме о несо-
измеримости стороны и диагонали квадрата, В то же время Евклиду
удалось построить логически замкнутую систему геометрии, в которой
считалось, что любой отрезок безгранично делим, а потому не сущест-
вует неделимых элементов пространства.
Книга Евклида подвела также итог длительному развитию идеи
бесконечности, приведшему к формированию, с одной стороны, поня-
тия о бесконечном ряде натуральных чисел, а с другой — понятия о
безгранично делимых геометрических фигурах (отрезках, кругах и
т.д.). Однако бесконечность понималась лишь как потенциальная воз-
можность продолжать определенный процесс (прибавления единицы к
натуральному числу, деления пополам отрезка и т.д.). Идея об акту-
альной (законченной) бесконечности изгонялась из работ Евклида и
его последователей (Архимеда, Аполлония и др.). Эта идея была дис-
кредитирована в результате открытия греческим философом Зеноном
затруднений, к которым вело ее использование. Например, Зенон «до-
казывал», что стрела не может пролететь свой путь, поскольку она
должна сначала пролететь половину пути, а до этого — половину по-
ловины и т.д. — значит, она никогда не сдвинется с места.
Поэтому формулы для объема шара и конуса, площади круга и т.д.
излагались без применения предельного перехода, без разложения на
бесконечно малые части, хотя для отыскания этих формул математики
применяли «запрещенные приемы». Архимед решил такие сложные
для тогдашней математики задачи, как отыскание объема сегмента па-
раболоида вращения и площади сектора архимедовой спирали.
26
Недостатком геометрического подхода к математике было то, что
он препятствовал развитию алгебры (хотя греки и умели, например, в
геометрической форме решать квадратные уравнения) — невозможно
было представить геометрически четвертую и высшие степени длины,
а кроме того, нельзя было складывать выражения разных степеней: эта
сумма геометрического смысла не имела.
По той же причине в греческой математике не было отрицательных
чисел и нуля, иррациональных чисел и буквенного исчисления. Лишь в
III в. н.э. в работах александрийского математика Диофанта появляют-
ся зачатки буквенного исчисления. Но этим работам не суждено было
иметь продолжения в греческой математике, гак как после принятия
христианства в V в. н.э. языческая культура, составной частью которой
была математика, оказалась разрушенной, а в 529 г. император Юсти-
ниан под страхом смертной казни запретил занятия математикой.
Центр математических исследований переместился на Восток — в
Индию, Китай и арабский мир. Индийские математики ввели нуль и
отрицательные числа, проводили исследования по комбинаторике
(Ариабхатта, V в. н.э.). Основной заслугой арабских математиков (аль-
Беруни, Омар Хайям, Гиясэддин Джемшид, IX—XIII вв. н.э.) следует
считать развитие тригонометрии (в связи с астрономическими иссле-
дованиями) и особенно создание новой области математики — алгебры.
Алгебра, которую теперь рассматривают как общее учение о фор-
мальных действиях и их свойствах, появилась у арабов как наука о
решении уравнений. Само слово «алгебра» арабского происхождения
и означало «восстановление», т.е. перенос отрицательных слагаемых в
другую часть уравнений.
С начала XIII в. вновь возрождаются математические исследования
в Европе. Но лишь в XVI в. были получены первые научные результа-
ты, превзошедшие достижения греков и арабов, — итальянские мате-
матики дель Ферро, Тарталья, Кардано, Феррари и другие вывели
формулы для решения уравнений третьей и четвертой степеней. Одно-
временно с этим формируется система алгебраических обозначений,
словесная алгебра постепенно заменяется буквенной. В начале XVII в.
в трудах французских и английских математиков (Виета, Декарта,
Гэрриота) завершается развитие алгебраической символики, создаются
правила буквенного исчисления. Одновременно с развитием символи-
ки происходит расширение понятия о числе: еще в середине XVI в. в
математике окончательно утверждаются отрицательные числа, а вско-
ре за тем появляются и комплексные числа (хотя они долгое время не
находили признания, поскольку не допускали истолкования известны-
ми в то время средствами). При этом оказалось, что правила буквенной
алгебры в равной мере применимы к числам любого вида.
2*
27
Важнейшую роль сыграли работы итальянского ученого Бомбелли
(XVI в.) и французского математика Р. Декарта (XVII в.), которые фак-
тически ввели идею действительного числа, освободив тем самым ал-
гебру от несвойственной ей геометрической одежды. Пользуясь этим,
Декарт, в отличие от греческих математиков, сводивших алгебраиче-
ские проблемы к геометрии, начал алгебраически решать геометриче-
ские задачи. Этим было положено начало аналитической геометрии.
4. Математика переменных величин. Началом третьего периода
развития математики следует считать работы Р. Декарта, в которых он
ввел понятие переменной величины Ф. Энгельс писал по этому поводу:
«Поворотным пунктом в математике была Декартова переменная
величина. Благодаря этому в математику вошли движение и тем са-
мым диалектика, и благодаря этому же стало немедленно необходимым
дифференциальное и интегральное исчисление, которое тотчас и воз-
никает и которое было в общем и целом завершено, а не изобретено
Ньютоном и Лейбницем».
Под влиянием запросов практики математики XVII в. переходят от
изучения постоянных величин к исследованию зависимостей между пе-
ременными величинами, т.е. к математическому описанию движения и
других процессов. Таким образом, третий период развития математики
является периодом математики переменных величин
Одним из основных достижений этого периода явилось введение
общего понятия функции, сделанное в конце XVII в. немецким мате-
матиком и философом Г.В. Лейбницем. В этом понятии нашла свое
отражение общефилософская идея о всеобщей связи явлений матери-
ального мира.
Следует отметить, что математические понятия переменной и
функции представляют собой не что иное, как абстракции конкретных
переменных величин (координат, скорости и ускорения движущегося
тела и т.д.) и конкретных зависимостей между ними (например, зако-
нов движения планет вокруг Солнца или законов свободного падения).
Значениями математической переменной являются числа. Исследова-
ние общих свойств зависимостей между переменными величинами
привело к созданию математического анализа.
Рассматривая вопросы геометрии и механики в конце XVII в., анг-
лийский физик и математик И. Ньютон и почти одновременно с ним
Г.В. Лейбниц создали основы дифференциального и интегрального ис-
числений. Они и их ученики развили аппарат математического анализа,
ставший одним из основных орудий в решении задач механики и гид-
родинамики, астрономии и оптики Триумфом методов математиче-
ского анализа явилось предсказание возвращения в 1759 г. кометы
Галлея. Математический анализ был в ту эпоху основным каналом
28
связи математики с естествознанием. Большие успехи в этом направ-
лении были достигнуты в XVIII—XIX столетиях: математики научи-
лись решать уравнения в частных производных, к которым сводились
многие вопросы математической физики, создали вариационное исчис-
ление, позволившее решать экстремальные задачи, недоступные для
первоначальных методов матемагического анализа, нашли истолкова-
ние и приложения для комплексных чисел. Большую роль в этих ис-
следованиях сыграли работы члена Петербургской академии наук
Л. Эйлера.
Следует отметить также возникновение и развитие теории вероят-
ностей, первые работы по которой появились в XVII в. Большой вклад
в нее сделали русские математики XIX в. П.Л. Чебышев, А.А. Марков,
А.М. Ляпунов и др.
5. Современный период развития математики. Для рассмотрен-
ных выше трех периодов развития математики характерна убежден-
ность в том, что эта наука непосредственно отражает свойства реаль-
ного мира, лишь в несколько идеализированной форме. Ни у кого не
возникало сомнения в том, что существует лишь одна геометрия, дан-
ная на все времена Евклидом и непосредственно отражающая свойства
реального пространства, что свойства производной полностью совпа-
дают с известными из физики свойствами скорости. Иными словами,
считали, что математические объекты нам даны и не в нашей власти
приписывать им произвольные свойства, так же как физик не может
изменить какое-нибудь природное явление. При таком подходе не
могло быть и речи об уклонении от изучения чисел и фигур.
Однако еще в конце XVII в. Лейбниц указывал на иные задачи ма-
тематической науки. Он считал, что «универсальная математика —
это, так сказать, логика воображения» и она должна изучать «все, что в
области воображения поддается точному определению». Главной ча-
стью так понимаемой математики была дпя него наука об абстрактных
соотношениях между математическими объектами, наука, в которой
изучают одинаковое и различное, похожее и непохожее, абсолютное и
относительное расположения, в то время как обычная математика за-
нимается большим и малым, единицей и многим, целым и частью.
Лейбниц ставил и задачу о развитии операций над высказываниями
Но уровень математической науки в то время был еще недостаточен
для решения столь грандиозных задач.
Лишь в начале XIX в. появляются первые работы, давшие новый
толчок математической мысли в направлении исследования предмета
математики и знаменовавшие зарождение нового, четвертого периода
истории математики. Первый удар классическим концепциям нанесло
построение в 20-х годах XIX в. гиперболической неевклидовой гео-
29
метрик, сделанное великим русским математиком Н.И. Лобачевским и
независимо от него (хотя и несколько позже) венгерским ученым
Я. Больяй.
Открытие неевклидовой геометрии потребовало отказа от претензий
предшествующих веков на «абсолютную истинность» евклидовой гео-
метрии, от точки зрения на аксиомы как на истины, не требующие доказа-
тельства в силу своей очевидности. Оказалось, что аксиомы скорее явля-
ются гипотезами, и речь идет о том, насколько построенные с их помо-
щью модели соответствуют материальному миру. Это послужило стиму-
лом к глубоким исследованиям в области оснований математики, к кри-
тике системы аксиом Евклида, к выяснению того, какими свойствами
может и должна обладать система аксиом. В дальнейшем это привело к
созданию аксиоматического метода, ставшего теперь одним из ведущих
методов познания не только в математике, но и в иных математизируе-
мых дисциплинах (математической экономике, математической лингвис-
тике и Т.Д.).
Важным этапом в развитии новых взглядов на математику явились
исследования Римана, показавшие неограниченное разнообразие гео-
метрических пространств, отличающихся друг от друга размерностью,
формулами для вычисления расстояний и т.д. Стали изучаться и про-
странства с комплексными координатами, а также пространства, эле-
ментами которых являются не точки, а прямые, окружности, сферы и
даже функции и последовательности (функциональные пространства).
Изучение функциональных пространств в дальнейшем привело к соз-
данию новой ветви математики — функционального анализа, в кото-
ром геометрические понятия и идеи применяются для решения задач
математического анализа.
Следует отметить, что восхождение от чувственного осязаемого,
реального пространства к абстрактным математическим пространст-
вам не означало отхода математики от отображения реального дейст-
вительного мира. Например, при создании в начале XX в. теории отно-
сительности были использованы геометрические идеи, разработанные за
полвека до того Б. Риманом, а в квантовой механике используют беско-
нечномерные пространства и линейные операторы в этих пространствах.
Качественные изменения произошли в начале XIX столетия и в ал-
гебре. В XVI—XVIII вв. алгебра занималась в основном решением
уравнений и систем уравнений, а также правилами преобразований
буквенных выражений, причем буквы в этих выражениях означали не-
которые числа. Таким образом, алгебра той эпохи была в своей основе
учением об общих свойствах арифметических действий над числами,
учением о формальных правилах преобразования выражений и реше-
ния уравнений.
30
Одиако к середине XIX в. понятие исчисления было расширено.
Различного вида операции начали производить не только над числами,
но и над векторами, кватернионами, матрицами, логическими выска-
зываниями и т.д. Правила этих действий отличались от привычных
правил действий над числами. Изучение таких исчислений привело к
необходимости исследовать общие свойства алгебраических операций
в произвольных множествах.
Изучение различных операций сочеталось с изучением таких ал-
гебраических структур, как группы и кольца, а позднее — поля, ре-
шетки и т.д. Эти структуры первоначально возникли из конкретных
задач алгебры и геометрии. Например, понятие группы было введено в
30-х годах XIX в. Э. Галуа в связи с задачей о разрешимости уравне-
ний в радикалах
В дальнейшем предметом алгебры становится изучение разного ро-
да алгебраических структур, порождаемых в множествах введением
различных операций. Этим значительно расширилось поле приложе-
ния алгебраических методов. Одна и та же алгебраическая теория (на-
пример, теория групп, теория коммутативных групп, теория колец,
теория полей и т.д.), описывающая определенный род алгебраических
структур, может применяться к любой структуре этого рода, в какой
бы предметной области она ни встретилась.
В конце XIX в. идеи теории групп стали применяться в геометрии.
Этот подход в геометрии был впервые сформулирован в 1872 г. не-
мецким математиком Ф. Клейном в его знаменитой Эрлангенской про-
грамме. Геометрия рассматривается Клейном как наука, изучающая
свойства фигур, не изменяющиеся при преобразованиях из той или
иной группы. Выбирая различные группы геометрических преобразо-
ваний (группы перемещений, подобий, аффинную, проективную, кон-
формную и т.д.), можно получить различные геометрии. А поскольку
отыскание инвариантов данной группы является алгебраической зада-
чей, то была установлена новая связь между алгеброй и геометрией.
Глубокие сдвиги произошли и в области математического анализа.
В ходе развития математики в XVIII в. не придавалось большого
внимания строгости рассуждения. Это привело к целому ряду
неясностей и даже к «скандалам в математике». Поэтому пришлось
критически пересмотреть основные понятия математического анализа,
начиная с понятия действительного числа. Лишь во второй половине
XIX в. это понятие оказалось «арифметизировано», т.е. сведено к
понятию натурального числа. Наряду с действительными числами в
математическом анализе начинают применять и комплексные числа,
что привело к созданию новой ветви математики — теории функций
комплексного переменного.
31
Критическому анализу были подвергнуты такие понятия математи-
ческого анализа, как «предел функции», «непрерывность», «производ-
ная», «интеграл». Им были даны определения, отличавшиеся большей
строгостью и общностью. Это позволило заметить, что, например, по-
нятия функции и геометрического преобразования весьма близки друг
к другу, и применить идею непрерывности в случаях, весьма далеких
от наглядности. Были уточнены понятия длины, площади и объема и
расширена область их применимости.
Исследования по теории интеграла и рядов Фурье привели к де-
тальному изучению разрывных функций, а позднее — к появлению
теории точечных множеств, т.е. множеств, состоящих из точек коор-
динатной прямой или плоскости.
Дальнейшее развитие теории множеств показало ее приложи-
мость к самым различным вопросам математики — алгебры и геомет-
рии, математического анализа и теории вероятностей. Общие методы и
понятия теории множеств позволили охватить с единой точки зрения
области математики, казавшиеся весьма удаленными друг от друга,
дали возможность сравнивать мощности различных множеств, т.е. как
бы «градуировать бесконечность».
Все сказанное привело к формированию нового взгляда на предмет
математики — стало ясно, что она изучает различные структуры, ко-
торые могут встречаться в различных предметных областях. Выяви-
лись общие идеи, лежащие в основе различных областей математики.
Начиная с этого момента выход на арену аксиоматического метода
становится общепризнанным фактом.
Важную роль в распространении этих идей сыграло завершение ра-
бот по аксиоматизации евклидовой геометрии. После критического
анализа аксиом Евклида первая полная система аксиом была создана
немецким ученым М. Пашем. В 1894 г. появилась книга Д. Гильберта
«Основания геометрии». В этой книге аксиомы геометрии были разби-
ты на группы и был исследован вопрос об их независимости, для чего
Гильберт построил самые разнообразные «геометрии», совсем непо-
хожие на евклидову. Таким образом, в области, рассматривавшейся до
того как одна из наиболее близких к действительности, была показана
возможность построения науки, исходя из произвольно выбранных по-
стулатов. Разумеется, этот произвол не следует понимать слишком бу-
квально — плодотворными оказываются лишь те системы аксиом, ко-
торые правильно отражают те или иные стороны действительности.
После указанных выше работ сложилась концепция математики,
которую академик А.Н. Колмогоров характеризует следующими двумя
тезисами:
А) В основе всей математики лежит чистая теория множеств.
32
Б) Специальные разделы математики занимаются структурами,
принадлежащими к тем или иным специальным родам структур Ка-
ждый род структур определяется соответствующей системой акси-
ом. Математика интересуется только теми свойствами структур,
которые вытекают из принятой системы аксиом, т е изучает
структуры только с точностью до изоморфизма
Точка зрения, выраженная в этих тезисах, получила наиболее пол-
ное отражение в работах группы современных французских математи-
ков (А. Вейль, Ж. Дьедонне и др.), п> бликующих свои труды под об-
щим псевдонимом «Николя Бурбаки». Ими выпускается многотомное
издание «Элементы математики», в котором наиболее важные разделы
современной математики рассматриваются с указанной выше точки
зрения (это издание еще далеко от завершения). Поэтому такую точку
зрения часто называют «бурбакистской», хотя в ее формировании
важную роль сыграли труды многих математиков XIX и XX вв., пи-
савших задолго до появления книг Н. Бурбаки.
Важной вехой в развитии теории вероятностей было создание ак-
сиоматики этой науки А.Н Колмогоровым. Благодаря этому было по-
казано, что теорию вероятностей можно рассматривать как теорию мер
особого вида, и потому к ней применимы методы теории функций дей-
ствительного переменного.
Систематическое применение аксиоматического метода позволило
выявить связи между областями математики, казавшимися очень дале-
кими друг от друга, найти пути преодоления тенденции к расщепле-
нию математики на почти независимые области и укрепить тем самым
единство математической науки. Оно дало ряд важных результатов
благодаря выявившейся возможности применять методы, выработан-
ные в одних областях математики, к иным областям, связанным с ними
единством структуры
6. Характерные черты современной математики и перспективы
ее развития. Развитие математики и расширение области ее примене-
ния показали, что в материальном мире существует ряд объектов и от-
ношений, математическое описание которых не сводится в чистом ви-
де к количественным отношениям и пространственным формам.
Выявилась роль таких математических структур, как эквивалентность,
порядок, близость и т.д. При этом стало ясно, что такие структуры
одинаково проявляют себя в различных предметных областях. Оказа-
лось далее, что наряду со структурами, непосредственно отражающи-
ми объекты и отношения реального мира, для многих приложений
нужны абстракции более высокого уровня.
Все это привело к тому, что данное Ф. Энгельсом определение
предмета математики было уточнено и приведено в соответствие с со-
33
временным состоянием науки — теперь речь идет не только о количе-
ственных отношениях и пространственных формах материального ми-
ра, а о любых формах и отношениях, взятых в отвлечении от их со-
держания. Но и эти абстрактные формы и отношения имеют в конеч-
ном счете прообразы в реальном мире.
Таким образом, в предмет математики теперь входят любые формы
и отношения действительного мира, которые объективно обладают та-
кой степенью независимости от содержания, что могут быть от него
полностью отвлечены и отражены в понятиях с такой ясностью и точ-
ностью, с сохранением такого богатства связей, чтобы дать основания
для чисто логического развития теории.
При этом в математике сейчас изучаются не только понятия, воз-
никшие при рассмотрении реальных объектов, но и свойства «мысли-
мых объектов» (например, шаров или спиралей в бесконечномерном
пространстве), математика изучает логически возможные чистые
формы, системы отношений. Главное в определении Энгельса, а
именно то, что математические понятия связаны с материальным
миром, а не являются продуктом деятельности «чистого сознания»,
сохранилось и теперь.
Предмет математики нельзя ни подменять формальными логиче-
скими схемами, ни низводить до уровня коллекции разрозненных фак-
тов. Математика есть учение об общих формах, свойственных реаль-
ному бытию, она создает постоянно развивающиеся теории, пригод-
ные для самых различных запросов естествознания и техники. Именно
это позволяет применять математические методы, разработанные при
решении задач одной области науки, к совершенно непохожим на них
задачам, относящимся к совсем иным областям знания.
Все сказанное показывает, что для современной математики ха-
рактерен весьма общий подход к предмету исследования Она абст-
рагируется как от конкретной природы объектов, так и от конкрет-
ного содержания отношений между ними. Для нее важна лишь
структура этих отношений. Роды структур, изучаемые современной
математикой, могут порождаться во множествах различной приро-
ды отношениями, отличными от количественных (в обычном их по-
нимании). Абстрактные математические пространства отражают
определенные формы действительности, однако эти формы дейст-
вительности не обязательно совпадают с пространственными фор-
мами в обычном их понимании.
Таким образом, расширение предмета математики привело к 'уше-
ственному расширению самого понятия количественных отношений и
пространственных форм. Содержащееся в определении Ф. Энгельса
34
выражение «количественные отношения и пространственные формы»
теперь следует понимать в более широком смысле, чем оно понима-
лось в период классической математики.
Следует отметить, что, несмотря на кажущуюся абстрактность мно-
гих разделов современной математики, она находит обширные приме-
нения в самых разных областях науки.
Серьезный толчок расширению области применения математики
дало создание во второй половине XX в. быстродействующих вычис-
лительных машин. Сейчас, когда их быстродействие измеряется мно-
гими миллионами операций в секунду, а память огромна, с помощью
таких машин можно решать задачи, о которых раньше невозможно
было и мечтать, настолько большой вычислительной работы они тре-
буют. В настоящее время вычислительные машины рассчитывают пу-
ти космических кораблей, позволяют моделировать работу атомных
реакторов, применяются для составления экономических планов и в
автоматических системах управления (АСУ), находят применения в
военном деле, управляют самолетами и т.д. Они во много миллионов
раз ускоряют формирование, поиск и обработку информации. Трудно
назвать область человеческой деятельности, не связанную так или
иначе с применением этих машин.
Создание быстродействующих вычислительных машин сделало
«прикладными» некоторые области математики, которые казались
раньше весьма далекими от какой-либо практики. В частности,
весьма важной для приложений оказалась математическая логика,
возникли новые отрасли математики (теория кодирования, теория
информации, теория алгоритмов, теория автоматов), так или иначе
связанные с вычислительными машинами. Бурное развитие получи-
ла конечная математика, связанная с изучением конечных мно-
жеств, почти заново была создана вычислительная математика. На
многие классические разделы математики пришлось смотреть под
иным углом зрения. Все это позволяет говорить о начале нового,
пятого периода в развитии математики, периода машинной матема-
тики.
Таким образом, математика сейчас переживает период бурного раз-
вития, диктуемого быстрым расширением областей ее применимости к
различным областям знания и техники. Как и в предыдущие периоды,
это развитие идет в следующих направлениях:
1) нахождение новых результатов в рамках уже определившихся поня-
тий —доказательство новых теорем о числах, функциях и тд.;
2) расширение предмета математики, связанное с включением в
нее новых форм и отношений;
35
3) развитие новых общих методов решения задач и доказательства
теорем;
4) восхождение к новым абстракциям, введение новых абстракт-
ных понятий;
5) углубление основных понятий, таких, как понятие множества,
алгоритма, доказуемости и т.д.
Мы видим, что развитие математики не сводится к количественно-
му росту, но включает глубокие качественные изменения. При этом
если последовательность развития математики определяется в значи-
тельной степени объективной логикой предмета (в этом находит свое
отражение относительная самостоятельность математической науки),
то темпы роста диктуются общими условиями, в частности потребно-
стями научно-технической революции.
Развитие математики является естественным ответом на все возрас-
тающую сложность и трудность проблем, с которыми она имеет дело.
Поскольку такие проблемы прямо или косвенно возникают при реше-
нии задач других областей науки, эта сложность математических про-
блем отражает все возрастающую сложность и разветвленность совре-
менного естествознания и наук об обществе.
Как и ранее, развитие математики в настоящее время происходит в
процессе борьбы многих сплетающихся в ней противоположностей:
конкретного и абстрактного, частного и общего, формального и со-
держательного, аксиоматического и конструктивного, конечного и
бесконечного, дискретного и непрерывного. Эта борьба противопо-
ложностей, развертывающаяся по законам, открытым материалистиче-
ской диалектикой, приводит к их постоянному разрешению и восста-
новлению на все более приближающихся к действительности ступенях
познания, ко все более глубокому и полному познанию объективной
реальности, идущему по восходящей линии.
Указанные выше и иные противоречия математической науки яв-
ляются следствиями ее основного противоречия. Математика изучает
отношения и формы, абстрагируясь от содержания. Но формы и отно-
шения не существуют вне содержания, а потому математические фор-
мы и отношения не могут быть абсолютно безразличны к содержанию.
Это и есть коренное противоречие в сущности математики, которое
наряду с противоречивостью понятия бесконечности является внут-
ренней движущей силой ее развития.
Как перед самой математикой, так и перед исследованиями по ее
основаниям лежит путь бесконечного развития и уточнения, а оконча-
тельное решение проблем оснований математики так или иначе упира-
ется в отношения этой науки к действительности.
36
Т. Фройденталь
АКСИОМАТИЧЕСКАЯ АБСТРАКЦИЯ’
Около 1870 года началось создание не только теории множеств, но
и современной аксиоматики, разумеется, в геометрии, ибо она издавна
была областью, в которой, естественно, возникала проблема дедуктив-
ного построения из основных положений — аксиом. Неевклидова гео-
метрия, послужившая толчком для развития аксиоматики, расцвела из
туманных начал около 1830 г. Аксиоматику проективной и комплекс-
ной проективной геометрии пытался создать Хр. К. Г. фон Штаудт в
40—50-х гт. Первую действительно полную аксиоматику евклидовой
геометрии предложил Паш. Он показал математикам, как следует фор-
мулировать аксиомы. Вскоре, однако, более глубокие «Основания
геометрии» Гильберта (1899) затмили работы Паша.
Смысл, который мы ныне, т.е. начиная с Гильберта, вкладываем в
слова «аксиома», «аксиоматика», совсем новый. Начиная с греков и до
философов начала XX в. под аксиомой понималось такое предложе-
ние, которое было недоказуемым, да и не требовало доказательства,
так как было основой и условием каждого доказательства, и было яс-
нее, очевиднее и более общим, чем то, что из него выводилось. Кое-
что, например постулат о параллельных, который в течение веков пы-
тались доказывать, не содержится в списке аксиом ни у Евклида, ни,
вообще говоря, у более поздних авторов. Паш также не говорит о та-
кой аксиоме, когда он имеет в виду основания геометрии; в француз-
ском и английском языках до самого нашего столетия сохранился
обычай говорить о постулате. По-видимому, Гельмгольц был первым,
кто назвал геометрические постулаты аксиомами (вероятно, вследст-
вие ложной интерпретации Канта); ему последовали Пуанкаре и Гиль-
берт, который в своих «Основаниях геометрии» ввел нынешнее упот-
ребление слов «аксиома» и «аксиоматика».
«Основания геометрии» Гильберта начинаются так: «Мы мыслим
три различные системы вещей, ... точки, ... прямые, ... плоскости.... Мы
мыслим точки, прямые и плоскости в определенных соотношениях ...,
как-то: «лежать», «между», «параллельный», «конгруэнтный», «непре-
рывный»... . Точное описание этих соотношений достигается аксиома-
ми геометрии».
Если мы ожидаем описания этих понятий, вроде «точка есть то, что
не имеет частей» (именно так записано у Евклида), то нас ждет раз-
очарование. У Гильберта нет таких явных описаний. Аксиомы дают
неявные описания, устанавливающие определенные свойства точек,
37
прямых, плоскостей и взаимосвязей между ними, вроде «существует
единственная прямая, которая проходит через две данные точки».
Фреге считал недостатком системы аксиом Гильберта невозмож-
ность установить с их помощью, что собой представляет точка; на-
пример, являются ли его — Фреге — карманные часы точкой. Гиль-
берт, напротив, подчеркнул, что в том и состоит суть аксиоматики, что
она позволяет вместо точек, прямых, плоскостей говорить о стульях,
столах и пивных кружках. Лишь свойства, явно указанные в аксиомах,
играют роль в дедуктивных рассуждениях. Это как в шахматах, где
свойства фигур определяются не их формой, а правилами игры.
Признание неявных определений было важным шагом, который
стал образцом всей современной методологии науки. Важность неяв-
ных определений была впервые подчеркнута математиком Жергоном
(1818). Тем самым был сделан решающий шаг на пути отхода от уче-
ния Аристотеля; выведение науки из точно сформулированных прин-
ципов было от Аристотеля до Жергона редко оспаривавшимся, но и
никогда не выполнявшимся даже приближенно идеалом.
Как только Гильберту удалось аксиоматически обосновать геомет-
рию Евклида и тем самым точно определить геометрические понятия,
аксиоматика получила новое направление, которое, впрочем, было уже
предопределено в «Основаниях геометрии» Гильберта. Важным наме-
рением Гильберта было выяснить, насколько существенны различные
аксиомы; что будет, если отказаться от той или иной аксиомы. Если
ничего не изменится, то аксиома является излишней. Если же она не
лишняя, то редуцированная система аксиом будет определять уже не
евклидову геометрию, а некоторый класс обобщенных, более слабых
геометрий, удовлетворяющих этой сокращенной системе аксиом. Как
раз такие системы аксиом, определяющие не единый объект, но удов-
летворяющие многим не изоморфным друг другу «моделям», оказа-
лись важными в дальнейшем. Собственно говоря, такие системы акси-
ом были известны и раньше, но никто не называл их аксиомами; ныне
их называют требованиями, которые налагаются на некоторый мате-
матический объект, чтобы он был группой, это также аксиомы, аксио-
мы группы, но сколь далеки они от традиционных аксиом!
История понятия группы является прекрасным примером возник-
новения подобных систем аксиом Лейтмотивом оживления геометрии
в XIX в. послужили геометрические преобразования. Были открыты
проективные, аффинные, эквиформные и т.д. преобразования, рас-
сматривались композиции таких преобразований, было установлено,
что эти преобразования образуют группы, еще до того, как было про-
изнесено это слово или кто-либо определил, что такое группа. Другие
группы, которые исследовали, также не зная еще, что такое группа, —
38
это группы перестановок. Таким образом, еще до того, как около 1870 г.
было сформулировано абстрактное понятие группы, в работах матема-
тиков встречались уже не только разнообразные группы, но и некото-
рая часть теории групп, сформулированная лишь для отдельных част-
ных случаев. Сама теория групп возникла как средство упорядочить
эти частные результаты; метод заключался в том, что общие для всех
групп свойства, к которым пришли позднее, — ассоциативность ум-
ножения, существование единицы и обратного элемента — были
сформулированы и названы аксиомами группы. Что такое группа, ус-
танавливается определенными требованиями, подобно тому как это
сделано в геометрической аксиоматике. Однако для аксиом евклидо-
вой геометрии есть, по сути дела, лишь одна модель — сама евклидова
геометрия; аксиомам группы удовлетворяют многие модели. Иногда
шутят, что аксиомы группы позволяют облегчить себе жизнь, объеди-
няя различные вещи в одну кучу.
Возникновение понятия группы может рассматриваться как образец
для описанного метода введения новых математических понятий. К
этому понятию нельзя было прийти, просто объединяя вместе все из-
вестные в то время примеры групп, а надо было выделить общие свой-
ства всех этих примеров. Аналогичным образом было введено в 1910 г.
Е. Штейницем понятие поля (исходя из полей рациональных, действи-
тельных и комплексных чисел, полей Галуа, р-адических чисел и т.д.).
С этого момента ведет свое летосчисление абстрактная алгебра. В
1914 г. было введено общее понятие линейного пространства, охва-
тившее многочисленные примеры ранее известных функциональных
пространств. В 30-х гт. это понятие под названием векторного простран-
ства было использовано для изложения аналитической геометрии.
Первыми областями математики, аксиоматизированными после
геометрии (и после Гильберта), оказались алгебра, примеры из кото-
рой приведены выше, и топология (Фреше, Хаусдорф). Множества то-
чек евклидова пространства, римановых поверхностей, многообразий
и множества функций были объединены вначале в метрические, а за-
тем в топологические пространства. Если абстрактная алгебра еще пи-
талась понятиями старой алгебры, то в топологии возникли свои фун-
даментальные понятия, которых не было в прежних специальных под-
ходах, — такие понятия, как полнота, компактность, сепарабельность,
или такие, которые можно правильно понять лишь с обобщенной точ-
ки зрения, — связность, размерность, произведение пространств и т.д.
Но то же самое относится в значительной мере и к алгебре.
Вероятно, еще более характерна «абстрактная» точка зрения в ана-
лизе, так как здесь в изобилии имеются «конкретные», т.е. формули-
руемые в старом анализе, результаты, полученные абстрактным путем,
39
которые невозможно было бы получить прежними методами. Пора-
зившим меня некогда примером могут служить почти-периодические
функции. Г. Бор называл непрерывную функциюf одной действитель-
ной переменной почти-периодической, если для каждого е > О сущест-
вует интервал длины I (е), в котором существует «почта-период» г (е),
такой, что [Дх + г (е)) -Дх)| < е для всех х. Это замечательное опреде-
ление. Должен признаться: будучи студентом, я однажды принимал
участие в семинаре по почти-периодическим функциям, но едва ли я
понял, что же собственно представляют собой эти функции. Позднее,
в один прекрасный день, я прочитал новую — абстрактную — форму-
лировку С. Бохнера: «Рассматривается линейное пространство Ф не-
прерывных ограниченных функций с нормой, равной верхней грани
значений функции; в этом пространстве рассматривается сдвиг Та (т.е.
(То /)(х) = fix + а)); функция f из Ф называется почти-периодической,
если пространство функций Taf имеет компактную оболочку».
У меня сразу все прояснилось; я тотчас понял все существенное в
определении Г. Бора и в его доказательстве. «Перевод» Бохнером оп-
ределения Бора на абстрактный язык оказался для меня убедительной4»
иллюстрацией моши абстрактного метода. Кстати, этот метод привел
меня не только к пониманию определения Бора, но и дальше, к пони-
манию почти-периодических функций на любых группах (а не только
на группе переносов на числовой прямой).
Примерно до конца 1920-х гт. аксиоматические стремления в ал-
гебре, топологии и анализе развивались более или менее независимо
друг от друга. Анализ, включавший в себя аксиоматические элементы
алгебры и топологии, дал толчок к комбинированию структур. Из-
вестные образования, как, например, поле действительных чисел,
можно рассматривать в качестве топологического поля, или в качестве
упорядоченного поля, или в качестве метрического поля, т.е. можно
образовать слияние двух или более структур, которые при уточнении
описания не должны противоречить друг другу. Топологическое поле
есть поле с топологией, причём операции поля непрерывны. Для упо-
рядоченного поля требуется наличие порядка, который сохраняется
при сложении и при перемножении положительных элементов. Метриче-
ское поле обладает нормой |...| с условиями: | а + Ь\ 5 |а| + |fr| и | afe| =
= |а| -|А|. Точно так же определяются топологические группы, группы
с мерой, линейные топологические пространства, метрические линей-
ные пространства. И здесь действует математическая абстракция, по-
зволяющая расчленить свойства объектов, способствующая большей
ясности и более глубокому пониманию. Абстракция полезна для по-
нимания элементарных свойств действительных чисел, для понимания
того, какие свойства зависят от аксиом кольца, какие — от аксиом по-
до
ля, от коммутативности умножения, от полноты, от локальной ком-
пактности и т.д.
МАТЕМАТИКА ПОНЯТИЙ И МАТЕМАТИКА АЛГОРИТМОВ
Имеется стакан белого вина и стакан красного; уровень вина в ста-
канах одинаков. Берут одну чайную ложку из стакана с красным вином
и вливают в стакан с белым, размешивают, затем чайную ложку смеси
вливают в стакан с красным вином. Чего больше: красного вина в ста-
кане с белым или белого вина в стакане с красным?
Эти количества одинаковы. Пусть объем стакана а, объем чайной
ложки Ь. После первого переливания. Треть тех, кто пытается решить
задачу таким путем, ошибаются. Лишь немногие рассуждают так: по-
сле всех переливаний количество жидкости в обоих сосудах одинако-
во; будем считать, что белое и красное вино не смешались; то количе-
ство красного вина, которое оказалось в сосуде с белым, отсутствует
(не хватает) в стакане с красным; значит, оно заменено белым. Поэто-
му красного вина в стакане с белым ровно столько же, сколько белого
вина в стакане с красным.
Первое решение алгоритмическое, второе — понятийное. Это лишь
один пример из многих, но пример весьма типичный. Он лишь на одно
мгновение ясно показывает различие между алгоритмической и поня-
тийной математикой. Ниже нам придется вернуться к дидактическому
значению этого различия. Здесь же мы остановимся на его историче-
ском аспекте.
Слово «алгоритм» увековечило память ал-Хорезми (Мохаммед ибн
Муса, VIH в.), который зафиксировал индо-арабский метод вычисле-
ний. Методы или, если угодно, рецепты вычислений называют алго-
ритмами. Алгебра Виета, аналитическая геометрия Декарта, диффе-
ренциальное и интегральное исчисление Лейбница являются такими
алгоритмами, и их создатели отдавали себе в этом отчет. Виета ясно
сказал об этом в своем введении; Декарт назвал геометрию в качестве
первого примера в своем «Рассуждении о методе»; Лейбниц был
одержим желанием находить алгоритмы, и это удалось ему столь пре-
восходно, что с помощью своего алгоритма он совершенно затмил
аналогичную по содержанию работу Ньютона; мощь алгоритма нигде
не проявляется столь ярко, как в дифференциальном и интегральном
исчислении. С проблемами, решение которых требовало гениальности
на уровне Архимеда или Гюйгенса, мог после Лейбница, используя его
алгоритм, шутя справиться любой посредственный математик.
Осуществление действенного алгоритма могло принести известное
ощущение мощи, но могло и удовлетворить потребность в игре. Так
41
расцвели алгоритмы, имевшие весьма ограниченную область дейст-
вия: начертательная геометрия, символический метод в теории инва-
риантов, Шубертов метод в исчислительной геометрии — только тот,
кто хоть однажды пользовался этим инструментом, может оценить, на-
сколько он захватывает. Ряды Фурье или более общие ортогональные ря-
ды, интеграл Фурье, вычеты, интегральные формулы Гаусса—Грина—
Стокса, функции Грина, исчисление Хивисайда, интеграл Лапласа —
эти термины позволяют вспомнить хорошо известные алгоритмы, поя-
вившиеся еще в XIX в.
Часто утверждают, что современная математика отличается от
классической усилением роли понятий за счет алгоритмического. По-
жалуй, верно, что самое поразительное новшество, с которого начина-
ется современная математика, — теория множеств, абстрактные ал-
гебра и анализ, топология — прямо-таки извержения понятий, про-
рвавшие застывшую лаву алгоритмического; это я уже неоднократно
подчеркивал ранее. Но когда-нибудь застынет и эта лава. Каждое но-
вое понятие таит в себе зародыш алгоритмического — в этом и заклю-
чается особенность математики.
Некогда арифметические действия были наукой. Лишь после того,
как они были механизированы, смогла свободнее развиваться теория
чисел. Без алгоритма дифференциального и интегрального исчисления
едва ли появился бы анализ. Алгоритмизируя математические методы,
их консолидируют. Было бы несправедливо противопоставлять алго-
ритмическую и понятийную математику или принижать одну форму,
возвеличивая другую; несправедливо также одну из форм считать «со-
временной», а другую — «устаревшей».
Систематизация и математизация. Коль скоро наука прошла пе-
риод накопления фактов, она переходит к упорядочению опыта. Не-
трудно указать сведения, упорядочение которых приводит к элемен-
тарной арифметике и геометрии. Математизацией мы назовем также
упорядочение действительности, если это выполняется математиче-
скими средствами. Однако математик часто сразу же отказывается от
рассмотрения действительности; он может сделать это в тех случаях,
когда логические взаимосвязи гарантируют быстрое достижение успе-
ха. Так собирается по крупицам математический опыт, который в
свою очередь снова должен быть систематизирован. Но какими сред-
ствами? Разумеется, математическими, — и таким образом математи-
зируется математика. Сначала в малом: что принять за определение и
что за теорему? Обосновать «это» — «тем» или наоборот? Доказать
«это» как особый случай «того» или начать с особого случая? А затем
перейти к общему: сознательному построению теории, аксиоматиче-
скому или явному виду?
42
Так поступали издавна Некоторые уравнения второй степени мож-
но рассматривать как уравнения кривых; эти кривые, как установил
еще Меиехм, являются коническими сечениями. Аполлоний начал с
конических сечений, чтобы ст них перейти к уравнениям. В новое
время снова повернули на 180° и поставили уравнения в начало. Одна-
ко в проективной геометрии конические сечения появляются раньше,
чем геометрическое место точек пересечения соответствующих пря-
мых, относящихся к рассматриваемому проективному пучку.
Ныне математизация математики — одно из основных занятий ма-
тематиков. Нет ни одной науки, в которой переработка, упорядочение
стали бы столь необходимы, как в математике. Кажется, что ничего не
должно повторяться; и тот, кто читает лекционный курс, перерабаты-
вает материал заново; почему нет, если это действительно ново, ори-
гинально и лучше, чем по-старому?
Эти поиски новшеств удаются в других науках гораздо меньше —
следовало бы сказать, совсем мало. Можно, скажем, заметить, что не-
которые главы теоретической физики десятилетиями, даже столетиями
переписываются из одного учебника в другой, причем авторы подчас
не замечают, что главы, появившиеся в разные периоды времени, про-
тиворечат друг другу или по содержанию, или по форме.
Тот, кто не проследил шаг за шагом постоянную реорганизацию
математики, может испытать трудности при попытке сразу переско-
чить всю последовательность ее развития. Тот, кто, не будучи матема-
тиком, привык применять в своей специальности математику своих
школьных лет, быстро приходит к неверному мнению о том, что такое
современная математика. Поразительно, что физики весьма скептиче-
ски относятся к той самой математике, которая не представляет за-
труднений для экономистов, психологов, лингвистов и других, именно
потому, что первые применяют математику издавна, а последние —
лишь недавно.
Выше уже подчеркивалось, что постоянное новое упорядочение не
каприз, а необходимость. Каждый знает, сколь стремительно развива-
ются науки. Чтобы овладеть ими, нужно привести наши знания в сис-
тему. К математике это относится так же, как и к другим наукам; в ма-
тематике это делается более осознанно и на более высоком уровне, чем
в какой-либо другой науке: ведь упорядочение в математике тоже ма-
тематическая деятельность. Едва ли сомнительно, что ныне математик
обозревает намного большую часть математики, чем его коллега пол-
века назад, — и это несмотря на рост математики, с одной стороны, и
благодаря новым формам организации — с другой. Из организацион-
ного опыта математиков могут вынести пользу на длительное время и
представители других наук, и математики могут помочь им в этом. В
43
недалеком будущем математики-прикладники будут заниматься упо-
рядочением материалов опыта и областей исследования и прежде все-
го математическим опытом формализации, т.е. формально-логическим
упорядочением.
В качестве систематизаторов математики наиболее известны Бур-
баки. Сколь убедительно упорядочена у иих математика! Столь неос-
поримо, что Пиаже смог «переоткрыть» бурбакистский порядок с по-
мощью психологического подхода. Бедный Пиаже! Пиаже не матема-
тик, и ои не мог знать, как мало можно полагаться на математика-
систематизатора. Еще до того, как Бурбаки закончили упорядочение
математики, было открыто значение категорий. Едва ли можно сомне-
ваться, что категории — инструмент нового порядка и что от бурбаки-
стского построения не останется камня на камне, если перестроить его
в стиле теории категорий, которая тоже когда-нибудь будет заменена
новым подходом к систематизации математики .
Между тем категории действительно замечательное средство для
упорядочения математики заново. Кто не знает, что такое категории,
пусть не очень сожалеет об этом; автор этих строк не очень уверен,
что знает их, также и потому, что эта теория еще только формируется.
Он может убедить себя и других, что знает, что такое категории, пре-
подавая их; но, несмотря на повторные усилия, ему это не удается. В
один прекрасный день он поймет, как это делается, найдет нужный
подход; кто-то другой продолжит, и, как водится, через 20 лет или еще
раньше первый семестр начнется с изучения категорий.
Если я не умею объяснить, что такое категории, то могу, пожалуй,
рассказать анекдот об одном профессоре математики, к которому
пришел некто с готовой диссертацией — не его ученик и даже не ма-
тематик, а инженер. В рукописи было около 30 страниц, и автор наде-
ялся, что она может быть принята в качестве диссертации. Профессор
спешил, он лишь бегло перелистал текст и сказал: «Это напоминает о
категориях. Вы знаете теорию категорий?» — «Нет», — ответил дис-
сертант и отправился изучать категории. С такой скоростью идут те-
перь дела. И чем современнее математика, тем она проще. Выясни-
лось, что работу объемом в 30 страниц с помощью категорий можно
изложить на трех страницах. Три странички составили бы бедноватую
диссертацию; но через некоторое время из них можно было бы опять
сделать тридцать, десятикратно увеличив содержание.
Приложения. Тот, кто прочитает эту главу, может подумать, что
современная математика лишь формализованный вариант прежней.
Это абсолютно неверно. В течение последних десятилетий не только
решены многие прежние проблемы, но в математике возникли и со-
вершенно новые области. Я усиленно подчеркиваю формальную сто-
44
рону, потому что это главное для обучения математике в школе. По
содержанию же школьная математика в ближайшем будущем едва ли
значительно превзойдет школу XIX в.
Правда, я должен сделать исключение в отношении того, что назы-
вают прикладной математикой. Возможно, что современные примеры
прикладной математики в школе превзойдут прежние — сейчас станет
ясно почему.
Я начал первую главу с прикладной математики или, скорее, с не-
посредственных применений математики, потому что это была исто-
рически первая математика — и я подчеркивал постоянное взаимо-
влияние математики и ее приложений друг на друга. Разве в наши дни
взаимосвязь математики и ее приложений изменилась? Вовсе нет;
львиная доля прикладной математики в естественных науках и в тех-
нике требует развития классических областей: алгебры, специальных
функций, интегралов, дифференциальных и интегральных уравнений,
вариационного исчисления весьма конкретного вида. При наличии со-
временной вычислительной техники эти области стали еще важнее,
ибо многие проблемы, которые раньше витали в облаках чистой тео-
рии, допускают теперь численные решения. Это, пожалуй, следует
подчеркнуть в противоположность тенденциям пренебрежительного
отношения к анализу в школьном и вузовском преподавании.
И еще нужно отметить, что среди тех, кто применяет математику,
особенно нелегко пришлось физикам. Около 1930 г. это стало особен-
но заметно в связи с усилением роли представлений групп и эрмито-
вых операторов в гильбертовых пространствах. Современная физика
живет такой математикой, новее же и в физике она не вполне прижи-
вается; редуцируют теорию групп (физики говорят: групповую чуму)
до классической алгебры и упускают при этом все преимущества
групповой трактовки, а также ослабляют, насколько возможно, суще-
ственные абстракции в абстрактном анализе. Несомненно, что физики
в своих стремлениях — с помощью специально для этого случая при-
думанных методов избежать современной математики и вернуться к
классическим методам — сами себя наказывают. В их же интересах
следует подчеркнуть смысл современной математики.
К современным приложениям математики нужно отнести также ма-
тематическую статистику, которая в нынешних формах также возник-
ла около 1930 г. В противоположность тому, что называется матема-
тической физикой, статистика является областью приложения весьма
элементарных разделов математики. Поэтому неудивительно, что ею
занимается множество людей, не получивших собственно математиче-
ского образования; статистика является полем деятельности ученых и
инженеров самых различных специальностей. После 1945 г. число ста-
45
тистиков стало стремительно расти; теперь оно не растет уже столь
быстро, но статистика была и остается весьма плодотворной областью
применения математики.
Наиболее поразительной новинкой среди прикладных математиче-
ских дисциплин является, однако, область, которую трудно определить
одним термином. Обычно используют выражение «исследование опе-
раций». Сюда относят теорию автоматов, логику контактных схем и
вычислительных устройств, теорию игр, математику средств связи и
теории информации, математический аппарат обработки числовых
данных и хранения информации, линейное программирование, кибер-
нетику и многое из теории графов. Однако вместо того, чтобы бро-
саться словами, я лучше приведу примеры задач, о которых идет речь;
некоторые из них могут показаться тривиальными или нечетко сфор-
мулированными, но они показывают наиболее существенное.
Как быстрее всего найти максимальный член последовательности?
Как быстрее упорядочить эти члены по величине? Каким приемом ре-
шить систему линейных уравнений с сотней неизвестных и как обсто-
ит дело с точностью результата? Как лучше всего построить контакт-
ную схему для заранее указанной цепи? Какие размеры должна иметь
телефонная станция, чтобы время ожидания (или потери переговоров)
не превышало определенных границ? Какие запасы товара должен
иметь торговец, чтобы наивыгоднейшим образом лавировать между
Сциллой («к сожалению, распродано») и Харибдой (залежалый товар)?
Целесообразно ли блефовать при игре в покер? В каком порядке ком-
мивояжер может кратчайшим путем посетить 50 указанных пунктов?
Как кратчайшим способом выявить фальшивую (более легкую) монету
среди множества одинаковых по массе? Как кодировать текст, чтобы
телеграфная передача обходилась возможно дешевле? Как расшифро-
вать тайнопись? Как уберечься от ошибок при передаче числовых по-
следовательностей? Как ослабить шумовые помехи при передаче сиг-
налов? Как уловить скрытую периодичность в шумовых помехах? Как
раскладывать пасьянс?
Надеюсь, что эти примеры скажут читателю больше, чем вышепри-
веденные названия. Здесь многократно встречаются проблемы, для
решения которых методы классической математики малоприменимы,
проблемы, каждая из которых требует особой теории; особенно отно-
сится это к «конечным» проблемам, т.е. таким, которые теоретически
могут быть решены за конечное число шагов, однако практически их
можно решить лишь при наличии подходящей стратегии — как раз той
стратегии, которая требуется в данной конкретной задаче.
Все это само по себе требует больших вычислительных установок,
для которых придумывают стратегии поиска; они в свою очередь так-
же требуют определенной стратегии.
46
Числовые расчеты издавна широко применялись в астрономии;
чтобы удовлетворить ее потребности, понадобились тригонометри-
ческие и логарифмические вычисления. Следующими вычислите-
лями оказались геодезисты и специалисты страхового дела, которые
разработали свой аппарат главным образом в XIX в.; к концу века
было разработано много методов вычислений, которые применяют-
ся и поныне. С распространением вычислительной техники век ло-
гарифмов окончился. Существенный перелом произошел после
1945 г.: лишь для ЭВМ с их невообразимым быстродействием стало
возможным рассмотрение многих проблем, к которым ранее не уда-
валось даже подступиться Тем самым вычислительная математика
колоссально расширилась и по содержанию. Нигде больше не выяв-
ляется столь четко, сколь разнообразно применяется математика:
теми, кто математизирует проблему; теми, кто знает формулы и де-
лает возможными вычисления; теми, кто переводит формулы на
язык ЭВМ; вычислительной машиной, которая обрабатывает полу-
ченные данные. Или иначе: создателем ЭВМ, разработчиками стра-
тегий, машинных языков, программ... Это очень разносторонняя
математика, которая используется при применении электронной
вычислительной техники.
Если говорить об областях применения, математика также очень
расширилась. Не стоит повторять, что везде и всюду применяются
ЭВМ. Точно так же везде, где обрабатываются статистические мате-
риалы, применяются математические методы. Вообще говоря, это не
методы классического анализа или математической физики, кото-
рые приспосабливают к потребностям новых областей применения.
Это проблемы комбинаторики, оптимизации, логики, организации,
т.е. проблемы, для решения которых нет готовых рецептов в суще-
ствующей литературе. Во всех науках произошли перевороты под
влиянием математики. Не решенные пока что проблемы примене-
ния ЭВМ для чтения и перевода текстов побудили лингвистов ис-
следовать структуры языка с совершенно новых точек зрения, ис-
ходя из математических принципов. Чтобы привлечь ЭВМ для ме-
дицинской диагностики, пришлось упорядочить симптомы с логи-
ческой точки зрения. Хозяйственные работники, предлагая крупные
экономические мероприятия, кладут в основу своих прогнозов ма-
тематические модели.
Так всплывает ужасающая картина, предсказывающая, что однаж-
ды нами начнут управлять вычислительные машины. Что это, химера
или реальность нашего завтра? Нет сомнений, что и ответ на этот во-
прос принадлежит математике точно так же, как решения дифферен-
циального уравнения.
47
<Р. Курант Т. (Роббинс
ЧТО ТАКОЕ МАТЕМАТИКА?5
Математика содержит в себе черты волевой деятельности, умозри-
тельного рассуждения и стремления к эстетическому совершенству. Ее
основные и взаимно противоположные элементы — логика н интуи-
ция, анализ и конструкция общность и конкретность. Как бы ни были
различны точки зрения, питаемые теми или иными традициями, только
совместное действие этих полярных начал и борьба за их синтез обес-
печивают жизненность, полезность и высокую ценность математиче-
ской науки.
Без сомнения, движение вперёд в области математики обусловлено
возникновением потребностей, в большей или меньшей мере носящих
практический характер Но раз возникшее, оно неизбежно приобретает
внутренний размах и выходит за границы непосредственной полезно-
сти. Совершающееся таким образом превращение прикладной науки в
теоретическую наблюдается в истории древности, но не в меньшей
степени также и в наши дни: достаточно принять во внимание тот
вклад, который сделан в современную математику инженерами и фи-
зиками.
Первые памятники математической письменности создаются на
Востоке: уже примерно четыре тысячи лет тому назад вавилоняне со-
брали обширный материал который мы склонны были бы в настоящее
время отнести к элементарной алгебре. Но как наука в современном
смысле слова математика возникает позднее на греческой почве, в пя-
том и четвёртом столетиях до нашей эры. Всё усиливающееся сопри-
косновение между Востоком и Грецией, начавшееся во времена Пер-
сидской империи и достигшее апогея в период, непосредственно сле-
дующий за экспедициями Александра, обеспечило для греков возмож-
ность перенять достижения вавилонян в области математики и астро-
номии. Математика не замедлила стать объектом философских дис-
куссий, обычных в греческих государствах-городах. Таким образом,
греческие мыслители осознали значительные трудности, связанные с
основными математическими концепциями — непрерывностью, дви-
жением, бесконечностью — и с проблемой измерения произвольных
величин данными заранее единицами. Но обнаружилась и решимость
преодолеть препятствия: возникшая в результате великолепного уси-
лия мысли эвдоксова теория геометрического континуума представля-
ет собой такое достижение, которое можно поставить в один ряд толь-
ко с современной теорией иррациональных чисел.
48
Хотя теоретико-постулативная тенденция незыблемо остаётся од-
ной из самых ярких особенностей греческой математики и как таковая
оказала беспримерное влияние на дальнейшее развитие науки, тем не
менее необходимо со всей энергией указать, что практические потреб-
ности и связь с физической реальностью участвовали никак ие в
меньшей мере в создании античной математики и что изложению, сво-
бодному от эвклидовой строгости, очень часто отдавалось предпочтение.
Не исключено, что именно слишком раннее открытие трудностей,
связанных с «несоизмеримыми» величинами, помешало грекам раз-
вить искусство численных операций, сделавшее в предшествовавшие
эпохи значительные успехи на Востоке. Вместо этого они стали искать
путей в дебрях чистой аксиоматической геометрии. Так началось одно
из странных блужданий в истории науки, и, может быть, упущены бы-
ли при этом блестящие возможности. Почти на два тысячелетия вес
греческой геометрической традиции задержал неизбежную эволюцию
идеи числа и буквенного исчисления, ставшего позднее фундаментом
точных наук.
После периода медленного накопления сил — с возникновением в
XVII столетии аналитической геометрии и дифференциального и ин-
тегрального исчислений — открылась бурная революционная фаза в
развитии математики и физики. В XVII и XVIII вв. греческий идеал
аксиоматической кристаллизации и систематической дедукции поту-
скнел и утерял своё влияние, хотя античная геометрия продолжала вы-
соко расцениваться. Логически безупречное мышление, отправляю-
щееся от отчётливых определений и «очевидных», взаимно ие проти-
воречащих аксиом, перестало импонировать новым пионерам матема-
тического знания. Предавшись подлинной оргии интуитивных дога-
док, перемешивая неоспоримые заключения с бессмысленными полу-
мистическими утверждениями, слепо доверяясь сверхчеловеческой
силе формальных процедур, они открыли новый математический мир,
полный несметных богатств. Но мало-помалу экстатическое состояние
мысли, упоённой головокружительными успехами, уступило место
духу сдержанности и критицизма. В XIX столетии сознание необхо-
димости консолидировать науку, особенно в связи с нуждами высшего
образования, после французской революции получившего широкое
распространение, повело к ревизии основ новой математики; в частно-
сти, внимание было направлено к дифференциальному и интегрально-
му исчислениям и к уяснению подразумеваемого анализом понятия
предела Таким образом, XIX в. не только стал эпохой новых успехов,
но и был ознаменован плодотворным возвратом к классическому
идеалу точности и строгости доказательств. В этом отношении грече-
ский образец был даже превзойдён. Ещё один раз маятник качнулся в
49
5 Зак 72
сторону логической безупречности и отвлечённости. В настоящее вре-
мя мы ещё, по-видимому, не вышли из этого периода, хотя позволи-
тельно надеяться, что установившийся прискорбный разрыв между
чистой математикой и её жизненными приложениями сменится эрой
более тесного единения. Приобретённый запас внутренних сил и, по-
мимо всего прочего, чрезвычайное упрощение, достигаемое на основе
ясного понимания, позволяют сегодня манипулировать математиче-
ской теорией таким образом, чтобы приложения не упускались из ви-
ду. Установить ещё раз органическую связь между чистым и приклад-
ным знанием, здоровое равновесие между абстрактной общностью и
полнокровной конкретностью — вот как нам представляется задача
математики в непосредственно обозримом будущем
0. Тиль Берт
МАТЕМАТИЧЕСКИЕ ПРОБЛЕМЫ И ИХ ИСТОЧНИКИ8
История учит, что развитие науки протекает непрерывно. Мы зна-
ем, что каждый век имеет свои проблемы, которые последующая эпоха
или решает, или отодвигает в сторону как бесплодные, чтобы заменить
их новыми. Чтобы представить себе возможный характер развития ма-
тематического знания в ближайшем будущем, мы должны перебрать в
нашем воображении вопросы, которые еще остаются открытыми, обо-
зреть проблемы, которые ставит современная наука и решения кото-
рых мы ждем от будущего. Такой обзор проблем кажется мне сегодня,
на рубеже нового столетия, особенно своевременным. Ведь большие
даты не только заставляют нас оглянуться на прошедшее, но и направ-
ляют нашу мысль в неизвестное будущее.
Невозможно отрицать глубокое значение, какое имеют определен-
ные проблемы для продвижения математической науки вообще, и важ-
ную роль, которую они играют в работе отдельного исследователя.
Всякая научная область жизнеспособна, пока в ней избыток новых
проблем. Недостаток новых проблем означает отмирание или прекра-
щение самостоятельного развития. Как вообще каждое человеческое
начинание связано с той или иной целью, так и математическое твор-
чество связано с постановкой проблем. Сила исследователя познается
в решении проблем: он находит новые методы, новые точки зрения, он
открывает более широкие и свободные горизонты
Трудно, а часто и невозможно заранее правильно оценить значение
отдельной задачи; ведь в конечном счете ее ценность определится
пользой, которую она принесет науке. Отсюда возникает вопрос: су-
50
шествуют ли общие признаки, которые характеризуют хорошую мате-
матическую проблему?
Один старый французский математик сказал: «Математическую
теорию можно считать совершенной только тогда, когда ты сделал ее
настолько ясной, что берешься изложить ее содержание первому
встречному». Это требование ясности и легкой доступности, которое
здесь так резко ставится в отношении математической теории, я бы
поставил еще резче в отношении математической проблемы, если она
претендует на совершенство; ведь ясность и легкая доступность нас
привлекают, а усложненность и запутанность отпугивают.
Математическая проблема, далее, должна быть настолько трудной,
чтобы нас привлекать, и в то же время не совсем недоступной, чтобы
не делать безнадежными наши усилия; она должна быть путеводным
знаком на запутанных тропах, ведущих к сокрытым истинам; и она за-
тем должна награждать нас радостью найденного решения.
Математики прошлого столетия со страстным рвением отдавались
решению отдельных трудных задач; они знали цену трудной задаче. Я
напомню только поставленную Иоганном Бернулли задачу о линии
быстрейшего падения. «Как показывает опыт, — говорит Бернулли,
оповещая о своей задаче, — ничто с такой силой не побуждает высо-
кие умы к работе над обогащением знания, как постановка трудной и в
то же время полезной задачи». И поэтому он надеется заслужить бла-
годарность математического мира, если он, следуя примеру таких му-
жей, как Мерсенн, Паскаль, Ферма, Вивиани и другие, которые (до не-
го) поступали так же, предложит задачу выдающимся аналитикам сво-
его времени, чтобы они могли на ней, как на пробном камне, испытать
достоинства своих методов и измерить свои силы. Этой задаче Бер-
нулли и другим аналогичным задачам обязано своим зарождением ва-
риационное исчисление.
Известно утверждение Ферма о том, что диофантово уравнение х" +
+ У = z" неразрешимо в целых числах х, у, z, если не считать известных
очевидных исключений Проблема доказательства этой неразреши-
мости являет разительный пример того, какое побуждающее влияние
на науку может оказать специальная и на первый взгляд малозначи-
тельная проблема. Ибо, побужденный задачей Ферма, Куммер пришел
к введению идеальных чисел и к открытию теоремы об однозначном
разложении чисел в круговых полях на идеальные простые множители —
теоремы, которая теперь, благодаря обобщениям на любую алгебрам
ческую числовую область, полученным Дедекиндом и Кронекером,
является центральной в современной теории чисел и значение которой
выходит далеко за пределы теории чисел в область алгебры и теории
функций
5"
51
Напомню еще об одной интересной проблеме — задаче трех тел. То
обстоятельство, что Пуанкаре предпринял новое рассмотрение и зна-
чительно продвинул эту трудную задачу, привело к плодотворным ме-
тодам и далеко идущим принципам, введенным этим ученым в небес-
ную механику, методам и принципам, которые сейчас признаются и
применяются также и в практической астрономии.
Обе упомянутые проблемы — проблема Ферма и проблема трех тел —
являются в нашем запасе проблем как бы противоположными полюса-
ми: первая представляет свободное достижение чистого разума, при-
надлежащее области абстрактной теории чисел, вторая выдвинута ас-
трономией и необходима для познания простейших основных явлений
природы.
Часто, однако, случается, что одна и та же специальная проблема
появляется в весьма различных областях математики. Так, проблема о
кратчайшей линии играет важную историческую и принципиальную
роль одновременно в основаниях геометрии, в теории кривых и по-
верхностей, в механике и в вариационном исчислении. А как убеди-
тельно демонстрирует Ф. Клейн в своей книге об икосаэдре, проблема
о правильных многогранниках имеет важное значение одновременно
для элементарной геометрии, теории групп, теории алгебраических и
теории линейных дифференциальных уравнений!
Чтобы осветить важность отдельных проблем, я позволю себе еще
сослаться на Вейерштрасса, считавшего большой удачей для себя то
стечение обстоятельств, которое позволило ему в начале своей науч-
ной деятельности заняться такой значительной проблемой, как про-
блема Якоби об обращении эллиптического интеграла.
После того как мы рассмотрели общее значение проблемы в мате-
матике, обратимся к вопросу о том, из какого источника математика
черпает свои проблемы. Несомненно, что первые и самые старые про-
блемы каждой математической области знания возникли из опыта и
поставлены над миром внешних явлений. Даже правила счета с целы-
ми числами были открыты на этом пути еще на ранней ступени куль-
турного развития человечества так же, как и теперь ребенок познает
применение этих правил эмпирическим методом То же относится к
первым проблемам геометрии — пришедшим к нам из древности зада-
чам удвоения куба, квадратуры круга, а также к старейшим проблемам
теории численных уравнений, теории кривых, дифференциального и
интегрального исчислений, вариационного исчисления, теории рядов
Фурье и теории потенциала, не говоря уже о всем богатстве проблем
собственно механики, астрономии и физики.
При дальнейшем развитии какой-либо математической дисциплины
человеческий ум, обнадеженный удачами, проявляет уже самостоя-
52
тельность; он сам ставит новые и плодотворные проблемы, часто без
заметного влияния внешнего мира, с помощью только логического со-
поставления, обобщения, специализирования, удачного расчленения и
группировки понятий и выступает затем сам на первый план как по-
становщик задач. Так возникли задача о простых числах и другие за-
дачи арифметики, теория Галуа, теория алгебраических инвариантов,
теория абелевых и автоморфных функций, и так возникали вообще
почти все тонкие вопросы современной теории чисел и теории функций
А между тем во время действия созидательной силы чистого мыш-
ления внешний мир снова настаивает на своих правах: он навязывает
нам своими реальными фактами новые вопросы и открывает нам но-
вые области математического знания. И в процессе включения этих
новых областей знания в царство чистой мысли мы часто находим от-
веты на старые нерешенные проблемы и таким путем наилучшим об-
разом продвигаем вперед старые теории. На этой постоянно повто-
ряющейся и сменяющейся игре между мышлением и опытом, мне ка-
жется, и основаны те многочисленные и поражающие аналогии и та
кажущаяся предустановленная гармония, которые математик так часто
обнаруживает в задачах, методах и понятиях различных областей знания
Остановимся еще кратко на вопросе о том, каковы могут быть об-
щие требования, которые мы вправе предъявить к решению математи-
ческой проблемы. Я имею в виду прежде всего требования, благодаря
которым удается убедиться в правильности ответа с помощью конеч-
ного числа заключений и притом на основании конечного числа пред-
посылок, которые кладутся в основу каждой задачи и которые должны
быть в каждом случае точно сформулированы. Это требование логиче-
ской дедукции с помощью конечного числа заключений есть не что
иное, как требование строгости проведения доказательств. Действи-
тельно, требование строгости, которое в математике уже вошло в по-
говорку, соответствует общей философской потребности нашего разу-
ма; с другой стороны, только выполнение этого требования приводит к
выявлению полного значения существа задачи и ее плодотворности.
Новая задача, особенно если она вызвана к жизни явлениями внешнего
мира, подобна молодому побегу, который может расти и приносить
плоды, лишь если он будет заботливо и по строгим правилам искусст-
ва садоводства взращиваться на старом стволе — твердой основе на-
шего математического знания.
Будет большой ошибкой думать при этом, что строгость в доказа-
тельстве — это враг простоты. Многочисленные примеры убеждают
нас в противоположном: строгие методы являются в то же время про-
стейшими и наиболее доступными Стремление к строгости как раз и
приводит к отысканию простейших доказательств Это же стремление
53
часто прокладывает путь к методам, которые оказываются более пло-
дотворными, чем старые менее строгие методы. Так, теория алгебраи-
ческих кривых благодаря более строгим методам функций комплекс-
ного переменного и целесообразному применению трансцендентных
средств значительно упростилась и приобрела большую цельность.
Далее, доказательство правомерности применения четырех элементар-
ных арифметических действий к степенным рядам, а также почленного
дифференцирования и интегрирования этих рядов и основанное на
этом признание степенного ряда, несомненно, значительно упростили
весь анализ, в частности теорию исключения и теорию дифференци-
альных уравнений (вместе с ее теоремами существования).
Но особенно разительный пример, иллюстрирующий мою мысль,
представляет вариационное исчисление. Исследование первой и вто-
рой вариаций определенного интеграла приводило к крайне сложным
вычислениям, а соответствующие исследования старых математиков
были лишены необходимой строгости. Вейерштрасс указал нам путь к
новому и вполне надежному обоснованию вариационного исчисления.
На примере простого и двойного интеграла я вкратце намечу в конце
моего доклада, как следование этому пути приводит в то же время к
поразительному упрощению вариационного исчисления вследствие
того, что для установления необходимых и достаточных критериев
максимума и минимума становится излишним вычисление второй ва-
риации и даже частично отпадает необходимость в утомительных умо-
заключениях, относящихся к первой вариации. Я уже не говорю о тех
преимуществах, которые возникают от того, что исчезает надобность
рассматривать лишь те вариации, для которых значения производных
функций меняются незначительно.
Предъявляя к полному решению проблемы требование строгости в
доказательстве, я хотел бы, с другой стороны, опровергнуть мнение о
том, что совершенно строгие рассуждения применимы только к поня-
тиям анализа или даже одной лишь арифметики. Такое мнение, под-
держиваемое иногда и выдающимися умами, я считаю совершенно
ложным. Такое одностороннее толкование требования строгости бы-
стро приводит к игнорированию всех понятий, возникших из геомет-
рии, механики, физики, приостанавливает приток нового материала из
внешнего мира и в конце концов приводит даже к отбрасыванию поня-
тия континуума и иррационального числа. А существует ли более
важный жизненный нерв, чем тот, который был бы отрезан от матема-
тики, если из нее изъять геометрию и математическую физику? Я, на-
против, считаю, что всякий раз, когда математические понятия зарож-
даются со стороны теории познания или в геометрии, или в естествен-
нонаучных теориях, перед математикой возникает задача исследовать
54
принципы, лежащие в основе этих понятий, и так обосновать эти поня-
тия с помощью полной и простой системы аксиом, чтобы строгость
новых понятий и их применимость к дедукции ни в какой мере не ус-
тупала старым арифметическим понятиям.
К новым понятиям относятся также новые обозначения. Мы их вы-
бираем таким образом, чтобы они напоминали те явления, которые по-
служили поводом для образования этих понятий. Так, геометрические
фигуры являются образами для напоминания пространственных пред-
ставлений и в качестве таковых применяются всеми математиками.
Кто не связывает с двумя неравенствами а > b > с между тремя вели-
чинами а, Ь, с образ тройки прямолинейно расположенных и следую-
щих друг за другом точек в качестве геометрической интерпретации
понятия «между»? Кто не пользуется образом вложенных друг в друга
отрезков и прямоугольников, если нужно провести полное и строгое
доказательство трудной теоремы о непрерывности функций или суще-
ствования предельной точки? Кто может обойтись без фигуры тре-
угольника, окружности с заданным центром или без тройки взаимно
перпендикулярных осей? Или кто хотел бы отказаться от образа век-
торного поля или семейства кривых, или поверхностей с их огибаю-
щей — понятий, которые играют такую существенную роль в диффе-
ренциальной геометрии, в теории дифференциальных уравнений, в ос-
новах вариационного исчисления и в других чисто математических
областях знания?
Арифметические знаки — это записанные геометрические фигуры, а
геометрические фигуры — это нарисованные формулы, и никакой матема-
тик не мог бы обойтись без этих нарисованных формул, так же как и не мог
бы отказаться при счете от заключения в скобки или их раскрытия или
применения других аналитических знаков.
Применение геометрических фигур в качестве строгого средства
доказательства предполагает точное знание и полное владение теми
аксиомами, которые лежат в основе теории этих фигур, и поэтому для
того, чтобы эти геометрические фигуры можно было включить в об-
щую сокровищницу математических знаков, необходимо строгое ак-
сиоматическое исследование их наглядного содержания. Подобно то-
му как при сложении двух чисел нельзя подписывать цифры слагае-
мых в неверном порядке, а нужно строго следовать правилам, т.е. тем
аксиомам арифметики, которым подчиняются арифметические дейст-
вия, так и операции над геометрическими образами определяются те-
ми аксиомами, которые лежат в основе геометрических понятий и свя-
зей между ними
Сходство между геометрическим и арифметическим мышлением
проявляется также и в том, что в арифметических исследованиях мы
55
так же мало, как и при геометрических рассмотрениях, прослеживаем
до конца цепь логических рассуждений, вплоть до аксиом. Напротив, в
особенности при первом подходе к проблеме, мы и в арифметике, со-
вершенно так же как и в геометрии, сначала пользуемся некоторым
мимолетным, бессознательным, не вполне отчетливым комбинирова-
нием, опирающимся на доверие к некоторому арифметическому чу-
тью, к действенности арифметических знаков, без чего мы не могли
бы продвигаться в арифметике точно так же, как мы не можем продви-
гаться в геометрии, не опираясь на силы геометрического воображе-
ния. Образцом арифметической теории, оперирующей строгим обра-
зом с геометрическими понятиями и знаками, может служить работа
Г. Минковского «Геометрия чисел».
Сделаем еще несколько замечаний относительно трудностей, кото-
рые могут представлять математические проблемы, и о преодолении
этих трудностей.
Если нам не удается найти решение математической проблемы, то
часто причина этого заключается в том, что мы не овладели еще дос-
таточно обшей точкой зрения, с которой рассматриваемая проблема
представляется лишь отдельным звеном в цепи родственных проблем.
Отыскав эту точку зрения, мы часто не только делаем более доступной
для исследования данную проблему, но и овладеваем методом, приме-
нимым и к родственным проблемам. Примерами могут служить вве-
денное Коши в теорию определенного интеграла интегрирование по
криволинейному пути и установление Куммером понятия идеала в
теории чисел. Этот путь нахождения общих методов наиболее удоб-
ный и надежный, ибо если ищут общие методы, не имея в виду какую-
нибудь определенную задачу, то эти поиски, по большей части, на-
прасны.
При исследовании математических проблем специализация играет,
как я полагаю, еще более важную роль, чем обобщение. Возможно,
что в большинстве случаев, когда мы напрасно ищем ответ на вопрос,
причина нашей неудачи заключается в том, что еще не разрешены или
не полностью решены более простые и легкие проблемы, чем данная
Тогда все дело заключается в том, чтобы найти эти более легкие про-
блемы и осуществить их решение наиболее совершенными средства-
ми, при помощи понятий, поддающихся обобщению. Это правило яв-
ляется одним из самых мощных рычагов для преодоления математи-
ческих трудностей, и мне кажется, что в большинстве случаев этот
рычаг и приводят в действие, подчас бессознательно.
Вместе с тем бывает и так, что мы добиваемся ответа при недоста-
точных предпосылках или идя в неправильном направлении и вслед-
ствие этого не достигаем цели. Тогда возникает задача доказать нераз-
56
решимость данной проблемы при принятых предпосылках и выбран-
ном направлении Такие доказательства невозможности проводились
еще старыми математиками, например, когда они обнаруживали, что
отношение гипотенузы равнобедренного прямоугольного треугольни-
ка к его катету есть иррациональное число. В новейшей математике
доказательства невозможности решений определенных проблем игра-
ют выдающуюся роль; там мы констатируем, что такие старые и труд-
ные проблемы, как доказательство аксиомы о параллельных, как квад-
ратура круга или решение уравнения пятой степени в радикалах, полу-
чили все же строгое, вполне удовлетворяющее нас решение, хотя и в
другом направлении, чем то, которое сначала предполагалось.
Этот удивительный факт наряду с другими философскими основа-
ниями создает у нас уверенность, которую разделяет, несомненно, ка-
ждый математик, но которую до сих пор никто не подтвердил доказа-
тельством, — уверенность в том, что каждая определенная математи-
ческая проблема непременно должна быть доступна строгому реше-
нию или в том смысле, что удается получить ответ на поставленный
вопрос, или же в том смысле, что будет установлена невозможность ее
решения и вместе с тем доказана неизбежность неудачи всех попыток
ее решить.
% 'БурБащ
АРХИТЕКТУРА МАТЕМАТИКИ7
МАТЕМАТИКА ИЛИ МАТЕМАТИКИ?
Дать в настоящее время общее представление о математической
науке — значит заняться таким делом, которое, как кажется, с самого
начала наталкивается на почти непреодолимые трудности благодаря
обширности и разнообразию рассматриваемого материала. В соответ-
ствии с общей тенденцией в науке с конца XIX в. число математиков и
число работ, посвященных математике, значительно возросло (статьи
по чистой математике, публикуемые во всем мире в среднем в течение
одного года, охватывают многие тысячи страниц). Не все они имеют,
конечно, одинаковую ценность; тем не менее после очистки от неиз-
бежных отбросов оказывается, что каждый год математическая наука
обогащается массой новых результатов, приобретает всё более разно-
образное содержание и постоянно дает ответвления в виде теорий, ко-
торые беспрестанно видоизменяются, пересзраиваются, сопоставляют-
ся и комбинируются друг с другом. Ни один математик не в состоянии
проследить это развитие во всех подробностях, даже если он посвятит
4 Зап 72
57
этому всю свою деятельность. Многие из математиков устраиваются в
каком-либо закоулке математической науки, откуда они и не стремят-
ся выйти, и не только почти полностью игнорируют веб то, что не ка-
сается предмета их исследований, но не в силах даже понять язык и
терминологию своих собратьев, специальность которых далека от них.
Нет такого математика, даже среди обладающих самой обширной эру-
дицией, который бы не чувствовал себя чужеземцем в некоторых об-
ластях огромного математического мира; что же касается тех, кто по-
добно Пуанкаре или Гильберту оставляет печать своего гения почти во
всех его областях, то они составляют даже среди наиболее великих
редчайшее исключение.
Поэтому даже не возникает мысли дать неспециалисту точное
представление о том, что даже сами математики не могут постичь во
всей полноте. Но можно спросить себя, является ли это обширное раз-
растание развитием крепко сложенного организма, который с каждым
днем приобретает всё больше и больше согласованности и единства
между своими вновь возникающими частями, или, напротив, оно яв-
ляется только внешним признаком тенденции к идущему всё дальше и
дальше распаду, обусловленному самой природой математики; не на-
ходится ли эта последняя на пути превращения в Вавилонскую баш-
ню, в скопление автономных дисциплин, изолированных друг от друга
как по своим методам, так и по своим целям и даже по языку? Одним
словом, существуют в настоящее время одна математика или несколь-
ко математик?
Хотя в данный момечт этот вопрос особенно актуален, ни в коем
случае не надо думать, что он нов; его ставили с первых же шагов ма*
тематической науки. Ведь, действительно, если даже не принимать в
расчет прикладной математики, между геометрией и арифметикой (по
крайней мере, в их элементарных разделах) существует очевидная раз-
ница в происхождении, поскольку последняя вначале была наукой о
дискретном, а первая — наукой о непрерывной протяженности (два
аспекта, которые были коренным образом противопоставлены друг
другу после открытия иррациональностей). Именно это открытие ока-
залось роковым для первой попытки унификации нашей науки —
арифметизации пифагорейцев («все вещи суть числа»).
Мы бы зашли слишком далеко, если бы от нас потребовали просле-
дить те превратности судьбы, которым подвергалась унитарная кон-
цепция математики от пифагорейцев до наших дней. Кроме того, это —
работа, к которой более подготовлен философ, чем ма1ематик, так как
общей чертой всех попыток объединить в единое целое математиче-
ские дисциплины — всё равно, идет ли речь о Платоне, о Декарте или
Лейбнице, об арифметизации или логистике XIX в., — является то, что
58
они делались в связи с какой-либо более или менее претенциозной фи-
лософской системой, причем исходным пунктом для них всегда слу-
жили априорные воззрения на отношения между математикой и двой-
ной действительностью внешнего мира и мира мысли. Самое лучшее,
что мы сумеем сделать, — это отослать читателя по этому вопросу к
историческому и критическому исследованию Л. Брюншвига «Этапы
математической философии». Наша задача более скромна и более точ-
но очерчена; мы намереваемся остаться внутри математики и искать
ответ на поставленный вопрос, анализируя ее собственное развитие.
ЛОГИЧЕСКИЙ ФОРМАЛИЗМ И АКСИОМАТИЧЕСКИЙ МЕТОД
После более или менее очевидного банкротства различных систем,
на которые мы указывали выше, в начале этого века, казалось, почти
полностью отказались от взгляда на математику как на науку, характе-
ризуемую единым предметом и единым методом; скорее наблюдалась
тенденция рассматривать ее как «ряд дисциплин, основывающихся на
частных, точно определенных понятиях, связанных тысячью нитей»,
которые позволяют методам, присущим одной из дисциплин, оплодо-
творять одну или несколько других. В настоящее время, напротив, мы
думаем, что внутренняя эволюция математической науки вопреки
внешности более чем когда-либо упрочила единство ее различных час-
тей и создала своего рода центральное ядро, которое является гораздо
более связным целым, чем когда бы то ни было. Существенное в этой
эволюции заключается в систематизации отношений, существующих
между различными математическими теориями; ее итогом явилось на-
правление, которое обычно называют «аксиоматическим методом».
Иногда говорят также «формализм» или «формалистический ме-
тод»; но необходимо с самого начала остерегаться путаницы, которую
вызывают эти недостаточно четко определенные слова и которая и без
того часто используется противниками аксиоматического метода. Ка-
ждому известно, что внешней отличительной чертой математики явля-
ется то, что она представляется нам той «длинной цепью рассужде-
ний», о которой говорил Декарт. Каждая математическая теория явля-
ется цепочкой высказываний, которые выводятся друг из друга со-
гласно правилам логики, во всем существенном совпадающей с логи-
кой, известной со времен Аристотеля под названием «формальной ло-
гики», соответствующим образом приспособленной к специфическим
потребностям математики. Таким образом, утверждение, что «дедук-
тивное рассуждение» является для математики объединяющим нача-
лом, — тривиальная истина. Но столь поверхностное замечание не
может, конечно, служить объяснением единства различных математи-
ческих теорий, точно так же, как нельзя, например, объединить в еди-
4-
59
ной науке физику и биологию под предлогом, что и та, и другая ис-
пользует экспериментальный метод. Способ рассуждения, заключаю-
щийся в построении цепочки силлогизмов, является только трансфор-
мирующим механизмом который можно применять независимо от то-
го, каковы посылки, к которым он применяется, и который, следова-
тельно, не может характеризовать природу этих последних. Другими
словами, это лишь внешняя форма, которую математик придает своей
мысли, орудие, делающее ее способной объединяться с другими мыс-
лями, и, так сказать, язык, присущий математике, но не более того.
Упорядочить словарь этого языка и уточнить его синтаксис — это зна-
чит сделать очень полезное дело, и эта работа и составляет действи-
тельно одну из сторон аксиоматического метода, а именно ту, которую
следует назвать логическим формализмом (или, как еще говорят, «ло-
гистикой»). Но — и мы настаиваем на этом — это только одна сто-
рона и при том наименее интересная.
То, что аксиоматика ставит перед собой в качестве основной цели
уразумение существа математики, именно этого не может дать логи-
ческий формализм, взятый сам по себе. Точно так же, как эксперимен-
тальный метод исходит из априорной уверенности в постоянстве зако-
нов природы, аксиоматический метод берет за точку опоры убеждение
в том, что если математика не является нанизыванием силлогизмов в
направлении, избранном наугад, то она тем более не является более
или менее хитрым искусством, состоящим из произвольных сближе-
ний, в котором господствует одна техническая ловкость. Там, где по-
верхностный наблюдатель видит лишь две или несколько теорий, со-
вершенно отличных друг от друга по своему внешнему виду и где
вмешательство гениального математика приводит к обнаружению со-
вершенно «неожиданной помощи», которую одна из иих может ока-
зать другой, там аксиоматический метод учит нас искать глубокие
причины этого открытия, находить общие идеи, скрывающиеся за де-
талями, присущими каждой из рассматриваемых теорий, извлекать эти
идеи и подвергать их исследованию.
ПОНЯТИЕ «СТРУКТУРЫ»
Какую форму приобретает эта процедура? Именно здесь аксиома-
тика больше всего сближается с экспериментальным методом. Черпая
из картезианского источника, она «разделяет трудности, чтобы лучше
их разрешить». В доказательствах какой-либо теории она стремится
разъединить главные пружины фигурирующих там рассуждений; за-
тем, беря каждое из соответствующих положений изолированно и воз-
водя его в общий принцип, она выводит из них следствия; наконец,
возвращаясь к изученной теории, она снова комбинирует предвари-
60
тельно выделенные составные элементы и изучает, как они взаимо-
действуют между собой. Конечно, нет ничего нового в этом классиче-
ском сочетании анализа и синтеза; вся оригинальность этого метода
заключается в том, как его применяют.
Чтобы проиллюстрировать примером только что описанную про-
цедуру, мы рассмотрим наиболее старую (и наиболее простую) аксио-
матическую теорию — теорию абстрактных групп. Рассмотрим сле-
дующие три операции: 1) сложение действительных чисел, при кото-
ром сумма двух действительных чисел (положительных, отрицатель-
ных и нуля) определена обычным образом; 2) умножение целых чисел
по простому модулю р, причем элементами, которые мы рассматрива-
ем, являются числа 1, 2, 3,... ,р - 1, а произведением двух таких чисел
является, по определению, остаток от деления на р их произведения в
обычном смысле; 3) «композицию» перемещений в евклидовом трех-
мерном пространстве, причем результатом этой композиции (или про-
изведением) двух перемещений Т и S (взятых в данном порядке) мы
будем считать, по определению, перемещение, полученное в результа-
те выполнения сначала перемещения Т, а затем S. В каждой из этих
трех теорий двум элементам х и у, взятым в данном порядке, рассмат-
риваемого множества (в первом случае множества всех действитель-
ных чисел, во втором — множества чисел 1,2,3,... ,р - 1, в третьем —
множества всех перемещений) ставится в соответствие (с помощью
особой для каждого множества процедуры) третий однозначно опре-
деленный элемент того же множества, который мы условимся во всех
трех случаях символически обозначать х т у (это будет сумма, если х и
у — действительные числа; их произведение по модулю р, если они —
натуральные числа £ р - 1; результат их композиции, если они явля-
ются перемещениями). Если теперь рассмотреть свойства этой «опе-
рации» в каждой из трех теорий, то обнаружится замечательный па-
раллелизм; внутри же каждой из этих теорий эти свойства зависят
друг от друга, и анализ логических связей между ними приводит к вы-
делению небольшого числа тех свойств, которые являются независи-
мыми (т.е. таких, что ни одно из них не является логическим следст-
вием остальных). Можно, например, взять три следующие свойства,
которые мы выразим с помощью наших символических обозначений,
но которые, конечно, легко перевести на язык каждой из них:
а) каковы бы ни были элементы х, у, z, (rcy)rz = rt(yrz) (ассоциа-
тивность операции хту);
Ь) существует элемент е такой, что для всякого элемента х выполняет-
ся равенство ехх = ххе = х (для «сложения действительных чисел —
число 0, для умножения по модулю р — число 1, для композиции пе-
61
ремещений — «тождественное перемещение», которое оставляет на
своем месте каждую точку пространства);
с) для каждого элемента х существует элемент х', такой, что ххх' =
= х'тх = е (для сложения действительных чисел — противоположное
число -х, для композиции перемещений — обратное перемещение, т.е.
такое, которое каждую точку, перемещенную смещением х, возвраща-
ет в исходное положение; для умножения по модулю р существование
х' следует из очень простого арифметического рассуждения).
Тогда мы устанавливаем, что те свойства, которые при помощи
общих обозначений возможно выразить одним и тем же образом в ка-
ждой из этих трех теорий, являются следствием трех предыдущих. На-
пример, поставим перед собой цель доказать, что из хху = xtz следует
у = z. Можно было бы это сделать в каждой из этих теорий, используя
рассуждения, специфические для данной теории. Но можно избрать
следующий образ действий, который применим ко всем трем случаям
Из соотношения хху = xxz мы выводим равенство х'х(хху) = x't(xtz)
(х’ имеет смысл, определенный выше). Далее, применяя «а», получим
(х'тх)ту = (хЧх)тг. Используя «Ь», запишем это соотношение в виде еху =
= erz, и, наконец, применяя «с», получаем у - z, что и требовалось до-
казать. В этом рассуждении мы полностью абстрагировались от при-
роды элементов х, у, z, т.е. нам незачем было знать, являются ли они
действительными числами, натуральными числами <. р - 1 или пере-
мещениями. Единственная посылка, которой мы пользовались, заклю-
чалась в том, что операция хху над элементами х, у удовлетворяет
свойствам «а», «Ь», «с». Для того чтобы избежать скучных повторе-
ний, приходят, таким образом, к мысли, что удобно раз и навсегда вы-
вести логические следствия из этих трех единственных свойств. Необ-
ходимо, конечно, для удобства речи принять общую терминологию.
Говорят, что множество, на котором определена операция хху, харак-
теризуемая тремя свойствами «а», «Ь», «с», снабжено структурой
группы (или, более коротко, является группой). Условия «а», «Ь», «с»
называются аксиомами группы, и вывести из них их следствия — зна-
чит построить аксиоматическую теорию групп.
Теперь можно объяснить, что надо понимать в общем случае под
математической структурой. Общей чертой различных понятий, объ-
единенных этим родовым названием, является то, что они применимы к
множествам элементов, природа которых не определена.
Чтобы определить структуру, задают одно или несколько отноше-
ний, в которых находятся его элементы (в случае групп — это отно-
шение хху = z между тремя произвольными элементами); затем посту-
лируют, что данное отношение или данные отношения удовлетворяют
62
некоторым условиям (которые перечисляют и которые являются ак-
сиомами рассматриваемой структуры) Построить аксиоматическую
теорию данной структуры — это значит вывести логические следствия
из аксиом структуры, отказавшись от каких-либо других предполо-
жений относительно рассматриваемых элементов (в частности от вся-
ких гипотез относительно их «природы»),
ОСНОВНЫЕ ТИПЫ СТРУКТУР
Отношения, являющиеся исходной точкой в определении структу-
ры, могут быть по своей природе весьма разнообразными. То отноше-
ние, которое фигурирует в групповых структурах, называют «законом
композиции»; это такое отношение между тремя элементами, которое
определяет однозначно третий элемент как функцию двух первых. Ко-
гда отношения в определении структуры являются «законами компо-
зиции», соответствующая структура называется алгебраической
структурой (например, структура поля определяется двумя законами
композиции с надлежащим образом выбранными аксиомами, сложе-
ние и умножение действительных чисел определяют структуру поля
на множестве этих чисел).
Другой важный тип представляют собой структуры, определенные
отношением порядка; на этот раз это — отношение между двумя эле-
ментами х, у, которое чаще всего мы выражаем словами «х меньше
или равно у» и которое мы будем обозначать в общем случае xRy.
Здесь больше не предполагается, что это отношение однозначно опре-
деляет один из элементов х, у как функцию другого. Аксиомы, кото-
рым оно подчиняется, таковы: а) для всех х xRx; Ь) из соотношении
xRy, yRx следует х = у; с) из соотношений xRy, yRz следует xRz. Оче-
видным примером множества, снабженного такой структурой, являет-
ся множество целых чисел (или множество действительных чисел),
причем здесь знак R заменяется на S. Но надо заметить, что мы не
включили в число аксиом аксиому, отражающую следующее свойство,
которое кажется неотделимым от того понятия порядка, каким мы
пользуемся в обыденной жизни: «каковы бы ни были х,у, имеет место
илихЯу илиуЯх». Другими словами, не исключается случай, когда два
элемента могут оказаться несравнимыми. На первый взгляд это может
показаться странным, но легко привести очень важные примеры
структур порядка, для которых имеет место именно это обстоятельст-
во. Именно с таким положением вещей мы сталкиваемся, когда X, Y
означают подмножества некоторого множества, aXRY означает «X со-
держится в У» или еще когда х, у являются натуральными числами, а
xRy означает «х делиту», или, наконец, когдаДх) или g(x) являются
действительными функциями, определенными на интервале а£х <,Ь,
63
аДх) R g(y) означает: «каково бы ни было х,/(х) £ g(x)». Эти примеры
в то же время показывают, сколь велико разнообразие областей, где
появляются структуры порядка, и заранее дают представление о том,
насколько интересно их изучение.
Мы скажем еще несколько слов о третьем важном типе структур —
топологических структурах (или топологиях)', в них находят абст-
рактную математическую формулировку интуитивные понятия окре-
стности, предела и непрерывности, к которым нас приводит наше
представление о пространстве. Усилия, необходимые для перехода к
абстракции, находящей свое выражение в аксиомах такой структуры,
требуются значительно большие по сравнению с тем, что имело место
в предыдущих примерах, и размеры настоящей статьи вынуждают нас
отослать читателей, желающих получить более подробные сведения
по этому вопросу, к специальной литературе.
СТАНДАРТИЗАЦИЯ МАТЕМАТИЧЕСКИХ ОРУДИИ
Мы думаем, что нами сказано достаточно для того, чтобы читатель
мог создать себе достаточно ясное представление об аксиоматическом
методе. Наиболее бросающейся в глаза его чертой, как это видно из
изложенного выше, является реализация значительной экономии мыс-
ли. «Структуры» являются орудиями математика; каждый раз, когда
он замечает, что между элементами, изучаемыми им, имеют место
отношения, удовлетворяющие аксиомам структуры определенного
типа, он сразу может воспользоваться всем арсеналом общих теорем,
относящихся к структурам этого типа, тогда как раньше он был бы
должен мучительно трудиться, выковывая сам средства, необходимые
для того, чтобы штурмовать рассматриваемую проблему, причем их
мощность зависела бы от его личного таланта и они были бы отягчены
часто излишне стеснительными предположениями, обусловленными
особенностями изучаемой проблемы. Таким образом, можно было бы
сказать, что аксиоматический метод является ничем иным, как «сис-
темой Тейлора» в математике.
Но это сравнение — недостаточное. Математик не работает подоб-
но машине; мы должны особенно подчеркнуть, что в рассуждениях
математика основную роль играет особая интуиция, отличная от обы-
денной чувственной интуиции и заключающаяся скорее в непосредст-
венном угадывании (предшествующем всякому рассуждению) нор-
мального положения вещей, которое, как кажется, он вправе ожидать
от математических объектов, ставших в результате его частого опери-
рования с ними столь же для него привычными, как и объекты реаль-
ного мира. Но ведь каждая структура сохраняет в своем языке интуи-
тивные отзвуки той специфической теории, откуда ее извлек аксиома-
64
тический анализ, описанный нами выше. И когда исследователь не-
ожиданно открывает эту структуру в изученных им явлениях, это для
него является как бы толчком, который сразу направляет интуитивный
поток его мыслей в неожиданном направлении, и в результате этого
математический ландшафт, по которому он движется, получает новое
освещение. Чтобы ограничиться старым примером, вспомним про-
гресс, осуществленный в начале XIX в. благодаря геометрической ин-
терпретации мнимых величин; с нашей точки зрения, это было обна-
ружение в множестве комплексных чисел хорошо известной тополо-
гической структуры — структуры евклидовой плоскости — со всеми
следующими отсюда возможностями приложений, — открытие, кото-
рое в руках Гаусса, Абеля, Коши и Рима не менее чем за одно столетие
обновило весь анализ.
Такие примеры умножились за последние 50 лет: пространство
Гильберта и более общие функциональные пространства, вводящие
топологические структуры в множества, элементами которых являют-
ся уже не точки, а функции', р-адические числа Гензеля, посредством
которых — еще более удивительное обстоятельство! — топология во-
царилась в той области, которая до этих пор считалась царством дис-
кретного, разрывного по преимуществу — в множестве целых чисел;
мера Хаара, безгранично расширившая область применения понятия
интеграла и способствовавшая весьма глубокому анализу свойств не-
прерывных групп, —таковы решающие моменты е прогрессе матема-
тики, те повороты, когда свет гения определял новое направление,
теории, обнаруживая в ней структуру, которая, как казалось a priori, не
играла там никакой роли.
Это говорит о том, что в настоящее время математика менее, чем
когда-либо, сводится к чисто механической игре с изолированными
формулами, более чем когда-либо интуиция безраздельно господству-
ет в генезисе открытий; но теперь и в дальнейшем в ее распоряжении
находятся могущественные рычаги, предоставленные ей теорией наи-
более важных структур, и она окидывает единым взглядом огромные
области, унифицированные аксиоматикой, в которых некогда, как ка-
залось, царил самый бесформенный хаос.
ОБЗОР В ЦЕЛОМ
Руководствуясь концепцией аксиоматики, попытаемся представить
теперь математический мир в целом. Конечно, мы более не распознаем
здесь традиционный порядок, который, подобно первым классифика-
циям видов животных, ограничивался тем, что расставлял рядом друге
другом теории, представляющие наибольшее внешнее сходство. Вме-
сто точно разграниченных разделов алгебры, анализа, теории чисел и
65
геометрии мы увидим, например, теорию простых чисел по соседству
с теорией алгебраических кривых или евклидову геометрию рядом с
интегральными уравнениями, и упорядочивающим принципом будет
концепция иерархии структур, идущей от простого к сложному, от
общего к частному.
В центре находятся основные типы структур, из которых мы только
что перечислили главнейшие, так сказать, порождающие структуры
(les structures — meres). В каждом из этих типов господствует уже дос-
таточное разнообразие, так как там надо различать наиболее общую
структуру рассматриваемого типа с наименьшим числом аксиом и
структуры, которые получаются из нее в результате ее обогащения до-
полнительными аксиомами, каждая из которых влечет за собой и но-
вые следствия. Именно таким образом теория групп, помимо тех об-
щих положений, которые справедливы для всех групп и зависят только
от аксиом, перечисленных выше, содержит, в частности, теорию ко-
нечных групп (в которой добавляют аксиому, гласящую, что число
элементов группы конечно), теорию абелевых групп (в которых имеем
хху = ytx, каковы бы ни были х, у), а также теорию конечных абелевых
групп (в которой предполагаются выполненными обе вышеуказанные
аксиомы). Точно так же среди упорядоченных множеств различают те,
в которых (как при упорядоченности в множестве целых или в множе-
стве действительных чисел) любые два элемента сравнимы и которые
называются линейно упорядоченными (totalement ordonnee); среди этих
последних особо изучают множества, называемые вполне упорядочен-
ными (в которых, так же как в множестве натуральных чисел, каждое
подмножество имеет «наименьший элемент»). Подобная же градация
существует и для топологических структур.
За пределами этого первоначального ядра появляются структуры,
которые можно было бы назвать сложными (multiples) и в которые
входят одновременно одна или несколько порождающих структур, но
не просто совмещенные друг с другом (что не дало бы ничего нового),
а органически скомбинированные при помощи одной или нескольких
связывающих их аксиом Именно такой характер носит топологиче-
ская алгебра, изучающая структуры, определяемые одним или не-
сколькими законами композиций и одной топологией, которые связа-
ны тем условием, что алгебраические операции являются непрерыв-
ными функциями (для рассматриваемой топологии) элементов, над ко-
торыми они производятся. Не менее важной является алгебраическая
топология, которая рассматривает некоторые множества точек про-
странства, определенные топологическими свойствами (симплексы,
циклы и т.д.), как элементы, над которыми производятся алгебраиче-
ские операции. Соединение структуры порядка и алгебраической
66
структуры точно так же изобилует результатами, приводя, с одной
стороны, к теории делимости идеалов, а с другой — к теории интегри-
рования и к «спектральной теории» операторов, где точно так же то-
пология играет свою роль.
Наконец, далее начинаются собственно частные теории, в которых
элементы рассматриваемых множеств, которые до сего момента в об-
щих структурах были совершенно неопределенными, получают более
определенную индивидуальность. Именно таким образом получают
теории классической математики: анализ функций действительного и
комплексного переменного, дифференциальную геометрию, алгебраи-
ческую геометрию, теорию чисел. Но они теряют свою былую авто-
номность и являются теперь перекрестками, на которых сталкиваются
и взаимодействуют многочисленные математические структуры,
имеющие более общий характер.
Чтобы сохранить правильную перспективу, необходимо после это-
го беглого обзора сейчас же добавить, что он должен рассматриваться
как весьма грубое приближение к истинному положению дел в мате-
матике. Он является одновременно схематическим, идеализированным
и застывшим
Схематическим — так как в деталях не всё идет так гладко
и планомерно, как это может представиться после того, что мы
рассказали. Между прочим, имеются неожиданные возвращения назад,
когда теория, носящая ярко выраженный частный характер, как,
например, теория действительных чисел, оказывает помощь, без
которой нельзя обойтись при построении какой-либо общей теории,
как, например, топологии или теории интегрирования.
Идеализированным — потому что далеко не во всех раз-
делах математики некоторая определенная часть каждой из основных
структур распознана и вмещена в четко очерченные границы. В неко-
торых теориях (например, в теории чисел) существуют многочислен-
ные изолированные результаты, которые до сего времени не умеют ни
классифицировать, ни связать удовлетворительным образом с извест-
ными структурами.
Наконец — застывшим, так как нет ничего более чуждого ак-
сиоматическому методу, чем статическая концепция науки, и мы не
хотели оставить у читателя впечатление, будто бы мы претендовали
дать очерк ее окончательного состояния. Структуры не остаются не-
изменными ни по их числу, ни по их сущности; вполне возможно, что
дальнейшее развитие математики приведет к увеличению числа фун-
даментальных структур; открыв плодотворность введения новых акси-
ом или новых сочетаний аксиом, можно заранее оценить значение этих
открытий, если судить о них по тем, которые дали уже известные
67
структуры. С другой стороны, эти последние ни в коем случае не яв-
ляются чем-то законченным, и было бы весьма удивительно, если бы
их жизненная сила была уже исчерпана.
Введя эти неизбежные поправки, можно лучше понять внутреннюю
жизнь математики, понять то, что создает ее единство и вносит в нее
разнообразие, понять этот большой город, чьи предместья не переста-
ют разрастаться несколько хаотическим образом на окружающем его
пространстве, в то время как центр периодически перестраивается,
следуя каждый раз всё более и более ясному плану и стремясь к всё
более и более величественному расположению, когда сносятся старые
кварталы с их лабиринтом переулков для того, чтобы проложить к пе-
риферии улицы всё более прямые, всё более широкие, всё более удобные.
ВОЗВРАЩЕНИЕ К ПРОШЛОМУ И ЗАКЛЮЧЕНИЕ
Концепция, которую мы только что пытались изложить, возникла не
сразу, а лишь в результате более чем полувековой эволюции и была
встречена не без сопротивления как со стороны философов, так и со сто-
роны математиков. Многие из этих последних долго не могли согласиться
рассматривать аксиоматику как что-либо большее, чем ненужные тонко-
сти логиков, неспособные оплодотворить какую-либо теорию. Эта крити-
ка объясняется, без сомнения, исторической случайностью: аксиоматиза-
ции, которые появились первыми и которые имели наибольший отклик
(аксиоматизации арифметики Дедекинда и Пеано, евклидовой геометрии
Гильберта), касались унивалентных теорий, т.е. таких, которые полно-
стью определялись совокупностью своих аксиом, причем система этих
аксиом не могла быть применена к какой-либо другой теории, кроме той,
из которой она была извлечена (в противоположность тому, что мы виде-
ли, например, в теории групп). Если бы это имело место для всех струк-
тур, то упрек в бесплодности, выдвинутый по адресу аксиоматического
метода, был бы полностью оправдан. Но этот последний доказал свою
мощь своим собственным развитием, и отвращение к нему, которое еще
встречается гам и сям, можно объяснить лишь тем, что разум по естест-
венной причине затрудняется допустить мысль, что в конкретной задаче
может оказаться плодотворной форма интуиции, отличная от той, которая
непосредственно подсказывается данными (и которая возникает в связи с
абстракцией более высокого порядка и более трудной).
Что касается возражений со стороны философов, то они относятся к
области, где мы не решаемся всерьез выступать из-за отсутствия ком-
петентности; основная проблема состоит во взаимоотношении мира
экспериментального и мира математического. То, что между экспери-
ментальными явлениями и математическими структурами существует
тесная связь, — это, как кажется, было совершенно неожиданным об-
68
разом подтверждено недавними открытиями современной физики, но
нам совершенно неизвестны глубокие причины этого (если только
этим словам можно приписать какой-либо смысл), и, быть может, мы
их никогда и не узнаем. Во всяком случае сделанное замечание могло
бы побудить философов в будущем быть более благоразумными при
решении этого вопроса. Перед тем как началось революционное разви-
тие современной физики, было потрачено немало труда из-за желания
во что бы то ни стало заставить математику рождаться из эксперимен-
тальных истин; но, с одной стороны, квантовая физика показала, что
эта «макроскопическая» интуиция действительности скрывает «мик-
роскопические» явления совсем другой природы, причем для их изу-
чения требуются такие разделы математики, которые, наверное, не
были изобретены с целью приложений к экспериментальным наукам, а
с другой — аксиоматический метод показал, что «истины», из которых
хотели сделать средоточие математики, являются лишь весьма част-
ным аспектом общих концепций, которые отнюдь не ограничивают
свое применение этим частным случаем. В конце концов, это интим-
ное взаимопроникновение, гармонической необходимостью которого
мы только что восхищались, представляется не более чем случайным
контактом наук, связи между которыми являются гораздо более скры-
тыми, чем это казалось a priori.
В своей аксиоматической форме математика представляется скоп-
лением абстрактных форм — математических структур, и оказывается
(хотя по существу и неизвестно, почему), что некоторые аспекты экс-
периментальной действительности как будто в результате предопреде-
ления укладываются в некоторые из этих форм. Конечно, нельзя отри-
цать, что большинство этих форм имело при своем возникновении
вполне определенное интуитивное содержание; но как раз сознательно
лишая их этого содержания, им сумели придать всю их действенность,
которая и составляет их силу, и сделали для них возможным приобре-
сти новые интерпретации и полностью выполнить свою роль в обра-
ботке данных.
Только имея в виду этот смысл слова «форма», можно говорить о
том, что аксиоматический метод является «формализмом». Единство,
которое ои доставляет математике, это — не каркас формальной логи-
ки, не единство, которое дает скелет, лишенный жизни. Это — пита-
тельный сок организма в полном развитии, податливый и плодотвор-
ный инструмент исследования, который сознательно используют в
своей работе, начиная с Гаусса, все великие мыслители-математики,
все те, кто, следуя формуле Лежен—Дирихле, всегда стремились
«идеи заменить вычислениями».
69
Вопросы и упражнения
для индивидуального осмысления
и коллективного обсуждения
1. Назовите основные периоды истории развития математики
2 Какие методы математических исследований характерны для перио-
да зарождения математики (до VII в до н.э )?
3. О довольно высоком уровне абстрактного мышления математиков
Древнего Мира свидетельствует выделение трех центральных математи-
ческих понятий — «фигура», «величина», «число». Приведите известные
вам математические факты, открытые математиками Древнего Мира.
4 Приведите примеры задач, которые умели решать вавилонские,
древнеегипетские, индусские математики Какие вам известны материаль-
ные источники, свидетельствующие об этих знаниях и умениях математи-
ков древности
5 Охарактеризуйте методы добывания математических знаний периода
математики постоянных величин (VII в. до н.э.—XVII в. до н.э ). Чем отли-
чался метод математических исследований древнегреческого философа и
математика Фалеса из Милета (VII—VI ев до н.э.) от методов, применяе-
мых его предшественниками. Приведите примеры доказательств, приписы-
ваемых Фалесу.
6 Какие математические открытия принадлежат школе пифагорейцев?
Разъясните утверждение пифагорейцев о том, что «все есть число» Какое
открытие показало несостоятельность попыток пифагорейцев свести всю
геометрию к натуральным числам? Покажите, что диагональ квадрата не-
соизмерима с его стороной.
7. Разъясните, какова роль древнегреческих философских школ (Платона
Аристотеля) в развитии математики Почему при входе в Академию Платона
была надпись: «Пусть сюда не входит тот, кто не знает геометрии...».
8 Объясните, почему считается, что знаменитые «Начала» Евклида
сыграли выдающуюся роль в формировании математики как теоретической
науки. В чем состояло влияние на Евклида (и на развитие геометрии в це-
лом) работ величайшего мыслителя древности Аристотеля?
9. В чем принципиальное отличие «Начал» Евклида от предшествую-
щих им математических работ? По рассказу Прокла, царь Птолемей спро-
сил Евклида, нельзя ли найти более короткий и менее утомительный путь к
изучению геометрии, чем его «Начала». Евклид ответил: «Нет царской до-
роги к геометрии!». Поясните, ссылаясь на структуру логической системы
«Начал» Евклида, это утверждение Подтвердите это высказывание Евк-
лида характеристикой истории многовековых попыток усовершенствования
евклидовой системы аксиом геометрии.
10 В чем состоят основные достижения известных представителей
Александрийской школы математиков Евклида, Архимеда, Аполлония
Пергского?
11 Расскажите о трех знаменитых задачах древности (о квадратуре
круга, о трисекции угла, об удвоении куба), истории их решения и влиянии
на развитие математики
12 Объясните причины упадка греческой цивилизации (в том числе и
математики)
70
13. В чем состоят основные достижения математиков древнего Востока —
Индии. Китая, арабского мира?
14. Различаете ли вы понятия «цифра» и «число»? Разъясните смысл
этих понятий Разъясните, что такое нумерация или система счисления
Какие системы счисления вы знаете*7 Расскажите об истории возникнове-
ния и развития систем счисления На фасаде дома латинскими цифрами
изображен год завершения его строительства MCMXIV. Какой это год? За-
пишите латинскими цифрами число 1917.
15. В чем состоит позиционный принцип записи числа Расскажите об
истории его разработки. Поясните этот принцип на примере записи числа в
десятичной системе счисления. Почему в вычислительной технике удобно
использовать двоичную систему счисления?
16. Расскажите о последовательности расширения понятия о числе
Сформулируйте условия, которые должны быть выполнены при расшире-
нии числового множества А до числового множества В Поясните смысл
выполнения этих условий на примере расширения множества целых чисел
до множества рациональных чисел
17. Расскажите о сущности аксиоматического метода. Сформулируйте
аксиомы множества N натуральных чисел. В чем смысл принципа матема-
тической индукции Расскажите о методе математической индукции, про-
иллюстрируйте его применение на примере
18. Эпоха Ренессанса характерна возрождением греческой мысли. Дай-
те анализ и приведите примеры достижений математики XVI—начала
XVII вв. итальянцев, французов, англичан (дель Ферро Тартанья Кардано,
Феррари, Виета, Декарт, Гэрриот и других) в областях решения уравнений,
завершения развития алгебраической символики, создания правил буквен-
ного исчисления, расширения понятия о числе
19. Дайте характеристику математики переменных величин Назовите
ведущие понятия математики переменных величин?
20 Назовите основные достижения ведущих основоположников мате
матики переменных величин Декарта Лейбница, Ньютона, Эйлера
21 Приведите основные факты из истории возникновения теории веро-
ятностей.
22 Как вы понимаете разделение математики на «чистую» и «приклад-
ную»? Приведите примеры результатов относящихся к каждой из облас-
тей, а также ярких представителей каждой области.
23. В чем смысл аксиоматического метода? Раскройте смысл таких по-
нятий, как основные (неопределяемые) понятия и отношения, аксиомы,
теоремы, система вксиом, полнота, непротиворечивость, независимость
аксиом. Расскажите о роли Давида Гильберта в создании аксиоматическо-
го метода.
24. Какими особенностями характеризуется современный период раз-
вития математики? Разъясните на примерах положения, характеризующие
особенности современной математики, сформулированные А.Н. Колмого-
ровым
А. В основе всей математики лежит чистая теория множеств,
Б. Специальные разделы математики занимаются структурами, при-
надлежащими к тем или иным специальным родам структур. Каждый род
структур определяется соответствующей системой аксиом Математика ин-
71
тересуется только теми свойствами структур, которые вытекают из приня-
той системы аксиом, т е изучает структуры только с точностью до изомор-
физма. (При ответе на этот вопрос воспользуйтесь статьей Н Бурбаки
«Архитектура математики», опубликованной в настоящем сборнике.)
25. В чем различия дискретной и непрерывной математики. Приведите
примеры дискретных и непрерывных ветвей математики?
26 Какие общие требования должны быть предъявлены (по мнению
Д. Гильберта) к решению математической проблемы?
27. Расскажите смысл понятия математической «структуры» и опишите
типы структур (по Н. Бурбаки).
28 Проанализируйте последний абзац статьи Н. Бурбаки, раскроите
роль аксиоматического метода в математике, прокомментируйте формулу
Лежен—Дирихле все великие мыслители-математики стремились «идеи
заменить вычислениями»
ЭЛЕМЕНТЫ МАТЕМАТИКИ
Великий архитектор Вселенной все более пред-
ставляется нам чистым математиком
Джеймс Джинс
Весь предшествующий опыт убеждает нас в
том, что природа представляет собой реализацию
простейших математических мыслимых элементов
Альберт Эйнштейн
Т. Фройденталь
ЛОГИКА*
Сорокалетний мужчина ищет заместителя для пешеходных прогу-
лок по предписанию врача Гарантируется высокий гонорар (объявле-
ние в швейцарской газете)
Сначала мне показалось, что это ваш брат. Когда вы приблизились, мне
казалось, что это вы сами. Теперь оказалось, что вы и есть ваш брат (разго-
вор при встрече)
Почему собака машет хвостом? Потому что собака очень тяжела и хвост
не может махать собакой.
Если женятся на своей собственной вдове, это не кровосмешение
(из юридического курса о наказаниях).
До рождества Христова годы считали в обратном порядке (из лекции по
истории).
Чему равен радиус окружности, длина которой 22 см, если можно счи-
тать, что л = 3 у ? (Из лекции по математике).
У кошки четыре лапы; нет кошки, у которой пять лап; значит, кошка
имеет девять лап.
Три мальчика + две девочки = пятеро детей = двум мальчикам +
+ трем девочкам.
73
Что такое логика? Познакомившись с этими примерами, каждый
скажет: «Это нелогично!» — и попытается логическим путем найти в
них противоречия. Однако они не имеют ничего общего с тем, что на-
зывают логикой в учебниках математики.
Среди эпиграфов нет такого примера, как:
Ни один император не является трубочистом,
встреча с трубочистом предвещает счастье,
значит, встреча ни с одним императором ие предвещает счастья
Такие примеры уже имеют нечто общее — и даже весьма много
общего — с тем, что издавна содержится в учебниках логики. Но они и
созданы лишь для того, чтобы оправдать существование этой логики.
Сборники задач, которые пришлось разработать и которые хотели про-
верять такой логикой, являются ужасным свидетельством того, что
происходит, когда некоторый предмет обучения изолируют от всей
системы и от реальной действительности. Формальная логика за по-
следние сто лет сильно изменилась, но примеры, которыми мы иллю-
стрируем ее нынешнюю форму, не намного улучшились. Для этого есть
свои причины.
Логика имеет нечто общее с мышлением; если мы делаем самый
процесс мышления предметом нашего мышления, то мы называем это
логикой.
Я знаю: то, что я здесь излагаю, звучит страшно старомодно. Все
специалисты по формальной логике сожрут меня живьем или, по мень-
шей мере, выразят сожаление. Ведь логика, скажут они, — это
изучение формальной системы. И все же я отваживаюсь на это. Я от-
важиваюсь назвать логикой нечто, что так называет каждый — также и
формальную логику, даже если и не рассматривается формальная ло-
гика непосредственно.
Схематизация и формализация. Мышление выражается словесно;
при этом часто произносят слова беззвучно, лишь про себя. Но мы не
отождествляем мыслей с их словесным выражением, как это иногда
делают формалисты и бихевиористы; ведь одна и та же мысль может
быть различными способами выражена словами, будь то на одном
языке или на разных языках. Однако мысль и ее словесное выражение
тесно связаны между собой. Если мы делаем мышление предметом
нашего мышления, то пользуемся логикой; при этом едва ли можно
избежать словесного выражения мышления — мы выражаем наше
мышление о процессе мышления опять-таки словесно Пожалуй, на
чем-то может быть поставлено ударение.
Мы многократно анализировали понятия и доказательства (вспом-
ним, например, теорему о перпендикулярах, проведенных к серединам
74
сторон треугольника), чтобы обнаружить их логическую структуру и
выражающиеся ими мысленные схемы, не размышляя относительно
каких-либо выводах относительно математического языка. С другой
стороны, мы анализировали словесные структуры (например, различ-
ные прилагательные при слове «группа») с выводами относительно
рассмотренных слов. Все это относится к логике. Однако для дидакти-
ки целесообразно различать эти две вещи. Я предлагаю говорить о
схематизации там, где мышление рассматривается в узком смысле как
предмет математической деятельности, и о формализации там. где
словесные формулировки принимают математический характер так,
что становится заметным стремление к математически безупречному
языку.
Я хотел бы также четко отделить одно от другого и хотел бы, чтобы
в моих разъяснениях всякий раз было ясно, о чем идет речь, ибо не-
возможно сначала аккуратно рассмотреть одно, а затем другое. Суще-
ствует процесс схематизации, при котором словесные выражения яв-
ляются средством, но не предметом исследования, и существует про-
цесс формализации, при котором язык математически анализируется
языковыми средствами, которые могут выражаться на том же или на
другом языке. Это верно и для учебного процесса: логика ни в коем
случае не означает лишь символической логики, а применение логиче-
ских символов вовсе не означает, что мы занимаемся логикой.
Логические схемы. То, что можно ныне считать надежным в логи-
ческих схемах, основано на анализе мыслительной деятельности, при
котором его, так сказать, разлагают на атомы. В традиционной логике
исходили из простых примеров повседневного мышления и под из-
вестным влиянием определенного языка строили определенные схемы;
в последнее время больше ориентируются на язык, развившийся из
математического мышления. Разумеется, анализируется не реальное, а
идеализированное мышление, однако в этом нет ничего из ряда вон
выходящего; мы всегда рассматриваем в математике идеализирован-
ные модели реальной действительности. Если же мы желаем приме-
нить результаты наших исследований — а применение и является
предметом обсуждения на занятиях, — то возникает вопрос, примени-
мо ли то, что изучено при анализе идеализированного мыслительного
процесса, к использованию и для улучшения реальных мыслительных
процессов. Насколько далеко простирается действенность идеализиро-
ванного мыслительного процесса, нужно всегда проверять мысленным
экспериментом. Ясно, что самый лучший анализ и синтез идеализиро-
ванного мыслительного процесса не помогают, если этот процесс не
укладывается в рамки реальности.
75
Конечно, дело не всегда обстоит столь уж плохо. Однако может
случиться, что результаты схематизированных действий окажутся ди-
дактически бездейственными, так как ход рассуждений будет разви-
ваться по совсем другой, более удобной схеме, которая не совпадает с
интересами логика. И все же то, что делает логик, может быть весьма
ценным. Если человек и не пожелает мыслить по данной схеме, ее
можно «привить» вычислительной машине.
Нет, это не шутка. Подоплекой, а в иных случаях даже основной
целью схематизации в течение последнего столетия является идея
придать математике такую форму, в которой с ней могла бы справить-
ся вычислительная машина.
Вообще-то нет уверенности, что это есть лучшая форма обучения
человека; напротив, это весьма маловероятно. Но стоит подумать, как
следует обучать, скажем, обслуживанию автозаправочной станции чело-
века и совершенно по-другому компьютер. Но коль скоро мы обучаем
людей, а не ЭВМ, то может быть лишь преимуществом, если мы всемер-
но используем, что наши школьники все же люди, а не автоматы.
Мы уже говорили о том, что обучение отдельным частным резуль-
татам анализа долгое время считалось высшей дидактической премуд-
ростью; элементы анализа могут оказаться важными, но лишь при ус-
ловии, что школьник может самостоятельно овладеть ими.
Как бы ни выглядели найденные нами логические схемы, всякий
раз возникают вопросы: являются ли схемы достаточными и, если
они окажутся достаточными, являются ли они целесообразными, ибо
может ведь случиться, что путем других группировок, более крупными
блоками, придут к другим понятиям
Но и это еще не все основные вопросы, так как схемы ведь нужно
применять, чтобы учить и учиться, а для этого нужно знать: как вве-
сти несхематизированное в рамки схемы?
То, что говорит нам формальная логика относительно форм мыш-
ления, может быть достаточным в следующем отношении; ряд матема-
тических выводов, если он вообще пригоден, можно подвергнуть та-
кой схематизации и можно проверить, действует ли он; при этом мож-
но убедиться, укладывается ли он в схему. Это и будет почти все воз-
можное. Схемы, конечно, могут быть в следующем смысле недоста-
точны: их едва ли можно применять, чтобы заполнить пробелы в ма-
тематических выводах, чтобы решить поставленную математическую
задачу, чтобы поставить задачи себе самому или кому-то другому.
Возможно, логические схемы достаточны, чтобы осознать, правильно
ли построено определение, но они не помогают предпочесть то или
иное определение для упорядочения некоторого поля. Возможно, что
удастся проанализировать или доказать очень простые математические
76
факты, применяя к ним все логические схемы в произвольном порядке,
но с их помощью никак нельзя осуществить глобальное упорядочение.
До сих пор мы едва ли занимались чем-либо, кроме изолированных
логических схем, — их ведь так легко формализовать, а тенденция ма-
тематической логики как раз и заключается в формализации. Но логи-
ческие схемы, которыми приходится заниматься в действительности,
не являются изолированными, как это бывает в формальной логике, и
мышление в них протекает гораздо более сложно. Большей частью
приходится рассматривать более крупные логические комплексы, ко-
торые гораздо труднее формализовать, и чем ближе мы подходим к
глобальному, тем больше логическая тактика уступает место логиче-
ской стратегии.
Я ни в коем случае не хотел бы утверждать, что в будущем каждая
логическая стратегия заменится формализацией, но известные и фор-
мализованные к настоящему моменту логические схемы ограничены
восприятием отдельных элементов или даже тем, что считается по-
следним этапом расчленения на составные элементы.
То, что на низших ступенях рассуждений было стратегией, может
быть на высших — тактикой. Скажем, рекомендации «если ты должен
доказать что-то, предположи сначала, что это неверно» или «если не-
что не известно, назови это иксом» являются до упорядочения логики
или соответственно алгебры стратегиями, которые вообще должны по-
зволить осуществить то упорядочение поля, которое затем будет на-
звано логикой высказываний или соответственно элементарной алгеб-
рой. Коль скоро эти упорядочения осуществлены, то глобально дейст-
вующие стратегии станут тактиками. Исходя из этой поэтапной зави-
симости расположения границы между тактикой и стратегией, было
бы, вероятно, полезным привести примеры стратегии на высших эта-
пах, чтобы показать, сколь мало помогает там формализация.
Вспомним, скажем, доказательство существования наибольшего об-
щего делителя двух целых чисел: ль и2. Издавна известен алгоритм Евк-
лида: большее число Л1 делят на меньшее и2 с остатком л3: Л| = ^1Л2 + и3.
Затем повторяют это действие с числами л2, л3,- л2 = ^2л3 + л4 и т.д.;
последний, не равный нулю остаток и является наибольшим общим
делителем d, в чем можно убедиться, выполняя действия в обратном
порядке, причем для d получается выражение d = Х|Л( + х2л2.
При последовательном делении числа л( и пъ последовательно за-
менялись меньшими числами. Путем линейного комбинирования мы
оказываемся внутри аддитивной группы целых чисел Н, порожденной
данными числами п\ и пг; d является наименьшим положительным
элементом в этой группе.
77
Теперь обратим доказательство — и это характерно для многих по-
добных доказательств — и оказывается, что мы вдруг ввели аддитив-
ную группу И и ищем в ней наименьший положительный элемент, ко-
торый по построению имеет форму d = jct п । + х2п2: следовательно, ка-
ждый делитель I чисел л( и п2 является также делителем d. Теперь ос-
тается лишь показать, что d является делителем чисел щ и пъ но суще-
ственно легче показать, что d является делителем всех элементов из Н —
опять-таки типичное рассуждение. Можно сказать так: данное числом
(еЯ) разделим на d с остатком г: у = qd + г, здесь у е H,d с H,qd е Н,
r = y-qd^Hu число г, как остаток от деления на d. меньше самого d,
а поэтому г = 0.
Но можно сделать это еще изящнее; если не каждый элементу g Н
делится на d, то рассмотрим наименьший «нарушитель» (т.е. число, не
делящееся на d) — число к. Итак, к с Н не делится на d и является
наименьшим положительным числом из всех таких чисел; но тогда k-d
тоже входит в Ни тоже не делится на d, причем к - d< к. Но, с другой
стороны, так как d было наименьшим положительным элементом из Н,
то число k-d является меньшим «нарушителем», чем само к. В этом
доказательстве заключены три стратегии, которые применимы и в дру-
гих случаях. Стоит заметить еще, что важный числовой алгоритм Евк-
лида и даже вообще деление с остатком ныне почти исчезли в качестве
способа доказательства. Об этом стоит пожалеть; в учебном процессе
следовало бы пользоваться обоими методами — понятийным и индук-
тивным.
Принципы минимума являются ценными стратегиями в теории чи-
сел. Скажем, при отыскании нормального вида квадратичных форм с
целыми коэффициентами или при построении базисов абелевых групп
пользуются этими принципами. Существуют понятие эквивалентности
и определенные операции, которые преобразуют объекты (т.е. квадра-
тичные формы) в им эквивалентные. Представители классов эквива-
лентности (нормальные формы) характеризуются определенными
уравнениями и неравенствами с параметрами (коэффициентами).
Можно показать, что каждый объект эквивалентен одному из объек-
тов-представителей, причем с помощью операций, сохраняющих экви-
валентность, отклонения от нормальной формы постепенно уменьша-
ются, пока не исчезнут окончательно.
Так поступали в давние времена. Теперь говорят: я заменяю неко-
торый объект ему эквивалентным так, что его отклонение от нормаль-
ной формы становится минимальным, — и показывают, что всякое
возможное отклонение можно еще уменьшить. Если некоторый объект
с минимальным отклонением от нормальной формы еще не является
нормальной формой, то рассматривают наименьший «нарушитель» и
78
поступают, как показано выше. Только здесь объекты не являются
упорядоченными по величине, как целые числа; приходится довольст-
воваться частными упорядочиваниями — опять-таки парадигматиче-
ская идея.
То, что строго монотонное отображение числовой прямой на себя
обязательно является непрерывным, можно нудно доказывать с помо-
щью «эпсилон—дельта». Ныне же поступают так: топологическая
структура множества действительных чисел определяется их структу-
рой порядка (именно потому, что определяемые порядком интервалы
образуют топологический базис); структура порядка при строго моно-
тонном отображении по определению инвариантна; следовательно,
инвариантна и топология, и, следовательно, такие отображения непре-
рывны.
Стратегии, которые здесь обнаруживаются и которые позволяют из
логической зависимости структур делать заключения об определенных
свойствах автоморфизма, имеют большое значение.
(Автор приводит специфические примеры из проективной геометрии
и из теории множеств, которые, по его мнению, дают представление о
том, что предвзятое мнение может иметь ослепляющее воздействие.)
Если анализ схемы мышления доведен до отдельных разобщенных
схем, то они могут быть достаточны лишь в ограниченном отношении,
но не в смысле целесообразности, которую мы можем апробировать
лишь практикой.
Это не означает, что разобщенные схемы не имеют ценности. Я еще
вернусь к тому, что они означают в учебном процессе. Но это еще не
все. Я не могу требовать от учителя, чтобы он преподавал такую логи-
ку, которой не овладели сами логики и которая существует лишь в той
полуосвоенной деятельности, которой они занимаются; нельзя этого
требовать и от авторов учебников. Но я все же хочу обратить внима-
ние на эти проблемы: каковы наши стратегии и можем ли мы осознать
их настолько, что они окажут влияние на преподавание? Может быть,
мы можем даже так сформулировать их, что и другие смогут исполь-
зовать их в учебном процессе.
Схематизация. Как уже сказано, с дидактической точки зрения
схематизация гораздо важнее, чем сами схемы. Многие из наших схем
еще едва осознаны. Не является ли это скорее полезным в дидактиче-
ском отношении, чем вредным? То, что нами не осознано, мы не мо-
жем сознательно распространять. Схемам, которые лишь неявно уло-
жились в нашем сознании, мы не готовы, к счастью, обучать других
Мы можем явно обучать лишь систематизации, но не собственно схе-
мам. К сожалению, при этом отдельно вести учет по каждой ступени
79
не удается. Схема мышления может быть уже нормализована так, что
учитель пользуется ею автоматически, тогда как для школьника она
оказывается целым событием Вот некоторые примеры
Логикой издавна занимаются в процессе обучения математике, будь
то в смысле схематизации или формализации. Каждый учитель то туг,
то там обучает логике. Это может делаться более или менее системати-
чески, но не существует другого дидактически оправданного пути к л>
гическим понятиям, кроме пути логической разведки, т.е. пути анализа
ситуаций, которые должны быть в этом случае мыслительными ситуа-
циями. Но мыслительные ситуации в повседневной жизни бывают часто
слишком простыми, и, как мы уже подчеркивали, слишком простые си-
туации не следует пытаться математизировать; более сложные ситуации
часто оказываются доступнее, так как в них обнаруживаются более ма-
тематизируемые шаги.
Нам неоднократно встречались такие ситуации в примерах, и мы
проводили логический анализ, как его должны проводить школьники
Я напомню теорему о перпендикулярах к серединам сторон треуголь-
ника с множеством поводов к логическому анализу. Там можно учить-
ся на многом: «необходимое и достаточное» — пара; если |Л£4| = \МВ\.
то точка М лежит на перпендикуляре, проведенном через середину от-
резка АВ; если точка М лежит на перпендикуляре, проведенном через
середину отрезка АВ, то |М4| = |А/В|; значение транзитивности отно-
шения; асимметризация симметричных высказываний; доказательство
инцидентности метрическими средствами.
«Необходимость—достаточность», однажды сформулированные, а
также транзитивность совершенствуются в разнообразных приложе-
ниях и становятся тактикой, а для учителя они уже давно служат так-
тикой с высшей точки зрения. Но это не дает учителю права требовать
той же схемы мышления и от ученика. Наоборот, исходя из таких си-
туаций, школьник должен скорее выработать у себя мысленную схему
«необходимо-и-достаточно» и схему транзитивности, чтобы в конце
концов, может быть, научиться их формализовать. Другие схемы мо-
гут надолго или даже навсегда оставаться неформализованными. При-
мерами этого могут служить третья и четвертая стратегии — обе они
представляют собой едва ли формализуемые на школьном уровне схемы.
Лучше всего издавна известны в школьном обучении схемы мыш-
ления в геометрии. Например, структурируются геометрические рас-
суждения — на определения, теоремы, условия, утверждения, доказа-
тельства; при построениях известны и некоторые другие аспекты.
Геометрия является в то же время образцом бездействия навязанных
схем. Это важные и типичные для математики вообще схемы, но они
не имеют ценности для школьника, который не испытал потребности в
80
схематизации на собственном опыте и потому не чувствует необходи-
мости схематизации. Кроме того, нет ведь никакого смысла диктовать
схему упорядочения неизвестного материала или материала, совсем не
требующего упорядочения Но традиционная дидактика часто идет
еще дальше; пытаются ввести формализацию, в ходе которой хотят
определить, что такое определение, теорема, условие, утверждение,
доказательство, построение
Доказательство от противного. Я хочу все же рассмотреть под-
робно одну схему мышления, нменно доказательство от противного.
Наряду с обращением доказательство от противного является тради-
ционным логическим предметом обучения геометрии. Это, собствен-
но, удивительно. При логически элементарном характере школьной
геометрии можно было думать, что доказательство от противного в
геометрии, которое рассматривается в школе, является излишним. Ес-
ли обратиться к учебникам, то наше предположение подтверждается
Доказательства от противного часто лишь кажутся таковыми. Вот то-
му пример
Нужно показать, что через три точки А, В, С, не лежащие на одной
прямой, проходит не более одной плоскости. Допустим, что сущест-
вуют две такие плоскости: а и 0. Разумеется, была введена аксиома, по
которой две плоскости, имеющие две общие точки Р и Q, имеют вме-
сте с ними и общую прямую PQ. Здесь можно использовать следствие:
прямые АВ, ВС и АС целиком принадлежат как плоскости а, так и
плоскости 0. Возьмем любую четвертую точку D е а, не лежащую ни
на одной из этих прямых; хотя бы одна из прямых DA, DB и DC не
окажется параллельной соответственно ВС АС или АВ, пусть, для оп-
ределенности, DA пересекает ВС в точке Е. Но точка Е лежит на ВС и,
следовательно, принадлежит плоскости 0; точка А также принадлежит
плоскости 0, а потому и вся прямая АЕ принадлежит плоскости 0.
А так как точка D лежит на прямой АЕ, то и точка D принадлежит
плоскости 0. Точно так же можно показать, что любая точка плоскости
а принадлежит и плоскости 0, а отсюда и следует, что плоскости а и 0
совпадают.
Является ли это доказательством от противного? Разумеется, нет.
Но обычно его рассматривают как доказательство от противного. При
этом начинают так: «Пусть а и 0 — две различные плоскости, прохо-
дящие через точки А В, С...». Вполне естественна склонность посту-
пать именно так. Но в действительности предположение а * 0 нигде не
используется в ходе доказательства. Точно так же можно при любом
доказательстве сделать особое предположение, которое, как выяснится
к концу доказательства, ложно Но эта ложность нигде в ходе доказа-
7 Зак 72 81
тельства не используется. По этой причине нельзя считать проведен-
ное доказательство доказательством от противного.
(Приведенное выше доказательство содержало еще исследование,
зависящее от того, не являются ли DA, DB или DC параллельными
противолежащим сторонам. Это выглядит как вывод от противного,
но легко может быть исключено. Разумеется, существуют геометриче-
ские системы, в которых это утверждение неверно, однако мы при-
держиваемся здесь рамок обычной геометрии.)
Другой пример. Чтобы показать, что известные прямые на плоско-
сти параллельны друг другу, предполагают, что они непараллельны и
выводят из этого противоречие.
Является ли это доказательством от противного? Я полагаю, нет.
Параллельные определены негативно, как прямые, не пересекающиеся
между собой. Прямой метод показать, что это пересечение не имеет
места, — это предположить, что такое пересечение налицо. Я не на-
звал бы это настоящим доказательством от противного. Подобный
пример: чтобы доказать, что 41 — иррациональное число, допуска-
ют, что 41 =plq при целых puq.
Когда из «Если |Я4| = |РВ|, то точка Р лежит на перпендикуляре,
проведенном через середину отрезка АВ» выводят: «Если точка Р не
лежит на перпендикуляре, проведенном через середину отрезка АВ, то
\РА\ * |РВ|», то это тоже не является доказательством от противного.
Переход от одного из этих высказываний к другому происходит по
контрапозиции (если р q, то q -> р. а хотя этот принцип является
основой доказательства от противного, сам по себе он еще не является
таким доказательством, р —> q означает, что из истинности р вытекает
истинность q: но тогда без всяких искусственных выводов ясно, что из
ложности q немедленно вытекает и ложность р Конечно, как и все
простые вещи, можно усложнить и это, скажем с помощью цепочки.
Дано, что р -> q\ предположим, что q неверно, т.е. q ; утверждается,
что р. Предположим, что верно р, т.е. само р; тогда из условия выте-
кает q, что противоречит предположению. Поэтому р неверно, т.е. р.
Здесь, чтобы подвести к доказательству от противного, потрачено
много слов впустую ради того, что гораздо проще, чем доказательство
от противного.
Любопытно, что учебники, рассматривающие доказательство от
противного, часто даже не упоминают о схеме контрапозиции.
В одном учебнике я нашел объяснение; при доказательстве от про-
тивного начинают с того, что перечисляют все мыслимые относитель-
82
но утверждения теоремы, допущения; все они поочередно исследуют-
ся. По мысли этого автора, будет доказательством от противного дока-
зательство некоторой теоремы о треугольнике, если сначала проверя-
ется, верна ли она для остроугольного треугольника, затем для прямо-
угольного и, наконец, для тупоугольного. Разумеется, это не есть дока-
зательство от противного, хотя исследование различных случаев мо-
жет завуалировать доказательство от проти ного. При доказательстве
от противного рассматривается только одно предположение, именно,
что утверждение теоремы неверно. Логически доказательство от против-
ного основывается на контрапозиции, т.е. на эквивалентности: р -> q и
Цитированный же автор имеет в виду метод, основанный на экви-
валентности: [(р v q) —> г] и [(р -> г) л (? “> О)-
Это, конечно, тоже не есть доказательство от противного — больше
того, это грубая ошибка, если, для того чтобы доказать нечто, предпо-
лагают это верным. Не стоит разъяснять, что то, что еще только требу-
ется доказать, нельзя заранее предполагать верным.
Если начать с требуемого высказывания р и шаг за шагом заменять
его эквивалентными высказываниями q, г, s, т.е. так, чтор <-> q; q <-» r\
г <-> s, причем истинность s очевидна, то истинность р доказана. Это,
собственно, даже больше, чем требуется. Чтобы обосновать доказа-
тельство, можно ограничиться требованиями p<-q, q<-r, r<-s
Если допустить ложное высказывание, то это может дорого обой-
тись. Это верно, что рано или поздно мы столкнемся с противоречием.
Если же, исходя из р, мы никогда не придем к противоречию, то р, во
всяком случае, непротиворечиво, и мы можем спокойно принять его
как истинное. Однако здесь мы не можем быть уверены в непротиво-
речивости; для этого следовало бы для каждого метода вывода пока-
зать, что из р не вытекает противоречия, но ведь проверить можно
лишь некоторые методы.
Откуда же берется это «допустим, что утверждение верно»? Может
быть, из анализа фигур геометрических построений, где начинают с
«Допустим, что АВС — искомый треугольник». Или из текстовых за-
дач: «Пусть искомое число фншек равно х». Затем для неизвестного х
получают уравнение Ф(х) = 0, откуда, скажем, находятх =13. Обычно
это означает лишь, что если решение существует, то оно должно быть
равно 13. Действительно ли число 13 решает задачу, нужно еще прове-
рить. Даже если бы математические аргументы были обратимы, можно
было еще думать, что некоторые числа в условии задачи не учтены и
не использованы в форме математических условий.
т
83
Что же такое действительно доказательство от противного? На это
еще труднее ответить, чем на вопрос, что такое доказательство. Точно
объяснить это можно только с помощью формальной теории доказа-
тельств, но там опять-таки вследствие жесткой формализации можно
получить совсем не те ответы, которые ожидаются. Нужно все же
больше следовать своим чувствам, если хотят рассказать, что такое
доказательство от противного, но тогда нужно принять во внимание,
что исследования различных случаев могут маскировать доказательст-
во от противного.
Место, где вводится доказательство от противного, можно найти,
листая учебник и замечая, где в некоторой фигуре поблизости от
сплошной прямой появляется пунктирная. В тексте можно прочитать
нечто вроде «Допустим, что прямая проходит через точку Р ..», и, чтобы
сделать это допущение наглядным, автор пытается его якобы изобра-
зить. В той стадии, когда школьник еще колеблется, стараясь понять со-
отношение между логикой и наглядностью, это является весьма сомни-
тельной иллюстрацией доказательства от противного.
Как я уже говорил, все доказательства от противного можно ис-
ключить из элементарной геометрии. Нужно ли исключить их и из
учебного процесса?
Отнюдь нет. Это вряд ли удастся. Доказательства «от противного»
растут и множатся как головы у гидры: на месте каждой отрубленной
головы вырастают семь новых. Однако роль доказательств от против-
ного совсем не та, которую им приписывают авторы учебников. Дока-
зательство от противного является и должно являться выражением
свободной активности школьников.
Аргументация «от противного» является общеизвестной деятель-
ностью («Петер, очевидно, дома, ибо иначе засов не был бы отодви-
нут»); школьник затрудняющийся, оставшись наедине с предложенной
задачей, начинает самостоятельно искать аргументы типа «...если бы
это было не так, то должно было бы быть...».
Доказательство от противного имеет прежде всего эвристическую
функцию. Я покажу это еще на одном примере.
Я рисую квадратную решетку на плоскости (т.е. множество точек с
целыми координатами). Вокруг каких точек существует нетривиаль-
ное вращение плоскости, преобразующее решетку в себя? Разумеется,
вы укажете эти точки: узлы решетки, середины сторон и центры
квадратов (клеток). Но как обосновать, что это решение полное?
Невольно начинают так: «Пусть, скажем...»
Пусть, скажем, Р — точка, лежащая на линии решетки АВ и притом
ближе к А. чем к В, тогда Р ближе к А, чем к какому-либо другому уз-
лу решетки, а потому для точки А не найдется точки, в которую могла
84
бы перейти точка А при вращении Если же Р лежит внутри квадрата
ABCD и не на перпендикуляре, проведенном через середину стороны
АВ. то...
После всего этого пытаются, конечно, исключить обходные пути и
избежать выводов, полученных путем рассуждений от противного. До-
казательства от противного являются, так сказать, черновыми. А учеб-
ник геометрии или урок геометрии тщательно отрабатываются, пока не
будут подготовлены набело; доказательство от противного не подходит
для них. Если учитель захочет рассказать школьнику, что такое доказа-
тельство от противного, то он должен не приводить примера, а поста-
раться поймать школьника на таком доказательстве и довести до его
сознания то, что он делает бессознательно.
Однако преобразовывать по известной схеме каждое доказательст-
во от противного в прямое доказательство, чтобы очистить геометрию
от небрежностей и затем насильственно вводить немотивированное
доказательство от противного лишь потому, что школьник должен
хоть раз увидеть его, — бессмысленно. Доказательство от противного
должно быть пережито школьником раньше, чем оно показано ему.
От схематизации к формализации. В недавно упомянутых при-
мерах речь шла о мыслительной схеме, и язык там играл второстепен-
ную роль. Но раньше встречались уже примеры, где главным был
язык. «Величайший поэт среди художников и величайший художник
среди поэтов» показывает логические ходы, таящиеся в языке; наш
язык пока еще не стал математическим, и правильно понимать его оз-
начает формализовать в математическом направлении; лишь когда это
сделано, известно, собственно, где расположены определения и как
протекают выводы. Конечно, то, что рассказывают традиционным ма-
тематическим языком, можно формализовать еще больше, и иной раз
это оказывается полезным; но от еще не математизированного языка
гораздо более далекий путь к формализации.
Я должен еще раз подчеркнуть, что нет смысла преподавать логи-
ческий формализм, независимый от материала, которому он должен
придавать форму. Это, разумеется, относится к любому формализму,
но логический формализм в этом смысле особенно опасен. Можно так на-
тренировать учащихся, что они будут увлеченно и уверенно решать труд-
нейшие задачи, и можно даже гордиться такими успехами обучения.
Я сказал «можно», но это происходит и на самом деле. Это стерили-
зованная математика, если такую деятельность, которую с успехом мо-
жет выполнить и ЭВМ, вообще можно назвать математикой
Если я говорил об ужасающих сборниках задач старой логики, то я
Должен добавить, что и сборники задач по новой логике им не уступа-
65
ют. В этом заключается проклятие изоляции. Логика может быть по-
лезна, если она не применяется только внутри себя самой. Логикой как
самоцелью пусть уж занимаются логики. Школьник же должен нау-
читься распознавать логические схемы и формы в теоремах и доказа-
тельствах, должен научиться применять логические схемы в формули-
ровке этих форм. Но прежде всего он должен научиться извлекать
пользу из этой логики в словесных ситуациях нематематического ха-
рактера. Многочисленные примеры логико-языковых ситуаций не слу-
чайно приводились там, где говорилось о математике как о дисципли-
не ума
Логика традиционно представляла собой упражнения в силлогиз-
мах, а за несколько веков лишь немногие заметили, что с одними сил-
логизмами далеко не уедешь. Ведь силлогизм лишь формализует
структуру «субъект—предикат» и не позволяет даже сделать такой
вывод, как:
Лошадь — животное;
значит, голова лошади есть голова животного.
Прежние логики знали, пожалуй, о существовании отношений, но
из философских соображений не придавали им значения. Такие выво-
ды можно формализовать лишь с помощью функций и многозначных
предикатов.
По традиции логика связана с геометрией; если присмотреться по-
ближе, станет ясным, что силлогизмы не очень помогают; однако ни-
кто не догадался использовать эту связь и, наоборот, приспособить ло-
гику к геометрии. Геометрия всегда была экспериментальным полем
для логики. Если просмотреть учебники и методики хотя бы начала
60-х гт., то никто не усомнится, что геометрия действительно пред-
ставляет собой материал для логических упражнений; в алгебре о ло-
гике не было и речи.
В алгебре школьнику преподносят хорошо действующую систему
правил преобразований данных выражений с заранее определенной
целью. В геометрии нет таких надежных схем. Волчьи ямы в алгебре
(скажем, деление на нуль или умножение обеих частей неравенства на
отрицательное число) исключаются не путем логического анализа, а с
помощью специально предусмотренных правил.
В классической школьной практике слово «алгебра» можно объяс-
нить как «руководство к заполнению схем» или, еще резче,
«...заготовленных бланков». Заготовленный текст запечатлен в глуби-
нах памяти школьника; он должен написать лишь то, что должно сто-
ять в оставленных промежутках. Результат напоминает восприятие те-
лефонного разговора, когда мы слышим только одного из собеседни-
86
ков: «Да... да-а... нет... да... три... нет». При хорошей сообразительно-
сти удается, может быть, по тону и по выражению лица говорящего
догадаться, о чем говорит второй собеседник. Ежегодно, просматривая
выпускные работы гимназистов, я поражаюсь догадливости учителя,
который знает, какую заготовку заполняет школьник в каждом кон-
кретном случае. Ибо это и есть проклятие алгебры: существуют не-
сколько, даже много заготовок, и взаимопонимание не достигается, если
один считает, что данный формуляр представляет собой налоговую дек-
ларацию, а другой считает его бланком для почтового перевода.
В геометрии тоже имеются заранее заготовленные бланки, но их не
удается заполнять механически; здесь дело зашло не так далеко, как в
алгебре. Это одна из причин, по которой геометрия предпочтительнее
в качестве логических упражнений в школе, чем алгебра.
Геометрическое доказательство, которое хоть куда-то годится, яв-
ляется последовательным рассуждением. Задача же по алгебре — это
лишь упражнение в заполнении пробелов. Чтобы школьники при ре-
шении задачи по алгебре получили такую логическую практику, как в
геометрии, учитель должен предъявить к решению алгебраических за-
дач такие же формальные требования, как и к геометрическим доказа-
тельствам (и это отнюдь не исключено, ибо тот, кто решает алгебраи-
ческую задачу, занимается ведь и доказательством). Разумеется, для
школьника было бы скучно воспроизводить весь хранящийся в глуби-
не памяти формуляр дословно (а учителю было бы скучно читать это).
Но этого и не требуется. Так же как начиная с Виета (примерно с 1600 г.)
существует алгебраическая символика, так начиная с Пеано (примерно
с 1900 г.) существует символика логическая. К счастью, она теперь
прививается. Если мы ее применяем, то это не значит, что мы занима-
емся логикой, но это может облегчить логические рассуждения.
Весьма поучительно исследование формуляров, которые находятся
перед глазами школьников, когда они решают алгебраическую задачу.
Я перепечатываю два примера, заимствованных у ван Дормолена. Речь
идет о двух решениях следующей задачи
«Доказать, что функция Зх2 + 12х имеет минимум. Найти этот ми-
нимум и значение х, при котором он достигается».
Решение I. Зх2 + 12х = 3(х + 2)2 - 12 имеет минимум -12, который
достигается при х = -2. Обоснование: (х + 2)2 должно быть равно ну-
лю; при х = -2 это выражение равно нулю, умножаем его на 3 — все
еще 0, затем прибавляем -12 и получаем минимум, за который можно
принять число -12.
Решение II. Выражение Зх2 + 12х есть квадратное выражение. Вы-
нося за скобку 3, мы не изменим выражение. В скобках будет тогда
х2 + 4х; чтобы это выражение было равно (х + 2)2, надо прибавить 4;
87
чтобы не изменить его величину, нужно вычесть 4; эту величину (-4)
нужно также умножить на 3, тогда получится 3(х + 2)2- 12, и это рав-
но Зх2 + 12х. Выражение имеет минимум, равный -12, ибо квадрат
всегда положителен или равен нулю. Так как этот квадрат умножается
на 3, то он по меньшей мере равен нулю; именно при х = -2 мы получаем
3(-2 + 2)2 - 12, и это будет -12.
Это, как мне кажется, поучительные примеры. Логический ход рас-
суждений перемежается с бихевиористическим. Почему? Потому, что
так требует установленный порядок, — вполне естественный ответ в
алгебре. Школьнику внушают формулу, и это означает, что формали-
зация, как это часто бывает, вводится слишком рано, не в качестве за-
ключительной фазы учебного процесса, а еще до достижения той ста-
дии, содержание которой подлежит формализации.
В геометрии это несколько сложнее. Если логику отождествляют
со схематизацией, то геометрия ближе к логике, чем алгебра. Алгебра
традиционно формализована гораздо сильнее, чем геометрия; в гео-
метрии гораздо больше ссылаются на мыслительные схемы, тогда как
в алгебре можно далеко продвинуться путем овладения языком. Это
является также причиной, по которой ныне часто отказываются от тя-
гостной геометрии с ее трудно поддающимися обучению мыслитель-
ными схемами и пытаются так алгебраизировать геометрию, чтобы ею
можно было овладеть, как и алгеброй, с помощью языка. Это — жела-
ние избежать трудностей, которое сказывается, коль скоро школьнику
приходится применять математику, после того как он ознакомился с
ней лишь в форме бессодержательных словесных упражнений.
Поскольку геометрия вызывает склонность к схематизации, а ал-
гебра — к формализации, то можно понять тесную связь геометрии с
логикой, коль скоро формализация еще не признана математической и
ценной в математическом отношении деятельностью. Вместе с возрас-
танием роли символической логики упало признание логического ста-
тута алгебры. Однако никого не удивляет, что мы здесь многократно
заимствовали примеры схематизации из геометрии, тогда как примеры
формализации чаще относились к алгебре.
Формализация в области высказываний. Если записывают урав-
нение вроде х2 - Зх + 2 = 0, то школьники склонны воспринимать это
как х = 1 и х = 2 (причем «и» лишь произносится, но не записывается).
Учитель, принимающий это буквально, замечает: «х = 1 и х = 2 не мо-
жет быть верным одновременно». Тогда привычный к таким поправ-
кам школьник отвечает: «Я считаю, что может быть х = 1 или х = 2».
Учитель заключает проблему моралью: «Если ты считаешь "или", то
так и следует написать».
88
Я спросил бы учителя' «Почему вы предлагаете писать слово
«или», если уже много десятилетий для этого применяется знак v? Вы
же не предлагаете писать словами "корень из, скобка, а плюс бе, скоб-
ка закрывается, в квадрате*'9» Но это еще не все: <ос = 1 и х = 2» — то-
же верный ответ, спрашивается лишь почему. В процессе обучения
геометрии учитель математики считает своей задачей мешать своему
коллеге — учителю родного языка. Там полагается ставить вопросы и
давать ответы полными предложениями. В алгебре же, наоборот, он
довольствуется любым бессвязным набором слов, можно даже сказать,
восклицаний. Ибо в алгебре существует формуляр, предписывающий,
что следует делать. Если учитель пишет х2 - Зх + 2 = 0, то школьник
уже знает, что он должен определить значения х, удовлетворяющие
этому уравнению; если уравнение имеет вид х2 - Зах + 2а2 = 0, то
школьник будет определять, чему равен х, но, упаси боже, не а. Одна-
ко в таком случае нельзя запрещать и школьнику считать, что учитель
может удовольствоваться в качестве ответа полусловом. Ответ «х = 1 и
х = 2» является верным, если школьник подразумевает под этим «х = 1
есть решение и х = 2 тоже решение». Или
[(х = 1) —> (х2 — Зх + 2 = 0)] л [(х = 2) —> (х2 — Зх + 2 = 0)],
что эквивалентно записи
[(х= 1) v(х = 2)]-> (х2’-3х + 2 = 0).
Единственное, что при этом может ответить учитель и что было бы
целесообразным, — это задать вопрос: «И никаких других решений?»
Ибо лишь после этого можно записать:
(х2 - Зх + 2 = 0) -> [(х = 1) v (х = 2)].
Я хотел бы пояснить этим, что может означать логическая симво-
лика. Я вовсе не требую, чтобы каждое алгебраическое вычисление
записывалось с помощью логической и теоретико-множественной
символики, ибо даже в тиши кабинетов и в математических работах
мы этого не делаем. Но из текста должно быть по меньшей мере ясно,
что из чего вытекает и связана ли данная переменная квантором суще-
ствования или всеобщности либо она свободна. Не следует на каждом
шагу называть логические законы или математические аксиомы и
леммы, оправдывающие этот шаг, не следует повторять все условия
или, скажем, представлять решение уравнения в форме цепочки ра-
венств между множествами, записанными с помощью фигурных ско-
бок. Но четкая формулировка с помощью логических символов облег-
чает и делает возможными такие рассуждения, как приведенные выше
относительно «и» и пили».
6 За, 72
69
В традиционном обучении алгебре решение уравнений выполняет-
ся путем последовательной, шаг за шагом, замены данного уравнения
ему эквивалентными. Это совершенно неестественный метод, изобре-
тенный школьными педагогами, чтобы уберечь своих учеников от
ошибок. Этот метод возможен лишь в простейших случаях; ио даже и
тогда он часто оказывается слишком сложным. Естественный путь за-
ключается в том, что из данного уравнения
7х + 1 +7х + 4 =ylx + 9
выводятся следствия, которые шаг за шагом постепенно приводятся к
виду, решаемому явно, скажем
(Зх + 28)х = 0.
Решение выполняется не на основе эквивалентности, а данное
уравнение рассматривается лишь как необходимое условие; следова-
тельно,
Vx +1 + Vx + 4 = Vx + 9 -> (Зх + 28)х = 0.
Затем делают проверку, подставляют вместо х полученные значе-
ния, чтобы убедиться, удовлетворяют ли они уравнению и какие
именно, т.е. исследуют, насколько верна стрелка и в обратном направ-
лении.
Разумеется, при решении квадратных уравнений с числовыми ко-
эффициентами проверку можно опустить, ибо известно, что по обще-
му правилу все решения такого уравнения могут быть найдены по
формуле и как именно. Но это — исключение. Каждый знает, как
можно вообще облегчить себе жизнь, считая данное уравнение лишь
необходимым условием. Это особенно понятно, если уравнение воз-
никло из реальной задачи и, следовательно, если вначале математизи-
руется реальная проблема. Но часто мы отнюдь не уверены, что учте-
ны все условия, а потому вполне нормально, если затем некоторые из
математически допустимых решений отвергаются как «физически не-
приемлемые»; это означает лишь, что математический «перевод» фи-
зической проблемы оказался неполным. И конечно, вполне естествен-
но, что школьника следует приучить к критическому анализу полу-
ченных математическим путем решений
Если уравнение решают с помощью эквивалентности, то промежу-
точный текст оказывается излишним. Но, во всяком случае, нужно
указать, что является неизвестным, которое школьник должен опреде-
лить, ибо почему это обязательно должно быть обозначено через х?
(х — эпидемия прежней символики уравнений перешла теперь и на
теоретико-множественную символику; в 999 случаях из 1000 речь идет
90
о множестве таких х, которые ...)• Из текста должно также вытекать,
чем должно быть решение; если их окажется несколько, то должно
быть ясно видно «и» и «или».
Если решение уравнений протекает не в прокрустовом ложе экви-
валентности, то требуется больше. Нужно ясно указать, что из чего
следует, заменяется ли одно равенство другим с помощью конъюнк-
ции или дизъюнкции и т.п. Все это можно коротко и точно выразить с
помощью логической символики. Однако это не означает, что логико-
символический аппарат автономен. Если используются символы, то
ясно, что они означают. То, что mp-^qwq-^r можно заключить,
что р -> г, нет необходимости формулировать в общем виде, и при ис-
пользовании таких выводов не обязательно ссылаться на общие прави-
ла, так как стрелки означают ведь нечто вполне определенное. Для от-
рицания конъюнкций и дизъюнкций не требуется общих правил, ибо
это есть осмысленные операции. Конечно, и здесь не нужно преувели-
чивать. Определенные правила выявятся в процессе применения; этим
можно воспользоваться и сформулировать их в общем виде. Но не
стоит заходить далеко, вырывать логическую символику из осмыслен-
ного контекста и развивать в виде бессмысленной самостоятельной
области.
Я обещал разъяснить, почему абстрагирование логики от ее осмыс-
ленного содержания дидактически невозможно на школьном уровне. Я
должен был, собственно, сказать: мне не известен ни один удачный
эксперимент такого абстрагирования (исключая логику, которая с са-
мого начала отделена от какого-либо содержания и преподается имен-
но в таком виде). Собственно, проблема здесь, я полагаю, еще не изу-
чена, может быть, даже не замечена. Она заключается в том, что сим-
волико-логический метод представляет резкие отличия от логических
обычаев обиходного языка
Известно, что математики придают слову «или» более определен-
ный смысл, чем в обычном обиходном языке, — это всегда нераздели-
тельное «или»; известно, что математики позволяют себе считать вы-
сказывание «элементы х из V обладают свойством F(x)» верным даже
тогда, когда множество К пусто. Известно, что в обиходе высказыва-
ние считается неверным, если оно говорит о данном предмете меньше,
чем о нем известно или должно быть известно («8 + 4=11 или 12»
считается неверным и даже рассматривается как ошибочное, хотя с
формальной точки зрения оно является верным).
Импликация. Гвоздем проблемы является импликация «если...,
то...», которая задается стрелкой. Из высказываний р и q образуются
составные высказывания pvq, p^q иногда также с использованием
6-
91
отрицания pvq, p^q и т.п. Известно, что подразумевается под v
(«или») и под л («и») Относительно же «->» дело обстоит иначе. Хо-
телось бы воспринимать р -> q как высказывание, если р и q — выска-
зывания. Это не сложно, если «р = идет дождь» и «9 = на улицах мок-
ро»; тогда образуется правильно понимаемое высказывание «если идет
дождь, то на улицах мокро». Сложнее, если «р = идет дождь» и «q = (2 х
х 2 = 4)» или «q = (2 -2 = 6)». Когда в обиходной речи (даже в матема-
тически обиходной речи) употребляется «если — то», имеют в виду не
взаимосвязь вроде «или» или «и», а как бы хотят сказать: «если я
знаю, что это произошло, то могу сделать заключение, что то тоже
произошло». Но такое неясное утверждение малопригодно для форма-
лизации, и, кроме того, действительно существует потребность рас-
сматривать предложения типа «если .... то ...» как нечто равноценное
предложениям типа «или» и типа «и».
В математике часто встречаются определения, в которых заключен
критерий действенности предложения типа «если — то». Например:
А с. В означает, что каждый элемент А является и элементом В;
формализовано:
АсВ означает Vx (х с А) -» (х 6 В).
Как же здесь понимать «->»? Формально можно ответить: не иначе,
как путем составления таблицы истинности для «—>». Нужно опреде-
лить значения р -> q для не определенных конкретно р и q, т.е. функ-
ции этих puq без учета их конкретного содержания. Это действитель-
но весьма формальная точка зрения. Для «р впереди q», или «р позади
q», или «р вместе с q» нельзя, конечно, определить значения, не зная,
что такое р и q; я не знаю даже, имеют ли эти выражения смысл (мож-
но возразить, что это несущественно, ибо «если идет дождь, то 2 -2 =
4» тоже не имеет смысла, и действительно, на это нечего ответить).
Если же отказаться от выяснения содержания р и q, то единствен-
ное, что остается и от чего нельзя отказаться, — это нх значения ис-
тинности. Дизъюнкцию н конъюнкцию можно удовлетворительно
объяснить с помощью таблиц истинности. Почему же не сделать этого
и для «->»? Мы уже условились, что «р —» (р тогда и только тогда счи-
тается неверным, когдар верно и (несмотря на это) q ложно. Иначе го-
воря, (р —* q) эквивалентно р v q. Это весьма разумно, но все же име-
ет такие последствия, как то, что высказывания если Земля — планета,
то 2 -2 = 4; если Солнце — планета, то 2 -2 = 4, если Солнце — пла-
нета, то 2 -2 = 5 считаются верными. Это неплохо, но можно сказать,
что все это бесплодные истины, ибо посылка и заключение являются
своеобразными высказываниями, относительно которых и без того из-
92
вестно, истинны они или ложны Иначе обстоит дело, еслир»ч сами
зависят от переменных В этом случае известна зависимость между
множествами и высказываниями, а именно для любого множества V
высказывание, содержащее переменную х, ру : х е V верно тогда и
только тогда, когда х е V; переменная х должна перемещаться в опре-
деленном универсальн >м пространстве V Тем самым устанавливается
соответствие между логическими операциями л, v, и теоретико-
множественными операциями Г), U, V Его можно проиллюстрировать с
помощью диаграмм Венна, но ошибочно мнение некоторых авторов
учебников, что здесь речь идет не об иллюстрации, а о доказательстве, —
это порочный круг
(Далее автор истолковывает импликацию с помощью включения
подмножеств, дает теоретико-множественное истолкование другим
логическим отношениям и операциям )
Логически все обстоит прекрасно и симметрично, но психологиче-
ски порочно Трудно привыкнуть к тому, чтобы переводить на теоре-
тико-множественный язык не только знаки объединения, пересечения,
отрицания, но также и знак «-»>, притом как множество, а не как от-
ношение между множествами Это связано с нестатичным операцио-
нальным характером, присущим импликации «если-то»
Лошадь —животное,
значит, голова лошади есть голова животного.
Подставляем 3 Тогда 2х = 6.
Эти «значит» и «тогда» записываются не с помощью символа «-»>,
а с помощью значка «|-». Запись р -> q читается «если р, то <?», это
предложение на том же языке, к которому относятся р и q Если при-
меняется знак « |-», то мы оказываемся над этим языком, р |- q может,
скажем, означать, что если предположить р верным, то q тоже будет
верно или даже что q можно вывести из р
Правда, если установлено р |- q, то можно также утверждать и р —» q;
если q верно при условии наличия р, то можно показать, что р —> q,
безусловно, верно Однако р —> q выполняет совсем другие задачи, а
не только подтверждает зависимость q от р Если р ложно, то мало
смысла писатьр |- q, в то же времяр —>q сохраняет значение и в слу-
чае, когда р случайно ложно, а именно в этом случае р —> q истинно
Более того, это условие может быть полезным
Приведем следующий пример- (Л с В) означает Vxf(x е А) -> (х с В)]
Если А пусто, то х е А всегда ложно; значит, (х е А) -> (х е В) все-
гда истинно, а потому А е В справедливо. Итак, пустое множество яв-
ляется подмножеством любого другого Это весьма целесообразное
93
свойство. Оно само собой напрашивается, коль скоро пустое множест-
во вообще допустимо.
При теоретико-множественной интерпретации логической терми-
нологии Аристотеля пустого множества не возникает; «Все квирксы—
кворксы» может быть у него верным, лишь если существует хоть один
квиркс, и это верно также для «все квирксы — квирксы». Для нас, на-
оборот, второе высказывание верно, как бы мы ни понимали слово
«квиркс», а первое верно, если квирксы вообще не существуют.
Все летающие слоны откладывают яйца
рассматривается современными логиками как тривиально верное, ибо
летающих слонов не существует; Аристотель не согласился бы с этим.
Если бы существовал хоть один летающий слон, мы были бы согласны
с Аристотелем; высказывание было бы тогда уже не тривиально вер-
ным, следовало бы проверить, откладывает ли этот летающий слон
яйца. Но поскольку множество летающих слонов пусто, мы можем с
полным правом выдумать нх.
Те, которые, если заболит голова, сразу бегут к врачу
образуют некоторое множество; в него входят и люди, у которых ни-
когда не болит голова.
Те, которые, когда лгут, краснеют
включает также тех, кто никогда не лжет.
Кто при окрике не остановится, будет застрелен
грозит также тем, кого не окрикнули.
Температура воды — 20°
означает, что, если в нее опустить термометр, то ртуть остановится на от-
метке 20°, — это определение утверждает, что температура воды равна
20° даже и в том случае, если я вообще не опущу термометр в воду.
Разумеется, неверно, что нужно делать такие заключения. Обиход-
ный язык имеет свои правила, и эти правила тоже можно оправдать, но
не в строго формализованной системе. Высказывания обиходного
языка нельзя заменить их значениями истинности, и взаимосвязи меж-
ду высказываниями нельзя найти по таблицам истинности. Все это
намного сложнее, чем в сильно формализованном искусственном язы-
ке, который недостаточен даже для математической деятельности.
Весьма неприятно, что формально-логическое применение импли-
кации столь отлично от обиходного языка. Некоторые путают, и долю
этих некоторых можно считать достаточно большой. Часто бывает,
что в импликациях делают ошибки, когда они встречаются в зависимых
предложениях, как, скажем, в одной из частей определения; даже весьма
очевидные ошибки, такие, как утверждение, чтох + х + 5 = 0 —> х = 1, яв-
ляется ложным (в области действительных чисел), часто можно найти
в учебниках.
94
Более утонченным является нечто вроде
V(a,i)(Vx{(x2 + ах + b = 0) -> [(х = 1) v (х = 2)]} -> [(а = -3) л (Ь = 2)]).
Если из х2 + ах + b = 0 следует, что х = 1 или х = 2, то должно
быть а = -3 и b = 2. Это высказывание неверно, так как, например,
х1 + 1 = 0 -> [(х = 1) v (х = 2)] является верным.
Я уже обращал внимание на ошибки, встречающиеся во всей учеб-
ной литературе при использовании фигурных скобок для «множества
таких х, что ...». С импликацией в придаточных предложениях проис-
ходит нечто подобное. В то же время выражение «множество таких х,
что...» совершенно безопасно, если оно встречается в неформализо-
ванном языке. Однако такие выражения совершенно несовместимы с
требованиями формализованного языка. Желание выразить формали-
зованным языком то, что не усвоено, является хвастовством и псевдо-
ученостью.
Я столь подробно остановился на этих вещах, потому что некото-
рые авторы учебников не понимают, сколь они трудны и как долго
нужно готовиться, перед тем как начать преподавать этот предмет.
Нечто вроде символики импликации будет хорошо действовать в
простых контекстах, именно там, где не очень далеко отходят от оби-
ходного языка. Однако отделить логический формализм от содержа-
ния, чтобы оперировать им, не оглядываясь на смысловое содержание,
бессмысленно, коль скоро мы так ограничиваем импликации. Я не ут-
верждаю, что этому невозможно научить школьника, но тогда его при-
дется учить чисто формально, и это останется формальным без
всякого содержания, если даже и будет действовать. Однако, зачем
нужно такое обучение, остается неясным.
Я отнюдь не против того, чтобы показать школьнику таблицу ис-
тинности для р -> q, чтобы логически показать эквивалентность р —> q
и pvq. но не следует требовать, чтобы это было для школьника и
психологически эквивалентно, ибо психологически это неэквивалент-
но и для нас, занимающихся математикой.
(Развивая мысли о синтаксисе алгебраического языка в разделе
«Формализация — структура математического языка», автор считает
все известные ему попытки формализации синтаксиса математическо-
го языка совершенно неудовлетворительными Если связи между
сложными выражениями формализованного языка не будут показаны
в процессе обучения — а на школьном уровне сделать этого не удает-
ся, — то автор считает нецелесообразным преподнесение этих тонко-
стей школьникам без необходимых разъяснений.)
Если школьник должен будет изучать формализацию — а я уверен,
что в будущем формализация станет важным видом деятельности ма-
05
тематиков, — то он должен вжиться в примеры возникновения форма-
лизации, прочувствовать на своем опыте потребность в этом, а не про-
сто познакомиться с конечным результатом. Эти осознанные действия
с языком должны, кроме того, внести вклад и в обучение самому языку.
Я уже упоминал бросающийся в глаза аспект алгебраического язы-
ка формул, — это структурирование с помощью расстановки скобок.
Эта их роль понятна лишь немногим. Если верить учебникам, скобки
для того и существуют, чтобы раскрывать их и вводить вновь. То, что
нечто подобное скобкам должно играть роль средства структурирова-
ния и при формализации, почти не упоминается в весьма примитивных
фрагментах формализованного языка; едва ли можно увидеть намного
больше, чем фигурные скобки для «множества таких х, что ...», да и
это лишь еще один очень плохой пример, ибо здесь весьма неосмотри-
тельно применен знак препинания, чтобы выразить взаимосвязь пере-
менных.
Я уже указывал, что обиходный язык знает совсем другие средства
синтаксического структурирования: флексии, предлоги, сослагатель-
ное наклонение, придаточные предложения и довольно произвольную
пунктуацию. Еще чаще синтаксическая структура определяется по
смыслу. Только смысл, а не синтаксическая структура указывает, что в
выражении «горячие сосиски и лимонад» скобки должны быть постав-
лены иначе, чем в выражении «спелые яблоки и груши». В математике
же нельзя отбросить скобки в надежде, что их место определится по
смыслу. В математике всегда больше используются формальные мето-
ды. 4 (5 + 3) имеет не меньший смысл, чем 4 '5 + 3, и в данном слу-
чае нужно точно знать, какой вариант имеется в виду, а это можно ука-
зать только путем введения скобок.
Коренным образом отличаются обиходный и математический язы-
ки в действиях с переменными, т.е. с многозначными именами. Было
бы безнадежной затеей дать каждой вещи особое имя; поэтому помимо
имен собственных люди издавна придумали так называемые имена на-
рицательные; словом «камень» можно назвать каждый камень, словом
«мышь» — каждую мышь; если потребуется, можно различать этот
камень и тот камень, эту мышь и ту мышь. Так должны былн вести
преподавание первые геометры: «соединим эту точку с той», «пере-
сечем эту прямую той окружностью». Затем придумали помечать
точки буквами, а прямым, параллелограммам, окружностям давать ал-
горитмические имена (названия). В алгебре придумали значки для не-
известной величины и ее степеней, переняли из геометрии обозначе-
ния неопределенных величин буквами. Применение переменных стало
ныне в математике единообразным. Если переменная «камень» может
обозначать только камни, а переменная «мышь» — только мышей, то
96
переменные а, b. с, .... х. у, г, .. А, В, С,.. , а, Р, у,... применяются уни-
версально, причем ограничения вводятся лишь от случая к случаю (во
всяком случае, переменная «+» может означать только сложение, пе-
ременная «>» — только отношение порядка).
(Автор приводит примеры обозначений переменных и связей между
ними, применяемых в математике, причем указательную связь {этот,
тот) считает не относящейся к математике и не формализуемой.)
При подготовке учителей мы исходим из аксиомы, что тот, кто обу-
чает, должен знать больше, чем только то, чему он обучает. Это
«больше» относится не только к объему материала. Учитель должен
знать то, чему он обучает, еще и в форме, отличной от той, по которой
он обучает. Он должен владеть не только большим объемом материа-
ла, но и более высокой логической формой понимания этого материа-
ла. А для этого он должен почувствовать логическую глубину мате-
риала. В этом ему может помочь логика, если она будет изучена глуб-
же, чем только доказательства от противного, обращение теоремы, эк-
вивалентность и т.п. Учитель математики не должен преподавать ло-
гику, а должен пользоваться логикой, уметь помочь школьнику осоз-
нать ту логику, которой тот пользуется.
От учителя следует потребовать большего: чтобы он стоял выше им
самим избранного метода изложения материала и чтобы он сам осоз-
нал этот метод. И даже выполнению самого этого требования может
помочь логический анализ. Не в тривиальном смысле, т.е. потому, что
это есть логическая структура, которая определяет избранный метод, а
потому, что в процессе логического анализа может быть осознана сту-
пень сознания и определено ее логическое отношение.
'Колмогоров
О ЯЗЫКЕ МАТЕМАТИЧЕСКИХ ЗНАКОВ*
Термы и формулы. На практике для выражения своих мыслей ма-
тематики пользуются как словами обычного языка, так и записями, со-
ставленными из специальных логических в математических знаков.
Существуют глубокие причины того, что мысль, выраженная полно-
стью на искусственно созданном математиками символическом языке
без обращения к обычной живой речи, часто оказывается трудно вос-
принимаемой. Но принципиально важно понять, что любое матема-
тическое рассуждение может быть формализовано, т.е. полностью
записано знаками, способ употребления которых регламентирован яв-
но сформулированными правилами.
97
В этом пункте мы занимаемся «грамматикой» языка логических и
математических знаков. Знаки и комбинации знаков; имеющие само-
стоятельный смысл, бывают четырех сортов.
1. Записи, являющиеся обозначением какого-либо определенного
предмета. Так, записи
2; 3-1; 4:2; !°°Г-»”1
1001+999
являются разными обозначениями одного и того же числа два, буква
N и запись {л : п е Z, л > 0} являются обозначениями одного и того же
множества всех натуральных чисел.
2. Записи, которые содержат знаки переменных и превращаются в
обозначения определенных предметов при замене всех входящих в них
переменных записями первого рода, т е. именами определенных пред-
метов Таковы сами знаки, объявленные нами знаками переменных х,
у, z и т.п.; знаки переменных, возможными значениями которых
являются числа х + у, (х-17)/(х + 17), х-1, знаки переменных, воз-
можными значениями которых являются точки плоскости [ЛВ] (отре-
зок), (АВ) (прямая), АВ (вектор), знаки переменных, возможными зна-
чениями которых являются прямые: Sz (симметрия с осью I).
3. Высказывания — записи, относительно которых имеет опреде-
ленный смысл вопрос, истинны они или ложны. Пример истинного вы-
сказывания: (10012 - 9992) /(1001 + 999) = 2.
Пример ложного высказывания: 2 + 2 = 5.
4. Записи, которые содержат знаки переменных и превращаются в
высказывания при замене всех входящих в них переменных именами
определенных предметов Например, х + у - 3, (АВ) A (CD) - Е (пря-
мые (АВ) и (CD) пересекаются в точке Е).
Записи первых двух сортов называются термами, а третьего и
четвертого сорта — формулами. Термы, не содержащие перемен-
ных, являются именами предметов, а формулы, не содержащие пере-
менных, высказываниями.
Правила построения термов и формул. Строго говоря, не сущест-
вует одного универсального языка математических знаков. Разные авто-
ры пользуются несколько разными языками. Существуют сложившиеся
традиции различного употребления одних и тех же знаков в разных отде-
лах математики. Но математик в каждом данном рассуждении должен
точно знать законы того языка, на котором он в данное время говорит.
Прежде всего, это чисто формальные правила образования термов и
формул.
98
Разберем в виде примера высказывание
{л:л бЛГ,|л-2|<2}= {1,2,3}. (1)
Строение этого высказывания можно изобразить родословным де-
ревом (рис. 1).
В первом поколении мы имеем простые термы N, л, 1,2, 3
1/7-21 <2
{п:п ьН, |л—2{<2}«-{};2^3}
Рис. 1
Из них 2V, 1, 2 и 3 являются именами предметов, ал — пе-
ременной. Во втором поколении из термов л и N, соединенных
знаком принадлежности е, получается формула л е N, содержащая
переменную п. Из термов л и 2, соединенных знаком вычитания «-»,
получается терм л — 2, содержащий переменную л Из термов 1, 2 и 3,
разделенных запятыми и заключенных в фигурные скобки, получается
терм (1, 2, 3} В третьем и четвертом поколениях из терма л - 2 после-
довательно получаются терм |л - 2| и формула |л - 2| < 2. Они тоже со-
держат переменную л.
Но в пятом поколении происходит нечто замечательное. Терм л и
формулы л е N, |л - 2 | < 2, содержащие переменную л, перемещаются
в надлежащие места схемы {терм : формула, формула}, и в результате
получается терм, являющийся обозначением вполне определенного
множества. Этот терм {л : л е N, |л - 2| < 2} не содержит пере-
менных, так как схема его образования «связывает» все перемен-
ные терма, стоящего перед двоеточием. (Иногда говорят, что наш терм
«не содержит свободных переменных». Но законна терминология, по
которой связанные переменные совсем «не входят» в полученный по-
сле «связывания» терм. Ее мы и будем держаться.)
В шестом поколении из двух термов, соединенных знаком равенст-
ва, получается высказывание (1).
Заметьте, что при образовании термов и формул, кроме знаков ис-
ходных простых термов, нам понадобились вспомогательные знаки —
запятые, фигурные скобки, двоеточие, вертикальные прямые черточки,
знаки принадлежности, неравенства, равенства. Перечислим все схемы
построения термов и формул, которыми мы пользовались:
99
1)терм е терм -» формула,
2) терм — терм -> терм,
3) {терм, терм, терм} -» терм,
4) |терм| -> терм,
5) терм < терм -> формула,
6) {терм : формула, формула} —> терм,
7) терм = терм -> формула.
По поводу всех этих схем при
полном описании нашего языка
математических знаков должна
быть указана судьба входящих в
исходные термы и формулы пе-
ременных (какие из них связыва-
ются и какие остаются входящи-
ми во вновь образованные термы
и формулы). В наших семи схе-
мах переменные связываются
только в схеме 1. Правило связы-
вания было уже высказано: связываются все переменные, входящие в
терм перед двоеточием Примеры: в терм {(х, у) : х < а, у < Ь} входят
переменные а и Ь, но не входят переменные х и у. Если придать а и b
определенные значения, то получится обозначение квадранта число-
вой плоскости, изображенного на рис. 2.
Бессмысленные термы. Типы переменных. Из терма х у можно
образовать терм 1 : 0, положив х = 1, у - 0. Можно ли назвать запись
1:0 термом? Ведь делить на нуль нельзя. Оказывается, что разумно не-
сколько изменить определение терма и все-таки считать 1:0 термом. В
качестве термов, не содержащих переменных, мы допустим и бес-
смысленные выражения, образованные по правилам принятого нами
математического языка. А как поступить с формулой 1:0 = 2?
Мы будем считать ее ложным высказыванием. Вообще, фор-
мула. не содержащая переменных, для которой хотя бы, один из
термов, участвовавших в ее образовании, бессмыслен, считается
ложной.
Можно вполне корректно построить математический язык, в кото-
ром имеется только один вид переменных, вместо которых разрешает-
ся подставлять любые термы. Естественно, однако, что при этом полу-
чится очень много бессмысленных формул. Например, если знак «<»
понимается только в смысле неравенства между действительными
числами, то терм (Z — множество целых чисел) {х: х < Z} не имеет
смысла, а формула 1723 < Z ложна.
100
Можно уменьшить возможности получения бессмысленных термов
и часто упростить записи, введя несколько типов переменных, ус-
ловившись, например, что в данном рассуждении буквы i, J, к. I. т. п,
р q. г, s обозначают переменные, допускающие в качестве значений
только натуральные числа буквы же a, b, с. d. е, f, g, о, t. х. у, г. и, v, w
резервировать для переменных, могущих принимать любые дейст-
вительные значения, итп Соответственно делятся и термы и в
правилах образования термов и формул оговаривается, какого типа
термы можно вставлять на те или иные места схем
Логические операции ндд высказываниями и формулами. 1 —> 'll
(отрицание высказывания 71) — «'ll ложно»
2 . 'll л В (конъюнкция высказываний Т/ и 2?) — «оба высказыва-
ния 'll и “В истинны»
3 'll v В (дизъюнкция высказываний 71 н В) — «хотя бы одно
(может быть, и оба) из высказываний 'll и В истинно».
4 'll о В (эквивалентность) — «оба высказывания 'll и В ис-
тинны. или оба ложны»
Если формулы 'll и В содержат переменные, то смысл формул -> 'll.
'll л В, 'll v В, 'll О® определяется тем, что, заменив в них все
переменные какими-либо определенными значениями, получают вы-
сказывания, смысл которых указан выше.
Например, (х=у) о (х + у = 2) превращается в истинную формулу
а) при подстановке х = у = 1,
б) при любой подстановке х = а, у = Ь, где о* А иа +А #2
Если 'll о В превращается в истинное высказывание при любой
подстановке вместо всех входящих в 'll и В переменных любых опре-
деленных значений, то формулы 'll и В называются равносильными
Введем теперь операцию (такое толкование знака р не общеприня-
то, но, кажется, удобно) pU, при помощи которой из каждой форму-
лы получается высказывание Знак |- читается «превращается в ис-
тинное высказывание при любой подстановке вместо всех входящих в
'll переменных определенных значений». Ясно, что равносильность
формул 'll и В записывается в виде |- ('ll О В)
5. Импликацию двух высказываний 'll и В 'll => В будем считать
ложной в том случае, когда 'll истинно, а В ложно, во всех
же остальных случаях будем считать, что 71 => В истинно Как и для
первых четырех логических операций отсюда выводится и смысл им-
пликации 71 => В для формул, содержащих переменные Высказывание
|- (71 => В) читается «формула В является следствием формулы 71»
Кванторы V и 3. Знак |- связывает все переменные в следующей
за ним формуле Следующие две операции связывают лишь неко-
101
торые переменные. Запись V х читается «для всех х», Зх читается
«существует такое х, что».
Например, Зл (и е N л а^ nb) есть формула с двумя переменны-
ми, а
V а V b {а > 0 л b е R) => 3 п(п е N л па > Ь) — (1)
высказывание, называемое «аксиомой Архимеда».
Вместо (I) можно писать
V а > О, b g R 3 л g N {па > Ь). (2)
Но соблюдайте корректность в употреблении кванторов V и 3.
Общеприняты, строго говоря, лишь схемы
V х у... формула -» формула,
Зх Зу... формула -> формула,
где х, у,... — одна или несколько переменных. Приведя пример (2) мы,
впрочем, допустили выходящие за пределы этих схем вольности.
О скобках. Еще в младших классах вы познакомились с правилами
употребления скобок для указания порядка выполнения арифметиче-
ских действий. Это частный случай применения скобок для указания
порядка построения термов и формул. Например, формулы (А => В) => С
и А => (В => С) имеют разный смысл. Существуют правила, позволяю-
щие избегать излишне большого числа скобок. Например, по аналогии
с правилом, по которому умножение делается ранее сложения,
можно условиться, что при отсутствии скобок конъюнкция формул
выполняется до дизъюнкции, и писать (А лВ) v (А лВ) просто в виде
А /\BvCaD.
Но, не владея четкими правилами, всегда лучше поставить избы-
точные скобки, чем сделать свои записи двусмысленными.
71Т Данциг
символыи
Под алгеброй в самом общем смысле в современной математике
понимается наука, которая имеет дело с операциями, записанными в
символической форме. Рассматриваемая в столь широком плане ал-
гебра не только пронизывает своими идеями всю математику, но и
распространяет их на логику и даже философию. Определенная таким
образом алгебра является столь же древней, как и способность челове-
ка к отвлеченному мышлению, как его умение различать понятия «не-
который» и «каждый».
102
В данной статье, однако, нас будет интересовать алгебра в гораздо
более ограниченном смысле — та часть алгебры, которая носит очень
точное название теории уравнений. Название «алгебра» впервые было
применено именно в этом узком смысле. Слово это пришло из араб-
ского языка. Ал — это определенный артикль; гебар — глагол «уста-
навливать». До сих пор слово алгебриста сохранило в испанском язы-
ке (на который оказал влияние арабский язык мавров) значение «кос-
топрав».
Почти в каждой стране алгебра последовательно проходила в своем
развитии три стадии: риторики, сокращений и символов. Риторическая
алгебра характеризуется полным отсутствием каких бы то ни было
символов, если, конечно, не иметь в виду, что сами слова могут ис-
пользоваться в их символическом значении. До сих пор риторическая
алгебра проявляется в таких утверждениях, как «сумма не зависит от
порядка слагаемых», которое в символической форме может быть за-
писано а + b = Ь + а.
Алгебра сокращений, типичным примером которой является древ-
неегипетская алгебра, представляет собой дальнейшее развитие рито-
рической. Некоторые слова из-за частого употребления постепенно
стали подвергаться сокращениям. Со временем эти сокращения дос-
тигли такой формы, когда уже трудно было установить их забытое
первоначальное значение, и они потеряли всякую видимую связь с на-
званиями обозначаемых ими математических действий. Так сокраще-
ние превратилось в условный знак.
Это можно проиллюстрировать историей математических знаков
«+» или «-». В средневековой Европе последняя операция сперва обо-
значалась написанным полностью словом «minus», затем его первой
буквой «т» над которой ставилась черточка. Наконец, сама буква ис-
чезла и осталась одна только черточка. Знак «+» тоже возник в резуль-
тате аналогичных метаморфоз.
Поворотным пунктом в истории алгебры явилась работа, написан-
ная в конце шестнадцатого столетия французом Виетом, который под-
писывался латинизированным именем Францискус Виета. Его великое
открытие представляется нам сегодня совсем простым. Оно описыва-
ется самим автором в следующих словах:
«Здесь мы будем придерживаться правила, которое позволит нам
отличать данные величины от неизвестных или искомых: введем сим-
волику очеиь простую по своей природе и легко постижимую, заклю-
чающуюся, например, в обозначении неизвестной величины через А
или другую гласную, а данные величины через В, С, G или другие со-
гласные».
юз
Такая система гласных—согласных продержалась очень недолго.
Менее чем через полстолетия после смерти Виета была опубликована
«Геометрия» Декарта, в которой для известных величин употребля-
лись первые буквы алфавита, а для неизвестных — его последние бук-
вы. Картезианская нотация (т.е. способ обозначения чисел, предло-
женный Декартом. — Ред.) не только вытеснила нотацию Виета, но и
дожила до сегодняшнего дня.
Несмотря на то, что принцип выбора букв, который использовался
Виета, не привился, основная идея его предложения была принята.
Введение букв для обозначения чисел в математике — «логистика
специоза», как он сам назвал ее и которая сыграла столь значительную
роль в развитии математики, является величайшей заслугой Виета.
Нам сейчас даже трудно себе представить истинную ценность идеи
Виета. Разве буквенная нотация не представляет собой простую фор-
мальность, в лучшем случае удобный способ сокращения? Действи-
тельно, есть определенная экономия в записи (а + b)2 = а2 + 2аЬ + Ь2,
но дает ли эта запись нам нечто такое, чего бы не было в словесном
утверждении «квадрат суммы двух слагаемых равен сумме квадратов
этих слагаемых и их удвоенного произведения»?
Буквенную нотацию постигла судьба всех чрезвычайно удачных
нововведений. Повсеместное ее использование привело к тому, что
сейчас трудно себе представить время, когда прибегали к менее удоб-
ным методам. Сегодня формулы, в которых фигурируют буквы, обо-
значающие числа и другие величины, стали самым обычным делом, и
возможность оперировать символами кажется большинству людей
почти врожденным свойством мыслящего человека. Но она стала
столь естественной только благодаря постоянному упражнению. Во
времена Виета эта нотация воспринималась как коренным образом
противоречащая вековым традициям.
В чем же сила такой символики?
Прежде всего, буквы освободили алгебру от подчиненности слову.
Не только в том смысле, что без буквенной нотации всякое обладаю-
щее некоторой общностью алгебраическое утверждение превращается
в длинный поток слов со всей присущей человеческой речи неточно-
стью и многозначностью смысла. Это, конечно, очень важное обстоя-
тельство, но еще важнее, что буква свободна от ограничений, нало-
женных на слова. «А» Виета или наш «х» существуют независимо от
того, какой конкретный объект скрывается за ними, в то время как со-
кращенный условный знак переносит свой первоначальный смысл на
то, что он обозначает. Поэтому буквенная символика не есть простая
формальность.
104
Во-вторых, над буквенными выражениями очень удобно произво-
дить действия и с их помощью преобразовывать одну формулу в дру-
гую, эквивалентную ей. Преобразования соотношений для алгебры
важнее, чем сокращение записи.
До появления буквенной символики можно было говорить лишь об
индивидуальных выражениях. Каждое из выражений (как, например,
2х + 3; Зх - 5; х2 + 4х + 7; Зх2 - 4х + 5) имело свои особенности и к ка-
ждому нужен был свой подход. Буквенная нотация позволила перейти
от индивидуального к коллективному, от «некоторого» ко «всякому».
Линейная функция ах + Ь, квадратичная функция ах2 + Ьх + с стали
рассматриваться теперь с единой точки зрения. Это позволило постро-
ить общую теорию функций, которая является базисом всей приклад-
ной математики.
Но самое важное из того, что дала «логистика специоза» — и это
нас будет интересовать в данной статье — роль, которую она сыграла
в формировании обобщенной концепции числа.
Имея дело с серией численных уравнений типа:
(I) х + 4 = 6; (П) х + 6 = 4;
2х = 8; 2х = 5;
х2 = 9, х2 = 7,
можно ограничиться заявлением (как это и делали средневековые ал-
гебраисты), что первую группу уравнений решить возможно, а вторую—
невозможно.
Но когда мы рассматриваем буквенные уравнения такого же типа:
х + b = а\
Ьх = а;
Я
х
то сама неопределенность коэффициентов заставляет писать символи-
ческие решения уравнений:
х = а - Ь;
х= alb',
х= п4а.
После этого уже невозможно настаивать, что выражение а - Ь име-
ет смысл только, если а больше, чем Ь, что а!b не существует, если b
не является делителем а, и что а есть число, если а не представляет
точную п-ю степень. Сам акт написания бессмыслицы придает ей
смысл и трудно становится отрицать существование того, что получи-
ло какое-то название. Более того, если а > Ь, а — кратное Ь; а — точ-
ная л-я степень какого-то числа, то для действий, обозначаемых сим-
волами а - Ь; а/Ь\ а ; существуют твердые правила. Поэтому рано
или поздно, благодаря тому факту, что во внешнем виде этих выраже-
105
ний нет ничего такого, что указывало бы на их законность или неза-
конность, мы приходим к выводу — ничего не случится, если мы бу-
дем считать эти символы нормальными числами. А отсюда всего один
шаг до признания этих символических выражений существующими
вообще всегда. Современную арифметику отличает от довиетовской
именно разница представлений о «невозможности». До семнадцатого
столетия алгебраисты вкладывали в это слово абсолютный смысл.
Имея дело лишь с нормальными числами при выполнении арифмети-
ческих операций, они считали возможность или ограниченную воз-
можность существенным свойством этих операций.
Так, прямые действия арифметики — сложение (а + Ь), умножение
(ab) и возведение в степень аь — были всегда возможными, в то время
как обратные действия — вычитание (а - Ь), деление (а/b) и извлече-
ние корня (Va) — были возможными лишь при определенных огра-
ничениях. Довиетовские алгебраисты удовлетворялись констатацией
этих фактов и не отваживались на более глубокий анализ проблемы.
Сегодня нам известно, что возможность и невозможность — понятия
весьма относительные, что они возникают не как проявление фундамен-
тальных свойств действий, а просто как следствие ограничений, нало-
женных традицией. Устранив эти ограничения, мы устраним и невоз-
можность той или иной операции. Прямые действия арифметики произ-
водят впечатление всегда возможных потому, что они требуют от нас
сделать лишь несколько дополнительных шагов в последовательность на-
туральных чисел, которая априорно предполагается бесконечной. От-
бросьте это предположение, ограничьте множество натуральных чисел
тем или иным пределом (например, числом 1000), и такие действия, как
925 + 125 или 67 -15 станут невозможными, а соответствующие выраже-
ния бессмысленными.
Или представим себе, что мы ограничились рассмотрением только
нечетных чисел. Умножение в этом случае будет возможно всегда, ибо
произведение двух нечетных чисел есть число нечетное. Однако сло-
жение в таком ограниченном множестве окажется вообще невозмож-
ным, ибо сумма двух нечетных чисел никогда не бывает нечетным
числом.
В случае, если рассматривать одни лишь простые числа, умноже-
ние будет вообще невозможно по той очевидной причине, что произ-
ведение двух простых чисел никогда не бывает простым, в то время
как сложение возможно будет лишь для таких редких случаев, когда
одно из слагаемых есть простое число 2, а второе является меньшим в
паре «близнецов» (соседних простых чисел, различающихся на 2 —
Ред.), как это имеет место в случае 2 + 11 = 13.
106
Количество примеров можно было бы увеличить, но даже приве-
денных здесь достаточно, чтобы вскрыть относительную природу слов
«возможный», «невозможный» и «бессмысленный». Но коль скоро мы
признаем эту относительность, то естественным становится желание
выяснить — нельзя ли так расширить область обратных действий,
чтобы оии, подобно прямым, стали всегда возможными.
В такую расширенную область операций вычитания достаточно
включить кроме натуральных чисел отрицательные числа и нуль; на-
зывается эта область полем целых чисел.
Точно так же добавление положительных и отрицательных дробей
делает всегда возможной операцию деления.
Все эти числа — целые числа, дроби, положительные и отрица-
тельные, нуль — составляют область рациональных чисел. Как часть в
нее входит совокупность натуральных чисел арифметики. Четыре ос-
новных арифметических действия, которые раньше производились над
целыми числами, по аналогии оказывается возможным распростра-
нить и на эти обобщенные числа.
Это обобщение проходит совершенно гладко, без всяких противо-
речий. и если пока исключить единственный случай, который мы сей-
час рассмотрим, можно утверждать, что сумма, разность, дробь от де-
ления и степень всякого рационального числа есть также число рацио-
нальное. Этот чрезвычайно важный факт выражается обычно в сле-
дующей форме — множество рациональных чисел замкнуто по отно-
шению к основным действиям арифметики.
Единственное и весьма существенное исключение состоит в невоз-
можности деления на нуль. Такое деление равносильно решению
уравнения х • 0 = а. Если а не есть нуль, то решение невозможно, ибо
мы вынуждены, определяя число нуль, приписать ему следующее
свойство: а • 0 = 0. Поэтому не существует рационального числа, для кото-
рого х • 0 = а.
С другой стороны, уравнение х • 0 = 0 удовлетворяется при любом
рациональном значении х. Следовательно, х есть в данном случае не-
определенная величина. И если у нас нет никакой другой информации
по этому вопросу, мы должны рассматривать 0/0 как символ, обозна-
чающий всякое рациональное число, а символ а/0 как символ, не
обозначающий никакого рациональною числа.
Подводя итог сказанному, мы можем выдвинуть следующее крат-
кое утверждение: если а, b и с — рациональные числа, и а не есть
нуль, то всегда существует рациональное число х, причем только одно,
которое удовлетворяет уравнению ах + b = 0.
Это уравнение, называемое «линейным», представляет собой про-
стейший тип уравнений. Следующим по сложности является квддрат-
107
ное уравнение, затем кубическое, четвертой степени и т.д. Общее ал-
гебраическое уравнение степени и, где под и понимается наивысшая
степень неизвестного, есть ах" + Ьх? '1 + сУ " 2 + ... + рх +q = 0.
Но и оно не исчерпывает бесконечного многообразия уравнений,
которые могут быть также экспоненциальными, тригонометрически-
ми, логарифмическими, эллиптическими и т.д. Все последние типы
уравнений охватываются весьма емким термином «трансцендентные».
Пригодно ли поле рациональных чисел для того, чтобы придать
смысл всем этим уравнениям? Абсолютно непригодно. Мы можем
ожидать все большего и большего усложнения множества чисел по
мере включения в рассмотрение новых уравнений. Однако это услож-
нение не является произвольным, в природе заложен некий механизм
расширения числового поля, фундаментальная идея, дающая общую
его схему.
Эта идея иногда носит название принципа перманентности. Впер-
вые она была ясно сформулирована в 1867 г. немецким математиком
Германом Ханкелем, но ее зачатки содержались уже в работах сэра
Уильяма Гамильтона — одного из оригинальнейших и продуктивней-
ших умов девятнадцатого столетия.
Я сформулирую этот принцип в форме определения.
Бесконечное множество символов называется числовым полем, и
каждый элемент этого множества называется числом при условиях:
— если среди элементов множества содержится последователь-
ность натуральных чисел;
— если мы можем установить некий критерий, с помощью которо-
го получаем возможность всегда установить, равны ли два элемента
между собою, а если не равны, то какой из них больше, а какой мень-
ше; в случае, когда элементы являются натуральными числами, этот
критерий превращается в известное правило сравнения натуральных
чисел;
— если для любых двух элементов множества мы можем дать схе-
му сложения и умножения, которая подчиняется перестановочному,
сочетательному и распределительному законам и которая превращает-
ся в схему этих действии над натуральными числами, когда символы
являются таковыми.
Эти очень общие положения оставляют открытым вопрос о том, как
принцип перманентности применяется в конкретных случаях. Гамильтон
указал для этого метод, который он назвал методом алгебраических пар.
Мы можем проиллюстрировать его на рациональных числах.
Если а кратно Ь, то символ а / b обозначает операцию деления а на
Ь. Так, 9/3 =3 означает, что частное отданного деления есть 3. Мож-
но ли для любых двух таких операций устанавливать, являются ли их
108
результаты равными, а если нет, то какой из них больше, а какой
меньше; причем устанавливать без выполнения самих операций? Да,
мы имеем следующий критерий:
а / b = с / d, если ad = be,
критерий сравнения а/b>c/d, если ad>bc,
а/b < cld, если ad <bc.
Мы можем пойти даже дальше и, не выполняя указанных операций,
установить правила манипуляций для данных отношений:
а с ad + Ьс
сложение: — + — =-------;
b d bd
а с ас
умножение: = —.
Z b d bd
Теперь нам уже не нужно ставить условие, что а должно быть
кратным Ь. Будем рассматривать как символ нового поля определен-
ным образом расположенных математических объектов. Эти символи-
ческие объекты зависят от двух целых чисел а и Ь, поставленных друг
по отношению к другу в определенном порядке. В этом множестве пар
мы можем ввести критерий сравнения, упомянутый выше, т.е. мы мо-
жем утверждать, например, что
— = —, так как 20 х 12 = 15 х 16
15 12
4 5
— > — , так как 4 х 4 > 3 х 5.
3 4
Определим действия над этими парами в согласии с правилами, ко-
торые, как было показано, удовлетворяют нас в случае, когда а кратно
b и с кратно d, т.е. будем утверждать, например, что
2 4 (2х5) + (3х4) = 22
3 + 5~ 3x5 ”15’
2 4 2x4 8
3Х 5 " 3x5 “ 15 ’
Мы удовлетворим, таким образом, всем требованиям принципа
перманентности, а именно:
— новое поле содержит натуральные числа как подполе, так как мы
12 3 4
можем записать всякое натуральное число в виде пары: ; у; у;;
— новое поле имеет критерий сравнения, который сводится к кри-
терию сравнения натуральных чисел, когда a lb и c/d есть нату-
ральные числа;
109
— существуют две операции над новым полем, которые обладают
свойствами сложения и умножения и сводятся к ним в случае, когда
а /Ь и с/d есть натуральные числа. Это и означает, что наши новые
объекты удовлетворяют всем новым требованиям принципа. Они до-
казали свое право получить почетный титул «чисел». Они, таким обра-
зом, получили призвание, и поле чисел, старых и новых, получило на-
звание поля рациональных чисел
На первый взгляд может показаться, что принцип перманентности
оставляет такую свободу в выборе операций, определяющих обобщен-
ные числа, что этот слишком уж широкий охват не имеет особой прак-
тической ценности. Однако предположение, что натуральные числа
входят как часть в новое поле и что операции над всеми числами
должны подчиняться одинаковым законам (таким же, как и для нату-
ральных чисел), накладывают в действительности столь серьезные ог-
раничения, удовлетворять которым могут лишь весьма специальные
поля.
Позицию арифметики, в которой сформулирован принцип перма-
нентности, можно сравнить с политикой государства, склонного к экс-
пансии, но желающего всюду соблюдать те фундаментальные законы,
на которых оно зиждется. Эти две различных цели — экспансия, с од-
ной стороны, и сохранение порядков и унификация, с другой, — опре-
деляют условия присоединения новых стран к союзу.
Первый пункт принципа перманентности соответствует положе-
нию, что центральное государство союза задает тон всему союзу. Для
каждого гражданина этого государства существует некий «табель о
рангах», и этот табель распространяется на всех граждан вновь при-
соединенных стран. Это соответствует второму пункту принципа пер-
манентности.
Наконец, предполагается, что законы, определяющие взаимоотно-
шения между гражданами каждой отдельной страны, входящей в союз,
строятся по типу отношений, установленных в ведущем государстве
этого союза.
Разумеется, я не хочу, чтобы читатель воспринимал эту аналогию
буквально. Она приведена лишь потому, что может вызвать ассоциа-
ции из более знакомой всем сферы и убедить в том, что принцип пер-
манентности не является надуманным и искусственным.
Рассуждения, которые помогли нам сконструировать область ра-
циональных чисел, были характерны для первых этапов того истори-
ческого процесса, который получил название арифметизации матема-
тики. Это движение, начатое Вейерштрассом в шестидесятых годах
прошлого века, имело своей целью принципиальное отделение чисто
математической концепции таких терминов, как «число», «соответст-
110
вие» и «множество», от интуитивных представлений, связанных с ни-
ми и родившихся в результате долгого использования этих понятий в
геометрии и механике.
В частности, механика, по мнению сторонников формальной шко-
лы, наложила такой сильный отпечаток на математическое мышление,
что даже при самом тщательном выборе слов в формулировках все
равно чувствуется механическое значение, скрытое в глубине, и это
оказывает влияние на наши рассуждения. Беда в том, что слова чело-
веческой речи суть нечто, связанное с определенным содержанием, в
то время как целью математики является «очищенное» мышление.
Но как можно избежать употребления человеческой речи? Ответ
заключен в слове «символ». Только используя символический язык, не
захваченный еще влиянием расплывчатых идей о времени, простран-
стве, непрерывности, господствующих в нашем подсознании и зату-
манивающих рассуждение, — только так мы можем надеяться поста-
вить математику на крепкое логическое основание.
В этом заключается платформа школы, заложенной итальянцем
Пеано и такими представителями современной математики, как Бер-
тран Рассел и Альфред Норт Уайтхед. В фундаментальном труде этих
ученых «Principia Mathematica» авторы попытались сконструировать
весь базис математики, отталкиваясь лишь от наиболее глубоких, фун-
даментальных предпосылок и опираясь исключительно на строгие
принципы логики. Использование символики не оставило места в этой
книге для тех расплывчатых ассоциаций, которые всегда связаны со
словами людской речи.
Признаюсь, что мне лично не импонирует крайний формализм
школы Пеано — Рассела, что я никогда не чувствовал вкуса к их ме-
тодам символической логики и что все мои многократные попытки ус-
воить их символизм всегда кончались неудачей, смущением и отчая-
нием. Это индивидуальное мое качество, разумеется, оказывало влия-
ние на мое мнение, и это — важная причина, по которой я не излагаю
здесь своих предубеждений.
Тем не менее эти предубеждения не заставили меня недооценивать
роли математической символики. Я считаю, что колоссальное значе-
ние этой символики заключается не в создании стерильности и полном
запрещении интуиции человеческого мышления, а в неограниченной
возможности использовать эту интуицию для создания новых форм
мышления.
Чтобы убедиться в этом, нет необходимости обращаться к слож-
ным техническим терминам современной математики. Достаточно бо-
лее известной, но и более тонкой символики языка. Ибо, поскольку наш
язык пригоден для формулировки точных высказываний, он является
111
ничем иным, как системой символов, риторической алгеброй высшего
ранга. Существительные есть не что иное, как символы классов объек-
тов, глаголы символизируют отношения, а предложения являются ут-
верждениями, связывающими эти классы. Но будучи абстрактными,
символами классов, слова обладают способностью пробуждать в во-
ображении картину конкретного элемента, представляющего класс.
Именно в этой двойственности функции слов и заключено зерно кон-
фликта, который возникает между логикой и интуицией.
То, что верно по отношению к словам вообще, верно, в частности,
и по отношению к тем словам, которые обозначают натуральные чис-
ла. Благодаря тому, что они способны вызывать в нашем воображении
конкретные множества, они кажутся нам настолько глубоко связан-
ными с реальностью, что приобретает как бы абсолютное значение.
Тем не менее в том смысле, в каком они употребляются в арифметике,
они есть не более, как символы, подчиняющиеся определенным пра-
вилам действий.
Но как только мы приходим к признанию символической природы
натуральных чисел, они сразу же теряют свой абсолютный характер.
Их внутреннее родство и сходство с более обширным классом объек-
тов, ядром которого они являются, становятся совершенно очевидным.
Наряду с этим в новом освещении последовательное расширение кон-
цепции числа начинает выглядеть не как некий искусственный и ус-
ловный трюк, а как необходимый и неизбежный процесс, шаг за ша-
гом углубляющий наше познание.
<Р. 'Курант, Т. (Роббинс
АЛГЕБРА МНОЖЕСТВ5
1. Общая теория. Понятие класса, или совокупности, или множе-
ства объектов есть одно из самых фундаментальных в математике.
Множество определяется некоторым свойством, или атрибутом U, ко-
торым должен или обладать, или не обладать каждый рассматривае-
мый объект; те объекты, которые обладают свойством U, образуют
множество А. Так, если мы рассматриваем целые числа и свойство U
заключается в том, чтобы «быть простым», то соответствующее мно-
жество А состоит из всех простых чисел 2,3, 5,7, ...
Математическое исследование множеств базируется на том обстоя-
тельстве, что множества, комбинируясь в результате выполнения не-
которых операций, образуют новые множества — так же как числа,
комбинируясь между собой в процессе сложения и умножения, обра-
112
зуют новые числа. Изучение операций над множествами включает
«алгебру множеств», которая имеет много общего с обыкновенной чи-
словой алгеброй, хотя кое в чём и отличается от неё. Тот факт, что ал-
гебраические методы могут быть применены к изучению нечисловых
объектов, каковы множества, иллюстрирует большую общность идей
современной математики. В последнее время выяснилось, что алгебра
множеств бросает новый свет иа многие области математики, как, на-
пример, теорию меры и теорию вероятностей; она полезна также при
систематизации математических понятий и выяснении их логических
связей.
В дальнейшем I будет обозначать некоторое постоянное множество
объектов, природа которых безразлична и которое мы можем называть
«универсальным множеством» (или, если угодно, «условной вселен-
ной»), а А, В, С,... будут какие-то подмножества/. Если / есть совокуп-
ность всех натуральных чисел, то А. скажем, может обозначать мно-
жество всех чётных чисел, В — множество всех нечётных чисел, С —
множество всех простых чисел и т.д. Если I обозначает совокупность
всех точек на плоскости, то А может быть множеством точек внутри
какого-то круга, В — множеством точек внутри другого круга и т.д. В
число «подмножеств» нам удобно включить само / и также «пустое»
множество О, не содержащее никаких элементов. Цель, которую пре-
следует такое искусственное расширение, заключается в сохранении
того положения, что каждому свойству U соответствует некоторое
множество элементов из /, обладающих этим свойством. В случае, ес-
ли U есть универсально выполняемое свойство, примером которого
может служить (если речь идёт о числах) свойство удовлетворять три-
виальному равенству х = х, то соответствующее подмножество / будет
само /, так как каждый элемент обладает таким свойством; с другой
стороны, если U есть какое-то внутренне противоречивой свойство
(вроде х х х), то соответствующее подмножество не содержит вовсе
элементов, оно — «пустое» и обозначается символом О
Говорят, что множество А есть подмножество множества В, коро-
че, «А входит в Я», или «В содержит Л», если во множестве Л нет тако-
го элемента, который не был бы также во множестве В. Этому соот-
ношению соответствует запись А с В, или BzjA.
Например, множество Л всех целых чисел, делящихся на 10, есть
подмножество множества В всех целых чисел, делящихся на 5, так как
каждое число, делящееся на 10, делится также на 5. Соотношение
А с В не исключает соотношения В с. А. Если имеет место и то и дру-
гое, то мы пишем Л “ В.
Это означает, что каждый элемент Л есть вместе с тем элемент В, и
обратно, так что множества А и В содержат как раз одни и те же эле-
менты.
9 Зап 72
113
Соотношение А с В между множествами во многих отношениях
напоминает соотношение a S b между числами. В частности, отметим
следующие свойства этого соотношения:
1)ЛсЛ;
2)еслиАсВнВсА, тоА = В;
3) если А а В и В g С, то А с С.
По этой причине соотношение А а. В иногда называют «отношени-
ем порядка». Главное отличие рассматриваемого соотношения от со-
отношения а £ b между числами заключается в том, что между всяки-
ми двумя заданными (действительными) числами а и Ь непременно
осуществляется по меньшей мере одно из соотношений а <Ь или b S а,
тогда как для соотношения А а. В между множествами аналогичное
утверждение неверно. Например, если А есть множество, состоящее из
чисел 1, 2, 3, А = {1, 2, 3},аВ — множество, состоящее из чисел 2, 3,
4, В = {2, 3, 4}, то не имеет места ни соотношение А с. В, ни соотно-
шение В с Л По этой причине говорят, что подмножества А, В, С, ..
множества / являются «частично упорядоченными», тогда как дейст-
вительные числа а, Ь, с,.., образуют «вполне упорядоченную» сово-
купность.
Заметим, между прочим, что из определения соотношенияАсВ
следует, что, каково бы ни было подмножество А множества 7,
4)0 а А;
5)Ас!.
Свойство 4) может показаться несколько парадоксальным, но, если
вдуматься, оно логически строго соответствует точному смыслу опре-
деления знака а. В самом деле, соотношение О с А нарушалось бы
только в том случае, если бы пустое множество О содержало элемент,
который не содержался бы в А', но так как пустое множество не содер-
жит вовсе элементов, то этого быть не может, каково бы ни было А.
Мы определим теперь две операции над множествами, формально
обладающие многими алгебраическими свойствами сложения и умно-
жения чисел, хотя по своему внутреннему содержанию совершенно
отличные от этих арифметических действий. Пусть А и В — какие-то
два множества. Под «объединением», или «логической суммой», А и В
понимается множество, состоящее из тех элементов, которые содер-
жатся или в А, или в В (включая и те элементы, которые содержатся и
в Л, и в В). Это множество обозначается А + В. Под «пересечением»,
или «логическим произведением», А и В понимается множество, со-
стоящее из тех элементов, которые содержатся и в А, и в В. Это мно-
жество обозначается АВ. Проиллюстрируем приведенные определения
114
примером. Возьмём опять в качестве А и В множества А = {1, 2, 3}, В =
= {2,3,4}. Тогда А+ В = {1,2, 3,4},АВ = {2, 3].
Среди важных алгебраических свойств операций А + В и АВ пере-
числим следующие. Читатель сможет проверить их справедливость,
исходя из определения самих операций:
6)Л + В = В + А; 7)АВ = ВА;
8) Л + (В + С) = (А + В) + С; 9)A(BQ = (АВ)С;
10) Л + Л = Л; 11)ЛЛ =Л;
12) А(В + С) = АВ + АС; 13) Л + (ВС) = (Л + В)(А + С);
14) Л + 0=Л; 16) А +1 = 1; 15)А1=А; 17) АО = О;
18) соотношение А с. В эквивалентно каждому из двух соотноше-
ний А + В = В. АВ = А
Проверка всех этих законов — дело самой элементарной логики.
Например, правило 10) констатирует, что множество элементов, со-
держащихся или в А, или в А, есть как раз множество А; правило 12)
констатирует, что множество тех элементов, которые содержатся в А и
вместе с тем содержатся или в В или в С, совпадает со множеством
элементов, которые или содержатся одновременно в А и в В. или со-
держатся одновременно в Л и в С. Логические рассуждения, исполь-
зуемые при доказательствах подобного рода правил, удобно иллюст-
рируются, если мы условимся изображать множества Л, В, С,... в виде
некоторых фигур на плоскости и будем очень внимательны в том от-
ношении, чтобы не упустить ни одной из возникающих логически
возможностей, когда речь идёт о наличии общих элементов двух мно-
жеств или, напротив, наличии в одном множестве элементов, которые
не содержатся в другом.
Объединение и пересечение множеств
Читатель, несомненно, обратил внимание на то обстоятельство, что
законы 6), 7), 8), 9) и 12) внешне тождественны с хорошо знакомыми
коммутативным, ассоциативным и дистрибутивным законами обыкно-
венной алгебры. Отсюда следует, что все правила обыкновенной ал-
гебры, вытекающие из этих законов, действительны также в алгебре
множеств. Напротив, законы 10), 11) и 13) не имеют своих аналогов в
обыкновенной алгебре, и они придают алгебре множеств более про-
стую структуру.
9*
115
Например, формула бинома в алгебре множеств сводится к про-
стейшему равенству (А + В)" = (А + В) -(А + В)... (А + В) = А + В, кото-
рое следует из закона И). Законы 14), 15) и 17) говорят о том, что
свойства множеств О и 7 по отношению к операциям объединения в
пересечения множеств весьма похожи на свойства чисел 0 и 1 по от-
ношению к операциям числовых действий сложения и умножения. Но
закон 16) не имеет аналога в числовой алгебре
Остается дать определение ещё одной операции в алгебре мно-
жеств. Пусть А — какое-нибудь подмножество универсального множе-
ства I. Тогда под дополнением А в I понимается множество всех эле-
ментов I, которые не содержатся в А. Для этого множества мы введём
обозначение А'. Так, если / есть множество всех натуральных чисел, а
А — множество всех простых чисел, то А' есть множество, состоящее
из всех составных чисел и числа 1. Операция перехода от Л кА', для ко-
торой нет аналога в обыкновенной алгебре, обладает следующими свой-
ствами:
19)Л+Л' = 7; 20)ЛЛ'=0;
21)0'= 7; 22)7'= 0;
23)Л" = Л;
24) Соотношение Ас В эквивалентно соотношению В'с А';
25) (А + В)' = А'В';
26) (АВ)'= А' + В'.
Опять мы предоставляем проверку этих свойств читателю.
Законы 1) — 26) лежат в основе алгебры множеств. Они обладают за-
мечательным свойством «двойственности» в следующем смысле
Если в одном из законов 1)—26) символы с и zj, О и I, + и • пере-
ставляются между собой (поскольку они встречаются), в результате
получается опять один из тех же законов. Например, закон 6) пере-
ходит в закон 7), 12) — в 13), 17) — в 16) и т.д. Отсюда следует, что
каждой теореме, которая может быть выведена из законов 1)—26),
соответствует другая «двойственная» ей теорема, получающаяся из
первой посредством указанных перестановок символов. В самом де-
ле, так как доказательство первой теоремы состоит из последова-
тельного применения (на различных стадиях проводимого рассуж-
дения) некоторых из законов 1)—26), то применение на соответст-
вующих стадиях «двойственных» законов составит доказательство
«двойственной» теоремы.
2. Применение к математической логике. Проверка законов ал-
гебры множеств основывалась на анализе логического смысла соот-
ношения А с Ви операций А + В, АВ и А'. Мы можем теперь обратить
116
этот процесс и рассматривать законы 1)—26) как базу для «алгебры
логики». Скажем точнее: та часть логики, которая касается множеств,
или, что то же, свойств, или атрибутов, рассматриваемых объектов,
может быть сведена к формальной алгебраической системе, основан-
ной на законах 1)—26) Логическая «условная вселенная» определяет
множество Г, каждое свойство, или атрибут, U определяет множе-
ство А, состоящее из тех объектов в I, которые обладают этим ат-
рибутом. Правила перевода обычной логической терминологии на
язык множеств ясны из следующих
«Пли А или В»
«И А и В»
«Не Л»
«Ни А, ни В»
«Не сразу А и В»
«Всякое А есть В», или «Если
А, то В», или «Из А следует В»
«Какое-то А есть В»
«Никакое А не есть В»
«Какое-то А не есть В»
«Нет никакого А»
В терминах алгебры множеств
щий, что «если всякое А есть В и вс
примеров:
А + В
АВ
А'
(А + В)', или, что то же, Л'В'
(ЛВ)', или, что то же, Л' + В'
ЛсВ
лв*о
лв = о
ЛВ'*0
Л =0
силлогизм «Barbara», обозначаю-
якое В есть С, то всякое Л есть С»,
принимает простой вид:
3) Если ЛсВиВсС, тоЛсС.
Подобным образом «закон противоречия», утверждающий, что
«объект не может одновременно обладать и не обладать некоторым
свойством», записывается в виде:
20)ЛЛ' = 0,
и «закон исключённого третьего», говорящий, что «объект должен или
обладать, или не обладать некоторым свойством», записывается:
19) Л + Л' = /.
Таким образом, та часть логики, которая выразима в терминах сим-
волов а, + , • и ’, может трактоваться как формальная алгебраическая
система, подчинённая законам 1)—26). На основе слияния логическо-
го анализа математики и математического анализа логики создалась
новая дисциплина «математическая логика», которая в настоящее вре-
мя находится в процессе бурного развития.
С аксиоматической точки зрения заслуживает внимания тот заме-
чательный факт, что утверждения 1)—26) вместе со всеми прочими
теоремами алгебры множеств, могут быть логически выведены из сле-
дующих трёх равенств:
117
А+В = В+ А',
27) (А + В)+ С = А + (В+С);
(А'+ ВУ + (А'+ В)’=А.
Отсюда следует, что алгебра множеств может быть построена как
чисто дедуктивная теория, вроде евклидовой геометрии, на базе этих
трёх положений, принимаемых в качестве аксиом. Если эти аксиомы
приняты, то операция АВ и соотношение А а. В определяются в тер-
минах А + В и А': АВ обозначает множество (А' + В')', Ас В обознача-
ет, что А + В = В.
Совершенно иного рода пример математической системы, в кото-
рой выполняются все формальные законы алгебры множеств, даётся
системой восьми чисел 1, 2, 3, 5, 6, 10, 15, 30: здесь а + Ь обозначает,
по определению, общее наименьшее кратное а и b, аЬ — общий наи-
больший делитель а и Ь, а с Ъ — утверждение «.Ь делится на а» на’ —
число 30/а. Существование таких примеров повлекло за собой изуче-
ние общих алгебраических систем, удовлетворяющих законам 27). Та-
кне системы называются «булевыми алгебрами» — в честь Джорджа
Буля (1815—1864), английского математика и логика, книга которого
«Ап investigation of the laws of thought» (Исследование законов мыш-
ления) появилась в 1854 г.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ БЕСКОНЕЧНОГО
1. Основные понятия. Последовательность натуральных чисел
1, 2, 3, ... представляет собой первый и самый важный пример беско-
нечного множества. Не нужно видеть ничего таинственного в том, что
она — бесконечная, что у неё «нет конца»: как бы велико ни было на-
туральное число л, можно построить другое, за ним следующее число,
ещё большее, л + 1. Но при переходе от прилагательного «бесконеч-
ный», означающего просто-напросто «не имеющий конца», к сущест-
вительному «бесконечность» никоим образом не следует привносить
допущения, чти «бесконечность», обыкновенно изображаемая особым
символом «оо», может быть рассматриваема как обыкновенное число.
Нельзя включить символ «со» в числовую систему действительных чи-
сел, вместе с тем не нарушая основных законов арифметики. И, тем не
менее, идея бесконечности пронизывает всю математику, так как ма-
тематические объекты изучаются обыкновенно не как индивидуумы —
каждый в отдельности, а как члены классов или совокупностей, со-
держащих бесчисленное множество элементов одного и того же типа;
таковы совокупности натуральных чисел, действительных чисел или
же треугольников на плоскости. Именно по этой причини возникает
118
необходимость в точном математическом анализе бесконечного Со-
временная теория множеств, созданная Георгом Кантором и его шко-
лой в конце XIX столетня, приступив к разрешению этой задачи, дос-
тигла значительных успехов. Канторова теория множеств глубоко
проникла во многие области математики и оказала на них огромное
влияние; она стала играть особо выдающуюся роль в исследованиях,
связанных с логическим и философским обоснованием математики.
Исходным в канторовой теории является общее понятие совокупности
или множества. При этом имеется в виду собрание объектов (элемен-
тов), которое определяется некоторым правилом, позволяющим с пол-
ной определённостью судить о том, входит ли данный объект в число
элементов собрания или не входит. Примерами могут служить множе-
ство всех натуральных чисел, множество всех периодических деся-
тичных дробей, множество всех действительных чисел или множество
всех прямых в трёхмерном пространстве.
Для того чтобы сравнивать множества с точки зрения «количества»
содержащихся в них элементов, нужно ввести основное в этой теории
понятие «эквивалентности» множеств. Если элементы двух множеств
А и В могут быть приведены в попарное сопоставление такого рода,
что каждому элементу множества А сопоставлен один и только один
элемент множества В и каждому элементу множества В сопоставлен
один и только один элемент множества А, то установленное таким об-
разом соответствий называется взаимно однозначным, а о самих мно-
жествах А и В тогда говорят, что они между собой эквивалентны По-
нятие эквивалентности в случае конечных множеств совпадает с
обыкновенным понятием числового равенства, так как два конечных
множества в том и только в том случае могут быть приведены во вза-
имно однозначное соответствие, если содержат одно и то же число
элементов. На этом и основывается, нужно заметить, идея счёта: когда
мы «считаем» элементы множества, то процесс счёта как раз и заклю-
чается в установлении взаимно однозначного соответствия между
элементами множества и числами 1,2,.... л.
Чтобы установить эквивалентность двух конечных множеств, ино-
гда нет необходимости «считать» элементы. Так, например, не считая,
можно утверждать, что конечное множество кругов единичного ра-
диуса эквивалентно множеству их центров.
Перенося понятие эквивалентности на бесконечные множества,
Кантор имел в виду создать «арифметику» бесконечного. Множество
действительных чисел и множество точек на прямой линии — эквива-
лентны, так как после того, как выбраны начало и единичный отрезок,
данная прямая становится «числовой прямой», и каждой её точке Р в
119
качестве координаты взаимнс однозначно сопоставляется некоторое
совершенно определённое действительное число х. Р <-> х.
Чётные числа образуют истинное подмножество множества всех
натуральных чисел, а все целые числа образуют истинное подмноже-
ство множества всех рациональных чисел. (Говоря об «истинном» под-
множестве некоторого множества S. мы имеем в виду некоторое мно-
жество S', состоящее из элементов множества S, но не из всех его эле-
ментов.) Совершенно ясно, что если данное множество конечно, т.е.
содержит какое-то число п элементов, и не более того, то оно не мо-
жет быть эквивалентно никакому своему истинному подмножеству,
так как всякое истинное его подмножество содержало бы самое боль-
шее п - 1 элементов. Но если данное множество содержит бесконеч-
ное число элементов, то, как это ни парадоксально, оно может быть
эквивалентно некоторому своему истинному подмножеству Напри-
мер, схема
1 2 3 4 5 ... п ...
т ? t ? т т
X I 4, 'Г 4' X
2 4 6 8 10 ... 2п ...
устанавливает взаимно однозначное соответствие между множеством
натуральных чисел и множеством всех чётных целых положительных
чисел, и эти два множества оказываются эквивалентными, хотя второе
есть истинное подмножество первого. Такое противоречие с ходячей
истиной «целое больше своей части» показывает, какие сюрпризы нас
ждут в области «арифметики бесконечного».
2. Счетность множества рациональных чисел и несчетность
континуума. Одно из первых открытий Кантора в области анализа
бесконечного заключалось в том, что множество рациональных чисел
(содержащее в качестве истинного подмножества бесконечное множе-
ство натуральных чисел и потому само бесконечное) эквивалентно
множеству натуральных чисел. На первый взгляд кажется странным,
что всюду плотное множество рациональных чисел не более богато
элементами, чем множество натуральных чисел, элементы которого
«рассеяны» редко и стоят на значительном расстоянии один от друго-
го. И в самом деле, с сохранением порядка возрастания нельзя распо-
ложить положительные рациональные числа так, как это можно сде-
лать с натуральными: самое маленькое число а будет первым, сле-
дующее за ним по величине b вторым, и т.д.; дело в том, что рацио-
нальные числа расположены везде плотно и потому нн для одного из
них нельзя указать «следующего по величине». Но Кантор заметил,
120
что если отказаться от требования «располагать по величине», то тогда
оказывается возможным расставить все рациональные числа в ряд гь г2,
rj, г4, .... подобный ряду натуральных чисел. Такое расставление в ряд
множества предметов называют иногда денумерацией («исчислением»)
множества; множества, для которых денумерация может быть выполнена,
называются исчислимыми, или счётными Указывая один из способов де-
нумерации множества рациональных чисел и устанавливая, таким обра-
зом, его счётность, Кантор тем самым показал, что это множество эквива-
лентно множеству натуральных чисел, так как схема
1 2 3 4 ... п ...
Г| г2 г3 г4 ... г„ ...
создаёт взаимно однозначное соответствие между двумя множества-
ми. Мы укажем, далее, один из возможных способов денумерации
множества рациональных чисел.
Каждое рациональное число записывается в виде а/Ь, где а и Ь —
целые числа; все эти числа могут быть расположены по такой таблице,
чтобы число а/b стояло в а-й строчке и в b-м столбце. Например, 3/4
станет в третьей строчке и в четвёртом столбце таблицы. Предполо-
жим, что все свободные места, или «клеточки», в таблице заполнены
соответствующими числами, н затем мы проведем по таблице непре-
рывную ломаную линию, которая пройдёт через все клеточки. Начи-
ная с 1, мы сделаем сначала один шаг вправо и получим 2 в качестве
второго члена последовательности; затем по диагонали налево и вниз —
получим третий член 1/2; следующий шаг прямо вниз даст нам четвёр-
тый член 1/3; потом движемся по диагонали вправо и вверх через 2/2 к
3; вправо — к 4; по диагонали влево и вниз через 3/2 и 2/3 к 1/4, и т.д.,
как показано ниже на схеме.
Денумерация рациональных чисел
8 Зак 72
121
В результате движение по ломаной линии приводит к последова-
тельности рациональных чисел 1, 2, 1/2, 1/3, 2/2, 3, 4, 3/2, 2/3, 1/4, 1/5,
2/4, 3/3,4/2,5,...
Если мы выбросим теперь все дроби, у которых числитель и знаме-
натель имеют отличные от 1 общие делители, то останется последова-
тельность, в которой каждое рациональное число встретится один и в
точности один раз: 1, 2, 1/2, 1/3, 3,4, 3/2, 2/3, 1/4, 1/5, 5, ...
Так устанавливается, что множество всех рациональных чисел яв-
ляется счётным. Принимая во внимание, что рациональные числа вза-
имно однозначно связаны с рациональными точками числовой прямой,
можно также сказать, что множество рациональных точек на число-
вой прямой обладает свойством счетности.
Упражнения. 1. Покажите, что множество всех целых, положитель-
ных и отрицательных чисел — счётное. Покажите, что множество всех рацио-
нальных, положительных и отрицательных, чисел — счётное.
2. Покажите, что если 5 и Т — счётные множества, то множество S + Т —
также счётное. То же покажите для суммы трёх, четырёх и вообще п мно-
жеств; покажите, наконец, что множество, составленное посредством сложе-
ния счётного множества счётных множеств, также счётное.
Раз оказалось, что множество рациональных чисел счётное, то могло
бы возникнуть подозрение, что и всякое бесконечное множество также
счётное, и на этом, естественно, закончился бы весь анализ бесконечного.
Но это совсем не так. Тому же Кантору принадлежит открытие высокой
значительности: множество всех действительных (рациональных и ир-
рациональных) чисел — несчетное. Другими словами, совокупность всех
действительных чисел — совершенно иного, так сказать, более высокого,
«типа бесконечности», чем совокупность одних только целых или одних
только рациональных чисел. Принадлежащее Кантору остроумное «кос-
венное» доказательство этого факта стало моделью для многих иных до-
казательств в математике. Идея рассуждения такова. Мы исходим из до-
пущения, что все действительные числа удалось перенумеровать, распо-
лагая их в виде последовательности, и после этого демонстрируем число,
которое никак не может быть числом этой последовательности. Отсюда
возникает противоречие: ведь было предположено, что все действитель-
ные числа вошли в состав последовательности, и эго предположение
должно быть признано ложным, если хотя бы одно число оказывается за
пределами последовательности. Таким образом обнаруживается несо-
стоятельность утверждения, что все действительные числа поддаются
«денумерации» и ничего другого не остаётся, как только признать вместе
с Кантором, что множество действительных чисел неисчислимо.
Однако проведём это рассуждение на самом деле. Мы допускаем,
что все действительные числа, представленные в виде бесконечных
122
десятичных дробей, расположены в порядке последовательности, или
списка:
1-е число N\, а\ а2 а3а4а3...
2-е число Л/j, bi b2 Ь3Ь*Ь3...
3-е число Nj, Cj с2 с3 .
где буквы N обозначают целую часть, а строчные буквы представляют
собой десятичные знаки, стоящие вправо от запятой. Мы допускаем,
что эта последовательность дробей охватывает все действительные
числа. Существенной частью доказательства является построение — с
помощью «диагональной процедуры» — такого нового числа, относи-
тельно которого можно показать, что оно не входит в наш список.
Построим такое число. Для этого возьмём первую цифру после за-
пятой а. какую угодно, но отличную от alt а также от 0 и 9 (последнее,
чтобы избежать затруднений, возникающих из равенств вроде сле-
дующего: 0,999.. = 1,000...), затем вторую цифру b возьмём отличной
от b2, а также от 0 и 9; третью цифру с — отличной от с3, и т.д. (для
большей определённости можно условиться в следующем; мы берём
а = 1, если только О| * 1, а в случае at = 1 возьмём а = 2; и аналогично
для всех прочих цифр b, с, d, е, ..). Теперь рассмотрим число
z = 0, abcde...
Это новое число z, наверное, не входит в список; действительно,
оно не равно первому числу, стоящему в списке, так как от него отли-
чается первой цифрой после запятой, оно не равно второму числу, так
как от него отличается второй цифрой после запятой, и вообще отлич-
но от л-го числа по списку, так как от него отличается л-й цифрой по-
сле запятой. Итак, в нашем списке, составленном будто бы из всех
действительных чисел, нет числа z. Значит, множество всех действи-
тельных чисел неисчислимо.
Читателю может придти в голову мысль, что неисчислимость кон-
тинуума обусловливается неограниченной протяжённостью прямой
линии и что конечный отрезок прямой будет содержать лишь счётное
множество точек. Чтобы убедиться в ложности такого предположения,
достаточно установить, что весь числовой континуум в целом эквива-
лентен некоторому конечному отрезку, скажем, единичному отрезку
от 0 до 1, с исключением конечных точек. Получить необходимое для
этой цели взаимно однозначное соответствие можно, например, сгибая
конечный отрезок в точках 1/3 и 2/3 и затем проектируя так, как по-
казано ниже на рисунке. Отсюда видно, что даже конечный отрезок
содержит неисчислимое множество точек.
а-
123
Взаимно однозначное соответствие Взаимно однозначное соответствие
между точками согнутого отрезка между точками двух интервалов
и точками прямой линии различной длины
Упражнение. Показать, что любой интервал [А, £] числовой прямой
эквивалентен любому другому интервалу [С, О].
Стоит привести ещё другое доказательство неисчислимости конти-
нуума, носящее, возможно, более интуитивный характер. Достаточно
(принимая во внимание последнее доказанное предложение) сосредо-
точить внимание на точках единичного отрезка от 0 до 1. Доказатель-
ство, впрочем, как и раньше, будет «косвенное» Предположим, что
множество всех точек названного отрезка может быть расположено в
виде последовательности
ai,a2,a3... (1)
Покроем точку отрезком, длина которого пусть будет равна 1/10,
точку а2 — отрезком длины 1/102 и т.д. Если бы все точки единичного
отрезка входили в последовательность (1), то весь единичный отрезок
оказался бы покрытым бесконечным множеством таких отрезков (мо-
жет быть, частью перекрывающихся), длины которых суть 1/10,
1/102... (Беды нет, если некоторые из наложенных отрезков выйдут за
пределы основного единичного отрезка.) Сумма всех длин наложен-
ных отрезков равна 1/10 + 1/102 + 1/103 + ... = (1/10) (1/(1 -1/10)) = 1/9.
Итак, допущение, что последовательность (1) содержит все дейст-
вительные точки единичного отрезка, приводит к заключению, что
весь этот отрезок, длина которого равна 1, можно покрыть множеством
промежутков с общей длиной 1/9; с интуитивной точки зрения это — не-
лепость. Это рассуждение мы позволим себе рассматривать как дока-
зательство, хотя строго логически тут был бы нужен более глубокий
анализ.
Приведённое только что рассуждение, между прочим, позволяет
установить одну теорему, имеющую большое значение в современной
«теории меры». Заменяя упомянутые выше промежутки меньшими
промежутками — длины е/10" , где е — произвольно малое положи-
тельное число, мы убедимся, что всякое счётное множество точек на
прямой может быть покрыто множеством отрезков с общей длиной
е/9. Так как е — произвольно мало, то и е/9 может быть сделано столь
124
малым, сколь нам угодно. Пользуясь фразеологией «теории меры», мы
скажем, что счётное множество точен имеет меру нуль.
Упражнение. Дсказать аналогичную теорему для счётного множе-
ства точек на плоскости, заменяя длины отрезков площадями квадратов.
3. «Кардинальные числа» Кантора. Резюмируем полученные ре-
зультаты. Число элементов конечного множества А не может равняться
числу элементов другого конечного множества В, если А содержит
больше элементов, чем В. Но если мы заменим понятие «множеств
имеющих одно и то же конечное число элементов», более общим по-
нятием «эквивалентных множеств», то — в случае бесконечных мно-
жеств — предыдущее утверждение уже не будет справедливо: множе-
ство всех целых чисел содержит «больше» элементов, чем множество
всех чётных чисел, а множество всех рациональных чисел — «боль-
ше» элементов, чем множество всех целых чисел; и, однако, как мы
видели, все эти множества эквивалентны. Можно было бы заподоз-
рить, что все бесконечные множества между собой эквивалентны, но
Кантор опроверг это предположение: существует множество — кон-
тинуум действительных чисел, — которое не эквивалентно никакому
счётному множеству.
Итак, существуют по меньшей мере два различных «типа беско-
нечности >: счётная бесконечность натуральных чисел и несчётная бес-
конечность континуума. Если два множества А и В, конечные или
бесконечные, эквивалентны, мы скажем, иначе, что им соответствует
одно и то же кардинальное число. В случае конечных множеств карди-
нальное число сводится к обыкновенному натуральному числу, но по-
нятие кардинального числа носнт более общий характер. Далее, если
случится, что множество А эквивалентно некоторому подмножеству
(части) множества В, но само В неэквивалентно ни множеству А. нн
какой бы то ни было его части, то говорят, следуя Кантору, что мно-
жеству В соответствует большее кардинальное число, чем множеству
А. Это употребление термина «число» также согласуется с обычным
употреблением в случае конечных множеств. Множество целых чисел
есть подмножество множества всех действительных чисел, тогда как
множество действительных чисел не эквивалентно ни множеству це-
лых чисел, ни какому бы то ни было его подмножеству (оно ни счёт-
ное, ни конечное). Значит, по данному определению, континууму дей-
ствительных чисел соответствует большее кардинальное число, чем
множеству натуральных чисел.
4. Косвенный метод доказательства. Теория кардинальных чисел
представляет собой лишь один из аспектов общей теории множеств, соз-
данной Кантором несмотря на наличие сурового критицизма со сто-
125
стороны наиболее выдающихся математиков того времени. Многие из
критиков, например Пуанкаре и Кроне кер, возражали против неопре-
делённости общего понятия «множества» и против неконструктивного
характера рассуждений, применявшихся при определении некоторых
множеств.
Возражения против неконструктивных рассуждений относятся к
тем доказательствам, которые можно было бы назвать «существенно
косвенными». Сами по себе «косвенные» доказательства есть самый
обыкновенный элемент математического мышления: желая установить
истинность предложения А. мы провизорно допускаем, что справедли-
во иное предложение А', противоположное А, затем некоторая цепь
рассуждений приводит нас к утверждению, противоречащему Л', и тем
самым обнаруживается несостоятельность предложения А'. Тогда, на
базе основного логического принципа «исключённого третьего», из
нелепости Л' следует истинность А.
В разных местах этой книги (речь идет о книге Р. Куранта и Г Роб-
бинса «Что такое математика» — сост.) читатель найдёт рад таких
примеров, для которых косвенное доказательство легко может быть
превращено в прямое, но «косвенная» форма создаёт преимущества
краткости и освобождает от рассмотрения подробностей, имеющих
второстепенный интерес с точки зрения поставленной ближайшей це-
ли. Но попадаются и такие теоремы, для которых до настоящего вре-
мени не удалось дать иных доказательств, кроме косвенных. О некото-
рых из этих теорем можно даже сказать, что, по-виднмому, по самой
природе теорем прямые, конструктивные их доказательства принципи-
ально невозможны. Не раз бывали случаи в истории математики, когда
все усилия математиков были направлены в сторону конструкции ре-
шения тех или иных проблем, разрешимость которых предполагалось
установить, и вот кто-нибудь приходил, если так можно выразиться, со
стороны и ликвидировал все трудности с помощью «косвенного» не-
конструктивного рассуждения.
Когда речь идёт о доказательстве существования объекта опреде-
лённого типа, то есть существенное различие между тем, чтобы по-
строить осязаемый пример объекта, и тем, чтобы доказать, что из не-
существования объекта можно вывести противоречивые заключения
В первом случае получается осязаемый объект, во втором — ничего,
кроме противоречия. В недавнее время некоторые математики (из чис-
ла имеющих большие заслуги) провозгласили более или менее полное
устранение из математики всех неконструктивных доказательств. Да-
же если бы выполнение этой программы признать желательным, необ-
ходимо указать, что это повлекло бы за собой в настоящую эпоху
чрезвычайные усложнения, и можно было бы даже опасаться, что в
126
процессе совершающихся потрясений подверглись бы разрушению
существенные части организма математики. Поэтому не представляет-
ся удивительным, что школа «интуиционистов», принявшая упомяну-
тую программу, встретила упорное сопротивление и что даже наибо-
лее ортодоксальные интуиционисты не всегда в состоянии жить со-
гласно своим убеждениям.
6. Парадоксы бесконечного. Хотя бескомпромиссная позиция, за-
нятая интуиционнстами, с точки зрения большинства математиков яв-
ляется слишком экстремистской, волей-неволей приходится согла-
ситься, что для внешне прекрасной теории бесконечных множеств
возникла серьёзная угроза, когда в пределах самой этой теории обна-
ружились совершенно открытые логические парадоксы. Очень скоро
было замечено, что неограниченная свобода в пользовании понятием
«множество» неизбежно ведёт к противоречиям Мы приведём здесь
один из парадоксов, предложенный Бертраном Рёсселом. Вот в чём он
заключается.
Весьма многие множества не содержат себя в качестве элемента.
Например, множество А всех целых чисел содержит в качестве эле-
ментов только целые числа; так как само А не есть целое число, а есть
множество целых чисел, то А себя в качестве элемента не содержит.
Условимся называть такие множества «ординарными». Но могут су-
ществовать и такие множества, которые содержат себя в качестве эле-
мента. Рассмотрим, например, множество S, определённое следующим
образом: «S содержит в качестве элементов все множества, которые
можно определить посредством предложения, содержащего меньше
двадцати слов». Так как само множество 5 определяется предложени-
ем, содержащим меньше двадцати слов, то выходит, что оно является
элементом множества. Такие множества назовём «экстраординарны-
ми». Как бы то ни было, большинство множеств — ординарные; мы
попробуем не встречаться с дурно ведущими себя экстраординарными
множествами и будем рассматривать только множество всех ординар-
ных множеств. Обозначим его буквой С. Каждый элемент С есть
множество, притом ординарное множество. Но вот возникает вопрос:
само множество С — ординарное или экстраординарное? Несомненно,
оно должно быть или тем, или другим. Если С — ординарное множе-
ство, то оно содержит себя в качестве элемента, так как С определено
как множество всех ординарных множеств. Раз дело обстоит так, зна-
чит, С — экстраординарное множество, так как экстраординарными,
согласно определению, названы множества, содержащие себя в каче-
стве элемента. Получается противоречие. Значит, С должно быть экст-
раординарным множеством Но тогда множество С содержит в качест-
127
ве элемента себя, т.е. экстраординарное множество, а это противоре-
чит, определению С как множества всех ординарных множеств. Итак,
мы видим, что уже одно только допущение существования множества
С внутренне противоречиво.
7. Основания математики. Парадоксы вроде вышеприведённого
побудили Рёссела и других подвергнуть систематическому изучению
основания математики и логики. Конечная цель этих исследований за-
ключается в создании для математических рассуждений такой логиче-
ской базы, относительно которой можно было бы доказать, что она
свободна от возможных противоречий, и которая вместе с тем была бы
достаточно обширной, чтобы из неё можно было путём дедукции вы-
вести всё, что в математике признаётся существенным или хотя бы
многое из того. Поскольку такой самонадеянной цели достигнуть не
удавалось (а может быть, её и нельзя достигнуть), математическая ло-
гика как особый предмет привлекала внимание всё возрастающего
числа исследователей. Многие относящиеся сюда проблемы необхо-
димо признать крайне трудными, хотя формулировки их вполне про-
сты. В качестве примера назовём гипотезу континуума, утверждаю-
щую, что не существует множества, для которого кардинальное число
больше, чем кардинальное число множества натуральных чисел, но
меньше, тем кардинальное число множества действительных чисел. Из
этой гипотезы можно вывести много интересных следствий, но сама
гипотеза до наших дней не была ни доказана, ни опровергнута. Впро-
чем, не так давно Курт Гёдель доказал, что если система обычных по-
стулатов, лежащих в основе теории множеств, не содержит противоре-
чий, то в таком случае расширенная система постулатов, получающая-
ся при добавлении гипотезы континуума, также не содержит противо-
речий. Вопросы, рассматриваемые в математической логике, в конеч-
ном счёте упираются в один основной вопрос: что понимать под суще-
ствованием в математике? К счастью, существование самой математи-
ки не зависит от того, найден ли удовлетворительный ответ на этот
вопрос. Школа «формалистов», во главе которой стоял великий мате-
матик Гильберт, утверждает, что в математике «существование» озна-
чает «свободу от противоречия». Если принять эту точку зрения, то
очередной и необходимой задачей является как раз построение систе-
мы постулатов, из которых всю математику можно было бы вывести
путём логической дедукции, и доказательство того, что эти постулаты
не могут привести ни к какому противоречию. Недавние результаты
Гёделя и других как будто бы показывают, что такая программа, по
крайней мере в той форме, в какой она была намечена самим Гильбер-
том, не может быть осуществлена. Весьма многозначительно то об-
128
стоятельство, что гильбертова теория формализированного построе-
ния математики существенно опирается на интуитивные процедуры.
Тем или иным путём, в открытой или в скрытой форме, даже прикры-
тая самым безупречным формалистическим, логическим, аксиомати-
ческим одеянием, конструктивная интуиция всегда остаётся самым
жизненным элементом в математике.
fW. Т&ц, С <Улам
МЕРА’
Проблема измерения величин областей на плоскости и в трехмер-
ном пространстве, состоящая в том, что этим областям нужно припи-
сать числа, выражающие их площади или объемы, восходит к самым
истокам математики. Греки создали стройную теорию площадей мно-
гоугольников и объемов многогранников. Интегральное исчисление
(которое берет начало в некоторых исследованиях Архимеда) распро-
странило эту теорию на широкий класс областей, ограниченных кри-
выми линиями и искривленными поверхностями.
Однако в процессе дальнейшего развития математики этого оказа-
лось недостаточно: понадобилось приписать меры множествам более
широкого класса. Так появилась общая теория меры, разработанная
Борелем и Лебегом. Но и это обобщение не достаточно полно: суще-
ствуют множества, которым нельзя приписать меру Лебега (т.е. эти
множества неизмеримы)- Чтобы построить неизмеримые множества,
приходится применять знаменитую аксиому выбора, согласно которой
из любой заданной совокупности непересекающихся множеств можно
образовать новое множество, выбрав по одному элементу из каждого
множества исходной совокупности. Хотя эта аксиома звучит вполне
безобидно, многие ее следствия могут показаться странными и пара-
доксальными.
Теория меры имеет важные применения в теории вероятностей.
Многие математические идеи, которые сейчас кажутся принадле-
жащими алгебре или анализу, обязаны своим происхождением зада-
чам, возникшим из геометрии. Так обстоит дело и с понятием меры и
измерения.
К рассмотрению длины отрезка прямой или дуги кривой, площади
или объема области привели, вероятно, самые первые попытки расши-
рить рамки использования чисел, которое ранее сводилось лишь к пе-
ресчету отдельных предметов. Эти понятия в своем первоначальном
виде появились уже в самых ранних математических работах вавило-
нян, египтян, греков.
129
Евклид занимался главным образом площадями многоугольников и
объемами многогранников. При этом использовались две аксиомы.
1. Если многоугольники (многогранники) конгруэнтны, то их пло-
щади (объемы) равны.
2. Если многоугольник (многогранник) допускает разбиение на ко-
нечное число неперекрывающихся многоугольников (многогранников)
Ль Аг,--, А„, то его площадь (объем) равна сумме площадей (объемов)
составляющих Л1, Аъ .... А„
Если, кроме того, выбран некоторый определенный квадрат (соот-
ветственно куб), площадь (соответственно объем) которого принята за
единицу, то каждому многоугольнику (многограннику) можно одно-
значно приписать число, выражающее в выбранных единицах его
площадь (объем).
Однако даже для нахождения площади круга приходится выйти из
безопасной области конечного и ввести в полной мере бесконечную
операцию перехода к пределу. В древности самый большой вклад в
нахождение площадей и объемов фигур, ограниченных кривыми ли-
ниями и искривленными поверхностями, внес Архимед; есть все осно-
вания полагать, что Архимед полностью осознавал всю тонкость по-
нятия предела. Эти исследования Архимеда, без сомнения, явились
началом интегрального исчисления, хотя вычисление площадей и объ-
емов было в полной мере систематизировано лишь во времена Ньюто-
на и его последователей.
Интегральное исчисление позволяет приписать площади, объемы и
длины лишь сравнительно «смирным» множествам. Оно не дает ника-
ких средств измерять, например, такие множества, как совокупность
всех точек (х, у) с рациональными координатами, заключенными меж-
ду 0 и 1. Но вопрос об измерении таких множеств и не поднимался,
пока проблематика интегрального исчисления отражала в основном
нужды физики и геометрии.
В конце 19-го века возникли задачи, которые привели к необходи-
мости приписать численную меру значительно более широкому классу
множеств. Возросший интерес к вопросам сходимости и расходимости
привлек внимание к множествам сходимости и расходимости и к про-
блеме определения их «размеров». Канторовская теория множеств,
ставшая краеугольным камнем всей современной математики, возник-
ла в результате изучения Кантором тригонометрических рядов и их
множеств сходимости.
Проблема меры формулируется совсем просто. Мы хотим уметь
приписывать некоторому множеству А неотрицательное число т(А),
называемое его мерой, так, чтобы выполнялись следующие условия
130
1. Если Ai, А2, ... — непересекающиеся измеримые множества (т.е.
каждому А„ можно сопоставить его меру т(А,)), то и их объединение
А\ U А2 U — (т.е. множество, состоящее из элементов всех множеств
А\. Аг,...) измеримо; при этом m(At U А2 U ...) = т(А,) + т(А2) + ...
2. Если А и В — измеримые множества и А содержится в В (А с В),
то их разность В-А (т.е. множество всех точек из В, не принадлежащих
А) тоже измерима. Тогда, согласно свойству 1, т(В -А) = т(В) - т(А).
3. Некоторое множество Е считается имеющим меру 1 (единичное
множество): w(F)= 1.
4. Если два множества конгруэнтны, то их меры равны (при усло-
вии, что множества измеримы).
При изучении множеств точек на прямой за Е принимают некото-
рый отрезок, на плоскости — квадрат, в пространстве — куб. Такой
выбор диктуется желанием, чтобы меры, приписываемые «смирным»
множествам, совпадали с мерами, сопоставленными им раньше в гео-
метрии или в интегральном исчислении.
Можно ли существенно расширить класс измеримых множеств, ес-
ли приписывать меры в соответствии с перечисленными правилами?
Ответом служит уверенное «да», при условии (в этой ситуации ре-
шающем), что в правиле 1 допускается бесконечное число множеств Л,.
Если, следуя Евклиду, допустить лишь конечное число множеств А,
(в этом случае мера называется конечно аддитивной), мы почти ниче-
го не выиграем, и расширение класса «смирных» множеств будет со-
всем незначительным. Например, можно показать, что множество то-
чек единичного квадрата с рациональными координатами окажется
неизмеримым, т.е. ему нельзя будет приписать никакой меры, не впа-
дая при этом в противоречие.
Ситуация коренным образом изменится, если рассматривать вполне
аддитивную меру, т.е. допускать в правиле 1 бесконечное число мно-
жеств А,. В этом случае класс измеримых множеств существенно вырас-
тет, и почти все множества, использовавшиеся в классической и воз-
никшие в современной математике, окажутся измеримыми.
Вполне аддитивная мера была введена в начале 20-го века Эмилем
Борелем и Анри Лебегом и стала источником наиболее строгой и пло-
дотворной линии исследования в математике. Мера Лебега — одно из
самых мощных средств современного анализа.
Насколько же общей является эта мера? Всякое ли множество на
прямой измеримо? Витали первым показал, что даже мере Лебега
свойственны определенные ограничения, т.е. существуют множества
точек, для которых она не определена. Поясним это, рассматривая для
простоты множество на окружности, а не на прямой; существо дела от
этого не меняется. (Два множества на окружности конгруэнтны, если
131
они совмещаются при некотором повороте этой окружности.) Опреде-
лим на окружности множество точек (углов) Z, которому нельзя при-
писать меру так, чтобы выполнялись перечисленные выше условия
Пусть х — некоторая точка окружности Рассмотрим все точки, кото-
рые получаются из х поворотом окружности на углы, составляющие
рациональную часть от 2л Эти углы образуют счетное множество,
обозначим их аь а 2, .... ая,Множество всех углов круга можно раз-
бить на попарно непересекающиеся классы С, в каждый из которых
попадают «рационально сравнимые» углы, т.е. углы, отличающиеся
друг от друга на рациональные величины. Эти классы не имеют общих
элементов. Выберем теперь из каждого класса в точности одну точку и
обозначим полученное множество через Z. Поворачивая затем множе-
ство Z на углы alt а2, .... мы получим новые множества, причем все
они попарно не пересекаются Совокупность всех точек всех этих
множеств есть множество всех точек окружности. Кроме того, количе-
ство этих множеств счетно и все они конгруэнтны, ибо получаются
одно из другого поворотом на углы СХ|, а.2, ... . Итак, мы получили
счетную совокупность множеств Z, Z(, ..., Z„, ..., которые попарно не
пересекаются, конгруэнтны и их объединением является вся окруж-
ность, которую мы можем выбрать в качестве единичного множества
Е, т(Е) = 1. Какова же мера множества Z? Допустим, что она равна 0.
Тогда и любое другое множество этой совокупности имеет меру 0, а их
счетное объединение должно иметь меру 1, так как = 1. Следова-
тельно, в этом случае нарушается аксиома аддитивности. Если же
мера множества Z положительна, то мы получим сумму бесконеч-
ного числа одинаковых положительных слагаемых; такая сумма не
может равняться 1, что снова является нарушением аксиомы адди-
тивности.
Итак, мы указали множество, которому нельзя приписать меру. Это
еще одно доказательство невозможности, свидетельствующее о том,
что процесс обобщения, как везде в математике, должен продолжаться.
Однако при определении множества Витали мы воспользовались
крайне неконструктивным приемом. В самом деле, мы выбирали по
одному элементу из каждого класса С Но как? Классы С определены
слишком неявно, чтобы можно было указать явное правило выбора из
этих элементов. И все же нас не покидает ощущение, что такой выбор
элемента из каждого класса и объединение этих элементов в новое
множество должны быть дозволены, даже если мы неспособны дать
конкретное предписание, как выполнить эту задачу.
Выход из этой дилеммы указал в начале 20-го века Эрнест Церме-
ло. Он предложил узаконить «построения», подобные описанному
выше, приняв следующую общую аксиому
132
Если задана совокупность С непересекающихся множеств, то мож-
но образовать множество Z, выбрав по одному элементу из каждого
множества этой совокупности.
Эта аксиома известна под названием аксиомы выбора. С самого
своего рождения она была предметом горячих дебатов, поскольку
многие ее следствия выглядят весьма странными и парадоксальными.
Так, например, Банах и Тарский доказали, что две сферы Si и S2
различных радиусов можно разбить на одно и то же конечное число
попарно не пересекающихся множеств:
Si =At + Л2 + ... + Ап,
S2 =Bi + В2 + ... + В„
так, чтобы А, было конгруэнтно В„ при любом 1 = 1,2,..., п Этим мно-
жествам нельзя приписать никакие меры, ибо, составляя их вместе
одним способом, мы получаем большую сферу, а используя другое
пространственное расположение — меньшую! Между прочим, на
плоскости такое разбиение невозможно. Как показал Банах, для всех
подмножеств плоскости можно найти конечно аддитивную меру, об-
ладающую тем свойством, что меры конгруэнтных множеств равны.
Попытки обобщить меру Лебега были вызваны необходимостью.
Как мы уже говорили, математики включали в рассмотрение множест-
ва все более и более общего вида. Например, в теории тригонометри-
ческих рядов можно было сформулировать теоремы, верные для всех
действительных чисел, за исключением некоторого специального мно-
жества. При этом желательно было установить, пользуясь какими-то
строго определенными понятиями, что множество этих исключи-
тельных точек в некотором смысле мало и им можно пренебречь. В
несчетном континууме точек можно «пренебрегать» счетными множе-
ствами, считая их малыми, однако в большинстве случаев
исключительные множества оказываются несчетными, но имеющими
лебегову меру нуль Многие утверждения теории вероятностей
выполняются «с вероятностью единица» (или «почти достоверно»)
Это попросту означает, что они верны для «почти всех» точек
некоторого подходящего множества, т.е. для всех его точек, за
исключением множества меры нуль. Некоторые важные теоремы
статистической механики устанавливают свойства динамических
систем, верные лишь для почти всех начальных условий.
Одно последнее замечание. Понятие меры находится в полном со-
гласии с самой примитивной интуицией. Аксиома выбора, всего-
навсего позволяющая рассматривать множество Z элементов, выбран-
ных по одному из каждого множества некоторого семейства непересе-
кающихся множеств, звучит настолько естественно, что кажется почти
133
L
тривиальной. И тем не менее эта аксиома приводит к парадоксу Бана-
ха—Тарского!
Вот почему оказался совершенно необходимым критический пере-
смотр логических оснований теории множеств, а вопрос существова-
ния математических «созданий» стал серьезной проблемой.
Если, как заявил Пуанкаре, существовать — это только быть сво-
бодным от противоречия, то у нас нет другого выхода, кроме как нау-
читься уживаться с неприятностями вроде неизмеримых множеств или
разбиений Банаха—Тарского.
Л- Яуанг&ре
ПРОСТРАНСТВО И ГЕОМЕТРИЯ21
Начнем с маленького парадокса.
Существа, разум которых был бы подобен нашему и которые име-
ли бы такие же органы чувств, как и мы, но которые не получили бы
никакого предварительного воспитания, могли бы получить от соот-
ветственно подобранного внешнего мира такие впечатления, что им
пришлось бы построить геометрию иную, чем евклидова, и разместить
явления этого внешнего мира в пространстве неевклидовом или даже в
пространстве четырех измерений.
Для нас, ум которых сформировался под влиянием окружающего
нас мира, не составило бы никакой трудности отнести к нашему евк-
лидову пространству явления этого нового мира, если бы мы были в
него внезапно перенесены. И, напротив, если бы существа из того ми-
ра были перенесены к нам, они должны были бы отнести наши явле-
ния к неевклидовому пространству.
Но ведь с небольшими усилиями этого же могли бы достигнуть и мы.
Тот, кто всю свою жизнь посвятил бы такой задаче, может быть,
оказался бы в состоянии представить себе четвертое измерение.
Пространство геометрическое и пространство представлений.
Часто говорят, что образы внешних предметов локализованы в про-
странстве, что они даже не могут образоваться иначе как при этом ус-
ловии. Говорят также, что это пространство, которое таким образом
служит готовым кадром наших ощущений и представлений, тождест-
венно с пространством геометров, всеми свойствами которого оно об-
ладает.
Всем, кто так думает, предыдущая фраза должна показаться крайне
странной. Но надо рассмотреть, не обманываются ли они некоторой
иллюзией, которую более глубокий анализ мог бы рассеять.
134
Каковы, прежде всего, свойства пространства в собственном смыс-
ле? Я хочу сказать — того пространства, которое является предметом
геометрии и которое я назову пространством геометрическим. Вот
некоторые из наиболее существенных его свойств:
1. Оно непрерывно.
2. Оно бесконечно.
3. Оно имеет три измерения.
4. Оно однородно, т.е. все точки его тождественны между собой.
5. Оно изотропно, т.е. все прямые, которые проходят через одну и
ту же точку, тождественны между собой.
Сравним теперь его с кадром наших представлений и ощущений,
который я мог бы назвать пространством представлений
Пространство визуальное. Рассмотрим сначала чистб зрительное
впечатление, обусловливаемое изображением, возникающим на сет-
чатке. Краткий анализ показывает, что это изображение непрерывно,
но обладает только двумя измерениями; это уже составляет отличие
между пространством геометрическим и тем, что можно было бы на-
звать чисто визуальным пространством. Далее, этот образ заключен в
ограниченном кадре.
Наконец, существует еще одно отличие, не менее важное: это чис-
то визуальное пространство неоднородно Различные точки сетчатки —
независимо от изображений, которые могут на них возникать, — играют
не одну и ту же роль. Никак нельзя считать желтое пятно тождественным
с точкой, лежащей у края сетчатки. В самом деле, здесь не только самый
предмет производит гораздо более живые впечатления, но здесь, как и во
всяком ограниченном кадре, точка, занимающая центр кадра, не будет ка-
заться тождественной с точкой, близкой к одному из краев.
Более глубокий анализ, без сомнения, показал бы нам, что эта не-
прерывность визуального пространства и его два измерения суть не
более чем иллюзия; этот анализ еще более отдалил бы визуальное про-
странство от геометрического. Но мы ограничимся здесь только этим
замечанием, следствия из которого были достаточно рассмотрены в
главе «Математическая величина и опьгг».
Однако зрение позволяет нам оценивать расстояния и, следова-
тельно, воспринимать третье измерение. Но всякий знает, что это вос-
приятие третьего измерения сводится к ощущению усилия, сопровож-
дающему аккомодацию, которую надо выполнить, и к ощущению, со-
провождающему то схождение обеих глазных осей, которое необхо-
димо для отчетливого восприятия предмета.
Мы имеем здесь мускульные ощущения, совершенно отличные от
ощущений зрительных, которые дали нам познание первых двух изме-
135
рений. Таким образом, третье измерение выступит перед нами не в той
же роли, какую играют два других. А следовательно, то, что можно
назвать полным визуальным пространством, не есть пространство
изотропное.
Правда, оно имеет как раз три измерения, т.е. элементы наших зри-
тельных ощущений (по крайней мере те из них, которые, слагаясь, об-
разуют представление протяженности) будут вполне определены, ко-
гда известны три из них; выражаясь математическим языком, они бу-
дут функциями трех независимых переменных.
Но исследуем предмет несколько ближе. Третье измерение откры-
вается нам двумя различными способами: благодаря усилию при ак-
комодации и вследствие схождения глазных осей.
Эти два рода показаний, без сомнения, всегда согласованы друг с
другом. Между ними существует постоянное соотношение; выражаясь
математически, две переменные, измеряющие оба типа мускульного
ощущения, не выступают перед нами в качестве независимых, или
еще, — чтобы не прибегать к математическим понятиям достаточно
высокой сложности, — мы можем снова воспользоваться языком пре-
дыдущей главы и выразить тот же факт следующим образом: если два
ощущения схождения осей А и В неразличимы, то и два соответствен-
но сопровождающих их ощущения аккомодации А' и В' будут также
неразличимы.
Но такое соотношение ощущений — это, так сказать, опытный
факт; ничто не мешает a priori допустить обратное, и если окажется,
что это обратное действительно имеет место, если эти два типа мус-
кульных ощущений изменяются независимо один от другого, то мы
должны будем ввести новую независимую переменную, и «полное ви-
зуальное пространство» выступит перед нами как физическая непре-
рывность четырех измерений.
Я даже прибавлю, что это представляет собою факт внешнего опы-
та. Ничто не мешает предположить, что существо, имеющее ум, по-
добный нашему, и такие же органы чувств, как н мы, помещено в ми-
ре, куда свет достигает, только пройдя через преломляющие среды
сложной формы. Тогда два показания, служащие нам для оценки рас-
стояний, перестали бы быть связанными постоянным соотношением.
Существо, которое получило бы в подобном мире воспитание своих
чувств, без сомнения, приписало бы полному визуальному простран-
ству четыре измерения.
Пространство тактильное н пространство моторное. «Тактиль-
ное пространство» еще более сложно, чем визуальное, и еще более, чем
оно, удаляется от пространства геометрического. Бесполезно было бы по-
вторять для осязания анализ, проведенный мною относительно зрения.
136
Но вне данных зрения и осязания существуют другие ощущения,
которые так же, как и эти ощущения, и даже более способствуют обра-
зованию понятия пространства. Это — те всем известные ощущения,
которыми сопровождаются все наши движения и которые обыкновен-
но называются мускульными.
Соответствующий им кадр (le cadre) образует то, что можно назвать
моторным пространством.
Каждый мускул дает происхождение особому ощущению, способ-
ному делаться больше или меньше, так что совокупность наших мус-
кульных ощущений будет зависеть от стольких переменных, сколько у
нас мускулов. С этой точки зрения моторное пространство имело бы
столько измерений, сколько мы имеем мускулов.
Я знаю, мне тотчас скажут, что если мускульные ощущения спо-
собствуют образованию понятия пространства, то это потому, что мы
имеем чувство направления каждого движения, и оно является состав-
ной частью ощущения. Если бы это было так, если бы мускульное
ощущение не могло зародиться иначе, как сопутствуемое геометриче-
ским чувством направления, то геометрическое пространство было бы
формой, присущей нашей способности к ощущению. Но когда я ана-
лизирую свои ощущения, я этого совершенно не замечаю. Я вижу, что
ощущения, соответствующие движениям того же направления, связа-
ны в моем уме простой ассоциацией идей. К этой ассоциации идей и
сводится то, что мы называем «чувством направления». Следователь-
но, этого чувства нельзя было бы найти в единичном ощущении.
Эта ассоциация крайне сложна, так как сокращение того же муску-
ла может отвечать, смотря по положению членов, движениям самых
различных направлений.
Она, кроме того, очевидно, является приобретенной; как все ассо-
циации идей, она есть результат привычки-, эта привычка сама вытека-
ет из крайне многочисленных опытов, не подлежит никакому сомне-
нию, что если бы воспитание наших чувств происходило в иной среде,
где мы получали иные впечатления, то возникли бы иные привычки, и
наши мускульные ощущения были бы ассоциированы по иным законам.
Характерные черты пространства представлений. Таким обра-
зом, пространство представлений в своих трех формах — визуального,
тактильного и моторного пространства — существенно отличается от
геометрического пространства.
Оно ни однородно, ни изотропно; нельзя даже сказать, что оно име-
ет три измерения.
Часто говорят, что мы «проектируем» в геометрическое простран-
ство предметы наших внешних восприятий, что мы «локализуем» их.
137
Имеет ли это смысл и какой? Должно ли это обозначать, что мы пред-
ставляем себе внешние предметы в геометрическом пространстве?
Наши представления суть только воспроизведение наших ощуще-
ний, поэтому они могут разместиться только в том же кадре, в каком и
последние, т.е. в пространстве представлений.
Нам так же невозможно представлять себе внешние тела в геомет-
рическом пространстве, как невозможно художнику рисовать на пло-
ской картине предметы с их тремя измерениями.
Пространство представлений есть только образ геометрического
пространства — образ, видоизмененный некоторым родом перспекти-
вы; мы не можем представить себе предметы иначе, как подчиняя их
законам этой перспективы.
Мы не представляем себе, следовательно, внешних тел в геометри-
ческом пространстве, но мы рассуждаем об этих телах, как если бы
они были помещены в геометрическом пространстве.
С другой стороны, когда говорят, что мы «локализуем» данный
предмет в данной точке пространства, что хотят этим сказать?
Это просто означает, что мы представляем себе движения, ко-
торые надо совершить, чтобы достигнуть этого предмета.
И пусть не говорят, что для того, чтобы представить себе эти дви-
жения, их надо проектировать сначала в пространство и что понятие
пространства должно, следовательно, существовать раньше.
Когда я говорю, что мы представляем себе эти движения, я хочу
сказать только, что мы представляем себе мускульные ощущения, ко-
торые сопровождают их и которые вовсе не имеют геометрического
характера, а следовательно, отнюдь не предполагают предсуществова-
ния понятия пространства.
Изменения состояния и изменения положения. Но, скажут, если
идея геометрического пространства не присуща нашему уму и, с дру-
гой стороны, если никакое из наших ощущений не может нам доста-
вить ее, то как она могла возникнуть?
Это — тема нашего ближайшего исследования. Оно потребует у
нас некоторого времени; но я Могу резюмировать в нескольких словах
конечную цель рассуждения, которое мне предстоит развить.
Никакое из наших ощущений, взятое в отдельности, не могло бы
привести нас к идее пространства, мы пришли к ней, только изучая
законы, по которым эти ощущения следуют друг за другом. Мы ви-
дим прежде всего, что наши впечатления подвержены изменению; но
между изменениями, которые мы констатируем, мы скоро бываем вы-
нуждены делать различие.
Мы говорим, или что некоторые предметы, вызывающие эти впе-
чатления, изменили свое состояние, или что они изменили свое поло-
жение — что они просто переместились.
13а
Меняет ли предмет свое состояние или только положение, это пе-
редается нам всегда одним и тем же способом: изменением во всем со-
ставе впечатлений.
Каким же образом мы могли прийти к различению обоих измене-
ний? Если произошло только изменение положения, то мы можем вос-
становить прежнюю совокупность впечатлений, совершая движения,
ставящие нас в то же относительное положение к подвижному пред-
мету. Мы компенсируем таким образом происшедшее изменение, вос-
станавливая начальное состояние обратным изменением.
Так, если речь идет о зрении и если предмет перемещается перед
нашими глазами, мы можем за ним «следить глазами» и удерживать
его изображение в той же точке сетчатки посредством соответствен-
ных движений глазного яблока.
Эти движения мы сознаем, так как они являются волевыми и со-
провождаются мускульными ощущениями; но это не значит, что мы
представляем их происходящими в геометрическом пространстве.
Именно этим характеризуется изменение положения, и оно отлича-
ется от изменения состояния тем, что всегда может быть компенсиро-
вано указанным способом.
Следовательно, может случиться, что мы переходим от системы
впечатлений А к системе В двумя различными способами: 1) непроиз-
вольно и без каких-либо мускульных ощущений — когда перемещает-
ся предмет; 2) произвольно и при наличии мускульных ощущений —
когда предмет неподвижен, но перемещаемся мы таким образом, что
предмет имеет по отношению к нам относительное движение.
Если дело происходит указанным образом, то переход от системы
впечатлений А к системе В есть только изменение положения.
Отсюда следует, что зрение и осязание не могли бы нам дать поня-
тие пространства без помощи «мускульного чувства».
Это понятие не могло бы образоваться не только из единичного
ощущения, но даже из ряда ощущений; кроме того, существо непод-
вижное никогда не могло бы приобрести его, так как, если бы оно не
имело возможности компенсировать своими движениями эффектов,
зависящих от изменений положения внешних предметов, оно не имело
бы никакого основания отличать их от изменений состояния. Оно не
могло бы также приобрести это понятие, если бы движения его не бы-
ли произвольными или если бы они не сопровождались некоторыми
ощущениями.
Условия компенсации. Каким образом возможно явление такого
рода, что два изменения, не зависящие друг от друга, взаимно компен-
сируются?
139
Ум, знакомый уже с геометрией, рассуждал бы так. Для того чтобы
произошла компенсация, очевидно, нужно, чтобы различные части
внешнего предмета, с одной стороны, и различные органы наших
чувств, с другой, приходили после двойного изменения опять в то же
относительное положение. А для этого надо, чтобы различные части
внешнего предмета равным образом сохранили друг к другу то же са-
мое относительное положение и чтобы то же имело место для взаим-
ного расположения различных частей нашего тела.
Другими словами, при первом изменении внешний предмет должен
перемещаться как неизменное твердое тело; то же самое должно про-
изойти с системой нашего тела при втором изменении, компенсирую-
щем первое.
При этих условиях компенсация может произойти. Но мы, не буду-
чи еще знакомы с геометрией, — потому что у нас еще не образова-
лось понятие пространства, — не можем рассуждать таким образом;
мы не можем предвидеть a priori, возможна ли компенсация. Но опыт
учит нас, что она иногда имеет место, и это — тот опытный факт, из
которого мы исходим для различения изменений состояния от измене-
ний положения.
Твердые тела н геометрия. Среди окружающих нас предметов
есть такие, которые часто испытывают перемещения, способные быть
компенсированными соответственным (коррелятивным) движением
нашего собственного тела. Это — тела твердые.
Другие предметы, форма которых способна изменяться, испытыва-
ют подобные перемещения (изменения положения без изменения фор-
мы) только в исключительных случаях. Когда тело перемещается, из-
меняя форму, мы уже не можем соответственными движениями при-
вести органы наших чувств в то же относительное положение к этому
телу; следовательно, мы более не в состоянии восстановить начальную
совокупность впечатлений.
Только позднее и вследствие новых опытов мы научаемся разлагать
тела переменной формы на меньшие элементы такого рода, что каж-
дый из них перемещается почти по тем же законам, что и твердые те-
ла. Мы таким образом отличаем «деформации» от других изменений
состояния; при таких деформациях каждый элемент испытывает про-
стое изменение положения, которое может быть компенсировано, но
изменение, испытываемое всей совокупностью элементов, более глу-
боко и уже не способно компенсироваться коррелятивным движением.
Подобное понятие, будучи уже очень сложным, могло явиться
только относительно поздно; кроме того, оно не могло бы зародиться,
если бы наблюдение твердых тел уже не научило нас отличать изме-
нения положения.
140
Следовательно, если бы не было твердых тел в природе, не было
бы и геометрии.
Другое замечание также заслуживает того, чтобы на нем остано-
виться. Вообразим твердое тело, занимающее сначала положение а и
затем переходящее в положение р; в первом своем положении оно про-
изведет на нас систему впечатлений Л и во втором — систему впечатле-
ний В. Пусть имеется теперь второе твердое тело, качественно вполне
отличное от первого, например, иного цвета. Предположим еще, что
оно переходит от положения а', в котором оно производит на нас сис-
тему впечатлений А', к положению р', котором оно вызывает в нас сис-
тему впечатлений В'.
Вообще, ни система Л не будет иметь ничего общего с системой Л',
ни система В с системой В' Переход от системы Л к системе В и пере-
ход от системы Л' к системе В' суть, следовательно, два изменения, ко-
торые сами по себе, вообще говоря, ничего общего не имеют. Между
тем и то и другое изменение мы рассматриваем как перемещения; бо-
лее того, мы рассматриваем их как то же самое перемещение. Каким
образом это происходит?
Это — просто потому, что и то и другое перемещение может быть
компенсировано одним и тем же коррелятивным движением нашего
тела.
Следовательно, не что иное, как «коррелятивное движение», со-
ставляет единственную связь между двумя явлениями, которые иначе
мы никогда и не подумали бы сближать.
С другой стороны, наше тело, благодаря огромному числу его со-
членений и мускулов, может предпринимать множество различных
движений; но не все они способны «компенсировать» изменение
внешних предметов; к этому способны только те, при которых или все
наше тело, или по крайней мере те из органов наших чувств, которых
касается дело, перемещаются как целое, т.е. не изменяя относительных
положений, — подобно твердому телу.
Итак:
1. Мы должны прежде всего различать две категории явлений. Од-
ни, непроизвольные, не сопровождаемые мускульными ощущениями,
приписываются нами внешним предметам; это суть внешние измене-
ния. Другие, противоположного характера, которые мы приписываем
движениям нашего собственного тела, суть изменения внутренние.
2. Мы замечаем, что известные изменения каждой из этих катего-
рий могут быть компенсированы коррелятивным изменением другой
категории.
3. Среди внешних изменений мы отличаем те, которые имеют кор-
релятивное изменение в другой категории; мы называем их перемеще-
141
ниями; среди изменений внутренних мы также отличаем те, которые
имеют коррелятивное изменение в первой категории. Таким образом,
благодаря этой взаимности определяется особый класс явлений, кото-
рые мы называем перемещениями
Законы этих явлений и составляют предмет геометрии.
Закон однородности. Первый из этих законов есть закон однород-
ности.
Предположим, что благодаря внешнему изменению а мы пришли
от системы впечатлений А к системе В; потом это изменение а ком-
пенсировано соответственным волевым движением р так, что мы
пришли опять к системе А
Предположим теперь, что другое внешнее изменение а' снова при-
водит нас от системы А к системе В.
Опыт учит нас тогда, что это изменение а', как и а, способно ком-
пенсироваться коррелятивным волевым движением р' и что это дви-
жение р' соответствует тем же мускульным ощущениям, что и движе-
ние р, которое компенсировало а.
Именно этот факт и выражается обыкновенно словами: простран-
ство однородно и изотропно.
Можно сказать также, что движение, происшедшее один раз, может
повториться второй раз, третий раз и т.д., не меняя своих свойств.
В первой главе, где мы изучали природу математического умозак-
лючения, мы видели, какое важное значение следует приписать возмож-
ности повторять неопределенное число раз одну и ту же операцию.
Именно от этого повторения математическое умозаключение при-
обретает свою силу; и если эта сила распространяется также на гео-
метрические факты, то это — благодаря закону однородности.
Для полноты изложения надо было бы присоединить к закону од-
нородности множество других аналогичных законов; я не хочу вхо-
дить по поводу их в подробности, но математики резюмируют их од-
ним словом, говоря, что перемещения образуют «группу».
Неевклидов мир. Если бы геометрическое пространство выступа-
ло в качестве кадра для каждого нашего представления, взятого в от-
дельности, то было бы невозможно представить себе образ, отделен-
ный от этого кадра, и мы не могли бы ничего изменить в нашей гео-
метрии.
На деле это не так: геометрия есть только резюме законов, по кото-
рым эти образы следуют друг за другом. В таком случае ничто не ме-
шает нам вообразить себе ряд представлений, во всем подобных на-
шим обычным представлениям, но следующих друг за другом по за-
конам, отличным от тех, к которым мы привыкли. Поэтому понятно, что
142
существа, умственное воспитание которых проходило бы в такой сре-
де, где эти законы не выполняются, могли бы иметь геометрию, в зна-
чительной степени отличную от нашей.
Вообразим, например, мир, заключенный внутри большой сферы и
подчиненный следующим законам. Температура здесь не равномерна;
она имеет наибольшее значение в центре и понижается но мере удале-
ния от него, делаясь равной абсолютному нулю на шаровой поверхно-
сти, которая является границей этого мира.
Я определю в точности даже закон, по которому изменяется эта
температура. Пусть R будет радиус граничной поверхности, г — рас-
стояние рассматриваемой точки от центра сферы. Абсолютная темпе-
ратура пусть будет пропорциональна R2 - А
Я предположу далее, что в этом мире все тела имеют один и тот же
коэффициент расширения, именно такой, что длина какой-нибудь ли-
нейки пропорциональна абсолютной температуре.
Наконец, я предположу, что предмет, перенесенный из одной точки
в другую, где температура иная, тотчас же приходит в состояние теп-
лового равновесия со своей новой средой. В этих допущениях нет ни-
чего ни противоречивого, ни немыслимого.
В таком случае движущийся предмет будет все уменьшаться по ме-
ре приближения к граничной сфере. Теперь заметим, что хотя этот мир
ограничен с точки зрения нашей обычной геометрии, тем не менее он
будет казаться бесконечным для его обитателей.
В самом деле, когда они пожелали бы приблизиться к граничной
сфере, они охлаждались бы и становились бы все меньше и меньше.
Поэтому шаги их постоянно укорачивались бы, и они никогда не мог-
ли бы достигнуть граничной сферы.
Если для нас геометрия есть не что иное, как изучение законов, по
которым движутся неизменные твердые тела, то для этих воображае-
мых существ она была бы изучением законов, по которым движутся
твердые тела, изменяющиеся вследствие тех различий в температуре,
о которых я только что говорил.
Без сомнения, и в нашем мире реальные твердые тела также испы-
тывают изменения формы и объема вследствие нагревания и охлажде-
ния. Но устанавливая основы геометрии, мы пренебрегаем этими из-
менениями, так как, помимо того, что они крайне незначительны, они
еще беспорядочны и, следовательно, кажутся нам случайными.
В воображаемом нами мире это было бы уже не так; эти изменения
следовали бы правильным и очень простым законам. С другой сторо-
ны, различные твердые составные части тела обитателей этого мира
испытывали бы такие же изменения формы и объема
143
Я сделаю еще другое допущение. Я предположу, что свет здесь
проходит через среды различной преломляющей способности, именно
такие, что показатель преломления обратно пропорционален R2 -
Легко видеть, что в этих условиях световые лучи были бы не прямоли-
нейными, а круговыми.
Чтобы оправдать все предыдущее, мне остается показать, что из-
вестные изменения, происходящие в положении внешних предметов,
могут быть компенсированы коррелятивными движениями чувствую-
щих существ, которые заселяют этот воображаемый мир; таким обра-
зом, может быть восстановлен первоначальный комплекс впечатлений,
испытываемых этими существами.
Предположим в самом деле, что предмет перемещается, деформи-
руясь: не как неизменное твердое тело, но как твердое тело, испыты-
вающее неравномерные расширения, в точности соответствующие до-
пущенному выше закону изменения температур. Для краткости я по-
зволю себе называть подобное движение неевклидовым перемещением
Если по соседству находится чувствующее существо, его впечатле-
ния будут изменены благодаря перемещению предмета, но оно будет в
состоянии восстановить их в прежнем виде, передвигаясь само надле-
жащим образом Достаточно, чтобы в результате система, состоящая
из предмета и чувствующего существа, рассматриваемая как одно те-
ло, испытала одно из тех особых перемещений, которые я назвал не-
евклидовыми. Это возможно, если допустить, что члены этих существ
расширяются по тому же закону, что и другие тела заселяемого нми
мира.
Хотя с точки зрения нашей обычной геометрии тела окажутся по-
сле такого перемещения деформированными и различные их части от-
нюдь не возвратятся в прежнее относительное расположение, но мы
увидим, что впечатления чувствующего существа окажутся теми же.
В самом деле, если взаимные расстояния различных частей и могли
измениться, тем не менее части, бывшие вначале в соприкосновении,
опять будут в соприкосновении. Следовательно, осязательные впечат-
ления не изменятся. С другой стороны, если учесть гипотезу о прелом-
лении и кривизне световых лучей, мы убедимся, что и зрительные впе-
чатления останутся прежними.
Итак, наши воображаемые существа должны будут, как и мы, клас-
сифицировать наблюдаемые ими явления и выделить из них «измене-
ния положения», которые можно компенсировать соответственным
волевым движением.
Если они создадут геометрию, то она не будет, подобно нашей,
изучением движений наших неизменных твердых тел; это будет наука
об изменениях положения, изменениях, которые они выделят в особую
144
группу и которые будут представлять не что иное, как «неевклидовы
перемещения». Это будет неевклидова геометрия.
Таким образом, такие же существа, как мы, воспитание которых
происходило бы в подобном мире, имели бы геометрию, отличную от
нашей.
Мир четырех измерений. Так же, как неевклидов мир, можно
представить себе мир четырех измерений
Чувство зрения, даже при единственном глазе, в соединении с мус-
кульными ощущениями, сопровождающими движения глазного ябло-
ка, могло бы оказаться достаточным для познания пространства трех
измерений.
Образы внешних предметов рисуются на сетчатке, которая является
картиной двух измерений; это — перспективные изображения.
Но так как эти предметы, а также и наш глаз, подвижны, то мы по-
следовательно видим различные перспективные изображения одного и
того же тела, схваченные с нескольких различных точек зрения.
В то же время мы убеждаемся, что переход от одного перспектив-
ного изображения к другому часто сопровождается мускульными
ощущениями. Если переходы от перспективы А к перспективе В и от
перспективы А' к перспективе В' сопровождаются одними и теми же
мускульными ощущениями, то мы сближаем их между собой как опе-
рации одной и той же природы.
Изучая затем законы, по которым сочетаются между собой эти опе-
рации, мы убеждаемся в том, что они образуют группу, которая имеет
такую же структуру, как и группа движений неизменных твердых тел.
Но мы видели, что именно из свойств этой группы мы извлекли по-
нятие геометрического пространства и пространства трех измерений
Мы понимаем, таким образом, как идея пространства трех измере-
ний могла возникнуть из наблюдения этих перспективных изображе-
ний, хотя каждое из них имеет только два измерения; дело в том, что
они следуют друг за другом по определенным законам
Теперь таким же образом, как на плоскости можно сделать пер-
спективное изображение фигуры трех измерений, можно сделать изо-
бражение фигуры четырех измерений на экране трех (или двух) изме-
рений. Для геометра эта задача в высшей степени простая.
Можно также получить несколько перспективных изображений од-
ной и той же фигуры с нескольких различных точек зрения. Мы можем
легко представить себе эти перспективные изображения, так как они
имеют только три измерения.
Вообразим, что различные перспективные изображения одного и
того же предмета следуют одно за другим и что переход от одного к
другому сопровождается мускульными ощущениями
11 Зак 72
145
Ясно, что два из таких переходов будут рассматриваться нами как
две операции одной и той же природы, если они будут связаны с та-
кими же мускульными ощущениями.
Теперь ничто не мешает нам вообразить себе, что эти операции со-
четаются по любому заданному закону, например так, что образуют
группу такой же структуры, как и группа движений неизменного твер-
дого тела четырех измерений.
В таком представлении нет ничего невозможного, и однако это как
раз такие же щущения, которые испытывало бы существо, обладаю-
щее сетчаткой двух измерений и возможностью перемещаться в про-
странстве четырех измерений.
В этом именно смысле допустимо говорить о возможности пред-
ставить себе четвертое измерение.
Было бы невозможно представить себе этот вид пространства
Гильберта, о котором мы говорили в предыдущей главе, так как это
пространство уже не является непрерывностью второго порядка. Сле-
довательно, оно слишком глубоко отличается от нашего обычного
пространства.
Выводы. Мы видим, что опыт играет необходимую роль в проис-
хождении геометрии; но было бы ошибкой заключить, что геометрия —
хотя бы отчасти — является экспериментальной наукой.
Если бы она была экспериментальной наукой, она имела бы только
временное, приближенное — и весьма грубо приближенное! — значе-
ние Она была бы только наукой о движении твердых тел. Но на самом
деле она не занимается реальными твердыми телами; она имеет своим
предметом некие идеальные тела, абсолютно неизменные, которые яв-
ляются только упрощенным и очень отдаленным отображением ре-
альных тел.
Понятие об этих идеальных телах целиком извлечено нами из недр
нашего духа, и опыт представляет только повод, побуждающий нас
его использовать.
Предмет геометрии составляет изучение лишь частной «группы»
перемещений, но общее понятие группы существует раньше в нашем
уме (dans notre esprit), по крайней мере в виде возможности. Оно при-
суще нам не как форма нашего восприятия, а как форма нашей спо-
собности суждений. Надо только среди всех возможных групп вы-
брать ту, которая служила бы, так сказать, эталоном, с которым мы
соотносили бы реальные явления. Опыт направляет нас при этом вы-
боре, но не делает его для нас обязательным; он показывает нам не то,
какая геометрия наиболее правильна, а то, какая наиболее удобна
Читатель заметит, что я был бы в состоянии описывать фантасти-
ческие миры, которые я представлял себе выше, не переставая пользо-
ваться языком обыкновенной геометрии
146
И в самом деле, мы не изменили бы его, даже если бы были пере-
несены в такой мир.
Существа, получившие там свое развитие, нашли бы без сомнения
более удобным создать геометрию, отличную от нашей, которая луч-
ше соответствовала бы их впечатлениям. Что же касается нас, то на-
верное даже при наличии тех же впечатлений мы нашли бы более
удобным не изменять наших привычек.
Норден
ОТКРЫТИЕ ЛОБАЧЕВСКОГО
И ЕГО МЕСТО В ИСТОРИИ НОВОЙ ГЕОМЕТРИИ10
1. Открытие неевклидовой геометрии. Со времен первых про-
должателей и комментаторов Евклида проблема пятого постулата его
«Начал» и связанная с ней теория параллельных линий стали цен-
тральной проблемой обоснования геометрии. Интерес к ней не слабел
в течение двух тысячелетий, и доказательство пятого постулата на ос-
нове других постулатов Евклида считалось единственно приемлемым
путем решения этой проблемы.
Бурное развитие математической мысли сказалось и в оживлении
интереса к вопросам обоснования геометрии во Франции и Германии
XVIII в. Но если во Франции проблема постулата Евклида рассматри-
валась как проблема методики (Лежандр), то геометры Германии свя-
зывали ее с вопросами методологии или, по выражению Гаусса, «ме-
тафизики пространства».
Вопрос о происхождении геометрических истин был также одним
из центральных вопросов теории познания Канта, оказавшей длитель-
ное влияние на представителей немецкой точной науки XVIII—XIX вв.
Утверждая, что основные положения геометрии имеют априорное, до-
опытное происхождение и коренятся в «чистом воззрении», Кант при-
соединяется, собственно говоря, к распространенному взгляду, со-
гласно которому постулаты должны обладать признаком самоочевид-
ности. С этой точки зрения проблема пятого постулата вставала с но-
вой остротой. Только этот постулат явно не обладал самоочевидно-
стью, а возможность его доказательства представлялась равносильной
возможности априорного обоснования всей геометрии
Именно так ставит вопрос Гаусс (1777—1855) в своем письме к
Фаркашу Больаи от 16.XI1.1799. Однако уверенность в возможности
доказательства постулата Евклида еще долго не покидает Гаусса: об
этом он определенно пишет Фаркашу Больаи еще в 1804 г., и только в
IT-
147
1817 г. он первый раз <в письме к Ольберсу) выражает свои сомнения.
Важно отметить, что эти сомнения Гаусс сразу же распространяет и на
возможность априорного обоснования геометрии, отмечая, что «гео-
метрию приходится ставить в один ранг не с арифметикой, сущест-
вующей чисто a priori, а скорее с механикой».
Следующие годы являются переломными в истории взглядов Гаус-
са на теорию параллельных, но только внешний толчок, связанный с
получением заметки Швейкарта, заставил его в первый раз с достаточ-
ной определенностью высказать свои новые взгляды. Действительно, в
письме к Герлингу по поводу этой заметки, в которой Швейкарт до-
пускает существование Астральной геометрии, Гаусс говорит, что все
это списано из его души.
С еще большей определенностью Гаусс утверждает в 1824 г. (в
письме в Тауринусу), что геометрия, основанная на предположении,
противоречащем постулату Евклида, «совершенно последовательна»
(in sich selbst consequent). В это время ему уже известны многие из ее
основных фактов, и тем не менее он не только не высказывает публич-
но своих взглядов, но и определенно просит Тауринуса не обнародо-
вать их. Лишь в 1831 г. Гаусс сообщает Шумахеру о своем желании
записать свои результаты. Сохранилось несколько черновых набро-
сков Гаусса по неевклидовой геометрии, но эта работа не была им за-
кончена возможно, потому, что уже в марте 1832 г. он получил экзем-
пляр «Аппендикса» Яноша Больаи.
Здесь уместно сделать краткий обзор тех фактов неевклидовой гео-
метрии, которые были известны Гауссу. Он знал, что при переходе к
новой геометрии определение параллельных линий, принятое в обыч-
ной геометрии, нужно заменить более сложным, но зато не зависящим
от пятого постулата Евклида. Это определение и основанные на нем
доказательства свойств параллельных и были изложены им в заметке
1831 г. Ему было известно, что в неевклидовой геометрии сумма углов
треугольника отличается от 180° и что мера этого различия пропор-
циональна площади треугольника. Вследствие этого не существует
подобных треугольников, но зато существует абсолютная мера длины.
Можно считать также, что еще в 1819 г. Гаусс владел основными фор-
мулами гиперболической тригонометрии; об этом свидетельствует
формула, приведенная им в письме к Герлингу, которая выражает
площадь асимптотического треугольника через константу Швейкарта
С. Существует также набросок Гаусса, расшифрованный Штеккелем и
относимый им к 40-м гт., содержащий вывод формул сферической и
гиперболической тригонометрии, основанный на рассмотрении беско-
нечно малых фигур.
148
В течение своей жизни Гаусс не только не публиковал своих иссле-
ований по неевклидовой геометрии, но и не отозвался публично о ра-
ботах Больаи и Лобачевского. Его странная сдержанность обычно объ-
ясняется опасениями встретить непонимание современников. Однако
нельзя недооценивать еще одного важного фактора, который объясня-
ет и то, что период сомнений Гаусса в возможности существования не*
евклидовой геометрии растянулся почти на четверть века. Этим фак-
тором являлись, по нашему мнению, философские воззрения Гаусса,
который был первоначально уверен в априорном характере всей мате-
матики и отходил с позиций априоризма в геометрии весьма неуверен-
но, непоследовательно и неохотно.
С иных, чисто материалистических позиций подходил к теории па-
раллельных гениальный творец неевклидовой геометрии Николай
Иванович Лобачевский. Еще в обозрении преподавания 1824 г. он го-
ворил, что основания математики «должны быть несомнительные для
нас истины, первые понятия о природе вещей, которые, будучи раз
приобретены, сохраняются навсегда...». В дальнейшем он еще уточня-
ет этот тезис и прямо говорит, что источником приобретения этих по-
нятий является опыт. «Первыми данными без сомнения будут всегда
те понятия, которые мы приобретаем в природе посредством наших
чувств».
Суждение же о всех других понятиях, которые Лобачевский назы-
вает составными, должно вытекать логически из свойств основных или
простых понятий.
Исходя из этих общих принципов, Лобачевский подходит к выбору
основных понятий геометрии. Он предлагает считать основным объек-
том геометрии тело, а основным отношением между телами — их при-
косновение Все остальные объекты, как-то поверхность, линия, плос-
кость, прямая, точка и т.д., должны быть определены через эти основ-
ные понятия.
Эту точку зрения Лобачевский приводил во всех своих работах, на-
чиная с неизданного курса лекций 1816—1817 гт., и развивает подроб-
но в 1835 г в своем фундаментальном сочинении «Новые начала
геометрии с полной теорией параллельных». Хотя замысел
Лобачевского перестроить основы геометрии и не может считаться в
этой ее части вполне удавшимся, мы относимся с уважением к смелой
п пытке великого геометра преодолеть те трудности в основаниях
геометрии, которые были осознаны и разрешены значительно позже на
основе изучения наиболее ценного из наследия Лобачевского и прежде
всего его гениальной теории параллельных.
Важность этой теории была осознана Лобачевским еще в первые
годы его университетского преподавания. В первом из дошедших до
149
нас обозрений 1822 г. он пишет: «Другого рода трудность в геометрии
представляет параллелизм линий, трудность до сих пор непобедимую,
но между тем заключающую в себе истины ощутительные, вне всякого
сомнения, и столь важные для целой науки, что никак не могут быть
обойдены».
С общей точки зрения, принятой Лобачевским, пятый постулат то-
же занимает особое место среди основных положений геометрии, но
не по недостатку очевидности, а потому, что он говорит о сложных,
«составных» понятиях и не вытекает прямо из непосредственно на-
блюдаемых свойств геометрических тел.
Вследствие этого Лобачевский присоединяется к общему мнению о
том, что постулат Евклида требует проверки, и первоначально мыслит
эту проверку в виде доказательства, которое и пытается построить.
Однако в отличие от всех своих предшественников он очень скоро по-
нял бесплодность этих попыток и встал на совершенно новый путь.
«Напрасное старание со времен Евклида в продолжении двух тысяч
лет заставляло меня подозревать, — пишет он в своем сочинении «Но-
вые начала геометрии с полной теорией параллельных», — что в самих
понятиях еще не заключается той истины, которую хотели доказывать
и которую проверить, подобно другим физическим законам, могут
лишь опыты».
Однако в соответствии со сложной природой пятого постулата его
проверка должна опираться на сложный эксперимент, требующий ма-
тематической базы. Но эта база сама уже не может основываться на
постулате Евклида, она должна быть геометрией, отличной от геомет-
рии Евклида. Эту геометрию и разработал Лобачевский, назвав ее пер-
воначально «воображаемой» Сочинение Лобачевского, посвященное
этому вопросу, «О началах геометрии» было опубликовано в 1829 г. и
содержало изложение доклада, представленного физико-математи-
ческому факультету Казанского университета 11 (23) февраля 1826 г.
В этом сочинении он исходит из предположения, что «угол парал-
лелизма» не является прямым, как в геометрии Евклида, а представля-
ет собой функцию F(a) соответствующего отрезка. Указывая далее на
то, что на предельной поверхности будет иметь место геометрия Евк-
лида, он прямо переходит к выводу основных формул тригонометрии
Этот вывод Лобачевский завершает, определив конечное выражение
функции F(a) и показав, что оно содержит некоторое неопределенное
постоянное число е, зависящее от выбора единицы длины. Далее Ло-
бачевский показывает, что для треугольников, длина стороны которых
мала по сравнению с радиусом кривизны пространства, приближенно
справедливы формулы евклидовой геометрии; это позволяет ему впо-
следствии говорить, что «воображаемая Геометрия обнимает употре-
150
бительную Геометрию как частный случай, к которому переходим,
принимая линии бесконечно малыми».
С другой стороны, свойства фигур «воображаемой геометрии» от-
личаются от свойств соответствующих фигур геометрии Евклида тем
больше, чем больше их размеры. Этот факт предопределяет характер
того эксперимента, который должен быть поставлен для оправдания
возможности пользоваться геометрией Евклида. Рассматриваемые фи-
гуры должны быть наибольшими из всех доступных наблюдению и
поэтому их следует искать в астрономии.
Коснемся теперь тех астрономических фактов, на которых Лоба-
чевский основывается в своих дальнейших рассуждениях.
Наименьший из годичных параллаксов земной орбиты всё же будет
заведомо больше угла параллелизма, соответствующего ее диаметру.
Пользуясь этим, можно найти нижнюю границу для радиуса кри1 изны
пространства. Подставив найденное граничное значение в формулы
гиперболической тригонометрии, мы можем решать такие треугольни-
ки, сторона которых совпадает с диаметром земной орбиты, а одна из
вершин совмещается со звездами больших параллаксов.
Исходя из значений параллаксов, известных в его время, Лобачев-
ский показывает, что отклонения геометрии указанных треугольников
от геометрии Евклида ничтожно малы, и приходит к следующему за-
ключению:
«После этого можно воображать, сколько эта разность, на которой
основана наша теория параллельных, оправдывает точность всех вы-
числений обыкновенной Геометрии и дозволяет принятые начала этой
последней рассматривать как бы строго доказанными».
Предложив метод обоснования евклидовой геометрии, Лобачев-
ский не считал, однако что он окончательно решил вопрос о строении
реального пространства. Об этом свидетельствуют, например, послед-
ние страницы его «Пангеометрии».
В «Новых началах геометрии» Лобачевский допускает также воз-
можность того, что его геометрия осуществляется в «тесной сфере мо-
лекулярных притяжений», если «некоторые силы в природе следуют
одной, другие своей особой Геометрии», предвосхищая некоторые
наиболее смелые гипотезы современной физики.
Будучи несомненно уверенным в логической безукоризненности
своей геометрии, Лобачевский тем не менее ставит вопрос о доказа-
тельстве ее непротиворечивости во всех своих работах и в особенно-
сти в сочинении «Воображаемая геометрия». Принимая без вывода ос-
новные уравнения своей тригонометрии, он доказывает, что, с одной
стороны, они не противоречат предложениям абсолютной геометрии, с
другой же стороны, из них вытекает основной факт неевклидовой гео-
метрии — сумма углов треугольников меньше двух прямых.
151
Одновременно с этим Лобачевский предпринимает огромные уси-
лия, направленные отчасти к той же цели: он строит аналитическую и
дифференциальную геометрию своего пространства и вычисляет дли-
ны дуг, площади поверхности и объемы. Сравнивая выражения этих
величин, полученные различными способами, он получает многочис-
ленные соотношения между определенными интегралами. Проверяя
эти соотношения аналитически, Лобачевский находит, таким образом,
новые подтверждения непротиворечивости своей системы.
Получение этих результатов необходимо еще и для другой цели Лоба-
чевского: расширения возможности приложения геометрии к анализу.
Мы не можем здесь остановиться подробнее на замечательном «Ап-
пендиксе» Яноша Больаи (1802—1860), который пришел к открытию
неевклидовой геометрии независимо от Гаусса и Лобачевского в конце
20-х гг. прошлого столетия. Отметим только, что эта работа выдающе-
гося венгерского геометра носит печать яркого своеобразия и написана
в блестящем, хотя и предельно сжатом стиле.
Открытия Лобачевского и Больаи не получили признания при их
жизни. Перелом наступил только в конце 60-х гг. прошлого столетия.
Чтобы описать этот перелом и те сложные взаимодействия, в которые
вступила идея неевклидовой геометрии после своего признания, нам
нужно вернуться к эпохе ее открытия.
2. Теория поверхностен н геометрия Римана. В 1827 г. вышел в
свет знаменитый мемуар Гаусса, положивший начало развитию диф-
ференциальной геометрии как самостоятельной научной дисциплины.
К основным идеям своего сочинения Гаусс пришел, с одной сторо-
ны, обобщая опыт своей практической работы по высшей геодезии; с
другой же стороны, несомненна и та роль, которую сыграли при его
создании размышления Гаусса об основаниях геометрии. Так, в письме
к Хансену (1825) Гаусс пишет, что его исследования о поверхностях
глубоко проникают в область метафизики пространства.
В своем мемуаре Гаусс разрабатывает метод криволинейных коор-
динат, вводит понятие сферического отображения, первую и вторую
квадратичные формы поверхности, устанавливает понятие наложимости
и изгибания, выделяет «абсолютные свойства» поверхности, составля-
ет ее деривационные уравнения, устанавливает понятие полной кри-
визны и доказывает, что она является инвариантом изгибания, и, нако-
нец, вводит полугеодезические ортогональные координаты.
Важнейшим из всего перечисленного следует считать выделение
абсолютных свойств поверхности, которые получили впоследствии на-
звание ее внутренней геометрии, и доказательство того, что полная
кривизна является инвариантом, принадлежащим этой геометрии.
152
К работам Гаусса непосредственно примыкают работы его ученика
Фердинанда Готлибовича Миндинга (1806—1885). В центре их стоит
проблема изгибания и внутренней геометрии поверхности. Мы оста-
новимся на четырех из них.
В первых двух работах Миндинг вводит понятие развертывания
линии па плоскость, которое было использовано впоследствии Леви-
Чивита и обобщено Картаном для определения связности вдоль кри-
вой. Миндинг показывает также, что геодезическая кривизна остается
неизменной при изгибании и равна полной кривизне линии, разверну-
той на плоскости.
В первой части третьей работы рассматриваются поверхности по-
стоянной гауссовой кривизны. Миндинг находит выражение линейно-
го элемента этих поверхностей и показывает, что каждая из них может
быть положена иа себя так, чтобы при этом совместились любые ее
две точки и любые направления, исходящие из этих точек. В заключе-
ние он указывает класс винтовых поверхностей постоянной кривизны
и поверхностей вращения, содержащих как частный случай и псевдо-
сферу.
Наконец, в последней заметке Миндинг замечает, что формулы
тригонометрии геодезических треугольников на поверхностях посто-
янной отрицательной кривизны могут быть получены из формул сфе-
рической тригонометрии заменой действительной постоянной 4k на
мнимую.
На эти результаты Миндинга и опирался Э. Бельтрами (1835—
1900) в своей работе 1868 г. «Опыт интерпретации неевклидовой
геометрии». Он обратил внимание на то, что поверхности постоянной
кривизны могут налагаться на себя с такой же степенью свободы, ко-
торая имеет место для движений плоскости и сферы по себе. С другой
стороны, геодезические линии этих поверхностей могут быть отобра-
жены на прямые линии плоскости, т.е. удовлетворяют (с известными
оговорками) тем же аксиомам, что и последние. Пользуясь, кроме того,
полученным им видом линейного элемента, Бельтрами показывает, что
для геодезических треугольников поверхности постоянной отрица-
тельной кривизны (например псевдосферы) имеет место пропорцио-
нальность дефекта и площади и справедливы формулы тригонометрии
Лобачевского. Все это приводит Бельтрами к заключению, что плани-
метрия Лобачевского может быть осуществлена в евклидовом про-
странстве как внутренняя геометрия поверхности постоянной отрица-
тельной кривизны.
Этот результат Бельтрами сыграл очень важную роль в процессе
распространения идей Лобачевского; он был воспринят, в сущности
10 Зак 72
153
говоря, как доказательство непротиворечивости неевклидовой геомет-
рии. Правда, в настоящее время мы не можем считать это доказатель-
ство вполне строгим. Впоследствии Гильберт (1862—1943) показал,
что в пространстве трех измерений не существует поверхностей по-
стоянной отрицательной кривизны, на которых осуществлялась бы
геометрия Лобачевского в целом. Но мысль о возможности такого ис-
толкования основных понятий неевклидовой геометрии в терминах
геометрии Евклида, при котором аксиомы первой становятся теорема-
ми последней, и об использовании интерпретации для доказательства
непротиворечивости сыграла и продолжает играть весьма важную
роль в вопросах обоснования геометрии и других дедуктивных систем.
Всеобщий интерес к вопросам обоснования геометрии, вызванный
работой Бельтрами, изданием писем Гаусса и переводами сочинений
Лобачевского на французский и итальянский языки, заставил обратить
внимание на речь Бернгарда Римана (1826—1866) «О гипотезах, ле-
жащих в основании геометрии», которая была произнесена им еще в
1854 г., но осталась незамеченной.
Развивая идею Гаусса о внутренней геометрии поверхности, Риман
рассматривает пространство п измерений как такое многообразие
элементов, каждый из которых определяется заданием системы значе-
ний п независимых переменных. Геометрия этого пространства опре-
деляется заданием квадратичной формы дифференциалов независимых
переменных, определяющей квадрат расстояния между бесконечно
близкими элементами многообразия. Задание этой основной квадра-
тичной формы позволяет ввести понятия длины дуги, кратчайших, или
геодезических, линий, угла, объема и т.д. Риман намечает такие пути,
по которым может быть получено обобщение понятия гауссовой кри-
визны как такого инварианта, который связан с каждой элементарной
площадкой его пространства. Тождественное обращение в нуль этого
инварианта характеризует пространство, линейный элемент которого
может быть приведен к сумме квадратов дифференциалов; такое про-
странство будет многомерным аналогом евклидова. Риман определяет
также более общий класс пространств, допускающих движения по себе
с таким же числом степеней свободы, как и в евклидовом пространст-
ве. Эти пространства характеризуются тем, что их кривизна не зависит
от направления площадки и сохраняет во всех точках пространства по-
стоянное значение.
Мы уже отмечали, что в сочинении «Воображаемая геометрия» Ло-
бачевский положил в основу изложения своей системы, наряду с по-
ложениями абсолютной геометрии, свои тригонометрические форму-
лы. Риман осуществил этот замысел Лобачевского в более закончен-
ном виде, показав возможность построения геометрии на чисто анали-
154
тической основе. Еще более непосредственная связь между системой
Римана и геометрией Лобачевского была обнаружена Бельтрами, ко-
торый показал, что трехмерное пространство Римана постоянной от-
рицательной кривизны совпадает с пространством Лобачевского. Этим
было дано второе и уже, в сущности говоря, безукоризненное доказа-
тельство непротиворечивости геометрии Лобачевского. Ее положения
получили аналитическое истолкование, в силу которого всякое проти-
воречие в геометрии Лобачевского оказалось бы и противоречием в
основах анализа.
3. Проективная метрика и «Эрлангенская программа». Перехо-
дя к рассмотрению взаимодействия неевклидовой и проективной гео-
метрии, мы должны отметить некоторые этапы развития последней.
Первая попытка систематического изложения проективной геометрии
принадлежит Понселе (1788—1867). Он последовательно опирается на
понятие бесконечно удаленных элементов, принцип двойственности и
свойства полярного соответствия и широко пользуется понятием мни-
мых элементов, хотя и не дает обоснования их теории. Проективная
геометрия была приведена в строгую и чисто синтетическую систему в
1847 г. Штаудтом (1798—1867). С другой стороны, еще в 1827 г. в
своем «Барицентрическом исчислении» Мёбиус (1790—1868) рас-
сматривает частные виды однородных координат. Систематическое
применение этих координат позволило Плюккеру (1801—1868) по-
строить аналитическую геометрию проективного пространства. Ему
же принадлежит важная мысль о том, что за элементы геометрии мо-
гут быть приняты, кроме точки, и другие геометрические образы. Ру-
ководствуясь этими соображениями, Плюккер строит линейчатую
геометрию, элементом которой является прямая трехмерного проек-
тивного пространства; с точки зрения такого выбора элемента про-
странство оказывается уже четырехмерным.
Кэли (1821—1895) положил аналитическую геометрию проектив-
ного пространства в основу геометрического истолкования теории
форм, т.е. однородных многочленов. Он связывает с бинарной формой
систему вещественных или мнимых точек прямой, однородные коор-
динаты которых обращают эту форму в нуль. Соответственным обра-
зом тернарная форма представляется кривой проективной плоскости и,
в частности, коническим сечением, если эта форма квадратична.
На этом пути Кэли приходит к фундаментальному понятию проек-
тивной метрики, фиксируя некоторую бинарную квадратичную фор-
му, он называет абсолютом пару точек, соответствующих ей на пря-
мой. Логарифм ангармонического отношения двух произвольных то-
чек этой прямой и точек абсолюта Кэли называет расстоянием между
IQ-
155
двумя данными точками, показав, что введенная им мера расстояний
аддитивна, т.е. подчиняется условию Dist (АВ) + Dist (ВС) = Dist (АС).
На плоскости абсолют задается кривой второго порядка, которая
своим пересечением с каждой прямой плоскости определяет абсолют
проективной метрики на этой прямой.
Кэли показал, что угловая метрика евклидова пространства может
рассматриваться как проективная метрика относительно мнимого ко-
нического сечения, расположенного в несобственной плоскости, а
метрика расстояний на прямой есть проективная метрика параболиче-
ского типа, абсолют которой совпадает с дважды взятой несобствен-
ной точкой этой прямой. Таким образом, евклидова геометрия оказы-
вается геометрией проективного пространства, в котором задан абсо-
лют в виде мнимой кривой второго порядка.
Опираясь на результат Кэли, Ф. Клейн (1849—1925) сделал сле-
дующий важный шаг. В своей работе «О так называемой неевклидовой
геометрии» он показал, что проективная метрика, определяемая дейст-
вительной кривой второго порядка, совпадает с метрикой пространст-
ва постоянной отрицательной кривизны. Этим путем была получена
проективная интерпретация плоскости Лобачевского. Точки этой
плоскости изображались точками, расположенными внутри кривой,
прямые — ее хордами, параллельные прямые — хордами с общим
концом. Неевклидова длина отрезка и угол между двумя прямыми ока-
зались при этом равными проективной мере их изображения.
В 1872 г. вышла знаменитая работа Клейна, которая получила в
дальнейшем название «Эрлангенской программы». В ней Клейн под-
вел итоги и наметил пути дальнейшего развития геометрии.
Центральная идея Эрлангенской программы связана с понятием
группы преобразований. Обобщая понятие группы алгебраических
подстановок, Софус Ли (1842—1899) создал теорию непрерывных
групп преобразований с ее многочисленными приложениями к теории
дифференциальных уравнений и геометрии. Клейн обращает внимание
на то, что уже движения, которыми пользуются в евклидовой и неевк-
лидовой геометрии для совмещения конгруэнтных фигур, подчиняют-
ся условиям, характеризующим группу: результат последовательного
выполнения двух движений есть движение и преобразование, обратное
движению, также есть движение. Тем же условиям подчиняются и
другие геометрические преобразования, например проективное.
Обобщая эти факты, Клейн приходит к расширенному пониманию
геометрии, формулируя ее задачу следующим образом:
Дано многообразие и в нем группа преобразований; нужно ис-
следовать те свойства образов, принадлежащих многообразию, ко-
торые не изменяются от преобразований группы.
156
Из этого общего определения следует, что существуют различные
геометрии. Они могут отличаться друг от друга характером элементов
рассматриваемого многообразия и строением группы. Последнее раз-
личие является наиболее существенным.
Самая общая группа, рассматриваемая Клейном, есть группа проек-
тивных преобразований; ей соответствует проективная геометрия
Подгруппа проективных преобразований трехмерного пространства,
переводящая в себя некоторую плоскость, есть группа, которой соот-
ветствует аффинная геометрия Подгруппа проективных преобразо-
ваний, переводящая в себя абсолют, т.е. некоторую поверхность вто-
рого порядка, определяет геометрию пространства постоянной кри-
визны. Если абсолют вырождается в кривую второго порядка, то мни-
мой кривой соответствует евклидова геометрия, а действительной —
так называемая псевдоевклидова геометрия, или, иначе говоря, гео-
метрия пространства Лоренца.
Геометрии могут различаться между собой и по характеру элемен-
та. Но это различие менее существенно, так как если группы этих гео-
метрий изоморфны, то каждому факту одной геометрии будет соответ-
ствовать аналогичный факт другой и каждую из них можно изучать на
основе другой. В этом сущность принципа перенесения, как его назы-
вает Клейн. Частным случаем этого принципа является уже принцип
двойственности проективной геометрии.
Второй, очень интересный пример, приводимый Клейном, — это
так называемая геометрия обратных радиусов, или конформная гео-
метрия Мёбиуса, как ее принято называть в настоящее время. Группа
этой геометрии (в случае двух измерений) может быть получена путем
добавления к движениям евклидовой плоскости подобных преобразо-
ваний и преобразований инверсии. Эти преобразования переводят кру-
ги и прямые в круги или прямые и сохраняют угол между ними.
К той же группе можно подойти и иначе. Каждой точке трехмерно-
го пространства отвечает на сфере окружность, по которой эта сфера
пересекается с полярной плоскостью точки. Проектируя стереографи-
чески точки сферы на плоскость, мы получим однозначное соответст-
вие между точками пространства и кругами или прямыми плоскости.
Тогда самому общему преобразованию плоскости, переводящему кру-
ги и прямые в круги или прямые, будет соответствовать проективное
преобразование пространства, переводящее в себя сферу, т.е. действи-
тельную поверхность второго порядка. Таким образом, группа круго-
вых преобразований плоскости изоморфна группе движений простран-
ства Лобачевского. Иначе говоря, круговая геометрия плоскости дает
еще одну интерпретацию геометрии пространства Лобачевского.
157
Отметим, что известная интерпретация планиметрии Лобачевского,
предложенная А. Пуанкаре (1854—1912), к которой он пришел незави-
симо от Клейна, легко может быть получена из этой общей схемы.
Аналогичным образом устанавливается связь между другими геомет-
риями: линейчатой и неевклидовой, пространства Лагерра и простран-
ства Лоренца и т.д.
Особое влияние оказала программа Клейна на развитие дифферен-
циальной геометрии. В конце XIX и начале XX столетия наряду с про-
ективно-дифференциальной геометрией возникли дифференциальные
геометрии неевклидова, аффинного и различных конформных про-
странств.
Несмотря на широту своего охвата, программа Клейна явно оставила в
стороне то направление развития геометрии, которое исходило из идей
Римана. Риманово пространство, вообще говоря, не допускало такой
группы преобразований в себя, которое сохраняет его основной инвари-
ант, т.е. квадрат линейного элемента Исключение в этом отношении
представляли только поверхности постоянной кривизны и еще некоторые
узкие специальные классы римановых пространств.
Глубокая связь с понятием группы, однако, существовала и здесь,
но она смогла быть обнаружена только впоследствии в результате обо-
гащения римановой геометрии с помощью понятия параллельного пе-
ренесения векторов (Леви-Чивита, 1917). Каждой точке риманова про-
странства можно отнести «касательное» евклидово пространство, а па-
раллельное перенесение векторов позволяет отобразить друг на друга
пространства, соответствующие двум различным точкам. Но это соот-
ветствие устанавливается не единым способом, а зависит от того пути,
который связывает две данные точки. Всякому изменению этого пути
отвечает некоторое отображение касательного евклидова пространства
на себя. Можно показать, что совокупность этих отображений образу-
ет группу, которая в случае риманова пространства будет группой
евклидовых вращений.
Э. Картан (1870—1953) называет эту группу группой голономии. С
этой же точки зрения он классифицирует различные типы пространств,
которые возникли как обобщение риманова пространства или были
построены, по аналогии с ним, Вейлем, Скоутеном, самим Картаном и
другими. Так, проективной, конформной, аффинной группам, группе
подобия и вращения, чистого подобия и чистого вращения соответст-
вуют пространства проективной, конформной, аффинной, вейлевой,
квазиевклидовой и римановой связности.
Мы не можем останавливаться здесь на освещении дальнейшего
развития геометрии. Отметим только, что до сих пор оно идет по пути
углубления и расширения сочетания групповой и дифференциально-
158
геометрической или более общей топологической точки зрения, харак-
терной для теории связности. Именно в этом сочетании состоит гео-
метрическая основа теории объектов, составных многообразий, рас-
слоенных пространств и т.д.
4. Аксиоматическое обоснование геометрии. Параллельно про-
цессу расширения содержания геометрии, который был вызван при-
знанием идей Лобачевского, шел процесс ее обоснования. Одной из
первых в этом направлении была замечательная работа Гельмгольца
(1821—1894) «О фактах, лежащих в основании геометрии». Гельм-
гольц рассматривает пространство как числовое многообразие, в кото-
ром некоторой системой аксиом определено движение. Анализу пред-
посылок Гельмгольца были посвящены интересные статьи Софуса Ли
и Пуанкаре.
Требования, сформулированные Гельмгольцем и Ли, давали воз-
можность строгого обоснования геометрии, но тем не менее предло-
женное ими решение вопроса не могло считаться окончательным. По-
ложив в основу понятие о пространстве как о числовом многообразии,
они приняли за исходный пункт геометрии итог ее длительного разви-
тия, нашедший свое выражение в создании координатного метода. Бо-
лее того, Гельмгольц и Ли предполагают, что движениям соответству-
ют такие преобразования координат, которые выражаются с помощью
дифференцируемых функций. Это требование еще менее элементарно
и ставит начала геометрии в зависимость от анализа.
Проблема построения такой аксиоматики, которая была бы доста-
точна для обоснования геометрии и вместе с тем элементарна, стала
предметом исследований многих геометров конца прошлого века Раз-
личные варианты их решения были даны Пашем (1882), Пеано (1889),
Веронезе (1891), Пиерри (1899), В.Ф. Каганом (1902). Система Вениа-
мина Федоровича Кагана (1809—1953) отличается особой простотой,
хотя и не является чисто геометрической: расстояние между двумя
точками, выражаемое числом, является одним из ее основных понятий.
Излагая свою систему, В.Ф. Каган произвел исчерпывающий анализ ее
полноты, непротиворечивости и независимости, основанный на ариф-
метических интерпретациях.
Решение задачи обоснования геометрии, которое до сих пор явля-
ется наилучшим, принадлежит Д. Гильберту. Опираясь главным обра-
зом на систему Паша, он значительно упростил се, сохранив полно-
стью ее чисто геометрический характер. В своем замечательном сочи-
нении «Основания геометрии» (1899) Гильберт разбил все аксиомы на
группы аксиом соединения, порядка, конгруэнтности, непрерывности
и параллельности и выяснил ту роль, которую играет каждая из этих
групп в логической структуре геометрии.
159
Особенно важны исследования Гильберта о том, что необходимо
потребовать для внесения в геометрию числа. Отказываясь от аксиом
порядка и непрерывности или части этих аксиом, Гильберт обосновы-
вает такие построения, которые обладают свойствами сложения и ум-
ножения алгебраического поля и позволяют определить положение
точки с помощью чисел, принадлежащих этому полю. Выполнение
всех аксиом Гильберта влечет за собой обращение этого поля в поле
вещественных чисел, т.е. возможность обоснования обычной аналити-
ческой геометрии, что и является, в сущности говоря, признаком пол-
ноты системы.
Решение задачи обоснования геометрии, поставленной со всей ост-
ротой еще Лобачевским, явилось исходным пунктом для исследований
по основаниям других разделов математики, которые играют такую
важную роль в ее современном развитии.
Вопросы и упражнения
для индивидуального осмысления
и коллективного обсуждения
1. Г Фройденталь пишет «Логика имеет нечто общее с мышлением, если
мы делаем самый процесс мышления предметом нашего мышления, то мы
называем это логикой». Сопоставьте это представление о логике с обще-
принятым определением предмета формальной логики. Изучив публикуемую
в хрестоматии статью «Логика», попытайтесь аргументировать приведенную
выше мысль Г. Фройденталя
2. Как вы понимаете такие мыслительные процессы, как схематизация и
формализация? Приведите примеры схематизации, если мышление рассмат-
ривать в узком смысле как предмет математической деятельности и формали-
зации, когда словесные формулировки принимают математический характер,
оформляясь в математически безупречный язык.
3. Что такое логическая схема? Приведите пример разработки логиче-
ской схемы, акцентируя анимание на таких вопросах: достаточна ли схема,
целесообразна ли она, как ввести в рамки этой схемы несхематизирован-
ные элементы?
4 Верно ли утверждение, что геометрия вызывает склонность к схемати-
зации, а алгебра — к формализации? Ответ попытайтесь проиллюстрировать
конкретными примерами систематизации и формализации из геометрии и ал-
гебры.
5. Разъясните и проиллюстрируйте примерами следующие формулы:
а) 1А (отрицание); б) А л В (конъюнкция); в) A v В (дизъюнкция); г) А <=> В
(эквивалентность); д) А => В (логическое следствие) (см. статью А Н. Кол-
могорова «О языке математических знаков»)
6 Смысл кванторов V и 3 состоит в следующем: Ух означает «для всех х»;
Эх означает «существует такое х, что». Прочитайте формализованную запись
«аксиомы Архимеда» Va Vb (а > 0 л b е R) => Зп (л с N л па > Ь). Составьте
формализованные записи двух—трех известных вам математических утвер-
160
ждений (см. опубликованную в хрестоматии статью А Н Колмогорова «О язы-
ке математических знаков»)
7. Изучите опубликованную в Хрестоматии статью Р. Куранта и Г. Робинса
«Алгебра множеств»:
а) определите понятие подмножество, опишите его свойства. проиллюст-
рируйте их примерами;
б) дайте определения теоретико-множественным операциям объединение
и пересечение множеств, опишите их свойства, проиллюстрируйте их приме-
рами и логическими кругами Эйлера—Венна;
в) дайте определение операции дополнения множества А в множестве В,
опишите ее свойства, проиллюстрируйте примерами и логическими кругами
Эйлера—Венна
г) приведите примеры применения правил перевода обычной логической
терминологии на теоретико-множественный язык.
8 Р Декарт в работе «Рассуждение о методе» пишет «Каждая решенная
мною задача становилась образцом, который служил впоследствии для реше-
ния других задач». Поясните эту мысль и проиллюстрируйте ее конкретным
примером.
9. Д. Пойа в книге «Математическое открытие» пишет «Мышление можно
назвать продуктивным, если оно приводит к решению данной конкретной за-
дачи; мышление можно назвать творческим, если оно создает средства для
решения будущих задач Чем больше число и чем шире разнообразие задач, к
которым применимы созданные средства, тем выше творческий уровень
мышления».
Порассуждайте на данную тему, проиллюстрировав свои мысли примера-
ми. Можете ли вы привести примеры явного проявления творческого мышле-
ния в случае, когда решаемая задача вообще решена не была?
10 Проиллюстрируйте примером из области математической деятель-
ности следующую мысль И Канта, высказанную им в работе «Критика чис-
того разума»' «Всякое человеческое познание начинается с созерцаний,
переходит от них к понятиям и заканчивается идеями» Какой смысл имеют
созерцания в математике? Возможен ли иной порядок умственной дея-
тельности в познании?
11. Покажите, что множество всех целых, положительных и отрицательных
чисел — счетное.
12. Покажите, что множество всех рациональных, положительных и отри-
цательных чисел — счетное.
13. Поясните и проиллюстрируйте примерами, что вы понимаете под фор-
мализацией высказываний. Прочитайте записи:
((х = 1) v (х = 2)]-♦ (х2-Зх + 2 = 0);
(?-Зх+ 2 = 0)-» «х = 1) v (х= 2)].
В чем отличие этих записей?
14. Поясните и проиллюстрируйте примерами, что вы понимаете под им-
пликацией. Поясните на примерах смысл понятий дизъюнкция и конъюнкция с
помощью таблиц истинности. Попытайтесь истолковать импликацию с помо-
щью включения подмножеств
15. Утверждение А с В означает, что каждый элемент А является и
элементом В. Эту запись можно формализовать: А с В означает
Vx (х е А) (х е В).
Формализуйте утверждения а) А г> В; б) А ш В.
161
16. Изучите опубликованную выше статью А.Н. Колмогорова «О языке ма-
тематических знаков». Перечислите и проиллюстрируйте примерами типы ма-
тематических знаков или их комбинаций Какие из них называют термами, а
какие формулами? Какие термы представляют собой имена предметов? Какие
формулы представляют собой высказывания?
17. Изучите опубликованную выше статью Р Куранта и Г. Роббинса «Ма-
тематический анализ бесконечного». Расскажите как сравнивают бесконеч-
ные множества с точки зрения «количества» содержащихся в них элементов.
Что означает эквивалентность двух множеств? Покажите на примере, что
множество, содержащее бесконечное число элементов, может быть эквива-
лентно некоторому своему истинному подмножеству
18 Покажите, что множество рациональных чисел счетно (воспользуйтесь
одним из способов денумерации рациональных чисел, описанным в статье Р
Куранта и Г. Роббинса «Математический анализ бесконечного»).
19 Покажите, что множество всех действительных чисел (объединения
рациональных и иррациональных чисел) несчетно (см опубликованную выше
статью Р. Куранта и Г. Роббинса «Математический анализ бесконечного»)
20 Покажите, что любой интервал числовой прямой эквивалентен любому
другому интервалу Покажите, что любой интервал числовой прямой эквива-
лентен числовой прямой. Объясните, что такое кардинальное число
21. Расскажите об известных вам парадоксах бесконечного
22. Изучите опубликованную выше статью М Каца и С Улама «Мера».
Расскажите в чем состоит проблема измерения величин. Сформулируйте ак-
сиомы метрического пространства. Приведите примеры метрических про-
странств.
23. Изучите опубликованную выше статью А.П. Нордена. Расскажите ос-
новные этапы разработки геометрии Лобачевского. В чем отличия в системах
аксиом геометрий Евклида и Лобачевского? Каким путем Лобачевский пытал-
ся обосновать непротиворечивость своей геометрии? В чем состоит револю-
ционное методологическое значение открытий Лобачевского. Больаи. Гаусса.
Гильберта в области геометрии?
24. Расскажите об Эрлангенской программе Феликса Клейна. Расскажите о
понятиях геометрическое преобразование, группа, группа преобразований
Прокомментируйте мысль Ф Клейна о том. что геометрия — это наука, изу-
чающая инварианты групп геометрических преобразований.
25 Какие группы геометрических преобразований аы знаете? Приведите
примеры. Назовите основные инварианты следующих групп геометрических
преобразований: движений, подобий, аффинных преобразований.
26 С помощью логических кругов Эйлера—Венна приведите с группо-
вой точки зрения классификацию следующих геометрий: движений, подо-
бий. аффинной геометрии, перспективной геометрии, топологии.
27. Расскажите о работе Д. Гильберта по обоснованию геометрии. Как вы
понимаете такие свойства системы аксиом, как непротиворечивость, полнота,
независимость? Как доказываются эти свойства?
28. Что вы понимаете под моделью геометрии? Приведите примеры моде-
лей евклидовой геометрии и геометрии Лобачевского Расскажите как. по ва-
шему мнению, геометрия помогает изучению реального физического про-
странства.
362
МАТЕМАТИКА В СОВРЕМЕННОМ МИРЕ
Вечная загадка мира — его познаваемость
Альберт Эйнштейн
И вот сам Господь, который был слишком благ,
оставаться праздным, затеял игру в символы, посы-
лая знаки своего подобия в мир Поэтому я и осмели-
ваюсь думать, что вся природа и благословенное не-
бо записаны на языке искусства геометрии
Иоган Кеплер
<Р. %урант
МАТЕМАТИКА В СОВРЕМЕННОМ МИРЕ11
Возросшая роль математики в современном мире прежде всего ска-
залась в резком увеличении числа математиков. С 1900 г. число членов
профессиональных математических объединений в США увеличилось
примерно в 30 раз. К 1964 г. 4800 человек были удостоены ученых
степеней. За последние 25 лет число специалистов-математиков, рабо-
тающих вне университетов — в промышленности и государственных
учреждениях — увеличилось в 12 раз. В настоящее время деятельность
десятков тысяч людей самой различной квалификации тесно связана с
математикой. В колледжах в 1962 г. число студентов-математиков бы-
ло втрое больше, чем в 1956 г. Математика перестала быть предметом
занятий только академической элиты; теперь профессия математика
стала одной из наиболее распространенных, привлекая к себе все
большее число одаренных людей. Значительно расширились область
математических исследований и программа математического образо-
вания. Математический аппарат проник далеко за пределы собственно
математики: в физику, новые отрасли техники, биологию и даже в
экономику и другие социальные науки. Счетные машины и вычисли-
тельная техника способствовали появлению новых областей научных
исследований, имеющих, несомненно, чрезвычайно важное (хотя и не
полностью еще осознанное) значение как для самой математики, так и
для всех наук, органически связанных с ней.
163
Роль математики в современной жизни лучше всего можно оценить
при поэтапном сравнении успехов ее развития. Всего три столетия на-
зад основы математического мышления зиждились на геометрии,
унаследованной нами от древних народов и лишь незначительно про-
двинувшейся за два тысячелетия. Затем началось стремительное и ра-
дикальное преобразование математики. Строгий аксиоматический де-
дуктивный стиль геометрии уступил место интуитивному индуктив-
ному подходу, а чисто геометрические понятия — представлениям о
числе и алгебраической операции, воплощенным в аналитической гео-
метрии и математическом анализе, а также в механике. Небольшая
группа ученых, относившихся к так называемой математической ари-
стократии, теперь стала ведущей в науке. Ко времени Великой фран-
цузской революции математические науки достигли такого расцвета,
что число людей, активно занимающихся научной деятельностью, значи-
тельно возросло. Появилась учебная литература, позволившая ознако-
миться с новыми достижениями математики; университеты стали систе-
матически готовить специалистов в области естественных наук и матема-
тики. Открылись новые перспективы развития человеческих знаний.
«Классическая» математика, возникшая в XVII в., и по сей день со-
храняет свое огромное значение и ведущее положение. Некоторые из
самых плодотворных работ появились в результате уточнения и обоб-
щения двух основных понятий математического анализа: понятия
функции (взаимной зависимости двух или более переменных) и поня-
тия предела, вводящего интуитивное представление о непрерывности в
жесткие рамки строгого исследования. В чрезвычайно расширившейся
области современной математики мы постоянно сталкиваемся с поня-
тиями математического анализа, в частности с теорией дифференци-
альных уравнений (как обычных, так и в частных производных), —
этим важнейшим инструментом исследования скорости изменения
различных величин. В трех последующих статьях (речь идет о статьях
сборника, из которого взята данная статья Р. Куранта, см. коммента-
рии составителя) на языке, по возможности доступном читателю-
нематематику, рассматривается роль арифметики, геометрии и алгеб-
ры в современной математике. Мы увидим, как далеко продвинулась в
своем развитии геометрия с появлением понятий функции и числового
континуума; ее наиболее молодые отрасли — топология и дифферен-
циальная геометрия — стоят сейчас в ряду самых активных и «совре-
менных» разделов математики. Теории вероятностей посвящена само-
стоятельная статья, так как эта область математики нашла широчайшее
применение в науке и технике, а также позволила выразить на языке
математики некоторые важные, еще не решенные проблемы филосо-
фии науки.
164
Для современной математики характерно закрепление достигнутых
результатов в духе математической строгости. Такой подход привел к
более интенсивной разработке оснований математики, детальному вы-
яснению структуры самой математики и смысла «существования»
объектов математического мышления.
Развитие математической науки неизбежно повлекло за собой спе-
циализацию и обособление; математика оказалась под угрозой потери
единства и внутренней взаимосвязи. Представители различных отрас-
лей математики стали хуже понимать друг друга, а связь математики с
остальными науками заметно ослабла. Тем не менее благодаря моло-
дым талантам, пользовавшимся решительной поддержкой общества,
которое осознало возрастающую роль математики, были достигнуты
значительные успехи, а растущий объем математических исследова-
ний повлек за собой лавину публикаций и многочисленные конферен-
ции математиков. В связи с этим появилась настоятельная потребность
в четком понимании существа математики, ее проблем и целей, а так-
же в отыскании идей, которые смогли бы объединить людей самых
различных интересов.
На вопрос «Что такое математика?» невозможно дать обстоятель-
ный ответ на основе одних лишь только философских обобщений, се-
мантических определений или с помощью обтекаемого газетно-
журнального многословия. Также как нельзя дать общее определение
музыке или живописи: никто не может оценить эти виды искусства, не
понимая, что такое ритм, гармония и строй в музыке или форма, цвет и
композиция в живописи. Для понимания же сути математики еще в
большей степени необходимо подлинное проникновение в составляю-
щие ее элементы.
Принимая во внимание все вышесказанное, можно тем не менее
дать математике некоторое общее определение. Часто говорят, что
цель математики — это последовательное абстрагирование, логически
строгая аксиоматическая дедукция и последующее еще более широкое
обобщение. Такая характеристика содержит лишь долю правды, по-
скольку она ограничивается однобоким, а порой и карикатурным изо-
бражением действительности. Прежде всего математика никак не вла-
деет монополией на абстракцию. Понятие массы, скорости, силы, на-
пряжения, тока — все это абстрактные идеализации физической ре-
альности. Так что такие математические понятия, как точка, простран-
ство, число и функция, едва ли много более абстрактны.
Система строгой дедукции из аксиом, принятая Евклидом в его
«Началах», столь длительное время оказывавшая влияние на матема-
тику, является заманчивой формой, в которую часто выкристаллизо-
вывается конечный продукт математической мысли, поскольку это да-
165
ет возможность добиться максимального успеха в осознании и упоря-
дочении математического содержания и в обнажении его структуры
Однако излишнее акцентирование именно этой стороны математики
сбивает с правильного пути, если конструктивным элементам, индук-
ции, воображению, а также трудно уловимому процессу мышления,
называемому интуицией, отводится лишь второстепенная роль. Прав-
да, дедуктивный метод, отправляющийся от аксиом, на первый взгляд
довольно догматических, позволяет при изучении математики быстро
овладеть значительными ее «территориями». Однако конструктивный
метод Сократа, идущий от частного к общему и избегающий догмати-
ческого подхода, прокладывает независимой творческой мысли не-
сравненно более надежный путь.
Точно так же, как дедукция должна дополняться интуицией, стрем-
ление к последовательному обобщению должно сдерживаться и урав-
новешиваться бережным и любовным отношением к частностям. От-
дельные задачи не следует низводить до отдельных иллюстраций ве-
личественных общих теорий. В действительности же почти все они
возникают из рассмотрения частных проблем; и если такие теории не
служат для разъяснения и систематизации более узких частных вопро-
сов, они не имеют смысла.
Взаимосвязь общего с частным, дедукции с конструктивным под-
ходом, логики с воображением — именно они и составляют самую
сущность живой математики. Может оказаться, что в основе какого-то
конкретного достижения лежит только один из перечисленных аспек-
тов. Однако всякое перспективное достижение, несомненно, содержит
все эти аспекты. Проиллюстрируем нашу мысль следующим образным
сравнением: мы стартуем с Земли (конкретная задача) и, сбросив бал-
ласт излишней информации, устремляемся на крыльях абстракции в
заоблачные высоты, где в разреженной атмосфере управление и на-
блюдение становятся легче. Затем наступает решающее испытание —
приземление; теперь нужно установить, достигнуты ли поставленные
цели (что происходит снова на «Земле», т.е. мы снова рассматриваем
конкретную реальность, но теперь уже с новой точки зрения). Иными
словами, полет в область абстрактной общности должен исходить из
конкретного и частного и завершаться конкретным и частным.
Эти положения ярко и убедительно показывают пути развития ма-
тематической науки. Иоганн Кеплер с прозорливостью настоящего ди-
агноста сумел абстрагировать из массы наблюдений Тихо Браге эллип-
тическую форму планетных орбит. Дальнейшее абстрагирование по-
зволило Исааку Ньютону вывести из этой модели закон всемирного
тяготения и дифференциальные уравнения механики. На этом весьма
высоком уровне, уже не отягощенном математическими абстракциями,
166
механика обрела неограниченную свободу и, снизойдя до конкретных
«земных» задач, продолжала добиваться успеха за успехом в областях,
лежащих далеко за пределами небесной механики, откуда она ведет
свое начало.
Подобным образом Майкл Фарадей установил в теории электро-
магнетизма ряд экспериментальных фактов, которые он связал воеди-
но, дав им собственное остроумное толкование. Это позволило вскоре
абстрагировать несколько математических качественных законов элек-
тромагнетизма. После того как эти законы были сформулированы для
некоторых простых частных случаев, Джеймс Клерк Максвелл открыл
весьма общий количественный закон, связывающий магнитные и элек-
трические силы, а также скорости их изменения системой дифферен-
циальных уравнений. Эти уравнения, абстрагированные и освобож-
денные от всего частного и конкретного, могут вначале показаться
слишком недоступными для использования. Однако вскоре становится
ясно, что уход Максвелла в высокие сферы абстракции проложил пе-
ред наукой путь к дальнейшему развитию по многим направлениям.
Раскрытие волновой природы электромагнитных явлений на основе
уравнений Максвелла вдохновило Генриха Герца на проведение экс-
перимента по распространению радиоволн, что в свою очередь приве-
ло к появлению отрасли техники совершенно нового типа и открыло
перед исследователями широкие горизонты. В результате стали возни-
кать новые направления; среди них отметим, например, ныне бурно
развивающуюся науку — магнитную гидродинамику.
Нельзя сказать, что уравнения Максвелла — это продукт последо-
вательного дедуктивного мышления. Еще в меньшей степени его от-
крытие может быть приписано чисто индуктивному сократовскому
методу. Вернее всего было бы причислить Максвелла к тем редким
умам, которые способны уловить сходство и провести параллели меж-
ду весьма отдаленными, внешне, казалось бы, совсем не связанными
фактами и встать на новую, более глубокую точку зрения, объединяя
явно разнородные элементы в единую систему.
В собственно математике соответствующая линия в развитии — от
конкретного и частного через абстракцию снова к конкретному и част-
ному — придает теории свой определенный смысл и значение. Чтобы
оценить роль этого основополагающего вывода, необходимо помнить,
что слова «конкретный», «абстрактный», «частный», «общий» в мате-
матике не имеют ни постоянного, ни абсолютного значения. Они отно-
сятся главным образом к рамкам нашего мышления, к уровню нашего
знания и характеру математического предмета. Например, мы охотно
принимаем за «конкретное» то, что уже давно стало привычным. Что
же касается слов «обобщение» и «абстракция», то они описывают не
167
статическую ситуацию или конечный результат, а живой, динамиче-
ский процесс перехода от некоторого конкретного уровня к какому-то
другому — «высшему».
Иногда плодотворные открытия в математике возникают совер-
шенно неожиданно, без особых видимых усилий: новые горизонты
появляются при абстрагировании от конкретного материала и раскры-
тии существенных по своей структуре элементов. Аксиоматика безот-
носительно к ее евклидовой форме подразумевает именно этот про-
цесс. Один из последних примеров плодотворного применения абстрак-
ции — это обобщение Джоном фон Нейманом и рядом других ученых
«спектральной» теории Давида Гильберта, обобщение, которое и при-
вело от частного случая «ограниченных» линейных операторов к «не-
ограниченным» операторам.
Этот далеко идущий результат можно проследить по ряду последо-
вательных операций абстрагирования, начавшихся с основ аналитиче-
ской геометрии. Известно, что в трехмерном пространстве с координа-
тами X|, х2, xj плоскости описываются линейными уравнениями, а по-
верхности второго порядка (сфера, эллипсоид и пр.) — квадратными
уравнениями (т.е. такими, в которые неизвестные входят во второй
степени). Например, уравнение, записанное в общем виде как
Д^х,2 + Х2х2 + XjX, = 1, описывает поверхность второго порядка с цен-
тром в начале координат и тремя главными осями, направленными по
осям координат. Для эллипсоида «коэффициенты» Х|, к2, ^-з должны
быть заданы положительными числами и соответственно равны
Ма*,\1а\,\1 а}, где О|, аъ аз — три полуоси эллипсоида. Поверх-
ность эллипсоида составляют те и только те точки, которые удовле-
творяют такому уравнению.
Следует отметить, что алгебраизация геометрии позволяет нам без
особого труда перейти к пространству более чем трех измерений, ска-
жем, к пространству п измерений с координатами Х|, х2, .... х„. Как и
ранее, плоскости в таком пространстве снова описываются линейными
уравнениями, а поверхности второго порядка — уравнениями второго
порядка (квадратичными формами) относительно переменныххьх2,... ,х„.
Один из важнейших результатов «линейной алгебры» состоит в том,
что поверхности второго порядка могут быть приведены к «канони-
ческому» виду X(x2 + Х2х2 + ... + Хяхя =1 при помощи соответст-
вующего преобразования системы координат (или, что то же самое,
при движении рассматриваемой поверхности и фигуры); в результате
центр фигуры оказывается в начале координат, а ее главные оси на-
правлены по осям координат. Эта теорема является ключевой во мно-
168
гих приложениях, например в теории механических или электрических
систем, в которых п материальных точек или л элементов электриче-
ской цепи могут колебаться относительно положения равновесия.
Некоторые физики, не думая о строгом математическом обоснова-
нии, например лорд Рэлей, смело применяли этот вывод и для значи-
тельно более общих случаев, когда число измерений л становится
сколь угодно большим. Такой шаг на пути к дальнейшему обобщению
и абстракции элементарной математики оказался весьма полезным при
изучении колебательных систем, в которых точечные массы или эле-
менты электрической цепи не заданы конечным числом, а равномерно
распределены, скажем, по струне, мембране или линии электрической
передачи.
Гильберт, один из величайших математиков старшего поколения,
понял, что подобным квадратичным формам от бесконечно большого
числа переменных следует предоставить должное место и в общей ма-
тематической теории. При попытке сделать это он прежде всего обна-
ружил, что нужно ограничить область переменных требованием, что-
бы сумма их квадратов «сходилась», т.е. принимала конечное значе-
ние. Это утверждение можно сформулировать, пользуясь также тер-
минами «обобщенной» теоремы Пифагора. Тогда ограничение Гиль-
берта сводилось к требованию, чтобы всякая точка гильбертова про-
странства была удалена от начала координат на конечное расстояние
г = у + х2 +.... Далее Гильберт ввел квадратичную форму от беско-
нечно большого числа переменных — ограниченную форму — как
бесконечную двойную сумму вида а1|х12+а|2х1х2+аиХ|Хз +
+ ...+,...а22х^ +a2Jx2Xj +..., где индекс первой переменной в каждом
слагаемом (т.е. переменной Х| в первой строке, переменной х2 — во
второй и т.д.) стремится к бесконечности при переходе от одной стро-
ки к другой, а индекс второй переменной (т.е. х2 в первой строке, хз —
во второй и т.д.) стремится к бесконечности вдоль каждой строки. Эта
бесконечная сумма подчинена решающему ограничению: она должна
сходиться во всякой точке гильбертова пространства.
Оказывается, что в таком пространстве многие понятия из геомет-
рии конечного числа измерений, относящиеся к свойствам плоскостей
и поверхностей второго порядка, сохраняют свою силу. Именно так, в
частности, обстоит дело с приведением квадратичных форм к канони-
ческому виду (или, как говорят еще, к главным осям). Гильберт пока-
зал, что любая квадратичная форма указанного вида может быть при-
ведена к каноническому виду соответствующим вращением системы
координат. По аналогии со случаем конечного числа измерений Гиль-
169
берт назвал набор значений Xi, Х2, Х3..., появляющихся в этом канони-
ческом виде, «спектром» квадратичной формы.
Обобщая теорию главных осей обычных квадратичных форм ко-
нечного числа переменных на случай их бесконечного числа, Гильберт
открыл также много новых явлений, например возникновение непре-
рывного «математического спектра». Более того, работы Гильберта
сыграли немаловажную роль при возникновении квантовой механики.
Его термин «математические спектры» оказался связанным со спек-
трами энергетических состояний атомов и частиц, их образующих.
Правда, гильбертова теория квадратичных форм не совсем подходила
для решения проблем квантовой механики; как выяснилось, в этих це-
лях потребовались «неограниченные» формы.
Именно здесь вдохновленный Эрхардом Шмидтом фон Нейман,
который был склонен к абстрагированию больше, чем его предшест-
венники, сделал следующий решающий шаг в этом направлении. От-
казавшись от представления Гильберта о квадратичной форме как о
чем-то, что может быть выражено в конкретной алгебраической форме
(в виде бесконечной алгебраической суммы), фон Нейман взамен на-
шел такое абстрактное определение квадратичной формы, что сумел
избежать ограничений, налагаемых гильбертовым подходом. Так рас-
ширенная гильбертова спектральная теория смогла дать ответ на впол-
не реальные и конкретные запросы современной физики.
Теория групп, являясь центральной в современной математике,
прошла в своем развитии аналогичный путь последовательных обоб-
щений. Эта теория ведет свое начало от частной проблемы, привле-
кавшей к себе умы математиков еще в средние века. Речь идет об оты-
скании решений алгебраического уравнения степени выше второй ал-
гебраическим же путем, т.е. с помощью операций сложения, вычита-
ния, умножения, деления и извлечения корня. Теория квадратных
уравнений была известна еще в Древнем Вавилоне, а решение уравне-
ний третьей и четвертой степеней в общем виде было получено мате-
матиками эпохи Возрождения Джироламо Кардано и Никколо Тарта-
нья. Однако решение уравнений пятой и еще более высоких степеней
натолкнулось на непреодолимые трудности.
В начале XIX в. новое решительное наступление на эту крепость
повели Луи Лагранж, П. Руффини и Нильс Хенрик Абель, а также
Эварист Галуа, который использовал наиболее оригинальный метод.
Все они исходили из хорошо известных фактов. Во-первых, алгебраи-
ческое уравнение л-й степени вида аях" + ая_хх"~1 + ... + ахх + а0 =0
имеет п корней и, г2, ... г„. и, во-вторых, полный набор этих корней
определяет алгебраическое уравнение однозначно. Например, если 1 и
170
3 являются корнями некоего квадратного уравнения, то этим уравне-
нием будет (х - 1)(х - 3) = х - 4х + 3 =0 Коэффициенты такого урав-
нения представляют собой симметрические функции от его корней,
т.е. зависят от всей совокупности этих корней так, что порядок их ну-
мерации безразличен; например, если кубическое уравнение х3 + ах2 +
+ Ьх + с = 0 имеет своими корнями гь г2, гз, то его коэффициенты могут
быть записаны как -а = rt + r2 + r3, b = rtr2 + r2r3 + пл, -с = rtr2r3.
Из этой записи видно, что если поменять нумерацию корней, то на
коэффициентах а, Ь, с это никак не скажется.
Многолетняя работа над такими уравнениями позволила устано-
вить, что ключ к решению задачи выражения корней уравнения через
его коэффициенты лежит не только в изучении таких симметрических
выражений, но также в исследовании лишь частично симметрических
выражений и анализе симметрии, которыми они обладают. Выражение
Е - г\г2 + Г3Г4, например, не сохраняется при произвольных переста-
новках входящих в него символов г(, г2, г3, г4. Но если произвести за-
мену индекса 1 на 2 и индекса 3 на 4, то выражение Е не изменится,
или, как говорят в таких случаях, оно инвариантно по отношению к
такой перестановке. Если же поменять местами индексы 1 и 3, то по-
лученное при этом выражение будет уже отлично от Е С другой сто-
роны, последовательное осуществление двух перестановок, из которых
первая нарушает Е, а вторая снова его восстанавливает, может быть
принято за новую перестановку, по отношению к которой Е инвари-
антно. Совокупность таких перестановок, названная Галуа «группой»,
отражает внутреннюю симметрию, присущую выражению Е Раскры-
тие природы таких групп, по мнению проницательного Галуа, и есть
ключ к построению более глубокой теории алгебраических уравнений
Вскоре математики обнаружили применимость таких групп пере-
становок и к другим областям математики. Совокупность шести дви-
жений, например превращающих равносторонний треугольник вновь в
такой же треугольник, тоже образует группу. Другие группы также
оказались существенными элементами большинства областей матема-
тики.
Чтобы охватить такие группы во всех их видах и проявлениях еди-
ным понятием, а также предусмотреть многочисленные скрытые в них
возможности, потребовалось сформулировать основополагающее по-
нятие группы в наиболее абстрактной форме. Это и было сделано;
группой стали называть совокупность математических объектов, в ко-
торой правило «комбинирования» любых двух из них задавалось бы
так, чтобы в результате снова получался бы некоторый элемент S,
принадлежащий этой же совокупности. От этого правила требуется,
чтобы оно было ассоциативным [т.е. (ST)U должно быть равно S(7V)]
171
Далее в совокупность должен входить так называемый единичный
элемент I, который в комбинации с любым другим элементом сово-
купности S снова даст элемент S (т.е. IS = SI = S). Наконец, для каждо-
го своего элемента S наша совокупность должна содержать еще и «об-
ратный» элемент S"1, такой, что комбинация S3"' дает единичный эле-
мент (ЗУ1™/).
Такое абстрактное определение группы оставляет, конечно, полно-
стью открытым вопрос о конкретной «материальной» природе группы.
Элементами группы могут быть числа, вращения геометрических тел,
деформации пространства (подобного рода деформации могут, напри-
мер, определяться линейными или какими-либо иными преобразова-
ниями координат) или же, как было упомянуто выше, перестановки п
объектов.
Одним из главных достижений последних 150 лет было введение
понятия группы: в результате различные разделы математики обрели
ясность и единообразие. Много усилий направлялось на вспомога-
тельный, «высший» участок «линии развития»— на анализ структуры
абстрактных понятий. Это неизменно способствовало выяснению
строения конкретных областей математики, таких, как теория чисел и
алгебра. Одно из самых замечательных достижений в этом направле-
нии — знаменитая классификация различных разделов геометрии,
предложенная Феликсом Клейном в 70-х гг. прошлого столетия. Она
основана на инвариантности некоторых определенных геометрических
свойств по отношению к различным группам преобразований.
Абстрактная теория групп нашла блестящее применение в решении
еще более конкретных проблем физики элементарных частиц. Здесь
возможности теории групп обусловливаются наличием довольно запу-
танных групп явных и скрытых симметрий во взаиморасположениях и
взаимодействиях ядерных частиц. Успех теории групп в систематиза-
ции массы экспериментальных данных, а также в предсказании суще-
ствования новых элементарных частиц, очевидно, свидетельствует о
пользе абстракций в поисках вполне реальных истин.
Интуиция, этот неуловимый жизненный элемент, всегда активно
присутствует в творческой математике, побуждая и направляя даже
самое абстрактное мышление. Ее наиболее распространенная форма —
геометрическая интуиция — содействовала появлению многих важных
достижений математики последнего времени, как относящихся к са-
мой геометрии, так и вытекающих из работ в этой области. Тем не ме-
нее существует явная тенденция к подкреплению интуиции точными и
строгими рассуждениями.
Топология, самая юная и самая мощная ветвь геометрии, наглядно
демонстрирует плодотворное влияние противоречий между интуицией
172
и логикой. Располагая небольшим числом разрозненных, но, безус-
ловно, важных открытий (как, например, открытие односторонней
ленты Мёбиуса), составляющих ее «основной капитал», топология
только в XIX в. предстала как область серьезных научных исследова-
ний. Долгое время в ней почти полностью господствовала геометриче-
ская интуиция. Поверхности разрезались и склеивались для наглядно-
го представления математической сущности топологии как науки о
свойствах поверхностей, остающихся неизменными при произвольных
непрерывных деформациях. Однако уже на заре развития новой дис-
циплины Георг Фридрих Бернгард Риман сумел привлечь к ней вни-
мание ученых. В своей сенсационной работе по теории алгебраиче-
ских функций комплексного переменного (в состав такого переменно-
го входит мнимое число V-Т) показал, что для подлинного понима-
ния этих функций существенны топологические свойства некоторых
специальных поверхностей, называемых теперь римановыми поверх-
ностями.
На протяжении прошлого столетия математики открыли и подверг-
ли систематическому исследованию большое число топологических
свойств поверхностей двух, трех и, наконец, п измерений. В начале
XX в. Анри Пуанкаре и ряд других математиков построили велико-
лепное здание топологической теории, все еще ориентируясь на ин-
туицию. Эта работа была тесно связана с развитием теории групп и
нашла применение в других областях математики, а также сыграла
свою роль в переходе математической науки на более высокую сту-
пень. Ее результаты использованы в небесной механике, в частности
при построении орбит планет в пространстве, искривленном гравита-
ционными полями.
Но теперь ученых-топологов начало одолевать двойственное чув-
ство: с одной стороны, они ощущали потребность заключить геомет-
рическую интуицию в рамки современной математической строгости,
с другой — им совсем не хотелось терять убедительности и стройнос-
ти интуитивных геометрических выводов. В первом десятилетии на-
шего века с этой задачей справился почти в одиночку голландский ма-
тематик Л.Э.Я. Брауэр. Благодаря его огромным усилиям в топологии
теперь подход не менее строгий, чем в геометрии Евклида; и дальней-
шее развитие этой области математики происходило на основе логиче-
ски безупречных рассуждений.
В основе тех трудностей, с которыми столкнулся Брауэр, стояла
дилемма, возникшая в связи с понятием непрерывности. Каждый из
нас интуитивно имеет твердое представление о том, что такое непре-
рывность (например, мы можем без труда вообразить плавную кри-
вую). Однако каждый, кто начинает изучать дифференциальное исчис-
173
ление, теряет свою уверенность, как только требуется ввести понятие не-
прерывности в рамки строгой математической формулировки. В этой за-
даче невозможно избежать трудностей, так как геометрическая интуиция
дает нам такое представление о непрерывности, которое не совсем согла-
суется с математически логическим представлением о ней. Строгое опре-
деление приводит к появлению множества случаев, которые с точки зре-
ния нашей интуиции кажутся парадоксальными. Можно без труда, па-
пример, построить непрерывную линию (в точном соответствии с опре-
делением), не имеющую конечной длины (рис. 1), не имеющую опреде-
ленного направления ни в какой точке, или, скажем, линию, которая, на-
ходясь внутри квадрата, может виться без самопересечений, подходя
сколь угодно близко к любой его точке. Такие необычные построения по-
казывают, что нужно соблюдать большую осторожность при обоснова-
нии топологических свойств тех или иных поверхностей или других объ-
ектов, подвергающихся сложной непрерывной деформации.
Рис. 1. Бесконечный зигзаг составлен здесь из последовательно
взятых отрезков длиной 1, 1/2, 1/3, ... Последовательность дробей
не имеет конечной суммы, а значит, и сама линия не имеет конеч-
ной длины. [Сам по себе пример линии, не имеющей конечной дли-
ны, не должен поражать воображение: существуют ведь совсем
простые примеры таких линий (на той же фигуре) — бесконечный
горизонтальный луч, устремляющийся вправо от точки О. Если от-
резки ОЕЬ ЕгЕ), EtE} и т.д параллельны друг другу (равно как от-
резки £|£2, £j£«, £s£« и т.д.), то наш бесконечный зигзаг будет про-
стираться над всем бесконечным лучом, и нет ничего удивительно-
го, что у него (зигзага) нет конечной длины. Если, однако, посте-
пенно приближать направления звеньев зигзага к вертикальному
так, чтобы проекции этих звеньев на горизонтальный луч доста-
точно быстро убывали по длине, то можно добиться, чтобы не
имеющий конечной длины зигзаг был расположен над конечным
участком горизонтального луча Например, если нужно, чтобы дли-
на горизонтальной проекции отрезка О£( была 1/2 длина горизон-
тальной проекции отрезка £t£2 равнялась 1/4 и вообще длина гори-
зонтальной проекции каждого отрезка E,_tE„ (имеющего длину 1/п)
была 1/2", то весь бесконечный зигзаг мог бы уместиться в квадрате
со стороной единица]
174
Необходимость в такой осторожной аргументации не всегда стано-
вится интуитивно понятной тому, кто не занимается топологией. При-
мером может служить знаменитая теорема Жордана, утверждающая,
что на плоскости всякая непрерывная замкнутая линия без самопере-
сечений разграничивает ее на две четкие области — внутреннюю и
внешнюю (рис. 2). Любой научный работник, инженер или студент,
исходя из соображений здравого смысла, скажет, что попытка дока-
зать такую теорему представляет собой ненужное упражнение. Тем
не менее при написании своего классического учебника анализа
Жордан счел необходимым доказать это утверждение. Сколь же
тонкой оказалась эта проблема, если найденное Жорданом доказа-
тельство оказалось не безупречным! Равным образом никто не
усомнится в том, что размерность двумерной или трехмерной гео-
метрической фигуры не меняется при любых непрерывных дефор-
мациях. Однако строгое доказательство этого факта, исходящее из
общего предположения об абстрактной непрерывности, — одно из
главных достижений Брауэра.
Р и с. 2. Теорема Жордана утверждает, что любая замкнутая
линия, подобная той, что показана выше, разграничивает
внешнюю и внутреннюю области Прямая, проведенная из
внутренней области наружу, пересечет линию нечетное чис-
ло раз Прямая же, проведенная из внешней области, даст
четное число таких пересечений
175
Безусловно, можно избежать некоторых трудностей, возникающих
при введении понятия непрерывности, если на группу непрерывных
преобразований наложить некоторые ограничения (например, потре-
бовать «гладкости», или дифференцируемости, вместо чистой непре-
рывности). Это и было успешно исполнено. Дифференциальная топо-
логия (раздел топологии, занимающийся подобными рассмотрениями)
достигла за последнее время выдающихся результатов. Изучение пре-
образований, подчиненных требованиям «разумной» гладкости, при-
вело к установлению классификации топологических структур, суще-
ственно отличной от той, которая была получена при условии требо-
вания самой общей непрерывности.
Эти достижения поддерживают вполне естественный отход от стрем-
ления к не знающим границ обобщениям Идея таких обобщений стала
казаться заманчивой с тех пор, как Георг Кантор получил в конце про-
шлого века блестящие результаты в теории множеств. Некоторые великие
ученые, особенно Пуанкаре, жестоко преследовали эту идею, считая ее
чуть ли не угрозой всей математике, в частности потому, что она заводит
в дебри неразрешимых парадоксов. И, хотя воинствующий критицизм
Пуанкаре во многом был чересчур суровым и даже реакционным, тем не
менее он оказал известную пользу математикам конструктивного направ-
ления, занятым частными и вполне конкретными проблемами.
Математическая деятельность разных людей и даже одного и того
же человека определяется различными стимулами. Без сомнения, тес-
ные связи с физической реальностью важных разделов математики,
особенно анализа, вдохновляют и стимулируют математическую
мысль. То же относится и к другим реальностям. В теории чисел и ал-
гебре раскрывается загадочная реальность мира чисел, прочно связан-
ного с человеческим разумом. Более далекой от физической реально-
сти представляется нам реальность логических процессов, неотъемле-
мо входящих в математическое мышление. Тем не менее основные
идеи в работах по математической логике, мало известных широким
кругам, оказались весьма полезными для понимания и даже для конст-
руирования автоматических вычислительных устройств.
Иными словами, конкретные частные факторы должны стимулиро-
вать математику внести свой вклад в определенную сферу реальности.
Полет в абстракции должен означать нечто большее, чем просто взлет;
отрыв от земли неотделим от возвращения на землю, даже если один и
тот же пилот не в состоянии вести корабль через все фазы полета. Са-
мые отвлеченные, чисто математические занятия могут быть обуслов-
лены вполне ощутимой физической реальностью. То обстоятельство,
что математика — эта чистая эманация человеческого разума — мо-
жет столь эффективно помочь в понимании и описании физического
176
мира, требует особого разъяснения, и не случайно этот вопрос всегда
привлекал внимание философов. Оставляя философские вопросы в
стороне, следует, однако, признать, что взятые на себя математикой
обязательства по решению различных физических проблем или, на-
оборот, видимое отсутствие таких обязательств не может быть приня-
то за критерий установления различий между теми или иными видами
математики или разногласий, существующих между самими матема-
тиками.
На самом деле между «чистой» и «прикладной» математикой не-
возможно провести четкую грань. Поэтому-то в математике и не
должно быть разделения на касту верховных жрецов, поклоняющихся
непогрешимой математической красоте и внимающих только своим
склонностям, и на работников, обслуживающих их. Подобная «касто-
вость» — в лучшем случае симптом человеческой ограниченности,
удерживающей большинство людей от свободного странствования по
необъятным просторам человеческих интересов.
Одна и та же математическая проблема может быть решена по-
разному; приверженец строгого математического подхода (а стремле-
ние к таковому временами возникает у всякого человека, склонного к
научному мышлению) требует бескомпромиссного совершенства. Он
не допускает никаких пробелов в логике мышления и в решении по-
ставленных задач, а достигнутый результат, по его мнению, должен
быть венцом неразрывной цепи безупречных рассуждений. И если
сторонник такого подхода сталкивается с трудностями, которые ему
кажутся непреодолимыми, то он скорее попытается переформулиро-
вать задачу или даже поставить другую, родственную ей, трудности
которой он может преодолеть Существует и другой обходный путь-
заново определить то, что считалось «решением проблемы»; в дейст-
вительности подобная процедура представляет собой довольно общепри-
нятый предварительный шаг к под линному решению исходной задачи.
В исследованиях прикладного характера все выглядит по-иному
Прежде всего поставленную задачу нельзя с такой легкостью видоиз-
менить или обойти. Здесь требуется другое: дать правильный и на-
дежный с общечеловеческой точки зрения ответ. В случае необходи-
мости математик может пойти на компромисс: он должен быть готов
ввести догадки в цепь рассуждений, а также допустить известную по-
грешность в числовых значениях. Однако даже задачи в основном
практического направления, например о течениях с ударными волнами,
могут потребовать фундаментального математического исследования,
чтобы установить, корректно ли поставлена такая задача. В прикладных
исследованиях могут понадобиться и доказательства чисто математиче-
ских теорем существования, поскольку уверенность в том, что имеется
177
13 Зак 72
решение, может гарантировать достоверность используемой математиче-
ской модели. И наконец, в прикладной математике доминируют аппрок-
симации (приближения) — без них невозможно обойтись при переносе
реальных физических процессов на математические модели.
Обращение с реальностью, преобразованной в абстрактные мате-
матические модели, и оценка точности достигаемых при этом соответ-
ствий требуют интуитивных навыков, совершенствуемых опытом.
Часто необходимо как-то преобразовать исходную математическую
проблему, которая оказывается слишком сложной для решения совре-
менными методами. Это отчасти объясняет характер интеллектуально-
го риска и удовлетворение, которое испытывают математики, рабо-
тающие с инженерами и естествоиспытателями над решением реаль-
ных задач, возникающих всюду, куда проникает человек в своем
стремлении к познанию природы и управлению ею.
5И. 7С*дйн
МАТЕМАТИКА И ПОВЕДЕНИЕ ПРИРОДЫ1
Весь предшествующий опыт убеждает нас в
там, что природа представляет собой реализацию
простейших математически мыслимых элементов
Альберт Эйнштейн
Естествознание с античных времен определяло наше отношение к
природе, но его роль еще более возросла после того, как предсказания
важнейших научных теорий были многократно подтверждены опы-
том. Основные философские течения строились на физической науке
и, казалось бы, неопровержимых фактах, установленных ею.
Однако дальнейшее развитие физики и прежде всего создание тео-
рии электромагнетизма, теории относительности и квантовой механи-
ки вызвали необходимость пересмотра философских учений. В этой
главе мы кратко обрисуем и сопоставим некоторые из старых и более
новых направлений философии, формирующих наши взгляды на при-
роду. Умонастроение любой эпохи, мышление и поведение общества
определяются господствующим мировоззрением В современном об-
ществе представления об окружающем нас физическом мире во мно-
гом определяют всю систему наших взглядов.
Основное учение — имеющее, как мы увидим в дальнейшем, пер-
востепенное значение само по себе, — на которое в той или иной мере
опираются все остальные учения, получило название «механицизм».
Не претендуя на строгость, суть механицизма можно сформулировать
так: физический мир представляет собой гигантский механизм, части
178
которого взаимодействуют между собой. Механизм действует без сбо-
ев и ошибок, о чем свидетельствуют движения планет, регулярность
чередования приливов и отливов, предсказуемость солнечных и лун-
ных затмений. Части гигантского механизма — это непрерывно дви-
жущаяся материя. Движение обусловлено действием сил. Рассмотрим
эти понятия более подробно.
В основе механицизма лежит понятие материи как некоторой те-
лесной вещественной субстанции. Убеждение в том, что материя со-
ставляет основу всего сущего, восходит к древним грекам. Выдаю-
щиеся греческие философы наблюдали окружающий мир и, несмотря
на свои весьма ограниченные возможности, всеми доступными им
средствами исследовали природу. При этом они с готовностью пере-
ходили от немногочисленных наблюдений к широким философским
обобщениям. Так, Левкипп и Демокрит выдвинули идею о том, что
мир состоит из неразрушимых и неделимых атомов, существующих в
пустоте. Аристотель строил материю из «четырех элементов» — зем-
ли, воды, воздуха и огня, но не из настоящих земли, воды, воздуха и
огня, а из четырех сущностей, наделенных теми качествами, которые
мы воспринимаем посредством наших органов чувств в четырех ре-
альных аналогах этих «элементов».
Томас Гоббс, развивая несколько более грубый вариант того же
учения, утверждал:
«Мир, т.е. вся масса всех вещей, тслесен, иначе говоря, есть тело, и оно обла-
дает измерениями величины, а именно длиной, шириной и глубиной, ио каждая
часть тела также есть тело и также обладает измерениями. Следовательно, каждая
часть нашего мира есть тело, а то, что не есть тело, не есть часть мира, а посколь-
ку мир есть все — то, что не есть часть его, есть ничто и, следовательно, не
существует нигде».
Тело, продолжает Гоббс, есть нечто такое, что занимает простран-
ство; оно делимо, подвижно и ведет себя математически.
Таким образом, механицизм утверждает, что реальность — это все-
го лишь сложная машина, управляющая объектами в пространстве и
во времени. Так как мы сами составляем часть физической природы,
все человеческое должно быть объяснимо через понятия материи,
движения и математики.
Декарт, как мы уже отмечали, также утверждал, что все физические
явления можно объяснить с помощью понятий материи и движения.
По Декарту, материя действует на материю при непосредственном со-
прикосновении. Материя состоит из мельчайших невидимых частиц,
отличающихся по величине, форме и другим свойствам. Так как час-
тицы слишком малы и их нельзя видеть, для объяснения более круп-
номасштабных и потому доступных наблюдению явлений, например
движений планет вокруг Солнца, требовалось принять определенные
13-
179
гипотезы относительно поведения таких частиц. Понятие пустого про-
странства Декарт отвергал, заявляя, что ваза, совершенно пустая внут-
ри, должна была бы разрушиться.
Естествознанию картезианская философия (от латинизированного име-
ни Декарта — Картезий), которую разделяло большинство естествоиспы-
тателей доньютоновской эпохи, в частности Гюйгенс, отводила по сущест-
ву ту же функцию, а именно физическое объяснение явлений природы.
До начала XX в. все физики и философы придерживались убежде-
ния, что материя — первооснова и сущность физической реальности.
Вот что писал по этому поводу Ньютон в своей «Оптике»:
«При размышлении о всех этих, вещах мне кажется вероятным, что Бог внача-
ле дал материи форму твердых, массивных, непроницаемых, подвижных частиц
таких размеров и фигур и с такими свойствами и пропорциями в отношении к про-
странству, которые более всего подходили бы для той цели, для которой он их
создал. Эти первоначальные частицы, являясь твердыми, несравнимо тверже, чем
всякое пористое тело, составленное из них, настолько тверже, что они никогда не
изнашиваются и не разбиваются на куски Никакая обычная сила не способна раз-
делить то, что создал Бог при первом творению)
Так как движущаяся материя была ключом к математическому
описанию движения планет и свободно падающих тел, ученые попы-
тались распространить такое материалистическое объяснение на явле-
ния, природу которых они совсем не понимали. Тепло, свет, электри-
чество и магнетизм рассматривались как «невесомые» разновидности
материи; «невесомость» означала, что плотность материи этих видов
слишком мала и потому ее невозможно измерить. Например, тепловая
«материя» называлась калорической. Нагреваемое тело впитывало в
себя эту «материю», как губка воду. Электричество также считалось
материей в жидком состоянии: электрическая жидкость, или, точнее, две
электрические жидкости (положительно и отрицательно заряженные), те-
кущие по проводникам, и представляют собой электрический ток.
Предполагалось, что материя приводится в движение и обычно
поддерживается в этом состоянии действием сил. Бильярдный шар,
сталкиваясь с другим шаром, сообщает тому движение силой удара.
Для объяснения непрерывного движения планет Ньютон ввел силу тя-
готения. Для объяснения электрических и магнитных явлений Фара-
дей ввел электрические и магнитные силовые линии, которые считал
реально существующими.
Итак, имеются три основных понятия: материя, сила и движение.
Сила действует на материю, а движение есть не что иное, как поведе-
ние материи Следовательно, материя — наиболее фундаментальное
из названных понятий. Исходя из этого, философы провозгласили ма-
терию (поведение которой задано соответствующими математически-
ми законами) единственной реальностью.
180
К концу XVIII в. наиболее полное развитие получила одна область
физики, а именно механика. В знаменитой французской «Энциклопе-
дии» Д'Аламбер и Дидро весьма уверенно провозгласили, что механи-
ка — наука универсальная. По словам Дидро, «истинная система мира
познана, изложена и усовершенствована». Механика стала парадигмой
для более новых и быстро развивающихся областей науки.
Лейбниц, хотя и отстаивал механицизм как самоочевидную истину,
не мог удовлетвориться одним лишь этим направлением. Бог, энергия
и цель были одинаковы для него. В своей «Монадологии» (1714)
Лейбниц утверждал, что мир состоит из крохотных монад, каждая из
которых неделима и представляет собой сосредоточение энергии. В
каждой монаде заключено ее прошлое и будущее. Монады действуют
сообща в предустановленной гармонии, образуя более крупные орга-
низмы. Монады определяют внутренний динамизм вещей. Механи-
цизм же занимается рассмотрением внешних, пространственных и
других физических качеств вещей, например сил.
По утверждению великолепного физика, врача и математика Гер-
мана Гельмгольца (1821—1894), высказанному в одном из докладов,
вошедших в его «Популярные лекции о науке» (1869), конечная цель
естественных наук состоит в том, чтобы найти решение всех своих
проблем в механике. Вместе с тем Гельмгольц сознавал, что еще не
все элементы механики достаточно понятны, и признавал необходи-
мость обратить особое внимание на проблему природы сил:
«Таким образом, мы обнаруживаем в конечном счете, что задача физической
материальной науки состоит в сведении явлений природы к не подверженным из-
менениям силам отталкивания и притяжения между телами, величина которых за-
висит только от расстояния Разрешимость згой задачи есть условие познаваемо-
сти природы ... Ее [физической науки] миссия завершится, как только удастся
окончательно свести явления природы к простым силам и доказать, что такое све-
дение — единственное, допускаемое этими явлениями».
Гельмгольц выражает здесь благие, но несбыточные надежды, ибо
даже в то время, когда были написаны эти строки, физическая наука
располагала убедительными данными, свидетельствовавшими о том,
что не все явления можно объяснить, сводя их к массам, подвержен-
ным воздействию простых и понятных сил.
Ныне мы со всей очевидностью столкнулись с тем, что, возможно,
оставалось незамеченным в XIX в.: с участившимися случаями «не-
срабатывания» механицизма. Излагать результаты своих исследований
ученые стремятся по возможности ясно и понятно, но именно тогда, ко-
гда им удается достичь наибольшей ясности, они наиболее далеки от ис-
тины. Вплоть до конца XIX в. физики пребывали в уверенности, что все
явления природы допускают механистическое объяснение. А если какие-
181
то явления пока не удавалось объяснить в рамках механицизма, то, счита-
лось, со временем это будет сделано. Среди тех явлений, которые не на-
ходили механистического объяснения, особенно важными были действие
тяготения и распространение электромагнитных волн.
Что касается тяготения, то физики конца XIX в., разумеется, знали
о настойчивых попытках Ньютона дать объяснение этому явлению.
Каким образом сила притяжения со стороны Солнца действует на пла-
неты, находящиеся от него на расстоянии в миллионы и сотни мил-
лионов километров? Усилия Ньютона не увенчались успехом, и, как
бы подводя им итог, он изрек свое знаменитое: «Я не измышляю гипо-
тез». Механицизм не помог Ньютону.
Почему же ученые XVIII—XIX вв. столь ревностно придержива- .
лись механицизма? Возможно, что их не покидала надежда разгадать
природу тяготения. Однако более существенно другое: физики были
настолько ослеплены успехами ньютоновского направления в науке,
что упустили из виду проблему объяснения физической природы тяго-
тения. Воспользовавшись математическим выражением закона все-
мирного тяготения, они (в особенности Лагранж и Лаплас) настолько
преуспели в применении этого закона для объяснения ряда наблюдае-
мых аномалий в движениях небесных тел и в обнаружении новых яв-
лений, что проблема физической природы тяготения оказалась погре-
бенной под грудой математических «мемуаров» (как принято было на-
зывать тогда публикации). Ныне мы знаем, что тяготение (или грави-
тация) — научная фикция, происхождение которой в определенной
степени связано со способностью человека оказать силовое воздейст-
вие на различные предметы. Джордж Беркли подверг критике понятие
физической силы тяготения с общих позиций своей философии. В со-
чинении «Алсифрон, или Мелкий философ. В семи диалогах, содер-
жащих апологию христианской религии против тех, кого называют
свободомыслящими» (1732) он писал:
«Е ф р а н о р. ...Прошу тебя, Алсифрон, ие играй терминами: оставь слово
сила, изринь все прочее из своих мыслей, и ты увидишь, какова точная идея силы
Алсифрон. Под силой я понимаю в телах то, что вызывает движение и
другие ощутимые действия.
Е ф р а н о р. А не существует ли что-нибудь отличное от этих действий?
Алсифрон. Существует.
Е ф р а и о р. Тогда будь добр, исключи все, что отличается, и те действия, к
которым оно приводит, и поразмысли над тем, что такое сила в собственной, точ-
ной идее.
Алсифрон. Должен признаться, нелегкое это дело.
Е ф р а н о р. Поскольку ни ты, ни я не можем определить идею силы и посколь-
ку, как ты сам заметил, разум н способности людей во многом схожи, ьы можем пред-
положить, что и у других людей нет ясного представления об идее силы».
182
Резюмируя, можно сказать, что не только замечательные достиже-
ния самого Ньютона, но и сотни результатов, полученных его много-
численными последователями, стали возможными благодаря тому, что
их авторы полагались на математическое описание даже в случаях, ко-
гда физическое понимание явления полностью отсутствовало. По су-
ществу все эти естествоиспытатели принесли физическое понимание в
жертву математическому описанию и математическому предсказанию.
В этой связи уместно привести слова английского писателя Г.К. Чес-
тертона (1874—1936): «Мы узрели истину, и оказалось, что истина не
имеет [физического] смысла». Что же касается механицизма, то исто-
рия развития теории электромагнитного поля по существу повторяет
историю развития теории тяготения. Мы уже упоминали о том, что
Фарадей ввел понятие силовых линий для объяснения различных элек-
трических явлений, магнетизма и взаимодействия электрических
зарядов. Предполагалось, что со временем удастся доказать физиче-
скую реальность силовых линий. Но когда Максвелл распространил
«юрисдикцию» электрических и магнитных явлений на волны, спо-
собные распространяться на сотни и тысячи километров, силовые ли-
нии Фарадея оказались совершенно непригодными даже как средство
описания, потенциально обладающее физическим смыслом. Вместо
силовых линий Максвелл ввел понятие эфира, который был определен
как среда — носитель света, как среда, в которой распространяются
все электромагнитные волны, включая световые. Максвелл настойчи-
во пытался дать механистическое объяснение распространению элек-
тромагнитных волн, но все его усилия, как и попытки Ньютона объяс-
нить тяготение, оказались безуспешными. Верх одержали математиче-
ские уравнения.
Последующее развитие физики показало несостоятельность меха-
ницизма. Эфир как материальная субстанция был отвергнут. Его заме-
нили чисто математические законы. Вместо силы тяготения общая
теория относительности ввела геодезические в пространстве-времени.
Мы «признали» явление распространения электромагнитных волн, хо-
тя их физическая природа неизвестна. Нам пришлось также «принять»
дуализм волна—частица, противоречащий здравому смыслу, и, как по
мановению волшебной палочки, электроны, бывшие в атоме частица-
ми, вылетая из него, стали превращаться в волны. Особенно глубокого
пересмотра классической механики потребовали теория относитель-
ности и квантовая механика. Тем не менее эти изменения не столь
беспрецедентны, если проследить всю долгую историю развития есте-
ствознания с античных времен до создания классической механики
Ньютона, работ Лагранжа и Лапласа. Пересмотры аристотелевской и
183
схоластической механики и птолемеевой астрономии были в свое вре-
мя не менее революционны.
Вторжение новых идей в механистическую концепцию природы
явственно ощутимо в сетованиях лорда Кельвина, ведущей фигуры в
английских научных кругах второй половины XIX в.:
«Я никогда нс испытываю чувства полного удовлетворения до тех пор, пока
не построю механическую модель изучаемого объекта- Если мне это удается, то я
сразу все понимаю, в противном случае не понимаю. Мне хотелось бы понять приро-
ду света как можно полнее, не вводя вещей, которые я понимаю еще меньше»
Тем не менее Кельвину пришлось довольствоваться пониманием
света, далеко не соответствовавшим его желаниям.
Еще одно философское учение, неоднократно привлекавшееся для
объяснения поведения природы, основано на понятии причины и след-
ствия. Мы ищем причины, полагая, что знание причин позволит нам
получить желаемые следствия. Учение о причинности в чем-то более
смутная доктрина, чем механицизм. Причинность лишь констатирует
существование причины и следствия, но ничего не говорит о механиз-
ме связи между ними. На протяжении нескольких столетий (вплоть до
начала XX в.) причинность действительно подразумевала сущест-
вование некоего механизма. Многие явления происходят потому, что
причина и следствие связаны физическим механизмом, который
порождает следствие. В первоначальном варианте учение о при-
чинности предполагало непосредственный «контакт» между причиной
и следствием, т.е. их пространственную «смежность». Но вскоре поня-
тие причинности стали использовать и при рассмотрении дальнодей-
ствия (действия на расстоянии), например в случае тяготения.
Как большинство философских учений, учение о причинности за-
родилось в Древней Греции. Аристотель различал четыре типа при-
чин, действующих в мире: форму (эйдос, морфе); цель, т.е. «то, ради
чего»; материю («то, из чего»), илн субстрат, и источник движения,
или «творящее начало». Великий математик и естествоиспытатель Ар-
химед, умевший применять свои знания на практике, подчеркивал
значение принципа причинности, интерпретируя последнюю в духе
«творящего начала» Аристотеля. Согласно Архимеду, причинность
приводит к тому, что материя всюду и всегда ведет себя упорядоченно
и предсказуемо.
Выявление причинности в науке нового времени берет начало с
Галилея. Он говорил о земном тяготении как о причине движения зем-
ных тел, хотя ему пришлось отказаться от причинности, ограничив-
шись математическим описанием движений.
Ньютон и его современники разработали концепцию, сохранив-
шуюся по существу неизменной на протяжении следующих двух сто-
летий. Согласно этой концепции, причинность присуща самой приро-
184
де физического мира. Следуя такой концепции, Ньютон ввел универ-
сальную силу тяготения — как причину эллиптичности планетных ор-
бит (не будь всемирного тяготения, планеты двигались бы по прямо-
линейным траекториям). Лейбниц также говорил, что все, что случает-
ся, имеет свою причину.
Совершенно иное толкование причины и следствия предложил
Иммануил Кант. Находясь под сильным влиянием ньютоновской нау-
ки в ту эпоху, когда в Европе господствовали космологические "теории
Декарта, Кант вступил в защиту системы небесной механики и даже
существенно дополнил ее в работе «Всеобщая естественная история и
теория неба» (1755). В своем основном философском сочинении «Кри-
тика чистого разума» (1781) Кант утверждал, что причинность являет-
ся логической предпосылкой всего рационального мышления. По
Канту, разум не нуждается в подтверждении эмпирическими данными
Во втором издании «Критики чистого разума» (1787) Кант так
определил причинность: «Все изменения происходят по закону связи
причины и действия».
Все многочисленные концепции причинности различным образом
включают в себя идею связи (или сцепления), посредством которой
причина порождает следствие. Шотландский философ Дэвид Юм пы-
тался очистить причинность от какой бы то ни было метафизической
подоплеки. В действительности он поставил под сомнение само поня-
тие причинности. В работе «Исследование о человеческом познании»
(1793) Юм утверждал:
«Единственная непосредственная польза всех наук состоит в том, что они обу-
чают нас управлять будущими явлениями и регулировать их с помощью причин.
Обладающие сходством объекты всегда соединяются со сходными же — это мы
знаем из опыта, сообразуясь с последним, мы можем поэтому определить причину
как объект, за которым следует другой объект, причем все объекты, похожие на
первый, сопровождаются объектами, похожими иа второй».
В приведенном отрывке слово «объект» лучше всего интерпрети-
ровать как «явление». Юм утверждает, что ситуация С и последующая
ситуация Е связаны между собой как причина и следствие, если воз-
никновение ситуации С (или похожей ситуации) всегда влечет за со-
бой ситуацию Е (или подобную ей) и если ситуация Е возникает после
наступления ситуации С. В свое определение причинности Юм вклю-
чил слова «похожий», «подобный», так как хотел сделать причинность
экспериментально проверяемой и понимал, что определенная ситуа-
ция никогда не может повториться с абсолютной точностью.
Определив, что такое причинность, Юм приступил к критике этого
понятия. По убеждению Юма, сам по себе тот факт, что мы знаем о
следовании события А за событием В, даже если это следование мно-
гократно повторялось, отнюдь не доказывает, что и в будущем собы-
12 Зак 72
185
тие А неизменно будет следовать за событием В. Юм приходит к вы-
воду, что наша вера в причинность не более чем привычка, и с полным
основанием утверждает, что привычка не может служить подходящей
основой для веры.
Джон Стюарт Милль, наиболее известный английский философ
XIX в., поддержав отрицание причинности Юмом, добавил несколько
собственных идей. В сочинении «Система логики» (1843) Мнлль так
изложил свою концепцию причинности: «Закон причинности, главный
столп, на который опирается наука, есть не что иное, как знакомая ис-
тина об обнаруживаемой путем наблюдения неизменности следования
между каждым природным фактом и каким-то другим фактом, ему
предшествующим». Таким образом, Милль, подобно Юму, усматрива-
ет сущность причинности в «неизменности следования» и, подобно
Юму, подводит под причинность эмпирический базис. Милль лишает
причинность логической необходимости, отказываясь от идеи прину-
ждения. Он анализирует условия, при которых, по его мнению, можно
предположить существование причинно-следственных связей между
двумя событиями: событие-причина пространственно близко к собы-
тию-следствию; следствие во времени происходит непосредственно
после причины; событие-следствие имеет место всегда, когда проис-
ходит событие-причина. Милль не опровергает явно высказывание
Юма, что причинность — всего лишь привычка мышления. Для Мил-
ля причинность — это обобщение эмпирических данных. Индукция
служит основой некоторых обобщений, в частности законов природы.
Милль рассматривает также методы, которые позволяют выявить при-
чинную связь, например метод различий:
«Если в данном случае, когда происходит исследуемое явление, и в другом,
когда оно не происходит, все условия одинаковы, за исключением одного, которое
выполняется только в первом случае, то единственное условие, которым отлича-
ются два случая, и есть причина (илн неотъемлемая часть ее) указанного явления».
Это четко сформулированный принцип и поныне широко исполь-
зуется во многих областях науки. Например, эксперимент, проводи-
мый на лабораторных животных для проверки действия нового лекар-
ственного препарата, всегда ставится на двух группах животных, по-
добранных так, чтобы они были как можно более схожи по размерам,
возрасту, условиям содержания, кормления и т.д. Единственное разли-
чие между группами состоит в том, что животным одной из них дают
испытываемое лекарство, а животные другой (так называемой кон-
трольной) группы его не получают. Согласно методу различий, любой
эффект, наблюдаемый у животных первой группы, но не наблюдае-
мый у животных второй, можно считать причинно обусловленным
лекарством.
186
Еще более разрушительную атаку на причинность предпринял Бер-
тран Рассел, английский математик и философ, удостоенный в 1950 г.
Нобелевской премии по литературе. В работе «О понятии причины»
Рассел писал:
«Все философы, к какой бы школе они ни принадлежали, воображают, будто
причинность есть одна из фундаментальных аксиом науки, ио, как ни странно, в
столь передовой науке, как гравитационная астрономия, слово «причина» никогда
не встречается... Принцип причинности, как и многое другое, имеющее хождение
среди философов, кажется мне реликтом прошлого века, выжившим, подобно мо-
нархии, только потому, что его ошибочно сочли безвредным».
Называя причинность «реликтом прошлого века», Рассел заходит,
пожалуй, слишком далеко. Но так или иначе, несмотря на критику
Юма, Милля и Рассела, к концу XIX в. причинность в глазах естество-
испытателей поднялась до статуса самоочевидной истины, который
столетием раньше Кант придал ей, исходя из метафизических основа-
ний. Отношение к причинности, сложившееся в конце XIX в., доста-
точно четко выразил Герман Гельмгольц в своей «Физиологической
оптике»:
«Принцип причинности носит характер чисто логического закона даже в том,
что выводимые из него следствия относятся в действительности не к самому опы-
ту, а к пониманию опыта и, следовательно, не могут быть опровергнуты никаким
возможным опытом».
О том, как повлияло на толкование принципа причинности разви-
тие квантовой теории, мы расскажем дальше.
Поскольку причину того или иного явления удается установить не
всегда (например, мы не знаем, как образовались кометы), а механи-
цизм также не всегда может объяснить разнообразные явления, в XIX в.
господствующее положение приобрело философское учение под на-
званием «детерминизм». Различие между учением о причинности и
детерминизмом отмечал еще Декарт: следствие отстает во времени от
причины из-за ограниченности чувственных восприятий человека.
Causa sive ratio (причина есть не что иное, как разум). Суть детерми-
низма лучше всего пояснить с помощью аналогии. Если аксиомы евк-
лидовой геометрии заданы, то свойства окружности (например, ее
длина и площадь ограниченного ею круга) и вписанных углов полно-
стью определены как необходимые логические следствия. Говорят,
что Ньютон как-то спросил, зачем нужно выписывать теоремы евкли-
довой геометрии, если они очевидным образом следуют из аксиом. И
все же большинству людей требуется немало времени, чтобы доказать
каждую из теорем. Но хронологический порядок открытия новых гео-
метрических свойств, который, казалось бы, связывает аксиомы и тео-
ремы такой же временной последовательностью, как причину и след-
ствие, в действительности иллюзорен.
12*
187
Так же обстоит дело и с физическими явлениями, считал Декарт.
Для «божественного разума» все явления «сосуществуют» в одной ма-
тематической структуре. Но наши чувства в силу ограниченности их
возможностей распознают явления не одновременно, а одно за другим,
и поэтому мы одни явления принимаем за причины других. Отсюда
понятно, заявлял Декарт, почему математика позволяет предсказывать
будущее. Это становится возможным благодаря ранее полученным ма-
тематическим соотношениям. Именно математическое соотношение
дает самое ясное физическое объяснение реальности. Кратко можно
сказать, что реальный мир — это совокупность математически пред-
ставимых движений объектов в пространстве и времени, а Вселенная в
целом — огромная, гармоничная машина, построенная на основе ма-
тематических законов. Кроме того, многие философы, включая самого
Декарта, утверждали, что математические законы заданы раз и навсе-
гда, поскольку именно так сотворил мир сам Бог, а божья воля неиз-
менна. Независимо от того, удалось ли человеку проникнуть в сокро-
венные «замыслы Бога», мир функционировал по закону, н закономер-
ность процессов, происходящих в природе, не ставилась никем под
сомнение, по крайней мере до начала XIX в.
Ньютоновская концепция Вселенной, состоящей из твердых нераз-
рушаемых частиц, каждая из которых действует на другие с вполне
определенной, вычислимой силой, была положена в основу последова-
тельного и жесткого детерминизма французским астрономом и мате-
матиком маркизом Пьером Симоном де Лапласом. Ему принадлежит
ставшее классическим описание сущности детерминизма:
«Состояние Вселенной в данный момент можно рассматривать как результат
ее прошлого и как причину ее будущего. Разумное существо, которое в любой мо-
мент знало бы все движущие силы природы и взаимное расположение образую-
щих ее существ, могло бы — если бы его разум был достаточно обширен для того,
чтобы проанализировать все эти данные, — выразить одним уравнением движение
и самых больших тел во Вселенной, и мельчайших атомов. Ничто не осталось бы
сокрытым от него — оно могло бы охватить единым взглядом как будущее, так и
прошлое».
«Одно уравнение», охватывающее, по словам Лапласа, всю Вселен-
ную, поражает воображение, но детерминисты вполне довольствова-
лись и многочисленными формулами.
Сам того не ведая, Лаплас составил эпитафию механицизму и детер-
минизму. Он рисует нам фантастический сверхчеловеческий «разум», но
существование такого разума к делу не относится. Если Вселенная во все
времена, в прошлом и будущем, неукоснительно следует по жестко де-
терминированному пути, то она функционирует так в независимости от
того, знает об этом сверхчеловеческий разум или нет, ибо на Вселенную
Лапласа он не оказывает никакого влияния. Среди математиков и астро-
186
номов Лаплас пользовался огромным и вполне заслуженным авторите-
том, поэтому его концепция полностью детерминистической Вселенной
оказала на них большое воздействие.
Детерминизм завоевал столь прочные позиции, что философы ста-
ли подходить с детерминистической точки зрения к оценке деятельно-
сти человека как части природы. Идеи, волевые акты и действия чело-
века рассматривались как неизбежные проявления взаимодействия ма-
терии с материей. По мнению детерминистов, человеческая воля опре-
деляется внешними физическими и физиологическими причинами.
Гоббс, например, объяснял кажущуюся свободу воли следующим об-
разом. События извне воздействуют на наши органы чувств, а те в
свою очередь — на мозг Движения внутри мозга порождают то, что
мы называем аппетитом, восторгом или страхом, но все эти чувства —
не более чем наличие движений внутри мозга. Когда аппетит и отвра-
щение сталкиваются в противоборстве, наступает особое физическое
состояние, именуемое осмотрительностью. Одно движение одержива-
ет верх над другим, а мы говорим о проявлении свободы воли. Но в
действительности выбор преобладающего движения принадлежит не
личности. Мы видим результат, но не в состоянии осознать опреде-
ляющий его процесс. Свободы воли не существует. Это бессмыслен-
ный набор слов. Воля жестко ограничена действиями материи.
Вольтер в сочинении «Невежественный философа утверждал: «Было
бы очень странно, если бы вся природа, все планеты должны были под-
чиняться вечным законам, а одно небольшое существо, ростом в пять
локтей, презирая эти законы, могло бы действовать, как ему заблагорас-
судится».
Случай — не что иное, как слово, придуманное для обозначения из-
вестного действия неизвестной причины.
Этот вывод был настолько категоричен, что даже материалисты
попытались умерить его остроту. Некоторые из них утверждали, что
детерминированы только действия человека, но не его мысли. Введе-
ние такой «дихотомии» вряд ли облегчало ситуацию, ибо означало,
что человеческое мышление не влияет на человеческие поступки —
люди становились автоматами. Другие пытались найти новую интер-
претацию свободы, пытаясь сохранить хотя бы какое-то подобие ее.
Вольтер саркастически заметил в этой связи: «Быть свободным озна-
чает иметь возможность делать что угодно, а не хотеть что угодно».
С научной точки зрения утверждение «событие И определяет собы-
тие В» означает, что если задано событие А, то можно вычислить со-
бытие В и наоборот. Таким образом, применение детерминизма в точ-
ных науках можно охарактеризовать следующим образом: если со-
стояние некоторого множества объектов в произвольный момент вре-
189
мени задано, то состояние объектов того же множества в любой мо-
мент времени в прошлом илн будущем может быть определено путем
вычислений.
Естественнонаучная концепция детерминизма наиболее четко вы-
ражена функциональными соотношениями между переменными, т.е.
формулами. Ясно, что из функционального соотношения не следует
существования причинно-следственной связи.
Многое из того, чем занимаются точные науки, сводится к установ-
лению функциональных соотношений между переменными. Если та-
кого рода соотношение оказывается верным в широких пределах и вы-
ражает нечто важное относительно физического мира, то оно обретает
статус закона природы. Что касается детерминизма, то суть его кроет-
ся просто в постоянстве и надежности естественнонаучных законов.
При должном учете двух обстоятельств: 1) экспериментальные дан-
ные, на которые опираются эти законы, никогда не бывают идеально
точными; 2) все теоретические соотношения имеют «пробный харак-
тер» и подлежат пересмотру в свете новых открытий — детерминизм
означает не больше и не меньше как однородность природы.
Но детерминизму не была суждена долгая жизнь. В действиях име-
ются моменты нестабильного поведения (Максвелл называл такие
моменты особыми точками). Камень на вершине горы находится в не-
устойчивом положении: достаточно легкого толчка, чтобы он обру-
шился вниз, увлекая за собой лавину. Подобным образом спичка, вы-
зывающая лесной пожар, неосторожно брошенное слово, способное
привести к мировой катастрофе, крохотный ген, в зависимости от ко-
торого люди становятся мудрецами или идиотами, — все это примеры
явлений неустойчивости. Факторы неустойчивости пробивают брешь в
эволюции детерминистического мира: в моменты потери устойчивости
безотказно действовавшие ранее законы нарушаются и эффекты, пре-
небрежимо малые при других обстоятельствах, становятся домини-
рующими.
Максвелл предостерегал своих ученых коллег против недооценки
роли этих особых точек в научном познании:
«Таким образом, если те, кто культивирует физическую науку,... в погоне за се
волшебные зельем придут к изучению особых точек и неустойчивости, сменившей
непрерывность н стабильность вещей, то успехи естествознания, возможно, позво-
лят устранить предрасположение к детерминизму, проистекавшее единственно из
допущения, что физическая наука будущего — всего лишь увеличенное изображе-
ние физической науки прошлого».
Лидер физической науки своего времени Максвелл стал пророком
для следующего поколения ученых. Некоторые из его работ по кинети-
ческой теории газов способствовали закату детерминизма. Трещины и
пробелы, которые Максвелл увидел в детерминистической схеме, вско-
ре расширились, и детерминистический мир распался.
190
На смену детерминизму пришли статистические законы. Но прежде
чем углубиться в новые проблемы, необходимо выяснить, что мы по-
нимаем под статистическими законами. Приведем в качестве примера
лишь одну из задач, которые успешно решают математическая стати-
стика и теория вероятностей. Страховое дело получило в США широ-
кое развитие. Совершенно очевидно, что любая попытка предсказать,
исходя из первых принципов, когда умрет какой-то конкретный чело-
век, обречена на провал. Тем не менее, опираясь на данные о продол-
жительности жизни тысяч людей и используя методы теории вероят-
ности, страховые компании занимаются страхованием жизней, взимая
суммы, устраивающие и тех, кто выплачивает страховой полис, и ком-
панию, берущую на себя риск.
Применение статистических законов в физике началось со стати-
стической механики, где еще можно было предполагать, что, детально
описав миллионы столкновений молекул, ведущих себя детермини-
стически, мы могли бы, например, предсказать поведение газа; но это
число столь велико, что рассматривать подобные «коллективные эф-
фекты» можно только статистическими методами. Первым стал широ-
ко использовать статистические законы Людвиг Больцман в своих ра-
ботах по кинетической теории газов. Его подход был радикальным ша-
гом в эпоху, когда господствовали идеи механицизма и детерминизма,
и вызвал ожесточенные споры. Задачу физики Больцман видел не в
сборе эмпирических данных и последующей оценке их с точки зрения
известных законов и умозрительных построений, а в том, чтобы при-
вести наше мышление, идеи и понятия в соответствие с эмпирически-
ми данными. Статистическую механику Больцмана его современники
восприняли не более как измышления «математического террориста».
Процесс радиоактивности, кажущееся произвольным поведение
электронов одновременно и как волн, и как частиц, непредсказуемый
распад атомных ядер — все эти новые явления подрывали устои де-
терминизма. Невозможно было предсказать достоверно и поведение
квантов Планка, фотонов Эйнштейна или «скачки» электронов в моде-
ли атома Бора.
Сформулированный Гейзенбергом в 1927 г. принцип неопределен-
ности также сыграл важную роль в потрясении основ детерминизма. В
статье, опубликованной в 1927 г., Гейзенберг подверг критике и при-
чинность, и детерминизм: речь идет не о незыблемом законе (который
неверен), а о допущении:
«Мы в принципе не можем знать настоящее во всех его детерминированных
подробностях. Следовательно, все наше восприятие — это право произвести отбор
нз огромного числа возможностей и наложить ограниченна на будущие возможно-
сти. Поскольку статистический характер квантовой теорнн столь тесно связан с
191
неточностью нашего восприятия, возникает подозрение, что за воспринимаемым
статистическим миром скрывается другой «реальный» мир, в котором выполняет-
ся принцип причинности. Но такого рода умозрительные заключения представля-
ются нам... бесцельными н бесплодными. Физика должна давать только формаль-
ное описание связи между восприятиями. Гораздо более точная констатация ре-
альных фактов состоит в следующем: так как все эксперименты удовлетворяют за-
конам квантовой механики, она неопровержимо свидетельствует о том. что прин-
цип причинности не выполняется».
Принцип неопределенности Гейзенберга вовсе не сводится к ут-
верждению о том, что причинные связи квантовых явлений находятся
за пределами возможности их обнаружения; он со всей очевидностью
предполагает, что таких связей просто не существует. Именно к тако-
му выводу пришел сам Гейзенберг. С появлением принципа неопреде-
ленности классическая причинность и детерминизм утрачивают
смысл. Квантовая механика оперирует только статистическими поня-
тиями. Она не дает точного описания отдельной частицы и точного пред-
сказания ее поведения. Однако квантовая механика позволяет с высокой
точностью предсказывать поведение больших ансамблей частиц.
Рихард фон Мизес и другие ученые, размышляя над проблемами
квантовой механики, отстаивали идею недетерминированности реаль-
ного мира. Все детерминированные законы, по мнению этих исследо-
вателей, представляют собой не что иное, как приближенное и чисто
пассивное отражение вероятностных соотношений, подчиняющихся
законам случая. Отдельные процессы и события в атомном мире тем
самым ставятся «вне закона». Как указывал Эддингтон в книге «При-
рода физического мира» (1933), «физика сделала детерминизм не-
прочным».
В 1957 г. Ганс Рейхенбах в работе «Атом и космос» подчеркивал
точность вероятностной интерпретации всех физических результатов.
Наиболее вероятное и есть то, что лежит в пределах ошибки наблюде-
ния. Только в больших масштабах, когда огромное число атомов уча-
ствует в процессах, идущих с высокой вероятностью, мы можем счи-
тать явления практически достоверными. Но в принципе даже крупно-
масштабные процессы носят вероятностный характер. Понятия про-
странства, времени, вещества, силы, причинности и законов природы
заимствованы из обыденного человеческого опыта, приобретенного в
мире «средних размеров», и заведомо непригодны для описания явле-
ний на атомном уровне.
Долгое время одни выдающиеся физики (Борн, Бор и Паули) при-
держивались с незначительными вариациями точки зрения, что все яв-
ления природы подлежат лишь вероятностной интерпретации, тогда
как другие, не менее крупные физики (Планк, Эйнштейн, фон Лауэ, де
Бройль, Шрёдингер и др.) не соглашались с ними, придерживаясь кон-
192
цепций причинности и детерминизма, восходящих к классической ме-
ханике. Суть спора сводилась главным образом к следующему: являет-
ся ли статистический характер законов квантовой физики временной
«платой» за неполное знание и не уступят ли эти законы со временем
место другим, столь же детерминированным, как законы ньютонов-
ской механики, или же статистические законы объективны, т.е. не за-
висят от нашего знания и сознания, и соответствуют явлениям, реаль-
но происходящим в микромире.
Широко известно высказывание Эйнштейна, что «Бог не играет в
кости». Эту мысль Эйнштейн подчеркивал и в двух письмах, приве-
денных в книге Рональда У. Кларка «Эйнштейн: жизнь и времена». В
первом письме (1926), адресованном Максу Борну, говорится:
«Квантовая механика, безусловно, впечатляет. Но внутренний голос подсказы-
вает мне, что ее пока нельзя считать реальной. Теория многое говорит, но ни на
йоту не приближает нас к секрету Старика. Я, во всяком случае, убежден, что Он
не бросает кости».
Во втором письме, написанном гораздо позже и адресованном
Джеймсу Франку, Эйнштейн заявляет:
«Я могу еще, если на то пошло, понять, что Господь Бог мог сотворить мнр, в
котором нет законов природы. Короче говоря, хаос. Но то, что должны быть ста-
тистические законы с вполне определенными решениями, например законы, вы-
нуждающие Господа Бога бросать кости в каждом отдельном случае, я считаю в
высшей степени неудовлетворительным»
В сборнике «Мир, каким я вижу его» (1934) Эйнштейн говорит:
«Господь Бог изощрен, но не злонамерен». Кроме того, в коллектив-
ной статье, опубликованной в журнале Physical Review за 1935 г.,
Эйнштейн утверждает, что волновая механика неполна. По мнению
авторов статьи, со временем должна появиться статистическая кванто-
вая теория, аналогичная статистической механике: движения отдель-
ных частиц (например молекул газа) должны быть детерминированы,
но вследствие большого числа частиц эта теория должна использовать
статистику и теорию вероятностей. То же мнение выразил (1978) Поль
А.М. Дирак, английский физик, внесший значительный вклад в созда-
ние новой физики:
«Я думаю, вполне возможно, что в конечном счете правым окажется Эйн-
штейн, ибо существующую ныне форму квантовой механики не следует рассмат-
ривать как окончательную... Я считаю вполне возможным, что в будущем у нас
появится усовершенствованная квантовая механика, в которой произойдет возврат
к детерминизму, н тем самым подтвердится точка зрения Эйнштейна. Но такой
возврат к детерминизму возможен только ценой отказа от кое-каких основных
идей, которые мы сейчас принимаем, не подвергая ни малейшему сомнению Если
мы вернемся к детерминизму, то нам придется каким-то образом заплатить за это,
хотя сейчас трудно предугадать, каким именно».
193
Дирак, несомненно, прав, говоря о некоем идейном барьере, пре-
граждающем путь к развитию более полной детерминистической тео-
рии. Как сказано в «Опыте о человеке» Александра Поупа, «все дело
случая, пути которого неисповедимы...».
Ни Дирак, ни Эйнштейн не предложили альтернативной модели
квантовой теории. Другие критики вероятностного характера кванто-
вой механики, например физики Дэвид Бом (1957) и Шоичи Саката
(1978), также не смогли найти разумные альтернативные модели. Над
той же проблемой безрезультатно бились и другие выдающиеся уче-
ные. Но к настоящему моменту квантовая теория достигла в своем
развитии такого уровня, что решение проблемы вряд ли зависит от по-
лучения новых экспериментальных данных.
Хотя, имея дело с явлениями, в которых участвуют видимые или
осязаемые объекты, т.е. с явлениями «средних размеров», по опреде-
лению Рейхенбаха, физики по-прежнему используют детерминистиче-
ские законы классической механики, их отношение к детерминизму
при описании таких явлений претерпело глубокие изменения вследст-
вие новых открытий, ставших возможными благодаря квантовой ме-
ханике. Предполагается, что все происходит так, как происходит, по-
скольку вероятность этого весьма высока, а вероятность того, что это
должно быть иначе, весьма незначительна.
Механицизм, учение о причинности и детерминизм — лишь три из
большого числа философских направлений, испытавших на себе глубо-
кое воздействие последних научных открытий. В действительности таких
направлений в философии гораздо больше. Остановимся бегло еще на
некоторых.
Философия идеализма — это другой способ решения основной мета-
физической проблемы — нашего взаимоотношения с внешним миром.
Идеализм решает эту проблему, «обрубив» ее с одного конца, а именно
отрицая, как это делал Беркли, существование внешнего мира. Все наше
осознание внешнего мира в действительности происходит в нас самих;
следовательно, убеждение, что это осознание порождено внешними по
отношению к нам объектами, вполне может оказаться иллюзией. Когда
мы смотрим на дерево, оно существует в нашем сознании. Когда мы от-
ворачиваемся, дерево в нашем сознании перестает существовать. И если
мы вспоминаем его или слышим, как кто-то другой уверяет нас, что дере-
во по-прежнему стоит на том же месте, то и на этот раз не испытываем
ничего, кроме неких процессов, происходящих в нашем сознании.
Общая интуитивная реакция на идеализм — отвергнуть его как аб-
сурдное учение. «Грозный доктор» (английский писатель и лексикограф)
Сэмюэл Джонсон (1709—1784) считал, что всякий может опровергнуть
идеализм, пнув в его сторону большой камень. Но, несмотря на много-
194
численные усилия весьма авторитетных философов, идеализм так и не
был окончательно опровергнут. Существование чего-то, что не вызывало
бы чувственных восприятий ни в чьем сознании, невозможно доказать
экспериментально, поэтому физическое существование, независимое от
человека, следует считать бессмысленным. Более того, все, кто занимает-
ся естественными науками, должны быть идеалистами. Однако вся клас-
сическая наука прочно стоит на допущении о существовании внешнего
объективного мира. Ученые обычно сходятся на том, что природа их не
обманывает и созданная ими концепция реального внешнего мира обос-
нована.
Классический ученый, если подвергнуть сомнению его убеждение в
существовании объективного мира, ответил бы, что наблюдения не ока-
зывают сколько-нибудь заметного влияния на наблюдаемый объект. Та-
кой ученый стал бы утверждать, что наблюдатель действительно опреде-
ляет, каким объект был до наблюдения и каким станет после. Однако это
допущение классической физики выглядит в наши дни весьма шатким.
Наблюдения оказывают воздействие на наблюдаемые объекты, и, как по-
казал Гейзенберг, для элементарных компонентов нашего мира это воз-
действие отнюдь не является неощутимо слабым.
Классическая наука исходила из априорного предположения, что
внешний мир существует. Математические уравнения классической ме-
ханики, как принято было считать, описывают то, что реально происходит
во внешнем мире. Квантовая механика имеет свои математические урав-
нения, но они описывают наблюдения — не реальные частицы, а воздей-
ствие этих частиц на экраны, подобные телевизионным.
В отличие от идеализма философия логического позитивизма ут-
верждает, что истины строятся только на наблюдаемых фактах. Пози-
тивисты — антиметафизики, и, с их точки зрения, единственным ис-
точником осмысленного знания может быть опыт. Из него мы «извле-
каем» основные утверждения, которые затем можно развить с помо-
щью строгой дедукции. Но смысл любого утверждения тождествен
средствам, позволяющим проверить его. Джон Стюарт Милль, пред-
ставитель позитивистской философии, утверждал, что хотя знание мы
черпаем главным образом из ощущений, оно включает в себя и соот-
ношения, которые наделенный сознанием разум формулирует относи-
тельно данных чувственного опыта, например научные законы. Хотя
позитивисты, как и идеалисты, считают, что доказать существование
внешнего мира невозможно, они утверждают, что невозможно и про-
тивоположное, а именно доказать, что внешний мир не существует. По
своей сути позитивисты — эмпирики, проводящие резкое различие
между данными опыта и объектами мышления и отрицающие реаль-
ность последних.
195
Что же мы узнали из этого беглого обзора? Наша задача была простой:
показать, каким образом недавние достижения физической науки застав-
ляют нас все время пересматривать, казалось бы, давно устоявшиеся
представления. Мы хотели также отметить те изменения, которые эти
достижения вызвали в нашей собственной жизни и наших взглядах на
природу. Философия науки (или, если угодно, поведения природы) строит
на основе текущего научного знания широкие обобщения. Поскольку на-
ше знание со временем претерпевает изменения, должна изменяться и
философия науки. Следовательно, мы никогда не должны упускать из ви-
ду самую «сердцевину» естественнонаучных данных.
Цель нашей книги состояла в том, чтобы показать, в сколь значитель-
ной степени научное знание зависит от математики. Какой вывод из этого
следует, если учесть, что математика — это творение человеческого ра-
зума? Мы не в состоянии дать однозначный ответ на вопрос, упорядочена
ли природа, заложен ли в ее основе некий план и даже некая цель (как
счел бы Аристотель). Но мы можем с полной уверенностью заявить, что
самый могущественный из созданных человеком инструмент — матема-
тика — позволяет нам достичь определенного понимания сложного и
разнообразного мира природных явлений.
(Б/В. Тнеден^р
МАТЕМАТИКА — ЯЗЫК НАУКИ12
Известно изречение о том, что математика является значительно
большим, чем наука, поскольку она является языком науки. Эта фраза
требует небольшого пояснения, поскольку в США и странах Западной
Европы слово наука (science) употребляется в более узком смысле, чем
в нашей стране, а именно только для обозначения естественных дис-
циплин, и не включает в себя социальных и гуманитарных предметов.
В последние годы приведенное утверждение приобретает все большее
число сторонников, поскольку к математике за помощью обращаются
представители не только физики, но и многих других дисциплин —
астрономии, химии, экономики, медицины, археологии, социологии,
сельского хозяйства, организации производства. Математика при этом
позволяет давать точную формулировку возникающих проблем, уточ-
нять понятия, проверять соответствие теоретических положений с ре-
альным течением явлений. Многим становится ясно, что без совре-
менной математики с развитым логическим и вычислительным аппа-
ратом, с ее символикой был бы невозможен современный прогресс фи-
зики, космонавтики, авиации, метеорологии, радиотехники и других
дисциплин.
196
По-видимому, впервые четко и ясно о математике как языке науки
почти четыреста лет назад сказал великий естествоиспытатель про-
шлого Галилео Галилей. По его словам, философия, т.е. наши пред-
ставления о мироздании, написана в грандиозной книге — природе,
которая открыта для всех и каждого. Но прочесть и понять ее может
лишь тот, кто научился понимать ее язык и знаки, которыми она напи-
сана. Написана же она на математическом языке, а знаки ее — матема-
тические формулы. Несомненно, что с тех пор наука добилась огром-
ных успехов, а роль математики в науке неизмеримо выросла. Многие
успехи техники, экономики, организации производства, естествозна-
ния без широкого использования математики были бы просто невоз-
можны. Один из крупнейших физиков современности В. Гайзенберг
так охарактеризовал место математики в современной теоретической
физике: «Первичным языком, который вырабатывают в процессе ус-
воения фактов, является в теоретической физике обычно язык матема-
тики, а именно математическая схема, позволяющая физикам предска-
зывать результаты будущих экспериментов». (Гайзенберг В Физика и
философия. М., 1963. С. 140—144).
Для общения и выражения мыслей природа наделила людей вели-
чайшим средством — живым разговорным языком, который люди раз-
вили и научились фиксировать с помощью записи.
Язык на протяжении времени не остается неизменным, но приспо-
сабливается к условиям жизни, обогащает словарный запас, выраба-
тывает новые средства для выражения тончайших оттенков мысли, че-
ловеческих эмоций и реальных ситуаций. Мы на протяжении нашей
жизни испытали на себе воздействие развития языка. Чтобы убедиться
в этом, достаточно вспомнить, что сейчас уже обыденными стали сло-
ва колхозник, телевизор, спутник и многие другие. И тем не менее, не-
смотря на всю свою гибкость и многогранность, во многих случаях он
оказывается недостаточным и даже больше — неудовлетворительным —
средством общения. В различных областях деятельности вырабатыва-
ются как бы свои собственные языки, специально приспособленные
для точного и краткого выражения мыслей, системы действий, правил
поведения, свойственных определенным видам человеческой деятель-
ности. Для примера, хирург во время операции обращается к своим
помощникам совсем не так, как в обычном разговоре. Он произносит
отдельные слова, почти не пользуется сказуемыми. При постройке судов,
погрузке пароходов тоже говорят так, что непривычному человеку можно
и не понять, что хотят специалисты. Приведем еще один пример.
При выдаче рабочего задания на изготовление того или иного изде-
лия техники никогда не ограничиваются только словесным описанием.
Такое описание недостаточно определенно и грозит тем, что исполни-
197
тель может допустить разного рода ошибки. Для уточнения размеров,
формы и иных особенностей изделия необходим в первую очередь
чертеж, в котором указаны все необходимые размеры. В какой-то мере
чертеж является тем своеобразным языком, который приспособлен для
передачи необходимой информации, которую желает и должен сооб-
щить конструктор исполнителю. Чертеж не допускает разночтений и
позволяет в наглядной форме передавать огромную информацию, не-
обходимую для успешного выполнения работы. Эта форма общения
несравненно удобнее и экономнее обычной словесной, поскольку сло-
весное описание мало-мальски сложного конструктивного задания
было бы настолько громоздким, что в нем мог бы запутаться и сам ав-
тор. У чертежа имеется еще одно несомненное преимущество: его без
труда прочтет любой специалист, даже не владеющий родным языком
конструктора.
В науке особенно важны ясность и точность выражения мыслей.
Язык науки не должен создавать дополнительных трудностей при вос-
приятии сообщаемой информации, но должен доносить идеи и факты
в однозначном, не допускающем различных толкований виде. Без это-
го требования не может быть науки как системы знаний, не может
быть уверенности в том, что определенное утверждение или предпо-
ложение не было искажено при передаче сообщений или же в процес-
се рассуждений. Необходимо также предусмотреть все мыслимые ис-
ходы и не пропустить каких-либо возможностей, оставшихся за бор-
том перечисленных. Научное изложение должно быть кратким и
вполне определенным. Именно поэтому наука должна разрабатывать
собственный язык, способный максимально точно передавать свойст-
венные ей особенности. Вспомним, как четок и лаконичен язык хими-
ческих формул. Он позволяет химикам не только записывать ход хи-
мических процессов, но и предвидеть возможные соединения. Однако
этот язык, несмотря на всю его важность, не распространяется на дру-
гие области знания. В этом отношении язык математических формул
обладает несравненно большей универсальностью. Об этом прекрасно
было сказано французским физиком нашего века Луи де Бройлем:
»...где можно применить математический подход к проблемам, наука
вынуждена пользоваться особым языком, символическим языком, сво-
его рода стенографией абстрактной мысли, формулы которой, когда
они правильно записаны, по-видимому, не оставляют места ни для ка-
кой неопределенности, ни для какого неточного истолкования». (Де
Бройль Л. По тропам науки. М., 1962. С. 326).
Заметим, что математическая символика не только не оставляет
места для неточности выражения мысли и расплывчатого истолкова-
ния написанного, но позволяет вдобавок автоматизировать проведение
198
тех действий, которые необходимы для получения выводов. Мы про-
иллюстрируем эту мысль на двух простых примерах.
На протяжении XII — XVI вв. позиционная десятичная система за-
писи чисел завоевывала мир. Рассказывая о занятиях К. Маркса мате-
матикой, мы имели возможность привести его высокую оценку изо-
бретения этой системы для человечества. Пусть, для примера, нам
нужно сложить числа 3,1415926535 и 2,7182818284.
Обычным с первых лет школьной жизни способом мы находим, что
искомая сумма равна 5,8598744819. Десятичная позиционная система
записи обладает многими удобствами, в том числе и приспособленно-
стью к проведению арифметических операций. Фактически действия
сложения и вычитания производятся точно так же, как они производи-
лись с помощью простейшего арифметического инструмента — счет-
ной доски или русских счет. Мы уже говорили о том, что пользование
счетной доской по сути дела рано или поздно должно было привести к
десятичной позиционной системе счисления, однако люди этого не
замечали в течение столетий, если даже не тысячелетий.
Прежние системы записи чисел — старославянская с помощью
букв алфавита и римская — такими операционными возможностями
не обладали. Ведь при сложении двух чисел, записанных по римской
системе, — MMDCXXV и CCCXXIII — мы лишены оперативной на-
глядности. Еще хуже со сложением чисел в старославянской записи.
Для примера, числа 372 и 963 имеют такие записи в славянских обо-
значениях ТОВ и ЦЕГ. Спрашивается, разве эти обозначения помо-
гают действиям сложения, вычитания, а тем более умножения и деления?
Для множества очень важных вопросов строительной механики,
геодезии, физики, экономики, разных вопросов инженерного дела их
математическая формулировка сводится к решению систем линейных
алгебраических уравнений с соответствующим числом неизвестных.
Очень часто число этих уравнений весьма велико — семьсот, тысяча и
даже больше. В школьном обучении все учащиеся прошли через прак-
тику решения систем, состоящих из двух или трех уравнений, знают,
что в привычной алгебраической символике необходимые действия
осуществляются достаточно просто и трудности возникают лишь в
том случае, когда решающий допускает небрежность и совершает
ошибку. Более того, нет необходимости каждый раз производить ка-
кие-то особые рассуждения, поскольку они выполнены раз и навсегда
для всех подобных систем. Применение набора стандартных правил
позволяет без принципиальных затруднений довести решение каждой та-
кой задачи до конца. Конечно, и здесь тяготит «проклятие размерности» —
чем больше уравнений и соответственно неизвестных, тем технически
199
сложнее решение. Для современных же вычислительных машин тут
появляются трудности иного характера: поскольку машина производит
вычисления с определенной точностью, с увеличением числа операций
накапливаются ошибки вычислений.
Представим себе теперь на минуту, что мы лишены языка матема-
тических символов и в нашем распоряжении имеется только обычный
разговорный язык. В таком положении находятся, например, все, кто
должен решать алгебраические задачи арифметическими средствами.
При этом возникают немедленно ненужные осложнения. Каждая зада-
ча становится особой проблемой, для которой нужно разрабатывать
специальную систему рассуждений. Самый простой вопрос уже требу-
ет значительного умственного напряжения. Вспомним, как просто ре-
шаются сложные арифметические задачи, когда для их решения ис-
пользуются простейшие алгебраические символы, и как сложно ре-
шать их чисто арифметическим путем. А ведь мы рассмотрели сейчас
одну из самых простых задач, с которыми постоянно приходится стал-
киваться и в теории, и в практической деятельности.
В качестве второго примера рассмотрим вычисление площадей и
объемов, длин дуг и поверхностей. За две с лишним тысячи лет были
решены лишь несколько таких задач — были найдены площади пря-
моугольника, треугольника и, значит, площади любых многоугольни-
ков, а также круга и сегмента параболы. С открытием же интегрально-
го исчисления разыскание площадей, длин дуг, объемов тел преврати-
лось в чисто техническую проблему. Известно, что Кеплер нашел объ-
емы более восьмидесяти тел вращения. Если в древности разыскание
площади сегмента параболы потребовало гения Архимеда, то теперь
площади куда более сложных фигур способен разыскать любой сту-
дент высшего технического учебного заведения на втором году обучения.
Математическая символика позволяет выполнять и ряд других
функций: сжимать запись информации, делать ее легко обозримой, а
также удобной для последующей обработки. Это относится ко всей
математике, во всех ее разделах. Для примера, обширные статистиче-
ские сведения удается посредством таблиц и аппроксимирующих рас-
пределений сжать в короткую табличку или же в одну строку формулы.
В последние годы появилась новая линия в развитии формальных
языков, связанная с вычислительной техникой и использованием ЭВМ
для управления производственными процессами, информационными
системами, линиями связи, а также для решения экономических и ор-
ганизационных задач. При этом необходимо осуществить общение с
машиной, надо разработать такие правила, которые позволяли бы ей
самой в каждый момент самостоятельно выбирать правильное в дан-
ных условиях действие. Но машина не понимает обычную человече-
200
скую речь, с ней нужно проводить диалог на доступном ей языке. Этот
язык не должен допускать разночтений, неопределенности, недоста-
точности или чрезмерной избыточности сообщаемой информации. В
настоящее время разработан ряд формальных языков, с помощью ко-
торых машина однозначно воспринимает сообщаемую ей информацию
и действует с учетом создавшейся обстановки. Понятно, что сам про-
цесс управления производится не посредством только формальных
языков, но в первую очередь на базе разработанной математической
модели самого явления. Оба эти момента и делают электронные вы-
числительные машины столь гибким инструментом при выполнении
сложнейших вычислительных работ и при проведении последователь-
ностей логических операций.
Теперь вполне естественно задать себе следующий вопрос: не при-
ведут ли использование формальных языков н математизация наук к
отмиранию обычного языка в научных исследованиях и в практиче-
ском общении людей? Об этом мечтал еще Г. Лейбниц, когда считал,
что придет время и люди станут разрешать все спорные вопросы путем
вычислений. Мы, однако, должны дать на поставленный вопрос отри-
цательный ответ, поскольку как формальные языки, так и наш повсе-
дневный язык имеют лишь ограниченные возможности. У каждого из
них имеются свои сильные и слабые стороны. В результате каждая от-
расль науки, каждый вид деятельности, в том числе и общение между
людьми, вынуждены использовать и символические и обычные языки.
Чтобы проследить мысль собеседника во всех тонкостях, недостаточен
только математический язык формул, необходимы также пояснения,
изложенные на обычном разговорном языке. Мы знаем, что если бы
мы приступили к изложению курса математики в школе или педагоги-
ческом институте и пользовались только языком математических сим-
волов, то нас никто бы не понял и никто из наших учеников не узнал
бы, куда его ведут. Точно так же, если бы мы попытались изложить
тот же курс без математических символов и использовали только раз-
говорный язык, то и из этого ничего бы не получилось, но уже по дру-
гой причине. Дело в том, что язык формул прекрасно приспособлен к
получению логических следствий из первичных предпосылок, но он не
может вывести нас за пределы уже сложившихся понятий и представ-
лений. На математическом языке невозможно проведение далеко иду-
щих аналогий (но он может быть и действительно является полезным
для их получения) или неожиданных индуктивных выводов. Так его
сила превращается в какой-то степени в слабость. И здесь ему на по-
мощь приходит обычный неформализованный язык с его неисчерпае-
мым богатством оттенков и возможностей. В еще большей степени
сказывается сила обычного языка при выражении эмоций. В полной
201
мере сила неформализованного и формализованного математического
языков проявляется лишь при их совместном использовании. Тогда
удается подметить далеко идущие аналогии между явлениями и
имеющимися закономерностями, выясняется, что разные по своему
физическому характеру процессы подчиняются одним и тем же мате-
матическим законам.
Сейчас уместно сказать, что система математических знаков выра-
батывалась на протяжении столетий и удивительно, что многие при-
вычные нам всем обозначения, такие, как +, -, л, е и ряд других, поя-
вились сравнительно недавно. Так, знаки + и - были введены в упот-
ребление в Германии в XV в., а до этого употреблялись многие другие
обозначения, например р и т (от латинских слов plus и minus). Число п
было введено в употребление в 1706 г. английским математиком Джон-
сом, а число е свое обозначение получило от Л. Эйлера в 1736 г. Вообще
Л. Эйлер ввел ряд удачных обозначений, которые прижились и оста-
лись навсегда в науке и в практических применениях. Так, ему при-
надлежат обозначения i - -J-1, sinx, cosx, tgx, Ax —для прираще-
ния аргумента, Е для обозначения суммы, Дх) для обозначения функ-
ции. Знак lim для обозначения предела появился и вошел в употреб-
пение только в XX в., а еще у У. Гамильтона (1805—1865) обозначе-
ние было несколько иным, lim, которое не подчеркивает изменение
Я-®
аргумента п до бесконечности (или до другого предельного значения),
а считает п актуально бесконечным. Для школьного преподавателя по-
лезно знать, что обозначение степени а* было введено в 1637 г Р. Де-
картом (1596—1650), а корня Va — чешским математиком К. Ру-
дольфом (ок. 1500—1545). Для логарифма обозначение log в 1634 г.
ввел И. Кеплер (1571—1630). Символ arcsin х был введен лишь в 1772 г.
Ж. Лагранжем (1736—1813); им же были введены обозначения у’ и
/*{х) для производной (1770). Символы умножения и деления (• и :)
принадлежат Г. Лейбницу (1646—1716): второй символ был им пред-
ложен в 1684 г., а первый — в 1698. Знак абсолютной величины |а|
принадлежит К. Вейерштрассу (1815—1897), он ввел его в 1841 г.
Укажем еще на три символа =, < и >. Первый из них был предложен в
1557 г. английским математиком и врачом Р. Рекордом (1510—1558), а
два остальных — в 1631 г. английским математиком Т. Гарриотом
(1560—1621).
Мы не будем перечислять дальше даты рождения символов, кото-
рые уже укоренились в математике и широко используются в школь-
ной практике. Это тема особого разговора
202
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
Мы уже упоминали раньше о том, что, прежде чем какое-нибудь
явление природы, технический (или вообще какой-нибудь) процесс
подвергнуть математическому изучению, его упрощают, т.е. из всего
многообразия свойств, присущих явлению, вводят в рассмотрение
лишь некоторую их часть, а также делают некоторые предположения о
связях между характеристиками самого явления и внешней средой.
Такая упрощенная схема явления, или, как принято теперь говорить,
его модель, подвергается математической обработке. Чтобы модель
могла бьпъ изучена, вводятся в рассмотрение характеристики явления,
или, как принято говорить в инженерном деле, определяющие явление
параметры. Эти параметры могут быть числами, векторами, тензора-
ми, функциями и т.д.
В том случае, если для двух или нескольких явлений модели с фор-
мальных позиций оказываются одинаковыми, их математическое изу-
чение ничем не отличается, их математические модели совпадают.
Одновременно заслуживает быть отмеченным и то обстоятельство, что
для одного и того же явления можно создать не одну, а несколько раз-
личных моделей. История науки оставила нам в наследство множество
примеров такого рода. Скажем, в оптике рассматривались несколько
моделей распространения света: корпускулярная, волновая, электро-
магнитная. Для них были чисто математическим путем выведены мно-
гочисленные важные закономерности количественного характера, и
эти закономерности хорошо подтверждались экспериментальным пу-
тем. Каждая из названных моделей требовала особого математическо-
го подхода для своего развития и соответствующих специфических
математических средств исследования. Так, корпускулярная (геомет-
рическая) оптика использовала средства евклидовой геометрии и при-
вела к выводу законов преломления и отражения лучей света. Волно-
вая модель теории света потребовала новых математических идей —
рассмотрения тригонометрических функций — как для подтверждения
уже известных результатов, так и для вывода новых (явлений интер-
ференции и дифракции). Чисто аналитическим путем были открыты
первичные результаты, относящиеся к интерференции и дифракции,
которые ранее опытным путем не наблюдались. Волновая теория на-
вела на те эксперименты, которые блестяще подтвердили большую
близость этой модели к реальности. Геометрическая же оптика оказа-
лась бессильной для вывода новых явлений. Так были получены вес-
кие аргументы в пользу волновой теории. Однако корпускулярная мо-
дель распространения света не отмерла. Для определенного круга задач
она в вычислительном отношении даже предпочтительнее волновой.
203
Полезно еще раз подчеркнуть то, что модель не тождественна явле-
нию, она только дает некоторое приближенное представление об его
структуре. Эта модель может быть на первый взгляд очень грубой по
сравнению с полной жизни и разнообразия красок реальностью и тем
не менее давать вполне удовлетворительное описание действительно-
сти. Вспомним, что небесная механика со времени И. Кеплера н И. Нью-
тона исходила из такой модели устройства Солнечной системы: Солн-
це и планеты представляют собой материальные точки с соответст-
вующими массами и между ними действуют силы тяготения по закону
тхт2
г*
, где F|.2 — сила тяготения между небесными телами 1
и 2 с массами т{ и т2 и расстоянием между ними, равным r.f— посто-
янная тяготения. Материальные точки, моделирующие планеты, рас-
положены в их центрах тяжести.
Как ни груба такая модель на первый взгляд, она вполне удовле-
творительно описывает движения планет и дает возможность прогно-
зировать взаимное их положение на небосводе. Более того, за послед-
ние полтора столетия она дважды позволила путем вычислений пред-
сказать наличие в мире неизвестных планет Солнечной системы, до
того не наблюдавшихся астрономами. Исходя из «неправильностей» в
движении крайних планет Солнечной системы, было сделано предпо-
ложение, что они вызваны наличием еще одной неизвестной планеты.
Сравнив фактические отклонения с теми, которые получались в пред-
положении существования еще одной планеты, удалось вычислить не-
известные массу, расстояние до Солнца и положение на небосводе ги-
потетической планеты в заранее указанный момент. Так в 1846 г. была
открыта планета Нептун в результате вычислений, выполненных неза-
висимо друг от друга У. Неверье и Дж. Адамсом. Подобные же вычис-
ления, выполненные П. Лоуэлом, привели в 1930 г. к открытию девя-
той планеты Солнечной системы, получившей название Плутон.
Эта модель продолжает превосходно служить познанию и теперь, в
период начала космических исследований. Однако отсюда совсем не
следует, что она будет достаточна для всех случаев, которые встанут
перед наукой. Несомненно, что уже и сейчас имеются задачи, в кото-
рых эта первичная модель небесной механики недостаточна и требует
модификации или полной перестройки. Так, уже в начале нашего века
ньютоновско-кеплеровская модель строения Солнечной системы не
смогла объяснить возмущений в движении ближайшей к Солнцу пла-
неты Меркурий. Эти объяснения позволила найти молодая тогда част-
ная теория относительности А. Эйнштейна.
Заметим, что для науки мало создать математическую модель явле-
ния, т.е. перечислить исходные положения теории, необходимо найти
204
тот математический язык, на котором удается описать в точных коли-
чественных терминах эту модель. Для описанной нами модели Сол-
нечной системы такими терминами явились понятия математического
анализа и аналитической механики. Недаром Ньютону принадлежат
решительные шаги в создании той и другой ветвей математической
науки. Это, так сказать, исходный пункт существования математиче-
ской модели явления. Далее необходимо получить из сделанных пред-
посылок логические выводы. В рассмотренном нами примере модели
Солнечной системы такие выводы были получены в небесной механи-
ке — науке о движении небесных тел, принадлежащих Солнечной сис-
теме. Затем необходимо убедиться в том, что выводы развитой теории
подтверждаются действительностью (опытом, наблюдениями). Модель
явления хороша тем, что при ее опытной проверке мы можем прове-
рять каждую из четко сформулированных предпосылок.
Создание математической модели — важный этап познания, по-
скольку он позволяет четко формулировать наши представления о
структуре явления, характерных его особенностях, действующих в нем
связях. Мы перечисляем сделанные нами предположения, и в ходе
опытной проверки или же при сравнении реального течения процесса с
вычисленным на базе предположений модели у нас появляется воз-
можность оценить качество модели, так же как и каждого из сделан-
ных предположений.
Остановимся теперь на одном иллюстративном примере, связанном
с решением несложной, но важной инженерной задачи. В связи со зна-
чительной ролью технических систем в жизни общества все большее
значение придается в наше время увеличению надежности изделий
техники. Это достигается различными путями, одним из которых явля-
ется резервирование, т.е. введение излишних для работы изделия эле-
ментов. Эти дополнительные элементы вводятся в техническую систе-
му с одной-единственной целью — чтобы они вступали в работу в тот
момент, когда основной элемент системы откажет. Запасное колесо ав-
томобиля является как раз таким резервным элементом. Если вдобавок
отказавший элемент направляется сразу на восстановление, то такие
системы называются резервированными системами с восстановлени-
ем. Говорят, что резервированная система с восстановлением отказы-
вает тогда, когда основной элемент и все резервные окажутся в нера-
бочем состоянии. Задача, которая при этом возникает, состоит в сле-
дующем: насколько резервирование с восстановлением увеличивает
длительность безотказной работы системы?
Понятно, что так поставленная задача еще не представляет собой
математического вопроса, поскольку нам, в сущности, еще ничего не-
известно. Пока это только словесная формулировка. У нас же еще нет
205
базы, на которой мы можем строить логические рассуждения и выво-
дить формулы, пригодные для инженерных расчетов. Нам нужно
сформулировать математическую модель задачи. Само собой разуме-
ется, что она не может быть взята «с потолка», в ее основе должны
быть ранее проведенные наблюдения и инженерный опыт. В результа-
те длительных обсуждений с учетом длительных наблюдений и экспе-
риментов была предложена следующая математическая модель, кото-
рая теперь широко принята.
1. Длительность безотказной работы элемента является случайной
величиной с некоторым распределением вероятностей F(x).
2. Длительности безотказной работы последовательно включаемых
элементов — независимые случайные величины с одним и тем же рас-
пределением вероятностей.
3. Отказ элемента обнаруживается немедленно.
4. После отказа элемент немедленно направляется в ремонт.
5. Длительность ремонта — случайная величина, с некоторым рас-
пределением вероятностей G(x).
6. Если имеется хотя бы один исправный элемент, замена
отказавшего элемента на исправный происходит мгновенно.
7. Отремонтированный элемент немедленно поступает в резерв.
8. Длительность ремонта не зависима от того, как долго продол-
жался работоспособный период элемента, и от того, сколько ремонтов
осуществило восстанавливающее устройство.
9. Ремонт полностью восстанавливает свойства элемента.
Только что сформулированные предпосылки составляют математи-
ческую модель нашей задачи. Она уже может служить основой для не-
обходимых выводов.
В приведенной нами модели особую неудовлетворенность могут
вызвать пункты 4, 7, 9. Действительно, мы знаем, что каждая замена
неисправного элемента на исправный требует некоторого, порой даже
значительного, времени. Для того чтобы заменить у автомобиля коле-
со на запасное, нужно поднять на домкрате кузов автомобиля, отвер-
нуть гайки, снять колесо, надеть сменное, вновь закрутить гайки и
спрятать запаску в багажник. Точно так же направление в ремонт осу-
ществляется не мгновенно. Девятый пункт нашей модели предполага-
ет полное восстановление свойств отремонтированного элемента. К
сожалению, такое возможно только в течение сравнительно короткого
срока. Так, известно, что средняя длительность безотказной работы
отремонтированного автомобиля составляет лишь около 60% от сред-
ней длительности безотказной работы нового автомобиля. Можно из-
менить эти пункты модели и тем самым несколько усложнить модель,
а также полученные на ее основе результаты. Однако во многих случа-
206
ях рассмотренная нами модель дает вполне удовлетворительные ре-
зультаты, хорошо описывает реальную обстановку и дает возмож-
ность получать полезные для практики формулы и качественные
выводы. Мне известно, что эта модель нашла применение в ряде
ответственных задач управления технологическими процессами на
химических предприятиях, устройств практически безотказного
электроснабжения ответственных участков (операционных систем
управления и пр.)
Одной из самых древних математических моделей, несомненно,
является геометрия Евклида. Это модель окружающего нас простран-
ства и находящихся в нем предметов. Эта модель создавалась на про-
тяжении тысячелетий и несет безотказную службу человеческому зна-
нию в настоящее время, так же как будет ее нести и в будущем. Мате-
матические прямые, поверхности, линии, тела являются ни чем иным,
как отвлечением от реальных прямых, поверхностей тел, линий, про-
странственных предметов. Этот процесс отвлечения от наблюдаемой
реальности продолжался длительный срок и оказался очень полезным
для практической деятельности. История математики дает описание
того, как геометрические понятия возникли из практических задач из-
мерения полей, расстояний, подсчета объемов зернохранилищ. В связи
с этим становится непонятным утверждение А. Эйнштейна, помещен-
ное в его книге «Геометрия и опыт»: «...перед нами возникает загадка,
которая столь беспокоила исследователей всех времен. Почему
возможно такое превосходное соответствие математики с действитель-
ными предметами, если сама она является произведением только че-
ловеческой мысли, независимо от всякого опыта? Может ли человече-
ский разум без всякого опыта, путем только одного размышления, от-
крыть основу существующих вещей?»
Несомненно, что математика, в том числе и геометрия, является аб-
страктной наукой, предметом изучения которой являются объекты,
определяемые теми свойствами, которые им приписываются в опреде-
лениях и аксиомах. Однако сами эти определения и аксиомы появля-
ются не по свободной воле ученых, а на основе абстрагирования от
свойств реальных вещей. Именно это обстоятельство позволяет мате-
матике отражать в своих результатах свойства окружающего нас мира.
При создании науки царит не произвол с введением понятий, а глубо-
кий процесс отвлечения от несущественных (по тем или иным призна-
кам) характеристик явления. Для примера, геометрическое понятие
шара отвлечено от всех реальных свойств тел, выполненных из какого-то
материала — дерева, пластмассы, металла; от их массы, плотности,
упругих свойств и т.п. Мы отвлекаемся от всего этого и даже от реальной
формы, а придаем геометрическим телам идеальную форму. Это
207
позволяет нам делать выводы, относящиеся не только к идеализиро-
ванному шару, но и к реальным шарам
Точно так же понятие числа появилось в результате счета окру-
жающих нас предметов. Это абстрактная модель числа предметов. Она
создавалась на протяжении тысячелетий. Эту модель создали люди в
результате практической деятельности и абстрагирующей деятельно-
сти разума. Этот факт следует из наблюдений над первобытными пле-
менами, изучения материальной культуры народов прошлого, всего
здания истории математики. Удивительными в связи с этим кажутся
высказывания ряда далеко не ординарных представителей прошлого,
которые мы сейчас приведем.
Беркли (епископ): «Целые числа — это знаки, которые бог дал
людям, чтобы они правильно распоряжались вещами».
Кант (философ): «Понятие числа — врожденное понятие, кото-
рым человек располагает до всякого опыта».
Гельмгольц (физик): «На числа мы должны смотреть прежде
всего, как на ряд произвольно выбранных знаков».
Дедекинд (математик): «Понятие числа я считаю совершенно
независимым от представлений и воззрений на пространство и время:
для меня оно чистый продукт законов нашей мысли; числа суть сво-
бодные создания человеческого духа и они служат средством, дающим
нам легче и яснее постигать различие вещей».
Кронекер (математик): «Целые числа создал Господь Бог, все
остальное — дело рук человеческих».
С такими позициями мириться никак нельзя, не только потому, что
они ошибочны, но и потому, что они уводят мысль от необходимости
искать истинное происхождение вещей, мешают и в настоящем стро-
ить правильные пути решения стоящих перед человечеством задач. Я
приведу здесь слова профессора Московского университета М. Панке-
вича, произнесенные им 30 нюня 1792 г. в торжественной речи «Слово
о подлинной цели математических наук»:
«Отведенный от природы отвлеченными умозрениями, обольстив-
шийся ими до такой степени, что, забавляясь оными, не думал бы уже
больше о самих вещах, к рассмотрению коих первые должны быть пу-
тями и средством, подобен бы был тому, кто заставлен будучи уда-
литься на время из своего отечества в другие пределы... не помышлял
бы более о возвращении в оное».
Полезно заметить, что математические модели реальных явлений
базируются на определенных эмпирических фактах, но одновременно
являются результатом прогнозирующей мысли исследователя. Он раз-
мышляет не только о том, что уже известно, но и как может быть объ-
яснено неизвестное. В связи со сказанным мне кажется полезной сле-
208
дующая довольно большая цитата из доклада известного физика В. Гей-
зенберга «Традиции в науке», который он произнес в апреле 1973 г. на
симпозиуме, организованном Смитсоновским институтом и Нацио-
нальной академией наук США по случаю 500-летнего юбилея со дня
рождения Н. Коперника.
«Оглядываясь таким образом на историю, мы видим, что у нас, по-
видимому, очень мало свободы при выборе наших проблем. Ученые
связаны историческим процессом, и выбор их, по-видимому, ограни-
чен принятием решения — участвовать или нет в том развитии, кото-
рое произойдет с ними или без них».
Это важная позиция, которая соответствует концепциям историче-
ского материализма и направлена против позиций свободной воли в
развитии науки и ее понятий.
Далее Гейзенберг сказал:
«Существует всеобщее мнение, что наша наука [физика— Б.Г.] —
эмпирическая и что мы черпаем наши понятия и наши математические
построения из данных опыта. Если бы в этом заключалась вся правда,
то, приступая к изучению новой области, мы должны были бы вводить
лишь такие величины, которые можно непосредственно наблюдать, и
формулировать законы природы лишь посредством этих величин. В
молодости я верил, что именно такой философии следовал Эйнштейн в
своей теории относительности. Но когда я впоследствии спросил об
этом Эйнштейна, он ответил:
«Может быть, в этом и была моя философия. Но это все таки чепу-
ха. Никогда нельзя ограничиться в теории только наблюдаемыми ве-
личинами. Именно теория решает, что можно наблюдать».
В этом замечании он имел в виду, что когда мы переходим от непо-
средственных наблюдений, например черной линии на фотопластинке
или разряда в счетчике, — к явлениям, которые нас интересуют, мы
вынуждены пользоваться теорией и теоретическими понятиями. Мы
не можем отделять эмпирический процесс наблюдения от математиче-
ского построения и его концепции».
На мой взгляд, в этой цитате высказано очень важное суждение, ко-
торое еще не дошло до многих физиков и на которое математики прак-
тически ие обращают внимания. Математическая модель явления не
только создается на базе экспериментальных фактов и связанных с
ними физических теорий, но оказывает и обратное влияние на физику:
когда математическая модель создана, то она в довольно большой мере
определяет, что должно быть определено экспериментатором, какие
опыты следует ставить как для проверки теории, так и для обнаруже-
ния новых явлений, которые предсказывает новая теория В двадцатых
годах прошлого века после доклада, прочитанного О.Ж. Френелем в
15 Зак 72
209
Парижской Академии наук по волновой оптике, присутствующие ма-
тематики немедленно сделали выводы и заявили, что из его теории по-
лучаются такие-то явления, которые нужно подтвердить эксперимен-
том. Эти эксперименты были произведены и блестяще подтвердили
теорию. Вот пример того, как математическая модель заставляет экс-
периментаторов ставить новые опыты, подсказанные ею.
Подобная же картина имеет место не только в физике и в естест-
венных науках, ио и в технике, и в других областях применения мате-
матики: математическая модель в значительной мере предопределяет
тот экспериментальный материал, который следует собирать, а также
ту обработку результатов наблюдений, которую следует производить.
В настоящее время широко используется математическое модели-
рованием тогда, когда о физической структуре явления известно край-
не мало. В этом случае строится гипотетическая модель и на ее основе
выводятся следствия, уже доступные наблюдению. Понятно, что такие
гипотетические модели зачастую не оправдываются опытом. В этом
случае они живут недолго и быстро отмирают, уступив место другим
моделям, позволяющим точнее познать природу вещей. Два года назад
руководимая мной кафедра заключила договорные отношения с ин-
ститутом кабельной промышленности на предмет построения матема-
тической модели старения изоляции электрических кабелей. Модель
была нами предложена, на ее базе была построена математическая
теория и предвычислены те сроки, в которые изоляция должна прийти
в отказовое состояние. Прогнозы оправдались с поразительной точно-
стью. Теперь мы ставим перед собой новые задачи не только теорети-
ческого плана, но и чисто прикладные. В частности, из соображений
теории предложен метод значительного увеличения срока службы
изоляции. Этот вопрос еще не вышел из начальной стадии, но есть все
основания надеяться на успех. В данном примере речь идет как раз о
такой гипотетической модели, поскольку экспериментальные выводы
были весьма скудными.
Ценность гипотетических моделей неоспорима: они активизируют
работу мысли, наводят экспериментаторов на принципиально новые
эксперименты, позволяют продвигаться в познании реального мира и
его явлений. История науки показывает, сколь большую роль сыграли
научные гипотезы и построенные на их основе математические модели
явлений. Вспомним хотя бы гипотезу строения Солнечной системы,
предложенную Коперником. Вспомним, далее, модель строения атома,
разработанную Резерфордом. Эта модель исходила из мысли, что атом
построен примерно так же, как и Солнечная система: вокруг ядра ато-
ма вращаются по своим орбитам электроны. Сама модель оказалась
недостаточной, и дальнейшее развитие науки ее отмело, но она вызва-
210
ла к жизни многочисленные исследования, приведшие к современной
атомной физике и к первым шагам на пути освоения энергии, таящей-
ся в недрах атома.
В настоящее время возникает настоятельная необходимость обра-
тить особое внимание на построение математических моделей в био-
логии, медицине, социальных науках. Они изучают явления исключи-
тельно сложные по своей природе и нуждаются для этого во всех ме-
тодах, как уже разработанных наукой, так и тех, которые еще предсто-
ит разработать. На очереди разработка математических моделей педа-
гогики, ио это сложный и длительный процесс Для педагогических
целей особенно важны модели, в которых разрабатывались бы вопро-
сы, связанные с процессом мышления, сохранения внимания, работы
памяти, поведения коллектива. Пока удовлетворительного решения
этих вопросов еще нет, но если над ними упорно думать, то сдвинется
с мертвой точки наше знание и в этой важнейшей области работы.
%% Колмогоров
АВТОМАТЫ И ЖИЗНЬ*
Мой доклад «Автоматы и жизнь», подготовленный для семинара на-
учных работников и аспирантов механико-математического факультета
Московского государственного университета, вызвал интерес у самых
широких кругов слушателей. Популярное изложение доклада подготов-
лено моей сотрудницей по лаборатории вероятностных и статистических
методов МГУ Н.Г. Рычковой. Изложение это во всех существенных чер-
тах правильно, хотя иногда словесное оформление мысли, а следователь-
но, и некоторые ее оттенки принадлежат Н.Г. Рычковой.
Подчеркну основные идеи доклада, имеющие наиболее широкий
интерес.
I. Определение жизни как «особой формы существования белковых
тел» (Энгельс) было прогрессивно и правильно, пока мы имели дело
только с конкретными формами жизни, развившимися на Земле. В век
космонавтики возникает реальная возможность встречи с «формами
движения материи» (см. статью «Жизнь» в Большой Советской Эн-
циклопедии), обладающими основными практически важными для нас
свойствами живых и даже мыслящих существ, устроенных иначе. По-
этому приобретает вполне реальное значение задача более общего оп-
ределения понятия жизни
II. Современная электронная техника открывает весьма широкие
возможности моделирования жизни в мышления. Дискретный (ариф-
15-
211
метический) характер современных вычислительных машин и автома-
тов не создает в этом отношении существенных ограничений. Системы
из очень большого числа элементов, каждый из которых действует чисто
«арифметически», могут приобретать качественно новые свойства.
Ill. Если свойство той или иной материальной системы «быть жи-
вой» или обладать способностью «мыслить» будет определено чисто
функциональным образом (например, любая материальная система, с
которой можно разумно обсуждать проблемы современной науки или
литературы, будет признаваться мыслящей), то придется признать в
принципе вполне осуществимым искусственное создание живых и
мыслящих существ.
IV. При этом, однако, следует помнить, что реальные успехи ки-
бернетики и автоматики на этом пути значительно более скромны, чем
иногда изображается в популярных книгах и статьях. Например, при
описании «самообучающихся» автоматов или автоматов, способных
«сочинять» музыку или писать стихи, иногда исходят из крайне упро-
щенного представления о действительном характере высшей нервной
деятельности человека и, в частности, творческой деятельности.
V. Реальное продвижение в направлении понимания механизма
высшей нервной деятельности, включая и высшие проявления челове-
ческого творчества, естественно, не может ничего убавить в ценности
и красоте творческих достижений человека. Я думаю, что это и хотела
сказать редакция журнала «Техника — молодежи», сделав лозунг
«Материализм — это прекрасно!» одним из подзаголовков в изложе-
нии моего доклада.
25 августа 1961 г.
Я принадлежу к тем крайне отчаянным кибернетикам, которые не
видят никаких принципиальных ограничений в кибернетическом под-
ходе к проблеме жизни и полагают, что можно анализировать жизнь во
всей ее полноте, в том числе и человеческое сознание со всей его
сложностью, методами кибернетики.
Очень часто задают такие вопросы:
— Могут ли машины воспроизводить себе подобных и может ли в
процессе самовоспроизведения происходить прогрессивная эволюция,
приводящая к созданию машин, существенно более совершенных, чем
исходные?
— Могут ли машины испытывать эмоции: радоваться, грустить,
быть недовольными чем-нибудь, чего-нибудь хотеть?
— Могут ли, наконец, машины сами ставить перед собой задачи,
не поставленные перед ними их конструкторами?
212
Иногда пытаются отделаться от этих вопросов или обосновать от-
рицательные ответы на ннх, предлагая, например, определить понятие
«машина» как нечто, каждый раз искусственно создаваемое челове-
ком. При таком определении часть вопросов, скажем первый, автома-
тически отпадает. Но вряд ли можно считать разумным упорное неже-
лание разобраться в вопросах, действительно интересных и сложных,
прикрываясь насильственно ограниченным пониманием терминов.
Вопрос о том, можно ли на пути кибернетического подхода к ана-
лизу жизненных явлений создать подлинную, настоящую жизнь, кото-
рая будет самостоятельно продолжаться и развиваться, остается на-
сущной проблемой современности. Уже сейчас он актуален, годен для
серьезного обсуждения, ибо изучение аналогий между искусственны-
ми автоматами и настоящей живой системой уже сейчас служит прин-
ципом исследования самих явлений жизни, с одной стороны, и спосо-
бом, помогающим изыскивать пути создания новых автоматов — с
другой.
Есть и другой способ сразу ответить иа все эти вопросы. Он заклю-
чается в ссылке иа математическую теорию алгоритмов. Математикам
хорошо известно, что в пределах каждой формальной системы, доста-
точно богатой математически, можно сформулировать вопросы, кото-
рые кажутся содержательными, осмысленными и должны предпола-
гать наличие определенного ответа, хотя в пределах данной системы
такого ответа найти нельзя. Вот поэтому-то и провозглашается, что
развитие самой формальной системы есть задача машины, а обдумы-
вание правильного ответа на вопрос — это уже дело человека, пре-
имущественное свойство человеческого мышления.
Такая аргументация, однако, использует идеализированное толко-
вание понятия «мышление», с помощью которого можно легко дока-
зать, что не только машина, но и сам человек мыслить не могут. Здесь
предполагается, что человек может давать правильные ответы на лю-
бые вопросы, в том числе и на поставленные неформально, а мозг че-
ловека способен производить неограниченно сложные формальные
выкладки. Между тем нет никаких оснований представлять себе чело-
века столь идеализированным образом — как бесконечной сложности
организм, в котором умещается бесконечное количество истин. Чтобы
достичь такого положения, заметим в шутку, пришлось бы расселить
человечество по звездным мирам, чтобы, пользуясь бесконечностью
мира, организовать формальные логические выкладки в бесконечном
пространстве и даже передавать их по наследству. Тогда можно было
бы считать, что любой математический алгоритм человечество может
развить до бесконечности.
Но вряд ли эта аргументация имеет отношение к реальному вопро-
су. И уж во всяком случае это не возражение против постановки во-
213
проса о том, возможно ли создание искусственных живых существ,
способных к размножению и прогрессивной эволюции, в высших
формах обладающих эмоцией, волей и мышлением.
Этот же вопрос поставлен изящно, но формально математиком
Тьюрингом в его книге «Может ли машина мыслить?». Можно ли по-
строить машину, которую нельзя было бы отличить от человека? Такая
постановка как будто ничуть не хуже нашей и к тому же проще и ко-
роче. На самом же деле она не вполне отражает суть дела. Ведь, по
существу, интересен не вопрос о том, можно ли создать автоматы,
воспроизводящие известные нам свойства человека; хочется знать,
можно ли создать новую жизнь, столь же высокоорганизованную, хо-
тя, может быть, очень своеобразную и совсем непохожую на нашу. В
современной научной фантастике сейчас появляются произведения,
затрагивающие эти темы. Интересен и остроумен рассказ «Друг» в
сборнике Станислава Лема «Вторжение с Альдебарана» о машине,
пожелавшей управлять человечеством. Однако фантазия романистов
не отличается особой изобретательностью. И. А. Ефремов, например,
выдвигает концепцию, что «все совершенное похоже друг на друга».
Стало быть, у высокоорганизованного существа должны быть, по его
мнению, два глаза и нос, хотя, может быть, и несколько измененной
формы. В век космонавтики не праздно предположение, что нам, воз-
можно, придется столкнуться с другими живыми существами, весьма
высокоорганизованными и в то же время совершенно на нас непохо-
жими. Сможем ли мы установить, каков внутренний мир этих существ,
способны ли они к мышлению, присущи ли им эстетические пережи-
вания, идеалы красоты или чужды и т.п. Почему бы, например, высо-
коорганизованному существу не иметь вид тонкой пленки — плесени,
распластанной на камнях?
Что такое жизнь? Возможно ли искусственное разумное суще-
ство? Поставленный нами вопрос тесно связан с другими: а что такое
жизнь, что такое мышление, что такое эмоциональная жизнь, эстети-
ческие переживания? В чем, скажем, состоит отличие последних от
простых элементарных удовольствий — от пирога, например, или еще
чего-нибудь в этом роде? Если говорить в более серьезном тоне, то
можно сказать следующее: точное определение таких понятий, как во-
ля, мышление, эмоции, еще не удалось сформулировать. Но на естест-
веннонаучном уровне строгости такое определение возможно. Если
мы не признаем эту возможность, мы окажемся безоружными против
аргументов солипсизма.
Хотелось бы научиться на основании фактов поведения, например,
делать выводы о внутреннем состояния живого высокоорганизованно-
го существа.
214
Как изучать высшую нервную деятельность, используя кибернети-
ческий подход? Здесь открываются следующие пути; во-первых, мож-
но детально изучать само поведение животных или человека; во-
вторых, изучать устройство их мозга; можно, наконец, иногда доволь-
ствоваться и так называемым симпатическим пониманием. Если, ска-
жем, просто внимательно наблюдать кошку нли собаку, то, и не зная
науки о поведении и условных рефлексах, можно прекрасно понять,
что они думают и чего хотят. Несколько труднее достигнуть такого
понимания с птицами или, например, с рыбами, но вряд ли и это не-
возможно. Это вопрос не новый, частично он уже решен, частично
легко решаем, частично — трудно. Опыт индуктивного развития науки
говорит нам, что все вопросы, долго не находившие решения, посте-
пенно разрешаются, и вряд ли нужно думать, что именно здесь суще-
ствуют заранее установленные пределы, дальше которых продвинуть-
ся нельзя.
Если считать, что анализ любой высокоорганизованной системы
естественно входит в состав кибернетики, придется отказаться от рас-
пространенного мнения, что основы кибернетики включают в себя
лишь изучение систем, имеющих заранее назначенные цели. Часто ки-
бернетику определяют как науку, занимающуюся изучением управ-
ляющих систем. Считается, что все такие системы обладают общими
свойствами и свойство номер один у них — наличие цели. Это верно
лишь до тех пор, пока все, что мы выделяем в качестве организован-
ных систем, управляющих собственной деятельностью, похоже на нас
самих. Однако если мы хотим методами кибернетики изучать проис-
хождение таких систем, их естественную эволюцию, то такое опреде-
ление становится узким. Вряд ли кибернетика поручит какой-либо
другой науке выяснять, каким образом обычная причинная связь в
сложных системах путем естественного развития приводит к возмож-
ности рассматривать всю систему как действующую целесообразно.
Обычно понятие «действовать целесообразно» включает умение
охранять себя от разрушающих внешних воздействий или, скажем,
способность содействовать своему размножению. Спрашивается: кри-
сталлы действуют целесообразно или нет? Если «зародыш» кристалла
поместить в некристаллическую среду, будет ли он развиваться? Ведь
никаких отдельных органов у кристалла различить невозможно, стало
бьггь, это есть некая промежуточная форма. И существование таковых
неизбежно.
По-видимому, частные задачи, подобные этой, будут решать науки,
непосредственно с ними связанные. Опытом частных наук никак нель-
зя пренебрегать. Но исключить из содержания кибернетики общие
представления о причинных связях в целесообразно действующих сис-
215
темах, ставящих себе цели, так же нельзя, как нельзя, например, уже
при имитации жизни автоматами не считаться, скажем, с тем, что и
сами эти цели меняются в процессе эволюции, а вместе с этим изменя-
ется и представление о них.
Когда говорят, что организация механизма наследственности, по-
зволяющего живым организмам передавать свое целесообразное уст-
ройство потомкам, имеет целью воссоздать данный вид, придать ему
определенные свойства, а также возможности изменчивости, прогрес-
сивной эволюции, то кто же ставит эту цель? Или если рассматривать
систему в целом, то кто же, как не она сама, ставит перед собой цель
развития путем отсеивания негодных экземпляров и размножения со-
вершенных?
Подводя итоги, можно сказать, что изучение в общей форме воз-
никновения систем, в которых применимо понятие целесообразности,
есть одна из главных задач кибернетики. При этом изучение в общей
форме естественно предполагает знание, отвлеченное от деталей фи-
зического осуществления, от энергетики, химии, возможностей техни-
ки и т.п. Нас здесь интересует только, как возникает возможность со-
хранять и накапливать информацию.
Такая широкая постановка задачи содержит в себе много трудно-
стей, но отказаться от нее на современном этале развития науки уже
невозможно.
Если признавать важность задачи определения в объективных
обобщенных терминах существенных свойств внутренней жизни
(высшей нервной деятельности) какой-то незнакомой нам и непохожей
на нас высокоорганизованной системы, то нельзя ли тот же путь пред-
ложить и в применении к нашей системе — человеческому обществу?
Хотелось бы на общем языке, одном и том же для всех высокооргани-
зованных систем, уметь описывать и все явления жизни человеческого
общества. Представим себе воображаемого постороннего наблюдателя
иашей жизни, который совершенно не обладает ни симпатиями к нам,
ни умением понять, что мы думаем и переживаем. Он просто наблю-
дает большое скопление организованных существ и желает понять, как
оно устроено. Совершенно так же, как, скажем, мы наблюдаем мура-
вейник. Через некоторое время он, пожалуй, без особого труда сможет
понять, какую роль играет информация, содержащаяся, например, в
железнодорожных справочниках (человек теряет такой справочник и
не может попасть иа нужный поезд). Правда, наблюдателю пришлось
бы столкнуться с большими трудностями. Как, например, понять ему
следующую картину: множество людей приходит вечером в большое
помещение, несколько человек поднимаются на возвышение и начи-
нают делать беспорядочные движения, а остальные сидят при этом
216
спокойно; по окончании люди расходятся без всякого обсуждения.
Один из молодых математиков, может быть в шутку, приводит и дру-
гой пример необъяснимого поведения: люди заходят в помещение, там
получают бутылки с некоей жидкостью, после чего начинают бес-
смысленно жестикулировать. Постороннему наблюдателю будет труд-
но установить, что же это такое — просто разлад в машине, какая-то
пауза в ее непрерывной осмысленной работе, или же можно описать,
что происходит в этих двух случаях, и установить разницу между жми.
Оставив шутливый тон, сформулируем серьезно возникающую
здесь проблему: нужно научиться в терминах поведения осуществлять
объективное описание самого механизма, это поведение обусловли-
вающего, уметь различать отдельные виды деятельности высокоорга-
низованной системы. Впервые в нашей стране И.П. Павлов установил
возможность объективного изучения поведения животных и человека,
а также регулирующих это поведение мозговых процессов без всяких
субъективных гипотез, выраженных в психологических терминах.
Глубокое изучение предложенной проблемы есть не что иное, как пав-
ловская программа анализа высшей нервной деятельности в ее даль-
нейшем развитии.
Создание высокоорганизованных живых существ превосходит воз-
можности техники наших дней. Но всякие ограничительные тенден-
ции, всякое неверие или даже утверждение невозможности на рацио-
нальных путях достичь объективного описания человеческого созна-
ния во всей его полноте сейчас явились бы тормозом в развитии науки.
Разрешение этой проблемы необходимо, ибо уже истолкование разных
видов деятельности может служить толчком для развития машинной
техники и автоматики. С другой стороны, возможности объективного
анализа нервной системы сейчас столь велики, что не хочется заранее
останавливаться перед задачами любой трудности.
Если технические трудности будут преодолены, то вопрос о прак-
тической целесообразности осуществления соответствующей про-
граммы работ останется по меньшей мере спорным.
Однако в рамках материалистического мировоззрения не существу-
ет никаких состоятельных принципиальных аргументов против поло-
жительного ответа на наш вопрос. Более того, этот положительный от-
вет является сейчас современной формой убеждений о естественном
возникновении жизни и материальной основе сознания.
Дискретна или непрерывна мысль? В кибернетике и теории ав-
томатов сейчас наиболее разработана теория работы дискретных уст-
ройств, т.е. таких устройств, которые состоят из большого числа от-
дельных элементов и работают отдельными тактами. Каждый элеменз
может находиться в небольшом числе состояний, и изменение состоя-
14 Зам 72
217
ния отдельного элемента зависит от предыдущих состояний сравни-
тельно небольшого числа элементов. Так устроены электронные ма-
шины, так, предположительно, устроен и человеческий мозг. Считает-
ся, что мозг имеет таких отдельных элементов — нервных клеток —
1О10, а может быть, и еще больше. Несколько проще, но еще более
грандиозно в смысле объема устроен аппарат наследственности.
Иногда делают вывод, что кибернетика должна заниматься лишь
дискретными устройствами. Против такого подхода есть два возраже-
ния. Во-первых, реальные сложные системы — как многие машины,
так и все живые существа — действительно имеют определенные уст-
ройства, основанные на принципе непрерывного действия. Что касает-
ся машин, то таким примером может служить, скажем, руль автомоби-
ля и т.п. Если мы обратимся к человеческой деятельности — созна-
тельной, но не подчиненной законам формальней логики, т.е. деятель-
ности интуитивной или полуинтуитивной, например к двигательным
реакциям, то мы обнаружим, что большое совершенство и отточен-
ность механизма непрерывного движения построены на движениях
непрерывно-геометрического характера. Если человек совершает
тройной прыжок или прыжок с шестом или, например, готовится к
дистанции слалома, его движение должно быть заранее намечено как
непрерывное (для математиков: путь слаломиста оказывается даже
аналитической кривой). Можно полагать, однако, что это не есть ради-
кальное возражение против дискретных механизмов. Скорее всего ин-
туиция непрерывной линии в мозге осуществляется на базе дискретно-
го механизма.
Второе возражение против дискретного подхода заключается в сле-
дующем: заведомо человеческий мозг и даже, к сожалению, часто вы-
числительные машины, отнюдь не всегда действуют детерминирован-
ие — полностью закономерным образом. Результат их действия в не-
который момент (в данной ячейке) нередко зависит от случая. Желая
обойти эти возражения, можно сказать, что и в автоматы можно «вве-
сти случайность». Вряд ли имитирование случайности (т.е. замена
случая какими-то закономерностями, не имеющими отношения к делу)
может принести сколько-нибудь серьезный вред при моделировании
жизни. Правда, вмешательство случайности часто рассматривается не-
сколько примитивно: заготавливается достаточно длинная лента слу-
чайных чисел, которая затем используется для имитации случая в раз-
личных задачах. Но при частом употреблении эта заготовленная «слу-
чайность» в конце концов перестает быть случайностью. Исходя из
этих соображений, к вопросу имитации случая на автоматах следует
подходить с большой осторожностью. Однако принципиально это
вещь во всяком случае возможная.
218
Только что изложенная аргументация приводит нас к следующему
основному выводу.
Несомненно, что переработка информации и процессы управления
в живых организмах построены на сложном переплетении дискретных
(цифровых) и непрерывных механизмов, с одной стороны, детермини-
рованного и вероятностного принципов действия — с другой.
Однако дискретные механизмы являются ведущими в процессах
переработки информации И управления в живых организмах. Не суще-
ствует состоятельных аргументов в пользу принципиальной ограни-
ченности возможностей дискретных механизмов по сравнению с не-
прерывными.
Что такое «очень много»? Часто, сомневаясь в возможности мо-
делировать человеческое сознание на автоматах, говорят, что количе-
ство функций высшей нервной деятельности человека необъятно ве-
лико и никакая машина не может стать моделью сознательной челове-
ческой деятельности в полном ее объеме. Одних только нервных кле-
ток в коре головного мозга Ю10. Каково же должно быть число эле-
ментов в машине, имитирующей всю сложную высшую нервную дея-
тельность человека?
Эта деятельность, однако, связана не с разрозненными нервными
клетками, а с довольно большими агрегатами их. Невозможно пред-
ставить себе, чтобы, скажем, какая-нибудь математическая теорема
«сидела» в одной-единственной, специально для нее заготовленной
нервной клетке или даже в каком-то определенном числе их. По-
видимому, дело обстоит совершенно иначе. Наше сознание оперирует
небольшими количествами информации. Количество единиц инфор-
мации, которое человек воспринимает и перерабатывает в секунду, со-
всем невелико. Вот один несколько парадоксальный пример: слало-
мист, преодолевая дистанцию, в течение десяти секунд воспринимает
и перерабатывает значительно большую информацию, чем при других,
казалось бы, более интеллектуальных видах деятельности, во всяком
случае больше, чем математик пропускает через свою голову за сорок
секунд напряженной работы мысли. Вообще, вся сознательная жизнь
человека устроена как-то очень своеобразно и сложно, но когда зако-
номерности ее будут изучены, для моделирования ее потребуется го-
раздо меньше элементарных ячеек, чем для моделирования всего моз-
га, как это ни удивительно.
Какие же объемы информации могут создавать уже качественное
своеобразие сложных явлений, подобных жизни, сознанию и т.п.?
Можно разделить все числа на малые, средние, большие и сверх-
большие. Эта классификация нестрога, в рамках ее нельзя будет ска-
14-
219
зать, что такое-то число, например, среднее, а следующее за ним —
уже большое. Здесь числа делятся на категории с точностью до поряд-
ка величин. Но большая строгость нам здесь и не нужна. Каковы же
эти категории? Начнем с определений, понятных лишь математикам.
I Число А назовем малым, если практически возможно перебрать
все схемы из А элементов с двумя входами и выходами или выписать
для них все функции алгебры логики с А аргументами.
II Число Б называется средним, если мы оказываемся не в состоя-
нии перебрать практически все схемы из Б элементов, а можем пере-
брать лишь сами эти элементы или (что чуть-чуть сложнее) выра-
ботать систему обозначений для любой системы из Б элементов.
III. И, наконец, число В — большое, если мы не в состоянии прак-
тически перебрать такое число элементов, а можем лишь устано-
вить систему обозначений для этих элементов
IV. Числа будут сверхбольшими, если практически и этого нельзя
сделать; они нам, как мы увидим дальше, и не понадобятся
Поясним теперь эти определения на доступных примерах.
Пусть к одной электрической лампочке подсоединено три выключате-
ля, каждый из которых может находиться в левом (Л) или правом (П) по-
ложении. Тогда, очевидно, возможных совместных положений трех вы-
ключателей будет 23 = 8. Перечислим их для наглядности: 1) ЛЛЛ,
2) ЛПЛ, 3) ЛПП, 4) ЛЛП, 5) ПЛЛ, 6) ППЛ, 7) ПЛП, 8) ППП.
Проводку к нашим выключателям можно сделать таким образом,
что в каждом из выписанных положений лампочка может как гореть,
так и не гореть. Если произвести подсчет, то окажется, что различных
положений выключателей, сопровожденных такими отметками, будет
22’, т.е. 2* = 256. Справедливость этого последнего утверждения чи-
татель без труда может проверить самостоятельно, дополняя выписан-
ные положения выключателей знаками «горит», «не горит».
Тот факт, что такое упражнение под силу читателю и не займет у
него слишком много времени, и убеждает нас в том, что число 3 (чис-
ло выключателей) относится к малым. Если бы выключателей было не
3, а, скажем, 5, то пришлось бы выписать 22’ = 4 294 967 296 различ-
ных совместных положений выключателей, сопровожденных отмет-
ками «горит», «не горит». Вряд ли можно за какое-нибудь разумное
время практически проделать все это не сбившись. Поэтому число 5
уже нельзя считать малым.
Чтобы стал понятен термин «среднее число», приведем другой
пример. Представьте себе, что вас ввели в помещение, где находится
1000 человек, и предложили с каждым из них поздороваться за руку.
Правда, ваша рука после таких упражнений будет чувствовать себя
неважно, но практически (по времени) проделать такое упражнение
220
вполне возможно. Вы вполне сумеете, не сбившись, подойти к каждо-
му из тысячи и протянуть ему руку. А если бы последовало предложе-
ние всей тысяче присутствующих обменяться друг с другом рукопо-
жатиями, да еще каждой компании из трех человек внутри своего
кружка дополнительно обменяться рукопожатиями и т.д., то это ока-
залось бы немыслимым. Число 1000 и есть среднее. Можно сказать, что
мы «перебрали» тысячу элементов, отметив при этом каждого (рукопо-
жатием).
Совсем простым примером большого числа является число види-
мых звезд на небосклоне. Каждый знает, что невозможно пересчитать
звезды пальцем, а тем не менее существует каталог звездного неба
(т.е. выработана система обозначений), пользуясь которым мы в лю-
бой момент можем получить справку о нужной нам звезде.
Естественно, что вычислительная машина может, во-первых, доль-
ше работать не сбиваясь, а во-вторых, она составляет различные схе-
мы во много раз быстрее, чем человек. Поэтому в каждой категории
соответствующие числа для машины будут больше, чем для человека.
Числа Человек Машина
Малые 3 10
Средние 1000 10'°
Большие ю100 ю,ои
Что поучительного в этой таблице? Из нее видно, что хотя соответ-
ственные числа для машины гораздо больше, чем для человека, но ос-
таются близкого порядка с ними. Между же числами разных катего-
рий существует непроходимая грань: числа, средние для человека, не
становятся малыми для машины, так же как числа, большие для чело-
века, не становятся средними для машины. 103 несравненно больше,
чем 10, а 1О*00 безнадежно больше, чем 1О10. Заметим, что объем памя-
ти живого существа и даже машины характеризуется средними числа-
ми, а многие проблемы, решающиеся путем так называемого простого
перебора, — большими.
Здесь мы сразу выходим за пределы возможностей сравнения путем
простого перебора. Проблемы, которые не могут быть решены без боль-
шого перебора, останутся за пределами возможностей машины на сколь
угодно высокой ступени развития техники и культуры.
К этому выводу мы пришли, не обращаясь к понятию бесконечно-
сти. Оно нам не понадобилось и вряд ли понадобится при решении ре-
альных проблем, возникающих на пути кибернетического анализа
жизни. Зато важным становится другой вопрос: существуют ли про-
блемы, которые ставятся и решаются без необходимости большого пе-
221
ребора? Такие проблемы должны прежде всего интересовать киберне-
тиков, ибо они реально разрешимы.
Принципиальная возможность создания полноценных живых су-
ществ, построенных полностью на дискретных (цифровых) механиз-
мах переработки информации и управления, не противоречит принци-
пам материалистической диалектики. Противоположное мнение может
возникнуть лишь потому, что некоторые привыкли видеть диалектику
лишь там, где появляется бесконечность. При анализе явлений жизни
существенна, однако, не диалектика бесконечного, а диалектика боль-
шого числа.
Осторожно, увлекаемся! В настоящее время для кибернетики, по-
жалуй, больше, чем для всякой другой науки, важно, что о ней пишут.
Я не принадлежу к большим энтузиастам всей той литературы по ки-
бернетике, которая сейчас так широко издается, и вижу в ней большое
количество, с одной стороны, преувеличений, а с другой — упрощен-
чества.
Нельзя, конечно, сказать, что в этой литературе утверждается то, что
на самом деле недостижимо, но в ней часто встречаются восторженные
статьи, сами заглавия которых уже кричат об успехах в моделировании
различных сложных видов человеческой деятельности, которые в дей-
ствительности моделируются пока совсем плохо. Например, в амери-
канской кибернетической литературе и у нас, порой даже в совсем серь-
езных научных журналах, можно встретить работы о так называемом
машинном сочинении музыки (это не относится к работам Р. X. Зарипо-
ва). Под этим обычно подразумевается следующее: в память машины
«закладывается» нотная запись большого числа (скажем, 70) ковбойских
песен или, например, церковных гимнов; затем машина по первым че-
тырем нотам одной из этих песен отыскивает все те песни, где эти четы-
ре ноты встречаются в том же порядке и, случайным образом выбрав
одну из них, берет из нее следующую, пятую ноту. Теперь перед махш-
ной вновь четыре ноты (2, 3, 4 и 5), и она снова таким же способом осу-
ществляет поиски и выбор. Так машина как бы на ощупь «создает» не-
кую новую мелодию. При этом утверждается, что если в памяти маши-
ны были ковбойские песни, то и в ее творении слышится нечто «ковбой-
ское», а если это были церковные гимны, — то нечто «божественное».
Спрашивается, а что произойдет, если машина будет производить поиск
не по четырем, а по семи идущим подряд нотам? Поскольку в действи-
тельности двух произведений, содержащих семь одинаковых нот под-
ряд, почти не встретить, то, очевидно, «запев» семь нот из какой-нибудь
песни, машина вынуждена будет пропеть ее до конца. Если же, наобо-
рот, машине для собственного творчества достаточно знать только две
222
ноты (а произведений с двумя одинаковыми нотами сколько угодно), то
здесь ей представился бы такой широкий выбор, что вместо мелодии из
машины послышалась бы какофония звуков.
Вся эта несложная схема преподносится в литературе как «машин-
ное сочинение музыки», причем всерьез заявляется, что с увеличением
числа нот, нужных «для затравки», машина начинает создавать музыку
более серьезного, классического характера, а с уменьшением этого
числа переходит на современную, джазовую.
На сегодня мы еще очень далеки от осуществления анализа и опи-
сания высших форм человеческой деятельности, мы даже еще не нау-
чились в объективных терминах давать определения многих встре-
чающихся здесь категорий и понятий, а не только моделировать такие
сложные виды этой деятельности, к каким относится создание музыки.
Если мы не умеем понять, чем отличаются живые существа, нуждаю-
щиеся в музыке, от существ, в ней не нуждающихся, то, приступая
сразу к машинному сочинению музыки, мы окажемся в состоянии мо-
делировать лишь чисто внешние факторы.
«Машинное сочинение музыки» — это только пример упрощенного
подхода к проблемам кибернетики. Другой распространенный недос-
таток заключается в том, что сторонники кибернетики настолько ув-
леклись возможностями кибернетического подхода к решению любых
самых сложных задач, что позволяют себе пренебрегать опытом, нако-
пленным другими науками за долгие века их существования. Часто за-
бывают о том, что анализ высших форм человеческой деятельности
был начат давно и продвинулся довольно далеко. И хотя он и ведется в
других, не кибернетических терминах, но по существу объективен, и
его необходимо изучать и использовать. А то, что сумели сделать ки-
бернетики «голыми руками» и вокруг чего поднимают такую шумиху,
зачастую не выходит за рамки исследования самых примитивных яв-
лений. Однажды на вечере в московском Доме литераторов один из
участников вел с трибуны разговор о том, что наше время должно бы-
ло создать и уже создало новую медицину. Эта новая медицина есть
достояние и предмет изучения не медиков, а специалистов по теории
автоматического регулирования! Самое главное в медицине, по мне-
нию выступавшего, — это циклические процессы, происходящие в че-
ловеческом организме. А такие процессы как раз и описываются диф-
ференциальными уравнениями, изучаемыми в теории автоматического
регулирования. Так что изучать медицину в медицинских институтах
теперь вроде как устарело — ее надо передать в ведение втузов и ма-
тематических факультетов. Может быть, и верно, что специалисты по
теории автоматического регулирования могут сказать свое слово в
разрешении отдельных проблем, стоящих перед медициной. Но если
223
они захотят принять участие в этой работе, то прежде всего им потре-
буется колоссальная деквалификация, ибо опыт, накопленный меди-
циной, этой старейшей из наук, огромен, и для того чтобы сделать в
ней что-то серьезное, надо сначала овладеть им.
Почему только крайности? Вообще анализ высшей нервной дея-
тельности в кибернетике сосредоточен пока на двух крайних полюсах. С
одной стороны, кибернетики активно занимаются изучением условий
рефлексов, т.е. простейшего типа высшей нервной деятельности. Всем,
вероятно, известно, что такое условный рефлекс. Если два каких-нибудь
раздражителя многократно осуществляются одновременно друг с другом
(например, одновременно с подачей пищи включается звонок), то через
некоторое время уже один из этих раздражителей (звонок) вызывает от-
ветную реакцию организма (слюноотделение) на другой раздражитель
(подачу пищи). Это сцепление является временным и, если его не под-
креплять, постепенно исчезает. Значительная часть кибернетических про-
блем, которые известны сейчас под названием математической теории
обучения, охватывает такие очень простые схемы, которые не исчерпы-
вают и малой доли всей сложной высшей нервной деятельности человека
и в анализе самой условно-рефлекторной деятельности представляют со-
бой лишь начальную ее ступень.
Другой полюс — это теория формально-логических решений. Эта
сторона высшей нервной деятельности человека хорошо поддается изу-
чению математическими методами, и с созданием вычислительной тех-
ники и вычислительной математики исследования такого рода быстро
двинулись вперед. И здесь кибернетики во многом преуспели.
А все огромное пространство между этими двумя полюсами — самы-
ми примитивными и самыми сложными психическими актами (даже та-
кие простые формы синтетической деятельности, как, скажем, механизм
точно рассчитанного геометрического движения, о котором говорилось
выше, пока плохо поддаются кибернетическому анализу) — изучается
крайне мало, чтобы не сказать вовсе не изучается.
Кибернетика и язык. Особое положение сейчас занимает матема-
тическая лингвистика. Эта наука только еще создается и развивается
по мере накопления кибернетических проблем, связанных с языком.
Она имеет дело с анализом высших форм человеческой деятельности
скорее интуитивного, нежели формально-логического характера, ибо
эта деятельность плохо поддается точному описанию. Каждый знает,
что такое грамотно построенная фраза, правильное согласование слов
и т.п., но никто пока не может адекватно передать это знание машине.
Точный, логически и грамматически безукоризненный машинный пе-
ревод сейчас возможен был бы, пожалуй, только с латинского и на ла-
224
тинский язык, грамматические правила которого достаточно полны и
однозначны. Грамматические же правила новых, живых языков, по-
видимому, еще недостаточны для осуществления с их помощью ма-
шинного перевода. Необходимым здесь анализом занимаются уже
давно, и в настоящее время машинный перевод стал предметом широ-
ко и серьезно поставленной деятельности. Можно, пожалуй, сказать,
что именно на нем сосредоточено сейчас основное внимание матема-
тических лингвистов. Однако в теоретических работах по математиче-
ской лингвистике мало учитывается одно обстоятельство, а именно
тот факт, что язык возник значительно раньше формально-логического
мышления. Быть может, для теоретической науки одно из самых инте-
ресных исследований (в котором могут естественно сочетаться идеи
кибернетики, новый математический аппарат и современная логика)
есть исследование процесса образования слов как второй сигнальной
системы. Первоначально, при полном еще отсутствии понятий, слова
выступают в роли сигналов, вызывающих определенную реализацию.
Возникновение логики обычно относят к сравнительно недавнему
времени: по-видимому, только в Древней Греции было ясно понято и
сформулировано, что слова не просто являются обозначениями неких
непосредственных представлений и образов, но что от слова можно
отделить понятие. До настоящего, формально-логического, мышления
мысли возникали не формализованные в понятии, а как комбинирова-
ние слов, которые ведут за собой другие слова, как попытки непосред-
ственно зафиксировать проходящий перед нашим сознанием поток
образов и т.д. Проследить этот механизм выкристаллизовывания слов
как сигналов, несущих в себе комплекс образов, и создания на этой ба-
зе ранней логики — крайне благодарная область исследования, для
математика в частности, что, впрочем, неоднократно отмечалось в ки-
бернетической литературе.
Интересным может показаться и следующий вопрос: как формули-
руется логическая мысль у человека? Попробуем проследить этапы
этого процесса на примере работы математика над какой-нибудь про-
блемой. Сначала, по-видимому, возникает желание исследовать тот
или иной вопрос, затем какое-то приблизительное, неведомо откуда
возникшее представление о том, что мы надеемся получить в резуль-
тате наших поисков и какими путями нам, может быть, удастся этого
достичь, и уже на следующем этапе мы пускаем в ход свой внутрен-
ний «арифмометр» формально-логического рассуждения. Таков, по-
видимому, путь формирования логической мысли, такова схема про-
цесса творчества. Может, вероятно, представиться интересным не
только исследовать первую, интуитивную стадию этого процесса, но и
задаться целью создать машину, способную помочь человеку в про-
225
цессе творчества на стадии оформления мысли (математику, например,
на стадии оформления вычислений), поручить, скажем, такой машине
понимать и фиксировать в полном виде какие-то неясные, вспомога-
тельные наброски чертежей и формул, которые всякий математик ри-
сует на бумаге в процессе творческих поисков, или, например, воссоз-
давать по наброскам изображения фигур в многомерных пространст-
вах и т.п. Иными словами, интересно подумать о создании машин, ко-
торые, не подменяя человека, уже сейчас помогали бы ему в сложных
процессах творчества. Пока еще трудно даже представить себе, каким
образом и на каких путях такую машину можно было бы осуществить.
Но хотя пока еще эта задача и далека от своего разрешения, разговор
обо всех таких вопросах уже возник в кибернетической литературе,
что, по-видимому, можно только приветствовать.
Как можно уже увидеть нз нескольких приведенных здесь приме-
ров, различных проблем, связанных с пониманием объективного уст-
ройства самых тонких разделов высшей нервной деятельности челове-
ка, очень много. И все они заслуживают должного внимания киберне-
тиков.
Материализм — это прекрасно! В заключение следует остано-
виться на вопросах, касающихся, если можно так сказать, этической
стороны идей кибернетики. Встречающиеся часто отрицание и непри-
ятие этих идей проистекают из нежелания признать, что человек явля-
ется действительно сложной материальной системой, но системой ко-
нечной сложности и весьма ограниченного совершенства и поэтому
доступной имитации. Это обстоятельство многим кажется унизитель-
ным и страшным. Даже воспринимая эту идею, люди не хотят мирить-
ся с ней: такая картина всеобъемлющего проникновения в тайны чело-
века, вплоть до возможности, так сказать, «закодировать» его и «пере-
дать по телеграфу» в другое место, кажется им отталкивающей и пу-
гающей. Встречаются опасения и другого рода: а допускает ли вообще
наше внутреннее устройство исчерпывающее объективное описание?
Предлагалось, например, поставить перед кибернетикой задачу нау-
читься отличать по объективным признакам существа, нуждающиеся в
сюжетной музыке, от существ, в ней ие нуждающихся. А вдруг поана-
лизируем, поанализируем — и окажется, что и в самом деле нет ника-
кого разумного основания выделять такую музыку как благородную по
сравнению с другими созвучиями.
Мне представляется важным понимание того, что ничего унизи-
тельного и сграшного нет в этом стремлении постичь себя до конца.
Такие настроения могут возникать лишь из полузнания: реальное по-
нимание всей грандиозности наших возможностей, ощущение присут-
226
ствия вековой человеческой культуры, которая придет нам на помощь,
должно производить огромное впечатление, должно вызывать восхи-
щение! Все наше устройство в самих себе понятно, но понятно и то,
что это устройство содержит в себе колоссальные, ничем не ограни-
ченные возможности.
На самом деле нужно стремиться этот глупый и бессмысленный
страх перед имитирующими нас автоматами заменить О1ромным удов-
летворением тем фактом, что такие сложные и прекрасные вещи могут
быть созданы человеком, который еще совсем недавно находил про-
стую арифметику чем-то непонятным и возвышенным.
Л- ^Пуанкаре
ОПЫТ И ГЕОМЕТРИЯ21
1. В предыдущем я уже неоднократно старался показать, что прин-
ципы геометрии не являются фактами опыта и что, в частности, посту-
лат Евклида не мог бы быть доказан опытом. Какими бы доказатель-
ными ни представлялись мне вышеприведенные соображения, я счи-
таю нужным еще остановиться на этом вопросе, так как здесь мы
встречаем ложную идею, глубоко укоренившуюся во многих умах.
2. Пусть мы изготовили материальный круг, измерили его радиус и
окружность и желаем убедиться, равно ли отношение этих величин
числу л. Что мы делаем в этом случае? Мы производим опыт не над
свойствами пространства, а над свойствами как того материала, из ко-
торого приготовлен этот диск, так и того, из которого сделан метр,
служащий для измерений.
3. Геометрия и астрономия. Но вопрос ставят еще иначе. Если
справедлива геометрия Лобачевского, то параллакс очень удаленной
звезды будет конечным; если справедлива геометрия Римана, то он бу-
дет отрицательным. Эти результаты, по-видимому, допускают опыт-
ную проверку; можно было надеяться, что астрономические наблюде-
ния могут решить выбор между тремя геометриями.
Но то, что в астрономии называется прямой линией, есть просто
траектория светового луча. Если, следовательно, сверх ожидания, уда-
лось бы открыть отрицательные параллаксы или доказать, что все па-
раллаксы больше известного предела, то представлялся бы выбор ме-
жду двумя заключениями: мы могли бы или отказаться от евклидовой
геометрии, или изменить законы оптики и допустить, что свет распро-
страняется не в точности по прямой линии. Бесполезно добавлять, что
всякий счел бы второе решение более удобным.
227
Таким образом, евклидовой геометрии нечего опасаться новых
опытов.
4. Можно ли утверждать, чтобы некоторые явления, возможные в
евклидовом пространстве, были невозможны в неевклидовом, так что
опыт, констатируя эти явления, прямо противоречил бы гипотезе о не-
евклидовом пространстве? По моему мнению, подобный вопрос не
может возникнуть. С моей точки зрения, он вполне равносилен сле-
дующему вопросу, нелепость которого всякому бросится в глаза: су-
ществуют ли длины, которые можно выразить в метрах и сантиметрах,
но которых нельзя измерить туазами, футами и дюймами, — так что
опыт, констатируя существование этих длин, прямо противоречил бы
тому допущению, что существуют туазы, делящиеся на 6 футов.
Рассмотрим вопрос ближе. Допустим, что прямая линия в евклидо-
вом пространстве обладает некоторыми двумя свойствами, которые я
назову А и В что в неевклидовом пространстве она по-прежнему об-
ладает свойством А. но уже не обладает свойством В; допустим, нако-
нец, что в евклидовом — как и в неевклидовом — пространстве пря-
мая линия есть единственная линия, обладающая свойством А
Если бы это было так, то опыт мог бы решить выбор между гипоте-
зами Евклида и Лобачевского. Представим себе, что мы констатирова-
ли бы, что известный конкретный предмет, доступный опыту, напри-
мер пучок световых лучей, обладает свойством А; отсюда мы заклю-
чили бы, что он прямолинейный, и исследовали бы затем, обладает он
свойством В или нет.
Но это не так; не существует свойства, которое могло бы. как это
свойство А, быть абсолютным критерием, позволяющим признать, что
данная линия есть прямая, и отличить ее от всякой другой линии.
Скажут, например, что это свойство следующее: «прямая линия
есть такая линия, что фигура, часть которой она составляет, может
двигаться без изменения взаимных расстояний ее точек, причем все
точки этой линии остаются неподвижными».
В самом деле, здесь мы имеем свойство, которое и в евклидовом и
в неевклидовом пространстве принадлежит прямой и только прямой.
Но как узнать на опыте, обладает ли этим свойством тот или другой
конкретный предмет? Для этого понадобится измерить расстояния
между некоторыми его точками, но как убедиться, что та конкретная ве-
личина, которую я измерил своим материальным прибором, в точности
представляет собой абстрактное расстояние между этими точками?
Таким образом, мы лишь отодвинули трудность.
И действительно, свойство, которое я изложил, не есть свойство
лишь одной прямой линии, оно есть свойство как прямой, так и рас-
228
стояния. Чтобы оно могло служить абсолютным критерием, надо
иметь возможность установить не только то, что оно ие принадлежит
никакой иной линии, кроме прямой, и принадлежит расстоянию, но
еше то, что оно не принадлежит никакой Другой линии, кроме прямой,
и никакой другой величине, кроме расстояния. А именно это неверно.
Поскольку невозможно указать конкретный опыт, который мог бы
быть истолкован в евклидовой системе и не мог бы быть истолкован в
системе Лобачевского, то я могу заключить: никогда никакой опыт не
окажется в противоречии с постулатом Евклида, но зато и никакой
опыт не будет никогда в противоречии с постулатом Лобачевского.
5. Итак, евклидова (или неевклидова) геометрия никогда не может
оказаться в прямом противоречии с опытом. Но этого недостаточно.
Возникает вопрос: не может ли случиться, что ее можно будет согла-
совать с опытом лишь путем нарушения принципа достаточного осно-
вания и принципа относительности пространства?
Объяснюсь подробнее. Рассмотрим какую-нибудь материальную
систему; мы обратим внимание, с одной стороны, на «состояние» раз-
личных тел этой системы (например, на их температуру, электриче-
ский потенциал и т.д.), с другой стороны — на их положение в про-
странстве; и среди данных, которые позволяют определить это поло-
жение, мы различим еще взаимные расстояния этих тел, определяю-
щие их относительные положения, и условия, которые определяют аб-
солютное положение системы и ее абсолютную ориентировку в про-
странстве.
Законы явлений, которые будут происходить в этой системе, могут
зависеть от состояния этих тел и их взаимных расстояний; но вследст-
вие относительности и пассивности пространства они не будут зави-
сеть от абсолютного положения и абсолютной ориентировки системы.
Другими словами, состояние тел и их взаимные расстояния в какой-
нибудь момент будут зависеть только от состояния этих же тел и их
взаимных расстояний в начальный момент; но они ни в каком случае
не будут зависеть от абсолютного начального положения системы и ее
абсолютной начальной ориентировки. Это свойство для краткости я
буду называть законом относительности
Я говорил до сих пор как геометр, следующий Евклиду. Всякий
опыт, как я уже сказал, допускает истолкование на почве евклидовой
гипотезы; но он допускает его и на почве гипотезы неевклидовой. Мы
произвели ряд опытов; мы их истолковали на основании евклидовой
гипотезы и нашли, что это истолкование согласно с «законом относи-
тельности».
Истолкуем их теперь по неевклидовой гипотезе. Это всегда воз-
можно; отличие же лишь в том, что в этом новом истолковании неевк-
229
лидовы расстояния между отдельными телами вообще не будут теми
же, что евклидовы расстояния в первом истолковании
Но будут ли истолкованные таким новым способом опыты по-
прежнему оставаться в согласии с нашим «законом относительности»?
И если это согласие не сохранится, то не будем ли мы все-таки вправе
сказать, что опыт доказал неправильность неевклидовой геометрии?
Легко видеть, что это опасение напрасно; в самом деле, для того
чтобы можно было приложить закон относительности во всей строго-
сти, надо было бы приложить его ко всей Вселенной. Если же иметь в
виду только часть этой Вселенной и если абсолютное положение этой
части изменилось, то и расстояния ее относительно других тел Все-
ленной также изменились, следовательно, их влияние на рассматри-
ваемую часть Вселенной могло увеличиться или уменьшиться; а это
может изменить законы происходящих здесь явлений.
Но если система, о которой у нас идет речь, есть вся Вселенная, то
опыт бессилен дать нам указания о ее абсолютном положении и ори-
ентировке в пространстве. Все, что могут обнаружить наши инстру-
менты, сколь бы совершенны они ни были, — это состояние различ-
ных частей Вселенной и их взаимные расстояния.
Таким образом, наш закон относительности может быть формули-
рован так:
Отсчеты, которые мы можем производить в какой-нибудь момент
на наших инструментах, будут зависеть только от отсчетов, которые
мы могли бы произвести на тех же инструментах в начальный момент.
Но подобная формулировка не зависит ни от какого истолкования
опытов. Если закон верен в евклидовом истолковании, он будет верен
также и в неевклидовом истолковании.
Я позволю себе по этому поводу сделать маленькое отступление.
Выше я говорил о данных, определяющих положение различных тел
системы; мне следовало бы сказать также о данных, определяющих их
скорости; тогда мне пришлось бы различать, с одной стороны, ско-
рость, с которой изменяются взаимные расстояния различных тел, а с
другой — скорости переноса и вращения системы, т.е. скорости, с ко-
торыми изменяются ее абсолютное положение и ориентировка.
Для полного удовлетворения ума надо был бы закон относитель-
ности формулировать так
Состояние тел и их взаимные расстояния в какой-нибудь момент,
так же, как и скорости, с которыми изменяются эти расстояния в тот
же момент, зависят только от состояния этих тел, их взаимных рас-
стояний в начальный момент, а также от скоростей, с которыми по-
следние изменялись в этот начальный момент; но они не будут зави-
сеть ни от начального абсолютного положения системы, ни от ее абсо-
230
лютной ориентировки, ни от скоростей, с которыми изменялись это
абсолютное положение и ориентировка в начальный момент.
К сожалению, закон, сформулированный таким образом, не находится
в согласии с опытами, по крайней мере с обычным их истолкованием.
Представим себе человека, перенесенного на некоторую планету,
где небо постоянно закрыто густым покровом облаков, так что никогда
не видно других светил; пусть жизнь этой планеты течет так, как если
бы она была изолирована в пространстве. Все же этот человек мог бы
заметить ее вращение, измеряя, например, ее сжатие (это производится
обыкновенно при помощи астрономических наблюдений, но могло бы
быть произведено и средствами чисто геодезическими) или повторяя
опыт Фуко с маятником. Следовательно, абсолютное вращение этой
планеты могло бы быть обнаружено.
Факт этот смущает философа, ио физик вынужден его принять. Из-
вестно, что из этого факта Ньютон заключил о существовании абсо-
лютного пространства; я никак не могу согласиться с таким заключе-
нием; причины этого я покажу в третьей части, так как я не хотел бы
касаться такого трудного вопроса мимоходом.
Таким образом, мне поневоле пришлось в формулировку закона от-
носительности ввести скорости всякого рода среди данных, опреде-
ляющих состояние тел.
Во всяком случае, трудность эта остается одной и той же как для
геометрии евклидовой, так и для геометрии Лобачевского; поэтому я
особенно не был обеспокоен ею и упомянул о ней только к случаю.
Что важно, так это вывод: опыт не может решить выбор между Евкли-
дом и Лобачевским.
Итак, как ни взглянуть на дело, невозможно найти разумное осно-
вание для геометрического эмпиризма.
6. Опыты обнаруживают только взаимные отношения тел; никакой
опыт не даст и не может дать указаний об отношениях тел к простран-
ству или о взаимных отношениях различных частей пространства.
«Да, — скажете вы на это, — единичный опыт недостаточен, так
как он дает только одно уравнение со многими неизвестными; но когда
я произведу достаточное количество опытов, я буду иметь достаточно
уравнений, чтобы вычислить все мои неизвестные».
Но недостаточно знать высоту грот-мачты, — возражаю я, — чтобы
вычислить возраст капитана. Определив все размеры корпуса корабля,
вы будете иметь много уравнений, но все-таки вы ие узнаете этого воз-
раста. Все ваши измерения, относящиеся к частям корабельного
корпуса, не могут обнаружить вам ничего, кроме того, что касается
этих частей. Точно так и ваши опыты, как бы многочисленны они ни
231
были: указывая только на взаимные отношения тел, они не скажут нам
ничего о взаимных отношениях различных частей пространства.
7. Вы скажете, что если опыты относятся к телам, то они относятся
по крайней мере к геометрическим свойствам тел.
Но, прежде всего, — что вы понимаете под геометрическими свой-
ствами тел? Допустим, что здесь речь идет об отношениях тел к про-
странству; но эти свойства недоступны опытам, которые касаются
только взаимного отношения между телами. Одного этого замечания
было бы достаточно, чтобы показать, что речь идет о другом.
Постараемся прежде всего понять смысл выражения: геометриче-
ские свойства тел. Когда я говорю, что тело слагается из нескольких
частей, я думаю, что этим я не высказываю суждения о геометриче-
ском свойстве; это осталось бы справедливым, даже если бы я усло-
вился пользоваться неподходящим названием точек для наименьших
рассматриваемых мною частей.
Когда я говорю, что такая-то часть такого-то тела находится в со-
прикосновении с такой-то частью другого какого-нибудь тела, я вы-
сказываю предложение, касающееся взаимных отношений этих двух
тел, но не их отношений к пространству.
Я думаю, вы согласитесь со мной, что здесь мы имеем дело не с
геометрическими свойствами; по крайней мере, вы, наверно, согласи-
тесь, что эти свойства независимы от каких бы то ни было понятий
метрической геометрии.
После этого представим себе, что имеется твердое тело, состоящее
из восьми тонких железных стержней ОА, ОВ, ОС, OD, ОЕ, OF, OG и
ОН, соединенных вместе своими концами О.
Пусть, с другой стороны, мы имеем второе твердое тело, например
кусок дерева, на котором отметим чернилами три маленьких пятныш-
ка; я назову их а, Р, у.
Пусть мы убедились затем, что можно привести в соприкосновение
аРу с AGO (т.е. одновременно а с А, Р с G, у с О), потом — что после-
довательно можно привести в соприкосновение офу с BGO, CGO,
DGO. EGO, FGO, затем с AHO, ВНО, СНО. DHO, ЕНО. FHO, потом ау
последовательно с АВ, ВС, CD, DE, EF, FA.
Вот опытные факты, в которых можно удостовериться, не имея на-
перед никакого знания о форме или метрических свойствах простран-
ства. Они никоим образом не относятся к «геометрическим свойствам
тел». И эти факты будут невозможны, если тела, над которыми экспе-
риментируют, движутся, следуя группе такой же структуры, как груп-
па Лобачевского (я хочу сказать — по законам движения твердых тел
в геометрии Лобачевского). Значит, достаточно этих фактов, чтобы
232
убедиться, что тела эти движутся, следуя евклидовой группе, или, по
крайней мере, что они движутся не в соответствии с группой Лобачев-
ского.
Что эти факты совместимы с евклидовой группой, легко убедиться,
стоит только представить себе аРу неизменяемым твердым телом на-
шей обычной геометрии, имеющим форму прямоугольного треуголь-
ника, а точки А, В, С, D, Е, F.G, Н — вершинами многогранника, обра-
зованного двумя правильными шестигранными пирамидами нашей
обыкновенной геометрии, имеющими общим основанием ABCDEF, а
вершинами — одна G, другая Н.
Предположим теперь, что вместо предыдущих фактов мы наблю-
дали, что можно опять-таки наложить офу последовательно на AGO,
BGO. CGO. DGO, EGO, FGO, AHO, BHO, CHO, DHO, EHO, FHO. a
потом можно ар (отнюдь не ау) наложить последовательно на А В, ВС,
CD, DE, EFhFA
Вот опытные факты, которые можно было бы наблюдать, если бы
неевклидова геометрия была правильна и если бы аРу и OABCDEFGH
были неизменяемыми твердыми телами: первое — в форме прямо-
угольного треугольника, а второе — в форме двойной правильной
шестигранной пирамиды соответствующих размеров.
Итак, эти новые факты невозможны, раз тела движутся, следуя евк-
лидовой группе; но они стали бы возможны, если бы допустить, что
тела движутся подобно группе Лобачевского. Их было бы, следова-
тельно, достаточно (если бы они наблюдались), чтобы убедиться, что
рассматриваемые тела не движутся, следуя евклидовой группе.
Таким образом, не вводя никакой гипотезы о форме и природе про-
странства, об отношениях тел к пространству, не приписывая телам
никакого геометрического свойства, я нашел факты, позволяющие мне
показать, что доступные опытам тела, в одном случае движутся, сле-
дуя структуре группы Евклида, в другом — следуя структуре группы
Лобачевского.
Однако нельзя сказать, что первый ряд фактов может составить
опыт, доказывающий, что пространство является евклидовым, а вто-
рой — опыт, доказывающий, что пространство неевклидово.
В самом деле, можно было бы представить себе тела, движущиеся
таким образом, что они осуществляют второй ряд фактов. Доказатель-
ством служит то, что любой механик мог бы их построить, если бы он
захотел взять на себя этот труд и если бы придавал этому значение.
Однако из этого вы не заключили бы, что пространство неевклидово,
тем более, что обыкновенные твердые тела продолжали бы существо-
вать и тогда, когда механик построил бы странные тела, упомянутые
мною: так что пришлось бы даже заключить, что пространство являет-
ся одновременно евклидовым и неевклидовым.
233
Предположим, например, что мы имеем большую сферу радиуса R
и что температура убывает от центра к поверхности этой сферы по за-
кону, о котором я говорил, описывая неевклидов мир (см. статью
А. Пуанкаре «Пространство и геометрия» в данной хр. — ГД.).
Мы могли бы иметь тела, расширением которых можно было бы
пренебречь и которые вели бы себя как обыкновенные неизменяемые
твердые тела; с другой стороны, мы могли бы иметь тела очень растя-
жимые, которые вели бы себя как неевклидовы твердые тела. Мы могли
бы иметь две двойные пирамиды OABCDEFGH и O'A'B'C'D'E'F'G'H’ и
два треугольника а₽у и а'Р'у1. Первая двойная пирамида была бы пря-
молинейной, вторая — криволинейной; треугольник аРу был бы сде-
лан из нерастяжимого, а треугольник а'Р'у1 — из очень растяжимого
вещества.
Тогда можно было бы обнаружить первый ряд фактов с двойной
пирамидой ОАН и треугольником аРу и второй — с двойной пирами-
дой О'А'Н1 и треугольником а'Р'у1. И тогда опыт, по-видимому, убеж-
дал бы сначала, что евклидова геометрия истинна, а затем — что она
ложна.
Таким образом, опыты относятся не к пространству, а к телам.
8. Добавление. Для полноты мне следовало бы еще сказать о во-
просе очень тонком, который потребовал бы подробного развития; я
ограничусь здесь только резюмированием того, что я изложил в
«Revue de Metaphysique et de Morale» и в «The Monist». Что мы хотим
сказать, когда говорим, что пространство имеет три измерения?
Мы видели важность тех «внутренних изменений», которые нам
открываются нашими мускульными ощущениями. Они могут служить
для характеристики различных положений нашего тела. Возьмем за
начальное одно из этих положений А. Когда мы переходим от этого
начального положения к какому-нибудь другому положению В, мы
испытываем ряд мускульных ощущений S, и этим рядом S определит-
ся В. Однако заметим, что часто мы рассматриваем два ряда S и S' как
определяющие одно и то же положение В (потому что начальное и ко-
нечное положение А и В остаются теми же, но промежуточные поло-
жения и соответствующие ощущения могут различаться) Как же мы
узнаем об эквивалентности этих двух рядов? Это возможно потому,
что они могут служить для компенсации одного и того же внешнего
изменения, или, более общо, потому, что когда речь идет о компенса-
ции внешнего изменения, один из рядов может быть заменен другим.
Среди этих рядов мы выделили те, которые одни могут компенси-
ровать внешнее изменение и которые мы назвали «перемещениями».
Так как мы не можем различать два слишком близких перемещения,
то совокупность этих перемещений представляет характерные черты
234
физической непрерывности; опыт учит нас, что эта физическая непре-
рывность имеет шесть измерений; но мы не знаем еще, сколько изме-
рений имеет пространство само по себе; нам надо решить сначала дру-
гой вопрос.
Что такое точка пространства? Все думают, что знают это, но это
только иллюзия. Когда мы стараемся представить себе точку про-
странства, то она выступает в виде черного пятна на белой бумаге или
как белое пятно от мела на черной доске; это всегда объект. Поэтому
вопрос должен быть поставлен следующим образом: что значит, когда
я говорю, что предмет В находится в той же точке, которую только что
занимал предмет Л? И еще: какой критерий позволит мне узнать это?
Я хочу этим сказать, что хотя сам я не шевелился (о чем свидетель-
ствует мое мускульное чувство), но мой указательный палец, который
только что касался предмета А, теперь касается предмета В Я мог бы
воспользоваться другими критериями, например средним пальцем или
чувством зрения. Но первый критерий достаточен, я знаю, что если он
отвечает утвердительно, то все другие критерии дадут тот же ответ. Я
знаю это из опыта — я не могу знать этого a priopi.
Поэтому-то я говорю также, что осязание не может действовать на
расстоянии; это — только другой способ выражения того же экспери-
ментального факта. И если я говорю, наоборот, что зрение действует
на расстоянии, то это значит, что критерий, доставляемый зрением,
может отвечать утвердительно, тогда как другие отвечают отрица-
тельно
В самом деле, пусть некоторый предмет даже после удаления дает
свое отображение в той же точке сетчатки. Тогда зрение дает положи-
тельный ответ: предмет пребывает в той же точке, но осязание отвеча-
ет отрицательно, ибо палец, только что касавшийся предмета, теперь
уже больше его не касается. Если бы опыт показал нам, что касание
одним пальцем дает отрицательный ответ, тогда как касание другим —
положительный, то мы сказали бы то же самое: что осязание действует
на расстоянии.
Итак, для каждого положения моего тела мой указательный палец
определяет некоторую точку; это и только это определяет точку про-
странства.
Каждому положению соответствует, таким образом, одна точка; но
часто бывает, что та же точка соответствует нескольким различным
положениям (например, в том случае, когда мы говорим, что наш па-
лец не двигался, между тем как остальная часть тела переместилась).
Мы выделяем, следовательно, среди изменений положения такие, при
которых палец не двигается. Как мы приходим к этому? Только благо-
даря тому, что мы часто замечаем, как при этих изменениях предмет,
находящийся в контакте с пальцем, не разрывает этого контакта.
235
Отнесем к одному и тому же классу все те положения, которые вы-
текают одни" из других путем одного из выделенных нами таким обра-
зом изменений. Всем положениям одного и того же класса будет соот-
ветствовать одна и та же точка пространства. Поэтому каждому классу
будет соответствовать точка, и каждой точке — класс. Но можно ска-
зать: то, к чему относится опыт, не есть точка; это есть указанный
класс изменений или лучше — соответственный класс мускульных
ощущений.
И когда мы говорим, что пространство имеет три измерения, мы
хотим просто сказать, что совокупность этих классов выступает перед
нами с характерными чертами физической непрерывности трех изме-
рений.
Мог бы показаться заманчивым тот вывод, что именно опыт пока-
зал нам, сколько измерений ймеет пространство. Но в действительно-
сти наши опыты имели здесь дело еще не с пространством, а с нашим
телом и с его отношениями к соседним предметам. Кроме того, они
слишком грубы.
В нашем уме предсуществовала скрытая идея известного числа
групп: это — те группы, теорию которых создал Ли. Какую из них мы
выберем в качестве как бы эталона, с которым будем сравнивать ре-
альные явления? И, выбрав эту группу, какую из ее подгрупп мы возь-
мем для характеристики точки пространства? Раньше нами руководил
опыт, показывая, какой выбор лучше соответствует свойствам нашего
тела. Но тут его роль ограничивается.
Опыт предков. Часто говорят, что если индивидуальный опыт не
мог породить геометрию, то это не относится к опыту всего человече-
ского вида. Но что под этим понимается? Не хотят ли этим сказать, что
если мы не в состоянии доказать постулат Евклида, то наши предки
могли это сделать? Ни в коем случае. Этим хотят сказать, что в силу
естественного отбора наш ум приспособился к условиям внешнего ми-
ра, что он усвоил себе геометрию, наиболее выгодную для вида, или,
другими словами, наиболее удобную. Но это соответствует нашим вы-
водам о том, что геометрия не истинна, а только выгодна.
Вопросы и упражнения
для индивидуального осмысления
и коллективного обсуждения
1. Какими фактами вы можете доказать утверждение о возросшей роли мате-
матики в современном мире?
2. Известно, что классическая математика возникла в XVII в. и по сей день со-
храняет свое огромное значение и ведущее положение. Какие ветви математики
относят к классической математике и в чем проявляется их важное значение?
236
3 Попытайтесь подтвердить примерами утверждение Р Куранта:
«Взаимосвязь общего с частным, дедукции с конструктивным подходом,
логики с воображением — именно они и составляют самую сущность жи-
вой математики».
4. Проиллюстрируйте одним—двумя примерами из статьи Р Куранта мысль о
том. что ведущая линия в развитии математики—от конкретного и частного через
абстракцию снова к конкретному и частному — предает теории определенный
смысл и значение
5 Дайте характеристику основных постулатов философского учения, именуе-
мого «механизмом». Почему ученые XVIII—XIX вв. (в первую очередь математики
и физики) столь ревностно придерживались механизма? Подтвердите свои ут-
верждения примерами из публикуемых выше фрагментов из книги М Клайна
«Математика. Поиск истины»
6. Какие достижения физики и математики доказали несостоятельность меха-
низма? Расскажите и проиллюстрируйте примерами из публикуемых выше фраг-
ментов из книги М Клайна «Математика Поиск истин» разлжные концепции при-
чинности.
7. В чем различия между учением о причинности и детерминизмом. Сопос-
тавьте в связи с этим мнения Декарта, Лапласа, Гоббса, Вольтера, Максвелла,
Планка, Больцмана, Бора, Гейзенберга, Эйнштейна (см. разд «Математика и по-
ведение природы» из книги М Клайна «Математика. Поиск истины»),
8. Покажите, как каждое из основных философских учений (по выбору) —ме-
ханизм, учение о причинности, детерминизм, философия идеализма, философия
логического позитивизма — испытывает на себе глубочайиме воздействия по-
следних научных открытий. Подтвердите в своем анализе примерами справедли-
вость утверждения М. Клайна: «...Мы можем с полной уверенностью заявить, что
самый могущественный из созданных человеком инструмент — математика —
позволяет нам достичь определенного понимания сложного «разнообразия мира
природных явлений».
9. Примерами из книги М Клайна «Математика. Поиск истины» попытайтесь
подтвердить следующую мысль А. Эйнштейна: «Весь предшествующий опыт
убеждает нас в том, что природа представляет собой реализацию простейших
математически мыслимых элементов».
10. Охарактеризуйте особенности научного языка, отличающего его от языка
обыденного или языка литературного произведения. В чем сила и слабость мате-
матического языка в сравнении с неформализованным языком с его неисчерпае-
мым богатством оттенков и возможностей. Приведите примеры математических
символов (знаков умножения и деления, абсолютной величины, равенства и не-
равенства —больше, меньше, корня, производной функции) и назовите кем и ко-
гда они были введены
11. Что такое математическая модель? Приведите примеры математических
моделей (например, по книге Б.В. Гнеденко «Математика и математическое обра-
зование в современном мире»)
12. Попытайтесь раскрыть смысл изречения: «Математика значительно боль-
ше, чем наука, поскольку она является языком науки». Проиллюстрируйте свои
утверждения примерами.
13. Приведите примеры практического использования математики (по выбору)
в теории надежности, управления качеством массовой продукции, в транспортных
237
задачах, сельском хозяйстве (воспользуйтесь, например, названной выие книгой
Б В Гнеденко).
14. Изучите раздел «Автоматы и жизнь» из книги А.Н. Колмогорова «Матема-
тика —наука и профессия» и попытайтесь ответить на вопросы:
а) Что такое жизнь? Какими способами можно изучать высшую нервную дея-
тельность, используя кибернетический подход?
б) Дискретна или непрерывна мысль?
в) Чем занимается математическая лингвистика?
15 Прочитайте раздел «Геометрия на сфере и геология» из названной выше
книги А.Н Колмогорова. Попытайтесь поразмышлять о возможностях применения
методов геометрии на сфере для изучения геолошческих проблем
МАТЕМАТИКА И ВОСПИТАНИЕ УМА
Боги открыли людям не все В поиск пустившись,
люди сами открыли немало
Ксенофон
То. что вы вынуждены были открыть сами, ос-
тавляет в вашем уме дорожку, которой вы можете
снова воспользоваться, когда в этом возникает не-
обходимость
Г. Лихтенберг
Мудрость рождается из пристального наблю-
дения за тем, как растут люди.
Конфуций
fi.'H. Т(рлмогоров
О МАТЕМАТИЧЕСКИХ СПОСОБНОСТЯХ*
Необходимость специальных способностей для изучения и понима-
ния математики часто преувеличивают. Впечатление исключительной
трудности математики иногда создается ее плохим, чрезмерно фор-
мальным изложением на уроке. Обычные средние человеческие спо-
собности вполне достаточны, чтобы при хорошем руководстве или по
хорошим книгам не только усвоить математику, преподающуюся в
средней школе, но и разобраться, например, в началах дифференци-
ального и интегрального исчислений. Тем не менее, когда дело идет о
выборе математики в качестве основной специальности, вполне есте-
ственно желание проверить математические способности, или, как го-
ворят иногда, математическую «одаренность». Ведь несомненно, что
разные люди воспринимают математические рассуждения, решают ма-
тематические задачи или — на более высокой ступени — приходят к
новым математическим открытиям с различной скоростью, легкостью
и успехом. И, конечно, следует стремиться к тому, чтобы из миллио-
нов нашей молодежи специалистами-математиками становились имен-
но те, кто в этой области будет работать наиболее успешно.
239
Поэтому содействие выдвижению математически одаренной моло-
дежи является одной из важных задач школьных математических
кружков, математических олимпиад и других мероприятий по пропа-
ганде математических знаний и распространению интереса к само-
стоятельным занятиям математикой. Не следует спешить с чрезмерно
ранним созданием для отдельных молодых людей репутации матема-
тических «талантов». Но вовремя подтолкнуть советом или премиро-
ванием на олимпиаде способных математиков в сторону выбора мате-
матики в качестве своей дальнейшей работы необходимо.
В чем же заключаются эти способности? Следует прежде всего
подчеркнуть, что успех в математике меньше всего основан на меха-
ническом запоминании большого числа фактов, отдельных формул и
т.п. Хорошая память в математике, как и во всяком другом деле, явля-
ется полезной, но никакой особенной, выдающейся памятью большин-
ство крупных ученых-математиков не обладало.
В частности, фокусники, запоминающие длинные ряды многознач-
ных чисел и складывающие или перемножающие их в уме, совсем не
могут служить примером людей с хорошими математическими спо-
собностями в серьезном смысле слова.
Умение производить алгебраические вычисления, в смысле умело-
го преобразования сложных буквенных выражений, нахождения удач-
ных путей для решения уравнений, не подходящих под стандартные
правила, и т.п., уже ближе соприкасается с теми способностями, кото-
рые часто требуются от математика в серьезной научной работе.
Принято даже думать, что исключительно большое развитие таких
вычислительных, или, иногда говорят, «алгоритмических» способно-
стей, является характерным для одного из нескольких основных типов
математической одаренности.
В школьной алгебре с трудностями, требующими для своего пре-
одоления такого рода способностей, школьники прежде всего сталки-
ваются при разложении алгебраических выражений на множители.
Среди задач на эту тему приведем две: разложить на множители вы-
ражения х5 + х + 1 и а + а5 + 1; эти задачи дают представление о том,
что иногда разложение очень простых выражений на множители тре-
бует большого остроумия.
Далее основной областью применения этого рода способностей ста-
новится решение уравнений. Однако везде, где это возможно, математи-
ки стремятся сделать изучаемые ими проблемы геометрически нагляд-
ными. В средней школе достаточно ясно видно, насколько полезны гра-
фики для изучения свойств функций. Поэтому читатель не удивится ут-
верждению, что геометрическое воображение, или, как говорят, «гео-
метрическая интуиция», играет большую роль при работе почти во всех
разделах математики, даже самых отвлеченных.
240
В школе обычно с большим трудом дается наглядное представле-
ние пространственных фигур. Надо, например, быть очень уж хоро-
шим математиком (по сравнению с обычным школьным уровнем),
чтобы, закрыв глаза, без чертежа ясно представить себе, какой вид
имеет пересечение поверхности куба с плоскостью, проходящей через
центр куба и перпендикулярной одной из его диагоналей
В задаче: В куб вложено два правильных тетраэдра так, что че-
тыре вершины куба служат вершинами одного из них, а остальные
четыре вершины куба — вершинами другого Какую долю куба со-
ставляет объем общей части этих тетраэдров? Вся трудность за-
ключается в том, чтобы наглядно понять, что за фигура получается при
пересечении тетраэдров.
При решении следующих задач:
Около сферы описан пространственный четырехугольник. Дока-
зать, что точки касания лежат в одной плоскости.
Доказать, что сумма расстояний от произвольной внутренней
точки правильного тетраэдра до его граней есть величина посто-
янная,
Доказать, что прямые, соединяющие середину высоты правильно-
го тетраэдра с вершинами основания, взаимно перпендикулярны
тоже очень существенна геометрическая интуиция, хотя здесь уже
больше остается и на долю твердого знания тех теорем, которые при-
дется применить при доказательстве, и на долю умения логически рас-
суждать.
Искусство последовательного, правильно расчлененного логиче-
ского рассуждения является также существенной стороной математи-
ческих способностей
В школе для развития этого искусства служит систематический
курс геометрии с ее определениями, теоремами и доказательствами.
Но часто наибольшую трудность для школьников в отношении пони-
мания точного смысла сложной логической конструкции представляет
принцип математической индукции, изучаемый в конце курса алгебры.
Многие не в состоянии ясно увидеть реальное содержание этого прин-
ципа за нагромождением слов «если» и «то».
Понимание и умение правильно применять принцип математиче-
ской индукции является хорошим критерием логической зрелости, ко-
торая совершенно необходима математику.
Умение последовательно, логически рассуждать в незнакомой об-
становке приобретается с трудом. На математических школьных олим-
пиадах самые неожиданные трудности возникают именно при
решении задач, в которых не предполагается никаких предваритель-
17 Заж 72
241
ных знаний из школьного курса, но требуется правильно уловить
смысл вопроса и рассуждать последовательно. Уже такой шуточный
вопрос затрудняет многих десятиклассников: в хвойном лесу 800 000
елей и ни на одной из них не более 500 000 игл; доказать, что по край-
ней мере у двух елей число игл точно одинаково (сравните с задачей: в
500 ящиках лежат яблоки, причем в ящике помещается не более 240
яблок; доказать, что по крайней мере 3 ящика содержат по одинако-
вому числу яблок).
В следующих задачах:
Какое наибольшее число острых углов может иметь выпуклый
многоугольник, имеющий п сторон? и Доказать, что выпуклый 13-
угольник нельзя разрезать на параллелограммы, а также в задаче
Сколько раз в сутки стрелки часов перпендикулярны друг другу?
тоже главная трудность не в сложности, а в необычности тех способов
рассуждения, которые требуется применить.
Различные стороны математических способностей встречаются в
разных комбинациях. Уже исключительное развитие одной из них
иногда позволяет приходить к неожиданным и замечательным откры-
тиям, хотя чрезмерная односторонность, конечно, опасна. Само собой
разумеется, что никакие способности не помогут без увлечения своим
делом, без систематической повседневной работы.
Математические способности проявляются обычно довольно рано и
требуют непрерывного упражнения. Полный отрыв от математики в
течение нескольких лет после средней школы часто оказывается труд-
но поправимым. Работа чертежника, лаборанта, обращение с машино-
строительными деталями, сборка радиоаппаратуры и т.п., по-
видимому, содержат в себе много элементов, родственных с работой
математика, например, в смысле развития пространственного вообра-
жения и функционального мышления. Соприкосновение на работе с
современной техникой может пробудить более сознательный интерес к
приложениям математики. Но мы очень советуем молодым людям,
намеревающимся поступить на математическое отделение универ-
ситета, проработав после школы несколько лет на производстве, за-
ранее заниматься математикой и не только путем подготовки к
вступительным экзаменам (для чего при всех университетах суще-
ствуют специальные подготовительные курсы), но и путем участия
в математических кружках и олимпиадах и самостоятельного чте-
ния Иначе никакие льготы для «производственников» при поступ-
лении в вузы не помогут им во время работы в университете не от-
стать от своих товарищей, пришедших со свежими знаниями и ув-
лечениями прямо из школы.
242
Хинчин
О ВОСПИТАТЕЛЬНОМ ЭФФЕКТЕ УРОКОВ МАТЕМАТИКИ1’
I. КУЛЬТУРА МЫСЛИ
1. Правильность мышления. Роль и значение математики в воспита-
нии навыков закономерного и безошибочного мышления всеми признаны
в такой мере, что нередко приходится встречаться с утверждениями, буд-
то приучение к строгому в логическом отношении ходу мыслей есть пер-
вая и основная задача учителя математики, так что в сравнении с нею д а-
же ознакомление учащихся с самим содержанием математической науки
отодвигается на второй план (что, несомненно, следует признать уже
вредным перегибом). Однако как раз потому, что эта воспитательная
функция уроков математики приобрела характер банальности, именно в
этом направлении мы слышим много высказываний, приводим по гото-
вому трафарету, без достаточного обдумывания В результате внимание
сосредоточивается на небольшом числе привычных (а подчас и набивших
оскомину), хотя и важных, но по своему значению частных и узких во-
просов, вроде пресловутого различения между прямыми и обратными
теоремами. Между тем остаются в тени вопросы более общего принципи-
ального значения.
Я думаю, что основным общим моментом воспитательной функции
математического образования — моментом, который в значительной
степени обусловливает собою все остальное, — служит приучение
воспитываемых к полноценности аргументации.
В обыденной жизни, даже в «любительских» (не строго научных)
принципиальных спорах, мы, защищая какое-либо утверждение, до-
вольствуемся обычно одним-двумя аргументами, говорящими в его
пользу. Противник может привести в ответ несколько аргументов, го-
ворящих против нашего утверждения Однако обычно ни та, ни другая
аргументация не бывает исчерпывающей; противники продолжают
изыскивать новые аргументы, каждый в пользу своей точки зрения, и
спор продолжается.
Примерно так же протекают и научные дискуссии в тех областях
знания, которые не входят в число так называемых точных наук; ко-
нечно, аргументация здесь бывает, как правило, более полной, чем в
обыденных спорах; но почти никогда не удается сделать ее исчерпы-
вающей, не допускающей никаких возражений и тем самым ликвиди-
рующей самую дискуссию.
Иначе обстоит дело в математике. Здесь аргументация, не обла-
дающая характером полной, абсолютной исчерпанности, оставляющая
хотя бы малейшую возможность обоснованного возражения, беспо-
17-
243
щадно признается ошибочной и отбрасывается как лишенная какой бы
то ни было силы. В математике нет и не может быть «наполовину до-
казанных» и «почти доказанных» утверждений: либо полноценность
аргументации такова, что никакие споры о правильности доказываемо-
го утверждения более невозможны, либо аргументация вообще полно-
стью отсутствует.
Изучая математику, школьник впервые в своей жизни встречает
столь высокую требовательность к полноценности аргументации. Вна-
чале оиа удивляет, отталкивает, пугает его, кажется ему излишней,
сверхмерной, педантичной. Но постепенно, день за днем, он к ней при-
выкает. Хороший учитель много может сделать для того, чтобы этот
процесс протекал и быстрее, и продуктивнее. Он приучит своих учени-
ков к взаимной критике; когда один из них что-либо доказывает или
решает какую-либо задачу перед всем классом, все остальные должны
напряженно искать возможных возражений и немедленно их
высказывать. Ученик, который «отобьется» от таких возражений, за-
ставит умолкнуть всех своих критиков, неизбежно испытает законную
радость победы. Вместе с тем он ясно почувствует, что именно логи-
ческая полноценность аргументации была тем оружием, которое дало
ему эту победу. А раз почувствовав это, он неизбежно научится ува-
жать это оружие, постарается, чтобы оно всегда было при нем. И,
конечно, не только в математических, но и в любых других дискуссиях
он все больше и настойчивее будет стремиться к полноценности аргу-
ментации. Каждый раз перед ним будет вставать задача — по возмож-
ности обезоружить своих противников, в полной мере используя весь
запас аргументов, какие вообще возможны в данной ситуации.
Этот воспитывающий процесс имеет решающее значение для логи-
ческой культуры мышления, в особенности если учесть, что учащийся
привыкает быть беспощадно требовательным к полноценности аргу-
ментации не только в споре, но и в своем собственном мышлении.
Процесс этот протекает повседневно на наших глазах у многих тысяч
школьников. Он неизбежно возникает и идет своим путем без нашего
специального вмешательства, но это не значит, что мы вправе пустить
его на самотек; в нашей власти сделать его и более быстрым, и более
полным по богатству и прочности достижений; а раз мы можем, то мы
и должны это делать; вопрос о том, какими приемами наиболее эффек-
тивно можно добиться этих целей, есть уже методическая задача, ко-
торую мы не имеем возможности рассматривать здесь детально.
Общий принцип борьбы за полноценность аргум нтации получает
в ходе интеллектуального развития учащегося целый ряд типичных по
своей форме конкретных разновидностей, важнейшие из которых мы
теперь перечислим.
244
1. Борьба против незаконных о б о б щ е н и й. На-
туралист, подметив наличие какого-либо свойства (признака) у ряда осо-
бей данного вида, с чистой научной совестью объявляет этот признак об-
щим для всего рассматриваемого вида, и никто не упрекнет его за это: та-
кого рода индуктивные заключения представляют собою один из основ-
ных методологических стержней естественных наук. Конечно, и в этих
науках координирующая и осмысливающая теоретическая мысль воз-
можна и необходима; но как исходным пунктом, так и решающей провер-
кой всякого заключения здесь всегда остаются наблюдение и опыт, осу-
ществляемые над отдельными экземплярами.
В математике дело обстоит принципиально иначе. Если мы прове-
рили, что несколько десятков (или хотя бы и несколько миллионов)
наудачу выбранных нами треугольников обладают каким-нибудь
свойством, мы еще не вправе признать это свойство принадлежащим
всем треугольникам. Такое заключение было бы не до конца обосно-
ванным, а в математической науке все, что обосновано до конца, рас-
ценивается как абсолютно необоснованное. Только исчерпывающее
общее доказательство может дать уверенность в том, что данный при-
знак действительно является общим свойством всех треугольников.
Чему же может и должна научить школьника та суровая критика по
адресу не вполне обоснованных обобщений, с какой он встречается в
математике? Конечно, он не должен стараться переносить такого рода
требования на выводы других наук и тем более на практические жиз-
ненные ситуации. Требование абсолютной полноты индукции специ-
фично для математического метода и совершенно невыполнимо ни в
естественных науках, ни в практической жизни Но привычка с крити-
ческой тщательностью проверять законность всякого обобщения, при-
вычка твердо помнить, что замеченное во многих случаях еще не обя-
зано тем самым иметь место во всех случаях и что закономерности,
установленные на основе хотя бы и многих единичных наблюдений и
опытов, требуют поэтому все новой и новой проверки, — все эти важ-
нейшие методологические навыки, необходимые в любой научной и
практической деятельности, в значительной степени воспитываются и
укрепляются вместе с повышением математической культуры.
Это процесс, который мы каждодневно видим происходящим на
наших глазах.
2. Борьба против необоснованных анало-
гий. Заключения по аналогии служат обычным и законным приемом
установления новых закономерностей как в эмпирических науках, так и
в обыденной жизни. Если, допустим, естествоиспытатель помнит, что
все встречавшиеся ему до сих пор виды, обладавшие признаками А и В,
обладали также и признаком С, и если он нашел новый вид, у которого
245
обнаружены признаки Л и В, то он, естественно, заключит, что этот но-
вый вид обладает также и признаком С. Такое заключение по аналогии
значительно выигрывает в убедительности, если к чисто эмпирическим
данным, описанным выше, присоединяются, как это часто бывает, ка-
кие-либо теоретические соображения, заставляющие предполагать, что
совместное наличие признаков А, В и С является не случайным, а обос-
новано теми или другими общими принципиальными соображениями.
Но только в математике возможно — и вместе с тем совершенно необ-
ходимо — требовать, чтобы эти принципиальные соображения были до-
ведены до степени исчерпывающего доказательства. Либо мы со всей
строгостью доказали, что из наличия признаков А и В с неизбежностью
вытекает и наличие признака С; либо, если нам не удалось доказать это-
го с исчерпывающей полнотой, нам запрещается делать из наличия при-
знаков А и В какие бы то ни было выводы относительно признака С. Но
в первом случае (т.е. когда доказана теорема «Из А и В следует С») про-
стое применение этой общей теоремы к конкретным частным случаям
уже вряд ли может быть названо заключением по аналогии. Будет, та-
ким образом, правильно сказать, что в математике заключения по анало-
гии категорически запрещены (что не должно, конечно, умалять огром-
ного эвристического значения заключений по аналогии), в то время как
в эмпирических науках и практической деятельности заключениям по
аналогии принадлежит почетная роль одного из основных приемов вы-
вода новых закономерностей. Поэтому снова встает вопрос о том, что
же в этом отношении могут дать уроки математики для воспитания об-
щей культуры мышления. И снова проходится ответить на это то же, что
и прежде: математическая вышколенность ума, привыкшего к тому, что
заключение по аналогии может служить лишь эвристическим приемом,
который сам по себе еще не имеет доказательной силы, неизбежно при-
учает прошедшего эту школу человека и во всех других областях мыш-
ления относиться к такого рода заключениям с большой осторожно-
стью, памятуя, что во всех таких случаях нельзя без основательной про-
верки считать полученное заключение твердо установленным. Каждый
из нас испытал в свое время на себе воспитывающее влияние этой осо-
бенности математического мышления, и каждодневно мы наблюдаем,
как влияние это содействует повышению мыслительной культуры на-
ших воспитанников. Критическое отношение к заключениям по анало-
гии есть один из важнейших показателей, отличающих правильно вос-
питанное научное и практическое мышление от первобытного, обыва-
тельского, и занятия математикой всегда служат одним из основных
средств воспитания этого важнейшего показателя.
3. Борьба за полноту дизъюнкций. Когда матема-
тик доказывает какое-либо общее свойство всех треугольников, то
246
иногда ему приходится проводить доказательство отдельно для остро-
угольных, прямоугольных и тупоугольных треугольников. Известно,
как часто в таких случаях начинающие делают ошибки, в особенности
в тех случаях, когда рассуждение сопровождается ссылкой на чертеж;
чертится, например, остроугольный треугольник, и рассуждение опи-
рается на добавочные построения, которые либо невозможны, либо те-
ряют доказательную силу, если выбранный треугольник имеет тупой
угол. В математике такое рассуждение признается ошибочным, так как
здесь нарушено основное требование полноты дизъюнкции: не преду-
смотрены все возможные разновидности данной ситуации, одна из них
выпала из поля зрения.
В обыденных, не научных рассуждениях это требование нарушает-
ся на каждом шагу. Рассмотрев две-три наиболее часто встречающиеся
или наиболее бросающиеся в глаза разновидности данной ситуации и
убедившись, что в каждом из этих случаев мы неизбежно встречаемся
с некоторым событием А, мы заключаем, что это событие А сопутству-
ет данной ситуации во всех случаях, хотя на самом деле данная ситуа-
ция может иметь, кроме двух-трех изученных нами, еще десяток дру-
гих разновидностей, и среди этих разновидностей, скинутых нами со
счета, могут быть и такие, в которых наступление события Л вовсе не-
обязательно. Мы говорим, например, что ученика Иванова вообще
нельзя дисциплинировать, потому что на него испытанным образом не
действуют ни ласка, ни угрозы. Мы забываем при этом, что лаской и
угрозами не исчерпываются еще все разновидности приемов дисцип-
линирующего воздействия, что существует еще, например, метод спо-
койного убеждения и что, стало быть, наша дизъюнкция страдает не-
полнотой. Мы часто наблюдаем, как начинающий, рассмотрев при ис-
следовании какого-нибудь уравнения случай, когда некоторый данный
коэффициент положителен, а затем случай, когда этот коэффициент
отрицателен, тем самым считает, что он провел исследование во всех
случаях, забывая, что изучаемый коэффициент может оказаться рав-
ным нулю. Здесь также мы видим неполноту дизъюнкции, которая может
привести и фактически приводит к тяжелым ошибкам в выводах.
В противоположность тем двум требованиям, которые мы рассмат-
ривали выше, требование полноты дизъюнкции, учета всех возможных
разновидностей изучаемой ситуации является необходимой принад-
лежностью не только математического, но и .всякого правильного
мышления. Аргументация, в которой не учтены все имеющиеся воз-
можности, всегда оставляет место для законных возражений и потому
не может быть признана полноценной. Военачальник, предпринимая
какой-либо маневр, при учете его последствий должен предвидеть все
возможные ответы врага; просмотр хотя бы одного из них может ока-
247
заться гибельным. Юридический кодекс в каждой статье обязательно
должен охватывать все мыслимые разновидности данной ситуации,
иначе он ставит судью перед необходимостью решать дела по своему
произволу.
Но нигде требование безукоризненной чистоты дизъюнкций не вы-
ставляется так явно и категорически, как в математике; и никто не об-
рушивается с такой быстротой и беспощадностью на замеченный про-
смотр в дизъюнкции, как вышколенный математик.
Вот почему уроки математики должны воспитывать и действитель-
но воспитывают в мышлении учащихся этот важнейший закон пра-
вильного рассуждения в несравненно большей мере, чем занятия дру-
гими предметами.
4. Борьба за полноту и выдержанность клас-
сификации. Классифицирует не только ученый-теоретик в своем
кабинете; классификацией приходится очень часто заниматься и прак-
тическому работнику: инженеру, врачу, учителю, статистику, агроно-
му. Общеизвестно, что невышколенный ум склонен допускать, произ-
водя классификацию, ряд типических ошибок; наиболее распростра-
ненными из таких ошибок являются нарушение полноты классифика-
ции и нарушение ее выдержанности, единопринципности. Нарушение
полноты классификации состоит в том, что остаются понятия, не вхо-
дящие ни в один из названных классов, и что, стало быть, названы не
все классы. Простые примеры: на вопрос «Какие ты знаешь растения?»
школьник отвечает: «Травы и деревья», забывая о кустарниках, ли-
шайниках и многих других типах; войсковые части делятся на сухо-
путные, водные и воздушные (упускаются интендантские, части связи
и многие другие); натуральные числа делятся на простые и составные
(упускается число 1); вещественные числа делятся на положительные
и отрицательные (упускается нуль).
Требование полноты классификации формально аналогично рас-
смотренному нами выше требованию полноты дизъюнкции, но, конеч-
но, отлично от него по содержанию. Там шла речь об обязательности
охвата всех могущих возникнуть ситуаций, здесь же — о необходимо-
сти перечисления всех разновидностей некоторого понятия. Но здесь,
как и там, явно и неукоснительно требование полноты классификации
провозглашается в математике преимущественно перед всеми другими
науками, и потому уроки математики более всех других воспитывают
в школьнике этот обязательный элемент правильного мышления.
Требование выдержанности классификации состоит в том, чтобы
она проводилась по единому принципу, по единому признаку. Это
требование, при строго правильном мышлении совершенно обязатель-
ное, очень часто нарушается не только в обывательских рассуждениях,
248
но и в серьезной практике. Вот простые примеры такой невыдержан-
ной классификации: суда делятся на весельные, парусные, моторные и
военные; очевидно, классификация начата по принципу различных
движущих сил, и последняя рубрика этот принцип нарушает; другой
пример: обувь подразделяют на кожаную, брезентовую, резиновую и
модельную — та же картина Конечно, подобного рода перечисления
не всегда претендуют на роль классификации, и в таких случаях со-
блюдение единого принципа необязательно (например, объявление:
завод приглашает на работу плотников, штукатуров, женщин и подро-
стков). Но во всех случаях, когда такому перечислению приписывается
классифицирующая функция, невыдержанность разделяющего прин-
ципа вызовет такую неотчетливость всей схемы, которая может при-
вести и к теоретическим смешениям, и к практической путанице. По-
этому логически вышколенный ум всегда ощущает недостаток выдер-
жанности классификации как существенный дефект рассуждения. И
снова наиболее чувствительна к этому дефекту математическая наука,
и поэтому именно на уроках математики школьник преимущественно
развивает в себе эту потребность видеть всякую классификацию вы-
держанной, построенной на едином классифицирующем принципе.
Я перечислил те моменты в борьбе за правильность мышления и
полноценность аргументации, которые представляются мне наиболее
важными. Как уже было сказано выше, я не могу входить в этой статье
в обсуждение тех методических приемов, с помощью которых учитель
математики может достигнуть наибольшего успеха в деле воспитания
у своих учеников перечисленных мною моментов правильного мыш-
ления. Но я считаю необходимым сделать по этому вопросу одно ме-
тодическое замечание общего характера (для опытного учителя, впро-
чем, совершенно очевидное), все те требования правильного мышле-
ния, о которых шла речь выше, должны воспитываться в учащихся ис-
подволь, от случая к случаю, без излишнего педалирования; не может
быть и речи о том, чтобы посвящать специальный урок, например,
борьбе с незаконными аналогиями; такая постановка дела может толь-
ко безнадежно погубить весь ожидаемый эффект. Надо, напротив,
всемерно избегать во всем этом деле общих рассуждении и обращать
внимание учащихся на тот или другой логический момент исключи-
тельно на базе ярко убедительного конкретного материала. Потреб-
ность в логической полноценности аргументации воспитывается не
постоянным надоедающим напоминанием о необходимости этой пол-
ноценности, а показом на конкретных примерах (поводы к которым
дает почти каждый урок), как несоблюдение этого требования ведет к
ошибкам и неувязкам. Надо не отвлеченно проповедовать полноцен-
ность аргументации, а приучить учащегося к тому, что каждый пробел
16 Зак 72
249
в аргументации немедленно вызывает придирчивый вопрос со стороны
учителя или, что много лучше, со стороны товарищей.
Я не буду говорить здесь о том, что следует использовать уроки ма-
тематики для правильного понимания различия между прямым и об-
ратным утверждениями, а также и ряда других аналогичных различе-
ний. С одной стороны, об этом так много уже писалось, что вряд ли я
смог прибавить здесь что-нибудь новое. С другой стороны, мне пред-
ставляется, что этого рода моменты, будучи, конечно, обязательными
для логически правильного мышления, все же по своему частному,
специальному характеру не имеют вне математики столь существенно-
го значения, как те значительно более общие принципы, которые я пе-
речислил выше.
2. Стиль мышления. Помимо специфических, особо строгих тре-
бований к логической правильности умозаключений, математика от-
личается от других преподаваемых в школе наук также и стилем сво-
его мышления. Стиль этот, хотя и претерпевает на протяжении веков,
и даже десятилетий, довольно значительные изменения, все же имеет
некоторые общие для всех эпох непреходящие черты, заметно отли-
чающие его от стилей, принятых в других науках.
Утвердившийся в той или другой науке стиль мышления не являет-
ся, как можно было бы думать, только внешним и потому второсте-
пенным фактором, имеющим лишь эстетическую ценность и не могу-
щим поэтому существенно влиять на развитие данной науки. Напро-
тив, стилем мышления в значительной степени определяется отчетли-
вость теоретических связей, простота и ясность научных конструкций,
наглядная конкретность понятий и многое другое, от чего в свою оче-
редь зависят эффективность, плодотворность научных дискуссий и на-
учного преподавания, а вместе с тем и темпы развития науки.
Среди тех особых черт, которые присущи стилю математического
мышления, имеется ряд таких, которым свойственно весьма общее и
широкое значение; такая черта, если она усваивается представителем
какой-нибудь другой науки или практическим деятелем, оказывает не-
редко весьма существенные услуги как его собственному мышлению,
так и усвоению его трудов учениками и последователями. Читая сочи-
нения какого-либо из крупнейших классиков в другой научной облас-
ти, математик подчас с некоторым удивлением восклицает: «Да ведь
он мыслит совсем по-нашему!»; удивление происходит оттого, что
обычно в этой научной области принят совсем иной стиль мышления,
имеющий очень мало общего с математическим.
Но если усвоение некоторых черт математического мышления спо-
собно облагородить мыслительный стиль и в других областях знания и
250
практической деятельности, сделать этот стиль более мощным и про-
дуктивным орудием мысли, то очевидно, что не следует пренебрегать
использованием уроков математики для приучения молодых умов к
постепенному усвоению этих черт, к тому, чтобы эти черты стали
прочными навыками их мышления — сначала в пределах математики,
а потом и за ее пределами. Для того чтобы это осуществить, надо в
первую очередь постараться со всей тщательностью выявить те черты
стиля математической мысли, о которых здесь идет речь.
В основе каждого правильно построенного хода мыслей независи-
мо от предметного содержания его лежит такая формально-логическая
схема, которая ощущается вышколенным умом как некий логический
костяк, стройный и закономерный, обросший тем или другим конкрет-
ным содержанием. Независимо от стиля мышления эта логическая
схема должна быть закономерной, лишенной пробелов: без этого рассуж-
дение становится недоброкачественным и должно быть отвергнуто.
Однако роль и положение этого логического скелета в данном ходе
мыслей бывают весьма различны и существенным образом зависят
именно от стиля мышления. В одних случаях логическая схема стано-
вится определяющим, руководящим моментом мышления, так что
мыслящий все время имеет ее перед глазами и сообразно с нею выби-
рает и направляет последовательные этапы рассуждения. В других,
напротив, логический костяк остается затушеванным, мысль в гораздо
большей степени направляется запросами конкретного содержания,
роль логики сводится к последующему контролю, да и этот контроль в
письменном или устном изложении часто только подразумевается и
явно не проводится; логическая схема как целое остается вне поля зре-
ния мыслящего. Разумеется, встречаются нередко и стили мышления,
промежуточные между двумя указанными.
Для математики характерно доведенное до предела доминирование
логической схемы рассуждения; математик, потерявший, хотя бы вре-
менно, из виду эту схему, вообще лишается возможности научно мыс-
лить. Эта своеобразная черта стиля математического мышления, в
столь полной мере не встречающаяся ни в одной другой науке, имеет в
себе много ценного. Очевидно, что она в максимальной степени по-
зволяет следить за правильностью течения мысли и гарантирует от
ошибок; с другой стороны, она заставляет мыслящего при каждой
дизъюнкции иметь перед глазами всю совокупность имеющихся воз-
можностей и обязывает его учесть каждую из них, не пропуская ни
одной (такого рода пропуски вполне возможны и фактически часто
наблюдаются при других стилях мышления). Поэтому приобретенные
на уроках математики стилистические навыки, связанные с указанной
чертой, имеют существенное значение для повышения общей культу-
ры мышления учащихся.
16*
251
Очень интересным и ярким примером мышления в далекой от ма-
тематики области, и тем не менее чрезвычайно насыщенного этой чер-
тою, могут служить произведения Маркса. Читателя, который после
изучения экономических трудов других ученых раскрывает «Капи-
тал», с первых страниц поражает железная, непреклонная логика его
строк. Логическая схема с ее неумолимыми требованиями не только
определяет ход мысли автора, но и настойчиво убеждает читателя, ко-
торый не может уйти от ее направляющего влияния. Этот необычный
для экономического сочинения стиль, почти приближающийся к мате-
матическому, неизменно вызывает в читателе ощущение прочности,
надежности, предельной убедительности и в то же время много помо-
гает ему в усвоении читаемого.
Второй характерной чертой математического стиля мышления, о
которой здесь должно быть упомянуто, является его лаконизм, созна-
тельное стремление всегда находить кратчайший, ведущий к данной
цели логический путь, беспощадное отбрасывание всего, в чем нет аб-
солютной необходимости для безупречной полноценности аргумента-
ции. Математическое сочинение хорошего стиля не терпит никакой
воды, никаких украшающих, ослабляющих логическое напряжение
разглагольствований, отвлечений в сторону; предельная скупость, су-
ровая строгость мысли и ее изложения составляют неотъемлемую чер-
ту математического мышления. Черта эта имеет большую ценность не
только для математического, но и для любого другого серьезного рас-
суждения; лаконизм, стремление не допускать ничего излишнего, по-
могает и самому мыслящему, и его читателю или слушателю полно-
стью сосредоточиться на данном ходе мыслей, не отвлекаясь побоч-
ными представлениями и не теряя непосредственного контакта с ос-
новной линией рассуждения.
Корифеи науки, как правило, мыслят и выражаются лаконично во
всех областях знания, даже тогда, когда мысль их создает и излагает
принципиально новые идеи. Какое величественное впечатление произ-
водит, например, благородная скупость мысли и речи величайших
творцов физики: Ньютона, Эйнштейна, Нильса Бора! Может быть,
трудно найти более яркий пример того, какое глубокое воздействие
может иметь на развитие науки именно стиль мышления ее творцов.
Для математики лаконизм мысли является непререкаемым, канони-
зированным веками законом. Всякая попытка обременить изложение
необязательно нужными (пусть даже приятными и увлекательными
для слушателей) картинами, отвлечениями, разглагольствованиями за-
ранее ставится под законное подозрение и автоматически вызывает
критическую настороженность. И поэтому именно уроки математики
призваны дать учащимся, предпочтительно перед другими предмета-
252
ми, навыки лаконичного, прямого, не знающего отвлечении, не обре-
мененного никакими излишними элементами мышления.
Далее, для стиля математического мышления характерна четкая
расчлененность хода рассуждения. Если, например, при доказательст-
ве какого-либо предложения мы должны рассмотреть четыре возмож-
ных случая, из которых каждый может разбиваться на то или другое
число подслучаев, то в каждый момент рассуждения математик дол-
жен отчетливо помнить, в каком случае и подслучае его мысль сейчас
обретается и какие случаи и подслучаи ему еще остается рассмотреть.
При всякого рода разветвленных перечислениях математик должен в
каждый момент отдавать себе отчет в том, для какого родового поня-
тия он перечисляет составляющие его видовые понятия, обыденном,
не научном мышлении мы весьма часто наблюдаем в таких случаях
смешение и перескоки, приводящие к путанице и ошибкам в рассуж-
дении. Часто бывает, что человек начал перечислять виды одного ка-
кого-нибудь рода, а потом незаметно для слушателей (а часто и для
самого себя), пользуясь недостаточной логической отчетливостью рас-
суждения, перескочил в другой род и заканчивает заявлением, что те-
перь оба рода расклассифицированы; а слушатели или читатели не
знают, где пролегает граница между видами первого и второго рода.
Для того чтобы сделать такие смешения и перескоки невозможны-
ми, математики издавна широко пользуются простыми внешними
приемами нумерации понятий и суждений, иногда (но гораздо реже)
применяемыми и в других науках. Те возможные случаи или те родо-
вые понятия, которые надлежит рассмотреть в данном рассуждении,
заранее перенумеровываются; внутри каждого такого случая те под-
лежащие рассмотрению подслучаи, которые он содержит, также пере-
нумеровываются (иногда для различения с помощью какой-либо дру-
гой системы нумерации). Перед каждым абзацем, где начинается рас-
смотрение нового подслучая, ставится принятое для этого подслучая
обозначение (например, П 3 — это означает, что здесь начинается рас-
смотрение третьего подслучая второго случая или описание третьего
вида второго вида, если речь идет о классификации). И читатель знает,
что до тех пор, покуда он не натолкнется на новую числовую рубрику,
все излагаемое относится только к этому случаю и подслучаю. Само
собой разумеется, что такая нумерация служит лишь внешним прие-
мом, очень полезным, но отнюдь не обязательным, и что суть дела не в
ней, а в той отчетливой расчлененности аргументации или классифи-
кации, которую она и стимулирует, и знаменует собой.
Наконец, следует упомянуть еще об одной чисто внешней традиции
математического стиля, могущей при надлежащих условиях приобре-
сти воспитательное значение, которым нельзя пренебрегать. Я имею в
253
виду свойственную математике скрупулезную точность символики.
Каждый математический символ имеет строго определенное значение;
замена его другим символом или перестановка на другое место, как
правило, влечет за собою искажение, а подчас и полное уничтожение
смысла данного высказывания. Учащийся, не привыкший еще отно-
ситься с достаточной требовательностью к точности устной речи и
письменного изложения, вначале может с некоторым легкомыслием
отнестись к неуклонным и настойчивым приглашениям учителя мате-
матики — вести математическую запись с абсолютной точностью; эти
требования могут даже показаться ему педантичными и вызвать на-
смешку. Однако он очень быстро убедится на собственном опыте, что
несоблюдение безукоризненной точности символической записи в ма-
тематике влечет за собой немедленную расплату: он сам теряет воз-
можность понять смысл записанного, вынужден гадать, угадывает не-
верно и либо получает неправильный ответ, либо вообще лишает себя
возможности решить задачу. В лучшем случае ему ценою значитель-
ных усилий удастся восстановить правильную запись и шествовать
дальше, отправляясь от нее.
Убедившись таким образом, что точность символической записи
соответствует его собственным интересам, он начинает следить за со-
бою в этом направлении, и постепенно строгая правильность матема-
тической символики становится его привычкой. Но такого рода при-
вычка, приобретенная в какой-либо одной сфере мышления, неизбеж-
но приводит к воспитанию и общего стиля мышления учащегося; он
начинает точнее выражаться и в устной речи, и в письменном изложе-
нии; в частности, он уделяет больше внимания правописанию, орфо-
графические ошибки переживаются им с такой же остротой и таким же
беспокойством, как математические. Мы неизменно наблюдаем, что
ученики, научившиеся требовательно относиться к точности матема-
тической символики, легче и быстрее перестают делать орфографиче-
ские ошибки. И я не знаю, возможно ли окончить школу, обладая тре-
буемой для аттестата зрелости математической культурой и не нау-
чившись в то же время писать совершенно безошибочно.
Заканчивая эту статью, посвященную вопросам воспитательного
воздействия уроков математики на культуру мышления учащихся, я
предвижу естественное и законное недоумение читателя по поводу то-
го, что мною нигде даже не затронута проблема развития элементов
диалектического мышления. Я считаю себя обязанным дать по этому
вопросу краткое разъяснение.
Маркс и Энгельс с полным основанием утверждали, что математи-
ка не только дает для законов диалектического мышления богатейший
иллюстративный материал, но систематически способствует развитию
254
диалектических навыков мыслительного процесса. Однако, как это не-
однократно отмечалось основоположниками марксизма, в полной мере
это может быть отнесено лишь к так называемой высшей математике,
т.е. к математике переменных величин. Именно здесь мы приучаемся к
математическому исследованию явлений природы и процессов техни-
ки в их живой изменчивости, а не статической неподвижности. Имен-
но здесь величины исследуются в их взаимной зависимости (понятие
функции), а не в отрыве друг от друга. Нигде с такой наглядностью,
как здесь, мы не видим в действии переход количества в качество,
диалектический синтез первоначально антагонистических противопо-
ложностей и другие основные принципы диалектики. И это одна из
важнейших причин (впрочем, далеко не единственная), заставляющих
нас признать абсолютно необходимым введение элементов высшей
математики в курс средней школы.
Но пока мы только боремся за это. Что же касается преподаваемой
в школе элементарной математики, то и она, конечно, как всякая под-
линная и живая наука, не лишена диалектических элементов. Но здесь
они выступают разрозненно и с малой мощностью, и говорить о них в
статье, посвященной лишь основным рычагам воспитательного воз-
действия уроков математики, я не решился.
II. МОРАЛЬНЫЕ МОМЕНТЫ В ВОСПИТАНИИ
О роли и значении уроков математики в воспитании правильного и
дисциплинированного мышления говорилось и писалось очень много.
Напротив о влиянии математических занятий на формирование личности
учащегося не сказано почти ничего. Это вполне понятно, по абстрактно-
сти своего предмета математическая наука не может давать учащемуся
тех непосредственных впечатлений, этически воздействующих и форми-
рующих характер образов, картин, эмоций, какими располагает, скажем,
история или литература Было бы, однако, весьма поверхностно делать
отсюда вывод, что в деле формирования нравственной личности школь-
ника уроки математики вообще должны быть скинуты со счетов. По мо-
ему многолетнему опьпу, работа над усвоением математической науки
неизбежно воспитывает — исподволь и весьма постепенно — в молодом
человеке целый ряд черт, имеющих яркую моральную окраску и способ-
ных в дальнейшем стать важнейшими моментами в его нравственном об-
лике. Сделать этот процесс более активным и результаты его более проч-
ными — достойная задача для учителя. Но прежде всего надо тщательно
разобраться в том, что это за черты и какие особенности математической
работы способны их воспитывать.
1. Честность н правдивость. В обывательских тяжбах всякого ро-
да каждая из спорящих сторон исходит, как правило, из желательного
255
ей, выгодного для нее решения вопроса и с большей или меньшей изо-
бретательностью изыскивает возможно более убедительную аргумен-
тацию для решения вопроса в свою пользу. В зависимости от эпохи,
среды и содержания спора стороны при этом апеллируют к тому или
другому высшему авторитету — общечеловеческой морали, «естест-
венному» праву, священному писанию, юридическому кодексу, дейст-
вующим правилам внутреннего распорядка, а часто и к высказываниям
отдельных авторитетных ученых или признанных политических руко-
водителей. Все мы много раз наблюдали, с какой страстностью ведут-
ся подобного рода споры и какой убежденностью дышит, по-
видимому, аргументация каждой из сторон; можно подумать, что та-
кой тяжущийся действительно обуреваем желанием найти и отстоять
истинное, справедливое, отвечающее духу и букве признанного в ка-
честве арбитра авторитетного источника решение.
Но хорошо известно, что эту картину мы часто наблюдаем не в од-
них только обывательских тяжбах. В точности те же черты являет под-
час и научная дискуссия. Выводы, с полной убежденностью сделанные
одним ученым, с такою же убежденностью оспариваются другими; за-
вязывается полемика, в которой каждая из сторон находит все новые и
новые аргументы в пользу своей позиции — даже вновь поставленные
опьггы часто говорят каждому из спорящих как раз то, что ему жела-
тельно. В ходе полемики каждая из сторон не только стремится все бо-
лее и более усиливать свою собственную позицию, но и старается раз-
личными средствами дискредитировать позицию противной стороны,
доходя иногда и до попыток персональной дискредитации. И лишь
сравнительно редко бывает, чтобы в такой затянувшейся полемике од-
на из спорящих сторон нашла честность и мужество признать свою
позицию ошибочной.
Субъективные основания такого рода явлений в жизни науки легко
понять: они ничем, к сожалению, не отличаются по своей непригляд-
ности от субъективных оснований самых мелочных обывательских
стычек. Что касается объективных оснований возможности подобного
рода научных ситуаций, то и их нетрудно найти: в эмпирических нау-
ках всякая новая, еще не окончательно установленная закономерность
фигурирует, по крайней мере временно, в качестве «рабочей гипоте-
зы»; покуда вопрос не решен окончательно, имеются обычно как сооб-
ражения (опытные и теоретические), говорящие в пользу этой гипоте-
зы, так и такие, которые говорят против нее. Из двух ученых один мо-
жет поставить своей задачей собрать как можно больше аргументов,
поддерживающих такую гипотезу, а другой — заняться собиранием
фактов и соображений, способных вызвать к ней недоверие. Дело проис-
ходит как в уголовном процессе, где перед обвинителем и защитником
256
ставятся задачи собрать, привести в порядок и изложить все аргументы,
соответственно говорящие за и против виновности подсудимых.
Само собою разумеется, что так поставленная научная дискуссия
сама по себе не содержит еще ничего морально одиозного: собрать с
возможною полностью все имеющиеся аргументы за и против данной
«рабочей гипотезы» — это во всех случаях приносило пользу прогрес-
су науки; нет, очевидно, ничего предосудительного и в том, что сбор
аргументов за и против гипотезы выполняется двумя различными уче-
ными (или группами ученых), если только обе стороны подходят к
своей задаче добросовестно, руководствуясь исключительно желанием
способствовать отысканию объективной истины. Моральный одиум,
этическое неблагополучие начинаются там, где в своих выводах уче-
ный перестает руководствоваться интересами объективной истины, а
стремится поставить эти выводы — сознательно, полусознательно или
бессознательно — на службу своим личным интересам — своему уп-
рямству, своему честолюбию, своему корыстолюбию, когда аргумен-
тация приводится с пристрастием, «притягивается за волосы», необъ-
ективно акцентируется, точь-в-точь как в мелком сутяжничестве или в
обывательских дрязгах. Такая деградация научного спора в иных слу-
чаях ложится мрачным пятном даже на крупнейших представителей
научной мысли; среди же ученых меньшего ранга она представляет
собою, к сожалению, довольно распространенное явление.
Одна только математическая наука полностью от всего этого из-
бавлена. Она не знает «рабочих гипотез» — предложений, истинность
которых может подлежать дискуссии. Пока предложение не доказано,
оно вообще никак не входит в сокровищницу науки, никому не придет
в голову его отстаивать; если же оно доказано, то истинность его ни-
как не может быть подвергнута сомнению, оно является абсолютно
общеобязательным. Никаких промежуточных ситуаций математика не
знает. Полемизировать, например, в защиту неполноценного доказа-
тельства в математике может только неуч, шарлатан или душевно-
больной (все три категории действительно время от времени встреча-
ются, достаточно вспомнить так называемых ферматистов, рыцарей
квадратуры круга и трисекции угла); но такой «защитник» немедлен-
но, единогласно и беспощадно разоблачается научным миром. Никакая
аргументация с пристрастием или тенденцией, никакое «притягивание
за волосы» ни при каких обстоятельствах не могут в математике иметь
успеха. Разумеется, это относится только к содержанию самой матема-
тической науки; в вопросах логического или философского обоснова-
ния математики дискуссии возможны и даже неизбежны; возможны (и,
к сожалению, нередки) и споры персонального характера, связанные с
развитием математики (например, по вопросам приоритета).
257
Каждый математик рано привыкает к тому, что в его науке всякая
попытка по тем или иным мотивам действовать тенденциозно, заранее
склоняясь к тому или другому решению вопроса и прислушиваясь
только к аргументам, говорящим в пользу избранного решения, —
всякая такая попытка заведомо обречена на неудачу, и ничего, кроме
разочарования, пытающемуся принести не может. Такое положение,
при котором неправильная или не до конца правильная аргументация
могла бы оказаться выгодной для аргументирующего, здесь просто
принципиально невозможно. Поэтому математик быстро привыкает к
тому, что в его науке выгодна только правильная, объективная, ли-
шенная всякой тенденциозности аргументация, что успех может при-
нести только непредубежденное, беспристрастное напряжение мысли.
И независимо от своего общего морального уровня он в своей научной
работе всегда руководствуется исключительно соображениями объек-
тивной истинности.
Но эту черту, естественно развивающуюся у ьатематика-специалиста, в
известной степени воспитывает в себе, занимаясь математикой, и каждый
неспециалист, в частности каждый школьник. Ему хорошо известно, что
втереть очки учителю математики невозможно, что никакой апломб и ни-
какое красноречие не помогут ему выдать незнание за знание, неполноцен-
ную аргументацию за полноценную. И как бы лжив он ни был в других от-
ношениях, в математике он остережется отстаивать неверное утверждение
или неправильное доказательство.
Но и здесь, как это часто бывает, моральные навыки, приобретен-
ные в какой-либо одной области, в известной мере переносятся и на
другие сферы мышления и практической деятельности. Теоретическая
честность, ставшая для математика непреложным законом его научно-
го мышления и профессиональной (в частности, педагогической) дея-
тельности, довлеет над ним во всех его жизненных функциях — от аб-
страктных рассуждений до практического поведения.
Я всегда интересовался этой чертою и много раз наблюдал, как она
развивается в людях под влиянием серьезного научного общения, в ча-
стности под воздействием уроков математики. Это очень радостная и
морально возвышающая картина, когда человек постепенно преодоле-
вает в себе отвратительную мещанскую привычку — подчинять зако-
ны мышления своим личным, мелким, корыстным интересам, теорети-
чески защищать все то и только то, что ему практически выгодно; ко-
гда он научается уважать объективную правильность аргументации
как высшую духовную и культурную ценность и все чаще и со все бо-
лее легким сердцем жертвовать ради нее своими личными интересами.
Доведенная до предела, эта черта представляет собою не что иное, как
честность и правдивость — одно из лучших украшений нравственной
личности человека.
258
2. Настойчивость и мужество. Добросовестная и серьезная работа
над приобретением и укреплением знаний в любой научной области
требует систематического напряжения умственных усилий, настойчи-
вости в преодолении трудностей, мужественной встречи неудач; по-
этому такая работа при правильном руководстве неизбежно воспиты-
вает у учащегося соответственные черты характера: трудолюбие,
усидчивость, упорство в преследовании намеченной цели, умение не
останавливаться перед трудностями и не впадать в уныние при неуда-
чах. Непосредственно ясно, какое решающее значение имеют все эти
черты для развития морально и общественно полноценной человече-
ской личности и с каким вниманием должен поэтому учитель следить
за максимальным использованием своих уроков в целях воспитатель-
ного воздействия в указанном направлении. Те возможности, которы-
ми для этого располагают предметы школьного обучения, весьма мно-
гочисленны и многообразны, и нет такого предмета, в специфических
чертах которого не было бы заложено особых, именно этому предмету
свойственных движущих рычагов такого воспитательного воздейст-
вия. Наша задача здесь, естественно, должна состоять в указании тех
черт математики как школьного преподавания, которые, отличая ее от
других предметов школьного преподавания, способствуют развитию у
учащихся разумной настойчивости и сознательного мужества — этих
неоценимых качеств будущего борца.
Прежде всего я хочу здесь отметить четкую определенность по-
ставленной цели, желаемого и требуемого результата каждого матема-
тического задания. Если заданием служит сочинение исторического
или литературного содержания, то нельзя указать момента, когда такое
задание дефинитивно закончено выполнением — возможности допол-
нения и усовершенствования, систематических улучшений всякого ро-
да здесь почти безграничны; с другой стороны, учащийся не чувствует
себя здесь достаточно компетентным для авторитетной оценки своей
работы: то, что ему представляется в его сочинении вполне удачным,
может встретить совсем иную оценку со стороны учителя. Вся эта, по
существу, данного задания неизбежная неопределенность, расплывча-
тость в оценке законченности и качества проделанной работы должна,
несомненно, оказывать некоторое расслабляющее влияние на волевое
напряжение еще мало вышколенного молодого ума.
В математике дело обстоит иначе. Если заданием служит решение за-
дачи или доказательство теоремы, то тем самым указывается с полной
определенностью и тот момент, когда задание может считаться оконча-
тельно выполненным: когда решена задача или доказана теорема; все ос-
тальное — изложение найденного решения, правильность и аккуратность
записи и т.п. — имеет и в глазах учителя, и в глазах ученика лишь второ-
259
степенное, не решающее значение. Равным образом и качество работы
здесь оценивается с однозначной определенностью: задача должна быть
решена верно, теорема должна быть доказана правильно. Проверить от-
сутствие логических ошибок в своем рассуждении ученик может и дол-
жен уметь сам; в случае задачи он знает даже определенные приемы про-
верки решения. Легко понять, какое стимулирующее влияние на упорст-
во, настойчивость в достижении цели может оказать и действительно ока-
зывает эта четкая определенность показателей результата. Победа здесь
так же непосредственно ощутительна, как в шахматной партии или спор-
тивном состязании, и сам учащийся может с такой же уверенностью за-
фиксировать и оценить свое достижение, как и его авторитетный учитель.
Вторая, значительно более глубокая и важная черта математиче-
ских заданий, которую я хочу здесь отметить, состоит в присущем им
в значительном большинстве случаев творческом характере. В то вре-
мя как в большинстве других областей знания выполнение задания, за
немногими исключениями, требует от учащегося лишь определенных
знаний и навыков — в лучшем случае еще умения стройно и стили-
стически правильно излагать эти знания, — решение математической
задачи, как правило, предполагает изобретение специально ведущего к
поставленной цели рассуждения и тем самым становится — пусть
весьма скромным — творческим актом. Именно этот творческий, ис-
следовательский характер математических заданий более чем что-либо
другое влечет к себе молодые силы растущего и крепнущего интеллек-
та учащегося. Тот, кто изведал благородную радость творческого дос-
тижения, никогда уже не пожалеет усилий, чтобы вновь ее испытать.
Никакие трудности его не остановят, сила его порыва и устремления,
его усидчивость и выдержка в преодолении препятствий будут креп-
нуть с каждым новым достижением, а неудачи, ошибки, временные
крушения и поражения он научится встречать, как подобает истинно-
му борцу, не опуская перед ними руки, а черпая в них источник и сти-
мул для все новых и новых напряжений мысли и воли.
Заключение. 1. Я сознательно полностью оставил в стороне важ-
нейший для темы настоящей статьи вопрос о значении уроков матема-
тики для формирования мировоззрения учащихся. Я сделал это по той
же причине, по какой в свое время отказался от рассмотрения вопроса
об использовании уроков математики для воспитания навыков диалек-
тического мышления: ознакомление с идеями и методами математиче-
ской науки имеет фундаментальное мировоззренческое значение, но
львиная доля воспитательного эффекта в этом направлении принадле-
жит математике переменных величин, так называемой высшей мате-
матике, с которой, по выражению Энгельса, в математику входит диа-
260
лектика и которая, к сожалению, все еще почти целиком остается за
бортом наших школьных программ. Поистине не стоит при этих усло-
виях говорить о влиянии на формирование мировоззрения той диалек-
тически худосочной части математической науки, которая в настоящее
время находит себе приют в нашем школьном преподавании. О тех же
мощных сдвигах, направляющих и формирующих мировоззрение, ко-
торые может произвести и фактически часто производит изучение
высшей математики, можно сказать очень много.
2. В этой статье я не касался методических вопросов. Я говорил
только о том, какие особенности математической науки и для воспита-
ния каких именно качеств интеллекта или моральной личности учаще-
гося могут и должны быть использованы, но нигде не касался вопроса
о том, как это может быть сделано. Мой опыт говорит мне, что это об-
стоятельство может вызвать недовольство в некоторых кругах читате-
лей; вероятно, я не гарантирован от набивших уже оскомину упреков в
том, что моя статья «ничего не дает учителю» и советов «повернуться
лицом» и т.д. Поэтому я считаю необходимым сделать по этому пово-
ду следующее краткое разъяснение.
1) Я считаю, что составление сколько-нибудь детальных методиче-
ских указаний по рассматриваемым мною в настоящей статье вопро-
сам действительно совершенно излишне. Сколько-нибудь заметный
воспитательный эффект уроки математики (как и всякой другой науки)
могут дать только при том условии, что учитель, во-первых, достаточ-
но хорошо знает свою науку, ее методологию и ее историю, во-вторых,
имеет достаточный педагогический такт и опыт и, наконец, в-третьих,
сам обладает в достаточной мере всеми теми качествами, которые он
собирается воспитывать в своих учениках. Учителю, который сам не
умеет мыслить абсолютно отчетливо, никакие методические шпаргал-
ки не помогут воспитать ясность мысли в учащихся.
И напротив, если учитель стоит на высоте своей задачи, если он в
полной мере обладает всеми перечисленными выше качествами, то
никакие методические разработки по воспитательным вопросам ему
заведомо не нужны: в каждом отдельном случае он с легкостью и не-
принужденностью сам найдет наиболее эффективный путь к постав-
ленной цели. Навязывание ему определенной конкретной методики
было бы для такого учителя только помехой в работе.
2) Если, таким образом, я считаю составление детальных методиче-
ских указаний по затронутым мною вопросам практически бесцель-
ным, то, может быть, было бы полезно все же дать по ним ряд общих
методических советов; я думаю, что было бы хорошо, если бы моя ста-
тья побудила кого-либо из наших лучших учителей-методистов выска-
заться по этому вопросу и сделать достоянием младших товарищей
261
некоторые общие выводы из своего опыта. В этом они во всяком слу-
чае компетентнее меня, и здесь я со всей необходимой скромностью
должен уступить им слово.
3. Наконец, я хочу попытаться заранее оградить себя еще от одного
рода упреков, которые я предвижу и которые обычно бывают основа-
ны на недоразумении. Так как я говорил о воспитательном эффекте
уроков математики, то мне, естественно, пришлось перечислять одну
за другой именно те черты математической науки, которые в воспита-
тельном отношении дают ей то или другое преимущество перед дру-
гими дисциплинами. В этом ведь и состояла моя задача. Но когда по-
ступаешь таким образом, то у недостаточно вдумчивого читателя соз-
дается впечатление, будто бы ты поставил своей целью превознесение
математики над всеми другими науками и вся твоя статья сплошь ут-
верждает, что единственно подлинная наука есть именно математика,
все же другие дисциплины страдают теми или другими изъянами и
науками могут быть названы лишь с известной оговоркой. Уважаемые
коллеги — представители других наук — начинают чувствовать себя
несправедливо обиженными и подвергают твою работу яростной кри-
тике, доказывая, что другие науки ничуть не хуже и что всеми пре-
имуществами, которыми в моем представлении монопольно обладает
математика, на самом деле в такой же мере наделены и все прочие
дисциплины.
С первым пунктом этого заявления я целиком и полностью согла-г
сен: другие науки действительно ничем не хуже математики; более то-
го, представители этих других наук обычно вызывают во мне глубо-
чайшее уважение тем, что творят великие ценности в таких областях, в
которых творчество, на мой взгляд, неимоверно трудно, гораздо труд-
нее, чем в математике. Но ведь в моей статье я нигде ни разу не назы-
ваю математику лучшей из наук! Напротив, я несколько раз со всею
скромностью подчеркиваю, что как орудие воспитания математика
прежде всего отмечена такой особенностью, значение которой для
данной цели очевидным образом отрицательно, — она абстрактна,
предметом ее служат не сами вещи и явления реального мира, а лишь
абстрагированные от них количественные отношения и пространст-
венные формы. Это обстоятельство, как я несколько раз подчеркиваю
в своей статье, делает для математики воспитательную задачу значи-
тельно труднее, чем для других школьных дисциплин. Но зато матема-
тика в некоторых других отношениях отмечена такими чертами, кото-
рые создают ей воспитательные возможности более значительные, чем
у этих других дисциплин. И то, что я в своей работе соответственно
моей задаче сосредоточиваю внимание читателя именно на этих чер-
тах, никак не может, конечно, означать какого-либо гипостазирования
математики, превознесения ее выше всех других наук.
262
Я отдаю математической науке лишь то, что ей принадлежит по
праву, с полной откровенностью признавая и те ее черты, которые в
отношении к данной цели составляют ее слабость. Но за те преимуще-
ства, которые я ей приписываю, я уж действительно готов драться до
конца. И если уважаемые коллеги пожелают утверждать, что та или
другая конкретная черта, по моему утверждению монопольно или пре-
имущественно присущая математике, на самом деле является в такой
же мере достоянием и всех других научных дисциплин, то здесь я где
угодно и когда угодно готов держать ответ в полной уверенности, что
смогу отстоять правильность моего утверждения перед любым компе-
тентным и беспристрастным судом.
Сойер
О КРАСОТЕ И СИЛЕ14
Нельзя быть настоящим математиком, не буду-
чи немного поэтом.
К. Вейерштрасс
Мудрость рождается из пристального наблю-
дения за тем. как растут люди
Конфуций
СФЕРА МАТЕМАТИКИ
Немногие представляют себе, как огромна сфера действия совре-
менной математики. Вероятно, было бы легче овладеть всеми сущест-
вующими языками, чем всеми математическими знаниями, известны-
ми в настоящее время. Мне кажется, что все языки можно было бы
выучить за одну человеческую жизнь; а всю математику, конечно, нет.
К тому же объем математических знаний не остается неизменным.
Ежегодно публикуются все новые открытия. Например, в 1951 г. для
реферативного изложения всех математических статей, вышедших за
год, потребовалось 900 печатных страниц крупного формата. Только
за январь упомянуто 451 название, причем реферировались статьи и
книги, рассматривающие новые проблемы; лишь в немногих из них
упоминались известные факты.
Человеку, желающему быть в курсе всего нового в математике,
пришлось бы прочитывать ежедневно около 15 статей, весьма боль-
ших по объему и содержащих сложные математические выкладки.
Трудно даже мечтать о выполнении подобной задачи.
Открытия, которые делают математики, столь разнообразны по сво-
ему характеру, что однажды кто-то, видимо, в отчаянии предложил
263
определить математику как «все, чем занимаются математики». Каза-
лось, что только такое широкое определение может охватить все, что
относится к математике. Математики решают проблемы, которые в
прошлом не считались математическими, и трудно предсказать, чем
они еще будут заниматься в будущем.
Точнее было бы определение: «Математика — это классификация
всех возможных задач и методов их решения». Это определение, по-
жалуй, тоже расплывчато, так как оно охватывало бы даже такие руб-
рики, как газетные объявления «Обращайтесь со всеми вашими сер-
дечными заботами к тете Минни», что мы никак не имеем в виду.
Для целей нашей книги достаточно было бы определение: «Мате-
матика — это классификация и изучение всех возможных закономер-
ностей». Слово «закономерность» здесь используется в таком смысле,
с которым многие могут не согласиться; а именно, в самом широком
смысле, как название любого рода закономерностей, которые могут
быть познаны умом Жизнь, особенно интеллектуальная жизнь, воз-
можна лишь потому, что в мире существуют определенные законо-
мерности. Птица, например, различает черные и желтые полоски осы;
человек знает, что растение развивается из посаженного в землю семе-
ни. В обоих случаях существует осознанная закономерность.
Закономерность — это наиболее стабильная характеристика посто-
янно меняющегося мира. Сегодняшний день не может быть похож на
вчерашний. Нельзя увидеть дважды одно и то же лицо под одним и
тем же углом зрения. Узнавание возможно не потому, что опыт точно
повторяется, а потому, что в огромном разнообразии жизненных явле-
ний можно распознать определенные закономерности. Такую постоян-
ную закономерность мы имеем в виду, когда говорим «мой велосипед»
или «река Темза», хотя велосипед довольно быстро изнашивается, а
воды реки непрерывно переливаются в море.
Любая математическая теория должна непременно сочетать в себе
мощь метода, обусловливающую возможность применений к естест-
венным наукам, и красоту, стройность, столь привлекательную для
ума. Нам кажется, что наше определение математики удовлетворяет
обоим этим требованиям. Вся наука зиждется на закономерностях,
имеющихся в природе; для практики важна классификация этих зако-
номерностей. С другой стороны, ум должен получать удовольствие
при изучении и познании закономерностей, поскольку необходимость
и желание всегда связаны в природе. Если следование законам приро-
ды характерно как для человека, так и для животных, то естественно
ожидать, что подчинение закономерностям доставляет удовольствие, та-
кое же, как удовлетворение любой другой человеческой потребности.
264
Интересно заметить, что «чистые» математики, движимые только
чувством стройности и математической формы, часто приходили к вы-
водам, которые в дальнейшем оказывались чрезвычайно важными для
науки. Греки изучали свойства эллипса более чем за тысячу лет до то-
го, как Кеплер использовал их идею для определения траектории пла-
нет. Математический аппарат теории относительности был создан за
тридцать—пятьдесят лет до того, как Эйнштейн нашел для него при-
менение в физике. Подобных примеров можно было бы привести мно-
го. С другой стороны, много стройных теорий и проблем, которые лю-
бой «чистый» математик причислит к математике, возникли в связи с
физикой.
КАКИЕ ЗАКОНОМЕРНОСТИ ЛЮБИТ ПРИРОДА?
Еще один интересный факт. Мы иногда встречаем одну и ту же за-
кономерность в разных областях природы, как если бы число законо-
мерностей было крайне лимитировано. Закономерность, которую ма-
тематики обозначают Av, встречается более чем в десятке различных
областей науки. Она возникает в связи с такими явлениями, как тяго-
тение, свет, звук, теплота, магнетизм, электростатика, электрический
ток, электромагнитные излучения, морские волны, полет самолета, ко-
лебания упругих тел и строение атома, не говоря уже об одной чисто
математической теории первостепенной важности — теории функций
комплексного переменного.
Практики часто допускают ошибку, рассматривая все эти проявле-
ния Av по отдельности. Это приводит к излишней трате сил. Мы здесь
имеем дело не с двенадцатью отдельными теориями, а с одной теори-
ей, имеющей 12 применений. Здесь везде проявляется одна и та же за-
кономерность. Физически ее применения различны, математически —
одинаковы.
Идея наличия одной и той же закономерности в различных услови-
ях очевидна. Остается только придумать для нее соответствующее на-
звание; и вот мы имеем один из самых общих терминов современной
математики — изоморфный, т.е. «имеющий одну и ту же форму». Ни-
что не доставляет математику большего наслаждения, чем открытие,
что две вещи, которые он ранее считал совершенно различными, ока-
зываются математически идентичными, изоморфными. «Математика, —
говорит Пуанкаре, — это искусство называть разные вещи одним и
тем же именем».
Возникает вопрос: «Чем вызвано то, что эта закономерность встре-
чается так часто?» Здесь мы уже лавируем на грани математического
мистицизма. Окончательного ответа на этот вопрос быть не может.
Предположим, мы доказали, что эта закономерность имеет ряд
265
свойств, делающих ее особенно подходящей; но тогда бы неминуемо
возник следующий вопрос: «Почему же природа предпочитает именно
эти свойства?» — и так без конца. Тем не менее на вопрос, почему
именно закономерность Av встречается так часто, можно частично от-
ветить.
Невозможность дать окончательный ответ на вопрос «Почему Мир
устроен так, а не иначе?» вовсе не означает, что такая постановка во-
проса абсолютно бесполезна. Нам, может быть, удастся показать в бу-
дущем, что все научные законы, открытые до сих пор, имеют ряд об-
щих свойств. Математик, изучающий закономерности этих общих
свойств, имеет все основания надеяться, что его работа окажется по-
лезной для будущих поколений; хотя, конечно, абсолютной уверенно-
сти в этом быть не может — ни в чем нельзя быть абсолютно уверен-
ным. Кроме того, он может надеяться удовлетворить таким образом
свою собственную потребность в глубоком проникновении в законы
Вселенной.
МАТЕМАТИК КАК КОНСУЛЬТАНТ
Практики, как правило, не имеют представления о математике как о
способе классификации всех проблем. Обычно они стремятся изучать
только те разделы математики, которые уже оказались полезными для
их специальности. Поэтому они совершенно беспомощны перед но-
выми задачами. Вот тогда-то они и обращаются за помощью к матема-
тикам. (Это разделение труда между инженерами и математиками, ве-
роятно, оправдано; жизнь слишком коротка для того, чтобы одновре-
менно изучать и абстрактную теорию и инженерное дело.) Встреча ма-
тематика и инженера обычно очень забавна. Инженер, ежедневно имея
дело с машинами, настолько привыкает к ним, что не может понять
чувств человека, видящего машину впервые. Он забрасывает своего
консультанта-математика огромным количеством подробностей, кото-
рые для того ровным счетом ничего не значат. Через некоторое время
инженер приходит к выводу, что математик — абсолютный невежда и
что ему нужно объяснять простейшие вещи, как ребенку или Сократу.
Но как только математик поймет, что делает машина или что от нее
требуется, он переводит задачу на язык математических терминов. По-
сле этого он может заявить инженеру одно из трех:
1) что задача известна и уже решена;
2) что это новая задача, которую он может попытаться решить;
3) что это одна из тех задач, которую математики безуспешно пы-
тались решить, и что еще могут пройти века, прежде чем будет сделан
хотя бы шаг к ее решению, и что поэтому инженеру придется решать
ее эмпирически.
266
К сожалению, третий случай встречается удручающе часто. Но пер-
вый и второй случаи также довольно часты, и вот тогда-то математик,
благодаря его знанию закономерностей, может принести пользу в тех
областях, о которых он в некотором смысле ничего не знает.
Математик, желающий консультировать инженеров, должен поэто-
му изучать не только те задачи, которые уже встречались; он также
должен быть готов анализировать задачи, которые только еще могут
возникнуть. Можно считать, что практические задачи образуют в из-
вестном смысле определенный тип задач. Например, очень часто прак-
тическая задача принимает форму дифференциального уравнения. Не-
которые дифференциальные уравнения мы умеем решать, а другие
нет. Поэтому математик стремится расширить свой арсенал, изучая те
дифференциальные уравнения, которые пока еще не решены; это не-
избежно поставит перед ним ряд фундаментальных вопросов, напри-
мер: «Какая разница между уже решенными и нерешенными диффе-
ренциальными уравнениями? В чем состоит трудность их решения?»
Но не всегда практическую задачу удается отнести к какому-либо
математическому типу. Иногда возникают задачи, совершенно не по-
хожие на уже встречавшиеся. Ключ к их решению может быть найден
совершенно случайно Они даже могут напомнить какую-нибудь за-
дачку, решенную на досуге. В подобном случае такая задача может
лечь в основу новой крупной теории. Впрочем, эта доктрина, как и все
доктрины, может привести к заблуждениям. Человек может потратить
всю свою жизнь на решение пустяковых задач, теша себя надеждой,
что они, возможно, станут началом новых областей математики. И так,
конечно, может случиться; все зависит от умения определить, что мо-
жет оказаться важным, и нет правила, которое позволило бы судить о
правильности выбора. Любой математик согласится, что существуют
теории, которые до сих пор не нашли практического применения, но
чувствуется, что они являются очень важной частью математики. Ра-
бота над ними свидетельствует не об отходе от главного направления,
а как раз об обратном — о борьбе за развитие математики. Когда-
нибудь эти теории, «подобно эллипсу», найдут своего Кеплера и, «по-
добно тензорному анализу», своего Эйнштейна. Но, во всяком случае,
ими подготовлен мощный аппарат для решения определенного класса
задач, если возникнет такая необходимость.
МАТЕМАТИК КАК ХУДОЖНИК
Я пишу и представляю себе, как «чистый математик» читает эту
книгу со все возрастающим недовольством. Даже если предположить,
что у него хватило терпения дочитать до сих пор, он, наверное, гово-
рит: «Вы рассматриваете математику как нечто приносящее практиче-
скую пользу. Но математика не прикладная наука, она важна сама по
267
себе. Важна не полезность математики, а ее стройность. Прикладная
математика — это самая скучная часть математики. Посмотрите-ка на
людей, работающих над теорией чисел, не имеющей никакого прак-
тического применения, — вы предложили бы им заниматься бух-
галтерией?»
Этой точке зрения, которой придерживаются многие крупные ма-
тематики, можно противопоставить утилитарный, бюрократический
взгляд на математику. Согласно этой немного пуританской точке зре-
ния математики должны стыдиться своей приверженности к красоте и
стройности, и им следует заниматься лишь решением неотложных
практических задач, получаемых от практиков.
Обе точки зрения несовершенны. Ясно, что следование любой из
них до логического конца явилось бы роковым и для математики, и
для технического прогресса.
Давайте рассмотрим вначале точку зрения «математика ради мате-
матики» и проанализируем как частный пример ее применение к по-
ложению в стране Золотой Берег. Золотой Берег — это страна, где жи-
вут умные, жизнерадостные люди. Не надо думать, что это несчастная
страна, но все же это страна, которая нуждается во многом. Во многих
местах плохое водоснабжение, отсутствует канализация, распростра-
нены заразные болезни, не хватает продуктов питания, некоторые дети
хронически недоедают. Так как же в этих условиях мы можем оправ-
дать расходы математического факультета нового университета?
Ссылками на стройность математики? В таких условиях защищать
расходы на факультет математики только на основании прелести ма-
тематики было бы верхом бессердечия. Математика имеет культурную
ценность, но ее ценность состоит вовсе не в том, чтобы любоваться
новыми закономерностями, с полным безразличием ко всему окру-
жающему. Совершенно очевидно, что практическая сила математики
как прикладной науки для техники, биологии и медицины имеет пер-
востепенное значение в любой развивающейся стране. Красота без си-
лы — бессмысленна.
Следует также сказать несколько слов в защиту математика-
художника. Полезность без красоты бессильна. Работа, которой зани-
маются только ради ее результата, без какого бы то ни было удоволь-
ствия от самого процесса работы, может оказаться выполненной пло-
хо. Инженер иногда начинает изучать математику потому, что она по-
лезна для него как для специалиста, но если он больше ничем не инте-
ресуется, если он не увлечется самим предметом, математика мало ему
поможет.
Утилитарный подход к математике оправдан лишь в одном отно-
шении; он признает тот факт, что математик — человек, что он зави-
268
сит от усилий других людей: ему нужна пища, одежда, кров и очаг—
и за все это он должен как-то отплатить обществу. Такую постановку
вопроса легче всего принимают нематематики: администраторы и на-
логоплательщики. Вообще, соображения полезности приводят к за-
ключению, что математики нужны; но они не показывают путей, как
их создавать. Было бы весьма желательным, чтобы Сахара покрылась
дубовыми рощами, в тени которых отдыхали бы путешественники, но
одного желания мало, чтобы там выросли деревья. Математикам, как и
деревьям, нужны условия, пригодные для роста.
Можно, конечно, возразить, что люди не деревья, что если человек
понимает, что нужно что-то сделать, он в состоянии приняться за это.
Эта мысль справедлива лишь в определенных пределах. Социальные
условия в какой-нибудь стране могут быть благоприятны для развития
математики; если стране срочно нужны математики и все об этом зна-
ют, тогда математика может там процветать. Но это все же не отвечает
на вопрос, как начинается это процветание. Внешних побудительных
факторов, будь то хороших или плохих, еще недостаточно. Такие чув-
ства, как жажда денег, стремление к славе или любовь к человечеству,
не могут сделать из человека великого композитора. Многим молодым
людям хотелось бы сидеть за пианино и импровизировать перед вос-
торженной толпой. Но многие ли способны на это? — Желать — еще
не значит уметь. Чтобы сочинять музыку, нужно любить музыку, а не
успех (или, во всяком случае, музыку не меньше, чем успех). А чтобы
стать математиком, нужно увлекаться прелестью закономерностей и логи-
ческой стройностью законов. Эго не значит, конечно, что такое увлечение
должно быть единственной страстью, у вас могут быть и другие цели, вы
можете заниматься другими делами, но если вы не попадете под очарова-
ние математики, вы в математике ничего не совершите.
В этом смысле точка зрения математика-художника ближе к жизни,
чем отношение математика-бюрократа. Первый, по крайней мере, по-
нимает, как люди становятся математиками. Как чистый художник,
так и чистый бюрократ ошибаются или, во всяком случае, не совсем
правы. Если бы обучение математике должно было основываться
лишь на одной из этих теорий, то можно сказать с уверенностью, что
теория художника принесла бы гораздо меньше вреда. Художник мо-
жет быть анархистом, представителем богемы или даже бродягой, но
он, по крайней мере, живой человек, а без жизни нет роста. И если та-
кой человек научит детей любить свой предмет, то всегда остается на-
дежда, что его ученики в зрелом возрасте обратят свои способности на
полезные дела. Но если вы отдадите их в руки человека с крайне ути-
литарными взглядами, то они, наверное, не принесут никакой пользы
обществу, так как растеряют все свои способности.
269
КАКИМИ КАЧЕСТВАМИ ДОЛЖЕН ОБЛАДАТЬ МАТЕМАТИК?
Не представляю себе, как можно довольство-
ваться знаниями, полученными из вторых рук. хотя
чужое знание может нас кое-чему научить, мудр
бываешь лишь своей собственной мудростью
Монтень, О педантизме
Для всех математиков, характерна дерзость ума. Математик не лю-
бит, когда ему о чем-нибудь рассказывают, он сам хочет дойти до все-
го. Конечно, зрелый математик, узнав о каком-нибудь великом откры-
тии, поинтересуется, в чем оно состоит, и не станет терять время на то,
чтобы открывать уже открытое. Но я имею в виду юных математиков,
у которых дерзость ума проявляется особенно сильно. Если вы, на-
пример, преподаете геометрию девяти-десятилетним ребятам и рас-
сказываете им, что никто еще не смог разделить угол на три равные
части при помощи линейки и циркуля, вы непременно увидите, что
один-два мальчика останутся после уроков и будут пытаться найти
решение. То обстоятельство, что в течение двух тысяч лет никто не
решил эту задачу, не помешает им надеяться, что они смогут это сде-
лать в течение часового перерыва на обед. Это, конечно, не очень
скромно, но и не свидетельствует об их самонадеянности. Они просто
готовы принять любой вызов. А ведь в действительности уже доказа-
но, что невозможно разделить угол на три равные части при помощи
линейки и циркуля. Их попытка найти решение — того же рода, что
попытка представить в виде рациональной дроби p/q.
Хороший ученик всегда старается забежать вперед. Если вы ему
объясните, как решать квадратное уравнение дополнением до полного
квадрата, он непременно захочет узнать, можно ли решить кубическое
уравнение дополнением до полного куба. Остальные ученики класса
не задают подобных вопросов. С них хватит и квадратных уравнений,
они не ищут дополнительных трудностей.
Вот это желание исследовать является второй отличительной чер-
той математика. Это одна из сил, содействующих росту математика.
Математик получает удовольствие от знаний, которыми уже овладел,
и всегда стремится к новым знаниям.
Эту мысль можно пояснить на примере дробных показателей сте-
пени из школьного курса алгебры. Легко представить себе человека,
который, поверхностно познакомившись с дробными и отрицатель-
ными показателями степени, начнет недоумевать, зачем все это нужно.
Ведь приходится преодолевать столько логических трудностей! Мне
представляется, что тот, кто открыл дробные показатели степени, сна-
чала работал над целыми показателями и получил такое большое
270
удовлетворение от этой работы, что ему захотелось развить этот раз-
дел, и он готов был взять на себя логический риск. Ведь на первых по-
рах новое открытие почти всегда является вопросом веры и лишь
позднее, когда становится ясным, что это действительно открытие,
приходится находить логическое оправдание, которое удовлетворит
самых придирчивых критиков.
Я уже говорил об интересе к закономерностям — третьем необхо-
димом качестве математика. Уже в самом начале арифметики встре-
чаются закономерности. Например, из четырех одинаковых камней
можно сложить квадрат, а из пяти — нельзя. Математические, как и
музыкальные, способности проявляются очень рано, с четырех лет, а
иногда и раньше. Один малыш однажды сказал мне: «Мне нравится
слово September [сентябрь], ведь получается sEptEmbEr». Сам я нико-
гда не замечал закономерного чередования гласных и согласных в
этом слове. Оно действительно совершенно симметрично. Такому ре-
бенку, конечно, понравится арифметика.
В таблице умножения имеется один элементарный пример законо-
мерности. Обычно дети любят умножать на 2 и на 5, потому что по-
следние цифры ответа легко запомнить: при умножении на 2 всегда
получаются четные цифры, а при умножении на 5 еще проще: всегда О
или 5. Но даже в умножении на 7 есть свои закономерности. Если мы
посмотрим на последние цифры произведении 7, 14, 21, 28, 35, 42, 49,
56, 63, 70, т.е. на 7, 4, 1, 8, 5, 2, 9, 6, 3, 0, то увидим, что разность меж-
ду последующей и предыдущей цифрами составляет. -3, +7; -3, -3, +7;
-3, -3, -3. В этом ряду чувствуется совершенно определенный ритм.
Если прочесть последние цифры ответов при умножении на 7 в обрат-
ном порядке, то мы получаем последние цифры от умножения на 3.
Даже в начальной школе можно развить навык наблюдения за ма-
тематическими закономерностями. Большая часть ранних работ Гаус-
са явилась следствием его привычки делать вычисления и анализиро-
вать полученные результаты. Эрмит, один из крупнейших француз-
ских математиков, также подчеркивал, как часто наблюдательность
ведет к математическим открытиям. Правда, одной наблюдательности
мало, чтобы стать великим математиком.
Так же как умение замечать арифметические закономерности по-
могает школьнику решать арифметические примеры, умение наблю-
дать закономерности в алгебре помогает избегать ошибок или обна-
руживать описки.
Например, условием равенства корней квадратного уравнения вида
ах2 + 2Ьх + с = 0 является Ь2 - ас = 0. (Читателю, возможно, более зна-
комо условие Ь2 - 4ас для уравнения ах2 + Ьх + с = 0.) Подобное же ус-
ловие можно найти для равенства корней кубического уравнения. Ку-
271
бическое уравнение имеет три корня; спрашивается, в каком случае
два из них равны.
Для уравнения ах3 + ЗЬх2 + Зсх + d ~ О условием равенства двух
корней будет (be - ad)2 - 4(ас - b2)(bd - с2) = 0. Это условие можно
также записать в виде а2^ - 6abcd + 4b3d + 4ас3 - ЗЬ2сг = 0.
Если вы проанализируете левые части указанных условий, то обя-
зательно заметите следующие закономерности:
1) общее количество множителей в каждом члене выражения оди-
наково. Например, в выражении Ь2 - ас каждый член состоит из двух
букв, умноженных друг на друга, т.е. степень каждого члена равна
двум. В более длинном условии для равенства двух корней кубическо-
го уравнения каждый член содержит четыре буквы, умноженные друг
на друга; например, b3d есть сокращенное bbbd',
2) в этих выражениях имеется также равновесие другого рода, хотя
эта вторая закономерность не сразу заметна: равновесие между буква-
ми, которые стоят раньше или позже в алфавите. Например, в условии
для кубического уравнения имеются члены abed и ad2 = aadd. Срав-
ним их вторые буквы. В члене aadd вторая буква есть а, в члене abed
вторая буква есть Ь. Буква а стоит в алфавите раньше, чем Ь. Но спра-
ведливость торжествует: если мы посмотрим на третьи буквы этих
выражений, то видим, что aadd содержит d, в то время как abed со-
держит с; буква d стоит в алфавите позже с. Равновесие совершенно точ-
ное: а стоит перед b,ad после с. То же самое равновесие сохраняется во
всех членах. Эго можно проверить следующим образом Оценим каждую
из букв а, Ь, с, d определенным количеством очков: а = 0, b = 1, с = 2,
d = 3. Тогда сумма очков в каждом члене будет равна 6; например, для
abed имеем 0+1+2 + 3=6, для ас3 0 + 2 + 2 + 2 = 6.
Число очков, сопоставленное данной букве, называют ее весом; та-
ким образом, вес каждого члена равен 6. В выражении Ь2 - ас вес каж-
дого члена равен 2;
3) сумма численных коэффициентов в каждом выражении равна
нулю. Действительно, в Ь2- ас коэффициентами являются числа +1 и -1,
сумма которых равна нулю, а в выражении t/d2 - 6abcd + 4b3d + 4ас3 -
- ЗЬ2с2 — числа 1, -6,4,4, -3, которые в сумме также дают 0. Другими
словами, если в приведенных выражениях положить а = b = с = d=
то эти выражения обратятся тождественно в нуль.
Эти три свойства дают возможность проверить нашу вниматель-
ность и аккуратность. Свойство (1) позволяет проверить, не ошиблись
ли мы при написании показателей степеней букв, поскольку из-за та-
кого рода ошибки количество букв в различных членах может ока-
заться неодинаковым (если, конечно, мы не допустили две взаимно
компенсирующиеся ошибки). Свойство (2) дает возможность избежать
272
ошибки при переписывании буквенных символов. Если, например, на
каком-то этапе работы мы написали d вместо а, это изменит вес дан-
ного члена. Свойство (3) спасает нас от ошибок при сложении членов.
Положим, мы пропустили один член при сложении. Тогда, придав
всем буквам значение 1, мы не получим в сумме 0 и тем самым сразу
обратим внимание на ошибку.
Такой тип контроля не дает еще полного представления о математике.
Посмотреть на ответ и проверить, получена ли ожидаемая симметрия или
равновесие, — это одна из вещей, которые математик делает почти бес-
сознательно. Просто удивительно, как редко детей учат анализировать
именно так. То и дело на экзаменах ученики сдают работы, в которых от-
веты имеют «какую-то странную форму», — как любил выражаться отец
Браун у Честертона. Применения этого типа контроля гораздо шире, чем
специальный вид проверки, о котором мы говорили.
ПРИМЕР ГЕОМЕТРИЧЕСКОЙ ЗАКОНОМЕРНОСТИ
В школьном курсе геометрии встречается уравнение х2 =
= (ас + bd)(ad + be) !(ab + cd), где x, a, b, с и d обозначают длины от-
резков на рис.1.
Рис. 1
Этот результат легко доказать, выразив cos£) и cosS через стороны
треугольников PQR и PSR. Сумма косинусов углов Qu S должна быть
равна 0, поскольку Q + 5 = 180° (вписанный четырехугольник), и по-
этому cos S' = -cos Q. Полученное уравнение затем разрешается отно-
сительно х2.
В этом доказательстве нет ничего интересного, но примечательна
закономерность результата.
Четыре предмета можно разбить попарно тремя различными спо-
собами. Так, если четверо играют в бридж, то Л и В могут играть про-
тив С и D, или А и С против В и D или же А и D против В иС Никак
иначе сгруппировать нельзя.
Алгебраические выражения ab + cd, ас + bd, ad + be также состав-
лены на основе группировки символов a, b,c,d в пары и последующе-
• 9 Зак 72
273
го сложения этих пар. Таким путем можно составить три, и только три,
выражения (считая, конечно, что cd + ab — это то же самое, что ab + cd).
В приведенной выше формуле встречаются все три выражения: два —
в числителе, третье — в знаменателе.
Я не собираюсь здесь вдаваться в вопрос, почему это получается
именно так. Мне хочется только подчеркнуть, что формула благодаря
такой закономерности легко запоминается.
СМЫСЛ И ОБОБЩЕНИЕ
Иногда, рассматривая какое-нибудь произведение искусства, мы
восхищаемся его красотой и чувствуем его значительность, но не мо-
жем сказать, в чем они состоят. Лучше и не пытаться это делать. Один
поэт протестовал против варварского обычая заставлять детей пере-
сказывать стихи своими словами. Он говорил, что единственный спо-
соб объяснить содержание стихотворения — это написать лучшее сти-
хотворение. А от детей этого, конечно, требовать нельзя.
Но в математике, как правило, бывает иначе. Если нам встречается
закономерность, мы обязательно спрашиваем: «Почему она встречает-
ся? Что она означает?» И мы обычно можем найти ответы на эти во-
просы. Итак, всякий раз, когда появляется закономерность, математик
чувствует, что он обязан узнать, почему она появляется.
Мы можем объяснить, например, почему условие равенства корней
должно обладать указанными выше тремя свойствами. Я лишь намечу
общую идею, опустив алгебраические подробности (которые в дейст-
вительности совсем просты).
Рассмотрим кубическое уравнение, которое я для краткости напи-
шу в виде fix) = 0. Первый график, показанный на рис. 2, а, представ-
ляет функцию у = fix) в случае, когда корни уравнения — действи-
тельные и различные. Если эту кривую сместить вверх так, чтобы точ-
ки В и С совпали, мы получим вторую кривую, изображенную на
рис. 2, б, которая соответствует кубическому уравнению с двумя кор-
нями. Между прочим, мы можем легко проверить равенство корней
при помощи вычисления. В точке Е величины у и dy/dx равны 0. Из-
вестно, что равные корни получаются в том случае, когда уравнение
dy/dx =f(x) = 0 имеет общий корень с исходным у равнением fix) = 0..
274
Теперь представьте себе, что вторая кривая (рис. 26) нарисована на
куске резины. Предположим, что резину растягивают вертикально.
Уравнение кривой приняло бы тогда вид у = АДх). Очевидно, что если
исходная кривая касалась оси х (как это должно быть при равных кор-
нях), то новая кривая, полученная при вертикальном растяжении, так-
же бы ее касалась. Иначе говоря, если уравнение _Дх)=0 имеет равные
корни, то это же справедливо и для уравнения АДх) = 0. Рассматривая
вопрос о влиянии множителя к на константы а, Ь, с и d, т.е. на коэф-
фициенты многочлена Дх), нетрудно видеть, что необходимым усло-
вием равенства корней является свойство (1) — все члены должны
иметь одну и ту же степень.
Точно так же не повлияет на общий вид кривой растяжение по оси
абсцисс. Она будет по-прежнему касаться оси х. Отсюда мы можем за-
ключить, что если уравнение Дх) = 0 имеет равные корни, то иДАх) = 0
тоже имеет равные корни. Это приводит нас к свойству (2) — все чле-
ны должны иметь одинаковый вес.
Свойство (3) оказывается самым простым. Если мы положим а = Ь =
- с = d = 1, то квадратное уравнение примет вид х2 + 2х + 1 = 0, а куби-
ческое х1 + Зх2 + Зх + 1 = 0. Эти уравнения короче можно записать как
(х + 1)2 = О и (х + I)5 = 0 соответственно; отсюда очевидно, что они
имеют повторяющийся корень -1. (Все три корня кубического уравне-
ния равны -1; для наших целей было бы достаточно, если бы только
два из них были равны -1.)
Таким образом, свойства (1) и (2) справедливы для любого условия,
которое сохраняется при вертикальном и горизонтальном растяжениях
(т.е. при изменении масштабов по осям у и х соответственно); свойст-
во (3) справедливо для любого условия, которое выполняется для
уравнения (х + 1)" = 0.
Эти выводы являются большим шагом вперед по сравнению с тем
моментом, когда мы просто подметили свойства (1), (2) и (3). Мы их
интерпретировали и знаем теперь, когда и почему они сохраняются.
Все это позволяет нам применить свойства (1), (2) и (3) не только
для проверки условия равенства корней, но и для других целей. На-
пример, если мы имеем кубическое уравнение с тремя корнями, то
можем исследовать, при каких условиях один корень окажется точно
посредине между двумя другими. Для соответствующей кривой (рис.
2а) это означало бы, что точка В делит отрезок АС пополам. Это свой-
ство не нарушалось бы при изменении масштабов как по вертикали,
так и по горизонтали. Оно справедливо и для уравнения (х +1)’ = 0, по-
тому что в этом случае точки А, В и С совпадают с х = -1 и, таким об-
разом, В оказывается серединой отрезка АС. Следовательно, алгебраи-
ческое выражение этого условия должно обладать свойствами (I), (2)
и (3); и действительно, оно имеет ожидаемый вид: 2Z? - ЗаЬс + а а = 0.
19*
275
Это пример обобщения — одного из самых важных факторов раз-
вития математики. Мы начали от наблюдения, касавшегося только
условия равенства корней, а закончили принципом, который применим
к гораздо более широкому классу условий. Ценность такого
обобщения очевидна. Чем шире круг вопросов, к которым применим
какой-нибудь общий принцип, тем чаще он нам поможет выпутаться
из затруднений. Пуанкаре говорил: «Предположим, я занялся сложным
вычислением и с большим трудом, наконец, получил результат, но все
мои усилия окажутся напрасными, если они не помогут предвидеть ре-
зультат в других аналогичных вычислениях, если они мне не дадут
возможность проводить их с уверенностью, избегая тех ошибок и за-
блуждений, с которыми я должен был мириться в первый раз».
ОБОБЩЕНИЕ И ПРОСТОТА
После обобщения результат становится более полезным. Вас, воз-
можно, удивит, что обобщение почти всегда также упрощает резуль-
тат. Более общий вывод легче воспринять, чем менее общий.
Иллюстрацией может послужить следующая тривиальная задача:
«В одном стакане десять ложек воды, в другом — десять ложек вина.
Ложку воды из первого стакана переливают во второй. Смесь энергич-
но взбалтывается, затем ложку полученной смеси переливают в г ер-
вый стакан. Спрашивается, чего будет больше: вина в первом стакане
или воды во втором?».
Очевидно, для того чтобы ответить на этот вопрос, можно проде-
лать следующее вычисление. После того как ложку воды перелили во
второй стакан, там стало 10 ложек вина и 1 ложка воды, т.е. всего 11
„ , 10
ложек жидкости. Таким образом, одна ложка смеси содержит — лож-
ки вина и ложки воды. Переливаем одну ложку смеси в первый
_ 1 10
стакан: в нем теперь оказывается воды 9—, а вина — ложки; во вто-
11 11
10 п 1
ром стакане останется — ложки воды и 9— ложки вина. Итак, мы
11 11
видим, что количество вина в первом стакане в точности равно коли-
честву воды во втором стакане.
Этот результат может показаться случайным, но если вы измените
условия задачи, вы убедитесь, что всегда будут получаться одинако-
вые количества. Если дано х ложек воды и х ложек вина, то количество
вина, которое попадет в первый стакан, неизменно будет оказываться
равным количеству воды, попавшему во второй. Даже если начать с
276
неравных количеств жидкости в стаканах, например с х ложек воды и у
ложек вина, и затем проделать все процедуры, как в первоначальной
задаче, то в конце концов вина в первом стакане будет столько же,
сколько воды во втором.
Это хороший пример математической безвкусицы. При четком и
хорошем математическом доказательстве результат не появляется не-
ожиданно в последней строчке, его логическая неизбежность должна
быть видна на протяжении всего хода доказательства.
Приведенная выше тривиальная задача использует своего рода мас-
кировку. В ней даются ненужные сведения, отвлекающие ваше внима-
ние от существа задачи. Лишним условием является предложение:
«Смесь энергично взбалтывается». На самом деле существенно лишь
то, что мы переливаем ложку жидкости из первого стакана во второй, а
затем ложку смеси из второго стакана в первый. Совершенно не важ-
но, какую жидкость переливают, важно лишь, что в конце концов оба
стакана содержат такое же количество жидкости, как и в самом начале.
А если это действительно так, то в первый стакан влили ровно столько
вина, сколько нужно, чтобы заместить взятую оттуда воду. Конечно
же, вода, взятая из первого стакана, обнаружится во втором. Количест-
ва жидкости должны быть равны; и ни дроби, ни алгебра здесь ни
при чем.
В общем виде эта задача выглядит так: имеется стакан воды и ста-
кан вина, мы производим ряд операций с этими жидкостями так, что в
итоге количество жидкости в каждом стакане равно первоначальному,
тогда количество воды, попавшее в вино, должно равняться количест-
ву вина в воде.
Это настолько очевидно, что едва ли стоит об этом говорить. Об-
щий вид задачи гораз. > проще, чем проделанные ранее вычисления.
Область применения задачи в общем виде гораздо шире. Вы можете
переливать ложки жидкости из одного стакана в другой и обратно
сколько угодно раз, и все же общий принцип останется неизменным.
Таким образом, исследование задачи состоит в том, чтобы отбро-
сить все лишние данные и оставить только существенно необходимые
условия. Чем меньше данных, тем легче найти решение. Общая теоре-
ма редко содержит что-нибудь запутанное; ее цель — обратить ваше
внимание на действительно важные факты.
В элементарной математике мы встречаем смесь всяких важных и
неважных деталей. В высшей математике мы пытаемся разделить раз-
личные элементы и изучить каждый в отдельности. В этом смысле
высшая математика, пожалуй, гораздо проще, чем элементарная.
По всей вероятности, самый известный пример упрощения через
обобщение представляет теорема Гильберта о конечном базисе. В 1868 г.
277
Гордая путем трудоемких вычислений доказал некую теорему, кото-
рую я здесь не собираюсь излагать. Она утверждала, что некоторые
специальные совокупности многочленов обладают определенным
свойством. В 1890 г. Гильберт доказал этот же результат очень просто
и без всяких вычислений. Это ему удалось сделать потому, что он от-
бросил 90 процентов информации, использованной Горданом. Он до-
казал также, что теорема справедлива не только для этих специальных
классов многочленов, но и для любых классов многочленов вообще!
Мы перешли от забавного к великому. Насколько тривиальна и ог-
раничена задачка о воде и вине, настолько глубока и всеобъемлюща
теорема Гильберта. Оба эти случая иллюстрируют один и тот же
принцип: «Большая степень обобщения и большая простота неотдели-
мы друг от друга» — и тем самым еще раз показывают огромные воз-
можности математики сводить под одну крышу совершенно разные
объекты.
Но нельзя судить о важности какого-либо математического иссле-
дования по отдельным частным задачам. Примером тому может слу-
жить топология. Топологию иногда называют «резиновой геометрией»
— геометрией фигур, нарисованных на растягивающемся листе. В не-
котором смысле это так — она действительно рассматривает свойства
таких фигур. Но ее значение связано с тем, что на эластичном листе
нет постоянной длины. Там не может быть теорем, подобных теореме
Пифагора. Можно лишь делать выводы типа: «эта кривая непрерывна,
а та — разделена на две отдельные части». Непрерывность — это ос-
новное свойство, изучаемое топологией. В ней говорится о таких свой-
ствах, которые сохраняются при непрерывных преобразованиях. Так
как существует очень много вещей, допускающих такого рода преоб-
разования, топология охватывает широкий круг вопросов. Она все
больше привлекает как чистых математиков, так и инженеров; с ее по-
мощью можно доказать ряд удивительных результатов. Она сочетает в
себе наивысшую степень обобщения с максимальной простотой.
УНИФИКАЦИЯ
Все, о чем мы говорили выше, имело целью расширить область во-
просов, подвластных математике. Исследование, открытие закономер-
ностей, объяснение смысла каждой закономерности, изобретение но-
вых закономерностей по образу уже известных — все эти виды дея-
тельности расширяют область действия математики. С практической
точки зрения становится исключительно трудным следить за всеми
полученными результатами, и нельзя сказать, чтобы нагромождение не
связанных между собой теорем представляло отрадное зрелище. Буду-
278
чи и деловыми людьми и художниками одновременно, математики
чувствуют потребность собрать все эти разрозненные результаты.
Не удивительно, что вся история математики состоит из чередующихся
процессов «расширений» и «сокращений». Например, внимание математи-
ков привлекает какая-нибудь задача, пишутся сотни статей, каждая из ко-
торых освещает лишь одну сторону истины. Вопрос разрастается. Затем ка-
кой-нибудь гений, опираясь на все данные, собранные с таким трудом, за-
являет: «Все, что мы знаем, станет почти очевидным, если посмотреть на
это вот с такой точки зрения». После этого никому, кроме историков мате-
матики, нет уже необходимости изучать сотни отдельных статей. Разроз-
ненные выводы объединяются в одну простую доктрину, важные факты
отделяются от шелухи, и прямой путь к желаемому выводу открыт для
всех. Объем сведений, которые нужно изучать, сократился. Но это еще не
конец. После того как новый метод стал всеобщим достоянием, возникают
новые вопросы, для решения которых он недостаточен, и снова начинаются
поиски ответов, снова публикуются статьи, снова начинается процесс
«расширения».
Если бы можно было свести все знания к двум общим законам, матема-
тик не был бы удовлетворен. Он ие успокоился бы до тех пор, пока не дока-
зал бы, что оба эти закона основываются на одном принципе. Но тогда он
стал бы несчастным, так как ему нечего было бы делать. К счастью, пер-
спектива такого застоя совершенно невероятна; решение одной проблемы
всегда создает новую проблему. Всегда есть и всегда будут материалы для
изучения и трудности, которые нужно преодолевать.
Каким путем это происходит, можно видеть на замечательном примере
унификации, относящемся примерно к 1900 г. Тогда обнаружилось, что
большинство ранее изучавшихся функций являются частными случаями
одного класса функций — класса гипергеометрических функций. С тех пор
теория гипергеометрических функций является мощным средством объе-
динения разрозненных математических знаний. Затем эти функции были
изучены с новых сторон. Было, между прочим, доказано, что их особые
свойства обусловлены тем, что они имеют три особые точки (незачем объ-
яснять здесь, что такое «особая точка»). Итак, функции с простыми свойст-
вами имеют три или менее особые точки; именно такими функциями зани-
малась классическая математика. Но здесь сразу возникал вопрос: какими
же свойствами будет обладать функция с четырьмя особыми точками? Этот
вопрос по существу не решен до сих пор.
И так будет всегда. И если бы оказалось, что вся существующая мате-
матика рассматривает только явления со свойствами А, В и С, математики
немедленно спросили бы: «А что случится, если какой-нибудь предмет
будет обладать только одним из этих свойств? А если ни одним из них?»
И снова погрузились бы в работу.
279
(D. УГойя
УМСТВЕННАЯ РАБОТА15
Мариотт говорит, что человеческий разум по-
добен шкатулке: думая, вы раскачиваете эту шка-
тулку, пока из нее что-нибудь не выпадет. Таким об-
разом, нет сомнения в том. что результат размыш-
ления в какой-то степени зависит от случая. Я бы
добавил, что человеческий разум еще больше похо-
дит на сито: когда вы думаете, вы раскачиваете
сито, пока сквозь него не просыплются какие-то
мелкие частицы. По мере того как они проходят,
ваше настороженное внимание подхватывает те из
них. которые кажутся относящимися к делу. Вот
еще одна аналогия чтобы поймать вора, комендант
города приказывает всему населению продефилиро-
вать мимо ворот, у которых дожидается ограблен-
ный человек. При этом, чтобы сберечь время и
уменьшить хлопоты, можно использовать какое-
нибудь средство отбора Если ограбленный утвер-
ждает. что вор был мужчиной, а не женщиной и.
кроме того, взрослым, а не юношей или ребенком, то
те, которых это не касается, освобождаются от
прохождения через ворота
Лейбниц, Opuscules, с. 170
1. Как мы думаем. Решающий задачу должен знать свой ум. а ат-
лет — свое тело примерно так же, как жокей знает своих лошадей. Я
представляю себе, что жокей изучает лошадей не с точки зрения чис-
той науки, а для того, чтобы добиться от них лучших результатов на
соревнованиях, что его больше интересуют особенности и капризы той
определенной лошади, с которой он должен выступить, чем общая фи-
зиология или психология лошади как таковая.
То, что вы сейчас начинаете читать — не глава из учебника психо-
логии; неточно было бы назвать это и беседой между интересующими-
ся решением задач лицами об особенностях их ума, подобно тому как
жокен могли бы обсуждать особенности своих лошадей; и все же это
гораздо больше похоже на беседу, чем на формальное изложение оп-
ределенных фактов.
2. Стремление решить задачу. Существенным ингредиентом про-
цесса решения всякой задачи является желание, стремление, реши-
мость ее решить. Задача, которой вы предполагаете заняться, которую
вы достаточно хорошо поняли, — это еще не совсем ваша задача. Она
260
становится по-настоящему вашей, действительно овладевает вами, ко-
гда вы твердо решили заняться ею как следует и стремитесь решить ее
Задача может увлечь вас больше или меньше, ваше желание решить
ее может быть более или менее сильным. Но я утверждаю, что пока
оно не станет очень сильным, ваши шансы решить по-настоящему
трудную задачу будут ничтожны.
Стремление решить задачу плодотворно уже само по себе, так как
оно, в конечном счете, может привести к решению и, безусловно, дает
толчок вашим мыслям.
3. Направленность мышления. Вы можете «плениться» какой-
нибудь задачей в точном смысле этого слова: задача сама «берет вас в
плен», вы не в состоянии от нее избавиться, она преследует вас всюду
Иногда задача овладевает решающим настолько, что он становится
рассеянным, перестает понимать вещи, кажущиеся очевидными окру-
жающим его людям, забывает вещи, которые никто из них никогда не
забыл бы Ньютон, напряженно работая над своими проблемами, часто
забывал пообедать.
Да, действительно, внимание решающего задачу избирательно. Оно
отказывается задерживаться на вещах, которые кажутся не относящи-
мися к его задаче, и видит издалека мельчайшие вещи, имеющие к ней
какое-то отношение. Это — направленное, «настороженное» внима-
ние, как выразился Лейбниц.
4. Близость решения. Учащийся сдает письменный экзамен по ма-
тематике. От него не требуют, чтобы он решил все предложенные за-
дачи, но он должен решить возможно большее их число. В такой си-
туации лучшей стратегией, возможно, будет следующая: начать с бег-
лого обзора всех задач и отобрать те, которые кажутся более доступ-
ными.
При этом, конечно, предполагается, что учащийся способен в ка-
кой-то степени оценить трудность задачи, что он может в какой-то ме-
ре «прикинуть психологическое расстояние», отделяющее его от ре-
шения. В самом деле, всякий серьезно занимающийся какой-нибудь
задачей должен живо ощущать близость решения и скорость своего
продвижения к конечной цели Возможно, что он не выражает этого
словесно, но он определенно чувствует: «дело идет на лад, решение
где-то рядом», или «дело тянется ужасно медленно, до решения еще
очень далеко», или «я отупел, нет никакого прогресса», «я сползаю в
сторону и лишь удаляюсь от решения».
5. Предвидение. Как только мы начинаем серьезно заниматься ка-
кой-нибудь задачей, нас что-то побуждает заглядывать вперед, мы пы-
таемся предвидеть, что будет дальше: мы ждем чего-то, мы стремимся
18 Зак 72
281
угадать контур решения. Этот контур может быть более или менее рас-
плывчатым, он может быть даже в какой-то степени неправильным,
хотя на самом деле не так уж часто он бывает очень неправильным.
Всем занимающимся решением задач приходится строить догадки
или выдвигать предположения, однако между догадками наивного ре-
шающего и вдумчивого человека имеется разница.
Наивный человек ожидает прозрения, почесывая затылок или грызя
карандаш; надеясь на приход блестящей идеи, он очень мало делает
(или даже вовсе ничего не делает) для того, чтобы ускорить этот при-
ход. А когда желанная идея появляется и приносит правдоподобную
догадку, он сразу ухватывается за нее почти без (или совсем без) вся-
кой критики, рассматривая ее как готовое решение.
Вдумчивый же человек относится к своим догадкам более скепти-
чески. Его первоначальной догадкой может быть: «Их имеется 25» или
«Я должен сказать ему то-то и то-то». Но вслед за этим он проверяет
свою догадку и даже может изменить ее: «Нет, не 25. Дай-ка лучше
попробую 30», или «Нет. Говорить ему то-то и то-то нет смысла пото-
му, что он может возразить мне так-то и так-то. Но тогда я мог бы ска-
зать ему, что ...». Идя по этому пути при помощи «проб и ошибок»,
пользуясь последовательными приближениями, решающий может, в
конце концов, подойти к правильному ответу, выбрать соответствую-
щий план решения.
Еще более вдумчивый и опытный решающий, когда ему не удается
получить полностью весь ответ, пытается угадать какую-то его часть,
какую-нибудь его характерную черту, какое-то приближение к реше-
нию или хотя бы некоторую деталь этого приближения. Затем он ста-
рается расширить свою догадку, одновременно отыскивая возможно-
сти для ее проверки; тем самым он старается привести свою догадку в
соответствие с наиболее полными сведениями, которыми он обладает
на данном этале решения.
Как менее опытному, так и более опытному решающему, безуслов-
но, хотелось бы прийти к по-иастоящему хорошей догадке, выдвинуть
по-настоящему плодотворную идею.
И каждый из них хотел бы знать, как велики шансы на то, что его
догадка верна. Эти шансы не могут быть точно взвешены (и здесь не
место для разбора проблематических возможностей их оценки). Одна-
ко во многих случаях у решающего может быть определенное ощуще-
ние перспективности своей догадки. Даже совсем наивные люди, не
знающие, что такое доказательство, могут испытывать сильнейшие
ощущения по поводу своих догадок; вдумчивые люди могут различать
в своих ощущениях тонкие оттенки; но кто бы ни высказывал догадку,
у него всегда имеется какое-то представление о ее вероятной судьбе.
282
Итак, помимо ощущения того, что относится и что не относится к рас-
сматриваемой задаче, помимо ощущения близости решения, мы отме-
чаем в мышлении решающего существование еще одной разновидно-
сти ощущения: предвидения.
Относится ли это соображение к делу? Далеко ли еще до решения?
Насколько хороша эта догадка? — Такие вопросы сопутствуют ре-
шающему на каждом шагу, они более ощущаются, нежели формули-
руются в явном виде, и ответы на них также больше чувствуются, чем
высказываются. Направляют ли подобные вопросы действия решаю-
щего или только сопровождают их? Являются ли они причиной или
только симптомами? — Это мне неизвестно, но я знаю, что если по-
добные ощущения у вас не возникают, то вы еще по-настоящему не
заинтересовались своей задачей.
6. Область поисков. Я редко расстаюсь со своими наручными ча-
сами, но когда это случается, у меня всегда появляется забота о том,
как их найти. Потеряв свои часы, я по привычке начинаю искать их в
некотором совершенно определенном месте: на своем письменном
столе или на какой-нибудь полке, где я обычно кладу свои мелкие ве-
щи, или еще в каком-то третьем месте, если мне удалось вспомнить,
что я снял свои часы именно там.
Такое поведение типично. Как только мы серьезно заинтересова-
лись своей задачей, мы стараемся наметить контур, внутри которого
следует искать ее решение. Этот контур может быть неопределенным,
он может быть почти неосязаемым, но именно он определяет наши бу-
дущие действия. Конечно, попытки решения могут быть различными,
но по существу же все они похожи друг на друга, все они лежат внутри
этого заранее намеченного (возможно, не вполне сознательно) конту-
ра. Если ни одна из испробованных попыток решения не дает резуль-
тата, мы чувствуем себя обескураженными, ничто другое не приходит
на ум; мы не в состоянии выйти за пределы намеченного контура. Ведь
мы ищем не вообще какое-то решение, а вполне определенное реше-
ние, решение, которое должно находиться внутри нашего ограничен-
ного контура. Мы не ищем решения где-то по всему свету, а внутри
ограниченной области поисков.
Итак, по-видимому, поиски решения целесообразно начинать внут-
ри какой-то подходящим образом ограниченной области. Когда я пы-
таюсь найти свои пропавшие часы, целесообразно искать их, конечно,
не где-то во вселенной, или где-то в городе, или где-то в доме, а имен-
но на письменном столе, где я находил их неоднократно в прошлом.
Безусловно, целесообразно начинать поиски неизвестного в ограниченной
области, но неразумно упорствовать и продолжать там поиск, когда ста-
новится все более и более ясным, что решения в этой области нет.
1в-
283
7. Промежуточные решения. Процесс решения задачи может но-
сить созерцательный характер; у недостаточно способных людей он
иногда превращается в бесплодное высиживание. Иногда же о нем
можно говорить как о длинной, извилистой, напряженной дороге к це-
ли, каждый поворот которой отмечен принятием того или иного про-
межуточного решения. Эти промежуточные решения подсказываются
(или, возможно, только сопровождаются) ощущением того, что отно-
сится и что не относится к задаче, ожиданием близости решения, рос-
том или затуханием надежды, Свои промежуточные решения и вне-
запно возникающие ощущения решающий редко выражает в словес-
ной форме, но иногда это все-таки случается:
«А ну-ка, попробую взглянуть сюда».
«Нет, здесь вряд ли есть на что смотреть. Попробую-ка лучше за-
глянуть туда».
«Здесь тоже немного увидишь, но в воздухе определенно чем-то
пахнет. Попытаюсь присмотреться к этому поближе».
Одним из важнейших типов промежуточного решения является
решение о расширении области поиска, об отбрасывании ограничения,
узость которого начинает нас стеснять.
8. Мобилизация и организация. Мы мало что знаем об особенно-
стях умственной деятельности человека, решающего задачу. Слож-
ность этой деятельности может быть неизмеримой, но одна ее сторона
видна совершенно ясно: по мере того как решающий продвигается
вперед, он накапливает все больше и больше сведений об изучаемом
объекте.
Попробуем сравнить взгляды решающего на математическую зада-
чу в начале и в конце его работы. Когда задача только еще возникла,
картина проста: решающий видит ее обособленной, либо без всяких
подробностей, либо с очень малыми подробностями; возможно, что он
различает только главные ее части — неизвестное, данные и условие,
или предпосылку и заключение. Картина же, которую он видит в кон-
це, совсем другая: она сложна, снабжена такими дополнительными
подробностями и деталями, о связи которых с рассматриваемой зада-
чей решающий вначале и не подозревал. На исходной, лишенной дета-
лей фигуре появились вспомогательные линии, введены вспомога-
тельные неизвестные, использованы знания, приобретенные решаю-
щим в прошлом, — это главным образом теоремы, имеющие отноше-
ние к рассматриваемой задаче. Решающий никак не мог предвидеть в
самом начале, когда он только приступал к решению задачи, что
именно эти теоремы окажутся ему полезными.
Откуда же берутся все эти материалы, вспомогательные элементы,
теоремы и т.д.? Их накопил решающий в своей памяти, и теперь ему
284
предстоит извлечь их оттуда и целенаправленно приспособить к реше-
нию своей задачи. Такое привлечение сведений мы будем называть мо-
билизацией, а их приспособление к решаемой задаче — организацией.
Процесс решения задачи подобен строительству дома. Сначала
нужно собрать необходимый материал, чего само по себе еще недоста-
точно: куча камней — это еще не дом. Чтобы построить дом или ре-
шение, надо сложить части вместе и организовать их в целое, к кото-
рому мы стремимся.
Практически мобилизацию невозможно отделить от организации;
они дополняют друг друга как аспекты единого сложного процесса —
процесса умственной работы, конечной целью которого является ре-
шение. Работа эта, если она проводится интенсивно, вводит в дело все
наши материальные ресурсы, требует применения всей гаммы наших
умственных способностей и содержит в себе неисчерпаемое множест-
во аспектов. Возможно, нам следует здесь поддаться искушению и вы-
делить некоторые операции из всего многообразия умственных опера-
ций, являющихся элементами умственной работы, и описать их в та-
ких терминах, как изоляция и комбинация, распознавание и вспомина-
ние, перегруппировка и пополнение.
В ближайших параграфах делается попытка описать эти операции.
Конечно, читатель не должен ожидать здесь встречи со строгими и
четкими различиями между понятиями или с жесткими и исчерпы-
вающими определениями.
9. Распознавание и вспоминание. Решая задачу, мы бываем очень
рады, если нам удается распознать какой-нибудь знакомый элемент.
Так, например, при изучении геометрической фигуры мы можем обна-
ружить не замеченный ранее треугольник или пару подобных тре-
угольников, или еще какую-нибудь хорошо знакомую конфигурацию.
Исследуя алгебраическую формулу, мы можем заметить полный квад-
рат или какое-нибудь другое знакомое сочетание. Конечно, нам может
встретиться и несколько более сложная ситуация, распознание которой
оказалось бы очень полезно; возможно, мы даже не знаем, как следо-
вало бы ее назвать, и у нас еще нет для нее формального определения,
но она кажется нам поразительно знакомой и важной.
Если нам удалось распознать на изучаемой фигуре некоторый тре-
угольник, то у нас есть достаточно оснований для того, чтобы почув-
ствовать удовлетворение. В самом деле, нам известно несколько тео-
рем о треугольниках, мы решали различные задачи на треугольники и
возможно, что та или другая из знакомых нам теорем или какое-
нибудь из найденных ранее решений окажутся пригодными и для рас-
сматриваемой задачи. Обнаружив, распознав этот треугольник, мы ус-
285
танавливаем тем самым связь с обширной областью ранее приобре-
тенных знаний, один из участков которой может оказаться в настоя-
щий момент полезным. Таким образом, распознавание может, вообще
говоря, побуждать нас к вспоминанию чего-то полезного для решения
задачи, к мобилизации относящихся к рассматриваемому вопросу све-
дений.
10. Пополнение и перегруппировка. Допустим, что мы распозна-
ли на фигуре треугольник и что нам удалось вспомнить теорему о тре-
угольниках, которая имеет некоторые шансы оказаться полезной в рас-
сматриваемой ситуации. Предположим далее, что для того чтобы
иметь возможность применить эту теорему на практике, нам пришлось
добавить на треугольнике кое-какие вспомогательные линии, напри-
мер высоту. Мобилизованные нами потенциально полезные элементы,
будучи присоединены к нашей концепции задачи, могут, вообще гово-
ря, обогатить ее, придать ей более законченный вид, ликвидировать
пробелы, устранить ее недостатки, одним словом, пополнить ее.
Подобное пополнение приносит с собой новый материал в наше
понимание задачи и является важным шагом в ее организации. Иногда,
однако, удается добиться значительного успеха в организации реше-
ния и без добавления нового материала за счет одного лишь изменения
расположения уже имеющихся элементов, путем изучения соотноше-
ний между ними в новой диспозиции, путем перестановки или пере-
группировки их. Перегруппировав элементы, мы меняем «структуру»
нашего понимания задачи. Итак, перегруппировка означает изменение
структуры.
Изложим наши соображения более конкретно. Ключом к решению
геометрической задачи может оказаться проведение вспомогательной
линии. Но иногда решающий шаг можно сделать и без введения каких
бы то ни было новых линий, ограничиваясь уже имеющимися, но рас-
сматривая их по-иному. Так, например, мы можем заметить, что неко-
торые прямые образуют два подобных треугольника. Рассматривая та-
кую знакомую конфигурацию, мы обнаруживаем не замеченные до
этого соотношения между ее элементами, мы видим их сгруппирован-
ными по-иному, мы фиксируем новую структуру, мы созерцаем фигу-
ру как более организованное, более гармоничное, более перспективное
целое — мы придали материалу задачи новую форму.
Перегруппировка может повлечь за собой изменение акцента в на-
шем понимании задачи. Элементы и соотношения, стоящие до пере-
группировки на переднем плане, могут уступить свои привилегиро-
ванные места и отойти на задний план; они могут отступить даже так
далеко, что практически выпадут из процесса решения. Для лучшей
286
организации процесса решения мы должны время от времени кое-что
отбрасывать из недавно считавшегося относящимся к делу. Однако в
целом мы, вообще говоря, больше добавляем, чем отбрасываем.
11. Изоляция и комбинация. При изучении сложного целого наше
внимание может привлекать то одна, то другая деталь. Мы сосредото-
чиваемся на какой-то определенной детали, мы фокусируем на ней
свое внимание, делаем на нее упор, выделяем ее из ее окружения —
одним словом, изолируем ее. Затем световое пятно передвигается и
выделяет другую деталь — мы изолируем новую деталь и т.д.
После того как изучен ряд деталей и произведена соответствующая
их переоценка, может снова возникнуть потребность представить себе
всю ситуацию в целом. В самом деле, после переоценки отдельных де-
талей «образ целого» («appearance of the whole», «vue d'ensemble», «Ge-
stalt») мог измениться. Комбинированный эффект переоценки роли
некоторых деталей может вылиться в новую мысленную картину об-
щей ситуации, новую, более гармоничную комбинацию всех деталей.
Изоляция и комбинация, дополняя друг друга, могут продвинуть
процесс решения. Изоляция деталей приводит к распаду целого на час-
ти, а последующая комбинация их снова объединяет части в целое, бо-
лее или менее отличающееся от исходного. Разлагая целое на состав-
ные части, а затем воссоединяя их по-иному, снова разлагая и снова
воссоединяя по-иному, мы заставляем эволюционировать наше пони-
мание задачи, переходя к более перспективной ситуации.
12. Диаграмма. Графическое резюме соображений, изложенных в
предыдущих параграфах, дано на рис. 1. Оценку полезности этой схе-
мы мы предоставляем читателю. Девять терминов расположены в виде
квадрата; один из них помещен в центре, четыре — в четырех верши-
нах и еще четыре выписаны на сторонах квадрата.
Рис. 1. Как мы думаем
287
Мобилизация и организация представлены как противоположные
концы одной и той же (горизонтальной) диагонали квадрата, так как
практически эти операции дополняют друг друга. Мобилизация извле-
кает из нашей памяти относящиеся к делу элементы, а организация це-
ленаправленно увязывает их друг с другом.
Изоляция и комбинация представлены как противоположные концы
другой (вертикальной) диагонали, так как практически эти операции
дополняют друг друга. Изоляция выделяет конкретную деталь из ок-
ружающего ее целого, комбинация воссоединяет рассеянные детали в
осмысленное целое.
Стороны, исходящие из вершины, отведенной мобилизации, поме-
чены словами распознайте и вспомните, так как практически
мобилизация элементов, имеющих отношение к задаче, часто
начинается с распознавания некоторого элемента, содержащегося в
задаче, и заключается во вспоминании связанных с ним и уже
знакомых нам других элементов.
Стороны, исходящие из вершины, отведенной организации, поме-
чены словами пополните и перегруппируйте, так как практически ор-
ганизация означает пополнение нашего понимания задачи, придание
ему определенной законченности путем добавления новых деталей и
ликвидации пробелов; она означает также перегруппировку, пере-
стройку во всей нашей концепции задачи.
Читая термины, расположенные вдоль сторон квадрата, слева на-
право, мы следуем от мобилизованных деталей к организованному це-
лому; только что распознанная деталь, тщательно изолированная и
помещенная в фокусе нашего внимания, может вызвать перестройку
всей концепции задачи. Точно так же деталь, которую нам удалось
вспомнить и которая оказалась полезной при комбинировании, обога-
щает наше понимание задачи и пополняет целое.
В процессе решения задачи прозрение (или предвидение) является
центром нашей деятельности; поэтому соответствующая точка поме-
щена в центре нашего символического квадрата. Мы движемся, моби-
лизуя и организуя, изолируя и комбинируя, распознавая и вспоминая
элементы различного вида, перегруппировывая и пополняя нашу кон-
цепцию задачи, стараясь предвидеть решение или какую-нибудь его
характерную черту, или участок ведущего к нему пути. Если предви-
дение, прозрение приходит внезапно, подобно вспышке, то мы называ-
ем его вдохновением или блестящей идеей; обладание такой идеей —
наше самое сокровенное желание.
Мыслительные операции, отраженные на рис. 1, принимают более
определенные формы, когда их рассматривают на каком-нибудь кон-
кретном материале. Мы сейчас перечислим четыре мыслительные
288
операции, соответствующие четырем сторонам нашего квадрата, кото-
рые имеют важное значение для решения математических задач.
Распознайте Перегруппируйте
используйте определения преобразуйте задачу
Вспомните Пополните.
знакомые теоремы и задачи введите вспомогательные элементы
Отметим еще одно обстоятельство. Продвижение решающего задачу
сопровождается ощущением направленности действий, чувством близо-
сти решения, ощущениями, характеризующими успешность его догадок
Обсуждая этот вопрос, мы попутно указывали, что более вдумчивые по-
ди отличаются более дифференцированными ощущениями. Мне не хоте-
лось бы обойти здесь молчанием одно, скорее, умозрительное замечание:
некоторые из оттенков этих ощущений могут быть связаны с мыслитель-
ными операциями, отображенными на рис. 1.
Мы радуемся, когда наше понимание задачи оказывается хорошо
сбалансированным и гармоничным, когда оно содержит все необхо-
димые детали, и притом только хорошо знакомые детали. Если в гар-
моничном целом встречается большое разнообразие деталей, идея ре-
шения кажется близкой. Употребляя эти термины, мы, как мне кажет-
ся, выражаем, что те или другие из рассмотренных выше операций хо-
рошо двигают дело вперед или даже приводят к цели. Наша концепция
задачи кажется хорошо уравновешенной, если не ощущается необхо-
димости в перегруппировке ее элементов, она кажется внутренне со-
гласованной, если не нужно вспоминать детали, если одна из них
легко вызывает в памяти другие. Если нет необходимости в попол-
нении концепции задачи, она представляется нам законченной; если
все детали распознаны, она кажется нам знакомой и близкой От-
четливость в восприятии деталей обеспечивается их предваритель-
ной изоляцией и сосредоточением внимания на каждой из них в от-
дельности, а гармоничность концепции в целом является следстви-
ем удачной комбинации деталей. Мы говорим, что идея близка, ко-
гда чувствуем уверенное продвижение к тому, что можно назвать
прозрением
Имея в виду систематизировать эти благоприятные признаки ус-
пешного продвижения, расположим их на схеме так, чтобы их взаим-
ное расположение было таким же, как у соответствующих терминов на
квадрате, изображенном на рис 1. Таким образом, мы размещаем на-
ши семь терминов подобно тому, как располагаются четыре стороны
квадрата и три важные точки на его вертикальной диагонали. Вот эта
схема.
289
Детали удачно
изолированы:
отчетливость деталей
Детали удачно
распознаны:
ощущение понимания
концепции задачи
Детали удачно
сгруппированы:
хорошая
уравновешенность
концепции задачи
Прозрение
близость решающей
идеи
Удачное вспомннанне:
внутренняя согласован-
ность задачи
Удачное пополнение:
полнота концепции
задачи
Удачная комбинация-
гармоничность
концепции в целом
13. Часть подсказывает целое. Мимо меня прошел по улице маль-
чишка, насвистывающий какой-то мотив. Я сумел уловить только один
или два такта мелодии, которая мне очень нравится, но которой я дав-
но не слышал. И вдруг эта мелодия, пополненная памятью, вытеснила
все заботы и праздные мысли, забивавшие до этого мою голову.
Описанное маленькое событие является хорошей иллюстрацией
«ассоциации идей», явления, описанного еще Аристотелем, а после не-
го — многими другими авторами. Хорошее описание этого явления
дает Брэдли: «Каждая часть отдельно взятого состояния ума, будучи
воспроизведенной, стремится восстановить все остальное». Так, в на-
шем случае один такт вызвал сначала общее впечатление о мелодии, а
затем, понемногу, восстановил и все остальные такты. Вот еще одна
характеристика ассоциации идей, в которой, правда, недостает дета-
лей, но которую легко запомнить: «Часть подсказывает целое». Усло-
вимся рассматривать эту краткую фразу как удобное сокращение более
точной формулировки Брэдли. Заметьте себе важные слова: «стремит-
ся» и «подсказывает».
Утверждения «Часть подсказывает целое», «Часть стремится вос-
становить целое», «По части есть надежда восстановить целое» могут
считаться приемлемыми, но фраза «Часть восстанавливает целое» со-
вершенно неприемлема для выражения «закона ассоциации», ибо этот
закон выражает не утверждение о восстановлении целого, а только на-
дежду, шанс, тенденцию. Нам известно кое-что также о силе этой тен-
денции: если часть ставится в центр внимания, то она более эффектив-
но наводит на мысль о целом; совокупность нескольких частей более
эффективно подсказывает целое, чем любая часть, взятая в отдельно-
290
сти. Эти добавления очень важны для понимания роли ассоциации
идей в умственной деятельности решающего.
Рассмотрим один очень схематический пример. Некоторая матема-
тическая задача может быть быстро решена при помощи одной имею-
щей решающее значение теоремы D, тогда как без применения этой
теоремы задача решается с большим трудом. Вначале решающий даже
не подозревает, что теорема D имеет какое-то отношение к его задаче,
хотя он достаточно знаком с этой теоремой как таковой. Как решаю-
щий может догадаться о том, что теорема D играет решающую роль?
Здесь могут быть разные случаи.
Сравнительно прост тот случай, когда предложенная задача и тео-
рема имеют общую составную часть. Испробовав сначала одно, а за-
тем другое, решающий обнаруживает эту составную часть, изолирует
ее и сосредоточивает на ней свое внимание; в результате у него появ-
ляется шанс вспомнить или «восстановить» с помощью общей части
целиком всю теорему D.
Менее прост случай, когда задача в ее первоначальной концепции и
имеющая решающее значение теорема D не имеют общей компонен-
ты. В этом случае может существовать еще одна теорема С, известная
решающему, которая имеет одну компоненту — общую с нашей зада-
чей, а другую компоненту — общую с теоремой D; тогда решающий
может добраться до D, соприкоснувшись сначала с С, а затем перейдя
от С к D.
Ясно, что цепочка ассоциаций может быть и более длинной: пред-
ложенная задача может находиться в таком «контакте по ассоциации»
с А, А с В, В с С н, наконец, С с D. Чем длиннее цепочка, тем дольше
должен решающий «встряхивать ящик» или «раскачивать сито», пока,
в конце концов, не выпадает желанная теорема D.
Встряхивание ящика или раскачивание сита можно рассматривать
как метафорический способ описания умственной деятельности ре-
шающего (см. эпиграф). В предыдущих параграфах, содержание кото-
рых подытожено на рис. 1, мы пытались интерпретировать эту дея-
тельность менее метафорически. Это была достаточно правдоподобная
интерпретация различных видов упомянутой деятельности; с их по-
мощью решающий пытается установить необходимые контакты по ас-
социации.
В самом деле, распознавая элемент, решающий вводит его в рассу-
ждение, с которым этот элемент имеет тесный контакт по ассоциации.
Каждый вновь мобилизованный элемент, присоединяемый к концеп-
ции задачи, дает решающему шансы на привлечение других элемен-
тов, с которыми он контактирует по ассоциации. Когда решающий
изолирует элемент и сосредоточивает на нем свое внимание, имеется
291
много шансов на то, что тем самым будут привлечены другие элемен-
ты из той же категории вещей. Перегруппировка может сблизить эле-
менты, которые в своей совокупности могут привлечь по ассоциации
нечто большее, чем каждый элемент в отдельности.
Однако трудно было бы объяснить мыслительные процессы, проте-
кающие в голове решающего, одними только ассоциациями, помимо
ассоциативных заимствований должно существовать и нечто другое,
помогающее отличать относящиеся к делу элементы и комбинации
элементов от не относящихся к делу, нужное от ненужного, полезное
от бесполезного.
ДИСЦИПЛИНА УМА 15
Метод состоит в размещении и упорядочении
того, на что должно быть направлено острие ума в
целях открытия какой-либо истины
Декарт,
Правила для руководства ума
Правило V, Избранные произведения, стр. 95
1. Как надо думать. В предыдущей статье была сделана попытка
описать типичные особенности умственной деятельности лица, ре-
шающего (математическую или нематематическую) задачу. Но являет-
ся ли типичное также и рациональным? Наша умственная работа мо-
жет протекать так, но должна ли она протекать именно так?
На эти вопросы, в силу их неопределенной общности, довольно
трудно дать однозначный ответ; однако для того, чтобы указать ос-
новную тенденцию этой статьи, они нам нужны. Руководствуясь опы-
том умственной работы решающего, попытаемся перечислить умст-
венные операции (шаги, процедуры и т.д.), которые обычно бывают
полезны при решении задач; при этом мы будем стараться указать ме-
сто каждой из таких операций в процессе решения задачи.
Мы выразим эти, как правило, полезные операции, применяемые
для решения задач, в коротком, сжатом виде, используя для этого
«стандартные» вопросы и рекомендации. Читателю должно быть ясно,
что подобные вопросы и рекомендации можно интерпретировать
двояко: либо как цитаты из разговора решающего с самим собой, либо
как обращения более опытного учителя к учащемуся, которому он хо-
чет помочь.
2. Концентрация внимания на цели. Когда вам нужно решить за-
дачу, вы о ней часто вспоминаете, может быть даже настолько часто,
что она превращается в навязчивую идею. Однако вы должны не про-
292
сто думать о своей задаче — думать некоторым, так сказать, неопре-
деленным образом, — вы должны быть постоянно обращены к своей
задаче, предельно ясно видеть ее перед собой и прежде всего задавать
себе основной вопрос: Что требуется?
В процессе решения задачи найдется много удобных случаев для
постановки этого вопроса. Когда вы забрались чересчур глубоко в
один из боковых ходов, который может, в конце концов, оказаться ту-
пиком или увести вас далеко от цели, когда ваши мысли начали блуж-
дать, бывает очень важно снова спросить себя: Что требуется? — и
снова тем самым поставить цель в центр вашего внимания.
Целью задачи на нахождение является неизвестное. Чтобы сосре-
доточить свое внимание на этой цели, спросите себя: Что представ-
ляет собой неизвестное? Целью задачи на доказательство является за-
ключение, вывод, — в этом случае соответствующий вопрос будет
иметь форму: В чем состоит заключение?
После того как вы стали ясно различать цель своей задачи, т.е. ис-
комый объект, необходимо приступить к инвентаризации всего, что
вы имеете в своем распоряжении, с тем, чтобы выделить объекты, кото-
рые с некоторой вероятностью могут быть использованы для достижения
цели; таким образом, вы должны спросить себя: Что у нас имеется?
Допустим, что вы хотите установить связь между двумя элемента-
ми, проложить себе путь от одного элемента к другому; вам может
помочь здесь поочередное рассмотрение этих элементов — вы начи-
наете с одного из них, а затем переходите к другому, так что часто у
вас оказывается возможность задавать упомянутые выше вопросы по-
следовательно: Что требуется? Что мы приобрели?
Применительно к задачам на нахождение эти вопросы звучат так:
Что представляет собой неизвестное? Что дано? В чем состоит ус-
ловие? Применительно к задачам на доказательство эти вопросы будут
такими: В чем состоит заключение? В чем состоит условие (предпо-
сылка)?
Почему так важны эти вопросы? Потому что они побуждают нас
обращать внимание на указанные элементы задачи. Согласно Декарту
(см. эпиграф) метод решения задачи состоит в том, чтобы направлять
свое внимание на все относящиеся к делу элементы, один за другим, в
надлежащей последовательности. У нас мало сомнений в том, что глав-
ные части задачи на нахождение (неизвестное, данное и условие) и глав-
ные части задачи на доказательство [заключение и условие (предпосыл-
ка)] являются относящимися к делу элементами задачи. Иногда они бы-
вают настолько важными, что кажется необходимым приступить к их
рассмотрению как можно раньше; после того как вы хорошо поняли за-
дачу в целом, переносите свое внимание на ее главные части.
293
3. Оценка перспектив. Решающий, серьезно занимающийся своей
задачей, остро чувствует близость цели и скорость своего продвиже-
ния к ней; так же остро ощущает он любую перемену, влияющую на
перспективы его плана. Но иногда оказывается желательным несколь-
ко выйти за границы одних лишь ощущений, более трезво оценить
свои возможности решения задачи, «диагнозировать» задачу, оценить
перспективы, — именно такова тенденция нижеследующих вопросов.
Некоторые задачи бывают безнадежными. Если задача безнадежна,
не следует позволять себе слишком глубоко в нее втягиваться, — и
здесь мы спрашиваем: Существует ли вообще ответ на поставлен-
ный вопрос? Имеется ли ясный, разумный ответ? Если ответ суще-
ствует, сумею ли я его найти?
Когда мы имеем дело с задачей на нахождение, мы должны спра-
шивать: Существует ли решение? Можно задавать и более дифферен-
цированные вопросы: Существует ли одно-единственное решение или
же их имеется несколько, или же решения нет вовсе? Строго ли дос-
таточно условие для определения неизвестного, или оно чрезмерно,
или оно недостаточно?
Когда мы имеем дело с задачей на доказательство, соответствую-
щие вопросы таковы: Верна ли теорема или она ложна? Можно зада-
вать вопросы и более дифференцированно: Верна ли теорема? Не
требуется ли для справедливости теоремы, чтобы условие было более
сильным? Правильно ли сформулирована теорема? Не достаточно ли
для справедливости теоремы более слабого условия? и т.д.
На самом деле мы не можем дать определенного ответа ни на один
из только что сформулированных вопросов до того, как не закончим
своей работы, т.е. не решим задачи. Но эти вопросы по самому своему
существу и не предполагают строго определенных ответов — они рас-
считаны только на предположительные ответы, на догадку. Пытаясь
угадать правильно, мы можем уточнить свою позицию относительно
рассматриваемой задачи, а к этому мы как раз и стремимся. Предыду-
щие вопросы сформулированы в лаконичной форме, обычной для бе-
седы, для разговора. Более осторожная (и более точная) постановка
вопросов такова: Имеется ли (и велика ли) вероятность того, что
существует ответ или решение задачи? Сформулированная теорема
может быть как верной, так и ложной, что более вероятно?
В какой момент, как скоро'должны мы начать ставить подобные
вопросы? На этот счет нет (и не может, не должно быть) никакого же-
сткого или поспешного правила. Очень часто они являются продолже-
нием вопросов из п. 2, относящихся к главным частям задачи.
4. Блуждания: поиски подхода. Конечная цель подсказывает сред-
ства; изучение цели (неизвестного, заключения) может помочь найти
подход к решению задачи. Мы уже знаем, что одни вопрос порождает
294
другой; Что требуется? Что представляет собой неизвестное? Ка-
ким образом можно найти подобное неизвестное? Какие требуются
данные, чтобы получить такое неизвестное? Именно эти вопросы
могут явиться началом пути, основанного на продвижении в обратном
направлении; так, например, если в предложенной задаче мы сумели
разглядеть «данные», позволяющие получить неизвестное, то можно
принять их за отвечающую постановке вспомогательной задачи «проме-
жуточную» цель и тем самым начать продвижение от конца к гвчалу.
В задаче на доказательство соответствующие вопросы будут таки-
ми: Что требуется? В чем состоит заключение? Как можно полу-
чить такое заключение? Из какого условия (предпосылки) можно вы-
вести подобное заключение?
Вместо того чтобы перенести ударение на неизвестное (или на за-
ключение теоремы), мы можем сосредоточить свое внимание на дан-
ных (или предпосылке): Что дано? Для чего могут пригодиться та-
кие данные? Что можно вывести из таких данных? Для задач на до-
казательство существует аналогичная цепочка вопросов: В чем состо-
ит условие (предпосылка)? Для чего может пригодиться такое усло-
вие? Что можно вывести из такого условия? Эти вопросы могут
явиться началом подхода, основанного на продвижении в прямом на-
правлении.
К сожалению, часто оказывается, что мы не в состоянии составить
удовлетворительный план — ни план, связанный с продвижением в
прямом направлении, ни план движения в обратном направлении. На
этот случай у нас в запасе имеются другие вопросы, которые могут
помочь найти подход к решению задачи; вот некоторые из них (их
можно с успехом задавать в самом начале работы): К какому типу от-
носится рассматриваемая задача? Не родственна ли она какой-
нибудь другой известной задаче? Не похожа ли она на какую-нибудь
знакомую задачу? Пытаясь классифицировать задачу, стараясь обна-
ружить ее связь или сходство с известными нам задачами, можно на-
пасть на знакомый метод, подходящий к рассматриваемой задаче, а
тогда уже есть с чего начинать — мы видим первый участок пути, ко-
торый, возможно, ведет к решению.
Пытаясь отыскать полезного «родственника» нашей задачи, укажем
сразу же те связи («родственные отношения») между задачами, которые
чаще всего оказываются полезными: Известна ли вам какая-нибудь род-
ственная данной задача7 Не можете ли вы придумать какую-нибудь
близкую к данной задачу? Аналогичную задачу? Более общую задачу?
Более частную задачу? Существует, однако, опасность, что подобные
вопросы уведут нас далеко в сторону от правильного пути; поэтому
обычно бывает более полезным задавать их несколько позже, когда суть
295
задачи отпечаталась в нашем сознании совершенно ясно и хорошо за-
крепилась в нем, т.е. тогда, когда нет риска, сознательно удаляясь от за-
дачи, вовсе потерять ее из виду.
5. Блуждания: может быть, есть более обнадеживающий аспект
задачи? Когда вы имеете дело с материальными объектами (напри-
мер, собираетесь спилить сук), вы автоматически занимаете наиболее
удобное для работы положение. Подобным же образом следует посту-
пать, сталкиваясь с любой задачей: вы должны стараться занять такую
позицию, чтобы можно было подойти к задаче с самой удобной или
наиболее доступной ее стороны. Вы обдумываете задачу, поворачи-
ваете ее в своей голове и так, и этак; попытайтесь же стать с той сто-
роны, с какой задача кажется проще. Аспект задачи, с которого вы
начинаете работу над ней, может оказаться не самым благоприят-
ным. Сформулирована ли задача так просто, так ясно, так «наводя-
ще», как это только и возможно сделать? Не смогли бы вы сформу-
лировать задачу иначе?
Конечно, вам хотелось бы сформулировать задачу лучше (преобра-
зовать ее в эквивалентную задачу), чтобы она казалась более знако-
мой, более привлекательной, более доступной, более перспективной.
Цель вашей работы состоит в том, чтобы заполнить разрыв между
тем, что вам требуется, н тем, что вы имеете, связать неизвестное с
данными, заключение с условием (предпосылкой). Не можете ли вы
изменить формулировку задачи так, чтобы неизвестное и данные, ус-
ловие и заключение как бы сблизились?
Видоизмените заключение или предпосылку, или обе эти части за-
дачи одновременно, но сделайте это так, чтобы они стали ближе друг к
другу. Видоизмените неизвестное или данные (условие) задачи, или
даже всю задачу в целом, но сделайте это так, чтобы неизвестное и
данные оказались стоящими друг к другу ближе, чем раньше.
По мере того как решение продвигается вперед, на изучаемой фи-
гуре появляются новые линии; постройка, которую воздвигает ре-
шающий в своем уме, пополняется новыми деталями и связями.
Каждое преобразование задачи может внести в нее новые элемен-
ты. Одним из важных способов введения нового материала в концеп-
цию задачи является возврат к определениям
Допустим в качестве примера, что мы имеем дело с усеченной пи-
рамидой. Что представляет собой усеченная пирамида? Как она опре-
деляется? — Усеченной пирамидой называется часть полной пирами-
ды, остающаяся при отсечении от нее плоскостью, параллельной ос-
нованию, некоторой меньшей пирамиды. Это определение вводит е
рассмотрение два новых тела: полную пирамиду и малую пирамиду — и
296
нам может показаться выгодным включение той или другой из этих
пирамид, или даже обеих сразу, в нашу концепцию задачи.
Возвращаясь к определениям элементов, встречающихся в условии за-
дачи, мы тем самым вводим новые элементы, которые в свою очередь так-
же привлекают новые элементы; продолжая действовать в таком же духе и
дальше, мы развертываем концепцию задачи все шире. Этот процесс раз-
вертывания условия задачи часто подводит нас ближе к решению, хотя это
бывает и не всегда — иногда он только загромождает задачу ненужными
деталями.
Существует много заслуживающих внимания способов преобразования
условий задач; одни из них приложимы только к некоторым частным слу-
чаям, другие — более универсальны.
6. Блуждания: поиски полезных сведений. Процесс решения задачи
существенно зависит от установления связи между этой задачей и соответ-
ствующими элементами накопленного вами ранее запаса знаний. Когда мы
пытаемся изложить задачу иначе, в более перспективной форме, то в дейст-
вительности мы ищем именно такую связь; при этом отправным пунктом
служит сама задача, и мы стараемся пробить окружающие ее облака, рабо-
тая над нею «изнутри». Но эту связь можно искать и с другого конца, пыта-
ясь обнаружить вовне какую-нибудь полезную частицу знаний — так ска-
зать, приближаясь к задаче «извне».
Обозреть все когда-либо накопленные нами знания невозможно! По-
этому следует начать с обследования тех областей наших знаний, связь ко-
торых с рассматриваемой задачей более вероятна.
Если область, к которой принад лежит рассматриваемая задача, вам зна-
кома, то вы должны знать ее «ключевые пункты» — факты, которыми ве-
роятнее всего придется воспользоваться. Подготовьте их так, как хороший
рабочий готовит свои любимые инструменты д ля работы, т.е. так, чтобы до
них было легко дотянуться.
Если вы имеете дело с задачей на нахождение, особого внимания
заслуживают задачи с тем же неизвестным; одна из таких задач может
стать отправным пунктом для продвижения в обратном направлении
Если же перед вами задача на доказательство, то в качестве возмож-
ных отправных пунктов особого внимания заслуживают теоремы,
имеющие то же заключение, что и теорема, интересующая вас в дан-
ный момент.
Какие факты являются здесь ключевыми9 Нет ли задачи (жела-
тельно уже решенной) с подобным неизвестным? Нет ли теоремы
(желательно ранее доказанной) с таким же заключением9 Имеются
хорошие шансы на то. что эти вопросы помогут извлечь из запаса на-
копленных вами знаний какой-нибудь полезный элемент; с них и ре-
297
комендуется начинать, если вы хотите собрать воедино все нужное
вам для решения задачи. Если же эти вопросы окажутся бесплодными,
вам, возможно, придется обратиться к более сложным или более тон-
ким фактам или рассмотренным ранее задачам, имеющим какой-либо
другой общий элемент с данной задачей, — вовсе не обязательно, что-
бы это было только неизвестное или заключение! Нет сомнения, что в
вашем запасе знаний имеются элементы, которые можно использовать
в рассматриваемой задаче, — но как они с ней связаны? Как подоб-
раться к ним? Вы можете испробовать обобщение, специализацию,
аналогию; вы можете рыться во всей области знания, к которой при-
надлежит ваша задача, особенно, если область эта в вашей голове не
так уж велика.
Конечно, чем ваши знания шире и чем лучше они упорядочены, тем
более имеется шансов на то, что вам удастся найти нужные элементы.
7. Блуждания: может быть, ситуацию следует переоценить? До-
пустим, что вы не удовлетворены тем, как продвигается ваша работа.
Различные идеи, приходившие вам в голову, потерпели фиаско, разно-
образные пути, которыми вы пробовали идти, все завели вас в тупик.
Созерцаемая вами фигура, вся концепция, задачи в ее нынешнем со-
стоянии, запутана и темна, перегружена деталями и вместе с тем не-
полна; какой-то существенный элемент, какое-то важное звено в ней
отсутствует.
Беда может состоять в том, что вы все время обследуете боковые
ходы и тупики, обременяя себя тем самым не относящимся к делу ма-
териалом. Попытайтесь вернуться назад к первоначальной, неприкра-
шенной, концепции задачи взгляните еще раз на неизвестное, на дан-
ные и условие задачи, на ее предпосылку и заключение. Приняли ли вы
во внимание полностью все условия? Использовали ли вы все данные? Уч-
ли ли вы целиком всю предпосылку? Использовали ли вы все ее части?
Эти вопросы особенно уместны, если вы заранее уверены в том, что для
определения неизвестного нужны все данные и все части условия задачи
или что для вывода заключения необходима целиком вся предпосылка.
Даже если у вас такой твердой уверенности нет и вы только подозреваете,
что все данные и все пункты условия или предпосылки могут быть сущест-
венны, то и в этом случае подобные вопросы будут оправданы и могут
принести пользу. Они напоминают, что вам следовало бы попытаться ис-
пользовать то данное или тот пункт, который вы до сих пор упускали из
виду, и, таким образом, могут подвести вас к недостающему звену.
Беда может состоять также в том, что вы недостаточно отчетливо пред-
ставляете себе значение основных терминов, содержащихся в условии за-
дачи. Понятны ли вам — представили ли вы себе наглядно — все понятия,
298
являющиеся неотъемлемыми частями задачи7 Этот вопрос может побу-
дить вас вернуться назад к определениям некоторых понятий и, таким об-
разом, навести на мысль о расширении концепции задачи; есть надежда,
что он поможет вам более удовлетворительно сформулировать условие за-
дачи и найти новые полезные элементы.
8. Искусство ставить вопросы. В предыдущих пунктах мы дали обзор
типичных мыслительных операций или умственных «шагов» решающего
задачу. Описание каждого такого шага имело своей кульминацией вопрос
(или совет, напечатанный курсивом), который может служить концентри-
рованным выражением данного конкретного шага решающего, его изо-
бражением в миниатюре. Важно понимать, как решающий задачу (или
учитель) может использовать эти вопросы.
Каждый из приведенных выше вопросов, будучи задан в надлежащее
время и в надлежащем месте, может стимулировать правильный ответ
верную идею, хорошо направленное движение мысли, которые могут про-
двинуть вперед решение. Итак, вопрос может сыграть роль стимулятора
(химики в таких случаях говорят о «катализаторах»), ускоряющего желае-
мую реакцию. Подобные вопросы представляют собой как бы индукторы
идей.
Конечно, в некоторых случаях можно не знать, какой именно вопрос
следовало бы задать. Но тогда вы можете перебирать их од ин за другим до
тех пор, пока, в конце концов, не дойдете до такого вопроса, который ока-
жется полезным. Таким образом, вы можете использовать предыдущие
пункты как каталог подходящих вопросов, как контрольный перечень их.
Нельзя, однако, пользоваться этим перечнем беспорядочно, выбирая
вопросы наугад; нельзя им пользоваться также механически, переби-
рая вопросы в одном, незыблемо установленном, порядке. Обращай-
тесь с этим перечнем вопросов так, как опытный рабочий на произ-
водстве обращается с ящиком с инструментами. Он окидывает внима-
тельным взглядом работу, которую ему предстоит выполнить, а затем
выбирает инструмент Возможно, что ему придется испробовать несколько
инструментов, пока он найдет нужный, но и в этом случае он не станет вы-
нимать инструменты из ящика наугад или в механически установленном
порядке: он выбирает их с рассудком. Таким же должен быть выбор нуж-
ного вопроса из всего множества вопросов, перечисленных в настоящей
статье.
Конечно, рабочий скорее всего приобрел мастерство благодаря
длительному опыту и внимательному наблюдению за работой других.
Таким же путем можете научиться применять собранные здесь вопро-
сы и вы. Строгого и жесткого правила, регулирующего их употребле-
ние, не существует. Однако если за этими вопросами стоит ваш лич-
299
ный опыт, основанный на успехах и неудачах, и если вы отдаете себе
полный отчет в цели, к которой стремитесь, то имеется много шансов
на то, что вы подберете хороший вопрос.
У хорошего рабочего инструменты всегда находятся в исправном со-
стоянии и лежат в ящике в полном порядке. Если вопросы и лежащие в их
основе типичные мыслительные операции, описанные в настоящей статье,
известны вам не по книгам, а по опыту, если вы хорошо поняли их роль в
процессе решения задач, то есть много шансов на то, что вы сумеете обра-
щаться с задачами более профессионально, менее неловко, не пользуясь
случайными приемами, которые употребит в подобном случае профан
Возможно, что всякий вид дисциплины ума заключается во владении
совокупностью вопросов и в правильном их употреблении. Но как можно
изучить искусство постановки вопросов? Подчиняется ли оно каким-либо
правилам?
Вопросы и упражнения
для индивидуального осмысления
и коллективного обсуждения
1 . Предложите свои комментарии и примеры к следующим качествам
математика (по У.У. Сойеру), дерзость ума, желание исследовать; интерес
к закономерностям.
2 . Известно, насколько важна в математике роль обобщений. С помо-
щью обобщения мы избавляемся от ненужных сведений, отвлекающих
наше внимание от существа задачи, сосредотачиваем его на действитель-
но важных фактах. С помощью обобщений математика сводит под одну
крышу совершенно разные объекты, унифицирует объекты и закономерно-
сти Покажите на математических примерах такую роль обобщений и про-
иллюстрируйте справедливость и закономерность принципа: «Большая
степень обобщения и большая простота неотделимы друг от друга».
3 . Ничто не доставляет математику большего наслаждения, чем откры-
тие, что две вещи, которые он раньше считвл совершенно различными,
оказываются математически идентичными, изоморфными. Проиллюстри-
руйте примерами мысль А Пуанкаре: «Математика — это искусство назы-
вать разные вещи одним и тем же именем».
4 . Какие способности человека А.Н. Колмогоров относит к математиче-
ским? Проиллюстрируйте мнение А.Н. Колмогорова примерами из биогра-
фий известных вам математиков (см. раздел «О математических способ-
ностях» из книги А Н Колмогорова «Математика — наука и профессия»).
5 Дайте комментарий и проиллюстрируйте примерами следующие ка-
чества математического мышления, характеризуемые А.Я Хинчиным как
культура мысли полноценность аргументации; борьба против незаконных
обобщений, необоснованных аналогий, за полноту дизъюнкций, за полноту
и выдержанность классификации, стиль мышления.
300
6 . А.Я. Хинчин считает, что наряду с воспитанием правильного и дисци-
плинированного мышления математическое образование формирует у че-
ловека такие моральные качества, как честность и правдивость, настойчи-
вость и мужество. Согласны ли вы во всем с аргументацией автора? Про-
иллюстрируйте свое мнение примерами.
7 Изучите раздел «Умственная работа» из книги Д Пойа «Математиче-
ское открытие» Вспомните свою работу над решением какой-нибудь гео-
метрической задачи и постарайтесь осмыслить, присутствовали ли в этом
процессе такие этапы, как мобилизация и привлечение вашего опыта, про-
зрение, синтезирование в целое отдельных частей или фактов, распозна-
вание объектов, их перегруппировка, установление связей с другими по-
добными задачами. Опишите свой опыт или приведите примеры из книги Д.
Пойа.
8 Изучите раздел «Дисциплина ум*а» из книги Д. Пойа «Математическое
открытие». Из собственного опыта решения задач или из книги Д Пойа
приведите примеры таких процессов мышления: концентрация внимания
на цели, оценка перспектив, блуждания (поиски подхода, более обнадежи-
вающего аспекта задачи, полезных сведений, возможностей переоценки
ситуации).
9 В чем состоит, по мнению Д. Пойа. искусство ставить перед собой
вопросы при решении задач? Подтвердите примером мнение Декарта,
сформулированное им в Правилах для руководства ума: «Метод состоит в
размещении и упорядочении того, на что должно быть неправлено острие
ума в целях открытия какой-либо истины».
10 По мнению Д Пойа, мышление можно считать продуктивным, если
оно приводит к решению данной конкретной задачи, мышление можно на-
звать творческим, если оно создает средства для решения будущих задач.
Чем больше число и чем шире разнообразие задвч, к которым применимы
созданные средства, и чем шире круг таких задач, тем выше творческий
уровень мышления. Проиллюстрируйте мысль Д. Пойа примерами созда-
ния средств (разработки теорий и методов) из истории математики.
МАТЕМАТИКА И ПСИХОЛОГИЯ
Здравый смысл — это толща предрассудков, ус-
певших отложиться в нашем сознании к восемна-
дцати годам.
Альберт Эйнштейн
Я скажу. что при таких-то обстоятельствах
нашел доказательство такой-то теоремы; эта
теорема получит какое-то варварское название, ко-
торое многие из вас не поймут, но это не важно
для психолога важна не теорема, а обстоятельства.
А. Пуанкаре
Математика черпает свою силу в умении исклю-
чать все лишнее в процессе мышления и в удиви-
тельной способности экономить мыслительную ра-
боту.
Эрнст Мах
СТРУКТУРЫ МАТЕМАТИЧЕСКИЕ
И ОПЕРАТОРНЫЕ СТРУКТУРЫ МЫШЛЕНИЯ1*
I
Станем на практическую точку зрения педагога, задачей которого
является преподавание математических истин, или на теоретическую
точку зрения эпистемолога (эпистемология — наука о законах позна-
ния — Г.Д.), размышляющего о сущности математических объектов,
тогда центральная проблема представится в двух аспектах: порождены
ли математические соотношения деятельностью ума или эта деятель-
ность только открывает их, как некую внешнюю реальность, действи-
тельно существующую. Эта проблема, такая же древняя, как восточная
философия, с современной точки зрения может быть поставлена, как
одна из проблем психологии и даже психологии ребенка. Одна из за-
дач изучения умственного развития заключается в том, чтобы устано-
вить: достаточны ли действия субъектов и операции мысли для полу-
чения конструкции математических объектов или эти последние были
902
открыты извне, как физические сущности с их объективными свойст-
вами. Таковыми являются также объекты, созданные синтагмами язы-
ка, присущими социальной группе данного индивидуума. (Нам из-
вестно, что взаимосвязь между объектами логико-математическими и
лингвистическими признается значительным числом логистов и осно-
вана или на теории конвенционалистов, или на теории платоников).
И вот если методы приближения к разрешению этой вечной про-
блемы могут быть улучшены путем обращения к генетической психо-
логии, то сами понятия проблемы были недавно обновлены благодаря
работам Бурбаки в области строения математики и благодаря фунда-
ментальной роли, отведенной в этих работах понятию «структуры».
Основой общего здания математики долгое время считались неко-
торые простые объекты, рассматриваемые более или менее изолиро-
ванно друг от друга. Это были целые числа, которые Кронеккер при-
писывал самому богу, противопоставляя их всем остальным числам,
изобретенным человечеством. Это были точка, линия и т.д., компози-
ции которых порождали пространство. Но это всегда были вещи, дан-
ные сами в себе, которые наш разум привлекал или для созерцания,
если ои еще не осознал роли операций, или для манипуляций над ни-
ми, если он употреблял их как простые элементы, как средства произ-
водства, которые использует каменщик, чтобы зацементировать пер-
воначальный материал при постройке стены или дома.
Но если в основу положить понятие структуры и если благодаря
ему познание переходит одновременно от простого к сложному и от
общего к частному, то перспективы будут совершенно иные.
Структура, как например «группа», есть система операторная, и
возникает вопрос, существуют ли до нее эти чрезвычайно разнородные
элементы, над которыми оперирует структура, т.е., другими словами,
имеют ли они значение достаточно независимое от нее или, наоборот,
они суть результат действия структуры — действия не вполне ясного
вначале, потому что порядок сознания противоположен порядку гене-
зиса, которым определяются эти элементы. Более точно, психологиче-
ская проблема (а это единственная, которую мы будем иметь в виду)
заключается в том, чтобы выяснить: или объекты, служащие элемен-
тами структуры, представляют собою результат операций, которые их
породили, или они предшествовали операциям, последовательно
включаясь в них.
Перестройка, которую вносит идея структуры в ход определений и
доказательств, играет существенную роль в этом отношении. Вместо
того чтобы определять элементы изолированно, путем соглашения или
конструктивно, структурное определение состоит в том, чтобы харак-
теризовать их путем операторных взаимоотношений, которыми опре-
деляются их функции в системе.
зоз
Структурное определение элемента будет иметь место при доказа-
тельстве существования этого элемента, так как он рассматривается,
как принадлежащий к системе, состоящей из отдельных взаимозави-
симых между собою частей. Таким образом, принцип аксиоматической
полноты системы дается с самого начала, и эта полнота будет обяза-
тельно операторной природы. То же самое происходит и в системе
чистых отношений, каковыми являются структуры порядка: если про-
изведение двух отношений есть тоже отношение, то это значит, что
они координированы между собою операциями логики отношений.
Не менее замечательны преобразования, полученные благодаря
введению понятия структуры в «архитектуру» математических наук,
другими словами, в порядок, в конструкцию или преемственность
многочисленных классов, которые можно различать в этих абстракт-
ных объектах. По этому поводу можно сказать, что введение структур
представляет собою прогресс, аналогичный тому, какого сравнитель-
ная анатомия добилась в биологии, установив классификацию, осно-
ванную на внутренних генетических связях, по сравнению с классифи-
кацией, опирающейся на внешние признаки в их разрозненной статич-
ности. Если отправляться от нескольких основных структур, то даль-
нейшее движение состоит в их дифференциации от общего к частному
и в комбинировании их друг с другом от простого к сложному. Так по-
лучается конструкция, заменяющая прежнее внешнее сочетание от-
дельных областей науки серией систем, подчиненных друг другу, со-
гласно вышеуказанным двум методам получения. Отсюда следует сно-
ва принцип полной подчиненности элементов или классов элементов
динамике конструкции в собственном смысле слова.
Отметим также большой интерес для психологии математической
мысли к методу открытия структур — и это нас вновь приведет к ис-
ходной альтернативе: либо строение математики есть результат рабо-
ты мысли, или идеальные объекты действительно существуют и наш
разум схватывает их как бы извне. На первый взгляд наблюдения за
попытками математика получить фундаментальные структуры, кажет-
ся, приводят ко второму из этих положений. Далекий от того, чтобы
обнаружить их сразу, он замечает аналогии, получаемые от сравнения
друг с другом форм рассуждений в областях, не имеющих заметного
сходства друг с другом, потом, в известной степени индуктивно и ис-
ходя из экспериментальных фактов, он находит общие методы, вплоть
до выделения наиболее общих законов искомой структуры И только
тогда вступает в дело аксиоматика, т.е. применение этих общих зако-
нов к частным теориям путем прогрессивной дифференциации. Более
того, переход от первоначальных структур к структурам вторичным
совершается путем комбинаций многочисленных структур, и здесь эта
304
комбинация не есть еще дедукция, потому что для каждой новой
структуры нужно использовать новые аксиомы, чтобы в нее можно
было бы включить но ые элементы.
Хотя этот переход к открытию структур является до некоторой сте-
пени индуктивным, он все же раскрывает отношения структуры к эле-
ментам, которые она упорядочивает. Если, исторически, эти элементы
кажутся данными до открытия структуры и если эта последняя играет
таким образом существенную роль рефлективного инструмента, пред-
назначенного выявлять их наиболее общие свойства, то не надо забы-
вать, что психологически порядок осознавания противоположен по-
рядку генезиса: то, что является первым в порядке сознания, будет по-
следним в рефлективном анализе, потому что субъект осознает резуль-
таты умственных построений до того, как они постигаются внутрен-
ними механизмами.
Мы далеки от того, чтобы выдвигать определенный аргумент в
пользу независимости «структур» по отношению к работе мышления.
Их позднее и как бы индуктивное открытие заставляет, наоборот,
предполагать их первоначальный и порождающий характер. Н если
эти основные мысли выразить в терминах анализа, то мы убедимся,
что обратное предложение не будет обязательно верным и возникает
проблема: как избавиться от случайных связей между первоначальны-
ми структурами математики и операторными структурами, которые, с
точки зрения умственного развития, можно рассматривать как основ-
ные части логико-математической конструкции. Это и требуется те-
перь рассмотреть с точек зрения психогенезиса.
Три фундаментальные структуры, на которых покоится здание ма-
тематики, по определению Бурбаки, суть алгебраические структуры,
прототипом которых является «группа», структуры порядка, к кото-
рым относятся использующаяся сейчас с таким успехом (излишне да-
же в некоторых случаях) «решетка», и структуры топологические.
Число три не является исчерпывающим, и развитие математики мо-
жет его увеличить. Но при настоящем состоянии знаний эти три струк-
туры являются неприводимыми по отношению друг к другу и играют
таким образом роль основных структур.
Большой интерес вызывает тот факт, что если проследить до самых
истоков психологическое развитие арифметических и геометрических
операций в сознании ребенка и особенно операций логических, осуще-
ствляющих в них все необходимые предварительные условия, то вновь
находят все этапы — вначале фундаментальные тенденции к органи-
зации целого или системы, вне которой элементы не имеют ни значе-
ния, ни вообще существования, а затем распределение этих систем со-
вокупностей по трем типам, которые в точности соответствуют струк-
21 Зак. 72
305
турам алгебраическим, структурам порядка и топологии. Это мы и со-
бираемся показать, рассматривая их одну за другой, чтобы выявить
потом основной смысл этого совпадения.
II
Нужно прежде всего напомнить, что понятие структуры формиро-
валось в течение нескольких десятилетий, независимо от современной
эволюции математических дисциплин, как одно из привычных поня-
тий психологии познавательных функций (восприятие и рассудок). В
совершенно различных областях психологи вынуждены были допус-
тить, что «естественное» течение ума, состоящее в отыскании перво-
начальных элементов и выведении новых путем сочетания с другими,
покоилось на ошибочных аналогиях с материальным производством. В
области восприятий, в частности, где действие поля сознания можно
легко проанализировать экспериментально, пришли к выводу, что так
называемые элементы суть всегда продукты диссоциации или вычле-
нения из целого внутри начальной совокупности и что ни одно частное
соотношение не может быть выделено без выявления с самого начала
характерных структурных свойств совокупности.
В специальной области рассудка, которая одна нас здесь интересу-
ет, обобщения играют ту же самую роль, но они представляют здесь
иную форму, чем в области восприятий. Ум выявляется, по существу,
как координация действий. Эти последние суть вначале просто мате-
риальные или чувственно двигательные процессы (без вмешательства
символики и отображения), но уже и тогда они несут в себе схемы, ко-
торые допускают определенные структуры обобщения. Потом с по-
мощью функциональной символики, и особенно с помощью умствен-
ных и языковых отображений, действия прогрессивно самоуглубляют-
ся, и после более или менее длительного периода транспозиции между
материальным актом и актом воспроизведения (период, который мы
назовем периодом подготовительной мысли между двумя и семью—
восемью годами) они преобразуются в действия в собственном смысле
этого слова и представляются тогда под типичной формой структур-
ных совокупностей, характерных для интеллекта.
Чтобы понять сущность этих операторных структур, надо исходить
из основного факта, что в противоположность процессам перцепции,
которые необратимы, потому что зависят от формы возможных компо-
зиций, ум с самого начала опирается на обратимость, значение кото-
рой в процессе развития все время увеличивается. Без сомнения, на-
чальные чувственно-двигательные действия тоже необратимы, потому
что они направлены к единственной практической цели, которую они
стремятся достигнуть. Но, начиная с момента координации чувствен-
306
но-двигательных схем, ум становится способным к известной подвиж-
ности в прямом и обратном направлении, и тогда можно видеть появ-
ление обратимости более или менее систематической, которая обна-
руживается в области представлений. В этом новом плане обратимость
еще далека до полного завершения. В продолжение всей подготови-
тельной фазы субъект больше рассуждает конфигурациями, чем пре-
образованиями, и вопрос состоит в том, чтобы научить его мыслить,
чего он достигает в действии (например, представляет себе систему
перемещений после того, как он уже выучился совершать это матери-
ально). Точно так же представления, возникающие в течение всего
раннего периода детства, заключают в себе систематические трудно-
сти в отношении обратимости и, следовательно, в сохранении элемен-
тарных инвариантов (длина, расстояние, непрерывные совокупности,
физические величины и т.д.). Но, начиная с этой дооперативной фазы,
все более и более регулированное действие ведет к постоянному ис-
правлению ошибок, исходящих от начальной необратимости, и прихо-
дит таким образом к оперативной обратимости.
Появление первых систематических действий к семи—восьми го-
дам указывает на переход к состоянию равновесия, к которому стре-
милась мысль в продолжение предшествующей начальной фазы, и на-
до хорошо понять это отношение прогрессивного равновесия между
фазой дооперативной и первым оперативным периодом (от 7—8 до
11—12 лет), чтобы не рассматривать эту последнюю как безусловно
начальную форму.
Зарождающиеся операции, таким образом, подготовлены чувствен-
но двигательными координациями и регулярными дооперативными
отображениями и обнаруживают тогда следующие свойства. Они суть
действия в буквальном смысле, являясь продолжением материальных
предшествующих действий, но в то же время внутренне мыслимых,
благодаря способности выражаться символически. Они по существу
обратимы, т.е., другими словами, операции и действия могут развер-
тываться в двух направлениях, и понимание одного из этих направле-
ний вызывает ipso facto (в силу самого факта — Г.Д.) понимание дру-
гого. И особенно важно то, что с самого начала они являются связан-
ными с одной и той же системой: не существует изолированной опе-
рации потому, что изолированное действие не будет операцией. Опе-
рация, таким образом, необходимо сочетается с другими операциями,
и сама их природа отвечает этому свойству мобильной и обратимой
композиции внутри системы. Таким образом, операторные структу-
ры появляются, как только появляются операции, а структура целого
не является последующим продуктом композиции между дооператив-
ными операциями, потому что действие, вначале необратимое, стано-
21-
307
вится операторным и обратимым только внутри структуры и под
влиянием своей собственной организации.
Прежде чем перейти к детальному рассмотрению типов структур,
отметим еще, что обратимость, составляя, без сомнения, фундамен-
тальный закон композиции, свойственный уму, представляется с само-
го начала (т.е. от схем чувственно-двигательных) под двумя формами —
взаимодополняющими и неприводимыми: обращение, или отрицание,
и взаимность. Когда ребенок от 10 до 12 месяцев, начинающий сис-
тематическим образом организовывать перемещения в ближайшем к
нему пространстве, переместил предмет из А в В, он может аннулиро-
вать это преобразование обратной транспозицией, переводя предмет
обратно из В в Л, что в итоге эквивалентно нулевому движению. Но он
может также оставить предмет в В, а сам переместиться из Л в В, что
воспроизведет начальное положение, когда предмет был против его
собственного тела.
В этом случае движение предмета не было аннулировано, но оно
просто компенсировалось путем соответствующего перемещения соб-
ственного тела, что составило другое преобразование. Не имея наме-
рения заключить в логические нормы поведение ребенка, отметим все
же, что эта существенная разница между отрицанием и обращением и
между взаимностью и компенсацией определяет с самого начала две
формы обратимости, которые будут находиться рядом в продолжение
всего развития и которые превратятся в синтез в единой системе толь-
ко в формальных операциях после 11—12 лет, когда построится груп-
па четырех форм суждений (которые, если мы используем пример пе-
ремещений, только тогда позволят ребенку координировать в одно все
перемещения по двум системам отсчета сразу — одно мобильное, дру-
гое неподвижное).
Теперь мы уже сможем уточнить, в каком смысле три фундамен-
тальные структуры Бурбаки соответствуют элементарным структурам
мышления, формальным продолжением которых они являются.
ill
Алгебраические структуры, а именно «группы», соответствуют
операторным механизмам ума, подчиненным первым из двух форм
обратимости, которую мы называем инверсией, или отрицанием (про-
изведение операции на обратную есть тождественная операция, или
нулевое преобразование).
В этом отношении необходимо обратить серьезное внимание на тот
факт, что, как бы ни запаздывало открытие понятия группы в матема-
тике (XIX век), такая структура изображает в действительности опре-
деленные, наиболее характерные для мышления механизмы.
308
Вспомним с этой точки зрения четыре элементарных свойства
группы: произведение двух элементов группы дает также элемент
группы; всякой прямой операции соответствует одна и только одна
обратная; существует операция тождества и последовательные компо-
зиции ассоциативны. Выраженные на языке интеллектуальных дейст-
вий эти четыре свойства означают: 1) координация двух систем дейст-
вия составляет новую схему, присоединяемую к предыдущим; 2) коор-
динация может по желанию осуществляться или быть упраздненной
или, прощё говоря, интеллектуальное действие (операция) может раз-
виваться в двух направлениях; 3) при возвращении к исходной точке
мы находим эту точку неизменной; 4) к одной и той же данной точке
можно прийти различными путями, причем сама точка останется не-
изменной. В общем смысле «группа» есть символический перевод не-
которых определенных фундаментальных свойств действия мышле-
ния: возможность координации действий, возможность возвращения и
отходов. Но, более того, собственные преобразования группы всегда
связаны с определенными инвариантами, откуда следует, что построе-
ние группы идет параллельно с построением инвариантов, которые к
ней относятся. Что касается непосредственных форм организации, ко-
торые осуществляются мышлением в процессе своего развития, то
первоначальной необратимости операций соответствует отсутствие
сохранения их, а построению обратимых структур соответствует вы-
работка сохранения понятий в построенной таким образом области.
Начиная с чувственно-двигательного уровня, эти процессы можно
рассматривать путем практического предвосхищения (связанного с
ближайшим пространством) того, чем станут эти операции в области
представления или мышления. Так, в продолжение первых месяцев
существования перемещения не могут быть организованы в «группу»,
потому что они сосредоточены на собственном теле и являются след-
ствием определенных систематических ошибок, вызванных этим
эгоцентризмом. На этом уровне нет также еще постоянных объектов
на пути собственного действия. К концу первого года, наоборот,
появляется одновременное осуществление этой экспериментальной
группы перемещений, уже упомянутых Пуанкаре (но которые он
считал врожденными, тогда как они составляют конечную устойчивую
чувственно-двигательную форму организации), и выработка схемы
постоянных предметов (в функции последовательных локализаций,
каковыми являются приближения и удаления).
Развитие предметного мышления в период дооперативиой фазы и
на уровне первых конкретных операций (7—11 лет) дает аналогичную
картину. Пока имеется необратимость мысли, мы не сможем получить
понятие постоянства даже в областях наиболее простых наблюдений
309
(сохранение совокупности в случаях изменения конфигурации ее эле-
ментов; сохранение эквивалентности между двумя соответственными
совокупностями, когда одни элементы рассматриваются с точки зре-
ния других, не представляя больше оптического соответствия; сохра-
нение равенства длин двух твердых стержней, когда один из них не-
много смешен по отношению к другому; сохранение расстояния меж-
ду двумя неподвижными элементами, когда новые элементы вставля-
ются между ними и т.д.). Напротив, строение первых предметных об-
ратимых структур к 7—8 годам фактически влечет за собою перера-
ботку соответствующих понятий постоянства.
Бесполезно производить здесь описание многочисленных обрати-
мых структур алгебраического типа, которые мы отметили в другом
месте, при переработке ребенком 6—8 лет понятий целого числа, про-
ективных или евклидовых прямых, геометрической меры, времени и
т.д. Важно напомнить, что каждая из этих конструкций предполагает
предварительную логическую переработку применением логики клас-
сов и что первые операции этой логики, которые доступны ребенку,
требуют для их осуществления определенных структур алгебраическо-
го типа, еще не идентичных с группой, но представляющих все же не-
которые из ее свойств.
Возьмем в качестве примера включение частного класса А в общий
класс В Кажется, нет ничего легче понять действие такого включения,
если все элементы расположены одновременно в одном и том же поле
восприятия. Пусть, например, В равно совокупности нескольких дере-
вянных шариков, А равно части В, образуемой из 20 коричневых ша-
риков, и А' равно другой части, образуемой из 2—3 белых шариков.
Между тем достаточно спросить у ребенка, будет ли все В более или
менее многочисленно, чем большая часть А (или «имеется ли здесь
больше шариков из дерева или больше шариков коричневых?» и т.д.),
чтобы заметить оперативную сложность этого действия включения. До
7 лет в среднем ребенок ответит, что А одерживает верх над В, и это
потому, что тотчас же, как В разлагается на части, это целое, как тако-
вое, уже не существует, а то, что остается от В, есть только другая
часть А' («имеется больше коричневых, чем деревянных, потому что
осталось всего два белых», говоря так, ребенок все же знает, что ко-
ричневые шарики тоже из дерева). Чтобы установить отношение Л < В,
ребенок должен пройти через обратимую операцию А + А' = В, откуда
А = В -А' и А' = В-А И только тогда достигается обратимость логи-
ческого сложения и вычитания классов, когда целое В сохраняет неза-
висимость от подразделений, которые можно в нем усмотреть. Други-
ми словами, включение части в целое уже само предполагает в себе
предварительную алгебраическую структуру.
310
Из чего состоит эта структура? Ее наиболее простая форма, кото-
рую мы называем структурой элементарных «группировок», может
быть иллюстрирована, например, классификациями или суммарными
группировками классов.
Основные из этих операций суть:
1) Л + А' = В\ В + В' = С, С + С = D и т.д., где все классы одного и
того же порядка разъединены (А А' = 0; В В’ - 0 и т.д.),
2)-Л-Л’ = -В,откудаЛ' = В-Л ит.д.,
3)Л-Л = 0,
4) А + А = А (тавтология),
5) ассоциативность, ограниченная в нетавтологических операциях:
(А +АГ) + В' = А + (А' + ВГ), ноА + (А-А)*(А +А)-А
В этих структурах мы узнаем определенные преобразования, об-
щие с «группой», такие, как +А, -А и 0. Но ассоциативность, с одной
стороны, ограничена, а с другой — преобразования осуществляются
только над смежным классом, т.е. над классом непосредственно выс-
шим. Эти два ограничения, естественно, сильно уменьшают общность
этой структуры. Но с точки зрения генетической она представляется
не менее интересной, потому что выявляет, без сомнения, необходи-
мость перехода через алгебраические структуры для получения наибо-
лее простых логических конструкций.
Отметим также, что некоторые формы научной мысли принадле-
жат структурам этого типа, например зоологическая классификация, в
которой мы находим каждый из этих признаков, включая и смежность
(нельзя расчленить два таких класса, как «верблюды» и «черви», что-
бы сделать из них новый класс, не проходя через серию выключения
типа: А' + С = D - В' и т.д.).
С другой стороны, мы видим, что эти структуры образуют с точки
зрения структуры порядка неполные сетки, потому что все внутренние
границы между классами одного и того же порядка нулевые. Но с ин-
тересующей нас здесь точки зрения возникновения структур от меха-
низмов непосредственного развития ума, гораздо важнее найти вне
структур главное значение определенных первоначальных форм орга-
низации, которые выявляют их примитивный характер, так как они
ускользнули от формулировок логистов и математиков.
IV
Структуры порядка, к которым мы теперь обратимся, суть так на-
зываемые структуры отношений, а не действий: таковы, например,
«сетка» и «решетка». Примем некоторые условия. Без сомнения, мож-
но полностью определить сетку в терминах отношений вместо введе-
ния операций + и х : в этом случае мы рассматриваем как основные
311
понятия «х предшествует у» или «у следует за х», вместо того чтобы
получить их из операций хху=хих+у=у Но даже при рассмотре-
нии отношений между полуупорядоченными элементами остается все
же то, что транзитивность, «если х предшествует у, у предшествует z, а
потому х предшествует z», состоит в соединении двух операций в од-
ну, которую мы будем рассматривать как операцию аддитивную, но
произведенную над отношениями.
Но сетка не есть только операторная структура: в действительности
она является еще и структурой обратимой. Большое психологическое
значение этих систем заключается в том, что их обратимость не явля-
ется под обшей формой инверсии или отрицания. (Лишь некоторые
виды дистрибутивных сеток являются определенным образом допол-
нительными и обладают, таким образом, «дополнительными элемен-
тами первого и второго рода».) Главная обратимость, свойственная
сетке, есть «взаимность». Действительно, сетка заключает в себе закон
двойственности, который состоит в том, чтобы менять знаки х и +
точно так же, как отношения «предшествует» и «следует». Применим
теперь закон двойственности в следующем примере, обозначая символом
-> отношение «предшествует» и символом <— отношение «следует»:
1) АВ -> А и АВ -> В. А —> (А + В) и В -> (А + В),
откуда
2) (АВ) -» (А + В).
в силу двойственности в этом случае имеем:
3) (А + В) ч- (АВ).
Итак, констатируем, что (3) совсем не является отрицанием (2), но,
наоборот, оно является простым обращением отношения (2).
В основном закон двойственности, свойственный сетке, не приво-
дит к инверсии или отрицанию, как это имело место в алгебраических
структурах, но к перемене, основанной на взаимности, т.е. переста-
новке порядка. В то время как инверсия приводит к отрицанию самой
операции, независимо от отношения порядка, взаимность возвращает-
ся к изменению порядка, без отрицания операций в действии.
Структуры порядка так же фундаментальны для механизма мыш-
ления, как структуры групп (или другие смежные структуры), и легко
показать, как мы делали для этих последних, что они формируются на
дооперативном уровне, начиная с действий чувственно-двигательных,
и a fortiori (тем более — ГД.) в течение всего периода зрительных
представлений от 2 до 7—8 лет. Но ограничимся характеристикой ро-
ли, которую они играют на уровне конкретных операций (7—11 лет),
до появления словесных или формальных операций (11—12 лет) и вы-
явлением роли их взаимоотношений на этом первом оперативном
уровне по сравнению с алгебраическими структурами.
312
Структуры порядка образуются в продолжение этого периода от 7
до 11 лет системами отношений. В то время как элементарные группи-
ровки классов покоятся на методе обратимости, группы отношений
покоятся на другом принципе, а именно на взаимности.
Наиболее простым примером этих самовозникающих систем, разви-
тие которых можно проследить на чувственно-двигательной деятельно-
сти и которые достигаются в периоде равновесия (т.е. на своем опера-
тивном уровне) в возрасте 6—7 лет, являются связи асимметричных
транзитивных отношений или «качественной серийности». Начиная с
чувственно-двигательного уровня, когда ребенок от 1,5 до 2 лет строит
башню, кладя в основание ее самые большие кубики и продолжая стро-
ить во все уменьшающемся порядке, можно сказать, что он вырабатыва-
ет путем проб (попытки и неудачи) практическую схему, подготавли-
вающую серийность. Но здесь мы имеем только эмпирическую схему,
основанную на воспринимаемой конфигурации и на бросающемся в
глаза неравенстве объектов. Если вместо этих элементов, разница в ве-
личине между которыми заметна с первого взгляда, мы предоставим ре-
бенку элементы, которые нужно более детально сравнивать попарно
(например, 10 стержней от 10 до 19 см, расположенных в беспорядке),
то должны будем констатировать, что систематическая серийность есть
нечто другое, чем серийность эмпирическая и что она предполагает
комплекс операторных действий. Действительно, после серии подгото-
вительных этапов (совокупностей маленьких серий, не координирован-
ных между собою, с последующими исправлениями) ребенок придет к
ним, но только в возрасте 6,5—7 лет, открывая метод, который на этот
раз обеспечит конструкцию полной и точной серийности без проб и
ошибок; он ищет путем сравнения самый маленький из всех стержней —
А и кладет его; он отыскивает путем таких же сравнений самый малень-
кий из оставшихся — стержень В и кладет его рядом с А; он отыскивает
стержень С — самый маленький из еще не определенных стержней и
т.д. Выявляющийся здесь метод предполагает понимание следующих
отношений: (I) что какой-нибудь элемент Е будет больше всех предше-
ствующих: Е > А, В, С, D; (II) что этот же самый элемент меньше всех
последующих: E<F, G, Hu т.д. Более того, существенно отметить, что
на уровне серий, производя пробы, ребенок вовсе не будет уверен в
транзитивности неравенств: после того как он увидел рядом два элемен-
та А < В и два элемента В < С, он может не заметить отношение А < С,
если от него спрятать А, оставив на виду С. Напротив, открытие двух
отношений Е > D, С и т.д. и Е < F, G и т.д. влечет ipso facto транзитив-
ность — (III) А < С, если А < В и В < С.
Если мы захотим установить отношения, используемые ребенком в
процессе этого упорядочения, то найдем структуру, аналогичную
20 Зак 72
313
классификации, но только опирающуюся на одни отношения. Назовем
через а отношение А < В. через Ь — отношение А < С, через с — отно-
шение А < D и т.д. и назовем через а' отношение В<С, через Ь' — от-
ношение С < D и т.д. Тогда будем иметь:
1) а + а'= b, Ь + Ь’= с и т.д.,
2) b - а' = аг, и т.д.,
3) а - а = О,
4) а + а' = а
и S) неполная ассоциативность.
Заметим, однако, что, если вычитание классов А - А = 0 дает нуле-
вой класс, что является свойством обращения, вычитание отношений
а - а = 0 дает разность 0, причем это вычитание не является той же са-
мой операцией, потому что разность 0 обозначает эквивалентность.
Композиция в области отношений состоит просто в чтении отношений
между крайними элементами двух отрезков сопоставленных серийно-
стей: А(а)В + В(а')С = А(Ь)С и обратная операция перемены порядка:
А(Ь)С - В^а^С = А(Ь)С + С(а)В = А(а)В С этой точки зрения обрати-
мость в действии в таких системах покоится на взаимности, а не на от-
рицании: вот поэтому а—а приводит к эквивалентности, а не к нуле-
вому отношению.
Таким образом, можно утверждать, что от 7 до 11 лет на уровне
конкретных операций (элементарные сочетания классов и отношений
между самими предметами путем противопоставления словесных вы-
ражений действию) структуры классов зависят от обращений (алгеб-
раические структуры), а структуры отношений — от взаимности
(структуры порядка). Но существуют ли эти два типа структур в своем
первоначальном периоде без связи между собою или, наоборот, можно
указать некоторую связь, существующую между обеими системами?
С точки зрения психологии мыслительных операций, оставляя в
стороне случайную закономерность первоначальных операторных сис-
тем, необходимо сделать существенное замечание: если опираться на
известное различие между объемом и содержанием понятия, то, есте-
ственно, нужно принять (с чем согласен весь мир), что объем понятия
определяется системами классов, в которых имеет место обращение,
приводящее к алгебраическим структурам, тогда как содержание поня-
тия всегда определяется системами отношений (что не всегда замеча-
ется). Все свойства, включенные в содержание понятия, определяются
суждениями, по внешнему виду безусловными (деревья суть «дере-
вянные», трава есть «зеленая» и т.д.) или вполне очевидными отноше-
ниями (рожденные прежде старше рожденных после и т.д.). Отсюда
ясно, что о сказуемых первого типа возможно мыслить лишь в терми-
нах отношений: «зеленый» означает или качество более или менее се-
314
рийное — континуум цветов от желтого или голубого к зеленому, или
качество, общее различным предметам: «зеленый» есть, таким обра-
зом, психологическое отношение асимметричное или симметричное в
зависимости от контекста.
С этой точки зрения между структурами классов, основанных на
обратимости, и структурами отношений, основанных на взаимности,
существует тесная связь, обусловленная связью между объемом и со-
держанием понятий.
Вот поэтому четыре основных условия группы, которые мы могли
различить в структурах классов на уровне конкретных операций
(группы аддитивные и мультипликативные и в формах взаимноодно-
значного или однозначного его соответствия), соответствуют почлен-
но четырем элементарным условиям отношений. Другими словами,
одни и те же совокупности элементов могут быть образованы в струк-
туры или по форме классов, или по форме отношений, что обеспечи-
вает психологическую общность системы. Но с точки зрения опера-
торной структуры на уровне конкретных операций не существует
структур, которые соединяли бы все эти свойства в одну и ту же сис-
тему преобразований и которые таким образом обеспечивали бы син-
тез обратимости и взаимности.
Этот синтез двух фундаментальных форм обратимости осущест-
вится только на последнем этапе равновесия в развитии логических
операций, т.е., другими словами, в стадии операций над суждениями, о
которых мы будем говорить ниже.
v
Если алгебраические структуры и структуры порядка кажутся глубоко
укоренившимися в психологическую деятельность умственных операций,
можно ли то же самое сказать о структурах топологических?
Особенно интересно по этому поводу констатировать, что порядок
формирования геометрических понятий и операций в самостоятель-
ном развитии ребенка абсолютно не соответствует историческому по-
рядку этапов геометрии и больше приближается к порядку преемст-
венности основных групп, с которыми связаны различные виды про-
странств. Исторически метрическая евклидова геометрия опередила на
несколько веков проективную геометрию, а топология получила свою
самостоятельность в эпоху еще более позднюю. С точки зрения ос-
новных групп, наоборот, топология является первой, а за ней уже идет
метрическая евклидова геометрия (как переход к общей геометрии) и
геометрия проективная (эта последняя присоединяется к евклидовой
метрике посредством связывающих звеньев — аффинной геометрии и
геометрии подобия). И вот, хотя ребенок и не отходит, естественно, от
315
20*
топологических главных схем (потому, что его топологические интуи-
ции зависят от определенных перспективных условий, быстро заклю-
чаемых в структуры по евклидову методу), не менее удивительно, что
при первых попытках рисования ребенок не различает квадратов, ок-
ружностей, треугольников и других метрических фигур, но прекрасно
различает фигуры открытые и замкнутые, положение «вне» или «внут-
ри» по отношению к границе (включая сюда и положение «на грани-
це»), разделение и соседство (не различая расстояния) и т.д.
Исходя, таким образом, от интуиции фундаментальной топологии,
он ориентируется в дальнейшем в направлении проективных структур
и структур метрических.
С чисто операторной точки зрения наряду с операциями над классами
и отношениями, которые одни составляют логические операции действия
на уровне конкретных операций, надо различать те, которые мы называем
«операциями инфралогическими». В то время как логическая операция
исходит от индивидуального объекта и, расширяясь, примыкает к клас-
сам, независимым от пространственных конфигураций составляющих их
элементов, операция инфралогическая, наоборот, расчленяет предмет,
взятый в отдельности, или его заново составляет по отношению к его
элементам. Этот метод композиции отличается от предыдущего введени-
ем континуума и конфигураций Отличные по их структуре от логических
операций, операции инфралогические ие предшествуют им во времени.
На уровне дооперативном нет никакой разницы между первыми инфра-
логическими и первыми логическими интуициями, тогда как на уровне
конкретных операций оба вида структур образуются параллельно. Инте-
ресно отметить этот параллелизм на уровне первых операторных струк-
тур, потому что, как бы ни были скромно и незаметно построены элемен-
тарные формы операторных организаций, можно там распознать корни
этого родства или, вернее, глубокой взаимодополнительности между то-
пологическими структурами и структурами алгебраическими, которая
стала очевидной лишь благодаря последним открытиям в топологии.
VI
Не будет преувеличением утверждать, что операторные структуры
мышления, формируясь, выявляют с самого начала наличие трех
больших типов систем, соответствующих в математике алгебраиче-
ским структурам, структурам порядка и структурам топологическим.
Отметим, между прочим, что очень скоро материнские структуры ко-
ординируются между собою и порождают посредством межструктур-
ных композиций определенные, более поздние структуры, значение
которых будет не менее важным для конструкции логических и мате-
матических понятий.
316
На уровне конкретных операций, связанных с действиями над пред-
метами и заключающими только определенные операции над классами
и отношениями (элементарные «группировки»), не существует еще ж-
каких структурных ансамблей, которые соединяли бы в одну и ту же
систему преобразований чистые обращения в алгебраические структуры
и чистые взаимности в структуры порядка. Но к 11—12 годам в среднем
к этим конкретным операциям прибавляется совокупность новых опе-
раций, опирающихся на этот раз на предложения, а не на предметы, и
эти операции над суждениями составляют тогда двойную структуру
групп и сеток, причем каждый из этих двух аспектов привлекает в свою
очередь чистое обращение в алгебраические структуры и чистую вза-
имность в структуры порядка.
Группа, которая теперь начинает действовать, содержит четыре
преобразования (группа Клейна), которые можно определить следую-
щим образом в операциях над предложениями:
(1) Обращение, или отрицание, N операции есть ее дополнение в
базовой совокупности, например:
#(pvg) = pvq ={р q) или# (ро q) = (pz> <?) = (р q).
(2) Взаимность R операции есть та же операция, но между отрица-
тельными предложениями, например:
Л (р v q) = ( р v q ) = (р /q) ил и R (р => q) = ( р z> q ) = (q =>р).
Отметим, что взаимность возвращает опять к перемене порядка
терминов включения, что имеет общее значение, потому что вся опе-
рация над суждениями может принять вид включения.
Пример:
(pv9) = (pz>g)HnH/?(pz>9) = (gz? p) = (p/g).
(3) Корреляция С операции есть результат замены (v) и (•) в нор-
мальной форме этой операции. Например,
C(pvg) = (р V9) (9V р) = (р vg) = (p q).
C(p^q) = (pvq) (pvq) (pvq) = (pq)-
(4) Тождественное преобразование I оставляет операцию неиз-
менной. Имеем коммутативную группу:
NR = С; NC = R-, RC = #; NRC = /.
Например, в случае р z> q имеем:
N(qzjp) -{pq) = C(pz>q) будет NR = С,
#( p • q)~ (qz3p) = Rip a q) будет NC = R,
317
Р * 9) = (Р ’ 9 ) ~ N(p я) будет RC = N,
Я( Р ’ 9) = (Р 9 ) и МР 9 ) ~ (Р => 9) будет NRC = I.
Таким же образом поступаем с тройничными операциями и т.д. В
определенных случаях (диагонали двойничных, тройничных и т.д.
операций в таблице) имеем: R = N и С = I или R = 1 и С = N, но обра-
щение N, естественно, всегда отличается от I
Констатируем, что эта группа INRC, которая составляет алгебраи-
ческую структуру, все же заключает в себе взаимности, которые со-
ставляют обратимую форму структур порядка. Психологически эта
группа осуществляет одновременно синтез и форму конечного равно-
весия двух операторных структур, до этих пор различных и основан-
ных одна — на обращении, другая — на взаимности.
Но система операций над суждениями составляет в то же время
сетку: вся совокупность операций предполагает внутреннюю границу,
определяемую их общей частью (), например (р = q) (р v q) = (р q),
и внешнюю границу, определяемую их объединением (v), например
(Р 9) v (Р ’ 9) = (Р = 9)- Только из того факта, что эта сетка дополнительна
она допускает операции обращения. Между прочим, и это важно подчерк-
нуть, две данные операции, их внутренняя граница (= BJ) и внешняя грани-
ца (= BS) вместе составляют группу, которая не является группой INRC, но
которая ей изоморфна и состоит из преобразований, которые мы назовем
la, Na, Ra. Са и которые определим следующим образом.
Дана двухчленная операция р v q. Ее можно рассматривать как со-
стоящую из двух единичных операций р и q, связанных составляющей
операцией (v). Рассмотрим также трехчленную операцию:
(Р q r)v(p q r)v(p q r)v(p -q r)=[(q^p) (par)],
которую можно рассматривать как состоящую из двух двойных опе-
раций (q z> р) и (р о г), связанных составляющими операциями ( ). Мы
назовем тогда Ja, Na, Ra и Са преобразования J, N, R и С, связанные с
составляющей операцией. Если теперь мы назовем х и у две какие-то
операции сетки, BJ — их внутреннюю границу и BS — их внешнюю
границу, то будем иметь группу:
(Ia)xy( = BJ) и
(Na)x/y = xv у
(Ла)х -у
(Ca)xvy(=BS)
(fa) х v у (= BS),
(Na) = х -у,
(Ra) xJy = xv у,
(Ca)xy(=BJ).
тогда имеем*
Ca(BJ) = BSh Ca(BS) = BJ.
318
Дальше имеем:
Na(BJ) = Яд(В5) и Na(BS) = Ra(BJ).
И все обычные преобразования группы:
Na(x • у)= RaCa(x у); Na Ra Са(х -у) =(х -у) = х • у и т.д.
Другими словами, если группа INRC включает взаимность, то сетка
операций над суждениями включает обращение и допускает структуру
группы для фундаментальных отношений между границами и опера-
циями, которые они соединяют.
Итак, с точки зрения генетической эта двойная структура группы и
сетки, которую составляют операции над суждениями есть только
присоединение элементарных структур к группировкам, которые, как
мы видели, представляют несовершенные группы, группы неассоциа-
тивные целые и полусетки.
Переход от группы классов и отношений к структуре группы и сет-
ки операций иад суждениями может действительно рассматриваться
как результат обратимости комбинаторных операций, замещаемых в
операциях просто аддитивных или мультипликативных. Другими сло-
вами, в простых включениях, классификациях и т.д. сетка представля-
ет собою «совокупность частей» путем комбинирования псп этих
частей между собою. Но такая комбинаторная композиция сама поро-
ждает классификацию: совокупность частей, которые составляют
двойную структуру сетки и группы, о которых идет речь, является ре-
зультатом совокупности возможных классификаций, приложенных к
элементам группировки, переведенные на язык предложений.
VII
Нам остается прийти к заключению, которое мы можем сделать ли-
бо с точки зрения общего представления математики, влияние которой
должен учитывать воспитатель, хочет он этого или нет, либо с точки
зрения практических применений.
Что касается первого из этих двух вопросов, то существенная про-
блема заключается в том, чтобы узнать: должен ли преподаватель сле-
довать строгой логике в платоновском духе, чтобы быть на уровне со-
временной математики, или он может рассматривать математическую
мысль как продолжение непосредственных конструкций ума и таким об-
разом исходить в преподавании и от психологии так же, как и от логики.
Если психологические данные, на которые мы опираемся, точны,
то конфликт между логизмом и психологизмом кажется подлежащим
некоторому ослаблению при условии все же введения некоторого чис-
ла понятий, нужных для того, чтобы отделить «психологию» от «пси-
хологизма» и «логику» от «логизма».
319
«Психологизм» есть попытка основать логику на психологических
законах: «Для психологии, — сказал Л. Апостел, — логические законы
суть законы психологические, и они описывают реальные умозаклю-
чения или как наиболее частые, или как наиболее нормальные, или как
наиболее легко осуществимые практически». Проще говоря, психоло-
гизм есть метод применения психологии в области, где она уже не
компетентна, потому что психологические законы опираются на кон-
статацию фактов, а законы логики управляют нормативными или де-
дуктивными необходимостями.
Обратно, «логизм» есть вторжение размышлений логика в область
фактов. Он состоит, например, в утверждении, что ум конкретного ин-
дивидуума (касается ли это самих ученых или школьников, начинаю-
щих изучать математику) достигает логической строгости только сле-
дуя определенным этапам, понимание сущностей, подчинение инди-
видуума правилам языка, усвоенным извне, и т.д.
Если мы предоставим психологии заботу изучать факты, а логике —
анализировать основания, получится то, что эти две науки будут иметь
между собою больше контактов, чем при помощи философских «из-
мов», в которых их хотели согласовать. Эти контакты полезны воспи-
тателю более, чем посторонние доктринерские противодействия на той
же ступени тех же самых наук.
Психология действительно протягивает руку логике в том, что ум
непосредственно ориентирован на организацию определенных опера-
торных структур, изоморфным таким же или некоторым частям мате-
матических структур, которые математики кладут в начало их конст-
рукций или которые логики находят в системах, перерабатываемых
ими. Но этот частный изоморфизм не означает, что логические прави-
ла суть законы мысли. Структуры совокупностей, на которые ориен-
тируется ум в процессе своего развития, не соответствуют ни направ-
ляющим структурам (или имеющих форму a priori), ни структурам фи-
зическим, полученным эмпирически: это суть только законы равнове-
сия под формой систем возможных операций, из которых лишь неко-
торые активизируются в функции окружающих физических или соци-
альных условий. Это те возможности, которыми располагает логика
для изучения извне полных совокупностей, свободно снабжая их осно-
вами, которыми она располагает: это не значит, что мы хотим сохра-
нить пункты трения между дедуктивным анализом, с одной стороны, а
с другой — экспериментальными определениями возможностей или
невозможностей, которыми характеризуются формы равновесия, соот-
ветственные различным уровням организации ума. Без сомнения, ал-
гебраическая техника логиста в психологии может быть и полезной
320
при описании форм равновесия и структур, но это не значит, что мож-
но без церемоний прилагать законы логики к законам мысли.
Что же касается того, будет ли логик искать некоторых контактов с
психологией, то история будущих исследований ответит нам на этот
вопрос. Некоторые логики продолжают относиться недоверчиво к
психологизму в целом, как, например, наш друг Бет, который в своей
интересной главе уточнит свои позиции. Зададим еще вопрос: «Лежит
ли боязнь психологизма в основе самой логики, или же она заключает-
ся в зачатках логизма, бессознательно ведущего логика к выбору в
психологической области одной концепции преимущественно перед
другой тем же методом, которым индивидуум приходит к достижению
логических связей?». Некоторые логики, как Апостел, отмечают раз-
личие между традиционным психологизмом и другими более тонкими
средствами психологии- «...мы не утверждаем, как психологи XIX в.
(Зигварт, Гейман, Вундт, Эрдман), что логические законы суть законы
мысли. Мы только говорим, что существуют такие законы мысли, что
в известной социальной структуре и для индивидуумов, обладающих
определенными качествами, мы можем обязательно (с физической не-
обходимостью) заставить их признать наши заключения, если они
признали наши посылки, лишь бы мы производили определенные опера-
ции, подчиненные на всех этапах правилам корректного доказательства».
В общем, весьма возможно, что актуальные работы об отношениях
между логикой и языком кончаются признанием того, что сам язык
проникает своими корнями в области, где его структуры отражают
структуры логики в операторных системах более глубоких, чем связи,
существующие между одними только вербальными символами.
Коротко — будущее взаимоотношений между психологией и логи-
кой остается широко открытым и не будет зависеть от предвзятых
мнений прошлого. С практической точки зрения для воспитателя не
стоит вопрос о выборе между методом формальным, основанным на
логике, и методом активным, основанным на психологии: цель препо-
давания математики остается все время в достижении логической
строгости и точно так же — в достаточном понимании формальной
стороны математики. Но только одна психология способна снабдить
педагогов такими данными, чтобы и эта строгость и этот формализм
были бы обязательно достигнуты. Нельзя считать доказанным, что,
пользуясь с самого начала формальным методом, мы не придем в кон-
це концов к псевдоформализму или к скороспелому словесному фор-
мализму, и в этом заключится опасность применения метода, пренеб-
регающего законами умственного развития.
В действительности, если здание математики покоится на «струк-
турах», которые соответствуют существующим структурам мышления.
321
то дидактическую математику нужно основывать только на прогрес-
сивной организации операторных структур. Психологически операции
происходят от действий, которые, самоуглубляясь, координируются в
структуры. Напрасно думать, что обращение к начальным действиям
компрометирует высшую строгость и поощряет эмпиризм. Эмпиризм
получается тогда, когда воспитатель заменяет математическое доказа-
тельство физическим экспериментом с простым запоминанием полу-
ченных результатов. Но как только эксперимент служит средством ко-
ординации действий, то абстракция переносится на сами эти действия,
а не на предмет эксперимента, подготавливая ум к дедукции, а не про-
тиводействуя ей. Если все знание ребенка предполагает эксперимент
для своего осуществления, то это психологическое утверждение не оп-
равдывает эмпиризма, потому что существуют две формы эксперимен-
та: эксперимент физический, ведущий к абстракции свойств, взятых от
самих предметов, и эксперимент логико-математический с абстракци-
ей по отношению к действиям или операциям, осуществляемым над
предметами, а ие по отношению к самому предмету, как он есть Та-
ким образом, обращение к эксперименту и действию и в общем смыс-
ле так называемая активная педагогика не компрометирует ни в чем
высшую дедуктивную строгость, но, наоборот, подготовляет ее, созда-
вая ей реальную, а не только вербальную базу.
Т. ‘Бирхофф
ПСИХОЛОГИЯ МАТЕМАТИКИ17
Арифметическое позиаиие. Перехожу теперь к своим последним
вопросам. Как мыслят математики9 Могут ли вычислительные маши-
ны моделировать только более простые и более рутинные мыслитель-
ные процессы математиков? Или их можно программировать для вы-
полнения основной части математической деятельности людей? Мой
тезис гласит, что для того, чтобы выполнять нерутинные математиче-
ские задачи экономнее или эффективнее людей, вычислительные ма-
шины должны управляться вышестоящими математиками, обладаю-
щими глубоким пониманием их ограничений.
Начну с первого вопроса: как мыслят математики (о математике).
Математическое мышление начинается в раннем детстве и сначала
имеет дело с арифметикой. Прежде чем научиться арифметике, необ-
ходимо научиться считать. Это делается очень легко повторением
слышимых звуков (механическое подражание) . На гретьем году жиз-
ни большинство детей может воспроизводить последовательности фо-
322
нем достаточно хорошо, чтобы сказать «раз, два, три четыре, пять»
так же легко, как «абракадабра». Играя же .в прятки, многие из нас
учатся в восьмилетием возрасте считать до 100 за каких-то 20 секунд,
без всякого понукания со стороны взрослых.
Сосчитать множество предметов U, сопоставляя его члены с после-
довательными ординальными числами, без повторений или пропусков,
требует большего умения. Ребенок должен помнить, говоря каждое чис-
ло к, каково множество 5(A) cz U уже сосчитанных вещей; подозреваю,
что эта способность зависит от зрительных или осязательных воспри-
ятий конкретных предметов. Проверка того, что мощность л множества
U не зависит от порядка, в каком перечисляются его элементы, требует
индуктивного рассуждения и еще большей зрелости. Только после про-
ведения такого опыта и уяснения его принципа ребенок действительно
понимает значение кардинальных чисел. По наблюдениям Пиаже, это
происходит нормально к семи годам. Подозреваю, что примерно в том
же возрасте дети приобретают и способность с первого взгляда опреде-
лять мощность множеств, имеющих менее чем л элементов, где л в
большинстве случаев равно «семи плюс или минус два», как отмечено
Дж. А. Миллером.
Усвоив способ счета в десятичной системе и его значение, дети го-
товы к изучению арифметических действий, также в десятичной сис-
теме. Опять-таки легче всего путем механического повторения они за-
печатлевают в памяти таблицы сложения и умножения для 10 деся-
тичных цифр (45 правил на таблицу) и правила сложения, умножения,
вычитания и деления положительных целых чисел в десятичной нуме-
рации.
Теперь дети готовы к изучению обыкновенных и десятичных дро-
бей и отрицательных чисел. Традиционным мерилом усвоения ариф-
метики была способность учащегося быстро и точно выполнять с ни-
ми сложные символические вычисления (например, деление столб-
цом) — то, что вычислительные машины могут, очевидно, делать по-
точным способом гораздо лучше и дешевле нас. Недаром профессио-
нальные арифметики прим няли механические сумматоры и множители с
XVIII столетия!
В так называемой новой математике происходит здоровое переме-
щение внимания с вычислительных упражнений на понятия и логику
арифметики. Думаю, однако, что новый упор был опять односторон-
ним: на первый план выдвинули оперирование лишенными смысла
символами согласно искусственным правилам и пренебрегли более
глубокой (и более важной) идеей величины.
Как указывал Гельмгольц, эта идея коренится в физическом опыте
и рабочих приемах измерения (Messen). Аксиомы упорядоченной
323
группы могут рассматриваться как эмпирические свойства величины.
К 13 годам учащиеся обычно имеют хорошие представления о при-
ближении и порядках величины, от крайне малой до крайне большой.
Важна также способность переводить словесные задачи и реальные
жизненные ситуации в символическую математическую форму и, об-
ратно, чувствовать значение таких арифметических утверждений, как
«он зарабатывает 3 доллара в час» или «процентная ставка равна 6%».
Эта способность, конечно, составляет существо прикладной арифметики.
Подозреваю, что дети резко различаются по своему арифметиче-
скому мышлению, и не только быстротой, но и тем, какое относитель-
ное значение они придают трем сторонам арифметики: умению опери-
ровать с числами, логическому рассуждению и практической полезно-
сти. Итак, мне кажется, что между математиками уже в детстве суще-
ствуют значительные различия.
Алгебра и геометрия. В юношестве, во время ознакомления с ал-
геброй и геометрией, дифференциация между людьми по их матема-
тическому мышлению, несомненно, резко возрастает. Так, потенци-
альные чистые математики склонны думать об алгебре как о некото-
рой игре, подчиненной определенным правдоподобным правилам, где
цель состоит в том, чтобы перенести х на одну сторону уравнения, ос-
тавив на другой только символы известных величин. Для потенциаль-
ных прикладных математике алгебра представляет собой громоздкий
инструмент, позволяющий находить ответы на интересные вопросы
неочевидными методами.
Указанное различие интересов поднимает много трудных педаго-
гических вопросов, в отношении которых я не имею твердых убежде-
ний. Но мне хотелось бы сопоставить весьма расходящиеся между со-
бой взгляды Эйлера, Гельмгольца и Пеано на основания алгебры; эти
взгляды иллюстрируют существование разных типов математиков.
Для Эйлера после усвоения арифметики увидеть истину алгебраи-
ческих манипуляций так легко, что достаточно указать необходимые
приемы; алгебра была для него прямым разысканием правильных от-
ветов. Гельмгольц, с другой стороны, отводил основное положение
постулатам для действительных чисел (GroQen), но рассматривал их
истинность как нечто непосредственно открываемое физическим опы-
том. Наконец, для Пеано важно было вывести законы алгебры из ми-
нимального числа формальных допущений с помощью чистой логики
(словесных или символических манипуляций).
Геометрическое познание. Геометрия — старейшая (и простей-
шая) отрасль математической физики. Прежде чем приступить к ее
систематическому изучению, дети должны координировать, вербали-
324
зировать и рационализировать огромное богатство зрительного и ося-
зательного опыта, относящегося к пространству и пространству-
времени (!) в обыденной жизни. Например, они должны научиться
распознавать прямую линию, чего они в первые годы жизни, вероятно,
не умеют делать.
Подозреваю, что по этой причине реакции учащихся на формаль-
ную школьную геометрию особенно разнообразны: они рационализи-
ровали свой опыт разными способами. Действительно, даже для зре-
лых математиков существуют весьма различные пути рационализации
геометрических фактов, которые все являются правильными.
Наиболее известны из них графический подход Эвклида и коорди-
натный подход Декарта. Промежуточный подход, предложенный мо-
им отцом, проще их обоих, после усвоения арифметики, и широко ис-
пользуется в современной американской средней школе. Этот проме-
жуточный подход основан на простых аксиомах о расстояниях и уг-
лах, измеряемых линейкой и транспортиром.
Психологические вопросы. Было бы интересно сравнить назван-
ные подходы с психологической точки зрения. Единственное извест-
ное мне психологическое исследование оснований геометрии принад-
лежит Гельмгольцу.
Гельмгольц показал, что значительная часть геометрии выводится
из следующих двух легко проверяемых физических фактов: 1) про-
странство X трехмерно и 2) всякое твердое тело S' может свободно пе-
ремещаться в пространстве, с сохранением неизменных расстояний
между парами точек (жесткое движение). Иными словами, можно пе-
реместить любую точку р тела S в любое положение, затем вращать S
непрерывно вокруг этого положения, перемещая любую точку q в лю-
бое положение q' на том же расстоянии от р, что и q, и затем, наконец,
вращать S свободно вокруг оси p~q .
Гельмгольц привел эти законы как аксиомы, в духе Эвклида. Разу-
меется, такая психофизическая интерпретация аксиоматических осно-
ваний геометрии весьма далека от взгляда на геометрические аксиомы
как на простые правила игры в доказательство теорем. К сожалению,
требуется очень изощренная аргументация, чтобы показать, что ак-
сиомы Гельмгольца (дополненные аксиомой подобия) действительно
содержат в себе все о геометрии. Поэтому его аксиомы не составляют
такого хорошего исходного пункта для изучения геометрии, как ак-
сиомы Эвклида.
Мне кажется, что сложность геометрии типична для высшей кон-
тинуальной математики и что усвоение и проверка ее истин включают
трудную задачу координации нескольких весьма различных человече-
ских способностей. Психологически она отнюдь не представляет со-
бой (логической) игры по предписанным правилам.
325
Обучающие машины? Неумирающий миф о роботах имеет много
вариантов; последний из них рисует нам обучающую машину с вы-
числительным устройством вместо мозга. Этот миф пропагандируется
следующим широко разрекламированным заявлением: «Через не-
сколько лет миллионы школьников будут пользоваться ... личным по-
печением наставника, столь же знающего и чуткого, как Аристотель».
Хотя в сфере вычислительной техники опасно заниматься пророчест-
вом, я думаю, что мы можем смело поубавить красок в этой радужной
картине.
В действительности речь идет не об обучающей машине как тако-
вой, а лишь о (программированном) полумашинном обучении, об обу-
чении с участием машины (computer aided instruction). Далее, для того
чтобы «персонализировать» такое обучение, необходимо дополнить
хитроумно запрограммированную машину дистанционными внешни-
ми устройствами и графическими пультами, которые сейчас стоят
очень дорого. Иными словами, нужна система разделения времени, в
которой «центральный процессор отвечает последовательно на запро-
сы пользователей, но так быстро, что каждому из них машина кажется
находящейся в его полном распоряжении». Утверждение, что такое
«разделение времени» стало теперь действительностью, просто невер-
но; мы не имеем пока ни малейшего представления о том, во что
обошлась бы «публичная информационная система, взаимодействую-
щая с пультами дома, в школе и в конторе».
Если пренебречь стоимостью оборудования (которая может значи-
тельно снизиться), то кажется очевидным, что упражнения по арифме-
тике в начальной школе и по геометрии в средней допускают эффек-
тивную механизацию. Более того, для коррективной работы с детьми,
имеющими психологические трудности, безличность индивидуализи-
рованного общения человека и машины может представлять сущест-
венную положительную ценность. Наконец, ценным побочным про-
дуктом механизированных уроков является объективная статистиче-
ская информация об отдельных учащихся. Было бы гораздо быстрее,
надежнее и удобнее собирать и обрабатывать такую информацию че-
рез вычислительные машины, чем через учителей. Разумно обрабо-
танная, эта информация могла бы помочь воспитателям в выделении
типов учащихся и в повышении эффективности программированного
обучения. Это было бы, вероятно, особенно легко в математике —
сравнительно устоявшемся предмете. .
Конечно, программированное обучение не требует многопро-
граммной работы машины в «режиме беседы». Как указал Скиннер,
самой большой проблемой при обучении арифметике является выбор
и «программирование» серии вопросов, которая позволит учащимся
326
выработать эффективные математические реакции при встрече с лю-
бой из 25—40 тысяч возможных арифметических задач разных уров-
ней сложности. Эти вопросы можно изложить в специальных книгах
или на контрольных карточках; их не надо хранить в машинной памя-
ти или проецировать на экран. Ответы можно также заранее записать;
их не надо вводить в машину через входное устройство.
Если оставить в стороне вопросы стоимости, то важнейшими огра-
ничениями обучающих машин будут поэтому ограничения самого
программированного обучения, механизировано оно или нет. Теперь я
опишу некоторые из них.
Прежде всего, на коррективном уровне машина (подобно книге или
магнитофонной записи лекции) может повторно предлагать ученику
стандартное объяснение и находить индивидуальные ошибки, но она
не способна дать диагноз его умственных и эмоциональных проблем.
Ошибки часто вызываются мечтами и наблюдением за ужимками со-
седних учеников.
Далее, как программированное обучение может создать мотива-
цию? Даже дети должны инстинктивно понимать, что все, чему может
научить машина, она может и лучше сделать. Тогда зачем тратить на
это силы? Вычислительные машины никогда не смогут подготовить
людей к занятию важных мест в автоматизированном обществе.
Наконец, что важнее всего, как можно программировать усвоение
понятий, т.е. значений слов? Я попытался убедить вас, что централь-
ное понятие арифметики есть величина. Это понятие относится как к
описаниям «10 миль», «50 тонн», «один акр», «один час», «два мил-
лиона долларов», так и к разнице между годичными процентными
ставками в 3 и 10%! Как может научить машина смыслу величины?
Я также привлек ваше внимание ко многим различным возможным
логическим подходам к геометрии и упомянул о скромном успехе
лучшей существующей машинной программы для решении ориги-
нальных задач в эвклидовой планиметрии. Было бы, наверное, намного
труднее программировать обучение, которое эффективно и систематиче-
ски сообщало бы учащимся, как решать широкий класс таких задач.
Вопрос разнообразия, к которому я еще вернусь, имеет много ас-
пектов. Надо ли унифицировать преподавание математики и науки по-
средством одной «оптимальной» программы, применяемой в нацио-
нальном или во всемирном масштабе? Сомневаюсь, думаю, что разно-
образие оправдано и благоприятствует математическому творчеству.
Если желать разнообразия, то кажется весьма маловероятным, что ка-
кая-то одна программа окажется наилучшей; и для всех типов учащих-
ся, следовательно, необходимо разработать и рекомендовать целый
набор программ для машинного обучения.
327
По изложенным выше причинам я полагаю, что полезность обу-
чающих машин в математическом образовании будет в предстоящие
годы ограничиваться в значительной мере заданием, исправлением и
оценкой индивидуальных механизированных упражнений на элемен-
тарном уровне. Кроме того, даже для этого пульты с разделением време-
ни должны экономически конкурировать со стандартными карточками и
бланками, которые могут очень дешево исправляться и анализироваться
поточным способом по существу одинаковыми машинными программа-
ми или свободно исправляться учащимися по таблицам ключей.
Признавая ясно эти ограничения, я думаю вместе с тем, что вычис-
лительные машины могут сделать ценный и возрастающий вклад в ма-
тематическое образование.
Математическое открытие. Один из увлекательных и спорных
вопросов касается степени, в какой искусно программированные ма-
шины могут участвовать в математическом творчестве. Мне кажется
очевидным, что это превосходный пример потребности в высокораз-
витом «симбиозе человека и машины, при котором каждый партнер
делает то, что он может делать лучше».
Не надо быть творческим математиком, чтобы понять, о чем идет
речь. Ибо, как заметил Адамар, «между работой ученика, решающего
задачу по алгебре или геометрии, и изобретательской работой разница
лишь в уровне!» Подобным образом Пойя начинает свое предисловие
заявлением: «Крупное научное открытие дает решение крупной про-
блемы, но и в решении любой задачи присутствует крупица открытия».
Очевидно, доказательство математических теорем зависит очень
сильно (если не исключительно) от дедуктивной логики, и математики
обладают острой и необычайно точной способностью отличать пра-
вильный дедуктивный шаг от неправильного. Эта способность тысячи
раз пускается в ход в цепочках силлогизмов, где одна логическая
ошибка может быть роковой. Думаю, что эта способность состоит по
существу в распознавании определенных допустимых схем предложе-
ний; ее можно было бы назвать чувством дедуктивной логики. Конеч-
но, это не одно из наших четырех или пяти внешних чувств; это одно
из наших внутренних чувств, подобно чувству душевного равновесия
или возбуждения, которое, вероятно, также связано с церебральными
процессами. Подобно им и нашему музыкальному чувству тона (высо-
ты и тембра) оно может быть весьма обострено упражнением.
Так как цифровые вычислительные машины — конечные автоматы
с двоичными элементами, то, по моему мнению, они могут нам по-
мочь прежде всего при доказательстве теорем дискретной математики.
В частности, думаю, что симбиоз человека и машины будет наиболее
эффективным при доказательстве теорем по логике, арифметике (тео-
328
рии чисел) и родственным областям алгебры и комбинаторики. Одна-
ко даже в этих областях наше восхищение логикой не должно приво-
дить нас к недооценке математики других чувств.
И правда, хотя можно думать о людях как о гибридных вычисли-
тельных машинах, в действительности они представляют собой нечто
гораздо большее. По сравнению с людьми даже гибридные (последова-
тельностные) вычислительные машины оказываются весьма ограничен-
ными, если их рассматривать как личности. Они имеют рутинный ум:
они догматичны, лишены воображения и привязаны к шаблону. Они не
способны воспринимать даже очевиднейшие количественные факты об
окружающем континууме, если только они не снабжены специальным
арифметическим устройством (и не консультируются с численным
аналитиком). Это устройство позволяет им заменять человеческих «фе-
номенальных вычислителей», которые, однако, и сами обычно не обла-
дают математическим восприятием.
Думается, математикам следовало бы попытаться рассеять популяр-
ное представление, что они такие же невосприимчивые автоматы! Им
следовало бы опровергнуть идею, что между ними и играющими или
доказывающими теоремы машинами различие лишь в степени; разли-
чие это качественное. Им следовало бы восстать против обвинения, что
их единственное важное умственное качество есть искусство опериро-
вания символами и числами согласно данным правилам! Разве менее
важна их способность оперировать понятиями, в смысле теории геш-
тальтов?
Так, даже элементарная теория чисел была безмерно обогащена
понятиями (диофантова) приближения и кристаллической решетки
(геометрия чисел), а наши знания о распределении простых чисел ос-
нованы прежде всего на понятиях асимптотической оценки и ком-
плексного анализа (наглядное представление нулей функции ^(/) на
комплексной плоскости). Было бы, по-видимому, весьма нелегко за-
программировать вычислительную машину для такой же хорошей ко-
ординации этих понятий, как у тонкого математика. (Уместио напом-
нить, что «пространственные группы» кристаллических решеток были
все определены методами, основанными на наглядных представлени-
ях, задолго до строго определения «групп» через постулаты!)
Ограниченная роль, которую играет двоичная логика в процессе
математического открытия, резко подчеркивается в единственных из-
вестных мне психологических исследованиях творчества в математи-
ке: Адамара и Пойя. Так, Пойя отмечает: «Стараясь решить задачу, мы
поочередно рассматриваем различные ее аспекты, так как в нашей ра-
боте очень существенно видоизменение задачи». Подобным образом
Адамар детально описывает ряд весьма различных психологических
329
подходов к математическому творчеству. Логико-игровой подход он
связывает с поверхностностью: «Совершенно естественно говорить об
уме более интуитивном, когда зона комбинирования идей находится
глубоко, и об уме логическом, если эта зона расположена достаточно
поверхностно». На следующей странице он указывает на важность ма-
тематических восприятий раннего детства для зрелого творчества:
«Очевиднейшим фактом наблюдения является то, что в нашем раннем
детстве происходят чрезвычайно совершенная организация и синтез
обычных ощущений, протекающие в самых глубоких слоях нашего
бессознательного и, значит, с очень большой скоростью» — и говорит
о Tojd, «как сильно различаются ученые по способу использования ум-
ственных образов или других конкретных представлений».
Поверхностность идеи, что математическое открытие есть игра,
вполне доступная для вычислительных машин, высмеивалась многими
другими выдающимися математиками. Так, по мнению Э. В. Бета, од-
на из немногих вещей, с которыми вычислительные машины могут
хорошо справиться, — это более или менее тривиальные обобщения
теорем (т.е. проверка гипотез). Л. Куффиньяль замечает довольно ед-
ко, что «Бурбаки создан для игры в Бурбаки». Как указывал Вейль, тео-
ремы математики суть содержательные истины; их словесное выражение
относится к математической истине примерно так же, как набальзамиро-
ванное человеческое тело в похоронном заведении — к живому человеку.
Конструирование посредством машины. С психологической
точки зрения, математика имеет много общего с музыкой и изобрази-
тельными искусствами. В обоих случаях важная роль принадлежит
тонкому эстетическому чувству. Как заметил фон-Нейман: «...Рождение
математических идей из опыта, хотя генеалогия этого подчас длинна и
запутанна, достаточно хорошо приближает истину... Но как только эти
идеи сформулировались, математика начинает жить своей собственной
жизнью, и ее лучше уподоблять какой-нибудь творческой дисциплине,
движимой почти исключительно эстетическими мотивами...». О том же
писал и Г.Г. Харди: «Математик, подобно живописцу или поэту, — соз-
датель форм... Первое испытание — красота».
Поэтому возможность механизации доказательства теорем пред-
ставляет лишь один аспект более широкой проблемы механизации ху-
дожественного конструирования. Я хочу высказать несколько кратких
замечаний по поводу этой восхитительной (для некоторых специали-
стов по машинам), хотя и ужасающей (для большинства людей искус-
ства) перспективы, прежде чем вернуться к математике. Мне особенно
хочется сделать это потому, что мой отец, Джордж Д. Биркгофф, свы-
ше сорока лет тому назад глубоко размышлял о возможности автома-
тического конструирования.
330
Излагая свои идеи математикам в прекрасном Палаццо Веккио во
Флоренции, мой отец начал с того, что напомнил определение эстети-
ческого качества, предложенное в XVI11 в. Гемстергейсом. По этому
определению, оно состоит в «сообщении возможно большего числа
представлений в возможно меньшее время» Как это близко к духу
нынешнего нашего симпозиума по оптимизации!
В книге «Эстетическая мера» мой отец разработал количественный
подход к эстетическому качеству М иа основе формулы М = О/С, в ко-
торой числитель О толковался как мера «порядка», а знаменатель С —
как мера «сложности», или усилий понимания. Этот анализ был сделан
во многом в том же духе интроспективной психологии, в каком Буль
исследовал законы логики.
Мой отец даже конструировал по формуле пробные вазы, мелодии
и поэмы (хотя и без помощи вычислительной машины) Однако он
предупреждал, что «полное количественное применение основной
формулы осуществимо только тогда, когда элементы порядка пре-
имущественно формальны». Хотя он руководствовался при конструи-
ровании формулами, он видел в этом не более чем трюк, tour de force,
и ни на минуту не допускал, что искусство может выиграть от таких
опытов.
Во всякой эстетической деятельности, будь то художественное кон-
струирование или творческая чистая математика, труднее всего выби-
рать между бесчисленными альтернативами. Так, в творческой мате-
матике, согласно Пуанкаре и Адамару, «бессознательное порождает и
сравнивает многочисленные сочетания, из которых сознание исследует
лишь небольшое меньшинство». Затем Адамар подчеркивает аналогию
с художественным творчеством и приводит следующие слова Поля
Валери: «Для того чтобы изобретать, надо быть в двух лицах. Один
образует комбинации, другой выбирает... То, что называют гением, яв-
ляется не столько заслугой того, кто комбинирует, сколько характери-
зует способность второго оценивать только что произведенную про-
дукцию и использовать ее». Правила, управляющие этим выбором (в
искусстве или математике), «предельно деликатны и тонки, их почти
невозможно выразить точными словами; они легче чувствуются, чем
формулируются; можно ли при таких условиях представить себе аппа-
рат, который их применяет автоматически?» (Пуанкаре).
Думаю поэтому, что «теоретики» вычислительных машин, которые
дерзко предлагают автоматизировать изобретение, должны тщательно
взвешивать свои слова. Как показал мой отец, самая трудная задача при
механизации конструирования состоит в открытии формулы эстетиче-
ской ценности, которая позволила бы надежно отбирать лучшее среди
механически порожденных конструкций! Для художественного конст-
331
руирования главнейшее требование — хороший вкус, а он, по общему
мнению, не поддается определению. Необходимо также предупредить
порождение нехудожественных конструкций, чтобы не тратить времени
на оценку негодного. До тех пор, пока хороший вкус и нехудожественное
не будут определены в математических терминах, вычислительные ма-
шины могут программироваться для моделирования чертежников и пиа-
нистов, но не художников или композиторов.
Итак, я очень сомневаюсь, что «цифровая вычислительная машина
будет писать музыку, которая будет признаваться критиками имеющей
значительную эстетическую ценность», даже если оставить в стороне
предсказанный 1967 год. Самое лучшее, некоторые специалисты по
вычислительным машинам и некоторые критики могут найти эти ма-
шины полезными для анализа, модификации и рекомбинации отрыв-
ков их произведений. И правда, вычислительные машины уже доказа-
ли свою полезность конструкторам в изобразительных искусствах при
таком символическом взаимодействии.
Точно так же не вызывает сомнения возможность написать про-
грамму, которая доказывала бы любое число истинных теорем — вы-
ражающих, например, булевы тождества. Но как научить машину от-
бирать важные теоремы? Или вести порождение в такой последова-
тельности, чтобы леммы были налицо, когда в них нужда? Или избе-
гать бесконечного повторения мелких вариаций на ту же тему? До сего
времени не было предложено никакого метода выполнения этих задач,
ни на каком уровне.
Наконец, почти во всех опубликованных математических доказа-
тельствах опускается изрядная часть второстепенных подробностей.
Как запрограммировать машину, чтобы при печатании ответа она
опускала «тривиальные» детали (сокращая общий объем)? Не может
ли случиться, что при оптимальном симбиозе человека и машины в
доказательстве теорем на долю машины придется в первую очередь
именно проверка таких деталей?
Все вышеизложенное укрепляет меня в мысли, что будет весьма
нелегко механизировать художественные творения математики — не
говоря уже об изящных искусствах
Зрительное воображение. Математики широко различаются меж-
ду собой по степени, в какой они обращаются к зрительному вообра-
жению при открытии и доказательстве теорем. Однако тот факт, что
оно играет важную роль, кажется мне очевидным в силу нашего по-
стоянного употребления слова «показать» (demonstrate, show) вместо
«доказать» (prove). Даже в абстрактной дискретной математике зрение
помогает действиям с символами. Возьмем, например, нынешнюю по-
332
пулярность «погони за диаграммами» в алгебре (особенно в теории
гомологии и категорий).
Как могли Декарт и Гильберт думать иначе? Возможно, на Декарта
повлиял его блестящий успех в замене чертежей в эвклидовой геомет-
рии алгеброй многочленов. Гильберт также находился под чарами де-
картовой геометрии; в своих работах по логике он не раз ссылается на
то, что непротиворечивость аксиом Эвклида можно доказать аналитиче-
ски, определяя абстрактно точки как пары или тройки чисел (х, у),
(х, у, z). (Как это далеко от идей Гельмгольца об «основаниях» геомет-
рии!) На Гильберта мог повлиять еще и его собственный успех в при-
менении аксиомы выбора для неконструктивного доказательства ал-
гебраических теорем. Во всяком случае, мнения Гильберта и Декарта
односторонни. Это было ясно Адамару, заметившему: «Но Декарт не
доверяет этому вмешательству воображения и желает полностью ис-
ключить его из науки ... Недавно знаменитым математиком Гильбер-
том на совершенно другой основе была дана более строгая трактовка
принципов геометрии, которые ... были освобождены от всякого об-
ращения к интуиции. Логически всякое вмешательство геометриче-
ского смысла исключено. Так ли обстоит дело с психологической точ-
ки зрения? Конечно, нет ... Фигуры появляются на каждой странице»
(книги Гильберта).
В предисловии к другой книге Гильберт сам подчеркивает, что «на-
глядное понимание играет первенствующую роль в геометрии». То же
справедливо и для классического аксиоматического изложения проек-
тивной геометрии, несмотря на введение произвольных полей координат.
Многие современные алгебраические и дифференциальные геомет-
ры, с другой стороны, целиком примкнули к Гильберту. Они считают,
что геометрия переросла реальное, трехмерное пространство Л5, в ко-
тором нам доводится жить, или даже наш пространственно-временной
континуум R*. Вместо того они хотят изучать общие свойства, спра-
ведливые для всех множеств (w-мерных многообразий) комплексных
векторов решений х = (хь .... х„) произвольной системы л—т незави-
симых полиномиальных уравнений. Ясным признаком их равнодушия
к геометрии в каком-либо физическом смысле является отсутствие в
их книгах рисунков реальных кривых или поверхностей.
Было бы бесплодно спорить о достоинствах этих разных подходов
к геометрии; я упоминаю их прежде всего для иллюстрации различий
между математиками. Кажется интереснее вернуться к основному во-
просу: в какой мере можно основать анализ на одной только логике?
Классический анализ. Вскоре после того как Декарт открыл при-
менение координатной геометрии («geometric analytique») для пред-
333
ставления кривых и поверхностей алгебраическими формулами, был
изобретен математический анализ («analyse infinitesimale», сокращен-
ный позже в «analyse») для определения их наклонов, площадей, каса-
тельных, углов пересечения и других видимых свойств. На протяже-
нии последующих 150 лет анализ продолжал существенно опираться в
своем развитии на зрительную и физическую интуицию.
Действительно, ни Эйлер, ни Коши никогда не характеризовали
системы действительных чисел формально (как единственное полное
упорядоченное поле); не знали они и того, что она несчетна. Эйлер на-
верное представлял себе действительное число наглядно, то как беско-
нечную десятичную дробь, то как точку на начерченной прямой с на-
несенной на нее шкалой.
Не давал он и общего определения слова «функция». Он просто на-
глядно представлял себе различные задания функций, формулами,
графиками, таблицами приближенных численных значений, и после-
довательностью коэффициентов степенного ряда, и особыми геомет-
рическими или физическими условиями, которым можно дать лишь
бледные парафазы в символической логике. Для него (как и для меня!)
существует замечательный факт, что эти различные представления
могут заменять друг друга в столь многих приложениях, — факт,
допускающий бесчисленные проверки.
Далее, связывая интуитивно континуальные свойства функций с
последовательностями коэффициентов (обыкновенно рациональных
чисел, в интересных случаях) их степенных рядов, Эйлер пришел к
использованию производящих функций для решения задач по комби-
наторному анализу и теории чисел. Эта плодотворная идея, возможно,
и не возникла бы у него в век, когда различие между аналитическими
и бесконечно дифференцируемыми функциями было неясно, если бы
он настаивал на подробном формальном доказательстве каждого ут-
верждения.
Логическая строгость в анализе. Потребность в большей логиче-
ской строгости в анализе впервые обнаружилась после 1755 г., когда
Даниил Бернулли, отправляясь от математической теории колебания
струны, высказал догадку, что «любая» (разумная) периодическая
функция может быть разложена в то, что сегодня называют ее рядом
Фурье. Эта догадка была оспорена д'Аламбером, Эйлером и Лагран-
жем, но время показало, что их возражения были неосновательны.
Эта неосновательность стала очевидной около 1815г., когда Фурье
дал поразительные примеры, показывающие, что сходящиеся ряды
гладких (даже аналитических!) функций могут иметь негладкие пре-
делы. Используя Эйлерово понятие ортогональности, Фурье также дал
334
и правдоподобные интуитивные аргументы в пользу того, что «вся-
НЮ
кая» функция fix) с конечным J|/(x)]dx может быть представлена как
—о
интеграл (Фурье)
J А(к)cos kxdk + J B(A)sin fcrrflt.
о 0
Этот результат (интегральная теорема Фурье) способствовал воз-
никновению теории слуховых ощущений Гельмгольца.
Спор о разложимости в ряды Фурье вынудил математиков дать яс-
ные определения понятий функций, непрерывности и сходимости. Од-
нако, как часто бывает в математической физике, строгость пришла в
последнюю очередь. Только в 1829 г. Дирихле дал достаточно строгое
дедуктивное доказательство догадки Бернулли, основанное на ясных
определениях «непрерывной функции» и «сходимости». Это привело,
наконец, около 1850 г. к общей теории «интегрируемости» Римана.
Поиски большей теоретической строгости и общности в основани-
ях анализа продолжались вплоть до I мировой войны. Они привели к
современной характеристике действительного континуума как единст-
венного полного упорядоченного поля и, наконец, к теории интегри-
рования Лебега. В этой теории, значительно более общей, нежели тео-
рия Римана, существенную роль играет классическая теорема Кантора
о том, что действительный континуум несчетен: множество R всех
действительных чисел невозможно расположить в последователь-
ность. Иными словами, мощность с действительного континуума бес-
конечно превосходит мощность бесконечной последовательности,
равную Ко.
Канторов рай. Блестящий результат Кантора был лишь одним из
применений его фундаментальной общей теории бесконечных мно-
жеств, которая, казалось, была чисто дедуктивной и освобождала дис-
куссии о действительном континууме от нужды в зрительной интуи-
ции и от мистицизма. Как другое применение своей общей теории,
Кантор также нашел, что с = лк° для любого целого л > 1, и показал,
что с = с" для любого положительного целого числа: пространства лю-
бых размерностей можно поставить во взаимно однозначное соответ-
ствие.
Следует, однако, сказать, что идеи и методы Кантора завоевали
признание не сразу. Кронекер был настолько подозрительным к Кан-
торовым методам, что задержал их публикацию, и Кантор сам был в
них не совсем уверен.
335
Парадокс Ришара. Действительно, теория множеств Кантора при-
вела к ряду парадоксов и глубоких вопросов, нерешенных и по сей
день. Рассмотрим, например, задачу определения всех действительных
чисел. Очевидно, что если дан любой конечный «алфавит» знаков, со-
держащий буквы, цифры, знаки препинания и пробелы, то можно пе-
речислить в бесконечной последовательности все мыслимые словес-
ные определения: существует только конечное множество определе-
ний длины л. С другой стороны, как мы уже говорили, Кантор показал,
что действительные числа нельзя расположить в последовательность.
Следовательно, лишь небольшая часть действительных чисел допус-
кает определение словами: язык, пригодный для печатания на пишу-
щей машинке, недостаточен для того, чтобы охарактеризовать каждое
число (каждую точку континуума) индивидуально. Этот весьма непри-
ятный факт именуется парадоксом Ришара.
Логики посвятили немало усилий описанию (счетного) множества
W с R всех действительных чисел, (рекурсивно) определимых через
конечные выражения. Так как существует биекция b: R действи-
тельных чисел х на подмножества S с. Р множества Р всех положи-
тельных целых чисел, то существует и соответствующее множество
b(W) определимых множеств положительных целых чисел. Аналогич-
ным способом задаются «определимые» подмножества любого счетно-
го множества (например, Z или Q). Можно определить также множест-
во всех определимых функций/. U -> V из любого счетного множества
в любое другое счетное множество, потому что существует биекция 0:
R —> Р^.
На фоне этих определений легко формулируется вывод Тьюринга
(называемый часто тезисом Черча): каждое определимое действитель-
ное число вычислимо на машине Тьюринга и обратно. Определимость
и вычислимость тем самым эквивалентны.
Континуум-гипотеза. Наконец, Кантор попал в тупик. Хотя он по-
лагал, что между Ко и с нет ни одного бесконечного кардинального
числа, — иначе говоря, что с есть второе наименьшее бесконечное
кардинальное число (К0, — он никогда не мог это доказать. Вейершт-
расс и Гильберт, хотя и очень глубокие и строгие аналитики, верили
оба, что доказали эту догадку, так называемую континуум-гипотезу.
Недавно Поль Коэн доказал чисто интуитивными математическими
методами, что континуум-гипотезу нельзя ни доказать, ни опроверг-
нуть в рамках существующей формальной логики.
Как могли Вейерштрасс и Гильберт так сильно обмануться? По-
добно этому, как мог великий логик Фреге работать годами над осно-
ваниями логики лишь для того, чтобы, наконец, узнать от Рассела о
336
противоречивости своих методов? По моему мнению, эти примеры
просто иллюстрируют опасность опоры исключительно на чистую де-
дуктивную логику.
Все это, конечно, не уменьшает важности строгого построения ана-
лиза. Безусловно, надо стараться проверять интуицию логикой; Ада-
мар соглашается, что зрительная интуиция и здравый смысл подвер-
жены ошибкам. Я лишь подчеркиваю опасность делать анализ исклю-
чительно логическим. В этом духе Вейль заметил, что, был» может,
«только жалкая часть» классического анализа допускает строгое дока-
зательство с осмысленным содержанием (sinnerfullte Inhalt) Подоб-
ным образом Уайтхед и Рассел признаются, что даже в их шедевре
«доказательства более ранних предложений даются без пропуска како-
го-либо шага, но по мере продвижения работы доказательства посте-
пенно сокращаются». При этом для построения R им понадобилось
три толстых тома, написанных в весьма сжатой символике.
Рассмотрение этих фактов убедило меня, что одна лишь формаль-
ная логика недостаточна для математического анализа и хотя некото-
рые его формальные аспекты поддаются механизации, многие его су-
щественнейшие понятия являются зрительными. Как писал фон-
Нейман: «Анализ обладает наиболее развитым математическим аппа-
ратом и является наиболее разработанной областью математики. Та-
ким образом, формальная логика в силу самого существа своего под-
хода отрезана от наиболее разработанных частей математики ...».
Как дальнейший косвенный довод в мою пользу, я хочу обратить
ваше внимание на существование двух неклассических (еретических?)
современных версий анализа, по меньшей мере столь же логических и
непротиворечивых каждая, как классический анализ Римана, Вейер-
штрасса и Пуанкаре. Это, соответственно, конструктивный анализ и
нестандартный анализ. Первый ведет свое начало от логического ин-
туиционизма Л.Э.И. Броуэра (отважного противника Гильбертова
формализма); он крайне сдержан, даже жеманен в том, что разрешает.
Второй следует либеральной традиции Лейбница и Кантора и крайне
снисходителен по отношению ко внутренне непротиворечивым моде-
лями реальности. В полное нарушение Вейерштрассова пуризма он
свободно говорит о «бесконечно малом» и «бесконечно большом», без
всяких е и 8.
Прикладная математика. Хотя вычислительные машины сделали
пока немного для художественного конструирования или чистой ма-
тематики. они уже свыше десяти лет служат необходимыми орудиями
прикладной математики. Дело, по-видимому, в том, что критерии оп-
тимизации промышленного конструирования носят объективный ха-
23 За* 72
337
рактер: получить максимальное количество обыкновенно значит до-
биться и минимальной стоимости! Это обстоятельство сделало вычис-
лительные машины (искусно программируемые численными аналити-
ками) незаменимыми при оптимальном конструировании ядерных ре-
акторов, размещении нефтяных скважин и выводе спутников на орбиту.
Я не вижу в этом ничего удивительного. Что меня удивляет, так это
позиция некоторых специалистов по вычислительной технике, кото-
рые, имея чрезмерно упрощенное понятие о человеческом мозге, пы-
таются умалить эти достижения. Такие чистые «специалисты» подоб-
ны тем чистым математикам, которые, будучи всего лишь прикладны-
ми логиками, настойчиво умаляют значение прикладной математики и
с радостью уморили бы ее до смерти. Лично я в области вычислитель-
ной техники считаю более неотложной задачей попытаться улучшить
условия человеческой жизни, чем пытаться моделировать человече-
ский мозг. Как бы увлекательны ни были такие попытки моделирова-
ния с точки зрения чистой психологии, с реалистической точки зрения
они еще очень слабы.
Даже математический мозг человека, как я старался убедить вас,
далеко не сводится к логической машине. В согласии с замечанием
фон-Неймана о «рождении математических идей из опыта» я сказал
бы, что математика обретает глубину, когда люди пытаются приме-
нить дискретные методы счета и логики к геометрии. Это привело к
открытию Пифагором существования иррациональных чисел и позже
к фундаментальному понятию дедекиндовых сечений.
Это также обогатило теорию чисел, придав более глубокое содер-
жание понятию «диофантова уравнения». Теория чисел была револю-
ционизирована еще раз, когда Гаусс и его современники нашли на-
глядное представление алгебраических чисел на комплексной плоскости.
Теория функций Римана также была обязана своим происхождени-
ем геометрической и даже физической интуиции. Этот пример иллю-
стрирует зависимость анализа не только от нашего зрительного вооб-
ражения, но и от нашей физической интуиции относительно явлений
тепла, света, электричества и магнетизма. Как сказал Фурье: «Глубо-
кое изучение природы — вот самый обильный источник математиче-
ских открытий». В прошлом физическая интуиция оказывалась гораз-
до надежнее, чем формальная математика, когда требовалось узнать,
какие задачи о дифференциальных уравнениях в частных производных
хорошо поставлены. Кроме того, физическая интуиция была источни-
ком таких фундаментальных математических понятий, как устойчи-
вость, векторное поле, функция Грина, ортогональное разложение,
собственные функции, характеристика и зона зависимости.
338
Наконец, если физическая интуиция была источником многих глу-
бочайших идей чистой математики, насколько важнее она для при-
кладной, постоянно сталкивающейся с новыми проблемами жизни,
безмерной глубины и сложности. Как хочешь пробуй укротить их ло-
гикой — что-то всегда ускользнет. В механике жидкостей, например,
хорошо известно, что убедительные логические аргументы часто бы-
вали обманчивыми и вели к парадоксам (Г. Биркгофф. Гидродинамика.
Методы, факты, подобия. М., 1963), решение которых подвергло бы
суровому испытанию искусство не одного софиста!
Может случиться, что со временем физическая интуиция станет иг-
рать меньшую роль как в чистой, так и в прикладной математике. Но
это будет лишь потому, что мы живем в век, когда приложения мате
матики выходят за границы физики и техники и начинают проникать в
химию, биологию, экономику и административные науки. Я предска-
зываю, что исследование этих предметов, стимулируемое показаниями
всех наших чувств, внешних и внутренних, а не только нашим чувст-
вом логики, приведет к новым и важным математическим понятиям.
Симбиоз человека и машины. Рассмотренные выше данные ка-
жутся несовместимыми с идеей, что роботообразные «думающие ма-
шины» заменят со временем людей, даже в чистой математике. Вместо
этого мы можем предвидеть все более растущий симбиоз человека и
машины, в котором каждый партнер выполняет задачи, наиболее для
него подходящие. Определить, какие это задачи, будет нелегко. Быть
может, здесь пригодится данный Пойя совет, что математическое
«изобретение и обучение следовало бы изучить ... методами экспери-
ментальной психологии». Только руководствуясь глубоким и благо-
желательным пониманием психологии человеческих математиков, так
же как и особенностей цифровых вычислительных машин, мы достиг-
нем эффективного взаимодействия человека и машины в решении
проблем завтрашней чистой и прикладной математики.
Итак, я полагаю, что вычислительные машины станут ценным ору-
дием исследования и что они окажут помощь в понимании психологи-
ческих процессов человеческого обучения, доказательства теорем, иг-
ры и перевода с одного языка на другой. Но думаю также, что усилия
заменить человеческое мышление статически или динамически про-
граммируемыми вычислениями будут ограничены областями, где име-
ется ясная экономическая и социальная отдача.
Это может свести роль чистых специалистов по вычислительным
машинам к роли техников, оптимизирующих взнос машин в общую
работу. Чтобы сделать симбиоз человека и машины подлинно эффек-
тивным, наше общество будет нуждаться в прикладных математиках,
23*
339
которые как численные аналитики следили бы за приближениями,
производимыми при моделировании континуумов, и, что еще важнее,
соотносили бы выход вычислительных машин с решаемыми на них
научными и техническими задачами.
Думаю, что эта потребность открывает перед Обществом промыш-
ленной и прикладной математики одну из величайших его возможно-
стей — поддержать и стимулировать профессиональное развитие та-
ких прикладных математиков, способных к глубокому общению с
другими учеными и инженерами и знакомыми с мощью и ограниче-
ниями цифровых машин. Люди, обладающие этими способностями,
призваны стать вождями завтрашнего математического мира, но их
будет крайне трудно найти и развить!
Т. Хан
КРИЗИС ИНТУИЦИИ11
Истину никогда не высказать, ее никогда не
поймут, в нее никогда не поверят.
Вильям Блейк
Низменные умы, подобно стенам, противостоят
всем обстрелам, и хотя иногда, возможно, ясность
сильного аргумента производит на них некоторое
впечатление, все же они твердо сопротивляются
воему врагу — истине, — не давая ей овладеть со-
бой и подчинить себе
Джон Лик
Сколько раз я повторял вам. что как только вы
исключите все невозможное, то оставшееся, как бы
н вероятно оно ни выглядело, будет истиной
Артур Конан Дойль
Из всех выдающихся философов Иммануил Кант был несомненно
тем, который придавал интуиции особое значение в формировании че-
ловеческого знания. Он обратил внимание на то, что в основе нашего
познания лежат два противоположных фактора- пассивный фактор
простого восприятия и активный фактор внутреннего постижения. В
своей «Критике чистого разума», в начале «Трансцендентальной тео-
рии о началах, часть вторая: Трансцендентальная логика», он пишет:
«Наше знание возникает из двух основных источников души, первый
из них есть способность получать представления (восприимчивость к
впечатлениям), а второй — способность познавать через эти представ-
ления предмет (спонтанность понятий). Посредством первой способ-
340
ности предмет нам дается, а посредством второй он мыслится в от-
ношении к представлению (как одно лишь определение души). Следо-
вательно, созерцания и понятия суть начала всякого нашего познания,
так что ни понятия без соответствующего им некоторым образом со-
зерцания, ни созерцание без понятий не могут дать знание». Итак, ко-
гда с помощью интуиции мы получаем впечатления — это пассивный
процесс; когда же мы используем их в нашем мышлении — это про-
цесс активный. Далее, согласно Канту, нужно различать две составные
части интуиции. Одна из них — эмпирическая, апостериорная часть,
она возникает из опыта и формирует содержание интуиции: цвет,
звук, запах и осязательные ощущения (ощущение твердого, мягкого,
шероховатого и т.д.). Другая часть — чисто априорная, не зависящая
от какого бы то ни было опыта; она определяет форму интуиции. Мы
располагаем двумя такими чисто интуитивными формами — это про-
странство, интуитивная форма внешнего восприятия, посредством
которой мы «создаем картину окружающего мира», и время, интуи-
тивная форма наших внутренних ощущений, «посредством которой
наш ум воспринимает самое себя или свое состояние».
Как я сказал, в системе Канта чистая интуиция играет исключи-
тельно важную роль. Кант считал, что математика основана на чистой
интуиции, а не на разуме. Геометрия, в том виде, в каком ее изучали с
античных времен, имеет дело со свойствами пространства, которые
полностью и совершенно точно сообщаются нам интуицией; арифме-
тика (изучение действительных чисел) покоится на нашей чистой и со-
вершенно точной интуиции времени. Эти интуитивные ощущения
чистого пространства и чистого времени образуют то априорное об-
рамление, в которое мы заключаем физические явления, представлен-
ные нам опытом. Всякое физическое событие имеет свое точно опре-
деленное время и место, где оно происходит.
Какими бы привлекательными ни казались эти идеи на первый
взгляд и как бы полно ни отражали уровень знаний того времени,
дальнейшее развитие науки сильно поколебало самую основу кантов-
ской теории.
Идеи Канта относительно физического пространства и времени со-
гласуются с ньютоновской физикой, занимавшей господствующее по-
ложение не только в кантовские времена но и до совсем недавних лет.
Первый удар кантовская концепция получила со стороны теории отно-
сительности Эйнштейна. Согласно Канту, пространство и время не
имеют друг с другом ничего общего, так как возникают из разных ис-
точников. Пространство есть интуитивная форма внешнего воспри-
ятия, а время — внутреннего восприятия. В нас заложено абсолютное
стационарное пространство и абсолютное время, которое движется со-
341
вершенно независимо от пространства. Теория относительности, на-
против, утверждает, что не существует абсолютного пространства и
абсолютного времени, а существует сочетание пространства и времени —
физическая Вселенная — и только она имеет абсолютный смысл
Еще более серьезный удар кантовской концепции о пространстве и
времени как априорных компонентах интуиции нанесли недавние от-
крытия в физике. Мы уже видели, что, по Канту, всякое физическое
событие должно быть локализовано в пространстве и времени. Но то-
гда возникает такая трудность. Мы узнаем о физических событиях по-
средством опыта, или эксперимента, но всякий эксперимент неточен и
всякое наблюдение связано с ошибками. Поэтому возникает противо-
речие: всякое физическое событие происходит в точно такое-то время
и в точно таком-то месте пространства, но мы не можем узнать ни это-
го времени, ни этого пространства. Возьмем, к примеру, круглый ку-
сок мела. Если выбрана единица длины, то расстояние между любыми
двумя точками мела выражается действительным числом. Представим,
что мы измерили расстояния между каждыми двумя точками этого
куска мела и назвали наибольшее из расстояний диаметром. Предпо-
ложив, что этот мел занимает точно определенную часть пространства,
данную нам в интуиции, мы вправе спросить: «Является ли диаметр
рациональным или же он выражается иррациональным числом?» На
этот вопрос никогда нельзя ответить, так как рациональные числа рас-
положены настолько близко к иррациональным, что отличие их не на-
блюдаемо и не фиксируемо с помощью эксперимента. То есть концеп-
ция, которую можно назвать классической, приводит к появлению не-
разрешимых проблем, и поэтому мы должны охарактеризовать эту
концепцию как метафизическую.
Долгое время эта трудность не принималась всерьез. В ответ на по-
добного рода критику отвечали примерно следующее: «Даже если вся-
кое отдельное измерение неточно и сопровождается ошибками, сам
метод измерений непрерывно совершенствуется. Давайте же вообра-
зим некий физический объект, который мы измеряем снова и снова со
все возрастающей точностью. Результаты таких измерений, каждое из
которых немного ошибочно, тем не менее неограниченно приближа-
ются к некоторому предельному значению, которое и представляет со-
бой точное значение измеряемой величины». Вряд ли такой аргумент
можно признать удовлетворительным с философской точки зрения, а
новейшие концепции в науке позволяют считать его неудовлетвори-
тельным также и с чисто физической точки зрения. С чисто физиче-
ской точки зрения говорить о точной локализации физического объек-
та во времени и пространстве невозможно. Но поскольку невозможно
определить положение объекта в пространстве и времени с точностью,
342
превышающей некоторую границу, то приходится сделать следующий
вывод: доктрина абсолютной локализации объекта в пространстве и
времени является метафизической доктриной, а следовательно, она
лишена смысла. Так, последние революционизирующие изменения в
физической науке потрясли многих (в том числе и физиков), привык-
ших к догматическому и метафизическому образу мышления. Однако
для вдумчивого человека, искушенного в эмпирической философии,
здесь нет ничего парадоксального. Он воспримет все это как нечто
близкое его духу, как значительный шаг вперед в направлении «физи-
кализации» физики, очищения ее от метафизических элементов.
После этого краткого обзора физической стороны вопроса мы пе-
рейдем к математике, где возражения кантовской доктрине сформиро-
вались значительно раньше, чем в физике. С этого момента я буду го-
ворить только на тему «Математика и интуиция» и, более того, остав-
лю вне поля зрения ряд важных и трудных проблем. Я не буду обсуж-
дать серьезнейший и сильнейший аргумент против кантовского тезиса
том, что арифметика — наука о числах — основана на чистой ин-
туиции, связанный с именем Бертрана Рассела и заключающийся в до-
казательстве того, что арифметика, в полном противоречии с тезисом
Канта, принадлежит исключительно миру разума и логики. Я ограничу
свою лекцию темой «Геометрия и интуиция» и постараюсь показать,
как даже в той ветви математики, которая считается основной и пер-
воначальной, роль интуиции постепенно сходит на нет, чтобы, нако-
нец, окончательно исчезнуть.
Один из выдающихся результатов, имеющих отношение к нашей
теме, состоит в открытии кривых, которые в полном противоречии с
основанными на интуиции взглядами, господствовавшими ранее, не
имеют касательной ни в одной своей точке. В дальнейшем мы увидим,
что это свойство эквивалентно следующему: материальная точка мо-
жет двигаться таким образом, что ни в какой момент времени не обла-
дает определенной скоростью. Математики были немало потрясены
этим фактом, когда в 1861 г. о нем сообщил берлинский коллега Карл
Веиерштрасс. Но рукопись, находящаяся в архиве Венской нацио-
нальной библиотеки, показывает, что этот факт был известен намного
раньше австрийскому философу, богослову и математику Бернарду
Больцано. Поскольку некоторые из относящихся к данному вопросу
понятий имеют прямое отношение к основам дифференциального ис-
числения, созданного Ньютоном и Лейбницем, я скажу сначала не-
сколько слов о фундаментальных идеях этой отрасли математики.
Ньютон исходил из понятия скорости. Вообразите точку, движу-
щуюся по прямой линии, как это показано на рис. 1, а В момент вре-
мени t движущаяся точка находится, скажем, в положении q Как нуж-
343
но понимать выражение «скорость движущейся точки в момент вре-
мени г»? Если мы определим положение точки в какой-то другой мо-
мент времени I' (пусть в этот момент точка занимает положение q'), то
мы можем определить и путь qq', пройденный точкой за интервал вре-
мени между t и /'. После этого разделим проделанный точкой путь qq'
на время между / и ('и в результате получим так называемую среднюю
скорость движущейся точки между t и t'. Разумеется, эта средняя ско-
рость не есть скорость в момент t. Средняя скорость может был», на-
пример, очень большой, хотя скорость в момент t чрезвычайно мала —
это случится, если точка начнет двигаться очень быстро на второй
части нашего интервала. Однако если выбрать момент /' достаточно
близко к моменту t, то средняя скорость даст хорошее приближение к ис-
тинной скорости в точке t, причем это приближение будет тем лучше, чем
меньше временной интервал между t и t'. Ньютон, размышляя об этих
вещах, думал примерно так: пусть момент t' выбирается все ближе и бли-
же к Z, тогда средняя скорость между t и (' будет становиться все ближе и
ближе к некоторому значению то есть, если говорить языком математи-
ки будет приближаться к некоторому пределу, этот предел мы и назовем
«скоростью движущейся точки в момент времени /». Другими словами,
скорость в момент t есть предельное значение средней скорости между t и
/', когда/'неограниченно приближается к /.
Лейбниц начал с так назы-
ваемой проблемы касательной.
Рассмотрим кривую, изобра-
женную на рис. 1,6. Каков ее
наклон (относительно горизон-
тали) в точке р? Выберем неко-
торую соседнюю точку р' на
этой же кривой и определим
«средний наклон» кривой меж-
ду точками р и р'. Для этого
разделим высоту (на рисунке это отрезок р"р), на которую поднимает-
а
О’
q
о
ся кривая на данном участке, на горизонтальную проекцию этого уча-
стка (на рисунке это отрезок р р"», который показывает, как далеко мы
уйдем в горизонтальном направлении, если будем двигаться вдоль
кривой от точки р к точке р). Средний наклон кривой на участке рр'
не равен, конечно, наклону в точке р (на нашем рисунке наклон в точ-
ке р явно больше, чем средний наклон между р и р). Тем не менее, ес-
ли мы выберем точку р' достаточно близко к точке р, то получим хо-
рошее приближение к искомой величине, и это приближение будет
тем лучше, чем ближе точка р' расположена к точке р Далее можно
рассуждать, как и в случае ньютоновской задачи о скорости если точка р'
344
начнет неограниченно приближаться к точке р, средний наклон между
р и р' будет стремиться к некоторому пределу; этот предел мы и назо-
вем «наклоном кривой в точке р». Иначе, наклон в точке р есть пре-
дельное значение среднего наклона между р и р' при условии, что точ-
ка р' неограниченно приближается к точке р. «Касательной к кривой в
точке р» мы назовем прямую, проходящую черезр и имеющую тот же
наклон, что и кривая в этой точке.
Нетрудно заметить удивительное сходство между процедурой оты-
скания наклона кривой и процедурой определения скорости точки в
данный момент времени. Идентичность этих процедур становится со-
вершенно ясной, если обратиться к изображению движения точки (на-
пример, поезда) на диаграмме время—путь. Фундаментальная задача
дифференциального исчисления состоит в следующем нам известен
путь движущейся точки, нужно найти ее скорость в любой момент
времени. Можно сформулировать эту задачу и по-другому: дана кри-
вая, нужно вычислить ее наклон в каждой точке (или же построить
касательную в любой наперед заданной точке). Мы рассмотрим более
подробно проблему касательной, имея постоянно в виду, что все вы-
воды и результаты с таким же правом могут быть отнесены к проблеме
измерения скорости.
Мы говорили, что если точ-
ка р' неограниченно приближа-
ется к точке р, то средний на-
клон все ближе и ближе подхо-
дит к некоторому предельному
значению, которое и представ-
ляет собой наклон кривой в
точке р. Теперь настало время
задать вопрос: будет ли это
верно для всякой кривой? Для
обиходных кривых, изучав
шихся с древних времен, это
несомненно верно. Но совсем несложный пример показывает, что все
же это не будет верным для любой кривой. Посмотрим на кривую,
изображенную на рис. 2; она имеет волнообразную форму, и количест-
во волн в районе точки р бесконечно велико. Длина волны, так же как
и ее амплитуда, неограниченно уменьшается при приближении к точке
р Используя описанный выше метод, мы можем попытаться найти на-
клон кривой в точке р. В соответствии с нашей методикой мы возьмем
некоторую, близкую к точке р. точку р' и найдем средний наклон кри-
вой на участке рр'. Когда точка р' начнет двигаться к точке р, то сред-
ний наклон сначала будет уменьшаться* когда/?' занимала положение
22 Зак 72
345
Pi, наклон был равен 1, когда же р' займет положение ръ наклон станет
равным нулю. При дальнейшем движении точки р’ некоторое время
будет продолжаться уменьшение наклона: когда р' придет в положе-
ние рз, наклон станет отрицательным (-1). Но вот когда точка двинет-
ся дальше в своем приближении к р, то наклон снова начнет возрас-
тать: при достижении точкой р' положения р4 он станет опять равным
нулю, а при достижении ps будет равным единице. При дальнейшем
приближении р' к р весь цикл повторится, и так будет происходить
бесчисленное количество раз: при прохождении точкой р' очередной
волны (а волн бесконечно много) наклон будет меняться от единицы
до минус единицы и обратно. Ясно, что не может быть речи о дости-
жении средним наклоном какого-то фиксированного предела в точке
р Другими словами, наша кривая в точке р не имеет касательной.
Этот довольно простой пример иллюстрирует, что кривая не обяза-
на иметь касательную в каждой своей точке. Но интуиция подсказыва-
ет нам, что точки, в которых кривая «теряет» касательную, являются
особыми точками, и они должны располагаться изолированно друг от
друга, а между ними должны находиться обычные точки, в которых
касательные существуют. В нас живет незыблемая убежденность, что
всякая кривая имеет касательную если не во всех, то в подавляющем
большинстве своих точек. Знаменитый физик и математик Ампер, чей
вклад в теорию электромагнетизма хорошо известен, пытался даже
доказать это. Конечно, его доказательство содержало ошибку, но было
большой неожиданностью, когда Вейерштрасс объявил о существова-
нии кривой, не имеющей касательной ни в одной точке. Оригинальная
кривая Вейерштрасса очень сложна и хитроумна, и я не буду пытаться
рассказать здесь о ней. Но последующее развитие математических мето-
дов дало возможность создавать кривые такого типа более простым спо-
собом, и это позволяет объяснить по крайней мере идею построения.
а б в
Рис 3
Начнем с простой кривой, изображенной на рис. 3, а, состоящей из
двух отрезков прямых. Теперь заменим левый отрезок ломаной лини-
ей, состоящей из шести одинаковых по длине отрезков (рис. 3, б): пер-
348
вый поднимается вверх, доходя до половины высоты первоначального
отрезка, второй опускается вниз, третий и четвертый оба идут вверх
(образуя вместе как бы один отрезок двойной длины), пятый идет
вниз, шестой снова поднимается вверх. Аналогичным образом мы за-
меним второй отрезок первоначальной кривой ломаной линией из
шести отрезков: первый опускается из самой верхней точки до поло-
вины высоты исходного отрезка, второй поднимается обратно вверх,
третий и четвертый идут вниз, пятый — снова вверх, шестой — вниз.
Теперь к каждому из образующихся 12 отрезков применим тот же са-
мый метод замены («восходящие» отрезки будем заменять по первому
правилу, «нисходящие» — по второму), в результате чего получим
ломаную, состоящую уже из 72 отрезков; эта ломаная изображена на
рис. 3, в. Далее, представим себе, что эта процедура повторяется снова
и снова, каждый раз будет получаться все более сложная линия. Мож-
но строго доказать (хотя я не буду делать здесь этого), что последова-
тельность геометрических объектов, построенных таким образом, бу-
дет неограниченно приближаться к некоторой кривой, которая и обла-
дает нужным нам свойством: ни в одной своей точке она не имеет ка-
сательной. Свойство этой линии интуитивн । совершенно непостижи-
мо; уже после нескольких первых шагов ее построения мы получаем
такую сложную кривую, что наша интуиция становится бессильной и
не может предвидеть каких-то ее свойств. Тем более не может интуи-
ция предсказать, что за кривая получится в пределе. И только разум,
только строгий логический анализ может следовать за указанным про-
цессом до самого конца и помогает познать свойства, получающиеся в
пределе. На этом примере видно, что если бы мы судили о кривой на
основании интуиции, мы неизбежно впали бы в ошибку, поскольку
интуиция отказывается признать существование кривой, не имеющей
ни в одной своей точке касательной.
Этот первый пример неуспеха интуиции был связан с дифференци-
альным исчислением. Второй наш пример относится к области инте-
грального исчисления. Основная задача дифференциального исчисле-
ния такова: дана кривая, отыскать ее касательную в любой точке, или —
дан путь точки, отыскать ее скорость в любой данный момент време-
ни. Фундаментальная задача интегрального исчисления прямо проти-
воположна: дан наклон кривой в каждой точке, построить саму кри-
вую, или — дана скорость материальной точке в каждый момент вре-
мени, найти путь этой точки. Эта задача, конечно, имеет смысл только
в том случае, когда наклон действительно определяет самое кривую
или когда скорость точки определяет ее путь. Более точно следует ска-
зать так: если по прямой линии из одной и той же точки в один и тот
же момент времени начнут двигаться две материальные точки и если
22*
347
скорости их движения в любой момент времени будут одинаковыми,
то будут ли эти материальные точки двигаться синхронно, то есть все
время совпадать друг с другом? Другая постановка вопроса: если две
кривые проходят через одну и ту же точку и всюду имеют равный на-
клон, то будут ли они сливаться повсюду или же могут разойтись? Ин-
туиция подсказывает нам, что при данных условиях движущиеся точ-
ки будут совпадать, а кривые — сливаться, однако логический анализ
показывает, что это не обязательно должно быть так. Интуитивный
ответ, конечно, верен для обычных кривых и движений, но интуиция
обманывает нас в более сложных случаях. К сожалению, у нас нет
сейчас времени, чтобы углубляться в детали этого вопроса, и нам при-
дется ограничиться лишь утверждением, что и здесь интуиция оказы-
вается бессильной.
Приведенные нами примеры ошибок интуиции были связаны с ма-
тематическим анализом — дисциплиной, которая более известна под
названием «высшая математика». Чтобы не создалось мнения, будто
интуиция подводит нас только в высших областях математики, я пред-
лагаю рассмотреть случаи таких ошибок, относящиеся к элементар-
ным областям.
Понятие кривой лежит в самой основе геометрии. Каждый человек
вполне уверен, что он ясно представляет себе, что такое кривая. С
древних времен это понятие пояснялось так: «Кривая есть геометриче-
ская фигура, вычерчиваемая движущейся точкой». Но, внимание! В
1890 г. итальянский математик Джузеппе Пеано (известный также
своими исследованиями в логике) доказал, что геометрические фигу-
ры, вычерчиваемые движущейся точкой, могут включать в себя целые
участки плоскости. В качестве примера можно представить себе такое
движение точки, когда в конечное время она пройдет через любую
точку квадрата. Но ведь никто не додумается до того, чтобы назвать
кривой сплошной квадрат. С помощью нескольких рисунков я поста-
раюсь объяснить общую идею построения такой заполняющей квадрат
кривой.
Разобьем квадрат на четыре одинаковые части, как это показано на
рис. 4, а. и соединим центры этих маленьких квадратов; далее, вообра-
зим точку, движущуюся по полученной линии с постоянной скоро-
стью, так, что она проходит эту линию за единицу времени. Затем раз-
делим каждый из четырех малых квадратов (рис. 4, б) на четыре еще
меньших квадрата и соединим центры этих 16 квадратов таким же
способом, как мы соединяли центры четырех квадратов раньше. Снова
вообразим движущуюся по полученной линии точку и снова придадим
ей мысленно такую постоянную скорость, чтобы она проходила свой
путь за ту же единицу времени. Повторим процедуру еще раз (рнс. 4, в),
348
разбив каждый из 16 квадратов, изображенных на рис. 4, б, еще на че-
тыре квадрата, соединив центры полученных 64 квадратов нашим спо-
собом и заставив воображаемую точку пробегать полученную линию
за единицу времени. Нетрудно сообразить, что процедуру можно про-
должать и далее; на рис. 5 изображена одна из более поздних стадий про-
цесса, когда первоначальный квадрат разбит уже на 4096 маленьких квад-
ратов. Можно доказать строго, что в предел нашего процесса мы
получим кривую, заполняющую квадрат, а точка, бегущая по этой кри-
вой, пройдет через каждую точку квадрата, затратив на все движение од-
ну единицу времени. Такое движение не может быть постигнуто интуи-
Наряду с геометрическими объектами, которые никто бы не осме
лился назвать кривыми (например, квадрат) и которые тем не менее
могут быть порождены движением точки, существуют и такие геомет-
рические объекты, которые каждый без колебаний зачислит в кривые,
но которые нельзя строить таким образом. Возьмем, например, фигу-
ру, изображенную на рис. 6. Это — волнообразная кривая, которая в
области, прилегающей к отрезку ab, содержит бесчисленное количест-
во волн, длина которых неограниченно уменьшается, но амплитуда
остается постоянной.
Рис 5
Ь
Р и с. б
349
Легко доказать, что эта фигура, несмотря на свой линейный харак-
тер, не может быть вычерчена движением точки: не существует такого
способа движения точки, чтобы она пробегала все волны этой кривой
за конечное время
Теперь естественно возникают два вопроса.
1. Если доброе старое определение кривой отказывается служить в
некоторых случаях, то какое новое определение могло бы оказаться
более полезным?
2. Если множество геометрических объектов, порождаемых движе-
нием точки, не совпадает с множеством всех кривых, то как следует
определить первое из этих множеств?
На оба вопроса современной наукой даны удовлетворительные от-
веты. Я отложу пока рассмотрение первого и кратко остановлюсь на
втором вопросе. Он разрешен с помощью новой геометрической кон-
цепции «связности в бесконечно малом» или «локальной связности».
Рассмотрим некоторые кривые, которые могут быть вычерчены дви-
жением точки, например такие, как прямая, окружность, квадрат (рис. 7).
Обратим внимание в каждой из этих кривых на точки р и q, находя-
щиеся очень близко друг к другу.
Очевидно, что в каждом из трех случаев мы можем двигаться от
точки р к точке q, не отрываясь от кривой и оставаясь все время близко
к обеим этим точкам. Это свойство (должным образом уточненное) и
называется «связностью в малом». Кривая, изображенная на рис. 6, не
обладает этим свойством. Возьмем на ней две соседние точки р и q.
Чтобы пройти от первой точки к соседней, не отрываясь от кривой, не-
обходимо описать бесконечно много волн, расположенных между
этими точками, и наш путь не будет пролегать вблизи точек pnq, по-
скольку все волны имеют одинаковую амплитуду. Важно понять, что
именно «связность в малом» есть основная характеристика кривой, ко-
торая может быть вычерчена движением точки. Прямая, окружность,
квадрат могут быть вычерчены движущейся точкой, потому что им
свойственна связность в малом; кривая, представленная рис. 6, не мо-
жет быть вычерчена движением точки, поскольку она не является
связной в малом.
Приведем еще один пример беспомощности интуиции даже в самых
элементарных геометрических вопросах. Рассмотрим карту (рис. 8), изо-
бражающую три соседних государства. На ней имеются линии, обо-
значающие границу между двумя странами, и есть точки, в которых
сходятся границы сразу трех стран, так называемые тройные точки,
отмеченные на рисунке буквами а и Ь. Интуиция с несомненностью
говорит нам, что такие тройные точки на любой карте расположены
изолированно, поскольку подавляющее большинство граничных точек —
350
«двойные». Но вот в 1910 г. голландский математик Л. Брауэр показал,
как можно построить карту, в которой все граничные точки будут трой-
ными Попытаемся коротко объяснить, как это может быть сделано.
Р и с. 9
Начнем с карты, изображенной на рис. 9, а, на которой имеются
три страны, — «полосатая» (А), «в крапинку» (В) и «зачерненная» (С).
Область, оставшаяся белой, — это ничейная, не занятая пока террито-
рия. Страна А, желая использовать эту землю д ля своих нужд, захватыва-
ет на ней коридор шириной в одну милю, как это показано на рис. 9, б. Не
желая вовлекаться в конфликты с соседями, страна Л формирует кори-
дор так, чтобы он не угрожал странам В и С. После такой акции перво-
го государства страна В решает, что и ей следует сделать нечто подоб-
ное, и она оккупирует коридор на оставшейся ничейной земле (как это
показано на рис. 9, в) шириной в полмили, также не примыкающий к
соседним странам. Затем страна С, не желая отстать от соседей, тоже
захватывает на нейтральной земле коридор шириной в треть мили, не
соприкасающийся с чужими землями (рис. 9, г). Страна Л, решив, что
ее перехитрили, переходит к захвату еще одного коридора на остав-
шейся нейтральной земле шириной в четверть мили, не соприкасаю-
щегося с уже занятыми территориями. Далее процесс продолжается:
страна В оккупирует коридор шириной в одну пятую мили, страна С —
шириной в одну шестую мили и так далее. И раз мы уж дали волю
своей фантазии, представим, что стран? А потребовался год для захва-
та первого коридора, страна В затратила на приобретение своего пер-
вого коридора полгода, страна С захватила свой первый коридор на
четверть года, следующая акция (со стороны страны А) заняла одну
восьмую года и так далее; каждая следующая акция требовала ровно
351
вдвое меньше времени, чем предшествующая. В этом случае, как лег-
ко вычислить, раздел нейтральной земли займет ровно два года, после
чего незанятой территории не останется. Но самое интересное то, что
на полученной таким образом карте не будет ни одной граничной точ-
ки, которая принадлежала бы только двум странам — в каждой гра-
ничной точке будут сходиться земли всех трех государств. Снова ин-
туиция неспособна постичь эту ситуацию, но логика заставляет нас
признать ее осуществимость. И здесь интуиция уводит нас от истины.
Поскольку интуиция оказывается столь ненадежной во многих слу-
чаях, поскольку утверждения, которые, согласно интуиции, должны
быть истинными, часто оказываются ложными при строгой логиче-
ской проверке, математики стали относиться к интуиции все более по-
дозрительно. Они убедились, что, основываясь на интуиции, верить
математическим утверждениям, особенно тем, которые относятся к
фундаментальным понятиям, очень опасно. Возникло требование из-
гнать интуицию из математического рассуждения и полностью фор-
мализовать математику. Другими словами, каждое новое математиче-
ское понятие должно определяться логически, каждое математическое
доказательство должно использовать лишь строгую логику. Провозве-
стниками этой программы были Опост Коши (1789—1857), Бернард
Больцано (1781—1848), Карл Вейерштрасс (1815—1897), Георг Кан-
тор (1845—1918) и Рихард Дедекинд (1831—1916). Конечно, я упомя-
нул только самых выдающихся ученых.
Задача полной формализации математики и сведения ее к логике
сложна и трудна, она означает не что иное, как перестройку древней
науки снизу доверху. Утверждения, которые прежде считались интуи-
тивно очевидными, теперь нужно было строго доказать. Вот пример
такого утверждения: «Всякий замкнутый несамопересекающийся мно-
гоугольник делит плоскость на две части». Эта теорема имеет длинное
и очень сложное доказательство. Еще сложнее доказательство анало-
гичной теоремы для пространства: «Всякий замкнутый несамопересе-
кающийся многогранник делит пространство на две части».
Как пример априорного синтетического суждения, основанного на
чистой интуиции, Кант приводит высказывание, что пространство
трехмерно. Но по современным воззрениям это заявление нуждается в
строгом логическом анализе. Прежде всего нужно определить абсо-
лютно четко, что такое «размерность» геометрической фигуры или
«множества точек», а затем доказать, что пространство, фигурирую-
щее в обычной геометрии, оно же ньютоновское физическое про-
странство, удовлетворяет этому определению, то есть действительно
является трехмерным. До недавнего времени такое доказательство не
удавалось найти, но в 1922 году оно одновременно было дано венским
352
математиком К. Менгером и русским математиком П. Урысоном (по-
следний трагически погиб в расцвете своих творческих сил — он уто-
нул, купаясь в море). Я приведу здесь в общих чертах идею определе-
ния размерности точечного множества.
а
Р и с. 10
о
Точечное множество называется нульмерным (имеющим нулевую
размерность), если около каждой его точки существует произвольная
окрестность, в границах которой не содержится ни одной точки этого
множества; например, любое множество, состоящее из конечного чис-
ла точек, нульмерно (см. рис. 10, а). Но существуют и значительно бо-
лее сложные точечные множества нулевой размерности, содержащие
бесконечно много точек. Множество точек называется одномерным,
если вокруг каждой его точки можно построить произвольную окрест-
ность, в границах которой будет содержаться совокупность точек
множества, имеющего нулевую размерность. Всякая прямая, всякая
фигура, образованная из конечного числа прямых, всякая окружность,
всякий эллипс, короче, всякая геометрическая конфигурация, которую
мы обычно характеризуем как линию, является одномерной в этом
смысле (рис. 10, 6). Но и фигура, изображенная на рис. 6, которая не
может быть вычерчена движением точки, тоже является одномерной,
согласно данному определению. Точно так же точечное множество, не
являющееся ни нульмерным, ни одномерным, называется двумерным,
если около каждой его точки существует произвольная окрестность, в
границах которой содержится одномерная совокупность точек множе-
ства. Всякая плоскость, всякая часть плоскости, ограниченная много-
угольником или окружностью, всякая сферическая поверхность —
иными словами, всякая геометрическая фигура, которую мы обычно
считаем поверхностью, является в этом смысле двумерной.Точечное
множество, не являющееся ни нульмерным, ни одномерным, ни дву-
мерным, называется трехмерным, если для каждой его точки сущест-
вует такая произвольная окрестность, что в границах этой окрестности
будет содержаться двумерная совокупность точек множества. Можно
доказать, хотя это и довольно сложно, что наше обычное пространство
по изложенной здесь теории является трехмерным.
Эта же теория дает возможность решить и вторую нашу проблему —
определить понятие кривой. Существенной характеристикой кривой
353
оказывается ее одномерность. Но помимо этого, теория позволяет про-
вести чрезвычайно строгое и тонкое исследование всякой кривой, о
чем я и хочу сейчас коротко рассказать. Точка кривой называется
концевой точкой, если вокруг нее можно построить произвольную ок-
рестность, в границах которой содержится только одна точка кривой
(это — точки а и b на рис. 10, в). Точка кривой, не являющаяся конце-
вой точкой, называется обыкновенной точкой, если граница некоторой
произвольной малой ее окрестности содержит ровно две точки кривой
(точка с на рис. 10, в). Точка кривой называется точкой ветвления, ес-
ли сколь угодно малая произвольная окрестность этой точки имеет в
своих границах больше двух точек кривой (точка d на рис. 10, в).
Интуиция говорит нам, что концевые точки на кривой, как и точки
ветвления, в некотором смысле исключительные точки, поэтому они
могут появляться лишь в отдельных местах, и уж конечно, не сущест-
вует кривой, которая состояла бы целиком из концевых точек или то-
чек ветвления. Это интуитивное заключение подтверждается логиче-
ским анализом для концевых точек, но если говорить о точках ветвле-
ния, то оно оказывается ложным. Польский математик В. Серпинский
доказал в 1915 году, что существуют кривые, состоящие целиком из
точек ветвления. Убедимся наглядно, что такая кривая действительно
имеется.
Представим себе, что мы вписали в равносторонний треугольник
другой равносторонний треугольник, вдвое меньший, как это показано
на рис. 11, а. Пусть внутренняя часть меньшего треугольника «вы-
брошена», то есть остается фигура, состоящая их трех треугольников
(выброшенная часть зачернена на рис. 11, а). Проделаем то же самое
для каждого их этих трех треугольников (рис. 11,6); после этого мы
получим фигуру, состоящую из девяти треугольников. В каждый из
этих девяти треугольников снова впишем еще меньшие треугольники,
так что образуется фигура, содержащая 27 маленьких треугольников.
Представим, что этот процесс продолжается бесконечно (на рис. 11, в
изображен пятый этап, когда получена фигура, состоящая из 243 тре-
угольников). Точки исходного треугольника, которые сохранятся на
сколь угодно далеком этапе этого процесса, образуют в пределе кри-
вую, к которой будет приближаться наша все время реконструируемая
конфигурация. Все точки этой кривой, за исключением вершин перво-
начального треугольника А, В и С, будут точками ветвления. Теперь
уже нетрудно получить кривую, которая состоит целиком из точек
ветвления — например, можно деформировать полученную только что
кривую таким образом, чтобы точки А, В и С соединились в одну точку.
Но хватит примеров. Давайте подведем некоторые итоги сказанному.
Снова и снова мы убеждались, что в геометрических вопросах, да-
354
же в очень простых и элементарных, интуиция является крайне нена-
дежной. На нее нельзя полагаться и использовать как основу в матема-
тике. Пространство в геометрии — не форма чистой интуиции, а логи-
ческая конструкция.
а б в
Р и cl 1
Открывается путь для построения других непротиворечивых логи-
ческих конструкций в виде пространств, отличающихся от простран-
ства обычной геометрии, — пространств, в которых так называемый
евклидов постулат о параллельных заменен противоположным посту-
латом (неевклидовы пространства), пространств с равномерностью,
превышающей три, неархимедовых пространств. Я скажу несколько
слов о последних.
Возможность измерения длины отрезка действительным числом и
все вытекающие отсюда последствия, например, выбор начала коор-
динат и введение координаты для каждой точки, как это делается в
аналитической геометрии, основаны на так называемом постулате Ар-
химеда. Этот постулат звучит так: если даны два отрезка, то всегда
существует кратное длины первого, которое больше второго отрезка. В
логических конструкциях постулат Архимеда заменен противополож-
ным, то есть, что существуют длины, превосходящие любые кратные
данной длины. Следовательно, в этих пространствах существуют бес-
конечно большие и бесконечно малые длины (при условии, что имеет-
ся некая единица длины), в то время как в обычном пространстве та-
ких длин не имеется. В неархимедовых пространствах длины можно
измерять, поэтому в них возможны построения аналитической геомет-
рии. Конечно, действительные числа обычной арифметики там будут
малопригодными; в них используется «неархимедова» числовая сис-
тема, которая может использоваться для вычислений с таким же успе-
хом, как действительные числа обычной арифметики.
Но что мы можем противопоставить обычному возражению, будто
многомерные, неевклидовы, неархимедовы геометрии, хотя и безуко-
ризненны с точки зрения логической конструкции, но бесполезны как
средство осмысления нашего опыта, поскольку они «неинтуитивны».
355
Не является ли полезным только обычное трехмерное, евклидово, ар-
химедово пространство, ибо только оно не противоречит нашей ин-
туиции. Мой ответ на это — и он является главным пунктом всей моей
лекции — состоит в том, что обычная геометрия несомненно является
высшим проявлением нашей интуиции. Дело в том, что всякая геомет-
рия — трехмерная, наряду с многомерной, евклидовой и неевклидо-
вой, архимедовой и неархимедовой — представляет собой логическую
конструкцию. Традиционная физика в ответе за то, что до недавнего
времени для организации нашего опыта мы использовали исключи-
тельно единственную логическую конструкцию, называемую трехмер-
ным, евклидовым, архимедовым пространством. В течение нескольких
столетий, до наших дней это пространство выполняло свое назначение
великолепно, поэтому мы все более и более привыкали к его использо-
ванию. Эта привычка к обычной геометрии и объясняет, почему мы
склонны считать такую геометрию «интуитивной», а всякое отклоне-
ние от такой геометрии считать «интуитивно невозможным». Но мы
убедились, что интуитивно невозможные факты имеются и в самой
обычной геометрии. Они обнаруживаются тогда, когда мы больше не
ограничиваем себя геометрическими понятиями, с которыми мы хо-
рошо знакомы, а размышляем вместо этого о вещах, над которыми мы
не привыкли задумываться.
Современная физика убедилась в полезности таких логических кон-
струкций, как многомерная и неевклидова геометрия, для описания
нашего опыта. (Хотя мы не имеем пока сведений об использовании не-
архимедовой геометрии, такое использование, разумеется, не исклю-
чено в будущем.) Но эти открытия в теоретической физике настолько
новы, что мы не успели еще научиться обращению с подобными логи-
ческими конструкциями, и выглядят они как вызов интуиции.
Теория сферообразной Земли тоже когда-то бросала вызов интуи-
ции. Эта теория долгое время решительно отвергалась на том основа-
нии, что существование антиподов противоречит интуиции. Но посте-
пенно мы привыкли к этой идее, и сегодня уже никто не отвергает ее.
Физические понятия также представляют собой логические струк-
туры, и здесь мы тоже можем четко видеть, как те из понятий, которые
привычны нам и часто используются, получают статус «интуитивно
ясных», в то время как редко используемые понятия не удостаиваются
этого статуса. Понятие «вес» настолько широко используется в прак-
тике, что почти каждый считают его интуитивным. Но понятие «мо-
мент инерции» употребляется только специалистами, поэтому боль-
шинство людей не считает его интуитивным. Однако среди физиков-
экспериментаторов и инженеров, повседневно с ними работающих,
оно приобрело такой же статус интуитивно ясного, как и понятие
356
«вес». То же можно сказать о понятии «разность потенциалов», интуи-
тивном для электротехников и неинтуитивном для остальных людей.
Использование многомерной и неевклидовой геометрии для упоря-
дочения результатов опыта все более и более оправдывает себя, по-
этому мы все больше начинаем привыкать к этим логическим конст-
рукциям. Если их начнут изучать в школе, если, так сказать, мы нач-
нем впитывать их с молоком матери, как изучаем сейчас евклидову
геометрию, то никто и не подумает сказать, что эти геометрии проти-
воречат интуиции. Они будут считаться заслуживающими статуса ин-
туитивных, точно так же, как сегодня утверждена в этом статусе евк-
лидова геометрия, Хотя утверждение Канта, будто интуиция априорна,
ошибочно, но создается она силой привычки и основана на психологи-
ческой инерции нашего мышления.
Л- Луанирре
МАТЕМАТИЧЕСКОЕ ТВОРЧЕСТВО1’
Генезис математического творчества является проблемой, которая
должна вызывать живейший интерес у психолога. Кажется, что в этом
процессе человеческий ум меньше всего заимствует из внешнего мира
и действует, или только кажется действующим, лишь сам по себе и
сам над собой. Поэтому, изучая процесс математической мысли, мы
можем надеяться постичь нечто самое существенное в человеческом
сознании.
Это было понято уже давно, и несколько месяцев назад журнал
«Математическое образование», издаваемый Лезаном и Фэром, опуб-
ликовал вопросник, касающийся умственных привычек и методов ра-
боты различных математиков. К тому моменту, когда были опублико-
ваны результаты этого опроса, мой доклад был в основном уже подго-
товлен, так что я практически не мог ими воспользоваться. Отмечу
лишь, что большинство ответов подтвердило мои заключения; я не го-
ворю об единогласии, так как при всеобщем опросе на него и нельзя
надеяться.
Первый факт, который должен нас удивлять, или, вернее, должен
был бы удивлять, если бы к нему не привыкли, следующий: как полу-
чается, что существуют люди, не понимающие математики? Если ма-
тематики используют лишь логические правила, которые принимаются
всеми разумными людьми; если математика основана на принципах,
которые являются общими для всех людей и которые никто, не будучи
сумасшедшим, не станет отрицать, то как получается, что есть люди,
совершенно не приемлющие математики?
357
Тот факт, что не все способны на открытие, не содержит ничего та-
инственного. Можно понять еще и то, что не все могут запомнить до-
казательство, которое когда-то узнали. Но то .обстоятельство, что не
всякий человек может понять математическое рассуждение, когда ему
его излагают, кажется совершенно удивительным. И тем не менее лю-
дей, которые лишь с большим трудом воспринимают эти рассуждения,
большинство; это неоспоримо, и опыт учителя средней школы под-
тверждает это.
И далее, как возможна ошибка в математике? Нормальный разум не
должен совершать логической ошибки, и тем не менее есть очень тон-
кие умы, которые не ошибутся в коротком рассуждении, подобном
тем, с которыми ему приходится сталкиваться в обыденной жизни и
которые не способны провести или повторить без ошибки более длин-
ные математические доказательства, хотя в конечном счете последние
являются совокупностью маленьких рассуждений, совершенно анало-
гичных тем, которые эти люди проводят так легко. Нужно ли приба-
вить, что и сами хорошие математики не являются непогрешимыми?
Ответ, как мне кажется, напрашивается сам собой. Представим себе
длинный ряд силлогизмов, у которых заключения первых служат по-
сыпками следующих; мы способны уловить каждый из этих силлогиз-
мов, и в переходах от посылки к рассуждению мы не рискуем оши-
биться. Но иной раз проходит много времени между моментом, когда
некоторое предложение мы встречаем в качестве заключения силло-
гизма, и моментом, когда мы вновь с ним встретимся в качестве по-
сылки другого силлогизма, когда много звеньев в цепи рассуждений, и
может случиться, что предложение забыто или, что более серьезно, за-
быт его смысл. Таким образом, может случиться, что предложение за-
меняют другим, несколько от него отличным, или что его применяют в
несколько ином смысле, и это приводит к ошибке.
Если математик должен воспользоваться некоторым правилом, ес-
тественно, он сначала его доказывает, и в момент, когда это доказа-
тельство свежо в его памяти, он прекрасно понимает его смысл и пре-
делы применения и поэтому не рискует его исказить. Но затем, дове-
ряя своей памяти, он применяет его механически, и если память его
подведет, то правило может быть применено неверно. В качестве про-
стого и почти вульгарного примера можно привести тот факт, что мы
часто ошибаемся в вычислении, так как забыли таблицу умножения.
С этой точки зрения математические способности должны были бы
сводиться к очень надежной памяти или к безупречному вниманию.
Это качество подобно способности игрока в вист запоминать сбро-
шенные карты; или — на более высоком уровне — способности шах-
матиста, который должен рассмотреть большое число комбинаций и
358
все их держать в памяти. Каждый хороший математик должен был бы
быть одновременно хорошим шахматистом и обратно; точно так же он
должен бы быть хорошим вычислителем. Действительно, так иногда
случается и, например, Гаусс был одновременно гениальным геомет-
ром и рано проявившим себя очень хорошим вычислителем.
Но есть исключения, хотя я, пожалуй, не прав, называя это исклю-
чениями, так как иначе исключения оказались бы более многочислен-
ными, чем правила. Напротив, это Гаусс был исключением. Что каса-
ется меня, то я вынужден признать свою совершенную неспособность
выполнить сложение без ошибки. Я был бы также очень плохим шах-
матистом; я мог бы хорошо рассчитать, что, совершив такой-то ход, я
подвергся бы такой-то опасности; я рассмотрел бы много других хо-
дов, которые я отбросил бы по другим причинам, и кончил бы тем, что
совершил бы рассмотренный ход, забыв между делом об опасности,
которую я раньше предвидел.
Одним словом, у меня неплохая память, но она недостаточна, что-
бы сделать меня хорошим шахматистом. Почему же она меня не под-
водит в трудном математическом рассуждении? Это, очевидно, пото-
му, что она руководствуется общей линией рассуждения. Математиче-
ское рассуждение не есть простая совокупность силлогизмов; это сил-
логизмы, помещенные в определенном порядке, и порядок, в котором
эти элементы расположены, гораздо более важен, чем сами элементы.
Если я чувствую этот порядок так, что вижу все рассуждение в целом,
то мне не страшно забыть один из элементов: каждый из них встанет
на место, которое ему приготовлено, причем без всякого усилия со
стороны памяти. Когда я изучаю некоторое утверждение, мне кажется,
что я мог бы сам его открыть, или, вернее, если это иллюзия и я недос-
таточно силен, чтобы открыл» его, я переоткрываю его во время изу-
чения.
Отсюда можно сделать вывод, что это интуитивное чувство мате-
матического порядка, которое позволяет нам угадать гармонию и
скрытые соотношения, доступно не всем людям. Одни не способны к
этому деликатному и трудному для определения чувству и не облада-
ют памятью и вниманием сверх обычных; и они совершенно неспо-
собны понимать серьезную математику; таковых большинство. Другие
обладают этим чувством в малой степени, но они имеют хорошую па-
мять и способны на глубокое внимание. Они запомнят наизусть детали
одну за другой, они смогут понять математику и иногда ее применять,
но они неспособны творить. Наконец третьи в большей или меньшей
степени обладают той специальной интуицией, о которой я говорил, и
они могут не только понимать математику, но и творить в ней и пы-
таться делать открытия с большим или меньшим успехом в зависимо-
359
сти от степени развития этой интуиции, несмотря на то, что их память
не представляет собой ничего особенного.
Что же такое в действительности изобретение в математике? Оно
состоит не в том, чтобы создавать новые комбинации из уже извест-
ных математических фактов. Это мог бы делать любой, но таких ком-
бинаций было бы конечное число, и абсолютное большинство из них
не представляло бы никакого интереса. Творить это означает не созда-
вать бесполезных комбинаций, а создавать полезные, которых ни-
чтожное меньшинство. Творить — это уметь распознавать, уметь вы-
бирать.
Как делать этот выбор, я объяснял в другом месте: математические
факты, которые заслуживают того, чтобы быть изученными, — это та-
кие, которые по своей аналогии с другими фактами могут нас подвести
к познанию математического закона, подобно тому, как эксперимен-
тальные факты подводят нас к познанию физического закона. Это та-
кие факты, которые открывают нам связь между другими законами,
известными уже давно, но ошибочно считавшимися не связанными
друг с другом.
Среди выбранных комбинаций наиболее плодотворными часто ока-
зываются те, которые составлены из элементов, взятых из очень дале-
ких друг от друга областей. Я не хочу сказать, что для того, чтобы сде-
лать открытие, достаточно сопоставить как можно более разношерст-
ные факты*, большинство комбинаций, образованных таким образом,
было бы совершенно бесполезным, но зато некоторые из них, хотя и
очень редко, бывают наиболее плодотворными из всех.
Я уже говорил, что изобретение — это выбор; впрочем, это слово,
может быть, подобрано не совсем точно, — здесь приходит в голову
сравнение с покупателем, которому предлагают большое количество
образцов товаров, и он исследует их один за другим, чтобы сделать
свой выбор. В математике образцы столь многочисленны, что всей
жизни не хватит, чтобы их исследовать. Выбор происходит не таким
образом. Бесплодные комбинации даже не придут в голову изобрета-
телю. В поле зрения его сознания попадают лишь действительно по-
лезные комбинации и некоторые другие, имеющие признаки полезных,
которые он затем отбросит.
Все происходит так, как если бы ученый был экзаменатором второ-
го тура, который должен экзаменовать лишь кандидатов, успешно
прошедших испытания в первом туре. Но все то, что я до сих пор го-
ворил, можно заметить или заключить, лишь достаточно вдумчиво
вчитываясь в труды по математике.
Настало время продвинуться немного вперед и посмотреть, что же
происходит в самой душе математика. Я полагаю, что лучшее, что
360
можно для этого сделать, это привести собственные воспоминания. Я
припомню и расскажу вам, как я написал первую свою работу об ав-
томорфных функциях. Я прошу прощения за то, что буду вынужден
употреблять специальные термины, но это не должно вас пугать, так
как вам их понимать совсем необязательно. Я, например, скажу, что
при таких-то обстоятельствах нашел доказательство такой-то теоремы;
эта теорема получит варварское название, которое многие из вас не
поймут, но это не важно: для психолога важна не теорема, а обстоя-
тельства.
В течение двух недель я пытался доказать, что не может существо-
вать никакой функции, аналогичной той, которую я назвал впоследст-
вии автоморфной. Я был, однако, совершенно не прав; каждый день я
садился за рабочий стол, проводил за ним час или два, исследуя боль-
шое число комбинаций, и не приходил ни к какому результату.
Однажды вечером, вопреки своей привычке, я выпил черного кофе;
я не мог заснуть; идеи теснились, я чувствовал, как они сталкиваются,
пока две из них не соединились, чтобы образовать устойчивую комби-
нацию. К утру я установил существование одного класса этих функ-
ций, который соответствует гипергеометрическому ряду; мне остава-
лось лишь записать результаты, что заняло только несколько часов. Я
хотел представить эти функции в виде отношения двух рядов, и эта
идея была совершенно сознательной и обдуманной, мной руководила
аналогия с эллиптическими функциями. Я спрашивал себя, какими
свойствами должны обладать эти ряды, если они существуют, и мне
без труда удалось построить эти ряды, которые я назвал тета-
автоморфными.
В этот момент я покинул Кан, где тогда жил, чтобы принять уча-
стие в геологической экскурсии, организованной Горной школой. Пе-
рипетии этого путешествия заставили меня забыть о моей работе.
Прибыв в Кутаис, мы сели в омнибус для какой-то прогулки; в мо-
мент, когда я встал на подножку, мне пришла в голову идея, без вся-
ких, казалось бы, предшествовавших раздумий с моей стороны, идея о
том, что преобразования, которые я использовал, чтобы определить
автоморфные функции, были тождественны преобразованиям неевк-
лидовой геометрии. Из-за отсутствия времени я не сделал проверки,
так как, с трудом сев в омнибус, я тотчас же продолжил начатый раз-
говор, но я уже имел полную уверенность в правильности сделанного
открытия. По возвращении в Кан я на свежую голову и для очистки
совести проверил найденный результат.
В то время я занялся изучением некоторых вопросов теории чисел,
не получая при этом никаких существенных результатов и не подозре-
вая, что это может иметь малейшее отношение к прежним исследова-
361
ниям. Разочарованный своими неудачами, я поехал провести несколь-
ко дней на берегу моря и думал совсем о другой вещи. Однажды, когда
я прогуливался по берегу, мне так же внезапно, быстро и с той же
мгновенной уверенностью пришла на ум мысль, что арифметические
преобразования квадратичных форм тождественны преобразованиям
неевклидовой геометрии.
Возвратившись в Кан, я думал над этим результатом, извлекая из
него следствия; пример квадратичных форм мне показал, что сущест-
вуют автоморфные группы, отличные от тех, которые соответствуют
гипергеометрическому ряду; я увидел, что могу к ним применить тео-
рию тета-автоморфных функций и что, следовательно, существуют ав-
томорфные функции, отличающиеся от тех, которые соответствуют ги-
пергеометрическому ряду—единственные, которые я знал до тех пор.
Естественно, я захотел построить все эти функции; я предпринял
систематическую осаду и успешно брал одно за другим передовые ук-
репления. Оставалось, однако, еще одно, которое держалось и взятие
которого означало бы падение всей крепости. Однако сперва ценой
всех моих усилий я добился лишь того, что лучше понял, в чем состо-
ит трудность проблемы, и это уже кое-что значило. Вся эта работа бы-
ла совершенно сознательной.
Затем я переехал в Мон-Валерьян, где я должен был продолжать
военную службу. Таким образом, занятия у меня были весьма разно-
образны. Однажды, во время прогулки по бульвару, мне вдруг пришло
в голову решение этого трудного вопроса, который меня останавливал.
Я не стал пытаться вникать в него немедленно и лишь после оконча-
ния службы вновь взялся за проблему. У меня были все элементы и
мне оставалось лишь собрать их и привести в порядок. Поэтому я сра-
зу и без всякого труда полностью написал эту работу.
Я ограничусь лишь этим одним примером. Бесполезно их умно-
жать, так как относительно других моих исследований я мог бы рас-
сказать вещи совершенно аналогичные, и наблюдения, приводимые
другими математиками в ответах на вопросы журнала «Математиче-
ское образование», только подтверждает мои.
То, что вас удивит прежде всего, это видимость внутреннего озаре-
ния, являющаяся результатом длительной неосознанной работы; роль
этой бессознательной работы в математическом изобретении мне ка-
жется несомненной и ее следы можно найти и в других случаях, когда
это менее очевидно. Часто, когда работают над трудным вопросом, с
первого раза не удается ничего хорошего, затем наступает более или
менее длительный период отдыха, а потом снова принимаются задело.
В течение первого получаса дело вновь не двигается, а затем вдруг
нужная идея приходит в голову. Можно было бы сказать, что созна-
362
тельная работа стала более плодотворной, так как была прервана и от-
дых вернул уму его силу и свежесть. Но более вероятно предположить,
что этот отдых был заполнен бессознательной работой и что результат
этой работы внезапно явился математику точно так, как это было в
случае, который я рассказывал; только озарение вместо того, чтобы
произойти во время прогулки или путешествия происходит во время
сознательной работы, но совершенно независимо от этой работы, ко-
торая, самое большее, играет роль связующего механизма, переводя
результаты, полученные во время отдыха, но оставшиеся неосознан-
ными, в осознанную форму.
Есть еще одно замечание по поводу условий этой бессознательной
работы: она возможна или, по крайней мере, плодотворна лишь в том
случае, когда ей предшествует и за ней следует сознательная работа
Приведенный мной пример подтверждает в достаточной мере, что эти
внезапные вдохновения происходят лишь после нескольких дней соз-
нательных усилий, которые казались абсолютно бесплодными, когда
предполагаешь, что не сделано ничего хорошего и когда кажется, что
выбран совершенно ошибочный путь. Эти усилия, однако, не являются
бесполезными, как это думают, они пустили в ход бессознательную
машину, без них она не пришла бы в действие и ничего бы не произвела.
Необходимость второго периода сознательной работы после озаре-
ния еще более понятна. Нужно использовать результаты этого озаре-
ния, вывести из них непосредственные следствия, привести в порядок,
отредактировать доказательство. Но особенно необходимо их прове-
рить. Я вам уже говорил о чувстве абсолютной уверенности, которое
сопровождает озарение; в рассказанных случаях оно не было ошибоч-
ным и чаще всего так и бывает; но следует опасаться уверенности, что
это правило без исключения; часто это чувство нас обманывает, не
становясь при этом менее ярким, и заметить это можно лишь при по-
пытке строго сознательно провести доказательство. Особенно я на-
блюдал такие факты в случае, когда идеи приходят в голову утром или
вечером в постели, в полусознательном состоянии.
Таковы факты; рассмотрим теперь выводы, которые отсюда следу-
ют. Как вытекает из предыдущего, или мое «бессознательное я» или,
как это называют, мое подсознание, играет основную роль в математи-
ческом творчестве. Но обычно рассматривают подсознательные про-
цессы как явления, чисто автоматические. Мы видим, что работа ма-
тематика не является просто механической и ее нельзя было бы дове-
рить машине, сколь бы совершенной она ни была Здесь дело не толь-
ко в том, чтобы применять правила и создавать как можно больше
комбинаций по некоторым известным законам. Комбинации, получен-
ные таким образом, были бы слишком многочисленными, громоздки-
363
ми и бесполезными. Истинная работа ученого состоит в выборе этих
комбинаций, так чтобы исключить бесполезные или, вернее, даже не
утруждать себя их созданием. И правила, которыми нужно руково-
дствоваться при этом выборе, предельно деликатны и тонки, их почти
невозможно выразить точными словами; они легче чувствуются, чем
формулируются; как можно при таких условиях представить себе ап-
парат, который их применяет автоматически?
Отсюда перед нами возникает первый вопрос: «Я — подсознатель-
ное» нисколько не является низшим по отношению к «я — сознатель-
ному», оно не является чисто автоматическим, оно способно здраво
судить, оно имеет чувство меры и чувствительность, оно умеет выби-
рать и догадываться. Да что говорить, оно умеет догадываться лучше, чем
мое сознание, так как преуспевает там, где сознание этого не может.
Короче, не стоят ли мои бессознательные процессы выше чем мое
сознание? Вы понимаете важность моего вопроса. Э. Бутру вам пока-
зал в докладе, сделанном здесь же два месяца назад, как этот вопрос
возникает при совершенно других обстоятельствах и какие следствия
вытекают из утвердительного ответа. Не вытекает ли такой утверди-
тельный ответ из фактов, которые я только что вам изложил? Я утвер-
ждаю, что не могу с этим согласиться. Итак, исследуем еще раз факты
и посмотрим, не содержат ли они другого объяснения.
Несомненно, что комбинации, приходящие на ум в виде внезапного
озарения после достаточно длительной бессознательной работы,
обычно полезны и глубоки, как будто они прошли уже первый отбор.
Значит ли это, что подсознание образовало только эти комбинации ин-
туитивно, догадываясь, что лишь они полезны, или оно образовало и
многие другие, которые были лишены интереса и остались неосознан-
ными?
При этой второй точке зрения все комбинации формируются меха-
низмом подсознания, но в поле зрения сознания попадают лишь пред-
ставляющие интерес. Но и это еще очень непонятно. Каковы причины
того, что среди тысяч результатов деятельности нашего подсознания
есть лишь некоторые, которые призваны пересечь его порог, в то вре-
мя как все прочие остаются по ту сторону? Не просто ли случай дает
им эту привилегию? Конечно нет. К примеру, среди всех ощущений,
действующих на наши органы чувств, только самые интенсивные об-
ращают на себя наше внимание, по крайней мере, если это внимание
не обращено на них по другим причинам. В более общем случае среди
бессознательных идей привилегированными, т.е. способными стать
сознательными, являются те, которые прямо или косвенно наиболее
глубоко воздействуют на наши чувства.
364
Может вызвать удивление обращение к чувствам, когда речь идет о
математических доказательствах, которые, казалось бы, связаны только с
умом. Но это означало бы, что мы забываем о чувстве математической
красоты, чувстве гармонии чисел и форм, геометрической выразительно-
сти. Эго настоящее эстетическое чувство, знакомое всем настоящим ма-
тематикам. Воистину, здесь налицо чувство!
Но каковы математические характеристики, которым мы
приписываем свойства красоты и изящества и которые способны
возбудить в нас своего рода эстетическое чувство? Это те, элементы
которых гармонически расположены таким образом, что ум без усилия
может их охватывать целиком, угадывая детали. Эта гармония служит
одновременно удовлетворением наших эстетических чувств и
помощью для ума, она его поддерживает и ею он руководствуется. Эта
гармония дает нам возможность предчувствовать математический
закон. Итак, как это было сказано выше, единственными фактами,
способными обратить на себя наше внимание и быть полезными,
являются те, которые подводят нас к познанию математического
закона. Таким образом, мы приходим к следующему выводу: полезные
комбинации это в точности наиболее красивые, т.е. те, которые
больше всего воздействуют на это специальное чувство
математической красоты, известное всем математикам и недоступное
профанам до такой степени, что они часто склонны смеяться над ним.
Что же, таким образом, происходит? Среди многочисленных комбина-
ций, образованных нашим подсознанием, большинство безынтересно и
бесполезно, но потому они и не способны подействовать на наше эстетиче-
ское чувство; они никогда не будут нами осознаны; только некоторые яв-
ляются гармоничными и потому одновременно красивыми и полезными;
они способны возбудить нашу специальную геометрическую интуицию,
которая привлечет к ним наше внимание и таким образом даст им возмож-
ность стать осознанными
Эго только гипотеза, но есть наблюдение, которое ее подтверждает вне-
запное озарение, происходящее в уме математика, почти никогда его не
обманывает, но иногда случается, что оио не выдерживает проверки, и тем
не менее почти всегда замечают, что если бы эта ложная идея оказалась
верной, то она удовлетворила бы наше естественное чувство математиче-
ского изящества.
Таким образом, это специальное эстетическое чувство играет роль ре-
шета, и этим объясняется, почему тот, кто лишен его, никогда не станет на-
стоящим изобретателем.
Однако преодолены не все трудности; ясно, что пределы сознания очень
узки, а что касается подсознания, то его пределов мы не знаем и потому не
слишком возражаем против предположения, что оно может образовать в
365
короткое время столько комбинаций, сколько сознательное существо не
смогло бы рассмотреть за всю жизнь. Эти пределы тем не менее существу-
ют, но правдоподобно предположить, что подсознание могло бы образо-
вать все возможные комбинации, число которых испугало бы воображение,
и это кажется и необходимым, так как если бы оно образовывало их мало и
делало бы это случайным образом, то маловероятно, чтобы «хорошая»
комбинация, которую надо выбрать, находилась среди них.
Для объяснения надо учесть первоначальный период сознательной ра-
боты, который предшествует плодотворной бессознательной работе. Про-
шу извинить меня за следующее грубое сравнение. Представим себе буду-
щие элементы наших комбинаций как что-то похожее на атомы — крючоч-
ки Эпикура Во время полного отдыха мозга эти атомы неподвижны, они
как будто прикреплены к стене; этот полный отдых может продолжаться
неопределенное время, атомы при этом не встречаются и, следовательно,
никакое их сочетание не может осуществиться. Во время же кажущегося
отдыха и бессознательной работы некоторые из них оказываются отделен-
ными от стены и приведенными в движение. Они перемещаются во всех
направлениях пространства, вернее, — помещения, где они заперты, так же,
как туча мошек или, если вы предпочитаете более ученое сравнение, как га-
зовые молекулы в кинетической теории газов. При взаимном столкновении
могут появиться новые комбинации.
Какова же роль первоначальной сознательной работы? Она состоит,
очевидно, в том, чтобы мобилизовать некоторые атомы, отделить их от
стены и привести в движение. Считают, что не сделано ничего хорошего,
так как эти элементы передвигали тысячами разных способов с целью най-
ти возможность их сочетать, а удовлетворительной комбинации найти не
удалось. Но после того импульса, который им был сообщен по нашей воле,
атомы больше не возвращаются в свое первоначальное неподвижное со-
стояние. Они свободно продолжают свой танец.
Но наша воля выбирала их не случайным образом, цель была вполне
определена, выбранные атомы были не первые попавшиеся, а те, от кото-
рых разумно ожидать искомого решения. Атомы, приведенные в движение,
начинают испытывать соударения и, следовательно, образовывать сочета-
ния друг с другом или с теми атомами, которые ранее были неподвижны и
были задеты при их движении. Я еще раз прошу у вас извинения за гру-
бость сравнения, но я не знаю другого способа, для того чтобы объяснить
свою мысль.
Как бы то ни было, у созданных комбинаций хотя бы одним из элемен-
тов служит атом, выбранный по нашей воле. И очевидно, что среди них на-
ходятся те комбинации, которые я только что назвал «хорошими». Может
быть, в этом содержится возможность уменьшить парадоксальность перво-
начальной гипотезы.
366
Другое наблюдение. Никогда не бывает, чтобы результатом бессозна-
тельной работы было полностью проведенное и достаточно длинное вы-
числение, даже если его правила заранее установлены. Казалось бы, под-
сознание должно быть особенно расположено к совершенно механической
работе. Если, например, вечером подумать о сомножителях, то можно было
бы надеяться, что при пробуждении будешь знать произведение или что ал-
гебраическое вычисление, например проверка, могло бы производиться
бессознательно. Но опыт опровергает это предположение. Единственное,
что получаешь при озарении, являющимся результатом бессознательной
работы, это отравные точки для подобных вычислений; что касается са-
мих вычислений, то их надо производить во время второго периода созна-
тельной работы, следующего за озарением; тогда проверяют результаты и
выводят из них следствия. Правила вычислений строги и сложны, они тре-
буют дисциплины, внимания и воли и, следовательно, сознания. В подсоз-
нании же царит, напротив, то, что я называю свободой, если можно назвать
этим словом простое отсутствие дисциплины и беспорядок, рожденный
случаем. Но только этот беспорядок рождает неожиданные комбинации.
Я сделаю последнее замечание; когда я выше излагал вам некоторые
личные наблюдения, я говорил о бессонной ночи, во время которой я рабо-
тал как бы против своей воли; такие случаи часты и необязательно, чтобы
причиной такой ненормальной мозговой активности было физическое воз-
буждение, как было в случае, о котором я говорил. Кажется, что в этих слу-
чаях присутствуешь при своей собственной бессознательной работе, кото-
рая стала частично ощутимой для сверхвозбужденного сознания и которая
не изменила из-за этого своей природы. При этом начинаешь смутно разли-
чать два механизма или, если угодно, два метода работы этих двух «я». И
психологические наблюдения, которые я мог при этом сделать, как мне ка-
жется, подтверждают в основных чертах те взгляды, которые я вам здесь
изложил.
Эти взгляды несомненно нуждаются в проверке, так как несмотря ни на
что остаются гипотетичными; вопрос, однако, столь интересен, что я не
раскаиваюсь в том, что изложил их вам.
>¥Q Ядамар
РАЗЛИЧНЫЕ ТИПЫ МАТЕМАТИЧЕСКИХ УМОВ20
Случай здравого смысла. Начнем с начала, а именно с людей,
рассуждающих просто здраво: мы можем сказать, что у них бессозна-
тельное играет большую роль и что они лишь немного пользуются по-
следующей работой сознания.
367
Кроме того, случается, что их бессознательное является поверхно-
стным, и его результаты несущественно отличаются от нормального
рассуждения. Так, Спенсер, напомнив классический силлогизм: «Вся-
кий человек смертен; Петр — человек; значит Петр смертен», предпо-
лагает, что вам рассказали о человеке в возрасте 90 лет, который зате-
вает постройку для себя нового дома. Этот силлогизм действительно
присутствует в вашем краевом сознании и разница лишь в форме меж-
ду этим последним и ходом мысли (ходом мгновенным, как обычно в
бессознательном), который вас приводит к выводу, что этот человек
неразумен. То же самое может иметь место и для многих простых ма-
тематических умозаключений
Но в ряде других случаев пути здравого смысла могут сильно отли-
чаться от тех, по которым может пойти четко сформулированное рас-
суждение. Особенно это касается вопросов конкретной природы, на-
пример геометрических и механических. Наши представления по та-
ким вопросам, усвоенные в раннем детстве, по-видимому, глубоко за-
прятаны в бессознательном; мы не можем их знать точно, и вероятно,
что часто они содержат эмпирические выводы, полученные не путем
рассуждения, а из чувственного опыта. Приведем несколько примеров.
Представим себе, что мы бросили перед собой «материальную точ-
ку» (т.е. крохотное тело, как, например, очень маленький шарик), ко-
торая будет продолжать двигаться благодаря своей начальной скоро-
сти и своему весу. Здравый смысл нам говорит, что это движение бу-
дет происходить в вертикальной плоскости, которая проходит через
начальное направление броска. В этом случае почти несомненно, что
подсознание использует «принцип достаточного основания», так как
нет никаких оснований для того, чтобы точка в своем движении от-
клонилась скорее вправо, чем влево от этой плоскости.
Математическое доказательство, как оно классически излагается в
курсах теоретической механики, основано на совершенно ином прин-
ципе и использует несколько теорем дифференциального и интеграль-
ного исчисления. Надо, однако, заметить, что доказательство, которое
нам дает «здравый смысл», можно превратить в совершенно строгое,
используя общую теорему (также относящуюся к интегральному ис-
числению), которая гласит, что в условиях, изложенных выше (при за-
данных величине и направлении скорости), движение определено од-
нозначно. Эта теорема может в свою очередь быть строго доказана, но
это доказательство приводится лишь в более строгих курсах инте-
грального исчисления, так что в обычном обучении способ, подска-
занный здравым смыслом, действительно кажется менее элементар-
ным, чем другой.
Рассмотрим теперь два геометрических примера. Если я хочу не-
прерывным движением точки описать и плоскости кривую, то здравый
368
смысл подсказывает, что во всех ее точках (кроме, может быть, не-
скольких исключительных точек) кривая будет иметь касательную
(другими словами, в каждый момент движение обязательно происхо-
дит во вполне определенном направлении). Мы не знаем, как здравый
смысл — т.е. наше бессознательное — приходит к такому выводу; мо-
жет быть, благодаря опыту, т.е. вспоминая кривые, которые мы при-
выкли видеть; или, как это предполагает Ф. Клейн, смешивая геомет-
рические кривые, которые не имеют толщины, с кривыми, которые мы
реально можем провести и которые всегда имеют некоторую толщину.
В действительности вывод ошибочен: математики умеют строить не-
прерывные кривые, которые нигде не имеют касательной.
В качестве второго примера рассмотрим замкнутую плоскую кри-
вую, которая не имеет «двойных точек», т.е. нигде не пересекается са-
ма с собой. Для здравого смысла очевидно, что такая кривая, какова
бы ни была ее форма, делит плоскость либо на две различные области,
либо более чем на две. Точно не известно, как здравый смысл прихо-
дит к такому выводу, и вероятно, что здесь снова налицо вмешательст-
во эмпиризма. На этот раз заключение (теорема Жордана) правильно,
но, несмотря на его очевидность для нашего здравого смысла, его до-
казательство очень трудное.
С помощью таких примеров можно понять, что, по крайней мере
для некоторого класса вопросов, связанных с основами, невозможно с
уверенностью полагаться на нашу обычную пространственную интуи-
цию: так же, как геометрические свойства могут быть сведены к свой-
ствам аналитическим благодаря аналитической геометрии, рассужде-
ния всегда должны быть полностью арифметизованы или, по крайней
мере, необходимо убедиться, что такая арифметизация возможна, даже
если она для краткости не проводится. Слова Паскаля «Все, чего не
может геометрия, ие можем и мы» заменены современными математи-
ками словами «Все, чего не может арифметика, не можем и мы».
Например, доказательство теоремы Жордана, сформулированной
выше, является удовлетворительным лишь тогда, когда оно полностью
арифметизовано.
Вторая стадия — изучение математики. После этой стадии здра-
вого смысла приходит следующая стадия — научная. Мы видели, что
она характеризуется наличием тройной операции: проверки результа-
та, его «завершения» и особенно его подготовки к использованию, что
требует формулировки результата-эстафеты. Мы видели, что это су-
щественно, во-первых, для того, чтобы иметь уверенность в приобре-
тенных таким образом знаниях, и для того, во-вторых, чтобы иметь
возможность их плодотворно использовать.
24 Зак. 72
369
Эти особенности помогут нам понять, что происходит, с точки зрения
психологии, при переходе от первой стадии ко второй; другими словами,
понять то, что происходит при изучении математики.
Известно, до какой степени обычным делом здесь являются полное
непонимание и полный крах. Впрочем, я буду очень краток в этом во-
просе, так как он основательно рассмотрен Пуанкаре. Прежде чем его
обсуждать, небесполезно заметить, что изучение математики уже вхо-
дит в тему нашего исследования. Между работой ученика, решающего
задачу по алгебре или геометрии, и изобретательской работой разница
лишь в уровне, в качестве, так как обе работы аналогичного характера.
Как получается, что столько учеников неспособны к этому виду ра-
боты, неспособны понимать математику? Пуанкаре рассмотрел имен-
но этот вопрос, и он ярко показал, какова здесь действительная причи-
на, источник которой — тот смысл, который следовало бы придавать
слову «понимать».
«Понять доказательство теоремы, — значит ли это исследовать по-
следовательно каждый из силлогизмов, из которых она состоит, и кон-
статировать, что он корректен и соответствует правилам игры? Да, для
некоторых; установив это, они скажут: я понял.
Но не для большинства. Почти все остальные являются гораздо бо-
лее требовательными, они хотят знать не только, все ли силлогизмы в
доказательстве верны, но также почему они связываются в таком по-
рядке, а не в другом. Так как они считают это порождением каприза, а
не ума, постоянно и сознательно стремящегося к цели, они считают,
что не поняли.
Несомненно, они не вполне отдают себе отчет в том, чего требуют,
и они не сумели бы сформулировать свое желание, но если они не
удовлетворены, то они смутно чувствуют что им чего-то не хватает
Легко понять связь между сказанным и нашими предыдущими рас-
смотрениями. Чтобы преподавать устно или письменно, надо дать каж-
дую часть доказательства в совершенно осознанном виде, в соответствии
с одновременными стадиями проверки и «завершения», которые мы опи-
сали выше. При этом, думая о будущих следствиях, обычно стараются
увеличить число результатов-эстафет. При таком подходе (который ка-
жется наилучшим для получения ясного и строгого представления у на-
чинающего) не остается ничего от синтеза, важность которого мы под-
черкнули ранее. Этот синтез является для нас поводырем, без которого
мы были бы как слепые, умеющие ходить, но никогда не знающие на-
правления, в котором надо идти.
Те, кто может видеть такой синтез, «понимают математику». В про-
тивном случае имеются две тактики, отмеченные Пуанкаре (см. выше),
и обычно вторая тактика преобладает: студент чувствует, что чего-то
370
не хватает, но никак не может понять, в чем же дело; если он не пре-
одолеет эту трудность, все потеряно.
В первом из указанных Пуанкаре случаев студент, не найдя никако-
го подхода для синтеза, обходится без последнего. Хотя это и позволя-
ет ему продолжать учебу (часто в течение многих лет), его случай с
некоторой точки зрения хуже, чем у другого; тот понимает, по крайней
мере, существование трудности. Так как требуется все больше и боль-
ше математиков для различных областей, такой тип студента встреча-
ется часто. Однажды я опрашивал студента, который, руководствуясь
своим здравым смыслом, знал верный ответ на мой вопрос, но не ду-
мал, что он всегда вправе так ответить, и не отдавал себе отчета в том,
что указания его подсознания могли быть легко преобразованы в пра-
вильное и строгое доказательство.
Любопытные примеры такого типа часто встречаются среди сту-
дентов, занимающихся дифференциальным и интегральным исчисле-
нием. Чаще всего они задают себе вопрос, можно ли опираться на та-
кую теорему или формулу и выполнены ли условия ее применимости;
и они иной раз из-за этого причиняют себе немало хлопот, в то время
как здравый смысл указывает, что ответ практически очевиден... и с
другой стороны, они пренебрегают такой предосторожностью в тон-
ких вопросах, заслуживающих внимательного исследования! Это за-
мечание и другие аналогичные могут при случае оказаться полезными в
педагогике.
Логические и интуитивные умы. Политический аспект вопро-
са. Поговорив о студентах, перейдем к самим математикам, способ-
ным не только понимать математические теории, но и выдвигать но-
вые. Они отличаются не только от студентов, но и между собой. Было
подчеркнуто основное различие: некоторые математики «интуитив-
ны», другие — «логики». Об этом различии говорил Пуанкаре, так же
как и немецкий математик Клейн. Доклад Пуанкаре на эту тему начи-
нается так: «Одни прежде всего заняты логикой; читая их работы, ду-
маешь, что они продвигались вперед шаг за шагом с методичностью
Вобана, который готовит штурм крепости, ничего не оставляя на волю
случая. Другие руководствуются интуицией и с первого удара доби-
ваются побед, но иногда ненадежных, так же, как отчаянные кавалери-
сты авангарда».
Клейи доходит до введения в вопрос политики; он утверждал в 1893 г.:
«кажется, что сильная пространственная интуиция присуща тевтон-
ской науке, в то время как чисто логический критический дух более
развит в латинской и еврейской расах». Такое утверждение противоре-
чит фактам, что будет ясно видно, когда мы перейдем к примерам. Не-
24*
371
сомненно, что, говоря об этом, Клейн недвусмысленно рассматривает
интуицию с ее таинственным характером как нечто высшее по отно-
шению к прозаическому пути логики, и он, очевидно, счастлив провоз-
гласить такое превосходство своих соотечественников. Совсем недав-
но мы были свидетелями того, как нацисты провозгласили этот особый
вид этнографии, мы видим, что нечто подобное существовало уже в
1893 г.!
Такую тенденциозную интерпретацию фактов находишь всякий
раз, когда в игру вступают националистические и расистские страсти.
В начале первой мировой войны один из наших самых крупных уче-
ных и историков науки физик Дюгем был, точно так же, как и Клейн,
сбит с толку, но в противоположном смысле. В достаточно подробной
статье он изображает немецких ученых, особенно математиков, как
людей, лишенных интуиции или даже как сознательно ее отметающих.
Особенно трудно понять, как он может так характеризовать Римана,
который несомненно является одним из наиболее типичных примеров
интуитивного ума. Утверждение Дюгема в 1915 г. мне кажется столь
же необоснованным, как и утверждение Клейна в 1893 г. Если бы тот
или другой был прав, то из всего сказанного читатель сделал бы вы-
вод, что либо французы, либо немцы никогда не делали важных от-
крытий. Единственная тенденция, в которой я мог бы упрекнуть с этой
точки зрения немецкую математическую школу, состоит в системати-
ческих попытках — мало обоснованных и несколько педантичных
(особенно под влиянием Клейна) — утверждать, что в некоторых до-
казательствах анализа и в его арифметических приложениях предпоч-
тительнее употреблять ряды, чем интегралы. Как раз в этих вопросах
использование рядов кажется более логичным и использование инте-
гралов более интуитивным. В этой тенденции проявляется, может
был», еще некоторый национализм, так как ряды использовались зна-
менитым Вейерштрассом — совершенно очевидным представителем
логических умов, — репутация которого и влияние на немецких уче-
ных были огромны, в то время как Коши и Эрмит в аналогичных слу-
чаях вводили интегралы (что делал, впрочем, и Риман).
Точка зрения Пуанкаре на это различие. Пуанкаре — более муд-
ро, я полагаю, — не переводит вопроса в политический план. Напро-
тив, он показывает, насколько сомнительна эта точка зрения, и, чтобы
проиллюстрировать противоположность этих двух видов умов, он
сравнивает между собой двух французов, затем двух немцев.
Выше я был полностью согласен с идеями Пуанкаре, но на этот раз
я с ним разойдусь во взглядах. Мы цитировали первую фразу его док-
лада, воспроизведем теперь вторую.
372
«Отнюдь не обсуждаемый ими вопрос заставляет их использовать
тот или другой метод. Если часто об одних говорят, что они а на-
лит и к и, а других называют геометрами, то это не мешает то-
му, что первые остаются аналитиками, даже когда занимаются вопро-
сами геометрии, в то время как другие являются геометрами, даже ес-
ли занимаются чистым анализом. Сама природа их ума делает их «ло-
гиками» или «интуитивистами», и они не могут переродиться, когда
принимаются за новую тему».
Что мы должны думать, сравнивая эти два абзаца? Дважды было под-
черкнуто различие между интуицией и логикой, но на совершенно различ-
ных, хотя и имеющих друг к другу некоторое отношение, основаниях.
Эго становится еще более очевидным при рассмотрении примеров, дан-
ных Пуанкаре. Жозефу Бертрану, который совершенно очевидно имеет
конкретные пространственные представления по всем вопросам, он проти-
вопоставляет Эрмита, чьи глаза «кажутся лишенными контакта с миром» и
который ищет «видение истины изнутри, а не снаружи» (там же).
Конечно, Эрмит не имел привычки думать конкретно. Он испыты-
вал своего рода ненависть к геометрии и однажды, как ни странно, уп-
рекнул меня в том, что я опубликовал мемуар по геометрии. Естест-
венно, его собственные работы по конкретным вопросам редки и не
относятся к числу его самых замечательных. Таким образом, в соот-
ветствии со вторым заявлением Пуанкаре Эрмит должен рассматри-
ваться как математик с логическим складом ума.
Но считать Эрмита логиком! Ничто не может мне казаться менее
правдоподобным. Казалось, что методы всегда рождались в его уме
каким-то таинственным образом. На его лекциях в Сорбонне — кото-
рые мы слушали с неизменным восторгом — он любил начинать свои
рассуждения словами: «Начнем с тождества...»; затем он писал форму-
лу, точность которой можно было гарантировать, но ни происхожде-
ния которой, ни метода открытия он не объяснял — и мы не могли о
них догадаться. Это качество его ума отчетливо проявилось при от-
крытии им знаменитых квадратичных форм: в этом вопросе возможны
два случая и очевидно, что их свойства совершенно различны. В пер-
вом случае «приведение» было известно со времен Гаусса. Казалось,
что никому не могло прийти в голову применить ко второму случаю
выкладки, используемые в первом, так как они, видимо, не имели с
ним ничего общего; казалось совершенно абсурдным, что они могут и в
этом случае привести к решению; и тем не менее, посредством своего ро-
да колдовства, они к нему привели. Механизм этого исключительного яв-
ления был несколькими годами позднее частично объяснен с помощью
геометрической интерпретации (данной, естественно, не Эрмитом, а
Клейном); но для меня она стала совершенно ясной лишь после того, как
373
я познакомился с соответствующей концепцией Пуанкаре, в одной из его
первых заметок. Я не могу себе представить более совершенного типа ин-
туитивного ума, чем Эрмит. Итак, пример Эрмита неукоснительно пока-
зывает, что два определения интуиции и логики, данные Пуанкаре, не
совпадают, по крайней мере не вполне совпадают, что в какой-то мере
признал сам Пуанкаре именно в связи с примером Эрмита.
Двумя немецкими математиками, которых сравнивает Пуанкаре,
являются Вейерштрасс и Риман. Несомненно, что, как заключает Пу-
анкаре, Риман — типичный интуитивист, а Вейерштрасс — типичный
логик. Но по поводу этого последнего Пуанкаре замечает: «Можно
просмотреть все его книги, и вы не найдете в них ни одного чертежа».
Здесь допущена одна фактическая ошибка. Действительно, почти ни в
одном из мемуаров Вейерштрасса нет чертежей; существует лишь од-
но исключение, но оно существует и находится в одном из его самых
замечательных и наиболее сжатых произведений, которое производит
наиболее яркое впечатление совершенства: я говорю о его фундамен-
тальном методе в вариационном исчислении. Вейерштрасс там поме-
щает один единственный чертеж и, опираясь на него, все дальнейшее
выводит глубоко логическим методом, который является несомненно
ему свойственным; так что достаточно каждому, кто хорошо знает ма-
тематические методы, бросить взгляд на этот чертеж, чтобы восстано-
вить весь ход рассуждений. Но для построения этой фигуры требова-
лась, естественно, начальная интуиция. Это было тем более трудным и
гениальным актом, что требовалось порвать с общепринятыми мето-
дами, которые непрерывно приносили все новые успехи со времен
изобретения исчисления бесконечно малых; в частности, Лагранж ус-
пешно применил исчисление бесконечно малых для получения первой
части решения, но больше никому не удавалось его правильно допол-
нить. Вейерштрасс показал, что для получения результата надо полно-
стью отойти от традиционных методов и оперировать непосредственно.
Как видно, в действительности этот случай является ярким приме-
ром того общего факта, что логика идет вслед за начальной интуицией.
Вопросы и упражнения
для индивидуального осмысления
и коллективного обсуждения
1 . В соответствии с классификацией Н Бурбаки здание математики по-
коится на трех типах фундаментальных структур: алгебраических, порядка
и топологических. Приведите по одному примеру структур каждого типа
2 . Что Жан Пиаже понимает под «операторными структурами»?
3 . Прокомментируйте и постарайтесь примерами подтвердить или оп-
ровергнуть мысль Жана Пиаже о том. что порядок формирования геомет-
374
рических понятий и операций в самостоятельном развитии ребенка абсо-
лютно не соответствует историческому порядку этапов геометрии и боль-
ше приближается к порядку преемственности основных групп, с которыми
связаны различные виды пространств.
4 Что вы понимаете под интуицией? Как Кант трактует апостериорную
и априорную части интуиции? Какова роль интуиции в познании вообще, в
математике в частности?
5 Согласно Канту, пространство и время возникают из различных ис-
точников и поэтому не имеют друг с другом ничего общего: пространство
есть интуитивная форма внешнего восприятия, а время — внутреннего
восприятия. Покажите, опираясь на аргументы Г. Хана, как теория относи-
тельности Эйнштейна и другие недавние открытия в физике и математике
разрушили эти утверждения.
6 Покажите на примерах ненадежность утверждений, которые согласно
интуиции должны быть истинными или кажутся таковыми, но на самом де-
ле при строгой логической проверке оказываются ложными.
7 Известно, что в математике существуют три типа парадоксов: 1) про-
тиворечия и абсурдные утверждения, являющиеся следствиями непра-
вильных рассуждений; 2) теоремы, которые кажутся странными и неверо-
ятными, но которые, будучи доказанными логически безукоризненно,
должны быть приняты как верные, несмотря на то что они выходят за пре-
делы нашей интуиции и воображения; 3) парадоксы, связанные с противо-
речиями теории множеств или логические парадоксы. Приведите примеры
парадоксов каждого из названных типов.
8 . В чем вы видите отличия «логических » и «интуитивных» умов?
9 Прокомментируйте и проиллюстрируйте примерами следующее вы-
сказывание Пуанкаре: «Если часто об одних говорят, что они аналитики, а
других называют геометрами, то это не мешает тому, что первые остают-
ся аналитиками даже когда занимаются вопросами геометрии, в то время
как другие являются геометрами, даже если занимаются частым анализом
Сама природа их ума делает их «логиками» и «интуитивистами», и они не
могут переродиться, когда принимаются за новую тему». Покажите на при-
мерах, что в математике логика всегда идет вслед за начальной интуицией
10 . Проиллюстрируйте примерами протекание процессов математиче-
ского мышления в умах разного типа по классификации Ж. Адамара.
11 Дайте характеристику процессу математического творчества или
математическому открытию (по А. Пуанкаре) Покажите, какую роль играло
в этом процессе «бессознательное я» или подсознание автора и какова
роль первоначальной сознательной работы.
12 . Прокомментируйте следующие мысли Жана Пиаже: «В действи-
тельности, если здание математики покоится на структурах, которые соот-
ветствуют существующим структурам мышления, то дидактическую мате-
матику нужно основывать только на прогрессивной организации оператор-
ных структур...».
«Психологически операции происходят от действий, которые, самоуг-
лубляясь, координируются в структуры ...».
«Эмпиризм получается тогда, когда воспитатель заменяет математиче-
ское доказательство физическим экспериментом с простым запоминанием
полученных результатов...».
375
«Таким образом, обращение к эксперименту и действию и в общем
смысле так называемая активная педагогика не комментирует ни в чем
высшую дедуктивную строгость, но. наоборот подготовляет ее. создавая
ей реальную, а не только вербальную базу».
Как эти мысли Ж. Пиаже могут повлиять на методику преподавания ма-
тематики?
13 - Расскажите о роли «зрительного воображения» и пространственно-
го мышления в математике и в процессе обучения математике. Свой рас-
каэ проиллюстрируйте примерами из школьных курсов арифметики, алгеб-
ры. геометрии.
14 . Проведите анализ работы Г. Биркгоффа «Математика и психоло-
гия» Расскажите, как мыслят математики (о математике), какие существу-
ют особенности и различия в образе мышления математиков теоретикоа
прикладников, аналитиков, геометров.
15 . Может ли компьютер моделировать только более простые и более
рутинные мыслительные процессы математиков? Или их можно програм-
мировать для выполнения основной части математической деятельности
людей? Верно ли до сих пор в эпоху появления современных ЭВМ мнение
Г. Биркгоффа. высказанное им в 1969 г о том, что «для того, чтобы выпол-
нять нерутинные математические задачи экономнее и эффективнее лю-
дей, вычислительные машины должны управляться вышестоящими мате-
матиками, обладающими глубоким пониманием их ограничений?»
16 Как вы представляете себе возможности участия компьютера в про-
цессе математического творчества? Прокомментируйте мысль Г. Бирк-
гоффа, что такое участие — превосходный пример потребности в высоко-
развитом «симбиозе человека и машины, при котором каждый партнер де-
лает то, что он может делать лучше».
17 . Попытайтесь аргументировать следующее утверждение Г. Бирк-
гоффа: «С психологической точки зрения, математика имеет много общего
с музыкой и изобразительными искусствами. В обоих случаях важная роль
принадлежит тонкому эстетическому чувству». Какова роль и возможности
конструирования посредством компьютера в математическом творчестве,
музыке, изобразительных искусствах?
18 Расскажите о соотношении наглядности и логической строгости в
геометрии и анализе. Проиллюстрируйте свои утверждения примерами.
19 Расскажите об известных вам парадоксах теории множеств В чем
суть континуум-гипотезы?
20 Составьте тезисы двух следующих разделов доклада Г. Биркгоффа
по книге «Математика и психология»: А. Дискретная математика и психоло-
гия: Б Континуальная математика и психология.
КОММЕНТАРИИ СОСТАВИТЕЛЯ
1 Публикуемые отрывки взяты из книги выдающегося американского матема-
тика и популяризатора науки Мориса Клайна «Математика. Поиск истины» (Пер.
с ангя. М.: Мир, 1988). Имя этого автора хорошо известно в России по изданной
ранее его книге «Математика. Утрата определенности» (М.: Мир, 1984), которая
до сих пор пользуется заслуженным авторитетом.
В своих книгах автор ярко и увлекательно рассказывает о роли математики в
сложном многовековом процессе познания человеком окружающего мира, се мес-
те и значении в науках, в первую очередь в физике
Работы М Клайна особый интерес могут представлять для всех, кто интересу-
ется историей и методологией математики.
2 Публикуемый историко-математический очерк составлен известным совет-
ским математиком и педагогом Н Я. Виленкиным. Очерк представляет собой вто-
рой параграф первой главы книги «Современные основы школьного курса мате-
матики» (М ' Просвещение, 1980). Вся первая глава, называемая «Методические
основы математики», написана Н Я Виленкиным с использованием статей и книг
А.Д Александрова, А Н. Колмогорова, Н. Бурбаки, К. А. Рыбникова.
Хотя книга написана для студентов-математиков, она может представлять ин-
терес для специалистов многих направлений, а также любителей математики, же-
лающих глубже осмыслить изученный в школе курс.
3 Предлагаемые фрагменты взяты из разделе «Математика сегодня» книги за-
мечательного немецкого математика и педагога Г. Фройденталя (Математика как
педагогическая задача. Ч. I, М.: Просвещение, 1982). Особый интерес эта книга,
изданная в двух частях, представляет для учителей математики или родителей,
желающих активно участвовать в математическом воспитании своих детей. Изла-
гаемые в книге идеи могут быть полезны всем любителям математики, желающим
глубже проникнуть в суть математических понятий, идей или методов Например,
в первой части книги читатель познакомится с трактовкой автора таких понятий,
как математическая традиция, математика сегодня, математическая строгость,
упорядочение и др., различными подходами в развитии понятия о числе.
4 Публикуемый материал представляет собой один из разделов книги извест-
ного математика и педагога Ганса Фройденталя «Математика как педагогическая
задача», ч. II (Пер. с нем. М.: Просвещение, 1983). В книге, изданной в России в
двух частях, обсуждаются, в основном, проблемы преподавания математики. Од-
нако в связи с тем, что автор подвергает глубокому анализу различные пути изло-
жения многих ведущих математических разделов, идей, методов, книга будет пэлезна
многим любителям математики. Широкий диапазон обсуждаемых в книге вопросов,
стремление автора заставить читателя самостоятельно задуматься над ними и искать
наилучшие пути для их разрешения усиливают привлекателлость данной книги.
5 Предлагаемые тексты публикуются по книге известных американских мате-
матиков Р Куранта и Г. Роббинса «Что такое математика» (Пер. с англ. М.; Л.:
ОГИЗ. Гос. изд. техн.-теор. литературы, 1947).
В книге в доступной и оригинальной форме изложены основы теории чисел,
алгебры, математического анализа, геометрии, топологии. Изложение сопровож-
дается разбором многочисленных содержательных задач. Акцент авторами дела-
ется на раскрытии идей и методов математики.
377
* Перевод отрывке из вводной часта доклада великого математика Давида
Гильберт публикуется по книге «Хрестоматия по истории математики» (Под. ред
А.П. Юшкевича. М.: Просвещение, 1976).
Доклад Д. Гильберта «Mathematische Probleme» был произнесен почта самый
канун XX столетия — 8 августа 1900 г. на II Международном конгрессе математи-
ков в Париже и в том же году напечатан в «Gottinger Nechrichten» В своем докла-
де Гильберт выдвинул 23 задачи, от исследования которых он ожидал больших
успехов в общем прогрессе математики Произведенный Гильбертом отбор ока-
зался почта во всех случаях замечательно удачным; решение поставленных им
вопросов, растянувшееся на десятки лет (и для некоторых проблем еше не полу-
ченное), стимулировало творчество многих выдающихся ученых и повлекло зв со-
бой создание целых новых разделов математики Доклад Гильберта заслуживает с
этой точки зрения специального изучения. Заметим, что ученые России внесли
крупный вклад в решение ряда поставленных Гильбертом проблем.
7 Статья «Архитектуре математики» написана группой французских математи-
ков, публикующих свои работы под общим псевдонимом Николай Бурбаки Соз-
данный этой группой фундаментальный многотомный труд по современной мате-
матике под общим названием «Элементы математики» переведен на многие языки
мира и пользуется необычайной популярностью и авторитетом.
Текст статьи публикуется с небольшими сокращениями по сб Математическое
просвещение. I960, № 5. В этом же сборнике читатель может познакомиться со
статьей П. Халмоша, рассказывающей более подробно об авторах, скрывающихся
под псевдонимом Н. Бурбаки.
* Публикуемые фрагменты взяты из первых двух глав книги крупнейшего ма-
тематика XX в Андрея Николаевиче Колмогорова «Математика — наука и про-
фессия» (М.' Наука, 1988). Книга представляет собой сборник избранных статей
автора, содержащий разнообразный материал о сущности профессии математика,
ее фундаментальных понятиях, о связях математики с другими науками и физи-
кой, о теории вероятностей, алгоритме Евклида, 10-й проблеме Гильберта и мно-
гих других вопросах математики и математического образования.
9 Предлагаемый очерк о математическом понятии «мера» написан видными аме-
риканскими математиками Марком Кацем и Станиславом Уламом Нами этот текст
взят из книпг М. Кац, С. Улам Математика и логика. Ретроспектива и перспектива
(М : Мир, 1971), написанной авторами для издательства «Британская энциклопедия»,
которое готовило к изданию серию обзоров о состоянии и перспективах развития раз-
личных наук. В книге особое внимание уделено взаимодействию и взаимозависимости
математики и других наук.
10 Статья А.П. Нордена «Открытие Лобачевского и его место в истории новой
геометрии» открывает сборник классических работ по геометрии Лобачевского и
развитию его идей (Об основаниях геометрии. Гос. изд-во технико-теоретической
литературы М., 1956). В 1893 г., к столетнему юбилею со дня рождения Лобачев-
ского, Казанское физико-математическое общество выпустило в свет сборник «Об
основаниях геометрии» Сборник содержал переводы шести важнейших работ,
посвященных интерпретации геометрии Лобачевского и развитию ее идей (работы
Римана, Гельмгольца, Пуанкаре, переписке Гаусса с Шумахером) Через дв» года
сборник был переиздан с добавлением знаменитого мемуара Гаусса «Общие ис-
следования о кривых поверхностях».
378
К столетию со дня смерти Лобачевского государственное издательство техни-
ко-теоретической литературы повторяет издание Казанского физико-математи-
ческого общества, дополнив его 22 классическими работами по геометрии Лоба-
чевского и развитию ее идей. Из этого издания и азята статья А.П. Нордеиа. Все
три сборника давно стали библиографической редкостью.
11 Статья известного математика Р Куранта публикуется по сборнику «Мате-
матика в современном мире» (М Мир, 1967), представляющем собой полный пе-
ревод тематического номера журнала «Сайентифик Америкен» Другие статьи в
нем написаны такими известными учеными, как Филип Дж Дейвис, Морис Клайн,
У У. Сойер, Марк Кац, У.В Куайн, Ф Дж Дайсон, Эдуард Ф Мур. Ричард Стоун,
Ричард Беллман, Станислав М Улам Книга в целом не утеряла интерес до сих
пор для всех любителей математики.
11 Предлагаемые тексты взяты из книги известного советского математика и
педагога Б. В. Гнеденко «Математика и математическое образование в современ-
ном мире» (М.; Просвещение, 1985) В книге освещается значение математики в
современном мире, ее роль в образовании и общественном прогрессе Ознакомле-
ние с публикуемыми в хрестоматии двумя параграфами сформируют у читателя
лишь представление о характере книги и, надеемся, вызовут интерес к ознакомле-
нию с другими разделами книги проблемам математического образования, роли
математики в современном мире, примерами ее практического использования
” Статья известного советского математика А.Я. Хинчина публикуется с неболь-
шими сокращениями по тексту из сборника «Повышение эффективности обучения
математике» (М Просвещение, 1969). Эту статью можно квалифицировать как луч-
шее, что написано в России о воспитательных возможностях занятий математикой
Несмотря на то что впервые эта статья была опубликовано достаточно давно (Матема-
тическое просвещение. М., 1961, ып. 6), ее воспитательный потенциал до сих пор ве-
лик и далеко не до конца реализован преподавателями и родителями
14 Публикуемые материалы представляют собой отрывки из первых двух глав
книги известного математика и педагога У.У. Сойера «Прелюдия к математике»
(рассказ о некоторых любопытных и удивительных областях математики с пред-
варительным анализом математического склада ума и целей математики), пер. с
англ. М.: Просвещение, 1972. Изучение книги позволит любителям математики
познакомиться с многими ее областями, примыкающими к курсам средней школы,
развить и углубить изучаемые в школе идеи и методы.
15 Предлагаемые тексты азяты из книги выдающегося математика, психолога и
педагога Дж Пойа «Математическое открытие» (Пер. с англ. М.. Нвука, 1970).
Эта книга продолжает линию, начатую автором двумя более ранними его кни-
гами «Как решать задачу» и «Математика и правдоподобные рассуждения» (оии
также были переведены иа русский язык). Для общей характеристики всей книги
приведу для читателя лишь названия ее глав. Ч. I: Частные методы, Метод двух
геометрических мест. Метод Декарта, Рекурсия, Суперпозиция, ч II На пути к
общему методу — О задачах. Расширение области применения методов. Геомет-
рическое представление процесса решения. План и программа. Задачи внутри за-
дач, Зарождение идеи. Умственная работа. Дисциплина ума. Законы открытия9 Об
учении, преподавании и обучении преподавателя, Догадкв и научный метод.
Надеемся, что перечисление названий глав вызовет интерес у читателя к книге
в целом
379
14 Публикуемая работа известного французского психолога Жанв Пиаже пред-
ставляет собой первую главу результатов коллективной работы Международной
комиссии по изучению и улучшению преподавания математики (Ж. Пиаже, Э. Бет,
Ж. Дьедонне, А. Лихиерович, Г. Шоке, К. Гаттеньо. Преподавание математики.
Пер. с франц. Гос. уч.-пед. изд. МЛ РСФСР, М.;, 1960). Публикуемый доклад, сде-
ланный Ж. Пиаже иа конференции в Решепте близ Милана в 1952 г., был посвя-
щен обсуждению с психологической точки зрения выступления известного мате-
матика Дьедонне об изучении математических структур (с общим понятием струк-
туры и типами структур читатель может познакомиться по публикуемой в данной
хрестоматии статье Николая Бурбаки «Архитектура математики»). В мзванной выше
книге опубликованы и другие не менее интересные статьи членов Международной
комиссии.
17 Приведенные тексты взяты из книги известного современного американско-
го математика Гаррета Биркгоффа (Garret Birkhoff) «Математике и психология»
(Пер. с англ. М.: Советское радио, 1977). Книга интересна тем, что в ней с доста-
точно широких современных позиций обсуждаются связи между математикой и
психологией, возможности «механизации» математического мышления Вскрывая
ограничения вычислительной техники (конечно же, созданной к моменту выхода в
свет английского издания этой книги в 1969 г.), автор рекомендует к использова-
нию их в «симбиозе» с людьми. Несмотря ив научно-популярный характер, книга
будет интересна всем, кто интересуется вопросами кибернетики и прикладной ма-
тематики, особенно их методологическими и философскими аспектами В книге
Г. Биркгоффа содержатся многочисленные ссылки на научные источники, кото-
рые мы в публикуемых фрагментах опустили.
11 Предлагаемая статья Ганса Хана посвящена анализу роли интуиции в мате-
матическом сознании На ярких математически содержательных примерах автор
показывает, сколь ненадежной оказывается интуиция во многих случаях, как часто
утверждения, которые, согласно интуиции, должны быть истинными, оказываются
ложными при строгой логической проверке.
Статья публикуется по сборнику: «Математики о математике». М; Знание, 1972.
19 Предлагаемая статья выдающегося математика Анри Пуанкаре (1854—1912)
представляет собой изложение его доклада Психологическому обществу в Пари-
же. Многие исследователи сущности и процесса математического творчества ана-
лизировали, комментировали этот доклад и ссылались на него. В частности, идеи
А. Пуанкаре существенным образом развил известный математик XX столетия
Ж. Адамар в работе «Исследование математики», отрывки из которой также пуб-
ликуются в данной книге.
10 Публикуемый очерк о различных типах математических умов был взят из
переведенной с французского на русский книги выдающегося математика XX сто-
летия Жака Адамара «Исследования психологии процесса изобретения в области
математики» (Сов. радио. М., 1970) Книга представляет собой переработанный и
дополненный перевод на французский язык курса лекций, прочитанных в 1943 г.
Ж. Адамаром в «Свободной школе высших исследований» в Нью-Йорке В книге
автор часто ссылается на известный доклад выдающегося математика А. Пуанкаре
«Математическое творчество», также публикуемый в настоящей хрестоматии. Со-
ставитель надеется, что ознакомление с публикуемым отрывком вызовет у читате-
ля интерес и желание обратиться к ознакомлению со всей книгой Жака Адамара.
380
11 Статьи Анри Пуанкаре «Пространство и время» и «Опыт и геометрия» пуб-
ликуются по его книге «О науке», изданной в издательстве «Наука» в 1983 году.
Эти статьи являются главами книги «Наука и гипотеза». Помимо названной книги
в том «О науке» вошли еше три книги А. Пуанкаре; «Ценность науки», «Наука и
метод», «Последние мысли». Несмотря на то, что все эти книги посвящены анали-
зу путей познания в математике, механике, физике они, безусловно, будут полез-
ны широкому кругу читателей, интересующихся процессом познания и творчест-
ва, философией и методологией науки.
и Статья известного американского математика Тобиуса Данцига взята из его
книги «Числа — язык науки» (иа русском языке она была опубликована в брошю-
ре «Математики о математике», изданной в серии XIX «Математика Кибернети-
ка» в 1967 году). В этой книге автор убедительно показывает, что математическая
символика не только помогает стенографировать математические рассуждения, ио
в случае ее адекватности может существенным образом стимулировать прогресс
математической мысли.
Источники
Адамар Ж. Исследование психологии процесса изобретения в области матема-
тики. М., 1970.
БиркгоффГ Математика и психология. М., 1977.
Ггейзер Г Роберт И, Розов Н Математика и информатика. Программа обще-
образовательного курса. М , 2000.
Гчеденко Б Математика и математическое образование в современном мире
М.. 1971.
Кац М. Улам С. Математика и логика Ретроспектива и перспектива М , 1971.
Клайн М. Математика Поиск истины М., 1988.
Колмогоров А. Математика— наука и профессия. М., 1988.
Курант Р, Роббинс Г Что такое математика М; Л., >947.
Математика в современном мире Сб М., 1967.
Математики о математике. М., 1972.
Математическое просвещение. М., 1960. Вып. 5.
Об основаниях геометрии: Сб. классических работ по геометрии Лобачевского
и развитию ее идей / Ред. и вступ. ст. А П. Нордена М., 1956.
Повышение эффективности обучения математике в школе / Сб под ред Г Глей-
зера М., 1989.
ПойяД Математическое открытие / Под. ред. И М. Яглома М., 1970
Преподавание математике. Сб. Пособие для учителей. М., 1960.
Современные основы школьного курса математики. М., 1980.
Пуанкаре А. О науке. М., 1983.
Сойер У Прелюдия к математике. М., 1972.
Фройденталь Г Математика как педагогическая задача / Под. ред. Н.Я. Ви-
ленкина. М., 1982 Ч. I; 1983 Ч. И.
Хрестоматия по математике. Арифметика и алгебра. Теория чисел. Геометрия /
Под ред А П. Юшкевича. М., 1976.
Хрестоматия по истории математики Математический анализ. Теория вероят-
ностей / Под ред А П. Юшкевича. М., 1977.
Дополнительная литература
Азевич А Двадцать уроков гармонии: гуманитарно-математический курс. М.,
1998.
Болтянский В , Ефремович В. Очерк основных идей топологии Математиче-
ское просвещение. М.. 1957. Вып. 2, 1958. Вып. 3; 1959. Вып 4; 1961. Вып. 6.
Борель Э. Вероятность и достоверность. М., 1961.
Бурбаки Н Очерки по истории математики. М., 1963.
Вейль Г Математическое мышление. М., 1989.
Вейль Г Философия математики М ; Л., 1934
Вилейтнер Г. История математики от Декарта до середины XIX столетия. М.. 1966.
Винер НЯ — математик. М., 1970.
Глейзер Г История математики в школе. М., 1981. IV—VI кл., 1982. VII—
VIII кл.; 1983 IX—Хкл
Клайн М Математика. Утрата определенности. М., 1984.
Колмогоров А. Математика. БСЭ, 3-е изд. Т. 15.
Лакатош И. Доказательства и опровержения М., 1967.
Радимахер Г, Теплиц О Числа и фигуры Опыты математического мышления
М., 1962
Шикин Е.. Шикин Г. Гуманитариям о математике. М , 1999.
382
Составитель Г.Д. Глейзер
МАТЕМАТИКА
ХРЕСТОМАТИЯ
ПО ИСТОРИИ. МЕТОДОЛОГИИ, ДИДАКТИКЕ
Корректор Л Я Сидорова
Оригинал-макет подготовила ИА. Пеннер
ISBN 5-204-00249-9
Изд. лицензия № 021079 от 28.10.96.
Изд. № 2011. Сдано в набор 03.01.01. Подписано в печать 29.03.01.
Формат 60x90/16. Печать офсетная. Бумага офсетная. Гарнитура «Таймс».
Уч.-изд. л. 23,7. Усл. печ. л. 24,0. Тираж 3000 экз. Зак. 72
Издательство УРАО
Москва, Б. Полянка, 58
Те л./фак с (095) 245-33-43
Отпечатано с готового оригинал-макета в ГУП «Облиздаъ
248640, Калуга, пл. Старый торг, 5