Автор: Тишин В.В.
Теги: компьютерные технологии математика задачи по математике дискретная математика
ISBN: 978-5-9775-0232-0
Год: 2008
Текст
I I
скр
магемет ка
в примерах и задачах
Множества, декартовы произведения,
соответствия, отношения
■ Булевы функции
■ Теория алгоритмов •
m Предикаты
■ Комбинаторика
■ Конечные автоматы
1. :■:■ t
1
р-**'
Mw
в. в. Тишин
Дискретная
в примерах и задачах
Допущено учебно-методическим советом по прикладной математике
и информатике УМО по классическому университетскому образованию
в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по специальности и направлению "Прикладная математика
и информатика" и по направлению "Информационные технологии"
Санкт-Петербург
«БХВ-Петербург»
2008
УДК 681.3.06(075.8)
ББК 32.973.26-018.2я73
Т47
Тишин В. В.
Т47 Дискретная математика в примерах и задачах. — СПб.:
БХВ-Петербург, 2008. — 352 с: ил. — (Учебная литература
для вузов)
ISBN 978-5-9775-0232-0
Учебное пособие составлено на основании материалов
лекционного курса, содержит краткую теорию, варианты заданий и примеры
решения по следующим разделам дискретной математики: множества,
декартовы произведения, соответствия, отношения, булевы функции,
теория алгоритмов, П1)едикаты, комбинаторика, конечные автоматы.
Даны основные определения, необходимые для выполнения заданий.
Для каждого типа задач предлагается по 30 вариантов заданий,
приводится подробный образец решения.
Для преподавателей и студентов технических вузов
и университетов, аспирантов, научных работников и инженеров
УДК 681.3.06(075.8)
ББК32.973.26-018.2я73
Группа подготовки издания:
Главный редактор Екатерина Кондукова
Зам. главного редактора Татьяна Лапина
Зав. редакцией Григории Добин
Компьютерная верстка Ната,1ьи Караваевой
Корректор Виктория Пиотровская
Дизайн серии Инны Тачиной
Оформление обложки £/7е«ь/ Беляевой
Фото Кирилла Сергеева
Зав. производством Николай Тверских
Лицензия ИД № 02429 от 24.07.00. Подписано в печать 07.07.08.
Формат 60x90Vie. Печать офсетная. Усл. печ. л. 22.
Тираж 2500 экз. Заказ № 3332
"БХВ-Петербург", 194354, Санкт-Петербург, ул. Есенина, 5Б.
Санитарно-эпидемиологическое заключение на продукцию
№ 77.99.60.953.Д.003650.04.08 от 14.04.2008 г. выдано Федеральной службой
по надзору в сфере защиты прав потребителей и благополучия человека.
Отпечатано с готовых диапозитивов
в ГУП "Типография "Наука"
199034, Санкт-Петербург, 9 линия, 12
ISBN 978-5-9775-0232-0 © Тишин в. в., 2008
© Оформление, издательство "БХВ-Петербург", 2008
Оглавление
Предисловие 1
Глава 1. Множества, графики, соответствия, отношения 5
1.1. Операции над множествами 5
1.2. Графики 36
1.3. Соответствия 45
1.4. Отношения 60
Глава 2. Булевы функции 73
2.1. Булевы функции. Суперпозиции 73
2.2. Булевы функции и теория множеств 83
2.3. Нормальные формы и полиномы 93
2.4. Классы Поста 102
2.5. Минимизация нормальных форм всюду определённых
булевых функций 116
2.6. Частичные функции и схемы 126
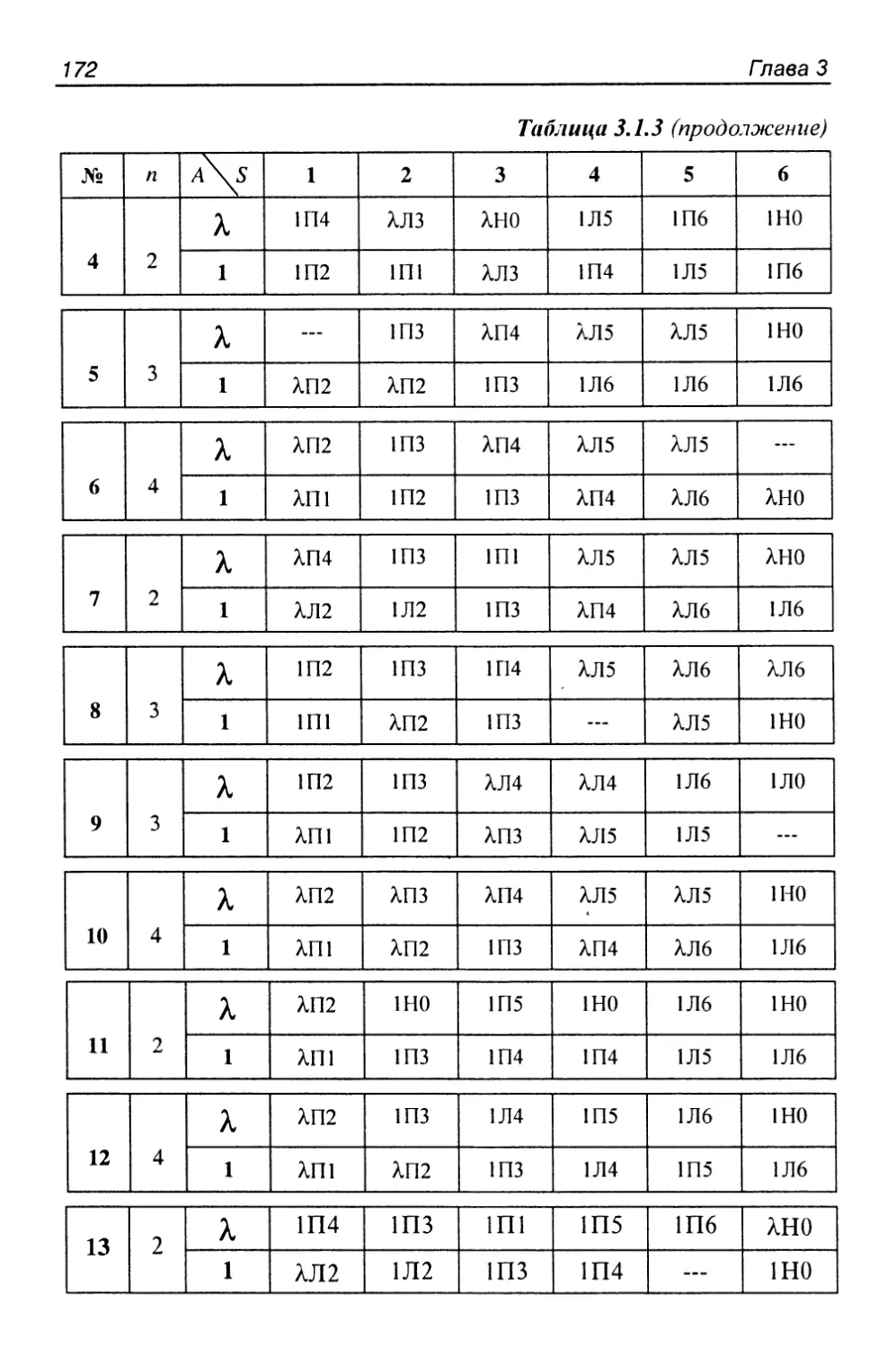
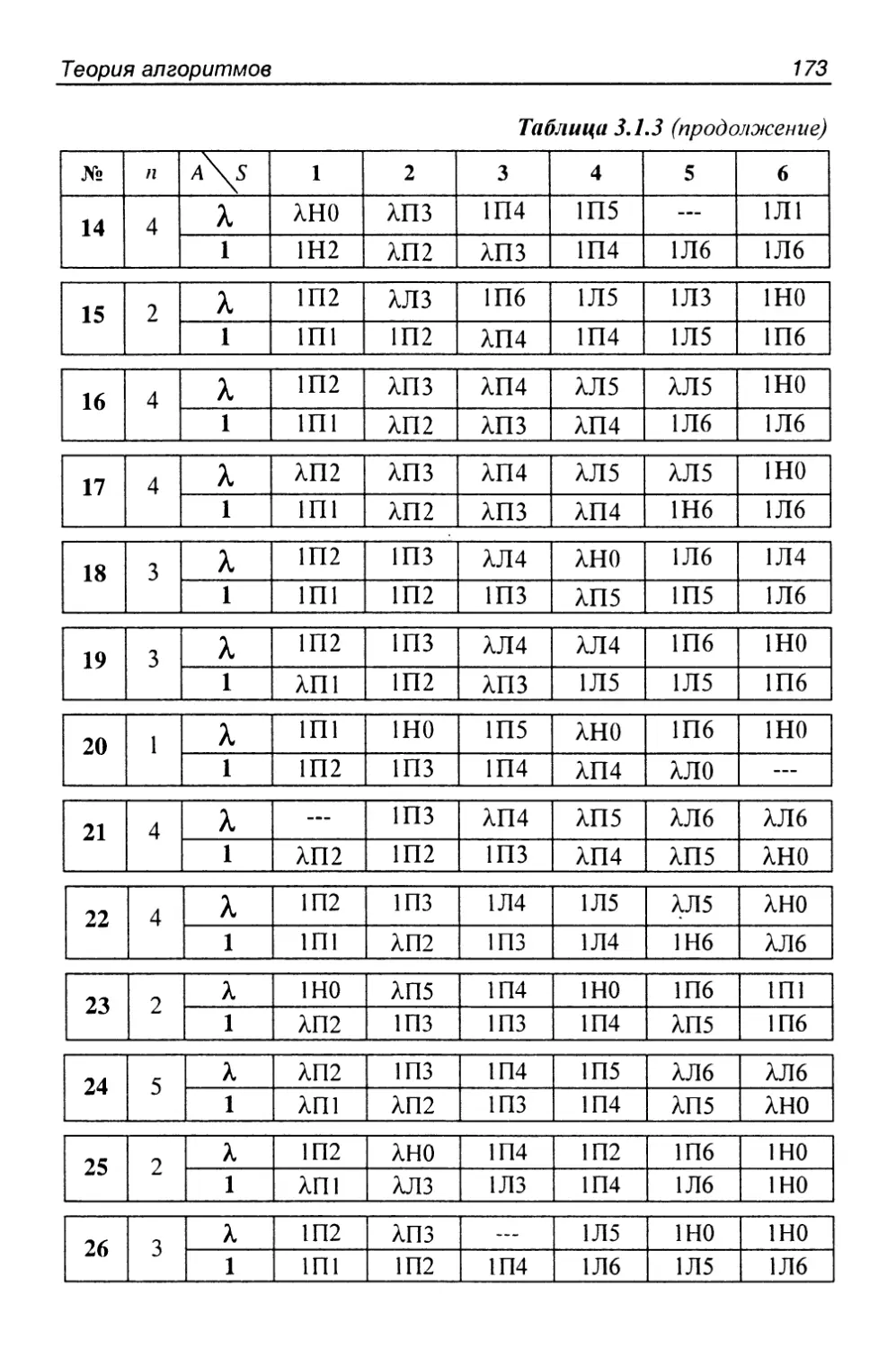
Глава 3. Теория алгоритмов 163
3.1 Машины Тьюринга 163
3.2. Нормальные алгоритмы 179
3.3. Рекурсивные функции 189
Глава 4. Предикаты 197
4.1. Предикаты 197
\\/ Оглавление
Глава 5. Комбинаторика 211
5.1. Сочетания, размещения, перестановки 211
5.2. Бином Ньютона и полиномиальная формула 217
5.3. Формула включений и исключений 226
5.4. Задачи о распределениях 231
5.5. Арифметический треугольник 235
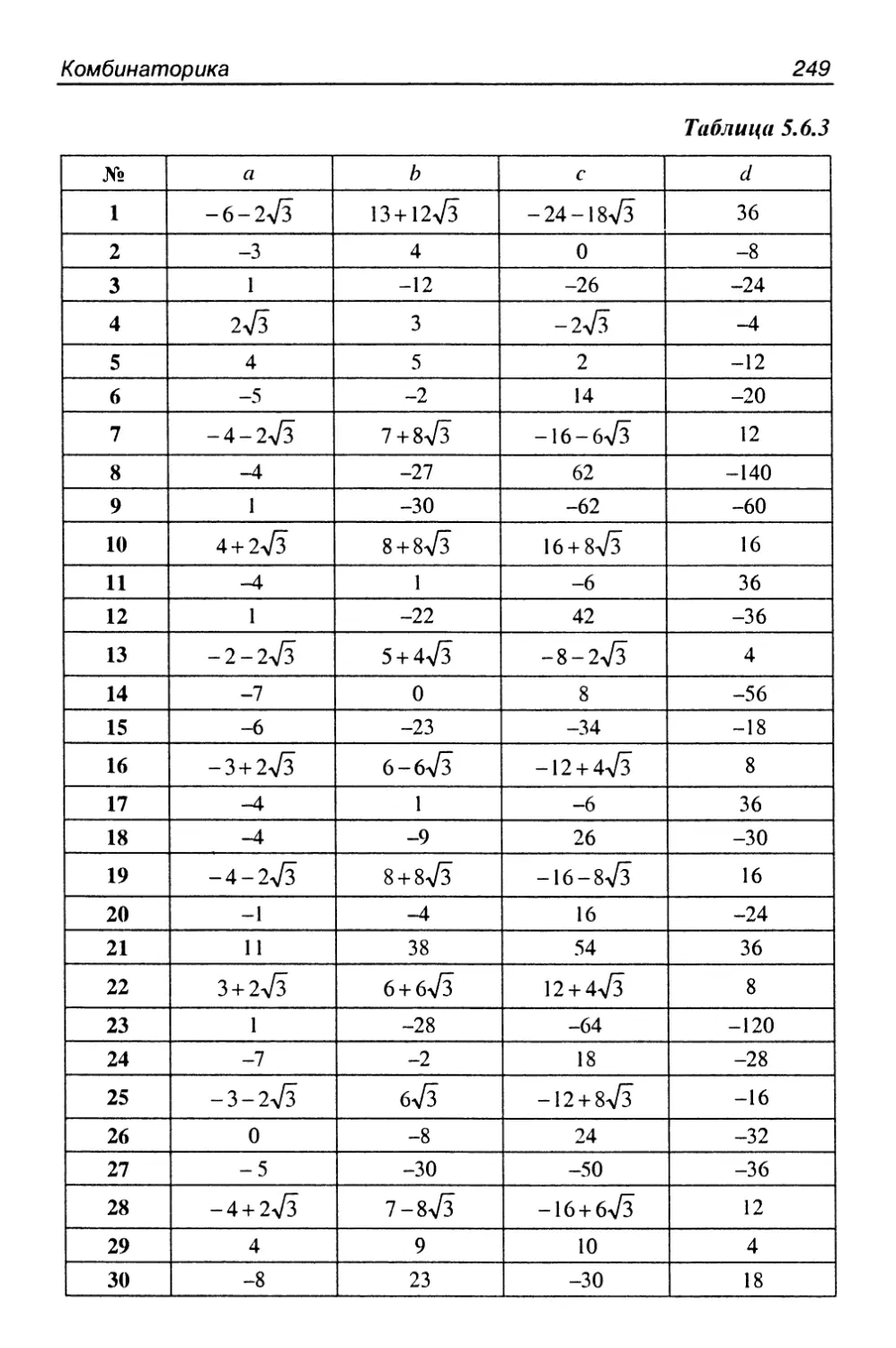
5.6. Рекуррентные соотношения 243
Глава 6. Конечные автоматы 255
6.1. Автоматы Мили 255
6.2. Частичные автоматы 269
6.3. Реализация автоматов схемами 284
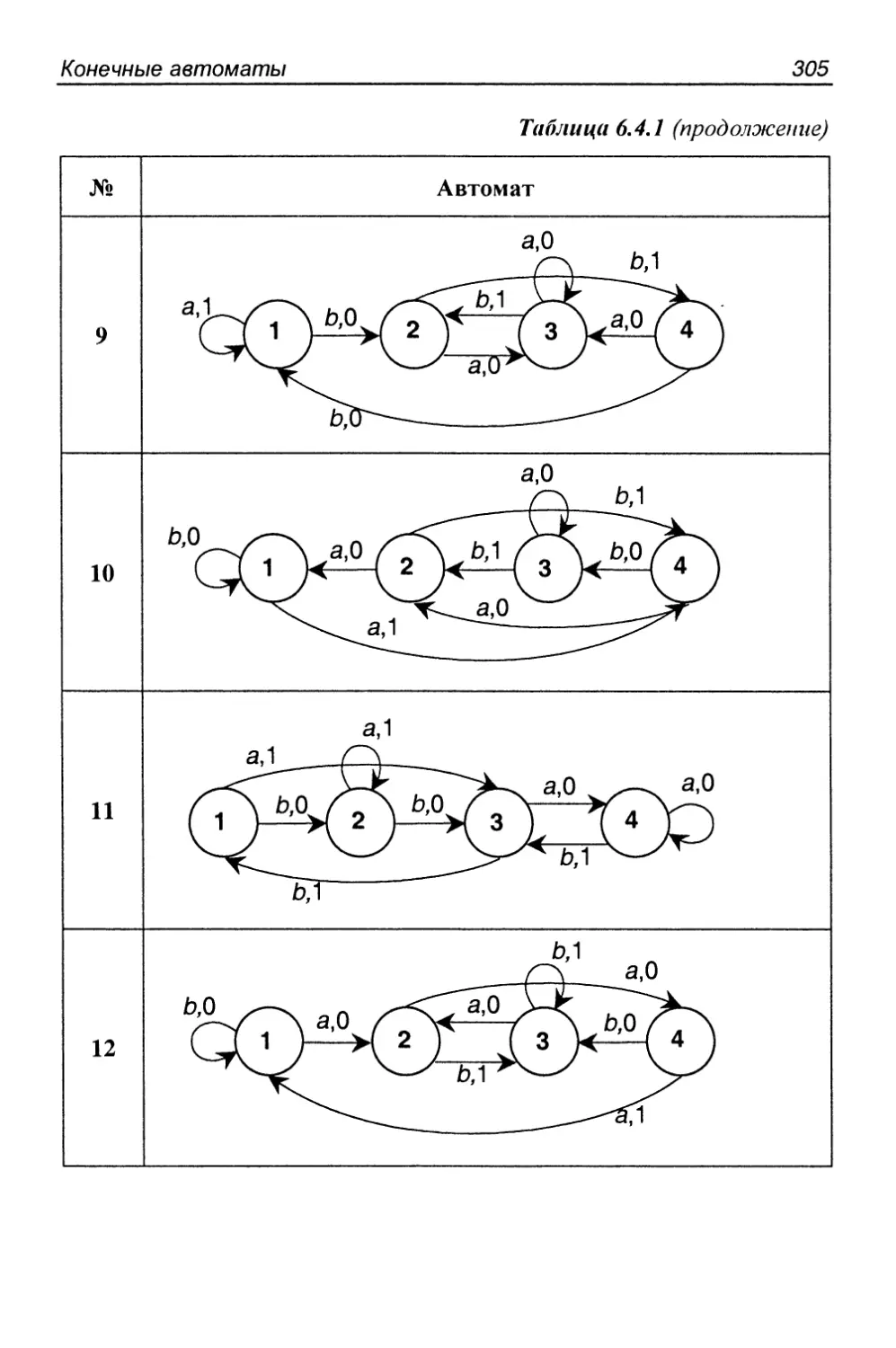
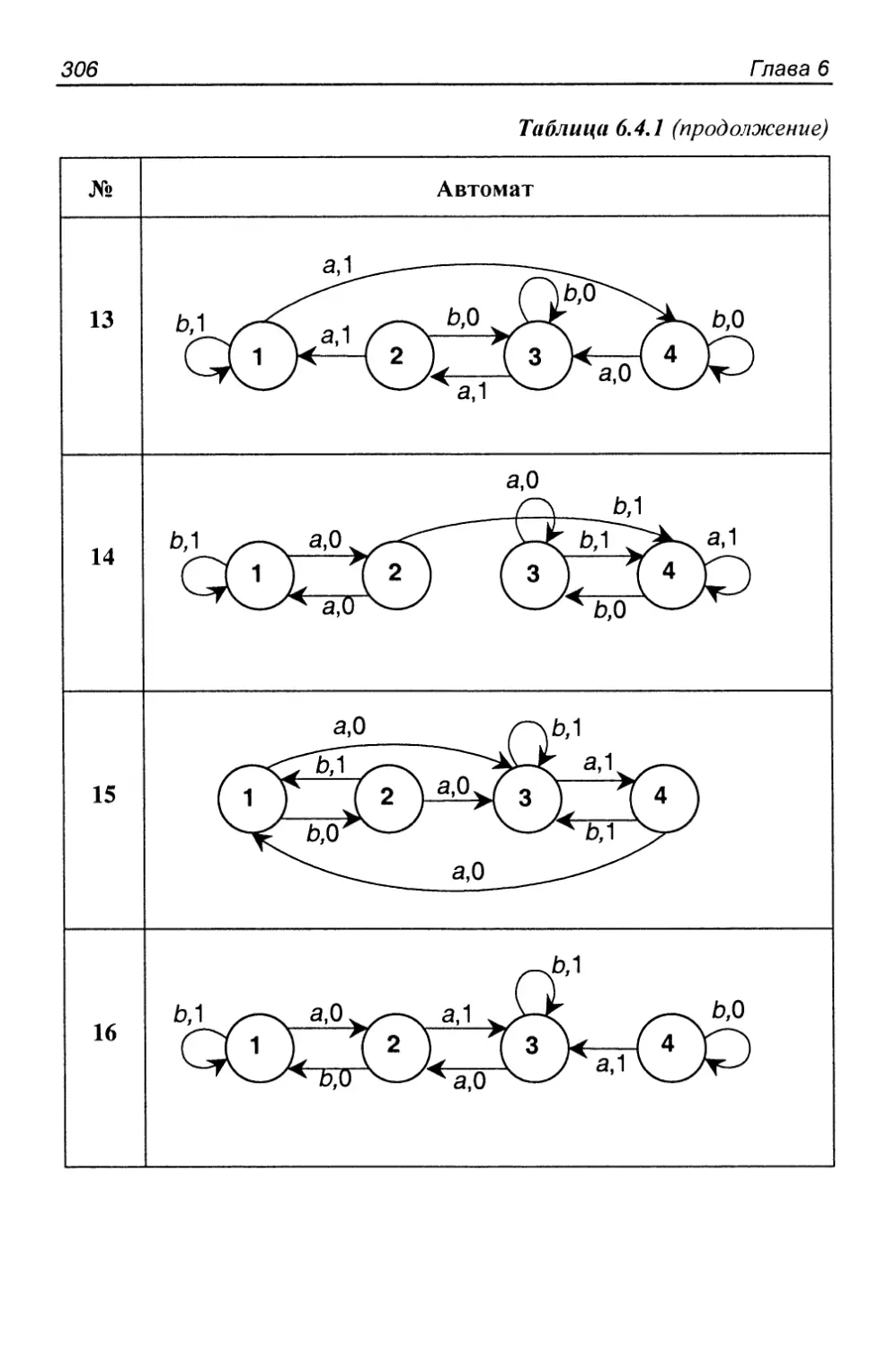
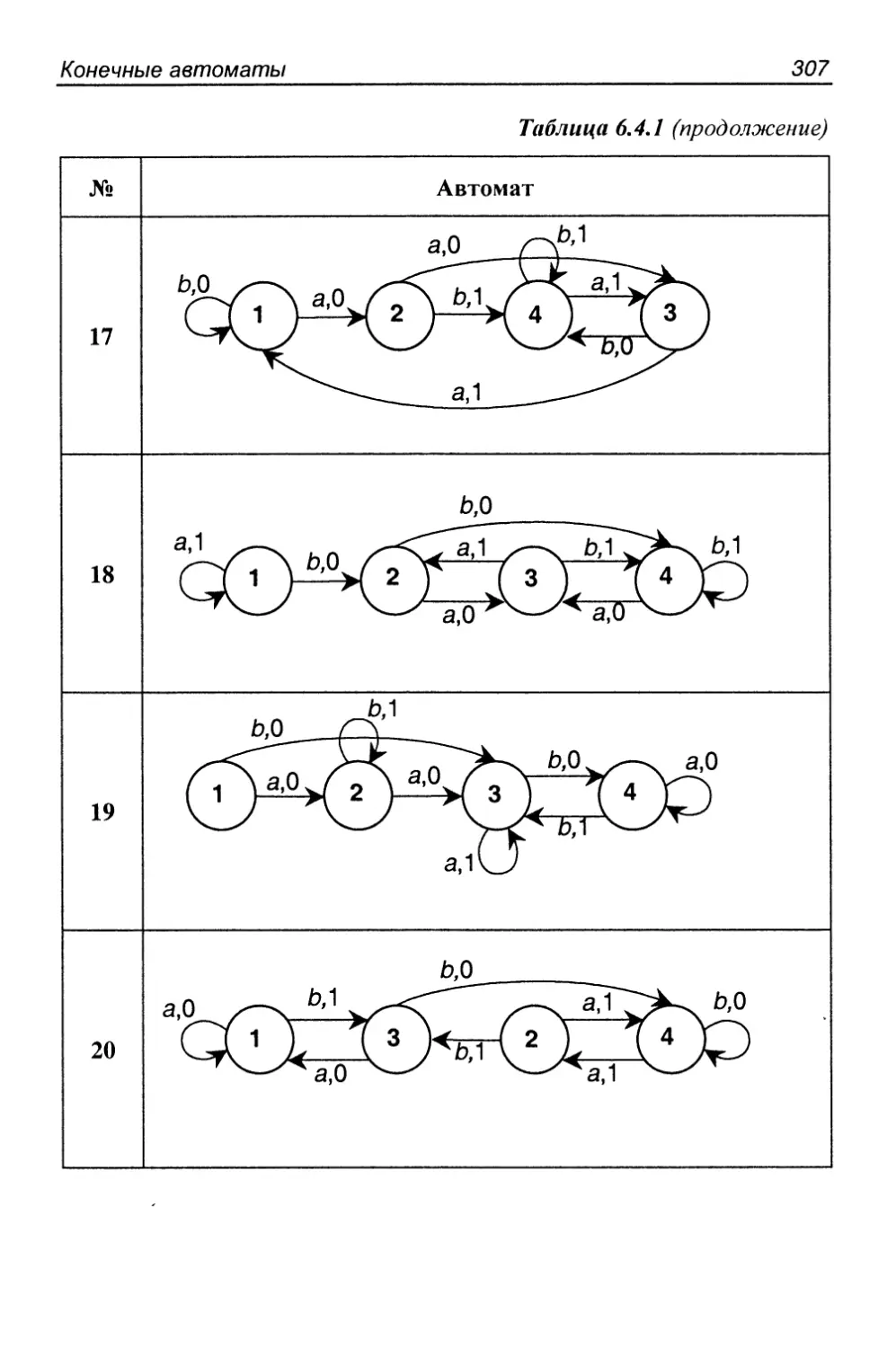
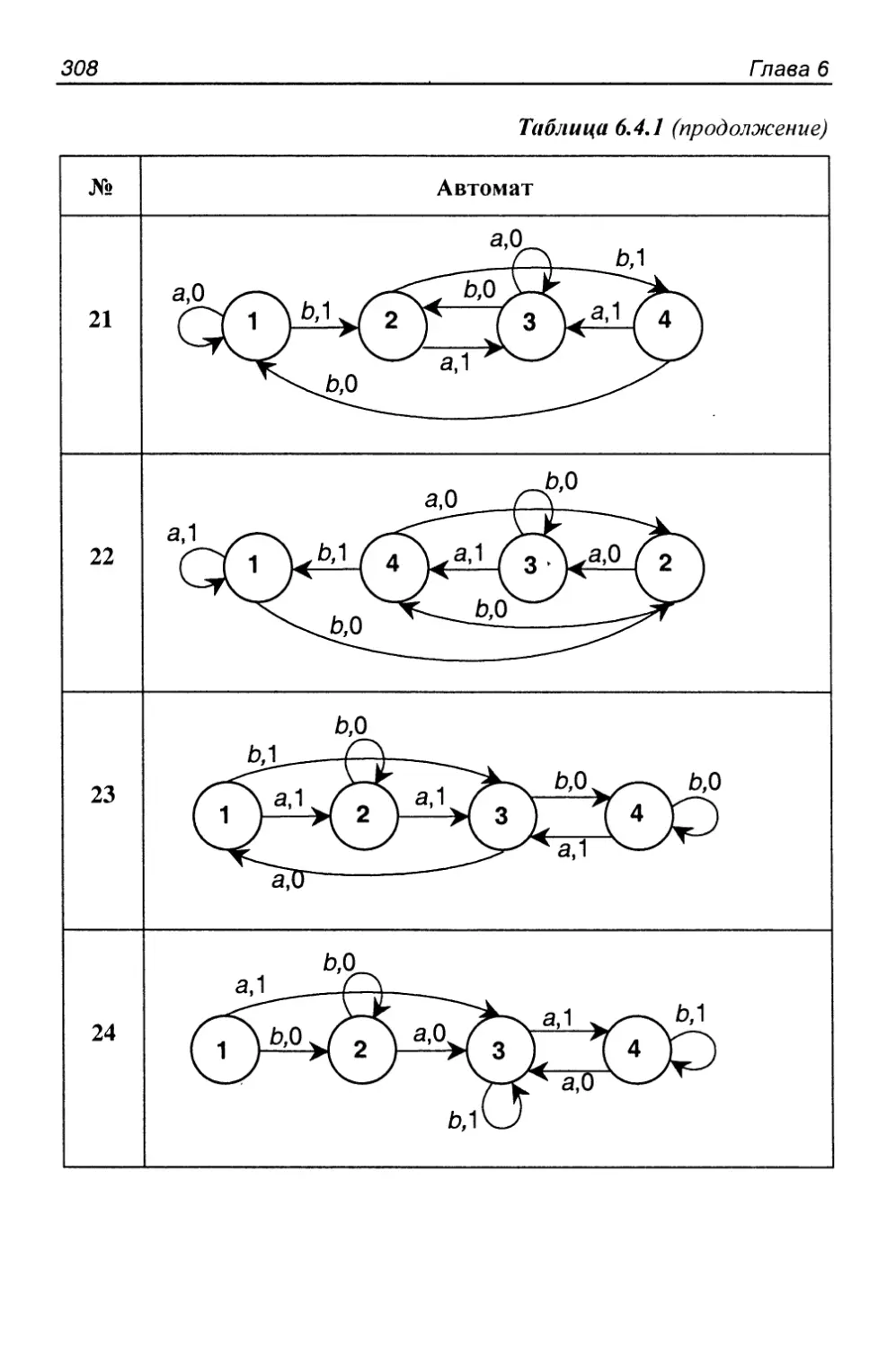
6.4. Распознавание множеств автоматами 300
Список литературы 337
Предисловие
Дискретная математика — одно из самых динамично
развивающихся направлений современной математики, и тотальная
компьютеризация всех областей нашей жизни приводит к
постоянному росту спроса как на программистов, так и на
специалистов, разрабатывающих математические основы компьютерных
технологий.
Важным моментом усвоения математики и овладения её
методами является самостоятельная работа учащегося. Система
индивидуальных заданий активизирует самостоятельную работу
студентов и способствует более глубокому освоению курса и
отработке приёмов решения задач.
Всем, имеющим отношение к преподаванию дискретной
математики, знакомы, ставшие классическими, задачники:
"Задачи и упражнения по дискретной математике" Г. П. Гаврилова
и А. А. Сапоженко, "Алгебра логики в задачах" С. Г. Гиндикина,
а также "Задачи по теории множеств, математической
логике и теории алгоритмов" И. А. Лаврова и Л. Л. Максимовой, но
в настоящее время ощущается потребность в задачниках по
дискретной математике, содержащих серии однотипных задач для
выполнения студентами индивидуальных заданий.
Настоящий сборник отражает многолетний опыт работы
автора, приобретённый им в Самарском государственном
аэрокосмическом университете им. С. П. Королёва при чтении лекций,
а также при ведении практических занятий по курсам
"Дискретная математика" и "Математическая логика и теория
алгоритмов".
Предисловие
Система индивидуальных заданий, практикуемая в СГАУ
с 80-х годов прошлого века, хорошо себя зарекомендовала. При
проведении практических занятий студенты активно участвуют в
решении и разборе задач, аналогичных тем, что им придётся
выполнять индивидуально. Большинство разделов курса дискретной
математики подкреплено и проиллюстрировано
индивидуальными заданиями, и самостоятельное решение студентами задач
помогает им лучше усвоить теорию и получить практические
навыки работы с объектами, являющимися предметом изучения
дискретной математики. Выполнение комплекса задач,
вошедших в данное пособие, даёт возможность студентам освоить
базовые понятия дискретной математики, прочувствовать связи
между ними и отработать приёмы решения основных типов задач
данного предмета.
Каждое задание даётся в 30 вариантах, и для каждого задания
в сборнике приведён образец решения, что может помочь
студентам внимательно разобрать предлагаемые способы решения задач
и грамотно оформить выполненные индивидуальные задания.
Данное пособие может быть также полезно для вузов,
практикующих заочную форму обучения, а также для всех энтузиастов,
решивших изучить дискретную математику самостоятельно.
Пособие состоит из 6 глав:
□ Множества, графики, соответствия, отношения;
□ Булевы функции;
□ Теория алгоритмов;
□ Предикаты;
□ Комбинаторика;
□ Конечные автоматы.
В начале каждой главы вводятся понятия, даются определения
и формулировки теорем, используемых при выполнении заданий,
что практически исключает необходимость привлечения
дополнительной литературы по рассматриваемой тематике.
Некоторые задачи, вошедшие в пособие, возникли
"тиражированием" идей, встречавшихся в классических задачниках по
дискретной математике, другие — в процессе чтения автором курсов
Предисловие
''Дискретная математика", ''Основы дискретной математики"
и "Математическая логика и теория алгоритмов" в Самарском
государственном аэрокосмическом университете им. С. П.
Королёва и общения со студентами.
Приношу благодарность всем, вдохновившим меня на этот
труд: авторам, идеи которых получили развитие в данной книге,
и своим студентам, чья заинтересованность и свежесть взгляда
повлияли на материал, представленный в данном сборнике.
Глава 1
Множества, графики,
соответствия, отношения
1.1. Операции над множествами
Запись хе А означает, что элемент х принадлелсит
множеству А. Если X не является элементом множеств Л, то пишут
х^ А или XG л. Два множества А w В считаются равными,
если они состоят из одних и тех же элементов. Будем писать Д = В,
если АиВ равны и А^ В в противном случае.
Множество называется пустым и обозначается 0, если оно не
содержит элементов.
Будем говорить, множество Л во/очено в множество В, и
писать AqB, если каждый элемент множества Л является
элементом множества В. В этом случае А называется подмноэюеством
множества В. Считается, что для любого А справедливо
включение 0 с Д.
Если ДсВи АфВ,то будем писать ЛсВ и говорить, что
множество А строго включено во множество В.
Семейство всех подмножеств данного множества А
обозначается Р{А).
Мощностью конечного множества А будем называть число
его элементов. Мощность конечного множества А
обозначается |Л|.
Объединением мнолсеств А и В называется множество
ЛиВ = {л'|;сЕЛ или jcgB}.
Глава
Пересечением множеств Л и В называется множество
Ar\B^[x\xG. Л и хЕ В].
Разностью множеств Av\Bназывается множество
А\В = [х\хе: л и хб В).
Если все рассматриваемые множества являются
подмножествами некоторого универсачьного множества U , то разность U \А
называется дополнением А и обозначается Л .
Симметрической разностью множеств Лий называется
множество A^B = {A\B)KJ{B\A).
Будем говорить, что множества Л и В находятся в общем
положении, и писать Л QDВ, если существуют такие элементы а,Ь,с,
что as Аи а^ В, ЬеВи b€ В, се А и се В.
Задание 1.1.1
1. Справедливо ли в общем случае утверждение: если ЛаВ
и В(ЗС и CyD,TO Л50?
2. Может ли при некоторых Л, В, С и D выполниться набор
условий: ЛаВ и В(ЗС и CyD и Л50?
Таблица LL1
№
1
2
3
4
5
6
7
8
9
10
а
с
е
с
G
С
е
6
G
G
G
Р
G
G
С
С
с
G
С
G
С
С
Y
с
с
G
6
G
6
С
С
6
с
8
с
G
G
С
С
С
с
с
с
с
№
11
12
13
14
15
16
17
18
19
20
а
G
С
С
с
G
С
С
6
с
G
Р
G
G
С
G
G
С
G
С
С
G
Y
с
с
с
G
G
G
С
С
С
с
S
G
G
G
С
G
С
G
G
С
G
№
21
22
23
24
25
26
27
28
29
30
а
G
С
G
С
С
G
G
С
G
С
Р
С
с
G
С
G
С
С
G
С
С
Y
с
G
С
С
G
G
С
С
С
G
S
С
G
С
G
С
G
G
С
С
с
Множества, графики, соответствия, отношения 7
Примеры решения задания 1.1.1
Пример 1.
а) Справедливо ли в общем случае утверэюдение :
если А а В, В qC и С (Z D, то AqD ?
Пусть хе А. Так как Ad В, из определения включения
следует, что XG В. Так как xG Ви BqC, то xg С. Так как xG С
и C(zD, то XG D. Итак, из того, что произвольный элемент
XG А следует, что xG D. На основании определения заключаем,
что Л с D, то есть данное утверждение верно.
б) Моэюет при некоторых А, В, С и D выполняться набор
условий: Ad В, BdC и CdD, и AdD ?
Да, может. Это следует из справедливости утверждения в
пункте а).
Примером могут служить множества Л = {jc}, В = С = {х,у},
D = {x,y,z}. Тогда {x}d[x,y}, {x,y}d{x,y}, {х,у} d{x,y,z}
и {x}d{x,y,z}.
Пример 2.
а) Справедливо ли в общем случае утверэюдение:
если Ad В, BgC и Се D, то AdD ?
Пусть Л = {х}, В = {х,у}, C = {[x,y},z}, D = [{{x,y},z}M-
Тогда {x}d{x,y} и {x,y}G {{x,y},z}G {{{x,y},z},w}.
Но в то же время неверно, что {х}с{{{х,y},z},w}, так как
единственный элемент х множества А не является элементом
множества D, состоящего из элементов {{х,у},г}и w. Итак,
утверждение из нашего примера 2а) в общем случае неверно.
б) Моэюет ли при некоторых А, В, С и D выполняться набор
условий: Ad В, Вес, CeD и AdD ?
Да, может. Например, А = 0, В = {х}, С = {{х},у},
D = {{{x},y},z}.
Тогда 0 с {х}, {х}е{{х},у], {{x},y}G{{{x},y},z} и в то же
время 0c{{{x},y},z}.
8
Глава 1
Задание 1.1.2
Для универсального мнол<ества t/ ={ -5, - 4, - 3, - 2, -1,1,2,3,4,5},
множества Л, заданного списком, и для В, являющегося
множеством корней уравнения х"^ + сие' +^х -f у-^ + S = О.
1. Найти множества: Л и Я, ВпЛ, А\В, В\А, Л д В, В,
С = (А А В) А А.
2. Выяснить, какая из пяти возможностей выполнена для
множеств А и С: Ad С, или С (Z А, или А = С, или АпС = 0,
или AGDB.
3. Найти Р{В) и \Р{В)\.
№
1
2
1 ^
4
5
6
7
8
9
10
11
12
13
14
15
А
-1,1,4,3
-1,1,2,3
-1,1,3,4
-1,1,2,3
-2,1,3,4
-1,1,4,5
-3,-1,1,2
-4,-1,1,2
-2,-1,3,5
-3,-1,1,2
-2,2,3,4
-3,-1,2,4
-1,-3,2,3
-4,-3,1,2
-5,-1,1,3
а
1
7
-2
0
0
3
-2
0
3
5
2
-2
-5
1
6
Р
-12
13
-12
-17
-11
-9
-7
-И
-7
1
-7
-15
1
-7
0
Y
-28
-3
18
36
-18
-23
20
18
-15
-21
-20
-4
21
-13
-22
5
-16
-18
27
-20
-8
-12
-12
-8
18
-18
-12
20
-18
-6
15
Хо
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
А
-1,1,2,3
-1,1,3,2
-2,-1,2.4
-1,1,2,3
-1,1,2,3
-3,5,3,4
1,2,3,4
-1,-2,1,2
-1,2,5,4
-1,-2,-3,1
1,4,2,3
-1,1,2,4
-1,1,2,3
-1,4,2,3
-1,2,3,4
а
-3
-7
-1
-4
-5
-И
-6
-3
0
-4
3
1
-2
-4
3
Таблица 1.1.2
Р
-3
12
-7
3
-3
39
8
-2
-9
-10
-3
-12
-4
-2
1
Y
7
4
13
4
13
-49
6
12
-4
28
-7
4
2
12
-3
5
6
-16
-6
-4
10
20
9
-8
12
-15
6
16
3
9
-2
Множества, графики, соответствия, отношения 9^
Пример решения задания 1.1.2
Решим задание 1.1.2 для А = {1,-2,3,-4} и уравнения
/-7хЧбхЧ32х-32 = 0.
Сначала найдём множество В корней данного уравнения.
Подбором устанавливаем, что корнем исходного многочлена
X -1х^ Л-вх +32х-32 является 1; поделив этот многочлен на
х-1, получим многочлен х -6х +32.
Также подбором устанавливаем, что -2 является корнем мно-
гочлена х -6х +32 и делим этот многочлен на х + 2. Получим
многочлен X -8х + 16. Его корни совпадают и равны 4.
Итак, множество В найдено, ^ = {-2,1,4}.Теперь решаем
пункты 1—3 данного задания.
1. ДиЯ = {-4,-2,1,3,4}, 5 п Л = {-2,1},
Л\В = {-4,3}, В\Л-{4},
A^B = {-4,3,4}, ~В = {-5,-4,-3,-1,2,3,5},
С=(ЛдВ)дЛ = {-4,3,4}д{ 1,-2,3,-4} ={4}и{ 1,-2}={-2,1,4}.
2. Так как -4g Л и -4^ С, 4g Си 4^ А, 1g Д п С, значит,
AdDB.
3. Р(В) = {0,{-2},{1},{4},{-2,1},{-2,4},{1,4},{-2,1,4}}.
Как видим, Р{В) содержит 8 элементов, т. е. | Р{В) |= 8.
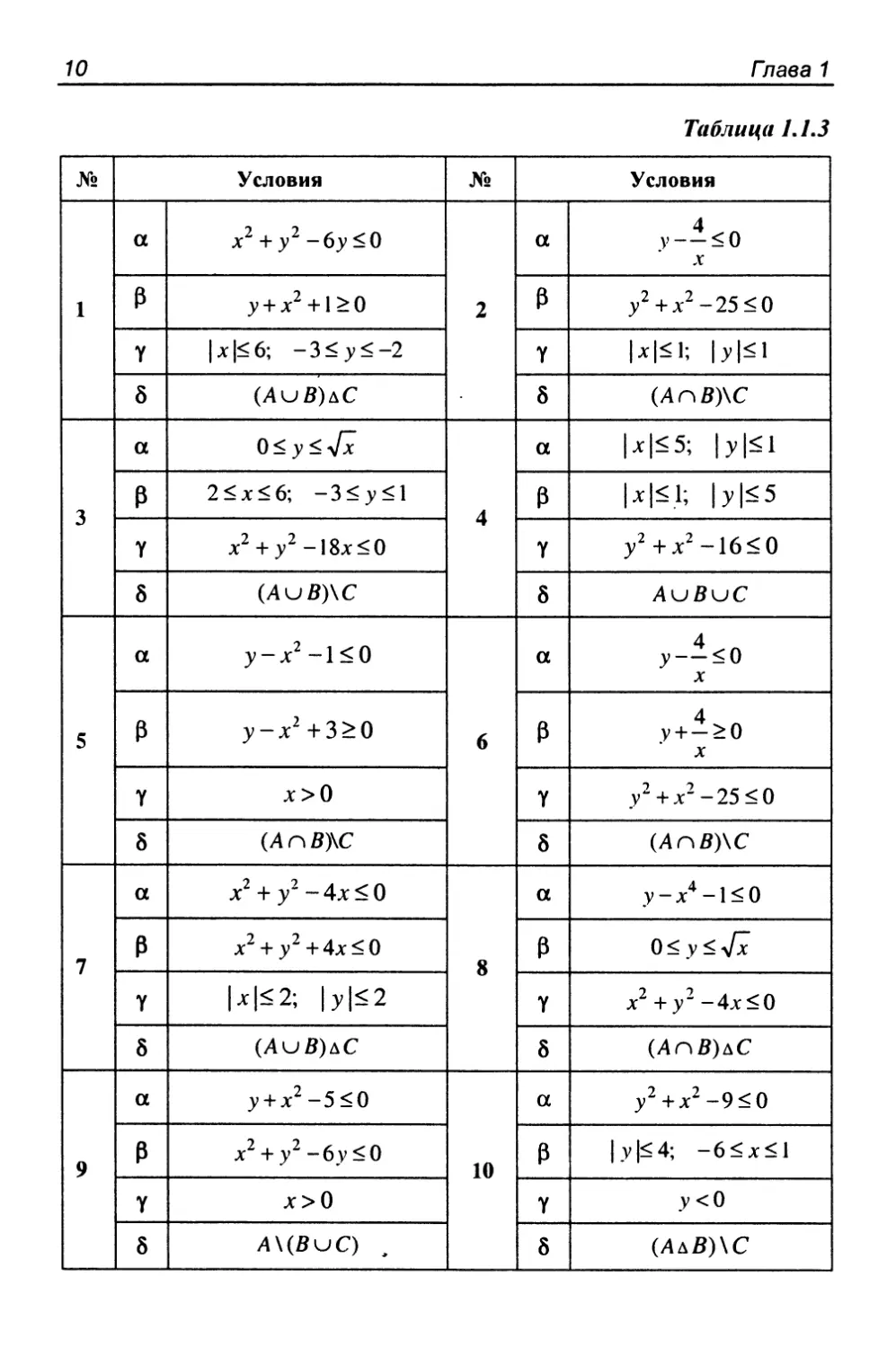
Задание 1.1.3
Пусть Л, В и С — множества точек плоскости, координаты
которых удовлетворяют условиям а, (3 и Y соответственно.
Изобразите в системе координат хОу множество D, полученное из
множеств А, В и С по формуле 5.
10
Глава 1
Таблица!, 1.3
№
1
3
5
7
9
Условия
а
р
Y
5
а
Р
Y
5
а
Р
Y
6
а
Р
Y
S
а
Р
Y
8
л:Ч>;^-6>'<0
>' + л:Ч1>0
|л:|<6; -3<>^<-2
{АиВ)^С
0<у<^
2<л:<6; -3<>'<1
л:Ч>;^-18л:<0
{АиВ)\С
у-х^-1<0
у-х^+3>0
х>0
{АпВ)\С
х^ + у'-4х<0
х^-\-у^-\-Лх<0
U|<2; |з;|<2
(AuB)aC
у + х^-5<0
л:Ч>'^-6у<0
х>0
А\(ВиС)
№
2
4
6
8
10
Условия
а
р
Y
5
а
Р
Y
6
а
Р
Y
S
а
Р
Y
8
а
Р
Y
8
4
v--<0
л:
/ + л'^-25<0
|^|<1; \у\<\
{АпВ)\С
|х|<5; |>;|<1
|х|<1; |з;|<5
/+jc'-16<0
Aui5uC
4
>;--<0
л:
4
у + ->0
л:
.уЧл:--25<0
{АпВ)\С
.у-/-1<0
0<y<^Jx
х^ + у'-4х<0
{АпВ)аС
у^ + х^-9<0
|у|<4; -6<л:<1
>'<0
(АаВ)\С
Множества, графики, соответствия, отношения
11
Таблица 1.1.3 (продолэ/сение)
Хо
11
13
15
17
19
1
Условия
а
Р
Y
5
а
р
Y
8
а
Р
Y
S
а
Р
Y
6
а
Р
Y
5
.Y-V>0
л- + >'<0
1 '^ ^ А
(AAi5)uC
у < sin .Y
У>0,5
У>-2
(Лд5)пС
у--<0
у + ->0
Л'
у>1
(Дп5)\С
.Г + >;--25<0
4
у — <0
л'- + .у--4<0
(A\i5)uC
|л-|<5; |у|<1
|х|<1; |у|<5
jc4.v'<16
{A^B)^C
Хо
12
14
16
18
20
Условия
а
Р
Y
8
а
Р
Y
6
а
Р
Y
8
а
Р
Y
5
а
Р
Y
5
у + л-^-6<0
|л'|>2; |у|>2
х<у
АслВслС
.V < у + 3
л- > у - 3
|х|<5; |у|<2
{Аг\В)\С 1
jc'^ + _y^ + 6y<0
>; + л-- + 1>0
|л:|<4; -4<у<-2 1
А(Л(В\С) 1
0<y<V^
2<л'<6; -3<у<1
л:Чу^-18л-<0
(ДдВ)аС
л-^-у-2>0
А-^-у + 4>0
у > 1
{АглВ^\С
12
Глава 1
Таблица LL3 (окончание)
Хо
21
23
25
27
29
Условия
а
Р
Y
8
а
Р
Y
5
а
Р
Y
5
а
Р
Y
8
а
Р
Y
8
|^v|<5; Lv|^5
4
v + ->4
4
X
Л\{Вг\С)
х^-у>0
х+у>0
\х\<2', \у\<2
(AaB)uC
\х\<4; \у\<4
х' + у^< 25
>'>0
Аг\(В\С)
у-х^^+4>0
\х\<2; -4<v<0
jc4>;'<l
{ЛиВ)\С
4
у — <0
X
jc4>;^-25<0
|х|<4; |Я^З
Дп(5\С)
№
22
24
26
28
30
Условия
а
Р
Y
5
а
р
Y
8
а
Р
Y
5
а
Р
Y
S
а
Р
Y
5
v + x'-5<0
.\:4>;--6>;<0
у>0
(ДдБ)пС 1
у + л:--6<0
х^ + у-^<4
х< у
(Л\В)г\С
X > COS у
л: < 0,5
у>0
(Дд5)пС
у-л'^-1<0
>;-,\:Чз>0
хЧуЧз
{АпВ)\С
2<л:<6; -3<у<1
0<y<^[I
х"-\2х + у^'<0
(АаВ)аС
Множества, графики, соответствия, отношения
13
Пример решения задания 1.1.3
Пусть Л, В и С — множества точек плоскости,
координаты которых удовлетворяют условиям х+2>у, х^ + у^<4 и
IX |< 2; I у 1^ 2 соответственно. Изобразите в системе
координат xQy мноэюество D, полученное из мнолсеств А, В и С по
формуле A\{B^C).
Множество В представляет из себя множество точек круга
радиуса 2 с центром в начале координат, включающего границу,
А - множество точек плоскости, расположенных выше и на
прямой y = jc-f2, и С — множество точек, лежащих внутри и на
границе квадрата | ^v |< 2; | у |< 2 .
Отметим горизонтальной штриховкой множество 5дС,
а вертикальной — множество А (рис. 1.1.3, а).
Удалив из области, помеченной вертикальной штриховкой,
точки области, помеченной горизонтальной штриховкой, мы получим
множество точек, образующих D. Изобразим результат, отметив
точки множества D вертикальной штриховкой (рис. 1.1.3,6).
1 i ii
Hii П
iiiiiii
^mf 0
^f\\
-i
Л
2 \
>
Рис. 1.1.3
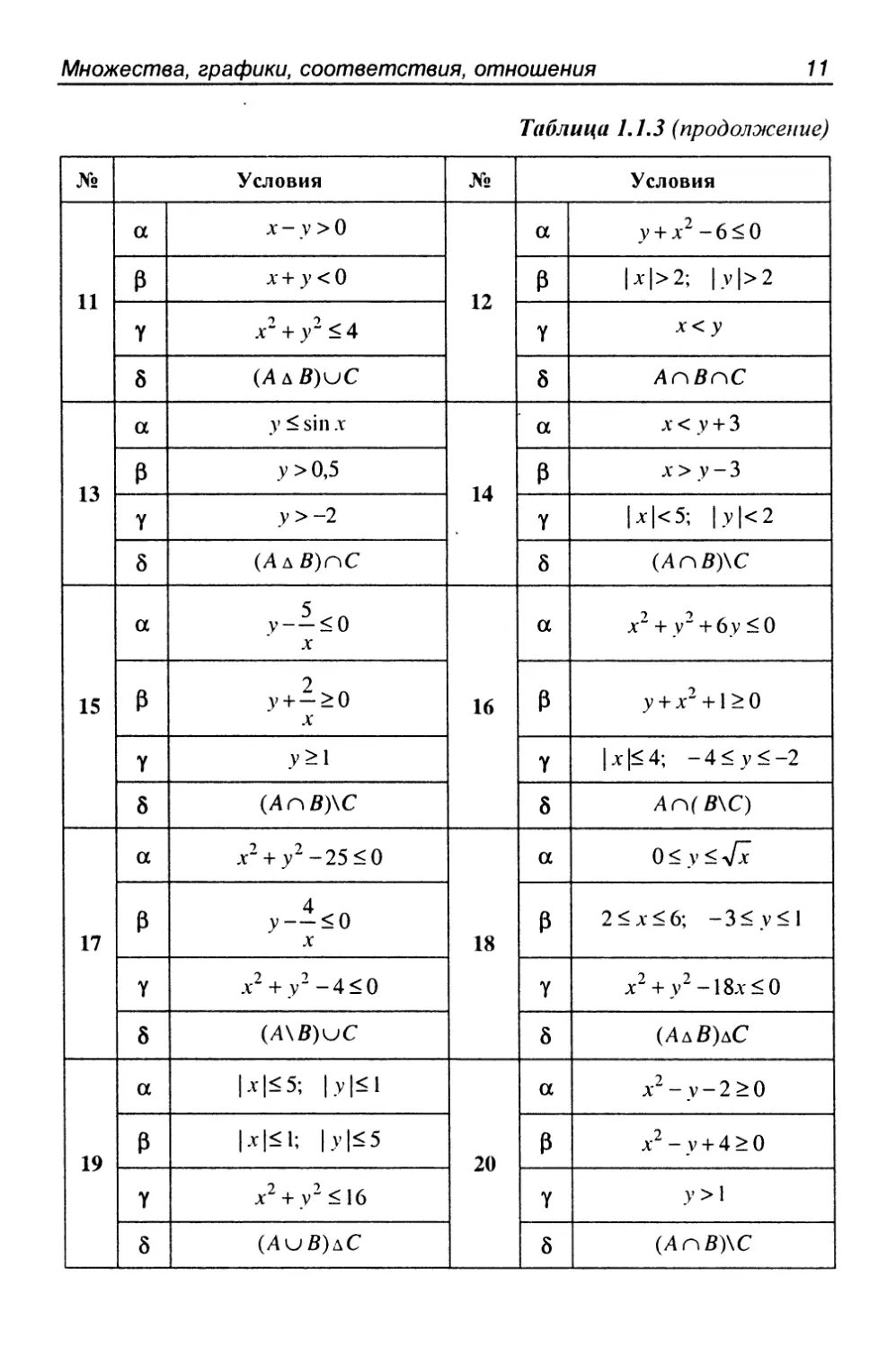
Задание 1.1.4
1. Существуют ли множества Д, В, X такие, что выполняется
набор условий а?
2. Существуют ли множества Л^, £, Р такие, что выполняется
набор условий (3?
14
Глава 1
Таблица LL4
№
1
1 ^ 1
1 ^ 1
4
1 ^
6
7
1 ^
9
1 ^^
11
12
13
14
15
16
17
18
19
20
21
22
а
Х\^ = Д\/^ = Ли^ = 0, ВФ0
В = ЛиВ = Х\В = 0, АслВфО!)
i5\A = AnA'=0, i5nA'^0
i5\X=X\A = 0, i5^0
Дп5 = ДиХ =0, в\Х 9^0
Д\Х=5\Л = Х\Д = 0, 59^0
д\х =5\д = д = 0, х^0
Д\Х=(5\Д)ПХ=0, Х\Д9^0
Х\^ = (/?\Д)пХ=0, Х\Д9^0
Д = X\5 = iB\X=0, 5^0
(X\Д)\iB = iB\Д = XUiB = 0, Д9^0
в\Х=ДпХ=0,5?^0
д = л:=(5\д)\х=0,в7ь0
ДпХ=5\Д = 0, X 7^0
Д\iB = X\Д = 0, X\B^(Z)
Аг\Х^~ХпЛ^В\А^О:>, ЛпВчь0
ВпХ =ЛиВ = 0, Х\Д^0
В\А = В\Х=Х\В = 0, ВФ0
ХпВ = {Х\В)\Л = 0, Х\А^0
ЛпВ = Х\Л = 0, В\АФ0
Х\5 = Д\Х=0, А\Вф0
Д\iB = Д\X=0, Х\ВФ0
Р
N\E = N\P = 0, Е\Рф0
E\P = N\E = 0, N\P^0
NnE = EuN = P = 0, N Ф0
P\E = N\E = 0, (PnE)\N^0
P\N = E = N\P = 0, N^0
Pr\N=iN\P)\E = 0, N\E^0 1
NuE = Er\P = 0, P\N^0
PnN = E\P = P\N = 0, ЕФ0 1
E\N = NnE = N\P = 0, N Ф0 1
P\N = PuE = 0, NnE^0
N\E = E\P = P\E = 0, E\N^0 1
PnNnE = N\P = 0, NnE^0 1
N\P = EnP = 0, ЕФ0 1
P\E = N\E = NuE = 0, Ei^0
P\N = N\P = P\E = 0, ~ЁФ0
N\P = (NnP)\E = 0, N\E^0 1
j P\E = N\E = NnP = 0, РФ0
P\N = N(^P = 0, РПЕФ0
E\P = NnE = 0, P\N Ф0
N\P = E\N=1^ = 0, 'РФ0
E = N^E = P\E = 0, Nr\E^0
E\P = N\P = Ny^P = 0, P:^0
Множества, графики, соответствия, отношения
15
Таблица 1,1.4 (окончание)
1 №
23
24
25
26
27
28
29
30
а
z?\a: = a\a:=0, {ВпХ)\афо:>
в\А^х =a\b = q:>, Д7ь0
^пД = (Д\в)\А:=0, Д\Х7Ь0
AuA'=A:ni5 = 0, i5\A9i0
5nA = A:\i5 = e\A = 0, X 9^0
х\д = дпа: =д\5 = 0, Д7Ь0
i5\Д = 5uX=0, ДпА:9^0
ДпА: =i5uД = 5 = 0, Д9^0
р
N\E = E\P = 0, N фО) 1
PnN = PuE = 0, N\E^0
P\E = N\P = E\P = 0, Nit0
P\E = N\P = ^ = 0, 1^0
P\E = {N\P)r\E = 0, Е\Рф0
E\N=(N\P)nE = 0, Е\Рф0
'p = E\N = N\E = 0, N^<Z>
N\P = PnE = 0, N(^E^0
Пример решения задания 1.1.4
7. Существуют ли миоэюества А, В, X такие, что
выполняется набор условий: Аи В = 0, ХдЛ = 0, В\А^0 ?
Изобразим множества А, В, X в
виде прямоугольников, расположенных на
плоскости в общем положении, и
поставим в каждой области, на которые
плоскость разбита прямоугольниками,
по одному символу: символ 4,
например, обозначает список всех элементов,
попавших во множества Л и Я, но не
попавших в X, и т. д. Теперь составим
множества Л, ^, X и универсальное
множество и (рис. 1.1.4):
и = {1,2,3,4,5,6,7,8}, А = {1,2,4,5}, В = {4,5,6,7}, X = {2,3,5.7}.
Изменим множества А, В, X так, чтобы выполнились условия
нашего задания.
fl
}
(а
1
/
2
к
Л
г
4
15
)
3
>
щ
6
л
х]]
Рис. 1.1.4
Из того, что A\jB-0>^ следует, что множество f/ \(ЛU5)
не должно содержать элементов, т. е. из V удаляем 8 и 3.
16
Глава 1
Чтобы выполнилось условие X д Л = 0, нужно удалить
элементы списков 1, 4, 7. Тогда получится, что множества Д, В, X
и f/имеют следующий вид: А = {2,5} = X, В = {5,6}, t/= {2,5,6}.
Заметим, что для этих множеств В\А = [в] ^ 0.
Если под символами 2, 5 и 6 будем понимать
соответствующие числа, то мы получим конкретный пример множеств А, В,
X, для которых выполнены все условия заданного набора
требований.
2. Существуют ли множества TV, £, Р такие, что выполняется
набор условий: E\N = Р\Е = 0, Р\Л^^0?
Попробуем построить множества N, Е, Р так же, как мы это
делали в п. 1. Пусть /V = {1,2,4,5}, £ = {4,5,6,7}, F = {2,3,5,7}.
Чтобы выполнилось условие E\N = 0, удаляем элементы
списков 6, 7. Для выполнения условия Р\Е = 0 удаляем элементы
из списков 2, 3. Но тогда множество P\N не будет содержать
элементов. Итак, мы показали, что этот набор условий
противоречив, т. е. не существует множеств Л^, Е, Р таких, что
выполнены условия упражнения.
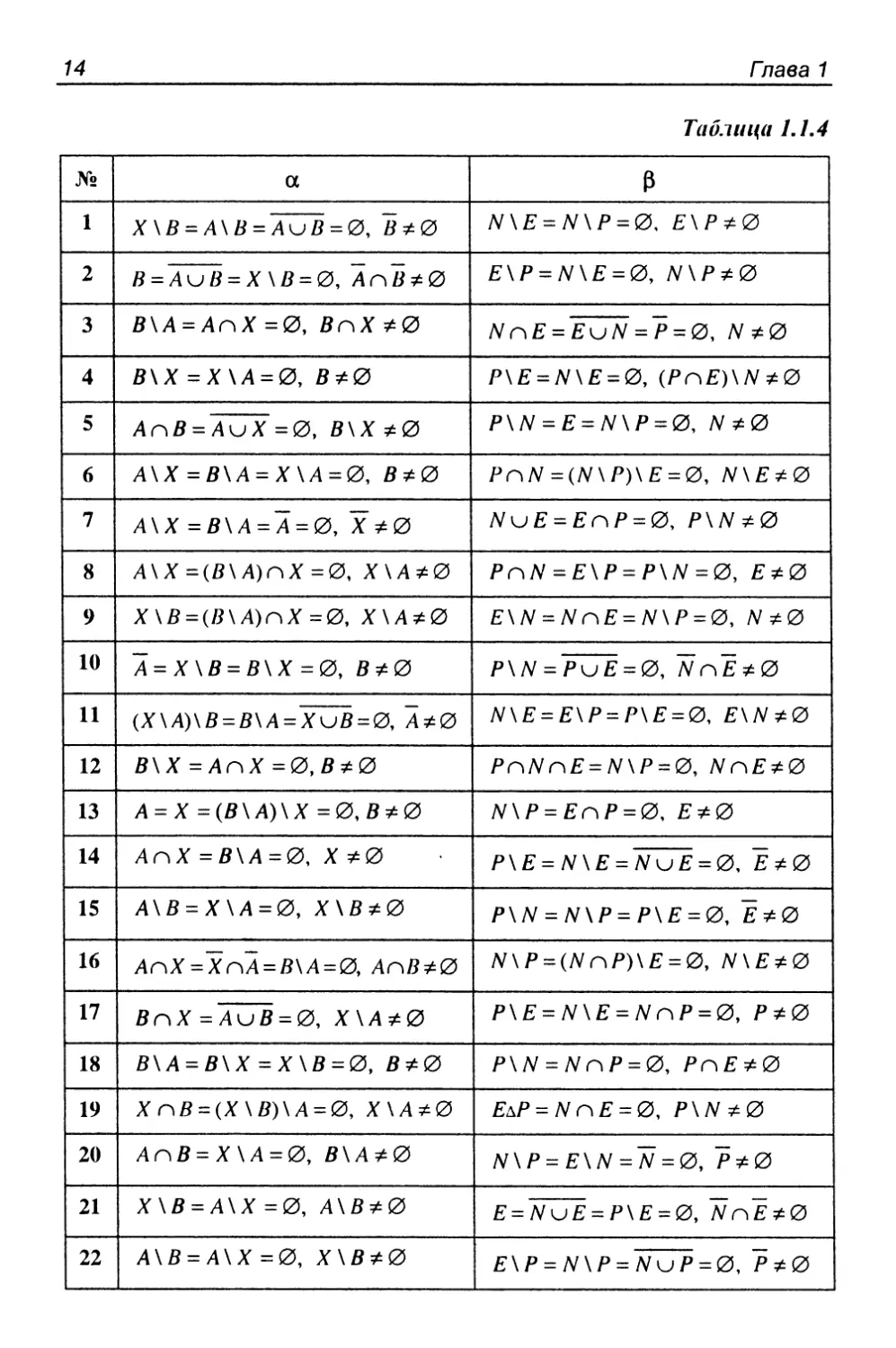
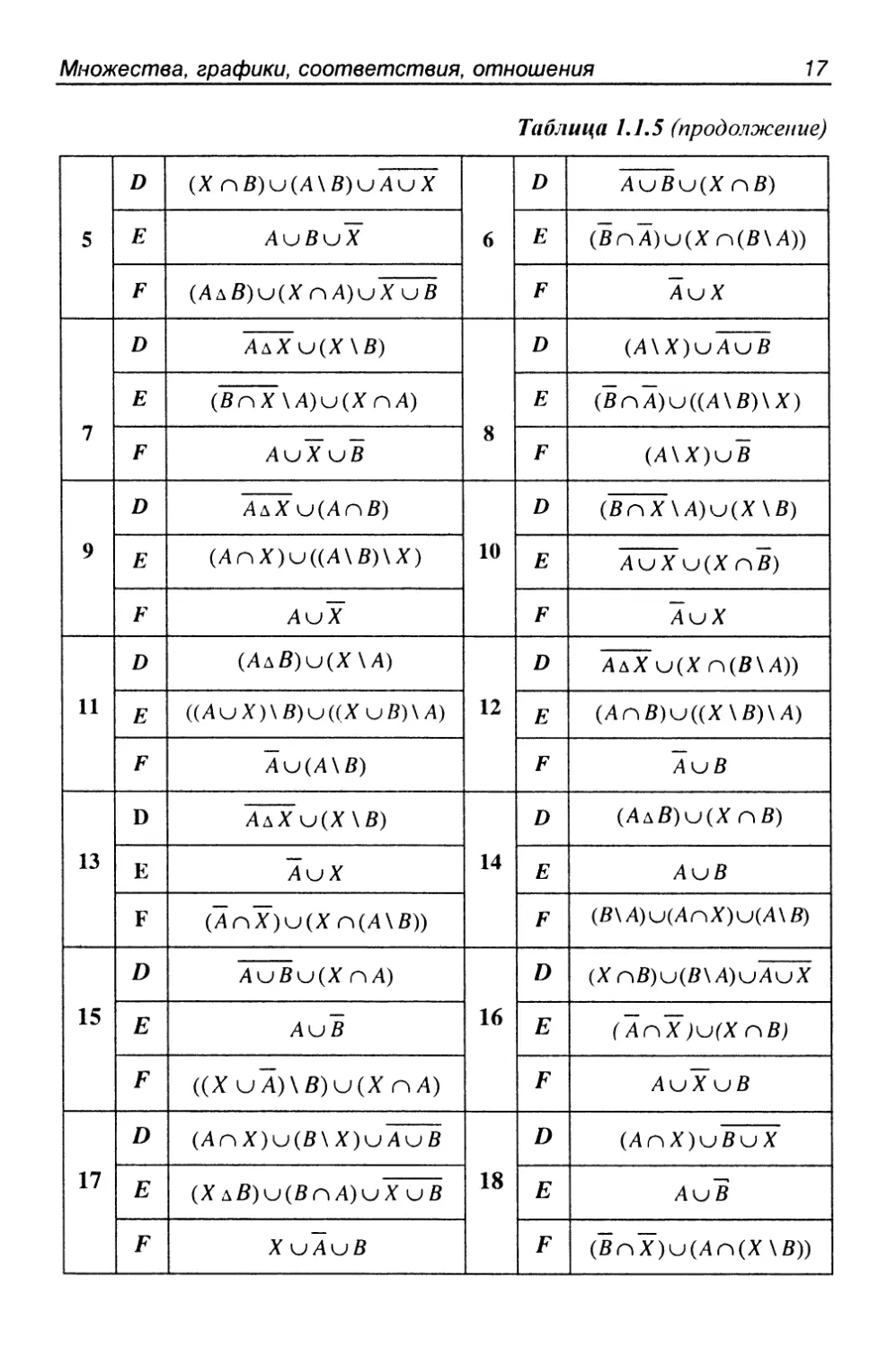
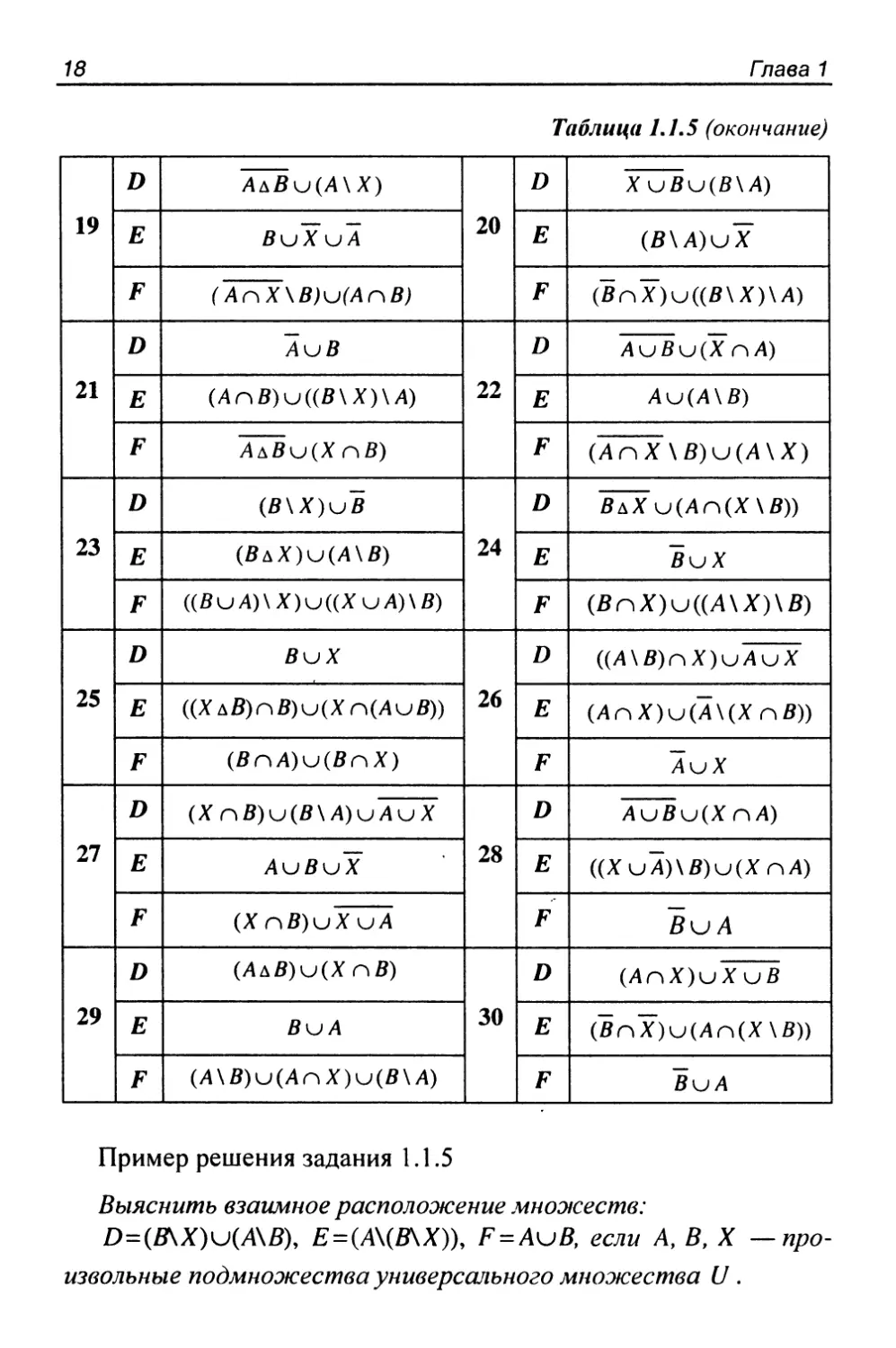
Задание 1.1.5
Выяснить взаимное расположение множеств D, £, F, если
Ау В, X — произвольные подмножества универсального
множества и.
Таблица LJ.5
1
3
D
Е
F
D
Е
F
Ви'х
(ВпХ)и(х\(ЛпВ))
(Вп^)и(Вп{Х\А))
(ДдХ)и(5пД)
ЛиХ
(Л\Х)и(Вг\Х)и(Х\А)
2
4
D
Е
F
D
Е
F
{A(^B)Kj(A\X)uB^X
А^ЪиХ
(Вп'Х)и(Вг\А)
{ВпХ)иАиХ
((Ви'Х)\А)и{Х пВ)
ДиХ
Множества, графики, соответствия, отношения
17
Таблица LJ.5 (продолэюение)
5
7
9
11
13
15
17
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
(X nB)Kj(A\B)yjAuX
ЛиВ^'х
(A^B)u{XnЛ)yJXuB
'АлХи(Х\В)
{ВпХ\А)и(ХпЛ)
ЛиХиЪ
АаХу^(ЛпВ)
(ЛпХ)и{{А\В)\Х)
ЛиХ
(ААВ)и(Х\А)
((АиХ)\В)^((ХиВ)\А)
Ди(Д\5)
AaXu(X\B)
ЛиХ
{Ап'Х)и{Хп{А\В))
АиВи(Х пА)
АиЪ
((ХиЛ)\5)и(ХпЛ)
(АпХ)и{В\Х)у^А^В
{X^B)u{BnA)uXuB
XuAUiB
6
8
10
12
14
16
18
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
AuB(j{X г\В)
(Вп'А)и(Хп(В\А))
ДиХ
(А\Х)иАиВ
(Вг\^)и{(А\В)\Х)
{А\Х)иЪ
(Вг\Х\А)^(Х\В)
ДиХи(ХпЯ)
ДиХ 1
ДAXu(Xn(i5\Д))
iAnB)yji(X\B)\A) 1
'aub
(АаВ)^(Хг\В)
А^В
(в\Д)и(ДпХ)и(Д\в)
(XniB)u(Z?\Д)uДuX
('Ап'Х)и(ХпВ)
ДuX"uiB
(ДnX)UiBuX
Аи'в
(^nx")u(Дn(X\iB))
18
Глава 1
Таблица L1.5 (окончание)
19
21
23
25
27
29
D
Е
t
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
AaBu{A\X)
fiuYuA
(АпХ\В)и(АпВ)
JuB
(АпВ)^{(В\Х)\А)
ААВи{ХпВ)
{В\Х)^'В
(BaX)u{A\B)
{{BuA)\X)u{{XuA)\B)
ВиХ
{(Х АВ)пВ)и{Х п(АиВ))
(ВпА)и{Вг\Х)
(ХпВ)и(В\А)иАиХ
AuBuJ
(ХпВ)иХиА
(ААВ)и{ХпВ)
ВиА
(А\В)и(АпХ)и{В\А)
20
22
24
26
28
30
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
ХиВи{В\А)
(£?\Л)иХ"
(BnJ)u(iB\X)\A)
АиВи(ХпА)
Аи(А\В) 1
(АпХ\В)и(А\Х)
ВАХи{Ап(Х\В))
luX
{ВпХ)и{{А\Х)\В)
({А\В)пХ)иАиХ
(АпХ)и(А\(ХпВ))
ЛиХ
АиВи(ХпА)
((Хи^)\В)и(Хг\А)
ВиЛ
{АпХ)иХ^В
(Вп'Х)и(Ап(Х\В))
1иД
Пример решения задания 1.1.5
Выяснить взаимное располоэюеиие миосисеств:
D=(B\X)u(A\B\ Е = (Л\{В\Х)), F = AuB, если Л, В, X
—произвольные подмнолсества универсального мноэюества U .
Множества, графики, соответствия, отношения
19
Возьмём множества Л, В, X, находящиеся в общем
положении:
Л = {1,2,4,5}, В = {4,5,6,7}, Х = {2,3,5,7}. В нашем случае, как
и при решении задания 1.1.3, цифры обозначают
соответствующие списки переменных. Тогда В\Х ={4,6}, А\В = {1,2},
Д\(В\Х) = {1,2,5}, Ли В = {1,2,4,5,6,7}, (iB\ Х)и(Л\В) = {1,2,4,6},
то есть D = {1,2,4,6}, £ = {1,2,5}, F = {1,2,4,5,6,7}.
Итак, видим, что включения DqF и EqF выполняются
для произвольных множеств А, В, X.
Если символы 1,2,4,5,6,7 обозначают соответствующие числа,
имеем, что 4g D и 4^ £, 5е £ и 5^ D, 1g DnE, то есть
множества ОиЕ могут находиться в общем положении.
Задание 1.1.6
Проверить, что для любых множеств Л, В, С выполнение
включения а влечёт выполнение включения (3.
Таблица I.L6
Хо
1
2
3
4
5
6
7
8
9
10
а
AnBQC
AnBQC
AnBQC
AnBQC
AnBQC
AqB^jC
AqBuC
AqBuC
AqBuC
AqBuC
P 1
AuBQiAAB)u{Ar\C)
A\Cq{A\B)uC 1
AaCq{A\B)^C
iB\C)u{A\C)QAAB
BQ(B\A)y^C
AACQ(AnB)uC
A\BQAnC
A^BqBuC
{A\B)u(AnC)QC
(A\C)u{B\C)qB
20
Глава 1
Таблица 1.1.6 (окончание)
Хо
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
а
Дс^иС
AUiBcC
ДивсС
Ди^сС
A^jBcC
ЛоВ\С
ЛоВ\С
ЛиВаС
Ди^сС
A^BqC
B\CqA
B\CqA
B\CqA
B\CqA
B\CqA
B\CqA
BqC\A
BqC\A
BqC\A
BqC\A
P
(А\В)\Сс:С\А
ААВс:(АпВ)иС
Ar\Cc:Au{B\A)
АпВс{Вг\С)и(АпС)
В\АсВглС
АглВсА\С
СпВаВХА
AaC(zC\A
iB\C)u{A\B)QAr\C
BqAu(C\A)
AuBQiBr\C)uA
В\С(^С^{АглВ)
iB\Дc(C\Д)u(Дni5)
i5cCu(iBnД)
iBдCcCuД
iBcCu(Д\C)
Дu(fi\C)cД\iB
(Д\iB)u((iB\C)\Д)cД
(iB\C)u(5\Д)CiBnC
CUiBc(C\Д)u(C\б)
Множества, графики, соответствия, отношения
21
Пример решения задания 1.1.6
Доказать, что для любых миоэ/сеств А, В, С выполнение
включения А \ В с С влечёт выполнение включения СдДс(ЛпВ)иС.
Возьмём множества Д, В, С, находящиеся в общем
положении: Л = { 1,2,4,5}, В = {4,5,6,7}, С = {2,3,5,7}. В нашем случае,
как и при решении предыдущих заданий, цифры обозначают
соответствующие списки переменных.
Тогда Д\В = {1,2},из включения Л \ В с С следует, что
список 1 пуст, Л = {2,4,5}. Рассмотрим C^A и (AnBjuC.
СдЛ = {3,4,7}, (ЛпВ)иС = {2,3,4,5,7}. Так как {3,4,7} с
с {2,3,4,5,7}, имеем, что включение СдЛ с(ЛпВ)иСдоказано
в предположении, что выполнено включение А\В с,С.
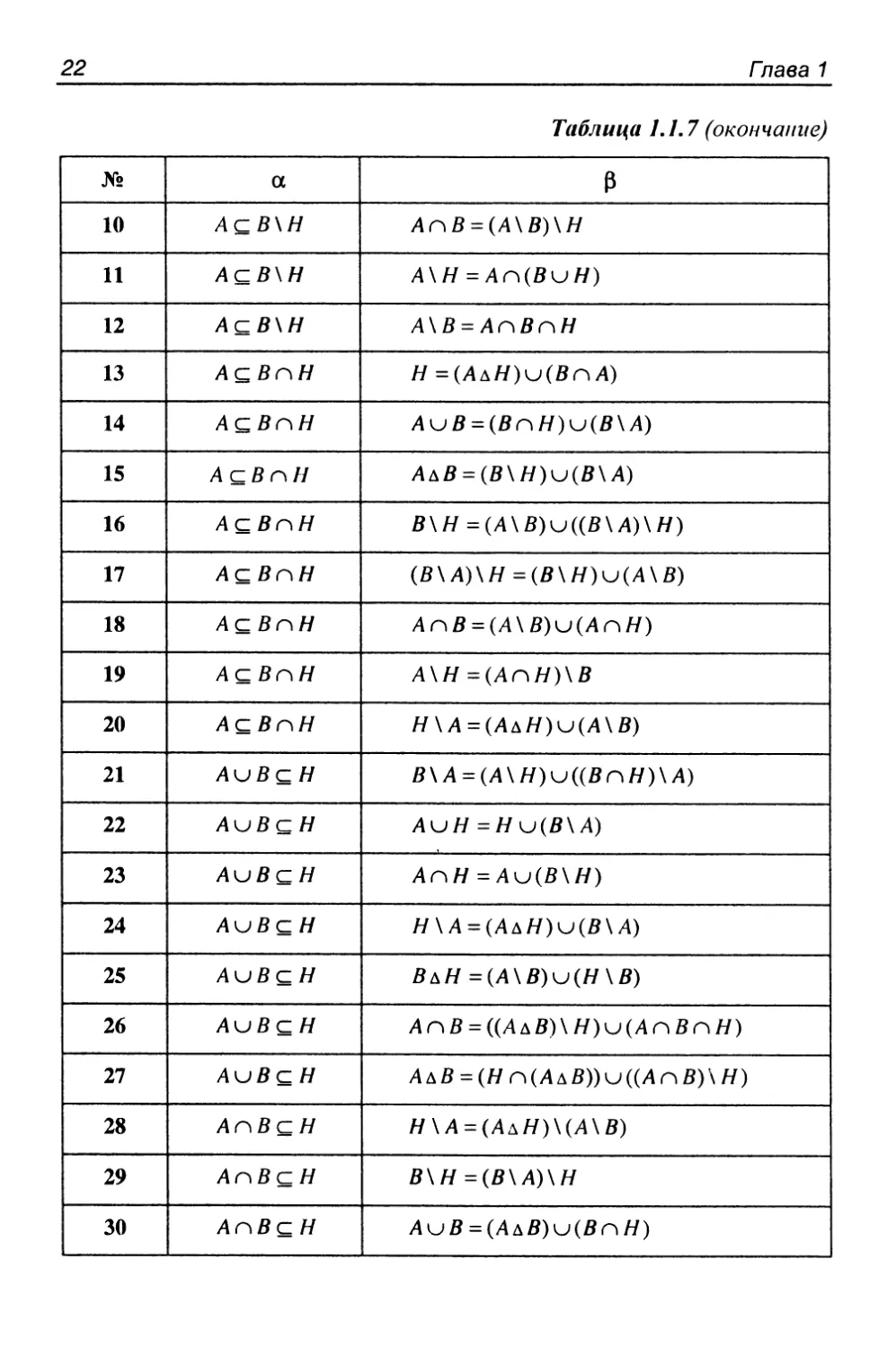
Задание 1.1.7
Для произвольных множеств Л, В, Н проверить, является ли
выполнение включения а необходимым и достаточным условием
выполнения равенства (3.
Таблица I.L7
Хо
1
2
3
4
5
6
7
8
9
а
AQB\H
AqB\H
aqb\h
aqb\h
AqB\H
AqB\H
AqB\H
aqb\h
AqB\H
p
H\A = Hyj{A\B)
H =(Н\А)и({А\В)\Н)
АпВ = {А\Н)и(А\В)
B = iA^B)u(A\H)
А^В = (В\Н)и{В\А)
B\A = (A^B)u{BnH)
A\H =Н^{АпВ)
А\В = {В\А)^{И(ЛВ)
AkjH ={Н\А)и((АглВ)\Н)
22
Глава 1
Таблица LL7 (окончание)
Г № 1
1 ^^
1 ^^
1 ^^
1 ^^
1 ^^
1 15
1 ^^
1 ^'^
1 ^^
1 ^^
1 20
1 ^^
1 22
1 ^-^
1 ^^
1 ^^
1 26
1 ^'^
1 28
1 29
1 30
а
aqb\h 1
AqB\H I
AqB\H
AQBnH
AQBnH
A(zBr\H
AdBnH
AdBnH
AczBnH
AQBnH
AQBnH
AuBqH
AuBqH
AuBqH
AuBqH
AuBqH
AuBqH
AuBqH
AnBQH
AnBQH
AnBQH
P 1
AnB = {A\B)\H 1
A\H = An{BuH) 1
A\B = AnBr\H 1
H -{AAH)u(BnA) 1
Ди5-(5пЯ)и(5\Л) 1
ААВ-(В\Н)и(В\А) 1
В\Н ={A\B)u{(B\A)\H) 1
(B\A)\H -{В\Н)и(А\В) 1
Дп5-(Д\в)и(ДпЯ) 1
A\H ={АпН)\В 1
Я\Д = (ДдЯ)и(Д\в) 1
5\Д = (Д\Я)и((5пЯ)\Д)
АиН =Ни{В\А) 1
АпН =Аи(В\И) 1
//\Д = (ДдЯ)и(5\Д)
ВаН ={А\В)и(Н\В)
АпВ = {{ААВ)\Н)и{АпВпН)
ААВ = {Нп(ААВ))и{(АпВ)\Н)
Н\А = (АаН)\(А\В)
В\Н =(В\А)\Н
А^В = (ААВ)и{Вг\Н)
Множества, графики, соответствия, отношения 23^
Пример решения задания 1.1.7
Для произвольных мнолсеств А, В, Н проверить, является ли
выполнение включения Ли В Q Н необходимым и достаточным
условием выполнения равенства ЛаН =(В\Л)и(Я\Д).
Рассмотрим множества А. В, Н : Л = {1,2,4,5}, В = {4,5,6,7},
Я ={2,3,5,7}. В нашем случае, как и при решении
предыдущих заданий, цифры обозначают соответствующие списки
переменных.
1. Посмотрим, какие множества мы получим, если потребуем
выполнения условия AkjBqH. ДиВ = { 1,2,4,5,6,7} и, чтобы
было выполнено включение AkjBqH, списки 1, 4, 6 должны
быть пусты, и множества А, В, Н будут таковы: Д = {2,5},
В = {5,7}, Я ={2,3,5,7}. Тогда (В\ Л)и(//\ Л) = {7}и{3,7} =
= {3,7}, ЛдЯ={3,7} и равенство ЛдЯ =(В\ Л)и(Я \ Д)
выполнено.
2. Посмотрим, какой вид примут множества Л = {1,2,4,5},
В = {4,5,6,7}, Н = {2,3,5,7}, чтобы выполнилось равенство
ЛдЯ=(В\Л)и(Я\Л).
ЛдЯ ={1,3,4,7}, (В\Л)и(Я\Л) = {6,7}и{3,7} = {3,6,7}.
Для выполнения равенства Л д Я = (В \ Л) и (// \ Л) нужно,
чтобы списки 1, 4 и 6 были пусты, и мы приходим к тем же
множествам, что и в п. 1, т. е. Л ={2,5}, й = {5,7}, Я={2,3,5,7}.
Видим, что в этом случае ЛиВ = {2,5,7} с Я.
Значит, доказано, что для любых множеств Л, В, Я
выполнение включения AkjBqH является необходимым и
достаточным условием выполнения равенства АаН = (В\Л)и(Я\Л).
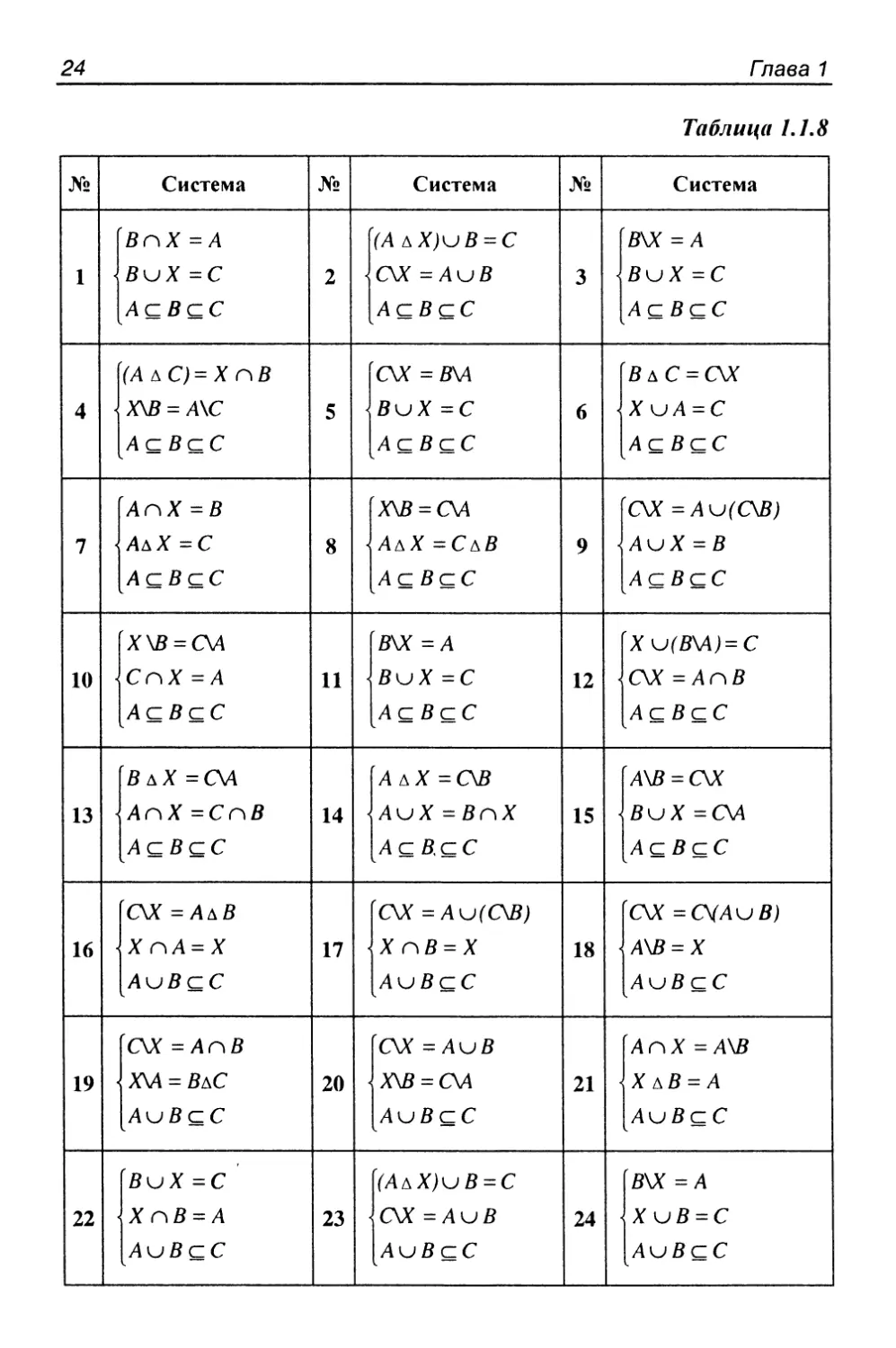
Задание 1.1.8
Решить систему соотношений относительно множества X и
указать условия совместности системы.
24
Глава 1
Таблица 1.1.8
Х2
1
4
7
10
13
16
19
22
Система
<
'
'
■
'Вг\Х=Л
ВиХ=С
AqBqC
(АаС)=ХпВ
х\в = л\с
[aqB(oC
АпХ =В
АаХ =С
[aqBqC
Х\В = С\А
СпХ =А
AqBqC
ВаХ =С\А
АпХ =Сг\В
AqBqC
С\Х =АаВ
X пА = Х
AuBqC
\СХХ =АпВ
Х\А = Вас
[a^BqC
\ВиХ =С
\Хг\В = А
[auBqC
Хо
2
5
8
11
14
17
20
23
Система
\
<
'
■
(AaX)uB = C
С\Х=АиВ
AqBqC
С\Х =В\А
ВиХ=С
AqBqC
Х\В = С\А
АаХ=СаВ
[aqBqC
В\Х=А
В^Х =С
AqBqC
АаХ=С\В
А^Х =Вг\Х
AqB.qC
'С\Х =Аи(С\В)
ХпВ = Х
AuBqC
С\Х =АиВ
Х\В = С\А
AuBqC
\(AaX)uB = C
\с\Х =AuB
[auBqC
Xs
3
6
9
12
15
18
21
24
Система
\
<
'
'
-
В\Х =A
В^Х=С
AqBqC
BaC = C\X
X^A = C
AqBqC
'C\X=A^(C\B)
AuX = B
AqBqC
'Xu(B\A}=C
C\X=AnB
AqBqC
A\B = C\X
ByjX=CM
AqBqC
'C\X =C\(AuB)
A\B = X
A(jBqC
Ar\X=A\B
XaB = A
AuBqC
\B\X =A
\xuB = C
[a^bqc
Множества, графики, соответствия, отношения
25
Таблица LL8 (окончание)
Хо
25
28
Система
■
Хи(В\А)=С
ОХ =АглВ
AuBqC
СМ = ХаВ
(AaB)uX =С
A(jBqC
Хо
26
29
Система
■
■
СМ = Х аВ
ХпА=ВпС
AuBqC
АпХ=СаВ
XVi = B\C
AkjBqC
№
27
30
Система
'
СМ = ХаВ
ХиВ=АпХ
A^BqC
СХХ=АаС
ХиВ = С
АиВ^С
А
К
1
Г
5
9
Й1
^7
6^
ч ,
у
4
^
8
X
В
J
Рис. 1.1.8
Пример решения задания 1.1.8
Решить задание 1.1.8 для системы
В аС = X п Л
Х\С = Л п 5
[С Q Л п В.
I. Построим множества общего
положения Д,В,Х и множество С
(рис. 1.1.8) такие, что CQAnB и
С(П)Х .
Символом 1 обозначим список
элементов множества А, не попавших ни в одно из множеств В,
С, X, символом 7 — список элементов, попавших в каждое
из множеств А, В, С, X и т. д. Будем иметь: Л = { 1,2,3,5,6,7},
В = {2,3,4,6,7,8}, С = {3,7}, X = {5,6,7,8,9}.
1. ВлС = {2,4,6,8}, ХпЛ = {5,6,7}. Эти множества равны
в силу первого уравнения системы, значит, списки
элементов 2,4,5,7 и 8 пусты. Получили: Л = {1,3,6}, В = {3,6}, С = {3},
Х={6,9}.
2. X \ С = {6,9}, An В = {3,6}. Данные множества равны в силу
второго уравнения системы, следовательно, списки элементов 3
и 9 пусты, и наши множества примут вид:
Д = {1,6}, В = {6}, С = 0, Х={6},
Видим, что X = В , В с Л, С = 0.
26
Глава 1
II. Проверим, что множество X = В является решением
исходной системы.
Если С = 0 и ВQ А,то СQAnB и можно записать:
В = {Ь}, А = {а,Ь}, где а,Ь —списки элементов.
Пусть л: =В = {Ь}, тогда: ЯлС = В\С = {Z?},
Х\С = Х ={Ь}, {b}[b} = A\X, СпХ={а,Ь} = ЛпВ.
Видим, что все соотношения системы удовлетворяются, т.е.
множество X - В является решением исходной системы при
выполнении условий В с Л, С = 0.
Ответ: X =В. В Q А, С = 0.
Задание 1.1.9
Решить систему уравнений относительно множества X и
указать условия совместности системы или доказать её
несовместность.
Таблица ]. 1.9
№
1
4
7
10
Система
■
■
■
АиХ=ВпХ
АпХ =СиХ
Д\Х =С\А
АиХ =В\Х
Х\В = СиХ
В\Х =АпС
А\Х =С\В
X\C = AyjB
ВпХ=Хг\С
Вг\С = В\Х
А\(ВиС)=С\В
х«
2
5
8
П
Система
■
■
•
А\Х=Х\В
XVi = C\X
ВиХ =Х\А
АиХ =ВаС
Х\С = ВиХ
ВпХ =С\А
ВиХ =Вг\С
АиС=СпХ
АиВ=ХпС
i
Х\С = А\В
А\С = ХпС
(В\Х )\А = А\С
№
3
6
9
12
Система
-
'
•
АпХ=В\Х
Х\А = СиХ
Х\С = АиВ
В\С = АаХ
В\Х=А\С
СпХ=АпВ
'Аг\Х=Вг\А
С\Х=АиВ
'а = а\в
СиХ =А\В
АпВ=В^С
В\А = ХпС
Множества, графики, соответствия, отношения
27
Таблица 1,1.9
Хо
13
16
19
22
25
28
Система
'<
'
С\Х-А\В
ВиС=ХпС
ХиВ=ХпВ
ВпХ=С\Х
Х\В = АиХ
Х\А = СиВ
С\А = ВаХ
С\Х =В\А
АпХ =ВпС
•
.
ВпХ=СпВ
А\Х =СиВ
Ъ = В\С
АиХ = В\С
Br\C = A(jC
С\В = ХпА
\СиХ =А\Х
\х\А = ВиХ
[с\в = х\с
№
14
17
20
23
26
29
1 _,..
Система
<
-
•
■
И
ВиХ=СпХ
ВпХ=АиХ
В\Х =А\В
B^jX =С\Х
Х\С = АиХ
В\А = Х\В
С\Х -ВпА
В\Х =А\С
Х\А = ВиС
Сг\Х = ХпА
АпС = С\Х
В\(СиА) = А\С
Д\Х =В\С
СиА = Аг\Х
[ХиС = ХпС
\А\Х=СпВ
\С\Х =В\А
[Х\В = АиС
№
15
18
21
24
27
30
Система
•i
'
•
В\Х = Х\С
Х\В = А\Х
CnJ=X\B
BkjX=CaA
X\A = CuX
СпХ=А\В
'СиХ=Сг\А
ВиА=АпХ
ВиС=ХпА
Х\А = В\С
В\А = ХпА
(С\Х )\В = В\А
С\Х=Х\А
Х\С = В\Х
[АиХ=Х\С
\ВиХ =С\А
\АпС = АиВ
[а\С = ХпВ
Пример решения задания 1.1.9
UaX =В\С
Решить задание 1.1.9 для системы \СпХ = Akj X.
[В\Х =А\Х
Построим множества общего положения Л, В, С, X,
являющиеся подмножествами универсального множества U. Для этого
выпишем все 16 различных двоичных наборов размерности 4.
28
Глава 1
Пусть разряды этих наборов слева направо соответствуют
множествам Л, В, С, X (табл. 1.1.9).
Символом 1 обозначим список элементов универсального
множества U, не попавших ни в одно из множеств А, В, С, X,
символом 4 — список элементов, не попавших ни в А, ни в В,
но попавших в Си X, и т. д. Будем иметь:
г/={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16},
А = {9,10,11,12,13,14,15,16},
В = {5,6,7,8,13,14,15,16}, Та6.и,аи.9
С = {3,4,7,8,11,12,15,16},
X ={2,4,6,8,10,12,14,16}.
1. АдХ ={2,4,6,8,9,11,13,15},
Я\С = {5,6,13,14}. Эти
множества равны в силу первого
уравнения системы, значит, списки
элементов 2, 4, 5, 8, 9, 11, 14 и 15
пусты. Получили: А = {10,12,13,16},
В = {6,7,13,16}, С = {3,7Д2,16},
X ={6,10,12,16}.
2. СпХ ={12,16},
AuX ={6,10,12,13,16}.
Данные множества равны в силу
второго уравнения системы,
следовательно, списки элементов 6, 10,
13 пусты, и наши множества
примут вид:
А = {12,16},В = {7,16},
X ={12,16}, С = {3,7,12,16}.
3. В\Х={7}, А\Х =0, в силу
третьего уравнения системы получаем, что список 7 пуст, и
С = {3,12,16}, В = {16}, А = {12,16} = Х, t/={ 1,ЗД2,16}.
Видим, что X = Л, В с А с С с f/.
Хо
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
Л
0
0
0
0
0
0
0
0
в
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
с
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
X
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Множества, графики, соответствия, отношения
29
II. Проверим, что множество X = А является решением
исходной системы.
Если выполнены включения BcAcCcf/, то можно
записать:
В = [Ь}, А = {а,Ь}, С = {а,Ь,с}, U ={а,Ь,с,и}, где а,Ь,с,и —
списки элементов.
Пусть Х=А = [а,Ь}, тогда: АаХ =0 = В\С,
В\Х=0 = А\Х, CnX={a,b} = AyjX.
Видим, что все уравнения системы удовлетворяются, т. е.
множество X = А является решением исходной системы при
выполнении включений В Q AqC qU.
Ответ: X = А, BqAqCqU.
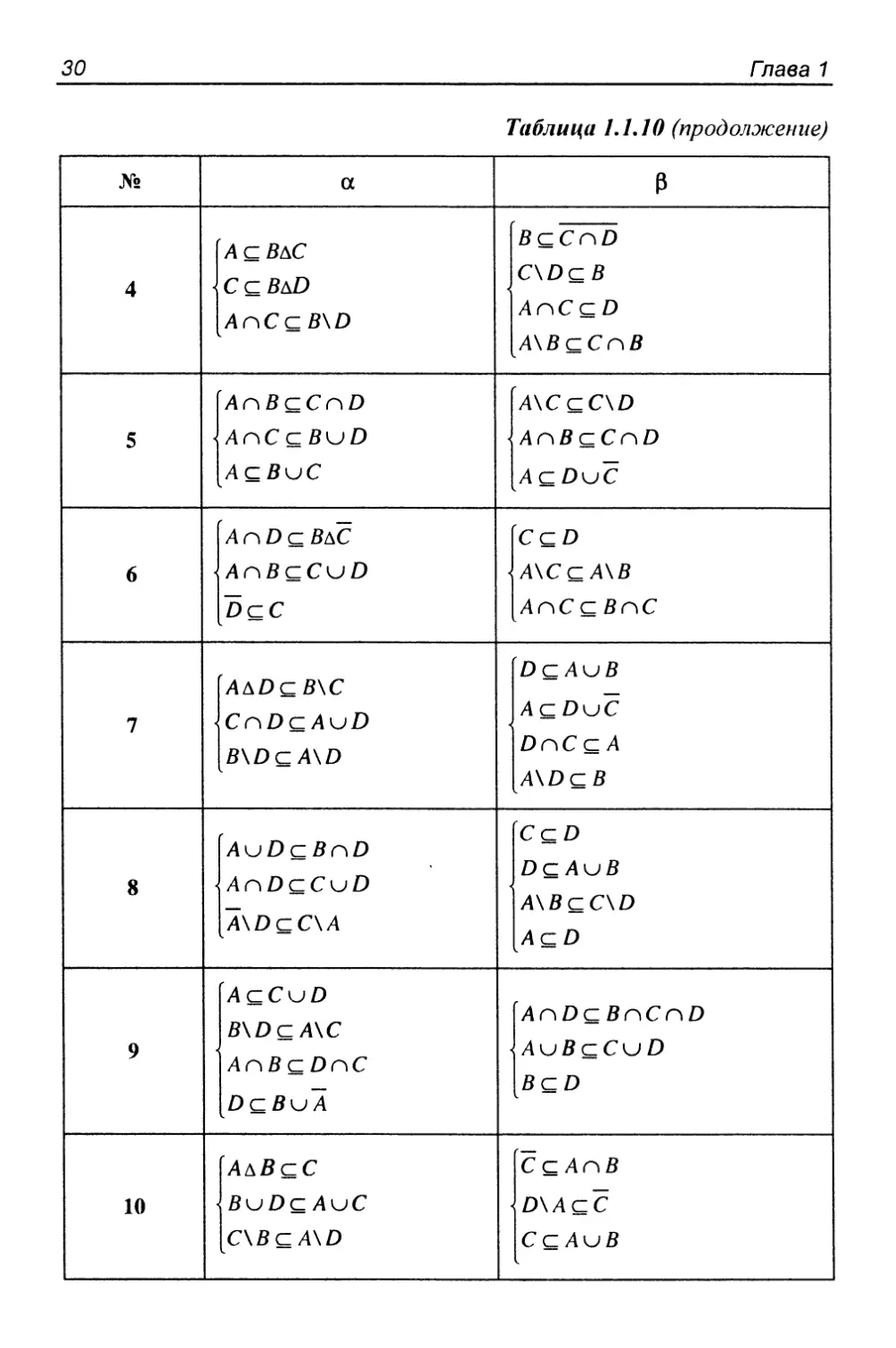
Задание 1.1.10
Для произвольных множеств Д, В, С, D проверить
равносильность систем а и (3.
Таблица 1.1.10
Хо
1
2
3
а
•
AuBqC
CuBqA^jD
c^aqb^d
AnCQB
CnBQA^D
AuBqCuD
BnDQA^C
AqBuC
CuDqAuB
P
■
ДиОсД\5
B\CqA\C
B(zAuD
AqC^D
(BnC)\AQCuD
(BnA)\CQ(B\A)\D
DnAQCXB
D\BQAnD
ЪQB\A
: Зак 3332
30
Глава 1
Таблица 1.1,10 (продолэк:еиие)
№
4
5
6
7
8
9
10
а
\а с B^C
\ С с Bad)
[AnC(zB\D
[AADCiBXC
\сглО^А^В
\b\dqa\d
JAnDcCuD
[д\ОсС\Д
[AcCuD
Lb\DcA\C
[Да£?сС
jiBuDcAuC
[c\iBcA\D
P
liBcCnD
C\DCiB
JAnCcD
[a\ccc\d
[acDuC
\a\cc^a\b
[АпС^ВслС
{DqAkjB
JacDuC
IDnCcA
[AXDCiB
JDcAUiB
д\всс\о
[дсО
JAuiScCuD
[c с Д n iB
\d\aq'c
\cqAkjB
Множества, графики, соответствия, отношения
31
Таблица LL10 (продолэюение)
№
11
12
13
14
15
16
17
а
^
•
•
DuCqBuA
DuBqCuA
BnDQC
DnCQB^A
BuCqDuA
CnAQBAD
BqCuD
DuAqCuB
•
•
BqCaD
DqCaA
BnDQC\A
CnBQAnD
BdDqCuA
BqDuC
AnBQ CaD
CnBQAuD
TiQD
A^BQC\D
AnDQAuB
C\AqB^
P
^
^
•
•
•
^
BuAqB\C
C\DqB\D
BQCnD
'CqBuA
BqDuA
(CnD)\BQDuA
(Cr\B)\DQ(C\B)r\J
BnAQD\C
A\CQBnA
CqC\B
CQDnA
D\AqiC
BnDQA
B\CQDnC
B\DqD\A
CnBaAnD
В^А^Ъ
DqA
B\DqB\C
BnDQDnC
AqCuB
BqA(j3
AnDQB
B\AqC
32
Глава 1
Таблица 1.1.10 (продоллсение)
№
18
19
20
21
22
23
24
а
\Ar\BQA(jD
[BAqD\B
{BqA^D
\c\aqb\d
\CnBQDr\A
[aqDuB
IcuAqBuD
[d\cqb\a
[DuCcA
IduAqBuC
JAuCcDufi
[cnAQD
\DnAQBuC
IduCqB^A
[DnBQCAA
[CcAuD
WqBqC
\buAqDuC
iCQA^D
IaqD^B
[cnAQD\B
P
\DqA
JAcCufi
\b\cqd\a
[bqA
UnBQAnCnD
IckjBqAuD
[cqa
[DcCni5
\а\в^Ъ
\d\aqc\a
\cQAnD
IDqBuC
\cqBuA
](AnD)\CQBuA
[(CnD)\AQ(D\B)\C
\BnCQA\D
\B\DQBnC
[DqD\C
\DQBr\A
\a\BqD
\Cr\AQB
[c\D^DnA
Множества, графики, соответствия, отношения
33
Таблица LLIO (окончание)
№ 1
25
26
27
28
29
30
а
{CnDQAnB
\cr\AQDuB
\CnBQD^A
IcnDQAuB
[BqA 1
ICaBqD\A
lAnBQCuB
[D\BqC\B
ic^BQDnB
IcnBQA^B
[C\BqA\C
ICqAuB
\d\BqC\A
\cnDQBnA
[i5cAuC 1
[CaDcA
[a\d^c\b
P 1
{c\aqa\b
\cr\DQAnB
Uqb
\cMqC\D
[cnAQDnA
[i5cCuD
|Ani5cC
[cViBcD 1
IAqB
\bqCuD
\c\dqa\b
[c^B
{Cr\BQBr\Dr\A
Id^cqBua
[DqB
[лсСпО
\b\cqJ
McCuD
Пример решения задания 1.1.10
Проверить равносильность систем
BnDQЛпС
BnAQDuC (*)и
BdDuA
Е\А сЛ\С
BnD Q АпС (**).
ВсСиЛ
34 Глава 1
I. Возьмём множества общего положения Л, В, С, D,
являющиеся подмножествами универсального множества U,
воспользовавшись техникой, описанной в решении примера 1.1.9. Будем
иметь:
[/={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16},
А = {9,10,11,12,13,14,15,16}, В = {5,6,7,8,13,14,15,16},
С = {3,4,7,8,11,12,15,16}, D = {2,4,6,8,10,12,14,16}.
I. Рассмотрим включения, вошедшие в систему (*).
BnD = {6,8,14,16}, ЛпС = { 11,12,15,16}.
По условию, {6,8,14,16} с {11,12,15,16} => список 6,8,14 пуст.
Значит, Л = {9,10,11,12,13,15,16}, В = {5,7,13,15,16},
С = {3,4,7,11,12,15,16}, D = {2,4,10,12,16}.
ВпЛ = {13,15,16}, Due = {2,3,4,7,10,11,12,15,16}.
Так как {13,15,16} с {2,3,4,7,10,11,12,15,16}, то {13} =0.
Множества А и В можно записать так:
А = {9,10,11,12,15,16}, В = {5,7,15,16}.
И, наконец, В с D U Л, то есть
{5,7,15,16} с {2,4,9,10, 11,12,15,16}=> {5,7} = 0.
Итак, множества А, В, С и D таковы: А = {9,10,11,12,15,16},
В = {15,16}, С = {3,4,11,12,15,16}, D = {2,4,10,12,16}.
Проверим при полученных А, В, С и D выполнение
включений (**):
В\А =0, поэтому включение В\А с А\С выполняется
независимо от вида множества А\С.
BnD = {16}, АпС = {11,15,16}, значит, BnDQAnC и
второе включение также выполнено.
Наконец, А = {1,2,3,5,6,7,8,13,14},
CuA = {l,2,3,4,5,6,7,8,ll,12,13,14,15,16} и BcCuA.
Получили, что все множества А, В, С и D,
удовлетворяющие системе включений (*), удовлетворяют также системе (**).
Множества, графики, соответствия, отношения 35_
2. Пусть теперь выполняется система (**).
Так же, как и в первой части доказательства, возьмём множества
А = {-Х9,Х10»-^11Д'12'-^13'-^14'-^15'-^1б}' 5 = {-^5'-^6'-'^7»-^8'-^13»-^14'-^'15'-^1б}'
B\A = {x^,X(^,X'j,x^}, { Л\С = {X(),XiQ,x^T„x^^}, И из выполнения
включения В\Л с А\С следует, что [х^,Х(^,х^,х^} = 0.
Рассматриваемые множества примут вид:
и ={^1,Х2,^з»-^4'-^9'-^10'-^11'-^12'-^13'-^14»-^15'-^'1б}'
Л = {Х9'-^10'-^11'-^12»-^'13»-^14'-^15'-^1б}' ^ -{^^\3'^\Л'^\5'^\())^
С = {Х2,Х^,Х^^,Х^2'^\5'^\в}\ ^ = {-^2'-^4'-^10»-^12'-^14>-^1б}-
5nD = {х,4Д1б}, ЛПС = {л, 1,Л-,2Д,5Д1б}-
Из включения BnDQ АпС следует, что {х^^} = 0, значит,
и ={^1,^2'-^'3'-^4>-^*9>-^10'-^11»-^12'-^13'-^15'-^^1б}'
А = {^9'-^10'-^11'-^12'-^13'-'^'15'-^1б}' ^-{-^13'-^15'-^1б}'
С = {^3'-^4'-^11'-^12'-^15''^1б}' ^ - {•^2'-^^4>-^10»-^12>-^'1б}-
А - {^1 Д2'-^'3'-^4'-^5'-^6'-^'7'-^'8 }'
С U Л = {Х|,д:2,Л'з>-^4>-^5'-^6'-^7'-^8'-^1 Ь^\Ъ^\Ъ^^\^ 1 '
Из включения В с С и Л следует, что {х^-х^} = 0, значит,
и ={^1,Х2,А'зД'4»-^9'-^10»-^11'-^12>-^15»^'1б}»
А = {А9»-^10'-^11'-^'12'-^'15'-^1б}' ^-{^\Ъ^^\^\^
С = {АЗ'-^4'-^11'-^12'-^15'-^'1б}' ^ -{-^2>-^4'-^10>-^12'-^1б}-
Проверим для этих множеств выполнение включений
системы (*): Br\D-{xy^Q^\, { AnC = {xii,Xi2,Xi5»-^i6} и включение
Br\D^Ar\C выполнено.
{ iBnA = {Xi5,X,6}, { ОиС = {Х2,Хз,Х4,Х,оД11,Х,2,Х,5,Х|б}, ВКЛЮ-
чение Br\Ac,DKJC выполнено.
И, наконец, DuЛ = {x2,X4,X9Xio,Aii,Xi2»-^i5'-^16} и BcDuA
также верно. Итак, доказано, что системы (*) и (**) равносильны.
36
Глава 1
1.2. Графики
Декартовым произведением множеств Л^,А2,...,Л,^ называется
множество А] хА2Х...хА,^ ={{а^,а2,...,а^^)\а^ е Ai,...,a,^ ^ АЛ •
Проекцией вектора {ai,a2,...,a,^) на ось / называется
координата а/. Проекцией миолсества А векторов на ось будем
называть множество проекций векторов из А на эту ось.
Графиком будем называть подмножество декартова
произведения двух множеств.
Инверсией графика Р будем называть график
p-^={{a,b)\{b,a)GP}.
Композицией графиков Р и Q называется график
PoQ = {(a,b)\3^{{a.x)eP и (x.b)GQ)}.
Задание 1.2.1
1. Проверить справедливость равенства а для множеств
А = {1,2}, В = {2,3},С = {1,3}.
2. Выяснить, верно ли равенство а для произвольных Л, В, С.
Таблица 1.2.1
№
1
2
3
4
5
6
7
8
а
ЛхС = (Лх(С\5))и(Лх(Сп5))
ДхС = (Лх(Сп5))и(ЛхС)
Ах{В ^C) = {Ax{BкJC)\{Ax{C глВ))
ДхС = (Дх(С\в))и(ДхС)
Ах(ВиС)^{АхВ)^(Ах{С\В))
Ax{C\B) = {AxC)^{Ax{Cr^B))
AxC = (Ax(CUiB))n(AxC)
Ax{Cr^{B^C)) = {AxC)^(Ax{Cr^B))
Множества, графики, соответствия, отношения
37
Таблица 1.2.1 (окончание)
Хо
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1 26
1 ^'^
1 28
1 29
1 30
а
Лх(С\В) = {АхС)\{Ах(Сг\В)) 1
Лх(ВиС) = {Лх{ВАС))и(Лх(ВпС)) 1
ЛхС = {Ах{С и В))\{Лх(В\С)) 1
Ax(iBnC) = (AxC)\(Ax(C\iB)) 1
Лх(В Г\С) = (Лх(В иС))\(Лх{В аС)) 1
Ax(C\iB) = (Ax(iBuC))\(AXiB) 1
iBxA = (iBx(A\C))u(^x(AnC)) 1
BxA = (Bx(Ar\C))(j(BxA)
BxA = (BxA)u(Bx(A\C))
Bx{AuC) = (Bx(A\C))u{BxC)
BxA = {BxA)r\(Bx(AuC))
Bx{A\C) = (BxA)\(Bx{AnC))
Bx A = {Bx{Au C))\(Bx{C\ A))
Bx(AnC) = {BxA)\{Bx(A\C))
Вх(А\С) = (ВхА)а(Вх(Аг\С))
Bx(A\C) = iBx{AKjC))\{BxC)
СхВ = (Сх{В\А))и(Сх{ВпА))
CxB = (Cx{BnA))u{CxB)
Cx(AAB) = {Cx(AuB)\{Cx(AnB))
CxB = {Cx{B\A))u{CxB)
Cx(AuB) = (CxA)^(Cx(B\A))
Cx(A\B) = {CxA)A{Cx(AnB))
38 Глава 1
Пример решения задания 1.2.1
7. Проверить справедливость равенства
Сх(5\А) = (СхЯ)д(Сх(ЛпВ)) для множеств
Д = {1,2}, В = {2,3},С = {1,3}.
2. Выяснить, верно ли равенство
Сх(В\А) = {СхВ)а(Сх(АпВ)) для произвольных Л, В, С.
1. Для нашего случая
Сх(В\Л) = {1,3}х({2,3}\{1,2}) = {1,3}х{3} = {(1,3),(3,3)}.
Сх(ЛпВ) = {1,3}х({1,2}п{2,3}) = {1,3}х{2} = {(1,2),(3,2)}.
СхВ = {1,3}х{2,3} = {(1,3),(1,2),(3,2),(3,3)}.
(СхВ)д(Сх(ЛпВ)) =
={(1,3),(1,2Ш,2ШЗ)}Д{(1,2Ш,2)}={(1,3),(3,3)}.
Итак, мы убедились, что в нашем примере равенство
выполнено. Проверим это для общего случая.
2. Пусть A = {a,d}, B = [b,d}, С = {с}, где a,b,c,d —списки
элементов.
Тогда Cx(B\A) = [c}x{b} = {{c,b)}, где [(с,Ь)} —множество
пар элементов, первая компонента которых входит в список с,
а вторая — в список Ь.
AnB = {d},
(CxB)A{Cx(AnB)) = {(c,bUc,d)}^{(c,d)} = {(c,b)}.
Как видно, множества Сх(В\А) и (СхВ)^(Сх(АпВ))
состоят из пар одинакового вида, следовательно, равенство
Сх(В\А) = (СхВ)^{Сх(АпВ)) для произвольных Л, В, С.
Задание 1.2.2
Для данного графика Р найти :
P"^ Рор, р-^Р, пр2(Р"^оР)хпр,(РоР).
Множества
, графики, соответствия, отношения
39
Таблица 1.2,2
1 Хо
1 1
1 ^
1 ^
1 "^
5
1 ^
1 '^
1 ^
1 ^
1 ^^
1 ^^
1 ^^
1 ^"^
1 ^"^
1 ^^
16
17
1 ^^
1 ^^
1 20
1 ^^
1 22
1 ^"^
1 ^"^
Р 1
(1,2), (1,3), (4,2), (2,3), (3,3)
(2,2), (4,4), (1,2), (3,1), (3,4) 1
(1,2), (2,3), (3,1), (2,2), (3,2) 1
(3,3), (3,2), (2,2), (12), (3,1) 1
(0,1), (1,1), (1,0), (0 2), (2,1) 1
(5,4), (2,4), (4,4), (3,2), (5,3)
(1,1), (1,2), (2,3), (3,1), (3,2) 1
(1,3), (3,1), (2,2), (1,2), (1,4)
(3,8), (8,4), (4,4), (8,3), (4,3)
(0,2), (2,3), (3,3), (3,0), (0,0) 1
(1,5), (5,2), (2,2), (1 1),(1,3)
(0,2), (0,3), (0,0), (1,2), (2,3)
(а,Ь1 {а,с), (d.b), {с,с), {Ь,с)
(Ь,Ь\ (d,d\ {a,bl (с,а), {c,d)
(a,b\ ib,c), (с,а), (Ь,Ь), {c,b)
(сс), (c,bl (b,bl (a,b), (ca)
(e,a), (a,a), {a,e), {e,b), (b,a)
{f,d\ (b.dl (d,d), icbl (f,c)
{a,al (a.b\ {b,c\ (ca), (c.b)
{a,cl (c,«), (b,bl (a,b\ (a,d)
(c,g\ (g,d), id,d\ {g,c), {d,c)
{e,b), (b,c), {c,c), {c,e), (e,e)
{a,f\ {f,b), {b,bl {a,a), (а,с)
(e.b), {e,c), (e.e), {a,b\ (b.c)
40
Глава 1
Таблица L2.2 (окончание)
1 №
1 ^^
26
27
1 28
1 29
30
Р 1
(jc,^),Cv,z), (г,)'), (<^z), (V.Z) 1
(у,у)ЛгЛ (х,у1 {z,x)Az,t)
{х,у)Лу,:Х (z,x\ {y,y)Az,y)
{z,z)Az,y\ (у,у). {x,y)Az,x)
it,x)Ax,xl (x,tl (t,y)Ay,x)
(w,0, (v,0, (t,t). (z,y\ (w,z)
Пример решения задания 1.2.2
Для данного графика Р = {(1,1),(1,2),(2,3),(2,2)} найти: Р~\
РоР, Р~^ оР^пр^(Р~^оР)хпр^(РоР),
По определению инверсии, (2,1)g Р~\ так как (1,2)е Р.
Итак далее, получаем : Р"' ={(1,1),(2,1),(3,2),(2,2)}.
По определению композиции, (1,3)е РоР, так как
существует 2, причём (1,2)еР и (2,3) е Р. Продолжая дальше строить
композицию, получим: Ро Р = {(1Д),(1,2),(1,3),(2,3),(2,2)}.
Аналогично получаем
Р-^Р = {(1,1),(2,2),(1,2),(2,1),(2,3),(3,2),(3,3)}.
Вспоминая определение проекции множества векторов на
ось, получим: пр2(Р~^ о Р) = { 1,2,3},аналогично найдём другую
проекцию:
пр,(Ро Р) = {1,2}, и, наконец, можем написать:
пр,(р-^ о Р) X пр, (Ро Р) = {(1,1),(1,2),(2,1),(2,2),(3,1),(3,2)}.
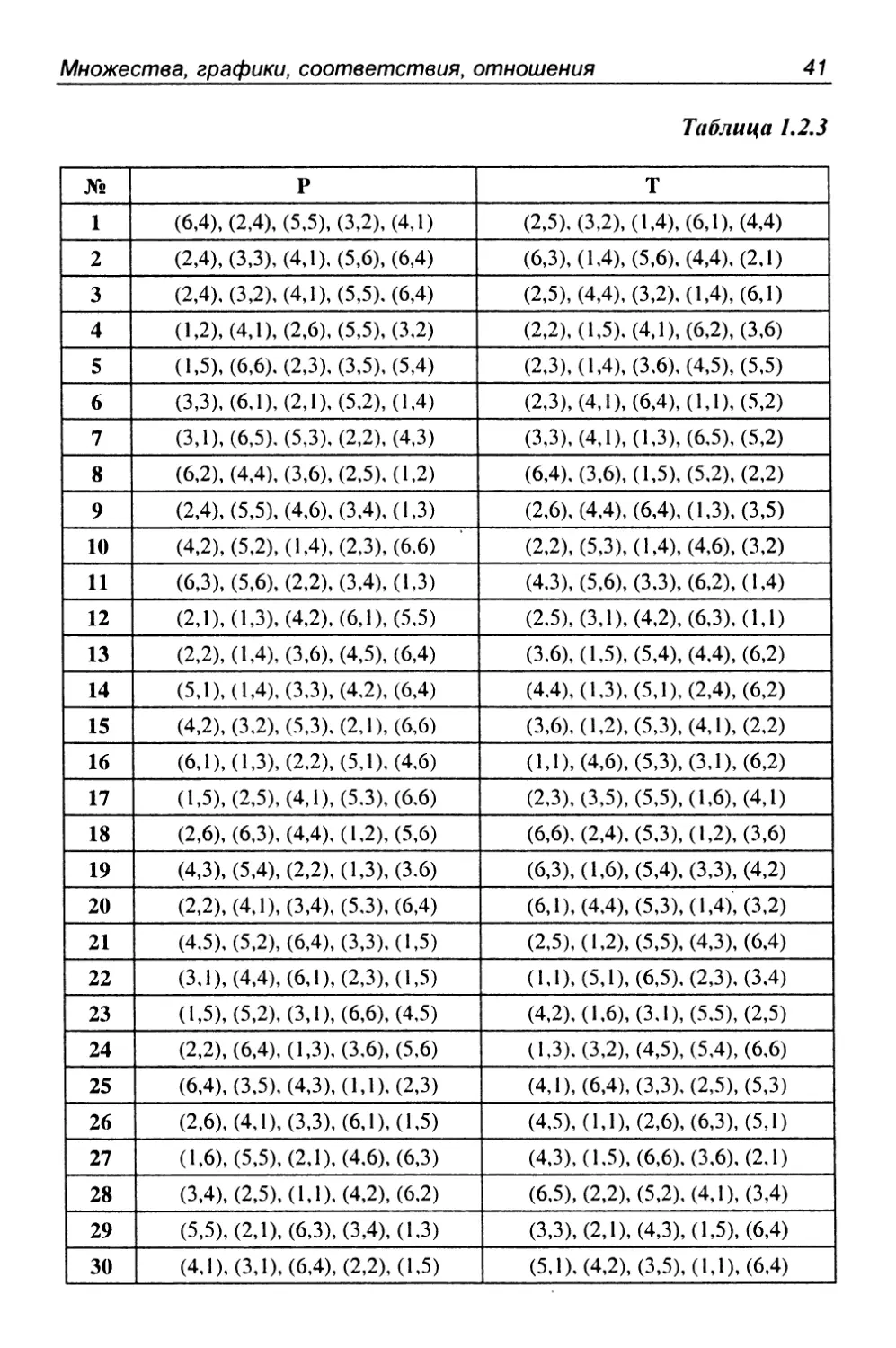
Задание 1.2.3
Для данных графиков Р и Г решить относительно графика X
уравнение X ^ Р = Т при условии, что | X |= 6, npi Х = прз А' =
= {1,2,3,4,5,6}. Для каждого найденного X указать РоХ.
Множества, графики, соответствия, отношения
41
Таблица 1.2.3
1 •'^°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
1 30
Р
(6,4), (2.4), (5,5), (3,2), (4,1)
(2,4), (3,3), (4,1). (5,6), (6,4)
(2,4). (3,2). (4,1), (5,5). (6,4)
(1,2), (4,1), (2,6), (5,5), (3,2)
(1,5), (6,6). (2,3). (3,5), (5,4)
(3,3), (6,1). (2,1), (5.2), (1,4)
(3,1), (6,5), (5,3), (2,2), (4,3)
(6,2), (4,4), (3,6), (2,5), (1,2)
(2,4), (5,5), (4,6), (3,4), (1,3)
(4,2), (5,2), (1,4), (2,3), (6.6)
(6,3), (5,6), (2,2), (3,4), (1,3)
(2,1), (1,3), (4,2), (6,1), (5,5)
(2,2), (1,4), (3,6), (4,5), (6,4)
(5,1), (1,4), (3,3), (4,2), (6,4)
(4,2), (3,2), (5,3), (2,1), (6,6)
(6,1), (1,3), (2,2), (5,1), (4.6)
(1,5), (2,5), (4,1), (5,3). (6.6)
(2.6), (6,3), (4,4), (1,2), (5,6)
(4,3), (5,4), (2,2), (1,3), (3.6)
(2,2), (4,1), (3,4), (5,3), (6,4)
(4.5). (5,2), (6,4), (3,3), (1,5)
(3,1), (4,4), (6,1), (2,3), (1,5)
(1,5), (5,2), (3,1), (6,6), (4.5)
(2,2), (6,4), (1,3). (3,6), (5,6)
(6,4), (3,5). (4,3), (1,1), (2,3)
(2,6), (4,1), (3,3), (6,1), (1,5)
(1,6), (5,5), (2,1), (4,6), (6,3)
(3,4), (2,5), (1,1), (4,2), (6.2)
(5,5), (2,1), (6,3), (3,4), (1,3)
(4.1). (3,1), (6,4), (2,2). (1.5)
т 1
(2.5). (3.2), (1,4), (6,1), (4,4)
(6,3), (1,4), (5,6), (4,4), (2,1)
(2,5), (4,4), (3,2), (1,4), (6,1)
(2,2), (1,5). (4,1), (6,2), (3,6)
(2,3), (1,4), (3.6), (4,5), (5,5)
(2,3), (4,1), (6,4), (1,1), (5,2)
(3,3), (4,1), (1,3), (6,5), (5,2)
(6,4), (3,6), (1,5), (5.2), (2,2)
(2,6), (4,4), (6,4), (1,3), (3,5)
(2,2), (5,3), (1,4), (4,6), (3,2)
(4,3), (5,6), (3,3), (6,2), (1,4)
(2,5), (3,1), (4,2), (6,3), (1,1)
(3,6), (1,5), (5,4), (4,4), (6,2)
(4.4), (1,3), (5,1), (2,4), (6,2)
(3,6), (1,2), (5,3), (4,1), (2,2)
(1,1), (4,6), (5,3), (3,1), (6,2)
(2,3), (3,5), (5,5), (1,6), (4,1)
(6,6), (2,4), (5,3), (1,2), (3,6)
(6,3), (1,6), (5,4), (3,3), (4,2)
(6,1), (4,4), (5,3), (1,4), (3,2)
(2,5), (1,2), (5,5), (4,3), (6,4)
(1,1), (5,1), (6,5), (2,3), (3.4)
(4.2), (1,6), (3.1), (5.5), (2,5)
(1,3). (3,2), (4,5), (5,4), (6,6)
(4,1), (6,4), (3,3), (2,5), (5,3)
(4,5), (1,1), (2,6). (6.3), (5,1)
(4,3), (1,5), (6,6), (3,6), (2,1)
(6,5), (2,2), (5,2). (4,1), (3,4)
(3,3), (2,1), (4,3), (1,5), (6,4)
1 (5,1), (4,2), (3,5), (1,1), (6,4)
42 Глава 1
Пример решения задания 1.2.3
Для данных графиков Р = {(5,3),(1»3),(4,4,),(2,1),(3,6)} и
Т = {(1,4),(2,1),(6,3),(5,6),(3,3)} решить относительно
графика X уравнение ХоР = Т при условии, что \Х\=6, npjX =
= пр2Х= {1,2,3,4,5,6}. Для калсдого найденного X указать
РоХ.
Для каждой пары (а,Ь)еТищем пару (x,b)G Р. Если такая
пара существует, то (а,х) может принадлежать графику X.
Запишем множество А, составленное из пар вида (а,х):
А = {(1,4),(2,2),(6Д),(6,5),(5,3),(ЗД),(3,5)}.
Так как 4Епр2Х, то пара (4,х)е X. Очевидно, что х = 6, так
как иначе в графике Т нашлась бы пара, начинающаяся на 4.
Составим X, добавляя к паре (4,6) пары из графика А так,
чтобы выполнилось условие задачи. Получим:
X, = {(1,4),(2,2),(6,1),(5,3),(3,5),(4,6)},
Х2={(1,4),(2,2),(6,5),(5,3),(3,1),(4,6)}.
Проверкой убеждаемся в том, что Х^ и Xj являются
решениями исходного уравнения. Согласно определению композиции,
выпишем РоХ^ и РоХ,: РоХ^ ={(1,5),(2,4),(ЗД),(4,6),(5,5)},
РоХ2={(1Д),(2,4),(3,5),(5,1),(4,6)}.
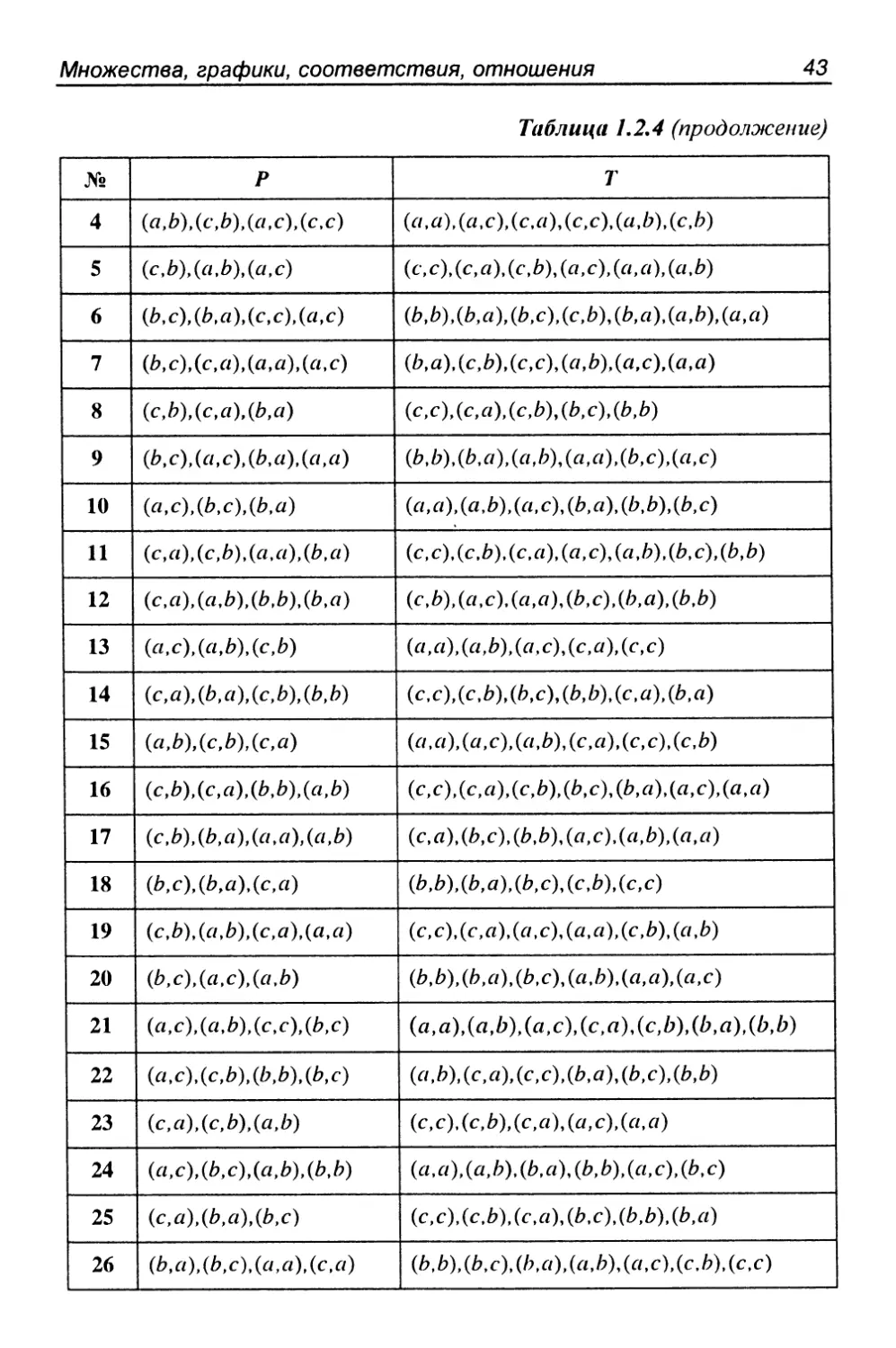
Задание 1.2.4
Для графиков Ри Г из соотношения РоХ=Т найти
график X наименьшей возможной мощности.
Таблица 1.2.4
№
1
2
3
Р
(a,b),(a,c),(b,b),ic,b)
(a,b),(h,c),{c,c)Xc,b)
(b,a),ib,c),(a,c)
Т
(а,а),(а,с),(а,Ь),{Ь,а),{Ь,с),(с,а),(с,с)
(ax)Xb,a)Xb,b),(c,a),{c,b)Xc,c)
{b,b),{b,c),{b,a\{a,b),{a,a)
Множества, графики, соответствия, отношения
43
Таблица 1.2.4 (продолэюеиие)
1 ^'
1 "^
1 ^
1 ^
1 "^
1 ^
1 ^
10
1 ^^
1 ^^
1 ^"^
1 ^"^
1 ^^
1 ^^
1 ^^
1 ^^
1 ^^
1 20
1 ^^
1 22
1 ^"^
1 ^"^
1 ^^
1 26
Р
(а,Ь),{с,Ь),{а,с),(сх)
(c,b),(a,b),(a,c)
(b,c),{b,a),{c,c),{a,c)
(b,c),(c,a),{a,a),{a,c)
{c,b),{c,a\{b,a)
ib,c),(ci,c),{b,a),{ci,a)
{а,с),(Ьх)ЛЬ.а)
{с,а),{с,Ь),(ам),{Ь,а)
{c,a),(a,b),{b,b)Xb,a)
{a,c),(a,bUc,b)
{c,a),(b,a),{c,b),(b,h)
{a,b),{c,b),{c,d)
(c,b),{c,a),{b,b),{a,b)
{c,b),{b,a),{a,a),{a,b)
(b,c),(b,a),(c,a)
{c,b)Aci>b),{c,a),{a,d)
{b,c),{a,c),{a^b)
(a,c),(a,b),{c,cUb,c)
iax),(c,b),{b,b),{b,c)
ic,a),{c,b),{a,b)
{a,c),{b,c),{a,b),{b,b)
{c,a),(b,aUb,c)
(b,a),(b,c)Xa,a),{c.a)
T 1
{a,a),{cix),{c,ci),(c,c),(ci,b),(c,b)
(c,c),(c,a),(c,b),{a,c),(a,a),(a,b)
(b,b),{b,a),{b,c),{c,b)Xb,a)Xa,b),{a,a) 1
{b,d),{c,b),{c,c)Xa,b)Xa,c),{a,a) 1
{c,c),{c,d),{c,b\{b,c),{b,b) 1
{b,b)XbM),{ci,h)Xa,a),{b,c),{a,c) 1
{a,ci),{a,b),{a,c\{b,a\{b.b),{b,c) 1
{c,c)Xc,b)Xc,ci)Xa,c)M.b),{b,c),(b,b) 1
{c,b),{ci,c),{a,a)Xb,c),{b,a),{b,b) 1
{ci,a),{a,b),{a,c),{c,a),{c,c)
{cx),ic,bUb,cUb,b)Xc.a),ib.a) 1
{a,a),(a,c),(a,b),{c,a),{c,c)Xc,b)
(c,c),ic,a)Xc,b),{b,c),(b,a),(a,c),{a,a)
ic,a),{b,c),(b,b),(a,c),{a,b),{a,ci) 1
{b,b),{b,a),{b,c\{c,bUc,c)
(c,c),(c,a),{ci,c),ia,a),(c,b),(ci,b)
{b,b),{b,a)Xb,c)M^b),(a,a),{a,c)
(a,a),{a,b)Xa,c),{c,a),{c,b),(b,a).(b,b)
{ci.b),{c,a),{c,c),{b,a)Xb,c),{b,b)
(c,c),(c,b),(c,a),(ci,c),(a,a)
{a,a),{ci.b)Xb,a),(b,b),ia,c),{bx)
1 {c,c),{c,b).(c,a),ibx),(b,b).(b,a)
(b,b),{b,c\(b,a),{ci,b)Xax),{c,b)Xcx)
44
Глава 1
Таблица L2.4 (окончание)
1 №
1 ^'^
1 28
1 29
1 30
Р
(Ь,а),{а,с),{с,с)Хс,а)
(а,Ь)Ха,с),ф,с)
(b,a)Xc,a)Xb,c),{cx)
(a,b),{a,a),{c,a)
Г 1
{b,c)Xa,b)Xa,a)Xc,b),(c,a)Xcx) 1
{a,a),{a,c),{a,b)Xb,a)Xb,b) 1
{b,b),(b,c),{c,bUc,c),{b,a),(c,a) 1
(a,«),(«,c),(fl,Z?),(c,c),(c,/?),(c,a)
Пример решения задания 1.2.4
Для графиков Р = {(b,a),(c,a)Xc,b)} и
Т = {(b,b),(byC),(b,a),(c,b)Xc,c),(cM)} из соотношения
РоХ=Т найти график X наименьшей возмолсиоймощности.
Найдём инверсию графика Р: Р~^ ={{a,b),(a,c),(b,c)}.
Пусть X — график наименьшей мощности, являющийся
решением уравнения РоХ=Т. Из определения композиции
графиков и минимальности X следует, что пр2Р= пр, X = {а,Ь}.
Найдём композицию графика Р~'с левой и правой частями
равенства Ро X =Т . Получим:
{(a,b)Xa,cUb,c)}о{{b,aUc,ci\(c,b)}o X = Р'^ оТ,ияи
{(a,a)Xb,bUa,b\(b,a)}o X = Р~^ оТ , откуда
{(а.а)ХЬ.Ь)}о X u[(a,bUka)}o X =Р~^ оТ ,
Из равенства пр^Р= пр, X ={а,Ь} и определения композиции
графиков следует, что {{a,a)Xb,b)}o X = X .
Значит, верно равенство X и{(а,а)ХЬ,Ь)}о X = Р~^ о Г .
Итак, график Р~ о 7 кроме пар графика X может содержать
также пары графика {(а,а)ХЬ,а)}о X , не попавшие в X .
Выпишем все пары, попавшие в график Р~ ^Т .
Р-' оТ = {(aM(a.c)Xb,c)}o{(b,b)Xkc)Xb,aUc,bUc,c)Xc,^^^
= {(a,b)Xa,c)Xa,a)Xb,b)Xb,c)Xka)}.
Множества, графики, соответствия, отношения
45
Выберем из этого графика пары, образующие X .
Для этого изобразим таблицу, в заголовках столбцов выписав
пары графика Р~^ о Г, а в заголовках строк — пары графика Т
(табл. 1.2.4а).
Таблица 1.2.4а
bb
be
ba
cb
ее
ea
ab
*
*
ae
*
*
aa
' *
*
bb
*
be
*
ba
*
Для каждой пары (u,v)e P ^ ^T звёздочкой отметим пары из Т,
попавшие в композицию Р~^ о{(и^у)}. Далее, выберем
наименьшее число столбцов таблицы так, чтобы для любой строки в
выбранном наборе нашёлся столбец, имеющий символ "*" в данной
строке, причём Р~ ° {(w, v)} не должен иметь пар, не входящих в Т.
В нашем примере видно, что такой набор образуют
столбцы, помеченные комбинациями аЬ,ае,аа, следовательно,
X ={аЬ,ае,аа}.
1.3. Соответствия
Соответствием между множествами X и Y будем называть
тройку объектов: Г = (X,Y,G), где X — область отправления
соответствия, Y — область прибытия соответствия, G — график
соответствия, причём G qX хУ.
46 Глава 1
Областью определения соответствия будем называть npj G.
Областью значений соответствия будем называть np^G.
Соответствие называется всюду определённым, если пр, G = X,
Соответствие называется сюръективным, если np^G = Y.
Соответствие будем называть функциональным, или функцией,
если его график не содержит пар с одинаковыми первыми и
различными вторыми координатами.
Соответствие называется инъективным, если его график не
содержит пар с одинаковыми вторыми и различными первыми
координатами.
Соответствие называется отобралсением X в Y, если оно
всюду определено и функционально.
Соответствие называется отобралсением X на Y, если оно
всюду определено, функционально и сюръективно.
Соответствие называется взаимно однозначным, если оно
функционально и инъективно.
Соответствие называется биекцией, если оно всюду
определено, сюръективно, функционально и инъективно.
Образом мнолсества А при данном соответствии называется
множество Г{В) = [у\{х,у)^0 и хЕ А}.
Прообразом мнолсества В при данном соответствии
называется множество r~\B) = [x\{x,y)iE:G и у^В).
Множества называются равномощными, если между ними
можно установить биекцию.
Множество называется счётным, если оно равномощно
множеству натуральных чисел.
Множество называется континуальным, если оно равномощно
множеству действительных чисел отрезка [0,1].
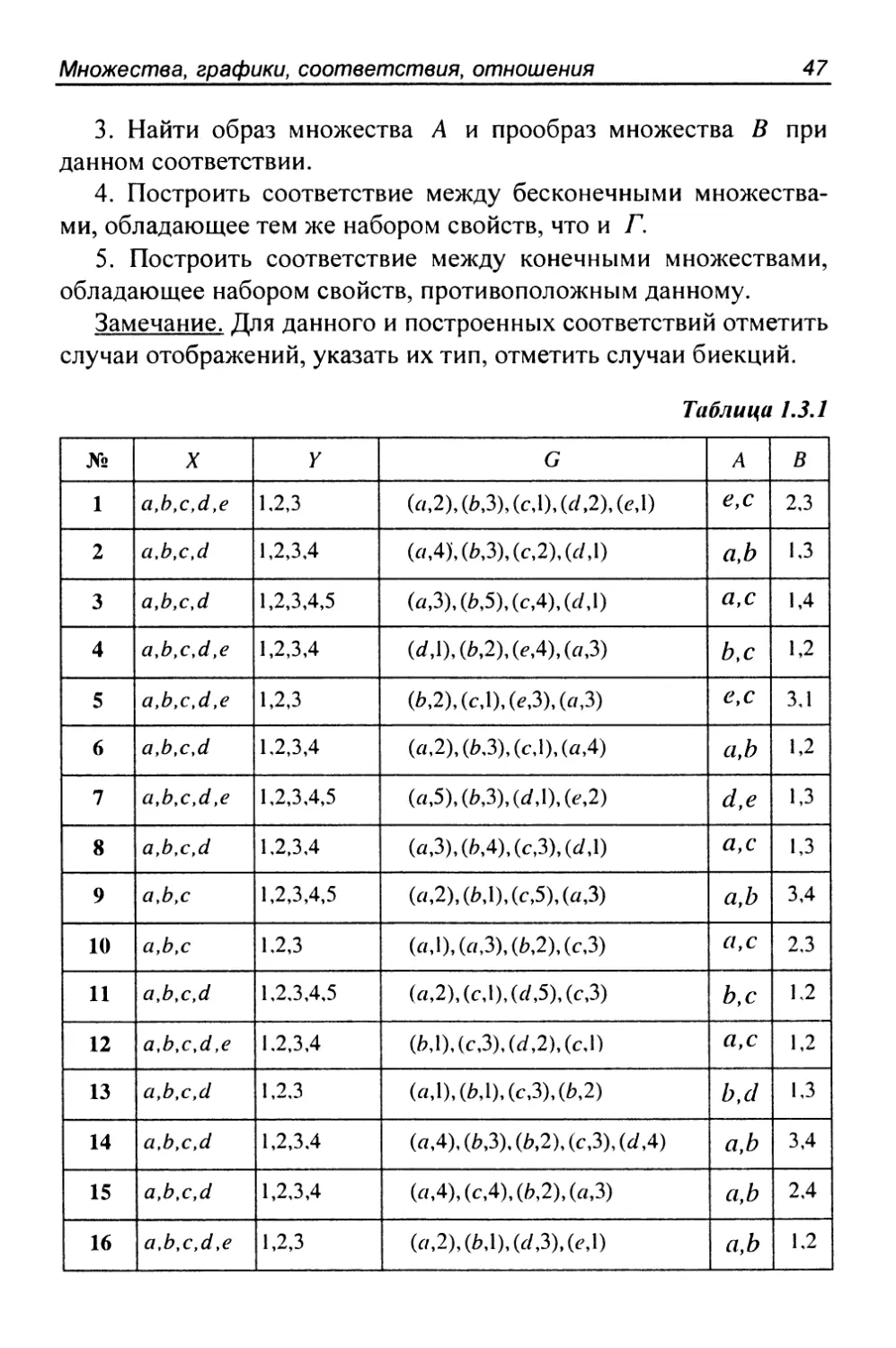
Задание 1.3.1
Дано соответствие Г = {X,Y,G).
1. Изобразить соответствие в виде графа.
2. Выяснить, какими из 4 основных свойств (всюду
определённость, сюръективность, функциональность, инъективность)
обладает Г.
Множества, графики, соответствия, отношения
47
3. Найти образ множества А и прообраз множества В при
данном соответствии.
4. Построить соответствие между бесконечными
множествами, обладающее тем же набором свойств, что и Г.
5. Построить соответствие между конечными множествами,
обладающее набором свойств, противоположным данному.
Замечание. Для данного и построенных соответствий отметить
случаи отображений, указать их тип, отметить случаи биекций.
№
1
2
3
4
5
6
7
8
9
10
11
12
1 ^^
1 ^"^
1 ^^
1 ^^
X
a,b,c,d,e
a,b,c,d
a,b,c,d
a,b,c,d,e
a,b,c,d,e
a,b,c,d
a,b,c,d,e
a,b,c,d
a,b,c
a,b,c
a,b,c,d
a,b,c,d,e
a,b,c,d
a,b,c,d
a,b,c,d
a,b,c,d,e
Y
1,2,3
1,2,3,4
1,2,3,4,5
1,2,3,4
1,2,3
1,2,3,4
1,2,3,4,5
1,2,3,4
1,2,3,4,5
1,2,3
1,2,3,4,5
1,2,3,4
1,2,3
1,2,3,4
1,2,3,4
1,2,3
Таблица 1,3.1
G
(a,2),(W),(c,l),(r/,2),(e,l)
(r/,4),(W),(c,2),(./,l)
(a,3),(Z7,5),(c,4),(J,l)
{dM{baUeAUa.3)
(Ь,2)Лс,\)ЛеЛ(с1,3)
(аЛ)ЛЬЗ)Лс,\)ЛаА)
(«,5),(W),W,1),(6',2)
(a,3),(M),(c,3),(J,l)
(./,2),(Z7,l),(c,5),(a,3)
(«,!), (r/,3),(W),(c,3)
(«,2),(c,l),W,5),(c,3)
(/7,l),(c,3),W,2),(c,l)
(аЛфЛисЗиЬЛ)
(a,4),(W),(W),(c,3),W,4)
(«,4),(c,4),(^,2),(«,3)
iaaUbAUd,3),(eA)
A
e,c
a,b
a,с
b,c
e,c
a,b
d,e
a,с
a,b
a,с
b,c
a,с
b,d
a,b
a,b
a,b
В 1
2,3
1,3
1,4 1
1,2
3,1
1,2
1,3
1,3
3,4
2,3
1,2
1,2
1,3
3,4
2,4
Ь2
48
Глава 1
Таблица 1.3.1 (окончание)
1 №
1 ^'^
1 ^^
1 ^^
1 20
1 ^^
1 22
1 23
1 ^"^
1 ^^
1 26
1 27
1 28
1 29
1 30
X
a,b,c,d
a,b,c,d
a,b,c
a,b,c,d
a,b,c.d
a,b,c,d
a,b,c,d
a,b,c
a,b,c,d,e
a,b,c,d
a,b,c,d,e
a,b,c,d
\a,b,c
a,b,c
Y
1,2,3,4
1,2,3,4
1,2,3,4,5
1,2,3,4
1,2,3
1,2,3
1,2,3,4
1,2,3,4
1,2,3
1,2,3,4
1,2,3,4,5
1,2,3,4
1,2,3,4,5
1,2,3
G
(Z7,3),(a,2),(c,2),W,l)
(«,3),(c,2),(J,l),(c,4)
(./,2),(Z7,5),(c,4),(W)
(a,l),(W),(«,2),(c,4)
(a,3),(W),(c,l),W,2)
(a,l),(W),(c,2),(«,2)
(a,3),(M),(c,l),W,2)
(fl,3),(^,l),(c,2),(c,l)
(c,2),(^,l),(a,3),(Z7,3)
(Z7,2),(c,3),(J,l),(M)
{Ь.5)ЛсЛ(еМ(а.2)
(Z7,3),(c,4),(J,3),(a,l)
(Z7,2),(c,l),(a,5),(W)
(Z7,l)',(Z7,3),(c,2),(fl,3)
A
a,с
c,d
a,b
a,b
c,d
c,d
a,b
a, с
a,d
b,c
a,e
b,d
kc
a,b
b\
1,4 1
2,3
2,5
2,3
1,3
2,3
1,4 1
4,2
3,1
1,2
1,3
3,1
4,3
2,3
Пример решения задания 1.3.1
Решим задание 1.3.1 для соответствия
r = (XXG), если X={a,b,c,d},
К = {1,2,3,4,5},
С = {(л,2),(Ь,1),(Ь,5),(^,4)},
А = {а,Ь}, В = {3,4}.
I. Изобразим соответствие в виде графа
(рис. 1.3.1, а).
Рис. 1.3.1, а
Множества, графики, соответствия, отношения
49
2. Выясним, какими из свойств обладает данное соответствие,
а) Соответствие не всюду определено, так как
up^G = {a,b,d}4^X.
(3) Соответствие не сюръективно, так как np^G = {1,2,4,5} ^ Y.
у) Соответствие не функционально, так как его график
содержит две пары (Ь,1)и (Ь,5) с одинаковыми первыми и
различными вторыми координатами.
5) Соответствие инъективно, так как его график G не
содержит пар с одинаковыми вторыми и различными первыми
координатами.
3. Найдём образ Г(А)и прообраз Г~ (В).
Г(Л) = { 1,2,5}, так как Л = {«,Ь} и {(a,2),(Z?,l),(b,5)} cG .
r~\B) = {d}, так как В = {3,4} и только (r/,4)EG.
4. Построим соответствие между бесконечными множествами,
обладающее тем же набором свойств, что и данное соответствие.
Пусть А:=[0,2], г = (-сх.,+оо), G = {(x,y)\x' +у^ =1 и х>0}.
Покажем, что это
соответствие (рис. 1.3.1, б) обладает тем же
набором свойств, что и данное.
а) Построенное соответствие
не всюду определено, так как
ир^С = т]ФХ.
(3) Построенное соответствие
не сюръективно, так как
np^G = [-l,l]^r.
у) Построенное соответствие
не функционально, т. к.,
например, (0,1)gG и (0,-1)eG.
5) Соответствие инъективно, так как его график не содержит
пар с различными первыми и одинаковыми вторыми
координатами.
Рис. 1.3.1,6
50
Глава 1
5. Построим соответствие между
конечными множествами, чтобы оно было
всюду определено, сюръективно,
функционально и не инъективно, изобразим
его в виде графа (рис. 1.3.1, в) и
аналитически:
r = ({M,v},{w},{(M,w),(v,w)}).
Рис. 1.3.1, в
Покажем, что это соответствие
обладает требуемым набором свойств,
что и данное.
а) Действительно, это соответствие всюду определено, так как
np,G = X ={m,v}.
(3) Соответствие сюръективно, так как np^G = {w} = Y.
Y) Соответствие функционально, так как в его графике нет
пар с одинаковыми первыми и различными вторыми
координатами.
5) Соответствие не инъективно, так как его график состоит из
двух пар (m,w)h , (v,w) с различными первыми и одинаковыми
вторыми координатами.
Так как построенное соответствие всюду определено,
сюръективно и функционально, оно является отображением X
на Y.
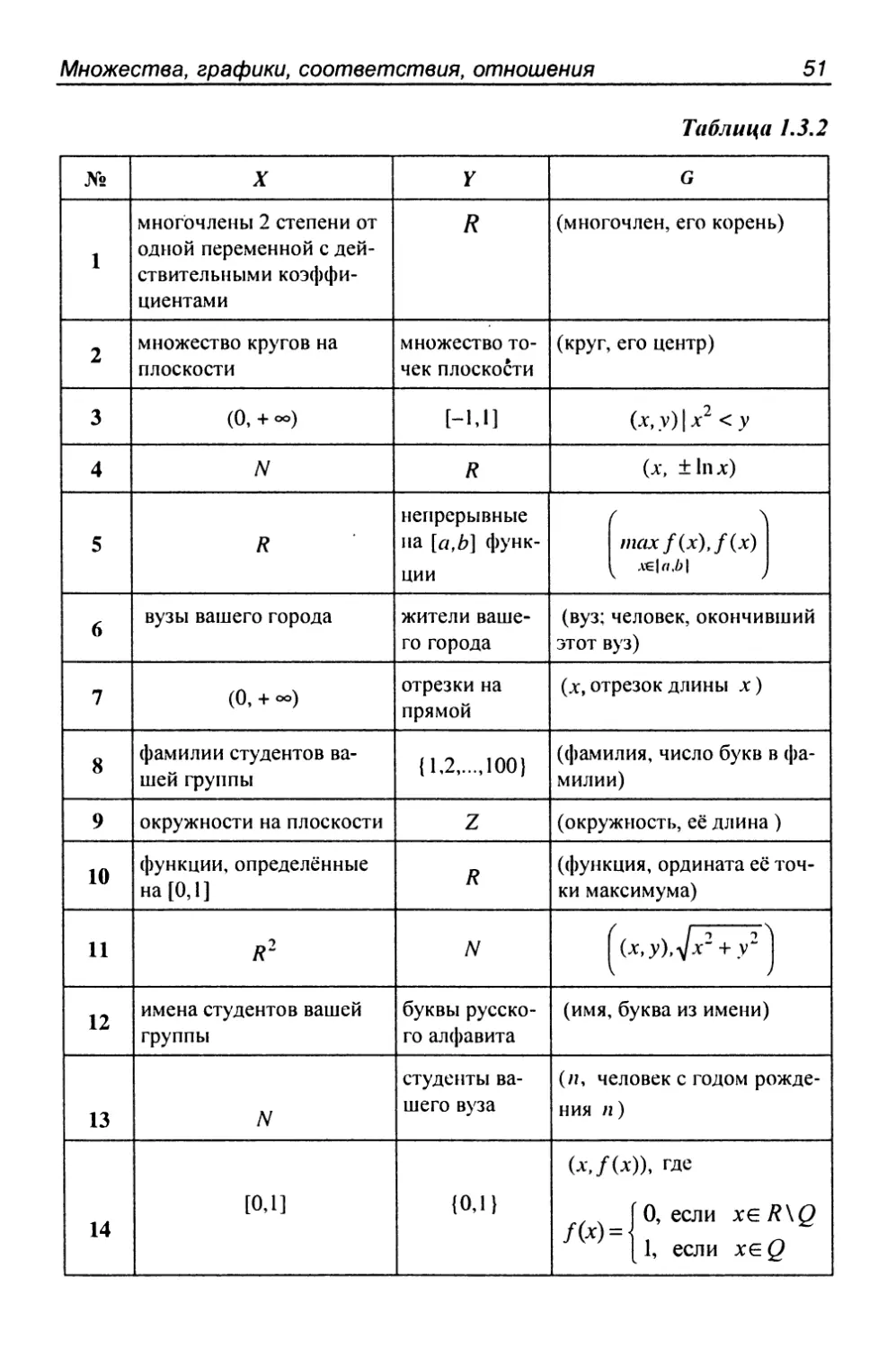
Задание 1.3.2
Для соответствия Г = (X,Y,G)
1. Определить набор свойств, которыми обладает данное
соответствие.
2. Построить соответствие между конечными множествами
с набором свойств, противоположным данному, изобразив
соответствие аналитически и в виде графа.
Замечание. Отметить случаи отображений и биекций.
Множества, графики, соответствия, отношения
51
Таблица 1.3.2
№
1
2
3
4
5
6
7
8
1 ^
10
11
12
1 ^^
14
^
многочлены 2 степени от
одной переменной с
действительными
коэффициентами
множество кругов на
плоскости
(0, + оо)
N
R
вузы вашего города
(0, + оо)
фамилии студентов
вашей группы
окружности на плоскости
функции, определённые
на [0,1]
R'
имена студентов вашей
группы
N
[0,1]
Y
R
множество
точек плоскости
[-1,1]
R
непрерывные
па [а,Ь]
функции
жители
вашего города
отрезки на
прямой
{1,2,...,100)
Z
R
N
буквы
русского ал{|)авита
студенты
вашего вуза
{0,1}
G
(многочлен, его корень)
(круг, его центр)
(х,у)\х^<у
(л-, ±lnjc) 1
( Л
max fix), fix)
(вуз; человек, окончивший
этот вуз)
(х, отрезок длины х)
(фамилия, число букв в
фамилии)
(окружность, её длина)
(функция, ордината её
точки максимума)
ix,y),ylx^ + y^
]
(имя, буква из имени)
(/?, человек с годом
рождения /2 )
(л,/(л-)), где
, , f 0, если хЕ R\Q
[ 1, если хе Q
52
Глава 1
Таблица 1.3.2 (окончание)
Хо
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
JV
/?
окружности на плоскости
[P{U)f
[0,1]
R
P(U)
{0,1,2}
[1,3]
пары окружностей на
плоскости
множество книг в
библиотеке вашего вуза
(-4,4)
мужчины вашего города
[PiU)f
политические партии
вашего города
Р(и\ где и =[12 40}
пары прямых на
плоскости
Y
^10
прямые на
плоскости
P(U)
R'
функции,
непрерывные
на [0,1]
[P(U)f
N
R.
R'
Z
tl.6]
женщины
вашего города
PiU)
жители вашего
города
N
R
G
Onaxai,iai,a2,:,aio))
1<;<10
(окружность, касательная
к этой окружности)
{(Л,В,С1ЛпВпС)
(х,(х,у)|л'- +v- = l)
ni,f(x)\fninf( X ) = т
[ 0<v<l J
{D,(AB,C)\AuBkjC = D)
(х, у)\х — остаток от
деления у на 3
ix,y)\{x-2f + iy-2f<\
(пара окружностей,
координаты точки пересечения
этих окружностей)
(книга, число страниц в этой
книге)
(x,^)|v = |a--2|+1
(х,у)\х ^ у состоят или
когда-либо состояли друг
с другом в законном браке
i(A,B),A\B)
((партия), (человек, состоя-
ший в этой партии))
(Д,|Д|),где AeP(U)
(пара прямых, абсцисса
точки пересечения прямых)
Множества, графики, соответствия, отношения 5£
Пример решения задания 1.3.2
Решим задание 1.3.2 для соответствия Г = (X,Y,G), если
X = N, Y — MHOJfcecmeo непрерывных на [а,Ь] (рункций, а
график Gзадан так: G = \{J,f{x))\J = \ f{x)dx>.
1. Определим набор свойств, которым обладает данное
соответствие.
а) Для любого натурального числа п можно рассмотреть
непрерывную функцию f(x) = . Тогда, вычисляя определён-
Ь-а
ный интеграл, будем иметь:
h b
dx= dx=
^ h-п h-nJ h-
x\
a ■
n(b - a)
= n .
b-a
Итак, доказано, что данное соответствие является всюду
определённым.
(3) Так как для некоторых непрерывных функций на [а,Ь]
определённый интеграл не выражается натуральным числом, то
данное соответствие не является сюръективным.
у) Покажем, что две различные функции могут иметь на
рассматриваемом промежутке одинаковое значение определённого
интеграла. Для этого можно рассмотреть функции
fM = - и g(x) = -z J.
b-a b -а^
Для f{x) определённый интеграл не отрезке [а,Ь], как мы
уже выяснили, равен п. Найдём соответствующий интеграл
для g{x)\
^ ^ 2пх . Ъг х^
lg(x)dx=l— -dx
а
Ь'-а' Ь'-а' 2
Итак, доказано, что соответствие, описанное в условии
задания, не является функциональным.
54
Глава 1
5) Так как для каждой функции её определённый интеграл на
данном промежутке находится однозначно, данное соответствие
является инъективным.
2. Построим соответствие между конечными множествами,
чтобы оно было не всюду определено, сюръективно,
функционально и не инъективно.
Пусть Г = ({аЛс}А1}ЛЫ)ХЪЛ)}
(рис. 1.3.2).
Покажем, что построенное
соответствие обладает требуемым набором
свойств.
а) Соответствие Г не всюду
определено, так как элемент с, входящий в
область отправления, не имеет образа при
данном соответствии.
(3) Соответствие Г сюръективно, так как его область
прибытия {1} совпадает с областью значений.
Y) Соответствие Г функционально, так как его график не
содержит пар с равными первыми и различными вторыми
координатами.
6) Соответствие Г не инъективно. так как в его графике пары
(аЛ) и (Ь,1) имеют различные первые и одинаковые вторые
координаты.
Рис. 1.3.2
Задание 1.3.3
Установить биекцию между множествами
Таблица 1.3.3
№
1
2
3
Множества
{{х,у)\х'-^у^<\} и
{(х,у)\х^ + у^<\}
[0,1] и R
[0,+оо)и[0,1]
Хо
4
5
6
Множества
N и множество многочленов
3" степени с натуральными
коэффициентами
R и [0,+ оо)
{Uv)|x4/ = i}H[0,i)
Множества, графики, соответствия, отношения
55
Таблица 1.3.3 (окончание)
№
7
8
9
10
11
12
13
14
15
16
17
18
Множества
все окружности на плоскости и
/?Х/?Х(0,+оо)
{(х,у)\-^<х<^,0<у<п}
и R^
еп[о,1]и е^п[о,1]'
(0,1) и [^,7Г]
[0, +оо) и (а,/?)
все интервалы на прямой и
полуплоскость, расположенная
ниже линии у = х
{{х,у)\х^ + у^^<\} и
{(a',v)|x4v^<100}
Q и Qn[0,+oo)
[0,1] и (2,5)
полуокружность без концевых
точек и луч (0, +«>)
(-00,0) и R
N v\ 0^
Хо
19
20
21
•22
23
24
25
26
27
28
29
30
Множества
Q и множество всех
многочленов с рациональными
коэффициентами
(0,1) и 7?
Q^Q" 1
сфера с выколотой точкой и
вся плоскость
{{х,у)\х''- + у^'<А] и
{(jc,>')|a'' + />4}
Q и еп[0,1]
R и[1,+оо)и{-10)
iV и iV^
все последовательности
натуральных чисел и все
возрастающие последовательности
натуральных чисел
N и множество всех
многочленов с натуральными
коэффициентами
R и R\Q
QwN^
56
Глава 1
Пример решения задания 1.3.3
Установить биещию мелсду миолсествами [0,1] и (0,1).
' 1 1 1
Будем считать, что ^=[0,1], К = (0,1). Пусть А--
2 3 п
B = J 0,l,-,-,...,-,...i = Au{0.1}. Очевидно, что X\B = Y\A,
[ 2 3 п j
X =Х\ВиВ, Y = Y\AuA.
Установим биекцию между множествами Х\Ви У\А, как
тождественное соответствие f{x) = х.
Биекцию между множествами А и В зададим так:
1
1
/(0)=-, /(1) = ~, /!
^О
v2,
i^i
о^
кЬ
-1 ^
/
1
п) п + 2
Таким образом, между X и Y установлена биекция:
X,
1
2'
1
п + 2'
при jc^O, х^ \ —
1 п
при jc = 0
при jce \ —
[п
HEN
ПЕ N
f(x) =
Изобразим график этой биекции в декартовой системе
координат (рис. 1.3.3).
>
1
1/2
1/3
1 /А
1/5
0
^7
1 -yf/-—^ — Ч
/^ I ' '•
[ 1/4 1/3 Г/2
1 *
Рис. 1.3.3
Задание выполнено.
Множества, графики, соответствия, отношения
57
Задание 1.3.4
Доказать, что множество:
Таблица 1.3,4
№
1
2
3
4
5
6
7
1 ^
1 ^
1 ^^
1 ^^
1 ^^
1 ^^
1 ^"^
1 ^^
16
Условие
всех многочленов от л: с рациональными коэффициентами счётно
всех пар рациональных чисел счётно
всех многочленов от х с целыми коэффициентами счётно
всех кругов на плоскости, радиусы которых и координаты центра
являются рациональными числами — счётно
попарно непересекающихся замкнутых кругов на плоскости не более
чем счётно
всех многочленов п -и степени от х с рациональными
коэффициентами счётно
всех многочленов п -й степени от х с целыми коэффициентами
счётно
попарно непересекающихся прямоугольников на плоскости не более
чем счётно
всех окружностей на плоскости, радиусы которых и координаты
центра являются целыми числами — счётно
полученное объединением счётного числа конечных множеств — не
более, чем счётно
полученное объединением счёпного числа счётных множеств —
счётно
рациональных чисел интервала (0,1) — счётно
непересекающихся окружностей на плоскости может быть
континуально
всех действительных чисел интервала (0,1), в десятичном разложении
которых на четвёртом месте стоит цифра 7 — континуально
точек разрыва монотонно убывающей на [а,Ь] функции — не более
чем счётно
точек плоскости, расстояние между любыми элементами которого
больше 3. не более чем счётно
58
Глава 1
Таблица L3.4 (окончание)
Х2
Условие
17
попарно непересекающихся открытых интервалов на прямой не более
чем счётно
18
полученное объединением счётного числа непустых попарно
непересекающихся конечных множеств, счётно
19
всех конечных последовательностей натуральных чисел — счётно
20
всех конечных подмножеств счетного множества — счетно
21
попарно непересекающихся букв Г на плоскости может быть
континуально
22
попарно непересекающихся букв L на плоскости может быть
континуально
23
попарно непересекающихся букв Г на плоскости не более чем счётно
24
счётно, если каждое из множеств Д|,Д2>---'А
25
чисел вида 2" -3'" —счётно, если пе N и те N
26
иррациональных чисел интервала (0,1) — несчётно
27
всех бесконечных последовательностей, составле1П4ЫХ из нулей и
единиц — континуально
28
всех корней \н10гочленов третьей степени с натуральными
коэффициентами — счётно
29
функций вида f :Е" -^ Е, где £ = {0,1}, п = 1,2,3,... — счётно
30
полученное объединением конечного числа счётных множеств — счёпю
Пример решения задания 1.3.4
Доказать, что мноэюество всех конечных
последовательностей, составленных из элементов некоторого счётного мно-
лсества, счётно.
Пусть множество А счётно, А=^{а1,а2,...,ац,...}. Обозначим
через В/^ множество конечных последовательностей длины /:,
составленных из элементов множества Л, ks N. Покажем для
любого к, что множество Bj^ —счётно.
Множества, графики, соответствия, отношения
59
Пусть
bj; =а^,а^,..„а^
к
^3 =^1,«2 —^1
h+\ =^i,rti,...,«2
сумма индексов у Лу равна к.
сумма индексов у Д/ равна Л +1,
> — сумма индексов у ai равна к-hi и т. д.
Таким образом, любая конечная последовательность длины к,
составленная из элементов счётного множества, получит свой номер.
Выпишем элементы множеств Bf. в виде бесконечной
таблицы, где kG Л^(табл. 1.3.4).
bl-
b^
\
bf
■^b[
i
-bl
^b\-
Таблица L3.4
^-
t
bl
t
^bl
>bl ...
i
bl ...
i
by..
Будем обходить таблицу по
маршруту, помеченному
стрелками.
По мере продвижения по
этому маршруту будем
навешивать номера: Ь\ -1, Ь\- 2,
Ь] - 3, Ь^ - 4. и т. д.
Имеем, что для любых индексов i,p последовательность Ь[
получит когда-нибудь единственный номер.
Таким образом, установлена биекция между множеством,
составленным из элементов Ь[, и множеством индексов Л^,
то есть доказана счётность множества всех конечных
последовательностей, составленных из элементов некоторого счётного
множества А.
60 Глава 1
1.4. Отношения
Бинарным отношением на множестве А называется пара
Ф = {А,С), где А —область задания отношения, G —график
отношения, причём G Q Л .
Если (x,y)GG, то будем писать хфу и говорить, что х и у
вступают в отношение ф. Если х и уне вступают в
отношение ф, будем писать х(ру.
Диагональю множества А называется график
A^={{x,x)\xgA}.
Свойства отношений :
1. Рефлексивность: V^.^ д (х(рх).
2. Антирефлексивность: V^^ д (^фх).
3. Симметричность: "^хеЛ^уеЛ^^^У ~^ З^Ф-^) •
4. Антисимметричность: "^хеА^уел (-^ФЗ^'З^Ф-^ "~> -^ = 3^) или
равносильное определение: ^^.^д\/^^д (хф};д '^ 3^ —> З^Ф ■^)-
5. Транзитивность: V^^д\/^.^д\/„^д (хф);,уфг —> х(р z).
6. Связность: "^хеА^уеА(^'^ У ~^ ^^У или уф;с).
Эти свойства можно определить с помощью графиков
отношений:
1. Дд QG, 2. Дд nG = 0, 3. G = G~\
4. GnG"^ сДд, 5. GoGcG, 6. Л^Дд cGuG"'.
Если даны два отношения: Ф=(А,С) и Ч^ = (Л,Г),то
операции над этими отношениями сводятся к операциям над их
графиками:
Ou4^ = (A,GuF), OnW = (A,GnF\ 0\W = (A,G\FI
Ф^W = (A,G^F\ Ф = (Л,Л'\0).
'Множества, графики, соответствия, отношения
61
Отношение называется отношением частичного порядка, если
оно рефлексивно, антисимметрично и транзитивно.
Отношение называется отношением линейного порядка, если
оно является отношением частичного порядка и связно.
Отношение называется отношением строгого порядка, если
оно антирефлексивно, антисимметрично и транзитивно.
Отношение называется отношением строгого линейного
порядка, если оно — связное отношение строгого порядка.
Отношение называется отношением эквивалентности, если
оно рефлексивно, симметрично и транзитивно.
Классом эквивалентности, поролсдённым элементом х,
называется множество всех элементов из Л, вступающих с jc в
отношение эквивалентности.
Фактор-мноэ^сеством множества А по отношению
эквивалентности ф называется множество всех различных классов
эквивалентности, которое обозначается Л/ф.
Мощность фактор-множества Л/ф называется индексом
разбиения, порождённого отношением ф.
Задание 1.4.1
Проверить для произвольных отношений Ф=(А,С) и
4^ = (A,F) справедливость утверждения: "Если отношения Ф
и Ч^ обладают свойством а , то отношение Ф также обладает
свойством а".
Обозначения: 1— рефлексивность, 2 — антирефлексивность,
3 — симметричность, 4 — антисимметричность, 5 —
транзитивность, 6 — связность.
Таблица 1.4.1
№
1
2
3
4
а
2
2
2
2
т
0KJ4'
0r\W
ф\^
ФлУ^
№
5
6
7
8
а
2
2
3
3
т
фо^
ф-'
фуиЧ"
Фп^
Хо
9
10
И
12
а
3
3
3
3
т J
ф\^^
Фа^
фо^
ф-'
; Зак. 3332
62
Глава 1
Таблица 1.4,1 (окончание)
Хо
13
14
15
16
17
18
а
4
4
4
4
4
4
Т
ФиЧ"
0nW
Ф\¥
Ф^W
0r\W
Ф-'
х«
19
20
21
22
23
24
а
5
5
5
5
5
5
т 1
0KJW
Фп'Г
Ф\Ч'
Фд!/^
фо^
Ф-'
№
25
26
27
28
29
30
а
6
6
6
6
6
6
т
Фи!^^
Фп^
Ф\¥
Фд!^^
фо^
ф-'
Примеры решения задания 1.4.1
Пример 1.
Проверить для произвольных оптошетш Ф = {А,С) и
4^ = (A,F) справедливость утверэк:дения: ''Если отношения Ф и
W транзитивны, то отношение фо^ таклсе транзитивно'\
Пусть (m'={A,GF), G = {(fl,b)}, F = {{b,c)]. Тогда
G о F - Л^ \[{ах)}= {(aM)Xci,bUh,aUb,bUc,aUc,bUb,cUc,c)}.
Отношение фоЧ^ не транзитивно, так как его график G^F
содержит пары (а,Ь)и (/?,с),но не содержит пару (а,с). Значит,
в общем случае утверждение, приведённое в примере I, неверно.
Пример 2.
Проверить для произвольных отношений Ф = {А,С) и
W ='{A,F) справедливость утверэ/сдения: ''Если отношения Ф
и W рефлексивны, то отношение Фи¥ такэюерефлексивно".
Для рефлексивных отношений Ф и Ч^ выполнены условия:
Дд qG, A^Q F, Значит, выполнено таюке включение:
Дд cGuF, а это и означает, что отношение ФиН^ таюке
рефлексивно. То есть мы показали, что утверждение примера 2 верно
для произвольных отношений Ф и Ч'.
Множества, графики, соответствия, отношения
63
Задание 1.4.2
1. Выяснить, какими из свойств: рефлексивность,
антирефлексивность, симметричность, антисимметричность, транзитивность,
связность обладает данное отношение Ф = (A,G).
2. Выяснить, что представляет из себя отношение фоф,
ФoФ"^
3. Построить на конечном множестве отношение, обладающее
таким же набором свойств, что и данное. Изобразить его графом
и аналитически.
4. Построить на бесконечном множестве отношение,
обладающее набором свойств, противоположным данному. В случае
невозможности построения доказать противоречивость набора
требований.
Замечание. В случае отношений эквивалентности указать
классы эквивалентности, фактор-множество, индекс разбиения. В
случае отношений частичного или линейного порядка указать
максимальные, минимальные, а также наибольшие и наименьшие
элементы (если они существуют).
Таблица L4.2
Хо
1
2
3
4
5
6
А
множество студентов вашего вуза
P{U)y где и — множество точек
плоскости
множество окружностей на
плоскости
жители России на начало этого
года
жители России на начало этого
года
прямые в пространстве
G
хц> у <=> X,у учатся на одном
курсе
ДфiB <^ Аг\В = 0
л: ф V <=> А' касается у
х(р у <=>А и у — супруги
X ф у <=> А и V состоят в
одной и той же политической
партии
X (р у ^=> X и у имеют хотя бы
одну общую точку
64
Глава 1
Таблица 1.4.2 (продолэюеиие)
\ ^ 1
7
8
9
10
1 ^^
1 ^^
1 ^^
14
1 ^^
1 ^^
1 ^'^
18
1 ^^
20
1 ^^
1 22
23
А 1
жители России на начало этого
года
N
P(N)
R
{iai,a2 aJ|a,E{0,l}}
R'
R
жители России на начало этого
года
[0,4]
R
N
Р((У), где и — множество точек
плоскости
жители России на начало этого
года
[0,2]
N'
N
непрерывные на [0,1] функции
G 1
jc ф у <=> X и у разного
возраста
д- ф у <=> JC и у имеют
одинаковый остаток от деления на 3
Лц>В <^ \Л\=^В\
хц> у <=^ 2х> у"
д' ф У <=> X и у отличаются
только в одной координате
(а у b ) <^ x = z или y = t
2 2
х(р у <^ X + у =1
х(^ у <=> X старше у
х(^у <^ х>2у + \
хц> у <=> g7^ и у имеют
одинаковую целую часть
х(^ у <=> х- у кратно трём
Дф5<=>Див — в общем
положении
д ф -у <=> у — тёща для X
х(^у<^х+у<\
{x,y)(p{zj)<^xt = yz.
х(^ у<^ х+ у крат1ю трём
11
f(x)i^g(x)<;^jf(x)dx=jg(x)dx
0 0
Множества, графики, соответствия, отношения
65
Таблица L4.2 (окончание)
№
24
25
1 26
1 ^'^
1 28
1 ^^
1 30
А
/?"
жители России на начало этого
года
R
читатели библиотеки вашего вуза
Р(6^),где и —множество точек
плоскости
векторы на плоскости
жители России на начало этого
года
G 1
Ц,...,Л„)ф(/7|,...,/?,,)<=>
<=> [max л,-, 1 </</?} =
= {niaxbi, \<i<n}
Я' ф -у «=> А" — отец для .у
х(^ у <=^ х = 2 у + 3
х(^ у<^ X и у прочитали одну
и ту же книгу
Лфв <t=> ЛиВ = 0
а(^Ь <^ \а\ = \Ь\
Л' ф у <=> X — внук у
Пример решения задания 1.4.2
Решить задание 1.4.2 для случая, когда А — множество
теннисистов, участвующих в турнире, где каждый теннисист должен
сыграть с каждым ровно три партии. Пусть х(р у означает, что х
обыграл у по результатам личных встреч.
1. Выясним, какими из основных свойств обладает данное
отношение.
1 . Отношение ф не является рефлексивным, так как
найдётся теннисист, не обыгравший сам себя.
2. Отношение ф является антирефлексивным, так как
каждый теннисист не обыграл сам себя.
3 . Отношение ф не является симметричным, так как
найдётся пара теннисистов л* и )^ такая, что х обыграл у по очкам в
личных встречах, а у не обыграл х.
66 Глава 1
4. Отношение ф является антисимметричным, так как если
X обыграл у, то у обязательно не обыграл х.
5. Отношение ф не яляется транзитивным, так как может
сложиться ситуация, когда х обыграл у, у обыграл z, и в то же
время Z, обыграл х.
6. Отношение ф является связным, так как любая пара
спортсменов должна сыграть между соболи и выявить победителя.
2. Выясним, что из себя представляют отношения фоф
и фоф'.
По определению композиции, хфофу означает, что
найдётся Z такой, что хфг и z^y. То есть в отношение фоф будут
вступать такие пары спортсменов х и у, для которых найдётся
теннисист ^ такой, что х обыграл г, а г обыграл у.
Рассуждая аналогично, получим, что в отношение фоф' будут
вступать такие пары спортсменов х и у, для которых найдётся
теннисист Z такой, что х обыграл z, а z проиграл у. То есть
график отношения фоф' будут образовывать пары, составленные
из теннисистов, для которых найдётся хотя бы один спортсмен,
которого они оба обыграли в турнире.
3. Построим на конечном множестве
отношение, обладающее таким же
набором свойств, что и данное.
Пусть Ф = {{аЛс],{{а,b\{b,с\{с,а)}).
Изобразим это отношение в виде графа
(рис. 1.4.2):
1. Это отношение не является
рефлексивным, так как ащ.
2. Отношение антирефлексивно,
так как афа и Ьф и сфс.
3. Отношение не симметрично, так как а(^Ь и Ьщ.
4. Отношение антисимметрично, так как а(рЬ и &фа, бфс
и ci^h , сфа и афс.
Множества, графики, соответствия, отношения 67_
5. Отношение не транзитивно, так как а(рЬ и &фс, но ац)с,
6. Отношение связно, так как любая пара различных
элементов из множества {а,Ь,с} вступает в отношение ф в том
или ином порядке.
4. Построим на бесконечном множестве отношение
рефлексивное, не антирефлексивное, симметричное, не
антисимметричное, транзитивное и не связное.
Пусть Л=(0,+оо), хф у означает, что хиу имеют одинаковую
дробную часть.
1. Отношение рефлексивно, так как любое число имеет
одинаковую дробную часть само с собой.
2. Отношение не антирефлексивно, так как найдётся число
(например, 1,32), имеющее одинаковую дробную часть само
с собой.
3. Отношение симметрично, так как если хи у имеют
одинаковую дробную часть, то у их также имеют одинаковую
дробную часть.
4. Отношение ф не антисимметрично, так как, например,
числа 1,78 и 4,78 не равны, и в то же время 4,78 ф 1,78 и
1,78 ф 4,78.
5. Отношение является транзитивным, так как если х
и у имеют одинаковую дробную часть, у и z имеют одинаковую
дробную часть, то х и z. таюке имеют ту же самую дробную
часть.
6. Отношение не связно, так как, например, 3,1^1,6 и
3,1ф1,6 и 1,6фЗ,1 .
Это отношение рефлексивно, симметрично и транзитивно,
значит, оно является отношением эквивалентности. Классами
эквивалентности являются множества {xjxjr,-х,„ Е Z}. Индекс
разбиения, соответствующего данному отношению
эквивалентности — континуальный, так как мощность
фактор-множества Л/ф равна мощности всевозможных дробных частей, то есть
множеству точек промежутка (0,1).
68
Глава 1
Задание 1.4.3
Провести факторизацию ^отображения / : X -^ К, если
X ={a,b,c,d,e}, К = { 1,2,3,4,5,6}, а значения f(x) заданы
таблицей.
Таблица 1.4,3
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1 ^'^
1 ^^
1 ^^
1 20
1 ^^
1 22
/(«)
1
I
4
2
1
3
5
1
2
6
4
5
3
4
5
4
6
5
6
3
5
2
fib)
3
2
3
3
2
2
5
6
3
3
3
1
5
3
2
1
1
3
4
2
6
1
/(с)
1
5
4
6
2
3
4
3
2
6
2
1
3
2
5
4
6
5
1
3
6
2
/(^/)
4
5
2
2
4
2
5
1
3
2
3
6
5
1
3
2
1
3
1
2
1
3
/W 1
3 1
1 1
4 1
3 1
5
3 1
6 1
3
4
6
4
5
5
3
2
4
1
3
4
2
5
2
Множества,
графики, соответствия, отношения
69
Таблица 1.4.3 (окончание)
№
1 ^^
1 ^"^
1 ^^
1 26
1 27
1 28
1 29
1 30
f{a)
5
3
5
2
4
3
2
4
/(^)
5
1
3
4
3
1
2
5
/W
4
3
3
2
4
1
3
6
/(^)
5
2
6
5
1
4
2
4
f(e)
4
2
3
2
3
5
3
6
Пример решения задания 1.4.3
Провести факторизацию отобралсения f: X -^Y, если
X ={a,b,c,d,e}, К = { 1,2,3,4,5,6}, а значения /(л) таковы:
/(fl) = 2;/(b) = 5;/(с) = 2;/(г/) = 4;
Рассмотрим на множестве X отношение Ф, которое
определим так: Х1фл*2 «=> f(x\) - fixi). Это — отношение
эквивалентности, которое порождает разбиение множества X на классы
эквивалентности.
В нашем примере имеем: [л] = Lc] = {а,с};
[d] = {d}\ [b] = [е] = [b,e]. Эти классы образуют фактор-множество
множества X по отношению ф: X /{^ = {[a,c},{d},{b,e]}.
Заметим, что индекс разбиения множества X равен 3. Введём
соответствие так: g{a) = g{c) = [a,c}, g{d) = {d}, g(b) = g{e) = [b,e}. Легко
заметить, что g является отображением Х на Х /ф. Для
исходного отображения f{x) областью значений является множество
/(Х) = {2,4,5}.
Рассмотрим соответствие h следующего вида:
/г; Х/ф-^/(Х), заданное равенствами: /i({a,c}) = 2,/2({J}) = 4,
h{{b,e]) = 5. Это соответствие всюду определено, сюръективно,
функционально и инъективно, то есть /г-биекция между
множествами Х/ф и f{X).
70
Глава 1
Рассмотрим, наконец, соответствие е: f{X)-^Y , е{х) = х.
Это соответствие всюду определено, функционально и инъектив-
но, то есть е(х) является взаимно-однозначным отображением
fiX) в Y.
Итак, исходное соответствие /(х) можно представить в виде
композиции соответствий g,h и е. В построении этой
композиции и заключается факторизация отображения /.
Задание 1.4.4
Для данного отношения Ф = ({1,2,3,4,5},G) проделать
следующее:
1. Изобразить Ф графом.
2. Достроить Ф до отношения эквивалентности, указать
фактор-множество.
3. Достроить Ф до отношения частичного порядка, указать
максимальные, минимальные элементы, а также пары
несравнимых элементов.
4. Достроить Ф до отношения линейного порядка, указать
наибольший и наименьший элементы.
5. Достроить Ф до отношения строгого порядка.
6. Достроить Ф до отношения строгого линейного порядка.
Замечание: отношение достраивается с помощью введения
минимально необходимого числа дополнительных рёбер.
Таблица 1.4.4
Хо
1
2
3
4
5
6
G
(1,2), (3,2), (2,4)
(2,1), (5,1), (4,2)
(1,2), (3,4), (4,5)
(3,1), (2,5), (5,4)
(1,5), (5,4), (4,3)
(2,3), (3,5), (5,1)
№
7
8
9
10
11
12
G
(1,2). (4,3), (4,5)
(3,5), (4,2), (1,2)
(1,2), (2,3), (2,4), (4,5)
(1,2), (2,3), (4,5), (5,3)
(1,2), (1,5), (1,4)
(1,2), (1,3), (3,2), (4,5)
Множества, графики, соответствия, отношения
71
Хо
13
14
15
16
17
18
19
20
21
G
(1,2), (2,3), (3,4), (5,5)
(4,3), (5,1), (1,2)
(1,3), (3,4), (1,4), (2,5)
(2,3), (4,3), (3,5)
(3,2), (1,2), (5.3)
(2,3), (4,5), (5,1)
(4,2), (3,1), (1,5)
(2,1), (1,5), (5,4)
(3,4), (4,1), (1,2)
Хо
22
23
24
25
26
27
28
29
30
Таблица 1.4.4 (окончание)
G
(2,3), (5,4), (5,1)
(4,1), (5,3), (2,3)
(2,3), (4,5), (3,4), (1,1)
(4,3), (3,1), (1,2)
(5,2), (2,4), (4,3), (1,1)
(3,4), (1,5), (5,2)
(5,4), (4,3), (5,3), (2,1)
(2,4), (3,4), (4,1)
(4,2), (5,2), (1,4)
Пример решения задания 1.4.4
Решим задание для
Ф = ({1,2,3,4,5}, {(1л ал (5,ш
Изобразим граф отношения Ф
(рис. 1.4.4, а).
2. Достроим Ф до отношения
эквивалентности Ф,, добавляя
минимально возможное число рёбер,
обозначим график полученного
отношения эквивалентности через
С]. Тогда G| будет иметь вид:
{(1,2), (1,3), (5,4), (1,1), (2,2), (3,3),
(4,4), (5,5), (2,1), (3,1), (4,5), (2,3),
(3,2)}.
Изобразим граф отношения Ф,
(рис. 1.4.4, в).
Укажем фактор-множество для
А = { 1,2,3,4,5} по отношению Ф,:
Л/ф| ={{1,2,3},{4,5}}. Отметим,
что индекс разбиения множества А
равен 2.
Рис. 1.4.4, а
(Г
•б
Рис. 1.4.4, в
72
Глава 1
&
к>
b
Рис. 1.4.4, с
3. Достроим Ф до отношения частичного порядка Ф2,
обозначив график этого отношения через ^2-
G2 = {(1 Д),(2,2),(3,ЗХ(4,4),(5,5),(1,2),(1,3),(5,4)}.
Изобразим граф Ф^ (рис. 1.4.4, с).
Минимальными элементами здесь
являются 1 и 5, максимальными
элементами — 2, 3 и 4.
Пары несравнимых элементов:
{1,4}, {1,5}, {2,4}, {2,5}, {3,4},
{3,5}, {2,3}.
4. Достроим Ф до отношения
линейного порядка Ф3, обозначив
график этого отношения через G^-
G3 =G2U{(2,3),(4,1),(4,2),(4,3), (5,1),(5,2),(5,3)}.
Изобразим граф отношения Ф3
(рис. 1.4.4, d).
Наибольшим элементом здесь
является 3, а наименьшим — 5.
5. Само исходное отношение Ф
является отношением строгого
порядка, так что достраивать его нет
необходимости.
6. Достроим Ф до отношения
строгого линейного порядка Ф^,
обозначив график этого отношения через G^.
С4=Сз\Ад={(5,4),(5,1),(5,2),(5,3),(4,1),(4,3),(4,3),(1,2),(1,3),(3,2)}.
Изобразим граф отношения Ф^
(рис. 1.4.4, е).
Задание выполнено.
Рис. 1.4.4, d
Рис. 1.4.4, е
Глава 2
Булевы функции
2.1. Булевы функции.
Суперпозиции
Булевой функцией (сокращенно бф) называется функция вида
f:E'^-^E, где £ = {0,1}, т.е. /(х^,Х2,...х,^), принимающая
значения О, 1 и аргументы которой могут принимать значения О, 1.
Множество всех булевых функций будем обозначать через ^2-
В таблице, задающей бф, наборы значений переменных
пишут в определенном порядке — лексикографическом, который
совпадает с порядком возрастания наборов, рассматриваемых как
числа в двоичной системе счисления.
Булевы функции, заданные табл. 2.1а и 2.1 в, будем считать
элементарными.
Используются обозначения:
g^(x) = 0 — константа О
g2(x) = l — константа 1
gi,{x) = X — толсдественная
функция
g^M = X — отрицание
Для отрицания употребляется также обозначение --ос.
Таблица 2.1а
X
0
1
^1
0
0
82
1
1
^3
0
1
^4
1
0
74
Глава 2
Таблица 2.1в
X
1 ^
1 ^
1 1
1 1
У
0
1
0
1
/*!
0
0
0
1
л
0
1
1
1
А
1
1
0
1
f,
1
0
1
1
/5
0
1
1
0
/б
1
0
0
1
л
1
1
1
0
/8
1
0
0
0
/9
0
0
1
0
/ю
0 1
1 1
0 1
0 1
/i(^>у) = Х' у — конъюнкция, употребляются также
обозначения xAyw х&у.
/2(-^'.v)--^^ У —дизъюнкция f^{x,y) = х-^ у —импликация
1а^ХуУ)-У-^х — импликация
fs (^' У) = Х"^ У — слоэк:ение по модулю два
/б С-^' у) - -^ ^"^ У — эквиваленция /^ (jc, у) = х | >> — штрих
Шеффера
hi^^y)-^^ У — стрелка Пирса /9(х,у) = х-/> у — запрет
/\о(^'У) = У-^^^ -^запрет
Наборы м и V значений переменных называются соседними
по i - той переменной, если они отличаются только / - той
координатой, то есть имеют вид:
и = (ai,(22v..<3/-i,0,^,+iv..,<3„), v = (a,,a2'-"^/-i'l''^/+i""'^/i)-
Переменная х^ называется фиктивной переменной бф/, если
для любых наборов и, v соседних по / -той переменной,
выполняется равенство f(u) = f(v).
Переменная х,- называется существенной переменной бф /,
если существуют хотя бы одна пара и, v наборов значений
переменных, соседних по / -той переменной, такая, что справедливо
неравенство f(u) ^ /(v).
Суперпозицией функций f\,---,f,n называется бф,
полученная с помощью подстановок этих функций друг в друга на места
Булевы функции 75_
переменных, а таюке с помощью переименования переменных.
Выражение, описывающее суперпозицию, называется формулой.
Некоторые основные равносильности:
Х'у = ух 1
\— коммутативные законы
XV у = yvх\
Х'(уч) = (х-у)-1 ]
>— ассог{иативные законы
xv(yv z) = (xv y)v ZJ
x-(yvz) = (x'y)v(x'z) ]
> — дистриоутивные законы
xw{y'z) = (xvy)'(x\/z) J
X-X = x\
> — законы идемпотентности
xwх-X J
x-O = 0 хЛ = х 1
\ — тоэюдества с константами
xwQ = X jcvl = l J
X'( XV у ) = x\
\ — законы поглощения
xw{х- у ) = X \
X' у = XW y\
1_ > — законы де Моргана
xw у = х- у J
X V X = 1 — закон искчючённого третьего
X • X = О — закон противоречия
х-х — закон двойного отрицания
х- у V х = yv X — правшо вычёркивания
Задание 2.1.1
Построить таблицу данной булевой функции /(х, у, z)
76
Глава 2
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/(^,>',z)
Х-\-у AZ-^ XW Z
{x\y)-^zrKy + x
{x-^ y)-\-z'^X
xw у + z <r^ у
xw у -^ z + у
xw y-^z/\y
{x i v) V Л* —> z
{X Ay -^ Z)^ X-\- у
{x\y)/\z-^ y^X
{x-^ у /\ z) ■\-X
xw у /\z—^ x/\y
(x+y) + (zvjc)
xw y-\-z—^ у
(xi y) + z'^X
{xw у -^ z) + y
Xo
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Таблица 2,1.1
f(x,y,z.)
X<r^ y + ZV у
XV у AZ + у
(X+ y)AZV X
{x-^ y) + (z V >;)
{x\y)AZVX
(x -» v) + z<r^ у
(xi y)<^ z + у
{XV y) + z-^ у
X A y + Z—^ X
(x + {yiz,)) + y
x—^yvy + z
{x\y) + {y-^ZAx)
x—^ у a{xv y + z)
y + Z <-^ ZAXV X
XAy-^Z<r^y+Z
Пример решения задания 2.1.1
Построить таблш(у булевой фуикг^ии, заданной формулой
f(x,y,z) = Х-^ у AZV-лХ
Выпишем в таблицу под символами переменных все наборы
значений, которые эти переменные принимают, а под символами
булевых операций будем выписывать значения функций,
соответствующие этим наборам.
Булевы функции
77
Для наглядности сверху проставим числа, указывающие
порядок выполнения действий, а снизу с помощью стрелок
покажем, над какими столбцами производятся действия и куда
пишется результат выполнения этих действий. Самой булевой
функции f{x,y,z) будет соответствовать столбец, обведённый
двойной рамкой.
X 1
0
0
0
0
1
1
1
1
-^
1
1
1
1
0
0
0
1
"^^
i
1 у
0
0
I
I
0
0
I
1
1^^
л
0
0
0
1
0
0
0
1
▲
Z.
0
1
0
1
0
1
0
1
V
1
1
1
1
0
0
0
1
[^ .
—1
1
1
1
1
0
0
0
0
i V
X 1
0
0
0
0
1
1
1
1
Итак, мы нашли, что исходная формула задаёт булеву
функцию f(x,y,z), имеющую вектор значений (1111 0001).
Задание 2.1.2
Написать таблицу функции h{x, у), являющейся суперпозицией
функций /„ и /;,, если /, =(1001 0111), /г =(0110 1011),
/з=(1110 ОНО), /4 = (0111 ООН),/5= (1100 0111),
/б =(1001 0100),/7 =(1011 0101),/8= (1000 ОНО),
/9 = (1010 0110), /,о = (0101 1000).
78
Глава 2
Таблица 2.1.2
JNo
1
2
3
4
5
6
7
8
17
18
19
20
21
22
23
п
1
2
1
3
3
4
2
5
7
5
5
10
10
7
8
к
2
1
2
5
2
3
3
2
8
9
10
9
5
9
7
/Па-, .у) 1
Ли>Л(А.А,у),>') 1
fni^Jkiy^-^^'y)'^) 1
Л(у,Л(А,у,А),х) 1
Л(а,/^(>',лс,Д>') 1
Л(>'.Л(А,у,А'),х) 1
/n(A,A(>'>v,A),y) 1
Л(А,Л(л-,у.у).у) 1
/,,(v,-\:./^Cr.x.>'))
/п(У'/к(^'У'^)'У)
/Л-^.Л(У'-^'^'),у)
fniyJki^^y'^)'-"^)
л (А,л (.V,л, у), у)
/п(Л(А,А,у).}',А)
/«(Л(-У>У>а),.\:,у)
/ДЛСа.дчуХу,^)
№
9
10
И
12
13
14
15
16
24
25
26
27
28
29
30
/7
5
3
4
2
5
9
7
8
7
6
9
2
3
10
8
к
4
2
3
4
7
8
5
7
8
7
2
10
9
7
3
/7(Л-,У) 1
/,i(A'(A'.y.yXA,y) 1
fn(x,x,f,^ix,y,y)) 1
/Ла.у./^(у,л-,у)) 1
Л(а.Д(л',у,у),у)
Л(а,.у,/^(у,.г..\:))
/«(v,y'A('^'>''A')) 1
Л (а, у, Л (л, у, у)) 1
Л(А,х,Д(у.л'.у)) 1
Л(Л-(а,у.а),а-,у)
/п{/к(У>У^^)'У"'^)
/п(^^к(У'У'^)'У)
/,Да.у,Л(а,.У,а))
fnifkiy'y^^"^)'^'^)
//,(V'A,/^(x,y,x))
Л (А> Л (у, у, л), у)
Пример решения задания 2.1.2
Написать таблицу функции /i(jc,y) = /2(y,y,/i(A:,y,Jc)).
Сначала запишем таблицу функций /i и /2 (табл. 2.1.2а).
Таблица 2.1.2а
xyz
000
001
010
/1
1
0
0
/2
0
1
1
л-уг
011
100
101
/l
1
0
1
/2
0
1
0
^yz
ПО
111
/1
1
1
/2
1
1
Булевы функции
79
Составим таблицу функции /г(;с,з;).Для этого запишем
формулу, задающую функцию/г(х,у), выпишем под символами
переменных все наборы значений, которые эти переменные
принимают, а под символами булевых функций будем выписывать
значения функций, соответствующие этим наборам.
Заключительный столбец, задающий функцию /г, обведём
двойной рамкой.
Таблица 2.1.2Ь
1
г{ X,
0
0
1
1
v) =
0
1
0
1
/2(
1
1
1
Л
У'
0
1
0
1
у, М ^
0
1
0
1
1
0
1
1
У'
0
0
1
1
х)]
0
1
0
1
1
0
0
1
1
Итак, /г(л:,у) = (1111).
Задание 2.1.3
Для данной функции f(x, у, z)
1. Выяснить, какие её переменные являются существенными,
а какие — фиктивными.
2. Выразить/(х, у, г) формулой, содержащей только
существенные переменные.
Таблица 2.1.3
Хо
1
2
3
4
f{x,y.z)
1011 1011
ООП 1100
0101 1111
1000 1000
Хо
5
6
7
8
f(x.y,z.)
1010 0000
1100 1111
0010 0010
1100 0011
Хо
9
10
и
12
f(x,y,z.)
0000 1010
1001 1001
0101 0000
1100 1100
80
Глава 2
Таблица 2.1.3 (окончание)
№
13
1 ^"^
1 ^^
16
17
18
f{x,y,z)
0100 0100
11110011
0000 0101
0000 0011
00110000
1101 1101
Хо
19
20
21
1 22
23
24
f{x.yr<)
11110101
01110111
10100101
00110011
1011 1011
1111 1100
№
25
26
27
28
29
30
/Ov,v.z)
01100110
10101111
1010 1010
июню
0001 0001
ООП 1111
Пример решения задания 2.1.3
Для данной функции f(x, у, z) = (0101 1010)
1. Выяснить, какие её переменные являются сугцествениыми,
а какие — фиктивными.
2. Выразить f(x,y,z) формулой, содерэ/сагцей только
существенные переменные.
Таблица 2.1.За
X
0
0
0
0
у
0
0
1
1 .
Z.
0
1
0
1
./■
0
1
0
1
X
1
1
1
1
У
0
0
1
1
Z
0
1
0
1
./■ 1
1
0
1
0
1. Переменная х является существенной
для данной бф, так как, например, наборы
(0,0,0) и (1,0,0) являются соседними по
переменной X и /(0,0,0)9^/(1,0,0).
Переменная z является существенной
для данной бф, так как, например, наборы
(0,0,0) и (0,0,1) являются соседними по
переменной Z и /(0,0,0)^/(0,0,1).
Таблица 2.1.Зв
X
0
0
1
1
-
0
1
0
1
./•
0
I
1 '
0
Булевы функции
81
Переменная у является фиктивной для данной бф, так как на
всех наборах, соседних по переменной у, значения функции
равны, то есть выполняются равенства:
/(ОДО) = /(0,1,0), /(1,0,0) = /(1,1,0), /(0,0,1) = /(0,1,1),
/(1,0,1) = /(Ul).
2. Выпишем таблицу функции /, как функцию только от
существенных переменных (табл. 2.1 .Зв).
Видим, что функция f(x, z.) = x-hz.
Задание 2.1.4
1. Написать таблицу булевой функции f(x,y,z), заданной
формулой.
2. Найти фиктивные переменные данной функции.
3. Преобразовать данную формулу в эквивалентную ей, но не
содержащую фиктивных переменных.
Таблица 2.1.4
Хо
1
2
3
4
5
6
7
8
9
f(x,y,z)
xyzvXV yv ZVxyvXуz
xyzv yzvxwxv yw z
X у z^ X у \/ x\/ у у z"^ X у z
xyzyxwywxyz'^xwywz
у г V xy z V Л" V z V .v>' v x v >• v z
Л" V z V .vv >; V Л' V vv z V xyz
jc >' z V xy z V x V V V xyz
jc д' z V д'г V jcz V X V V V z
A'v z V X V >? V xyz V X V V V z
X2
10
11
12
13
14
15
16
17
18
f{x,y,z) 1
A'V Z\/ yZW xy V Л' V V
JC Д' Z V X V V V Z V VZ V JC уZ
xyz'^xys/yz'^xwywz
у Z V A' V ^ V A V у V Z V A V Z
A V Z V у V Z V A' \/ yW Z^ xy Z
X Z V A V Z V A V у V Z V A Д' Z V V Z
A у Z V у V Z V A Д' Z V A V у V Z
AVZVA>'ZV>;VZVA>'Z
AVZVAZVA>'VAV>'VZ
82
Глава 2
Таблица 2.1.4 (окончание)
Хо
19
20
21
22
23
24
f(^,y,z)
xyzvzvyvxyzvxvyvz
xyzvxzvyzvyvz
xyzvXV yvzvxzvxyz
XV yv zvxy zvxyzVXV yvz
xzv xyzv xyz V Л' V yv z
xyzvXV zvxyzvXV yvz
Xa
25
26
27
28
29
30
f{x,y,z) 1
xyv xyzv xyz V xzv XV yv z
xyzv XV zv xyzv XV yv z
xyzv xyzv XV у V zv xyz
X у zv X у V XV у V zv у z
xyzv XV zv XV yv zv xyz
xy zv xyv XV zv xz
Выполним задание 2.1.4 для функции
f{^.y,z) = xyw yzwxyzw yzw xw yw z
1. При отыскании таблицы значений для Таблица 2.1.4а
данной функции (табл. 2.1.4а) заметим, что из
определения дизъюнкции и конъюнкции
следует, что для построения таблицы функции,
имеющей вид дизъюнкции нескольких
выражений, нужно найти единичные наборы для
каждого из этих выражений, тогда объединение
множеств единичных наборов и даст множество
единичных наборов исходной функции.
2. Рассмотрим пары наборов, соседних по
переменной л:, и значения функции на этих
наборах:
/(0,0,0) = /(1,0,0) = 0; /(0,0,1) = /(1,0,1) = 1;
/(0,1,0) = /(1,1,0) = 1; /(0,1,1) = /(1,1,1) = 1.
Значит, х — фиктивная переменная.
Так как /(0,0,0) ^ /(0,0,1), значит, z — существенная
переменная.
Неравенство /(0,0,0)^/(0,1,0) показывает, что v — также
существенная переменная.
xyz
000
001
010
Oil
100
101
НО
111
/
0
1
1
1
0
1
1
1
Булевы функции 83_
3. Преобразуем формулу к виду, не содержащему фиктивной
переменной.
/ ( X,y,Z ) = X -^ у А Z V -1 X
= xyvyzvyzvxyz = xyv(yvy)zvxyz = xyvl-zvxyz =
= xyvzvxyz = xyvzvxy=z'yxyvxy=z'y(xvx)y =
= zvl-v = zv>'.
Итак, f{x,y,z) = zv у.
2.2. Булевы функции
и теория множеств
Пусть множества В^,В2,.,В,^^ составлены из множеств
А|,Л2'---»Аг с помощью формул, содсржащих теоретико-
множественные операции и, п, \, А , -•
Тогда любому из множеств В^, i = l,...,m можно поставить
в соответствие булеву функцию /^(ai,fl2v^,i)» i = U...,m,
полученную из формулы, задающей Яу, заменой имён множеств Д
на символы переменных а,, символ и заменяется на v, п на л, \
на -/>, Д на +, знак дополнения — понимается, как отрицание.
Тогда В^^В2<^ fx=f2. В, с iB2 <^ /i -> /2 = 1,
Если между множествами В,,Й2»-»Вшзаписано соотношение,
содержащее, кроме символов теоретико-множественных
операций, символы: X (декартово произведение), с (включение), =
(равенство), 0 (пустое множество), U (универсальное
множество), то в соответствующей формуле для булевой функции
делается замена х на л, с на -^, = на <->, 0 на О, t/ на 1.
Тогда исходное соотношение будет истинным для любых
множеств В|,В2»--» 5/71 тогда и только тогда, когда
соответствующая этому соотношению булева функция будет тождественно
равна 1.
84
Глава 2
Задание 2.2.1
Выяснить взаимное расположение множеств D, £, F, если
Л, В, С — произвольные подмножества универсального
множества и.
Таблица 2.2.1
1
3
5
7
9
11
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
ВиС
(ВпС)и(С\{ЛпВ))
(Вг\С)и(Вг\{С\А))
(ЛАС)и{Вг\Л)
АиС
{А\С)и(Вг\С)и(С\А)
{СпВ)и{А\В)иАиС
A(jBuC
{ААВ)и(СпА)иСиВ
JICuiCXB)
(ВпС\А)и{СпА)
АиСи'в
ААСи{Аг\В)
{АпС)и{(А\В)\С)
ДиС
(ААВ)и(С\А)
i(AuO\B)ui(C^B)\A)
Ди(Д\в)
2
4
6
8
10
12
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
{АпВ)и{А\С)иВиС
ЛивиС
(Вг\С)^(ВпА)
(iBnC)uAuC
ЦВиС)\А)^{Сг\В)}
ДиС
АиВи{С пВ)
(^nД)u(Cn(iB\Д))
ДиС
(Д\C)uДuiB
(5пД)и((Д\5)\С)
(Д\С)и^
{ВпС\А)и{С\В)
ДиСи(Спв)
ДиС
дICu(Cn(iB\Д))
(ДniB)u((C\в)\Д)
ДUiB
Булевы функции
85
Таблица 2.2.1 (продолэ/сепие)
13
15
17
19
21
23
25
27
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
A^C^{X\B)
ДиС
(AnC)u(Cn(A\iB))
Диви(СпД)
A^l
((CuA)\iB)u(CnA))
(AnC)u(iB\C)uAUiB
{C^B)^{Br^A)^CuB
СиЛиВ
AaBu{A\C)
BuCu'a
(Аг\С\В)и(Аг\В)
JuB
(АпВ)и((В\С)\А)
ААВи{Сг\В)
(В\С)иЪ
{BaC)kj{A\B)
((ВиА)\С)и({СиА)\В)
ВиС
((Сдв)пв)и(Сп(Диад
{ВпА)и(ВпС)
{СпВ)и(В\А)иАиС
АиВиС
(СпВ)иСиА
14
16
18
20
22
24
26
28
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
D
Е
F
{ААВ)и(СпВ) 1
АиВ 1
{В\А)и{АпС)и(А\В) 1
(Сг\В)и{В\А)иАиС
(АпС)и{СпВ)
АиСиВ
(AnC)UiBuC
Див
(ВпС)и{Аг\(С\В))
СиВу^(В\А)
(В\А)иС
(ВпС)и({В\С)\А)
АиВи(СпА)
Аи(А\В)
{АпС\В)^{А\С)
'в^и(Аг\(С\В))
'ВиС
(ВпС)и({А\С)\В)
({А\В)пС)^АиС
(Аг\С)и(А\(Сг\В))
ЛиС
АиВи(СпА)
((CuA)\iB)u(Cn^)
Ъ^А
86
Глава 2
Таблица 2,2.1 (окончание)
29
D
Е
F
{AAB)(j(CnB)
ВиЛ
(Л\В)и{ЛпС)и{В\Л)
30
D
Е
F
(ДпС)иСив
(ВпС)и(Лп(С\В))
ЯиД
Примеры решения задания 2.2.1
Пример 1.
Выяснить взаимное расположение множеств D=(B\Qu{A\B),
E=A\(B\Q, F = AuB. если А, В, С —произвольные
подмножества универсального множества U.
Найдём соответствующие булевы функции:
fp(a,h,c) = (b-f^c)via-^b), fi:(a,b,c) = a-f^(b-f^ с),
fj7{a,b,c) = avb и, построив таблицы, найдём векторы
значений этих функций:
^=(0010 1110), Д =(0000 1101), /^.-(0011 1111).
Так как множество единичных наборов функций /q и Д
строго включены в множество единичных наборов функции /^7,
to/o->/f=1 и/£->/^=1, но fo^fr^ /£^/^, значит,
DqF и EqF.
Выясним взаимное расположение множеств D и Е:
/о(0,1,0) = 1 и Д(0,1,0) = О =^DzE
/о(1ДД) = 0 и /^(1,1,1) = 1 =^££D \ =^ Е(П)0,
^(1,0,0) = 0 и /^(1,0,0) = 1 =^DnE^0
Пример 2.
Решить задание 2.2.2 для множеств £ = ВдСи(В\Л),
D=AuCu(BnQu(BnC), F = BuC
Найдём соответствующие булевы функции и векторы их
значений:
f^=b-\-cv(b-^a) = (lOn 1001)
fi)='aVlv{bAc)v(bvc) = (lOll 1001)
ff,=bvc = ilOll 1011).
Булевы функции
87
Так как/^ =/d' ^^ E = D. Заметим, что /^ "^ fr^ и,
построив таблицу, можем убедиться, что /^ -^ /,, = 1.
Значит, справедливы соотношения: Е = D Q F.
Задание 2.2.2
Проверить, что для любых множеств А, В, С выполнение
включения а влечёт выполнение включения (3.
Таблица 2.2.2
Х2
1
2
3
4
5
6
7
8
9
10
И
12
13
14
1 ^^
1 ^^
1 ^'^
а
АпВоС
AcsBqC
АпВаС
AnBQC
AdBqC
AqBuC
AqBuC
AQBy^C
AqB(jC
AqBuC
AqB^jC
AuBqC
A^BqC
AuBqC
A^jBqC
AqB\C
AqB\C
P 1
А^Во(ААВ)и(Аг\С)
A\CQiA\B)KjC 1
AACc:iA\B)yjC 1
iB\C)u{A\C)QA^B 1
Bq{B\A)uC 1
AACQiAnB)uC
A\BQAnC 1
AuBqBuC
(A\B)uiAnC)QC
iA\C)uiB\C)QB
{A\B)\CqC\A
AABQ(AnB)^C
AnCQA^{B\A)
АпВо{Вг\С)и(Аг\С)
B\AQBnC
AnBQA\C
Cr\BQB\A
88
Глава 2
Таблица 2.2,2 (окончание)
1 №
1 ^^
1 ^^
1 20
1 ^^
1 22
1 ^^
1 ^"^
1 ^^
1 26
1 ^'^
1 28
1 29
1 30
а
AuBqC
AkjBqC
A(jBqC
B\CqA
B\CqA
B\CqA
B\CqA
B\C^A
B\CqA
BqC\A
BqC\A
BqC\A
BqC\A
P
AaCqC\A 1
{B\C)u{A\B)QAr\C 1
BqAu(C\A) 1
AUiBc(iBnC)uA
BACQC^iAnB)
B\AQ(C\A)u{AnB) 1
iBcCu(iBnA)
iBACcCuA
5сСи(Д\С)
Au(iB\C)cA\iB
(A\iB)u((iB\C)\A)cA
(iB\C)u(iB\A)CiBnC
CUiBc(C\A)u(C\iB)
Пример решения задания 2.2.2
Проверить, что для любых миолсеств Л, В, С
выполнение включения A\BqC влечёт выполнение включения
СдДс(ДпВ)иС.
Составим булеву функцию, соответствующую высказыванию,
которое надо доказать:
f( a,b,c ) = {{а ф b) -^ с) -^ (с + а -^ а Abv с).
Построим таблицу, убедимся, что заключительный столбец,
являющийся вектором значений функции f(a,b,c), состоит из
одних единиц, что доказывает справедливость требуемого
утверждения.
Булевы функции
89
Задание 2.2.3
Для произвольных множеств А, В, Н проверить, является ли
выполнение включения а необходимым и достаточным
условием выполнения равенства (3.
Таблица 2.2.3
№
1
2
3
4
5
б
7
1
1 8
!
!
! 9
1 10
1
11
1
! 12
13
1
! 14
1 15
16
17
18
19
1
а
AqB\H 1
AqB\H
AqB\H
AqB\H
AqB\H
AqB\H
AqB\H
AqB\H
AqB\H
AqB\H
AqB\H
AqB\H
AQBnH
AQBnH
AQBnH
AQBnH
AQBnH
AQBnH
AQBnH
P 1
H\A = Hu{A\B) 1
Н=(Н\А)и((А\В)\Н) 1
AnB = {A\H)u(A\B) 1
В = (ААВ)и(А\Н) 1
AuB = {B\H)u{B\A) 1
В\А = (АаВ)^{ВпН) 1
AaH = Ни{АпВ) 1
ААВ = {В\А)и{НпВ) 1
Au^=(//\A)u((Ani5)\^) 1
АпВ = (А\В)\Н 1
А\Н = Ап(В^Н) 1
А\В = АпВпН
Н =(ААН)и(ВпА) 1
AUiB = (iBn//)u(iB\A)
AaB = {B\H)u{B\A)
В\Н =(А\В)и((В\А)\Н)
{В\А)\Н =(В\Н)и(А\В)
АпВ = (А\В)и(АпН)
А\Н ={АпН)\В
90
Глава 2
Таблица 2.2.3 (окончание)
1 Хо
1 20
1 ^^
1 22
1 ^^
1 ^^
1 ^^
1 26
1 27
1 28
1 29
1 30
а
Дсвп/У
АиВаН
ЛиВсН
AkjBclH
AkjBqH
AuBqH
AkjB^H
AuBqH
AnBQH
AnBQH
AnBQH
P -
H\A-iAAH)yjiA\B) 1
B\A-{A\H)u{{BnH)\A) 1
AuH -Ни(В\А) 1
АпН -Аи(В\Н) 1
^\A = (AA^)u(iB\A) 1
BaH =(А\В)и{Н\В) 1
^niB = ((AAiB)\^)u(AniBn^) 1
AA5 = (^n(AAiB))u((AniB)\^)
^\A = (AA^)\(A\iB)
B\H =(В\А)\Н
AuB = {AAB)u(Br\H)
Пример решения задания 2.2.3
Для произвольных миоэюеств Л, В, Н проверить, является ли
выполнение включения Akj В qH необходимым и достаточным
условием выполнения равенства A^H ={B\A)kj(H\A).
Составим булеву функцию, соответствующую высказыванию,
которое надо доказать:
f{a,b,h) = {(а vb)-^h)^{a + h^ {{b -/^a)v{h-f^ а))).
Построим таблицу, убедимся, что заключительный столбец,
являющийся вектором значений функции f{a,bjt), состоит из
одних единиц, что доказывает справедливость требуемого
утверждения.
Булевы функции
91
Задание 2.2.4
Выяснить, верно ли равенство а для произвольных А, В, С.
Таблица 2.2,4
№ 1
1 1
2 1
3
4
1 ^
1 ^ '
1 '^
8
1 ^
1 ^^
1 ^^
1 ^^
13
1 ^"^
1 ^^
1 ^^
1 ^'^
18
1 ^^
20
а
AxC = (Ax(C\iB))u(Ax(CniB)) 1
АхС = (Лх{СпВ))и{АхС)
Лх{ВАС) = (Лх{ВиС)\{Лх{СпВ)) 1
AxC = (Ax(C\iB))u(AxC) 1
Лх(ВиС) = (ЛхВ)и(Лх(С\В)) 1
Ax(C\iB) = (AxC)A(Ax(CniB)) 1
ЛхС = {Лх{СиВ))г\(АхС) 1
Ax(Cn(iBAC)) = (AxC)A(Ax(Cne)) 1
Ax(C\iB) = (AxC)\(Ax(CniB)) 1
Ax(B^C) = {Ax(BAC))yjiAx(BnC)) 1
А X С = (Л X (С u iB)) \ (Д X (iB \ О) 1
Ах{В ПС) = {АхС)\(Ах{С\ В)) 1
Ax(finC) = (Ax(iBuC))\(Ax(iBAC)) 1
Ax(C\iB) = (Ax(iBuC))\(Ax5) 1
ВхА = {Вх{А\С))и(Вх{АпС)) 1
iBXy4 = (iBx(AnC))u(iBxA)
iBxA = (iBxA)u(iBx(A\C))
Вх{АиС) = {Вх{А\С))^{ВхС)
BxA = (BxA)r\(Bx(AuC)) 1
5x(A\C) = (iBxA)\(iBx(AnC))
92
Глава 2
Таблица 2.2.4 (окончание)
1 №
1 ^^
1 22
1 ^^
1 ^"^
1 ^^
1 26
1 27
1 28
1 29
1 30
а
ВхЛ = {Вх(АиС))\{Вх(С\Л)) 1
Вх(АпС) = {ВхЛ)\(Вх{А\С)) 1
iBx(A\C) = (iBxA)A(iBx(AnC)) 1
Вх(А\С) = (Вх{ЛиС))\(ВхС) 1
CXiB = (Cx(iB\A))u(Cx(iBnA)) 1
CXi5 = (Cx(iBnA))u(Cxe) 1
Сх(ААВ) = {Сх(АиВ)\{Сх{АпВ)) 1
CXiB = (Cx(e\A))u(CXiB) 1
Cx{AuB) = {CxA)u(Cx(B\A)) 1
Cx(iB\A) = (CXiB)\(Cx(AniB)) 1
Пример решения задания 2.2.4
Выяснить, верно ли равенство
Сх(В\А) = (СхВ)а(Сх(ЛпВ)) для произвольных А, В, С-
Составим булеву функцию, соответствующую высказыванию,
которое надо доказать:
f(a,b,c) = {сА(Ьфа))<г^{сАЬ) + {сА{аА Ь)).
Построим таблицу, убедимся, что заключительный столбец,
являющийся вектором значений функции f{a,b,c), состоит из
одних единиц, что доказывает справедливость требуемого
утверждения.
Булевы функции 93
2.3. Нормальные формы
и полиномы
Возведение в степень булевых переменных определяется так:
1 о ~
X = Л', X = X .
Элементарной конъюнкцией называется выражение
X.' -х. - -...-х.'", где все переменные, вошедшие в состав
I 3 III
конъюнкции, различны, m > 1.
Дизъюнктивной нормальной формой (ДНФ) данной булевой
функции называется её представление в виде дизъюнкции
некоторых элементарных конъюнкций.
Для любой булевой функции /(xi,X2,...,-^„) справедлива ^о/?-
мула дизъюнктивного разлолсения по совокупности переменных:
X\,X2,---Xf^) — V Xj -Xj^'-'-'X^ ' j\^a^,...,cij.,X].j^^,...,x,^).
Заметим, что эта формула остаётся справедливой и для
разложения не только по первым к переменным.
Совершенной дизъюнктивной нормальной формой (СДНФ)
данной булевой функции называется её представление в виде:
/(Х„Л,,...Х„)= V Х^^-Х^-...-Х^''.
{ах,а1,...Дп)
/(fl,,rt2.-.fl„)=l
Элементарной дизъюнкцией называется выражение
х.^ VX. - V...VX.'", где все переменные, вошедшие в состав
дизъюнкции, различны, m > 1.
Для любой булевой функции /(Х],л'2,...,^„) справедлива фор-
мула конъюнктивного разлоэюения по совокупности переменных:
Конъюнктивной нормальной формой (КНФ) данной булевой
функции называется её представление в виде конъюнкции
некоторых элементарных дизъюнкций.
4 Зак. 3332
94
Глава 2
Совершенной конъюнктивной нормальной формой (СКНФ)
данной булевой функции называется её представление в виде:
f(a^,a2,....aj=0
Полиномом Жеголкина буя^ъой функции f(Xl,X2,^..,x,^)
называется её представление в виде суммы по модулю два некоторых
элементарных конъюнкций и, быть может, константы 1.
Полином Жегалкина может быть найден с помощью формулы
(<7,,a2,...,rt„)
fia^,a2....,a„)=\
В которой нужно раскрыть скобки и упростить выражение с
помощью соотношений:
x-(y + z) = x-y + x-z, х + 1 = х, х + 0=^х, х + х = 0.
Задание 2.3.1
Преобразовать f(xi,X2,x;^,x^), используя формулу
дизъюнктивного разложения по совокупности переменных л',^, jc^.,
представляя получаемые функции от двух переменных формулами
над множеством элементарных связок: отрицание, конъюнкция,
дизъюнкция, импликация, сумма по модулю два, эквиваленция,
запрет, штрих Шеффера, стрелка Пирса.
Таблица 2.3.1
Хо
1
2
3
4
5
/
ОНО 1110 1101 1001
оно 1110 1101 1001
оно 1110 1101 1001
оно 1110 1101 1001
оно 1110 1101 1001
п
1
1
1
2
2
к
2
3
4
3
4
Хо
6
7
8
9
10
/
ОНО 1110 1101 1001
1010 1110 оно 0101
1010 1110 оно 0101
1010 1110 оно 0101
1010 1110 оно 0101
п
3
1
1
1
2
к
4
2
3
4
3
Булевы функции
95
Таблица 2,3,1 (окончание)
№
11
12
13
14
15
16
17
18
19
20
/
1010 1110 оно 0101
1010 1110 оно 0101
1100 0100 0111 оно
1100 0100 0111 оно
1100 0100 01 н оно
1100 0100 0111 оно
1100 0100 0111 оно
1100 0100 0111 оно
1110 0111 0101 1011
1110 0111 0101 1011
п
2
3
1
1
1
2
2
3
1
1
к
4
4
2
3
4
3
4
4
2
3
Хо
21
22
23
24
25
26
27
28
29
30
/
1110 0111 0101 1011
\\\0 ОН! 0101 1011
1110 0111 0101 1011
1110 0111 0101 1011
1010 оно 1111 0111
1010 оно 1111 0111
1010 оно 1111 0111
1010 оно 1111 0111
1010 оно 1111 0111
1010 оно 1111 0111
п
1
2
2
3
1
1
1
2
2
3
к
4
3
4
4
2
3
4
3
4
4
Пример решения задания 2.3.1
Разложим функцию f(xi,X2,x^,x^)= (0100 0111 1000 1011)
попеременным Х2,х^.
Для этого случая формула дизъюнктивного разложения
примет вид:
f(xi,X2jX'^,x^)— V Х2' 'х^"^ - f(x^,a2,X2,ci^)—
(«2'«4)
(«2'«4 J
= V Х2^ •Х4^ •/(x,,fl2'-^3'^4)= ^2 ••^4 •/(•^1'0'-^3'0)V
(0.0)
(0,1)
(1,0)
(1,1)
"^ -^2 • 4 • f(^\ Д-^3'!) ^ 4 • 4 • /(-^1 Д.-^З'О) V ^2 • 4 • /(-^1 Д»-^3'1) =
96
Глава 2
vx^'X^ ' f{x^Xx^,0)v х^' х^- /(х^Хх^Л)
Запишем таблицу функции /{х^,Х2,Хт^,х^) и с её помощью
составим таблицы всех четырёх функций от переменных Х|, х^.
Таблица 2.3.1а
^\
0
0
0
0
0
0
0
0
Х2
0
0
0
0
1
1
1
1
■^3
0
0
1
1
0
0
1
1
^4
0
1
0
1
0
1
0
1
/
0
1
0
0
0
1
1
1
■^1
Л'2
0
0
0
0
1
1
1
1
■^3
0
0
1
1
0
0
1
1
ч
0
1
0
1
0
1
0
1
/
1
0
0
0
1
0
1
1
Таблица 2.3.1b
^\
0
0
1
1
^3
0
1
0
1
/(^1,0,^3.0)
0
0
1
0
/(^1,0,^3.0
1
0
0
0
f(x„lx^,0)
0
1
1
1
f(x„lx^,\)
1 1
1
0
1
Булевы функции
97
Как мы видим, /(jc, Д;сз,0) = х, -/> Хз, /(jci,0,jc3,1) = Xj i Х3,
/(jci,l,jc3,0) = Xi V X3, /(x,,l,jc3,l) = Xi -^ X3, значит, можно записать
ответ:
f(x^,X2,X2,X^) = X2-X4'{Xi 4^X2) V Х2 ' Х^ • (х, ix^)^
V Х2- X4'(XiV X^)V ^2 • ^4 • (Х| —> Х^) •
Задание 2.3.2
1. Выяснить вопрос о равносильности ДНФ /1,/2,/з
сведением их к СДНФ.
2. Преобразовать с помощью дистрибутивных законов /2
в КНФ, упростить полученное выражение.
Таблица 2.3.2
Хо
1
2
3
4
5
6
7
8
9
1 ^^^
1 ^^
/i
a:>'v.v>'V д'г
д'г VXZVA7Z v>'.v
>' Z V JCZ V X Д'
xyzvxzv xyz.
yzv xyv yzv zx
yzvxyzvxyz
xy zv xzv yzv xyz
X yz vxyv yz vxzv xyz
yzv xyv yzv xyz
xyz V xzv yzv xyz
xyzvyzvxyvxyz
/2
xyv xz
у XV xyv yz
yzv xyv yxv yz
xy zv zv xy
yxv yzv xz
xzv x у
yxv yxv xz
yxv yxv z
yx V yx V xz
yx V >;д: V xz
yxv yxv X
/3 1
yv z
zxv yv xz
xyzv xyzvx
xyv yz
yxv yzv xz
X V xyz
zxV yxv z
yzv yzv xz
yvz
XV yz
yzv yzvX
98
Глава 2
Таблица 2.3.2 (окончание)
1 Хо
1 ^^
1 ^^
1 ^"^
1 ^^
1 ^^
1 ^'^
1 ^^
1 ^^
1 20
1 ^^
1 22
1 ^-^
1 ^"^
1 ^^
1 26
1 ^'^
1 28
1 29
1 30
/i
xyzv yxvxyzv у z
yzvzxvzy
zyv zyxv xyv xz
zyv yzv xzv xz
xyzv xyv xyz
xzvxyvxzv yz
xzv xyzv xyz
xy V xyz V xz V X yz
xyzv yz V л:>' V x yz
xzvxzv xyzv yz
xyz V xz V xy V xyz
X yzv xzv xy V xy z
xyz VxzvxyzV у z
xyv xz
xzv yv Xyz
xyvxzvyz
xyzv xyzv xy
yzv xy zv xyv xy z
xz V yv xz
/2
V-vV yzv z
yx V yz
zyvyzvxz
zyv yzv xz V zx
yzv XV xyz
xy V xzv у z
yxv yz
xyv yzV yz
yzv yzvX
xyv yzv yz
xyv yzv yz
' yv yzv yz
yzv XV xz
xy V xy z
xy V xz
xy V yzv xy V xz
yzv xz
yzv xzv xz
xy zv xzv xyzv yz
/з
yxvzxvzx
XV Z
yxv xyv z
xyz V V V xyz
xzv yz
xz V xy V yz
yvxyz
xvxyvyz
xz V xy V xz
XV Z
yv xz
xz V yv xz
xy V л'>' V V z
yzv xyzv xyz
xyzv xyzv yz
yz V xy V xz
xyz V z
yzvyvxz
xyv xyv yz
Булевы функции 99_
Пример решения задания 2.3.2
Решим задание 2.3.2 для
Mx,y,z)^xyv yzvxz, f2{x,y,z) = xvxyzvyz,
f2{x,y,z) = xyv xzv zy.
1. Преобразуем данные функции в СДНФ:
f\(x,y,z) = xyv yzvxz = xy-lvl'yzvx-l-z =
= xy-(zv z)v{xvx)-yzv x-(yv у)- z =
= xyzv xyzv xyz V xyzv xyz V xyz.
f2{x,y,z) = XV XyZV yZ = X-{yv y)-{zv z)v XyZV {XV x)yz =
= xyz V xyzv xyzv xy zv xyz V xyz V xyz =
- xyz V xyz V xyzv xyzv xyz V xyz^
/з(х,y,z) = xyvxzv zy-xy{zV z)vx{y V y^zV(л-Vx)zy =
= xyz V xyzv xyzv xyzv xyz V X yz.
Сравнивая СДНФ этих функций, делаем вывод, что
/1-/3'^/2-
2. Преобразуем /2 в КИФ. Воспользуемся одним из
дистрибутивных законов:
ЛС-^» У'^) = -^ V (х • у • z) V (>; • z) =
={xv XV y)'{xv yv y)-{xv zv у)'{х\/ XV z)'{xv yv 7)'{xv zv z)-
= {\y y)' {x w \)' {xw zw y) • {\w z) • {xw у w z) • {xw \) =
= \'\-{xv zv y)-\'{xw yw z)'\= {xv zv y){x V у V z).
Задание 2.3.3
1. Найти двумя способами полином функции, заданной век-
торно.
2. Найти СДНФ.
3. СКНФ данной функции.
100
Гпава 2
Таблица 2.3.3
№
1 1
1 ^
1 ^
4
5
6
7
8
9
10
/
1001 0111
оно 1011
1110 оно
0111 1001
1100 0111
1001 0100
1011 0101
1000 оно
1010 оно
0101 1000
х«
11
12
13
14
15
16
17
18
19
20
/
ООН 1000
0001 оно
1101 1010
0101 1100
1110 1101
0010 1000
1010 1101
0010 оно
1010 0111
0101 1001
Хо
21
22
23
24
25
26
27
28
29
30
f
0111 1001
0100 1010
ООН 1000
1000 0111
оно ООН
0111 1010
1101 0111
ООН 1110
1101 1000
оно 0101
Пример решения задания 2.3.3
Решить задание 2.3.3 для функции f{x, у, z,) = (0001 0101).
Запишем таблицу данной функции в развёрнутом виде.
Таблица 2.3.3а
X
0
0
0
0
1
1
1
1
у
0
0
1
1
0
0
1
1
Z
0
1
0
1
0
1
0
1
/
0
0
0
1
0
1
0
1
Булевы функции 101
Способ 1. Найдём полином Жегалкина данной функции,
исходя из формулы:
f(x.y,z)= J^ix + a)(y + h){z + c).
Получим: ^^^^^^^^^ Х(.-ь«)(, + Ь)(, + с) =
(0,1,и
(1,0,1)
(1,1,1)
= (А' + 1)(у + 0)(г + 0) + (х + 0)(у + 1)(г + 0) + (х + 0)(у+0)(г+0) =
= (л: + l)yz -^ х(у-^ l)z-^ xyz = xyz-\г XZ-^ xyz-^ yz-^ xyz =
= XZ + yz + xyz.
f(x,y,z) = xz + yz + xyz. Итак, f{x,y,z) = xz + yz + xyz.
Способ 2. Применим метод неопределённых коэффициентов.
Будем искать полином для данной функции в виде:
fix, у, z) = aQ + а^х + а2У + a^^z + а^ху + a^xz + ct^yz + a^xyz. (*)
Используя таблицу функции, будем подставлять наборы
значений переменных и значения функции в соотношение (*) и
последовательно находить неопределённые коэффициенты а^:
/(0,0,0) = 0 = ^ +^1 О + а, О + Оз 0 + ^4 0 + ^5 0 + ^6 -0 + ^ -0 =
— а^=> aq = о,
/(0,0,1) = 0 = 04-аз-1 =>аз=0,
/(0,1,0) = О = 04-flt, 1 = ^2 => ^2 =0'
/(0,1,1) = 1 = о + «6 • 1 = ^6 => «6 = 1'
/(1,0,0) = 0 = 0 + ^^1 •l = flt,=> а^ =0,
/(1,0,1) = 1 = О 4- а, • 1 4- (2з • 1 + (25 • 1 = (25 => <25 = 1,
/(l,l,0) = 0 = 04-(2i •1 + (22-1 + (24-1 = (24=> а^ =0,
/(1,1,1) = 1 = ^0 + «1 • 1 4- (22 • 1 + «3 • 1 4- (24 • 1 + (25 • 1 + (2^ • 1 + (27 • 1 =
= 04-(25-14-(2б-1 + (271==04-1 + 1 + (27 =(27 => а^=\.
102 Глава 2
Получили, что
f{x,y,z) = 0 + 0'X + 0-y + 0'xy + l-xz + l'yz + l-xyz =
= xz + yz + xyz.
Как и следовало ожидать, результаты, найденные различными
способами, совпали. Итак, f(x, у, z) = xz + yz + xyz.
Найдём СДНФ данной функции:
f(x,y,z)= V x"y'z' =^x^'y'z' =x'y'z' vx'y'z' vx'y'z' =
{n,b,() (Ql.l)
fia,b,r)=\ (l.Ql)
(M.l)
= xyz V xyz V xyz .
Найдём СКНФ:
f(x,y,z)= A (jc^v/vz^)= A(jc^v/vz^) =
ia,b,c) (0,0,0)
f(a,b,c)=0 (0.0,1)
(0,1.0)
(1.0,0)
(1.1,0)
= (x vyvz')-U^vy vz^)-U'v/vz^).(/vy vz^).(/vy^vz') =
= ixv yv z)'{xv yv z)-{xv yv z)'{xv yv z)-(xv yv z).
2.4. Классы Поста
Классами Поста называются следующие классы:
Класс функций, сохраляюгцих константу 0:
7Ь = {/еР2 1/(0.0 0) = 0}.
Класс функций, сохраняющих константу 1:
71={/бР2 1/(и,...Д) = 1}.
Класс линейных функций'.
l^ = {f^ P2\f(x^,X2,...,x,^) = aQ-\-a^x^+... + a,^x,,}.
Класс самодвойственных функций:
Булевы функции
103
Говорят, что набор а предшествует набору (3, и пишут
а =^(3, если ai<bi для / = 1,2,.--,'^.
Класс монотонных функций:
M={/eP2|V„Vp а^^-^/(а)</ф)}.
Замыканием множества булевых функций и называется
множество всех суперпозиций функций класса и, которое
обозначается [и].
Класс и назы^а^тся функ11ионально замкнутым, Qcnn [и] = и.
Теорема. Классы Поста функционально замкнуты.
Класс функций и называется функционально полным, если
Класс функций и называется функционально полным в
слабом смысле, если добавление в и констант О и 1 превращает его
в функционально полный класс.
Теорема Поста. Множество булевых функций и является
функционально полным тогда и только тогда, когда для каждого
из классов Поста найдётся во множестве и функция, не
принадлежащая этому классу.
Задание 2.4.1
Доопределить функции f(x,y,z), g(x,y,z), h(x,y,z) так,
чтобы /еМ, gsL, heS.
Если построение какой-либо функции невозможно,
докажите это.
Выясните вопрос о принадлежности построенных функций
к классам Гд и TJ.
Таблица 2.4,1
Хо
1
2
3
/
(-10- 1---)
(---0 1---)
(---0 -10-)
8
(-10- -0-0)
(0--- 110-)
(---0 0-10)
1г
(-0-- 11-1)
(1 1-- 10--)
(- 1 -- 0 1 -0)
104
Гпава 2
Таблица 2.4.1 (окончание)
1 ^' 1
1 "^ 1
1 ^ 1
1 ^
1 7
1 ^
1 ^
1 ^^
1 ^^
1 1^
1 13
1 ^"^
1 ^^
1 ^^
1 ^'^
1 ^^
1 ^^
1 20
1 ^^
1 22
1 ^^
1 ^"^
1 ^^
I 26
1 ^'^
1 28
1 29
1 30
/ 1
(- 1 0-)
(---0 -0 1-)
(-- 1- -0--)
(-0-0 1 ---)
(-1-1 --0-)
(-01- -0--)
(---0 1- 1 -)
(- 1 0 1)
(0--0 1 ---)
(0- 1- -0--)
(0 1 0-)
(---0 1-- 1 )
(--1- -0- 1 )
(-1 1 0-)
(--00 1 ---)
(-0 1 - -0--)
(- 1-- 0-0-)
(---0 1- 1-)
(--1 1 -0--)
(- 10 0-)
(-01 - -0--)
(-0-0 1 ---)
(-1-1 --0-)
(-0-0 1---)
(--1 1 -0--)
(- 1 -- 01 1-)
(---0 1 1--)
8 1
(0 1-0 - 1--)
(0-10 --- 1 )
(-0 1 - - 1 - 1)
( 1 --- 00 1 -)
(--- 11-01)
(10-1 -0--)
(1-01 ---0)
( 1 - 1 - --00)
(--00 1 -0-)
(--10 1 - 1 -)
(-00- 1 - 1 -)
(0--- 00 1-)
(-10- 0--1)
(0--1 -0-0)
(--1 - 11-0)
(---0 01-0)
( 1--0 - 1 - 1)
(--0- 00- 1 )
(---1 10-1)
(1--- 110-)
(-01 - 1--0)
(-1-0 1-01)
(1--0 -01-)
(01-1 -0--)
(-10- 1-0-)
(01-- 1-0-)
(-0-- 101-)
h 1
(10 1- 1 ---)
(--10 --01 )
(-1-0 - 1-0)
(-00- 1 -- 1 )
(- 1 -- 10-0)
(0--- 101-)
( 1 -- 1 -00-)
( 1 - 1 0 --1 -)
(--10 --00)
(-10- 0--1)
(11-1 -0--)
(-0 1 0 --- 1 )
(-1-- 1 0-0)
(00- 1 - 1 --)
(00-0 -0--)
(01 -- 0 1 --)
(0-10 --0-)
(--- 1-0 10)
(- 1 -- 1 0-0)
(0--1 - 10-)
(-1-0 -0-1)
(1--0 -10-)
(--0 1 --11)
(0-00 --0-)
(0-- 1 -0 1-)
(-101 ---0)
(00-0 -0--)
Булевы функции
105
Пример решения задания 2.4.1
Решгт задание 2,4.1 для / =(-101--0-), ^=(---1-010),
/г = (1-10--1-).
Изобразим развёрнутую таблицу
данных функций.
Доопределим функцию /,
используя определение монотонной функции.
Так как /(1,1,0) = О, то на всех
наборах, предшествующих набору (1Д,0),
функция / тоже должна равняться О,
т.е./(0Д0) = /(1Д0) = 0.
Так как /(0Д1) = 1, то на всех
наборах, которым предшествует набор
(0,0,1), функция / должна принять
значение 1, т. е. /(1Д1) = /(1,1,1) = 1.
Получаем: /(х,у,г) = (01010101).
Доопределим функцию g,
учитывая, что она — линейная. Общий вид линейной функции от
переменных x,y,z имеет вид: g{x,y,z)-ciQ + ci^x-\-a2y-^a2^z.
Будем подставлять наборы значений аргументов, на которых
функция определена.
xyz.
000
001
010
Oil
100
1 101
ПО
1 ^^^
Таблица 2,4,1а
f
-
1
0
1
-
-
0
-
8
-
-
-
1
-
0
1
0
h
1
-
1
0
-
-
1
-
Получим систему соотношений:
l = aQ + ai'0 + a2'l + a^-l
0 = ^0 + й^1 ■ 1 + й^2 * О + ^3 * ^
1 = ^0 + fli • 1 + й^2 • 1 + ^3 * О
О = ^0 + ^1 • 1 + ^2 • 1 + «3 * 1
или <
Заменяя fltg "^ ^i "•" ^2 на 1 в 4 уравнении системы, имеем:
l + a^ =0 => ^3-1-
106 Глава 2
Сложив первые три уравнения и учитывая, что х + х = 0,
получим: fltg+0-0 =^ ^0-1-
Подставляя в 1 уравнение найденные значения а^ и а^,
получим: О + й^2 +1 = 1 или й^2 +1 - 1' откуда «2 - О-
Подставив значения а^^ и а-т, ъо 2 уравнение, получим:
0 + flt| +1 = 0 или fl^i +1 = 0, откуда щ =1.
Итак, g{x,y,z) = 0 + l-x + 0-y + l-z = x + z.
Исходя из этой формулы, найдём значения функции g на тех
наборах, на которых она была не определена: g(0,0,0) = 0 + 0 = 0;
g(0,0,l) = 0 + l = l; ^(0,1,0) = 0 + 0 = 0; g(l,0,0) = l + 0 = l.
В итоге имеем: g(x,у,г) = (01011010).
Доопределим функцию /г, используя определение
самодвойственной функции. Так как наборы (0,0,0) и (1,1 И)
противоположны и /г(0,0,0) = 1 => /г(1,1,1) = 0.
Противоположными парами наборов значений переменных
являются также (0,0,1) и (1,1,0), (0,1,0) и (1,0,1), (0,1,1) и (1,0,0).
Используя известные значения функции /г, получим:
/г(0,0,1) = /г(1,1,0) = 1 = 0, /г(1,0,1) = /г(0,1,0) = 1 = 0.
Итак, /г(х,};,г) = (10101010).
Так как /(0,0,0) = g(0,0,0) = 0^/z(0,0,0), то /еГо, g^T^.
h^To.
Так как g(l,l,l) = /i(l,l,l) = 0, /(1,1,1) = 1,то /еГ,, g€T^,
Задание 2.4.2
1. Можно ли из функции f{x,y,z) с помощью суперпозиций
получить g{x,y,z) ?
2. Верно ли, что f{x,y,z)^[g]l {[g] — замыкание класса
[8))-
Булевы функции
107
Таблица 2,4.2
Хо
1
2
3
4
S
6
7
8
9
10
11
12
13
14
15
/
10010110
10010100
0111 1010
1101 1010
оно 1111
1000 0110
оно 1110
1000 0110
1100 0111
10100110
1110 1000
1000 0000
0111 1110
1110 0000
11101111
8
11100110
11010100
1000 0110
1010 1010
10100110
1001 1000
1001 0010
1101 1001
1001 1110
10010110
1100 1000
1100 0011
11010000
1011 0010
1100 0010
Хо
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/
10100100
0101 1110
1101 0000
1100 0001
1001 1000
1011 0010
1000 1100
1001 оно
1100 1110
1100 0011
1001 оно
0111 1010
11010000
11Н01Н
1000 1000
g 1
1000 1110 1
1011 0000
11010100
1101 1000 1
1110 1000 1
1100 оно
ООН 1010 J
11110010
1000 0001
1001 1000
1101 1100
1001 1010
1110 1000
1010 1000
10010110
Пример решения задания 2.4.2
Решим задание 2.4.2 д.чя функций / = (10010100),
5 =(1001 ОНО).
Проверим f{x,y,z) на принадлежность к классам Поста.
/(0Д0) = 1 =* /£Го;/(1,и) = 1 ^ /gr,;
(0,0,0)=<(0,0,1)и /(0Д0)>/(0Д1) =* /€М;
(0,0,1) и (1,1,0) — противоположные наборы,
/(0Л1) =/(1,1,0)^/6 5;
108 Глава 2
f(x,y,z) = ix + l)iy + l)iz + l) + (x-hl)yz + x(y + l)z =
= l + x+y + z + xy + xz + yz + xyz + xyz + yz + xyz + xz =
= l + x+ y + z + xy + xyz.
Так как в полиноме функции / присутствуют конъюнкции, то
Итак, мы видим, что функция f(x,y,z) не принадлежит ни
одному из классов Поста, значит, система {/}функционально
полна, и с помощью суперпозиций из / можно получить любую
булеву функцию, в частности, gix,y,z).
Проверяя значения функции g(x,y,z) на всех парах
противоположных наборов, видим:
^(ОДО) = 1 = g(l,l,l), g(0,0,l) = О = gillO),
^(0,1,0) = 1 = g(lAl), 8(0X1) = 1 = ^(1,0,0).
Значит, gs S.
Так как S — функционально замкнутый класс, то [g] с 5, но
/^5, значит, f^[gl
Задание 2.4.3
Для функций /(х,у,г)и g(x,y,z) выяснить вопрос об их
принадлежности к классам Tq, Г], L, 5, М.
В случае, если некоторая функция представляет из себя
функционально полный класс, выразить из неё с помощью
суперпозиций константы 0,1, отрицание и конъюнкцию ху.
В случае, если некоторая функция представляет из себя
функционально полный в слабом смысле класс, выразить из неё
с помощью суперпозиций и фиксирования переменных
отрицание и конъюнкцию ху.
Полученные результаты проверить с помощью построения
таблиц.
Булевы функции
109
Таблица 2,4,3
№
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
/
11000111
1110 1010
0100 1101
1111 0100
оно 1001
1000 0010
1011 1101
1111 1010
1000 0001
1101 1100
0010 0000
1001 0000
0111 1110
1110 0000
1110 1111
8
1101 1000
00110101
1100 1110
10010110
11010100
0000 1101
1100 0100
0101 1111
1110 1010
0001 1010
1100 1000
1000 0011
1101 0000
1011 ООП
1100 0010
Ха
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/
0010 0100
1101 1110
11010000
1100 0001
1001 1000
1011 ООН
1000 1100
00010110
1100 1110
1100 0011
1001 ню
0111 1010
1101 0000
1111 0111
1000 1100
8
1000 1110
10110011
11010100
Н01 1110
1110 1000
11000110
ООН 1010
11110010
1000 0001
1101 1100
0101 0100
1011 1010
1110 1001
1011 1100
1001 0111
Пример решения задания 2.4.3
Решим задание 2.4.3 для функций
/ = (0010 1000), g=(1001 0010).
Выпишем развёрнутую таблицу
функций f и g (табл. 2.4.3а).
1. Исследуем функцию f(x,y,z).
Проверим f(x,y,z) на принадлежность к классам
Поста.
/(0,0,0) = О =^ fsTo.
Заметим, что отсюда следует, что {/} не
является функционально полным классом.
/(1,1,1) = о ^ /г г,.
Таблица 2,4,3 а
xyz
000
001
010
ОН
100
101
НО
111
/
0
0
1
0
1
0
0
0
8
1
0
0
1
0
0
1
0
110 Глава 2
Так как наборы (0,0,0) и (1,1J) противоположны
h/(0,0,0) = /(U1), то f^S,
Имеем, что (0,1,0) =^ (0,1,1), но /(0.1,0) > /(0.1,1),значит,
f€M.
Найдём полином для f(x,y,z):
f(x,y,z)= S (x + a){y + b)(z + c)={x + i)y(z + i) + x(y + l)(z + l) =
(0,1.0)
(1Д0)
= xyz + xy + yz + 3^ + xyz + xy + xz + x = XZ + yz + x+ y.
Так как полином функции / содержит конъюнкцию, то
/€L.
Как было отмечено ранее, {/} не является функционально
полным классом, но, так как функция / нелинейна и
немонотонна, {/} — функционально полный в слабом смысле класс.
Выразим из / отрицание с помощью фиксирования
переменных. На соседних наборах (0,1,0) и (0,1,1) нарушается
монотонность, рассмотрим функцию р(х) = /(0,1, jc).
Найдём все значения функции р(х):
/7(0) =/(0,1,0) = 1, /7(1) = /(0,1,1) = О =^ Р(Х) = Х.
Отрицание построено, х = f(OXx).
Для построения конъюнкции зафиксируем одну переменную и
переобозначим оставшиеся переменные так, чтобы полином
принял вид
xy + ou + Pv + Y' где a,p,Y^{0,l}.
Например, можно сделать так: f(l,y,x) = l'X + xy + l + y =
= ху + х + у + 1. в этом случае а = Р = у=1.
Введём функцию h(x,у) = f(ly + a,x + ^) + a^ + y = f{hv,х) =
= /(1,/(0,1, у),/(0,1, Л')).
Найдём значения функции h на всех её наборах.
/2(0,0) = /(1,/(0,1,0),/(0,1,0)) = /(1,1,1) = 0;
/2(0,1) = /(1/(0,1,1),/(0,1,0)) = /(1,0,1) = 0;
Булевы функции Ш_
/2(1,0) = /(1,/(0Д,0),/(0Д,1)) = /(1Д,0) -0;
hill) = /(1,/(0ДД),/(0ДД)) = /(1Д0) = 1.
Как видим, таблица функции h{x,y) совпадает с таблицей
конъюнкции, следовательно, х- у = /(1,/(0,1,>'),/(0,1,х)).
2. Исследуем g(x,y,z) на принадлежность к классам Поста.
8(0,0,0) = 1 =^ g^To.
^(1ДД)-0 =^ g^T,.
Наборы (1,0,1) и (0,1,0) противоположны и
^(1Д1) = ^(0Д,0) ^ g^S.
Так как (0,0,0)^(0,0,1), но g(0,0,0) > g(0,ОД) => g^M.
Найдём полином для g(x,y,z):
g(x,y,z) = {x-^l)(y + l){x + l) + (x + l)yz + xy(z + l) =
= xyz + xy + xz + yz + x + y + z + l + xyz + yz + xyz + xy =
= l + x + y + z + xz + xyz.
Так как в полиноме функции g содержится конъюнкция,
то g^L
Итак, функция g не принадлежит ни одному из пяти классов
поста, значит, {g} —функционально полный класс.
Выразим из g отрицание с помощью одних лишь
суперпозиций. Рассмотрим функцию s(x) = g(x,x,x).
Найдём все значения функции s(x):
5(0) = g(0,0,0) = l, 5(1) = ^(1ДД) = 0 =^ s(x) = x.
Отрицание построено, х = g(x,x.x).
Строим константу 0. Для этого возьмём набор из пары
противоположных наборов, на которых функция g равна О, например,
(1,0,1), и рассмотрим функцию о(х):
о{х) = g{x\x^,x^) = g{x,x,x) = g(x,g(x,x,x),x).
112 Глава 2
Найдём значения функции о(х) на её наборах.
0(0) - 5(0,5(0Д0),0) - 5(0,1,0) = 0;
o(l) = g(l,5(Ul),l) = 5(1.0,1)-0.
Константа О построена, g(x,g(x,x,x),x) = 0.
Для построения константы 1 возьмём отрицание от функции
о{х) и обозначим полученную функцию через е{х).
е(х) = g(o(x)Mx),oM) =
= g(g(x,gix,x,x,),x),g(x,g(x,x,x,\x),g(x,g(x,x,x,),x)).
Итак, койстанта 1 получена,
g(g(x,g{x,x,x,),x),g(x,g(x,x,x,),x\gix,g(x,x,x,),x)) = l.
Для построения конъюнкции зафиксируем переменную г,
придав ей значение 1.
Получим: g(x,y,l) = l + x+y + l + x-l + xy'l = xy + y + U т. е. мы
получили выражение вида ху + сих-\-^у + у, где а = у = 0, (3 = 1.
Рассмотрим функцию к{х,у) = g(jc + (3,y+ а,1) + а(3 + у =
= g(x + ly,l) + 0-l + 0= g{g(x,x,x),y,l) =
= g(g(x,x,xXy,g{g(x,g(x,x,x),xlg(x,g(x,x,x),xXg(x,g{x,x,xlx))).
Найдём значения функции к на всех её наборах.
^(0,0) = ^(^(ОДО)Д g(giO, g(0,0,0),0), g(0, g(0,0,0),0), g(0, g(OAO)m=
= gm g(g(OXOl g(OXOl g(OXO)) = gdOfi) = 0;
^(0,1)=g(^(o,o,o),i, gigio, g(om\oig(o, g(o,o,o),o), g(o, ^(одо),о)))=
= gdX g(g(0X0lg(0X0l giOXO))) = gdX g(0,0,0)) = ^(Ш) = 0;
^(1,0)=^(^(1,и)д g(g(i gaxmx gn giumx gd gaxnm=
=g(OA gigumi g(imi gdom = gm, ^содо»=^(од1)=o;
^(U)=g(g(ixi)x g(g(i gdxmi gii gdxmi g(i gnuim=
=g(ox g(gmi\ giiOM giiom = g(ox ^(одд))=^(o,i,i)=i.
Булевы функции
113
Как видим, таблица функции к(х,у) совпадает с таблицей
конъюнкции, следовательно,
^'^'У = gigix, X, х\ у, g(g(x, g{x. А', х\ х\ g(x, g(x, X, х\ Л'), g(x, g(x, X, х\ х))).
Задание 2.4.4
Подсчитать число различных булевых функций от п
переменных, принадлежащих данному множеству Л.
Таблица 2.4,4
Хо
1
2
3
4
5
6
7
8
9
10
А
{LuTo)\T,
iSuTo)\T,
5иГоиГ,
(5иГо)пГ,
S ^T^
{LuTO\To
LaT^
(5пГо)иГ1
(5пГ,)иГо
(SuL)\To
Хо
11
12
13
14
15
16
1 ^'^
18
19
20
А
S aL
(SnL)uro
(SnL)uT^
(SuL)nr,
(SuL)nro
(Luro)nS
(Ln7o)uS
(Lur,)nS
(Lnr,)uS
(Suro)nL
Xo
21
22
23
24
25
26
27
28
29
30
A
(5nri)uL
(riU7o)nL
(r,nro)uL
(Lnro)u(Snr,)
(Snri)\(Lnro)
(7iu7b)\S
(7]u7b)\L
аиГо)\5
7b\(SuL)
(Го\5)\Г,
Примеры решения задания 2.4.4
Пример 1. Подсчитать число
различных булевых функций от п переменных,
принадлежащих множеству L \ (Гд п 5).
rOi)
Т^'^и 5^"^
Обозначим через Lr
соответственно множества линейных,
сохраняющих ноль и самодвойственных
Рис. 2.4.4, а
114 Глава 2
функций от п переменных. Изобразим множества u'^\ ^о и
5^^^^ схематично (рис. 2.4.4, а).
Заштрихованная область соответствует функциям искомого
класса. Очевидно, выполнено равенство:
16'\{Т^"^ пЗ^"^)И L^'^\-\L^"^ пТ^"^ nS^"^\.
Каждая функция из L^"^имеет вид: а^ + а^Х1 +02X2+... + а,^х,^.
Поставим в соответствие каждой такой функции вектор её
двоичных коэффициентов {а^,а^,а2,"-,а^^). Очевидно, что это
соответствие — биекция, значит, количество различных линейных
функций от п переменных равно количеству различных
двоичных наборов размерности /14-1, т.е. 2"^ , итак, |L(/i)|=2"^.
Если линейная функция сохраняет константу О, то
fl^o + ^i •0 + й^2 0 + ..-Ь^л 0 = 0 => «0-0' и она имеет вид
щх^ + а2Х2+.'. + a^Xjy Для самодвойственной функции
выполняется свойство/(х1,...,Х/0 =/(^i,...,A',j). Учитывая, что x = x + U
посмотрим, как будет выглядеть это равенство в случае
линейной, сохраняющей ноль функции:
ai(X] +l)-f «2(^2 +l) + ... + an(x^j^ +1) = l + flt|X| +^^2^2 +--- + «/i^/2-
Раскроем скобки:
flt,X, +a^+ a2X2 + flt2 + - + ^^n +«/1 = 1 + «1-^1 + «2-^2 + - + ^n^n-
Прибавим no модулю 2 к обеим частям полученного равенства
выражение fltiXj 4-й^2-^2 "•"••• "^«л-^/м учтём, что х + х = 0. Тогда
после упрощений будем иметь: щ+а2 + ...-^ а,^=\. (*)
Из коэффициентов а^,а2,...,а,^ произвольным образом можно
назначать п-1 коэффициент, а значение /1-го коэффициента
однозначно определяется из равенства (*). Итак, между
множеством булевых функций класса l}'^"^ пТ^ nS^"^ и множеством
двоичных векторов размерности п-1 существует биекция,
значит, верно равенство | L^"^ пТ^'^^ п5^"^ |= Г~^.
Булевы функции
115
В итоге получаем:
I 6''^ \ (Т^'^ п 5^"^) Н б'^ I -1 L^'^ пТ^"^ п S^'^ I = Г^' - Г-' =
Пример 2. Подсчитать число различных булевых функций от
п переменных, принадлежащих множеству ^иГ^.
Обозначим через 5 "^ и Т^ соответственно множества
самодвойственных и сохраняющих единицу функций от п переменных.
Изобразим множества 5^"^ и Tj^"^
(рис. 2.4.4, б).
Очевидно,
Пусть /g5^"\ gG7/'^ h^S^"^rM^"\
изобразим таблицы этих функций. ^*ж. 2.4.4, б
Таблица 2.4.4а
'^1
0
0
0
1
1
1
■^2
0
0
1
0
1
1
^п-\
0
0
1
0
1
1
^п
0
1
1
0
0
1
/
щ
«2
a^j,-i
-^а^и-х
-nCh
-п«1
8
Ьх
h
^"-i
1
h
0
Cl
V'-i
-iC2„.,_i
-nC,
1
(/0 rj.{n)
:(«) ,^t(»)
Значит, мощности множеств 5^ % Г, и 5^ ^ г\Т^ ^ равны со
о 2"-' о2"-1 о2""'-1
ответственно 2,2 и 2
2''-! о2""'-1 02""'-1 . ^2"-\
Витоге: |5^"^иГ;"М=2' +2' "^-2" "'=2" "42
116 Глава 2
2.5. Минимизация нормальных форм
всюду определённых
булевых функций
Элементарная конъюнкция Е называется гшпликанпюй
булевой функции /, если E-^f = l.
Импликанта Е называется простой, если при удалении
любой буквы из неё она перестаёт быть импликантой булевой
функции /.
Сокрагцённой ДНФ называется ДНФ, состоящая из всех
простых импликант данной булевой функции.
Ядровая импликанта — импликанта, удаление которой из
ДНФ некоторой булевой функции / приводит к ДНФ, не
равносильной /.
Минимальная ДНФ данной функции / — ДНФ, имеющая
наименьшее число символов переменных из всех ДНФ,
задающих функцию /.
Тупиковой ДНФ функции / называется такая её ДНФ,
состоящая из простых импликант, что удаление из неё любой
конъюнкции нарушает равносильность ДНФ данной функции.
Слоэююстъю ДНФ (КНФ) называется количество символов
переменных, использованных в записи формулы.
Сокращённая ДНФ может быть получена из СДНФ
последовательным применением, пока это возможно, формулы неполного
склеивания Kuv Ки = Kuv Ки v К, г. затем — формулы
поглощения Kuv К = К.
Задание 2.5.1
Для данной функции /(x,v,z,w), заданной векторно,
проделать следующее:
1. Записать её СДНФ и СКНФ.
2. Методом Квайна найти сокращённую ДНФ.
Булевы функции
117
3. Для сокращённой ДНФ построить матрицу Квайна, указать
ядровые импликанты.
4. С помощью матрицы Квайна найти минимальную ДНФ,
указать её сложность.
5. Найти минимальную ДНФ данной функции с помощью карт
Карнау, сравнить полученный результат с ДНФ, найденной в п. 4.
№
1
2
3
4
5
6
7
8
9
10
/
1111 0101 ООП 1101
1101 1110 1010 1110
0111 0001 1111 1101
1011 1111 1111 1000
1101 0101 1101 1111
1111 1110 10100011
1111 00100111 1110
1100 11101111 1011
11000110 1111 0111
1011 1111 11100010
х»
11
12
13
14
15
16
''
18
19
20
1....
/
01001110 1101 1111
1111 11100111 1100
1000 1011 1111 1111
1111 1101 11100001
1101 0111 1100 1110
1011 1111 1010 1101
1001 1101 1010 1111
11100110 1111 1100
ООП 1011 1010 1111
1111 оно 1110 1110
Хо
21
22
23
24
25
26
27
28
29
30
Таблица 2.5.1
f
1011 1111 0001 nil
1110 1100 nil 1001
1001 ion nil 1010
nil 1110 01110011
1010 nil 0111 0011
1110 0110 nil 1100
0111 0111 0101 1011
1101 nil 1110 1010
nil 0011 0111 0111
1110 1110 1010 1101
Пример решения задания 2.5.1
Решим задание 2.5.1 для (pyuKifuu
/(x,y,z,w) = (1101 1010 1101 1100).
1. Изобразим таблицу функции / в
виде двумерной таблицы — карты
Карнау (табл. 2.5.1а).
\ч ZW
00
01
11
10
Таблица 2.5.1а
00
1
1
1
1
01
1
0
1
1
11
1
0
0
1
10
0
1
0
0
118 Глава 2
Найдём СДНФ данной функции:
{a,b,c,cl)
fia,b,c,cJ)=\
= x'yW V x'yW V x'y'z'w' V x%'z'w' V x'y'z'w' V
xy z^v xy zwv xy zwv xyzy^v xyzwv xy z^^^'V xy zwv
V jc>> z w V X уz w V д: yz w.
Найдём СКНФ данной функции:
/(jC,y,Z,w)= A (jC^v/vz'vw^) = (A'4y VZ^Vw')a
fiaA(,d)=0
Л (Jc4 / V z' V W^) Л (X^ V y% Z^ V W^) Л (/ V у' V Z^ V W^) Л
/0 0 0 1ч /0 о о Оч
л(х vy VZ vw)a(x vy vz vw) =
= (x V у V z V w) л (jc V у V z V w) л (x V у V z V vv) л (x V у V z V w) л
= (jc V у V z V w) л (x V у V z V w).
2. Построим сокращённую ДНФ из СДНФ, используя
формулы неполного склеивания и поглощения. Для удобства, вместо
символов переменных будем работать только с показателями
степеней переменных.
Например, вместо xz будем употреблять набор О - 1 - . Тогда
СДНФ функции будет соответствовать множество всех её
единичных наборов. Выпишем единичные наборы данной булевой
функции в таблицу, разбив их на группы в соответствии с
количеством единичных компонент в наборах.
Тогда для применения формулы неполного склеивания
достаточно просмотреть всевозможные пары наборов, входящих в
соседние группы. Результаты склеивания наборов из 1 полосы
поместим во II полосе, а наборы, участвующие в склеиваниях,
пометим крестиком. Во второй полосе снова применяем,
насколько возможно, операцию склеивания, записывая результаты
в III полосу и т. д. После завершения процедуры склеивания все
Булевы функции
119
простые импликанты попадут в таблицу и не будут помечены
крестиком. Помеченные же конъюнкции поглотятся на этапе
применения формулы поглощения.
Таблица 2,5, lb
0000 +
0001 +
0100 +
1 000 +
0011 +
0 110 +
1001 +
1 1 00 +
10 11 +
110 1 +
1 I полоса
000 - +
0 -00 +
-000 +
00-1 +
0 1 -0
-001 +
1 00 - +
- 100 +
1 -00 +
-011 +
10 - 1 +
1-01 +
1 1 0 - +
II полоса
-00-
- -00
-0-1
1 -0-
III полоса
Сокращённая ДНФ данной булевой функции имеет вид:
XyWV yzV ZWV yWV XZ .
3. Для получения из сокращённой ДНФ минимальной ДНФ
изобразим следующую таблицу — матрицу Квайна (табл. 2.5.1с).
Ядровыми импликантами будут 1, 4 и 5, так как для каждой из
них найдётся единичный набор, на котором она одна принимает
значение 1.
4. Выбираем наименьшее число столбцов таких, чтобы для
каждой строки из данной таблицы и хотя бы одной единицы
в этой строке нашёлся бы по крайней мере один столбец из
множества выбранных столбцов, который содержит эту единицу.
Тогда дизъюнкция членов, сопоставленных всем выбранным
столбцам, является минимальной ДНФ.
120
Глава 2
Таблица 2,5.1с
№ простой
им пли канты
\v простые
\v им пли канты
единичные \.
наборы \s^
0000
0001
ООН
0100
ОНО
1000
1001
1011
1 1100
1 1101
1
xyw
1
1
9
yz
1
1
1
1
3
zw
1
1
1
1
4
yw
1
1
1
1
5
xz
1
1
1
1
Для выбора наименьшего числа столбцов, удовлетворяющих
перечисленным выше требованиям, составляем символическое
выражение (2v3)-(2v4)-4-(lv3)-l-(2v3v5)-(2v4v5)-4.(5v3)-5.
Приведём это символическое выражение к ДНФ, используя
дистрибутивный закон и формулу поглощения (Av В)- Л = А.
Получим: (2v3)4.1-5 = 24-l-5v3-4.1-5.
Сопоставим каждой символической
конъюнкции тупиковую ДНФ и
выберем из них кратчайшую.
В нашем примере символической
конъюнкции 2-4-1-5 соответствует
ДНФ xywv yzv ywv XZ , а
символической конъюнкции 3-41-5 —
jcyvvv zwv ^'vvvxz . Каждая из полу-
Таблица 2.5.1d
00
01
11
10
00
' ll
nt
:| 1 !
:Lxi
01
1
iLl
\~V
'il
[Lu
11
1
Ы
0
0
1 11
10
0
kz:
0
0
Булевы функции
121
ченных ДНФ является минимальной для данной булевой
функции и имеет сложность, равную количеству символов
переменных в формуле, т. е. сложность 9.
5. Найдём минимальную ДНФ с помощью карты Карнау
(табл. 2.5.Id).
Задача нахождения минимальной ДНФ с помощью карты
Карнау сводится к задаче покрытия всех единиц карты Карнау
прямоугольниками возможно больших размеров, причём
разрешается использовать только прямоугольники, площади которых
являются натуральными степенями двойки. При построении
покрытия не забываем, что карта Карнау как бы наклеена на
поверхность тора, т. е. её левая и правая, а также верхняя и нижняя
границы отождествляются. В нашем примере все единицы
покрываются четырьмя прямоугольниками: прямоугольник 1x2,
соответствующий конъюнкции xyw, прямоугольник 1x4,
соответствующий конъюнкции zw, и два квадрата, соответствующих
импликантам xz nyw. Значит, минимальная ДНФ,
соответствующая этому покрытию, равна xywv г w v yvv v xz .
Задание 2.5.2
Для функций f{x,y,z),g(x,y,z,w),h(x,y,z,w,t) найти
минимальные ДНФ и минимальные КНФ с помощью карт Карнау,
указать сложности минимальных ДНФ.
Таблица 2.5.2
№
1
2
3
/
1011
1100
0111
1010
1001
1001
8
11101110
1111 0001
1111 0010
1111 0111
1101 1001
1111 ООП
h
1011 1110 1100 1111
11110001 0101 1100
1100 1011 1011 1110
1110 1011 0111 1111
1011 1111 ООП 0001
оно 1101 1011 1110
122
Глава 2
Таблица 2.5.2 (продолэюеиие)
1 Хо
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/
1110
1110
1010
1111
оно
1111
1000
1101
0111
оно
1110
ООН
0111
0101
1000
1111
1011
0111
ООН
1101
1011
0111
0111
0101
0111
1110
1111
оно
g
1011 1010
1111 1110
1101 1100
ни 1101
1111 1011
ООН 1101
1010 1111
\0\\ 1110
1100 1110
1100 1111
1101 1011
1111 1101
10101110
1110 1111
1001 0001
1110 1110
1101 1011
1110 1110
0111 1011
ООН 1110
1000 0110
1111 1110
1011 1101
ООН 0111
1100 1100
0111 1100
00110111
1111 1011
h 1
1100 1100 1110 1111 1
1000 1111 1011 1111 1
11010011 1111 1101 1
1110 1101 0111 1100 1
1011 1100 1111 1000 1
0111 1011 11100101 1
1100 11100111 1111 1
0001 1111 1011 0111 1
1010 1110 1111 liOl 1
0111 1001 1110 0000 1
1001 1100 1101 1111 1
1101 1111 0001 1011
1010 11100111 1110
ООН 111001100101
0101 1Н01Н00111
0111 1110 1101 оно
10100111 1101 1111
1000 1111 1110 1001
1001 1100 1110 1111
1100 1111 1010 0000
оно 1101 1111 1101
1111 1011 0111 1110
1010 1111 1011 1101
0111 1110 1101 1110
1101 0111 1101 1011
0111 1110 1111 0000
0101 1000 1111 1100
1000 1110 1110 0111
Булевы функции
123
Таблица 2.5.2 (окончание)
Хо
18
19
20
21
22
23
24
25
26
27
28
29
30
/
0111
1001
1000
1110 J
0111
1001
0101
1100
0111
0101
1001
оно
0001
1100
1000
1110
1110
0101
1101
1100
1110
оно
0001
1111
1100
ООН
8 1
1100 1100 1
1110 0011 1
0111 1110
ООН 1110
10101110
1111 1101
11110011
1011 1111
Н 00 0000
1110 1101
1101 1110
1101 1111
1100 1110
0111 1111
10100111
1110 1100
1101 1001
1111 0111
ООН ООН
1011 1111
10100101
1111 1011
11010111
11100110
01101101
1111 1000
h 1
01001111 11010111 1
1111 0101 1110 1101 1
0001 1111 1011 1101 1
0010 1111 1000 1000
10110001 1111 1100 1
0111 1001 1110 1110
1001 1011 1100 1110 1
0001 0111 1011 1000
1011 1111 1101 0111 1
1110 11100111 0001
0111 1110 11100011 1
1111 ООН 1001 1111
1010 1111 1101 1100
1111 1010 1101 оно
0111 0111 10100011 1
1111 0010 1010 1111
оно 1111 1110 1010 1
01100110 1101 0010
1001 1110 1001 1111
0010 1001 1111 ООН
0111 1011 1011 1111
1111 1011 0010 1111
1101 0100 1111 0111
1110 0110 1111 1000
0111 1010 11100111
11100111 11100110
124
Глава 2
Таблица 2.5.2а
Л7\|
00
01
11
10
0
км
Тп
1
щ\
1
гл
шГ
1
"о;
Таблица 2.5.2Ь
Пример решения задания 2.5.2
Решим задание 2.5.2 для функций f(x, у, z) = (0111 0011),
g(x,y,z,w) = (llll 1101 1010 0000),
/zU3;,z,w,0 = (llll 0111 1010 ОНО 1111 0111 1010 1010).
Карта Карнау для функции fix,y,z) от трёх переменных имеет
такой вид (табл. 2.5.2а).
Мы считаем её как бы наклеенной на
поверхность цилиндра, т. е. отождествляем
верхнюю часть карты Карнау с нижней.
При отыскании минимальной ДНФ
единицы карты Карнау покрываем
прямоугольниками вида 2x2 и 1x2, отвечающим им-
пликантам у и xz соответственно,
получаем минимальную ДНФ yv xz . Её
сложность равна 3.
Для нахождения минимальной
КИФ покрываем нули карты Карнау
двумя прямоугольниками
размерами 1x2, которые соответствуют
элементарным дизъюнкциям yvx
и yvz.B результате получаем
минимальную КНФ (yvx)-(yvz).
При нахождении минимальной
ДНФ функции g(x,y,z,w)
заполняем карту Карнау и
покрываем единицы карты
прямоугольниками возможно больших размеров
(табл. 2.5.2Ь).
Получим минимальную ДНФ:
yWV XZV XW.
Сложность минимальной ДНФ
равна 6.
Отыщем минимальную КНФ функции g(x,y,z,\\^). Для этого
произведём покрытие нулей карты Карнау (табл. 2.5.2с).
00
01
11
10
00
гтН
LlJ
0
1
01
7т1
Jjj
0
0
11
"~Г|
^
0
0
10
1
0
0
1
Таблица 2.5.2с
00
01
И
10
00
1
1
щ
1
01
1
1
Го~
То'
11
1
1
~0]
0
10
1
0
0
3^
_Т2
Булевы функции
125
Минимальная КНФ будет иметь вид:
(XV y)-(xvw)-(yv zvw).
Рассмотрим функцию
h(x,y,z,wj) = (mi 0111 1010 НИ 0111 1010 1010).
Карту Карнау для пяти переменных можно воспринимать, как
"двухслойную" карту Карнау для функции от 4 переменных, где
верхний слой соответствует значениям х = 0, а нижний - jc = l,
причём клетки, образующие "двухслойный" прямоугольник,
соответствуют импликантам, в которых переменная х отсутствует.
Двухслойные прямоугольники будем изображать жирными
линиями, а однослойные — тонкими (табл. 2.5.2d).
Все единицы карты Карнау могут быть покрыты тремя
двухслойными прямоугольниками и двумя однослойными.
Минимальная ДНФ будет иметь вид: ztv ytv xzwt v xyt.
Её сложность равна 13.
Таблица 2.5.2е
xyz\
000
001
ОН
010
100
101
111
НО
00
1
-jj
Чг
0
ll
1
~v
^r-|
■~п
-Ч
Таблица 2.5.2d
01
ГТ"
[|i ]
[it
0
п—
1
1 л
0
0
11
1
1
0
10
П"П'
гтт
\ 1 1
0 in
—ч
1
^
и
0
ы
ш
ГТ|
Ьо
K==i
000
001
он
010
100
101
111
но J
00
1
Ш1
0
V
1
Id 1
V
1
01
1
1
1
1 0
1
1^1 [
1
0
D
11
1
1
1 ^1
о|
ч^
1
f 1\
0 1
~рг|
10
Для отыскания минимальной КНФ покроем
прямоугольниками нули карты Карнау (табл. 2.5.2е).
Все нули карты Карнау могут быть покрыты тремя
двухслойными прямоугольниками и двумя однослойными.
Минимальная КНФ будет иметь вид:
(у V wvt)-(yv zvt)-(yvzvwvt)-(xvyvt)'(xvzvwvt).
5 Зак 3332
126 Глава 2
2.6. Частичные функции и схемы
Частичной функцией называется функция, определённая не на
всех наборах своих переменных.
Простой импликантой частичной функции f
называется элементарная конъюнкция К, для которой выполняются
условия:
1)3^/^(а) = 1, /(а) = 1;
2) У^/(Д) = 0-^ Кф) = ^-
3) если из импликанты К удалить любую букву, получится
формула К' такая, что З^А:'(7) = 1 /(7) = 0.
Доопределением частичной функции / будем называть всюду
определённую функцию g, значения которой совпадают со
значениями функции / на тех наборах, на которых функция /
определена.
Критерий существования декомпозиции заданного вида:
Частичная функция / представляется в виде
f{u,v,w) = g{u,w,h{u,v)) тогда и только тогда для каждого
фиксированного набора а значений переменных из множества и
таблица функции /ot(v,w) допускает доопределение до таблицы,
содержащей столбцы не более двух различных типов.
Контактной схемой называется неориентированный граф,
каждому ребру {контакту) которого приписан символ
переменной в некоторой степени и выделены две вершины, которые
называются полюсами.
Частная производная булевой функции /(xi,X2,...,jc,J по
переменной Xi определяется так:
/л-, ~/(xi,...,x/_iA^/+iv..,^,i) + /(^i,--.,^/_iJ,^,4i,--.,^^).
Тестом относительно множества G-[gi] попарно различных
булевых функций называется множество наборов значений
переменных Т такое, что V.V^,^,3^^7'(<?/(^)'^ ^Д^))-
Булевы функции
127
Задание 2.6.1
1. Реализовать частичную функцию f(x,y,z,w) формулами
над базисом конъюнкция, дизъюнкция, отрицание четырьмя
способами:
а) методом Квайна; б) исходя из минимальной ДНФ,
найденной с помощью карт Карнау; в) исходя из минимальной КНФ,
найденной с помощью карт Карнау; г) методом
последовательного разложения по переменным xyzw.
2. Для простейшего представления построить схему из
функциональных элементов типа конъюнкция, дизъюнкция,
отрицание.
3. Реализовать простейшее представление контактной схемой.
4. Проверить возможность разделительной декомпозиции
функции f(x,y,z,w) в виде g(u,v,h(p,t)), где u,v,pj —некоторая
перестановка переменных xyzw.
Если декомпозиция указанного вида возможна, реализовать её
схемой с ветвлениями из функциональных элементов типа
конъюнкция, дизъюнкция, отрицание. Указать сложность
построенной схемы.
Таблица 2.6.1
№
1
2
3
4
5
6
7
8
9
10
f(x,y,z,w)
--01 1 - И -0--0110
1-- 1 0-0-010--01 -
-0-1-001 -- 1 1 10- 1
11 --0- 11- 1 - 1 - 100
-- 100- 11--01 - 101
1 --1 01 ---100- по
0- 110-10 10-- 1 - 1 -
10-1-100 10-- 10--
- 10- 101 -- 1 -0 11 -0
1--0- по- 1 -0 11 -0
Ха
11
12
13
14
15
16
17
18
19
20
f{x,y,z,w)
-1 -0-011 1 -- 1 -Oil
11 --01 -0-01 -Oil -
1 -- 101 - 1 -- 10 00- I
-ОЮ- 1 -001-1 - 1-0
0-0- 11 - 1 - ПО 1 -- 1
1 --0 1 - 11 -0-0 110-
0--0 1 - 1 - 1110 1 - П
11 ---0-1 -0100- 10
0-11 1 --1 0-1 -00- 1
1 - 10---0 11 -ООП -
128
Глава 2
Таблица 2.6.1 (окончание)
IVo
21
22
1 23
24
25
fix,y,z,w)
01- 1 -10-011 --01 -
-- 1-01-0 00- 1 111 -
0- 1 -- 1 -00- 11 -001
- 1 0--011 1 - 10--01
1 --01 - 1 -- 1010- 10
No
\ 26
27
28
29
30
fix,y,z,w)
- 0 - 0 - 111 1-0-00-1
11 -00- 10--0-00- 1
--0 1 1-11-0-0-001
10---011 1 --0 11 - 1
- 1 - 1 0- 11 0- 1 - 101 -
00
01
11
10
00
-
0
1
-
01
1
1
1
-
11
1
-
0
-
To"l
0
-
-
0
Пример решения задания 2.6.1 Таблица 2.6.1а
Решим задание 2.6.1 для функции
/(jc,>',z,w) = (-10101 О- 11-0).
Запишем таблицу функции / в
виде карты Карнау (табл. 2.6.1а).
Для отыскания сокращённой ДНФ
выпишем в список Mq все нулевые
наборы функции, а в М| —
единичные наборы (табл. 2.6.1b).
Будем перебирать все единичные
наборы из списка Mj, который
запишем в виде первого столбца. Для
каждого из единичных наборов
будем заменять последовательно его
символы на неопределённый символ
"-" и смотреть, не будет ли
совпадать с точностью до
неопределённого символа полученная комбинация с каким-либо набором,
вошедшим в список Mq. Если совпадение есть, переходим к
следующему символу, а если нет — помечаем набор "крестиком",
выписываем результат замены во второй столбец и переходим
к следующему символу или к следующему набору.
Таблица 2.6.1b
Mo
0010
0100
1010
1111
Ml
0001
ООП
0101
1100
1101
Булевы функции
129
Затем совершаем
аналогичную процедуру
над наборами из
второго столбца и так далее.
В результате наборы,
не помеченные
крестиком, будут
соответствовать простым им-
пликантам, из которых
состоит сокращенная
ДНФ (табл. 2.6.1с).
Итак, простые им-
пликанты нашей
функции таковы:
xyw, yz у xw , zw ,
yw, xz.
a) Изобразим
матрицу Квайна (табл. 2.6.Id),
в которой строки
соответствуют единичным
наборам функции, а столбцы
Таблица 2.6.1с
Ml
000 1 +
0011 +
0 10 1 +
1 1 00 +
1 110 1 +
000-+ !
00- 1 +
--0 1 +
-00 1 +
-0 11 +
0-11 +
-101 +
0 1-1 +
1 -00 +
1 1 -0
j 110-+
1-0 1 +
-00- 1
0-- 1
--0 1
-0- 1
1-0-
1 столбец 2 столбец 3 столбец
простым импликантам.
Таблица 2.6. Id
0001
ООП
0101
1100
1 1101
xyw
1
У^-
1
XW
1
1
1
ZW
1
1
1
yw
1
1
xz
1
1
Как видим, ядровых импликант нет. Для нахождения
минимальной ДНФ составим символическую КИФ, каждая элемен-
130
Глава 2
тарная дизъюнкция которой соответствует единичному набору
нашей функции, которую преобразуем затем в ДНФ. Получим:
(2v3v4v5)-(3v5)-(3v4)-(lv6)-(4v6) = (3v5-4)-(6vl.4) =
= 3-6v54-6v3-14v5-14.
Видим, что наименьшую длину имеет символическая
конъюнкция 3-6, которая соответствует минимальной ДНФ xwv xz..
Сложность найденной минимальной ДНФ равна 4.
б) При нахождении минимальной ДНФ с помощью карты
Карнау (табл. 2.6.1е), мы доопределяем функцию/так, чтобы
покрытие имело более простой вид.
Таблица 2,6.1 е
Таблица 2,6.1/
\^ ZW 1
00
01
11
10
00 1
-0
0
1 1
1 -7 1
01
IT"
1
-l\
1 11
1 1
-7
0
1 '^
10
0 1
-0
-0
0 ^
\^ ZW
00
01
11
10
00
-0
0
1
-7
01 1
1
1
1
-7
11
1
-7
ПГ"
|-0
10
Го"
1 -0
-0 1
0 1
Тогда все единицы покроются двумя квадратами 2x2 xwn xz,
соответствующая минимальная ДНФ совпадает с ДНФ,
найденной в п. а).
в) Для отыскания минимальной КНФ покрываем нули карты
Карнау (табл. 2.6.1/) двумя квадратами 2x2: xvw и xv z -
Соответствующая минимальная КНФ такова: (х vw) • (jc v z).
Сложность её равна 4.
г) Проведём разложение по набору переменных xyzw. На
первом этапе, раскладывая по переменной х, имеем:
f(x, y,z,w) = X' /(О, у, г, w) V X • /(1, у, Z, w).
Изобразим таблицы функций /(0,y,z,w) и f(ly,z,w)
(табл. 2.6. Ig).
Булевы функции
131
Таблица 2. б. Ig
y7.\V
001
010
1 oil
100
101
/(0,y,z,vv)
1
0
1
1
1
yzw
010
100
i 101
111
/(0,y.z,w)
0 i
1
1
0
Каждая ИЗ функций /(0,y,z,w) и f{\,y,z,w) не доопределима
до константы, но /(l,v,z,w) доопределима до г.
Изобразим таблицы (табл. 2.6. Ih) функций /(0,0, z,w) и
/(0.1,z,w).
Таблица 2.6.Ih
yzw
01
10
11
/(0,v,z.hO
1
0
1
yzw
00
01
/(0,.v,r.nv)
1
1
Видим, что /(0,0,z,w) и /(0,I,z,vv) доопределимы до w и 1
соответственно.
Получаем разложение исходной функции:
f{x,y,Z,w) = X'{y'WW уЛ)\/ X-Z = X-{WW у)\/ X'Z .
Во время упрощений мы
применяли тождества с константами и правило у
вычёркивания. Сложность полученной о
формулы оказалась равной 5.
2) В качестве простейшего
представления возьмём минимальную ДНФ
XWW XZ и реализуем её схемой из
функциональных элементов (рис. 2.6.1, а).
Реализуем ту же минимальную ДНФ
контактной схемой (рис. 2.6.1, Ь).
Рис. 2.6.1, а
132
Глава 2
3) Реализуем ту же минимальную
ДНФ контактной схемой (рис. 2.61, Ь).
4) Запишем двумерную таблицу
функции / (табл. 2.6.1 i).
Видим, что таблица допускает
доопределение до строк только двух типов
(табл. 2.6.Ij).
Таблица 2,6,11
Рис. 2.6.1, b
Таблица 2,6, Ij
N^ zw
ху \
00
01
11
10
00
-
0
1
-
01
1
1
1
-
11
1
-
0
-
10
0
-
-
0
ху \
00
01
10
11
00
-0
0
-0
1
01
1
1
-1
1
10
0
-0
0
-0
и
1
-/
-/
0
I тип
1тии
I тип
11тип
Значит, /(^,y,z,w) допускает разделительную декомпозицию
вида f(x,y,z,w) = g(z,w,h(x,y)).
Найдём вид функций g и h.
h( ) = i ^' Qcnw набор {х, у) соответствует строке I типа,
[О, если набор {х,у) соответствует строке II типа,
т.е. /2(х,у) = (1110), h{x,y) = XW у .
Строкам I типа соответствует функция ф(г, w) = (0101) = w.
Строкам II типа соответствует функция \|/(z, w) = (1101) = z
Тогда функция / выражается через /г, ф, \|/ так:
/(х, V, г, w) = h{x, у) • ф( г, w) V h{x, у) • \|/(z, w) =
= {xw y)'ww{xw у)- z .
Соответствующая схема из функциональных элементов с
ветвлениями будет иметь вид (рис. 2.6.1, с).
Булевы функции
133
Рис. 2.6.1, с
Сложность схемы равна количеству функциональных
элементов, её образующих, т. е. 8.
Задание 2.6.2
1. Представить функцию /(х^,Х2,Хт^,х^,х^) декомпозицией
вида g(xi,Xi^,Xp,h(xi,x,fj,x,i)), где Xi,xi^,Xp,Xi,x„i,x,^ —некоторая
перестановка переменных Х], ^2»-^з»-^4»-^5 •
2. Реализовать найденную декомпозицию схемой с
ветвлениями, используя функциональные элементы типа отрицание,
конъюнкция и дизъюнкция. Указать сложность полученной схемы.
3. Построить минимальную ДНФ с помощью карт Карнау,
указать сложность найденной формулы.
Таблица 2.6.2
Хо
1
2
3
4
5
6
/
1
2
3
4
5
1
/(Xl,A'2,A'3,JC4,-X5)
1 -01
1 - 1 -
110-
-011
0- 10
-001
1101
00-0
01 -0
-000
-000
--01
10--
0-01
1 -11
- Ill
10-0
1 -01
1 -0-
-001
0-00
-000
01 - 1
- 101
1 -1 -
--0-
1 -11
1- 10
0010
--11
111 -
11 -0
oil -
100-
- и -
1 --1
000-
01-1
111 -
11 -0
--11
00-0
-on
0-01
011-
-001
-11 -
001 -
134
Гпава 2
Таблица 2.6.2 (окончание)
Хо 1
7 1
8 1
9
10
11
12
13
14
15
1 ^^
17
1 ^^
1 ^^
1 20
1 ^^
1 22
1 ^"^
1 ^"^
1 ^^
1 26
1 ^"^
1 28
1 29
1 30
/
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
1
2
3
4
5
-11-1
- 1 -0 1
0-1-1
-010
10--
--11
1 -00
--11
00-0
-00-
111 -
- 10-
001 -
0- 1-
10- 1
-1 -1
1100
0- И
-01 -
1001
111 -
- 100
001-
0- 10
0-00 1
ою- 1
00--
-00-
11-1
00-0
- 100
00-0
00-0
1 -01
00-0
01 -0
-000
000-
110-
0-0-
- 10-
-000
0-00
11 -1
0-00
01 --
0000
00--
/Ст,,Х2,Л
0-- 1 1
11 -- 1
01 - 1 1
-1 -- 1
-001
-001
1-11
011 -
1010
-0- 1
0-0-
1 -11
-111
101 -
1 -01
-0--
-111
0- 11
-0-0
1 -01
0-01
1111
01 - 1
101 -
-00-1
01 -0 1
0-00 1
0101
1 -01
0001
01 -0
-00-
0-01
110-
000-
0-00
00-0
01 - 1
,- 101
0001
010-
0-00
0-01
--0-
0-01
010-
00-0
01 - 1
:з>-^4-^'5)
00-0
11 --
10--
-01 -
-1 -1
--00
1 -1 -
1010
0- 10
m -
000-
1 -11
101 -
00-0
- Ill
-0-0
-1 -1
1- 10
-01 -
1 -11
00--
1 -1 -
10-0
001 -
- 10- 1
Olio 1
10- 1 1
0- 11 1
11-1
1-00
oil -
-001
- Ill
11 -1
1 -00
-- 10
1001
01 - 1
-11 -
1100
0- 10
10- 1
0-- 1
1 -1 -
110-
01-0
1001
0111
1
- 101 1
--11 1
1-1-1
-1-1
0-0-
010-
1--1
- 110
1 -11
000-
- 101
111 -
1 -1 -
11-1
0-00
-1 -1
1 -11
111 -
1 -11
0-00
0101
1111
--1 -
-1 -1
- 10- 1
Olio 1
100- 1
1 --1 1
0- 11 1
- 101 1
0- 10 1
-0- 1 1
--1-1
0-- 1 1
0-0- 1
Olio 1
1001 1
111 - 1
ООП 1
0101 1
-1-0
10- 1
1-11
0- 1 -
01 - 1
0- 10 1
10- 1
111 -
Булевы функции
135
Пример решения задания 2.6.2
Решим задание 2.6.2 для i = 5 и функ1{ии
/и,,Х2,хз,Х4,Х5) = (10-1 0--0 --01 -1-- 0-10 ОЮ- 1--0 --1-).
Выпишем значения функции / в виде таблицы (табл. 2.6.2а):
Х^Х2
Х-7,Х^Х^
00
01
10
и
000
1
-
0
1
001
0
-
-
-
010
-
0
1
-
011
1
1
0
0
100
0
-
0
-
Таблица
101
-
1
1
-
110
0
-
0
1
12.6.2а
111
-
-
-
-
Выясним, возможна ли декомпозиция вида
/==^(-^5'-^1>-^2>М^5'-^3'-^4))
(*)
ИЛИ
Для этого выпишем двумерные таблицы функции / для
^5 = О и ^5 - ^ ^^^^ чтобы в заголовках строк и столбцов были
написаны наборы х^Х2 и х^х^ соответственно. Получим
(табл. 2.6.2b).
Х^Х2 \s^
00
01
11
10
00
1
-
0
1
01
-
0
1
-
11
0
-
0
-
10
0
-
0
1
00
01
11
10
00
0
-
-
-
Таблица 2.6.2b
01
1
1
0
0
11
-
1
1
-
10
-
-
-
-
^5 =0
•^5 =1
136
Глава 2
Как видим, таблица функции /,соответствующая х^ =0, не
доопределима так, чтобы использовались столбцы только двух
типов, и не доопределима до вида, в котором используются
строки только двух типов. Значит, декомпозиция вида (*) или (^'^)
невозможна.
Проверим, допустима ли декомпозиция вида
f = g(xs,X2,X2,h{x^,x^,x^)) или f = g(x^,x^,x^,h(x^,X2,X2)).
Для этого выпишем двумерные таблицы функции / для
^5 = О и ^5 = 1 так, чтобы в заголовках строк и столбцов были
написаны наборы ^2^3 и ■^1-^4 соответственно. Получим (табл. 2.6.2с).
:0
Таблица 2.6.2с
00
01
И
10
00
1
0
-0
-1
I
01
-7
0
0
-/
I
11
0
0
1
-1
II
10
1
0
-0
1
I
\ ХзЛ'4
00
01
11
10
00
0
-/
-0
1
1
01
1
-7
1
-0
II
11
-7
1
-7
-0
II
10
0
-7
0
-7
I
^5 =1
Видим, что в этом случае обе таблицы допускают
доопределение до столбцов двух типов.
Для ^5 = О столбцам I типа соответствует функция
ф^ \х2,х^,) = {\00\)-хгхъ VX2X3, а столбцу II типа — функция
^^^\Х2,Х^) = Ф\0\) = Х2.
Введём функцию
/,(0)/ ^ = J ^' ^^^^ набор (хх,х^) соответствует столбцам Iтипа;
[о,если набор (jci,jc4) соответствует столбцам IIтипа.
Булевы функции 137
Вектор значений h^ \xi,x^) равен (1101), значит,
h {x^,X^) = Xi V Х4
/(х,,Х2,Хз,Х4,0) = /1^'\х,,Х4)-ф^'Ч^2.^'з)^/г^'Ч^„^4)-¥^'Ч^2>^з) =
= (XiVX^)(x^X^ VX2X3)VX, VX4 •Х2
Рассмотрим таблицу, соответствующую х^ =1.
Столбцам I типа соответствует функция
Ф^ ^(х2,Хз) = (0101) = ХЗ' столбцам II типа — функция
V^4x2,X3) = (1110) = X2VX3.
Введём функцию
.14 fl, если набор {х^,х^) соответствует столбцам 1типа;
[О, если набор {xi,x^) соответствует столбцам Птипа.
Вектор значений h^\xi,x^) равен (1001), значит,
h^^\x^,X^) = Х\Х4 V Х^Х^.
f(x^,X2,X2,x^,l) = h^^\x^,x^)'(f>^^\x2,x^)vh^^\x^,x^)-\\f^^\x2,X2^) =
= (Х^Х^ V X^X^)x^VXyX^ vA',X4-(-^2 "^-^з) •
Получаем искомое представление для / :
/ (X| ,Х2^Х2,Х^,Х^) = Х5 ' J \Х\, А^2'-^3'-^4»^) ^ ^5 ' J ^^\ ?-^2'-^3'-^4'^) ~
=~хДх, w'~x^){x~x^ wx,Xi)\/x^ ^y~x^' x,}w х^{(х^х^ w x^x;)x^w~x ~х ^ "^^iX^'ix, VX3)).
2. Реализуем это представление схемой с ветвлениями.
Ввиду громоздкости полученного выражения реализуем
схемами S^ (рис. 2.6.2, а) и S^ (рис. 2.6.2, Ь)
соответственно /(хрХ2,Хз,Х4'0) и /(xi,X2,X3,X4,l), а саму функцию
реализуем блок-схемой 5 (рис. 2.6.2, с).
Сложность построенной схемы равна 24.
138
Глава 2
А-, Х4 Х^ X. Л-2 ^3
X, Л'^ А' Л'| ^4 Х-\ Х')
(и и и
Рис. 2.6.2, b
Рис. 2,6.2, с
3. Найдём минимальную ДНф
с помощью карты Карнау
(табл. 2.6.2d).
Все единицы карты Карнау
могут быть покрыты двумя
двухслойными
прямоугольниками и тремя однослойными.
Минимальная ДНФ будет
иметь вид:
Аз • ^5 V ^2 • Аз • ^4 • ^5 V А] • А2
• 'Аз * Х^ V А| • Х^ • А^ V А| • А2 ' А^
Её сложность равна 16.
Таблица 2,6,2d
\. А4А5
OOP
001
oil
010
100
101
111
110
00
_ц
0
-' -
-
0
0
^
lJ
01 1
0
'-
1
- J
- 1
Ti
j:
■
11
ГТ
T^
-
LL
0
П
-
0
10 1
JED
0 1
- 1
0 1
q1
0 1
П
Lr [
Булевы функции
139
Задание 2.6.3
1. С помощью частных производных найти оптимальный для
метода каскадов порядок дизъюнктивного разложения функции
f(x,y,z,w) ПО её переменным на первых двух этапах.
2. Используя результаты п. 1, построить контактную схему
методом каскадов, указать сложность построенной контактной схемы.
Таблица 2,6.3
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1 1^
f{x,y,z,w) 1
1110 ОНО 1010 1101 1
ООП 1100 1101 0111
ОНО 1101 1100 1111
1110 0111 1100 0111
0010 1110 1111 ООН
1110 1101 0010 1111
1110 1010 0010 оно
1110 1000 1111 оно
1101 оно 1110 0001
1011 0111 1010 оно i
1101 0001 0010 1111
1110 0100 1110 1001
0001 1000 1100 оно
1101 1111 0010 1101
1001 1101 ООН 1000
Хо
16
17
18
19
20
21
22
23
24
25
26
27
28
29
1 30
/(^,>
0111 0101
0010 1011
ООН 1110
0101 1010
0101 1101
0010 1101
1110 1101
0010 1010
оно 1001
0010 0000
0010 1010
0101 1101
^z,w)
1101 1111 1
1101 1110 1
1101 0000 1
1111 1101 1
1110 ООН
1001 оно
0101 1010
1110 1111
1100 1101
1000 1110
0001 1111
0000 1011
1101 1000 оно 1110
1000 1010
1101 0111
0101 1001
1101 ООН
Пример решения задания 2.6.3
Решим задание 2.6.3 для
функции /(х, V, Z, w) =
= (1010 0100 0100 1010).
Запишем таблицу функции
fix,y,z,^) в виде карты Карнау
(табл. 2.6.3а).
00
01
11
10
00
1
0
1
0
Таблица
01
0
1
0
1
11
0
0
0
0
2.6.3 а
10
1
0
1
0
140
Глава 2
Найдём полином Жегалкина:
/(a',v,z,vv)= Y.(^ + a)(y + b)(z + c)(w + d) =
{a,b,c,d)
f{a,b,c,d)=\
= l + x+ y + w + xzw + yzw.
Определим оптимальный для метода каскадов порядок
разложения.
По определению, Л (^,>',г,w) = /(О, у, z, w) + /(1, у, z, w).
Таблица для /д. имеет вид
(табл. 2.6.3b).
Видим, что I /^ 1= 6.
Аналогично,
fyix,y,z,\0) = f(x,O,z,w) + f(xXz,w)'
Таблица для fy имеет вид
(табл. 2.6.3с).
Видно, что I fy \= 6.
Продолжаем отыскание
частных производных.
/^ (x,y,z,w) = fix, у,о, w) н- fix, уХ w).
Таблица для /, имеет вид (Табл. 2.6.3d).
Заметим, что | /, |= 2.
И далее, f^Xxj,z,w) = fix, у, z,0) + fix, у, z,l).
Таблица для /^^ имеет вид (табл. 2.6.3е).
Таблица 2.6.3d Таблица 2.6.3е
0
1
1
1
Таблица 2.6.3b
01
1
1
11
0
0
10
1
1
Таблица 2.6.3с
\^^^ Z.W
0
1
00
1
1
01
1
1
11
0
0
10
1
1
ху\
00
01
11
10
0
1
1
1
1
1
0
1
0
1
\. Z
00
01
11
10
0
1
1
1
1
1
0
1
0
1
Булевы функции
141
Как видно, I f^,, \= 6.
Так как набольшее число единиц в таблице имеют Д., Д,
и /^,, то на 1 и 2 этапах метода каскадов разложение ведём по
любой из переменных x,y,w. Выберем, например, в качестве
первой переменной, по которой будем проводить разложение, х,
а второй — W.
Получим: /(jc,у,z,w) = X'/(О,у,г,w)vх• /(1,у,z,w).
Выпишем таблицы функций /(0,y,z,vv) и /(l,y,z,w)
(табл. 2.6.3f).
Таблица 2.6.3/
^v ZW
у \^
0
1
00
1
0
01
0
1
11
0
0
10
1
0
1 V \s^
0
1
00
0
1
01
1
0
И
0
0
10
0
1
3. Строим контактную схему методом
каскадов (рис. 2.6.3, а).
На втором этапе разложение ведём по
переменной W.
Рис. 2.6.3, а
= w-(l + y + 0 + 0)vw(l+}; + l + };z) =
= w-(l+ у) vw(y + yz) = w-yvwy-(l + z) = w-yvwy-z-
/i(y,^,w) = w/|(y,z,0)vw/i(y,z,l) =
= w-(y + 0)vw(y + l + z + yz)= vv-y vw-/|i(y,z).
Осталось разложить функцию /ii(y,z).
f\\(y^z) = z-fu(y^O)vz'fu(y,l) = z-(y + l)vz-(y + l + l'\-y) =
= z-y vz-0 = z-y.
142
Глава 2
Изобразим полученную контактную схему (рис. 2.6.3, Ь).
W
X ^^-•С
^^.У
Or
W
Рис. 2.6.3, b
JO
У
Сложность построенной схемы равна количеству контактов
в ней, т. е. 8.
Задание 2.6.4
Для функции f{x,y,z,t). заданной своей ДНФ:
1. Построить таблицу данной булевой функции.
2. Найти минимальную ДНФ. Исходя из минимальной ДНФ,
построить контактную схему.
3. Построить контактную схему методом каскадов, отыскав
оптимальный порядок разложения переменных с помощью
частных производных.
4. Исходя из простейшей контактной схемы, построить
минимальный тест для нахождения неисправности:
а) для вариантов с чётными номерами — типа замыкания
ровно одного контакта;
б) для вариантов с нечётными номерами —типа размыкания
ровно одного контакта.
Таблица 2,6.4
№
1
2
3
f(x,y,z,t)
xyzv xyz. V xyz.t V yzt
xyzt V xzt V xyzt V xzt V yz
xyzt V xyzt V xyzt V xzt
Xo
4
5
6
f{x,y,z,t)
xyztvxzfvxyzt
xyzt V xyzt V xzt
xzt V xyzt vyztv yzt
Булевы функции
143
Таблица 2.6.4 (окончание)
Хо
7
8
9
10
11
12
13
14
15
16
17
18
f(x,y^z,t) 1
xyzt V хуг V xyzt V XV? V г/
xyz.tv xytv xyzt
xyz.t V xy zt V X yt
xyzt V xyzt V xyzt V xyt
xzt V xytv xztv xyzt
xyzt V xyzv xy zt V xyzv xt
xyzt V xyzv xyzt
xyz.t V xyzt V xyz
xyzt vxyztv xyz V Л' yzt
xyt V xyzv xyzt V xyt
xyz.t V yztv xyzt V xyz V xy
xyztV yztV xyzt
JVo
19
20
21
22
23
24
25
26
27
28
29
30
f{x,y,zj) 1
хд'г? V yzr V jcvr/
X vzr w xy ztv xy ztv yzt
xyt wxytw xyzt V yzt
xyzt V xztv xyzt V xztv yt
xyzt V xyzv xyzt
xyzt V xyzt V yzt
xyzt V xy ztv xyzt V yzt
xztv xztv xyzt V yzt
xyzt V xytv xyzt V xyt V yz
xyztv yztv xyzt
xyzt V xyzt V xzt
xyzt V xyztv xyztv xyz
Таблица 2.6.4a
Пример решения задания 2.6.4
Решим задание 2.6.4 для
f{x,y,z,t) = x yzt \^ xyw xytv xzt, выбрав в п. 4 неисправность
типа размыкания ровно одного
контакта.
1. Построим таблицу функции
f{x,y,z,t) в виде карты Карнау
(табл. 2.6.4а).
2. Все единицы карты Карнау
покрываем тремя прямоугольниками.
Соответствующая минимальная
ДНФ будет иметь вид yzt w xtw xz.
\^ zt
xy\.
00
01
11
10
00
0
0
rv
I 1
01
0
0
Til
ilJ
11
0
0
"T|
1J
10
1 ^ 1
0
0
1 11
144
Глава 2
Рис. 2.6.4, а
Упростим формулу:
yzt V xtv xz = yzt V x{t V z).
Реализуем это представление
контактной схемой (рис. 2.6.4, а).
3. При отыскании оптимального порядка
разложения по методу каскадов заметим, что
1л1=б,|/;и2,|/:|=2, i/;i=2.
Так что на первом шаге разложение будем производить по
переменной х, а на втором этапе можно проводить разложение
по любой оставшейся переменной, например, по у.
Получаем:
f(x,y,zJ) = X'fiO,y,zJ)vx'f(ly,z,t) =
= X• (yzt) VX'iyv ytv zt) =
= Xyzt \^ X• (у V t V zt) = Xyzt V X• (у V t V z).
Разложение no у нет необходимости делать.
Строим контактную схему (рис. 2.6.4, Ь).
4. Так как контактная схема, полученная в п. 2, имеет более
простой вид, будем работать с ней.
Занумеруем все контакты схемы (рис. 2.6.4, с).
Рис. 2.6.4, b
Неисправность типа размыкания контакта означает, что при
любых значениях аргументов соответствующий контакт
разомкнут, т. е. реализует функцию 0. Разомкнутый контакт будем изо-
Булевы функции 145
бражать пунктирной линией, а замкнутый — сплошной. Для
каждого из единичных наборов функции на соответствующем
изображении контактной схемы полюсы соединены цепью
контактов из сплошных линий. На каждом же из нулевых наборов
функции такой цепи не найдётся.
Пусть fo{x,y,zJ) = f{x,y,z,t), а при неисправности /-го
контакта схема реализует функцию fj{x,y,zj).
Если исправно работающая контактная схема на некотором
наборе аргументов принимает значение О, значит, на её
изображении между полюсами нет цепи из сплошных линий. Ясно, что
при наличии неисправности типа размыкания контакта на том же
наборе аргументов полюсы контактной схемы тем более не
соединены цепью из сплошных линий. Значит, на всех нулевых
наборах функции f{x,y,z,t) все функции fi{x,y,z,t), / = 1,2,...,6
также принимают значение, равное 0.
При построении теста нас не интересуют наборы аргументов,
на которых значения всех функций совпадают, поэтому напишем
таблицу всех функций fi{x,y,zj),
/ = 1,2,...,6, вписывая в неё только те
наборы аргументов, на которых
исходная функция равна 1.
При заполнении таблицы для
каждого набора аргументов изобразим
схему. Например, для набора (0,0,1,0)
схема примет вид (рис. 2.6.4, d). Рис. 2.6.4, d
Видим, что цепь из сплошных
линий, соединяющая полюсы схемы,
разрывается, если разомкнут 4, 5 или 6 контакт, т. е. на наборе
(0,0,1,0) значение О принимают функции /4, /5 и/^. Изобразим
вид контактной схемы на всех единичных наборах функции
f(x,y,zj) (рис. 2.6.4, е).
Заполняем "таблицу неисправностей", вписывая для каждого
набора аргументов нули в столбцы, соответствующие функциям с
номерами, записанными в кружочках. Получим следующую
таблицу (табл. 2.6.4b).
146
Глава 2
(К0А1)
/ .
(1Д1Л)
о, Ц, /^ ( у о -X.. ^£^Ii.IX
(1,0.0,0)
'%
/t
^..а=
V
/1
(1Л1,0)
(1
\
v
ДАО)
/
X f
ф
\ т
V^>™
~ (Ъ
"' , ^\
1...Л
/
/
/1
..V
.V г t \
/.
{1,1,0,1)
т\
/ -
/ t
(1,1,1.1)-^ :
^—-v,^
^ Xt J \
\ '-1^ ^3j /
А Z /г
Рис. 2.6.4, е
Таблица 2.6,4b
xyzi
0100
1000
1001
1010
1011
1100
1101
nil
/о
/i
1
0
0
1
0
0
0
0
fl
1
0
1
1
1
0
1
1
/з
1
1
1
1
0
1
1
0
h
0
1
1
0
1
1
1
1
/5
0
1
1
0
1
1
1
1
/б
0
1
1
0
1
1
1
1
Видим, что некоторые столбцы таблицы совпадают. Это озна-
чаеТ;, что неисправности типа размыкания одного контакта
неотличимы в случае разомкнутости 4, 5 или 6 контактов.
Объединяем неотличимые неисправности в классы
неисправностей.
Получим 5 классов:
^0={/о}' ^1 ={/]}' ^2 ={/2}' ^3={/з}' ^4={/4>/5>/б}-
Булевы функции
147
Строим таблицу классов неисправностей, таблицу, не
содержащую одинаковых столбцов.
Отметим, что если в таблице присутствуют одинаковые
строки, то мы ничего не потеряем, если для каждого набора
одинаковых строк оставим одного представителя, удалив остальные
строки из таблицы.
Получим (табл. 2.6.4с):
Выясним, какие из
наборов 1-5 войдут в
минимальный тест. Для этого
выпишем все сочетания индексов
{i,k} и для каждого
сочетания укажем номера наборов,
на которых отличаются
функции gi и g^.
ОД
Хо
1
2
3
4
5
xyz.t
0100
1000
1001
1010
1111
^0
Таблица 2.6.4с
S\
1
0
0
1
0
S2
1
0
1
1
1
<?3
1
1
1
1
0
^4
0
1
1
0
1
Будем иметь:
1,4
2v3v5
2,3 2,4
02
2 '
03,
5 '
3,4
0,4
1,2
1,3
lv4 3v5 2v3
Iv2v3v4v5 2v5 Iv2v4 Iv4v5
Теперь составим символическую КНФ из "знаменателей"
полученных выражений Kj. Будем иметь:
A'7-=(2v3v5)-2-5-(lv4)-(3v5)-(2v3)-(lv2v3v5)-(2v5)-
•(Iv2v4)-(lv4v5).
Упростим полученное выражение, применяя формулу
поглощения.
Получим: Kj =2-5-{\wА).
С помощью дистрибутивного закона преобразуем это
выражение в ДНФ, тогда каждой символической конъюнкции будет
соответствовать минимальный тест. Имеем:
A:7- = 2-5-(1v4) = 2-5-1v2-5-4.
В качестве минимального теста можно взять, например,
совокупность 1, 2 и 5 наборов, т. е. найден минимальный тест
Г,,,,, ={(0,1,0,0), (1,0,0.0), (1,1,1,1)}.
148
Глава 2
Задание 2.6.5
1. Построить таблицу значений функции, реализуемой данной
контактной схемой.
2. Найти минимальную ДНФ с помощью карты Карнау,
построить на её основе контактную схему, равносильную
исходной.
Таблица 2.6.5
Булевы функции
149
Таблица 2.6.5 (продолэюеиие)
150
Глава 2
Таблица 2.6.5 (продолэ^сение)
Булевы функции
151
Таблица 2.6.5 (продолэ^сение)
10
11
152
Глава 2
Таблица 2.6.5 (продолжение)
12
13
14
Булевы функции
153
Таблица 2,6.5 (продолэюение)
15
16
17
154
Глава 2
Таблица 2.6.5 (продолжение)
18
19
20
Булевы функции
155
Таблица 2.6.5 (продолэюейие)
21
22
23
156
Глава 2
Таблица 2.6.5 (продолжение)
24
25
26
Булевы функции
157
Таблица 2,6.5 (продолэюеиие)
27
28
29
бЗак 3332
158
Глава 2
Таблица 2.6.5 (окончание)
Пример решения задания 2.6.5
Решим задание 2.6.5 для
контактной схемы.
Рассмотрим вид
контактной схемы на всех 8 наборах
переменных x,y,z, изображая
разомкнутые контакты
пунктирной линией, а замкнутые —
сплошной.
Рассмотрим набор (0,0,0).
Видим, что в данном
случае между полюсами нет
маршрута, составленного из
сплошных линий, значит, на
Булевы функции
159
этом наборе функция, реализованная данной схемой, равна нулю,
ЛОЛО) = 0.
Рассмотрим изображение схемы на остальных наборах:
/(0,0,1) = О
Д0,1,0) = 1
Л0ЛЛ)=1
160
Глава 2
л-^
Л1Л0)=1
л-^
Л1Д1)=1
Л1Д,0) = 1
Булевы функции
161
Л1ДД) = 0
Запишем найденные значения функции
Дх,у,г) в карту Карнау (табл. 2.6.5а).
Минимальная ДНФ: ху v xz v ху.
Преобразуем формулу: xyvxzv ху =
= xyvxlz'^y]. Соответствующая
контактная схема имеет вид:
Таблица 2.6.5а
00
01
11
10
0
0
1
1
1
1
0
1
1
1
Задание выполнено.
Глава 3
Теория алгоритмов
3.1. Машины Тьюринга
Машиной Тьюринга называется пятёрка объектов
7 = (Л,5,5,У,|1), где А-[а^,а2\...,а^^] —алфавит',
5 = {^0''^1'---''^ш} —мноэюество внутренних состояний,
причём 5q —заключительное, 3. s^ —//д'ча^ь/ш^ состояния.
5: Л X 5 —> 5 — функция перехода;
V : А X 5 —> Л — функция выхода;
\1\ AxS -^ {Я, Д Н] — функция управления.
Командой машины Тьюринга называется запись вида
a^^Si —^apDsj, где а^ , D, Sj —значения на наборе (aj^Sj)
функций 5, jUH V соответственно.
Программой машины Тьюринга называется набор всех её
команд.
Работа машины Тьюринга связана с бесконечной лентой,
разбитой на ячейки, причём в каждой ячейке может быть записан
один символ некоторого алфавита, причём X является символом
пустой ячейки.
Работа машины Тьюринга над словом а, записанным на ленте,
проходит следующим образом:
машина Тьюринга начинает свою работу всегда в состоянии
5], а её считывающее устройство расположено над первым слева
символом слова, записанного на ленте;
считав символ в ячейке, обозреваемой считывающим
устройством машины Тьюринга, она печатает в эту ячейку символ,
164 Глава 3
найденный с помощью функции выхода V, двигается вдоль ленты
вправо, влево или остаётся на месте, в случае, если функция [i
принимает значения П, Л или Н соответственно и переходит
в состояние, определяемое с помощью функции перехода 5; при
переходе машины Тьюринга в состояние Sq считают, что она
закончила работу над словом а и говорят, что машина Тьюринга
применима к слову а.
Если машина Тьюринга при работе над словом а не переходит
в состояние Sq, то говорят, что она не применима к слову а.
Конфигурацией машины Тьюринга называется запись а| ha2 .
•ч
где b — символ ячейки, обозреваемой считывающим
устройством машины Тьюринга, находящейся в состоянии Si^. а а^
и а^— слова, записанные на ленте соответственно левее и правее
символа Ь.
Кодом машины Тьюринга называется запись набора её команд
в алфавите {*,!}, позволяющая однозначно восстанавливать
каждую команду.
Машина Тьюринга называется салюпримеиимой (несалюпри-
менимой), в случае, ели она применима (не применима) к своему
коду.
Числовой функцией называется функция вида
/:yVo^->/Vo, kGN.
Изобраэ/сением набора аргументов (.Г|,.Г2,...,Лд) называется
запись вида l''^^W^^W^^X.,l\'''^^ (*), где Г" =11...1.
Числовая функция /(xi,A-2,...,A'jrO называется вычислимой по
Тьюрингу, если существует машина Тьюринга, применимая к
любому слову вида ('^), переводящая его в слово 1^^ , где
Задание 3.1.1
1. Построить машину Тьюринга, применимую ко всем словам
•^1-^2"-^/г ^ алфавите {а,Ь}и переводящую их в слово а.
Теория алгоритмов
165
2. Проверить работу машины Тьюринга над некоторыми
словами.
Таблица 3.1,1
№
1
2
3
4
5
6
7
8
1 ^
10
1 ^^
1 ^^
1 ^^
14
1 ^^
1 ^^
1 ^"^
1 ^^
1 ^^
20
а 1
■'^1^2---^п-Л^п-\ \
л-|Ал'з...х„ }, если Хо =«, л--5Л'4....г„, если лч =Ь
л'|Л-)...л',,, если в данном слове количество букв л нечётно,
bb, если четно
a'i>uv3X..Xt„, если /Z нечётно, Aja^.-.-V,,, если /2 —четно
Аз а А|
A,A2...A,,_iA,jA„_i...A|
haba, Qc.iH слово начинается на Ьа,
A-jA'2...A,// В других случаях
Z?A-j...A,j, если А„ =а, ^^, если а„ =Ь
аЬ, если /2 —четно, а,^, если /г —нечётно
а'\ если А„_1 =л, AiA2...A„_2aZ?, если a„_i =Z?
А,АзА2А4А5...А„
<r/AjA2...A,j_2^
а, если /?<4, Aj...a,,, если /г > 3
г/ а, если в данном слове число букв нечётно,
A-,A2...A,j_,, если четно
A,A2...A„_iA„A,,, если А2=Л, А,...А„, ССЛИ Ао = ^
bab, если слово начинается на aZ?, AjAt в других случаях
AiA-,...A,j^, если П четно, ^AiA2...A„, ССЛИ /2 НСЧёТНО
аЬ, если а2 =л, Ai...a„_i, если а^ =Ь
аХа, если п —нечётно, AjA2...a,,_jA,,a,^, если /? —четно
а'\ если Aj =<:/, А2, если Aj =Ь
166
Глава 3
Таблица 3. L1 (окончанне)
№
1 ^^
1 22
1 ^^
24
25
1 26
1 ^'^
1 28
1 29
1 30
а 1
^\-^2-'^п-\ 1
CL\{kx^X^...X,^
^\^п^2^Ъ-"^п-\ 1
Ь''ху..х^
(аЬГ
X\X2...X,^_2X,^_^X,^_lX,^ 1
A'j, если п —нечётно, .г^, если п —
- четно
^п^п-\"-^\ 1
XiA'2...JC,j_2Ajc„_jX„ 1
fif^, если слово начинается на Ьа, х^.
..д:„_1 в других случаях
Пример решения задания 3.1.1
Решить задание 3.1.1 для
а-{х,^, если х,^_^ =а, й"~ х„, если х,^_^ =Ь, (/2>1).
1. Опишем работу алгоритма, решающего эту задачу.
Будем обозначать состояния машины Тьюринга числами
0,1,2..., причём 1 — начальное, а О — заключительное состояния.
Вначале с помощью команд (дД)—>аП1; (b,l)—^bU\
проходим до конца слова, не изменяя его символов.
Признаком окончания слова будет считывание X в первом
состоянии.
С помощью команд (Л,1)—>ЛЛ2; (а,2)—>лЛЗ; (Ь,2)-^ЬЛЗ
движемся влево, не изменяя последнего символа слова.
Если в состоянии 3 считываем символ а, значит, x„_i = а,
нужно стирать все символы слова а, кроме последнего. Это
можно сделать с помощью команд (л,3)—> ^Л4; (л,4)-^ ЛЛ4; (М)->
ЛЛ4. Если в состоянии 4 считывается Л, значит, вся работа
проделана, и пора останавливаться с помощью команды (Л,4)—>ЛНО.
Теория алгоритмов
167
Если в состоянии 3 считываем символ Ь, значит, x,j_i =b,
нужно все символы, кроме х,^, заменять буквами Ь. Это делаем
с помощью команд (Ь,3)-^ЬЯ5; (а,5)-^ЬЯ5; (b,5)-^bJ]5. Если
в состоянии 5 считывается X, значит, все символы исходного
слова пройдены, можно переходить в состояние О с помощью
команды (^,5) -^ ЛНО.
Запишем программу найденной машины Тьюринга в виде
таблицы:
Таблица 3,1.1(1
a\s
X
а
b
1
А,Л2
aU\
mi
2
-
аПЗ
ЬЯЗ
3
-
ХЛ4
ЬЯ5
4
хт
ХЛ4
АЛ4
5
АНО
ЬЯ5
ЬЯ5
2. Проверим работу построенной машины Тьюринга над
словом abba:
abba, abba, abba, abba, abbaX, abba, abba, abba,
11 1 1 2 3 5 5
Xbbba, Xbbba.
5 0
Итак, в слове abba предпоследний символ — b, и все буквы
исходного слова, кроме последней, заменены буквой Ь.
Проверим работу построенной машины Тьюринга над словом
bbaaa:
bbaaa, bbaaa, bbaaa, bbaaa, bbaaa, bbaaaX, bbaaa,
1111112
bbaaa, bbaXa, bbXXa, bXXXa, XXXXXa, XXXXXa.
3 4 4 4 4 0
В слове bbaaa предпоследний символ — a, и все буквы
исходного слова, кроме последней, заменены пустыми символами X.
Итак, проверка сделана, результат работы машины Тьюринга
удовлетворяет требованиям, которые ставились в условии задачи.
168 Глава 3
Задание 3.1.2
1. Построить машину Тьюринга, вычисляющую числовую
функцию /(xi,X2,...,^,i)-
2. Проверить работу построенной машины над некоторыми
наборами значений переменных.
Таблица 3.L2
Хо
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/(JC1,A-2,...,JC„)
f{x,y,z) = x + y
f{x,y,z) = y^3
f(x,y) = [x-у,ест\ л'>>', 0, если х<у}
f{x,y,z,w) = 4
/(х,у) = {0,есяи х>у, 1,если л'<,у}
/(x,>',z) = {z-3,если z>3, 0,если z<3}
f(x,y,z,w) = у + z + \
f{x,y,z) = {Oyecnv\ х = 0, у, если х^О}
f{x,y) = {y-x,Qcm\ jc<>', 0,если х>у}
/U>>') = {2, если >'>1, ^,если >'<1}
f{x,y,z) = y + 3+z
/U,>') = {0, если Х9^0, у + 1, если х = 0}
/(■^.>') = {-^,если X—четно; д', если л-—нечётно}
f(x,y) = [x + y,Qcnv\ .г>>;, 0, если х<у}
f(x,y,z.) = {z + \,ecnH z?^0, 0, если z = 0}
/(л,>') = {0,если X—четно; 1 если л-—нечётно}
f(x,y,z) = 2y
/(д:,.у, z) = {w, если х = 0, 2, если .V9i0}
/{ХуУ) = {х-2,сся1\ лс>2, 0, если х<2}
Теория алгоритмов
169
Таблица 3.L2 (окончание)
1 №
1 20
21
22
23
1 ^"^
1 ^^
26
27
28
29
30
/(A',,X2,...,JCJ
/(х.>') = 2х + 1 1
/(х, д') = {х,если X—четно; 0, если х—нечётно)
/(х, у) = {0, если лт = 0, х+ у, если ху ФО}
f(x,y,z) = y + 3
f(x,y) = {\,ecm Л'= 0, 0, если .V7t 0}
/(.V,y,Z,H') = Z + W
f(x,у) = {у,если Л' = 1, Л' + 2, если хФ\}
/(х,у,г) = {х+у,если ZT^O; у, если г = 0}
/(х, y,z,w) = {z, если л'>1; vv, если х<\]
f(x,y,z) = 2z
f{Xy у) = {5, если х+ у> 2, 0, если лч- у <2}
Пример решения задания 3.1.2
Решить задание 3.1.2 для f(x, у) = х + 2у.
1. Внутренние состояния машины Тьюринга, которую
требуется построить, будем обозначать числами 0,1,2..., причём 1 —
начальное, а О — заключительное состояния.
Набор значений аргументов (х,у) изображается словом
Аргумент X должен остаться без изменения, этого можно
добиться с помощью команды (1,1)-^1П1. Когда в первом
состоянии встретится символ Я, значит, мы попали на символ,
разделяющий изображения аргументов, переходим в состояние 2,
а сам символ X пока оставляем без изменений с помощью
команды (;1,1)-^Ш2.
Далее, набор единиц, изображающий аргумент j;, проходим до
конца. Для этого добавим команды (1,2)-^1П2; (Л,2)-^ЯЛЗ.
170
Глава 3
Теперь с помощью "челночного" алгоритма удвоим
количество единиц в блоке, изображающем вторую переменную.
Расширим алфавит, введя метку #. Считая, что к единиц
блока продублированы, рассмотрим, как будет дублироваться к + 1-я
у+1-к к к
единица. Г'^^^.!...!!...!!...!. Заменим очередную единицу из
блока, изображающего вторую переменную, меткой # и будем
двигаться вправо ((1,3)-^#П4; (1,4)—>1П4), пока не встретим пустую
ячейку, заполним её единицей и пойдём влево ((Л,4)-^1Л5;
(1,5)-^1Л5), пока не встретим метку, заменим её единицей,
перейдём к следующему символу слева, вернувшись в состояние 3
((#,5)-^1ЛЗ).
Когда в третьем состоянии считается X, значит, блок,
изображающий вторую переменную, продублирован. Заменим
разделяющий символ единицей ((^,3)—>1Л5) и пойдём на начало
полученного блока из x + l-\-l-\-2(y^l) = x + 2y + 4 единиц. Когда
в состоянии 5 встретится X, значит, пора идти вправо, стирать три
лишние единицы, ведь для изображения числа х + 2у требуется
х-\-2у + 1 единиц. Для этого добавим команды (Л,5)-^Ш6;
(1,6)-^Ш7; (1,7)-^Ш8; (l,8)-^;iH0 .
Запишем все команды полученной машины Тьюринга в виде
таблицы.
Таблица 3.1,2(1
a\s
X
1
#
1
хт
1П1
-
2
АЛЗ
1П2
-
3
1Л5
#П4
-
4
1Л5
1П4
-
5
XU6
1Л5
1ЛЗ
6
-
АП7
-
7
-
АП8
-
8
-
АНО
-
В клетках таблицы, помеченных неопределённым символом —
можно вписать любые команды, т. к. до их исполнения дело всё
равно не дойдёт.
Теория алгоритмов
171
2. Проверим работу алгоритма над изображением набора
переменных (0,1), т. е. над словом IXU:
ail, an, ail, an, aia, aia, ai#x, ai#i,
112 2 2 3 4 5
aiii, a#n, a#ii, a#ia, a#iii, a#iii, a#iii,
3 4 4 4 5 5 5
anil, 11', ;ll^;lll^;lll^;lll^;l;llll.
8 0
l^^l^
5 5 6 7
Итак, в результате осталось три единицы, которые являются
изображением числа 2.
Заметим, что /(0,1) = 0 + 2-1 = 2, так что на ленте получено
то, что и нужно было получить.
Задание 3.1.3
1. Написать формулу числовой функции /(xi,jC2,...,^,i),
вычислимой машиной Тьюринга с множеством внутренних
состояний {0,1,2,3,4,5,6}, где О — заключительное, а 1 — начальные
состояния, если машина задана своей программой.
2. Проверить работу машины Тьюринга с некоторым набором
значений аргументов.
Таблица 3,1,3
Хо
1
п
4
дХ^^
X
1
1
1П2
АП1
2
1ПЗ
1П2
3
ХП4
1ПЗ
4
ХП5
АП4
5
Х}\5
ХМ
6
хно
Ало
2
2
X
1
™
1П2
1П5
хт
ХП4
хт
ХНО
хш
—
1П6
хно
Х\\6
3
3
X
1
хт
лП1
хт
хт
А,Л4
1ПЗ
1Н0
XY\5
1Л6
1П5
1Л4
1Л6
172
Глава 3
Таблица 3.1.3 (продолэюение)
№
4
п
2
дЧ^ 1
X
1
1
1П4
1П2
2
хяз
1П1
3
хно
хяз
4
1Л5
1П4
5
1П6
1Л5
6 1
1Н0 1
1П6 1
5
3
X
1
—
хт
1ПЗ
ХП2
XUA
1ПЗ
лЛ5
1Л6
ХЛ5
1Л6
1Н0 1
1Л6 1
6
4
X
1
хт
хп\
1ПЗ
1П2
XU4
ШЗ
ХЛ5
XU4
А,Л5
ХЛ6
...
хт
7
2
я
1
XU4
ХЛ2
1ПЗ
1Л2
1П1
1ПЗ
ХЛ5
ХП4
ХЛ5
ХЛ6
хт
1Л6 1
8
3
X
1
1П2
1П1
1ПЗ
ХП2
1Г14
1ПЗ
АЛ5
...
ХЛ6
ХЛ5
хяв
1Н0 1
9
3
X
1
1П2
ХП1
1ПЗ
1П2
ХЯА
хт
ХЯ4
ХЛ5
1Л6
1Л5
1Л0 1
...
10
4
X
1
хт
хт
хт
хт
хш
1ПЗ
ХЛ5
хт
ХЛ5
ХЛ6
1Н0 1
1Л6
11
2
X
1
хт
хи\
1Н0
1ПЗ
1П5
1П4
1Н0
1П4
1Л6
1Л5
1Н0
1Л6
12
4
X
1
хт
хп\
1 1ПЗ
XU2
1Л4
1ПЗ
1П5
1Л4
1 1Л6
1П5
1Н0
1Л6 1
13
2
X
1
1П4
XJ12
1ПЗ
1Л2
1П1
1ПЗ
1П5
1П4
1П6
...
1 хно
1Н0
Теория алгоритмов
173
Таблица 3.1.3 (продомлсение)
1 ^-
14
п
4
■4\5
Л
1
1
хно
1Н2
2
хпз
ХП2
3
Ш4
ХПЗ
4
1П5
Ш4
5
...
1Л6
6 1
1Л1
1Л6 1
15
2
Л
1
1П2
1П1
хлз
1П2
1П6
ХП4
1Л5
1П4
1ЛЗ
1Л5
ШО 1
Ш6 1
16
4
Л
1
1П2
1П1
ХПЗ
ХП2
ХП4
ХПЗ
ХЛЗ
ХП4
ХЛЗ
1Л6
ШО 1
1Л6 1
17
4
Л
1
ХП2
1П1
ХПЗ
ХП2
ХП4
ХПЗ
ХЛЗ
ХП4
ХЛЗ
1Н6
ШО 1
1Л6 1
18
3
л
1
1П2
1П1
1ПЗ
1П2
ХЛ4
ШЗ
ХНО
ХПЗ
1Л6
ШЗ
1Л4
1Л6 1
19
3
х
1
1П2
ХП1
1ПЗ
1П2
ХЛ4
ХПЗ
ХЛ4
1Л5
Ш6
1Л5
ШО 1
1П6 1
20
1
л
1
1П1
1П2
1Н0
1ПЗ
1П5
1П4
ХНО
ХП4
Ш6
хло
1Н0
1
21
4
л
1
—
ХП2
ШЗ
1П2
ХП4
1ПЗ
ХПЗ
ХП4
ХЛ6
ХПЗ
ХЛ6
ХНО
22
4
х
1
1П2
1П1
ШЗ
ХП2
1Л4
ШЗ
1Л5
1Л4
ХЛ5
Ш6
ХНО
ХЛ6
23
2
X
1
1Н0
ХП2
ХП5
ШЗ
Ш4
ШЗ
1Н0
Ш4
Ш6
ХПЗ
Ш1
Ш6
24
5
1 ^
1 1
ХП2
хт
ШЗ
ХП2
Ш4
ШЗ
Ш5
104
ХЛ6
ХПЗ
ХЛ6
ХНО
25
2
X
1 1
1П2
ХП1
ХНО
ХЛЗ
Ш4
1ЛЗ
Ш2
Ш4
Шб
1Л6
ШО
ШО
26
3
1 ^
1 1
1П2
1П1
ХПЗ
Ш2
...
Ш4
1Л5
1Л6
ШО
1Л5
ШО
1Л6
174
Глава 3
Таблица 3, J.3 (окончание)
№
27
п
2
дХ^^
X
1
1
1П2
1П1
2
—
1ПЗ
3
1Н0
1П4
4
1Л5
1П4
5
1П6
1Л5
6
1ПЗ
1П6
28
3
X
1
1П2
1Л1
1ЛЗ
1П2
1П4
1ЛЗ
1Л5
1П4
1П6
1Л5
хно
1П6
29
3
X
1
ХП2
ХП1
—
хпз
ХП4
1ПЗ
ХЛ5
ХП4
ХЛ5
ХЛ6
1Н0
1Л6
30
2
X
1
1П2
1П1
ХЛ5
1ПЗ
ХЛ4
1П2
1Н0
ХЛ4
1Л6
1Л5
1П0
ХЛ6
Пример решения задания ЗЛ.З
Решить задание 3.1.3 для f{xi,X2), вычислимой на машине
Тьюринга, заданной своей программой.
Таблица 3.1.3а
a\s
X
1
1
—
ХП2
2
ХПЗ
1ПЗ
3
1Л4
1ПЗ
4
1Ы0
1Л4
5
ХН6
ХПЗ
6
П-10
...
Рассмотрим последовательность конфигураций данной
машины Тьюринга при работе над изображением набора значений
аргументов (Х|,Х2).
Рассмотрим случаи: \) х^^О.
12 3 3
4 "'"4 'о
Итак, в результате работы машины Тьюринга над
изображением набора аргументов получился блок из a'i4-X2 4-3 единиц,
которые служат изображением числа Xi+X2+ 2.
Теория алгоритмов
175
2) х^=0.
В этом случае последовательность конфигураций будет
выглядеть так:
lXl''^\Xkl''^\Xn''\XW~\ ... ,1ДД, 1.
1 2 5 5 5 5 6 0
В этом случае осталась одна единица, которая служит
изображением числа 0.
х^+Х2+ 2, если JC] ^ О,
Ответ: /(л'|,Х2) =
О, если Xi =0.
Задание 3.1.4
1. По данному коду N(T) восстановить программу машины
Тьюринга.
2. Выяснить, является ли машина Т самоприменимой или не-
самоприменимой.
При составлении N(T) использована следующая кодировка:
П —1,Л—Р, Н—РД—1М —Р, * — 1\
So — 1\ S^ — 1\ S2 — Р.
Таблица 3.1.4
Хо
1
2
3
4
5
N{T)
1 8* 1 4* 1 5* 1 :^ 1 9:^::^ 1 8:^:1 5:^ 16:^:1:^:1 8** 18:^1 6:^:1 4* l2:j:l8:j::i: l9*
l4*l4*lЗ:^:l9:^::^:l9:^:l5:^:l5*l:^:l9:„:^:l9:^:l6:^:l4:„l:^:l8
l8*l4:j:l4:Cl:j:l7:j::j:l8:^l5:i:l6*l*l9:^:i:l8:j:l6:Cl5*l2:j:l9:j::j: l9*
[4*14:^:1:^:1 8:i::i:l9:i:l5:i:l 5*1 :i:l8*:i.l9:f: 16^: l5:^l:i:l9
I8*i4:cl4:cl*l8**i8:icl5:icl6*i2*i7**i8*i6*i5*i3*i7** i9*
l4*i4*i3*i7**i9*i 5*16:,! *l9**i9*i 6*16*1*18
18* 14:), 14* i2:i, 19** 18* 15* 16* 12* 18** 18* 16* 15* 13* 18*:}:
I9*i4:f:l4*i*i9**i9*i5:,l6*i2*i8**i9^l6*i4:,l*l8
I8*l4*l4*l2*l7**l8*l5*l6*l2*l9**l8:^l6:j:l6*l3*l9:^:i:
I9*i4*i4*i2*i8**i9*i5*i5*i2*i7.-i:*i9*i6*i5*i*i9
176
Глава 3
Таблица 3.J.4 (продолж:ение)
№
6
7
8
9
10
11
12
13
14
15
16
17
/v(r)
I4*l4^1^l7:i:^l9:i:l5:i:|5:i,l3;„l9^:^l9^l6:i:l6^l*l8
1 8* l4* 1 4:^: 1 3;„ 1 9^:^: ] 8:^: 1 5:^: l4sj, 1 3:}: 1 8** 1 8^ 1 6sj, 1 6^ 1 :}: [ 8*:^:
I4^l4:i:l2:i:l9:i:^l9^l5:i,l6:^l2*l8:^^l9^l6*l4:i:[^l8
1 8^ 1 4я« [4:}: [ 3:}c 1 7:}c:}: 1 8:}: 1 5:jj 1 5;|: 1 3^ l9:{;:}: 1 8:j: 1 6:j: 1 6^ 1 :}: 1 9:}:5(j
I4*l4:i:bl8*^l9:i:l5,^l6;^l3^|9:i:^l9^l6=,,l5*l.-^.l8
1 8:j, 1 4:j. 1 4^ 1 3 :}: 1 8:}::j, 1 8:j: ] 5:j: 1 4^ 1 ^ 1 7^^ 1 8ji; [ 6:j, 1 6:j, 1 2:}c 1 7:j:^
l4*i4*bi7*^l9^l5^l4*l*l8*:i:l9^l6Hci6^1:i:l9
1 8я« 1 4:j. 1 4^ 1 ^ 1 9:j::j: 1 8:j: 1 5* 1 4^ 1 ^ 1 8:}::^: 1 8^ 1 6^ 1 6:}: 1 2^. 1 8^},*
l4*l4*|2Hcl8:i:^l9:i:l5*l5:i:l3:i:l7:i:H.l9:i:l6:j:l4*l:i:l9
1 84:14^, 1 5^ 1 ^i, 1 7:j:* 1 8:^: 1 5:^: l4* 1 ^ 1 9:^:* 1 8^ 1 6:^: l6:i: I 2:^: l9:i:*
4*l4^l2^l9**i9^l5Hci6:i:l^l9^^l9*l6^l5^l2*l7
I4^l6*l2:i:l7:i;*l9:i:l5*l4:i:l^l9:i::i:l9:i,l6:j,[6:i:l2*l8
l9* 1
l9*
l9* 1
l9*
l9* 1
l9*|
19*
I4^l2*i8^^l8:i:l6*l6*l3*i8^:i:
I9*l4*l6*l3*l8:j::i:l9:i:l5^l5:i:l2:i:[8=,,*l9:j:l6*l4^l2:i:l8
I8*l4*l5:i:l2=,,l7;^:i:l8:i:l5:i:l4^l2*l9^:i:l8*l6*l4*l3:i:l9^* 1
9*l4*l6*l3:i:l9:i::i:l9*l5*l6*l2:i:l8^^l9:i:l6:i:l5:j:l2^l8
I9*l4:}:l6:i:l3:i:l7**l9:j:l5*l4^l3:i:l7**l9^l6:i:l6:i:l2:i:l8
1 8:}c 1 4:jc 1 5:}: 1 3 :j: 1 9я«5Ц 1 8:}: 1 5:ij 1 4:j: 1 2^ 1 85j<:f: 1 8^ 1 6:f: 14,^ J ^ 1 8:}::j:
l9*l4:i:l6:i:l*l9^*l9:i:l5^l4^l2H.l9H.*l9*l6^l4*l2*l9
10:j<l4:j«lJ:j:l3:j:[7:j::j:|0:j:lJ:j:
i9*i4*i6*i*i8**i9h=i5»i5*i3*i9**19*i6*i5*i2*i9
Теория алгоритмов
177
Таблица 3.1.4 (окончание)
№
18
19
20
21
22
23
24
25
26
27
28
29
30
N{T) 1
[Oii:\4^\6:^:\^\l^^\0^\5^\5^\3r^,\9:^:^\S^\6^\4i^\2^\9^:^
{9:^:14*16:^:12:^:18** l9*l 5* i4:i:l2^l7^^l9*l6^15^1^19
1 8* 1 4:j: I 6:j: 1 ^ 1 8*:}: 1 8^ 1 5:^: 1 5^ 1 :}: 1 7:C:j: 1 8:(, 1 6:C l4:i, 1 3* 1 7:„:i:
l9:i.l4:i:l5*l2:i:l7:i::i:l9:j:l5:i:l5:Cl2:i:l9:C:„l9*l6=,,l6:^l:i:l8
1 8:}: 1 4:j, 1 6:}: 1 2^. 1 9^:j. 1 8:j: 1 5:j< 1 5:j, 1 :1c 1 8:}c:{; 1 8:}: I 6:}: 1 4:j: 1 3^ 1 8:}::}:
l9:Cl6*l4:^Ul9
1 8* 1^* 1 6:}: 1 2:j: 1 7:^:.^ 1 8:{, 1 5:С 1 5ц, 1 :i: I 9^:}: 1 8:^ 1 6:С 1 5:С 1 3:k 1 9:^::),
l9:i:|4:i:l5:i:l3:j.l8:^:i:l9:i:l5:i:l6:Cl2:{,l9:i,:^l9:Cl6:Cl5:j:l:i,l7
1 Osi<}4:j: 10:j:l2:j: 10:i«:j:l Osjsl J:js 1 J:j: lZ:j: l7:(j^-l 0:j:10:fclJ;}:l :j<l '*i«*i«
1 9* 1 4:C 1 5 :j: 1 3 :i: 1 7:^::^: 1 9:^: 1 5 :C 1 5 :}: 1 2:j: 1 9:i,.<: 1 9^ 1 6:), 1 6:^: 1 :i: I 9
1 8:}: l4:j: 1 6:i, 1 2:}: 1 9:}::}: 1 84; 1 5:(« 1 5:}: 1 2:j: 1 8:j;:,j 1 8:i« 1 6^. 1 5:j: 1 :(, 1 8:}::}:
1 9:1. 1 4:^ 1 5:i, 1 :C l9:i::i, 1 9:^: 1 5:^: 1 6:i, 1 3:}: 1 8:i,:C 1 9:^: 1 6:}: 1 4:}: 1 2:^: 1 9
10:J:14:J:16:J:13:J:17:J::J:10:J:1J:J:15:J:12:1j19.^:J:18:(c16:jj1J:{;1:J:19:J:5{;
I9*l4:i:l5:i:l:^l8:i::cl9:j:l5:i:l4:j:|3:i:l8:i,*l9:i,l6*l5:i:l3:cl8
I 8:C 1 4:), 1 6:), 1 3:^: 1 8:ic* 1 8:), 1 5:ic I 6:), 1 3:„ 1 7:„^ 1 8:j: 1 6:^ 1 5* 1 2:^: 1 7:1,4:
1 9:}: 1 4:}: I 5:}: 1 >»: 1 7:^:), I 9:^: 1 5:C 1 5:^ 1 :i: 1 8:i,:i, 1 9:^ 1 6:^ 1 6:), 1 3:^ 1 7
1 8:ic l4:i, l6:i: 1 :i: l9:i::i: 1 8* 1 5:C 1 6:^: I 3:„ 1 8:^::^: 1 8:„ 1 6* 1 5:C 1 2:), 1 8:^::^:
1 9:ic 1 4:j, 1 5:^: 1 2:„ 1 9:^:}: 1 9:^: 1 5:^: 1 6:^: 1 3:;: 1 7:^:), 1 9:^: 1 6:^: 1 4:1, 1 3:j: 1 8
1 8:1, l4:^ 1 5:j, 1 :(, 1 7:j::j: 1 8:}: 1 5:}: 1 6:j, 1 3:i: 1 9:1,:,: 1 8:(c 1 6:}, 1 5:), 1 2:{; l9:j::j:
I9:^l4:„l5:„l3:i:l8.^:^l9:„l5:i,l5:,l*l9:,:;,l9:f:l6:,l5:,l*l8
1 8:j: 1 4:f: 1 4:}: 1 :„ 1 8:}:::, 1 8:}:1 5:„ 1 6:„ 1 :i, I 7^:„ 1 8:}: 1 6:i, 1 5.-1, 1 3:„ 1 7:j::j:
I9:}:l4:i:l4:i,l2:„l7**l9:i:l5:^l4:„l,-^.l8:i::j,l9:i,l6:„l6:„l2:i,l7
178
Глава 3
Таблица 3.1.4а
Пример решения задания 3.1.4
Решить задание 3.1.4 для данного кода N{T):
* 19:1. 14* 15:1. 13* 17:1.:1. 19:1. 15:1. 14^.12^.19^.^1: 19:1. 16:1. 15* 1:1. 18.
1. Заменим каждый блок единиц символом по описанному
в условии задачи правилу. Одной звёздочкой разделяются
символы одной команды, а двумя звёздочками — отдельные команды
машины Тьюринга.
Например, комбинации I8*i4*i4*i*i8 соответствует команда
(X,Si)—>А,П^|. Заменяя таким
образом коды всех команд их
стандартной записью, изобразим
программу машины Тьюринга в виде
таблицы (табл. 3.1.4а).
2. Запишем
последовательность конфигураций машины
Тьюринга при работе над своим
кодом, обозначив через А слово,
полученное из кода машины
Тьюринга, начиная с 10-го символа.
1 iJ ^^А, ХУ^^^А, 1 }^^А.
S2 S2 Sq
Как видим, при работе над своим кодом машина Тьюринга
перешла в своё заключительное состояние, значит, она является
самоприменимой.
д\5
X
1
*
•^1
s^Xn
1П5,
*Л52
52
1Н.0
ЛЛ52
1П5|
Теория алгоритмов 179_
3.2. Нормальные алгоритмы
Пусть А — алфавит, не содержащий символов "." и "-^'\
Обыкновенной формулой подстановок называется запись вида
Р —^Q, где Р и Q — некоторые слова в алфавите А.
Заключительной формулой подстановок называется запись
вида Р -^ .Q, где Pv\ Q — некоторые слова в алфавите А.
Нормальной схемой подстановок над алфавитом А называет-
ся запись вида
P2^d2Q2
где f), Qi — слова в алфавите Л,
di — либо пустое место, либо символ "." .
Нормачъным алгоритмом над алфавитом В называется пара
(Д,5) такая, что В^А, S — нормальная схема над
алфавитом В.
Работа нормального алгоритма над словом R состоит из
отдельных шагов, в результате которых получаются слова
R = Ri,R2,...,Ri,... Слово /?/^1 получается из слова R^ так:
просматривается нормальная схема подстановок и из неё
выбирается самая верхняя формула, левая часть которой входит
в слово Ri. Пусть, например, это будет формула Pj —>djQj.
Затем первое вхождение Pj в слово R^ заменяется на Qj, что
и даёт слово R^^^.
Работа нормального алгоритма над словом R заканчивается
в двух случаях:
1) существует / такое, что слово Ri получено с помощью
заключительной формулы подстановки;
2) существует i такое, что ни одна из левых частей
нормальной схемы подстановок не входит в слово /?,.
И в том, и в другом случаях слово /?, объявляется
результатом работы нормального алгоритма над словом R и говорят, что
нормальный алгоритм применим к слову R.
180 Глава 3
Изобраэюеиием набора аргументов (л'1,л'2,...,Х;,) называется
запись вида Г'^^'^l'^^^ ^1'^^''^...*Г'^^\ (*) где Г=П^1.
Числовая функция /(xi,X2,.--,a'/,) называется вычислимой по
Маркову, если существует нормальный алгоритм, применимый к
любому слову вида (^), переводящий его в слово 1-^^ , где
Задание 3.2.1
1. Построить нормальный алгоритм, применимый ко всем
словам XiX2'--Xi^ В алфавите {д,Ь} и переводящий их в слово а.
2. Проверить работу построенного нормального алгоритма над
некоторыми словами.
Таблица 3.2.1
Хо
1
2
3
4
5
6
7
8
9
10
а
аЬ, если /2<3, ax^Xj.-.x^, если п>3
аа, если в данном слове число букв b нечётно. Х|Л"2...л-,,_1, если
четно
XiA'2...x„_|jc^jX„, если Х2=а, х^Х2...х,^Ь, если х^^Ь
abb, если слово начинается на аЬ, х^х^ в остальных случаях
х^...х,^Ь, если п —четно, Ьх^...х,^, если п —нечётно
аЬ, если Х2 =а, Xi....v,j_|, если х^^Ь
а^а, если п —нечётно, Xi...a"„_iX„a-„, если п —четно
а", если А| =а, Xi, если Aj =Z?
А,...А„а"
^^2 *Ai ♦Аз *...*А^
Теория алгоритмов
181
Таблица 3,2.1 (окончание)
Хо
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
а
.VjA-„.l-2X3...X^,_lA-^
Z?"av..x„ I
{abf 1
Л-,Л-2...А'„*А'„_, *X,,_2 1
Aj =f *Аз...А'„_1, если Аз =a, A3A4...A,,, если X2=b
Aj...A,j, если в исходном слове количество букв а нечётно, aba, если
четно
А, *Аз *А5 ^-^...^ А„, если п нсчётно. А1А2...А„,если п четно
Aj ax-^bx-i^cLx^b... А„
A'j А2Аз...А^_1 A„A,j_i ...Aj
baba, если слово начинается на Ьа,
А|А2...А„я в других случаях
/?AiA2...A„, если А,, =а, bbb,Qcnvi x^j=b
ab, если п —нечётно, а,,_1А,,, если п —четно
а\ если А^_1 =а, AiA2...a„_2«^, если х,^_^ -Ь
A'l A3 А2 А4 А'з... А„_2 A,j A,j_i
aVj Aj A2A2.. .A„_2 A„_2^
bb, если «<3, Ai...A„_i, если п>Ъ
AiA2...A„«, если n —нечётно. bx^...x,^, если n —четно
^"а,...а.
A2*A, >^A2*A,
A,j A„_i...A2A'l A2A3...A^j_i A,,
182
Глава 3
Пример решения задания 3.2.1
Решить задание 3.2.1 для
a = {x,j, если x,j_i =а\ Ь'^~^х,^, если л',^_, -Ь], {п>\).
1. Опишем работу нормального алгоритма, решающего эту задачу.
Последней в схеме подстановок запишем формулу -^ а , тогда
слово JCiX2"-^/i перейдёт в ou:iX2...a',^. Затем с помощью формул
подстановок аа—>аа, ab—^ba символ а прейдёт на конец
слова: XiX2..-x,^a.
для разбора варианта х^^_^=а введём формулы подстановок
aba-^^b, ааа-^^а, а(3-^(3, (3—>.
Для разбора случая х,,_, -Ь введём формулы подстановок
bba-^ybb, baa-^yba, ay-^yb, by-^yb, y-^.
Запишем нормальную схему подстановок:
аа —>ла
ab-^ba
aba -^ (ЗЬ
ааа -^ (За
«(3-^(3
bba -> ybb
baa -^ yba
ay-^yb
by-^yb
->a
2. Проверим работу построенного нормального алгоритма над
словами abba и bbaaa:
_abba, aabba, aabba, ababa, abbaa, abbaa,
abyba, aybba, ybbba, bbba.
Теория алгоритмов
183
_bbaaa, apbaaa, babaaa, bbaaaa, bbaaaa, bbaaaa,
bbaaaa, bba^, bb^, fepa, pa, a.
Видим, что нормальный алгоритм работает так, как и
требовалось.
Задание 3.2.2
1. Построить нормальный алгоритм, вычисляющий данную
числовую функцию /.
2. Проверить работу построенного нормального алгоритма над
некоторыми наборами значений переменных.
Таблица 3,2.2
№
1
2
3
4
5
6
7
8
9
10
11
12
13
/
/(a-,v,z) = 2.v + z
/U>у) = {у- А'> если V > Л", 0, если ,у < л}
fix,y,z,w) = {4, если X —четно; х, если х
нечётно }
f(x:,y) = {l, если л>у; 0, если л'< v}
f{x,y,z) = {z-?>, еслиг>3; 0, если .■:<3}
/(.г, у, Z, vv) = л' +3 V + 3vv
f(x,y,z) = {0, если х = 0; у, если хфО]
f(x,y) = {x-y, если л->у; 1, если х<у]
f{x,y,z) = {3, если >>1; х. если .v<l}
f(x,y,z.) = y + z + 4
f(x,y,z) = {0, еслих7^0; у + 1, если .х: = 0}
f(x,y) = {x, если X —четно; 2у, если х —
- нечётно}
f{x,y,z) = {x+ у, если л->у; 0, если л-<у}
184
Глава 3
Таблица 3,2.2 (окончание)
№
14
15
16
17
18
19
20
21
22
23
24
1 ^^
1 26
1 27
1 28
1 29
1 30
/
f(x,y,z) = {z + \, если z;tO; 0, если :. = 0}
f(x,y)-{^^ если Л' —четно; 2, если л- —нечётно}
fix,y,z) = 3y + z
f{x,y,z,w) = {w, если л' = 0; 2, если л-?^0}
/(■^» Д') = {-^ - 2, если лс > 2; 0, если л- < 2}
/и,у) = 4л- + 1
/(■^»>') = {-^» если X —четно; 0, если х — нечётно}
fix,у) = {0, если ху = 0; л- + ,v, если .vv^0}
f(x,y,z.) = {y + 2, если >'>1; 0, если v<l}
/(jc,v) = {l,jc= 1;0,если л-^1}
f(x,y,z,w) = 2y + w
f(x,y,z) = niin{x,y}
f(x,y,z) = {z-2, еслиг>2; 0, если г. <2}
/(л'.у) = {у-X, если у > х\ 2, если v < л}
f{x,y,z.w) = x^y-\-[w/2]
f{x,y,z) = {\, если Z —четно; 2х-^у, если z —нечётно}
fix, у, Z, w) = л- + 2 у + 3z + 4
Пример решения задания 3.2.2
Решить задание 3.2.2 для f{x,y)-x-\-2y.
Вначале мы имеем запись изображения набора аргументов
Теория алгоритмов
185
Последней формулой подстановки мы введём символ а: —> а.
Получим слово al^"^' ^^l^^K
Затем с помощью подстановки а 1-^1 а оно преобразуется
в слово Г^^* а * 1'^^'. Сотрём а и разделительную звёздочку: а*-^(3.
Удвоим количество единиц в блоке, изображающем второй
аргумент: р1->11р. После выполнения всех перечисленных выше
подстановок окажется запись, содержащая
х + 1 + 2(у + 1) = х + 2у + 3 единицы. Сотрём лишние две единицы
и закончим работу подстановкой 1 iP-^.
fal->la
Запишем нормальную схему подстановок: \
(31-^11(3
11(3->.
2. Проверим работу алгоритма над изображением набора
переменных (0,1), т. е. над словом 1*11:
1*11,а1*11, 1а*11, 1(311, 111(31, 11111(3, 111.
Итак, осталось три единицы, которые являются изображением
числа 2, что и ожидалось, т. к. /(ОД) = 0 + 21 = 2.
Задание 3.2.3
1. Написать формулу для функции >'=/(xi,X2,...,^,j),
вычисляемой нормальным алгоритмом.
2. Проверить работу алгоритма над некоторым набором
значений аргументов.
Таблица 3.2.3
Хо
1
п
3
/
*-^11 .
all->la
№
2
п
2
f
al->la
а* ->(3
(31->Y
Y1->Y
Y-^.
->а
186
Глава 3
Таблица 3.2,3 (продолэ1сеиие)
№
3
5
7
9
11
п
2
3
2
3
4
/
1
]
<
al—> а
а * -> Р
pl-^lip
Р*->а
а->.111
—)а
'1*1—>*
*1^р
*->.1
Pl-^P
р^.1
f * 1 ->1 *
Р1->1(3
yl-^Y
Y->.
[->a
Xo
4
6
8
10
12
n
2
3
2
3
3
/ 1
\
<
al-^lla
(311-^.
(31-^.1111
1 ** ->a
al-^ 11 a
a->.
1*-^P
IP^PIII
P->.i
[l->.l
:^ :^ г^Л ^^ ^ ^
^ ^ :Jc ^ 1
**l-^a
al—>a
'
al 1-^p
al^Y
P1->P
P*^P
P^.l
yl^lY
Y*—>Y
Y-^.ll
Теория алгоритмов
187
Таблица 3.2.3 (продолэ^сение)
Хо
13
15
17
19
п
3
3
3
3
/ 1
^
-
^ 1 * 1 ->1 *
* * —> а
al 1-> 1а
а 1->.
а->.
al->la
а* ->(3
(31-^111(3
Y 1->Y
Y->.
->а
all->ll(3
(31->1(3
al->Y
Y 1-^Y
Y "^-^ Y
Y^.ll
->a
al-^a
a*l->(3
(3111-^1(3
(311*->.11
(31*->.l
(3*->.
->a
Xo
14
16
18
20
n
3
2
2
2
/ 1
^
-
■
^
11 a->l a
1 al->l Y
Y 1->1 Y
Y *—^•
al->(3
(31->(3
(3*->.ll
1 *—>a
7-^.
al-^111 a
a*-^(3
(31->11(3
(3->.lll
->a
al-^la
a*-^(3
(31->111(3
(3->.ll
->a
188
Глава 3
Таблица 3,2.3 (окончание)
№
21
23
25
27
29
/1
2
3
3
2
2
/
^
<
^
■
аа 1 -> аа
аа * —> аа
аа ->. 11
all->(3
(31->(3
1 a-^al
1 *->al *
**1—>a
al l-> la
a 1-^.
a->.
al->ll a
a*l-^(3
a*—>p
P^.ll
—)a
■al->ipia
a* 1^
—>a
Xo
22
24
26
28
30
/2
2
2
3
2
3
/
<
'
'
■
al^lp
Pl^la
a*—>Y
Yl->11 Y
Y^.
P*^5
611-^61
al-^ip
Pl^la
a* —> Y
P*l^.
Y1 -^ Y
Y^.
—>a
'1*1^1*
al^ 111 a
a—>.
11*11^.11
*^P
pl-^lip
,1P^-
al-^a
a*-^(3
(31-^11(3
-^a
Теория алгоритмов 189
Пример решения задания 3.2.3
Решить задание 3.2.3 для f{x,y,z), вычисляемой нормальным
[*1->а
алгоритмом с данной, схемой подстановок: J ^ ~^
[al—>а
1. Вначале мы имеем запись изображения набора аргументов
Г^^ ^1^"^^ *1^^ . Запишем последовательность слов,
получающихся при работе данного нормального алгоритма над словом
\'^^^\У ^V-^\ l^^^alMl\ P^^oll-^-^ar', P^^all>'-'al\
...X'^'aa\V-\ I'^^Wl^-, l-^^''aall^-'\..., Г^^--^>аа, i'^-^K
Итак, в результате работы нормального алгоритма над
изображением набора аргументов получилось слово из х + 2г +1
единиц, которое служит изображением числа x + 2z.
Значит, искомая функция имеет вид f(x,y,z) = x + 2Z'
2. Проверим работу алгоритма над изображением набора
аргументов (2,0,1): 1 ИИ* И, 111аИ1, 1И gg 1Л И11 gg. 11111.
В результате получено изображение числа 4.
Но /(2,0,1) = 2 +2-1 = 4. Так что нормальный алгоритм
получил то, что и должен был получить.
3.3. Рекурсивные функции
Числовой функцией называется функция вида f: Nl^ —^ Nq,
где Л^о={ОД'2,3,...}.
Исходными функциями называются числовые функции
следующих видов:
1) о(х) = 0 — нулевая функция;
2) s(x) = х + 1 — функция следования:
3) /^'(jcj, A'2,...,x,j) = Xj. — функция выбора аргумента.
7 Зак 3332
190 Глава 3
Cynepno3utfueu функций /i(X|,X2,...,x„), /2(Х|,л'2,...,а'„), ...,
fk(xi,X2,...,xJ, 8(У\,У2^-'^Ук) называется функция /i(a',,X2,...,x„) =
^(/lUb-^2---^/i)'/2(-^l-^2--^/Jv..,A(Ai,X2,...,X„)), причём h
определена только на тех наборах {а^,а2,...,а,^), на которых
определены /,(а,,й^2,-,«„), /2(«i,«2—«/zX— fd^x^^i^-^^n)'
^(/l(«b«2--«/iX/2(«b«2--«/i)-vA(«l>«2-->«n))-
Говорят, что числовая функция /(.Ti,A2,...,jc,j) получена из
числовых функций g(xi,A2,...,x,j_i), /z(a:i,X2,...,x,j,X/,+i) с помощью
примитивной рекурсии, если выполняются два условия;
1) /(x,,A2,...,A,,_,,0) = g(x,,X2,...,x,j_|);
2) /(Xl,X2,...,X^^_l,У + l) = /г(x,,A2,...,X,J_,,}^/Ul,X2,...,A-,,_,,y)).
Операция минимизации по / -той переменной функции
g(Ai,A2,...,A,^) обозначается |1^,(^(а,,А2,...,а'у_|,з^,а^+,,...,л',^) = а^) и
определяется так:
Рассмотрим соотношение ^(А|,а'2,...,А/_1,>',А/+1,.-.,а,,) = а,, (*)
которое будем рассматривать, как уравнение относительно у.
Это уравнение будем решать подбором, подставляя вместо v
последовательно числа 0,1,2, и т.д. Возможны случаи:
1) на некотором шаге левая часть соотношения (*) не
определена. В этом случае считаем, что на наборе (А],А2,...,а,^)
операция минимизации не определена.
2) На каждом шаге левая часть соотношения (*) определена,
но ни при каких у равенство не выполнится. В этом случае
также считаем, что на наборе (ai,A2,...,a,j) операция минимизации
не определена.
3) Левая часть соотношения (*) определена при
у = 0,у = \,..,, y = z-\,y = z, но при y<z равенство (*) не
выполнялось, а при у = Z оно выполняется. В этом случае число z
считается значением операции минимизации на наборе
(Ai,A2,...,A,j).
Примитивно-рекурсивной называется числовая функция,
которая может быть получена из исходных за конечное число ша-
Теория алгоритмов
191
гов с помощью применения операции суперпозиции и
примитивной рекурсии.
Частично-рекурсивной называется числовая функция, которая
может быть получена из исходных с помощью применения
конечного числа раз операций суперпозиции, примитивной
рекурсии и минимизации.
Задание 3.3.1
Найти функцию f(x,y), полученную из функций g(x) и
h(x,y,z) по схеме примитивной рекурсии.
Таблица 3.3.1
№
1
2
3
4
5
6
7
8
9
10
11
1 12
13
14
15
g{x)
х'
2
X
X
1
X
0
/
X
X
3
1
1
0
X
h(x,y,z)
XZ.
^х
x + y-z
x+ z
x{y + \)z
x-^z
у + г. +1
ifz-x'
zx
y^z
z>'''
Xy-hX
X
z
x^ + z
xyz + XZ
Xo
16
17
18
19
20
21
22
23
24
25
26
1 27
28
29
30
^W
X
X
2x
X
0
0
X
0
X
X
x'
0
0
1
0
li(x,y,z,)
z" 1
3x
z
2x+z
x-z
x + 2y
x + y + z
4z-x'~
\z-x\
x-\- у
zy-^z
3y + z
y^ + z
x+y' + z
z + 3v
x-y-\-z
192 Глава 3
Пример решения задания 3.3.1
Решить задание 3,3.1 для фуик1(ий:
g(x) = х^; 1г{х, V, z.) = (y + 2)xz.
Найдём несколько значений функции / •
f(x,0) = g{x) = x^'.
f{xX) = /z(jc,0,/(x,0)) = h(xfl,x^) = 2'X-x^ = 2x^\
fix,2) = h{xXf{xA))--h(xX2x^) = 3-x-2x^ =3\x'^',
f{x,3) = h(x,2,f(x,2)) = h(x,2,3\x'^) = 4'X-3\x'^=4\x\
Возникает предположение, что f(x,y) = {y-hl)\x^^ ; (1)
Докажем формулу (1) методом математической индукции,
проведя индукцию по у:
1) Проверка при у = 0.
f(x,0) = x^=(0-hl)\x^^^.
Да, при у = 0 формула (1) верна.
2) Допустим, что предложение (1) верно при у = п, т. е.
допустим, что верна формула f(x,n) = (n + l)\x"^^'', (2)
3) Докажем, что предложение (1) верно при у = п + 1, т. е.
докажем справедливость формулы f{x,n + l) = {п + 2)\х^^'^ (3)
Выразим f(x,n + l) с помощью схемы примитивной рекурсии:
f(x,n + l) = hix,n,f(x,n)) = h(x,nXn + l)\x"^^) =
= (п + 2)'Х'(п + 1)\х''^^={п + 2)\х''^^.
Итак, в предположении справедливости формулы (2) доказана
формула (3).
На основании метода математической индукции утверждаем,
что предложение (1) справедливо для всех У^ ^о-
Ответ: /(х,у) = {у + 1)\хУ''^.
Теория алгоритмов
193
Задание 3.3.2
Найти функции, получаемые из данной числовой функции
/(xi,X2,...,x,j) с помощью операции минимизации по каждой её
переменной.
Таблица 3.3.2
№
1
2
3
4
5
1 ^
1 '^
1 ^
1 ^
1 ^^
1 ^^
1 ^^
13
14
15
п
4
3
3
4
3
3
3
4
3
4
3
4
4
4
4
/Ui,.x:2,...,xJ
•^1'^2 "^ "^'з
2'' (2а-2 +1)
Xl(X2 + l)
-^3
^1-2x2
Х|^ + 3^2
2 1
JC|X2 + 1
JCj + ^2 - 2^3
^lfe-1)'
^,+—
■'^З
2(л-,-л-2)
A'l -Л'2Л'з
хГ-^х,
Х^{Х2-\)Х^
л/'^1 " •^2-^3
Хо 1
16 1
17 1
18
19
1 20
1 ^^
22
1 ^^
1 ^"^
1 ^^
26
1 ^"^
1 28
29
1 30
/г
4
3
3
4
3
4
4
3
4
3
4
3
4
3
4
/(Xl,A'2,...,JCj
2
}[х^+2фс2
Xi+log 2X2
i+-^'2-^3
З-^'+л/^
A'l + ^2 - 2а'з
-W Aj ~ A2 + A3
1
A2'^i
•^W-^2 ~-^3
V^-4^=
Зл-,-4
^3
iiAi + A-)
X\X2 - у A3
2
6AiA2+/gA-3
194 Глава 3
Пример решения задания 3.3.2
Решить задание 3.3.2 для функции f {х^,Хо,Х2,х^) = Х2 .
1) Минимизируем данную функцию по переменной х^.
у
Рассмотрим уравнение -^2 --^V (1)
а) Если ^2 = Xj, то при подстановке вместо у нуля получаем
верное равенство.
б) Если ^2 ^х,, ^3 ^1, то при подстановке в уравнение (1)
вместо 3^ единицы в левой части уравнения (1) появляется
неосмысленное выражение — дробь —, значит, в этом случае опера-
ция минимизации не определена.
в) Еслил:з=1, но Х2<х^, уравнение (1) примет вид
Это уравнение не может выполниться ни при каких уе Nq.
г) Если ^3 =1, но ^2 >Хр то при у = л*2 -х^ равенство (1)
выполнится.
[о, если Х2 =х^\
не определено, если х^ ^1, Xj^/^ х^
не определено, если х^ =1, Х2< х^
[Х2 - ^1, если Хз =1, ^2 - -^1 •
Итак, \i^
X.
2) Минимизируем данную функцию по переменной Х2-
Рассмотрим уравнение У = -^2 • (2)
^3
Если х, =0, а ^3 ^0, то уравнение (2) примет вид у = Х2 и
имеет решением число ^2.
Теория алгоритмов
195
Если X, Ф О, то на самом первом шаге, при подстановке
вместо у нуля, в левой части соотношения (2) возникает
отрицательное число, т. е. неосмысленное выражение.
г Х2, если Х| = О, х^'^О;
Итак, \Ху
у-
^1 _
'^2
не определено в остальных случаях.
3) Минимизируем данную функцию по переменной Х3.
Рассмотрим уравнение ^2 -^'з-
(3)
Это уравнение на самом первом шаге, при подстановке вместо
V нуля теряет смысл, значит, операция минимизации по третьей
переменной [i^,
у
нигде не определена.
4) Минимизируем данную функцию по переменной х^.
Рассмотрим уравнение ^2
--^ = х.
(4)
Если набор переменных таков, что левая часть соотношения
(4) имеет смысл и равенство (4) выполнено, то можно считать,
что оно выполнено при "подстановке" в соотношение (4)
переменной V на самом первом шаге, т. е. при у = 0.
В остальных случаях значение операции минимизации не
определено. Итак,
1^)
-^'1 _
Х2 - ^4
^3
О, если Х2 —- = х^\
не определено в остальных случаях.
Глава 4
Предикаты
4.1. Предикаты
Предикатом называется функция, область значений которой
включена во множество Е = {ОД}.
Предикат Р называется толсдественно истинным (толсде-
ственно лоэюным), если на всех наборах своих переменных он
принимает значение 1(0).
Предикат называется выполнимым, если на некотором наборе
своих переменных он принимает значение 1.
Предикатом \/ ^^P{xi,X2,...,x,j) называется предикат
T(x2,".,x,j), который принимает значение 1 на тех и только тех
наборах (а2,...,а,^), при которых предикат Р(х1,а2,...,а^^)
—тождественно истинный.
Предикатом З^^^Р(х^,Х2,...,х,^) называется предикат
/?(x2,...,x,J, который принимает значение 1 на тех и только тех
наборах {а2,...,а,^), при которых предикат P(jCi,flt2>---»«,i)
выполним.
Если предикат P(>',Xi,X2,...,x,j) таков, чтоуЕ {^^рЬз,...,^^.}, то
\/yP(y,X^,X2,...,xJ= P{b^,X^,X2,...,X,,)AP{b2,X^,X2,...,xjA...
...AP{b^,X^,X2,...,xJ.
ЗуР(у,Х^,Х2,...,Х,^)= P(fti,X,,X2,...,xJvP(Z?2,Xi,X2,...,xJv...
198
Глава 4
Теоремы об отрицании кванторов:
Для любого предиката Р{у,х^,...,х,^) справедливы формулы
V^P(>;,x,,X2,...,xJ = 3,,F(v..Vi,A-2,...,A'J.
Говорят, ЧТО предикатная формула находится в приведённой
форме, если в ней используются лишь операции квантификации,
отрицания, конъюнкции, дизъюнкции, причём отрицание
относится лишь к предикатным буквам.
Говорят, предикатная формула находится в предварённой
нормальной форме, если она имеет вид Д^^0,,^...0/^^ (Л), где D —
либо квантор общности, либо квантор существования, А —
формула, находящаяся в приведённой форме, не содержащая кванторов.
Задание 4.1.1
Построить п — местные предикаты на множестве М такие,
что выполнено условие а. (Л — множество всех людей)
Таблица 4. /. /
Хо
1
i ^
3
4
5
6
7
8
9
п
3
2
3
3
3
3
3
2
3
м
RxZxR
ZxA
ZxZxN
AxZxN
NxRxR
AxNxA
RxNxZ
RxR
ZxZxR
a
P(x,y,n) = \, P(1,v,zM-^g(V2-1,z) —выполним
P(0, >; j = 0, Р(х,у) -> -nQ(\,y) — выполним
Р(л-,-3,2; — выполним, P(x, у, z) ^ 6(2,1, г.) = 0
Р(л'Д.-:)=1, P(x.>',2)v-n(2UAz) —выполним
P(x,\,z ) = 0, -iP(x, у, z.) л б( 1, у, z) — выполним
P(x,y,z.) —выполним, P(x,20,z.)-^-nQix,20,z.) = 0
P(2,\,z.) = 0, P{x,y-\)<-^-nQ(nX2) —выполним
P{x,y) —выполним. -nP(x,^I2)-^Q(x,y) = 0
Д-1,2,г) = 1, /'(A',v,V3)->-.e(0,v,z) —выполним
Предикаты
199
Таблица 4,LI (окончание)
1 Хо
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/г
3
3
3
3
3
3
3
2
3
3
3
3
2
3
3
3
2
3
3
3
3
м
AxAxR^
NxZxN
AxNxN
RxNxN
RxRxN
AxRxN
RxRxZ
AxN
NxNxN
RxRxN
NxRxZ
RxRxA
RxR
RxNxR
AxAxA
ZxZxN
AxN
NxZxR
ZxZxN
AxAxZ
ZxNxR
a
P{x,y,3) —выполним, P(x,y,z)v-^Q{x,y^6) = \
P(2,v,rJ = l. -пб(1.у,3)->^(л:,-1,г) —выполним
P{x, у A) — выполним. P{x2, z) V -iQ(x, y,3) = 1
P(jc,3,4) = 0, -.P{x, v,2) ^ -^Qix,3, z) = \ 1
P(^|3-5,z) —выполним, P(x,y,2)л-nQix,^fЗ,z.) = \
Р(х,у,\9) = \, P{x,3,z.)-^Q{x,yJ) = 0 1
P{n,e,z) —выполним, -,P(jc,>;,-l) + g(jc,2,z) = 1
P{x,\ 80) = 0, P(x, v) V -.e(jc,20) — выполним
Р(2, у Л) — выполним, -пР(х, у, Z.) ^ G(2,3, z) = \
Р(х, у,3) = 1, Р{х, у, z) л Q{x, у,3) — выполним
Pix,0,z.) — выполним, Р(х, у-4) -> -^Qix,3, z) = 0
P{3,3,z) = 0, P(x,yf\9,z.)vQ{x,у,z)—выполним
P(10,>;) —выполним. -^P{x,y,) <-^Q(20,y) = l
Р(л/3,у,г.) = 1, Pix,y,z)-^Q{\,y,z.)-выполним
P(x, V, z.) — выполним, P(x, V, z) + Q(x, y,z) = \
P{x-3,2) = 0, P(x,)',z)V-.6(2,1,z)—выполним
Р(х,\0) = \, P(x,,v)v6(x,2) —выполним
P(x, y,S) — выполним, P{3A, z) V -iQix, y, z) = 0
P(9-9,z) = 0, -,P(l,v,z)->e(x,>',z)—выполним
P(x,y-2) —выполним. P(x,y,z)<r^-nQ(x,y,z) = \
P{6,y,z.) = \, P{x,2,z.)AQ{x,y,3) —выполним
200 Глава 4
Пример решения задания 4.1.1
Построить трёхместные предикаты Р и 2 на множестве
NxNxZ такие, что Р(1,у-3) — выполним, и
Пусть Р(х, у,г):(д: + 2у-г кратно 4);
Q(x,y,z)'.(x + y-h z-^5 — нечётное число).
Тогда Р(1, у-3) = Т(у) :(2у + 4 кратно 4).
Г(1) = (2 + 4 кратно 4) = 0; Г(1) = (4 + 4 кратно 4) = 1.
Значит, Т(у) = Р{1,у,-3) —выполнимый предикат.
Обозначим S{x, у, z) = Р(х, у, z) -^ QU,1, z).
Покажем, что S(x, y,z) = 0.
Предикат S(x,y,z) может принять значение 1 лишь на таком
наборе (а,Ь,с), при котором Р(а,Ь,с) = 1 и Q(a,l,c) =0, т. е.
а + 2Ь-с кратно 4 и а + 1 + с + 5 —нечётное число.
Запишем эти высказывания в равносильной форме:
\а + 2Ь-с = Am
\ , где m,/iG Z.
[а + \ + с + 5 = 1п-\
Но тогда, складывая уравнения этой системы, получим:
2а + 26 + 6 = 4т + 2п -1, или Am + 2/2 -2a-2b-l, откуда
2{2m-\-n-a-b)-l. В левой части этого равенства стоит чётное
число, а в правой — нечётное. Значит, ни при каких значениях
переменных x,y,z предикат S{x,y,z) не может принимать
значения I, следовательно, S'(x,y,z) = P(x,y,z)—>Q(jc,1,z) = 0.
Задание 4.1.2
Выяснить местность и тип предиката, каждый аргумент
которого принимает значения из множества М.
Предикаты
201
Таблица 4.1.2
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
М
Z
/?
iV
/?
iV
z
/?
iV
/?
z
R
N
R
Z
N
P 1
V,Cy + .v-z>2)
3^\/^Xxy = z-x)
\/^3^X-'cyz = yz)
V^V^>V^)
3,3,{zx = y^)
V,3,(A'Z = ^)
3,V,Cv + 2^>)^+z) 1
V^(x^ + M>0)
УДДл'- + г'>2и+у)')
V^.V,(a' + .v + z>V^)
3,(a43^z = 7)
V^.V^xz = .y')
V,3,(yx+vz<0)
3^,(>; + z>x + 2v)
V^(x" -y" > A+z)
№
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
M
R
Z
N
z
R
Z
N
R
Z
R
N
Z
R
N
Z
P 1
3y\f^{yx- =3yA+z)
3,V/2y + x>A:+z^-)
V^A-2y<z-y)
V,3,(A+y + z = 5) 1
3,V/xy-2A^-z>0)
V,3,Uy = xz) 1
3,\f^{xy-zx<0) 1
3..(av + z" >2ау)
V^.(xz = y)
V,3,(xz-/-z>0)
3^(y + AZ = 4)
V,3,(.v^- + yz>0)
3y(yx-xyz>0)
V,3,(^>V)
3^.{xz + yx = \)
Пример решения задания 4.1.2
Выяснить местность и тип предиката Р = \/^З^Х^У = х ),
каждый аргумент которого принимает значения из множества Z.
Из определения операции навешивания кванторов следует, что
предикат Р зависит от переменной z.
202
Глава 4
Так как предикат у-0 = 1 не является выполнимым,
следовательно, высказывание 3^(>'0 = 1) ложно. Значит, предикат
^у{У'^-^) не является тождественно истинным предикатом
относительно X, следовательно, высказывание V^.3^,(у-О = х)
ложно, то есть Р(0) = 0.
Для произвольного Xq предикат относительно у з^-1 = л:о
выполним (приу = Хо ), значит, высказывание 3^{у Л = Xq)
истинно. Следовательно, в виду произвольности х^, имеем, что
предикат Зу{уЛ = х ) — тождественно-истинный. Но тогда вы-
сказывание ^^^{у Л = х ) истинно, то есть Р(1) = 1.
Так как Р(0) = О, а Р(1) = 1, P{z) — выполнимый предикат.
Задание 4.1.3
Найти значение высказывания а, полученного из
трёхместного предиката, определённого на множестве М.
Таблица 4,1,3
№
1
2
3
4
5
6
7
М
Z
R
N
R
N
Z
R
Р
\f,{x-^y-z>2)
3\f y{xy = z-x)
\f^3y{xyz^yz)
\/-i^Jxyz. > 4x)
3,3 y(zx = y^)
\/,3yixz = y)
3y\/,{x + 2y>y + z)
№
8
9
10
11
12
13
14
M
N
R
Z
R
N
R
Z
P
V^.r+|jcyz|>0)
У,Зу(х'+г'>2{х + уУ-)
\/,\/y{x-\-y + z>^Jxyz.)
3^(x-+3yz=l)
V,V,(xz=v^-)
\/,3.(yx+yz<0)
3yiy + z>x + 2y)
Предикаты
203
Таблица 4.1.3 (окончание)
№
15
16
17
18
19
20
21
22
М
N
R
Z
N
Z
R
Z
N
Р
\f ^{х' -у- >x^z)
З^М ^{ух- =Ъух-^7)
3\f^X2y^x>x-^z')
\f^Xx-2y<z-y)
V,3,(A'+y + z = 5)
3^V,(a7-2a--z>0)
\/д.Э.. {xy = xz)
3,y^{xy-zx<0)
№
23
24
25
26
27
28
29
30
M
R
Z
/?
iV
z
/?
iV
z
p
3-^{xy + z~ >2xy)
\J,3^xz = y)
V,3,(Az-rz>0)
3,(>' + AZ = 4)
V,.3_Cr + vz>0)
3y{yx-xyz>0)
УД_(г.>х/)
3,(aZ+ VA=I)
Пример решения задания 4.1.3
Найти значение высказывания ЗуМ^3^{х-z^ >у),
определённого на множестве R.
3,V,3,(x-z^>y) = 0 <^
<=» предикат относительно у \/^3^{x-z ^у) не выполним <=»
<=» для произвольного >'о высказывание \/^3.{х- z^ > у^ )ложно <=>
<=» для произвольного >'о предикат 3^{x-z ^Уо) —не является
тождественно-истинным относительно х <=>
<=> для произвольного Vq высказывание 3^(y^-l-z > Уо)
ложно <=> З.(г <-1) = 0 <=> предикат z <-1 не является
выполнимым.
А он действительно не является выполнимым, т. к. любое
действительное число в чётной степени не может быть меньше, чем -1.
Итак, получено, что исходное высказывание ложно.
204
Глава 4
Задание 4.1.4
Предикаты Р и б определены на множестве {а,Ь,с].
1. Найти предикат, равносильный предикату R, но не
содержащий кванторов.
2. Выяснить, может ли предикат R быть выполнимым, но не
тождественно истинным.
Таблица 4.1.4
№
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/?
\/,\/„P{x,y)^3^,Q{y.z) 1
v,33,pu>')^33.v,eu^,z) 1
3,V^.P(>;,z)AV,eUv)
V^(P(x,>^)aQ(>',z))
3,P(A',>^)vV,3,G(>',z)
V,3,P(x,.y) + G(x,z) 1
3,P(:c,z)->V,.33.e(^.x) 1
3y^XP(x.z)vQ(y,x))
y,3,P{y,x)^Q{x,z.)
V_P(jc,z)v3,V,e(.v,z)
3^P(x,z)a3,V^G(^,>;)
y,3yP{x,y)^3,Q(x,z)
3yy,Pix,y)vy^Q(x,z)
\3,3,P(x,y)^y,Q{x,z)
\y,P(x,z)A3,3,Q(x,y)
Xo
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
R
3,v,p(x,^)+v^_e(z,A-)
V,P(y,z)->3,V,2(>;,z) 1
3,v,P(x,^)vV^_2Uz) 1
3,V,(P(x.z)AV,e(.v,z))
y,P(x,y)v3,y,Q{x,z.) 1
V3,PUz)->3,e(A',^)
3,P(A.v) + V,3,e(^,z)
V^.P(A,v)v3^_e(x,z) 1
3,P(.v,z)A3,V^,eU.v)
y,3,P(x,y)v3,Q(y,z)
y,P{x,y)^y3yQ(y,z)
3,Pix,z.)-^3,^yQ{x,y)
y,^^P(y,z.)vy^Q(x,z)
V,P(v,z)aV,3,2(a-,z)
3,3/(^,z)^V,e(y,z)
Предикаты
205
Пример решения задания 4.1.4
Решим задание 4.1.4 для предиката Уy3^P(z,y) + 'B^Q(x,y).
По свойствам предикатов, определённых на конечных
множествах, имеем:
V^P(z,y) + 3,eUy) =
= 3yP{a,y)A3yP(b,y)A3yP(c,y) +
+ 3,GU,v) =
iPia,a)v P(a,b)v P(a,c))A(P{b,a)v P(b,b)v P(b,c))A
A (Pic a) V P(c, b) V P(c, c)) + (Q{a,y) v Q(b,y) v Q(c,y)),
Пусть P(z,y) — тождественно-ложный предикат. Тогда
высказывание ложно, так как конъюнкция и дизъюнкция ложных
высказываний ложна, и выражение: \/ y3.P(z.y) + 3^Q(x,y)
равносильно выражению 3^Q(x,y).
Если положить Q(a,a) = Q(a,b) = Q(a,c) = 0 и Q(b,a) = l, то
/?(fl) = 0 + (OvOvO) = 0; /?(b) = 0 + (lv...) = l.
Итак, предикат R(y) может быть выполнимым, но не
тождественно истинным.
Задание 4.1.5
1. Представить в приведённой форме предикат D варианта №.
2. Представить в предварённой нормальной форме предикат
D варианта № + 1.
Таблица 4,1,5
Хо
1
2
3
D 1
\/,P{x,y,z.)-^i3^,\/^Q{x,y,t)\R(x,y))
{3,3yR{y,x,z)vT{x,y))iy,Pix,y,z.)
(y^3J{x^y)^ Rix^z)) \З^Р(х,у)
206
1 Xo
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Таблица 4.1.
Глава 4
5 (продолэюение)
D 1
{3yyP{y,z,t)\R{x,y,z))A3J{x,yj) 1
(V^V/U3;,0>t3,.PU,v))|/?U,v,z)
(З^Р(л', >;, z) i V,3,/?( V,z,/)) л Т(х, у)
\^yRix,y,t)-^3y^P{x,y,z)vT{x,y)
{y,3yP(x,zJ)\y,R(x,y,z))\T{x,y)
(3,y,Pix,y,z)iyj{x,yj))vR{y,z)
(V,V,/?U.v,z)|3,5(x,^))-^P(y,z)
(3,V,P(.v,y,z)i3,/?Cv.>',r))|r(.v,z)
V^3^PU,v,r)A3,3,r(x,y.r)<-^V,/?(A:,r)
(3,P(x,);) 1 y^3^Mx,y.z))vyyjix,y)
i\/^3yR{x,y.z)i\/y-Tix,y,z))vP{y,z.)
3,^fyP(z,x,y)-^{3^R{x.t,z)\T(x,y))
(V,V,P(x, z) i 3.R{x. y, z)) л T{x, z)
(3,V,/?(A',y.r) |3,P(x,)4z))vr(y.z)
V,3,./?(jc.r) -> 3.P{x,z) л V ,Т(л-,у)
(3,V^.P(>;,A,r)|eUy.z))->V,rCv,y)
(V,3,PUy.z)|rUr))|V,/?Cv.y)
{3,УуР{х,у,г) -> 3,Г(л'.>-)) -> /?(л-,г)
(y,yyP{x,y,t)\3,nx,y))vQ(x,y,z)
Предикаты
1 Хо
23
24
25
26
27
28
29
30
Таблица
207
4.1.5 (окончание)
D 1
(P(^,);,z)| УДТ(х,);,0)лУ,/?и,^) 1
{V,3, Р{х, y,z)iy ,Q{x, у, z)) -^ 3,Г(х, Z)
i3,yyP{x,y,z)v3,Q(x,y,t))\Six,y,z) 1
3,,/?U>;.z)A(V,V^_e(^,z,r)iP(z.x,^))
V,3,PU,v,z)->(/?U^,r)|3,V^.rUz.^))
3,P(x,>;,z) -> 3,V^e(r,v,z)v /?(x, v,r)
3,V,P(x,y,r)Ar(>',z,r)->V,.V^_GUv,r)
3,P(x.z.v)v(V,3,eU^,r)|/?Uv))
Пример решения задания 4.1.5
1. Представить в приведённой форме предикат
\f3,P{x^y^z)^R{y,z).
Воспользуемся формулой a<-^b = a-bvа-Ь.
\/3,P{x,y,z)^R{y^) =
V 3., Дх, V, Z) • R{y. z) V V 3,PU, у, z) • /?(};, z).
Воспользуемся теоремами об отрицании кванторов. Получим:
3.V^.P(x,y,z)-/?Cv,z)vV_3^P(x,y,z)-/?Cy,z). Так как кроме
кванторов, символов конъюнкции, дизъюнкции и отрицания
в формуле не используются другие символы предикатных
операций, а отрицание относится лишь к предикатным буквам,
приведённая форма получена.
2. Представить в предварённой нормальной форме предикат
3^P(x,y,z)-^y,3,R(x,y,z) i Т{х, г).
Воспользуемся формулами а —> b = av Ь, aib-a-b и а = а.
208 Глава 4
Получим: З^Р(х, у, z) -^ V ,3,./?(x, v, г) i Т{х, z) =
= 3,Р(х, у. Z) -^ V ,3 ,Я{х, у. Z) ■ Т{х. z) ■
= (a,FU, у, z) -^ V,3,, R(x, у, z)) ■ Т(х, z)
- (3,Р{х, y.z)v V.,3,/?(x, у. z)) ■ Т{х, z).
Переобозначим переменные:
(3. Р(х, ,y,z)v УЧ Rix,, у,, Z)) ■ Пх, Z) =
= (V,,, Р(х,, у,Z) V V ,^3,. Р(Х2, .V,, г)) • Т(х,z).
Теперь можно вынести все кванторы в начало формулы:
V,, V,^3^, {{Р(х,, у, Z) V V, R(x,, у,, г)) • Т{х, z)).
Предварённая нормальная форма получена.
Задание 4.1.6
1. Записать с помощью кванторов высказывание а.
2. Составить высказывание "не а".
3. Привести пример доказательства на основании
высказывания "не а".
Хо
1
2
3
4
5
6
7
Таблица 4,1.6
а
функция f{x) непрерывна на (а,Ь)
числовая последовательность {а,^} имеет пределом -о©
функция f(x) равномерно непрерывна на (а,Ь)
функция f(x) дифференцируема в точке xq
функция f(x) ограничена на R
векторы линейного векторного пространства линейно зависимы
функция f{x) непрерывна в точке л^
Предикаты 209
Таблица 4.L6 (окончание)
Ха
числовой ряд с общим членом а^^ сходится к сумме S
функциональная последовательность /,Дл") сходится поточечно к /(л)
на {а,Ь)
10
функциональная последовательность /„(.v) сходится равномерно к
f(x) на {а,Ь)
11
функция /(л) стремится к -оо при .v—>+оо
12
числовая последовательность {а,,} ограничена сверху
13
функция /(л) монотонна на [а,Ь\
14
точка xq является точкой минимума функции /(х)
15
бинарное отношение ф является связным
16
числовая последовательность [а,^] фундаментальна
17
функция f{x) непрерывна хотя бы в одной точке интервала {а,Ь)
18
функция /(х) стремится к числу а при jc—>-
19
функция достигает наибольшего значения на отрезке в точке Xq
20
бинарное отношение ф является антисимметричным
21
функция /(л) разрывна хотя бы в одной точке интервала {а,Ь)
11
функция /(л') имеет в точке х^ конечный скачок
23
булева функция /(.Yj,jct,...,x^,) монотонна и сохраняет О
24
множество А является собственным подмножеством В
25
булева функция /(a'j,a'9,...,x„) является двойственной к функции
26
функция f{x) имеет на отрезке [а,Ь] конечное число точек разрыва
27
число siipX является точной верхней гранью числового множества X
28
функция /(х) имеет в точке aq бесконечный скачок
29
график R является композицией графиков Р w Q
30
множества А w В находятся в общем положении
210 Глава 4
Пример решения задания 4.1.6
Решим задание 4.1.6 для высказывания а: числовая
последовательность {a,j} является бесконечно малой.
1. Запишем данное определение а с помощью кванторов,
представив предикатную формулу в предварённой нормальной
форме:
VgByv\/,Д8>0-^(п> N -^\a,j \<г)).
2. Возьмём отрицание от этого определения, применив
формулу а —> b = а-Ь, а также теоремы об отрицании кванторов:
= ЗеЗуу V„(8 > О -> (уг > /V -^1 а,^ \< г)) =
= 3,V^3,(8>0-^(/i>/V-^|flJ<8)) =
= З^УууЗ,^ (8 > о л п > yV -^1 а,^ \< 8) =
= З^У дгЗ,^ (8 > О л п > Л^ л] a,j |< 8) =
= 3gVдгЗ,^ (8 > О л /1 > Л^Л I (2,J> 8).
Отрицание от а получено, то есть получено определение того,
что числовая последовательность {^t,, }не является бесконечно
малой.
3. Докажем на основании полученного определения, что
числовая последовательность с общим членом а^^ =( — 1)" -п не
является бесконечно малой.
Действительно, существует 8 = 0,5, причём для любого Л^
найдётся п = N + 1. Очевидно, п > N.
Тогда|а„|Н(-1)"-п'И«'^0'5.
Доказательство закончено.
Глава 5
Комбинаторика
5.1. Сочетания, размещения,
перестановки
Пусть имеется п предметов, отмеченных числами 1,2,...,/i.
Из этих предметов выбираем один, записываем число, на нём
изображённое, а сам предмет либо возвращаем назад (в этом
случае говорят о выборе с возвращением), либо он убирается
и больше не может быть выбран (в этом случае говорят о выборе
без возвращения). Повторяем эту процедуру к раз.
Запись, полученная в результате всех действий, называется
выборкой из /2 элементов по к.
Запись, полученная по схеме выбора с возвращением,
называется выборкой с повторениями, а запись, полученная по схеме
выбора без возвращений, называется выборкой без повторений.
Если две выборки, отличающиеся только порядком записи
символов, считают различными, то говорят о размещении из п
элементов по к.
Если две выборки, отличающиеся только порядком записи
символов, считают совпадающими, то говорят о сочетании из п
элементов по к.
—к
Через An обозначают число различных размещений с
повторениями из п элементов по к.
An =п
212_ Глава 5
Через A,j обозначают число различных размещений без
повторений из п элементов по к.
к "'
А -•
{п-к)\
1ИСЛ0
рений из п элементов по к
Через С,1 обозначают число различных сочетаний без повто-
к\{п-к)\
Через Сп обозначают число различных сочетаний с
повторениями из п элементов по к.
Размещение из п элементов по п называется перестановкой
п элементов. Число различных перестановок п элементов
обозначают Р,^.
Пусть имеется к^ элементов 1-го типа, к2 элементов 2-го
типа,..., А:,,^ элементов m-vo типа, причём элементы одного типа
считаем неразличимыми. Тогда мы будем говорить, что у нас
имеются перестановки с повторениями, и количество таких
перестановок выражается числом.
(/:,+/:2+...-f/:,J!
P(k,^2^„.,kJ=-
L^-kJ- -к '
Задание 5.1.1
Сколькими способами из колоды карт в 36 листов можно
выбрать неупорядоченный набор из 5 карт так, чтобы в этом наборе
было бы точно:
Комбинаторика
213
Таблица 5,1.1
1 ^- 1
1
2
3
4
5
6
1 "^
1 ^
9
10
И
1 ^^
13
14
15
1 ^^
1 ^"^
18
19
20
21
22
23
24
25
26
27
28
29
1 30
Условия
1 король, 2 дамы, 1 пиковая карта
1 крестовая карта. 2 дамы, нет червей
хотя бы 4 крестовые карты, 1 туз
3 ламы, 2 крестовые карты
1 бубновая карта, 2 кресговых, 1 дама
2 бубновые, 2 крестовые карты, 1 т\'з
по крайней мере 4 пиковые карты, 1 дама
2 карты чёрной масти, 2 дамы
1 туз, 1 валет, 1 карта красной масти
3 туза, 3 карты чёрной масти
1 дама, 1 карта пик, 2 крестовых карты
2 дамы, 2 туза, 1 карта пиковой масти
дама и король одной масти, 1 пиковая карта
1 король, 2 дамы, 1 карта красной масти
не меньше 4 красных карт. 2 туза
2 чёрных карты, 1 карта червей, 1 туз
3 короля, 2 бубновых карты
1 король, 1 дама. 1 крестовая карта
2 крестовых карты, 1 бубновая, 1 дама
1 бубновая карта, 2 дамы, нет червей
3 бубновых карты, 2 дамы, 1 валет
2 туза, не меньше 3 пиковых карт
2 карты красной масти. 3 туза
2 дамы, 1 бубновая карта, 1 пиковая карта
1 валет, нет дам, 3 черные карты
2 туза, по крайней мере 4 красные карты
валет и дама черной масти, не более 1 туза
1 туз, 3 дамы, не больше 2 карт красной масти
2 крестовые карты, хотя бы 2 туза
2 дамы, 1 король, нет червей
214 Глава 5
Пример решения задания 5.1.1
Сколькими способами из колоды карт в 36 листов моэюю
выбрать неупорядоченный набор из 5 карт так, чтобы в этом
наборе было бы точно два туза, одна дама, одна бубновая карта.
Рассмотрим случаи:
1. Среди пяти выбранных карт есть бубновая дама.
Бубновую даму можно выбрать единственным способом, два
туза будут выбираться из трёх, т. к. бубновый туз не может быть
выбран, и число способов выбора двух тузов равно С^ = 3, к
выбранным трём картам надо добавить до пяти ещё две карты так,
чтобы они не были дамами, тузами и бубновыми картами.
Таких карт в колоде 21 штука. Число неупорядоченных выбо-
21! 21-20
рок из 21 по 2 без повторений равно С^, = —- = 210.
По правилу произведения, число способов выбора 5 карт, среди
которых есть бубновая дама, равно 1 • 3 • 210 = 630.
2. Среди пяти выбранных карт есть бубновый туз.
Бубнового туза можно выбрать единственным способом,
второго туза к нему можно добавить тремя способами, выберем
любую даму из трёх, т. к. бубновую даму выбирать не имеем права,
этот выбор может быть сделан тремя способами, к выбранным
трём картам надо добавить до пяти ещё две карты так, чтобы они
не были дамами, тузами и бубновыми картами. Число способов
выбора этих двух карт, как уже рассматривалось раньше, равно
210. По правилу произведения, число способов выбора 5 карт,
среди которых есть бубновый туз, равно 1 • 3 • 3 • 210 = 1890.
3. Среди пяти выбранных карт нет бубнового туза и бубновой
дамы.
Выбираем одну даму из трёх (три способа), два туза из трёх
(Сз =3 способа), одну бубновую карту, не являющуюся тузом
или дамой (семь способов) и одну карту, не являющуюся тузом,
дамой или бубновой картой (21 способ). Число комбинаций
равно 3 •3.7-21 = 1323.
Комбинаторика
215
Общее число способов выбора 5 карт, удовлетворяющих
требованиям задачи, по правилу суммы, составит 630 + 1890 +
+ 1323 = 3843.
Ответ: 3843 способа.
Задание 5.1.2
Сколько различных слов можно получить перестановкой букв
слова а?
Таблица 5.1.2
Хо
1
2
3
4
5
6
1 "^
8
9
10
1 ^^
1 ^^
1 ^^
14
1 ^^
1 ^^
а
атаман
ворон
интернирование
взбрыкнул
пастух
околоток
криминал
переходим
перешеек
диктатура
катастрофа
танкетка
комитет
парламент
диссидент
полумера
Условие
согласные идут в алфавитном порядке, но буквы "«'
не стоят рядом
две буквы "о" не стоят рядом
согласные и гласные чередуются, гласные идут в
алфавитном порядке
между двумя гласными находятся 3 согласные
между двумя гласными расположены 2 согласные
ровно 3 буквы ^'о" не идут подряд
пятое и седьмое места заняты согласными
согласные и гласные чередуются
четыре буквы "е" не идут подряд
как гласные, так и согласные идут в алфавитном
порядке
не меняется порядок согласных букв
запрещено буквосочетание "а«ш"
гласные не стоят рядом и разделяются буквами "т"
согласные идут в алфавитном порядке, гласные —
в порядке, обратном алфавитному
гласные чередуются с парами согласных
не встречается буквосочетание '"мурло''
216
Глава 5
Таблица 5.L2 (окончание)
1 Хо
17
1 ^^
1 ^^
1 20
1 ^^
1 22
1 ^-^
1 ^"^
1 ^^
1 26
27
1 28
1 29
1 30
а
министр
передел
приватизация
салага
президент
кишмиш
полномочия
логарифм
ультиматум
переворот
капитуляция
легитимность
белиберда
коммунизм
Условие
нельзя сказать, что согласные ил>т в а^афавитном
порядке
в начале и в конце слова стоит согласная буква
чередуются пары гласных и согласных букв
буква '*д" идёт непосредственно после "с"
согласные ид>т в алфавитном порядке
одинаковые буквы не ид>т друг за другом
никакие гласные не стоят рядом
второе, четвёртое и шестое места заняты согласными
между буквами '*т*' стоят все гласные и только они
не больше одной пары одинаковых букв стоят рядом
слово начинается с буквы "а", чередуются гласные и
согласные буквы
не присутствуют буквосочетания ^'ггимн" и ''тост''
между буквами "б" стоит блок из четырёх гласных
не встречается сочетание букв "мукгГ
Пример решения задания 5.1.2
Сколько различных слов моэ/сио получить перестановкой букв
слова огород так, чтобы три буквы "о " не стоячи бы рядом?
Общее количество различных слов, полученных
перестановкой букв слова огород, равно
Р(3,Ш) = <1±1±112)1Л = 6^5.4 = 120.
ЗМММ! 3!
Если в каком-то слове все три буквы "о" стоят рядом, то
тройную "о" можно считать единым символом, и количество слов,
в которых три буквы "о" стоят рядом, равно Р(4) = 4! =24.
В итоге получаем: 120 - 24 = 96.
Ответ: 96 слов.
Комбинаторика
217
5.2. Бином Ньютона
и полиномиальная формула
Некоторые свойства биномиальных коэффициентов:
1)С:=С:=1; С:^СГ=п;
3) С,^ = С^_, + C^J — свойство арифметического треуголъни-
своиство симметричности;
-1
ка\
с:+с:+с1+...+с:=2" \
4) ^ , ^ > — Свойства сумм.
c:-ci+c!,-...+i-iyc:=o\
Справедлива формула бинома Ньютона:
п
Справедлива также полиномиальная формула:
IciENq k,„ENQ
А-,+...+А' =/г
P{k^,k2,.'.,kni) = —\ ;—f— — полиномиальные коэф-
к,Щ\:..-к„:.
фициенты.
Задание 5.2.1
Найти наибольший член разложения бинома {а + 6)".
Таблица 5.2. J
№
1
2
а
лД
лД
b
3
10
п
17
17
№
3
4
flt
лД
3
b
2
7б
п
13
12
1 №
5
6
flt
V^
3
ь
3
Vio
'^
15
19
218
Глава 5
Хо
7
8
9
10
11
12
13
14
а
ViT
3
V8
4
Vi^
4
V7
3
b
4
лД2
3
2^3
3
Vi3
2,5
л/з
п
14
13
12
И
13
10
21
18
№
15
16
17
18
19
20
21
22
а
>Д
2,2
V6
3,5
Vio
3,2
Vio
2.8
b
3
V7
2,5
VFT
3,3
#
2,8
V7
Таблица
и
10
13
11
10
13
9
15
19
Xo
23
24
25
26
27
28
29
30
5.2.7 (окончание)
a
V3
2,8
V7
2,3
V7
3.5
V^
3,2
b
1,9
V6
2,5
#
2,7
^Гз
2,3
Vio
л
18
17
16
20
18
15
17
20
Пример решения задания 5.2.1
Найти наибольший член разлолсеиия бииома (1 +
Пусть Т/. — наибольший член разложения бинома
(l + ^/3)'«', r,=cfoo-l"'""*-(V3/'- Тогда 7,>7;_, и П>Т,^,.
„ fc*oo-(V3)*>c*o^'-(V3)*-"'
Получаем систему неравенств: J '"" '""
\c'-(s/bf>c:^-i^r,
или
100!
к\{100-ку.
100!
А:!(100-А:)!
■фу
100!
(А;-1)!(101-А:)!
■iSf
>•
100!
(A: + 1)!(99-Jt)!
•(ТзГ
Комбинаторика
219
После сокращений имеем:
Тз
1
101-А:
1 Vi
>
или
\(101-к)у/з>к
l)t + l>(100-)t)V3'
откуда
100-/: к + 1
\к(1 + у1з)<101у[з
к(1 + у1з)>100у[з-1
получаем
^ looVs-i , loiVs ^
двойное неравенство для к : р— < к < j=r. Подставляя
1 + V3 1 + V3
приближённое значение v3 = 1,732, получим: 63,135<к<64,64
Единственное целое значение к, удовлетворяющее этому
двойному неравенству, равно 64.
Следовательно, наибольший член разложения бинома имеет
номер к, равный 64 и 7^4 = cfoo • l'^^^^ *(V3)^^ = ■
100! 3З2
64I-36!
Ответ: ^3
64I-36!
Задание 5.2.2
Из данной пропорции найти х иу.
Хо
1
2
3
4
5
Пропорция
С>;^^:СУ:СУ-^ =3:3:2 1
С^^^:СУ^^: СУ =42:35:20
/^v+l./^y ./^у-1_д.с.д
Таблица 5.2.2
№
6
7
8
9
10
Пропорция
C>"'':Cj':Cr*=21:14:6
Cr':Cf':Ci'=3:5:5
/-У+2 . >r.y+l . ^у _9.д.с
С>'''':С;:СГ'=14:8:3
220
Глава 5
Таблица 5.2.2 (окончание)
Хо
11
12
13
14
15
16
17
18
19
20
Пропорция
СУ^':С^^^:СУ =5:3:1
СУ^{:СУ^1:СУ^^=5:6:5
^л+1 -^.v+l -^x+l -^■'*- ' -^
Cf':C^':C>'"' =6:14:21
С;;.^^:С^^^:СУ, =24:9:2
С^:ПСу:1:СУ,, =2S:\2:3
Су:1:СУ,,:СУ-1 =6:3:1
СУ^^:СУ:СУ~^ =12:45:20
СУ^^:СУ^^:СУ=\4:\0:5
Су:^:С>;:1:СУ,,=28:24:\5
№
21
22
23
24
25
26
27
28
29
30
Пропорция
^л-+1 -^.v+l •^-л+1 - l*^--^-^
СУ^^:СУ:СУ~^ =\5:24:2Я
СУ^":СУ^^:СУ =1:1:5
Су:^:Су:1:С:,,=6:1:6
С:::1:СУ,,:СУ:1 =5:5:3
СУ^^:СУ:СУ-^ =\:1:2\
СУ^':СУ^^:СУ =42:35:20
Су:^:С;::1 :С1,=45:20:6
Су:1:СУ,,:СУ;1 =55:22:6
\сУ^^:СУ:СУ-^ =3:4:3
Пример решения задания 5.2.2
Из данной пропорции С^'^ : С ^ : С ^~ =2:2:1
найти X и у.
Записав отдельно отношение первого члена пропорции ко
второму и второго к третьему, после сокращения получим:
XI
г!
х- у
{у + 1)\(х-у-1)\ у\(х-у)\ y + l
х\ х\ X - V + I
уКх-у)\ (у-1)\{х- у + 1)\
Комбинаторика
221
В силу условия задачи мы приходим к системе:
Решив её, получим: х = 5, у = 2.
Ответ:
у = 2.
х- у
1
У + 1
X - у + I
= 2.
Задание 5.2.3
Вычислить данные суммы.
Хо
1
2
3
4
5
6
7
8
1 ^
1 ^^
11
Таблица 5.2.3
Сумма
С,',+2С„ЧЗС,^+...+ «С 1
4С„Ч 7С,^ + lOC,t +... + (3/i - 2)С
c; + 2c3+3c,t+...+(/,-i)c: 1
C«+3Ci+5C; + ...+ (2«-l)Cr'
-2с,',+зс,7-4с„Ч...+(-1)"(«+1)с;;
с,',-2С„- + ЗС,^-... + (-!)"-'„с
3C'+5C,;+7C,^+... + (2«-l)C,r'
2С,',+7С„- + 12С,^+... + (5/г-3)С;;
ЗС," „ + 7С^^, +1 ICl^ +... + (4/, - 1)С:„
5С°+8С,'+11С;+... + (3/.-1)С:-'
Ci^i+2C„\,+3C,^„+... + (« + l)C:,'
8 Зак. 3332
222
Глава 5
Таблица 5.2,3 (окончание)
1 №
12
1 ^^
1 ^"^
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Сумма
cix+2ci,+3c^,,,+...+nc:::i |
С-2с,',.,+зс,?.,-...+(-!)"-'<;:,' 1
С,^ -ЗС1+5С^, -...+ Ы)"(2п-3)С::
С,'+5С,;+9С,^+... + (4,1-3)С;
4С,?+, + 7С„^, + 10С„^, +... + (3« + ос:? 1
зс1, + 5с1, + 1с1, +...+{111 + з)с;;,'
cl.^ - 2с,:„ + зс1, -...+(-1)" (/I+1)с;;:'
5С + 8с,',„+1 ici, +...+(ЗУ,+2)с;;;,'
C'.i -ЗС,^., +5С -... + (-1)-'(2/,- 1)С:'
2с^.,+зс,].,+<.,+...+(«-1)с;;:,'
2с'_, + 7с,^, +12с„з_, +...+(5/. - 8)с;:,'
C;?.,+2C,^.,+3Ci+... + („-2)C::,'
ЗС1, - 4С„\, + 5С,^, -... + (-1)" (,«+ 2)C"„:l
4С,? - 7С1 +1 ОС* -... + (-1)" (Зп - 2)С
5с„^,+9с1^+1 зС +...+(4п+1)с;;:,'
3Ci -7С^ + 11С^-...+ (-!)"-'(4/1-1)С;
с„^-2с>зс*-...+(-1)"(«-1)с;;
2с„Чзс,^+4с*+...+(«-ос;-'
2С,^ + 7С„^ + 12С* + ... + (5;г -8)С;,'
Комбинаторика 223
Пример 1 решения задания 5.2.3
Вычислить сумму
Cli + ЗС,?+2 + 5С,^+2 + - + (2п + 3)С:| (п > -1).
Обозначим искомую сумму через 5. Тогда
S -1 = -1 • С + С1, + ЗС + 5С1, +... + (2п + 3)С,^. (*)
Учитывая свойство С^ =С"~\ можем переписать (*) в виде:
5 -1 - (2п + 3)С + (2п + 1)С1, +... + d - с::',. (**)
Сложив равенства (*) и (**), получим:
25-2 = (2п + 2)С^+2 +
+ (2п + 2)С;,^2 + ••• + (2п + 2)С1 + (2n + 2)0^,
откуда 2(5 -1) = (2п + 2)(С°+2 + ^,',+2 + - + С+2 )• Разделим
обе части равенства на 2 и используем свойство
С°+с',+... + С,"; = 2"'. Получим: S-1 = {п + 1)-2"*\ откуда
5=(n + l)-2"+4l.
Ответ: (n + l)-2""^4l.
Пример 2 решения задания 5.2.3
Вычислить сумму
Cl2 - ЗС,?+2 + 5Cl2 + - + (-1)" (2п + 3)С:| (« > -1).
Обозначим искомую сумму через S. Тогда
5 +1 = С°,2 + С;„2 - ЗС^,2 + 5Cl2 +... + (-1)" (2п + 3)С1-
Можно считать, что 5 +1 = / '(\), где
/Чл-) = -^+с'^2-зс;?+2^' +
+ 5Cl2x' -... + (-1)" (2п + 3)С;::|х'"^'.
224
Глава 5
Тогда одна из первообразных для f'(x) будет иметь вид:
X
ит fix)-—\С„+2-С„+2^ +С„+2-^ -... + (-1) С„+2-« ).
Свернув сумму по формуле бинома Ньютона, получим:
/w=-
(l-Jc2)"+2
Тогда /' (х) =
(l-jc^)"^'(2nx43jc4l)
2 1
Если/1 = -1, /'W-^^, /(1)-2.
X'
Если п>-1, /'W =
а-хЪ^'-^Сг/исЧЗл'Ч!)
= 0.
х=\
Учитывая, что 5 = f'{l)-l, получаем ответ.
Ответ: если п = -1, то 5 = 1, если /i > -1, то S = -1.
Задание 5.2.4
Найти коэффициент при х в разложении данного
выражения Р по полиномиальной формуле, полученный после
раскрытия скобок и приведения подобных членов.
№
1
2
3
к
23
96
80
Р
{2 + х'-х'У'
(\ + x'-x''f
(4-хЧхТ
№
4
5
6
к
130
66
48
Таблица 5.2.4
Р
{x'-2 + x'f'
{x'-x'+3f'
{\ + x'-x'f'
Комбинаторика
225
Таблица 5,2.4 (окончание)
№
7
8
9
10
11
12
13
14
15
16
17
18
к
114
30
18
22
112
46
48
40
132
34
96
57
Р 1
Q-^jc'Ux'f'
иЧз-л-Ъ"
(2 + л-^-хЪ^
(3-хЧл-^У^
(4 + ;с'Ч/)-'
(1-/+Л'^)'^
(3 + х^"-л'^У^
(хЧЗ-.ИУ^
(2-л-Ч..^Ъ-'
(4 + х--хЪ''
(1 + /_V'^)24
(2-хЧл-Ъ'^
№
19
20
21
22
23
24
25
26
27
28
29
30
А-
60
9
44
27
56
68
60
17
150
120
34
300
Р 1
(\ + х''-х'У'
{5-х-х'У'
(2 + л-»«-/У
{З^х' + хУ
(2-.,Чл'^)-^
(Ux''-хТ
i2-xUx'y'
(l-x + x'f
{2-х'-х'Г'
(л-'Ч/-ЗУ^
U2-x42/^
(;,10_з + .,14)31
Пример решения задания 5.2.4
Найти коэффициент при х' в разлоэюении выралсения
(3-х +х ) по полиномиачъной формуле, полученный после
раскрытия скобок и приведения подобных членов.
Общий член разложения по полиномиальной формуле имеет
вид: Г' •{-х'^Т '{x^f 'Р{т,п,к\ с:;;:С,:с;=2:3:з.
Для отыскания всех случаев, в которых возникает х^°, решаем
в целых неотрицательных числах уравнение 2п + 5к = 30.
226
Глава 5
Выразим к: к =6 . Видно, что к принимает целые
значения, если п кратно 5. Выпишем все такие случаи:
п = 0 => к =6\ п=5 => к=4\
п = 10 => к = 2\ п = 15 => к=0.
Для каждой найденной пары значений /г, Означение т
находим из уравнения m+ /! + /: =19. Получим 4 набора {т\п\к)\
(13;0;6), (10;5;4), (7;10;2Х (4;15;0).
Слагаемые, содержащие х^^, таковы:
Ъ^^-i-x^f'ix^f • Р(13Д6); 3^^-{-x^)^-ix^f • F(10,5,4);
З'^ '{-x^)^^'(x^f'P(7,iO,2)\ 3^-{-x^y^'(x^f'P{4A5,0).
В итоге, коэффициент при х имеет вид:
19!
513
>10
- + -
13!0!6! 10!5!4! 7!10!2! 4!15!0!
Ответ: 19!
>13
)10
- + -
13!0!6! 10!5!4! 7!10!2! 4!15!0!
5.3. Формула включений
и исключений
Пусть имеется Л^ предметов, которые могут обладать
свойствами ai,a2,..-,oc„. Обозначим через N{a^,a2,"-,oik)
количество предметов, обладающих набором свойств а,,^^,...,^^, а
через yV(ai,a2,...,al) — количество предметов, не обладающих ни
одним из свойств а,,а2,...,а^. Тогда справедлива формула
включений и исключений:
A^(ai,a2,...,a,i) = yV-yV(a,)~yV(a2)-...-A^(a,j)+A^(a,,a2) +
+ Л^(а1,аз)+...+УУ(а,,_,,ап)-Л^(а,,а2,аз)-...4-(-1У'Л^(а,,а2,...,а,,).
Комбинаторика
227
Количество перестановок п различных предметов, при
которых ни один предмет не стоит на своём первоначальном месте,
выражается числом D,^ =/i!-C,j(/i-l)!-fС,Д/i-2)!-... + (-!)"С"
/
или D„ = т
1 1
- + -
i---f----f...-f(-ir-
1! 2! 3! п\
Количество перестановок п различных предметов, при
которых ровно к предметов стоят на своих первоначальных местах,
выражается числом D,^f^ =Q '^п-к-
Задание 5.3.1
Сколько натуральных чисел от 1 до 10000 не делится ни на а,
ни на (3, ни на у, ни на 5?
№
1
2
3
4
5
6
7
8
9
10
а
4
2
3
6
5
3
2
3
11
11
Р
5
3
4
7
8
4
4
7
3
8
Y
6
4
5
3
9
5
5
6
9
5
5
7
- 5
8
2
4
6
7
11
10
4
№
11
12
13
14
15
16
17
18
19
20
а
7
8
3
13
3
11
17
2
3
13
Р
9
5
8
9
5
8
2
5
4
2
Y
5
2
16
5
6
3
3
4
6
3
5
3
9
7
3
13
2
4
17
17
4
№
21
22
23
24
25
26
27
28
29
30
а
2
2
11
3
4
19
5
11
12
23
Таблица 5.3.1
Р
5
8
7
6
8
5
6
3
3
2
Y
4
5
9
5
19
10
7
9
5
8
5
13
13
3
4
3
2
8
5
19
7
Пример решения задания 5.3.1
Сколько натуральных чисел от 1 до 10000 не делится ни на 2,
ни на 4, ни на 5, ни на 9 ?
228
Глава 5
Очевидно, что если число не делится на 2, то оно и подавно не
будет делиться на 4. Поэтому число 4 в условии можно просто
опустить.
Заметим, что на 2 делится каждое второе натуральное число,
на 5 — каждое пятое, на 9 — ка>1<дое девятое, на 2 и на 5 —
каждое 10-е и т. д. Воспользуемся формулой включений и
исключений, обозначив искомое число через М, а через[гг] будем
обозначать целую часть числа а. Получим:
М =10000-
10000
10000
2
-
10000
5
-
10000
9
+
10000
10
+
45
10000
90
10000
= 10000 - 5000 - 2000 -1111 + 1000 + 555 +
+ 222-111 = 3555.
Ответ: 3555 чисел.
Задание 5.3.2
Подсчитать количество различных перестановок цифр
данного числа а, при которых никакие п одинаковых цифр не идут
друг за другом.
Таблица 5.3.2
№
I
2
3
4
5
6
7
8
9
10
п
3
2
2
3
2
3
2
2
2
3
а
4244522
6858757
1249248
32331252
46749679
53233252
383448
78959681
443536
3884383
№
И
12
13
14
15
16
17
18
19
20
п
2
2
3
2
3
2
2
2
3
2
а
5612651
7434276
23992921
78974894
13341134
565262
49129258
352366
1887181
6556373
№
21
22
23
24
25
26
27
28
29
30
п
2
3
2
3
2
2
2
3
2
2
а
4954512
37665363
42535234
17721212
534354
52566314
134534
9395339
3744753
825824
Комбинаторика
229
Пример решения задания 5.3.2
Подсчитать количество различных перестановок цифр числа
123132, при которых никакие 2 одинаковые цифры не идут друг
за другом.
Общее количество различных перестановок цифр числа
123132 равно Р(2,2,2) = —^ = —= 90.
2!2!2! 8
Если две какие-то одинаковые цифры стоят рядом, мы можем
считать эту двойную цифру единым символом. Тогда количество
перестановок, содержащих этот символ, равно
Р(2,2Д) = -
5!
120
= 30.
2!2!1! 4
Заметим, что количество таких случаев равно С1 = 3.
Аналогично, количество перестановок, в которых присутст-
4! 24
вуют пара двойных символов, равно Р(2,1,1):
= 12,
2!1!1! 2
количество таких случаев равно Сз = 3, а общее число
перестановок, образованных парами одинаковых цифр, равно
P(U1) = 3! = 6.
В итоге, применяя формулу включений и исключений, будем
иметь: 90-3-30-f 312-6 = 30.
Ответ: 30 перестановок.
Задание 5.3.3
Сколько существует перестановок п различных предметов,
при которых на своих первоначальных местах окажутся ровно к
или ровно т предметов?
№
1
2
/2
9
8
к
1
6
т
3
5
№
3
4
п
1
6
к
3
2
т
4
3
№
5
6
Таблица
п
9
8
к
6
3
5.3.3
т
4
5
230
Глава 5
Таблица 5.3.3 (окончание)
№
7
8
9
10
11
12
13
14
п
1
6
9
8
7
6
9
8
/:
3
3
5
4
2
1
4
2
т
5
4
3
2
3
4
2
5
№
15
16
17
18
19
20
21
22
п
1
6
9
8
7
6
9
8
к
4
2
5
3
1
3
3
2
т
2
1
2
4
3
1
4
6
№
23
24
25
26
27
28
29
30
п
1
6
9
8
7
6
9
8
к
2
4
3
4
5
2
6
6
т
6
2
5
6
2
5
3
3
Пример решения задания 5.3.3
Сколько существует перестановок 9 различных предметов,
при которых на своих первоначальных местах окажутся ровно 2
или ровно 6 предметов?
Количество различных перестановок девяти предметов, при
которых на своих первоначальных местах окажутся ровно 2
предмета, равно D92, а количество различных перестановок девяти
предметов, при которых на своих первоначальных местах
окажутся ровно 6 предметов, равно Dq б- Применяя правило суммы,
а также формулу для вычисления D, j., имеем:
09,2+^9,6=^9^^7+^9^^3 =
9!
2!7!
7!
1_1 l._i_ JL_JL JL_i_
1!"^2! 3!"^4! 5!"^6! 7!
-f
6!3! 1! 2! 3! 7!2!
9! 9!
1854 + —--2:
6!3!
66912.
Ответ: 66912 перестановок.
Комбинаторика 231
5.4. Задачи о распределениях
Пусть имеется п шаров, которые распределяются по к
ящикам. Тогда количество способов распределения для различных
случаев равно:
1) шары различимы, ящики различимы, все ящики непусты:
к-\
C/*(n,)t) = 2(-iyd(it-/)";
/=о
2) шары различимы, ящики различимы, допускаются пустые
ящики:
f/(/z,)t) = )t";
3) шары различимы, ящики неразличимы, все ящики непусты:
V * (/1, А:) = ;
к\
4) шары различимы, ящики неразличимы, допускаются пустые
ящики:
к
5) шары неразличимы, ящики различимы, все ящики непусты:
6) шары неразличимы, ящики различимы, допускаются пустые
ящики:
Пп,к) = С^;1_,;
7) шары неразличимы, ящики неразличимы, все ящики непусты:
W'^in,k) = W(n-k,k)\
8) шары неразличимы, ящики неразличимы, допускаются
пустые ящики:
к
W{n,k) = lliW^(nJ).
Последняя пара совместно рекурсивных формул позволяет
сводить вычисления количества способов распределения при
больших значениях пик к меньшим значениям этих переменных.
232
Глава 5
Задание 5.4.1
Сколькими способами можно распределить п различных
открыток в к
1) различных;
2) неразличимых конвертов, если:
а) все конверты непусты;
б) допускаются пустые конверты. (Всего рассмотреть 4 случая.)
Таблица 5.4.1
№
1
2
3
4
5
6
п
11
10
9
8
7
12
к
5
5
5
5
5
4
№
7
8
9
10
11
12
п
11
10
9
8
7
12
к
4
4
4
4
4
6
№
13
14
15
16
17
18
/Z
И
10
9
8
7
12
к
3
3
6
6
3
3
№
19
20
21
22
23
24
/I
И
10
9
8
7
12
/:
6
6
3
3
6
7
№
25
26
27
28
29
30
п
11
10
9
8
13
12
к
1
1
7
7
3
5
Пример решения задания 5.4.1
Решить задачу 5.4.1 для п-Ь, к =4.
1а) Если конверты различимы, и все они должны быть
непусты, то число способов распределения равно
f/*(6,4) = C^4^-Ci34c^2^-C^=4096-4-729-f6-64-4 = 1560;
16) если конверты различимы и допускаются пустые
конверты, то число способов распределения равно (/(6,4) = 4 = 4096;
2а) если конверты неразличимы и все они должны быть
непусты, то число способов распределения равно
V. (6,4) = i^i<5:fi = 1^ = 65;
4! 24
26) если конверты неразличимы и допускаются пустые
конверты, то число способов распределения равно
V(6,4) = V * (6,4) + V * (6,3) + V * (6,2) + V * (6,1) =
Комбинаторика
233
^^ t/*(6,3) и* (6,2) ,,,,^„
3!
2!
^65-f^^'^ "^^'' ''^''^ 4-^^'^ "^^+СГ^
6 2 '
^, 1-729-3-64 + 3 64-2 , ^^ ^^ ^, , ,^^
= 65 + + + 1 = 65 + 90 + 31 + 1 = 187.
6 2
Ответ: 1а) 1560; 16) 4096; 2а) 65; 26) 187.
Задание 5.4.2
Сколькими способами можно представить число п в виде к
а) неотрицательных
б) положительных целых слагаемых, если представления,
отличающиеся только порядком слагаемых, считаются: 1)
различными, 2) одинаковыми. (Всего рассмотреть 4 варианта.)
Таблица 5.4.2
№
1
2
3
4
5
6
/I
12
11
10
9
8
7
/:
5
5
5
5
5
5
№
7
8
9
10
11
12
/1
12
11
10
9
8
7
/:
4
4
4
4
4
4
№
13
14
15
16
17
18
/I
12
11
10
9
8
7
/:
6
3
3
6
6
3
№
19
20
21
22
23
24
11
12
11
10
9
8
7
к
3
6
6
3
3
6
№
25
26
27
28
29
30
п
12
11
10
9
8
13
к
1
1
1
1
1
3
Пример решения задания 5.4.2
Решить задачу 5.4.2 для ^г = 13, к = А.
Данная задача равносильна задаче распределения 13
неразличимых шаров (т. е. единиц, образующих число 13) по 4 ящикам
(4 слагаемым).
1а) Если слагаемые неотрицательны, а представления,
отличающиеся только порядком слагаемых, считаются различными,
234 Глава 5
то количество различных способов представления числа 13 в ви-
4-1 3 16!
де суммы 4 слагаемых равно Г(13,4) = С13+4-1 = Qg ~ '~~ ~ ^^0.
16) Если слагаемые положительны, а представления,
отличающиеся только порядком слагаемых, считаются различными, то
количество различных способов представления числа 13 в виде
4-1 3 12!
суммы 4 слагаемых равно r*(13,4)==Ci3_i =Ci2=—^ = 220.
2а), 26). Для. нахождения количества различных способов
представления числа 13 в виде суммы 4 слагаемых, если
представления, отличающиеся только порядком слагаемых,
считаются различными, нужно найти числа IV(13,4) и для случаев
неотрицательных и положительных слагаемых соответственно.
Заметим, что W*(/i,l)=lV(n,l)=l; если п = к, то W*(/i,/:) = l;
если п<к, то W *(/!,/:) = О,
значит, W * (1,2) = W * (1,3) = W * (1,4) = 0;
И/(1,2) = И/*(1,2) + Ж* (1,1) = 0 + 1 = 1,
аналогично, И^(1,3) = И^(1,4) = 1.
И/* (2,1) = IV* (2,2) = 1; lV*(2,3) = iy*(2,4) = 0;
И/(2,2) = 1У*(2,1) + 1У*(2,2) = 1 + 1 = 2;
lV(2,3) = iy*(2,l) + iy*(2,2) + lV*(2,3) = l+ 1 + 0 = 2;
аналогично, И^(2,4) = 2;
lV*(3,2) = Vy(3-2,2) = iy(l,2) = l.
Продолжим вычисление коэффициентов W(n,k) и И^*(п,/:),
заполним таблицу, в левом верхнем углу каждой клетки будем
писать значение W(n,k), а в правом нижнем углу — IV*(«,/:).
Получим табл. 5.4.2а. Как видно из таблицы, W*(13,4) = 18,
1У(13,4) = 39.
Комбинаторика
235
Таблица 5,4.2а
п /
/к
1
2
3
1 4
5
6
7
От
1
вет: 1г
2
I
0
2
1
2
1
3
2
3
2
4
3
4
3
1) 560;
3
1
0
2
0
3
1
4
1
5
2
7
3
8
4
16)2:
4
1
0
2
0
3
0
5
1
6
1
9
2
11
3
Ю; 2а)
/к
8
9
10
И
12
13
1
2
5
4
5
4
6
5
6
5
7
6
7
6
3
10
5
12
7
14
8
16
10
19
2
21
14
4
15
5
18
6
23
9
27
11
34
15
39
18
5.5. Арифметический
треугольник
Коэффициентами обобщённого арифметического
треугольника называются числа, которые определяются так:
С,„(1Д)-
fl, если к<т-1;
Если п > 1, то
С„,{п,к) = -
О, если к > т-1.
q„(/2-U)+QXn-U-l)+...+QX"-l,0), ^^^'^^ к<т-1\
Qj(/z-l,/:)-fQj(n-l,/:-l)+...+Qj(/i-l,/:-m+l), если к >т-1.
236
Глава 5
Теорема: Число Qj(/i,/:) равно количеству ^-разрядных чисел
в т -ичной системе счисления, сумма цифр которых равна к
(если допускаются числа, начинающиеся с 0).
Свойства коэффициентов обобщённого арифметического
треугольника:
1) С2(пД)-С^
2) C„i{n,k) = Cf,i{nXm-l)n-k) (свойство симметричности);
3) C^,j(n,0)-hC„j{n,l)+...+C^,j{n,(rn-l)n) = m'^ (свойство суммы).
Задание 5.5.1
Наносятся т цифр 1,2,.., т на т различных шаров (на
каждый шар пишем ровно одну цифру), после чего шары помещаем
в мешок. Из мешка наудачу извлекаем шар, записываем число,
изображённое на нём, и возвращаем шар в мешок. Эта процедура
повторяется п раз.
Сколько существует различных случаев, при которых сумма
выписанных чисел оказалась бы равной к ?
Хо
1
2
3
4
5
6
7
8
9
10
т
13
11
9
7
5
3
12
10
8
6
п
4
4
5
5
6
9
4
5
5
5
к
21
20
21
22
19
18
21
16
21
16
№
11
12
13
14
15
16
17
18
19
20
т
4
13
11
9
7
5
3
12
10
8
п
1
4
4
5
5
6
9
4
5
5
к
18
20
19
22
21
18
17
20
15
22
Хо
21
22
23
24
25
26
27
28
29
30
Таблица 5.5.1
т
6
4
13
11
9
7
5
3
12
19
/2
5
7
4
4
5
5
6
9
4
5
к
15
19
19
21
20
20
17
16
19
14
Комбинаторика
237
Пример решения задания 5.5.1
Решить задачу 5.5.1 для m = S, п = 4, к = 21.
Перейдём от шаров, помеченных цифрами 1,2,...,8, к шарам,
помеченным цифрами 0,1,2,...,7. Тогда сумме 21, полученной
"старыми" метками, будет соответствовать сумма, образованная
"новыми" метками, которая равна 21 - 4 = 17. Тогда каждой
"новой" записи будет соответствовать некоторое 4-значное число
в 8-ичной системе счисления, причём некоторые числа могут
начинаться и с нулей. Общее количество 4-разрядных чисел
в 8-ичной системе счисления, сумма цифр которых равна 17,
выражается коэффициентом Cg(4,17).
По свойству симметричности, Cg (4,17) = С8(4,7-4-17) =
= С8(4,11). Найдём коэффициент С8(4,11), построив
арифметический треугольник 8 порядка (табл. 5.5.1а).
Таблица 5.5.1а
п^^Л
1
2
3
4
0
1
1
1
1
1
2
3
2
1
3
6
3
1
4
10
4
1
5
15
5
1
6
21
6
1
7
28
7
1
8
36
8
0
7
42
9
0
6
46
10
0
5
48
11
0
4
48
284
С8(4,11) = 15 4-214-28 4-36 4-42 4-46 4-48 4-48 = 284.
Ответ: 284 случая.
Задание 5.5.2
Игральная кость бросается п раз. Во сколько раз число
способов набора суммы в р очков превышает число способов набора
суммы в к очков?
238
Глава 5
х«
1
2
3
4
5
6
7
8
9
10
п
5
5
5
4
5
5
5
4
5
5
Р
18
19
16
17
17
21
19
15
15
20
/:
20
21
14
18
15
13
И
23
23
13
Хо
11
12
13
14
15
16
17
18
19
20
п
5
4
5
5
5
4
5
5
5
4
Р
19
12
14
15
13
15
14
15
16
16
к
15
21
22
21
23
12
23
24
20
И
Хо
21
22
23
24
25
26
27
28
29
30
Таблица 5.5.2
п
5
5
5
4
5
5
5
4
5
5
Р
16
13
18
17
19
20
16
15
17
18
к
24
24
15
10
12
14
24
21
23
13
Пример решения задания 5.5.2
Решить задачу 5.5.2 для п = 4, р = 13, к =П.
Перейдём от кости, грани которой помечены символами
1,2,...,6, к кости, грани которой помечены цифрами 0,1,...,5. Тогда
суммам в 13 и 17 очков, полученным с помощью обычной кости,
будут соответствовать суммы в 13-4 = 9и 17-4= 13 очков,
полученные с помощью кости с нестандартной разметкой. Но
результаты бросаний нестандартной кости, выписанные подряд,
можно воспринимать как четырёхзначное число в шестеричной
системе счисления.
Количества четырёхзначных чисел в шестеричной системе
счисления, с суммами цифр 9 и 13, равны соответственно Q(4.9)
и Сб(4ДЗ). Заметим, что Q(4,13) = Q(4,5-4-13) = Q(4,7). Для
нахождения этих чисел построим обобщенный арифметический
треугольник шестого порядка (табл. 5.5.2а). Видим, что
Q(4,7) = 104, Сб(4,9) = 140.
Комбинаторика
239
Таблица 5,5,2а
п\к
I 1
1 ^
1 3
1 ^
0
1
1
1
1
1
2
3
2
1
3
6
3
1
4
10
4
1
5
15
5
1
6
21
6
0
5
25
7
0
4
27
104
8
0
3
27
9 1
0 1
2 1
25 1
140 1
ii^ = ^. 1,346.
104 26
Ответ: в 1,346 раза.
Задание 5.5.3
Запускается п волчков, у каждого из которых по т граней
с нанесёнными на них числами p,p-f 1,...,/?+ т-1. Сколькими
способами эти волчки могут упасть, набрав сумму в к очков,
если волчки : 1) различимы? 2) неразличимы?
Если число способов не превосходит 10, выписать их.
Таблица 5,5,3
№
1
2
3
4
5
6
7
8
9
[ю
п
1
5
5
5
6
5
5
5
5
5
т
3
4
5
7
3
4
5
7
3
4
Р
2
3
5
2
2
4
5
3
4
3
^
24
26
20
21
21
30
26
27
26
24
№
11
12
13
14
15
16
17
18
19
20
п
4
5
7
4
5
4
6
5
5
5
/«
5
7
3
4
5
7
3
4
5
7
Р
4
2
3
6
2
3
3
3
3
3
к
25
23
30
33
22
26
28
25
28
25
Хо
21
22
23
24
25
26
27
28
29
30
п
5
5
5
5
8
5
5
5
7
5
т
3
4
5
7
3
4
5
7
3
4
Р
5
2
4
2
2
5
5
3
3
5
к
32
22
34
24
27
30 1
39
24
29
36
240
Глава 5
Пример решения задания 5.5.3
Запускается 4 волчка, у каоюдого из которых по 4 грани с
нанесёнными на них числами 5,6,7,8. Сколькими способами эти
волчки могут упасть, набрав сумму в 25 очков, если волчки:
1) различимы ? 2) неразличимы ?
Перейдём от данных волчков к волчкам, грани которых
помечены цифрами 0,1,2,3. Тогда сумме 13, полученной с помощью
исходных волчков, будет соответствовать сумма 25-5-4 = 5 для
''новых" волчков. В дальнейшем будем говорить только о
волчках с новой разметкой. Рассмотрим случаи:
1) волчки различимы.
В этом случае каждому способу набора волчками суммы
в 5 очков соответствует четырёхзначное число в четверичной
системе счисления, сумма
п\к
1
2
3
4
0
1
1
1
1
1
2
3
2
1
3
6
3
1
4
10
4
0
3
12
5
0
2
12
40
цифр которого равна 5, и
количество таких чисел
равно С4(4,5). Для
нахождения этих чисел построим
обобщенный
арифметический треугольник
четвёртого порядка (табл. 5.5.3а).
Как видим, С4(4,5) = 40.
2) волчки неразличимы.
В этом случае введём
функцию /„(/гД), где /„Д/гД)
суммы к на п волчках, если т
личина баллов.
Очевидно, что справедливо рекуррентная формула
f,n (^' ^) - /.-1 ('^ ^) + Л,-1 {п-1к- т) +
+Х._, {п -2, к- 2т) + .../„,_, {п -t,k- tm\
Таблица 5.5.3а
количество способов набора
• максимальная выпавшая ве-
где t =
т
Для нашего случая будем иметь:
/з(4,5) = /2(4.5) + /2(3,2).
/2 (4-5) = /, (4,5) + /, (3,3) + /, (2.1) = 0 + 1 + 1 = 2.
/2(3,2) = /,(3.2)+ /,(2,0) = 1 + 1 = 2.
Комбинаторика
241
В итоге получим: /з(4,5) - /2(4,5) + /2(3,2) = 2 + 2 = 4.
Выпишем 4 возможные комбинации:
0+0+2+3 , 0+1+1+3, 0+1+2+2, 1+1+1+2.
Ответ: 1) 40 способов; 2) 4 способа.
Задание 5.5.4
Сколькими способами можно оплатить марками бандероль на
сумму к рублей, если есть неограниченное число марок
достоинством в а,Ь,с рублей и два способа, отличающиеся только
порядком наклейки марок, считаются
1) различными? 2) одинаковыми?
Если число способов не превосходит 10, выписать их в явном
виде.
Хо
1
2
3
4
5
6
7
8
9
10
к
25
25
25
25
25
25
24
24
24
24
а
3
6
4
2
3
8
3
6
3
2
b
5
5
3
5
4
3
5
5
4
5
с
1
2
6
7
7
2
7
2
6
7
№
11
12
13
14
15
16
17
18
19
20
к
24
24
26
26
26
26
26
26
23
23
а
3
8
3
2
4
5
4
2
3
5
ib
4
3
7
5
3
2
7
3
5
6
с
7
2
5
6
6
7
3
8
7
2
Хо
21
22
23
24
25
26
27
28
29
30
Таблица 5.5.4
к
23
23
23
23
27
27
27
27
27
27
а
4
2
7
3
5
2
3
7
7
8
b
6
1
3
8
3
6
4
2
4
3
с
3
5
4
2
7
5
6
5
3
2
Пример решения задания 5.5.4
Решим задание 5.5.4 для к = 20, а = 6, Ь = 5, с = 3.
1) Пусть f(k) означает число способов, которыми можно
оплатить сумму в к рублей марками достоинством в 6, 5 и 3 рубля,
если есть неограниченное число марок достоинством в 6, 5, 3 рубля
242 Гпава 5
и два способа, отличающиеся только порядком наклейки марок,
считаются различными. Тогда справедлива рекуррентная формула
f{k) = f{k-6) + f(k-5) + f(k-3).
Эта формула позволяет вычислять значения функции в точке
к через значения функции в точках к-6, к-5, к-Ъ.
Очевидно, что при Л<0 f{k) = 0. Далее, /(0)=1, /(1) = 0,
/(2) = О, /(3) = 1, /(4) = О, /(5) = 1, /(6) = 2;
/(7) = /(1)4-/(2) 4-/(4) = 0 + 0 +0 = 0;
/(8) = /(2) + /(3) + /(5) = 0 + 1 + 1 = 2;
/(9) = /(3) + /(4) + /(6) = 1 + 0 + 2 = 3;
/(10) = /(4) + /(5) + /(7) = 0 + 1 + 0 = 1;
/(И) = /(5) + /(6) + /(8) = 1 + 2 + 2 = 5;
/(12) = /(6) + /(7) + /(9) = 2 + 0 + 3 = 5;
/(14) = /(8) + /(9) + /(11) = 2 + 3 + 5 = 10;
/(15) = /(9) + /(10) + /(12) = 3 + 1 + 5 = 9;
/(17) = /(11) + /(12) + /(14) = 5 + 5 + 10 = 20;
/(20) = /(14) + /(15) + /(17) = 10 + 9 + 20 = 39.
Итак, /(20) = 39.
2) Пусть g{k\ni,ii2,...,np) означает число способов, которыми
можно оплатить сумму в к рублей марками достоинством
в щ,п2,>..,Пр рублей, если есть неограниченное число марок
каждого достоинства и два способа, отличающиеся только порядком
наклейки марок, считаются одинаковыми.
Для нашего случая справедлива рекуррентная формула:
^(20;6,5,3) = g(20;5,3) + ^(14;5,3) + ^(8;5,3) 4- ^(2;5,3) •
Первое слагаемое в правой части этой формулы соответствует
случаю, когда 6-рублёвые марки не участвуют в оплате суммы,
второе — когда ровно одна 6-рублёвая марка участвует в оплате
суммы и т. д.
Комбинаторика 243
Очевидно, 4TOg(2;53) = 0, а для каждого из остальных
слагаемых составим рекуррентную формулу:
g(20;53) = g(20;3) + g(15;3) + g(10;3) + g(5;3) + ^Ч0;3);
g(14;5,3) - g(14;3) + g(9;3) + g(4;3); g(8;5,3) = g(8;3) + g(3;3).
^ /14 Ц'если к кратно n\
Понятно, что g{k\n) = <
[О, если к не кратно п.
Поэтому имеем:
g(20;5,3) = 0 + 1 + 0 + 0 +1 = 2; g(14;5,3) = 0 + 1 + 0 = 1;
g(8;5,3) = 0 + 1 = 1; g(20;6,5,3) = 2 +1 +1 + 0 = 4.
Выпишем соответствующие представления:
20 = 5 + 5 + 5 + 5;
20 = 6 + 6 + 5 + 3;
20 = 6 + 5 + 3 + 3 + 3;
20 = 5 + 3 + 3 + 3 + 3 + 3.
Ответ: 1) 39 способов; 2) 4 способа.
5.6. Рекуррентные соотношения
Рекуррентным соотношением к-го порядка называется
формула, позволяющая выражать значения члена
последовательности с номером п (п>к) через члены этой последовательности
с номерами п-1, я-2,..., п-к.
Решением рекуррентного соотношения называется числовая
последовательность, обращающая его в верное равенство при
подстановке в него формулы общего члена последовательности.
Начальными условиями рекуррентного соотношения к -го
порядка называются первые к членов последовательности,
являющейся решением данного рекуррентного соотношения.
Линейным однородным рекуррентным соотношением к-го
порядка с постоянными коэффициентами называется
соотношение вида
f{n + k) = a^'f{n + k-\) + a2'f{n + k-2)^... + af^-f{n). (*)
244 Глава 5
Общим решением соотношения {^) называется такое его
решение, которое содержит к произвольных постоянных, путём
подбора которых можно удовлетворить любым начальным условиям.
Характеристическим уравнением соотношения {^) называется
уравнение х - а^-х ~ -\-a2-х~ -f...-fflt^,. (**)
Теорема: Общее решение соотношения (*) имеет вид:
f{n) = A, +Л2 +.- + Л^.
где А. =С.х\ если х —действительный корень первой
кратности уравнения (**), где Q — произвольные постоянные.
А, =х" -(С,,, +«С,, +п^С,з +... + п"-'С,,„),
если X — действительный корень кратности т уравнения (**),
где С,,,C,2v.-,C,,„, —произвольные постоянные;
Л. = г" (cos пф • D. + sin /1ф • Е.),
если r(cos9±/sin ф) —комплексно-сопряжённая пара, каждый
член которой является корнем первой кратности уравнения (**)
и D., £.— произвольные постоянные;
+ 5Шпф-(£/,, +«£,,2 +/г'£,з +.: + n"~'E.Jl
если r(cosф±/sinф) — комплексно-сопряжённая пара, каждый
член которой является корнем кратности т уравнения (**) и
D,,, D- 2 v,^>;, £"/,1, £/,2 V.-£",.„, — произвольные постоянные.
Задание 5.6.1
Найти общее решение рекуррентного соотношения 5-го
порядка
f(n + 5) = a'f(n + 4) + b-f(n + 3) + c-fin + 2) + d'fin + l) + e-f{n).
Комбинаторика
245
JNo
1
2
3
4
5
6
7
8
9
10
И
12
13
14
I ^^
fl
2
-11
2
9
3
6
7
15
5
5
-2
-2
-6
1
2
b
10
-30
6
-26
ь
-11
-7
-83
-2
-4
9
11
-6
14
17
с
-8
22
-4
20
-27
2
-19
205
-14
-16
22
40
16
-6
-70
d
-33
95
-13
24
32
12
16
-216
3
32
-4
44
15
-45
92
е
-18
-75
-6
-32
-12
-8
20
80
9
-16
-24
16
-18
-27
-40
Хо
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
а
-1
0
4
2
-2
-6
-4
3
6
4
-6
0
8
11
7
h
11
18
3
11
10
-6
3
13
-6
0
-5
19
-12
-23
5
Таблица
с
29
-4
-34
-40
8
20
34
-11
-20
-14
16
-34
-2
47
-35
d
26
-57
52
44
-33
39
52
-24
39
17
12
-12
13
24
-4
5.6.1
е
8
-36
-24 1
-16
18
18
24
20
-18
-6
-16
40
-6
36
28
Пример решения задания 5.6.1
Найти общее решение рекуррентного соотношения 5-го
порядка
/(« + 5) = 4./(/г + 4)-4./(« + 3)-2./(/1 + 2) + 5./(п + 1)-2./(п).
Запишем характеристическое уравнение данного соотношения:
;с^-4/+4x42x^-5x4-2 = 0.
Непосредственной подстановкой убеждаемся, что Xj = 1 —
корень характеристического уравнения.
Понизим степень уравнения, поделив характеристический
многочлен на х-1 по схеме Горнера:
1
1
1
-4
-3
4
1
2
3
-5
-2
2
0
246
Глава 5
В результате деления получили уравнение четвёртой степени:
Заметим, что ^2 = 1 является корнем и этого уравнения,
разделим левую часть уравнения на х-1:
1
1
1
-3
-2
1
-1
3
2
-2
0
Получено уравнение х^ -2х' -л+ 2 = 0, которое также
имеет хз =1 своим корнем. Понижаем степень уравнения:
1
1
1
-2
-1
-1
-2
2
0
В результате имеем квадратное уравнение х^ -х-2 = 0,
которое имеет корни ^4 - "^ и Хз = 2.
По теореме о виде общего решения линейного однородного
рекуррентного соотношения с постоянными коэффициентами,
запишем общее решение:
/(П) = 1".(С, +пС2+/1^Сз)4-(-1У^С4 4-С5-2'' =
= с, + пС^ + пС^ + (- \УС, 4- Q • 2\
Ответ: /(п) = Q 4-пСз+ п^Сз 4-(-1ГС4 4-С5-2".
Задание 5.6.2
Найти общее решение рекуррентного соотношения 5-го
порядка
/(п + 5) = а-/(n + 4) + b-/(;i + 3) + c-/(n +2) +J./(n+ !) + (?•/(«).
Комбинаторика
247
Хо
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1 ^^
а
2
2л/з
2
2
-7л/Т
-2
4
4л/3
4
-4
-4л/3
-4
2
2л/3
2
h
-?
-4
-4
7
-4
-4
-8
-16
-16
-8
-16
-16
-2
-4
-4
с
8
-3
-4
5
-6
-1
-5
2
3
-2
4
6
-8
27
1
^
-16
6л/3
8
10
-12л/з
-2
20
-8>/з
-12
-8
16л/3
24
16
-54Л
-2
^
16
-12
-16
10
-24
-4
-40
32
48
-16
64
96
-16
108
4
Х2
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
а
2
2л/3
2
-2
-2л/3
-2
4
4л/3
4
-4
-4л/з
-4
-2
-2л/3
-2
Z?
-2
-4
-4
-2
-4
-4
-8
-16
-16
-8
-16
-16
-2
-4
-4
Таблица 5,6,2
с
5
-6
7
-8
3
-27
-1
4
2
-3
1
-10
-1
3
-5
d
-10
12л/3
-14
-16
6л/3
-54
4
-16v/3
-8
-12
4л/3
-40
-2
бл/З
-10
е
10
-24
28 1
-16
12
-108
-8
64
32
-24
16
-160
-2
12
-20
Пример решения задания 5.6.2
Найти общее решение рекуррентного соотношения 5-го
порядка
f(n + 5) = 2S'f(n + 4)-4-f(n + 3)-
-2./(п + 2) + 4л/з/(п + 1)-8/(п).
Запишем характеристическое уравнение данного
соотношения: х^ - iSx"^ + Ах^ + 2х^ - aSx + 8 = 0.
С помощью группировки разложим левую часть на множители:
х\х^ -2л/Зх + 4) + 2(х~ -2л/Зх + 4) = 0,
или
(хЧ2)(л--2л/Зх + 4) = 0.
248
Глава 5
Рассмотрим два случая:
/(Л+271^)
Если к=^Зп + 1, то x = -yJ2, при к = 3п и к=Зп-1 получаем
пару комплексно-сопряжённых чисел с модулями, равными v2,
и аргументами ф = ±— .
Соответствующие слагаемые в общем
решении будут иметь вид:
q(-^\(^(c,cos^^C,sm^
3 ^ 3
2) л-^-2л/Зл: + 4 = 0 =;> x^^^=S±i
Рис. 5.6.2
Изобразим число v3+/ на
комплексной плоскости для нахождения его модуля и аргумента (рис. 5.6.2).
Видим, ЧТО г = 2, ф =—.
6
Соответствующие слагаемые в общем решении будут иметь
2/2
C.cos — + Csin-
6 ' 6
В итоге получаем общее решение
исходного рекуррентного соотношения.
Ответ:
/(м) = С,(Ч/2)"+(^2)"
' юг юг^
Q cos— + С sin —
3 ' 3
+2"! C4COS— + Qsm —
6 6
Задание 5.6.3
Найти общий вид решения рекуррентного соотношения 4-го
порядка Х,^^4 + ^^п+З "^ 1^^п+2 + ^-^n+l + d^n "= О' ^С-^И Ло = 0.
Комбинаторика
249
Таблица 5,6.3
1 №
1 1
2
3
4
5
6
1 '^
8
9
1 ^^
11
12
1 ^^
14
15
16
17
18
L ^^
20
21
22
23
24
1 ^^
26
27
1 28
29
1 30
й
-6-2V3 1
-3
1
2V^
4
-5
-4-2л/з
-^
1
4 + 2л/3
-4
1
-2-2л/з
-7
-6
-3 + 2л/з
-4
-4
-4-2л/з
-1
11
3 + 2л/з
1
-7
-3-2л/з
0
-5
-4 + 2>/з
4
-8
h 1
13 + 12V3 1
4
-12
3
5
-2
7 + 8л/з
-27
-30
8 + 8л/з
1
-22
5 + 4>/з
0
-23
6-6л/з
1
-9
8 + 8л/з
-4
38
б+бТз
-28
-2
бТз
-8
-30
7-8>/з
9
23
с
-24-18V3 1
0
-26
-2л/з
2
14
-16-6л/3
62
-62
16 + 8л/з
-6
42
-8-2V3
8
-34
-12 + 4л/з
-6
26
-16-8V3
16
54
12 + 4>/з
-64
18
-12 + 8л/з
24
-50
-16 + 6л/3
10
-30
d 1
36 1
-8
-24
-4 1
-12
-20
12 1
-140
-60
16 1
36
-36
4
-56
-18
8 1
36
-30
16 1
-24
36
8
-120
-28
-16
-32
-36
12
4
18
250
Глава 5
Пример решения задания 5.6.3
Найти обгций вид решения рекурреитного соотношения 4-го
порядка jc,^+4 ~ 3^/2-1-3 ~ 8х„+1 + 24 = О, если х^ = 0.
Запишем характеристическое уравнение данного соотношения:
Непосредственной подстановкой убеждаемся, что х^=1 —
корень характеристического уравнения.
Понизим степень уравнения, поделив характеристический
многочлен на 1бл/з^ по схеме Горнера:
2
1
1
-3
-1
0
-2
-8
-12
24
0
В результате деления получили уравнение третьей степени:
x^-x^-2a'-12 = 0.
Заметим, что Х2'=Ъ является корнем этого уравнения,
разделим левую часть уравнения на х-Ъ\
3
1
1
-1
2
-2
4
-12
0
Получено уравнение х^ + 2х + 4 = О, которое имеет корни
д:зд=-1±/л/з.
Комплексное число имеет модуль г = 2 и аргумент
2я
Запишем общее решение исходного рекуррентного
соотношения: х„ =С,2" +С2З" +2"( Cjcos—+ C4sin —
Комбинаторика
251
Учтём начальное условие xq =0:
О = С, 2' + С 3' + 2' (C3COSO + C4sin0),
откуда С, = -С2 - Сз..
Подставляя выражение для в формулу общего решения,
получим ответ.
Ответ:
JC =(-С-С)-2''+С,3"+2''
^ 271/1 ^ . 2пп
C3COS 4- C4Sin
Задание 5.6.4
Найти общее решение рекуррентного соотношения 4-го
порядка
f(n + 4) = a-f(n + 3) + ^-f{n + 2) + y'f(n + l) + 8-f(n)
с заданными начальными условиями /(0), /(1), /(2), /(3).
Таблица 5.6.4
Хо
1
2
3
4
5
6
7
8
9
10
11
12
а
5
-1
-6
3
7
1
4
5
11
6
3
0
р
-1
7
0
3
-12
7
-3
3
-39
-8
2
9
Y
-21
13
22
-7
-4
-13
-4
-13
49
-6
-12
4
6 1 /(0)
18
6
-15
-6
16
3
1
5
3
4
6 3
4 1 0
-10 1 3
-20 2
9 1 1
8 6
-12 1 5
/0)
8
6
-4
-3
-3
3
-3
3
0
3
7
-3
/(2)
8
1
19
12
-1
4
3
0
-11
17
7
19
/(3)
38
44
-54
-3
-19
7
3
15
-58
51
3
-37
252
Глава 5
Таблица 5.6.4 (окончание)
1 Хо
13
14
15
16
17
18
19
20
21
22
23
24 .
25
26
27
28
29
1 30
а
-1
-7
2
0
0
-3
2
0
-3
-5
-2
2
6
4
5
2
3
-1
\^
12
-13
12
17
И
9
7
11
7
-1
7
15
-8
-3
12
3
-1
7
Y
28
3
-18
-36
18
23
-20
-18
15
21
20
4
-6
-4
-44
-8
-3
13
6
16
18
-27
20
8
12
12
8
-18
18
12
-20
9
4
-80
4
2
6
/(0)
-2
2
4
4
1
3
1
4
6
2
3
4.
4
-2
4
0
-1
2
/0)
-1
1
2
3
3
4
2
1
3
3
-6
3
0
3
-4
5
-6
1
/(2)
9
7
4
-1
-8
21
2
-1
17
-3
14
-1
20
-13
36
-16
-3
-6
/(3) 1
-29 1
-17 1
50 1
-13 1
15
50
-2
-1
-15
33
-34
19
48
-25
16
19
-22
15
Пример решения задания 5.6.4
Найти решение рекуррентного соотношения 4-го порядка
/(/1 + 4) = 6-/(n + 2) + 8-/(h + l) + 3-/(n) с начальными
условиями /(0) = 0; /(1) = -6; /(2) = ^; /(3) = -34.
Запишем характеристическое уравнение данного
соотношения: X -6х -8х-3 = 0. Подстановкой убеждаемся, что х^=-1 —
корень характеристического уравнения. Понизим степень
уравнения, поделив характеристический многочлен на х + 1 по схеме
Горнера:
-1
1
1
0
-1
-6
-5
-8
-3
-3
0
Комбинаторика
253
В результате деления получили уравнение третьей степени:
X -X -5х-3 = 0.
Заметим, что Х2 = -1 также является корнем этого уравнения,
разделим левую часть уравнения на x + l:
-1
1
1
-1
-2
-5
-3
-3
0
Получено уравнение х' - 2х - 3 = О, которое имеет корни
Общее решение исходного соотношения имеет вид:
f(n) = (-iy\A + Bn + Cn^)-hD3'\
Учтём начальные условия, получим систему линейных
уравнений:
A + D = -34
-A-B-C + 3D = -6
A + 2B + 4C + 9D = -4
-A-3B-9C + 21D = -34.
Решив эту систему, будем иметь: A = U В = 2, С = 0, D = -l.
Подставив найденные значения констант в формулу общего
решения, получим: /(/г) = (-1)"(1 + 2п + 0-п^)-1'3'\
Ответ: /(/|) = (-1УЧ1 + 2/|)-3".
9 Зак. 3332
Глава 6
Конечные автоматы
6.1. Автоматы Мили
Автоматом Мили будем называть пятерку объектов
S = (A,Q,V,8,X), где Д = {flti,...,flt,J —входной алфавит;
Q-[Q\ »---»^ш } — мнолсество внутренних состояний;
V = {vj,..., v^,} — выходной алфавит;
Ъ\ AxQ-^Q — функция переходов;
X'.AxQ-^V — функция выхода.
Таблица, задающая функции переходов и выхода, называется
таблицей состояний автомата.
Диаграммой состояний автомата Мили называется
ориентированный граф, в котором количество вершин равно количеству
состояний данного автомата Мили и помечено символами
внутренних состояний; дуга, выходящая из любой вершины q^ и
заходящая в вершину Qj, помечена символами Uj, v,., причём
^(^^Qi) = Qj^ Maf,qi) = v,.
Автомат Мили называется инициальным, если он всегда
начинает свою работу из одного и того же состояния (q^).
Автомат Мили называется неинициальным, если он может
начинать свою работу из любого своего состояния.
Работа автомата Мили связана с двумя бесконечными
лентами, разбитыми на ячейки, причём в каждой ячейке может быть
записан один символ некоторого алфавита.
256 Глава 6
Работа автомата Мили над словом а, записанным на входной
ленте, проходит следующим образом:
1) считав символ в ячейке входной ленты, обозреваемой
считывающим устройством автомата Мили, он печатает в ячейку
входной ленты символ, найденный с помощью функции выхода v,
двигается вдоль ленты вправо и переходит в состояние,
определяемое с помощью функции перехода 5;
2) работа автомата продолжается до тех пор, пока все ячейки,
содержащие символы данного слова, не будут пройдены.
Тактом времени называют промежуток, за который конечный
автомат обрабатывает одну ячейку.
Дешифратором называется инициальный конечный автомат,
выходным алфавитом которого является множество {0,1},
причём на вход подаётся бесконечная последовательность символов
некоторого алфавита и символ 1 печатается в том и лишь в том
случае, если в данный момент времени считывающее устройство
автомата обозревает последний символ уже считанного слова а,
фиксированного для данного автомата, а на ленте записано слово,
в которое входит а. Слово а называется кодовой комбинацией
этого автомата.
Неинициальный автомат называется сильно связным, если для
любых состояний автомата qi и cjj найдётся слово а такое, что
автомат, начавший работу в состоянии д., при считывании слова
а переходит в состояние qj.
Состояния qi и qj, неинициальных автоматов Л] и ^2
называются эквивалентными, если для любого слова а, составленного
из букв входного алфавита, выходные слова, полученные при
работе автоматов Aj и Л^' запущенных соответственно из
состояний qi и qi^ над словом а, равны.
Автоматы Aj и Л2 называются эквивалентными, если для
любого состояния qi автомата Aj найдётся эквивалентное ему
состояние qi^ автомата Л2, а также, если для любого состояния
qj. автомата Л2 найдётся эквивалентное ему состояние q^
автомата Д.
Конечные автоматы
257
Автомат Л,„/^ называется мингшачъным для автомата Л, если
он является эквивалентным автомату А и содержит наименьшее
число внутренних состояний среди всех автоматов,
эквивалентных автомату А,
Задание 6.1.1
По данной кодовой комбинации а построить дешифратор с
входным алфавитом {х, у] и записать его:
1) диаграммой состояний;
2) таблицей состояний.
Таблица 6,1.1
№
1
2
3
4
5
6
7
8
9
10
а
ххуххуух
ухуххуху
>^Л'>^>^Л'Х VA'
хухххуху
хххуххух
ухуууххх
ху у X у уху
уху у у у XX
Xу уухуху
ухууухху
№
11
12
13
14
15
16
17
18
19
20
а
у уху у XXX
хуууххуу
ууххуу ух
хуххууху
ууухххуу
X у X у у X у X
у XX уху у у
хххуууху
>^Л'V VXA-УЛ"
ху уххуу X
№
21
22
23
24
25
26
27
28
29
30
а
уххуухху
УУУУХуху
хуу уху XX
ухухухух
ху уху XXX
ххуухуу у
ууухуухх
хххуухух
ууухххху
ухухххух
Пример решения задания 6.1.1
Решим задание 6.1.1 для а = ху у хуухх.
Составим диаграмму состояний дешифратора, содержаш,его
8 внутренних состояний (по количеству символов кодовой
комбинации).
Пусть начальное состояние— ^j.Определим X{x,q^)-Y, для
остальных случаев значение функции выходов равно 0.
258
Глава 6
Функцию переходов зададим следующим образом:
В дальнейшем, если XiX2...x^ (k^S) — начало кодовой
комбинации, то Hxi^,qj,) = qi^^i, в остальных случаях 5(x/^,q/^) = qp,
где р — наименьший номер, т^акой, что слово x^x^^i...x^
является начальным отрезком кодовой комбинации.
Получаем: b{y,q^) = q^, d{x,q^) = q2, d(y,q2) = q^,
b{x,q2)-q2-> т. к. в слове хх последний символ может служить
началом кодовой комбинации, а при получении одного символа
кода мы переходим во 2 состояние.
Далее имеем: 8(у,^з)-^4' 3(х,(7з) = ^2' 'Г- ^- ^ слове хул:
последний символ может служить началом кодовой
комбинации, а при получении одного символа кода мы переходим во 2
состояние.
Найдя, действуя аналогично, значения функции переходов на
остальных наборах переменных, получим диаграмму состояний
(рис. 6.1.1, а):
Рис. 6.1.1, а
Конечные автоматы
259
Теперь запишем таблицу состояний дешифратора:
Таблица 6.1.1 а
a\q
X
У
Я1
<72,0
'h.O
Я2
<72.0
<?з.О
Яз
42-0
94.0
<74
<75.0
91.0
<75
92-0
%.о
%
92.0
97.0
97
98.0
91.0
98
92.1
9б.О
Задание полностью выполнено.
Задание 6.1.2
Для данного конечного автомата, заданного таблично, со
множеством внутренних состояний {1,2,3,4,5,6,7,8,9}, входным
алфавитом {а,Ь} и выходным алфавитом {х,у}:
1. Выяснить, является ли автомат сильно связным.
2. Построить эквивалентный минимальный автомат,
3. Гфоверить работу исходного и минимального автоматов над
словом "bbabaab'\
Таблица 6,1.2
№ I
аХ
а
Ь
1
4,х
7,.У
2
\У
4, У
3
7,-х:
9.x
4
5,jc
9, у
5
%,х
7, У
6
7,л'
9,3'
7
2, У
8,jc
8
5,х
9, У
9
2,У
5,х
№2
>^
а
Ь
1
2,А'
5,3'
2
6, У
9,x
3
8, У
9,А-
4
7,.У
5,л-
5
4,v
6,х
6
Ъ,х
7, У
7
4,А-
8, У
8
2,х
6, У
9
3,у
8, Л'
260
Глава 6
Таблица 6,1.2 (продолсисение)
№3
^
а
b
1
2,х
3,А-
2
1,х
4,х
3
З,}'
1.x
4
5.x
2,х
5
4.x
3,х
6
8,х
3.x
7
3,У
8, У
8
6.x
8,х
9 1
З.у
4, У
№4
р^
а
b
1
5,А'
8,>'
2
3,v
6, А
3
7,х
5,v
4
8,х
7,v
5
1у
7,У
6
9.x
1у
7
4. У
8, У
8
3,у
5, У
9 1
4.V
6,х
№5
рч
а
b
1
3,х
2,л'
2
8,.v
5,л'
3
4,х
5,х
4
l-v
5.x
5
8.x
2,х
6
7. У
8, У
7
6. у
8, У
8
9, У
8,х
9 1
9. У
8. у
№6
рЧ
а
b
1
2,v
7,3'
2
4,}^
3,v
3
9,v
г у
4
5,v
3,3'
5
4,v
7,v
6
7. у
9.x
7
9, У
4, У
8
з.у
9,х
9
8.x
9.У
№7
|>^
а
b
1
2,д:
3,х
2
4,х
6,.Y
3
2.x
1.x
4
2.x
3.V
5
9.x
3,v
6
9.У
7.x
7
8.x
1.У
8
7,х
б.х
9
7.x
6.x
№8
>^
а
b
1
2,х
5, А
2
4,х
Ъ,х
3
4.x
2,х
4
3.x
5,^
5
6,v
6.V
6
7.x
5,v
7
6.x
7,х
8
7.x
5.x
9
7.x
5.x
Конечные автоматы
' 261
Таблица 6.1.2 (продолэюение)
№9
^
а
b
1
2,х
\^У
2
3,х
гу
3
4,л'
3,}^
4
5,А
7,^
5
4,А
5,V
6
4,А
7,А
7
8, А
6, А
8
5, А
9,}^
9 1
8, А
9,А
№10
>^
а
b
1
2,х
3,.v
2
\,х
Хх
3
4,А
5.А'
4
5,А
6,.v
5
4,v
9о'
6
7.А
^У
7
6,}^
8,v
8
6, А
7,А
9 1
6, А
5,А
№11
р^
а
b
1
2, А'
1х
2
1,х
Ъ,х
3
7,А
2,х
4
3,А
5, А
5
3,А
4, А
6
5, А
7,}^
7
6,}^
7,}^
8
4,А
1.У
9 1
\,х
7,У
№12
рХ
а
b
1
2, у
9, У
2
(>,у
Ъ,у
3
5,}^
6,v
4
4,А
3,А
5
6,}^
3,}^
6
8, А
4,}^
7
8,}^
6,}^
8
9,}^
7,}^
9 1
8.А
4,А
№13
р^
а
b
1
2,x
3,х
2
4,А'
6,х
3
2,А
\,х
4
2,А
3,}^
5
9, А
3,v
6
9,.V
7, А
7
8.А
1.}^
8
7,А
6, А
9
7,А
6,А
№14
рЧ
а
b
1
3,.у
7,>;
2
2,v
3,jc
3
1>^
7,)^
4
5,А
4,А
5
5,v
6,)^
6
7,>;
5,3"
7
гу
Ъ,у
8
8,)^
9.>;
9
5,v
8,3;
262
Глава 6
Таблица 6,1.2 (продолэ/сение)
№15
>^
а
b
1
2,х
1л'
2
4,х
5,х
3
4,х
5,х
4
3,х
5.}^
5
5,.у
6, у
6
7.x
5, У
7
6.x
5.x
8
7.x
9.x
9 1
7.x
8.x
№16
р^Ч
а
b
1
1у
2.x
2
1.}^
5,х
3
4,v
2,х
4
Ъ,у
9.x
5
6.x
8.x
6
5,У
2, у
7
8. У
9, У
8
7.x
5.x
9 1
4, У
8.x
№17
рч
а
b
1
4.jc
2,х
2
5,х
2,х
3
3,х
5,}'
4
9,х
2,х
5
3,У
8, У
6
6,х
7, У
7
6, У
8,У
8
7.x
2.x
9 1
9.x
8.x
№18
рЧ
а
b
1
2,у
1у
2
1у
^,У
3
2, у
Ъ,у
4
5,х
4,v
5
з,у
4, У
6
6,х
9.x
7
8, У
4, У
8 '
7, У
9.}^
9
5,У
8,У
№19
рХ
а
b
1
• 1.JC
2,х
2
3.x
9,х
3
2,х
6.x
4
6.x
5,}^
5
5,х
6.x
6
4, У
5.x
7
7.x
5,х
8
9,х
З.у
9
8,У
3.x
№20
рЧ
а
b
1
2,>;
1 з,>;
2
1.3^
3,у
3
6,}^
2,х
4
4,.У
6, У
5
7,у
5.У
6
З.у
4.x
7
7.x
8,х
8
7, У
9, У
9
7.У
8, у
Конечные автоматы
263
Таблица 6J.2 (продолэюение)
№21
^
а
b
1
\,х
г У
2
3,jc
7,х
3 1
2,А'
5,х
4
3,.у
4,л'
5
6,х
4,х
6
5,х
4,х
7
7,х
4,х
8
9,х
7,х
9 1
8,х
6,х
№22
р^
а
b
1
\,х
2,х
2
3,У
5,}^
3
4,}^
5,х
4
3,}^
5,х
5
2,v
4,х
6
9,У
4,х
7
7,}^
8,х
8
9.У
1.x
9 1
7,.У 1
8,}^
№23
рч
а
b
1
2,х
4,д:
2
1х
4,х
3
4,х
2, У
4
4,х
4,А'
5
5,х
6,х
6
7,х
6,х
7
6,х
6,х
8
7,х
5,v
9 1
9,У
8,3'
№24
рЧ
а
b
1
2,х
1у
2
1у
3.x
3
5,jc
4,JC
4
2,х
2,х
5
6.x
4,х
6
5,х
7,х
7
9,х
6,х
8
9,х
8.}^
9
8,}^
6,х
№25
рЧ
а
b
1
2,х
8,}^
2
5, У
6,.У
3
2,х
5, У
4
9,jc
5,.v
5
4,х
7..V
6
6,х
1у
7
4,х
8,.У
8
3,х
гу
9
8,У
6,>;
№26
р^
а
b
1
3,х
L^^}^
2
3,);
в,х
3
l,x
5,)^
4
4,А'
7,>;
5
1.}^
гу
6
9,}^
1>^
7
^,У
8,);
8
3,>;
5,>;
9
4,>;
6,х
264
Глава 6
Таблица 6,1,2 (окончание)
№27
^
а
Ъ
1
2,х
8,}^
2
5,х
1,У
3
7,х
9.}^
4
9,х
5, У
5
6, У
1У
6
4,х
8,.v
7
6, У
6,.У
8
з,у
9.x
9 1
1у
6, У
№28
pN^
а
b
1
^,У
9, У
2
6,v
5,х
3
1^У
4,А'
4
3,jc
1>^
5
2,х
9, У
6
5,х
г У
7
4,л'
8,v
8
5,л-
6.V
9 1
З.У
1у
№29
рЛ
а
Ь
1
4,x
2,х
2
7,jc
1,х
3
l,.v
5,х
4
2,}^
7,}^
5
2,JC
З.л-
6
1,х
6,х
7
6, У
9, У
8
9.x
8,х
9
8,у
7,У
№30
1^
а
Ь
1
2,х
3,х
2
1,Л'
j 5,)^
3
5,.v
L^'^
4
7,х
9,х
5
3,л-
2,х
6
5,л-
1У
7
S,x
4,3^
8
9,х
7,х
9
4,х
8, J
Пример решения задания 6.1.2
Решим задание 6.1.2 для автомата, заданного таблицей
состоянии.
Таблица 6,1,2а
>^
а
b
1
5,х
2, У
2
3,у
1,х
3
7,х
9, У
4
5,х
8, У
5
6, У
7,х
6
9,х
5, У
7
6, У
5,х
8
4, У
3,х
9
1.У
4.x
Конечные автоматы 265
1. Выясним, является ли автомат сильно связным. Для этого
изобразим диаграмму состояний данного автомата, опуская
пометки дуг и объединяя пары противоположно направленных дуг,
соединяющих одинаковые вершины графа. Получим:
Рис. 6.1.2
Построим в полученном графе циклический маршрут:
1->2->3->7->6->5-^7->6->9->4->8->3->9->1
Из возможности построения такого маршрута следует, что из
любого состояния автомата достижимо любое состояние этого же
автомата, то есть автомат является сильно связным.
2. Для построения минимального эквивалентного автомата
выявим все пары эквивалентных состояний данного автомата.
Для этого построим треугольную таблицу, где каждой паре
различных состояний соответствует одна клетка. Если для какой-
нибудь пары состояний одному значению входного сигнала
соответствуют различные выходные символы, следовательно, эта
пара состояний не является эквивалентной, и в соответствующую
клетку мы ставим крест. Получим (табл. 6.1.2Ь).
Далее, в незачеркнутые клетки выписываем пары состояний,
в которые переходит автомат из состояний, соответствующих
этой клетке, при подаче на вход одинаковых входных символов.
266
Глава 6
Таблица 6.1,2b
Таблица 6,1,2с
X
57
29
28
X
59
25
X
X
36
X
36
15
34
13
13
14
57
X
79
59
X
58
59
X
46
37
1 6
47
X
46
35
1 6
45
14
34
Конечные автоматы
267
Из этого правила записи есть два исключения:
1) не выписываем пары одинаковых состояний;
2) не выписываем пару, соответствующую заполняемой клетке.
Будем иметь (табл. 6.1.2с).
Затем, если внутри какой-нибудь клетки выписана пара,
соответствующая зачёркнутой ранее клетке, то клетка с этой парой
также зачёркивается. Окончательно имеем (табл. 6.1.2d).
Таблица 6.1.2d
2
3
4
5
6
7
8
9
X
57
29
28
X
X
y^i^
34
1 3
1 3
14
57
89
X
X
/^ТК,
14
34
1
8
Здесь каждой незачёркнутой клетке соответствует пара
эквивалентных состояний, которые мы объединяем в классы
эквивалентности:
1' = {1,3,4}; 2' = {2,8,9}; З' = {5,7}; 4' = {6}.
Строим минимальный автомат с четырьмя внутренними
состояниями Г, 2', З', 4'.
Для построения таблицы состояний минимального автомата
поступаем следующим образом: чтобы найти значение функций
перехода и выхода, например, на наборе (а,Г), выбираем из
класса эквивалентности Г любого представителя. Пусть это будет
268
Глава 6
состояние 3. Из таблицы состояний исходного автомата мы
имеем, что Х(а,3) = X,значит, определим также функцию выхода
минимального автомата: Х(а,1') = х. Из таблицы состояний
исходного автомата имеем, что 5(а,3) = 7. Но Те {5,7}=3', значит, будем
считать, что 5(л,3) = 3'.
Найдя значения функций перехода и выхода на всех наборах
перемененных, заполним таблицу состояний минимального
автомата (табл. 6.1.2е).
Таблица 6.1,2е
>r;
а
b
\
Ъ',х
2\у
1
У,у
\\х
1
3
^\У
З',л-
1
4
2',х
3',v
3. Проверим работу исходного автомата над словом abbabaab.
Пусть исходный автомат начинает свою работу, например, из 1
состояния:
Входное слово
Состояния
Выходное слово
1
а
5
X
b
7
X
b
5
X
а
6
У
b
5
У
а
6
у
а
9
X
b
4
X
Так как 1€{1,3,4}=Г, то минимальный автомат запускаем из
состояния Г. Получим:
Г
а
3'
X
b
3'
X
b
3'
X
а
4'
У
b
3'
У
а
4'
У
а
2'
X
b
1'
X
Как мы видим, результатом работы исходного и
минимального автоматов над словом abbabaab является одно и то же
слово хххууухх.
Конечные автоматы 269
6.2. Частичные автоматы
Автомат Мили называется частичным автоматом, если хотя
бы одна из функций перехода или выхода не является всюду
определённой.
Говорят, что слово а применимо к. состоянию q^
неинициального автомата, если функция переходов автомата, начавшего
работу в состоянии qi над словом а, может быть не определена
лишь после считывания последнего символа слова а.
Будем рассматривать слова одинаковой длины в алфавите,
содержащем неопределённый символ '' - ".
Слово а покрывает слово Р, если слово Р может быть
получено из а заменой некоторого множества (может быть, пустого)
символов неопределёнными символами.
Слово а совместимо со словом Р, если существует слово у,
покрывающее как слово а, так и слово р.
Через 5(а,^) будем обозначать выходное слово, полученное
в результате работы над словом а неинициального автомата 5,
запущенного из состояния q. Если на некотором наборе
аргументов значение выходной функции не определено, то в
соответствующей позиции выходного слова ставим неопределённый символ.
Состояние q' автомата S' покрывает состояние q автомата
5, если любое слово а, применимое к состоянию q, будет также
применимо к состоянию q\ причём S'(a,q') будет покрывать
S(a,qy
Частичный автомат S' покрывает автомат 5, если для
любого состояния q автомата S найдётся покрывающее его
состояние q' автомата S'.
Автомат, покрывающий частичный автомат S и имеющий
наименьшее возможное число внутренних состояний среди всех
автоматов, покрывающих 5, называется л/г///ш^а/7ьныл/для S.
Состояния q и q' частичного автомата S называются
совместимыми, если для любого слова а, применимого к
состояниям <7 и q\ слова S'(a,q') и S(a,q) будут совместимы.
270
Глава 6
Множество попарно совместимых состояний автомата
называется группой совмеатшоспт этого автомата.
Группа совместимости называется максимальной, если при
добавлении в неё любого состояния, она перестаёт быть группой
совместимости.
Класс групп совместимости автомата S называется
группировкой, если любое состояние автомата S попадает хотя бы в
одну группу совместимости.
Группировка, состоящая из всех максимальных групп
совместимости данного автомата, называется максимальной
группировкой данного автомата.
Группировка называется замкнутой, если для любой группы
совместимости Q^, этой группировки, для любого символа
входного алфавита а и для любых состояний q и q' из группы
совместимости Q^, либо хотя бы одно из значений 5(а,г/')и
5(а,(7)не определено, либо 5(а,г/')и 5(а, г/) определены и из
того, что 5(а,^) принадлежит некоторой группе совместимости
2^^., следует, что и 5(а,^') также принадлежит 2^^.
Задание 6.2.1
Для слов a,b,c,d:
1. Указать пары {х,у) такие, что х покрывает у.
2. Указать все пары совместимых слов.
3. Указать все пары несовместимых слов.
4. Найти слово е, не попавшее в множество {а,Z?,с,с/}такое,
что е покрывает не менее двух слов из множества {a,b,c,d}.
Таблица 6.2,1
№
1
2
3
4
а
_ 10-0-1—0
1„_01 —1"
-01101--10-1
01-1-1-01-01
b
1-0-11-10-0
— 11-1-100
-1-0—10-
-1-1—0-0-
с
-101-0--11-0
—00-1-10
__1_0—01-
01 — 1-1-0-
d
-01-0-11-0
1-0011-101
-011-1—0-1
01-1—001-
Конечные автоматы
271
Таблица 6.2.1 (окончание)
1 ^-
1 ^
1 ^
1 ^
1 ^
1 ^
1 ^^
1 ^^
1 ^^
1 ^^
1 ^"^
1 ^^
1 ^^
1 ^"^
1 ^^
1 ^^
1 20
1 ^^
1 22
1 ^^
1 ^"^
1 ^^
1 26
1 ^"^
1 28
1 29
1 30
л
_1._01-—01
0-1-1-00" 1
„0-1-0-0-
01-1-0-10-11
01-01—-1-
10-101-011-
—0-101-0-
„1-01-1-
-01 — 1-0-0-
-1-010-0-011
1„01—00-1
-01—0-1-1
1-0—1-1-1
10-10-10-1-
-1-011-01-1
-1-0-01-1
01 — 1-00—
010-01-1-00
—01 — 10-1
-10-0-10-
0-1110-01-0
0—111—0
1 10-10-011-1
10-0-10-1-1
111-001-101
1„00-0—0
b
0-1-1-1-0-
-1-1-1—1-
-10-11-0-100
-1-1-0—10
— 11-0-010
-0-10-01-
0-1-010—1
-1-010-110-
1—1-00110
-1-01-0-11
1-1011-00-1
-01—0-1101
-10-0-10-
"1-0-10-01-
-1-01-0—1
10-0-1-1-0-
01-1 — 10-
-10-10-1-0
1„01—00-
-0-11-1-1-
0-11—0—
0-1-111-0-0
101-01-10-0
0-10-011-0
-11-00—1
11-00-101-10
с
01-101-11-01 1
-1—01-10-
0-0-0-1-11
— 11-0-1-0
— 10-1 — 10
1—1-1-1-1-
-11-1-1-0-
-1-10-01-
-010-1-0001
0-01-1-1-
-10-1-00-
10-1-1—01
-1-0-01-0-
10-0-1-1"
-ЬО-О-Ю-О
-0-0-01-0-
0-1-0-0-1-
-10-0-1-0-
11-011-00-1
-10-10-101-
-1-00-10-0
1 -01-101-0-0
1-10-01-1
-0-1-1-1-1
1 11—0-1-10-
1 _1_0-1-11-
d 1
-101 — 1-0- 1
01-1-1-0011 1
-1-1-0-00 1
-1-11-0-1010 1
01-101 — 10 1
1 —1-1-0-1- 1
0-11-0101-01
„1-10-1-0- 1
-0-0-1-0-1 1
—0-0-0-11 1
-1000—0-1 1
-1—0-1-0- 1
-110-0110-1 1
-0-1-10-1- 1
—0-1-0-"1 1
10-0-101-01
011-01-001-
01—01-1-0
-1-0-1-00-1
-0-10—01-
-11-0-01-
— 1-1-1-0-
-0-10—1-1
10-10-1011-1
111-1101-001
1 111-0-000-10
272 Гпаеа 6
Пример решения задания 6.1.2
Решим задание 6.1.2 для а = 101- 01 -0; Ь= И- - 1- О -;
с= -0--0--0; d= 1-1--1-0.
1. Слово а покрывает слово с, т. к. если первую, третью
и шестую единицы слова а заменить неопределённым символом
"-\ то получим слово с.
Слово а покрывает слово d, т. к. если второй и пятый символ
слова а заменить неопределённым символом "-", то получим
слово d.
2. Совместимыми парами слов будут пары {а,с], {ci,d},
{c,d}, т. к. для каждой из этих пар слово а покрывает каждое
слово этой пары.
Совместимой является также пара [b,d}, т. к. существует
слово /= 111-1100, покрывающее как слово Ь, так и слово d.
3. Парами несовместимых слов являются пары [а,Ь} и {с,Ь},
т. к. слова а и с имеют вторым символом О, а слово b имеет на
втором месте 1.
4. Примером слова е может быть слово 101101-0, которое
покрывает слова а, с и d.
Задание 6.2.2
Для частичного неинициального автомата, заданного
таблично, со множеством внутренних состояний {1,2,3,4,5,6,7,8,9},
входным алфавитом {(7,/?} и выходным алфавитом {х,у}:
1. Найти слово а длины не меньшей 7, такое, что а применимо
к некоторому состоянию q, но любое слово, полученное из а
приписыванием справа одной буквы, не применимо к q.
2. Построить максимальную группировку.
3. Построить покрывающий автомат на основе максимальной
группировки.
4. Построить покрывающий автомат с помощью Т —
алгоритма, убедиться, что каждый класс совместимости попадает
в некоторый максимальный класс совместимости группировки,
построенной в п. 2.
Конечные автоматы
273
5. Проверить работу построенных различных автоматов над
словом а из п. 1.
Таблица 6.2,2
№1
^
а
Ь
1
2,-
-,х
2
-,Л'
6-
3
—
1.Л'
4
2-
-.,v
5
-,х
3,}^
6
9,v
-Л
7
8,х
-3^
S
7,х
9 1
-,х
6-
№2
[^
а
Ь
1
2,-
2
4,x
-,х
3
4,-
2,-
4
3,х
-}^
5
6,3'
6,У
6
-,х
5,-
7
-,х
-,-^
8
7,х
5,-
9 1
-,х
№3
Р>^
а
Ь
1
2,х
-^у
2
-,х
1,У
3
4,-
3,-
4
-,х
7-
5
5,3'
6
4,х
-,х
7
8,х
6-
8
5,3^
9,У
9 1
-,х
9.x
№4
рХ
а
Ь
1
3,х
2
1,-
-,х
3
4,х
5,-
4
5,-
-,v
5
4,.V
9-
6
7,х
-3^
7
6, У
8,.У
8
-,х
7,х
9 1
6,-
№5
рЛ
а
Ь
1
2,х
-,x
2
7-
3,-
3
2.x
4
3-
-,-^
5
-,х
4,х
6
5,х
Ъу
7
6,.У
7,-
8
4-
9
1,Л'
7,:^
№6
рЧ
а
Ь
1
2,>;
->^
2
6-
3,)^
3
6-
4
4,х
3,х
5
6,.у
3,3^
6
-,х
6,3^
7
9,-
8
8,3^
6,-
9
-,х
I 4,)-
274
Глава 6
Таблица 6,2.2 (продолэюение)
№7
>^
'^ а
b
1
2,х
5,-
2
6,х
3
-,х
4-
4
1,х
~'У
5
8-
4,}^
6
1,х
-,х
7
6,}^
8-
8
7,>'
9 1
8,.v
9- 1
№8
р^
а
b
№9
pN^
а
1 ^
1
3,}^
1
2,-
1л:
2
2,-
3,х
2
5,х
3
-^у
7,v
3
4-
-,х
4
5..V
4,-
4
3,х
5,}^
5
5,v
(^^У
5
5,3'
-^у
6
—
5-
6
-,х
5,v
7
7-
3,.V
7
6-
5,х
8
8.V
9-
8
1,х
9-
9 1
5,v
8-
9 1
-,х
8,х
№10
|>^
а
1 ^
1
1,-
2,х
2
- >^
5,-
3
2,х
4
3,}^
9,л'
5
6,х
-,х
6
5-
2, у
1
8,3^
8
1,х
5,-
9
8,х
№11
рХ
а
1 ^
1
4.д:
2
5-
2,х
3
3,д:
-^у
4
9-
-,л:
5
\У
8,-
6
6,.v
7.)^
7
-,.v
8
7,.\:
2-
9
9-
8,х
№12
рХ
а
1 ^
1
2,>;
2
1,-
^,У
3
2,>;
3-
4
-,х
4-
5
3,)^
—
6
в,х
9,х
7
8,>;
4-
8
-V
9.V
9
5-
8,>;
Конечные автоматы
275
Таблица 6.2.2 (продолэюение)
№13
ач.
а
b
1
1-
2,х
2
З..Х
3
2,-
6, л:
4
-,х
5, У
5
5,-
6-
6
- 3^
5,х
7
7,л'
8
9,-
3,.v
9 1
8,v
-,х
№14
рЧ
а
b
1
2,}^
3-
2
-^у
-^у
3
6,-
2,JC
4
4-
5
7,.v
6-
6
3,У
7
1,х
S,x
8
-^у
9, У
9 1
7,- 1
8,v
№15
рч.
а
b
1
\,х
-^у
2
3-
1,х
3
2,х
4
-, V
4,Jc
5
6,Л'
4,-
6
4,л'
7
7-
4,-
8
9.x
7-
9 1
6,х
№16
рл
а
1 ^
1
l,Jt
2,-
2
-^у
3,У
3
5,х
4
3,}^
5
2,-
4-
6
9,}^
-,х
7
7,.V
8,.v
8
9,}^
9
7-
8,}^
№17
рХ
а
1 ^
1
2-
4,х
2
1,-v
3
-,Л'
2, У
4
4,-
4,х
5
5,А'
6-
6
7-
-,.v
7
6,л-
8
7,х
5, У
9
->^
8-
№18
рх
а
1 ^
1
2,-
1у
2
1>^
3-
3
5,х
4
2,-
5,х
5
6,-
4.JC
6
-,х
7,-
7
9-
6,х
8
9,х
-^у
9
~'V
6,х
276
Глава 6
Таблица 6,2,2 (продолэюение)
№19
><о^
^
b
1
4,х
->^
2
-,у
4,-
3
7,х
9,х
4
5,-
9,у
5
8,х
- >'
6
7-
7
2,}^
8,х
8 1
-,х
9-
9 1
->.у
5.x 1
№20
рч.
а
b
1
2,х
- >^
2
- >^
9,х
3
8.V
—
4
7-
5,х
5
4-
6,х
6
-у
7,}^
7
4,х
- 3^
8
6,3'
9 1
3.V
8.x
Х«21
F^
а
1 ^
1
2,х
-,х
2
1,-
4,х
3
3,}^
—
4
5,х
2-
5
4-
3.x
6
-,х
3-
7
3,}^
8,v
8
6.x
8.-
9 1
-.у
4, У 1
№22
1^
а
1 ^
1
5-
3,х
2
9,х
-,х
3
—
8,х
4
7,}^
5,}^
5
-..V
6,-
6
2,х
-,х
7
8,}^
5-
8
9, У
9
2,У
3,-
№23
1^
а
1 ^
1
3,х
2,-
2
8-
5,-
3
5,х
4
1.x
-,х
5
8,х
2-
6
1 7,.у
"•^
7
6,}^
8..V
8
->у
8.x
9
^"
8.V
№24
рЧ
а
1 ^
1
2,у
->у
2
4,>;
3,-
3
9,-
2,v
4
^'^
5
4,-
7,.у
6
-'V
9,х
7
90'
Г 4-
8
3.-
-,х
9
8.x
9,v
Конечные автоматы
277
Таблица 6.2.2 (окончание)
№25
^
а
h
1
-,х
2
З.л'
3
-..V
—
4
6,х
7,-
5
5- 1
-у
6
—
2, у
7
-,Л'
-,х
8
6,у
7,-
9 1
8. У
-у
№26
рч
а
b
1
-,Л'
- >^
2
5,л-
7-
3
—
9,>'
4
9,-
5
6,.У
1,-
6
4,х
8-
7
6-
6, У
8
-,х
9 1
4, У
№27
рч
а
I ^
1
2-
2
6, У
-,х
3
7-
4,х
4
-,л'
1.У
5
2,-
6
5.Л'
7-
7
-'У
8
5,-
6, У
9 1
З.У
1-
№28
Р^
а
1 ^
1
4,л'
2-
2
7-
1,л-
3
-,х
5,х
4
-^у
7,>'
5
2,х
3-
6
-.Л'
6,л-
7
6, У
-«У
8
9,л-
8,л-
9 1
8,У
7, У
№29
рл
а
1 ^
1
2,.t
-,Л'
2
1-
5,v
3
5,.г
1у
4
7-
5
3,.v
-,.Y
6
5,х
1у
7
-,х
4,у
8
9-
7,jc
9 1
8,.v
№30
>^
а
1 ^
1
I 4,>;
2
7,v
-'У
3
1,-
1 5,.\:
4
1 ^~
6,А'
5
-'У
[^.У
6
5, у
7
1,А'
1 3,А'
8
7,>'
-у
9
~' •^'
1,х
278
Глава 6
Пример решения задания 6.2.2
Решим задание 6.2.2 для автомата, заданного своей таблицей
состоянии:
Таблица 6,2.2а
^
а
b
1
2-
2
3,л'
- }'
3
Iv
4
5, А'
5
в,х
6
-,х
1
\-
4,}^
8
5.}^
—
9
-,х
6-
1. Построение слова а начнём "с конца", т. е. сначала выберем
в таблице клетку, в которой происходит переход в
неопределённое состояние, например, клетку {а,Ъ). В третье состояние можно
перейти из второго при появлении входного сигнала а. Во второе
можно перейти из первого при подаче на вход сигнала а и т. д.
В результате можно получить слово а-аааЬааа, причём
автомат над этим словом будем запускать из состояния 7. Проверим
работу автомата над словом а:
7
а
1
-
а
2
-
а
3
X
b
1
У
а
2
-
а
3
X
а
-
-
Как видим, слово а применимо к состоянию 7, но любое
слово, полученное из а приписыванием справа хотя бы одного
символа, не будет применимо к состоянию 7, т. к. при подаче
последнего символа слова а автомат, запущенный из 7 состояния,
перешёл в неопределённое состояние.
2. Строим максимальную группировку. Сначала выявим с
помощью треугольной таблицы все пары совместимых состояний.
Правило заполнения таблицы остаётся таким же, как и для всюду
определённых автоматов. На первом этапе получим (табл. 6.2.2Ь).
Конечные автоматы
279
Таблица 6.2.2Ь
2
3
4
5
6
7
8
23
25
12
1 ^^
35
13
X
14
16
1 5
X
^^^<
1 5
46
><|
Потом, заметив, что клетка (2,5) зачёркнута, ставим крест
также и на клетку (1,4), куда попала пара (2,5). Таким же образом
кресты получат и клетки (1,8), (2,4) и (3,7). Окончательно имеем
(табл. 6.2.2с):
bxJX]
23
Таблица 6.2,2с
Итак, каждой незачёркнутой клетке таблицы соответствует
пара совместимых состояний.
280 Глава 6
Построение максимальной группировки проведём по
алгоритму, содержащему количество шагов, равным числу внутренних
состояний автомата:
а) на нулевом шаге выписываем все состояния, объединяя их
в один класс;
б) на / -том шаге просматриваем / -ый столбец треугольной
таблицы.
Если какой-либо класс внутренних состояний, полученный на
предыдущем шаге, не содержит состояния с номером /,то этот
класс переписываем без изменений.
Если класс содержит / -е состояние, но все остальные
состояния этого класса совместимы с / -тым, то этот класс также
переписывается без изменений.
Если класс содержит / -е состояние вместе с состояниями,
несовместимыми с / -м, то этот класс делится на две части: одна
получается из этого класса удалением состояния с номером /,
а другая — удалением из этого класса всех состояний, не
совместимых с / -ым.
Если на каком-то шаге образуется два класса, один из которых
является собственным подмножеством другого, то меньший
удаляется из рассмотрения.
В результате работы этого алгоритма получается
максимальная группировка.
Применим алгоритм к нашему примеру. Работа алгоритма
будет состоять из 9 шагов. Выпишем классы, получающиеся на
каждом шаге:
0) {1,2,3,4,5,6,7,8,9}.
1) {2,3,4,5,6,7,8,9}, {1,2,3,5,6,7,9}.
2) {3,4,5,6,7,8,9}, {2,3,7,9}, {1,3,5,6,7,9}, {1,2,3,7,9}.
3) {4,5,6,7,8,9}, {3,4,8,9}, {1,5,6,7,9}, {1,3,9}, {1,2,7,9},
{1,2,3,9}.
V) {5,6,7,8,9}, {4,5,6,7,9}, {3,8,9}, {3,4,9}, {1,5,6,7,9}, {1,2,7,9},
{1,2,3,9}.
'S)'{6,7,8,9}, {5,6,8,9}, {4,6,7,9}, {4,5,6,9}, {3,8,9}, {3,4,9},
{1,6,7,9}, {1,5,6,9}, {1,2,7,9}, {1,2,3,9}.
6) {7,8,9}, {6,8,9}, {5,6,8,9}, {4,7,9}, {4,6,9}, {4,5,6,9}, {3,8,9},
{3,4,9}, {1,7,9}, {1,6,9}, {1,5,6,9}, {1,2,7,9}, {1,2,3,9}.
Конечные автоматы
281
7) {7,8,9}, {5,6,8,9}, {4,7,9}, {4,5,6,9}, {3,8,9}, {3,4,9}, {1,6,9},
{1,5,6,9}, {1,2,7,9}, {1,2,3,9}.
'8) {7,9},'{7,8},'{5,6,9}', {5,6,8}, {4,7,9}, {4,5,6,9}, {3,9}, {3,8},
{3,4,9}, {1,6,9}, {1,5,6,9}, {1,2,7,9}, {1,2,3,9}.
Заметим, что на втором, третьем, шестом и восьмом шагах
происходило удаление классов, являющихся собственными
подмножествами некоторых других классов. В результате получена
максимальная группировка:
{{7,8}, {5,6,8}, {4,7,9}, {4,5,6,9}, {3,8}, {3,4,9}, {1,5,6,9},
{1,2,7,9}, {1,2,3,9}}.
3. Обозначим группы совместимости:
1' = {7,8}; 2' = {5,6,8}; 3* = {4,7,9}; 4' = {4,5,6,9}; 5' = {3,8};
6' = {3,4,9}; 7' = {1,5,6,9}; 8' = {1,2,7,9}; 9' = {1,2,3,9}.
Построим автомат S^ с входным алфавитом {а,Z?}, выходным
алфавитом [х,у} и множеством внутренних состояний
{ Г,2',3',4',5',б',7',8',9'} на основе исходного частичного автомата.
Для построения таблицы состояний покрывающего автомата
поступаем следующим образом:
чтобы найти значение функции выхода, например, на наборе
(а,Г), смотрим значения функции выхода исходного автомата на
наборах (а,7) и (а,8). Видим, что X(aJ) не определена, и
X(a,S) = у. Значит, считаем, что Х(а,Г) = у.
Для нахождения значения 5(а,Г) отметим, что исходный
автомат из состояний 7 и 8 при подаче входного символа а
переходит в 1 и 5 состояния, которые попали в класс 7*. Значит, будем
считать, что 8(а,Г) = Т.
Продолжая аналогично, построим таблицу состояний
покрывающего автомата S^.
Таблица 6.2.2d
>-^
а
b
1'
Г,у
4',}^
2'
4',У
2',х
з'
7',л'
4',v
4'
Т,х
1',х
5'
7',у
7',у
6'
7',л-
7',У
7'
8',х
1',х
8'
S\x
4',У
9'
9',х
7',У
282 Глава 6
4. Рассмотрим Т -алгоритм построения покрывающего
автомата:
а) Выявляем все пары совместимых состояний (например, с
помощью треугольной таблицы).
б) Выписываем все состояния автомата в порядке возрастания
индексов. Вычёркиваем все состояния, несовместимые с первым,
выбираем следующее по порядку возрастания индексов невы-
черкнутое состояние, зачёркиваем все состояния, несовместимые
с ним, и т. д. В результате получим некоторую группу
совместимости.
Составляем из вычеркнутых состояний список по порядку
возрастания номеров и проделываем с ним ту же
последовательность действий, что была описана в предыдущем абзаце.
Если мы повторим эту процедуру до тех пор, пока это
возможно, получим группировку.
в) Начинаем строить покрывающий автомат, в котором
каждой группе совместимости соответствует некоторое внутреннее
состояние. Если группировка замкнута, такое построение
возможно, и полученный автомат будет искомым.
Если группировка не замкнута, строим на её основе
замкнутую группировку, расширяя, в случае необходимости, группы
совместимости или добавляя новые группы совместимости.
После получения замкнутой группировки строим
покрывающий автомат, сопоставляя каждой полученной группе
совместимости внутреннее состояние автомата.
Применим Т -алгоритм к нашему автомату. Пары
совместимых состояний у нас уже найдены, поэтому сразу переходим к п. б)
алгоритма. Напишем полученную последовательность групп
состояний:
1 2 34^^^^ 9, 4 5 6 \^, 7 8.
Итак, найдена группировка: {{1,2,3,9}, {4,5,6}, {7,8}}.
Проверим группировку на замкнутость, пробуя построить
автомат 5*2 с входным алфавитом {а,Ь], выходным
алфавитом {х,у} и множеством внутренних состояний {1",2",3"}, где
1"={ 1,2,3,9); 2"={4,5,6};3"={7,8}.
Конечные автоматы
283
Видим, что при подаче на вход сигнала b исходный автомат
переходит из состояний 1, 2, 3 и 9 либо в неопределённое
состояние, либо в 1 или 6. Состояния 1 и 6 вместе не входят ни в какую
группу совместимости построенной группировки, и группу 2
нельзя расширить, добавив в неё состояние 1, т. к. оно
несовместимо с состоянием 4, вошедшим в 2".
Итак, добавим новое состояние 4"= {1,6}.
Далее видим, что из состояний 7 и 8 под действием сигнала а
исходный автомат переходит в состояния 1 и 5, которые также не
вошли ни в одну группу совместимости построенной
группировки. Заметим, что состояния 1, 5 и 6 совместимы, поэтому группа
4"={1,6} может быть расширена добавлением состояния 5,
значит, 4" примет вид 4"={ 1,5,6}.
Заметим, что при подаче сигнала а из состояний 1, 5, 6
исходный автомат переходит либо в неопределённое состояние,
либо во 2 состояние, а при подаче b — либо в неопределённое
состояние, либо в состояние 6. Каждое из этих состояний входит
в одну из новых групп совместимости. Значит, построенная
группировка замкнута. Строим таблицу автомата 5*2 ( табл. 6.2.2е).
Таблица 6.2.2е
аХ,
а
b
1"
У\х
^",У
2"
2".х
2",х
3"
4",}^
2",У
4"
1",-
4",Л'
Заметим, что l' = {7,8} с 9' = {1,2,3,9}; 2" = {4,5,6} с 4' =
= {4,5,6,9};
3" = {7,8} с 1' = {7,8}; 4" = {1,5,6} с {1,5,6,9}.
Итак, мы убедились, что каждый класс совместимости
попадает в максимальный класс совместимости группировки,
построенной в п. 2.
5. Проверим работу полученных автоматов над словом а из
п. 1 данного задания.
284
Глава 6
Так как 7е Г, автомат 5| надо запускать из состояния Г.
Г
а
i
у
а
8'
X
а
8'
Л'
Z?
4'
>^
с/
7'
X
а
8'
X
г/
8'
X
Заметим, что слово уххуххх, полученное в результате
работы автомата 5,, запущенного из состояния Г над словом а,
покрывает слово —л:у-Х-,полученное в результате работы
исходного автомата, запущенного из состояния 7 над а.
Так как 7еЗ , автомат 5*2 будем запускать из состояния 3 .
з"
а
4"
V
а
Г'
-
а
Г'
X
b
4"
у
а
l"
-
а
Г'
X
а
Г'
X
Также видим, что слово у-ху-хх, полученное в результате
работы автомата ^2, запущенного из состояния З" над словом а,
покрывает слово —ху-х-, полученное в результате работы
исходного автомата, запущенного из состояния 7 над а.
6.3. Реализация
автоматов схемами
Функциональным элементом называется
устройство, имеющее п упорядоченных отрезков
вверху, которые называются входами, и один
отрезок внизу, называемый выходом
функционального элемента.
Функциональный элемент изображается так:
Конечные автоматы
285
На входы функционального элемента могут подаваться
сигналы двух типов, причём при подаче набора сигналов на входы
элемента задержки, на выходе мгновенно возникает сигнал
одного из этих типов, причём каждый набор входных сигналов
однозначно определяет значение выходного сигнала.
Элементом задерэюки называется конечный автомат,
имеющий два внутренних состояния, входной и выходной алфавиты
которого имеют по два символа и совпадают, и который
осуществляет задержку входного сигнала на один такт времени.
Элемент задержки изображается так: |
Верхний отросток называется входом, а нижний —
выходом элемента задержки.
Полюсами называется упорядоченный набор кружков,
помеченных символами различных переменных.
Схема из функциональных элементов
и элементов задерэюки определяется
индуктивно:
а) совокупность полюсов (кружков,
помеченных символами переменных)
есть схема\ все полюсы являются её вершинами',
б) результат присоединения к вершинам схемы всех входов
некоторого элемента (функционального элемента или элемента
задержки) есть схема\ вершинами новой схемы являются все
вершины исходной схемы и выход присоединённого элемента,
а полюсами — все полюсы исходной схемы;
А'/
О
о
о
а)
i_
т
ш
W
? • ?
1 Е
61) 62) в)
в) результат присоединения выхода задержки к
некоторому полюсу Xi есть схема\ её вершинами являются все вершины
ЮЗак. 3332
286
Глава 6
исходной схемы, за исключением х-, а полюсами — все полюсы
исходной схемы, кроме Х/. Операция, соответствующая пункту в),
называется введением обратной связи.
Задание 6.3.1
1. Построить таблицу состояний автомата, осуществляющего
автоматное отображение а в р.
2. Провести минимизацию, построить диаграмму состояний
минимизированного автомата, проверить работу полученного
автомата над словом а.
3. Провести кодировку в двоичные коды символов входного
и выходного алфавитов, множества внутренних состояний
автомата, написать "физическую" таблицу состояний
минимизированного автомата.
4. Построить минимальные ДНФ, реализующие функции
переходов и функцию выхода автомата.
5. Построить схему из функциональных Э1пементов типа
конъюнкция, дизъюнкция, отрицание и элементов задержки,
реализующих данный автомат.
Замечание. Если схема получается сложная, можно
реализовать отдельно схемами функции переходов и выхода и
изобразить блок — схему автомата.
Таблица 6.3.1
№
1
2
3
4
5
6
7
а
abbacccab
bacaabacb
caaabcbba
acbcacbbc
cacabbbac
baabccbcc
bacaaccba
p
uppinipppu
upuppuppu
iippuupupu
upppupuup
iippuuppuu
pupuupppu
puuupuiipp
№
8
9
10
11
12
13
14
a
caacaabbb
bciccabbcc
caabcbacb
bcK^ccbaaa
accbbccab
caabbbaca
bcaccbbba
p
puuppuiipp
ppiiuuppup
upupppuuu
piiuuupppp
upuppuupu
puiiupuupu
upuppuuup
Конечные автоматы
287
№
15
16
17
18
19
20
21
22
а
ababbcccb
bcbaaccbb
abbccaabc
baabcbbac
acbccbabc
baaccbabc
cabcbcbaa
bcbabccba
p
iiuppupupp
pupuupppu
upppupppu
puiiupupuu
upupuppuu
puuppuppp
upupupppu
pupuupppp
№
23
24
25
26
27
28
29
30
Таблица 6.3,1 (окончание)
a
acbbbbcca
hacbbcaba
cibbcabcaa
cbcbacibcc
aaccbcacb
bbbcbabac
aabacabba
aabbbcaac
p
pupupiiupu
upupppuup
puuppuuup
ppiiupuppp
uuupuupup
ppuuppuiip
ppppiippiiu
ppuupuppu
Пример решения задания 6.3.1
Решим задание 6.3.1 для а= abccbbbac, Р = иириррирр.
1. Строим таблицу состояний инициального частичного
автомата, осуществляющего автоматное отображение а в р. Автомат
будет иметь входным алфавитом множество {а,Ь,с}, выходным
алфавитом — множество {и,р} и число состояний, равное
количеству символов в словах а и р. Будем обозначать состояния
автомата цифрами от 1 до 9.
Функцию переходов зададим следующим образом:
5(аД) = 2, 5(^7,1) и 5(сД) не определены. В дальнейшем, если
Х|Х2,...,х^ (к<9) —начало слова а, то 5(xi^,k) = k + l, в
остальных случаях 5(х/,Д) не определена.
Функцию выходов зададим так: если XiX2,...,x^^ (к <9) начало
слова а, то 5(xj^,k) = yj., где yj^ — к -и символ слова Р; в
остальных случаях 6(xj.,k) не определена.
Получим таблицу состояний автомата (табл. 6.3.1а).
2. Сначала строим треугольную таблицу для нахождения пар
совместимых состояний (табл. 6.3.lb).
288
Глава 6
Таблица 6,3,1а
>^
а
b
с
1
2,w
2
Хи
3
4,Р
4
5,11
5
6,р
6
7,Р
7
8,w
8
9,р
9
->Р
^^
@
^
38
рд
Таблица 6,3, lb
^u^
i>^>^
Проведём минимизацию с помощью Т -алгоритма:
1 2 34^ ^7 8,9, 4 5 ^8, 6.
Обозначим: Г = {1,2,3,7,9}; 2' = {4,5,8}; 3'= {3,6,8}.
Строим таблицу покрывающего автомата (табл. 6.3.1с):
Проверим работу полученного автомата на словом а:
Таблица 6.3.1с
7~-^--^
а
b
с
1'
У.Р
у,и
2\Р
i
i'.p
У.Р
2', и
3'
У,Р
У.Р
2',Р
Конечные автоматы
289
Проверим работу полученного автомата над словом а:
Г
а
Г
и
b
з'
и
с
2'
Р
с
2'
и
b
3'
р
b
г
р
b
3'
и
а
Г
Р
с
2'
Р
3. Проведём кодировку двоичными кодами символов входного
и выходного алфавитов, символов множества внутренних
состояний автомата:
а -00, b -01, с -И, и -О, р -1,
1'-00, 2'-01,3'-И.
Запишем "физическую" таблицу состояний автомата, т. е.
таблицу состояний, в которой символы состояний, символы
входного и выходного алфавитов заменены их двоичными кодами:
Таблица 6.3, Id
00
01
11
00
00,0
11,0
01,1
01
00,1
11,1
01,0
и
00,1
00,1
01,1
4. Будем рассматривать эту таблицу как сводную таблицу двух
функций переходов д^^з' соответствующих старшим и младшим
разрядам двоичных кодов состояний и функции выхода у,
которые зависят от четырёх переменных х^,Х2, cj^, ^72-
Для каждой из этих функций найдём минимальную ДНФ с
помощью карт Карнау.
Запишем в карту Карнау таблицу значений функции q^, выписав
значения старших разрядов двоичных кодов состояний автомата,
взятые из "физической" таблицы переходов, заменяя значения, на
которых Qi не определена, прочерками (табл. 6.3.1е).
290
Глава 6
Таблица 6,3, le
1 ^л
^1^2
1 00
1 ^^
1 ^^
1 ^^
00
0
п
0
-
01
0
п
0
-
и
0
0
0
-
10 1
1
-
-
-
Имеем: q^ = х\-Х2 'q\ •
Аналогично, построим карту Карнау для функции ^^(табл. 6.3.If).
Таблица 6,3,1/
00
i ^^
11
L ^^
00
0
Г"
'1
. 1
^ч
01
0
1
1
-
11
0
0
1
-
10
-
-
>
_^
Получаем: qi- Ц^ ^2' Я\ •
Строим карту Карнау для функции выхода (табл. 6.3. Ig).
Таблица 6,3,Ig
Х|Х2 ^ .^^^^
00
01
11
10
00
0
0
~1
_ -
01
Г~\
L_j
0
-
и
гп
_L^
1
Vz
10
_л
-
-
=eJ
Конечные автоматы
291
Имеем: y = q\^x^- q 2 ^ ^\ 'Qi-
Итак, Qi = х\ •Х2' q\ , Ц2- Ц^ ^2' Ч \ •> У-Ч\^^\' Яг ^ ^^ ' ^2 •
5. Строим схему из функциональных элементов типа
конъюнкция, дизъюнкция, отрицание и элементов задержки.
f~
Y,
1
3,
^=
^
"о
4
Л
32
Л/
V
\л
Задание 6.3.2
1. Удалить из данной схемы задержки и написать формулы
для функций ^1, ^2' ^3' .V-
2. Построить таблицы для функций, найденных в п. 1.
3. Свести таблицы, найденные в п. 2, в одну, провести кодировку.
4. Провести минимизацию автомата.
5. Для минимального автомата провести обратную кодировку,
написать "физическую" таблицу переходов и выхода.
6. С помощью карт Карнау написать формулы функций
перехода и выхода.
7. Реализовать найденные функции схемами из
функциональных элементов типа конъюнкция, дизъюнкция и отрицание.
8. Изобразить схему из функциональных элементов типа
конъюнкция, дизъюнкция, отрицание и задержек, реализующую
минимальный конечный автомат.
292
Глава 6
Таблица 6.3.2
Конечные автоматы
293
Таблица 6.3.2 (продолэюение)
10
11
12
294
Глава 6
Таблица 6.3.2 (продолжение)
13
/ yN^ y^
3,
З2 З3
У
14
15
16
17
18
Конечные автоматы
295
Таблица 6.3.2 (продолжение)
19
20
21
22
23
24
296
Глава 6
Таблица 6.3.2 (окончание)
25
26
27
28
29
30
Конечные автоматы
297
Пример решения задания 6.3.2
Решим задание 6.3.2 для данной схемы (рис. 6.3.2):
Рис. 6.3.2, а
1. Удалим задержки (рис. 6.3.2, а), введём три новых полюса
^Р^2 и ^3' соответствующих выходам задержек, а входам
задержек будут соответствовать вершины^,, q2 ^ Q3- Проведём
анализ схемы, напишем формулы для функций q^^Qi^R^ ^ У-
q^=xvqi\ q2-^\ q^^XAq^ ах = 0\ y = xvq^vq2.
2. Напишем таблицы найденных функций.
Таблица для <?, =xv q^ (табл. 6.3.2а).
Таблица 6.3,2а
0
1
000
0
1
001
0
1
010
0
1
011
0
1
100
1
1
101
1
1
110
1
I
111
1
1
298
Глава 6
Таблица для (/2 =х (табл. 6.3.2Ь).
Таблица 6.3.2Ь
0
1
000
1
0
001
1
0
010
1
0
oil
1
0
100
1
0
101
1
0
по
1
0
111
1
0
Таблица для y = xwq^wcj2 (табл. 6.3.2с).
Таблица 6,3,2с
X ^^\^
0
1
000
0
1
001
1
1
010
л
1
011
1
1
100
1
1
101
1
1
110
1
1
111
1
1
3. Сведём построенные таблицы в одну (табл. 6.3.2d).
Таблица 6,3,2d
\s^^2^3
X \v
0
1
000
010,0
100,1
001
010,1
100,1
010
010,1
100,1
oil
010,1
100,1
100
110,1
100,1
101
110,1
100,1
110
110,1
100,1
111
110,1
100,1
Закодируем наборы значений q\q2Q3 •
000-1; 001-2; 010-3; 011-4; 100-5;
101-6; 110-7; 111-8.
Перепишем сводную таблицу, заменяя трёхразрядные
двоичные наборы их кодами (табл. 6.3.2е).
Таблица 6,3,2е
0
1
1
2,0
5,1
2
2,1
5,1
3
2,1
5,1
4
2,1
5,1
5
7,1
5,1
6
7,1
5,1
7
7,1
5,1
8
7,1
5,1
Конечные автоматы
299
4. Минимизируем полученный автомат по числу внутренних
состояний. Строим треугольную таблицу (табл. 6.3.2f).
Таблица 6,3.2/
2
3
4
5
6
7
8
27
27
27
27
27
27
27
27
27
27
27
12 3 4
Из построенной таблицы видно,
что все состояния, кроме первого,
эквивалентны между собой.
Запишем классы эквивалентности: Г =
{1}; 2'= {2,3,4,5,6,7,8}. Изобразим
таблицу состояний минимального
автомата (табл. 6.3.2g).
5. Проведём обратную кодировку:
Г — 0; 2' — 1, запишем
"физическую" таблицу состояний автомата
(табл. 6.3.2h).
6. Ввиду простоты примера, нет
необходимости использовать карты
Карнау, функция перехода —
тождественная единица, которая может
Таблица 6.3.2g
X"-v^
0
1
Г
2',0
2М
2
2\\
2М
Таблица 6.3,2h
х"^^^.^
0
1
0
1,0
1,1
1
1,1
1,1
300
Глава 6
быть реализована формулой q = xvх, функция выхода
описывается формулой y = xvq\
7—8. Изобразим схему из функциональных элементов и
задержек, реализующую минимальный автомат (рис. 6.3.2, б).
Рис. 6.3.2, б
6.4. Распознавание множеств
автоматами
Автоматом Мура называется пятерка S = (A,Q,V,5,[i), где
A = {ai,...,a^} —входной алфавит', Q = {q\,---,q,n} —мноэюество
внутренних состояний', V = {Vj,..., v^^,} — выходной алфавит',
5: ЛX2 —>2 — функция переходов', \i:Q—^V — функция
отметок.
Конечные автоматы 301
Автоматом без выхода называется пятерка S = (A,Q,6,q^, F),
где Л = {«!,...,«„} —входной алфавит; Q = {c]\,---,g,n} —мнолсе-
ство внутренних состояний; Ъ\ AxQ-^Q — функция
переходов; Q\^Q — начальное состояние; F qQ — мноэюество
заключительных состояний.
Событием называется множество Е такое, что Е с Л*, где
А * —мноэюество слов в алфавите А.
Элементарным событием называется слово, состоящее из
одной буквы.
Событие Е представилю автоматом без выхода S, если
автомат при работе над словом а переходит в одно из своих
заключительных состояний тогда и только тогда, когда а принадлежит Е.
Конкатенацией слов а и Р называется слово, полученное из
данных слов выписыванием всех символов слова а, а затем —
всех символов слова р.
Конкатенацией событий Е^ и £2 называется событие
Ej о Е2, которое определятся так: Е, о ^2 = {aia2 | aj е Ej и
а2 е ^2}.
Итерацией события Е называется событие Е*,
определяющееся так: Е* = {^и Ей ЕЕU Е^ U...U Е^ U...}, где е
—пустое слово, Е = Ео Ео...о Е —регулярная степень.
к
Регулярным называется событие, которое может быть
получено из элементарных событий с помощью применения
конечного числа раз операций конкатенации, объединения и
итерации.
Источником будем называть ориентированный граф, в
котором:
1) выделено некоторое множество начальных вершин и
некоторое множество конечных вершин, имеющих, возможно,
непустое пересечение;
302 Глава 6
2) над каждым ребром графа стоит или буква из входного
алфавита, или пустое слово.
Источник Н представляет событие Е, если Е состоит
из тех и только тех слов, которые соответствуют всем
маршрутам из начальных вершин источника в заключительные
вершины.
Исток — вершина, из которой дуги только выходят; сшок: —
вершина, в которую дуги только заходят.
Детермтшровапиый источник — источник, имеющий ровно
одну начальную вершину, не имеющий пустых рёбер, причём для
любой вершины h источника и любого символа а входного
алфавита существует единственная дуга, выходящая из вершины h
и помеченная символом а.
Недетерминированным автоматом называется пятерка
'S'= (^,!2»5;^,^, ,F), где Д = {«!,...,(2^} — входной алфавит-,
Q = {q\,.'.,q„i] — MHOJfcecmeo внутренних состояний',
5^ : AxQ—^ P(Q) — функция переходов, где P{Q) —
множество всех подмножеств множества Q\ q]S Q —
начальное состояние', FqQ —мноэюество заключительных
состояний.
Задание 6.4.1
1. Написать таблицу состояний данного автомата.
2. Считая автомат неинициальным, построить эквивалентный
автомат Мура. Проверить работу данного и построенного
автоматов над одним и тем же словом.
Конечные автоматы
303
Таблица 6,4.1
№
Автомат
'осшгз^^^
сЕЙ'
304
Глава 6
Таблица 6,4.1 (продолэн:еи11е)
№
Автомат
а,1
•ад-<^^:Ш5
Конечные автоматы
305
Таблица 6,4,1 (продолэюеине)
№
Автомат
10
11
12
306
Глава 6
Таблица 6,4,1 (продолэюение)
№
Автомат
13
а,0
14
'qoS^^
а,0
15
ьл
SI>2QS
а,0
16
Ь,1 ^—ч а,0^^>-^ а,1
оДГ^^—^""^^
Ь,1
Ь,0
' ^^'
Конечные автоматы
307
Таблица 6.4,1 (продолэюение)
№
Автомат
17
Ь,0
18
00^4^35
19
Ь.О^^.-^ а,0
20
308
Глава 6
Таблица 6.4.1 (продолэюение)
№
Автомат
21
22
23
(^5#$);К)Р'
24
ОЭр
Конечные автоматы
309
Таблица 6.4.1 (продолэ/сение)
№
Автомат
а,0
25
"бЭМ^Э^
26
■аЭЭ1Й1$"€б
27
28
•bo5di^^g)3
310
Глава 6
№
29
30
Таблица 6.4.1 (окончание)
Автомат
^•QOf!
^ ^^ b,0
aJ__
^-^ ъ,о^^
а,1
а.0_ ГЛ ^
^^^
Г~\'^
2 ) Р>1 >( 3 ) Л 4 )
—^ v_^< ь,1 V^
Пример решения задания 6.4.1 .
Решим задание 6.4.1 для автомата, заданного своей
диаграммой состояний:
Jb,1
^^^^=5й5Эй
Изобразим таблицу данного автомата (табл. 6.4.1а).
Таблица 6.4,1а
"г-^--^
а
b
1
3,0
2,0
2
3,0
2,1
3
4,0
1,0
4
3,1
4,1
Конечные автоматы
311
По данному неинициальному автомату Мили S строим
эквивалентный ему автомат Мура S' следующим образом:
автомат S' содержит 4-2 + 4=12 состояний, каждое из
которых мы будем помечать двумя символами. Состояния автомата
S' обозначим так: ^'1,*2, *3, *4, cd, bU al, hi, аЪ, ЬЪ, а4, М.
Функция отметок |Li на состояниях *1, *2, *3, *4 не определена,
а её значения на состояниях al, /?!,...,/;4 задаются с помощью
функции выходов X автомата S: \x(iii) = X(uJ), где 1</<4,
ие {а,Ь}.
То есть |Li(al) = X{a,i) = О,..., \х{Ь4) = ХфА) = 1.
Функция переходов 5' на состояниях, содержащих в
изображении символ *, определяется так: 5'(w,^:n') =^</, ие{а,Ь}, 1</<4.
В остальных случаях первый символ имени нового состояния
совпадает со считываемым символом входного алфавита, а
второй символ имени нового состояния определяется с помощью
функции переходов 5 автомата S: b\u,vi) = iij\ где u,ve{a,b}.
Получим: 5'(<:/,*1) = г/1, 5'(/?,л1) = 62, т.к. 5((7,1) = 2, и т. д.
Запишем таблицу состояний полученного автомата Мура.
ц
Л^е
а
h
-
*1
а\
Ы
-
*2
а2
Ь2
-
*3
аЗ
ЬЪ
-
>i4
а4
ЬА
0
а\
аЪ
ЬЪ
0
ь\
а2
Ь2
0
ci2
аЗ
ЬЗ
1
/р2
а2
Ь2
0
аЗ
а\
Ь4
Таблица 6,4.lb
0
ЬЗ
а\
Ь\
1
а4
аЗ
ЬЗ
1
Ь4
а\
Ь\
Проверим работу исходного автомата над словом baaba,
запустив его из 2 состояния:
2
b
2
1
а
3
0
а
4
0
b
4
1
а
3
1
312
Глава 6
Построенный автомат Мура запускаем из состояния ^2:
*2
b
Ь2
1
а
а2
0
а
аЪ
0
b
Ь4
1
а
аА
1
Как видим, результаты работы обоих автоматов совпали.
Задание 6.4.2
1. Построить диаграмму автомата без выхода,
представляющего конечное событие Е, используя, по возможности, меньшее
число внутренних состояний.
2. Изобразить найденный автомат таблицей переходов,
отметив в ней заключительные состояния.
3. Минимизировать построенный автомат или убедиться, что
построенный автомат — минимальный.
4. Проверить работу полученного автомата над словом из
множества Е и над словом, не попавшим в Е.
Таблица 6.4.2
№
1
2
3
4
5
6
7
1 8
9
10
11
12
Е 1
bbb, abb, baba, baaa
abab, aa, abb, bbab
aaab, abab, baa, aab
bba, abba, aaba, bb
aab, baab, bbba, aaab
baaa, aaa, bbab, baab
abab, bba, aaba, aba
bbaa, aaa, baba, aabaa
aab, bbba, bba, aabab
aba, bbab, abb, baba
bbba, abb, baba, bba
aaab, bbab, aaa, bab
№
13
14
15
16
17
18
19
20
21
22
23
24
E 1
aaba, bab, aaa, bbaba
aba, bba, aaba, bab
aaa, bba, babba, abab
bbba, abba, aab, baa
aaba, bab, bbaba, aba
bab, aabb, aab, baaa
aaa, baab, bab, aabaa
baaba, bab, aaba, aa
bab, aaba, bbba, aaa
baba, aab, bbab, bbb
aab, abba, aaab, bbba
abb, baab, bbab, baaa
Конечные автоматы
313
Таблица 6,4,2 (окончание)
№
25
26
27
Е
ааа, abba, bba, babbb
bba, babb, aab, abaa
aba, baab, bbaba, bba
№
28
29
30
E
aaa, baa, ababa, baab
aab, bab, abbb, baab
baa, abaa, bbab, abbba
Пример решения задания 6.4.2
1. Решим задание 6.4.2 для события Е = [aba, bbab, baa, abbb).
Изобразим диаграмму состояний автомата без выхода (рис. 6.4.2)
с начальным состоянием 1, изобразив заключительное состояние
двойным кружком так, чтобы каждому слову из множества Е
соответствовал маршрут из начального состояния в
заключительное, и такие маршруты находились бы лишь для слов из
множества Е.
Рис. 6.4.2
2. Запишем таблицу состояний, соответствующую полученной
диаграмме.
314
Глава 6
Таблица 6.4.2а
>^
а
1 ^
1
2
5
2
8
3
3
4
9
@
10
10
5
8
6
6
7
10
7
10
4
8
4
10
9
10
4
10
10
10
3. Проверим автомат на минимальность, считая, что
заключительным состояниям соответствуют выходные символы одного
типа, а всем остальным состояниям — выходные символы
другого типа.
Составим таблицу, расставив кресты в клетках,
соответствующих парам состояний разного-вида.
Таблица 6.4.2Ь
2
3
4
5
6
7
8
9
10
2 10
53
24
59
28
56
27
5 10
2 10
45
24
5 10
2 10
45
8 10
5 10
4 10
59
3 6
8 10
7 10
3 10
34
4 10
3 10
34
3 10
48
69
47
9 10
9 10
49
9 10
4 10
49
4 10
9 10
78
6 10
8 10
46
48
6 10
8 10
46
8 10
6 10
7 10
4 10
47
7 10
4 10
7 10
4 10
4 10
4 10
4 10
4 10
Конечные автоматы
315
Продолжим процедуру минимизации. Окончательно получим
таблицу (табл. 6.4.2с).
2
3
4
5
6
7
8
9
10
^
А\
[/^К.
W
А\
\у
/К
^2 щ/
/45\
/бИК
\и/^
/45\
\8 ip/
W
/5К
\/
/l\
^'^'^S
\j in/
y2^lb\
/34\
^a^ib\
W
A>
N47/
y/i\^
Nnj/^
/49\
у9К)\
\l0^
/49\
^бИК
\ш^
/4 6\
\4&/
y^lK
/4б\
/6KK
N7 K>/
уиК
/iX
\/
A\
/f^\
/4ИК
/4K\
Таблица 6,4,2c
у/ик
/410\
^1(\
Видим, что состояния 7 и 9 эквивалентны. Переходим к
минимальному автомату, состояния которого соответствуют классам
эквивалентности данного автомата.
Получим: ]'={!}, 2' = {2}, 3' = {3}, 4' = {4}, 5' = {5}, 6' = {6},
7'={7,9},8'={8},9'={10}.
Изобразим таблицу состояний минимального автомата
(табл. 6.4.2d).
316
Глава 6
Таблица 6.4.2d
[><
1 а
1 ^
Г
2'
5'
2'
8'
3'
3'
4'
7'
4'
9'
9'
5'
8'
6'
6'
7'
9'
Г
9'
4'
8'
4'
9'
9' 1
9' 1
9' 1
4. Проверим работу автомата над словом, вошедшим в Е,
например, bbab:
Г
b
5*
b
6*
а
7'
Z?
4'
В результате на последнем шаге произошёл переход в
заключительное состояние 4-
Проверим работу автомата над словом, не вошедшим в Е,
например, baab:
Г
b
5'
а
8'
b
9'
Ь
9'
В результате работы автомата над словом baab автомат оказался
в состоянии 9\ которое не является заключительным, чего и
следовало ожидать.
Задание 6.4.3
Изобразить недетерминированный источник,
соответствующий недетерминированному автомату, заданному таблицей
переходов, с входным алфавитом {a,b]v\ множеством внутренних
состояний {1,2,3,4,5}. При построении использовать возможно
меньшее число дуг. В построенном недетерминированном
источнике желательно присутствие хотя бы одного пустого ребра.
Если построить соответствующий недетерминированный
источник с пустым ребром невозможно, докажите это.
Конечные автоматы
317
Таблица 6.4.3
№
>-^
С1
b
1
0
3,4
2
1
3,5
3
2,3,4
0
4
1
3,5
5 1
3,4
2,4
№2
>-^
а
b
1
1,5
0
2
1,3,4,5
2,4
3
0
2,3,4
4
1
0
5
3
4,5
№3
>^-Л
а
1 ^
1
0
3,4,5
2
0
1,3
3
4
2,3,5
4
0
1,2
5
1,2,4
2,3,5
№4
рг-^
а
b
1
1,3,4,5
4
2
2,3,4
3
3
0
1,5
4
0
2,4
5 1
1,3,5
4
№5
ПГ--е^
а
1 ^
1
0
1,2,3
2
2,3
1,4,5
3
0
1,5
4
3,4
0
5
4,5
2,3
№6
р--^
а
1 ^
1
1,2,3
3
2
0
2,3,4
3
3,4
1 ^
4
1,2
2,5
5
0
3,4
11 Зак. 3332
318
Глава 6
Таблица 6.4.3 (продолжение)
№7
>-^
а
ь
1
0
1,4,5
2
0
1,2,4
3
3
4,5
4
0
1,3
5 1
2,3,4
1,3
№8
|>-^
а
b
1
1,2
2,4
2
0
1,3,5
3
3,5
0
4
3,4
0
5 1
1,2,3,5
1,2
№9
Г>-^
а
b
1
2,3,4,5
3
2
3,4
2,5
3
0
3
4
0
1,5
5 1
2,4,5
3
№10
р--^
а
b
1
0
1,3,4
2
2
3,4
3
1,3,4,5
2,5
4
5
0
5
0
2,4
№11
Г>^
а
b
1
1,2
1,5
2
1,2,3
1,5
3
1,2,3
3
4
0
4,5
5
1,4
1,2,3
№12
р-^
а
1 ^
1
0
1,3,4
2
3,4
2,4,5
3
0
2,4
4
0
1,4,5
5
2
1,3,4,5
Конечные автоматы
319
Таблица 6.4.3 (продолэк:еиие)
№13
>-<
а
b
1
1,4
0
2
1,3,4,5
0
3
3,4
1,2,4,5
4
1,3 ^
1,2,4,5
5 1
0 1
1,3
№14
>-^
а
b
1
1,2,5
3
2
3
0
3
1,2,5
3,4
4
1,3
1,2,5
5 1
3
0 1
№15
Г>-^
а
b
1
1,3,4
1,2,3
2
2,3
0
3
1,3
4
4
0
1,2,5
5 1
1,3,4,5
1,2,3
№16
Г>^
а
b
1
0
1,3,4
2
0
1,2
3
0
3,4,5
4
2,3
1,2
5
3,4,5
2,3,4,5
№17
рГ--^
а
b
1
1,3
1,3,5
2
1,3
1,3,5
3
1,4,5
0
4
1,2
0
5
3,4
1
№18
р--^
а
1 ^
1
2,4
1 ^
2
3,4
1,2,3,4
3
0
1Л5
4
0
3,4
5
1,2,4,5
3
320
Глава 6
Таблица 6.4.3 (продолэюение)
№19
7--<
а
b
1
3,5
1,2,5
2
3,5
0
3
1,2,4
3,5
4
1,2,4
0
5
3,4
1,2
№20
р^^-
а
b
1
1,3
1,2,3
2
0
1,3,4
3
1,2,3,4
1,2,3
4
3
0
5 1
1,3
5 1
№21
Р^-^
а
b
1
2,5
1,4,5
2
1
2,3
3
1,5
0
4
0
1,3,4
5 1
1,2,5
1,2,4,5
№22
рг-^
а
1 ^
1
1,3
0
2
2,3,4
0
3
1,2,4
3,5
4
1,2,3
0
5 1
1,2,3,4
1,3,5
№23
рГ---е^
а
1 ^
1
5
3,4,5
2
1,3,4
2,3,4
3
5
3,4,5
4
1,3
0
5
2,4
0
№24
Р^-^
а
1 ^
1
1,2,4
3,4
2
0
1,3,4
3
3,4
3,4,5
4
0
3,4,5
5-
1,5
3,4
Конечные автоматы
321
Таблица 6.4.3 (окончание)
№25
>-^1
^'
h
1
0
1,2,4
2
1,3
0
3
1,3,5
0
4
3,4
1,3,4
5 1
1,3,5
1,3
№26
Г>-^
а
b
1
1,4
1,4,5
2
3,4
2,3
3
0
1,2
4
4,5
0
5 1
0
0
}(^.ll
р--^
а
b
1
4
0
2
3,5
1,2,3
3
0
1,2,3
4
1,3
1,3,4
5 1
5
2,3
№28
р--^
а
b
1
2
4,5
2
0
3,5
3
1,3,5
5
4
0
2,4
5 1
1,3,5
0
№29
Р^-^
а
b
1
13
1,2
2
4
1,3
3
1,2,3
0
4
3
4,5
5 1
0
[ 5
№30
р-^
а
1 ^
1
0
1,2
2
2
3,4
3
1,5
2,3
4
1,5
2,3,4,5
5
2,5
0
322
Глава 6
Пример решения задания 6.4.3
Решим задание 6.4.3 для недетерминированного автомата,
заданного таблицей переходов:
Таблица 6.4,3а
7---^
а
b
1
2,4,5
3,5
2
3
0
3
5
3,4,5
4
4,5
0
5
4,5
0
Выясним, можно ли построить недетерминированный
источник, соответствующий данному недетерминированному
автомату, содержащий пустое ребро.
Если недетерминированный источник содержит пустую дугу,
выходящую из / -той вершины и заходящую в /: -ю вершину, то,
очевидно, должны выполняться два условия:
1) /-тая вершина не встречается в какой-либо клетке таблицы
автомата без к -той вершины;
2) множество вершин, в которое можно попасть, считав любой
символ входного алфавита, из вершины к, включено во
множество вершин, в которое можно попасть из вершины /, считав тот
же символ.
Первое из этих условий выполняется для пар вершин (2;4),
(2;5) и (4;5), но второе условие выполняется только для пары
(4;5). Будем строить
недетерминированный источник с пустой
дугой, выходящей из 4 вершины
и заходящей в 5 вершину.
Получим:
Конечные автоматы
323
Задание 6.4.4
1. Изобразить источник с одним истоком, представляющий
событие а.
2. Записать таблицу соответствующего недетерминированного
автомата.
3. Построить таблицу детерминированного автомата,
эквивалентного автомату, полученному в п. 2.
4. Провести переобозначение классов внутренних состояний и
записать таблицу автомата без выхода в стандартном виде.
5. Взять по одному слову из события а и ле а, проверить
представление автоматом этих слов.
Таблица 6.4.4
№
1
2
3
4
5
6
7
8
9
L ^^
п
12
13
14
15
16
L ^'^
L ^^
19
1 20
а
(be U а * h){b * иса) * {а U be)
{aub"^с){сU/?л*)* (сUса)
(са U b'^){ab и be) * (Z? и ас*)
(aZ? U c*)(Z? u flfc) * (a u Z?) 1
(Z?c u a*)(Z? u a * c) * (a u c)
{ac u Z?*)((7Z? u bc'^^a u Z?) *
0fl U с * /?)(fl * Ubc) * (Z? U ac)
(a * ubc){b uc''ci)'^'{au be)
{b * ua) * (aZ? u с * a)(Z? u c)
(/? u с * a)(a u/?c) * (Z? * uc)
(Z?c u a*)(a u be) * (Z? * uac)
(a u cZ?*)(r/ u Z?/?) * (c u «/?)
(/?Z? u e'^){ae u Z?*) * (a u Z?)
(a * uba){ae u /?*) * (c u ab)
{ab u c*)(a u ^c*) * (Z? u bb)
{a u Z?*)(ac * ub) * (/:?Z? u a)
(Z? u л * c)(Z?c u a) * (cc u Z?)
(«c u b''){bb u c*) * {cie u /?)
(a u c*) * (Z?c u a*)(Z? u a)
(aa u Z?*)(ac u b) * (ac u a*)
324
Глава 6
Таблица 6,4.4 (окончание)
1 №
21
22
23
24
25
26
27
28
29
30
а 1
(be * ua)(cc ^h)^{hu ас)
{c'^uhc){buaay{auh)
(ab u с*) ^^ (be u л)(с u /?/?)
{bucic^)(bucia)'^{cub)
(b * ucr/)(c u Z?fl*) * (/? u a * л)
(a * с u b){bc * u/?) * (ла u /?(?*)
(cZ? u Z?) * (a u bc'^Xac u a) *
(c * « u Z?)(Z? u bci) * (a u cb)
{bu a^ c){b^' cu a)"" {cbu ab"")
ib'^aub){buca)'^(aub)
Пример решения задания 6.4.4
Решим задание 6.4.4 для события
а = (Ь^ \Jcb){ba ис^^)^^(аи be),
1. Изобразим источник, учитывая, что конкатенации слов
соответствует последовательное соединение источников,
представляющих данные слова, объединению — параллельное
соединение, а итерации — зацикливание, так, чтобы каждому слову из
события а соответствовал бы маршрут из начальной вершины
источника в заключительную. Получим:
Рис. 6.4.4
Конечные автоматы
325
2. Строим таблицу полученного недетерминированного
автомата. В клетке, соответствующей состоянию cji и символу
входного алфавита и, будем писать список вершин, в которые можно
попасть из вершины д., считав по пути символ и. Так, например,
из вершины 2, считав по пути символ Ь, можно попасть в
вершины 2,4,5 и 7. Получим таблицу переходов
недетерминированного автомата (табл. 6.4.4а).
Таблица 6,4.4а
>-^
а
b
с
1
6
2,4,5,7
3,4
2
6
2,4,5,7
4
3
0
4
0
4
6
5,7
4
5
4
0
0
6
0
0
0
7
0
0
6
Таблица 6ААЬ
3. Строим вспомогательную таблицу следующим образом:
в заголовке первого столбца выпишем номер начальной
вершины (в нашем случае это — 1), а также номера всех вершин,
в которые можно попасть из начальной
вершины по пустым рёбрам (в нашем случае —
это вершины 2 и 4). Заголовки строк, как и в
предыдущей таблице, помечаем символами
входного алфавита а, Ь, с. Далее, в клетку,
соответствующую входному сигналу и и
списку состояний 1, 2, 4, запишем объединение
содержимого клеток, находящихся на
пересечении строки, помеченной символом и, и находящихся на
пересечении строки, помеченной символом и, и столбцов 1, 2 и 4.
Получим (табл. 6.4.4Ь).
Затем дополним таблицу тремя столбцами, пометив их
полученными списками. В нашем случае — это 6; 2,4,5,7 и 3,4. Новые
образовавшиеся клетки заполним по тому же правилу, по
которому мы заполняли клетки первого столбца.
Получим (табл. 6.4.4с).
а
b
с
1,2,4
6
2,4,5,7
3,4
326
Глава 6
Таблица 6.4,4с
а
1 ^
с
1,2,4
6
2,4,5,7
3,4
6
0
0
0
2,4,5,7
4,6
2,4,5,7
4,6
3,4 1
6 1
4,5,7 1
4 1
Продолжим построение таблицы до тех пор, пока будем
получать новые столбцы. В итоге имеем (табл. 6.4.4d).
Таблица 6A.4d
а
b
с
1,2,4
6
2,4,5,7
3,4
6
0
0
0
2,4,5,7
4,6
2,4,5,7
4,6
3,4
6
4,5,7
4
0
0
0
0
4,6
6
5,7
4
4,5,7
4,6
5,7
4,6
4
6
5,7
4
5,7
4
0
6
На основе полученной таблицы строим детерминированный
автомат без выхода, с алфавитом {а,Ьх], в котором состояния
будут соответствовать спискам, проставленным в заголовках
столбцов в построенной таблице, начальному состоянию будет
соответствовать список, которым помечен первый столбец, а
заключительным состояниям будут соответствовать списки, в
которые вошла заключительная вершина источника (вершина 6
в нашем случае). Проведём переобозначение: 1,2,4 — Г; 6 — 2';
2,4,5,7 — 3'; 3,4 — 4'; 0 — 5'; 4,6 — б'; 4,5,7 — 7'; 4 — 8'; 5,7 — 9'.
Перепишем таблицу, заменив списки номерами \\ 2'»--» 9*.
Получим (табл. 6.4.4е).
Таблица 6.4,4е
>-^
а
b
с
1'
2'
3'
4'
2'
5'
5'
5'
3'
2'
3'
6'
4'
2'
7'
8'
5'
5'
5'
5'
6'
2'
9'
8'
7'
6'
9'
6'
8'
2'
9'
8'
9'
8'
5'
2'
Конечные автоматы
327
Проверим работу построенного детерминированного
автомата без выхода с начальным состоянием Г и
заключительными состояниями 2' и 6' над словом cbbaccbc, вошедшим в
событие а:
1'
с
4'
b
Т
b
9'
а
8'
с
8'
с
8'
с
8'
b
9'
с
2'
Как мы видим, в результате работы над словом, вошедшим
в событие а, произошёл переход в состояние 2', являющееся
заключительным для нашего автомата.
Возьмём слово, не попавшее в а, например, аЬЬЬас, проверим
работу над ним построенного автомата без выхода:
Г
а
2'
b
5'
b
5'
b
5'
а
5'
с
5'
Как мы видим, в результате работы над словом, не
вошедшим в событие а, произошёл переход в состояние 5', не
являющееся заключительным для нашего автомата, что и следовало
ожидать.
Задание 6.4.5
1. Пользуясь алгоритмом Макнотона-Ямады, провести анализ
конечного автомата, заданного диаграммой переходов.
Начальное состояние — 1.
2. Убедиться для некоторого маршрута из начальной в
конечную вершину соответствующего детерминированного источника,
что слово а, связанное с этим маршрутом, принадлежит
построенному событию.
Для произвольного слова из построенного события указать
маршрут из начальной в конечную вершину.
328
Глава 6
Таблица 6.4.5
№
Конечные автоматы
329
Таблица 6.4.5 (продолэюеиие)
№
0Й1«
10
330
Глава 6
Таблица 6,4,5 (продолж:ение)
№
автомат
11
12
а,Ь ^-^ «
(1Х=Ш=&
13
14
15
Конечные автоматы
331
Таблица 6,4.5 (продолjfcenue)
№
автомат
16
17
18
19
20
332
Глава 6
Таблица 6.4.5 (продолжение)
№
автомат
21
22
23
24
b ^^ а
b ^у^--ч ^
ссхдадао
25
Конечные автоматы
333
Таблица 6.4.5 (окончание)
№
автомат
26
27
28
29
30
334
Глава 6
Пример решения задания 6.4.5
Рис. 6.4.5
Рассмотрим множества: Ejj ={а\5(a,q^)-Qj)
4 = 4"'^4"'(4"')*4"'''^>о-
(1)
(2)
Согласно теореме Макнотона-Ямады, числа E^j образуют
слова, соответствующие маршрутам из /-той вершины в у-ю
вершину, причём в этих маршрутах номера вершин, проходимых
внутри маршрута, не превосходят к.
В нашем случае начальная вершина — 1, заключительная — 2,
обш.ее количество вершин равно 3, значит, данный автомат
представляет событие £12 •
Найдём события по формулам (1):
£0 = е- Е^2 = С1\ Е^^ = Ь; Е^^ = 0; Е^2 = ci\
где е — пустое слово (не путать с пустым событием 0).
События найдём по формуле (2):
£,', = Ef, U £,'',(£f,)*£,", =eKJee^e = e;
En = £12 ^ ^и (^u )*E^2=a^ee*a = a\Ja = a;
£,'з = E^^ u £f, {E^^ )* E^^=bKjee*b = b^b = b\
e\\ = £21 ^ £^2i(£n)*^n =0u0e*e = 0u0 = 0;
£22=^22^^2l(£n)*^12=«^0^*« = «^0 = «'.
Конечные автоматы 335
E\^=E^^uE^^(E^^)*E^^=bube^<e = bub = b\
El,=E',,uE^,{E^^yE^,=e^be^b = eubb.
Выразим £^2' посмотрим, какие события, помеченные
верхним индексом 2, нам надо найти: Е^^ = Е^^ и Е^^(Е^^УЕ^2-
Найдём каждое из событий, присутствующих в правой части
последнего равенства:
2 1 11*1
Е\2 - Е\2 '^£'12(^22)^22 - а^аа^^^а\
Е^^ = Е1^^Е12(Е\2УЕ\з=Ьиаа^Ь\
Е^^ = Е\^иЕ12(Е^^2У'Е\з=е^ЬЬи(а^Ьа)а^Ь\
£з^2 = ^32 ^ ^32 (^22 )*^22 = ((^ ^ Ьо) KJ {aKj Ьа)а "^ а.
Итак, получаем регулярное выражение:
^12 = ^12*^^13(^33) ^32 =
= auaa^au(buaa^b)(eubbu(auba)a^b)'^(a\jbau(a\jba)a'^a).
2. Рассмотрим какой-нибудь маршрут из первой вершины во
вторую, например: 1—>2—>2—>3—>2. Этому маршруту
соответствует слово ааЬа. Проверим, присутствует ли оно в событии Е{2-
3 7 *
Если в событии £|2 взять слово ааЬ, в (£33) взять ^, а в
2 3
£'з2С-^ово а, то конкатенация этих слов, вошедшая в £,2, и будет
равна ааЬа.
3. Возьмём какое-нибудь слово из события, например, bbbbaa.
Рассмотрим маршрут, соответствующий этому слову:
b b b b а a
1->3->1->3->1->2->2.
Действительно, при считывании слова bbbbaa, начав
движение из 1 вершины, мы оказались во 2, заключительной, вершине.
Список литературы
Г. Виленкин Н. Я., Виленкин А. Н., Виленкин П. А.
Комбинаторика. — М,: ФИМА, МЦНМО, 2006.
2. Гаврилов Г. П., Сапоженко А. А. Сборник задач по
дискретной математике. — М.: ФИЗМАТЛИТ, 2005.
3. Ерусалимский Я. М., Дискретная математика: Теория, задачи,
приложения. — М.: Вузовская книга, 2005.
4. Капитонова Ю. В., Кривой С. Л., Летичевский А. А., Луцкий Г. М.
Лекции по дискретной математике. — СПб.: БХВ-Петербург,
2004.
5. Карпов В. Г., Мощенский В. А. Математическая логика и
дискретная математика. — Минск: Вышэйшая школа, 1977.
6. Кузнецов О. П., Адельсон-Вельский Г. М. Дискретная
математика для инженера. — М.: Энергоатомиздат, 1988.
7. Лавров И. А., Максимова Л. Л. Задачи по теории множеств,
математической логике и теории алгоритмов. — М.: Наука,
1984.
8. Мощенский В. А. Лекции по математической логике. —
Минск, Изд-во Белорус, университета, 1973.
9. Нефёдов В. Н., Осипова В. А. Курс дискретной
математики. — Изд-во МАИ, 1992.
10. Новиков Ф. А. Дискретная математика для программистов. —
СПб.: Питер, 2004.
И. Шиханович Ю. А. Введение в современную математику. —
М.: Наука, 1965.
12. Шоломов Л. А. Основы теории дискретных логических и
вычислительных устройств.— М.: Наука, 1980.
в. и. Смирнов
УРС
высшей
математики
«... составляющей успеха
представляемой книги был непревзойденный
педагогический дар Владимира Ивановича.
До преклонных лет он был одним из
любимейших лекторов на физическом
факультете. Книги, написанные им, читаются
просто и увлекательно, даже те
страницы, где проводятся громоздкие
вычисления. И все это с сохранением
достаточной строгости изложения».
Академик РАН Л. Д. Фаддеев
Фундаментальный учебник по высшей математике, выдержавший множество изданий,
отличается, с одной стороны, систематичностью и строгостью изложения, а с другой
простым языком, подробными пояснениями и многочисленными примерами,
иллюстрирующими теорию.
Более полувека используется в различных учебных заведениях в качестве основного
учебника, высоко ценится математиками.
В первом томе изложены функциональная зависимость и теория
пределов, понятие о производной и интеграле, ряды и их приложения
к приближенным вычислениям, функции нескольких переменных,
комплексные числа, начала высшей алгебры и интегрирование
функции.
Во втором томе рассматриваются обыкновенные
дифференциальные уравнения, линейные дифференциальные уравнения и
дополнительные сведения по теории дифференциальных уравнений;
кратные и криволинейные интегралы, несобственные интегралы и
интегралы, зависящие от параметра; векторный анализ и теория
поля; основы дифференциальной геометрии; ряды Фурье;
уравнения с частными производными математической физики.
ГРИФ: Допущено Научно-методическим советом по математике министерства образования
и науки Российской Федерации в качестве учебника для студентов механико-математических
и физико-математических факультетов университетов и технических высших учебных заведений
www.bhv.ru
Шапорев С. Д.
Дискретная математика.
Курс лекций и практических занятий
Магазин "Новая техническая книга"
СПб., Измайловский пр., д. 29, тел.: (812) 251-41-10
www.techkniga.corT>
Отдел оптовых поставок
E-mail: opt@bhv.spb.su
ДИСКРЕТНАЯ
МАТЕМАТИКА
Пособие представляет собой учебный
курс, включающий лекции и практические
занятия по трем разделам, изучаемым в
курсе дискретной математики: теории
множеств, комбинаторике и теории
графов. Благодаря многолетнему опыту
преподавания автор излагает вопросы теории
сжато, но в то же время достаточно для
освоения курса, просто и доступно.
Обсуждается основная система аксиом для
теории множеств, рассматриваются
основные типы задач комбинаторики,
приведены наиболее употребительные
оптимизационные алгоритмы теории графов.
Весь теоретический материал рассматривается на конкретных
практических задачах и упражнениях. Приводятся подробные решения более
четырехсот задач, предложенных в книге. Весь материал изложен на
высоком методическом уровне и рассчитан на студентов технических
вузов, изучающих дискретную математику.
Шапорев Сергей Дмитриевич, доктор физико-математических наук,
профессор, заведующий кафедрой прикладной математики и информатики
Балтийского государственного технического университета «Военмех».
Член Ассоциации математиков вузов Северо-Запада. Автор более 50
работ по небесной механике и вычислительной математике.
Учебная литература
издательства "БХВ-Петербург"
www.bhv.ru В продаже:
Магазин "Новая техническая книга": СПб., Измайловский пр., д. 29, тел.:
(812)251-41-10
www.techkniga.com
Отдел оптовых поставок: e-mail: opt@bhv.spb.su
Серия "Для студента"
Герман О., Герман Ю. Программирование на Java и С# 512 с.
Дунаев В. Базы данных. Язык SQL для студента, 2-е изд. 320 с.
Едомский Ю. Техника Web-дизайна 400 с.
Магда Ю. UNIX для студента 480 с.
Пахомов Б.Си Borland C++ Builder для студента 448 с.
Побегайло А. C/C++ для студента 528 с.
Половко А. Derive для студента 352 с.
Половко А., Бутусов П. MATLAB для студента 320 с.
Половко А. Mathematica для студента 368 с.
Пономаренко С. Adobe Photoshop CS2 для студента 464 с.
Рудикова Л. Microsoft Excel для студента 368 с.
Рудикова Л. Базы данных. Разработка приложений 496 с.
Рудикова Л. Microsoft Word для студента 400 с.
Скотт К. Java для студента 448 с.
Федорова А. CorelDRAW для студента 528 с.
Федорова А. Adobe Illustrator для студента 640 с.
Серия "На примерах"
Богданов М. Visual Basic 2005 на примерах 592 с.
Васильев А. Mathcad 13 на примерах 528 с.
Васильев А. Excel 2007 на примерах 656 с.
Дударева Н. SolidWorks 2007 на примерах 528 с.
Катаев С. Программирование в Microsoft Excel на примерах 320 с.
Катаев С. 1С:Предприятие 8. Учимся программировать на 336 с.
примерах
Кирьянов д. Adobe Premiere Pro 2 на примерах 240 с.
Кирьянов Д. Pinnacle Studio Plus 11 на примерах 224 с.
Кузнецов М. MySQL на примерах 592 с.
Кузнецов В. 1С:Бухгалтерия 7.7. Ускоренный курс на примерах 304 с.
Климов А. JavaScript на примерах 256 с.
Левковец Л. Autodesk Inventor. Базовый курс на примерах 400 с.
Левковец Л. AutoCAD 2008. Базовый курс на примерах 480 с.
Левковец Л. Adobe Photoshop CS3. Базовый курс на примерах 592 с.
Левковец Л. Adobe InDesign CS3. Базовый курс на примерах 512 с.
Мержевич В. HTML и CSS на примерах 448 с.
Пестриков В., Маслобоев А. Delphi на примерах 496 с.
Пирогов В. Ассемблер на примерах 416 с.
Погорелов В. AutoCAD 2008 на примерах 256 с.
Поляк-Брагинский А. Администрирование сети на примерах - 2- 432 с.
е изд.
Потопахин В. Язык С. Освой на примерах 320 с.
Сибрина Т. Adobe Photoshop CS3 на примерах 496 с.
Слепченко О. Macromedia Flash Professional 8 на примерах 416 с.
Слепченко К. Flash CS3 на примерах 480 с.
Талалай П. K0MnAC-3D V9 на примерах 592 с.
Серия "В задачах и примерах"
Культин Н. Delphi .NET в задачах и примерах 256 с.
Культин Н., Цой Л. C/C++ Builder в задачах и примерах 336 с.
Культин Н. Turbo Pascal в задачах и примерах 256 с.
Культин Н. С# в задачах и примерах 240 с.
Сафронов И. Бейсик в задачах и примерах 400 с.
Сафронов И. Visual Basic в задачах и примерах, 2-е изд. 320 с.
Серия "Учебное пособие"/ "Учебник"/«Учебник для вузов»
Амосов В. Схемотехника и средства проектирования цифровых 560 с.
устройств
Бармасов А. Курс общей физики для природопользователей. 416 с.
Механика
Барсегян А. Технологии анализа данных: Data Mining, Visual 384 с.
Mining, Text Mining, OLAP
Бертяев В. Теоретическая механика на базе Mathcad. 752 с.
Практикум
Боев В. Моделирование систем. Инструментальные средства 368 с.
GPSS World
Бойко В. Схемотехника электронных систем. Микропроцессоры 464 с.
и микроконтроллеры
Бойко В. Схемотехника электронных систем. Цифровые 512 с.
устройства
Бойко В. Схемотехника электронных систем. Аналоговые и 450 с.
импульсные устройства
Большаков В. Инженерная и компьютерная графика. Практикум 592 с.
Бутиков Е. Оптика: Учебное пособие для студентов физических 480 с.
специальностей вузов
Васильев А. Микроконтроллеры. Разработка встраиваемых 304 с.
приложений
Вуль В. Электронные издания (+дискета) 560 с.
Гольдштейн Б. Системы коммутации, 2-е изд. 314 с.
Гомоюнов К. Транзисторные цепи 240 с.
Грушвицкий Р. и др. Проектирование систем на микросхемах 608 с.
программируемой логики
Грушвицкий Р. и др. Проектирование систем на микросхемах 650 с.
с программируемой структурой, 2-е изд.
Гуревич А. Физика твердого тела 320 с.
Давыдов В. C++. Технологии программирования 672 с.
Даугавет И. Теория приближенных методов. Линейные 288 с.
уравнения, 2-е изд.
Демидович Е. Основы алгоритмизации и программирования. 440 с.
Язык СИ
Жмакин А. Архитектура ЭВМ 320 с.
Ивановский Р. Теория вероятностей и математическая 528 с.
статистика. Основы, прикладные аспекты с примерами и
задачами в среде Mathcad
Иглин С. Математические расчеты на базе Matlab 640 с.
Ирвин Дж., Харль Д. Передача данных в сетях: инженерный 448 с.
подход
Иртегов Д. Введение в сетевые технологии 560 с.
Иртегов Д. Введение в операционные системы. — 2-е изд., 1040 с.
перераб. и доп.
Колесов Ю., Сениченков Ю. Моделирование систем. 224 с.
Динамические и гибридные системы
Колесов Ю., Сениченков Ю. Моделирование систем. Объектно- 192 с.
ориентированный подход
Колесов Ю., Сениченков Ю. Моделирование систем. Практикум 352 с.
по компьютерному моделированию
Кочетов В., Кочетов М., Павленко А. Сопротивление 544 с.
материалов, 3-е изд.
Крылов В., Самохвалова С. Теория телетрафика и ее 288 с.
приложения
Кубенский А. Структуры и алгоритмы обработки данных: 464 с.
объектно-ориентированный подход и реализация на C++ (+CD)
Литвиненко Н. Технология программирования на C++. 288 с.
Начальный курс
Лурье Б., Энрайт П. Классические методы автоматического 640 с.
управления
Макаров Е. Сопротивление материалов на базе Mathcad (+CD) 512 с.
Максименко А. Эксплуатация строительных и дорожных машин 400 с.
Малыхина М. Базы данных: основы, проектирование, 512 с.
использование, 2-е изд.
Малыхина М. Программирование на языке высокого уровня. 544 с.
Turbo Pascal
Миронов Д. Компьютерная графика в дизайне 560 с.
Молдовян Н. Практикум по криптосистемам с открытым ключом 304 с.
Никулин Е. Основы теории автоматического управления. 640 с.
Частотные методы анализа и синтеза систем
Никулин Е. Компьютерная геометрия и алгоритмы машинной 560 с.
графики
Опалева Э., Самойленко В. Языки программирования и методы 480 с.
трансляции
Петров Ю. История и философия науки. Математика, 448 с.
вычислительная техника, информатика
Погорелов В. Строительная механика тонкостенных 528 о.
конструкций
Порев В. Компьютерная графика 432 с.
Поршнев С. Вычислительная математика. Курс лекций 320 с.
Поршнев С, Беленкова И. Численные методы на базе Mathcad 464 с.
Пышкин Е. Основные концепции и механизмы объектно- 640 с.
ориентированного программирования
Рапаков Г., Ржеуцкая С. Программирование на языке Pascal 480 с.
Сафронов И. Бейсик в задачах и примерах 224 с.
Сеннов А. Курс практической работы на ПК 576 с.
Смирнов В. Курс высшей математики. Том I - 24-е изд. 624 с.
Смирнов В. Курс высшей математики. Том II - 24-е изд. 848 с.
Солонина А. Цифровая обработка сигналов. Моделирование в 816 с.
MATLAB
Солонина А. Основы цифровой обработки сигналов. 608 с.
Курс лекций
Солонина А., Улахович Д., Яковлев Л. Алгоритмы и процессоры 464 с.
цифровой обработки сигналов
Сорокина С. и др. Программирование драйверов и систем 256 с.
безопасности
Стешенко В. P-CAD. Технология проектирования печатных плат 720 с.
Сырецкий Г. Информатика. Фундаментальный курс. Том I. 832 с.
Основы информатики и вычислительной техники
Сырецкий Г. Информатика. Фундаментальный курс. Том II. 848 с.
Информационные технологии и системы
Угрюмов Е. Цифровая схемотехника, 2-е изд. 800 с.
Ускова О. и др. Программирование алгоритмов обработки 192 с.
данных
Файншмидт В. Дифференциальное и интегральное исчисление 224 с.
функций одного аргумента
Файншмидт В. Дифференциальное и интегральное исчисление 208 с.
функций нескольких аргументов
Хабибуллин И. Программирование на языке высокого уровня. 512 с.
C/C++
Хейфец А. 3-d технологии построения чертежа. AutoCAD, 3-е 256 с.
изд.
Хейфец А. Инженерная компьютерная графика AutoCAD 336 с.
Хрящев В., Шипова Г. Моделирование и создание чертежей в 224 с.
системе AutoCAD
Частиков А. и др. Разработка экспертных систем. Среда CLIPS 608 с.
Черноруцкий И. Методы принятия решений 416 с.
Черняк А. и др. Математика для экономистов на базе Mathcad 496 с.
Черняк А. и др. Высшая математика для экономистов на базе 608 с.
Mathcad. Общий курс
Шапорев С. Дискретная математика. Курс лекций и 400 с.
практических занятий
Шапорев С. Математическая логика. Курс лекций и 416 с.
практических занятий
Шапорев С. Информатика. Теоретический курс и практические 480 с.
занятия
Шелест В. Программирование 592 с.
Щука А. Электроника - 2-е изд. 752 с.
Юревич Е. Основы робототехники, 2-е изд. (+CD-ROM) 416 с.
Юревич Е. Теория автоматического управления, 3-е изд. 560 с.
Книги издательства "БХВ-Петербург'
в продаже:
www.bhv.ru
Магазин "Новая техническая книга": СПб., Измайловский пр., д. 29, тел.:
(812)251-41-10
www.techkniga.com
Отдел оптовых поставок: e-mail: opt@bhv.spb.su
Серия «В подлиннике»
Андреев А. и др. Microsoft Windows ХР. Home Edition и Professional. 640 с.
Русские версии
Андреев А. и др. Microsoft Windows 2000 Professional. Русская 752 с.
версия
Андреев А. и др. Microsoft Windows 2000 Server и Professional. 1056 с.
Русские версии
Андреев А. и др. Microsoft Windows ХР. Руководство 848 с.
администратора
Бергер А. Microsoft® SQL Server 2005 Analysis Services. OLAP и 928 с.
многомерный анализ данных
Борри X. Firebird: руководство разработчика баз данных 1104 с.
Бурлаков М. CorelDRAW 11 720 с.
Бурлаков М. Создание видеоклипов 1216 с.
Бурлаков М. 3ds Мах 9. Энциклопедия пользователя 1024 с.
Бурлаков М. 3ds Мах 2008 1168 с.
Давыдов С, Ефимов А. IntelliJ IDEA. Профессиональное 800 с.
программирование на Java (+CD-ROM)
Долженков В., Колесников Ю. Microsoft Excel 2002 1072 с.
Дронов В. Adobe Dreamweaver CS3 816 с.
Дубовцев А. Microsoft .NET (+CD-ROM) 704 с.
Дударева Н. SolidWorks 2007 1328 с.
Дунаев В. HTML, скрипты и стили 832 с.
Закер К. Компьютерные сети. Модернизация и поиск 1088 с.
неисправностей
Касперски К. Искусство дизассемблирования 896 с.
Кирьянов Д. Mathcad 12 576 с.
Кирьянов Д. Adobe Premiere Pro CS3 640 с.
Клепинин В. Visual FoxPro 9.0
Колесниченко О., Шишигин И. Аппаратные средства PC, 5-е изд.
Котеров Д., Костарев А. РНР 5
Матросов А. и др. HTML 4.0
Ноутон П. Java 2
Пауэлл Т. Web-дизайн, 2-е изд.
Полещук Н. AutoCAD 2004. Разработка приложений и адаптация
Полещук Н. AutoCAD 2005
Пономаренко С. Adobe Illustrator CS
Пономаренко С. Adobe Illustrator CS3
Пономаренко С. Adobe Photoshop CS
Пономаренко С. Adobe Photoshop CSS Extended
Стахнов A. Linux, 2-е изд.
Тозик В. ArchiCAD и архитектурная графика
Тозик В. 3ds Мах 9: трехмерное моделирование и анимация
Тайц А. М., Тайц А. А. Adobe PageMaker 7.0
Тайц А. М., Тайц А. А. CorelDRAW Graphics Suite 11: все программы
пакета
Трасковский А. BIOS
Фаронов В. Turbo Pascal
Фаронов В. Система программирования Delphi
Чекмарев А. Microsoft® Windows Vista. Руководство администратора
Шлее М. Qt. Профессиональное программирование на C++
1216с.
1152 с.
1120 с.
672 с.
1072 с.
1072 с.
624 с.
944 с.
768 с.
752 с.
928 с.
1072 с.
944 с.
592 с.
1056 с.
784 с.
1200 с.
544 с.
1056 с.
912 с.
784 с.
544 с.
..^-,.-.--■::..--.-''У^Ч.-'.:^-^ А!?'''''''"'v'* ' '"' .J
Магазин-салон
<<НОВАЯкТЕХНИНЕСКАЯ КНИГА»
190005, Санкт-Петербург, Измайловский пр., 29
В МАГАЗИНЕ ПРЕДСТАВЛЕНА
ЛИТЕРАТУРА
ПО
компьютерным технологиям
радиотехнике и электронике
физике и математике
строительству и архитектуре
транспорту
машиностроению
и другим
естественно-научным
и техническим направлениям
у^ Низкие цены
^ Прямые поставки
^ от издательств
х/ Ежедневное
пополнение
ассортимента
^ Подарки и скидки
покупателям
Тел.: (812) 251-41-10, e-mail: trade@techkniga.com
,:;.11ГП|1ГЛС11111
>^
Тишин Владимир Викторович, доцент
кафедры прикладной математики
Самарского государственного аэро-космического
университета им. С. П. Королева. Имеет
более чем тридцатилетний опыт
лекционной и практической деятельности, в том
числе по курсам «Дискретная математика» и
«Математическая логика и теория
алгоритмов».
Дискретная
математика
в примерах и задачах
Учебное пособие составлено на
основании материалов лекционного курса,
содержит краткую теорию, варианты
заданий и примеры решения по
следующим разделам дискретной мате-
мати и: множества, декартовы
произведения, соответствия, отношения,
булевы функции, теория алгоритмов,
предикаты, комбинаторика, конечные
автоматы. Даны все основные
определения, необходимые для
выполнения заданий. Для каждого типа
задач предлагается по 30 вариантов
заданий, приводится подробный образец
решения.
Незаменимо при составлении
индивидуальных заданий, а также при
заочной форме обучения.
Предназначено для преподавателей и
студентов университетов и
технических вузов, аспирантов, научных
работников и инженеров, а также для
самостоятельного изучения дискретной
математики.
БХВ-ПЕТЕРБУРГ
194354.
Санкт-Петербург,
ул. Есенина, 5Б
E-mail: mail@bhv.ru
Internet: www.bhv.ru
Тел./сЬакс: (812) 591-6243
»
ISBN 978-5-9775-0232-0
9 117 8 5 97 7115 02 3 2 01