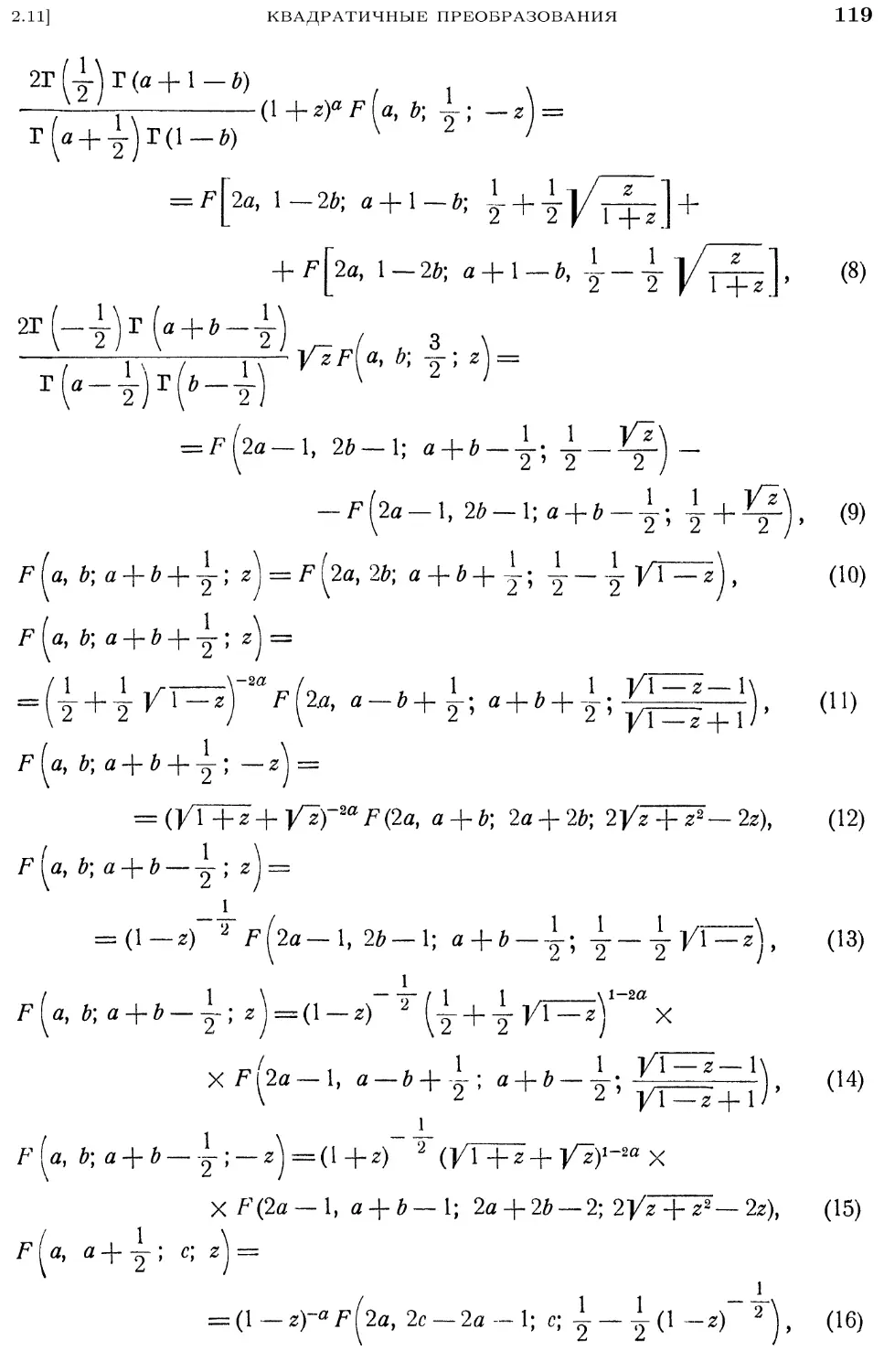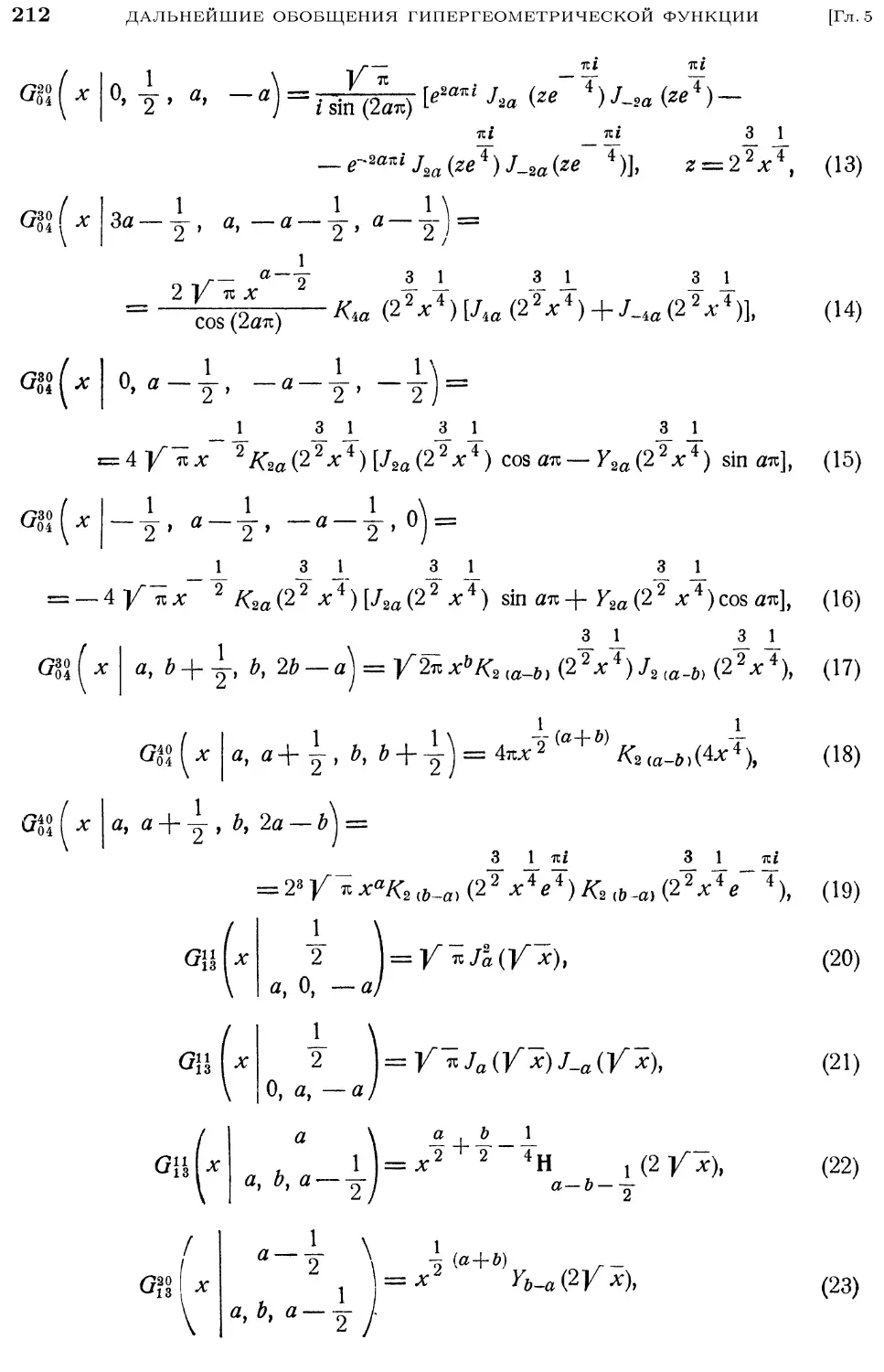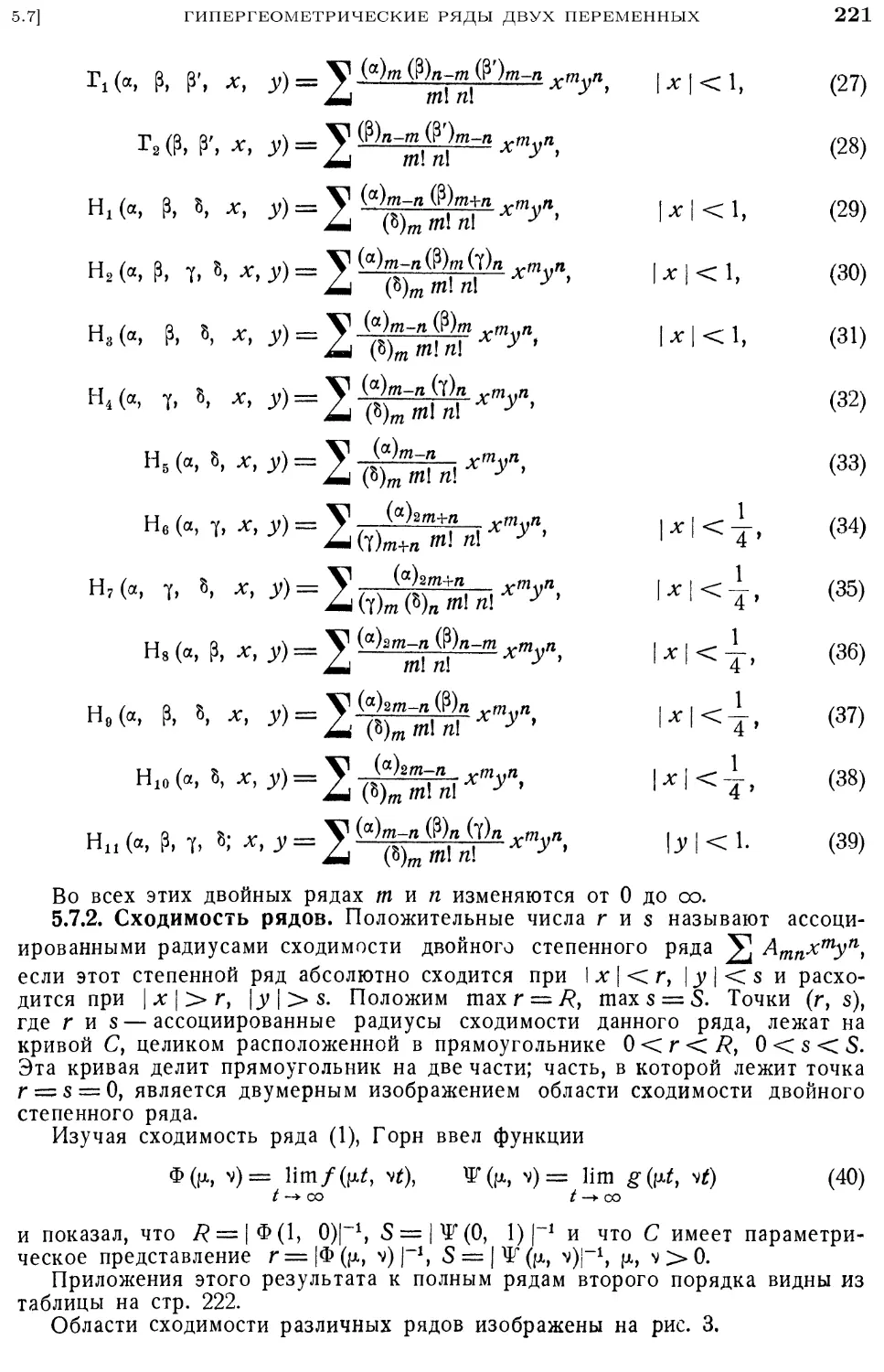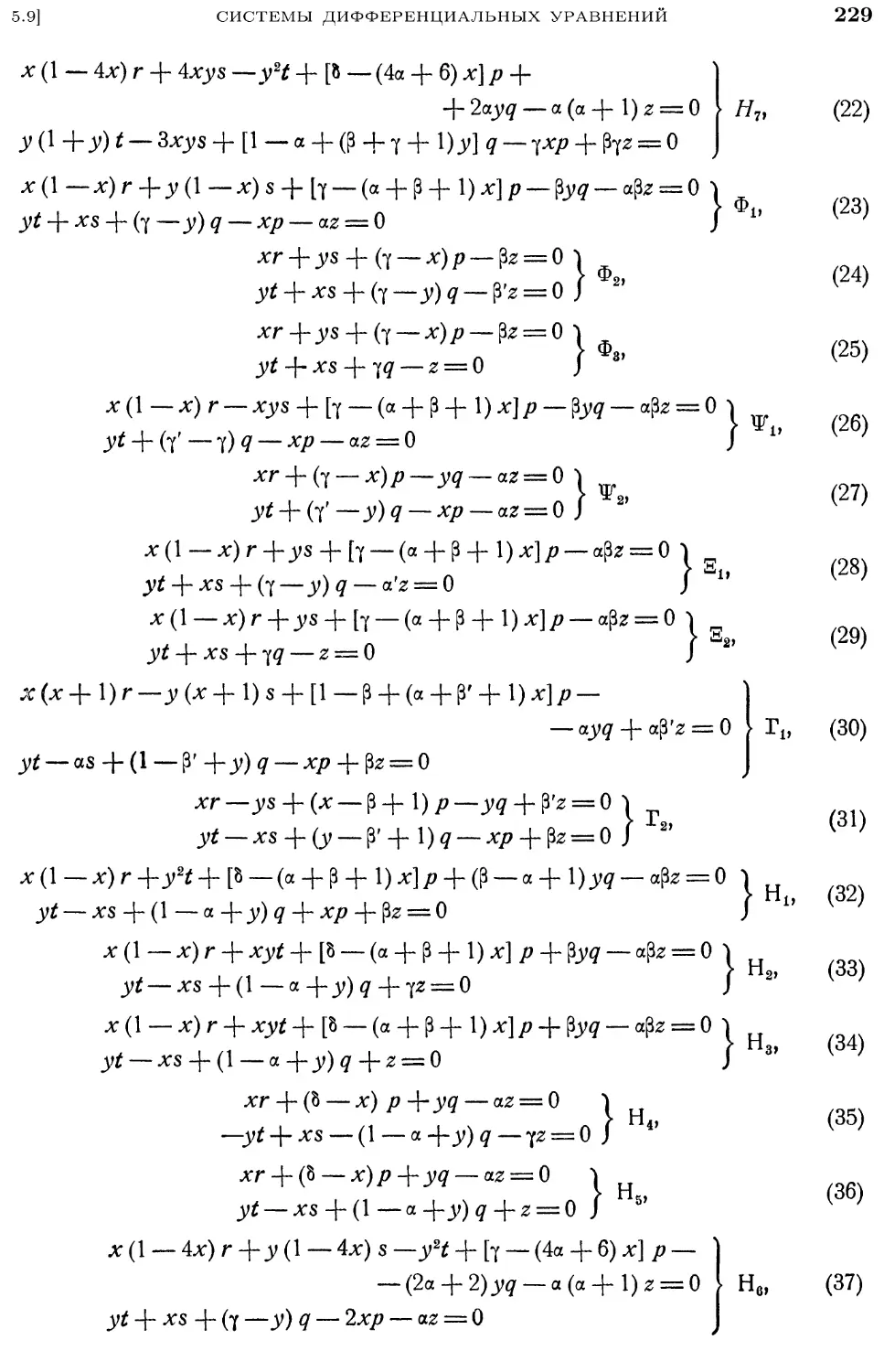Этот труд посвящен памяти
ГАРРИ БЕЙТМЕНА,
создавшего столь грандиозный
проект и продвинувшего свой
замысел столь далеко по пути
к завершению

HIGHER
TRANSCENDENTAL
FUNCTIONS
Volume 1
BASED, IN PART, ON NOTES LEFT BY
HARRY BATEMAN
AND COMPILED BY THE
STAFF OF THE BATEMAN MANUSCRIPT PROJECT
DIRECTOR ARTHUR ERDELYI
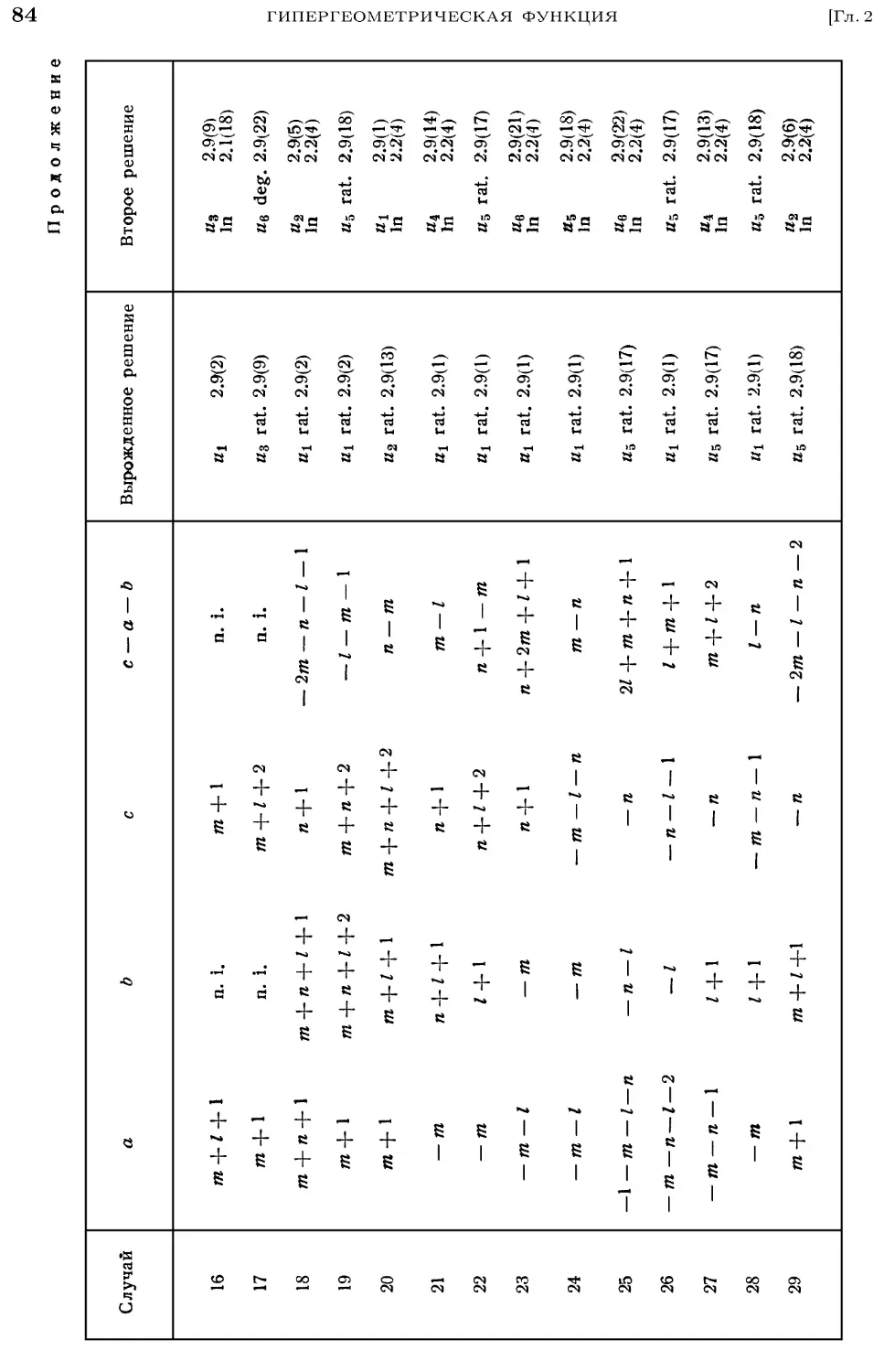
NEW YORK TORONTO LONDON
MC GRAW-HILL BOOK COMPANY, INC.
1953

СПРАВОЧНАЯ МАТЕМАТИЧЕСКАЯ БИБЛИОТЕКА
Г. БЕЙТМЕН и А. ЭРДЕЙИ
ВЫСШИЕ
ТРАНСЦЕНДЕНТНЫЕ
ФУНКЦИИ
ГИПЕРГЕОМЕТРИЧЕСКАЯ
ФУНКЦИЯ
ФУНКЦИИ ЛЕЖАНДРА
Перевод с английского
Н. Я. ВИЛЕНКИНА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1966

517.2 @83)
Б 41
УДК 517.5@83)
АННОТАЦИЯ
Настоящая книга представляет собой перевод первого
тома вышедшего в США трехтомного издания под названием
«Высшие трансцендентные функции», являющегося наиболее
полным из существующих ныне трудов по теории
специальных функций. В отличие от других справочных пособий она
содержит не только все формулы по теории специальных
функций, полученные к концу 40-х годов, но и сжато
изложенную теорию этих функций. По полноте охвата материала
книга уникальна. В ней изложена как теория
классических специальных функций, так и теория автоморфных
функций, эллиптических функций и интегралов, специальных
функций дискретного аргумента, функций Мейера и Мак-
Роберта и т. д. Приведена весьма полная библиография
но специальным функциям.
Книга явится настольной для физиков-теоретиков и
экспериментаторов, инженеров-исследователей, математиков-
прикладников и т. д.
ШТАБ ПО ОСУЩЕСТВЛЕНИЮ ПРОЕКТА БЕЙТМЕНА
Директор
АРТУР ЭРДЕЙИ
Руководство штаба:
ВИЛЬГЕЛЬМ МАГНУС, ФРИЦ ОБЕРХЕТТИНГЕР,
ФРАНЧЕСКО Д. ТРИКОМИ
Ассистенты:
Д. Б е р т и н, Д. Л. Т о м с о н,
В. Б. Ф а л к с, Мария А. В е б е р,
А. Р. Харви, Е. Л. У и т н е й

ОГЛАВЛЕНИЕ
От переводчика 9
Введение 11
Глава 1
ГАММА-ФУНКЦИЯ
1.1. Определение гамма-функции „ . . . 15
1.2. Функциональные уравнения, которым удовлетворяет Г (z) 17
1.3. Выражение некоторых бесконечных произведений через гамма-функцию 19
1.4. Некоторые бесконечные ряды, связанные с гамма-функцией 21
1.5. Бета-функция 23
1.5.1. Определенные интегралы, выражаемые через бета-функцию 24
1.6. Выражения гамма- и бета-функций в виде контурных интегралов 28
1.7. Функция ф {z) 30
1.7.1. Функциональные уравнения для ф(г) 31
1.7.2. Интегральные представления для ty{z) 31
1.7.3. Теорема Гаусса 34
1.7.4. Некоторые бесконечные ряды, связанные с функцией фB) 34
1.8. Функция G (z) 35
1.9. Выражения для функции In Г (г) 36
1.9.1 Ряды Куммера для In Г (z) 38
1.10. Обобщенная дзета-функция 40
оо
1.11. Функция Ф(г, s,v)= ^ (v + n)~s2n 42
я = 0
1.11.1. Дилогарифм Эйлера 46
1.12. Дзета-функция Римана 47
1.13. Числа и многочлены Бернулли 50
1.13.1. Многочлены Бернулли высшего порядка 54
1.14. Числа и многочлены Эйлера 55
1.14.1. Многочлены Эйлера высшего порядка 57
1.15. Некоторые интегральные формулы, связанные с многочленами Эйлера и Бернулли . . 58
1.16. Полигамма-функция 59
1.17. Некоторые выражения для \пТ (\ -{- z), <\> (I ~\- z), G (\ -{- z) и Т (z) 60
1.18. Асимптотические разложения 61
1.19. Интегралы Меллина —Бернса 63
1.20. Разложения некоторых тригонометрических функций в степенные ряды 65
1.21. Некоторые другие разложения и символы 67
Глава 2
ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ
Часть первая. Теория
2.1. Гипергеометрический ряд 69
2.1.1. Гипергеометрическое уравнение 69
2.1.2. Элементарные соотношения 70
2.1.3. Основные интегральные представления 72

2.1.4. Аналитическое продолжение гипергеометрического ряда 74
2.1.5. Квадратичные и кубичные преобразования 76
2.1.6. F (а, b; с; z) как функция параметров 80
2.2. Вырожденный случай гипергеометрического уравнения 81
2.2.1. Частное решение 81
2.2.2. Полное решение в вырожденном случае 82
2.3. Полное решение и асимптотическое разложение в общем случае 85
2.3.1. Линейно независимые решения гипергеометрического уравнения в
невырожденном случае 85
2.3.2. Асимптотические разложения 86
2.4. Интегралы, выражающие или содержащие гипергеометрические функции 89
2.5. Различные результаты 93
2.5.1. Производящая функция 93
2.5.2. Произведения гипергеометрических рядов 93
2.5.3. Соотношения, содержащие биномиальные коэффициенты и неполную бета-
функцию 96
2.5.4. Непрерывные дроби 98
2.5.5. Частные случаи гипергеометрической функции 99
2.6. Уравнение Римана 100
2.6.1. Редукция гипергеометрического уравнения 100
2.6.2. Квадратичные и кубичные преобразования 102
2.7. Конформные преобразования 103
2.7.1. Группа гипергеометрического уравнения 103
2.7.2. Функция Шварца 105
2.7.3. Униформизация 108
2.7.4. Нули 108
Часть вторая. Формулы 109
2.8. Гипергеометрический ряд 109
2.9. Ряды Куммера и соотношения между ними 113
2.10. Аналитическое продолжение 116
2.11. Квадратичные преобразования и преобразования высших степеней 118
2.12. Интегралы , . 123
Глава 3
ФУНКЦИИ ЛЕЖАНДРА
3.1. Введение 125
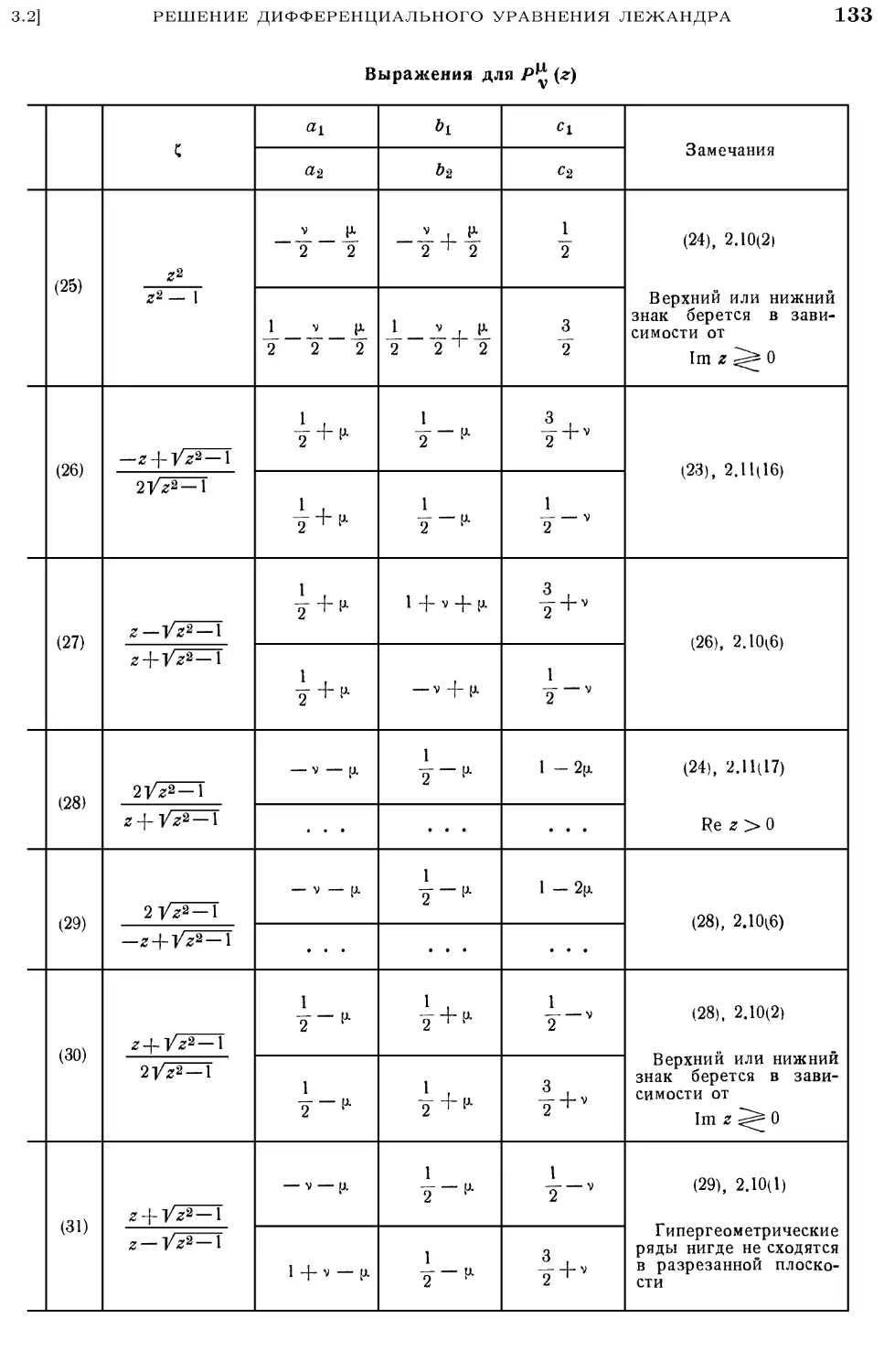
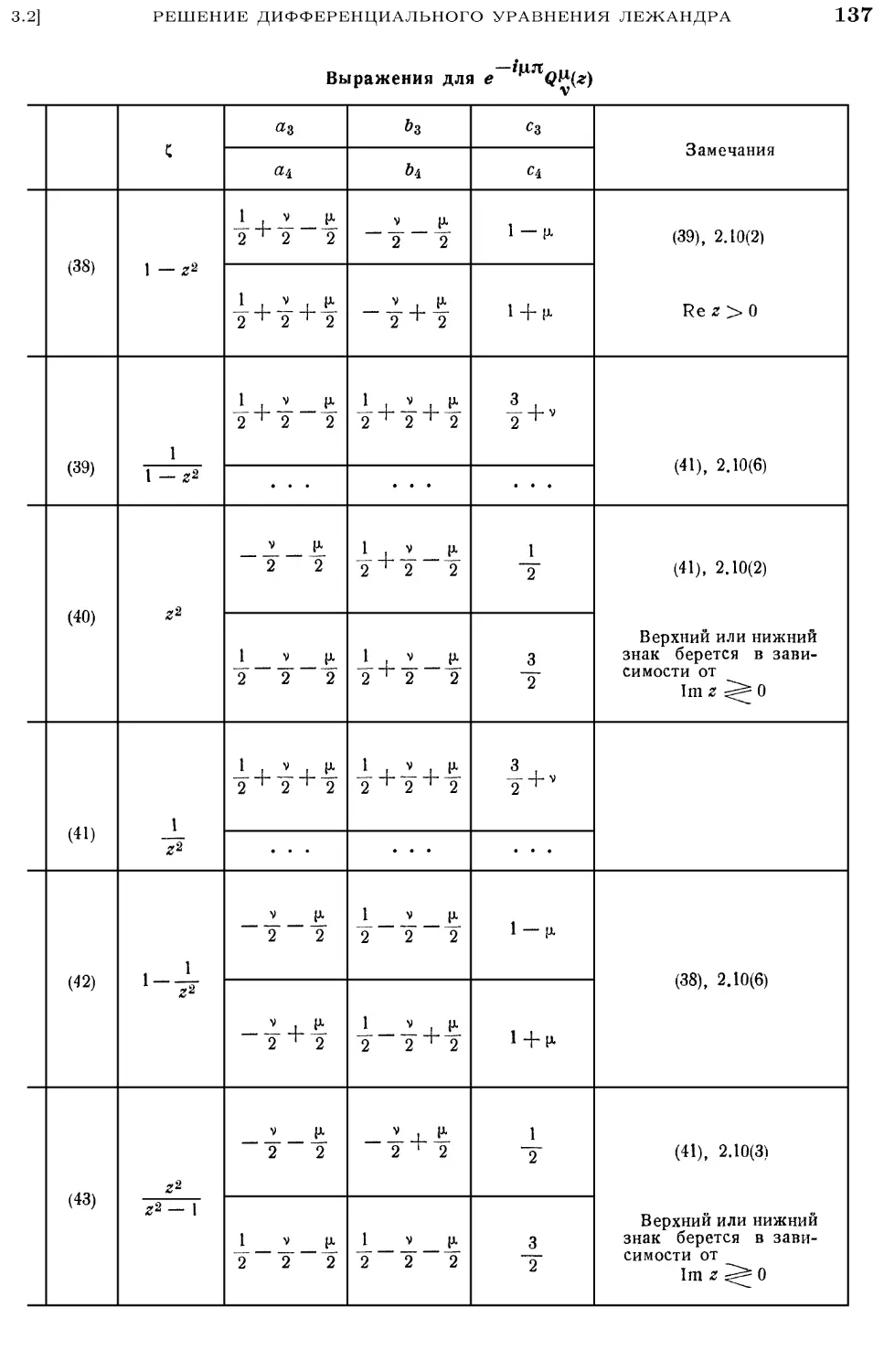
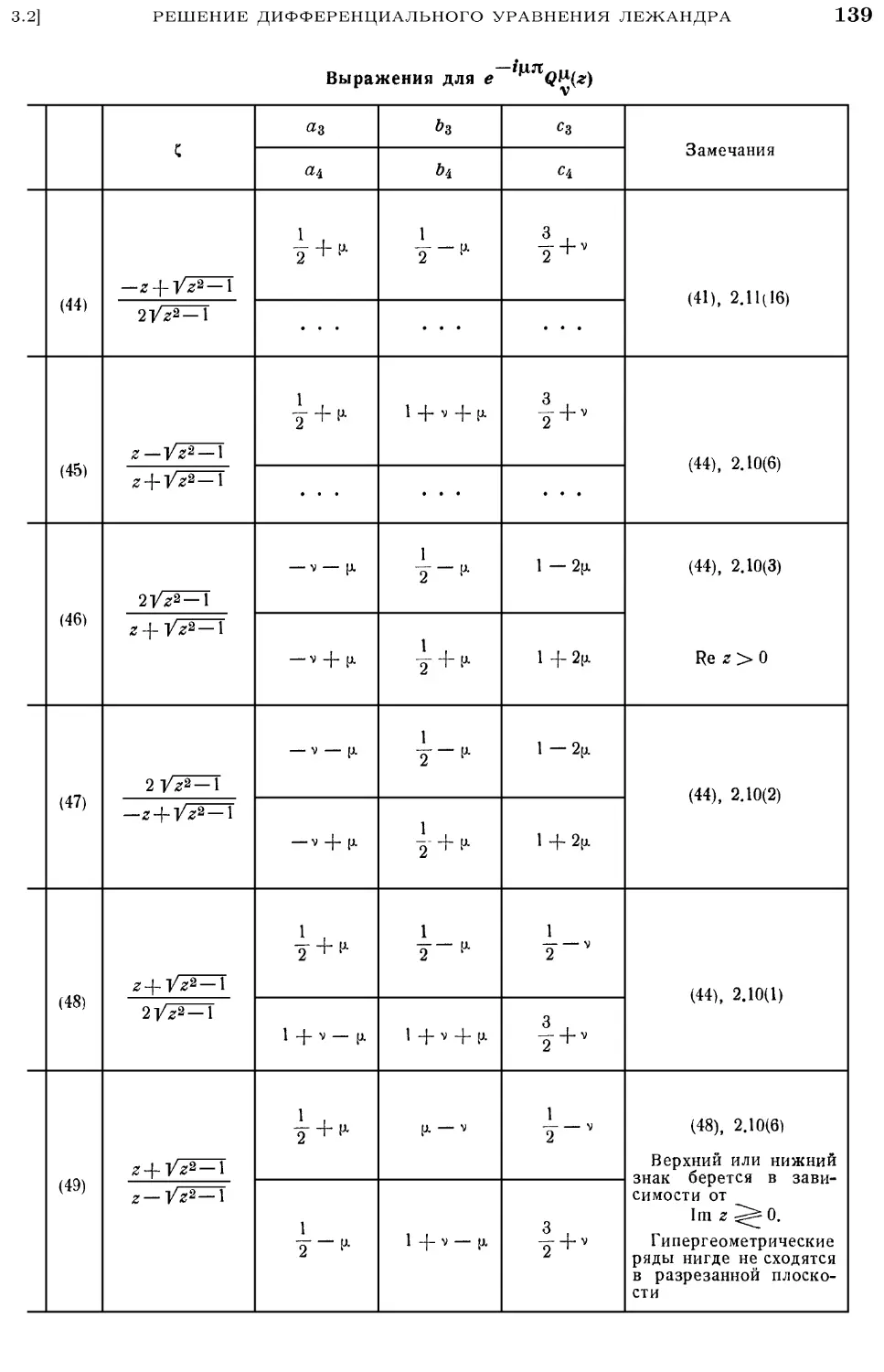
3.2. Решение дифференциального уравнения Лежандра 126
3.3.1. Соотношения между функциями Лежандра 140
3.3.2. Некоторые дальнейшие связи с гипергеометрическим рядом 142
3.4. Функции Лежандра на разрезе 143
3.5. Тригонометрические разложения для Р^(соs 6) и Q^(cos 6) 146
3.6.1. Частные значения (л и v , 148
3.6.2. Многочлены Лежандра 151
3.7. Интегральные представления 155
3.8. Соотношения между смежными функциями Лежандра 161
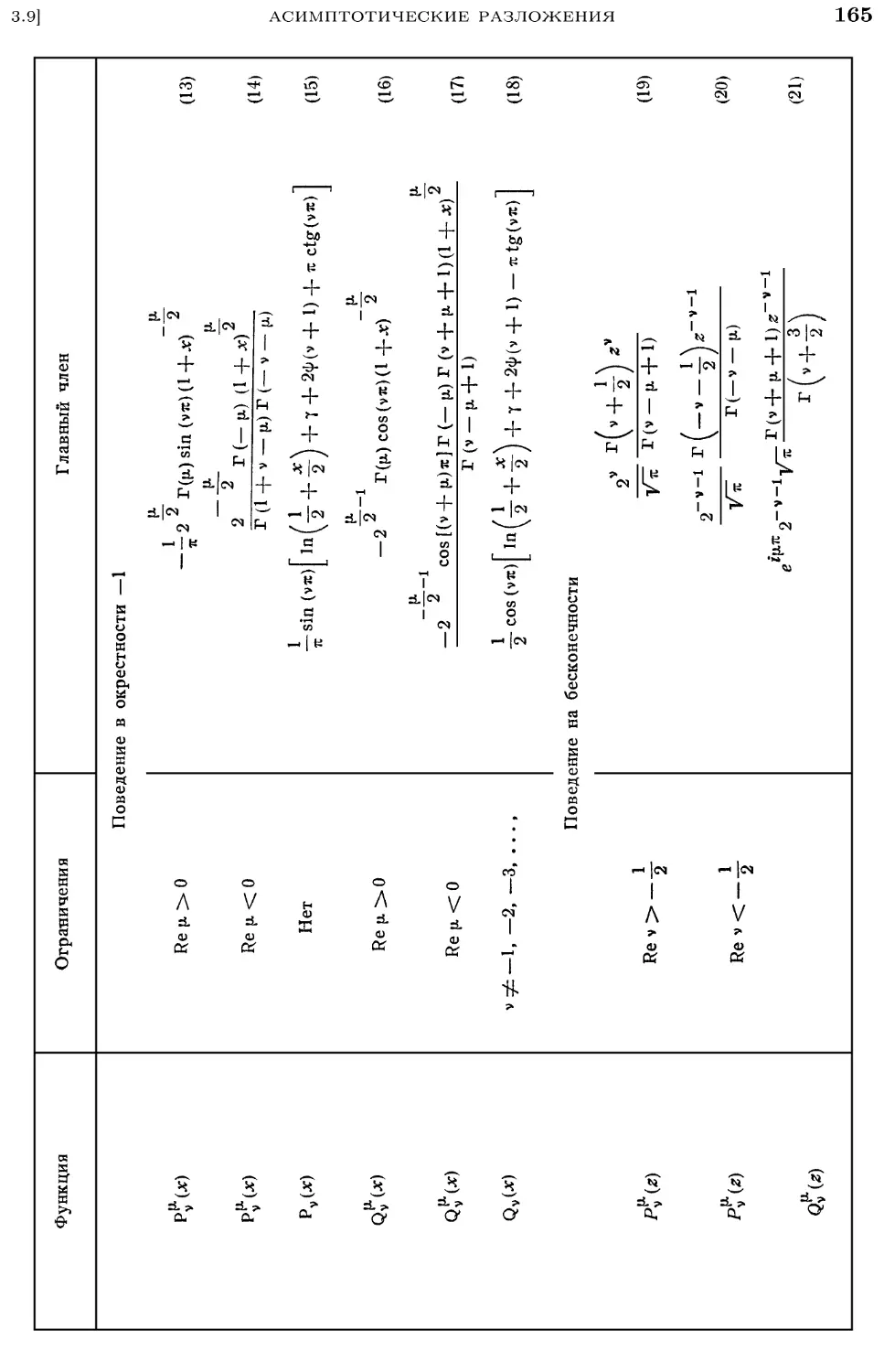
3.9.1. Асимптотические разложения 163
3.9.2. Поведение функций Лежандра вблизи особых точек 164
3.10. Разложения по функциям Лежандра 165
3.11. Теоремы сложения 169
3.12. Интегралы, содержащие функции Лежандра 170
3.13. Функции кольца или тороидальные функции 174
3.14. Функции конуса 176
3.15. Функции Гегенбауэра 177
3.15.1. Многочлены Гегенбауэра 177
3.15.2. Функции Гегенбауэра 180
3.16. Некоторые другие обозначения 181

Глава 4
ОБОБЩЕННЫЙ ГИПЕРГЕОМЕТРИЧЕСКИЙ РЯД
4.1. Введение 183
4.2. Дифференциальные уравнения 184
4.3. Тождества и рекуррентные соотношения 185
4.4. Обобщенный гипергеометрический ряд, аргумент которого равен единице в случае
р = q _j_ 1 188
4.5. Преобразования , F при значениях аргумента, отличных от единицы 190
4.6. Интегралы 192
4.7. Некоторые частные результаты 193
4.8. Базисные гипергеометрические ряды 195
Глава 5
ДАЛЬНЕЙШИЕ ОБОБЩЕНИЯ ГИПЕРГЕОМЕТРИЧЕСКОЙ ФУНКЦИИ
5.1. Различные обобщения 199
Е-ф ункция Мак-Роберта 200
5.2. Определение ^-функции 200
5.2.1. Рекуррентные соотношения 201
5.2.2. Интегралы 202
G-функция Мейера 203
5.3. Определение G-функции 203
5.3.1. Простые тождества 203
5.4. Дифференциальные уравнения 205
5.4.1. Асимптотические разложения 207
5.5. Ряды и интегралы 208
5.5.1. Ряды (/-функций 208
5.5.2. Интегралы, содержащие (/-функции 20Э
5.6. Частные случаи (/-функции 210
Гипергеометрические функции многих переменных 218
5.7. Гипергеометрические ряды двух переменных 218
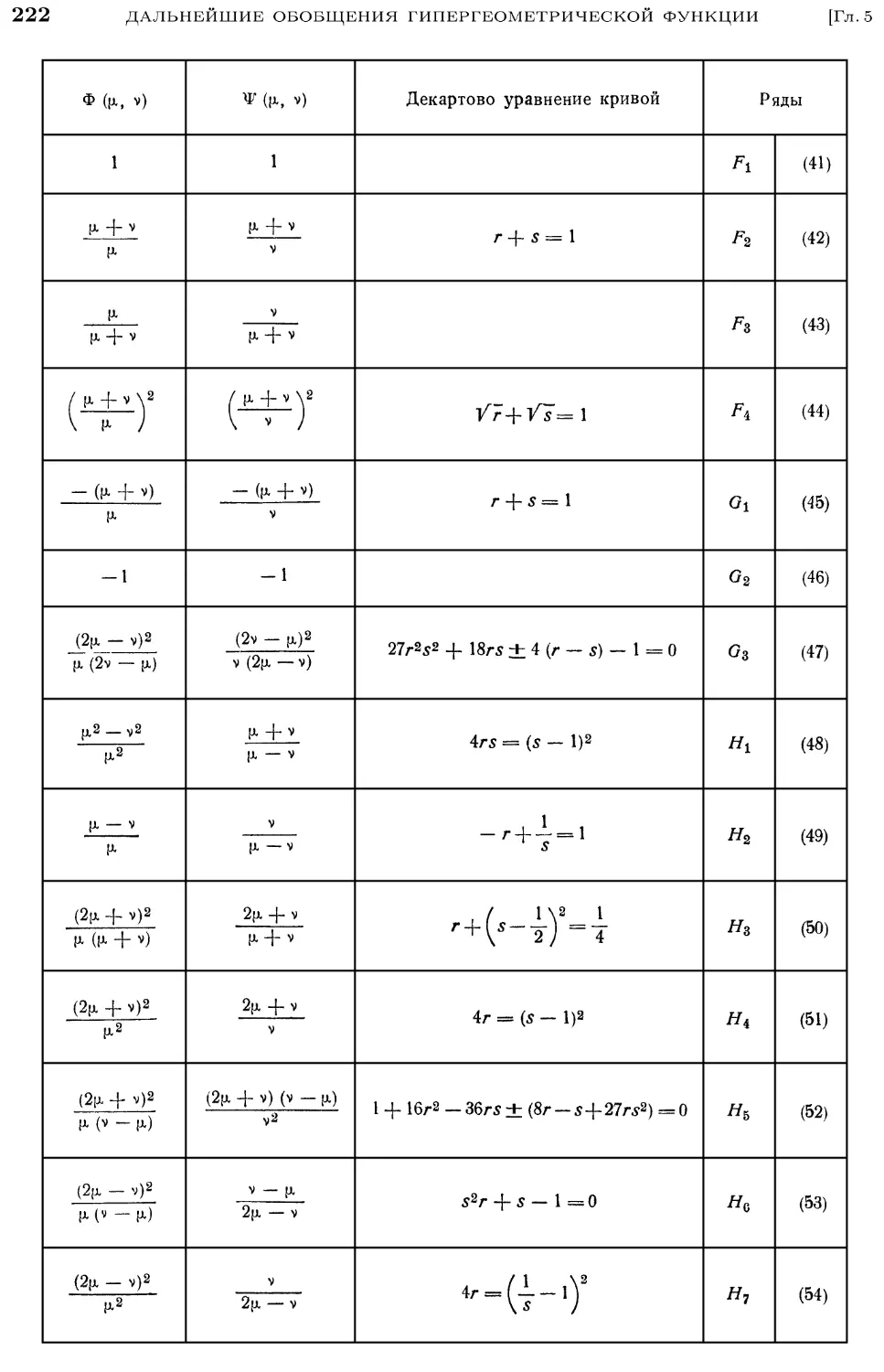
5.7.1. Список Горна 219
5.7.2. Сходимость рядов 221
5.8. Интегральные представления 224
5.8.1. Двойные интегралы типа Эйлера 224
5.8.2. Обычные интегралы типа Эйлера 225
5.8.3. Двойные интегралы типа Меллина — Бернса 228
5.9. Системы дифференциальных уравнений в частных производных 226
5.9.1. Исследования Айнса 230
5.10. Формулы приведения 231
5.11. Преобразования 232
5.12. Символические формы и разложения 234
5.13. Частные случаи 236
5.14. Другие ряды 236
Глава 6
ВЫРОЖДЕННАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ
6.1. Предварительные замечания 237
6.2. Дифференциальные уравнения 238
6.3. Общее решение вырожденного уравнения в окрестности начальной точки 241
6.4. Элементарные соотношения для функций Ф 242
6.5. Основные интегральные представления 243
6.6. Элементарные соотношения для функции W 245
6.7. Фундаментальная система решений для вырожденного гипергеометрического
уравнения 246
6.7.1. Логарифмический случай 247
6.8. Дальнейшие свойства функции W 249
6.9. Функции Уиттекера 251
6.9.1. Функции Бесселя 252
6.9.2. Другие частные случаи вырожденной гипергеометрической функции 253

6.10. Преобразование Лапласа и вырожденная гипергеометрическая функция 256
6.11. Интегральные представления 259
6.11.1. Функция Ф 259
6.11.2. Функция W 260
6.11.3. Функции Уиттекера 262
6.12. Разложения по многочленам Лагерра и функциям Бесселя 263
6.13. Асимптотическое поведение 265
6.13.1. Поведение при больших значениях |лг| 265
6.13.2. Большие значения параметров 266
6.13.3. Большие значения переменного и параметра 268
6.14. Теоремы умножения 271
6.15. Ряды и интегральные формулы 272
6.15.1. Ряды 272
6.15.2. Интегралы 273
6.15.3. Произведения вырожденных гипергеометрических функций 274
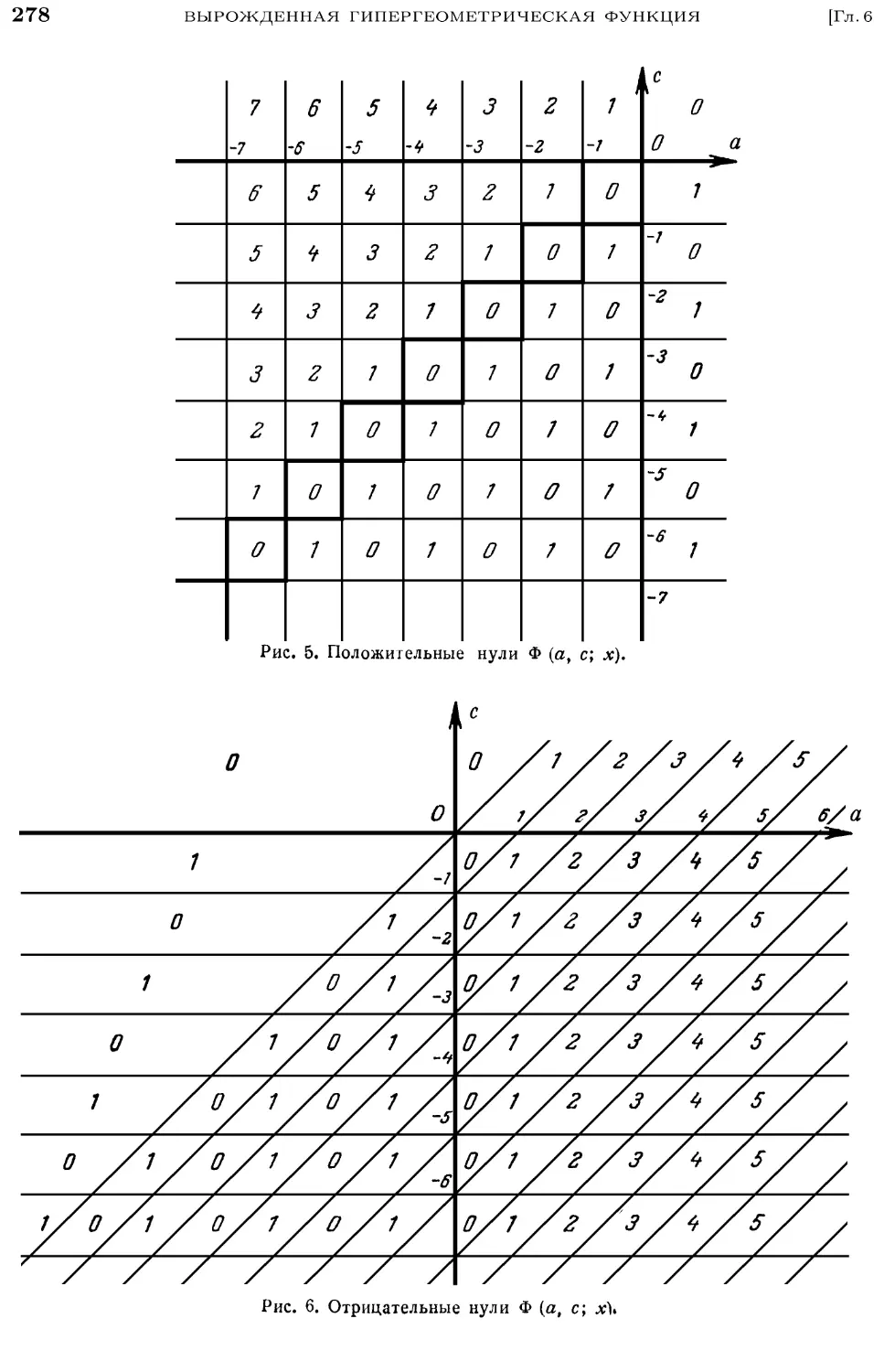
6.16. Вещественные нули для вещественных а и с 277
6.17. Дескриптивные свойства при вещественных а, с, х 279
Цитированная литература 281
Именной указатель 289
Предметный указатель 290
Указатель обозначений 293

ОТ ПЕРЕВОДЧИКА
Вряд ли есть необходимость много говорить о важности специальных
функций для любого ученого и инженера, имеющего дело с практическим
применением дифференциальных уравнений. Решение самых разных задач,
относящихся к теплопроводности и динамике, электромагнитным колебаниям и
аэромеханике, квантовой механике и теории потенциала, приводит к
специальным функциям. Чаще всего они появляются при решении дифференциальных
уравнений в частных производных методом разделения переменных.
Разнообразие задач, приводящих к специальным функциям, вызвало
быстрый рост числа функций, применяемых в приложениях. Уже давно
появились многочисленные руководства по теории специальных функций.
К числу таких руководств, сравнительно полно охватывающих
состояние науки на период составления, принадлежит известный «Курс
современного анализа» Уиттекера и Ватсона (Физматгиз, 1961—1962). Ряд книг
посвящен теории отдельных классов специальных функций (функций Бесселя,
Лежандра, Матье и т. д.). Однако объем этих книг делает их не слишком
удобными для использования (например, трактат Ватсона по функциям
Бесселя содержит почти 800 страниц). Поэтому наряду с монографиями стали
появляться справочники, содержащие формулы и самые краткие пояснения
(одним из лучших справочников такого типа является книга: И. С. Град-
штейн и И. М. Рыжик, Таблицы интегралов, сумм, рядов и произведений,
изд. 4, Физматгиз, 1963). Но такими справочниками можно пользоваться,
лишь владея уже теорией соответствующего класса функций.
Предлагаемая вниманию читателя книга занимает как бы
промежуточное положение между этими двумя типами изданий. Она содержит краткие,
но весьма ясно написанные выводы основных свойств изучаемых функций, по
которым человек, не владеющий теорией, может ее изучить. Но, кроме того,
в нее включены многочисленные списки формул, касающихся наиболее
важных специальных функций. Наконец, каждая глава книги сопровождается
списком использованной литературы (помещенным в конце книги), что
позволяет читателю найти дополнительную информацию об изучаемых функциях.
Эта книга была задумана (в несколько ином и более обширном виде)
профессором Калифорнийского технологического института Гарри Бейтменом,
одним из крупнейших американских специалистов в области классического
анализа и его приложений к аэро- и гидромеханике, электромагнитной
теории, термодинамике, геофизике и т. д. В течение двух десятков лет он
собирал рассеянные по различным монографиям и периодической литературе
сведения о специальных функциях: их свойствах, интегральных и иных
представлениях, связях между различными классами специальных функций,
определенных интегралах, содержащих специальные функции, и т. д. В
результате этой работы была составлена гигантская картотека, содержавшая почти
все, что касалось указанных вопросов, а также теории дифференциальных
уравнений математической физики, интегральных уравнений и т. д.

Последовавшая в 1946 г. смерть Бейтмена прервала его работу над
задуманной энциклопедией классического анализа. Для обработки собранного
материала был создан штаб во главе с известным английским математиком
А. Эрдейи, в который вошли немецкие ученые В. Магнус и Ф. Оберхеттингер
и итальянский математик Ф. Трикоми.
Эти ученые вместе с руководимой ими группой молодых математиков
создали, используя материалы Бейтмена, уникальный труд по теории
специальных функций и интегральных преобразований. Он состоит из трех томов
под общим названием «Высшие трансцендентные функции» и двух томов
«Интегральных преобразований». Первые три тома охватывают все важные
классы специальных функций: гамма- и бета-функции, гипергеометрическая
функция и вырожденная гипергеометрическая функция, всевозможные
обобщения гипергеометрических функций (функции Мейера, Мак-Роберта и Др.)»
функции и многочлены Лежандра, функции Бесселя, функции
параболического цилиндра, неполная гамма-функция, интегральный синус и косинус,
интеграл вероятности, всевозможные классы ортогональных многочленов от
одного и нескольких переменных, гармонические функции нескольких
переменных, эллиптические функции и интегралы, автоморфные функции, функции
Ламе и Матье, дзета-функция Римана и т. д. Для каждого из этих классов
функций даны рекуррентные соотношения, дифференциальные уравнения,
интегральные представления, асимптотические формулы, различные теоремы
сложения, неравенства и т. д.
Как уже говорилось, к этому трехтомнику примыкает двухтомник
«Интегральные преобразования». Он содержит подробные таблицы для
преобразования Фурье (обычного, а также по синусам и косинусам), Лапласа
(прямого и обратного), Меллина, Ганкеля, Канторовича — Лебедева, Гильберта,
Стильтьеса и многочисленных других интегральных преобразований. Таким
образом, пять томов справочника охватывают в своей совокупности почти
весь гигантский материал, накопленный в теории специальных функций и
интегральных преобразований за двухсотлетнюю историю их развития (до
конца 40-х годов). По полноте охвата материала и плотности информации
справочник не имеет себе равных в мировой литературе.
Несомненно, что эта энциклопедия классического математического
анализа окажется полезной весьма широкому кругу читателей. Физики-теоретики
и экспериментаторы, исследователи в области прикладного анализа и
уравнений математической физики, инженеры, сталкивающиеся с решением
дифференциальных уравнений, будут пользоваться этой книгой наряду с
математиками самых различных специальностей.
Настоящий выпуск содержит теорию гипергеометрической функции и ее
обобщений и частных случаев (в частности, функций и многочленов
Лежандра). Кроме того, в нем изложена теория гамма- и бета-функций.
Для облегчения пользования книгой многие применяемые авторами
обозначения были заменены на обозначения, принятые в Советском Союзе
(например, мы пишем arcsin х вместо sin х, In x вместо log л: и т. д.).
Доктор физико-математических наук, профессор
Н. Виленкин

ВВЕДЕНИЕ
Предлагаемая вниманию читателя книга является первой частью труда,
который может рассматриваться как современная версия знаменитого
«Курса современного анализа» Уиттекера и Ватсона, точнее, второй части этого
курса, посвященной теории трансцендентных функций. Бейтмен (который был
учеником Уиттекера) задумал свой «Путеводитель по функциям» в
гигантских масштабах. Кроме детального изложения свойств наиболее важных
функций, труд должен был содержать историю их возникновения, основные
относящиеся к ним формулы и библиографию, касающуюся всех
специальных функций. Эти функции были каталогизированы и расклассифицированы
в зависимости от способа их определения: с помощью степенных рядов,
производящих функций, бесконечных произведений, последовательного
дифференцирования, неопределенных интегралов, определенных интегралов,
дифференциальных уравнений, разностных уравнений, функциональных
уравнений, тригонометрических рядов, рядов по ортогональным функциям и
интегральных уравнений. Таблицы интегральных представлений специальных
функций и таблицы значений для некоторых новых функций должны были
войти в этот «Путеводитель». Наконец, он должен был содержать подробные
таблицы определенных интегралов от специальных функций и список
таблиц значений для этих функций.
Трудно переоценить значение задуманного Бейтменом труда. Не имеющая
себе равных осведомленность его в математической литературе, как
современной, так и давно опубликованной, а также его непревзойденное усердие
должны были сделать этот труд наиболее авторитетным изложением
широкой области классического анализа и, во многих отношениях,
устанавливающим общепризнанные стандарты — своеобразным Большим оксфордским
словарем для теории специальных функций.
Реалистическая оценка наших возможностей и отведенного времени
привела к коренному пересмотру планов Бейтмена. Лишь сам Бейтмен обладал
достаточной эрудицией для того, чтобы охватить теорию всех функций.
Таким образом, нам пришлось ограничиться изложением (вероятно, менее
подробным, чем это было задумано Бейтменом) самых существенных свойств
тех специальных функций, которые мы рассматривали как наиболее важные.
Разумеется, происшедшее в результате этого пересмотра обеднение
содержания книги весьма прискорбно. Однако мы позволяем себе надеяться, что
оно в некоторой мере уравновешивается достигнутым в результате
сокращением объема и большей прозрачностью структуры. Мы надеемся, что
хотя получившаяся книга по широте охвата материала уступает задуманной
Бейтменом, но в пределах намеченной нами сферы она окажется более
удобной для использования.
Составление книги. Изложим кратко, как была написана эта
книга. Сначала мы составили подробный перечень содержания книги. После
этого каждый из руководящих работников штаба взял на себя написание
определенных глав. В выполнении этой задачи им помогали более молодые
сотрудники штаба. Однако главной обязанностью последних было составле-

ние таблиц интегральных преобразований, которые будут опубликованы
отдельно. Наконец, написанные главы были просмотрены и отредактированы,
чтобы достигнуть их согласованности. Из шести глав, вошедших в первую
часть книги, Магнус писал гл. 2 и 4, Оберхеттингер — 1 и 3, Эрдейи — 5 и Три-
коми — 6. Взаимозависимость отдельных глав делала желательным
сотрудничество авторов. Например, в теории функций Лежандра используются
гипергеометрические ряды и, в соответствии с этим, Магнус и Оберхеттингер
планировали свою работу так, чтобы достичь необходимой согласованности.
Точно так же взаимозависимы гл. 2, 4 и 5, а потому Магнус и Эрдейи
согласовывали свои планы.
В результате получился труд, содержащий главы весьма различного
характера. Различие в изложении зависит в некоторой степени от индивидуальных
вкусов основных авторов, но в значительно большей степени от того, что
каждый класс функций требовал особого подхода. В тех случаях, когда
рассматриваемые функции часто встречаются и имеют важные приложения, мы
старались давать достаточно подробное дедуктивное изложение,
сопровождаемое ссылками на литературу. Такие главы носят скорее характер учебника,
за исключением того, что доказательства в них часто лишь намечаются,
а не проводятся детально. С другой стороны, в случаях, когда изучаемые
функции не играют большой роли в прикладной математике, мы
ограничивались кратким изложением сведений об этих функциях, не выводя, как
правило, их свойств. Наиболее характерным примером такого стиля изложения
в этом томе является, вероятно, гл. 5. Встречаются и функции, общая теория
которых может быть весьма кратко изложена, но практическое применение
их связано с громадным набором формул, которые трудно изложить в
удобном виде. В этих случаях мы включали в главу списки соответствующих
формул либо как часть текста, либо как дополнение к главе. В связи с этим надо
отметить, что, насколько нам известно, воспроизведенная в гл. 2 таблица
Гурса всех квадратичных преобразований гипергеометрического ряда была
ранее весьма труднодоступной; это же справедливо и относительно полного
анализа вырожденного случая гипергеометрического уравнения (см. 2.2.2).
В случае функций Бесселя проблема состояла в том, что результаты,
полученные до 1922 г., были полно и систематично изложены в известном
трактате Ватсона, в то время как многочисленные результаты, полученные после
1922 г., были рассеяны по различным источникам. В этом случае мы приняли
решение менее подробно излагать результаты, содержащиеся в книге Ватсона,
сосредоточив усилия на результатах, которые не были столь легко доступны
читателю. Коротко говоря, практически каждый класс функций требовал
особого подхода, и мы без колебаний решали возникавшие проблемы
индивидуально в каждом случае. Для каждого случая мы искали решение, казавшееся
нам наилучшим, жертвуя во многих случаях единством изложения.
Каждая глава сопровождается списком литературы *), содержащим не
только материалы, на которых было основано изложение в этой главе, но и
те, которые необходимы читателю для поисков дальнейшей информации.
Степень полноты этих списков зависела от индивидуальных вкусов авторов,
а также от степени важности и характера функций. Следует отметить,
однако, что ни в одном случае список литературы не исчерпывает всей
библиографии, относящейся к данному классу функций. Задача составления
систематической библиографии, относящейся к изучаемым функциям,
неразрешима с помощью имевшихся в наличии сил; кроме того, такая библиография
слишком увеличила бы объем книги.
Мы старались включать в эту книгу в основном функции, встречающиеся
в прикладной математике. Выбор включаемых функций, равно как и выбор
обозначений, делался исходя из принятого в математике. Например, для вы-
) Весь список литературы вынесен в конец книги. Прим. ред.

рожденной гипергеометрической функции есть много обозначений. Мы
использовали лишь два из них, обычно применяемые в математических работах,
и кратко указали на другие обозначения; однако мы не касались обозначений,
используемых в квантовой механике. Мы исключали малоизученные в
математике специальные функции даже в тех случаях, когда для них существуют
подробные таблицы, или они полезны в некоторых практических вопросах.
С другой стороны, мы включили некоторые специальные функции, которых
обычно не касаются в трудах подобного рода, например функции,
встречающиеся в теории чисел, или некоторые специальные виды автоморфных
функций. Главы, посвященные этим функциям, следует рассматривать как пробные,
и мы вполне отдаем себе отчет в том, насколько проблематичным является
такое добавление к обычному семейству специальных функций.
По большей части мы не смогли широко использовать обширные заметки
Бейтмена; нам оказалось легче составить разделы, касающиеся различных
функций, используя свои знания об этих функциях и дополняя их путем
обычных поисков в доступной нам литературе. Однако в некоторых случаях
заметки Бейтмена были широко использованы. Глава о производящих функциях
возникла благодаря составленному Бейтменом каталогу производящих
функций, и при ее составлении мы широко пользовались этим каталогом.
Обозначения и ссылки. При выборе обозначений возникли
своеобразные затруднения. Существуют специальные функции, например функции
Бесселя первого рода, для которых есть общепринятые стандартные
обозначения. В то же время в некоторых случаях, например для вырожденных
гипергеометрических функций, имеется много существенно различных и
независимых обозначений. Наиболее затруднительные проблемы возникали в связи
с функциями, для которых более или менее одинаковые символы
применяются в нескольких различных смыслах. Многочлены Эрмита обычно
обозначают через Нп(х) или Неп(х), но иногда этими символами обозначают
многочлены, возникающие при повторном дифференцировании функции ехр (—х2),
( 2\
а иногда — при повторном дифференцировании ехр ( ~-1. Кроме того, одни
авторы включают множитель п\, а другие этого не делают. Мы старались
придерживаться на протяжении всей книги одних и тех же обозначений.
Наиболее существенное отклонение от этого принципа произошло для
вырожденной гипергеометрической функции: в большей части книги мы обозначаем
ее 1F1, но в гл. 6 (и некоторых следующих главах) тот же ряд обозначается
символом Ф (а второе решение вырожденного гипергеометрического
уравнения— символом *Р).
Насколько это возможно, мы следовали обычным обозначениям. Для
функций Бесселя были использованы обозначения, применявшиеся Ватсоном в его
монументальном труде, для ортогональных многочленов мы использовали
обозначения Сеге (за исключением обозначения С^для ультрасферических
многочленов). Что касается функций Лежандра, то мы, следуя книгам Янке —
Эмде и Магнуса — Оберхеттингера, а также некоторым другим авторам,
различали определение функций Лежандра, применимое для отрезка [—1, 1],
и определение, применимое во всей комплексной плоскости, исключая этот
отрезок. В сомнительных случаях мы использовали обозначения, примененные
в более удобных или более обширных таблицах. Мы придерживались
обозначений, применяемых в таблицах, и в случаях, когда считали, что с
математической точки зрения предпочтительнее были бы иные обозначения. Все
обозначения истолковываются в том месте, где они впервые встречаются. В конце
тома приложены указатель обозначений, который должен помочь читателю
выяснить смысл каждого обозначения, применяемого в этой книге, и
предметный указатель, в котором приведены обозначения для любой функции,
встречающейся в тексте.

Многие главы книги можно читать независимо от остальных, но
встречаются и многочисленные перекрестные ссылки. Внутри каждого пункта
равенства обозначаются просто с помощью номеров. Если данное равенство
используется в другом пункте, оно обозначается с помощью номера пункта,
дополненного номером равенства. Таким образом C) обозначает равенство
C) пункта, в котором делается ссылка, а 2.1C) обозначает ссылку на
равенство C) из пункта 2.1. Ссылки на литературу даются путем указания фамилии
автора и года публикации.
Сложность и объем выполненной работы делают тщетной надежду на то,
что нам удалось полностью избежать ошибок в выводах и опечаток.
Подписавшийся будет благодарен за все исправления, которые могут оказаться
весьма полезными в случае, если понадобится второе издание книги.
В заключение я хочу выразить благодарность от имени всего штаба
проекта Калифорнийскому технологическому институту и особенно декану
Е. Ватсону за то, что они начали эту работу и оказывали нам большую
поддержку во всех проблемах, с которыми нам пришлось сталкиваться.
Я выражаю также благодарность всем моим коллегам, без содействия которых
этот труд не мог бы появиться в свет.
А Эрдейи

ГЛАВА 1
ГАММА-ФУНКЦИЯ
1.1. Определение гамма-функции
Функция Г (z) может быть определена одним из следующих выражений:
A)
B)
C)
где
D)
обозначает постоянную Эйлера — Маскерони. Определение A) было
использовано Эйлером, B) (в несколько иных обозначениях) — Гауссом и C) — Вей-
ерштрассом.
Заменяя в формуле A) t на st (s вещественно и положительно),
получаем
E)
Можно показать [см. 1.5 C4)], что эта формула остается справедливой
и для комплексных значений s, если в качестве пути интегрирования взять
луч, выходящий из начала координат и наклоненный к оси абсцисс иод
углом 5.

Таким образом, имеем
F)
Если 0<Re2<l, то это равенство остается справедливым при arg s -j- 5 =
•к
_ I
~~— 2 '
Из равенств B) и C) видно, что гамма-функция является аналитической
функцией от z всюцу, кроме точек z = О, —1, —2, ... Из A) следует, что
G)
где Q (z) — целая функция. Разлагая е~~ь в степенной ряд и почленно
интегрируя, получаем
(8)
Следовательно, функция Г (z) имеет простые полюсы в точках г — — п (п=.
= 0, 1, 2, ...) с вычетами tl^l [см. 1.17 A1)].
Покажем теперь, что выражения A), B), C) представляют одну и ту же
функцию.
Если п — натуральное число и Re z >> 0, то, почленно интегрируя по
частям, получаем
а поэтому, по теореме Таннери,
Таким образом, A) эквивалентно B). Равенство C) может быть выведено
из равенства B) следующим образом. Из B) вытекает, что
или

и окончательно
Если вещественная часть z отрицательна и п -f-1 >> Re (—z)^>n}
/г = 0,1,2, ..., то функция Г (z) может быть представлена интегралом
Коши — Заальшютца (Уиттекер — Ватсон, 1962, п. 12.21):
1.2. Функциональные уравнения, которым удовлетворяет Г(г)
Интегрируя 1.1 A) по частям, получаем
т. е.
Следовательно, если п — натуральное число, то
Отсюда следует
D)
Так как
мы получаем
Из выражения 1.1 C) следует, что
и, так как
(см. Фихтенгольц, т. II, стр. 379), то
E)

Отсюда следует, что
или
Из E) и B) следует
Из G), B) и C) вытекает
Полагая в равенствах F) и A) z = -^9 получаем
Докажем теперь формулу умножения Гаусса — Лежандра
(И)
Из 1.1 B) следует, что
A2)
где
Так как
то мы получаем
Обозначим правую часть этого равенства через —. Очевидно, что К не за-
висит от z. Поэтому К можно вычислить, положив, например, в равенстве
A3) 2 = —. Таким образом,

или
Перемножая последние два равенства и принимая во внимание F),
получаем
а потому
A4)
Из равенства A3), определяющего К> видно, что АГ>0, а потому из A2),
A3) и A4) следует равенство A1).
Случай т = 2 в равенстве A1) дает формулу Лежандра для удвоения
аргумента Г (z):
A5)
1.3. Выражение некоторых бесконечных произведений
через гамма-функцию
Из 1.1 B) следует, что
и так как Г —] = 1/ я, то
A)

Из формулы 1.1 C) находим
B)
и, следовательно,
C)
Из B) получаем
D)
Формула Меллина
E)
легко доказывается следующим образом. Из 1.7C) следует, что
откуда, в силу равенства B), вытекает искомая формула E).
Положим теперь в формуле удвоения Лежандра 1.2A5) последовательно
z — 2~1v, 2~2 v, ... , 2~п v и перемножим полученные п равенств. После
сокращения мы придем к формуле
Это равенство, в силу 1.2A), эквивалентно равенству
Полагая п-*оо, получаем формулу Кнара
F)
Соотношение
G)

является обобщением хорошо известной формулы 1.2 D). Его легко
проверить, использовав выражение 1.1 C) для каждой гамма-функции, входящей
в правую часть, и заметив, что
Наконец, рассмотрим выражение
где bu b2, #3, ... , bk не являются натуральными числами. Необходимое
условие абсолютной сходимости этого бесконечного произведения состоит
в том, что
Это условие также является достаточным, и если оно выполнено, то,
воспользовавшись соотношениями 1.1C) и 1.2A), получим
(8)
1.4. Некоторые бесконечные ряды, связанные с гамма-функцией
Формула Дуголла
может быть доказана следующим образом.
Ясно, что ряд 5 является суммой вычетов функции
соответствующих полюсам 2 = 0, ±1, ±2, ... функции ctg (nz). Для
больших значений | z | из 1.18D) и 1.2E) следует, что асимптотическое
значение функции

равно za+b~c~d, если — тс < arg .г < тс, и равно
если — тс < arg (— г) < тс.
Рассмотрим на плоскости z последовательность концентрических
окружностей радиусов гп таких, что расстояние каждой из окружностей от
множеств нулей функций sin [тс (z-\- a)], sin [тс (г + Ь)] и sin (%z) превосходит
фиксированное положительное число. На этих окружностях выражение
ограничено, причем верхняя граница не зависит от гп. Следовательно,
интегралы
взятые вдоль этих окружностей, стремятся к нулю, когда гп—>со. Поэтому
сумма всех вычетов функции f(z) равна нулю, и, таким образом, 5 равно
сумме вычетов в полюсах функций T(z-\-a) и Г {г + Ь), взятой с обратным
знаком. Вычет f(z) в полюсе г = — (а-\-т), т = 0, 1, 2, ... , равен
а потому сумма вычетов в полюсах функции Г (г + а), в силу формулы
Гаусса 2.1 A4), равна
Чтобы получить сумму в полюсах функции Г (г + Ь), достаточно в
полученном выражении вместо а написать Ь, а вместо Ь написать а. Ясно, что
сумма двух получившихся выражений равна A).
Формула
B)
легко проверяется путем разложения подынтегрального выражения в
формуле 1.5A) в степенной ряд и почленного интегрирования.
Кроме того, справедливы следующие формулы (доказательство см. в 2.4):
C)

D)
(определение (а)п см. стр. 67).
1.5. Бета-функция
Бета-функция определяется с помощью интеграла
о)
v
Делая подстановку t= у-г-—, получаем выражение
B)
из которого легко следует, что
C)
Отсюда имеем
D)
Умножив обе части равенства
(см. 1.1 D)) на Vх \ проинтегрировав по v от 0 до оо и изменив порядок
интегрирования, получим

откуда
E)
Таким образом, найдено выражение бета-функции через гамма-функцию.
Следующие функциональные уравнения для бета-функции легко выводятся
из равенств D) и E) (см. 1.2):
F)
G)
(8)
n, m — целые положительные. (9)
1.5.1. Определенные интегралы, выражаемые через бета-функцию.
Многие определенные интегралы легко сводятся с помощью
соответствующих подстановок к бета-функциям. Приведем некоторые примеры:
A0)
A1)
A2)
A3)
A4)
A5)

A6)
A7)
A8)
Подставляя вместо переменной интегрирования тригонометрические и
гиперболические функции, получаем интегралы, содержащие эти функции:
A9)
B0)
B1)
B2)
B3)
B4)

B5)
B6)
B7)
B8)
Формула B7) известна как формула Рамануджана.
Формулы A2), A3), A7) и A9) вытекают из A); A1) из B); A0) и B6) из
C); A4), A5), B0) и B1) из A1); A6) и B2) из A2); A8) из A6); B4) из A7);
B3) из B2); B5) из B4); B7) и B8) из B6). Все они получаются путем
несложных подстановок или выбора специальных значений параметров. Очевидно,
что формулы A1), B0) и A2), A6), B1), B2) остаются справедливыми для
всех комплексных значений Ь, если считать, что комплексная плоскость
разрезана по вещественной оси от—1 до — оо или от 0 до — оо соответственно.
С помощью контурного интегрирования можно выразить через гамма-
функцию следующие тригонометрические интегралы. Рассмотрим интеграл
где С — контур, состоящий из верхней полуокружности | г | = 1 и ее
диаметра с вырезами в точках z = 0, ± 1, причем радиус этих вырезов равен е.
Устремляя е к нулю, получаем (см. Nielsen, 1906, стр. 158) следующий
результат:
B9)
Пусть контур С состоит из полуокружности |z| = l, лежащей в правой
полуплоскости, и из отрезка, соединяющего точки z = -\-i, z = — / с
вырезами в точках г = 0, ±: /; если устремить радиусы вырезов к нулю, то,
вычисляя интеграл
получим
C0)
Другие интегралы такого вида приведены в формулах 2.4F)—2.4A0).

Теперь рассмотрим интеграл
где контур С состоит из отрезка вещественной оси от -)-е До + #> ДУги
окружности z = Rei(? от ср = О до ср = р ( — -?-<Р ^тг)» отрезка от г =/?е'Р
до ее'Р и дуги окружности г = sei(? от ср = р до ср = 0. Так как значение
интеграла по этому контуру равно нулю, то полагая е—*0 и У?—*>оо,
получаем
Полагая р = с cos p, ^ = csinp, выводим отсюда
Полагая p-|-^ = s, arctg — = arg s, получаем
и, следовательно, имеет место более общее равенство
C4)
Из C2) следует
C5)
C6)

Если р~>у ис>0, то
C7)
C8)
Далее, получаем
C9)
D0)
1.6. Выражения гамма- и бета-функций в виде
контурных интегралов
Обозначим через интеграл, взятый вдоль контура С, который
начинается в точке С, обходит начало координат против часовой стрелки и
возвращается в исходную точку. При этом предполагается, что все особые точки
подынтегральной функции, кроме ? = 0, лежат вне контура С.
@+)
Рассмотрим интеграл ^ eH~z dt, в котором начальное и конечное значе-
— оо
ния аргумента t равны ссответственно —тс и -|- ъ. Будем считать, что
контур С состоит из нижнего берега разреза, идущего от — оо до — р,
окружности ? = p?'cf>(—л^ср^тг) и верхнего берега разреза от —р до — оо. Мы
получим тогда
где / означает интеграл, взятый вдоль окружности |tf| = p. Так как при
Re г < 1 интеграл / стремится к нулю, когда р стремится к нулю, то,
принимая во внимание 1.1 A), получаем
а)
Отсюда при помощи 1.2F) выводим представление Ганке ля для гамма-
функции
B)

Так кад< обе части этого равенства являются целыми функциями от г, то
равенство справедливо для всех значений г.
Если заменить в равенстве A) г на 1—2, то получим
C)
Равенство C) может быть записано в виде
D)
Точно таким же образом может быть получено более общее выражение,
если рассмотреть контурный интеграл
и воспользоваться равенством 1.5C4). В интеграле в качестве начального и
конечного значений arg t берут соответственно 8 и 2тс + 5. Тогда
E)
Заменив s на 1 — s и использовав 1.2F), получаем равенство
F)
которое справедливо для всех значений s.
Наконец, рассмотрим интеграл
взятый вдоль замкнутого контура, который начинается в точке А
вещественной оси t, лежащей между 0 и 1, и состоит из петли, обходящей точку
t=l в положительном направлении; петли, обходящей ^ = 0 в
положительном направлении; петли, обходящей ^=1 в отрицательном направлении, и
петли, обходящей ? = 0 в отрицательном направлении. При обходе этого
контура, функция f(t) пол)чает в точке Л свое первоначальное значение.
Это значение положительно, и мы считаем, что его аргумент равен нулю.
Первую петлю составим из отрезка прямой от точки Л до точки 1 — р,
малой окружности 11 — 1 | = р и отрезка от 1 — р до Л. Аналогично составим
вторую петлю. Третью и четвертую выберем так, чтобы они отличались от
первой и второй только направлением обхода. Положив р—*0, получим

Следовательно,
G)
Эта формула установлена нами при Rex>0, Re_y>0, где лги у не являются
целыми числами. Но, в силу принципа аналитического продолжения, она
верна при всех х и у, за исключением целых значений. Доказанная формула
была получена Похгаммером.
Проведя аналогичные рассуждения, можно представить функцию В (х, у)
в виде интеграла, взятого вдоль простой петли,
(8)
(9)
1.7. Функция
Через ф (z) обозначают логарифмическую производную Г-функции
A)
Из равенств 1.1B) и 1.1C) получаем представления этой функции:
B)
C)
Функция ф (г) мероморфна и имеет простые полюсы в точках 2 = 0, —1,
-2, ...
Очевидно,
D)
Из равенства 1.3B), в котором взято u = z, #=1, получаем
E)
Из равенств C) и E) находим
F)

Из равенств F) и 1.1A) следует
G)
1.7.1. Функциональные уравнения для <Ь(г). Из равенств 1.2A),
1.2B), 1.2F) и 1.2A1) получаем
(8)
(9)
A0)
(И)
A2)
1.7.2. Интегральные представления для ty(z). Формула
A3)
легко проверяется путем разложения A—г) в ряд, почленного
интегрирования и применения равенства C).
Подстановка t = e~x дает
A4)
Следовательно,
Из A1) получаем формулу для *\>(z), справедливую при Re«<l,
A5)

или
A6)
Интегральная формула Гаусса
A7)
может быть доказана следующим образом. Проинтегрируем равенство
по л: от 1 до п. Мы получим
A8)
Подставляя это выражение в B) и используя соотношение
находим
Первый из интегралов в правой части равенства не зависит от п, а второй
стремится к нулю, когда п—*оо. Тем самым формула A7) доказана.
Полагая в A7) 2=1, получаем интегральную формулу для постоянной
Эйлера
A9)
Полагая ^ = In (I -J- а:) и Ь = In A + А), получаем из A7)
Так как первый из пределов в правой части равен нулю, то получаем

формулу Дирихле
B0)
Таким образом, мы доказали, что
Первый интеграл следует из равенства B0), а второй получается путем
интегрирования выражения t~le~f— ^(l+^T1 вдоль контура,
охватывающего первую четверть круга с центром в начале координат и имеющего
вырез около начала координат.
Из равенств B0) и B1) получаем
Выражения Бине
B2)
B3)
B4)
B5)
легко вытекают из A7) и A8). Более общее выражение
B6)
легко выводится из B5) путем интегрирования выражения
вдоль границы сектора, вырезанного в начале координат, как при выводе
1.5C1).
Из 1.9(9) получаем формулу
B7)

которая также была доказана Бине. Следовательно,
B8)
1.7.3. Теорема Гаусса. Положив в A3) 2 = — , где 0 </?<#, р и q —
целые, и сделав подстановку t = t>9, получаем
Так как
то R(p) может быть разложена в сумму элементарных дробей:
Подставляя это выражение в R(v) и интегрируя, получаем (Bohmer, 1939,
стр. 77)
B9)
Штрих указывает, что в случае, когда q — четное число, последнее
слагаемое в сумме надо умножить на -у. Таким образом, если г является
положительной правильной дробью, то значение ф (г) может быть выражено
как конечная комбинация элементарных функций. С помощью равенства A0)
этот результат может быть распространен на все рациональные значения г.
Эта теорема доказана Гауссом.
1.7.4. Некоторые бесконечные ряды, связанные с функцией
Если положить
то из равенства 1.7(8) следует, что
Таким образом, мы имеем

Следовательно, если а не является целым отрицательным числом, то
разложение функции ф (а -\- z) в ряд факториалов сходится при Re (a + z) > 0 и
имеет вид (Norlund, 1924, стр. 261)
C0)
Функциональное уравнение 1.7A0) полезно для суммирования некоторых
рядов. Мы имеем, например,
C1)
C2)
C3)
1.8. Функция G(z)
Функция G (z) определяется равенством
A)
Из 1.7A3) и 1.7A4) следует, что
B)
C)
Рассмотрим интеграл взятый вдоль контура, который был
использован при выводе 1.5C1). Мы получим с помощью этого интеграла
более общее представление
D)

или
E)
Разложив в равенстве B) функцию (\-\-1) * в ряд и проинтегрировав по
частям, получим
Используя равенства A) и 1.7A), можно получить следующие
функциональные уравнения:
G)
(8)
т— четное, (9)
т — нечетное. A0)
1.9. Выражения для функции In Г (г)
Из 1.7A7) получаем формулу Мальмстена
A)
а из 1.7B5)
B)
Так как (см. Уиттекер—Ватсон, 1962, п. 12,31)
C)

то мы получаем первое выражение Бине для In Г (г)
D)
или более общее выражение (см. 1.5A), а также 1.7B5), 1.7B6))
Из 1.2F) получаем
и, следовательно,
Складывая A) и F), получаем
Так как
то из первого выражения Бине D) легко следует, что
(8)
Наконец, выведем второе выражение Бине для In Г (г)
(9)
Из 1.7C) следует, что

Применим теперь формулу суммирования Плана (Lindelof, 1905, стр. 61)
Эта формула справедлива, если
1) Функция /(С) регулярна при ReC^O, ^ = z-\-it.
2) Равенство =0 выполняется равномерно при Ог<т;<оо.
3)
Полагая в равенстве A1) получаем
A2)
Дважды интегрируя от 1 до г, получаем
A3)
где А и В — постоянные интегрирования. Чтобы определить их, заметим, что
Ot при лг^О, а потому при положительных z имеем
Выражение в правой части стремится к нулю, если z —«-со по
положительной полуоси, поэтому, в силу оценки (8), получаем А = 0, В = -~- In Bтг).
Этим доказано равенство (9).
1.9.1. Ряды Куммера для In Г (г). Функция In Г (г), 0<л:<1 может
быть разложена в ряд Фурье. Мы используем известные разложения Фурье
(Bromwich), 1947, стр. 356, 393 и 370 соответственно):

Подставим эти разложения в равенство G), положив в немг = л:. Мы
получим
В силу равенств 1.7B1) и 1.7A8), этот интеграл равен Bтгя)~1 [7 + In Bтш)],
поскольку для третьего слагаемого имеем
Таким образом мы доказали, что
A4)
Этот ряд называется рядом Куммера.
Аналогичное представление для ф (х) дано Лерхом (Nielsen, 1906, стр. 204)
A5)
Из A4) вытекают интегральные формулы
A7)
A8)
Далее, имеем
A9)
Эта формула может быть доказана след) ющим образом.

Из формулы умножения 1.2A1) следует
Если устремить в этом выражении т к оо, заменить Г (тх) асимптотическим
выражением 1.18A) и заметить, что
то получим A9).
Заменяя в равенстве A9) х соответственно на лг+1, х-j-2, x-f-3, ... э
х-\-п—1 и складывая полученные равенства, приходим к более общему
соотношению
B0)
1.10. Обобщенная дзета-функция
Обобщенная дзета-функция определяется при Re s >> 1 равенством
Она удовлетворяет функциональному уравнению
B)
Так как при Res>0 и Ret;>0 из 1.1E) следует, что
то
C)
Рассмотрим интеграл

взятый вдоль контура кругового сектора, вырезанного в начале координат
(см. 1.5A)). Мы получим более общее представление
D)
Используя обозначения п. 1.6, можно переписать равенство C) в виде
контурного интеграла
E)
Этот интеграл дает представление для ? (s, v\ справедливое во всей
плоскости s, за исключением точек s = 1, 2, 3, ... Из этой формулы может быть
получено разложение Гурвица функции
С (s, v) в ряд. Рассмотрим интеграл
взятый вдоль замкнутого контура,
изображенного на рис. 1. Этот контур
начинается в точке t — {2N-\-\)K и состоит
из окружности К и петли L. При этом
радиус окружности равняется BN-\-\) n
(N—целое), а петля L не охватывает то-
чек t= ±. 2nit нь 4тг/, ±: бтг/, ... В
области, ограниченной контуром С,
подынтегральная функция E) аналитична и
однозначна, за исключением точек ±; 2nit ± 4nif
... , ±2Nni} в которых она имеет
простые полюсы. В силу теоремы о вычетах,
где R к R'n являются вычетами подынтегральной функции соответственно
в точках 2пш и —2#тг/:
Если Re s <0 и 0 <г;^ 1, то интеграл вдоль Af, стремится к нулю, когда
N—*co. Поэтому, в силу F), получаем формулу Гурвица
F)

Наконец, полагая в формуле суммирования Плана 1.9A1) f(y)=s(y -\- v)~s,
получаем
G)
Это — представление Эрмита для С (s, v).
Из равенства G) видно, что функция С (s, v) имеет только одну особую
точку (простой полюс с вычетом 1) в конечной части плоскости s.
Следовательно (см. 1.7B7)),
(8)
(9)
Продифференцировав G) по s, положив затем s = 0 и применив 1.9(9),
пол>чаем
A0)
В частном случае, когда s = —т (т = 0, 1, 2, ...), имеем
со
где Br(v) — многочлен Бернулли (см. 1.13C)). Чтобы доказать эту формулу,
заметим, что если s — целое число, то подынтегральная функция в равенстве E)
является однозначной функцией от t\ это позволяет применить теорему Коши.
Если s = — т (ш = 0, 1, 2, ...), то пол)чаем
Таким образом, вычет подынтегральной функции в точке ? = 0 равен rV_?J*,
откуда и следует равенство A1).
1.11. Функция
Функция
A)

удовлетворяет уравнению
B)
Поскольку
то из 1.1E) вытекает интегральная формула
C)
Rez;>0H либо \г | ^ 1, 27М, Re s>0, либо 2 = 1, Re s > 1.
Проведем разрез в плоскости z вдоль положительной полуоси от точки
1 до оо. При Re s > 0 и Rez>>0 функция Ф является аналитической функщ ей
от z в разрезанной ^-плоскости.
Другое представление в виде определенного интеграла может быть
получено из определения A) и формулы суммирования Плана 1.9A1)
D)
При 2 = 1 снова получаем формулу Эрмита 1.10G).
Полагая в C) z = e^t получаем формулу Липшица
Функция Ф может быть представлена в виде контурного интеграла
E)
В этой формуле, как и в аналогичном месте п. 1.6, контур не охватывает ни
одной из точек t = \п г ± 2пшу * = 0, 1, 2, ..., в которых подынтегральная
функция в равенстве E) имеет полюсы. Для любого фиксированного s, не
являющегося натуральным числом, равенство E) определяет Ф как
аналитическую функцию от z, регулярную в разрезанной плоскости, а для любого
фиксированного г в разрезанной плоскости Ф является аналитической
функцией от s, регулярной всюду, кроме, быть может, точек s = l, 2, 3, ... (мы
предполагаем, что Ret;>0).

Как и в предыдущем пункте, наша функция может быть разложена в ряд.
Чтобы получить это разложение, рассмотрим интеграл
взятый по контуру С, составленному из окружности /^радиуса BN-\-\)tz
(N—натуральное число) и петли Z,, охватывающей начало координат.
Центром круга в этом случае является точка t = lnz} zz?\y причем все точки
вида t = In г ± 2аш, я = 0, 1, 2, ..., должны лежать вне петли. Устремляя TV
к бесконечности, замечаем, что при Res<0 и 0<г/^1 интеграл по
окружности К стремится к нулю. Следовательно,
rjieRn = z~1(—tn)s~1e~{v~1)tn является вычетом подынтегральной функции
в полюсе t = tn = In г -f- 2аш. Таким образом,
F)
Но
Сравнивая это равенство с равенством A), получаем формулу
преобразования Лерха для функции Ф (z, s, v)
G)
Если в формуле F) воспользоваться биномиальным разложением
то получим

Суммируя по п и используя формулу Гурвица 1.10F), получаем
(8)
Если s — положительное число, s = mf то сначала положим s = m-fe и
пол>чим из 1.17A1) и 1.10(9)
Полагая е —* 0, получаем из равенства (8)
(9)
Штрих означает, что член, для которого п = т — 1, должен быть опущен.
В случае, когда s=l, получаем простое равенство
A0)
Из 1.8F) следует, что
Если s — отрицательное целое число, s = —т (т=\> 2, 3, ...), то,
используя равенства 1.10A1) и (8), получаем выражение для Ф через многочлены
Бернулли
(И)
Наконец, из (8) и A0) выводим
A2)
A3)
Свойства функции
A4)
легко могут быть выведены из равенств A)—A3). Если s = —т (т= 1, 2, 3, ...),

то получаем из A1) и 1.13G)
A5)
где Вт+г+1 — числа Бернулли.
С помощью преобразования Лерха 1.11G) получаем соотношение )Конкье
Наконец, имеем
A7)
A8)
Эти равенства задают аналитическое продолжение ряда A4) в область,
лежащую вне круга сходимости | г | = 1.
Разрежем плоскость г вдоль вещественной оси от 1 до оо и обозначим
через F0(z) главную ветвь F(z) в разрезанной ^-плоскости [0 < arg (z— 1) <
<2тг]. Из формулы A6) следует, что разность между значениями F0(z)
в соответствующих точках верхнего и нижнего берегов разреза имеет вид
A9)
Следовательно, при переходе через разрез из верхней полуплоскости в
нижнюю получаем для продолжения Ft (z) функции Fo (z) формулу
B0)
Аналогичная формула для обратного процесса продолжения имеет вид
B1)
Относительно дальнейших свойств функции F (z, s) см. Truesdell, 1945, стр. 144.
1.11.1. Дилогарифм Эйлера. Дилогарифм Эйлера определяется формулой
которая является частным случаем формулы A4).
Из равенства A8) следует соотношение
B2)
B3)
Обозначим главную ветвь функции L2 (z) через Lf (z) [0 < arg (z — 1) < 2n].
Тогда из равенств A9) и B0) следует, что для любой ветви
Относительно дальнейших свойств см. О. Holder, 1928, стр. 312. Другие
специальные случаи формулы A4) см. Ramanujan, 1927, стр. 40, 336; Rogers,
1905 и Sandham, 1949.

1.12. Дзета-функция Римана
Полагая в формуле 1.10A) г/=1, получаем дзета-функцию Римана
A)
Следовательно,
B)
C)
Таким образом, получаем следующие интегральные представления для
функции ?(s) (см. 1.10C) и 1.11C)):
D)
E)
F)
Из 1.11A) и 1.11C) имеем
G)
(8)
Из равенств 1.10E) и 1.11E) с помощью A), B) и C) вытекают следующие
представления функции С (s) в виде контурных интегралов:
(9)
A0)
A1)

где
Контур в (9) и A1) не содержит ни одной из точек вида t — ± 2пш, а в
формуле A0) — ни одной из точек вида t = Bn—1)тм.
Из A) и 1.10G) получаем
A2)
Следовательно (Lindelof, 1905, стр. 103),
A3)
A4)
A5)
Эти формулы были выведены Иенсеном. Интегралы в формулах A2) и A5)
определяют аналитическую функцию для всех значений s.
Приведем и другие интегральные представления (Bruijn, 1937)
Эти формулы справедливы при 0<Res<l, функция ф(т) определена
в 1.16A). Далее

Докажем, наконец, представление Римана для функции С (s),
A6)
где
и б3 является эллиптической 8-функцией. Интеграл в формуле A6) задает
аналитическую функцию от s при всех значениях s.
Из 1.1E) следует, что
Таким образом,
С помощью преобразования Якоби для тета-функции (Уиттекер и Ватсон,
1962, § 21, 51) выводим, что
Подставив это выражение в интеграл, получаем
и, сделав в первом интеграле подстановку -~ = Г> приходим к формуле A6).
Относительно других интегральных представлений см. Ramanujan, 1927,
стр. 72; Харди, 1949.
Разложение функции С (s) в степенной ряд имеет вид (Hardy, 1912, стр. 215;
Kluyver, 1927, стр. 185)
A7)
где
Положив в формулах 1.10(8)—1.10A1) v = \f получаем
A8)
A9)

и (см. 1.13G))
B0)
или
B1)
B2)
Положив в равенстве Гурвица г>=1, получаем функциональное
уравнение Римана для ?()
B3)
или, в силу 1.2F),
B4)
Введем новую функцию, определив ее равенством
B5)
Из доказанного следует, что она удовлетворяет условию
B6)
Эта функция известна, как ^-функция Римана. Относительно асимптотических
представлений дзета-функции см. Hutchinson, 1925, Titchmarsh, 1935, 1936.
Ряд других результатов имеется в книге Титчмарша, 1947.
Для функции
B7)
подобной дзета-функции, из 1.11A) и 1.11C) следует, что
B8)
Положив в преобразовании Лерха 1.11G) z = —1, г> = -к-, мы получаем
следующее функциональное уравнение для L (s):
B9)
Относительно дальнейших свойств см. Lichtenbaum, 1931, стр. 641.
1.13. Числа и многочлены Бернулли
Числа Бернулли Вп определяются равенством

а многочлены Бернулли Вп(х) — равенством
B)
Так как левая часть равенства B) имеет вид
то, перемножая степенные ряды, пол}чаем
C)
Очевидно, что
D)
Дифференцируя равенство B) по л: и сравнивая коэффициенты при
одинаковых степенях лг, получаем
E)
Из равенства B) следует, что
Следовательно,
и вообще
F)
Отсюда вытекает, что
G)
Так как
то, перемножая степенные ряды, приходим к рекуррентной формуле для
многочленов Бернулли
(8)
Из E) и F) следует

Поэтому
A0)
Из равенства F) получаем теоремы умножения и соотношения симметрии
для Вп(х) (см. Fort, 1948, стр. 32, 34)
(И)
A2)
Многочлены Бернулли могут быть разложены в тригонометрические ряды.
Для Вх (х) из формулы C) находим
A3)
Ряды Фурье для В/г(х) при k > 1 легко получаются с помощью вычетов.
Рассмотрим \f(z) dz, r%ef(z) = z~kexz(ez— I)" (k — натуральное число, k >• 1),
<:
а контур С является (большой) окружностью с радиусом B7V + 1) % (N— целое)
и центром в начале координат. Полюсами подынтегральной функции являются
точки zr=z2izir (r = 0, z±z 1, ±2, ...). Вычеты функции f(z) при г = ±1,
it 2, ... равны Bшг)~ке2™гх. Из равенства B) видно, что вычет при 2 = 0
равен Bk(x)jk\. Если 0^л:-<:1, то интеграл по окружности С при N—*co
стремится к нулю; поэтому, в силу теоремы о вычетах,
Штрих означает, что надо опустить член, соответствующий значению г = 0.
Отсюда вытекают разложения (я=1, 2, 3, ... ; O^x^l)
A4)
A5)
Полагая л; = 0, получаем следующие разложения для чисел Бернулли (см.
также Schwatt, 1932, стр. 143):
A6)
A7)
Равенства D) и (8) позволяют получить рекуррентные формулы для чисел
Бернулли
A8)

Из A8) и C) имеем
A9)
Численные значения для В2п вплоть до В4о и рекуррентные соотношения
можно найти в книге Ramanujan, 1927, стр. 1.
Из A4), A5) и 1.11D) вытекают следующие интегральные представления
для многочленов Бернулли:
B0)
B1)
Используя равенство A6) и 1.12B2), получаем выражения чисел Бернулли
через дзета-функцию Римана 1.12A)
B2)
B3)
Из 1.12D) —1.12(8) получаем интегральные представления для В»п (п=\,
2, 3, ...)
B4)
B5)
B6)
B7)
B8)
Дальнейшие результаты можно найти в книгах Nielsen, 1923 и Ramanujan,
1927, стр. 1.

1.13.1. Многочлены Бернулли высшего порядка. Числа и многочлены
Бернулли порядка т определяются соответственно равенствами
B9)
C0)
Здесь т — натуральное число, <xj ат — любые параметры и
C1)
При т=1 и aj = 1 формулы B9) и C0) сводятся соответственно к A) и B).
Очевидно, что
C2)
C3)
Из B9) и C0) следует
C4)
Введем обозначения
C5)
и
C6)
Можно показать, что
C7)
Таким образом, из C0) следует
C8)
Числа и многочлены Бернулли порядка —т (т = 1, 2, 3,...)
определяются соответственно формулами
C9)
D0)
Оба разложения сходятся во всей плоскости z.

Из C5) и D0) получаем при х==—?
D1)
где
D2)
И в этом случае
D3)
Полное изложение теории чисел и многочленов Бернулли высшего порядка
имеется в книге Norlund, 1922 и 1924, гл. VI.
Случай 04 = а2 = ... = аот= 1 полностью изучен в книге Milne-Thomson,
1933, гл. VI.
1.14. Числа и многочлены Эйлера
Числа Эйлера Еп и многочлены Еп(х) определяются равенствами
0)
B)
Дифференцируя равенство B) по х и приравнивая коэффициенты при zn,
получаем
C)
Если записать левую часть равенства B) в виде
и перемножить степенные ряды, то пол>чим
D)
Если же положить в этой формуле х = — } то
E)
Из B) вытекает

и, следовательно,
Используя тождество
получаем из B) и 1.13 B)
G)
Следовательно, из 1.13A1), 1.13A2) вытекают следующие соотношения:
т — нечетное; (8)
т — четное; (9)
A0)
Из
получаем рекуррентную формулу
или A1)
Точно так же как в 1.13, можно получить разложение многочленов
Эйлера в ряды Фурье. Для этого рассмотрим интеграл 2 С z~k~1exz(ez-\- I) dz,
С
взятый вдоль окружности с центром в начале координат и радиусом 2Nn
(N—целое число). Из равенства B) следует, что вычет подынтегральной
функции в точке 2 = 0 равен k' ^ ' . Отсюда следует, что
A2)
A3)
Из E), A2) и A3) имеем
A4)
A5)

или, используя обозначения 1.12B7),
A6)
Равенство
после перемножения степенных рядов в правой части равенства позволяет
получить рекуррентную формулу для чисел Эйлера
A7)
Применяя A4), находим
Интегральное представление для Е2п получается путем замены LBn-\- 1)
в равенстве A6) выражением 1.12B8)
A8)
Разложения Фурье A2) и A3) могут быть заменены интегральными
выражениями. В результате получаются равенства
A9)
B0)
(Относительно дальнейших результатов см. Nielsen, 1923.)
1.14.1. Многочлены Эйлера высшего порядка. Числа и многочлены
Эйлера определяют при помощи равенств
B1)
B2)
Ряд в формуле B1) сходится при | г | < -^Ы, а ряд в B2) — при
|г|-<;те jot/l, где величина \а{\ определена формулой 1.13C1). В формулах B1)

и B2) т — натуральное число, a alt ... , ат— любые параметры. Частный
случай т = 1, о^ = 1 был рассмотрен в 1.14.
Ясно, что из B1), B2) и 1.13C5) следует
B3)
Числа и многочлены Эйлера порядка —т (т = 1, 2, 3, ...) определяют
при помощи равенств
B4)
B5)
причем оба разложения сходятся во всей плоскости z. Относительно
дальнейших деталей см. Norlund, 1922 и 1924, гл. VI. Случай а1 = а2=...
... = am=l полностью изучен в книге Milne-Thomson, 1933, гл. VI.
1.15. Некоторые интегральные формулы, связанные
с многочленами Эйлера и Бернулли
Из результатов предыдущих двух пунктов могут быть выведены
некоторые интегральные соотношения. Во-первых, равенство 1.13A) может быть
записано в виде
A)
Если заменить здесь В2п по формулам 1.13B4) и 1.13B7), то получим
B)
C)
Если в 1.13B) заменить Вг (х) выражениями 1.13B0) и 1.13B1), а в 1.14B)
заменить Е^х) выражениями 1.14A9) и 1.14B0), то получим
D)

1.16. Полигамма-функция
Определение:
A)
B)
Следующие функциональные уравнения являются следствиями
результатов 1.7.1 и 1.8:
C)
D)
E)
F)
G)
(8)
Имеют место также следующие выражения:
(9)
A0)
Если заменить здесь функции ф(Л) (z) и G{n) (z) их интегральными
представлениями, то получим выражения функций С и Ф в виде определенных
интегралов.

1.17. Некоторые выражения для 1пГA+^)>
G(l+*) и Г(г)
Разложение 1пГA-(-г) по формуле Тейлора имеет вид
A)
ИЛИ
B)
(см. 1.16(9) и 1.12A)).
Полагая 2=1, получаем выражение
для постоянной Эйлера.
Если в равенстве
C)
D)
(см. 1.7C)) воспользоваться разложением
то получим
E)
Аналогично из 1.8F) получаем
F)
где \г |< 1, оA) = 1п2 и при
Составим суммы ФО+^ + ФО—г) и (?A+2) + (?A—г) и запишем
их с помощью E) и (о), принимая во внимание 1.8G), 1.8(8), 1.7A0) и 1.7A1).

Мы получим
G)
(8)
Используя 1.7A), выводим из равенства G)
(9)
Разложив первое слагаемое в правой части по формуле
пол>чаем
A0)
Формулы (9) и A0) справедливы, если | г | < 1.
Наконец, пол}чим выражения для Г (г) и ф (г) в окрестностях точек
z = — m (m = 0, 1, 2, ...). Из 1.2F) имеем
Разлагая =гт] \ в Ряд Тейлора в окрестности точки z = —т и используя
1A z)
1.13C6), пол)чаем
(И)
Аналогично из 1.7A1), 1.13C1) и 1.16(9) находим
A2)
1.18. Асимптотические разложения
Заменим в формуле 1.9E) часть подынтегрального выражения, стоящую
в квадратных скобках, правой частью равенства 1.15A). Поскольку
выполнены условия леммы Ватсона, полученное равенство можно почленно
проинтегрировать. В результате получается следующее асимптотическое разложение

(ряд Стирлинга):
О)
Это равенство эквивалентно
B)
(Формула B) может быть непосредственно пол\чена из контурного интеграла
1.6B) с помощью метода наискорейшего спуска. Этот вывод и оценку
остаточного члена в формулах A) и B) см. в статье Watson, 1920, стр. 1.)
Из равенств A) и B) вытекает ряд асимптотических формул, например,
C)
D)
E)
В связи с формулой C) см. также A2), а в связи с формулой D) см. A3).
В формулах C), D) и E) а и р являются произвольными фиксированными
комплексными числами и — те < arg z < тс. Имеем также
х, у — вещественные. (б)
Из формулы A) вытекает асимптотическое разложение для ф (z)
G)
Подынтегральная функция в 1.10D) может быть представлена в виде
(см. 1.15A))
(8)
Следовательно, из 1.10C) пол>чаем асимптотическое разложение для функции
C(s, v), справедливое для больших | v | и | arg v | < тс:
(9)

Полагая s == лг —{— 1, получаем асимптотическое разложение для ф(л) (г)
(см. формулу 1.16(9)).
Наконец, выведем асимптотическое разложение для In Г (г), пол}ченное
Бине. Представим подынтегральную функцию в первом выражении Бине
1.9D) в виде
(мы заменили функцию ef в числителе левой части равенства ее
разложением в степенной ряд). Так как, в силу 1.10C),
то получаем равенство
A0)
Это и есть формула Бине.
Аналогичное выражение дает формула Бернсайда (Wilton, 1922, стр. 90)
an
Для левых частей равенств C) и D) могут быть получены полные
асимптотические разложения. Они имеют вид
A2)
A3)
Эти разложения выведены Бернсом (Barnes, 1899, стр. 64) и Ван-Энгеном
(Van Engen, 1938) соответственно.
1.19. Интегралы Меллина—*Бернса
Из всех интегралов, для которых подынтегральное выражение содержит
Г-функцию, наиболее важными являются так называемые интегралы
Меллина— Бернса. Эти интегралы были впервые введены Пинчерле в 1888 г.;
Меллин развил их теорию (см. МеШп A910), где даны также ссылки на более

ранние работы). Они были использованы для полного интегрирования
гипергеометрического дифференциального уравнения Е. В. Бернсом (Е. W.
Barnes, 1908), см. также 2.1.3.
Интеграл
A)
является типичным интегралом Меллина — Бернса. Здесь предполагается,
что 7 — вещественное число, все числа Ар Вр Ср Dj положительны и
что путь интегрирования представляет собой параллельную мнимой оси
прямую, некоторые отрезки которой заменены дугами для обхода полюсов
подынтегральной функции. Исследование, изложенное здесь, основано на
работе Диксона и Феррара (Dixon, Ferrar, 1936).
Введем следующие обозначения:
B)
C)
D)
E)
Для исследования сходимости интеграла A) используем асимптотическое
представление гамма-функции 1.18F). Пусть
s = а -\- Н (а, t — вещественное), z = Re1® (R > 0, Ф — вещественное).
Тогда абсолютное значение подынтегральной функции при больших
значениях 111 может быть задано выражением
(в)
Возможны четыре типа сходимости интегралов A).
Первый тип: а > 0. Интеграл абсолютно сходится при | Ф |< -~- и
определяет функцию, аналитическую в секторе | argz | < min {%, -~-J. (Точка z — 0
при этом исключается.)
Второй тип: а = 0, р^О. Тогда интеграл A) расходится при
комплексных значениях z. При z > 0 он абсолютно сходится, если 7 выбрано так, что
G)

При этом существует аналитическая функция от 2, определенная в области
|arg2|<7t и принимающая на положительной полуоси значения,
определяемые равенством A).
Третий тип: а = [3 = 0, Х< — 1. В этом случае условие G) выполняется
при любом значении 7- Интеграл абсолютно сходится при всех
положительных z (но не при комплексных г) и задает непрерывную функцию от z
(О <с z <; оо). В этом случае существуют две аналитические функции: одна
из них регулярна в любой области, содержащейся в | arg z \ < я, | г | > р,
и при 2>р выражается интегралом A); другая регулярна в любой области,
содержащейся в | arg 2 | < те, 0 < | z | < р, и при 0 < г < р выражается
интегралом (I). Эти две функции, вообще говоря, отличны друг от друга.
Четвертый тип'. а = [3 = О, — 1 =^ X < 0. Интеграл сходится (вообще говоря,
условно) при 0<z<p и при г > р, причем существуют две аналитические
функции с теми же свойствами, что и в предыдущем случае. В точке г = р
имеем разрыв, и в этой точке интеграл может не существовать. Однако он
имеет в этой точке главное значение в смысле Коши. Характер разрыва и
главные значения исследованы в работе Диксона и Феррара (Dixon, Ferrar,
1936).
Иногда встречаются кратные интегралы аналогичной структуры.
Примером интеграла типа Меллина — Бернса является (Уиттекер — Ватсон, 1962,
п. 14.52):
(В)
Путь интегрирования выбран так, чтобы полюсы функции Г G— s) Г E— s)
лежали справа, а полюсы функции Г (а -\- s) Г ({J -f- s) — слева от пути
интегрирования. При этом предполагается, что числа а, р, 7, Ь таковы, что ни
один полюс из первого множества не совпадает ни с одним полюсом из
второго множества (дальнейшие примеры можно найти: 2.1A5), п. 7.3.6 и Ra-
manujan, 1927, стр. 216).
1.20. Разложения некоторых тригонометрических функций
в степенные ряды
Из 1.13A) вытекают многочисленные разложения тригонометрических
функций в степенные ряды (см. также аналогичные разложения, полученные
Шваттом (Schwatt, 1932)). Например,
B)

C)
D)
E)
F)
Положим
G)
(8)
Сравнение с D) и E) показывает, что
(9)
A0)
Интегральное представление для коэффициентов C2n-i и D2n может быть
получено из 1.13B4)—1.13B8).
Разложения более общие, чем указанные выше, получаются из
результатов, изложенных в 1.13.1 и 1.14.1 (Norlund, 1922, стр. 196). Приведем два
примера:
(И)
A2)
Оба разложения сходятся при |?|<я. Использовав обозначения,
примененные в 1.13A), получим
A3)

1.21. Некоторые другие разложения и символы
Для Г-функции и связанных с ней функций применяются также
некоторые другие обозначения, а именно (см. 1.2):
факториал П (z) = z\ =Г (г + 1); A)
7 — постоянная Эйлера 1.1D); B)
символ Ганкеля
C)
символ Крампа
D)
символ Похгаммера
E)
биномиальный коэффициент
F)
Числа Бернулли Вп часто определяются с помощью разложения
G)
Из 1.13A) и 1.13A6) следует, что для определенных таким образом чисел
Вп имеем
(8)
и, следовательно,
(9)
Многочлены Бернулли часто обозначают через Фп(х) и определяют
равенством
A0)
Переход к нашим обозначениям 1.13B) осуществляется по формуле

и, следовательно, в силу 1.13C),
A2)
Если определить числа Эйлера Еп равенством
A3)
то очевидно, что из 1.14A) и 1.14A4) следует
A4)

ГЛАВА 2
ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ
ЧАСТЬ ПЕРВАЯ. ТЕОРИЯ
2.1. Гипергеометрический ряд
2.1.1. Гипергеометрическое уравнение. Если однородное линейное
дифференциальное уравнение второго порядка имеет не более трех особых точек,
можно, не теряя общности, считать, что ими являются точки 0, со, 1. Если
все эти особые точки «правильны» (см. Уиттекер и Ватсон, 1961, п. 10.3), то
уравнение может быть приведено к виду (см. Уиттекер и Ватсон, 1961,
п. 10.72)
О)
где я, Ь, с не зависят от г. Это уравнение называют гипергеометрическим,
Будем называть я, Ъ, с параметрами уравнения; они могут быть любыми
комплексными числами.
Положим
иными словами,
Если сфО, —1, —2, ..., то выражение
B)
является решением дифференциального уравнения A), регулярным в точке
2 = 0.
Если с == — /г, где п = 0, 1,2,..., то
C)

Функцию 2^i (aJ Ь\ с; г) называют гипергеометрическим рядом от
переменной z с параметрами а, Ъ, с. Индексы в 2FX обычно опускают, если нет
опасности смешать эту функцию с другими типами обобщенных
гипергеометрических рядов (см. гл. 4, 5).
Определим дополнительно гипергеометрический ряд в случае с== — т
(т = 0, 1, 2, ... ), когда разложение B) теряет смысл.
Если а = — п или Ь = — п, где п = О, 1, 2, ..., причем с = — т, где т = я,
п-j-l, п + 2, ..., то положим
D)
Функции C) и D) являются решениями уравнения A). Таким образом,
если —а или —Ь — неотрицательные целые числа, гипергеометрическое
уравнение имеет решение, являющееся многочленом от z (когда а = —т
или Ь = — т и с = — я, где п = 0, 1, 2, ... и т = п + 1, п + 2, ..., то ряд C)
обрывается).
Если a u b отличны от 0, —1, —2, ..., то гипергеометрический ряд B)
(или C) в случае с = — п) абсолютно сходится для всех значений, лежащих
внутри круга | z \ < 1. Так как из 1.18D) следует, что
E)
то, применяя признак Раабе (см. Фихтенгольц, т. II, стр. 275), получаем для
гипергеометрического ряда следующий результат:
абсолютно сходится
условно сходится
расходится
при
при
при
г
z
z
= 1,
если Re(a
?1, если O^Re
если 1 ^ Re
_|_ & — с) < 0,
4 {а -\-Ь — с) < 1,
j (a -f- ^ — с).
2.1.2. Элементарные соотношения. Из определения B) вытекает, что
F(a, Ь\ с; z) = F(b, а; с; z).
Шесть функций
F(a± 1, Ь\ с; z\ F(a, b ± 1; с; z), F(a, b;c+\; z)
называются смежными с функцией F(a, b\ с; z). Между F(a, b\ c; z) и
любыми двумя смежными с ней функциями существует линейная зависимость,
коэффициенты которой являются линейными функциями от z. Существуют
15 соотношений этого типа, которые были найдены впервые Гауссом.
Полную таблицу этих соотношений см. 2.8C1)—2.8D5). Одно из них таково:
cF(a,b—\; с; г) + (a — b)z F (a, b;c + \; z) = cF(a~\, b; с; z). (б)
Чтобы проверить соотношение F), разложим обе части его в степенные

ряды. Коэффициент при zn в левой части имеет вид
что и доказывает равенство F).
Если /, т, п — целые числа, то функция
F {а + U Ь + го; с + п; г)
может быть выражена путем повторного применения соотношений Гаусса
как линейная комбинация функции F (а, Ь\ с; г) и одной из смежных функций
с коэффициентами, являющимися рациональными функциями от я, Ъ, с, z.
Разумеется, мы должны считать, что с и с-{-п отличны от 0, —1, —2,...
Функции F(a, Ь\ с\ z) и F{а -\- /, Ь -j- m, с -\- п; z) называют ассоциированными
рядами. Можно показать, что если значения третьего параметра отличны
от 0, —1, —2, ..., то любые три ассоциированных ряда связаны линейной
однородной зависимостью, коэффициенты которой являются многочленами
(Poole, 1936, стр. 91).
Имеют место следующие соотношения:
G)
(9)
Соотношение (9) выведено Якоби (Jacobi, 1859). Полный список подобных
формул см. 2.8B0) —2.8B7). Чтобы доказать (8) и (9), введем операторы
Мы имеем
и так как для любой аналитической функции
(см. Poole, 1936, стр. 93), то равенство (8) доказано.
Чтобы получить (9), запишем равенство A) в виде
D[z(\—z) MDu] = abMu,
где M = zc~1(\—z)a+b~c. Из равенства G) следует, что Dn~1F(a1 b; с; z)
удовлетворяет гипергеометрическому уравнению, в котором а, Ь и с
заменены на а-\-п—1, Ъ-\-п—1, с-\-п—1. Отсюда получаем рекуррентную
формулу
D [zn A — z)nMDnF] = (a + п — 1) (Ъ + п — 1) [г A - z)]n -1
и, следовательно,
— z)n MDnF\ = (а)п (b)n MF.

Применяя снова G) и предполагая, что F не является многочленом степени,
меньшей чем я, то есть что (а)п(Ь)пф0, получаем (9).
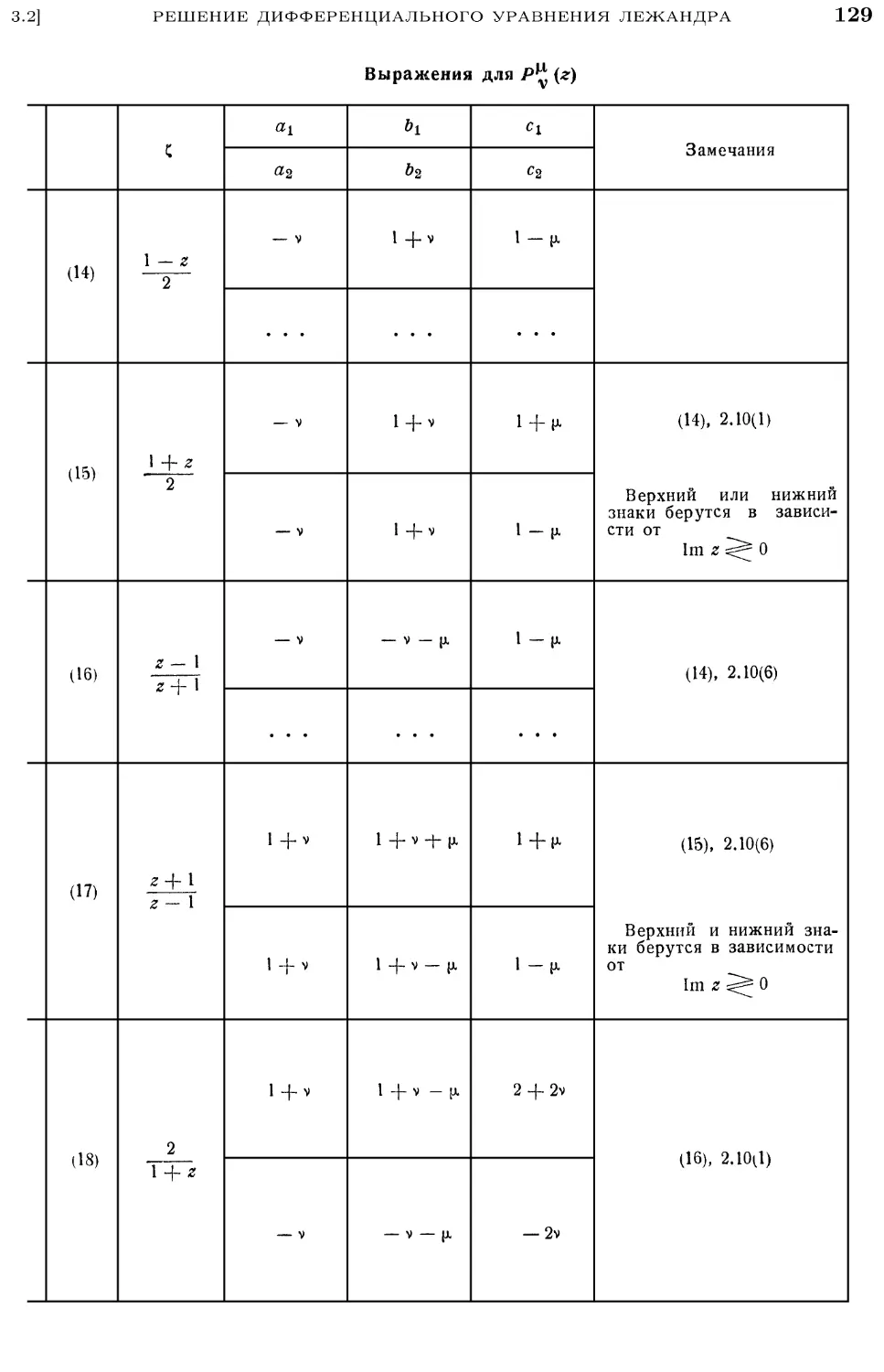
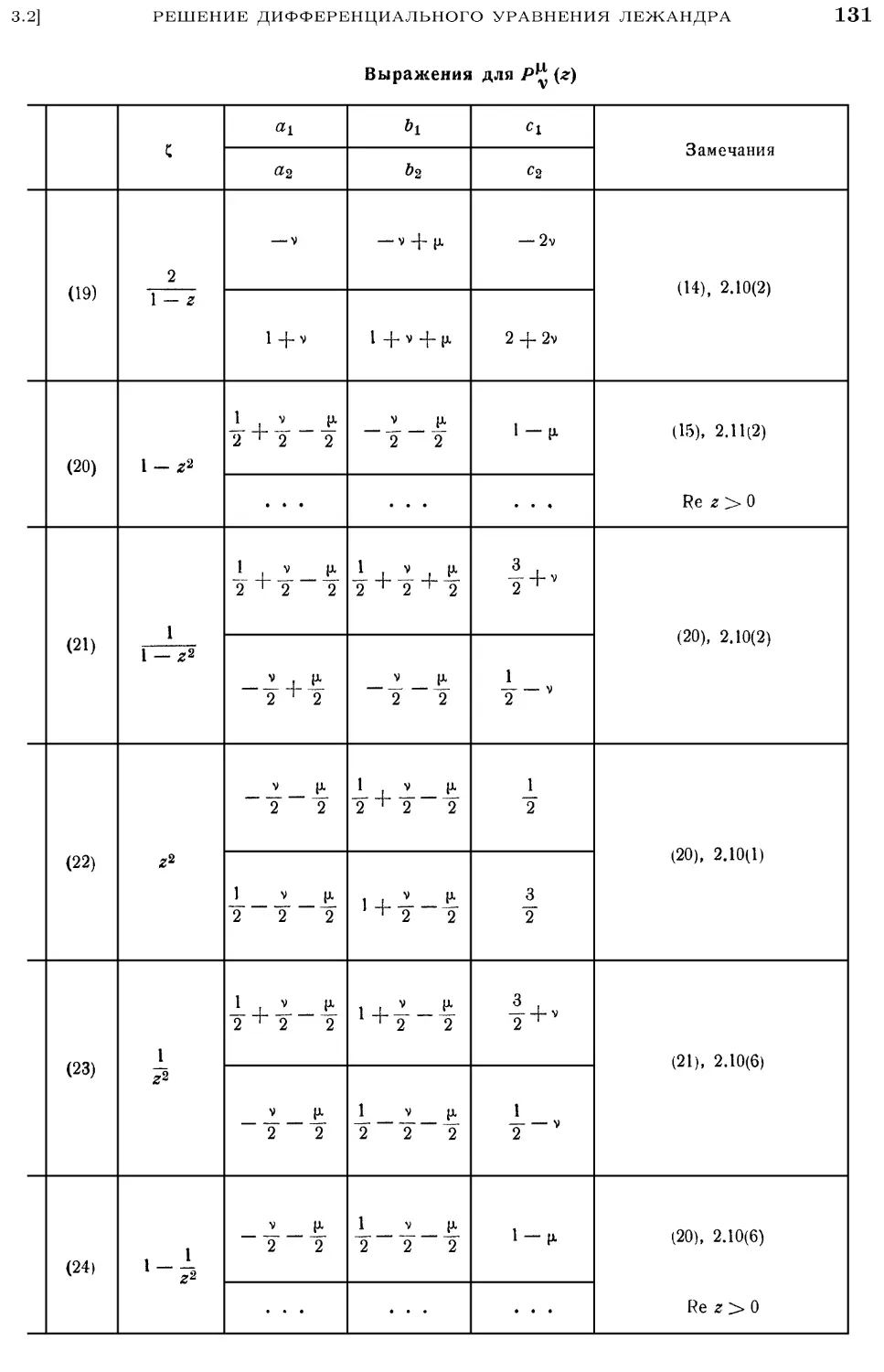
Общая теория уравнения Римана (см. 2.6.1 и Poole, 1936) показывает,
что вообще должно быть 24 решения уравнения A), имеющих вид
zP(l — z)° F{a\ b", с", г'),
где р, а, а\ Ь\ с' являются линейными функциями от а, Ь, с а г и zf связаны
дробно-линейным преобразованием. Полный список этих 24 соотношений
(которые были выведены Куммером) см. Goursat, 1881, и формулы 2.9A) —
2.9B4). Любые три из этих решений связаны линейной зависимостью с
постоянными коэффициентами. Формулы зависимостей см. Goursat, 1881 и
формулы 2.9B5) — 2.9D4). Эти соотношения могут быть использованы для
аналитического продолжения гипергеометрического ряда (доказательство
см. 2.1.4).
2.1.3. Основные интегральные представления. Если Re с > Re b > 0,
то имеет место формула Эйлера
A0)
Правая часть этого равенства является однозначной аналитической функцией
от г в области |arg(l—2)|<тс; таким образом, равенство A0) дает
аналитическое продолжение для F (а, Ь; с; z). Чтобы доказать равенство A0) при
|г|<1, разложим A—tz)~a в биномиальный ряд и почленно
проинтегрируем полученное разложение. Мы получим бета-интегралы, которые могут
быть вычислены с помощью 1.5A) — 1.5E).
Из тождества
(И)
следует, что выражение в правой части равенства A) является решением
дифференциального уравнения A). Полагая s=—t, получаем, что при
Re b > 0, Re (в + 1 —- с) >0 и | arg г \ < п
является решением дифференциального уравнения A). Подстановка s = —-—
приводит этот интеграл к виду
Следовательно,
A2)

также является решением гипергеометрического уравнения. Более того,
любой интеграл вида
является решением уравнения A), если либо контур С замкнут на
римановой поверхности подынтегральной функции, либо концы контура являются
нулями функции tb (\ —t)c~b A —tz)~a~l. Разлагая A —tz)~a в биномиальный
ряд и применяя контурные интегралы 1.6F)—1.6(8) для бета-функции,
получаем
A3)
Во всех случаях мы предполагаем, что путь интегрирования начинается
в точке римановой поверхности для ^"^(l—tH^'1 (\— tz)~af в кот.орой t
вещественно, 0^ t^ 1 и tb, (I—t)c~b — главные значения этих функций,
а A — tz)~a определена так, что A —tz)~a—* 1, когда 2 — 0.
Если положить 2 = 1, то правая часть равенства A0) станет
бета-интегралом, и из 1.5A) и 1.5E) вытекает, что
A4)
Докажем непосредственно, что равенство A4) остается справедливым
при более слабых ограничениях на параметры: достаточно потребовать,
чтобы с ф 0, —1,-2, ... и Re (с — а— #)>0. Из рекуррентной формулы
и замечания к формуле 2.1.1E) вытекает, что при т=1, 2, 3, ... имеют
место равенства

при условии, что
Это условие выполняется, так как для Re (с — а — Ь) > 0, в силу E), имеем
при п-+со
и потому
ПрИ 2-Й.
Таким образом, при /я—>оо имеем
что вместе с 1.18D) доказывает равенство A4).
Второй вид интегральных представлений для гипергеометрического ряда
дан Бернсом (Е. W. Barnes, 1908); он построил свою теорию
гипергеометрической функции на основе представления
A5)
где |arg(—2)|<я, а путь интегрирования имеет, если это необходимо,
такие изгибы, чтобы он отделял полюсы подынтегральной функции в точках
s = 0, 1, 2, ... от полюсов в точках s = — а — п, s = — Ь — п (п = 0, 1,2,...).
Такой путь интегрирования всегда может быть найден при условии, что как
а, так и Ь отличны от 0, —1, —2, ... Если определить
при с = — п (я = 0, 1, 2, ...) как
A6)
то равенство A5) сохраняет силу и при этих значениях с.
Для того чтобы доказать равенство A5), достаточно заметить, что при
| z | •< 1 интеграл в правой части можно вычислить с помощью вычетов и
представить его как сумму вычетов подынтегральной функции в полюсах
s = 0, 1, 2, ... (поведение подынтегральной функции на бесконечности легко
следует из асимптотических формул 1.18).
2.1.4. Аналитическое продолжение гипергеометрического ряда.
Интегралы в формулах A0), A3), A5) определяют аналитическую функцию от z,
которая однозначна в области | arg (—г)\<.щ то есть во всей ^-плоскости,
за исключением точек положительной полуоси. Эти интегралы могут служить
для аналитического продолжения функции F (а, Ь; с; z) в область | arg (— z) \ <ж
Для обозначения аналитического продолжения F (а, Ь\ с; г) будем
использовать снова F(af Ь\ с; z). Только теперь этот символ обозначает ветвь
(главную ветвь) аналитической функции, порожденной гипергеометрическим рядом.

Исключим полиномиальный случай, когда а или Ь равны 0, —1, —2 ...,
и определим при с = 0, — 1, —2, ... — т/\'— с помощью формулы A6).
Вычислим интеграл, стоящий в правой части равенства A5) как сумму
вычетов подынтегральной функции в полюсах s — — а — /, s = — b-^ k, где
k, / = 0, 1, 2, ... Сначала рассмотрим случай, когда а — Ъ не является целым
числом, а потому порядок полюсов равен единице. ]Мы получим
A7)
где а — Ь не является целым числом и где | arg (—г)\<с.ъ.
Если Ь = а-\- т> где т = 0, 1, 2, ... , то подынтегральная функция A5)
имеет простые полюсы в точках s = — а — /г(& = 0, 1, ... , т—1) (и не
имеет, вообще говоря, простых полюсов, если т = 0); в точках s = —а—т~1
(/ = 0, 1, 2, ...) она имеет полюсы второго порядка, и потому
A8)
Сумма в соотношении A8) при т = 0 считается равной нулю. Если
с = а-\- т + U где / = 0, 1, 2, ... , то формула A8) становится справедливой
лишь после предельного перехода, в результате чего получаем
A9)

Здесь
при / = 0 или /я = 0 полагают равными нулю и
Если с — а или с — Ъ являются отрицательными целыми числами, то
F(a, Ь\ с; г) является элементарной функцией от z. В частности, имеем
B0)
где гипергеометрический ряд в правой части является многочленом, если
/ = 0, 1, 2, ... Для того чтобы доказать формулу B0), заметим, что при
подстановках
B1)
интегралы Эйлера A0) или A2) преобразуются в интегралы того же самого
вида. Отсюда получаем
B2)
B3)
< 1; так как правая
Соотношение B2) справедливо, если | г | < 1 и
часть равенства B2) определена при Re2<-H-, то это равенство можно
использовать для аналитического продолжения F(af b; с; z) в полуплоскость
Re z<z~2' Равенство B3) справедливо лишь при | z | < 1 и если а, Ь, с — а
или с — Ь не являются неположительными целыми числами.
Из равенств A7) — B3) и комбинаций этих формул (см. п. 2.9 и 2.10)
можно получить полное аналитическое продолжение для F(a, b; с; г)
в область |arg(l—z) \ < тс. Отсюда следует, что в любой точке z = zOf
кроме точек z0 = exp ( ± — J, функция F(a, b; c; z) может быть вычислена
с помощью ряда, который сходится с быстротой геометрической прогрессии.
При z0 = exp (± ~) ряды A7) — B3) сходятся либо условно, либо так, как
ряды 2 znn~R, где k > 1 — постоянная.
2.1.5. Квадратичные и кубичные преобразования. Равенства A7) — B3)
можно рассматривать как линейные преобразования F(ay b; с; г). Если а, Ъ,с
не удовлетворяют дополнительным условиям, то не существует
преобразований высшего поряцка, то есть преобразований, при которых переменные
были бы связаны нелинейными соотношениями.
Квадратичные преобразования существуют тогда и только тогда, когда
либо одно из чисел
dt(l-c), ±(a — b), +(a + b — c)

FaBHO Vs» либо два из них равны друг другу. Основные формулы даны
ауссом и Куммером:
B4)
B5)
B6)
B7)
В формуле B6) выбрана ветвь функции "J/1 —г , принимающая
положительные значения, если z— вещественное число и z <c 1. Следствием равенств
B7) и 2.10A) является
B8)
Ряцы в обеих частях равенств B4) — B8) сходятся в некоторой окрестности
точки 2 = 0. Каждая формула справедлива в наибольшей связной области,
содержащей точку 2 = 0, в которой ряды, входящие в эту формулу, сходятся.
Например, формула B7) справедлива, когда | z | < у (j/2"—1), но не имеет
места, если г(Чу, 1), хотя обе части равенства B7) имеют смысл в этом
случае. С учетом этого ограничения формулы B4) — B8) также могут быть
использованы для аналитического продолжения функции, заданной рядом,
стоящим в одной части равенства, в область, где сходится ряд, стоящий
в другой части равенства. При этом можно воспользоваться линейными
преобразованиями.
Полный список квадратичных преобразований см. Е. Goursat, 1881 и
2.11A)—2.11C6).
Квадратичные преобразования являются следствиями общей теории Р-урав-
нений Римана (см. Poole, 1936, и 2.6B)). Мы докажем формулы B4)—B8),
показав, что обе части этих формул удовлетворяют гипергеометрическому
уравнению. Например, легко показать, что F[at b\ # + #+тг; 4z(l— г)\

удовлетворяет уравнению A), если принять в нем за значения параметров
числа 2а, 2Ь и а-\-b -\--^. Далее, ясно, что при 2 = 0 обе части
равенства B7), равно как и их первые производные, принимают одинаковые
значения. Но из 2.2B) и 2.3A) следует, что если с отлично от 0, —1, —2, ...,
то уравнение A) имеет единственное решение, однозначное и регулярное
в окрестности точки z = 0. Поэтому обе части равенства B7) должны
совпадать, за исключением, быть может, случая, когда а -\- Ь-\- -у = 0, —1, —2, ...
Применяя линейные преобразования к равенству B7), получаем
остальные формулы B4)—B8). Существует также прямое доказательство этих
преобразований. Например, для того чтобы доказать равенство B5), мы можем
поступить следующим образом (см. Bailey, 1935): запишем равенство B3) в виде
A— z)a+b-cF(a; Ь\ с; z) = F(c — a, c — b; с; z), B9)
разложим обе части равенства в ряды по степеням г и сравним
коэффициенты при zn. Получим
и, следовательно,
C0)
Эта формула называется формулой Заальшютца. Так как правая часть
равенства B5) имеет вид
то коэффициент при zn равен
В силу соотношений
C1)
и формулы Заальшютца C0), это выражение можно записать в виде
Тем самым равенство B5) доказано.

Применяя B2) к правой части равенства B5), получаем
Если вместо г ввести новое переменное , то получим соотношение,
эквивалентное B6).
Прежде чем доказывать B4), убедимся, что
C2)
Это равенство эквивалентно равенству
C3)
что можно проверить путем замены переменной 2 на .Из B6)
следует, что правая часть равенства C2) равна
и, следовательно, B4) вытекает из B6) и C2). Чтобы доказать C2),
применим равенство A0), из которого следует, что
C4)
Поскольку интеграл в правой части равенства остается неизменным, если
подставить —г вместо z и 1—t вместо t, то он является четной функцией
от г. Поэтому подстановка 1—2? = cos0 преобразует правую часть
равенства C4) в
Разлагая выражение в квадратных скобках в ряд по степеням cos 0 и
вычисляя получающиеся бета-интегралы по формуле 1.5A9), получаем
В силу

находим, что это выражение равно
Применяя формулу удвоения Г-функции к выражению, стоящему за знаком
суммы, убеждаемся, что получившееся выражение совпадает с правой частью
равенства C2).
Если два из параметров гипергеометрической функции могут принимать
любые значения, то возможны лишь линейные и квадратичные
преобразования.
Кубические преобразования гипергеометрического уравнения существуют,
либо если
1 — с = ± (а — Ь) = ± (с — а — Ь\
либо если два из чисел
±A—с), ±(а — Ь), ±(с — а — Ь)
равны третьему из этих чисел.
Доказательства основных результатов, которые будут приведены в 2.11,
см. Е. Goursat, 1881 и G. N. Watson, 1909.
Существуют преобразования четвертой и шестой степеней, при которых
один из трех параметров может принимать любое значение (см. Goursat, 1881
и п. 2.11). Преобразования других степеней существуют лишь тогда, когда
a, b и с являются некоторыми рациональными числами. В этих случаях
решения гипергеометрического уравнения являются алгебраическими
функциями (см. 2.7.2 и Goursat, 1938).
2.1.6. F(a, b; с; z) как функция параметров. Во многих случаях
удобнее доказывать те или иные соотношения (например, формулы для линейных
преобразований) для гипергеометрических рядов при некоторых
ограничениях (например, неравенствах) на параметры; так, формулу B2) легче
вывести из формулы A0) при условии Re с> Re #> 0, чем применить для
вывода этой формулы равенство A3), не накладывающее каких-либо
ограничений на параметры. В этой связи весьма удобен метод аналитического
продолжения по параметрам.
Нетрудно проверить, что если z0 фиксировано, причем | z0| < 1, то
функция • р / ч'— является целой аналитической функцией от а, Ь и с. В
самом деле, в этом случае гипергеометрический ряд равномерно сходится
в любой конечной области (комплексного) пространства изменения
параметров а, Ь, с. Из B2) следует, что это же утверждение справедливо для всех
20 таких, что Re20<-2~.
Приведем выражения гипергеометрической функции при некоторых
частных значениях г:

Другие формулы см. 2.8D6) — 2.8E6). Многие из результатов этого типа
могут быть получены из формул преобразования гипергеометрических рядов
путем прямого вычисления интегральных представлений или из разложения
на простейшие дроби. Известны некоторые случаи, когда требуются более
сложные доказательства, например для формулы
Относительно этого и более общих результатов см. Mitra, 1943.
2.2. Вырожденный случай гипергеометрического уравнения
2.2.1. Частное решение. Вообще точки 2 = 0, оо, 1 являются точками
ветвления решений гипергеометрического уравнения 2.1A). Возьмем
некоторое решение u^z) уравнения 2.1A), разложим его по степеням г — 20 и
продолжим аналитически их вдоль замкнутой кривой, которая обходит хотя бы
одну из точек ветвления 0, 1 и возвращается в точку 20. Мы получим
тогда решение вида и = А^ -(- Х2и2, где At и Х2 — постоянные, а их и и2 —
линейно независимые решения уравнения 2.1A). Вообще говоря, Х2 отлично
от нуля, а потому все решения уравнения 2.1A) могут быть получены из
какого-либо одного путем аналитического продолжения. Но может случиться,
что для любого контура L выполняется равенство А2 = 0. В этом случае
говорят о вырожденном случае и называют решение ии обладающее этим
свойством, вырожденным решением.
Если при обходе точки 2 = 0 или 2 = 1 соответственно по петлям Ц+}
или Z,(j"} (в положительном направлении) решение их умножается
соответственно на e2%i? или e27ti(S, то функция
является однозначной функцией от 2, регулярной при всех конечных
значениях 2, за исключением, быть может, точек 2 = 0 и 2=1, в которых м*
может иметь полюс. В соответствии с общей теорией уравнений Фукса (см.
Poole, 1936) ии а следовательно и и*, не может иметь существенной
особенности в точке 2 = оо. Следовательно, и* должно быть рациональной
функцией, которая может иметь полюсы лишь в точках 2 = 0, оо, 1; таким
образом, в вырожденном случае щ имеет вид
где рп(г) — многочлен степени п такой, что рп@) ^0 и рп(\)-?0.
Из общей теории Р-уравнений Римана следует (см. Winston, 1895 и
п. 2.7.1), что уравнение 2.1A) имеет решение вида A) тогда и только тогда,
когда одно из чисел
а, Ь, с — а, с — Ь B)
является целым. Это условие эквивалентно тому, что по крайней мере одно
из восьми чисел ±, (с — 1) ± (а — b) + (a-\-b — с) является нечетным целым,

Если ровно одно из четырех чисел
±2, ..., то одна из двух функций
B) является целым и
±: 1,
C)
имеет вид A), поскольку тогда один из четырех рядов C) обрывается.
2.2.2. Полное решение в вырожденном случае. Мы укажем два линейно
независимых решения гипергеометрического уравнения в вырожденном
случае. Эти решения могут быть выражены через 24 ряда Куммера (см. 2.9A)—
2.9B4)). Чтобы получить также аналитическое продолжение этих решений
в область | arg (— z) | <C я, мы используем формулу
где F(\, 1; 2; z) =— 2~ЧпA—z). Полезно заметить, что если с = а, то
D)
E)
является решением уравнения 2.1A), причем это выражение может быть
представлено в виде
(б)
Если / <С 2, последняя сумма равна нулю.
Чтобы доказать равенство D), достаточно применить 2.1G) к 2.1(9);
формула F) элементарна.
Выбор двух линейно независимых решений из рядов Куммера зависит от
того, сколько из величин B) являются целыми.
При разборе различных случаев будут применяться следующие
обозначения:
/, т, п обозначают неотрицательные целые числа;
п. i. означает, что величина не является целой;
deg. означает, что решение имеет вид A);
rat. указывает, что решение является рациональной функцией;
In 2.1A9) указывает, что аналитическое продолжение решения может
"быть осуществлено с помощью формулы 2.1A9) и приводит
к логарифму;
щ 2.9A) указывает на один из 24 рядов Куммера и означает,
например, что следует взять первую из шести функций и
использовать выражение 2.9A).

Если решение имеет хотя бы одно аналитическое продолжение,
содержащее логарифмы, то это указывается в таблице на стр. 83—84.
Так как гипергеометрическое уравнение симметрично относительно а и Ь,
можно предположить в этой таблице, что
1) если а или Ь — целое, то целым числом является а;
2) если с — а или с — Ь — целые, то целым числом является с — а;
3) если Ь — а — целое, то Ь — а^>0.
2.3. Полное решение и асимптотическое разложение
в общем случае
2.3.1. Линейно независимые решения гипергеометрического
уравнения в невырожденном случае. Предположим теперь, что ни одно из чисел
а, Ьу с — а, с — Ь не является целым. Тогда два линейно независимых
решения u1(zI u2(z) уравнения 2.1A) могут быть получены из любого не равного
тождественно нулю решения с помощью аналитического продолжения вдоль
пути, обходящего одну из точек 2 = 0, со, 1. Если с не является целым
числом, можно положить
о)
Если а — Ь и с — а — Ь также не являются целыми числами, аналитическое
продолжение решений ut (z), u2 (z) может быть выполнено с помощью
формул 2.10A) — 2.10F). Если а — b — целое число, но с не является целым
числом, то формула 2.1A8) дает аналитическое продолжение решений u1(z) и
u2(z) в окрестности точки 2 = со, а если с — а — Ь — целое число, то при
|?|/ / = 0, 1, 2, ..., имеем
B)
где
и где равно нулю, если / = 0.
Этот результат может быть получен из формулы 2.10A), если положить
с = а-\-Ъ-\-1-\-г и перейти к пределу при г—>0.
Точно так же получаем в этом случае для решения и2
C)

где
и равно нулю, если /==0.
Наконец, если с = а + Ъ — /, где / = 0, 1, 2, ... и с не является целым
числом, то для их {г) имеем
D)
где
и где означает нуль, если / = 0.
Соответствующая формула для и2 получается путем замены а и Ь
соответственно на 1 + / — я, \-\-l — Ь.
Если с — целое число, то можно положить
Ф)
F)
G)
(8)
Аналитическое продолжение решений их (z) и и2 (z) в окрестности точек
2 = 0, z = od или z=\ можно осуществить с помощью формул 2.10A)—
2.10A5), поскольку в настоящем пункте мы предполагаем, что ни одно из
чисел а, Ь, с — а, с — Ь не является целым.
2.3.2. Асимптотические разложения. Поведение решений
гипергеометрического уравнения при больших значениях | z \ полностью описывается
с помощью формул, дающих аналитическое продолжение этих решений
в окрестности точки z = co. За исключением случая, когда а — Ъ — целое
число, каждое решение и (z) может быть представлено в виде
(9)
где Xj и Х2 — постоянные; если же а — Ь — целое число, то z~a или z~b надо
еще умножить на In z.
Поведение функции F(ay Ь\ с; z) при больших значениях | а |, \Ь\, \с\
было исследовано Перроном (О. Perron, 1916—1917) и Ватсоном (G. N.
Watson, 1918).
Если а, Ь и z — фиксированные числа и \с\ — большое число, такое, что
I arg с | ^ п —е» е > 0, то при | z | < 1 имеем
A0)

Если |г|>1, то аналогичное выражение с несколько иным видом
остаточного члена имеет место и при |arg(l — г)|<тс, Re с —* оо. В этом случае,
когда |с|-*оо и Ь фиксировано, то Re с > Re b. При достаточно большом
значении п имеем также Re (b + n) > О- Положим
(И)
и разложим параметры на вещественную и мнимую части: a = a-\-ia't
#==p-|-jp', c = Y + fY- Тогда при 0<c:s, t^l получим оценку
где М зависит от г и означает либо минимум, либо максимум выражения
|l-sto|.
Отсюда следует
Формула 1.18E) позволяет оценить последние три сомножителя, являющиеся
отношениями гамма-функций. В результате получаем
A2)
где [а (я) зависит от п, a, b и от Im z, если Re z > 0. Этим доказано
равенство A0) (где вместо О (| с I"") при достаточно больших значениях п надо
взять | Р/г+1 |).
Но тогда A0), очевидно, верно и при п=\, 2, ..., поскольку каждый
член асимптотического ряда A0) сравним с | ря+1 |. Более общие результаты
см. Т. М. MacRobert, 1923, где равенство A0) доказано для области argo-л;.
Если а, с и z — фиксированные числа, сфЬ, —1, —2, ..., 0 < | г | < 1 и
S
A3)
если \b\—>оо так, что ^ < arg bz < -~-, то
Асимптотическая формула для вырожденной гипергеометрической функции
большого аргумента (см. гл. 6 или Уиттекер—Ватсон, 1962, 17.3) дает
A4)

ft n * Зтс
Аналогично, если ^- <С arg bz <С-^-, то
A5)
Для случая, когда более чем один из параметров стремится к
бесконечности, Г. Н. Ватсон (G. N. Watson, 1918) получил следующие результаты.
Пусть 5 определяется равенством г ± Y*2—1=?±* и пусть
где верхний или нижний знаки берутся в случаях ImzJjO. Тогда для
больших значений I XI
где | arg X | ^ те— Ь, &;>0, а также
A7)
где верхний или нижний знаки берутся в случаях Im^^O и где |Х| —
большое число, ?== ?+ /
Здесь arctgx означает главную ветвь этой функции, то есть

Другие случаи, когда а, Ь, с (или их модули) велики, изучены Лайтхил-
лом (М. J. Lighthill, 1947), Зейфертом (Н. Seifert, 1947) и Черри (Т. М.
Cherry, 1950а, Ь). Случай, когда a = jpv, b = fa, с=1, где р, v вещественны,
причем р фиксировано, a v—*оо, был рассмотрен Зоммерфельдом (Зоммерфельд,
1956).
2.4. Интегралы, выражающие или содержащие
гипергеометрические функции
Интеграл Эйлера 2.1.A0) не может быть преобразован в себя с помощью
элементарных подстановок так, чтобы стало очевидным соотношение
F(a, Ь\ с; z) = F(b, а; с; г).
Однако это соотношение элементарно вытекает из разложения в
гипергеометрический ряд. Виртингер (Wirtinger, 1902) указал тройной интеграл для
функции F, который делает очевидной симметрию относительно а и Ь. С
той же самой целью А. Эрдейи (A. Erdelyi, 1937b) вывел двойной интеграл
A)
который вытекает из формул 2.1A0) и 1.5A1).
Г. Бейтмен (Н. Bateman, 1909) (см. также A. Erdelyi, 1937) доказал, что
B)
Это утверждение может быть получено путем разложения F(a, Ь\ s; xz)
в ряд по степеням xz, почленного интегрирования и применения
формул 1.5A) и 1.5E).
С помощью дробного интегрирования по частям были получены
следующие обобщения интеграла B) (A. Erdelyi, 1939):
C)
Комбинируя интегральные прецставления 2.1A0) и 2.1A5) с линейными и

квадратическими преобразованиями гипергеометрического ряца, получаем
большое число интегральных формул. Исходя, например, из 2.1A5),
заменяя z на —z и применяя формулу преобразования Меллина, получаем
D)
где c^0t — 1, —2, ... и Res<0, Re(tf + s)>0> Re(? + s)>°- Разлагая
правую часть равенства D) в сумму двух интегралов, взятых соответственно
от 0 до 1 и от 1 до оо, применяя 2.1A7) к подынтегральной функции во
втором интеграле и делая подстановки —z и —z вместо z} получаем
где надо взять либо верхние, либо нижние знаки. Если теперь исключить
третий интеграл путем комбинации формул с верхними и нижними знаками,
а
получаем, полагая s = w—-~-,
E)
Первое равенство в E) справедливо, если Re (a -\-b — с) < 1. Второе равен-

ство справедливо, если, кроме того, Re (у it тем >0 и Re A —
Формула принимает особенно простой вид, если с — а=\—Ь.
Имеет место равенство
В частности, если a = v -f-^ + 1, 2{л = лг, 2v=y, то из 1.5A3) (при в=1,
Ь = —1, v = e2iB) следует, что
G)
Для доказательства формулы F) надо сделать в левой части этой формулы
подстановку em = t и применить интегральное представление Эйлера 2.1A0).
При Re jJL >—~-, Rev>—^- из формулы F) вытекает, что
(8)
где положено
В частности, мы имеем при 2{л —т = 0, 1, 2, ... и

Комбинируя квадратичное преобразование 2.1B4) с формулой 2.1A0)
получаем
(9)
Если /г = 0, 1, 2, ..., имеем
A0)
Это может быть доказано следующим образом. Запишем разложение
и разложим правую часть по биному Ньютона
Если перемножить ряды и собрать коэффициенты при е— i(?n} то получим A0).
Имеет место также формула
(И)
Она получается путем разложения подынтегральной функции в
биномиальный ряд и почленного интегрирования. Если | а | > | Ь |, то
соответствующая формула может быть получена при замене а на —а и 6 на —6. Однако
аналитическое продолжение гипергеометрической функции в A1) в область
й
т- >1 не совпадает со значением интеграла, стоящего в правой части
равенства.

2.5. Различные результаты
2.5.1. Производящая функция. Если /г = 0, 1,2,... , то F(—п, а + /г; с; z)
являются многочленами Якоби (см. гл. 10 об ортогональных многочленах).
Для этих многочленов производящей функцией будет
о)
где
и 5—И, когда s—>(). Разложение в левой части равенства A) сходится, если
|s|<l и |1—2z | < 1. В случае Rec>0 можно доказать равенство A)
путем подстановки в интеграле 2.1A0) u = t(\—tz)(\—ty1. Эта
подстановка дает
B)
где
Применяя формулу обращения для преобразования Меллина, получаем
C)
где р — соответственно выбранное вещественное число. Подынтегральная
функция в правой части равенства C) имеет полюсы при
? = — п (/t = 0, 1, 2, ...).
Из результатов п. 2.3 следует, что можно применить теорему о вычетах,
которая и приводит к равенству A) при s = — и. Ограничения, наложенные
на с, могут быть сняты путем аналитического продолжения обеих частей
равенства A) по с.
Равенство C) можно рассматривать как непрерывную линейную
производящую функцию для F(by a — b\ c\ z). Относительно билинейной
производящей функции и многих связанных с этим результатов см. A. Erdelyi, 1941.
Метод, с помощью которого было доказано равенство A), позволяет также
установить, что
2.5.2. Произведения гипергеометрических рядов. Кели, Opp (Ceyley,
Огг, 1899) и Бейли (Bailey, 1935) доказали ряд тождеств, которые были
обобщены Берчнеллом и Ченди (J. L. Burchnall, T. W. Chaundy, 1948).
(Доказательство см. в последней работе.) Результат Кели и Орра заключается в том,

что если
то
D)
Берчнелл и Ченди доказали формулы умножения и удвоения
E)
(б)
G)
Все эти формулы справедливы, если | z | < 1, и если все входящие в них
гипергеометрические ряды имеют смысл, то есть если 2с и с отличны от
о 1 9
и, i, -6, ...
Формулы Берчнелла и Ченди, имеющие вид теорем сложения (см. Burch-
nall, Chaundy, 1940), таковы:

Они справедливы, если [ z |, | С | и либо | z + С — zC |, либо | z + С | меньше 1,
причем сфО, —1, —2, ...
Некоторые билинейные соотношения были доказаны Мейснером (J. Meix-
ner, 1941), например,
(8)
(9)
A0)
Все эти формулы справедливы, если s, z и С таковы, что аргументы всех
четырех гипергеометрических функций, входящих в эти формулы, отличны
от 1 и оо, причем величина \s\ достаточно мала. Если с, -у—*-0, —1,—2,...,
то для получения формулы, имеющей смысл, надо сначала умножить обе
части равенства на [Г (с)]'1 или [Г ft)], или на оба эти выражения, после
чего с или 7, или оба эти выражения устремить к 0, —1, —2, ... В качестве

частного случая полученных формул имеем
A2)
Так как F(a, b\ b\ z) = (l—z)~a, то при c = y = — X одна из этих сумм
конечна. Полагая в формулах (8) и (9) С = 0, получаем
Наконец, если положить С = 0 в формуле A2), получаем A).
Обобщая соотношения Лежандра в теории эллиптических интегралов,
Эллиот (Е. В. Elliot, 1904) доказал
A3)
Если X = fA = v = 0, то из формулы A3) следует соотношение Лежандра.
Этот результат был также обобщен Диксоном (A. L. Dixon, 1905).
2.5.3. Соотношения, содержащие биномиальные коэффициенты и
неполную бета-функцию. Определим зависящий от и многочлен С^ при
помощи равенства
A4)
Тогда имеем

и, в силу 2.1 A4),
A5)
Так как
то имеем также
Комбинируя это равенство с A5), получаем
Равенства A5) и A6) называют «теоремой Лерха».
Положив в формуле 2.1B5) z = — 1 и применив равенство 2.1A4),
получим
Если положить я = — w, где т — целое число, то получим
Точно так же линейные и квадратичные преобразования
гипергеометрического ряда могут быть использованы для того, чтобы вычислить в
замкнутом виде некоторые суммы, содержащие биномиальные коэффициенты. При
этом используются следующие методы:
1) придание специальных значений г,
2) выбор в качестве а или Ь отрицательных целых чисел,
3) сравнение коэффициентов при одной и той же степени z в различных
выражениях для гипергеометрического ряда, например в обеих частях
равенства 2.1 B2) или другого равенства подобного типа.
Например, из равенства 2.1A4) следует, что F(n> —п; 1; 1) =0. Это
может быть записано в вице следующего равенства:
Другим примером является формула Заальшютца 2.1 CQ).

Усеченный биномиальный ряд
можно выразить через два гипергеометрических ряда. Именно
или
Неполная бета-функция- В математической статистике используются
функции
Вх(р> Я) называют неполной бета-функцией. Имеют место формулы
Следующие рекуррентные соотношения вытекают из 2.8C1) — 2.8D5)
(относительно приложений см. Т. A. Bancroft, 1949):
2.5.4. Непрерывные дроби. Гаусс в 1812 г. (см. Gauss, 1876) разложил
отношения некоторых ассоциированных гипергеометрических рядов в
непрерывные дроби. Типичным примером является разложение

где
Если положить # = 0, получим непрерывную дробь для F(a} 1; с; z).
2.5.5. Частные случаи гипергеометрической функции. Во многих
случаях гипергеометрический ряд оказывается разложением некоторой
элементарной функции. В вырожденном случае по крайней мере одно из решений
уравнения 2.1 A) является элементарной функцией. Результаты вида
могут быть получены с помощью квадратичного преобразования 2.1 B4)
путем предельного перехода Ь—*0. Различные другие случаи, когда F (а, Ь; с; z)
является элементарной функцией, указаны в формулах 2.8D) — 2.8A7). Все
эти формулы либо непосредственно проверяются, либо могут быть
выведены с помощью линейных и квадратичных преобразований. Многие классы
специальных функций выражаются через гипергеометрическую функцию.
Эти случаи, а также некоторые другие особые случаи для
гипергеометрической функции, указаны в следующей таблице.
Частные случаи гипергеометрической функции
Параметры а, Ь, с
Два из чисел
1 - с, ±(а - Ъ), ±(с — а — Ь)
равны другому числу или одно из них
равно +; -jr-
—п, п -f 2v; v + -i- (« = 0,1,2,...)
— я, a-f^J 7 (л = 0, 1, 2, ...)
-j , -j , 1 ИЛИ
~ "J' If' [
1 1 1
-r-, — , — или нуль
(/, m, «= 1, 2, 3, . . .)
Отношение двух ре олений 2.1A)
Одно из чисел
а, Ь, с — а, с — b — целое
с — а = 1
Переменное
1-я
2
1 -г
2
Z
Z
Название
Функции
Лежандра
Многочлены
Гегенбауэра
Многочлены
Якоби
Полные
эллиптические интегралы
Обратная авто-
морфная функция
Вырожденный
случай
Неполная
бета-функция
Глава
3
10, 11
10, 11
13
14
2.2
2.5.3

2.6. Уравнение Римана
2.6.1. Редукция гипергеометрического уравнения. Доказательства
теорем этого пункта см. в книгах: Пууль (Е. G. С. Poole, 1936), или Кратцер
и Франц, 1963, или Голубев, 1961. Если однородное дифференциальное
уравнение второго порядка имеет только три особые точки, причем эти особые
точки являются правильными (см. Кратцер и Франц, 1963), то уравнение
может быть записано в виде
A)
Зцесь аП} а'п, zn— постоянные, такие, что 24 = z2i zb = z3, но г^фг^фг^-ф
фг„ и
B)
Особыми точками являются z=zzn (л=1, 2, 3); постоянные ад, ап
называют показателями, соответствующими особой точке г = zn. Мы попускаем
случай, когда одна из особых точек бесконечно удалена, и коэффициенты
du ...
при -г- и и ъ уравнении A) получаются путем соответствующего предель-
ctz
ного перехода.
Уравнение A) называют уравнением Римана. Применяют также название
«уравнение Папперитца».
Постоянные \п = ап — ап называют разностью показателей. Если ни
одна из них не является целой, то уравнение A) имеет два линейно
независимых решения u1(z)i u2(z), которые в окрестности точки z = zn имеют
вид
C)
Здесь vm и v'm могут зависеть от z1} z2, z3, но не зависят от г, причем
v0 ф 0, v'o ф 0. Если оцна или несколько разностей показателей — целые
числа, то один или оба ряда C) содержат логарифмические члены. Ниже
мы сведем уравнение A) к гипергеометрическому уравнению. Поэтому
отсылаем читателя к предыдущим пунктам, где изложены детали
логарифмического случая.
Полное множество решений уравнения A) обозначается символом
D)

Риман показал, что
E)
F)
где
G)
и Л, В, С, D являются произвольными постоянными, такими, что AD — СВ ф О
(см. Б. Риман, 1948). Из равенства E) следует, что решение уравнения A),
умноженное на
также удовлетворяет уравнению Римана. Разумеется, индексы 1, 2, 3 в E)
можно переставлять. Если zn = co) то z— zn в равенстве E) надо заменить
единицей.
Если числа zv z2} zz заданы, то можно найти такие четыре постоянные
Л, В} С, D, удовлетворяющие условию AD — ВСфО, что С17 С2, С3 являются
тремя любыми наперед заданными числами. Таким образом, из равенства (б)
следует, что с помощью дробно-линейного преобразования независимой
переменной можно преобразовать уравнение A) в уравнение Римана,
имеющее особенности в заданных точках Сь С2, С3.
Комбинируя E) и F), получаем
(8)
Гипергеометрическое уравнение 2.1A) является частным случаем уравнения
Римана. Поэтому множество решений гипергеометрического уравнения
может быть записано в виде
Равенство (8) позволяет, таким образом, свести более общее уравнение
Римана к частному случаю 2.1 A). Так как существуют 24 различных способа

преобразования гипергеометрического уравнения в себя, это сведение не
является однозначно определенным. К этому можно прийти также
следующим образом. Гипергеометрическое уравнение выделяется среди всех
уравнений риманова типа тем, что его особенности находятся в точках 0, со, 1,
причем разности показателей в этих точках равны 1 — с, а — Ь, с — а — Ь
соответственно и один из показателей в точках 2 = 0 и 2 = 1 равен нулю.
Шесть возможных перестановок особых точек даются шестью
дробно-линейными преобразованиями
A0)
Умножим решение уравнения Римана с особыми точками 2 = 0, со, 1 на
гРA—z)x. Тогда можно выбрать числа р и т так, чтобы один из
показателей в точках 2 = 0 и 2 = 1 равнялся нулю. Поскольку в каждой из точек
мы можем приравнять нулю оцин из двух показателей, получаем 2-2-6 = 24
преобразовании уравнения 2.1 A) в себя. Это приводит к 24 решениям вида
где 2* — одно из преобразований A0) и я*, Ь*, с* — линейные функции от
а, Ь, с. Эти решения называют рядами Куммера; они даны в формулах
2.9A) — 2.9B4). Эти 24 решения можно разбить на шесть множеств так,
чтобы четыре ряда, принадлежащих каждому множеству, задавали одну и
ту же функцию; шесть получающихся функций, вообще говоря, различны.
Мы будем обозначать их и1} и2, ... , и6.
Любые три из них связаны линейными соотношениями с постоянными
коэффициентами. Возникающие 20 линейных соотношений (справедливых в
полуплоскости Re 2 > 0) указаны в формулах 2.9B5) — 2.9D4).
2.6.2. Квадратичные и кубичные преобразования. Следующие
соотношения вытекают из квадратичных и кубичных преобразований
гипергеометрического ряда:
(И)
где
A2)
где «з + аз = ~5~ и w — ехР (~о" 1 • О^а соотношения были открыты Рима-

ном и исследованы Э. Гурса (Е. Goursat, 1881) (см. также Е. W. Barnes, 1908
и G. N. Watson, 1909).
В некоторых случаях существуют также преобразования высшей степени,
причем все входящие в них постоянные являются рациональными числами.
Относительно этого см. Е. Goursat, 1881, 1938.
2.7. Конформные преобразования
(См. Е. Goursat, 1936, 1938.)
2.7.1. Группа гипергеометрического уравнения. Если ни одна из
разностей показателей 1 — с, b — я, с — а — b не является целой, то формулы
A)
определяют два линейно независимых решения уравнения 2.1 A), которые
однозначны и регулярны в области
1
у. Однако для обоих
решеZ 2
ний по крайней мере одна из трех точек 0, оо и 1 является точкой
ветвления. Рассмотрим, что происходит с решением A), когда z описывает любой
замкнутый контур, начинающийся и оканчивающийся, например, в точке
2 =-у и обходящий одну или несколько точек ветвления. Эту задачу можно
свести к следующей: что происходит при обходе контуров Сш и Сш,
начинающихся и оканчивающихся в точке 2 = — и обходящих один раз в
положительном направлении точки 2 = 0 и 2 = 1 соответственно. Обхоц любой
петли сводится к обходу одной или нескольких петель С@),СA) и С('о„ С|1}, где
штрих означает обход в отрицательном направлении. Из формул 2.9B5) —
2.9D4) легко следует, что их и и2 преобразуются при обходах по контурам
С@) и Сш следующим образом:
B)
C)
где

Доказательство формулы B) очевидно. Для того чтобы доказать
формулу C), будем исходить из формулы (см. 2.10A))
Отсюда следует
Из этих равенств имеем
Здесь
Чтобы закончить доказательства формул C), достаточно повторно применить
основные соотношения для гамма-функции.
Обход по любому замкнутому контуру, начинающемуся и
оканчивающемуся в фиксированной точке, скажем z = -~-} приводит к линейному
преобразованию решений их и и2) множество всех этих преобразований
образует группу гипергеометрического уравнения. Все преобразования группы
могут быть получены путем композиции преобразований, соответствующих
формулам B) и C). Обычно множество дробно-линейных преобразований для
¦ х / ч также называют группой гипергеометрического уравнения. Если с
отлично от 0, ±1, ±2, ..., то B) и C) всегда имеют смысл. Очевидно, что
если хотя бы одно из чисел я, Ь, с — а, с — b — целое, то либо ии либо и2
лишь умножается на постоянный множитель при обходе по любому
замкнутому контуру. Это приводит к вырожденному случаю, который был
исследован в п. 2.2. Если с — целое число, то может оказаться необходимым
модифицировать соотношения B) и C). Для этого можно использовать равенства
2.1A8), 2.1A4), 2.2D), а также 2.10G) —2.10A5). Например, в невырожденном
случае а = Ь = -^, с= 1 все три разности показателей 1 — с, Ь — ау с — a — b

равны нулю. В этом случае можно положить
Тогда получаем
D)
E)
Этот результат может быть выведен из соотношения
F)
получаемого из 2.1A5) с помощью метода, использованного в п. 2.1.4.
Б. Риман показал (см. Poole, 1936), что ассоциированные
гипергеометрические уравнения имеют одну и ту же группу дробно-линейных подстановок.
Отсюда было выведено, что существуют линейные соотношения между любыми
тремя ассоциированными гипергеометрическими рядами, коэффициенты
которых являются рациональными функциями независимой переменной.
2.7.2. Функция Шварца (см. Kampe de Feriet A937), Poole A936)).
Начиная отсюда, будем обозначать разности показателей через
1 — с = Х, b — а = {л, с — а — b = v. G)
Если и является решением гипергеометрического уравнения, то функция
удовлетворяет уравнению
(8)
где
(9)
Определим производную Шварца {w, z} равенством
и положим
где ух и у2— два линейно независимых решения уравнения (8). Тогда имеем
(Ю)

Если С является функцией от 2, то справедливо тождество Кели
(id
Кроме того,
A2)
где Л, В, С, D — такие постоянные, что AD—ВС^О. Следовательно, если
, то
Это показывает, что если w (z) является решением уравнения A0), то
-^—4—r также удовлетворяет этому уравнению. При этом можно доказать,
LiW -\- и
что все решения уравнения A0) имеют вид дробно-линейной комбинации от
w. Следовательно, если известны два линейно независимых решения
уравнения (8), можно найти все решения уравнения A0). С другой стороны, если
w(z) — решение уравнения A0), то w(z) не может быть постоянным, за
исключением случая X2 = {л2 = v2 = 1. Исключим этот случай. Тогда функции
A3)
являются двумя линейно независимыми решениями уравнения (8).
Обозначим через s (ji, v, X; z) полное множество решений уравнения A0)
и назовем s общей функцией Шварца. Частные функции Шварца будут
обозначаться через S (fx, v, X; z). Можно показать, что функция s (X, jx, v; z)
мероморфна в окрестности любой точки, отличной от точек zzfiO, оо, 1, и
что соответствие между whs локально взаимно однозначно. Это вытекает
ds ds~l
из того, что -г- или, если s имеет полюс, ~— отлично от нуля в точках
dz dz
oo, 1. Последнее утверждение следует из равенства
в котором второй сомножитель постоянен.
Рассмотрим частный случай, когда X, jx, v вещественны. Используя
теоремы об ассоциированных гипергеометрических рядах (см. п. 2.1.2 и 2.7.2),
можно показать, что в случае, когда 1-\-т-\-п — четное число, функции
связаны с гипергеометрическими функциями, имеющими одну и ту же группу.
Среди этих функций есть множество, называемое приведенным, для которого
Г. А. Шварц (Н. A. Schwarz, 1873) показал, что приведенная функция
т —5(Х, fx, \>; z) отображает верхнюю полуплоскость Imz^O на
треугольник До т-плоскости, ограниченный тремя дугами окружностей (некоторые из

них могут вырождаться в отрезки прямой). Внутренние углы треугольника Ао
в точках, соответствующих точкам 2 = 0, со, 1., равны Хя, fin, чп.
Из принципа симметрии Шварца следует, что полная система ветвей
функции t = S(X, (jl; v; z) отображает плоскость z на риманову поверхность,
лежащую над т-плоскостью, которая состоит из Ао и всех треугольников,
получаемых из Ао с помощью следующей конструкции. Пусть задана
окружность (или прямая линия как предельный случай окружности). Отобразим
т-плоскость на себя с помощью подстановки
где т' — точка, соответствующая т, и т — комплексно сопряжено с т;
заметим, что для точек окружности т = т'. Назовем это преобразование
инверсией относительно окружности. Выполняя инверсии относительно
окружностей, ограничивающих Ао, получим три новых треугольника At, A2, А3,
которые также ограничены дугами окружностей. Из этих треугольников At,
А2, А3 мы получим новые треугольники, вновь выполняя инверсии
относительно окружностей, которые их ограничивают. Если никакие два из
полученных таким путем треугольников не перекрываются друг с другом, то
функция t = S(X, fx; v; г) имеет однозначную мероморфную обратную
функцию
A4)
которую называют автоморфной функцией. Необходимым условием для
существования функций ср с такими свойствами является то, что X, jx, v
должны быть либо равными нулю, либо обратными величинами к целым числам.
Существуют 15 приведенных множеств значений X, ji, v, при которых
s (X, {л, v; z) — алгебраическая функция. Эти множества были указаны
Г. А. Шварцем (Н. A. Schwarz, 1873). Список Шварца (в котором номер 1
содержит на самом деле бесконечно много случаев) приведен в следующей
таблице. Здесь п, р — неотрицательные целые числа и 2р^п.
Таблица Шварца
1 8
2 9
3 10
4 П
5 12
6 13
7 14
15

В случае 1 (при р = \) обратная функция ср(Х, p., v; т) рациональна. В
частности, можно положить
В случае X={a = v = 0 получаем частный вид автоморфной функции,
положив
Соответствующая обратная функция г (т) обычно обозначается %2 (т) и
называется эллиптической модулярной функцией. Этой функции посвящена
обширная литература. См. гл. 14, а также Klein, Fricke, 1890, 1892; об общих
автоморфных функциях см. Fricke, Klein, 1897. Явное выражение для %2 (т)
/ft \4
имеет вид %2(т) = ЙМ , где
являются регулярными функциями от т тогда и только тогда, когда Im т > 0
(см. Уиттекер и Ватсон, 1962, п. 21.7, 22.3).
2.7.3. Униформизация. Введем вместо переменной г переменную т по
формуле
(см. 2.7.2). Тогда F (а, Ь; с; г) станет однозначной функцией от г-, которая
определена и регулярна в полуплоскости 1тт>0. Виртингер (Wirtinger,
1902, 1903) доказал формулу
A5)
где
Функции 8; (и, т)(/=1, 2, 3, 4) являются четырьмя тета-функциями Якоби
(см. гл. 13). Если не выполнены условия Re c> Re Ь > 0 (см. 2.1.3), то
интеграл в A5) надо заменить контурным интегралом.
2.7.4. Нули. Пусть и (а, Ь\ с; г) — однозначная ветвь решения уравнения
2.1A), которая определена в полуплоскости 2^0 с возможным исключением

точек 0, оо, 1. Тогда, если А — заданная постоянная, то уравнение
имеет лишь конечное число решений относительно z. Это вытекает из того,
что решения уравнения 2.1A) могут быть разложены в окрестности особых
точек 0, со, 1 в соответствии с формулами 2.10A) — 2.10E). Отсюда следует,
что поведение и в окрестности этих точек определяется лишь членом вида
или
где го = О, со, 1, причем г — z0 заменяется на я, если 20 = со. Это озна-
и
чает, что отношение — стремится к конечному пределу, отличному от нуля,
vo
если z—*z0. Следовательно, A6) имеет лишь конечное число решений в
достаточно малой окрестности 0, оо, 1 (если мы ограничимся областью
lmz^>0 и, следовательно, однозначной ветвью vo). В оставшейся части
верхней полуплоскости функция и регулярна и, следовательно, равенство A6)
может иметь лишь конечное число решений.
В случае, когда а, Ь, с — вещественные числа, число нулей [то есть
решений уравнения A6) при Л = 0] однозначной ветви и (а, Ь\ с\ г) было
определено Гурвицем (Hurwitz, 1907), Ван Флеком (Van Vleck, 1901, 1902) и Гер-
глотцем (Herglotz, 1917). Методы, использованные этими авторами, тесно
связаны с результатами, выражаемыми формулами 2.7A) и 2.7B).
Для многочленов
где а, 7 вещественны и y>0, a я+1 — ч>>0 все нули вещественны и лежат
на промежутке 0<г<1 (о многочленах Якоби см. гл. 10).
ЧАСТЬ ВТОРАЯ. ФОРМУЛЫ
2.8. Гипергеометрический ряд
0)
B)
Если с = — т — /, где т, 1 = 0, 1, 2,... , то имеем
C)
Некоторые элементарные функции, которые могут быть выражены с
помощью гипергеометрического ряда (см. 2.2.1 и 2.5.5):
D)

Усеченный биномиальный ряд имеет вид
A2)
A3)
A4)
A5)
A6)
Элементарные соотношения
A8)
A9)
B0)
B1)

B2)
B3)
B4)
B5)
B6)
B7)
Соотношения между смежными гипергеометрическими рядами в случае,
когда два параметра постоянны:
B8)
B9)
C0)
15 соотношений Гаусса между смежными функциями (F обозначает
F(a,b;c;z) и F(a ± 1), F(b±A) и F(c±\) обозначают соответственно
F(a ± 1, Ь\ с; г), F(a, Ь±\; с; г), F(a, b; с ± 1; г))
C1)
C2)
C3)
C4)
C5)
C6)
C7)
C8)
C9)
D0)

D1)
D2)
D3)
D4)
D5)
Формулы для частных значений z
D6)
D7)
D8)
D9)
E0)
E1)
E2)
E3)

E4)
E5)
E6)
2.9. Ряды Куммера и соотношения между ними
24 решения Куммера для гипергеометрического уравнения имеют вид
A)
B)
C)
D)
E)
F)
G)
(8)
(9)
A0)
(И)
A2)
A3)
A4)

A5)
A6)
A7)
A8)
A9)
B0)
B1)
B2)
B3)
B4)
Любые три из функций ии ..., «в связаны друг с другом линейным
соотношением с постоянными коэффициентами. Это приводит к двадцати
соотношениям, а именно
B5)
B6)
B7)
B8)
B9)
C0)
C1)

C2)
C3)
C4)
C5)
C6)
C7)
C8)
C9)
D0)
D1)
D2)
D3)
D4)
Эти соотношения справедливы для всех значений а, Ь, с, для которых
гамма-множители, стоящие в числителях, конечны, и для всех значений г
для которых соответствующие ряды сходятся, причем Im г > 0. Первые
восемь из этих соотношений связывают три из функций ttv и2, ..., uQ, не
имеющих общей области определения. Последние двенадцать соотношений
выражают функцию, которая определена в области Д через две функции,

каждая из которых определена в одной и той же области D', причем ф
Эти формулы могут быть использованы для аналитического продолжения.
Если Im г < 0, то знаки аргументов в экспоненциальных множителях
формул B5)—D4) должны быть изменены на противоположные.
2.10. Аналитическое продолжение
Здесь приведены основные формулы для аналитического продолжения
гипергеометрического ряда. Общим считается случай, когда 1—с, Ъ — а и
с — Ъ — а не являются целыми (см. также 2.9A)—2.9D) и 2.9C)—2.9D4))
A)
B)
C)
D)
Коэффициенты Alf A2, Вх и В2 имеют следующий вид:
E)
F)
Аналитическое продолжение F(a, b; с; z) в логарифмическом случае
(числа /, т, п неотрицательные целые)
G)
с — а — не целое;
(8)

причем сумма от нуля до от —1 для /п = 0 считается равной нулю,
A0)
(И)
A2)
A3)
где при /л = 0 считается равным нулю,
A4)

A5)
где при /я = 0 считается равным нулю.
Вырожденному случаю (одно из чисел а, Ь, с — а, с — Ъ — целое)
посвящен п. 2.2.2.
2.11. Квадратичные преобразования и преобразования
высших степеней
Все квадратичные преобразования могут быть выведены из линейных
преобразований п. 2.9 и преобразований специального вида, указываемых
ниже (относительно области, где справедливы эти формулы, см. п. 2.1.5):
0)
B)
C)
D)
E)
F)
Таблица Гурса квадратичных преобразований. Мы выбираем здесь для
квадратного корня ветвь, принимающую положительные и вещественные
значения, если г вещественно и 0^2<1. Все формулы справедливы в
некоторой окрестности точки 2 = 0.
G)

(8)
(9)
A0)
(И)
A2)
A3)
A4)
A5)
A6)

A7)
A8)
A9)
B0)
B1)
B2)
B3)
B4)
B5)
B6)
B7)
B8)
B9)
C0)

C1)
C2)
C3)
C4)
C5)
C6)
Кубические преобразования. Эти преобразования сводятся к
преобразованиям C7), C8) и C9) с помощью 2.10A)—2.10F) и 2.11A)—2.11F)
C7)
C8)
Знаки нь ставятся при Im (— w) ^ 0.

Имеем также
C9)
Гурса (Е. Goursat, 1881) дал большой список кубических преобразований.
Мы воспроизводим здесь лишь рациональные преобразования:
D0)
D1)
D2)
D3)
D4)
D5)
D6)
D7)

2.12. Интегралы
A)
B)
C)
D)
E)
F)
G)
(8)

(9)
A0)
(П)
A2)
A3)
A4)
A5)
Формулы G)—A5) справедливы, если
Re о Re Ь > 0.
Относительно других интегралов см. 2.4A)—2.4A0), 2.1C4), 2.1C5) и 3.7,
где функции Лежандра могут быть выражены через гипергеометрические
функции. Относительно интегралов, приводящих к гипергеометрическим
функциям, см. также гл. 7 (интегралы Сонина—Шафхейтлина и связанные
с ними интегралы).

ГЛАВА 3
ФУНКЦИИ ЛЕЖАНДРА
3.1. Введение
_JL
Выражение (а2— 2ar cos 7 + г2) 2 задает потенциал в точке Р,
образованный зарядом, помещенным в точке Л. Здесь г и а — расстояния точек Р
и Л соответственно от точки О, и 7— угол, под которым виден отрезок РА
из точки О. Разложение этого выражения по возрастающим степеням г
имеет вид
A)
Коэффициенты Pw(cosy) этого разложения зависят лишь от cos 7 (то есть не
зависят от а и г) и являются многочленами степени п от cos 7- Эти многочлены
были введены в 1784 г. Лежандром и называются многочленами Леэюандра.
Многочлены Лежандра и связанные с ними функции встречаются,
например, при решении уравнения Лапласа, волнового уравнения или уравнения
теплопроводности в сферических координатах г, 0, ср, определяемых форму-
В этих координатах
и решение уравнения ДК=0 имеет вид V = R(r) Г@) F(cp), где R, T, F
зависят только от г, 0, ср соответственно. При этом Т удовлетворяет
обыкновенному дифференциальному уравнению
B)
где (х и v — постоянные, возникающие при разделении переменных.
Подстановка C=cos0 приводит уравнение B) к уравнению Лежандра степени v
и порядка fx
C)
Это же самое дифференциальное уравнение возникает для задачи потенциала
в сфероидальных и тороидальных координатах; см. п. 3.13 и 3.14.

В случае сферических координат число ?=cos6 вещественно и лежит
на отрезке [—1, 1]. Для того чтобы потенциал был однозначной функцией,
которая непрерывна и имеет непрерывные частные производные на сфере
г = const, числа fx и v должны быть целыми. Однако уравнение C)
встречается и в других задачах, когда нет необходимости ограничиваться лишь
значениями С на отрезке [ — 1, 1] и целыми значениями [х и v. Поэтому мы
будем изучать уравнение C) при произвольных вещественных или
комплексных значениях чисел С, fx, v.
Уравнение Лежандра встречается также в теории гипергеометрических
функций. В этой теории установлено, что если гипергеометрический ряд
Гаусса допускает квадратичное преобразование, то гипергеометрическое
дифференциальное уравнение может быть сведено к уравнению C).
Совершенно иной подход используется в теории ортогональных
многочленов. Многочлены Лежандра РЯ(С) являются ортогональными на отрезке
[—1, 1] многочленами, соответствующими весу /?(л:)= 1. Отсюда возникает
связь с теорией интерполяции и механическими квадратурами. Ортогональные
многочлены с весовой функцией A — ?2)а на отрезке [ — 1, 1] также могут
быть выражены через функции Лежандра (см. гл. 10). В этой главе основой
для изучения функций Лежандра будет дифференциальное уравнение C).
3.2. Решение дифференциального уравнения Лежандра
Функции Лежандра являются решениями дифференциального уравнения
Лежандра
где z, v, fx могут принимать любые значения.
Подстановка w = (z2—1)^/2г/ преобразует уравнение A) к виду
B)
Если выбрать за независимое переменное С = -~ ^-, то это дифферен-
циальное уравнение примет вид
Это уравнение совпадает с уравнением Гаусса 2.1A), где a = fx— v, ? = fx
—j— V —|— 1 И С = fX -f- 1.
Следовательно, в силу 2.3A), функция
C)
является решением уравнения A).
Если сделать подстановку ? = 22, уравнение B) примет вид
D)

Это также уравнение гипергеометрического типа, где а = -9" 0х + v + 1)>
# = —(fx— v), c = ~2-- Следовательно, в силу 2.9(9), уравнение A) имеет
решение
Функции PJ (z) и Qy(z) называют соответственно функциями Лежандра
первого и второго рода. Они однозначны и регулярны на 2-плоскости,
разрезанной вдоль вещественной оси от 1 до оо. Будем считать, что
и F)
Дифференциальное уравнение Лежандра остается неизменным, если заме-
[ть fx на —fx, z на —z и v на —1—v. Следовательно, функции
также являются решениями уравнения A) (см. также п. 3.3.1).
Применяя формулы 2.1B3) к C) и E), получаем
G)
(8)
(о сл)чае, когда у или fx или оба индекса являются положительными целыми
числами, см. п. 3.6).
Используя формулы преобразования гипергеометрической функции,
данные в п. 2.10, можно выразить функции в формулах C) и E) различными
способами в виде
(9)
(Ю)
где С является функцией от z и зависит от выбора преобразования.
Различные выражения вида (9) и A0) указаны в формулах A4)—D9). Последний
столбец каждой таблицы указывает метод вывода данного выражения из
других. Например, A5) получается с помощью 2.10A) к 14. (Далее см. стр. 140.)

Выражения для Р** (г)
A4)
A3)
A6)
A7)
A8)

Выражения для Р^ (г)
Замечания
A4)
A4), 2.10A)
A5)
Верхний или нижний
знаки берутся в зависи-
сти от
lm 2$^ 0
A6) A4), 2.10F)
A5), 2.10F)
A7)
Верхний и нижний
знаки берутся в зависимости
от
A8) A6), 2.10A)

Выражения для Р** (г)
A9)
B0)
B1)
B2)
B3)
B4)

B2)
B3)
Выражения для Р** (г)
Замечания
A9) A4), 2.10B)
A5). 2.1 Ц2)
B0)
Re z>0
B1) B0), 2.10B)
B0), 2.10A)
B0), 2.10F)
B4)
Re z>0

B5)
B6)
B7)
B8)
B9)
C0)
C1)
Выражения для />** (г)

Выражения для Р^ (г)
Замечания
B4), 2.10B)
Верхний или нижний
знак берется в
зависимости от
Im z^O
B6) B3), 2.11A6)
B7) B6), 2.10F)
B4), 2.11A7)
B8)
Re z>0
B9) B8), 2.10F)
B8), 2.10B)
Верхний или нижний
знак берется в
зависимости от
B9), 2.10A)
Гипергеометрические
ряды нигде не сходятся
в разрезанной
плоскости

Выражения для е
C2)
C3)
C4)
C5)
C6)
C7)

Выражения для е (
Замечания
C2) C7), 2.10B)
C6), 2.10B)
v ' Верхний или нижний
знак берется в
зависимости от
lm г =JJO
C4) C6), 2.10A)
C5) C6), 2.10C)
C6) D1), 2.11A7)
C7) C6), 2.10F)

Выражения для е (}Щ
C8)
C9)
D0)
D1)
D2)
D3)

Выражения для е ^
Замечания
C9), 2.10B)
C8)
Re г > 0
C9) D1), 2.10F)
D1), 2.10B)
D0)
Верхний или нижний
знак берется в
зависимости от
\mz >0
D1)
D2) C8), 2.10F)
D1), 2.10C)
D3)
Верхний или нижний
знак берется в
зависимости от
Im z 5=5=0

Выражения для е
D4)
D5)
D6)
D7)
D8)
D9)

Выражения для е Я
D4)
Замечания
D1), 2.11A6)
{45) W' 2-10F)
D4), 2.10C)
D6)
Re z>0
D7)
D4), 2.10B)
D8)
D8), 2.10F)
Верхний или нижний
знак берется в зави-
симости от
Im z^O.
Гипергеометрические
ряды нигде не сходятся
в разрезанной
плоскости

Таблица содержит 36 различных гипергеометрических рядов, каждый
из которых является решением уравнения A). Если применить к каждому
из этих рядов преобразование 2.1B3), то получим 36 других
гипергеометрических рядов. Таким путем получаются 72 решения Олбрихта
дифференциального уравнения A) (Olbricht, 1888, стр. 1). Во всех этих формулах положено.
(И)
и, следовательно,
A2)
где верхний или нижний знаки берутся в соответствии со знаком Im z.
Из A) следует, что определитель Вронского
должен иметь вид -j -2. Значение постоянной можно получить, положив
2 = 0. Используя B2) и D0), получим
A3)
На стр. 128—139 приведена таблица разложений, имеющих форму равенств
(9) и A0).
3.3.1. Соотношения между функциями Лежандра. Из 3.2C) вытекает,
что
A)
Из 3.2E) и 3.2(8) следует
B)
Из 3.2E) в силу 3.2B3) вытекает, что
C)
Из 3.2C2) и 3.2C) следует
D)
потому
E)
F)
Таким образом, если ц = т (т = 1, 2,3, ...), то
G)

Из E) и C) выводим
(8)
или, в силу 1.2F),
(9)
Из 3.2A5), 3.2C) и 3.2C2) имеем
A0)
или
A1)
Следовательно, заменяя z на —z, получаем
A2)
В формулах A0), A1), A2) верхний или нижний знак выбирается в
зависимости от \mz JjO.
Если заменить в формуле 3.2C) z на , v на —[а—- и [i на
— v—у и сравнить с 3.2D4), то получим формулу Уиппла
A3)
которая эквивалентна формуле
A4)
Когда z изменяется вдоль линии, соединяющей точку вещественной оси,
такую, что 2>1, с точкой мнимой оси, выражение изменяется
вдоль линии, соединяющей точку вещественной оси с точкой разреза,
лежащей между нулем и единицей. Так как функция Лежандра второго рода
имеет разрыв на разрезе, то нужно ввести ограничение Re z > 0.

3.3.2. Некоторые дальнейшие связи с гипергеометрическим рядом.
Из 3.2C) и A1) следует, что
A5)
и, следовательно, в силу B)
A6)
где верхний или нижний знак выбран в зависимости от
Из F), 3.2C) и A6) следует:
A7)
где верхний или нижний знак берется в зависимости от Imz^jO.
Представления A5) — A7) не относятся к типам 3.2(9) и 3.2A0), поскольку входящие
в них гипергеометрические функции зависят от различных переменных.
Если в 3.2D4) г обходит точку + 1 в отрицательном направлении,
получим новую ветвь функции, которую будем обозначать Q^B, 1—). В силу
3.2A1)
A8)
Если точка г лежит на вещественной оси справа от 1 или слева от—1, то
аргумент гипергеометрической функции вещественен и больше 1.

Из 3.2C2) имеем для той же функции
A9)
Из A9), 3.2C2) и 3.2C) вытекает, что
B0)
Следовательно, в силу A8) и 3.2D4)
B1)
Далее, из (9), B0) и 3.2D4) имеем
B2)
Выражения B1) и B2) также не относятся к формулам типа 3.2(9) и 3.2A0).
3.4. Функции Лежандра на разрезе
Во многих приложениях нужны функции Лежандра при z = x, где
— 1<л:<1. Отрезок [—1, 1] будем называть в этом пункте «разрезом»
и будем считать, что— 1 <.х <С 1. Для четного целого числа из 3.2C) следует,
что значения Р? (г) на обеих сторонах разреза равны между собой. В этом
случае достаточно провести разрез вдоль вещественной оси от—1 до — оо.
Во всех остальных случаях функции Р^ (х — ДО) и Р^ (х -\- ДО) различны
(через f(x ± ДО) обозначим lim f(x ± /e), е>0). Чтобы избежать двузнач-

ности, обычно пользуются модифицированными решениями уравнения 3.2A).
Будем обозначать их Р^(лг) и Q4(x):
О)
B)
В этих обозначениях формулы для PJ и Q^, соответствующие аналогичным
формулам для Р^ и Q^, могут быть получены из формул предыдущего
пункта путем замены: г—1 на A — х)е—т, г2—1 на A—х^)е±1ж и г-)-1
на х -{¦ 1 (— 1 < х <с 1) в соответствии с г = х ±« 0.
Для этих функций справедливы следующие соотношения:
C)
D)
E)
F)
G)
(8)
(9)
A0)
(И)

A2)
A3)
A4)
A5)
A6)
A7)
A8)
Равенство
C)
D)
E)
F)
G)
(8
(9)
(Ю)
(И)
A2)
A3)
A4)
A5)
A6)
A7)
A8)
следует из:
3.2C) и 3.2A2)
3.2C) и 3.2A2)
C) и D)
A), C) и D)
F)
F) и 3.2C2)
(8) и B)
B) и 3.2C2)
3.2B2), A) и 3.2A2)
3.2D0) и 3.2A2)
3.3D), A) и (9)
3.3A0), G) и (9)
3.3A2), B) и C)
3.3C), E) и B)
A3)
3.3B), (9) и B)
При целых га и п из A4) и A5) следует, что
A9)

При х = 0 из A1) и A2) вытекает
B0)
B1)
Так как , то из A1) и A2) следует
B2)
B3)
Следовательно, из равенств B0) — B3) имеем
B4)
Так как из п. 3.2 следует, что
то постоянную С можно вычислить, положив лг = О и использовав
равенство B4). Получаем
B5)
3.5. Тригонометрические разложения для Pv(cos0) hQv(cos6)
Положив в 3.2D5) 2 = cos0±;/O, ]/i2 — \=е 2 sin 0, получим
A)

Следовательно, в силу 3.4(8) и 2.1B),
B)
Точно так же из 3.4B) следует
C)
Оба ряда сходятся при 0 < 0 < п. Точно так же получаем из 3.2D4)
D)
и, следовательно, в силу 3.4(8), 3.4B) и 2.1B),
E)
(в)

Из равенства D) можно усмотреть, что разложения E) и (б) сходятся при
|-<6<:~. Из формул 3.4E) и 3.2B0), 3.2G) и 3.2C) соответственно
получаем
G)
(8)
(9)
Формула для P~[x(cos0), удобная, если 0 мало (MacDonald, 1914, стр. 220),
имеет вид
A0)
Здесь и /х(°0 означает функцию Бесселя (см. гл. 7).
Это выражение может быть получено, если записать 3.4F) в виде
и выразить через степень ^ + -9".
3.6.1. Частные значения ju, и v. Если jj.— положительное целое число,
1х = т(т = \, 2, 3, ...), то из 3.3G) и 3.2G) следует
A)
и из 3.4E) и A):
B)
Теперь рассмотрим случай, когда %• — целое число. Из равенства 3.3A)
следует, что достаточно рассмотреть случай, когда м = п — неотрицательное
целое число. Будем различать следующие три случая:
1) Если р. — не является натуральным числом, то гипергеометрический
ряд в 3.2C) есть многочлен степени п относительно z.

2) Если fx = /я, m=l, 2, 3,... и п^>т, то справедливы формулы A) и
B) и гипергеометрические ряды, входящие в эти формулы, являются
многочленами степени п—т относительно г.
3) Если р. = /я, т= 1, 2, 3, ... и /я > я, то функции Р^ (г) и Р^ (х)
тождественно равны нулю. Однако Г(м — М-+1)Р^B) и Г(м — [*+1) Р^(х)
стремятся к конечным пределам, когда {л —* /я, %> —> я.
Принято писать: PJ (z) = Pv B) и т. д. Часто Pv B) и Qv B) называют
функциями Лежандра, Р% (z) и QjJ* B) — присоединенными функциями Ле-
жандра.
Из 3.2G) имеем
C)
Если продифференцировать равенство C) т раз по z (/я = 1, 2, 3, ...) и
принять во внимание 2.1G), 1.20E), 3.2G) и 3.3G), то получим
D)
и, следовательно, в силу 3.3A1) и 3.2(8),
E)
Из D), E), 3.4B) и 3.4E) следует
F)
G)
Далее, из C), 2.1G) и 3.2G)
(8)
(9)
A0)
Если {х — натуральное число, fx = /n(w = l, 2, 3, ...), то выражение 3.2C2)
теряет смысл и его значение определяют с помощью правила Лопиталн.

В результате (Гобсон, 1952, стр. 205) получаем
(И)
где
Если р. — отрицательное целое число, то можно использовать 3.3B) и A1).
При т = 0 A1) дает
Если при этом м — натуральное число, v = п (л = 1, 2, 3,...), то
(см. также 3.6.2).
Из 3.2A6), 3.2B0), 3.2B6), 3.2C6), 3.2C7) и 3.2D4) соответственно вытекает,
что если п = 0, 1,2,..., то выражения для функций Р~_?_п, РЦ~^2/г~^1,
состоят из конечного числа
слагаемых. В частности,
A2)

A3)
и из 3.2A6)
A4)
Используя 3.3A3) и 3.3A4), можно вывести из равенств A1) и A4) много
дальнейших формул.
3.6.2. Многочлены Лежандра. Если м. = 0 и %• — целое число, возникает
особо важный частный случай функций Лежандра (см. также п. 10.10). Можно
считать, что целое число v неотрицательно. Из 3.2B2) получаем при п = 0,
1, 2,...
A5)
или в обоих случаях
A6)
Это равенство может быть записано в виде
A7)
Выведенную формулу называют формулой Родрига.
Таким образом, Рп (z) является многочленом степени п относительно z и
имеет ту же четность, что и п,
Эти многочлены называются многочленами Лежанцра. Они образуют
ортогональную систему функций на отрезке [— 1, 1]; их корни вещественны,
просты и лежат между — 1 и 1 (см. также гл. 10).

Из 3.5B) и 3.5C) имеем
A8)
A9)
Из 3.2D0) следует, что
где верхний или_нижний знак берется в соответствии с ImzJjO. Так как
1 —^ = (^— 1) еты , то
B0)
и из 3.4A2)
B1)
Равенства 3.2A3) дают при [л = 0 и м = я
следовательно,
B2)
где путь интегрирования не должен пересекать разрез. Так как Ро (t) = 1
(см. 3.6C)), то равенство B2) при п = 0 согласуется с равенством B0).
Многочлен Рп (t) имеет степень п и различные корни; обозначим их,
например, через tlt t2) ..., tn. При этом, так как Рп(\) = (— \)п Рп {— 1) = 1,
ни один из этих корней не равен ±. 1. Разлагая на простейшие дроби, имеем
И, следовательно, из B2)
B3)

или
B4)
где Wn_! (z) — многочлен степени п—1. Так, например,
B5)
Из формулы B4) видно, что функция Qn(z) имеет логарифмические точки
ветвления в г = ± 1, но не имеет точки ветвления на бесконечности. Поэтому
любая ветвь функции однозначна и регулярна в плоскости г, разрезанной
вдоль вещественной оси от — 1 до 1.
Из B4) и 3.4B) следует
B6)
Подставляя B4) в уравнение Лежандра 3.2A), при ;л = 0, получаем, что
функции Wn-u п== 1, 2, 3, ... , удовлетворяют уравнению
B7)
Отсюда можно вывести, что (Гобсон, 1952, стр. 56)
B8)
Эта формула принадлежит Кристоффелю.
Далее, пусть г — любая точка плоскости w, не лежащая на вещественной
оси между — 1 и 1. Применим теорему Коши к
области, ограниченной контурами Ct и С2,
изображенными на рис. 2. Мы получим тогда
Если устремить радиус окружности С2 к
бесконечности, то, в силу 3.2E), имеем \ —>¦ О, а вклад по
дугам окружностей в \ стремится к нулю вместе с
Ci
радиусами этих окружностей. Таким образом, имеем

Так как выражение в квадратных скобках равно niPn(v)f получаем
интегральное представление Неймана
B9)
Записывая формулу B9) в виде
C0)
и сравнивая с B4), получаем, что
C1)
Обобщением формулы Неймана B9) является следующая формула (Gor-
mley, 1934, стр. 149):
C2)
v -j- fji = 0, 1, 2, ..., Re {л < 1 не лежит на отрезке вещественной оси [— 1, 1].
Другое обобщение (Wrinch, 1930, стр. 1037)
у z не лежит на вещественной оси между —1 и 1, я, т — целые.
Производящая функция для многочленов Лежандра имеет вид
C3)
Это легко может быть установлено путем разложения функции C3) в ряц
соответственно по возрастающим и убывающим степеням h и применения
формулы A6) (обозначения см. п. 3.15).
С другой стороны, если z = ch (a -{- iv) (a, v вещественны), то ряд
сходится при | h | <с е—и. Подставляя сюда выражение C0) для Qn (z) и
используя C3), получаем

или
C4)
Из 3.4B) следует, что
C5)
Дальнейшие результаты в случае целых значений (л и %> см. в гл. 10 и 11,
а относительно результатов о присоединенных функциях Лежандра, для
которых сумма степени и порядка является натуральным числом, см. п. 3.15
и MacRobert, 1943, стр. 1; 1947, стр. 332.
3.7. Интегральные представления
Из 3.2G) и 2.12A0) вытекает, во-первых, чго
A)
где г не лежит на вещественной оси между — 1 и оо.
Точно так же из 3.2D5) и 2.12A4)
B)
C)
Обе формулы справедливы, если Re (v ± {л -f- 1) >» 0.
Делая в интервале C) подстановку ev = ch a -f-sh а ch t и применяя 3.3B),
получаем
D)
Далее, из 3.2C6) и 2.12(8) следует, что если г не лежит на вещественной

оси между —1 и 1, то
E)
F)
Из F) вытекает
G)
Поэтому, после подстановки ch a -f- sh a cos t = ev, имеем
(8)
Другие интегральные представления пол>чаются в результате
рассмотрения интеграла , взятого вдоль контура
прямоугольника с вершинами (± с, 0) и (± с, Ы), в котором сделаны вырезы
в точках (± а, 0). Устремляя с—>оо и используя равенство (8), получаем
интегральное представление для P^(cha). Заменим в формуле v на —1—v
и сложим пол)чающиеся выражения, после чего применим 3.3A). В
результате получим
(9)

Если в формуле 7.8F) заменить / , (t) выражением 7.3C1) и изменить
V+2"
порядок интегрирования, то получим
A0)
где z не должно быть точкой вещественной оси, лежащей между 1 и со.
Следовательно, из 3.3(9) имеем
где г не является точкой вещественной оси между — 1 и — оо.
Применяя преобразование Уиппла 3.3A3) к A1), получаем
A2)
Применяя 3.3A4) к A0), имеем
A3)

Следовательно, если {л — целое число, ii = m(m = 0, 1, 2, ...)(см. п. 1.2.3), то
A4)
Это равенство может быть записано в виде
A5)
Делая подстановку ? = Ф — ф, получаем
A6)
A7)
В случае, когда ф = 0, A6) может быть распространено на все значения
т и Rev>— I (Erdelyi, 1941, стр. 351).
В сл>чае /и = 0 обобщение формулы A6) имеет вид (Уиттекер — Ватсон,
1962, п. 15.71)
A8)
Другие выражения для Р^ {г) могут быть выведены из полученных здесь
результатов с помощью 3.3A).
С помощью 3.4E), 3.4(8) и 3.4B) можно получить аналогичные выражения
для Р^ (х) и QiJ* (л:). Из 3.4(8) и B) получаем, полагая г = cos 0,
A9)

Из 3.4B) и B) имеем
B0)
Из 3.4(8) и A2), а также из 3.4B) и A2) получаем соответственно
B1)
B2)
Обе формулы справедливы, если Re(v±n)> — 1, чф—1, —2, —3, ...
Из 3.4E) и F) следует
B3)
и из 3.4E) и A3) следует
B4)

Из 3.4E), A6) и A7) вытекает
B5)
B6)
В случае у < 0 < л выражение в правой части равенств B5) и B6) может
быть вычислено с помощью 3.4A4).
Делая подстановку cos 0 -f- i sin 0 cost = e*v1 выводим из B3)
B7)
Эта формула называется формулой Мелера—Дирихле.
Далее (Copson, 1945, стр. 81)
B8)
Формула
B9)
справедлива, если Re \x ;> 0 и г не является вещественным числом, лежащим
на отрезке [— 1, 1]. Она может быть легко выведена из 3.6C) и 2.1G). Инте-
г
грал ^ (t—\)п (z — ty-'1 dt, который встречается в доказательстве, может
быть вычислен с помощью подстановки
t = v(z~\) + \
и формулы 1.5A). Его значение равно

Точно так же имеет место равенство
C0)
вытекающее из 3.6C), 1.5A3) и 3.4E).
Аналогично имеем
C1)
Последнее равенство вытекает из 3.2E), 1.5B) с помощью подстановки
t — vz -f- z.
Далее, из 3.2D5) и 2.12A5) имеем
C2)
Соответствующие выражения для PJ'Oz), Qj"(cos6) и P^(cos6) выводятся
с помощью формул 3.3(9), 3.4B) и 3.4(8) соответственно.
Формула
C3)
может быть доказана, если записать
разложить подынтегральное выражение в ряд, почленно проинтегрировать
и использовать равенства 1.5A2), 2.1B) и 3.2G). Относительно выражений
функций Лежандра с помощью контурных интегралов см. Гобсон, 1952,
стр. 177—194, 226—234, 258.
3.8. Соотношения между смежными функциями Лежандра
Рекуррентные формулы для функций Лежандра могут быть выведены при
помощи соотношения Гаусса между смежными гипергеометрическими
функциями (см. 2.8). Так, из 3.2A4) и 2.8C0) вытекает, что
0)

из 3.2B8) и 2.8B8)— что
B)
из 3.2B4) и 3.2D) —что
C)
Следующие формулы выводятся из формул A) — C):
D)
E)
F)
G)
(8)
Дифференцируя 3.2G) и применяя 2.1G), получаем
(9)
Исключая отсюда с помощью F) Р^^), получаем
A0)
Легко установить, что формулы A) —A0) справедливы также для
Принимая во внимание, что , получаем
следующие рекуррентные соотношения для функций Лежандра на разрезе:
(И)
A2)
A3)
A4)
A5)
A6)
A7)

A8)
A9)
Легко установить, что формулы A1) — A9) справедливы для QJ (х).
Из B) вытекают первая и вторая формулы суммирования Кристоффеля
B0)
B1)
3.9.1. Асимптотические разложения. Если г не является вещественным
числом, большим 1, то даже в случае, когда гипергеометрический ряд
F(a, Ь\ с; г) расходится, он является асимптотическим разложением по с при
больших положительных значениях Re с. Следовательно, при фиксированных
г и v и Re ц —> оо формулы 3.3A7), 3.3A6), 3.2C) и 3.3A5) дают
асимптотические разложения функций Р^ (z\ Q^ (z), P~ ^ (z), Q~ ^ (z) соответственно.
Первое, второе и четвертое разложения справедливы для всех значений z,
за исключением точек вещественной оси между — оо и —1, а также 1 и оо,
а формула 3.2C) справедлива для всех значений z, кроме точек
вещественной оси между —оо и —1.
При фиксированных z и {а и Rev—> со формулы 3.3B1), 3.2D4), 3.3B1)
вместе с 3.3A) и 3.3B2) дают соответственно асимптотические разложения
функций P^(z), Q^{z), P^lv (z) и Q^v(z). Первое, третье и четвертое
разложения справедливы для всех значений z, кроме точек вещественной оси
между —оо и —1, оо и 1, а разложение 3.2D4) справедливо для всех
значений z, кроме точек вещественной оси между —оо и -\- 1.
Разложения 3.5E) и 3.5F) являются асимптотическими разложениями
по v функций P^(cos0) и Q^ (cos 6) соответственно, которые справедливы
в области е^б^тх — е, е>0. Таким образом,
A)
B)
Для малых значений 0 см. 3.5A0). Формула 3.5(9) дает асимптотическое
разложение ФУНКЦИИ Р~^(СО8 0) ПО (JL.

Поведение функций Лежандра в окрестности одной из особых точек 1, — 1
или оо может быть исследовано с помощью разложений п. 3.2, 3.4 и 3.6.
Результаты, включая ограничения, которые налагаются на параметры, указаны в
таблице на стр. 164, 165. Этой таблицей пользуются следующим образом. Равенство
C), например, показывает, что в окрестности точки z = 1 функция Р^ {г) равна
плюс члены высшего порядка относительное — 1 при
условии, что fjL не
из 3.2C).
Равенство
C)
D)
E)
F)
G)
(8)
(9)
(Ю)
(И)
A2)
является натуральным числом.
Выводится из
3.2C)
3.6A)
3.2C2)
3.2C2)
3.2C6) и 2.10A4)
3.4F)
3.6B)
3.4A0)
3.4A0)
G), 3.4B) и 3.2A2)
Равенство
A3)
A4)
A5)
A6)
A7)
A8)
A9)
B0)
B1)
с>тот результат
Выводится из
3.4A4), (8) и A0)
3.4A4), (8) и A1)
3.4A4), (8) и A2)
3.4A5), A0) и (8)
3.4A5), A1) и (8)
3.4A5), A2) и (8)
3.2A8)
3.2A8)
3.2E)
ЗЛО. Разложения по функциям Лежандра
Некоторые интегральные представления функций Лежандра имеют вид
коэффициентов Фурье и могут быть использованы для суммирования
некоторых рядов Фурье.
Пусть при фиксированном 0, O<0<'ji,
Коэффициенты Фурье для f(v) могут быть вычислены при помощи 3,7B7).
Отсюда вытекает разложение

Заменяя v на %—0 и 6 на %— v, получаем отсюда, что
Аналогично из 3.7B7) вытекает
B)
Если разложить (z—cosv) в ряд Фурье (z фиксировано и не
является точкой вещественной оси между — 1 и 1), то с помощью 3.7A0)
получим
C)
где г не лежит на вещественной оси между — 1 и 1.
Далее из 3.7A6) следует
D)
Следовательно, положив ср = 0, заменив v на —v-—1 и воспользовавшись
3.3A) и 1.2C), получим

Разложение Дуголла
F)
может быть доказано следующим образом. Будем исходить из формулы
G)
которая легко устанавливается при вычислении контурного интеграла
взятого по окружности с центром в начале координат и радиусом (jV + -~-) тс
— натуральное число). Применив теорему Коши и перейдя к пределу при
-*оо, получаем G). Подставив G) в 3.7B7), проинтегрировав по частям и
заменив /л на —/а, получаем формулу F).
Далее, из формулы 3.7B7) имеем
Применив G) и проинтегрировав по частям, находим
(8)
Далее, положив в формуле (8){х = 0 и \ = т (т — натуральное число),
проинтегрировав т раз по х и применив 3.6F), выводим, что
(9)
(Об аналогичных разложениях см. Mac Robert, 1934.)

Из асимптотических разложений 3.3B1) и 3.2D4) для Рп (z) и Qn(z)
соответственно (см. 3.9A)) получаем, что при условии
первая часть равенства 3.8B1) стремится к 1, когда п—*оо. Отсюда
получается формула Гейне
A0)
О многих других формулах см. Dougall, 1919; Darling, 1923; Prasad, 1930,
стр. 64—67, 159; 1931; Shabde, 1931, 1932, 1933; Banerjee, 1932; MacRobert,
1934, 1935, 1936.
3.11. Теоремы сложения
Соотношение
A)
может быть выведено следующим образом. Из равенств 3.10D), 3.10E) и
теоремы Парсеваля (Титчмарш, 1951, стр. 470) следует, что ряд
сходится к
причем последнее выражение, в силу 3.7A8), равно
Отсюда и вытекает равенство A).
Далее (Гобсон, 1952, стр. 358), в силу 3.4A4), имеем
B)
— вещественное.

Поэтому из 3.4A4) вытекает
C)
— вещественное.
Из A) и 3.3A1) следует
D)
t, t' — вещественные, \<f<t, v ф — 1, — 2, — 3, ..., ф — вещественное
(аналогичные разложения см. Cowling, 1940, стр. 222).
3.12. Интегралы, содержащие функции Лежандра
Еслии>?(я) и w\(z) означают решения дифференциального уравнения
Лежандра 3.2A) с параметрами \>, /а и с, р соответственно, то из 3.2A),
3.8A0) и 3.8A9) вытекает, что
О)
Когда /л = р=О, из A) и 3.8G) следует
B)
Если через wv и wa обозначить две функции Лежандра на разрезе, то из
A) и 3.8A7) получим
C)
Следующие результаты легко могут быть получены из B) и C) с помощью

формул п. 3.9.2.
D)
E)
F)
G)
В частности, при v = n, а = т (п и т — целые)

A4)
A5)
A6)
A7)
В формулах A5) —A7) использовано обозначение
Если в формуле A) jx = р = т, \> = /г, с==/ (/, т, п — натуральные числа),
то получаем из 3.9 (8), 3.9A0) и 3.4A9)
A8)
Аналогично, если т, п, !, k — неотрицательные целые числа, то из A)
следует
A9)
B0)
B1)

B2)
Далее, имеем
B3)
Это равенство может быть доказано путем подстановки 3.2C) и 2.1B) и
почленного интегрирования. Применяя 1.5A) и 2.1B3), находим сначала,
что
откуда соотношение B3) вытекает в силу формулы 2.8E0).
Берне (Barnes, 1908, стр. 183 и далее) доказал, что
B4)
B5)
т — натуральное;
B6)
— натуральное.

Приведем еще несколько интегралов, содержащих функции Лежандра
и тригонометрические функции (MacRobert, 1940, стр. 95, 96; 1947, стр. 366,
367):
B7)
B8)
B9)
Кроме того (Shabde, 1945, стр. 51), имеем
C0)
Другие интегралы, содержащие функции Лежандра, см. в гл. 7, а также
в работах: Bailey, 1931, стр. 187; Banerjee, 1940, стр. 25; Barnes, 1908,
стр. 179 — 204; В. N. Bose, 1944, стр. 125; S. К. Bose, 1946, стр. 177; Dhar,
Shabde, 1932, стр. 177; MacRobert, 1936, стр. 203; 1940, стр. 95; 1947, стр. 336,
367; Meijer, 1939, стр. 930; Prasad, 1930, стр. 33; Shabde, 1934, стр. 41; Sircar,
1927, стр. 244. Об интегралах по индексам см. MacRobert, 1934, 1935.
3.13. Функции кольца или тороидальные функции
Функции кольца или тороидальные функции возникают, когда
уравнение Лапласа ДК=0 преобразуют к тороидальным координатам (yj, 0, <р)

Подстановка s = chf] и 1/ = (спт]—cos 6)t/(s, 0, <р) преобразует
уравнение ДК = 0 в уравнение
B)
Если v = vx (s) v2 (8) vz (<p), то получаем следующее дифференциальное
уравнение для t/x:
C)
где v и [х — параметры разделения переменных. В соответствии,с 3.2A),
решениями уравнения C) являются
D)
Поведение этих решений при больших значениях yj следует из 3.2B8) и 3.2D5):
E)
F)
Специальными случаями решений D) являются
G)
(8)
(9)
/Си Е — полные эллиптические интегралы первого и второго рода
соответственно (см. также Darling, 1923; Lowry, 1926; Airey, 1935).
Все другие формулы, свойства и представления для тороидальных
функций вытекают из ранее полученных формул этой главы. О теореме
разложения, содержащей тороидальные функции, см. Banerjee, 1938; 1942.

3.14. Функции конуса
Дифференциальное уравнение
A)
(р — вещественный параметр) является частным случаем уравнения 3.2A),
где v = — у + W-
Решениями уравнения A) являются
и B)
Функциями конуса называют решения уравнения A) при вещественных
значениях аргумента, меньших по модулю, чем 1,
и C)
Основные свойства этих функций могут быть получены из общих свойств
функций P^(cos6) и Q^(cos6). Например, из 3.5G) и 3.5(8) следует
D)
E)
Отсюда видно, что функции конуса первого вида положительны при
вещественных значениях р. Специальным случаем формулы E) является формула
К—полный эллиптический интеграл первого рода (см. также Darling, 1923;
Lowry, 1926; Airey, 1935).
Формулы, аналогичные соответственно формуле Неймана 3.6B9) и
формуле Гейне 3.10(9) были установлены Мелером (Mehler, 1881, стр. 193):
(в)
G)

Эти формулы являются частным случаем следующей формулы обращения
(Mehler, 1881, стр. 192; В. А. Фок, 1943):
(8)
(9)
Все другие свойства и представления функций конуса вытекают из
формул предыдущих пунктов этой главы. См. также Mehler 1881 и
Neumann, 1881. О теореме разложения, содержащей функции конуса, см. Вапег-
jee, 1938, стр. 30.
3.15. Функции Гегенбауэра
3.15.1. Многочлены Гегенбауэра. Многочлены Гегенбауэра С„(г) при
целых значениях п определяются как коэффициенты при hn в разложении
функции A—2hz-\-h2)~^ по степеням h (см. также п. 10.9):
A)
Так как
то коэффициент при hn в разложении A) имеет вид
B)
и из 1.2C), 1.20E) и 2.1B) получаем, что
C)
Из C) и 3.2G) следует
D)

Из D) и 3.B2) вытекает
E)
F)
Из C), E) и F) имеем
G)
Из 3.2B3) получаем
(8)
(9)
Таким образом, доказано, что
A0)
Из (9) следует
(И)
Тригонометрическое разложение для C^(coscp) может быть получено
следующим образом. Запишем тождество
A2)
и разложим как левую часть, так и оба сомножителя справа по степеням Л.
Тогда получим
Сравнивая коэффициенты при hn в обеих частях, получаем

или
A3)
Если п — четное число, то в этой формуле надо взять лишь половину
последнего члена (соответствующего т = ~~\. Из формулы A3) следует
A4)
Из тождества
получаем
A5)
Для того чтобы получить соотношения ортогональности для многочленов
Гегенбауэра
A7)
перепишем интеграл в левой части по формуле A0) в виде
Интегрируя п раз по частям и используя равенство A1), получим A6) и A7).
Из равенств A6) и A7) получаем, поскольку CJ (л:) = 1,
A8)

Теорема сложения для функций C*n(z) была установлена Гегенбаузром
(Gegenbauer, 1893, стр. 942)
A9)
Из A8) и A9) следует, что
B0)
(О дальнейших интегральных формулах см. Ватсон, 1949, стр. 412—414.)
3.15.2. Функции Гегенбауэра. Из 2.1A) видно, что функция C), где п
заменено на а (а произвольно), является решением дифференциального
уравнения
B1)
Таким образом, можно определить функции Гегенбауэра для любого (в том
числе и комплексного) значения а с помощью формул C) или D), где п
заменено на а.
Из D), 3.7F), 3.7(8) и 3.7C4) вытекает соответственно, что
B2)
B3)
B4)
О дальнейших интегральных представлениях см. Dinghas, 1950.

Применяя формулу обращения преобразования Меллина к последнему
соотношению, получаем
B5)
Из D) и п. 3.8 следует, что
B6)
B7)
B8)
B9)
C0)
Из 3.3A) и D) вытекает
C1)
Легко найти, что вторым решением дифференциального уравнения Геген-
бауэра B1) является
C2)
Функция D^(z) удовлетворяет тем же самым рекуррентным соотношениям,
что и Cl (z).
Соотношение между D^(z) и C^(z)y аналогичное соотношению Кристоф-
феля между Qn (z) и Рп (z) (см. 3.6B4), 3.6B8)), дано Ватсоном (Watson, 1938)
C3)
3.16. Некоторые другие обозначения
Множитель ещ>к в определении Q^ (z) 3.2E) часто опускают (Мак-Роберт).
В определении Q^ (z), данном Бернсом, множитель ег^п в 3.2(8) заменен
кроме того, множитель е^к в левой части равенства 3.4B) опущен.

Присоединенные функции Лежандра по Феррару (MacRobert, 1947,
стр. 307) обозначаются Т^(х) и тождественны Р^(лг) (—1<л:<1).
Иное обозначение для функций Гегенбауэра было использовано Чу и
Стреттоном (Chu, Stratton, 1941). Вместо D) и C2) имеем соответственно
Эти функции удовлетворяют следующему дифференциальному уравнению:

ГЛАВА 4
ОБОБЩЕННЫЙ ГИПЕРГЕОМЕТРИЧЕСКИЙ РЯД
4.1. Введение
Гипергеометрический ряд Гаусса F(a, 3; с; г) может быть обобщен путем
введения р параметров, играющих ту же роль, что а и Ь, и q параметров,
играющих ту же роль, что с. При этом получается ряд
A)
который называют обобщенным гипергеометрическим рядом. Ряд Гаусса
в этих обозначениях имеет вид
Зцесь
B)
и г — комплексное переменное. Вообще говоря (то есть за исключением
некоторых целых значений параметра, для которых ряд состоит из конечного
числа членов или не имеет смысла), ряд pFq сходится для всех конечных
ей ес р ^ сс р |z|cl ес р q \ \
), р pq
значений z, если р ^q, сходится при |z|<cl, если р = q -\- \, и расходится
при всех г ф. О, если р >> q -f- 1.
Числа ах, ... , ар называют параметрами числителя, а числа рх, ... , р^—
параметрами знаменателя.
Ряды pFq не являются единственными обобщениями ряда Гаусса.
Гипергеометрическое уравнение есть линейное дифференциальное уравнение типа
Фукса, в то время как ряд A) удовлетворяет линейному дифференциальному
уравнению, которое, вообще говоря, не является уравнением типа Фукса.
Таким образом, дифференциальные уравнения можно использовать, чтобы
ввести другое обобщение, которое является решением уравнения типа Фукса
высшего порядка. В связи с этим Л. Похгаммер A870) изучил наиболее
общее однородное линейное дифференциальное уравнение я-го порядка
с особыми точками а1У а2, ... , аю оо такое, что общее решение в
окрестности любой особой точки tfv (v=l, 2, ... , п) имеет вид

где с0, cv ... , сп_2 и с'о — произвольные постоянные. Аналогично
разложение общего решения при больших значениях г имеет вид
где g01 ... , gn_2 и g'o — произвольные постоянные. Можно показать, что
дифференциальное уравнение однозначно определяется этими требованиями.
Исходной точкой иного обобщения является s-функция Шварца (см. 2.7.2),
которая отображает полуплоскость на треугольник, образованный тремя
дугами окружности. Коппенфельс (Koppenfels, 1937, 1939) изучил функции,
отображающие на полуплоскость область, ограниченную четырьмя дугами
окружности, такую, что два из углов криволинейного четырехугольника
ТС у Л Зл у Зп Зл
равны -у, а другие два либо -г и у, либо "о" и ~9~*
Райт (Е. М. Wright, 1935, 1940) изучил асимптотическое поведение
суммы
при больших значениях \z\. Здесь (Зг и ^ — вещественные положительные
числа такие, что
Если все р./ и рг равны единице, этот ряд отличается от pFq лишь
постоянным множителем.
Гипергеометрические ряды Гейне будут изучены в п. 4.8. Дальнейшие
обобщения см. в гл. 5.
На протяжении этой главы будут соблюдаться следующие условия:
Значения q параметров рь ... , р^ в pFq отличны от 0, — 1, —2, ...
Если переменная г в q+1Fq не равна единице, то предполагается, что
И<1.
Если переменная г в q+lFq равна единице, то мы предполагаем
Если переменная г в pFq равна единице, она будет опускаться.
4.2. Дифференциальные уравнения
Функция pFq определена равенством 4.1A). Этот ряд был введен Клаузе-
ном (Clausen, 1Б28) для случая р = 3, q = 2. Обозначение введено Похгам-
мером и модифицировано Бернсом. Если одно из чисел аг является целым
неположительным, то ряд состоит из конечного числа членов (случаи, когда
одно из р^ является целым неположительным, исключены).

Если р = q -f- 1 и
0)
то ряд 4.1A) при s > 1 сходится на всей окружности | г \ = 1. Если 1 :> s > О,
он сходится при всех г таких, что | г | = 1, г ф 1, а если s^<0, то
расходится на всей окружности |2| = 1. Доказательство аналогично тому, которое
приведено в 2.1.1 для 2FV
Пусть 5 означает оператор 2--. Тогда функция u=pFq удовлетворяет
дифференциальному уравнению
B)
которое эквивалентно общему уравнению вида
C)
ИЛИ
D)
где ап, Ьп — постоянные, апф0 и D = — Для уравнения C) 2 = 0 и
2 = оо— особые точки, причем 2 = 0— правильная особая точка (см. Уитте-
кер и Ватсон, 1961, п. 10.3). Уравнение D) является уравнением типа Фукса
с правильными особыми точками 0, оо, 1. О множестве линейно независимых
решений в окрестностях точек 2 = 0 и 2 = оо см. п. 5.4. Здесь, как и в
большей части литературы, рассматривается лишь общий случай, когда ни одно
из чисел р^ и ни одна из разностей рг— р0, ar — as (rzfis) не являются
целыми числами.
В случае p^q Берне (Е. W. Barnes, 1906) дал асимптотическое
разложение для решений B) в «общем» случае (см. выше). Похгаммер (L. Pochhammer,
1893b) рассмотрел различные формы уравнений B) и C) и дал полное
множество линейно независимых решений в виде кратных интегралов. В частности,
случаи # = 3 и q — 4 (p^q) были изучены Похгаммером (Pochhammer,
1893а, 1895, 1898).
В случае p = q + 1 Похгаммер (Pochhammer 1888b) изучил уравнения B)
и D) в общем случае и указал кратные интегралы, которые являются
решениями в окрестностях точек 2 = 0, оо, 1. Он указал также, что существуют/?
линейно независимых решений, которые однозначны в окрестности точки
2 = 1. Для /7 = 3, q = 2 это было доказано Гурса (Е. Goursat, 1883, 1884).
Томе (Thomae, 1896) указал связь между полными множествами линейно
независимых решений в точках 2 = 0 и z = oo при/? = 3, q = 2. Это было
сделано при всех значениях p(=q-\-\) Смитом (F. С. Smith, 1938, 1939),
который изучил также различные частные случаи, когда некоторые из
решений уравнений B) и D) выражаются через логарифм (все или некоторые из
разностей р^ — р5 могут быть целыми, но р^ — аи сами р^ не являются целыми;
все или некоторые разности аг — as — целые, но аг — р^ и сами аг не являются
целыми).
Если v(z) удовлетворяет уравнению B) и если эта функция может быть
выражена как преобразование Лапласа аналитической функции w (t) такой,

что lim w(t) = 0,
то w (t) удовлетворяет дифференциальному уравнению
E)
О других результатах, касающихся дифференциальных уравнений, которым
удовлетворяют функции, выражаемые обобщенными гипергеометрическими
рядами, см. Chaundy, 1943.
4.3. Тождества и рекуррентные соотношения
Клаузен (Т. Clausen, 1828), доказал, что
A)
Он показал, также, что это — единственный случай, когда квадрат F(a, Ь\ с; z)
выражается в виде функции bF2 от аргумента z. Более общий результат
получен Э. Гурса (Е. Goursat, 1883). Он доказал, что F(a, Ь\ с; z)F(a', b'\ c'\ z)
является функцией pFq аргумента z лишь тогда, когда либо
а' = а -\- 1 — с, Ь' = Ь -\-1 — с, с' = 2 — с,
с~а~Ь = п + ~1 л = 0, ±1, ±2, ...,
либо а — а\ Ь — Ъ', с — с' — целые и с -\- с' — а — а' — Ъ — Ь' = п, где я = 0,
1, 2, ...
В. Н. Бейли (W. N. Bailey, 1928) дал новое доказательство для этого и
аналогичных результатов Орра, Приса (Огг, Ргеесе, 1924) и Рамануджана и
дополнил их некоторыми новыми формулами. Имеем
B)
C)
D)
E)
F)

(8)
(9)
Ряд в формуле D) сходится лишь в случае, когда а или {J являются
неположительными целыми, но формула D) формально справедлива для всех
значений а, р в том смысле, что при формальном перемножении степенных
рядов в левой части равенства получается правая часть равенства.
Остальные формулы справедливы по крайней мере, если |г|<1.
Соответствующие формулы Кели и Орра (см. 2.5D)) можно найти у Бейли
(Bailey, 1935). Следующая формула принадлежит Дарлингу (Н. В. С. Darling
1932) (см. также Bailey, 1935):
-\- произведение,
получаемое перестановкой 8 и г. A0)
Другие результаты, связанные с тождествами Кели и Орра, см. в п. 2.5.2
и Burchnall, Chaundy, 1948. Большое число разложений гипергеометрических
функций в ряды по другим гипергеометрическим функциям было получено
Ченди (Т. W. Chaundy, 1942, 1943). Простейшими случаями являются:
(И)

A2)
A3)
A4)
A5)
Ряды в формуле A5) расходятся, за исключением случая, когда они состоят
из конечного числа членов. Однако коэффициенты при соответствующих
степенях z в обеих частях равенства совпадают.
Две функции pFq называются смежными, если их аргументы и параметры
имеют одни и те же значения, за исключением одного параметра, значения
которого могут отличаться на ± 1. Существуют 2р-\-q линейно независимых
линейных соотношений между фиксированной функцией pFq и ее 2 (р -\- q)
смежными функциями. Коэффициенты этих соотношений являются линейными
функциями переменного и многочленами от параметра. Эти соотношения
были получены Е. Рейнвиллом (Е. Rainville, 1945) для случая, когда все
параметры знаменателя отличны от 0, —1, —2, ... и + 1
4.4. Обобщенный гипергеометрический ряд, аргумент
которого равен единице в случае p = q-\-l
Стандартные типы обобщенных гипергеометрических рядов. Если
параметры q+1Fq (аг; р^; г) таковы, что
A)
то ряд называют рядом вида Заальшютца. Если
B)
то ряд называют вполне уравновешенным. Если все равенства в B), за
исключением одного, выполняются, то ряд называют почти уравновешенным.
Тогда, не меняя самого ряда, можно упорядочить параметры так, чтобы
нарушение равенства сумм пары параметров встретилось или для первой
или для последней пары; соответственно этому ряд q^\Fq называют почти
уравновешенным первого или второго рода соответственно.

Теорема Заальшютца
* = <>, 1, 2, ..., C)
которая была доказана в п. 2.1.5 (см. 2.1 C0)), позволяет вычислить сумму
любого конечного ряда BF2 вида Заальшютца. Для бесконечных рядов BF2
вида Заальшютца имеем (Saalschutz, 1891, Bailey, 1935, стр. 21)
D)
Эта формула является частным случаем большого числа линейных
соотношений между тремя рядами SF2, полное исследование таких соотношений
имеется у Бейли (Bailey, 1935, гл. III).
Каждый вполне уравновешенный ряд 3F2 при г = 1 может быть
просуммирован с помощью гамма-функций. Результат имеет вид
E)
Это — теорема Диксона (см. Dixon, 1903; Watson, 1924; Bailey, 1937;
MacRobert, 1939). Кроме того 8F2 может быть вычислено при г = 1 в
следующих случаях:
(б)
(теорема Ватсона, см. Whipple, 1925) и
G)
(теорема Уаппла, см. Whipple, 1925).

Теорема Дуголла позволяет просуммировать конечный вполне
уравновешенный ряд 7Fe ПРИ 2=1 и специальных значениях второго параметра:
(8)
где \+2a = b + c + d + e — п и /i = 0, 1, 2, ... (Dougall, 1907).
Существует целое семейство преобразований ряда g+iFg при 2 = 1, то
есть формул, позволяющих выразить один из таких рядов через один или
несколько других (часто при других значениях q). Простым примером
является соотношение
(9)
которое позволяет преобразовать обрывающийся почти уравновешенный
ряд 4FS второго рода в bF4. Об этом и других более сложных результатах
см. Bailey, 1935, гл. Ill— VI; Whipple, 1935, 1937; MacRobert, 1939; Mitra, 1942;
Bose, 1944.
4.5. Преобразования q+1Fq при значениях аргумента,
отличных от единицы
В общем случае q>\ не известно никаких линейных преобразований
для g+iFgt за исключением связи между обобщенными гипергеометрическими
рядами от аргументов г и г, которые являются решениями одного и того
же дифференциального уравнения (см. Thomae, 1869; F. С. Smith, 1938, 1939).
В некоторых случаях существуют квадратичные и кубичные
преобразования для sF2i например
A)
(Whipple, 1927) и
B)

Эта формула была доказана Бейли (Bailey, 1929). Бейли указал также
линейное преобразование почти уравновешенной функции BF2 первого вида:
C)
Берчнелл (Burchnall, 1948) доказал, что вполне уравновешенная функция
BF2 аргумента х может быть выражена как сумма рядов BF2 аргумента
AJ
Ах '
В некоторых случаях q+1Fq можно вычислить для аргумента, не равного
единице, например
D)
(см. Bailey, 1935, стр. 28, а также Bailey, 1929).
Некоторые частные случаи: формулы, выведенные в п. 4.4 и в этом
пункте, содержат большое число результатов, которые трудно было бы
установить непосредственно и которые были уже давно отмечены в литературе.
Например, 4.4E) дает (при а = Ь = с = —п)
E)
Если подставить в 4.4(8) Ь = \ -\- а-\- п и перейти к пределу при я—+оо,
ПОЛ}ЧИМ
(в)
Специальным случаем этого равенства является формула Дуголла — Ра-
мануджана
G)

которая имеет место при Re (х-\-у + 2+ 1) >0. Другим следствием
формулы F) (при я = 1, с = \—ху d = e = \) является
(8)
Ряд в левой части равенства сходится, если Rex>l. Много результатов
для других частных случаев указаны Бейли (Bailey, 1935, примеры на
стр. 96, 97) и Харди (Hardy, 1923).
Усеченный гипергеометрический ряд
можно двумя различными способами выразить через 3F2:
Если 2 = 1, имеем
(см. Bailey, 1935, стр. 93, 94). Соответствующие формулы существуют для
усеченного ряда 8F2 и для специальных усеченных рядов 7FQ при г = 1
(см. Bailey, 1935, стр. 94, 95).
4.6. Интегралы
Интегралы, аналогичные интегральному представлению Эйлера в п. 2.1.3,
были получены для случая общего гипергеометрического ряда pFQ Похгам-
мером (Pochhammer, 1893b), Эрдейи (Erdelyi, 1937) (см. также 5.2B)) и
Б. Г. Певным A940) для интегральных соотношений вида 2.4B).
Распространение интегрального представления Бернса 2.1A5) на случай общего ряда
pFg может быть выведено из результатов п. 5.3 и 5.6.
Многие определенные интегралы могут быть выражены через один или
несколько рядов pFq. Например, преобразование Лапласа pFqi р ^ я, есть

Формула Ченкера (Shanker, 1946) дает преобразование Ганкеля для
где
Другие частные результаты можно найти в п. 4.7 и у Эрдейи (Erdelyi, 1938).
4.7. Некоторые частные результаты
Г. Бейтмен (Н. Bateman, 1933, 1934) и Пастернак (Pasternack, 1939)
исследовали многочлены от г вида
Бейтмен (Bateman, 1936) изучил многочлены Zn(z) и J%'v(z), определяемые
равенствами
Результаты Бейтмена были обобщены Пастернаком (Pasternack, 1937) и
Райсом (S. О. Rice, 1939). Последний ввел функцию
где п = 0, 1, 2, ... и ?,/?, v — комплексные переменные, причем р ф — п — 1,
— п — 2, ... Райе установил, что

Производящая функция для Нп имеет вид
Если Qn (г) определено равенством 3.6B4), то
Если п—> со, то асимптотическое выражение для Нп(%, р, 1) имеет вид
Рейнвилл (Rainville, 1945) дал рекуррентные соотношения для функций J%v
и показал, что функции Нп (?, /?, v) удовлетворяют рекуррентному
соотношению, которое содержит четыре члена
Фазенмайер (М. С. Fasenmyer, 1947) доказала, что
и изучила многочлены
Производящая функция для этих многочленов имеет вид
где
О рекуррентных соотношениях, рядах и интегралах, содержащих fn,
см. Fasenmyer, 1947, а также Chaundy, 1943. Простым частным результатом
является интегральное представление для функции Бейтмена Zn (z):

где Ln(z) означает п-й многочлен Лагерра (см. гл. 10), и
Эрдейи (Erdelyi, 1938) доказал разложение
где
Это разложение справедливо при 11 | > 1, | z | < 1, [л ф 0, ±1, ±2, ...
Кралл и Фринк (Krall, Frink, 1949) изучили класс многочленов уп(а, z).
Согласно Рейнвиллу, они могут быть записаны в виде
где я = 0, 1, 2, ... и а—1^0, —Ь —2, ... Функции уп (a, z) являются
ортогональными многочленами на единичной окружности,
соответствующими весовой функции
Они могут быть выражены через функции Уиттекера W^ ^ (z) (см. 6.9E))
в виде
О рекуррентных соотношениях, дифференциальном уравнении и других
результатах для уп (a, z) см. Krall, Frink, 1949.
4.8. Базисные гипергеометрические ряды
Приведенное ниже изложение теории базисных обобщенных
гипергеометрических рядов следует гл. 8 книги Бейли (Bailey, 1935). Пусть q —
параметр, принадлежащий области \q\ < 1. Введем для всех а и q
обозначения
A)
B)

(В литературе более принято обозначение [а]п для (а) п где явно не
участвует q.)
Тогда
C)
является функцией от г и г + s + l параметров а1У ..., ar; pt, ..., р5; q,
которая сводится к
если r = s+l и q—*1. Функция 2ФХ была впервые изучена Гейне (Е. Heine,
1878, стр.97—125); ГФ5 называют базисным гипергеометрпческим рядом.
По-видимому, представляет интерес лишь случай r = s + l. О базисных
гипергеометрических рядах двух переменных см. п. 5.14.
Простейшим случаем является ряд jOq (a; z\ обобщающий
биномиальный ряд. Можно показать, что
D)
и поэтому
(см. Bailey, 1935, стр. 66). Другими элементарными случаями являются
F)
G)
(8)
Если разделить равенство (8) на Yz и заменить q, z на qs, q exp Bi
где х вещественно, то мнимая часть ряда дает

где sn и означает эллиптическую функцию Якоби модуля k, a k, К и q
связаны соотношениями
(9)
A0)
Этот результат есть часть теории эллиптических тета-функций, см. гл. 11.
Многие из результатов теории обобщенных гипергеометрических рядов
имеют аналоги в теории базисных гипергеометрических рядов. Это
справедливо, в частности, для теорем о вполне уравновешенных рядах. Аналогом
теоремы Дуголла является теорема Джексона
(И)
где bcde = a2qN~^1 и N = I, 2, 3, ... Из-за присутствия в стоящей слева
функции четырех элементов qYai —qVai Vai —Vа общий член ряда со-
1 —— ап^^
держит множитель —:—-—. Другой важный результат (аналогичный
теореме Уиппла) был доказан Ватсоном (Watson, 1929)
A2)
где ряд справа конечен, а слева сходится. Более общие результаты есть у
Бейли (Bailey, 1935, 1936, 1947а, b, 1948a, b). Анализ состояния теории
также дан Бейли A947а, 1948b).

Среди следствий равенства A1) отметим базисные аналоги теорем Зааль-
згаа 4.4C). Гаусса 2.U14) и 2.9 B). Именно
шютца 4.4C), Гаусса 2.1A4) и 2.9B). Именно
Большое число тождеств может быть выведено из A2). Среди них
укажем тождество Эйлера
тождества Роджерса — Рамануджана
и результат Гаусса
Доказательства и другие результаты см. у Бейли (Bailey, 1935).
Базисный аналог формулы Куммера 2.8D7) был доказан Даумом (Da
um, 1942). Результат имеет вид
где

ГЛАВА 5
ДАЛЬНЕЙШИЕ ОБОБЩЕНИЯ ГИПЕРГЕОМЕТРИЧЕСКОЙ
ФУНКЦИИ
5.1. Различные обобщения
Изучение классического гипергеометрического ряда
о)
стимулировало изучение многих функций и рядов. Эта глава посвящена тем
обобщениям, которые обычно рассматривают как гипергеометрические
функции. Другие обобщения, например функции Матье и Ламе, будут изучены
в дальнейших главах.
Обобщенный гипергеометрический ряд
B)
где
C)
а параметры таковы, что по крайней мере одно из определений C) имеет
смысл, был изучен в гл. 4. Здесь будем рассматривать B) как формальный
степенной ряд, не обращая внимания на то, сходится он или нет.
Обычно определяют наиболее общий (формальный) гипергеометрический
ряд как формальный степенной ряд, такой, что отношение двух
последовательных коэффициентов является (фиксированной) рациональной функцией
индекса. Более точно
D)
где Р и Q — многочлены; мы предполагаем, что
где Qj — такой многочлен, что Р(п) и Qi(ft-j-l) не имеют общих
множителей. Степени многочленов Р и Qj равны соответственно р и q. Разложение
Р и Qj на линейные множители позволяет выразить D) с помощью символа

pFq, так что, по сути дела, B) является наиболее общим (формальным)
гипергеометрическим рядом.
Дифференциальное уравнение, которому удовлетворяет ряд D), может
быть записано с помощью дифференциального оператора
E)
Мы имеем Ьхп = пхп, и поэтому для любого полиномиального оператора
с постоянными коэффициентами /'E) хп = /\п) хп\ Таким образом, ряд D)
удовлетворяет дифференциальному уравнению
F)
порядок которого равен max(/?, q-\-1) и особыми точками при рфц\
являются 0 и сю, а при р —q-\-\ —точки 0, оо и некоторая третья
конечная точка.
Для обобщенной гипергеометрической функции возникают две задачи:
1) интерпретировать B), если p>>q-\-\ и ряд расходится для любого хфО,
и 2) найти фундаментальную систему решений уравнения F) в окрестности
каждой особой точки.
Другие обобщения связаны с базисными гипергеометрическими
функциями, о которых см. гл. 4.
Гипергеометрические функции двух или большего числа переменных
определяются точно так же (см. п. 5.7).
^-ФУНКЦИЯ МАК-РОБЕРТА
6.2. Определение ^-функции
^-функция Мак-Роберта возникла в связи с попыткой придать смысл
символу pFg при р > q -f-1. Когда р ^ q -f- 1, полагаем
где х ф О, если р < #, и | х | > 1, если р = q -\-1.
"~" "^ " ' 1 полагаем
B)
где | х | < 1, если р = q -\- 1. Штрих у произведения означает, что
опускается множитель Г (аг — аг), звездочка в F означает, что опускается
параметр аг — аг -\- 1; пустое произведение интерпретируется как единица;
нулевые и целые отрицательные значения аг исключаются. Будем предполагать

на протяжении всей главы, что эти условия выполнены. Асимптотическое
разложение для B) при х-»оо,
дается правой частью равенства A). Первоначально (MacRobert, 1937 —
1938) ^-функция была определена с помощью кратного интеграла
C)
где | arg x \<Zn, p ^ q -\-\ и аг и р5 таковы, что интеграл сходится. Можно
доказать эквивалентность определений B) и C) (MacRobert, 1937—1938).
Родственными функциями являются Р-функция, которая получается,
если записать B) в виде
D)
а также две другие функции Q и Я, связанные соответственно с Р и Е
(MacRobert, 1937—1938). Функцию Е (р; ar : q; p5 : х) обозначают также
Многие частные случаи ^-функции возникают из ряда A) с помощью
формул, изученных или указанных в гл. 4. Из B) и C) .также вытекают
некоторые интересные частные случаи. Среди них наиболее важными
являются выражение модифицированной функции Бесселя третьего рода
E)
(MacRobert, 1937—1938, формула A2)) и ^-функции Уиттекера
F)
(MacRobert,-1941, формула B5)). Следует отметить, что функция Wk,m(ix)X
X Wfjim (— ix) также может быть выражена через ^-функцию, равно как
и другие комбинации (MacRobert, 1941, A5)). Сама ^-функция является
частным случаем (/-функции Мейера (см. 5. 6B)).
5.2.1. Рекуррентные соотношения. Основная система рекуррентных
формул была дана Мак-Робертом (MacRobert, 1941, равенства B0)—B4)).

Тремя наиболее важными формулами являются
G)
(8)
(9)
5.2.2. Интегралы. Многие интегралы, содержащие гипергеометрические
функции, могут быть выражены через ^-функцию. Типичным примером
(MacRobert, 1937—1938, формула B1)) является
A0)
Эта формула может быть доказана путем подстановки
в левую часть равенства и применения равенства C).
Интеграл
может быть вычислен с помощью интегрирования в комплексной области.
Интегрирование ведется вдоль контура, ограничивающего прямоугольник
с вершинами 0, 1, 1 + ik, ik (k > 0). В этом контуре сделаны вырезы в
точках 0 и 1, после чего радиусы вырезов устремляются к нулю, a k — к
бесконечности и применяется равенство A0) (MacRobert, 1937—1938, B3), там
же указаны многие другие интегралы).
Интегралы, содержащие ^-функцию, были изучены Мак-Робертом (Mac-
Robert, 1941). Наиболее важными являются интегралы типа Эйлера и
Лапласа, однако, кроме них, есть многие более общие интегралы. Типичными
примерами являются
A2)
A3)

Если p = q-\-\} то равенства верны при условии, что точка % = х лежит
внутри петли; если р < q или р = q и х > 1, правая часть сводится к
A4)
Доказательство этих формул основано на определении ^-функции;
формулы A), B) или C) применяются в зависимости от значений р и q.
Q-ФУНКЦИЯ МЕЙЕРА
5.3. Определение G-функции
(/-функция Мейера, так же как и ^-функция Мак-Роберта, возникает при
интерпретации символа pFq, где/? ># + 1, и не противоречит
интерпретации, даваемой ^-функцией. При этом все важные частные решения
гипергеометрического дифференциального уравнения 5.1 (б) могут быть выражены
с помощью G-функции.
Первоначально (Meijer, 1936) G-функция была определена способом,
напоминающим 5.2B). Позже (Meijer, 1941b, 1946) это определение было
заменено определением с помощью интеграла типа Меллина — Бернса (см. 1.19).
Последнее определение предпочтительнее, поскольку оно оставляет
большую свободу выбора значений р и q. Здесь мы дополним определение
Мейера, так чтобы оно охватывало все значения р и q без каких-либо
(нетривиальных) ограничений на т и п.
Определим
A)
где пустое произведение интерпретируется как 1, 0 ^tn^q, O^n^p и
параметры таковы, что полюсы Г(bj—s), / = l,...,m, не совпадают ни с
одним полюсом ГA — tf? + s)> k = 1,..., п. Будем предполагать, что эти
ограничения всегда выполнены. В тех случаях, когда это не приведет к
недоразумению, будем для краткости писать
и даже G(x).
Для пути интегрирования L возможны три различных варианта.
Во-первых, путь L можно выбрать так, что он идет от
— /со до + *°°> оставляя все полюсы функций Г (bj—s),
] = 1,..., m, справа, а все полюсы функций Г A —ak -f- s), k = лп
= 1, n, слева. Интеграл сходится, если р ~f- q < 2 (т -f- п) к '
и | аг§ х | < ((т + п — -^ р — ^ <7J п.

Во-вторых, в качестве L можно взять петлю,
начинающуюся и оканчивающуюся в точке -\-со и охватывающую все
полюсы функций Г (bj— s), j = 1,..., m, в отрицательном на- /g\
правлении, но не охватывающую ни одного полюса функций
Г A — ak -)- s), k = 1,..., п. Интеграл сходится, если g^l и
либо p<q, либо р = q и | х \ < 1.
Наконец, в-третьих, в качестве L можно взять петлю,
начинающуюся и оканчивающуюся в точке — оо и охватывающую все
полюсы функций Г A — а,ъ + s), k = 1 ,... , п, в положительном ,,>.
правлении, но не охватывающую ни одного полюса функций ^ '
T(bj—s), j = 1, ..., т. Интеграл сходится, если /? :> 1 и либо
p>q, либо p = q и |*| > 1.
Мы будем в дальнейшем предполагать, что значения параметров и
переменной х выбраны так, что хотя бы одно из трех определений B)^ C) и D)
имеет смысл. В случае, когда имеют смысл несколько определений, они
приводят к одинаковым результатам, так что не может возникнуть никаких
недоразумений.
Сг-функция является аналитической функцией от х. Она симметрична
относительно параметров аи ..., ап, равно как и параметров an + li ..., ар,
Ьъ ..., Ьт и ?т+1, ..., Ьд.
В соответствии с C) интеграл может быть вычислен как сумма вычетов.
Если никакие два значения bj, 7 = 1, ..., tn, не отличаются на целое число,
то все полюсы являются полюсами первого порядка и
E)
р < q или р = q и | х \ < 1.
Точно так же, если никакие два а^ k= 1, ..., п, не отличаются на целое
число, то из D) следует
F)
<7</? или q=p и |лг|>1.
В этих разложениях предполагается, что выполнены условия,
соответствующие условиям для 5. 2 B).

5.3.1. Простые тождества. Если одно из ар у = 1, ..., п, равйо одному
из bp j = т -\-1, ..., q (или одно из Ь-р у==1, ..., /я, равно одному из
аР 7 = ^+1» -•, р), то G-функция сводится к функции меньшего порядка:
р, q и п (или р, q и гп) могут быть уменьшены на единицу;
G)
является такой формулой приведения, остальные формулы ей подобны.
Очевидно, что замена переменной в интеграле A) дает
(8)
(9)
A0)
В равенстве A0) была использована формула удвоения для Г-функции.
Существует соответствующая формула, в которой используется теорема
умножения 1.2A1) для Г-функции.
Наиболее важной из этих формул является формула (9), поскольку она
позволяет преобразовать G-функцию, для которой р > q, в функцию, где
p<.q. Поэтому, не теряя общности, можно считать p^q. Примерами
Других почти очевидных соотношений являются
(И)
A2)
A3)

A4)
5.4. Дифференциальные уравнения
Из 5.3A) следует, что G(x) удовлетворяет линейному
дифференциальному уравнению
A)
Ясно, что любое уравнение вида 5. 2 F) может быть сведено к этому виду
путем замены переменной. Порядок уравнения A) равен max (p, q), причем
из 5.3(9) следует, что можно считать р ^ q. Решения уравнения A) были
изучены Мейером (Meijer, 1946).
Если р <С qy то у уравнения A) только две особые точки: х —0, оо;
х — 0 является правильной особой точкой, х = со— неправильной.
Фундаментальная система q линейно независимых решений уравнения A) в
окрестности точки х = О состоит из функций
B)
В окрестности неправильной особой точки переменную х надо
рассматривать в секторе. Мейер определяет два целых числа k и g так, что
C)
И
D)
при /г=?, g + 1, ... , g + q— p — 1, где & = ^' если ^==^+1' и ?=zil>
если q^p-\-2. Тогда, если х лежит в секторе, определенном
неравенствами C) и D), р функций
Л = 1, ... ,/?, E)
и q —р функций
b=g,g+l g + q-P + h F)
образуют фундаментальную систему решений уравнения A).

р = #, то точка х = со также является правильной особой точкой
и, при условии C), фундаментальная система определяется функциями
E). В этом случае х = (—\)Р-т-п также является правильной особой
точкой, однако в литературе не указано фундаментальной системы в
окрестности этой точки.
Еслир>#, то можно использовать 5.3 (9) для того, чтобы свести
дифференциальное уравнение к рассмотренным здесь случаям; х = 0 и х = оо
меняются ролями.
Во всяком случае, из равенства A) ясно, что при любых фиксированных
р, q, а1} ..., ар, bv ..., bq все (р + \)(q + 1) функций
G)
удовлетворяют одному и тому же дифференциальному уравнению.
5.4.1. Асимптотические разложения. Будем предполагать, что р ^ q,
результаты для р > q могут быть получены с помощью формулы 5.3 (9),
если поменять ролями точки х = 0 и х —оо. Некоторые целые значения
комбинаций параметров исключаются, равно как и некоторые другие случаи,
например случай, когда коэффициент главного члена асимптотического
разложения равен нулю.
Точка х = 0 является особой точкой дифференциального уравнения A),
и поведение G(x) в окрестности этой точки следует из 5.3E). Имеем
при х-*0, (8)
rjxep^q Hp = minRe^ при Л = 1, 2, ..., т. Точка л: = со является
неправильной особой точкой для уравнения A), а потому поведение G(x) при
х—*оо имеет значительно более сложный характер. Изучение этого
поведения было начато Бернсом (Barnes, 1907 и другие статьи), продолжено
многими авторами (среди них Мак-Роберт (MacRobert, 1937—1938)) и закончено
Мейером (С. S. Meijer, 1946). Детальные результаты слишком сложны,
чтобы излагать их здесь, и мы ограничимся лишь кратким резюме (Meijer,
1946, § 18).
Если х—> оо, то G-функция растет, как степенная функция, если р <С q и
(9)
или если
q=zp-\-\, k — некоторое целое и
A0)
Если же при х—>оо и p<.q будет
то G-функция экспоненциально убывает. При тех же условиях относительно
х} р и q (/-функция имеет экспоненциальный рост в следующих областях:
Если q~>zp-\-% то следует взять либо
(i) и A2)
либо
(ii) причем на arg x не накладывается ограничений.

Если #=/?-|»1> то пусть к— целое число, причем
В этом случае следует взять либо
(О A3)
либо
(ii) причем нет ограничений на целое число к.
Если p = q} то из 5.3F) следует, что функция при х-+со имеет
степенной рост.
Более полные и детальные результаты см. у Мейера (Meijer, 1946, § 18).
5.5. Ряды и интегралы
Среди различных функциональных соотношений для (/-функции наиболее
важными являются ряды и интегралы. Изучено сравнительно мало рядов
(/-функций; число же известных интегралов весьма значительно. Здесь будет
приведено лишь несколько примеров. Более детальные результаты имеются
в оригинальных статьях, большей частью принадлежащих К. С. Мейеру.
5.5.1. Ряды (/-функций. Первую группу разложений по (/-функциям
образуют четыре теоремы умножения (Meijer, 1941b)
О)
B)
C)
D)
которые выражают G (кх) в виде бесконечных рядов по G (х). Если р <.q и
/я = 1, то ограничение (X — 1) <с 1 в равенстве A) может быть опущено.
Аналогичное замечание применимо к C), если я=1, p>q.
Вторую группу рядов образуют так называемые формулы разложения
(Meijer, 1946). Они служат для того, чтобы выразить (^-функции в виде ли-

нейной комбинации С/-функций с теми же значениями р и q> но с другими т
и л, и весьма полезны при изучении решений дифференциального уравнения
5.4A). Например, четыре формулы разложения (Meijer, 1946, теорема 5)
выражают G™ в виде линейной комбинации v функций вида G^lq, p. функций
вида Gp'gl~l и еще к — (х — v функций того же типа при соответствующих
ограничениях на k, /, т, п, р> q, [a, v.
5.5.2. Интегралы, содержащие (/-функции. Наиболее важными
интегралами являются те, которые выражают свойства С/-функций
относительно интегральных преобразований. Преобразование Эйлера задается
формулой
E)
Если
G)
то E) следует из 5.3A), а если р < q (или p = q и | х \ < 1) и выполнено
условие G), то из 5.3E). Если а равно одному из чисел Ьп+1, ... , bq или р
равно одному из чисел alf..., ап> то E) приводит к важному
функциональному уравнению для G™q.
Поведение G™q при преобразовании Лапласа вытекает из формулы
(8)
справедливой, например, при условиях F) и G), причем часть, относящаяся
к р, может быть опущена.
Поведение С/-функции при преобразовании Меллина видно из 5.3A)
с условием 5.3B). Некоторые интегралы от произведений С/-функций могут
быть вычислены с помощью теоремы о свертке для преобразований
Меллина и Лапласа. Некоторые такие интегралы были вычислены Мейером
(Meijer, 1936). Мейер указал также обобщение формулы E).
Преобразование Ганкеля задается формулой
(9)

справедливой, например, при условиях F) и
A0)
Во всех этих формулах введение контурных интегралов позволяет
ослабить ограничение на а (или на р в E)). Возможны и другие условия
справедливости преобразования Ганкеля, но, за исключением некоторых случаев,
рассмотренных в работах Мейера, полного исследования не проведено.
Последний интеграл, содержащий (модифицированную) функцию Бесселя,
имеет вид
(И)
Эта формула справедлива, например, при условиях (б) и
A2)
Более слабые условия были даны в частном случае Мейером (Meijer, 1936,
равенство E8)).
5.6. Частные случаи G-функции
Очевидно, что
Сравнивая с 5.2B) и 5.3E), получаем
B)
Важность (/-функции в значительной степени связана с возможностью
выразить через (/-символ большое число специальных функций, встречаю-

щихся в прикладной математике. Поэтому каждая формула, выведенная для
С/-функции, является образцом, по которому можно получить большое число
соотношений для функций Бесселя, Лежандра, Уиттекера, для их комбинаций
и родственных им функций. Для этого можно использовать следующий список
частных случаев С/-функции, составленный на основе многочисленных работ
Мейера:
C)
D)
E)
F)
G)
(8)
(9)
A0)
A2)

A3)
A4)
A5)
A6)
A7)
A8)
A9)
B0)
B1)
B2)
B3)

B4)
B5)
B6)
B7)
B8)
B9)
C0)
C1)
C2)
C3)
C4)
C5)
C6)

C7)
C8)
C9)
D0)
D1)
D2)
D3)
Следующие комбинации специальных функций могут быть выражены через
G-функцию:
D4)
D5)

D6)
D7)
D8)
D9)
E0)
E1)
E2)
E3)
E4)
E5)
E6)

E7)
E8)
E9)
F0)
F1)
F2)
F3)
F4)
F5)

F6)
F7)
F8)
F9)
G0)
G1)
G2)
G3)

G4)
G5)
В работах Мейера можно найти много аналогичных формул, в частности,
формулы для функций Лежандра и для многих обобщений
гипергеометрической функции.
ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
5.7. Гипергеометрические ряды двух переменных
Большие успехи в изучении теории гипергеометрического ряда одного
переменного стимулировали развитие соответствующих теорий для рядов от
двух или многих переменных. Аппель определил в 1880 г. четыре ряда
Ft— Fi (см. ниже равенства F) — (9)), каждый из которых аналогичен ряду
Гаусса F(a, fj, f, x). Пикар указал, что один из этих рядов тесно связан
с функцией, изученной Похгаммером в 1870 г., а Пикар и Гурса построили
теорию рядов Аппеля, которая аналогична теории Римана для гауссовского
гипергеометрического ряда. Гумберт изучил вырожденный
гипергеометрический ряд двух переменных. Изложение этих результатов французской школы
со ссылками на оригинальную литературу содержатся в монографии Аппеля
и Кампе-де-Ферье (Appell, Kampe de Feriet, 1926), которая является
основным трудом в этой области. Эта работа содержит также обширную
библиографию, содержащую все существенные работы до 1926 г. Список работ,
данный в этой главе, в основном является дополнением к библиографии
Аппеля и Кампе-де-Ферье.
Горн (Horn, 1889) дал следующее общее определение: двойной
степенной ряд
о)
является гипергеометрическим рядом, если два отношения
и B)
— рациональные функции от т и п. Горн изучил сходимость
гипергеометрических рядов от двух переменных и установил систему дифференциальных
уравнений в частных производных, которым они удовлетворяют.
Частным случаем гипергеометрического ряда, изученным многими
авторами, в частности Меллином, является ряд, для которого Лтп есть гамма-
произведение, то есть
C)
где а/ — произвольные вещественные или комплексные постоянные и Ui и
vi — любые целые числа, которые могут быть положительными,
отрицательными или нулями. Возникает вопрос об описании наиболее общего типа

рядов, удовлетворяющих определению Горна. Очевидно, что / и g должны
удовлетворять при всех /я, я = 0, 1, 2, ... условию
D)
Это условие должно выполняться тождественно по т и п, поскольку обе
л
части равенства D) равны ¦ mj"b n+i ; легко видеть, что любая пара рацио-
Атп
нальных функций от т и п, удовлетворяющая условию D), порождает
гипергеометрический ряд.
Биркеланд (Birkeland, 1927) установил, что любое рациональное решение
функционального уравнения D) может быть разложено на линейные
множители, что приводит к выражению Атп через произведение гамма-функций.
Оре заметил (Ore, 1929), что теорема Биркеланда не обладает полной
общностью, и дал (Ore, 1930) полное исследование рациональных решений
уравнения D). Из результатов Оре вытекает, что наиболее общей формой
для Лтп является
где R — фиксированная рациональная функция от т и щ аи Ь —
постоянные и 7/тш — произведение гамма-функций. Это эквивалентно тому, что
наиболее общий гипергеометрический ряд от двух переменных получается
путем применения рационального дифференциального оператора
к гипергеометрическому ряду вида
Поэтому достаточно рассматривать ряды типа Горна—Биркеланда.
5.7.1. Список Горна. Горн положил
E)
где F, F> G, G'— многочлены от т и п, имеющие соответственно степени
Pt P'j %•> Я'- При этом предполагается, что F имеет множитель т -\- 1, a G'—
множитель я+1; F и F не имеют общих множителей, за исключением,
быть может, т-\- 1, a G и G' не имеют общих множителей, за исключением,
быть может, п-\-\. Наибольшее из четырех чисел />,//, q, q' называют
порядком гипергеометрического ряда. Горн исследовал, в частности,
гипергеометрические ряды второго порядка. Он установил, что, кроме некоторых
рядов, выражаемых через ряды от одного переменного или через
произведения двух гипергеометрических рядов, каждый из которых зависит от
одного переменного, существуют 34 существенно различных сходящихся
ряда порядка 2 (Horn, 1931, исправления см. у Borngasser, 1933).
Существуют 14 полных рядов, для которых р=р' = q = q' =2:
F)
G)

(8)
(9)
A0)
(И)
A2)
A3)
A4)
A5)
A6)
A7)
A8)
A9)
и существуют 20 вырожденных рядов, которые являются предельными
формами для полных рядов и для которых />s?p' = 2, q-^q' = 2, причем
р и q не могут одновременно равняться двум:
B0)
B1)
B2)
B3)
B4)
B5)
B6)

B7)
B8)
B9)
C0)
C1)
C2)
C3)
C4)
C5)
C6)
C7)
C8)
C9)
Во всех этих двойных рядах тип изменяются от 0 до оо.
5.7.2. Сходимость рядов. Положительные числа г и s называют
ассоциированными радиусами сходимости двойного степенного ряда ^ Л
если этот степенной ряд абсолютно сходится при I х | < г, |^|<s и
расходится при | х | > г, |.y|>s. Положим maxr = /?, maxs = S. Точки (г, s),
где г и s — ассоциированные радиусы сходимости данного ряда, лежат на
кривой С, целиком расположенной в прямоугольнике 0 < г < /?, 0 < s < S.
Эта кривая делит прямоугольник на две части; часть, в которой лежит точка
г = s = 0, является двумерным изображением области сходимости двойного
степенного ряда.
Изучая сходимость ряда A), Горн ввел функции
D0)
и показал, что /? = |ФA, О)!, S = |*F@, I) |-1 и что С имеет
параметрическое представление г = |Ф(p., v) \~\ 5 = |?(jjl, v)], p., v > 0.
Приложения этого результата к полным рядам второго порядка видны из
таблицы на стр. 222.
Области сходимости различных рядов изображены на рис. 3.

> ((л, v) W ((л, v) Декартово уравнение кривой Ряды
Fi D1)
F2 D2)
^з D3)
F4 D4)
01 D5)
02 D6)
03 D7)
Ях D8)
Щ D9)
Я3 E0)
Я4 E1)
Я5 E2)
Яс E3)
Я7 E4)

Рис. 3.

Для вырожденных рядов либо функция Ф, либо функция W тождественно
равна нулю и область сходимости значительно проще. Неравенства,
необходимые для сходимости, указаны в формулах B0) — C9).
5.8. Интегральные представления
Гипергеометрические функции двух переменных, как и соответствующие
функции одного переменного, могут быть выражены либо интегралами типа
Эйлера — Лапласа, либо интегралами типа Меллина — Бернса. Эти интегралы
являются в рассматриваемом случае двойными. Так как двойные интегралы
менее удобны, чем обычные, и плохо приспособлены для интегрирования
дифференциальных уравнений, представляется естественным найти простые
интегралы, выражающие эти функции. Такие представления могут быть
найдены во всех случаях, но подынтегральная функция в большинстве из них
содержит гипергеометрическую функцию одного переменного или
произведение таких функций.
Список Горна слишком обширен, и здесь невозможно привести полный
перечень интегральных представлении. Мы укажем интегральные
представления лишь для функций Аппеля, но надо иметь в виду, что подобные
представления существуют для всех функций Горна. Многие из этих
представлений даны в работах, имеющихся в списках литературы. Интегральные
представления полезны для аналитического продолжения гипергеометрических
рядов двух переменных, теории их преобразования, а также для
интегрирования гипергеометрических систем дифференциальных уравнений в частных
производных.
5.8.1. Двойные интегралы типа Эйлера. Если использовать разложение
в ряды и применить либо интеграл Эйлера первого рода для бета-функции
или соответствующий двойной интеграл, то легко получаются интегральные
представления
B)
C)
(Appell, Kampe de Feriet, 1926, гл. 2).

Изучение функции t\ значительно сложнее, и, по-видимому, для нее не
существует достаточно простого интегрального представления. Из большого
числа предложенных для нее двойных интегралов простейшим представляется
интеграл Берчнелла и Ченди (Burchnall, Chaundy, 1940, равенство F8))
D)
Во всех этих интегральных представлениях предполагается, что \х\ и \у |
достаточно малы, чтобы как ряды, так и интегралы сходились.
5.8.2. Обычные интегралы типа Эйлера. Пикар отметил, что функция
F\ может быть представлена с помощью обычного интеграла в виде
E)
Это представление имеет то большое преимущество, что оно легко
преобразуется в контурный интеграл, применимый для отрицательных значений Re a
и Re G — а), и что оно является наилучшим средством для полного
интегрирования связанной с функцией Fl системы дифференциальных уравнений
в частных производных. Равенство E) показывает, что преобразование
Эйлера функции Fl является произведением функции от х на функцию от^у.
Применимость и полезность равенства E) связаны с этим свойством.
Существуют соответствующие соотношения для F2 и Fz (Erdelyi, 1848)
(б)
где р + р' = а -j- 1 и путь интегрирования является двойной петлей Похгам-
мера A + , 0 + , 1 —, 0 —) такой, что вдоль нее 11 \ > | х | и | 1 — t \ > | у\;
далее
G)
где р + р' = 7- В° всех случаях путем специального выбора р можно
выразить одну из гипергеометрических функций в подынтегральном выражении
через элементарные функции, но при общих значениях параметров
невозможно выразить все подынтегральное выражение через элементарные
функции.
Функция Ft, как и выше, является более трудной для изучения: неизвестно
ни одного обычного интеграла, позволяющего факторизовать Fv С другой

стороны, известно интегральное представление (Erdelyi, 1941, равенство C))
(8)
в котором вдоль контура выполняется неравенство Это
представление сравнительно просто и является полезным для интегрирования
системы дифференциальных уравнений в частных производных, связанной
с функцией Fv
5.8.3. Двойные интегралы типа Меллина — Бернса. Согласно Аппелю
и Кампе-де-Ферье четыре интегральных представления могут быть записаны
в едином виде
(9)
где контуры интегрирования имеют вырезы обычного вида (см. п. 2.1.3); Ф
и W в этих четырех случаях выражаются формулами
A0)
(Н)
A2)
A3)
Интегралы такого типа были использованы Меллином при изучении
гипергеометрических функций.
5.9. Системы дифференциальных уравнений в частных
производных
Ряды где и
F, F', G, G' являются такими же многочленами, как и в 5.7E),
удовлетворяют системе линейных дифференциальных уравнений в частных
производных. Эту систему можно записать с помощью дифференциальных операторов
в виде
B)

В дальнейшем ограничимся рассмотрением гипергеометрических функций
второго порядка. В этом случае получаем два дифференциальных уравнения
в частных производных второго порядка.
Эти два уравнения совместны (так как гипергеометрическая функция
удовлетворяет обоим), и из общей теории таких систем (см., например,
Appell, Kampe de Feriet, 1926, гл. 3) вытекает, что они имеют не более
четырех, а может быть, и меньше, линейно независимых решений. Полное
изучение показывает, что системы линейных дифференциальных уравнений в
частных производных, связанные с восемью рядами
C)
из списка Горна, имеют лишь три линейно независимых решения, в то время
как остальные 26 систем обладают четырьмя линейно независимыми решениями
каждая. Для систем, связанных с функциями
D)
одно из решений является элементарной функцией вида х?у° со следующими
значениями р и а:
Ряды
о3 E)
Я3, Н8 F)
Яв, Н8 G)
В следующем списке дифференциальных уравнений в частных
производных г является искомой функцией от х и у
(8)
(9)
A0)
(И)
A2)

A3)
A4)
A5)
A6)
07)
A8)
A9)
B0)
B1)

B2)
B3)
B4)
B5)
B6)
B7)
B8)
B9)
C0)
C1)
C2)
C3)
C4)
C5)
C6)
C7)

C8)
C9)
D0)
D1)
D2)
В монографии Аппеля и Кампе-де-Ферье рассмотрены некоторые из этих
систем дифференциальных уравнений в частных производных. Дальнейшие
результаты принадлежат другим авторам, в частности Горну, Борнгессеру,
Берчнеллу и Эрдейи. Для каждой системы известны отдельные решения,
однако полной совокупности всех фундаментальных решений до сих пор
не известно, за исключением систем Fx и G2 (Эрдейи, не опубликовано),
F4 (Burchnall, 1939; Erdelyi, 1941) и Фх, Ф2, Гх (Erdelyi, 1939, 1940).
При работе с такими системами дифференциальных уравнений в частных
производных возникают трудности двух типов. Во-первых, общая
аналитическая теория систем дифференциальных уравнений в частных производных
находится в неудовлетворительном состоянии; в частности, очень мало
известно о поведении решений в окрестности точек, где пересекаются более
чем две особые кривые или в которых две особые кривые касаются.
Во-вторых, препятствием является слишком большое число возникающих
различных систем. Вторая трудность может быть заметно уменьшена путем
использования результатов теории преобразований (см. и. 5.11). Эта теория
позволяет, за возможным исключением систем
D3)
свести каждую систему для гипергеометрического ряда второго порядка
к системе для F2 или к ее частным и предельным случаям.
5.9.1. Исследования Айнса. Айне (Ince, 1942) изучил систему уравнений
D4)
в которой а, Ь, с, d, e, f—многочлены от х и аи bu cu du eu f1 —
многочлены от у. Он сделал некоторые дополнительные предположения о
коэффициентах а, Ь, ... , еи f1} обеспечивающие, что система D4) имеет четыре
линейно независимых решения, что эти решения симметричны по х и у

(с соответствующей перестановкой постоянных параметров) и что особые
кривые определяются коэффициентами при вторых частных производных
в D4). При этих предположениях он доказал, что система D4) сводится
к системе для F2 или к частным и предельным случаям этой системы.
5.10. Формулы приведения
При некоторых исключительных обстоятельствах гипергеометрические
функции двух переменных могут быть выражены через более простые
функции, например через гипергеометрические функции одного переменного или
через элементарные функции. В этих случаях мы говорим о приводимых
гипергеометрических функциях и о формулах приведения. Исключительные
обстоятельства сводятся либо к тому, что параметры гипергеометрического
ряда удовлетворяют одному или нескольким соотношениям, либо к тому,
что два переменных связаны некоторым соотношением. В последнем случае
соотношение является обычно уравнением особой кривой для системы
дифференциальных уравнений в частных производных, связанной с изучаемым рядом.
Некоторые тривиальные формулы приведения очевидны. Если в функциях
Ft и F2, или Fs, или Ф2 имеем C' = 0 или если у = 0 в любом из рядов, то
гипергеометрический ряд от двух переменных может быть выражен с
помощью ряда одного переменного. Такие тривиальные приведения в
дальнейшем не будут рассматриваться.
Приводимость при частных значениях параметров.
Следующие формулы приведения могут быть доказаны либо путем
разложения в бесконечные ряды и сравнения коэффициентов, либо с помощью
интегральных представлений:
о)
B)
C)
D)
E)
F)
G)
(8)
(9)

Относительно A), B) и D) см. Appell, Kampe de Feriet, 1926, гл. I;
относительно C), E), F), G) и (8) см. Bailey, 1935, гл. 9 и примеры;
относительно (9) см. Erdelyi, 1948, стр. 384. В указанной литературе имеются
некоторые другие случаи приводимости.
Приводимость при частных значениях переменной
Методы, используемые в этом случае, примерно те же, что и в
предыдущем случае. Однако известных результатов значительно меньше.
Монография Аппеля и Кампе-де-Ферье дает лишь
A0)
A1)
Оба соотношения являются непосредственным следствием 5.8 E),
5.11. Преобразования
Несмотря на то, что, по сути дела, есть лишь один гипергеометрический
ряд второго порядка от одного переменного (именно, ряд Гаусса), теория
его преобразований весьма обширна (см. п. 2.9 — 2.11). Поскольку число
гипергеометрических рядов второго порядка от двух переменных велико,
полное множество их преобразований исчисляется сотнями. Мы приведем
лишь немногие из них. Лучшим средством для вывода этих (и других)
преобразований являются интегральные представления рассматриваемых
функций. С целью получения желаемых результатов применяются замена
переменной интегрирования или деформация контура интегрирования. Для
интегральных представлений, таких, как 5.8F), в которых подынтегральная
функция содержит гипергеометрическую функцию одного переменного, весьма
полезно использование теории преобразований гипергеометрических
функций одного переменного.
Приведем сначала преобразования рядов в ряды того же типа:
0)
B)
C)
D)
E)
F)
G)
(8)

Все эти преобразования соответствуют преобразованиям Эйлера для
обычных гипергеометрических рядов 2.9D). Ни для одного из других полных
гипергеометрических рядов от двух переменных не известно простого
преобразования такого типа.
Существуют также преобразования рядов в ряды того же типа, дающие
аналитические продолжения, например
(9)
Наконец, при специальных значениях параметров встречаются квадратичные
преобразования и преобразования высших степеней. Все эти
преобразования приведены в монографии Аппеля и Кампе-де-Ферье (гл. I и II).
Далее, существуют преобразования гипергеометрических рядов от двух
переменных в гипергеометрические ряды других типов. Есть два вида
таких преобразований. Один служит для аналитического продолжения ряда
с помощью ряда другого типа, а второй дает формулы приведения,
показывающие, что при некоторых частных значениях параметров ряды
выражаются через более простые, например имеющие меньшее число параметров.
Наиболее известным примером аналитического продолжения с помощью
другого гипергеометрического ряда является преобразование
A0)
где сумма состоит из четырех слагаемых, в которых X, ja, p, а равны
соответственно а, а', р, р'; а, р', р, а'; р, а', а, р', и р, р' а, а'. Наиболее известным
примером приведения является
В следующих двух таблицах дается сжатое изложение различных
известных преобразований полных рядов, то есть рядов, обозначенных в списке
Горна через F, G, Н. Соответствующие формулы и подобные преобразования
вырожденных рядов можно найти в следующих работах: монография Appell,
Kampe de Feriet, 1926; Bailey, 1935, гл. IX и примеры; Burchnall, Chaundy,
1940, 1941 (где преобразования не установлены в явном виде, а получены
как вырожденные случаи разложений) и Erdelyi, 1948.
Аналитические продолжения
Ряды Переменные Выражаются через функции С переменными
F. х.у F2 Li-
^8 Х,у Щ ~, -У
# % У

Преобразования и формулы приведения для частных
значений параметра
Ряды Ограничения Преобразуются в С ограничениями
Ft р' + 7 = а + 1 F, р = 7'
Fo а = у Fi нет
f2 7 + 7' =а +1 О2 нет
p = P' и 7+7' = а + 1 F4 7 + T
p = pf и y 4- Yf = а + 1 01 нет
7 + 7' —« + 1=2 —P = 2 —P' G3 нет
a-fa' = Y fi нет
a-fp = l иа-}-а' = 7 //з нет
FA p+ + 4 p + Y
Я2 e = 2,3 H7 нет
Я2 p = vHa + S==s Я! a4-S = s
H2 y H- 8 «= 1, S + s = a #6 нет
Например, первая строка в этой таблице показывает, что если в ряде
^i (a> Р> Р'> 7J х> У) выполняется условие р' —|— у = « -(- 1, то он может быть
выражен через ряд FA (a, p, ?, т"» х» ^)» гДе новые a, p, y, т' (в Л) зависят
от параметров Fv так что в F4 p = <(', а ^ и у в F4 зависят от
переменных в /^
Эта таблица показывает, что ряды Fv F3, Gv G2, G3, H2, Я3, #4, Нв и Я7
при любых значениях параметров могут быть выражены через F2 и,
следовательно, вырожденные ряды, которые являются их предельными случаями,
могут быть выражены через предельные случаи F2. Таким образом,
получен следующий результат: все гипергеометрические ряды второго порядка
от двух переменных, за возможным исключением Fi} Hv Нь и Hv могут
быть выражены через F2 или его частные и предельные формы. Это
приводит к- соответствующей теореме для систем дифференциальных уравнений
в частных производных, связанных с этими рядами (см. также п. 5. 9). До сих
пор неизвестно, являются ли при произвольных значениях параметра ряды
FA, Hx и #5 независимыми от г2 и, следовательно, от других. Однако это
кажется правдоподобным.
5.12. Символические формы и разложения
Берчнелл и Ченди (Burchnall, Chaundy, 1940, 1941) ввели операторы
С помощью этих операторов можно представить функции от F1 до F± в виде
B)
C)
D)
E)

Таким образом, с помощью операторов Д и у функции Аппеля факторизу-
ются, Берчнелл и Ченди получили также преобразования функций Аппеля,
имеющие вид
F)
G)
(8)
и некоторые другие.
Эти символические формы были использованы для нахождения
разложений функций Аппеля по другим функциям, а также функций Аппеля по
произведениям обычных гипергеометрических функций и обратно. Чтобы дать
пример, заметим, что, в силу формулы Гаусса 2.8 D6), для F(a, p ; -у; 1)
имеем символическую запись
Таким образом,
и, следовательно, B) приводит к разложению
(9)
Используя обращение B) в виде
и соответствующее разложение А (а), наряду с (9) получаем формулу
A0)
Это разложение может быть доказано без использования символических
методов, путем сравнения коэффициентов при одинаковых степенях х и у в
обеих частях.
С помощью этого метода Берчнелл и Ченди получили 15 пар
разложений, содержащих функции Аппеля и обычные гипергеометрические функции,
а также значительное число разложений, содержащих гипергеометрические
ряцы высшего порядка и вырожденные гипергеометрические ряды Гумберта
Ф, W и Е. Полезны также методы интегральных представлений (таких, как
5.8 D)) и формул интегрирования.
Существует много других разложений, содержащих функции Аппеля
и обычную гипергеометрическую функцию. Особенно важной является

билинейная производящая функция для многочленов Я к оби
где (Bailey, 1935, стр. 102,
пример 19).
5.13. Частные случаи
Обобщая многочлены Якоби на случай двух переменных, Аппель изучил
следующие семейства многочленов (т и п — неотрицательные целые числа):
A)
B)
C)
Последние два семейства образуют биортогональную систему в области
х, з>гЭ:О, х+з'^! с весом х^'У'".
Ряды
D)
(которые могут быть выражены через F2) и
E)
встречаются в исследованиях по гиперсферическим гармоникам.
Все эти частные случаи изучены в монографии Аппеля и Кампе-де-Ферье.
5.14. Другие ряды
Гипергеометрические ряды высшего порядка от двух переменных
изучались Меллином, Биркеландом, Кампе-де-Ферье (см. Appell, Kampe de Feriet,
1926, гл. IX) и Берчнеллом и Ченди (Burchnall, Chaundy, 1941, Burchnall, 1942
и Chaundy, 1942). Гипергеометрические ряды от трех переменных были
изучены Горном (Horn, 1889); ряды от п переменных — Лауричелла (Appell, Kampe
de Feriet, гл. VII) и Эрдейи (Erdelyi, 1937, 1939 а). Частные случаи рядов
Лауричелла встречаются в исследовании по гиперсферическим гармоникам.
Обобщение базисных гипергеометрических рядов на случай двух
переменных дано Джексоном (Jackson, 1942, 1944).

ГЛАВА 6
ВЫРОЖДЕННАЯ ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ
6.1. Предварительные замечания
Положим в гипергеометрическом ряде Гаусса
х
2 = -т-, и предположим, что ни а, ни с не являются ни нулем, ни
отрицательным целым числом. Мы получим степенной ряд по х, радиус
сходимости которого равен | Ь J и который определяет аналитическую функцию с
особыми точками х — 0, Ь и оо. Если # —оо, то в пределе получаем целую
функцию, для которой особая точка л: = оо возникает в результате слияния
( \
двух особых точек для F\ а, Ь\ с; -т-j. Таким образом, появляется ряд
Куммера
В обозначениях, используемых для обобщенных гипергеометрических рядов
4.1A) эта функция запишется как lFl (а; с; х). Но в этой главе и в
следующих двух главах ряд A) будет обозначаться символом Гумберта
Иногда также применяют обозначение М(а, с, х).
Ряд A) удовлетворяет дифференциальному уравнению
B)
Подстановка
C)
приводит B) к стандартной форме Уиттекера
D)

Каждое из этих уравнений называют вырожденным гипергеометрическим
уравнением и любое решение их называют вырожденной гипергеомет-
оической функцией; а и с (или k и \i) называют параметрами, х—
переменной.
В этой главе изучение вырожденной гипергеометрической функции
будет основано на уравнении B), но некоторые наиболее важные результаты
будут даны в обозначениях Уиттекера.
6.2. Дифференциальные уравнения
Уравнение 6.1B) является однородным линейным дифференциальным
¦ уравнением второго порядка, коэффициенты которого линейно зависят от
независимого переменного. Можно показать, что, обратно, любое такое
дифференциальное уравнение может быть проинтегрировано с помощью
вырожденной гипергеометрической функции. Пусть
A)
является таким дифференциальным уравнением. Если ао = а1 = а2 = О, то
уравнение имеет постоянные коэффициенты и может быть проинтегрировано
в элементарных функциях. Исключим этот случай. Тогда преобразование
B)
приводит уравнение A) к виду
C)
где
D)
Если можно определить X, \l и h так, что
то уравнение C) сводится к 6.1 B). В других случаях замена независимой
переменной сводит C) к вырожденному гипергеометрическому уравнению
или к уравнению Бесселя. Результаты указаны в таблице на следующей
странице, где <?/ (а, с, х) обозначает любое решение 6.1B) и Cv (x) — любое
решение уравнения Бесселя
E)
Сведение уравнения A) к вырожденному гипергеометрическому
уравнению не является однозначно определенным, поскольку 6.1 B) может быть
различными методами преобразовано к уравнению того же типа. Если
положить
A0)

Приведение уравнения
Предположения Параметры
F)
G)
(8)
(9)
то дифференциальное уравнение 6.1 B) преобразуется в
(И)
Это есть дифференциальное уравнение для <?7 (а, •/, ?), если
р = 0или1— с, /z = 0 или 1, ХA—2Л)=1,
a = l (a —he)+ 9, Т = с + 2р. A2)
Таким образом, если считать тождественное преобразование, уравнение
6.1 B) может быть четырьмя различными путями преобразовано в уравнение
того же самого вида.
Вырожденное гипергеометрическое уравнение является однородным
линейным дифференциальным уравнением второго порядка с правильной
особой точкой лг = О, причем его коэффициенты регулярны при всех хфО
(включая лг = оо). Каждое такое уравнение может быть приведено (Tricomi, 1948)
к виду
A3)
и легко показать, что (исключая тривиальный случай, когда уравнение A3)
решается в элементарных функциях) интегрирование A3) приводит к
вырожденной гипергеометрической функции или функциям Бесселя. Будем
различать два случая уравнения A3).
Если а2 ф 4а, имеем
A4)

где
A5)
и &>(¦*., (х, х) является решением 6.1D); если а2 = 4<х, то
A6)
где
A7)
Уравнение
A8)
в котором р^О — любое число, сводится к уравнению A3) подстановкой
A9)
И, следовательно, сводится к вырожденному гипергеометрическому
уравнению. Более общая форма может быть получена из A8), если положить
B0)
У удовлетворяет уравнению
B1)
Например, если y(X) = hX°, то получаем, что уравнение
B2)
при условии
B3)
может быть проинтегрировано с помощью вырожденной
гипергеометрической функции.
Следует отметить, что сами функции Бесселя являются частным случаем
вырожденной гипергеометрической функции (см. 6.9.1). Поэтому все
нетривиальные случаи дифференциальных уравнений этого пункта могут быть
проинтегрированы с помощью вырожденной гипергеометрической функции.

Основными линейными дифференциальными уравнениями второго
порядка, которые могут быть проинтегрированы с помощью вырожденной
гипергеометрической функции, являются A), A3), A8), а также уравнение B2) при
условиях B3).
6.3. Общее решение вырожденного уравнения в окрестности
начальной точки
Будем изучать вырожденное гипергеометрическое уравнение в виде
A)
Одним из решений уравнения является
B)
и преобразования 6. 2. A0), 6. 2 A2) дают три других решения, а именно
C)
D)
E)
Из их поведения вблизи лг = О следует, что, если с не является целым
числом, то решения yt и у2 линейно независимы. Следовательно, в этом
случае общее решение может быть записано в виде
где А и В — произвольные постоянные. Особый случай, когда с — целое
число, будет изучен позже (см. 6. 7. 1).
С другой стороны, как yv так и у3 являются решениями уравнения A),
причем оба они регулярны при х = 0 и у1@)=у3@) = \. Так как (при
нецелом с) дифференциальное уравнение может иметь не более одного такого
решения, то имеет место равенство yt =y8 или
Это соотношение называется преобразованием Куммера. Точно так же,
в силу преобразования Куммера, у2=у*-
Преобразование Куммера есть предельный случай преобразования Эйлера
для гипергеометрического ряда (см. 2.1 B2)) и является весьма важным
соотношением. При его выводе мы предположили, что число с — не целое, но
преобразование справедливо (по непрерывности) и при целых
положительных с.
Если ур и уд являются решениями уравнения A), их определитель
Вронского
(8)

должен иметь вид JKpqexx~c, где постоянная Kpq может быть вычислена с
помощью первых двух членов разложений функции у в ряд. Получаем
(9)
Все другие определители Вронского для этих четырех решений
тождественно равны нулю.
6.4. Элементарные соотношения для функции Ф
Как и в теории гипергеометрических рядов Гаусса, четыре функции
о)
называются смежными с функциями Ф = Ф(а, с; х). Функция Ф и любые
две смежные с ней функции связаны линейной зависимостью. Шесть
формул, описывающих эти зависимости, могут быть выведены из соотношений
Гаусса между смежными функциями (см. 2.1.2); их также можно
проверить путем сравнения коэффициентов при одинаковых степенях х. Они
имеют следующий вид:
B)
C)
D)
E)
F)
G)
Эти соотношения не являются независимыми. Из любых двух соотношений,
например B) и D), при помощи простых операций могут быть выведены
все остальные.
Любая функция Ф(а-\-т, с-\-п; х), где т и п — целые числа,
называется ассоциированной с Ф(а, с; х). Путем последовательного применения
соотношений между смежными функциями легко доказать, что любые две
ассоциированные функции связаны однородным линейным соотношением,
коэффициенты которого являются многочленами от х.
С помощью почленного дифференцирования получаем
(8)
или ф' = — Ф (а +, с +). Применяя это соотношение повторно, получаем,
с
что производные любого порядка функции Ф являются ассоциированными
функциями и, следовательно, любые три производные связаны однородным
линейным соотношением, коэффициенты которого являются многочленами
от х. Дифференциальное уравнение 6.1 B) является простейшим примером
такого соотношения. Комбинируя (8) с соотношениями между смежными
функциями, получаем
(9)

Дальнейшими полезными формулами являются
A0)
A2)
A3)
A4)
6.5. Основные интегральные представления
Известно, что однородное линейное дифференциальное уравнение,
коэффициенты которого являются линейными функциями независимого
переменного, может быть проинтегрировано с помощью интеграла Лапласа.
Интегральное представление
A)
легко проверяется путем разложения еха по степеням х. Это представление
позволяет найти решение уравнения 6.1B) в виде интеграла следующей
формы:
что может быть получено также с помощью метода Лапласа. Подставим это
выражение в 6.1B) и используем тождество
Мы получим, что если кривая С не проходит через особые точки
подынтегральной функции и если начальное и конечное значения функции e~xtta(\ +
-|- t)c~a конечны и равны друг другу, то интеграл удовлетворяет уравнению
6.1B). Если Re о Re а > 0, то в качестве С можно выбрать интервал @,—1).
Это показывает, что A) удовлетворяет 6.1B). Если Re a > 0, то в качестве
пути интегрирования можно выбрать луч, выходящий из начала координат.

Положим
B)
Это равенство определяет решение уравнения 6.1B) в полуплоскости
Rex>0. Область определения может быть расширена путем поворота пути
интегрирования. Таким образом,
C)
Здесь предполагается, что функции ta l и A + t)c~a~l принимают главные
значения. Позже будет показано, что условия Rea>0, соответственно Rec>
> Re a > 0, могут быть опущены, если ввести в формулы 6.11B) и 6.11A)
контурные интегралы.
Другой тип интегральных представлений использует интегралы Мелли-
на—Бернса (см. 1.19). Формула
D)
может быть проверена путем вычисления интеграла как суммы вычетов
подынтегральной функции в полюсах Г (— s).
Соответствующее представление для ? получается путем подстановки
в B)
Перестановка порядка интегрирования допустима, если -\ + Re a > 0, и дает
Вычисляя последний интеграл, получаем

или, несколько изменяя обозначения,
E)
При выводе были сделаны более строгие ограничения, чем это необходимо.
Ослабление условий, наложенных в E), делается с помощью аналитического
продолжения. Условия, наложенные на параметры в D) и E), могут быть
ослаблены, если соответственно изменить путь интегрирования. В самом
деле, равенство D) (при любом -у) справедливо, если а не равно нулю или
отрицательному целому числу, при условии, что контур интегрирования
соответственно изогнут, если это необходимо, так, чтобы он отделял
полюсы Г(—s) от полюсов T(a-\-s). Точно так же равенство E) справедливо
(при любом y)> если ни а, ни а — с -{-1 не равны нулю или отрицательному
целому числу, при условии, что путь интегрирования отделяет полюсы
I(a-|-s) от полюсов Г(—s) ГA — с — s). Условия на arg x не могут быть
ослаблены.
Можно проверить, что функции D) и E) удовлетворяют уравнению
6.1 B) (Уиттекер и Ватсон, 1961—1962, 16.4).
Из E) имеем
F)
Если с не является целым числом, то полюсы Г(—s)I(l — с — s) —
простые. Вычисление E) как суммы вычетов подынтегральной функции в этих
полюсах приводит к важному соотношению
G)
между функциями Ф и ?.
6.6. Элементарные соотношения для функции ЧГ
Функция W была введена Трикоми A927), который обозначил ее через
G. Она связана с функциями Ft (Meixner, 1933), ?(а, р : : х) (MacRobert, 1941)
и 2^о (а> Р»' х) (Erdelyi, 1939) соотношениями
A)
B)
C)
?(а, с; х) является многозначной функцией от х, и обычно будет
рассматриваться главная ветвь этой функции в плоскости, разрезанной вдоль
отрицательной вещественной полуоси. При —^^«р^^- она определяется
равенством 6.5C).

Многие элементарные соотношения для функции W непосредственно
вытекают из соответствующих соотношений 6.4 для Ф
D)
E)
(б)
G)
(8)
(9)
A0)
(И)
A2)
A3)
A4)
A5)
6.7. Фундаментальная система решений для вырожденного
гипергеометрического уравнения
В п. 6.3 были указаны четыре решения ylt ... ,у4 вырожденного
гипергеометрического уравнения. Из результатов п. 6.5 и п. 6.3 вытекает, что
четыре других решения определяются формулами
A)
B)
C)
D)
В п. 6.3 была изучена связь между четырьмя решениями^!, ...,^4- В частности,
было показано, что если с не является целым числом, то yt =уг и у2 ==^4
образуют фундаментальную систему решений уравнений б. 1 B). Теперь
осталось изучить четыре решения уъ, ...,у8. В этом пункте будем предполагать,
что с не является целым числом. Особый случай будет изучен в следующем
пункте.
Из 6.5 (б) следует, что
Уъ = .Уе и з>8 = — e~h%c Ун E)
где е ^ sign (Im х) = 1, если 1тл'>0, = —1, если 1тх<0 (этим
обозначением будем пользоваться на протяжении данного пункта). Множитель eitKli"c}

связан с условием, определяющим xl~c. Таким образом, остаются четыре,
вообще говоря, различных решения^ = .Уз» У 2 = У» Уь=Ув и Уч = ei7t? (С~1} Уз-
Все эти решения определены, если с не является целым числом. Их
определители Вронского, см. 6.3(8), имеют вид Wpg = KPq ex х~с, где
Вообще, -то есть если с, а, с — а не являются целыми числами, любые
два из этих четырех решений различны и образуют фундаментальную систему.
Однако если п означает неотрицательное целое число и а = — п, то Wib
тождественно равно нулю, а потому^ иуъ отличаются друг от друга лишь постоянным
множителем; 6.5G) показывает, что это действительно так. Аналогично, если
а = 1 -\- п, то совпадают у2 и у7; если с — а = — п, совпадают yt и у7, а если
с — а== 1 -\-п, то у2 и уъ отличаются друг от друга лишь постоянным
множителем. Если с — целое число, то либо у1} либо у2 не определено и не может быть
использовано. Значение Wbl было выведено из VP12 и 6.5G) при условии, что
с не является целым числом. Однако, в силу непрерывности, оно справедливо
и для целых значений с. Так как оно не обращается в нуль тождественно по
х, то уъ и у7 при всех обстоятельствах образуют фундаментальную систему
решений уравнения 6. 1 B).
Выражение для W через Ф дано формулой 6.5G). Обратное выражение
Ф через W получается путем записи выражения, аналогичного
выражению 6.5G) для з>7> и исключения одной из двух Ф-функций. Результат имеет вид
G)
Аналогичная формула имеет место для у2. Из G) и 6.5 G) могут быть
получены следующие соотношения между решениями вырожденного
гипергеометрического уравнения:
(8)
(9)
A0)
(И)
6.7.1. Логарифмический случай. Функция Ф (а, с; х) является целой
функцией от х, а также целой функцией от а. Рассматриваемая как функция
от с, функция Ф имеет полюсы и соответственно этому не определена
в точках с = 0, —1, —2, ... Однако имеет место соотношение
A2)

показывающее, что функция Ф* = — -n/ \— является целой функцией
от обоих параметров и от переменной. Эта функция и в других отношениях
имеет более простое поведение, например, некоторые из формул
дифференцирования в п. 6.4 упрощаются, если выразить их через Ф*.
Отсюда следует, что если с является целым числом, то функция Ф дает
лишь одно решение вырожденного уравнения. Если с=1, то ух и у2
совпадают. Если с = 2, 3, ..., то у2 не существует. Хотя выражение -р/0—-
1 (z — с)
стремится к конечному пределу, когда с приближается к одному из целых
чисел, больших 1, равенство A2) показывает, что этот предел отличается
от з>1 лишь числовым множителем и, следовательно, не приводит к новому
решению. При с = 0, —1, —2, ... ситуация аналогична, за исключением того,
что yt и у2 меняются ролями. Если с является целым числом, то j^i или у2
дают одно решение, а второе решение содержит логарифмические члены.
Оно может быть получено с помощью обычного метода Фробениуса.
Отправным пунктом другого подхода к особому случаю является
функция W. Интегральное представление 6.5C) определяет функцию W для всех
значений с и показывает, что она всегда удовлетворяет вырожденному
гипергеометрическому уравнению. Если с не является целым числом, то 6.5G)
дает разложение для W" по возрастающим степеням х. Если с—целое число,
то достаточно рассмотреть случай, когда с=1-|-я> где я = 0, 1, 2, ... При
с = 1 -f~ я оба члена в правой части 6.5 G) обращаются в бесконечность и
разложение по возрастающим степеням х может быть получено либо путем
непосредственного предельного перехода с —*>п-\-\ в 6.5G), либо прямо с
помощью 6.5E). Опишем кратко второй метод.
Если с = п 4-1, то подынтегральная функция в 6.5E) имеет простые
полюсы в точках s=—я, —я+1, ..., —1 и двойные полюсы в точках
s = 0, 1, 2, ... (если я = 0, то имеются только двойные полюсы). Вычет
функции r@-j-s)r(—s)T(—я— s)x~s в простом полюсе s = r—я, г = 0,
1, ..., п — 1, равен
вычет в двойном полюсе s = r, r = 0, 1, 2, ..., равен
где ty(z) — логарифмическая производная для Г (г) (см. 1.7). Вычисляя
интеграл 6.5E) как сумму вычетов подынтегральной функции в полюсах,
лежащих справа от пути интегрирования, получаем
A3)
Если я = 0, последняя сумма опускается. Соответствующее разложение для
ЧГ (а, 1 — я; х) получается из A3) и 6.5F).

Некоторые формулы в логарифмическом случае упрощаются. Например,
покажем, что функция
A4)
при целых значениях с может быть выражена через вырожденную
гипергеометрическую функцию.
Так как
где ф (z) — логарифмическая производная в гамма-функции, то почленное
дифференцирование 6.1 A) дает
Сравнивая с A3), при п = 0 получаем
A5)
Соответствующий результат для f(\-\-n) при я = 0, 1, 2, ... может быть
получен с помощью 6.4A3).
6.8. Дальнейшие свойства функции ЧГ
Подобно функции Ф функция W является предельным случаем
гипергеометрической функции Гаусса. Именно
A)
/ с\
(Erdelyi, 1939). Доказательство основано на 6.5G) и разложении F[\ по
возрастающим степеням х.
Поведение функции W при малых х может быть изучено с помощью
6.5G), 6.7A3) и соответствующих формул, когда с равно нулю или является
отрицательным целым числом. Результаты сведены в таблицу:
W (а, с; х) при малых х
B)
C)
D)
E)

Порядок остаточного члена виден из следующей таблицы:
R - О (а)
G)
(8)
(9)
A0)
(П)
A2)
A3)
В соответствии с условием п. 6.6 отрицательная вещественная полуось
является разрезом для функции 41". Обозначим через /(—S-j-Ю) предел
/(—? + fy)> когда т)—*0, принимая положительные значения, и аналогично
определим /(—? — /0). Из 6.5G) следует
A4)
где 5>0 и всюду надо брать верхние, либо нижние знаки. В частности,
A5)
Так как вывод этой формулы основан на 6.5G), то сначала приходится
исключать целые значения с. По непрерывности формула остается
справедливой и при с = 1, 0, —1, —2, ... При с = 2, 3, 4, ... правая часть

принимает неопределенный вид, но если записать ее в виде
то с можно устремить к \-\-n (# = 1, 2, ...). Это приводит к равенству
A6)
Функция ?(я, с, х) однозначна в следующих случаях: 1) если я = 0, —1,
— 2, ...; в этом сл>чае W является многочленом от х и, в силу 6.5G),
кратно Ф и 2) если с = п-\-\, я = 1, 2, ..., и а является одним из целых
1, 2, ..., п\ в этом случае 6.7A2) показывает, что W — многочлен от х~х.
Поведение W, когда х обходит вокруг начала координат, видно из
формулы
A7)
6.9. Функции Уиттекера
Для некоторых целей удобнее использовать обозначения Уиттекера. Уит-
текер записывает вырожденные уравнения в стандартной форме 6.1D). Из
6.2A3), где
видно, что
где х = —0 + -^-, р = -к—-н-. Двумя решениями уравнения Уиттекера
являются функции Уиттекера
A)
B)
Следовательно,
C)
D)
Имеем также в обозначениях 6.6C)
E)

Дальнейшие решения уравнения Уиттекера 6.1A4) могут быть получены из
п. 6.3 и 6.7. Обозначая соответствующие решения 6.1B) и 6.1D) теми же
самыми индексами, имеем
(в)
Преобразование Куммера 6.3G) показывает, что
G)
где е = 1, если Im(x)>0, и е=—1, если Im(x)<0. Преобразование 6.5F)
показывает, что
(8)
Уиттекер определяет решение М равенством A), а определение W
основывает на интегральном представлении, эквивалентном 6.5B).
Бухгольц (Buchholz, 1943 и дальнейшие работы) использует обозначения
6.9.1. Функции Бесселя. Если х = О, уравнение Уиттекера 6.1D) легко
сводится к уравнению Бесселя 6.2E). Результат выражается формулой
В обозначениях 6.1B) это соответствует случаю с = 2я. Связь между
функциями Бесселя и вырожденной гипергеометрической функцией выражается
следующими формулами, в которых использованы обычные обозначения для
функций Бесселя (см. Ватсон, 1949)
(9)
A0)
(И)
A2)

(Для Щ2) изменить i на — i.)
A3)
A4)
A5)
Функции Бесселя встречаются также как предельный случай
вырожденных гипергеометрических функций. Выполняя почленно предельный переход,
получаем
Соответствующий результат для функции W может быть получен при
нецелых с из 6.5G). Из формулы Стирлинга или из 1.18D), имеем
Этот результат вместе с формулами A6) и 6.5G) показывает, что
A7)
Аналогично доказательство равенств
A8)
A9)
6.9.2. Другие частные случаи вырожденной гипергеометрической
функции. Соотношение
Ф (а, а; х) = е* B0)
очевидно. Многие другие специальные функции также могут быть выражены
через вырожденную гипергеометрическую функцию. Первую группу таких
функций образует неполная гамма-функция и связанные с ней функции.

В силу 6.5B) и 6.5F), а также 6.5G) и 6.3G), получаем
B1)
B2)
Для интеграла вероятностей имеем
B3)
B4)
Для интегральной показательной функции, интегральной
логарифмической функции, интегральных синуса и косинуса и интегралов Френеля
имеем
B5)
B6)
B7)
B8)
B9)
C0)

Функции параболического цилиндра из гл. 8 также являются
вырожденными гипергеометрическими функциями:
C1)
Их частным случаем являются многочлены Эрмита
C2)
где п — неотрицательное целое число.
Далее ЧГ (а, 0; х) = х W (а +1, 2; х) связана с функцией Бейтмена
' где v = -^—у. Первоначально Бейтмен положил
C3)
при вещественных значениях х и \>. Тогда
для х > 0. C4)
Это равенство полезно рассматривать как определение функции k в
разрезанной плоскости. По первоначальному определению Бейтмена kv (—х) =
= &_v (*). Эта формула перестает быть справедливой, если использовать
определение C4). Вместо нее имеем
C5)
Если а — отрицательное целое число, то ф и f являются многочленами
от х, связанными с обобщенными многочленами Лагерра из гл. 10
C6)
Так называемая функция Лагерра при произвольных значениях \> является
просто иной записью для вырожденных гипергеометрических функций (Pin-
пеу, 1946)
C7)
Если с — а—1—неотрицательное целое число, то xc~14f(ay с; х) является
многочленом и
C8)

Можно доказать (Erdelyi, 1937f), что вырожденное уравнение тогда и только
тогда имеет решение, являющееся конечной комбинацией элементарных
функций, когда либо а, либо с — а — целое число.
Важное значение имеют многочлены Пуассона — Шарлье (Сеге, 1962),
встречающиеся в теории вероятностей. Они могут быть выражены с
помощью вырожденной гипергеометрической функции в виде
C9)
Так называемая функция Торонто (Heatley, 1943) определяется
равенством
D0)
Следующая таблица дает информацию относительно наиболее важных
частных и предельных случаев вырожденной гипергеометрической функции.
Частные случаи вырожденной гипергеометрической функции
Параметры Функции
а = \, 2, ... Неполная гамма-функция и ее частные случаи
а = 0, — 1, —2, ..• Многочлены Лагерра
а->оо Функции Бесселя
с = 0, с = 2 /г-функция Бейтмена
c=-—f c=~ Функции параболического цилиндра
с —а Элементарные функции, неполная гамма-функция
с —а=\, 2, 3, ... Ф —многочлены Лагерра
ЧГ — неполная гамма-функция
с = 2а Функция Бесселя
с =а = 1 Интегральная экспонента и связанные с ней функции
1 Ч
Интеграл вероятностей и связанные с ним функции
6.10. Преобразование Лапласа и вырожденная
гипергеометрическая функция
Для преобразования Лапласа функции F(t) будем использовать
обозначение
0)
Часто будем писать короче: L{F}. Из теории преобразования Лапласа
известно, что если L{Fl} и L{F2} абсолютно сходятся, то имеет место
теорема умножения
B)
Далее известно, что комплексная формула обращения
C)

справедлива, например, если L {F} абсолютно сходится при Re s = y, а
функция F(x) имеет ограниченное изменение и непрерывна в некоторой
окрестности точки t Бесконечный интеграл понимается, вообще, в смысле главного
значения Коши, то есть как lim , когда Л—>со. Однако если функция/(s)
абсолютно интегрируема на прямой Res = 7, можно просто писать в
формуле C)
Известно много пар преобразований Лапласа, в которые входит
вырожденная гипергеометрическая функция. Можно переписать формулу 6.5B) в 'виде
D)
Далее, при Re b> 0 и Re s > max @, Re ft), | s | > | k |, имеем
E)
Первая формула может быть получена либо путем почленного
интегрирования степенного ряда для функции ф, либо из формулы 6.5A) и интеграла
Эйлера для гипергеометрического ряда Гаусса. Вторая формула получается
с помощью преобразования Эйлера первой формулы. Если k — отрицательное
вещественное число, то при условии, что Re a > Re b, можно перейти в
формуле E) к пределу, когда s —*- со. При b = с E) принимает более простой вид
Из E), 6.5G) и 2.9C3) вытекает, что
G)
Этот результат может быть записан во многих эквивалентных формах и
может быть распространен с помощью аналитического продолжения на
полуплоскость Res>0. Если Re a > Re b, можно перейти в формуле G) к
пределу, когда s —* + 0.
Другие пары преобразований Лапласа вытекают из первого
экспоненциального интеграла Вебера
(8)

Точно так же
(9)
Соотношение
A0)
эквивалентно интегральному представлению функции W% ^ данному
К. С. Мейером.
Другая пара преобразований
В обозначениях Уиттекера основные формулы могут быть записаны
следующим образом:
A2)
A3)
A4)
Из теоремы умножения B) и формулы F) вытекает интегральная
теорема сложения для функции Ф:
A5)

Отметим особо частный случай а'= 0:
A6)
6.11. Интегральные представления
В этом пункте основные интегральные представления будут обобщены
путем введения контурных интегралов, а также будут получены дальнейшие
интегральные представления.
6.11.1. Функция Ф. Интегральное представление 6.5A) основано на
интеграле Эйлера первого рода 1.5A) для бета-функции. Ограничения, наложенные
на параметры, могут быть сняты полностью или частично путем введения
контурных интегралов, как это было сделано в п. 1.6. Применяя вместо 1.5A)
формулы 1.6F), 1.6G) или 1.6(8), приходим к интегральным представлениям
A)
B)
C)
В формуле A) контур интегрирования является двойной петлей (рис. 4),
начинающейся в точке А между 0 и 1 на вещественной оси t, обходящей
Рис. 4. Области сходимости.
сначала точку t — \ в положительном направлении, потом ^ = 0 в
положительном направлении, далее t=\ в отрицательном направлении и, наконец,
^ = 0 в отрицательном направлении и заканчивающейся в точке А При этом
в начальной точке полагают arg? = arg(l—t) = 0.
В интеграле B) контур является петлей, которая начинается и
заканчивается в точке ^ = 0 и обходит точку 1 в положительном направлении.

Это же имеет место в формуле C), где 0 и 1 меняются ролями. Все степени
понимаются в формулах B) и C) в смысле главного значения.
Функция Ф может быть также выражена через функции Бесселя. Из
6.10A6), где 7 = 2а, и 6.9A0) имеем
D)
E)
Дальнейшие интегральные представления могут быть получены с помощью
комплексной формулы обращения 6.10C), преобразования Лапласа 6.10E),
где /г=1, и 6.10F)
F)
G)
Если в формуле F) Ь = п-{-\, я = 0, 1, ... , то подынтегральная функция
является однозначной функцией от s, и путь интегрирования может быть
заменен замкнутым контуром, например кругом,
(8)
6.11.2. Функция W. Аналогичное исследование функции ? приводит к
следующим интегральным представлениям:
(9)
в начальной точке пути;
A0)

A1)
A2)
При х > О из формулы 6.5B) вытекает следующее интегральное
представление. Предположим, что Retf>0, Re с < 1 и л:>0. Тогда можно
преобразовать путь интегрирования в отрезок вещественной оси от точки ? = 0 до
?=—— и луч от t = 2~ д0 i=z—2" + го°- Вдоль (о, =-) положим
t~ueii:, вдоль (—рг-, ^- + ioo) положим
\ Z Z I
Тогда получим
Аналогичная формула получается, если путь интегрирования деформируется
в отрезок (о, —-^-J, вдоль которого теперь полагаем t = ue~ii:t и луч
(— -7г у —у—/оо), вдоль которого ? = -9- к-. Вычитая вторую формулу
\ 2 Z J Z COS и
из первой, получим
A3)
Условие Retf>0, использованное при выводе, может быть снято путем
аналитического продолжения. Однако некоторое ограничение на а должно
быть наложено для того, чтобы обойти полюсы гамма-функции. Формула A3)
соответствует интегральному представлению 6,9B9) для /г-функции Бейтмена.

Мейер (С. S. Meijer, 1938, 1941) дал два следующих интегральных
представления:
A4)
A5)
6.11.3. Функции Уиттекера. Основные интегральные представления для
вырожденных гипергеометрических функций Уиттекера таковы:
A6)
A7)
A8)
A9)

1 . 1 ,
где ни y + ^ + M* ни "о~ + % — М-не являются целыми положительными, а путь
интегрирования отделяет полюсы Г (s) от полюсов
6.12. Разложения по многочленам Лагерра и функциям Бесселя
Для вырожденной гипергеометрической функции, помимо разложений
в степенные ряцы, бывают полезны другие разложения.
Положим в формуле 6.11(9)ср = 0, с = а-\-\, ? = у-^—, Получим
A)
Но
B)
является хорошо известной производящей функцией для обобщенных
многочленов Лагерра (Сеге, 1962, E.1.9)). Так как ряд сходится лишь внутри
единичного круга |и|<1, пишем =lim , v —> 1—, и подставляем
B). Так как
то получаем
и, в силу теоремы Абеля о непрерывности степенных рядов, имеем
C)
где бесконечные ряды сходятся. Из известной оценки для обобщенных
многочленов Лагерра (Сеге, 1962, теорема 7.6.4) видно, что если а <-^-,
то ряд сходится в любом конечном положительном отрезке для х. С другой
стороны, используя преобразование 6.5F), имеем
D)

где ряд сходится (для положительных х), если а>—^-. Вне положительной
вещественной полуоси оба ряда расходятся. Разложения B) и D)
принадлежат Трикоми. Другое разложение по многочленам Лагерра
E)
является обобщением разложения B) и при х = -^у дает разложение
функции Ф на отрицательной полуоси по многочленам Лагерра. Оно принадлежит
Эрдейи (Erdelyi, 1937a, равенство E.7)).
Трикоми (Tricomi, 1947, 1949) дал два разложения функции Ф по
функциям Бесселя. Эти разложения полезны для изучения поведения функции Ф
при больших значениях параметра. Первое разложение имеет вид
F)
где а вещественно, h^>0 и коэффициенты Лт определяются с помощью
производящей функции
G)
Из асимптотического представления функции Бесселя большого порядка
видно, что бесконечный ряд F) сходится одновременно с рядом
и, следовательно, абсолютно и равномерно сходится в каждой ограниченной
области комплексной плоскости х. Из G) имеем
(8)
и рекуррентное соотношение
(9)
для вычисления остальных А. Поэтому
(Ю)
и если я = я = 0, 1, 2, ..., то

Функции А являются многочленами от я, a, h и степень Ат по а равна
\~2\i если h^t-^fn Го" > если Л =-у ([&]—наибольшее целое, меньшее
или равное #). Наиболее удобным значением для h является -~-,
Второе разложение Трикоми имеет вид
(И)
где х= -к--\- 2 —а является параметром Уиттекера и Лт(х, X) —
коэффициенты в разложении
A2)
Трикоми (Tricomi, 1950) показал с помощью рассуждений, похожих на
примененные в связи с формулой F), что бесконечный ряц в A1) сходится во
всей плоскости х. Кроме того, разложение A1) может быть применено для
приближенного вычисления функции Ф при больших значениях х. Из A2)
имеем
A3)
где Ап является многочленом степени по %. Также
A4)
Дальнейшие детали см. Tricomi, 1949.
6.13. Асимптотическое поведение
Асимптотическое поведение вырожденной гипергеометрической функции
различно в зависимости от того, что принимает большее значение:
переменное, один из параметров, оба параметра или, наконец, все три величины.
Полный список результатов пока еще не получен.
Исследования основаны или на интегральных представлениях или же
непосредственно на дифференциальном уравнении, или на подходящем
разложении в бесконечный ряд.
6.13.1. Поведение при больших значениях | х |. Поведение
вырожденной гипергеометрической функции, когда х—*оо, может быть изучено с

помощью основных интегральных представлений. Если положить в 6.5C)
и оценить интеграл, содержащий RN, то получим, что
Этот же результат может быть получен из 6.5E) путем сдвига пути
интегрирования влево, вычисления вычетов, когда мы проходим через полюсы
T(a-\-s), и оценки оставшегося интеграла. Заметим, что этот результат
находится в соответствии с 6.6C). В самом деле (расходящийся) формальный
степенной ряд 2F0 является асимптотическим разложением в
соответствующем секторе для аналитической функции, определенной формулой 6.6C).
Поведение функции Ф может быть выведено из 6.7G)
B)
е==1, если Imx>0, е ===== — 1, если х<0, х-»оо, — % < arg х < тс.
В частности, если Rex—*со, то
C)
а если Rex—*» — оо, то
6.13.2. Большие значения параметров. Если с —* оо, в то время как а и
х ограничены, то поведение функции Ф описывается формулой 6.1A).
В частности,
Ф(а, с; х)=\ + О(]с]~1), я, х ограничены, с-*оо. D)
о, в то время как с— а и х ограничены, то 6.3G) дает требуе-
ие. В частности,
(я, с) ^) = ^[1 + О(|сГ1)], с —а, х ограничены, с-*со. E)

Поведение функции 4f в этом случае может быть выведено с помощью
6.5G), 1.18C) и 1.18D)
F)
я, х ограничены, с-* со, |arg с\ ^тс — е, |arg(— с)\ ^тс — е, s > о.
Соответствующие результаты, когда с—*оо, а с — а и х остаются
ограниченными, вытекают из 6.5F).
Случай а—*оо более труден. Перрон (Perron, 1921) обосновал изучение
этого случая на интегральном представлении типа Лапласа и применил метод
наискорейшего спуска. Среди дальнейших исследователей отметим Трикоми
(Tricomi, 1947), который нашел, что при некоторых ограничениях его
разложение 6.12A1) является асимптотическим, а также- Тейлора (Taylor, 1939),
который использовал метод Лангера для асимптотического представления
решений дифференциального уравнения. Результаты Тейлора будут описаны
в 6.13.3. Если |*| и \х\~ * ограничены, положение дел заметно упрощается.
В следующих ниже формулах с, х и х~ 1 ограничены, а —* со. Более удобно
выражать формулы через
G)
Предполагается, что | arg x— argx|<Tc. Имеем тогда следующую таблицу,
где е — некоторое положительное число:
arg х между
(8)
A0)
(И)
Асимптотическая формула для Ф при тех же самых предположениях
получается из 6.7 G)
A2)

При целом s мы имеем
A3)
A4)
Для Ф Тейлор дал также асимптотическую формулу, справедливую
равномерно в окрестности точки *=:0. Если ъх ограничено, то
A5)
с, х, х ограничены, х—*оо.
Случай, когда а, с и с — а одновременно стремятся к бесконечности, не
исследован полностью, однако известно, что если
A6)
где а, р — фиксированные, возможно комплексные, числа, а Л и В —
фиксированные положительные числа, причем v —> со, пробегая положительные
значения, то имеет место формула
A7)
Здесь использовано сокращенное обозначение ? = -~ ¦ ¦ и = Л
Л -4- и
АИ
/ . См. также 6.13.3.
6.13.3. Большие значения переменного и параметра. Если а
ограничено, с—»-со и х—*оо так, что | х | <с | с |, то поведение функции Ф может
быть изучено с помощью формулы 6.1A). Положим л; = с? 0|?|1
— е(е>0) и используем 1.18D). Тогда имеем при с —* со
A8)
а ограничено,
Соответствующая формула при ограниченном с — а и с, х—*оо может быть
получена с помощью преобразования Куммера, формула для W — с
помощью 6.5G).
Если а и х неограниченно возрастают, поведение вырожденных
гипергеометрических функций более сложно. Тейлор (Taylor, 1939) применил метод

Лангера, чтобы вывести асимптотические формулы для вырожденных
гипергеометрических функций из дифференциального уравнения. Положим снова
A9)
Тейлор вводит вспомогательное переменное
B0)
Здесь аргументы чисел х, х и х— 4х равны нулю, если эти числа
положительны, а для других значений аргументы получаются с помощью
аналитического продолжения, при котором выполняется условие | arg х—arg x | <$:
г^я. Тейлор изучил сначала асимптотическое поведение функции W при
условии, что $—*оо, причем существуют также постоянные г и N такие,
что 0<r^l, iV>0 и | х | > N | х |~1+2г, когда х —>со. Его результаты в
этом случае имеют следующий вид:
arg S между
B1)
B2)
B3)
B4)
При ограниченном 5 или х — 4x = O(|x|d) Тейлор получил
асимптотическую формулу
B5)
Для Ф Тейлор получил
B6)
с, arg xt arg x ограничены,

Если хл: велико, функция Бесселя может быть выражена через
элементарные функции
где ct и с2 такие же, как в A3) и A4).
Далее, при больших а и х разложение Трикоми 6.12 A0) является
асимптотическим представлением, если х—> оо и л: = О(|*|Р) для некоторого р<
<-_- (Tricomi, 1949).
о
Случай, когда оба параметра и переменные велики, не изучен еще
систематически. Эрдейи (Erdelyi, 1938) применил метод наискорейшего спуска
к интегральным представлениям типа Лапласа для того, чтобы исследовать
поведение вырожденных гипергеометрических функций, когда
Л, В, X—вещественные, B7)
и либо
B8)
либо
B9)
Вещественные числа Л, В, X, а также числа а, р, ?, которые могут
принимать и комплексные значения, считаются фиксированными, когда v—*oo
вдоль положительной полуоси. Квадратное уравнение по t
Xt(t + \) — A(t+\) — Bt = 0 C0)
имеет в обоих рассматриваемых случаях два различных вещественных корня.
В случае B8) обозначим через tx (единственный) положительный корень, а
в случае B9) — через t2 (единственный) корень уравнения C0), лежащий
между —1 и 0. Положим тогда
C1)
Эта величина положительна в обоих случаях. Тогда имеем
C2)
C3)
Эти формулы могут быть выведены соответственно из 6.5B) и 6.5A).

6.14. Теоремы умножения
Разложение Тейлора
с одной стороны, и разложение
являющееся частным случаем разложения Лагранжа (Уиттекер и Ватсон,
1961, 7.32), с другой, являются источниками «теорем умножения» для функ-
dn fix) dn \хп f(x)]
ций, для которых известны либо все — п , либо все и п • При-
ил (XX
меняя формулы из п. 6.4 и 6.6, получаем следующие формулы умножения:
A)
B)
C)
D)
E)
F)
Все эти формулы могут быть переписаны как формулы сложения, если
положить А = 1+~, \х — х -\-у. Следующая формула умножения
X
G)
принадлежит Эрдейи (Erdelyi, 1936c). Здесь g—любой параметр, который
не может принимать лишь отрицательных нечетных значений. Ряд Гаусса F,
входящий в формулу G), является многочленом Якоби и превращается
в ультрасферический многочлен, если g = 2c—1, и в многочлен Лежандра,
если g = c=l.

6.15. Ряды и интегральные формулы
За последние 20 лет было получено большое число соотношений,
содержащих бесконечные ряды или интегралы вырожденных гипергеометрических
функций. Здесь нет единой теории и полное изложение всех результатов
было бы неосуществимо. Мы приведем некоторые примеры наиболее
интересных результатов и некоторые ссылки на литературу. Эти ссылки далеки
от того, чтобы быть исчерпывающими, и дальнейшие работы могут быть
найдены, в частности, в английской и индийской периодической литературе.
6.15.1. Ряды. Многие из рядов, содержащих вырожденные
гипергеометрические функции, которые изучены в настоящее время, имеют одну из
следующих трех форм:
A)
B)
C)
Некоторые из найденных результатов приведены в следующей таблице:
Коэффициенты Сумма
D)
E)
F)
G)
(8)

Об этих и других связанных с ними результатах см. Erdelyi, 1936 в. с;
1937 а, с. В (б)
(9)
Дальнейшие ряды см. в 6.15.3.
6.15.2. Интегралы. Неопределенные интегралы, содержащие вырожденные
гипергеометрические функции, получают из формул дифференцирования
п. 6.4 и 6.6. Многие определенные интегралы могут быть выведены из
формул п. 6.10.
Если k = —1 и Retf>Re#>0 в 6.10E) или если Re a > Re Ь > 0 и
в 6.10G), то можно положить s—"bo. Таким образом,
A0)
(П)
Эти формулы являются формулами обращения Меллина для 6.5D) и 6.5E).
Другие интегральные формулы таковы:
A2)
A3)
(это — обращение преобразования Ганкеля для 6.15 A9)), взаимная формула
A4)

Теорема сложения Магнуса (Magnus, 1946), имеющая вид
A5)
и формула
A6)
тесно связаны с обращением преобразования Стильтьеса для 6.8A5). Отметим
еще некоторые результаты Мейснера (Meixner, 1933). Интегралы по
параметрам были также вычислены Эрдейи (Erdelyi, 1941) и Бухгольцем
(Buchholz, 1947, 1948, 1949).
Другие типы интегралов возникают при изучении нулей вырожденных
гипергеометрических функций. Цветков, 1941, доказал, что для любых двух
нулей ?, f] функции Ф имеем
и для любых двух нулей ?, т\ функции Ф имеем
Отметим также формулу обращения с ядром
Из
вытекает при некоторых предположениях
6.15.3. Произведения вырожденных гипергеометрических функций.
При изучении произведений вырожденных гипергеометрических функций
часто используют обобщенные геометрические ряды (см гл. 5). В этом
пункте будут рассмотрены некоторые сл>чаи, в которых такое обобщение
не нужно.

Некоторые наиболее важные интегральные представления таковы:
A7)
где L — петля, начинающаяся и заканчивающаяся в точке —со и обходящая
особенности подынтегральной функции, то есть четыре точки s = ± -~- х ±
± -у-уу в положительном направлении, а также
A8)
A9)
B0)
B1)
Можно добавить следующие интегральные формулы:
B2)
B3)

B4)
где либо
либо
Эти и многие другие интегралы могут быть найдены в работах Эрдейи и
особенно Мейера. Эрдейи (Erdelyi, 1936d) выразил также интеграл
через гипергеометрическую функцию Лауричелла от п переменных.
Некоторые бесконечные ряды, содержащие вырожденные
гипергеометрические функции, таковы:
B5)
B6)
B7)

B8)
B9)
Эти ряды взяты из работ Эрдейи, где исследованы также другие ряды. См.
также Burchnall, Chaundy, 1940, 1941.
6.16. Вещественные нули для вещественных а и с
Из 6.9A) и 6. 9B) вытекает, что нули функции М%^ совпадают с нулями
функции Ф, а нули tvXt{JL— с нулями ?, исключая, быть может, х = 0, оо.
Если а и с вещественны, то Ф имеет лишь конечное число
вещественных нулей, а ? — лишь конечное число положительных нулей. В самом деле,
на любом конечном отрезке лежит лишь конечное число нулей, а, в силу
6.13A) и 6.9C), нет нулей при достаточно больших значениях \х\. Из
дифференциального уравнения Уиттекера 6. 1 D) можно вывести, что при
вещественных значениях а и с каждая вырожденная гипергеометрическая
функция имеет лишь конечное число нулей.
Более детальное изучение числа вещественных нулей для Ф(я, с; х),
где а ис вещественны (Kienast, 1921), основано на том обстоятельстве, что
при некоторых предположениях либо функции Ф(а-\-\—у, с; х) (/ =
= 0, 1,...,/п+1), либо функции <P(a-{-j, с; х) (/ = 0, 1,..., п) образуют
ряд Штурма. Результаты Кинаста удобно изображать в виде
диаграммы, где (вещественная) (я, с)-плоскость разделена на области, внутри
которых функция Ф имеет заданное число или положительных, или
отрицательных нулей (рис. 5, 6). В следующих диаграммах вертикальные линии
отнесены к областям, расположенным справа от них, а наклонные линии —
к областям, лежащим слева от них. Вдоль горизонтальных линий с =
= 0, — 1, — 2,... функция ф не определена.
Положительные нули для ?(я, с; х) могут быть изучены таким же
образом. Однако для отрицательных вещественных х функция ?, вообще
говоря, принимает комплексные значения и отлична от нуля (см. 6. 8A4)).
Равенства 6.5B) и 6.5F) показывают, что функция W не может иметь
положительных нулей, если а и с вещественны и либо а :> 0, либо а — с +
-f-1 >0. Если —я<я<1 — п, п= 1,2,..., функции 4f(a-\-j, с; х\ j =
= 0,1,..., я, образуют ряд Штурма; все эти функции положительны при
больших положительных значениях х} а их знак, когда х—>0, выясняется
из формул 6.8 B) и 6.8E). Полученная отсюда информация может быть
представлена в виде следующей ниже диаграммы (рис. 7). Эти
результаты совпадают с результатами, полученными Милном (Milne, 1915) и
Цветковым, 1941 а.
Приближенные выражения для нулей были даны Трикоми (Tricomi, 1947).
Из 6.12A1) вытекает, что если ?г—r-й положительный корень
функции Ф(я, с; х) и jc^ur — r-й положительный корень для Jc-i(x)i то при

Рис. 5. Положительные нули Ф (а, с; х).
Рис. 6. Отрицательные нули Ф (а, с;

больших значениях %
A)
Шмидт (Schmidt, 1937) нашел аналогичный результат и показал, что ряд,
первые два члена которого даются формулой A), сходится при достаточно
Рис. 7. Положительные нули W (а, с; х).
больших значениях | а |; r-й положительный корень может быть
приблизительно выражен так:
B)
Дальнейшие детали относительно нулей содержатся в цитированных выше
работах Трикоми и Цветкова.
Комплексные корни (для вещественных а и с) были изучены Цветковым,
19416, и Трикоми (Tricomi, 1950a).
6.17. Дескриптивные свойства при вещественных а, с, х
Результаты п. 6. 16 вместе с формулами дифференцирования, такими как
6.4A0) и 6.6A1), дают информацию относительно числа и приближенного
положения нулей, точек экстремума и точек перегиба для вырожденных
гипергеометрических функций, когда я, с, х, а следовательно, Ф и ?
вещественны. Теорема Сонина — Пойя (Сеге, 1962) определяет поведение
величин последовательных максимумов и минимумов. Запишем уравнение 6.1B) в

самосопряженной форме
а)
и применим эту теорему. Мы получим, что экстремальные значения, или,
точнее, их абсолютные значения, образуют возрастающую или убывающую
последовательность, в зависимости от того, является ли
B)
убывающей или возрастающей функцией от х. Поэтому последовательные
максимумы от \у\ возрастают, если
я>0, х<с 2~ или я<0, х>с 9~,C)
и убывают, если
а>0, ^>с-уили с<0, х<с--. D)
Рассмотрим функции Уиттекера MXl ^ и WXt ^
Пусть
о? — отрезок
Применим к 6.1 D) теорему Сонина — Пойя.
Последовательные относительные максимумы
| z ) возрастают, если
%>0 и х лежит вне <?/ \
или | E)
х <0 и х лежит внутри ,#, J
и убывают, если
х >0 и х лежит внутри <?? \
или | F)
х <0 и х лежит вне <?7. J
Величина дальнейших экстремальных значений может быть приближенно
вычислена с помощью асимптотических представлений, развитых в п. 6.13.
В качестве примера изучим
G)
при вещественных х. В обозначениях Уиттекера % = 5, ^ = 0. В силу 6.4 A0)
(8)
Ясно, что з>@) = 1, /@) = — 4,5, и так как Г(— 4,5)<0, то из 6.13C)
следует, что у (— со) = со, / (— со) = со, у (со) = — со, у' (со) = — со. В
силу диаграммы п. 6.16, у имеет пять положительных нулей и не имеет
отрицательных нулей. В силу 6.16B), нули функции у имеют приближенные
значения 0,3; 1,5; 3,7; 6,9; 10,6 и, в силу 6.16B) и (8), экстремальными
точками являются л: = 0,9; 2,8; 5,8; 9,9. Кроме того, поскольку во всех этих
точках выполнено условие B), то максимумы |^| образуют возрастающую
последовательность. Набросок графика для у, основанный на этой
информации, изображен на рис. 8.

ЦИТИРОВАННАЯ ЛИТЕРАТУРА
К главе 1
Barnes E. W., 1899: Messenger of Math. 29, 64—128.
Barnes E.W., 1906: Proc. London Math. Soc. B) 4, 284-316.
Barnes E. W., 1908: Proc. London Math. Soc. B) 6, 141—177.
B6hmer Eugen, 1939: Differenzengleichungen und bestimmte Integrate, Leipzig.
Bromwich T. J. Га., 1947: An introduction to the theory of infinite series, Macmillan & Co.,
Ltd., London.
В r u i j n N. G., 1937: Mathematica, Zutphen B5, 170—180.
D i x о n A. L. and F e r r a r W. L., 1936: Quart. J. Math., Oxford Ser. 7, 81—96.
Engen van H., 1938: Tohoku Math. J. 45, 124—129.
Fort Tomlinson, 1948: Finite differences, Oxford.
Hardy G. H., 1912: Quart. J. Math. 43, 215—216.
H o 1 d e r Otto, 1928: Ber. Verh. Sachs. Akad. Wiss. Math. Phys. Kl. 80, 312—325.
H u t с h i n s о n J. I., 1925: Trans. Amer. Math. Soc. 27, 49—60.
Hutchinson J. I., 1929: Trans. Amer. Math. Soc. 31, 222—344.
I n g h a m A. E., 1932: The distribution of prime numbers, Cambridge.
К 1 u у v e r J. C., 1927: Quart. J. Math. 50, 185—192.
Lichtenbaum Paul, 1931: Math. Z. 33, 641—647.
Lindelof Ernst, 1905: Le Calcul des Residus, Gauthier—Villars.
M e 11 i n H. J., 1910: Math. Ann. 68, 305—337.
Milne-Thomson L. M., 1933: The calculus of finite differences, Macmillan & Co., Ltd.,
London.
Nielsen Niels, 1906: Handbuch der Theorie der Gamma-Funktion, B. G. Teubner, Leipzig.
Nielsen Niels, 1923: Traite elementaire des nombres de Bernoulli, Gauthier — Villars.
N o r 1 u n d N. E., 1922: Acta Math. 43, 121-196.
N o r 1 u n d N. E., 1924: Vorlesungen tiber Differenzenrechnung, Springer.
R a m a n u j a n Srinivasa, 1927: Collected papers, Cambridge.
Rasch G., 1931: Ann. of Math. 32, 591-599.
Rogers L. S., 1905: Proc. London Math. Soc. 4, 169—189.
R о w e С. Н., 1931: Ann. of Math. 32, 10—16.
S a n d h a m H. F., 1949: J. London Math. Soc. 24, 83—91.
S с h w a 11 I. S., 1932: J. Math. Pure Appl. IX, 143—151.
S h a s t r i N. A., 1938: Philos. Mag. 25, 930—950.
T i t с h m a r s h E. C, 1935: Proc. Roy. Soc. London 151, 234—255.
T i t с h m a r s h E. C, 1936: Proc. Roy. Soc. London 157, 261—263.
Tricomi Francesco, 1950: Rend. Semin. Mat. Torino 9, 343—351.
T r u e s d e 11 С A., 1945: Ann. of Math. 46, 114—157.
Watson G. N., 1920: Quart. J. of Pure and Applied Math. 48, 1—18.
Wilton F. R., 1922: Messenger of Mathematics 52, 90—93.
Гельфонд А. О., Исчисление конечных разностей, Физматгиз, 1959.
Титчмарш Э., Дзета-функция Римана, ИЛ, 1948.

Уиттекер Э., В а т с о н Г., Курс современного анализа, Физматгиз, т. I, 1961; т. II, 1962.
Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, Физматгиз,
т. I, 1962; т. II, 1962; т. III, 1963.
X а р д и Г., Сходящиеся ряды, ИЛ, 1949.
К главе 2
Bailey W. N., 1935a: Generalized hypergeometric series, Cambridge.
Bailey W. N., 1935b: Proc. London Math. Soc. B) 38, 377—384.
Bancroft T. A., 1949: Ann. Math. Statistics 20, 451—455.
Barnes E. W., 19Э7: Trans. Cambridge Philos. Soc. 20, 253—279.
Barnes E. W., 1908: Proc. London Math. Soc. B) 6, 141—177.
Bateman Harry, 1909: Trans. Cambridge Philos. Soc. 21, 171-196. In particular p. 184.
В г о m w i с h T. J., 1947: An introduction to the theory of infinite series, Macmillan & Co.,
Ltd., London.
Burchnall J. L. and Chaundy T. W., 1940: Quart. J. Math., Oxford Ser. 11, 249—270.
Burchnall J. L. and Chaundy T. W., 1948: Proc. London Math. Soc. B) 50, 56—74.
Chaundy T. VV. см. Bur chnall J. L.
Cherry T. M., 1950a: Trans. Amer. Math. Soc. 68, 224—257.
Cherry Т. М., 1953b: Proc. Roy. Soc. London Ser. A 1202, 507—522.
D i x о n A. L., 1905: Proc. London Math. Soc. B) 3, 206—224.
Elliot E. В., 1904: Messenger of Math. 33, 31—40.
Erdelyi Arthur, 1937a: Quart. J. Math., Oxford Ser. 8, 200—213.
Erdelyi Arthur, 1937b: Quart. J. Math., Oxford Ser. 8, 267-277.
Erdelyi Arthur, 1939: Quart. J. Math., Oxford Ser. 10, 176-189.
Erdelyi Arthur, 1941: Proc. Roy. Soc. Edinburgh, Sect. A 61, 61—70.
Fricke Robert and Klein Felix, 1897—1912: Vorlesungen uber die Theorie der Auto-
morphen Funktionen, Vol. 2, B. G., Teubner, Leipzig.
Gauss C. F., 1876: Werke, Vol. Ill, Konigliche Gesellschaft der Wissenschaften, Gottingen.
Goursat Edouard, 1881: Ann. Sci. Ecole Norm. Sup. B) 10, 3—142.
Goursat Edouard, 1884: Math. Ann. 24, 445—460.
Goursat E d о u a r d, 1887: J. Math. Pures Appl. D) 3, 255-305.
Goursat Edouard, 1888: Acta Soc. Sci. Fennicae 15, 47—127.
Goursat Edouard, 1936: Proprietes generates de L'equation d'Euler et de Gauss (Actua-
lites scientifiques et industrielles 333), Paris.
Goursat Edouard, 1938: Integrates Algebriques, Probleme d'inversion (Actualites
scientifiques et industrielles 692), Paris.
H e rg 1 о t z G. A., 1917: Ber. Sachs. Ges. Wissensch., Leipzig 69, 510—534.
Heymann Woldemar, 1899: Z. Math. u. Physik 44, 280—288.
Hurwitz Adolf, 1890: Nachr. Ges. Wiss., Gottingen, 557-564.
Hurwitz Adolf, 1891: Math. Ann. 38, 452—458.
Hurwitz Adolf, 1906: Nachr. Ges. Wiss., G5ttingen, lib-Ill.
Hurwitz Adolf, 1907: Math. Ann. 64, 517—560.
J а с о b i С G. J., 1859: J. Reine Angew. Math. 56, 144—165.
Kampe de FerietM. J., 1937: La Fonction Hypergeometrique (Memorial des sciences
mathematiques, Fascicule 85). Gauthier—Villars.
Klein Felix and Fricke Robert, 1890—1892: Vorlesungen uber die Theorie der ellipti-
schen Modulfunktionen Vol. 2, B. G. Teubner, Leipzig.
Klein Felix, 1933: Vorlesungen uber die hypergeometrische Funktion, B. G. Teubner,
Leipzig.
L i g h t h i 11 M. J., 1947: Proc. Roy. Soc. London Ser. A191, 341—351.
M а с R о b e r t Т. М., 1923: Proc. Edinburgh Math. Soc. 42. 84—88.
Mehlenbacher L. E., 1938: Amer. J. Math. 60, 120-128.
Meixner Joseph, 1941: Deutsche Math. 6, 341—349.

М е 111 n H. J., 1895: Uber die fundamental Wichtigkeit des Satzes von Cauchy fiir die
Theorien der Gamma und der hypergeometrischen Funktionen, Acta Soc. Sci. Fennicae
20, № 12.
M i t r a S. C, 1943: J. Indian Math. Soc. (N. S.) 7, 102—109.
О r r W. Ma. F., 1899: Trans. Cambridge Philos. Soc. 17, 1-15.
Perron Oskar, 1916—1917: S. — B. Heidelberger Akad. Wiss. No. 9, 1916, No. 1, 1917.
P ool e E. G. C., 1936: Introduction to the theory of linear differential equations, Oxford.
S с h w a r z H. A., 1873: J. Reine Angew. Math. 75, 292—335.
Seifert Herbert, 1947: Math. Ann. 120, 75-126.
Snow Chester, 1942: The hypergeometric and Legendre functions with applications to
integral equations of potential theory, National Bureau of Standards.
T r u e s d e 1 1 С A., 1948: An essay toward a unified theory of special functions based upon
the functional equation OF (z, a)/dz = F (z, a-\-1), Princeton University Press, Princeton, N. Y.
Van V 1 e с к Е. В., 1902: Trans. Amer. Math. Soc. 3, 110—131.
Watson G. N., 1909. Quart. J. Math. 41, 70-79.
Watson G. N., 1918: Trans. Cambridge Philos. Soc. 22, 277—303.
WinstonM., 1895: Math. Ann. 46, 159.
Wirtinger Wilhelm, 1902: Akad. Wiss. Wien. S. - B. Ila, III, 894-900.
W i r t i n g e r Wilhelm, 1903: Akad. Wiss. Wien. S. - B. Ila, 112, 1721-1733.
Голубев В. В., Однозначные аналитические функции. Автоморфные функции, Физматгиз,
1961.
Зоммерфельд А., Строение атома и спектры, Гостехиздат, 1956.
Кратцер А., Франц К., Трансцендентные функции, ИЛ, 1963.
Р и м а н Б., Сочинения, Гостехиздат, 1948.
Уиттекер Э., В а т с о н Г., Курс современного анализа, Физматгиз, т, I, 1961; т. II, 1962.
К главе 3
Airey J. R., 935: Philos. Mag. 19. 177-178.
Bailey W. N., 1931: Proc. Cambridge Philos. Soc. 27, 184-189, 381—386.
Bailey W. N., 1938: J. London Math. Soc. 13, 167—169.
В a n e r j e e D. P., 1932: Bull. Calcutta Math. Soc. 24, 89—94.
В a n e r j e e D. P., 1938: Proc. Cambridge Philos. Soc. 34, 30—32.
В a n e r j e e D. P., 1940: J. Indian Math. Soc. 4, 25—28.
В a n e r j e e D. P., 1942: Amer. J. Math. 64, 72—80.
Barnes E. W., 1908: Quart. J. Math., Oxford Ser. 39, 97—204.
Bateman Harry, 1932: Partial differential equations of mathematical physics, Cambridge.
Bateman Harry and Rice S. O., 1938: Amer. J. Math. 60, 297—308.
В о s e B. N., 1944: Bull. Calcutta Math. Soc. 36, 125—132.
Bose S. K., 1946: Bull. Calcutta Math. Soc. 38, 177—184.
С h u L. J. and S t r a 11 о n J. A., 1941: J. Math. Physics 20, 259—309.
С о о k e R. G., 1925: Proc. London Math. Soc. B) 23, XIX-XX.
С о p s о n E. Т., 1945: Proc. Edinburgh Math. Soc. B) 7, 81—82.
CowlingT.G., 1940: Quart. J. Math., Oxford Ser. 11, 222—224.
D a r 1 i n g H. B. C, 1923: Quart. J. Math. 49, 289—303.
D h a r S. C. and S h a b d e N. G., 1932: Bull. Calcutta Math. Soc. 24, 177—186.
Dinghas Alexander, 1950: Math. Z. 53, 76—83.
Dougall John, 1919; Proc. Edinburgh Math. Soc. 37, 33—47.
Erdelyi Arthur, 1941: Philos. Mag. G) 32, 351—352.
Gegenbauer L#> 1893: Wiener Sitzungsberichte 102, 942.
G о r m 1 e у P. G., 1934: J. London Math. Soc. 9, 149—152.
Heine E m i 1, 1878, 1881: Theorie der Kugelfunktionen, G. Riemer, Berlin.
Lense Josef, 1950: Kugelfunktionen, Akademische Verlagsgesellschaft.
Lowry H. V., 1926: Philos. Mag. 2, 1184—1187.
M а с D о n a 1 d H. M., 1911: Proc. London Math. Soc. 13, 220—221.
MacRobert T. M., 1932: Philos. Mag. G) 14, 632—656.

MacRobertT.M., 1934: Proc. Roy. Soc. Edinburgh 54, 135-144.
MacRobert Т. М., 1935: Proc. Roy. Soc. Edinburgh 55, 85—90.
M а с R о b e r t Т. М., 1936: Proc. Roy. Soc. Edinburgh 57, 19—23.
MacRobert Т. М., 1936: Philos. Mag. G) 27, 703-705.
MacRobert Т. М., 1940: Quart. J. Math., Oxford Ser. 11, 95-100.
MacRobert T. M., 1943: Quart. J. Math., Oxford Ser. 14, 1—4.
MacRobert Т. М., 1947: Spherical harmonics, Methuen.
M e h 1 e r F. G., 1881: Math. Ann. 18, 161—194.
M e i j e r С S., 1939: Nederl. Akad. Wetensch., Proc. 42, 930-947.
Neumann C, 1881: Ann. 18, 195—236.
Olbricht R., 1887: Nova Acta Acad. Leop. 52, 1—48.
Prasad Ganesh, 1930: Proc. Benares Math. Soc. 12, 33—42.
Prasad Ganesh, 1930 (Vol. 1) and 1932 (Vol. 2): A treatise on spherical harmonics and
the functions of Bessel and Lame, Benares Math. Soc, India.
Prasad Ganesh, 1930: Bull. Calcutta Math. Soc. 22, 159—170.
Prasad Ganesh, 1931: Bull. Calcutta Math. Soc. 23, 155—182.
S h a b d e N. G., 1931: Bull. Calcutta Math. Soc. 23, 23—44, 155—182.
S h a b d e N. G., 1932: Bull. Calcutta Math. Soc. 24, 53-60.
S h a b d e N. G., 1933: Bull. Calcutta Math. Soc. 25, 23—30.
S h a b d e N. G., 1934: Proc. Edinburgh Math. Soc. 4, 41—46.
S h a b d e N. G., 1939: Bull. Calcutta Math. Soc. 31, 87—90.
S h a b d e N. G., 1940: Bull. Calcutta Math. Soc. 32, 121—124.
S h a b d e N. G., 1945: Proc. Benares Math. Soc. 7, 51—53.
Sircar H., 1927: Proc. Edinburgh Math. Soc. 1, 244—245.
T i t с h m a r s h E. C, 1932: The theory of functions, Oxford.
Watson G. N., 1938: Quart. J. Math., Oxford Ser. 9, 123-140.
Wrinch D., 1930: Philos. Mag. G) 10, 1037-1043.
Ват сон Г., Теория бесселевых функций, т. I, ИЛ, 1949.
Г о б с о н Е., Теория сферических и эллипсоидальных функций, ИЛ, 1952.
Уиттекер Э., В а т с о н Г., Курс современного анализа, Физматгиз, т. I, 1961; т. II, 1962.
Ф о к В. А., 1943: Доклады АН СССР 39, 253—256.
К главе 4
Bailey W. N., 1928: Proc. London Math. Soc. B) 28, 242—254.
Bailey W. N., 1929: Proc. London Math. Soc. B) 29, 503—516.
Bailey W. N., 1935: Generalized hypergeometric series (Cambridge Tracts, No 32),
Cambridge.
Bailey W. N., 1936: Quart. J. Math., Oxford Ser. 7, 105—115.
Bailey W. N., 1937: Quart. J. Math., Oxford Ser 8, 113-114.
Bailey W. N., 1947a: Quart. J. Math., Oxford Ser. 18, 157-166.
Bailey W. N., 1947b: Proc. London Math. Soc. B) 49, 421—435.
Bailey W. N.. 1948a: Proc. London Math. Soc. B) 50, 1—10.
Bailey W. N.. 1948b: J. London Math. Soc. 22, 237-240.
Barnes E. W., 1906: Proc. London Math. Soc. B) 5, 59-116.
Bateman Harry, 1933: Tohoku Math. J. 37, 23—38.
Bateman Harry, 1934: Ann. Math. 35, 767-775.
Bateman Harry, 1936: Duke Math. J. 2, 569—577.
В о s e B. N.. 1944: J. Indian Math. Soc. (N. S.) 8, 120-128.
В u r с h n a 1 1 J. L.. 1948: J. London Math. Soc. 23, 253—257.
Burchnall J. L. and Chaundy T. W., 1948: Proc. London Math. Soc. B) 50, 56—74.
Chaundy T. W., 1942: Quart. J. Math., Oxford Ser. 13, 159—171.
Chaundy T. W., 1943: Quart. J. Math., Oxford Ser. 14, 55—78.
Clausen Thomas, 1828: J. Reine Angew. Math. 3. 89—91.
Darling H. В. С, 1932: Proc. London Math. So:. B) 34, 323—339.

Daum J. A., 1942: Bull. Amer. Math. Soc. 48, 711—713.
Dixon A. C, 1903: Proc. London Math. Soc. A) 35, 285—289.
Dougall John, 1907: Proc. Edinburgh Math. Soc. 25, 114-132.
Erdelyi Arthur, 1937: Quart. J. Math., Oxford Ser. 8, 267-277.
Erdelyi Arthur, 193S: Monatsh. Math. Phys. 46, 132-156.
Erdelyi Arthur, 1939: Monatsh. Math. Phys. 47, 87-103.
Fasenmyer Mary Celine, 1947: Bull. Amer. Math. Soc. 53, 806—812.
Goursat Edouard, 1883: Ann. Sci. Ecole Norm. Sup. Ser. 2, 12, 261— 235, 395—430.
Goursat Edouard, 1884: Acta Math. 5, 97-120.
Hardy G. H., 1923: Proc. Cambridge Philos. Soc. 21, 492—503.
Heine Emil, 1878: Handbuch der Kugelfunktionen. Theorie und Anwendungen, G. Riemer,
Berlin.
Hill M. J. M., 1907: Proc. London Math. Soc. B) 5, 335-341.
Koppenfels Werner von, 1937: Akad. Wiss. Wien, S. - B. 146, 11 -22.
Koppenfels Werner von, 1939: J. Reine Angew. Math. 181, 83—124.
К r a 11 H. L. and F r i n к О г г i n, 1949: Trans. Amer. Math. Soc. 65, 100—115.
MacRobert T. M., 1939: Philos. Mag. G) 27, 579—581 and G) 28, 488—492.
M i t r a S. C, 1942: J. Indian Math. Soc. (N. S.) 6, 84—86 and 81—83; see also Math. Rev. 4, 141.
Pasternack S., 1937: Proc. Nat. Acad. Sci. USA 23, 91—94.
Pasternack S., 1939: Philos. Mag. G) 28, 209—226.
Pochhammer Leo, 1870: J. Reine Angew. Math. 71, 316—352.
Pochhammer Leo, 1871: J. Reine Angew. Math. 73, 135—157.
Pochhammer Leo, 1883a: Math. Ann. 32, 353—371.
Pochhammer Leo, 1883b: J. Reine Angew. Math. 102, 76-159.
Pochhammer Leo, 1891: Math. Ann. 38, 586—597.
Pochhammer Leo, 1893a: Math. Ann. 41, 197—218.
Pochhammer Leo, 1893b: J. Reine Angew. Math. 112, 58—86.
Pochhammer Leo, 1895: Math. Ann. 46, 584—605.
Pochhammer Leo, 1898: Math. Ann. 50, 285—302.
P г е е с е С. Т., 1924; Proc. London Math. Soc. B) 22, 370—380.
R a i n v i 11 e E. D., 1945: Bull. Amer. Math. Soc. 51, 714—723.
Rice S. O., 1939: Duke Math. J. 6, 108-119.
S a a 1 s с h ii t z L., 1891: Z. Math. u. Phys. 36, 278—295, 321—327.
Shanker Hari, 1946: J. London Math. Soc. 21, 194—198.
Shanker Hari, 1947: J. London Math. Soc. 22, 112—115.
Smith F. C, 1938: Bull. Amer. Math. Soc. 44, 429—433.
Smith F. C, 1939: Bull. Amer. Math. Soc. 45, 629-636.
T h о m a e J., 1869: Math. Ann. 2, 427-444.
Thomae J., 1879: J. Reine Angew. Math. 87, 222-349.
Watson G. N.. 1924: Proc. London Math. Soc. B) 22, XXXII-XXXIII.
WatsonG.N,, 1929: J. London Math. Soc. 4, 4—9.
W h i p p 1 e F. J. W., 1925: Proc. London Math. Soc. B) 23, 104-114.
Whipple F. J. W., 1927: Proc. London Math. Soc. B) 26, 257—272.
Whipple F. J. W., 1935: Proc. London Math. Soc. B) 40, 336—344.
Whipple F. J. W., 1937: Proc. London Math. Soc. B) 42, 410—421.
Wright E. M,, 1935: J. London Math. Soc. 10, 287—293.
Wright E. M., 1940: Proc. London Math. Soc. B) 46, 389—408.
Певный Б. Г., 1940: Доклады АН СССР 28, 310—312.
Уиттекер Э., Ватсон Г., Курс современного анализа, Физматгиз, т. I, 1961; т. И. 1962.
К главе 5
А р р е 11 Paul and Kampe de Feriet M. J., 1926: Fonctions hyperge6metriques et
hyperspheriques. Polynomes d'Hermite, Gauthier—Villars.
В a i 1 e у W. N., 1935: Generalized hypergeometric series (Cambridge Tracts in Mathematics
and Mathematical Physics No 32), Cambridge.

Barnes E. W,, 1907: Proc. London Math. Soc. B) 5, 59—116.
Barnes E. W., 1908: Proc. London Math. Soc. B) 6, 141—177.
Barnes E. W., 1908: Trans. Cambridge Philos. Soc. 20, 253—279.
Birkeland Richard, 1927: C. R. Acad. Sci. Paris 185, 923—925.
Borngasser Ludwig, 1933: Cber hypergeometrische Funktionen zweier Veranderlichen,
Dissertation, Darmstadt.
Burctinall J. L., 1939: Quart. J. Math., Oxford Ser. 10, 145—150.
В u г с h n a 1 1 J. L., 1942: Quart. J. Math., Oxford Ser. 13, 90—106.
В u г с h n a 1 1 J. L. and С h a u n d у T. W., 1940: Quart. J. Math. Oxford Ser. 11, 249-270.
Burchnall J. L. and Chaundy T. W., 1941: Quart. J. Math., Oxford Ser. 12, 112—
128.
Chaundy T. W., 1942: Quart. J. Math., Oxford Ser. 13, 159—171.
Erdelyi Arthur, 1937: Akad. Wiss. Wien, S-B IIa, 146, 431-467.
Erdelyi Arthur, 1939: Proc. Roy. Soc. Edinburgh 59, 224—241.
Erdelyi Arthur: 1939a: Nieuw Arch. Wiskunde B) 20, 1—34.
Erdelyi Arthur, 1940: Proc. Roy. Soc. Edinburgh 60, 344—361.
Erdelyi Arthur, 1941: Quart. J. Math., Oxford Ser. 11, 63—77.
Erdelyi Arthur, 1948: Proc. Roy. Soc. Edinburgh, Sect. A 62, 378—385.
Horn Jakob, 1889: Math. Ann. 34, 544—600.
Horn Jakob, 1931: Math. Ann. 105, 381—407.
Horn Jakob, 1935: Math. Ann. Ill, 638—677.
Horn Jakob, 1936: Math. Ann. 113, 242-291.
Horn Jakob, 1938: Math. Ann. 115, 435—455.
Horn Jakob, 1938a: Monatsh. Math. Phys. 47, 186—194.
Horn Jakob, 1939: Monatsh. Math. Phys. 47, 359—379.
I n с e E. L., 1942: Proc. Roy. Soc. Edinburgh A 61, 195-209.
Jackson F. H., 1942: Quart. J. Math. 13, 69-82.
Jackson F. H., 1944: Quart. J. Math. 15, 49—61.
M а с R о b e r t Т. М., 1937—1938: Proc. Roy. Soc. Edinburgh 58, 1—13.
M а с R о b e r t T. M.( 1941: Philos. Mag. G) 31, 254—260.
M а с R о b e r t Т. М., 1942: Quart. J. Math., Oxford Ser. 12, 65—68.
M а с R о b e r t T. M., 1948: Philos. Mag. G) 39, 466—471.
M e i j e r C. S., 1936: Nieuw Arch. Wiskunde B) 18, 10—39.
M e i j e r С S., 1940: Nederl. Akad. Wetensch., Proc. 43, 198-210 and 366-378.
M e i j e r C.S., 1941a: Nederl. Akad. Wetensch., Proc. 44, 82-92, 186-194, 298-307, 442-451
and 590—598.
M e i j e r С S., 1941b: Nederl. Akad. Wetensch., Proc. 44, 435-441 and 599-603.
M e i j e r С S., 1941c: Nederl. Akad. Wetensch., Proc. 44, 1062-1070.
M e i j e r С S., 1946: Nederl. Akad. Wetensch., Proc. 49, 344—456, 457—469, 632—641, 765—772,
936—943, 1063—1072, 1165—1175.
Ore О у s t e i n, 1929: С R. Acad. Sci. Paris 189, 1238—1240.
Ore О у s t e i n, 1930: J. Math. Pure and Appl. (9) 9, 311—326.
К главе 6
A i г е у J. R. and Webb H. A., 1918: Philos. Mag. F) 36, 129—141.
A p p e 11 Paul and К a m p ё d e F ё r i e t M. J., 1926: Fonctions hypergeometriques et
hyperspheriques. Polynomes d'Hermite, Gauthier-Villars.
Archibald W. J., 1938: Philos. Mag. G) 26, 415—419.
Bailey W. N.. 1937: Quart. J. Math., Oxford Ser. 8, 51-53.
Bateman Harry, 1931: Trans. Amer. Math. Soc. 33, 817—831.
Bock P. L., 1939: Compositio Math. 7, 123—134.
Buchholz Herbert, 1943: Z. Angew. Math. Mech. 23, 47—58 and 101—118.
Buchholz Herbert, 1947: Z. Physik 124, 196-218.
Buchholz Herbert, 1948: Ann. Physik F) 2, 185-210.

Buchholz Herbert, 1949: Math. Z. 52, 355—383.
В u г с h n a 11 J. L. and Chaundy T. W., 1940: Quart. J. of Math. 11, 249—270.
В u г с h n a 11 J. L. and С h a u n d у Т. W,, 1941: Quart. J. of Math. 12, 112—128.
Cailer Charles, 1920: Enseignement Math. 21, 224—225, 255—259.
С h a p p e I ! G. E., 1924/25: Proc. Edinburgh Math. Soc. 43, 117—130.
D h a r S. C, 1933: Bull. Calcutta Math. Soc. 26, 57—64.
Erdelyi Arthur, 1936a: Math. Ann. 113, 357—362.
Erdelyi Arthur, 1936b: Nederl. Akad. Wetensch., Proc. 39, 1092—1098.
Erdelyi Arthur, 1936c: Monatsh. Math. Phys. 45, 31—52.
Erdelyi Arthur, 1936d: Math. Z. 42, 125—143.
Erdelyi Arthur, 1937a: Math. Z. 42, 125—143, 641—670.
Erdelyi Arthur, 1937b: Akad. Wies. Wien., S—B. Ha, 146, 431—467.
Erdelyi Arthur, 1937c: Monatsh. Math. Phys. 45, 251 -279.
Erdelyi Arthur, 1937d: Quart. J. Math., Oxford Ser. 8, 200—213.
Erdelyi Arthur, 1937e: Monatsh. Math. Phys. 46, 132—156.
ErdelyiArthur, 1937f: Monatsh. Math. Phys. 46, 1—9.
Erdelyi Arthur, 1938a: J. London Math. Soc. 13, 146—154.
E r d e 1 у i Arthur, 1938b: Philos. Mag. G) 26, 871-877.
Erdelyi Arthur, 1938c: Nederl. Akad. Wetensch., Proc. 41, 481—486.
Erdelyi Arthur, 1^38d: Casopis Pest. Mat. Fys. 67, 240-248.
Erdelyi Arthur, 1939a: Compositio Math. 7, 340—353 and 6, 336—347.
Erdelyi Arthur, 1939b: Quart. J. Math., Oxford Ser. 10, 176—189.
Erdelyi Arthur, 1939c: Proc. Benares Math. Soc. 1, 39—53.
Erdelyi Arthur, 1939d: J. Indian Math. Soc. 3, 169-181.
Erdelyi Arthur, 1940: Nieuw. Arch. Wiskunde 20, 1—38.
Erdelyi Arthur, 1941: Proc. Roy. Soc. Edinburgh 61, 61—70.
Fisher E., 1935: Proc. Nat. Acad. Sci. USA 21, 529-533.
О h e о r g h i u G. Т., 1938: Bull. Sci. Ecole Polytech. Timosoara 8, 17—27.
Giraud Georges, 1942: С R. Acad. Sci. Paris 214, 649—651.
Gordon W., 1928: Ann. Physik 48, 180.
Gran О 1 s s о n R., 1937: Ing. Arch. 8, 99—103.
Gupta H. C, 1943: Proc. Nat. Acad. Sci. India Sect. A 13, 225—231.
H e a 11 e у A. H., 1943: Trans. Roy. Soc. Canada C) 37, 13—29.
Howell W. J., 1939: Philos. Mag. G) 28, 493-495.
Humbert Pierre, 1921: C. R. Acad. Sci. Paris 173, 217—219.
Kienast Alfred, 1921: Denkschr. Schw. Naturf. Gesell. 57, 247—325.
К u m m e r E. E., 1837: J. Reine Angew. Math. 17, 228-242.
Lowan Arnold and HorensteinW., 1942: J. Math. Phys. Mass. Inst. Tech. 21, 264—283.
M а с R о b e r t T. M., 1919/20: Proc. Roy. Soc. Edinburgh 42, 8Э—96.
M а с R о b e r t T. M., 1938: Philos. Mag. G) 26, 82—93.
M а с R о b e r t Т. М., 1941: Philos. Mag. G) 26, 82—93.
Magnus Wilhelm, 1941: Z. Physik 48, 343—356.
Magnus Wilhelm, 1946: Nachr. Ges. Wiss., Gottingen, 4—5.
M e i j e r C. S., 1934: Nederl. Akad. Wetensch., Proc. 37, 805—812.
M e i j e r С S., 1935a: Quart. J. Math., Oxford Ser. 6, 241—248.
M e i j e r C.S, 1935b: Nederl. Akad. Wetensch., Proc 38, 528—535.
M e i j e r C.S, 1936a: Nederl. Akad. Wetensch, Proc. 39, 394—403 and 519-527,
M e i j e r С S., 1936b: Math. Ann. 112, 469-489.
M e i jer C.S., 1937: Nederl. Akad. Wetensch., Proc. 40, 133—141 and 871-879.
M e i j e r C. S., 1938: Nederl. Akad. Wetensch., Proc. 41, 42—44, 275—277, 624—633, 744—755,
879—888 and 1108—1114.
M e i j e r C.S., 1941: Nederl. Akad. Wetensch., Proc. 44, 81-92, 186-194, 298-307, 436-451 and
590—598.
Meixner Joseph, 1933: Math. Z. 36, 677-707.
Milne Archibald, 1914/15: Proc. Edinburgh Math. Soc. 33, 48—64.
M it r a S. C, 1928: Tohoku Math. J. 29, 321-325.

Mit r a S. С, 1942: J. Indian Math. Soc. (N. S.) 6, 84—86 and 81—83.
Mohan Brij, 1943: Proc. Benares Math. Soc. 4, 59—60.
P a s r i с h a B. R., 1943: Proc. Benares Math. Soc. 4, 61—69.
Perron Otto, 1921: J. Reine Angew. Math. (Crelle) 151, 63—78.
Pinney Edmund, 1946: J. Math. Physics 25, 49—79.
Pochhammer Leo, 1890: Math. Ann. 35, 495—526.
P о о 1 e E. О. С, 1935: Proc. London Math. Soc. B) 38, 542—552.
P о о 1 e E, G. C, 1938: Quart. J. Math., Oxford Ser. 9, 230-233.
Schmidt Harry, 1937: J. Reine Angew. Math. (Crelle) 176, 250—252.
Shanker Hari, 1939: J. Indian Math. Soc. 3, 228-230.
Shanker Hari, 1943: Proc. Benares Math. Soc. 4, 51—57.
Shanker Hari, 1946: J. London Math. Soc. 21, 194—198.
S h a r m a J. L., 1938: Philos. Mag. G) 25, 491—504.
Ser J., 1937: Bull. Sci. Math. B) 61, 74—81.
Ser J., 1938: Bull. Sci. Math. B) 62, 171-182.
Sexl Theodor, 1929: Z. Physik 56, 62-93.
Taylor W. C, 1939: J. Math. Phys. Mass. Inst. Tech. 18, 34—49.
Tricomi Francesco, 1947: Ann. Mat. Рига Appl. (IV) 26, 141—175.
Tricomi Francesco, 1949: Ann. Mat. Рига Appl. D) 28, 263—290.
Tricomi Francesco, 1950a: Math. Z. 52, 669—675.
Tricomi Francesco, 1950b: Expansion of the hypergeometric function in series of
confluent ones.
Watson G. N., 1922: A treatise on the theory of Bessel functions, MacMillan, 100.
Зоммерфельд А., Строение атома и спектры, Гостехиздат, 1956.
Cere Г., Ортогональные многочлены, Физматгиз, 1962.
Т р и к о м и Ф., Дифференциальные уравнения, ИЛ, I960.
Уиттекер Э., ВатсонГ., Курс современного анализа, Физматгиз, т. I, 1961; т. II, 1962.
Цветков Г. Е., 1941а: Доклады АН СССР 32, 10-12.
Цветков Г. Е., 19416: Доклады АН СССР 33, 290—291.

ИМЕННОЙ УКАЗАТЕЛЬ
Айне 230
Аппель 218, 230, 236
Бейли 93, 186, 191
Бейтмен 89, 193, 255
Берне 63, 64, 74, 173, 181, 184, 185, 207
Берчнелл 93, 94, 225, 230, 234, 235, 236
Бине 63
Биркеланд 219, 236
Борнгессер 230
Бухгольц 252, 274
Ван-Флек 109
Ван-Энген 63
Ватсон 86, 88, 181, 197
Вейерштрасс 15
Виртингер 89, 108
Гаусс 15, 34, 70, 77, 98
Гегенбауэр 180
Герглотц 109
Горн 218, 219, 221, 230, 236
Гумберт 218
Гурвиц 109
Гурса 103, 185, 186, 218
Дар л инг 187
Даум 198
Джексон 236
Диксон 96
Зейферт 88
Зоммерфельд 89
Иенсен 48
Кампе-де-Ферье 230, 236
Кели 93
Кинаст 277
Клаузен 184, 186
Коппенфельс 184
Крал л 195
Кристоффель 153
Куммер 72, 77
Лайтхилл 88
Лауричелла 236
Лежандр 125
Лерх 39
Мак-Роберт 201, 207
Мейер 206, 207, 208, 209, 276
Мейснер 95, 274
Мелер 176
Меллин 64, 236
Милн 277
Оре 219
Орр 93
Пастернак 193
Певный 192
Перрон 86, 267
Пикар 218, 225
Пинчерле 63
Похгаммер 30, 183, 184, 185, 192
Райе 193
Райт 184
Рейнвилл 188, 194
Риман 102, 103, 105
Смит 185
Тейлор 268, 269
Томе 185
Трикоми 245, 264, 265, 277, 279
Уиттекер 251, 252
Фазенмайер 1Э4
Фринк 195
Цветков 274, 277, 279
Ченди 93, 94, 187, 225, 234, 235, 236
Черри 88
Шварц 106, 107
Шмидт 279
Эйлер 15
Эллиот 96
Эрдейи 89, 192, 195, 230, 264, 270, 271, 274, 276
Якоби 71

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоморфная функция 107
обратная 99
, частный вид 108
Асимптотические разложения 61, 62, 63
Ассоциированные ряды 71
Бейтмена ^-функция 255, 261
Бейтмена — Пастернака многочлены 193
Бернсайда формула для In Г (г) 63
Бернулли многочлены 51, 67, 68
— —, интегральные представления 53, 58
порядка т и — т 54
, рекуррентная формула 51
, ряды Фурье 52
, соотношения симметрии 52
, теоремы умножения 52
— числа 50, 52, 53, 67
, выражение через С E) 53
, интегральные представления 53
— — порядка т и — т 54
, рекуррентные формулы 52
Берчнелла и Ченди формулы умножения
гипергеометрических рядов 94
Бесселевы функции 201, 211, 240, 252, 264
Бесселя дифференциальное уравнение 238
Бета-функция 23, 24
— неполная 98, 99
—, контурные интегралы 28
—, определенные интегралы 24
Бине выражения для In Г (z) 37, 63
для ф (z) 33, 34
Биномиальный коэффициент 67
— ряд, обобщение 196
усеченный 98, ПО
Вырожденный гипергеометрический ряд — см.
гипергеометрический ряд вырожденный
Гамма-функция 15, 16, 17
—, бесконечные произведения 19
—, — ряды 21
—, контурные интегралы 28
—, логарифмическая производная 30
—, представление Ганкеля 28
—, функциональные уравнения 17
Ганкеля представление для гамма-функции 28
— символ 67
Гаусса гипергеометрический ряд — см.
гипергеометрический ряд соотношения между
смежными гипергеометрическими рядами
111, 112
— теорема для ф (z) 34
Гаусса — Лежандра формула умножения 18
Гегенбауэра дифференциальное уравнение 180
— многочлены 99, 177
, соотношения ортогональности 179
— —, теорема сложения 180
Гегенбауэра многочлены, тригонометрическое
разложение 178
— функции 180, 181, 182
Гейне формула 169
Гипергеометрическая функция 70, 109
вырожденная 237, 238, 241
, асимптотическое поведение 265—270
, ассоциированная функция 242
, вещественные нули 277
, дескриптивные свойства 279
, дифференциальное уравнение Уитте-
кера 238
_ , интеграл вероятностей 254
— —, — Френеля 254
_ , интегралы 273
, интегральная логарифмическая
функция 254
_ , — показательная функция 254
_ , интегральные косинус и синус 254
_ , — представления 243, 259, 260—262
_ , — теоремы сложения 258
_ , логарифмический случай 247
, многочлены Пуассона 256
__ , — Эрмита 255
__ , неполная гамма-функция 253
— —г преобразование Куммера 241
_ , — Лапласа 256—258
_ , произведение 275
— , разложение по многочленам Лагерра
и функциям Бесселя 263—265
_ _ —., ряды 272
_ , свойства функции Ф и W 247—250
__ , связь с функцией Бесселя 252
_ — —, смежные функции 242
_ , теорема сложения 274
_ , теоремы умножения 272
— —, функции Бесселя 252
_ , — параболического цилиндра 255
, - Уиттекера 251, 262
— —, функция Бейтмена 255
— , — Лагерра 255
— , — Торонто 256
— , частные случаи 253—256
, элементарные соотношения 242, 245
f обобщения 183, 199, 200
смежная 70
— , соотношения Гаусса 111, 112
Гипергеометрический ряд 70, 109
, аналитическое продолжение 74, 76, 116,
117
— — ассоциированный, разложение в
непрерывные дроби 98
базисный 195, 196, 200
, аналоги теорем Гаусса, Дуголла,
Заальшютца, Куммера, Уиппла 197—198
вполне уравновешенный 197
нескольких переменных 236

Гипергеометрический ряд базисный,
обобщение биномиального ряда 196
, обозначение 195
, случай г = 5 + 1
, теорема Джексона 197
, тождество Роджерса — Рамануджана
198
, — Эйлера 198
— , элементарные случаи 196
— —, выражение некоторых элементарных
функций 109, ПО
вырожденный 81—85
— — —, асимптотическое разложение 87, 88
двух переменных 218
второго порядка (полный и
вырожденный) 219-221
, двойные интегралы типа Мелли-
на — Бернса, Эйлера 224, 226
— — — —, интегральные представления 224—
226
, исследования Айнса 230
— 1 общие интегралы типа Эйлера
225
— — , преобразования 232—234
, системы дифференциальных
уравнений в частных производных 226—230
, сходимость 221, 222
, формулы приведения 231, 232
, интегральные представления 72, 73, 74,
89—92, 123, 124
как функция параметров 80
обобщенный 183, 199
аргумента единица 184, 189, 190
базисный 196, 197
вида Заальшютца 188
вполне уравновешенный 188, 190
, дифференциальные уравнения 183,
185, 200
для частного случая G-функции 210
, интегральные представления 192
, квадратичные преобразования для
8F2 190
, конечность 183
, кубичные преобразования для 3^2 190
, многочлены Бейтмена и Пастернака
193
— , обобщение биномиального ряда 196
, обозначения Похгаммера— Бернса 184
, почти уравновешенный 188, 190
, преобразование Ганкеля 193
, — Лапласа 192
— — —, преобразования квадратичные и
кубичные 190
( _ линейные 188, 191
, рекуррентные соотношения 186, 187
смежный 188
, сходимость 183, 185
, теорема Ватсона 189
, — Диксона 189
, — Дуголла 190
—, — Уиппла 189
, тождества 185
, формула Дуголла—Рамануджана 191
, — Ченкера 193
, 1^1 (а, с; х) 237
, частные случаи 191, 193
— —, преобразования квадратичные 76, 77,
102, 118—121
, - кубичные 80, 102, 121-122
, — линейные 75, 76
, рекуррентная формула 71
, соотношения 110—111
— — усеченный 192
— —, формула Эйлера 72
, частные случаи 92, 112—113
Гипергеометрическое дифференциальное
уравнение 69, 70, 71, 101
вырожденное 238, 239
, общее решение 241
, фундаментальная система решений
246
обобщенное 183, 185
Группа гипергеометрического
дифференциального уравнения 104
Гумберта символ 237
Гурвица формула для СE, v) 41
Гурса таблица квадратичных преобразований
* 118-121
кубичных преобразований 122
О-функция Мейера — см. Мейера G-функ-
ция
Дзета-функция обобщения 40
, представление Эрмита 42
, формула Гурвица 41
— Римана — см. Римана дзета-функция
Дирихле формула для ф (г) 33
Дуголла разложение по функциям Лежандра
168
— формула 21
/Г-функция Мак-Роберта — см. Мак-Роберта
Е- функция
Жонкье соотношение для F (z, s) 46
Заальшютца формула 78
Инверсия относительно окружности 107
Интеграл — см. соответствующее название
Кели тождество 106
Кнара формула 20
Кольца функции 174, 175
Конуса функции 176
Крампа символ 67
Кристоффеля формулы суммирования для
функций Лежандра 163
Кси-функция Римана — см. Римана кси-функ-
ция
Куммера ряды 102, 113—115, 237
для In Г (г) 38, 39
Лежандра многочлены 125, 126, 151
, производящая функция 154
, формула Родрига 151
— уравнение 125, 126
— формула для удвоения аргумента Г (z) 19
— функции 99, 126, 149
— —, асимптотические разложения 163
, интегралы 170—174
, интегральные представления 154, 155—
160
на разрезе 143, 144, 145, 162, 163
первого и второго рода 127—139
, поведение вблизи особых точек 163—165
присоединенные 149, 182
, разложения 166—168
рекуррентные соотношения 140—141, 162
, связь с гипергеометрическим рядом 127,
142, 143
, теоремы сложения 169—170
, тригонометрические разложения 146, 147
, формула Гейне 169
, — Уиппла 141
, формулы суммирования Кристоффеля
163
, частные случаи 148—155

Лерха преобразование для Ф(г, 5, v) 44
— теорема 97
Липшица формула для Ф{г, s, v) 43
Логарифмическая производная Г-функции 30
Мак-Роберта ^-функция 200, 201
, интегральные представления 202—203
, рекуррентные соотношения 202
, родственные функции 201
, частные случаи 201
Мальмстена формула для In T(z) 36
Мейера G-функция 203, 204
, асимптотические разложения 207
, дифференциальные уравнения 206
, интегральные преобразования 209
, преобразование Ганкеля 209
, пути интегрирования 203, 204
, ряды 208, 209
, свойства 207
, теоремы умножения 208
, тождества 205
, формулы разложения 209
, частные случаи 201, 210—218
Мелера — Дирихле формула 160
Меллина — Бернса интегралы 63, 64, 65
Меллина формула 20
Многочлен — см. соответствующее название
Неймана интегральное представление для
многочленов Лежандра 154
Обобщенный гипергеометрический ряд — см.
гипергеометрический ряд обобщенный
Олбрихта решения уравнения Лежандра 140
Папперитца дифференциальное уравнение 100
Параметры гипергеометрического уравнения
69
Плана формула суммирования 38
Показатели, соответствующие особой точке 100
Полигамма-функции 59
Порядок гипергеометрического ряда 219
Похгаммера символ 67
Произведения гипергеометрических рядов 94—
96
Производная Шварца 105
Разность показателей 100
Рамануджана формула 26
Решения гипергеометрического
дифференциального уравнения 69, 70, 72,73, 81—85, 101
— дифференциального уравнения Римана 101
Римана дзета-функция 47, 49
, интегральные представления 47, 48
, контурные интегралы 47, 48
, разложение в ряд 49
— дифференциальное уравнение 100
— кси-функция 50
Родрига формула для многочленов Лежандра
151
Ряд — см. соответствующее название
Стирлинга ряд 62
5-функция Шварца 184
Таблица — см. соответствующее название
Тождество — см. соответствующее название
Тороидальные координаты 174
— функции 174, 175
Тригонометрические функции, разложение в
степенные ряды 65, 66
Уиппла формула для функций Лежандра 141
Уиттекера lF-функция 201, 251, 262
Факториал U(z) 67
Формула — см. соответствующее название
Функция F {z, s) 45
, соотношение Жонкье 46
— Ф {z, s, v) 42
, выражение через многочлены Бернулли
45
, интегральные формулы 43
, контурный интеграл 43
, преобразование Лерха 44
, разложение в ряд 44
, формула Липшица 43
— G (г) 35
, функциональные уравнения 36
— L (s) 50
, функциональное уравнение 50
— In Г (z) 36
, выражения Бине 37
, интегральные формулы 39
, ряды Куммера 38, 39
, формула Мальмстена 36
— ф (г) 30
, бесконечные ряды 34
, выражение Бине 33, 34
— —, интегральная формула Гаусса 32
, интегральные представления 31
, теорема Гаусса 34
, формула Дирихле 33
» функциональные уравнения 31
— см. также соответствующее название
Число — см. соответствующее название
Шварца производная 105
— 5-функция 184
— таблица 107
— функция общая 106
— — частная 106
Эйлера дилогарифм 46
— многочлены 55, 56
, интегральные формулы 58
порядка т и — т 57, 58
, рекуррентная формула 56
, ряд Фурье 56
— постоянная 15. 32, 60
— —, интегральная формула 32
— формула для гипергеометрического ряда 72
— числа 55, 56, 57, 68
, интегральное представление 57
порядка т и — т 57
— —, рекуррентная формула 57
Эллиптическая модулярная функция 108
Эллиптические интегралы полные 99
Эрмита представление для С {s,v) 42
Якоби многочлены 92, 99
, обобщение 236
, производящая функция 93
, билинейная 236

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
(а) — Похгаммера символ 67
В — Бернулли числа 50
в(?> 55
Вп (х) — Бернулли многочлены 51
bJJ° (х | а1( . . . , ап) 55
В(*, у) — бета-функция 23
в (Р> Я) — бета-функция неполная 98
с^— Крампа символ 67
Ci {x) — интегральный косинус 254
С(х) — Френеля интеграл 254
С™ — биномиальный коэффициент 67
Cv (z) — Гегенбауэра многочлен 177
Cv U). Z)^ (z) — Гегенбауэра функции 180,
^ 181
D (x) — функция параболического цилиндра
V255
~ г ~dz ' ~~ ~d~z
С (s, v) — дзета-функция обобщенная 40
С E) — Римана дзета-функция 47
Е (р; ar : q; pg : х) или Е (а^ ... , а : pv ...
..., р : л:) — Мак-Роберта ^-функция 200,201
Еп — Эйлера число 55
Е^т' (aj ... ат) — Эйлера число порядка т
57, 58
Е (х) — Эйлера многочлен 55
^п ^х I ai ''' ат) ~ Э^леРа многочлен
порядка т 57, 58
— Ei (— л:) — интегральная показательная
функция 254
Erf (л:) — интеграл вероятностей 254
F(a, b; с; z) или F\ (a, b; с; z) —
гипергеометрическая функция 70, 74
г/7! (а, Ь; с, г) ~ /Ч — Гаусса ги-
L с J
пергеометрический ряд 183
[а , .... а ; .г"]
¦^ — гипергеометрический
ряд обобщенный 183
/Ч F\(. . , , х, у) —
гипергеометрический ряд двух переменных 219, 220
<& {а, с; х) 238
ГФ5 — гипергеометрический ряд базисный 196
Ф {а, с; х) — гипергеометрическая функция
вырожденная 237
Фп W ~ Бернулли многочлены 67
Ф ([1, v), W ([1, v) 221, 222
Ф {г, s, v) 42
G (г) 35
() 59
C?i, G2, Gg (• • • » Jf» У) — гипергеометрический
ряд двух переменных 220
Qp,
:), G(x) — Мейера G-функция 203
Г (z) — гамма-функция 15
7 — постоянная Эйлера 15
Нп (х) — Эрмита многочлен 255
#1, . .. , Н7 (. . . , х, у) —
гипергеометрические ряды двух переменных 220
Нп E. Р) v) 193
1„ (Р> 9) 98
J"' (z) ~ Бейтмена многочлен 193
п
&v (*) — Бейтмена функция 255, 261
? (s) — Римана кси-функция 50
L E) 50
}' Z { F } ~ ЛаПЛаСа
Lq (z) — Эйлера дилогарифм 46
Ln {z) — Лагерра п-й многочлен 195
li(x) — интегральный логарифм 255
М {а, с; х) — вырожденная
гипергеометрическая функция 237
М , W — Уиттекера функция 251

(Л), A (h), 8, 8' — Берчнелла и Ченди
операторы 234
ац а2 а8 г \ — множество решений урав-
а[ ar2 a8 J
нения Римана 100
Р^(С) — Лежандра многочлены 125, 126
P^{z) — Лежандра функция первого рода 127
Q^ (г) — Лежандра функция второго рода 127
Р^ , (ch i\), Q^1 , (ch т]) — тороидальные
v__ v——
функции 175
Р^ (cos 8), Q11 (cos 6) — функции
конуса 176
И (г) 67
ф (г) — логарифмическая производная Г-функ-
ции 30
ф(я)(г) 59
5(jf) — Френеля интеграл 254
5([х, v, X; г) — Шварца общая функция 106
5(jx, v, X; г) — Шварца частная функция 106
Si (x) — интегральный синус 254
Т^ (х) — Лежандра присоединенные функции
(обозначение по Феррари) 182
т = «S @, 0, 0; z) — частный вид автоморфной
функции 107
х2 (т) — эллиптическая модулярная функция
108
и1( и2» • • • » «о — Куммера ряды 102
(г», /г) — Ганкеля символ 67
№^ m (x) — Уиттекера W-функция 201
{ W, z } — Шварца производная 105
Уп (a, z) 195
z = (р (X, |А, v; r) — автоморфная функция 107
Z (х) — Бейтмена многочлен 193

Г. Бейтмен и А. Эрдейи
Высшие трансцендентные функции.
Гипергеометрическая функция.
Функции Лежандра.
М., 1965 г., 296 стр. с илл.
Редактор Ворновицкий М. Я.
Техн. редактор Шкляр С. Я.
Корректор Серкина А. Ф.
Сдано в набор 16/II 1965 г. Подписано к печати
24/V 1965 г. Бумага 60X90Vie. Физ. печ. л. 18,5.
Условн. печ. л. 18,5. Уч.-изд. л. 19,81. Тираж
14 000 экз. Цена книги 1 р. 14 к. Заказ № 1556.
Издательство «Наука»
Главная редакция физико-математической
литературы.
Москва, В-71, Ленинский проспект, 15
Ленинградская типография № 1 «Печатный Двор»
им. А. М. Горького «Главполиграфпрома»
Государственного комитета Совета Министров СССР
по печати, Гатчинская, 26.